CLRS Solutions Manual
CLRS_Solutions_Manual
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 511 [warning: Documents this large are best viewed by clicking the View PDF Link!]
Chapter 1
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 1.1-1
An example of a real world situation that would require sorting would be if
you wanted to keep track of a bunch of people’s file folders and be able to look
up a given name quickly. A convex hull might be needed if you needed to secure
a wildlife santuary with fencing and had to contain a bunch of specific nesting
locations.
Exercise 1.1-2
One might measure memory usage of an algorithm, or number of people
required to carry out a single task.
Exercise 1.1-3
An array. It has the limitation of requiring a lot of copying when resizing,
inserting, and removing elements.
Exercise 1.1-4
They are similar since both problems can be modeled by a graph with
weighted edges and involve minimizing distance, or weight, of a walk on the
graph. They are different because the shortest path problem considers only
two vertices, whereas the traveling salesman problem considers minimizing the
weight of a path that must include many vertices and end where it began.
Exercise 1.1-5
If you were for example keeping track of terror watch suspects, it would be
unacceptable to have it occasionally bringing up a wrong decision as to whether
a person is on the list or not. It would be fine to only have an approximate
solution to the shortest route on which to drive, an extra little bit of driving is
not that bad.
1

Exercise 1.2-1
A program that would pick out which music a user would like to listen to
next. They would need to use a bunch of information from historical and pop-
ular preferences in order to maximize.
Exercise 1.2-2
We wish to determine for which values of nthe inequality 8n2<64nlog2(n)
holds. This happens when n < 8 log2(n), or when n≤43. In other words,
insertion sort runs faster when we’re sorting at most 43 items. Otherwise merge
sort is faster.
Exercise 1.2-3
We want that 100n2<2n. note that if n= 14, this becomes 100(14)2=
19600 >214 = 16384. For n= 15 it is 100(15)2= 22500 <215 = 32768. So,
the answer is n= 15.
Problem 1-1
We assume a 30 dday month and 365 day year.
1 Second 1 Minute 1 Hour 1 Day 1 Month 1 Year 1 Century
lg n21×10626×10723.6×10928.64×1010 22.592×1012 23.1536×1013 23.15576×1015
√n1×1012 3.6×1015 1.29 ×1019 7.46 ×1021 6.72 ×1024 9.95 ×1026 9.96 ×1030
n1×1066×1073.6×1098.64 ×1010 2.59 ×1012 3.15 ×1013 3.16 ×1015
nlg n189481 8.64 ×1064.18 ×1088.69 ×1092.28 ×1011 2.54 ×1012 2.20 ×1014
n21000 7745 60000 293938 1609968 5615692 56176151
n3100 391 1532 4420 13736 31593 146679
2n19 25 31 36 41 44 51
n! 9 11 12 13 15 16 17
2

Chapter 2
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 2.1-1
31 41 59 26 41 58
31 41 59 26 41 58
31 41 59 26 41 58
26 31 41 59 41 58
26 31 41 41 59 58
26 31 41 41 58 59
Exercise 2.1-2
Algorithm 1 Nonincreasing Insertion-Sort(A)
1: for j= 2 to A.length do
2: key =A[j]
3: // Insert A[j] into the sorted sequence A[1..j −1].
4: i=j−1
5: while i > 0 and A[i]< key do
6: A[i+ 1] = A[i]
7: i=i−1
8: end while
9: end for
10: A[i+ 1] = key
Exercise 2.1-3
On each iteration of the loop body, the invariant upon entering is that there
is no index k < j so that A[k] = v. In order to procede to the next iteration of
the loop, we need that for the current value of j, we do not have A[j] = v. If
the loop is exited by line 5, then we have just placed an acceptable value in i
on the previous line. If the loop is exited by exhausting all possible values of j,
then we know that there is no index that has value j, and so leaving NIL in i
is correct.
1

1: i=NIL
2: for j= 1 to A.length do
3: if A[j] = vthen
4: i=j
5: return i
6: end if
7: return i
8: end for
Exercise 2.1-4
Input: two n-element arrays Aand Bcontaining the binary digits of two
numbers aand b.
Output: an (n+ 1)-element array Ccontaining the binary digits of a+b.
Algorithm 2 Adding n-bit Binary Integers
1: carry = 0
2: for i=1 to n do
3: C[i] = (A[i] + B[i] + carry) (mod 2)
4: if A[i] + B[i] + carry ≥2then
5: carry = 1
6: else
7: carry = 0
8: end if
9: end for
10: C[n+1] = carry
Exercise 2.2-1
n3/1000 −100n2−100n+ 3 ∈Θ(n3)
Exercise 2.2-2
Input: An n-element array A.
Output: The array Awith its elements rearranged into increasing order.
The loop invariant of selection sort is as follows: At each iteration of the for
loop of lines 1 through 10, the subarray A[1..i −1] contains the i−1 smallest
elements of Ain increasing order. After n−1 iterations of the loop, the n−1
smallest elements of Aare in the first n−1 positions of Ain increasing order,
so the nth element is necessarily the largest element. Therefore we do not need
to run the loop a final time. The best-case and worst-case running times of
selection sort are Θ(n2). This is because regardless of how the elements are
initially arranged, on the ith iteration of the main for loop the algorithm always
inspects each of the remaining n−ielements to find the smallest one remaining.
2

Algorithm 3 Selection Sort
1: for i= 1 to n−1do
2: min =i
3: for j=i+ 1 to ndo
4: // Find the index of the ith smallest element
5: if A[j]< A[min]then
6: min =j
7: end if
8: end for
9: Swap A[min] and A[i]
10: end for
This yields a running time of
n−1
X
i=1
n−i=n(n−1) −
n−1
X
i=1
i=n2−n−n2−n
2=n2−n
2= Θ(n2).
Exercise 2.2-3
Suppose that every entry has probability pof being the element looked for.
Then, we will only check kelements if the previous k−1 positiions were not
the element being looked for, and the kth position is the desired value. Taking
the expected value of this distribution we get it to be
(1 −p)A.length +
A.length
X
k=1
k(1 −p)k−1pk
Exercise 2.2-4
For a good best-case running time, modify an algorithm to first randomly
produce output and then check whether or not it satisfies the goal of the al-
gorithm. If so, produce this output and halt. Otherwise, run the algorithm as
usual. It is unlikley that this will be successful, but in the best-case the running
time will only be as long as it takes to check a solution. For example, we could
modify selection sort to first randomly permut the elements of A, then check if
they are in sorted order. If they are, output A. Otherwise run selection sort as
usual. In the best case, this modified algorithm will have running time Θ(n).
Exercise 2.3-1
If we start with reading accross the bottom of the tree and then go up level
by level.
3 41 52 26 38 57 9 49
3 41 26 52 38 57 9 49
3 26 41 52 9 38 49 57
3 9 26 38 41 49 52 57
3

Exercise 2.3-2
The following is a rewrite of MERGE which avoids the use of sentinels. Much
like MERGE, it begins by copying the subarrays of Ato be merged into arrays
Land R. At each iteration of the while loop starting on line 13 it selects the
next smallest element from either Lor Rto place into A. It stops if either L
or Rruns out of elements, at which point it copies the remainder of the other
subarray into the remaining spots of A.
Algorithm 4 Merge(A, p, q, r)
1: n1=q−p+ 1
2: n2=r−q
3: let L[1, ..n1] and R[1..n2] be new arrays
4: for i= 1 to n1do
5: L[i] = A[p+i−1]
6: end for
7: for j= 1 to n2do
8: R[j] = A[q+j]
9: end for
10: i= 1
11: j= 1
12: k=p
13: while i6=n1+ 1 and j6=n2+ 1 do
14: if L[i]≤R[j]then
15: A[k] = L[i]
16: i=i+ 1
17: else A[k] = R[j]
18: j=j+ 1
19: end if
20: k=k+ 1
21: end while
22: if i== n1+ 1 then
23: for m=jto n2do
24: A[k] = R[m]
25: k=k+ 1
26: end for
27: end if
28: if j== n2+ 1 then
29: for m=ito n1do
30: A[k] = L[m]
31: k=k+ 1
32: end for
33: end if
4
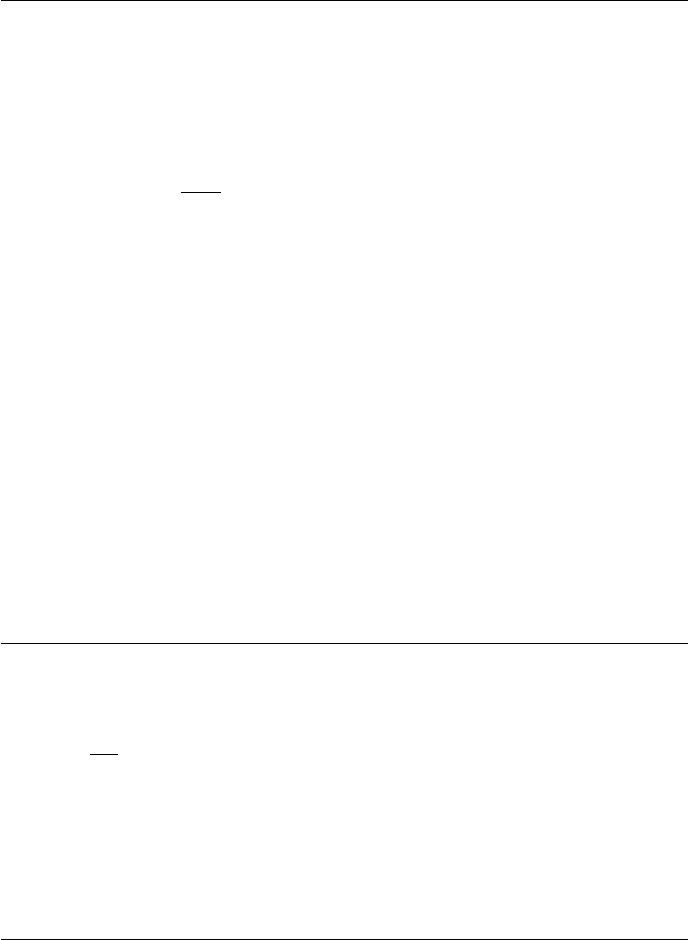
Exercise 2.3-3
Since nis a power of two, we may write n= 2k. If k= 1, T(2) = 2 = 2 lg(2).
Suppose it is true for k, we will show it is true for k+ 1.
T(2k+1) = 2T2k+1
2+ 2k+1 = 2T2k+ 2k+1 = 2(2klg(2k)) + 2k+1
=k2k+1 + 2k+1 = (k+ 1)2k+1 = 2k+1 lg(2k+1) = nlg(n)
Exercise 2.3-4
Let T(n) denote the running time for insertion sort called on an array of size
n. We can express T(n) recursively as
T(n) = Θ(1) if n≤c
T(n−1)I(n) otherwise
where I(n) denotes the amount of time it takes to insert A[n] into the sorted
array A[1..n −1]. As seen in exercise 2.3-5, I(n) is Θ(log n).
Exercise 2.3-5
The following recursive algorithm gives the desired result when called with
a= 1 and b=n.
1: BinSearch(a,b,v)
2: if thena > b
3: return NIL
4: end if
5: m=ba+b
2c
6: if thenm=v
7: return m
8: end if
9: if thenm<v
10: return BinSearch(a,m,v)
11: end if
12: return BinSearch(m+1,b,v)
Note that the initial call should be BinSearch(1, n, v). Each call results in
a constant number of operations plus a call to a problem instance where the
quantity b−afalls by at least a factor of two. So, the runtime satisfies the
recurrence T(n) = T(n/2) + c. So, T(n)∈Θ(lg(n))
Exercise 2.3-6
5

A binary search wouldn’t improve the worst-case running time. Insertion
sort has to copy each element greater than key into its neighboring spot in the
array. Doing a binary search would tell us how many how many elements need
to be copied over, but wouldn’t rid us of the copying needed to be done.
Exercise 2.3-7
1: Use Merge Sort to sort the array Ain time Θ(nlg(n))
2: i= 1
3: j=n
4: while i<jdo
5: if A[j] + A[j] = Sthen
6: return true
7: end if
8: if A[i] + A[j]< S then
9: i=i+ 1
10: end if
11: if A[i] + A[j]> S then
12: j=j−1
13: end if
14: end while
15: return false
We can see that the while loop gets run at most O(n) times, as the quantity
j−istarts at n−1 and decreeases at each step. Also, since the body only consists
of a constant amount of work, all of lines 2-15 takes only O(n) time. So, the
runtime is dominated by the time to perform the sort, which is Θ(nlg(n)).
We will prove correctness by a mutual induction. Let mi,j be the proposition
A[i] + A[j]< S and Mi,j be the proposition A[i] + A[j]> S. Note that because
the array is sorted, mi,j ⇒ ∀k < j, mi,k, and Mi,j ⇒ ∀k > i, Mk,j .
Our program will obviously only output true in the case that there is a valid
iand j. Now, suppose that our program output false, even though there were
some i, j that was not considered for which A[i] + A[j] = S. If we have i > j,
then swap the two, and the sum will not change, so, assume i≤j. we now have
two cases:
Case 1 ∃k, (i, k) was considered and j < k. In this case, we take the smallest
such k. The fact that this is nonzero meant that immediately after considering
it, we considered (i+1,k) which means mi,k this means mi,j
Case 2 ∃k, (k, j) was considered and k < i. In this case, we take the largest
such k. The fact that this is nonzero meant that immediately after considering
it, we considered (k,j-1) which means Mk,j this means Mi,j
Note that one of these two cases must be true since the set of considered
points separates {(m, m0) : m≤m0< n}into at most two regions. If you are
in the region that contains (1,1)(if nonempty) then you are in Case 1. If you
6

are in the region that contains (n, n) (if non-empty) then you are in case 2.
Problem 2-1
a. The time for insertion sort to sort a single list of length kis Θ(k2), so, n/k
of them will take time Θ( n
kk2) = Θ(nk).
b. Suppose we have coarseness k. This meas we can just start using the usual
merging procedure, except starting it at the level in which each array has size
at most k. This means that the depth of the merge tree is lg(n)−lg(k) =
lg(n/k). Each level of merging is still time cn, so putting it together, the
merging takes time Θ(nlg(n/k)).
c. Viewing kas a function of n, as long as k(n)∈O(lg(n)), it has the same
asymptotics. In particular, for any constant choice of k, the asymptotics are
the same.
d. If we optimize the previous expression using our calculus 1 skills to get k, we
have that c1n−nc2
k= 0 where c1and c2are the coeffients of nk and nlg(n/k)
hidden by the asymptotics notation. In particular, a constant choice of kis
optimal. In practice we could find the best choice of this kby just trying
and timing for various values for sufficiently large n.
Problem 2-2
1. We need to prove that A0contains the same elements as A, which is easily
seen to be true because the only modification we make to Ais swapping
its elements, so the resulting array must contain a rearrangement of the
elements in the original array.
2. The for loop in lines 2 through 4 maintains the following loop invari-
ant: At the start of each iteration, the position of the smallest element of
A[i..n] is at most j. This is clearly true prior to the first iteration because
the position of any element is at most A.length. To see that each iter-
ation maintains the loop invariant, suppose that j=kand the position
of the smallest element of A[i..n] is at most k. Then we compare A[k] to
A[k−1]. If A[k]< A[k−1] then A[k−1] is not the smallest element
of A[i..n], so when we swap A[k] and A[k−1] we know that the smallest
element of A[i..n] must occur in the first k−1 positions of the subarray,
the maintaining the invariant. On the other hand, if A[k]≥A[k−1] then
the smallest element can’t be A[k]. Since we do nothing, we conclude that
the smallest element has position at most k−1. Upon termination, the
smallest element of A[i..n] is in position i.
7

3. The for loop in lines 1 through 4 maintain the following loop invariant:
At the start of each iteration the subarray A[1..i −1] contains the i−1
smallest elements of Ain sorted order. Prior to the first iteration i= 1,
and the first 0 elements of Aare trivially sorted. To see that each iteration
maintains the loop invariant, fix iand suppose that A[1..i −1] contains
the i−1 smallest elements of Ain sorted order. Then we run the loop in
lines 2 through 4. We showed in part b that when this loop terminates,
the smallest element of A[i..n] is in position i. Since the i−1 smallest
elements of Aare already in A[1..i −1], A[i] must be the ith smallest
element of A. Therefore A[1..i] contains the ismallest elements of Ain
sorted order, maintaining the loop invariant. Upon termination, A[1..n]
contains the nelements of Ain sorted order as desired.
4. The ith iteration of the for loop of lines 1 through 4 will cause n−i
iterations of the for loop of lines 2 through 4, each with constant time
execution, so the worst-case running time is Θ(n2). This is the same as
that of insertion sort; however, bubble sort also has best-case running time
Θ(n2) whereas insertion sort has best-case running time Θ(n).
Problem 2-3
a. If we assume that the arithmeticcan all be done in constant time, then since
the loop is being executed ntimes, it has runtime Θ(n).
b. 1: y= 0
2: for i=0 to n do
3: yi=x
4: for j=1 to n do
5: yi=yix
6: end for
7: y=y+aiyi
8: end for
This code has runtime Θ(n2) because it has to compute each of the powers
of x. This is slower than Horner’s rule.
c. Initially, i=n, so, the upper bound of the summation is −1, so the sum
evaluates to 0, which is the value of y. For preservation, suppose it is true
for an i, then,
y=ai+x
n−(i+1)
X
k=0
ak+i+1xk=ai+x
n−i
X
k=1
ak+ixk−1=
n−i
X
k=0
ak+ixk
At termination, i= 0, so is summing up to n−1, so executing the body of
the loop a last time gets us the desired final result.
8

d. We just showed that the algorithm evaluated Σn
k=0akxk. This is the value of
the polynomial evaluated at x.
Problem 2-4
a. The five inversions are (2,1), (3,1), (8,6), (8,1), and (6,1).
b. The n-element array with the most inversions is hn, n −1,...,2,1i. It has
n−1 + n−2 + . . . + 2 + 1 = n(n−1)
2inversions.
c. The running time of insertion sort is a constant times the number of inver-
sions. Let I(i) denote the number of j < i such that A[j]> A[i]. Then
Pn
i=1 I(i) equals the number of inversions in A. Now consider the while
loop on lines 5-7 of the insertion sort algorithm. The loop will execute once
for each element of Awhich has index less than jis larger than A[j]. Thus,
it will execute I(j) times. We reach this while loop once for each iteration
of the for loop, so the number of constant time steps of insertion sort is
Pn
j=1 I(j) which is exactly the inversion number of A.
d. We’ll call our algorithm M.Merge-Sort for Modified Merge Sort. In addition
to sorting A, it will also keep track of the number of inversions. The algorithm
works as follows. When we call M.Merge-Sort(A,p,q) it sorts A[p..q] and
returns the number of inversions amongst the elements of A[p..q], so left
and right track the number of inversions of the form (i, j) where iand jare
both in the same half of A. When M.Merge(A,p,q,r) is called, it returns the
number of inversions of the form (i, j) where iis in the first half of the array
and jis in the second half. Summing these up gives the total number of
inversions in A. The runtime is the same as that of Merge-Sort because we
only add an additional constant-time operation to some of the iterations of
some of the loops. Since Merge is Θ(nlog n), so is this algorithm.
Algorithm 5 M.Merge-Sort(A, p, r)
if p<rthen
q=b(p+r)/2c
lef t =M.M erge −Sort(A, p, q)
right =M.M erge −Sort(A, q + 1, r)
inv =M.M erge(A, p, q, r) + left +right
return inv
end if
return 0
9

Algorithm 6 M.Merge(A,p,q,r)
inv = 0
n1=q−p+ 1
n2=r−q
let L[1, ..n1] and R[1..n2] be new arrays
for i= 1 to n1do
L[i] = A[p+i−1]
end for
for j= 1 to n2do
R[j] = A[q+j]
end for
i= 1
j= 1
k=p
while i6=n1+ 1 and j6=n2+ 1 do
if L[i]≤R[j]then
A[k] = L[i]
i=i+ 1
else A[k] = R[j]
inv =inv +j// This keeps track of the number of inversions between
the left and right arrays.
j=j+ 1
end if
k=k+ 1
end while
if i== n1+ 1 then
for m=jto n2do
A[k] = R[m]
k=k+ 1
end for
end if
if j== n2+ 1 then
for m=ito n1do
A[k] = L[m]
inv =inv +n2// Tracks inversions once we have exhausted the right
array. At this point, every element of the right array contributes an inversion.
k=k+ 1
end for
end if
return inv
10

Chapter 3
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 3.1-1
Since we are requiring both fand gto be aymptotically non-negative, sup-
pose that we are past some n1where both are non-negative (take the max of the
two bounds on the n corresponding to both fand g). Let c1=.5 and c2= 1.
0≤.5(f(n) + g(n)) ≤.5(max(f(n), g(n)) + max(f(n), g(n)))
= max(f(n), g(n)) ≤max(f(n), g(n)) + min(f(n), g(n)) = (f(n) + g(n))
Exercise 3.1-2
Let c= 2band n0≥2a. Then for all n≥n0we have (n+a)b≤(2n)b=cnb
so (n+a)b=O(nb). Now let n0≥−a
1−1/21/b and c=1
2. Then n≥n0≥−a
1−1/21/b
if and only if n−n
21/b ≥ −aif and only if n+a≥(1/2)a/bnif and only if
(n+a)b≥cnb. Therefore (n+a)b= Ω(nb). By Theorem 3.1, (n+a)b= Θ(nb).
Exercise 3.1-3
There are a ton of different funtions that have growth rate less than or equal
to n2. In particular, functions that are constant or shrink to zero arbitrarily
fast. Saying that you grow more quickly than a function that shrinks to zero
quickly means nothing.
Exercise 3.1-4
2n+1 ≥2·2nfor all n≥0, so 2n+1 =O(2n). However, 22nis not O(2n). If
it were, there would exist n0and csuch that n≥n0implies 2n·2n= 22n≤c2n,
so 2n≤cfor n≥n0which is clearly impossible since cis a constant.
Exercise 3.1-5
1

Suppose f(n)∈Θ(g(n)), then ∃c1, c2, n0,∀n≥n0,0≤c1g(n)≤f(n)≤
c2g(n), if we just look at these inequalities saparately, we have c1g(n)≤f(n)
(f(n)∈Ω(g(n))) and f(n)≤c2g(n) (f(n)∈O(g(n))).
Suppose that we had ∃n1, c1,∀n≥n1, c1g(n)≤f(n) and ∃n2, c2,∀n≥
n2, f(n)≤c2g(n). Putting these together, and letting n0= max(n1, n2), we
have ∀n≥n0, c1g(n)≤f(n)≤c2g(n).
Exercise 3.1-6
Suppose the running time is Θ(g(n)). By Theorem 3.1, the running time is
O(g(n)), which implies that for any input of size n≥n0the running time is
bounded above by c1g(n) for some c1. This includes the running time on the
worst-case input. Theorem 3.1 also imlpies the running time is Ω(g(n)), which
implies that for any input of size n≥n0the running time is bounded below by
c2g(n) for some c2. This includes the running time of the best-case input.
On the other hand, the running time of any input is bounded above by
the worst-case running time and bounded below by the best-case running time.
If the worst-case and best-case running times are O(g(n)) and Ω(g(n)) respec-
tively, then the running time of any input of size nmust be O(g(n)) and Ω(g(n)).
Theorem 3.1 implies that the running time is Θ(g(n)).
Exercise 3.1-7
Suppose we had some f(n)∈o(g(n)) ∩ω(g(n)). Then, we have
0 = lim
n→∞
f(n)
g(n)=∞
a contradiction.
Exercise 3.1-8
Ω(g(n, m)) = {f(n, m) : there exist positive constants c, n0,and m0such that f(n, m)≥cg(n, m)
for all n≥n0or m≥m0}
Θ(g(n, m)) = {f(n, m) : there exist positive constants c1, c2, n0,and m0such that c1g(n, m)≤f(n, m)
≤c2g(n, m) for all n≥n0or m≥m0}
Exercise 3.2-1
Let n1< n2be arbitrary. From fand gbeing monatonic increasing, we
know f(n1)< f(n2) and g(n1)< g(n2). So
f(n1) + g(n1)< f(n2) + g(n1)< f (n2) + g(n2)
2

Since g(n1)< g(n2), we have f(g(n1)) < f(g(n2)). Lastly, if both are nonega-
tive, then,
f(n1)g(n1) = f(n2)g(n1)+(f(n2)−f(n1))g(n1)
=f(n2)g(n2) + f(n2)(g(n2)−g(n1)) + (f(n2)−f(n1))g(n1)
Since f(n1)≥0, f(n2)>0, so, the second term in this expression is greater
than zero. The third term is nonnegative, so, the whole thing is< f(n2)g(n2).
Exercise 3.2-2
alogb(c)=a
loga(c)
loga(b)=c1
loga(b)=clogb(a).
Exercise 3.2-3
As the hint suggests, we will apply stirling’s approximation
lg(n!) = lg p(2πn n
en1+Θ1
n
=1
2lg(2πn) + nlg(n)−nlg(e) + lg Θn+ 1
n
Note that this last term is O(lg(n)) if we just add the two expression we get
when we break up the lg instead of subtract them. So, the whole expression is
dominated by nlg(n). So, we have that lg(n!) = Θ(nlg(n)).
lim
n→∞
2n
n!= lim
n→∞
1
√2πn(1 + Θ( 1
n)) 2e
nn
≤lim
n→∞ 2e
nn
If we restrict to n > 4e, then this is
≤lim
n→∞
1
2n= 0
lim
n→∞
nn
n!= lim
n→∞
1
√2πn(1 + Θ( 1
n))en= lim
n→∞ O(n−.5)en≥lim
n→∞
en
c1√n
≥lim
n→∞
en
c1n= lim
n→∞
en
c1
=∞
Exercise 3.2-4
The function dlog ne! is not polynomially bounded. If it were, there would
exist constants c,a, and n0such that for all n≥n0the inequality dlog ne!≤
cnawould hold. In particular, it would hold when n= 2kfor k∈N. Then
3
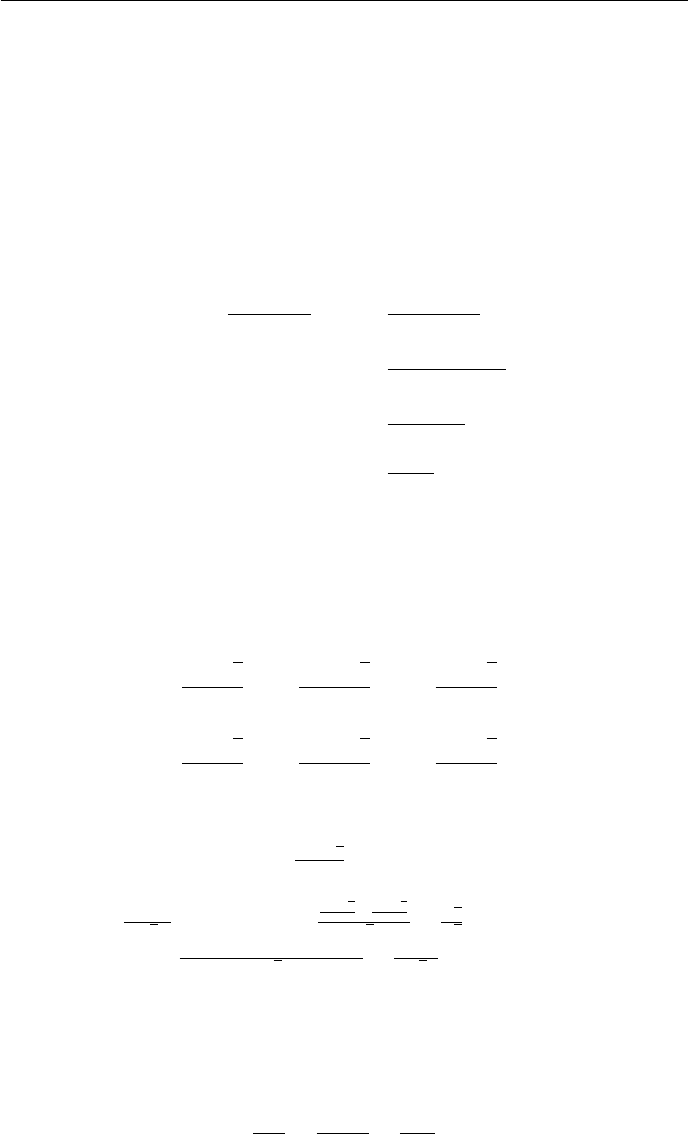
this becomes k!≤c(2a)k, a contradiction since the factorial function is not
exponentially bounded.
We’ll show that dlog log ne!≤n. Without loss of generality assume n= 22k.
Then this becomes equivalent to showing k!≤22k, or 1 ·2···(k−1) ·k≤
4·16 ·28···22k, which is clearly true for k≥1. Therefore it is polynomially
bounded.
Exercise 3.2-5
Note that lg∗(2n) = 1 + lg∗(n), so,
lim
n→∞
lg(lg∗(n))
lg∗(lg(n)) = lim
n→∞
lg(lg∗(2n))
lg∗(lg(2n))
= lim
n→∞
lg(1 + lg∗(n))
lg∗(n)
= lim
n→∞
lg(1 + n)
n
= lim
n→∞
1
1 + n
= 0
So, we have that lg∗(lg(n)) grows more quickly
Exercise 3.2-6
φ2= 1 + √5
2!2
=6+2√5
4= 1 + 1 + √5
2= 1 + φ
ˆ
φ2= 1−√5
2!2
=6−2√5
4= 1 + 1−√5
2= 1 + ˆ
φ
Exercise 3.2-7
First, we show that 1 + φ=6+2√5
4=φ2. So, for every i,φi−1+φi−2=
φi−2(φ+ 1) = φi. Similarly for ˆ
φ.
For i= 0, φ0−ˆ
φ0
√5= 0. For i= 1, 1+√5
2−1−√5
2
√5=√5
√5= 1. Then, by induction,
Fi=Fi−1+Fi−2=φi−1+φi−2−(ˆ
φi−1+ˆ
φi−2)
√5=φi−ˆ
φi
√5.
Exercise 3.2-8
Let c1and c2be such that c1n≤kln k≤c2n. Then we have ln c1+ ln n=
ln(c1n)≤ln(kln k) = ln k+ ln(ln k) so ln n=O(ln k). Let c3be such that
ln n≤c3ln k. Then n
ln n≥n
c3ln k≥k
c2c3
4
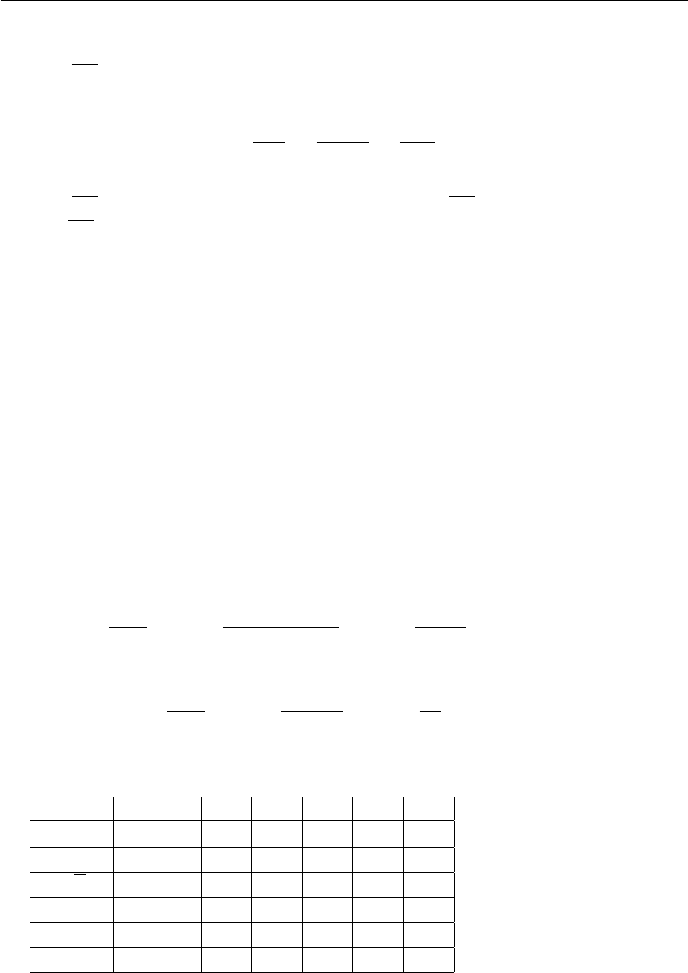
so that n
ln n= Ω(k). Similarly, we have ln k+ ln(ln k) = ln(kln k)≤ln(c2n) =
ln(c2) + ln(n) so ln(n) = Ω(ln k). Let c4be such that ln n≥c4ln k. Then
n
ln n≤n
c4ln k≤k
c1c4
so that n
ln n=O(k). By Theorem 3.1 this implies n
ln n= Θ(k). By symmetry,
k= Θ n
ln n.
Problem 3-1
a. If we pick any c > 0, then, the end behavior of cnk−p(n) is going to infinity,
in particular, there is an n0so that for every n≥n0, it is positive, so, we
can add p(n) to both sides to get p(n)< cnk.
b. If we pick any c > 0, then, the end behavior of p(n)−cnkis going to infinity,
in particular, there is an n0so that for every n≥n0, it is positive, so, we
can add cnkto both sides to get p(n)> cnk.
c. We have by the previous parts that p(n) = O(nk) and p(n) = Ω(nk). So, by
Theorem 3.1, we have that p(n) = Θ(nk).
d.
lim
n→∞
p(n)
nk= lim
n→∞
nd(ad+o(1))
nk<lim
n→∞
2adnd
nk= 2adlim
n→∞ nd−k= 0
e.
lim
n→∞
nk
p(n)= lim
n→∞
nk
ndO(1) <lim
n→∞
nk
nd= lim
n→∞ nk−d= 0
Problem 3-2
A B O o ΩωΘ
lgkn nyes yes no no no
nkcnyes yes no no no
√n nsin nno no no no no
2n2n/2no no yes yes no
nlog cclog nyes no yes no yes
log(n!) log(nn) yes no yes no yes
Problem 3-3
5
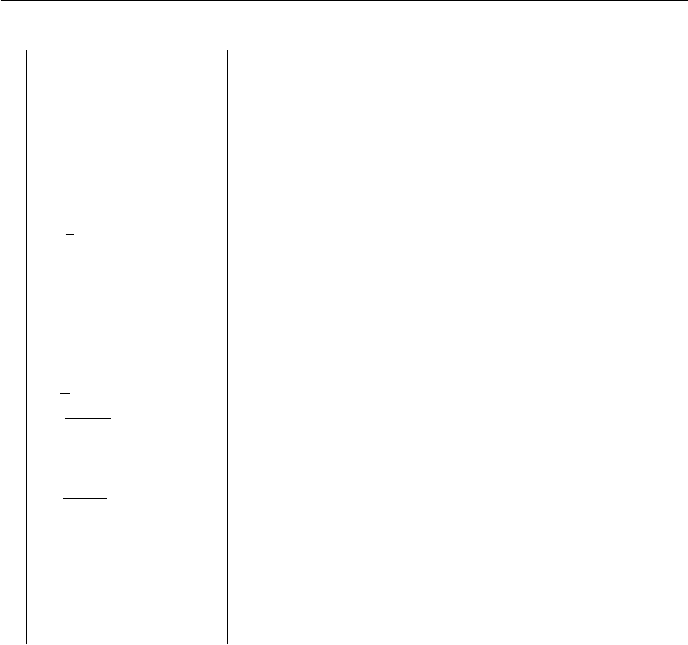
a.
22n+1
22n
(n+ 1)!
n!
n2n
en
2n
3
2n
(lg(n))!
nlg(lg(n)) lg(n)lg(n)
n3
n24lg(n)
nlg(n) lg(n!)
2lg(n)n
(√2)lg(n)
2√2 lg(n)
lg2(n)
lg(n)
plg(n)
ln(ln(n))
2lg∗(n)
lg∗(n) lg∗(lg(n))
lg(lg∗(n)
1n1/lg(n)
The terms are in decreasing growth hrate by row. Functions in the same row
are Θ of eachother.
b.
f(n) = g1(n)! nmod 2 = 0
0nmod 2 = 1
Problem 3-4
a. False. Counterexample: n=O(n2) but n26=O(n).
b. False. Counterexample: n+n26= Θ(n).
c. True. Since f(n) = O(g(n)) there exist cand n0sucht hat n≥n0implies
f(n)≤cg(n) and f(n)≥1. This means that log(f(n)) ≤log(cg(n)) =
log(c) + log(g(n)). Note that the inequality is preserved after taking logs
because f(n)≥1. Now we need to find dsuch that f(n)≤dlog(g(n)). It
will suffice to make log(c) + log(g(n)) ≤dlog(g(n)), which is achieved by
taking d= log(c) + 1, since log(g(n)) ≥1.
6

d. False. Counterexample: 2n=O(n) but 22n6= 2nas shown in exercise 3.1-4.
e. False. Counterexample: Let f(n) = 1
n. Suppose that cis such that 1
n≤c1
n2
for n≥n0. Choose ksuch that kc ≥n0and k > 1. Then this implies
1
kc ≤c
k2c2=1
k2c, a contradiction.
f. True. Since f(n) = O(g(n)) there exist cand n0such that n≥n0implies
f(n)≤cg(n). Thus g(n)≥1
cf(n), so g(n) = Ω(f(n)).
g. False. Counterexample: Let f(n) = 22n. By exercise 3.1-4, 22n6=O(2n).
h. True. Let gbe any function such that g(n) = o(f(n)). Since gis asymp-
totically positive let n0be such that n≥n0implies g(n)≥0. Then
f(n) + g(n)≥f(n) so f(n) + o(f(n)) = Ω(f(n)). Next, choose n1such
that n≥n1implies g(n)≤f(n). Then f(n) + g(n)≤f(n) + f(n) = 2f(n)
so f(n) + o(f(n)) = O(f(n)). By Theorem 3.1, this implies f(n) + o(f(n)) =
Θ(f(n)).
Problem 3-5
a. Suppose that we do not have that f=O(g(n)). This means that ∀c >
0, n0,∃n≥n0, f(n)> cg(n). Since this holds for every c, we can let it be
arbitrary, say 1. Initially, we set n0= 1, then, the resulting nwe will call
a1. Then, in general, let n0=ai+ 1 and let ai+1 be the resulting value
of n. Then, on the infinite set {a1, a2, . . .}, we have f(n)> g(n), and so,
f=∞
Ω(g(n))
This is not the case for the usual definition of Ω. Suppose we had f(n) = n2(n
mod 2) and g(n) = n. On all the even values, g(n) is larger, but on all the
odd values, f(n) grows more quickly.
b. The advvantage is that you get the result of part a which is a nice property. A
disadantage is that the infinite set of points on which you are making claims
of the behavior could be very sparse. Also, there is nothing said about the
behavior when outside of this infinite set, it can do whatever it wants.
c. A function fcan only be in Θ(g(n)) if f(n) has an infinite tail that is non–
negative. In this case, the definition of O(g(n)) agrees with O0(g(n)). Sim-
ilarly, for a funtion to be in Ω(g(n)), we need that f(n) is non-negative for
some infinite tail, on which O(g(n)) is identical to O0(g(n)). So, we have
athat in both directions, changing Oto O0does not change anything.
7
d. Suppose f(n)∈∼
Θ(g(n)), then ∃c1, c2, k1, k2, n0,∀n≥n0,0≤c1g(n)
lgk1(n)≤
f(n)≤c2g(n) lgk2(n), if we just look at these inequalities saparately, we have
c1g(n)
lgk1(n)≤f(n) (f(n)∈∼
Ω(g(n))) and f(n)≤c2g(n) lgk2(n) (f(n)∈∼
O(g(n))).
Now for the other direction. Suppose that we had ∃n1, c1, k1∀n≥n1,c1g(n)
lgk1(n)≤
f(n) and ∃n2, c2, k2,∀n≥n2, f(n)≤c2g(n) lgk2(n). Putting these to-
gether, and letting n0= max(n1, n2), we have ∀n≥n0,c1g(n)
lgk1(n)≤f(n)≤
c2g(n) lgk2(n).
Problem 3-6
f(n)c f∗
c(n)
n−1 0 dne
log n1 log∗n
n/2 1 dlog(n)e
n/2 2 dlog(n)e − 1
√n2 log log n
√n1 undefined
n1/32 log3log2(n)
n/ log n2 Ω log n
log(log n)
8

Chapter 4
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 4.1-1
It will return the least negative position. As each of the cross sums are
computed, the most positive one must have the shorest possible lengths. The
algoritm doesn’t consider length zero sub arrays, so it must have length 1.
Exercise 4.1-2
Algorithm 1 Brute Force Algorithm to Solve Maximum Subarray Problem
lef t = 1
right = 1
max =A[1]
curSum = 0
for i= 1 to ndo // Increment left end of subarray
curSum = 0
for j=ito ndo // Increment right end of subarray
curSum =curSum +A[j]
if curSum > max then
max =curSum
lef t =i
right =j
end if
end for
end for
Exercise 4.1-3
The crossover point is at around a length 20 array, however, the times were
incredibly noisy and I think that there was a garbage collection during the run,
so it is not reliable. It would probably be more effective to use an acutal profiler
for measuring runtimes. By switching over the way the recursive algorithm
handles the base case, the recursive algorithm is now better for smaller values of
n. The chart included has really strange runtimes for the brute force algorithm.
These times were obtained on a Core 2 duo P8700 and java 1.8.0.51.
1
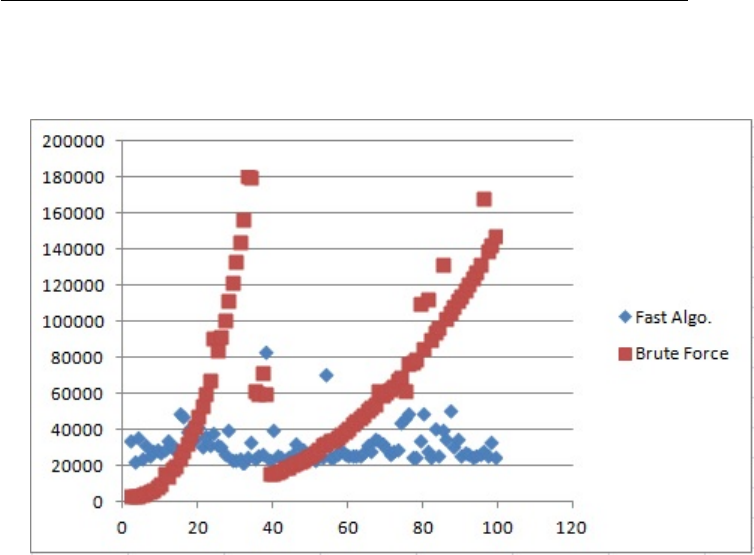
In the chart of runtimes, the x axis is the length of the array input. The y
axis is the measured runtime in nanoseconds.
Exercise 4.1-4
First do a linear scan of the input array to see if it contains any positive
entries. If it does, run the algorithm as usual. Otherwise, return the empty
subarray with sum 0 and terminate the algorithm.
Exercise 4.1-5
See the algorithm labeled linear time maximum subarray.
Exercise 4.2-1
2

Algorithm 2 linear time maximum subarray(A)
1: M=−∞
2: lowM, highM=null
3: Mr= 0
4: lowr= 1
5: for ifrom 1 to A.length do
6: Mr+ = A[i]
7: if Mr> M then
8: lowM=lowr
9: highM=i
10: M=Mr
11: end if
12: if Mr<0then
13: Mr= 0
14: lowr=i+ 1
15: end if
16: return (lowM, highM, M )
17: end for
S1= 8 −2=6
S2= 1 + 3 = 4
S3= 7 + 5 = 12
S4= 4 −6 = −2
S5= 1 + 5 = 6
S6= 6 + 2 = 8
S7= 3 −5 = −2
S8= 4 + 2 = 6
S9= 1 −7 = −6
S10 = 6 + 8 = 14
P1= 6
P2= 8
P3= 72
P4=−10
P5= 48
P6=−12
P7=−84
3

C11 = 48 −10 −8−12 = 18
C12 = 6 + 8 = 14
C21 = 72 −10 = 62
C22 = 48 + 6 −72 + 84 = 66
So, we get the final result:
18 14
62 66
Exercise 4.2-2
As usual, we will assume that nis an exact power of 2 and Aand Bare n
by nmatrices. Let A[i..j][k..m] denote the submatrix of Aconsisting of rows i
through jand columns kthrough m.
Exercise 4.2-3
you could pad out the input matrices to be powers of two and then run the
given algorithm. Padding out the the next largest power of two (call it m) will
at most double the value of n because each power of two is off from wach other
by a factor of two. So, this will have runtime
mlg 7 ≤(2n)lg 7 = 7nlg 7 ∈O(nlg 7)
and
mlg 7 ≥nlg 7 ∈Ω(nlg 7)
Putting these together, we get the runtime is Θ(nlg 7).
Exercise 4.2-4
Assume that n= 3mfor some m. Then, using block matrix multiplication,
we obtain the recursive running time T(n) = kT (n/3) +O(1). Using the Master
theorem, we need the largest integer ksuch that log3k < lg 7. This is given by
k= 21.
Exercise 4.2-5
If we take the three algorithms and divide the number of multiplications
by the side length of the matrices raised to lg(7), we approximately get the
4

Algorithm 3 Strassen(A, B)
if A.length == 1 then
return A[1] ·B[1]
end if
Let Cbe a new nby nmatrix
A11 = A[1..n/2][1..n/2]
A12 = A[1..n/2][n/2+1..n]
A21 = A[n/2+1..n][1..n/2]
A22 = A[n/2+1..n][n/2+1..n]
B11 = B[1..n/2][1..n/2]
B12 = B[1..n/2][n/2+1..n]
B21 = B[n/2+1..n][1..n/2]
B22 = B[n/2+1..n][n/2+1..n]
S1=B12 −B22
S2=A11 + A12
S3=A21 + A22
S4=B21 −B11
S5=A11 + A22
S6=B11 + B22
S7=A12 −A22
S8=B21 + B22
S9=A11 −A21
S10 =B11 + B12
P1=Strassen(A11, S1)
P2=Strassen(S2, B22)
P3=Strassen(S3, B11)
P4=Strassen(A22, S4)
P5=Strassen(S5, S6)
P6=Strassen(S7, S8)
P7=Strassen(S9, S10)
C[1..n/2][1..n/2] = P5+P4−P2+P6
C[1..n/2][n/2+1..n] = P1+P2
C[n/2+1..n][1..n/2] = P3+P4
C[n/2+1..n][n/2+1..n] = P5+P1−P3−P7
return C
5

following values
3745
3963
4167
This means that, if used as base cases for a Strassen Algorithm, the first one
will perform best for very large matrices.
Exercise 4.2-6
By considering block matrix multiplication and using Strassen’s algorithm as
a subroutine, we can multiply a kn×nmatrix by an n×kn matrix in Θ(k2nlog 7)
time. With the order reversed, we can do it in Θ(knlog 7) time.
Exercise 4.2-7
We can see that the final result should be
(a+bi)(c+di) = ac −bd + (cb +ad)i
We will be multiplying
P1= (a+b)c=ac +bcP2=b(c+d) = bc +bdP3= (a−b)d=ad +bd
Then, we can recover the real part by taking P1−P2and the imaginary part
by taking P2+P3.
Exercise 4.3-1
Inductively assume T(n)≤cn2, were cis taken to be max(1, T (1)) then
T(n) = T(n−1) + n≤c(n−1)2+n=cn2+ (1 −2c)n+ 1 ≤cn2+ 2 −2c≤cn2
The first inequality comes from the inductive hypothesis, the second from the
fact that n≥1 and 1 −2c < 0. The last from the fact that c≥1.
Exercise 4.3-2
We’ll show T(n)≤3 log n−1, which will imply T(n) = O(log n).
T(n) = T(dn/2e)+1
≤3 log(dn/2e)−1+1
≤3 log(3n/4)
= 3 log n+ 3 log(3/4)
≤3 log n+ log(1/2)
= 3 log n−1.
6

Exercise 4.3-3
Inductively assume that T(n)≤cn lg nwhere c= max(T(2)/2,1). Then,
T(n)=2T(bn/2c) + n≤2cbn/2clg(bn/2c) + n
≤cn lg(n/2) + n=cn(lg(n)−1) + n=cn(lg(n)−1 + 1
c)≤cn lg(n)
And so, T(n)∈O(nlg(n)).
Now, inductively assume that T(n)≥c0nlg(n) where c0= min(1/3, T (2)/2).
T(n) = 2T(bn/2c) + n≥2c0bn/2clg(bn/2c) + n≥c0(n−1) lg((n−1)/2) + n
=c0(n−1)(lg(n)−1−lg(n/(n−1))) + n
=c0n(lg(n)−1−lg(n/(n−1)) + 1
c0)−c0(lg(n)−1−lg(n/(n−1)))
≥c0n(lg(n)−2 + 1
c0−(lg(n−1) −1)
n)≥c0n(lg(n)−3 + 1
c0)≥c0nlg(n)
So, T(n)∈Ω(n). Together with the first part of this problem, we get that
T(n)∈Θ(n).
Exercise 4.3-4
We’ll use the induction hypothesis T(n)≤2nlog n+ 1. First observe that
this means T(1) = 1, so the base case is satisfied. Then we have
T(n)=2T(bn/2c) + n
≤2((2n/2) log(n/2) + 1) + n
= 2nlog(n)−2nlog 2 + 2 + n
= 2nlog(n) + 1 + n+ 1 −2n
≤2nlog(n)+1.
Exercise 4.3-5
If nis even, then that step of the induction is the same as the “inexact”
recurrence for merge sort. So, suppose that nis odd, then, the recurrence is
T(n) = T((n+ 1)/2) + T((n−1)/2) + Θ(n). However, shifting the argu-
ment in nlg(n) by a half will only change the value of the function by at most
1
2·d
dn (nlg(n)) = lg(n)
2+ 1, but this is o(n) and so will be absorbed into the Θ(n)
term.
Exercise 4.3-6
7

Choose n1such that n≥n1implies n/2 + 17 ≤3n/4. We’ll find cand d
such that T(n)≤cn log n−d.
T(n)=2T(bn/2c+ 17) + n
≤2(c(n/2 + 17) log(n/2 + 17) −d) + n
≤cn log(n/2 + 17) + 17clog(n/2 + 17) −2d+n
≤cn log(3n/4) + 17clog(3n/4) −2d+n
=cn log n−d+cn log(3/4) + 17clog(3n/4) −d+n.
Take c=−2/log(3/4) and d= 34. Then we have T(n)≤cn log n−d+
17clog(n)−n. Since log(n) = o(n), there exists n2such that n≥n2im-
plies n≥17clog(n). Letting n0= max{n1, n2}we have that n≥n0implies
T(n)≤cn log n−d. Therefore T(n) = O(nlog n).
Exercise 4.3-7
We first try the substitution proof T(n)≤cnlog34.
T(n)=4T(n/3) + n≤4c(n/3)log34+n= 4cnlog34+n
This clearly will not be ≤cnlog34as required.
Now, suppose instead that we make our inductive hypothesis T(n)≤cnlog34−
3n.
T(n) = 4T(n/3) + n≤4(c(n/3)log34−n) + n=cnlog34−4n+n=cnlog34−3n
as desired.
Exercise 4.3-8
Suppose we want to use substitution to show T(n)≤cn2for some c. Then
we have
T(n)=4T(n/2) + n
≤4(c(n/2)2) + n
=cn2+n,
which fails to be less than cn2for any c > 0. Next we’ll attempt to show
T(n)≤cn2−n.
T(n)=4T(n/2) + n
≤4(c(n/2)2−n) + n
=cn2−4cn +n
≤cn2
8
provided that c≥1/4.
Exercise 4.3-9
Consider nof the form 2k. Then, the recurrence becomes
T(2k)=3T(2(k/2)) + k
We define S(k) = T(2k). So,
S(k)=3S(k/2) + k
We use the inductive hypothesis S(k)≤(S(1) + 2)klog23−2k
S(k) = 3S(k/2) + k≤3(S(1) + 2)(k/2)log23−3k+k= (S(1) + 2)klog23−2k
as desired. Similarly, we show that S(k)≥(S(1) + 2)klog23−2k
S(k)=3S(k/2) + k≥(S(1) + 2)klog23−2k
So, we have that S(k) = (S(1) + 2)klog23−2k. Translating this back to T,
T(2k)=(T(2) + 2)klog23−2k. So, T(n) = (T(2) + 2)(lg(n))log23−2 lg(n).
Exercise 4.4-1
Since in a recursion tree, the depth of the tree will be lg(n), and the number
of nodes that are ilevels below the root is 3i. This means that we would estimate
that the runtime is Plg(n)
i=0 3i(n/2i) = nPlg(n)
i=0 (3/2)i=n(3/2)lg(n)−1
.5≈nlg(3).
We can see this by performing a substutiton T(n)≤cnlg(3) −2n. Then, we
have that
T(n)=3T(nbn/2c) + n
≤3cnlg(3)/2lg(3) −3n+n
=cnlg(3) −n
So, we have that T(n)∈O(nlg(3)).
Exercise 4.4-2
As we construct the tree, there is only one node at depth d, and its weight
is n2/(2d)2. Since the tree has log(n) levels, we guess that the solution is
roughly Plog n
i=0 n2
4i=O(n2). Next we use the substitution method to verify that
T(n)≤cn2.
T(n) = T(n/2) + n2
≤c(n/2)2+n2
= ( c
4+ 1)n2
≤cn2
9

provided that c≥4/3.
Exercise 4.4-3
Again, we notice that the depth of the tree is around lg(n), and there are 4i
vertices on the ith level below the root, so, we have that our guess is n2. We
show this fact by the substitution method. We show that T(n)≤cn2−6n
T(n)=4T(n/2 + 2) + n
≤4c(n2/4+2n+ 4 −3n−12) + n
=cn2−4cn −32c+n
Which will be ≤cn2−6 so long as we have −4c+ 1 ≤ −6 and c≥0. These
can both be satisfied so long as c≥7
4.
Exercise 4.4-4
The recursion tree looks like a complete binary tree of height nwith cost 1 at
each node. Thus we guess that the solution is O(2n). We’ll use the substitution
method to verify that T(n)≤2n−1.
T(n)=2T(n−1) + 1
≤2(2n−1−1) + 1
= 2n−1.
Exercise 4.4-5
The recursion tree looks like one long branch and off of it, branches that
jump all the way down to half. This seems like a pretty full tree, we’ll we’ll
guess that the runtime is O(n2). To see this by the substitution method, we try
to show that T(n)≤2nby the substitution method.
T(n) = T(n−1) + T(n/2) + n
≤2n−1+√2n+n
≤2n
Now, to jsutfiy that this is acutally a pretty dight bound, we’ll show that we
can’t have any polynomial upper bound. That is, if we have that T(n)≤cnk
then, when we substitute into the recurrence, we get that the new coeffient for
nkcan be as high as c(1+ 1
2k) which is bigger than cregardless of how we choose
c.
Exercise 4.4-6
10
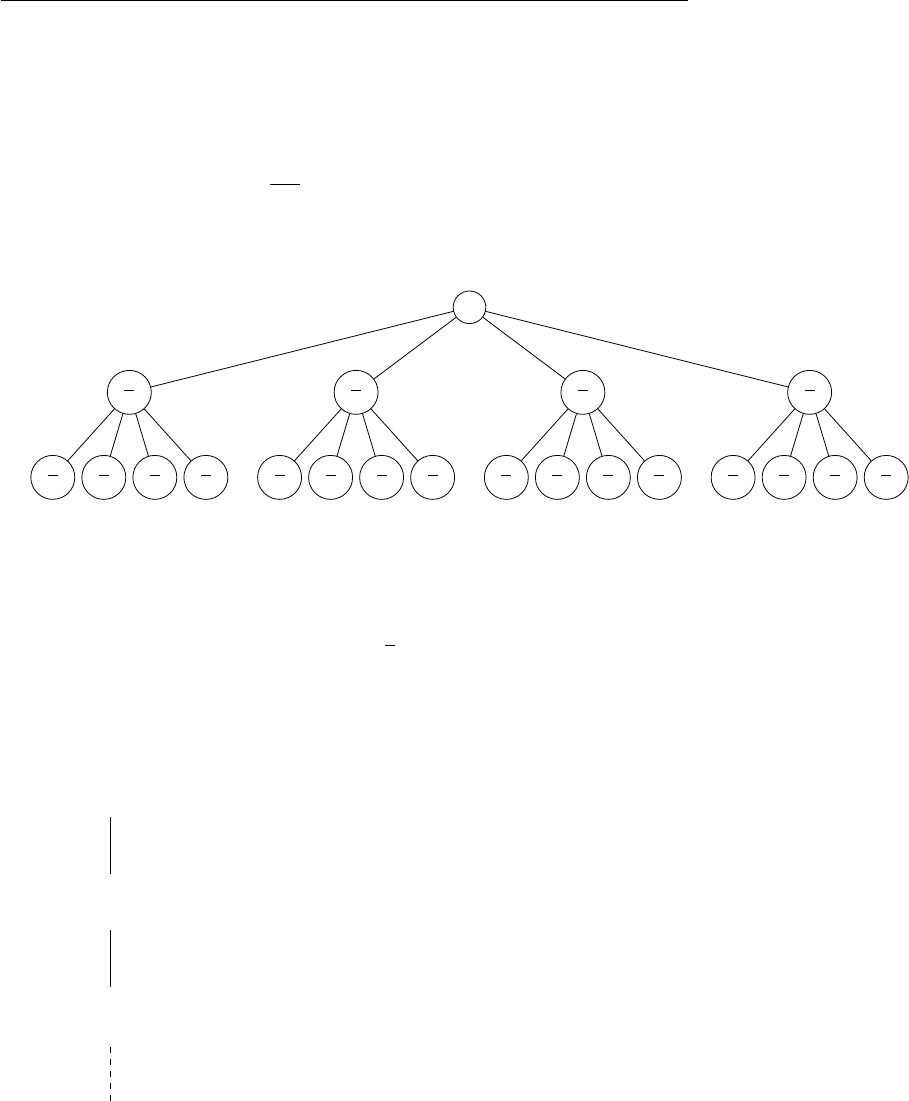
Examining the tree in figure 4.6 we observe that the cost at each level of the
tree is exactly cn. To find a lower bound on the cost of the algorithm, we need
a lower bound on the height of the tree. The shortest simple path from root to
leaf is found by following the left child at each node. Since we divide by 3 at
each step, we see that this path has length log3n, so the cost of the algorithm
is cn(log3n+ 1) ≥cn log3n=c
log3nlog n= Ω(nlog n).
Exercise 4.4-7
Here is an example for n= 4.
n
n
2
n
4
n
4
n
4
n
4
n
2
n
4
n
4
n
4
n
4
n
2
n
4
n
4
n
4
n
4
n
2
n
4
n
4
n
4
n
4
We can see by an wasy substitution that the answer is Θ(n2). Suppose that
T(n)≤c0n2then
T(n)=4T(bn/2c) + cn
≤c0n2+cn
which is ≤c0n2whenever we have that c0+c
n≤1, which, for large enough nis
true so long as c0<1. We can do a similar thing to show that it is also bounded
below by n2.
Exercise 4.4-8
T(a) + cn
T(a) + c(n−a)
T(a) + c(n−2a)
T(1)
11

Since each node of the recursion tree has only one child, the cost at each
level is just the cost of the node. Moreover, there are dn/aelevels in the tree.
Summing the cost at each level we see that the total cost of the algorithm is
dn/ae−1
X
i=0
T(a) + c(n−ia) = dn/aeT(a) + cdn/aen−cadn/ae(dn/ae − 1)
2.
To compute the asymptotoics we can assume nis divisible by aand ignore
the ceiling functions. Then this becomes
c
2an2+ (T(a)/a +c/2)n= Θ(n2).
Exercise 4.4-9
Since the sum of the sizes of the two children is αn + (1 −α)n=n, we would
guess that this behaves the same way as in the analysis of merge sort, so, we’ll
try to show that it has a solution that is T(n)≤c0nlg(n)−cn.
T(n) = T(αn) + T((1 −α)n) + cn
≤c0αn(lg(α) + lg(n)) −cαn +c0(1 −α)n(lg(1 −α) + lg(n)) −c(1 −α)n+cn
=c0nlg(n) + c0n(αlg(α) + (1 −α) lg(1 −α))
≤c0nlg(n)−c0n
Where we use the fact that xlg(x) is convex for the last inequality. This
then completes the induction if we have c0≥cwhich is easy to do.
Exercise 4.5-1
a. Θ(√n)
b. Θ(√nlg(n))
c. Θ(n)
d. Θ(n2)
Exercise 4.5-2
Recall that Strassen’s algorithm has running time Θ(nlg 7). We’ll choose
a= 48. This is the largest integer such that log4(a)<lg 7. Moreover,
2<log4(48) so there exists > 0 such that n2< nlog4(48)−. By case 1 of
the Master theorem, T(n) = Θ(nlog4(48)) which is asymptotically better than
Θ(nlg 7).
12

Exercise 4.5-3
Applying the method with a= 1, b = 2, we have that Θ(nlog12) = Θ(1). So,
we are in the second case, so, we have a final result of Θ(nlog12lg(n)) = Θ(lg(n)).
Exercise 4.5-4
The master method cannot be applied here. Observe that logba= log24=2
and f(n) = n2lg n. It is clear that cases 1 and 2 do not apply. Furthermore,
although fis asymptotically larger than n2, it is not polynomially larger, so
case 3 does not apply either. We’ll show T(n) = O(n2lg2n). To do this, we’ll
prove inductively that T(n)≤n2lg2n.
T(n)=4T(n/2) + n2lg n
≤4((n/2)2lg2(n/2)) + n2lg n
=n2(lg n−lg 2)2+n2lg n
=n2lg2n−n2(2 lg n−1−lg n)
=n2lg2n−n2(lg n−1)
≤n2lg2n
provided that n≥2.
Exercise 4.5-5
Let =a= 1, b = 3, and f= 3n+ 23nχ{2i:i∈N}where χAis the indicator
function of the set A. Then, we have that for any number nwhich is three times
a power of 2, we know that
f(n)=3n < 2n+n=f(n/3)
And so, it fails the regularity condition, even though f∈Ω(n) = Ω(nlogb(a)+).
Exercise 4.6-1
njis obtained by shifting the base brepresentation jpositions to the right,
and adding 1 if any of the jleast significant positions are non-zero.
Exercise 4.6-2
Assume that n=bmfor some m. Let c1and c2be such that c2nlogbalgkn≤
f(n)≤c1nlogbalgkn. We’ll first prove by strong induction that T(n)≤nlogbalgk+1 n−
dnlogbalgknfor some choice of d≥0. Equivalently, that T(bm)≤amlnk+1(bm)−
13

damlgk(bm).
T(bm) = aT (bm/b) + f(bm)
≤a(am−1lgk+1(bm−1)−dam−1lgkbm−1) + c1amlgk(bm)
=≤amlgk+1(bm−1)−damlgkbm−1+c1amlgk(bm)
=≤am[lg(bm)−lg b]k+1 −dam[lg bm−lg b]k+c1amlgk(bm)
=amlgk+1(bm)−damdlgkbm−am d
k−1
X
r=0 k
rlgr(bm)(−lg b)k−r+
k
X
r=0 k+ 1
rlgr(bm)(−lg(b))k+1−r+c1lgk(bm)!
=amlgk+1(bm)−damlgkbm−am (c1−klg b) lgk(bm) +
k−1
X
r=0 k+ 1
rlgr(bm)(−lg(b))k+1−r+d
k−1
X
r=0 k
rlgr(bm)(−lg b)k−r!
≤amlgk+1(bm)−damlgkbm
for c1≥klg b. Thus T(n) = O(nlogbalgk+1 n). A similar analysis shows
T(n) = Ω(nlogbalgk+1 n).
Exercise 4.6-3
Suppose that fsatisfies the regularity condition, we want that ∃, d, k,∀n≥
k, we have f(n)≥dnlogba+. By the regularity condition, we have that for
sufficiently large n,af(n/b)≤cf(n). In particular, it is true for all n≥bk. Let
this be our kfrom above, also, =−logb(c). Finally let dbe the largest value
of f(n)/nlogb(a)+between bk and b2k. Then, we will prove by induction on
the highest iso that bikis less than nthat for every n≥k, f(n)≥dnlogba+.
By our definition of d, we have it is true for i= 1. So, suppose we have
bi−1k < n ≤bik. Then, by regularity and the inductive hypothesis, cf (n)≥
af(n/b)≥ad n
blogb(a)+. Solving for f(n), we have
f(n)≥ad
cn
blogba/c =a/c
blogb(a/c)dnlogb(a)+=dnlogb(a)+
Completing the induction.
Problem 4-1
a. By Master Theorem, T(n)∈Θ(n4)
b. By Master Theorem, T(n)∈Θ(n)
c. By Master Theorem, T(n)∈Θ(n2lg(n))
d. By Master Theorem, T(n)∈Θ(n2)
e. By Master Theorem, T(n)∈Θ(nlg(7))
14

f. By Master Theorem, T(n)∈Θ(n1/2lg(n))
g. Let d=mmod 2, we can easily see that the exact value of T(n) is
j=n/2
X
j=1
(2j+d)2=
n/2
X
j=1
4j2+ 4jd +d2=n(n+ 2)(n+ 1)
6+n(n+ 2)d
2+d2n
2
This has a leading term of n3/6, and so T(n)∈Θ(n3)
Problem 4-2
a. 1. T(n) = T(n/2) + Θ(1). Solving the recursion we have T(N) = Θ(lg N).
2. T(n) = T(n/2)+Θ(N). Solving the recursion we have T(N) = Θ(Nlg N).
3. T(n) = T(n/2) + Θ(n/2). Solving the recursion we have T(N) = Θ(N).
b. 1. T(n)=2T(n/2) + cn. Solving the recursion we have T(N) = Θ(Nlg N).
2. T(n) = 2T(n/2) + cn + 2Θ(N). Solving the recursion we have T(N) =
Θ(Nlg N) + Θ(N2) = Θ(N2).
3. T(n)=2T(n/2) + cn + 2c0n/2. Solving the recursion we have T(N) =
Θ(Nln N).
Problem 4-3
a. By Master Theorem, T(n)∈Θ(nlog3(4))
b. We first show by substitution that T(n)≤nlg(n).
T(n)=3T(n/3)+n/ lg(n)≤cn lg(n)−cn lg(3)+n/ lg(n) = cn lg(n)+n(1
lg(n)−clg(3)) ≤cn lg(n)
now, we show that T(n)≥cn1−for every > 0.
T(n)=3T(n/3) + n/ lg(n)≥3c/31−n1−+n/ lg(n)=3cn1−+n/ lg(n)
showing that this is ≤cn1−is the same as showing
3+n/(clg(n)) ≥1
Since lg(n)∈o(n) this inequality holds. So, we have that The function is
soft Theta of n, see problem 3-5.
15
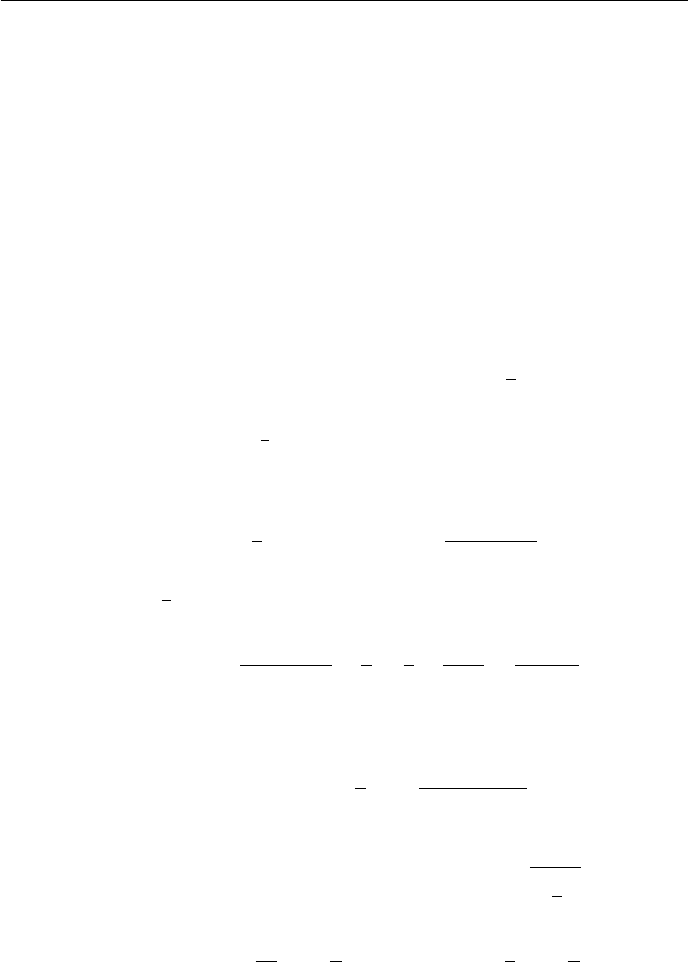
c. By Master Theorem, T(n)∈Θ(n2.5)
d. it is Θ(nlg(n)). The subtraction occurring inside the argument to Twon’t
change the saymptotics of the solution, that is, for large nthe division is
so much more of a change than the subtraction that it is the only part that
matters. once we drop that subtraction, the solution comes by the master
theorem.
e. By the same reasoning as part 2, the function is O(nlg(n)) and Ω(n1−) for
every and so is soft theta of n, see problem 3-5.
f. We will show that this is O(n) by substitution. We want that T(k)≤ck for
k < n, then,
T(n) = T(n/2) + T(n/4) + T(n/8) + n≤7
8cn +n
So, this is ≤cn so long as 7
8c+ 1 ≤cwhich happens whenever c≥8.
g. Recall that χAdenotes the indicator function of A, then, we see that the
sum is
T(0) +
n
X
j=1
1
j=T(0) + Zn+1
1
n+1
X
j=1
χ(j,j+1)(x)
jdx
However, since 1
xis monatonically decreasing, we have that for every i∈Z+,
sup
x∈(i,i+1)
n+1
X
j=1
χ(j,j+1)(x)
j−1
x=1
i−1
i+ 1 =1
i(i+ 1)
So, our expression for T(n) becomes
T(N) = T(0) + Zn+1
11
x+O(1
bxc(bxc+ 1)dx
We deal with the error term by first chopping out the constant amount
between 1 and 2 and then bound the error term by O(1
x(x−1) ) which has
an antiderivative (by method of partial fractions) that is O(1
n). so,
T(N) = Zn+1
1
dx
x+O(1
n= lg(n) + T(0) + 1
2+O(1
n)
This gets us our final answer of T(n)∈Θ(lg(n))
h. we see that we explicity have
T(n) = T(0) +
n
X
j=1
lg(j) = T(0) + Zn+1
1
n+1
X
j=1
χ(j,j+1)(x) lg(j)dx
16

Similarly to above, we will relate this sum to the integral of lg(x).
sup
x∈(i,i+1)
n+1
X
j=1
χ(j,j+1)(x) lg(j)−lg(x)
= lg(j+ 1) −lg(j) = lg j+ 1
j
So,
T(n)≤Zn
i
lg(x+ 2) + lg(x)−lg(x+ 1)dx = (1 + O(1
lg(n)))Θ(nlg(n))
i. See the approach used in the previous two parts, we will get T(n)∈Θ(li(n)) =
Θ( n
lg(n))
j. Let ibe the smallest iso that n1
2i<2. We recall from a previous problem
(3-6.e) that this is lg(lg(n)) Expanding the recurrence, we have that it is
T(n) = n1−1
2iT(2) + n+n
i
X
j=1
1∈Θ(nlg(lg(n)))
Problem 4-4
a. Recall that F0= 0, F1= 1, and Fi=Fi−1+Fi−2for i≥2. Then we have
F(z) = ∞
X
i=0
Fizi
=F0+F1z+∞
X
i=2
(Fi−1+Fi−2)zi
=z+z∞
X
i=2
Fi−1zi−1+z2∞
X
i=2
Fi−2zi−2
=z+z∞
X
i=1
Fizi+z2∞
X
i=0
Fizi
=z+zF(z) + z2F(z).
b. Manipulating the equation given in part (a) we have F(z)−zF(z)−z2F(z) =
z, so factoring and dividing gives
F(z) = z
1−z−z2.
Factoring the denominator with the quadratic formula shows 1 −z−z2=
(1 −φz)(1 −ˆ
φz), and the final equality comes from a partial fraction decom-
position.
17
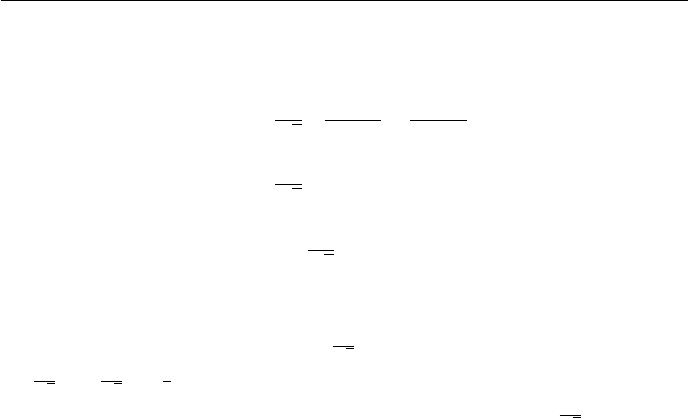
c. From part (b) and our knowledge of geometric series we have
F(z) = 1
√51
1−φz −1
1−ˆ
φz
=1
√5 ∞
X
i=0
(φz)i−∞
X
i=0
(ˆ
φz)i!
=∞
X
i=0
1
√5(φi−ˆ
φi)zi.
d. From the definition of the generating function, Fiis the coefficient of ziin
F(z). By part (c) this is given by 1
√5(φi−ˆ
φi). Since |ˆ
φ|<1 we must have
|ˆ
φi
√5|<|ˆ
φ
√5|<1
2. Finally, since the Fibonacci numbers are integers we see
that the exact solution must be the approximated solution φi
√5rounded to
the nearest integer.
Problem 4-5
a. The strategy for the bad chips is to always say that other bad chips are good
and other good chips are bad. This mirrors the strategy used by the good
chips, and so, it would be impossible to distinguish
b. Arbitrarily pair up the chips. Look only at the pairs for which both chips
said the other was good. Since we have at least half of the chips being good,
we know that there will be at least one such pair which claims the other is
good. We also know that at least half of the pairs which claim both are good
are actually good. Then, just arbirarily pick a chip from each pair and let
these be the chips that make up the sub-instance of the problem
c. Once we have indentified a single good chip, we can just use it to query every
other chip. The recurrence from before for the number of tests to find a good
chip was
T(n)≤T(n/2) + n/2
This has solution Θ(n) by the Master Theorem. So, we have the problem
can be solved in O(n) pairwise tests. Since we also neccesarily need to look
at at least half of the chips, we know that the problem is also Ω(n).
Problem 4-6
a. If an array Ais Monge then trivially it must satisfy the inequality by taking
k=i+ 1 and l=j+ 1. Now suppose A[i, j] + A[i+ 1, j + 1] ≤A[i, j + 1] +
A[i+ 1, j]. We’ll use induction on rows and columns to show that the array
18

is Monge. The base cases are each covered by the given inequality. Now fix i
and j, let r≥1, and suppose that A[i, j]+A[i+1, j+r]≤A[i, j+r]+A[i+1, j].
By applying the induction hypothesis and given inequality we have
A[i, j] + A[i+ 1, j +r+ 1] ≤A[i, j +r] + A[i+ 1, j]−A[i+ 1, j +r]
+A[i, j +r+ 1] + A[i+ 1, j +r]−A[i, j +r]
=A[i+ 1, j] + A[i, j +r+ 1]
so it follows that we can extend columns and preserve the Monge property.
Next we induct on rows. Suppose that A[i, j] + A[k, l]≤A[i, l] + A[k, j].
Then we have
A[i, j] + A[k+ 1, l]≤A[i, l] + A[k, j]−A[k, l] + A[k+ 1, l] by assumption
≤A[i, l] + A[k, j]−A[k, l] + A[k, l] + A[k+ 1, l −1] −A[k, l −1] by given inequality
=A[i, l]+(A[k, j] + A[k+ 1, l −1]) −A[k, l −1]
≤A[i, l] + A[k, l −1] + A[k+ 1, j]−A[k, l −1] by row proof
=A[i, l] + A[k+ 1, j].
b. Change the 7 to a 5.
c. Suppose that there exist iand ksuch that i<kbut f(i)> f(k). Since
Ais Monge we must have A[i, f(k)] + A[k, f(i)] ≤A[k, f (k)] + A[i, f(i)].
Since f(i) gives the position of the leftmost minimum element in row i,
this implies that A[i, f(k)] > A[i, f (i)]. Moreover, A[k, f(k)] ≤A[k, f(i)].
Combining these with the Monge inequality implies A[i, f(i)] + A[k, f(i)] <
A[k, f(i)]+A[i, f(i)], which is impossible since the two sides are equal. There-
fore no such iand kcan exist.
d. Linearly scan row 1 indices 1 through f(2) for the minimum element of row
1 and record as f(1). Next linearly scan indices f(2) through f(4) of row
3 for the minimum element of row 3. In general, we need only scan indices
f(2k) through f(2k+ 2) of row 2k+ 1 to find the leftmost minimum element
of row 2k+ 1. If mis odd, we’ll need to search indices f(m−1) through nto
find the leftmost minimum in row m. By part (c) we know that the indices
of the leftmost minimum elements are increasing, so we are guaranteed to
find the desired minimum from among the indices scanned. An element of
column jwill be scanned Nj+1 times, where Njis the number of isuch that
f(i) = j. Since Pn
j=1 Nj=n, the total number of comparisons is m+n,
giving a running time of O(m+n).
e. Let T(m, n) denote the running time of the algorithm applied to an mby n
matrix. T(m, n) = T(m/2, n) + c(m+n) for some constant c. We’ll show
19

T(m, n)≤c(m+nlog m)−2cm.
T(m, n) = T(m/2, n) + c(m+n)
≤c(m/2 + nlog(m/2)) −2cm +c(m+n)
=c(m/2 + nlog m)−cn +cn −cm
≤c(m+nlog m)−cm
so by induction we have T(m, n) = O(m+nlog m).
20

Chapter 5
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 5.1-1
We may of been presented the candidates in increasing order of goodness.
This would mean that we can apply transitivity to determine our preference
between any two candidates
Exercise 5.1-2
Algorithm 1 RANDOM(a,b)
1: n=dlg(b−a+ 1)e
2: Initialize an array Aof length n
3: while true do
4: for i= 1 to ndo
5: A[i] = RANDOM(0,1)
6: end for
7: if Aholds the binary representation of one of the numbers in athrough
bthen
8: return number represented by A
9: end if
10: end while
Each iteration of the while loop takes ntime to run. The probability that
the while loop stops on a given iteration is (b−a+ 1)/2n. Thus the expected
running time is the expected number of times run times n. This is given by:
nX
i≥1
i1−b−a+ 1
2ni−1b−a+ 1
2n=nb−a+ 1
2n 2n
b−a+ 12
=n2n
b−a+ 1 =O(lg(b−a)).
Exercise 5.1-3
Clearly since aand bare IID, the probability this algorithm returns one is
equal to the probability it returns 0. Also, since there is a constant positive
probabiltiy (2p(p−1)) that the algorithm returns on each iteration of the for
1

1: for all eternity do
2: a= BiasedRandom
3: b= BiasedRandom
4: if a>bthen
5: return 1
6: end if
7: if a<bthen
8: return 0
9: end if
10: end for
loop. This program will expect to go through the loop a number of times equal
to:
∞
X
j=0
j(1 −2p(p−1))j(2p(p−1)) = 2p(p−1)(1 −2p(p−1))
(2p(p−1))2=1−2p(p−1)
2p(p−1)
Note that the formula used for the sum of jαjcan be obtained by differentiawt-
ing both sides of the geometric sum formula for αjwith respect to α
Exercise 5.2-1
You will hire exactly one time if the best candidate is presented first. There
are (n−1)! orderings with the best candidate first, so, it is with probability
(n−1)!
n!=1
nthat you only hire once. You will hire exactly ntimes if the candi-
dates are presented in increasing order. This fixes the ordering to a single one,
and so this will occur with probability 1
n!.
Exercise 5.2-2
Since the first candidate is always hired, we need to compute the probability
that that exactly one additional candidate is hired. Since we view the cadidate
ranking as reading an random permutation, this is equivalent to the probability
that a random permutation is a decreasing sequence followed by an increase,
followed by another decreasing sequence. Such a permutation can be thought
of as a partition of [n] into 2 parts. One of size kand the other of size n−k,
where 1 ≤k≤n−1. For each such partition, we obtain a permutation with
a single increase by ordering the numbers each partition in decreasing order,
then concatenating these sequences. The only thing that can go wrong is if the
numbers nthrough n−k+ 1 are in the first partition. Thus there are n
k−1
permutations which correspond to hiring the second and final person on step
k+ 1. Summing, we see that the probability you hire exactly twice is
Pn−1
k=1 n
k−1
n!=2n−2−(n−1)
n!=2n−n−1
n!.
2

Exercise 5.2-3
Let Xjbe the indicator of a dice coming up j. So, the expected value of a
single dice roll Xis
E[X] =
6
X
j=1
jPr(Xj) = 1
6
6
X
j=1
j
So, the sum of ndice has probability
E[nX] = nE[X] = n
6
6
X
j=1
j=n6(6 + 1)
12 = 3.5n
Exercise 5.2-5
Let Xi,j for i < j be the indicator of A[i]> A[j]. Then, we have that the
expected number of inversions is
E
X
i<j
Xi,j
=X
i<j
E[Xi,j ] =
n−1
X
i=1
n
X
j=i+1
Pr(A[i]> A[j]) = 1
2
n−1
X
i=1
n−i
=n(n−1)
2−n(n−1)
4=n(n−1)
4.
Exercise 5.2-4
Let Xbe the number of customers who get back their own hat and Xibe the
indicator random variable that customer igets his hat back. The probability
that an individual gets his hat back is 1
n. Then we have
E[X] = E"n
X
i=1
Xi#=
n
X
i=1
E[Xi] =
n
X
i=1
1
n= 1.
Exercise 5.3-1
We modify the algorithm by unrolling the i= 1 case.
1: swap A[1] with A[Random(1,n)]
2: for i from 2 to n do
3: swap A[i] with A[Random(i,n)]
4: end for
Modify the proof of the lemma by starting with i= 2 instead of i= 1. This
entirely sidesteps the issue of talking about 0- permutations.
3

Exercise 5.3-2
The code does not do what he intends. Suppose A= [1,2,3]. If the algo-
rithm worked as proposed, then with nonzero probability the algorithm should
output [3,2,1]. On the first iteration we swap A[1] with either A[2] or A[3].
Since we want [3,2,1] and will never again alter A[1], we must necessarily swap
with A[3]. Now the current array is [3,2,1]. On the second (and final) iteration,
we have no choice but to swap A[2] with A[3], so the resulting array is [3,1,2].
Thus, the procedure cannot possibly be producing random non-identity permu-
tations.
Exercise 5.3-3
Consider the case of n= 3 in running the algorithm, three IID choices will
be made, and so you’ll end up having 27 possible end states each with equal
probability. There are 3! = 6 possible orderings, these shuld appear equally
often, but this can’t happen because 6 does not divide 27
Exercise 5.3-4
Fix a position jand an index i. We’ll show that the probability that A[i]
winds up in position jis 1/n. The probability B[j] = A[i] is the probability
that dest =j, which is the probability that i+offset or i+offset −nis equal
to j, which is 1/n. This algorithm can’t possibly return a random permutation
because it doesn’t change the relative positions of the elements; it merely cycli-
cally permutes the whole permutation. For instance, suppose A= [1,2,3]. If
offset = 1, B= [3,2,1]. If offset = 2, B= [2,3,1]. If v= 3, B= [1,2,3]. Thus,
the algorithm will never produce B= [1,3,2], so the resulting permutation can-
not be uniformly random.
Exercise 5.3-5
Let Xi,j be the event that P[i] = P[j]. Then, the event that all are unique
is the compliment of there being some pair that are equal, so, we must show
that Pr(∪i,j Xi,j )≤1/n. We start by applying a union bound
Pr(∪i<kXi,j )≤
n−1
X
i=1
n
X
j=i+1
Pr(Xi,j ) =
n−1
X
i=1
n
X
j=i+1
1
n3
Where we use the fact that any two indices will be equal with probability equal
to one over the size of the probability space being drawn from, which is n3.
=
n−1
X
i=1
n−i
n3=n(n−1)
n3−n(n−1)
2n3=n−1
2n2<1
n
4
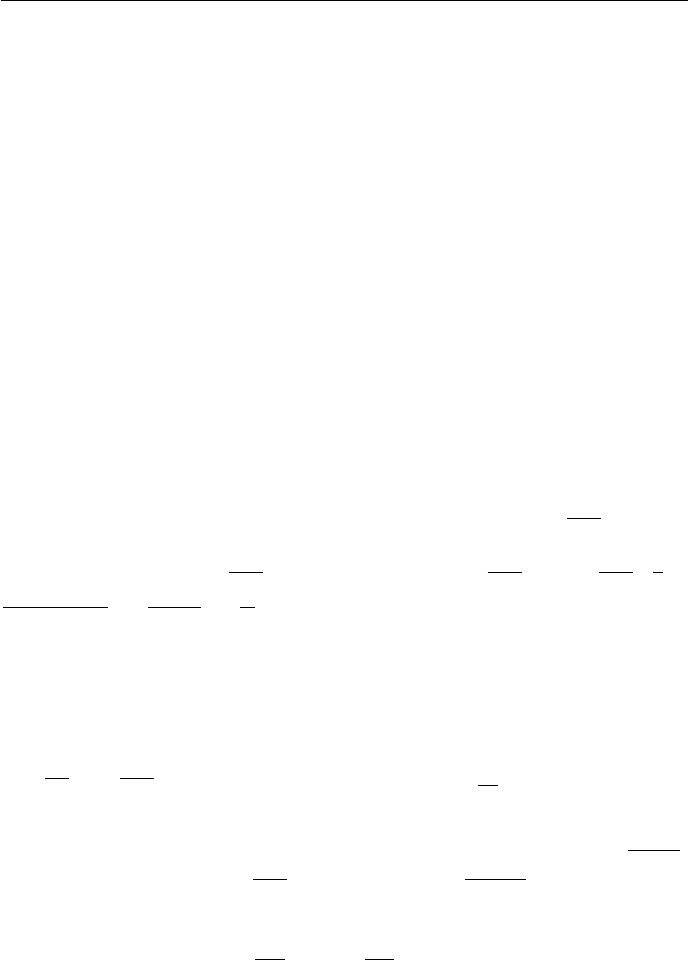
Exercise 5.3-6
After the completion of the for loop, check whether or not two or more priori-
ties are identical. Suppose that kof them are identical. Then call RAN DOM (1, k3)
ktimes to introduce a relative ordering on the kidentical entries. Some entries
mmay still be identical, so simply call RAN DOM(1, m3) that many times
to introduce a relative ordering on these indentical entries. For example, if
the first sequence of numbers we get is 1,1,1,3,4,5,5, we’ll need to order the
1’s and the 5’s. For the 1’s, we’ll call RANDOM(1,27) 3 times. Suppose
it produces 23,14,23. Then we’ll call RANDOM(1,8) twice to sort the 23’s.
Suppose it gives 3,5. Then the relative ordering of 23,14,23 becomes 2,1,3, so
the new relative ordering on the original array is 2,1,3,4,5,6,6. Now we call
RANDOM(1,8) twice to sort the 6’s. If the first number is larger than the
second, our final array will be 2,1,3,4,5,7,6.
Exercise 5.3-7
We prove that it produces a rawndom msubset by induction on m. It is
obviously true if m= 0 as there is only one size msubset of [n]. Suppose Sis a
uniform m−1 subset of n−1, that is, ∀j∈[n−1],Pr[j∈S] = m−1
n−1. Then, if
we let S0denote the returned set, suppose first j∈[n−1], Pr[j∈S0] = Pr[j∈
S] + Pr[j6∈ S∧i=j] = m−1
n−1+ Pr[j6∈ S] Pr[i=j] = m−1
n−1+1−m−1
n−11
n=
n(m−1)+n−m
(n−1)n=nm−m
(n−1)n=m
n. Since the constructed subset contains each of
[n−1] with the correct probability, it must also contain nwith the correct
probability because the probabilities sum to 1.
Exercise 5.4-1
The probability that none of npeople have the same birthday as you is
(1 −1
365 )n=364n
365n. This falls below zero when n≥log 364
365 (.5) ≈252.6 so, when
n= 253. Since you are also a person in the room, we add one to get the final
anwer of 254.
The probability that k of the n people have july 4 as a birthday is n
k364n−k
365 .
In particular, for k= 0 it is 364n
365nand for k= 1 it is n364n−1
365n. Adding these up
and solving for nto have the sum drop less than a half, we get
364
365n1 + n
364< .5
This is difficult to solve analytically, but because of the LHS’s monotonicity, the
answer can be found rather quickly by using a gallop search to be n= 612.
Exercise 5.4-2
We compute directly from the definition of expectation. Let Xdenote the
5
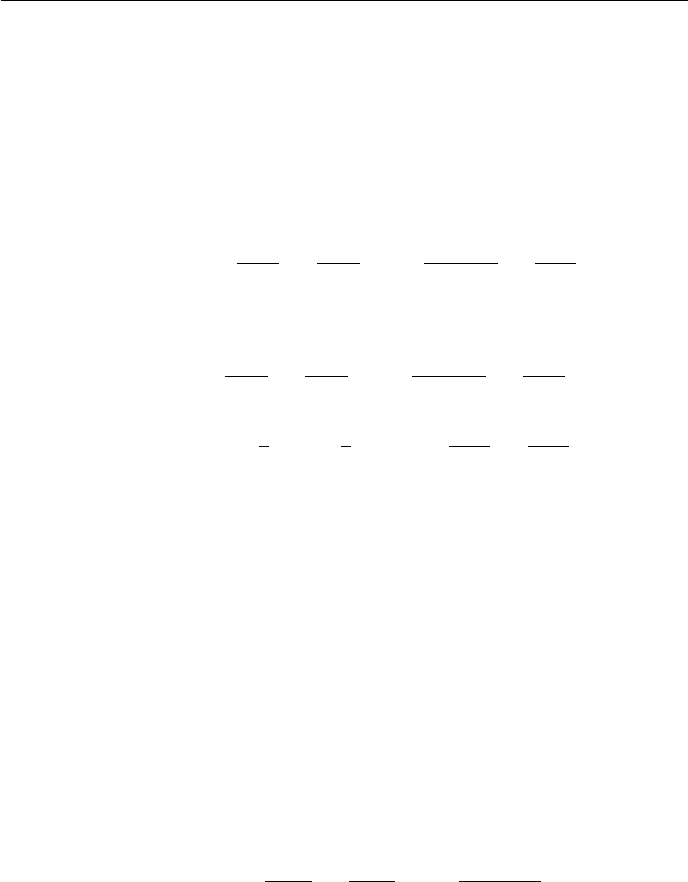
number of balls tossed until some bin contains two balls.
E[X] =
b+1
X
i=2
iP (X=i).
The probability that itosses are required is the probability that the first i−1
tosses go into unique bins, so we have
P(X=i)=1·b−1
bb−2
b· · · b−i+ 2
bi−1
b.
Thus
E[X] =
b+1
X
i=2
ib−1
bb−2
b· · · b−i+ 2
bi−1
b
=
b+1
X
i=2
i1−1
b1−2
b· · · 1−i−2
bi−1
b.
Exercise 5.4-3
Pairwise independence is sufficient. All the independence is used for is to
show that Pr(bi=r∧bj=r) = Pr(bi=r) Pr(bj=r). This is a result of
pairwise independence.
Exercise 5.4-4
We can compute ”likely” in two ways. The probability that at least three
people share the same birthday is 1 minus the probability that none share the
same birthday, minus the probability that any number of pairs of people share
the same birthday. Let n= 365 denote the number of days in a year and kbe
the number of people at the party. As computed earlier in the section, we have
P(all unique birthdays) = 1·n−1
nn−2
n· · · n−k+ 1
n≤e−k(k−1)/2n.
Next we compute the probability that exactly ipairs of people share a birth-
day. There are k
2k−2
2· · · k−2i+2
2ways to choose an ordered collection of i
pairs from the kpeople, n
iways to select the set of birthdays the pairs will
share, and the probability that any such ordered subset has these precise birth-
days is (1/n2)i. Multiplying by the probability that the rest of the birthdays
6

are different and unique we have
P(exactly ipairs of people share birthdays) = k
2k−2
2· · · k−2i+2
2n
i
n2in−i
nn−i−1
n· · · n−k+i+ 1
n
≤k!n
i
2i(k−2i)!n2i1−i
n1−i+ 1
n· · · 1−k−i−1
n
≤k!n
i
2i(k−2i)!n2ie−(k−1)(k−2i−1)/2n
Thus,
P(≥3 people share a birthday) ≤1−e−k(k−1)/2n−k!n
i
2i(k−2i)!n2ie−(k−1)(k−2i−1)/2n.
This is pretty messy, even with the simplifying inequality 1 + x≤ex, so
we’ll do another analysis, this time on expectation. We’ll determine the value
of krequired such that the expected number of triples (i, j, m) where person
i, person j, and person mshare a birthday is at least 1. Let Xijm be the
indicator variable that this triple of people share a birthday and Xdenote the
total number of triples of birthday-sharers. Then we have
E[X] = X
distinct triples (i,j,m)
E[Xijm] = k
31
n2.
To make E[X] exceed 1 we need to find the smallest ksuch that k(k−1)(k−
2) ≥6(365)2, which happens when k= 94.
Exercise 5.4-5
Since to be a k-permutation, we need that no letter appears repeated, it is
equivalent to the birthday problem with k people and n days. So, this probability
is given on the top of page 132 to be:
k−1
Y
i=1 1−i
n
Problem 5.4-6
Let Xibe the indicator variable that bin iis empty after all balls are tossed
and Xbe the random variable that gives the number of empty bins. Then we
have
E[X] =
n
X
i=1
E[Xi] =
n
X
i=1 n−1
nn
=nn−1
nn
.
7
Now let Xibe the indicator variable that bin icontains exactly 1 ball after
all balls are tossed and Xbe the random variable that gives the number of bins
containing exactly 1 ball. Then we have
E[X] =
n
X
i=1
E[Xi] =
n
X
i=1 n
1n−1
nn−11
n=nn−1
nn−1
because we need to choose which toss will go into bin i, then multiply by the
probability that that toss goes into that bin and the remaining n−1 tosses
avoid it.
Exercise 5.4-7
We split up the nflips into n/s groups where we pick s= lg(n)−2 lg(lg(n)).
We will show that at least one of these groups comes up all heads with proba-
bility at least n−1
n. So, the probability the group starting in position icomes
up all heads is:
Pr(Ai,lg(n)−2 lg(lg(n))) = 1
2lg(n)−2 lg(lg(n)) =lg(n)2
n
Since the groups are based of of disjoint sets of IID coinflips, these probabilities
are indipendent. so,
Pr(^
i
¬Ai,lg(n)−2 lg(lg(n))) = Y
i
Pr(¬Ai,lg(n)−2 lg(lg(n)))
=1−lg(n)2
n
n
lg(n)−2 lg(lg(n))
≤e−lg(n)2
lg(n)−2 lg(lg(n)) =1
ne
−2 lg(lg(n)) lg(n)
lg(n)−2 lg(lg(n))
=n−1−2 lg(lg(n))
lg(n)−2 lg(lg(n)) < n−1
Showing that the probability that there is no run of length at least lg(n)−
2 lg(lg(n)) to be <1
n.
Problem 5-1
a. We will show that the expected increase from each increment operation is
equal to one. Suppose that the value of the counter is currently i. Then, we
will increase the number represented from nito ni+1 with a probability of
1
ni+1−ni, leaving the value alone otherwise. Multiplying these together, we
get that the expected increase is ni+1 −ni
ni+1−ni−1.
b. For this choice of ni, we have that at each increment operation, the proba-
bility that we change the value of the counter is 1
100 . Since this is a constant
with respect to the current value of the counter i, we can view the final re-
sult as a minomial distribution with a p value of .01. Since the variance of
a binomial distribution is np(1 −p), and we have that each success is worth
100 instead, the variance is going to be equal to .99n.
8

Problem 5-2
a. Assume that Ahas nelements. Our algorithm will use an array Pto track
the elements which have been seen, and add to a counter ceach time a new
element is checked. Once this counter reaches n, we will know that every
element has been checked. Let RI(A) be the function that returns a random
index of A.
Algorithm 2 RANDOM-SEARCH
Initialize an array Pof size ncontaining all zeros
Initialize integers cand ito 0
while c6=ndo
i=RI(A)
if A[i] == xthen
return i
end if
if P[i] == 0 then
P[i]=1
c=c+ 1
end if
end while
return A does not contain x
b. Let Nbe the random variable for the number of searches required. Then
E[N] = X
i≥1
iP (iiterations are required)
=X
i≥1
in−1
ni−11
n
=1
n
1
1−n−1
n2
=n.
c. Let Nbe the random variable for the number of searches required. Then
E[N] = X
i≥1
iP (iiterations are required)
=X
i≥1
in−k
ni−1k
n
=k
n
1
1−n−k
n2
=n
k.
9

d. This is identical to the ”How many balls must we toss until every bin con-
tains at least one ball?” problem solved in section 5.4.2, whose solution is
b(ln b+O(1)).
e. The average case running time is (n+ 1)/2 and the worst case running time
is n.
f. Let Xbe the random variable which gives the number of elements examined
before the algorithm terminates. Let Xibe the indicator variable that the
ith element of the array is examined. If iis an index such that A[i]6=xthen
P(Xi) = 1
k+1 since we examine it only if it occurs before every one of the k
indices that contains x. If iis an index such that A[i] = xthen P(Xi) = 1
k
since only one of the indices corresponding to a solution will be examined.
Let S={i|A[i] = x}and S0={i|A[i]6=x}. Then we have
E[X] =
n
X
i=1
E[Xi] = X
i∈S
P(Xi) + X
i∈S0
P(Xi) = k
k+n−k
k+ 1 =n+ 1
k+ 1 .
Thus the average case running time is n+1
k+1 . The worst case happens when
every occurrence of xis in the last kpositions of the array. This has running
time n−k+ 1.
g. The average and worst case running times are both n.
h. SCRAMBLE-SEARCH works identically to DETERMINISTIC-SEARCH,
except that we add to the running time the time it takes to randomize the
input array.
i. I would use DETERMINISTIC-SEARCH since it has the best expected
runtime and is guaranteed to terminate after nsteps, unlike RANDOM-
SEARCH. Moreover, in the time it takes SCRAMBLE-SEARCH to randomly
permute the input array we could have performed a linear search anyway.
10
Chapter 6
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 6.1-1
At least 2hand at most 2h+1 −1. Can be seen because a complete binary
tree of depth h−1 has Σh−1
i=0 2i= 2h−1 elements, and the number of elements
in a heap of depth his between the number for a complete binary tree of depth
h−1 exclusive and the number in a complete binary tree of depth hinclusive.
Exercise 6.1-2
Write n= 2m−1 + kwhere mis as large as possible. Then the heap consists
of a complete binary tree of height m−1, along with kadditional leaves along
the bottom. The height of the root is the length of the longest simple path to
one of these kleaves, which must have length m. It is clear from the way we
defined mthat m=blg nc.
Exercise 6.1-3
If there largest element in the subtee were somewhere other than the root,
it has a parent that is in the subtree. So, it is larger than it’s parent, so, the
heap property is violated at the parent of the maximum element in the subtree
Exercise 6.1-4
The smallest element must be a a leaf node. Suppose that node xcontains
the smallest element and xis not a leaf. Let ydenote a child node of x. By
the max-heap property, the value of xis greater than or equal to the value of
y. Since the elements of the heap are distinct, the inequality is strict. This
contradicts the assumption that xcontains the smallest element in the heap.
Exercise 6.1-5
Yes, it is. The index of a child is always greater than the index of the parent,
so the heap property is satisfied at each vertex.
1
Exercise 6.1-6
No, the array is not a max-heap. 7 is contained in position 9 of the array, so
its parent must be in position 4, which contains 6. This violates the max-heap
property.
Exercise 6.1-7
It suffices to show that the elements with no children are exactly indexed
by {bn/2c+ 1, . . . , n}. Suppose that we had an iin this range. It’s childeren
would be located at 2iand 2i+ 1 but both of these are ≥2bn/2c+ 2 > n and so
are not in the array. Now, suppose we had an element with no kids, this means
that 2iand 2i+ 1 are both > n, however, this means that i > n/2. This means
that i∈ {bn/2c+ 1, . . . , n}.
Exercise 6.2-1
27 17 3 16 13 10 1 5 7 12 4 8 9 0
27 17 10 16 13 3 1 5 7 12 4 8 9 0
27 17 10 16 13 8 1 5 7 12 4 3 9 0
Exercise 6.2-2
Algorithm 1 MIN-HEAPIFY(A,i)
1: l=LEF T (i)
2: r=RIGHT (i)
3: if l≤A.heap −size and A[l]< A[i]then
4: smallest =l
5: else smallest =i
6: end if
7: if r≤A.heap −size and A[r]< A[smallest]then
8: smallest =r
9: end if
10: if smallest 6=ithen
11: exchange A[i] with A[smallest]
12: MAX-HEAPIFY(A, smallest)
13: end if
The running time of MIN-HEAPIFY is the same as that of MAX-HEAPIFY.
Exercise 6.2-3
The array remains unchanged since the if statement on line line 8 will be
false.
2

Exercise 6.2-4
If i > A.heap −size/2 then land rwill both exceed A.heap −size so the
if statement conditions on lines 3 and 6 of the algorithm will never be satisfied.
Therefore largest =iso the recursive call will never be made and nothing will
happen. This makes sense because inecessarily corresponds to a leaf node, so
MAX–HEAPIFY shouldn’t alter the heap.
Exercise 6.2-5
Iterative Max Heapify(A, i)
while i<A.heap-size do
l=LEFT(i)
r=LEFT(i)
largest =i
if l≤A.heap-size and A[l]> A[i]then
largest =l
end if
if l≤A.heap-size and A[r]> A[i]then
largest =r
end if
if largest 6=ithen
exchange A[i] and A[largest]
elsereturn A
end if
end while
return A
Exercise 6.2-6
Consider the heap resulting from Awhere A[1] = 1 and A[i] = 2 for
2≤i≤n. Since 1 is the smallest element of the heap, it must be swapped
through each level of the heap until it is a leaf node. Since the heap has height
blg nc, MAX-HEAPIFY has worst-case time Ω(lg n).
Exercise 6.3-1
5 3 17 10 84 19 6 22 9
5 3 17 22 84 19 6 10 9
5 3 19 22 84 17 6 10 9
5 84 19 22 3 17 6 10 9
84 5 19 22 3 17 6 10 9
84 22 19 5 3 17 6 10 9
84 22 19 10 3 17 6 5 9
3

Exercise 6.3-2
If we had started at 1, we wouldn’t be able to guarantee that the max-heap
property is maintained. For example, if the array Ais given by [2,1,1,3] then
MAX-HEAPIFY won’t exchange 2 with either of it’s children, both 1’s. How-
ever, when MAX-HEAPIFY is called on the left child, 1, it will swap 1 with 3.
This violates the max-heap property because now 2 is the parent of 3.
Exercise 6.3-3
All the nodes of height hpartition the set of leaves into sets of size between
2h−1+ 1 and 2h, where all but one is size 2h. Just by putting all the children
of each in their own part of trhe partition. Recall from 6.1-2 that the heap has
height blg(n)c, so, by looking at the one element of this height (the root), we
get that there are at most 2blg(n)cleaves. Since each of the vertices of height h
partitions this into parts of size at least 2h−1+ 1, and all but one corresponds
to a part of size 2h, we can let kdenote the quantity we wish to bound, so,
(k−1)2h+k(2h−1+ 1) ≤2blg(n)c≤n/2
so
k≤n+ 2h
2h+1 + 2h+ 1 ≤n
2h+1 ≤ln
2h+1 m
Exercise 6.4-1
4
5 13 2 25 7 17 20 8 4
5 13 20 25 7 17 2 8 4
5 25 20 13 7 17 2 8 4
25 5 20 13 7 17 2 8 4
25 13 20 5 7 17 2 8 4
25 13 20 8 7 17 2 5 4
4 13 20 8 7 17 2 5 25
20 13 4 8 7 17 2 5 25
20 13 17 8 7 4 2 5 25
5 13 17 8 7 4 2 20 25
17 13 5 8 7 4 2 20 25
2 13 5 8 7 4 17 20 25
13 2 5 8 7 4 17 20 25
13 8 5 2 7 4 17 20 25
4 8 5 2 7 13 17 20 25
8 4 5 2 7 13 17 20 25
8 7 5 2 4 13 17 20 25
4 7 5 2 8 13 17 20 25
7 4 5 2 8 13 17 20 25
2 4 5 7 8 13 17 20 25
5 4 2 7 8 13 17 20 25
2 4 5 7 8 13 17 20 25
4 2 5 7 8 13 17 20 25
2 4 5 7 8 13 17 20 25
Exercise 6.4-2
We’ll prove the loop invariant of HEAPSORT by induction:
Base case: At the start of the first iteration of the for loop of lines 2-5 we
have i=A.length. The subarray A[1..n] is a max-heap since BUILD-MAX-
HEAP(A) was just called. It contains the nsmallest elements, and the empty
subarray A[n+1..n] trivially contains the 0 largest elements of Ain sorted order.
Suppose that at the start of the ith iteration of of the for loop of lines 2-5,
the subarray A[1..i] is a max-heap containing the ismallest elements of A[1..n]
and the subarray A[i+ 1..n] contains the n−ilargest elements of A[1..n] in
sorted order. Since A[1..i] is a max-heap, A[1] is the largest element in A[1..i].
Thus it is the (n−(i−1))th largest element from the original array since the
n−ilargest elements are assumed to be at the end of the array. Line 3 swaps
A[1] with A[i], so A[i..n] contain the n−i+ 1 largest elements of the array,
and A[1..i −i] contains the i−1 smallest elements. Finally, MAX-HEAPIFY
is called on A, 1. Since A[1..i] was a max-heap prior to the iteration and only
the elments in positions 1 and iwere swapped, the left and right subtrees of
node 1, up to node i−1, will be max-heaps. The call to MAX-HEAPIFY will
place the element now located at node 1 into the correct position and restore the
5

max-heap property so that A[1..i −1] is a max-heap. This concludes the next
iteration, and we have verified each part of the loop invariant. By induction,
the loop invariant holds for all iterations.
After the final iteration, the loop invariant says that the subarray A[2..n]
contains the n−1 largest elements of A[1..n], sorted. Since A[1] must be the
nth largest element, the whole array must be sorted as desired.
Exercise 6.4-3
If it’s already sorted in increasing order, doing the build max heap-max-heap
call on line 1 will take Θ(nlg(n)) time. There will be niterations of the for loop,
each taking Θ(lg(n)) time because the element that was at position iwas the
smallest and so will have blg(n)csteps when doing max-heapify on line 5. So,
it will be Θ(nlg(n)) time.
If it’s already sorted in decreasing order, then the call on line one will only
take Θ(n) time, since it was already a heap to begin with, but it will still take
nlg(n) peel off the elements from the heap and re-heapify.
Exercise 6.4-4
Consider calling HEAPSORT on an array which is sorted in decreasing order.
Every time A[1] is swapped with A[i], MAX-HEAPIFY will be recursively called
a number of times equal to the height hof the max-heap containing the elements
of positions 1 through i−1, and has runtime O(h). Since there are 2knodes at
height k, the runtime is bounded below by
blg nc
X
i=1
2ilog(2i) =
blg nc
X
i=1
i2i= 2 + (blg nc − 1)2blg nc= Ω(nlg n).
Exercise 6.4-5
Since the call on line one could possibly take only linear time (if the input
was already a max-heap for example), we will focus on showing that the for loop
takes n log n time. This is the case because each time that the last element is
placed at the beginning to replace the max element being removed, it has to
go through every layer, because it was already very small since it was at the
bottom level of the heap before.
Exercise 6.5-1
The following sequence of pictures shows how the max is extracted from the
heap.
1. Original heap:
6
15
13
5
4 0
12
6 2
9
8
1
7
2. we move the last element to the top of the heap
1
13
5
4 0
12
6 2
9
8 7
3. 13 >9>1 so, we swap 1 and 13.
13
1
5
4 0
12
6 2
9
8 7
4. Since 12 >5>1, we swap 1 and 12.
7
13
12
5
4 0
1
6 2
9
8 7
5. Since 6 >2>1, we swap 1 and 6.
13
12
5
4 0
6
1 2
9
8 7
Exercise 6.5-2
The following sequence of pictures shows how 10 is inserted into the heap,
then swapped with parent nodes until the max-heap property is restored. The
node containing the new key is heavily shaded.
1. Original heap:
8
15
13
5
4 0
12
6 2
9
8
1
7
2. MAX-HEAP-INSERT(A,10) is called, so we first append a node assigned
value −∞:
15
13
5
4 0
12
6 2
9
8
1−∞
7
3. The key value of the new node is updated:
15
13
5
4 0
12
6 2
9
8
110
7
4. Since the parent key is smaller than 10, the nodes are swapped:
9
15
13
5
4 0
12
6 2
9
10
1 8
7
5. Since the parent node is smaller than 10, the nodes are swapped:
15
13
5
4 0
12
6 2
10
9
1 8
7
Exercise 6.5-3
Heap-Minimum(A)
1: return A[1]
Heap-Extract-Min(A)
1: if A.heap-size <1then
2: Error “heap underflow”
3: end if
4: min =A[1]
5: A[1] = A[A.heap −size]
6: A.heap −size − −
7: Min-heapify(A,1)
8: return min
Heap-decrease-key(A,i,key)
10

1: if key ¿ A[i] then
2: Error “new key larger than old key”
3: end if
4: A[i] = key
5: while i > 1 and A[P arent(i)] < A[i]do
6: exchange A[i] with A[P arent(i)]
7: i=P arent(i)
8: end while
Min-Heap-Insert(A,key)
1: A.heap −size + +
2: A[A.heap −size] = ∞
3: Heap-Decrease-Key(A,A.heap-size,key)
Exercise 6.5-4
If we don’t make an assignment to A[A.heap −size] then it could contain
any value. In particular, when we call HEAP-INCREASE-KEY, it might be the
case that A[A.heap −size] initially contains a value larger than key, causeing
an error. By assigning −∞ to A[A.heap −size] we guarantee that no error will
occur. However, we could have assigned any value less than or equal to key to
A[A.heap −size] and the algorithm would still work.
Exercise 6.5-5
Initially, we hve a heap and then only change the value at ito make it
larger. This can’t invalidate the ordering between iand it’s children, the only
other thing that needs to be related to iis that iis less than it’s parent, which
may be false. Thus we have the invariant is true at initalization. Then, when
we swap iwith its parent if it is larger, since it is larger than it’s parent, it must
also be larger than it’s sibling, also, since it’s parent was initally above its kids
in the heap, we know that it’s parent is larger than it’s kids. The only relation
in question is then the new iand it’s parent. At termination, iis the root, so it
has no parent, so the heap property must be satisfied everywhere.
Exercise 6.5-6
Replace A[i] by key in the while condition, and replace line 5 by “A[i] =
A[P AREN T (i)].” After the end of the while loop, add the line A[i] = key.
Since the key value doesn’t change, there’s no sense in assigning it until we
know where it belongs in the heap. Instead, we only make the assignement of
the parent to the child node. At the end of the while loop, iis equal to the
position where key belongs since it is either the root, or the parent is at least
11

key, so we make the assignment.
Exercise 6.5-7
Have a field in the structure that is just a count of the total number of
elements ever added. When adding an element, use the current value of that
counter as the key.
Exercise 6.5-8
The algorithm works as follows: Replace the node to be deleted by the last
node of the heap. Update the size of the heap, then call MAX-HEAPIFY to
move that node into its proper position and maintain the max-heap property.
This has running time O(lg n) since the number of times MAX-HEAPIFY is
recursively called is as most the height of the heap, which is blg nc.
Algorithm 2 HEAP-DELETE(A,i)
1: A[i] = A[A.heap −size]
2: A.heap −size =A.heap −size + 1
3: MAX-HEAPIFY(A,i)
Exercise 6.5-9
Construct a min heap from the heads of each of the klists. Then, to find
the next element in the sorted array, extract the minimum element (in Olg(k)
time). Then, add to the heap the next element from the shorter list from which
the extracted element originally came (also O(lg(k)) time). Since finding the
next element in the sorted list takes only at most O(lg(k)) time, to find the
whole list, you need O(nlg(k)) total steps.
Problem 6-1
a. They do not. Consider the array A=h3,2,1,4,5i. If we run Build-Max-
Heap, we get h5,4,1,3,2i. However, if we run Build-Max-Heap’, we will get
h5,4,1,2,3iinstead.
b. Each insert step takes at most O(lg(n)), since we are doing it ntimes, we
get a bound on the runtime of O(nlg(n)).
Problem 6-2
a. It will suffice to show how to access parent and child nodes. In a d-ary array,
PARENT(i) = bi/dc, and CHILD(k, i) = di −d+ 1 + k, where CHILD(k, i)
gives the kth child of the node indexed by i.
12

b. The height of a d-ary heap of nelements is with 1 of logdn.
c. The following is an implementation of HEAP-EXTRACT-MAX for a d-ary
heap. An implementation of DMAX-HEAPIFY is also given, which is the
analog of MAX-HEAPIFY for d-ary heap. HEAP-EXTRACT-MAX con-
sists of constant time operations, followed by a call to DMAX-HEAPIFY.
The number of times this recursively calls itself is bounded by the height of
the d-ary heap, so the running time is O(dlogdn). Note that the CHILD
function is meant to be the one described in part (a).
Algorithm 3 HEAP-EXTRACT-MAX(A) for a d-ary heap
1: if A.heap −size < 1then
2: error “heap underflow”
3: end if
4: max =A[1]
5: A[1] = A[A.heap −size]
6: A.heap −size =A.heap −size −1
7: DMAX-HEAPIFY(A,1)
Algorithm 4 DMAX-HEAPIFY(A,i)
1: largest =i
2: for k= 1 to ddo
3: if CHILD(k, i)≤A.heap −size and A[CHILD(k, i)] > A[i]then
4: if A[CHILD(k, i)] > largest then
5: largest =A[CHILD(k, i)]
6: end if
7: end if
8: end for
9: if largest 6=ithen
10: exchange A[i] with A[largest]
11: DMAX-HEAPIFY(A, largest)
12: end if
d. The runtime of this implementation of INSERT is O(logdn) since the while
loop runs at most as many times as the height of the d-ary array. Note that
when we call PARENT, we mean it as defined in part (a).
e. This is identical to the implementation of HEAP-INCREASE-KEY for 2-ary
heaps, but with the PARENT function interpreted as in part (a). The run-
time is O(logdn) since the while loop runs at most as many times as the
height of the d-ary array.
13
Algorithm 5 INSERT(A,key)
1: A.heap −size =A.heap −size + 1
2: A[A.heap −size] = key
3: i=A.heap −size
4: while i > 1 and A[P AREN T (i)< A[i]do
5: exchange A[i] with A[P AREN T (i)]
6: i=P AREN T (i)
7: end while
Algorithm 6 INCREASE-KEY(A,i,key)
1: if key < A[i]then
2: error “new key is smaller than current key ”
3: end if
4: A[i] = key
5: while i > 1 and A[P AREN T (i)< A[i]do
6: exchange A[i] with A[P AREN T (i)]
7: i=P AREN T (i)
8: end while
Problem 6-3
a.
2 3 4 5
8 9 12 14
16 ∞ ∞ ∞
∞ ∞ ∞ ∞
b. For every i, j,Y[1,1] ≤Y[i, 1] ≤Y[i, j]. So, if Y[1,1] = ∞, we know that
Y[i, j] = ∞for every i, j. This means that no elements exist. If Yis full, it
has no elements labeled ∞, in particular, the element Y[m, n] is not labeled
∞.
c. Extract-Min(Y,i,j), extracts the minimum value from the young tableau Y0
obtained by Y0[i0, j0] = Y[i0+i−1, j0+j−1]. Note that in running this
algorithm, several accesses may be made out of bounds for Y, define these
to return ∞. No store operations will be made on out of bounds locations.
Since the largest value of i+jthat this can be called with is n+m, and
this quantity must increase by one for each call, we have that the runtime is
bounded by n+m.
d. Insert(Y,key) Since i+jis decreasing at each step, starts as n+mand is
bounded by 2 below, we know that this program has runtime O(n+m).
e. Place the n2elements into a Young Tableau by calling the algorithm from
part d on each. Then, call the algorithm from part c n2to obtain the numbers
in increasing order. Both of these operations take time at most 2n∈O(n),
and are done n2times, so, the total runtime is O(n3)
14

1: min =Y[i, j]
2: if Y[i, j + 1] = Y[i+ 1, j] = ∞then
3: Y[i, j] = ∞
4: return min
5: end if
6: if Y[i, j + 1] < Y [i+ 1, j]then
7: Y[i, j] = Y[i, j + 1]
8: Y[i, j + 1] = min
9: return Extract-min(y,i,j+1)
10: else
11: Y[i, j] = Y[i+ 1, j]
12: Y[i+ 1, j] = min
13: return Extract-min(y,i+1,j)
14: end if
1: i=m,j=n
2: Y[i, j] = key
3: while Y[i−1, j]> Y [i, j] or Y[i, j −1] > Y [i, j]do
4: if Y[i−1, j]< Y [i, j −1] then
5: Swap Y[i, j] and Y[i, j −1]
6: j− −
7: else
8: Swap Y[i, j] and Y[i−1, j]
9: i− −
10: end if
11: end while
15

f. Find(Y,key). Let Check(y,key,i,j) mean to return true if Y[i, j] = key, oth-
erwise do nothing
i=j= 1
while Y[i, j]< key and i<mdo
Check(Y,key,i,j)
i++
end while
while i > 1 and j < n do
Check(i,j)
if Y[i, j]< key then
j++
else
i–
end if
end while
return false
16
Chapter 7
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 7.1-1
13 19 9 5 12 8 7 4 21 2 6 11
13 19 9 5 12 8 7 4 21 2 6 11
13 19 9 5 12 8 7 4 21 2 6 11
9 19 13 5 12 8 7 4 21 2 6 11
9 5 13 19 12 8 7 4 21 2 6 11
9 5 13 19 12 8 7 4 21 2 6 11
9 5 8 19 12 13 7 4 21 2 6 11
9 5 8 7 12 13 19 4 21 2 6 11
9 5 8 7 4 13 19 12 21 2 6 11
9 5 8 7 4 13 19 12 21 2 6 11
9 5 8 7 4 2 19 12 21 13 6 11
9 5 8 7 4 2 6 12 21 13 19 11
9 5 8 7 4 2 6 11 21 13 19 12
Exercise 7.1-2
If all elements in the array have the same value, PARTITION returns r. To
make PARTITION return q=b(p+r)/2cwhen all elements have the same
value, modify line 4 of the algorithm to say this: if A[j]≤xand j(mod2) =
(p+ 1)(mod2). This causes the algorithm to treat half of the instances of the
same value to count as less than, and the other half to count as greater than.
Exercise 7.1-3
The for loop makes exactly r−piterations, each of which takes at most
constant time. The part outside the for loop takes at most constant time. Since
r−pis the size of the subarray, PARTITION takes at most time proportional
to the size of the subarray it is called on.
Exercise 7.1-4
To modify QUICKSORT to run in nonincreasing order we need only modify
line 4 of PARTITION, changing ≤to ≥.
1

Exercise 7.2-1
By definition of Θ, we know that there exists c1, c2so that the Θ(n) term
is between c1nand c2n. We make that inductive hypothesis be that c1m2≤
T(m)≤c2m2for all m<n, then, for large enough n,
c1n2≤c1(n−1)2+c1n≤T(n−1) + Θ(n)
=T(n) = T(n−1) + Θ(n)≤c2(n−1)2+c2n≤c2n2
Exercise 7.2-2
The running time of QUICKSORT on an array in which evey element has the
same value is n2. This is because the partition will always occur at the last po-
sition of the array (Exercise 7.1-2) so the algorithm exhibits worst-case behavior.
Exercise 7.2-3
If the array is already sorted in decreasing order, then, the pivot element is
less than all the other elements. The partition step takes Θ(n) time, and then
leaves you with a subproblem of size n−1 and a subproblem of size 0. This
gives us the recurrence considered in 7.2-1. Which we showed has a solution
that is Θ(n2).
Exercise 7.2-4
Let’s say that by “almost sorted” we mean that A[i] is at most cpositions
from its correct place in the sorted array, for some constant c. For INSERTION-
SORT, we run the inner-while loop at most ctimes before we find where to insert
A[j] for any particular iteration of the outer for loop. Thus the running time
time is O(cn) = O(n), since cis fixed in advance. Now suppose we run QUICK-
SORT. The split of PARTITION will be at best n−cto c, which leads to O(n2)
running time.
Exercise 7.2-5
The minimum depth corresponds to repeatedly taking the smaller subprob-
lem, that is, the branch whoose size is proportional to α. Then, this will fall to
1 in ksteps where 1 ≈(α)kn. So, k≈logα(1/n) = −lg(n)
lg(α). The longest depth
corresponds to always taking the larger subproblem. we then have and identical
expression, replacing αwith 1 −α.
Exercise 7.2-6
2

Without loss of generality, assume that the entries of the input array are
distinct. Since only the relative sizes of the entries matter, we may assume
that Acontains a random permutation of the numbers 1 through n. Now fix
0< α ≤1/2. Let kdenote the number of entries of Awhich are less than
A[n]. PARTITION produces a split more balanced than 1 −αto αif and
only if αn ≤k≤(1 −α)n. This happens with probability (1−α)n−αn+1
n=
1−2α+ 1/n ≈1−2α.
Exercise 7.3-1
We analyize the exprected run time because it represents the more typical
time cost. Also, we are doing the expected run time over the possible random-
ness used during computation because it can’t be produced adversatially, unlike
when doing expected run time over all possible inputs to the algorithm.
Exercise 7.3-2
In the worst case, RANDOM returns the index of the largest element each
time it’s called, so Θ(n) calls are made. In the best case, RANDOM returns
the index of the element in the middle of the array and the array has distinct
elements, so Θ(lg n) calls are made.
Exercise 7.4-1
By definition of Θ, we know that there exists c1, c2so that the Θ(n) term
is between c1nand c2n. We make that inductive hypothesis be that c1m2≤
T(m)≤c2m2for all m<n, then, for large enough n,
c1n2≤c1max
q∈[n]n2−2n(q+ 2) + (q+ 1)2+ (q+ 1)2+n
= max
q∈[n]c1(n−q−2)2+c1(q+ 1)2+c1n
≤max
q∈[n]T(n−q−2) + T(q+ 1) + Θ(n)
=T(n)
Similarly for the other direction
Exercise 7.4-2
We’ll use the substitution method to show that the best-case running time
is Ω(nlg n). Let T(n) be the best-case time for the procedure QUICKSORT on
an input of size n. We have the recurrence
T(n) = min
1≤q≤n−1(T(q) + T(n−q−1)) + Θ(n).
Suppose that T(n)≥c(nlg n+ 2n) for some constant c. Substituting this guess
3

into the recurrence gives
T(n)≥min
1≤q≤n−1(cq lg q+ 2cq +c(n−q−1) lg(n−q−1) + 2c(n−q−1)) + Θ(n)
=cn
2lg(n/2) + cn +c(n/2−1) lg(n/2−1) + cn −2c+ Θ(n)
≥(cn/2) lg n−cn/2 + c(n/2−1)(lg n−2) + 2cn −2cΘ(n)
= (cn/2) lg n−cn/2+(cn/2) lg n−cn −lg n+ 2 + 2cn −2cΘ(n)
=cn lg n+cn/2−lg n+ 2 −2c+ Θ(n)
Taking a derivative with respect to qshows that the minimum is obtained when
q=n/2. Taking clarge enough to dominate the −lg n+ 2 −2c+ Θ(n) term
makes this greater than cn lg n, proving the bound.
Exercise 7.4-3
We will treat the given expression to be continuous in q, and then, any ex-
tremal values must be either adjacent to a critical point, or one of the endpoints.
The second derivative with respect to qis 4, So, we have that any ciritcal points
we find will be minima. The expression has a derivative with respect to q of
2q−2(n−q−2) = −2n+ 4q+ 4 which is zero when we have 2q+ 2 = n. So,
there will be a minima at q=n−2
2. So, the maximal values must only be the
endpoints. We can see that the endpoints are equally large because at q= 0, it
is (n−1)2, and at q=n−1, it is (n−1)2+ (n−n+ 1 −1)2= (n−1)2.
Exercise 7.4-4
We’ll use the lower bound (A.13) for the expected running time given in the
section:
E[X] =
n−1
X
i=1
n
X
j=i+1
2
j−i+ 1
=
n−1
X
i=1
n−i
X
k=1
2
k
≥
n−1
X
i=1
2 ln(n−i+ 1)
= 2 ln n−1
Y
i=1
n−i+ 1!
= 2 ln(n!)
=2
lg elg(n!) ≥cn lg n
for some constant csince lg(n!) = Θ(nlg n) by Exercise 3.2-3. Therefore
RANDOMIZED-QUICKSORT’s expected running time is Ω(nlg n).
4

Exercise 7.4-5
If we are only doing quick-sort until the problem size becomes ≤k, then, we
will have to take lg(n/k) steps, since, as in the original analysis of randomized
quick sort, we expect there to be lg(n) levels to the recursion tree. Since we
then just call quicksort on the entire array, we know that each element is within
kof its final position. This means that an insertion sort will take the shifting
of at most kelements for every element that needed to change position. This
gets us the running time described.
In theory, we should pick kto minimze this expression, that is, taking a
derivative with respect to k, we want it to be evaluating to zero. So, n−n
k= 0,
so k∼1
n2. The constant of proportianality will depend on the relative size of
the constants in the nk term and in the nlg(n/k) term. In practice, we would
try it with a large number of input sizes for various values of k, because there
are gritty properites of the machine not considered here such as cache line size.
Exercise 7.4-6
For simplicity of analysis, we will assume that the elements of the array A
are the numbers 1 to n. If we let kdenote the median value, the probability of
getting at worst an αto 1 −αsplit is the probability that αn ≤k≤(1 −α)n.
The number of “bad” triples is equal to the number of triples such that at least
two of the numbers come from [1, αn] or at least two of the numbers come from
[(1 −α)n, n]. Since both intervals have the same size, the probability of a bad
triple is 2(α3+3α2(1−α)). Thus the probability of selecting a “good” triple, and
thus getting at worst an αto 1−αsplit, is 1−2(α3+3α2(1−α)) = 1+4α3−6α2.
Problem 7-1
a. We will be calling with the parameters p= 1, r=|A|= 12. So, throughout,
x= 13.
i j
13 19 9 5 12 8 7 4 11 2 6 21 0 13
6 19 9 5 12 8 7 4 11 2 13 21 1 11
6 13 9 5 12 8 7 4 11 2 19 21 2 10
6 13 9 5 12 8 7 4 11 2 19 21 10 2
And we do indeed see that partition has moved the two elements that are
bigger than the pivot, 19 and 21, to the two final positions in the array.
b. We know that at the beginning of the loop, we have that i<j, because
it is true initially so long as |A| ≥ 2. And if it were to be untrue at some
iteration, then we would of left the loop in the prior iteration. To show that
we won’t access outside of the array, we need to show that at the beginning
of every run of the loop, there is a k > i so that A[k]≥x, and a k0< j so
that A[j0]≤x. This is clearly true because initially iand jare outside the
bounds of the array, and so the element xmust be between the two. Since
5

i < j, we can pick k=j, and k0=i. The elements ksatisfies the desired
relation to x, because the element at position jwas the element at position
iin the prior iteration of the loop, prior to doing the exchange on line 12.
Similarly, for k0.
c. If there is more than one run of the main loop, we have that j < r because
it decreases by at least one with every iteration.
Note that at line 11 in the first run of the loop, we have that i= 1 because
A[p] = x≥x. So, if we were to terminate after a single iteration of the main
loop, we must also have that j= 1 < p.
d. We will show the loop invariant that all the elements in A[p..i] are less than
or equal to x which is less than or equal to all the elements of A[j..r]. It is
trivially true prior to the first iteration because both of these sets of elements
are empty. Suppose we just finished an iteration of the loop during which j
went from j1to j2, and iwent from i1to i2. All the elements in A[i1+1..i2−1]
were < x, because they didn’t cause the loop on lines 8 −10 to terminate.
Similarly, we have that all the elements in A[j2+ 1..j1−1] were > x. We
have also that A[i2]≤x≤A[j2] after the exchange on line 12. Lastly, by
induction, we had that all the elements in A[p..i1] are less than or equal to
x, and all the elements in A[j1..r] are greater than or equal to x. Then,
putting it all together, since A[p..i2] = A[p..i1]∪A[i1+1..i2−1]∪ {A[i2]}and
A[j2..r] = ∪{A[j2]}∪A[j2+1..j1−1]∪A[j1..r], we have the desired inequality.
Since at termination, we have that i≥j, we know that A[p..j]⊆A[p..i], and
so, every element of A[p..j] is less than or equal to x, which is less than or
equal to every element of A[j+ 1..r]⊆A[j..r].
e. After running Hoare-partition, we don’t have the guarentee that the pivot
value will be in the position j, so, we will scan through the list to find the
pivot value, place it between the two subarrays, and recurse
Problem 7-2
a. Since all elements are the same, the initial random choice of index and swap
change nothing. Thus, randomized quicksort’s running time will be the same
as that of quicksort. Since all elements are equal, PARTITION(A, P, r) will
always return r−1. This is worst-case partitinoing, so the runtime is Θ(n2).
b. See the PARTITION’ algorithm for modifications.
c. See the RANDOMIZED-PARTITION’ algorithm for modifications.
d. Let dbe the number of distinct elements in A. The running time is dominated
by the time spent in the PARTITION procedure, and there can be at most d
calls to PARTITION. If Xis the number of comparisons performed in line 4
of PARTITION over the entire execution of QUICKSORT’, then the running
6
Quicksort(A,p,r)
1: if p<rthen
2: x=A[p]
3: q=HoareP artition(A, p, r)
4: i= 0
5: while A[i]6=xdo
6: i=i+ 1
7: end while
8: if i≤qthen
9: exchange A[i] and A[q]
10: else
11: exchange A[i] and A[q+ 1]
12: q=q+ 1
13: end if
14: Quicksort(A,p,q-1)
15: Quicksort(A,q+1,r)
16: end if
Algorithm 1 PARTITION’(A,p,r)
1: x=A[r]
2: exchange A[r] with A[p]
3: i=p−1
4: k=p
5: for j=p+ 1 to r−1do
6: if A[j]< x then
7: i=i+ 1
8: k=i+ 2
9: exchange A[i] with A[j]
10: exchange A[k] with A[j]
11: end if
12: if A[j] = xthen
13: k=k+ 1
14: exchange A[k] with A[j]
15: end if
16: end for
17: exchange A[i+ 1] with A[r]
18: return i+ 1 and k+ 1
Algorithm 2 RANDOMIZED-PARTITION’
1: i=RANDOM(p, r)
2: exchange A[r] with A[i]
3: return PARTITION’(A,p,r)
7

Algorithm 3 QUICKSORT’(A,p,r)
1: if p<rthen
2: (q, t) = RANDOM IZED −P ART IT ION 0
3: QUICKSORT’(A,p,q-1)
4: QUICKSORT’(A,t+1,r)
5: end if
time is O(d+X). It remains true that each pair of elements is compared
at most once. If ziis the ith smallest element, we need to compute the
probability that ziis compared to zj. This time, once a pivot xis chosen
with zi≤x≤zj, we know that ziand zjcannot be compared at any
subsequent time. This is where the analysis differs, because there could be
many elements of the array equal to zior zj, so the probability that ziand
zjare compared decreases. However, the expected percentage of distinct
elements in a random array tends to 1 −1
e, so asymptotically the expected
number of comparisons is the same.
Problem 7-3
a. Since the pivot is selected as a ranom element in the array, which has size n,
the probabilities of any particular element being selected are all equal, and
add to one, so, are all 1
n. As such, E[Xi] = Pr[i smallest is picked ] = 1
n.
b. We can apply linearity of expectation over all of the events Xi. Suppose we
have a particular Xibe true, then, we will have one of the sub arrays be
length i−1, and the other be n−i, and will of couse still need linear time
to run the partition procedure. This corresponds exactly to the summand in
equation (7.5).
c.
E"n
X
q=1
Xq(T(q−1) + T(n−q) + Θ(n))#=
n
X
q=1
E[Xq(T(q−1) + T(n−q) + Θ(n))]
=
n
X
q=1
(T(q−1) + T(n−q) + Θ(n))/n = Θ(n) + 1
n
n
X
q=1
(T(q−1) + T(n−q))
= Θ(n) + 1
n n
X
q=1
T(q−1) +
n
X
q=1
T(n−q)!
= Θ(n) + 1
n n
X
q=1
T(q−1) +
n
X
q=1
T(q−1)!= Θ(n) + 2
n
n
X
q=1
T(q−1)
= Θ(n) + 2
n
n−1
X
q=0
T(q) = Θ(n) + 2
n
n−1
X
q=2
T(q)
8

d. We will prove this inequality in a different way than suggested by the hint. If
we let f(k) = klg(k) treated as a continuous function, then f0(k) = lg(k)+1.
Note now that the summation written out is the left hand approximation of
the integral of f(k) from 2 to nwith step size 1. By integration by parts,
the antiderivative of klg kis
1
ln(2) k2
2ln(k)−k2
4
So, plugging in the bounds and subtracting, we get n2lg(n)
2−n2
4 ln(2) −1.
Since fhas a positive derivative over the entire interval that the integral is
being evaluated over, the left hand rule provides a underapproximation of
the integral, so, we have that
n−1
X
k=2
klg(k)≤n2lg(n)
2−n2
4 ln(2) −1≤n2lg(n)
2−n2
8
where the last inequality uses the fact that ln(2) >1/2.
e. Assume by induction that T(q)≤qlg(q) + Θ(n). Combining (7.6) and (7.7),
we have
E[T(n)] = 2
n
n−1
X
q=2
E[T(q)] + Θ(n)≤2
n
n−1
X
q=2
(qlg(q) + T heta(n)) + Θ(n)
≤2
n
n−1
X
q=2
(qlg(q)) + 2
n(nΘ(n)) + Θ(n)
≤2
n(1
2n2lg(n)−1
8n2) + Θ(n) = nlg(n)−1
4n+ Θ(n) = nlg(n) + Θ(n)
Problem 7-4
a. We’ll proceed by induction. For the base case, if Acontains 1 element then
p=rso the algorithm terminates immediately, leave a single sorted element.
Now suppose that for 1 ≤k≤n−1, TAIL-RECURSIVE-QUICKSORT cor-
rectly sorts an array Acontaining kelements. Let Ahave size n. We set
qequal to the pivot and by the induction hypothesis, TAIL-RECURSIVE-
QUICKSORT correctly sorts the left subarray which is of strictly smaller
size. Next, pis updated to q+1 and the exact same sequence of steps follows
as if we had originally called TAIL-RECURSIVE-QUICKSORT(A,q+1,n).
Again, this array is of strictly smaller size, so by the induction hypothesis it
correctly sorts A[q+ 1...n] as desired.
9
b. The stack depth will be Θ(n) if the input array is already sorted. The right
subarray will always have size 0 so there will be n−1 recursive calls before
the while-condition p<ris violated.
c. We modify the algorithm to make the recursive call on the smaller subarray
to avoid building pushing too much on the stack:
Algorithm 4 MODIFIED-TAIL-RECURSIVE-QUICKSORT(A,p,r)
1: while p<rdo
2: q=PARTITION(A, p, r)
3: if q < b(r−p)/2cthen
4: MODIFIED-TAIL-RECURSIVE-QUICKSORT(A, p, q −1)
5: p=q+ 1
6: else
7: MODIFIED-TAIL-RECURSIVE-QUICKSORT(A, q + 1, r)
8: r=q−1
9: end if
10: end while
Problem 7-5
a. piis the probability that a randomly selected subset of size three has the
A0[i] as it’s middle element. There are 6 possible orderings of the three ele-
ments selected. So, suppose that S0is the set of three elements selected. We
will compute the probability that the second element of S0is A0[i] among all
possible 3-sets we can pick, since there are exactly six ordered 3-sets corre-
sponding to each 3-set, these probabilities will be equal. We will compute
the probability that S0[2] = A0[i]. For any such S0, we would need to select
the first element from [i−1] and the third from {i+ 1, . . . , n}. So, there are
(i−1)(n−i) such 3-sets. The total number of 3-sets is n
3=n(n−1)(n−2)
6.
So,
pi=6(n−i)(i−1)
n(n−1)(n−2)
b. If we let i=n+1
2, the previous result gets us an increase of
6(n−1
2)(n−n+1
2)
n(n−1)(n−2) −1
n
in the limit ngoing to infinity, we get
lim
n→∞
6(bn−1
2c)(n−bn+1
2c)
n(n−1)(n−2)
1
n
=3
2
10

c. To save the messiness, suppose nis a multiple of 3. We will approximate the
sum as an integral, so,
2n/3
X
i=n/3
pi≈Z2n/3
n/3
6(−x2+nx +x−n)
n(n−1)(n−2) dx =6(−7n3/81 + 3n3/18 + 3n2/18 −n2/3)
n(n−1)(n−2)
Which, in the limit n goes to infinity, is 13
27 which is a constant that is larger
than 1/3 as it was in the original ranomized quicksort implementation.
d. Since the new algorithm always has a “bad” choice that is within a constant
factor of the original quicksort, it will still have a reasonable probability that
the randomness leads us into a bad situation, so, it will still be nlg n.
Problem 7-6
a. Our algorithm will be essentially the same as the modified randomized quick-
sort written in problem 2. We sort the ai’s, but we replace the comparison
operators to check for overlapping intervals. The only modifications needed
are made in PARTITION, so we will just rewrite that here. For a given
element xin position i, we’ll use x.a and x.b to denote aiand birespectively.
Algorithm 5 FUZZY-PARTITION(A,p,r)
1: x=A[r]
2: exchange A[r] with A[p]
3: i=p−1
4: k=p
5: for j=p+ 1 to r−1do
6: if bj< x.a then
7: i=i+ 1
8: k=i+ 2
9: exchange A[i] with A[j]
10: exchange A[k] with A[j]
11: end if
12: if bj≥x.a or aj≤x.b then
13: x.a = max(aj, x.a) and x.b = min(bj, x.b)
14: k=k+ 1
15: exchange A[k] with A[j]
16: end if
17: end for
18: exchange A[i+ 1] with A[r]
19: return i+ 1 and k+ 1
When intervals overlap we treat them as equal elements, thus cutting down
on the time required to sort.
11

b. For distinct intervals the algorithm runs exactly as regular quicksort does, so
its expected runtime will be Θ(nlg n) in general. If all of the intervals overlap
then the condition on line 12 will be satisfied for every iteration of the for
loop. Thus the algorithm returns pand r, so only empty arrays remain to
be sorted. FUZZY-PARTITION will only be called a single time, and since
its runtime remains Θ(n), the total expected runtime is Θ(n).
12

Chapter 8
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 8.1-1
We can construct the graph whoose vertex set is the indices, and we place
an edge between any two indices that are compared on the shortest path. We
need this graph to be connected, because otherwise we could run the algorithm
twice, once with everything in one component less than the other componenet,
and a second time with the everything in the second component larger. As long
as we mainatin the same relative ordering of the elements in each component,
the algorithm will take exactly the same path, and so produce the same result.
This means that there will be no difference in the output, even though there
should be. For a graph on nvertices, it is a well known that at least n−1 edges
are neccesary for it to be connected, as the addition of an edge can reduce the
number of connected components by at least one, and the graph with no edges
has nconnected components.
So, it will have depth at least n−1.
Exercise 8.1-2
Since lg(k) is monotonically increasing, we use formula A.11 to approximate
the sum:
Zn
0
lg(x)dx ≤
n
X
k=1
lg(k)≤Zn+1
1
lg(x)dx.
From this we obtain the inequality
nln(n)−n
ln 2 ≤
n
X
k=1
lg(k)≤(n+ 1) ln(n+ 1) −n
ln 2
which is Θ(nlg n).
Exercise 8.1-3
Suppose to a contradiction that there is a c1so that for every n≥k, at least
half of the inupts of length nhave depth at most c1n. However, there are
less than 2c1n+1 elements in the tree of depth at most c1n. However, 1/2n!>
1/2(n/e)n>2c1n+1 so long as n>e2c1. This is a contradiction.
1

To have a 1/n fraction of them with small depth, similarly, we get a contra-
diction because 1/nn!>2c1n+1 for large enough n.
To make an algorithm that is linear for a 1/2nfraction of inputs, we yet
again get a contradiction because 2−nn!>(n/2e)n>2c1n+1 for large enough
n.
The moral of the story is that n! grows very quickly.
Exercise 8.1-4
We assume as in the section that we need to construct a binary decision tree
to represent comparisons. Since each subsequence is of length k, there are k!n/k
possible output permutations. To compute the height hof the decision tree we
must have k!n/k ≤2h. Taking logs on both sides and using exercise 2 this gives
h≥(n/k) lg(k!) ≥(n/k)kln k−k
ln 2 =nln(k)−n
ln 2 = Ω(nlg k).
Exercise 8.2-1
We have that C=h2,4,6,8,9,9,11i. Then, after successive iterations of the
loop on lines 10-12, we have B=h,,,,,2,,,,,i,B=h,,,,,2, , 3, , , i,B=
h, , , 1, , 2, , 3, , , i, and at the end, B=h0,0,1,1,2,2,3,3,4,6,6i
Exercise 8.2-2
Suppose positions iand jwith i<jboth contain some element k. We con-
sider lines 10 through 12 of COUNTING-SORT, where we construct the output
array. Since j > i, the loop will examine A[j] before examining A[i]. When it
does so, the algorithm correctly places A[j] in position m=C[k] of B. Since
C[k] is decremented in line 12, and is never again incremented, we are guaran-
teed that when the for loop examines A[i] we will have C[k]< m. Therefore
A[i] will be placed in an earlier position of the output array, proving stability.
Exercise 8.2-3
The algorithm still works correctly. The order that elements are taken out
of Cand put into Bdoesn’t affect the placement of elements with the same key.
It will still fill the interval (C[k−1], C[k]] with elements of key k. The question
of whether it is stable or not is not well phrased. In order for stability to make
sense, we would need to be sorting items which have information other than
their key, and the sort as written is just for integers, which don’t. We could
think of extending this algorithm by placing the elements of Ainto a collection
of elments for each cell in array C. Then, if we use a FIFO collection, the mod-
ification of line 10 will make it stable, if we use LILO, it will be anti-stable.
Exercise 8.2-4
2

The algorithm will begin by preprocessing exactly as COUNTING-SORT
does in lines 1 through 9, so that C[i] contains the number of elements less than
or equal to iin the array. When queried about how many integers fall into a
range [a..b], simply compute C[b]−C[a−1]. This takes O(1) times and yields
the desired output.
Exercise 8.3-1
Starting with the unsorted words on the left, and stable sorting by progres-
sively more important positions.
COW SEA T AB BAR
DOG T EA BAR BIG
SEA MOB EAR BOX
RU G T AB T AR COW
ROW RUG SEA DIG
MOB DOG T EA DOG
BOX DIG DIG EAR
T AB BIG BIG F OX
BAR BAR M OB MOB
EAR EAR DOG N OW
T AR T AR COW ROW
DIG COW ROW RUG
BIG ROW NOW SEA
T EA N OW BOX T AB
NOW BOX F OX T AR
F OX F OX RUG T EA
Exercise 8.3-2
Insertion sort and merge sort are stable. Heapsort and quicksort are not. To
make any sorting algorithm stable we can preprocess, replacing each element of
an array with an ordered pair. The first entry will be the value of the element,
and the second value will be the index of the element. For example, the array
[2,1,1,3,4,4,4] would become [(2,1),(1,2),(1,3),(3,4),(4,5),(4,6),(4,7)]. We
now interpret (i, j)<(k, m) if i<kor i=kand j < m. Under this definition
of less-than, the algorithm is guaranteed to be stable because each of our new
elements is distinct and the index comparison ensures that if a repeat element
appeared later in the original array, it must appear later in the sorted array.
This doubles the space requirement, but the running time will be asymptotically
unchanged.
Exercise 8.3-3
After sorting on digit i, we will show that if we restrict to just the last i
digits, the list is in sorted order. This is trivial for i= 1, because it is just
claiming that the digits we just sorted were in sorted order. Now, suppose it’s
3

true for i−1, we show it for i. Suppose there are two elements, who, when
restricted to the ilast digits, are not in sorted order after the i’th step. Then,
we must have that they have the same i’th digit because otherwise the sort of
digit iwould put them in the right order. Since they have the same first digit,
their relative order is determined by their restrictions to their last i−1 dig-
its. However, these were placed in the correct order by the i−1’st step. Since
the sort on the i’th digit was stable, their relative order is unchanged from the
previous step. This means that they are in the correct order still. We use sta-
bility to show that being in the correct order prior to doing the sort is preserved.
Exercise 8.3-4
First run through the list of integers and convert each one to base n, then
radix sort them. Each number will have at most logn(n3) = 3 digits so there
will only need to be 3 passes. For each pass, there are npossible values which
can be taken on, so we can use counting sort to sort each digit in O(n) time.
Exercise 8.3-5
Since a pass consists of one iteration of the loop on line 1 −2, only dpasses
are needed. Since each of the digits can be one of ten decimal numbers, the
most number of piles that would be needed to be kept track of is 10.
Exercise 8.4-1
The sublists formed are h.13, .16i,h.20i,h.39i,h.42i,h.53i,h.64i,h.71, .79i,
h.89i. Putting them together, we get h.13, .16, .20, .39, .42, .53, .64, .71, .79, .89i
Exercise 8.4-2
In the worst case, we could have a bucket which contains all nvalues of the
array. Since insertion sort has worst case running time O(n2), so does Bucket
sort. We can avoid this by using merge sort to sort each bucket instead, which
has worst case running time O(nlg n).
Exercise 8.4-3
Xis 0 or 2 with probability a quarter each, and 1 with probability 2. Note
that E[X] = 1, so, E2[x] = 1. Also, X2takes 0 or 4 with probability a quarter
each, and 1 with probability a half. So, E[X2] = 1.5.
Exercise 8.4-4
Define ri=qi
nand ci={(x, y)|ri−1≤x2+y2≤ri}for i= 1,2, . . . , n.
The ciregions partition the unit disk into nparts of equal area, which we will
4

use as the buckets. Since the points are uniformly distributed on the disk and
each region has equal area, bucket sort will run in expected time Θ(n).
Exercise 8.4-5
We have to pick our bounds for our buckets in bucket sort in such a way
that there is approximately equal probability that an element drawn from the
dirstibution will be any one of the buckets. To do this, we can perform a binary
search to find the Dyadic rationals with denominator at least a constant fraction
of n. Finding each of these takes only lg(n) time. Then, these form the bounds
for a bucket sort. There are an expected constant number of elements in any
one of these buckets, so just use any sort you want at this point.
Problem 8-1
a. There are n! possible permutations of the input array because the input
elements are all distinct. Since each is equally likely, the distribution is uni-
formly supported on this set. So, each occurs with probability 1
n!and corre-
sponds to a different leaf because the program needs to be able to distinguish
between them.
b. The depths of particular elements of LT(resp. RT) are all one less than their
depths when considered elements of T. In particular, this is true for the leaves
of the two subtrees. Also, {LT, RT }form a partition of all the leaves of T.
So, if we let L(T) denote the leaves of T,
D(T) = X
`∈L(T)
DT(`) = X
`∈L(LT )
DT(`) + X
`∈L(RT )
DT(`) =
X
`∈L(LT )
(DLT (`) + 1) + X
`∈L(RT )
(DRT (`) + 1) =
X
`∈L(LT )
DLT (`) + X
`∈L(RT )
DRT (`) + k=D(LT ) + D(RT ) + k
c. Suppose we have a Twith kleaves so that D(T) = d(k). Let i0be the
number of leaves in LT . Then, d(k) = D(T) = D(LT ) + D(RT ) + kbut, we
can pick LT and RT to minimize the external path length
d. We treat ias a continuous variable, and take a derivative to find critical
points. The given expression has the following as a derivative with respect
to i1
ln(2) + lg(i) + 1
ln(2) −lg(k−i) = 2
ln(2) + lg i
k−i
which is zero when we have i
k−i= 2−2
ln(2) = 2−lg(e2)=e−2. So, (1 + e−2)i=
k, so, i=k
1+e−2.
5

Since we are picking the two subtrees to be roughtly equal size, the total depth
will be order lg(k), with each level contributing k, so the total external path
length is at least klg(k).
e. Since before we that a tree with kleaves needs to have external length klg(k),
and that a sorting tree needs at least n! trees, a sorting tree must have
external tree length at least n! lg(n!). Since the average case run time is the
depth of a leaf weighted by the probability of that leaf being the one that
occurs, we have that the run time is at least n! lg(n!)
n!= lg(n!) ∈Ω(nlg(n))
f. Since the expected runtime is the average over all possible results from the
random bits, if every possible fixing of the randomness resulted in a higher
runtime, the average would have to be higher as well.
Problem 8-2
Algorithm 1 O(n) and Stable(A)
a. Create a new array C
index = 1
for i= 1 to ndo
if A[i] == 0 then
C[index] = A[i]
index =index + 1
end if
end for
for i= 1 to ndo
if A[i] == 1 then
C[index] = A[i]
index =index + 1
end if
end for
This algorithm first selects all the elements with key 0 and puts them in the
new array Cin the order in which they appeared in A, then selects all the
elements with key 1 and puts them in Cin the order in which they appeared
in A. Thus, it is stable. Since it only makes two passes through the array, it
is O(n).
The algorithm maintains the 0’s seen so far at the start of the array. Each
time an element with key 0 is encountered, the algorithm swaps it with the
position following the last 0 already seen. This is in-place and O(n), but not
stable.
c. Simply run BubbleSort on the array.
6

Algorithm 2 O(n) and in place(A)
b. index = 1
for i= 1 to ndo
if A[i] == 0 then
Swap A[i] with A[index]
index =index + 1
end if
end for
d. Use the algorithm given in part a. For each of the b-bit keys it takes O(n)
and is stable, as is required by Radix-Sort. Thus, the total running time will
be O(bn).
e. Create the array Cas done in lines 1 through 5 of counting sort. Create an
array Bwhich is a copy of C, then run lines 7 through 9 on B. In other
words, C[i] gives the number of elements in Awhich are equal to i, and B[i]
gives the number of elements in Awhich are less than or equal to i, so given
an element, we can correctly identify where it belongs in the array. While
the element in position i doesn’t belong there, swap it with the element in
the place it belongs. Once an element which belongs in position iappears,
increment i. The preprocessing takes O(n+k) time, the total number of
swaps is at most n, and we iterate through the whole array once, so the
overall runtim is O(n+k). This algorithm has the advantage of sorting in
place, however it is no longer stable like counting sort.
Problem 8-3
a. First, sort the integer by their lengths. This can be done efficiently using a
bucket sort, where we make a bucket for each possible number of digits. We
sort each these uniform length sets of integers using radix sort. Then, we
just concatenate the sorted lists obtained from each bucket.
b. Make a bucket for every letter in the alphabet, each containing the words
that start with that letter. Then, forget about the first letter of each of the
words in the bucket, concatenate the empty word (if it’s in this new set of
words) with the result of recursing on these words of length one less. Since
each word is processed a number of times equal to it’s length, the runtime
will be linear in the total number of letters.
Problem 8-4
a. Select a red jug. Compare it to blue jugs until you find one which matches.
Set that pair aside, and repeat for the next red jug. This will use at most
Pn−1
i=1 i=n(n−1)/2 = O(n2) comparisons.
7

b. We can imagine first lining up the red jugs in some order. Then a solution
to this problem becomes a permutation of the blue jugs such that the ith
blue jug is the same size as the ith red jug. As in section 8.1, we can make a
decision tree which represents comparisons made between blue jugs and red
jugs. An internal node represents a comparison between a specific pair of
red and blue jugs, and a leaf node represents a permutation of the blue jugs
based on the results of the comparison. We are interested in when one jug
is greater than, less than, or equal in size to another jug, so the tree should
have 3 children per nod. Since there must be at least n! leaf nodes, the deci-
sion tree must have height at least log3(n!). Since a solution corresponds to
a simple path from root to leaf, an algorithm must make at least Ω(nlg n)
comparisons to reach any leaf.
c. We use an algorithm analogous to randomized quicksort. Select a blue jug
at random. Partition the red jugs into those which are smaller than the blue
jug, and those which are larger. At some point in the comparisons, you will
find the red jug which is of equal size. Once the red jugs have been divided by
size, use the red jug of equal size to partition the blue jugs into those which
are smaller and those which are larger. If kred jugs are smaller than the
originally chosen jug, we need to solve the original problem on input of size
k−1 and size n−k, which we will do in the same manner. A subproblem of
size 1 is trivially solved because if there is only one red jug and one blue jug,
they must be the same size. The analysis of expected number of comparisons
is exactly the same as that of randomized-quicksort given on pages 181-184.
We are running the procedure twice so the expected number of comparisons
is doubled, but this is absorbed by the big-O notation. In the worst case,
we pick the largest jug each time, which results in Pn
i=2 i+i−1 = n2
comparisons.
Problem 8-5
a. Since each of the averages will be of sets of a single element, so, wach element
will be ≤than the next element. So, this is the usual definition of sorted
b. h1,6,2,7,3,8,4,9,10i
c. Suppose we have A[i]≤A[i+k] for all appropriate i. Then, every element in
the sum Pi+k−1
j=iA[j] has a corresponding element in the sum Pi+k−1
j=iA[j]
that it is less than. This means the sums must have the desired ineqality.
Now, suppose that we had the array was k-sorted. This means that
i+k−1
X
j=i
A[j]≤
i+k
X
j=i+1
but, if we subtract off all the terms that both sums have in common, we get:
A[i]≤A[i+k]
8

d. We can do quicksort until we are down to subarrays of size at most k. In
exercise 7.4-5, this was shown to take time O(nlg(n/k). Note that this
much work is all that is needed because we only need show that elements
separated by kpositions are in different blocks which is true because they
are ≤kpositions wide.
e. Consider the lists, which, for every i∈ {0, . . . , k −1}, are Li=hA[i], A[i+
k], . . . , A[i+bn/kck]i. Note that by part c, if Ais k−sorted, then we must
have each Liis sorted. Then, by 6.5-9, we can merge them all into a single
sorted array in the desired time.
f. Let t(k, n) be the time required to k-sort arrays of length n. Then, we have
that, for every k, we can sort an array by first ksorting it and then applying
the previous part in time t(n, k) + nlg(k). If t(n, k) were o(nlg(n)), then we
would have a contradiction to the comparison based sorting lower bounds.
Problem 8-6
a. There are 2n
nways to divide 2nnumbers into two sorted lists, each with n
numbers.
b. Any decision tree to merge two sorted lists must have at least 2n
nleaf nodes,
so it has height at least lg 2n!
n!n!. We’ll use the inequalities derived in Exercise
8.1-2 to bound this:
lg 2n!
n!n!= lg((2n)!) −2 lg(n!)
=
2n
X
k=1
lg(k)−2
n
X
k=1
lg(k)
≥2nln(2n)−2n
ln 2 −2(n+ 1) ln(n+ 1) −n
ln 2
= 2n+ 2nlg(n)−2nlg(n+ 1) −2 lg(n+ 1)
= 2n+ 2nlg(n/(n+ 1)) −2 lg(n+ 1)
= 2n−o(n).
c. If we don’t compare them, then there is no way to distinguish between the
original unmerged lists and the unmerged lists obtained by swapping those
two items between lists. In the case where the two elements are different we
require a different action to be taken in order to correctly merge the lists, so
the two must be compared.
d. Let list A= 1,3,5, ..., 2n−1 and B= 2,4,6,...,2n. By part c, we must
compare 1 with 2, 2 with 3, 3 with 4, and so on up until we compare 2n−1
with 2n. This amounts to a total of 2n−1 comparisons.
9

Problem 8-7
a. Since we claim that A[p] is the smallest value placed at a wrong location,
everything that has value less than or equal to A[p] is in it’s correct spot, and
so, cannot be placed where A[p] should of been. This means that A[q]≥A[p].
Also, if we had that A[q] = A[p]. Then it wouldn’t be an error to have A[q] in
the spot that should of had A[q]. This gets us A[q]> A[p]. Since we are only
considering arrays with 0-1 values, this means that we must have 0 = A[p]
and 1 = A[q].
b. It fails to sort Bcorrectly because there is some position that A[p] was moved
to that was greater than where it should of been, this means that A[q] is to
the left of it, which shows the array is unsorted.
c. All of the even steps in the algorithm do not even look at the values of the
cells, they just push them around. The odd steps are also oblivious because
we can just use the oblivious compare exchange version of insertion sort givin
at the beginning of the problem.
d. After step 1, we know that each column looks like some number of zeroes
followed by some number of ones. Suppose that column ihad zizeroes in
it. Then, after the reshaping step, we know that each of the columns will
contribute dzi/(r/s)ezeroes to the first zimod scolumns, and one less to
the rest. In particular, since the number of zeros contributed to each of the
columns after step 2 only has a single jump by one, the sum over each must
only change by at most s. Then, after sorting, this means that there will
only be sdirty rows.
e. From the prior part, we know that before step 4, there are at most sdirty
rows, with a total of s2elements in them. So, after step 4, these dirty
elements will map to some bottom part of a column, some of another column,
and then some top part of a column. with everything to the left being zero,
and everything to the right being one.
f. From the previous part, we have that there are at most s2values that may
be bad. Also, r≥2s2. Then, there are two cases. The first is that the
dirty region spans two columns, in this case, we have that after step 6, the
dirty region is entirely in one column. So, after doing step 7, we have that
the column that was dirty has a clean top half, and the array is sorted, so,
it remains sorted when applying step 8. The second case is that the dirty
region is entirely in one column. If this is the case, then, after sorting in step
5, the array is already sorted, and the only dirty column has a clean first
half. So, it will mainatain it’s being sorted after performing steps 6-8.
g. The proof is very similar to the way that part e was shown. There must be
some care taken with how the transformation in steps 2 and 4 are changed.
We would need that r≥2s2−2s, since a dirty region of 2s−1 rows cor-
responds to a dirty region (when read column major) of size 2s2−s. we
10

could simply pad the array with a number of rows with all zero, to bring the
number of rows up to a multiple of s. Then, take away that many zeroes
from the final answer.
11
Chapter 9
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 9.1-1
In this problem, we will be recursing by dividing the array into two equal
size sets of elements, we will neglect taking floors and ceilings. The analysis will
be the same but just a bit uglier if we don’t assume that n is a power of 2.
Break up the elements into disjoint pairs. Then, compare each pair, consider
only the smallest elements from each. From among this set of elements, the re-
sult to the original problem will be either what had been paired with the smallest
element, or what what is the second smallest element of the sub-problem. Doing
this will get both the smallest and second smallest element. So, we get the recur-
rence T(n) = T(n/2)+n/2+1 and T(2) = 1. So, solving this recurrence, we will
use the substitution method with T(n)≤n+dlg(n)e−2, it agrees with the base
case, and, T(n) = n/2+T(n/2)+1 ≤n/2+n/2+dlg(n/2)e−2+1 = n+dlg(n)e−2
as desired.
Exercise 9.1-2
Initially, all nnumbers are potentially either the maximum or minimum.
Let MAX be the set of numbers which are potentially the maximum and MIN
denote the set of numbers which are potentially the minimum. Say we compare
two elements aand b. If a≤b, we can remove afrom MAX and remove bfrom
MIN, so we reduce the counts of both sets by 1. If we compare two elements
in MIN, we reduce the size of MIN by 1, and if we compare two elements in
MAX, we can reduce the size of MAX by 1. Thus, the first type of comparison
is optimal. There are dn/2esuch comparisons which can be made until MIN
and MAX are disjoint, and the sets will have sizes dn/2eand bn/2c. Within
each of these, only the second and third types of comparisons can be made, each
reducing the set size by 1, so we require a total of dn/2e − 1 + bn/2c − 1 = n−2
comparisons. Adding this to initial dn/2ecomparisons gives d3n/2e − 2.
Exercise 9.2-1
Calling a zero length array would mean that the second and third arguments
are equal. So, if the call is made on line 8, we would need that p=q−1. which
1

means that q−p+ 1 = 0 .However, iis assumed to be a nonnegative num-
ber, and to be executing line 8, we would need that i<k=q−p+ 1 = 0,
a contradiction. The other possibility is that the bad recursive call occurs on
line 9. This would mean that q+ 1 = r. To be executing line 9, we need that
i>k=q−p+ 1 = r−p. This would be a nonsensical original call to the array
though because we are asking for the ith element from an array of strictly less
size.
Exercise 9.2-2
The probability that Xkis equal to 1 is unchanged when we know the max of
k−1 and n−k. In other words, P(Xk=a|max(k−1, n−k) = m) = P(Xk=a)
for a= 0,1 and m=k−1, n −kso Xkand max(k−1, n −k) are independent.
By C.3-5, so are Xkand T(max(k−1, n −k)).
Exercise 9.2-3
Algorithm 1 ITERATIVE-RANDOMIZED-SELECT
while p<rdo
q=RANDOMIZED −P ART IT ION (A, p, r)
k=q−p+ 1
if i=k then
return A[q]
end if
if i<kthen
r=q−1
else
p=q
i=i−k
end if
end while
return A[p]
Exercise 9.2-4
When the partition selected is always the maximum element of the array we
get worst-case performance. In the example, the sequence would be 9, 8, 7, 6,
5, 4, 3, 2, 1, 0.
Exercise 9.3-1
It will still work if they are divided into groups of 7, because we will still
know that the median of medians is less than at least 4 elements from half of the
dn/7egroups, so, it is greater than roughly 4n/14 of the elements. Similarly, it
2

is less than roughly 4n/14 of the elements. So, we are never calling it recursively
on more than 10n/14 elements. So, T(n)≤T(n/7) + T(10n/14) + O(n). So,
we can show by substitution this is linear. Suppose T(n)< cn for n<k, then,
for m≥k,T(m)≤T(m/7) + T(10m/14) + O(m)≤cm(1/7 + 10/14) + O(m).
So, as long as we have that the constant hidden in the big-Oh notation is less
than c/7, we have the desired result.
Suppose now that we use groups of size 3 instead. So, For similar reasons,
we have that the recurrence we are able to get is T(n) = T(dn/3e) + T(4n/6) +
O(n)≥T(n/3) + T(2n/3) + O(n). So, we will show it is ≥cn lg(n).
T(m)≥c(m/3) lg(m/3) + c(2m/3) lg(2m/3) + O(m)≥cm lg(m) + O(m).
So, we have that it grows more quickly than linear.
Exercise 9.3-2
We know that the number of elements greater than or equal to xand the
number of elements less than or equal to xis at least 3n/10 −6. Then for
n≥140 we have
3n/10 −6 = n
4+n
20 −6≥n/4 + 140/20 −6 = n/4+1≥ dn/4e.
Exercise 9.3-3
We can modify quicksort to run in worst case nlg(n) time by choosing our
pivot element to be the exact median by using quick select. Then, we are guar-
anteed that our pivot will be good, and the time taken to find the median is on
the same order of the rest of the partitioning.
Exercise 9.3-4
Create a graph with nvertices and draw a directed edge from vertex ito
vertex jif the ith and jth elements of the array are compared in the algorithm
and we discover that A[i]≥A[j]. Observe that A[i] is one of the i−1 smaller
elements if there exists a path from xto iin the graph, and A[i] is one of the
n−ilarger elements if there exists a path from ito xin the graph. Every vertex
imust either lie on a path to or from xbecause otherwise the algorithm can’t
distinguish between i≤xand i≥x. Moreover, if a vertex ilies on both a path
to xand a path from xthen it must be such that x≤A[i]≤x, so x=A[i]. In
this case, we can break ties arbitrarily.
Exercise 9.3-5
To use it, just find the median, partition the array based on that median. If
iis less than half the length of the original array, recurse on the first half, if iis
half the length of the array, return the element coming from the median finding
3

black box. Lastly, if iis more than half the length of the array, subtract half
the length of the array, and then recurse on the second half of the array.
Exercise 9.3-6
Without loss of generality assume that nand kare powers of 2. We first
find the n/2th order statistic, in time O(n) using SELECT, then reduce the
problem to finding the k/2th quantiles of the smaller n/2 elements and the
k/2th quantiles of the larger n/2 elements. Let T(n) denote the time it takes
the algorithm to run on input of size n. Then T(n) = cn + 2T(n/2) for some
constant c, and the base case is T(n/k) = O(1). Then we have:
T(n)≤cn + 2T(n/2)
≤2cn + 4T(n/4)
≤3cn + 8T(n/8)
.
.
.
≤log(k)cn +kT (n/k)
≤log(k)cn +O(k)
=O(nlog k).
Exercise 9.3-7
Find the n/2−k/2 largest element in linear time. Partition on that ele-
ment. Then, find the klargest element in the bigger subarray formed from the
partition. Then, the elements in the smaller subarray from partitioning on this
element are the desired knumbers.
Exercise 9.3-8
Without loss of generality, assume nis a power of 2.
Algorithm 2 Median(X,Y,n)
if n==1 then
return min(X[1], Y [1])
end if
if X[n/2] < Y [n/2] then
return Median(X[n/2+1...n], Y [1...n/2], n/2)
else
if X[n/2] ≥Y[n/2] then
return Median(X[1...n/2], Y [n/2+1...n], n/2)
end if
end if
Exercise 9.3-9
4

If nis odd, then, we pick the y coordinate of the main pipeline to be equal
to the median of all the y coordinates of the wells. if nis even, then, we can
pick the y coordinate of the pipeline to be anything between the y coordinates
of the wells with y-coordinates which have order statistics b(n+ 1)/2cand the
d(n+ 1)/2e. These can all be found in linear time using the algorithm from this
section.
Problem 9-1
a. Sorting takes time nlg(n), and listing them out takes time i, so the total
runtime is O(nlg(n) + i)
b. Heapifying takes time nlg(n), and each extraction can take time lg(n), so,
the total runtime is O((n+i) lg(n))
c. Finding and partitioning around the ith largest takes time n. Then, sorting
the subarray of length icoming from the partition takes time ilg(i). So, the
total runtime is O(n+ilg(i)).
Problem 9-2
a. Let mkbe the number of xismaller than xk. When weights of 1/n are as-
signed to each xi, we have Pxi<xkwi=mk/n and Pxi>xkwi= (n−mk−
1)/2. The only value of mkwhich makes these sums <1/2 and ≤1/2 re-
spectively is when dn/2e − 1, and this value of xmust be the median since
it has equal numbers of x0
iswhich are larger and smaller than it.
b. First use mergeSort to sort the xi’s by value in O(nlog n) time. Let Sibe
the sum of the weights of the first ielements of this sorted array and note
that it is O(1) to update Si. Compute S1, S2, . . . until you reach ksuch that
Sk−1<1/2 and Sk≥1/2. The weighted median is xk.
c. We modify SELECT to do this in linear time. Let xbe the median of medi-
ans. Compute Pxi<x wiand Pxi>x wiand check if either of these is larger
than 1/2. If not, stop. If so, recurse on the collection of smaller or larger
elements known to contain the weighted median. This doesn’t change the
runtime, so it is Θ(n).
d. Let pbe the minimizer, and suppose that pis not the weighted median. Let
be small enough such that < mini(|p−pi|), where we don’t include kif
p=pk. If pmis the weighted median and p < pm, choose > 0. Otherwise
5

choose < 0. Then we have
n
X
i=1
wid(p+, pi) =
n
X
i=1
wid(p, pi) + X
pi<p
wi−X
pi>p
wi!<
n
X
i=1
wid(p, pi)
since the difference in sums will take the opposite sign of epsilon.
e. Observe that
n
X
i=1
wid(p, pi) =
n
X
i=1
wi|px−(pi)x|+
n
X
i=1
wi|py−(pi)y|.
It will suffice to minimize each sum separately, which we can do since we
choose pxand pyindividually. By part e, we simply take p= (px, py) to be
such that pxis the weighted median of the x-coordinates of the pi’s and py
is the weighted medain of the y-coordiantes of the pi’s.
Problem 9-3
a. If i≥n/2, then just use the algorithm from this chapter to get the answer in
time T(n). If i < n/2, then, we can compare disjoint pairs of elements from
the list, and then we know that the ith smallest is in the set of elements that
are smaller in each pair. So, we can recurse, this gets us runtime in this case
of bn/2c+Ui(dn/2e) + T(2i). Note that the last term comes from the fact
that the ith smallest could of also been any of the elements paired with the
ith smallest elements from the subproblem.
b. By the Substitution method, suppose that Ui(n) = n+cT (2i) lg(n/i) for
smaller n, then, there are two cases based on whether or not i < n/4. If it
is, Ui(n) = bn/2c+Ui(dn/2e) + T(2i)≤n/2 + n/2 + cT (2i) lg(n/2i) + T(2i).
This then satisfies the recurrence if we have that c≥1. The other case is that
n/4≤i < n/2. In this case, we have that Ui(n) = n/2 + T(dn/2e) + T(2i)≤
n/2 + 2T(2i), which works if we have c≥2. So, we can just pick c= 2, and
both cases of the recurrence go through.
c. From the previous part, if iis a constant, the O(T(2i) lg(n/i)) becomes
T(lg(n)). So, Ui(n) = n+O(T(2i) lg(n/i)) = n+O(lg(n)).
d. From part c, we just substitute in n/k for ito get Ui(n) = n+O(T(2i) lg(n/i)) =
n+O(T(2n/k) lg k).
Problem 9-4
6

a. We only need to worry about what happens when we select a pivot element
which is between min(zi, zj, zk) and max(zi, zj, zk), since at this point we
will either select zior zjand compare them, select an element between zi
and zjand never compare them, or select an element between zkand the
[zi, zj] interval, so that we will will never again be selecting pivots from a
range containing ziand zj. We split into three cases. If zk≤zi< zjthen
E(Xijk) = 2
j−k+1 . If zi≤zk< zjthen E(Xijk ) = 2
j−i+1 . If zi< zj≤zk
then E(Xijk) = 2
k−i+1 .
b.
E[Xk]≤
n
X
i=1
n
X
j=1
E[Xijk]
=
k
X
i=1
n
X
j=k
2
j−i+ 1 +
n
X
i=k+1
n
X
j=i+1
2
j−k+ 1 +
k−2
X
i=1
k−1
X
j=i+1
2
k−i+ 1.
For the second term, fix some value m. The term 2
m−k+1 will appear once
for every time jdoesn’t exceed m, so m−(k+ 1) times in the sum. For the
third term, each term in the sum doesn’t depend on jso we can rewrite it
as 2 Pk−2
i=1
k−i−1
k−i+1 . This gives
E[Xk]=2
k
X
i=1
n
X
j=k
1
j−i+ 1 +
n
X
j=k+1
j−k−1
j−k+ 1 +
k−2
X
i=1
k−i−1
k−i+ 1
.
c. We can bound the summands of the second and third terms from (b) by 1,
so the total contribution of these terms is n−(k+ 1) + 1 + k−2 = n−2.
For the first double sum, consider a term of the form 1
cfor some c. There
are at most cof these, because we must have j−i=c−1. The largest term
which appears is 1 and the smallest term which appears is 1
n, so the double
sum contributes a total of at most n. Thus, E[Xk]≤2(n+n−2) ≤4n.
d. The running time of RANDOMIZED-SELECT is dominated by the time
spent in RANDOMIZED-PARTITION, whose running time is dominated by
comparisons. By part (c) we know that the expected number of comparisons
over the entire algorithm, including recursions, is O(n).
7

Chapter 10
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 10.1-1
4
4 1
413
4 1
418
4 1
Exercise 10.1-2
We will call the stacks Tand R. Initially, set T.top = 0 and R.top =n+ 1.
Essentially, stack Tuses the first part of the array and stack Ruses the last
part of the array. In stack T, the top is the rightmost element of T. In stack R,
the top is the leftmost element of R.
Algorithm 1 PUSH(S,x)
1: if S== Tthen
2: if T.top + 1 == R.top then
3: error “overflow”
4: else
5: T.top =T.top + 1
6: T[T.top] = x
7: end if
8: end if
9: if S== Rthen
10: if R.top −1 == T.top then
11: error “overflow”
12: else
13: R.top =R.top −1
14: T[T.top] = x
15: end if
16: end if
1
Algorithm 2 POP(S)
if S== Tthen
if T.top == 0 then
error “underflow”
else
T.top =T.top −1.
return T[T.top + 1]
end if
end if
if S== Rthen
if R.top == n+ 1 then
error “underflow”
else
R.top =R.top + 1.
return R[R.top −1]
end if
end if
Exercise 10.1-3
4
4 1
413
1 3
138
3 8
Exercise 10.1-4
Algorithm 3 ENQUEUE
if Q.head == Q.tail + 1, or Q.head == 1 and Q.tail == Q.length then
error “overflow”
end if
Q[Q.tail] = x
if Q.tail == Q.length then
Q.tail = 1
else
Q.tail =Q.head + 1
end if
Exercise 10.1-5
As in the example code given in the section, we will neglect to check for
overflow and underflow errors.
2
Algorithm 4 DEQUEUE
if Q.tail == Q.head then
error “underflow”
end if
x=Q[Q.head]
if Q.head == Q.length then
Q.head = 1
else
Q.head =Q.head + 1
end if
return x
Algorithm 5 HEAD-ENQUEUE(Q,x)
Q[Q.head] = x
if Q.head == 1 then
Q.head =Q.length
else
Q.head =Q.head −1
end if
Algorithm 6 TAIL-ENQUEUE(Q,x)
Q[Q.tail] = x
if Q.tail == Q.length then
Q.tail = 1
else
Q.tail =Q.tail + 1
end if
Algorithm 7 HEAD-DEQUEUE(Q,x)
x=Q[Q.head]
if Q.head == Q.length then
Q.head = 1
else
Q.head =Q.head + 1
end if
Algorithm 8 TAIL-DEQUEUE(Q,x)
x=Q[Q.tail]
if Q.tail == 1 then
Q.tail =Q.length
else
Q.tail =Q.tail −1
end if
3

Exercise 10.1-6
The operation enqueue will be the same as pushing an element on to stack
1. This operation is O(1). To dequeue, we pop an element from stack 2. If stack
2 is empty, for each element in stack 1 we pop it off, then push it on to stack 2.
Finally, pop the top item from stack 2. This operation is O(n) in the worst case.
Exercise 10.1-7
The following is a way of implementing a stack using two queues, where pop
takes linear time, and push takes constant time. The first of these ways, consists
of just enqueueing each element as you push it. Then, to do a pop, you dequque
each element from one of the queues and place it in the other, but stopping
just before the last element. Then, return the single element left in the original
queue.
Exercise 10.2-1
To insert an element in constant time, just add it to the head by making it
point to the old head and have it be the head. To delete an element, it needs
linear time because there is no way to get a pointer to the previous element in
the list without starting at the head and scanning along.
Exercise 10.2-2
The PUSH(L,x) operation is exactly the same as LIST-INSERT(L,x). The
POP operation sets xequal to L.head, calls LIST-DELETE(L,L.head), then
returns x.
Exercise 10.2-3
In addition to the head, also keep a pointer to the last element in the linked
list. To enqueue, insert the element after the last element of the list, and set it
to be the new last element. To dequeue, delete the first element of the list and
return it.
Exercise 10.2-4
First let L.nil.key =k. Then run LIST-SEARCH’ as usual, but remove the
check that x6=L.nil.
Exercise 10.2-5
To insert, just do list insert before the current head, in constant time. To
search, start at the head, check if the element is the current node being in-
spected, check the next element, and so on until at the end of the list or you
4

found the element. This can take linear time in the worst case. To delete, again
linear time is used because there is no way to get to the element immediately
before the current element without starting at the head and going along the list.
Exercise 10.2-6
Let L1be a doubly linked list containing the elements of S1and L2be a
doubly linked list containing the elements of S2. We implement UNION as fol-
lows: Set L1.nil.prev.next =L2.nil.next and L2.nil.next.prev =L1.nil.prev
so that the last element of L1is followed by the first element of L2. Then set
L1.nil.prev =L2.nil.prev and L2.nil.prev.next =L1.nil, so that L1.nil is the
sentinal for the doubly linked list containing all the elements of L1and L2.
Exercise 10.2-7
Algorithm 9 REVERSE(L)
a=L.head.next
b=L.head
while a6=NIL do
tmp =a.next
a.next =b
b=a
a=tmp
end while
L.head =b
Exercise 10.2-8
We will store the pointer value for L.head separately, for convenience. In
general, AXOR (AXOR C) = C, so once we know one pointer’s true value
we can recover all the others (namely L.head) by applying this rule. Assuming
there are at least two elements in the list, the first element will contain exactly
the address of the second.
Algorithm 10 LISTnp-SEARCH(L,k)
p=NIL
x=L.head
while x6=NIL and x.key 6=kdo
temp =x
x=pXORx.np
p=temp
end while
To reverse the list, we simply need to make the head be the “last” ele-
5
Algorithm 11 LISTnp-INSERT(L,x)
x.np =L.head
L.nil.np =xXOR(L.nil.npXORL.head)
L.head =x
Algorithm 12 LISTnp-Delete(L,x)
L.nil.np =L.nil.npXORL.headXORL.head.np
L.head.np.np =L.head.np.npXORL.head
ment before L.nil instead of the first one after this. This is done by setting
L.head =L.nil.npXORL.head.
Exercise 10.3-1
A multiple array version could be L= 2,
/34567/
12 4 8 19 5 11
/2 3 4 5 6
A single array version could be L= 4,
12 7 /4 10 4 8 13 7 19 16 10 5 19 13 11 /16
Exercise 10.3-2
Algorithm 13 Allocate-Object()
if free == NIL then
error “out of space”
else
x=free
free =A[x+ 1]
end if
Exercise 10.3-3
Allocate object just returns the index of some cells that it’s guarenteed to
not give out again until they’ve been freed. The prev attribute is not modified
because only the next attribute is used by the memory manager, it’s up to the
code that calls allocate to use the prev and key attributes as it sees fit.
Exercise 10.3-4
For ALLOCATE-OBJECT, we will keep track of the next available spot in
the array, and it will always be one greater than the number of elements being
stored. For FREE-OBJECT(x), when a space is freed, we will decrement the
6
Algorithm 14 Free-Object(x)
A[x+ 1] = free
free =x
position of each element in a position greater than that of xby 1 and update
pointers accordingly. This takes linear time.
Exercise 10.3-5
See the algorithm COM P ACT IF Y −LIST (L, F )
Exercise 10.4-1
18
12
7 4
5
10
2 21
Note that indices 8 and 2 in the array do not appear, and, in fact do not
represent a valid tree.
Exercise 10.4-2
See the algorithm PRINT-TREE.
Exercise 10.4-3
Exercise 10.4-4
See the algorithm PRINT-TREE.
Exercise 10.4-5
See the algorithm INORDER-PRINT’(T)
Exercise 10.4-6
Our two pointers will be lef t and right. For a node x,x.lef t will point to
the leftmost child of xand x.right will point to the sibling of ximmediately to
its right, if it has one, and the parent of xotherwise. Our boolean value b, stored
at x, will be such that b=depth(x) mod 2. To reach the parent of a node,
simply keep following the “right” pointers until the parity of the boolean value
changes. To find all the children of a node, start by finding x.left, then follow
7

Algorithm 15 COMPACTIFY-LIST(L,F)
if n=m then
return
end if
e= max{maxi∈[m]{|key[i]|},maxi∈L{|key[i]|}}
increase every element of key[1..m] by 2e
for every element of L, if its key is greater than e, reduce it by 2e
f= 1
while key[f]< e do
f+ +
end while
a=L.head
if a>mthen
next[prev[f]] = next[f]
prev[next[f]] = prev[f]
next[f] = next[a]
key[f] = key[a]
prev[f] = prev[a]
F REE −OBJECT (a)
f+ +
while key[f]< e do
f+ +
end while
end if
while a6=L.head do
if a>mthen
next[prev[f]] = next[f]
prev[next[f]] = prev[f]
next[f] = next[a]
key[f] = key[a]
prev[f] = prev[a]
F REE −OBJECT (a)
f+ +
while key[f]< e do
f+ +
end while
end if
end while
8

Algorithm 16 PRINT-TREE(T.root)
if T.root == N IL then
return
else
Print T.root.key
PRINT-TREE(T.root.left)
PRINT-TREE(T.root.right)
end if
Algorithm 17 INORDER-PRINT(T)
let S be an empty stack
push(S, T )
while S is not empty do
U=pop(S)
if U6=NIL then
print U.key
push(S, U.lef t)
push(S, U.right)
end if
end while
Algorithm 18 PRINT-TREE(T.root)
if T.root == N IL then
return
else
Print T.root.key
x=T.root.left −child
while x6=NIL do
PRINT-TREE(x)
x=x.right −sibling
end while
end if
9

Algorithm 19 INORDER-PRINT’(T)
a=T.left
prev =T
while a6=Tdo
if prev =a.left then
print a.key
prev =a
a=a.right
else if prev =a.right then
prev =a
a=a.p
else if prev =a.p then
prev =a
a=a.lef t
end if
end while
print T.key
a=T.right
while a6=Tdo
if prev =a.left then
print a.key
prev =a
a=a.right
else if prev =a.right then
prev =a
a=a.p
else if prev =a.p then
prev =a
a=a.lef t
end if
end while
10

the “right” pointers until the parity of the boolean value changes, ignoring this
last node since it will be x.
Problem 10-1
For each, we assume sorted means sorted in ascending order
unsorted, single sorted, single unsorted, double sorted, double
SEARCH(L, k)n n n n
IN SERT (L, x) 1 1 1 1
DELET E(L, x)n n 1 1
SUCCESSOR(L, x)n1n1
P REDECESSOR(L, x)n n n 1
MINIMUM(L, x)n1n1
MAXIMU M(L, x)n n n 1
Problem 10-2
In all three cases, MAKE-HEAP simply creates a new list L, sets L.head =
NIL, and returns Lin constant time. Assume lists are doubly linked. To realize
a linked list as a heap, we imagine the usual array implementation of a binary
heap, where the children of the ith element are 2iand 2i+ 1.
a. To insert, we perform a linear scan to see where to insert an element such
that the list remains sorted. This takes linear time. The first element in the
list is the minimum element, and we can find it in constant time. Extract-min
returns the first elment of the list, then deletes it. Union performs a merge
operation between the two sorted lists, interleaving their entries such that
the resulting list is sorted. This takes time linear in the sum of the lengths
of the two lists.
b. To insert an element xinto the heap, begin linearly scanning the list until
the first instance of an element ywhich is strictly larger than x. If no such
larger element exists, simply instert xat the end of the list. If ydoes exist,
replace yt by x. This maintains the min-heap property beause x≤yand y
was smaller than each of its children, so xmust be as well. Moreover, xis
larger than its parent because ywas the first element in the list to exceed
x. Now insert y, starting the scan at the node following x. Since we check
each node at most once, the time is linear in the size of the list. To get the
minimum element, return the key of the head of the list in constant time.
To extract the minimum elemet, we first call MINIMUM. Next, we’ll replace
the key of the head of the list by the key of the second smallest element y
in the list. We’ll take the key stored at the end of the list and use it to
replace the key of y. Finally, we’ll delete the last element of the list, and call
MIN-HEAPIFY on the list. To implement this with linked lists, we need to
step through the list to get from element ito element 2i. We omit this detial
from the code, but we’ll consider it for runtime analysis. Since the value of
ion which MIN-HEAPIFY is called is always increasing and we never need
11
to step through elements multiple times, the runtime is linear in the length
of the list.
Algorithm 20 EXTRACT-MIN(L)
min =MINIMUM(L)
Linearly scan for the second smallest element, located in position i.
L.head.key =L[i]
L[i].key =L[L.length].key
DELETE(L, L[L.length])
MIN-HEAPIFY(L[i], i)
return min
Algorithm 21 MIN-HEAPIFY(L[i],i)
1: l=L[2i].key
2: r=L[2i+ 1].key
3: p=L[i].key
4: smallest =i
5: if L[2i]6=NIL and l < p then
6: smallest = 2i
7: end if
8: if L[2i+ 1] 6=NIL and r < L[smallest]then
9: smallest = 2i+ 1
10: end if
11: if smallest 6=ithen
12: exchange L[i] with L[smallest]
13: MIN-HEAPIFY(L[smallest],smallest)
14: end if
Union is implemented below, where we assume Aand Bare the two list
representations of heaps to be merged. The runtime is again linear in the
lengths of the lists to be merged.
c. Since the algorithms in part b didn’t depend on the elements being distinct,
we can use the same ones.
Problem 10-3
a. If the original version of the algorithm takes only t iterations, then, we have
that it was only at most t random skips though the list to get to the desired
value, since each iteration of the original while loop is a possible random
jump followed by a normal step through the linked list.
b. The for loop on lines 2-7 will get run exactly t times, each of which is constant
runtime. After that, the while loop on lines 8-9 will be run exactly Xttimes.
So, the total runtime is O(t+E[Xt]).
12

Algorithm 22 UNION(A,B)
1: if A.head =NIL then
2: return B
3: end if
4: i= 1
5: x=A.head
6: while B.head 6=N IL do
7: if B.head.key ≤x.key then
8: Insert a node at the end of list Bwith key x.key
9: x.key =B.head.key
10: Delete(B, B.head)
11: end ifx=x.next
12: end while
13: return A
c. Using equation C.25, we have that E[Xt] = P∞
i=1 P r(Xt≥i). So, we need
to show that P r(Xt≥i)≤(1 −i/n)t. This can be seen because having Xt
being greater than imeans that each random choice will result in an element
that is either at least isteps before the desitred element, or is after the
desired element. There are n−isuch elements, out of the total nelements
that we were pricking from. So, for a single one of the choices to be from
such a range, we have a probability of (n−i)/n = (1 −i/n). Since each of
the selections was independent, the total probability that all of them were
is (1 −i/n)t, as desired. Lastle, we can note that since the linked list has
length n, the probability that Xtis greater than nis equal to zero.
d. Since we have that t > 0, we know that the function f(x) = xtis increasing,
so, that means that bxct≤f(x). So,
n−1
X
r=0
rt=Zn
0brctdr ≤Zn
0
f(r)dr =nt+1
t+ 1
e.
E[Xt]≤
n
X
r=1
(1 −r/n)t=
n
X
r=1
t
X
i=0 t
i(−r/n)i=
t
X
i=0
n
X
r=1 t
i(−r/n)i
=
t
X
i=0 t
i(−1)i ni−1 +
n−1
X
r=0
(r)t!/n ≤
t
X
i=0 t
i(−1)ini−1 + ni+1
i+ 1/n
≤
t
X
i=0 t
i(−1)ini
i+ 1 =1
t+ 1
t
X
i=0 t+ 1
i+ 1(−n)i≤(1 −n)t+1
t+ 1
f. We just put together parts b and e to get that it runs in time O(t+n/(t+1)).
But, this is the same as O(t+n/t).
13

g. Since we have that for any number of iterations tthat the first algorithm takes
to find its answer, the second algorithm will return it in time O(t+n/t). In
particular, if we just have that t=√n. The second algorithm takes time
only O(√n). This means that tihe first list search algorithm is O(√n) as
well.
h. if we don’t have distinct key values, then, we may randomly select an element
that is further along than we had been before, but not jump to it because
it has the same key as what we were currently at. The analysis will break
when we try to bound the probability that Xt≥i.
14
Chapter 11
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 11.1-1
Starting from the first index in T, keep track of the highest index so far that
has a non NIL entry. This takes time O(m).
Exercise 11.1-2
Start with a bit vector bwhich contains a 1 in position kif kis in the dy-
namic set, and a 0 otherwise. To search, we return true if b[x] == 1. To insert
x, set b[x] = 1. To delete x, set b[x] = 0. Each of these takes O(1) time.
Exercise 11.1-3
You could have each entry in the table be either a pointer to a doubly linked
list containing all the objects with that key, or NIL if there are none. search
just returns the first element in the list corresponding to the given key. Since
all the elements in the list have that same key, it doesn’t matter which search
returns. Insert just adds to the start of teh doubly linked list. Finally, deletion
can be done in constant time in a doubly linked list, see problem 10-1
Exercise 11.1-4
The additional data structure will be a doubly linked list Swhich will be-
have in many ways like a stack. Initially, set Sto be empty, and do nothing
to initialize the huge array. Each object stored in the huge array will have two
parts: the key value, and a pointer to an element of S, which contains a pointer
back to the object in the huge array. To insert x, add an element yto the stack
which contains a pointer to position xin the huge array. Update position A[x]
in the huge array Ato contain a pointer to yin S. To search for x, go to position
xof Aand go to the location stored there. If that location is an element of S
which contains a pointer to A[x], then we know xis in A. Otherwise, x /∈A. To
delete x, delete the element of Swhich is pointed to by A[x]. Each of these takes
O(1) and there are at most as many elements in Sas there are valid elements
in A.
1
Exercise 11.2-1
Under the assumption of simple uniform hashing, we will use linearity of
expectation to compute this. Suppose that all the keys are totally ordered
{k1, . . . , kn}. Let Xibe the number of ` > kiso that h(`) = h(ki). Note, that
this is the same thing as Pj>i P r(h(kj) = h(ki)) = Pj>i 1/m = (n−i)/m.
Then, by linearity of expectation, the number of collisions is the sum of the
number of collisions for each possible smallest element in the collision. The
expected number of collisions is Pn
i=1 n−i
m=n2−n(n+1)
2
m=n2−n
2m
Exercise 11.2-2
Label the slots of our table be 0,1,2,...,8. Numbers which appear to the
left in the table have been inserted later.
0∅
1 10, 19, 28
2 20
3 12
4∅
5 5
6 33, 15
7∅
8 17
Exercise 11.2-3
Both kinds of searches become expected runtime of Θ(1 + lg(α)). Insertions
and deletions stay Θ(1 + α) because the time to insert into or delete from a
sorted list is linear.
Exercise 11.2-4
The flag in each slot of the hash table will be 1 if the element contains a
value, and 0 if it is free. The free list must be doubly linked. Seach is un-
modified, so it has expected time O(1). To insert an element x, first check if
T[h(x.key)] is free. If it is, delete T[h(x.key)] and change the flag of T[h(x.key)]
to 1. If it wasn’t free to begin with, simply insert x.key at the start of the list
stored there. To delete, first check if x.prev and x.next are NIL. If they are,
then the list will be empty upon deletion of x, so insert T[h(x.key)] into the free
list, update the flag of T[h(x.key)] to 0, and delete xfrom the list it’s stored in.
Since deletion of an element from a singly linked list isn’t O(1), we must use a
doubly linked list. All other operations are O(1).
Exercise 11.2-5
There is a subset of size n hashing to the same spot, because if each spot only
2

had n−1 elements hashing to it, then the universe could only be size (n−1)m.
The worst case searching time would be if all of the elements that we put in
the hashtable were this subset of size n all going to the same spot, which is linear.
Exercise 11.2-6
Choose one of the mspots in the hash table at random. Let nkdenote
the number of elements stored at T[k]. Next pick a number xfrom 1 to L
uniformly at random. If x < nj, then return the xth element on the list. Oth-
erwise, repeat this process. Any element in the hash table will be selected with
probability 1/mL, so we return any key with equal probability. Let Xbe the
random variable which counts the number of times we must repeat this process
before we stop and pbe the probability that we return on a given attempt. Then
E[X] = p(1+α)+(1−p)(1+E[X]) since we’d expect to take 1+αsteps to reach
an element on the list, and since we know how many elements are on each list, if
the element doesn’t exist we’ll know right away. Then we have E[X] = α+ 1/p.
The probability of picking a particular element is n/mL =α/L, so we have
E[X] = α+L/α =L(α/L + 1/α) = O(L(1 + 1/α)) since α≤L.
Exercise 11.3-1
If every element also contained a hash of the long character string, when
we are searching for the desired element, we’ll first check if the hashvalue of
the node in the linked list, and move on if it disagrees. This can increase the
runtime by a factor proportional to the length of the long character strings.
Exercise 11.3-2
Compute the value of the first character mod m, add the value of the second
character mod m, add the value of the third character mod mto that, and so
on, until all rcharacters have been taken care of.
Exercise 11.3-3
We will show that each string hashes to the sum of it’s digits mod 2p−1.
We will do this by induction on the length of the string. As a base case, suppose
the string is a single character, then the value of that character is the value of
kwhich is then taken mod m. Now, for an inductive step, let w=w1w2where
|w1| ≥ 1 and |w2|= 1. Suppose, h(w1) = k1. Then, h(w) = h(w1)2p+h(w2)
mod 2p−1 = h(w1) + h(w2) mod 2p−1. So, since h(w1) was the sum of all
but the last digit mod m, and we are adding the last digit mod m, we have the
desired conclusion.
Exercise 11.3-4
The keys 61, 62, 63, 64, and 65 are mapped to locations 700, 318, 936, 554,
3
and 172 respectively.
Exercise 11.3-5
As a simplifying assumption, assume that |B|divides |U|. It’s just a bit
messier if it doesn’t divide evenly.
Suppose to a contradiction that > 1
|B|−1
|U|. This means that for all
pairs k, ` in U, we have that the number nk,` of hash functions in Hthat
have a collision on those two elements satisfies nk,` ≤|H|
|B|−|H|
|U|. So, summing
over all pairs of elements in U, we have that the total number is less than≤
|H||U|2
2|B|−|H||U|
2.
Any particular hash function must have that there are at least |B||U|/|B|
2=
|B||U|2−|U||B|
2|B|2=|U|2
2|B|−|U|
2colliding pairs for that hash function, summing over
all hash functions, we get that there are at least |H| |U|2
2|B|−|U|
2colliding pairs
total. Since we have that there are at most some number less than this many,
we have a contradiction, and so must have the desired restriction on .
Exercise 11.3-6
Fix b∈Zp. By exercise 31.4-4, hb(x) collides with hb(y) for at most n−1
other y∈U. Since there are a total of ppossible values that hbtakes on, the
probability that hb(x) = hb(y) is bounded from above by n−1
p. Since this holds
for any value of b,His ((n-1)/p)-universal.
Exercise 11.4-1
This is what the array will look like after each insertion when using linear
probing:
10
22 10
22 31 10
22 4 31 10
22 4 15 31 10
22 4 15 28 31 10
22 4 15 28 17 31 10
22 88 4 15 28 17 31 10
22 88 4 15 28 17 59 31 10
For quadradic probing, it will look identical until there is a collision on
inserting the fifth element. Then, it is
22 4 15 31 10
22 4 28 15 31 10
22 17 4 28 15 31 10
22 88 17 4 28 15 31 10
22 88 17 4 28 15 31 10
4

Note that there is no way to insert the element 59 now, because the offsets
coming from c1= 1 and c2= 3 can only be even, and an odd offest would be
required to insert 59 because 59 mod 11 = 4 and all the empty positions are at
odd indices.
For double hashing, it is the same as linear probing.
Exercise 11.4-2
Algorithm 1 HASH-DELETE(T,k)
i=HASH −SEARCH(T, k)
T[i] = DELET ED
We modify INSERT by changing line 4 to: if T[j] == NIL or T[j] ==
DELET ED.
Exercise 11.4-3
For the α= 3/4 case, we just plug into theorems 11.6 and 11.8 respectively
to get that for a unsuccessfull search, the expected number of probes is bounded
by 4. And for a sucessfull search, the expected number of probes is bounded by
4
3ln(4).
For α= 7/8. The bound for expected number of probes of unsucessfull is 8,
and for sucessfull is 8
7ln(8).
Exercise 11.4-4
Write h2(k) = dc1and m=dc2for constants c1and c2. When we have ex-
amined (1/d)th of the table entries, this corresponds to m/d =c2of them. The
entry that we check at this point is [h1(k)+(m/d)h2(k)] mod m= [h1(k) +
(m/d)(dc1)] mod m≡h1(k). When d= 1, we may have to examine the entire
hash table.
Exercise 11.4-5
We will try to find a rational solution, let α=m/n. Using theorems 11.6
and 11.8, we have to solve the equation
1
1−α=2
αln( 1
1−α)
Unfortunately, this trancendental equation cannot be solved using simple
techniques. There is an exact solution using the Lambert W function of
1
2
1+2LambertW (−1,−(1
2)∗exp(−1
2))
LambertW (−1,−(1
2)∗exp(−1
2))
5
Which evaluates to approximately α=.7153.
Exercise 11.5-1
Let Aj,k be the event that jand khash to different things. Due to uniform
hashing, P r(Aj,k) = m−1
m. Also, we can say that there is a negative correlation
between the events. That is, if we know that several pairs of elements hashed
to the same thing, then we can only decrease the likelyhood that some other
pair hashed to different things. This gets us that the probability that all events
happen is ≤the probability that the all happened if they were independent, so,
P r(∩j,kAj,k)≤m−1
m(n
2)
≤e−1/m
n(n−1)
2=e
−n(n−1)
2m
So, if we have that that nexceeds m, the −n2/(2m) term is much bigger than
the n/2mterm, so, the exponent is going to −∞, which means the probability
is going to 0.
Problem 11-1
a. The index for each probe is computed uniformly from among all the possible
indices. Since we have n≤m/2, we know that there are at least half of the
indices empty at any stage. So, for more than kprobes to be required, we
would need that in each of kfirst probes, we probed a vertex that already had
an entry, this has probability less than 1/2, so the probability of it happening
each time is <1/(2k).
b. Using the result from the previous part with k= 2 lg(n), we have that the
probability that so many probes will be required is
<2−2 lg(n)= 2lg(n−2)=n−2=1
n2
c. We apply a union bound followed by the results of the previous part
P r{X > 2 lg(n)}=P r{∨iXi>2 lg(n)} ≤ X
i
P r{Xi>2 lg(n)} ≤ X
i
1
n2=n
n2=1
n
d. The longest possible length of a probe sequence is n, as we would try check-
ing every single entry already placed in the array. We also know that the
probability that a sequence of length more than 2 lg(n) is required is ≤1/n.
So, we have that the largest the expected value can be is
E[X]≤P r{X≤2 lg(n)}2 lg(n)+P r{X > lg(n)}n=n−1
n2 lg(n)+ 1
nn= 2 lg(n)+1−2lg(n)
n∈O(lg(n))
Problem 11-2
6

a. Let Qkdenote the probability that exactly kkeys hash to a particular
slot. There are n
kways to select the kkeys, they hash to that spot with
probability 1
nk, and the remaining n−kkeys hash to the remaining n−1
slots with probability n−1
nn−k. Thus,
Qk=1
nkn−1
nn−kn
k.
b. The probability that the slot containing the most keys contains exactly k
is bounded above by the probability that some slot contains kkeys. There are
nslots which we could select to contain those k, so Pk≤nQk.
c. Using the fact that n
k≤ne
kkwe have Qk≤(n−1)n−k
nnne
kk≤ek/kk.
d. By part (b), we have Pk≤nQk<1/n2.
e. This comes from computing expectation by conditioning, and bound-
ing Mfrom above by nin the first term. From the bound in (d) we have
nP (M > clg n
lg lg n)<1. For the second term, Pd
i=1 P(M=i)≤1 where
d=clg n/ lg lg n, so the asymptotic expectation follows.
Problem 11-3
a. At each step, we are increasing the amount we increase by by 1, so, this leads
to the “Gauss numbers” which have formula i2+i
2. So, we have c1=c2=1
2.
b. To show that this algorithm examines every number, we will show that every
number that it examines is distinct. Then, since it examines mnumbers
total, this will imply that every number is visited. Suppose that we visited
the same position on rounds iand i0, then,
h(k) + i+i2
2≡h(k) + i0+i02
2mod m
Which means i+i2
2≡i0+i02
2mod m
So,
i+i2≡i0+i02mod 2m
Rearranging,
i−i0≡i2−i02= (i+i0)(i−i0) mod 2m
Which would mean,
1≡(i+i0) mod 2m
7

However, there are only mrounds, so, we have that
1 = i+i0
Which is not possible because this would only corrsepond to having the first
(i= 0) and second(i= 1) rounds be probing the same position. This could
only happen if m= 1. and if m= 1, then we wouldn’t even have the second
round occur. So, we have our contradiction and so every probe was to a
distinct position, meaning every position was probed.
c.
Problem 11-4
a. Let k, l ∈Ube arbitrary. Then P(h(k) = h(l)) = P(< h(k), h(l)>=<
x, x >) for some x∈[m]. Since hcomes from a set of 2-unifersal hash functions,
this is equally likely to be any of the m2sequences. There are mpossible values
of xwhich would cause a collision, so the probability of collision is m
m2=1
m.
b. The probability of collision is 1
p, so His universal. Now consider the tuple
z=<0,0,...,0>. Then ha(x) = hb(x) = 0 for any a, b ∈U, so the sequence
< z, x(2) >is equally likely to be any of psequences starting with 0, but can’t
be any of the other p2−psequences, so His not 2-universal.
c. Let x, y ∈Ube fixed, distinct n-tuples. As aiand brange over Zp,h0
ab(x)
is equally likely to achieve every value from 1 to psince for any sequence a, we
can let bvary from 1 to p−1. Thus, < h0
ab(x), h0
ab(y)>is equally likely to be
any of the p2sequences, so His 2-universal.
d. Since His 2-universal, there are pother functions which map mto h(m),
and the adversary has no way of knowing which one of these Alice and Bob
have agreed on in advance, so the best he can do is try one of them, which will
succeed in fooling Bob with probability 1/p.
8
Chapter 12
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 12.1-1
Anytime that a node has a single child, treat it as the right child, with the
left child being NIL
10
4
1 5
17
16 21
10
4
1 5
16
17
21
1
5
1
4
10
16
17
21
4
1 5
10
16
17
21
2

1
4
5
10
16
17
21
Exercise 12.1-2
The binary-search-tree property guarantees that all nodes in the left subtree
are smaller, and all nodes in the right subtree are larger. The min-heap prop-
erty only guarantees the general child-larger-than-parent relation, but doesn’t
distinguish between left and right children. For this reason, the min-heap prop-
erty can’t be used to print out the keys in sorted order in linear time because
we have no way of knowing which subtree contains the next smallest element.
Exercise 12.1-3
Our solution to exercise 10.4-5 solves this problem.
Exercise 12.1-4
We call each algorithm on T.root. See algorithms PREORDER-TREE-
WALK and POSTORDER-TREE-WALK.
Exercise 12.1-5
Suppose to a contradiction that we could build a BST in worst case time
o(nlg(n)). Then, to sort, we would just construct the BST and then read off the
3

Algorithm 1 PREORDER-TREE-WALK(x)
if x6=NIL then
print x
PREORDER-TREE-WALK(x.left)
PREORDER-TREE-WALK(x.right)
end if
return
Algorithm 2 POSTORDER-TREE-WALK(x)
if x6=NIL then
POSTORDER-TREE-WALK(x.left)
POSTORDER-TREE-WALK(x.right)
print x
end if
return
elements in an inorder traversal. This second step can be done in time Θ(n) by
Theorem 12.1. Also, an inorder traversal must be in sorted order because the
elements in the left subtree are all those that are smaller than the current ele-
ment, and they all get printed out before the current element, and the elements
of the right subtree are all those elements that are larger and they get printed
out after the current element. This would allow us to sort in time o(nlg(n)) a
contradiction
Exercise 12.2-1
option ccould not be the sequence of nodes explored because we take the
left child from the 911 node, and yet somehow manage to get to the 912 node
which cannot belong the left subtree of 911 because it is greater. Option eis
also impossible because we take the right subtree on the 347 node and yet later
come across the 299 node.
Exercise 12.2-2
See algorithms TREE-MINIMUM and TREE-MAXIMUM.
Algorithm 3 TREE-MINIMUM(x)
if x.lef t 6=NIL then
return T REE −MINIMUM(x.left)
else
return x
end if
4
Algorithm 4 TREE-MAXIMUM(x)
if x.right 6=NIL then
return T REE −MAXIMUM(x.right)
else
return x
end if
Exercise 12.2-3
Algorithm 5 TREE-PREDECESSOR(x)
if x.lef t 6=NIL then
return TREE-MAXIMUM(x.left)
end if
y=x.p
while y6=NIL and x== y.left do
x=y
y=y.p
end while
return y
Exercise 12.2-4
Suppose we search for 10 in this tree. Then A={9},B={8,10}and C=∅,
and Professor Bunyan’s claim fails since 8 <9.
8
NIL 10
9NIL
Exercise 12.2-5
Suppose the node xhas two children. Then it’s successor is the minimum
element of the BST rooted at x.right. If it had a left child then it wouldn’t be
the minimum element. So, it must not have a left child. Similarly, the prede-
cessor must be the maximum element of the left subtree, so cannot have a right
child.
Exercise 12.2-6
5

First we establish that ymust be an ancestor of x. If yweren’t an ancestor
of x, then let zdenote the first common ancestor of xand y. By the binary-
search-tree property, x<z<y, so ycannot be the successor of x.
Next observe that y.left must be an ancestor of xbecause if it weren’t, then
y.right would be an ancestor of x, implying that x > y. Finally, suppose that
yis not the lowest ancestor of xwhose left child is also an ancestor of x. Let
zdenote this lowest ancestor. Then zmust be in the left subtree of y, which
implies z < y, contradicting the fact that yis the successor if x.
Exercise 12.2-7
To show this bound on the runtime, we will show that using this procedure,
we traverse each edge twice. This will suffice because the number of edges in a
tree is one less than the number of vertices.
Consider a vertex of a BST, say x. Then, we have that the edge between
x.p and xgets used when successor is called on x.p and gets used again when it
is called on the largest element in the subtree rooted at x. Since these are the
only two times that that edge can be used, apart from the initial finding of tree
minimum. We have that the runtime is O(n). We trivially get the runtime is
Ω(n) because that is the size of the output.
Exercise 12.2-8
Let xbe the node on which we have called TREE-SUCCESSOR and ybe the
kth successor of x. Let zbe the lowest common ancestor of xand y. Successive
calls will never traverse a single edge more than twice since TREE-SUCCESSOR
acts like a tree traversal, so we will never examine a single vertex more than
three times. Moreover, any vertex whose key value isn’t between xand ywill
be examined at most once, and it will occur on a simple path from xto zor y
to z. Since the lengths of these paths are bounded by h, the running time can
be bounded by 3k+ 2h=O(k+h).
Exercise 12.2-9
If x=y.lef t then calling successor on xwill result in no iterations of the
while loop, and so will return y. Similarly, if x=y.right, the while loop for call-
ing predecessor(see exercise 3) will be run no times, and so ywill be returned.
Then, it is just a matter of recognizing what the problem asks to show is exactly
that y is either predecessor(x) or successor(x).
Exercise 12.3-1
The initial call to TREE-INSERT-REC should be NIL,T.root,z
Exercise 12.3-2
6

Algorithm 6 TREE-INSERT-REC(y,x,z)
if x6=NIL then
if z.key < x.key then
TREE-INSERT-REC(x,x.left,z)
else
TREE-INSERT-REC(x,x,right,z)
end if
end if
z.p = y
if y== NIL then
T.root = z
else if z.key < y.key then
y.left = z
else
y.right = z
end if
The nodes examined in the while loop of TREE-INSERT are the same as
those examined in TREE-SEARCH. In lines 9 through 13 of TREE-INSERT,
only one additional node is examined.
Exercise 12.3-3
The worst case is that the tree formed has height nbecause we were inserting
them in already sorted order. This will result in a runtime of Θ(n2). In the best
case, the tree formed is approximately balanced. This will mean that the height
doesn’t exceed O(lg(n)). Note that it can’t have a smaller height, because a
complete binary tree of height honly has Θ(2h) elements. This will result in a
rutime of O(nlg(n). We showed Ω(nlg(n)) in exercise 12.1-5.
Exercise 12.3-4
Deletion is not commutative. In the following tree, deleting 1 then 2 yields
a different from the one obtained by deleting 2 then 1.
2
1 4
3NIL
Exercise 12.3-5
7

Our insertion procedure follows closely our solution to 12.3-1, the difference
being that once it finds the position to insert the given node, it updates the
succ fields appropriately instead of the p field of z.
Algorithm 7 TREE-INSERT’(y,x,z)
if x6=NIL then
if z.key < x.key then
TREE-INSERT’(x,x.left,z)
else
TREE-INSERT’(x,x,right,z)
end if
end if
if y== NIL then
T.root = y
else if z.key < y.key then
y.left = z
x.succ = y
else
y.right = z
z.succ = y.succ
y.succ = z
end if
Our Search procedure is unchanged from the version given in the previous
section
We will assume for the deletion procedure that all the keys are distinct, as
that has been a frequent assumption throughout this chapter. This will however
depend on it. Our deletion procedure first calls search until we are one step away
from the node we are looking for, that is, it calls TREE-PRED(T.root,z.key)
Algorithm 8 TREE-PRED(x,k)
if k < x.key then
y=x.lef t
else
y=x.right
end if
if y== NIL then
throw error
else if y.key =kthen
return x
else
return TREE-PRED(y,k)
end if
It can use this TREE-PRED procedure to comput u.p and v.p in the TRANS-
8
PLANT procedure. Since TREE-DELETE only calls TRANSPLANT a con-
stant number of times, increasing the runtime of TRANSPLANT to O(h) in
this way causes the runtime of the new TREE-DELETE procedure to be O(h).
Exercise 12.3-6
Update line 5 so that yis set equal to TREE-MAXIMUM(z.left). To imple-
ment the fair strategy, we could randomly decide each time TREE-DELETE is
called whether or not to use the predecessor or successor.
Exercise 12.4-1
Consider all the possible positions of the largest element of the subset of
n+ 3 of size 4. Suppose it were in position i+ 4 for some i≤n−1. Then, we
have that there are i+3 positions from which we can select the remaining three
elements of the subset. Since every subset with different largest element is dif-
ferent, we get the total by just adding them all up (inclusion exclusion principle).
Exercise 12.4-2
To keep the average depth low but maximize height, the desired tree will be
a complete binary search tree, but with a chain of length c(n) hanging down
from one of the leaf nodes. Let k= log(n−c(n)) be the height of the complete
binary search tree. Then the average height is approximately given by
1
n
n−c(n)
X
i=1
lg(i)+(k+ 1) + (k+ 2) + . . . + (k+c(n))
≈lg(n−c(n)) + c(n)2
2n.
The upper bound is given by the largest c(n) such that lg(n−c(n))+ c(n)2
2n=
Θ(lg n) and c(n) = ω(lg n). One function which works is √n.
Exercise 12.4-3
Suppose we have the elements {1,2,3}. Then, if we construct a tree by a
random ordering, then, we get trees which appear with probabilities some mul-
tiple of 1
6. However, if we consider all the valid binary search trees on the key
set of {1,2,3}. Then, we will have only five different possibilities. So, each will
occur with probability 1
5, which is a different probability distribution.
Exercise 12.4-4
The second derivative is 2xln2(2) which is always positive, so the function
is convex.
9

Exercise 12.4-5
Suppose that when quikcksort always selects it’s elements to be in the middle
n1−k/2of the elements each time. Then, the size of the problem shrinks by a
power of at least (1−k/2) each time. So, the greatest depth of recursion dwill be
so that n(1−k/2)d≤2, solving for d, we get (1 −k/2)d≤logn(2) = lg(2)/lg(n),
so, d≤log1−k/2(lg(2))−log1−k/2(lg(n) = log1−k/2(lg(2))−lg(lg(n))/lg(1−k/2).
Let A(n) deonte the probabiltiy that when quicksorting a list of length n,
some pivot is selected to not be in the middle n1−k/2of the numbers. This
doesn’t happen with probability 1
nk/2. Then, we have that the two subproblems
are of sizen1, n2with n1+n2=n−1 and max{n1, n2} ≤ n1−k/2. So, A(n)≤
1
nk/2+T(n1) + T(n2) So, since we bounded the depth by O(1/lg(n)) let {ai,j }i
be all the subproblem sizes left at depth j. So, A(n)≤1
nk/2PjPi1
a
Problem 12-1
a. Each insertion will add the elemement to the right of the rightmost leaf
because the inequality on line 11 will always evaluate to false. This will
result in the runtime being Pn
i=1 i∈Θ(n2)
b. This strategy will result in each of the two children subtrees having a differ-
ence in size at most one. This means that the height will be Θ(lg(n)). So,
the total runtime will be Pn
i=1 lg(n)∈Θ(nlg(n))
c. This will only take linear time since the tree itself will be height 0, and a
single insertion into a list can be done in constant time.
d. The worst case performance is that every random choice is to the right (or
all to the left) this will result in the same behavior as in the first part of this
problem, Θ(n2)
To compute the expected runtime informally, just notice that when randomly
choosing, we will pick left roughly half the time, so, the tree will be roughly
balanced, so, we have that the depth is roughly lg(n), so the expected runtime
will be nlg(n).
Problem 12-2
The word at the root of the tree is necessarily before any word in its left or
right subtree because it is both shorter, and the prefix of, every word in each of
these trees. Moreover, every word in the left subtree comes before every word
in the right subtree, so we need only perform a preorder traversal. This can be
done recursively, as shown in exercise 12.1-4.
Problem 12-3
a. Since we are averaging over all nodes xthe value of d(x, T ), it is 1
nPx∈Td(x, T ),
but by definition, this is 1
nP(T).
10

b. Every non-root node has a contribution of one coming from the first edge from
the root on its way to that node, every other edge in this path is counted
by looking at the edges within the two subtrees rooted at the child of the
original root. Since there are n−1 non-root nodes, we have
P(T) = X
x∈T
d(x, T ) = X
x∈TL
d(x, T ) + X
x∈TR
d(x, T ) =
X
x∈TL
(d(x, TL)+1)+ X
x∈TR
(d(x, TR)+1) = X
x∈TL
d(x, TL)+ X
x∈TR
d(x, TR)+n−1 =
P(TL) + P(TR) + n−1
c. When we are randomly building our tree on n keys, we have npossibilities
for the first element that we add to the tree, the key that will belong to
the eventual root. Suppose that it had order statistic i+ 1 for some iin
{0,...n−1}. Then, we have that all the smaller elements will be to the
left and all the larger elements will be in the subree to the right. However,
they will all be in random order relative to eachother, so, we will have P(i) =
E[P(TL)] and P(n−i−1) = E[P(TR)]. So, we have have the deisred ineqality
by averaging over the order statistic of the first term put into the BST.
d.
1
n
n−1
X
i=0
P(i)+P(n−i−1)+n−1 = 1
n n−1
X
i=0
P(i) +
n−1
X
i=0
P(n−i−1) +
n−1
X
i=0
(n−1)!
Then, we do the substitution j=n−i−1 and do the simple thing of summing
a constant for the third sum to get
=1
n
n−1
X
i=0
P(i) +
n−1
X
j=0
P(j) + n(n−1)
=2
n
n−1
X
i=0
P(i) + n−1
e. Our recurrence from the previous part is exactly the same as eq (7.6) which
we showed in problem 7-3.e to have solution Θ(nlg(n))
f. Let the first pivot selected be the first element added to the binary tree. Since
every element is compared to the root, and every element is compared to the
first pivot, we have what we want. Then, let the next pivot for the left (resp.
right) subarrays be the first element that is less than (resp. greater than)
the root. Then, we have that the two subtrees form the same partition of the
remaining elements as the two subarrays left form. We can than continue to
recurse in this way. Since if holds at the first element, and the problems have
the same recursive structure, we have that it holds at every element.
Problem 12-4
11

a. There is a single binary tree on one vertex consisting of just a root, so b0= 1.
To count the number of binary trees with nnodes, we first choose a root from
among the nvertices. If the root node we have chosen is the ith smallest
element, the left subtree will have i−1 vertices, and the right subtree will
have n−ivertices. The number of such left and right subtrees are counted by
bi−1and bn−irespectively. Summing over all possibly choices of root vertex
gives:
bn=
n
X
k=1
bk−1bn−k=
n−1
X
k=0
bkbn−k−1.
b.
B(x) =
∞
X
n=0
bnxn
= 1 +
∞
X
n=1
bnxn
= 1 +
∞
X
n=1
n−1
X
k=0
bkbn−k−1xn
= 1 + x
∞
X
n=1
n−1
X
k=0
bkxkbn−k−1xn−k−1
= 1 + x
∞
X
n=0
n
X
k=0
bkxkbn−kxn−k
= 1 + xB(x)2.
Applying the quadratic formula and noting that the minus sign is to be taken
so that B(0) = 0 proves the result.
c. Using the Taylor expansion of √1−4xwe have:
B(x) = 1
2x 1−
∞
X
n=0
1
1−2n2n
nxn!
=−1
2x
∞
X
n=1
1
1−2n2n
nxn
=1
2
∞
X
n=1
1
2n−12n
nxn−1
=1
2
∞
X
n=0
1
2n+ 12n+ 2
n+ 1 xn.
12

Extracting the coefficient from xnand simplifying yields the result.
d. The asymptotic follows from applying Sirling’s formula to bn.
13
Chapter 13
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 13.1-1
8
4
2
1 3
6
5 7
12
10
9 11
14
13 15
We shorten NIL to N so that it can be more easily displayed in the document.
The following has black height 2.
8
4
2
1
N N
3
N N
6
5
N N
7
N N
12
10
9
N N
11
N N
14
13
N N
15
N N
The following has black height 3
1
8
4
2
1
N N
3
N N
6
5
N N
7
N N
12
10
9
N N
11
N N
14
13
N N
15
N N
Lastly, the following has black height 4.
8
4
2
1
N N
3
N N
6
5
N N
7
N N
12
10
9
N N
11
N N
14
13
N N
15
N N
Exercise 13.1-2
If the inserted node is red then it won’t be a red-black tree because 35 will
be the parent of 36, which is also colored red. If the inserted node is black it
will also fail to be a red-black tree because there will be two paths from node
38 to T.nil which contain different numbers of black nodes, violating property
5. In the picture of the tree below, the NIL nodes have been omitted for space
reasons.
2
26
17
14
10
7
3
12
16
15
41
30
28 38
35
36
39
47
Exercise 13.1-3
It will. There was no red node introduced, so 4 will still be satisfied. Since
the root is in every path from the root to the leaves, but no others. 5 will be
satisfied because the only paths we will be changing the number of black nodes
in are those coming from the root. All of these will increase by 1, and so will
all be equal. 3 is trivially preserved, as no new leaves are introduced. 1 is also
trivially preserved as only one node is changed and it is not changed to some
mysterious third color.
Exercise 13.1-4
The possible degrees are 0 through 5, based on whether or not the black
node was a root and whether it had one or two red children, each with either
one or two black children. The depths could shrink by at most a factor of 1/2.
Exercise 13.1-5
Suppose we have the longest simple path (a1, a2,...as) and the shortest sim-
ple path (b1, b2, . . . , bt). Then, by propery 5 we know they have equal numbers
of black nodes. By property 4, we know that neither contains a repeated red
node. This tells us that at most bs−1
2cof the nodes in the longest path are red.
3

This means that at least ds+1
2eare black, so, t≥ ds+1
2e. So, if, by way of con-
tradiction, we had that s > t∗2, then t≥ ds+1
2e≥d2t+2
2e=t+1 a contradiction.
Exercise 13.1-6
In a path from root to leaf we can have at most one red node between any
two black nodes, so maximal height of such a tree is 2k+1, where each path from
root to leaf is alternating red and black nodes. To maximize internal nodes, we
make the tree complete, giving a total of 22k+1 −1 internal nodes. The smallest
possible number of internal nodes comes from a complete binary tree, where
every node is black. This has 2k+1 −1 internal nodes.
Exercise 13.1-7
Since each red node needs to have two black children, our only hope at
getting a large number of internal red nodes relative to our number of black
internal nodes is to make it so that the parent of every leaf is a red node. So,
we would have a ratio of 2
3if we have the tree with a black root which has red
children, and all of it’s grandchildren be leaves. We can’t do better than this
because as we make the tree bigger, the ratio approaches 1
2.
The smallest ratio is acheived by having a complete tree that is balanced
and black as a raven’s feather. For example, see the last tree presented in the
solution to 13.1-1.
Exercise 13.2-1
See the algorithm for RIGHT-ROTATE.
Algorithm 1 RIGHT-ROTATE(T,x)
y = x.left
x.left = y.right
if y.right 6=T.nil then
t.right.p = x
end if
y.p = x.p
if x.p == T.nil then
T.root = y
else if x == x.p.left then
x.p.left = y
else
x.p.right = y
end if
y.right =x
x.p =y
4

Exercise 13.2-2
We proceed by induction. In a tree with only one node, the root has nei-
ther a left nor a right child, so no rotations are valid. Suppose that a tree on
n≥0 nodes has exactly n−1 rotations. Let Tbe a binay search tree on n+ 1
nodes. If T.root has no right child then the root can only be involved in a right
rotation, and the left child of Thas nverties, so it has exactly n−1 rotations,
yielding a total of nfor the whole tree. The arugment is identical if T.root has
no left child. Finally, suppose T.root has two children, and let kdenote the
number of nodes in the left subtree. Then the root can be either left or right
rotated, contributing 2 to the count. By the induction hypothesis, T.lef t has
exactly k−1 rotations and T.right has exactly n−k−1−1 rotations, so there
are a total of 2+k−1+n−k−1−1 = npossible rotations, completing the proof.
Exercise 13.2-3
the depth of cdecreases by one, the depth of bstays the same, and the depth
of aincreases by 1.
Exercise 13.2-4
Consider transforming an arbitrary n-node BT into a right-going chain as
follows: Let the root and all successive right children of the root be the elements
of the chain initial chain. For any node xwhich is a left child of a node on the
chain, a single right rotation on the parent of xwill add that node to the chain
and not remove any elements from the chain. Thus, we can convert any BST to
a right chain with at most n−1 right rotations. Let r1, r2, . . . , rkbe the sequence
of rotations required to convert some BST T1into a right-going chain, and let
s1, s2, . . . , smbe the sequence of rotations required to convert some other BST
T2to a right-going chian. Then k < n and m<n, and we can convert T1to
T2be performing the sequence r1, r2, . . . , rk, s0
ms0
m−1, . . . , s0
1where s0
iis the op-
posite rotation of si. Since k+m < 2n, the number of rotations required is O(n).
Exercise 13.2-5
Consider the BST for T2to be
8
4
NIL NIL
NIL
5
And let T1be
8
NIL 4
NIL NIL
Then, there are no nodes for which its valid to call right rotate in T1. Even
though it is possible to right convert T2into T1, the reverse is not possible.
For any BST T, define the quantity f(T) to be the sum over all the nodes of
the number of left pointers that are used in a simple path from the root to that
node. Note that the contribution from each node is O(n). Since there are only n
nodes, we have that f(T) is O(n2). Also, when we call RIGHT-ROTATE(T,x),
then the contribution from xdecreases by one, and the contribution from all
other elements remain the same. Since f(T) is a quantity that decreases by
exactly one with every call of RIGHT-ROTATE, and begins O(n2), and never
goes negative, we know that there can only be at most O(n2) calls of RIGHT-
ROTATE on a BST.
Exercise 13.3-1
If we chose to set the color of zto black then we would be violating property
5 of being a red-black tree. Because any path from the root to a leaf under z
would have one more black node than the paths to the other leaves
Exercise 13.3-2
41
N N
41
38
N N
N
6
38
31
N N
41
N N
38
31
12
N N
N
41
N N
38
19
12
N N
31
N N
41
N N
7
38
19
12
8
N N
N
31
N N
41
N N
Exercise 13.3-3
For the z being a right child case, we append the black height of each node to
get
C:k
A:k
αB:k
βγ
D:k
δ
which goes to
8
C:k+1
A:k
αB:k
βγ
D:k
δ
note that while the black depths of the nodes may of changed, they are still
well defined, and so they still satisfy condition 5 of being a red-black tree. Sim-
ilar trees for when z is a left child.
Exercise 13.3-4
First observe that RB-INSERT-FIXUP only modifies the child of a node if
it is already red, so we will never modify a child which is set to T.nil. We just
need to check that the parent of the root is never set to red. Since the root and
the parent of the root are automatically black, if zis at depth less than 2, the
while loop will be broken. We only modify colors of nodes at most two levels
above z, so the only case we need to worry about is if zis at depth 2. In this
case we risk modifying the root to be red, but this is handled in line 16. When
zis updated, it will either the root or the child of the root. Either way, the
root and the parent of the root are still black, so the while condition is violated,
making it impossibly to modify T.nil to be red.
Exercise 13.3-5
Suppose we just added the last element. Then, prior to calling RB-INSERT-
FIXUP, we have that it is red. In all of the fixup cases for an execution of the
while loop, we have that the resulting tree fragment contains a red non-root
node. This node will not be later made black on line 16 becuse it isn’t the root.
Exercise 13.3-6
We need to remove line 8 from RB-INSERT and modify RB-INSERT-FIXUP.
At any point in RB-INSERT-FIXUP we need only keep track of at most 2 an-
cestors: z.p and z.p.p. We can find and store each of these nodes in log ntime
and use them for the duration of the call to RB-INSERT-FIXUP. This won’t
change the running time of RB-INSERT.
9
Exercise 13.4-1
There are two ways we may of left the while loop of RB-DELETE-FIXUP.
The first is that we had x=T.root. In this case, we set x.color =BLACK onl
ine 23. So, we must have that the root is black. The other case is that we ended
the while loop because we had x.color == RED, but had that x6=T.root. This
rules out case 4, because that has us setting x=T.root. In case 3, we don’t
set xto be red, or change xat all, so it coudn’t of been the last case run. In
case 2, we set nothing new to be RED, so this coudn’t lead to exiting the while
loop for this reason. In case 1, we make the sibling black and rotate it into the
position of the parent. So, it wouln’t be possible to make the root red in this
step because the only node we set to be red, we then placed a black node above.
Exercise 13.4-2
Suppose that both xand x.p are red in RB-DELETE. This can only happen
in the else-case of line 9. Since we are deleting from a red-black tree, the other
child of y.p which becomes x0ssibling in the call to RB-TRANSPLANT on line
14 must be black, so xis the only child of x.p which is red. The while-loop
condition of RB-DELETE-FIXUP(T,x) is immediately violated so we simply
set x.color =black, restoring property 4.
Exercise 13.4-3
38
19
12
8
N N
N
31
N N
41
N N
10
38
19
12
N N
31
N N
41
N N
38
19
N31
N N
41
N N
38
31
N N
41
N N
38
N41
N N
11
41
N N
N
Exercise 13.4-4
Since it is possible that wis T.nil, any line of RB-DELETE-FIXUP(T,x)
which examines or modifies wmust be included. However, as described on page
317, xwill never be T.nil, so we need not include those lines.
Exercise 13.4-5
Our count will include the root (if it is black).
Case 1: The count to each subtree is 2 both before and after
Case 2: The count to the subtrees αand βis 1+count(c) in both cases,
and the count for the rest of the subtrees goes from 2+count(c) to 1+count(c).
This decrease in the count for the other subtreese is handled by then having x
represent an additional black.
Case 3: The count to and ζis 2+count(c) both before and after, for all the
other subtrees, it is 1+count(c) both before and after
Case 4: For αand β, the count goes from 1+count(c) to 2+count(c). For
γand δ, it is 1+count(c)+count(c’) both before and after. For and ζ, it is
1+ count(c) both before and after. This increase in the count for αand βis
because xbefore indicated an extra black.
Exercise 13.4-6
At the start of case 1 we have set wto be the sibling of x. We check on line
4 that w.color == red, which means that the parent of xand wcannot be red.
Otherwise property 4 is violated. Thus, their concerns are unfounded.
Exercise 13.4-7
Suppose that we insert the elements 3,2,1 in that order, then, the resulting
tree will look like
12
2
1
NIL NIL
3
NIL NIL
Then, after deleting 1, which was the last element added, the resulting tree is
2
NIL 3
NIL NIL
however, the tree we had before we inserted 1 in the first place was
3
2
NIL NIL
NIL
These two red black trees are clearly different
Problem 13-1
a. We need to make a new version of every node that is an ancestor of the node
that is inserted or deleted.
b. See the algorithm, PERSISTENT-TREE-INSERT
c. Since the while loop will only run at most htimes, since the distance from
xto the root is increasing by 1 each time and bounded by the height. Also,
since each interation only takes a constant amount of time and uses a constant
amount of additional space, we have that both the time and space complexity
are O(h).
d. When we insert an element, we need to make a new version of the root. So,
any nodes that point to the root must have a new copy made so that they
13

Algorithm 2 PERSISTENT-TREE-INSERT(T,k)
x=T.root
if x==NIL then
T.root = new node(key =k)
end if
while x6=NIL do
y=x
if k¡x.key then
x= x.left
y.left = copyof(x)
else
x= x.right
y.right = copyof(x)
end if
end while
z = new node(key = k, p = y)
if k ¡ y.key then
y.left = z
else
y.right = z
end if
point to the new root. So, all nodes of depth 1 must be copied. Similarly,
all nodes that point to those must have new copies so that have the correct
version. So, all nodes of depth 2 must be copied. Similarly, all nodes must
be copied. So, we have that we need at least Ω(n) time and additional space.
e. Since the rebalancing operations can only change ancestors, and children of
ancestors we only have to allocate at most 2hnew nodes for each insertion,
since the rest of the tree will be unchanged. This is of course assuming
that we don’t keep track of the parent pointers. This can be acheived by
following the suggestions in 13.3-6 applied to both insert and delete. That is,
we perform a search for the element where we store the O(h) elements that
are either ancestors or children of ancestors. Since these are the only nodes
under consideration when doing the insertion and deletion procedure, then
we can know their parents even though we aren’t keeping track of the parent
pointers for each node. Since the height stays O(lg(n)), then, we have that
everything can be done in O(lg(n)).
Problem 13-2
a. When we call insert or delete we modify the black-height of the tree by at
most 1 and we can modify it according to which case we’re in, so no addi-
tional storage is required. When descending through T, we can determine
the black-height of each node we visit in O(1) time per node visited. Start by
14

determining the black height of the root in O(log n) time. As we move down
the tree, we need only decrement the height by 1 for each black node we
see to determine the new height which can be done in O(1). Since there are
O(log n) nodes on the path from root to leaf, the time per node is constant.
b. Find the black-height of T1in O(log n) time. Then find the black-height of
T2in O(log n) time. Finally, set z=T1.root. While the black height of z
is strictly greater than T2.bh, update zto be z.right if such a child exists,
otherwise update zto be z.left. Once the height of zis equal to T2.bh, set y
equal to z. The runtime of the algorithm is O(log n) since the height of T1,
and hence the number of iterations of the while-loop, is at most O(log n).
c. Let Tdenote the desired tree. Set T.root =x,x.left =y,y.p =x,
x.right =T2.root and T2.root.p =x. Every element of Tyis in T1which
contains only elements smaller than xand every element of T2is larger than
x. Since Tyand T2each have the binary search tree property, Tdoes as well.
d. Color xred. Find yin T1, as in part b, and form T=Ty∪ {x} ∪ T2as
in part c in constant time. Call T’ = RB-TRANSPLANT(T,y,x). We have
potentially violated the red black property if y’s parent was red. To remedy
this, call RB-INSERT-FIXUP(T’, x).
e. In the symmetric situation, simply reverse the roles of T1and T2in parts b
through d.
f. If T1.bh ≥T2.bh, run the steps outlined in part d. Otherwise, reverse the
roles of parts T1and T2in d and then proceed as before. Either way, the
algorithm takes O(log n) time because RB-INSERT-FIXUP is O(log n).
Problem 13-3
a. Let T(h) denote the minimum size of an AVL tree of height h. Since it is
height h, it must have the max of it’s children’s heights is equal to h−1. Since
we are trying to get as few notes total as possible, suppose that the other
child has as small of a height as is allowed. Because of the restriction of AVL
trees, we have that the smaller child must be at least one less than the larger
one, so, we have that T(h)≥T(h−1) + T(h−2) + 1 where the +1 is coming
from counting the root node. We can get inequality in the opposite direction
by simply taking a tree that acheives the minimum number of number of
nodes on height h−1 and on h−2 and join them together under another
node. So, we have that T(h) = T(h−1) + T(h−2) + 1. Also, T(0) = 0,
15

T(1) = 1. This is both the same recurrence and initial conditions as the
Fibonacci numbers. So, recalling equation (3.25), we have that
T(h) = φh
√5+1
2≤n
Rearranging for h, we have
φh
√5−1
2≤n
φh≤√5n+1
2
h≤lg(√5) + lg(n+1
2)
lg(φ)∈O(lg(n))
b. Let UNBAL(x) deonte x.left.h - x.right.h. Then, the algorithm BALANCE
does what is desired. Note that because we are only rotating a single element
at a time, the value of UNBAL(x) can only change by at most 2 in each step.
Also, it must eventually start to change as the tree that was shorter becomes
saturated with elements. We also fix any breaking of the AVL property that
rotating may of caused by our recursive calls to the children.
Algorithm 3 BALANCE(x)
while |UN BAL(x)|>1do
if UN BAL(x)>0then
RIGHT-ROTATE(T,x)
else
LEFT-ROTATE(T,x)
end if
BALANCE(x.left)
BALANCE(x.right)
end while
c. For the given algorithm AVL-INSERT(x,z), it correctly maintains the fact
that it is a BST by the way we search for the correct spot to insert z. Also, we
can see that it maintains the property of being AVL, because after inserting
the element, it checks all of the parents for the AVL property, since those
are the only places it could of broken. It then fixes it and also updates the
height attribute for any of the nodes for which it may of changed.
d. Since both for loops only run for O(h) = O(lg(n)) iterations, we have that
that is the runtime. Also, only a single rotation will occur in the second while
loop because when we do it, we will be decreasing the height of the subtree
rooted there, which means that it’s back down to what it was before, so all
of it’s ancestors will have unchanged heights, so, no further balancing will be
required.
16

Algorithm 4 AVL-INSERT(x,z)
w = x
while w6=NIL do
y = w
if z.key > y.key then
w= w.right
else
w = w.left
end if
end while
if z.key > y.key then
y.right = z
if y.left = NIL then
y.h = 1
end if
else
y.left = z
if y.right = NIL then
y.h = 1
end if
end if
while y6=xdo
y.h = 1 + max{y.left.h, y.right.h}
if y.lef t.h > y.right.h + 1 then
RIGHT-ROTATE(T,y)
end if
if y.right.h > y.left.h + 1 then
LEFT-ROTATE(T,y)
y= y.p
end if
end while
17

Problem 13-4
a. The root ris uniquely determined because it must contain the smallest prior-
ity. Then we partition the set of nodes into those which have key values less
than rand those which have values greater than r. We must make a treap
out of each of these and make them the left and right children of r. By in-
duction on the number of nodes, we see that the treap is uniquely determined.
b. Since choosing random priorities corresponds to inserting in a random order,
the expected height of a treap is the same as the expected height of a ran-
domly built binary search tree, Θ(log n).
c. First insert a node as usual using the binary-search-tree insertion procedure.
Then perform left and right rotations until the parent of the inserted node
no longer has larger priority.
d. The expected runtime of TREAP-INSERT is Θ(log n) since the expected
height of a treap is Θ(log n).
e. To insert x, we initially run the BST insert procedure, so xis a leaf node.
Every time we perform a left rotation, we increase the length of the right
spine of the left subtree by 1. Every time we perform a right rotation, we
increase the length of the left spine of the right subtree by 1. Since we only
perform left and right rotations, the claim follows.
f. If Xik = 1 then the properties must hold by the binary-search-tree property
and the definition of treap. On the other hand, suppose y.key < z.key <
x.key implies y.priority < z.priority. If ywasn’t a child of xthen taking
zto be the lowest common ancestor of xand ywould violate this. Since
y.priority > x.priority,ymust be a child of x. Since y.key < x.key,yis in
the left subtree of x. If yis not in the right spine of the left subtree of xthen
there must exist some zsuch that y.priority > z.priority > x.priority and
y.key < z.key < x.key, a contradiction.
g. We need to compute the probability that the conditions of part f are satisfied.
For all z∈[i+ 1, k −1] we must have x.priority < y.priority < z.priority.
There are (k−i−1)! ways to permute the priorities corresponding to these z,
out of (k−i+1)! ways to permute the priorities corresponding to all elements
in [i, k]. Cancelation gives P{Xik}=1
(k−i+1)(k−i).
18
h. We use part g then simplify the telescoping series:
E[C] =
k−1
X
j=1
E[Xjk]
=
k−1
X
j=1
1
(k−j+ 1)(k−j)
=
k−1
X
j=1
1
j(j+ 1)
=
k−1
X
j=1
1
j−1
j+ 1
= 1 −1
k.
i. A node yis in the left spine of the right subtree of xif and only if it would
be in the right spine of the left subtree of xin the treap where every node
with key kis replaced by a node with key n−k. Replacing kby n−kin the
expectation computation of part h gives the result.
j. By part e, the number of rotations is C+D. By linearity of expectation,
E[C+D]=2−1
k−1
n−k+1 ≤2 for any choice of k.
19
Chapter 14
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 14.1-1
The call sequance is:
OS −SELECT (T.root, 10)
OS −SELECT (T.root.lef t, 10)
OS −SELECT (T.root.lef t.right, 2)
OS −SELECT (T.root.lef t.right.lef t, 2)
OS −SELECT (T.root.lef t.right.lef t.right, 1)
Then, we have that the node (with key 20) that is returned is T.root.lef t.right.lef t.right
Exercise 14.1-2
OS-RANK(T,x) operates as follows. ris set to 0 and yis set to x. On the
first iteration of the while loop, yis set to the node with key 38. On the second
iteration, ris increased to 2 and yis set to the node with key 30. On the third
iteration, yis set to the node with key 41. On the fourth iteration ris increased
to 15 and yis set to the node with key 26, the root. This breaks the while loop,
and rank 15 is returned.
Exercise 14.1-3
See the algorithm OS-SELECT’
Exercise 14.1-4
See the algorithm RECURSIVE-OS-KEY-RANK.
Exercise 14.1-5
The desired result is OS-SELECT(T,OS-RANK(T,x)+i). This has runtime
O(h), which by the properties of red black trees, is O(lg(n)).
Exercise 14.1-6
First perform the usual BST insertion procedure on z, the node to be in-
serted. Then add 1 to the rank of every node on the path from the root to z
1

Algorithm 1 O
S-SELECT’(x,i)
r = x.left.size
while i6=rdo
if i>rthen
x = x.right
i = i-r
else
x=x.left
end if
r = x.left.size
end while
return x
Algorithm 2 RECURSIVE-OS-KEY-RANK(T,k)
1: if T.root.key == kthen
2: Return T.root.lef t.size + 1
3: else if T.root.key > k then
4: Return RECU RSIV E −OS −KEY −RAN K(T.root.left, k)
5: else
6: Return RECU RSIV E −OS −KEY −RAN K(T.root.right, k) +
T.root.lef t.size + 1
7: end if
2

such that zis in the left subtree of that node. Since the added node is a leaf,
it will have no subtrees so its rank will always be 1. When a left rotation is
performed on x, its rank within its subtree will remain the same. The rank
of x.right will be increased by the rank of x, plus one. If we perform a right
rotation on a node y, its rank will decrement by y.left.rank + 1. The rank of
y.lef t will remain unchanged. For deletion of z, decrement the rank of every
node on the path from zto the root such that zis in the left subtree of that
node. For any rotations, use the same rules as before.
Exercise 14.1-7
See the algorithm INV-COUNT(L). It does assume that all the elements of
the list are distinct. To adapt it to the not neccesarily distinct case, each time
that the we do the search, we should be selecting the element with that key that
comes first in an inorder traversal.
Algorithm 3 INV-COUNT(L)
Construct an order statistic tree Tfor all the elements in L
t=−|L|
for ifrom 0 to |L| − 1do
t=t+OS −RANK(T, SEARCH(T, L[i]))
remove the node corresponding to L[i] from T
end for
return t
Exercise 14.1-8
Choose a point on the circle and assign it key value 1. The rank of any point
will be its position when read in the sequence starting with point 1, and reading
clockwise around the circle. Next, we label each point with a key. Reading
clockwise around the circle, if a point’s chordal companion has a key, assign it
the same key. Otherwise, assign it the next lowest unused integer key value.
Then use the algorithm given in the solution to problem 2-4 d to count the
number of inversions (based on key value), with the caveat that an inversion
from key ito key j(with i > j)doesn’t count if the rank of the companion of i
is smaller than the rank of j.
Exercise 14.2-1
Along all the nodes in an inorder traversal, add a prev and succ pointer. If
we keep the head to be the first node, and, make it circularly linked, then this
clearly allows for the four operations to work in constant time. We still need
to be sure to maintain this linked list structure throughout all the tree modifi-
cations. Suppose we insert a node into the BST to be a left child, then we can
3

insert it into this doubly linked list immediately before it’s parent, which can
be done in constant time. Similarly, if it is a right child, then we would insert it
immediately after its parent. Deletion of the element is just the usual deletion
in a linked list.
Exercise 14.2-2
Since the black height of a node depends only on the black height and color
of its children, Theorem 14.1 implies that we can maintain the attribute with-
out affecting the asymptotic performance of the other red-black tree operations.
The same is not true for maintaining the depths of nodes. If we delete the root
of a tree we could potentially have to update the depths of O(n) nodes, making
the DELETE operation asymptotically slower than before.
Exercise 14.2-3
After performing the rotate operation, starting at the deeper of the two nodes
that were moved by the rotate, say x, set x.f =x.lef t.f ⊗x.a⊗x.right.f . Then,
do the same thing for the higher up node in the rotation. For size, instead set
x.size =x.left.size +x.right.size + 1 and then do the same for the higher up
node after the rotation.
Exercise 14.2-4
The following algorithm runs in Θ(m+ lg n) time. There could be as many
as O(lg n) recursive calls to locate the smallest and largest elements necessary
to print, and every other constant time call will print one of the mkeys between
aand b. We can’t do better than this because there are mkeys to output, and
to find a key requires lg ntime to search.
Algorithm 4 RB-ENUMERATE(x,a,b)
if a≤x.key ≤bthen
print x
end if
if a≤x.key and x.lef t 6=NIL then
RB −EN UMERAT E(x.lef t, a, b)
end if
if x.key ≤band x.right 6=NIL then
RB −EN UMERAT E(x.right, a, b)
end if
Return
Exercise 14.3-1
after rearranging the nodes, starting with the lower of the two nodes moved,
4

set it’s max attribute to be the maximum of its right endpoint and the the two
max attributes of its children. Do the same for the higher up of the two moved
nodes.
Exercise 14.3-2
Change the weak inequality on line 3 to be strict.
Exercise 14.3-3
Consider the usual interval search given, but, instead of breaking out of the
loop asa soon as we have an overlap, we just keep track of the most recently
seen overlap, and keep going in the loop until we hit T.nil. We then return the
most recently seen overlap. We have that this is the overlapping interval with
minimum left end point because the search always goes to the left it contains an
overlapping interval, and the left children are the ones with smaller left endpoint.
Exercise 14.3-4
Algorithm 5 INTERVAL(T,i)
if T.root overlaps ithen
Print T.root
end if
if T.root.lef t 6=T.nil and T.root.left.max ≥i.low then
INTERVAL(T.root.left,i)
end if
if T.root.right 6=T.nil and T.root.right.max ≥i.low and T.root.right.key ≤
i.high then
INTERVAL(T.root.right,i)
end if
The algorithm examines each node at most twice and performs constant
time checks so the runtime cannot excede O(n). If a recursive call is made on
a branch of the tree, then that branch must contain an overlapping interval, so
the runtime also cannot excede O(klg n) since the height is at most nand there
are kintervals in the output list.
Exercise 14.3-5
We could modify the interval tree insertion procedure to, once you find a
place to put the given interval, then we perforn an insertion procedure based on
the right hand endpoints. Then, to perform INTERVAL-SEARCH-EXACTLY(T,i)
first perform a search for the left hand endpoint, then, perform a search for the
right hand endpoint based on the BST rooted at this node for the right hand
5

endpoint, stopping the search if we ever come across a element with a different
left hand endpoint.
Exercise 14.3-6
Store the elements in a red-black tree, where the key value is the value of
each number itself. The auxiliary attribute stored at a node xwill be the min
gap between elements in the subtree rooted at x, the maximum value contained
in subtree rooted at x, and the minimum value contained in the subtree rooted
at x. The min gap at a leaf will be ∞. Since we can determine the attributes of
a node xusing only the information about the key at x, and the attributes in
x.lef t and x.right, Theorem 14.1 implies that we can maintain the values in all
nodes of the tree during insertion and deletion without asymptotically affecting
their O(lg n) performance. For MIN-GAP, just check the min gap at the root,
in constant time.
Exercise 14.3-7
Let Lbe the set of left coordinates of rectangles. Let Rbe the set of right
coordinates of rectangles. Sort both of these sets in O(nlg(n)) time. Then, we
will have a pointer to Land a pointer to R. If the pointer to Lis smaller, call
interval search on Tfor the up-down interval corresponding to this left hand
side. If it contains something that intersects the up-down bounds of this rect-
angle, there is an intersection, so stop. Otherwise add this interval to Tand
increment the pointer to L. If Ris the smaller one, remove the up-down interval
that that right hand side corresponds to and increment the pointer to R. Since
all the interval tree operations used run in time O(lg(n)) and we only call them
at most 3ntimes, we have that the runtime is O(nlg(n)).
Problem 14-1
a. Suppose we have a point of maximum overlap p. Then, as long as we imagine
moving the point pbut don’t pass any of the endpoints of any of the intervals,
then we won’t be changing the number of intervals containing p. So, we just
move it to the right until we hit the endpoint of some interval, then, we have
a point of maximum overlap that is the endpoint of an interval.
b. We will present a simple solution to this problem that runs in time O(nlg(n))
which doesn’t augment a red-black tree even though that is what is suggested
by the hint. Consider a list of elements so that each element has a integer
x.pos and a field that says whether it is a left endpoint or a right endpoint
x.dir =Lor R. Then, sort this list on the pos attribute of each element.
Then, run through the list with a running total of how many intervals you
are currently in, subtracting one for each right endpoint and adding one for
each left endpoint. Also keep track of the running max of these values, and
6

the endpoint that has that value. Then, this point that attains the running
max is what should be returned.
Problem 14-2
a. Create a circular doubly linked list. Continue to advance mplaces in the
list (not counting the sentinal), followed by printing and deleting the current
node, until the list is empty. Since mis a constant and we advance at most
mn places, the runtime is O(n).
b. Begin by creating an order statistic tree for the given elements, where rank
starts at 0 and ends at n−1, the rank of a node is its position in the original
order minus 1, and we store each element’s value in an attribute x.value.
Print the element with rank m(n)−1, then delete it from the tree. Then
proceed as follows: If you’ve just printed the kth value which had rank r,
delete that node from the tree, and the (k+ 1)st value to be printed will have
rank r−1 + m(n) mod (n−k). Since deletion and lookup take O(lg n) and
there are nnodes, the runtime is O(nlg n).
7

Chapter 15
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 15.1-1
Procede by induction. The base case of T(0) = 20= 1. Then, we apply the
inductive hypothesis and recall equation (A.5) to get that
T(n) = 1 +
n−1
X
j=0
T(j) = 1 +
n−1
X
j=0
2j= 1 + 2n−1
2−1= 1 + 2n−1=2n
Exercise 15.1-2
Let p1= 0, p2= 4, p3= 7 and n= 4. The greedy strategy would first cut
off a piece of length 3 since it has highest density. The remaining rod has length
1, so the total price would be 7. On the other hand, two rods of length 2 yield
a price of 8.
Exercise 15.1-3
Now, instead of equation (15.1), we have that
rn= max{pn, r1+rn−1−c, r2+rn−2−c, . . . , rn−1+r1−c}
And so, to change the top down solution to this problem, we would change
MEMOIZED-CUT-ROD-AUX(p,n,r) as follows. The upper bound for i on line
6 should be n−1 instead of n.Also, after the for loop, but before line 8, set
q= max{q−c, p[i]}.
Exercise 15.1-4
Create a new array called s. Initialize it to all zeros in MEMOIZED-CUT-
ROD(p,n) and pass it as an additional argument to MEMOIZED-CUT-ROD-
AUX(p,n,r,s). Replace line 7 in MEMOIZED-CUT-ROD-AUX by the following:
t=p[i] + MEM OIZED −CU T −ROD −AUX(p, n −i, r, s). Following this,
if t>q, set q=tand s[n] = i. Upon termination, s[i] will contain the size of
the first cut for a rod of size i.
1
Exercise 15.1-5
The subproblem graph for n= 4 looks like
4
2
0 1
3
1 2
0 1
The number of vertices in the tree to compute the nth Fibonacci will follow
the recurrence
V(n) = 1 + V(n−2) + V(n−1)
And has initial condition V(1) = V(0) = 1. This has solution V(n) =
2∗F ib(n)−1 which we will check by direct substitution. For the base cases,
this is simple to check. Now, by induction, we have
V(n) = 1 + 2 ∗F ib(n−2) −1+2∗F ib(n−1) −1=2∗F ib(n)−1
The number of edegs will satisfy the recurrence
E(n) = 2 + E(n−1) + E(n−2)
and having base cases E(1) = E(0) = 0. So, we show by induction that we have
E(n)=2∗F ib(n)−2. For the base cases it clearly holds, and by induction, we
have
E(n) = 2 + 2 ∗F ib(n−1) −2+2∗F ib(n−2) −2=2∗F ib(n)−2
We will present a O(n) bottom up solution that only keeps track of the the
two largest subproblems so far, since a subproblem can only depend on the so-
lution to subproblems at most two less for Fibonacci.
Exercise 15.2-1
An optimal parenthesization of that sequence would be (A1A2)((A3A4)(A5A6))
which will require 5 ∗50 ∗6+3∗12 ∗5+5∗10 ∗3+3∗5∗6+5∗3∗6 =
1500 + 180 + 150 + 90 + 90 = 2010.
Exercise 15.2-2
2

Algorithm 1 DYN-FIB(n)
prev = 1
prevprev = 1
if n≤1then
return 1
end if
for i=2 upto n do
tmp = prev + prevprev
prevprev = prev
prev = tmp
end for
return prev
Algorithm 2 MATRIX-CHAIN-MULTIPLY(A,s,i,j)
if i== jthen
Return Ai
end if
Return MATRIX-CHAIN-MULTIPLY(A,s,i,s[i,j]) ·MATRIX-CHAIN-
MULTIPLY(A,s,s[i,j]+1,j)
The following algorithm actually performs the optimal multiplication, and
is recursive in nature:
Exercise 15.1-3
By indution we will show that P(n) from eq (15.6) is ≥2n−1∈Ω(2n). The
base case of n=1 is trivial. Then, for n≥2, by induction and eq (15.6), we have
P(n) =
n−1
X
k=1
P(k)P(n−k)≥
n−1
X
k=1
2k2n−k= (n−1)(2n−1) ≥2n−1
So, the conclusion holds.
Exercise 15.2-4
The subproblem graph for matrix chain multiplication has a vertex for each
pair (i, j) such that 1 ≤i≤j≤n, corresponding to the subproblem of finding
the optimal way to multiply AiAi+1 · · · Aj. There are n(n−1)/2 + nvertices.
Vertex (i, j) is connected by an edge directed to vertex (k, l) if k=iand
k≤l < j or l=jand i<k≤j. A vertex (i, j) has outdegree 2(j−i). There
are n−kvertices such that j−i=k, so the total number of edges is
n−1
X
k=0
2k(n−k).
3
Exercise 15.1-5
We count the number of times that we reference a different entry in mthan
the one we are computing, that is, 2 times the number of times that line 10
runs.
n
X
l=2
n−l+1
X
i=l
i+l−2
X
k=i
2 =
n
X
l=2
n−l+1
X
i=1
(l−1)2 =
n
X
l=2
2(l−1)(n−l+ 1)
=
n−1
X
l=1
2l(n−l)
= 2n
n−1
X
l=1
l−2
n−1
X
l=1
l2
=n2(n−1) −(n−1)(n)(2n−1)
3
=n3−n2−2n3−3n2+n
3
=n3−n
3
Exercise 15.2-6
We proceed by induction on the number of matrices. A single matrix has no
pairs of parentheses. Assume that a full parenthesization of an n-element ex-
pression has exactly n−1 pairs of parentheses. Given a full parenthesization of
an n+ 1-element expression, there must exist some ksuch that we first multiply
B=A1· · · Akin some way, then multiply C=Ak+1 · · · An+1 in some way, then
multiply Band C. By our induction hypothesis, we have k−1 pairs of paren-
theses for the full parenthesization of Band n+ 1 −k−1 pairs of parentheses
for the full parenthesization of C. Adding these together, plus the pair of outer
parentheses for the entire expression, yields k−1+ n+1−k−1 +1 = (n+1) −1
parentheses, as desired.
Exercise 15.3-1
The runtime of of enumerating is just n∗P(n), while is we were running
RECURSIVE-MATRIX-CHAIN, it would also have to run on all of the internal
nodes of the subproblem tree. Also, the enumeration approach wouldn’t have
as much overhead.
Exercise 15.3-2
Let [i..j] denote the call to Merge Sort to sort the elements in positions i
through jof the original array. The recursion tree will have [1..n] as its root,
and at any node [i..j] will have [i..(j−i)/2] and [(j−i)/2 + 1..j] as its left
4

and right children, respectively. If j−i= 1, there will be no children. The
memoization apprach fails to speed up Merge Sort because the subproblems
aren’t overlapping. Sorting one list of size nisn’t the same as sorting another
list of size n, so there is no savings in storing solutions to subproblems since
each solution is used at most once.
Exercise 15.3-3
This modification of the matrix-chain-multiplication problem does still ex-
hibit the optimal substructure property. Suppose we split a maximal multipli-
cation of A1, . . . , Anbetween Akand Ak+1 then, we must have a maximal cost
multiplication on either side, otherwise we could substitute in for that side a
more expensive multiplication of A1, . . . , An.
Exercise 15.3-4
Suppose that we are given matricies A1, A2, A3, and A4with dimensions
such that p0, p1, p2, p3, p4= 1000,100,20,10,1000. Then p0pkp4is minimized
when k= 3, so we need to solve the subproblem of multiplying A1A2A3,
and also A4which is solved automatically. By her algorithm, this is solved
by splitting at k= 2. Thus, the full parenthesization is (((A1A2)A3)A4).
This requires 1000 ·100 ·20 + 1000 ·20 ·10 + 1000 ·10 ·1000 = 12,200,000
scalar multiplications. On the other hand, suppose we had fully parenthesized
the matricies to multiply as ((A1(A2A3))A4). Then we would only require
100 ·20 ·10 + 1000 ·100 ·10 + 1000 ·10 ·1000 = 11,020,000 scalar multiplications,
which is fewer than Professor Capulet’s method. Therefore her greedy approach
yields a suboptimal solution.
Exercise 15.3-5
The optimal substructure property doesn’t hold because the number of pieces
of length iused on one side of the cut affects the number allowed on the other.
That is, there is information about the particular solution on one side of the
cut that changes what is allowed on the other.
To make this more concrete, suppose the rod was length 4, the values were
l1= 2, l2=l3=l4= 1, and each piece has the same worth regardless of length.
Then, if we make our first cut in the middle, we have that the optimal soultion
for the two rods left over is to cut it in the middle, which isn’t allowed because
it increases the total number of rods of length 1 to be too large.
Exercise 15.3-6
First we assume that the commission is always zero. Let kdenote a currency
which appears in an optimal sequence sof trades to go from currency 1 to
currency n.pkdenote the first part of this sequence which changes currencies
from 1 to kand qkdenote the rest of the sequence. Then pkand qkare both
5

optimal sequences for changing from 1 to kand kto nrespectively. To see this,
suppose that pkwasn’t optimal but that p0
kwas. Then by changing currencies
according to the sequence p0
kqkwe would have a sequence of changes which is
better than s, a contradiction since swas optimal. The same argument applies
to qk.
Now suppose that the commisions can take on arbitrary values. Suppose we
have currencies 1 through 6, and r12 =r23 =r34 =r45 = 2, r13 =r35 = 6, and
all other exchanges are such that rij = 100. Let c1= 0, c2= 1, and ck= 10 for
k≥3. The optimal solution in this setup is to change 1 to 3, then 3 to 5, for
a total cost of 13. An optimal solution for changing 1 to 3 involves changing 1
to 2 then 2 to 3, for a cost of 5, and an optimal solution for changing 3 to 5 is
to change 3 to 4 then 4 to 5, for a total cost of 5. However, combining these
optimal solutions to subproblems means making more exchanges overall, and
the total cost of combining them is 18, which is not optimal.
Exercise 15.4-1
An LCS is h1,0,1,0,1,0i. A concise way of seeing this is by noticing that the
first list contains a “00” while the second contains none, Also, the second list
contains two copies of “11” while the first contains none. Inorder to reconcile
this, any LCS will have to skip at least three elements. Since we managed to
do this, we know that our common subsequence was maximal.
Exercise 15.4-2
The algorithm PRINT-LCS(c,X,Y) prints the LCS of Xand Yfrom the
completed table by computing only the necessary entries of Bon the fly. It
runs in O(m+n) time because each iteration of the while loop decrements
either ior jor both by 1, and halts when either reaches 0. The final for loop
iterates at most min(m, n) times.
Exercise 15.4-3
Exercise 15.4-4
Since we only use the previous row of the ctable to compute the current
row, we compute as normal, but when we go to compute row k, we free row k−2
since we will never need it again to compute the length. To use even less space,
observe that to compute c[i, j], all we need are the entries c[i−1, j], c[i−1, j −1],
and c[i, j −1]. Thus, we can free up entry-by-entry those from the previous row
which we will never need again, reducing the space requirement to min(m, n).
Computing the next entry from the three that it depends on takes O(1) time
and space.
Exercise 15.4-5
Given a list of numbers L, make a copy of Lcalled L0and then sort L0. Then,
6

Algorithm 3 PRINT-LCS(c,X,Y)
n=c[X.length, Y.length]
Initialize an array sof length n
i=X.length and j=Y.length
while i > 0 and j > 0do
if xi== yjthen
s[n] = xi
n=n−1
i=i−1
j=j−1
else if c[i−1, j]≥c[i, j −1] then
i=i−1
else
j=j−1
end if
end while
for k= 1 to s.length do
Print s[k]
end for
Algorithm 4 MEMO-LCS-LENGTH-AUX(X,Y,c,b)
m = |X|
n = |Y|
if c[m, n]! = 0 or m== 0 or n== 0 then
return
end if
if xm== ynthen
b[m, n] =-
c[m,n] =MEMO-LCS-LENGTH-AUX(X[1,. . . , m-1],Y[1,. . . ,n-1],c,b) +1
else if MEMO −LCS −LEN GT H −AUX(X[1, . . . , m −1], Y, c, b)≥
MEM O −LCS −LEN GT H −AUX(X, Y [1, . . . , n −1], c, b)then
b[m, n] =↑
c[m,n] =MEMO-LCS-LENGTH-AUX(X[1,. . . , m-1],Y,c,b)
else
b[m, n] =←
c[m,n] =MEMO-LCS-LENGTH-AUX(X,Y[1,. . . ,n-1],c,b)
end if
Algorithm 5 MEMO-LCS-LENGTH(X,Y)
let c be a (passed by reference) |X|by |Y|array initiallized to 0
let b be a (passed by reference) |X|by |Y|array
MEMO-LCS-LENGTH-AUX(X,Y,c,b)
return c and b
7

just run the LCS algorithm on these two lists. The longest common subsequnce
must be monotone increasing because it is a subsequence of L0which is sorted.
It is also the longest monotonte increasing subsequence because being a subse-
qucene of L0only adds the restriction that the subsequence must be monotone
increasing. Since |L|=|L0|=n, and sorting Lcan be done in o(n2) time, the
final running time will be O(|L||L0|) = O(n2).
Exercise 15.4-6
The algorithm LONG-MONOTONIC(S) returns the longest monotonically
increasing subsequence of S, where Shas length n. The algorithm works as
follows: a new array Bwill be created such that B[i] contains the last value of
a longest monotonically increasing subsequence of length i. A new array Cwill
be such that C[i] contains the monotonically increasing subsequence of length
iwith smallest last element seen so far. To analyze the runtime, observe that
the entries of Bare in sorted order, so we can execute line 9 in O(log(n)) time.
Since every other line in the for-loop takes constant time, the total run-time is
O(nlog n).
Algorithm 6 LONG-MONOTONIC(S)
1: Initialize an array Bof integers length of n, where every value is set equal
to ∞.
2: Initialize an array Cof empty lists length n.
3: L= 1
4: for i= 1 to ndo
5: if A[i]< B[1] then
6: B[1] = A[i]
7: C[1].head.key =A[i]
8: else
9: Let jbe the largest index of Bsuch that B[j]< A[i]
10: B[j+ 1] = A[i]
11: C[j+ 1] = C[j]
12: C[j+ 1].insert(A[i])
13: if j+ 1 > L then
14: L=L+ 1
15: end if
16: end if
17: end for
18: Print C[L]
Exercise 15.5-1
Run the given algorithm with the initial arguemnt of i= 1 and j=m[1].length.
Exercise 15.5-2
8
Algorithm 7 CONSTRUCT-OPTIMAL-BST(root,i,j)
if i>jthen
return nil
end if
if i== jthen
return a node with key kiand whose children are nil
end if
let nbe a node with key kroot[i,j]
n.left = CONSTRUCT-OPTIMAL-BST(root,i,root[i,j]-1)
n.right = CONSTRUCT-OPTIMAL-BST(root,root[i,j]+1,j)
return n
After painstakingly working through the algorithm and building up the ta-
bles, we find that the cost of the optimal binary search tree is 3.12. The tree
takes the following structure:
5
2
1 3
NIL 4
7
6NIL
Exercise 15.5-3
Each of the Θ(n2) values of w[i, j] would require computing those two sums,
both of which can be of size O(n), so, the asymptotic runtime would increase
to O(n3).
Exercise 15.5-4
Change the for loop of line 10 in OPTIMAL-BST to “for r=r[i, j −1] to
r[i+ 1, j]”. Knuth’s result implies that it is sufficient to only check these values
because optimal root found in this range is in fact the optimal root of some
binary search tree. The time spent within the for loop of line 6 is now Θ(n).
This is because the bounds on rin the new for loop of line 10 are nonoverlap-
ping. To see this, suppose we have fixed land i. On one iteration of the for
loop of line 6, the upper bound on ris r[i+ 1, j] = r[i+ 1, i +l−1]. When
we increment iby 1 we increase jby 1. However, the lower bound on rfor
the next iteration subtracts this, so the lower bound on the next iteration is
9

r[i+ 1, j + 1 −1] = r[i+ 1, j]. Thus, the total time spent in the for loop of line 6
is Θ(n). Since we iterate the outer for loop of line 5 ntimes, the total runtime
is Θ(n2).
Problem 15-1
Since any longest simple path must start by going through some edge out of
s, and thereafter cannot pass through sbecause it must be simple, that is,
LONGEST (G, s, t) = 1 + max
s∼s0{LONGEST (G|V\{s}, s0, t)}
with the base case that if s=tthen we have a length of 0.
A naive bound would be to say that since the graph we are considering is
a subset of the vertices, and the other two arguments to the substructure are
distinguished vertices, then, the runtime will be O(|V|22|V|). We can see that
we can actually will have to consider this many possible subproblems by taking
|G|to be the complete graph on |V|vertices.
Problem 15-2
Let A[1..n] denote the array which contains the given word. First note that
for a palindrome to be a subsequence we must be able to divide the input word
at some position i, and then solve the longest common subsequence problem on
A[1..i] and A[i+ 1..n], possibly adding in an extra letter to account for palin-
dromes with a central letter. Since there are nplaces at which we could split the
input word and the LCS problem takes time O(n2), we can solve the palindrome
problem in time O(n3).
Problem 15-3
First sort all the points based on their x coordinate. To index our subprob-
lem, we will give the rightmost point for both the path going to the left and
the path going to the right. Then, we have that the desired result will be the
subproblem indexed by v,v where vis the rightmost point. Suppose by symme-
try that we are further along on the left-going path, that the leftmost path is
going to the ith one and the right going path is going until the jth one. Then,
if we have that i>j+ 1, then we have that the cost must be the distance from
the i−1st point to the ith plus the solution to the subproblem obtained where
we replace iwith i−1. There can be at most O(n2) of these subproblem, but
solving them only requires considering a constant number of cases. The other
possibility for a subproblem is that j≤i≤j+ 1. In this case, we consider for
every kfrom 1 to jthe subproblem where we replace iwith kplus the cost from
kth point to the ith point and take the minimum over all of them. This case
requires considering O(n) things, but there are only O(n) such cases. So, the
final runtime is O(n2).
10

Problem 15-4
First observe that the problem exhibits optimal substructure in the following
way: Suppose we know that an optimal solution has kwords on the first line.
Then we must solve the subproblem of printing neatly words lk+1, . . . , ln. We
build a table of optimal solutions solutions to solve the problem using dynamic
programming. If n−1 + Pn
k=1 lk< M then put all words on a single line for an
optimal solution. In the following algorithm Printing-Neatly(n), C[k] contains
the cost of printing neatly words lkthrough ln. We can determine the cost
of an optimal solution upon termination by examining C[1]. The entry P[k]
contains the position of the last word which should appear on the first line of
the optimal solution of words l1, l2, . . . , ln. Thus, to obtain the optimal way to
place the words, we make LP[1] the last word on the first line, lP[P[1]] the last
word on the second line, and so on.
Algorithm 8 Printing-Neatly(n)
1: Let P[1..n] and C[1..n] be a new tables.
2: for k=ndownto 1 do
3: if Pn
i=kli+n−k < M then
4: C[k] = 0
5: end if
6: q=∞
7: for j= 1 downto n−kdo
8: if Pj
m=1 lk+j+j−1< M and (M−Pj
m=1 lk+j+j−1)+C[k+j+1] < q
then
9: q= (M−Pj
m=1 lk+j+j−1) + C[k+j+ 1]
10: P[k] = k+j
11: end if
12: end for
13: C[k] = q
14: end for
Problem 15-5
a. We will index our subproblems by two integers, 1 ≤i≤mand 1 ≤j≤n.
We will let iindicate the rightmost element of xwe have not processed and
jindicate the rightmost element of ywe have not yet found matches for. For
a solution, we call EDIT (x, y, i, j)
b. We will set cost(delete) = cost(insert) = 2, cost(copy) = −1, cost(replace) =
1, and cost(twiddle) = cost(kill) = ∞. Then a minimum cost translation of
the first string into the second corresponds to an alignment. where we view
a copy or a replace as incrementing a pointer for both strings. A insert as
putting a space at the current position of the pointer in the first string. A
11

Algorithm 9 EDIT(x,y,i,j)
let m=x.length and n=y.length
if i=mthen
return (n-j)cost(insert)
end if
if j=nthen
return min{(m−i)cost(delete), cost(kill)}
end if
o1, . . . , o5initialized to ∞
if x[i] = y[j] then
o1=cost(copy) + EDIT (x, y, i + 1, j + 1)
end if
o2=cost(replace) + EDIT (x, y, i + 1, j + 1)
o3=cost(delete) + EDIT (x, y, i + 1, j)
o4=cost(insert) + EDIT (x, y, i, j + 1)
if i<m−1 and j < n −1then
if x[i] = y[j+ 1] and x[i+ 1] = y[j]then
o5=cost(twiddle) + EDIT (x, y, i + 2, j + 2)
end if
end if
return mini∈[5]{oi}
delete operation means putting a space in the current position in the second
string. Since twiddles and kills have infinite costs, we will have neither of
them in a minimal cost solution. The final value for the alignment will be
the negative of the minimum cost sequence of edits.
Problem 15-6
The problem exhibits optimal substructure in the following way: If the root r
is included in an optimal solution, then we must solve the optimal subproblems
rooted at the grandchildren of r. If ris not included, then we must solve
the optimal subproblems on trees rooted at the children of r. The dynamic
programming algorithm to solve this problem works as follows: We make a
table Cindexed by vertices which tells us the optimal conviviality ranking of a
guest list obtained from the subtree with root at that vertex. We also make a
table Gsuch that G[i] tells us the guest list we would use when vertex iis at
the root. Let Tbe the tree of guests. To solve the problem, we need to examine
the guest list stored at G[T.root]. First solve the problem at each leaf L. If
the conviviality ranking at Lis positive, G[L] = {L}and C[L] = L.conviv.
Otherwise G[L] = ∅and C[L] = 0. Iteratively solve the subproblems located
at parents of nodes at which the subproblem has been solved. In general for a
12

node x,
C[x] = min
X
yis a child of x
C[y],X
yis a grandchild of x
C[y]
.
The runtime of the algorithm is O(n2) where nis the number of vertices,
because we solve nsubproblems, each in constant time, but the tree traversals
required to find the appropriate next node to solve could take linear time.
Problem 15-7
a. Our substructure will consist of trying to find suffixes of s of length one less
starting at all the edges leaving ν0with label σ0. if any of them have a
solution, then, there is a solution. If none do, then there is none. See the
algorithm VITERBI for details.
Algorithm 10 V IT ERBI(G, s, ν0)
if s.length = 0 then
return ν0
end if
for edges (ν0, ν1)∈Vfor some ν1do
if σ(ν0, ν1) = σ1then
res =V IT ERBI(G, (σ2, . . . , σk), ν1)
if res != NO-SUCH-PATH then
return ν0, res
end if
end if
end for
return NO-SUCH-PATH
Since the subproblems are indexed by a suffix of s (of which there are only
k) and a vertex in the graph, there are at most O(k|V|) different possible
arguments. Since each run may require testing a edge going to every other
vertex, and each iteration of the for loop takes at most a constant amount of
time other than the call to PROB=VITERBI, the final runtime is O(k|V|2)
b. For this modification, we will need to try all the possible edges leaving from
ν0instead of stopping as soon as we find one that works. The substructure is
very similar. We’ll make it so that instead of just returning the sequence, we’ll
have the algorithm also return the probability of that maximum probability
sequence, calling the fields seq and prob respectively. See the algorithm
PROB-VITERBI
Since the runtime is indexed by the same things, we have that we will call
it with at most O(k|V|) different possible arguments. Since each run may
13

Algorithm 11 P ROB −V IT ERBI(G, s, ν0)
if s.length = 0 then
return ν0
end if
let sols.seq =N O −SUCH −P AT H, and sols.prob = 0
for edges (ν0, ν1)∈Vfor some ν1do
if σ(ν0, ν1) = σ1then
res =P ROB −V IT ERBI(G, (σ2, . . . , σk), ν1)
if p(ν0, ν1)·res.prob >=sols.prob then
sols.prob =p(ν0, ν1)·res.prob and sols.seq =ν0, res.seq
end if
end if
end for
return sols
require testing a edge going to every other vertex, and each iteration of the
for loop takes at most a constant amount of time other than the call to
PROB=VITERBI, the final runtime is O(k|V|2)
Problem 15-8
a. If n > 1 then for every choice of pixel at a given row, we have at least 2
choices of pixel in the next row to add to the seam (3 if we’re not in column
1 or n). Thus the total number of possibilities is bounded below by 2m.
b. We create a table D[1..m, 1..n] such that D[i, j] stores the disruption of an
optimal seam ending at position [i, j], which started in row 1. We also create
a table S[i, j] which stores the list of ordered pairs indicating which pixels
were used to create the optimal seam ending at position (i, j). To find the
solution to the problem, we look for the minimum kentry in row mof table
D, and use the list of pixels stored at S[m, k] to determine the optimal seam.
To simplify the algorithm Seam(A), let M IN(a, b, c) be the function which
returns −1 if ais the minimum, 0 if bis the minimum, and 1 if cis the mini-
mum value from among a, b, and c. The time complexity of the algorithm is
O(mn).
Problem 15-9
The subproblems will be indexed by contiguous subarrays of the arrays of
cuts needed to be made. We try making each possible cut, and take the one
with cheapest cost. Since there are mto try, and there are at most m2possible
things to index the subproblems with, we have that the mdependence is that
the solution is O(m3). Also, since each of the additions is of a number that
14

Algorithm 12 Seam(A)
Initialize tables D[1..m, 1..n] of zeros and S[1..m, 1..n] of empty lists
for i= 1 to ndo
S[1, i] = (1, i)
D[1, i] = d1i
end for
for i= 2 to mdo
for j= 1 to ndo
if j== 1 then //Handles the left-edge case
if D[i−1, j]< D[i−1, j + 1] then
D[i, j] = D[i−1, j] + dij
S[i, j] = S[i−1, j].insert(i, j)
else
D[i, j] = D[i−1, j + 1] + dij
S[i, j] = S[i−1, j + 1].insert(i, j)
end if
else if j== nthen //Handles the right-edge case
if D[i−1, j −1] < D[i−1, j]then
D[i, j] = D[i−1, j −1] + dij
S[i, j] = S[i−1, j −1].insert(i, j)
else
D[i, j] = D[i−1, j] + dij
S[i, j] = S[i−1, j].insert(i, j)
end if
end if
x=MIN(D[i−1, j −1], D[i−1, j], D[i−1, j + 1])
D[i, j] = D[i−1, j +x]
S[i, j] = S[i−1, j +x].insert(i, j)
end for
end for
q= 1
for j= 1 to ndo
if D[m, j]< D[m, q]then q=j
end if
end for
Print the list stored at S[m, q].
15

is O(n), each of the iterations of the for loop may take time O(lg(n) + lg(m)),
so, the final runtime is O(m3lg(n)). The given algorithm will return (cost,seq)
where cost is the cost of the cheapest sequence, and seq is the sequence of cuts
to make
Algorithm 13 CUT-STRING(L,i,j,l,r)
if l=rthen
return (0,[])
end if
mincost =∞
for k from i to j do
if l+r+CUT −ST RIN G(L, i, k, l, L[k]).cost +CUT −
ST RING(L, k, j, L[k], j).cost < mincost then
mincost =l+r+CUT −ST RIN G(L, i, k, l, L[k]).cost +CUT −
ST RING(L, k, j, L[k], j).cost
minseq =L[k] concatenated with the sequence returned fromCUT −
ST RING(L, i, k, l, L[k]) and from CUT −ST RIN G(L, i, k, l, L[k])
end if
end for
return (mincost,minseq)
Problem 15-10
a. Without loss of generality, suppose that there exists an optimal solution
Swhich involves investing d1dollars into investment kand d2dollars into
investement min year 1. Further, suppose in this optimal solution, you
don’t move your money for the first jyears. If rk1+rk2+. . . +rkj >
rm1+rm2+. . . +rmj then we can perform the usual cut-and-paste maneau-
ver and instead invest d1+d2dollars into investment kfor jyears. Keeping
all other investments the same, this results in a strategy which is at least
as profitable as S, but has reduced the number of different investments in a
given span of years by 1. Continuing in this way, we can reduce the optimal
strategy to consist of only a single investment each year.
b. If a particular investment strategy is the year-one-plan for a optimal investe-
ment strategy, then we must solve two kinds of optimal suproblem: either
we maintain the strategy for an additional year, not incurring the money-
moving fee, or we move the money, which amounts to solving the problem
where we ignore all information from year 1. Thus, the problem exhibits
optimal substructure.
c. The algorithm works as follows: We build tables Iand Rof size 10 such that
I[i] tells which investment should be made (with all money) in year i, and
16

R[i] gives the total return on the investment strategy in years ithrough 10.
Algorithm 14 Invest(d,n)
Initialize tables Iand Rof size 11, all filled with zeros
for k= 10 downto 1 do
q= 1
for i= 1 to ndo
if rik > rqk then // inow holds the investment which looks best for
a given year
q=i
end if
end for
if R[k+ 1] + drI[k+1]k−f1> R[k+ 1] + drqk −f2then //If revenue is
greater when money is not moved
R[k] = R[k+ 1] + drI[k+1]k−f1
I[k] = I[k+ 1]
else
R[k] = R[k+ 1] + drqk −f2
I[k] = q
end if
end for
Return Ias an optimal strategy with return R[1].
d. The previous investment strategy was independent of the amount of money
you started with. When there is a cap on the amount you can invest, the
amount you have to invest in the next year becomes relevant. If we know
the year-one-strategy of an optimal investment, and we know that we need
to move money after the first year, we’re left with the problem of investing a
different initial amount of money, so we’d have to solve a subproblem for every
possible initial amount of money. Since there is no bound on the returns,
there’s also no bound on the number of subproblems we need to solve.
Problem 15-11
Our subproblems will be indexed by and integer i∈[n] and another integer
j∈[D]. iwill indicate how many months have passed, that is, we will restrict
ourselves to only caring about (di, . . . , dn). jwill indicate how many machines
we have in stock initially. Then, the recurrence we will use will try producing
all possible numbers of machines from 1 to [D]. Since the index space has size
O(nD) and we are only running through and taking the minimum cost from D
many options when computing a particular subproblem, the total runtime will
be O(nD2).
17

Problem 15-12
We will make an N+1 by X+1 by P+1 table. The runtime of the algorithm
is O(NXP ).
18

Algorithm 15 Baseball(N,X,P)
Initialize an N+ 1 by X+ 1 table B
Initialize an array Pof length N
for i= 0 to Ndo
B[i, 0] = 0
end for
for j= 1 to Xdo
B[0, j]=0
end for
for i= 1 to Ndo
for j= 1 to Xdo
if j < i.cost then
B[i, j] = B[i−1, j]
end if
q=B[i−1, j]
p= 0
for k= 1 to pdo
if B[i−1, j −i.cost] + i.value > q then
q=B[i−1, j −i.cost] + i.value
p=k
end if
end for
B[i, j] = q
P[i] = p
end for
end for
Print: The total VORP is B[N, X] and the players are:
i=N
j=X
C= 0
for k= 1 to Ndo //Prints the players from the table
if B[i, j]6=B[i−1, j]then
Print P[i]
j=j−i.cost
C=C+i.cost
end if
i=i−1
end for
Print: The toal cost is C
19
Chapter 16
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 16.1-1
The given algorithm would just stupidly compute the minimum of the O(n)
numbers or return zero depending on the size of Sij . There are a possible
number of subproblems that is O(n2) since we are selecting iand jso that
1≤i≤j≤n. So, the runtime would be O(n3).
Exercise 16.1-2
This becomes exactly the same as the original problem if we imagine time
running in reverse, so it produces an optimal solution for essentially the same
reasons. It is greedy because we make the best looking choice at each step.
Exercise 16.1-3
As a counterexample to the omtimality of greedily selecting the shortest,
suppose our activity times are {(1,9),(8,11),(10,20)}then, picking the shortest
first, we hahve to eliminate the other two, where if we picked the other two
instead, we would have two tasks not one.
As a counterexample to the optimality of greedily selecting the task that
conflicts with the fewest remaining activities, suppose the activity times are
{(−1,1),(2,5),(0,3),(0,3),(0,3),(4,7),(6,9),(8,11),(8,11),(8,11),(10,12)}. Then,
by this greedy strategy, we would first pick (4,7) since it only has a two con-
flicts. However, doing so would mean that we would not be able to pick the
only optimal solution of (−1,1),(2,5),(6,9),(10,12).
As a counterexample to the optimality of greedily selecting the earliest start
times, suppose our activity times are {(1,10),(2,3),(4,5)}. If we pick the ear-
liest start time, we will only have a single activity, (1,10), whereas the optimal
solution would be to pick the two other activities.
Exercise 16.1-4
Maintain a set of free (but already used) lecture halls Fand currently busy
lecture halls B. Sort the classes by start time. For each new start time which
you encounter, remove a lecture hall from F, schedule the class in that room,
1

and add the lecture hall to B. If Fis empty, add a new, unused lecture hall
to F. When a class finishes, remove its lecture hall from Band add it to F.
Why this is optimal: Suppose we have just started using the mth lecture hall
for the first time. This only happens when ever classroom ever used before is
in B. But this means that there are mclasses occurring simultaneously, so it is
necessary to have mdistinct lecture halls in use.
Exercise 16.1-5
Run a dynamic programming solution based off of the equation (16.2) where
the second case has “1” replaced with “vk”. Since the subproblems are still
indexed by a pair of activities, and each calculation requires taking the minimum
over some set of size ≤ |Sij | ∈ O(n). The total runtime is bounded by O(n3).
Exercise 16.2-1
A optimal solution to the fractional knapsack is one that has the highest
total value density. Since we are always adding as much of the highest value
density we can, we are going to end up with the highest total value density.
Suppose that we had some other solution that used some amount of the lower
value density object, we could substitute in some of the higher value density
object meaning our original solution coud not of been optimal.
Exercise 16.2-2
Suppose we know that a particular item of weight wis in the solution. Then
we must solve the subproblem on n−1 items with maximum weight W−w.
Thus, to take a bottom-up approach we must solve the 0-1 knapsack problem
for all items and possible weights smaller than W. We’ll build an n+ 1 by
W+ 1 table of values where the rows are indexed by item and the columns
are indexed by total weight. (The first row and column of the table will be
a dummy row). For row icolumn j, we decide whether or not it would be
advantageous to include item iin the knapsack by comparing the total value of
of a knapsack including items 1 through i−1 with max weight j, and the total
value of including items 1 through i−1 with max weight j−i.weight and also
item i. To solve the problem, we simply examine the n, W entry of the table to
determine the maximum value we can achieve. To read off the items we include,
start with entry n, W . In general, proceed as follows: if entry i, j equals entry
i−1, j, don’t include item i, and examine entry i−1, j next. If entry i, j doesn’t
equal entry i−1, j, include item iand examine entry i−1, j −i.weight next.
See algorithm below for construction of table:
Exercise 16.2-3
At each step just pick the lightest (and most valuable) item that you can
pick. To see this solution is optimal, suppose that there were some item jthat
we included but some smaller, more valuable item ithat we didn’t. Then, we
could replace the item jin our knapsack with the item i. it will definitely fit
2

Algorithm 1 0-1 Knapsack(n,W)
1: Initialize an n+ 1 by W+ 1 table K
2: for j= 1 to Wdo
3: K[0, j]=0
4: end for
5: for i= 1 to ndo
6: K[i, 0] = 0
7: end for
8: for i= 1 to ndo
9: for j= 1 to Wdo
10: if j < i.weight then
11: K[i, j] = K[i−1, j]
12: end if
13: K[i, j] = max(K[i−1, j], K[i−1, j −i.weight] + i.value)
14: end for
15: end for
because iis lighter, and it will also increase the total value because iis more
valuable.
Exercise 16.2-4
The greedy solution solves this problem optimally, where we maximize dis-
tance we can cover from a particular point such that there still exists a place
to get water before we run out. The first stop is at the furthest point from
the starting position which is less than or equal to mmiles away. The problem
exhibits optimal substructure, since once we have chosen a first stopping point
p, we solve the subproblem assuming we are starting at p. Combining these two
plans yields an optimal solution for the usual cut-and-paste reasons. Now we
must show that this greedy approach in fact yields a first stopping point which
is contained in some optimal solution. Let Obe any optimal solution which has
the professor stop at positions o1, o2, . . . , ok. Let g1denote the furthest stopping
point we can reach from the starting point. Then we may replace o1by g2to
create a modified solution G, since o2−o1< o2−g1. In other words, we can
actually make it to the positions in Gwithout running out of water. Since G
has the same number of stops, we conclude that g1is contained in some optimal
solution. Therefore the greedy strategy works.
Exercise 16.2-5
Consider the leftmost interval. It will do no good if it extends any further
left than the leftmost point, however, we know that it must contain the leftmost
point. So, we know that it’s left hand side is exactly the leftmost point. So, we
just remove any point that is within a unit distance of the left most point since
3

they are contained in this single interval. Then, we just repeat until all points
are covered. Since at each step there is a clearly optimal choice for where to
put the leftmost interval, this final solution is optimal.
Exercise 16.2-6
First compute the value of each item, defined to be it’s worth divided by its
weight. We use a recursive approach as follows: Find the item of median value,
which can be done in linear time as shown in chapter 9. Then sum the weights
of all items whose value exceeds the median and call it M. If Mexceeds W
then we know that the solution to the fractional knapsack problem lies in taking
items from among this collection. In other words, we’re now solving the frac-
tional knapsack problem on input of size n/2. On the other hand, if the weight
doesn’t exceed W, then we must solve the fractional knapsack problem on the
input of n/2 low-value items, with maximum weight W−M. Let T(n) denote
the runtime of the algorithm. Since we can solve the problem when there is only
one item in constant time, the recursion for the runtime is T(n) = T(n/2) + cn
and T(1) = d, which gives runtime of O(n).
Exercise 16.2-7
Since an idential permutation of both sets doesn’t affect this product, sup-
pose that Ais sorted in ascending order. Then, we will prove that the product
is maximized when Bis also sorted in ascending order. To see this, suppose
not, that is, there is some i < j so that ai< ajand bi> bj. Then, consider
only the contribution to the product from the indices iand j. That is, abi
iabj
j,
then, if we were to swap the order of b1and bj, we would have that contribution
be abj
iabi
j. we can see that this is larger than the previous expression because
it differs by a factor of ( aj
ai)bi−bjwhich is bigger than one. So, we couldn’t of
maximized the product with this ordering on B.
Exercise 16.3-1
If we have that x.freq =b.freq, then we know that bis tied for lowest
frequency. In particular, it means that there are at least two things with lowest
frequency, so y.freq =x.f req. Also, since x.f req ≤a.freq ≤b.freq =x.f req,
we must have a.freq =x.freq.
Exercise 16.3-2
Let Tbe a binary tree corresponding to an optimal prefix code and suppose
that Tis not full. Let node nhave a single child x. Let T0be the tree obtained
by removing nand replacing it by x. Let mbe a leaf node which is a descendant
of x. Then we have
4

cost(T0)≤X
c∈C\{m}
c.freq·dT(c)+m.f req(dT(m)−1) <X
c∈C
c.freq·dT(c) = cost(T)
which contradicts the fact that Twas optimal. Therefore every binary tree
corresponding to an optimal prefix code is full.
Exercise 16.3-3
An optimal huffman code would be
00000001 →a
0000001 →b
000001 →c
00001 →d
0001 →e
001 →f
01 →g
1→h
This generalizes to having the first nFibonacci numbers as the frequencies
in that the nth most frequent letter has codeword 0n−11. To see this holds, we
will prove the recurrence
n−1
X
i=0
F(i) = F(n+ 1) −1
This will show that we should join together the letter with frequency F(n) with
the result of joining together the letters with smaller frequencies. We will prove
it by induction. For n= 1 is is trivial to check. Now, suppose that we have
n−1≥1, then,
F(n+ 1) −1 = F(n) + F(n−1) −1 = F(n−1) +
n−2
X
i=0
F(i) =
n−1
X
i=0
F(i)
See also Lemma 19.2.
Exercise 16.3-4
Let xbe a leaf node. Then x.freq is added to the cost of each internal node
which is an ancestor of xexactly once, so its total contribution to the new way
of computing cost is x.freq ·dT(x), which is the same as its old contribution.
Therefore the two ways of computing cost are equivalent.
5

Exercise 16.3-5
We construct this codeword with monotonically increasing lengths by always
resolving ties in terms of which two nodes to join together by joining together
those with the two latest occurring earliest elements. We will show that the
ending codeword has that the least frequent words are all having longer code-
words. Suppose to a contradiction that there were two words, w1and w2so that
w1appears more frequently, but has a longer codeword. This means that it was
involved in more merge operation than w2was. However, since we are always
merging together the two sets of words with the lowest combined frequency, this
would contradict the fact that w1has a higher frequency than w2.
Exercise 16.3-6
First observe that any full binary tree has exactly 2n−1 nodes. We can
encode the structure of our full binary tree by performing a preorder traversal
of T. For each node that we record in the traversal, write a 0 if it is an internal
node and a 1 if it is a leaf node. Since we know the tree to be full, this uniquely
determines its structure. Next, note that we can encode any character of C
in dlg nebits. Since there are ncharacters, we can encode them in order of
appearance in our preorder traversal using ndlg nebits.
Exercise 16.3-7
Instead of grouping together the two with lowest frequency into pairs that
have the smallest total frequency, we will group together the three with lowest
frequency in order to have a final result that is a ternary tree. The analysis of
optimality is almost identical to the binary case. We are placing the symbols
of lowest frequency lower down in the final tree and so they will have longer
codewords than the more frequently occurring symbols
Exercise 16.3-8
For any 2 characters, the sum of their frequencies exceeds the frequency of
any other character, so initially Huffman coding makes 128 small trees with 2
leaves each. At the next stage, no internal node has a label which is more than
twice that of any other, so we are in the same setup as before. Continuing in this
fashion, Huffman coding builds a complete binary tree of height lg(256) = 8,
which is no more efficient than ordinary 8-bit length codes.
Exercise 16.3-9
If every possible character is equally likely, then, when constructing the Huff-
man code, we will end up with a complete binary tree of depth 7. This means
that every character, regardless of what it is will be represented using 7 bits.
This is exactly as many bits as was originally used to represent those characters,
so the total length of the file will not decrease at all.
6

Exercise 16.4-1
The first condition that Sis a finite set is a given. To prove the second
condition we assume that k≥0, this gets us that Ikis nonempty. Also, to
prove the hereditary property, suppose A∈ Ikthis means that |A| ≤ k. Then,
if B⊆A, this means that |B| ≤ |A| ≤ k, so B∈ Ik. Lastly, we porove the
exchange property by letting A, B ∈ Ikbe such that |A|<|B|. Then, we can
pick any element x∈B\A, then, |A∪ {x}| =|A|+ 1 ≤ |B| ≤ k, so, we can
extend Ato A∪ {x}∈Ik.
Exercise 16.4-2
Let c1, . . . , cmbe the columns of T. Suppose C={ci1, . . . , cik}is depen-
dent. Then there exist scalars d1, . . . , dknot all zero such that Pk
j=1 djcij= 0.
By adding columns to C and assigning them to have coefficient 0 in the sum,
we see that any superset of Cis also dependent. By contrapositive, any subset
of an independent set must be independent. Now suppose that Aand Bare
two independent sets of columns with |A|>|B|. If we couldn’t add any col-
umn of Ato be whilst preserving independence then it must be the case that
every element of Ais a linear combination of elements of B. But this implies
that Bspans a |A|-dimensional space, which is impossible. Therefore our in-
dependence system must satisfy the exchange property, so it is in fact a matroid.
Exercise 16.4-3
Condition one of being a matroid is still satisfied because the base set hasn’t
changed. Next we show that I0is nonempty. Let Abe any maximal element of
Ithen, we have that S−A∈ I0because S−(S−A) = A⊆Awhich is maximal
in I. Next we show the hereditary property, suppose that B⊆A∈ I0, then,
there exists some A0∈ I so that S−A⊆A0, however, S−B⊇S−A⊆A0so
B∈ I0.
Lastly we prove the exchange property. That is, if we have B, A ∈ I0and
|B|<|A|we can find an element xin A−Bto add to Bso that it stays
independent. We will split into two cases.
Our first case is that |A|=|B|+ 1. We clearly need to select xto be the
single element in A−B. Since S−Bcontains a maximal independent set
Our second case is if the first case does not hold. Let Cbe a maximal inde-
pendent set of Icontained in S−A. Pick an aribitrary set of size |C| − 1 from
some maximal independent set contained in S−B, call it D. Since Dis a subset
of a maximal independent set, it is also independent, and so, by the exchange
property, there is some y∈C−Dso that D∪ {y}is a maximal independent
set in I. Then, we select xto be any element other than yin A−B. Then,
S−(B∪{x}) will still contain D∪{y}. This means that B∪{x}is independent
in (I)0
7

Exercise 16.4-4
Suppose X⊂Yand Y∈ I. Then (X∩Si)⊂(Y∩Si) for all i, so
|X∩Si| ≤ |Y∩Si| ≤ 1 for all 1 ≤i≤k. Therefore Mis closed under inclusion.
Now Let A, B ∈ I with |A|=|B|+ 1. Then there must exist some j
such that |A∩Sj|= 1 but B∩Sj|= 0. Let a=A∩Sj. Then a /∈Band
|(B∪ {a})∩Sj|= 1. Since |(B∪ {a})∩Si|=|B∩Si|for all i6=j, we must
have B∪ {a}∈I. Therefore Mis a matroid.
Exercise 16.4-5
Suppose that Wis the largest weight that any one element takes. Then,
define the new weight function w2(x) = 1 + W−w(x). This then assigns a
strictly positive weight, and we will show that any independent set that that
has maximum weight with respect to w2will have minimum weight with respect
to w. Recall Theorem 16.6 since we will be using it, suppose that for our
matriod, all maximal independent sets have size S. Then, suppose M1and M2
are maximal independent sets so that M1is maximal with respect to w2and
M2is minimal with respect to w. Then, we need to show that w(M1) = w(M2).
Suppose not to achieve a contradiction, then, by minimality of M2,w(M1)>
w(M2). Rewriting both sides in terms of w2, we have w2(M2)−(1 + W)S >
w2(M1)−(1+W)S, so, w2(M2)> w2(M1). This however contradicts maximality
of M1with respect to w2. So, we must have that w(M1) = w(M2). So, a
maximal independent set that has the largest weight with respect to w2also
has the smallest weight with respect to w.
Exercise 16.5-1
With the requested substitution, the instance of the problem becomes
ai1234567
di4243146
wi10 20 30 40 50 60 70
We begin by just greedily constructing the matroid, adding the most costly
to leave incomplete tasks first. So, we add taks 7,6,5,4,3. Then, in order to
schedule tasks 1 or 2 we need to leave incomplete more important tasks. So,
our final scedule is h5,3,4,6,7,1,2ito have a total penalty of only w1+w2= 30.
Exercise 16.5-2
Create an array Bof length ncontaining zeros in each entry. For each ele-
ment a∈A, add 1 to B[a.deadline]. If B[a.deadline]> a.deadline, return that
the set is not independent. Otherwise, continue. If successfully examine every
element of A, return that the set is independent.
8

Problem 16-1
a. Always give the highest denomination coin that you can without going over.
Then, repeat this process until the amount of remaining change drops to 0.
b. Given an optimal solution (x0, x1, . . . , xk) where xiindicates the number of
coins of denomination ci. We will first show that we must have xi< c for
every i<k. Suppose that we had some xi≥c, then, we could decrease
xiby cand increase xi+1 by 1. This collection of coins has the same value
and has c−1 fewer coins, so the original solution must of been non-optimal.
This configuration of coins is exactly the same as you would get if you kept
greedily picking the largest coin possible. This is because to get a total value
of V, you would pick xk=bV c−kcand for i < k,xib(V modci+1)c−ic. This
is the only solution that satisfies the property that there aren’t more than c
of any but the largest denomination because the coin amounts are a base c
representation of V modck.
c. Let the coin denominations be {1,3,4}, and the value to make change for be
6. The greedy solution would result in the collection of coins {1,1,4}but
the optimal solution would be {3,3}.
d. See algorithm MAKE-CHANGE(S,v) which does a dynamic programming
solution. Since the first forloop runs n times, and the inner for loop runs k
times, and the later while loop runs at most n times, the total running time
is O(nk).
Problem 16-2
a. Order the tasks by processing time from smallest to largest and run them in
that order. To see that this greedy solution is optimal, first observe that the
problem exhibits optimal substructure: if we run the first task in an optimal
solution, then we obtain an optimal solution by running the remaining tasks
in a way which minimizes the average completion time. Let Obe an optimal
solution. Let abe the task which has the smallest processing time and let b
be the first task run in O. Let Gbe the solution obtained by switching the
order in which we run aand bin O. This amounts reducing the completion
times of aand the completion times of all tasks in Gbetween aand bby the
difference in processing times of aand b. Since all other completion times
remain the same, the average completion time of Gis less than or equal to
the average completion time of O, proving that the greedy solution gives an
optimal solution. This has runtime O(nlg n) because we must first sort the
elements.
b. Without loss of generality we my assume that every task is a unit time task.
Apply the same strategy as in part (a), except this time if a task which we
9

Algorithm 2 MAKE-CHANGE(S,v)
Let numcoins and coin be empty arrays of length v, and any any attempt to
access them at indices in the range −max(S),−1 should return ∞
for i from 1 to v do
bestcoin =nil
bestnum =∞
for c in S do
if numcoins[i−c]+1< bestnum then
bestnum = numcoins[i-c]
bestcoin = c
end if
end for
numcoins[i] = bestnum
coin[i] = bestcoin
end for
let change be an empty set
iter = v
while iter > 0do
add coin[iter] to change
iter =iter −coin[iter]
end while
return change
would like to add next to the schedule isn’t allowed to run yet, we must skip
over it. Since there could be many tasks of short processing time which have
late release time, the runtime becomes O(n2) since we might have to spend
O(n) time deciding which task to add next at each step.
Problem 16-3
a. First, suppose that a set of columns is not linearly independent over F2then,
there is some subset of those columns, say Sso that a linear combination of
Sis 0. However, over F2, since the only two elements are 1 and 0, a linear
combination is a sum over some subset. Suppose that this subset is S0, note
that it has to be nonempty because of linear dependence. Now, consider the
set of edges that these columns correspond to. Since the columns had their
total incidence with each vertex 0 in F2, it is even. So, if we consider the
subgraph on these edges, then every vertex has a even degree. Also, since
our S0was nonempty, some component has an edge. Restrict our attention
to any such component. Since this component is connected and has all even
vertex degrees, it contains an Euler Circuit, which is a cycle.
Now, suppose that our graph had some subset of edges which was a cycle.
Then, the degree of any vertex with respect to this set of edges is even, so,
10

when we add the corresponding columns, we will get a zero column in F2.
Since sets of linear independent columns form a matroid, by problem 16.4-2,
the acyclic sets of edges form a matroid as well.
b. One simple approach is to take the highest weight edge that doesn’t complete
a cycle. Another way to phrase this is by running Kruskal’s algorithm (see
Chapter 23) on the graph with negated edge weights.
c. Consider the digraph on [3] with the edges (1,2),(2,1),(2,3),(3,2),(3,1)
where (u, v) indicates there is an edge from uto v. Then, consider the two
acyclic subsets of edges B= (3,1),(3,2),(2,1) and A= (1,2),(2,3). Then,
adding any edge in B−Ato Awill create a cycle. So, the exchange property
is violated.
d. Suppose that the graph contained a directed cycle consisting of edges corre-
sponding to columns S. Then, since each vertex that is involved in this cycle
has exactly as many edges going out of it as going into it, the rows corre-
sponding to each vertex will add up to zero, since the outgoing edges count
negative and the incoming vertices count positive. This means that the sum
of the columns in Sis zero, so, the columns were not linearly independent.
e. There is not a perfect correspondence because we didn’t show that not con-
taining a directed cycle means that the columns are linearly independent,
so there is not perfect correspondence between these sets of independent
columns (which we know to be a matriod) and the acyclic sets of edges
(which we know not to be a matroid).
Problem 16-4
a. Let Obe an optimal solution. If ajis scheduled before its deadline, we can
always swap it with whichever activity is scheduled at its deadline without
changing the penalty. If it is scheduled after its deadline but aj.deadline ≤j
then there must exist a task from among the first jwith penalty less than
that of aj. We can then swap ajwith this task to reduce the overall penalty
incurred. Since Ois optimal, this can’t happen. Finally, if ajis scheduled
after its deadline and aj.deadline > j we can swap ajwith any other late
task without increasing the penalty incurred. Since the problem exhibits the
greedy choice property as well, this greedy strategy always yields on optimal
solution.
b. Assume that MAKE-SET(x) returns a pointer to the element xwhich is
now it its own set. Our disjoint sets will be collections of elements which
have been scheduled at contiguous times. We’ll use this structure to quickly
find the next available time to schedule a task. Store attributes x.low and
x.high at the representative xof each disjoint set. This will give the earliest
and latest time of a scheduled task in the block. Assume that UNION(x, y)
11

maintains this attribute. This can be done in constant time, so it won’t af-
fect the asymptotics. Note that the attribute is well-defined under the union
operation because we only union two blocks if they are contiguous. Without
loss of generality we may assume that task a1has the greatest penalty, task
a2has the second greatest penalty, and so on, and they are given to us in the
form of an array Awhere A[i] = ai. We will maintain an array Dsuch that
D[i] contains a pointer to the task with deadline i. We may assume that the
size of Dis at most n, since a task with deadline later than ncan’t possibly
be scheduled on time. There are at most 3ntotal MAKE-SET, UNION, and
FIND-SET operations, each of which occur at most ntimes, so by Theorem
21.14 the runtime is O(nα(n)).
Algorithm 3 SCHEDULING-VARIATIONS(A)
1: Initialize an array Dof size n.
2: for i= 1 to ndo
3: ai.time =ai.deadline
4: if D[ai.deadline]6=N IL then
5: y= FIND-SET(D[ai.deadline])
6: ai.time =y.low −1
7: end if
8: x= MAKE-SET(ai)
9: D[ai.time] = x
10: x.low =x.high =ai.time
11: if D[ai.time −1] 6=NIL then
12: UNION(D[ai.time −1], D[ai.time])
13: end if
14: if D[ai.time + 1] 6=NIL then
15: UNION(D[ai.time], D[ai.time + 1])
16: end if
17: end for
Problem 16-5
a. Suppose there are mdistinct elements that could be requested. There may be
some room for improvement in terms of keeping track of the furthest in future
element at each position. If you maintain a (double circular) linked list with
a node for each possible cache element and an array so that in index ithere
is a pointer corresponding to the node in the linked list corresponding to the
possible cache request i. Then, starting with the elements in an arbitrary
order, process the sequence hr1, . . . , rnifrom right to left. Upon processing a
request move the node corresponding to that request to the beginning of the
linked list and make a note in some other array of length nof the element at
the end of the linked list. This element is tied for furthest-in-future. Then,
just scan left to right through the sequence, each time just checking some
12

set for which elements are currently in the cache. It can be done in constant
time to check if an element is in the cache or not by a direct address table.
If an element need be evicted, evict the furthest-in-future one noted earlier.
This algorithm will take time O(n+m) and use additional space O(m+n).
If we were in the stupid case that m > n, we could restrict our attention to
the possible cache requests that actually happen, so we have a solution that
is O(n) both in time and in additional space required.
b. Index the subproblems c[i, S] by a number i∈[n] and a subset S∈[m]
k.
Which indicates the lowest number of misses that can be achieved with an
initial cache of Sstarting after index i. Then,
c[i, S] = min
x∈{S}(c[i+ 1,{ri} ∪ (S− {x})] + (1 −χ{ri}(x)))
which means that xis the element that is removed from the cache unless it is
the current element being accessed, in which case there is no cost of eviction.
c. At each time we need to add something new, we can pick which entry to
evict from the cache. We need to show the there is an exchange property.
That is, if we are at round iand need to evict someone, suppose we evict x.
Then, if we were to instead evict the furthest in future element y, we would
have no more evictions than before. To see this, since we evicted x, we will
have to evict someone else once we get to x, whereas, if we had used the
other strategy, we wouldn’t of had to evict anyone until we got to y. This
is a point later in time than when we had to evict someone to put xback
into the cache, so we could, at reloading y, just evict the person we would of
evicted when we evicted someone to reload x. This causes the same number
of misses unless there was an access to that element that wold of been evicted
at reloading xsome point in between when xany ywere needed, in which
case furthest in future would be better.
13
Chapter 17
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 17.1-1
It woudn’t because we could make an arbitrary sequence of MULT IP U SH(k), MU LT IP OP (k).
The cost of each will be Θ(k), so the average runtime of each will be Θ(k) not
O(1).
Exercise 17.1-2
Suppose the input is a 1 followed by k−1 zeros. If we call DECREMENT
we must change kentries. If we then call INCREMENT on this it reverses these
kchanges. Thus, by calling them alternately ntimes, the total time is Θ(nk).
Exercise 17.1-3
Note that this setup is similar to the dynamic tables discussed in section
17.4. Let nbe arbitrary, and have the cost of operation ibe c(i). Then,
n
X
i=1
c(i) =
dlg(n)e
X
i=1
2i+X
i≤nnot a power of 2
1≤
dlg(n)e
X
i=1
2i+n= 21+dlg(n)e−1+n≤4n−1+n≤5n∈O(n)
So, since to find the average, we divide by n, the average runtime of each com-
mand is O(1).
Exercise 17.2-1
To every stack operation, we charge twice. First we charge the actual cost
of the stack operation. Second we charge the coase of copying an element later
on. Since we have the size of the stack never excede k, and there are always
koperations between backups, we always overpay by at least enough. So, the
ammortized cost of the operation is constant. So, the cost of the n operation is
O(n).
Exercise 17.2-2
1

Assign the cost 3 to each operation. The first operation costs 1, so we have
a credit of21. Now suppose that we have nonnegative credit after having per-
formed the 2ith operation. Each of the 2i−1 operations following has cost 1.
Since we pay 3 for each, we build up a credit of 2 from each of them, giving us
2(2i−1) = 2i+1 −2 credit. Then for the 2i+1th operation, the 3 credits we pay
gives us a total of 2i+1 + 1 to use towards the actual cost of 2i+1, leaving us
with 1 credit. Thus, for any operation we have nonnegative credit. Since the
amortized cost of each operation is O(1), an upper bound on the total actual
cost of noperations is O(n).
Exercise 17.2-3
For each time we set a bit to 1, we both pay a dollar for eventually setting
it back to zero (in the usual manner as the counter is incremented). But we
also pay a third dollar in the event that even after the position has been set
back to zero, we check about zeroing it out during a reset operation. We also
increment the position of the highest order bit (as needed). Then, while doing
the reset operation, we will only need consider those positions less significant
than the highest order bit. Because of this, we have at least paid one extra
dollar before, because we had set the bit at that position to one at least once for
the highest order bit to be where it is. Since we have only put down a constant
ammortized cost at each setting of a bit to 1, the ammortized cost is constant
because each increment operation involves setting only a single bit to 1. Also,
the ammortized cost of a reset is zero because it involves setting no bits to one.
It’s true cost has already been paid for.
Exercise 17.3-1
Define Φ0(D) = Φ(D)−Φ(D0). Then, we have that Φ(D)≥Φ(D0) implies
Φ0(D) = Φ(D)−Φ(D0)≥Φ(D0)−Φ(D0) = 0. and Φ0(D0) = φ(D0)−Φ(D0) =
0. Lastly, the ammortized cost using Φ0is ci+Φ0(Di)−Φ0(Di−1) = ci+(Φ(Di)−
Φ(D0)) −(Φ(Di)−Φ(Di−1)) = ci+ Φ(Di)−Φ(Di−1) which is the ammortized
cost using Φ.
Exercise 17.3-2
Let Φ(Di) = k+ 3 if i= 2k. Otherwise, let kbe the largest integer such
that 2k≤i. Then define Φ(Di) = Φ(D2k) + 2(i−2k). Also, define Φ(D0) = 0.
Then Φ(Di)≥0 for all i. The potential difference Φ(Di)−Φ(Di−1) is 2 if iis
not a power of 2, and is −2k+ 3 if i= 2k. Thus, the total amortized cost of n
operations is Pn
i=1 ˆci=Pn
i=1 3=3n=O(n).
Exercise 17.3-3
Make the potential function be equal to nlg(n) where nis the size of the
min-heap. Then, there is still a cost of O(lg(n)) to insert, since only an amount
2

of ammortization that is about lg(n) was spent to increase the size of the heap
by 1. However, since extract min decreases the size of the heap by 1, the actual
cost of the operation is offset by a change in potential of the same order, so only
a constant amount of work is needed.
Exercise 17.3-4
Since Dn=sn,D0=s0, and the amortized cost of nstack operations start-
ing from an empty stack is is O(n), equation 17.3 implies that the amortized
cost is O(n) + sn−s0.
Exercise 17.3-5
Suppose that we have that n≥cb. Since the counter begins with b1’s,
we’ll make all of our ammortized cost 2 + 1
c. Then the additional cost of 1
cover
the course of noperations amounts to paying an extran
c≥bwhich was how
much we were behind by when we started. Since the ammortized cost of each
operation is 2 + 1
cit is in O(1) so the total cost is in O(n).
Exercise 17.3-6
We’ll use the accounting method for the analysis. Assign cost 3 to the
ENQUEUE operation and 0 to the DEQUEUE operation. Recall the imple-
mentation of 10.1-6 where we enqueue by pushing on to the top of stack 1, and
dequeue by popping from stack 2. If stack 2 is empty, then we must pop every
element from stack 1 and push it onto stack 2 before popping the top element
from stack 2. For each item that we enqueue we accumulate 2 credits. Before
we can dequeue an element, it must be moved to stack 2. Note: this might
happen prior to the time at which we wish to dequeue it, but it will happen
only once overall. One of the 2 credits will be used for this move. Once an item
is on stack 2 its pop only costs 1 credit, which is exactly the remaining credit
associated to the element. Since each operation’s cost is O(1), the amortized
cost per operation is O(1).
Exercise 17.3-7
We’ll store all our elements in an array, and if ever it is too large, we will
copy all the elements out into an array of twice the length. To delete the larger
half, we first find the element mwith order statistic d|S|/2eby the algorithm
presented in section 9.3. Then, scan through the array and copy out the ele-
ments that are smaller or equal to minto an array of half the size. Since the
delete half operation takes time O(|S|) and reduces the number of elemnts by
b|S|/2c ∈ Ω(|S|), we can make these operations take ammortized constant time
by selecting our potential function to be linear in |S|. Since the insert opera-
tion only increases |S|by one, we have that there is only a constant amount of
work going towards satisfying the potential, so the total ammortized cost of an
3

insertion is still constant. To output all the elements just iterate through the
array and output each.
Exercise 17.4-1
By theorems 11.6-11.8, the expected cost of performing insertions and searches
in an open address hash table approaches infinity as the load factor approaches
one, for any load factor fixed away from 1, the expected time is bounded by
a constant though. The expected value of the actual cost my not be O(1) for
every insertion because the actual cost may include copying out the current val-
ues from the current table into a larger table because it became too full. This
would take time that is linear in the number of elements stored.
Exercise 17.4-2
First suppose that αi≥1/2. Then we have
ˆci= 1 + (2 ·numi−sizei)−(2 ·numi−1−sizei−1)
= 1 + 2 ·numi−sizei−2·numi−2 + sizei
=−2.
On the other hand, if αi<1/2 then we have
ˆci= 1 + (sizei/2−numi)−(2 ·numi−1−sizei−1)
= 1 + sizei/2−numi−2·numi−2 + sizei
=−1 + 3
2(sizei−2·numi)
≤ −1 + 3
2(sizei−(sizei−1))
≤1.
Either way, the amortized cost is bounded above by a constant.
Exercise 17.4-3
If a resizing is not triggered, we have
ˆci=Ci+ Φi−Φi−1
= 1 + |2·numi−sizei|−|2·numi−1−sizei−1|
= 1 + |2·numi−sizei|−|2·numi+ 2 −sizei|
≤1 + |2·numi−sizei|−|2·numi−sizei|+ 2
= 3
However, if a resizing is triggered, suppose that αi−1<1
2. Then the actual
cost is numi+ 1 since we do a deletion and move all the rest of the items. Also,
4

since we resize when the load factor drops below 1
3, we have that sizei−1/3 =
numi−1=numi+ 1.
ˆci=ci+φi−Φi−1
=numi+1+|2·numi−sizei|−|2·numi−1−sizei−1|
≤numi+1+2
3sizei−1−2·numi−(sizei−1−2·numi−2)
=numi+ 1 + (2 ·numi+ 2 −2·numi)−(3 ·numi+ 3 −2·numi)
= 2
The last case, that we had the load factor was greater than or equal to 1
2,
will not trigger a resizing because we only resize when the load drops below 1
3.
Problem 17-1
a. Initialize a second array of length nto all trues, then, going through the
indices of the original array in any order, if the corresponding entry in the
second array is true, then swap the element at the current index with the
element at the bit-reversed position, and set the entry in the second array
corresponding to the bit-reversed index equal to false. Since we are running
revk< n times, the total runtime is O(nk).
b. Doing a bit reversed increment is the same thing as adding a one to the
leftmost position where all carries are going to the left instead of the right.
See the algorithm BIT-REVERSED-INCREMENT(a)
Algorithm 1 BIT-REVERSED-INCREMENT(a)
let m be a 1 followed by k-1 zeroes
while m bitwise-AND a is not zero do
a = a bitwise-XOR m
shift m right by 1
end whilereturn m bitwise-OR a
By a similar analysis to the binary counter (just look at the problem in a
mirror), this BIT-REVERSED-INCREMENT will take constant ammortized
time. So, to perform the bit-reversed permutation, have a normal binary
counter and a bit reversed counter, then, swap the values of the two counters
and increment. Do not swap however if those pairs of elements have already
been swapped, which can be kept track of in a auxillary array.
c. The BIT-REVERSED-INCREMENT procedure given in the previous part
only uses single shifts to the right, not arbitrary shifts.
Problem 17-2
5

a. We linearly go through the lists and binary search each one since we don’t
know the relationship between one list an another. In the worst case, every
list is actually used. Since list ihas length 2iand it’s sorted, we can search
it in O(i) time. Since ivaries from 0 to O(lg n), the runtime of SEARCH is
O((lg n)2).
b. To insert, suppose we must change the first m1’s in a row to 0’s, followed
by changing a 0 to a 1 in the binary representation of n. Then we must com-
bine lists A0, A1, . . . , Am−1into list Am, then insert the new item into list
Am. Since merging two sorted lists can be done linearly in the total length
of the lists, the time this takes is O(2m). In the worst case, this takes time
O(n) since mcould equal k. However, since there are a total of 2mitems the
amortized cost per item is O(1).
c. Find the smallest msuch that nm6= 0 in the binary representation of n. If
the item to be deleted is not in list Am, remove it from its list and swap
in an item from Am, arbitrarily. This can be done in O(lg n) time since we
may need to search list Akto find the element to be deleted. Now simply
break list Aminto lists A0, A1, . . . , Am−1by index. Since the lists are already
sorted, the runtime comes entirely from making the splits, which takes O(m)
time. In the worst case, this is O(lg n).
Problem 17-3
a. Since we have O(x.size) auxiliary space, we will take the tree rooted at xand
write down an inorder traversal of the tree into the extra space. This will
only take linear time to do because it will visit each node thrice, once when
passing to its left child, once when the nodes value is output and passing to
the right child, and once when passing to the parent. Then, once the inorder
traversal is written down, we can convert it back to a binary tree by selecting
the median of the list to be the root, and recursing on the two halves of the
list that remain on both sides. Since we can index into the middle element of
a list in constant time, we will have the recurrence T(n)=2T(n/2)+1, which
has solution that is linear. Since both trees come from the same underlying
inorder traversal, the result is a BST since the original was. Also, since the
root at each point was selected so that half the elements are larger and half
the elements are smaller, it is a 1/2-balanced tree.
b. We will show by induction that any tree with ≤α−d+delements has a
depth of at most d. This is clearly true for d= 0 because any tree with
a single node has depth 0, and since α0= 1, we have that our restriction
on the number of elements requires there to only be one. Now, suppose
that in some inductive step we had a contradiction, that is, some tree of
6

depth dthat is αbalanced but has more than α−delements. We know that
both of the subtrees are alpha balanced, and by being alpha balanced at the
root, we have root.left.size ≤α·root.size which implies root.right.size >
root.size −α·root.size −1. So, root.right.size > (1 −α)root.size −1>
(1 −α)α−d+d−1=(α−1−1)α−d+1 +d−1≥α−d+1 +d−1 which is a
contradiction to the fact that it held for all smaller values of dbecause any
child of a tree of depth dhas depth d−1.
c. The potential function is a sum of ∆(x) each of which is the absolute value
of a quantity, so, since it is a sum of nonnegative values, it is nonnegative
regardless of the input BST.
If we suppose that our tree is 1/2−balanced, then, for every node x, we’ll
have that ∆(x)≤1, so, the sum we compute to find the potential will be
over no nonzero terms.
d. Suppose that we have a tree that has become no longer αbalanced be-
cause it’s left subtree has become too large. This means that x.left.size >
αx.size = (α−1
2)x.size +1
2α.size. This means that we had at least c(α−
1
2)x.size units of potential. So, we need to select c≥1
α−1
2
.
e. Suppose that our tree is αbalanced. Then, we know that performing a search
takes time O(lg(n)). So, we perform that search and insert the element that
we need to insert or delete the element we found. Then, we may have made
the tree become unbalanced. However, we know that since we only changed
one position, we have only changed the ∆ value for all of the parents of
the node that we either inserted or deleted. Therefore, we can rebuild the
balanced properties starting at the lowest such unbalanced node and working
up. Since each one only takes ammortized constant time, and there are
O(lg(n)) many trees made unbalaced, tot total time to rebalanced every
subtree is O(lg(n)) ammortized time.
Problem 17-4
a. If we insert a node into a complete binary search tree whose lowest level is
all red, then there will be Ω(lg n) instances of case 1 required to switch the
colors all the way up the tree. If we delete a node from an all-black, com-
plete binary tree then this also requires Ω(lg n) time because there will be
instances of case 2 at each iteration of the while-loop.
b. For RB-INSERT, cases 2 and 3 are terminating. For RB-DELETE, cases 1
and 3 are terminating.
c. After applying case 1, z’s parent and uncle have been changed to black and
z’s grandparent is changed to red. Thus, there is a ned loss of one red node,
7

so Φ(T0) = Φ(T)−1.
d. For case 1, there is a single decrease in the number of red nodes, and thus
a decrease in the potential function. However, a single call to RB-INSERT-
FIXUP could result in Ω(lg n) instances of case 1. For cases 2 and 3, the
colors stay the same and each performs a rotation.
e. Since each instance of case 1 requires a specific node to be red, it can’t
decrease the number of red nodes by more than Φ(T). Therefore the po-
tential function is always non-negative. Any insert can increase the number
of red nodes by at most 1, and one unit of potential can pay for any struc-
tural modifications of any of the 3 cases. Note that in the worst case, the
call to RB-INSERT has to perform kcase-1 operations, where kis equal
to Φ(Ti)−Φ(Ti−1). Thus, the total amoritzed cost is bounded above by
2(Φ(Tn)−Φ(T0)) ≤n, so the amortized cost of each insert is O(1).
f. In case 1 of RB-INSERT, we reduce the number of black nodes with two red
children by 1 and we at most increase the number of black nodes with no red
children by 1, leaving a net loss of at most 1 to the potential function. In
our new potential function, Φ(Tn)−Φ(T0)≤n. Since one unit of potential
pays for each operation and the terminating cases cause constant structural
changes, the total amortized cost is O(n) making the amortized cost of each
RB-INSERT-FIXUP O(1).
g. In case 2 of RB-DELETE, we reduce the number of black nodes with two red
children by 1, thereby reducing the potential function by 2. Since the change
in potential is at least negative 1, it pays for the structural modifications.
Since the other cases cause constant structural changes, the total amortized
cost is O(n) making the amortized cost of each RB-DELETE-FIXUP O(1).
h. As described above, whether we insert or delete in any of the cases, the po-
tential function always pays for the changes made if they’re nonterminating.
If they’re terminating then they already take constant time, so the amortized
cost of any operation in a sequence of minserts and deletes is O(1), making
the toal amortized cost O(m).
Problem 17-5
a. Since the heuristic is picked in advance, given any sequence of requests given
so far, we can simulate what ordering the heuristic will call for, then, we will
pick our next request to be whatever element will of been in the last position
8

of the list. Continuing until all the requests have been made, we have that
the cost of this sequence of accesses is = mn.
b. The cost of finding an element is = rankL(x) and since it needs to be swapped
with all the elements before it, of which there are rankL(x)−1, the total
cost is 2 ·rankL(x)−1.
c. Regardless of the heuristic used, we first need to locate the element, which
is left where ever it was after the previous step, so, needs rankLi−1(x). After
that, by definition, there are titranspositions made, so, c∗
i=rankLi−1(x)+t∗
i.
d. If we perform a transposition of elements yand z, where yis towards the
left. Then there are two cases. The first is that the final ordering of the list
in L∗
iis with yin front of z, in which case we have just increased the number
of inversions by 1, so the poitential increases by 2. The second is that in L∗
Iz
occurs before y, in which case, we have just reduced the number of inversions
by one, reducing the potential by 2. In both cases, whether or not there is
an inversion between yor zand any other element has not changed, since
the transposition only changed the relative ordering of those two elements.
e. By definition, Aand Bare the only two of the four categories to place
elements that precede xin Li−1, since there are |A|+|B|elements preceding
it, it’s rank in Li−1is |A|+|B|+ 1. Similarly, the two categories in which
an element can be if it precedes xin L∗
i−1are Aand C, so, in L∗
i−1,xhas
rank |A|+|C|+ 1.
f. We have from part d that the potential increases by 2 if we transpose two
elements that are being swapped so that their relative order in the final
ordering is being screwed up, and decreases by two if they are begin placed
into their correct order in L∗
i. In particular, they increase it by at most 2.
since we are keeping track of the number of inversions that may not be the
direct effect of the transpositions that heuristic Hmade, we see which ones
the Move to front heuristic may of added. In particular, since the move to
front heuristic only changed the relative order of xwith respect to the other
elements, moving it in front of the elements that preceded it in Li−1, we only
care about sets Aand B. For an element in A, moving it to be behind A
created an inversion, since that element preceded xin L∗
i. However, if the
element were in B, we are removing an inversion by placing xin front of it.
g. First, we apply parts b and f to the expression for ˆcito get ˆci≤2·rankL(x)−
1+2(|A|−|B|+t∗
i). Then, applying part e, we get this is = 2(|A|+|B|+1)−1+
2(|A|−|B|+t∗
i)=4|A|−1+2t∗
i≤4(|A|+|C|+1)+4t∗
i= 4(rankL∗
i−1(x)+t∗
i).
Finally, by part c, this bound is equal to 4c∗
i.
h. We showed that the ammortized cost of each operation under the move to
front heuristic was at most four times the cost of the operation using any
other heuristic. Since the ammortized cost added up over all these operation
is at most the total (real) cost, so we have that the total cost with movetofront
is at most four times the total cost with an arbitrary other heuristic.
9
Chapter 18
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 18.1-1
If we allow t= 0, then, since we only know that internal nodes have to have
at least t−1 keys, it may be the case that some internal nodes represent no
keys, a bad situation indeed.
Exercise 18.1-2
The possible values of tare 2 and 3. Every non-root node has at least 1
(resp. 2) keys and at most 3 (resp. 5) keys. The value of tcannot exceed 3
since some nodes have only 2 keys.
Exercise 18.1-3
3
1,2 4,5
4
1,2,3 5
4
2
1 3
5
1
2
1 4
3 5
2
13,4,5
2,4
1 3 5
Exercise 18.1-4
The maximum number of nodes is achieved when every node has 2tchildren.
In this case, there are 1 + 2t+ (2t)2+. . . + (2t)h=1−(2t)h+1
1−2tnodes. Since every
node has at most 2t−1 keys, there are at most (2t)h+1 −1 keys.
Exercise 18.1-5
We would get a t=2 B-tree. It would have one, two, or three keys depending
on if it has zero, one, or two red children respectively. Suppose that the left
child is red, then it’s keys becomes the first one, and that red node’s children
become the first and second children of the new node. Similarly, if it is the right
child that is red, that key becomes the last key listed with the new node, and
the red nodes children become the second to last and last children of the new
node.
Exercise 18.2-1
F
FS
FQS
2
Q
FK S
Q
CFK S
FQ
C KL S
FQ
C HKL S
FQ
C HKL ST
FQ
C HKL STV
FQT
C HKL S VW
3
FQT
C K
H LM
S VW
FQT
C K
H LM
RS VW
FQT
C K
H LMN
RS VW
FQT
C KM
H L NP
RS VW
4
FQT
AC KM
H L NP
RS VW
FQT
ABC KM
H L NP
RS VW
FQT
ABC KM
H L NP
RS VWX
FQT
ABC KM
H L NP
RS W
V XY
5
FQT
B
A CD
KM
H L NP
RS W
V XY
FQT
B
A CD
KM
H L NP
RS W
V XYZ
FQT
B
A CDE
KM
H L NP
RS W
V XYZ
Exercise 18.2-2
Lines 1, 2, and 13 of B-TREE-SPLIT-CHILD guarantee that there are no
redundant DISK-WRITE operations performed in this part of the algorithm,
since each of these lines necessarily makes a change to nodes z,y, and xrespec-
tively. B-TREE-INSERT makes no calls to DISK-READ or DISK-WRITE. In
B-TREE-INSERT-NONFULL, we only reach line 8 after executing line 7, which
modifies x, so line 8 isn’t redundant. The only call to DISK-READ occurs at
line 12. Since calls to B-TREE-INSERT-NONFULL are made recursively on
successive children, line 12 will never be redundant. Thus, no redundant read
or write operations are ever performed.
Exercise 18.2-3
To find the minimum key, just always select the first child until you are on a
leaf, then return the first key. To find the predecessor of a given key, fist find it.
6

if it’s on a leaf then just return the preceding key. If it’s not a leaf, then return
the largest element(in an analogous way to finding minimum) of the child that
immediately precedes the key just found.
Exercise 18.2-4
The final tree can have as many as n−1 nodes. Unless n= 1 there cannot
ever be nnodes since we only ever insert a key into a non-empty node, so there
will always be at least one node with 2 keys. Next observe that we will never
have more than one key in a node which is not a right spine of our B-tree. This
is because every key we insert is larger than all keys stored in the tree, so it
will be inserted into the right spine of the tree. Nodes not in the right spine
are a result of splits, and since t= 2, every split results in child nodes with one
key each. The fewest possible number of nodes occurs when every node in the
right spine has 3 keys. In this case, n= 2h+ 2h+1 −1 where his the height of
the B-tree, and the number of nodes is 2h+1 −1. Asymptotically these are the
same, so the number of nodes is Θ(n).
Exercise 18.2-5
You would modify the insertion procedure by, in B-TREE-Insert, check if
the node is a leaf, and if it is, only split it if there twice as many keys stored
as expected. Also, if an element needs to be inserted into a full leaf, we would
split the leaf into two separate leaves, each of which doesn’t have too many keys
stored in it.
Exercise 18.2-6
If we use binary search rather than linear search, the CPU time becomes
O(log2(t) logt(n)) = O(log2(n)) by the change of base formula.
Exercise 18.2-7
By Theorem 18.1, we have that the height of a B-tree on nelements is
bounded by logt
n+1
2. The number of page reads needed during a search is at
worst the height. Since the cost per page access is now also a function of t,
the time required for the search is c(t) = (a+bt) logt
n+1
2. To minimize this
expression, we’ll take a derivative with respect to t.c0(t) = blogt
n+1
2−(a+
7
bt)ln(n+1
2)
tln(t)2. Then, setting this equal to zero, we have that
blogt
n+ 1
2= (a+bt)ln n+1
2
tln(t)2
bln n+ 1
2= (a+bt)ln n+1
2
tln(t)
tln(t) = (a
b+t)
t(ln(t)−1) = a
b
For our particular values of a= 5, and b= 10, we can solve this equation
numerically to get an approximate maxima of 3.18, so selecting t=3 will mini-
mize the worst case cost of a search in the tree.
Exercise 18.3-1
LPTX
AEJK NO QRS UV YZ
LQTX
AEJK NO RS UV YZ
LQT
AEJK NO RS UXYZ
Exercise 18.3-2
The algorithm B-TREE-DELETE(x, k) is a recursive procedure which deletes
key kfrom the B-tree rooted at node x. The functions PRED(k, x) and SUCC(k, x)
return the predecessor and successor of kin the B-tree rooted at xrespectively.
The cases where kis the last key in a node have been omitted because the pseu-
docode is already unwieldy. For these, we simply use the left sibling as opposed
8

to the right sibling, making the appropriate modifications to the indexing in the
for-loops.
Problem 18-1
a. We will have to make a disk access for each stack operation. Since each of
these disk operations takes time Θ(m), the CPU time is Θ(mn).
b. Since only every mth push starts a new page, the number of disk operations
is approximately n/m, and the CPU runtime is Θ(n), since both the contri-
bution from the cost of the disk access and the actual running of the push
operations are both Θ(n).
c. If we make a sequence of pushes until it just spills over onto the second page,
then alternate popping and pulling many times, the asymptotic number of
disk accesses and CPU time is of the same order as in part a. This is because
when we are doing that alternating of pops and pushes, each one triggers a
disk access.
d. We define the potential of the stack to be the absolute value of the difference
between the current size of the stack and the most recently passed multiple
of m. This potential function means that the initial stack which has size
0, is also a multiple of m, so the potential is zero. Also, as we do a stack
operation we either increase or decrease the potential by one. For us to have
to load a new page from disk and write an old one to disk, we would need
to be at least mpositions away from the most recently visited multiple of
m, because we would have had to just cross a page boundary. This cost of
loading and storing a page takes (real) cpu time of Θ(m). However, we just
had a drop in the potential function of order Θ(m). So, the ammortized cost
of this operation is O(1).
Problem 18-2
a. For insertion it will suffice to explain how to update height when we split
a node. Suppose node xis split into nodes yand z, and the median of x
is merged into node w. The height of wremains unchanged unless xwas
the root (in which case w.height =x.height + 1). The height of yor z
will often change. We set y.height = maxiy.ci.height + 1 and z.height =
maxiz.ci.height + 1. Each update takes O(t). Since a call to B-TREE-
INSERT makes at most hsplits where his the height of the tree, the total
time it takes to update heights is O(th), preserving the asymptotic running
time of insert. For deletion the situation is even simple. The only time the
height changes is when the root has a single node and it is merged with its
subtree nodes, leaving an empty root node to be deleted. In this case, we
update the height of the new node to be the (old) height of the root minus
1.
9

Algorithm 1 B-TREE-DELETE(x,k)
1: if x.leaf then
2: for i= 1 to x.n do
3: if x.keyi== kthen
4: Delete key kfrom x
5: x.n =x.n −1
6: DISK-WRITE(x)
7: Return
8: end if
9: end for
10: end if
11: i= 1
12: while x.keyi< k do
13: i=i+ 1
14: end while
15: if x.keyi== kthen // If kis in node xat position i
16: DISK-READ(x.ci)
17: if x.ci.n ≥tthen
18: k0=P RED(k, x.ci)
19: x.keyi=k0
20: DISK-WRITE(x)
21: B-TREE-DELETE(x.ci, k0)
22: Return
23: DISK-READ(x.ci+1)x.ci+1.n ≥t
24: k0=SUCC(k, x.ci)
25: x.keyi=k0
26: DISK-WRITE(x)
27: B-TREE-DELETE(x.ci+1, k0)
28: Return
29: y=x.ci
30: z=x.ci+1
31: m=y.n
32: p=z.n
33: y.keym+1 =k
34: for j= 1 to pdo
35: y.keym+1+j=z.keyj
36: end for
37: y.n =m+p+ 1
38: for j=i+ 1 to x.n −1do
39: x.cj=x.cj+1
40: end for
41: x.n =x.n −1
42: FREE(z)
43: DISK-WRITE(x)
44: DISK-WRITE(y)
45: DISK-WRITE(z)
46: B-TREE-DELETE(y, k)
47: Return
48: end if
49: end if
10

50: DISK-READ(x.ci)
51: if x.ci.n ≥tthen
52: B-TREE-DELETE(x.ci, k)
53: Return
54: DISK-READ(x.ci+1)x.ci+1.n ≥t
55: x.ci.keyt=x.keyi
56: x.ci.n =x.ci.n + 1
57: x.keyi=x.ci+1.key1
58: x.ci.ct+1 =x.ci+1.c1
59: x.ci.n =t
60: x.ci+1.n =x.ci+1.n −1
61: for j= 1 to x.ci+1.n do
62: x.ci+1.keyj=x.ci+1.keyj+1
63: end for
64: DISK-WRITE(x)
65: DISK-WRITE(x.ci)
66: DISK-WRITE(x.ci+1)
67: B-TREE-DELETE(x.ci, k)
68: y=x.ci
69: z=x.ci+1
70: m=y.n
71: p=z.n
72: y.keym+1 =x.keyi
73: for j= 1 to pdo
74: y.keym+1+j=z.keyj
75: end for
76: y.n =m+p+ 1
77: for j=i+ 1 to x.n −1do
78: x.cj=x.cj+1
79: end for
80: x.n =x.n −1
81: FREE(z)
82: DISK-WRITE(x)
83: DISK-WRITE(y)
84: DISK-WRITE(z)
85: B-TREE-DELETE(y, k)
86: if x.n == 0 then //This occurs when the root contains no keys
87: Free(x)
88: end if
89: Return
90: end if
11

b. Without loss of generality, assume h0≥h00 . We essentially wish to merge T00
into T0at a node of height h00 using node x. To do this, find the node at
depth h0−h00 on the right spine of T0. Add xas a key to this node, and T00
as the additional child. If it should happen that the node was already full,
perform a split operation.
c. Let xibe the node encountered after isteps on path p. Let libe the in-
dex of the largest key stored in xiwhich is less than or equal to k. We
take k0
i=xi.keyliand T0
i−1to be the tree whose root node consists of the
keys in xiwhich are less than xi.keyli, and all of their children. In general,
T0
i−1.height ≥T0
i.height. For S00 , we take a similar approach. They keys
will be those in nodes passed on pwhich are immediately greater than k,
and the trees will be rooted at a node consisting of the larger keys, with the
associated subtrees. When we reach the node which contains k, we don’t
assign a key, but we do assign a tree.
d. Let T1and T2be empty trees. Consider the path pfrom the root of Tto k.
Suppose we have reached node xi. We join tree T0
i−1to T1, then insert k0
i
into T1. We join T00
i−1to T2and insert k00
iinto T2. Once we have encountered
the node which contains kat xm.keyk, join xm.ckwith T1and xm.ck+1 with
T2. We will perform at most 2 join operations and 1 insert operation for each
level of the tree. Using the runtime determined in part (b), and the fact that
when we join a tree T0to T1(or T00 to T2respectively) the height difference
is T0.height −T1.height. Since the heights are nondecreasing of successive
tree that are joined, we get a telescoping sum of heights. The first tree has
height h, where his the height of T, and the last tree has height 0. Thus,
the runtime is O(2(h+h)) = O(lg n).
12
Chapter 19
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 19.2-1
First, we take the subtrees rooted at 24, 17, and 23 and add them to the
root list. Then, we set H.min to 18. Then, we run consolidate. First this has
its degree 2 set to the subtree rooted at 18. Then the degree 1 is the subtree
rooted at 38. Then, we get a repeated subtree of degree 2 when we consider the
one rooted at 24. So, we make it a subheap by placing the 24 node under 18.
Then, we consider the heap rooted at 17. This is a repeat for heaps of degree 1,
so we place the heap rooted at 38 below 17. Lastly we consider the heap rooted
at 23, and then we have that all the different heaps have distinct degrees and
are done, setting H.min to the smallest, that is, the one rooted at 17.
The three heaps that we end up with in our root list are:
23
17
38
41
30
and
1
18
24
26
35
46
21
52
39
Exercise 19.3-1
A root in the heap became marked because it at some point had a child
whose key was decreased. It doesn’t add the potential for having to do any
more actual work for it to be marked. This is because the only time that
markedness is checked is in line 3 of cascading cut. This however is only ever
run on nodes whose parent is non NIL. Since every root has NIL as it parent,
line 3 of cascading cut will never be run on this marked root. It will still cause
the potential function to be larger than needed, but that extra computation
that was paid in to get the potential function higher will never be used up later.
Exercise 19.3-2
Recall that the actual cost of FIB-HEAP-DECREASE-KEY is O(c), where
cis the number of calls made to CASCADING-CUT. If ciis the number of
calls made on the ith key decrease, then the total time of ncalls to FIB-HEAP-
DECREASE-KEY is Pn
i=1 O(ci). Next observe that every call to CASCADING-
CUT moves a node to the root, and every call to a root node takes O(1). Since
no roots ever become children during the course of these calls, we must have
that Pn
i=1 ci=O(n). Therefore the aggregate cost is O(n), so the average, or
amortized, cost is O(1).
Exercise 19.4-1
Add three nodes then delete one. This gets us a chain of length 1. Then, add
three nodes, all with smaller values than the first three, and delete one of them.
Then, delete the leaf that is only at depth 1. This gets us a chain of length
2. Then, make a chain of length two using this process except with all smaller
keys. Then, upon a consolidate being forced, we will have that the remaining
heap will have one path of length 3 and one of length 2, with a root that is
unmarked. So, just run decrease key on all of the children along the shorter
path, starting with those of shorter depth. Then, extract min the appropriate
number of times. Then what is left over will be just a path of length 3. We can
2

continue this process ad infinitum. It will result in a chain of arbitrarily long
length where all but the leaf is marked. It will take time exponential in n, but
that’s none of our concern.
More formally, we will make the following procedure linear(n, c) that makes
heap that is a linear chain of nnodes and has all of its keys between cand c+2n.
Also, as a precondition of running linear(n, c), we have all the keys currently in
the heap are less than c. As a base case, define linear(1, c) to be the command
insert(c). Define linear(n+ 1, c) as follows, where the return value list of nodes
that lie on the chain but aren’t the root
S1=linear(n, c)
S2=linear(n, c + 2n)
x.key =−∞
insert(x)
extractmin()
for each entry in S1, delete that key
The heap now has the desired structure, return S2
Exercise 19.4-2
Following the proof of lemma 19.1, if xis any node if a Fibonacci heap,
x.degree =m, and xhas children y1, y2, . . . , ym, then y1.degree ≥0 and
yi.degree ≥i−k. Thus, if smdenotes the fewest nodes possible in a node
of degree m, then we have s0= 1, s1= 2, . . . , sk−1=kand in general,
sm=k+Pm−k
i=0 si. Thus, the difference between smand sm−1is sm−k. Let {fm}
be the sequence such that fm=m+ 1 for 0 ≤m < k and fm=fm−1+fm−k
for m≥k. If F(x) is the generating function for fmthen we have F(x) =
1−xk
(1−x)(1−x−xk). Let αbe a root of xk=xk−1+ 1. We’ll show by induction that
fm+k≥αm. For the base cases:
fk=k+ 1 ≥1 = α0
fk+1 =k+ 3 ≥α1
.
.
.
fk+k=k+(k+ 1)(k+ 2)
2=k+k+1+k(k+ 1)
2≥2k+1+αk−1≥αk.
In general, we have
fm+k=fm+k−1+fm≥αm−1+αm−k=αm−k(αk−1+ 1) = αm.
Next we show that fm+k=k+Pm
i=0 fi. The base case is clear, since
fk=f0+k=k+ 1. For the induction step, we have
fm+k=fm−1−k+fm=k+
m−1
X
i=0
fi+fm=k+
m
X
i=0
fi.
3

Observe that si≥fi+kfor 0 ≤i<k. Again, by induction, for m≥kwe
have
sm=k+
m−k
X
i=0
si≥k+
m−k
X
i=0
fi+k≥k+
m
X
i=0
fi=fm+k
so in general, sm≥fm+k. Putting it all together, we have:
size(x)≥sm
≥k+
m
X
i=k
si−k
≥k+
m
X
i=k
fi
≥fm+k
≥αm.
Taking logs on both sides, we have
logαn≥m.
In other words, provided that αis a constant, we have a logarithmic bound on
the maximum degree.
Problem 19-1
a. It can take actual time proportional to the number of children that x had
because for each child, when placing it in the root list, their parent pointer
needs to be updated to be NIL instead of x.
b. Line 7 takes actual time bounded by x.degree since updating each of the
children of x only takes constant time. So, if cis the number of cascading
cuts that are done, the actual cost is O(c+x.degree).
c. From the cascading cut, we marked at most one more node, so, m(H0)≤
1 + m(H) regardless of the number of calls to cascading cut, because only
the highest thing in the chain of calls actually goes from unmarked to marked.
Also, the number of children increases by the number of children that xhad,
that is t(H0) = x.degree +t(H). Putting these together, we get that
Φ(H0)≤t(H) + x.degree + 2(1 + m(H))
d. The asymptotic time is Θ(x.degree) = Θ(lg(n)) which is the same asyptotic
time that was required for the original deletion method.
Problem 19-2
4

a. We proceed by induction to prove all four claims simultaneously. When
k= 0, B0has 20= 1 node. The height of B0is 0. The only possible depth
is 0, at which there are 0
0= 1 node. Finally, the root has degree 0 and
it has no children. Now suppose the claims hold for k.Bk+1 is formed by
connecting two copies of Bk, so it has 2k+ 2k= 2k+1 nodes. The height of
the tree is the height of Bkplus 1, since we have added an extra edge con-
necting the root of Bkto the new root of the tree, so the height is k+ 1. At
depth iwe get a contribution of k
i−1from the first tree, and a contribution
of k
ifrom the second. Summing these and applying a common binomial
identity gives k+1
i. Finally, the degree of the root is the sum of 1, and the
degree of the root of Bk, which is 1 + k. If we number the children left to
right by k, k −1,...,0, then the first child corresponds to the root of Bkby
definition. The remaining children correspond to the proper roots of subtrees
by the induction hypothesis.
b. Let n.b denote the binary expansion of n. The fact that we can have at most
one of each binomial tree corresponds to the fact that we can have at most
1 as any digit of n.b. Since each binomial tree has a size which is a power of
2, the binomial trees required to represent nnodes are uniquely determined.
We include Bkif and only if the kth position of n.b is 1. Since the binary
representation of nhas at most blg nc+ 1 digits, this also bounds the number
of trees which can be used to represent nnodes.
c. Given a node x, let x.key,x.p,x.c, and x.s represent the attributes key,
parent, left-most child, and sibling to the right, respectively. The pointer
attributes have value NIL when no such node exists. The root list will be
stored in a singly linked list. MAKE-HEAP() is implemented by initializing
an empty list for the root list and returning a pointer to the head of the
list, which contains NIL. This takes constant time. To insert: Let xbe a
node with key k, to be inserted. Scan the root list to find the first msuch
that Bmis not one of the trees in the binomial heap. If there is no B0, sim-
ply create a single root node x. Otherwise, union x, B0, B1, . . . , Bm−1into
aBmtree. Remove all root nodes of the unioned trees from the root list,
and update it with the new root. Since each join operation is logarithmic in
the height of the tree, the total time is O(lg n). MINIMUM just scans the
root list and returns the minimum in O(lg n), since the root list has size at
most O(lg n). EXTRACT-MIN finds and deletes the minimum, then splits
the tree Bmwhich contained the minimum into its component binomial trees
B0, B1, . . . , Bm−1in O(lg n) time. Finally, it unions each of these with any
existing trees of the same size in O(lg n) time. To implement UNION, sup-
pose we have two binomial heaps consisting of trees Bi1, Bi2, . . . , Bikand
Bj1, Bj2, . . . , Bjmrespectively. Simply union corresponding trees of the same
size between the two heaps, then do another check and join any newly cre-
ated trees which have caused additional duplicates. Note: we will perform at
5

most one union on any fixed size of binomial tree so the total running time
is still logarithmic in n, where we assume that nis sum of the sizes of the
trees which we are unioning. To implement DECREASE-KEY, simply swap
the node whose key was decreased up the tree until it satisfies the min-heap
property. To implement DELETE, note that every binomial tree consists of
two copies of a smaller binomial tree, so we can write the procedure recur-
sively. If the tree is a single node, simply delete it. If we wish to delete from
Bk, first split the tree into its constituent copies of Bk−1, and recursively call
delete on the copy of Bk−1which contains x. If this results in two binomial
trees of the same size, simply union them.
d. The Fibonacci heap will look like a binomial heap, except that multiple copies
of a given binomial tree will be allowed. Since the only trees which will ap-
pear are binomial trees and Bkhas 2knodes, we must have 2k≤n, which
implies k≤ blg nc. Since the largest root of any binomial tree occurs at the
root, and on Bkit is degree k, this also bounds the largest degree of a node.
e. INSERT and UNION will no longer have amortized O(1) running time be-
cause CONSOLIDATE has runtime O(lg n). Even if no nodes are consoli-
dated, the runtime is dominated by the check that all degrees are distinct.
Since calling UNION on a heap and a single node is the same as insertion, it
must also have runtime O(lg n). The other operations remain unchanged.
Problem 19-3
a. If k < x.key just run the decrease key procedure. If k > x.key, delete the
current value xand insert x again with a new key. Both of these cases only
need O(lg(n)) ammortized time to run.
b. Suppose that we also had an additional cost to the potential function that
was proportional to the size of the structure. This would only increase when
we do an insertion, and then only by a constant amount, so there aren’t any
worries concerning this increased potential function raising the ammortized
cost of any operations. Once we’ve made this modification, to the potential
function, we also modify the heap itself by having a doubly linked list along
all of the leaf nodes in the heap. To prune we then pick any leaf node, re-
move it from it’s parent’s child list, and remove it from the list of leaves.
We repeat this min(r, H.n) times. This causes the potential to drop by an
amount proportianal to rwhich is on the order of the actual cost of what just
happened since the deletions from the linked list take only constant amounts
of time each. So, the ammortized time is constant.
Problem 19-4
6

a. Traverse a path from root to leaf as follows: At a given node, examine the
attribute x.small in each child-node of the current node. Proceed to the child
node which minimizes this attribute. If the children of the current node are
leaves, then simply return a pointer to the child node with smallest key. Since
the height of the tree is O(lg n) and the number of children of any node is at
most 4, this has runtime O(lg n).
b. Decrease the key of x, then traverse the simple path from xto the root by
following the parent pointers. At each node yencountered, check the at-
tribute y.small. If k < y.small, set y.small =k. Otherwise do nothing and
continue on the path.
c. Insert works the same as in a B-tree, except that at each node it is assumed
that the node to be inserted is “smaller” than every key stored at that node,
so the runtime is inherited. If the root is split, we update the height of the
tree. When we reach the final node before the leaves, simply insert the new
node as the leftmost child of that node.
d. As with B-TREE-DELETE, we’ll want to ensure that the tree satisfies the
properties of being a 2-3-4 tree after deletion, so we’ll need to check that
we’re never deleting a leaf which only has a single sibling. This is handled in
much the same way as in chapter 18. We can imagine that dummy keys are
stored in all the internal nodes, and carry out the deletion process in exactly
the same way as done in exercise 18.3-2, with the added requirement that we
update the height stored in the root if we merge the root with its child nodes.
e. EXTRACT-MIN simply locates the minimum as done in part a, then deletes
it as in part d.
f. This can be done by implementing the join operation, as in Problem 18-2 (b).
7

Chapter 20
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 20.1-1
To modify these structure to allow for multiple elements, instead of just
storing a bit in each of the entries, we can store the head of a linked list rep-
resenting how many elements of that value that are contained in the structure,
with a NIL value to represent having no elements of that value.
Exercise 20.1-2
All operations will remain the same, except instead of the leaves of the tree
being an array of integers, they will be an array of nodes, each of which stores
x.key in addition to whatever additional satellite data you wish.
Exercise 20.1-3
To find the successor of a given key k from a binary tree, call the procedure
SUCC(x, T.root). Note that this will return NIL if there is no entry in the tree
with a larger key.
Exercise 20.1-4
The new tree would have height k. INSERT would take O(k), MINI-
MUM, MAXIMUM, SUCCESSOR, PREDECESSOR, and DELETE would take
O(ku1/k).
Exercise 20.2-1
See the two algorithms, PROTO-vEB-MAXIMUM and PROTO-vEB-PREDECESSOR.
Exercise 20.2-2
When we delete a key, we need to check membership of all keys of that
cluster to know how to update the summary structure. There are √uof these,
and each membership takes O(lg lg u) time to check. With the recursive calls,
recurrence for running time is
1

Algorithm 1 SUCC(k,x)
if k < x.key then
if x.lef t == NIL then
return x
else
if SUCC(k, x.left) == NIL then
return x
else
return SUCC(k,x.left)
end if
end if
else
if x.right == NIL then
return NIL
else
return SUCC(k,x.right)
end if
end if
Algorithm 2 PROTO-vEB-MAXIMUM(V)
if V.u == 2 then
if V.A[1] == 1 then
return 1
else if V.A[0] == 1 then
return 0
else
return NIL
end if
else
max-cluster = PROTO-vEB-MAXIMUM(V.summary)
if max-cluster ==NIL then
return NIL
else
off set =P ROT O −vEB −MINIMUM(V.cluster[max −cluster])
return index(max −cluster, offset)
end if
end if
2

Algorithm 3 PROTO-vEB-PREDECESSOR(V,x)
if V.u==2 then
if x==1 and V.A[0] ==1 then
return 0
else
return NIL
end if
else
off set =P ROT O−vEB−P REDECESSOR(V.cluster[high(x)], low(x))
if off set 6=NIL then
return index(high(x),offest)
else
pred-cluster = PROTO-vEB-PREDECESSOR(V.summary,high(x))
if pred-cluster ==NIL then
return NIL
else
return index(succ-cluster, PROTO-vEB-
MAXIMUM(V.cluster[pred-cluster]))
end if
end if
end if
T(u) = T(√u) + O(√ulg lg u).
We make the substitution m= lg uand S(m) = T(2m). Then we apply the
Master Theorem, using case 3, to solve the recurrence. Substituting back, we
find that the runtime is T(u) = O(√ulg lg u).
Exercise 20.2-3
We would keep the same as before, but insert immediately after the else, a
check of whether n= 1. If it doesn’t continue as usual, but if it does, then we
can just immediately set the summary bit to zero, null out the pointer in the
table, and be done immediately. This has the upside that it can sometimes save
up to lg lg u. The procedure has the big downside that the number of elements
that are in the set could be as high as lg(lg(u)), in which case lg(u) many bits
are needed to store n.
Exercise 20.2-4
The array Afound in a proto van Emde Boas structure of size 2 should now
support integers, instead of just bits. All other pats of the structure will remain
the same. The integer will store the number of duplicates at that position. The
modifications to insert, delete, minimum, successor, etc... will be minor. Only
the base cases will need to be updated.
3

Algorithm 4 PROTO-vEB-DELETE(V, x)
if V.u == 2 then
V.A[x] = 0
else
PROTO-vEB-DELETE(V.cluster[high(x)], low(x))
inCluster =F alse
for i=high(x)·√uto (high(x) + 1) ·√u−1do
if PROTO-vEB-MEMBER(V.cluster[high(x)], i)then
inCluster =T rue
Break
end if
end for
if inCluster == F alse then
PROTO-vEB-DELETE(V.summary, high(x))
end if
end if
Exercise 20.2-5
The only modification necessary would be for the u=2 trees. They would
need to also include a length two array that had pointers to the corresponding
satellite data which would be populated in case the corresponding entry in A
were 1.
Exercise 20.2-6
This algorithm recursively allocates proper space and appropriately initial-
izes attributes for a proto van Emde Boas structure of size u.
Algorithm 5 Make-Proto-vEB(u)
V=allocate-node()
V.u =u
if u== 2 then
Allocate-Array A of size 2
V.A[1] = V.A[0] = 0
else
V.summary = Make-Proto-vEB(√u)
for i= 0 to √u−1do
V.cluster[i] = Make-Proto-vEB(√u)
end for
end if
4

Exercise 20.2-7
For line 9 to be executed, we would need that in the summary data, we
also had a NIL returned. This could of either happened through line 9, or 6.
Eventually though, it would need to happen in line 6, so, there must be some
number of summarizations that happened of V that caused us to get an empty
u=2 vEB. However, a summarization has an entry of one if any of the corre-
sponding entries in the data structure are one. This means that there are no
entries in V, and so, we have that Vis empty.
Exercise 20.2-8
For MEMBER the runtime recurrence is T(u) = T(u1/4) + O(1), whose so-
lution is again O(lg lg(u)). For MINIMUM, T(u) = 2T(u1/4) + O(1). Making a
substitution and applying case 1 of the master theorem, this is O(√lg u). For
SUCCESSOR, T(u)=2T(u1/4) + O(lg u). By case 3 of the master theorem,
this is O(lg u). For INSERT, T(u) = 2T(u1/4) + O(1). This is the same as
MINIMUM, which is O(√lg u). To analyze DELETE, we need to update the
recurrence to reflect the fact that DELETE depends on MEMBER. The new
recurrence is T(u) = T(u1/4) + O(u1/4lg lg u). By case 3 of the master theorem,
this is O(u1/4lg lg u).
Exercise 20.3-1
To support duplicate keys, for each u=2 vEB tree, instead of storing just a
bit in each of the entries of its array, it should store an integer representing how
many elements of that value the vEB contains.
Exercise 20.3-2
For any key which is a minimum on some vEB, we’ll need to store its satel-
lite data with the min value since the key doesn’t appear in the subtree. The
rest of the satellite data will be stored alongside the keys of the vEB trees of
size 2. Explicitly, for each non-summary vEB tree, store a pointer in addition
to min. If min is NIL, the pointer should also point to NIL. Otherwise, the
pointer should point to the satellite data associated with that minimum. In a
size 2 vEB tree, we’ll have two additional pointers, which will each point to the
minimum’s and maximum’s satellite data, or NIL if these don’t exist. In the
case where min=max, the pointers will point to the same data.
Exercise 20.3-3
We define the procedure for any uthat is a power of 2. If u= 2, then, just
slap that fact together with an array of length 2 that contains 0 in both entries.
If u= 2k>2, then, we create an empty vEB tree called Summary with
u= 2dk/2e. We also make an array called cluster of length 2dk/2ewith each
5

entry initialized to an empty vEB tree with u= 2bk/2c. Lastly, we create a min
and max element, both initialized to NIL.
Exercise 20.3-4
Suppose that xis already in Vand we call INSERT. Then we can’t satisfy
lines 1, 3, 6, or 10, so we will enter the else case on line 9 every time, causing an
infinite loop. Now suppose we call DELETE when xisn’t in V. If there is only
a single element in V, lines 1 through 3 will delete it, regardless of what element
it is. To enter the elseif of line 4, xcan’t be equal to 0 or 1 and the vEB tree
must be of size 2. In this case, we delete the max element, regardless of what
it is. Since the recursive call always puts us in this case, we always delete an
element we shouldn’t. To avoid these issue, keep and updated auxiliary array A
with uelements. Set A[i] = 0 if iis not in the tree, and 1 if it is. Since we can
perform constant time updates to this array, it won’t affect the runtime of any
of our operations. When inserting x, check first to be sure A[x] == 0. If it’s
not, simply return. If it is, set A[x] = 1 and proceed with insert as usual. When
deleting x, check if A[x] == 1. If it isn’t, simply return. If it is, set A[x]=0
and proceed with delete as usual.
Exercise 20.3-5
Similar to the analysis of (20.4), we will analyze:
T(u)≤T(u1−1/k) + T(u1/k) + O(1)
This is a good choice for analyis because for many operations we first check
the summary vEB tree, which will have size u1/k (the second term). And then
possible have to check a vEB tree somewhere in cluster, which will have size
u1−1/k(the first term). We let T(2m) = S(m), so the equation becomes
S(m)≤S(m(1 −1/k)) + S(m/k) + O(1).
If k > 2 the first term dominates, so by master theorem, we’ll have that S(m)
is O(lg(m)), this means that Twill be O(lg(lg(u))) just as in the original case
where we took squareroots.
Exercise 20.3-6
Set n=u/ lg lg u. Then performing noperations takes c(u+nlg lg u) time
for some constant c. Using the aggregate amoritzed analysis, we divide by nto
see that the amortized cost of each operations is c(lg lg u+ lg lg u) = O(lg lg u)
per operation. Thus we need n≥u/ lg lg u.
Problem 20-1
6
a. Lets look at what has to be stored for a vEB tree. Each vEB tree contains
one vEB tree of size +
√uand +
√uvEB trees of size 1
√u. It also is storing
three numbers each of order O(u), so they need Θ(lg(u)) space each. Lastly,
it needs to store +
√umany pointers to the cluster vEB trees. We’ll combine
these last two contributions which are Θ(lg(u)) and Θ( +
√u) respectively into
a single term that is Θ +
√u. This gets us the recurrence
P(u) = P(+
√u) + +
√uP (−
√u) + Θ(√u)
Then, we have that u= 22m(which follows from the assumption that √uwas
an integer), this equation becomes
P(u) = (1 + 2m)P(2m) + Θ(√u) = (1 + √u)P(√u) + Θ(√u)
as desired.
b. We recall from our solution to problem 3-6.e (it seems like so long ago now)
that given a number n, a bound on the number of times that we need to take
the squareroot of a number before it falls below 2 is lg(lg(n)). So, if we just
unroll out recurrence, we get that
P(u)≤
lg(lg(u))
Y
i=1
(u1/2i+ 1)
P(2) +
lg(lg(u))
X
i=1
Θ(u1/2i)(u1/2i+ 1)
The first product has a highest power of ucorresponding to always multi-
plying the first terms of each binomial. The power in this term is equal to
Plg(lg(u))
i=1 1
2iwhich is a partial sum of a geometric series whose sum is 1. This
means that the first term is o(u). The order of the ith term in the summation
appearing in the formula is u2/2i. In particular, for i= 1 is it O(u), and for
any i > 1, we have that 2/2i<1, so those terms will be o(u). Putting it all
together, the largest term appearing is O(u), and so, P(u) is O(u).
c. For this problem we just use the version written for normal vEB trees, with
minor modifications. That is, since there are entries in cluster that may not
exist, and summary may of not yet been initialized, just before we try to
access either, we check to see if it’s initialized. If it isn’t, we do so then.
d. As in the previous problem, we just wait until just before either of the two
things that may of not been allocated try to get used then allocate them if
need be.
e. Since the initiallizations performed only take constant time, those modifica-
tions don’t ruin the the desired runtime bound for the original algorithms
already had. So, our responses to parts c and d are O(lg(lg(n))).
f. As mentioned in the errata, this part should instead be changed to O(nlg(n))
space. When we are adding an element, we may have to add an entry to a
dynamic hash table, which means that a constant amount of extra space
7

Algorithm 6 RS-vEB-TREE-INSERT(V,x)
if V.min == N IL then
vEB-EMPTY-TREE-INSERT(V,x)
else
if x < V.min then
swap V.min with x
end if
if V.u > 2then
if V.summary == N IL then
V.summary =CREAT E −NEW −RD −vEB −T REE(+
√V.u)
end if
if lookup(V.cluster, low(x)) == N IL then
insert into V.summary with key high(x) what is returned by
CREAT E −N EW −RD −vEB −T REE(−
√V.u)
end if
if vEB−T REE −MINIMUM(lookup(V.cluster, high(x))) == NIL
then
vEB-TREE-INSERT(V.summary,high(x))
vEB-EMPTY-TREE-INSERT(lookup(V.cluster,high(x)),low(x))
else
vEB-TREE-INSERT(lookup(V.cluster,high(x)),low(x))
end if
end if
if x > V.max then
V.max =x
end if
end if
8

Algorithm 7 RS-vEB-TREE-SUCCESSOR(V,x)
if V.u == 2 then
if x== 0 and V.max == 1 then
return 1
else
return NIL
end if
else if V.min 6=NIL and x < V.min then
return V.min
else
if lookup(V.cluster, low(x)) == N IL then
insert into V.summary with key high(x) what is returned by
CREAT E −N EW −RD −vEB −T REE(−
√V.u)
end if
max-low = vEB-TREE-MAXIMUM(lookup(V.cluster,high(x)))
if max −low 6=N IL and low(x)< max −low then
returnindex(high(x), vEB −T REE −
SUCCESSOR(lookup(V.summary, high(x)), low(x)))
else
if V.summary == N IL then
V.summary =CREAT E −NEW −RD −vEB −T REE(+
√V.u)
end if
succ−cluster =vEB−T REE−SU CCESSOR(V.summary, high(x))
if succ-cluster==NIL then
return NIL
else
returnindex(succ −cluster, vEB −T REE −
MINIMUM(lookup(V.summary, succ −cluster)))
end if
end if
end if
9

would be needed. If we are adding an element to that table, we also have to
add an element to the RS-vEB tree in the summary, but the entry that we
add in the cluster will be a constant size RS-vEB tree. We can charge the cost
of that addition to the summary table to the making the minimum element
entry that we added in the cluster table. Since we are always making at least
one element be added as a new min entry somewhere, this ammortization
will mean that it is only a constant amount of time in order to store the new
entry.
g. It only takes a constant amount of time to create an empty RS-vEB tree.
This is immediate since the only dependence on u in CREATE-NEW-RS-
vEB-TREE(u) is on line 2 when V.u is initialized, but this only takes a
constant amount of time. Since nothing else in the procedure depends on u,
it must take a constant amount of time.
Problem 20-2
a) By 11.5, the perfect hash table uses O(m) space to store melements. In a
universe of size u, each element contributes lg uentries to the hash table, so
the requirement is O(nlg u). Since the linked list requires O(n), the total
space requirement is O(nlg u).
b) MINIMUM and MAXIMUM are easy. We just examine the first and last
elements of the associated doubly linked list. MEMBER can actually be
performed in O(1), since we are simply checking membership in a perfect
hash table. PREDECESSOR and SUCCESSOR are a bit more complicated.
Assume that we have a binary tree in which we store all the elements and
their prefixes. When we query the hash table for an element, we get a pointer
to that element’s location in the binary search tree, if the element is in the
tree, and NULL otherwise. Moreover, assume that every leaf node comes
with a pointer to its position in the doubly linked list. Let xbe the number
whose successor we seek. Begin by performing a binary search of the prefixes
in the hash table to find the longest hashed prefix ywhich matches a prefix
of x. This takes O(lg lg u) since we can check if any prefix is in the hash table
in O(1). Observe that ycan have at most one child in the BST, because if it
had both children then one of these would share a longer prefix with x. If the
left child is missing, have the left child pointer point to the largest labeled
leaf node in the BST which is less than y. If the right child is missing, use
its pointer to point to the successor of y. If If yis a leaf node then y=x, so
we simply follow the pointer to xin the doubly linked list, in O(1), and its
successor is the next element on the list. If yis not a leaf node, we follow its
predecessor or successor node, depending on which we need. This gives us
O(1) access to the proper element, so the total runtime is O(lg lg u). INSERT
and DELETE must take O(lg u) since we need to insert one entry into the
hash table for each of their bits and update the pointers.
10

c) The hash table has lg uentries for each of the n/ lg ugroups, so it stores a
total of nentries, making it size O(n). There are n/ lg ubinary trees of size
lg u, so they take O(n) space. Finally, the linked list takes O(n/ lg u) space.
Thus, the total space requirement is O(n).
d) For MINIMUM: Starting with the linked list, locate the minimum represen-
tative. This is O(1) since we can just look at the start of the doubly linked
list. Then use the hash table to find its corresponding binary tree in O(1).
Since this binary tree contains lg(u) elements and is balanced, its height is
lg lg u, so we can find its minimum in O(lg lg u). The procedure is similar for
MAXIMUM.
e) We start by finding the smallest representative greater than or equal to x.
To do this, store the representatives in the structure described above, with
runtimes given in parts a and b, and call SUCCESSOR(x) to find the proper
binary search tree to look in. Since n≤uwe can do this in O(lg lg u). Next
we search the binary search tree for x. Since its height is lg u, the total
runtime is O(lg lg u).
f) Again, if we can find the largest representative greater than or equal to x,
we can determine which binary tree contains the predecessor or successor of
x. To do this, just call PREDECESSOR or SUCCESSOR on xto locate the
appropriate tree in O(lg lg u). Since the tree has height lg u, we can find the
predecessor or successor in (Olg lg u).
g) Insertion and deletion into a binary tree of height lg uis Ω(lg lg u). In addi-
tion to this, we may have to update the representatives of the groups which
can only increase the running time. representatives.
h) We can relax the requirements and only impose the condition that each
group has at least 1
2lg uelements and at most 2 lg uelements. If a red-black
tree is too big, we split it in half at the median. If a red-black tree is too
small, we merge it with a neighboring tree. If this causes the merged tree to
become too large, we split it at the median. If a tree splits, we create a new
representative. If two trees merge, we delete the lost representative. Any
split or merge takes O(lg u) since we have to insert or delete an element in
the data structure storing our representatives, which by part b takes O(lg u).
However, we only split a tree after at least lg uinsertions, since the size of one
of the red-black trees needs to increase from lg uto 2 lg uand we only merge
two trees after at least (1/2) lg udeletions, because the size of the merging
tree needs to have decreased from lg uto (1/2) lg u. Thus, the amortized cost
of the merges, splits, and updates to representatives is O(1) per insertion or
deletion, so the amortized cost is O(lg lg u) as desired.
11

Chapter 21
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 21.1-1
EdgeP rocessed
initial {a} {b} {c} {d} {e} {f} {g} {h} {i} {j} {k}
(d, i){a} {b} {c} {d, i} {e} {f} {g} {h} {j} {k}
(f, k){a} {b} {c} {d, i} {e} {f, k} {g} {h} {j}
(g, i){a} {b} {c} {d, i, g} {e} {f, k} {h} {j}
(b, g){a} {b, d, i, g} {c} {e} {f, k} {h} {j}
(a, h){a, h} {b, d, i, g} {c} {e} {f, k} {j}
(i, j){a, h} {b, d, i, g, j} {c} {e} {f, k}
(d, k){a, h} {b, d, i, g, j, f, k} {c} {e}
(b, j){a, h} {b, d, i, g, j, f, k} {c} {e}
(d, f){a, h} {b, d, i, g, j, f, k} {c} {e}
(g, j){a, h} {b, d, i, g, j, f, k} {c} {e}
(a, e){a, h, e} {b, d, i, g, j, f, k} {c}
So, the connected components that we are left with are {a, h, e},{b, d, i, g, j, f, k},
and {c}.
Exercise 21.1-2
First suppose that two vertices are in the same connected component. Then
there exists a path of edges connecting them. If two vertices are connected by
a single edge, then they are put into the same set when that edge is processed.
At some point during the algorithm every edge of the path will be processed, so
all vertices on the path will be in the same set, including the endpoints. Now
suppose two vertices uand vwind up in the same set. Since every vertex starts
off in its own set, some sequence of edges in Gmust have resulted in eventually
combining the sets containing uand v. From among these, there must be a
path of edges from uto v, implying that uand vare in the same connected
component.
Exercise 21.1-3
Find set is called twice on line 4, this is run once per edge in the graph, so,
we have that find set is run 2|E|times. Since we start with |V|sets, at the end
1

only have k, and each call to UNION reduces the number of sets by one, we
have that we have to of made |V| − kcalls to UNION.
Exercise 21.2-1
The three algorithms follow the english description and are provided here.
There are alternate versions using the weighted union heuristic, suffixed with
WU.
Algorithm 1 MAKE-SET(x)
Let o be an object with three fields, next, value, and set
Let L be a linked list object with head = tail = o
o.next = NIL
o.set = L
o.value = x
return L
Algorithm 2 FIND-SET(x)
return o.set.head.value
Algorithm 3 UNION(x,y)
L1= x.set
L2 = y.set
L1.tail.next = L2.head
z = L2.head
while z.next 6=NIL do
z.set = L1
end while
L1.tail = L2.tail
return L1
Exercise 21.2-2
Originally we have 16 sets, each containing xi. In the following, we’ll replace
xiby i. After the for loop in line 3 we have:
{1,2},{3,4},{5,6},{7,8},{9,10},{11,12},{13,14},{15,16}.
After the for loop on line 5 we have
{1,2,3,4},{5,6,7,8},{9,10,11,12},{13,14,15,16}.
Line 7 results in:
2

Algorithm 4 MAKE-SET-WU(x)
L = MAKE-SET(x)
L.size = 1
return L
Algorithm 5 UNION-WU(x,y)
L1= x.set
L2 = y.set
if L1.size ≥L2.size then
L = UNION(x,y)
else
L = UNION(y,x)
end if
L.size = L1.size + L2.size
return L
{1,2,3,4,5,6,7,8},{9,10,11,12},{13,14,15,16}.
Line 8 results in:
{1,2,3,4,5,6,7,8},{9,10,11,12,13,14,15,16}.
Line 9 results in:
{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}.
FIND-SET(x2) and FIND-SET(x9) each return pointers to x1.
Exercise 21.2-3
During the proof of theorem 21.1, we concluded that the time for the n
UNION operations to run was at most O(nlg(n)). This means that each of
them took an ammortized time of at most O(lg(n)). Also, since there is only
a constant actual amount of work in performing MAKE-SET and FIND-SET
operations, and none of that ease is used to offest costs of UNION operations,
they both have O(1) runtime.
Exercise 21.2-4
We call MAKE-SET ntimes, which contributes Θ(n). In each union, the
smaller set is of size 1, so each of these takes Θ(1) time. Since we union n−1
times, the runtime is Θ(n).
Exercise 21.2-5
3
For each member of the set, we will make its first field which used to point
back to the set object point instead to the last element of the linked list. Then,
given any set, we can find its last element by going ot the head and following the
pointer that that object maintains to the last element of the linked list. This
only requires following exactly two pointers, so it takes a constant amount of
time. Some care must be taken when unioning these modified sets. Since the
set representative is the last element in the set, when we combine two linked
lists, we place the smaller of the two sets before the larger, since we need to
update their set representative pointers, unlike the original situation, where we
update the representative of the objects that are placed on to the end of the
linked list.
Exercise 21.2-6
Instead of appending the second list to the end of the first, we can imag-
ine splicing it into the first list, in between the head and the elements. Store
a pointer to the first element in S1. Then for each element xin S2, set
x.head =S1.head. When the last element of S2is reached, set its next pointer
to the first element of S1. If we always let S2play the role of the smaller set,
this works well with the weighted-union heuristic and don’t affect the asymp-
totic running time of UNION.
Exercise 21.3-1
18
24
26
35
46
21
52
39
Exercise 21.3-2
To implement FIND-SET nonrecursively, let xbe the element we call the
function on. Create a linked list Awhich contains a pointer to x. Each time we
most one element up the tree, insert a pointer to that element into A. Once the
root rhas been found, use the linked list to find each node on the path from
the root to xand update its parent to r.
Exercise 21.3-3
4

Suppose that n0= 2kis the smallest power of two less than n. To see that
this sequences of operations does take the required amount of time, we’ll first
note that after each iteration of the for loop indexed by j, we have that the
elements x1, . . . , xn0are in trees of depth i. So, after we finish the outer for
loop, we have that x1. . . xn0all lie in the same set, but are represented by a tree
of depth k∈Ω(lg(n)). Then, since we repeatedly call FIND-SET on an item
that is lg(n) away from its set representative, we have that each one takes time
lg(n). So, the last for loop alltogther takes time mlg(n).
Algorithm 6 Sequence of operations for Exercise 21.3-3
for i=1..n do
MAKE-SETxi
end for
for i= 1..k do
for j= 1..n0−2i=1by2ido
UNION(xi,xi+2j−1)
end for
end for
for i= 1..m do
FIND-SET(x1)
end for
Exercise 21.3-4
In addition to each tree, we’ll store a linked list (whose set object contains
a single tail pointer) with which keeps track of all the names of elements in the
tree. The only additional information we’ll store in each node is a pointer x.l to
that element’s position in the list. When we call MAKE-SET(x), we’ll also cre-
ate a new linked list, insert the label of xinto the list, and set x.l to a pointer
to that label. This is all done in O(1). FIND-SET will remain unchanged.
UNION(x, y) will work as usual, with the additional requirement that we union
the linked lists of xand y. Since we don’t need to update pointers to the head,
we can link up the lists in constant time, thus preserving the runtime of UNION.
Finally, PRINT-SET(x) works as follows: first, set s= FIND-SET(x). Then
print the elements in the linked list, starting with the element pointed to by
x. (This will be the first element in the list). Since the list contains the same
number of elements as the set and printing takes O(1), this operation takes
linear time in the number of set members.
Exercise 21.3-5
Clearly each MAKE-SET and LINK operation only takes time O(1), so,
supposing that n is the number of FIND-SET operations occuring after the
making and linking, we need to show that all the FIND-SET operations only
5

take time O(n). To do this, we will ammortize some of the cost of the FIND-
SET operations into the cost of the MAKE-SET operations. Imagine paying
some constant amount extra for each MAKE-SET operation. Then, when do-
ing a FIND-SET(x) operation, we have three possibilities. First, we could have
that xis the representative of its own set. In this case, it clearly only takes
constant time to run. Second, we could have that the path from x to its set’s
representative is already compressed, so it only takes a single step to find the set
representative. In this case also, the time required is constant. Lastly, we could
have that x is not the representative and it’s path has not been compressed.
Then, suppose that there are knodes between xand its representative. The
time of this find-set operation is O(k), but it also ends up compressing the paths
of knodes, so we use that extra amount that we paid during the MAKE-SET
operations for these knodes whoose paths were compressed. Any subsequent
call to find set for these nodes will take only a constant amount of time, so we
would nver try to use the work that ammortization amount twice for a given
node.
Exercise 21.4-1
The initial value of x.rank is 0, as it is initialized in line 2 of the MAKE-
SET(x) procedure. When we run LINK(x,y), whichever one has the larger rank
is placed as the parent of the other, and if there is a tie, the parent’s rank is
incremented. This means that after any LINK(y,x), the two nodes being linked
satisfy this strict inequality of ranks. Also, if we have that x6=x.p, then, we
have that xis not its own set representative, so, any linking together of sets that
would occur would not involve x, but that’s the only way for ranks to increase,
so, we have that x.rank must remain constant after that point.
Exercise 21.4-2
We’ll prove the claim by strong induction on the number of nodes. If
n= 1, then that node has rank equal to 0 = blg 1c. Now suppose that the
claim holds for 1,2, . . . , n nodes. Given n+ 1 nodes, suppose we perform a
UNION operation on two disjoint sets with aand bnodes respectively, where
a, b ≤n. Then the root of the first set has rank at most blg acand the root
of the second set has rank at most blg bc. If the ranks are unequal, then the
UNION operation preserves rank and we are done, so suppose the ranks are
equal. Then the rank of the union increases by 1, and the resulting set has rank
blg ac+ 1 ≤ blg(n+ 1)/2c+ 1 = blg(n+ 1)c.
Exercise 21.4-3
Since their value is at most blg(n)c, we can represent them using Θ(lg(lg(n)))
bits, and may need to use that many bits to represent a number that can take
that many values.
6

Exercise 21.4-4
MAKE-SET takes constant time and both FIND-SET and UNION are bounded
by the largest rank among all the sets. Exercise 21.4-2 bounds this from about
by blg nc, so the actual cost of each operation is O(lg n). Therefore the actual
cost of moperations is O(mlg n).
Exercise 21.4-5
He isn’t correct, suppose that we had that rank(x.p)> A2(rank(x)) but
that rank(x.p.p) = 1 + rank(x.p), then we would have that level(x.p) = 0, but
level(x)≥2. So, we don’t have that level(x)≤level(x.p) even though we have
that the ranks are monotonically increasing as we go up in the tree. Put another
way, even though the ranks are monotonically increasing, the rate at which they
are increasing (roughly captured by the level vales) doesn’t have to, itself be
increasing.
Exercise 21.4-6
First observe that by a change of variables, α0(2n−1) = α(n). Earlier in the
section we saw that α(n)≤3 for 0 ≤n≤2047. This means that α0(n)≤2 for
0≤n≤22046, which is larger than the estimated number of atoms in the observ-
able universe. To prove the improved bound of O(mα0(n)) on the operations, the
general structure will be essentially the same as that given in the section. First,
modify bound 21.2 by observing that Aα0(n)(x.rank)≥Aα0(n)(1) ≥lg(n+ 1) >
x.p.rank which implies level(x)≤α0(n). Next, redefine the potential replacing
α(n) by α0(n). Lemma 21.8 now goes through just as before. All subsequent
lemmas rely on these previous observations, and their proofs go through exactly
as in the section, yielding the bound.
Problem 21-1
a.
index value
1 4
2 3
3 2
4 6
5 8
6 1
b. As we run the for loop, we are picking off the smallest of the possible elements
to be removed, knowing for sure that it will be removed by the next unused
EXTRACT-MIN operation. Then, since that EXTRACT-MIN operation is
used up, we can pretend that it no longer exists, and combine the set of
things that were inserted by that segment with those inserted by the next,
7

since we know that the EXTRACT-MIN operation that had separated the
two is now used up. Since we proceed to figure out what the various extract
operations do one at a time, by the time we are done, we have figured them
all out.
c. We let each of the sets be represented by a disjoint set structure. To union
them (as on line 6) just call UNION. Checking that they exist is just a matter
of keeping track of a linked list of which ones exist(needed for line 5), initially
containing all of them, but then, when deleting the set on line 6, we delete
it from the linked list that we were maintaining. The only other interaction
with the sets that we have to worry about is on line 2, which just amounts
to a call of FIND-SET(j). Since line 2 takes ammorized time α(n) and we
call it exactly ntimes, then, since the rest of the for loop only takes constant
time, the total runtime is O(nα(n)).
Problem 21-2
a. MAKE-TREE and GRAFT are both constant time operations. FIND-
DEPTH is linear in the depth of the node. In a sequence of moperations the
maximal depth which can be achieved is m/2, so FIND-DEPTH takes at most
O(m). Thus, moperations take at most O(m2). This is achieved as follows:
Create m/3 new trees. Graft them together into a chain using m/3 calls to
GRAFT. Now call FIND-DEPTH on the deepest node m/3 times. Each call
takes time at least m/3, so the total runtime is Ω((m/3)2) = Ω(m2). Thus the
worst-case runtime of the moperations is Θ(m2).
b. Since the new set will contain only a single node, its depth must be zero
and its parent is itself. In this case, the set and its corresponding tree are in-
distinguishable.
Algorithm 7 MAKE-TREE(v)
v= Allocate-Node()
v.d = 0
v.p =v
Return v
c. In addition to returning the set object, modify FIND-SET to also return
the depth of the parent node. Update the pseudodistance of the current node
vto be v.d plus the returned pseudodistance. Since this is done recursively, the
running time is unchanged. It is still linear in the length of the find path. To
implement FIND-DEPTH, simply recurse up the tree containing v, keeping a
running total of pseudodistances.
d. To implement GRAFT we need to find v’s actual depth and add it to the
pseudodistance of the root of the tree Siwhich contains r.
8

Algorithm 8 FIND-SET(v)
if v6=v.p then
(v.p, d) = F IND −SET (v.p)
v.d =v.d +d
Return (v.p, v.d)
else
Return (v, 0)
end if
Algorithm 9 GRAFT(r,v)
(x, d1) = FIND-SET(r)
(y, d2) = FIND-SET(v)
if x.rank > y.rank then
y.p =x
x.d =x.d +d2 + y.d
else
x.p =y
x.d =x.d +d2
if x.rank == y.rank then
y.rank =y.rank + 1
end if
end if
e. The three implemented operations have the same asymptotic running
time as MAKE, FIND, and UNION for disjoint sets, so the worst-case runtime
of msuch operations, nof which are MAKE-TREE operations, is O(mα(n)).
Problem 21-3
a. Suppose that we let ≤LCA to be an ordering on the vertices so that u≤LCA v
if we run line 7 of LCA(u) before line 7 of LCA(v). Then, when we are
running line 7 of LCA(u), we immeduatle go on to the for loop on line 8.
So, while we are doing this for loop, we still haven’t called line 7 of LCA(v).
This means that v.color is white, and so, the pair {u,v}is not considered
during the run of LCA(u). However, during the for loop of LCA(v), since
line 7 of LCA(u) has already run, u.color = black. This means that we will
consider the pair {u,v}during the running of LCA(v).
It is not obvious what the ordering ≤LCA is, as it will be implementation
dependent. It depends on the order in which child vertices are iterated in
the for loop on line 3. That is, it doesn’t just depend on the graph structure.
b. We suppose that it is true prior to a given call of LCA, and show that
9

this property is preserved throughout a run of the procedure, increasing the
number of disjoint sets by one by the end of the procedure. So, supposing
that uhas depth dand there are ditems in the disjoint set datastructure
before it runs, it increases to d+1 disjoint sets on line 1. So, by the time we
get to line 4, and call LCA of a child of u, there are d+1 disjoint sets, this
is exactly the depth of the child. After line 4, there are now d+ 2 disjoint
sets, so, line 5 brings it back down to d+ 1 disjoint sets for the subsequent
times through the loop. After the loop, there are no more changes to the
number of disjoint sets, so, the algorithm terminates with d+1 disjoint sets,
as desired. Since this holds for any arbitrary run of LCA, it holds for all runs
of LCA.
c. Suppose that the pair uand vhave the least common ancestor w. Then, when
running LCA(w), u will be in the subtree rooted at one of w’s children, and v
will be in another. WLOG, suppose that the subtree containing uruns first.
So, when we are done with running that subtree, all of their ancestor values
will point to wand their colors will be black, and their ancestor values will
not change until LCA(w) returns. However, we run LCA(v) before LCA(w)
returns, so in the for loop on line 8 of LCA(v), we will be considering the
pair {u, v}, since u.color == BLACK. Since u.ancestor is still w, that is
what will be output, which is the correct answer for their LCA.
d. The time complexity of lines 1 and 2 are just constant. Then, for each
child, we have a call to the same procedure, a UNION operation which only
takes constant time, and a FIND-SET operation which can take at most
ammortized inverse Ackerman’s time. Since we check each and every thing
that is adjacent to ufor being black, we are only checking each pair in Pat
most twice in lines 8-10, among all the runs of LCA. This means that the
total runtime is O(|T|α(|T|) + |P|).
10
Chapter 22
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 22.1-1
Since it seems as though the list for the neighbors of each vertex vis just an
undecorated list, to find the length of each would take time O(out −degree(v)).
So, the total cost will be Pv∈VO(outdegree(v)) = O(|E|+|V|). Note that the
|V|showing up in the asymptotics is necessary, because it still takes a constant
amount of time to know that a list is empty. This time could be reduced to
O(|V|) if for each list in the adjacency list representation, we just also stored
its length.
To compute the in degree of each vertex, we will have to scan through all
of the adjacency lists and keep counters for how many times each vertex has
appeared. As in the previous case, the time to scan through all of the adjacency
lists takes time O(|E|+|V|).
Exercise 22.1-2
The adjacency list representation:
1:2,3
2:1,4,5
3:1,6,7
4:2
5:5
6:3
7:3.
1

The adjacency matrix representation:
0110000
1001100
1000011
0100000
0100000
0010000
0010000
.
Exercise 22.1-3
For the adjacency matrix representation, to compute the graph transpose,
we just take the matrix transpose. This means looking along every entry above
the diagonal, and swapping it with the entry that occurs below the diagonal.
This takes time O(|V|2).
For the adjacency list representation, we will maintain an initially empty
adjacency list representation of the transpose. Then, we scan through every list
in the original graph. If we are in the list corresponding to vertex vand see u
as an entry in the list, then we add an entry of vto the list in the transpose
graph corresponding to vertex u. Since this only requires a scan through all of
the lists, it only takes time O(|E|+|V|)
Exercise 22.1-4
Create an array Aof size |V|. For a list in the adjacency list corresponding
to vertex v, examine items on the list one by one. If any item is equal to v,
remove it. If vertex uappears on the list, examine A[u]. If it’s not equal to
v, set it equal to v. If it’s equal to v, remove ufrom the list. Since we have
constant time lookup in the array, the total runtime is O(V+E).
Exercise 22.1-5
From the adjacency matrix representation, if we take the square of the ma-
trix, we are left an edge between all pairs of vertices that are separated by a
path of exactly 2, so, to get the desired notion of the square of a graph, we also
just have to add in the vertices that are separated by only a single edge in G,
that is the entry u, v in the final resulting matrix should be one iff either G2[u, v]
or G[u, v] are one. Taking the square of a matrix can be done with a matrix
multiplication, which at the time of writing, can be most efficiently done by the
Coppersmith-Windograd algorithm which takes time O(|V|2.3728639). Since the
other operation for computing the final result only takes time O(|V|2), the total
runtime is O(|V|2.3728639).
If we are given an adjacency list representation, we can find the desired re-
sulting graph by first computing the transpose graph GTfrom exercise 22.1-3
in O(|V|+|E|) time. Then, our initally empty adjacency list representation of
2

G2will be added to as follows. As we scan though the list of each vertex, say
v, and see a entry going to u, then we add uto the list corresponding to v, but
also add uto the list of everything on v’s list in GT. This means that we may
take as much as O(|E||V|+|V|) time since, we have to spend potentially |V|
time as we process each edge.
Exercise 22.1-6
Start by examining position (1,1) in the adjacency matrix. When examining
position (i, j), if a 1 is encountered, examine position (i+ 1, j). If a 0 is encoun-
tered, examine position (i, j + 1). Once either ior jis equal to |V|, terminate.
I claim that if the graph contains a universal sink, then it must be at vertex
i. To see this, suppose that vertex kis a universal sink. Since kis a universal
sink, row kin the adjacency matrix is all 0’s, and column kis all 1’s except for
position (k, k) which is a 0. Thus, once row kis hit, the algorithm will continue
to increment juntil j=|V|. To be sure that row kis eventually hit, note that
once column kis reached, the algorithm will continue to increment iuntil it
reaches k. This algorithm runs in O(V) and checking whether or not iin fact
corresponds to a sink is done in O(V). Therefore the entire process takes O(V).
Exercise 22.1-7
We have two cases, one for the diagonal entries and one for the non-diagonal
entries.
The entry of [i, i] for some irepresents the sum of the in and ourt degrees of
the vertex that icorresponds to. To see this, we recall that an entry in a matrix
product is the dot product of row iin Band column iin BT. But, column i
in BTis the same as row iin B. So, we have that the entry is just row iof B
dotted with itself, that is
|E|
X
j=1
b2
ij
However, since bij only takes values in {−1,0,1}, we have that b2
ij only takes
values in {0,1}, taking zero iff bi,j is zero. So, the entry is the sum of all nonzero
entries in row iof B, Since each edge leaving iis −1 and each edge going to i
is 1, we are counting all the edges that either leave or enter i, as we wanted to
show.
Now, suppose that our entry is indexed by [i, j] where i6=j. This is the dot
product of row iin Bwith column jin BT, which is row jin B. So, the entry
is equal to
|E|
X
k=1
bi,k ·bj,k
Each term in this sum is −1 if kgoes between iand j, or 0 if it doesn’t. Since
we can’t have that two different vertices ar both on the same side of an edge,
3

no terms may ever be 1. So, the entry is just -1 if there is an edge between i
and j, and zero otherwise.
Exercise 22.1-8
The expected loopup time is O(1), but in the worst case it could take O(V).
If we first sorted vertices in each adjacency list then we could perform a binary
search so that the worst case lookup time is O(lg V), but this has the disadvan-
tage of having a much worse expected lookup time.
Exercise 22.2-1
vertex d π
1∞NIL
2 3 4
3 0 NIL
4 2 5
5 1 3
6 1 3
Exercise 22.2-2
These are the results when we examine adjacent vertices in lexicographic
order:
Vertex d π
r 4 s
s 3 w
t 1 u
u 0 NIL
v 5 r
w 2 t
x 1 u
y 1 u
Exercise 22.2-3
As mentioned in the errata, the question should state that we are to show
that a single bit suffices by removing line 18. To see why it is valid to remove
line 18, consider the possible transitions between colors that can occur. In par-
ticular, it is impossible for a white vertex to go straight to black. This is because
inorder for a vertex to be colored black, it must of been assigned to uon line
11. This means that we have to of enqueued the vertex in the queue at some
point. This can only occur on line 17, however, if we are running line 17 on a
vertex, we have to of run line 14 on it, giving it the color GRAY. Then, notice
that the only testing of colors that is done anywhere is on line 13, in which we
test whiteness. Since line 13 doesn’t care if a vertex is GRAY or BLACK, and
4

we only ever assign black to a gray vertex, we don’t affect the running of the
algorithm at all by removing line 18. Since, once we remove line 18, we ever
assign BLACK to a vertex, we can represent the color by a single bit saying
whether the vertex is WHITE or GRAY.
Exercise 22.2-4
If we use an adjacency matrix, for each vertex uwe dequeue we’ll have to
examine all vertices vto decide whether or not vis adjacent to u. This makes
the for-loop of line 12 O(V). In a connected graph we enqueue every vertex of
the graph, so the worst case runtime becomes O(V2).
Exercise 22.2-5
First, we will show that the vale dassigned to a vertex is independent of
the order that entries appear in adjacency lists. To do this, we rely on theorem
22.5 which proves correctness of BFS. In particular, that we have ν.d =δ(s, ν)
at the end of the procedure. Since δ(s, ν) is a property of the underlying graph,
no matter which representation of the graph in terms of adjacency lists that we
choose, this value will not chage. Since the dvalues are equal to this thing that
doesn’t change when we mess with the adjacency lists, it too doesn’t change
when we mess with the adjacency lists.
Now, to show that πdoes depend on the ordering of the adjacency lists, we
will be using Figure 22.3 as a guide. First, we note that in the given worked out
procedure, we have that in the adjacency list for w,tprecedes x. Also, in the
worked out procedure, we have that u.π =t. Now, suppose instead that we had
xpreceding tin the adjacency list of w. Then, it would get added to the queue
before t, which means that it would uas it’s child before we have a chance to
process the children of t. This will mean that u.π =xin this different ordering
of the adjacency list for w.
Exercise 22.2-6
Let Gbe the graph shown in the first picture, G0= (V, Eπ) be the graph
shown in the second picture, and 1 be the source vertex. Let’s see why Eπcan
never be produced by running BFS on G. Suppose that 2 preceeds 5 in the
adjacency list of 1. We’ll dequeue 2 before 5, so 3.π and 4.π must both equal 2.
However, this is not the case. Thus, 5 must have preceded 2 in the adjacency
list. However, this implies that 3.π and 4.π both equal 5, which again isn’t true.
Nonetheless, it is easily seen that the unique simple path in G0from 1 to any
vertex is a shortest path in G.
5

4
5
1
2
3
4
5
1
2
3
Exercise 22.2-7
This problem is basically just a obfuscated version of two coloring. We will
try to color the vertices of this graph of rivalries by two colors, “babyface” and
“heel”. To have that no two babyfaces and no two heels have a rivalry is the
same as saying that the coloring is proper. To two color, we perform a breadth
first search of each connected component to get the d values for each vertex.
Then, we give all the odd ones one color say “heel”, and all the even d values a
different color. We know that no other coloring will succeed where this one fails
since if we gave any other coloring, we would have that a vertex vhas the same
color as v.π since vand v.π must have different parities for their dvalues. Since
we know that there is no better coloring, we just need to check each edge to see
if this coloring is valid. If each edge works, it is possible to find a designation,
if a single edge fails, then it is not possible. Since the BFS took time O(n+r)
and the checking took time O(r), the total runtime is O(n+r).
Exercise 22.2-8
Suppose that aand bare the endpoints of the path in the tree which achieve
the diameter, and without loss of generality assume that aand bare the unique
pair which do so. Let sbe any vertex in T. I claim that the result of a single BFS
will return either aor b(or both) as the vertex whose distance from sis greatest.
To see this, suppose to the contrary that some other vertex xis shown to be
furthest from s. (Note that xcannot be on the path from ato b, otherwise we
could extend). Then we have d(s, a)< d(s, x) and d(s, b)< d(s, x). Let cdenote
the vertex on the path from ato bwhich minimizes d(s, c). Since the graph is in
fact a tree, we must have d(s, a) = d(s, c) + d(c, a) and d(s, b) = d(s, c) + d(c, b).
6

(If there were another path, we could form a cycle). Using the triangle inequality
and inequalities and equalities mentioned above we must have
d(a, b)+2d(s, c) = d(s, c) + d(c, b) + d(s, c) + d(c, a)< d(s, x) + d(s, c) + d(c, b).
I claim that d(x, b) = d(s, c) + d(s, b). It not, then by the triangle inequality
we must have a strict less-than. In other words, there is some path from xto
bwhich does not go through c. This gives the contradiction, because it implies
there is a cycle formed by concatenating these paths. Then we have
d(a, b)< d(a, b)+2d(s, c)< d(x, b).
Since it is assumed that d(a, b) is maximal among all pairs, we have a con-
tradiction. Therefore, since trees have |V| − 1 edges, we can run BFS a single
time in O(V) to obtain one of the vertices which is the endpoint of the longest
simple path contained in the graph. Running BFS again will show us where the
other one is, so we can solve the diameter problem for trees in O(V).
Exercise 22.2-9
First, the algorithm computes a minimum spanning tree of the graph. Note
that this can be done using the procedures of Chapter 23. It can also be done
by performing a breadth first search, and restricting to the edges between vand
v.π for every v. To aide in not double counting edges, fix any ordering ≤on the
vertices before hand. Then, we will construct the sequence of steps by calling
MAKE −P AT H(s) where swas the root used for the BFS.
Algorithm 1 MAKE-PATH(u)
for v adjacent to u in the original graph, but not in the tree such that u≤v
do
go to v and back to u
end for
for v adjacent to u in the tree, but not equal to u.π do
go to v
perform the path proscribed by MAKE-PATH(v)
end for
go to u.π
Exercise 22.3-1
For directed graphs:
from\to BLACK GRAY W HIT E
BLACK Allkinds Back, Cross Back, Cross
GRAY T ree, F orward, Cross T ree, F orward, Back Back, Cross
W HIT E Cross, T ree, F orward Cross, Back allkinds
For undirected graphs, note that the lower diagonal is defined by the upper
diagonal:
7
from\to BLACK GRAY W HIT E
BLACK Allkinds Allkinds Allkinds
GRAY −T ree, F orward, Back Allkinds
W HIT E − − Allkinds
Exercise 22.3-2
The following table gives the discovery time and finish time for each vetex
in the graph.
Vertex Discovered Finished
q 1 16
r 17 20
s 2 7
t 8 15
u 18 19
v 3 6
w 4 5
x 9 12
y 13 14
z 10 11
The tree edges are: (q, s),(s, v),(v, w),(q, t),(t, x),(x, z),(t, y),(r, u). The
back edges are: (w, s),(y, q),(z, x). The forward edge is: (q, w). The cross
edges are: (u, y),(r, y).
Exercise 22.3-3
As pointed out in figure 22.5, the parentheses structure of the DFS of figure
22.4 is (((())()))(()())
Exercise 22.3-4
Treat white vertices as 0 and non-white vertices as 1. Since we never check
whether or not a vertex is gray, deleting line 3 doesn’t matter. We need only
know whether a vertex is white to get the same results.
Exercise 22.3-5
a. Since we have that u.d < v.d, we know that we have first explored ubefore
v. This rules out back edges and rules out the possibility that vis on a tree
that has been explored before exploring u’s tree. Also, since we return from v
before returning from u, we know that it can’t be on a tree that was explored
after exploring u. So, This rules out it being a cross edge. Leaving us with
the only possibilities of being a tree edge or forward edge.
To show the other direction, suppose that (u, v) is a tree or forward edge. In
8

that case, since voccurs further down the tree from u, we know that we have
to explored ubefore v, this means that u.d < v.d. Also, since we have to of
finished vbefore coming back up the tree, we have that v.f < u.f . The last
inequality to show is that v.d < v.f which is trivial.
b. By similar reasoning to part a, we have that we must have v being an ancestor
of uon the DFS tree. This means that the only type of edge that could go
from u to v is a back edge.
To show the other direction, suppose that (u, v) is a back edge. This means
that we have that vis above uon the DFS tree. This is the same as the
second direction of part a where the roles of u and v are reversed. This means
that the inequalities follow for the same reasons.
c. Since we have that v.f < u.d, we know that either vis a descendant of uor
it comes on some branch that is explored before u. Similarly, since v.d < u.d,
we either have that uis a descendant of vor it comes on some branch that
gets explored before u. Putting these together, we see that it isn’t possible
for both to be descendants of each other. So, we must have that vcomes on
a branch before u, So, we have that uis a cross edge.
To See the other direction, suppose that (u, v) is a cross edge. This means
that we have explored vat some point before exploring u, otherwise, we
would have taken the edge from uto vwhen exploring u, which would make
the edge either a forward edge or a tree edge. Since we explored vfirst, and
the edge is not a back edge, we must of finished exploring vbefore starting
u, so we have the desired inequalities.
Exercise 22.3-6
By Theorem 22.10, every edge of an undirected graph is either a tree edge
or a back edge. First suppose that vis first discovered by exploring edge (u, v).
Then by definition, (u, v) is a tree edge. Moreover, (u, v) must have been dis-
covered before (v, u) because once (v, u) is explored, vis necessarily discovered.
Now suppose that visn’t first discovered by (u, v). Then it must be discovered
by (r, v) for some r6=u. If uhasn’t yet been discovered then if (u, v) is explored
first, it must be a back edge since vis an ancestor of u. If uhas been discovered
then uis an ancestor of v, so (v, u) is a back edge.
Exercise 22.3-7
See the algorithm DFS-STACK(G). Note that by a similar justification to
22.2-3, we may remove line 8 from the original DFS-VISIT algorithm without
changing the final result of the program, that is just working with the colors
white and gray.
Exercise 22.3-8
9

Algorithm 2 DFS-STACK(G)
for every u∈G.V do
u.color = WHITE
u.π = NIL
end for
time = 0
S is an empty stack
while there is a white vertex u in Gdo
S.push(u)
while S is nonempty do
v=S.pop
time++
v.d = time
for all neighbors w of v do
if w.color == WHITE then
w.color = GRAY
w.π = v
S.push(w)
end if
end for
time++
v.f = time
end while
end while
10

Consider a graph with 3 vertices u,v, and w, and with edges (w, u),(u, w),
and (w, v). Suppose that DFS first explores w, and that w’s adjecency list has
ubefore v. We next discover u. The only adjacent vertex is w, but wis already
grey, so ufinishes. Since vis not yet a descendent of uand uis finished, vcan
never be a descendent of u.
Exercise 22.3-9
Consider the Directed graph on the vertices {1,2,3}, and having the edges
(1,2),(1,3),(2,1) then there is a path from 2 to 3, however, if we start a DFS
at 1 and process 2 before 3, we will have 2.f = 3 <2=2.d which provides a
counterexample to the given conjecture.
Exercise 22.3-10
We need only update DFS-VISIT. If Gis undirected we don’t need to make
any modifications. We simply note that lines 11 through 16 will never be exe-
cuted.
Algorithm 3 DFS-VISIT-PRINT(G,u)
1: time =time + 1
2: u.d =time
3: u.color =GRAY
4: for each v∈G.Adj[u]do
5: if v.color == white then
6: Print “(u, v) is a Tree edge”
7: v.π =u
8: DFS-VISIT-PRINT(G, v)
9: else if v.color == grey then
10: Print “(u, v) is a Back edge”
11: else
12: if v.d > u.d then
13: Print “(u, v) is a Forward edge”
14: else
15: Print “(u, v) is a Cross edge”
16: end if
17: end if
18: end for
Exercise 22.3-11
Suppose that we have a directed graph on the vertices {1,2,3}and having
edges (1,2),(2,3) then, 2 has both incoming and outgoing edges. However, if we
pick our first root to be 3, that will be in it’s own DFS tree. Then, we pick our
11
second root to be 2, since the only thing it points to has already been marked
BLACK, we wont be exploring it. Then, picking the last root to be 1, we don’t
screw up the fact that 2 is along in a DFS tree despite the fact that it has both
an incoming and outgoing edge in G.
Exercise 22.3-12
The modifications work as follows: Each time the if-condition of line 8 is
satisfied in DFS-CC, we have a new root of a tree in the forest, so we update
its cc label to be a new value of k. In the recursive calls to DFS-VISIT-CC, we
always update a descendent’s connected component to agree with its ancestor’s.
Algorithm 4 DFS-CC(G)
1: for each vertex u∈G.V do
2: u.color =white
3: u.π =NIL
4: end for
5: time = 0
6: k= 1
7: for each vertex u∈G.V do
8: if u.color == white then
9: u.cc =k
10: k=k+ 1
11: DFS-VISIT-CC(G,u)
12: end if
13: end for
Algorithm 5 DFS-VISIT-CC(G,u)
1: time =time + 1
2: u.d =time
3: u.color =GRAY
4: for each v∈G.Adj[u]do
5: v.cc =u.cc
6: if v.color == white then
7: v.π =u
8: DFS-VISIT-CC(G, v)
9: end if
10: end for
11: u.color =black
12: time =time + 1
13: u.f =time
Exercise 22.3-13
12

This can be done in time O(|V||E|). To do this, first perform a topological
sort of the vertices. Then, we will contain for each vertex a list of it’s ancestors
with in degree 0. We compute these lists for each vertex in the order starting
from the earlier ones topologically. Then, if we ever have a vertex that has the
same degree 0 vertex appearing in the lists of two of its immediate parents, we
know that the graph is not singly connected. however, if at each step we have
that at each step all of the parents have disjoint sets of degree 0 vertices as
ancestors, the graph is singly connected. Since, for each vertex, the amount of
time required is bounded by the number of vertices times the in degree of the
particular vertex, the total runtime is bounded by O(|V||E|).
Exercise 22.4-1
Our start and finish times from performing the DFS are
label d f
m1 20
q2 5
t3 4
r6 19
u7 8
y9 18
v10 17
w11 14
z12 13
x15 16
n21 26
o22 25
s23 24
p27 28
And so, by reading off the entries in decreasing order of finish time, we have
the sequence p, n, o, s, m, r, y, v, x, w, z, u, q, t.
Exercise 22.4-2
The algorithm works as follows. The attribute u.paths of node utells the
number of simple paths from uto v, where we assume that vis fixed throughout
the entire process. To count the number of paths, we can sum the number of
paths which leave from each of u’s neighbors. Since we have no cycles, we will
never risk adding a partially completed number of paths. Moreover, we can
never consider the same edge twice amongst the recursive calls. Therefore, the
toal number of executions of the for-loop over all recursive calls is O(V+E).
Calling SIMPLE-PATHS(s, t) yields the desired result.
13

Algorithm 6 SIMPLE-PATHS(u,v)
1: if u== vthen
2: Return 1
3: else if u.paths 6=N IL then
4: Return u.paths
5: else
6: for each w∈Adj[u]do
7: u.paths =u.paths+ SIMPLE-PATHS(w, v)
8: end for
9: Return u.paths
10: end if
Exercise 22.4-3
We can’t just use a depth first search, since that takes time that could be
worst case linear in |E|. However we will take great inspiration from DFS, and
just terminate early if we end up seeing an edge that goes back to a visited ver-
tex. Then, we should only have to spend a constant amount of time processing
each vertex. Suppose we have an acyclic graph, then this algorithm is the usual
DFS, however, since it is a forest, we have |E|≤|V| − 1 with equality in the
case that it is connected. So, in this case, the runtime of O(|E|+|V|)O(|V|).
Now, suppose that the procedure stopped early, this is because it found some
edge coming from the currently considered vertex that goes to a vertex that
has aleady been considered. Since all of the edges considered up to this point
didn’t do that, we know that they formed a forest. So, the number of edges
considered is at most the number of vertices considered, which is O(|V|). So,
the total runtime is O(|V|).
Exercise 22.4-4
This is not true. Consider the graph Gconsisting of vertices a, b, c, and d.
Let the edges be (a, b),(b, c),(a, d),(d, c),and (c, a). Suppose that we start the
DFS of TOPOLOGICAL-SORT at vertex c. Assuming that bappears before
din the adjacency list of a, the order, from latest to earliest, of finish times is
c, a, d, b. The “bad” edges in this case are (b, c) and (d, c). However, if we had
instead ordered them by a, b, d, c then the only bad edges would be (c, a). Thus
TOPOLOGICAL-SORT doesn’t always minimizes the number of “bad” edges.
Exercise 22.4-5
Consider having a list for each potential in degree that may occur. We
will also make a pointer from each vertex to the list that contains it. The
initial construction of this can be done in time O(|V|+|E|) because it only
requires computing the in degree of each vertex, which can be done in time
14

O(|V|+|E|) (see problem 22.1-3). Once we have constructed this sequence of
lists, we repeatedly extract any element from the list corresponding to having in
degree zero. We spit this out as the next element in the topological sort. Then,
for each of the children cof this extracted vertex, we remove it from the list that
contains it and insert it into the list of in degree one less. Since a deletion and an
insertion in a doubly linked list can be done in constant time, and we only have
to do this for each child of each vertex, it only has to be done |E|many times.
Since at each step, we are outputting some element of in degree zero with respect
to all the vertices that hadn’t yet been output, we have successfully output a
topological sort, and the total runtime is just O(|E|+|V|). We also know that
we can always have that there is some element to extract from the list of in
degree 0, because otherwise we would have a cycle somewhere in the graph. To
see this, just pick any vertex and traverse edges backwards. You can keep doing
this indefinitely because no vertex has in degree zero. However, there are only
finitely many vertices, so at some point you would need to find a repeat, which
would mean that you have a cycle.
If the graph was not acyclic to begin with, then we will have the problem of
having an empty list of vertices of in degree zero at some point. That is, if the
vertices left lie on a cycle, then none of them will have in degree zero.
Exercise 22.5-1
It can either stay the same or decrease. To see that it is possible to stay
the same, just suppose you add some edge to a cycle. To see that it is possible
to decrease, suppose that your original graph is on three vertices, and is just
a path passing through all of them, and the edge added completes this path
to a cycle. To see that it cannot increase, notice that adding an edge cannot
remove any path that existed before. So, if uand vare in the same connected
component in the original graph, then there are a path from one to the other,
in both directions. Adding an edge wont disturb these two paths, so we know
that uand vwill still be in the same SCC in the graph after adding the edge.
Since no components can be split apart, this means that the number of them
cannot increase since they form a partition of the set of vertices.
Exercise 22.5-2
The finishing times of each vertex were computed in exercise 22.3-2. The
forest consists of 5 trees, each of which is a chain. We’ll list the vertices of each
tree in order from root to leaf: r,u,q−y−t,x−z, and s−w−v.
Exercise 22.5-3
Professor Bacon’s suggestion doesn’t work out. As an example, suppose that
our graph is on the three vertices {1,2,3}and consists of the edges (2,1),(2,3),(3,2).
Then, we should end up with {2,3}and {1}as our SCC’s. However, a possible
DFS starting at 2 could explore 3 before 1, this would mean that the finish
15

time of 3 is lower than of 1 and 2. This means that when we first perform the
DFS starting at 3. However, a DFS starting at 3 will be able to reach all other
vertices. This means that the algorithm would return that the entire graph is a
single SCC, even though this is clearly not the case since there is neither a path
from 1 to 2 of from 1 to 3.
Exercise 22.5-4
First observe that Cis a strongly connected component of Gif and only if
it is a strongly connected component of GT. Thus the vertex sets of GSCC and
(GT)SCC are the same, which implies the vertex sets of ((GT)SCC )Tand GSCC
are the same. It suffices to show that their edge sets are the same. Suppose
(vi, vj) is an edge in ((GT)SCC )T. Then (vj, vi) is an edge in (GT)SCC . Thus
there exist x∈Cjand y∈Cisuch that (x, y) is an edge of GT, which implies
(y, x) is an edge of G. Since components are preserved, this means that (vi, vj)
is an edge in GSCC . For the opposite implication we simply note that for any
graph Gwe have (GT)T=G.
Exercise 22.5-5
Given the procedure given in the section, we can compute the set of vertices
in each of the strongly connected components. For each vertex, we will give it an
entry SCC, so that v.SCC denotes the strongly connected component (vertex
in the component graph) that v belongs to. Then, for each edge (u, v) in the
original graph, we add an edge from u.SCC to v.SCC if one does not already
exist. This whole process only takes a time of O(|V|+|E|). This is because the
procedure from this section only takes that much time. Then, from that point,
we just need a constant amount of work checking the existence of an edge in
the component graph, and adding one if need be.
Exercise 22.5-6
By Exercise 22.5-5 we can compute the component graph in O(V+E) time,
and we may as well label each node with its component as we go (see exercise
22.3-12 for the specifics), as well as creating a list for each component which
contains the vertices in that component by forming an array Asuch that A[i]
contains a list of the vertices in the ith connected component. Then run DFS
again, and for each edge encountered, check whether or not it connects two
different components. If it doesn’t, delete it. If it does, determine whether it is
the first edge connecting them. If not, delete it. This can be done in constant
time per edge since we can store the component edge information in a kby k
matrix, where kis the number of connected components. The runtime of this
is thus O(V+E). Now the only edges we have are a minimal number which
connect distinct connected components. The last step is place edges within the
connected compoenents in a minimal way. The fewest edges which can be used
to create a connected component with nvertices is n, and this is done with a
16

cycle. For each connected component, let v1, v2, . . . , vkbe the vertices in that
component. We find these by using the array Acreated earlier. Add in the
edges (v1, v2),(v2, v3),...,(vk, v1). This is linear in the number of vertices, so
the total runtime is O(V+E).
Exercise 22.5-7
First compute the component graph as in 22.5-5. Then, in order to have
that every vertex either has a path to or from every other vertex, we need
that this component graph also has this property. Since this is acyclic, we can
perform a topological sort on it. For this to be the case, we want that there
is a single path through this dag that hits every single vertex. This can only
happen in the DAG if each vertex has an edge going to the vertex that appears
next in the topological ordering. See the algorithm IS-SEMI-CONNECTED(G).
Algorithm 7 IS-SEMI-CONNECTED(G)
Compute the component graph of G, call it G0
Perform a topological sort on G0to get the ordering of its vertices
v1, v2, . . . , vk.
for i=1..k-1 do
if there is no edge from vito vi+1 then
return FALSE
end if
end for
return TRUE
Problem 22-1
a) 1. If we found a back edge, this means that there are two vertices, one a
descendant of the other, but there is already a path from the ancestor to
the child that doesn’t involve moving up the tree. This is a contradiction
since the only children in the bfs tree are those that are a single edge
away, which means there cannot be any other paths to that child because
that would make it more than a single edge away. To see that there are
no forward edges, We do a similar procedure. A forward edge would mean
that from a given vertex we notice it has a child that has already been
processed, but this cannot happen because all children are only one edge
away, and for it to of already been processed, it would need to have gone
through some other vertex first.
2. An edge is placed on the list to be processed if it goes to a vertex that has
not yet been considered. This means that the path from that vertex to
the root must be at least the distance from the current vertex plus 1. It
is also at most that since we can just take the path that consists of going
to the current vertex and taking its path to the root.
17

3. We know that a cross edge cannot be going to a depth more than one less,
otherwise it would be used as a tree edge when we were processing that
earlier element. It also cannot be going to a vertex of depth more than
one more, because we wouldn’t of already processed a vertex that was
that much further away from the root. Since the depths of the vertices in
the cross edge cannot be more than one apart, the conclusion follows by
possibly interchanging the roles of uand v, which we can do because the
edges are unordered.
b) 1. To have a forward edge, we would need to have already processed a vertex
using more than one edge, even though there is a path to it using a single
edge. Since breadth first search always considers shorter paths first, this
is not possible.
2. Suppose that (u, v) is a tree edge. Then, this means that there is a path
from the root to vof length u.d + 1 by just appending (u, v) on to the
path from the root to u. To see that there is no shorter path, we just
note that we would of processed vsooner, and so wouldn’t currently have
a tree edge if there were.
3. To see this, all we need to do is note that there is some path from the root
to vof length u.d + 1 obtained by appending (u, v) to v.d. Since there is a
path of that length, it serves as an upper bound on the minimum length
of all such paths from the root to v.
4. It is trivial that 0 ≤v.d, since it is impossible to have a path from the
root to vof negative length. The more interesting inequality is v.d ≤u.d.
We know that there is some path from vto u, consisting of tree edges,
this is the defining property of (u, v) being a back edge. This means that
is v, v1, v2, . . . , vk, u is this path (it is unique because the tree edges form
a tree). Then, we have that u.d =vk.d+1 = vk−1.d+2 = · · · =v1.d +k=
v.d +k+ 1. So, we have that u.d > v.d.
In fact, we just showed that we have the stronger conclusion, that 0 ≤
v.d < u.d.
Problem 22-2
a. First suppose the root rof Gπis an articulation point. Then the removal of
rfrom Gwould cause the graph to disconnect, so rhas at least 2 children
in G. If rhas only one child vin Gπthen it must be the case that there
is a path from vto each of r’s other children. Since removing rdisconnects
the graph, there must exist vertices uand wsuch that the only paths from
uto wcontain r. To reach rfrom u, the path must first reach one of r’s
children. This child is connect to vvia a path which doesn’t contain r. To
reach w, the path must also leave rthrough one of its children, which is also
reachable by v. This implies that there is a path from uto wwhich doesn’t
contain r, a contradiction.
18

Now suppose rhas at least two children uand vin Gπ. Then there is no
path from uto vin Gwhich doesn’t go through r, since otherwise uwould
be an ancestor of v. Thus, removing rdisconnects the component containing
uand the component containing v, so ris an articulation point.
b. Suppose that vis a nonroot vertex of Gπand that vhas a child ssuch that
neither snor any of s’s descendents have back edges to a proper ancestor
of v. Let rbe an ancestor of v, and remove vfrom G. Since we are in the
undirected case, the only edges in the graph are tree edges or back edges,
which means that every edge incident with stakes us to a descendent of s,
and no descendents have back edges, so at no point can we move up the
tree by taking edges. Therefore ris unreachable from s, so the graph is
disconnected and vis an articulation point.
Now suppose that for every child of vthere exists a descendent of that child
which has a back edge to a proper ancestor of v. Remove vfrom G. Every
subtree of vis a connected component. Within a given subtree, find the
vertex which has a back edge to a proper ancestor of v. Since the set Tof
vertices which aren’t descendents of vform a connected component, we have
that every subtree of vis connected to T. Thus, the graph remains connected
after the deletion of vso vis not an articulation point.
c. Since vis discovered before all of its descendants, the only back edges which
could affect v.low are ones which go from a descendant of vto a proper an-
cestor of v. If we know u.low for every child uof v, then we can compute
v.low easily since all the information is coded in its descendents. Thus, we
can write the algorithm recursively: If vis a leaf in Gπthen v.low is the
minimum of v.d and w.d where (v, w) is a back edge. If vis not a leaf, vis
the minimum of v.d,w.d where wis a back edge, and u.low, where uis a
child of v. Computing v.low for a vertex is linear in its degree. The sum of
the vertices’ degrees gives twice the number of edges, so the total runtime is
O(E).
d. First apply the algorithm of part (c) in O(E) to compute v.low for all v∈V.
If v.low =v.d if and only if no descendent of vhas a back edge to a proper
ancestor of v, if and only if vis not an articulation point. Thus, we need
only check v.low versus v.d to decide in constant time whether or not vis an
articulation point, so the runtime is O(E).
e. An edge (u, v) lies on a simple cycle if and only if there exists at least one
path from uto vwhich doesn’t contain the edge (u, v), if and only if remov-
ing (u, v) doesn’t disconnect the graph, if and only if (u, v) is not a bridge.
19

f. A edge (u, v) lies on a simple cycle in an undirected graph if and only if
either both of its endpoints are articulation points, or one of its endpoints
is an articulation point and the other is a vertex of degree 1. Since we can
compute all articulation points in O(E) and we can decide whether or not a
vertex has degree 1 in constant time, we can run the algorithm in part dand
then decide whether each edge is a bridge in constant time, so we can find
all bridges inO(E) time.
g. It is clear that every nonbridge edge is in some biconnected component, so
we need to show that if C1and C2are distinct biconnected components,
then they contain no common edges. Suppose to the contrary that (u, v)
is in both C1and C2. Let (a, b) be any edge in C1and (c, d) be any edge
in C2. Then (a, b) lies on a simple cycle with (u, v), consisting of the path
a, b, p1, . . . , pk, u, v, pk+1, . . . , pn, a. Similarly, (c, d) lies on a simple cycle with
(u, v) consisting of the path c, d, q1, . . . , qm, u, v, qm+1, . . . , ql, c. This means
a, b, p1, . . . , pk, u, qm, . . . , q1, d, c, ql, . . . , qm+1, v, pk+1 , . . . , pn, a is a simple cy-
cle containing (a, b) and (c, d), a contradiction. Thus, the biconnected com-
ponents form a partition.
h. Locate all bridge edges in O(E) time using the algorithm described in part f.
Remove each bridge from E. The biconnected components are now simply
the edges in the connected components. Assuming this has been done, run
the following algorithm, which clearly runs in O(E) where Eis the number
of edges originally in G.
Algorithm 8 BCC(G)
1: for each vertex u∈G.V do
2: u.color =white
3: end for
4: k= 1
5: for each vertex u∈G.V do
6: if u.color == white then
7: k=k+ 1
8: VISIT-BCC(G,u, k)
9: end if
10: end for
Problem 22-3
a. First, we’ll show that it is necessary to have in degree equal out degree for
each vertex. Suppose that there was some vertex vfor which the two were
not equal, suppose wlog that in-degree - out-degree = a ¿ 0. Note that we
20

Algorithm 9 VISIT-BCC(G,u,k)
1: u.color =GRAY
2: for each v∈G.Adj[u]do
3: (u, v).bcc =k
4: if v.color == white then
5: VISIT-BCC(G, v, k)
6: end if
7: end for
may assume that in degree is greater because otherwise we would just look
at the transpose graph in which we traverse the cycle backwards. If vis the
start of the cycle as it is listed, just shift the starting and ending vertex to
any other one on the cycle. Then, in whatever cycle we take going though
v, we must pass through vsome number of times, in particular, after we
pass through it atimes, the number of unused edges coming out of vis zero,
however, there are still unused edges goin in that we need to use. This means
that there is no hope of using those while still being a tour, becase we would
never be able to escape vand get back to the vertex where the tour started.
Now, we show that it is sufficient to have the in degree and out degree equal
for every vertex. To do this, we will generalize the problem slightly so that
it is more amenable to an inductive approach. That is, we will show that
for every graph Gthat has two vertices vand uso that all the vertices have
the same in and out degree except that the indegree is one greater for uand
the out degree is one greater for v, then there is an Euler path from vto u.
This clearly lines up with the original statement if we pick u=vto be any
vertex in the graph. We now perform induction on the number of edges. If
there is only a single edge, then taking just that edge is an Euler tour. Then,
suppose that we start at v and take any edge coming out of it. Consider the
graph that is obtained from removing that edge, it inductively contains an
Euler tour that we can just post-pend to the edge that we took to get out of v.
b. To actually get the Euler circuit, we can just arbitrarily walk any way that
we want so long as we don’t repeat an edge, we will necessarily end up with
a valid Euler tour. This is implemented in the following algorithm, EULER-
TOUR(G) which takes time O(|E|). It has this runtime because the for loop
will get run for every edge, and takes a constant amount of time. Also, the
process of initializing each edge’s color will take time proportional to the
number of edges.
Problem 22-4
Begin by locating the element vof minimal label. We would like to make
u.min =v.label for all usuch that u v. Equivalently, this is the set of ver-
21

Algorithm 10 EULER-TOUR(G)
color all edges white
let (v, u) be any edge
let L be a list containing just v.
while there is some white edge (v, w) coming out of vdo
color (v,w) black
v = w
append vto L
end while
tices uwhich are reachable from vin GT. We can implement the algorithm as
follows, assuming that u.min is initially set equal to N IL for all vertices u∈V,
and simply call the algorithm on GT.
Algorithm 11 REACHABILITY(G)
1: Use counting sort to sort the vertices by label from smallest to largest
2: for each vertex u∈Vdo
3: if u.min == NIL then
4: REACHABILITY-VISIT(u, u.label)
5: end if
6: end for
Algorithm 12 REACHABILITY-VISIT(u, k)
1: u.min =k
2: for v∈G.Adj[u]do
3: if v.min == NIL then
4: REACHABILITY-VISIT(v, k)
5: end if
6: end for
22
Chapter 23
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 23.1-1
Suppose that Ais an empty set of edges. Then, make any cut that has (u, v)
crossing it. Then, since that edge is of minimal weight, we have that (u, v) is
a light edge of that cut, and so it is safe to add. Since we add it, then, once
we finish constructing the tree, we have that (u, v) is contained in a minimum
spanning tree.
Exercise 23.1-2
Let Gbe the graph with 4 vertices: u, v, w, z. Let the edges of the graph be
(u, v),(u, w),(w, z) with weights 3, 1, and 2 respectively. Suppose Ais the set
{(u, w)}. Let S=A. Then Sclearly respects A. Since Gis a tree, its minimum
spanning tree is itself, so Ais trivially a subset of a minimum spanning tree.
Moreover, every edge is safe. In particular, (u, v) is safe but not a light edge for
the cut. Therefore Professor Sabatier’s conjecture is false.
Exercise 23.1-3
Let T0and T1be the two trees that are obtained by removing edge (u, v)
from a MST. Suppose that V0and V1are the vertices of T0and T1respectively.
Consider the cut which separates V0from V1. Suppose to a contradiction that
there is some edge that has weight less than that of (u, v) in this cut. Then, we
could construct a minimum spanning tree of the whole graph by adding that
edge to T1∪T0. This would result in a minimum spanning tree that has weight
less than the original minimum spanning tree that contained (u, v).
Exercise 23.1-4
Let Gbe a graph on 3 vertices, each connected to the other 2 by an edge,
and such that each edge has weight 1. Since every edge has the same weight,
every edge is a light edge for a cut which it spans. However, if we take all edges
we get a cycle.
1

Exercise 23.1-5
Let Abe any cut that causes some vertices in the cycle on once side of the
cut, and some vertices in the cycle on the other. For any of these cuts, we know
that the edge eis not a light edge for this cut. Since all the other cuts wont
have the edge ecrossing it, we won’t have that the edge is light for any of those
cuts either. This means that we have that eis not safe.
Exercise 23.1-6
Suppose that for every cut of the graph there is a unique light edge crossing
the cut, but that the graph has 2 spanning trees Tand T0. Since Tand T0are
distinct, there must exist edges (u, v) and (x, y) such that (u, v) is in Tbut not
T0and (x, y) is in T0but not T. Let S={u, x}. There is a unique light edge
which spans this cut. Without loss of generality, suppose that it is not (u, v).
Then we can replace (u, v) by this edge in Tto obtain a spanning tree of strictly
smaller weight, a contradiction. Thus the spanning tree is unique.
For a counter example to the converse, let G= (V, E) where V={x, y, z}
and E={(x, y),(y, z),(x, z)}with weights 1, 2, and 1 respectively. The unique
minimum spanning tree consists of the two edges of weight 1, however the cut
where S={x}doesn’t have a unique light edge which crosses it, since both of
them have weight 1.
Exercise 23.1-7
First, we show that the subset of edges of minimum total weight that con-
nects all the vertices is a tree. To see this, suppose not, that it had a cycle.
This would mean that removing any of the edges in this cycle would mean that
the remaining edges would still connect all the vertices, but would have a total
weight that’s less by the weight of the edge that was removed. This would con-
tradict the minimality of the total weight of the subset of vertices. Since the
subset of edges forms a tree, and has minimal total weight, it must also be a
minimum spanning tree.
To see that this conclusion is not true if we allow negative edge weights, we
provide a construction. Consider the graph K3with all edge weights equal to
−1. The only minimum weight set of edges that connects the graph has total
weight −3, and consists of all the edges. This is clearly not a MST because it is
not a tree, which can be easily seen because it has one more edge than a tree on
three vertices should have. Any MST of this weighted graph must have weight
that is at least -2.
Exercise 23.1-8
Suppose that L0is another sorted list of edge weights of a minimum span-
ning tree. If L06=L, there must be a first edge (u, v) in Tor T0which is of
smaller weight than the corresponding edge (x, y) in the other set. Without
2

loss of generality, assume (u, v) is in T. Let Cbe the graph obtained by adding
(u, v) to L0. Then we must have introduced a cycle. If there exists an edge on
that cycle which is of larger weight than (u, v), we can remove it to obtain a
tree C0of weight strictly smaller than the weight of T0, contradicting the fact
that T0is a minimum spanning tree. Thus, every edge on the cycle must be of
lesser or equal weight than (u, v). Suppose that every edge is of strictly smaller
weight. Remove (u, v) from Tto disconnect it into two components. There
must exist some edge besides (u, v) on the cycle which would connect these, and
since it has smaller weight we can use that edge instead to create a spanning
tree with less weight than T, a contradiction. Thus, some edge on the cycle has
the same weight as (u, v). Replace that edge by (u, v). The corresponding lists
Land L0remain unchanged since we have swapped out an edge of equal weight,
but the number of edges which Tand T0have in common has increased by 1.
If we continue in this way, eventually they must have every edge in common,
contradicting the fact that their edge weights differ somewhere. Therefore all
minimum spanning trees have the same sorted list of edge weights.
Exercise 23.1-9
Suppose that there was some cheaper spanning tree than T0. That is, we
have that there is some T00 so that w(T00 )< w(T0). Then, let Sbe the edges
in Tbut not in T0. We can then construct a minimum spanning tree of Gby
considering S∪T00 . This is a spanning tree since S∪T0is, and T00 makes
all the vertices in V0connected just like T0does. However, we have that
w(S∪T00 ) = w(S) + w(T00 )< w(S) + w(T0) = w(S∪T0) = w(T). This
means that we just found a spanning tree that has a lower total weight than a
minimum spanning tree. This is a contradiction, and so our assumption that
there was a spanning tree of V0cheaper than T0must be false.
Exercise 23.1-10
Suppose that Tis no longer a minimum spanning tree for Gwith edge
weights given by w0. Let T0be a minimum spanning tree for this graph. Then
we have we have w0(T0)< w(T)−k. Since the edge (x, y) may or may not be
in T0we have w(T0)≤w0(T0) + k < w(T), contradicting the fact that Twas
minimal under the weight function w.
Exercise 23.1-11
If we were to add in this newly decreased edge to the given tree, we would
be creating a cycle. Then, if we were to remove any one of the edges along this
cycle, we would still have a spanning tree. This means that we look at all the
weights along this cycle formed by adding in the decreased edge, and remove
the edge in the cycle of maximum weight. This does exactly what we want since
we could only possibly want to add in the single decreased edge, and then, from
there we change the graph back to a tree in the way that makes its total weight
3

minimized.
Exercise 23.2-1
Suppose that we wanted to pick Tas our minimum spanning tree. Then, to
obtain this tree with Kruskal’s algorithm, we will order the edges first by their
weight, but then will resolve ties in edge weights by picking an edge first if it is
contained in the minimum spanning tree, and treating all the edges that aren’t
in Tas being slightly larger, even though they have the same actual weight.
With this ordering, we will still be finding a tree of the same weight as all the
minimum spanning trees w(T). However, since we prioritize the edges in T, we
have that we will pick them over any other edges that may be in other minimum
spanning trees.
Exercise 23.2-2
At each step of the algorithm we will add an edge from a vertex in the tree
created so far to a vertex not in the tree, such that this edge has minimum
weight. Thus, it will be useful to know, for each vertex not in the tree, the edge
from that vertex to some vertex in the tree of minimal weight. We will store
this information in an array A, where A[u] = (v, w) if wis the weight of (u, v)
and is minimal among the weights of edges from uto some vertex vin the tree
built so far. We’ll use A[u].1 to access vand A[u].2 to access w.
Algorithm 1 PRIM-ADJ(G,w,r)
Initialize Aso that every entry is (NIL, ∞)
T={r}
for i= 1 to Vdo
if Adj[r, i]6= 0 then
A[i] = (r, w(r, i))
end if
end for
for each u∈V−Tdo
k= miniA[i].2
T=T∪ {k}
k.π =A[k].1
for i= 1 to Vdo
if Adj[k, i]6= 0 and Adj[k, i]< A[i].2then
A[i] = (k, Adj[k, i])
end if
end for
end for
Exercise 23.2-3
4

Prim’s algorithm implemented with a Binary heap has runtime O((V+
E) lg(V)), which in the sparse case, is just O(Vlg(V)). The implementation
with Fibonacci heaps is O(E+Vlg(V)) = O(V+Vlg(V)) = O(Vlg(V)). So,
in the sparse case, the two algorithms have the same asymptotic runtimes.
In the dense case, we have that the binary heap implementation has runtime
O((V+E) lg(V)) = O((V+V2) lg(V)) = O(V2lg(V)). The Fibonacci heap
implementation however has a runtime of O(E+Vlg(V)) = O(V2+Vlg(V)) =
O(V2). So, in the dense case, we have that the Fibonacci heap implementation
is asymptotically faster.
The Fibonacci heap implementation will be asymptotically faster so long
as E=ω(V). Suppose that we have some function that grows more quickly
than linear, say f, and E=f(V). The binary heap implementation will have
runtime O((V+E) lg(V)) = O((V+f(V)) lg(V)) = O(f(V) lg(V)). However,
we have that the runtime of the Fibonacci heap implementation will have run-
time O(E+Vlg(V)) = O(f(V) + Vlg(V)). This runtime is either O(f(V)) or
O(Vlg(V)) depending on if f(V) grows more or less quickly than Vlg(V) re-
spectively. In either case, we have that the runtime is faster than O(f(V) lg(V)).
Exercise 23.2-4
If the edge weights are integers in the range from 1 to |V|, we can make
Kruskal’s algorithm run in O(Eα(V)) time by using counting sort to sort the
edges by weight in linear time. I would take the same approach if the edge
weights were integers bounded by a constant, since the runtime is dominated by
the task of deciding whether an edge joins disjoint forests, which is independent
of edge weights.
Exercise 23.2-5
If there the edge weights are all in the range 1,...,|V|, then, we can imagine
adding the edges to an array of lists, where the edges of weight igo into the list
in index iin the array. Then, to decrease an element, we just remove it from the
list currently containing it(constant time) and add it to the list corresponding
to its new value(also constant time). To extract the minimum wight edge, we
maintain a linked list among all the indices that contain non-empty lists, which
can also be maintained with only a constant amount of extra work. Since all of
these operations can be done in constant time, we have a total runtime O(E+V).
If the edge weights all lie in some bounded universe, suppose in the range
1 to W. Then, we can just vEB tree structure given in chapter 20 to have the
two required operations performed in time O(lg(lg(W))), which means that the
total runtime could be made O((V+E) lg(lg(W))).
Exercise 23.2-6
For input drawn from a uniform distribution I would use bucket sort with
5

Kruskal’s algorithm, for expected linear time sorting of edges by weight. This
would achieve expected runtime O(Eα(V)).
Exercise 23.2-7
We first add all the edges to the new vertex. Then, we preform a DFS rooted
at that vertex. As we go down, we keep track of the largest weight edge seen so
far since each vertex above us in the DFS. We know from exercise 23.3-6 that in
a directed graph, we don’t need to consider cross or forward edges. Every cycle
that we detect will then be formed by a back edge. So, we just remove the edge
of greatest weight seen since we were at the vertex that the back edge is going
to. Then, we’ll keep going until we’ve removed one less than the degree of the
vertex we added many edges. This will end up being linear time since we can
reuse part of the DFS that we had already computed before detecting each cycle.
Exercise 23.2-8
Professor Borden is mistaken. Consider the graph with 4 vertices: a, b, c,
and d. Let the edges be (a, b),(b, c),(c, d),(d, a) with weights 1, 5, 1, and 5
respectively. Let V1={a, d}and V2={b, c}. Then there is only one edge
incident on each of these, so the trees we must take on V1and V2consist of
precisely the edges (a, d) and (b, c), for a total weight of 10. With the addition
of the weight 1 edge that connects them, we get weight 11. However, an MST
would use the two weight 1 edges and only one of the weight 5 edges, for a total
weight of 7.
Problem 23-1
a. To see that the second best minimum spanning tree need not be unique, we
consider the following example graph on four vertices. Suppose the vertices
are {a, b, c, d}, and the edge weights are as follows:
a b c d
a−143
b1−5 2
c4 5 −6
d3 2 6 −
Then, the minimum spanning tree has weight 7, but there are two spanning
trees of the second best weight, 8.
b. We are trying to show that there is a single edge swap that can demote our
minimum spanning tree to a second best minimum spanning tree.
In obtaining the second best minimum spanning tree, there must be some cut
of a single vertex away from the rest for which the edge that is added is not
light, otherwise, we would find the minimum spanning tree, not the second
best minimum spanning tree. Call the edge that is selected for that cut for
6

the second best minimum spanning tree (x, y). Now, consider the same cut,
except look at the edge that was selected when obtaining T, call it (u, v).
Then, we have that if consider T− {(u, v)}∪{(x, y)}, it will be a second
best minimum spanning tree. This is because if the second best minimum
spanning tree also selected a non-light edge for another cut, it would end up
more expensive than all the minimum spanning trees. This means that we
need for every cut other than the one that the selected edge was light. This
means that the choices all align with what the minimum spanning tree was.
c. We give here a dynamic programming solution. Suppose that we want to
find it for (u, v). First, we will identify the vertex xthat occurs immediately
after uon the simple path from uto v. We will then make max[u, v] equal to
the max of w((u, x)) and max[w, v].Lastly, we just consider the case that u
and vare adjacent, in which case the maximum weight edge is just the single
edge between the two. If we can find xin constant time, then we will have
the whole dynamic program running in time O(V2), since that’s the size of
the table that’s being built up.
To find xin constant time, we preprocess the tree. We first pick an arbitrary
root. Then, we do the preprocessing for Tarjan’s off-line least common an-
cestors algorithm(See problem 21-3). This takes time just a little more than
linear, O(|V|α(|V|)). Once we’ve computed all the least common ancestors,
we can just look up that result at some point later in constant time. Then,
to find the wthat we should pick, we first see if u=LCA(u, v) if it does
not, then we just pick the parent of uin the tree. If it does, then we flip the
question on its head and try to compute max[v, u], we are guaranteed to not
have this situation of v=LCA(v, u) because we know that uis an ancestor
of v.
d. We provide here an algorithm that takes time O(V2) and leave open if there
exists a linear time solution, that is a O(E+V) time solution. First, we
find a minimum spanning tree in time O(E+Vlg(V)), which is in O(V2).
Then, using the algorithm from part c, we find the double array max. Then,
we take a running minimum over all pairs of vertices u, v, of the value of
w(u, v)−max[u, v]. If there is no edge between u and v, we think of the weight
being infinite. Then, for the pair that resulted in the minimum value of this
difference, we add in that edge and remove from the minimum spanning tree,
an edge that is in the path from u to v that has weight max[u,v].
Problem 23-2
a. We’ll show that the edges added at each step are safe. Consider an un-
marked vertex u. Set S={u}and let Abe the set of edges in the tree so far.
Then the cut respects A, and the next edge we add is a light edge, so it is safe
for A. Thus, every edge in Tbefore we run Prim’s algorithm is safe for T. Any
edge that Prim’s would normally add at this point would have to connect two
7

of the trees already created, and it would be chosen as minimal. Moreover, we
choose exactly one between any two trees. Thus, the fact that we only have
the smallest edges available to us is not a problem. The resulting tree must be
minimal.
b. We argue by induction on the number of vertices in G. We’ll assume
that |V|>1, since otherwise MST-REDUCE will encounter an error on line 6
because there is no way to choose v. Let |V|= 2. Since Gis connected, there
must be an edge between uand v, and it is trivially of minimum weight. They
are joined, and |G0.V |=1=|V|/2. Suppose the claim holds for |V|=n. Let
Gbe a connected graph on n+ 1 vertices. Then G0.V ≤n/2 prior to the final
vertex vbeing examined in the for-loop of line 4. If vis marked then we’re done,
and if visn’t marked then we’ll connect it to some other vertex, which must be
marked since vis the last to be processed. Either way, vcan’t contribute an
additional vertex to G0.V , so |G0.V | ≤ n/2≤(n+ 1)/2.
c. Rather than using the disjoint set structures of chapter 21, we can simply
use an array to keep track of which component a vertex is in. Let Abe an array
of length |V|such that A[u] = vif v=F IND −SET (u). Then FIND-SET(u)
can now be replaced with A[u] and UNION(u, v) can be replaced by A[v] = A[u].
Since these operations run in constant time, the runtime is O(E).
d. The number of edges in the output is monotonically decreasing, so each
call is O(E). Thus, kcalls take O(kE) time.
e. The runtime of Prim’s algorithm is O(E+Vlg V). Each time we run
MST-REDUCE, we cut the number of vertices at least in half. Thus, af-
ter kcalls, the number of vertices is at most |V|/2k. We need to minimize
E+V/2klg(V/2k)+ kE =E+Vlg(V)
2k−V k
2k+kE with respect to k. If we choose
k= lg lg Vthen we achieve the overall running time of O(Elg lg V) as desired.
To see that this value of kminimizes, note that the V k
2kterm is always less than
the kE term since E≥V. As kdecreases, the contribution of kE decreases,
and the contribution of Vlg V
2kincreases. Thus, we need to find the value of k
which makes them approximately equal in the worst case, when E=V. To
do this, we set lg V
2k=k. Solving this exactly would involve the Lambert W
function, but the nicest elementary function which gets close is k= lg lg V.
f. We simply set up the inequality Elg lg V < E +Vlg Vto find that we
need E < Vlg V
lg lg V−1=OVlg V
lg lg V.
Problem 23-3
a. To see that every minimum spanning tree is also a bottleneck spanning tree.
Suppose that Tis a minimum spanning tree. Suppose there is some edge in
it (u, v) that has a weight that’s greater than the weight of the bottleneck
8

spanning tree. Then, let V1be the subset of vertices of Vthat are reach-
able from uin T, without going though v. Define V2symmetrically. Then,
consider the cut that separates V1from V2. The only edge that we could
add across this cut is the one of minimum weight, so we know that there
are no edge across this cut of weight less than w(u, v). However, we have
that there is a bottleneck spanning tree with less than that weight. This is a
contradiction because a bottleneck spanning tree, since it is a spanning tree,
must have an edge across this cut.
b. To do this, we first process the entire graph, and remove any edges that
have weight greater than b. If the remaining graph is selected, we can just
arbitrarily select any tree in it, and it will be a bottleneck spanning tree
of weight at most b. Testing connectivity of a graph can be done in linear
time by running a breadth first search and then making sure that no vertices
remain white at the end.
c. Write down all of the edge weights of vertices. Use the algorithm from section
9.3 to find the median of this list of numbers in time O(E). Then, run the
procedure from part b with this median value as the one that you are testing
for there to be a bottleneck spanning tree with weight at most. Then there
are two cases:
First, we could have that there is a bottleneck spanning tree with weight at
most this median. Then just throw the edges with weight more than the
median, and repeat the procedure on this new graph with half the edges.
Second, we could have that there is no bottleneck spanning tree with at
most that weight. Then, we should run the procedure from problem 23-2
to contract all of the edges that have weight at most this median weight.
This takes time O(Elg(lg(V))) and then we are left solving the problem on
a graph that now has half the vertices.
Problem 23-4
a. This does return an MST. To see this, we’ll show that we never remove an
edge which must be part of a minimum spanning tree. If we remove e, then
ecannot be a bridge, which means that elies on a simple cycle of the graph.
Since we remove edges in nonincreasing order, the weight of every edge on
the cycle must be less than or equal to that of e. By exercise 23.1-5, there is
a minimum spanning tree on Gwith edge eremoved.
To implement this, we begin by sorting the edges in O(Elg E) time. For each
edge we need to check whether or not T− {e}is connected, so we’ll need
to run a DFS. Each one takes O(V+E), so doing this for all edges takes
O(E(V+E). This dominates the running time, so the total time is O(E2).
9

b. This doesn’t return an MST. To see this, let Gbe the graph on 3 vertices
a,b, and c. Let the eges be (a, b), (b, c), and (c, a) with weights 3, 2, and 1
respectively. If the algorithm examines the edges in their order listed, it will
take the two heaviest edges instead of the two lightest.
An efficient implementation will use disjoint sets to keep track of connected
components, as in MST-REDUCE in problem 23-2. Trying to union within
the same component will create a cycle. Since we make |V|calls to MAKE-
SET and at most 3|E|calls to FIND-SET and UNION, the runtime is
O(Eα(V)).
c. This does return an MST. To see this, we simply quote the result from exer-
cise 23.1-5. The only edges we remove are the edges of maximum weight on
some cycle, and there always exists a minimum spanning tree which doesn’t
include these edges. Moreover, if we remove an edge from every cycle then
the resulting graph cannot have any cycles, so it must be a tree.
To implement this, we use the approach taken in part (b), except now we
also need to find the maximum weight edge on a cycle. For each edge which
introduces a cycle we can perform a DFS to find the cycle and max weight
edge. Since the tree at that time has at most one cycle, it has at most |V|
edges, so we can run DFS in O(V). The runtime is thus O(EV ).
10
Chapter 24
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 24.1-1
If we change our source to z and use the same ordering of edges to decide
what to relax, the d values after successive iterations of relaxation are:
s t x y z
∞ ∞ ∞ ∞ 0
2∞7∞0
2 5 7 9 0
2 5 6 9 0
2 4 6 9 0
The πvalues are:
s t x y z
NIL NIL NIL N IL N IL
z NIL z N IL NIL
z x z s NIL
z x y s NIL
z x y s NIL
Now, if we change the weight of edge (z, x) to 4 and rerun with sas the
source, we have that the d values after successive iterations of relaxation are:
s t x y z
0∞ ∞ ∞ ∞
0 6 ∞7∞
0 6 4 7 2
0 2 4 7 2
0 2 4 7 −2
The πvalues are:
s t x y z
NIL NIL NIL N IL N IL
NIL s NIL s NIL
NIL s y s t
NIL x y s t
NIL x y s t
1

Note that these values are exactly the same as in the worked example. The
difference that changing this edge will cause is that there is now a negative
weight cycle, which will be detected when it considers the edge (z, x) in the for
loop on line 5. Since x.d = 4 >−2 + 4 = z.d +w(z, x), it will return false on
line 7.
Exercise 24.1-2
Suppose there is a path from sto v. Then there must be a shortest such
path of length δ(s, v). It must have finite length since it contains at most |V|−1
edges and each edge has finite length. By Lemma 24.2, v.d =δ(s, v)<∞upon
termination. On the other hand, suppose v.d < ∞when BELLMAN-FORD ter-
minates. Recall that v.d is monotonically decreasing throughout the algorithm,
and RELAX will update v.d only if u.d +w(u, v)< v.d for some uadjacent
to v. Moreover, we update v.π =uat this point, so vhas an ancestor in the
predecessor subgraph. Since this is a tree rooted at s, there must be a path
from sto vin this tree. Every edge in the tree is also an edge in G, so there is
also a path in Gfrom sto v.
Exercise 24.1-3
Before each iteration of the for loop on line 2, we make a backup copy of the
current d values for all the vertices. Then, after each iteration, we check to see
if any of the d values changed. If none did, then we immediately terminate the
for loop. This clearly works because if one iteration didn’t change the values of
d, nothing will of changed on later iterations, and so they would all proceed to
not change any of the d values.
Exercise 24.1-4
If there is a negative weight cycle on some path from sto vsuch that u
immediately preceeds von the path, then v.d will strictly decrease every time
RELAX(u, v, w) is called. If there is no negative weight cycle, then v.d can
never decrease after lines 1 through 4 are executed. Thus, we just update all
vertices vwhich satisfy the if-condition of line 6. In particular, replace line 7
with v.d =−∞.
Exercise 24.1-5
Initially, we will make each vertex have a Dvalue of 0, which corresponds to
taking a path of length zero starting at that vertex. Then, we relax along each
edge exactly V−1 times. Then, we do one final round of relaxation, which if any
thing changes, indicated the existence of a negative weight cycle. The code for
this algorithm is identical to that for Bellman ford, except instead of initializing
the values to be infinity except at the source which is zero, we initialize every d
value to be infinity. We can even recover the path of minimum length for each
2
vertex by looking at their πvalues.
Note that this solution assumes that paths of length zero are acceptable. If
they are not to your liking then just initialize each vertex to have a d value
equal to the minimum weight edge that they have adjacent to them.
Exercise 24.1-6
Begin by calling a slightly modified version of DFS, where we maintain the
attribute v.d at each vertex which gives the weight of the unique simple path
from sto vin the DFS tree. However, once v.d is set for the first time we will
never modify it. It is easy to update DFS to keep track of this without changing
its runtime. At first sight of a back edge (u, v), if v.d > u.d +w(u, v) then we
must have a negative-weight cycle because u.d +w(u, v)−v.d represents the
weight of the cycle which the back edge completes in the DFS tree. To print
out the vertices print v,u,u.π,u.π.π, and so on until vis reached. This has
runtime O(V+E).
Exercise 24.2-1
If we run the procedure on the DAG given in figure 24.5, but start at vertex
r, we have that the d values after successive iterations of relaxation are:
r s t x y z
0∞∞∞∞∞
05 3∞∞∞
0 5 3 11 ∞ ∞
0 5 3 10 7 5
0 5 3 10 7 5
0 5 3 10 7 5
The πvalues are:
r s t x y z
NIL NIL NIL N IL N IL N IL
NIL r r NIL NIL NIL
NIL r r s N IL NIL
NIL r r t t t
NIL r r t t t
NIL r r t t t
Exercise 24.2-2
When we reach vertex v, the last vertex in the topological sort, it must have
out-degree 0. Otherwise there would be an edge pointing from a later vertex to
an earlier vertex in the ordering, a contradiction. Thus, the body of the for-loop
of line 4 is never entered for this final vertex, so we may as well not consider it.
3

Exercise 24.2-3
Introduce two new dummy tasks, with cost zero. The first one having edges
going to every task that has no in edges. The second having an edge going to it
from every task that has no out edges. Now, construct a new directed graph in
which each egets mapped to a vertex veand there is an edge (ve, ve0) with cost
wif and only if edge egoes to the same vertex that e0comes from, and that
vertex has weight w. Then, every path through this dual graph corresponds to
a path through the original graph. So, we just look for the most expensive path
in this DAG which has weighted edges using the algorithm from this section.
Exercise 24.2-4
We will compute the total number of paths by counting the number of paths
whose start point is at each vertex v, which will be stored in an attribute
v.paths. Assume that initiall we have v.paths = 0 for all v∈V. Since all
vertices adjacent to uoccur later in the topological sort and the final vertex has
no neighbors, line 4 is well-defined. Topological sort takes O(V+E) and the
nested for-loops take O(V+E) so the total runtime is O(V+E).
Algorithm 1 PATHS(G)
1: topologically sort the vertices of G
2: for each vertex u, taken in reverse topologically sorted order do
3: for each vertex v∈G.Adj[u]do
4: u.paths =u.paths +1+v.paths
5: end for
6: end for
Exercise 24.3-1
We first have s as the source, in this case, the sequence of extractions from
the priority queue are: s, t, y,x,z. The d values after each iteration are:
s t x y z
03∞5∞
0 3 9 5 ∞
0 3 9 5 11
0 3 9 5 11
0 3 9 5 11
The πvalues are:
4
s t x y z
NIL s NIL NIL N IL
NIL s t s NIL
NIL s t s y
NIL s t s y
NIL s t s y
Now, if we repeat the procedure, except having z as the source, we have that
the d values are
s t x y z
3∞7∞0
3 6 7 8 0
3 6 7 8 0
3 6 7 8 0
3 6 7 8 0
The πvalues are:
s t x y z
z NIL z NIL NIL
z s z s N IL
z s z s N IL
z s z s N IL
z s z s N IL
Exercise 24.3-2
Consider any graph with a negative cycle. RELAX is called a finite number
of times but the distance to any vertex on the cycle is −∞, so DIJKSTRA’s
algorithm cannot possibly be correct here. The proof of theorem 24.6 doesn’t
go through because we can no longer guarantee that δ(s, y)≤δ(s, u).
Exercise 24.3-3
It does work correctly to modify the algorithm like that. Once we are at the
point of considering the last vertex, we know that it’s current d value is at at
least as large as the largest of the other vertices. Since none of the edge weights
are negative, its d value plus the weight of any edge coming out of it will be
at least as large as the d values of all the other vertices. This means that the
relaxations that occur will not change any of the d values of any vertices, and
so not change their πvalues.
Exercise 24.3-4
Check that s.d = 0. Then for each vertex in V\{s}, examine all edges com-
ing into V. Check that v.π is the minimum of u.d +w(u, v) for all vertices ufor
5

which there is an edge (u, v), and that v.d =v.π.d +w(v.π, v). If this is ever
false, return false. Otherwise, return true. This takes O(V+E) time. Now
we must check that this correctly checks whether or not the dand πattributes
match those of some shortest-paths tree. Suppose that this is not true. Let vbe
the vertex of smallest v.d value which is incorrect. We may assume that v6=s
since we check correctness of s.d explicitly. Since all edge weights are nonnega-
tive, vmust be preceeded by a vertex of smaller estimated distance, which we
know to be correct since vhas the smallest incorrect estimated distance. By
verifying that v.π is in fact the vertex which minimizes the distance of v, we
have ensured that v.π is correct, and by checking that v.d =v.π.d +w(v.π, v)
we ensure that the computation of v.d is accurate. Thus, if there is a vertex
which has the wrong estimated distance or parent, we will find it.
Exercise 24.3-5
Consider the graph on 5 vertices {a, b, c, d, e}, and with edges (a, b),(b, c),(c, d),(a, e),(e, c)
all with weight 0. Then, we could pull vertices off of the queue in the ordera, e, c, b, d.
This would mean that we relax (c, d) before (b, c). However, a shortest pat to
dis (a, b),(b, c),(c, d). So, we would be relaxing an edge that appears later on
this shortest path before an edge that appears earlier.
Exercise 24.3-6
We now view the weight of a path as the reliability of a path, and it is
computed by taking the product of the reliabilities of the edges on the path.
Our algorithm will be similar to that of DIJKSTRA, and have the same run-
time, but we now wish to maximize weight, and RELAX will be done inline by
checking products instead of sums, and switching the inequality since we want
to maximize reliability. Finally, we track that path from yback to xand print
the vertices as we go.
Exercise 24.3-7
Each edge is replaced with a number of edges equal to its weight, and one
less than that many vertices. That is, |V0|=P(v,u)∈Ew(v, u)−1. Similarly,
|E0|=P(v,u)∈Ew(v, u). Since we can bound each of these weights by W, we
can say that |V0| ≤ W|E| − |E|so there are at most W|E| − |E|+|V|vertices
in G0. A breadth first search considers vertices in an order so that uand v
satisfy u.d < v.d it considers ubefore v. Similarly, since each iteration of the
while loop in Dijkstra’s algorithm considers the vertex with lowest dvalue in
the queue, we will also be considering vertices with smaller dvalues first. So,
the two order of considering vertices coincide.
Exercise 24.3-8
6

Algorithm 2 RELIABILITY(G, r, x, y)
1: INITIALIZE-SINGLE-SOURCE(G, x)
2: S=∅
3: Q=G.V
4: while Q6=∅do
5: u= EXTRACT-MIN(Q)
6: S=S∪ {u}
7: for each vertex v∈G.Adj[u]do
8: if v.d < u.d ·r(u, v)then
9: v.d =u.d ·r(u, v)
10: v.π =u
11: end if
12: end for
13: end while
14: while y6=xdo
15: Print y
16: y=y.π
17: end while
18: Print x
We will modify Dijkstra’s algorithm to run on this graph by changing the
way the priority queue works, taking advantage of the fact that its members
will have keys in the range [0, W V ]∪ {∞}, since in the worst case we have to
compute the distance from one end of a chain to the other, with |V|vertices each
connected by an edge of weight W. In particular, we will create an array Asuch
that A[i] holds a linked list of all vertices whose estimated distance from sis i.
We’ll also need the attribute u.list for each vertex u, which points to u’s spot
in the list stored at A[u.d]. Since the minimum distance is always increasing,
kwill be at most V W , so the algorithm spends O(V W ) time in the while loop
on line 9, over all iterations of the for-loop of line 8. We spend only O(V+E)
time executing the for-loop of line 14 because we look through each adjacency
list only once. All other operations take O(1) time, so the total runtime of the
algorithm is O(V W ) + O(V+E) = O(V W +E).
Exercise 24.3-9
We can modify the construction given in the previous exercise to avoid having to
do a linear search through the array of lists A. To do this, we can just keep a set
of the indices of Athat contain a non-empty list. Then, we can just maintain
this as we move the vertices between lists, and replace the while loop in the
previous algorithm with just getting the minimum element in the set.
One way of implementing this set structure is with a self-balancing binary
search tree. Since the set consists entirely of indices of Awhich has length W,
the size of the tree is at most W. We can find the minimum element, delete an
element and insert in element all in time O(lg(W)) in a self balancing binary
7

Algorithm 3 MODIFIED-DIJKSTRA(G,w,s)
1: for each v∈G.V do v.d =V W + 1 v.π =N IL
2: end for
3: s.d = 0
4: Initialize an array Aof length V W + 2
5: A[0].insert(s)
6: Set A[V W + 1] equal to a linked list containing every vertex except s
7: k= 0
8: for i= 1 to |V|do
9: while A[k] = NIL do
10: k=k+ 1
11: end while
12: u=A[k].head
13: A[k].delete(u)
14: for each vertex v∈G.Adj[u]do
15: if v.d > u.d +w(u, v)then
16: A[v.d].delete(v.list)
17: v.d =u.d +w(u, v)
18: v.π =u
19: A[v.d].insert(v)
20: v.list =A[v.d].head
21: end if
22: end for
23: end for
8

serach tree.
Another way of doing this, since we know that the set is of integers drawn
from the set {1, . . . , W }, is by using a vEB tree. This allows the insertion,
deletion, and find minimum to run in time O(lg(lg(W)).
Since for every edge, we potentially move a vertex from one list to another,
we also need to possibly perform a deletion and insertion in the set. Also, at
the beginning of the outermost for loop, we need to perform a get min opera-
tion, if removing this element would cause the list in that index of Ato become
empty, we have to delete it from our set of indices. So, we need to perform a
set operation for each vertex, and also for each edge. There is only a constant
amount of extra work that has to be done for each, so the total runtime is
O((V+E) lg lg(W)) which is also O((V+E) lg(W)).
Exercise 24.3-10
The proof of correctness, Theorem 24.6, goes through exactly as stated in
the text. The key fact was that δ(s, y)≤δ(s, u). It is claimed that this holds
because there are no negative edge weights, but in fact that is stronger than is
needed. This always holds if yoccurs on a shortest path from sto uand y6=s
because all edges on the path from yto uhave nonnegative weight. If any had
negative weight, this would imply that we had “gone back” to an edge incident
with s, which implies that a cycle is involved in the path, which would only be
the case if it were a negative-weight cycle. However, these are still forbidden.
Exercise 24.4-1
Our vertices of the constraint graph will be {v0, v1, v2, v3, v4, v5, v6}. The
edges will be (v0, v1),(v0, v2),(v0, v3),(v0, v4),(v0, v5),(v0, v6),(v2, v1),(v4, v1),(v3, v2),(v5, v2),(v6, v2),(v6, v3),(v2, v4),(v1, v5),(v4, v5),(v3, v6)
with edge weights 0,0,0,0,0,0,1,−4,2,7,5,10,2,−1,3,−8 respectively. Then,
computing (δ(v0, v1), δ(v0, v2), δ(v0, v3), δ(v0, v4), δ(v0, v5), δ(v0, v6)), we get (−5,−3,0,−1,−6,−8)
which is a feasible solution by Theorem 24.9.
Exercise 24.4-2
There is no feasible solution because the constraint graph contains a negative-
weight cycle: (v1, v4, v2, v3, v5, v1) has weight -1.
Exercise 24.4-3
No, it cannot be positive. This is because for every vertex v6=v0, there is
an edge (v0, v) with weight zero. So, there is some path from the new vertex
to every other of weight zero. Since δ(v0, v) is a minimum weight of all paths,
it cannot be greater than the weight of this weight zero path that consists of a
single edge.
9

Exercise 24.4-4
To solve the single source shortest path problem we must have that for each
edge (vi, vj), δ(s, vj)≤δ(s, vi) + w(vi, vj), and δ(s, s) = 0. We we will use these
as our inequalities.
Exercise 24.4-5
We can follow the advice of problem 14.4-7 and solve the system of con-
straints on a modified constraint graph in which there is no new vertex v0. This
is simply done by initializing all of the vertices to have a d value of 0 before run-
ning the iterated relaxations of Bellman Ford. Since we don’t add a new vertex
and the nedges going from it to to vertex corresponding to each variable, we
are just running Bellman Ford on a graph with nvertices and medges, and so
it will have a runtime of O(mn).
Exercise 24.4-6
To obtain the equality constraint xi=xj+bkwe simply use the inequalities
xi−xj≤bkand xj−xi≤ −bk, then solve the problem as usual.
Exercise 24.4-7
We could avoid adding in the additional vertex by instead initializing the
d value for each vertex to be 0, and then running the bellman ford algorithm.
These modified initial conditions are what would result from looking at the ver-
tex v0and relaxing all of the edges coming off of it. After we would of processed
the edges coming off of v0, we can never consider it again because there are no
edges going to it. So, we can just initialize the vertices to what they would be
after relaxing the edges coming off of v0.
Exercise 24.4-8
Bellman-Ford correctly solves the system of difference constraints so Ax ≤b
is always satisfied. We also have that xi=δ(v0, vi)≤w(v0, vi) = 0 so xi≤0 for
all i. To show that Pxiis maximized, we’ll show that for any feasible solution
(y1, y2, . . . , yn) which satisfies the constraints we have yi≤δ(v0, vi) = xi. Let
v0, vi1, . . . , vikbe a shortest path from v0to viin the constraint graph. Then we
must have the constraints yi2−yi1≤w(vi1, vi2), . . . , yik−yik−1≤w(vik−1, vik).
Summing these up we have
yi≤yi−y1≤
k
X
m=2
w(vim, vim−1) = δ(v0, vi) = xi.
Exercise 24.4-9
10

We can see that the Bellman-Ford algorithm run on the graph whose con-
struction is described in this section causes the quantity max{xi} − min{xi}to
be minimized. We know that the largest value assigned to any of the vertices in
the constraint graph is a 0. It is clear that it won’t be greater than zero, since
just the single edge path to each of the vertices has cost zero. We also know
that we cannot have every vertex having a shortest path with negative weight.
To see this, notice that this would mean that the pointer for each vertex has
it’s p value going to some other vertex that is not the source. This means that
if we follow the procedure for reconstructing the shortest path for any of the
vertices, we have that it can never get back to the source, a contradiction to the
fact that it is a shortest path from the source to that vertex.
Next, we note that when we run Bellman-Ford, we are maximizing min{xi}.
The shortest distance in the constraint graphs is the bare minimum of what is
required in order to have all the constraints satisfied, if we were to increase any
of the values we would be violating a constraint.
This could be in handy when scheduling construction jobs because the quan-
tity max{xi} − min{xi}is equal to the difference in time between the last task
and the first task. Therefore, it means that minimizing it would mean that the
total time that all the jobs takes is also minimized. And, most people want the
entire process of construction to take as short of a time as possible.
Exercise 24.4-10
Consider introducing the dummy variable x. Let yi=xi+x. Then
(y1, . . . , yn) is a solution to a system of difference constraints if and only if
(x1, . . . , xn) is. Moreover, we have xi≤bkif and only if yi−x≤bkand xi≥bk
if and only if yi−x≥bk. Finally, xi−xj≤bif and only if yi−yj≤b. Thus, we
construct our constraint graph as follows: Let the vertices be v0, v1, v2, . . . , vn, v.
Draw the usual edges among the vi’s, and weight every edge from v0to another
vertex by 0. Then for each constraint of the form xi≤bk, create edge (x, yi)
with weight bk. For every constraint of the form xi≥bk, create edge (yi, x)
with weight −bk. Now use Bellman-Ford to solve the problem as usual. Take
whatever weight is assigned to vertex x, and subtract it from the weights of
every other vertex to obtain the desired solution.
Exercise 24.4-11
To do this, just take the floor of (largest integer that is less than or equal to)
each of the bvalues and solve the resulting integer difference problem. These
modified constraints will be admitting exactly the same set of assignments since
we required that the solution have integer values assigned to the variables. This
is because since the variables are integers, all of their differences will also be
integers. For an integer to be less than or equal to a real number, it is neces-
sary and sufficient for it to be less than or equal to the floor of that real number.
Exercise 24.4-12
11

To solve the problem of Ax ≤bwhere the elements of bare real-valued
we carry out the same procedure as before, running Bellman-Ford, but allow-
ing our edge weights to be real-valued. To impose the integer condition on
the xi’s, we modify the RELAX procedure. Suppose we call RELAX(vi, vj, w)
where vjis required to be integral valued. If vj.d > bvi.d +w(vi, vj)c, set vj.d =
bvi.d+w(vi, vj)c. This guarantees that the condition that vj.d−vi.d ≤w(vi, vj)
as desired. It also ensures that vjis integer valued. Since the triangle inequal-
ity still holds, x= (v1.d, v2.d, . . . , vn.d) is a feasible solution for the system,
provided that Gcontains no negative weight cycles.
Exercise 24.5-1
Since the induced shortest path trees on {s, t, y}and on {t, x, y, z}are in-
dependent and have to possible configurations each, there are four total arising
from that. So, we have the two not shown in the figure are the one consist-
ing of the edges {(s, t),(s, y),(y, x),(x, z)}and the one consisting of the edges
{(s, t),(t, y),(t, x),(y, z)}.
Exercise 24.5-2
Let Ghave 3 vertices s, x, and y. Let the edges be (s, x),(s, y),(x, y) with
weights 1, 1, and 0 respectively. There are 3 possible trees on these vertices
rooted at s, and each is a shortest paths tree which gives δ(s, x) = δ(s, y) = 1.
Exercise 24.5-3
To modify Lemma 24.10 to allow for possible shortest path weights of ∞
and −∞, we need to define our addition as ∞+c=∞, and −∞ +c=−∞.
This will make the statement behave correctly, that is, we can take the shortest
path from s to u and tack on the edge (u, v) to the end. That is, if there is a
negative weight cycle on your way to u and there is an edge from uto v, there
is a negative weight cycle on our way to v. Similarly, if we cannot reach vand
there is an edge from u to v, we cannot reach u.
Exercise 24.5-4
Suppose uis the vertex which first caused s.π to be set to a non-NIL value.
Then we must have 0 = s.d > u.d +w(u, s). Let pbe the path from s
to uin the shortest paths tree so far, and Cbe the cycle obtained by fol-
lowing that path from sto u, then taking the edge (u, s). Then we have
w(C) = w(p) + w(u, s) = u.d +w(u, s)<0, so we have a negative-weight
cycle.
Exercise 24.5-5
Suppose that we have a grap hon three vertices {s, u, v}and containing edges
12

(s, u),(s, v),(u, v),(v, u) all with weight 0. Then, there is a shortest path from
sto vof s, u, v and a shortest path from sto uof s, v, u. Based off of these, we
could set v.pi =uand u.π =v. This then means that there is a cycle consisting
of u, v in Gπ.
Exercise 24.5-6
We will prove this by induction on the number of relaxations performed. For
the base-case, we have just called INITIALIZE-SINGLE-SOURCE(G, s). The
only vertex in Vπis s, and there is trivially a path from sto itself. Now suppose
that after any sequence of nrelaxations, for every vertex v∈Vπthere exists
a path from sto vin Gπ. Consider the (n+ 1)st relaxation. Suppose it is
such that v.d > u.d +w(u, v). When we relax v, we update v.π =u.π. By the
induction hypothesis, there was a path from sto uin Gπ. Now vis in Vπ, and
the path from sto u, followed by the edge (u, v) = (v.π, v) is a path from sto
vin Gπ, so the claim holds.
Exercise 24.5-7
We know by 24.16 that a Gπforms a tree after a sequence of relaxation
steps. Suppose that Tis the tree formed after performing all the relaxation
steps of the Bellman Ford algorithm. While finding this tree would take many
more than V−1 relaxations, we just want to say that there is some sequence
of relaxations that gets us our answer quickly, not necessarily proscribe what
those relaxations are. So, our sequence of relaxations will be all the edges of T
in an order so that we never relax an edge that is below an unrelaxed edge in
the tree(a topological ordering). This guarantees that Gπwill be the same as
was obtained through the slow, proven correct, Bellman-Ford algorithm. Since
any tree on Vvertices has V−1 edges, we are only relaxing V−1 edges.
Exercise 24.5-8
Since the negative-weight cycle is reachable from s, let vbe the first vertex
on the cycle reachable from s(in terms of number of edges required to reach v)
and s=v0, v1, . . . , vk=vbe a simple path from sto v. Start by performing the
relaxations to v. Since the path is simple, every vertex on this path is encoun-
tered for the first time, so its shortest path estimate will always decrease from
infinity. Next, follow the path around from vback to v. Since vwas the first
vertex reached on the cycle, every other vertex will have shortest-path estimate
set to ∞until it is relaxed, so we will change these for every relaxation around
the cycle. We now create the infinite sequence of relaxations by continuing to
relax vertices around the cycle indefinitely. To see why this always causes the
shortest-path estimate to change, suppose we have just reached vertex xi, and
the shortest-path estimates have been changed for every prior relaxation. Let
x1, x2, . . . , xnbe the vertices on the cycle. Then we have xi−1.d +w(xi−1, x) =
xi−2.d +w(xi−2, xi−1) + w(xi−1, wi) = . . . =xi.d +Pn
j=1 w(xj)< w.d since the
13

cycle has negative weight. Thus, we must update the shortest-path estimate of
xi.
Problem 24-1
a. Since in Gfedges only go from vertices with smaller index to vertices with
greater index, there is no way that we could pick a vertex, and keep increas-
ing it’s index, and get back to having the index equal to what we started
with. This means that Gfis acyclic. Similarly, there is no way to pick an
index, keep decreasing it, and get back to the same vertex index. By these
definitions, since Gfonly has vertices going from lower indices to higher in-
dices, (v1, . . . , v|V|) is a topological ordering of the vertices. Similarly, for Gb,
(v|V|, . . . , v1) is a topological ordering of the vertices.
b. Suppose that we are trying to find the shortest path from sto v. Then,
list out the vertices of this shortest path vk1, vk2, . . . , vkm. Then, we have
that the number of times that the sequence {ki}igoes from increasing to
decreasing or from decreasing to increasing is the number of passes over the
edges that are necessary to notice this path. This is because any increasing
sequence of vertices will be captured in a pass through Efand any decreasing
sequence will be captured in a pass through Eb. Any sequence of integers
of length |V|can only change direction at most b|V|/2ctimes. However, we
need to add one more in to account for the case that the source appears later
in the ordering of the vertices than vk2, as it is in a sense initially expecting
increasing vertex indices, as it runs through Efbefore Eb.
c. It does not improve the asymptotic runtime of Bellman ford, it just drops
the runtime from having a leading coefficient of 1 to a leading coefficient of
1
2. Both in the original and in the modified version, the runtime is O(EV ).
Problem 24-2
1. Suppose that box x= (x1, . . . , xd) nests with box y= (y1, . . . , yd) and
box ynests with box z= (z1, . . . , zd). Then there exist permutations π
and σsuch that xπ(1) < y1, . . . , xπ(d)< ydand yσ(1) < z1, . . . , yσ(d)< zd.
This implies xπ(σ(1)) < z1, . . . , xπ(σ(d)) < zd, so xnests with zand the
nesting relation is transitive.
2. Box xnests inside box yif and only if the increasing sequence of dimen-
sions of xis componentwise strictly less than the increasing sequence of
dimensions of y. Thus, it will suffice to sort both sequences of dimensions
and compare them. Sorting both length dsequences is done in O(dlg d),
and comparing their elements is done in O(d), so the total time is O(dlg d).
14

3. We will create a nesting-graph Gwith vertices B1, . . . , Bnas follows. For
each pair of boxes Bi, Bj, we decide if one nests inside the other. If Bi
nests in Bj, draw an arrow from Bito Bj. If Bjnests in Bi, draw an
arrow from Bjto Bi. If neither nests, draw no arrow. To determine the
arrows efficiently, after sorting each list of dimensions in O(nd lg d) we
can sort all boxes’ sorted dimensions lexicographically in O(dn lg n) using
radix sort. By transitivity, it will suffice to test adjacent nesting relations.
Thus, the total time to build this graph is O(nd max lg d, lg n). Next, we
need to find the longest chain in the graph.
Problem 24-3
a. To do this we take the negative of the natural log (or any other base will also
work) of all the values cithat are on the edges between the currencies. Then,
we detect the presence or absence of a negative weight cycle by applying
Bellman Ford. To see that the existence of an arbitrage situation is equivalent
to there being a negative weight cycle in the original graph, consider the
following sequence of steps:
R[i1, i2]·R[i2, i3]· · · · · R[ik, i1]>1
ln(R[i1, i2]) + ln(R[i2, i3]) + · · · + ln(R[ik, i1]) >0
−ln(R[i1, i2]) −ln(R[i2, i3]) − · · · − ln(R[ik, i1]) <0
b. To do this, we first perform the same modification of all the edge weights as
done in part aof this problem. Then, we wish to detect the negative weight
cycle. To do this, we relax all the edges |V| − 1 many times, as in Bellman-
Ford algorithm. Then, we record all of the d values of the vertices. Then, we
relax all the edges |V|more times. Then, we check to see which vertices had
their dvalue decrease since we recorded them. All of these vertices must lie
on some (possibly disjoint) set of negative weight cycles. Call Sthis set of
vertices. To find one of these cycles in particular, we can pick any vertex in
Sand greedily keep picking any vertex that it has an edge to that is also in
S. Then, we just keep an eye out for a repeat. This finds us our cycle. We
know that we will never get to a dead end in this process because the set S
consists of vertices that are in some union of cycles, and so every vertex has
out degree at least 1.
Problem 24-4
a. We can do this in O(E) by the algorithm described in exercise 24.3-8 since
our “priority queue” takes on only integer values and is bounded in size by E.
15

b. We can do this in O(E) by the algorithm described in exercise 24.3-8 since
wtakes values in {0,1}and V=O(E).
c. If the ith digit, read from left to right, of w(u, v) is 0, then wi(u, v) =
2wi−1(u, v). If it is a 1, then wi(u, v) = 2wi−1(u, v) + 1. Now let s=
v0, v1, . . . , vn=vbe a shortest path from sto vunder wi. Note that any
shortest path under wiis necessarily also a shortest path under wi−1. Then
we have
δi(s, v) =
n
X
m=1
wi(vm−1, vm)
≤
n
X
m=1
[2wi−1(u, v) + 1]
≤2
n
X
m=1
wi−1(u, v) + n
≤2δi−1(s, v) + |V| − 1.
On the other hand, we also have
δi(s, v) =
n
X
m=1
wi(vm−1, vm)
≥
n
X
m=1
2wi−1(vm−1, vm)
≥2δi−1(s, v)
d. Note that every quantity in the definition of ˆwiis an integer, so ˆwiis
clearly an integer. Since wi(u, v)≥2wi−1(u, v), it will suffice to show that
wi−1(u, v) + δi−1(s, u)≥δi−1(s, v) to prove nonnegativity. This follows im-
mediately from the triangle inequality.
e. First note that s=v0, v1, . . . , vn=vis a shortest path from sto vwith
respect to ˆwif and only if it is a shortest path with respect to w. Then we
have
ˆ
δi(s, v) =
n
X
m=1
wi(vm−1, vm)+2δi−1(s, vm−1)−2δi−1(s, vm)
=
n
X
m=1
wi(vm−1, vm)−2δi−1(s, vn)
=δi(s, v)−2δi−1(s, v)
16

f. By part a we can compute ˆ
δi(s, v) for all v∈Vin O(E) time. If we have
already computed δi−1then we can compute δiin O(E) time. Since we can
compute δ1in O(E) by part b, we can compute δifrom scratch in O(iE)
time. Thus, we can compute δ=δkin O(Ek) = O(Elg W) time.
Problem 24-5
a. If µ∗= 0, then we have that the lowest that 1
kPk
i=1 w(ei) can be is zero.
This means that the lowest Pk
i=1 w(ei) can be is 0. This means that no cycle
can have negative weight. Also, we know that for any path from sto v, we
can make it simple by removing any cycles that occur. This means that it
had a weight equal to some path that has at most n−1 edges in it. Since we
take the minimum over all possible number of edges, we have the minimum
over all paths.
b. To show that
max
0≤k≤n−1
δn(s, v)−δk(s, v)
n−k≥0
we need to show that
max
0≤k≤n−1δn(s, v)−δk(s, v)≥0
Since we have that µ∗= 0, there aren’t any negative weight cycles. This
means that we can’t have the minimum cost of a path decrease as we increase
the possible length of the path past n−1. This means that there will be a
path that at least ties for cheapest when we restrict to the path being less
than length n. Note that there may also be cheapest path of longer length
since we necessarily do have zero cost cycles. However, this isn’t guaranteed
since the zero cost cycle may not lie along a cheapest path from s to v.
c. Since the total cost of the cycle is 0, and one part of it has cost x, in order to
balance that out, the weight of the rest of the cycle has to be −x. So, suppose
we have some shortest length path from s to u, then, we could traverse the
path from u to v along the cycle to get a path from sto uthat has length
δ(s, u) + x. This gets us that δ(s, v)≤δ(s, u) + x. To see the converse
inequality, suppose that we have some shortest length path from sto v.
Then, we can traverse the cycle going from vto u. We already said that this
part of the cycle had total cost −x. This gets us that δ(s, u)≤δ(s, v)−x.
Or, rearranging, we have δ(s, u) + x≤δ(s, v). Since we have inequalities
both ways, we must have equality.
d. To see this, we find a vertex vand natural number k≤n−1 so that δn(s, v)−
δk(s, v) = 0. To do this, we will first take any shortest length, smallest
number of edges path from sto any vertex on the cycle. Then, we will just
keep on walking around the cycle until we’ve walked along nedges. Whatever
17

vertex we end up on at that point will be our v. Since we did not change the
dvalue of vafter looking at length npaths, by part a, we know that there
was some length of this path, say k, which had the same cost. That is, we
have δn(s, v) = δk(s, v).
e. This is an immediate result of the previous problem and part b. part b says
that for all vthe inequality holds, so, we have
min
v∈Vmax
0≤k≤n−1
δn(s, v)−δk(s, v)
n−k≥0
The previous part says that there is some von each minimum weight cycle
so that
max
0≤k≤n−1
δn(s, v)−δk(s, v)
n−k= 0
which means that
min
v∈Vmax
0≤k≤n−1
δn(s, v)−δk(s, v)
n−k≤0
Putting the two inequalities together, we have the desired equality.
f. if we add tto the weight of each edge, the mean weight of any cycle becomes
µ(c) = 1
kPk
i=1(w(ei) + t) = 1
kPk
iw(ei)+kt
k=1
kPk
iw(ei)+t. This
is the original, unmodified mean weight cycle, plus t. Since this is how the
mean weight of every cycle is changed, the lowest mean weight cycle stays the
lowest mean weight cycle. This means that µ∗will increase by t. Suppose
that we first compute µ∗. Then, we subtract from every edge weight the
value µ∗. This will make the new µ∗equal zero, which by part e means that
minv∈Vmax0≤k≤n−1δn(s,v)−δk(s,v)
n−k= 0. Since they are both equal to zero,
they are both equal to each other.
g. By the previous part, it suffices to compute the expression on the previ-
ous line. We will start by creating a table that lists δk(s, v) for every
k∈ {1, . . . , n}and v∈V. This can be done in time O(V(E+V)) by
creating a |V|by |V|table, where the kth row and vth column represent
δk(s, v) when wanting to compute a particular entry, we need look at a num-
ber of entries in the previous row equal to the in degree of the vertex we
want to compute. So, summing over the computation required for each row,
we need O(E+V). Note that this total runtime can be bumped down to
O(V E) by not including in the table any isolated vertices, this will ensure
that E∈Ω(V) So, O(V(E+V)) becomes O(V E). Once we have this table
of values computed, it is simple to just replace each row with the last row
minus what it was, and divide each entry by n−k, then, find the min column
in each row, and take the max of those numbers.
Problem 24-6
18

We’ll use the Bellman-Ford algorithm, but with a careful choice of the order
in which we relax the edges in order to perform a smaller number of RELAX
operations. In any bitonic path there can be at most two distinct increasing se-
quences of edge weights, and similarly at most two distinct decreasing sequences
of edge weights. Thus, by the path-relaxation property, if we relax the edges
in order of increasing weight then decreasing weight three times (for a total of
six times relaxing every edge) the we are guaranteed that v.d will equal δ(s, v)
for all v∈V. Sorting the edges takes O(Elg E). We relax every edge 6 times,
taking O(E). Thus the total runtime is O(Elg E) + O(E) = O(Elg E), which
is asymptotically faster than the usual O(V E) runtime of Bellman-Ford.
19
Chapter 25
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 25.1-1
First, the slow way:
L(1) =
0∞∞∞−1∞
1 0 ∞2∞ ∞
∞2 0 ∞∞−8
−4∞ ∞ 0 3 ∞
∞7∞ ∞ 0∞
∞5 10 ∞ ∞ 0
L(2) =
0 6 ∞∞−1∞
−2 0 ∞2 0 ∞
3−3 0 4 ∞ −8
−4 10 ∞0−5∞
8 7 ∞9 0 ∞
6 5 10 7 ∞0
L(3) =
0 6 ∞8−1∞
−2 0 ∞2−3∞
−2−3 0 −1 2 −8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 5 0
L(4) =
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−3−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
L(5) =
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−6−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
1

Then, since we have reached L(n−1) we can stop since we know that since
there are no negative weight cycles, taking higher powers will not cause the
matrix to change at all. By the fast method, we get that
L(1) =
0∞∞∞−1∞
1 0 ∞2∞ ∞
∞2 0 ∞∞−8
−4∞ ∞ 0 3 ∞
∞7∞ ∞ 0∞
∞5 10 ∞ ∞ 0
L(2) =
0 6 ∞∞−1∞
−2 0 ∞2 0 ∞
3−3 0 4 ∞ −8
−4 10 ∞0−5∞
8 7 ∞9 0 ∞
6 5 10 7 ∞0
L(4) =
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−3−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
L(8) =
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−6−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
We stop since 8 ≥5 = n−1.
Exercise 25.1-2
This is consistent with the fact that the shortest path from a vertex to itself
is the empty path of weight 0. If there were another path of weight less than 0
then it must be a negative-weight cycle, since it starts and ends at vi.
Exercise 25.1-3
This matrix corresponds to the identity matrix in normal matrix multiplica-
tion. This is because anytime that we take a min of any number with infinity, we
get that same number back. Another way of seeing this is that we can interpret
this strange version of matrix multipllication as allowing any of our shortest
paths to be a path described by one matrix followed by a path described by the
other. However, the given matrix corresponds to there being no paths between
2

any of the vertices. This means that we won’t change any of the shortest paths
that are described by the matrix we are multiplying it by since we are allowing
nothing more for those paths.
Exercise 25.1-4
To verify associativity, we need to check that (WiWj)Wp=Wi(WjWp)
for all i, j, p, where we use the matrix multiplication defined by the EXTEND-
SHORTEST-PATHS procedure. Consider entry (a, b) of the left hand side. This
is:
min
1≤k≤n[WiWj]a,k +Wp
k,b = min
1≤k≤nmin
1≤q≤nWi
a,q +Wj
q,k +Wp
k,b
= min
1≤q≤nWi
a,q + min
1≤k≤nWj
q,k +Wp
k,b
= min
1≤q≤nWi
a,q + [WjWp]q,b
which is precisely entry (a, b) of the right hand side.
Exercise 25.1-5
We can express finding the shortest path from a single vertex with the mod-
ified version of matrix multiplication described in the section. We initially let
v1be a vector indexed by the vertices of the graph. It is infinity when the
corresponding vertex has no edge going to it from th esource vertex, s. It is
the weight of the edge going to it from sif there is one. Lastly, it is zero in
the entry corresponding to sitself. Essentially, we are only taking the row of
the Wmatrix that corresponds to s. Then, we define vi+1 =viW. Then, we
stop computing vionce we compute vn−1. This vector then contains the correct
shortest distances from the source to each vertex. Since each time we multiply
the vector by the matrix, we only have to consider the entries which are non-
infinite in W. There are only |E|+|V|of these non-finfinite entries. So, we
have that the time required for each time we mutiply the vector by the matrix,
we take time at most O(E). So, the total runtime would be O(EV ) just as in
Bellman-Ford. The similarities don’t stop there however. This is because vi
represents the shortest distance to each vector from susing at most iedges,
and each time we multiply by Wcorresponds to relaxing every edge.
Exercise 25.1-6
For each source vertex viwe need to compute the shortest-paths tree for vi.
To do this, we need to compute the predecessor for each j6=i. For fixed iand
j, this is the value of ksuch that Li,k +w(k, j) = Li,j . Since there are nvertices
whose trees need computing, nvertices for each such tree whose predecessors
need computing, and it takes O(n) to compute this for each one (checking each
possible k), the total time is O(n3).
3

Exercise 25.1-7
Exercise 25.1-8
We can overwrite matrices as we go. Let A?B denote multiplication defined
by the EXTEND-SHORTEST-PATHS procedure. Then we modify FASTER-
ALL-EXTEND-SHORTEST-PATHS(W). We initially create an nby nmatrix
L. Delete line 5 of the algorithm, and change line 6 to L=W ? W , followed by
W=L.
Exercise 25.1-9
For the modification, keep computing for one step more than the original,
that is, we compute all the way up to L(2k+1)where 2k> n −1. Then, if
there aren’t any negative weight cycles, then, we will have that the two matri-
ces should be equal since having no negative weight cycles means that between
any two vertices, there is a path that is tied for shortest and contains at most
n−1 edges. However, if there is a cycle of negative total weight, we know that
it’s length is at most n, so, since we are allowing paths to be larger by 2k≥n
between these two matrices, we have that we would need to have all of the ver-
tices on the cycle have their distance reduce by at least the negative weight of
the cycle. Since we can detect exactly when there is a negative cycle, based on
when these two matrices are different. This algorithm works. It also only takes
time equal to a single matrix multiplication which is littlee oh of the unmodified
algorithm.
Exercise 25.1-10
A negative-weight cycle appears when Wm
i,i <0 for some mand i. Each time
a new power of Wis computed, we simply check whether or not this happens,
at which point the cycle has length m. The runtime is O(n4).
Exercise 25.2-1
4

k Dk
0
0∞∞∞−1∞
1 0 ∞2∞ ∞
∞2 0 ∞∞−8
−4∞ ∞ 0 3 ∞
∞7∞ ∞ 0∞
∞5 10 ∞ ∞ 0
1
0∞∞∞−1∞
1 0 ∞2 0 ∞
∞2 0 ∞∞−8
−4∞ ∞ 0−5∞
∞7∞ ∞ 0∞
∞5 10 ∞ ∞ 0
2
0∞∞∞−1∞
1 0 ∞2 0 ∞
3 2 0 4 2 −8
−4∞ ∞ 0−5∞
8 7 ∞9 0 ∞
6 5 10 7 5 0
3
0∞∞∞−1∞
1 0 ∞2 0 ∞
3 2 0 4 2 −8
−4∞ ∞ 0−5∞
8 7 ∞9 0 ∞
6 5 10 7 5 0
4
0∞∞∞−1∞
−2 0 ∞2−3∞
0 2 0 4 −1−8
−4∞ ∞ 0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
5
0 6 ∞8−1∞
−2 0 ∞2−3∞
0 2 0 4 −1−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
6
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−6−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
Exercise 25.2-2
5

We set wij = 1 if (i, j) is an edge, and wij = 0 otherwise. Then we replace
line 7 of EXTEND-SHORTEST-PATHS(L,W) by l0
ij =l0
ij ∨(lik ∧wkj ). Then
run the SLOW-ALL-PAIRS-SHORTEST-PATHS algorithm.
Exercise 25.2-3
See the modified version of the Floyd-Warshall algorithm:
Algorithm 1 MOD-FLOYD-WARSHALL(W)
n= W.rows
D0=W
π0is a matrix with nil in every entry
for i=1 to n do
for j = 1 to n do
if i6=jand D0
i,j <∞then
π0
i,j =i
end if
end for
end for
for k=1 to n do
let Dkbe a new n×nmatrix.
let πkbe a new n×nmatrix
for i=1 to n do
for j = 1 to n do
if dk−1
ij ≤dk−1
i,k +dk−1
k,j then
dk
i,j =dk−1
i,j
πk
i,j =πk−1
i,j
else
dk
i,j =dk−1
i,k +dk−1
k,j
πk
i,j =πk−1
k,j
end if
end for
end for
end for
In order to have that π(k)
ij =l, we need that d(k)
ij ≥d(k)
il +wlj . To see
this fact, we will note that having π(k)
ij =lmeans that a shortest path from
ito jlast goes through l. A path that last goes through lcorresponds to
taking a chepest path from ito land then following the single edge from l
to j. However, This means that dil ≤dij −wij , which we can rearrange
to get the desired inequality. We can just continue following this inequality
around, and if we ever get some cycle, i1, i2,...ic, then we would have that
dii1≤dii1+wi1i2+wi2i3+· · · +wici1. So, if we subtract the common term
from both sides, we get that 0 ≤wici1+Pc−1
q=1 wiqiq+1 . So, we have that we
6

would only have a cycle in the precedessor graph if we ahvt that there is a zero
weight cycle in the original graph. However, we would never have to go around
the weight zero cycle since the constructed path of shortest weight favors ones
with a fewer number of edges because of the way that we handle the equality
case in equation (25.7).
Exercise 25.2-4
Suppose we are updating d(
ij k). To be sure we get the same results from
this algorithm, we need to check what happens to d(k−1)
ij ,d(k−1)
ik and d(k−1)
kj .
The d(k−1)
ij term will be unchanged. On the other hand, the other terms won’t
change because any shorest path from ito kwhich includes knecessarily in-
cludes it only once (since there are no negative-weight cycles) so it is the length
of a shortest path using only vertices 1 through k−1. Thus, updating in place
is okay.
Exercise 25.2-5
If we change the way that we handle the equality case, we willl still be gen-
erating a the correct values for the πmatrix. This is because updating the π
values to make paths that are longer but still tied for the lowest weight. Mak-
ing πij =πkj means that we are making the shortest path from ito jpasses
through kat some point. This has the same cost as just going from ito j, since
dij =dik +dkj .
Exercise 25.2-6
If there was a negative-weight cycle, there would be a negative number oc-
curring on the diagonal upon termination of the Floyd-Warshall algorithm.
Exercise 25.2-7
We can recursively compute the values of φ(k)
ij by, letting it be φ(k−1)
ij if d(k)
ik +
d(k)
kj ≥d(k−1)
ij , and otherwise, let it be k. This works correctly because it per-
fectly captures whether we decided to use vertex kwhen we were repeatedly
allowing ourselves use of each vertex one at a time. To modify Floyd War-
shall to compute this, we would just need to stick within the innermost for
loop, something that computes φ(k)
ij by this recursive rule, this would only be
a constant amount of work in this innermost for loop, and so would not cause
the asymptotic runtime to increase. It is similar to the s table in matrix-chain
multiplication because it is computed by a similar recurrence.
If we already have the n3values in φ(k)
ij provided, then we can reconstruct
the shortest path from ito jbecause we know that the largest vertex in the
path from ito jis φ(n)
ij , call it a1. Then, we know that the largest vertex in
the path before a1will be φ(a1−1)
ia1and the largest after a1will be φ(a1−1
a1j. By
7

continuing to recurse until we get that the largest element showing up at some
point is NIL, we will be able to continue subdividing the path until it is entirely
constructed.
Exercise 25.2-8
Create an nby nmatrix Afilled with 0’s. We are done if we can determine
the vertices reachable from a particular vertex in O(E) time, since we can just
compute this for each v∈V. To do this, assign each edge weight 1. Then we
have δ(v, u)≤ |E|for all u∈V. By Problem 24-4 (a) we can compute δ(v, u)
in O(E) for all u∈V. If δ(v, u)<∞, set Aij = 1. Otherwise, leave it as 0.
Exercise 25.2-9
First, compute the strongly connected components of the directed graph, and
look at it’s component graph. This component graph is going to be acyclic and
have at most as many vertices and at most as many edges as the original graph.
Since it is acyclic, we can run our transitive closure algorithm on it. Then,
for every edge (S1, S2) that shows up in the transitive closure of the compo-
nent graph, we add an edge from each vertex in S1to a vertex in S2. This takes
time equal to O(V+E∗). So, the total time required is ≤f(|V|,|E|)+O(V+E).
Exercise 25.3-1
v h(v)
1−5
2−3
3 0
4−1
5−6
6−8
8

u v ˆw(u, v)
1 2 NIL
1 3 NIL
1 4 NIL
1 5 0
1 6 NIL
2 1 3
2 3 NIL
2 4 0
2 5 NIL
2 6 NIL
3 1 NIL
3 2 5
3 4 NIL
3 5 NIL
3 6 0
4 1 0
4 2 NIL
4 3 NIL
4 5 8
4 6 NIL
5 1 NIL
5 2 4
5 3 NIL
5 4 NIL
5 6 NIL
6 1 NIL
6 2 0
6 3 18
6 4 NIL
6 5 NIL
So, the di,j values that we get are
0 6 ∞8−1∞
−2 0 ∞2−3∞
−5−3 0 −1−6−8
−4 2 ∞0−5∞
5 7 ∞9 0 ∞
3 5 10 7 2 0
Exercise 25.3-2
This is only important when there are negative-weight cycles in the graph.
Using a dummy vertex gets us around the problem of trying to compute −∞+∞
to find ˆw. Moreover, if we had instead used a vertex vin the graph instead of
9

the new vertex s, then we run into trouble if a vertex fails to be reachable from v.
Exercise 25.3-3
If all the edge weights are nonnegative, then the values computed as the
shortest distances when running Bellman-Ford will be all zero. This is because
when constructing G0on the first line of Johnson’s algorithm, we place an edge
of weight zero from sto every other vertex. Since any path within the graph
has no negative edges, its cost cannot be negative, and so, cannot beat the
trivial path that goes straight from sto any given vertex. Since we have that
h(u) = h(v) for every uand v, the reweighting that occurs only adds and sub-
tracts 0, and so we have that w(u, v) = ˆw(u, v)
Exercise 25.3-4
This doesn’t preserve shortest paths. Suppose we have a graph with vertices
a, b, c, d, e, and fand edges (a, b),(b, c),(c, d),(d, e),(a, e),(a, f ) with weights -1,
-1, -1, -1, -1, 1, and -2. Professor Greenstreet would add 2 to every edge weight
in the graph. Originally, the shortest path from ato ewent through vertices b,
c, and d. With the added weight, the new shortest path goes directly from ato
e. Thus, property 1 of ˆwis violated.
Exercise 25.3-5
By lemma 25.1, we have that the total weight of any cycles is unchanged as
a result of the reweighting procedure. This can be seen in a way similar to how
the last claim of lemma 25.1 was proven. Namely, we consider the cycle c as
a path that has the same starting and ending vertices, so, by the first half od
lemma 25.1, we have that
ˆw(c) = w(c) + h(v0)−h(vk) = w(c)=0
This means that in the reweighted graph, we still have that the same cycle as
before had a total weight of zero. Since there are no longer any negative weight
edges after we reweight, this is precicely the second property of the reweighting
procedure shown in the section. Since we have that the sum of all the edge
weights in cis still equal to zero, but each of them individually has a non-
negative weight, it must be the case that each of them individually is equal to
0.
Exercise 25.3-6
Let Ghave vertices a,b, and c, and edge (b, c) with weight 1, and let s=a.
When we try to compute ˆw(b, c), it is undefined because h(c) = h(b) = ∞. Now
suppose that Gis strongly connected, and further that there are no negative-
weight cycles. Since every vertex is reachable from every other, his well-defined
10

for any choice of source vertex. We need only check that ˆwsatisfies properties
1 and 2. For the first property, let p=hu=v0, v1, . . . , vk=vibe a shortest
path from uto vusing the weight function w. Then we have
ˆw(p) =
k
X
i=1
ˆw(vi−1, vi)
=
k
X
i=1
w(vi−1, vi) + h(vi−1)−h(vi)
= k
X
i=1
w(vi−1, vi)!+h(u)−h(v)
=w(p) + h(u)−h(v).
Since h(u) and h(v) are independent of p, we must have that wminimizes
w(p) if and only if ˆwminimizes ˆw(p). For the second property, the triangle in-
equality tells us that for any vertices v, u ∈Vwe have δ(v, u)≤δ(v, z)+w(z, u).
Thus, if we define h(u) = δ(v, u) then we have ˆw(z, u) = w(z, u) + h(z)−h(u)≥
0.
Problem 25-1
a. We can update the transitive closure in time O(V2) as follows. Suppose that
we add the edge (x1, x2). Then, we will consider every pair of vertices (u, v).
In order to of created a path between them, we would need some part of that
path that goes from uto x1and some second part of that path that goes from
x2to v. This means that we add the edge (u, v) to the transitive closure if
and only if the transitive closure contains the edges (u, x1) and (x2, v). Since
we only had to consider every pair of vertices once, the runtime of this update
is only O(V2).
b. Suppose that we currently have two strongly connected components, each
of size |V|/2 with no edges between them. Then their transitive closures
computed so far will consist of two complete directed graphs on |V|/2 vertices
each. So, there will be a total of |V|2/2 edges adding the number of edges in
each together.
Then, we add a single edge from one component to the other. This will
mean that every vertex in the component the edge is coming from will have
an edge going to every vertex in the component that the edge is going to.
So, the total number of edges after this operation will be |V|/2 + |V|/4. So,
the number of edges increased by |V|/4. Since each time we add an edge, we
need to use at least constant time, since there is no cheap way to add many
edges at once, the total amount of time needed is Ω(|V|2).
c. We will have each vertex maintain a tree of vertices that have a path to it and
a tree of vertices that it has a path to. The second of which is the transitive
11

closure at each step. Then, upon inserting an edge, (u,v), we will look at
successive ancestors of u, and add vto their successor tree, just past u. If we
ever don’t insert an edge when doing this, we can stop exploring that branch
of the ancestor tree. Similarly, we keep doing this for all of the ancestors of
v. Since we are able to short circuit if we ever notice that we have already
added an edge, we know that we will only ever reconsider the same edge at
most ntimes, and, since the number of edges is O(n2), the total runtime is
O(n3).
Problem 25-2
a. As in problem 6-2, the runtimes for a d-ary min heap are the same as
for a d-ary max heap. The runtimes of INSERT, EXTRACT-MIN, and
DECREASE-KEY are O(logdn), O(dlogdn), and O(logdn) respectively. If
d= Θ(nα) these become O(1/α), O(nα/α), and O(1/α) respectively. The
amortized costs for these operations in a FIbonacci heap are O(1), O(lg n),
and O(1) respectively.
b. Choose d=nε. Then implement Dijkstra’s algorithm using a d-ary min-
heap. The analysis from part (a) tells us that the runtime will be O(n/ε +
2n1+ε/ε) = O(n1+ε) = O(E).
c. Run the algorithm from part (b) once for each vertex of the graph.
d. Using the methods from section 25.3, create the graph G0with all nonnegative
edge weights using the weight function ˆw, proceed as in part (c), then convert
back to the original weight function.
12
Chapter 26
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 26.1-1
To see that the networks have the same maximum flow, we will show that
every flow through one of the networks corresponds to a flow through the other.
First, suppose that we have some flow through the network befor applying the
splitting procedure to the anti-symmetric edges. Since we are only changing
one of any pair of anti-symmetric edges, for any edge that is unchanged by the
splitting, we just have an identical flow going through those edges. Suppose
that there was some edge (u, v) that was split because it had an anti-symmetric
edge, and we had some flow, f(u, v) in the original graph. Since the capacity of
both of the two edges that are introduced by the splitting of that edge have the
same capacity, we can set f0(u, v) = f0(u, x) = f0(x, v). By constructing the
new flow in this manor, we have an identical total flow, and we also still have a
valid flow.
Similarly, suppose that we had some flow f0on the graph with split edges,
then, for any triple of vertices u, x, v that correspond to a split edge, we must
have that f0(u, x) = f0(x, v) because the only edge into xis (u, x) and the only
edge out of xis (x, v), and the net flow into and out of each vertex must be
zero. We can then just set the flow on the unsplit edge equal to the common
value that the flows on (u, x) and (x, v) have. Again, since we handle this on an
edge by edge basis, and each substitution of edges maintains the fact that it is
a flow of the same total, we have that the end result is also a valid flow of the
same total value as the original.
Since we have shown that any flow in one digraph can be translated into a
flow of the same value in the other, we can translate the maximum value flow
for one of them to get that it’s max value flow is ≤to that of the other, and do
it in the reverse direction as well to achieve equality.
Exercise 26.1-2
The capacity constraint remains the same. We modify flow conservation
so that each siand timust satisfy the “flow in equals flow out” constraint,
and we only exempt sand t. We define the value of a flow in the multiple-
source, multiple-sink problem to be
Pm
i=1 Pv∈Vf(si, v)−Pv∈Vf(v, si)
. Let
fi=Pv∈Vf(si, v)−Pv∈Vf(v, si). In the single-source flow network, set
1

f(s, si) = fi. This satisfies the capacity constraint and flow conservation, so it
is a valid assignment. The flow for the multiple-source network in this case is
|f1+f2+··· +fm|. In the single-source case, since there are no edges coming
into s, the flow is Pm
i=1 f(s, si). Since f(s, si) is positive and equal to fi, they
are equivalent.
Exercise 26.1-3
Suppose that we are in the situation posed by the question, that is, that
there is some vertex uthat lies on no path from sto t. Then, suppose that we
have for some vertex v, either f(v, u) or f(u, v) is nonzero. Since flow must be
conserved at u, having any positive flow either leaving or entering u, there is
both flow leaving and entering. Since udoesn’t lie on a path from sto t, we
have that there are two cases, either there is no path from sto uor(possibly
and) there is no path from uto t. If we are in the second case, we construct
a path with c0=u, and ci+1 is an successor of cithat has f(ci, ci+1) being
positive. Since the only vertex that is allowed to have a larger flow in than flow
out is t, we have that this path could only ever terminate if it were to reach
t, since each vertex in the path has some positive flow in. However, we could
never reach tbecause we are in the case that there is no path from uto t. If
we are in the former case that there is no path from sto u, then we similarly
define c0=u, however, we let ci+1 be any vertex so that f(ci+1, ci) is nonzero.
Again, this sequence of vertices cannot terminate since we could never arrive at
having sas one of the vertices in the sequence.
Since in both cases, we an always keep extending the sequence of vertices,
we have that it must repeat itself at some point. Once we have some cycle of
vertices, we can decrease the total flow around the cycle by an amount equal
to the minimum amount of flow that is going along it without changing the
value of the flow from sto tsince neither of those two vertices show up in the
cycle. However, by decreasing the flow like this, we decrease the total number
of edges that have a positive flow. If there is still any flow passing though u,
we can continue to repeat this procedure, decreasing the number of edges with
a positive flow by at least one. Since there are only finitely many vertices, at
some point we need to have that there is no flow passing through u. The flow
obtained after all of these steps is the desired maximum flow that the problem
asks for.
Exercise 26.1-4
Since f1and f2are flows, they satisfy the capacity constraint, so we have
0≤αf1(u, v)+(1−α)f2(u, v)≤αc(u, v)+(1−α)c(u, v) = c(u, v), so the new flow
satisfies the capacity constraint. Further, f1and f2satisfy flow conservation,
2

so for all u∈V− {s, t}we have
X
v∈V
αf1(v, u) + (1 −α)f2(v, u) = αX
v∈V
f1(v, u) + (1 −α)X
v∈V
f2(v, u)
=αX
v∈V
f1(u, v) + (1 −α)X
v∈V
f2(u, v)
=X
v∈V
αf1(u, v) + (1 −α)f2(u, v).
Therefore the flows form a convex set.
Exercise 26.1-5
A linear programming problem consists of a set of variables, a linear func-
tion of those variables that needs to be maximized, and a a set of constraints.
Our variables xewill be the amount of flow across each edge e. The function
to maximize is Peleaving sxe−Peentering sxe. The sum of these flows is
exactly equal to the value of the flow from sto t. Now, we consider constraints.
There are two types of constraints, capacity constraints and flow constraints.
The capacity constraints are just xe≤c(e) where ceis the capacity of edge
e. The flow constraints are that Peleaving vxe−Peentering vxe= 0 for all
vertices v6=s, t. Since this linear program captures all the same constraints,
and wants to maximize the same thing, it is equivalent to the max flow problem.
Exercise 26.1-6
Use the map to create a graph where vertices represent street intersections
and edges represent streets. Define c(u, v) = 1 for all edges (u, v). Since a
street can be traversed, start off by creating a directed edge in each direction,
then make the transformation to a flow problem with no antiparallel edges as
described in the section. Make the home the source and the school the sink. If
there exist at least two distinct paths from source to sink then the flow will be
at least 2 because we could assign f(u, v) = 1 for each of those edges. However,
if there is at most one distinct path from source to sink then there must exist a
bridge edge (u, v) whose removal would disconnect sfrom t. Since c(u, v) = 1,
the flow into uis at most 1. We may assume there are no edges into sor out
from t, since it doesn’t make sense to return home or leave school. By flow
conservation, this implies that f=Pv∈Vf(s, v)≤1. Thus, determining the
maximum flow tells the Professor whether or not his children can go to the same
school.
Exercise 26.1-7
We can capture the vertex constraints by splitting out each vertex into two,
where the edge between the two vertices is the vertex capacity. More formally,
3

our new flow network will have vertices {0,1}×V. It has an edge between 1 ×v
and 0 ×uif there is an edge (v, u) in the original graph, the capacity of such
an edge is just c(v, u). The edges of the second kind that the new flow network
will have are from 0 ×vto 1 ×vfor every vwith capacity l(v). This new flow
network will have 2|V|vertices and have |V|+|E|edges. Lastly, we can see that
this network does capture the idea that the vertices have capacities l(v). This
is because any flow that goes through vin the original graph must go through
the edge (0 ×v, 1×v) in the new graph, in order to get from the edges going
into vto the edges going out of v.
Exercise 26.2-1
To see that equation (26.6) equals (26.7), we will show that the terms that
we are throwing into the sums are all zero. That is, we will show that if
v∈V\(V1∪V2), then f0(s, v) = f0(v, s) = 0. Since v6∈ V1, then there is
no edge from sto v, similarly, since v6∈ V2, there is no edge from vto s. This
means that there is no edge connecting sand vin any way. Since flow can only
pass along edges, we know that there can be no flow passing directly between s
and v.
Exercise 26.2-2
The flow across the cut is 11 + 1 + 7 + 4 −4 = 19. The capacity of the cut
is 16 + 4 + 7 + 4 = 31.
Exercise 26.2-3
If we perform a breadth first search where we consider the neighbors of a vertex
as they appear in the ordering {s, v1, v2, v3, v4, t}, the first path that we will
find is s, v1, v3, t. The min capacity of this augmenting path is 12, so we send 12
units along it. We perform a BFS on the resulting residual network. This gets
us the path s, v2, v4, t. The min capacity along this path is 4, so we send 4 units
along it. Then, the only path remaining in the residual network is {s, v2, v4, v3}
which has a min capacity of 7, since that’s all that’s left, we find it in our BFS.
Putting it all together, the total flow that we have found has a value of 23.
Exercise 26.2-4
A minimum cut corresponding to the maximum flow is S={s, v1, v2, v4}
and T={v3, t}. The augmenting path in part (c) cancels flow on edge (v3, v2).
Exercise 26.2-5
Since the only edges that have infinite value are those going from the super-
source or to the supersink, as long as we pick a cut that has the supersource and
all the original sources on one side, and the other side has the supersink as well
as all the original sinks, then it will only cut through edges of finite capacity.
Then, by Corollary 26.5, we have that the value of the flow is bounded above
4

by the value of any of these types of cuts, which is finite.
Exercise 26.2-6
Begin by making the modification from multi-source to single-source as done
in section 26.1. Next, create an extra vertex ˆsifor each iand place it between s
and si. Explicity, remove the edge from sto siand add edges (s, ˆsi) and ( ˆsi, si).
Similarly, create an extra vertex ˆ
tifor each vertex tiand place it between tand
ti. Remove the edges (ti, t) and add edges (ti,ˆ
ti) and (ˆ
ti, t). Assign c( ˆsi, si) = pi
and c(ti,ˆ
ti) = qi. If a flow which satisfies the constraints exists, it will assign
f( ˆsi, si) = pi. By flow conservation, this implies that Pv∈Vf(si, v) = pi. Sim-
ilarly, we must have f(ti,ˆ
ti) = qi, so by flow conservation this implies that
Pv∈Vf(v, ti) = qi.
Exercise 26.2-7
To check that fpis a flow, we make sure that it satisfies both the capacity
constraints and the flow constraints. First, the capacity constraints. To see this,
we recall our definition of cf(p), that is, it is the smallest residual capacity of
any of the edges along the path p. Since we have that the residual capacity is
always less than or equal to the initial capacity, we have that each value of the
flow is less than the capacity. Second, we check the flow constraints, Since the
only edges that are given any flow are along a path, we have that at each vertex
interior to the path, the flow in from one edge is immediately canceled by the
flow out to the next vertex in the path. Lastly, we can check that its value is
equal to cf(p) because, while smay show up at spots later on in the path, it
will be canceled out as it leaves to go to the next vertex. So, the only net flow
from sis the inital edge along the path, since it (along with all the other edges)
is given flow cf(p), that is the value of the flow fp.
Exercise 26.2-8
Paths chosen by the while loop of line 3 go from sto tand are simple because
capacities are alway nonnegative. Thus, no edge into swill ever appear on an
augmenting path, so such edges may as well never have existed.
Exercise 26.2-9
The augmented flow does satisfy the flow conservation property, since the
sum of flow into a vertex and out of a vertex can be split into two sums each,
one running over flow in fand the other running over flow in f0, since we have
the parts are equal separately, their sums are also equal.
The capacity constraint is not satisfied by this arbitrary augmentation of
flows. To see this, suppose we only have the vertices sand t, and have a single
edge from sto tof capacity 1. Then we could have a flow of value 1 from sto
5

t, however, augmenting this flow with itself ends up putting two units along the
edge from sto t, which is greater than the capacity we can send.
Exercise 26.2-10
Suppose we already have a maximum flow f. Consider a new graph Gwhere
we set the capacity of edge (u, v) to f(u, v). Run Ford-Fulkerson, with the mod-
ification that we remove an edge if its flow reaches its capacity. In other words,
if f(u, v) = c(u, v) then there should be no reverse edge appearing in residual
network. This will still produce correct output in our case because we never
exceed the actual maximum flow through an edge, so it is never advantageous
to cancel flow. The augmenting paths chosen in this modified version of Ford-
Fulkerson are precisely the ones we want. There are at most |E|because every
augmenting path produces at least one edge whose flow is equal to its capacity,
which we set to be the actual flow for the edge in a maximum flow, and our
modification prevents us from ever destroying this progress.
Exercise 26.2-11
To test edge connectivity, we will take our graph as is, pick an arbitrary s
to be our source for the flow network, and then, we will consider every possible
other selection of our sink t. For each of these flow networks, we will replace
each (undirected) edge in the original graph with a pair of anti-symmetric edges,
each of capacity 1.
We claim that the minimum value of all of these different considered flow
networks’ maximum flows is indeed the edge connectivity of the original graph.
Consider one particular flow network, that is, a particular choice for t. Then,
the value of the maximum flow is the same as the value of the minimum cut
separating sand t. Since each of the edges have a unit capacity, the value of
any cut is the same as the number of edges in the original graph that are cut
by that particular cut. So, for this particular choice of t, we have that the
maximum flow was the number of edges needed to be removed so that sand
tare in different components. Since our end goal is to remove edges so that
the graph becomes disconnected, this is why we need to consider all n−1 flow
networks. That is, it may be much harder for some choices of tthan others to
make sand tend up in different components. However, we know that there is
some vertex that has to be in a different component than safter removing the
smallest number of edges required to disconnect the graph. So, this value for
the number of edges is considered when we have tbe that vertex.
Exercise 26.2-12
Since every vertex lies on some path starting from sthere must exist a cycle
which contains the edge (v, s). Use a depth first search to find such a cycle with
no edges of zero flow. Such a cycle must exist since fsatisfies conservation of
flow. Since the graph is connected this takes O(E). Then decrement the flow
6

of every edge on the cycle by 1. This preserves the value of the flow so it is
still maximal. It won’t violate the capacity constraint because f > 0 on every
edge of the cycle prior to decrementing. Finally, flow conservation isn’t violated
because we decrement both an incoming and outgoing edge for each vertex on
the cycle by the same amount.
Exercise 26.2-13
Suppose that your given flow network contains |E|edges, then, we were to
modify all of the capacities of the edges by taking any edge that has a postive
capacity and increasing its capacity by 1
|E|+1 . Doing this modification can’t get
us a set of edges for a min cut that isn’t also a min cut for the unmodified graph
because the difference between the value of the min cut and the next lowest cut
vale was at least one because all edge weights were integers. This means that
the new min cut value is going to be at most the original plus |E|
|E|+1 . Since this
value is more than the second smallest valued cut in the original flow network,
we know that the choice of cuts we make in the new flow network is also a
minimum cut in the original. Lastly, since we added a small constant amount
to the value of each edge, our minimum cut would have the smallest possible
number of edges, otherwise one with fewer would have a smaller value.
Exercise 26.3-1
First, we pick an augmenting path that passes through vertices 1 and 6. Then,
we pick the path going through 2 and 8. Then, we pick the path going through
3 and 7. Then, the resulting residual graph has no path from sto t. So, we
know that we are done, and that we are pairing up vertices (1,6),(2,8),and
(3,7). This number of unit augmenting paths agrees with the value of the cut
where you cut the edges (s, 3),(6, t),and (7, t).
Exercise 26.3-2
We proceed by induction on the number of iterations of the while loop of
Ford-Fulkerson. After the first iteration, since conly takes on integer values
and (u, v).f is set to 0, cfonly takes on integer values. Thus, lines 7 and 8 of
Ford-Fulkerson only assign integer values to (u, v).f . Assume that (u, v).f ∈Z
for all (u, v) after the nth iteration. On the (n+ 1)st iteration cf(p) is set to the
minimum of cf(u, v) which is an integer by the induction hypothesis. Lines 7
and 8 compute (u, v).f or (v, u).f. Either way, these the the sum or difference
of integers by assumption, so after the (n+ 1)st iteration we have that (u, v).f
is an integer for all (u, v)∈E. Since the value of the flow is a sum of flows of
edges, we must have |f| ∈ Zas well.
Exercise 26.3-3
The length of an augmenting path can be at most 2 min{|L|,|R|} + 1. To
7

see that this is the case, we can construct an example which has an augmenting
path of that length.
Suppose that the vertices of Lare {`1, `2,...`|L|}, and of Rare {r1, r2, . . . , r|R|}.
For convenience, we will call m= min{|L|,|R|}. Then, we will place the edges
{(`m, rm−1),(`1, r1),(`1, rm)} ∪ ∪i=m−1
i=2 {(`i, ri),(`i, ri−1)}
Then, after augmenting with the shortest length path min{|L|,|R|}−1 times,
we could end up having sent a unit flow along {(`i, ri)}i=1,...,m−1. At this point,
there is only a single augmenting path, namely, {s, `m, rm−1, `m−1, rm−2, . . . , `2, r1, `1, rm, t}.
This path has the length 2m+ 1.
It is clear that any simple path must have length at most 2m+ 1, since the
path must start at s, then alternate back and forth between Land R, and then
end at t. Since augmenting paths must be simple, it is clear that our bound
given for the longest augmenting path is tight.
Exercise 26.3-4
First suppose there exists a perfect matching in G. Then for any subset
A⊆L, each vertex of Ais matched with a neighbor in R, and since it is a
matching, no two such vertices are matched with the same vertex in R. Thus,
there are at least |A|vertices in the neighborhood of A. Now suppose that
|A|≤|N(A)|for all A⊆L. Run Ford-Fulkerson on the corresponding flow
network. The flow is increased by 1 each time an augmenting path is found, so
it will suffice to show that this happens |L|times. Suppose the while loop has
run fewer than Ltimes, but there is no augmenting path. Then fewer than L
edges from Lto Rhave flow 1. Let v1∈Lbe such that no edge from v1to
a vertex in Rhas nonzero flow. By assumption, v1has at least one neighbor
v0
1∈R. If any of v1’s neighbors are connected to tin Gfthen there is a path,
so assume this is not the case. Thus, there must be some edge (v2, v1) with
flow 1. By assumption, N({v1, v2})≥2, so there must exist v0
26=v0
1such that
v0
2∈N({v1, v2}). If (v0
2, t) is an edge in the residual network we’re done since
v0
2must be a neighbor of v2, so s, v1, v0
1, v2, v0
2, t is a path in Gf. Otherwise v0
2
must have a neighbor v3∈Lsuch that (v3, v0
2) is in Gf. Specifically, v36=v1
since (v3, v0
2) has flow 1, and v36=v2since (v2, v0
1) has flow 1, so no more flow
can leave v2without violating conservation of flow. Again by our hypothesis,
N({v1, v2, v3})≥3, so there is another neighbor v0
3∈R.
Continuing in this fashion, we keep building up the neighborhood v0
i, expand-
ing each time we find that (v0
i, t) is not an edge in Gf. This cannot happen L
times, since we have run the Ford-Fulkerson while-loop fewer than |L|times, so
there still exist edges into tin Gf. Thus, the process must stop at some vertex
v0
k, and we obtain an augmenting path s, v1, v0
1, v2, v0
2, v3, . . . , vk, v0
k, t, contra-
dicting our assumption that there was no such path. Therefore the while loop
runs at least |L|times. By Corollary 26.3 the flow strictly increases each time
by fp. By Theorem 26.10 fpis an integer. In particular, it is equal to 1. This
implies that |f|≥|L|. It is clear that |f|≤|L|, so we must have |f|=|L|. By
8

Corollary 26.11 this is the cardinality of a maximum matching. Since |L|=|R|,
any maximum matching must be a perfect matching.
Exercise 26.3-5
We convert the bipartite graph into a flow problem by making a new vertex
for the source which has an edge of unit capacity going to each of the vertices
in L, and a new vertex for the sink that has an edge from each of the vertices in
R, each with unit capacity. We want to show that the number of edge between
the two parts of the cut is at least L, this would get us by the max-flow-min-
cut theorem that there is a flow of value at least |L|. The, we can apply the
integrality theorem that all of the flow values are integers, meaning that we are
selecting |L|disjoint edges between Land R.
To see that every cut must have capacity at lest |L|, let S1be the side of the
cut containing the source and let S2be the side of the cut containing the sink.
Then, look at L∩S1. The source has an edge going to each of L∩(S1)c, and
there is an edge from R∩S1to the sink that will be cut. This means that we
need that there are at least |L∩S1|−|R∩S1|many edges going from L∩S1|to
R∩S2. If we look at the set of all neighbors of L∩S1, we get that there must
be at least the same number of neighbors in R, because otherwise we could sum
up the degrees going from L∩S1to Ron both sides, and get that some of the
vertices in Rwould need to have a degree higher than d. This means that the
number of neighbors of L∩S1is at least L∩S1, but we have that they are in
S1, but there are only |R∩S1|of those, so, we have that the size of the set of
neighbors of L∩S1that are in S2is at least |L∩S1|−|R∩S1|. Since each of these
neighbors has an edge crossing the cut, we have that the total number of edges
that the cut breaks is at least (|L|−|L∩S1|)+(|L∩S1|−|R∩S1|)+|R∩S1|=|L|.
Since each of these edges is unit valued, the value of the cut is at least |L|.
Exercise 26.4-1
When we run INITIALIZE-PREFLOW(G,s), s.e is zero prior to the for loop
on line 7. Then, for each of the vertices that shas an edge to, we decrease the
value of s.e by the capacity of that edge. This means that at the end, s.e is
equal to the negative of the sum of all the capacities coming out of s. This is
then equal to the negative of the cut value of the cut that puts son one side,
and all the other vertices on the other. The negative of the value of the min cut
is larger or equal to the negative of the value of this cut. Since the value of the
max flow is the value of the min cut, we have that the negative of the value of
the max flow is larger or equal to s.e.
Exercise 26.4-2
We must select an appropriate data structure to store all the information
which will allow us to select a valid operation in constant time. To do this, we
will need to maintain a list of overflowing vertices. By Lemma 26.14, a push or
9

a relabel operation always applies to an overflowing vertex. To determine which
operation to perform, we need to determine whether u.h =v.h + 1 for some
v∈N(u). We’ll do this by maintaining a list u.high of all neighbors of uin Gf
which have height greater than or equal to u. We’ll update these attributes in
the PUSH and RELABEL functions. It is clear from the pseudocode given for
PUSH that we can execute it in constant time, provided we have maintain the
attributes δf(u, v), u.e,cf(u, v), (u, v).f, and u.h. Each time we call PUSH(u, v)
the result is that uis no longer overflowing, so we must remove it from the list.
Maintain a pointer u.overflow to u’s position in the overflow list. If a vertex u
is not overflowing, set u.overf low =N IL. Next, check if vbecame overflowing.
If so, set v.overflow equal to the head of the overflow list. Since we can update
the pointer in constant time and delete from a linked list given a pointer to the
element to be deleted in constant time, we can maintain the list in O(1). The
RELABEL operation takes O(V) becaue we need to compute the minimum v.h
from among all (u, v)∈Ef, and there could be |V| − 1 many such v. We will
also need to update u.high during RELABEL. When RELABEL(u) is called,
set u.high equal to the empty list and for each vertex vwhich is adjacent to u,
if v.h =u.h + 1, add uto the list v.high. Since this takes constant time per
adjacent vertex we can maintain the attribute in O(V) per call to relabel.
Exercise 26.4-3
To run RELABEL(u), we need to take the min a number of things equal to
the out degree of u(and so taking this min will take time proportional to the out
degree). This means that since each vertex will only be relabeled at most O(|V|)
many times, the total amount of work is on the order of |V|Pv∈Voutdeg(v).
But the sum of all the out degrees is equal to the number of edges, so, we have
the previous expression is on the order of |V||E|.
Exercise 26.4-4
In the proof of 2 =⇒3 in Theorem 26.6 we obtain a minimum cut by letting
S={v∈V|there exists a path from sto vin Gf}and T=V−S. Given a
flow, we can form the residual graph in O(E). Then we just need to perform
a depth first search to find the vertices reachable from s. This can be done in
O(V+E), and since |E|≥|V| − 1 the whole procedure can be carried out in
O(E).
Exercise 26.4-5
First, construct the flow network for the bipartite graph as in the previous
section. Then, we relabel everything in L. Then, we push from every vertex in
Lto a vertex in R, so long as it is possible. keeping track of those that vertices
of Lthat are still overflowing can be done by a simple bit vector. Then, we
relabel everything in Rand push to the last vertex. Once these operations have
been done, The only possible valid operations are to relabel the vertices of L
10

that weren’t able to find an edge that they could push their flow along, so could
possibly have to get a push back from Rto L. This continues until there are no
more operations to do. This takes time of O(V(E+V)).
Exercise 26.4-6
The number of relabel operations and saturating pushes is the same as before.
An edge can handle at most knonsaturating pushes before it becomes saturated,
so the number of nonsaturating pushes is at most 2k|V||E|. Thus, the total num-
ber of basic operations is at most 2|V|2+ 2|V||E|+ 2k|V||E|=O(kV E).
Exercise 26.4-7
This won’t affect the asymptotic performance, in fact it will improve the
bound obtained in lemma 16.20 to be that no vertex will ever have a height
more than 2|V| − 3. Since this lemma was the source of all the bounds later,
they carry through, and are actually a little bit (not asymptotically) better
(lower).
To see that it won’t affect correctness of the algorithm. We notice that the
reason that we needed the height to be as high as it was was so that we could
consider all the simple paths from sto t. However, when we are done initializ-
ing, we have that the only overflowing vertices are the ones for which there is
an edge to them from s. Then, we only need to consider all the simple paths
from them to t, the longest such one involves |V| − 1 vertices, and, so, only
|V|−2 different edges, and so it only requires that there are |V|−2 differences
in heights, since the set {0,1,...,|V| − 3}has |V| − 2 different values, this is
possible.
Exercise 26.4-8
We’ll prove the claim by induction on the number of push and relabel op-
erations. Initially, we have u.h =|V|if u=sand 0 otherwise. We have
s.h − |V|= 0 ≤δf(s, s) = 0 and u.h = 0 ≤δf(u, t) for all u6=s, so the claim
holds prior to the first iteration of the while loop on line 2 of the GENERIC-
PUSH-RELABEL algorithm. Suppose that the properties have been maintained
thus far. If the next iteration is a nonsaturating push then the properties are
maintained because the heights and existence of edges in the residual network are
preserved. If it is a saturating push then edge (u, v) is removed from the residual
network, which increases both δf(u, t) and δf(u, s), so the properties are main-
tained regardless of the height of u. Now suppose that the next iteration causes
a relabel of vertex u. For all vsuch that (u, v)∈Efwe must have u.h ≤v.h.
Let v0= min{v.h|(u, v)∈Ef}. There are two cases to consider. First, sup-
pose that v0.h < |V|. Then after the relabeling we have u.h = 1 + v0.h ≤
1 + min(u,v)∈Efδf(v, t) = δf(u, t). Second, suppose that v0.h ≥ |V|. Then after
relabeling we have u.h = 1+v0.h ≤1+|V|+min(u,v)∈Efδf(v, s) = δf(u, s)+|V|
which implies that u.h − |V| ≤ δ)f(u, s). Therefore the GENERIC-PUSH-
11

RELABEL procedure maintains the desired properties.
Exercise 26.4-9
What we should do is to, for successive backwards neighborhoods of t, rela-
bel everything in that neighborhood. This will only take at most O(V E) time
(see 26.4-3). This also has the upshot of making it so that once we are done
with it, every vertex’s height is equal to the quantity δf(u, t). Then, since we
begin with equality, after doing this, the inductive step we had in the solution
to the previous exercise shows that this equality is preserved.
Exercise 26.4-10
Each vertex has maximum height 2|V|−1. Since heights don’t decrease, and
there are |V|−2 vertices which can be overflowing, the maximum contribution
of relabels to Φ over all vertices is (2|V| − 1)(|V| − 2). A saturating push from
uto vincreases Φ by at most v.h ≤2|V| − 1, and there are at most 2|V||E|
saturating pushes, so the total contribution over all saturating pushes to Φ is
at most (2|V| − 1)(2|V||E|). Since each nonsaturating push decrements Φ by
at least on and Φ must equal zero upon termination, we must have that the
number of nonsaturating pushes is at most
(2|V|−1)(|V|−2) + (2|V|−1)(2|V||E|)=4|V|2|E|+ 2|V|2−5|V|+ 3 −2|V||E|.
Using the fact that |E|≥|V| − 1 and |V| ≥ 4 we can bound the number of
saturating pushes by 4|V|2|E|.
Exercise 26.5-1
When we initialize the preflow, we have 26 units of flow leaving s. Then,
we consider v1since it is the first element in the Llist. When we discharge it,
we increase it’s height to 1 so that it can dump 12 of it’s excess along its edge
to vertex v3, to discharge the rest of it, it has to increase it’s height to |V|+ 1
to discharge it back to s. It was already at the front, so, we consider v2. We
increase its height to 1. Then, we send all of its excess along its edge to v4. We
move it to the front, which means we next consider v1, and do nothing because
it is not overflowing. Up next is vertex v3. After increasing its height to 1, it
can send all of its excess to t. This puts v3at the front, and we consider the
non-overflowing vertices v2and v1. Then, we consider v4, it increases its height
to 1, then sends 4 units to t. Since it still has an excess of 10 units, it increases
its height once again. Then it becomes valid for it to send flow back to v2or to
v3. It considers v4first because of the ordering of its neighbor list. This means
that 10 units of flow are pushed back to v2. Since v4.h increased, it moves to
the front of the list Then, we consider v2since it is the only still overflowing
vertex. We increase its height to 3. Then, it is overflowing by 10 so it increases
its height to 3 to send 6 units to v4. It’s height increased so it goes to the front
12

of the list. Then, we consider v4, which is overflowing. it increases its height to
3, then it sends 6 units to v3. Again, it goes to the front of the list. Up next is
v2which is not overflowing, v3which is, so it increases it’s height by 1 to send
4 units of flow to t. Then sends 2 units to v4after increasing in height. The
excess flow keeps bobbing around the four vertices, each time requiring them to
increase their height a bit to discharge to a neighbor only to have that neighbor
increase to discharge it back until v2has increased in height enough to send all
of it’s excess back to s, this completes and gives us a maximum flow of 23.
Exercise 26.5-2
Initially, the vertices adjacent to sare the only ones which are overflowing.
The implementation is as follows:
Algorithm 1 PUSH-RELABEL-QUEUE(G,s)
1: INITIALIZE-PREFLOW(G, s)
2: Initialize an empty queue q
3: for v∈G.Adj[s]do
4: q.push(v)
5: end for
6: while q.head 6=NIL do
7: DISCHARGE(q.head)
8: q.pop()
9: end while
Note that we need to modify the DISCHARGE algorithm to push vertices
vonto the queue if vwas not overflowing before a discharge but is overflowing
after one. Between lines 7 and 8 of DISCHARGE(u), add the line “if v.e > 0,
q.push(v).” This is an implementation of the generic push-relabel algorithm,
so we know it is correct. The analysis of runtime is almost identical to that
of Theorem 26.30. We just need to verify that there are at most |V|calls to
DISCHARGE between two consecutive relabel operations. Observe that after
calling PUSH(u, v), Corollary 26.28 tells us that no admissible edges are enter-
ing v. Thus, once vis put into the queue because of the push, it can’t be added
again until it has been relabeled. Thus, at most |V|vertices are added to the
queue between relabel operations.
Exercise 26.5-3
If we change relabel to just increment the value of u, we will not be ruining
the correctness of the Algorithm. This is because since it only applies when
u.h ≤v.h, we won’t be every creating a graph where hceases to be a height
function, since u.h will only ever be increasing by exactly one whenever relabel
is called, ensuring that u.h + 1 ≤v.h. This means that Lemmatae 26.15 and
26.16 will still hold. Even Corollary 26.21 holds since all it counts on is that
13

relabel causes some vertex’s hvalue to increase by at least one, it will still work
when we have all of the operations causing it to increase by exactly one. How-
ever, Lemma 26.28 will no longer hold. That is, it may require more than a
single relabel operation to cause an admissible edge to appear, if for example,
u.h was strictly less than the hvalues of all its neighbors. However, this lemma
is not used in the proof of Exercise 26.4-3, which bounds the number of relabel
operations. Since the number of relabel operations still have the same bound,
and we know that we can simulate the old relabel operation by doing (possibly
many) of these new relabel operations, we have the same bound as in the origi-
nal algorithm with this different relabel operation.
Exercise 26.5-4
We’ll keep track of the heights of the overflowing vertices using an array and
a series of doubly linked lists. In particular, let Abe an array of size |V|, and let
A[i] store a list of the elements of height i. Now we create another list L, which
is a list of lists. The head points to the list containing the vertices of highest
height. The next pointer of this list points to the next nonempty list stored in
A, and so on. This allows for constant time insertion of a vertex into A, and also
constant time access to an element of largest height, and because all lists are
doubly linked, we can add and delete elements in constant time. Essentially, we
are implementing the algorithm of Exercise 26.5-2, but with the queue replaced
by a priority queue with constant time operations. As before, it will suffice to
show that there are at most |V|calls to discharge between consecutive relabel
operations.
Consider what happens when a vertex vis put into the priority queue. There
must exist a vertex ufor which we have called PUSH(u, v). After this, no ad-
missible edge is entering v, so it can’t be added to the priority queue again
until after a relabel operation has occurred on v. Moreover, every call to DIS-
CHARGE terminates with a PUSH, so for every call to DISCHARGE there is
another vertex which can’t be added until a relabel operation occurs. After |V|
DISCHARGE operations and no relabel operations, there are no remaining valid
PUSH operations, so either the algorithm terminates, or there is a valid relabel
operation which is performed. Thus, there are O(V3) calls to DISCHARGE.
By carrying out the rest of the analysis of Theorem 26.30, we conclude that the
runtime is O(V3).
Exercise 26.5-5
Suppose to try and obtain a contradiction that there were some minimum
cut for which a vertex that had v.h > k were on the sink side of that cut.
For that minimum cut, there is a residual flow network for which that cut is
saturated. Then, if there were any vertices that were also on the sink side of the
cut which had an edge going to vin this residual flow network, since it’s hvalue
cannot be equal to k, we know that it must be greater than ksince it could be
only at most one less than v. We can continue in this way to let Sbe the set
14

of vertices on the sink side of the graph which have an hvalue greater than k.
Suppose that there were some simple path from a vertex in Sto s. Then, at
each of these steps, the height could only decrease by at most 1, since it cannot
get from above kto 0 withour going through k, we know that there is no path
in the residual flow network going from a vertex in Sto s. Since a minimal cut
corresponds to disconnected parts of the residual graph for a maximum flow,
and we know there is no path from Sto s, there is a minimum cut for which S
lies entirely on the source side of the cut. This was a contradiction to how we
selected v,and so have shown the first claim.
Now we show that after updating the h values as suggested, we are still left
with a height function. Suppose we had an edge (u, v) in the residual graph. We
knew from before that u, h ≤v.h + 1. However, this means that if u.h > k, so
must be v.h. So, if both were above k, we would be making them equal, causing
the inequality to still hold. Also, if just v.k were above k, then we have not
decreased it’s hvalue, meaning that the inequality also still must hold. Since we
have not changed the value of s.h, and t.h, we have all the required properties
to have a height function after modifying the hvalues as described.
Problem 26-1
a. This problem is identical to exercise 26.1-7.
b. Construct a vertex constrained flow network from the instance of the escape
problem by letting our flow network have a vertex (each with unit capacity)
for each intersection of grid lines, and have a bidirectional edge with unit
capacity for each pair of vertices that are adjacent in the grid. Then, we will
put a unit capacity edge going from sto each of the distinguished vertices,
and a unit capacity edge going from each vertex on the sides of the grid to t.
Then, we know that a solution to this problem will correspond to a solution
to the escape problem because all of the augmenting paths will be a unit flow,
because every edge has unit capacity. This means that the flows through the
grid will be the paths taken. This gets us the escaping paths if the total flow
is equal to m(we know it cannot be greater than mby looking at the cut
which has sby itself). And, if the max flow is less than m, we know that the
escape problem is not solvable, because otherwise we could construct a flow
with value mfrom the list of disjoint paths that the people escaped along.
Problem 26-2
a. Set up the graph G0as defined in the problem, give each edge capacity 1,
and run a maximum-flow algorithm. I claim that if (xi, yj) has flow 1 in the
maximum flow and we set (i, j) to be an edge in our path cover, then the
result is a minimum path cover. First observe that no vertex appears twice
in the same path. If it did, then we would have f(xi, yj) = f(xk, yj) for
some i6=k6=j. However, this contradicts the conservation of flow, since the
15

capacity leaving yjis only 1. Moreover, since the capacity from sto xiis 1,
we can never have two edges of the form (xi, yj) and (xi, yk) for k6=j. We
can ensure every vertex is included in some path by asserting that if there
is no edge (xi, yj) or (xj, yifor some j, then jwill be on a path by itself.
Thus, we are guaranteed to obtain a path cover. If there are kpaths in a
cover of nvertices, then they will consist of n−kedges in total. Given a
path cover, we can recover a flow by assigning edge (xi, yj) flow 1 if and
only if (i, j) is an edge in one of the paths in the cover. Suppose that the
maximum flow algorithm yields a cover with kpaths, and hence flow n−k,
but a minimum path cover uses strictly fewer than kpaths. Then it must use
strictly more than n−kedges, so we can recover a flow which is larger than
the one previously found, contradicting the fact that the previous flow was
maximal. Thus, we find a minimum path cover. Since the maximum flow
in the graph corresponds to finding a maximum matching in the bipartite
graph obtained by considering the induced subgraph of G0on {1,2, . . . , n},
section 26.3 tells us that we can find a maximum flow in O(V E).
b. This doesn’t work for directed graphs which contain cycles. To see this,
consider the graph on {1,2,3,4}which contains edges (1,2),(2,3),(3,1), and
(4,3). The desired output would be a single path 4,3,1,2 but flow which
assigns edges (x1, y2), (x2, y3), and (x3, y1) flow 1 is maximal.
Problem 26-3
a. Suppose to a contradiction that there were some Ji∈T, and some Ak∈Ri
so that Ak6∈ T. However, by the definition of the flow network, there is an
edge of infinite capacity going from Akto Jibecause Ak∈Ri. This means
that there is an edge of inifinite capacity that is going across the given cut.
This means that the capacity of the cut is infinite, a contradiction to the
given fact that the cut was finite capacity.
b. Let T=Pici. This is the total possible gross revenue if we accept all jobs
and hire all experts. In the cut that corresponds to this, we we need to pat
c. (Of course if he just wanted to get the book done he could of used Michelle
and I and not had to pay anything)
Problem 26-4
a. If there exists a minimum cut on which (u, v) doesn’t lie then the maximum
flow can’t be increased, so there will exist no augmenting path in the residual
network. Otherwise it does cross a minimum cut, and we can possibly in-
crease the flow by 1. Perform one iteration of Ford-Fulkerson. If there exists
an augmenting path, it will be found and increased on this iteration. Since
the edge capacities are integers, the flow values are all integral. Since flow
strictly increases, and by an integral amount each time, a single iteration of
16

the while loop of line 3 of Ford-Fulkerson will increase the flow by 1, which
we know to be maximal. To find an augmenting path we use a BFS, which
runs in O(V+E0) = O(V+E).
b. If the edge’s flow was already at least 1 below capacity then nothing changes.
Otherwise, find a path from sto twhich contains (u, v) using BFS in O(V+
E). Decrease the flow of every edge on that path by 1. This decreases total
flow by 1. Then run one iteration of the while loop of Ford-Fulkerson in
O(V+E). By the argument given in part a, everything is integer valued
and flow strictly increases, so we will either find no augmenting path, or will
increase the flow by 1 and then terminate.
Problem 26-5
a. Since the capacity of a cut is the sum of the capacity of the edges going
from a vertex on one side to a vertex on the other, it is less than or equal to
the sum of the capacities of all of the edges. Since each of the edges has a
capacity that is ≤C, if we were to replace the capacity of each edge with C,
we would only be potentially increasing the sum of the capacities of all the
edges. After so changing the capacities of the edges, the sum of the capacities
of all the edges is equal to C|E|, potentially an overestimate of the original
capacity of any cut, and so of the minimum cut.
b. Since the capacity of a path is equal to the minimum of the capacities of each
of the edges along that path, we know that any edges in the residual network
that have a capacity less than Kcannot be used in such an augmenting
path. Similarly, so long as all the edges have a capacity of at least K, then
the capacity of the augmenting path, if it is found, will be of capacity at
least K. This means that all that needs be done is remove from the residual
network those edges whose capacity is less than Kand then run BFS.
c. Since Kstarts out as a power of 2, and through each iteration of the while
loop on line 4, it decreases by a factor of two until it is less than 1. There
will be some iteration of that loop when K= 1. During this iteration, we
will be using any augmenting paths of capacity at least 1 when running the
loop on line 5. Since the original capacities are all integers, the augmenting
paths at each step will be integers, which means that no augmenting path
will have a capacity of less than 1. So, once the algorithm terminates, there
will be no more augmenting paths since there will be no more augmenting
paths of capacity at least 1.
d. Each time line 4 is executed we know that there is no augmenting path of
capacity at least 2K. To see this fact on the initial time that line 4 is executed
we just note that 2K= 2·2blg(C)c>2·2lg(C)−1= 2lg(C)=C. Then, since an
augmenting path is limited by the capacity of the smallest edge it contains,
and all the edges have a capacity at most C, no augmenting path will have
a capacity greater than that. On subsequent times executing line 4, the loop
17

of line 5 during the previous execution of the outer loop will of already used
up and capacious augmenting paths, and would only end once there are no
more.
Since any augmenting path must have a capacity of less than 2K, we can
look at each augmenting path p, and assign to it an edge epwhich is any
edge whose capacity is tied for smallest among all the edges along the path.
Then, removing all of the edges epwould disconnect the residual network
since every possible augmenting path goes through one of those edge. We
know that there are at most |E|of them since they are a subset of the edges.
We also know that each of them has capacity at most 2Ksince that was the
value of the augmenting path they were selected to be tied for cheapest in.
So, the total cost of this cut is 2K|E|.
e. Each time that the inner while loop runs, we know that it adds an amount
of flow that is at least K, since that’s the value of the augmenting path. We
also know that before we start that while loop, there is a cut of cost ≤2K|E|.
This means that the most flow we could possibly add is 2K|E|. Combining
these two facts, we get that the most cuts possible is 2K|E|
K= 2|E| ∈ O(|E|).
f. We only execute the outermost for loop lg(C) many times since lg(2blg(C)c)≤
lg(C). The inner while loop only runs O(|E|) many times by the previous
part. Finally, every time the inner for loop runs, the operation it does can
be done in time O(|E|) by part b. Putting it all together, the runtime is
O(|E|2lg(C)).
Problem 26-6
a. Suppose Mis a matching and Pis an augmenting path with respect to M.
Then Pconsists of kedges in M, and k+ 1 edges not in M. This is because
the first edge of Ptouches an unmatched vertex in L, so it cannot be in
M. Similary, the last edge in Ptouches an unmatched vertex in R, so the
last edge cannot be in M. Since the edges alternate being in or not in M,
there must be exactly one more edge not in Mthan in M. This implies that
|M⊕P|=|M|+|P| − 2k=|M|+ 2k+ 1 −2k=|M|+ 1 since we must
remove each edge of Mwhich is in Pfrom both Mand P. Now suppose
P1, P2, . . . , Pkare veretx-disjoint augmenting paths with respect to M. Let
kibe the number of edges in Piwhich are in M, so that |Pi|= 2k+i+ 1.
Then we have
M⊕(P1∪P2∪. . .∪Pk) = |M|+|P1|+. . .+|Pk|−2k1−2k2−. . .−2kk=|M|+k.
To see that we in fact get a matching, suppose that there was some vertex v
which had at least 2 incident edges eand e0. They cannot both come from
M, since Mis a matching. They cannot both come from Psince Pis simple
and every other edge of Pis removed. Thus, e∈Mand e0∈P\M. However,
if e∈Mthen e∈P, so e /∈M⊕P, a contradiction. A similar argument
gives the case of M⊕(P1∪. . . ∪Pk).
18

b. Suppose some vertex in G0has degree at least 3. Since the edges of G0
come from M⊕M∗, at least 2 of these edges come from the same matching.
However, a matching never contains two edges with the same endpoint, so
this is impossible. Thus every vertex has degree at most 2, so G0is a disjoint
union of simple paths and cycles. If edge (u, v) is followed by edge (z, w) in
a simple path or cycle then we must have v=z. Since two edges with the
same endpoint cannot appear in a matching, they must belong alternately to
Mand M∗. Since edges alternate, every cycle has the same number of edges
in each matching and every path has at most one more edge in one matching
than in the other. Thus, if |M| ≤ |M∗|there must be at least |M∗|−|M|
vertex-disjoint augmenting paths with respect to M.
c. Every vertex matched by Mmust be incident with some edge in M0. Since
Pis augmenting with respect to M0, the left endpoint of the first edge of P
isn’t incident to a vertex touched by an edge in M0. In particular, Pstarts
at a vertex in Lwhich is unmatched by Msince every vertex of Mis incident
with an edge in M0. Since Pis vertex disjoint from P1, P2, . . . , Pk, any edge
of Pwhich is in M0must in fact be in Mand any edge of Pwhich is not
in M0cannot be in M. Since Phas edges alternately in M0and E−M0,
Pmust in fact have edges alternately in Mand E−M. Finally, the last
edge of Pmust be incident to a vertex in Rwhich is unmatched by M0. Any
vertex unmatched by M0is also unmatched by M, so Pis an augmenting
path for M.Pmust have length at least lsince lis the length of the shorest
augmenting path with respect to M. If Phad length exactly lthen this would
contradict the fact that P1∪. . .∪Pkis a maximal set of vertex disjoing paths
of length lbecause we could add Pto the set. Thus Phas more than ledges.
d. Any edge in M⊕M0is in exactly one of Mor M0. Thus, the only possible
contributing edges from M0are from P1∪. . . ∪Pk. An edge from Mcan
contribute if and only if it is not in exactly one of Mand P1∪. . . ∪Pk,
which means it must be in both. Thus, the edges from Mare redundant so
M⊕M0= (P1∪. . . ∪Pk) which implies A= (P1∪. . . ∪Pk)⊕P.
Now we’ll show that Pis edge disjoint from each Pi. Suppose that an edge
eof Pis also an edge of Pifor some i. Since Pis an augmenting path with
respect to M0, either e∈M0or e∈E−M0. Suppose e∈M0. Since Pis
also augmenting with respect to M, we must have e∈M. However, if eis in
Mand M0then ecannot be in any of the Pi’s by the definition of M0. Now
suppose e∈E−M0. Then e∈E−Msince Pis augmenting with respect to
M. Since eis an edge of Pi,e∈E−M0implies that e∈M, a contradiction.
Since Phas edges alternately in M0and E−M0and is edge disjoint from
P1∪. . . ∪Pk,Pis also an augmenting path for M, which implies |P| ≥ l.
Since every edge in Ais disjoint we conclude that |A| ≥ (k+ 1)l.
e. Suppose M∗is a matching with strictly more than |M|+|V|/(l+ 1) edges.
By part b there are strictly more than |V|/(l+ 1) vertex-disjoint augmenting
paths with respect to M. Each one of these contains at least ledges, so
19
it is incident on l+ 1 vertices. Since the paths are vertex disjoint, there
are strictly more than |V|(l+ 1)/(l+ 1) distict vertices incident with these
paths, a contradiction. Thus, the size of the maximum matching is at most
|M|+|V|/(l+ 1).
f. Consider what happens after interation number p|V|. Let M∗be a maximal
matching in G. Then |M∗| ≥ |M|so by part b, M⊕M∗contains at least
|M∗| − |M|vertex disjoing augmenting paths with respect to M. By part
c, each of these is also a an augmenting path for M. Since each has lenght
p|V|, there can be at most p|V|such paths, so |M∗|−|M| ≤ p|V|. Thus,
only p|V|additional iterations of the repeat loop can occur, so there are at
most 2p|V|iterations in total.
g. For each unmatched vertex in Lwe can perform a modified BFS to find the
length of the shortest path to an unmatched vertex in R. Modify the BFS
to ensure that we only traverse an edge if it causes the path to alternate
between an edge in Mand an edge in E−M. The first time an unmatched
vertex in Ris reached we know the length kof a shortest augmenting path.
We can use this to stop our search early if at any point we have traversed
more than that number of edges. To find disjoint paths, start at the vertics
of Rwhich were found at distance kin the BFS. Run a DFS backwards
from these, which maintains the property that the next vertex we pick has
distance one fewer, and the edges alternate between being in Mand E−M.
As we build up a path, mark the vertices as used so that we never traverse
them again. This takes O(E), so by part fthe total runtime is O(√V E).
20
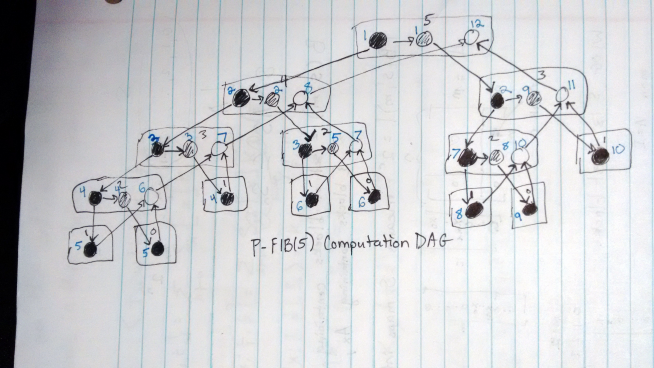
Chapter 27
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 27.1-1
This modification is not going to affect the asymptotic values of the span
work or parallelism. All it will do is add an amount of overhead that wasn’t
there before. This is because as soon as the F IB(n−2) is spawned the spawn-
ing thread just sits there and waits, it does not accomplish any work while it
is waiting. It will be done waiting at the same time as it would of been before
because the F IB(n−2) call will take less time, so it will still be limited by the
amount of time that the F IN(n−1) call takes.
Exercise 27.1-2
The computation dag is given in the image below. The blue numbers by
each strand indicate the time step in which it is executed. The work is 29, span
is 10, and parallelism is 2.9.
Exercise 27.1-3
1

Suppose that there are xincomplete steps in a run of the program. Since
each of these steps causes at least one unit of work to be done, we have that
there is at most (T1−x) units of work done in the complete steps. Then, we
suppose by contradiction that the number of complete steps is strictly greater
than b(T1−x)/P c. Then, we have that the total amount of work done during the
complete steps is P·(b(T1−x)/P c+1) = Pb(T1−x)/P c+P= (T1−x)−((T1−x)
mod P) + P > T1−x. This is a contradiction because there are only (T1−x)
units of work done during complete steps, which is less than the amount we
would be doing. Notice that since T∞is abound on the total number of both
kinds of steps, it is a bound on the number of incomplete steps, x , so,
TP≤ b(T1−x)/P c+x≤ b(T1−T∞)/P c+T∞
Where the second inequality comes by noting that the middle expression, as a
function of xis monotonically increasing, and so is bounded by the largest value
of xthat is possible, namely T∞.
Exercise 27.1-4
The computation is given in the image below. Let vertex uhave degree k,
and assume that there are mvertices in each vertical chain. Assume that this
is executed on kprocessors. In one execution, each strand from among the k
on the left is executed concurrently, and then the mstrands on the right are
executed one at a time. If each strand takes unit time to execute, then the total
computation takes 2mtime. On the other hand, suppose that on each time step
of the computation, k−1 strands from the left (descendents of u) are executed,
and one from the right (a descendent of v), is executed. If each strand take
unit time to executed, the total computation takes m+m/k. Thus, the ratio
of times is 2m/(m+m/k)=2/(1 + 1/k). As kgets large, this approaches 2 as
desired.
2

Exercise 27.1-5
The information from T10 applied to equation (27.5) give us that
42 ≤T1−T∞10 + T∞
which tell us that
420 ≤T1+ 9T∞
Subtracting these two equations, we have that 100 ≤8T∞.
If we apply the span law to T64, we have that 10 ≥T∞. Applying the work
law to our measurement for T4gets us that 320 ≥T1. Now, looking at the result
of applying (27.5) to the value of T10, we get that
420 ≤T1+ 9T∞≤320 + 90 = 410
a contradiction. So, one of the three numbers for runtimes must be wrong.
However, computers are complicated things, and its difficult to pin down what
can affect runtime in practice. It is a bit harsh to judge professor Karan too
poorly for something that may of been outside her control (maybe there was just
a garbage collection happening during one of the measurements, throwing it off).
Exercise 27.1-6
We’ll parallelize the for loop of lines 6-7 in a way which won’t incur races.
With the algorithm P−P ROD given below, it will be easy to rewrite the code.
For notation, let aidenote the ith row of the matrix A.
Algorithm 1 P-PROD(a,x,j,j’)
1: if j== j0then
2: return a[j]·x[j]
3: end if
4: mid = jj+j0
2k
5: a’ = spawn P-PROD(a,x,j,mid)
6: x’ = P-PROD(a,x,mid+1,j’)
7: sync
8: return a’+x’
Exercise 27.1-7
The work is unchanged from the serial programming case. Since it is flipping
Θ(n2) many entries, it does Θ(n2) work. The span of it is Θ(lg(n)) this is be-
cause each of the parallel for loops can have its children spawned in time lg(n),
so the total time to get all of the constant work tasks spawned is 2 lg(n)∈Θ(lg).
3

Algorithm 2 MAT-VEC(A,x)
1: n=A.rows
2: let ybe a new vector of length n
3: parallel for i= 1 to ndo
4: yi= 0
5: end
6: parallel for i= 1 to ndo
7: yi= P-PROD(ai, x, 1, n)
8: end
9: return y
Since the work of each task is o(lg(n)), that doesn’t affect the T∞runtime. The
parallelism is equal to the work over the span, so it is Θ(n2/lg(n)).
Exercise 27.1-8
The work is Θ(1 + Pn
j=2 j−1) = Θ(n2). The span is Θ(n) because in the
worst case when j=n, the for-loop of line 3 will need to execute ntimes. The
parallelism is Θ(n2)/Θ(n) = Θ(n).
Exercise 27.1-9
We solve for P in the following equation obtained by setting TP=T0
P.
T1
P+T∞=T0
1
P+T0
∞
2048
P+ 1 = 1024
P+ 8
1024
P= 7
1024
7=P
So we get that there should be approximately 146 processors for them to
have the same runtime.
Exercise 27.2-1
See the computation dag in the image below. Assuming that each strand
takes unnit time, the work is 13, the span is 6, and the parallelism is 13
6
4
Exercise 27.2-2
See the computation dag in the image below. Assuming each strand takes
unit time, the work is 30, the span is 16, and the parallelism is 15
8.
5
Exercise 27.2-3
We perform a modification of the P-SQUARE-MATRIX-MULTIPLY algo-
rithm. Basiglly, as hinted in the text, we will parallelize the innermost for loop
in such a way that there aren’t any data races formed. To do this, we will just
define a parallelized dot product procedure. This means that lines 5-7 can be
replaced by a single call to this procedure. P-DOT-PRODUCT computes the
dot dot product of the two lists between the two bounds on indices.
Using this, we can use this to modify P-SQUARE-MATRIX-MULTIPLY
Since the runtime of the inner loop is O(lg(n)), which is the depth of the
recursion. Since the paralel for loops also take O(lg(n)) time. So, since the
runtimes are additive here, the total span of this procedure is Θ(lg(n)). The
total work is still just O(n3) Since all the spawnging and recursing couls be re-
placed with the normal serial version once there anren’t enough free processors
to handle all of the spawned calls to P-DOT-PRODUCT.
Exercise 27.2-4
6

Algorithm 3 P-DOT-PROD(v,w,low,high)
if low == high then
return v[low] = v[low]
end if
mid = jlow+high
2k
x = spawn P-DOT-PROD(v,w,low,mid)
y = P-DOT-PROD(v,w,mid+1,high)
sync
return x+y
Algorithm 4 MODIFIED-P-SQUARE-MATRIX-MULTIPLY
n = A.rows
let C be a new n×nmatrix
parallel for i=1 to n do
parallel for j=1 to n do
ci,j = P-DOT-PROD(Ai,·, B·,j ,1, n)
end
end
return C
Assume that the input is two matrices Aand Bto be multiplied. For this
algorithm we use the function P-PROD defined in exercise 21.7-6. For notation,
we let Aidenote the ith row of A and A0
idenote the ith column of A. Here, C
is assumed to be a pby rmatrix. The work of the algorithm is Θ(prq), since
this is the runtime of the serialization. The span is Θ(log(p) + log(r) + log(q)) =
Θ(log(pqr)). Thus, the parallelism is Θ(pqr/ log(pqr), which remains highly
parallel even if any of p,q, or rare 1.
Algorithm 5 MATRIX-MULTIPLY(A,B,C,p,q,r)
1: parallel for i= 1 to pdo
2: parallel for j= 1 to rdo
3: Cij = P-PROD(Ai, B0
j,1, q)
4: end
5: end
6: return C
Exercise 27.2-5
Split up the region into four sections. Then, this amounts to finding the
transpose the uppoer left and lower right of the two submatrices. In adition to
that, you also need to swap the elements in the upper right with their transpose
position in the lower left. This dealing with the uppoer right swapping only
7

takes time O(lg(n2)) = O(lg(n)). In addition, there are two subproblems, each
of half the size. This gets us the recursion:
T∞(n) = T∞(n/2) + lg(n)
By the master theorem, we get that the total span of this procedure is
T∞∈O(lg(n). The total work is still the usual O(n2).
Exercise 27.2-6
Since Dkcannot be computed without Dk−1we cannot parallelize the for
loop of line 3 of Floyd-Warshall. However, the other two loops can be paral-
lelized. The work is Θ(n2), as in the serial case. The span is Θ(nlg n). Thus,
the parallelism is Θ(n/ lg n). The algorithm is as follows:
Algorithm 6 P-FLOYD-WARSHALL(W)
1: n=W.rows
2: D(0) =W
3: for k= 1 to ndo
4: let D(k)= (d(k)
ij ) be a new n×nmatrix
5: parallel for i= 1 to ndo
6: parallel for j= 1 to ndo
7: d(k)
ij = min(d(k−1)
ij , d(k−1)
ik +d(k−1)
kj
8: end
9: end
10: end for
11: return D(n)
Exercise 27.3-1
To coarsen the base case of P-MERGE, just replace the condition on line 2
with a check that n<kfor some base case size k. And instead of just copying
over the particular element of Ato the right spot in B, you would call a serial
sort on the remaining segment of Aand copy the result of that over into the
right spots in B.
Exercise 27.3-2
By a slight modification of exercise 9.3-8 we can find we can find the median
of all elements in two sorted arrays of total length nin O(lg n) time. We’ll
modify P-MERGE to use this fact. Let MEDIAN(T, p1, r1, p2, r2) be the func-
tion which returns a pair, q, where q.pos is the position of the median of all the
elements Twhich lie between positions p1and r1, and between positions p2and
r2, and q.arr is 1 if the position is between p1and r1, and 2 otherwise. The
first 8 lines of code are identical to those in P-MERGE given on page 800, so
8

we omit them here.
Algorithm 7 P-MEDIAN-MERGE(T, p1, r1, p2, r2, A, p3)
1: Run lines 1 through 8 of P-MERGE
2: q= MEDIAN(T, p1, r1, p2, r2)
3: if q.arr == 1 then
4: q2= BINARY-SEARCH(T[q.pos]), T, p2, r2)
5: q3=p3+q.pos −p1+q2−p2
6: A[q3] = T[q.pos]
7: spawn P-MEDIAN-MERGE(T, p1, q.pos −1, p2, q2−1, A, p3)
8: P-MEDIAN-MERGE(T, q.pos + 1, r1, q2+ 1, r2, A, p3)
9: sync
10: else
11: q2= BINARY-SEARCH(T[q.pos], T, p1, r1)
12: q3=p3+q.pos −p2+q2−p1
13: A[q3] = T[q.pos]
14: spawn P-MEDIAN-MERGE(T, p1, q2−1, p2, q.pos −1, A, p3)
15: P-MEDIAN-MERGE(T, q2+ 1, r1, q.pos + 1, r2, A, p3)
16: sync
17: end if
The work is characterized by the recurrence T1(n) = O(lg n)+2T1(n/2),
whose solution tells us that T1(n) = O(n). The work is at least Ω(n) since we
need to examine each element, so the work is Θ(n). The span satisfies the recur-
rence T∞(n) = O(lg n) + O(lg n/2) + T∞(n/2) = O(lg n) + T∞(n/2) = Θ(lg2n),
by exercise 4.6-2.
Exercise 27.3-3
Suppose that there are c different processors, and the array has length nand
you are going to use its last element as a pivot. Then, look at each chunk of size
dn
ceof entries before the last element, give one to each processor. Then, each
counts the number of elements that are less than the pivot. Then, we compute
all the running sums of these values that are returned. This can be done eas-
ily by considering all of the subarrays placed aout along the leaves of a binary
tree, and then summing up adjacent pairs. This computation can be done in
time lg(min{c, n}) since it’s the log of the number of leaves. From there, we can
compute all the running sums for each of the subarrays also in logarithmic time.
This is by keeping track of the sum of all more left cousins of each internal node,
which is found by adding the left sibling’s sum vale to the left cousing value of
the parent, with the root’s left cousing value initiated to 0. This also just takes
time the depth of the tree, so is lg(min{c, n}). Once all of these values are
computed at the root, it is the index that the subarray’s elements less than the
pivot should be put. To find the position where the subarray’s elements larger
9

than the root should be put, just put it at twice the sum value of the root minus
the left cousin value for that subarray. Then, the time taken is just O(n
c). By
doing this procedure, the total work is just O(n), and the span is O(lg(n)), and
so has parallelization of O(n
lg(n)). This whole process is split across the several
algoithms appearing here.
Algorithm 8 PPartition(L)
c= min{c, n}
pivot = L[n]
let Count be an array of length c
let r1,...rc+1 be roughly evenly spaced indices to L with r1= 1 and rc+1 =n
for i=1 . . . c do
Count[i] = spawn countnum(L[ri, ri+1 −1],pivot)
end for
sync
let Tbe a nearly complete binary tree whoose leaves are the elements of Count
whoose vertices have the attributes sum and lc
for all the leaves, let their sum value be the corresponding entry in Count
ComputeSums(T.root)
T.root.lc = 0
ComputeCousins(T.root)
Let Target be an array of length nthat the elements will be copied into
for i=1 . . . c do
let cousin be the lc value of the node in Tthat corresponds to i
spawn CopyElts(L,Target, cousin,ri, ri+1 −1)
end for
Target[n] = Target[T.root.sum]
Target[T.root.sum] = L[n]
return Target
Algorithm 9 CountNum(L,x)
ret = 0
for i=1 . . . L.length do
if L[i]< x then
ret++
end if
end for
return ret
Exercise 27.3-4
See the algorithm P-RECURSIVE-FFT. it parallelized over the two recursive
calls, having a parallel for works because each of the iterations of the for loop
10

Algorithm 10 ComputeSums(v)
if v is an internal node then
x = spawn ComputeSums(v.left)
y = ComputeSums(v.right)
sync
v.sum = x+y
end if
return v.sum
Algorithm 11 ComputeCousins(v)
if v6=NIL then
v.lc = v.p.lv
if v=v.p.right then
v.lc += c.p.left.sum
end if
spawn ComputeCousins(v.left)
ComputeCousins(v.right)
sync
end if
Algorithm 12 CopyElts(L1, L2, lc,lb,ub)
counter1 = lc+1
counter2 = lb
for i=lb . . . ub do
if L1[i]< x then
L2[counter1++] = L1[i]
else
L2[counter2++] = L1[i]
end if
end for
11

touch independent sets of variables. The span of the procedure is only Θ(lg(n))
giving it a parallelization of Θ(n)
Algorithm 13 P-RECURSIVE-FFT(a)
n=a.length
if n== 1 then
return a
end if
ωn=e2πi/n
ω= 1
a[0] = (a0, a2, . . . , an−2)
a[1] = (a1, a3, . . . , an−1)
y[0] = spawn P-RECURSIVE-FFT(a[0])
y[1] = P-RECURSIVE-FFT(a[1])
sync
parallel for k= 0, . . . , n/2−1do
yk=y[0]
k+ωy[1]
k
yk+(n/2) =y[0]
k−ωy[1]
k
ω=ωωn
end
return y
Exercise 27.3-5
Randomly pick a pivot element, swap it with the last element, so that it
is in the correct format for running the procedure described in 27.3-3. Run
partition from problem 27.3−3. As an intermediate step, in that procedure, we
compute the number of elements less than the pivot (T.root.sum), so keep track
of that value after the end of PPartition. Then, if we have that it is less than k,
recurse on the subarray that was greater than or equal to the pivot, decreasing
the order statistic of the element to be selected by T.root.sum. If it is larger
than the order statistic of the element to be selected, then leave it unchanged
and recurse on the subarray that was formed to be less than the pivot. A lot
of the analysis in section 9.2 still applies, except replacing the timer needed for
partitioning with the runtime of the algorithm in problem 27.3-3. The work is
unchanged from the serial case because when c= 1, the algorithm reduces to
the serial algorithm for partitioning. For span, the O(n) term in the equation
half way down page 218 can be replaced with an O(lg(n)) term. It can be seen
with the substitution method that the solution to this is logarithmic
E[T(n)] ≤2
n
n−1
X
k=bn/2c
Clg(k) + O(lg(n)) ≤O(lg(n))
So, the total span of this algorithm will still just be O(lg(n)).
12

Exercise 27.3-6
Let MEDIAN(A) denote a brute force method which returns the median
element of the array A. We will only use this to find the median of small arrays,
in particular, those of size at most 5, so it will always run in constant time. We
also let A[i..j] denote the array whose elements are A[i], A[i+ 1], . . . , A[j]. The
function P-PARTITION(A, x) is a multithreaded funciton which partitions A
around the input element xand returns the number of elements in Awhich are
less than or equal to x. Using a parallel for-loop, its span is logarithmic in the
number of elements in A. The work is the same as the serialization, which is Θ(n)
according to section 9.3. The span satisfies the recurrence T∞(n) = Θ(lg n/5) +
T∞(n/5)+Θ(lg n)+T∞(7n/10+6) ≤Θ(lg n)+T∞(n/5)+T∞(7n/10+6). Using
the substitution method we can show that T∞(n) = O(nε) for some ε < 1. In
particular, ε=.9 works. This gives a parallelization of Ω(n.1).
Algorithm 14 P-SELECT(A,i)
1: if n== 1 then
2: return A[1]
3: end if
4: Initialize a new array Tof length bn/5c
5: parallel for i= 0 to bn/5c − 1do
6: T[i+ 1] = MEDIAN(A[ibn/5c..ibn/5c+ 4])
7: end
8: if n/5 is not an integer then
9: T[bn/5c] = MEDIAN(A[5bn/5c..n)
10: end if
11: x= P-SELECT(T, dn/5e)
12: k= P-PARTITION(A, x)
13: if k== ithen
14: return x
15: else if i<kthen
16: P-SELECT(A[1..k −1], i)
17: else
18: P-SELECT(A[k+ 1..n], i −k)
19: end if
Problem 27-1
a. See the algorithm Sum-Arrays(A,B,C). The parallelism is O(n) since it’s work
is nlg(n) and the span is lg(n).
b. If grainsize is 1, this means that each call of Add-Subarray just sums a single
pair of numbers. This means that since the for loop on line 4 will run n
times, both the span and work will be O(n). So, the parallelism is just O(1).
13

Algorithm 15 Sum-Arrays(A,B,C)
n = jA.length
2k
if n=0 then
C[1] = A[1]+B[1]
else
spawn Sum-Arrays(A[1. . . n], B[1. . . n], C[1. . . n])
Sum-Arrays(A[n+1 . . . A.length],B[n+1 . . . A.length],C[n+1 . . . A.length])
sync
end if
c. Let gbe the grainsize. The runtime of the function that spawns all the other
functions is ln
gm. The runtime of any particular spawned task is g. So, we
want to minimize n
g+g
To do this we pull out our freshman calculus hat and take a derivative, we
get
0=1−n
g2
So, to solve this, we set g=√n. This minimizes the quantity and makes the
span O(n/g +g) = O(√n). Resulting in a parallelism of O(p(n)).
Problem 27-2
a. Our algorithm P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C,A,B) mul-
tiplies Aand B, and adds their product to the matrix C. It is assumed that
Ccontains all zeros when the function is first called.
b. The work is the same as the serialization, which is Θ(n3). It can also be found
by solving the recurrence T1(n) = Θ(n2)+8T(n/2) where T1(1) = 1. By
the mater theorem, T1(n) = Θ(n3). The span is T∞(n) = Θ(1) + T∞(n/2) +
T∞(n/2) with T∞(1) = Θ(1). By the master theorem, T∞(n) = Θ(n).
c. The parallelism is Θ(n2). Ignoring the constants in the Θ-notation, the
parallelism of the algorithm on 1000 ×1000 matrices is 1,000,000. Using P-
MATRIX-MULTIPLY-RECURSIVE, the parallelism is 10,000,000, which is
only about 10 times larger.
Problem 27-3
14

Algorithm 16 P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C,A,B)
1: n=A.rows
2: if n= 1 then
3: c11 = c11 + a11b11
4: else
5: Partition A,B, and Cinto n/2×n/2 submatrices
6: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C11, A11, B11)
7: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C12, A11, B12)
8: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C21, A21, B11)
9: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C22, A21, B12)
10: sync
11: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C11, A12, B21)
12: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C12, A12, B22)
13: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C21, A22, B21)
14: spawn P-MATRIX-MULTIPLY-RECURSIVE-SPACE(C22, A22, B22)
15: sync
16: end if
a. For the algorithm LU-DECOMPOSITION(A) on page 821, the inner for
loops can be parallelized, since they never update values that are read on later
runs of those loops. However, the outermost for loop cannot be parallelized
because across iterations of it the changes to the matrices from previous runs
are used to affect the next. This means that the span will be Θ(nlg(n)), work
will still be Θ(n3) and, so, the parallelization will be Θ( n3
nlg(n)) = Θ( n2
lg(n)).
b. The for loop on lines 7-10 is taking the max of a set of things, while recording
the index that that max occurs. This for loop can therefor be replaced with
a lg(n) span parallelized procedure in which we arrange the n elements into
the leaves of an almost balanced binary tree, and we let each internal node
be the max of its two children. Then, the span will just be the depth of this
tree. This procedure can gracefully scale with the number of processors to
make the span be linear, though even if it is Θ(nlg(n)) it will be less than
the Θ(n2) work later. The for loop on line 14-15 and the implicit for loop
on line 15 have no concurrent editing, and so, can be made parallel to have
a span of lg(n). While the for loop on lines 18-19 can be made parallel, the
one containing it cannot without creating data races. Therefore, the total
span of the naive parallized algorithm will be Θ(n2lg(n)), with a work of
Θ(n3). So, the parallelization will be Θ( n
lg(n)). Not as parallized as part (a),
but still a significant improvement.
c. We can parallelize the computing of the sums on lines 4 and 6, but cannot
also parallize the for loops containing them without creating an issue of
concurrently modifying data that we are reading. This means that the span
will be Θ(nlg(n)), work will still be Θ(n2), and so the parallelization will be
Θ( n
lg(n)).
15

d. The recurrence governing the amount of work of implemeting this procedure
is given by
I(n)≤2I(n/2) + 4M(n/2) + O(n2)
However, the two inversions that we need to do are independent, and the
span of parallelized matrix multiply is just O(lg(n)). Also, the n2work of
having to take a transpose and subtract and add matrices has a span of only
O(lg(n)). Therefore, the span satisfies the recurrence
I∞(n)≤I∞(n/2) + O(lg(n))
This recurrence has the solution I∞(n)∈Θ(lg2(n)) by exercise 4.6-2. There-
fore, the span of the inversion algorithm obtained by looking at the pro-
cedure detailed on page 830. This makes the parallelization of it equal to
Θ(M(n)/lg2(n)) where M(n) is the time to compute matrix products.
Problem 27-4
a. The algorithm below has Θ(n) work because its serialization satisfies the re-
currence T1(n)=2T(n/2) + Θ(1) and T(1) = Θ(1). It has span T∞(n) =
Θ(lg n) because it satisfies the recurrence T∞(n) = T∞(n/2) + Θ(1) and
T∞(1) = Θ(1).
Algorithm 17 P-REDUCE(x,i,j)
1: if i== jthen
2: return x[i]
3: else
4: mid =b(i+j)/2c
5: x=spawn P-REDUCE(x, i, mid)
6: y= P-REDUCE(x, mid + 1, j)
7: sync
8: return x⊗y
9: end if
b. The work of P-SCAN-1 is T1(n) = Θ(n2). The span is T∞(n) = Θ(n). The
parallelism is Θ(n).
c. We’ll prove correctness by induction on the number of recursive calls made to
P-SCAN-2-AUX. If a single call is made then n= 1, and the algorithm sets
y[1] = x[1] which is correct. Now suppose we have an array which requires
n+1 recursive calls. The elements in the first half of the array are accurately
16

computed since they require one fewer recursive calls. For the second half of
the array,
y[i] = x[1]⊗x[2]⊗. . .⊗x[i] = (x[1]⊗. . .⊗x[k])⊗(x[k+1]⊗. . .⊗x[i]) = y[k]⊗(x[k+1]⊗. . .⊗x[i]).
Since we have correctly computed the parenthesized term with P-SCAN-2-
AUX, line 8 ensures that we have correctly computed y[i].
The work is T1(n) = Θ(nlg n) by the master theorem. The span is T∞(n) =
Θ(lg2n) by exercise 4.6-2. The parallelism is Θ(n/ lg n).
d. Line 8 of P-SCAN-UP should be filled in by right ⊗t[k]. Lines 5 and 6 of
P-SCAN-DOWN should be filled in by vand v⊗t[k] respectively. Now we
prove correctness. First I claim that if line 5 is accessed after lrecursive calls,
then
t[k] = x[k]⊗x[k−1] ⊗. . . ⊗x[k− bn/2lc+ 1]
and
right =x[k+ 1] ⊗x[k+ 2] ⊗. . . x[k+bn/2lc].
If n= 2 we make a single call, but no recursive calls, so we start our base case
at n= 3. In this case, we set t[2] = x[2], and 2 −b3/2c+ 1 = 2. We also have
right =x[3] = x[2 + 1], so the claim holds. In general, on the lth recursive
call we set t[k] = P-SCAN-UP(x, t, i, k), which is t[b(i+k)/2c]⊗right. By
our induction hypothesis, t[k] = x[(i+k)/2] ⊗x[(i+k)/2−1] ⊗. . . ⊗x[(i+
k)/2− bn/2l+1c+ 1] ⊗x[(i+k)/2+1⊗. . . ⊗x[(i+k)/2 + bn/2l+1c]. This
is equivalent to our claim since (k−i)/2 = bn/2l+1c. A similar proof shows
the result for right.
With this in hand, we can verify that the value vpassed to P-SCAN-DOWN(v, x, t, y, i, j)
satisfies v=x[1] ⊗x[2] ⊗. . . ⊗x[i−1]. For the base case, if a single recur-
sive call is made then i=j= 2, and we have v=x[1]. In general, for
the call on line 5 there is nothing to prove because idoesn’t change. For
the call on line 6, we replace vby v⊗t[k]. By our induction hypothesis,
v=x[1] ⊗. . . ⊗x[i−1]. By the previous paragraph, if we are on the lth
recursive call, t[k] = x[i]⊗. . . ⊗x[k− bn/2lc+ 1] = x[i] since on the lth
recursive call, kand imust differ by bn/2lc. Thus, the claim holds. Since
we set y[i] = v⊗x[i], the algorithm yields the correct result.
e. The work of P-SCAN-UP satisfies T1(n)=2T(n/2) + Θ(1) = Θ(n). The
work of P-SCAN-DOWN is the same. Thus, the work of P-SCAN-3 satisfies
T1(n) = Θ(n). The span of P-SCAN-UP is T∞(n) = T∞(n/2) + O(1) =
Θ(lg n), and similarly for P-SCAN-DOWN. Thus, the span of P-SCAN-3 is
T∞(n) = Θ(lg n). The parallelism is Θ(n/ lg n).
Problem 27-5
17

a. Note that in this algorithm, the first call will be SIMPLE-STENCIL(A,A),
and when there are ranges indexed into a matrix, what is gotten back is a
view of the original matrix, not a copy. That is, changed made to the view
will show up in the original. We can set up a recurrence for the work, which
Algorithm 18 SIM P LE −ST EN CIL(A, A2)
let n1×n2be the size of A2.
let mi=ni
2for i= 1,2.
if m1== 0 then
if m2== 0 then
compute the value for the only position in A2based on the current
values in A.
else
SIM P LE −ST EN CIL(A, A2[1,1. . . m2])
SIM P LE −ST EN CIL(A, A2[1, m2+ 1 . . . n3])
end if
else
if m2== 0 then
SIM P LE −ST EN CIL(A, A2[1 . . . m1,1])
SIM P LE −ST EN CIL(A, A2[m1+ 1 . . . n1,1])
else
SIM P LE −ST EN CIL(A, A2[1 . . . m1,1. . . m2])
spawn SIMP LE −ST EN CIL(A, A2[m1+ 1 . . . n1,1. . . m2])
SIM P LE −ST EN CIL(A, A2[1 . . . m1, m2+ 1 . . . n2])
sync
SIM P LE −ST EN CIL(A, A2[m1+ 1 . . . n1, m2+ 1 . . . n2])
end if
end if
is just
W(n)=4W(n/2) + Θ(1)
which we can see by the master theorem has a solution which is Θ(n2). For
the span, the two middle subproblems are running at the same time, so,
S(n)=3S(n/2) + Θ(1)
Which has a solution that is Θ(nlg(3)), also by the master theorem.
b. Just use the implementation for the third part with b= 3The work has the
same solution of n2because it has the recurrence
W(n)=9W(n/3) + Θ(1)
The span has recurrence
S(n)=5S(n/3) + Θ(1)
Which has the solution Θ(nlog3(5))
18

Algorithm 19 GEN-SIMPLE-STENCIL(A,A2,b)
c. let n×mbe the size of A2.
if (n6= 0)&&(m6= 0) then
if (n== 1)&&(m== 1) then
compute the value at the only position in A2
else
let ni=in
bfor i= 1, . . . , b −1
let mi=im
bfor i= 1, . . . , b −1
let n0=m0= 1
for k=2, . . . b+1 do
for i=1, . . . k-2 do
spawn GEN−SIMP LE−ST EN CIL(A, A2[ni−1. . . ni, mk−i−1. . . mk−i], b)
end for
GEN−SIM P LE−ST EN CIL(A, A2[ni−1. . . ni, mk−i−1. . . mk−i], b)
sync
end for
for k=b+2, . . . , 2b do
for i=1,. . . ,2b-k do
spawn GEN−SIMP LE−ST EN CIL(A, A2[nb−k+i−1. . . nb−k+i, mb−i−1. . . mb−i], b)
end for
GEN−SIM P LE−ST EN CIL(A, A2[n3b−2k. . . n3b−2k+1i, m2k−2b. . . m2k−2b+1], b)
sync
end for
end if
end if
19

The recurrences we get are
W(n) = b2W(n/b) + Θ(1)
S(n) = (2b−1)W(n/b) + Θ(1)
So, the work is Θ(n2), and the span is Θ(nlgb(2b−1)). This means that the
parallelization is Θ(n2−lgb(2b−1)). So, to show the desired claim, we only need
to show that 2 −logb(2b−1) <1
2−logb(2b−1) <1
logb(2b)−logb(2b−1) <1
logb2b
2b−1<1
2b
2b−1< b
2b < 2b2−b
0<2b2−3b
0<(2b−3)b
This is clearly true because bis an integer greater than 2 and this right hand
side only has zeroes at 0 and 3
2and is positive for larger b.
Algorithm 20 BETTER-STENCIL(A)
d. for k=2,. . . , n+1 do
for i=1, . . . k-2 do
spawn compute and update the entry at A[i,k-i]
end for
compute and update the entry at A[k-1,1]
sync
end for
for k=n+2,. . . 2n do
for i=1, . . . 2n-k do
spawn compute and update the entries along the diagonal which have
indices summing to k
end for
sync
end for
This procedure has span only equal to the length of the longest diago-
nal with is O(n) with a factor of lg(n) thrown in. So, the parallelism is
O(n2/(nlg(n))) = O(n/ lg(n)).
Problem 27-6
20

a. The work law becomes E[TP]≥E[T1]/P . The span law becomes E[TP]≥
E[T∞]. The greedy scheduler bound becomes E[TP]≤E[T1]/P +E[T∞].
b. We’ll compute each.
E[T1]/E[TP] = 100 + 109·.99
.01 + 109·.99 ≈1
E[T1/Tp] = 100 + .99 = 100.99.
Since the algorithm almost always runs in the same amount of time, regard-
less of the increase in number of processors, and the speedup tells us how
many times faster something runs on Pprocessors than on 1, the expected
speedup should be approximately 1. Thus, E[T1]/E[TP] is the better defini-
tion.
c. As P→ ∞ the speedup should approach the parallelism, so it makes sense
to use a definition which agrees with part b in the limit.
d. Assume that PARTITION is implemented as described in exercise 27.3-3,
with work Θ(n) and span Θ(lg n). However, we will not modify anything
else about RANDOMIZED-PARTITION.
Algorithm 21 P-RANDOMIZED-QUICKSORT(A,p,r)
1: if p<rthen
2: q= RANDOMIZED-PARTITION(A, p, r)
3: spawn P-RANDOMIZED-QUICKSORT(a, P, Q −1)
4: RANDOMIZED-QUICKSORT(A, q + 1, r)
5: end if
e. The work is just the runtime of the serialization, which we know to have
expected time O(nlg n). For the span, our analysis will be similar to that of
RANDOMIZED-SELECT from page 216. Let Xkbe the indicator random
variable which is equal to 1 if A[p..q] has exactly kelements and 0 otherwise.
Then we have
T∞(n)≤
n
X
k=1
Xk·T∞(max(k−1, n −k)) + Θ(lg n).
By linearity of expectation this implies that
E[T∞(n)] ≤
n
X
k=1
1
nE[T∞(max(k−1, n −k))] + Θ(lg n).
Since each even term appears twice we can write this as
E[T∞(n)] ≤2
n
n−1
X
k=bn/2c
E[T∞(k)] + Θ(lg n).
21
We’ll show that E[T∞(n)] = O(n1−ε) for εsuch that 2−2ε−1
2−ε<1 by the
substitution method. Suppose that E[T∞(n)] ≤c1n1−ε. Then we have
E[T∞(n)] ≤2c1
n
n−1
X
k=bn/2c
k1−ε+ Θ(lg n)
≤2c1
nZn
k=bn/2c
x1−εdx + Θ(lg n)
=2c1
n
x2−ε
2−ε
n
k=bn/2c
+ Θ(lg n)
=c1n1−ε2−2ε−1
2−ε+ Θ(lg n).
Since the dominating term is strictly less than c1n1−ε, we can overcome the
Θ(lg n) term. Thus, E[T∞(n)] = O(n1−ε), so we achieve sublinear expected
time. The expected parallelization Ω(nlg n/n1−ε) = Ω(nεlg n).
22

Chapter 28
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 28.1-1
We get the solution:
3
14 −4·3
−7−5·(14 −4·3) + 6 ·3
=
3
2
1
Exercise 28.1-2
An LU decomposition of the matrix is given by
4−5 6
8−6 7
12 −7 12
=
100
210
321
4−5 6
0 4 −5
0 0 4
.
Exercise 28.1-3
First, we find the LUP decomposition of the given matrix
154
203
582
we bring the 5 to the top, and then divide the first column by 5, and use schur
complements to change the rest of the matrix to get
5 8 2
.4−3.2 2.2
.2 3.4 3.6
Then, we swap the third and second rows, and apply the schur complement to
get
5 8 2
.2 3.4 3.6
.4−3.2
3.42.2 + 11.52
3.4
1

This gets us the LUP decomposition that
L=
1 0 0
.2 1 0
.4−3.2
3.41
U=
5 8 2
0 3.4 3.6
002.2 + 11.52
3.4
P=
001
100
010
Using this, we can get that the solution must be
1 0 0
.210
.4−3.2
3.41
5 8 2
0 3.4 3.6
002.2 + 11.52
3.4
x1
x2
x3
=
5
12
9
Which, by forward substitution,
5 8 2
0 3.4 3.6
002.2 + 11.52
3.4
x1
x2
x3
=
5
11
7 + 35.2
3.4
So, finally by back substitution,
x1
x2
x3
=
−3
19
−1
19
49
19
Exercise 28.1-4
The LUP decomposition of a diagonal matrix Dis D=IDI where Iis the
identity matrix.
Exercise 28.1-5
A LU decomposition of a permutation matrix is letting Pbe the inverse per-
mutation matrix, and let both L and U be the identity matrix. Now, we need
show that this representation is unique. We know that the permutation matrix
Ais non-singular. This means that Uhas nonzero elements all along its diago-
nal. Now, suppose that there were some nonzero element off of the diagonal in
L, which is to say Li,j 6= 0 for i6=j. Then, look at row iin the product LU.
This has a nonzero entry both at column jand at column i. Since it has more
than one non-zero entry, it cannot be transformed into a permutation matrix
by permuting the rows. Similarly, we have that Ucannot have any off-diagonal
elements. Lastly, since we know that both Land Uare diagonal matrices, we
2

know that Lis the identity. Since Aonly has ones as its nonzero entries, and
LU =U. U must also only have ones as its nonzero entries. So, we have U
is the identity. This means that P A =I, which means that P=A−1. This
completes showing that the given decomposition is unique.
Exercise 28.1-6
The zero matrix always has an LU decomposition by taking Lto be any unit
lower-triangular matrix and Uto be the zero matrix, which is upper triangular.
Exercise 28.1-7
For LU decomposition, it is indeed necessary. If we didn’t run the last run
of the outermost for loop, unn would be left its initial value of zero instead of
being set equal to ann. This can clearly produce incorrect results, because the
LU decomposition of any non-singular matrix must have both Land Uhaving
positive determinant. However, if unn = 0, the determinant of Uwill be zero
by problem D.2-2.
For LUP-decomposition, the iteration of the outermost for loop that occurs
with k=nwill not change the final answer. Since πwould have to be a per-
mutation on a single element, it cannot be non-trivial. and the for loop on line
16 will not run at all.
Exercise 28.2-1
Showing that being able to multiply matrices in time M(n) implies being
able to square matrices in time M(n) is trivial because squaring a matrix is just
multiplying it by itself.
The more tricky direction is showing that being able to square matrices in
time S(n) implies being able to multiply matrices in time O(S(n)).
As we do this, we apply the same regularity condition that S(2n)∈O(S(n)).
Suppose that we are trying to multiply the matrices, Aand B, that is, find AB.
Then, define the matrix
C=I A
0B
Then, we can find C2in time S(2n)∈O(S(n)). Since
C2=I A +AB
0B
Then we can just take the upper right quarter of C2and subtract Afrom it to
obtain the desired result. Apart from the squaring, we’ve only done work that
is O(n2). Since S(n) is Ω(n2) anyways, we have that the total amount of work
we’ve done is O(n2).
3

Exercise 28.2-2
In this problem and the next, we’ll follow the approach taken in Algebraic
Complexity Theory by Burgisser, Claussen, and Shokrollahi. Let Abe an n×
nmatrix. Without loss of generality we’ll assume n= 2k, and impose the
regularity condition that L(n/2) ≤cL(n) where c < 1/2 and L(n) is the time it
takes to find an LUP decomposition of an n×nmatrix. First, decompose Aas
A=A1
A2
where A1is n/2 by n. Let A1=L1U1P1be an LUP decomposition of A1,
where L1is n/2 by n/2, U1is n/2 by n, and P1is nby n. Perform a block
decomposition of U1and A2P−1
1as U1= [U1|B] and A2P−1
1= [C|D] where
U1and Care n/2 by n/2 matrices. Since we assume that Ais nonsingular, U1
must also be nonsingular. Set F=D−CU−1
1B. Then we have
A=L10
CU−1
1In/2 U1B
0FP1.
Now let F=L2U2P2be an LUP decomposition of F, and let P=In/20
0P2.
Then we may write
A=L10
CU−1
1L2 U1BP −1
2
0U2P P1.
This is an LUP decomposition of A. To achieve it, we computed two LUP
decompositions of half size, a constant number of matrix multiplications, and a
constant number of matrix inversions. Since matrix inversion and multiplication
are computationally equivalent, we conclude that the runtime is O(M(n)).
Exercise 28.2-3
From problem 28.2-2, we can find a LU-decomposition algorithm that only
takes time O(M(n)). So, we run that algorithm and multiply together all of
the entries along the diagonal of U, this will be the determinant of the original
matrix.
Now, suppose that we have a determinant algorithm that takes time D(n),
we will show that we can find a matrix multiplication algorithm that takes time
O(D(n)). By the previous problem, it is enough to show that we can find matrix
inverses using at most 3 determinants and an additional Θ(n2) work.
Authors note on the second half of this problem: Typically we strive to
complete all the exercises independently as a way of gaining a greater under-
standing ourselves. For the second half of this problem, this was unfortunately
not something that we achieved. After been stuck for several weeks, I asked a
number of other graduate students, and even two professors, none were able
4

to help with how the proof went. One did however refer me to the book
Algebraic Complexity Theory by Burgisser, Claussen, and Shokrollahi. The
proof given here for the second half of the exercise was lifted from their section
16.4. This was one of the hardest exercises in the book.
Exercise 28.2-4
Suppose we can multiply boolean matrices in M(n) time, where we assume
this means that if we’re multiplying boolean matrices Aand B, then (AB)ij =
(ai1∧b1j)∨. . . ∨(ain ∧bnj ). To find the transitive closure of a boolean matrix
Awe just need to find the nth power of A. We can do this by computing A2,
then (A2)2, then ((A2)2)2), and so on. This requires only lg nmultiplications,
so the transitive closure can be computed in O(M(n) lg n).
For the other direction, first view Aand Bas adjacency matrices, and impose
the regularity condition T(3n) = O(T(n)), where T(n) is the time to compute
the transitive closure of a graph on nvertices. We will define a new graph whose
transitive closure matrix contains the boolean product of Aand B. Start by
placing 3nvertices down, labeling them 1,2, . . . , n, 10,20, . . . , n0,100 ,200 , . . . , n00 .
Connect vertex ito vertex j0if and only if Aij = 1. Connect vertex j0to vertex
k00 if and only if Bjk = 1. In the resulting graph, the only way to get from the
first set of nvertices to the third set is to first take an edge which “looks like”
an edge in A, then take an edge which “looks like ” an edge in B. In particular,
the transitive closure of this graph is:
I A AB
0I B
0 0 I
.
Since the graph is only of size 3n, computing its transitive closure can be
done in O(T(3n)) = O(T(n)) by the regularity condition. Therefore multiplying
matrices and finding transitive closure are are equally hard.
Exercise 28.2-5
It does not work necessarily over the field of two elements. The problem
comes in in applying theorem D.6 to conclude that ATAis positive definite. In
the proof of that theorem they obtain that ||Ax||2≥0 and only zero if every
entry of Ax is zero. This second part is not true over the field with two elements,
all that would be required is that there is an even number of ones in Ax. This
means that we can only say that ATAis positive semi-definite instead of the
positive definiteness that the algorithm requires.
Exercise 28.2-6
We may again assume that our matrix is a power of 2, this time with complex
entries. For the moment we assume our matrix Ais Hermitian and positive-
definite. The proof goes through exactly as before, with matrix transposes
5

replaced by conjugate transposes, and using the fact that Hermitian positive-
definite matrices are invertible. Finally, we need to justify that we can obtain the
same asymptotic running time for matrix multiplication as for matrix inversion
when Ais invertible, but not Hermitian positive-definite. For any nonsingular
matrix A, the matrix A∗Ais Hermitian and positive definite, since for any x
we have x∗A∗Ax =hAx, Axi>0 by the definition of inner product. To invert
A, we first compute (A∗A)−1=A−1(A∗)−1. Then we need only multiply this
result on the right by A∗. Each of these steps takes O(M(n)) time, so we can
invert any nonsingluar matrix with complex entries in O(M(n)) time.
Exercise 28.3-1
To see this, let eibe the vector that is zeroes except for a one in the ith
position. Then, we consider the quantity eT
iAeifor every i.Aeitakes each row
of Aand pulls out the ith column of it, and puts those values into a column
vector. Then, multiplying that on the left by eT
i, pulls out the ith row of this
quantity, which means that the quantity eT
iAeiis exactly the value of Ai,i. So,
we have that by positive definiteness, since eiis nonzero, that quantity must
be positive. Since we do this for every i, we have that every entry along the
diagonal must be positive.
Exercise 28.3-2
Let x=−by/a. Since Ais positive-definite we must have
0<[xy]TAx
y
= [xy]Tax +by
bx +cy
=ax2+ 2bxy +cy2
=cy2−b2y2
a
= (c−b2/a)y2.
Thus, c−b2/a > 0 which implies ca −b2>0, since a > 0.
Exercise 28.3-3
Suppose to a contradiction that there were some element aij with i6=j
so that aij were a largest element. We will use eito denote the vector that
is all zeroes except for having a 1 at position i. Then, we consider the value
(ei−ej)TA(ei−ej). When we compute A(ei−ej) this will return a vector
which is column iminus column j. Then, when we do the last multiplication,
6

we will get the quantity which is the ith row minus the jth row. So,
(ei−ej)TA(ei−ej) = aii −aij −aji +ajj
=aii +ajj −2aij ≤0
Where we used symmetry to get that aij =aji. This result contradicts the
fact that Awas positive definite. So, our assumption that there was a element
tied for largest off the diagonal must of been false.
Exercise 28.3-4
The claim clearly holds for matrices of size 1 because the single entry in the
matrix is positive the only leading submatrix is the matrix itself. Now suppose
the claim holds for matrices of size n, and let Abe an (n+1)×(n+1) symmetric
positive-definite matrix. We can write Aas
A=
A0w
v c
.
Then A0is clearly symmetric, and for any xwe have xTA0x= [x0]Ax
0>
0, so A0is positive-definite. By our induction hypothesis, every leading subma-
trix of A0has positive determinant, so we are left only to show that Ahas
positive determinant. By Theorem D.4, the determinant of Ais equal to the
determinant of the matrix
B=
c v
w A0
.
Theorem D.4 also tells us that the determinant is unchanged if we add a
multiple of one column of a matrix to another. Since 0 < eT
n+1Aen+1 =c, we
can use multiples of the first column to zero out every entry in the first row
other than c. Specifically, the determinant of Bis the same as the determinant
of the matrix obtained in this way, which looks like
C=
c0
w A00
.
By definition, det(A) = cdet(A00 ). By our induction hypothesis, det(A00 )>
0. Since c > 0 as well, we conclude that det(A)>0, which completes the proof.
7

Exercise 28.3-5
When we do an LU decomposition of a positive definite symmetric matrix, we
never need to permute the rows. This means that the pivot value being used
from the first operation is the entry in the upper left corner. This gets us that
for the case k= 1, it holds because we were told to define det(A0) = 1, getting
us, a11 =det(A1)/det(A0). When Diagonalizing a matrix, the product of the
pivot values used gives the determinant of the matrix. So, we have that the
determinant of Akis a product of the kth pivot value with all the previous
values. By induction, the product of all the previous values is det(Ak−1). So,
we have that if xis the kth pivot value, det(Ak) = xdet(Ak−1), giving us the
desired result that the kth pivot value is det(Ak)/det(Ak−1).
Exercise 28.3-6
First we form the Amatrix
A=
1 0 e
1 2 e2
1 3 lg 3 e3
1 8 e4
.
We’ll compute the pseudoinverse using Wolfram Alpha, then multiply it by
y, to obtain the coefficient vector
c=
.411741
−.20487
.16546
.
Exercise 28.3-7
AA+A=A((ATA)−1AT)A
=A(ATA)−1(ATA)
=A
A+AA+= ((ATA)−1AT)A((ATA)−1AT)
= (ATA)−1(ATA)(ATA)−1AT
= (ATA)−1AT
=A+
8

(AA+)T= (A(ATA)−1AT)T
=A((ATA)−1)TAT
=A((ATA)T)−1AT
=A(ATA)−1AT
=AA+
(AA+)T= ((ATA)−1ATA)T
= ((ATA)−1(ATA))T
=IT
=I
= (ATA)−1(ATA)
=A+A
Problem 28-1
a. By applying the procedure of the chapter, we obtain that
L=
1 0 0 0 0
−1 1 0 0 0
0−1 1 0 0
0 0 −110
000−1 1
U=
1−1 0 0 0
0 1 −1 0 0
0 0 1 −1 0
0 0 0 1 −1
0 0 0 0 1
P=
10000
01000
00100
00010
00001
b. We first do back substitution to obtain that
Ux =
5
4
3
2
1
9
So, by forward substitution, we have that
x=
5
9
12
14
15
c. We will set Ax =eifor each i, where eiis the vector that is all zeroes except
for a one in the ith position. Then, we will just concatenate all of these
solutions together to get the desired inverse.
equation solution
Ax1=e1x1=
1
1
1
1
1
Ax2=e2x2=
1
2
2
2
2
Ax3=e3x3=
1
2
3
3
3
Ax4=e4x4=
1
2
3
4
4
Ax5=e5x5=
1
2
3
4
5
This gets us the solution that
A−1=
11111
12222
12333
12344
12345
10

d. When performing the LU decomposition, we only need to take the max over
at most two different rows, so the loop on line 7 of LUP-DECOMPOSITION
drops to O(1). There are only some constant number of nonzero entries in
each row, so the loop on line 14 can also be reduced to being O(1). Lastly,
there are only some constant number of nonzero entries of the form aik and
akj . since the square of a constant is also a constant, this means that the
nested for loops on lines 16-19 also only take time O(1) to run. Since the
for loops on lines 3 and 5 both run O(n) times and take O(1) time each
to run(provided we are smart to not consider a bunch of zero entries in the
matrix), the total runtime can be brought down to O(n).
Since for a Tridiagonal matrix, it will only ever have finitely many nonzero
entries in any row, we can do both the forward and back substitution each
in time only O(n).
Since the asymptotics of performing the LU decomposition on a positive
definite tridiagonal matrix is O(n), and this decomposition can be used to
solve the equation in time O(n), the total time for solving it with this method
is O(n). However, to simply record the inverse of the tridiagonal matrix
would take time O(n2) since there are that many entries, so, any method
based on computing the inverse of the matrix would take time Ω(n2) which
is clearly slower than the previous method.
e. The runtime of our LUP decomposition algorithm drops to being O(n) be-
cause we know there are only ever a constant number of nonzero entries in
each row and column, as before. Once we have an LUP decomposition, we
also know that that decomposition have both Land Uhaving only a con-
stant number of non-zero entries in each row and column. This means that
when we perform the forward and backward substitution, we only spend a
constant amount of time per entry in x, and so, only takes O(n) time.
Problem 28-2
a. We have ai=fi(0) = yiand bi=f0
i(0) = f0(xi) = Di. Since fi(1) =
ai+bi+ci+diand f0
i(1) = bi+2ci+3diwe have di=Di+1 −2yi+1 +2yi+Di
which implies ci= 3yi+1 −3yi−Di+1 −2Di. Since each coefficient can be
computed in constant time from the known values, we can compute the 4n
coefficients in linear time.
b. By the continuity constraints we have f00
i(1) = f00
i+1(0) which implies that
2ci+ 6di= 2ci+1, or ci+ 3di=ci+1 . Using our equations from above, this is
equivalent to
Di+ 2Di+1 + 3yi−3yi+1 = 3yi+2 −3yi+1 −Di+2 −2Di+1.
Rearranging gives the desired equation
Di+ 4Di+1 +Di+2 = 3(yi+2 −yi).
11

c. The condition on the left endpoint tells us that f00
0(0) = 0, which implies
2c0= 0. By part a, this means 3(y1−y0) = 2D0+D1. The condition on the
right endpoint tells us that f00
n−1(1) = 0, which implies cn−1+ 3dn−1= 0. By
part a, this means 3(yn−yn−1) = Dn−1+ 2Dn.
d. The matrix equation has the form AD =Y, where Ais symmetric and
tridiagonal. It looks like this:
2 1 0 0 · · · 0
1 4 1 0 · · · 0
0.........· · · .
.
.
.
.
.· · · 1 4 1 0
0· · · 0 1 4 1
0· · · 0 0 1 2
D0
D1
D2
.
.
.
Dn−1
Dn
=
3(y1−y0)
3(y2−y0)
3(y3−y1)
.
.
.
3(yn−yn−2)
3(yn−yn−1)
.
e. Since the matrix is symmetric and tridiagonal, Problem 28-1 e tells us that
we can solve the equation in O(n) time by performing an LUP decomposition.
By part a of this problem, once we know each Diwe can compute each fiin
O(n) time.
f. For the general case of solving the nonuniform natural cubic spline problem,
we require that f(xi+1) = fi(xi+1 −xi) = yi+1,f0(xi+1) = f0
i(xi+1 −xi) =
f0
i+1(0) and f00 (xi+1) = f00
i(xi+1 −xi) = f00
i+1(0). We can still solve for each of
ai,bi,ci, and diin terms of yi,yi+1,Di, and Di+1 , so we still get a tridiagonal
matrix equation. The solution will be slightly messier, but ultimately it is
solved just like the simpler case, in O(n) time.
12
Chapter 29
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 29.1-1
c=
2
−3
3
A=
1 1 −1
−1−1 1
1−2 2
b=
7
−7
4
with m=n= 3
Exercise 29.1-2
One solution is (x1, x2, x3) = (6,1,0) with objective value 9. Another is
(5,2,0) with objective value 4. A third is (4,3,0) with objective value -1.
Exercise 29.1-3
N={1,2,3}
B={4,5,6}
A=
1 1 −1
−1−1 1
1−2 2
b=
7
−7
4
1

c=
2
−3
3
And v= 0.
Exercise 29.1-4
maximize −2x1−2x2−7x3+x4
subject to −x1+x2−x4≤ −7
x1−x2+x4≤7
−3x1+ 3x2−x3≤ −24
x1, x2, x3, x4≥0
Exercise 29.1-5
First, we will multiply the second and third inequalities by minus one to
make it so that they are all ≤inequalities. We will introduce the three new
variables x4, x5, x6, and perform the usual procedure for rewriting in slack form
x4= 7 −x1−x2+x3
x5=−8+3x1−x2
x6=−x1+ 2x2+ 2x3
x1, x2, x3, x4, x5, x6≥0
where we are sill tring to maximize 2x1−6x3. The basic variables are
x4, x5, x6and the nonbasic variables are x1, x2, x3.
Exercise 29.1-6
By dividing the second constraint by 2 and adding to the first, we have
0≤ −3, which is impossible. Therefore there linear program is infeasible.
Exercise 29.1-7
For any number r > 1, we can set x1= 2rand x2=r. Then, the restaints
become
−2r+r=−r≤ −1
−2r−2r=−4r≤ −2
2r, r ≥0
All of these inequalities are clearly satisfied because of our initial restriction
in selecting r. Now, we look to the objective function, it is 2r−r=r. So, since
2

we can select rto be arbitrarily large, and still satisfy all of the constraints, we
can achieve an arbitrarily large value of the objective function.
Exercise 29.1-8
In the worst case, we have to introduce 2 variables for every variable to en-
sure that we have nonnegativity constraints, so the resulting program will have
2nvariables. If each constraint is an equality, we would have to double the num-
ber of constraints to create inequalities, resulting in 2mconstraints. Changing
minimization to maximization and greater-than signs to less-than signs don’t
affect the number of variables or constraints, so the upper bound is 2non vari-
ables and 2mon constraints.
Exercise 29.1-9
Consider the linear program where we want to maximize x1−x2subject to
the constraints x1−x2≤1 and x1, x2≥0. clearly the objective value can never
be greater than one, and it is easy to achieve the optimal value of 1, by setting
x1= 1 and x2= 0. Then, this feasable region is unbounded because for any
number r, we could set x1=x2=r, and that would be feasible because the
difference of the two would be zero which is ≤1.
If we further wanted it so that there was a single solution that achieved the
finite optimal value, we could add the requirements that x1≤1.
Exercise 29.2-1
The objective is already in normal form. However, some of the constraints
are equality constraints instead of ≤constraints. This means that we need to
rewrite them as a pair of inequality constraints, the overlap of whose solutions
is just the case where we have equality. we also need to deal with the fact that
most of the variables can be negative. To do that, we will introduce variables
for the negative part and positive part, each of which need be positive, and
we’ll just be sure to subtract the negative part. dsneed not be changed in this
way since it can never be negative since we are not assuming the existence of
negative weight cycles.
d+
v−d−
v−d+
u+d−
u≤w(u, v)for every edge (u, v)
ds≤0
all variables are positive
Exercise 29.2-2
3

maximize dy
subject to dt≤ds+ 3
dx≤dt+ 6
dy≤ds+ 5
dy≤dt+ 2
dz≤dx+ 2
dt≤dy+ 1
dx≤dy+ 4
dz≤dy+ 1
ds≤dz+ 1
dx≤dz+ 7
d2= 0
Exercise 29.2-3
We will follow a similar idea to the way to when we were finding the shortest
path between two particular vertices.
maximize X
v∈V
dv
subject to dv≤du+w(u, v)for each edge (u,v)
ds= 0
The first type of constraint makes sure that we never say that a vertex is
further away than it would be if we just took the edge corresponding to that
constraint. Also, since we are trying to maximize all of the variables, we will
make it so that there is no slack anywhere, and so all the dvvalues will corre-
spond to lengths of shortest paths to v. This is because the only thing holding
back the variables is the information about relaxing along the edges, which is
what determines shortest paths.
Exercise 29.2-4
4

maximize fsv1+fsv2
subject to fsv1≤16
fsv2≤14
fv1v3≤12
fv2v1≤4
fv2v4≤14
fv3v2≤9
fv3t≤20
fv4v3≤7
fv4t≤4
fsv1+fv2v1=fv1v3
fsv2+fv3v2=fv2v1+fv2v4
fv1v3+fv4v3=fv3v2+fv3t
fv2v4=fv4v3+fv4t
fuv ≥0 for u, v ∈ {s, v1, v2, v3, v4, t}
Exercise 29.2-5
All we need to do to bring the number of constraints down from O(V2) to
O(V+E) is to replace the way we index the flows. Instead of indexing it by
a pair of vertices, we will index it by an edge. This won’t change anything
about the analysis because between pairs of vertices that don’t have an edge
between them, there definitely won’t be any flow. Also, it brings the number
of constraints of the first and third time down to O(E) and the number of
constraints of the second kind stays at O(V).
maximize X
edges e coming out of s
fe−X
edges e going into s
fs
subject to f(u,v)≤c(u, v)for each edge (u,v)
X
edges e leaving u
fe=X
edges e entering u
fefor each edge u∈V− {s, t}
fe≥0 for each edge e
Exercise 29.2-6
Recall from section 26.3 that we can solve the maximum-bipartite-matching
problem by viewing it as a network flow problem, where we append a source s
and sink t, each connected to every vertex is Land Rrespectively by an edge
with capacity 1, and we give every edge already in the bipartite graph capacity
5

1. The integral maximum flows are in correspondence with maximum bipartite
matchings. In this setup, the linear programming problem to solve is as follows:
maximize X
v∈L
fsv
subject to fuv ≤1 for each u, v ∈ {s} ∪ L∪R∪ {t}=V
X
v∈V
fvu =X
v∈V
fuv for each u∈L∪R
fuv ≥0 for each u, v ∈V
Exercise 29.2-7
As in the minimum cost flow problem, we have constaints for the edge capac-
ities, for the conservation of flow, and nonegativity. The difference is that the
restraint that before we required exactly dunits to flow, now, we require that
for each commodity, the right amount of that comodity flows. the conservation
equalities will be applied to each different type of commodity independently. If
we super script fthat will denote the type of commodity the flow is describing,
if we do not superscript it, it will denote the aggregate flow.
We want to minimize X
u,v∈V
a(u, v)fuv
The capacity constraints are that
X
i∈[k]X
u,v∈V
fi
uv ≤c(u, v)
The conservation constraints are that for every i∈[k], for every u∈V\
{si, ti}.
X
v∈V
fi
u,v =X
v∈V
fi
v,u
Now, the constraints that correspond to requiring a certain amount of flow
are that for every i∈[k].
X
v∈V
fi
si,v −X
v∈V
fi
v,si=d
Now, we put in the constraint that makes sure what we called the aggregate
flow is actually the aggregate flow, so, for every u, v ∈V,
fu,v =X
i∈[k]
fi
u,v
Finally, we get to the fact that all flows are nonnegative, for every u, v ∈V,
6

fu,v ≥0
Exercise 29.3-1
We subtract equation (29.81) from equation (29.79). This gets us
0 = v−v0+X
j∈N
(cj−c0
j)xj
which can be rearranged to
X
j∈N
c0
jxj= (v−v0) + X
j∈N
cjxj
Then, by applying Lemma 29.3, we get that for every j, we have cj=c0
jand
also, (v−v0) = 0, so v=v0.
Exercise 29.3-2
The only time vis updated in PIVOT is line 14, so it will suffice to show
that ceˆ
be≥0. Prior to making the call to PIVOT, we choose an index esuch
that ce>0, and this is unchanged in PIVOT. We set ˆ
bein line 3 to be bl/ale.
The loop invariant proved in Lemma 29.2 tells us that bl≥0. The if-condition
of line 6 of SIMPLEX tells us that only the noninfinite δimust have aie >0,
and we choose lto minimize δl, so we must have ale >0. Thus, ceˆ
be≥0, which
implies vcan never decrease.
Exercise 29.3-3
To show that the two slack forms are equivalent, we will show both that they
have equal objective functions, and their sets of feasible solutions are equal.
First, we’ll check that their sets of feasible solutions are equal. Basically
all we do to the constraints when we pivot is take the non-basic variable, e,
and solve the equation corresponding to the basic variable lfor e. We are then
taking that expression and replacing ein all the constraints with this expression
we got by solving the equation corresponding to l. Since each of these algebraic
operations are valid, the result of the sequence of them is also algebraically
equivalent to the original.
Next, we’ll see that the objective functions are equal. We decrease each cj
by ceˆaej , which is to say that we replace the non-basic variable we are making
basic with the expression we got it was equal to once we made it basic.
Since the slack form returned by PIVOT, has the same feasible region and
an equal objective function, it is equivalent to the original slack form passed in.
Exercise 29.3-4
7

First suppose that the basic solution is feasible. We set each xi= 0 for
1≤i≤n, so we have xn+i=bi−Pn
j=1 aij xj=bias a satisfied constraint.
Since we also require xn+i≥0 for all 1 ≤i≤m, this implies bi≥0. Now
suppose bi≥0 for all i. In the basic solution we set xi= 0 for 1 ≤i≤nwhich
satisfies the nonnegativity constraints. We set xn+i=bifor 1 ≤i≤mwhich
satisfies the other constraint equations, and also the nonnegativity constraints
on the basic variables since bi≥0. Thus, every constraint is satisfied, so the
basic solution is feasible.
Exercise 29.3-5
First, we rewrite the linear program into it’s slack form, we want to maximize
18x1+ 12.5x2, given the constraints
x3= 20 −x1−x2
x4= 12 −x1
x5= 16 −x2
x1, x2, x3, x4, x5≥0
Then, we take the initial basic solution, we get that x1=x2= 0 and x3= 20,
x4= 12, and x5= 16, with a value of the objective function of 0. Now, we pick
x1as our non basic variable in the simplex method. Of all of our ∆ values, we
get that the smallest corresponds to x4, so, we pivot to x4from x1. This gets
us that we want to maximize 216 −18x4+ 12.5x2subject to the constraints:
x3= 8 + x4−x2
x1= 12 + x4
x5= 16 −x2
x1, x2, x3, x4, x5≥0
Then, we need to select x2as our non-basic variable, which gets us that we
should pivot to x3, which gets us that the objective is 316 −5.5x4−12.5x3and
the constraints are
x2= 8 + x4−x3
x1= 12 + x4
x5= 8 −x4+x3
x1, x2, x3, x4, x5≥0
We now stop since no more non-basic variables appear in the objective with
a positive coefficient. Our solution is (12,8,0,0,8) and has a value of 316. Going
back to the standard form we started with, we just disregard the values of x3
8

through x5and have the solution that x1= 12 and x2= 8. We can check that
this is both feasible and has the objective achieve 316.
Exercise 29.3-6
The first step is to convert the linear program into slack form. We’ll intro-
duce the slack variables x3and x4. We have:
z= 5x1−3x2
x3= 1 −x1+x2
x4= 2 −2x1−x2.
The nonbasic variables are x1and x2. Of these, only x1has a positive
coefficient in the objective function, so we must choose xe=x1. Both equations
limit x1by 1, so we’ll choose the first one to rewrite x1with. Using x1=
1−x3+x2we obtain the new system
z= 5 −5x3+ 2x2
x1= 1 −x3+x2
x4= 2x3−2x2.
Now x2is the only nonbasic variable with positive coefficient in the objective
function, so we set xe=x2. The last equation limits x2by 0 which is most
restrictive, so we set x2=x3−x4
2. Rewriting, our new system becomes
z= 5 −3x3−x4
x1= 1 −x4
2
x2=x3−x4
2.
Every nonbasic variable now has negative coefficient in the objective func-
tion, so we take the basic solution (x1, x2, x3, x4) = (1,0,0,0). The objective
value this achieves is 5.
Exercise 29.3-7
First, we convert this equation to the slack form. Doing so doesn’t change
the objective, but the constraints become
9

z=−x1−x2−x3
x4=−10000 + 2x1+ 7.5x2+ 3x3
x5=−30000 + 20x1+ 5x2+ 10x3
x1, x2, x3, x4, x5≥0
Also, since the objective is to minimize a given function, we’ll change it over
to maximizing the negative of that function. In particular maximize −x1−x2−
x3. Now, we note that the initial basic solution is not feasible, because it would
leave x4and x5being negative. This means that finding an initial solution
requires using the method of section 29.5. The auxiliary linear program in slack
form is
z=−x0
x4=−10000 + 2x1+ 7.5x2+ 3x3+x0
x5=−30000 + 20x1+ 5x2+ 10x3+x0
x0, x1, x2, x3, x4, x5≥0
We choose x0as the entering variable and x5as the leaving variable, since
it is the basic variable whose value in the basic solution is most negative. After
pivoting, we have the slack form
z=−30000 + 20x1+ 5x2+ 10x3−x5
x0= 30000 −20x1−5x2−10x3+x5
x4= 20000 −18x1+ 2.5x2−7x3+x5
x0, x1, x2, x3, x4, x5≥0
The associated basic solution is feasible, so now we just need to repeatedly
call PIVOT until we obtain an optimal solution to Laux. We’ll choose x2as our
entering variable. This gives
z=−x0
x2= 6000 −4x1−2x3+x5/5−x0/5
x4= 35000 −28x1−12x3+ (3/2)x5−x0/2
x0, x1, x2, x3, x4, x5≥0
This slack form is the final solution to the auxiliary problem. Since this
solution has x0= 0, we know that our initial problem was feasible. Furthermore,
since x0= 0, we can just remove it from the set of constraints. We then restore
the oritinal objective function, with appropriate substitutions made to include
only the nonbasic variables. This yields
10

z=−6000 + 3x1+x3−x5/5
x2= 6000 −4x1−2x3+x5/5
x4= 35000 −28x1−12x3+ (3/2)x5
x1, x2, x3, x4, x5≥0
This slack form has a feasible basic solution, and we can return it to SIM-
PLEX. We choose x1as our entering variable. This gives
z=−2250 −(2/7)x3−(3/28)x4−(11/280)x5
x1= 1250 −(3/7)x3−(1/28)x4+ (3/56)x5
x2= 1000 −(2/7)x3+ (1/7)x4−(1/70)x5
x1, x2, x3, x4, x5≥0.
At this point, all coefficients in the objective function are negative, so the ba-
sic solution is an optimal solution. This solution is (x1, x2, x3) = (1250,1000,0).
Exercise 29.3-8
Consider the simple program
z=−x1
x2= 1 −x1.
In this case we have m=n= 1, so m+n
n=2
1= 2, however, since the
only coefficients of the objective function are negative, we can’t make any other
choices for basic variable. We must immediately terminate with the basic solu-
tion (x1, x2) = (0,1), which is optimal.
Exercise 29.4-1
By just transposing A, swapping band c, and switching the maximization
to a minimization, we want to minimize 20y1+ 12y2+ 16y3subject to the
constraints
y1+y2≥18
y1+y3≥12.5
y1, y2, y3≥0
Exercise 29.4-2
11

By working through each aspect of putting a general linear program into
standard form, as outlined on page 852, we can show how to deal with trans-
forming each into the dual individually. If the problem is a minimization instead
of a maximization, replace cjby −cjin (29.84). If there is a lack of nonneg-
ativity constraint on xjwe duplicate the jth column of A, which corresponds
to duplicating the jth row of AT. If there is an equality constraint for bi, we
convert it to two inequalities by duplicating then negating the ith column of AT,
duplicating then negating the ith entry of b, and adding an extra yivariable.
We handle the greater-than-or-equal-to sign Pn
i=1 aij xj≥biby negating ith
column of ATand negating bi. Then we solve the dual problem of minimizing
bTysubject to ATy≥cand y≥0.
Exercise 29.4-3
First, we’ll convert the linear program for maximum flow described in equa-
tion (29.47)-(29.50) into standard form. The objective function says that cis a
vector indexed by a pair of vertices, and it is positive one if sis the first index
and negative one if sis the second index (zero if it is both). Next, we’ll modify
the constraints by switching the equalities over into inequalities to get
fu,v ≤c(u, v) for each u, v ∈V
X
u∈V
fvu ≤X
u∈V
fuv for each v∈V− {s, t}
X
u∈V
fvu ≥X
u∈V
fuv for each v∈V− {s, t}
fu,v ≥0 for each u, v ∈V
Then, we’ll convert all but the last set of the inequalities to be ≤by multi-
plying the third line by −1.
fu,v ≤c(u, v) for each u, v ∈V
X
u∈V
fvu ≤X
u∈V
fuv for each v∈V− {s, t}
X
u∈V
−fvu ≤X
u∈V
−fuv for each v∈V− {s, t}
fu,v ≥0 for each u, v ∈V
Finally, we’ll bring all the variables over to the left to get
12

fu,v ≤c(u, v) for each u, v ∈V
X
u∈V
fvu −X
u∈V
fuv ≤0 for each v∈V− {s, t}
X
u∈V
−fvu −X
u∈V
−fuv ≤0 for each v∈V− {s, t}
fu,v ≥0 for each u, v ∈V
Now, we can finally write down our Aand b.Awill be a |V|2×|V|2+2|V|−4
matrix built from smaller matrices A1and A2which correspond to the three
types of constraints that we have (of course, not counting the non-negativity
constraints). We will let g(u, v) be any bijective mapping from V×Vto |V|2.
We’ll also let hbe any bijection from V− {s, t}to [|V| − 2]
A=
A1
A2
−A2
Where A1is defined as having its row g(u, v) be all zeroes except for having
the value 1 at at the g(u, v)th entry. We define A2to have it’s row h(u) be equal
to 1 at all columns jfor which j=g(v, u) for some vand equal to −1 at all
columns jfor which j=g(u, v) for some v. Lastly, we mention that bis defined
as having it’s jth entry be equal to c(u, v) if j=g(u, v) and zero if j > |V|2.
Now that we have placed the linear program in standard form, we can take
its dual. We want to minimize P|V|2+2|V|−2
i=1 biyigiven the constraints that all
the yvalues are non-negative, and ATy≥c.
Exercise 29.4-4
First we need to put the linear programming problem into standard form,
as follows:
13

maximize X
(u,v)∈E
−a(u, v)fuv
subject to fuv ≤c(u, v) for each u, v ∈V
X
v∈V
fvu −X
v∈V
fuv ≤0 for each u∈V− {s, t}
X
v∈V
fuv −X
v∈V
fvu ≤0 for each u∈V− {s, t}
X
v∈V
fsv −X
v∈V
fvs ≤d
X
v∈V
fvs −X
v∈V
fsv ≤ −d
fuv ≥0.
We now formulate the dual problem. Let the vertices be denoted v1, v2, . . . , vn, s, t
and the edges be e1, e2, . . . , ek. Then we have bi=c(ei) for 1 ≤i≤k,bi= 0 for
k+ 1 ≤i≤k+ 2n,bk+2n+1 =d, and bk+2n+2 =−d. We also have ci=−a(ei)
for 1 ≤i≤k. For notation, let j.left denote the tail of edge ejand j.right
denote the head. Let χs(ej) = 1 if ejenters s, set it equal to -1 if ejleaves s,
and set it equal to 0 if ejis not incident with s. The dual problem is:
minimize
k
X
i=1
c(ei)yi+dyk+2n+1 −dyk+2n+2
subject to yj+yk+ej.right −yk+j.left −yk+n+ej.right +yk+n+ej.lef t
−χs(ej)yk+2n+1 +χs(ej)yk+2n+2 ≥ −a(ej)
where jruns between 1 and k. There is one constraint equation for each edge ej.
Exercise 29.4-5
Suppose that our original linear program is in standard form for some A, b, c.
Then, the dual of this is to minimize Pm
i=1 biyisubject to ATy≥cThis can be
rewritten as wanting to maximize Pm
i=1(−bi)yisubject to (−A)Ty≤ −c. Since
this is a standard form, we can take its dual easily, it is minimize Pn
j=1(−cj)xj
subject to (−A)x≥ −b. This is the same as minimizing Pn
j=1 cjxjsubject to
Ax ≤b, which was the original linear program.
Exercise 29.4-6
Corollary 26.5 from Chapter 26 can be interpreted as weak duality.
14

Exercise 29.5-1
For line 5, first let (N, B, A, b, c, v) be the result of calling PIVOT on Laux
using x0as the entering variable. Then repeatedly call PIVOT until an optimal
solution to Laux is obtained, and return this to (N, B, A, b, c, v). To remove
x0from the constraints, set ai,0= 0 for all i∈B, and set N=N\{0}. To
restore the original objective function of L, for each j∈Nand each i∈B, set
cj=cj−ciaij .
Exercise 29.5-2
In order to enter line 10 of INITIALIZE-SIMPLEX and begin iterating the
main loop of SIMPLEX, we must have recovered a basic solution which is fea-
sible for Laux. Since x0≥0 and the objective function is −x0, the objective
value associated to this solution (or any solution) must be negative. Since the
goal is to aximize, we have an upper bound of 0 on the objective value. By
Lemma 29.2, SIMPLEX correctly determines whether or not the input linear
program is unbounded. Since Laux is not unbounded, this can never be returned
by SIMPLEX.
Exercise 29.5-3
Since it is in standard form, the objective function has no constant term, it
is entirely given by Pn
i=1 cixi, which is going to be zero for any basic solution.
The same thing goes for its dual. Since there is some solution which has the
objective function achieve the same value both for the dual and the primal,
by the corollary to the weak duality theorem, that common value must be the
optimal value of the objective function.
Exercise 29.5-4
Consider the linear program in which we wish to maximize x1subject to the
constraint x1<1 and x1≥0. This has no optimal solution, but it is clearly
bounded and has feasible solutions. Thus, the Fundamental theorem of linear
programming does not hold in the case of strict inequalities.
Exercise 29.5-5
The initial basic solution isn’t feasible, so we will need to form the auxiliary
linear program:
15

maximize −x0
subject to x1−x2−x0≤8
−x1−x2−x0≤ −3
−x1+ 4x2−x0≤2
x1, x2, x0≥0.
Then we write this linear program in slack form:
z=−x0
x3= 8 −x1+x2+x0
x4=−3 + x1+x2+x0
x5= 2 + x1−4x2+x0
x1, x2, x3, x4, x5, x0≥0.
Next we make one call to PIVOT where x0is the entering variable and x4
is the leaving variable. This gives:
z=−3 + x1+x2−x4
x0= 3 −x1−x2+x4
x3= 11 −2x1+x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
The basic solution is feasible, so we repeatedly call PIVOT to get the optimal
solution to Laux. We’ll choose x1to be our entering variable and x0to be the
leaving variable. This gives
z=−x0
x1= 3 −x0−x2+x4
x3= 5 + 2x0+ 2x2−x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
The basic solution is now optimal for Laux, so we return this slack form to
SIMPLEX, set x0= 0, and update the objective function which yields
16

z= 3 + 2x2+x4
x1= 3 −x2+x4
x3= 5 + 2x2−x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
We’ll choose x2as our entering variable, which makes x5our leaving variable.
PIVOT then gives
z= 5 + (7/5)x4−(2/5)x5
x2= 1 + (1/5)x4−(1/5)x5
x1= 2 + (4/5)x4+ (1/5)x5
x3= 7 −(3/5)x4−(2/5)x5
x1, x2, x3, x4, x5, x0≥0.
We’ll choose x4as our entering variable, which makes x3our leaving variable.
PIVOT then gives
z= (64/3) −(7/3)x3−(4/3)x5
x4= (35/3) −(5/3)x3−(2/3)x5
x2= (10/3) −(1/3)x3−(1/3)x5
x1= (34/3) −(4/3)x3−(1/3)x5
x1, x2, x3, x4, x5, x0≥0.
Now all coefficients in the objective function are negative, so the basic solu-
tion is the optimal solution. It is (x1, x2) = (34/3,10/3).
Exercise 29.5-6
The initial basic solution isn’t feasible, so we will need to form the auxiliary
linear program:
maximize −x0
subject to x1+ 2x2−x0≤4
−2x1−6x2−x0≤ −12
x2−x0≤1
x1, x2, x0≥0.
Then we write this linear program in slack form:
17

z=−x0
x3= 4 −x1−2x2+x0
x4=−12 + 2x1+ 6x2+x0
x5= 1 −x2+x0.
Next we make one call to PIVOT where x0is the entering variable and x4
is the leaving variable. This gives:
z=−12 + 2x1+ 6x2−x4
x3= 16 −3x1−8x2+x4
x0= 12 + x4−2x1−6x2
x5= 13 −2x1−8x2+x4.
The basic solution is (x0, x1, x2, x3, x4, x5) = (12,0,0,16,0,13) which is fea-
sible for the auxiliary program. Now we need to run SIMPLEX to find the
optimal objective value to Laux. Let x1be our next entering variable. It is
most constrainted by x3, which will be our leaving variable. After PIVOT, the
new linear program is
z=−4/3 + (2/3)x2−(2/3)x3−(1/3)x4
x1= 16/3−(8/3)x2−(1/3)x3+ (1/3)x4
x0= 4/3−(2/3)x2+ (2/3)x3+ (1/3)x4
x5= 7/3−(8/3)x2+ (2/3)x3+ (1/3)x4.
Every coefficient in the objective function is negative, so we take the basic
solution (x0, x1, x2, x3, x4, x5) = (4/3,16/3,0,0,0,7/3) which is also optimal.
Since x06= 0, the original linear program must be infeasible.
Exercise 29.5-7
The initial basic solution isn’t feasible, so we will need to form the auxiliary
linear program:
18

maximize −x0
subject to −x1+x2−x0≤ −1
−x1−x2−x0≤ −3
−x1+ 4x2−x0≤2
x1, x2, x0≥0.
Then we write this linear program in slack form:
z=−x0
x3=−1 + x1−x2+x0
x4=−3 + x1+x2+x0
x5= 2 + x1−4x2+x0
x1, x2, x3, x4, x5, x0≥0.
Next we make one call to PIVOT where x0is the entering variable and x4
is the leaving variable. This gives:
z=−3 + x1+x2−x4
x0= 3 −x1−x2+x4
x3= 2 −2x2+x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
Let x1be our entering variable. Then x0is our leaving variable, and we
have
z=−x0
x1= 3 −x0−x2+x4
x3= 2 −2x2+x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
The basic solution is feasible, and optimal for Laux, so we return this and
run SIMPLEX. Updating the objective function and setting x0= 0 gives
19

z= 3 + 2x2+x4
x1= 3 −x2+x4
x3= 2 −2x2+x4
x5= 5 −5x2+x4
x1, x2, x3, x4, x5, x0≥0.
We’ll choose x2as our entering variable, which makes x3our leaving variable.
This gives
z= 5 −x3+ 2x4
x2= 1 −(1/2)x3+ (1/2)x4
x1= 2 + (1/2)x3+ (1/2)x4
x5= (5/2)x3−(3/2)x4
x1, x2, x3, x4, x5, x0≥0.
Next we use x4as our entering variable, which makes x5our leaving variable.
This gives
z= 5 + (7/3)x3−(4/3)x5
x4= (5/3)x3−(2/3)x5
x2= 1 + (1/3)x3−(1/3)x5
x1= 2 + (4/3)x3−(1/3)x5
x1, x2, x3, x4, x5, x0≥0.
Finally, we would like to choose x3as our entering variable, but every co-
efficient on x3is positive, so SIMPLEX returns that the linear program is un-
bounded.
Exercise 29.5-8
We first put the linear program in standard form:
maximize x1+x2+x3+x4
subject to 2x1−8x2−10x4≤ −50
−5x1−2x2≤ −100
−3x1+ 5x2−10x3+ 2x4≤ −25
x1, x2, x3, x4≥0.
20

The initial basic solution isn’t feasible, so we will need to form the auxiliary
linear program. It is given below in slack form:
z=−x0
x5=−50 −2x1+ 8x2+ 10x4+x0
x6=−100 + 5x1+ 2x2+x0
x7=−25 + 3x1−5x2+ 10x3−2x4+x0.
The index of the minimum biis 2, so we take x0to be our entering variable
and x6to be our leaving variable. The call to PIVOT on line 8 yields
z=−100 + 5x1+ 2x2−x6
x5= 50 −7x1+ 8x2+ 10x4+x6
x0= 100 −5x1−2x2+x6
x7= 75 −2x1−7x2+ 10x3−2x4+x6.
Next we’ll take x2to be our entering variable and x5to be our leaving
variable. The call to PIVOT yields
z=−225/2 + (27/4)x1−(10/4)x4+ (1/4)x5−(5/4)x6
x2=−50/8 + (7/8)x1−(10/8)x4+ (1/8)x5−(1/8)x6
x0= 225/2−(27/4)x1+ (10/4)x4−(1/4)x5+ (5/4)x6
x7= 475/4−(65/8)x1+ 10x3+ (54/8)x4−(7/8)x5+ (15/8)x6.
The work gets rather messy, but INITIALIZE-SIMPLEX does eventually
give a feasible solution to the linear program, and after running the simplex
method we find that (x1, x2, x3, x4) = (175/11,225/22,125/44,0) is an optimal
solution to the original linear programming problem.
Exercise 29.5-9
1. One option is that r= 0, s≥0 and t≤0. Suppose that r > 0, then, if we
have that sis non-negative and tis non-positive, it will be as we want.
2. We will split into two cases based on r. If r= 0, then this is exactly when
tis non-positive and sis non-negative. The other possible case is that r
is negative, and tis positive. In which case, because ris negative, we can
always get rx as small as we want so sdoesn’t matter, however, we can never
make rx positive so it can never be ≥t.
21

3. Again, we split into two possible cases for r. If r= 0, then it is when tis non-
negative and sis non-positive. The other possible case is that ris positive,
and sis negative. Since ris positive, rx will always be non-negative, so it
cannot be ≤s. But since ris positive, we have that we can always make rx
as big as we want, in particular, greater than t.
4. If we have that r= 0 and tis positive and sis negative. If ris nonzero,
then we can always either make rx really big or really small depending on
the sign of r, meaning that either the primal or the dual would be feasable.
Problem 29-1
a. We just let the linear inequalities that we need to satisfy be our set of con-
straints in the linear program. We let our function to maximize just be a
constant. The solver for linear programs would fail to detect any feasible
solution if the linear constraints were not feasible. If the linear programming
solver returns any solution at all, we know that the linear constraints are
feasible.
b. Suppose that we are trying to solve the linear program in standard form with
some particular A, b, c. That is, we want to maximize Pn
j=1 cjxjsubject to
Ax ≤band all entries of the x vector are non-negative. Now, consider the
dual program, that is, we want to minimize Pm
i=1 biyisubject to ATy≥cand
all the entries in the yvector are nonzero. We know by Corollary 29.9, if x
and yare feasible solutions to their respective problems, then, if we have that
their objective functions are equal, then, they are both optimal solutions.
We can force their objective functions to be equal. To do this, let ckbe
some nonzero entry in the cvector. If there are no nonzero entries, then
the function we are trying to optimize is just the zero function, and it is
exactly a feasibility question, so we we would be done. Then, we add two
linear inequalities to require xk=1
ckPm
i=1 biyi−Pn
j=1 cjxj. This will
require that whatever values the variables take, their objective functions will
be equal. Lastly, we just throw these in with the inequalities we already had.
So, the constraints will be:
Ax ≤b
ATy≥c
xk≤1
ck
m
X
i=1
biyi−
n
X
j=1
cjxj
xk≥1
ck
m
X
i=1
biyi−
n
X
j=1
cjxj
x1, x2, . . . , xn, y1, y2,...ym≥0
22

We have a number of variables equal to n+mand a number of constraints
equal to 2+2n+2m, so both are polynomial in n and m. Also, any assignment
of variables which satisfy all of these constraints will be a feasible solution to
both the problem and its dual that cause the respective objective functions to
take the same value, and so, must be an optimal solution to both the original
problem and its dual. This of course assumes that the linear inequality
feasibility solver doesn’t merely say that the inequalities are satisfyable, but
actually returns a satisfying assignment.
Lastly, it is necessary to note that if there is some optimal solution x, then,
we can obtain an optimal solution for the dual that makes the objective
functions equal by theorem 29.10. This ensures that the two constraints we
added to force the objectives of the primal and the dual to be equal don’t
cause us to change the optimal solution to the linear program.
Problem 29-2
a. An optimal solution to the LP program given in (29.53) - (29.57) is (x1, x2, x3) =
(8,4,0). An optimal solution to the dual is (y1, y2, y3) = (0,1/6,2/3). It is
then straightforward to verify that the equations hold.
b. First suppose that complementary slackness holds. Then the optimal objec-
tive value of the primal problem is, if it exists,
n
X
k=1
ckxk=
n
X
k=1
m
X
i=1
aikyixk
=
m
X
i=1
n
X
k=1
aikxkyi
=
m
X
i=1
biyi
which is precisely the optimal objective value of the dual problem. If any xj
is 0, then those terms drop out of them sum, so we can safely replace ckby
whatever we like in those terms. Since the objective values are equal, they
must be optimal. An identical argument shows that if an optimal solution
exists for the dual problem then any feasible solution for the primal problem
which satisfies the second equality of complementary slackness must also be
optimal.
Now suppose that xand yare optimal solutions, but that complementary
slackness fails. In other words, there exists some jsuch that xj6= 0 but
Pm
i=1 aij yi> cj, or there exists some isuch that yi6= 0 but Pn
j=1 aij xj< bi.
In the first case we have
23

n
X
k=1
ckxk<
n
X
k=1
m
X
i=1
aikyixk
=
m
X
i=1
n
X
k=1
aikxkyi
=
m
X
i=1
biyi.
This implies that the optimal objective value of the primal solution is strictly
less than the optimal value of the dual solution, a contradiction. The argu-
ment for the second case is identical. Thus, xand yare optimal solutions if
and only if complementary slackness holds.
c. This follows immediately from part b. If xis feasible and ysatisfies conditions
1, 2, and 3, then complementary slackness holds, so xand yare optimal. On
the other hand, if xis optimal, then the dual linear program must have an
optimal solution yas well, according to Theorem 29.10. Optimal solutions
are feasible, and by part b xand ysatisfy complementary slackness. Thus,
conditions 1, 2, and 3 hold.
Problem 29-3
a. The proof for weak duality goes through identically. Nowhere in it does it
use the integrality of the solutions.
b. Consider the linear program given in standard form by A= (1), b=1
2and
c= (2). The highest we can get this is 0 since that’s that only value that x
can be. Now, consider the dual to this, that is, we are trying to minimize x
2
subject to the constraint that x≥2. This will be minimized when x= 2, so,
the smallest solution we can get is 1.
Since we have just exhibited an example of a linear program that has a
different optimal solution as it’s dual, the duality theorem does not hold for
integer linear program.
c. The first inequality comes from looking at the fact that by adding the re-
striction that the solution must be integer valued, we obtain a set of feasible
solutions that is a subset of the feasible solutions of the original primal linear
program. Since, to get IP , we are taking the max over a subset of the things
we are taking a max over to get P, we must get a number that is no larger.
The third inequality is similar, except since we are taking min over a subset,
the inequality goes the other way.
The middle equality is given by Theorem 29.10.
24

Problem 29-4
Suppose that both systems are solvable, let xdenote a solution to the first
system, and ydenote a solution to the second. Taking transposes we have
xTAT≤0T. Right multiplying by ygives xTc=xTATy≤0T, which is a
contradiction to the fact that cTx > 0. Thus, both systems cannot be simul-
taneously solved. Now suppose that the second system fails. Consider the
following linear program:
maximize 0xsubject to ATy=cand y≥0
and its corresponding dual program
minimize −cTxsubject to Ax ≤0.
Since the second system fails, the primal is infeasible. However, the dual
is always feasible by taking x= 0. If there were a finite solution to the dual,
then duality says there would also be a finite solution to the primal. Thus, the
dual must be unbounded. Thus, there must exist a vector xwhich makes −cTx
arbitrarily small, implying that there exist vectors xfor which cTxis strictly
greater than 0. Thus, there is always at least one solution.
Problem 29-5
a. This is exactly the linear program given in equations (29.51) - (29.52) except
that the equation on the third line of the constraints should be removed, and
for the equation on the second line of the constraints, u should be selected
from all of Vinstead of from V\ {s, t}.
b. If a(u, v)>0 for every pair of vertices, then, there is no point in sending any
flow at all. So, an optimal solution is just to have no flow. This obviously
satisfies the capacity constraints, it also satisfies the conservation constraints
because the flow into and out of each vertex is zero.
c. We assume that the edge (t, s) is not in Ebecause that would be a silly edge
to have for a maximum flow from sto t. If it is there, remove it and it won’t
decrease the maximum flow. Let V0=Vand E0=E∪ {(t, s)}. For the
edges of E0that are in E, let the capacity be as it is in Eand let the cost be
0. For the other edge, we set c(t, s) = ∞and a(t, s) = −1. Then, if we have
any circulation in G0, it will be trying to get as much flow to go across the
edge (t, s) in order to drive the objective function lower, the other flows will
have no affect on the objective function. Then, by Kirchhoff’s current law
(a.k.a. common sense), the amount going across the edge (t, s) is the same
as the total flow in the rest of the network from sto t. This means that
maximizing the flow across the edge (t, s) is also maximizing the flow from
sto t. So, all we need to do to recover the maximum flow for the original
network is to keep the same flow values, but throw away the edge (t, s).
25

d. Suppose that sis the vertex that we are computing shortest distance from.
Then, we make the circulation network by first starting with the original
graph, giving each edge a cost of whatever it was before and infinite capacity.
Then, we place an edge going from every vertex that isn’t s to sthat has a
capacity of 1 and a cost of −|E|times the largest cost appearing among all
the edge costs already in the graph. Giving it such a negative cost ensures
that placing other flow through the network in order to get a unit of flow
across it will cause the total cost to decrease. Then, to recover the shortest
path for any vertex, start at that vertex and then go to any vertex that is
sending a unit of flow to it. Repeat this until you’ve reached s.
26

Chapter 30
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 30.1-1
(56)x6−8x5+ (8 −42)x4+ (−80 + 6 + 21)x3+ (−3−6)x2+ (60 + 3)x−30
which is
56x6−8x5−34x4−53x3−9x2+ 63x−30
Exercise 30.1-2
Let Abe the matrix with 1’s on the diagonal, −x0’s on the super diag-
onal, and 0’s everywhere else. Let qbe the vector (r, q0, q1, . . . , xn−2). If
a= (a0, a1, . . . , an−1) then we need to solve the matrix equation Aq =ato
compute the remainder and coefficients. Since Ais tridiagonal, Problem 28-1
(e) tells us how to solve this equation in linear time.
Exercise 30.1-3
For each pair of points, (p, A(p)), we can compute the pair (1
p, Arev (1
p)). To
do this, we note that Arev (1
p) = Pn−1
j=0 an−1−j1
pj=Pn−1
j=0 aj1
pn−1−j=
p1−nPn−1
j=0 ajpj=p1−nA(p) since we know what A(p) is, we can compute
Arev (1
p) of course, we are using the fact that p6= 0 because we are dividing
by it. Also, we know that each of these points are distinct, because 1
p=1
p0im-
plies that p=p0by cross multiplication. So, since all the x values were distinct
in the point value representation of A, they will be distinct in this point value
representation of Arev that we have made.
Exercise 30.1-4
Suppose that just n−1 point-value pairs uniquely determine a polynomial P
which satisfies them. Append the point value pair (xn−1, yn−1) to them, and let
P0be the unique polynomial which agrees with the npairs, given by Theorem
30.1. Now append instead (xn−1, y0
n−1) where yn−16=y0
n−1, and let P00 be the
1

polynomial obtained from these points via Theorem 30.1. Since polynomials
coming from npairs are unique, P06=P00. However, P0and P00 agree on the
original n−1 point-value pairs, contradicting the fact that Pwas determined
uniquely.
Exercise 30.1-5
First, we show that we can compute the coefficient representation of Qj(x−
xj) in time Θ(n2). We will do it by recursion, showing that multiplying Qj<k(x−
xj) by (x−xk) only takes time O(n), since this only needs to be done ntimes,
this gets is total runtime of O(n). Suppose that Pk−1
i=0 kixiis a coefficient
representation of Qj<k(x−xj). To multiply this by (x−xk), we just set
(k+ 1)i=ki−1−xkkifor i= 1,...k and (k+ 1)0=−xk·k0. Each of these
coefficients can be computed in constant time, since there are only linearly many
coefficients, then, the time to compute the next partial product is just O(n).
Now that we have a coefficient representation of Qj(x−xj), we need to
compute, for each kQj−k(x−xj), each of which can be computed in time θ(n)
by problem 30.1-2. Since the polynomial is defined as a product of things con-
taining the thing we are dividing by, we have that the remainder in each case is
equal to 0. Lets call these polynomials fk. Then, we need only compute the sum
Pkykfk(x)
fk(xk). That is, we compute f(xk) each in time Θ(n), so all told, only
Θ(n2) time is spent computing all the f(xk) values. For each of the terms in the
sum, dividing the polynomial fk(x) by the number fk(xk) and multiplying by
ykonly takes time Θ(n), so total it takes time Θ(n2). Lastly, we are adding up
npolynomials, each of degree bound n−1, so the total time taken there is Θ(n2).
Exercise 30.1-6
If we wish to compute P/Q but Qtakes on the value zero at some of these
points, then we can’t carry out the “obvious” method. However, as long as all
point value pairs (xi, yi) we choose for Qare such that yi6= 0, then the approach
comes out exactly as we would like.
Exercise 30.1-7
For the set A, we define the polynomial fAto have a coefficient representa-
tion that has aiequal zero if i6∈ Aand equal to 1 if i∈A. Similarly define fB.
Then, we claim that looking at fC:= fA·fBin coefficient form, we have that
the ith coefficient, ciis exactly equal to the number of times that iis realized as
a sum of elements from Aand B. Since we can perform the polynomial multi-
plication in time O(nlg(n)) by the methods of this chapter, we can get the final
answer in time O(nlg(n)). To see that fChas the nice property described, we’ll
look at the ways that we could end up having a term of xiappear. Each con-
tribution to that coefficient must come from there being some kso that ak6= 0
and bi−k6= 0, because the powers of x attached to each are additive when we
2
multiply. Since each of these contributions is only ever 1, the final coefficient is
counting the total number of such contributions, therefore counting the number
of k∈Asuch that i−k∈B, which is exactly what we claimed fCwas counting.
Exercise 30.2-1
ωn/2
n=e2πi/nn/2=eπi =−1 = ω2
Exercise 30.2-2
The DFT is (6,−2i−2,−2,2i−2).
Exercise 30.2-3
We want to evaluate both of the functions at the fourth roots of unity, that is,
±1,±i. We have an initial call of RECU RSIV E−FFT((−10,1,−1,7,0,0,0,0)).
This causes a call of RECU RSIV E −FFT((−10,−1,0,0)), which evaluates to
(−11,−10−i, −9,−10+i). It also causes a call of RECURSIV E−FFT((1,7,0,0))
which returns (8,1+7i, −6,1−7i). Now, in evaluating the original function call,
we have y0=−11+8 = −3, y4=−19. Then, we change ωto ω8=1+i
√2, and have
y1=−10−i+1+i
√2(1+7i) = −10−i−3√2+4√2iand y5=−10−i+3√2−4√2.
At the next value of k, we get y2=−9−6iand y6=−9+6i. Lastly, we compute
y3=−10 + i+ 3√2+4√2iand y7=−10 + i−3√2−4√2i. So, the vector re-
turned is (−3,−10 −i−3√2+4√2i, −9−6i, −10 + i+ 3√2+4√2i, −19,−10 −
i+ 3√2−4√2i, −9+6i, −10 + i−3√2−4√2i). Similarly, if we wanted to
compute the FFT of the other polynomial, we’d get the FFT of B is given by
(5,3−7√2+√2i, 3−14i, 3+7√2+√2i, 1,3+7√2−√2i, 3+14i, 3−7√2−√2i).
Then, we just multiply together these point value representations to get that
the product of Aand Bhas the point value representation of
(−15,
4 + 62√2+(−65 + 9√2)i,
−111 + 108i,
4−62√2 + (65 + 9√2)i,
−19,
4−62√2+(−65 + −9√2)i,
−111 −108i,
4 + 62√2 + (65 −9√2)i)
Interpolating this polynomial using equation (30.11), we get
3
a0=1
8
7
X
k=0
yk=−30
a1=1
8
7
X
k=0
ykω−k
8= 63
a2=1
8
7
X
k=0
ykω−2k
8=−9
a3=1
8
7
X
k=0
ykω−3k
8=−53
a4=1
8
7
X
k=0
ykω−4k
8=−34
a5=1
8
7
X
k=0
ykω−5k
8=−8
a6=1
8
7
X
k=0
ykω−6k
8= 56
a7=1
8
7
X
k=0
ykω−7k
8= 0
Giving us the polynomial
56x6−8x5−34x4−53x3−9x2+ 63x−30
The same as in problem 30.1-1.
Exercise 30.2-4
Exercise 30.2-5
To show that our algorithm for nbeing a power of 3 works, we will first
prove an analogue of the halving lemma. In particular, for na power of 3, that
the cube of the nth complex roots of unity are the n/3 complex (n/3)th roots
of unity. First, we note that by the cancellation lemma, (ωk
n)3=ωk
n/3.
(ωk+n/3
n)3=ω3k+n
n
=(ωk
n)3
Now, we write A(x) = Pn−1
j=0 ajxj, and define A[i]=Pn/3−1
j=0 ai+3jxjfor i=
4

Algorithm 1 RECURSIVE-FFT-INV(y)
1: n=y.length
2: if n== 1 then
3: return y/n
4: end if
5: wn=e2πi/n
6: w= 1/n
7: y[0] = (y0, y2, . . . , yn−2)
8: y[1] = (y1, y3, . . . , yn−1)
9: a[0] = RECURSIVE-FFT-INV(y[0])
10: a[1] = RECURSIVE-FFT-INV(y[1])
11: for k= 0 to n/2−1do
12: ak=a[0]
k+wa[1]
k
13: ak+(n/2) =a[0]
k−wa[1]
k
14: w=wwn
15: end for
16: return a
1,2,3. Then, we can see that
A(x) = A[0](x3) + xA[1](x3) + x2A[2](x3)
The recurrence we get is
T(n)=3T(n/3) + Θ(n)
= Θ(nlg(n))
Exercise 30.2-6
Using this different value of ω, and viewing the value modulo m, we will
use the same definition of the DFT. First, notice that this choice of ωhas the
correct behavior, that is, ωn= (2tn/2)2≡ −12= 1. To see that DF T −1is well
defined, we can just notice that if we take two different sets of coefficients, say
{ak}and {bk}, if we get the same evaluations at each of the npoints, we get
that the polynomial Pn−1
j=0 (aj−bj)xkhas nzeroes, even though it is only degree
n−1, a contradiction to the fundamental theorem of Algebra (which works over
an arbitrary ring, so it works in Zm.
Now, to see that the DFT is well defined, suppose we have a single set of
coefficients then it has to give the same evaluations at the various points, so it
has to give a single evaluation after being viewed mod m.
Exercise 30.2-7
We just do a bunch of multiplications. More seriously, let Pi,0(x)=(x−zi−1)
for i= 1, . . . , n. Then, we compute the following products, Pi,k =Pi,k−1·
P2i,k−1, for any i≤n/(2k). If we ever index outside of the already defined
5

Algorithm 2 POW3FFT(a)
n = a.length
if n==1 then
return a
end if
ωn=e2πi/n
ω= 1
a[0] = (a0, a3, a6...,an−3)
a[1] = (a1, a4, a7...,an−2)
a[2] = (a2, a5, a8...,an−1)
y[0] =P OW 3FFT(a[0])
y[1] =P OW 3FFT(a[1])
y[2] =P OW 3FFT(a[2])
for k=0,1. . . n/2-1 do
yk=yk[0] + ωy[1]
k+ω2y[2]
k
yk+n/3=yk[0] + ω3ωy[1]
k+ω2
3ω2y[2]
k
yk+2n/3=yk[0] + ω2
3ωy[1]
k+ω3ω2y[2]
k
ω=ωωn
end for
return y
Pi,k values, we pretend that the value we get is 1. Then, our final answer will
be P1,blg(n)c+1. We have that obtaining a polynomial in this way that has the
recurrence where we nrepresents the time required to do it for a polynomial of
degree bound n that has zeroes at ngiven points.
T(n) = 2T(n/2) + Θ(nlg(n))
Which, we know by exercise 4.6-2, has a solution of T∈Θ(nlg2(n)).
Exercise 30.2-8
Define a polynomial P(x) of degree bound 2nby P(x) = P2n−1
j=0 bjxjwhere
bj=ajzj2/2if j≤n−1 and 0 for j≥n. Define Q(x) = P2n−1
j=0 cjxjwhere
cj=z−j2/2. We can compute their product in time O(2nlg 2n) = O(nlg n). If
we let dkbe the coefficient on xkin their product, for k≥nwe have
dk=
k
X
j=0
bjck−j=
n−1
X
j=0 ajzj2/2z−(k−j)2/2.
By setting yk=zk2/2dkin linear time, we can compute the chirp transform
in O(nlg n).
6

Exercise 30.3-1
By calling BIT-REVERSE-COPY, we get that A= (0,4,3,7,2,5,−1,9).
after the first pass of the outermost, loop, when s= 1, we have that the array
is A= (4,−4,10,−4,7,−3,8,−10). The value at the end of the next iteration
of the outermost loop is (14,−3−3i, −8,−3−3i, 15,3 + 4i, −13,3−4i). Then,
on the last iteration, we get our final answer of
A= (19,
−4−4i+7
√2−13
√2i,
−6 + i,
−4+4i−7
√2−13
√2i,
−1,
−4−4i−7
√2+13
√2i,
−6−i,
−4+4i+7
√2+13
√2i)
Exercise 30.3-2
We can consider ITERATIVE-FFT as working in two steps, the copy step
(line 1) and the iteration step (lines 4 through 14). To implement in inverse
iterative FFT algorithm, we would need to first reverse the iteration step,
then reverse the copy step. We can do this by implementing the INVERSE-
INTERATIVE-FFT algorithm exactly as we did with the FFT algorithm, but
this time creating the iterative version of RECURSIVE-FFT-INV as given in
exercise 30.2-4.
Exercise 30.3-3
It computes a twiddle factor for each iteration of the innermost for loop.
Since there are n/m iterations of the loop on line 6 and, for each m/2 iterations
of the innermost loop, there are a total of n/(2s)·2s−1=n/2 twiddle factors.
If we, before line 6 compute all of the powers < m/2 of ωm, we won’t have to
do any computation of them later on. These are the only twiddle factors that
will show up, and so, we only compute m/2 = s2/2=2s−1of them.
Exercise 30.3-4
First observe that if the input to a butterfly operation is all zeros, then
7

so is the output. Our initial input will be (a0, a1, . . . , an−1) where ai= 0 if
0≤i≤n/2−1, and iotherwise. By examining the diagram on page 919, we
see that the zeros will propogate as half the input to each butterfly operation
in the final stage. Thus, if any of the output values are 0 we know that one of
the yk’s is zero, where k≥n/2−1. If this is the case, then the faulty butterfly
added occurs along the wire connected to yk. If none of the output values are
zero, the faulty butterfly adder must occur as one which only deals with the
first n/2−1 wires. In this case, we rerun the test with input such that ai=i
if 0 ≤i≤n/2−1 and 0 otherwise. This time, we will know for sure which of
the first n/2−1 wires touches the faulty butterfly adder. Since only lg nadders
touch a given wire, we have reduced the problem of size nto a problem of size
lg n. Thus, at most 2 lg?n=O(lg?n) tests are required.
Problem 30-1
a. Similar to problem 4.2-7,
(a+b)(c+d) = ac +cb +ad +cd
So, we compute that product, we also compute ac and cd. This gets us the
the product of the two polynomials is
acx2+ ((a+b)(c+d)−ac −cd)x+cd
b. Assume that nis a power of two, if it isn’t, then just bump it up to the nearest
power of two, since the degree bound can be higher than the degree of the
polynomials. Suppose that we want to multiply the polynomials A1(x) =
Pn−1
j=1 aj,1xjand A2(x) = Pn−1
j=1 aj,2xj.
In the first method, we’ll set Hi(x) = Pn−1
j=n
2aj,ixjand Li(x) = Pn/2−1
j=0 aj,ixj
for i= 1,2. Then, we have that Ai(x) = Hi(x)xn/2+Li(x) for i= 1,2. Then,
by the method of the first part of this problem, we have that
A1(x)·A2(x)=(H1(x)·H2(x))xn
+ ((H1(x) + L1(x)) ·(H2(x) + L2(x)) −H1(x)·H2(x)−L1(x)·L2(x))xn/2
+L1(x)·L2(x)
So, the runtime of this procedure for degree bound nis, by the master theo-
rem:
HL(n) = 3HL(n/2) + Θ(n)
= Θ(nlg(3))
8

Now, for the second method, we write Oi(x) = Pn/2−1
j=0 a2j+1,ixjand Ei(x) =
Pn/2−1
j=0 a2j,ixjfor i= 1,2. Then, we have that for both values of i,Ai=
xOi(x2) + Ei(x2). So,
A1(x)·A2(x) =x2(O1(x2)·O2(x2))
+x((O1(x2) + E1(x2))(O2(x2) + E1(x2)) −O1(x2)·O2(x2)−E1(x2)·E2(x2))
+E1(x2)·E2(x2)
So, again, we only need to do three multiplies, each with a degree bound of
half. So, the runtime for this, call it OE(n) is
OE(n) = 3OE(n/2) + Θ(n)
= Θ(nlg(n))
c. Suppose that we want to multiply two integers A1=Pblg(A1)c
k=0 ak,12kand
A2=Pblg(A2)c
k=0 ak,22k. Then, we’ll associate to these polynomials fi=
Pblg(Ai)c
k=0 ak,ixi. Then, we exactly have that fi(2) = Ai. So, to find A1·A2,
all we need do is multiply the polynomials f1and f2and evaluate their prod-
uct at 2. Since both of their degrees are bounded by n, we can multiply them
in time Θ(nlg(3)) by the previous part. evaluating them also only takes linear
time, so doesn’t change the total runtime.
Problem 30-2
a. The sum of two Toeplitz matrices is Toeplitz, but the product is not.
b. Let Abe a Toeplitz matrix. We can use a vector of length 2n−1 to represent
it, given by: (c0, . . . , c2n−2) = (an,1, an−1,1, . . . , a2,1, a1,1, a1,2, . . . , aa,n). To
add two Toeplitz matrices, simply add their associated vectors.
c. We can interpret this as the multiplication of two polynomials. Specifically,
let P(x) = c0+c1x+. . . +c2n−1x2n−2. Let (b0, b1, . . . , bn−1) be the vector
of length nby which we wish to multiply, and let ykdenote the kth entry
of the vector which results from the multiplication. Let Q(x) = b0xn−1+
b1xn−2+. . .+bn−1. Then the coefficient on xn−k+n−1in P(x)Q(x) is given by
Pn−1
i=0 cn−k+ibi=Pn−1
i=0 ak,ibi=yk. Since we can multiply the polynomials
in O(nlg n) and the needed results are just some of the coefficients, we can
multiply a Toeplitz matrix by an n-vector in O(nlg n).
d. We can view matrix multiplication as simply multiplication by an nvector
carried out ntimes. If bjis the jth column of the second matrix, then Abj
is the jth column of the resulting matrix. By part c, this can be done in
O(n2lg n) time, which is asymptotically faster than even Strassen’s algo-
rithm.
9

Problem 30-3
a.
yk1,...,kd=
n1−1
X
j1=0 ···
nd−1
X
jd=0
aj1,...jdωj1k1
n1···ωjdkd
nd
=
nd−1
X
jd=0 ···
n1−1
X
j1=0
aj1,...jdωj1k1
n1···ωjdkd
nd
=
nd−1
X
jd=0 ···
n2−1
X
j2=0
n1−1
X
j1=0
aj1,...jdωj1k1
n1
ωj2k2
n2···ωjdkd
nd
So, the thing inside the parentheses is a one dimensional Fourier transform
that must be computed for every possible term of the outer sums, that is,
must be computed n2n3···nd=n/n1times because in each term the a
values might be different. Once that is computed we’ve decreased the number
of sums by 1. This means that by keeping on applying this, we can keep
decreasing the number of dimensions until the problem is solved. We are
actually only needing to do n/(Qi≤kni) of the DFT’s along dimension k
instead of the larger number stated in the problem of n/ni.
b. We can exchange the order of summation however we please because none of
the indices of summation ever appear in the bounds for a different summation
sign.
c. The time to do each DFT along the kth dimension is O(nklg(nk)), since we
only need to do it at most n/(Qj≤knj) times, the runtime of all of them
in dimension kis at most O(n/(Qj<k nj) lg(nk)). Also, note that we may
assume that all of the nkvalues are at least two, because otherwise doing
that DFT would be trivial. So, the total time is on the order of
d
X
k=1
n/
Y
j<k
nj
lg(nk)≤lg(n)
d
X
k=1
n/
Y
j<k
nj
≤lg(n)
d
X
k=1
n/2k−1
< n lg(n)
Which is independent of d.
Problem 30-4
10

a. It is straightforward to check that A(t)(x0) = t!bt. Since A(t+1)(x0) = (t+
1)A(t)(x0)bt+1/bt, we can compute each next term in constant time from the
previous, so computing A(t)(x0) for t= 0,1, . . . , n −1 takes O(n) time.
b. We just need to perform an inverse FFT procedure on the npoint-value pairs
A(x0+wk
n) = Pn−1
j=0 bjwkj
n. This takes O(nlg n).
c. Let χ(x) = 1 if x≥0 and 0 otherwise. Using the binomial theorem we have
A(x0+wk
n) =
n−1
X
j=0
aj
j
X
r=0 j
rwkr
nxj−r
0
=
n−1
X
j=0
aj
n−1
X
r=0
j!
r!(j−r)!wkr
nxj−r
0χ(j−r)
=
n−1
X
r=0
wkr
n
r!
n−1
X
j=0
ajj!xj−r
0χ(j−r)
(j−r)!
=
n−1
X
r=0
wkr
n
r!
n−1
X
j=0
f(j)g(r−j).
d. Let s(r) = Pn−1
j=0 f(j)g(r−j) in O(n) time. Letting bj=s(r)
r!. Then we
need only compute the DFT of the coefficient vector (b0, b1, . . . , bn−1), which
can be done in O(nlg n). By part b, once we have these evaluations we can
compute the derivatives in O(nlg n) time as well.
Problem 30-5
a. First, note that because the degree of x−zis one, A(x)mod(x−z) will be
a constant. By the definition of modular arithmetic for polynomials(or any
Euclidean Domain), there is some polynomial f(x) so that A(x) = f(x)(x−
z)+(A(x) mod (x−z)). So, if we evaluate this expression at z, the first
term goes to zero, and we have that A(z) = A(x) mod (x−z).
b. Pkk(x)=(x−xk) so, by the previous part, Qkk =A(xk). The degree of
P0,n−1is equal to nwhich is higher than the degree of A. Therefore modding
out by it doesn’t change the value value of A(x) at all. That is, if we were to
write A(x) = f(x)P0,n−1+Q0,n−1, the only acceptable value of f(x) is zero,
otherwise there would be a too high degree term on the right.
c. Suppose we write A(x) = f1(x)Pij (x) + Qij (x). Then, we take Qij=
f2(x)Pik + (Qij (x) mod Pik). Since we have that Pik is a product over a
smaller set of irreducible factors than Pij , we can write A(x)=(f1(x)Qj
`=k+1(x−
x`) + f2)Pik + (Qij (x) mod Pik). Since we can write it as a remainder of A
11

after dividing by Pik, we have that Amod Pik =Qij (x) mod Pik, which is
to say, Qik =Qij (x) mod Pik.
We basically do the same thing to show the other equality. Suppose that
Qij =f3Pkj +(Qij (x) mod Pkj ), then A(x)=(f1Q`=k−1
`=i(x−x`)+f3)Pkj +
(Qij (x) mod Pkj ) and so, Qkj =Amod Pkj = (Qij (x) mod Pkj ).
d. Initially, we know what the value of Q0,n−1is, since it is just A(x). Suppose
that nis a power of 2, since it makes the analysis easier to do, if it is not
a power of two, then bump up the degree bound to the nearest value of 2,
since we have that (2n) + lg2(2n)∈O(nlg2(n)), doing this increase of the
degree bound will not change the asymptotics of the algorithm. Since we
have that the number of points we are evaluating at is equal to the degree
bound, just pick arbitrary points to pad the original set of points with and
then disregard their values once they are computed. The idea is to cut in half
0, . . . , n −1, by computing Q0,n/2−1and Qn/2,n−1using the rule from the
previous part until you arrive at having to compute Qii for some i, which by
part b is equal to A(xi). Since the computing of each of the Qvalues before
the end is only a matter of computing two polynomial remainders, the time
to do this is given by the recurrence
T(n) = 2T(n/2) + Θ(nlg(n))
Even though the master theorem doesn’t apply to this recurrence, exercise
4.6-2 tells us that T∈Θ(nlg2(n)).
Problem 30-6
a. By the prime number theorem, the number of primes between 1 and N
is approximately 1
ln(N). This means that between 1 and nlg(n), we can
expect that a random number will be prime with probability 1
lg(nlg(n)) =
1
lg(n)+lg(lg(n)) ≈1
lg(n). Also, we are considering lg(n) numbers between 1 and
nlg(n) + 1 that are one more than a multiple of n, so, the expected number
of prime numbers of that form with k≤lg(n) is one, so, by the poisson
paradigm, we would think that with probability at least about 1
e, there is a
prime number of that form with k≤lg(n).
Sine the value of pis expected to be about nlg(n), it has a length of about
lg(nlg(n)) = lg(n) + lg(lg(n)).
b.
c.
d.
12
Chapter 31
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 31.1-1
By the given equation, we can write c= 1 ·a+b, with 0 ≥b<a. By the
definition of remainders given just below the division theorem, this means that
bis the remainder when c is divided by a, that is b=cmod a.
Exercise 31.1-2
Suppose that there are only finitely many primes p1, p2, . . . , pk. Then p=
p1p2···pk+ 1 isn’t prime, so there must be some piwhich divides it. However,
pi·(p1···pi−1pi+1 ···pk)< p and p·(p1···pi−1pi+1 ···pk+ 1) > p, so pican’t
divide p. Since this holds for any choice of i, we obtain a contradiction. Thus,
there are infinitely many primes.
Exercise 31.1-3
a|bmeans there exists k1∈Zso that k1a=b.b|cmeans there exists k2∈Z
so that k2b=c. This means that (k1k2)a=c. Since the integers are a ring,
k1k2∈Z, so, we have that a|c.
Exercise 31.1-4
Let g= gcd(k, p). Then g|kand g|p. Since pis prime, g=por g= 1. Since
0< k < p,g < p. Thus, g= 1.
Exercise 31.1-5
By Theorem 31.2, since gcd(a, n) = 1, there exist integers p, q so that
pa +qn = 1, so, bpa +bqn =b. Since n|ab, there exists an integer kso that
kn =ab. This means that knp +pqn = (k+q)pn =b. Since ndivides the left
hand side, it must divide the right hand side as well.
Exercise 31.1-6
1

Observe that p
k=p!
k!(p−k)! =p(p−1)···(p−k+1)
k!. Let q= (p−1)(p−2) ···(p−
k+ 1). Since pis prime, k!6 |p. However, we know that p
kis an integer because
it is also a counting formula. Thus, k! divides pq. By Corollary 31.5, k!|q. Write
q=ck!. Then we have p
k=pc, which is divisible by p.
By the binomial theorem and the fact that p|p
kfor 0 < k < p,
(a+b)p=
p
X
k=0 p
kakbp−k≡ap+bp(mod p).
Exercise 31.1-7
First, suppose that x=yb + (xmod b), (xmod b) = za + ((xmod b)
mod a), and ka =b. Then, we have x=yka + (xmod b)=(yk +z)a+ ((x
mod b) mod a). So, we have that xmod a= ((xmod b) mod a).
For the second part of the problem, suppose that xmod b=ymod b.
Then, by the first half of the problem, applied first to x and then to b, x
mod a= (xmod b) mod a= (ymod b) mod a=ymod a. So, x≡y
mod a.
Exercise 31.1-8
We can test in time polynomial in βwhether or not a given β-bit number
is a perfect kth power. Then, since two to the βth power is longer than the
number we are given, we only need to test values of kbetween 2 and β, thereby
keeping the runtime polynomial in β.
To check whether a given number nis a perfect kth power, we will be using
a binary search like technique. That is, if we want to find the k-th root of a
number, we initially know that it lies somewhere between 0 and the number
itself. We then look at the number of the current range of number under con-
sideration, raise it to the kth power in time polynomial in β. We can do this
by the method of repeated squaring discussed in section 31.6. Then, if we get a
number larger than the given number when we perform repeated squaring, we
know that the true kth root is in the lower half of the range in consideration,
if it is equal, it is the midpoint, if larger, it is the upper half. Since each time,
we are cutting down the range by a factor of two, and it is initially a range of
length Θ(2β), the number of times that we need to raise a number the the kth
power is Θ(β). Putting it all together, with the O(β3) time exponentiation, we
get that the total runtime of this procedure is O(β5).
Exercise 31.1-9
For (31.6), we see that aand bin theorem 31.2 which provides a characteri-
zation of gcd appear symmetrically, so swapping the two won’t change anything.
For (31.7), theorem 31.2 tells us that gcd’s are defined in terms of integer
linear combinations. If we had some integer linear combination involving a and
2

b, we can changed that into one involving (-a) and b by replacing the multiplier
of a with its negation.
For (31.8), by repeatedly applying (31.6) and (31.7), we can get this equality
for all four possible cases based on the signs of both aand b.
For(31.9), consider all integer linear combinations of aand 0, the thing we
multiply by will not affect the final linear combination, so, really we are just
taking the set of all integer multiples of aand finding the smallest element.
We can never decrease the absolute value of a by multiplying by an integer
(|ka|=|k||a|), so, the smallest element is just what is obtained by multiplying
by 1, which is |a|.
For (31.10), again consider possible integer linear combinations na +mka,
we can rewrite this as (n+km)a, so it has absolute value |n+km||a|. Since the
first factor is an integer, we can’t have it with a value less than 1 and still have
a positive final answer, this means that the smallest element is when the first
factor is 1, which is achievable by setting n= 1, m = 0.
Exercise 31.1-10
Consider the prime factorization of each of a,b, and c, written as a=
p1p2. . . pkwhere we allow repeats of primes. The gcd of band cis just the
product of all pisuch that piappears in both factorizations. If it appears multi-
ple times, we include it as many times as it appears on the side with the fewest
occurrances of pi. (Explicitly, see equation 31.13 on page 934). To get the gcd
of gcd(b, c) and a, we do this again. Thus, the left hand side is just equal to the
intersection (with appropriate multiplicities) of the products of prime factors
of a,b, and c. For the right hand side, we consider intersecting first the prime
factors of aand b, and then the prime factors of c, but since intersections are
associative, so is the gcd operator.
Exercise 31.1-11
Suppose to a contradiction that we had two different prime decomposition.
First, we know that the set of primes they both consist of are equal, because if
there were any prime pin the symmetric difference, pwould divide one of them
but not the other. Suppose they are given by (e1, e2, . . . , er) and (f1, f2, . . . , fr)
and suppose that ei< fifor some position. Then, we either have that pei+1
i
divides aor not. If it does, then the decomposition corresponding to {ei}is
wrong because it doesn’t have enough factors of pi, otherwise, the one corre-
sponding to {fi}is wrong because it has too many.
Exercise 31.1-12
Standard long division runs in O(β2), and one can easily read off the re-
mainder term at the end.
3

Exercise 31.1-13
First, we bump up the length of the original number until it is a power of two,
this will not affect the asymptotics, and we just imagine padding it with zeroes
on the most significant side, so it does not change its value as a number. We
split the input binary integer, and split it into two segments, a less significant
half `and an more significant half m, so that the input is equal to m2β/2+`.
Then, we recursively convert mand `to decimal. Also, since we’ll need it later,
we compute the decimal versions of all the values of 22iup to 2β. There are
only lg(β) of these numbers, so, the straigtforward approach only takes time
O(lg2(β)) so will be overshadowed by the rest of the algorithm. Once we’ve
done that, we evaluate m2β/2+`, which involves computing the product of two
numbers and adding two numbers, so, we have the recurrence
T(β) = 2T(β/2) + M(β/2)
Since we have trouble separating Mfrom linear by a nfor some epsilon, the
analysis gets easier if we just forget about the fact that the difficulty of the
multiplication is going down in the subcases, this concession gets us the runtime
that T(β)∈O(M(β) lg(β)) by master theorem.
Note that there is also a procedure to convert from binary to decimal that
only takes time Θ(β), instead of the given algorithm which is Θ(M(β) lg(β)) ∈
Ω(βlg(β)) that is rooted in automata theory. We can construct a deterministic
finite transducer between the two languages, then, since we only need to take as
many steps as there are bits in the input, the runtime will be linear. We would
have states to keep track of the carryover from each digit to the next.
Exercise 31.2-1
First, we show that the expression given in equation (31.13) is a common
divisor. To see that we just notice that
a= (
r
Y
i=1
pei−min(ei,fi)
i)
r
Y
i=1
pmin(ei,fi)
i
and
b= (
r
Y
i=1
pfi−min(ei,fi)
i)
r
Y
i=1
pmin(ei,fi)
i
Since none of the exponents showing up are negative, everything in sight is
an integer.
Now, we show that there is no larger common divisor. We will do this by
showing that for each prime, the power can be no higher. Suppose we had some
common divisor dof aand b. First note that dcannot have a prime factor that
doesn’t appear in both aor b, otherwise any integer times dwould also have
that factor, but being a common divisor means that we can write both aand
bas an integer times d. So, there is some sequence {gi}so that d=Qr
i=1 pgi
i.
4

Now, we claim that for every i,gi≤min(ei, fi). Suppose to a contradiction
that there was some iso that gi>min(ei, fi). This means that deither has
more factors of pithan aor than b. However, multiplying integers can’t cause
the number of factors of each prime to decrease, so this is a contradiction, since
we are claiming that dis a common divisor. Since the power of each prime in d
is less than or equal to the power of each prime in c, we must have that d≤c.
So, cis a GCD.
Exercise 31.2-2
We’ll create a table similar to that of figure 31.1:
a b ba/bcd x y
899 493 1 29 -6 11
493 406 1 29 5 -6
406 87 4 29 -1 5
87 58 1 29 1 -1
58 29 2 29 0 1
29 0 - 29 1 0
Thus, (d, x, y) = (29,−6,11).
Exercise 31.2-3
Let cbe such that a=cn+(amod n). If k= 0, it is trivial, so suppose k <
0. Then, EUCLID(a+kn,n) goes to line 3, so returns EU CLID(n, a mod n).
Similarly, EU CLID(a, n) = EUCLID((amod n) + cn, n) = EU CLID(n, a
mod n). So, by correctness of the Euclidean algorithm,
gcd(a+kn, n) = EUCLID(a+kn, n)
=EUCLID(n, a mod n)
=EUCLID(a, n)
=gcd(a, n)
Exercise 31.2-4
Algorithm 1 ITERATIVE-EUCLID(a,b)
1: while b > 0do
2: (a, b) = (b, a mod b)
3: end while
4: return a
Exercise 31.2-5
We know that for all k, if b < Fk+1 < φk+1/√5, then it takes fewer than k
steps. If we let k= logφb+ 1, then, since b<φlogφb+2/√5 = φ2
√5·b, we have
that it only takes 1 + logφ(b) steps.
5

We can improve this bound to 1+logφ(b/ gcd(a, b)). This is because we know
that the algorithm will terminate when it reaches gcd(a, b). We will emulate the
proof of lemma 31.10 to show a slightly different claim that Euclid’s algorithm
takes krecursive calls, then a≥gcd(a, b)Fk+2 and b≥gcd(a, b)Fk+!. We will
similarly do induction on k. If it takes one recursive call, and we have a > b,
we have a≥2 gcd(a, b) and b= gcd(a, b).
Now, suppose it holds for k−1, we want to show it holds for k. The
first call that is made is of EUCLID(b, a mod b). Since this then only needs
k−1 recursive calls, we can apply the inductive hypothesis to get that b≥
gcd(a, b)Fk+1 and amod b≥gcd(a, b)Fk. Since we had that a>b, we have
that a≥b+ (amod b)≥gcd(a, b)(Fk+1 +Fk) = gcd(a, b)Fk+2 completing the
induction.
Since we have that we only need ksteps so long as b < gcd(a, b)Fk+1 <
gcd(a, b)φk+1. we have that logφ(b/ gcd(a, b)) < k + 1. This is satisfied if we set
k= 1 + logφ(b/ gcd(a, b))
Exercise 31.2-6
Since Fk+1 mod Fk=Fk−1we have gcd(Fk+1, Fk) = gcd(Fk, Fk−1). Since
gcd(2,1) = 1 we have that gcd(Fk+1, Fk) = 1 for all k. Moreover, since Fkis
increasing, we have bFk+1/Fkc= 1 for all k. When we reach the base case of
the recursive calls to EXTENDED-EUCLID, we return (1,1,0). The following
returns are given by (d, x, y) = (d0, y0, x0−y0). We will show that in general,
EXTENDED-EUCLID(Fk+1, Fk) returns (1,(−1)k+1Fk−2,(−1)kFk−1). We have
already shown dis correct, and handled the base case. Now suppose the claim
holds for k−1. Then EXTENDED-EUCLID(Fk+1, Fk) returns (d0, y0, x0−y0)
where d0= 1, y0= (−1)k−1Fk−2,x0= (−1)kFk−3, so the algorithm returns
(1,(−1)k−1Fk−2,(−1)kFk−3−(−1)k−1Fk−2) = (1,(−1)k+1Fk−2,(−1)k(Fk−3+Fk−2)
= (1,(−1)k+1Fk−2,(−1)kFk−1)
as desired.
Exercise 31.2-7
To show it is independent of the order of its arguments, we prove the fol-
lowing swap property, for all a, b, c, gcd(a, gcd(b, c)) = gcd(b, gcd(a, c)). By
applying these swaps in some order, we can obtain an arbitrary ordering on the
variables (the permutation group is generated by the set of adjacent transposi-
tions). Let aibe the power of the ith prime in the prime factor decomposition
of a, similarly define biand ci. Then, we have that
6

gcd(a, gcd(b, c)) = Y
i
pmin(ai,min(bi,ci))
i
=Y
i
pmin(ai,bi,ci)
i
=Y
i
pmin(bi,min(ai,ci))
i
= gcd(b, gcd(a, c))
To find the integers {xi}as described in the problem, we use a similar
approach as for EXTENDED-EUCLID.
Exercise 31.2-8
From the gcd interpretation given in equation (31.13), it is clear that lcm(a1, a2) =
a1·a2
gcd(a1,a2). More generally, lcm(a1, . . . , an) = a1···an
gcd(···(gcd(gcd(a1,a2),a3),...),an). We
can compute the denominator recursively using the two-argument gcd opera-
tion. The algorithm is given below, and runs in O(n) time.
Algorithm 2 LCM(a1, . . . , an)
x=a1
g=a1
for i= 2 to ndo
x=x·ai)
g= gcd(g, ai)
end for
return x/g
Exercise 31.2-9
For two numbers to be relatively prime, we need that the set of primes
that occur in both of them are disjoint. Multiplying two numbers results in
a number whoose set of primes is the union of the two numbers multiplied.
So, if we let p(n) denote the set of primes that divide n. By testing that
gcd(n1n2, n3n4) = gcd(n1n3, n2n4) = 1. We get that (p(n1)∪p(n2)) ∩(p(n3)∪
(n4)) = (p(n1)∪p(n3))∩(p(n2)∪(n4)) = ∅. Looking at the first equation, it gets
us that p(n1)∩p(n3) = p(n1)∩p(n4) = p(n2)∩p(n3) = p(n2)∩p(n4) = ∅. The
second tells, among other things, that p(n1)∩p(n2) = p(n3)∩p(n4) = ∅. This
tells us that the sets of primes of any two elements are disjoint, so all elements
are relatively prime.
A way to fiew this that generalizes more nicely is to consider the complete
graph on nvertices. Then, we select a partition of the vertices into two parts.
Then, each of these parts corresponds to the product of all the numbers cor-
responding to the vertices it contains. We then know that the numbers that
7
any pair of vertices that are in different parts of the partition correspond to
will be relatively prime, because we can distribute the intersection across the
union of all the prime sets in each partition. Since partitioning into two parts is
equivalent to selecting a cut, the problem reduces to selecting lg(k) cuts of Kn
so that every edge is cut by one of the cuts. To do this, first cut the vertex set
in as close to half as possible. Then, for each part, we recursively try to cut in
in close to half, since the parts are disjoint, we can arbitrarily combine cuts on
each of them into a single cut of the original graph. Since the number of time
you need to divide nby two to get 1 is blg(n)c, we have that that is the number
of times we need to take gcd.
Exercise 31.3-1
+40123
0 0123
11230
2 2301
3 3012
·51234
11234
22413
33142
44321
Then, we can see that these are equivalent under the mapping α(0) = 1,
α(1) = 3, α(2) = 4, α(3) = 2.
Exercise 31.3-2
The subgroups of Z9and {0},{0,3,6}, and Z9itself. The subgroups of Z∗
13
are {1},{1,3,9},{1,3,4,9,10,12},{1,5,8,12},{1,12}and Z∗
13 itself.
Exercise 31.3-3
Since Swas a finite group, every element had a finite order, so, if a∈S0,
there is some number of times that you can add it to itself so that you get the
identity, since adding any two things in S0gets us something in S0, we have
that S0has the identity element. Assiciativity is for free because is is a propert
of the binary operation, no the space that the operation draws it’s arguments
from. Lastly, we can see that it contains the inverse of every element, because
we can just add the element to itself a number of times equal to one less than
its order. Then, adding the element to that gets us the identity.
Exercise 31.3-4
8

The only prime divisor of peis p. From the definition of the Euler phi
function, we have
φ(pe) = pe1−1
p=pe−1(p−1).
Exercise 31.3-5
To see this fact, we need to show that the given function is a bijection. Since
the two sets have equal size, we only need to show that the function is onto.
To see that it is onto, suppose we want an element that maps to x. Since Z∗
n
is a finite abelian group by theorem 31.13, we can take inverses, in particu-
lar, there exists an element a−1so that aa−1= 1 mod n. This means that
fa(a−1x) = aa−1xmod n= (aa−1mod n)(xmod n) = xmod n. Since we
can find an element that maps to any element of the range and the sizes of
domain and range are the same, the function is a bijection. Any bijection from
a set to itself is a permutation by definition.
Exercise 31.4-1
First, we run extended Euclid on 35,50 and get the result (5,−7,10). Then,
our initial solution is −7∗10/5 = −14 = 36. Since d= 5, we have four other
solutions, corresponding to adding multiples of 50/5 = 10. So, we also have
that our entire solution set is x={6,16,26,36,46}.
Exercise 31.4-2
If ax ≡ay mod nthen a(x−y)≡0 mod n. Since gcd(a, n) = 1, ndoesn’t
divide aunless n= 1, in which case the claim is trivial. By Corollary 31.5,
since ndivides a(x−y), ndivides x−y. Thus, x≡ymod n. To see that the
condition gcd(a, n) is necessary, let a= 3, n= 6, x= 6, and y= 2. Note that
gcd(a, n) = gcd(3,6) = 3. Then 3 ·6≡3·2 mod 6, but 6 6= 2 mod 6.
Exercise 31.4-3
it will work. It just changes the initial value, and so changes the order in
which solutions are output by the program. Since the program outputs all val-
ues of xthat are congruent to x0mod n/b, if we shift the answer by a multiple
of n/b by this modification, we will not be changing the set of solutions that
the procedure outputs.
Exercise 31.4-4
The claim is clear if a≡0 since we can just factor out an x. For a6= 0,
let g(x) = g0+g1x+. . . +gt−1xt−1. In order for f(x) to equal (x−a)g(x)
we must have g0=f0(−a)−1,gi= (fi−gi−1)(−a)−1for 1 ≤i≤t−1 and
9

gt−1=ft. Since pis prime, Z∗
p={1,2, . . . , p −1}so every element, includ-
ing −a, has a multiplicative inverse. It is easy to satisfy each of these equa-
tions as we go, until we reach the last two, at which point we need to satisfy
both gt−1= (ft−1−gt−2)(−a)−1and gt−1=ft. More compactly, we need
ft= (ft−1−gt−2)(−a)−1. We will show that this happens when ais a zero of
f.
First, we’ll proceed inductively to show that for 0 ≤k≤t−1 we have
ak+1gk=−Pk
i=0 fiai. For the base case we have ag0=−f0, which holds.
Assume the claim holds for k−1. Then we have
ak+1gk=ak+1(fk−gk−1)(−a)−1
=−akfk+akgk−1
=−akfk−
k−1
X
i=0
fiai
=
k
X
i=0
fiai
which completes the induction step. Now we show that we can satisfy the
equation given above. It will suffice to show that −atft=at−1(ft−1−gt−2).
at−1(ft−1−gt−2) = at−1ft−1−at−1gt−2
=at−1ft−1+
t−2
X
i=0
fiai
=
t−1
X
i=0
fiai
=−atft
where the second equality is justified by our earlier claim and the last equality
is justified because ais a zero of f. Thus, we can find such a g.
It is clear that a polynomial of degree 1 can have at most 1 distinct zero
modulo psince the equation x=−ahas at most 1 solution by Corollary 31.25.
Now suppose the claim holds for t > 1. Let fbe a degree t+ 1 polynomial.
If fhas no zeros then we’re done. Otherwise, let abe a zero of f. Write
f(x) = (x−a)g(x). Then by the induction hypothesis, since gis of degree t,g
has at most tdistinct zeros modulo p. The zeros of fare aand the zeros of g,
so fhas at most t+ 1 distinct zeros modulo p.
Exercise 31.5-1
10

These equations can be viewed as a single equation in the ring Z+
5×Z11+,
in particular (x1, x2) = (4,5). This means that xneeds to be the element in
Z55+that corresponds to the element (4,5). To do this, we use the process de-
scribed in the proof of Theorem 31.27. We have m1= 11, m2= 5, c1= 11(11−1
mod 5) = 11, c2= 5(5−1mod 11) = 45. This means that the corresponding
solution is x= 11 ·4 + 45 ·5 mod 55 = 44 + 225 mod 55 = 269 mod 55 = 49
mod 55. So, all numbers of the form 49 + 55kare a solution.
Exercise 31.5-2
Since 9 ·8·7 = 504, we’ll be working mod 504. We also have m1= 56,
m2= 63, and m3= 72. We compute c1= 56(5) = 280, c2= 63(7) = 441, and
c3= 72(4) = 288. Thus, a= 280 + 2(441) + 3(288) mod 504 = 10 mod 504.
Thus, the desired integers xare of the form x= 10 + 504kfor k∈Z.
Exercise 31.5-3
Suppose that x≡a−1mod n. Also, xi≡xmod niand ai≡amod ni.
What we then want to show is that xi≡a−1
imod ni. That is, we want that
aixi≡1 mod ni. To see this, we just use equation 31.30. To get that ax
mod ncorresponds to (a1x1mod n1, . . . , akxkmod nk). This means that 1
corresponds to (1 mod n1,...,1 mod nk). This is telling us exactly what we
needed, in particular, that aixi≡1 mod ni.
Exercise 31.5-4
Let f(x) = f0+f1x+. . .+fdxd. Using the correspondence of Theorem 31.27,
f(x)≡0 mod nif and only if Pd
i=0 fijxi
j≡0 mod njfor j= 1 to k. The
product formula arises by constructing a zero of fvia choosing x1, x2, . . . , xk
such that f(xj)≡0 mod njfor each j, then letting xbe the number associated
to (x1, . . . , xk).
Exercise 31.6-1
element order
1 1
2 10
3 5
4 5
5 5
6 10
7 10
8 10
9 5
10 2
11
The smallest primitive root is 2, and has the following values for ind11,2(x)
xind11,2(x)
1 10
2 1
3 8
4 2
5 4
6 9
7 7
8 3
9 6
10 5
Exercise 31.6-2
To perform modular exponentiation by examining bits from right to left,
we’ll keep track of the value of a2ias we go. See below for an implementation:
Algorithm 3 MODULAR-EXPONENTIATION-R-to-L(a, b, n)
c= 0
d= 1
s=a
let hbk, bk−1, . . . , b0ibe the binary representation of b
for i= 0 to kdo
if bi== 1 then
d=s·dmod n
c= 2i+c
end if
s=s·smod n
end for
return d
Exercise 31.6-3
Since we know φ(n), we know that aφ(n)≡1 mod nby Euler’s theorem.
This tells us that a−1=aφ(n)−1because aa−1=≡aaφ(n)−1≡aφ(n)≡1 mod n.
Since when we multiply this expression times a, we get the identity, it is the
inverse of a. We can then compute nφ(n)efficiently, since φ(n)< n, so can be
represented without using more bits than was used to represent n.
Exercise 31.7-1
For the secret key’s value of ewe compute the inverse of d= 3 mod φ(n) =
280. To do this, we first compute φ(280) = φ(23)φ(7)φ(5) = 4 ·6·4 = 96. Since
12

any number raised to this will be one mod 280, we will raise it to one less than
this. So, we compute
395 ≡3(32)47
≡3(9(92)23)
≡3(9(81(812)11))
≡3(9(81(121(1212)5)))
≡3(9(81(121(81(812)2
≡3·9·81 ·121 ·81 ·81
≡3·9·121
≡187 mod 280
Now that we know our value of e, we compute the encryption of M= 100
by computing 100187 mod 319, which comes out to an encrypted message of 122
Exercise 31.7-2
We know ed = 1 mod φ(n). Since d < φ(n) and e= 3, we have 3d−1 =
k(p−1)(q−1) for k= 1 or 2. We have k= 1 if 3d−1< n and k= 2 if
3d−1> n. Once we’ve determined k,p+q=n−(3d−1)/k + 1, so we can
now solve for p+qin time polynomial in β. Replacing q−1 by (p+q)−p−1
in our earlier equation lets us solve for pin time polynomial in βsince we need
only perform addition, multiplication, and division on numbers bounded by n.
Exercise 31.7-3
PA(M1)PA(M2)≡Me
1Me
2
≡(M1M2)e
≡PA(M1M2) mod n
So, if the attacker can correctly decode 1
100 of the encrypted messages, he
does the following. If the message is one that he can decrypt, he is happy, de-
crypts it and stops. If it is not one that he can decrypt, then, he picks a random
element in Zm, say xencrypts it with the public key, and multiplies that by the
encrypted text, he then has a 1
100 chance to be able to decrypt the new message.
He keeps doing this until he can decrypt it. The number of steps needed follows
a geometric distribution with a expected value of 100. Once he’s stumbled upon
one that he could decrypt, he multiplies by the inverses of all the elements that
he multiplied by along the way. This recovers the final answer, and also can be
done efficiently, since for every x,xn−2is x−1by Lagrange’s theorem.
13

Exercise 31.8-1
Suppose that we can write n=Qk
i=1 pei
i, then, by the Chinese remainder the-
orem , we have that Zn∼
=Zpe1
1× ··· × Zpe1
1. Since we had that nwas not a
prime power, we know that k≥2. This means that we can take the elements
x= (pe1
1−1,1,...,1) and y= (1, pe2
2−1,1,...,1). Since multiplication in the
product ring is just coordinate wise, we have that the squares of both of these
elements is the all ones element in the product ring, which corresponds to 1 in
Zn. Also, since the correspondence from the Chinese remainder theorem was
a bijection, since xand yare distinct in the product ring, they correspond to
distinct elements in Zn. Thus, by taking the elements corresponding to xand y
under the Chinese remainder theorem bijection, we have that we have found two
squareroots of 1 that are not the identity in Zn. Since there is only one trivial
non-identity squareroot in Zn, one of the two must be non-trivial. It turns out
that both are non-trivial, but that’s more than the problem is asking.
Exercise 31.8-2
Let c= gcd(···(gcd(gcd(φ(pe1
1), φ(pe2
2)), φ(pe3
3)), . . .), φ(per
r)). Then we have
λ(n) = φ(ee1
1)···φ(per
r)/c =φ(n)/c. Since the lcm is an integer, λ(n)|φ(n).
Suppose pis prime and p2|n. Since φ(p2) = p2(1 −1
p) = p2−p=p(p−1),
we have that p must divide λ(n). however, since pdivides n, it cannot divide
n−1, so we cannot have λ(n)|n−1.
Now, suppose that is the product of fewer than 3 primes, that is n=pq
for some two distinct primes p < q. Since both pand qwere primes, λ(n) =
lcm(φ(p), φ(q)) = lcm(p−1, q −1). So, mod q−1, λ(n)≡0, however, since
n−1 = pq −1=(q−1)(p) + p−1, we have that n−1≡p−1 mod q−1.
Since λ(n) has a factor of q−1 that n−1 does not, meaning that λ(n)6 |n−1.
Exercise 31.8-3
First, we prove the following lemma. For any integers a, b, n, gcd(a, n)·
gcd(b, n)≥gcd(ab, n). Let {pi}be an enumeration of the primes, then, by
Theorem 31.8, there is exactly one set of powers of these primes so that a=
Qipai
i,b=Qipbi
i, and n=Qipni
i.
gcd(a, n) = Y
i
pmin(ai,ni)
i
gcd(b, n) = Y
i
pmin(bi,ni)
i
gcd(ab, n) = Y
i
pmin(ai+bi,ni)
i
14

We combine the first two equations to get:
gcd(a, n)·gcd(b, n) = Y
i
pmin(ai,ni)
i!· Y
i
pmin(bi,ni)
i!
=Y
i
pmin(ai,ni)+min(bi,ni)
i
≥Y
i
pmin(ai+bi,ni)
i
= gcd(ab, n)
Since xis a non-trivial squareroot, we have that x2≡1 mod n, but x6= 1
and x6=n−1. Now, we consider the value of gcd(x2−1, n). By theorem 31.9,
this is equal to gcd(n, x2−1 mod n) = gcd(n, 1−1) = gcd(n, 0) = n. So, we
can then look at the factorization of x2−1=(x+ 1)(x−1) to get that
gcd(x+ 1, n) gcd(x−1, n)≥n
However, we know that since xis a nontrivial squareroot, we know that
1< x < n −1 so, neither of the factors on the right can be equal to n. This
means that both of the factors on the right must be nontrivial.
Exercise 31.9-1
The Pollard-Rho algorithm would first detect the factor of 73 when it con-
siders the element 84, when we have x12 because we then notice that gcd(814 −
84,1387) = 73.
Exercise 31.9-2
Create an array Aof length n. For each xi, if xi=j, store iin A[j]. If jis
the first position of Awhich must have its entry rewritten, set tto be the entry
originally stored in that spot. Then count how many additional xi’s must be
computed until xi=jagain. This is the value of u. The running time is Θ(t+u).
Exercise 31.9-3
Assuming that pedivides n, by the same analysis as sin the chapter, it will
take time Θ(pe/2). To see this, we look at what is happening to the sequence
mod pn.
15

x0
i+1 =xi+1 mod pe
=fn(xi) mod pe
= ((x2−1) mod n) mod pe
= (x2−1) mod pe
= (x0
i)2−1 mod pe
=fpe(x0
i)
So, we again are having the birthday paradox going on, but, instead of hop-
ing for a repeat from a set of size p, we are looking at all the equivalence classes
mod pewhich has size pe, so, we have that the expected number of steps be-
fore getting a repeat in that size set is just the squareroot of its size, which is
Θ(√pe) = Θ(pe/2).
Exercise 31.9-4
Problem 31-1
a. If aand bare both even, then we can write them as a= 2(a/2) and b= 2(b/2)
where both factors in each are integers. This means that, by Corollary 31.4,
gcd(a, b) = 2 gcd(a/2, b/2).
b. If ais odd, and bis even, then we can write b= 2(b/2), where b/2 is an
integer, so, since we know that 2 does not divide a, the factor of two that
is in bcannot be part of the gcd of the two numbers. This means that we
have gcd(a, b) = gcd(a, b/2). More formally, suppose that d= gcd(a, b).
Since dis a common divisor, it must divide a, and so, it must not have any
even factors. This means that it also divides aand b/2. This means that
gcd(a, b)≤gcd(a, b/2). To see the reverse, suppose that d0= gcd(a, b/2),
then it is also a divisor of aand b, since we can just double whatever we need
to multiply it by to get b/2. Since we have inequalities both ways, we have
equality.
c. If aand bare both odd, then, first, in analoge to theorem 31.9, we show
that gcd(a, b) = gcd(a−b, b). Let dand d0be the gcd’s on the left and right
respectively. Then, we have that there exists n1, n2so that n1a+n2b=d,
but then, we can rewrite to get n1(a−b) + (n1+n2)b=d. This gets
us d≥d0. To see the reverse, let n0
1, n0
2so that n0
1(a−b) + n0
2b=d0.
We rewrite to get n0
1a+ (n0
2−n0
1)b=d0, so we have d0≥d. This means
that gcd(a, b) = gcd(a−b, b) = gcd(b, a −b). From there, we fall into the
case of part b. This is because the first argument is odd, and the second
is the difference of two odd numbers, hence is even. This means we can
halve the second argument without changing the quantity. So, gcd(a, b) =
gcd(b, (a−b)/2) = gcd((a−b)/2, b).
16

d. See the algorithm BINARY-GCD(a,b)
Algorithm 4 BINARY-GCD(a,b)
if amod 2 ≡1then
if bmod 2 ≡1then
return BINARY-GCD((a−b)/2, b)
else
return BINARY-GCD(a, b/2)
end if
else
if bmod 2 ≡1then
return BINARY-GCD(a/2, b)
else
return 2·BINARY-GCD(a/2, b/2)
end if
end if
Problem 31-2
a. We can imagine first writing aand bin their binary representations, and then
performing long division as usual on these numbers. Each time we compute
a term of the quotient we need to perform a multiplication of aand that
term, which takes lg bbit operations, followed by a subtraction from the first
bterms of awhich takes lg bbit operations. We repeat this once for each
digit of the quotient which we compute, until the remainder is smaller than
b. There are lg qbits in the quotient, plus the final check of the remainder.
Since each requires lg bbit operations to perform the multiplication and sub-
traction, the method requires O((1 + lg q) lg b) bit operations.
b. The reduction requires us to compute amod b. By carrying out ordinary
“paper and penil” long division we can compute the remainder. The time to
do this, by part a, is bounded by k(1 + lg q)(lg b) for some constant k. In the
worst case, qhas lg a−lg bbits. Thus, we get the bound k(1+lg a−lg b)(lg b).
Next, we compute µ(a, b)−µ(b, a mod b) = (1 +lg a)(1+ lg b)−(1+lg b)(1 +
lg(amod b). This is smallest when amod bis small, so we have a lower
bound of (1 + lg a)(1 + lg b)−(1 + lg b). Assuming lg b≥1, we can take c=k
to obtain the desired inequality.
c. As shown in part (b), EUCLID takes at most c(µ(a, b)−µ(b, amodb)) op-
erations on the first recursive call, at most c(µ(b, a mod b)−µ(amod b, b
mod (amod b)) operations on the second recursive call, and so on. Summing
over all recursive calls gives a telescoping series, resulting in cµ(a, b)+O(1) =
O(µ(a, b)). When applies to two β-bit inputs the runtime is O(µ(a, b)) =
O((1 + β)(1 + β)) = O(β2).
17

Problem 31-3
a. Mirroring the proof in chapter 27, we first notice that in order to solve
F IB(n), we need to compute F IB(n−1) and F IB(n−2). This means
that the recurrence it satisfies is
T(n) = T(n−1) + T(n−2) + Θ(1)
We find it’s solution using the substitution method. Suppose that the Θ(1)
is bounded above by c2and bounded below by c1. Then, we’ll inducively
assume that T(k)≤cFk−c2kfor k < n. Then,
T(n) = T(n−1) + T(n−2)
≤cFn−1−c2(n−1) + cFn−2−c2(n−2) + c2
=cFn−c2n+ (4 −n)c2
≤cFn−c2n
Where the last inequality only holds if we have that n≥4,but since small
values can just be absorbed into the constants, we are allowed to assume this.
To show that T∈Ω(Fn), we again use the substitution method. Suppose
that T(k)≥cFk+c1kfor k < n. Then.
T(n) = T(n−1) + T(n−2)
≥cFn−1+c1(n−1) + cFn−2+c1(n−2) + c1
=cFn+c1n+ (n−4)c1
≥cFn−c1n
Again, this last inequality only holds if we have n≥4, but small cases can
be absorbed into the constants, we may assume that n≥4.
b. This problem is the same as exercise 15.1-5.
c. For this problem, we assume that all integer multiplications and additions
can be done in unit time. We will show first that
0 1
1 1 k
=Fk−1Fk
FkFk+1
Where we start We will proceed by induction. Then,
18

0 1
1 1 k+1
=0 1
1 1 0 1
1 1 k
=0 1
1 1 Fk−1Fk
FkFk+1
=FkFk−1+Fk
Fk−1+FkFk+Fk+1
=FkFk+1
Fk+1 Fk+2
completing the induction. Then, we just show that we can compute the
given matrix to the power n−2 in time O(lg(n)), and look at it’s bottom
right entry. We will use a technique similar to section 31.6, that is, we will
use the idea of iterated squaring in order to obtain high powers quickly.
First, we should note that using 8 multiplications and 4 additions, we can
multiply any two square matrices. This means that matrix multiplications
can be done in constant time, so, we only need to bound the number of those
in our algorithm. Run the algorithm MATRIX-POW(A,n-2) and extract
the bottom left argument. We can see that this algorithm only takes time
O(lg(n)) because in each step, we are halving the value of n, and within each
step, we are only performing a constant amount of work, so the solution to
T(n) = T(n/2) + Θ(1)
is O(lg(n)) by the master theorem.
Algorithm 5 MATRIX-POW(A,n)
if n%2 = 1 then
return A·MATRIX-POW(A2,n−1
2)
else
return MATRIX-POW(A2, n/2)
end if
d. Here, we replace the assumption of unit time additions and multiplications
with having it take time Θ(β) to add and Θ(β2) to multiply two βbit num-
bers. For the naive approach, We are adding a number which is growing
exponentially each time, so, the recurrence becomes
T(n) = T(n−1) + T(n−2) + Θ(n)
Which has the same solution 2n. Which can be seen by a substitution argu-
ment. Suppose that T(k)≤c2kfor k < n. Then,
19

T(n) = T(n−1) + T(n−2) + Θ(lg(n))
≤c(1
2+1
4)2n+ Θ(lg(n))
=c2n−c2n−2+ Θ(lg(n))
≤c2k
Since we had that it was Ω(2n) in the case that the term we added was Θ(1),
and we have upped this term to Θ(lg(n)), we still have that T(n)∈Ω(2n).
This means that T(n)∈Θ(2n).
Now, considering the memoized version. We have that our solution has to
satisfy the recurrence
M(n) = M(n−1) + Θ(n)
This clearly has a solution of Pn
i=2 n∈Θ(n2) by equation (A.11) where it is
trivial to obtain Rx dx.
Finally, we reanalyze our solution to part (c). For this, we have that we are
performing a constant number of both additions and multiplications. This
means that, because we are multiplying numbers that have value on the order
of φn, hence have order nbits, our recurrence becomes
P(n) = P(n/2) + Θ(n2)
Which has a solution of Θ(n2).
Though it is not asked for, we can compute Fibonacci in time only Θ(nlg(n))
because multiplying integers with βbits can be done in time βlg(β) using
the fast Fourier transform methods of the previous chapter.
Problem 31-4
a. Since pis prime, Theorem 31.32 implies that Z∗
pis cyclic, so it has a generator
g. Thus, g2, g4, . . . , gp−1are all distinct. Moreover, each one is clearly a
quadratic residue so there are at least (p−1)/2 residues. Now suppose that
ais a quadratic residue and a=g2k+ifor some i. Then we must also have
a=x2for some x, and x=gmfor some m, since gis a generator. Thus,
g2m=g2k+i. By the discrete logarithm theorem we must have 2m= 2k+ 1
mod φ(p). However, this is impossible since φ(p) = p−1 which is even, but
2mand 2k+ 1 differ by an odd amount. Thus, precisely the elements of the
form g2ifor i= 1,2,...,(p−1)/2 are quadratic residues.
b. If ais a quadratic residue modulo pthen there exists xsuch that a(p−1)/2=
(x2)(p−1)/2=xp−1=1=a
p. On the other hand, suppose ais not a
20

quadratic residue. Then a=g2i+1 for some iand a(p−1)/2=g2i+1(p−1)/2=
g(p−1)/22i+1 = (−1)2i+1 =−1 mod p. To see why g(p−1)/2=−1, recall
that Theorem 31.34 tells us that g=±1. Since gis a generator, powers of g
are distinct. Since gp−1= 1, we must have g(p−1)/2=−1.
To determine whether a given number ais a quadratic residue modulo p, we
simply compute a(p−1)/2mod pand check if it is 1 or -1. We can do this
using the MODULAR-EXPONENTIATION function, and the number of bit
operations is O((lg p)3).
c. If p= 4k+ 3 and ais a quadratic residue then a2k+1 = 1 mod p. Then we
have (ak+1)2=a2k+2 =aa2k+1 =a, so ak+1 is a square root of a. To find the
square root, we use the MODULAR-EXPONENTIATION algorithm which
has O((lg p)3) bit operations.
d. Run the algorithm of part b repeatedly until a non-quadratic residue is found.
Since only half the elements of Z∗
pare residues, after kruns this approach
will find a nonresidue with probability 1−2−k. The expected number of runs
is P∞
k=1 k·2−k= 2, so the expected number of bit operations is O((lg p)3).
21

Chapter 32
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 32.1-1
We let (i, j) denote that the algorithm checks index iof the text against index
jof the pattern. We’ll let p(s) indicate that the matching algorithm reported
an occurrence with a shift of s. The algorithm has the following execution on
T= 000010001010001 and P= 0001.
s= 0 (0,0) (1,1) (2,2) (3,3)
s= 1 (1,0) (2,1) (3,2) (4,3) p(1)
s= 2 (2,0) (3,1) (4,2)
s= 3 (3,0) (4,1)
s= 4 (4,0)
s= 5 (5,0) (6,1) (7,2) (8,3) p(5)
s= 6 (6,0) (7,1) (8,2)
s= 7 (7,0) (8,1)
s= 8 (8,0)
s= 9 (9,0) (10,1)
s= 10 (10,0)
s= 11 (11,0) (12,1) (13,2) (14,3) p(11)
Exercise 32.1-2
We know that one occurrence of Pin Tcannot overlap with another, so
we don’t need to double-check the way the naive algorithm does. If we find an
occurrence of Pkin the text followed by a nonmatch, we can increment sby k
instead of 1. It can be modified in the following way:
Exercise 32.1-3
For any particular value of s, the probability that the ith character will need
to be looked at when doing the string comparison is the probability that the
first i−1 characters matched, which is 1
di−1. So, by linearity of expectation,
summing up over all sand i, we have that the expected number of steps is, by
equation (A.5),
1

Algorithm 1 DISTINCT-NAIVE-STRING-MATCHER(T, P )
n=T.length
m=P.length
k= 0
while s≤n−mdo
i= 1
if T[s] == P[1] then
k=s
i= 0
while T[k+i] == P[i] and i<mdo i=i+ 1
if i== mthen
Print “Pattern occurs with shift” k
end if
end while
end if
s=s+i
end while
(n−m+ 1)
m
X
i=1
1
di−1= (n−m+ 1) (d−m−1)
(d−1−1)
= (n−m+ 1)(1−d−m
1−d−1)
≤(n−m+ 1) 1
1−d−1
≤(n−m+ 1) 1
1−1
2
= 2(n−m+ 1)
Exercise 32.1-4
We can decompose a pattern with g−1 gap characters into the form a1a2
· · · ag. Since we only care whether or not the pattern appears somewhere, it
will suffice to look for the first occurrance of a1, followed by the first occurrance
of a2which comes anywhere after a1, and so on. If the pattern Phas length m
and the text has length nthen the runtime of the naive strategy is O(nm).
Exercise 32.2-1
Since the string 26 only appears once in the text, to find the number of
spurious hits, we will find the total number of hits and subtract 1. when we
compute the hash of the pattern we get (20 + 6) mod 11 ≡26 mod 11 ≡4
mod 11.
2
We get the following hashes of various shift values:
s ts
0 9
1 3
2 8
3 4
4 4
5 4
6 4
7 10
8 9
9 2
10 3
11 1
12 9
13 2
14 5
Since there were 4 hits, three of them must of been spurious.
Exercise 32.2-2
We first tackle the case where each of the kpatterns has the same length m.
We first compute the number associated to each pattern in O(m) time, which
contributes O(km) to the runtime. In line 10 we make kchecks, one for each
pattern, which contributes O(n−m+ 1)km time. Thus, the total runtime is
O(km(n−m+ 1). For patterns of different lenghts l1, l2, . . . , lk, keep an array
Asuch that A[i] holds the number associated to the first lidigits of T, mod
q. We’ll have to update each of these each time the outer for-loop is executed,
but it will allow us to immediately compare any of the pattern numbers to the
appropriate text number, as done in line 10.
Exercise 32.2-3
We use the same idea of maintaining a hash of the pattern and computing
running hashes of the text. However, updating the hash at each step can take
time as long as Θ(m) because the number of entries which are both entering
and leaving the hashed window is 2m, and you have to at least look at all of
them as they come in and leave. This would get us a total expected runtime
(occurring not too many spurious hits of (n−m+ 1)2·m, and still the same
worst case as the trivial algorithm, which is (n−m+ 1)2·m2.
In order to compute this hash, we will be giving each entry of the window
a power of dthat unique to its position. The entry in row i, column jwill be
multiplied by dm2−mi+j. Then, moving to the right, we multiply the value of
the hash by d, subtract off the scaled entries that were in the left column, and
3

add in the entries that are in the right column, also appropriately scaled by
what row they are in. Similarly for shifting the window up or down. Again, all
of this arithmetic is done mod some large prime.
Exercise 32.2-4
Suppose A(x) = B(x). Then Pn−1
i=0 (ai−bi)xi≡0 mod q. Since qis
prime, Exercise 31.4-4 tells us that this equation has at most n−1 solutions
modulo q. Since each of the qchoices for xis equally likely, the probabil-
ity that we pick one of the potential n−1 which make the equation hold is
(n−1)/q < (n−1)/1000n < 1/1000. However, if the files are the same then
ai=bifor all i, so A(x) = B(x).
Exercise 32.3-1
The states will be {0,1,2,3,4,5,6}and having a transition function given
by
state a b
0 1 0
1 2 0
2 2 3
3 4 0
4 2 5
5 1 0
The sequence of states for Tis 0,1,2,2,3,4,5,1,2,3,4,2,3,4,5,1,2,3, and
so finds two occurrences of the pattern, one at s= 1 and another at s= 9.
Exercise 32.3-2
See picture below for the 22 state automaton.
4

Exercise 32.3-3
The state transition function looks like a straight line, with all other edges
going back to either the initial vertex (if it is not the first letter of the patter) or
the second vertex (if it is the first letter of the pattern). If it were to go back to
any later state, that would mean that some suffix of what we had constructed
so far(which was a prefix of P) was a prefix of the copy of Pthat we are next
trying to find.
Exercise 32.3-4
We can construct the automaton as follows: Let Pkbe the longest prefix
which both Pand P0have in common. Create the automaton Ffor Pkas usual.
Add an arrow labeled P[k+1] from state kto a chain of states k+1, k+2,...,|P|,
and draw the appropriate arrows, so that δ(q, a) = σ(Pqa). Next, add an arrow
labeled P0[k+ 1] from state kto a chain of states (k+ 1)0,(k+ 2)0,...,|P0|0.
Draw the appropriate arrows so that δ(q, a) = σ(P0
qa).
Exercise 32.3-5
To create a DFA that worked with gap characters, construct the DFA so that
it has |P|+ 1 states. let mbe the number of gap characters Suppose that the
positions of all the gap characters within the pattern pare given by gi, and let
g0= 0, gm=|P|+ 1. Let the segment of pattern occurring after gap character
ibut before the i+ 1 gap character be called Pi. Then, we will imagine that we
are trying to match each of these patterns in sequence, but if we have trouble
matching some particular pattern, then we can not undo the success we enjoyed
in matching earlier patterns.
More concretely, suppose that we have (Qi, qi,0, Ai,Σi, δi) is the DFA corre-
5
sponding to the pattern Pi. Then, we will construct our DFA so that Q=tiQi,
q0=q0,0,A=Am+1, Σ = ∪iΣi, and δis described below. If we are at state
q∈Qiand see character a, if q6∈ Ai, we just go to the state proscribed by
δi(q, a). If, however, we have that q∈Ai, then, δ(q, a) = δi+1(qi+1,0, a). This
construction achieves the description given in English above.
Exercise 32.4-1
The prefix function is:
i π(i)
1 0
2 0
3 1
4 2
5 0
6 1
7 2
8 0
9 1
10 2
11 0
12 1
13 2
14 3
15 4
16 5
17 6
18 7
19 8
Exercise 32.4-2
The largest π∗[q] can be is q−1. This is tight because if Pconsists of a the
letter arepeated mtimes, the π∗[q] = q−1 for all q.
Exercise 32.4-3
Suppose that at position i, you have the value of the prefix function is π[i].
Then, if i−π[i]≥ |P|, this means that there is an occurrence of |P|starting at
position i−π[i].
A simpler way to achieve a similar result is to expand the alphabet by one,
making it so that some character cdoes not occur in either Por T, then com-
pute the prefix array of P cT , then, the prefix function is bounded by |P|and
any time that it reaches that bound, we have that there is an occurrence of
the pattern, since we know that any prefix containing the ccannot be a proper
6

suffix of any other prefix.
Exercise 32.4-4
To show that the running time of KMP-MATCHER is O(n), we’ll show that
the total number of executions of the while loop of line 6 is O(n). Observe that
for each iteration for the for loop of line 5, qincreases by at most 1, in line 9.
This is because π(q)< q. On the other hand, the while loop decreases q. Since
qcan never be negative, we must decrease qfewer than ntimes in total, so the
while loop executes at most n−1 times. Thus, the total runtime is O(n).
Exercise 32.4-5
Basically, each time that we have to execute line 7, we have that we are
decreasing qby at least 1. Since the only place that we ever increase the value
of qis on line 9, and then we are only increasing it by 1, each of these runs of
line 5 are paid for by the times we ran 9.
Using this as our motivation, we let the potential function be proportional
to the value of q. This means that when we execute line 9, we pay a constant
amount to raise up the potential function. And when we run line 7, we decrease
the potential function which reduces the ammortized cost of an iteration of the
while loop on line 6 to a zero ammortized cost. The only other time that we
change the value of q is on line 12, which only gets run once per execution of
the outer for loop anyways and the ammortization is in our favor there.
Since the ammortized cost under this potential function of each iteration of
the outermost for loop is constant, and that loop runs ntimes, the total cost of
the algorithm is Θ(n).
Exercise 32.4-6
We’ll prove this by induction on the number of recursive calls to π0. The
behavior is identical to πif we are in the first or third cases (base cases) of
the definition of π0, so the behavior is correct for a single call. Otherwise,
π0[q] = π0[π[q]]. The conditions of case 2 imply that the while loop of line 6
will execute an additional time after the update of line 7, so it is equivalent to
setting q=π[π[q]], and then continuing with the while loop as usual. Since
π0recurses on π[q] one fewer times than on q, its behavior is correct on π[q],
proving that the modified algorithm is correct. KMP-MATCHER already runs
asymptotically as fast as possible, so this doesn’t constitute a runtime improve-
ment in the worst case. However, every time a recursive call to π0is made, we
circumvent having to check P[q+ 1] against T[i].
Exercise 32.4-7
If the lengths to Tand T0are different, they are obviously not cyclic rotations
of each other, so suppose that |T|=T0. Let our text be T T and our pattern
7
be T0. If and only if T0occurs in T T , then the two given strings are cyclic
rotations of each other. This can be done in linear time by the Knuth Morris
Pratt algorithm.
To see that being cyclic rotations means that T0occurs in T T , suppose that
T0is obtained from Tby cyclically shifting the right character to the left s
times. This means that the |T| − sprefix of Tis a suffix of T0, and the ssuffix
of Tis a prefix of T0. This means that T0occurs in T T with a shift of |T| − s.
Now, suppose that T0occurs in T T with a shift of s. This means that the s
suffix of Tis a prefix of T0, it also means that the |T| − scharacters left over in
T0are a prefix of T. So, they are cyclic rotations of each other.
Exercise 32.4-8
We have δ(q, a) = σ(Pqa), which is the length of the longest prefix of P
which is a suffix of Pqa. Let this be k. Then P[1] = P[q−k+ 2], P[2] = P[q−
k+ 3], . . . , P [k−1] = P[q], P [k] = a. On the other hand, δ(π[q], a) = σ(Pπ[q]a).
It is clear that σ(Pqa)≥σ(Pπ[q]a). However, π[q]≥k−1 and since P[k] = a,
we must have σ(Pπ[q]a)≥k. Thus, they are equal. If q6=mand P[q+ 1] = a
then δ(q, a) = q+ 1. We can now compute the transition function δin O(m|Σ|)
in the algorithm TRANSITION-FUNCTION, given below.
Algorithm 2 TRANSITION-FUNCTION(P, Σ)
π= COMPUTE-PREFIX-FUNCTION(P)
for a∈Σdo
δ(0, a) = 0
end for
δ(0, P [1]) = 1
for a∈Σdo
for q= 1 to mdo
if q== mor P[q+ 1] 6=athen
δ(q, a) = δ(π[q], a)
else
δ(q, a) = q+ 1
end if
end for
end for
Problem 32-1
a. First, compute the prefix array for the given pattern in linear time using the
method of section 32.4. Then, Suppose that π[i] = i−k. If k|i, we know that
kis the length of the primitive root, so, the word has a repetition factor of i
k.
We also know that there is no smaller repetition factor in this case because
otherwise we could include one more power of that root.
8
Now, suppose that we have knot dividing i. We will show that we can
only have the trivial repetition factor of 1. Suppose we had some repetition
yr=Pi. Then, we know that π[i]≥yr−1. however, if we have it strictly
greater than this, this means that we can write the y’s themselves as powers
because we have them aligning with themselves.
Since the only difficult step of this was finding the prefix function, which
takes linear time, the runtime of this procedure is linear.
b. To determine the probability that there is a repetition factor of r, we assign
whatever we want to the first i
rletters, and after that, all of the other letters
are determined. This means that position ihas a repetition factor of rwith
probability 1
2i(r−1)
r
for every rdividing i. By applying a union bound to this,
we have that the probability that Pihas a repetition factor of more than r
is bounded by
X
r0>r,r0|i
1
2i(r0−1)
r0
=1
2iX
r0>r,r0|i
2i/r0
=1
2i
bi/r
c
X
j=1
2j
≤2i/r
2i−1
= 2i/r−i+1
Then, applying the union bound over all values of i, we have the probability
that a repetition factor of at least ris bounded by
m
X
i=0
2i/r−i+1 = 2
m
X
i=1
2(1
r−1)i
= 21−2m+1
r−m−1
1−2(1
r−1)
≤21
2(1
r−1)
This shrinks quickly enough in r, that the expected value is finite, and since
there is no min the expression, we have the expected value is bounded by a
constant.
c. This algorithm correctly finds the occurrences of the pattern Pfor reasons
similar to the Knuth Morris Pratt algorithm. That is, we know that we
will only increase q ρ∗(P) many times before we have to bite the bullet and
9

increase s, and scan only be increased at most n−mmany times. It will
definitely find every possible occurrence of the pattern because it searches
for every time that the primitive root of Poccurs, and it must occur for P
to occur.
10

Chapter 33
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 33.1-1
Suppose first that the cross product is positive. We shall consider the an-
gles that both of the vectors make with the positive x axis. This is given
by tan−1(y/x) for both. Since the cross product is positive, we have that
0< x1y2−x2y1, which means that y1
x1<y2
x2. however, since arctan is a mono-
tone function, this means that the angle that p2makes with the positive xaxis
is greater than the angle that p1does, which means that you need to move in a
clockwise direction to get from p2to p1.
If the cross product is negative, this means that we have y1
x1>y2
x2which
means that the angle that p1makes is greater, which means that we need to go
counter clockwise from p2to get to p1.
Exercise 33.1-2
If the segment pipjis vertical, then pkcould be colinear with piand pj, but
lie directly below them. Then xi=xj=xk, so if we don’t also check the y
values we won’t catch that pkis not on the segment.
Exercise 33.1-3
The beauty of the fact that our sorting algorithms from earlier in the book
were only comparison based is that if we can implement a comparison operation
between any two elements that operates in constant time, then, we can use the
earlier comparison based sorting algorithms as a black box to work on our data.
So, what we need to do is, given two indices iand j, decide whether the
polar angle of piwith respect to p0is larger or smaller than the polar angle of
pjwith respect to p0. This can be done with a single cross product. That is,
we look at the cross product, (p1−p0)×(p2−p0). This is positive if we need
to turn left from p1to get to p2. That is, if it is positive, then the polar angle
is greater for p2than from p1. We similarly know that we are in the reverse
situation if we have that this cross product is negative. The only tricky thing is
that we could have two distinct elements piand pjso that the cross product is
still zero. The problem statement is unclear how to resolve these sorts of ties,
because they have the same polar angle. We could just pick some arbitrary
1

property of the points to resolve ties, such as we pick the point that is farther
away from p0to be larger. Since we have a total ordering on the points that
can be queried in constant time, we can use it in our O(nlg(n)) algorithms from
earlier on in the book.
Exercise 33.1-4
By Exercise 33.1-3 we can sort npoints according to their polar angles with
respect to a given point in O(nlg n) time. If points pi,pj, and pkare colinear,
then at two one of the following is true: (1) pjand pkhave the same polar angle
with respect to pi, (2) piand pkhave the same polar angle with respect to pj,
or (3) piand pjhave the same polar angle with respect to pk. Thus, it will
suffice to do as follows: For each point p, compute the polar angle of all other
points with respect to p. If there are any duplicates, those points are colinear.
Since we must do this for each point, the algorithm has runtime O(n2lg n).
Exercise 33.1-5
Because, as stated in this definition of convex polynomials, we cannot have
a vertex of a convex polygon be a convex combination of any two points of the
boundary of the polynomial. This means that as we enter a particular vertex,
we cannot have that it is colinear with the next vertex. Professor Amundsen’s
algorithm just rejects if both left and right turns are made. However, it should
also reject if there is ever any vertex where no turn is made, because that vertex
would then be a convex combination of the next and previous vertices.
Exercise 33.1-6
It will suffice to check whether or not the line segments p0p3and p1p2inter-
sect, where p3= (max(x1, x2), y0). We can do this in O(1).
Exercise 33.1-7
Starting from the point p0, pick an arbitrary direction, and consider the ray
coming out in that direction. Instead of just counting the intersections with the
sides of the polygon, we’ll also count all the vertices that the ray intersects. for
each side that it intersects, if it intersects the vertices at both sides, then we
don’t count that edge, because that means that the ray passes along that side.
Lastly, if the ray passes through any vertex where both sides touching that ver-
tex aren’t of the previous type, we flip the parity of the count. Lastly, we say it
is inside if the final count is odd. See the algorithm DETERMINE-INSIDE(P,p).
Exercise 33.1-8
Without loss of generality, assume that the interior of the polygon is to the
right of the first segment p0p1. We will examine segments of the polygon one at a
2

Algorithm 1 DETERMINE-INSIDE(P,p), P is a polygon, and p is a point
Let Sbe the set of sides that the right horizontal ray intersects
Let Tbe the set of vertices that the right horizontal ray intersects
Let Ube an empty set of sides
count = 0
for s∈Sdo
let p1and p2be the vertices at either side of s
if p1∈Tand p2∈Tthen
put sin U
end if
count++
end for
for x∈Tdo
let yand zbe the sides that xis touching
if y∈Uor z∈Uthen
count++
end if
end for
if count is odd then
return inside
else
return outside
end if
3
time. At any point, if we are at segment pipi+1 and if the next segment pi+1pi+2
of the polygon turns right then, then we can compute the are of 4pipi+1pi+2,
and reduce the problem to that of finding the area of the polygon without pi+1,
adding the area just computed. On the other hand, if we turn left then we
need to compute the area of the polygon without pi+1, but we need to subtract
the area of 4pipi+1pi+2. Since we can compute the area of a triangle given
its vertices in constant time, the runtime satisfies T(n) = T(n−1) + O(1), so
T(n) = O(n).
Exercise 33.2-1
Suppose you split your set of lines into two equal sets, each of size n/2.
Then, we will make half of them horizontal and close together, each above the
next. That is, we’ll put a horizontal line at y=1
kfor k= 1, . . . , n/2 extending
from −1 to 1. For the other half, we’ll put lines along x=1
kfor k= 1, . . . , n/2,
extending from -1 to 1. Then, we’ll have every line from the first set intersect
every line from the second set. Therefore the total number of intersections is
n2
4, which is Θ(n2).
Exercise 33.2-2
First suppose that aand bdo not intersect. Let as, af, bs, bfdenote the
left and right endpoints of aand brespectively. Without loss of generality,
let bhave the leftmost left endpoint. If bsasis to the right of bsbf, then a
is below b. Otherwise ais above b. Now suppose that aand bintersect. To
decide which segment is on top, we need to determine whether the intersection
occurs to the left or right of x. Assume that each point has xand yattributes.
For example, as= (as.x, as.y). The equation of the line through segment ais
y=m1(x−as.x)+as.y where m1=af.y−as.y
af.x−as.x . The equation of the line through
segment bis y=m2(x−bs.x) + bs.y where m2=bf.y−bs.y
bf.x−bs.x . Setting these equal
to each other gives
x=bs.y −m2bs.x −as.y +m1as.x
m1−m2
.
Let x=x0be the equation of the sweep line at which we want to test the
relationship between aand b. We need to determine whether or not x<x0, but
without using division. To do this, we’ll need to clear denominators. x<x0is
equivalent to
bs.y −m2bs.x −as.y +m1as.x < (m1−m2)x0
which is equivalent to this gross mess, which fortunately requires only addition,
subtraction, multiplication, and comparison, so it is numerically stable:
(af.x −as.x)(bf.x −bs.x)(bs.y −as.y)−(af.x −as.x)(bf.y −bs.y)bs.x + (bfx−bs.x)(af.y −as.y)as.x
<(bf.x −bs.x)(af.y −as.y)x0−(af.x −as.x)(bf.y −bs.y)x0.
4

Exercise 33.2-3
It looks like the moral of this book is that the only time that a professor
can be right is when he’s disagreeing with another professor. Professor Dixon
is correct.
It will not necessarily print the leftmost intersection first. The intersection
that it prints first will be the pair of lines such that both lines have their enpoints
show up first in the lexicographical ordering on line 2. An example is, suppose we
have the lines {{(0,1000),(2,2000)},{(0,1001),(2,1001)},{(0,0),(1,2)},{(0,2),(1,0)}}.
Then, the first two lines have the leftmost intersection, but the intersection be-
tween the last two lines will be printed out first.
The procedure will not necessarily display all intersections, in particular,
suppose that we have the line segments {{(0,0),(4,0)},{(0,1),(4,−2)},{(0,2),(4,−2)},{(0,3),(4,−1)}}.
There are intersections of the first line segment with each of the other line seg-
ments at 1,2, and 3. However, we cannot detect the intersection at 2 because the
line segment from (0,2) to (4,−2) is not adjacent to the horizontal line segment
in the red-black tree either when we process left endpoints or right endpoints.
Exercise 33.2-4
An nvertex polygon hp0, p1, . . . , nn−1iis simple if and only if the only in-
tersections of the segments p0p1, p1p2, . . . , pn−1p0of the boundary are between
consecutive segments pipi+1 and pi+1pi+2 at the point pi+1. We run the usual
ANY-SEGMENTS-INTERSECT algorithm on the segments which make up
the boundary of the polygon, with the modification that if an intersection is
found, we first check if it is an acceptable one. If so, we ignore it and proceed.
Since we can check this in O(1), the runtime is the same as ANY-SEGMENTS-
INTERSECT.
Exercise 33.2-5
Construct the set of line segments which correspond to all the sides of both
polygons, then just use the algorithm from this section to see if any pair of
them intersect. If we are in the fringe case that some segment is vertical, just
rotate the whole picture by some epsilon. This won’t change whether or not
there is an intersection.
Exercise 33.2-6
We can use a modified version of the intersecting-segments algorithm to
solve this problem. We’ll first associate left and right endpoints to each disk.
If disk Dhas radius rand center (x, y), define its left endpoint to be (x−r, y)
and its right endpoint to be (x+r, y). Begin by ordering the endpoints of the
disks first by left-right position. If two endpoints have the same x-coordinate,
then covertical left endpoints come before right endpoints. Within these, order
by y-coordinates from low to high. We’ll use the same event point schedule as
for the intersecting segments problem. Maintain a sweep-line status that gives
5

the relative order of the segments of the disks, where the segment associated
to each disk is the segment formed by its left and right endpoints. When we
encounter a left endpoint, we add the associated disk to the sweep-line status.
When we encounter a right endpoint, we delete the disk from the sweep-line
status. Consider the first time two disks become consecutive in the ordering.
Let their centers be (x1, y1) and (x2, y2), and their radii be r1and r2. Check
if (x2−x1)2+ (y2−y1)2≤(r1+r2)2. If yes, then the two circles intersect.
Otherwise they don’t. Since we can check this in O(1), and there are only 2n
points which are added, we make at most 4nchecks in total. Sorting the points
takes O(nlg n), so the total runtime is O(nlg n) + O(n) = O(nlg n).
Exercise 33.2-7
We preform a slight modification to what Professor Mason suggested in ex-
ercise 33.2-3. Once we have found an intersection, we then keep considering
elements further and further away in the red black tree until we no longer have
an intersection. Since all the tree operations only take time O(lg(n)), and we
are only doing an additional one on top of the original algorithm for each of the
intersections that we found, we have that the additional runtime is O(klg(n))
so, the total runtime is O((n+k) lg(n)).
Exercise 33.2-8
Suppose that at least 3 segments intersect at the same point. It is clear
that if ANY-SEGMENTS-INTERSECT returns true, then it must be correct.
Now we will show that it must return true if there is an intersection, even if
it occurs as an intersection of 3 or more segments. Suppose that there is at
least one intersection, and that pis the leftmost itnersection point, breaking
ties by choosing the point with the lowest y-coordinate. Let a1, a2, . . . , akbe
the segments that intersect at p. Since no intersections occur to the left of p,
the order given by Tis correct at all points to the left of p. Let zbe the first
sweep line at which some pair ai, ajis consecutive in T. Then zmust occur at
or to the left of p. Let ibe the smallest number such that there exists a jsuch
that aiand ajare consecutive in T, and assume that we choose the smallest j
possible, and let qbe the event point at which aiand ajbecome consecutive in
the total preorder. If pis on z, then we must have q=p, and at this point the
intersection is detected. As in the proof of correctness given in the section, the
ordering of our endpoints allows us to detect this even if pis the left endpoint
of aiand the right endpoint of aj. If pis not on zthen qis to the left of p, and
when we process qno other intersections have occurred, so the ordering in Tis
correct, and the algorithm correctly identifies the intersection between aiand aj.
Exercise 33.2-9
In the original statement of the problem, we are putting points with lower y-
coordinates first. This means that when we are processing our vertical segment,
6

we want its lower bound to of already been processed by the time we process
any of the left endpoints of other lines that may intersect the given line. Also,
we don’t want to remove the segment until we have already processed all the
right endpoints of the lines that may of intersected it, which means we want
it’s upper bound to be dealt with in the second pass (the right endpoint pass).
Again, since we process lower y-values first, this means that we have it added
to our tree before we process anything it could intersect and have it removed
after processing everything it could intersect.
If one or both of the segments are vertical at x in exercise 33.2-2, then test-
ing whether they intersect is just a matter of looking to see if the other line is
less than the upper bound and more than the lower bound at the given xvalue.
otherwise we just see if it’s more than the upper bound or less than the lower
bound to see which direction the inequality should go.
Exercise 33.3-1
To see this, note that p1and pmare the points with the lowest and high-
est polar angle with respect to p0. By symmetry, we may just show it for p1
and we would also have it for pmjust by reflecting the set of points across a
vertical line. To a contradiction, suppose we have the convex hull doesn’t con-
tain p1. Then, let pbe the point in the convex hull that has the lowest polar
angle with respect to p0. If pis on the line from p0to p1, we could replace it
with p1and have a convex hull, meaning we didn’t start with a convex hull. If
we have that it is not on that line, then there is no way that the convex hull
given contains p1, also contradicting the fact that we had selected a convex hull.
Exercise 33.3-2
Let our nnumbers be a1, a2, . . . , anand fbe a strictly convex function,
such as ex. Let pi= (ai, f(ai)). Compute the convex hull of p1, p2, . . . , pn.
Then every point is in the convex hull. We can recover the numbers them-
selves by looking at the x-coordinates of the points in the order returned by the
convex-hull algorithm, which will necessarily be a cyclic shift of the numbers
in increasing order, so we can recover the proper order in linear time. In an
algorithm such as GRAHAM-SCAN which starts with the point with minimum
y-coordinate, the order returned actually gives the numbers in increasing order.
Exercise 33.3-3
Suppose that pand qare the two furthest apart points. Also, to a con-
tradiction, suppose, without loss of generality that pis on the interior of the
convex hull. Then, construct the circle whose center is qand which has pon
the circle. Then, if we have that there are any vertices of the convex hull that
are outside this circle, we could pick that vertex and q, they would have a
higher distance than between pand q. So, we know that all of the vertices of
the convex hull lie inside the circle. This means that the sides of the convex
7

hull consist of line segments that are contained within the circle. So, the only
way that they could contain p, a point on the circle is if it was a vertex, but
we suppsed that pwasn’t a vertex of the convex hull, giving us our contradiction.
Exercise 33.3-4
We simply run GRAHAM-SCAN but without sorting the points, so the
runtime becomes O(n). To prove this, we’ll prove the following loop invariant:
At the start of each iteration of the for loop of lines 7-10, stack Sconsists of,
from bottom to top, exactly the vertices of CH(Qi−1). The proof is quite similar
to the proof of correctness. The invariant holds the first time we execute line 7
for the same reasons outline in the section. At the start of the ith iteration, S
contains CH(Qi−1). Let pjbe the top point on Safter executing the while loop
of lines 8-9, but before piis pushed, and let pkbe the point just below pjon
S. At this point, Scontains CH(Qj) in counterclockwise order from bottom to
top. Thus, when we push pi,Scontains exactly the vertices of CH(Qj∪ {pi}).
We now show that this is the same set of points as CH(Qi). Let ptbe any
point that was popped from Sduring iteration iand prbe the point just below
pton stack Sat the time ptwas popped. Let pbe a point in the kernel of P.
Since the angle ∠prptpimakes a nonelft turn and Pis star shaped, ptmust
be in the interior or on the boundary of the triangle formed by pr,pi, and p.
Thus, ptis not in the convex hull of Qi, so we have CH(Qi− {pt}) = CH(Qi).
Applying this equality repeatedly for each point removed from Sin the while
loop of lines 8-9, we have CH(Qj∪ {pi}) = CH(Qi).
When the loop terminates, the loop invariant implies that Sconsists of ex-
actly the vertices of CH(Qm) in counterclockwise order, proving correctness.
Exercise 33.3-5
Suppose that we have a convex hull computed from the previous stage
{q0, q1, . . . , qm}, and we want to add a new vertex, pin and keep track of how
we should change the convex hull. First, process the vertices in a clockwise
manner, and look for the first time that we would have to make a non-left to
get to p. This tells us where to start cutting vertices out of the convex hull. To
find out the upper bound on the vertices that we need to cut out, turn around,
start processing vertices in a clockwise manner and see the first time that we
would need to make a non-right. Then, we just remove the vertices that are in
this set of vertices and replace the with p. There is one last case to consider,
which is when we end up passing ourselves when we do our clockwise sweep.
Then we just remove no vertices and add pin in between the two vertices that
we had found in the two sweeps. Since for each vertex we add we are only
considering each point in the previous step’s convex hull twice, the runtime is
O(nh) = O(n2) where his the number of points in the convex hull.
Exercise 33.3-6
8

Algorithm 2 ONLINE-CONVEX-HULL
let P={p0, p1,...pm}be the convex hull so far listed in counterclockwise
order.
let pbe the point we are adding
i=1
while going from pi−1to pito p is a left turn and i6= 0 do
i++
end while
if i==0 then
return P
end if
j=i
while going from pi+1 to pito pis a right turn and j≥ido
j–
end while
if j < i then
insert p between pjand pi
else
replace pi,...pjwith p.
end if
First sort the points from left to right by xcoordinate in O(nlg n), breaking
ties by sorting from lowest to highest. At the ith step of the algorithm we’ll
compute Ci= CH({p1, . . . , pi}) using Ci−1, the convex hull computed in the
previous step. In particular, we know that the rightmost of the first ipoints will
be in Ci. The point which comes before piin a clockwise ordering will be the
first point qof Ci−1such that qpidoes not intersect the interior of Ci−1. The
point which comes after piwill be the last point q0in a clockwise ordering of the
vertices of Ci−1such that piq0does not intersect the interior of Ci−1. We can
find each of these points in O(lg n) using a binary search. Here, assume that q
and q0are given as the positions of the points in the clockwise ordering). This
follows because we’re searching a set of points which already forms a convex
hull, so the segments pjpiwill intersect the interior of Ci−1for the first k1
points, not intersect for the next k2points, and intersect for the last k3points,
where any of k1,k2, or k3could be 0. Once found, we can delete every point
between qand q0. Since a point is deleted at most once and we store things in
a red-black tree, the total runtime of all deletions is O(nlg n). Since we insert
a total of npoints, each taking O(lg n), the total runtime is thus O(nlg n). See
the algorithm below:
Exercise 33.4-1
The flaw in his plan is pretty obvious, in particular, when we select line l,
we may be unable perform an even split of the vertices. So, we don’t neccesar-
ily have that both the left set of points and right set of points have fallen to
roughly half. For example, suppose that the points are all arranged on a vertical
9

Algorithm 3 INCREMENTAL-METHOD(p1, p2, . . . , pn)
if n≤3then
return (p1, . . . , pn)
end if
Use Merge Sort to sort the points by increasing x-coordinate, breaking ties
by requiring increasing y-coordinate
Initialize an red-black tree Cof size 3 with entries p1, p2, and p3
for i= 4 to ndo
Let qbe the result of binary searching for the first point of Ci−1such that
qpidoesn’t intersect the interior of Ci−1
Let q0be the result of binary searching for the last point of Ci−1such that
q0pidoesn’t intersect the interior of Ci−1
Delete q+ 1, q + 2, . . . , q0−1 from C
Insert piinto C
end for
line, then, when we recurse on the the left set of points, we haven’t reduced the
problem size AT ALL, let alone by a factor of two. There is also the issue in
this setup that you may end up asking about a set of size less than two when
looking at the right set of points.
Exercise 33.4-2
Since we only care about the shortest distance, the distance δ0must be
strictly less than δ. The picture in Figure 33.11(b) only illustrates the case of a
nonstrict inequality. If we exclude the possibility of points whose xcoordinate
differs by exactly δfrom l, then it is only possible to place at most 6 points in
the δ×2δrectangle, so it suffices to check on the points in the 5 array positions
following each point in the array Y0.
Exercise 33.4-3
In the analysis of the algorithm, most of it goes through just based on the
triangle inequality. The only main point of difference is in looking at the num-
ber of points that can be fit into a δ×2δrectangle. In particular, we can cram
in two more points than the eight shown into the rectangle by placing points at
the centers of the two squares that the rectangle breaks into. This means that
we need to consider points up to 9 away in Y0instead of 7 away. This has no
impact on the asymptotics of the algorithm and it is the only correction to the
algorithm that is needed if we switch from L2to L1.
Exercise 33.4-4
We can simply run the divide and conquer algorithm described in the sec-
10

tion, modifying the brute force search for |P| ≤ 3 and the check against the
next 7 points in Y0to use the L∞distance. Since the L∞distance between two
points is always less than the euclidean distance, there can be at most 8 points
in the δ×2δrectangle which we need to examine in order to determine whether
the closest pair is in that box. Thus, the modified algorithm is still correct and
has the same runtime.
Exercise 33.4-5
We select the line lso that it is roughly equal, and then, we won’t run into
any issue if we just pick an aribitrary subset of the vertices that are on the line
to go to one side or the other. Since the analysis of the algorithm allowed for
both elements from PLand PRto be on the line, we still have correctness if we
do this. To determine what values of Y belong to which of the set can be made
easier if we select our set going to PLto be the lowest however many points
are needed, and the PRto be the higher points. Then, just knowing the index
of Ythat we are looking at, we know whether that point belonged to PLor to PR.
Exercise 33.4-6
In addition to returning the distance of the closest pair, the modify the al-
gorithm to also return the points passed to it, sorted by y-coordinate, as Y. To
do this, merge YLand YRreturned by each of its recursive calls. If we are at
the base case, when n≤3, simply use insertion sort to sort the elements by
y-coordinate directly. Since each merge takes linear time, this doesn’t affect the
recursive equation for the runtime.
Problem 33-1
a. We need just iteratively apply Jarvis march. The first march takes time
O(n|CH(Q1)|), the next time O(nCH(Q2)), and so on. So, since each point
in Q appears in exactly one convex hull, as we take off successive layers, we
have
X
i
O(n|CH(Qi)|) = O(nX
i
|CH(Qi)|) = O(n2)
b. Suppose that the elements r1, r2, r3,...r`are the points that we are asked
to sort. We will construct an instance of the convex layers problem, whose
solution will tell us what the sorted order of {ri}is. Since we can’t com-
parison sort quickly, and this would provide a solution of sorting based on a
convex layers algorithm, it would mean that we cannot find a convex layers
algorithm that takes time less than Ω(nlg(n)).
Suppose that all the {ri}are positive. If they aren’t, we can in linear time
find the one with the smallest value and subtract that value minus one from
11

each of them. We will select our 4`points to be
P={(ri,0)}∪{(0,±i)|i= 1,2,...`}∪{(−i, 0)|i= 1,2,...`}
Note that all of the points in this set are on the coordinate axes. So, every
layer will contain one point that lies on each of the four half axes coming out
of the origin. Looking at the points that lie on the positive xaxis, they will
correspond to the original points that we wanted to sort. Also, by looking at
the outermost layer and going inwards, we are reading off the points {ri}in
order of decreasing value. Since we have only increased the size of the problem
by a constant factor, we haven’t changed the asymptotics. In particular, if
we had some magic algorithm for convex layers that was o(nlg(n)), we would
then have an algorithm that was o(nlg(n)).
See also the solution to 33.3-2
Problem 33-2
a. Suppose that yi≤yi+1 for some i. Let pibe the point associated to yi.
In layer i,piis the leftmost point, so the x-coordinate of every other point
in layer iis greater than the x-coordinate of pi. Moreover, no other point
in layer ican have ycoordinate greater than pi, since that would imply it
dominates pi. Let qi+1 be the point of layer i+ 1 with y-coordinate yi+1 . If
qi+1 is to the left of pi, then qi+1 cannot be dominated by any point in Li
since every point in Liis to the right of and below pi. Moreover, if qi+1 is
to the right of pithen qi+1 dominates pi, which can’t happen. Thus, qi+1
cannot be weakly to the left or right of pi, a contradiction. Thus yi> yi+1.
b. First suppose j≤k. Then for 1 ≤i≤j−1 we have that (x, y) is dominated
by the point in layer iwith y-coordinate yi, so (x, y) is not in any of these
layers. Since (x, y) is the leftmost point and yj< y, and all other points
in layer jhave lower ycoordinate, no point in layer jdominates (x, y).
Moreover, since it is leftmost, no other point can be dominated by (x, y).
Thus, (x, y) is in Lj, as well as all other points previously in Lj. The other
layers are unaffected since we no longer consider (x, y) when computing them.
Thus the layers of Q0are identical to the maximal layers of Q, except that
Lj=Lj∪(x, y).
Now suppose j=k+ 1. Then (x, y) is dominated by each point in layer i
with y-coordinate yi, so it can’t be in any of the first klayers. This implies
that it is in a layer of its own, Lk+1 ={(x, y)}.
c. First sort the points by xcoordinate, with the highest corrdinate first. Pro-
cess the points one at a time. For each point, find the layer in which it
belongs as described in part b, creating a new layer if necessary. We can
maintain lists of the layers in sorted order by ycoordinate of the leftmost
element of each list. In doing so, we can decide which list each new point
belongs to in O(lg n) time. Since there are npoints to process, the runtime
12

after sorting is O(nlg n). The initial sorting takes O(nlg n), so the total
runtime is O(nlg n).
d. We’ll have to modify our approach to deal with points having the same x-
or y-coordinate. In particular, if two points have the same x-coordinate then
when we go to place the second one, the old algorithm would have us put
it in the same layer as the first one. We’ll compensate for this as follows.
Suppose we wish to add the point (x, y). Let jbe the minimum index such
that yj< y. If the x-coordinate of the leftmost point of Ljis equal to x,
then we need to create a new list L0which lives between Lj−1and Lj. Using
red-black trees we can update the information in O(lg n) time. Otherwise,
we add (x, y) to Ljas usual. If j=k+ 1, then create a new layer Lk+1.
Two points having the same y-coordinate doesn’t actually cause any difficulty
because of the strict inequality required for the check described in part b.
Problem 33-3
a. Take a convex hull of the set of all the ghostbusters and the ghosts. If the
convex hull doesn’t consist of either all ghosts or all busters, we can just
pick an edge of the convex hull that joins a buster and a ghost, Since all of
the other points lie on the same side of that line, the number of ghosts and
busters will be n-1 and so will be equal.
So, assume that the convex hull does not contain one of both types. Since
there is symmetry between ghosts and ghostbusters, suppose the convex hull
is entirely made of ghostbusters. Pick an arbitrary ghostbuster on the convex
hull, and that he’s facing somewhere inside the convex hull. Have him/her
initially pointing his proton pack just to the left the person furthest to his
right and have him slowly start turning left. We know that initially there
are more ghostbusters than ghosts to his right. We also know that by the
time he is just to the right of the person furthest to his left there are more
ghosts to his right than ghostbusters. This means at some point he must of
gone from having more ghostbusters to his right to having more ghosts to
his right. In order to have this happen he had to of just passed a ghost. So,
he is then paired up with that ghost.
b. We just keep iterating the first part of this procedure, applying it separately
to all the ghosts and ghostbusters to each of the sides of the line. We have
that no beam will cross because the beams for each stays entirely on that
side of the line. This gives us, for some n≤k > 0, the recurrence
T(n) = T(n−k) + T(k−1) + nlg(n)
This has the worst case when either kis really tiny or really close to n.
Therefore, the worst case solution to this recurrence is O(n2lg(n)).
Problem 33-4
13

a. Let abe given by endpoints (ax, ay, az) and (a0
x, a0
y, a0
z) and bbe given by
endpoints (bx, by, bz) and (b0
x, b0
y, b0
z). Compute, using cross products, whether
or not segments (ax, ay)(a0
xa0
y) and (bx, by)(b0
x, b0
y) intersect in constant time,
as described earlier in the chapter. If they do, then either aor bis above the
other one. If not, then they are unrelated. If they are related, we need to
determine which of aand bare on top. In this case, there exist λ1and λ2
such that
ax+λ1(a0
x−ax) = bx+λ2(b0
x−bx)
and
ay+λ1(a0
y−ay) = by+λ2(b0
y−by).
In other words, we get intersection when we project to the xy-plane. We
can solve for λ1and λ2. This requires division at first blush, but we shall
see in a moment that this isn’t necessary. In particular, ais above bif and
only if az+λ1(a0
z−az)≥bz+λ1(b0
z−bz). By multiplying both sides by
(a0
x−ax)(b0
y−by−(a0
y−ay)(b0
x−bx)) we clear all denominators, so we
need only perform addition, subtraction, multiplication, and comparison to
determine whether ais on top. Moreover, we can do this in constant time.
b. Make a graph whose vertices are each of the npoints. Find each pair of
overlapping sticks. If ais above b, then draw a directed edge from ato b.
Then perform a topological sort to determine an ordering of picking up the
sticks. If such an ordering exists, then we use it. Otherwise there is no legal
way to pick up the sticks. Since there could be as many as O(n2) instances
of a point abeing above a point b, there could be Θ(n2) edges in the graph,
so the runtime is O(n2).
Problem 33-5
a. Pick one point on one of the convex hulls, and look at the point on the other
that has the lowest polar angle. Then, start marching counter clockwise
around the first hull until it would require a non-right turn to go to the
point selected before. Do the same thing, picking a point and looking at the
point on the second polygon with highest polar angle, and keep marching
in a clockwise direction until getting to the particular point would require
a non-right. Cut out all the vertices between these two places we stopped
inclusive. In their place put the vertices of the other convex polygon that
are between to two selected vertices of it, inclusive.
b. Let P1be the first dn/2epoints, and let P2be the second bn/2cpoints. Since
the original set of points were selected independently from the sparse distri-
bution, both the sets P1and P2were selected from a sparse distribution.
This means that we have that |CH(P1)| ∈ O(n1−) and also, |CH(P2)| ∈
O(n1−). Then, by applying the procedure from part a, we have the re-
currence T(n)≤2T(n/2) + |CH(P1)|+|CH(P2)|= 2T(n/2) + O(n1−).
14

By applying the master theorem, we see that this recurrence has solution
T(n)∈O(n).
15

Chapter 34
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 34.1-1
Showing that LONGEST-PATH-LENGTH being polynomial implies that
LONGEST-PATH is polynomial is trivial, because we can just compute the
length of the longest path and reject the instance of LONGEST-PATH if and
only if k is larger than the number we computed as the length of the longest
path.
Since we know that the number of edges in the longest path length is between
0 and |E|, we can perform a binary search for it’s length. That is, we construct
an instance of LONGEST-PATH with the given parameters along with k=|E|
2.
If we hear yes, we know that the length of the longest path is somewhere above
the halfway point. If we hear no, we know it is somewhere below. Since each
time we are halving the possible range, we have that the procedure can require
O(lg(|E|)) many steps. However, running a polynomial time subroutine lg(n)
many times still gets us a polynomial time procedure, since we know that with
this procedure we will never be feeding output of one call of LONGEST-PATH
into the next.
Exercise 34.1-2
The problem LONGST-SIMPLE-CYCLE is the relation that associates each
instance of a graph with the longest simple cycle contained in that graph. The
decision problem is, given k, to determine whether or not the instance graph
has a simple cycle of length at least k. If yes, output 1. Otherwise output 0.
The language corresponding to the decision problem is the set of all hG, kisuch
that G= (V, E) is an undirected graph, k≥0 is an integer, and there exists a
simple cycle in Gconsisting of at least kedges.
Exercise 34.1-3
A formal encoding of the adjacency matrix representation is to first encode
an integer nin the usual binary encoding representing the number of vertices.
Then, there will be n2bits following. The value of bit mwill be 1 if there is an
edge from vertex bm/ncto vertex (m%n), and zero if there is not such an edge.
1

An encoding of the adjacency list representation is a bit more finessed. We’ll
be using a different encoding of integers, call it g(n). In particular, we will
place a 0 immediately after every bit in the usual representation. Since this
only doubles the length of the encoding, it is still polynomially related. Also,
the reason we will be using this encoding is because any sequence of integers
encoded in this way cannot contain the string 11 and must contain at least
one zero. Suppose that we have a vertex with edges going to the vertices in-
dexed by i1, i2, i3, . . . , ik. Then, the encoding corresponding to that vertex is
g(i1)11g(i2)11 · · · 11g(ik)1111. Then, the encoding of the entire graph will be
the concatenation of all the encodings of the vertices. As we are reading through,
since we used this encoding of the indices of the vertices, we won’t ever be con-
fused about where each of the vertex indices end, or when we are moving on to
the next vertex’s list.
To go from the list to matrix representation, we can read off all the adjacent
vertices, store them, sort them, and then output a row of the adjacency matrix.
Since there is some small constant amount of space for the adjacency list repre-
sentation for each vertex in the graph, the size of the encoding blows up by at
most a factor of O(n), which means that the size of the encoding overall is at
most squared.
To go in the other direction, it is just a matter of keeping track of the posi-
tions in a given row that have ones, encoding those numerical values in the way
described, and doing this for each row. Since we are only increasing the size of
the encoding by a factor of at most O(lg(n))(which happens in the dense graph
case), we have that both of them are polynomially related.
Exercise 34.1-4
This isn’t a polynomial-time algorithm. Recall that the algorithm from
Exercise 16.2-2 had running time Θ(nW ) where Wwas the maximum weight
supported by the knapsack. Consider an encoding of the problem. There is
a polynomial encoding of each item by giving the binary representation of its
index, worth, and weight, represented as some binary string of length a= Ω(n).
We then encode W, in polynomial time. This will have length Θ(lg W) = b.
The solution to this problem of length a+bis found in time Θ(nW ) = Θ(a∗2b).
Thus, the algorithm is actually exponential.
Exercise 34.1-5
We show the first half of this exercise by induction on the number of times
that we call the polynomial time subroutine. If we only call it zero times, all we
are doing is the polynomial amount of extra work, and therefore we have that
the whole procedure only takes polynomial time.
Now, suppose we want to show that if we only make n+ 1 calls to the
polynomial time subroutine. Consider the execution of the program up until
just before the last call. At this point, by the inductive hypothesis, we have
only taken a polynomial amount of time. This means that all of the data that
2

we have constructed so far fits in a polynomial amount of space. This means
that whatever argument we pass into the last polynomial time subroutine will
have size bounded by some polynomial. The time that the last call takes is then
the composition of two polynomials, and is therefore a polynomial itself. So,
since the time before the last call was polynomial and the time of the last call
was polynomial, the total time taken is polynomial in the input. This proves
the claim of the first half of the input.
To see that it could take exponential time if we were to allow polynomi-
ally many calls to the subroutine, it suffices to provide a single example. In
particular, let our polynomial time subroutine be the function that squares its
input. Then our algorithm will take an integer xas input and then square
it lg(x) many times. Since the size of the input is lg(x), this is only linearly
many calls to the subroutine. However, the value of the end result will be
x2lg(x)=xx= 2xlg(x)= 2lg(x)2lg(x)∈ω(22lg(x)). So, the output of the function
will require exponentially many bits to represent, and so the whole program
could not of taken polynomial time.
Exercise 34.1-6
Let L1, L2∈P. Then there exist algorithms A1and A2which decide L1
and L2in polynomial time. We will use these to determine membership in the
given languages. An input xis in L1∪L2if and only if either A1or A2returns 1
when run on input x. We can check this by running each algorithm separately,
each in polynomial time. To check if xis in L1∩L2, again run A1and A2,
and return 1 only if A1and A2each return 1. Now let n=|x|. For i= 1
to n, check if the first ibits of xare in L1and the last n−ibits of xare
in L2. If this is ever true, then x∈L1L2so we return 1. Otherwise return
0. Each check is performed in time O(nk) for some k, so the total runtime is
O(n(nk+nk)) = O(nk+1) which is still polynomial. To check if x∈L1, run
A1and return 1 if and only if A1returns 0. Finally, we need to determine if
x∈L∗
1. To do this, for i= 1 to n, check if the first ibits of xare in L1, and the
last n−ibits are in L∗
1. Let T(n) denote the running time for input of size n,
and let cnkbe an upper bound on the time to check if something of length nis
in L1. Then T(n)≤Pn
i=1 cnkT(n−i). Observe that T(1) ≤csince a single bit
is in L∗
1if and only if it is in L1. Now suppose T(m)≤c0mk0. Then we have:
T(n)≤cnk+1 +
n−1
X
i=0
c0ik0≤cnk+1 +c0nk0+1 =O(nmax k,k0).
Thus, by induction, the runtime is polynomial for all n. Since we have exhib-
ited polynomial time procedures to decide membership in each of the languages,
they are all in P, so Pis closed under union, intersection, concatenation, com-
plement, and Kleene star.
Exercise 34.2-1
3

To verify the language, we should let the certificate be the mapping ffrom
the vertices of G1to the vertices of G2that is an isomorphism between the
graphs. Then all the verifier needs to do is verify that for all pairs of vertices
uand v, they are adjacent in G1if and only if f(u) is adjacent to f(v) in G2.
Clearly it is possible to produce an isomorphism if and only if the graphs are
isomorphic, as this is how we defined what it means for graphs to be isomorphic.
Exercise 34.2-2
Since Gis bipartite we can write its vertex set as the disjoint union StT,
where neither Snor Tis empty. Since Ghas an odd number of vertices, ex-
actly one of Sand Thas an odd number of vertices. Without loss of generality,
suppose it is S. Let v1, v2, . . . , vnbe a simple cycle in G, with v1∈S. Since n
is odd, we have v1∈S,v2∈T, . . . , vn−1∈T,vn∈S. There can be no edge
between v1and vnsince they’re both in S, so the cycle can’t be Hamiltonian.
Exercise 34.2-3
Suppose that Gis hamiltonian. This means that there is a hamiltonian cycle.
Pick any one vertex vin the graph, and consider all the possibilities of deleting
all but two of the edges passing through that vertex. For some pair of edges
to save, the resulting graph must still be hamiltonian because the hamiltonian
cycle that existed originally only used two edges. Since the degree of a vertex
is bounded by the number of vertices minus one, we are only less than squaring
that number by looking at all pairs (n−1
2∈O(n2)). This means that we are
only running the polynomial tester polynomially many independent times, so
the runtime is polynomial. Once we have some pair of vertices where deleting
all the others coming off of vstill results in a hamiltonian graph, we will re-
member those as special, and ones that we will never again try to delete. We
repeat the process with both of the vertices that are now adjacent to v, testing
hamiltonicity of each way of picking a new vertex to save. We continue in this
process until we are left with only |V|edge, and so, we have just constructed a
hamiltonian cycle.
Exercise 34.2-4
This is much like Exercise 34.1-6. Let L1and L2be languages in NP, with
verification algorithms A1and A2. Given input xand certificate yfor a language
in L1∪L2, we define A3to be the algorithm which returns 1 if either A1(x, y)=1
or A2(x, y) = 1. This is a polynomial verification algorithm for L1∪L2, so NP is
closed under unions. For intersection, define A3to return 1 if and only if A1(x, y)
and A2(x, y) return 1. For concatenation, define A3to loop through i= 1 to n,
checking each time if A1(x[1..i], y[1..i]) = 1 and A1(x[i+1..n], y[i+1..n]) = 1. If
so, terminate and return 1. If the loop ends, return 0. This still takes polynomial
time, so NP is closed under concatenation. Finally, we need to check Kleene star.
Define A3to loop through i= 1 to n, each time checking if A1(x[1..i], y[1..i]) = 1,
4

and y[i+ 1..n] is a certificate for x[i+ 1..n] being in L∗
1. Let T(n) denote the
running time for input of size n, and let cnkbe an upper bound on the time to
verify that yis a certificate for x. Then T(n)≤Pn
i=1 cnkT(n−i). Observe that
T(1) ≤csince we can verify a certificate for a problem of length 1 in constant
time. Now suppose T(m)≤c0mk0. Then we have:
T(n)≤cnk+1 +
n−1
X
i=0
c0ik0≤cnk+1 +c0nk0+1 =O(nmax k,k0).
Thus, by induction, the runtime of A3is polynomial. Note that we only
needed to deal with the runtime recursion with respect to the length of x, since
it is assumed |y|=O(|x|c) for some constant c. Therefore NP is closed under
Kleene star.
A proof for closure under complement breaks down, however. If a certificate
yis given for input xand A1(x, y) returns false, this doesn’t tell us that yis a
certificate for xbeing in the complement of L1. It meerly tells us that ydidn’t
prove x∈L1.
Exercise 34.2-5
Suppose that we know that the length of the certificates to the verifier are
bounded by nk−1, we know it has to be bounded by some polynomial because
the vertifier can only look at polynomially many bits because it runs in poly-
nomial time. Then, we try to run the verifier on every possible assignment to
each bit of the certificates of length up to that much. Then, the runtime of this
will be a polynomial times 2nk−1which is little oh of 2nk.
Exercise 34.2-6
The certificate in this case would be a list of vertices v1, v2, . . . , vn, starting
with uand ending with v, such that each vertex of Gis listed exactly once and
(vi, vi+1)∈Efor 1 ≤i≤n−1. Since we can check this in polynomial time,
HAM-PATH belongs to NP.
Exercise 34.2-7
For a directed acyclic graph, we can compute the topological sort of the
graph by the method of section 22.4. Then, looking at this sorting of the
vertices, we say that there is a Hamiltonian path if as we read off the vertices,
each is adjacent to the next, and they are not if there is any pair of vertices so
that one is not adjacent to the next.
If we are in the case that each is adjacent to the next, then the topological
sort itself gives us the Hamiltonian path. However, if there is any pair of vertices
so that one is not adjacent to the next, this means that that pair of vertices do
not have any paths going from one to the other. This would clearly imply that
5

there was no Hamiltonian path, because the Hamiltonian path would be going
from one of them to the other.
To see the claim that a pair of vertices uand vthat are adjacent in a topo-
logical sort but are not adjacent have no paths going from one to the other,
suppose to a contradiction there were such a path from uto v. If there were any
vertices along this path they would have to be after usince they are descendants
of uand they would have to be before vbecause they are ancestors of v. This
would contradict the fact that we said uand vwere adjacent in a topological
sort. Then the path would have to be a single edge from uto v, but we said
that they weren’t adjacent, and so, we have that there is no such path.
Exercise 34.2-8
Let L0be the complement of TAUTOLOGY. Then L0consists of all boolean
formulas φsuch that there exists an assignment y1, y2, . . . , ykof 0 and 1 to the
input variables which causes φto evaluate to 0. A certificate would be such an
assignment. Since we can check what an assignment evaluates to in polynomial
time in the length of the input, we can verify a certificate in polynomial time.
Thus, L0∈NP which implies TAUTOLOGY ∈co-NP.
Exercise 34.2-9
A language is in coNP if there is a procedure that can verify that an input
is not in the language in polynomial time given some certificate. Suppose that
for that language we a procedure that could compute whether an input was in
the language in polynomial time receiving no certificate. This is exactly what
the case is if we have that the language is in P. Then, we can pick our procedure
to verify that an element is not in the set to be running the polynomial time
procedure and just looking at the result of that, disregarding the certificate that
is given. This then shows that any language that is in Pis in coNP , giving us
the inclusion that we wanted.
Exercise 34.2-10
Suppose NP 6= co-NP. Let L∈NP \co-NP. Since P⊂NP ∩co-NP, and L /∈
NP ∩co-NP, we have L /∈P. Thus, P 6= NP.
Exercise 34.2-11
As the hint suggests, we will perform a proof by induction. For the base
case, we will have 3 vertices, and then, by enumeration, we can see that the
only hamiltonian graph on three vertices is K3. For any connected graph on
three vertices, the longest the path connecting them can be is 2 edges, and so
we will have G3=K3, meaning that the graph Gwas hamiltonian.
Now, suppose that we want to show that the graph Gon n+ 1 vertices has
the property that G3is hamiltonian. Since the graph Gis connected we know
6

that there is some spanning tree by Chapter 23. Then, let vbe any internal
vertex of that tree. Suppose that if we were to remove the vertex v, we would
be splitting up the original graph in the connected components V1, V2, . . . , Vk,
sorted in increasing order of size. Suppose that the first `1of these components
have a single vertex. Suppose that the first `2of these components have fewer
than 3 vertices. Then, let vibe the vertex of Vithat is adjacent to vin the tree.
For i>`1, let xibe any vertex of Vithat is distance two from the vertex v. By
induction, we have hamiltonian cycles for each of the components V`2+1, . . . , Vk.
In particular, there is a hamiltonian path from vito xi. Then, for each iand j
there is an edge from xjto vi, because there is a path of length three between
them passing through v. This means that we can string together the hamilto-
nian paths from each of the components with i>`1. Lastly, since V1, . . . , V`all
consist of single vertices that are only distance one from v, they are all adjacent
in G3. So, after stringing together the hamiltonian paths for i>`1, we just
visit all of the single vertices in v1, v2, . . . , v`1in order, then, go to vand then
to the vertex that we started this path at, since it was selected to be adjacent
to v, this is possible. Since we have constructed a hamiltonian cycle, we have
completed the proof.
Exercise 34.3-1
The formula in figure 34.8b is
((x1∨x2)∧(¬(¬x3))) ∧(¬(¬x3)∨((x1)∧(¬x3)∧(x2))) ∧((x1)∧(¬x3)∧(x2))
We can cancel out the double negation to get that this is the same expression
as
((x1∨x2)∧(x3)) ∧((x3)∨((x1)∧(¬x3)∧(x2))) ∧((x1)∧(¬x3)∧(x2))
Then, the first clause can only be true if x3is true. But the last clause can
only be true if ¬x3is true. This would be a contradiction, so we cannot have
both the first and last clauses be true, and so the boolean circuit is not satis-
fiable since we would be taking the and of these two quantities which cannot
both be true.
Exercise 34.3-2
Suppose L1≤PL2and let f1be the polynomial time reduction function
such that x∈L1if and only if f1(x)∈L2. Similarly, suppose L2≤PL3and
let f2be the polynomial time reduction function such that x∈L2if and only
if f2(x)∈L3. Then we can compute f2◦f1in polynomial time, and x∈L1if
and only if f2(f1(x)) ∈L3. Therefore L1≤PL3, so the ≤Prelation is transitive.
7

Exercise 34.3-3
Suppose first that we had some polynomial time reduction from Lto ¯
L. This
means that for every xthere is some f(x) so that x∈Liff f(x)∈¯
L. This means
that x∈¯
Liff x6∈ Liff f(x)6∈ ¯
Liff f(x)∈L. So, our polytime computable
function for the reduction is the same one that we had from L≤P¯
L. We can
do an identical thing for the other direction.
Exercise 34.3-4
We could have instead used as a certificate a satisfying assignment to the
input variables in the proof of Lemma 34.5. We construct the two-input, poly-
nomial time algorithm Ato verify CIRCUIT-SAT as follows. The first input is
a standard encoding of a boolean combinational circuit C, and the second is a
satisfying assignment of the input variables. We need to compute the output
of each logic gate until the final one, and then check whether or not the out-
put of the final gate is 1. This is more complicated than the approach taken
in the text, because we can only evaluate the output of a logic gate once we
have successfully determined all input values, so the order in which we examine
the gates matters. However, this can still be computed in polynomial time by
essentially performing a breath-first search on the circuit. Each time we reach
a gate via a wire we check whether or not all of its inputs have been computed.
If yes, evaluate that gate. Otherwise, continue the search to find other gates,
all of whose inputs have been computed.
Exercise 34.3-5
We do not have any loss of generality by this assumption. This is because since
we bounded the amount of time that the program has to run to be polynomial,
there is no way that the program can access more than an polynomial amount
of space. That is, there is no way of moving the head of the turning machine
further than polynomially far in only polynomial time because it can move only
a single cell at a time.
Exercise 34.3-6
Suppose that ∅is complete for P. Let L={0,1}∗. Then Lis clearly in
P, and there exists a polynomial time reduction function fsuch that x∈ ∅
if and only if f(x)∈L. However, it’s never true that x∈ ∅, so this means
it’s never true that f(x)∈L, a contradiction since every input is in L. Now
suppose {0,1}∗is complete for P, let L0=∅. Then L0is in Pand there ex-
ists a polynomial time reduction function f0. Then x∈ {0,1}∗if and only if
f0(x)∈L0. However xis always in {0,1}∗, so this implies f0(x)∈L0is always
true, a contradiction because no binary input is in L0.
Finally, let Lbe some language in Pwhich is not ∅or {0,1}∗, and let L0
be any other language in P. Let y1/∈L0and y2∈L0. Since L∈P, there
8

exists a polynomial time algorithm Awhich returns 0 if x /∈Land 1 if x∈L.
Define f(x) = y1if A(x) returns 0 and f(x) = y2if A(x) returns 1. Then f
is computable in polynomial time and x∈Lif and only if f(x)∈L0. Thus,
L0≤PL.
Exercise 34.3-7
Since Lis in NP , we have that ¯
L∈coNP because we could just run our
verification algorithm to verify that a given x is not in the complement of L,
this is the same as verifying that xis in L. Since every coNP language has its
complement in NP, suppose that we let Sbe any language in coNP and let ¯
S
be its compliment. Suppose that we have some polynomial time reduction f
from ¯
S∈NP to L. Then, consider using the same reduction function. We will
have that x∈Siff x6∈ ¯
Siff f(x)6∈ Liff f(x)∈¯
L. This shows that this choice
of reduction function does work. So, we have shown that the compliment of any
NP complete problem is also NP complete. To see the other direction, we just
negate everything, and the proof goes through identically.
Exercise 34.3-8
To prove that a language Lis NP-hard, one need not actually construct the
polynomial time reduction algorithm Fto compute the reduction function ffor
every L0∈NP . Rather, it is only necessary to prove that such an algorithm
exists. Thus, it doesn’t matter that Fdoesn’t know A. If L0is in NP, we
know that Aexists. If Aexists, dependent on kand that big-oh constant, we
know that Fexists and runs in polynomial time, and this is sufficient to prove
CIRCUIT-SAT is NP-hard.
Exercise 34.4-1
Suppose that it is a circuit on two inputs, and then, we have n rounds of two
and gates each, both of which take both of the two wires from the two gates from
the previous round. Since the formulas for each round will consist of two copies
of the formulas from the previous round, it will have an exponential size formula.
Exercise 34.4-2
To make this more readable, we’ll just find the 3-CNF formula for each term
listed in the AND of clauses for φ0on page 1083, including the auxiliary variables
pand qas necessary.
9

y= (y∨p∨q)∧(y∨p∨ ¬q)∧(y∨ ¬p∨q)∧(y∨ ¬p∨ ¬q)
(y1↔(y2∧ ¬x2)) = (¬y1∨ ¬y2∨ ¬x2)∧(¬y1∨y2∨ ¬x2)∧(¬y1∨y2∨x2)∧(y1∨ ¬y2∨x2)
(y2↔(y3∨y4)) = (¬y2∨y3∨y4)∧(y2∨ ¬y3∨ ¬y4)∧(y2∨ ¬y3∨y4)∧(y2∨y3∨ ¬y4)
(y3↔(x1→x2)) = (¬y3∨ ¬x2∨x2)∧(y3∨ ¬x1∨ ¬x2)∧(y1∨x1∨ ¬x2)∧(y3∨x1∨x2)
(y4↔ ¬y5)=(¬x4∨ ¬y5∨q)∧(¬x4∨ ¬y5∨ ¬p)∧(x4∨y5∨p)∧(x4∨y5∨ ¬p)
(y5↔(y6∨x4)) = (¬y5∨y6∨x4)∧(y5∨ ¬y6∨ ¬x4)∧(y5∨ ¬y6∨x4)∧(y5∨y6∨ ¬x4)
(y6↔(¬x1↔x3)) = (¬y6∨ ¬x1∨ ¬x3)∧(¬y6∨x1∨x3)∧(y6∨ ¬x1∨x3)∧(y6∨x1∨ ¬x3).
Exercise 34.4-3
The formula could have Ω(n) free variables, then, the truth table corre-
sponding to this formula would a number of rows that is Ω(2n) since it needs to
consider every possible assignment to all the variables. This then means that
the reduction as described is going to incrase the size of the problem exponen-
tially.
Exercise 34.4-4
To show that the language L= TAUTOLOGY is complete for co-NP, it will
suffice to show that Lis NP-complete, where Lis the set of all boolean formu-
las for which there exists an assignment of input variables which makes it false.
We showed in Exercise 34.2-8 that TAUTOLOGY ∈co-NP, which implies L∈
NP. Thus, we need only show that Lis NP-hard. We’ll give a polynomial time
reduction from the problem of determining satisfiability of boolean formulas to
determining whether or not a boolean formula fails to be a tautology. In partic-
ular, given a boolean formula φ, the negation of φhas a satisfying assignment
if and only if φhas an assignment which causes it to evaluate to 0. Thus, our
function will simply negate the input formula. Since this can be done in poly-
nomial time in the length of the input, boolean satisfiability is polynomial time
reducible to L. Therefore Lis NP-complete. By Exercise 34.3-7, this implies
TAUTOLOGY is complete for co-NP.
Exercise 34.4-5
Since the problem is in disjunctive normal form, we can write it as ∨iφi
where each φilooks like the and of a bunch of variables and their negations.
Then, we know that the formula is satisfiable if and only if any one if the φiare
satisfiable. If a φicontains both a variable and its negation, then it is clearly not
satisfiable, as one of the two must be false. However, if each variable showing
up doesn’t have its negation showing up, then we can just pick the appropriate
value to assign to each variable. This is a property that can be checked in linear
time, by just keeping two bit vectors of length equal to the number of variables,
one representing if the variable has shown up negated and one for if the variable
10

has shown up without having been negated.
Exercise 34.4-6
Let Adenote the polynomial time algorithm which returns 1 if input xis
a satisfiable formula, and 0 otherwise. We’ll define an algorithm A0to give a
satisfying assignment. Let x1, x2, . . . , xmbe the input variables. In polynomial
time, A0computes the boolean formula x0which results from replacing x1with
true. Then, A0runs Aon this formula. If it is satisfiable, then we have re-
duced the problem to finding a satisfying assignment for x0with input variables
x2, . . . , xm, so A0recursively calls itself. If x0is not satisfiable, then we set x1
to false, and need to find a satisfying assignment for the formula x0obtained by
replacing x1in xby false. Again, A0recursively calls itself to do this. If m= 1,
A0takes a polynomial-time brute force approach by evaluating the fomula when
xmis true, and when xmis false. Let T(n) denote the runtime of A0on a for-
mula whose encoding is of length n. Note that we must have m≤n. Then we
have T(n) = O(nk) + T(n0) for some kand n0=|x0|, and T(1) = O(1). Since
we make a recursive call once for each input variable there are mrecursive calls,
and the input size strictly decreases each time, so the overall runtime is still
polynomial.
Exercise 34.4-7
Suppose that the original formula was ∧i(xi∨yi), and the set of variables were
{ai}. Then, consider the directed graph which has a vertex corresponding both
to each variable, and each negation of a variable. Then, for each of the clauses
x∨y, we will place an edge going from ¬xto y, and an edge from ¬yto x. Then,
anytime that there is an edge in the directed graph, that means if the vertex
the edge is coming from is true, the vertex the edge is going to has to be true.
Then, what we would need to see in order to say that the formula is satisfiable
is a path from a vertex to the negation of that vertex, or vice versa. The naive
way of doing this would be to run all pairs shortest path, and see if there is a
path from a vertex to its negation. This however takes time O(n2lg(n)), and
we were charged with making the algorithm as efficient as possible. First, run
the procedure for detecting strongly connected components, which takes linear
time. For every pair of variable and negation, make sure that they are not in
the same strongly connected component. Since our construction was symmet-
ric with respect to taking negations, if there were a path from a variable to
its negation, there would be a path going from its negation to itself as well.
This means that we would detect any path from a variable to its negation, just
by checking to see if they are contained in the same connected component or not.
Exercise 34.5-1
To do this, first, notice that it is in NP, where the certificate is just the
injection from G1into G2so that G1is isomorphic to its image.
Now, to see that it is NP complete, we will do a reduction to clique. That
11

is, to detect if a graph has a clique of size k, just let G1be a complete graph
on kvertices and let G2be the original graph. If we could solve the subgraph
isomorphism problem quickly, this would allow us to solve the clique problem
quickly.
Exercise 34.5-2
A certificate would be the n-vector x, and we can verify in polynomial time
that Ax ≤b, so 0-1 integer linear programming (01LP) is in NP. To prove that
01LP is NP-hard, we show that 3-CNF-SAT ≤P01LP. Let φbe 3-CNF formula
with ninput variables and kclauses. We construct an instance of 01LP as
follows. Let Abe a k+ 2nby 2nmatrix. For 1 ≤i≤k, set entry A(i, j) to -1
if 1 ≤j≤nand clause Cicontains the literal xj. Otherwise set it to 0. For
n+1 ≤j≤2n, set entry A(i, j) to -1 if clause Cicontains the literal ¬xj−n, and
0 otherwise. When k+ 1 ≤i≤k+n, set A(i, j) = 1 if i−k=jor i−k=j−n,
and 0 otherwise. When k+n+ 1 ≤i≤k+ 2n, set A(i, j) = −1 if i−k−n=j
or i−k−n=j−n, and 0 otherwise. Let bbe a k+ 2n-vector. Set the first
kentries to -1, the next nentries to 1, and the last nentries to -1. It is clear
that we can construct Aand bin polynomial time.
We now show that φhas a satisfying assignment if and only if there exists
a 0-1 vector xsuch that Ax ≤b. First, suppose φhas a satisfying assignment.
For 1 ≤i≤n, f xiis true, make x[i] = 1 and x[n+i] = 0. If xiis false, set
x[i] = 0 and x[n+i] = 1. Since clause Ciis satisfied, there must exist some
literal in it which makes it true. If it is xj, then x[j] = 1 and A(i, j) = −1, so we
get a contribution of -1 to the ith row of b. Since every entry in the upper kby
2nsubmatrix of Ais nonpositive and every entry of xis nonnegative, there can
be no positive contributions to the ith row of b. Thus, we are guaranteed that
the ith row of Ax is at most -1. The same argument applies if the literal ¬xj
makes clause itrue. For 1 ≤m≤n, at most one of xmand ¬xmcan be true,
so at most one of x[m] and x[m+n] can be true. When we multiply row k+m
by x, we get the number of 1’s among x[m] and x[m+n]. Thus, the (k+m)th
row of bis at most 1, as required. Finally, when we multiply row k+n+mof
Aby x, we get negative 1 times the number of 1’s among x[m] and x[m+n].
Since this is at least 1, the (k+n+m)th row of bis at most -1. Therefore all
inequalities are satisfied, so xis a 0-1 solution to Ax =b.
Next we must show that any 0-1 solution to Ax =bprovides a satisfying
assignment. Let xbe such a 0-1 solution. The inequalities ensured by the last
2nrows of bguarantee that exactly one of x[m] and x[n+m] is set equal to 1
for 1 ≤m≤n. In particular, this means that each xiis either true or false, but
not both. Let this be our candidate satisfying assignment. By the construction
of A, we get a contribution of -1 to row iof Ax every time a literal in Ciis true,
based on our candidate assignment, and a 0 contribution every time a literal is
false. Since row iof bis -1, this guarantees at least one literal which is true
per our assignment in each clause. Since this holds for each of the kclauses,
the candidate assignment is in fact a satisfying assignment. Therefore 01LP is
NP-complete.
12

Exercise 34.5-3
We will try to show a reduction to the 0-1 integer programming problem.
To see this, we will take our Afrom the 0-1 integer programming problem, and
tack on a copy of the n×nidentity matrix to its bottom, and tack on nones
to the end of bfrom teh 0-1 integer programming problem. This has the effect
of adding the restrictions that every entry of xmust be at most 1. However,
since, for every i, we needed xito be an integer anyways, this only leaves the
option that xi= 0 or xi= 1. This means that by adding these restrictions,
we have that any solution to this system will be a solution to the 0-1 integer
programming problem given by Aand b.
Exercise 34.5-4
We can solve the problem using dynamic programming. Suppose there are n
integers in S. Create a tby ntable to solve the problem just as in the solution
to the 0-1 knapsack problem described in Exercise 16.2-2. This has runtime
O(tn lg t), since without loss of generality we may assume that every integer in
Sis less than or equal to t, otherwise we know it won’t be included in the solu-
tion, and we can check for this in polynomial time. The extra lg tterm comes
from the fact that each addition takes O(lg t) time. Moreover, we can assume
that Scontains at most t2integers. If tis expressed in unary then the length of
the problem is at most O(t+t2lg t) = O(t3), since we express the integers in S
in binary. The time to solve it is O(t4). Thus, the time to compute the solution
is polynomial in the length of the input.
Exercise 34.5-5
We will be performing a reduction from the subset sum problem. Suppose
that Sand tare our set and target from our subset sum problem. Let xbe
equal to Ps∈Ss. Then, we will add the elements x+t, 2x−t. Once we have
added the elements, note that the sum of all of the elements in the new set S0
will be 4x. We also know that we cannot have both of the new elements that
we added be on same side of the partition, because they add up to 3xwhich is
three times all the other elements combined. Now, this set of elements will be
what we pass into our set partition solver. Note that since the total is 4x, each
side will add up to 2x. This means that if we look at the elements that on the
same side as, but not equal to 2x−t, they must add up to t. Since they were
also members of the original set S, this means that they are a subset with the
desired sum, solving the original instance of subset sum. Since it was proved in
the section that subset sum is NP-complete, this proves that the set-partition
problem is NP hard.
To see that it is in NP, just let the certificate be the set of elements of S
that forms one side of the partition. It is linear time to add them up and make
sure that they are exactly half the sum of all the elements in S.
13

Exercise 34.5-6
We’ll show that the hamiltonian-path problem HAM-PATH is NP-complete.
First, a certificate would be a list {v1, v2, . . . , vn}of the vertices of the path, in
order. We can check in polynomial time whether or not {vi, vi+1}is an edge for
1≤i≤n−1. Thus, HAM-PATH is in NP.
Next, we’ll show that HAM-PATH is NP-complete by showing that HAM-
CYCLE ≤PHAM-PATH. Let G= (V, E) be any graph. We’ll construct a graph
G0as follows. For each edge ei∈E, let Geidenote the graph with vertex set
Vand edge set E−ei. Let eihave the form {ui, vi}. Now, G0will contain one
copy of Geifor each ei∈E. Additionally, G0will contain a vertex xconnected
to u1, an edge from vito ui+1 for 1 ≤i≤ |E| − 1, and a vertex yand edge from
v|E|to y. It is clear that we can construct G0from Gin time polyomial in the
size of G.
If Ghas a hamiltonian cycle, then Geihas a hamilonian path starting at
uiand ending at vifor each i. Thus, G0has a hamiltonian cycle from xto y,
obtained by taking each of these paths one after another. On the other hand,
suppose Gfails to have a hamiltonian cycle. Since xand yhave degree 1, the
only way G0can have a hamiltonian path is if it starts at xand ends at y.
Moreover, since {v1, u2}is a cut edge, it must be in the hamiltonian path if it
exists. Since we can not traverse this edge a second time, any hamiltonian path
must start with a hamiltonian path from xto v1. However, this means there is
a hamiltonian path from u1to v1. Since {u1, v1}is an edge in G, this implies
there is a Hamiltonian cycle in G, a contradiction. Thus, Ghas a hamiltonian
cycle if and only if G0has a hamiltonian path. Therefore HAM-PATH is NP-
hard, so HAM-PATH is in fact NP-complete.
Exercise 34.5-7
The related decision problem is to, given a graph Gand integer kdecide
if there is a simple cycle of length at least kin the graph G. To see that this
problem is in NP , just let the certificate be the cycle itself. It is really easy just
to walk along this cycle, keeping track of what vertices you’ve already seen, and
making sure they don’t get repeated.
To see that it is NP-hard, we will be doing a reduction to Hamilton cycle.
Suppose we have a graph Gand want to know if it is Hamilton. We then create
an instance of the decision problem asking if the graph has a simply cycle of
length at least |V|vertices. If it does then there is a hamilton cycle. If there is
not, then there cannot be any hamilton cycle.
Exercise 34.5-8
A certificate would be an assignment to input variables which causes exactly
half the clauses to evaluate to 1, and the other half to evaluate to 0. Since
we can check this in polynomial time, half 3-CNF is in NP. To prove that it’s
14

NP-hard, we’ll show that 3-CNF-SAT ≤pHALF-3-CNF. Let φbe any 3-CNF
formula with mclauses and input variables x1, x2, . . . , xn. Let Tbe the formula
(y∨y∨¬y), and let Fbe the formula (y∨y∨y). Let φ0=φ∧T∧. . .∧T∧F∧. . .∧F
where there are mcopies of Tand 2mcopies of F. Then φ0has 4mclauses and
can be constructed from φin polynomial time. Suppose that φhas a satisfying
assignment. Then by setting y= 0 and the xi’s to the satisfying assignment,
we satisfy the mclauses of φand the m T clauses, but none of the Fclauses.
Thus, φ0has an assignment which satisfies exactly half of its clauses. On the
other hand, suppose there is no satisfying assignment to φ. The m T clauses
are always satisfied. If we set y= 0 then the total number of clauses satisfies
in φ0is strictly less than 2m, since each of the 2m F clauses is false, and at
least one of the φclauses is false. If we set y= 1, then strictly more than half
the clauses of φ0are satisfied, since the 3m T and Fclauses are all satisfied.
Thus, φhas a satisfying assignment if and only if φ0has an assignment which
satisfies exactly half of its clauses. We conclude that HALF-3-CNF is NP-hard,
and hence NP-complete.
Problem 34-1
a) The related decision problem should be to, given a graph and a number k
decide whether or not there is some independent set of size at least k. If we
take the compliment of the given graph, then it will have a clique of size at
least kif and only if the original graph has an independent set of size at least
k. This is because if we take any set of vertices in the original graph, then
it will be an independent set if and only if there are no edges between those
vertices. However, in the compliment graph, this means that between every
one of those vertices, there is an edge, which means they form a clique. So,
to decide independent set, just decide clique in the compliment.
b) We know that since all independent sets are subsets of the set of vertices,
then the size of the largest independent set will be an integer in the range
1..|V|. Then, we will perform a binary search on this space of valid sizes
of the largest independent set. That is, we pick the middle element, ask if
there is an independent set of that size, if there is, we know we are in the
upper half of this range of values for the size of the largest independent set,
if not, then we are in the lower half. The total runtime of this procedure to
find the size of the largest independent set will only be a factor of lg(|V||)
higher than the solution to the decision problem. Call the size of the largest
independent set k.
Now, for every pair of vertices, try adding an edge, and check if the proce-
dure from before determines that the size of the largest independent set has
decreased. If it hasn’t that means that that pair of vertices doesn’t prevent
us from attaining an independent set of the given size. That is, we aren’t in
the case that there is only one maximal set of the given size and that pair of
vertices belongs to it. So, add that edge to the graph, and continue in this
15

fashion for every pair of vertices. Once we are done, the size of the largest
independent set will be the same, and we will have that every edge is filled
in except for those going between an independent set of the given size. So,
we just list off all the vertices whose degree is less than |V| − 1 as being
members of our independent set.
c) Since every vertex has degree 2, and so self edges are allowed, the graph must
look like a number of disjoint cycles. We can then consider the independent
set problem separately for each of the cycles. If we have an even cycle, the
largest independent set possible is half the vertices, by selecting them to be
alternating. If it is an odd cycle, then we can do half rounded down, since
when we get back to the start, we are in the awkward place where there are
two unselected vertices between two selected vertices. It’s easy to see that
these are tight, because there is so little freedom in selecting an independent
set in a cycle. So, to calculate the size of the smallest independent set, look
at the sizes of each cycle ci, then, the largest independent set will have size
bci
2c.
d) First, find a maximal matching. This can be done in time O(V E) by
the methods of section 26.3. let f(x) be defined for all vertices that were
matched, and let it evaluate to the point that is paired with xin the maxi-
mal matching. Then, we do the following procedure. Let S1be the unpaired
points, Let S2=f(N(S1)) \S1, where we extend fto sets of vertices by just
letting it be the set containing all the pairs of the given points. Similarly,
define Si+1 =f(N(Si)) \∪i
j=1Sj. First, we need to show that this is well
defined. That means that we want to make sure that we always have that
every neighbor of Siis paired with something. Since we could get from an
unpaired point to something in Siby taking a path that is alternating from
being an edge in the matching and an edge not in the matching, starting
with one that was not, if we could get to an unpaired point from Si, that
last edge could be tacked onto this path, and it would become an augmenting
path, contradicting maximality of the original matching. Next, we can note
that we never have an element in some Siadjacent to an element in some Sj.
Suppose there were, then we could take the path from an unpaired vertex
to a vertex in Si, add the edge to the element in Sjand then take the path
from there to an unpaired vertex. This forms an augmenting path, which
would again contradict maximality. The process of computing the {Si}must
eventually terminate by becoming ∅because they are selected to be disjoint
and there are only finitely many vertices. Any vertices that are neither in an
Sior adjacent to one consist entirely of a perfect matching, that has no edges
going to picked vertices. This means that the best we can do is to just pick
everything from one side of the remaining vertices. This whole procedure of
picking vertices takes time at most O(E), since we consider going along each
edge only twice. This brings the total runtime to O(V E).
Thanks to John Chiarelli, a fellow graduate student at Rutgers, for helpful
discussion of this part of the problem.
16

Problem 34-2
a. We can solve this problem in polynomial time as follows. Let adenote the
number of coins of denomination xand bdenote the number of coins of
denomination y. Then we must have a+b=n. In order to divide the
money exactly evenly, we need to know if there is a way to make (ax +by)/2
out of the coins. In other words, we need to determine whether there exist
nonnegative integers cand dless than or equal to aand brespectively such
that cx +dy = (ax +by)/2. There are (a+ 1)(b+ 1) ≤(n+ 1)2many such
linear combinations. We can compute each one in time polynomial in the
length of the input numbers, and there are polynomially many combinations
to compute, so we can just check all combinations to see if we find one that
works.
b. We can solve this problem in polynomial time as follows. Start by arranging
the coins from largest to smallest. If there are an even number of the current
largest coin, distribute them evenly to Bonnie and Clyde. Otherwise, give the
extra one to Bonnie and then only give coins to Clyde until the difference
has been resolved. This clearly runs in polynomial time, so we just need
to show that this will always yield an even division if such a division is
possible. Suppose that for some input of coins which can be divided evenly,
the algorithm fails. Then there must exist a last time at which there were an
odd number of a denomination 2i, so that Bonnie got ahead and had 2imore
dollars than Clyde. At this point, we start giving coins only to Clyde. Since
every denomination decrease cuts the amount in half, it will never be the
case that Clyde had strictly less than Bonnie, was given an additional coin,
and then had an amount strictly greater than Bonnie. Thus, the sum of all
coins of size less than 2imust not exceed 2i. Since we assumed the coins can
be divided evenly, there exists b0, b1, . . . and c0, c1, . . . such that we assign
Bonnie bicoins of value 2iand Clyde cicoins of value 2i, and both receive
an equal amount. Now remove all coins of value smaller than 2i. Bonnie
now has P∞
k=ibk2kdollars and Clyde has P∞
k=ick2kdollars. Moreover, we
know that there is an uneven distribution of wealth at this point, and since
every coin has value at least 2i, the difference is at least 2i. Since the sum
of the smaller coins is strictly less than 2i, there is no way to distribute the
smaller coins to fix the difference, a contradiction since we started with an
even split! Thus, the proposed algorithm is correct.
c. This problem is NP-complete. First, an assignment of each check to either
Bonnie or Clyde represents a certificate which can be checked in polynomial
time by adding up the amounts on each of Bonnies checks, and ensuring
that it is equal to the sum of the amounts on each of Clyde’s checks. Next
we’ll show this problem, SPLIT-CHECKS is NP-hard by showing that SET-
PARTITION ≤PSPLIT-CHECKS. Let Sbe a set of numbers. We can think
of each one as giving the value of a check. If there exists a set A⊂Ssuch
that Px∈Ax=Px∈(S−A)x, then we can assign each check in Ato Bonnie
17

and each check in S−Ato Clyde to get an equal division. On the other
hand, if there is a way to evenly assign checks then we may just take Ato be
the set of checks given to Bonnie, so by contrapositive, if we can’t find a set
partition which evenly splits the set then we can’t evenly divide the checks.
Thus, the problem is NP-hard, so it is NP-complete.
d. An assignment of each check to either Bonnie or Clyde represents a certificate,
and we can check in polynomial time whether or not the total amounts given
to Bonnie and Clyde differ by at most 100. Thus, the problem is in NP. Next,
we’ll show it’s NP-hard by showing SET-PARTITION ≤PSPLIT-CHECKS-
100. Let S={s1, s2, . . . , sn}be a set, and let xS ={xs1, xs2, . . . , xsn}.
Choose x=101
mini,j si−sj. Then the difference between any two elements in xS
is more than 100. If there exists A⊂Ssuch that Ps∈As=Ps∈S−As, then
we give Bonnie all the checks in xA and Clyde all the checks in x(S−A), for
a perfectly even split of the money, which means the difference is less than
100. On the other hand, suppose there exists no such A. Then for any way of
splitting the elements of Sinto two sets, their sums will differ by at least the
minimum difference of elements in S. Thus, any way of splitting the checks
in xS will result in a difference of at least 101, so there is no way to split
them so that the difference is at most 100. Therefore SET-PARTITION ≤P
SPLIT-CHECKS-100, so the problem is NP-hard. Since we showed it is in
NP, it is also NP-complete.
Problem 34-3
a) To two color a graph, we will do it a connected component at a time, so,
suppose that the graph is a single component. Pick a vertex and color arbi-
trarily, and color that vertex that color. Then, we repeatedly find a vertex
that has a colored neighbor and color it the other color. If we are ever in
the case that a vertex has neighbors of both colors, then the graph is not
2-colorable. This procedure is able to 2-color if the graph is 2-colorable,
since the only point where our hand isn’t forced is at the beginning when
we pick a vertex and a color, but this choice is only a false one because of
the symmetry of the two colors. If it finds it is 2-colorable, it also outputs a
valid 2-coloring.
b) The equivalent decision problem is to, given a graph Gand an integer k
say if there is a coloring that uses at most kcolors. The easy direction
is showing that if the original problem is solvable in poly thime, then the
decision problem is solvable in poly time. To do this, just compute the
minimum number of colors needed and output true if this is ≤k.
The other direction is a bit harder. Suppose that we can solve the decision
problem in polynomial time, then, we will try to show how we can actually
compute the minimum number of colors needed. A trivial bound on the
number of colors needed is the number of vertices, because if each vertex has
it’s own color, then the coloring has to be valid. So, we perform a binary
18
search on the number of colors, starting with the range 1..|V|, halving it
each time until we are down to a single possible number of colors needed in
order to color the graph. This will only add a log factor to the runtime of
the decision problem, and so will run in polynomial time.
c) For this problem, we need to show that if we can solve the decision problem
quickly, then we can decide the language 3-COLOR quickly. This is just
a matter of running the decision procedure with the same graph and with
k= 3. This gets us the reduction we need to show that 3-COLOR being
NP-complete implies the decision problem is NP-hard. The decision problem
is in NP because we can just have the certificate explicitly be the coloring
of the vertices of the graph.
d) When we restrict the graph to the vertices xi,¬xi, RED, then we will obtain
aK3because of the literal edges. This means that all three colors must
show up in it. Since there is already c(RED), then the other two must be
c(T RU E) and c(F ALSE). No matter whether we choose xior ¬xito be
c(T RU E), we can just select the other one to be c(F ALSE), this gets us
that, if we only care about the literal edges, we always have a 3 coloring
regardless of whether we want each xito be true or false.
e) For convenience, we will call the vertices a, b, c, d, e from the figure, where
we are reading from top to bottom and left to right for vertices that are
horizontal from one another. Since we are trying to check that it is 3 colorable
if and only if at least one of x, y, z are c(T RU E), we can negate the only
if direction. That is, we suppose they are all colored c(F ALSE) and show
that the graph is not 3 colorable.
Suppose c(x) = c(y) = c(z) = c(F ALSE). Then, we have that the only
possibility for vertex eis to be c(RED). This means the only possibility for
cis to be c(F ALSE). However, this means that c(a)6=c(x) = c(F ALSE),
c(d)6=c(y) = c(F ALSE), and c(b)6=c(c) = c(F ALSE). So, we have a
contradiction because any K3must have one of each color, and none of the
vertices in this K3can be c(F ALSE). This shows that the graph is not
3-colorable.
For the other direction, we do not negate. So, we assume there is a vertex
colored c(T RU E) and we show that the graph is 3-colorable. We will split
into the following cases. Note that because xand yplay a symmetric role,
we can reduce the number of cases from 7 to 5
x y z a b c d e
c(T RU E)c(T RU E)c(T RU E)c(F ALSE)c(T RU E)c(F ALSE)c(RED)c(RED)
c(F ALSE)c(T RU E)c(T RU E)c(RED)c(T RU E)c(F ALSE)c(F ALSE)c(RED)
c(F ALSE)c(F ALSE)c(T RU E)c(RED)c(F ALSE)c(RED)c(T RU E)c(F ALSE)
c(T RU E)c(T RU E)c(F ALSE)c(F ALSE)c(T RU E)c(F ALSE)c(RED)c(RED)
c(F ALSE)c(T RU E)c(F ALSE)c(T RU E)c(RED)c(F ALSE)c(F ALSE)c(RED)
19

Then, in every case where at least one of the inputs is true, there is an
assignment of colors to the other vertices that produces a valid 3-coloring.
f) Suppose we are given any instance of 3-CNF-SAT, we will be using exactly
the same construction as described in the problem for the reduction. First,
we note that each of the vertices corresponding to a variable and its negation
must only have the colors c(T RUE) and c(F ALSE), and exactly one can be
c(T RU E) because of the literal edges. This means that each of the clause
vertices will only be colorable if we assign a color of true to one of the variable
vertices that are in the clause. This means that if we set each variable that
has c(xi) = c(T RU E) true and each variable that has c(¬xi) = c(T RU E)
to be false, we will of obtained an assignment that makes at least one of the
entries in each clause true, and so, is a satisfying assignment of the formula.
Since 3-CNF-SAT is NP-complete, this means that 3-COLOR is NP-hard.
To see that it is in NP, just let the certificate be the coloring. Checking the
coloring can be done in linear time.
Problem 34-4
a. For fixed k, does there exist a permutation σ∈Snsuch that if we run the
tasks in the order aσ(1), . . . , aσ(n), the total profit is at least k?
b. It is clear that the decision problem is in NP because we can view a certificate
as a permutation of the tasks. We then check the tasks in that order to see
if they have finished by their deadlines and what profit we incur, finally
comparing this to k.
c. Suppose that a particular task aiis the first to be performed. Then we solve
the subproblem of deciding whether there exists a solution to the problem
with tasks a1, . . . , ai−1, ai+1, . . . , an, each with their respective profits and
times, deadlines such that dj=dj−ti, and with total profit at least k−pi.
To find this out, we make a lookup table which keeps track of the optimal
schedule computed bottom-up.
d. There are 2npossible profits that could be made, based on whether or not
we finish each task by its deadline. We can binary search these for the
one with maximum profit which satisfies the decision problem, which we can
determine in polynomial time by part c. Since binary search takes lg(2n) = n,
we need only run the polynomial time algorithm of part c.ntimes before we
find the maximal kwhich solves the decision problem, and thus solves the
optimization problem.
20

Chapter 35
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise 35.1-1
We could select the graph that consists of only two vertices and a single
edge between them. Then, the approximation algorithm will always select both
of the vertices, whereas the minimum vertex cover is only one vertex. more
generally, we could pick our graph to be k edges on a graph with 2kvertices so
that each connected component only has a single edge. In these examples, we
will have that the approximate solution is off by a factor of two from the exact
one.
Exercise 35.1-2
It is clear that the edges picked in line 4 form a matching, since we can only
pick edges from E0, and the edges in E0are precisely those which don’t share an
endpoint with any vertex already in C, and hence with any already-picked edge.
Moreover, this matching is maximal because the only edges we don’t include are
the ones we removed from E0. We did this because they shared an endpoint
with an edge we already picked, so if we added it to the matching it would no
longer be a matching.
Exercise 35.1-3
We will construct a bipartite graph with V=R∪L. We will try to construct
it so that Ris uniform, not that Ris a vertex cover. However, we will make it
so that the heuristic that the professor (professor who?) suggests will cause us
to select all the vertices in L, and show that |L|>2|R|.
Initially start off with |R|=nfixed, and Lempty. Then, for each ifrom
2 up to n, we do the following. Let k=bn
ic. Select Sa subset of the vertices
of Rof size ki, and so that all the vertices in R−Shave a greater or equal
degree. Then, we will add kvertices to L, each of degree i, so that the union of
their neighborhoods is S. Note that throughout this process, the furthest apart
the degrees of the vertices in Rcan be is 1, because each time we are picking
the smallest degree vertices and increasing their degrees by 1. So, once this has
been done for i=n, we can pick a subset of Rwhose degree is one less than
the rest of R(or all of Rif the degrees are all equal), and for each vertex in
1
that set we picked, add a single vertex to Lwhose only neighbor is the one in
Rthat we picked. This clearly makes Runiform.
Also, lets see what happens as we apply the heuristic. Note that each vertex
in Ronly has at most a single vertex of each degree in L. This means that as
we remove vertices from Lalong with their incident edges, we will always have
that the highest degree vertex remaining in Lis greater or equal to the highest
degree vertex in R. This means that we can always, by this heuristic, continue
to select vertices from Linstead of R. So, when we are done, we have selected,
by this heuristic, that our vertex cover is all of L.
Lastly, we need to show that Lis big enough relative to R. The size of L
is greater or equal to Pn
i=2bn
icwhere we ignore any of the degree 1 vertices
we may of added to Lin our last step. This sum can be bounded below by
the integral Rn+1
i=2
n
xdx by formula (A.12). Elementary calculus tells us that this
integral evaluates to n(lg(n+ 1) −1), so, we can clearly select n > 8 to make it
so that
2|R|= 2n
< n(lg(8 + 1) −1)
≤n(lg(n+ 1) −1)
=Zn+1
i=2
n
xdx
≤
n
X
i=2
bn
ic
≤ |L|
Since we selected Las our vertex cover, and Lis more than twice the size of
the vertex cover R, we do not have a 2- approximation using this heuristic. In
fact, we have just shown that this heuristic is not a ρapproximation for any
constant ρ.
Exercise 35.1-4
If a tree consists of a single node, we immediately return the empty cover
and are done. From now on, assume that |V| ≥ 2. I claim that for any tree
T, and any leaf node von that tree, there exists an optimal vertex cover for T
which doesn’t contain v. To see this, let V0⊂Vbe an optimal vertex cover,
and suppose that v∈V0. Since vhas degree 1, let ube the vertex connected
to v. We know that ucan’t also be in V0, because then we could remove v
and still have an vertex cover, contradicting the fact that V0was claimed to
be optimal, and hence smallest possible. Now let V00 be the set obtained by
removing vfrom V0and adding uto V0. Every edge not incident to uor v
has an endpoint in V0, and thus in V00. Moreover, every edge incident to u
is taken care of because u∈V00. In particular, the edge from vto uis still
okay because u∈V00. Therefore V00 is a vertex cover, and |V00|=|V0|, so it is
2

optimal. We may now write down the greedy approach, given in the algorithm
GREEDY-VERTEX-COVER:
Algorithm 1 GREEDY-VERTEX-COVER(G)
1: V0=∅
2: let Lbe a list of all the leaves of G
3: while V6=∅do
4: if |V|== 1 or 0 then
5: return V0
6: end if
7: let vbe a leaf of G= (V, E), and {v, u}be its incident edge
8: V=V−v
9: V0=V0∪u
10: for each edge {u, w} ∈ Eincident to udo
11: if dw== 1 then
12: L.insert(w)
13: end if
14: E=E− {u, w}
15: end for
16: V=V−u
17: end while
As it stands, we can’t be sure this runs in linear time since it could take O(n)
time to find a leaf each time we run line 7. However, with a clever implementa-
tion we can get around this. Keep in mind that a vertex either starts as a leaf,
or becomes a leaf when an edge connecting it to a leaf is removed from it. We’ll
maintain a list Lof current leaves in the graph. We can find all leaves initially
in linear time in line 2. Assume we are using an adjacency list representation.
In line 4 we check if |V|is 1 or 0. If it is, then we are done. Otherwise, the tree
has at least 2 vertices which implies that it has a leaf. We can get our hands
on a leaf in constant time in line 7 by popping the first element off of the list
L, which maintains our leaves. We can find the edge {u, v}in constant time by
examining v’s adjacency list, which we know has size 1. As described above,
we know that visn’t contained in an optimal solution. However, since {u, v}
is an edge and at least one of its endpoints must be contained in V0, we must
necessarily add u. We can remove vfrom Vin constant time, and add uto V0
in constant time. Line 10 will only execute once for each edge, and since Gis a
tree we have |E|=|V| − 1. Thus, the total contribution of the for-loop of line
10 is linear. We never need to consider edges adjacent to usince u∈V0. We
check the degrees as we go, adding a vertex to Lif we discover it has degree
1, and hence is a leaf. We can update the attribute dwfor each win constant
time, so this doesn’t affect the runtime. Finally, we remove ufrom Vand never
again need to consider it.
3

Exercise 35.1-5
It does not imply the existence of an approximation algorithm for the max-
imum size clique. Suppose that we had in a graph of size n, the size of the
smallest vertex cover was k, and we found one that was size 2k. This means
that in the compliment, we found a clique of size n−2k, when the true size of
the largest clique was n−k. So, to have it be a constant factor approximation,
we need that there is some λso that we always have n−2k≥λ(n−k). However,
if we had that kwas close to n
2for our graphs, say n
2−, then we would have
to require 2≥λn
2+. Since we can make stay tiny, even as ngrows large,
this inequality cannot possibly hold.
Exercise 35.2-1
Suppose that c(u, v)<0 and wis any other vertex in the graph. Then, to
have the trianle inequality satisfied, we need c(w, u)≤c(w, v) + c(u, v). Now
though, subtract c(u, v) from both sides, we get c(w, v)≥c(w, u)−c(u, v)>
c(w, u) + c(u, v) so, it is impossible to have c(w, v)≤c(w, u) + c(u, v) as the
triangle inequality would require.
Exercise 35.2-2
Let mbe some value which is larger than any edge weight. If c(u, v) denotes
the cost of the edge from uto v, then modify the weight of the edge to be
H(u, v) = c(u, v) + m. (In other words, His our new cost function). First we
show that this forces the triangle inequality to hold. Let u,v, and wbe ver-
tices. Then we have H(u, v) = c(u, v) + m≤2m≤c(u, w) + m+c(w, v) + m=
H(u, w) + H(w, v). Note: it’s important that the weights of edges are nonneg-
ative.
Next we must consider how this affects the weight of an optimal tour. First,
any optimal tour has exactly nedges (assuming that the input graph has exactly
nvertices). Thus, the total cost added to any tour in the original setup is nm.
Since the change in cost is constant for every tour, the set of optimal tours must
remain the same.
To see why this doesn’t contradict Theorem 35.3, let Hdenote the cost of
a solution to the transformed problem found by a ρ-approximation algorithm
and H∗denote the cost of an optimal solution to the transformed problem.
Then we have H≤ρH∗. We can now transform back to the original problem,
and we have a solution of weight C=H−nm, and the optimal solution has
weight C∗=H∗−nm. This tells us that C+nm ≤ρ(C∗+nm), so that
C≤ρ(C∗)+(ρ−1)nm. Since ρ > 1, we don’t have a constant approximation
ratio, so there is no contradiction.
Exercise 35.2-3
4

From the chapter on minimum spanning trees, recall Prim’s algorithm. That
is, a minimum spanning tree can be found by repeatedly finding the nearest ver-
tex to the vertices already considered, and adding it to the tree, being adjacent
to the vertex among the already considered vertices that is closest to it. Note
also, that we can recusively define the preorder traversal of a tree by saying
that we first visit our parent, then ourselves, then our children, before returning
priority to our parent. This means that by inserting vertices into the cycle in
this way, we are always considering the parent of a vertex before the child. To
see this, suppose we are adding vertex vas a child to vertex u. This means that
in the minimum spanning tree rooted at the first vertex, vis a child of u. So,
we need to consider ufirst before considering v, and then consider the vertex
that we would of considered after vin the previous preoreder traversal. This
is precisely achieved by inserting vinto the cycle in such a manner. Since the
property of the cycle being a preoreder traversal for the minimum spanning tree
constructed so far is maintained at each step, it is the case at the end as well,
once we have finished considering all the vertices. So, by the end of the process,
we have constructed the preorder traversal of a minimum spanning tree, even
though we never explicity built the spanning tree. It was shown in the sec-
tion that such a Hamiltonian cycle will be a 2 approximation for the cheapest
cycle under the given assumption that the weights satisfy the triangle inequality.
Exercise 35.2-4
By Problem 23-3, there exists a linear time algorithm to compute a bottle-
neck spanning tree of a graph, and recall that every bottleneck spanning tree is
in fact a minimum spanning tree. First run this linear time algorithm to find a
bottleneck tree BT . Next, take full walk on the tree, skipping at most 2 con-
secutive intermediate nodes to get from one unrecorded vertex to the next. By
Exercise 34.2-11 we can always do this, and obtain a graph with a hamiltonian
cycle which we will call HB. Let Bdenote the cost of the most costly edge in
the bottleneck spanning tree. Consider the cost of any edge that we put into
HB which was not in BT . By the triangle inequality, it’s cost is at most 3B,
since we traverse a single edge instead of at most 3 to get from one vertex to the
next. Let hb be the cost of the most costly edge in HB. Then we have hb ≤3B.
Thus, the most costly edge in HB is at most 3B. Let B∗denote the cost of the
most costly edge an optimal bottleneck hamiltonian tour HB∗. Since we can
obtain a spanning tree from HB∗by deleting the most costly edge in HB∗, the
minimum cost of the most costly edge in any spanning tree is less than or equal
to the cost of the most costly edge in any hamiltonian cycle. In other words,
B≤B∗. On the other hand, we have hb ≤3B, which implies hb ≤3B∗, so the
algorithm is 3-approximate.
Exercise 35.2-5
To show that the optimal tour never crosses itself, we will suppose that it
did cross itself, and then show that we could produce a new tour that had
5

lower cost, obtaining our contradiction because we had said that the tour we
had started with was optimal, and so, was of minimal cost. If the tour crosses
itself, there must be two pairs of vertices that are both adjacent in the tour, so
that the edge between the two pairs are crossing each other. Suppose that our
tour is S1x1x2S2y1y2S3where S1, S2, S3are arbitrary sequences of vertices, and
{x1, x2}and {y1, y2}are the two crossing pairs. Then, We claim that the tour
given by S1x1y2Reverse(S2)y1x2S3has lower cost. Since {x1, x2, y1, y2}form
a quadrilateral, and the original cost was the sum of the two diagonal lengths,
and the new cost is the sums of the lengths of two opposite sides, this problem
comes down to a simple geometry problem.
Now that we have it down to a geometry problem, we just exercise our grade
school geometry muscles. Let Pbe the point that diagonals of the quadri-
lateral intersect. Then, we have that the vertices {x1, P, y2}and {x2, P, y1}
form triangles. Then, we recall that the longest that one side of a trian-
gle can be is the sum of the other two sides, and the inequality is strict if
the triangles are non-degenerate, as they are in our case. This means that
||x1y2|| +||x2y1|| <||x1P|| +||P y2|| +||x2P|| +||P y1|| =||x1x2|| +||y1y2||. The
right hand side was the original contribution to the cost from the old two edges,
while the left is the new contribution. This means that this part of the cost has
decreased, while the rest of the costs in the path have remained the same. This
gets us that the new path that we constructed has strictly better cross, so we
must not of had an optimal tour that had a crossing in it.
Exercise 35.3-1
Since all of the words have no repeated letters, the first word selected will
be the one that appears earliest on among those with the most letters, this is
“thread”. Now, we look among the words that are left, seeing how many let-
ters that aren’t already covered that they contain. Since “lost” has four letters
that have not been mentioned yet,and it is first among those that do, that is
the next one we select. The next one we pick is “drain” because it is has two
unmentioned letters. This only leave “shun” having any unmentioned letters,
so we pick that, completing our set. So, the final set of words in our cover is
{thread, lost, drain, shun}.
Exercise 35.3-2
A certificate for the set-covering problem is a list of which sets to use in
the covering, and we can check in polynomial time that every element of X
is in at least one of these sets, and that the number of sets doesn’t exceed k.
Thus, set-covering is in NP. Now we’ll show it’s NP-hard by reducing it from the
vertex-cover problem. Suppose we are given a graph G= (V, E). Let V0denote
the set of vertices of Gwith all vertices of degree 0 removed. To each vertex
v∈V, associate a set Svwhich consists of vand all of its neighbors, and let
F={Sv|v∈V0}. If S⊂Vis a vertex cover of Gwith at most kvertices, then
{Sv|v∈S∩V0}is a set cover of V0with at most ksets. On the other hand, sup-
6

pose there doesn’t exist a vertex cover of Gwith at most kvertices. If there were
a set cover Mof V0with at most ksets from F, then we could use {v|Sv∈M}
as a k-element vertex cover of G, a contradiction. Thus, Ghas a kelement
vertex cover if and only if there is a k-element set cover of V0using elements
in F. Therefore set-covering is NP-hard, so we conclude that it is NP-complete.
Exercise 35.3-3
See the algorithm LINEAR-GREEDY-SET-COVER. Note that everything
in the inner most for loop takes constant time and will only run once for each
pair of letter and a set containing that letter. However, if we sum up the number
of such pairs, we get PS∈F |S|which is what we wanted to be linear in.
Algorithm 2 LINEAR-GREEDY-SET-COVER(F)
compute the sizes of every S∈ F, storing them in S.size.
let Abe an array of length maxS|S|, consisting of empty lists
for S∈ F do
add Sto A[S.size].
end for
let A.max be the index of the largest nonempty list in A.
let Lbe an array of length | ∪S∈F S|consisting of empty lists
for S∈ F do
for `∈Sdo
add Sto L[`]
end for
end for
let Cbe the set cover that we will be selecting, initially empty.
let Tbe the set of letters that have been covered, initially empty.
while A.max > 0do
Let S0be any element of A[A.max].
add S0to C
remove S0from A[A.max]
for `∈S0\Tdo
for S∈L[`]do
Remove Sfrom A[A.size]
S.size = S.size -1
Add Sto A[S.size]
if A[A.max] is empty then
A.max = A.max-1
end if
end for
add `to T
end for
end while
7

Exercise 35.3-4
Each cxhas cost at most 1, so we we can trivially replace the upper bound
in inequality (35.12) by Px∈Scx≤ |S| ≤ max{|S|:S∈F}. Combining
inequality (35.11) and the new (35.12), we have
|C| ≤ X
S∈C∗X
x∈S
cx≤X
S∈C∗
max{|S|:S∈F}=|C∗|max{|S|:S∈F}.
Exercise 35.3-5
Suppose we pick the number of elements in our base set to be a multiple
of four. We will describe a set of sets on a base set of size 4, and then take n
disjoint copies of it. For each of the four element base sets, we will have two
choices for how to select the set cover of those 4 elements. For a base set con-
sisting of {1,2,3,4}, we pick our set of sets to be {{1,2},{1,3},{3,4},{2,4}},
then we could select either {{1,2},{3,4}} or {{1,3},{2,4}}. This means that
we then have a set cover problem with 4nsets, each of size two where the set
cover we select is done by nindependent choices, and so there are 2npossible
final set covers based on how ties are resolved.
Exercise 35.4-1
Any clause that contains both a variable and its negation is automatically
satisfied, since we always have x∨ ¬xis true regardless of the truth value of
x. This means that if we separate out the clauses that contain no variable and
its negation, we have an 8/7ths approximation on those, and we have all of the
other clauses satisfied regardless of the truth assignments to variables. So, the
quality of the approximation just improves when we include the clauses con-
taining variables and their negation.
Exercise 35.4-2
As usual, we’ll assume that each clause contains only at most instance of
each literal, and that it doesn’t contain both a literal and its negation. Assign
each variable 1 with probability 1/2 and 0 with probability 1/2. Let Yibe the
random variable which takes on 1 if clause iis satisfied and 0 if it isn’t. The
probability that a clause fails to be satisfied is (1/2)k≤1/2 where kis the
number of literals in the clause, so k≥1. Thus, P(Yi)=1−P(Yi)≥1/2. Let
Ybe the total number of clauses satisfied and mbe the total number of clauses.
Then we have
E[Y] =
m
X
i=1
E[Yi]≥m/2.
Let C∗be the number of clauses satisfied by an optimal solution. Then
C∗≤mso we have C∗/E[Y]≤m/(m/2) = 2. Thus, this is a randomized
8

2-approximation algorithm.
Exercise 35.4-3
Lets consider the expected value of the weight of the cut. For each edge,
the probability that that edge crosses the cut is the probability that our coin
flips came up differently for the two vertices that are in the edge. This happens
with probability 1
2. Therefore, by linearity of expectation, we know that the
expected weight of this cut is |E|
2. We know that for the best cut we can make,
the weight will be bounded by the total number of edges in the graph, so we
have that the weight of the best cut is at most twice the expected weight of this
random cut.
Exercise 35.4-4
Let x:V→R≥0be an optimal solution for the linear-programming relax-
ation with condition (35.19) removed, and suppose there exists v∈Vsuch that
x(v)>1. Now let x0be such that x0(u) = x(u) for u6=v, and x0(v) = 1. Then
(35.18) and (35.20) are still satisfied for x0. However,
X
u∈V
w(u)x(u) = X
u∈V−v
w(u)x0(u) + w(v)x(v)
>X
u∈V−v
w(u)x0(u) + w(v)x0(v)
=X
u∈V
w(u)x0(u)
which contradicts the assumption that xminimized the objective function.
Therefore it must be the case that x(v)≤1 for all v∈V, so the condition
(35.19) is redundant.
Exercise 35.5-1
Every subset of {1,2, . . . , i}can either contain ior not contain i. If it does
contain i, the sum corresponding to that subset will be in Pi−1+xi, since the
sum corresponding to the restriction of the subset to {1,2,3, . . .}will be in Pi−1.
If we are in the other case, then when we restrict to {1,2, . . . , i −1}we aren’t
changing the subset at all. Similarly, if an element is in Pi−1, that same subset
is in Pi. If an element is in Pi−1+xi, then it is in Piwhere we just make sure
our subset contains i. This proves (35.23).
It is clear that Lis a sorted list of elements less than Tthat corresponds
to subsets of the empty set before executing the for loop, because it is empty.
Then, since we made Lifrom elements in Li−1and xi+Li −1, we know that
it will be a subset of those sums obtained from the first ielements. Also, since
both Li−1and xi+Li−1were sorted, when we merged them, we get a sorted
9
list. Lastly, we know that it all sums except those that are more than tsince
we have all the subset sums that are not more than tin Li−1, and we cut out
anything that gets to be more than t.
Exercise 35.5-2
We’ll proceed by induction on i. When i= 1, either y= 0 in which case
the claim is trivially true, or y=x1. In this case, L1={0, x1}. We don’t lose
any elements by trimming since 0(1 + δ)< x1∈Z>0. Since we only care about
elements which are at most t, the removal in line 6 of APPROX-SUBSET-SUM
doesn’t affect the inequality. Since x1/(1 + ε/2n)≤x1≤x1, the claim holds
when i= 1. Now suppose the claim holds for i, where i≤n−1. We’ll show
that the claim holds for i+ 1. Let y∈Pi+1. Then by (35.23) either y∈Pi
or y∈Pi+xi+1. If y∈Pi, then by the induction hypothesis there exists
z∈Lisuch that y
(1+ε/2n)i+1 ≤y
(1+ε/2n)i≤z≤y. If z∈Li+1 then we’re done.
Otherwise, zmust have been trimmed, which means there exists z0∈Li+1 such
that z/(1 + δ)≤z0≤z. Since δ=ε/2n, we have y
(1+ε/2n)i+1 ≤z0≤z≤y, so
inequality (35.26) is satisfied. Lastly, we handle the case where y∈Pi+xi+1.
Write y=p+xi+1. By the induction hypothesis, there exists z∈Lisuch that
p
(1+ε/2n)i≤z≤p. Since z+xi+1 ∈Li+1, before thinning, this means that
p+xi+1
(1 + ε/2n)i≤p
(1 + ε/2n)i+xi+1 ≤z+xi+1 ≤p+xi+1,
so z+xi+1 well approximates p+xi+1. If we don’t thin this out, then we
are done. Otherwise, there exists w∈Li+1 such that z+xi+1
1+δ≤w≤z+xi+1.
Then we have
p+xi+1
(1 + ε/2n)i+1 ≤z+xi+1
1 + ε/2n≤w≤z+xi+1 ≤p+xi+1.
Thus, claim holds for i+ 1. By induction, the claim holds for all 1 ≤i≤n,
so inequality (35.26) is true.
Exercise 35.5-3
10
As we have many times in the past, we’ll but on our freshman calculus hats.
d
dn 1 +
2nn=
d
dnenlg(1+
2n)=
enlg(1+
2n)1 +
2n+n−
2n2
1 +
2n=
enlg(1+
2n) 1 +
2n2−
2n
1 +
2n!=
enlg(1+
2n) 1 +
2n+
2n2
1 +
2n!=
Since all three factors are always positive, the original expression is always
positive.
Exercise 35.5-4
We’ll rewrite the relevant algorithms for finding the smallest value, modify-
ing both TRIM and APPROX-SUBSET-SUM. The analysis is the same as that
for finding a largest sum which doesn’t exceed t, but with inequalities reversed.
Also note that in TRIM, we guarantee instead that for each yremoved, there
exists zwhich remains on the list such that y≤z≤y(1 + δ).
Algorithm 3 TRIM(L, δ)
1: let mbe the length of L
2: L0=hymi
3: last =ym
4: for i=m−1 downto 1 do
5: if yi< last/(1 + δ)then
6: append yito the end of L0
7: last =yi
8: end if
9: end for
10: return L’
Exercise 35.5-5
We can modify the procedure APPROX-SUBSET-SUM to actually report
the subset corresponding to each sum by giving each entry in our Lilists a piece
of satellite data which is a list the elements that add up to the given number
sitting in Li. Even if we do a stupid representation of the sets of elements, we
will still have that the runtime of this modified procedure only takes additional
11

Algorithm 4 APPROX-SUBSET-SUM(S, t, ε)
1: n=|S|
2: L0=hPn
i=1 xii
3: for i= 1 to ndo
4: Li= MERGE-LISTS(Li−1, Li−1−xi)
5: Li= TRIM(Li, ε/2n)
6: return from Lievery element that is less than t
7: end for
8: let z∗be the largest value in Ln
9: return z∗
time by a factor of the size of the original set, and so will still be polynomial.
Since the actual selection of the sum that is our approximate best is unchanged
by doing this, all of the work spent in the chapter to prove correctness of the
approximation scheme still holds. Each time that we put an element into Li,
it could of been copied directly from Li−1, in which case we copy the satellite
data as well. The only other possibility is that it is xiplus an entry in Li−1,
in which case, we add xito a copy of the satellite data from Li−1to make our
new set of elements to associate with the element in Li.
Problem 35-1
a. First, we will show that it is np hard to determine if, given a set of numbers,
there is a subset of them whose sum is equal to the sum of that set’s compli-
ment, this is called the partition problem. We will show this is NP hard by
using it to solve the subset sum problem. Suppose that we wanted to fund
a subset of {y1, y2,...yn}that summed to t. Then, we will run partition
on the set {y1, y2, . . . , yn,(Piyi)−2t}. Note then, that the sum of all the
elements in this set is 2 (Piyi)−2t. So, any partition must have both sides
equal to half that. If there is a subset of the original set that sums to t, we
can put that on one side together with the element we add, and put all the
other original elements on the other side, giving us a partition. Suppose that
we had a partition, then all the elements that are on the same side as the
special added element form a subset that is equal to t. This show that the
partition problem is NP hard.
Let {x1, x2, . . . , xn}be an instance of the partition problem. Then, we will
construct an instance of a packing problem that can be packed into 2 bins if
and only if there is a subset of {x1, x2,...xn}with sum equal to that of its
compliment. To do this, we will just let our values be ci=2xi
Pn
j=1 xj. Then,
the total weight is exactly 2, so clearly two bins are needed. Also, it can fit
in two bins if there is a partition of the original set.
b. If we could pack the elements in to fewer than dSebins, that means that the
total capacity from our bins is <bSc ≤ S, however, we know that to total
12

space needed to store the elements is S, so there is no way we could fit them
in less than that amount of space.
c. Suppose that there was already one bin that is at most half full, then when
we go to insert an element that has size at most half, it will not go into an
unused bin because it would be placed in this bin that is at most half full.
This means that we will never create a second bin that is at most half full,
and so, since we start off with fewer that two bins that are at most half full,
there will never be two bins that are at most half full (and so never two that
are less than half full).
d. Since there is at most one bin that is less than half full, we know that the
total amount of size that we have packed into our Pbins is >1
2(P−1). That
is, we know that S > 1
2(P−1), which tells us that 2S+1 > P . So, if we were
to have P > d2Se, then, we have that P≥ d2Se+1 = d2S+1e ≥ 2S+1 > P ,
which is a contradiction.
e. We know from part bthat there is a minimum of dSebins required. Also,
by part d, we know that the first fit heuristic causes us to sue at most d2Se
bins. This means that the number of bins we report is at most off by a factor
of d2Se
dSe≤2.
f. We can implement the first fit heuristic by just keeping an array of bins, and
each time just doing a linear scan to find the first bin that can accept it.
So, if we let Pbe the number of bins, this procedure will have a runtime of
O(P2) = O(n2). However, since all we needed was that there was at most
one bin that was less than half full, we could do a faster procedure. We keep
the array of bins as before, but we will keep track of the first empty bin and
a pointer to a bin that is less than half full. Upon insertion, if the thing we
inserted is more than half, put it in the first empty bin and increment it.
If it is less than half, it will fit in the bin that is less than half full, if that
bin then becomes more than half full, get rid of the less than half full bin
pointer. If there wasn’t a nonempty bin that was less than half full, we just
put the element in the first empty bin. This will run in time O(n) and still
satisfy everything we needed to assure we had a 2-approximation.
Problem 35-2
a. Given a clique Dof mvertices in G, let Dkbe the set of all k-tuples of
vertices in D. Then Dkis a clique in G(k), so the size of a maximum clique
in G(k)is at least that of the size of a maximum clique in G. We’ll show that
the size cannot exceed that.
Let mdenote the size of the maximum clique in G. We proceed by induction
on k. When k= 1, we have V(1) =Vand E(1) =E, so the claim is trivial.
Now suppose that for k≥1, the size of the maximum clique in G(k)is equal
to the kth power of the size of the maximum clique in G. Let ube a (k+ 1)-
tuple and u0denote the restriction of uto a k-tuple consisting of its first k
13

entries. If {u, v} ∈ E(k+1) then {u0, v0} ∈ E(k). Suppose that the size of the
maximum clique Cin G(k+1) =n>mk+1. Let C0={u0|u∈C}. By our
induction hypothesis, the size of a maximum clique in G(k)is mk, so since
C0is a clique we must have |C0| ≤ mk< n/m. A vertex uis only removed
from C0when it is a duplicate, which happens only when there is a vsuch
that u, v ∈C,u6=v, and u0=v0. If there are only mchoices for the last
entry of a vertex in C, then the size can decrease by at most a factor of m.
Since the size decreases by a factor of strictly greater than m, there must be
more than mvertices which appear among the last entries of vertices in C0.
Since C0is a clique, all of its vertices are connected by edges, which implies
all of these vertices in Gare connected by edges, implying that Gcontains a
clique of size strictly greater than m, a contradiction.
b. Suppose there is an approximation algorithm that has a constant approxi-
mation ratio cfor finding a maximum size clique. Given G, form G(k), where
kwill be chosen shortly. Perform the approximation algorithm on G(k). If n
is the maximum size clique of G(k)returned by the approximation algorithm
and mis the actual maximum size clique of G, then we have mk/n ≤c. If
there is a clique of size at least nin G(k), we know there is a clique of size
at least n1/k in G, and we have m/n1/k ≤c1/k. Choosing k > 1/logc(1 + ε),
this gives m/n1/k ≤1 + ε. Since we can form G(k)in time polynomial in k,
we just need to verify that kis a polynomial in 1/ε. To this end,
k > 1/logc(1 + ε) = ln c/ ln(1 + ε)≥ln c/ε
where the last inequality follows from (3.17). Thus, the (1+ε) approximation
algorithm is polynomial in the input size, and 1/ε, so it is a polynomial time
approximation scheme.
Problem 35-3
An obvious way to generalize the greedy set cover heuristic is to not just pick
the set that covers the most uncovered elements, but instead to repeatedly select
the set that maximizes the value of the number of uncovered points it covers
divided by its weight. This agrees with the original algorithm in the case that
the weights are all 1. The main difference is that instead of each step of the algo-
rithm assigning one unit of cost, it will be assigning wiunits of cost to add the set
Si. So, suppose that Cis the cover we selected by this heuristic, and C∗is an op-
timal cover. So, we will have |PSi∈C wi|=Px∈Xwicx≤PSi∈C∗Px∈Siwicx.
Then, Px∈Siwicx=wiPx∈Sicx≤wiH(|S|). So, |C| ≤ PSi∈C∗wiH(|Si|)≤
|PSi∈C∗wi|H(max(|Si|). This means that the weight of the selected cover is a
H(d) approximation for the weight of the optimal cover.
Problem 35-4
a. Let V={a, b, c, d}and E={{a, b},{b, c},{c, d}}. Then {b, c}is a maximal
matching, but a maximum matching consists of {a, b}and {c, d}.
14

b. The greedy algorithm considers each edge one at a time. If it can be added
to the matching, add it. Otherwise discard it and never consider it again.
If an edge can’t be added at some time, then it can’t be added at any later
time, so the result is a maximal matching. We can determine whether or not
to add an edge in constant time by creating an array of size |V|filled with
zeros, and placing a 1 in position iif the ith vertex is incident with an edge
in the matching. Thus, the runtime of the greedy algorithm is O(E).
c. Let Mbe a maximum matching. In any vertex cover C, each edge in M
must have the property that at least one of its endpoints is in C. Moreover,
no two edges in Mhave any endpoints in common, so the sice of Cis at least
that of M.
d. It consists of only isolated vertices and no edges. If an edge {u, v}were
contained in the subgraph of Ginduced by the vertices of Gnot in T, then
this would imply that neither unor vis incident on some edge in M, so
we could add the edge {u, v}to Mand it would still be a matching. This
contradicts maximality.
e. We can construct a vertex cover by taking the endpoints of every edge in M.
This has size 2|M|because the endpoints of edges in a matching are disjoint.
Moreover, if any edge failed to be incident to any vertex in the cover, this
edge would be in the induced subgraph of Ginduced by the vertices which
are not in T. By part d, no such edge exists, so it is a vertex cover.
f. The greedy algorithm of part (b) yields a maximal matching M. By part
(e), there exists a vertex cover of size 2|M|. By part (c), the size of this
vertex cover exceeds the sizeof a maximum matching, so 2|M|is an upper
bound on the size of a maximum matching. Thus, the greedy algorithm is a
2|M|/|M|= 2 approximation algorithm.
Problem 35-5
a. Suppose that the greatest processing time is pi. Then, any schedule must
assign the job Jito some processor. If it assigns Jito start as soon as
possible, it still won’t finish until piunits have passed. This means that
since the makespan is the time that all jobs have finished, it will at or after
pibecause it needs job Jito of finished. This problem can be viewed as a
restatement of (27.3), where we have an infinite number of processors and
assign each job to its own processor.
b. The total amount of processing per step of time is one per processor. Since
we need to accomplish Pipimuch work, we have to of spent at lest 1
mtimes
that amount of time. This problem is a restatement of equation (27.2).
c. See the algorithm GREEDY-SCHEDULE
Since we can perform all of the heap operations in time O(lg(m)), and we
need to perform one for each of our jobs, the runtime is in O(nlg(m)).
15

Algorithm 5 GREEDY-SCHEDULE
for every i= 1, . . . , m, let fi= 0. We will be updating this to be the latest
time that we have any task running on processor i.
put all of the fiinto a min heap, H
while There is an unassigned job Jido
extract the min element of H, let it be fj
assign job Jito processor Mj, to run from fjto fj+pi.
fj=fj+pi
add fjto H
end while
d. This is Theorem 27.1 and Corollary 27.2.
Problem 35-6
a. Let V={a, b, c, d}and E={{a, b},{b, c},{c, d},{b, d}} with edge weights
3, 1, 5, and 4 respectively. Then SG={{a, b},{c, d},{b, d}} =TG.
b. Let V={a, b, c, d}and E={{a, b},{b, c},{c, d}}.Then SG={{a, b},{c, d}} 6=
{{a, b},{b, c},{c, d}} =TG.
c. Consider the greedy algorithm for a maximum weight spanning tree: Sort the
edges from largest to smallest weight, consider them one at a time in order,
and if the edge doesn’t introduce a cycle, add it to the tree. Suppose that
we don’t select some edge {u, v}which is of maximum weight for u. This
means that the edge must introduce a cycle, so there is some edge {w, u}
which is already included in the spanning tree. However, we add edges in
order of decreasing weight, so w(w, u)> w(u, v) because edge weights are
distinct. This contradicts the fact that {u, v}was of maximum weight. Thus
SG⊆TG.
d. Since the edge weights are distinct, a particular edge can be the maximum
edge weight for at most two vertices, so |SG|≥|V|/2. Therefore |TG\SG| ≤
|V|/2≤ |SG|. Since every edge in TG\SGis nonmaximal, each of these has
weight less than the weight of any edge in SG. Let mbe the minimum weight
of an edge in SG. Then w(TG\SG)≤m|SG|, so w(TG)≤w(SG) + m|SG| ≤
2w(SG).Therefore w(TG)/2≤w(SG).
e. Let N(v) denote the neighbors of a vertex v. The following algorithm
APPROX-MAX-SPANNING produces a subset of edges of a minimum span-
ning tree by part (c), and is a 2-approximation algorithm by part (d).
Problem 35-7
a. Though not stated, this conclusion requires the assumption that at least one
of the values is non-negative. Since any individual item will fit, selecting
that one item would be a solution that is better then the solution of taking
16

Algorithm 6 APPROX-MAX-SPANNING-TREE(V, E)
1: T=∅
2: for v∈Vdo
3: max =−∞
4: best =v
5: for u∈N(v)do
6: if w(v, u)≥max then
7: v=u
8: max =w(v, u)
9: end if
10: end for
11: T=T∪ {v, u}
12: end for
13: return T
no items. We know then that the optimal solution contains at least one
item. Suppose the item of largest index that it contains is item i, then, that
solution would be in Pi, since the only restriction we placed when we changed
the instance to Iiwas that it contained item i.
b. We clearly need to include all of item j, as that is a condition of instance
Ij. Then, since we know that we will be using up all of the remaining space
somehow, we want to use it up in such a way that the average value of that
space is maximized. This is clearly achieved by maximizing the value density
of all the items going in, since the final value density will be an average of
the value densities that went into it weighted by the amount of space that
was used up by items with that value density.
c. Since we are greedily selecting items based off of the amount of value per
space, we only stop once we can no longer fit any more, and each time before
putting some faction of the item with the next least value per space, we
complete putting in the item we currently are. This means that there is at
most one item fractionally.
d. First, it is trivial that v(Qj)/2≥v(Pj)/2 since we are trying to maximize a
quantity, and there are strictly fewer restrictions on what we can do in the
case of the fractional packing than in the 1-0 packing. To see that v(Rj)≥
v(Qj)/2, note that among the items {1,2, . . . , j}, we have the highest value
item is vjbecause of our ordering of the items. We know that the fractional
solution must have all of item j, and there is some item that it may not
have all of that is indexed by less than j. This part of an item is all that
is thrown out when going from Qjto Rj. Even if we threw all of that item
out, it still wouldn’t be as valuable as item jwhich we are keeping, so, we
have retained more than half of the value. So, we have proved the slightly
stronger statement that v(Rj)> v(Qj)/2≥v(Pj)/2.
17

e. Since we knew that the optimal solution was the max of all the Pj(part a),
and we know that each Pjis at most 2Rj(part d), by selecting the max of all
the the Rj, we are obtaining a solution that is at most a factor of two less
than the optimal solution.
max
jRj≤max
jPj≤max
j2Rj
18

Appendix A
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise A.1-1
n
X
k=1
(2k−1) = 2
n
X
k=1
k−
n
X
k=1
1 = n(n+ 1) −n=n2
Exercise A.1-2
Using the harmonic series formula we have that
n
X
k=1
1
(2k−1) ≤1 +
n
X
k=1
1
2k= 1 + ln(√n) + O(1) = ln(√n) + O(1).
Exercise A.1-3
First, we recall equation (A.8)
∞
X
k=0
kxk=x
(1 −x)2
for |x|<1. Then, we take a derivative of each side, taking the derivative of the
left hand side term by term
∞
X
k=0
k·kxk−1=(1 −x)2+ 2x(1 −x)
(1 −x)4=(1 −x)+2x
(1 −x)3=(1 + x)
(1 −x)3
Lastly, since we have a xk−1instead of the xkthat we’d like, we’ll multiply both
sides of the equation by xto get the desired equality.
∞
X
k=0
k2xk=x(1 + x)
(1 −x)3
Exercise A.1-4
Using formula A.8 we have
1

∞
X
k=0
k−1
2k=−1 + 1
2
∞
X
k=0
k1
2k
=−1 + 1
2·1/2
1/4
=−1+1
= 0.
Exercise A.1-5
First, we’ll start with the equation
∞
X
k=0
yk=1
1−y
So long as |y|<1. Then, we’ll let y=x2to get
∞
X
k=0
(x2)k=1
1−x2
∞
X
k=0
xx2k=x
1−x2
∞
X
k=0
x2k+1 =x
1−x2
∞
X
k=0
(2k+ 1)x2k=(1 −x2)+2x2
(1 −x2)2
∞
X
k=0
(2k+ 1)x2k=1 + x2
(1 −x2)2
so long as |x|<1.
Exercise A.1-6
Let g1, g2, . . . , gnbe any functions such that gk(i) = O(fk(i)). By the defi-
nition of big-oh there exist constant c1, c2, . . . , cnsuch that gk(i)≤ckfk(i). Let
c= max1≤k≤nck. Then we have
n
X
k=1
gk(i)≤
n
X
k=1
ckfk(i)≤c
n
X
k=1
fk(i) = O n
X
k=1
fk(i)!.
Exercise A.1-7
2

lg n
Y
k=1
2·4k!
=
n
X
k=1
lg(2 ·4k)
=
n
X
k=1
lg(2) + klg(4)
= lg(2)
n
X
k=1
1!+ lg(4)
n
X
k=1
k!
=n+ 2n(n+ 1)
2
=n(n+ 2)
This means that we need to raise 2 to this quantity to get the desired product,
so out final answer is
2n(n+2) = 2n2·4n
Exercise A.1-8
We expand the product and cancel as follows:
n
Y
k=2
1−1/k2=
n
Y
k=2
(k−1)(k+ 1)
k2
=1·3
2·2·2·4
3·3·3·5
4·4··· (n−1) ·(n+ 1)
n·n
=n+ 1
2n.
Exercise A.2-1
Define a function f1=d1
x2eand f2= 1 + 1
x2. Note that we always have that
f1≤f2. Then we have that the desired summation is exactly equal to R∞
1f1
because the graph of f1is a bunch of rectangles of width 1 and height equal to
each of the terms in the sum. By monotonicity of integrals, we have that this
is ≤R∞
1f2= 2.
Exercise A.2-2
When n= 2mthe sum becomes n+n/2 + n/4 + . . . + 1 = 2n−1 = O(n).
There always exists a power of 2 which lies between nand 2nfor any choice of
n, so let n0denote the smallest power of 2 which is greater than or equal to n.
Then we have
3

blg nc
X
k=0 dn/2ke ≤
blg n0c
X
k=0 dn0/2ke= 2n0−1≤4n−1 = O(n).
Exercise A.2-3
Similar to the derivation of (A.10), we split up the interval [n] into blg(n)c − 1
pieces, with the ith starting at 1/2iand going to 1/2i+1. So, we have
n
X
k=1
1
k≥
lg(n)−1
X
i=0
2i−1
X
j=0
1
2i+j
≥
lg(n)−1
X
i=0
1
2i+1
=
lg(n)−1
X
i=0
1
2
=1
2lg(n)
Which gets us that the nth harmonic number is Ω(lg(n)).
Exercise A.2-4
Since k3is monotonically increasing we use bound A.11. For the upper
bound we have
n
X
k=1
k3≤Zn+1
1
x3dx
=x4
4
n+1
1
=(n+ 1)4−1
4.
For the lower bound we have
n
X
k=1
k3≥Zn
0
x3dx
=x4
4
n
0
=n4
4.
4

Exercise A.2-5
If we were to apply the integral approximation given in (A.12) directly to the
sum, then we would be trying to evaluate the integral
Zn
0
dx
x
Which is an improper integral that doesn’t have a finite value.
Problem A-1
a. Applying the integral approximation to this, we get that
Zn+1
1
xrdx ≤
n
X
k=1
kr≤Zn
0
xrdx(n+ 1)r+1 −1
r+ 1 ≤
n
X
k=1
kr≤nr+1
r+ 1
So, the given sum is nr+1(1
r+1 +o(1)).
b. We’ll split up the domain into lg(n) pieces. based on being between 1/2iand
1/2i+1. This gets us
k=n
X
k=1 ≥(k)s≥
blg(n)c
X
k=1
2k
X
i=1
(lg(2k+i))s≥
blg(n)c
X
k=1
2k
X
i=1
(lg(2k+1))s=
blg(n)c
X
k=1
2k(k+ 1)s
c.
5
Appendix B
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise B.1-1
FIrst we consider
A∩(B∪C) = (A∩B)∪(A∩C)
For the first picture, we can see that the shaded regions are all the regions
that are in A and also in either B or C, and so are in the set described on the
left hand side. Since the green and gray shaded regions are in both Aand B,
1
they are in the right hand side, also, the red and gray regions are in Aand C
and so are also in the right hand side. There aren’t any other regions that are
either both in A and B or both in A and C, so the shaded regions are the right
hand side of the equation as well.
Next we consider
A∪(B∩C) = (A∪B)∩(A∪C)
The ony regions in B∩Care blue and purple. All the other colored regions
are in A. So, the shaded regions are exactly the left hand side. To see what is
in the right hand side, we see what is both in A∪Band A∩C. Individually
both both contain all of the shaded regions plus one of the white regions. Since
the white region contained differs, their intersection is all of the shaded regions.
Exercise B.1-2
We’ll proceed by induction. The base case has already been taken care of
for us by B.2. Suppose that the claim holds for a collection of nsets. Then we
have
A1∩A2∩ ··· ∩ An∩An+1 = (A1∩A2∩ ··· ∩ An)∩An+1
=A1∩A2∩ ··· ∩ An∪An+1
=A1∪A2∪ ··· ∪ An∪An+1.
2

An identical proof with the roles of intersection and union swapped gives
the second result.
Exercise B.1-3
If we are taking the union over only two sets, then we are exactly in the case
of equation (B.3).
Now, proceed by induction. Suppose n > 2, we can write B= (A1∪A2∪
··· ∪ An−1). Then, we have
|A1∪A2∪ ··· ∪ An|=|B∪An|
=|B|+|An|−|B∩An|
=|B|+|An|−|B∩An|
=|B|+|An|−|(A1∪A2∪ ···An−1)∩An|
=|A1∩A2∩ ···An−1|+|An|−|(A1∩An)∪(A2∩An)∪ ···(An−1∩An)|
=
X
∅6=S⊆{1,2,...,n−1}
(−1)|S|−1|∩i∈SAi|
+|An|
−
X
∅6=S⊆{1,...,n−1}
(−1)|S|−1|An∩(∩i∈SAi)|
=
X
∅6=S⊆{1,2,...,n−1}
(−1)|S|−1|∩i∈SAi|+ (−1)|S||An∩(∩i∈SAi)|
+|An|
=
X
∅S⊆{1,2,...,n},S6=∅,S6={n}
(−1)|S|−1|∩i∈SAi|
+|A|
=
X
∅S⊆{1,2,...,n},S6=∅
(−1)|S|−1|∩i∈SAi|
Where to go from line 7 to line 8, we used the fact that every subset of
{1, . . . , n}can be counted as a subset of {1, . . . , n −1}, and then either contain-
ing or not containing the nth element. Since the empty subset of {1, . . . , n −1}
then corresponds both to the empty set and the singleton set {n}under this
correspondence, explaining why that value of S is dropped from the sum on line
8.
Exercise B.1-4
Let f(k)=2k+ 1. Then fis a bijection from Nto the set of odd natural
numbers, so they are countable.
3

Exercise B.1-5
For each of the elements of S, some subset of Scan either contain that element
or not contain that element. If the decision differs for any of the |S|many
elements, then you’ve just created a distinct set. Since we make a decision be-
tween two options |S|many times, the total number of possible sets is 2|S|. It
can be thought of as the number of leaves in a complete binary tree of depth |S|.
Exercise B.1-6
We define an n-tuple recursively as (a1, a2, . . . , an) = ((a1, a2, . . . , an−1), an).
Exercise B.2-1
To see that it is a partial ordering, we need to show it is reflexive, antisymmetric,
and transitive. To see that it is reflexive, we need to show S⊆S. That is, for
every x∈S,s∈S, which is a tautology. To see that it is antisymmetric, we
need that if S16=S2and S1⊆S2then S26⊆ S1. Since S16=S2there is some
element that is in one of them but not in the other. Since S16=S2, we know
that that element must be in S2because if it were in S1it would be in S2.
Since we have an element in S2not in S1, we have S26⊆ S1. Lastly, we show
transitivity, suppose S1⊆S2⊆S3. This means that any element that is in S1
is in S2. But since it is in S2, it is in S3. Therefore, every element in S1is in
S3, that is S2⊆S3.
To see that it is not a total order, consider the elements {1,2}and {2,3}.
Neither is contained in the other, so there is no proscribed ordering between
the two based off of inclusion. If it were a total ordering, we should be able to
compare any two elements, which we just showed we couldn’t.
Exercise B.2-2
For all positive integers awe have a−a= 0 ·nso the relation is reflexive.
If a−b=qn then b−a= (−q)nso the relation is symmetric. If a−b=qn and
b−c=pn then a−c=a−b+b−c= (q+p)nso the relation is transitive.
Thus, equivalence modulo nis an equivalence relation. This partitions the in-
tegers into equivalence classes consisting of numbers which differ by a multiple
of n.
Exercise B.2-3
a. Consider the set of vertices in some non-complete, non-empty graph where
we make two vertices related if they are adjacent or the same vertex.
b. Consider the vertices in a digraph where we have aRb if there is some possibly
empty path from ato b. For a concrete example, suppose we have only the
set {0,1}and the relations 0R0, 0R1, and 1R1.
c. Consider the relation that makes no two elements related. This satisfies both
4

the symmetric and transitive properties, since both of those require that cer-
tain elements are related to conclude that some particular other elements are
related.
Exercise B.2-4
Suppose that aRb. Since Ris an equivalence relation it is symmetric, so
bRa. Since Ris antisymmetric, aRb and bRa imply that a=b. Thus every
equivalence class is a singleton.
Exercise B.2-5
Professor Narcissus is full of himself! The relation that makes no two elements
related to each other is both symmetric and transitive, but is not reflexive.
Exercise B.3-1
a. Since fis injective, for every element in it’s range, there is at most one
element that maps to it. So, we proceed by induction on the number of
elements in the domain of the function. If there is only a single element
in the domain, since the function has to map to something, we have that
|B| ≥ 1 = |A|. Suppose that all functions that are on a domain of size n
satisfy this relation. Then, look at where that n+ 1st element gets mapped.
This point will never be mapped to by any of the other elements of the
domain. So, we can think of restricting the function to just the first n
elements, and use the inductive assumption to get the desired relation of the
two sets.
b. As a base case, assume that |B|= 1. Then, since the function is surjective,
some element must map to that, so, |A| ≥ 1 = |B|. Not, suppose it is true
for all function with a range of size at most n. Then, just look at all the
elements that map to the n+1st element, there is at least one by surjectivity.
This gets us that |A| ≥ 1 + |A0| ≥ 1 + |B0|=|B|.
Exercise B.3-2
When the domain and codomain are N, the function f(x) = x+ 1 is not
bijective because 0 is not in the range of f. It is bijective when the domain and
codomain are Z.
Exercise B.3-3
Define R−1by aR−1bif and only if bRa. This clearly swaps the domain and
range for the relation, and so, if Rwas bijective, it is the inverse function. If R
was not bijective, then R−1might not even be a function.
Exercise B.3-4
5

It is easiest to see this bijection pictorally. Imagine drawing out the ele-
ments of Z×Zas points in the plane. Starting from (0,0), move up one unit
to (0,1), then right one unit to (1,1), down 2 units through (1,0) to (1,−1),
then left, and so on, continuing in a spiraling fashion, hitting each point exactly
once, not skipping any as you move outwards. If point (i, j) is the kth point
which is hit, then let f(i, j)=(−1)kdk/2e. This gives a bijection from Z×Zto
Z, which implies that fhas an inverse g. The function gis the desired bijection.
Exercise B.4-1
Let f(u, v) be equal to 1 if ushook hands with v. Then, Pv∈Vdegree(v) =
Pv∈VPu∈Vf(v, u) then, since handshaking is symmetric, we are counting
both when ushakes vhand and when vshakes u’s hand. So, this sum is
Pe∈E2=2|E|.
Exercise B.4-2
Suppose that u=v0, v1, . . . , vk=vis a path pfrom uto v. If it is not sim-
ple, then it contains a cycle, so there exist iand jsuch that vi=vj. Let p0be
the path on vertices v0, v1, . . . , vi−1, vj, . . . , vk. This is a path from uto vwhich
contains at least one fewer cycles than before. We can continue this process
until the path contains no cycles. Similarly, suppose a directed graph contains
a cycle v0, v1, . . . , vk. If it is not simple, then there exist iand j6=ksuch that
vi=vj. Remove the vertices vi, vi+1, . . . , vj−1from the cycle to obtain a cycle
with at least one fewer duplicate vertices. Continuing with this process will
eventually produce a cycle with no repeated vertices except the first and last,
so it will be simple.
Exercise B.4-3
We proceed by induction on the number of vertices. If there is a single vertex,
then the inequality trivially holds since the left hand side is the size of a set and
the right hand side is zero. For the inductive case, pick one vertex in particular.
We know that that vertex must have at least one edge to the rest of the vertices
because the graph is connected. So, when we take the induced subgraph on the
rest of the vertices, we are decreasing the number of edges by at least one. So,
|E| ≥ 1 + |E0| ≥ 1 + |V0| − 1 = |V| − 1.
Exercise B.4-4
Every graph is reachable from itself by the empty path so the relation is re-
flexive. If vis reachable from uthen there exists a path u=v0, v1, . . . , vk=v.
Thus, vk, vk−1, . . . , v0is a path from vto u, so uis reachable from vand the
relation is symmetric. If vis reachable from uand wis reachable from vthen
by concatenation of paths, wis reachable from u, so the relation is transitive.
Therefore the “is reachable from” relation is an equivalence relation.
Exercise B.4-5
6
The undirected version of the graph in B.2(a) is on the same vertex set, but
has E={(1,2),(2,4),(2,5),(4,1),(4,5),(6,3)}. That is, we threw out the
antisymmetric edge, and the self edge. There is also a difference in that now
the edges should be viewed as unordered unlike before.
The directed version of B.2(b) looks the same, except it has arrows drawn
in. One from 2 to 1, one from 1 to 5, one from 2 to 5, and one from 3 to 6.
Exercise B.4-6
We create a bipartite graph as follows: Let V1be the set of vertices of
the hypergraph and V2be the set of hyperedges. For each hyperedge e=
{v1, v2, . . . , vk} ∈ V2, draw edges (e, vi) for 1 ≤i≤k.
Exercise B.5-1
There are three such rooted trees:
x
yz
x
y
z
x
z
y
The ordered trees are those listed above, in addition to the tree
x
zy
The Binary trees are all ten of the following:
x
y
NIL NIL
z
NIL NIL
7
x
y
z
NIL NIL
NIL
NIL
x
NIL y
z
NIL NIL
NIL
x
y
NIL z
NIL NIL
NIL
8
x
NIL y
NIL z
NIL NIL
x
z
NIL NIL
y
NIL NIL
x
z
y
NIL NIL
NIL
NIL
9
x
NIL z
y
NIL NIL
NIL
x
z
NIL y
NIL NIL
NIL
x
NIL z
NIL y
NIL NIL
Exercise B.5-2
Suppose vertex uis not on the unique path from v0to vand vis not on the
unique path from v0to u. Then there can’t be an edge from vto uor from uto
v, otherwise we would violate uniqueness. This implies that in the undirected
version of Gwhen we remove the arrows from the edges, there is still a unique
path from v0to every vertex. This implies that there exists a path between
every pair of vertices. Suppose the path from uto vis not unique. Then there
10

must be a path pfrom uto vwhich does not contain v0. Thus, the unique path
from v0to vdiffers from the path obtained by going from v0to u, then taking
p. This is a contradiction, because the path from v0to vis unique. By property
2 of Theorem B.2, Gis a free tree.
Exercise B.5-3
As a base case, consider the binary tree that consists of a single node. This
tree has no degree two nodes and one leaf, so, the number of degree two nodes
is one less than the number of leaves. As an inductive step, suppose it is true
for all binary trees with at most ndegree two nodes. Then, let Gbe a binary
tree with n+ 1 internal nodes. Let vbe the first node, possibly the leaf itself,
that is the child of a degree two node, and can be obtained by taking the parent
pointer from the leaf. Then, consider the tree obtained by removing vand all
its children. Doing so removes only one leaf, and it makes the parent of vdrop
to being degree 2. None of the children of vwere degree 2 because otherwise
we would of stopped earlier when we were selecting v. Since we have decreased
the number of degree two nodes and leaves both by 1, we have completed the
inductive case, because if |T0|is the modified tree, the number of leaves in Tis
one more than that in T0which means it is one more than the number of degree
2 nodes in T0, which is the number of degree two nodes in T.
Since a full binary tree has each internal node with degree two, this result
gets us that the number of internal nodes in a full binary tree is one more than
the number of leaves.
Exercise B.5-4
A tree with 1 node has height at least 0, so the claim holds for n= 1. Now
suppose the claim holds for n. Let Tbe a binary tree with n+ 1 nodes. Select
a leaf node and remove it. By our induction hypothesis, the resulting tree has
height at least blg nc. If n+1 is not a power of 2 then this is equal to blg(n+1)c,
so we are done. Otherwise, choose a leaf of greatest depth to remove. The re-
sulting tree has height at least blg nc. If the height in fact achieves that, then
the only possible tree is the complete binary tree on nvertices. Since every
internal node has two children, the only place the removed leaf could have come
from is from a leaf vertex. Adding a child to any leaf vertex increases the height
of the tree by 1. Since blg nc+ 1 ≥ blg(n+ 1)c, the claim holds.
Exercise B.5-5
We will perform structural induction. For the empty tree that has n= 0, the
equation is obviously satisfied. Now, let rbe the root of the tree T, and let TL
and TRbe the left and right subtrees respectively. By the inductive hypothesis,
we may assume that eL=iL+ 2nLand eR=iR+ 2nR. Then, since being
placed as a child of the root adds one to the depth of each of the nodes in both
11

TLand TR, we have that i=iL+iR+nL+nRand
e=eL+|leaves(TL)|+eR+|leaves(TR)|
=eL+eR+|leaves(T)|
=iL+ 2nL+iR+ 2nR+|leaves(T)|
=i+nL+nR+|leaves(T)|
=i+n−1 + |leaves(T)|
By problem B.5-3, since the tree is full, we know that |leaves(T)|is one more
than the number of internal nodes of T. So, e=i+2n, completing the induction.
Exercise B.5-6
We’ll proceed by strong induction on the number of nodes in the tree. When
n= 1, there is a single leaf which has depth 0, so we have Px∈Lw(x)=2−0= 1.
Now suppose the claim holds for a tree with at most nnodes and let Tbe a
tree on n+ 1 nodes. If the left or right subtree of Tis empty then the induction
hypothesis tells us that the subtree on the nonempty side satisfies the inequality
with respect to depth in that tree. Since the depth in the original tree is one
greater for each leaf, the claim holds. On the other hand, if Thas left and right
children, call the subtrees rooted at the children T1and T2. By the induction
hypothesis, the sums of the weights of their leaves are each less than or equal to
1. Since the depth of a node in Tis one greater than its depth in T1or T2, the
weight of each leaf in Tis halved. Thus, the sum of the weights of the leaves in
each subtree is bounded by 1/2, so the total sum of weights of leaves is bounded
by 1.
Exercise B.5-7
Suppose to a contradiction that there was some binary tree with more than 2
leaves that had no subtree with a number of leaves in the desired range. Since
L > 1, the root is not a leaf. Now, define the sequence x0=root,xi+1 is the
larger(more leaves) of the children of xi, until we have reached a root. Now,
we consider the number of leaves in the subtree rooted at each xi. For x0it
is L, which is too large, and at xh, it is 1 which is not too large. Now, we
keep incrementing from x0to x1to x2, and so on until we have some number
of leaves that falls in the desired range. If it happens we are done and have
contradicted the assumption that this binary tree didn’t have such a subtree.
Since it doesn’t that means there is some step where the number of leaves jumps
from more than 2L/3 to less than L/3, Since both of the children of the next
xiwere less than L/3, their sum cannot be more than 2L/3, a contradiction.
Problem B-1
a. If the tree is unrooted, pick an arbitrary node to be the root. Assign color 0
to all nodes that are at an even height, and assign color 1 to all nodes that
12

are at an odd height. Since the child of any node has height one greater,
there will never be two adjacent nodes that have received the same color.
b. We show the following implications in order to get equivalence of all three
1⇒2 Since the graph is bipartite, we can partition the vertices into two sets
Land Rso that there are no edges going between vertices in Land no
edges going between vertices in R. This means that we can assign color
0 to all vertices in Land color 1 to all vertices in Rwithout having any
edges going between two vertices of the same color.
2⇒3 Suppose to a contradiction that there was a cycle of odd length, but we
did have a valid two coloring. As we go along the cycle, each time we
go to the next vertex, the color must change because no two adjacent
vertices can have the same color. If we go around the cycle like this
though, we have just flipped the color an odd number of times, and
have returned back to the original color, a contradiction.
3⇒2 If Ghas no cycles of an odd length, then we can just perform the greedy
operation to two color. That is, we pick a vertex, color it arbitrarily,
then, for any vertex adjacent to a colored vertex, we color it the opposite
color. If this process doesn’t end up coloring everything, i.e. the graph
is disconnected, we repeat it. Since the only way this process could fail
is if there is an odd length cycle, it provides a two coloring, proving that
the graph is two colorable.
2⇒1 Partition the vertices based on what color they received. Since there
are no edges going between the vertices of the same color, there won’t
be any edges going between vertices that are in the same part in the
partition.
c. Consider the process where we pick an arbitrary uncolored vertex and color it
an arbitrary color that is not the color of any of its neighbors. Since a vertex
can only have at most dneighbors, and there are d+ 1 colors to choose from,
this procedure can always be carried out. Also, since we are maintaining at
each step that there are no two adjacent vertices that have been colored the
same, we have that the end result of all the coloring is also valid.
d. Let V0be the set of vertices whose degree is at least p|E|. The total number
of edges incident to at least one of these vertices is at least |V0|√|E|
2by exercise
B.4-1. Since this also has to be bounded by the total number of edges in the
graph, we have that |V0|√|E|
2≤ |E|, which gets us that |V0| ≤ 2p|E|. So,
we’ll assign all of the vertices in V0their own distinct color. Then, so long as
we color the rest of the edges with colors different from those used to color
V0, the edges between V0and the rest of the vertices won’t be important
for affecting the validity of the coloring. So, we look at the graph induced
on the rest of the vertices. This graph is degree at most p|E|because
we already removed all the vertices of high degree. This means that by
13

the previous part, we can color it using at most p|E|+ 1 colors. Putting
it together, the total number of colors used to obtain a valid coloring is
2p|E|+p|E+ 1 ∈O(p|E|) = O(p|V|).
Problem B-2
a. Any undirected graph with at least two vertices contains at least two vertices
of the same degree. Proof: Suppose every vertex has a different degree. Since
the degree of a vertex is bounded between 0 and n−1, the degrees of the
vertices must be exactly 0,1, . . . , n −1. However, if some vertex has degree 0
then no vertex can have degree n−1. Thus, some pair of vertices must have
the same degree.
b. Every undirected graph on 6 vertices contains 3 vertices which are all con-
nected to one another or 3 vertices among which there are no edges. Proof:
Suppose that we have a graph which doesn’t have this property. We’ll show
such a graph cannot exist. If vertex 1 has degree at least 3, then there can
be no edges among these vertices connected to 1. Otherwise there would be
a triangle. However, if there are no edges among these vertices then there
are at least 3 among which there are no edges. Thus vertex 1 must have
degree at most 2. Since there was nothing special about this vertex, the
same argument tells us that every vertex must have degree at most 2. Now
consider the graph G0= (V, E0) where E0={(u, v)|(u, v)/∈E}. Observe
that Ghas no 3 mutually connected or mutually disconnected vertices if and
only if G0does, so the same argument tells us that every vertex of G0has at
most degree 2, which implies that ever vertex of Ghas degree at least 4, a
contradiction.
c. The vertex set Vof any undirected graph can be partitioned into V=V1tV2
such that at least half of the neighbors of each v∈V1are in V2, and at least
half of the neighbors of each v∈V2are in V1. Proof: Consider an abritrary
partition V1tV2. For each edge (u, v) where u∈V1and v∈V2, do the
following: If uand valready have the property that more than half of their
neighbors are in the opposite partition, do nothing. If both uand vfail to
have this property, swap which partition uand vare in. Now suppose just one
vertex fails. Without loss of generality, suppose it is u. If vhas at least one
more than half its neighbors in V1, simply move uinto V1. Otherwise, swap u
and v. Each time we do this for an edge (u, v), the number of edges from V1
to V2strictly increases. For an edge (u, v) with uand vin the same partition,
if either uor vhas more than half its neighbors in its own partition, move
it to the other partition. If both do, just move u. Again, this will strictly
increase the number of edges between V1and V2. Keep picking edges and
repeating this process. Since the number of edges between V1and V2cannot
increase indefinitely, this process will eventually stop, and every vertex will
14

have the property that at least half its neighbors are in the opposite partition.
d. If every vertex of an undirected graph has degree at least |V|/2 then there
exists a way to draw the graph where the vertices all lie on a circle, and
vertices next to one another on the circle are always connected by an edge.
Proof: Let |V|=n. It is easy to check that the claim holds from n= 1,2,3.
We’ll proceed by induction on n. Supoose the claim holds for all graphs on
≤nvertices and let Gbe a graph on n+ 1 vertices such that each vertex has
degree at least (n+1)/2. If nis odd, consider the arrangement of the induced
subgraph on nvertices. There must exist some pair of adjacent vertices both
of which are connected to the (n+ 1)st vertex by an edge, so we may insert
it there. If nis even, it could be the case that vertex n+ 1 is connected to
every other vertex in the arrangement on nvertices. In this case, select a pair
of vertices which are separated by 2 edges on the circle, both of which are
connected to n+ 1. Replace the vertex vbetween them by n+ 1. Excluding
vertex n+ 1, its two adjacent vertices (on the circle), and v, there are n−3
remaining vertices. Since nis even, n−3 is odd. Since vis connected to at
least (n−3)/2 of these, there must exist 2 which are adjacent on the circle.
We can safely place vinbetween these to obtain the desired graph.
Problem B-3
a. Suppose that n≥4, as all smaller binary trees can be easily enumerated
and this fact checked for. Start at the root, let that be x0, then, let xi+1
be the larger child of xi, or it’s only child if there is just one. Eventually
this process will stop once it has reached a root. Let s(v) be the size of the
subtree rooted at v. Since we always pick the larger of the two subtrees, we
have that s(xi)≤2s(xi+1) + 1. So, if we have that s(xi+1)≤n/4, then, we
have that s(xi)≤2n/4 + 1 ≤3n/4. Since eventually this sequence goes to
1, which is below the range, and it starts at n, which is above, we must have
that at some point it dips below, the parent of this node is the one that we
need to snip off of the original tree to get the desired size subtree.
b. Take a binary tree on four vertices as follows:
x
y
a z
Where it is unimportant whether y is the left or right child of x. Then,
any cut that is made of the three edges in the graph results in there being
15
one set of vertices of size 3 that are connected and one vertex that is all by
its lonesome self. This means that the larger of the two sets the vertices is
partitioned into has size 3 = (3/4) ·n.
c. We will make a single cut to the original tree to take off a piece that is less
than or equal to bn
2c. As in part a, we let x0be the root, and let xi+1 be
the larger child of xi. We show that the size of the subtree rooted at xi, say
s(xi) can old drop by at most a factor of 3. To do this, we use the fact that
s(xi)≤2s(xi+1) + 1. So, if s(xi+1)≤s(xi)
3, then,
s(xi)≤2s(xi+1)+1≤2s(xi)
3+ 1
s(xi)
3≤1
s(xi)≤3
However, for there to even be a xi+1, it must have size at least one, so, even
then, we have that has dropped by at most a factor of 3.
This means that we can always select a tree that is less than a fact of three
below bn
2c. So, what we do is cut off that subtree, decrease the amount we
are trying to cut off by that amount, and then continue. Each cut doing this
procedure must decrease the most significant digit of the ternary representa-
tion of the amount need to be cut off by 1. This means that it needs at most
2 log3(n) many cuts, but this is O(lg(n)), so, we are done.
16

Appendix C
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise C.1-2
There are 2(2n)n-input, 1-output boolean functions and (2m)(2n)n-input,
m-output boolean functions.
Exercise C.1-4
The sum of three numbers is even if and only if they are all even, or exactly
two are odd and one is even. For the first case, there are 49
3ways to pick them.
For the second case, there are 50
249
1ways. Thus, the total number of ways to
select 3 distinct numbers so that their sum is even is
49
3+50
249
1.
Exercise C.1-6
We can prove this directly:
n
k=n!
k!(n−k)! =n
n−k
(n−1)!
k!(n−k−1)! =n
n−kn−1
k.
Exercise C.1-8
The following shows Pascal’s triangle with nincreasing down columns and
kincreasing across rows.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1615201561
Exercise C.1-10
1

Fix n. Then we have
n
k=n!
k!(n−k)! =n−k+ 1
k
n!
(k−1)!(n−k+ 1)! =n−k+ 1
kn
k−1.
Thus, we increase in kif and only if n−k+1
k≥1, which happens only when
n+ 1 ≥2k, or k≤ dn/2e. On the other hand, we decrease in kif and only if
n−k+1
k≤1, so k≥ bn/2c. Thus, the function is maximized precisely when kis
equal to one of these.
Exercise C.1-12
We’ll prove inequality C.6 for k≤n/2 by induction on k. For k= 0 we
have n
0= 1 ≤nn
00(n−0)(n−0) = 1. Now suppose the claim holds for k, and that
k < n/2. Then we have
n
k+ 1=n−k
k+ 1 n
k
≤n−k
k+ 1
nn
kk(n−k)(n−k)
=nn
(k+ 1)kk(n−k)(n−k−1) .
To show that this is bounded from above by nn
(k+1)k+1(n−k−1)(n−k−1) we need
ony verify that k+1
kk≤n−k
n−k−1n−k−1. This follows from the fact that the
left hand side, when viewed as a function of k, is increasing, and k < n/2 which
implies that k+ 1 ≤n−k. By induction, the claim holds. Using equation C.3,
we see that the claim extends to all 0 ≤k≤nsince the right hand side of the
inequality is symmetric in kand n−k.
Exercise C.1-14
Differentiating the entropy function and setting it equal to 0 we have
H0(λ) = lg(1 −λ)−lg(λ)=0,
or equivalently lg(1 −λ) = lg(λ). This happens when λ= 1/2. Moreover,
H00(1/2) = −4
ln(2) <0, so this is a local maximum. We have H(1/2) = 1, and
since H(0) = H(1) = 0, this is in fact a global maximum for H.
Exercise C.2-2
2

Let Bi=Ai\(∪i−1
k=1Ai). Then B1, B2, . . . are disjoint and A1∪A2∪. . . =
B1∪B2∪. . .. Moreover, Bi⊆Aifor each i, so P r(Bi)≤P r(Ai). By third
axiom of probability we have
P r(A1∪A2∪. . . =P r(B1∪B2∪. . .) = X
i≥1
P r(Bi)≤X
i≥1
P r(Ai).
Exercise C.2-4
We can verify this directly from the definition of conditional probability as
follows:
P r(A|B) + P r(A|B) = P r(A∩B)
P r(B)+P r(A∩B)
P r(B)=P r(B)
P r(B)= 1.
Exercise C.2-6
Let .a1a2a3. . . be the binary representation of a/b. Flip the fair coin repeat-
edly, associating 1 with heads and 0 with tails, until the first time that the value
of the ith flip differs from ai. If the value is greater than ai, output tails. If the
value is less than ai, output heads. Every number between 0 and .99999 . . . = 1
has the possibility to be represented, and is created by randomly choosing its
binary representation. The probability that we output tails is the probability
that our number is less than a/b, which is just a/b. The expected number of
flips is P∞
i=1 i2−i=2=O(1).
Exercise C.2-8
Suppose we have a biased coin which always comes up heads, and a fair
coin. We pick one at random and flip it twice. Let Abe the event that the
first coin is heads, Bbe the event that the second coin is heads, and Cbe the
event that the fair coin is the one chosen. Then we have P r(A∩B)=5/8 and
P r(A) = P r(B) = 3/4 so P r(A∩B)6=P r(A)P r(B). Thus, Aand Bare not
independent. However,
P r(A∩B|C) = P r(A∩B∩C)
P r(C)=(1/2)(1/2)(1/2)
1/2= 1/4
and
P r(A|C)·P r(B|C) = P r(A∩C)
P r(C)
P r(B∩C)
P r(C)=1/4
1/2
1/4
1/2= 1/4.
Exercise C.2-10
His chances are still 1/3, because at least one of Yor Zwould be executed,
so hearing which one changes nothing about his own situation. However, the
probability that Zis going free is now 2/3. To see this, note that the probability
3
that the free prisoner is among Yand Zis 2/3. Since we are told that it is not
Y, the 2/3 probability must apply exclusively to Z.
Exercise C.3-2
The probability that the maximum or minimum element is in a particular
spot is 1/n since the ordering is random. Thus, the expected index of the
maximum and minimum are the same, and given by:
E[X] =
n
X
i=1
i(1/n) = 1
n
n(n+ 1)
2=n+ 1
2.
Exercise C.3-4
Let Xand Ybe nonnegative random variables. Let Z=X+Y. Then Zis a
random variable, and since Xand Yare nonnegative, we have Z≥max(X, Y )
for any outcome. Thus, E[max(X, Y )] ≤E[Z] = E[X] + E[Y].
Exercise C.3-6
We can verify directly from the definition of expectation:
E[X] = ∞
X
i=0
i·P r(X=i)
≥∞
X
i=t
i·P r(X=i)
≥t∞
X
i=t
P r(X=i)
=t·P r(X≥t).
Dividing both sides by tgives the result.
Exercise C.3-8
The expectation of the square of a random variable is larger. To see this,
note that by (C.27) we have E[X2]−E2[X] = E[(X−E[X])2]≥0 since the
square of a random variable is a nonnegative random variable, so its expectation
must be nonnegative.
Exercise C.3-10
Proceeding from (C.27) we have
4

V ar[aX] = E[(aX)2]−E2[aX]
=E[a2X2]−a2E2[X]
=a2E[X2]−a2E2[X]
=a2(E[X2]−E2[X])
=a2V ar[X].
Exercise C.4-2
Let Xbe the number of times we must flip 6 coins before we obtain 3 heads
and 3 tails. The probability that we obtain 3 heads and 3 tails is 6
3(1/2)6=
5/16, so the probability that we don’t is 11/16. Moreover, Xhas a geometric
distribution, so by (C.32) we have
E[X] = 1/p = 16/5.
Exercise C.4-4
Using Stirling’s approximation we have b(k;n, p)≈√nnn
√2π√k(n−k)kk(n−k)n−kpkqn−k.
The binomial distribution is maximized at its expectation. Plugging in k=np
gives
b(np;n, p)≈√nnnpnp(1 −p)n−np
pnp(n−np)(np)np(n−np)n−np =1
√2πnpq .
Exercise C.4-6
There are 2ntotal coin flips amongst the two professors. They get the same
number of heads if Professor Guildenstern flips kheads and Professor Rosen-
crantz flips n−ktails. If we imagine flipping a head as a success for Professor
Rosencrantz and flipping a tail as a success for Professor Guildenstern, then
the professors get the same number of heads if and only if the total number of
successes achieved by the professors is n. There are 2n
nways to select which
coins will be a successes for their flipper. Since the outcomes are equally likely,
and there are 22n= 4npossible flip sequences, the probability is 2n
n/4n.
To verify the identity, we can imagine counting successes in two ways. The
right hand side counts via our earlier method. For the left hand side, we can
imagine first choosing ksuccesses for Professor Guildenstern, then choosing the
remaining n−ksuccesses for Professor Rosencrantz. We sum over all kto get
the total number of possibilities. Since the two sides of the equation count the
same thing they must be equal.
Exercise C.4-8
5

Let a1, a2, . . . , anbe uniformly chosen from [0,1]. Let Xibe the indicator
random variable that ai≤piand Yibe the indicator random variable that
ai≤p. Let X0=Pn
i=1 Xiand Y0=Pn
i=1 Yi. Then for any event we have
X0≤Y0, which implies P(X0< k)≥P(Y0< k). Let Ybe the number of suc-
cesses in ntrials if each trial is successful with probability p. Then Xhas the
same distribution as X0and Yhas the same distribution of Y0, so we conclude
that P(X < k)≥P(Y < k).
Exercise C.5-2
For Corollary C.6 we have b(i;n, p)/b(i−1; n, p)≤(n−k)p
kq . Let x=(n−k)p
kq .
Note that x < 1, so the infinite series below converges. Then we have
P r(X > k) =
n
X
i=k+1
b(i;n, p)
≤
n
X
i=k+1
xi−kb(k;n, p)
=b(k;n, p)
n−k
X
i=1
xi
≤b(k;n, p)∞
X
i=1
xi
=b(k;n, p)x
1−x
=b(k;n, p)(n−k)p
k−np .
For Corollary C.7, we use Corollary C.6 and the fact that x < 1 as follows:
P r(X > k)
P r(X > k −1) =P r(X > k)
P r(X > k) + P r(X=k−1) ≤xb(k;n, p)
xb(k;n, p) + b(k;n, p)<1
2.
Exercise C.5-4
Using Lemma C.1 and Corollary C.4 we have
6
k−1
X
i=0
piqn−i≤
k−1
X
i=0 n
ipiqn−i
=
k−1
X
i=0
b(i;n, p)
≤kq
np −kb(k;n, p)
≤kq
np −knp
kknq
n−kn−k
.
Exercise C.5-6
As in the proof of Theorem C.8, we’ll bound E[eα(X−µ)and substitute a
suitable value for α. First we’ll prove (with a fair bit of work) that if q= 1 −p
then f(α) = eα2/2−peαq −qe−αp ≥0 for α≥0. First observe that f(0) = 0.
Next we’ll show f0(α)>0 for α > 0. To do this, we’ll show that f0(0) = 0 and
f00(α)>0. We have
f0(α) = αeα2/2−pqeαq +pqe−αp
so f0(0) = 0. Moreover
f00(α) = α2eα2/2+eα2/2−pq(qeαq +pe−αp).
Since α2eα2/2>0 it will suffice to show that eα2/2≥pq(qeαq +pe−αp).
Indeed, we have
pq(qeαq +pe−αp)≤(1/4)(qeαq +pe−αp ≤(1/4)e−αp(eα+ 1) ≤(1/4)(eα+ 1)
so we need to show 4eα2/2≥eα+ 1. Since eα2/2>1, it is enough to show
3eα2/2≥eα. Taking logs on both sides, we need α2/2−α+ ln(3) ≥0. By
taking a derivative we see that this function is minimized when α= 1, where it
attains the value ln(3) −1/2>0. Thus, the original inequality holds. Now can
proceed with the rest of the proof. As in the proof of Theorem C.8, E[eα(X−µ)=
Qn
i=1 E[eα(Xi−pi)]. Using the inequality we just proved we have
E[eα(Xi−pi)] = pieαqi+qie−αpi≤eα2/2.
Thus, E[eα(X−µ)]≤Qn
i=1 eα2/2=enα2/2. By this and (C.43) and (C.44) we
have
P r(X−µ≥r)≤E[eα(X−µ)]e−αr ≤enα2/2−αr.
Finally, taking α=r/n gives the desired result.
7
Appendix D
Michelle Bodnar, Andrew Lohr
December 30, 2015
Exercise D.1-1
Let C=A+Band D=A−B. Then, since Aand Bare symmetric, we
know that aij =aji and bij =bji. We consider these two matrices Cand D
now.
cij =aij +bij
=aji +bji
=cji
dij =aij −bij
=aji −bji
=dji
Exercise D.1-2
From the definitions of transpose and matrix multiplication we have
(AB)T
ij = (AB)ji
=
n
X
k=1
ajkbki
=
n
X
k=1
bkiajk
= (BTAT)ij .
Therefore (AB)T=BTAT. This implies (ATA)T=AT(AT)T=ATA, so
ATAis symmetric.
Exercise D.1-3
1

Suppose that Aand Bare lower triangular, and let C=AB. Being lower
triangular, we know that for i < j,aij =bij = 0. To see that Cis lower
triangular,
cij =
n
X
k=1
aikbkj
=
j−1
X
k=1
aikbkj +
n
X
k=j
aikbkj
=
j−1
X
k=1
aik0 +
n
X
k=j
0bkj
=
j−1
X
k=1
0 +
n
X
k=j
0
= 0 + 0 = 0
Exercise D.1-4
Suppose row iof Phas a 1 in column j. Then row iof P A is row jof A,
so P A permutes the rows. On the other hand, column jof AP is column iof
A, so AP permutes the columns. We can view the product of two permutation
matrices as one permutation matrix permuting the rows of another. This pre-
serves the property that there is only a single 1 in each row and column, so the
product is also a permutation matrix.
Exercise D.2-1
I=I
AC =AB
B(AC) = B(AB)
(BA)C= (BA)B
IC =IB
C=B
Exercise D.2-2
Let Lbe a lower triangular matrix. We’ll prove by induction on the size
of the matrix that the determinant is the product of its diagonal entries. For
n= 1, the determinant is just equal to the matrix entry, which is the product
of the only diagonal element. Now suppose the claim holds for n, and let Lbe
(n+1)×(n+1). Let L0be the n×nsubmatrix obtained from Lby deleting the
2
first row and column. Then we have det(L) = L11 det(L0), since L1j= 0 for all
j6= 1. By the indution hypothesis, det(L0) is the product of the diagonal entries
of L0, which are all the diagonal entries of Lexcept L11. The claim follows since
we multiply this by L11.
We will prove that the inverse of a lower triangular matrix is lower trian-
gular by induction on the size of the matrix. For n= 1 every matrix is lower
triangular, so the claim holds. Let Lbe (n+ 1) ×(n+ 1) and let L0be the sub-
matrix obtained from Lby deleting the first row and column. By our induction
hypothesis, L0has an inverse which is lower triangular, call it L0−1. We will
construct a lower triangular inverse for L:
L−1=
1/l11 0· · · 0
a1
.
.
.L0−1
an
where we define airecursively by
a1=−L21/(L11L0
11) and ai=− L(i+1),1/L11 +
i−1
X
k=1
L0
ikak!/L0
ii.
It is straightforward to verify that this in fact gives an inverse, and it is
well-defined because Lis nonsingular, so Lii 6= 0.
Exercise D.2-3
We will show that it is invertible by showing that PTis its inverse. Suppose
that the only nonzero entry of row iis a one in column σ(i). This means that
the only nonzero entry in column iof PTis in row σ(i). If we let C=P P T,
then, for every iand j, we have that cij =Pn
k=1 pikpjk =piσ(i)pjσ(i). Since σ
is a bijection, we have that if i6=j, then σ(i)6=σ(j). This means that cij = 0.
However, if i=j, then cij = 1. That is, their product is the identity matrix.
This means that PTis the inverse of P.
Since a permutation matrix is defined as having exactly one one in each row
and column, we know that this is true of P. However, the set of rows of PTis
the set of columns of P, and the set of columns of PTare the set of rows of P.
Since all of those have exactly one one, we have that PTis a permutation matrix.
Exercise D.2-4
Assume first that j6=i. Let Cij be the matrix with a 1 in position (i, j), and
zeros elsewhere, and C=I+Cij . Then A0=CA, so A0−1=A−1C−1. It is easy
to check that C−1=I−Cij . Moreover, right multiplication by C−1amounts
to subtracting column ifrom column j, so the claim follows. The claim fails to
hold when i=j. To see this, consider the case where A=B=I. Then A0
is invertible, but if we subtract column ifrom column jof Bwe get a matrix
with a column of zeros, which is singular, so it cannot possibly be the inverse
3

of a matrix.
Exercise D.2-5
To see that the inverse of a marix that has only real entries must be real.
Imagine instead that that matrix was a matrix over R. Then, it will have a
inverse in this ring of matrices so long as it is non-singular. This inverse will
also be an inverse of the matrix when viewed as a matrix of C. Since inverses are
distinct, this must be its inverse, and is all real entries because it was originally
computed as a matrix that was in the set of real entry matrices.
To see the converse implication, just swap the roles, computing the inverse
of the inverse. This will be the original matrix.
Exercise D.2-6
We have (A−1)T= (AT)−1=A−1so A−1is symmetric, and (BABT)T=
(BT)TATBT=BABT.
Exercise D.2-5
We will consider the contrapositive. That is, we will show that a matrix has
rank less than nif and only if there exists a null vector.
Suppose that vis a null vector, and let a1, a2,...anbe the columns of A.
Since multiplying a matrix by a vector produces a linear combination of its
columns whoose coefficients are determined by the vector vthat we are multi-
plying by. Since vevaluates to zero, we have just found a linear combination of
the set of columns of Athat sums to zero. That is, the columns of Aare linearly
dependent, so the column rank is less than n, since the set of all vectors is not
linearly independent, the largest independent set must be a proper subset.
Now, suppose that the column rank is less than n. This means that there is
some set of column vectors which are linearly dependent. Let vibe the coeffi-
cient given to the ith column of Ain this linear combination that sums to zero.
Then, the vivalues combine into a null vector.
Exercise D.2-8
Let Abe m×pand Bbe p×n. Recall that rank(AB) is equal to the
minimum rsuch that there exist Fand Gof dimensions m×rand r×nsuch
that F G =AB. Let A0and A00 be matrices of minimum r0such that A0A00 =A
and the dimensions are m×r0and r0×p. Let B0and B00 be the corresponding
matrices for B, which minimize r00 . If r0≤r00 we have A0(A00 B0B00 ) = AB, so
r≤r0since rwas minimal. If r00 ≤r0we have (A0A00 B0)B00 =AB, so r≤r00 ,
since rwas minimal. Either way, rank(AB)≤min(rank(A),rank(B)).
The product of a nonsingular matrix and another matrix preserves the rank
of the other matrix. Since the rank of a nonsingular n×nmatrix is nand the
rank of an m×nor n×mmatrix is bounded above by min(m, n), the rank of
4

AB is bounded above by the minimum of nand the rank of the other matrix,
which is the minimum of the rank of each of the matrices.
Problem D-1
We’ll proceed by induction on n. If n= 1, then, the matrix is just the 1 ×1
matrix with it’s only entry 1. This clearly has a determinant of 1. Also, since
there is no way to pick distinct iand jin the product on the right hand side,
the product is just one as well.
Now, suppose it is true for n×nVandermonde matrices, we will show it
for (n+ 1) ×(n+ 1) Vandermonde matrices. Now, suppose that we, as the
hint suggests, starting at the second from rightmost column and working left,
add (−x0) times that column to the one to its right. Since the determinant is
unaffected by this sort of operation,we won’t be changing the determinant. For
every entry in the top row except the leftmost one, we have made it zero, since
it becomes xj−1
0−xj−2
0·x0= 0. This means that we can do a expansion by
minors along the top row to compute the determinant. The only nonzero term
in this is the top left column. This means that the determinant is the same as
the determinant of that one minor. Everything in the ith row of that minor has
a factor of (xi−x0). This means that if we take all those factors out, we have
Qn−1
i=1 (xi−x0), which are all the factors in the formula that include x0. Once
we take that factors out, we are left with a n×nVandermonde matrix on the
variables x1, . . . , xn−1. So, we know that it will contain all the other factors we
need to get the right hand side, completing the induction.
Problem D-2
a. Without loss of generality we may assume that the first rcolumns of A
are linearly independent. Then for x1and x2∈Snsuch that x1and x2
are not identical in the first rentries and have 0’s in the remaining entries
we have that Ax16=Ax2. This is because the first rentries of each are a
linear combination of the first rrows of A, and since they are independent
there can’t be two different linear combinations of them which are equal.
Since there are at least 2rnon-equivalent vectors x∈Sn, we must have
|R(A)| ≥ 2r. On the other hand, xis a vector which doesn’t have 0’s in the
coordinates greater than r. Then Ax =Pxiaiwhere aiis the ith column of
A. Since each of the last n−rcolumns of Ais in fact a linear combination of
the first rcolumns of A, this can be rewritten as a linear combination of the
first rcolumns of A. Since we have already counted all of these, |R(A)|= 2r.
If Adoesn’t have full rank then the range can’t include all 2nelements of
Sn, so Acan’t possibly define a permutation.
b. Let y∈R(A) and xr, xr+1, . . . , xn−1be arbitrary. Set z=Pn−1
i=raixi. Since
the first icolumns of Aspan the range of Aand zis in the range of A,y−zis
in the range of Aand there exist x0, x1, . . . , xr−1such that Pr−1
i=0 aixi=y−z.
Then we have Ax =y−z+z=y. Since the last n−rentries of xwere
5

arbitrary, |P(A, y)| ≥ 2n−r. On the other hand, there are 2relements in
R(A), each with at least 2n−rpreimages, which means there are at least
2r·2n−r= 2npreimages in total. Since |Sn|= 2n, there must be exactly
2n−rpreimages for each element of the range.
c. First observe that |B(S0, m)|is just the number of blocks which contain an
element of the range of S. Since the first mrows of Aonly affect the first
mpositions of Ax, they can affect the value of Ax by at most 2m−1, which
won’t change the block. Thus, we need only consider the last n−mrows.
Without loss of generality, we may assume that Sconsists of the first block
of Sn, so that only the first mcolumns of Aare relevant. Suppose that
the lower left (n−m)×msubmatrix of Ahas rank r. Then the range of
Ax consists of vectors of the form [∗,· · · ,∗, x0, x1,· · · xr−1,0,· · · ,0]T, where
there are m∗’s. There are 2m+rsuch vectors, spanning 2rblocks. Thus,
|B(S0, m)|= 2r. Since it is only the choice of x0, . . . , xr−1which determines
the block we’re in, and we can pick every possible combination, every block
must be hit the same number of times. Thus, the number of numbers in S
which map to a particular block is 2m/2r= 2m−r.
d. The number of linear permutations is bounded above by the number of pairs
(A, c) where Ais an n×nmatrix with entries in GF (2) and cis an n-
bit vector. There are 2n2+nof these. On the other hand, there are (2n)!
permutations of Sn. For n≥3, 2n2+n≤(2n)!.
e. Let n= 3 and consider the permutation π(0) = 0, π(1) = 1, π(2) = 2,
π(3) = 3, π(4) = 5, π(5) = 4, π(6) = 6 and π(7) = 7. Since A·0 + c= 0
we must have cbe the zero vector. In order for π(1) to equal 1, the first
column of Amust be [1 0 0]T. To have π(2) = 2, the second column of A
must be [0 1 0]T. To have π(3) = 3, the third column of Amust be [0 0 1]T.
This completely determines Aas the identity matrix, making it impossible
for π(4) = 5, so the permutation is not achievable by any linear permutation.
6