Dakota V6.7 User's Manual
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 364 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface
- Introduction
- Dakota Tutorial
- Parameter Study Capabilities
- Design of Experiments Capabilities
- Uncertainty Quantification Capabilities
- Optimization Capabilities
- Nonlinear Least Squares Capabilities
- Models
- Overview
- Single Models
- Recast Models
- Surrogate Models
- Overview of Surrogate Types
- Correction Approaches
- Data Fit Surrogate Models
- Procedures for Surface Fitting
- Taylor Series
- Two Point Adaptive Nonlinearity Approximation
- Linear, Quadratic, and Cubic Polynomial Models
- Kriging/Gaussian-Process Spatial Interpolation Models
- Artificial Neural Network (ANN) Models
- Multivariate Adaptive Regression Spline (MARS) Models
- Radial Basis Functions
- Moving Least Squares
- Piecewise Decomposition Option for Global Surrogate Models
- Surrogate Diagnostic Metrics
- Multifidelity Surrogate Models
- Reduced Order Models
- Surrogate Model Selection
- Nested Models
- Random Field Models
- Active Subspace Models
- Variables
- Interfaces
- Responses
- Inputs to Dakota
- Output from Dakota
- Advanced Methods
- Advanced Model Recursions
- Advanced Simulation Code Interfaces
- Parallel Computing
- Overview
- Single-level parallelism
- Multilevel parallelism
- Capability Summary
- Running a Parallel Dakota Job
- Specifying Parallelism
- Application Parallelism Use Cases
- Restart Capabilities and Utilities
- Simulation Failure Capturing
- Additional Examples
SAND2014-4633
Unlimited Release
July 2014
Updated November 13, 2017
Dakota, A Multilevel Parallel Object-Oriented Framework for
Design Optimization, Parameter Estimation, Uncertainty
Quantification, and Sensitivity Analysis:
Version 6.7 User’s Manual
Brian M. Adams, Mohamed S. Ebeida, Michael S. Eldred, Gianluca Geraci,
John D. Jakeman, Kathryn A. Maupin, Jason A. Monschke, J. Adam Stephens,
Laura P. Swiler, Dena M. Vigil, Timothy M. Wildey
Optimization and Uncertainty Quantification Department
William J. Bohnhoff
Radiation Transport Department
Keith R. Dalbey
Software Simulation and Data Processing Department
John P. Eddy
System Readiness and Sustainment Technologies Department
Joseph R. Frye, Russell W. Hooper
Multiphysics Applications Department
Kenneth T. Hu
W76-0/W88 Stockpile Systems Engineering Department
Patricia D. Hough, Mohammad Khalil
Quantitative Modeling and Analysis Department
Elliott M. Ridgway
Data-driven and Neural Computing
Sandia National Laboratories
P.O. Box 5800
Albuquerque, New Mexico 87185
Ahmad Rushdi
Electrical and Computer Engineering
University of California
One Shields Avenue
Davis, CA 95616-5294

4
Abstract
The Dakota toolkit provides a flexible and extensible interface between simulation codes and iterative analysis
methods. Dakota contains algorithms for optimization with gradient and nongradient-based methods; uncertainty
quantification with sampling, reliability, and stochastic expansion methods; parameter estimation with nonlinear
least squares methods; and sensitivity/variance analysis with design of experiments and parameter study methods.
These capabilities may be used on their own or as components within advanced strategies such as surrogate-
based optimization, mixed integer nonlinear programming, or optimization under uncertainty. By employing
object-oriented design to implement abstractions of the key components required for iterative systems analyses,
the Dakota toolkit provides a flexible and extensible problem-solving environment for design and performance
analysis of computational models on high performance computers.
This report serves as a user’s manual for the Dakota software and provides capability overviews and procedures
for software execution, as well as a variety of example studies.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Contents
Preface 17
1 Introduction 19
1.1 Motivation for Dakota Development ................................. 19
1.2 Dakota Capabilities .......................................... 19
1.3 Coupling Dakota to a Simulation ................................... 21
1.4 User’s Manual Organization ..................................... 22
1.5 Files Referenced in this Manual ................................... 23
1.6 Summary ............................................... 23
2 Dakota Tutorial 25
2.1 Quickstart ............................................... 25
2.1.1 Acquiring and Installing Dakota ............................... 25
2.1.2 Running Dakota with a simple input file ........................... 26
2.1.3 Examples of Dakota output .................................. 27
2.2 Dakota Input File Format ....................................... 29
2.3 Examples ............................................... 31
2.3.1 Rosenbrock Test Problem .................................. 32
2.3.2 Two-Dimensional Grid Parameter Study ........................... 32
2.3.3 Gradient-based Unconstrained Optimization ......................... 33
2.3.4 Uncertainty Quantification with Monte Carlo Sampling ................... 34
2.3.5 User Supplied Simulation Code Examples .......................... 37
2.3.5.1 Optimization with a User-Supplied Simulation Code - Case 1 .......... 37
2.3.5.2 Optimization with a User-Supplied Simulation Code - Case 2 .......... 41
2.4 Dakota Command-Line Options ................................... 42
2.5 Next Steps ............................................... 43

6 CONTENTS
2.5.1 Problem Exploration and Method Selection ......................... 43
2.5.2 Key Getting Started References ............................... 44
3 Parameter Study Capabilities 47
3.1 Overview ............................................... 47
3.1.1 Initial Values ......................................... 48
3.1.2 Bounds ............................................ 48
3.2 Vector Parameter Study ........................................ 49
3.3 List Parameter Study ......................................... 50
3.4 Centered Parameter Study ...................................... 51
3.5 Multidimensional Parameter Study .................................. 52
3.6 Parameter Study Usage Guidelines .................................. 54
3.7 Example: Vector Parameter Study with Rosenbrock ......................... 54
4 Design of Experiments Capabilities 57
4.1 Overview ............................................... 57
4.2 Design of Computer Experiments .................................. 58
4.3 DDACE ................................................ 59
4.3.1 Central Composite Design .................................. 59
4.3.2 Box-Behnken Design ..................................... 60
4.3.3 Orthogonal Array Designs .................................. 61
4.3.4 Grid Design .......................................... 62
4.3.5 Monte Carlo Design ..................................... 62
4.3.6 LHS Design .......................................... 62
4.3.7 OA-LHS Design ....................................... 62
4.4 FSUDace ............................................... 62
4.5 PSUADE MOAT ........................................... 63
4.6 Sensitivity Analysis .......................................... 64
4.6.1 Sensitivity Analysis Overview ................................ 64
4.6.2 Assessing Sensitivity with DACE .............................. 66
4.7 DOE Usage Guidelines ........................................ 67
5 Uncertainty Quantification Capabilities 69
5.1 Overview ............................................... 69
5.1.1 Summary of Dakota UQ Methods .............................. 69
Dakota Version 6.7 User’s Manual generated on November 13, 2017

CONTENTS 7
5.1.2 Variables and Responses for UQ ............................... 72
5.2 Sampling Methods .......................................... 72
5.2.1 Uncertainty Quantification Example using Sampling Methods ............... 74
5.2.2 Incremental Sampling .................................... 78
5.2.3 Principal Component Analysis ................................ 79
5.2.4 Wilks-based Sample Sizes .................................. 79
5.3 Reliability Methods .......................................... 79
5.3.1 Local Reliability Methods .................................. 81
5.3.1.1 Method mapping .................................. 81
5.3.2 Global Reliability Methods .................................. 82
5.3.3 Uncertainty Quantification Examples using Reliability Analysis .............. 83
5.3.3.1 Mean-value Reliability with Textbook ...................... 83
5.3.3.2 FORM Reliability with Lognormal Ratio ..................... 84
5.4 Stochastic Expansion Methods .................................... 89
5.4.1 Uncertainty Quantification Examples using Stochastic Expansions ............. 90
5.4.1.1 Polynomial Chaos Expansion for Rosenbrock .................. 90
5.4.1.2 Uncertainty Quantification Example using Stochastic Collocation ........ 90
5.5 Importance Sampling Methods .................................... 95
5.5.1 Importance Sampling Method based on Reliability Approach ................ 96
5.5.2 Gaussian Process Adaptive Importance Sampling Method ................. 96
5.6 Adaptive Sampling Methods ..................................... 97
5.6.1 Adaptive sampling based on surrogates ........................... 97
5.6.2 Adaptive sampling based on dart throwing .......................... 98
5.7 Epistemic Nondeterministic Methods ................................. 99
5.7.1 Interval Methods for Epistemic Analysis ..........................100
5.7.2 Dempster-Shafer Theory of Evidence ............................100
5.8 Bayesian Calibration Methods ....................................105
5.8.1 QUESO ............................................106
5.8.2 DREAM ...........................................107
5.8.3 GPMSA ............................................108
5.8.4 WASABI ...........................................108
5.8.5 Feature Comparison .....................................108
5.8.6 Bayesian Calibration Example ................................109
5.8.7 Calibrating the Observation Error Model ..........................111
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8 CONTENTS
5.8.8 Model Discrepancy ......................................111
5.8.9 Bayesian Experimental Design ................................114
5.8.9.1 One-at-a-time Implementation ..........................117
5.9 Uncertainty Quantification Usage Guidelines ............................118
6 Optimization Capabilities 121
6.1 Optimization Formulations ......................................121
6.1.1 Constraint Considerations ..................................123
6.2 Optimizing with Dakota: Choosing a Method ............................123
6.2.1 Gradient-Based Local Methods ...............................124
6.2.1.1 Method Descriptions ...............................124
6.2.1.2 Example ......................................125
6.2.2 Derivative-Free Local Methods ...............................125
6.2.2.1 Method Descriptions ...............................125
6.2.2.2 Example ......................................126
6.2.3 Derivative-Free Global Methods ...............................128
6.2.3.1 Method Descriptions ...............................128
6.2.3.2 Examples .....................................129
6.3 Additional Optimization Capabilities .................................133
6.3.1 Multiobjective Optimization .................................133
6.3.1.1 Multiobjective Example 1 .............................134
6.3.1.2 Multiobjective Example 2 .............................137
6.3.2 Optimization with User-specified or Automatic Scaling ...................139
6.3.2.1 Scaling Example ..................................141
6.4 Optimization Usage Guidelines ....................................141
6.5 Optimization Third Party Libraries ..................................144
7 Nonlinear Least Squares Capabilities 147
7.1 Overview ...............................................147
7.2 Nonlinear Least Squares Fomulations ................................148
7.3 Nonlinear Least Squares with Dakota ................................148
7.4 Solution Techniques ..........................................149
7.4.1 Gauss-Newton ........................................149
7.4.2 NLSSOL ...........................................149
7.4.3 NL2SOL ...........................................150
Dakota Version 6.7 User’s Manual generated on November 13, 2017

CONTENTS 9
7.4.4 Additional Features ......................................150
7.5 Examples ...............................................150
7.6 Usage Guidelines ...........................................152
8 Models 153
8.1 Overview ...............................................153
8.2 Single Models .............................................154
8.3 Recast Models .............................................154
8.4 Surrogate Models ...........................................154
8.4.1 Overview of Surrogate Types .................................154
8.4.2 Correction Approaches ....................................156
8.4.3 Data Fit Surrogate Models ..................................157
8.4.3.1 Procedures for Surface Fitting ...........................157
8.4.3.2 Taylor Series ....................................158
8.4.3.3 Two Point Adaptive Nonlinearity Approximation .................158
8.4.3.4 Linear, Quadratic, and Cubic Polynomial Models ................159
8.4.3.5 Kriging/Gaussian-Process Spatial Interpolation Models .............160
8.4.3.6 Artificial Neural Network (ANN) Models ....................163
8.4.3.7 Multivariate Adaptive Regression Spline (MARS) Models ............163
8.4.3.8 Radial Basis Functions ..............................164
8.4.3.9 Moving Least Squares ...............................164
8.4.3.10 Piecewise Decomposition Option for Global Surrogate Models .........164
8.4.3.11 Surrogate Diagnostic Metrics ...........................165
8.4.4 Multifidelity Surrogate Models ................................166
8.4.5 Reduced Order Models ....................................166
8.4.6 Surrogate Model Selection ..................................167
8.5 Nested Models ............................................167
8.6 Random Field Models .........................................168
8.7 Active Subspace Models .......................................169
9 Variables 171
9.1 Overview ...............................................171
9.2 Design Variables ...........................................171
9.2.1 Continuous Design Variables .................................171
9.2.2 Discrete Design Variables ..................................172
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10 CONTENTS
9.2.2.1 Discrete Design Integer Variables .........................172
9.2.2.2 Discrete Design String Variables .........................173
9.2.2.3 Discrete Design Real Variables ..........................173
9.3 Uncertain Variables ..........................................173
9.3.1 Aleatory Uncertain Variables .................................173
9.3.1.1 Continuous Aleatory Uncertain Variables .....................174
9.3.1.2 Discrete Aleatory Uncertain Variables ......................174
9.3.2 Epistemic Uncertain Variables ................................175
9.3.2.1 Continuous Epistemic Uncertain Variables ....................175
9.3.2.2 Discrete Epistemic Uncertain Variables ......................175
9.4 State Variables ............................................175
9.5 Management of Mixed Variables by Iterator .............................176
9.5.1 View .............................................176
9.5.2 Domain ............................................177
9.5.3 Precedence ..........................................177
9.6 Dakota Parameters File Data Format .................................177
9.6.1 Parameters file format (standard) ...............................178
9.6.2 Parameters file format (APREPRO) .............................179
9.7 The Active Set Vector .........................................181
9.7.1 Active set vector control ...................................181
10 Interfaces 183
10.1 Overview ...............................................183
10.2 Simulation Interfaces .........................................183
10.2.1 Direct Simulation Interface ..................................183
10.2.2 System Call Simulation Interface ..............................184
10.2.3 Fork Simulation Interface ..................................184
10.2.4 Syntax for Filter and Driver Strings .............................185
10.2.5 Fork or System Call: Which to Use? .............................185
10.3 Building a Black-Box Interface to a Simulation Code ........................186
10.3.1 Generic Script Interface Files ................................186
10.3.2 Adapting These Scripts to Another Simulation .......................192
10.3.3 Additional Examples .....................................193
10.4 Simulation Interface Components ..................................193
Dakota Version 6.7 User’s Manual generated on November 13, 2017

CONTENTS 11
10.4.1 Single analysis driver without filters .............................194
10.4.2 Single analysis driver with filters ...............................195
10.4.3 Multiple analysis drivers without filters ...........................196
10.4.4 Multiple analysis drivers with filters .............................197
10.5 Simulation File Management .....................................198
10.5.1 File Saving ..........................................198
10.5.2 File Tagging for Evaluations .................................199
10.5.3 Temporary Files .......................................199
10.5.4 File Tagging for Analysis Drivers ..............................200
10.5.5 Work Directories .......................................201
10.6 Parameter to Response Mapping Examples .............................202
10.7 Parameters and Results Files with dakota.interfacing ........................206
10.7.1 Creating Parameters and Results objects ...........................206
10.7.2 Parameters objects ......................................207
10.7.3 Results objects ........................................207
10.7.4 Response object .......................................208
10.7.5 dakota.interfacing Examples .................................208
11 Responses 211
11.1 Overview ...............................................211
11.1.1 Response function types ...................................211
11.1.2 Gradient availability .....................................212
11.1.3 Hessian availability ......................................212
11.1.4 Field Data ...........................................212
11.2 Dakota Results File Data Format ...................................213
11.3 Active Variables for Derivatives ...................................214
12 Inputs to Dakota 217
12.1 Overview of Inputs ..........................................217
12.1.1 Tabular Data Formats .....................................217
12.2 Data Imports .............................................218
12.2.1 AMPL algebraic mappings: stub.nl, stub.row, and stub.col .................218
12.2.2 Genetic algorithm population import .............................219
12.2.3 Calibration data import ....................................219
12.2.4 PCE coefficient import ....................................220
Dakota Version 6.7 User’s Manual generated on November 13, 2017

12 CONTENTS
12.2.5 Surrogate construction and evaluation data .........................220
12.2.6 Variables/responses import to post-run ............................220
13 Output from Dakota 223
13.1 Overview of Output Formats .....................................223
13.2 Standard Output ............................................223
13.3 Tabular Output Data ..........................................229
13.4 Graphics Output ............................................230
13.5 Error Messages Output ........................................230
13.6 Stochastic expansion exports .....................................232
13.7 Surrogate Model Exports .......................................232
13.8 Variables Output from Pre-run ....................................232
14 Advanced Methods 233
14.1 Overview ...............................................233
14.2 Hybrid Minimization .........................................233
14.3 Multistart Local Minimization ....................................234
14.4 Pareto Optimization ..........................................236
14.5 Mixed Integer Nonlinear Programming (MINLP) ..........................236
14.5.1 Example MINLP Problem ..................................239
14.6 Surrogate-Based Minimization ....................................241
14.6.1 Surrogate-Based Local Minimization ............................241
14.6.1.1 SBO with Data Fits ................................241
14.6.1.2 SBO with Multifidelity Models ..........................244
14.6.1.3 SBO with Reduced Order Models .........................244
14.6.2 Surrogate-Based Global Minimization ............................245
15 Advanced Model Recursions 249
15.1 Mixed Aleatory-Epistemic UQ ....................................249
15.1.1 Interval-valued probability (IVP) ...............................250
15.1.2 Second-order probability (SOP) ...............................251
15.1.3 Dempster-Shafer Theory of Evidence ............................253
15.2 Optimization Under Uncertainty (OUU) ...............................253
15.2.1 Nested OUU .........................................254
15.2.2 Surrogate-Based OUU (SBOUU) ..............................256
Dakota Version 6.7 User’s Manual generated on November 13, 2017

CONTENTS 13
15.2.3 Trust-Region Surrogate-Based OUU (TR-SBOUU) .....................256
15.2.4 RBDO ............................................257
15.2.5 Stochastic Expansion-Based Design Optimization ......................257
15.2.6 Epistemic OUU ........................................258
15.3 Surrogate-Based Uncertainty Quantification .............................258
16 Advanced Simulation Code Interfaces 261
16.1 Algebraic Mappings ..........................................261
16.2 Developing a Direct Simulation Interface ..............................264
16.2.1 Extension ...........................................264
16.2.2 Derivation ...........................................265
16.2.3 Sandwich ...........................................265
16.3 Existing Direct Interfaces to External Simulators ..........................266
16.3.1 Matlab ............................................266
16.3.1.1 Dakota/Matlab input file specification .......................266
16.3.1.2 Matlab .m file specification ............................267
16.3.2 Python ............................................268
16.4 Scilab Script and Direct Interfaces ..................................268
16.4.1 Scilab Script Interface ....................................270
16.4.2 Scilab Linked Interface ....................................271
16.4.3 Scilab Compiled Interface ..................................271
17 Parallel Computing 273
17.1 Overview ...............................................273
17.1.1 Categorization of parallelism .................................274
17.1.2 Parallel Dakota algorithms ..................................275
17.1.2.1 Parallel iterators ..................................275
17.1.2.2 Advanced methods ................................276
17.1.2.3 Parallel models ..................................277
17.2 Single-level parallelism ........................................277
17.2.1 Asynchronous Local Parallelism ...............................279
17.2.1.1 Direct function synchronization ..........................279
17.2.1.2 System call synchronization ............................279
17.2.1.3 Fork synchronization ...............................280
17.2.1.4 Asynchronous Local Example ...........................281
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14 CONTENTS
17.2.1.5 Local evaluation scheduling options .......................283
17.2.2 Message Passing Parallelism .................................283
17.2.2.1 Partitioning ....................................283
17.2.2.2 Scheduling .....................................284
17.2.2.3 Message Passing Example .............................285
17.2.3 Hybrid Parallelism ......................................286
17.2.3.1 Hybrid Example ..................................287
17.3 Multilevel parallelism .........................................289
17.3.1 Asynchronous Local Parallelism ...............................290
17.3.2 Message Passing Parallelism .................................290
17.3.2.1 Partitioning of levels ................................290
17.3.2.2 Scheduling within levels ..............................291
17.3.3 Hybrid Parallelism ......................................291
17.4 Capability Summary .........................................292
17.5 Running a Parallel Dakota Job ....................................293
17.5.1 Single-processor execution ..................................293
17.5.2 Multiprocessor execution ...................................293
17.6 Specifying Parallelism ........................................294
17.6.1 The interface specification ..................................295
17.6.2 The meta-iterator and nested model specifications ......................295
17.6.3 Single-processor Dakota specification ............................296
17.6.3.1 Example 1 .....................................296
17.6.3.2 Example 2 .....................................297
17.6.4 Multiprocessor Dakota specification .............................297
17.6.4.1 Example 3 .....................................297
17.6.4.2 Example 4 .....................................299
17.6.4.3 Example 5 .....................................301
17.7 Application Parallelism Use Cases ..................................302
17.7.1 Case 1: Massively Serial — Multiple serial analysis jobs ..................303
17.7.2 Case 2: Sequential Parallel — One parallel analysis job at a time ..............304
17.7.3 Case 3: Evaluation Tiling — Multiple simultaneous parallel analysis jobs .........304
17.7.3.1 Mpiexec server mode ...............................305
17.7.3.2 Relative node scheduling .............................305
17.7.3.3 Machinefile management .............................306
Dakota Version 6.7 User’s Manual generated on November 13, 2017

CONTENTS 15
17.7.4 Case 4: Evaluation Submission — Parallel analysis jobs submitted to a queue . . . . . . . 306
18 Restart Capabilities and Utilities 307
18.1 Restart Management .........................................307
18.2 The Dakota Restart Utility ......................................308
18.2.1 Print ..............................................309
18.2.2 To/From Neutral File Format .................................310
18.2.3 To Tabular Format ......................................311
18.2.4 Concatenation of Multiple Restart Files ...........................312
18.2.5 Removal of Corrupted Data .................................312
19 Simulation Failure Capturing 315
19.1 Failure detection ...........................................315
19.2 Failure communication ........................................316
19.3 Failure mitigation ...........................................316
19.3.1 Abort (default) ........................................316
19.3.2 Retry .............................................316
19.3.3 Recover ............................................316
19.3.4 Continuation .........................................317
19.4 Special values .............................................317
20 Additional Examples 319
20.1 Textbook ...............................................319
20.1.1 Gradient-based Constrained Optimization ..........................321
20.2 Rosenbrock ..............................................324
20.2.1 Least-Squares Optimization .................................324
20.3 Herbie, Smooth Herbie, and Shubert .................................327
20.3.1 Efficient Global Optimization ................................328
20.4 Sobol and Ishigami Functions ....................................328
20.5 Cylinder Head .............................................329
20.5.1 Constrained Gradient Based Optimization ..........................333
20.6 Container ...............................................336
20.6.1 Constrained Gradient Based Optimization ..........................337
20.7 Cantilever ...............................................338
20.7.1 Constrained Gradient Based Optimization ..........................339
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16 CONTENTS
20.7.2 Optimization Under Uncertainty ...............................340
20.8 Multiobjective Test Problems .....................................340
20.8.1 Multiobjective Test Problem 2 ................................341
20.8.2 Multiobjective Test Problem 3 ................................341
20.9 Morris .................................................347
20.9.1 Morris One-at-a-Time Sensitivity Study ...........................347
20.10Test Problems for Reliability Analyses ................................350
20.10.1 Log Ratio ...........................................350
20.10.2 Steel Section .........................................351
20.10.3 Portal Frame .........................................351
20.10.4 Short Column .........................................351
20.10.5 Steel Column .........................................352
20.11Test Problems for Forward Uncertainty Quantification ........................353
20.11.1 Genz functions ........................................353
20.11.2 Elliptic Partial differential equation with uncertain coefficients ...............354
20.11.3 Damped Oscillator ......................................355
20.11.4 Non-linear coupled system of ODEs .............................355
20.11.5 Experimental Design .....................................355
20.11.6 Bayes linear ..........................................356
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Preface
The Dakota project started in 1994 as an internal research and development activity at Sandia National Labora-
tories in Albuquerque, New Mexico. The original goal was to provide a common set of optimization tools for
a group of engineers solving structural analysis and design problems. Prior to the Dakota project, there was no
focused effort to archive optimization methods for reuse on other projects. Thus, engineers found themselves
repeatedly building new custom interfaces between the engineering analysis software and optimization software.
This was especially burdensome when using parallel computing, as each project developed a unique master pro-
gram to coordinate concurrent simulations on a network of workstations or a parallel computer. The initial Dakota
toolkit provided the engineering and analysis community at Sandia access to a variety of optimization algorithms,
hiding the complexity of the optimization software interfaces from the users. Engineers could readily switch
between optimization software packages by simply changing a few lines in a Dakota input file. In addition to
structural analysis, Dakota has been applied to computational fluid dynamics, nonlinear dynamics, shock physics,
heat transfer, electrical circuits, and many other science and engineering models.
Dakota has grown significantly beyond an optimization toolkit. In addition to its state-of-the-art optimization
methods, Dakota includes methods for global sensitivity and variance analysis, parameter estimation, uncertainty
quantification, and verification, as well as meta-level strategies for surrogate-based optimization, hybrid optimiza-
tion, and optimization under uncertainty. Available to all these algorithms is parallel computation support; ranging
from desktop multiprocessor computers to massively parallel computers typically found at national laboratories
and supercomputer centers.
As of Version 5.0, Dakota is publicly released as open source under a GNU Lesser General Public License and
is available for free download world-wide. See http://www.gnu.org/licenses/lgpl.html for more
information on the LGPL software use agreement. Dakota Versions 3.0 through 4.2+ were licensed under the GNU
General Public License. Dakota public release facilitates research and software collaborations among Dakota
developers at Sandia National Laboratories and other institutions, including academic, government, and corporate
entities. See the Dakota FAQ at http://dakota.sandia.gov/faq-page for more information on the
public release rationale and ways to contribute.
Dakota leadership includes Brian Adams (project lead), Mike Eldred (founder and research lead), Adam Stephens
(support manager), Dena Vigil (product owner), and Jim Stewart (business manager). For a listing of current
and former contributors and third-party library developers, visit the Dakota webpage at http://dakota.
sandia.gov.
Contact Information:
Brian M. Adams, Dakota Project Lead
Sandia National Laboratories
P.O. Box 5800, Mail Stop 1318
Albuquerque, NM 87185-1318
Web (including support information): http://dakota.sandia.gov

18 CONTENTS
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 1
Introduction
1.1 Motivation for Dakota Development
Computational models are commonly used in engineering design and scientific discovery activities for simulating
complex physical systems in disciplines such as fluid mechanics, structural dynamics, heat transfer, nonlinear
structural mechanics, shock physics, and many others. These simulators can be an enormous aid to engineers who
want to develop an understanding and/or predictive capability for complex behaviors typically observed in the
corresponding physical systems. Simulators often serve as virtual prototypes, where a set of predefined system
parameters, such as size or location dimensions and material properties, are adjusted to improve the performance
of a system, as defined by one or more system performance objectives. Such optimization or tuning of the
virtual prototype requires executing the simulator, evaluating performance objective(s), and adjusting the system
parameters in an iterative, automated, and directed way. System performance objectives can be formulated, for
example, to minimize weight, cost, or defects; to limit a critical temperature, stress, or vibration response; or
to maximize performance, reliability, throughput, agility, or design robustness. In addition, one would often
like to design computer experiments, run parameter studies, or perform uncertainty quantification (UQ). These
approaches reveal how system performance changes as a design or uncertain input variable changes. Sampling
methods are often used in uncertainty quantification to calculate a distribution on system performance measures,
and to understand which uncertain inputs contribute most to the variance of the outputs.
A primary goal for Dakota development is to provide engineers and other disciplinary scientists with a systematic
and rapid means to obtain improved or optimal designs or understand sensitivity or uncertainty using simulation-
based models. These capabilities generally lead to improved designs and system performance in earlier design
stages, alleviating dependence on physical prototypes and testing, shortening design cycles, and reducing product
development costs. In addition to providing this practical environment for answering system performance ques-
tions, the Dakota toolkit provides an extensible platform for the research and rapid prototyping of customized
methods and meta-algorithms [34].
1.2 Dakota Capabilities
Dakota delivers a variety of iterative methods and meta-algorithms, and the ability to flexibly interface them to
your simulation code. While Dakota was originally conceived to more readily interface simulation codes and
optimization algorithms, recent versions go beyond optimization to include other iterative analysis methods such

20 CHAPTER 1. INTRODUCTION
as uncertainty quantification with nondeterministic propagation methods, parameter estimation with nonlinear
least squares solution methods, and sensitivity/variance analysis with general-purpose design of experiments and
parameter study capabilities. These capabilities may be used on their own or as building blocks within more
sophisticated meta-algorithms such as hybrid optimization, surrogate-based optimization, optimization under un-
certainty, or mixed aleatory/epistemic UQ.
The principal classes of Dakota algorithms, with brief descriptions, are summarized here. For details, formula-
tions, and usage guidelines, see the referenced chapters.
•Parameter Studies (Chapter 3): Parameter studies employ deterministic designs to explore the effect of
parametric changes within simulation models, yielding one form of sensitivity analysis. They can help
assess simulation characteristics such as smoothness, multi-modality, robustness, and nonlinearity, which
affect the choice of algorithms and controls in follow-on optimization and UQ studies. Typical examples
include centered, one-at-a-time variations or joint variation on a grid.
•Design of Experiments (Chapter 4): Design and analysis of computer experiments (DACE) techniques
are often used to explore the parameter space of an engineering design problem, for example to perform
global sensitivity analysis. DACE methods can help reach conclusions similar to parameter studies, but the
primary goal of these methods is to generate good coverage of the input parameter space. Representative
methods include Latin hypercube sampling, orthogonal arrays, and Box-Behnken designs.
•Uncertainty Quantification (Chapter 5): Uncertainty quantification methods (also referred to as nonde-
terministic analysis methods) compute probabilistic information about response functions based on simu-
lations performed according to specified input parameter probability distributions. Put another way, these
methods perform a forward uncertainty propagation in which probability information for input parameters
is mapped to probability information for output response functions. Common approaches include Monte
Carlo sampling, reliability methods, and polynomial chaos expansions.
•Optimization (Chapter 6): Optimization solvers seek to minimize cost or maximize system performance,
as predicted by the simulation model, subject to constraints on input variables or secondary simulation re-
sponses. Categories of algorithms include gradient-based, derivative-free, and global optimization. Dakota
also includes capabilities for multi-objective trade-off optimization and automatic scaling of problem for-
mulations. Advanced Dakota approaches include hybrid (multi-method), multi-start local, and Pareto-set
optimization.
•Calibration (Chapter 7): Calibration algorithms seek to maximize agreement between simulation outputs
and experimental data (or desired outputs). They are used to solve inverse problems (often referred to as
parameter estimation or least-squares problems). Dakota approaches include nonlinear least squares and
Bayesian calibration.
Dakota includes a number of related advanced capabilities. Surrogate models are inexpensive approximate mod-
els that are intended to capture the salient features of an expensive high-fidelity model and include data fits,
multifidelity, and reduced-order model surrogates. They can be used to explore the variations in response quanti-
ties over regions of the parameter space, or they can serve as inexpensive stand-ins for optimization or uncertainty
quantification studies. Section 8.4 summarizes surrogate model mechanics in Dakota, while optimization methods
tailored to particular surrogate approaches are surveyed in Section 14.6.
Nested models permit layering one Dakota method over another, enabling algorithms like mixed epistemic-
aleatory or second-order UQ, optimization under uncertainty, or surrogate-based UQ. Additional information
on these nested approaches is provided in Section 8.5 and Chapter 15.
The methods and algorithms in Dakota are designed to exploit parallel computing resources such as those found
in a desktop multiprocessor workstation, a network of workstations, or a massively parallel computing platform.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
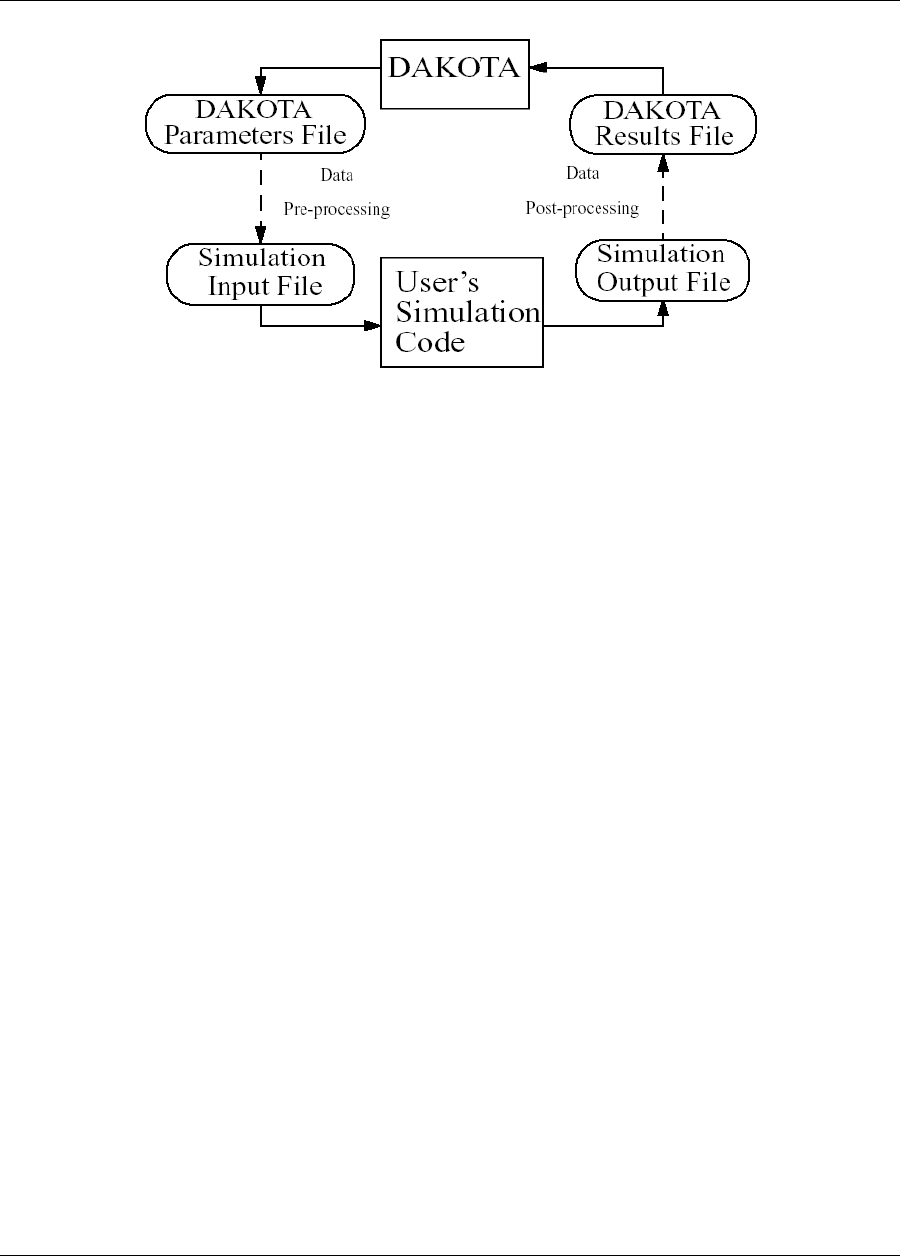
1.3. COUPLING DAKOTA TO A SIMULATION 21
Figure 1.1: The loosely-coupled or “black-box” interface between Dakota and a user-supplied simulation code.
This parallel computing capability is a critical technology for rendering real-world engineering design problems
computationally tractable. See Chapter 17.
Dakota also has emerging capabilities in solution verification and Bayesian calibration/UQ, which are documented
briefly in the Dakota Reference Manual, and in later sections of this manual.
In addition to its iterative methods and algorithms, Dakota also provides a graphical user interface that allows
you to manage your Dakota studies visually. Among other features, the GUI allows you to intuitively link your
Dakota study to a simulation model (see Section 1.3 below) as well as graphically plot output data from your
Dakota study. For the full Dakota GUI tutorial, please visit this link: https://dakota.sandia.gov/
content/dakota-gui-user-manual.
1.3 Coupling Dakota to a Simulation
A key Dakota advantage is access to a broad range of iterative capabilities through a single, relatively simple,
interface between Dakota and your simulator. Trying a different iterative method or meta-algorithm typically
requires changing only a few commands in the Dakota text input file and starting the new analysis. It does not
require intimate knowledge of the underlying software package integrated in Dakota, with its unique command
syntax and interfacing requirements. In addition, Dakota will manage concurrent executions of your computa-
tional model in parallel, whether on a desktop or high-performance cluster computer.
Figure 1.1 depicts a typical loosely-coupled relationship between Dakota and the simulation code(s). Such cou-
pling is often referred to as “black-box,” as Dakota has no (or little) awareness of the internal details of the
computational model, obviating any need for its source code. Such loose coupling is the simplest and most com-
mon interfacing approach Dakota users employ. Dakota and the simulation code exchange data by reading and
writing short data files. Dakota is executed with commands that the user supplies in a text input file (not shown
in Figure 1.1) which specify the type of analysis to be performed (e.g., parameter study, optimization, uncer-
tainty quantification, etc.), along with the file names associated with the user’s simulation code. During operation,
Dakota automatically executes the user’s simulation code by creating a separate process external to Dakota.
The solid lines in Figure 1.1 denote file input/output (I/O) operations inherent to Dakota or the user’s simulation
code. The dotted lines indicate passing or converting information that must be implemented by the user. As Dakota
Dakota Version 6.7 User’s Manual generated on November 13, 2017

22 CHAPTER 1. INTRODUCTION
runs, it writes out a parameters file containing the current variable values. Dakota then starts the user’s simulation
code (or, often, a short driver script wrapping it), and when the simulation completes, reads the response data from
a results file. This process is repeated until all of the simulations required by the iterative study are complete.
In some cases it is advantageous to have a close coupling between Dakota and the simulation code. This close
coupling is an advanced feature of Dakota and is accomplished through either a direct interface or a SAND (si-
multaneous analysis and design) interface. For the direct interface, the user’s simulation code is modified to
behave as a function or subroutine under Dakota. This interface can be considered to be “semi-intrusive” in that
it requires relatively minor modifications to the simulation code. Its major advantage is the elimination of the
overhead resulting from file I/O and process creation. It can also be a useful tool for parallel processing, by en-
capsulating all computation in a single executable. For details on direct interfacing, see Section 16.2. A SAND
interface approach is “fully intrusive” in that it requires further modifications to the simulation code so that an
optimizer has access to the internal residual vector and Jacobian matrices computed by the simulation code. In
a SAND approach, both the optimization method and a nonlinear simulation code are converged simultaneously.
While this approach can greatly reduce the computational expense of optimization, considerable software devel-
opment effort must be expended to achieve this intrusive coupling between SAND optimization methods and the
simulation code. SAND may be supported in future Dakota releases.
1.4 User’s Manual Organization
The Dakota User’s Manual is organized into the following major categories. New users should consult the Tutorial
to get started, then likely the Method Tour and Interfacing to select a Dakota method and build an interface to
your code.
•Tutorial (Chapter 2): How to obtain, install, and use Dakota, with a few introductory examples.
•Method Tour (Chapters 3through 7): Survey of the major classes of iterative methods included in Dakota,
with background, mathematical formulations, usage guidelines, and summary of supporting third-party
software.
•Models (Chapters 8through 11): Explanation of Dakota models, which manage the mapping from variables
through interfaces to responses, as well as details on parameter and response file formats for simulation code
interfacing.
•Input/Output (Chapters 12 and 13): Summary of input to Dakota, including tabular data, and outputs
generated by Dakota.
•Advanced Topics:
– Recursion with Components: Chapter 14 addresses component-based method recursions, and Chap-
ter 15 addresses component-based model recursions.
– Interfacing: Chapter 16 describes interfacing Dakota with engineering simulation codes in both
loose- and tightly-coupled modes.
– Parallelism: Chapter 17 describes Dakota’s parallel computing capabilities, with a summary of major
application parallel modes in Section 17.7.
– Fault Tolerance: Chapter 18 describes restart capabilities and utilities, and Chapter 19 explains ways
to detect and mitigate simulation failures.
•Additional Examples (Chapter 20): Supplemental example analysis problems and discussion.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

1.5. FILES REFERENCED IN THIS MANUAL 23
1.5 Files Referenced in this Manual
Dakota input files are shown in figures throughout the Manual. The filename is specified in the comments and un-
less specified otherwise, these files are available in the Dakota/examples/users directory, where Dakota
refers to the directory where Dakota was installed. Some of the input files have associated files, such as output or
tabular data, with the same base filename, and .sav appended to the names.
Additional files are referenced, and if the location differs then it will be specified in the text. A small number of
examples refer to files included only in the source directory, which is labeled Dakota Source. You will need a
copy of the source to view these files - see Section 2.1.1.
1.6 Summary
Dakota is both a production tool for engineering design and analysis activities and a research tool for the develop-
ment of new algorithms in optimization, uncertainty quantification, and related areas. Because of the extensible,
object-oriented design of Dakota, it is relatively easy to add new iterative methods, meta-algorithms, simulation
interfacing approaches, surface fitting methods, etc. In addition, Dakota can serve as a rapid prototyping tool for
algorithm development. That is, by having a broad range of building blocks available (i.e., parallel computing,
surrogate models, simulation interfaces, fundamental algorithms, etc.), new capabilities can be assembled rapidly
which leverage the previous software investments. For additional discussion on framework extensibility, refer to
the Dakota Developers Manual [2].
The capabilities of Dakota have been used to solve engineering design and optimization problems at Sandia Labs,
at other Department of Energy labs, and by our industrial and academic collaborators. Often, this real-world
experience has provided motivation for research into new areas of optimization. The Dakota development team
welcomes feedback on the capabilities of this software toolkit, as well as suggestions for new areas of research.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

24 CHAPTER 1. INTRODUCTION
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 2
Dakota Tutorial
2.1 Quickstart
This section provides an overview of acquiring and installing Dakota, running a simple example, and looking
at the basic output available. More detailed information about downloads and installation can be found on the
Dakota website http://dakota.sandia.gov.
2.1.1 Acquiring and Installing Dakota
Dakota operates on most systems running Unix or Linux operating systems as well as on Windows, natively in
a Command Prompt window, and (optionally) with the help of a Cygwin emulation layer. Dakota is developed
and most extensively tested on Redhat Enterprise Linux with GNU compilers, but additional operating systems
/ compiler combinations are tested nightly as well. See the Dakota website for more information on supported
platforms for particular Dakota versions.
Department of Energy users: Dakota may already be available on your target system. Sandia users should visit
http://dakota.sandia.gov/ for information on supported Dakota installations on engineering networks
and cluster computers, as well as for Sandia-specific downloads. At other DOE institutions, contact your system
administrator about Dakota availability. If Dakota is not available for your target platform, you may still download
Dakota as described below.
New users should visit https://dakota.sandia.gov/quickstart.html to get started with Dakota.
This typically involves the following steps:
1. Download Dakota.
You may download binary executables for your preferred platforms or you can compile Dakota from source
code. Downloads are available from http://dakota.sandia.gov/download.html.
2. Install Dakota.
Instructions are available from http://dakota.sandia.gov/content/install-dakota. Guid-
ance is also included in the Dakota source files, including Dakota Source/INSTALL. Further platfor-
m/operating system-specific guidance can be found in Dakota Source/examples/platforms.
3. Verify that Dakota runs.
To perform a quick check that your Dakota executable runs, open a terminal window (in Windows, cmd.exe),

26 CHAPTER 2. DAKOTA TUTORIAL
and type:
dakota -v
Dakota version information should display in your terminal window. For a more detailed description of
Dakota command line options, see Section 2.4.
4. Participate in Dakota user communities.
Join Dakota mail lists to get the most up-to-date guidance for downloading, compiling, installing, or run-
ning. For information about mail lists, getting help, and other available help resources, see
http://dakota.sandia.gov/content/get-help.
2.1.2 Running Dakota with a simple input file
This section is intended for users who are new to Dakota, to demonstrate the basics of running a simple example.
First Steps
1. Make sure Dakota runs. You should see Dakota version information when you type: dakota -v
2. Create a working directory
3. Copy rosen multidim.in from the Dakota/examples/users/ directory to the working direc-
tory – see Section 1.5 for help.
4. From the working directory, run dakota -i rosen multidim.in -o rosen multidim.out
> rosen multidim.stdout
What should happen
Dakota outputs a large amount of information to help users track progress. Four files should have been created:
1. The screen output has been redirected to the file rosen multidim.stdout.
The contents are messages from Dakota and notes about the progress of the iterator (i.e. method/algorithm).
2. The output file rosen multidim.out contains information about the function evaluations.
3. rosen multidim.dat is created due to the specification of tabular graphics data and
tabular graphics file. This summarizes the variables and responses for each function evaluation.
4. dakota.rst is a restart file. If a Dakota analysis is interrupted, it can be often be restarted without losing
all progress.
In addition to the files, some plots are created due to the specification of graphics. These can be helpful when
processing the data or diagnosing unexpected results. If your particular installation or build of Dakota does not
support graphics, you will instead get a warning to this effect.
Dakota has some data processing capabilities for output analysis. The output file will contain the relevant results.
In this case, the output file has details about each of the 81 function evaluations. For more advanced or customized
data processing or visualization, the tabular data file can be imported into another analysis tool.
What now?
•Assuming Dakota ran successfully, skim the three text files (restart files are in a binary format). These are
described further in Section 2.1.3.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.1. QUICKSTART 27
•This example used a parameter study method, and the rosenbrock test problem. More details about the
example are in Section 2.3.2 and the test problem is described in Sections 2.3.1 and 20.2.
•Explore the many methods available in Dakota in Chapters 3–7.
•Try running the other examples in the same directory. These are mentioned throughout the manual and are
listed in Table 2.1 for convenience.
•Learn the syntax needed to use these methods. For help running Dakota, see Section 2.4 and for input file
information, see Section 2.2.
•Learn how to use your own analysis code with Dakota in Chapter 16.
2.1.3 Examples of Dakota output
Beyond numerical results, all output files provide information that allows the user to check that the actual analysis
was the intended analysis. More details on all outputs can be found in Chapter 13.
Screen output saved to a file
Whenever an output file is specified for a Dakota run, the screen output itself becomes quite minimal consisting
of version statements, environment statements and execution times.
Output file
The output file is much more extensive, because it contains information on every function evaluation (See Figure
2.1). It is organized into three basic parts:
1. Information on the problem
For this example, we see that a new restart file is being created and Dakota has carried out a
multidim parameter study with 8 partitions for each of two variables.
2. Information on each function evaluation
Each function evaluation is numbered. Details for function evaluation 1 show that at input vari-
able values x1 = −2.0and x2 = −2.0, the direct rosenbrock function is being evaluated. There
is one response with a value of 3.609e+03.
3. Summary statistics
The function evaluation summary is preceded by <<<<<. For this example 81 total evalua-
tions were assessed; all were new, none were read in from the restart file. Correlation matrices
complete the statistics and output for this problem. Successful runs will finish with <<<<<
Iterator study type completed.
Tabular output file
For this example, the default name for the tabular output file dakota tabular.dat was changed in the input
file to rosen multidim.dat. This tab-delimited text file (Figure 2.1.3) summarizes the inputs and outputs to
the function evaluator. The first line contains the names of the variables and responses, as well as headers for the
evaluation id and interface columns.
%eval_id interface x1 x2 response_fn_1
Dakota Version 6.7 User’s Manual generated on November 13, 2017

28 CHAPTER 2. DAKOTA TUTORIAL
The number of function evaluations will match the number of evaluations listed in the summary part of the output
file for single method approaches; the names of inputs and outputs will match the descriptors specified in the input
file. The interface column is useful when a Dakota input file contains more than one simulation interface. In
this instance, there is only one, and it has no id interface specified, so Dakota has supplied a default value
of NO ID. This file is ideal for import into other data analysis packages.
{Writing new restart file dakota.rst
methodName = multidim_parameter_study
gradientType = none
hessianType = none
>>>>> Running multidim_parameter_study iterator.
Multidimensional parameter study for variable partitions of
8
8
------------------------------
Begin Function Evaluation 1
------------------------------
Parameters for function evaluation 1:
-2.0000000000e+00 x1
-2.0000000000e+00 x2
Direct function: invoking rosenbrock
Active response data for function evaluation 1:
Active set vector = { 1 }
3.6090000000e+03 response_fn_1
.
.
.
<<<<< Function evaluation summary: 81 total (81 new, 0 duplicate)
Simple Correlation Matrix among all inputs and outputs:
x1 x2 response_fn_1
x1 1.00000e+00
x2 1.73472e-17 1.00000e+00
response_fn_1 -3.00705e-03 -5.01176e-01 1.00000e+00
.
.
.
<<<<< Iterator multidim_parameter_study completed.}
Figure 2.1: Rosenbrock 2-D parameter study example: excerpt from output file
Dakota Version 6.7 User’s Manual generated on November 13, 2017
2.2. DAKOTA INPUT FILE FORMAT 29
%eval_id interface x1 x2 response_fn_1
1 NO_ID -2 -2 3609
2 NO_ID -1.5 -2 1812.5
3 NO_ID -1 -2 904
4 NO_ID -0.5 -2 508.5
Figure 2.2: Rosenbrock 2-D parameter study example: excerpt from tabular data file
2.2 Dakota Input File Format
See Section 1.5 for location of all files referenced in this manual.
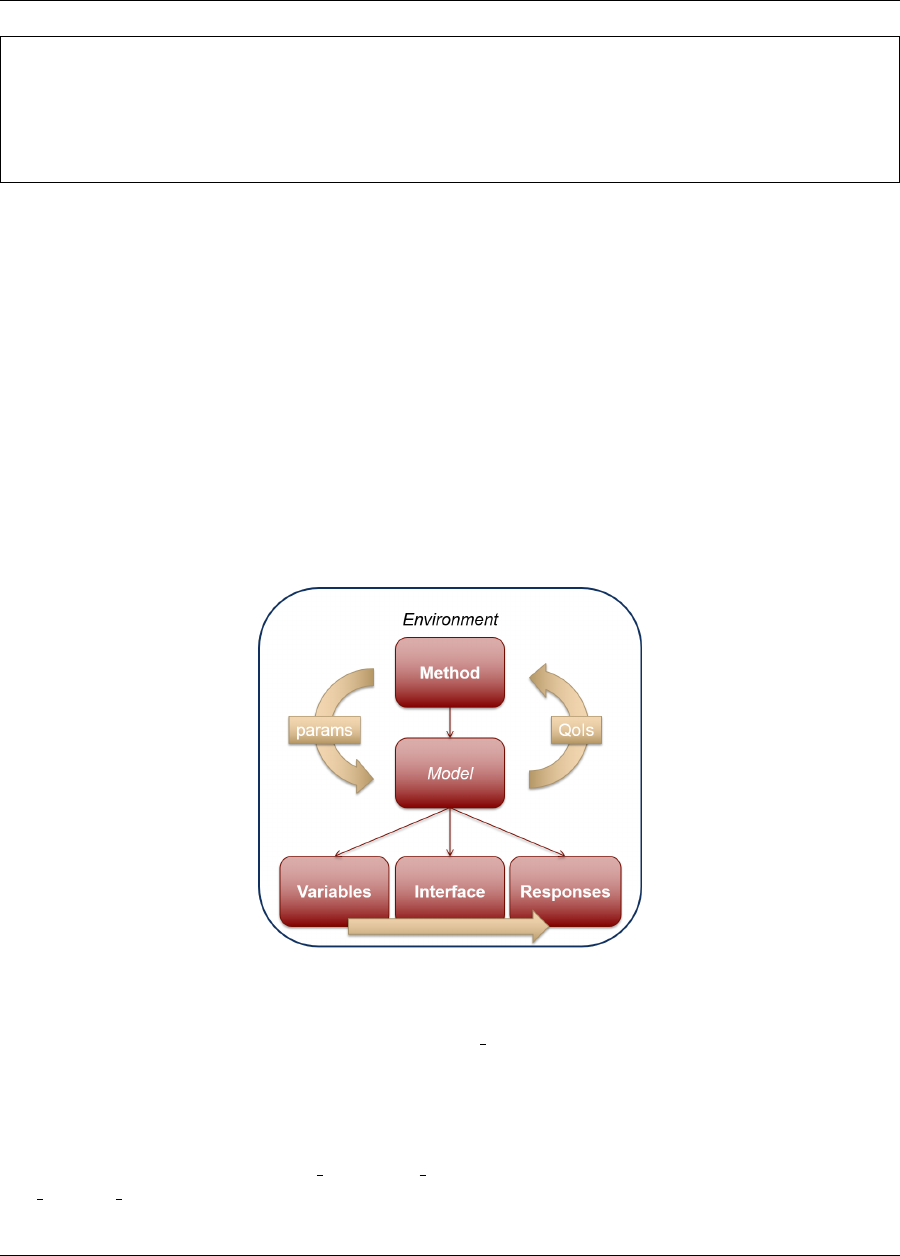
There are six specification blocks that may appear in Dakota input files. These are identified in the input file using
the following keywords: variables, interface, responses, model, method, and environment. While, these keyword
blocks can appear in any order in a Dakota input file, there is an inherent relationship that ties them together. The
simplest form of that relationship is shown in Figure 2.3 and can be summarized as follows: In each iteration of
its algorithm, a method block requests a variables-to-responses mapping from its model, which the model fulfills
through an interface. While most Dakota analyses satisfy this relationship, where a single method runs a single
model, advanced cases are possible and are discussed in Chapter 14.
Figure 2.3: Relationship between the six blocks, for a simple study.
As a concrete example, a simple Dakota input file, rosen multidim.in, is shown in Figure 2.4 for a two-
dimensional parameter study on Rosenbrock’s function. This input file will be used to describe the basic format
and syntax used in all Dakota input files. The results are shown later, in Section 2.3.2.
The first block of the input file shown in Figure 2.4 is the environment block. This keyword block is used
to specify the general Dakota settings such as Dakota’s graphical output (via the graphics flag) and the
tabular data output (via the tabular graphics data keyword). In advanced cases, it also identifies the
top method pointer that will control the Dakota study. The environment block is optional, and at most one
such block can appear in a Dakota input file.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

30 CHAPTER 2. DAKOTA TUTORIAL
# Dakota Input File: rosen_multidim.in
# Usage:
# dakota -i rosen_multidim.in -o rosen_multidim.out > rosen_multidim.stdout
environment
graphics
tabular_data
tabular_data_file = ’rosen_multidim.dat’
method
multidim_parameter_study
partitions = 8 8
model
single
variables
continuous_design = 2
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
response_functions = 1
no_gradients
no_hessians
Figure 2.4: Rosenbrock 2-D parameter study example: the Dakota input file.
The method block of the input file specifies which iterative method Dakota will employ and associated method
options. The keyword multidim parameter study in Figure 2.4 calls for a multidimensional parameter
study, while the keyword partitions specifies the number of intervals per variable (a method option). In
this case, there will be eight intervals (nine data points) evaluated between the lower and upper bounds of both
variables (bounds provided subsequently in the variables section), for a total of 81 response function evaluations.
At least one method block is required, and multiple blocks may appear in Dakota input files for advanced studies.
The model block of the input file specifies the model that Dakota will use. A model provides the logical unit
for determining how a set of variables is mapped through an interface into a set of responses when needed by
an iterative method. In the default case, the model allows one to specify a single set of variables, interface,
and responses. The model block is optional in this simple case. Alternatively, it can be explicitly defined as in
Figure 2.4, where the keyword single specifies the use of a single model in the parameter study. If one wishes to
perform more sophisticated studies such as surrogate-based analysis or optimization under uncertainty, the logical
organization specified in the model block becomes critical in informing Dakota on how to manage the different
components of such studies, and multiple model blocks are likely needed. See Chapter 8for relevant advanced
model specification details.
The variables block of the input file specifies the number, type, and characteristics of the parameters that will
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.3. EXAMPLES 31
be varied by Dakota. The variables can be classified as design variables, uncertain variables, or state variables.
Design variables are typically used in optimization and calibration, uncertain variables are used in UQ and sensi-
tivity studies, and state variables are usually fixed. In all three cases, variables can be continuous or discrete, with
discrete having real, integer, and string subtypes. See Chapter 9for more information on the types of variables
supported by Dakota. The variables section shown in Figure 2.4 specifies that there are two continuous design
variables. The sub-specifications for continuous design variables provide the descriptors “x1” and “x2” as well as
lower and upper bounds for these variables. The information about the variables is organized in column format
for readability. So, both variables x1and x2have a lower bound of -2.0 and an upper bound of 2.0. At least one
variables block is required, and multiple blocks may appear in Dakota input files for advanced studies.
The interface block of the input file specifies the simulation code that will be used to map variables into responses
as well as details on how Dakota will pass data to and from that code. In this example, the keyword direct
is used to indicate the use of a function linked directly into Dakota, and data is passed directly between the two.
The name of the function is identified by the analysis driver keyword. Alternatively, fork or system
executions can be used to invoke instances of a simulation code that is external to Dakota as explained in Section
2.3.5.2 and Chapter 16. In this case, data is passed between Dakota and the simulation via text files. At least one
interface block is required, and multiple blocks may appear in Dakota input files for advanced studies.
The responses block of the input file specifies the types of data that the interface will return to Dakota. They
are categorized primarily according to usage. Objective functions are used in optimization, calibration terms in
calibration, and response functions in sensitivity analysis and UQ. For the example shown in Figure 2.4, the as-
signment response functions = 1 indicates that there is only one response function. The responses block
can include additional information returned by the interface. That includes constraints and derivative information,
both discussed in Chapter 11. In this example, there are no constraints associated with Rosenbrock’s function,
so the keywords for constraint specifications are omitted. The keywords no gradients and no hessians
indicate that no derivatives will be provided to the method; none are needed for a parameter study. At least one
responses block is required, and multiple blocks may appear in Dakota input files for advanced studies.
We close this section with a list of rules regarding the formatting of the Dakota input file.
•“Flat” text only.
•Whitespace is ignored.
•Comments begin with # and continue to the end of the line.
•Keyword order is largely unimportant as long as major sections are respected and there is no ambiguity.
•Equal signs are optional.
•Strings can be surrounded by single or double quotes (but not “fancy” quotes).
•Scientific notation is fine.
Please see the Dakota Reference Manual [3] for additional details on this input file syntax.
2.3 Examples
This section serves to familiarize users with how to perform parameter studies, optimization, and uncertainty
quantification through their common Dakota interface. The initial examples utilize simple built in driver functions;
later we show how to utilize Dakota to drive the evaluation of user supplied black box code. The examples
presented in this chapter are intended to show the simplest use of Dakota for methods of each type. More advanced
examples of using Dakota for specific purposes are provided in subsequent, topic-based, chapters.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
32 CHAPTER 2. DAKOTA TUTORIAL
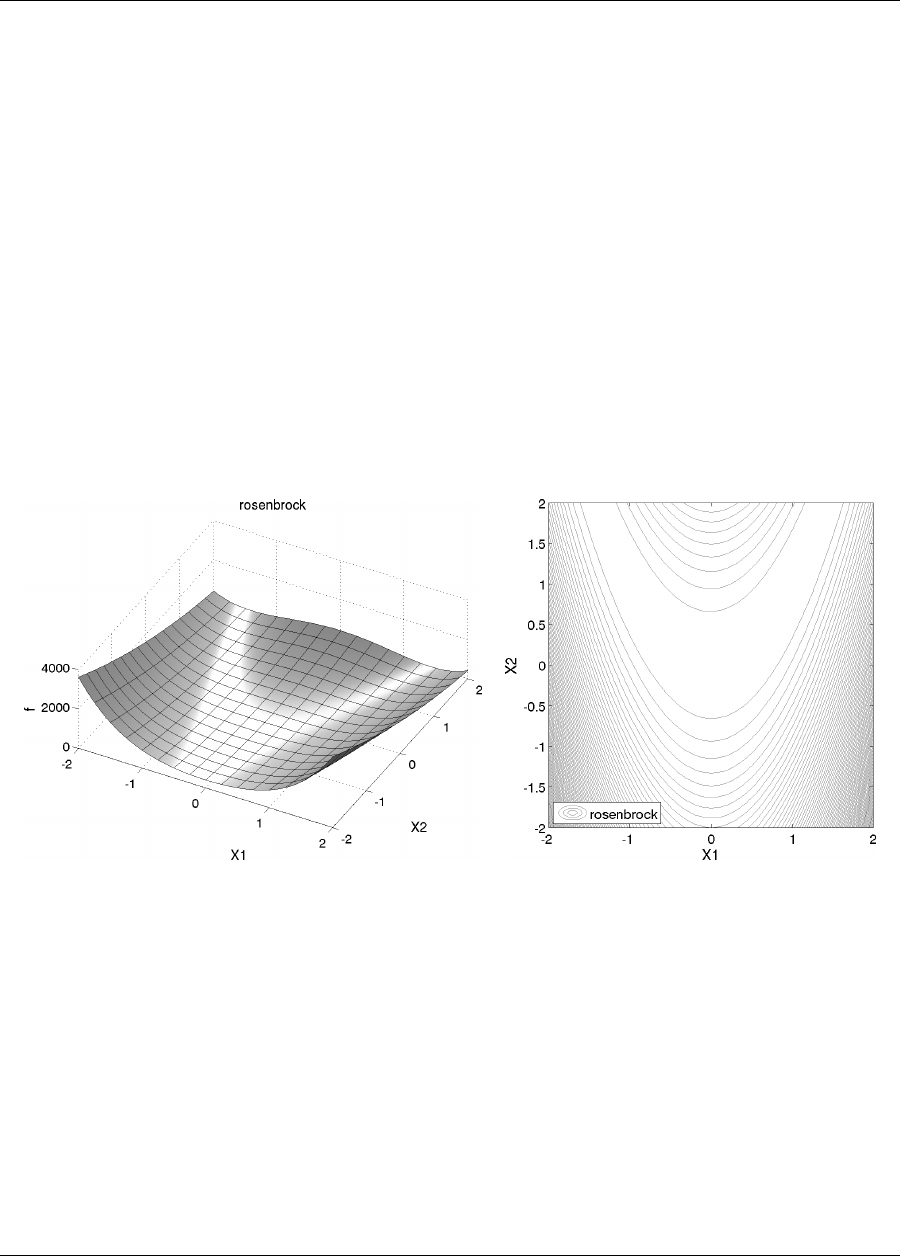
2.3.1 Rosenbrock Test Problem
The examples shown later in this chapter use the Rosenbrock function [115] (also described in [57], among other
places), which has the form:
f(x1, x2) = 100(x2−x2
1)2+ (1 −x1)2(2.1)
A three-dimensional plot of this function is shown in Figure 2.5(a), where both x1and x2range in value from −2
to 2. Figure 2.5(b) shows a contour plot for Rosenbrock’s function. An optimization problem using Rosenbrock’s
function is formulated as follows:
minimize f(x1, x2)
x∈ <2
subject to −2≤x1≤2(2.2)
−2≤x2≤2
(a) (b)
Figure 2.5: Rosenbrock’s function: (a) 3-D plot and (b) contours with x1on the bottom axis.
Note that there are no linear or nonlinear constraints in this formulation, so this is a bound constrained optimization
problem. The unique solution to this problem lies at the point (x1, x2) = (1,1), where the function value is zero.
Several other test problems are available. See Chapter 20 for a description of these test problems as well as further
discussion of the Rosenbrock test problem.
2.3.2 Two-Dimensional Grid Parameter Study
Parameter study methods in the Dakota toolkit involve the computation of response data sets at a selection of
points in the parameter space. These response data sets are not linked to any specific interpretation, so they may
consist of any allowable specification from the responses keyword block, i.e., objective and constraint functions,
Dakota Version 6.7 User’s Manual generated on November 13, 2017
2.3. EXAMPLES 33
least squares terms and constraints, or generic response functions. This allows the use of parameter studies in
direct coordination with optimization, least squares, and uncertainty quantification studies without significant
modification to the input file.
An example of a parameter study is the 2-D parameter study example problem listed in Figure 2.4. This is
executed by Dakota using the command noted in the comments:
dakota -i rosen_multidim.in -o rosen_multidim.out > rosen_multidim.stdout
The output of the Dakota run is written to the file named rosen multidim.out while the screen output, or
standard output, is redirect to rosen multidim.stdout. For comparison, files named rosen multidim.out.sav
and rosen multidim.stdout.sav are included in the Dakota/examples/users directory. As for
many of the examples, Dakota provides a report on the best design point located during the study at the end of
these output files.
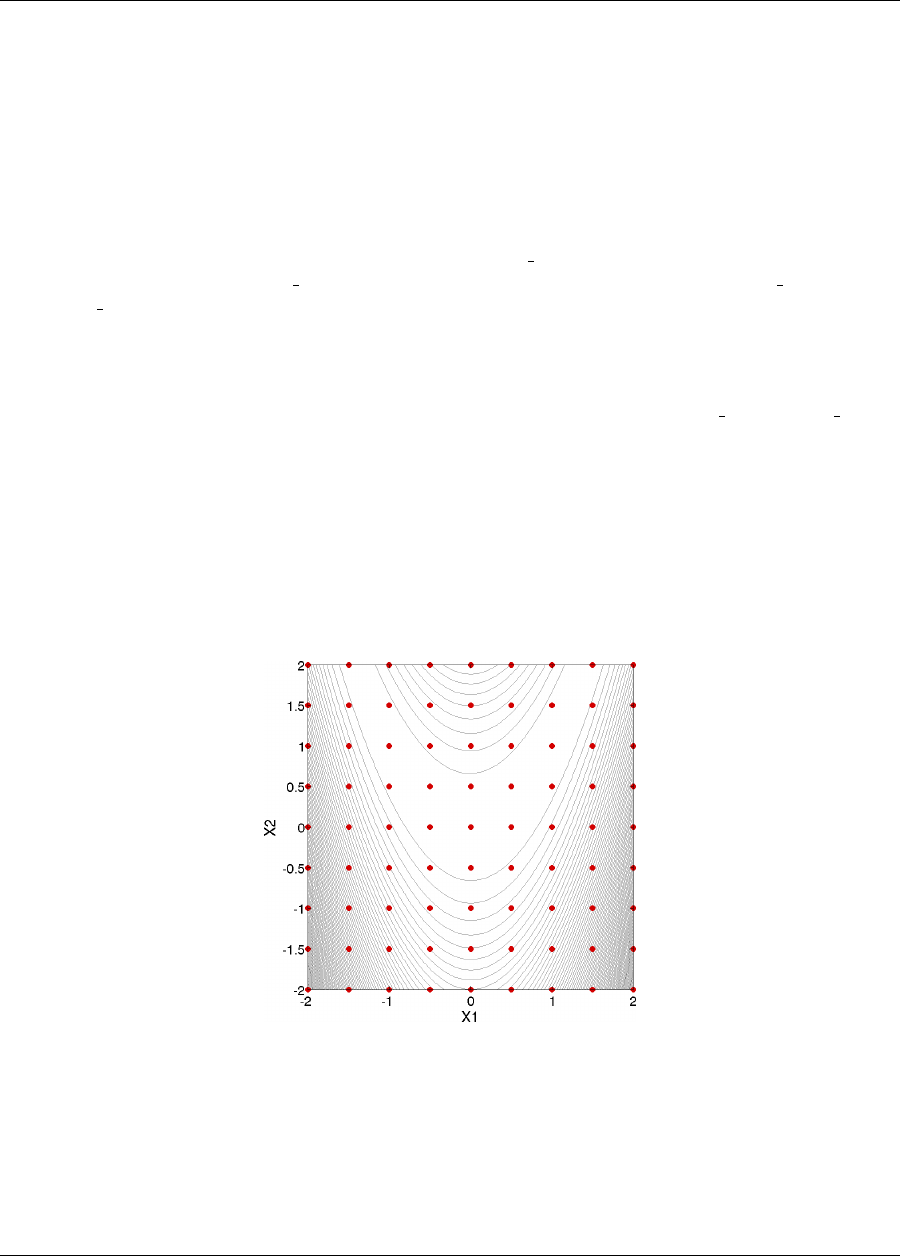
This 2-D parameter study produces the grid of data samples shown in Figure 2.6. In general, a multidimensional
parameter study lets one generate a grid in multiple dimensions. The keyword multidim parameter study
indicates that a grid will be generated over all variables. The keyword partitions indicates the number of grid
partitions in each dimension. For this example, the number of the grid partitions are the same in each dimension (8
partitions) but it would be possible to specify (partitions = 8 2), and have only two partitions over the second input
variable. Note that the graphics flag in the environment block of the input file could be commented out since,
for this example, the iteration history plots created by Dakota are not particularly instructive. More interesting
visualizations can be created by importing Dakota’s tabular data into an external graphics/plotting package. Com-
mon graphics and plotting packages include Mathematica, Matlab, Microsoft Excel, Origin, Tecplot, Gnuplot and
many others. (Sandia National Laboratories and the Dakota developers do not endorse any of these commercial
products.)
Figure 2.6: Rosenbrock 2-D parameter study example: location of the design points (dots) evaluated.
2.3.3 Gradient-based Unconstrained Optimization
Dakota’s optimization capabilities include a variety of gradient-based and nongradient-based optimization meth-
ods. This subsection demonstrates the use of one such method through the Dakota interface.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

34 CHAPTER 2. DAKOTA TUTORIAL
A Dakota input file for a gradient-based optimization of Rosenbrock’s function is listed in Figure 2.7. The
format of the input file is similar to that used for the parameter studies, but there are some new keywords in
the responses and method sections. First, in the responses block of the input file, the keyword block start-
ing with numerical gradients specifies that a finite difference method will be used to compute gradi-
ents for the optimization algorithm. Note that the Rosenbrock function evaluation code inside Dakota has the
ability to give analytical gradient values. (To switch from finite difference gradient estimates to analytic gra-
dients, uncomment the analytic gradients keyword and comment out the four lines associated with the
numerical gradients specification.) Next, in the method block of the input file, several new keywords have
been added. In this block, the keyword conmin frcg indicates the use of the Fletcher-Reeves conjugate gra-
dient algorithm in the CONMIN optimization software package [139] for bound-constrained optimization. The
keyword max iterations is used to indicate the computational budget for this optimization (in this case, a
single iteration includes multiple evaluations of Rosenbrock’s function for the gradient computation steps and the
line search steps). The keyword convergence tolerance is used to specify one of CONMIN’s convergence
criteria (under which CONMIN terminates if the objective function value differs by less than the absolute value
of the convergence tolerance for three successive iterations).
The Dakota command is noted in the file, and copies of the outputs are in the Dakota/examples/users
directory, with .sav appended to the name. When this example problem is executed using Dakota with graph-
ics support enabled, Dakota creates some iteration history graphics similar to the screen capture shown in Fig-
ure 2.8(a). These plots show how the objective function and design parameters change in value during the
optimization steps. The scaling of the horizontal and vertical axes can be changed by moving the scroll knobs on
each plot. Also, the “Options” button allows the user to plot the vertical axes using a logarithmic scale. Note that
log-scaling is only allowed if the values on the vertical axis are strictly greater than zero.
Figure 2.8(b) shows the iteration history of the optimization algorithm. The optimization starts at the point
(x1, x2)=(−1.2,1.0) as given in the Dakota input file. Subsequent iterations follow the banana-shaped val-
ley that curves around toward the minimum point at (x1, x2) = (1.0,1.0). Note that the function evaluations
associated with the line search phase of each CONMIN iteration are not shown on the plot. At the end of the
Dakota run, information is written to the output file to provide data on the optimal design point. These data in-
clude the optimum design point parameter values, the optimum objective and constraint function values (if any),
plus the number of function evaluations that occurred and the amount of time that elapsed during the optimization
study.
2.3.4 Uncertainty Quantification with Monte Carlo Sampling
Uncertainty quantification (UQ) is the process of determining the effect of input uncertainties on response metrics
of interest. These input uncertainties may be characterized as either aleatory uncertainties, which are irreducible
variabilities inherent in nature, or epistemic uncertainties, which are reducible uncertainties resulting from a lack
of knowledge. Since sufficient data is generally available for aleatory uncertainties, probabilistic methods are
commonly used for computing response distribution statistics based on input probability distribution specifica-
tions. Conversely, for epistemic uncertainties, data is generally sparse, making the use of probability theory
questionable and leading to nonprobabilistic methods based on interval specifications.
The subsection demonstrates the use of Monte Carlo random sampling for Uncertainty Quantification.
Figure 2.9 shows the Dakota input file for an example problem that demonstrates some of the random sampling
capabilities available in Dakota. In this example, the design parameters, x1 and x2, will be treated as uncertain
parameters that have uniform distributions over the interval [-2, 2]. This is specified in the variables block of
the input file, beginning with the keyword uniform uncertain. Another difference from earlier input files
such as Figure 2.7 occurs in the responses block, where the keyword response functions is used in place
of objective functions. The final changes to the input file occur in the method block, where the keyword
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.3. EXAMPLES 35
# Dakota Input File: rosen_grad_opt.in
# Usage:
# dakota -i rosen_grad_opt.in -o rosen_grad_opt.out > rosen_grad_opt.stdout
environment
graphics
tabular_data
tabular_data_file = ’rosen_grad_opt.dat’
method
conmin_frcg
convergence_tolerance = 1e-4
max_iterations = 100
model
single
variables
continuous_design = 2
initial_point -1.2 1.0
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
# analytic_gradients
numerical_gradients
method_source dakota
interval_type forward
fd_step_size = 1.e-5
no_hessians
Figure 2.7: Rosenbrock gradient-based unconstrained optimization example: the Dakota input file.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
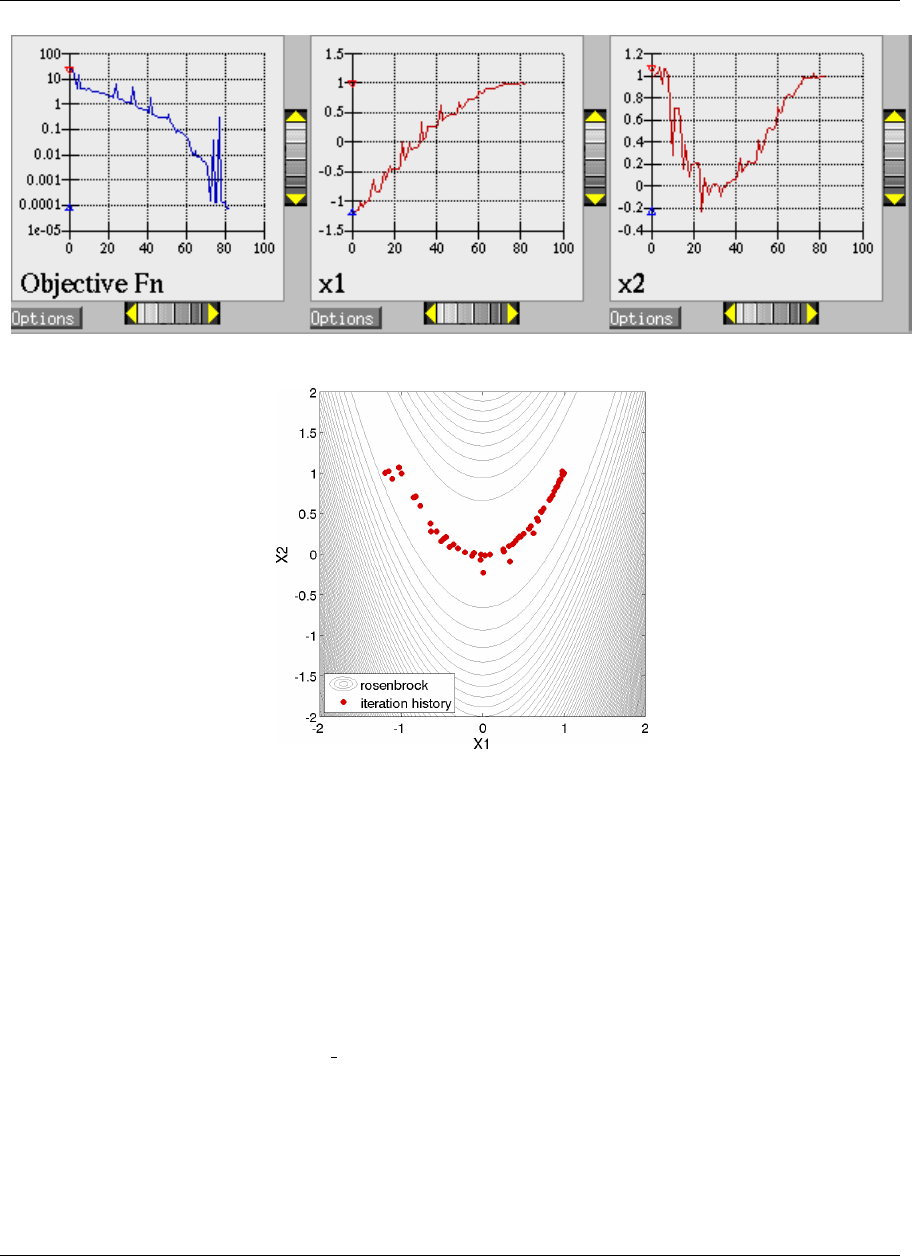
36 CHAPTER 2. DAKOTA TUTORIAL
(a)
(b)
Figure 2.8: Rosenbrock gradient-based unconstrained optimization example: (a) screen capture of the Dakota
graphics and (b) sequence of design points (dots) evaluated (line search points omitted).
sampling is used.
The other keywords in the methods block of the input file specify the number of samples (200), the seed for the
random number generator (17), the sampling method (random), and the response threshold (100.0). The seed
specification allows a user to obtain repeatable results from multiple runs. If a seed value is not specified, then
Dakota’s sampling methods are designed to generate nonrepeatable behavior (by initializing the seed using a
system clock). The keyword response levels allows the user to specify threshold values for which Dakota
will output statistics on the response function output. Note that a unique threshold value can be specified for each
response function.
In this example, Dakota will select 200 design points from within the parameter space, evaluate the value of
Rosenbrock’s function at all 200 points, and then perform some basic statistical calculations on the 200 response
values.
The Dakota command is noted in the file, and copies of the outputs are in the Dakota/examples/users
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.3. EXAMPLES 37
directory, with .sav appended to the name. Figure 2.10 shows example results from this sampling method. Note
that your results will differ from those in this file if your seed value differs or if no seed is specified.
As shown in Figure 2.10, the statistical data on the 200 Monte Carlo samples is printed at the end of the output
file in the section that starts with “Statistics based on 200 samples.” In this section summarizing moment-based
statistics, Dakota outputs the mean, standard deviation, skewness, and kurtosis estimates for each of the response
functions. For example, the mean of the Rosenbrock function given uniform input uncertainties on the input
variables is 455.4 and the standard deviation is 536.8. This is a very large standard deviation, due to the fact that
the Rosenbrock function varies by three orders of magnitude over the input domain. The skewness is positive,
meaning this is a right-tailed distribution, not a symmetric distribution. Finally, the kurtosis (a measure of the
“peakedness” of the distribution) indicates that this is a strongly peaked distribution (note that we use a central,
standardized kurtosis so that the kurtosis of a normal is zero). After the moment-related statistics, the 95% con-
fidence intervals on the mean and standard deviations are printed. This is followed by the fractions (“Probability
Level”) of the response function values that are below the response threshold values specified in the input file. For
example, 34 percent of the sample inputs resulted in a Rosenbrock function value that was less than or equal to
100, as shown in the line listing the cumulative distribution function values. Finally, there are several correlation
matrices printed at the end, showing simple and partial raw and rank correlation matrices. Correlations provide
an indication of the strength of a monotonic relationship between input and outputs. More detail on correlation
coefficients and their interpretation can be found in Section 5.2.1. More detail about sampling methods in general
can be found in Section 5.2. Finally, Figure 2.11 shows the locations of the 200 sample sites within the parameter
space of the Rosenbrock function for this example.
2.3.5 User Supplied Simulation Code Examples
This subsection provides examples of how to use Dakota to drive user supplied black box code.
2.3.5.1 Optimization with a User-Supplied Simulation Code - Case 1
Many of the previous examples made use of the direct interface to access the Rosenbrock and textbook test
functions that are compiled into Dakota. In engineering applications, it is much more common to use the fork
interface approach within Dakota to manage external simulation codes. In both of these cases, the communication
between Dakota and the external code is conducted through the reading and writing of short text files. For this
example, the C++ program rosenbrock.cpp in Dakota Source/test is used as the simulation code. This
file is compiled to create the stand-alone rosenbrock executable that is referenced as the analysis driver
in Figure 2.12. This stand-alone program performs the same function evaluations as Dakota’s internal Rosenbrock
test function.
Figure 2.12 shows the text of the Dakota input file named rosen syscall.in that is provided in the directory
Dakota/examples/users. The only differences between this input file and the one in Figure 2.7 occur in
the interface keyword section. The keyword fork indicates that Dakota will use fork calls to create separate Unix
processes for executions of the user-supplied simulation code. The name of the simulation code, and the names
for Dakota’s parameters and results file are specified using the analysis driver,parameters file, and
results file keywords, respectively.
The Dakota command is noted in the file, and copies of the outputs are in the Dakota/examples/users
directory, with .sav appended to the name.
This run of Dakota takes longer to complete than the previous gradient-based optimization example since the
fork interface method has additional process creation and file I/O overhead, as compared to the internal com-
munication that occurs when the direct interface method is used.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

38 CHAPTER 2. DAKOTA TUTORIAL
# Dakota Input File: rosen_sampling.in
# Usage:
# dakota -i rosen_sampling.in -o rosen_sampling.out > rosen_sampling.stdout
environment
graphics
tabular_data
tabular_data_file = ’rosen_sampling.dat’
method
sampling
sample_type random
samples = 200
seed = 17
response_levels = 100.0
model
single
variables
uniform_uncertain = 2
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’rosenbrock’
direct
responses
response_functions = 1
no_gradients
no_hessians
Figure 2.9: Monte Carlo sampling example: the Dakota input file.
To gain a better understanding of what exactly Dakota is doing with the fork interface approach, add the key-
words file tag and file save to the interface specification and re-run Dakota. Check the listing of the
local directory and you will see many new files with names such as params.in.1,params.in.2, etc., and
results.out.1,results.out.2, etc. There is one params.in.X file and one results.out.X file
for each of the function evaluations performed by Dakota. This is the file listing for params.in.1:
2 variables
-1.200000000000000e+00 x1
1.000000000000000e+00 x2
1 functions
1 ASV_1:obj_fn
2 derivative_variables
1 DVV_1:x1
2 DVV_2:x2
0 analysis_components
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.3. EXAMPLES 39
Statistics based on 200 samples:
Moment-based statistics for each response function:
Mean Std Dev Skewness Kurtosis
response_fn_1 4.5540183516e+02 5.3682678089e+02 1.6661798252e+00 2.7925726822e+00
95% confidence intervals for each response function:
LowerCI_Mean UpperCI_Mean LowerCI_StdDev UpperCI_StdDev
response_fn_1 3.8054757609e+02 5.3025609422e+02 4.8886795789e+02 5.9530059589e+02
Level mappings for each response function:
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e+02 3.4000000000e-01
Probability Density Function (PDF) histograms for each response function:
PDF for response_fn_1:
Bin Lower Bin Upper Density Value
--------- --------- -------------
1.1623549854e-01 1.0000000000e+02 3.4039566059e-03
1.0000000000e+02 2.7101710856e+03 2.5285698843e-04
Simple Correlation Matrix among all inputs and outputs:
x1 x2 response_fn_1
x1 1.00000e+00
x2 -5.85097e-03 1.00000e+00
response_fn_1 -9.57746e-02 -5.08193e-01 1.00000e+00
Partial Correlation Matrix between input and output:
response_fn_1
x1 -1.14659e-01
x2 -5.11111e-01
Simple Rank Correlation Matrix among all inputs and outputs:
x1 x2 response_fn_1
x1 1.00000e+00
x2 -6.03315e-03 1.00000e+00
response_fn_1 -1.15360e-01 -5.04661e-01 1.00000e+00
Partial Rank Correlation Matrix between input and output:
response_fn_1
x1 -1.37154e-01
x2 -5.08762e-01
Figure 2.10: Results of Monte Carlo Sampling on the Rosenbrock Function
Dakota Version 6.7 User’s Manual generated on November 13, 2017
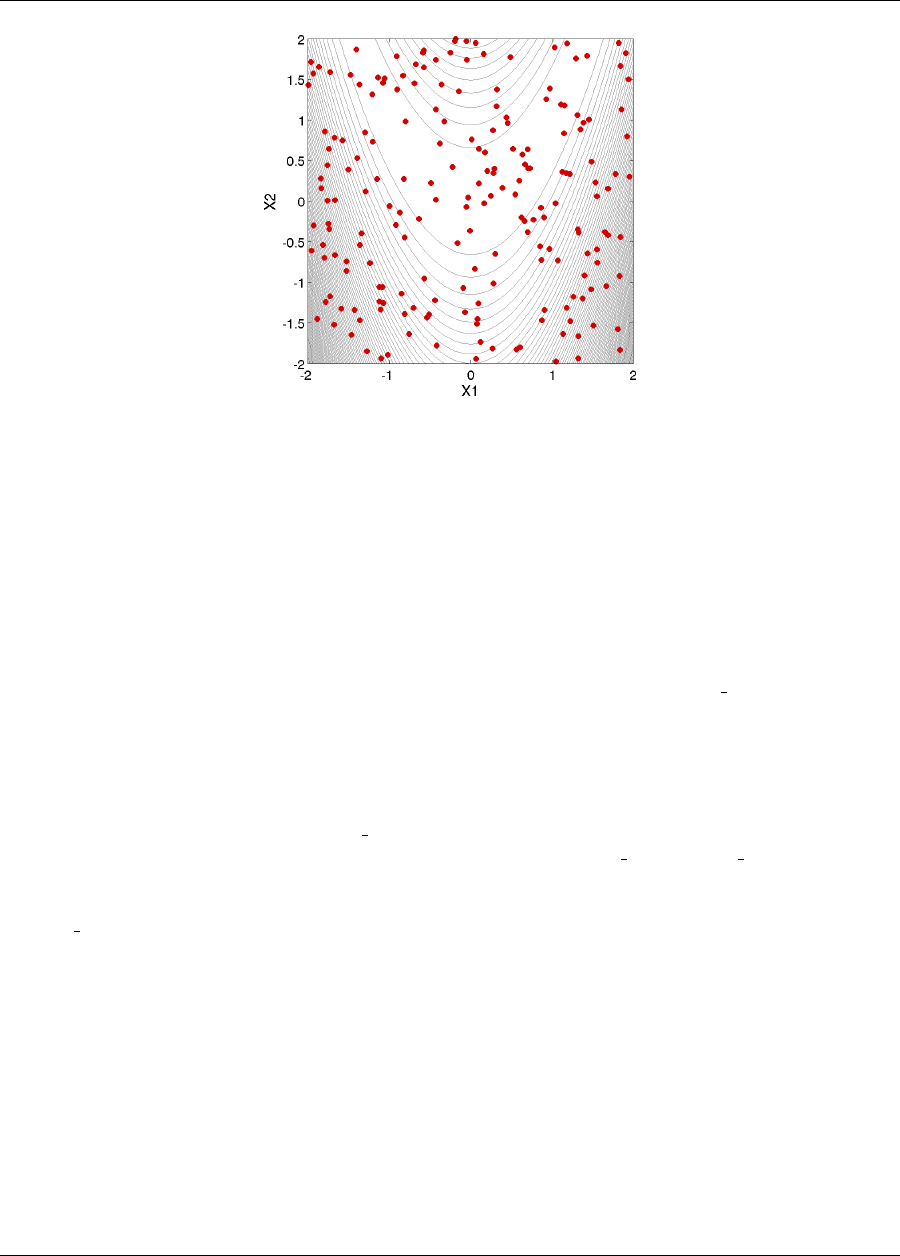
40 CHAPTER 2. DAKOTA TUTORIAL
Figure 2.11: Monte Carlo sampling example: locations in the parameter space of the 200 Monte Carlo samples
using a uniform distribution for both x1and x2.
The basic pattern is that of array lengths and string identifiers followed by listings of the array entries, where the
arrays consist of the variables, the active set vector (ASV), the derivative values vector (DVV), and the analysis
components (AC). For the variables array, the first line gives the total number of variables (2) and the “variables”
string identifier, and the subsequent two lines provide the array listing for the two variable values (-1.2 and 1.0)
and descriptor tags (“x1” and “x2” from the Dakota input file). The next array conveys the ASV, which indicates
what simulator outputs are needed. The first line of the array gives the total number of response functions (1)
and the “functions” string identifier, followed by one ASV code and descriptor tag (“ASV 1”) for each function.
In this case, the ASV value of 1 indicates that Dakota is requesting that the simulation code return the response
function value in the file results.out.X. (Possible ASV values: 1 = value of response function value, 2
= response function gradient, 4 = response function Hessian, and any sum of these for combinations up to 7
= response function value, gradient, and Hessian; see 9.7 for more detail.) The next array provides the DVV,
which defines the variable identifiers used in computing derivatives. The first line of the array gives the number
of derivative variables (2) and the “derivative variables” string identifier, followed by the listing of the two DVV
variable identifiers (the first and second variables) and descriptor tags (“DVV 1” and “DVV 2”). The final array
provides the AC array used to provide additional strings for use by the simulator (e.g., to provide the name of
a particular mesh file). The first line of the array gives the total number of analysis components (0) and the
“analysis components” string identifier, followed by the listing of the array, which is empty in this case.
The executable program rosenbrock reads in the params.in.X file and evaluates the objective function at the
given values for x1and x2. Then, rosenbrock writes out the objective function data to the results.out.X file.
Here is the listing for the file results.out.1:
2.420000000000000e+01 f
The value shown above is the value of the objective function, and the descriptor ‘f’ is an optional tag returned by
the simulation code. When the fork call has completed, Dakota reads in the data from the results.in.X file
and processes the results. Dakota then continues with additional executions of the rosenbrock program until the
optimization process is complete.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.3. EXAMPLES 41
2.3.5.2 Optimization with a User-Supplied Simulation Code - Case 2
In many situations the user-supplied simulation code cannot be modified to read and write the params.in.X
file and the results.out.X file, as described above. Typically, this occurs when the simulation code is a
commercial or proprietary software product that has specific input file and output file formats. In such cases, it
is common to replace the executable program name in the Dakota input file with the name of a Unix shell script
containing a sequence of commands that read and write the necessary files and run the simulation code. For
example, the executable program named rosenbrock listed in Figure 2.12 could be replaced by a Unix Bourne
or C-shell script named simulator script, with the script containing a sequence of commands to perform
# Dakota Input File: rosen_syscall.in
# Usage:
# dakota -i rosen_syscall.in -o rosen_syscall.out > rosen_syscall.stdout
environment
graphics
tabular_data
tabular_data_file = ’rosen_syscall.dat’
method
conmin_frcg
convergence_tolerance = 1e-4
max_iterations = 100
model
single
variables
continuous_design = 2
initial_point -1.2 1.0
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
fork
parameters_file = ’params.in’
results_file = ’results.out’
responses
objective_functions = 1
numerical_gradients
method_source dakota
interval_type forward
fd_step_size = 1.e-5
no_hessians
Figure 2.12: Dakota input file for gradient-based optimization using the fork call interface to an external rosen-
brock simulator.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

42 CHAPTER 2. DAKOTA TUTORIAL
the following steps: insert the data from the parameters.in.X file into the input file of the simulation code,
execute the simulation code, post-process the files generated by the simulation code to compute response data, and
return the response data to Dakota in the results.out.X file. The steps that are typically used in constructing
and using a Unix shell script are described in Section 10.3.
2.4 Dakota Command-Line Options
The Dakota executable file is named dakota (dakota.exe on Windows). If this command is entered at the
command prompt without any arguments, a usage message similar to the following appears:
usage: dakota [options and <args>]
-help (Print this summary)
-version (Print Dakota version number)
-input <$val> (REQUIRED Dakota input file $val)
-output <$val> (Redirect Dakota standard output to file $val)
-error <$val> (Redirect Dakota standard error to file $val)
-parser <$val> (Parsing technology: nidr[strict][:dumpfile])
-no_input_echo (Do not echo Dakota input file)
-check (Perform input checks)
-pre_run [$val] (Perform pre-run (variables generation) phase)
-run [$val] (Perform run (model evaluation) phase)
-post_run [$val] (Perform post-run (final results) phase)
-read_restart [$val] (Read an existing Dakota restart file $val)
-stop_restart <$val> (Stop restart file processing at evaluation $val)
-write_restart [$val] (Write a new Dakota restart file $val)
Of these available command line inputs, only the “-input” option is required, and “-input” can be omitted
if the input file name is the final item on the command line; all other command-line inputs are optional. The
“-help” option prints the usage message above. The “-version” option prints the version number of the
executable. The “-check” option invokes a dry-run mode in which the input file is processed and checked for
errors, but the study is not performed. The “-input” option provides the name of the Dakota input file. The
“-output” and “-error” options provide file names for redirection of the Dakota standard output (stdout)
and standard error (stderr), respectively. By default, Dakota will echo the input file to the output stream, but
“-no input echo” can override this behavior.
The “-parser” input is for debugging and will not be further described here. The “-read restart” and
“-write restart” options provide the names of restart databases to read from and write to, respectively.
The “-stop restart” option limits the number of function evaluations read from the restart database (the
default is all the evaluations) for those cases in which some evaluations were erroneous or corrupted. Restart
management is an important technique for retaining data from expensive engineering applications. This advanced
topic is discussed in detail in Chapter 18. Note that these command line options can be abbreviated so long as
the abbreviation is unique. Accordingly, the following are valid, unambiguous specifications: “-h”, “-v”, “-c”,
“-i”, “-o”, “-e”, “-re”, “-s”, “-w”, “-pr”, “-ru”, and “-po” and can be used in place of the longer forms
of the command line options.
To run Dakota with a particular input file, the following syntax can be used:
dakota -i dakota.in
or more simply
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.5. NEXT STEPS 43
dakota dakota.in
This will echo the standard output (stdout) and standard error (stderr) messages to the terminal. To redirect stdout
and stderr to separate files, the -o and -e command line options may be used:
dakota -i dakota.in -o dakota.out -e dakota.err
or
dakota -o dakota.out -e dakota.err dakota.in
Alternatively, any of a variety of Unix redirection variants can be used. The simplest of these redirects stdout to
another file:
dakota dakota.in > dakota.out
To run the dakota process in the background, append an ampersand symbol (&) to the command with an embedded
space, e.g.,
dakota dakota.in > dakota.out &
Refer to [6] for more information on Unix redirection and background commands.
The “-pre run”, “-run”, and “-post run” options instruct Dakota to run one or more execution phases,
excluding others. For example pre-run might generate variable sets, run (core run) might invoke the simulation
to evaluate variables and produce responses, and post-run might accept variable/response sets and analyzes the
results (for example, calculate correlations from a set of samples). Currently only two modes are supported and
only for sampling, parameter study, and DACE methods: (1) pre-run only with optional tabular output of variables:
dakota -i dakota.in -pre_run [::myvariables.dat]
and (2) post-run only with required tabular input of variables/responses:
dakota -i dakota.in -post_run myvarsresponses.dat::
2.5 Next Steps
After reading this chapter, you should understand the mechanics of acquiring, installing, and executing Dakota
to perform simple studies. You should have a high-level appreciation for what inputs Dakota requires, how it
behaves during interfacing and operation for a few kinds of studies, and what representative output is obtained.
To effectively use Dakota, you will need to understand the character of your problem, select a Dakota method to
help you meet your analysis goals, and develop an interface to your computational model.
2.5.1 Problem Exploration and Method Selection
Section 1.2 provides a high-level overview of the analysis techniques available in Dakota, with references to more
details and usage guidelines in the following chapters. Selecting an appropriate method to meet your analysis
goals requires understanding problem characteristics. For example, in optimization, typical questions that should
Dakota Version 6.7 User’s Manual generated on November 13, 2017

44 CHAPTER 2. DAKOTA TUTORIAL
be addressed include: Are the design variables continuous, discrete, or mixed? Is the problem constrained or un-
constrained? How expensive are the response functions to evaluate? Will the response functions behave smoothly
as the design variables change or will there be nonsmoothness and/or discontinuities? Are the response functions
likely to be multimodal, such that global optimization may be warranted? Is analytic gradient data available,
and if not, can gradients be calculated accurately and cheaply? Questions pertinent for uncertainty quantification
may include: Can I accurately model the probabilistic distributions of my uncertain variables? Are the response
functions relatively linear? Am I interested in a full random process characterization of the response functions, or
just statistical results?
If there is not sufficient information from the problem description and prior knowledge to answer these questions,
then additional problem characterization activities may be warranted. Dakota parameter studies and design of
experiments methods can help answer these questions by systematically interrogating the model. The resulting
trends in the response functions can be evaluated to determine if these trends are noisy or smooth, unimodal or
multimodal, relatively linear or highly nonlinear, etc. In addition, the parameter studies may reveal that one or
more of the parameters do not significantly affect the results and can be omitted from the problem formulation.
This can yield a potentially large savings in computational expense for the subsequent studies. Refer to Chapters 3
and 4for additional information on parameter studies and design of experiments methods.
For a list of all the example Dakota input files, see Table 2.1. All of these input files can be found in
Dakota/examples/users.
2.5.2 Key Getting Started References
The following references address many of the most common questions raised by new Dakota users:
•Dakota documentation and training materials are available from the Dakota website http://dakota.
sandia.gov.
•Dakota input file syntax (valid keywords and settings) is described in the Dakota Reference Manual [3].
•Example input files are included throughout this manual, and are included in Dakota distributions and
installations. See Section 1.5 for help finding these files.
•Detailed method descriptions appear in the Method Tour in Chapters 3through 7.
•Building an interface to a simulation code: Section 10.3, and related information on parameters file formats
(Section 9.6) and results file format (Section 11.2).
•Chapter 13 describes the different Dakota output file formats, including commonly encountered error mes-
sages.
•Chapter 18 describes the file restart and data re-use capabilities of Dakota.
•Documentation for getting started with the Dakota Graphical User Interface may be found here: https:
//dakota.sandia.gov/content/dakota-gui-user-manual.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

2.5. NEXT STEPS 45
Table 2.1: List of Example Input Files
Method Category Specific Method Input File Name Reference
parameter study multidimensional parameter study rosen multidim.in 2.4
parameter study vector parameter study rosen ps vector.in 3.3
design of comp exp moat (Morris) morris ps moat.in 20.22
uncertainty quantification random sampling rosen sampling.in 2.9
uncertainty quantification LHS sampling textbook uq sampling.in 5.2
uncertainty quantification polynomial chaos expansion rosen uq pce.in 5.14
uncertainty quantification stochastic collocation rosen uq sc.in 5.17
uncertainty quantification reliability Mean Value textbook uq meanvalue.in 5.8
uncertainty quantification reliability FORM logratio uq reliability.in 5.10
uncertainty quantification global interval analysis cantilever uq global interval.in 5.20
uncertainty quantification global evidence analysis textbook uq glob evidence.in 5.23
optimization gradient-based, unconstrained rosen grad opt.in 2.7
optimization gradient-based, unconstrained rosen syscall.in 2.12
optimization gradient-based, constrained textbook opt conmin.in 20.2
optimization gradient-based, constrained cantilever opt npsol.in 20.16
optimization gradient-based, constrained container opt npsol.in 13.1
optimization evolutionary algorithm rosen opt ea.in 6.3
optimization pattern search rosen opt patternsearch.in 6.1
optimization efficient global optimization (EGO) rosen opt ego.in 6.5
optimization efficient global optimization (EGO) herbie shubert opt ego.in 20.7
optimization multiobjective textbook opt multiobj1.in 6.6
optimization Pareto opt., moga mogatest1.in 6.8
optimization Pareto opt., moga mogatest2.in 20.17
optimization Pareto opt., moga mogatest3.in 20.19
optimization optimization with scaling rosen opt scaled.in 6.10
calibration nonlinear least squares rosen opt nls.in 20.4
calibration NLS with datafile textbook nls datafile.in
advanced methods hybrid minimization textbook hybrid strat.in 14.1
advanced methods Pareto minimization textbook pareto strat.in 14.4
advanced methods multistart minimization qsf multistart strat.in 14.2
advanced methods surrogate based global mogatest1 opt sbo.in 14.10
advanced methods surrogate based local rosen opt sbo.in 14.8
advanced models opt. under uncertainty (OUU) textbook opt ouu1.in 15.5
advanced models second order probability cantilever uq sop rel.in 15.2
advanced models sampling on a surrogate model textbook uq surrogate.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

46 CHAPTER 2. DAKOTA TUTORIAL
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 3
Parameter Study Capabilities
3.1 Overview
Dakota parameter studies explore the effect of parametric changes within simulation models by computing re-
sponse data sets at a selection of points in the parameter space, yielding one type of sensitivity analysis. (For a
comparison with DACE-based sensitivity analysis, see Section 4.6.) The selection of points is deterministic and
structured, or user-specified, in each of the four available parameter study methods:
•Vector: Performs a parameter study along a line between any two points in an n-dimensional parameter
space, where the user specifies the number of steps used in the study.
•List: The user supplies a list of points in an n-dimensional space where Dakota will evaluate response data
from the simulation code.
•Centered: Given a point in an n-dimensional parameter space, this method evaluates nearby points along
the coordinate axes of the parameter space. The user selects the number of steps and the step size.
•Multidimensional: Forms a regular lattice or hypergrid in an n-dimensional parameter space, where the
user specifies the number of intervals used for each parameter.
More detail on these parameter studies is found in Sections 3.2 through 3.5 below.
When used in parameter studies, the response data sets are not linked to any specific interpretation, so they may
consist of any allowable specification from the responses keyword block, i.e., objective and constraint functions,
least squares terms and constraints, or generic response functions. This allows the use of parameter studies in
alternation with optimization, least squares, and uncertainty quantification studies with only minor modification
to the input file. In addition, the response data sets may include gradients and Hessians of the response functions,
which will be catalogued by the parameter study. This allows for several different approaches to “sensitivity
analysis”: (1) the variation of function values over parameter ranges provides a global assessment as to the
sensitivity of the functions to the parameters, (2) derivative information can be computed numerically, provided
analytically by the simulator, or both (mixed gradients) in directly determining local sensitivity information at a
point in parameter space, and (3) the global and local assessments can be combined to investigate the variation of
derivative quantities through the parameter space by computing sensitivity information at multiple points.
In addition to sensitivity analysis applications, parameter studies can be used for investigating nonsmoothness in
simulation response variations (so that models can be refined or finite difference step sizes can be selected for

48 CHAPTER 3. PARAMETER STUDY CAPABILITIES
computing numerical gradients), interrogating problem areas in the parameter space, or performing simulation
code verification (verifying simulation robustness) through parameter ranges of interest. A parameter study can
also be used in coordination with minimization methods as either a pre-processor (to identify a good starting
point) or a post-processor (for post-optimality analysis).
Parameter study methods will iterate any combination of design, uncertain, and state variables defined over con-
tinuous and discrete domains into any set of responses (any function, gradient, and Hessian definition). Parameter
studies draw no distinction among the different types of continuous variables (design, uncertain, or state) or
among the different types of response functions. They simply pass all of the variables defined in the variables
specification into the interface, from which they expect to retrieve all of the responses defined in the responses
specification. As described in Section 11.3, when gradient and/or Hessian information is being catalogued in the
parameter study, it is assumed that derivative components will be computed with respect to all of the continuous
variables (continuous design, continuous uncertain, and continuous state variables) specified, since derivatives
with respect to discrete variables are assumed to be undefined. The specification of initial values or bounds is
important for parameter studies.
3.1.1 Initial Values
The vector and centered parameter studies use the initial values of the variables from the variables keyword
block as the starting point and the central point of the parameter studies, respectively. In the case of design
variables, the initial point is used, and in the case of state variables, the initial state is used (see the
Dakota Reference Manual [3] for default values when initial point or initial state are unspecified).
In the case of uncertain variables, initial values are inferred from the distribution specification: all uncertain
initial values are set to their means, where mean values for bounded normal and bounded lognormal are repaired
of needed to satisfy the specified distribution bounds, mean values for discrete integer range distributions are
rounded down to the nearest integer, and mean values for discrete set distributions are rounded to the nearest
set value. These parameter study starting values for design, uncertain, and state variables are referenced in the
following sections using the identifier “Initial Values.”
3.1.2 Bounds
The multidimensional parameter study uses the bounds of the variables from the variables keyword block to
define the range of parameter values to study. In the case of design and state variables, the lower bounds
and upper bounds specifications are used (see the Dakota Reference Manual [3] for default values when
lower bounds or upper bounds are unspecified). In the case of uncertain variables, these values are either
drawn or inferred from the distribution specification. Distribution lower and upper bounds can be drawn directly
from required bounds specifications for uniform, loguniform, triangular, and beta distributions, as well as from
optional bounds specifications for normal and lognormal. Distribution bounds are implicitly defined for histogram
bin, histogram point, and interval variables (from the extreme values within the bin/point/interval specifications)
as well as for binomial (0 to num trials) and hypergeometric (0 to min(num drawn,num selected)) vari-
ables. Finally, distribution bounds are inferred for normal and lognormal if optional bounds are unspecified, as
well as for exponential, gamma, gumbel, frechet, weibull, poisson, negative binomial, and geometric (which have
no bounds specifications); these bounds are [0, µ+3σ] for exponential, gamma, frechet, weibull, poisson, negative
binomial, geometric, and unspecified lognormal, and [µ−3σ,µ+ 3σ] for gumbel and unspecified normal.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

3.2. VECTOR PARAMETER STUDY 49
3.2 Vector Parameter Study
The vector parameter study computes response data sets at selected intervals along an n-dimensional vector in
parameter space. This capability encompasses both single-coordinate parameter studies (to study the effect of
a single variable on a response set) as well as multiple coordinate vector studies (to investigate the response
variations along some arbitrary vector; e.g., to investigate a search direction failure).
Dakota’s vector parameter study includes two possible specification formulations which are used in conjunction
with the Initial Values (see Section 3.1.1) to define the vector and steps of the parameter study:
final_point (vector of reals) and num_steps (integer)
step_vector (vector of reals) and num_steps (integer)
In both of these cases, the Initial Values are used as the parameter study starting point and the specification
selection above defines the orientation of the vector and the increments to be evaluated along the vector. In
the former case, the vector from initial to final point is partitioned by num steps, and in the latter case, the
step vector is added num steps times. In the case of discrete range variables, both final point and
step vector are specified in the actual values; and in the case of discrete sets (integer or real), final point
is specified in the actual values but step vector must instead specify index offsets for the (ordered, unique)
set. In all cases, the number of evaluations is num steps+1. Two examples are included below:
Three continuous parameters with initial values of (1.0, 1.0, 1.0), num steps = 4, and either final point =
(1.0, 2.0, 1.0) or step vector = (0, .25, 0):
Parameters for function evaluation 1:
1.0000000000e+00 c1
1.0000000000e+00 c2
1.0000000000e+00 c3
Parameters for function evaluation 2:
1.0000000000e+00 c1
1.2500000000e+00 c2
1.0000000000e+00 c3
Parameters for function evaluation 3:
1.0000000000e+00 c1
1.5000000000e+00 c2
1.0000000000e+00 c3
Parameters for function evaluation 4:
1.0000000000e+00 c1
1.7500000000e+00 c2
1.0000000000e+00 c3
Parameters for function evaluation 5:
1.0000000000e+00 c1
2.0000000000e+00 c2
1.0000000000e+00 c3
Two continuous parameters with initial values of (1.0, 1.0), one discrete range parameter with initial value of 5,
one discrete real set parameter with set values of (10., 12., 18., 30., 50.) and initial value of 10., num steps = 4,
and either final point = (2.0, 1.4, 13, 50.) or step vector = (.25, .1, 2, 1):
Parameters for function evaluation 1:
1.0000000000e+00 c1
1.0000000000e+00 c2
5 di1
Dakota Version 6.7 User’s Manual generated on November 13, 2017

50 CHAPTER 3. PARAMETER STUDY CAPABILITIES
1.0000000000e+01 dr1
Parameters for function evaluation 2:
1.2500000000e+00 c1
1.1000000000e+00 c2
7 di1
1.2000000000e+01 dr1
Parameters for function evaluation 3:
1.5000000000e+00 c1
1.2000000000e+00 c2
9 di1
1.8000000000e+01 dr1
Parameters for function evaluation 4:
1.7500000000e+00 c1
1.3000000000e+00 c2
11 di1
3.0000000000e+01 dr1
Parameters for function evaluation 5:
2.0000000000e+00 c1
1.4000000000e+00 c2
13 di1
5.0000000000e+01 dr1
An example using a vector parameter study is described in Section 3.7.
3.3 List Parameter Study
The list parameter study computes response data sets at selected points in parameter space. These points are
explicitly specified by the user and are not confined to lie on any line or surface. Thus, this parameter study
provides a general facility that supports the case where the desired set of points to evaluate does not fit the
prescribed structure of the vector, centered, or multidimensional parameter studies.
The user input consists of a list of points specification which lists the requested parameter sets in succes-
sion. The list parameter study simply performs a simulation for the first parameter set (the first nentries in the
list), followed by a simulation for the next parameter set (the next nentries), and so on, until the list of points has
been exhausted. Since the Initial Values will not be used, they need not be specified. In the case of discrete range
or discrete set variables, list values are specified using the actual values (not set indices).
An example specification that would result in the same parameter sets as in the second example in Section 3.2
would be:
list_of_points = 1.0 1.0 5 10.
1.25 1.1 7 12.
1.5 1.2 9 18.
1.75 1.3 11 30.
2.0 1.4 13 50.
For convenience, the points for evaluation in a list parameter study may instead be specified via the import points file
specification, e.g., ’import points file listpstudy.dat’, where the file listpstudy.dat may
be in freeform or annotated format 12.1.1. The ordering of the points is in input specification order, with both
active and inactive variables by default.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

3.4. CENTERED PARAMETER STUDY 51
3.4 Centered Parameter Study
The centered parameter study executes multiple coordinate-based parameter studies, one per parameter, centered
about the specified Initial Values. This is useful for investigation of function contours in the vicinity of a specific
point. For example, after computing an optimum design, this capability could be used for post-optimality analysis
in verifying that the computed solution is actually at a minimum or constraint boundary and in investigating the
shape of this minimum or constraint boundary.
This method requires step vector (list of reals) and steps per variable (list of integers) specifications,
where the former specifies the size of the increments per variable (employed sequentially, not all at once as
for the vector study in Section 3.2) and the latter specifies the number of increments per variable (employed
sequentially, not all at once) for each of the positive and negative step directions. As for the vector study described
in Section 3.2,step vector includes actual variable steps for continuous and discrete range variables, but
employs index offsets for discrete set variables (integer or real).
For example, with Initial Values of (1.0, 1.0), a step vector of (0.1, 0.1), and a steps per variable of
(2, 2), the center point is evaluated followed by four function evaluations (two negative deltas and two positive
deltas) per variable:
Parameters for function evaluation 1:
1.0000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 2:
8.0000000000e-01 d1
1.0000000000e+00 d2
Parameters for function evaluation 3:
9.0000000000e-01 d1
1.0000000000e+00 d2
Parameters for function evaluation 4:
1.1000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 5:
1.2000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 6:
1.0000000000e+00 d1
8.0000000000e-01 d2
Parameters for function evaluation 7:
1.0000000000e+00 d1
9.0000000000e-01 d2
Parameters for function evaluation 8:
1.0000000000e+00 d1
1.1000000000e+00 d2
Parameters for function evaluation 9:
1.0000000000e+00 d1
1.2000000000e+00 d2
This set of points in parameter space is depicted in Figure 3.1.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
52 CHAPTER 3. PARAMETER STUDY CAPABILITIES
Figure 3.1: Example centered parameter study.
3.5 Multidimensional Parameter Study
The multidimensional parameter study computes response data sets for an n-dimensional hypergrid of points.
Each variable is partitioned into equally spaced intervals between its upper and lower bounds (see Section 3.1.2),
and each combination of the values defined by these partitions is evaluated. As for the vector and centered studies
described in Sections 3.2 and 3.4, partitioning occurs using the actual variable values for continuous and discrete
range variables, but occurs within the space of valid indices for discrete set variables (integer or real). The number
of function evaluations performed in the study is:
n
Y
i=1
(partitionsi+ 1) (3.1)
The partitions information is specified using the partitions specification, which provides an integer list of the
number of partitions for each variable (i.e., partitionsi). Since the Initial Values will not be used, they need
not be specified.
In a two variable example problem with d1 ∈[0,2] and d2 ∈[0,3] (as defined by the upper and lower bounds
from the variables specification) and with partitions = (2,3), the interval [0,2] is divided into two equal-sized
partitions and the interval [0,3] is divided into three equal-sized partitions. This two-dimensional grid, shown in
Figure 3.2, would result in the following twelve function evaluations:
Parameters for function evaluation 1:
0.0000000000e+00 d1
0.0000000000e+00 d2
Parameters for function evaluation 2:
1.0000000000e+00 d1
0.0000000000e+00 d2
Parameters for function evaluation 3:
2.0000000000e+00 d1
0.0000000000e+00 d2
Parameters for function evaluation 4:
0.0000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 5:
Dakota Version 6.7 User’s Manual generated on November 13, 2017
3.5. MULTIDIMENSIONAL PARAMETER STUDY 53
Figure 3.2: Example multidimensional parameter study
1.0000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 6:
2.0000000000e+00 d1
1.0000000000e+00 d2
Parameters for function evaluation 7:
0.0000000000e+00 d1
2.0000000000e+00 d2
Parameters for function evaluation 8:
1.0000000000e+00 d1
2.0000000000e+00 d2
Parameters for function evaluation 9:
2.0000000000e+00 d1
2.0000000000e+00 d2
Parameters for function evaluation 10:
0.0000000000e+00 d1
3.0000000000e+00 d2
Parameters for function evaluation 11:
1.0000000000e+00 d1
3.0000000000e+00 d2
Parameters for function evaluation 12:
2.0000000000e+00 d1
3.0000000000e+00 d2
The first example shown in this User’s Manual is a multi-dimensional parameter study. See Section 2.3.2.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

54 CHAPTER 3. PARAMETER STUDY CAPABILITIES
3.6 Parameter Study Usage Guidelines
Parameter studies, classical design of experiments (DOE), design/analysis of computer experiments (DACE), and
sampling methods share the purpose of exploring the parameter space. Parameter Studies are recommended for
simple studies with defined, repetitive structure. A local sensitivity analysis or an assessment of the smoothness
of a response function is best addressed with a vector or centered parameter study. A multi-dimensional parameter
study may be used to generate grid points for plotting response surfaces. For guidance on DACE and sampling
methods, in contrast to parameter studies, see Section 4.7 and especially Table 4.4, which clarifies the different
purposes of the method types.
3.7 Example: Vector Parameter Study with Rosenbrock
This section demonstrates a vector parameter study on the Rosenbrock test function described in Section 2.3.1.
An example of multidimensional parameter study is shown in Section 2.3.2.
A vector parameter study is a study between any two design points in an n-dimensional parameter space. An input
file for the vector parameter study is shown in Figure 3.3. The primary differences between this input file and the
input file for the multidimensional parameter study are found in the variables and method sections. In the variables
section, the keywords for the bounds are removed and replaced with the keyword initial point that specifies
the starting point for the parameter study. In the method section, the vector parameter study keyword
is used. The final point keyword indicates the stopping point for the parameter study, and num steps
specifies the number of steps taken between the initial and final points in the parameter study.
Figure 3.4(a) shows the graphics output created by Dakota. For this study, the simple Dakota graphics are more
useful for visualizing the results. Figure 3.4(b) shows the locations of the 11 sample points generated in this study.
It is evident from these figures that the parameter study starts within the banana-shaped valley, marches up the
side of the hill, and then returns to the valley.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

3.7. EXAMPLE: VECTOR PARAMETER STUDY WITH ROSENBROCK 55
# Dakota Input File: rosen_ps_vector.in
environment
graphics
tabular_data
tabular_data_file = ’rosen_ps_vector.dat’
method
vector_parameter_study
final_point = 1.1 1.3
num_steps = 10
model
single
variables
continuous_design = 2
initial_point -0.3 0.2
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
no_gradients
no_hessians
Figure 3.3: Rosenbrock vector parameter study example: the Dakota input file – see
Dakota/examples/users/rosen ps vector.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
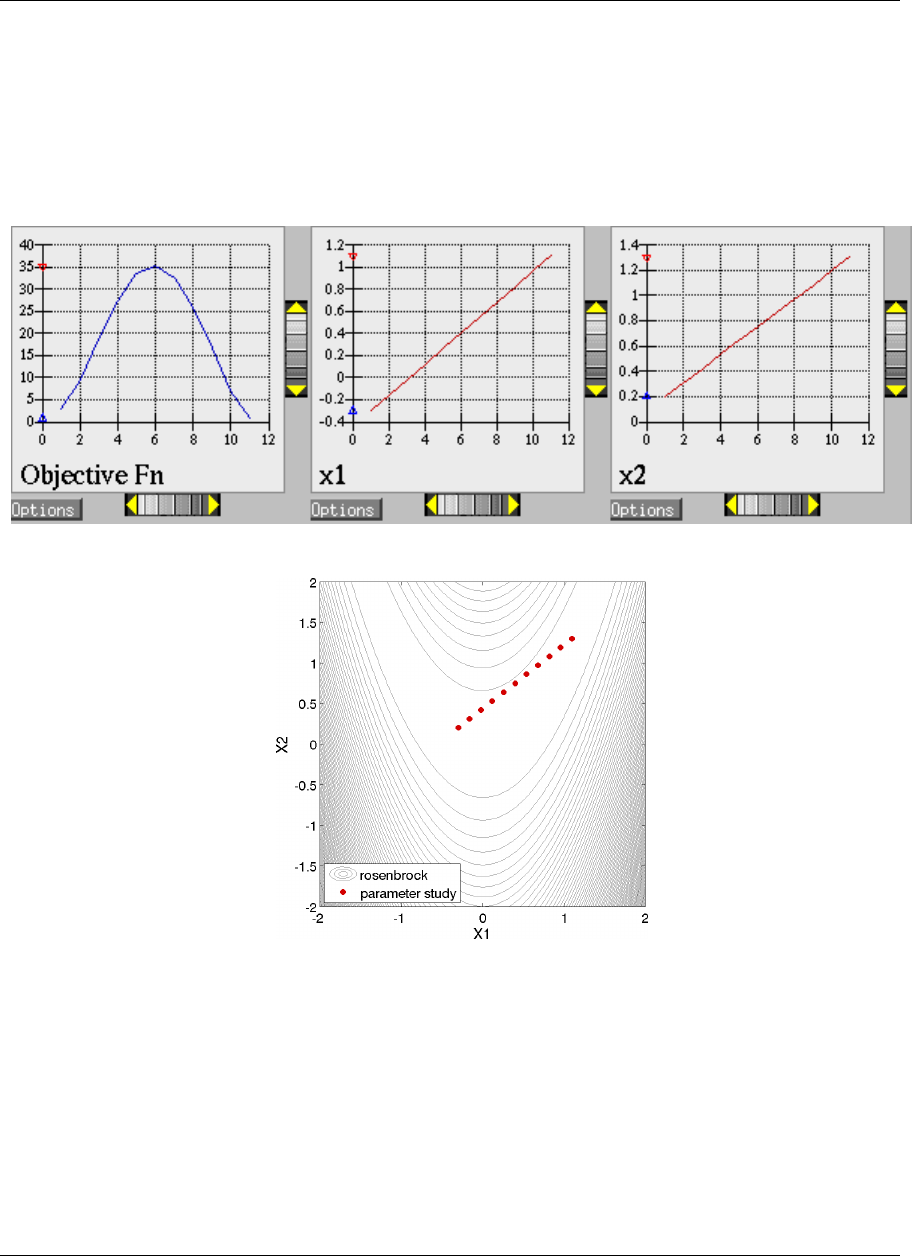
56 CHAPTER 3. PARAMETER STUDY CAPABILITIES
(a)
(b)
Figure 3.4: Rosenbrock vector parameter study example: (a) screen capture of the Dakota graphics and (b)
location of the design points (dots) evaluated.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 4
Design of Experiments Capabilities
4.1 Overview
Classical design of experiments (DoE) methods and the more modern design and analysis of computer experi-
ments (DACE) methods are both techniques which seek to extract as much trend data from a parameter space as
possible using a limited number of sample points. Classical DoE techniques arose from technical disciplines that
assumed some randomness and nonrepeatability in field experiments (e.g., agricultural yield, experimental chem-
istry). DoE approaches such as central composite design, Box-Behnken design, and full and fractional factorial
design generally put sample points at the extremes of the parameter space, since these designs offer more reliable
trend extraction in the presence of nonrepeatability. DACE methods are distinguished from DoE methods in that
the nonrepeatability component can be omitted since computer simulations are involved. In these cases, space
filling designs such as orthogonal array sampling and Latin hypercube sampling are more commonly employed
in order to accurately extract trend information. Quasi-Monte Carlo sampling techniques which are constructed
to fill the unit hypercube with good uniformity of coverage can also be used for DACE.
Dakota supports both DoE and DACE techniques. In common usage, only parameter bounds are used in selecting
the samples within the parameter space. Thus, DoE and DACE can be viewed as special cases of the more
general probabilistic sampling for uncertainty quantification (see following section), in which the DoE/DACE
parameters are treated as having uniform probability distributions. The DoE/DACE techniques are commonly
used for investigation of global response trends, identification of significant parameters (e.g., main effects), and
as data generation methods for building response surface approximations.
Dakota includes several approaches sampling and design of experiments, all implemented in included third-party
software libraries. LHS (Latin hypercube sampling) [132] is a general-purpose sampling package developed at
Sandia that has been used by the DOE national labs for several decades. DDACE (distributed design and analysis
for computer experiments) is a more recent package for computer experiments developed at Sandia Labs [137].
DDACE provides the capability for generating orthogonal arrays, Box-Behnken designs, Central Composite de-
signs, and random designs. The FSUDace (Florida State University’s Design and Analysis of Computer Ex-
periments) package provides the following sampling techniques: quasi-Monte Carlo sampling based on Halton
or Hammersley sequences, and Centroidal Voronoi Tessellation. Lawrence Livermore National Lab’s PSUADE
(Problem Solving Environment for Uncertainty Analysis and Design Exploration) [136] includes several methods
for model exploration, but only the Morris screening method is exposed in Dakota.
This chapter describes DDACE, FSUDace, and PSUADE, with a focus on designing computer experiments. Latin
Hypercube Sampling, also used in uncertainty quantification, is discussed in Section 5.2.

58 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
4.2 Design of Computer Experiments
What distinguishes design of computer experiments? Computer experiments are often different from physical
experiments, such as those performed in agriculture, manufacturing, or biology. In physical experiments, one
often applies the same treatment or factor level in an experiment several times to get an understanding of the
variability of the output when that treatment is applied. For example, in an agricultural experiment, several fields
(e.g., 8) may be subject to a low level of fertilizer and the same number of fields may be subject to a high level of
fertilizer to see if the amount of fertilizer has a significant effect on crop output. In addition, one is often interested
in the variability of the output within a treatment group: is the variability of the crop yields in the low fertilizer
group much higher than that in the high fertilizer group, or not?
In physical experiments, the process we are trying to examine is stochastic: that is, the same treatment may result
in different outcomes. By contrast, in computer experiments, often we have a deterministic code. If we run the
code with a particular set of input parameters, the code will always produce the same output. There certainly
are stochastic codes, but the main focus of computer experimentation has been on deterministic codes. Thus, in
computer experiments we often do not have the need to do replicates (running the code with the exact same input
parameters several times to see differences in outputs). Instead, a major concern in computer experiments is to
create an experimental design which can sample a high-dimensional space in a representative way with a minimum
number of samples. The number of factors or parameters that we wish to explore in computer experiments is
usually much higher than physical experiments. In physical experiments, one may be interested in varying a few
parameters, usually five or less, while in computer experiments we often have dozens of parameters of interest.
Choosing the levels of these parameters so that the samples adequately explore the input space is a challenging
problem. There are many experimental designs and sampling methods which address the issue of adequate and
representative sample selection.
There are many goals of running a computer experiment: one may want to explore the input domain or the
design space and get a better understanding of the range in the outputs for a particular domain. Another objective
is to determine which inputs have the most influence on the output, or how changes in the inputs change the
output. This is usually called sensitivity analysis. Another goal is to use the sampled input points and their
corresponding output to create a response surface approximation for the computer code. The response surface
approximation (e.g., a polynomial regression model, a Gaussian-process/Kriging model, a neural net) can then
be used to emulate the computer code. Constructing a response surface approximation is particularly important
for applications where running a computational model is extremely expensive: the computer model may take 10
or 20 hours to run on a high performance machine, whereas the response surface model may only take a few
seconds. Thus, one often optimizes the response surface model or uses it within a framework such as surrogate-
based optimization. Response surface models are also valuable in cases where the gradient (first derivative) and/or
Hessian (second derivative) information required by optimization techniques are either not available, expensive
to compute, or inaccurate because the derivatives are poorly approximated or the function evaluation is itself
noisy due to roundoff errors. Furthermore, many optimization methods require a good initial point to ensure
fast convergence or to converge to good solutions (e.g. for problems with multiple local minima). Under these
circumstances, a good design of computer experiment framework coupled with response surface approximations
can offer great advantages.
In addition to the sensitivity analysis and response surface modeling mentioned above, we also may want to do
uncertainty quantification on a computer model. Uncertainty quantification (UQ) refers to taking a particular set
of distributions on the inputs, and propagating them through the model to obtain a distribution on the outputs. For
example, if input parameter A follows a normal with mean 5 and variance 1, the computer produces a random
draw from that distribution. If input parameter B follows a weibull distribution with alpha = 0.5 and beta = 1, the
computer produces a random draw from that distribution. When all of the uncertain variables have samples drawn
from their input distributions, we run the model with the sampled values as inputs. We do this repeatedly to build
up a distribution of outputs. We can then use the cumulative distribution function of the output to ask questions
Dakota Version 6.7 User’s Manual generated on November 13, 2017

4.3. DDACE 59
such as: what is the probability that the output is greater than 10? What is the 99th percentile of the output?
Note that sampling-based uncertainty quantification and design of computer experiments are very similar. There
is significant overlap in the purpose and methods used for UQ and for DACE. We have attempted to delineate
the differences within Dakota as follows: we use the methods DDACE, FSUDACE, and PSUADE primarily for
design of experiments, where we are interested in understanding the main effects of parameters and where we
want to sample over an input domain to obtain values for constructing a response surface. We use the nondeter-
ministic sampling methods (sampling) for uncertainty quantification, where we are propagating specific input
distributions and interested in obtaining (for example) a cumulative distribution function on the output. If one
has a problem with no distributional information, we recommend starting with a design of experiments approach.
Note that DDACE, FSUDACE, and PSUADE currently do not support distributional information: they take an
upper and lower bound for each uncertain input variable and sample within that. The uncertainty quantification
methods in sampling (primarily Latin Hypercube sampling) offer the capability to sample from many distri-
butional types. The distinction between UQ and DACE is somewhat arbitrary: both approaches often can yield
insight about important parameters and both can determine sample points for response surface approximations.
Three software packages are available in Dakota for design of computer experiments, DDACE (developed at
Sandia Labs), FSUDACE (developed at Florida State University), and PSUADE (LLNL).
4.3 DDACE
The Distributed Design and Analysis of Computer Experiments (DDACE) package includes both classical design
of experiments methods [137] and stochastic sampling methods. The classical design of experiments methods
in DDACE are central composite design (CCD) and Box-Behnken (BB) sampling. A grid-based sampling (full-
factorial) method is also available. The stochastic methods are orthogonal array sampling [89] (which permits
main effects calculations), Monte Carlo (random) sampling, Latin hypercube sampling, and orthogonal array-
Latin hypercube sampling. While DDACE LHS supports variables with normal or uniform distributions, only
uniform are supported through Dakota. Also DDACE does not allow enforcement of user-specified correlation
structure among the variables.
The sampling methods in DDACE can be used alone or in conjunction with other methods. For example, DDACE
sampling can be used with both surrogate-based optimization and optimization under uncertainty advanced meth-
ods. See Figure 15.5 for an example of how the DDACE settings are used in Dakota.
The following sections provide more detail about the sampling methods available for design of experiments in
DDACE.
4.3.1 Central Composite Design
A Box-Wilson Central Composite Design, commonly called a central composite design (CCD), contains an em-
bedded factorial or fractional factorial design with center points that is augmented with a group of ’star points’
that allow estimation of curvature. If the distance from the center of the design space to a factorial point is ±1 unit
for each factor, the distance from the center of the design space to a star point is ±αwith |α|>1. The precise
value of αdepends on certain properties desired for the design and on the number of factors involved. The CCD
design is specified in Dakota with the method command dace central composite.
As an example, with two input variables or factors, each having two levels, the factorial design is shown in
Table 4.1 .
With a CCD, the design in Table 4.1 would be augmented with the following points shown in Table 4.2 if α= 1.3.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

60 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
Table 4.1: Simple Factorial Design
Input 1 Input 2
-1 -1
-1 +1
+1 -1
+1 +1
These points define a circle around the original factorial design.
Table 4.2: Additional Points to make the factorial design a CCD
Input 1 Input 2
0 +1.3
0 -1.3
1.3 0
-1.3 0
0 0
Note that the number of sample points specified in a CCD,samples, is a function of the number of variables in
the problem:
samples = 1 + 2 ∗N umV ar + 2NumV ar
4.3.2 Box-Behnken Design
The Box-Behnken design is similar to a Central Composite design, with some differences. The Box-Behnken
design is a quadratic design in that it does not contain an embedded factorial or fractional factorial design. In this
design the treatment combinations are at the midpoints of edges of the process space and at the center, as compared
with CCD designs where the extra points are placed at ’star points’ on a circle outside of the process space. Box-
Behken designs are rotatable (or near rotatable) and require 3 levels of each factor. The designs have limited
capability for orthogonal blocking compared to the central composite designs. Box-Behnken requires fewer runs
than CCD for 3 factors, but this advantage goes away as the number of factors increases. The Box-Behnken design
is specified in Dakota with the method command dace box behnken.
Note that the number of sample points specified in a Box-Behnken design, samples, is a function of the number
of variables in the problem:
samples = 1 + 4 ∗N umV ar + (NumV ar −1)/2
Dakota Version 6.7 User’s Manual generated on November 13, 2017
4.3. DDACE 61
4.3.3 Orthogonal Array Designs
Orthogonal array (OA) sampling is a widely used technique for running experiments and systematically testing
factor effects [75]. An orthogonal array sample can be described as a 4-tuple (m, n, s, r), where mis the number
of sample points, nis the number of input variables, sis the number of symbols, and ris the strength of the
orthogonal array. The number of sample points, m, must be a multiple of the number of symbols, s. The number
of symbols refers to the number of levels per input variable. The strength refers to the number of columns where
we are guaranteed to see all the possibilities an equal number of times.
For example, Table 4.3 shows an orthogonal array of strength 2 for m= 8, with 7 variables:
Table 4.3: Orthogonal Array for Seven Variables
Input 1 Input 2 Input 3 Input 4 Input 5 Input 6 Input 7
0000000
0001111
0110011
0111100
1010101
1011010
1100110
1101001
If one picks any two columns, say the first and the third, note that each of the four possible rows we might see
there, 0 0, 0 1, 1 0, 1 1, appears exactly the same number of times, twice in this case.
DDACE creates orthogonal arrays of strength 2. Further, the OAs generated by DDACE do not treat the factor
levels as one fixed value (0 or 1 in the above example). Instead, once a level for a variable is determined in the
array, DDACE samples a random variable from within that level. The orthogonal array design is specified in
Dakota with the method command dace oas.
The orthogonal array method in DDACE is the only method that allows for the calculation of main effects, speci-
fied with the command main effects. Main effects is a sensitivity analysis method which identifies the input
variables that have the most influence on the output. In main effects, the idea is to look at the mean of the response
function when variable A (for example) is at level 1 vs. when variable A is at level 2 or level 3. If these mean
responses of the output are statistically significantly different at different levels of variable A, this is an indication
that variable A has a significant effect on the response. The orthogonality of the columns is critical in performing
main effects analysis, since the column orthogonality means that the effects of the other variables ’cancel out’
when looking at the overall effect from one variable at its different levels. There are ways of developing orthog-
onal arrays to calculate higher order interactions, such as two-way interactions (what is the influence of Variable
A * Variable B on the output?), but this is not available in DDACE currently. At present, one way interactions
are supported in the calculation of orthogonal array main effects within DDACE. The main effects are presented
as a series of ANOVA tables. For each objective function and constraint, the decomposition of variance of that
objective or constraint is presented as a function of the input variables. The p-value in the ANOVA table is used
to indicate if the input factor is significant. The p-value is the probability that you would have obtained samples
more extreme than you did if the input factor has no effect on the response. For example, if you set a level of
significance at 0.05 for your p-value, and the actual p-value is 0.03, then the input factor has a significant effect
on the response.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

62 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
4.3.4 Grid Design
In a grid design, a grid is placed over the input variable space. This is very similar to a multi-dimensional
parameter study where the samples are taken over a set of partitions on each variable (see Section 3.5). The
main difference is that in grid sampling, a small random perturbation is added to each sample value so that the
grid points are not on a perfect grid. This is done to help capture certain features in the output such as periodic
functions. A purely structured grid, with the samples exactly on the grid points, has the disadvantage of not being
able to capture important features such as periodic functions with relatively high frequency (due to aliasing).
Adding a random perturbation to the grid samples helps remedy this problem.
Another disadvantage with grid sampling is that the number of sample points required depends exponentially on
the input dimensions. In grid sampling, the number of samples is the number of symbols (grid partitions) raised
to the number of variables. For example, if there are 2 variables, each with 5 partitions, the number of samples
would be 52. In this case, doubling the number of variables squares the sample size. The grid design is specified
in Dakota with the method command dace grid.
4.3.5 Monte Carlo Design
Monte Carlo designs simply involve pure Monte-Carlo random sampling from uniform distributions between the
lower and upper bounds on each of the input variables. Monte Carlo designs, specified by dace random, are a
way to generate a set of random samples over an input domain.
4.3.6 LHS Design
DDACE offers the capability to generate Latin Hypercube designs. For more information on Latin Hypercube
sampling, see Section 5.2. Note that the version of LHS in DDACE generates uniform samples (uniform between
the variable bounds). The version of LHS offered with nondeterministic sampling can generate LHS samples
according to a number of distribution types, including normal, lognormal, weibull, beta, etc. To specify the
DDACE version of LHS, use the method command dace lhs.
4.3.7 OA-LHS Design
DDACE offers a hybrid design which is combination of an orthogonal array and a Latin Hypercube sample.
This design is specified with the method command dace oa lhs. This design has the advantages of both
orthogonality of the inputs as well as stratification of the samples (see [111]).
4.4 FSUDace
The Florida State University Design and Analysis of Computer Experiments (FSUDace) package provides quasi-
Monte Carlo sampling (Halton and Hammersley) and Centroidal Voronoi Tessellation (CVT) methods. All three
methods natively generate sets of uniform random variables on the interval [0,1] (or in Dakota, on user-specified
uniform intervals).
The quasi-Monte Carlo and CVT methods are designed with the goal of low discrepancy. Discrepancy refers to the
nonuniformity of the sample points within the unit hypercube. Low discrepancy sequences tend to cover the unit
hypercube reasonably uniformly. Quasi-Monte Carlo methods produce low discrepancy sequences, especially if
Dakota Version 6.7 User’s Manual generated on November 13, 2017

4.5. PSUADE MOAT 63
one is interested in the uniformity of projections of the point sets onto lower dimensional faces of the hypercube
(usually 1-D: how well do the marginal distributions approximate a uniform?) CVT does very well volumetrically:
it spaces the points fairly equally throughout the space, so that the points cover the region and are isotropically
distributed with no directional bias in the point placement. There are various measures of volumetric uniformity
which take into account the distances between pairs of points, regularity measures, etc. Note that CVT does not
produce low-discrepancy sequences in lower dimensions, however: the lower-dimension (such as 1-D) projections
of CVT can have high discrepancy.
The quasi-Monte Carlo sequences of Halton and Hammersley are deterministic sequences determined by a set of
prime bases. A Halton design is specified in Dakota with the method command fsu quasi mc halton, and
the Hammersley design is specified with the command fsu quasi mc hammersley. For more details about
the input specification, see the Reference Manual. CVT points tend to arrange themselves in a pattern of cells that
are roughly the same shape. To produce CVT points, an almost arbitrary set of initial points is chosen, and then
an internal set of iterations is carried out. These iterations repeatedly replace the current set of sample points by
an estimate of the centroids of the corresponding Voronoi subregions [30]. A CVT design is specified in Dakota
with the method command fsu cvt.
The methods in FSUDace are useful for design of experiments because they provide good coverage of the input
space, thus allowing global sensitivity analysis.
4.5 PSUADE MOAT
PSUADE (Problem Solving Environment for Uncertainty Analysis and Design Exploration) is a Lawrence Liv-
ermore National Laboratory tool for metamodeling, sensitivity analysis, uncertainty quantification, and optimiza-
tion. Its features include non-intrusive and parallel function evaluations, sampling and analysis methods, an
integrated design and analysis framework, global optimization, numerical integration, response surfaces (MARS
and higher order regressions), graphical output with Pgplot or Matlab, and fault tolerance [136]. Dakota includes a
prototype interface to its Morris One-At-A-Time (MOAT) screening method, a valuable tool for global sensitivity
(including interaction) analysis.
The Morris One-At-A-Time method, originally proposed by M. D. Morris [103], is a screening method, designed
to explore a computational model to distinguish between input variables that have negligible, linear and additive,
or nonlinear or interaction effects on the output. The computer experiments performed consist of individually
randomized designs which vary one input factor at a time to create a sample of its elementary effects.
With MOAT, each dimension of a k−dimensional input space is uniformly partitioned into plevels, creating a grid
of pkpoints x∈Rkat which evaluations of the model y(x)might take place. An elementary effect corresponding
to input iis computed by a forward difference
di(x) = y(x+ ∆ei)−y(x)
∆,(4.1)
where eiis the ith coordinate vector, and the step ∆is typically taken to be large (this is not intended to be a
local derivative approximation). In the present implementation of MOAT, for an input variable scaled to [0,1],
∆ = p
2(p−1) , so the step used to find elementary effects is slightly larger than half the input range.
The distribution of elementary effects diover the input space characterizes the effect of input ion the output of
interest. After generating rsamples from this distribution, their mean,
µi=1
r
r
X
j=1
d(j)
i,(4.2)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

64 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
modified mean
µ∗
i=1
r
r
X
j=1 |d(j)
i|,(4.3)
(using absolute value) and standard deviation
σi=v
u
u
t
1
r
r
X
j=1 d(j)
i−µi2
(4.4)
are computed for each input i. The mean and modified mean give an indication of the overall effect of an input
on the output. Standard deviation indicates nonlinear effects or interactions, since it is an indicator of elementary
effects varying throughout the input space.
The MOAT method is selected with method keyword psuade moat as shown in the sample Dakota input deck in
Figure 4.1. The number of samples (samples) must be a positive integer multiple of (number of continuous de-
sign variables k+ 1) and will be automatically adjusted if misspecified. The number of partitions (partitions)
applies to each variable being studied and must be odd (the number of MOAT levels pper variable is partitions
+ 1, similar to Dakota multidimensional parameter studies). This will also be adjusted at runtime as necessary.
Finite user-specified lower and upper bounds are required and will be scaled as needed by the method. For more
information on use of MOAT sampling, see the Morris example in Section 20.9, or Saltelli, et al. [116].
4.6 Sensitivity Analysis
4.6.1 Sensitivity Analysis Overview
In many engineering design applications, sensitivity analysis techniques and parameter study methods are useful in
identifying which of the design parameters have the most influence on the response quantities. This information is
helpful prior to an optimization study as it can be used to remove design parameters that do not strongly influence
the responses. In addition, these techniques can provide assessments as to the behavior of the response functions
(smooth or nonsmooth, unimodal or multimodal) which can be invaluable in algorithm selection for optimization,
uncertainty quantification, and related methods. In a post-optimization role, sensitivity information is useful is
determining whether or not the response functions are robust with respect to small changes in the optimum design
point.
In some instances, the term sensitivity analysis is used in a local sense to denote the computation of response
derivatives at a point. These derivatives are then used in a simple analysis to make design decisions. Dakota
supports this type of study through numerical finite-differencing or retrieval of analytic gradients computed within
the analysis code. The desired gradient data is specified in the responses section of the Dakota input file and
the collection of this data at a single point is accomplished through a parameter study method with no steps.
This approach to sensitivity analysis should be distinguished from the activity of augmenting analysis codes to
internally compute derivatives using techniques such as direct or adjoint differentiation, automatic differentiation
(e.g., ADIFOR), or complex step modifications. These sensitivity augmentation activities are completely separate
from Dakota and are outside the scope of this manual. However, once completed, Dakota can utilize these analytic
gradients to perform optimization, uncertainty quantification, and related studies more reliably and efficiently.
In other instances, the term sensitivity analysis is used in a more global sense to denote the investigation of
variability in the response functions. Dakota supports this type of study through computation of response data
sets (typically function values only, but all data sets are supported) at a series of points in the parameter space.
The series of points is defined using either a vector, list, centered, or multidimensional parameter study method.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

4.6. SENSITIVITY ANALYSIS 65
# Dakota Input File: morris_ps_moat.in
environment
tabular_data
tabular_data_file ’dakota_psuade.0.dat’
method
psuade_moat
samples = 84
partitions = 3
seed = 500
variables
continuous_design = 20
lower_bounds = 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
upper_bounds = 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
interface
analysis_drivers = ’morris’
fork
asynchronous evaluation_concurrency = 5
responses
objective_functions = 1
no_gradients
no_hessians
Figure 4.1: Dakota input file showing the Morris One-at-a-Time method – see
Dakota/examples/users/morris ps moat.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

66 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
For example, a set of closely-spaced points in a vector parameter study could be used to assess the smoothness of
the response functions in order to select a finite difference step size, and a set of more widely-spaced points in a
centered or multidimensional parameter study could be used to determine whether the response function variation
is likely to be unimodal or multimodal. See Chapter 3for additional information on these methods. These more
global approaches to sensitivity analysis can be used to obtain trend data even in situations when gradients are
unavailable or unreliable, and they are conceptually similar to the design of experiments methods and sampling
approaches to uncertainty quantification described in the following sections.
4.6.2 Assessing Sensitivity with DACE
Like parameter studies (see Chapter 3), the DACE techniques are useful for characterizing the behavior of the
response functions of interest through the parameter ranges of interest. In addition to direct interrogation and
visualization of the sampling results, a number of techniques have been developed for assessing the parameters
which are most influential in the observed variability in the response functions. One example of this is the
well-known technique of scatter plots, in which the set of samples is projected down and plotted against one
parameter dimension, for each parameter in turn. Scatter plots with a uniformly distributed cloud of points indicate
parameters with little influence on the results, whereas scatter plots with a defined shape to the cloud indicate
parameters which are more significant. Related techniques include analysis of variance (ANOVA) [104] and
main effects analysis, in which the parameters which have the greatest influence on the results are identified
from sampling results. Scatter plots and ANOVA may be accessed through import of Dakota tabular results (see
Section 13.3) into external statistical analysis programs such as S-plus, Minitab, etc.
Running any of the design of experiments or sampling methods allows the user to save the results in a tabular
data file, which then can be read into a spreadsheet or statistical package for further analysis. In addition, we have
provided some functions to help determine the most important variables.
We take the definition of uncertainty analysis from [116]: “The study of how uncertainty in the output of a model
can be apportioned to different sources of uncertainty in the model input.”
As a default, Dakota provides correlation analyses when running LHS. Correlation tables are printed with the
simple, partial, and rank correlations between inputs and outputs. These can be useful to get a quick sense of how
correlated the inputs are to each other, and how correlated various outputs are to inputs. The correlation analyses
are explained further in Chapter 5.2.
We also have the capability to calculate sensitivity indices through Variance-based Decomposition (VBD). Variance-
based decomposition is a global sensitivity method that summarizes how the uncertainty in model output can be
apportioned to uncertainty in individual input variables. VBD uses two primary measures, the main effect sen-
sitivity index Siand the total effect index Ti. The main effect sensitivity index corresponds to the fraction of
the uncertainty in the output, Y, that can be attributed to input xialone. The total effects index corresponds to
the fraction of the uncertainty in the output, Y, that can be attributed to input xiand its interactions with other
variables. The main effect sensitivity index compares the variance of the conditional expectation V arxi[E(Y|xi)]
against the total variance V ar(Y). Formulas for the indices are:
Si=V arxi[E(Y|xi)]
V ar(Y)(4.5)
and
Ti=E(V ar(Y|x−i))
V ar(Y)=V ar(Y)−V ar(E[Y|x−i])
V ar(Y)(4.6)
where Y=f(x)and x−i= (x1, ..., xi−1, xi+1, ..., xm).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

4.7. DOE USAGE GUIDELINES 67
The calculation of Siand Tirequires the evaluation of m-dimensional integrals which are typically approximated
by Monte-Carlo sampling. More details on the calculations and interpretation of the sensitivity indices can be
found in [116]. In Dakota version 5.1, we have improved calculations for the calculation of the Siand Tiindices
when using sampling. The implementation details of these calculatiosn are provided in [148]. VBD can be
specified for any of the sampling or DACE methods using the command variance based decomposition.
Note that VBD is extremely computationally intensive when using sampling since replicated sets of sample values
are evaluated. If the user specified a number of samples, N, and a number of nondeterministic variables, M,
variance-based decomposition requires the evaluation of N(M+ 2) samples. To obtain sensitivity indices that
are reasonably accurate, we recommend that N, the number of samples, be at least one hundred and preferably
several hundred or thousands. Because of the computational cost, variance-based decomposition is turned off
as a default for sampling or DACE. Another alternative, however, is to obtain these indices using one of the
stochastic expansion methods described in Section 5.4. The calculation of the indices using expansion methods is
much more efficient since the VBD indices are analytic functions of the coefficients in the stochastic expansion.
The paper by Weirs et al. [148] compares different methods for calculating the sensitivity indices for nonlinear
problems with significant interaction effects.
In terms of interpretation of the sensitivity indices, a larger value of the sensitivity index, Si, means that the
uncertainty in the input variable ihas a larger effect on the variance of the output. Note that the sum of the main
effect indices will be less than or equal to one. If the sum of the main effect indices is much less than one, it
indicates that there are significant two-way, three-way, or higher order interactions that contribute significantly to
the variance. There is no requirement that the sum of the total effect indices is one: in most cases, the sum of the
total effect indices will be greater than one. An example of the Main and Total effects indices as calculated by
Dakota using sampling is shown in Figure 4.2
Global sensitivity indices for each response function:
response_fn_1 Sobol indices:
Main Total
4.7508913283e-01 5.3242162037e-01 uuv_1
3.8112392892e-01 4.9912486515e-01 uuv_2
Figure 4.2: Dakota output for Variance-based Decomposition
Finally, we have the capability to calculate a set of quality metrics for a particular input sample. These quality
metrics measure various aspects relating to the volumetric spacing of the samples: are the points equally spaced,
do they cover the region, are they isotropically distributed, do they have directional bias, etc.? The quality metrics
are explained in more detail in the Reference Manual.
4.7 DOE Usage Guidelines
Parameter studies, classical design of experiments (DOE), design/analysis of computer experiments (DACE), and
sampling methods share the purpose of exploring the parameter space. When a global space-filling set of samples
is desired, then the DOE, DACE, and sampling methods are recommended. These techniques are useful for scatter
plot and variance analysis as well as surrogate model construction.
The distinction between DOE and DACE methods is that the former are intended for physical experiments con-
taining an element of nonrepeatability (and therefore tend to place samples at the extreme parameter vertices),
whereas the latter are intended for repeatable computer experiments and are more space-filling in nature.
The distinction between DOE/DACE and sampling is drawn based on the distributions of the parameters. DOE/-
Dakota Version 6.7 User’s Manual generated on November 13, 2017

68 CHAPTER 4. DESIGN OF EXPERIMENTS CAPABILITIES
DACE methods typically assume uniform distributions, whereas the sampling approaches in Dakota support a
broad range of probability distributions.
To use sampling in design of experiments mode (as opposed to uncertainty quantification mode), an active view
override (e.g., active all) can be included in the variables specification (see Section 9.5.1) of the Dakota input
file.
Design of experiments method selection recommendations are summarized in Table 4.4.
Table 4.4: Guidelines for selection of parameter study, DOE, DACE, and sampling methods.
Method Applications Applicable Methods
Classification
parameter study sensitivity analysis, centered parameter study,
directed parameter space investigations list parameter study,
multidim parameter study,
vector parameter study
classical design physical experiments dace (box behnken,
of experiments (parameters are uniformly distributed) central composite)
design of computer variance analysis, dace (grid, random, oas, lhs, oa lhs),
experiments space filling designs fsu quasi mc (halton, hammersley),
(parameters are uniformly distributed) fsu cvt, psuade moat
sampling space filling designs sampling (Monte Carlo or LHS)
(parameters have general probability distributions) with optional active view override
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 5
Uncertainty Quantification Capabilities
5.1 Overview
At a high level, uncertainty quantification (UQ) or nondeterministic analysis is the process of characterizing input
uncertainties, forward propagating these uncertainties through a computational model, and performing statisti-
cal or interval assessments on the resulting responses. This process determines the effect of uncertainties and
assumptions on model outputs or results. In Dakota, uncertainty quantification methods specifically focus on
the forward propagation part of the process, where probabilistic or interval information on parametric inputs are
mapped through the computational model to assess statistics or intervals on outputs. For an overview of these
approaches for engineering applications, consult [73].
UQ is related to sensitivity analysis in that the common goal is to gain an understanding of how variations in
the parameters affect the response functions of the engineering design problem. However, for UQ, some or all
of the components of the parameter vector, are considered to be uncertain as specified by particular probability
distributions (e.g., normal, exponential, extreme value), or other uncertainty structures. By assigning specific
distributional structure to the inputs, distributional structure for the outputs (i.e, response statistics) can be inferred.
This migrates from an analysis that is more qualitative in nature, in the case of sensitivity analysis, to an analysis
that is more rigorously quantitative.
UQ methods are often distinguished by their ability to propagate aleatory or epistemic input uncertainty charac-
terizations, where aleatory uncertainties are irreducible variabilities inherent in nature and epistemic uncertainties
are reducible uncertainties resulting from a lack of knowledge. Since sufficient data is generally available for
aleatory uncertainties, probabilistic methods are commonly used for computing response distribution statistics
based on input probability distribution specifications. Conversely, for epistemic uncertainties, any use of proba-
bility distributions is based on subjective knowledge rather than objective data, and we may alternatively explore
nonprobabilistic methods based on interval specifications.
5.1.1 Summary of Dakota UQ Methods
Dakota contains capabilities for performing nondeterministic analysis with both types of input uncertainty. These
UQ methods have been developed by Sandia Labs, in conjunction with collaborators in academia [53,54,35,134].
The aleatory UQ methods in Dakota include various sampling-based approaches (e.g., Monte Carlo and Latin Hy-
percube sampling), local and global reliability methods, and stochastic expansion (polynomial chaos expansions

70 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
and stochastic collocation) approaches. The epistemic UQ methods include local and global interval analysis and
Dempster-Shafer evidence theory. These are summarized below and then described in more depth in subsequent
sections of this chapter. Dakota additionally supports mixed aleatory/epistemic UQ via interval-valued probabil-
ity, second-order probability, and Dempster-Shafer theory of evidence. These involve advanced model recursions
and are described in Section 15.1.
LHS (Latin Hypercube Sampling): This package provides both Monte Carlo (random) sampling and Latin
Hypercube sampling methods, which can be used with probabilistic variables in Dakota that have the following
distributions: normal, lognormal, uniform, loguniform, triangular, exponential, beta, gamma, gumbel, frechet,
weibull, poisson, binomial, negative binomial, geometric, hypergeometric, and user-supplied histograms. In addi-
tion, LHS accounts for correlations among the variables [82], which can be used to accommodate a user-supplied
correlation matrix or to minimize correlation when a correlation matrix is not supplied. In addition to a standard
sampling study, we support the capability to perform “incremental” LHS, where a user can specify an initial LHS
study of N samples, and then re-run an additional incremental study which will double the number of samples (to
2N, with the first N being carried from the initial study). The full incremental sample of size 2N is also a Latin
Hypercube, with proper stratification and correlation. Statistics for each increment are reported separately at the
end of the study.
Reliability Methods: This suite of methods includes both local and global reliability methods. Local methods
include first- and second-order versions of the Mean Value method (MVFOSM and MVSOSM) and a variety of
most probable point (MPP) search methods, including the Advanced Mean Value method (AMV and AMV2),
the iterated Advanced Mean Value method (AMV+ and AMV2+), the Two-point Adaptive Nonlinearity Approx-
imation method (TANA-3), and the traditional First Order and Second Order Reliability Methods (FORM and
SORM) [73]. The MPP search methods may be used in forward (Reliability Index Approach (RIA)) or inverse
(Performance Measure Approach (PMA)) modes, as dictated by the type of level mappings. Each of the MPP
search techniques solve local optimization problems in order to locate the MPP, which is then used as the point
about which approximate probabilities are integrated (using first- or second-order integrations in combination
with refinements based on importance sampling). Global reliability methods are designed to handle nonsmooth
and multimodal failure surfaces, by creating global approximations based on Gaussian process models. They
accurately resolve a particular contour of a response function and then estimate probabilities using multimodal
adaptive importance sampling.
Stochastic Expansion Methods: The development of these techniques mirrors that of deterministic finite element
analysis utilizing the notions of projection, orthogonality, and weak convergence [53], [54]. Rather than estimat-
ing point probabilities, they form an approximation to the functional relationship between response functions and
their random inputs, which provides a more complete uncertainty representation for use in multi-code simula-
tions. Expansion methods include polynomial chaos expansions (PCE), which employ multivariate orthogonal
polynomials that are tailored to representing particular input probability distributions, and stochastic collocation
(SC), which employs multivariate interpolation polynomials. For PCE, expansion coefficients may be evalu-
ated using a spectral projection approach (based on sampling, tensor-product quadrature, Smolyak sparse grid,
or cubature methods for numerical integration) or a regression approach (least squares or compressive sensing).
For SC, interpolants are formed over tensor-product or sparse grids and may be local or global, value-based or
gradient-enhanced, and nodal or hierarchical. In global value-based cases (Lagrange polynomials), the barycentric
formulation is used [11,88,79] to improve numerical efficiency and stability. Both sets of methods provide ana-
lytic response moments and variance-based metrics; however, CDF/CCDF probabilities are evaluated numerically
by sampling on the expansion.
Importance Sampling: Importance sampling is a method that allows one to estimate statistical quantities such
as failure probabilities in a way that is more efficient than Monte Carlo sampling. The core idea in importance
sampling is that one generates samples that are preferentially placed in important regions of the space (e.g. in
or near the failure region or user-defined region of interest), then appropriately weights the samples to obtain an
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.1. OVERVIEW 71
unbiased estimate of the failure probability.
Adaptive Sampling: The goal in performing adaptive sampling is to construct a surrogate model that can be used
as an accurate predictor of an expensive simulation. The aim is to build a surrogate that minimizes the error over
the entire domain of interest using as little data as possible from the expensive simulation. The adaptive sampling
methods start with an initial LHS sample, and then adaptively choose samples that optimize a particular criteria.
For example, if a set of additional possible sample points are generated, one criteria is to pick the next sample
point as the point which maximizes the minimum distance to the existing points (maximin). Another criteria is to
pick the sample point where the surrogate indicates the most uncertainty in its prediction.
Recently, Dakota added a new method to assess failure probabilities based on ideas from computational geometry.
Part of the idea underpinning this method is the idea of throwing “darts” which are higher dimensional objects
than sample points (e.g. lines, planes, etc.) The POF (Probability-of-Failure) darts method uses these objects to
estimate failure probabilities.
Interval Analysis: Interval analysis is often used to model epistemic uncertainty. In interval analysis, one assumes
that nothing is known about an epistemic uncertain variable except that its value lies somewhere within an interval.
In this situation, it is NOT assumed that the value has a uniform probability of occurring within the interval.
Instead, the interpretation is that any value within the interval is a possible value or a potential realization of that
variable. In interval analysis, the uncertainty quantification problem is one of determining the resulting bounds
on the output (defining the output interval) given interval bounds on the inputs. Again, any output response that
falls within the output interval is a possible output with no frequency information assigned to it.
We have the capability to perform interval analysis using either global or local methods. In the global approach,
one uses either a global optimization method (based on a Gaussian process surrogate model) or a sampling method
to assess the bounds. The local method uses gradient information in a derivative-based optimization approach,
using either SQP (sequential quadratic programming) or a NIP (nonlinear interior point) method to obtain bounds.
Dempster-Shafer Theory of Evidence: The objective of evidence theory is to model the effects of epistemic
uncertainties. Epistemic uncertainty refers to the situation where one does not know enough to specify a proba-
bility distribution on a variable. Sometimes epistemic uncertainty is referred to as subjective, reducible, or lack
of knowledge uncertainty. In contrast, aleatory uncertainty refers to the situation where one does have enough
information to specify a probability distribution. In Dempster-Shafer theory of evidence, the uncertain input vari-
ables are modeled as sets of intervals. The user assigns a basic probability assignment (BPA) to each interval,
indicating how likely it is that the uncertain input falls within the interval. The intervals may be overlapping,
contiguous, or have gaps. The intervals and their associated BPAs are then propagated through the simulation
to obtain cumulative distribution functions on belief and plausibility. Belief is the lower bound on a probability
estimate that is consistent with the evidence, and plausibility is the upper bound on a probability estimate that is
consistent with the evidence. In addition to the full evidence theory structure, we have a simplified capability for
users wanting to perform pure interval analysis (e.g. what is the interval on the output given intervals on the input)
using either global or local optimization methods. Interval analysis is often used to model epistemic variables in
nested analyses, where probability theory is used to model aleatory variables.
Bayesian Calibration: In Bayesian calibration, uncertain input parameters are described by a “prior” distribution.
The priors are updated with experimental data, in a Bayesian framework that involves the experimental data and
a likelihood function which describes how well each parameter value is supported by the data. After the process
of Bayesian calibration, the prior distribution becomes a posterior distribution. The posterior distribution of the
parameters represents the parameter values that have been updated with the data (e.g. the model, when run at
these parameters, should yield results that are consistent with the observational data).
Dakota Version 6.7 User’s Manual generated on November 13, 2017
72 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
5.1.2 Variables and Responses for UQ
All the UQ methods perform a forward uncertainty propagation in which probability or interval information for
input parameters is mapped to probability or interval information for output response functions. The mfunctions
in the Dakota response data set are interpreted as mgeneral response functions by the Dakota methods (with no
specific interpretation of the functions as for optimization and least squares).
Within the variables specification, uncertain variable descriptions are employed to define the parameter probability
distributions (see Section 9.3). The continuous aleatory distribution types include: normal (Gaussian), lognormal,
uniform, loguniform, triangular, exponential, beta, gamma, gumbel, frechet, weibull, and histogram bin. The
discrete aleatory distribution types include: poisson, binomial, negative binomial, geometric, hypergeometric,
and histogram point. The epistemic distribution type is interval for continuous variables. For epistemic discrete
variables, there are three types: integer range, integer set, and real set. When gradient and/or Hessian information
is used in an uncertainty assessment, derivative components are normally computed with respect to the active
continuous variables, which could be aleatory uncertain, epistemic uncertain, aleatory and epistemic uncertain, or
all continuous variables, depending on the active view (see Section 9.5).
5.2 Sampling Methods
Sampling techniques are selected using the sampling method selection. This method generates sets of samples
according to the probability distributions of the uncertain variables and maps them into corresponding sets of
response functions, where the number of samples is specified by the samples integer specification. Means,
standard deviations, coefficients of variation (COVs), and 95% confidence intervals are computed for the response
functions. Probabilities and reliabilities may be computed for response levels specifications, and response
levels may be computed for either probability levels or reliability levels specifications (refer
to the Method keywords section in the Dakota Reference Manual [3] for additional information).
Currently, traditional Monte Carlo (MC) and Latin hypercube sampling (LHS) are supported by Dakota and are
chosen by specifying sample type as random or lhs. In Monte Carlo sampling, the samples are selected
randomly according to the user-specified probability distributions. Latin hypercube sampling is a stratified sam-
pling technique for which the range of each uncertain variable is divided into Nssegments of equal probability,
where Nsis the number of samples requested. The relative lengths of the segments are determined by the nature
of the specified probability distribution (e.g., uniform has segments of equal width, normal has small segments
near the mean and larger segments in the tails). For each of the uncertain variables, a sample is selected randomly
from each of these equal probability segments. These Nsvalues for each of the individual parameters are then
combined in a shuffling operation to create a set of Nsparameter vectors with a specified correlation structure.
A feature of the resulting sample set is that every row and column in the hypercube of partitions has exactly one
sample. Since the total number of samples is exactly equal to the number of partitions used for each uncertain
variable, an arbitrary number of desired samples is easily accommodated (as compared to less flexible approaches
in which the total number of samples is a product or exponential function of the number of intervals for each
variable, i.e., many classical design of experiments methods).
Advantages of sampling-based methods include their relatively simple implementation and their independence
from the scientific disciplines involved in the analysis. The main drawback of these techniques is the large number
of function evaluations needed to generate converged statistics, which can render such an analysis computationally
very expensive, if not intractable, for real-world engineering applications. LHS techniques, in general, require
fewer samples than traditional Monte Carlo for the same accuracy in statistics, but they still can be prohibitively
expensive. For further information on the method and its relationship to other sampling techniques, one is referred
to the works by McKay, et al. [101], Iman and Shortencarier [82], and Helton and Davis [76]. Note that under
Dakota Version 6.7 User’s Manual generated on November 13, 2017
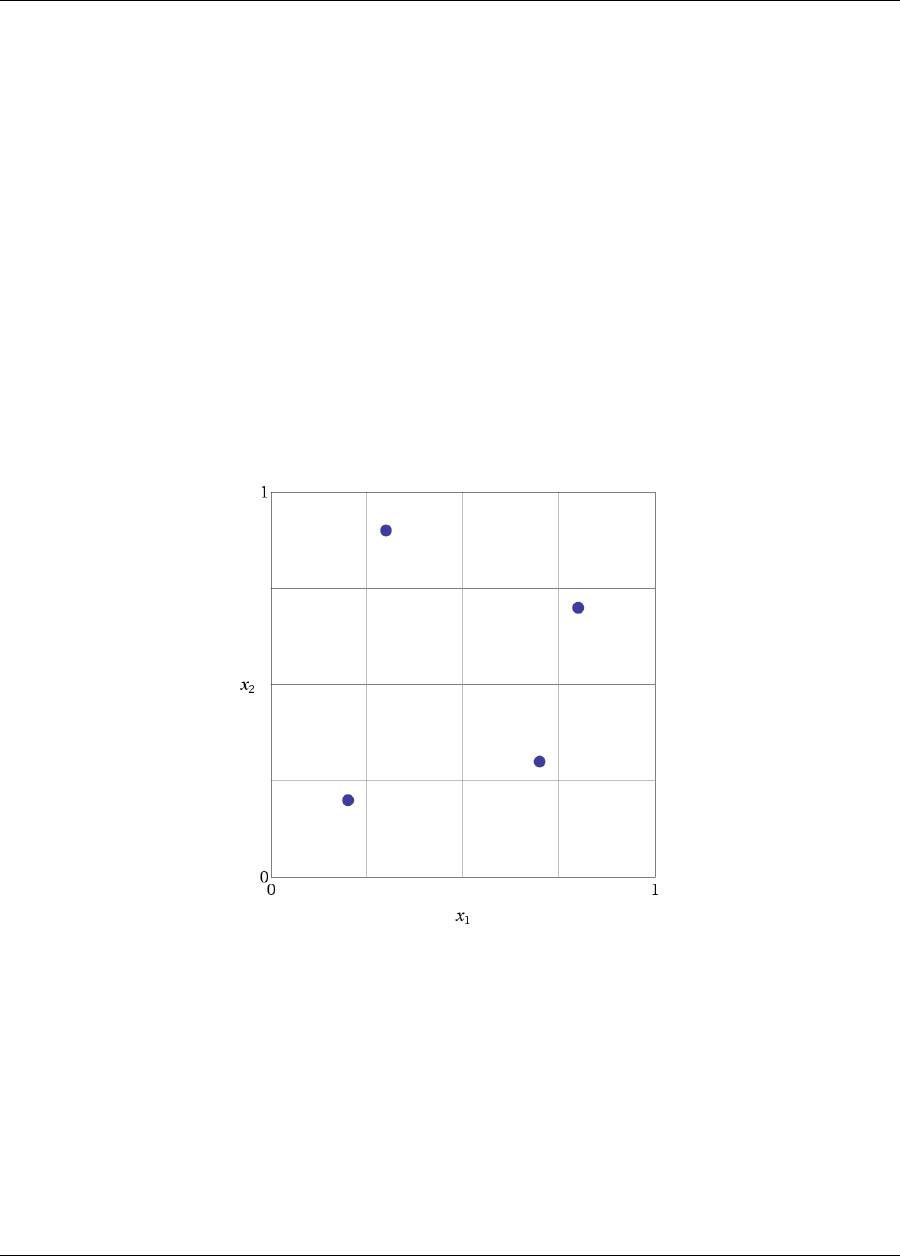
5.2. SAMPLING METHODS 73
certain separability conditions associated with the function to be sampled, Latin hypercube sampling provides a
more accurate estimate of the mean value than does random sampling. That is, given an equal number of samples,
the LHS estimate of the mean will have less variance than the mean value obtained through random sampling.
Figure 5.1 demonstrates Latin hypercube sampling on a two-variable parameter space. Here, the range of both
parameters, x1and x2, is [0,1]. Also, for this example both x1and x2have uniform statistical distributions.
For Latin hypercube sampling, the range of each parameter is divided into p“bins” of equal probability. For
parameters with uniform distributions, this corresponds to partitions of equal size. For ndesign parameters,
this partitioning yields a total of pnbins in the parameter space. Next, psamples are randomly selected in the
parameter space, with the following restrictions: (a) each sample is randomly placed inside a bin, and (b) for all
one-dimensional projections of the psamples and bins, there will be one and only one sample in each bin. In a
two-dimensional example such as that shown in Figure 5.1, these LHS rules guarantee that only one bin can be
selected in each row and column. For p= 4, there are four partitions in both x1and x2. This gives a total of
16 bins, of which four will be chosen according to the criteria described above. Note that there is more than one
possible arrangement of bins that meet the LHS criteria. The dots in Figure 5.1 represent the four sample sites in
this example, where each sample is randomly located in its bin. There is no restriction on the number of bins in
the range of each parameter, however, all parameters must have the same number of bins.
Figure 5.1: An example of Latin hypercube sampling with four bins in design parameters x1and x2. The dots are
the sample sites.
The actual algorithm for generating Latin hypercube samples is more complex than indicated by the description
given above. For example, the Latin hypercube sampling method implemented in the LHS code [132] takes into
account a user-specified correlation structure when selecting the sample sites. For more details on the implemen-
tation of the LHS algorithm, see Reference [132].
In addition to Monte Carlo vs. LHS design choices, Dakota sampling methods support options for incrementally-
refined designs, generation of approximately determinant-optimal (D-optimal) designs, and selection of sample
sizes to satisfy Wilks’ criteria.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

74 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
5.2.1 Uncertainty Quantification Example using Sampling Methods
The input file in Figure 5.2 demonstrates the use of Latin hypercube Monte Carlo sampling for assessing prob-
ability of failure as measured by specified response levels. The two-variable Textbook example problem (see
Equation 20.1) will be used to demonstrate the application of sampling methods for uncertainty quantification
where it is assumed that x1and x2are uniform uncertain variables on the interval [0,1].
The number of samples to perform is controlled with the samples specification, the type of sampling algorithm
to use is controlled with the sample type specification, the levels used for computing statistics on the response
functions is specified with the response levels input, and the seed specification controls the sequence of
the pseudo-random numbers generated by the sampling algorithms. The input samples generated are shown in
Figure 5.3 for the case where samples = 5 and samples = 10 for both random (◦) and lhs (+) sample types.
# Dakota Input File: textbook_uq_sampling.in
environment
tabular_data
tabular_data_file = ’textbook_uq_sampling.dat’
top_method_pointer = ’UQ’
method
id_method = ’UQ’
sampling
sample_type lhs
samples = 10
seed = 98765
response_levels = 0.1 0.2 0.6
0.1 0.2 0.6
0.1 0.2 0.6
distribution cumulative
variables
uniform_uncertain = 2
lower_bounds = 0. 0.
upper_bounds = 1. 1.
descriptors = ’x1’ ’x2’
interface
id_interface = ’I1’
analysis_drivers = ’text_book’
fork
asynchronous evaluation_concurrency = 5
responses
response_functions = 3
no_gradients
no_hessians
Figure 5.2: Dakota input file for UQ example using LHS – see
Dakota/examples/users/textbook uq sampling.in
Latin hypercube sampling ensures full coverage of the range of the input variables, which is often a problem with
Monte Carlo sampling when the number of samples is small. In the case of samples = 5, poor stratification
Dakota Version 6.7 User’s Manual generated on November 13, 2017
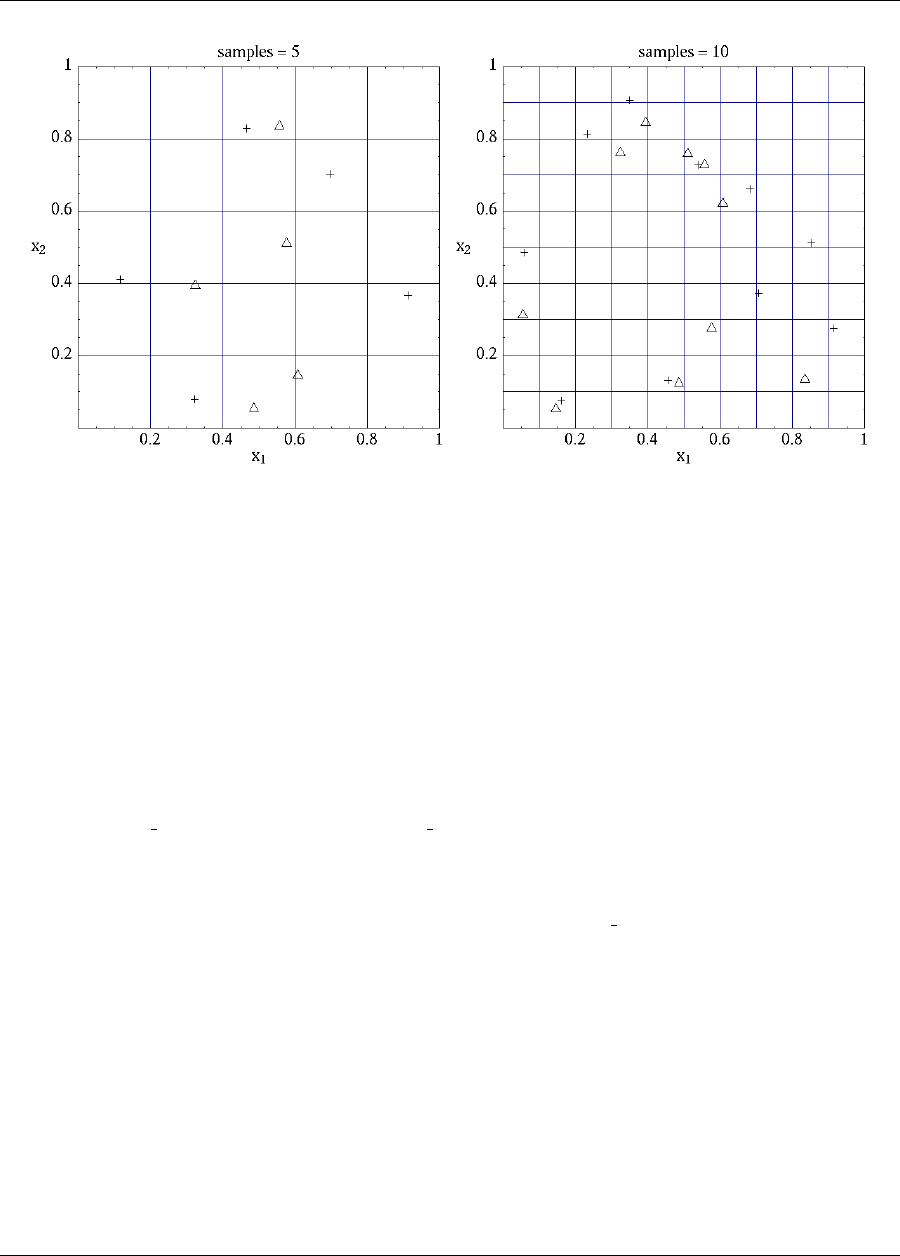
5.2. SAMPLING METHODS 75
Figure 5.3: Distribution of input sample points for random (4) and lhs (+) sampling for samples=5 and 10.
is evident in x1as four out of the five Monte Carlo samples are clustered in the range 0.35 < x1<0.55, and
the regions x1<0.3and 0.6< x1<0.9are completely missed. For the case where samples = 10, some
clustering in the Monte Carlo samples is again evident with 4samples in the range 0.5< x1<0.55. In both
cases, the stratification with LHS is superior.
The response function statistics returned by Dakota are shown in Figure 5.4. The first block of output specifies
the response sample means, sample standard deviations, and skewness and kurtosis. The second block of output
displays confidence intervals on the means and standard deviations of the responses. The third block defines
Probability Density Function (PDF) histograms of the samples: the histogram bins are defined by the lower and
upper values of the bin and the corresponding density for that bin. Note that these bin endpoints correspond
to the response levels and/or probability levels defined by the user in the Dakota input file. If
there are just a few levels, these histograms may be coarse. Dakota does not do anything to optimize the bin
size or spacing. Finally, the last section of the output defines the Cumulative Distribution Function (CDF) pairs.
In this case, distribution cumulative was specified for the response functions, and Dakota presents the
probability levels corresponding to the specified response levels (response levels) that were set. The default
compute probabilities was used. Alternatively, Dakota could have provided CCDF pairings, reliability
levels corresponding to prescribed response levels, or response levels corresponding to prescribed probability or
reliability levels.
In addition to obtaining statistical summary information of the type shown in Figure 5.4, the results of LHS
sampling also include correlations. Four types of correlations are returned in the output: simple and partial “raw”
correlations, and simple and partial “rank” correlations. The raw correlations refer to correlations performed
on the actual input and output data. Rank correlations refer to correlations performed on the ranks of the data.
Ranks are obtained by replacing the actual data by the ranked values, which are obtained by ordering the data
in ascending order. For example, the smallest value in a set of input samples would be given a rank 1, the next
smallest value a rank 2, etc. Rank correlations are useful when some of the inputs and outputs differ greatly in
magnitude: then it is easier to compare if the smallest ranked input sample is correlated with the smallest ranked
output, for example.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

76 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
Statistics based on 10 samples:
Sample moment statistics for each response function:
Mean Std Dev Skewness Kurtosis
response_fn_1 3.8383990322e-01 4.0281539886e-01 1.2404952971e+00 6.5529797327e-01
response_fn_2 7.4798705803e-02 3.4686110941e-01 4.5716015887e-01 -5.8418924529e-01
response_fn_3 7.0946176558e-02 3.4153246532e-01 5.2851897926e-01 -8.2527332042e-01
95% confidence intervals for each response function:
LowerCI_Mean UpperCI_Mean LowerCI_StdDev UpperCI_StdDev
response_fn_1 9.5683125821e-02 6.7199668063e-01 2.7707061315e-01 7.3538389383e-01
response_fn_2 -1.7333078422e-01 3.2292819583e-01 2.3858328290e-01 6.3323317325e-01
response_fn_3 -1.7337143113e-01 3.1526378424e-01 2.3491805390e-01 6.2350514636e-01
Probability Density Function (PDF) histograms for each response function:
PDF for response_fn_1:
Bin Lower Bin Upper Density Value
--------- --------- -------------
2.3066424677e-02 1.0000000000e-01 3.8994678038e+00
1.0000000000e-01 2.0000000000e-01 2.0000000000e+00
2.0000000000e-01 6.0000000000e-01 5.0000000000e-01
6.0000000000e-01 1.2250968624e+00 4.7992562123e-01
PDF for response_fn_2:
Bin Lower Bin Upper Density Value
--------- --------- -------------
-3.5261164651e-01 1.0000000000e-01 1.1046998102e+00
1.0000000000e-01 2.0000000000e-01 2.0000000000e+00
2.0000000000e-01 6.0000000000e-01 5.0000000000e-01
6.0000000000e-01 6.9844576220e-01 1.0157877573e+00
PDF for response_fn_3:
Bin Lower Bin Upper Density Value
--------- --------- -------------
-3.8118095128e-01 1.0000000000e-01 1.2469321539e+00
1.0000000000e-01 2.0000000000e-01 0.0000000000e+00
2.0000000000e-01 6.0000000000e-01 7.5000000000e-01
6.0000000000e-01 6.4526450977e-01 2.2092363423e+00
Level mappings for each response function:
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e-01 3.0000000000e-01
2.0000000000e-01 5.0000000000e-01
6.0000000000e-01 7.0000000000e-01
Cumulative Distribution Function (CDF) for response_fn_2:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e-01 5.0000000000e-01
2.0000000000e-01 7.0000000000e-01
6.0000000000e-01 9.0000000000e-01
Cumulative Distribution Function (CDF) for response_fn_3:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e-01 6.0000000000e-01
2.0000000000e-01 6.0000000000e-01
6.0000000000e-01 9.0000000000e-01
Figure 5.4: Dakota response function statistics from UQ sampling example.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.2. SAMPLING METHODS 77
Correlations are always calculated between two sets of sample data. One can calculate correlation coefficients
between two input variables, between an input and an output variable (probably the most useful), or between two
output variables. The simple correlation coefficients presented in the output tables are Pearson’s correlation co-
efficient, which is defined for two variables xand yas: Corr(x, y) = Pi(xi−¯x)(yi−¯y)
√Pi(xi−¯x)2Pi(yi−¯y)2. Partial correlation
coefficients are similar to simple correlations, but a partial correlation coefficient between two variables measures
their correlation while adjusting for the effects of the other variables. For example, say one has a problem with
two inputs and one output; and the two inputs are highly correlated. Then the correlation of the second input and
the output may be very low after accounting for the effect of the first input. The rank correlations in Dakota are
obtained using Spearman’s rank correlation. Spearman’s rank is the same as the Pearson correlation coefficient
except that it is calculated on the rank data.
Figure 5.5 shows an example of the correlation output provided by Dakota for the input file in Figure 5.2. Note that
these correlations are presently only available when one specifies lhs as the sampling method under sampling.
Also note that the simple and partial correlations should be similar in most cases (in terms of values of correlation
coefficients). This is because we use a default “restricted pairing” method in the LHS routine which forces near-
zero correlation amongst uncorrelated inputs.
Simple Correlation Matrix between input and output:
x1 x2 response_fn_1 response_fn_2 response_fn_3
x1 1.00000e+00
x2 -7.22482e-02 1.00000e+00
response_fn_1 -7.04965e-01 -6.27351e-01 1.00000e+00
response_fn_2 8.61628e-01 -5.31298e-01 -2.60486e-01 1.00000e+00
response_fn_3 -5.83075e-01 8.33989e-01 -1.23374e-01 -8.92771e-01 1.00000e+00
Partial Correlation Matrix between input and output:
response_fn_1 response_fn_2 response_fn_3
x1 -9.65994e-01 9.74285e-01 -9.49997e-01
x2 -9.58854e-01 -9.26578e-01 9.77252e-01
Simple Rank Correlation Matrix between input and output:
x1 x2 response_fn_1 response_fn_2 response_fn_3
x1 1.00000e+00
x2 -6.66667e-02 1.00000e+00
response_fn_1 -6.60606e-01 -5.27273e-01 1.00000e+00
response_fn_2 8.18182e-01 -6.00000e-01 -2.36364e-01 1.00000e+00
response_fn_3 -6.24242e-01 7.93939e-01 -5.45455e-02 -9.27273e-01 1.00000e+00
Partial Rank Correlation Matrix between input and output:
response_fn_1 response_fn_2 response_fn_3
x1 -8.20657e-01 9.74896e-01 -9.41760e-01
x2 -7.62704e-01 -9.50799e-01 9.65145e-01
Figure 5.5: Correlation results using LHS Sampling.
Finally, note that the LHS package can be used for design of experiments over design and state variables by
including an active view override in the variables specification section of the Dakota input file (see Section 9.5.1).
Then, instead of iterating on only the uncertain variables, the LHS package will sample over all of the active
variables. In the active all view, continuous design and continuous state variables are treated as having
uniform probability distributions within their upper and lower bounds, discrete design and state variables are
sampled uniformly from within their sets or ranges, and any uncertain variables are sampled within their specified
Dakota Version 6.7 User’s Manual generated on November 13, 2017

78 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
probability distributions.
5.2.2 Incremental Sampling
In many situations, one may run an initial sample set and then need to perform further sampling to get better
estimates of the mean, variance, and percentiles, and to obtain more comprehensive sample coverage. We call
this capability incremental sampling. Typically, a Dakota restart file (dakota.rst) would be available from
the original sample, so only the newly generated samples would need to be evaluated. Incremental sampling sup-
ports continuous uncertain variables and discrete uncertain variables such as discrete distributions (e.g. binomial,
Poisson, etc.) as well as histogram variables and uncertain set types.
There are two cases, incremental random and incremental Latin hypercube sampling, with incremental LHS being
the most common. One major advantage of LHS incremental sampling is that it maintains the stratification and
correlation structure of the original LHS sample. That is, if one generated two independent LHS samples and
simply merged them, the calculation of the accuracy of statistical measures such as the mean and the variance
would be slightly incorrect. However, in the incremental case, the full sample (double the original size) is a Latin
Hypercube sample itself and statistical measures and their accuracy can be properly calculated. The incremental
sampling capability is most useful when one is starting off with very small samples. Once the sample size is more
than a few hundred, the benefit of incremental sampling diminishes.
1. Incremental random sampling: With incremental random sampling, the original sample set with N1sam-
ples must be generated using sample type = random and samples = N1. Then, the user can du-
plicate the Dakota input file and add refinement samples = N2 with the number of new samples
N2to be added. Random incremental sampling does not require a doubling of samples each time. Thus,
the user can specify any number of refinement samples (from an additional one sample to a large
integer).
For example, if the first sample has 50 samples, and 10 more samples are desired, the second Dakota
run should specify samples = 50,refinement samples = 10. In this situation, only 10 new
samples will be generated, and the final statistics will be reported at the end of the study both for the
initial 50 samples and for the full sample of 60. The command line syntax for running the second sample
is dakota -i input60.in -r dakota.50.rst where input60.in is the input file with the
refinement samples specification and dakota.50.rst is the restart file containing the initial 50 samples.
Note that if the restart file has a different name, that is fine; the correct restart file name should be used.
This process can be repeated if desired,arbitrarily extending the total sample size each time, e.g, samples
= 50,refinement samples = 10 3 73 102.
2. Incremental Latin hypercube sampling: With incremental LHS sampling, the original sample set with N1
samples must be generated using sample type = lhs and samples = N1. Then, the user can du-
plicate the Dakota input file and add refinement samples = N1. The sample size must double each
time, so the first set of refinement samples must be the same size as the initial set. That is, if one starts with
a very small sample size of 10, then one can use the incremental sampling capability to generate sample
sizes of 20, 40, 80, etc.
For example, if the first sample has 50 samples, in the second Dakota run, the number of refinement samples
should be set to 50 for a total of 100. In this situation, only 50 new samples will be generated, and at the
end of the study final statistics will be reported both for the initial 50 samples and for the full sample
of 100. The command line syntax for running the second sample is dakota -i input100.in -r
dakota.50.rst, where input100.in is the input file with the incremental sampling specification
and dakota.50.rst is the restart file containing the initial 50 samples. Note that if the restart file has a
different name, that is fine; the correct restart file name should be used.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.3. RELIABILITY METHODS 79
This process can be repeated if desired, doubling the total sample size each time, e.g, samples = 50,
refinement samples = 50 100 200 400.
5.2.3 Principal Component Analysis
As of Dakota 6.3, we added a capability to perform Principal Component Analysis on field response data when
using LHS sampling. Principal components analysis (PCA) is a data reduction method and allows one to express
an ensemble of field data with a set of principal components responsible for the spread of that data.
Dakota can calculate the principal components of the response matrix of N samples * L responses (the field
response of length L) using the keyword principal components. The Dakota implementation is under
active development: the PCA capability may ultimately be specified elsewhere or used in different ways. For
now, it is performed as a post-processing analysis based on a set of Latin Hypercube samples.
If the user specifies LHS sampling with field data responses and also specifies principal components,
Dakota will calculate the principal components by calculating the eigenvalues and eigenvectors of a centered data
matrix. Further, if the user specifies percent variance explained = 0.99, the number of components that
accounts for at least 99 percent of the variance in the responses will be retained. The default for this percentage
is 0.95. In many applications, only a few principal components explain the majority of the variance, resulting in
significant data reduction. The principal components are written to a file, princ comp.txt. Dakota also uses
the principal components to create a surrogate model by representing the overall response as weighted sum of M
principal components, where the weights will be determined by Gaussian processes which are a function of the
input uncertain variables. This reduced form then can be used for sensitivity analysis, calibration, etc.
5.2.4 Wilks-based Sample Sizes
Most of the sampling methods require the user to specify the number of samples in advance. However, if one
specifies random sampling, one can use an approach developed by Wilks[149] to determine the number of
samples that ensures a particular confidence level in a percentile of interest. The Wilks method of computing the
number of samples to execute for a random sampling study is based on order statistics, eg considering the outputs
ordered from smallest to largest [149,108]. Given a probability level,α, and confidence level,
β, the Wilks calculation determines the minimum number of samples required such that there is (β∗100)%
confidence that the (α∗100)%-ile of the uncertain distribution on model output will fall below the actual (α∗
100)%-ile given by the sample. To be more specific, if we wish to calculate the 95% confidence limit on the
95th percentile, Wilks indicates that 59 samples are needed. If we order the responses and take the largest
one, that value defines a tolerance limit on the 95th percentile: we have a situation where 95% of the time,
the 95th percentile will fall at or below that sampled value. This represents a one sided upper treatment
applicable to the largest output value. This treatment can be reversed to apply to the lowest output value by
using the one sided lower option, and further expansion to include an interval containing both the smallest
and the largest output values in the statistical statement can be specified via the two sided option. Additional
generalization to higher order statistics, eg a statement applied to the N largest outputs (one sided upper) or
the N smallest and N largest outputs (two sided), can be specified using the order option along with value N.
5.3 Reliability Methods
Reliability methods provide an alternative approach to uncertainty quantification which can be less computa-
tionally demanding than sampling techniques. Reliability methods for uncertainty quantification are based on
Dakota Version 6.7 User’s Manual generated on November 13, 2017
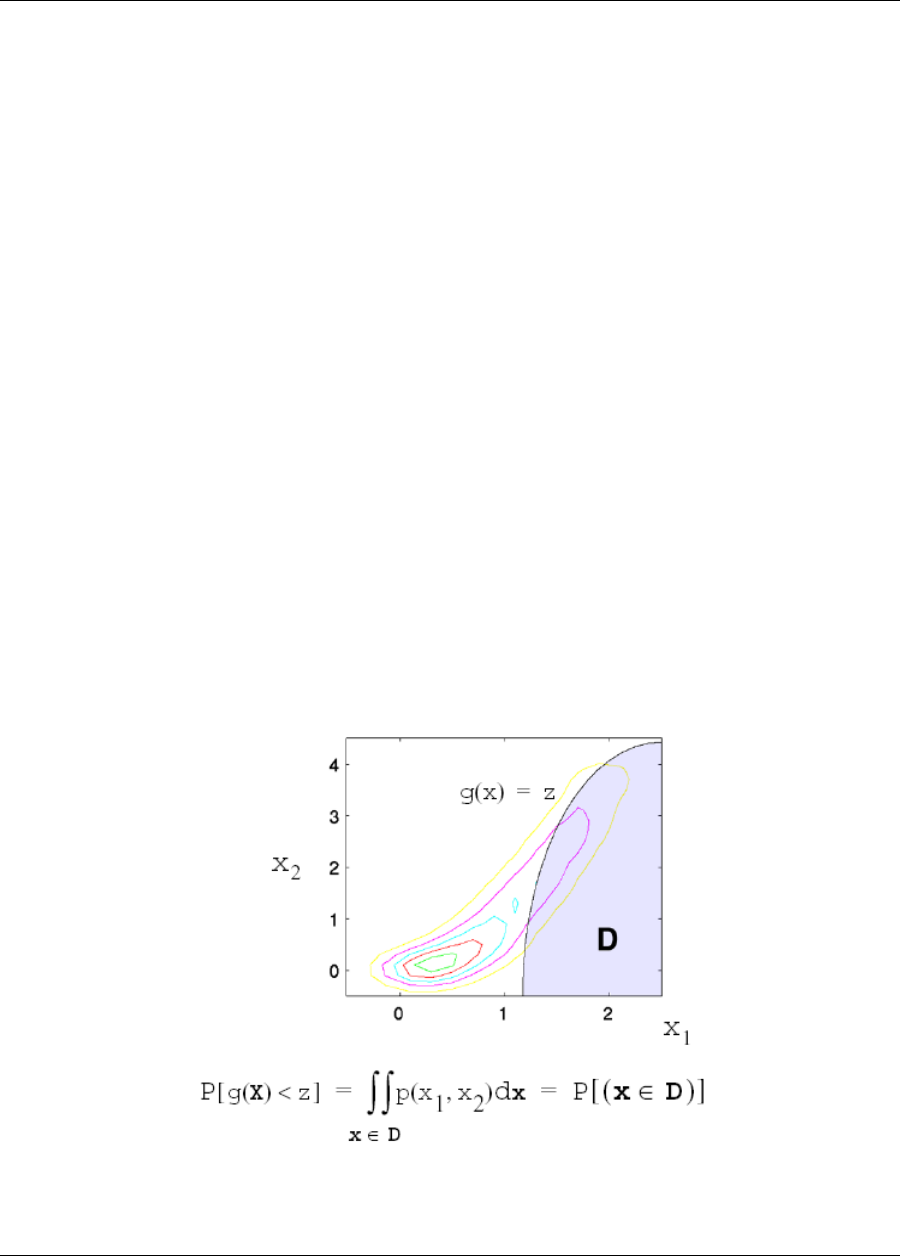
80 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
probabilistic approaches that compute approximate response function distribution statistics based on specified un-
certain variable distributions. These response statistics include response mean, response standard deviation, and
cumulative or complementary cumulative distribution functions (CDF/CCDF). These methods are often more ef-
ficient at computing statistics in the tails of the response distributions (events with low probability) than sampling
based approaches since the number of samples required to resolve a low probability can be prohibitive.
The methods all answer the fundamental question: “Given a set of uncertain input variables, X, and a scalar
response function, g, what is the probability that the response function is below or above a certain level, ¯z?” The
former can be written as P[g(X)≤¯z] = Fg(¯z)where Fg(¯z)is the cumulative distribution function (CDF) of the
uncertain response g(X)over a set of response levels. The latter can be written as P[g(X)>¯z]and defines the
complementary cumulative distribution function (CCDF).
This probability calculation involves a multi-dimensional integral over an irregularly shaped domain of interest,
D, where g(X)< z as displayed in Figure 5.6 for the case of two variables. The reliability methods all involve the
transformation of the user-specified uncertain variables, X, with probability density function, p(x1, x2), which
can be non-normal and correlated, to a space of independent Gaussian random variables, u, possessing a mean
value of zero and unit variance (i.e., standard normal variables). The region of interest, D, is also mapped to
the transformed space to yield, Du, where g(U)< z as shown in Figure 5.7. The Nataf transformation [28],
which is identical to the Rosenblatt transformation [114] in the case of independent random variables, is used in
Dakota to accomplish this mapping. This transformation is performed to make the probability calculation more
tractable. In the transformed space, probability contours are circular in nature as shown in Figure 5.7 unlike in
the original uncertain variable space, Figure 5.6. Also, the multi-dimensional integrals can be approximated by
simple functions of a single parameter, β, called the reliability index. βis the minimum Euclidean distance from
the origin in the transformed space to the response surface. This point is also known as the most probable point
(MPP) of failure. Note, however, the methodology is equally applicable for generic functions, not simply those
corresponding to failure criteria; this nomenclature is due to the origin of these methods within the disciplines
of structural safety and reliability. Note that there are local and global reliability methods. The majority of the
methods available are local, meaning that a local optimization formulation is used to locate one MPP. In contrast,
global methods can find multiple MPPs if they exist.
Figure 5.6: Graphical depiction of calculation of cumulative distribution function in the original uncertain variable
space.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
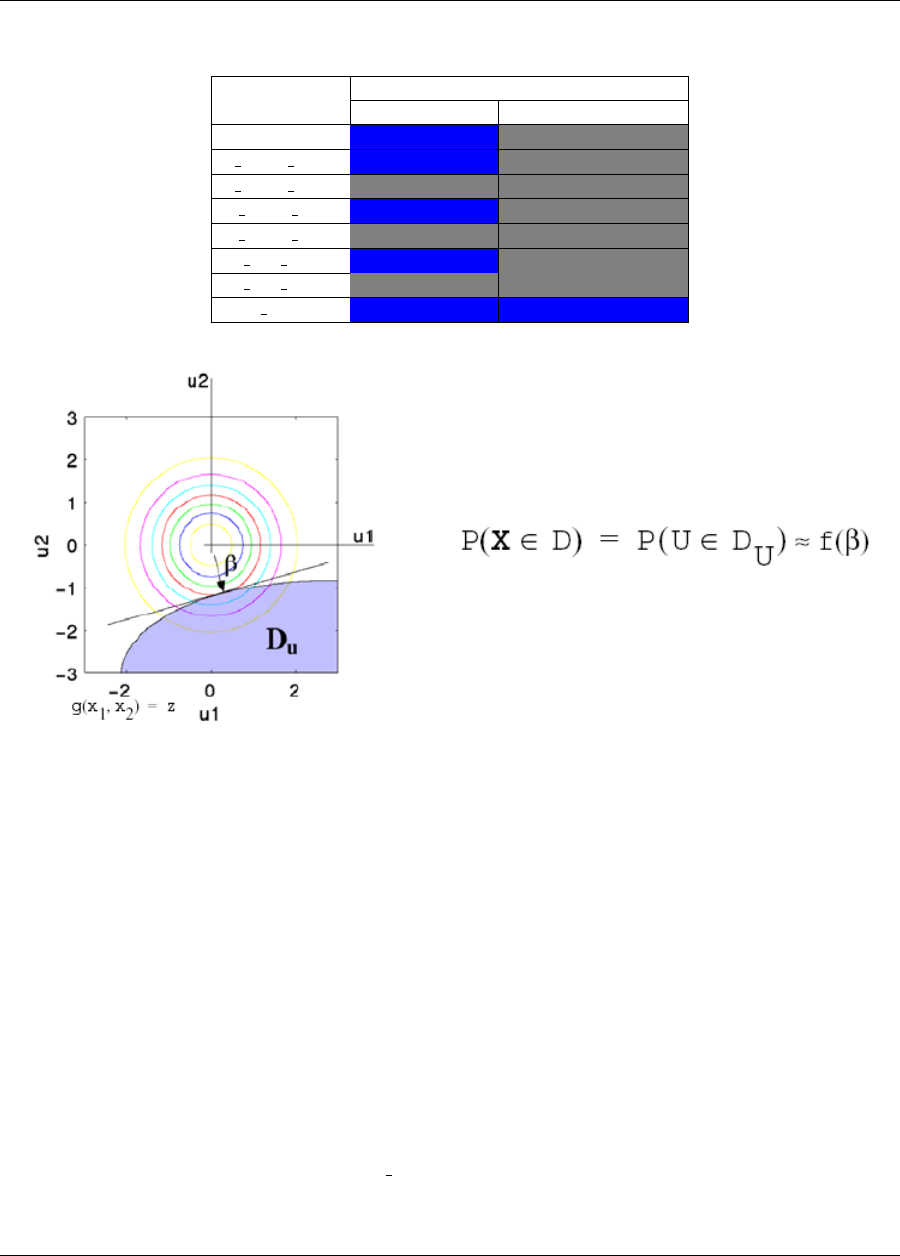
5.3. RELIABILITY METHODS 81
Table 5.1: Mapping from Dakota options to standard reliability methods.
Order of approximation and integration
MPP search First order Second order
none MVFOSM MVSOSM
x taylor mean AMV AMV2
u taylor mean u-space AMV u-space AMV2
x taylor mpp AMV+ AMV2+
u taylor mpp u-space AMV+ u-space AMV2+
x two point TANA
u two point u-space TANA
no approx FORM SORM
Figure 5.7: Graphical depiction of integration for the calculation of cumulative distribution function in the trans-
formed uncertain variable space.
5.3.1 Local Reliability Methods
The Dakota Theory Manual [4] provides the algorithmic details for the local reliability methods, including the
Mean Value method and the family of most probable point (MPP) search methods.
5.3.1.1 Method mapping
Given settings for limit state approximation, approximation order, integration approach, and other details pre-
sented to this point, it is evident that the number of algorithmic combinations is high. Table 5.1 provides a
succinct mapping for some of these combinations to common method names from the reliability literature, where
blue indicates the most well-known combinations and gray indicates other supported combinations.
Within the Dakota specification (refer to local reliability in the keywords section of the Reference Man-
ual [3]) within the Reference Manual), the MPP search and integration order selections are explicit in the method
specification, but the order of the approximation is inferred from the associated response specification (as is done
Dakota Version 6.7 User’s Manual generated on November 13, 2017

82 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
with local taylor series approximations described in Section 8.4.3.2). Thus, reliability methods do not have to be
synchronized in approximation and integration order as shown in the table; however, it is often desirable to do so.
5.3.2 Global Reliability Methods
Global reliability methods are designed to handle nonsmooth and multimodal failure surfaces, by creating global
approximations based on Gaussian process models. They accurately resolve a particular contour of a response
function and then estimate probabilities using multimodal adaptive importance sampling.
The global reliability method in Dakota is called Efficient Global Reliability Analysis (EGRA) [12]. The name
is due to its roots in efficient global optimization (EGO) [84,81]. The main idea in EGO-type optimization
methods is that a global approximation is made of the underlying function. This approximation, which is a
Gaussian process model, is used to guide the search by finding points which maximize the expected improvement
function (EIF). The EIF is used to select the location at which a new training point should be added to the Gaussian
process model by maximizing the amount of improvement in the objective function that can be expected by adding
that point. A point could be expected to produce an improvement in the objective function if its predicted value
is better than the current best solution, or if the uncertainty in its prediction is such that the probability of it
producing a better solution is high. Because the uncertainty is higher in regions of the design space with fewer
observations, this provides a balance between exploiting areas of the design space that predict good solutions, and
exploring areas where more information is needed.
The general procedure of these EGO-type methods is:
1. Build an initial Gaussian process model of the objective function.
2. Find the point that maximizes the EIF. If the EIF value at this point is sufficiently small, stop.
3. Evaluate the objective function at the point where the EIF is maximized. Update the Gaussian process
model using this new point. Go to Step 2.
Gaussian process (GP) models are used because they provide not just a predicted value at an unsampled point, but
also an estimate of the prediction variance. This variance gives an indication of the uncertainty in the GP model,
which results from the construction of the covariance function. This function is based on the idea that when input
points are near one another, the correlation between their corresponding outputs will be high. As a result, the
uncertainty associated with the model’s predictions will be small for input points which are near the points used
to train the model, and will increase as one moves further from the training points.
The expected improvement function is used in EGO algorithms to select the location at which a new training point
should be added. The EIF is defined as the expectation that any point in the search space will provide a better
solution than the current best solution based on the expected values and variances predicted by the GP model. It
is important to understand how the use of this EIF leads to optimal solutions. The EIF indicates how much the
objective function value at a new potential location is expected to be less than the predicted value at the current
best solution. Because the GP model provides a Gaussian distribution at each predicted point, expectations can
be calculated. Points with good expected values and even a small variance will have a significant expectation of
producing a better solution (exploitation), but so will points that have relatively poor expected values and greater
variance (exploration).
The application of EGO to reliability analysis, however, is made more complicated due to the inclusion of equality
constraints. In forward reliability analysis, the response function appears as a constraint rather than the objective.
That is, we want to satisfy the constraint that the response equals a threshold value and is on the limit state:
G(u) = ¯z. Therefore, the EIF function was modified to focus on feasibility, and instead of using an expected
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.3. RELIABILITY METHODS 83
improvement function, we use an expected feasibility function (EFF) [12]. The EFF provides an indication of
how well the response is expected to satisfy the equality constraint. Points where the expected value is close to
the threshold (µG≈¯z) and points with a large uncertainty in the prediction will have large expected feasibility
values.
The general outline of the EGRA algorithm is as follows: LHS sampling is used to generate a small number of
samples from the true response function. Then, an initial Gaussian process model is constructed. Based on the
EFF, the point with maximum EFF is found using the global optimizer DIRECT. The true response function is
then evaluated at this new point, and this point is added to the sample set and the process of building a new GP
model and maximizing the EFF is repeated until the maximum EFF is small. At this stage, the GP model is
accurate in the vicinity of the limit state. The GP model is then used to calculate the probability of failure using
multimodal importance sampling, which is explained below.
One method to calculate the probability of failure is to directly perform the probability integration numerically
by sampling the response function. Sampling methods can be prohibitively expensive because they generally
require a large number of response function evaluations. Importance sampling methods reduce this expense by
focusing the samples in the important regions of the uncertain space. They do this by centering the sampling
density function at the MPP rather than at the mean. This ensures the samples will lie the region of interest,
thus increasing the efficiency of the sampling method. Adaptive importance sampling (AIS) further improves the
efficiency by adaptively updating the sampling density function. Multimodal adaptive importance sampling [29]
is a variation of AIS that allows for the use of multiple sampling densities making it better suited for cases where
multiple sections of the limit state are highly probable.
Note that importance sampling methods require that the location of at least one MPP be known because it is
used to center the initial sampling density. However, current gradient-based, local search methods used in MPP
search may fail to converge or may converge to poor solutions for highly nonlinear problems, possibly making
these methods inapplicable. The EGRA algorithm described above does not depend on the availability of accurate
gradient information, making convergence more reliable for nonsmooth response functions. Moreover, EGRA has
the ability to locate multiple failure points, which can provide multiple starting points and thus a good multimodal
sampling density for the initial steps of multimodal AIS. The probability assessment using multimodal AIS thus
incorporates probability of failure at multiple points.
5.3.3 Uncertainty Quantification Examples using Reliability Analysis
In summary, the user can choose to perform either forward (RIA) or inverse (PMA) mappings when performing
a reliability analysis. With either approach, there are a variety of methods from which to choose in terms of limit
state approximations (MVFOSM, MVSOSM, x-/u-space AMV, x-/u-space AMV2, x-/u-space AMV+, x-/u-space
AMV2+, x-/u-space TANA, and FORM/SORM), probability integrations (first-order or second-order), limit state
Hessian selection (analytic, finite difference, BFGS, or SR1), and MPP optimization algorithm (SQP or NIP)
selections.
All reliability methods output approximate values of the CDF/CCDF response-probability-reliability levels for
prescribed response levels (RIA) or prescribed probability or reliability levels (PMA). In addition, mean value
methods output estimates of the response means and standard deviations as well as importance factors that attribute
variance among the set of uncertain variables (provided a nonzero response variance estimate).
5.3.3.1 Mean-value Reliability with Textbook
Figure 5.8 shows the Dakota input file for an example problem that demonstrates the simplest reliability method,
called the mean value method (also referred to as the Mean Value First Order Second Moment method). It is
Dakota Version 6.7 User’s Manual generated on November 13, 2017

84 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
specified with method keyword local reliability. This method calculates the mean and variance of the
response function based on information about the mean and variance of the inputs and gradient information at the
mean of the inputs. The mean value method is extremely cheap computationally (only five runs were required
for the textbook function), but can be quite inaccurate, especially for nonlinear problems and/or problems with
uncertain inputs that are significantly non-normal. More detail on the mean value method can be found in the
Local Reliability Methods section of the Dakota Theory Manual [4], and more detail on reliability methods in
general (including the more advanced methods) is found in Section 5.3.
Example output from the mean value method is displayed in Figure 5.9. Note that since the mean of both inputs
is 1, the mean value of the output for response 1 is zero. However, the mean values of the constraints are both
0.5. The mean value results indicate that variable x1 is more important in constraint 1 while x2 is more important
in constraint 2, which is the case based on Equation 20.1. The importance factors are not available for the first
response as the standard deviation is zero.
# Dakota Input File: textbook_uq_meanvalue.in
environment
#graphics
method
local_reliability
interface
analysis_drivers = ’text_book’
fork asynchronous
variables
lognormal_uncertain = 2
means = 1. 1.
std_deviations = 0.5 0.5
descriptors = ’TF1ln’ ’TF2ln’
responses
response_functions = 3
numerical_gradients
method_source dakota
interval_type central
fd_gradient_step_size = 1.e-4
no_hessians
Figure 5.8: Mean Value Reliability Method: the Dakota input file – see
Dakota/examples/users/textbook uq meanvalue.in
5.3.3.2 FORM Reliability with Lognormal Ratio
This example quantifies the uncertainty in the “log ratio” response function:
g(x1, x2) = x1
x2
(5.1)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.3. RELIABILITY METHODS 85
MV Statistics for response_fn_1:
Approximate Mean Response = 0.0000000000e+00
Approximate Standard Deviation of Response = 0.0000000000e+00
Importance Factors not available.
MV Statistics for response_fn_2:
Approximate Mean Response = 5.0000000000e-01
Approximate Standard Deviation of Response = 1.0307764064e+00
Importance Factor for TF1ln = 9.4117647059e-01
Importance Factor for TF2ln = 5.8823529412e-02
MV Statistics for response_fn_3:
Approximate Mean Response = 5.0000000000e-01
Approximate Standard Deviation of Response = 1.0307764064e+00
Importance Factor for TF1ln = 5.8823529412e-02
Importance Factor for TF2ln = 9.4117647059e-01
Figure 5.9: Results of the Mean Value Method on the Textbook Function
by computing approximate response statistics using reliability analysis to determine the response cumulative
distribution function:
P[g(x1, x2)<¯z](5.2)
where X1and X2are identically distributed lognormal random variables with means of 1, standard deviations of
0.5, and correlation coefficient of 0.3.
A Dakota input file showing RIA using FORM (option 7 in limit state approximations combined with first-order
integration) is listed in Figure 5.10. The user first specifies the local reliability method, followed by
the MPP search approach and integration order. In this example, we specify mpp search no approx and
utilize the default first-order integration to select FORM. Finally, the user specifies response levels or probabili-
ty/reliability levels to determine if the problem will be solved using an RIA approach or a PMA approach. In the
example figure of 5.10, we use RIA by specifying a range of response levels for the problem. The resulting
output for this input is shown in Figure 5.11, with probability and reliability levels listed for each response level.
Figure 5.12 shows that FORM compares favorably to an exact analytic solution for this problem. Also note that
FORM does have some error in the calculation of CDF values for this problem, but it is a very small error (on the
order of e-11), much smaller than the error obtained when using a Mean Value method, which will be discussed
next.
If the user specifies local reliability as a method with no additional specification on how to do the MPP
search (for example, by commenting out mpp search no approx in Figure 5.10), then no MPP search is
done: the Mean Value method is used. The mean value results are shown in Figure 5.13 and consist of approximate
mean and standard deviation of the response, the importance factors for each uncertain variable, and approximate
probability/reliability levels for the prescribed response levels that have been inferred from the approximate mean
and standard deviation (see Mean Value section in Reliability Methods Chapter of Dakota Theory Manual [4]).
It is evident that the statistics are considerably different from the fully converged FORM results; however, these
rough approximations are also much less expensive to calculate. The importance factors are a measure of the
sensitivity of the response function(s) to the uncertain input variables. A comparison of the mean value results
with the FORM results is shown in Figure 5.12. The mean value results are not accurate near the tail values of the
CDF, and can differ from the exact solution by as much as 0.11 in CDF estimates. A comprehensive comparison
of various reliability methods applied to the logratio problem is provided in [36].
Additional reliability analysis and design results are provided in Sections 20.10.1-20.10.5.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

86 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
# Dakota Input File: logratio_uq_reliability.in
environment
graphics
method
local_reliability
mpp_search no_approx
response_levels = .4 .5 .55 .6 .65 .7
.75 .8 .85 .9 1. 1.05 1.15 1.2 1.25 1.3
1.35 1.4 1.5 1.55 1.6 1.65 1.7 1.75
variables
lognormal_uncertain = 2
means = 1. 1
std_deviations = 0.5 0.5
initial_point = 0.6 1.4
descriptors = ’TF1ln’ ’TF2ln’
uncertain_correlation_matrix = 1 0.3
0.3 1
interface
analysis_drivers = ’log_ratio’
direct
# fork asynch
responses
response_functions = 1
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 1.e-4
no_hessians
Figure 5.10: Dakota input file for Reliability UQ example using FORM – see
Dakota/examples/users/logratio uq reliability.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
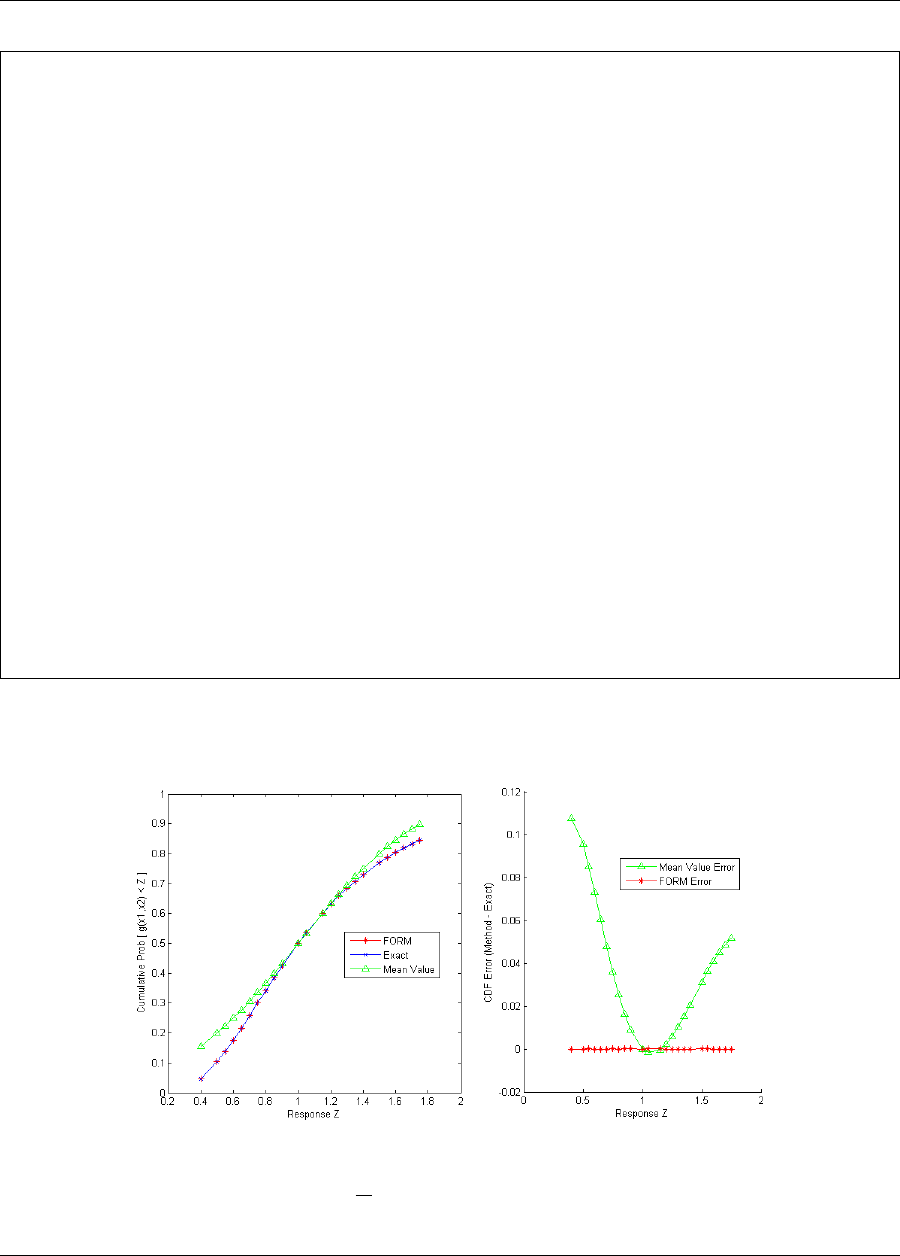
5.3. RELIABILITY METHODS 87
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index
-------------- ----------------- -----------------
4.0000000000e-01 4.7624085962e-02 1.6683404020e+00
5.0000000000e-01 1.0346525475e-01 1.2620507942e+00
5.5000000000e-01 1.3818404972e-01 1.0885143628e+00
6.0000000000e-01 1.7616275822e-01 9.3008801339e-01
6.5000000000e-01 2.1641741368e-01 7.8434989943e-01
7.0000000000e-01 2.5803428381e-01 6.4941748143e-01
7.5000000000e-01 3.0020938124e-01 5.2379840558e-01
8.0000000000e-01 3.4226491013e-01 4.0628960782e-01
8.5000000000e-01 3.8365052982e-01 2.9590705956e-01
9.0000000000e-01 4.2393548232e-01 1.9183562480e-01
1.0000000000e+00 5.0000000000e-01 6.8682233460e-12
1.0500000000e+00 5.3539344228e-01 -8.8834907167e-02
1.1500000000e+00 6.0043460094e-01 -2.5447217462e-01
1.2000000000e+00 6.3004131827e-01 -3.3196278078e-01
1.2500000000e+00 6.5773508987e-01 -4.0628960782e-01
1.3000000000e+00 6.8356844630e-01 -4.7770089473e-01
1.3500000000e+00 7.0761025532e-01 -5.4641676380e-01
1.4000000000e+00 7.2994058691e-01 -6.1263331274e-01
1.5000000000e+00 7.6981945355e-01 -7.3825238860e-01
1.5500000000e+00 7.8755158269e-01 -7.9795460350e-01
1.6000000000e+00 8.0393505584e-01 -8.5576118635e-01
1.6500000000e+00 8.1906005158e-01 -9.1178881995e-01
1.7000000000e+00 8.3301386860e-01 -9.6614373461e-01
1.7500000000e+00 8.4588021938e-01 -1.0189229206e+00
Figure 5.11: Output from Reliability UQ example using FORM.
Figure 5.12: Comparison of the cumulative distribution function (CDF) computed by FORM, the Mean Value
method, and the exact CDF for g(x1, x2) = x1
x2
Dakota Version 6.7 User’s Manual generated on November 13, 2017

88 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
MV Statistics for response_fn_1:
Approximate Mean Response = 1.0000000000e+00
Approximate Standard Deviation of Response = 5.9160798127e-01
Importance Factor for TF1ln = 7.1428570714e-01
Importance Factor for TF2ln = 7.1428572143e-01
Importance Factor for TF1ln TF2ln = -4.2857142857e-01
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
4.0000000000e-01 1.5524721837e-01 1.0141851006e+00 1.0141851006e+00
5.0000000000e-01 1.9901236093e-01 8.4515425050e-01 8.4515425050e-01
5.5000000000e-01 2.2343641149e-01 7.6063882545e-01 7.6063882545e-01
6.0000000000e-01 2.4948115037e-01 6.7612340040e-01 6.7612340040e-01
6.5000000000e-01 2.7705656603e-01 5.9160797535e-01 5.9160797535e-01
7.0000000000e-01 3.0604494093e-01 5.0709255030e-01 5.0709255030e-01
7.5000000000e-01 3.3630190949e-01 4.2257712525e-01 4.2257712525e-01
8.0000000000e-01 3.6765834596e-01 3.3806170020e-01 3.3806170020e-01
8.5000000000e-01 3.9992305332e-01 2.5354627515e-01 2.5354627515e-01
9.0000000000e-01 4.3288618783e-01 1.6903085010e-01 1.6903085010e-01
1.0000000000e+00 5.0000000000e-01 0.0000000000e+00 0.0000000000e+00
1.0500000000e+00 5.3367668035e-01 -8.4515425050e-02 -8.4515425050e-02
1.1500000000e+00 6.0007694668e-01 -2.5354627515e-01 -2.5354627515e-01
1.2000000000e+00 6.3234165404e-01 -3.3806170020e-01 -3.3806170020e-01
1.2500000000e+00 6.6369809051e-01 -4.2257712525e-01 -4.2257712525e-01
1.3000000000e+00 6.9395505907e-01 -5.0709255030e-01 -5.0709255030e-01
1.3500000000e+00 7.2294343397e-01 -5.9160797535e-01 -5.9160797535e-01
1.4000000000e+00 7.5051884963e-01 -6.7612340040e-01 -6.7612340040e-01
1.5000000000e+00 8.0098763907e-01 -8.4515425050e-01 -8.4515425050e-01
1.5500000000e+00 8.2372893005e-01 -9.2966967555e-01 -9.2966967555e-01
1.6000000000e+00 8.4475278163e-01 -1.0141851006e+00 -1.0141851006e+00
1.6500000000e+00 8.6405064339e-01 -1.0987005257e+00 -1.0987005257e+00
1.7000000000e+00 8.8163821351e-01 -1.1832159507e+00 -1.1832159507e+00
1.7500000000e+00 8.9755305196e-01 -1.2677313758e+00 -1.2677313758e+00
Figure 5.13: Output from Reliability UQ example using mean value.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.4. STOCHASTIC EXPANSION METHODS 89
5.4 Stochastic Expansion Methods
The development of these techniques mirrors that of deterministic finite element analysis through the utilization
of the concepts of projection, orthogonality, and weak convergence. The polynomial chaos expansion is based
on a multidimensional orthogonal polynomial approximation and the stochastic collocation approach is based
on a multidimensional interpolation polynomial approximation, both formed in terms of standardized random
variables. A distinguishing feature of these two methodologies is that the final solution is expressed as a func-
tional mapping, and not merely as a set of statistics as is the case for many nondeterministic methodologies. This
makes these techniques particularly attractive for use in multi-physics applications which link different analysis
packages. The first stochastic expansion method is the polynomial chaos expansion (PCE) [53,54]. For smooth
functions (i.e., analytic, infinitely-differentiable) in L2(i.e., possessing finite variance), exponential convergence
rates can be obtained under order refinement for integrated statistical quantities of interest such as mean, vari-
ance, and probability. Dakota implements the generalized PCE approach using the Wiener-Askey scheme [152],
in which Hermite, Legendre, Laguerre, Jacobi, and generalized Laguerre orthogonal polynomials are used for
modeling the effect of continuous random variables described by normal, uniform, exponential, beta, and gamma
probability distributions, respectively1. These orthogonal polynomial selections are optimal for these distribution
types since the inner product weighting function corresponds2to the probability density functions for these con-
tinuous distributions. Orthogonal polynomials can be computed for any positive weight function, so these five
classical orthogonal polynomials may be augmented with numerically-generated polynomials for other probabil-
ity distributions (e.g., for lognormal, extreme value, and histogram distributions). When independent standard
random variables are used (or computed through transformation), the variable expansions are uncoupled, allow-
ing the polynomial orthogonality properties to be applied on a per-dimension basis. This allows one to mix and
match the polynomial basis used for each variable without interference with the spectral projection scheme for
the response.
In non-intrusive PCE, simulations are used as black boxes and the calculation of chaos expansion coefficients for
response metrics of interest is based on a set of simulation response evaluations. To calculate these response PCE
coefficients, two primary classes of approaches have been proposed: spectral projection and regression. The spec-
tral projection approach projects the response against each basis function using inner products and employs the
polynomial orthogonality properties to extract each coefficient. Each inner product involves a multidimensional
integral over the support range of the weighting function, which can be evaluated numerically using sampling,
tensor-product quadrature, Smolyak sparse grid [124], or cubature [128] approaches. The regression approach
finds a set of PCE coefficients which best match a set of response values obtained from either a design of computer
experiments (“point collocation” [145]) or from a randomly selected subset of tensor Gauss points (“probabilistic
collocation” [135]). Various methods can be used to solve the resulting linear system, including least squares
methods for over-determined systems and compressed sensing methods for under-determined systems. Details of
these methods are documented in the Linear regression section of the Dakota Theory Manual [4] and the neces-
sary specifications needed to activate these techniques are listed in the keyword section of the Dakota Reference
Manual [3].
Stochastic collocation (SC) is another stochastic expansion technique for UQ that is closely related to PCE. As
for PCE, exponential convergence rates can be obtained under order refinement for integrated statistical quantities
of interest, provided that the response functions are smooth with finite variance. The primary distinction is that,
whereas PCE estimates coefficients for known multivariate orthogonal polynomial basis functions, SC forms
multivariate interpolation polynomial bases for known coefficients. The interpolation polynomials may be either
local or global and either value-based or gradient-enhanced (four combinations: Lagrange, Hermite, piecewise
linear spline, and piecewise cubic spline), and may be used within nodal or hierarchical interpolation formulations.
Interpolation is performed on structured grids such as tensor-product or sparse grids. Starting from a tensor-
1Orthogonal polynomial selections also exist for discrete probability distributions, but are not yet supported in Dakota.
2Identical support range; weight differs by at most a constant factor.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

90 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
product multidimensional interpolation polynomial in the value-based case (Lagrange or piecewise linear spline),
we have the feature that the ith interpolation polynomial has a value of 1 at collocation point iand a value of 0
for all other collocation points, leading to the use of expansion coefficients that are just the response values at
each of the collocation points. In the gradient-enhanced case (Hermite or piecewise cubic spline), SC includes
both type 1 and type 2 interpolation polynomials, where the former interpolate the values while producing zero
gradients and the latter interpolate the gradients while producing zero values (refer to [4] for additional details).
Sparse interpolants are weighted sums of these tensor interpolants; however, they are only interpolatory for sparse
grids based on fully nested rules and will exhibit some interpolation error at the collocation points for sparse
grids based on non-nested rules. A key to maximizing performance with SC is performing collocation using the
Gauss points and weights from the same optimal orthogonal polynomials used in PCE. For use of standard Gauss
integration rules (not nested variants such as Gauss-Patterson or Genz-Keister) within tensor-product quadrature,
tensor PCE expansions and tensor SC interpolants are equivalent in that identical polynomial approximations
are generated [22]. Moreover, this equivalence can be extended to sparse grids based on standard Gauss rules,
provided that a sparse PCE is formed based on a weighted sum of tensor expansions [20].
The Dakota Theory Manual [4] provides full algorithmic details for the PCE and SC methods.
5.4.1 Uncertainty Quantification Examples using Stochastic Expansions
5.4.1.1 Polynomial Chaos Expansion for Rosenbrock
A typical Dakota input file for performing an uncertainty quantification using PCE is shown in Figure 5.14. In this
example, we compute CDF probabilities for six response levels of Rosenbrock’s function. Since Rosenbrock is a
fourth order polynomial and we employ a fourth-order expansion using an optimal basis (Legendre for uniform
random variables), we can readily obtain a polynomial expansion which exactly matches the Rosenbrock function.
In this example, we select Gaussian quadratures using an anisotropic approach (fifth-order quadrature in x1and
third-order quadrature in x2), resulting in a total of 15 function evaluations to compute the PCE coefficients.
The tensor product quadature points upon which the expansion is calculated are shown in Figure 5.15. The tensor
product generates all combinations of values from each individual dimension: it is an all-way pairing of points.
Once the expansion coefficients have been calculated, some statistics are available analytically and others must be
evaluated numerically. For the numerical portion, the input file specifies the use of 10000 samples, which will be
evaluated on the expansion to compute the CDF probabilities. In Figure 5.16, excerpts from the results summary
are presented, where we first see a summary of the PCE coefficients which exactly reproduce Rosenbrock for a
Legendre polynomial basis. The analytic statistics for mean, standard deviation, and COV are then presented.
For example, the mean is 455.66 and the standard deviation is 606.56. The moments are followed by global
sensitivity indices (Sobol’ indices).This example shows that variable x1 has the largest main effect (0.497) as
compared with variable x2 (0.296) or the interaction between x1 and x2 (0.206). After the global sensitivity
indices, the local sensitivities are presented, evaluated at the mean values. Finally, we see the numerical results
for the CDF probabilities based on 10000 samples performed on the expansion. For example, the probability
that the Rosenbrock function is less than 100 over these two uncertain variables is 0.342. Note that this is a very
similar estimate to what was obtained using 200 Monte Carlo samples, with fewer true function evaluations.
5.4.1.2 Uncertainty Quantification Example using Stochastic Collocation
Compared to the previous PCE example, this section presents a more sophisticated example, where we use
stochastic collocation built on an anisotropic sparse grid defined from numerically-generated orthogonal poly-
nomials. The uncertain variables are lognormal in this example and the orthogonal polynomials are generated
Dakota Version 6.7 User’s Manual generated on November 13, 2017
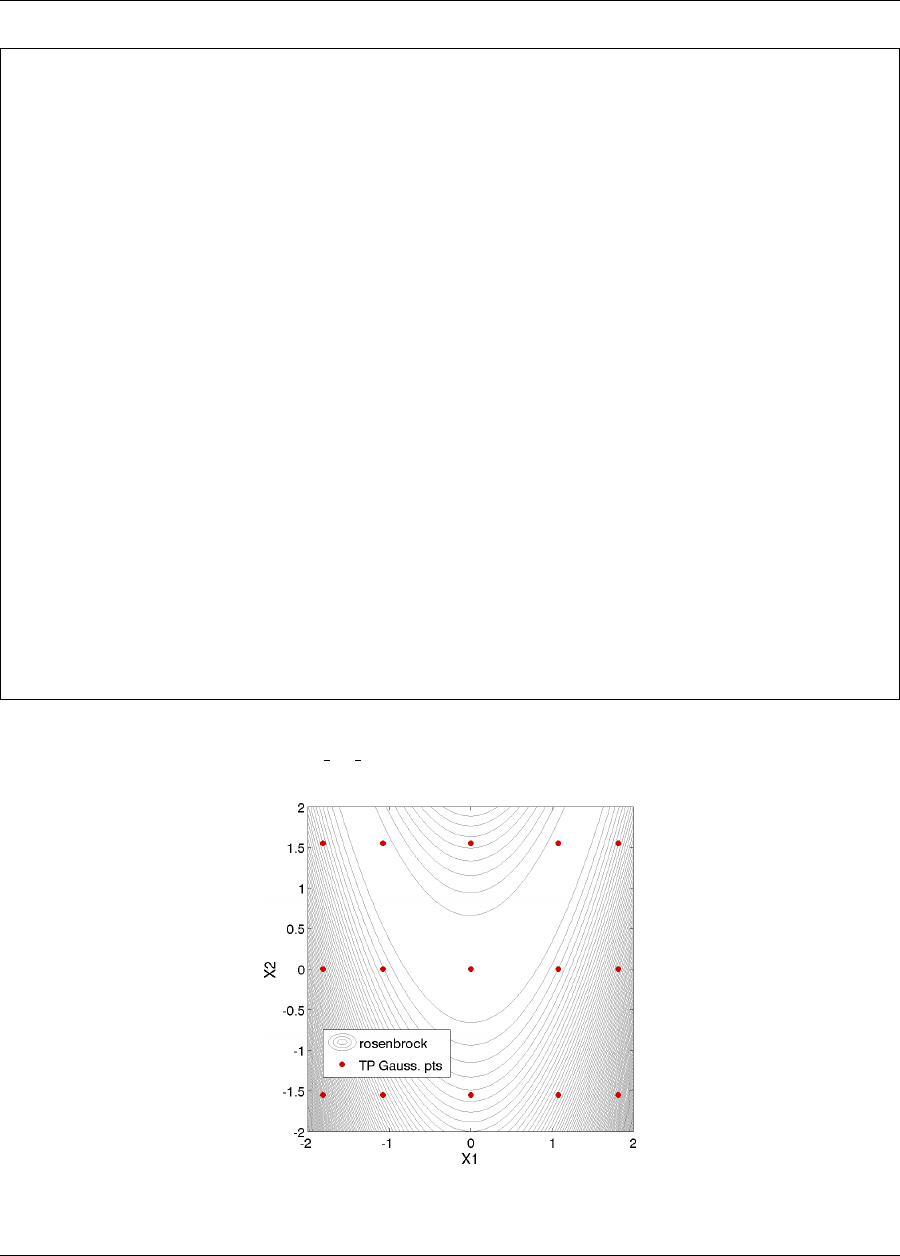
5.4. STOCHASTIC EXPANSION METHODS 91
# Dakota Input File: rosen_uq_pce.in
environment
#graphics
method
polynomial_chaos
quadrature_order = 5
dimension_preference = 5 3
samples_on_emulator = 10000
seed = 12347
response_levels = .1 1. 50. 100. 500. 1000.
variance_based_decomp #interaction_order = 1
variables
uniform_uncertain = 2
lower_bounds = -2. -2.
upper_bounds = 2. 2.
descriptors = ’x1’ ’x2’
interface
analysis_drivers = ’rosenbrock’
direct
responses
response_functions = 1
no_gradients
no_hessians
Figure 5.14: Dakota input file for performing UQ using polynomial chaos expansions – see
Dakota/examples/users/rosen uq pce.in
Figure 5.15: Rosenbrock polynomial chaos example: tensor product quadrature points.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

92 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
Polynomial Chaos coefficients for response_fn_1:
coefficient u1 u2
----------- ---- ----
4.5566666667e+02 P0 P0
-4.0000000000e+00 P1 P0
9.1695238095e+02 P2 P0
-9.9475983006e-14 P3 P0
3.6571428571e+02 P4 P0
-5.3333333333e+02 P0 P1
-3.9968028887e-14 P1 P1
-1.0666666667e+03 P2 P1
-3.3573144265e-13 P3 P1
1.2829737273e-12 P4 P1
2.6666666667e+02 P0 P2
2.2648549702e-13 P1 P2
4.8849813084e-13 P2 P2
2.8754776338e-13 P3 P2
-2.8477220582e-13 P4 P2
-------------------------------------------------------------------
Statistics derived analytically from polynomial expansion:
Moment-based statistics for each response function:
Mean Std Dev Skewness Kurtosis
response_fn_1
expansion: 4.5566666667e+02 6.0656024184e+02
numerical: 4.5566666667e+02 6.0656024184e+02 1.9633285271e+00 3.3633861456e+00
Covariance among response functions:
[[ 3.6791532698e+05 ]]
Local sensitivities for each response function evaluated at uncertain variable means:
response_fn_1:
[ -2.0000000000e+00 2.4055757386e-13 ]
Global sensitivity indices for each response function:
response_fn_1 Sobol indices:
Main Total
4.9746891383e-01 7.0363551328e-01 x1
2.9636448672e-01 5.0253108617e-01 x2
Interaction
2.0616659946e-01 x1 x2
Statistics based on 10000 samples performed on polynomial expansion:
Probability Density Function (PDF) histograms for each response function:
PDF for response_fn_1:
Bin Lower Bin Upper Density Value
--------- --------- -------------
6.8311107124e-03 1.0000000000e-01 2.0393073423e-02
1.0000000000e-01 1.0000000000e+00 1.3000000000e-02
1.0000000000e+00 5.0000000000e+01 4.7000000000e-03
5.0000000000e+01 1.0000000000e+02 1.9680000000e-03
1.0000000000e+02 5.0000000000e+02 9.2150000000e-04
5.0000000000e+02 1.0000000000e+03 2.8300000000e-04
1.0000000000e+03 3.5755437782e+03 5.7308286215e-05
Level mappings for each response function:
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e-01 1.9000000000e-03
1.0000000000e+00 1.3600000000e-02
5.0000000000e+01 2.4390000000e-01
1.0000000000e+02 3.4230000000e-01
5.0000000000e+02 7.1090000000e-01
1.0000000000e+03 8.5240000000e-01
-------------------------------------------------------------------
Figure 5.16: Excerpt of UQ output for polynomial chaos example.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.4. STOCHASTIC EXPANSION METHODS 93
from Gauss-Wigert recursion coefficients [121] in combination with the Golub-Welsch procedure [65]. The input
file is shown in Figure 5.17. Note that the dimension preference of (2,1) is inverted to define a γweighting vector
of (0.5,1) (and γof 0.5) for use in the anisotropic Smolyak index set constraint (see Smolyak sparse grids sec-
tion in Stochastic Expansion Methods chapter in Dakota Theory Manual [4]). In this example, we compute CDF
probabilities for six response levels of Rosenbrock’s function. This example requires 19 function evaluations to
calculate the interpolating polynomials in stochastic collocation and the resulting expansion exactly reproduces
Rosenbrock’s function. The placement of the points generated by the sparse grid is shown in Figure 5.18.
# Dakota Input File: rosen_uq_sc.in
environment
#graphics
method
stoch_collocation
sparse_grid_level = 3
dimension_preference = 2 1
samples_on_emulator = 10000 seed = 12347
response_levels = .1 1. 50. 100. 500. 1000.
variance_based_decomp #interaction_order = 1
output silent
variables
lognormal_uncertain = 2
means = 1. 1.
std_deviations = 0.5 0.5
descriptors = ’x1’ ’x2’
interface
analysis_drivers = ’rosenbrock’
direct
responses
response_functions = 1
no_gradients
no_hessians
Figure 5.17: Dakota input file for performing UQ using stochastic collocation – see
Dakota/examples/users/rosen uq sc.in
Once the expansion coefficients have been calculated, some statistics are available analytically and others must be
evaluated numerically. For the numerical portion, the input file specifies the use of 10000 samples, which will be
evaluated on the expansion to compute the CDF probabilities. In Figure 5.19, excerpts from the results summary
are presented. We first see the moment statistics for mean, standard deviation, skewness, and kurtosis computed
by numerical integration (see Analytic moments section in Stochastic Expansion Methods chapter in Dakota
Theory Manual [4]), where the numerical row corresponds to integration using the original response values and the
expansion row corresponds to integration using values from the interpolant. The response covariance (collapsing
to a single variance value for one response function) and global sensitivity indices (Sobol’ indices) are presented
next. This example shows that variable x1 has the largest main effect (0.99) as compared with variable x2 (0.0007)
or the interaction between x1 and x2 (0.005). Finally, we see the numerical results for the CDF probabilities based
on 10000 samples performed on the expansion. For example, the probability that the Rosenbrock function is less
Dakota Version 6.7 User’s Manual generated on November 13, 2017

94 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
Figure 5.18: Rosenbrock stochastic collocation example: sparse grid points.
than 100 is 0.7233. Note that these results are significantly different than the ones presented in Section 5.4.1.1
because of the different assumptions about the inputs: uniform[-2,2] versus lognormals with means of 1.0 and
standard deviations of 0.5.
5.5 Importance Sampling Methods
Importance sampling is a method that allows one to estimate statistical quantities such as failure probabilities (e.g.
the probability that a response quantity will exceed a threshold or fall below a threshold value) in a way that is
more efficient than Monte Carlo sampling. The core idea in importance sampling is that one generates samples
that preferentially samples important regions in the space (e.g. in or near the failure region or user-defined region
of interest), and then appropriately weights the samples to obtain an unbiased estimate of the failure probability
[126]. In importance sampling, the samples are generated from a density which is called the importance density:
it is not the original probability density of the input distributions. The importance density should be centered
near the failure region of interest. For black-box simulations such as those commonly interfaced with Dakota, it
is difficult to specify the importance density a priori: the user often does not know where the failure region lies,
especially in a high-dimensional space. [131]
More formally, we define the objective of importance sampling as calculating the probability, P, that the output
will exceed a threshold level. This is a failure probability, where the failure probability is defined as some scalar
function, y(X), exceeding a threshold, T, where the inputs, X, are randomly distributed with density, ρ(X).
When evaluating y(X)is sufficiently expensive or Pis sufficiently small, Monte Carlo (MC) sampling methods
to estimate Pwill be infeasible due to the large number of function evaluations required for a specified accuracy.
The probability of failure can be thought of as the mean rate of occurrence of failure. The Monte Carlo (MC)
estimate of Pis therefore the sample mean of the indicator function, I(X),
PMC =1
N
N
X
i=1
I(Xi)X∼ρ(X),(5.3)
where Nsamples, Xi, are drawn from ρ(X), and the indicator function I(X)is 1 if failure occurs and zero
otherwise.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.5. IMPORTANCE SAMPLING METHODS 95
Statistics derived analytically from polynomial expansion:
Moment-based statistics for each response function:
Mean Std Dev Skewness Kurtosis
response_fn_1
expansion: 2.5671972656e+02 2.0484189184e+03 2.7419241630e+02 1.9594567379e+06
numerical: 2.5671972656e+02 2.0484189184e+03 2.7419241630e+02 1.9594567379e+06
Covariance among response functions:
[[ 4.1960200651e+06 ]]
Global sensitivity indices for each response function:
response_fn_1 Sobol indices:
Main Total
9.9391978710e-01 9.9928724777e-01 x1
7.1275222945e-04 6.0802128961e-03 x2
Interaction
5.3674606667e-03 x1 x2
Statistics based on 10000 samples performed on polynomial expansion:
Level mappings for each response function:
Cumulative Distribution Function (CDF) for response_fn_1:
Response Level Probability Level Reliability Index General Rel Index
-------------- ----------------- ----------------- -----------------
1.0000000000e-01 1.8100000000e-02
1.0000000000e+00 8.7800000000e-02
5.0000000000e+01 5.8410000000e-01
1.0000000000e+02 7.2330000000e-01
5.0000000000e+02 9.2010000000e-01
1.0000000000e+03 9.5660000000e-01
Figure 5.19: Excerpt of UQ output for stochastic collocation example.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

96 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
Importance sampling draws samples from the importance density ρ0(X)and scales the sample mean by the im-
portance density:
PIS =1
N
N
X
i=1 I(Xi)ρ(Xi)
ρ0(Xi)X∼ρ0(X).(5.4)
This reduces the asymptotic error variance from:
σ2
errM C =
Eh(I(X)−P)2i
N(5.5)
to
σ2
errI S =
EI(X)ρ(X)
ρ0(X)−P2
N.(5.6)
Inspection of Eq. 5.6 reveals σ2
errI S = 0 if ρ0(X)equals the ideal importance density ρ∗(X),
ρ∗(X) = I(X)ρ(X)
P.(5.7)
However, ρ∗(X)is unknown a priori because I(X)is only known where it has been evaluated. Therefore, the
required Pin the denominator is also unknown: this is what we are trying to estimate.
If importance sampling is to be effective, the practitioner must be able to choose a good ρ0(X)without already
knowing I(X)everywhere. There is a danger: a poor choice for ρ0(X)can put most of the samples in unimportant
regions and make σ2
errI S much greater than σ2
errM C . In particular, importance sampling can be challenging for
very low probability events in high-dimensional spaces where the output yis calculated by a simulation. In these
cases, usually one does not know anything a priori about where the failure region exists in input space. We have
developed two importance sampling approaches which do not rely on the user explicitly specifying an importance
density.
5.5.1 Importance Sampling Method based on Reliability Approach
The first method is based on ideas in reliability modeling 5.3.1. An initial Latin Hypercube sampling is performed
to generate an initial set of samples. These initial samples are augmented with samples from an importance density
as follows: The variables are transformed to standard normal space. In the transformed space, the importance
density is a set of normal densities centered around points which are in the failure region. Note that this is similar
in spirit to the reliability methods, in which importance sampling is centered around a Most Probable Point (MPP).
In the case of the LHS samples, the importance sampling density will simply by a mixture of normal distributions
centered around points in the failure region.
This method is specified by the keyword importance sampling. The options for importance sampling are as
follows: import centers a sampling density at one of the initial LHS samples identified in the failure region. It
then generates the importance samples, weights them by their probability of occurence given the original density,
and calculates the required probability (CDF or CCDF level). adapt import is the same as import but is
performed iteratively until the failure probability estimate converges. mm adapt import starts with all of the
samples located in the failure region to build a multimodal sampling density. First, it uses a small number of
samples around each of the initial samples in the failure region. Note that these samples are allocated to the
different points based on their relative probabilities of occurrence: more probable points get more samples. This
early part of the approach is done to search for “representative” points. Once these are located, the multimodal
sampling density is set and then the multi-modal adaptive method proceeds similarly to the adaptive method
(sample until convergence).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.6. ADAPTIVE SAMPLING METHODS 97
5.5.2 Gaussian Process Adaptive Importance Sampling Method
The second importance sampling method in Dakota is the one we recommend, at least for problems that have a
relatively small number of input variables (e.g. less than 10). This method, Gaussian Process Adaptive Importance
Sampling, is outlined in the paper [24]. This method starts with an initial set of LHS samples and adds samples
one at a time, with the goal of adaptively improving the estimate of the ideal importance density during the process.
The approach uses a mixture of component densities. An iterative process is used to construct the sequence of
improving component densities. At each iteration, a Gaussian process (GP) surrogate is used to help identify areas
in the space where failure is likely to occur. The GPs are not used to directly calculate the failure probability; they
are only used to approximate the importance density. Thus, the Gaussian process adaptive importance sampling
algorithm overcomes limitations involving using a potentially inaccurate surrogate model directly in importance
sampling calculations.
This method is specified with the keyword gpais. There are three main controls which govern the behavior of
the algorithm. samples specifies the initial number of Latin Hypercube samples which are used to create the
initial Gaussian process surrogate. emulator samples specifies the number of samples taken on the latest
Gaussian process model each iteration of the algorithm. These samples are used in the construction of the next
importance sampling density. The default is 10,000 samples. The third control is max iterations, which
controls the number of iterations of the algorithm. Each iteration, one additional sample of the “true” simulation
is taken. Thus, if samples were set at 100 and max iterations were set to 200, there would be a total of
300 function evaluations of the simulator model taken.
5.6 Adaptive Sampling Methods
The goal in performing adaptive sampling is to construct a surrogate model that can be used as an accurate
predictor to some expensive simulation, thus it is to one’s advantage to build a surrogate that minimizes the error
over the entire domain of interest using as little data as possible from the expensive simulation. The adaptive part
alludes to the fact that the surrogate will be refined by focusing samples of the expensive simulation on particular
areas of interest rather than rely on random selection or standard space-filling techniques.
5.6.1 Adaptive sampling based on surrogates
At a high-level, the adaptive sampling pipeline is a four-step process:
1. Evaluate the expensive simulation (referred to as the true model) at initial sample points
2. Fit/refit a surrogate model
3. Create a candidate set and score based on information from surrogate
4. Select a candidate point to evaluate the true model and Repeat 2-4
In terms of the Dakota implementation, the adaptive sampling method currently uses Latin Hypercube sampling
(LHS) to generate the initial points in Step 1 above. For Step 2, we use a Gaussian process model. The user
can specify the scoring metric used to select the next point (or points) to evaluate and add to the set. We have
investigated several scoring metrics with which to evaluate candidate points for Step 3. There are some classical
ones such as distance (e.g. add a point which maximizes the minimum distance to all of the existing points). This
distance metric tends to generate points that are space-filling. We have investigated several methods that involve
Dakota Version 6.7 User’s Manual generated on November 13, 2017

98 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
interesting topological features of the space (e.g. points that are near saddle points). These are an area of active
investigation but are not currently included in Dakota. The fitness metrics for scoring candidate points currently
include:
Predicted Variance First introduced in [97] and later used in [120], this method uses the predicted variance of
the Gaussian process surrogate as the score of a candidate point. Thus, the adaptively chosen points will be
in areas of highest uncertainty according to the Gaussian process model.
Distance A candidate’s score is the Euclidean distance in domain space between the candidate and its nearest
neighbor in the set of points already evaluated on the true model. Therefore, the most undersampled area of
the domain will always be selected. The adaptivity of this method could be brought to question as it would
chose the exact same points regardless of the surrogate model used. However, it is useful to use to compare
other adaptive metrics to one that relies purely on space-filling in an equivalent context.
Gradient Similar to the above metric, a candidate’s nearest neighbor is determined as in the distance metric,
only now the score is the absolute value of the difference in range space of the two points. The range space
values used are predicted from the surrogate model. Though this method is called the gradient metric, it
actually does not take into account how close the candidate and its neighbor are in domain space. This
method attempts to evenly fill the range space of the surrogate.
Note that in our approach, a Latin Hypercube sample is generated (a new one, different from the initial sample)
and the surrogate model is evaluated at this points. These are the “candidate points” that are then evaluated
according to the fitness metric outlined above. The number of candidates used in practice should be high enough
to fill most of the input domain: we recommend at least hundreds of points for a low- dimensional problem. All
of the candidates (samples on the emulator) are given a score and then the highest-scoring candidate is selected to
be evaluated on the true model.
The adaptive sampling method also can generate batches of points to add at a time. With batch or multi-point
selection, the true model can be evaluated in parallel and thus increase throughput before refitting our surrogate
model. This proposes a new challenge as the problem of choosing a single point and choosing multiple points off
a surrogate are fundamentally different. Selecting the nbest scoring candidates is more than likely to generate a
set of points clustered in one area which will not be conducive to adapting the surrogate. We have implemented
several strategies for batch selection of points:
Naive Selection This strategy will select the nhighest scoring candidates regardless of their position. This tends
to group an entire round of points in the same area.
Distance Penalized Re-weighted Scoring In this strategy, the highest scoring candidate is selected and then all
remaining candidates are re-scored with a distance penalization factor added in to the score. Only points
selected within a round are used for the distance penalization. The factor is the same as used in the distance
penalization scoring metrics from [98]. First, compute all of the minimum distances from each remaining
candidate to the selected candidates. Then, determine the median value of these distances. If the smallest
distance, d, between a point and the selected set is less than the computed median distance its score is
unaltered, otherwise the score is multiplied by a value ρdetermined by the following equation:
ρ= 1.5∗d−0.5∗d3(5.8)
Topological Maxima of Scoring Function In this strategy we look at the topology of the scoring function and
select the nhighest maxima in the topology. To determine local maxima, we construct the approximate
Morse-Smale complex. If the number of local maxima is less than n, we revert to the distance strategy
above. As a further extension, one may want to filter low-persistence maxima, but to keep the framework
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.6. ADAPTIVE SAMPLING METHODS 99
general, we chose to omit this feature as defining a threshold for what deems a critical point as ”low
persistence” can vary drastically from problem to problem.
Constant Liar We adapt the constant liar strategy presented in [59] with the scoring metrics. The strategy first
selects the highest scoring candidate, and then refits the surrogate using a “lie” value at the point selected
and repeating until npoints have been selected whereupon the lie values are removed from the surrogate
and the selected points are evaluated on the true model and the surrogate is refit with these values.
The adaptive sampling method is specified by the method keyword adaptive sampling. There are many
controls, including the number of candidate samples to investigate each iteration (emulator samples), the
fitness metric used in scoring candidates (fitness metric), and the number of iterations to perform the adap-
tive sampling (max iterations). For batch selection of points, one specifies a batch selection strategy
and a batch size. The details of the specification are provided in the Dakota reference manual.
5.6.2 Adaptive sampling based on dart throwing
pof darts is a novel method for estimating the tail probability (Probability of Failure) based on random sphere-
packing in the uncertain parameter space. Random points are sequentially sampled from the domain and conse-
quently surrounded by protecting spheres, with the constraint that each new sphere center has to be outside all
prior spheres [31]. The radius of each sphere is chosen such that the entire sphere lies either in the failure or
the non-failure region. This radius depends of the function evaluation at the disk center, the failure threshold
and an estimate of the function gradient at the disk center. After exhausting the sampling budget specified by
build samples, which is the number of spheres per failure threshold, the domain is decomposed into two
regions. These regions correspond to failure and non-failure categories, each represented by the union of the
spheres of each type. The volume of the union of failure spheres gives a lower bound on the required estimate of
the probability of failure, while the volume of the union of the non-failure spheres subtracted from the volume of
the domain gives an upper estimate. After all the spheres are constructed, we construct a surrogate model, spec-
ified via a model pointer, and sample the surrogate model extensively to estimate the probability of failure
for each threshold.
pof darts handles multiple response functions and allows each to have multiple failure thresholds. For each
failure threshold pof darts will insert a number of spheres specified by the user-input parameter ”samples”.
However, estimating the probability of failure for each failure threshold would utilize the total number of disks
sampled for all failure thresholds. For each failure threshold, the sphere radii changes to generate the right spatial
decomposition. The POF-Darts method is specified by the method keyword pof darts. The sample budget
is specified by build samples. By default, the method employs a local approach to estimate the Lipschitz
constant per sphere.
The surrogate model used by the pof darts method for extensive sampling is specified using a model pointer,
and its parameters are therefore defined in that model. It can typically be any global surrogate in Dakota (e.g.,
Gaussian process, polynomial chaos expansion, polynomial regression, etc). POF-Darts can also use piecewise-
decomposed surrogates which build local pieces of the surrogate over different domain patches. The piecewise
decomposition option is a new capability added to Dakota to help construct surrogates in high-dimensional spaces,
using known function evaluations as well as gradient and Hessian information, if available. The piecewise decom-
position option is declared using the keyword domain decomp and currently supports polynomial, Gaussian
Process (GP), and Radial Basis Functions (RBF) surroagte models only. For example: a polynomial regres-
sion global surrogate is specified with model polynomial, its order is selected using surrogate order,
and the piecewise decomposition option is specified with domain decomp. The domain decomp option is
parametrized by a cell type set by default to Voronoi cells, an optional number of support layers, and
an optional discontinuity detection capability. See 8.4.3.10 for more details.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
100 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
5.7 Epistemic Nondeterministic Methods
Uncertainty quantification is often used as part of the risk assessment of performance, reliability, and safety of
engineered systems. Increasingly, uncertainty is separated into two categories for analysis purposes: aleatory
and epistemic uncertainty [109,77]. Aleatory uncertainty is also referred to as variability, irreducible or inherent
uncertainty, or uncertainty due to chance. Examples of aleatory uncertainty include the height of individuals
in a population, or the temperature in a processing environment. Aleatory uncertainty is usually modeled with
probability distributions, and sampling methods such as Latin Hypercube sampling in Dakota can be used to model
aleatory uncertainty. In contrast, epistemic uncertainty refers to lack of knowledge or lack of information about
a particular aspect of the simulation model, including the system and environment being modeled. An increase
in knowledge or information relating to epistemic uncertainty will lead to a reduction in the predicted uncertainty
of the system response or performance. For epistemic uncertain variables, typically one does not know enough
to specify a probability distribution on a variable. Epistemic uncertainty is referred to as subjective, reducible,
or lack of knowledge uncertainty. Examples of epistemic uncertainty include little or no experimental data for
a fixed but unknown physical parameter, incomplete understanding of complex physical phenomena, uncertainty
about the correct model form to use, etc.
There are many approaches which have been developed to model epistemic uncertainty, including fuzzy set theory,
possibility theory, and evidence theory. It is also possible to use simple interval analysis in an epistemic context.
Interval analysis and evidence theory are described in more detail below.
5.7.1 Interval Methods for Epistemic Analysis
In interval analysis, one assumes that nothing is known about an epistemic uncertain variable except that its value
lies somewhere within an interval. In this situation, it is NOT assumed that the value has a uniform probability
of occuring within the interval. Instead, the interpretation is that any value within the interval is a possible value
or a potential realization of that variable. In interval analysis, the uncertainty quantification problem is one of
determining the resulting bounds on the output (defining the output interval) given interval bounds on the inputs.
Again, any output response that falls within the output interval is a possible output with no frequency information
assigned to it.
We have the capability to perform interval analysis using either global interval est or local interval est.
In the global approach, one uses either a global optimization method or a sampling method to assess the bounds.
global interval est allows the user to specify either lhs, which performs Latin Hypercube Sampling
and takes the minimum and maximum of the samples as the bounds (no optimization is performed) or ego. In
the case of ego, the efficient global optimization method is used to calculate bounds. The ego method is de-
scribed in Section 6.2.3. If the problem is amenable to local optimization methods (e.g. can provide derivatives
or use finite difference method to calculate derivatives), then one can use local methods to calculate these bounds.
local interval est allows the user to specify either sqp which is sequential quadratic programming, or
nip which is a nonlinear interior point method.
Note that when performing interval analysis, it is necessary to define interval uncertain variables as described in
Section 9.3. For interval analysis, one must define only one interval per input variable, in contrast with Dempster-
Shafer evidence theory, where an input can have several possible intervals. Interval analysis can be considered
a special case of Dempster-Shafer evidence theory where each input is defined by one input interval with a
basic probability assignment of one. In Dakota, however, the methods are separate and semantic differences
exist in the output presentation. If you are performing a pure interval analysis, we recommend using either
global interval est or local interval est instead of global evidence or local evidence,
for reasons of simplicity.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.7. EPISTEMIC NONDETERMINISTIC METHODS 101
These interval methods can also be used as the outer loop within an interval-valued probability analysis for prop-
agating mixed aleatory and epistemic uncertainty – refer to Section 15.1.1 for additional details.
An example of interval estimation is shown in Figure 5.20, with example results in Figure 5.21. This example is
a demonstration of calculating interval bounds for three outputs of the cantilever beam problem. The cantilever
beam problem is described in detail in Section 20.7. Given input intervals of [1,10] on beam width and beam
thickness, we can see that the interval estimate of beam weight is approximately [1,100].
# Dakota Input File: cantilever_uq_global_interval.in
environment
tabular_data
# tabular_data_file = ’cantilever_uq_global_interval.dat’
method
global_interval_est ego
seed = 1234567
output verbose
variables
continuous_interval_uncertain = 2
num_intervals = 1 1
interval_probabilities = 1.0 1.0
lower_bounds = 1.0 1.0
upper_bounds = 10.0 10.0
descriptors ’w’ ’t’
continuous_state = 4
initial_state = 40000. 29.E+6 500. 1000.
descriptors = ’R’ ’E’ ’X’ ’Y’
interface
analysis_drivers = ’cantilever’
direct
responses
response_functions = 3
descriptors = ’weight’ ’stress’ ’displ’
no_gradients
no_hessians
Figure 5.20: Dakota input file for performing UQ using interval analysis – see
Dakota/examples/users/cantilever uq global interval.in
5.7.2 Dempster-Shafer Theory of Evidence
We have chosen to pursue evidence theory at Sandia as a way to model epistemic uncertainty, in part because
evidence theory is a generalization of probability theory. Evidence theory is also referred to as Dempster-Shafer
theory or the theory of random sets [109]. This section focuses on the use of Dempster-Shafer evidence theory
for propagating epistemic uncertainties. When aleatory uncertainties are also present, we may choose either to
discretize the aleatory probability distributions into sets of intervals and treat them as well-characterized epis-
Dakota Version 6.7 User’s Manual generated on November 13, 2017
102 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
------------------------------------------------------------------
Min and Max estimated values for each response function:
weight: Min = 1.0000169352e+00 Max = 9.9999491948e+01
stress: Min = -9.7749994284e-01 Max = 2.1499428450e+01
displ: Min = -9.9315672724e-01 Max = 6.7429714485e+01
-----------------------------------------------------------------
Figure 5.21: Excerpt of UQ output for interval example.
temic variables, or we may choose to segregate the aleatory uncertainties and treat them within an inner loop.
A nested Dempster-Shafer approach for propagating mixed aleatory and epistemic uncertainty is described in
Section 15.1.3.
In evidence theory, there are two complementary measures of uncertainty: belief and plausibility. Together, belief
and plausibility can be thought of as defining lower and upper bounds, respectively, on probabilities. Belief and
plausibility define the lower and upper limits or intervals on probability values. Typical plots of cumulative and
complementary cumulative belief and plausibility functions are shown in Figure 5.22 [77]. In evidence theory,
Figure 5.22: Example cumulative belief and plausibility distribution functions on left; complementary cumulative
belief and plausibility distribution functions on right
it is not possible to specify one probability value. Instead, there is a range of values that is consistent with the
evidence. The range of values is defined by belief and plausibility. Note that no statement or claim is made about
one value within an interval being more or less likely than any other value.
In Dempster-Shafer evidence theory, the uncertain input variables are modeled as sets of intervals. The user
assigns a basic probability assignment (BPA) to each interval, indicating how likely it is that the uncertain in-
put falls within the interval. The BPAs for a particular uncertain input variable must sum to one. The inter-
vals may be overlapping, contiguous, or have gaps. In Dakota, an interval uncertain variable is specified as
interval uncertain. When one defines an interval type variable in Dakota, it is also necessary to specify
the number of intervals defined for each variable with iuv num intervals as well the basic probability assign-
ments per interval, iuv interval probs, and the associated bounds per each interval, iuv interval bounds.
Figure 5.23 shows the input specification for interval uncertain variables. The example has two epistemic uncer-
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.7. EPISTEMIC NONDETERMINISTIC METHODS 103
tain interval variables. The first uncertain variable has three intervals and the second has two. The basic probability
assignments for the first variable are 0.5, 0.1, and 0.4, while the BPAs for the second variable are 0.7 and 0.3.
Note that it is possible (and often the case) to define an interval uncertain variable with only ONE interval. This
means that you only know that the possible value of that variable falls within the interval, and the BPA for that
interval would be 1.0. In the case we have shown, the interval bounds on the first interval for the first variable are
0.6 and 0.9, and the bounds for the second interval for the first variable are 0.1 to 0.5, etc.
# Dakota Input File: textbook_uq_glob_evidence.in
environment
tabular_data
tabular_data_file = ’textbook_uq_glob_evidence.dat’
method
global_evidence lhs
samples = 1000
seed = 59334
response_levels = 0.001 0.03 0.2 0.8 0.001 0.2 0.6 0.8
probability_levels = 0.25 0.5 0.75 0.25 0.5 0.75
distribution cumulative
output verbose
variables
continuous_interval_uncertain = 2
num_intervals = 3 2
interval_probabilities = 0.5 0.1 0.4 0.7 0.3
lower_bounds = 0.6 0.1 0.5 0.3 0.6
upper_bounds = 0.9 0.5 1.0 0.5 0.8
interface
analysis_drivers = ’text_book’
direct
responses
response_functions = 2
no_gradients
no_hessians
Figure 5.23: Dakota input file for UQ example using Evidence Theory – see
Dakota/examples/users/textbook uq glob evidence.in
Once the intervals, the BPAs, and the interval bounds are defined, the user can run an epistemic analysis by
specifying the method as either global evidence or local evidence in the Dakota input file. Both
of these methods perform Dempster-Shafer calculations: the difference is that the local method uses a local
optimization algorithm to calculate the interval bounds and the global method uses either sampling or a global
optimization approach to calculate an interval bound. These differences are discussed in more detail below. The
intervals and their associated BPAs are then propagated through the simulation to obtain cumulative distribution
functions on belief and plausibility. As mentioned above, belief is the lower bound on a probability estimate that
is consistent with the evidence, and plausibility is the upper bound on a probability estimate that is consistent with
the evidence.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

104 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
Figure 5.24 shows results for the first response function obtained when running the example in Figure 5.23. In
this example, there are 6 output intervals (as a result of the 2 interval input variables with 3 and 2 intervals, re-
spectively). The output intervals are ordered to obtain cumulative bound functions for both belief and plausibility.
The cumulative distribution function is presented for both belief (CBF) and plausibility (CPF). The CBF value is
the cumulative belief corresponding to a certain output value. For example, the belief that the output value is less
than or equal to 0.2 for response 1 is 0.27, and the plausibility that the output is less than or equal to 0.2 is 1 for
response 1. The belief that the output value is less than 0.6217 is 0.75, while the plausbility that the output is less
than 0.0806 is 0.75. The CBF and CPF may be plotted on a graph and interpreted as bounding the cumulative
distribution function (CDF), which is the probability that the output is less than or equal to a certain value. The
interval bounds on probability values show the value of epistemic uncertainty analysis: the intervals are usually
much larger than expected, giving one a truer picture of the total output uncertainty caused by lack of knowledge
or information about the epistemic input quantities.
Belief and Plausibility for each response function:
Cumulative Belief/Plausibility Functions (CBF/CPF) for response_fn_1:
Response Level Belief Prob Level Plaus Prob Level
-------------- ----------------- ----------------
1.0000000000e-03 0.0000000000e+00 0.0000000000e+00
3.0000000000e-02 0.0000000000e+00 2.7000000000e-01
2.0000000000e-01 2.7000000000e-01 1.0000000000e+00
8.0000000000e-01 9.3000000000e-01 1.0000000000e+00
Probability Level Belief Resp Level Plaus Resp Level
----------------- ----------------- ----------------
2.5000000000e-01 2.6187288772e-01 6.2609206069e-02
5.0000000000e-01 2.9829775860e-01 6.3736734971e-02
7.5000000000e-01 6.2173551556e-01 8.0596931719e-02
Figure 5.24: Results of an Epistemic Uncertainty Quantification using Evidence Theory.
As in other nondeterministic methods, with local evidence or global evidence, one can specify prob-
ability levels and response levels. If response levels are specified, the belief and plausibility function values
corresponding to those response levels are calculated (see Belief Prob Level and Plaus Prob Level in the tables
shown in Figure 5.24). Similarly, if probability levels are specified, these are first interpreted to be belief val-
ues, and the corresponding response levels are calculated (see Belief Resp Level); then they are interpreted to
be plausibility values and the corresponding response levels are calculated (see Plaus Resp Level in the table in
Figure 5.24). We have recently added the capability to support generalized reliability mappings in the evidence
methods. If the user specifies a generalized reliability level, it will be first converted to a probability, then inter-
preted as a belief and plausibility and the corresponding response levels will be calculated. Likewise, if response
levels are specified, the corresponding belief and plausibility values will be mapped to bounds on the generalized
reliability levels.
To elaborate on the differences between global evidence and local evidence: both of these methods
take the Dempster-Shafer structures specified on the inputs and calculate a resulting Dempster-Shafer structure on
the outputs (e.g. a cumulative belief and plausibility function). To calculate the belief and plausibility measures, it
is necessary to calculate the minimum and maximum of the response function in each “interval cell combination.”
For example, in a two variable problem, if the first variable had three intervals and associated BPAs assigned and
the second variable had two intervals and associated BPAs assigned, there would be 6 interval cells in total. In
each of these six cells, one needs to identify a minimum and maximum value of the response function. This is
easy to do if the function is monotonic in both variables, but in general it is not. We offer the capability to use
local optimization methods to calculate these bounds: local evidence allows the user to specify either sqp
Dakota Version 6.7 User’s Manual generated on November 13, 2017
5.8. BAYESIAN CALIBRATION METHODS 105
which is sequential quadratic programming, or nip which is a nonlinear interior point method. We also offer
the capability to use global methods to assess these interval cell bounds. global evidence allows the user
to specify either lhs, which performs Latin Hypercube Sampling and takes the minimum and maximum of the
samples within each cell as the bounds (no optimization is performed) or ego. In the case of ego, the efficient
global optimization method is used to calculate bounds. The ego method is described in Section 6.2.3. Note that
for a situation with many uncertain variables, each with a fairly complicated Dempster-Shafer structure described
by many intervals, there will be a huge number of interval calls, and the overall process of performing Dempster-
Shafer analysis will be extremely expensive. Reference [133] provides more details about the implementation of
the optimization methods to perform Dempster-Shafer calculations, as well as comparisons on test problems.
5.8 Bayesian Calibration Methods
In Bayesian calibration a “prior distribution” on a parameter is updated through a Bayesian framework involving
experimental data and a likelihood function. Bayesian inference theory is best left to other sources [86] and
only a brief summary is given here. In Bayesian methods, uncertain parameters are characterized by probability
density functions. These probability density functions define the permissible parameter values - the support, as
well as the relative plausibility of each permissible parameter value. In the context of calibration or any inference
step, the probability density function that describes knowledge before the incorporation of data is called the prior,
fΘ(θ).
When data are available, the likelihood function describes how well each parameter value is supported by the
data. Bayes Theorem [83], shown in Equation 5.9, is used for inference: to derive the plausible parameter values,
based on the prior probability density and the data d. The result is the posterior probability density function of
the parameters fΘ|D(θ|d). It is interpreted the same way as the prior, but includes the information derived from
the data.
fΘ|D(θ|d) = fΘ(θ)L(θ;d)
fD(d).(5.9)
The likelihood function is used to describe how well a model’s predictions are supported by the data. The likeli-
hood function can be written generally as:
L(θ;d) = F(q(θ)−d),
where θare the parameters of model quantity of interest q. The form of the function Fcan greatly influence
the results. The specific likelihood function used in Dakota is based on Gaussian probability density functions.
This means that we assume the difference between the model quantity (e.g. quantity of interest returned from a
computer simulation) and the experimental observations are Gaussian:
di=qi(θ) + i,(5.10)
where iis a random variable that can encompass both measurement errors on diand modeling errors associated
with the simulation quantity of interest qi, for each of nobservations.
If we assume that all experiments and observations are independent, then the probabilistic model defined by
Eq. (5.10) results in a likelihood function for θthat is the product of nnormal probability density functions:
L(θ;d) =
n
Y
i=1
1
σd√2πexp "−(di−qi(θ))2
2σd2#,(5.11)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

106 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
where σd2refers to the measurement error of the data, assumed constant across all data observations in this case.
We also support the more general case of a full covariance matrix, Σd, that specifies the covariance between each
observation iand j. In this case, the likelihood is commonly written in log form, where the log-likelihood is:
log L(θ;d)∝ −1
2rTΣd−1r,(5.12)
where ris the vector of residuals between the data points and the model quantity of interest, q(θ)−d.
Dakota admits four experiment variance type options to specify the measurement error covariance:
none for no measurement error specified (in this case, the variance is assumed to be one), scalar where a
constant value σd2is given for all observations, diagonal where a value is specified for the diagonal elements
of the covariance matrix Σdmeaning that each observation has its own measurement error but there are no cross
terms, and matrix where the full covariance matrix Σdis specified. The diagonal and matrix terms are
only available for field response data. In contrast to earlier versions of Dakota, all measurement error variance
should be specified with units of variance/covariance, not standard deviation.
Markov Chain Monte Carlo (MCMC) is the prototypical method used to estimate posterior parameter densities,
given the observational data and the priors. There are many references that describe the basic algorithm [55]
and this is an active research area. MCMC algorithms may require hundreds of thousands of steps to converge,
depending on dimensionality, response nonlinearity, and the desired set of posterior statistics. Since each iteration
involves an evaluation of the model to obtain q(θ), surrogate models of expensive simulations are often employed
to make the MCMC process tractable.
Dakota offers four approaches for Bayesian calibration: QUESO, DREAM, GPMSA, and WASABI. They are
specified with the bayes calibration keyword in combination with the queso,dream,gpmsa, or wasabi
selections, respectively. The QUESO and GPMSA methods use components from the QUESO library (Quantifi-
cation of Uncertainty for Estimation, Simulation, and Optimization) developed at The University of Texas at
Austin. It implements the Delayed Rejection and Adaptive Metropolis [71] (DRAM) algorithm, among others.
Algorithm variants selectively combine the delayed rejection and adaptive elements. The QUESO/GPMSA ca-
pability is based on the GPMSA Matlab toolbox developed at Los Alamos National Laboratory and uses tightly
integrated Gaussian process models during calibration. It’s Dakota implementation is in an early prototype stage.
DREAM uses an implementation of DiffeRential Evolution Adaptive Metropolis developed by John Burkardt.
The DREAM approach runs concurrent chains for global exploration, and automatically tunes the proposal covari-
ance during the process by a self-adaptive randomized subspace sampling [142]. The prototype WASABI method
is an MCMC-free Bayesian calibration approach. QUESO/DRAM and variants are the most well-developed
within Dakota.
5.8.1 QUESO
The QUESO library includes several sampling algorithm variants. One can use a standard Metropolis-Hastings
algorithm (metropolis hastings), adaptive Metropolis (adaptive metropolis) for adapting the pro-
posal covariance during the sampling, delayed rejection (delayed rejection) for backtracking from sample
rejections, the full DRAM (dram) which involves both delayed rejection and adaptive Metropolis, or a multi-level
algorithm (multilevel). This last option is not yet production-ready in Dakota.
With any choice of sampling algorithm, one may manually set the burn in period for the MCMC chain with
burn in samples. If a sub sampling period is specified, the MCMC chain is further filtered such that
only the sample at the beginning of each period is in the final MCMC chain. The sub sampling period
should therefore be greater than or equal to the correlation length of the samples.
With the QUESO method, one may run the MCMC sampling on the simulation model directly. However, if the
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.8. BAYESIAN CALIBRATION METHODS 107
model is expensive, use of a surrogate (emulator) model is recommended. Options include a Gaussian process, a
polynomial chaos expansion, or a stochastic collocation expansion.
The proposal covariance refers to the covariance structure of a multivariate normal distribution, which governs
sample generation in the chain. One may specify proposal covariance, followed by prior (the default),
values,filename, or derivatives. With the prior setting, the proposal covariance will be set to the
variance of the prior distributions of the parameters being calibrated. When specifying the proposal covariance
with input file values or from a separate file, the user may specify only the diagonals of the covariance matrix or
the full covariance matrix.
The derivatives option will use derivatives from the simulation or emulator model to form or approximate the
Hessian of the misfit function (the negative log likelihood). Especially when derivative information is available
inexpensively (e.g. from an emulator), the derivative-based proposal covariance forms a more accurate proposal
distribution, resulting in lower rejection rates and faster chain mixing. When using an emulator, the derivative-
based proposal covariance should be updated periodically using the posterior adaptive specification. This
will add simulation truth evaluations in areas of high-likelihood to the emulator training data, thus refining the
Hessian. For more detail about derivative-based formulations involving the misfit Hessian, refer to the Theory
Manual.
An additional control for QUESO is to perform a logit transformation (logit transform) which performs an
internal variable transformation from bounded domains to unbounded domains. This option can be helpful when
regions of high posterior density exist in the corners of a multi-dimensional bounded domain. In these cases, it
may be difficult to generate feasible samples from the proposal density, and transformation to unbounded domains
may greatly reduce sample rejection rates.
The pre solve option will perform a deterministic gradient-based optimization before the MCMC sampling
to get a good starting point for the chain. This pre-solve seeks to maximize the log-posterior (the log-likelihood
minus the log-prior) to identify the maximum a posteriori probability point, also called the MAP point. The
Markov Chain will then start at the MAP point, which can circumvent a lot of initial searching for high posterior
probability points. The pre-solve option can be used with an emulator or with no emulator.
Credible and prediction intervals will be calculated if probability levels is specified. Credible intervals
propagate uncertainties in parameter density information to the quantity of interest and quantify how well the
model fits the provided data, while prediction intervals propagate both parameter and experimental measurement
uncertainties and contain the next experimental or simulated observation with the specified probability. Further
details can be found in [123]. If probability levels is specified, credible intervals will always be calcu-
lated. Prediction intervals will only be calculated if experiment variance type is also specified in the
responses block. By specifying posterior stats, information-theoretic metrics may be calculated us-
ing the posterior distribution of parameters. If the kl divergence option is selected, the Kullback-Leibler
Divergence will be calculated between the posterior and the prior distributions such that
DKL =ZfΘ|D(θ|d) log fΘ|D(θ|d)
fΘ(θ)dθ.(5.13)
This quantity represents the amount of information gained about the parameters during the Bayesian update.
Further details regarding the calculation and use of DKL can be found in [4].
5.8.2 DREAM
For the DREAM method, one can define the number of chains used with the chains specification. The total num-
ber of generations per chain in DREAM is the number of samples divided by the number of chains. The number of
chains randomly selected to be used in the crossover each time a crossover occurs is crossover chain pairs.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

108 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
There is an extra adaptation during burn-in, in which DREAM estimates a distribution of crossover probabilities
that favors large jumps over smaller ones in each of the chains. Normalization is required to ensure that all of
the input dimensions contribute equally. In this process, a discrete number of candidate points for each crossover
value is generated, which can be specified with num cr. The gr threshold control is the convergence toler-
ance for the Gelman-Rubin statistic, which governs the convergence of the multiple chain process. The integer
jump step forces a long jump every jump step generations. For more details about these parameters, refer to
[142]. Credible and prediction intervals can be calculated by specifying probability levels, and statistics
regarding the posterior may be calculated by specifying posterior stats, as described in Section 5.8.1.
5.8.3 GPMSA
Core to GPMSA is the construction of a Gaussian process emulator from simulation runs collected at various
settings of input parameters. The emulator is a statistical model of the system response, and it is used to incor-
porate the observational data to improve system predictions and constrain or calibrate the unknown parameters.
The GPMSA code draws heavily on the theory developed in the seminal Bayesian calibration paper by Kennedy
and O’Hagan [86]. The particular approach developed by the Los Alamos group, and implemented in QUESO
and therefore Dakota, is provided in [78]. It includes an embedded discrepancy model and the ability to estimate
various hyper-parameters of the Gaussian process, observation error model, and discrepancy model. Dakota’s
GPMSA capability is an experimental prototype with a number of limitations. See the Dakota Reference Man-
ual [3] for more information.
5.8.4 WASABI
WASABI differs from the other Bayesian approaches in that it is not an MCMC-based approach. Instead, it is
based on the idea of “consistent Bayes” which is outlined in [14]. This approach to stochastic inference uses
measure-theoretic principles to construct a probability measure or density on model parameters that is consistent
with the model and the data. The idea is that the probability measure on the parameters, when “pushed-foward”
through the computational model, will give results that match the probability measure on the observational data.
We use a similar notation as with the Bayesian methods, but the interpretation is different here. The goal is to
identify the posterior density on the parameters, πpost(θ), which is equal to the prior density on the parameters
times a ratio. The numerator of the ratio, πobs
D, describes the relative likelihood that the output of the model
corresponds to the observed data D: this is the density of the data evaluated at the model output. q(θ)refers
to the model output. πqprior
Drefers to the push-forward of the prior through the model and represents a forward
propagation of uncertainty.
πpost(θ) = πprior (θ)πobs
D(q(θ))
πqprior
D(q(θ)).(5.14)
The Theory Manual [4] has more detail about the assumptions and mathematical foundations for this method.
Note a major difference in interpretation of the posterior results with respect to a standard Bayesian approach: In
a standard Bayesian approach, the posterior reflects an updated state of information about the prior distribution
on parameter values induced by the observational data. In consistent Bayes, the posterior reflects a stochastic
mapping of parameter values such that the posterior parameters, when pushed-forward through the model, give
results that are consistent with the density of the observational data. WASABI is a prototype capability. See the
Dakota Reference Manual [3] for more information.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.8. BAYESIAN CALIBRATION METHODS 109
Table 5.2: Capabilities of Bayesian methods in Dakota
Capability QUESO GPMSA DREAM WASABI
Prior Distributions Any continuous Any continuous Uniform only Uniform only
variable type variable type
Inference Type MCMC with DR, MCMC with DR, MCMC with MCMC-free
AM, DRAM, or MH AM, DRAM, or MH Differential Evolution interval analysis
Adaptive Metropolis
Can use PCE/SC Emulator Yes No Yes Yes
Can use GP Emulator Yes Yes (required) Yes Yes
Likelihood-based adaptive Yes No No No
emulator update
Initialize with MAP pre-solve Yes No No No
Proposal covariance prior, user, prior, user n/a n/a
options derivative-based
Can calibrate error Yes Yes (internal) Yes No
covariance multipliers
Supports standardized space Yes Yes Yes Yes
Logit transform Yes Yes No No
Posterior export samples samples samples samples, density
5.8.5 Feature Comparison
Table 5.2 compares the options available with the QUESO and DREAM implementations in Dakota.
5.8.6 Bayesian Calibration Example
To run a QUESO-based Bayesian calibration in Dakota, create a Dakota input file such as the one shown in
Figure 5.25. Here, the QUESO DRAM (delayed rejection adaptive metropolis) solver is selected. The num-
ber of samples = 1000 indicates how many points to generate in the acceptance chain3. This example uses the
mod cantilever algebraic model, so an emulator is not warranted. The proposal covariance used has diagonal
element values of 1.e6 and 0.1. Two credible and prediction intervals will be calculated for each model output: a
5/95 interval and a 10/90 interval. The calibration terms in the responses section refers to the number of outputs
that will be used in the calibration process: in this case, it is just two. The calibration data file has the observational
data: in this case, it is a freeform file (e.g. no header or annotation) with ten experiments. For each experiment,
there are two experiment values, one for stress and one for displacement, followed by two variance values for the
error associated with that experiment for each quantity of interest.
When the input file shown in 5.25 is run, Dakota will run the MCMC algorithm and generate a posterior sample
of θin accordance with Bayes Theorem 5.9 and the likelihood function 5.11. Dakota’s final output summary
reports an evaluation count summary and the best sample point visited during the MCMC process as measured by
maximum posterior probability (an estimate of the MAP point). The final output also summarizes the moments
of the posterior samples from the chain (e.g. mean of the chain, standard deviation of the chain samples, etc.), as
well as the credible and prediction intervals for each model output.
Auxilliary output is also generated to a directory called QuesoDiagnostics/ in the directory from which
Dakota is run. The file display sub0.txt contains diagnostic information regarding the MCMC process.
3If delayed rejection is active, the number of simulation evaluations will typically be higher due to backtracking.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

110 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
method,
bayes_calibration queso
chain_samples = 1000 seed = 348
dram # | delayed_rejection | adaptive_metropolis | metropolis_hastings
proposal_covariance
values 1.0e6 1.0e-1
diagonal
logit_transform # default is off
probability_levels 0.05 0.1
0.05 0.1
output debug
variables,
uniform_uncertain 2
upper_bounds 1.e8 10.0
lower_bounds 1.e6 0.1
initial_point 2.85e7 2.5
descriptors ’E’ ’w’
continuous_state 4
initial_state 3 40000 500 1000
descriptors ’t’ ’R’ ’X’ ’Y’
interface,
analysis_drivers = ’mod_cantilever’
direct
responses,
calibration_terms = 2
calibration_data_file = ’dakota_cantilever_queso.withsigma.dat’
freeform
num_experiments = 10
variance_type = ’scalar’ # read 2 scalar sigmas in each row
descriptors = ’stress’ ’displacement’
no_gradients
no_hessians
Figure 5.25: Dakota input file for UQ example using Bayesian Calibration
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.8. BAYESIAN CALIBRATION METHODS 111
The Matlab files contained in the QuesoDiagnostics directory contain the chain files. The files to load in
Matlab are raw chain.m or filtered chain.m, containing the full chain or the filtered chain values of the
parameters4. In addition, the accepted chain values that Dakota generates are written to a file in the run directory
called (by default) dakota mcmc tabular.dat. The first columns of this file are the posterior values of the
input variables. If burn in or sub sampling period are specified, the filtered acceptance chain is instead
written to the file dakota mcmc tabular.dat. This file contains the posterior values of the filtered MCMC
chain, as well as the values of state variables and the resulting model responses. Finally, if one wants to see
the likelihood of each point, specifying verbose output in the method section will result in the likelihoods being
printed.
5.8.7 Calibrating the Observation Error Model
As discussed in Section 12.2.3, Dakota accepts user information on the covariance Σdamong observation errors
and includes this in the likelihood formulation:
log L(θ;d)∝ −1
2rTΣd−1r.
In some cases, it can be helpful to fine tune the assumptions in this covariance during the calibration process.
Dakota supports calibrating one or more multipliers on the blocks of the error covariance. So if Σdis block
diagonal such that Σd=diag(Σd1, ..., ΣdN), we instead formulate as Σd=diag(m1Σd1, ..., mPΣdP)and
calibrate the multipliers mias hyper-parameters in the Bayesian inference process.
The supported modes for calibrating observation error multipliers are shown in Figure 5.26:one,per experiment,
per response, and both. Here, the two major blocks denote two experiments, while the inner blocks denote
five response groups (two scalar, three field). The priors on the hyper-parameters miare taken to be inverse
gamma distributions, with mean and mode approximately 1.0 and standard deviation approximately 0.1.
5.8.8 Model Discrepancy
Whether in a Bayesian setting or otherwise, the goal of model calibration is to minimize the difference between
the observational data diand the corresponding model response qi(θ). In the presence of scenario or configuration
variables x, Eq. 5.10 can be modified,
di(x) = qi(θ, x) + i,(5.15)
with the ensuing equations of the likelihood and Bayes Theorem updated likewise. The configuration variables
represent experimental settings, such as temperature or pressure, that may vary between experiments.
However, it is often the case that the agreement between the data and the model after calibration is not sufficiently
close. This is generally attributed to model form or structural error, and can be corrected to some extent with the
use of model discrepancy. The Kennedy and O’Hagan [86] formulation takes the form
di(x) = qi(θ, x) + δi(x) + i,(5.16)
where δi(x)represents the model discrepancy. It should be noted that the discrepancy depends only on the
configuration variables. Furthermore, one discrepancy model is calculated for each observable di,i= 1, . . . , n,
yielding δ1, . . . , δn. Future work includes developing a discrepancy model that accounts for field data so that a
single, global δ(x)will be approximated.
4The full chain will be output in cases of adaptive posterior refinement or proposal updating, since these use cases access the entire
acceptance chain to identify refinement data or restarting points, respectively.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
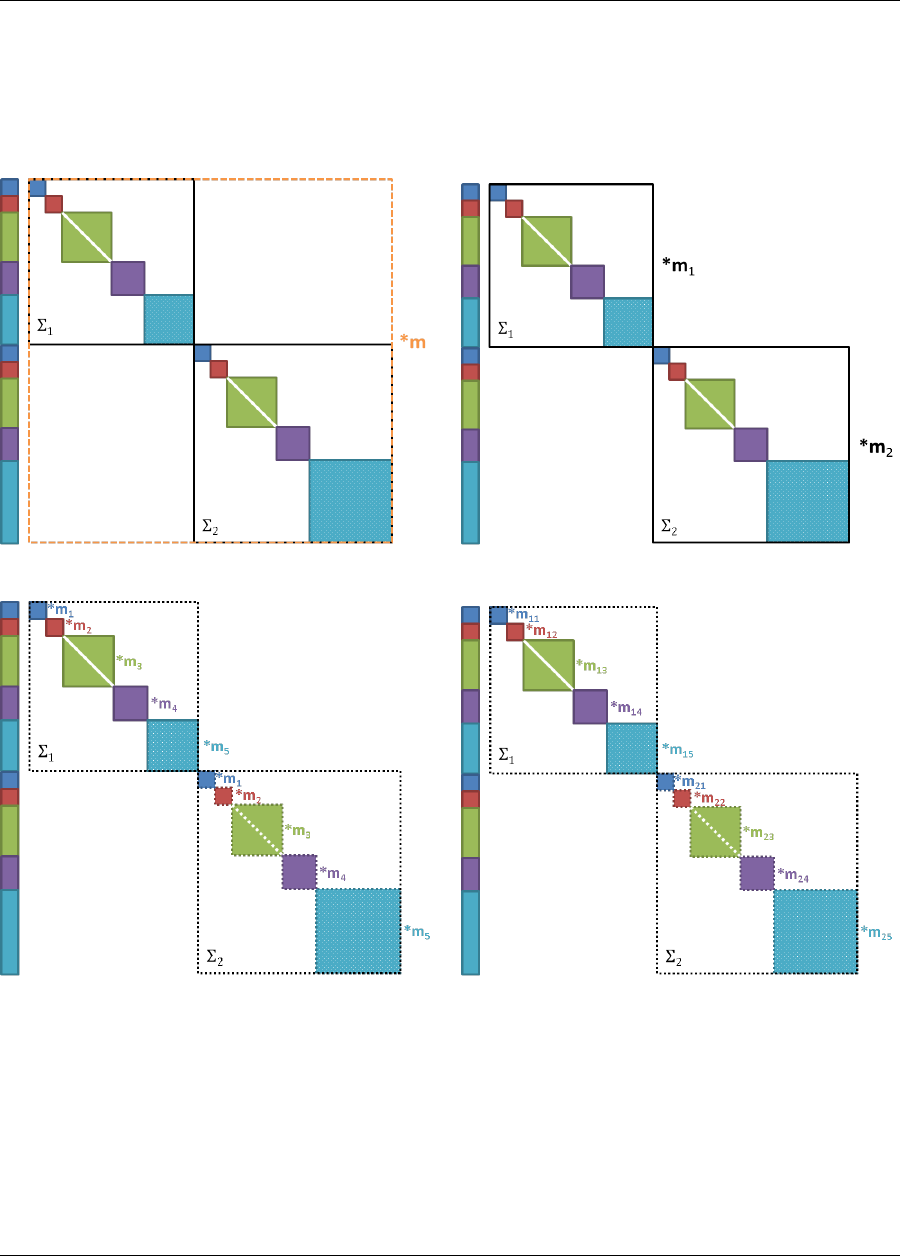
112 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
(a) (b)
(c) (d)
Figure 5.26: Calibrating observational error covariance multipliers: (a) one multiplier on whole user-provided
covariance structure, (b) multiplier per-experiment, (c) multiplier per-response, and (d) both..
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.8. BAYESIAN CALIBRATION METHODS 113
The current implementation of the model discrepancy capability in Dakota serves as a post-processing mechanism
after the completion of a Bayesian update. If model discrepancy is specified in the input file, Dakota will
perform the Bayesian update as detailed in the section above, and then begin the process of approximating δi. For
each observable diand for each configuration xj,
δi(xj) = di(xj)−qi(θ∗, xj),(5.17)
where θ∗is the average of the calibrated posterior distribution of the model parameters. The ith discrepancy
function will be built over the computed δi(xj),j= 1, . . . , m. Within the Dakota input file, the user may
specify the discrepancy type to be either a Gaussian process or polynomial regression model with the
gaussian process or polynomial commands, respectively. Additionally, the order of the trend func-
tion may be selected using the correction order command and choosing one of constant,linear,
or quadratic. Any specifications using these keywords will apply to all δi. By default, Dakota will build a
Gaussian process discrepancy model with a quadratic trend function. Information regarding how polynomial and
Gaussian process models are built can be found in Sections 8.4.3.4 and 8.4.3.5, respectively.
The user may specify new “prediction” configurations at which the corrected model should be calculated. For
each response and for each new configuration, qi(θ, xk,new ) + δi(xk,new)will be computed. The prediction
configurations can be specified in one of three ways. If num prediction configs is included, Dakota will
uniformly distribute the indicated number of prediction configurations throughout the domain of the configuration
variable that is given in the variables block of the input file. Alternatively, the user may explicitly list desired
prediction configuration locations within the input file following the prediction configs keyword, or in an
external file to be read in with the import prediction configs option. If none of these three options is
selected, Dakota will automatically calculate corrected model predictions at ten configurations, spread uniformly
in the configuration variable domain.
Calculations corresponding to each prediction configuration and to each observable will be output to tabular files.
The responses from the discrepancy model itself is output to dakota discrepancy tabular.dat. Those
from the corrected model are output to dakota corrected tabular.dat. The user may specify the output
file names for the discrepancy and corrected model tabular files using the export discrepancy file and
export corrected model file keywords, respectively.
Variance information corresponding to each specified configuration location and for each observable is also com-
puted. In a prediction setting, the variance calculated from the discrepancy model is additively combined with the
variance information provided with the experimental data, such that
Σtotal,i(x) = Σδ,i(x) + σ2
exp,iI(5.18)
for each observable i. Further details of how the variance Σδ,i(x)is computed for Gaussian process and polyno-
mial regression models can be found in the Dakota Theory Manual [4]. The experimental variance provided for
parameter calibration may vary for the same observable from experiment to experiment, thus σ2
exp,i is taken to be
the maximum variance given for each observable. That is,
σ2
exp,i = max
jσ2
i(xj),(5.19)
where σ2
i(xj)is the variance provided for the ith observable di, computed or measured with the configuration
variable xj.
When each corrected model value qi(θ∗, xk,new) + δi(xk,new)is considered, the variance calculated via 5.18
provides a prediction interval, similar to those described in Section 5.8.1. Including σ2
exp,i in the variance cal-
culation accounts for the uncertainty in the model predictions that arise due to uncertainties in the calibration
data. These prediction variances are output to the file dakota discrepancy variance tabular.dat by
Dakota Version 6.7 User’s Manual generated on November 13, 2017

114 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
default. The name of this file can be modified using the export corrected variance file keyword in
the input script.
Additional details and an illustrative example of these calculations are given in the Dakota Theory Manual [4].
5.8.9 Bayesian Experimental Design
The goal of experimental design is to add observational data to the Bayesian update that informs model parameters
and reduces their uncertainties. In Bayesian approaches, data from physical experiments is typically used to
calibrate a model. However, another common practice is to use responses or output from a high-fidelity model as
“truth data” in place of experimental data in a low-fidelity model calibration. This can be done in with a single
Bayesian calibration, or it can be done iteratively with the use of experimental design, where an initial set of
high-fidelity runs is augmented sequentially to find the next “best” high-fidelity design point at which to run the
high-fidelity model to add to the calibration data. The low-fidelity posterior parameter distribution is then updated
again using Bayesian calibration. The mutual information is used as the selection criterion to guide the process of
high-fidelity data acquisition.
In Dakota, design conditions, such as temperature or spatial location, can be specified using so-called configura-
tion variables. The design selection algorithm implemented in Dakota uses a user-specified high-fidelity code to
produce the “experimental” or observational data that is used in the calibration of the desired low-fidelity model.
The high-fidelity model is dependent only upon the design or configuration variables while the low-fidelity model
depends on both the design variables and uncertain model parameters.
An example Dakota input file that implements this Bayesian experimental design algorithm is shown in Fig-
ures 5.27-5.28. Note that there are three model blocks, one describing the model hierarchy and one each for
the high-fidelity and low-fidelity models. There are two variables,interface, and responses blocks
such that each model has its own specifications. The low-fidelity variables block contains information about
both the design variables, which are specified with continuous state, and the parameters to be updated via
Bayes’ Theorem 5.9, which are specified using one of the aleatory uncertain variable types discussed in Sec-
tion 9.3.1.1. In the high-fidelity variables block, only the continuous state parameters are included.
The specifications of the design variables should be consistent in both blocks. Each interface block should
point to the appropriate high- or low-fidelity code, and the responses blocks should contain consistent de-
tails about the responses from each code. For example, both of the models should return the same number of
calibration terms.
The mutual information experimental design algorithm is selected by specifying bayesian calibration,
queso, and experimental design within the method block of the input file, and the first model block
should contain the hierarchical specification of the surrogate keyword. The algorithm starts by per-
forming a Bayesian calibration using a number of data points, specified in Dakota by initial samples.
These initial data points can be pulled from external data using the calibration data file keyword in
the high-fidelity response block. In this case, num config variables should be specified and set to
the number of configuration variables captured in the variables blocks. Furthermore, for use in Bayesian
experimental design, calibration data file should contain the configuration variables and the corre-
sponding high-fidelity model responses. Scalar variance information may be included for the calibration data
through the use of the experimental variance type or simulation variance command within
the high-fidelity responses block. The former is applied to any user-provided data, such as through the
calibration data file keyword, while the latter applies only to those high-fidelity model responses pro-
duced by the high-fidelity code run by Dakota. Further information can be found in the Dakota Reference Man-
ual [3]. If the number of points taken from this file is less than initial samples, or if no such file is provided,
Latin Hypercube Sampling is used to draw samples of the design space, and the high-fidelity model is run at these
points to supplement the user-specified data. After this initial calibration, a set of design conditions (i.e. con-
Dakota Version 6.7 User’s Manual generated on November 13, 2017
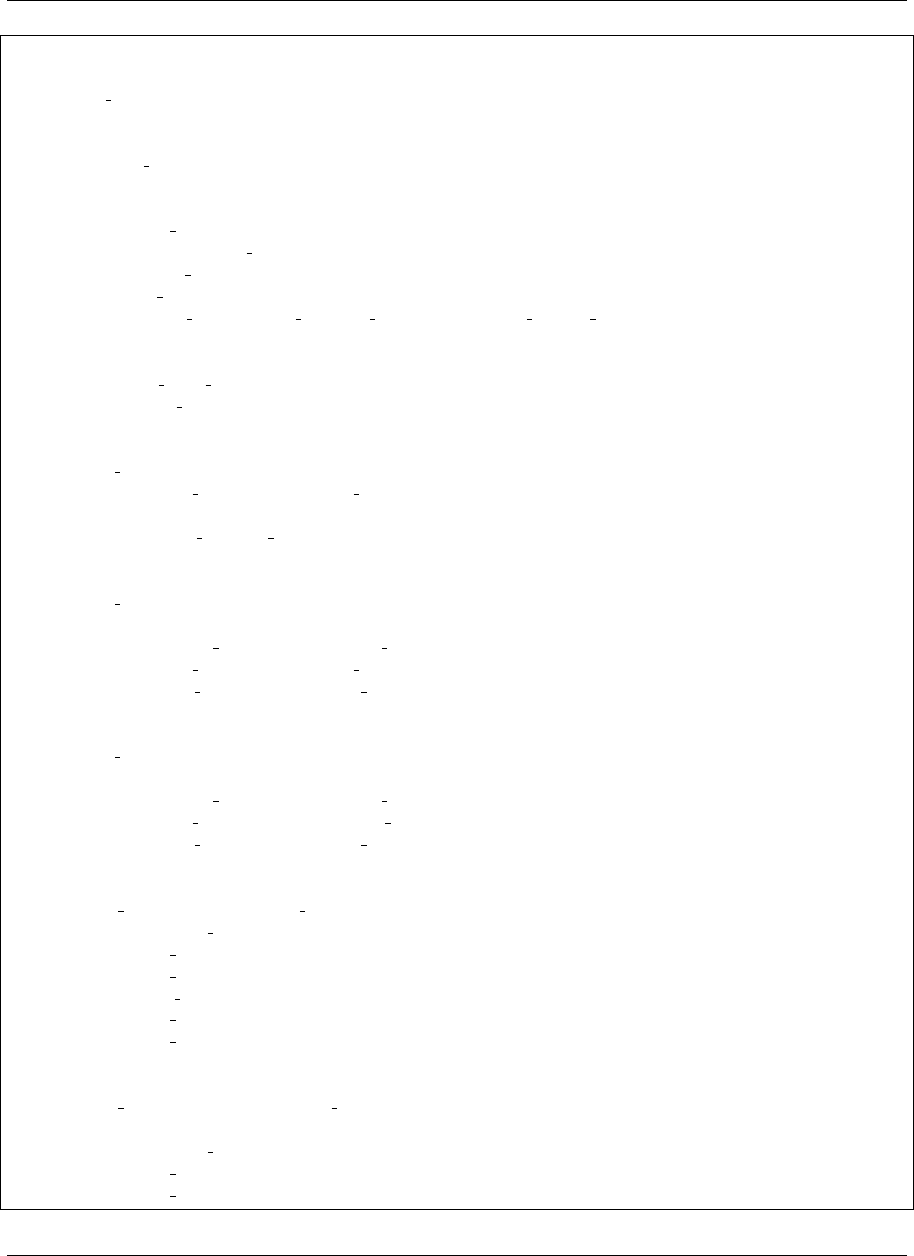
5.8. BAYESIAN CALIBRATION METHODS 115
environment
tabular data
method ,
b a y e s c a l i b r a t i o n que s o
dram
s e e d = 34785
c h a i n s a m p l e s = 500
experimental design
initial samples = 2
num candidates = 2
i m p o r t c a n d i d a t e p o i n t s f i l e = ’ d a k o t a b a y e s e x p d e s i g n . ca nd . d a t ’
freeform
# ks g2
max hifi evaluations = 1
m o d e l p o i n t e r = ’HIERARCH’
model ,
i d m o d e l = ’HIERARCH’
v a r i a b l e s p o i n t e r = ’ALL VARS’
s u r r o g a t e h i e r a r c h i c a l
ordered model fidelities = ’LF’ ’HF’
model ,
i d m o d e l = ’ LF ’
single
interface pointer = ’lofi IF ’
v a r i a b l e s p o i n t e r = ’ALL VARS’
r e s p o n s e s p o i n t e r = ’ l o f i r e s p ’
model ,
i d m o d e l = ’HF ’
single
interface pointer = ’hifi IF ’
v a r i a b l e s p o i n t e r = ’CONFIG VARS’
r e s p o n s e s p o i n t e r = ’ h i f i r e s p ’
variables ,
i d v a r i a b l e s = ’ALL VARS’
c o n t i n u o u s s t a t e = 1
u p p e r b o u n d s = 70
l o w e r b o u n d s = 10
uniform uncertain = 3
u p p e r b o u n d s 0 . 0 6 0 260
lower bounds 0 −8 0
variables ,
i d v a r i a b l e s = ’CONFIG VARS’
a c t i v e s t a t e
c o n t i n u o u s s t a t e = 1
u p p e r b o u n d s = 70
l o w e r b o u n d s = 10
Figure 5.27: Dakota input file for Bayesian Experimental Design.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
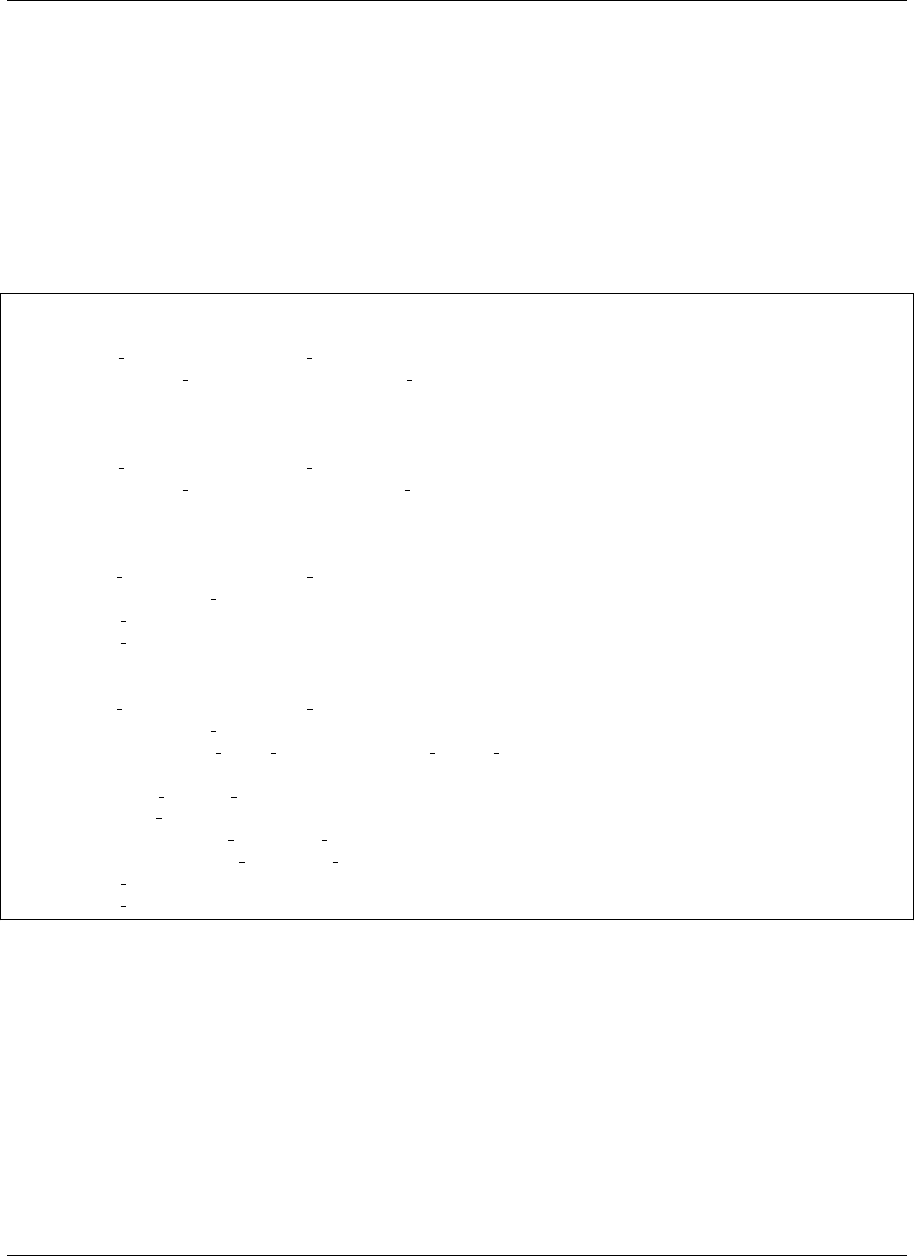
116 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
interface ,
i d i n t e r f a c e = ’ h i f i I F ’
a n a l y s i s d r i v e r s = ’ e x p d e s i g n h i g h ’
f o r k
interface ,
i d i n t e r f a c e = ’ l o f i I F ’
a n a l y s i s d r i v e r s = ’ e x p d e s i g n l o w ’
f o r k
r e s p o n s e s ,
i d r e s p o n s e s = ’ l o f i r e s p ’
c a l i b r a t i o n t e r m s = 1
no gradients
no hessians
r e s p o n s e s ,
i d r e s p o n s e s = ’ h i f i r e s p ’
c a l i b r a t i o n t e r m s = 1
c a l i b r a t i o n d a t a f i l e = ’ d a k o t a b a y e s e x p d e s i g n . d a t ’
freeform
num config variables = 1
n u m e x p e r i m e n t s = 2
experiment variance type = ’none ’
#experiment variance type = ’scalar ’
no gradients
no hessians
Figure 5.28: Dakota input file for Bayesian Experimental Design.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
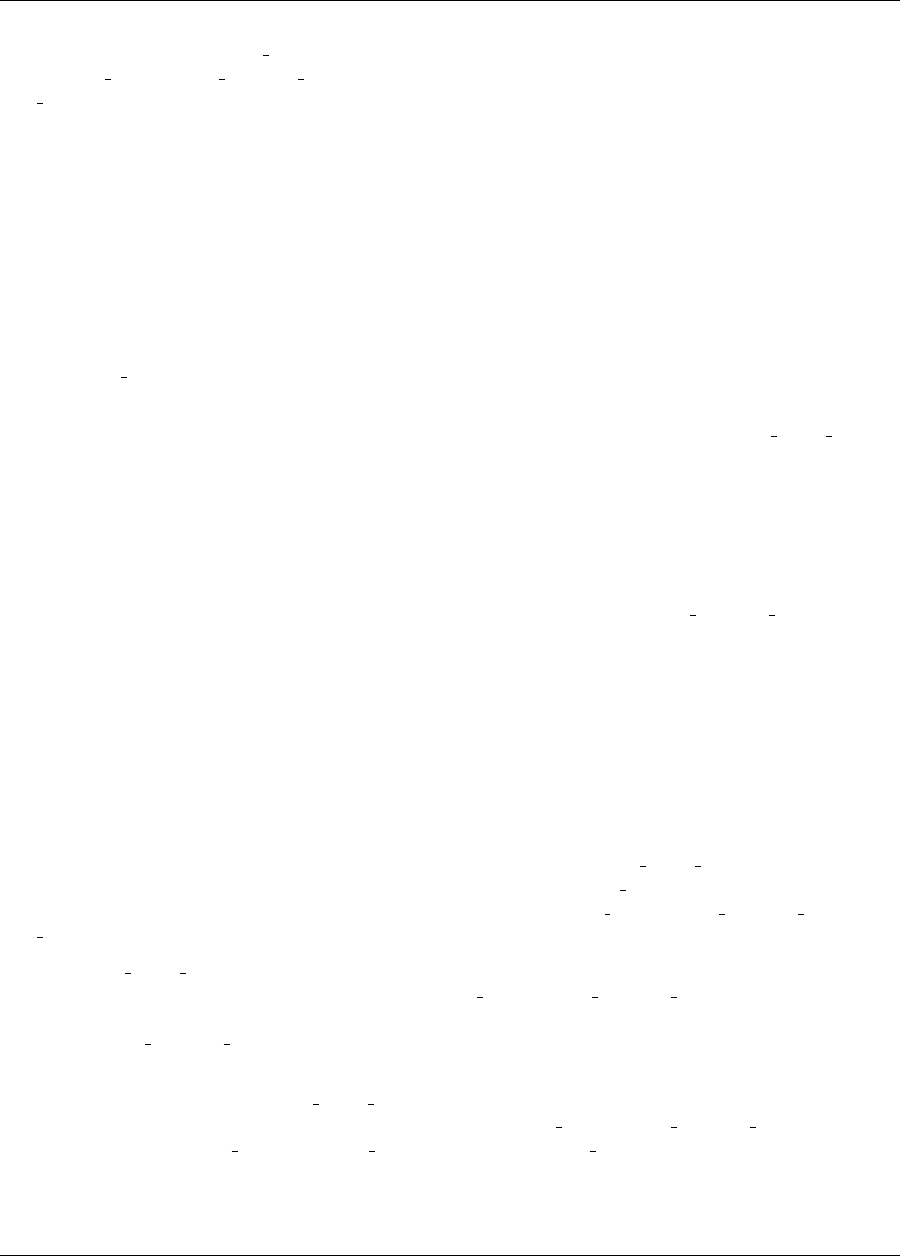
5.8. BAYESIAN CALIBRATION METHODS 117
figuration variables) of size num candidates is proposed. Users may specify these candidate points through
the import candidate points file command. Again, if the number of points in this file is less than
num candidates, or if no such file is provided, Latin Hypercube Sampling is used to draw samples of the
design space.
From these candidate designs, that which maximizes the mutual information with respect to the low-fidelity model
parameters is deemed “optimal.” The mutual information is approximated using the low-fidelity model and a k-
nearest neighbor algorithm, as detailed in [95]. This optimal design is used in the high-fidelity model to create
a new observation, which is appended to the initial data. This updated data is used to recalculate the Bayesian
posterior, and the process repeats until one of three stopping criteria are met. There are two algorithms that may
be used to calculate the mutual information, both of which are derived in [90]. The first algorithm discussed
therein is used as the default algorithm within Dakota; the second may be selected by including the keyword
ksg2 in the Dakota input script. Furthermore, the user may choose to include, during the computation of the
mutual information, a stochastic error term on the low-fidelity model responses. This is done by specifying
simulation variance in the responses block corresponding to the low-fidelity model. See the Dakota
Theory Manual [4] for more information regarding the implementation of the mutual information calculations.
There are three criteria by which this algorithm is considered complete. The user may specify max hifi evaluations,
which limits the number of high-fidelity model simulations Dakota will run. Note that this does not include any
simulations needed to perform the initial Bayesian calibration of the low-fidelity model parameters. Alternatively,
if the change in the mutual information from one iteration to the next is sufficiently small or if all candidate points
have been exhausted, the algorithm will terminate.
Progress of the algorithm will be reported to the screen with the rest of the Dakota output. Furthermore, a sum-
mary of the algorithm’s results, including, for each iteration, the optimal design, the mutual information, and the
corresponding high-fidelity model response, can be found in the file experimental design output.txt.
5.8.9.1 One-at-a-time Implementation
There may be some applications for which the high-fidelity model must be run independently of Dakota. This
algorithm may still be implemented in this case, however, it requires some extra work by the user to ensure that
the high-fidelity model information is properly communicated to Dakota, as a ”dummy” high-fidelity model code
must be supplied to Dakota. The data to be used in the initial Bayesian calibration should be gathered from the
high-fidelity model or physical experiment and imported via the calibration data file in the high-fidelity
responses block, and extra care should be taken to ensure that initial samples matches the number of
experiments in this file. It is also best, for this use-case, to use import candidate points file, with
num candidates exactly matching the number of candidate points in the file.
By setting max hifi evaluations to zero, Dakota will run the initial calibration of the low-fidelity model,
select the “optimal” design from those provided in import candidate points file, and exit without run-
ning the “dummy” high-fidelity model code. The selected design will be output to the screen, as well as to
experimental design output.txt, as detailed above. The high-fidelity model may then be run offline
with the newly selected design point.
The user must update calibration data file with the new high-fidelity data when it becomes available,
as well as remove the previously selected design point from import candidate points file. Within the
Dakota input file, initial samples,num experiments, and num candidates should be correspond-
ingly updated. Dakota may then be run again to yield the next optimal experimental design. It should be noted
that the stopping criteria will not be automatically evaluated by Dakota when one-at-a-time implementation is
used. The user must determine when the algorithm should be terminated.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
118 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
5.9 Uncertainty Quantification Usage Guidelines
The choice of uncertainty quantification method depends on how the input uncertainty is characterized, the com-
putational budget, and the desired output accuracy. The recommendations for UQ methods are summarized in
Table 5.3 and are discussed in the remainder of the section.
Table 5.3: Guidelines for UQ method selection.
Method Desired Problem Applicable Methods
Classification Characteristics
Sampling nonsmooth, multimodal response functions; sampling (Monte Carlo or LHS)
response evaluations are relatively inexpensive
Local smooth, unimodal response functions; local reliability (MV, AMV/AMV2,
reliability larger sets of random variables; AMV+/AMV2+, TANA, FORM/SORM)
estimation of tail probabilities
Global smooth or limited nonsmooth response; global reliability
reliability multimodal response; low dimensional;
estimation of tail probabilities
Adaptive smooth or limited nonsmooth response; importance sampling,
Sampling multimodal response; low dimensional; gpais, adaptive sampling,
estimation of tail probabilities pof darts
Stochastic smooth or limited nonsmooth response; polynomial chaos,
expansions multimodal response; low dimensional; stoch collocation
estimation of moments or moment-based metrics
Epistemic uncertainties are poorly characterized interval: local interval est,
global interval est, sampling;
BPA: local evidence, global evidence
Mixed UQ some uncertainties are poorly characterized nested UQ (IVP, SOP, DSTE) with epistemic
outer loop and aleatory inner loop, sampling
Sampling Methods
Sampling-based methods are the most robust uncertainty techniques available, are applicable to almost all simu-
lations, and possess rigorous error bounds; consequently, they should be used whenever the function is relatively
inexpensive to compute and adequate sampling can be performed. In the case of terascale computational simu-
lations, however, the number of function evaluations required by traditional techniques such as Monte Carlo and
Latin hypercube sampling (LHS) quickly becomes prohibitive, especially if tail statistics are needed.
Alternatively, one can apply the traditional sampling techniques to a surrogate function approximating the ex-
pensive computational simulation (see Section 15.3). However, if this approach is selected, the user should be
aware that it is very difficult to assess the accuracy of the results obtained. Unlike the case of surrogate-based
local minimization (see Section 14.6.1), there is no simple pointwise calculation to verify the accuracy of the
approximate results. This is due to the functional nature of uncertainty quantification, i.e. the accuracy of the
surrogate over the entire parameter space needs to be considered, not just around a candidate optimum as in the
case of surrogate-based local. This issue especially manifests itself when trying to estimate low probability events
such as the catastrophic failure of a system.
Reliability Methods
Local reliability methods (e.g., MV, AMV/AMV2, AMV+/AMV2+, TANA, and FORM/SORM) are more com-
putationally efficient in general than the sampling methods and are effective when applied to reasonably well-
behaved response functions; i.e., functions that are smooth, unimodal, and only mildly nonlinear. They can be
Dakota Version 6.7 User’s Manual generated on November 13, 2017

5.9. UNCERTAINTY QUANTIFICATION USAGE GUIDELINES 119
used to provide qualitative sensitivity information concerning which uncertain variables are important (with rel-
atively few function evaluations), or compute full cumulative or complementary cumulative response functions
(with additional computational effort). Since they rely on gradient calculations to compute local optima (most
probable points of failure), they scale well for increasing numbers of random variables, but issues with nons-
mooth, discontinuous, and multimodal response functions are relevant concerns. In addition, even if there is a
single MPP and it is calculated accurately, first-order and second-order integrations may fail to accurately capture
the shape of the failure domain. In these cases, adaptive importance sampling around the MPP can be helpful.
Overall, local reliability methods should be used with some care and their accuracy should be verified whenever
possible.
An effective alternative to local reliability analysis when confronted with nonsmooth, multimodal, and/or highly
nonlinear response functions is efficient global reliability analysis (EGRA). This technique employs Gaussian
process global surrogate models to accurately resolve the failure domain and then employs multimodal adaptive
importance sampling to resolve the probabilities. For relatively low dimensional problems (i.e, on the order
of 10 variables), this method displays the efficiency of local reliability analysis with the accuracy of exhaustive
sampling. While extremely promising, this method is still relatively new and is the subject of ongoing refinements
as we deploy it to additional applications.
Adaptive Sampling Methods
There are now a number of methods in Dakota which are tailored to estimating tail probabilities. These methods
include both standard importance sampling and Gaussian Process Adaptive Importance Sampling, as well as
adaptive sampling and the POF-darts method. These methods are suitable for smooth or limited non-smooth
responses, and work well in low dimensions. GPAIS and POF-darts utilize a Gaussian process surrogate model.
Stochastic Expansions Methods
The next class of UQ methods available in Dakota is comprised of stochastic expansion methods (polynomial
chaos and stochastic collocation), which are general purpose techniques provided that the response functions pos-
sess finite second order moments. Further, these methods capture the underlying functional relationship between a
key response metric and its random variables, rather than just approximating statistics such as mean and standard
deviation. This class of methods parallels traditional variational methods in mechanics; in that vein, efforts are
underway to compute rigorous error bounds of the approximations produced by the methods. Another strength of
these methods is their potential use in a multiphysics environment as a means to propagate the uncertainty through
a series of simulations while retaining as much information as possible at each stage of the analysis. The current
challenge in the development of these methods, as for other global surrogate-based methods, is effective scaling
for large numbers of random variables. Recent advances in adaptive collocation and sparsity detection methods
address some of the scaling issues for stochastic expansions.
Epistemic Uncertainty Quantification Methods
The final class of UQ methods available in Dakota are focused on epistemic uncertainties, or uncertainties re-
sulting from a lack of knowledge. In these problems, the assignment of input probability distributions when
data is sparse can be somewhat suspect. One approach to handling epistemic uncertainties is interval analysis
(local interval est and global interval est), where a set of intervals on inputs, one interval for
each input variable, is mapped to a set of intervals on outputs. To perform this process efficiently, optimiza-
tion methods can be used. Another related technique is Dempster-Shafer theory of evidence (Dakota methods
local evidence and global evidence), where multiple intervals per input variable (which can be over-
lapping, contiguous, or disjoint) are propagated, again potentially using optimization methods. The choice be-
tween local or global optimization methods for interval computation is governed by the same issues described in
Section 6.4.
Mixed Aleatoric and Epistemic Methods
For problems with a mixture of epistemic and aleatoric uncertainties, it is desirable to segregate the two uncer-
tainty types within a nested analysis, allowing stronger probabilistic inferences for the portion of the problem
Dakota Version 6.7 User’s Manual generated on November 13, 2017
120 CHAPTER 5. UNCERTAINTY QUANTIFICATION CAPABILITIES
where they are appropriate. In this nested approach, an outer epistemic level selects realizations of epistemic
parameters (augmented variables) and/or realizations of random variable distribution parameters (inserted vari-
ables). These realizations define the objective probabilistic analysis to be performed on the inner aleatoric level.
In the case where the outer loop involves propagation of subjective probability, the nested approach is known
as second-order probability and the study generates a family of CDF/CCDF respresentations known as a “horse
tail” plot. In the case where the outer loop is an interval propagation approach (local interval est or
global interval est), the nested approach is known as interval-valued probability (see also Section 8.5) .
In the case where the outer loop is an evidence-based approach (local evidence or global evidence),
the approach generates epistemic belief and plausibility bounds on aleatory statistics.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 6
Optimization Capabilities
Optimization algorithms work to minimize (or maximize) an objective function, typically calculated by the user
simulation code, subject to constraints on design variables and responses. Available approaches in Dakota include
well-tested and proven gradient-based, derivative-free local, and global methods for use in science and engineering
design applications. Dakota also offers more advanced algorithms, e.g., to manage multi-objective optimization or
perform surrogate-based minimization. This chapter summarizes optimization problem formulation, standard al-
gorithms available in Dakota (mostly through included third-party libraries, see 6.5), some advanced capabilities,
and offers usage guidelines.
6.1 Optimization Formulations
This section provides a basic introduction to the mathematical formulation of optimization, problems. The primary
goal of this section is to introduce terms relating to these topics, and is not intended to be a description of theory
or numerical algorithms. For further details, consult [7], [57], [72], [107], and [140].
A general optimization problem is formulated as follows:
minimize: f(x)
x∈ <n
subject to: gL≤g(x)≤gU
h(x) = ht(6.1)
aL≤Aix≤aU
Aex=at
xL≤x≤xU
where vector and matrix terms are marked in bold typeface. In this formulation, x= [x1, x2, . . . , xn]is an n-
dimensional vector of real-valued design variables or design parameters. The n-dimensional vectors, xLand xU,
are the lower and upper bounds, respectively, on the design parameters. These bounds define the allowable values
for the elements of x, and the set of all allowable values is termed the design space or the parameter space. A
design point or a sample point is a particular set of values within the parameter space.

122 CHAPTER 6. OPTIMIZATION CAPABILITIES
The optimization goal is to minimize the objective function,f(x), while satisfying the constraints. Constraints
can be categorized as either linear or nonlinear and as either inequality or equality. The nonlinear inequality
constraints,g(x), are “2-sided,” in that they have both lower and upper bounds, gLand gU, respectively. The
nonlinear equality constraints,h(x), have target values specified by ht. The linear inequality constraints create
a linear system Aix, where Aiis the coefficient matrix for the linear system. These constraints are also 2-sided
as they have lower and upper bounds, aLand aU, respectively. The linear equality constraints create a linear
system Aex, where Aeis the coefficient matrix for the linear system and atare the target values. The constraints
partition the parameter space into feasible and infeasible regions. A design point is said to be feasible if and only
if it satisfies all of the constraints. Correspondingly, a design point is said to be infeasible if it violates one or
more of the constraints.
Many different methods exist to solve the optimization problem given by Equation 6.1, all of which iterate on xin
some manner. That is, an initial value for each parameter in xis chosen, the response quantities,f(x),g(x),h(x),
are computed, often by running a simulation, and some algorithm is applied to generate a new xthat will either
reduce the objective function, reduce the amount of infeasibility, or both. To facilitate a general presentation of
these methods, three criteria will be used in the following discussion to differentiate them: optimization problem
type, search goal, and search method.
The optimization problem type can be characterized both by the types of constraints present in the problem
and by the linearity or nonlinearity of the objective and constraint functions. For constraint categorization, a hi-
erarchy of complexity exists for optimization algorithms, ranging from simple bound constraints, through linear
constraints, to full nonlinear constraints. By the nature of this increasing complexity, optimization problem cat-
egorizations are inclusive of all constraint types up to a particular level of complexity. That is, an unconstrained
problem has no constraints, a bound-constrained problem has only lower and upper bounds on the design pa-
rameters, a linearly-constrained problem has both linear and bound constraints, and a nonlinearly-constrained
problem may contain the full range of nonlinear, linear, and bound constraints. If all of the linear and nonlinear
constraints are equality constraints, then this is referred to as an equality-constrained problem, and if all of the
linear and nonlinear constraints are inequality constraints, then this is referred to as an inequality-constrained
problem. Further categorizations can be made based on the linearity of the objective and constraint functions. A
problem where the objective function and all constraints are linear is called a linear programming (LP) problem.
These types of problems commonly arise in scheduling, logistics, and resource allocation applications. Likewise,
a problem where at least some of the objective and constraint functions are nonlinear is called a nonlinear pro-
gramming (NLP) problem. These NLP problems predominate in engineering applications and are the primary
focus of Dakota.
The search goal refers to the ultimate objective of the optimization algorithm, i.e., either global or local optimiza-
tion. In global optimization, the goal is to find the design point that gives the lowest feasible objective function
value over the entire parameter space. In contrast, in local optimization, the goal is to find a design point that is
lowest relative to a “nearby” region of the parameter space. In almost all cases, global optimization will be more
computationally expensive than local optimization. Thus, the user must choose an optimization algorithm with an
appropriate search scope that best fits the problem goals and the computational budget.
The search method refers to the approach taken in the optimization algorithm to locate a new design point that
has a lower objective function or is more feasible than the current design point. The search method can be
classified as either gradient-based or nongradient-based. In a gradient-based algorithm, gradients of the response
functions are computed to find the direction of improvement. Gradient-based optimization is the search method
that underlies many efficient local optimization methods. However, a drawback to this approach is that gradients
can be computationally expensive, inaccurate, or even nonexistent. In such situations, nongradient-based search
methods may be useful. There are numerous approaches to nongradient-based optimization. Some of the more
well known of these include pattern search methods (nongradient-based local techniques) and genetic algorithms
(nongradient-based global techniques).
Dakota Version 6.7 User’s Manual generated on November 13, 2017
6.2. OPTIMIZING WITH DAKOTA: CHOOSING A METHOD 123
Because of the computational cost of running simulation models, surrogate-based optimization (SBO) methods
are often used to reduce the number of actual simulation runs. In SBO, a surrogate or approximate model is
constructed based on a limited number of simulation runs. The optimization is then performed on the surrogate
model. Dakota has an extensive framework for managing a variety of local, multipoint, global, and hierarchical
surrogates for use in optimization. Finally, sometimes there are multiple objectives that one may want to optimize
simultaneously instead of a single scalar objective. In this case, one may employ multi-objective methods that are
described in Section 6.3.1.
This overview of optimization approaches underscores that no single optimization method or algorithm works
best for all types of optimization problems. Section 6.4 offers guidelines for choosing a Dakota optimization
algorithm best matched to your specific optimization problem.
6.1.1 Constraint Considerations
Dakota’s input commands permit the user to specify two-sided nonlinear inequality constraints of the form gLi≤
gi(x)≤gUi, as well as nonlinear equality constraints of the form hj(x) = htj. Some optimizers (e.g., npsol ,
optpp ,soga, and moga methods) can handle these constraint forms directly, whereas other optimizers (e.g.,
asynch pattern search,dot , and conmin ,mesh adaptive search) require Dakota to perform an
internal conversion of all constraints to one-sided inequality constraints of the form gi(x)≤0. In the latter
case, the two-sided inequality constraints are treated as gi(x)−gUi≤0and gLi−gi(x)≤0and the equality
constraints are treated as hj(x)−htj≤0and htj−hj(x)≤0. The situation is similar for linear constraints:
asynch pattern search,npsol ,optpp ,soga, and moga methods support them directly, whereas
dot and conmin methods do not. For linear inequalities of the form aLi≤aT
ix≤aUiand linear equalities
of the form aT
ix=atj, the nonlinear constraint arrays in dot and conmin methods are further augmented
to include aT
ix−aUi≤0and aLi−aT
ix≤0in the inequality case and aT
ix−atj≤0and atj−aT
ix≤0
in the equality case. Awareness of these constraint augmentation procedures can be important for understanding
the diagnostic data returned from the dot and conmin methods. Other optimizers fall somewhere in between.
nlpql methods support nonlinear equality constraints hj(x)=0and nonlinear one-sided inequalities gi(x)≥
0, but does not natively support linear constraints. Constraint mappings are used with NLPQL for both linear and
nonlinear cases. Most coliny methods now support two-sided nonlinear inequality constraints and nonlinear
constraints with targets, but do not natively support linear constraints.
When gradient and Hessian information is used in the optimization, derivative components are most commonly
computed with respect to the active continuous variables, which in this case are the continuous design vari-
ables. This differs from parameter study methods (for which all continuous variables are active) and from non-
deterministic analysis methods (for which the uncertain variables are active). Refer to Section 11.3 for additional
information on derivative components and active continuous variables.
6.2 Optimizing with Dakota: Choosing a Method
This section summarizes the optimization methods available in Dakota. We group them according to search
method and search goal and establish their relevance to types of problems. For a summary of this discussion, see
Section 6.4.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

124 CHAPTER 6. OPTIMIZATION CAPABILITIES
6.2.1 Gradient-Based Local Methods
Gradient-based optimizers are best suited for efficient navigation to a local minimum in the vicinity of the ini-
tial point. They are not intended to find global optima in nonconvex design spaces. For global optimization
methods, see 6.2.3. Gradient-based optimization methods are highly efficient, with the best convergence rates
of all of the local optimization methods, and are the methods of choice when the problem is smooth, unimodal,
and well-behaved. However, these methods can be among the least robust when a problem exhibits nonsmooth,
discontinuous, or multimodal behavior. The derivative-free methods described in 6.2.2 are more appropriate for
problems with these characteristics.
Gradient accuracy is a critical factor for gradient-based optimizers, as inaccurate derivatives will often lead to
failures in the search or pre-mature termination of the method. Analytic gradients and Hessians are ideal but often
unavailable. If analytic gradient and Hessian information can be provided by an application code, a full Newton
method will achieve quadratic convergence rates near the solution. If only gradient information is available and
the Hessian information is approximated from an accumulation of gradient data, the superlinear convergence rates
can be obtained. It is most often the case for engineering applications, however, that a finite difference method
will be used by the optimization algorithm to estimate gradient values. Dakota allows the user to select the step
size for these calculations, as well as choose between forward-difference and central-difference algorithms. The
finite difference step size should be selected as small as possible, to allow for local accuracy and convergence, but
not so small that the steps are “in the noise.” This requires an assessment of the local smoothness of the response
functions using, for example, a parameter study method. Central differencing will generally produce more reliable
gradients than forward differencing but at roughly twice the expense.
Gradient-based methods for nonlinear optimization problems can be described as iterative processes in which a
sequence of subproblems, usually which involve an approximation to the full nonlinear problem, are solved until
the solution converges to a local optimum of the full problem. The optimization methods available in Dakota fall
into several categories, each of which is characterized by the nature of the subproblems solved at each iteration.
6.2.1.1 Method Descriptions
Conjugate Gradient methods require first derivative information and can only be applied to unconstrained prob-
lems. The subproblems entail minimizing a quadratic function over a space defined by the gradient and directions
that are mutually conjugate with respect to the Hessian, though the Hessian is never computed. There are several
variants of how those directions are defined. Those available in Dakota are the Fletcher-Reeves conjugate gradient
method (conmin frcg and dot frcg [141]) and the Polak-Ribiere conjugate gradient method (optpp cg).
We here provide a caution regarding dot frcg. In DOT Version 4.20, we have noticed inconsistent behavior of
this algorithm across different versions of Linux. Our best assessment is that it is due to different treatments of
uninitialized variables. As we do not know the intention of the code authors and maintaining DOT source code
is outside of the Dakota project scope, we have not made nor are we recommending any code changes to address
this. However, all users who use dot frcg in DOT Version 4.20 should be aware that results may not be reliable.
Sequential Quadratic Programming (SQP) methods are appropriate for nonlinear optimization problems with
nonlinear constraints. Each subproblem involves minimizing a quadratic approximation the Lagrangian subject
to linearized constraints. Only gradient information is required; Hessians are approximated by low-rank updates
defined by the step taken at each iterations. It is important to note that while the solution found by an SQP method
will respect the constraints, the intermediate iterates may not. SQP methods available in Dakota are dot sqp,
nlpql sqp, and npsol sqp [56]. The particular implementation in nlpql sqp [117] uses a variant with
distributed and non-monotone line search. Thus, this variant is designed to be more robust in the presence of
inaccurate or noisy gradients common in many engineering applications. Also available is a method related to
SQP: sequential linear programming (dot slp).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.2. OPTIMIZING WITH DAKOTA: CHOOSING A METHOD 125
Newton Methods can be applied to nonlinear optimization problems with nonlinear constraints. The subproblems
associated with these methods entail finding the solution to a linear system of equations derived by setting the
derivative of a second-order Taylor series expansion to zero. Unlike SQP methods, Newton methods maintain
feasibility over the course of the optimization iterations. The variants of this approach correspond to the amount
of derivative information provided by the user. The full Newton method (optpp newton) expects both gradients
and Hessians to be provided. Quasi-Newton methods (optpp q newton,dot bfgs) expect only gradients.
The Hessian is approximated by the Broyden-Fletcher-Goldfarb-Shanno (BFGS) low-rank updates. Finally, the
finite difference Newton method (optpp fd newton) expects only gradients and approximates the Hessian
with second-order finite differences.
Method of Feasible Directions (MFD) methods are appropriate for nonlinear optimization problems with non-
linear constraints. These methods ensure that all iterates remain feasible. Dakota includes conmin mfd [139]
and dot mmfd One observed drawback to conmin mfd is that it does a poor job handling equality constraints.
dot mmfd does not suffer from this problem, nor do other methods for constrained problems.
6.2.1.2 Example
We refer the reader to Section 2.3.3 for this example.
6.2.2 Derivative-Free Local Methods
Derivative-free methods can be more robust and more inherently parallel than gradient-based approaches. They
can be applied in situations were gradient calculations are too expensive or unreliable. In addition, some derivative-
free methods can be used for global optimization which gradient-based techniques (see 6.2.1), by themselves,
cannot. For these reasons, derivative-free methods are often go-to methods when the problem may be nonsmooth,
multimodal, or poorly behaved. It is important to be aware, however, that they exhibit much slower convergence
rates for finding an optimum, and as a result, tend to be much more computationally demanding than gradient-
based methods. They often require from several hundred to a thousand or more function evaluations for local
methods, depending on the number of variables, and may require from thousands to tens-of-thousands of function
evaluations for global methods. Given the computational cost, it is often prudent to use derivative-free methods
to identify regions of interest and then use gradient-based methods to home in on the solution. In addition to
slow convergence, nonlinear constraint support in derivative-free methods is an open area of research and, while
supported by many methods in Dakota, is not as refined as constraint support in gradient-based methods.
6.2.2.1 Method Descriptions
Pattern Search methods can be applied to nonlinear optimization problems with nonlinear. They generally walk
through the domain according to a defined stencil of search directions. These methods are best suited for effi-
cient navigation to a local minimum in the vicinity of the initial point; however, they sometimes exhibit limited
global identification abilities if the stencil is such that it allows them to step over local minima. There are two
main pattern search methods available in Dakota, and they vary according to richness of available stencil and the
way constraints supported. Asynchronous Parallel Pattern Search (APPS) [67] (asynch pattern search)
uses the coordinate basis as its stencil, and it handles nonlinear constraints explicitly through modification of
the coordinate stencil to allow directions that parallel constraints [68]. A second variant of pattern search,
coliny pattern search, has the option of using either a coordinate or a simplex basis as well as allow-
ing more options for the stencil to evolve over the course of the optimization. It handles nonlinear constraints
through the use of penalty functions. The mesh adaptive search [8], [1], [93] is similar in spirit to and falls
in the same class of methods as the pattern search methods. The primary difference is that its underlying search
Dakota Version 6.7 User’s Manual generated on November 13, 2017
126 CHAPTER 6. OPTIMIZATION CAPABILITIES
structure is that of a mesh. The mesh adaptive search also provides a unique optimization capability in
Dakota in that it can explicitly treat categorical variables, i.e., non-relaxable discrete variables as described in
Section 9.2.2. Furthermore, it provides the ability to use a surrogate model to inform the priority of function
evaluations with the goal of reducing the number needed.
Simplex methods for nonlinear optimization problem are similar to pattern search methods, but their search
directions are defined by triangles that are reflected, expanded, and contracted across the variable space. The
two simplex-based methods available in Dakota are the Parallel Direct Search method [27] (optpp pds) and the
Constrained Optimization BY Linear Approximations (COBYLA) (coliny cobyla). The former handles only
bound constraints, while the latter handles nonlinear constraints. One drawback of both simplex-based methods
is that their current implementations do not allow them to take advantage of parallel computing resources via
Dakota’s infrastructure. Additionally, we note that the implementation of COBYLA is such that the best function
value is not always returned to Dakota for reporting. The user is advised to look through the Dakota screen output
or the tabular output file (if generated) to confirm what the best function value and corresponding parameter
values are. Furthermore, COBYLA does not always respect bound constraints when scaling is turned on. Neither
bug will be fixed, as maintaining third-party source code (such as COBYLA) is outside of the Dakota project
scope.
AGreedy Search Heuristic for nonlinear optimization problems is captured in the Solis-Wets (coliny solis wets)
method. This method takes a sampling-based approach in order to identify search directions. Note that one ob-
served drawback to coliny solis wets is that it does a poor job solving problems with nonlinear constraints.
This algorithm is also not implemented in such a way as to take advantage of parallel computing resources via
Dakota’s infrastructure.
Nonlinear Optimization with Path Augmented Constraints (NOWPAC) is a provably-convergent gradient-
free inequality-constrained optimization method that solves a series of trust region surrogate-based subproblems
to generate improving steps. Due to its use of an interior penalty scheme and enforcement of strict feasibility,
nowpac [10] does not support linear or nonlinear equality constraints. The stochastic version is snowpac,
which incorporates noise estimates in its objective and inequality constraints. snowpac modifies its trust region
controls and adds smoothing from a Gaussian process surrogate in order to mitigate noise. Note that as opposed
to the stochastic version (snowpac), nowpac does not currently support a feasibility restoration mode, so it is
necessary to start from a feasible design. Also note that (s)nowpac is not configured with Dakota by default and
requires a separate installation of the NOWPAC distribution, along with third-party libraries Eigen and NLOPT.
6.2.2.2 Example
The Dakota input file shown in Figure 6.1 applies a pattern search method to minimize the Rosenbrock function.
We note that this example is used as a means of demonstrating the contrast between input files for gradient-based
and derivative-free optimization. Since derivatives can be computed analytically and efficiently, the preferred
approach to solving this problem is a gradient-based method.
The Dakota input file shown in Figure 6.1 is similar to the input file for the gradient-based optimization, ex-
cept it has a different set of keywords in the method block of the input file, and the gradient specification in
the responses block has been changed to no gradients. The pattern search optimization algorithm used,
coliny pattern search is part of the SCOLIB library [74]. See the Dakota Reference Manual [3] for more
information on the methods block commands that can be used with SCOLIB algorithms.
For this run, the optimizer was given an initial design point of (x1, x2) = (0.0,0.0) and was limited to 2000
function evaluations. In this case, the pattern search algorithm stopped short of the optimum at (x1, x2) =
(1.0,1,0), although it was making progress in that direction when it was terminated. (It would have reached the
minimum point eventually.)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.2. OPTIMIZING WITH DAKOTA: CHOOSING A METHOD 127
# Dakota Input File: rosen_opt_patternsearch.in
environment
graphics
tabular_data
tabular_data_file = ’rosen_opt_patternsearch.dat’
method
coliny_pattern_search
max_iterations = 1000
max_function_evaluations = 2000
solution_target = 1e-4
initial_delta = 0.5
threshold_delta = 1e-4
exploratory_moves basic_pattern
contraction_factor = 0.75
model
single
variables
continuous_design = 2
initial_point 0.0 0.0
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
no_gradients
no_hessians
Figure 6.1: Rosenbrock pattern search optimization example: the Dakota input file – see
Dakota/examples/users/rosen opt patternsearch.in
The iteration history is provided in Figures 6.2(a) and (b), which show the locations of the function evaluations
used in the pattern search algorithm. Figure 6.2(c) provides a close-up view of the pattern search function evalua-
tions used at the start of the algorithm. The coordinate pattern is clearly visible at the start of the iteration history,
and the decreasing size of the coordinate pattern is evident at the design points move toward (x1, x2) = (1.0,1.0).
While pattern search algorithms are useful in many optimization problems, this example shows some of the
drawbacks to this algorithm. While a pattern search method may make good initial progress towards an optimum,
it is often slow to converge. On a smooth, differentiable function such as Rosenbrock’s function, a nongradient-
based method will not be as efficient as a gradient-based method. However, there are many engineering design
applications where gradient information is inaccurate or unavailable, which renders gradient-based optimizers
ineffective. Thus, pattern search algorithms are often good choices in complex engineering applications when the
quality of gradient data is suspect.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
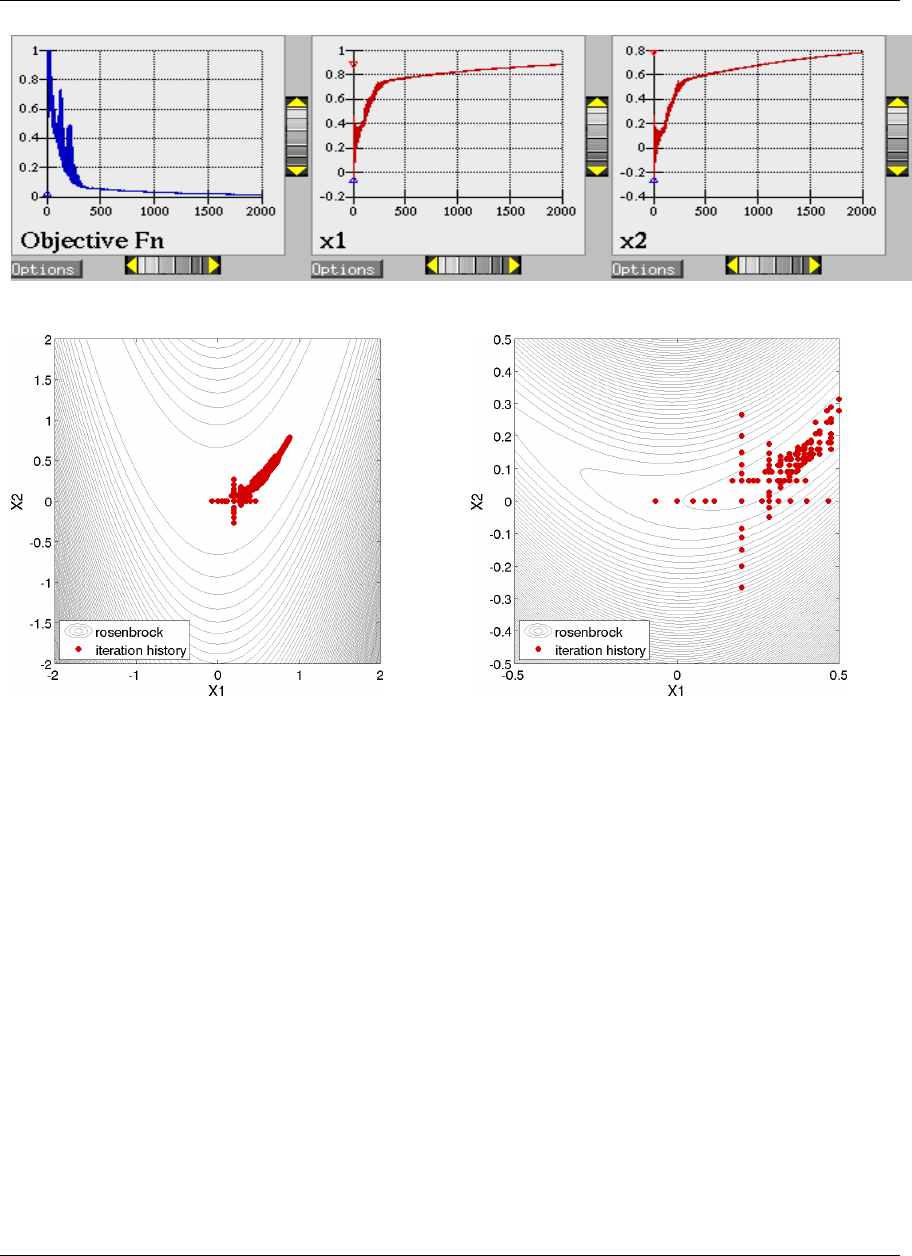
128 CHAPTER 6. OPTIMIZATION CAPABILITIES
(a)
(b) (c)
Figure 6.2: Rosenbrock pattern search optimization example: (a) screen capture of the Dakota graphics, (b)
sequence of design points (dots) evaluated and (c) close-up view illustrating the shape of the coordinate pattern
used.
6.2.3 Derivative-Free Global Methods
The discussion of derivative-free global methods is identical to that in 6.2.2, so we forego repeating it here. There
are two types of global optimization methods in Dakota.
6.2.3.1 Method Descriptions
Evolutionary Algorithms (EA) are based on Darwin’s theory of survival of the fittest. The EA algorithm starts
with a randomly selected population of design points in the parameter space, where the values of the design
parameters form a “genetic string,” analogous to DNA in a biological system, that uniquely represents each
design point in the population. The EA then follows a sequence of generations, where the best design points
in the population (i.e., those having low objective function values) are considered to be the most “fit” and are
allowed to survive and reproduce. The EA simulates the evolutionary process by employing the mathematical
analogs of processes such as natural selection, breeding, and mutation. Ultimately, the EA identifies a design point
(or a family of design points) that minimizes the objective function of the optimization problem. An extensive
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.2. OPTIMIZING WITH DAKOTA: CHOOSING A METHOD 129
discussion of EAs is beyond the scope of this text, but may be found in a variety of sources (cf., [72] pp. 149-
158; [64]). EAs available in Dakota include coliny ea,soga, and moga. The latter is specifically designed
for multi-objective problems, discussed further in 6.3. All variants can optimize over discrete variables, including
discrete string variables, in addition to continuous variables. We note that an experimental branch and bound
capability is being matured to provide a gradient-based approach to solving mixed variable global optimization
problems. One key distinction is that it does not handle categorical variables (e.g., string variables). The branch
and bound method is discussed further in Section 14.5.
DIvision of RECTangles (DIRECT) [51] balances local search in promising regions of the design space with
global search in unexplored regions. It adaptively subdivides the space of feasible design points to guarantee
that iterates are generated in the neighborhood of a global minimum in finitely many iterations. Dakota in-
cludes two implementations (ncsu direct and coliny direct. In practice, DIRECT has proven an ef-
fective heuristic for many applications. For some problems, the ncsu direct implementation has outper-
formed the coliny direct implementation. ncsu direct can accommodate only bound constraints, while
coliny direct handles nonlinear constraints using a penalty formulation of the problem.
Efficient Global Optimization (EGO) is a global optimization technique that employs response surface sur-
rogates [84,81]. In each EGO iteration, a Gaussian process (GP) approximation for the objective function is
constructed based on sample points of the true simulation. The GP allows one to specify the prediction at a new
input location as well as the uncertainty associated with that prediction. The key idea in EGO is to maximize an
Expected Improvement Function (EIF), defined as the expectation that any point in the search space will provide
a better solution than the current best solution, based on the expected values and variances predicted by the GP
model. It is important to understand how the use of this EIF leads to optimal solutions. The EIF indicates how
much the objective function value at a new potential location is expected to be less than the predicted value at
the current best solution. Because the GP model provides a Gaussian distribution at each predicted point, ex-
pectations can be calculated. Points with good expected values and even a small variance will have a significant
expectation of producing a better solution (exploitation), but so will points that have relatively poor expected val-
ues and greater variance (exploration). The EIF incorporates both the idea of choosing points which minimize the
objective and choosing points about which there is large prediction uncertainty (e.g., there are few or no samples
in that area of the space, and thus the probability may be high that a sample value is potentially lower than other
values). Because the uncertainty is higher in regions of the design space with few observations, this provides a
balance between exploiting areas of the design space that predict good solutions, and exploring areas where more
information is needed.
There are two major differences between our implementation and that of [84]: we do not use a branch and bound
method to find points which maximize the EIF. Rather, we use the DIRECT algorithm. Second, we allow for
multiobjective optimization and nonlinear least squares including general nonlinear constraints. Constraints are
handled through an augmented Lagrangian merit function approach (see Surrogate-Based Minimization chapter
in Dakota Theory Manual [4]).
6.2.3.2 Examples
Evolutionary algorithm: In contrast to pattern search algorithms, which are local optimization methods, evo-
lutionary algorithms (EA) are global optimization methods. As was described above for the pattern search al-
gorithm, the Rosenbrock function is not an ideal test problem for showcasing the capabilities of evolutionary
algorithms. Rather, EAs are best suited to optimization problems that have multiple local optima, and where
gradients are either too expensive to compute or are not readily available.
Figure 6.3 shows a Dakota input file that uses an EA to minimize the Rosenbrock function. For this example
the EA has a population size of 50. At the start of the first generation, a random number generator is used to
select 50 design points that will comprise the initial population. [A specific seed value is used in this example to
Dakota Version 6.7 User’s Manual generated on November 13, 2017

130 CHAPTER 6. OPTIMIZATION CAPABILITIES
# Dakota Input File: rosen_opt_ea.in
environment
graphics
tabular_data
tabular_data_file = ’rosen_opt_ea.dat’
method
coliny_ea
max_iterations = 100
max_function_evaluations = 2000
seed = 11011011
population_size = 50
fitness_type merit_function
mutation_type offset_normal
mutation_rate 1.0
crossover_type two_point
crossover_rate 0.0
replacement_type chc = 10
model
single
variables
continuous_design = 2
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
no_gradients
no_hessians
Figure 6.3: Rosenbrock evolutionary algorithm optimization example: the Dakota input file – see
Dakota/examples/users/rosen opt ea.in
generate repeatable results, although, in general, one should use the default setting which allows the EA to choose
a random seed.] A two-point crossover technique is used to exchange genetic string values between the members
of the population during the EA breeding process. The result of the breeding process is a population comprised
of the 10 best “parent” design points (elitist strategy) plus 40 new “child” design points. The EA optimization
process will be terminated after either 100 iterations (generations of the EA) or 2,000 function evaluations. The
EA software available in Dakota provides the user with much flexibility in choosing the settings used in the
optimization process. See [3] and [74] for details on these settings.
The EA optimization results printed at the end of this file show that the best design point found was (x1, x2) =
(0.98,0.95). The file ea tabular.dat.sav provides a listing of the design parameter values and objective
Dakota Version 6.7 User’s Manual generated on November 13, 2017
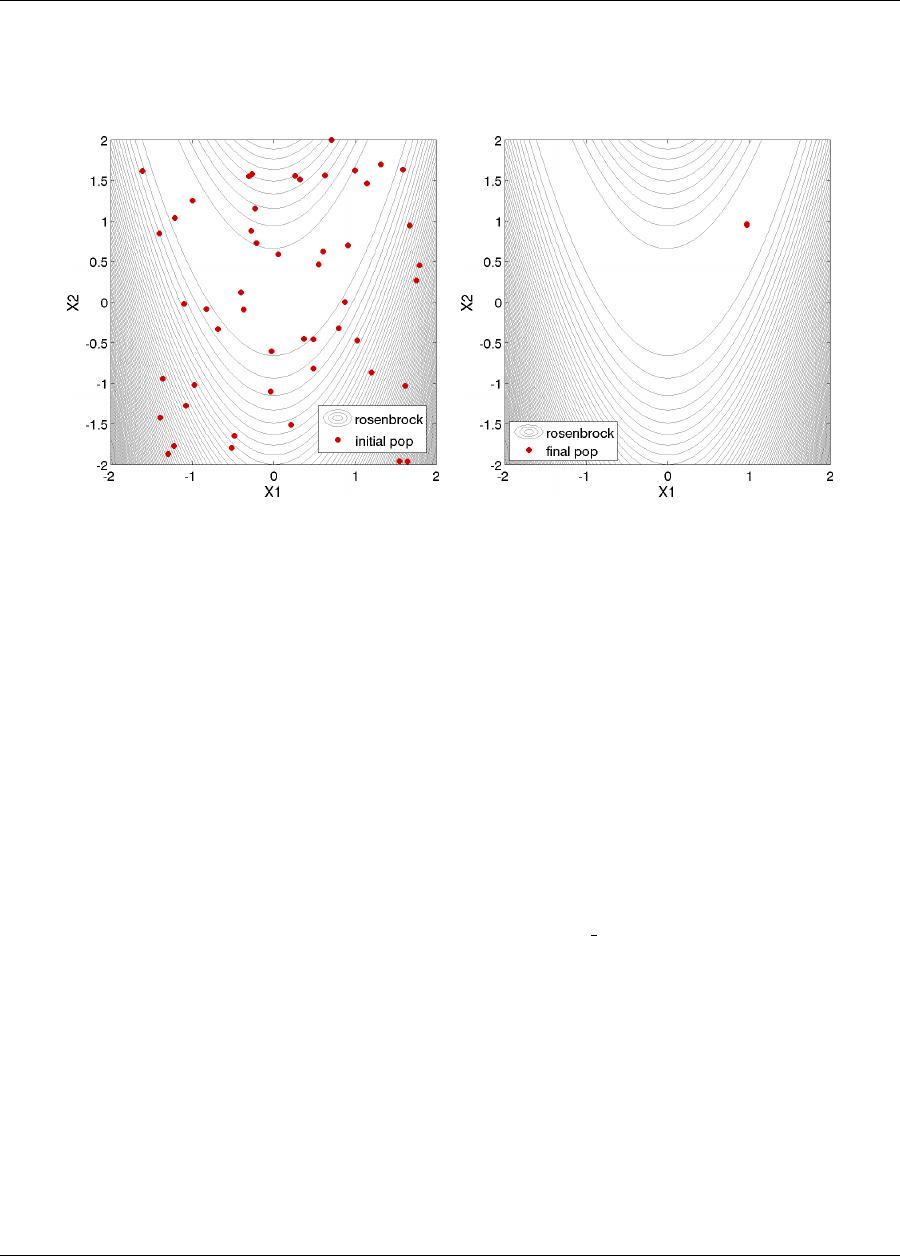
6.3. ADDITIONAL OPTIMIZATION CAPABILITIES 131
function values for all 2,000 design points evaluated during the running of the EA. Figure 6.4(a) shows the popu-
lation of 50 randomly selected design points that comprise the first generation of the EA, and Figure 6.4(b) shows
the final population of 50 design points, where most of the 50 points are clustered near (x1, x2) = (0.98,0.95).
(a) (b)
Figure 6.4: Rosenbrock evolutionary algorithm optimization example: 50 design points in the (a) initial and (b)
final populations selected by the evolutionary algorithm.
As described above, an EA is not well-suited to an optimization problem involving a smooth, differentiable objec-
tive such as the Rosenbrock function. Rather, EAs are better suited to optimization problems where conventional
gradient-based optimization fails, such as situations where there are multiple local optima and/or gradients are
not available. In such cases, the computational expense of an EA is warranted since other optimization methods
are not applicable or impractical. In many optimization problems, EAs often quickly identify promising regions
of the design space where the global minimum may be located. However, an EA can be slow to converge to the
optimum. For this reason, it can be an effective approach to combine the global search capabilities of a EA with
the efficient local search of a gradient-based algorithm in a hybrid optimization strategy. In this approach, the op-
timization starts by using a few iterations of a EA to provide the initial search for a good region of the parameter
space (low objective function and/or feasible constraints), and then it switches to a gradient-based algorithm (us-
ing the best design point found by the EA as its starting point) to perform an efficient local search for an optimum
design point. More information on this hybrid approach is provided in Section 14.2.
Efficient Global Optimization: The method is specified as efficient global. Currently we do not expose
any specification controls for the underlying Gaussian process model used or for the optimization of the expected
improvement function, which is currently performed by the NCSU DIRECT algorithm. The only item the user
can specify is a seed which is used in the Latin Hypercube Sampling to generate the initial set of points which
is used to construct the initial Gaussian process. An example specification for the EGO algorithm is shown in
Figure 6.5.
6.3 Additional Optimization Capabilities
Dakota provides several capabilities which extend the services provided by the optimization software packages
described in Sections 6.2.1 through 6.2.3. Those described in this section include:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

132 CHAPTER 6. OPTIMIZATION CAPABILITIES
# Dakota Input File: rosen_opt_ego.in
environment
tabular_data
tabular_data_file = ’rosen_opt_ego.dat’
method
efficient_global
seed = 123456
variables
continuous_design = 2
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
no_gradients
no_hessians
Figure 6.5: Dakota input file for the efficient global optimization example – see
Dakota/examples/users/rosen opt ego.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.3. ADDITIONAL OPTIMIZATION CAPABILITIES 133
•Multiobjective optimization: There are three capabilities for multiobjective optimization in Dakota. The
first is MOGA, described above in Section 6.2.3.1. The second is the Pareto-set strategy, described in
Section 14.4. The third is a weighting factor approach for multiobjective reduction, in which a composite
objective function is constructed from a set of individual objective functions using a user-specified set of
weighting factors. These latter two approaches work with any of the above single objective algorithms.
•Scaling, where any optimizer (or least squares solver described in Section 7.4), can accept user-specified
(and in some cases automatic or logarithmic) scaling of continuous design variables, objective functions (or
least squares terms), and constraints. Some optimization algorithms are sensitive to the relative scaling of
problem inputs and outputs, and this feature can help.
The Advanced Methods Chapter 14 offers details on the following component-based meta-algorithm approaches:
•Sequential Hybrid Minimization: This meta-algorithm allows the user to specify a sequence of mini-
mization methods, with the results from one method providing the starting point for the next method in
the sequence. An example which is useful in many engineering design problems involves the use of a
nongradient-based global optimization method (e.g., genetic algorithm) to identify a promising region of
the parameter space, which feeds its results into a gradient-based method (quasi-Newton, SQP, etc.) to
perform an efficient local search for the optimum point.
•Multistart Local Minimization: This meta-algorithm uses many local minimization runs (often gradient-
based), each of which is started from a different initial point in the parameter space. This is an attractive
approach in situations where multiple local optima are known to exist or may potentially exist in the param-
eter space. This approach combines the efficiency of local minimization methods with the parameter space
coverage of a global stratification technique.
•Pareto-Set Minimization: The Pareto-set minimization strategy allows the user to specify different sets
of weights for either the individual objective functions in a multiobjective optimization problem or the
individual residual terms in a least squares problem. Dakota executes each of these weighting sets as a
separate minimization problem, serially or in parallel, and then outputs the set of optimal designs which
define the Pareto set. Pareto set information can be useful in making trade-off decisions in engineering
design problems.
6.3.1 Multiobjective Optimization
Multiobjective optimization refers to the simultaneous optimization of two or more objective functions. Often
these are competing objectives, such as cost and performance. The optimal design in a multi-objective problem
is usually not a single point. Rather, it is a set of points called the Pareto front. Each point on the Pareto front
satisfies the Pareto optimality criterion, which is stated as follows: a feasible vector X∗is Pareto optimal if there
exists no other feasible vector Xwhich would improve some objective without causing a simultaneous worsening
in at least one other objective. Thus, if a feasible point X0exists that CAN be improved on one or more objectives
simultaneously, it is not Pareto optimal: it is said to be “dominated” and the points along the Pareto front are said
to be “non-dominated.”
There are three capabilities for multiobjective optimization in Dakota. First, there is the MOGA capability de-
scribed previously in Section 6.2.3.1. This is a specialized algorithm capability. The second capability involves
the use of response data transformations to recast a multiobjective problem as a single-objective problem. Cur-
rently, Dakota supports the simple weighted sum approach for this transformation, in which a composite objective
function is constructed from a set of individual objective functions using a user-specified set of weighting factors.
This approach is optimization algorithm independent, in that it works with any of the optimization methods listed
Dakota Version 6.7 User’s Manual generated on November 13, 2017
134 CHAPTER 6. OPTIMIZATION CAPABILITIES
previously in this chapter. The third capability is the Pareto-set meta-algorithm described in Section 14.4. This
capability also utilizes the multiobjective response data transformations to allow optimization algorithm inde-
pendence; however, it builds upon the basic approach by computing sets of optima in order to generate a Pareto
trade-off surface.
In the multiobjective transformation approach in which multiple objectives are combined into one, an appropriate
single-objective optimization technique is used to solve the problem. The advantage of this approach is that one
can use any number of optimization methods that are especially suited for the particular problem class. One
disadvantage of the weighted sum transformation approach is that a linear weighted sum objective will only find
one solution on the Pareto front. Since each optimization of a single weighted objective will find only one point
near or on the Pareto front, many optimizations need to be performed to get a good parametric understanding of
the influence of the weights. Thus, this approach can become computationally expensive.
A multiobjective optimization problem is indicated by the specification of multiple (R) objective functions in the
responses keyword block (i.e., the objective functions specification is greater than 1). The weighting
factors on these objective functions can be optionally specified using the weights keyword (the default is equal
weightings 1
R). The composite objective function for this optimization problem, F, is formed using these weights
as follows: F=PR
k=1 wkfk, where the fkterms are the individual objective function values, the wkterms are
the weights, and Ris the number of objective functions. The weighting factors stipulate the relative importance
of the design concerns represented by the individual objective functions; the higher the weighting factor, the more
dominant a particular objective function will be in the optimization process. Constraints are not affected by the
weighting factor mapping; therefore, both constrained and unconstrained multiobjective optimization problems
can be formulated and solved with Dakota, assuming selection of an appropriate constrained or unconstrained
single-objective optimization algorithm. When both multiobjective weighting and scaling are active, response
scaling is applied prior to weighting.
6.3.1.1 Multiobjective Example 1
Figure 6.6 shows a Dakota input file for a multiobjective optimization problem based on the “textbook” test prob-
lem. In the standard textbook formulation, there is one objective function and two constraints. In the multiobjec-
tive textbook formulation, all three of these functions are treated as objective functions (objective functions
= 3), with weights given by the weights keyword. Note that it is not required that the weights sum to a value of
one. The multiobjective optimization capability also allows any number of constraints, although none are included
in this example.
Figure 6.7 shows an excerpt of the results for this multiobjective optimization problem, with output in verbose
mode. The data for function evaluation 9 show that the simulator is returning the values and gradients of the three
objective functions and that this data is being combined by Dakota into the value and gradient of the composite
objective function, as identified by the header “Multiobjective transformation:”. This combination
of value and gradient data from the individual objective functions employs the user-specified weightings of .7,
.2, and .1. Convergence to the optimum of the multiobjective problem is indicated in this case by the gradient
of the composite objective function going to zero (no constraints are active).
By performing multiple optimizations for different sets of weights, a family of optimal solutions can be generated
which define the trade-offs that result when managing competing design concerns. This set of solutions is referred
to as the Pareto set. Section 14.4 describes an algorithm for directly generating the Pareto set in order to investigate
the trade-offs in multiobjective optimization problems.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.3. ADDITIONAL OPTIMIZATION CAPABILITIES 135
# Dakota Input File: textbook_opt_multiobj1.in
environment
tabular_data
tabular_data_file = ’textbook_opt_multiobj1.dat’
method
npsol_sqp
convergence_tolerance = 1.e-8
variables
continuous_design = 2
initial_point 0.9 1.1
upper_bounds 5.8 2.9
lower_bounds 0.5 -2.9
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’text_book’
direct
responses
objective_functions = 3
weights = .7 .2 .1
analytic_gradients
no_hessians
Figure 6.6: Example Dakota input file for multiobjective optimization – see
Dakota/examples/users/textbook opt multiobj1.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

136 CHAPTER 6. OPTIMIZATION CAPABILITIES
------------------------------
Begin Function Evaluation 9
------------------------------
Parameters for function evaluation 9:
5.9388064483e-01 x1
7.4158741198e-01 x2
(text_book /tmp/fileFNNH3v /tmp/fileRktLe9)
Removing /tmp/fileFNNH3v and /tmp/fileRktLe9
Active response data for function evaluation 9:
Active set vector = { 3 3 3 } Deriv vars vector = { 1 2 }
3.1662048106e-02 obj_fn_1
-1.8099485683e-02 obj_fn_2
2.5301156719e-01 obj_fn_3
[ -2.6792982175e-01 -6.9024137415e-02 ] obj_fn_1 gradient
[ 1.1877612897e+00 -5.0000000000e-01 ] obj_fn_2 gradient
[ -5.0000000000e-01 1.4831748240e+00 ] obj_fn_3 gradient
-----------------------------------
Post-processing Function Evaluation
-----------------------------------
Multiobjective transformation:
4.3844693257e-02 obj_fn
[ 1.3827084219e-06 5.8620632776e-07 ] obj_fn gradient
7 1 1.0E+00 9 4.38446933E-02 1.5E-06 2 T TT
Exit NPSOL - Optimal solution found.
Final nonlinear objective value = 0.4384469E-01
Figure 6.7: Dakota results for the multiobjective optimization example.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.3. ADDITIONAL OPTIMIZATION CAPABILITIES 137
6.3.1.2 Multiobjective Example 2
This example illustrates the use of multi-objective optimization based on a genetic algorithm method. This method
is called moga. It is based on the idea that as the population evolves in a GA, solutions that are non-dominated are
chosen to remain in the population. The MOGA algorithm has separate fitness assessment and selection operators
called the domination count fitness assessor and below limit selector respectively. This approach of
selection works especially well on multi-objective problems because it has been specifically designed to avoid
problems with aggregating and scaling objective function values and transforming them into a single objective.
Instead, the fitness assessor works by ranking population members such that their resulting fitness is a function of
the number of other designs that dominate them. The below limit selector then chooses designs by considering
the fitness of each. If the fitness of a design is above a certain limit, which in this case corresponds to a design
being dominated by more than a specified number of other designs, then it is discarded. Otherwise it is kept and
selected to go to the next generation. The one catch is that this selector will require that a minimum number of
selections take place. The shrinkage percentage determines the minimum number of selections that will
take place if enough designs are available. It is interpreted as a percentage of the population size that must go on
to the subsequent generation. To enforce this, the below limit selector makes all the selections it would make
anyway and if that is not enough, it relaxes its limit and makes selections from the remaining designs. It continues
to do this until it has made enough selections. The moga method has many other important features. Complete
descriptions can be found in the Dakota Reference Manual [3].
We demonstrate the MOGA algorithm on three examples that are taken from a multiobjective evolutionary algo-
rithm (MOEA) test suite described by Van Veldhuizen et. al. in [17]. These three examples illustrate the different
forms that the Pareto set may take. For each problem, we describe the Dakota input and show a graph of the Pareto
front. These problems are all solved with the moga method. The first example is presented below, the other two
examples are presented in the additional examples chapter 20.8.1 and 20.8.2.
In Van Veldhuizen’s notation, the set of all Pareto optimal design configurations (design variable values only) is
denoted P∗or Ptrue and is defined as:
P∗:= {x∈Ω|¬∃ x0∈Ω¯
f(x0)¯
f(x)}
The Pareto front, which is the set of objective function values associated with the Pareto optimal design configu-
rations, is denoted PF∗or PFtrue and is defined as:
P F ∗:= {¯u=¯
f= (f1(x), . . . , fk(x)) |x∈P∗}
The values calculated for the Pareto set and the Pareto front using the moga method are close to but not always
exactly the true values, depending on the number of generations the moga is run, the various settings governing
the GA, and the complexity of the Pareto set.
The first test problem is a case where Ptrue is connected and P Ftrue is concave. The problem is to simultaneously
optimize f1and f2given three input variables, x1,x2, and x3, where the inputs are bounded by −4≤xi≤4:
Figure 6.8 shows an input file that demonstrates some of the multi-objective capabilities available with the moga
method.
In this example, the three best solutions (as specified by final solutions =3) are written to the output.
Additionally, final results from moga are output to a file called finaldata1.dat in the directory in which you
are running. This finaldata1.dat file is simply a list of inputs and outputs. Plotting the output columns
against each other allows one to see the Pareto front generated by moga. Figure 6.9 shows an example of the
Pareto front for this problem. Note that a Pareto front easily shows the trade-offs between Pareto optimal solutions.
For instance, look at the point with f1 and f2 values equal to (0.9, 0.23). One cannot improve (minimize) the value
Dakota Version 6.7 User’s Manual generated on November 13, 2017

138 CHAPTER 6. OPTIMIZATION CAPABILITIES
# Dakota Input File: mogatest1.in
environment
graphics
tabular_data
tabular_data_file = ’mogatest1.dat’
method
moga
seed = 10983
max_function_evaluations = 2500
initialization_type unique_random
crossover_type shuffle_random
num_offspring = 2 num_parents = 2
crossover_rate = 0.8
mutation_type replace_uniform
mutation_rate = 0.1
fitness_type domination_count
replacement_type below_limit = 6
shrinkage_fraction = 0.9
convergence_type metric_tracker
percent_change = 0.05 num_generations = 40
final_solutions = 3
output silent
variables
continuous_design = 3
initial_point 0 0 0
upper_bounds 4 4 4
lower_bounds -4 -4 -4
descriptors ’x1’ ’x2’ ’x3’
interface
analysis_drivers = ’mogatest1’
direct
responses
objective_functions = 2
no_gradients
no_hessians
Figure 6.8: Multiple objective genetic algorithm (MOGA) example: the Dakota input file – see
Dakota/examples/users/mogatest1.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
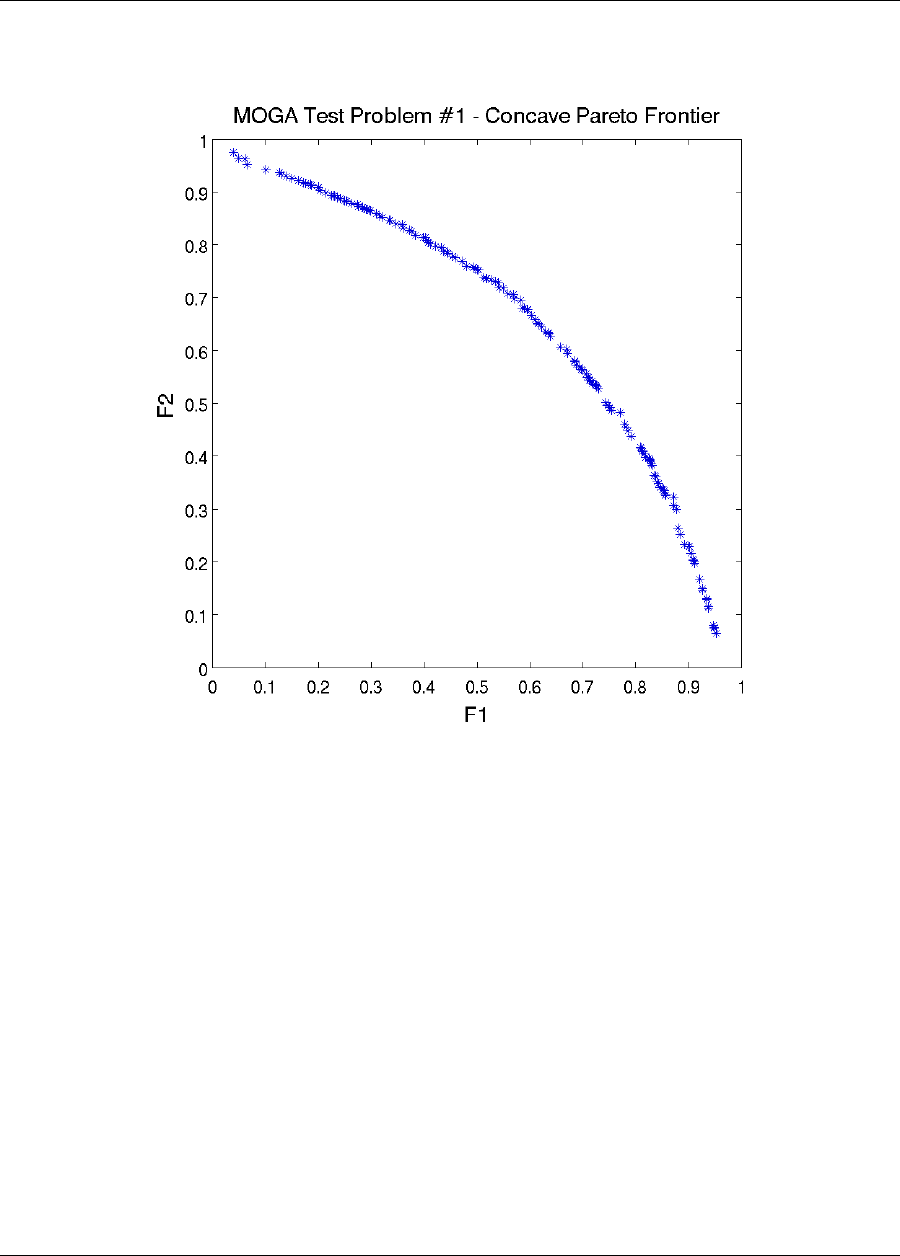
6.3. ADDITIONAL OPTIMIZATION CAPABILITIES 139
of objective function f1 without increasing the value of f2: another point on the Pareto front, (0.63, 0.63) represents
a better value of objective f1 but a worse value of objective f2.
Figure 6.9: Multiple objective genetic algorithm (MOGA) example: Pareto front showing trade-offs between
functions f1 and f2.
6.3.2 Optimization with User-specified or Automatic Scaling
Some optimization problems involving design variables, objective functions, or constraints on vastly different
scales may be solved more efficiently if these quantities are adjusted to a common scale (typically on the order
of unity). With any optimizer (or least squares solver described in Section 7.4), user-specified characteristic
value scaling may be applied to any of continuous design variables, functions/residuals, nonlinear inequality and
equality constraints, and linear inequality and equality constraints. Automatic scaling is available for variables or
responses with one- or two-sided bounds or equalities and may be combined with user-specified scaling values.
Logarithmic (log10) scaling is available and may also be combined with characteristic values. Log scaling is not
available for linear constraints. Moreover, when continuous design variables are log scaled, linear constraints are
not permitted in the problem formulation. Discrete variable scaling is not supported.
Scaling is enabled on a per-method basis for optimizers and least squares minimizers by including the scaling
keyword in the relevant method specification in the Dakota input deck. When scaling is enabled, variables, func-
tions, gradients, Hessians, etc., are transformed such that the optimizer iterates in scaled variable space, whereas
evaluations of the computational model as specified in the interface are performed on the original problem scale.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

140 CHAPTER 6. OPTIMIZATION CAPABILITIES
Therefore using scaling does not require rewriting the interface to the simulation code. When the scaling
keyword is omitted, all *scale types and *scales specifications described below are ignored in the cor-
responding method, variables, and responses sections. When the method output level is set above normal,
scaling initialization and diagnostic information will be printed.
Scaling for a particular variable or response type is enabled through the *scale types specification (see the
Reference Manual method section and references contained therein for a complete keyword list). Valid options
for this string specification include ’none’ (default), ’value’,’auto’, or ’log’, for no, characteristic
value, automatic, or logarithmic scaling, respectively (although not all types are valid for scaling all entities). If a
single string is specified with any of these keywords it will apply to each component of the relevant vector, e.g.,
cdv scale types = ’value’ will enable characteristic value scaling for each continuous design variable.
The user may additionally specify no, one, or a vector of characteristic scale values through the *scales
specification. These characteristic values are ignored for scaling type ’none’, required for ’value’, and
optional for ’auto’ and ’log’. If a single value is specified with any of these keywords it will apply to each
component of the relevant vector, e.g., cdv scales = 3.0 will apply a characteristic scaling value of 3.0 to
each continuous design variable.
When scaling is enabled, the following procedures determine the transformations used to scale each component
of a variables or response vector. A warning is issued if scaling would result in division by a value smaller in
magnitude than 1.0e10*DBL MIN. User-provided values violating this lower bound are accepted unaltered,
whereas for automatically calculated scaling, the lower bound is enforced.
•None (’none’): no scaling performed (*scales ignored) on this component.
•Characteristic value (’value’): the corresponding quantity is scaled (divided) by the required character-
istic value provided in the *scales specification, and bounds are adjusted as necessary. If the value is
negative, the sense of inequalities are changed accordingly.
•Automatic (’auto’): First, any characteristic values from the optional *scales specification are ap-
plied. Then, automatic scaling will be attempted according to the following scheme:
–two-sided bounds scaled into the interval [0,1];
–one-sided bounds or targets are scaled by a characteristic value to move the bound or target to 1, and
the sense of inequalities are changed if necessary;
–no bounds or targets: no automatic scaling possible for this component
Automatic scaling is not available for objective functions nor least squares terms since they lack bound
constraints. Further, when automatically scaled, linear constraints are scaled by characteristic values only,
not affinely scaled into [0,1].
•Logarithmic (’log’): First, any characteristic values from the optional *scales specification are ap-
plied. Then, log10 scaling is applied. Logarithmic scaling is not available for linear constraints. Further,
when continuous design variables are log scaled, linear constraints are not allowed.
Scaling for linear constraints specified through linear inequality scales or linear equality scales
is applied after any (user-specified or automatic) continuous variable scaling. For example, for scaling mapping
unscaled continuous design variables xto scaled variables ˜x:
˜xj=xj−xj
O
xj
M
,
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.4. OPTIMIZATION USAGE GUIDELINES 141
where xj
Mis the final component multiplier and xj
Othe offset, we have the following matrix system for linear
inequality constraints
aL≤Aix≤aU
aL≤Ai(diag(xM)˜x+xO)≤aU
aL−AixO≤Aidiag(xM)˜x≤aU−AixO
˜aL≤˜
Ai˜x≤˜aU,
and user-specified or automatically computed scaling multipliers are applied to this final transformed system,
which accounts for any continuous design variable scaling. When automatic scaling is in use for linear constraints
they are linearly scaled by characteristic values only, not affinely scaled into the interval [0,1].
6.3.2.1 Scaling Example
Figure 6.10 demonstrates the use of several scaling keywords for the textbook optimization problem. The con-
tinuous design variable x1 is scaled by a characteristic value of 4.0, whereas x2 is scaled automatically into
[0,1] based on its bounds. The objective function will be scaled by a factor of 50.0, then logarithmically, the first
nonlinear constraint by a factor of 15.0, and the second nonlinear constraint is not scaled.
6.4 Optimization Usage Guidelines
In selecting an optimization method, important considerations include the type of variables in the problem (contin-
uous, discrete, mixed), whether a global search is needed or a local search is sufficient, and the required constraint
support (unconstrained, bound constrained, or generally constrained). Less obvious, but equally important, con-
siderations include the efficiency of convergence to an optimum (i.e., convergence rate) and the robustness of the
method in the presence of challenging design space features (e.g., nonsmoothness).
Table 6.1 provides a convenient reference for choosing an optimization method or strategy to match the charac-
teristics of the user’s problem, where blank fields inherit the value from above. With respect to constraint support,
it should be understood that the methods with more advanced constraint support are also applicable to the lower
constraint support levels; they are listed only at their highest level of constraint support for brevity.
Gradient-based Methods
Gradient-based optimization methods are highly efficient, with the best convergence rates of all of the optimization
methods. If analytic gradient and Hessian information can be provided by an application code, a full Newton
method will provide quadratic convergence rates near the solution. More commonly, only gradient information
is available and a quasi-Newton method is chosen in which the Hessian information is approximated from an
accumulation of gradient data. In this case, superlinear convergence rates can be obtained. These characteristics
make gradient-based optimization methods the methods of choice when the problem is smooth, unimodal, and
well-behaved. However, when the problem exhibits nonsmooth, discontinuous, or multimodal behavior, these
methods can also be the least robust since inaccurate gradients will lead to bad search directions, failed line
searches, and early termination, and the presence of multiple minima will be missed.
Thus, for gradient-based optimization, a critical factor is the gradient accuracy. Analytic gradients are ideal, but
are often unavailable. For many engineering applications, a finite difference method will be used by the optimiza-
tion algorithm to estimate gradient values. Dakota allows the user to select the step size for these calculations,
as well as choose between forward-difference and central-difference algorithms. The finite difference step size
should be selected as small as possible, to allow for local accuracy and convergence, but not so small that the
steps are “in the noise.” This requires an assessment of the local smoothness of the response functions using, for
Dakota Version 6.7 User’s Manual generated on November 13, 2017

142 CHAPTER 6. OPTIMIZATION CAPABILITIES
# Dakota Input File: rosen_opt_scaled.in
environment
graphics
tabular_data
tabular_data_file = ’rosen_opt_scaled.dat’
method
conmin_frcg
scaling
output verbose
model
single
variables
continuous_design = 2
initial_point -1.2 1.0
lower_bounds -2.0 0.001
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
scale_types = ’value’ ’log’
scales = 4.0 0.1
interface
analysis_drivers = ’rosenbrock’
direct
responses
objective_functions = 1
primary_scale_types = ’value’
primary_scales = 50.0
analytic_gradients
no_hessians
Figure 6.10: Sample usage of scaling keywords in Dakota input specification – see
Dakota/examples/users/rosen opt scaled.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
6.4. OPTIMIZATION USAGE GUIDELINES 143
Table 6.1: Guidelines for optimization method selection.
Method Desired Problem Applicable Methods
Classification Characteristics
Gradient-Based Local smooth; continuous variables; no constraints optpp cg
smooth; continuous variables; dot bfgs, dot frcg, conmin frcg
bound constraints
smooth; continuous variables; npsol sqp, nlpql sqp, dot mmfd,
bound constraints, dot slp, dot sqp, conmin mfd,
linear and nonlinear constraints optpp newton, optpp q newton,
optpp fd newton,
weighted sums (multiobjective),
pareto set strategy (multiobjective)
Gradient-Based Global smooth; continuous variables; hybrid strategy,
bound constraints, multi start strategy
linear and nonlinear constraints
Derivative-Free Local nonsmooth; continuous variables; bound constraints optpp pds
nonsmooth; continuous variables; coliny cobyla,
bound constraints, coliny pattern search,
nonlinear constraints coliny solis wets,
nonsmooth; continuous variables; asynch pattern search,
bound constraints, surrogate based local
linear and nonlinear constraints
nonsmooth; continuous variables;
discrete variables; bound constraints, mesh adaptive search
nonlinear constraints
Derivative-Free Global nonsmooth; continuous variables; bound constraints ncsu direct
nonsmooth; continuous variables; coliny direct,
bound constraints, efficient global
nonlinear constraints
nonsmooth; continuous variables; surrogate based global
bound constraints,
linear and nonlinear constraints
nonsmooth; continuous variables, coliny ea
discrete variables; bound constraints,
nonlinear constraints
nonsmooth; continuous variables, soga,
discrete variables; bound constraints, moga (multiobjective)
linear and nonlinear constraints
Dakota Version 6.7 User’s Manual generated on November 13, 2017

144 CHAPTER 6. OPTIMIZATION CAPABILITIES
example, a parameter study method. Central differencing, in general, will produce more reliable gradients than
forward differencing, but at roughly twice the expense.
Non-gradient-based Methods
Nongradient-based methods exhibit much slower convergence rates for finding an optimum, and as a result, tend
to be much more computationally demanding than gradient-based methods. Nongradient local optimization meth-
ods, such as pattern search algorithms, often require from several hundred to a thousand or more function eval-
uations, depending on the number of variables, and nongradient global optimization methods such as genetic
algorithms may require from thousands to tens-of-thousands of function evaluations. Clearly, for nongradient
optimization studies, the computational cost of the function evaluation must be relatively small in order to obtain
an optimal solution in a reasonable amount of time. In addition, nonlinear constraint support in nongradient meth-
ods is an open area of research and, while supported by many nongradient methods in Dakota, is not as refined
as constraint support in gradient-based methods. However, nongradient methods can be more robust and more
inherently parallel than gradient-based approaches. They can be applied in situations were gradient calculations
are too expensive or unreliable. In addition, some nongradient-based methods can be used for global optimization
which gradient-based techniques, by themselves, cannot. For these reasons, nongradient-based methods deserve
consideration when the problem may be nonsmooth, multimodal, or poorly behaved.
Surrogate-based Methods
Approaches that seek to improve the effectiveness or efficiency of optimizers and least squares methods through
the use of surrogate models include the surrogate-based local, surrogate-based global, and efficient global meth-
ods. Section 14.6 provides further information on these approaches. The surrogate-based local approach (see
Section 14.6.1) brings the efficiency of gradient-based optimization/least squares methods to nonsmooth or poorly
behaved problems by smoothing noisy or discontinuous response results with a data fit surrogate model (e.g., a
quadratic polynomial) and then minimizing on the smooth surrogate using efficient gradient-based techniques.
The surrogate-based global approach (see Section 14.6.2) similarly employs optimizers/least squares methods
with surrogate models, but rather than localizing through the use of trust regions, seeks global solutions using
global methods. And the efficient global approach (see Section 6.2.3) uses the specific combination of Gaussian
process surrogate models in combination with the DIRECT global optimizer. Similar to these surrogate-based
approaches, the hybrid and multistart optimization component-based algorithms seek to bring the efficiency of
gradient-based optimization methods to global optimization problems. In the former case, a global optimization
method can be used for a few cycles to locate promising regions and then local gradient-based optimization is
used to efficiently converge on one or more optima. In the latter case, a stratification technique is used to disperse
a series of local gradient-based optimization runs through parameter space. Without surrogate data smoothing,
however, these strategies are best for smooth multimodal problems. Section 14.2 and Section 14.3 provide more
information on these approaches.
6.5 Optimization Third Party Libraries
As mentioned in 6, Dakota serves as a delivery vehicle for a number third-party optimization libraries. The
packages are listed here along with the license status and web page where available.
•CONMIN (conmin methods) License: Public Domain (NASA).
•DOT (dot methods) License: commercial; website: Vanderplaats Research and Development, http:
//www.vrand.com.Not included in the open source version of Dakota. Sandia National Laboratories
and Los Alamos National Laboratory have limited seats for DOT. Other users may obtain their own copy
of DOT and compile it with the Dakota source code.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

6.5. OPTIMIZATION THIRD PARTY LIBRARIES 145
•HOPSPACK (asynch pattern search) License: LGPL; web page: https://software.sandia.
gov/trac/hopspack.
•JEGA (soga,moga) License: LGPL
•NCSUOpt (ncsu direct) License: MIT
•NLPQL (nlpql methods) License: commercial; website: Prof. Klaus Schittkowski, http://www.
uni-bayreuth.de/departments/math/˜kschittkowski/nlpqlp20.htm). Not included
in the open source version of Dakota. Users may obtain their own copy of NLPQLP and compile it with the
Dakota source code.
•NPSOL (npsol methods) License: commercial; website: Stanford Business Software http://www.
sbsi-sol-optimize.com.Not included in the open source version of Dakota. Sandia National
Laboratories, Lawrence Livermore National Laboratory, and Los Alamos National Laboratory all have
site licenses for NPSOL. Other users may obtain their own copy of NPSOL and compile it with the Dakota
source code.
•NOMAD (mesh adaptive search) License: LGPL; website: http://www.gerad.ca/NOMAD/
Project/Home.html.
•OPT++ (optpp methods) License: LGPL; website: http://csmr.ca.sandia.gov/opt++.
•SCOLIB (coliny methods) License: BSD; website: https://software.sandia.gov/trac/
acro/wiki/Packages
Dakota Version 6.7 User’s Manual generated on November 13, 2017

146 CHAPTER 6. OPTIMIZATION CAPABILITIES
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 7
Nonlinear Least Squares Capabilities
7.1 Overview
Any Dakota optimization algorithm can be applied to calibration problems arising in parameter estimation, sys-
tem identification, and test/analysis reconciliation. However, nonlinear least-squares methods are optimization
algorithms that exploit the special structure of a sum of the squares objective function [57].
To exploit the problem structure, more granularity is needed in the response data than is required for a typical
optimization problem. That is, rather than using the sum-of-squares objective function and its gradient, least-
squares iterators require each term used in the sum-of-squares formulation along with its gradient. This means
that the mfunctions in the Dakota response data set consist of the individual least-squares terms along with any
nonlinear inequality and equality constraints. These individual terms are often called residuals when they denote
differences of observed quantities from values computed by the model whose parameters are being estimated.
The enhanced granularity needed for nonlinear least-squares algorithms allows for simplified computation of
an approximate Hessian matrix. In Gauss-Newton-based methods for example, the true Hessian matrix is ap-
proximated by neglecting terms in which residuals multiply Hessians (matrices of second partial derivatives) of
residuals, under the assumption that the residuals tend towards zero at the solution. As a result, residual function
value and gradient information (first-order information) is sufficient to define the value, gradient, and approxi-
mate Hessian of the sum-of-squares objective function (second-order information). See Section 7.2 for additional
details on this approximation.
In practice, least-squares solvers will tend to be significantly more efficient than general-purpose optimization
algorithms when the Hessian approximation is a good one, e.g., when the residuals tend towards zero at the
solution. Specifically, they can exhibit the quadratic convergence rates of full Newton methods, even though only
first-order information is used. Gauss-Newton-based least-squares solvers may experience difficulty when the
residuals at the solution are significant. Dakota has three solvers customized to take advantage of the sum of
squared residuals structure in this problem formulation. Least squares solvers may experience difficulty when the
residuals at the solution are significant, although experience has shown that Dakota’s NL2SOL method can handle
some problems that are highly nonlinear and have nonzero residuals at the solution.
148 CHAPTER 7. NONLINEAR LEAST SQUARES CAPABILITIES
7.2 Nonlinear Least Squares Fomulations
Specialized least squares solution algorithms can exploit the structure of a sum of the squares objective function
for problems of the form:
minimize: f(x) =
n
X
i=1
[Ti(x)]2
x∈ <n
subject to: gL≤g(x)≤gU
h(x) = ht(7.1)
aL≤Aix≤aU
Aex=at
xL≤x≤xU
where f(x)is the objective function to be minimized and Ti(x)is the ith least squares term. The bound, linear,
and nonlinear constraints are the same as described previously for (6.1). Specialized least squares algorithms are
generally based on the Gauss-Newton approximation. When differentiating f(x)twice, terms of Ti(x)T00
i(x)and
[T0
i(x)]2result. By assuming that the former term tends toward zero near the solution since Ti(x)tends toward
zero, then the Hessian matrix of second derivatives of f(x)can be approximated using only first derivatives of
Ti(x). As a result, Gauss-Newton algorithms exhibit quadratic convergence rates near the solution for those
cases when the Hessian approximation is accurate, i.e. the residuals tend towards zero at the solution. Thus, by
exploiting the structure of the problem, the second order convergence characteristics of a full Newton algorithm
can be obtained using only first order information from the least squares terms.
A common example for Ti(x)might be the difference between experimental data and model predictions for a
response quantity at a particular location and/or time step, i.e.:
Ti(x) = Ri(x)−Ri(7.2)
where Ri(x)is the response quantity predicted by the model and Riis the corresponding experimental data. In
this case, xwould have the meaning of model parameters which are not precisely known and are being calibrated
to match available data. This class of problem is known by the terms parameter estimation, system identification,
model calibration, test/analysis reconciliation, etc.
7.3 Nonlinear Least Squares with Dakota
In order to specify a least-squares problem, the responses section of the Dakota input should be configured us-
ing calibration terms (as opposed to objective functions as for optimization). The calibration
terms refer to the residuals (differences between the simulation model and the data). Note that Dakota expects
the residuals, not the squared residuals, and offers options for instead returning the simulation output to Dakota
together with a separate calibration data file, from which residuals will be calculated. Any linear or
nonlinear constraints are handled in an identical way to that of optimization (see Section 6.1; note that neither
Gauss-Newton nor NLSSOL require any constraint augmentation and NL2SOL supports neither linear nor non-
linear constraints). Gradients of the least-squares terms and nonlinear constraints are required and should be
specified using either numerical gradients,analytic gradients, or mixed gradients. Since
Dakota Version 6.7 User’s Manual generated on November 13, 2017

7.4. SOLUTION TECHNIQUES 149
explicit second derivatives are not used by the least-squares methods, the no hessians specification should
be used. Dakota’s scaling options, described in Section 6.3.2 can be used on least-squares problems, using the
calibration term scales keyword to scale least-squares residuals, if desired.
7.4 Solution Techniques
Nonlinear least-squares problems can be solved using the Gauss-Newton algorithm, which leverages the full
Newton method from OPT++, the NLSSOL algorithm, which is closely related to NPSOL, or the NL2SOL
algorithm, which uses a secant-based algorithm. Details for each are provided below.
7.4.1 Gauss-Newton
Dakota’s Gauss-Newton algorithm consists of combining an implementation of the Gauss-Newton Hessian ap-
proximation (see Section 7.2) with full Newton optimization algorithms from the OPT++ package [102] (see Sec-
tion 6.2.1.1). The exact objective function value, exact objective function gradient, and the approximate objective
function Hessian are defined from the least squares term values and gradients and are passed to the full-Newton
optimizer from the OPT++ software package. As for all of the Newton-based optimization algorithms in OPT++,
unconstrained, bound-constrained, and generally-constrained problems are supported. However, for the generally-
constrained case, a derivative order mismatch exists in that the nonlinear interior point full Newton algorithm will
require second-order information for the nonlinear constraints whereas the Gauss-Newton approximation only
requires first order information for the least squares terms. License: LGPL.
This approach can be selected using the optpp g newton method specification. An example specification
follows:
method,
optpp_g_newton
max_iterations = 50
convergence_tolerance = 1e-4
output debug
Refer to the Dakota Reference Manual [3] for more detail on the input commands for the Gauss-Newton algorithm.
The Gauss-Newton algorithm is gradient-based and is best suited for efficient navigation to a local least-squares
solution in the vicinity of the initial point. Global optima in multimodal design spaces may be missed. Gauss-
Newton supports bound, linear, and nonlinear constraints. For the nonlinearly-constrained case, constraint Hes-
sians (required for full-Newton nonlinear interior point optimization algorithms) are approximated using quasi-
Newton secant updates. Thus, both the objective and constraint Hessians are approximated using first-order
information.
7.4.2 NLSSOL
The NLSSOL algorithm is bundled with NPSOL. It uses an SQP-based approach to solve generally-constrained
nonlinear least-squares problems. It periodically employs the Gauss-Newton Hessian approximation to accelerate
the search. Like the Gauss-Newton algorithm of Section 7.4.1, its derivative order is balanced in that it requires
only first-order information for the least-squares terms and nonlinear constraints. License: commercial; see
NPSOL 6.2.1.1.
This approach can be selected using the nlssol sqp method specification. An example specification follows:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

150 CHAPTER 7. NONLINEAR LEAST SQUARES CAPABILITIES
method,
nlssol_sqp
convergence_tolerance = 1e-8
Refer to the Dakota Reference Manual [3] for more detail on the input commands for NLSSOL.
7.4.3 NL2SOL
The NL2SOL algorithm [25] is a secant-based least-squares algorithm that is q-superlinearly convergent. It adap-
tively chooses between the Gauss-Newton Hessian approximation and this approximation augmented by a correc-
tion term from a secant update. NL2SOL tends to be more robust (than conventional Gauss-Newton approaches)
for nonlinear functions and “large residual” problems, i.e., least-squares problems for which the residuals do not
tend towards zero at the solution. License: publicly available.
7.4.4 Additional Features
Dakota can calculate confidence intervals on estimated parameters. These are computed on a per-parameter basis;
they are not joint confidence intervals. The intervals reported are 95% intervals around the estimated parameters,
and are calculated as the optimal value of the estimated parameters +/−a t-test statistic times the standard error
(SE) of the estimated parameter vector. The SE is based on a linearization approximation involving the matrix of
the derivatives of the model with respect to the derivatives of the estimated parameters. In the case where these
gradients are extremely inaccurate or the model is very nonlinear, the confidence intervals reported are likely to
be inaccurate as well. (Confidence intervals cannot be calculated when the number of least-squares terms is less
than the number of parameters to be estimated, or when using vendor numerical gradients.) See [119] and [143]
for more details about confidence intervals, and note that there are alternative approaches such as Bonferroni
confidence intervals and joint confidence intervals based on linear approximations or F-tests.
Least squares calibration terms (responses) can be weighted. When observation error variance is provided along-
side calibration data, its inverse is applied to yield the typical variance-weighted least squares formulation. Alter-
nately, the calibration terms weights specification can be used to weight the squared residuals. (Nei-
ther set of weights are adjusted during calibration as they would be in iteratively re-weighted least squares.)
When response scaling is active, it is applied after error variance weighting and before weights application.
The calibration terms keyword documentation in the Dakota Reference Manual [3] has more detail about
weighting and scaling of the residual terms.
7.5 Examples
Both the Rosenbrock and textbook example problems can be formulated as nonlinear least-squares problems.
Refer to Chapter 20 for more information on these formulations.
Figure 7.1 shows an excerpt from the output obtained when running NL2SOL on a five-dimensional problem.
Note that the optimal parameter estimates are printed, followed by the residual norm and values of the individual
residual terms, followed by the confidence intervals on the parameters.
The analysis driver script (the script being driven by Dakota) has to perform several tasks in the case of parameter
estimation using nonlinear least-squares methods. The analysis driver script must: (1) read in the values of
the parameters supplied by Dakota; (2) run the computer simulation with these parameter values; (3) retrieve the
results from the computer simulation; (4) compute the difference between each computed simulation value and the
Dakota Version 6.7 User’s Manual generated on November 13, 2017
7.5. EXAMPLES 151
<<<<< Iterator nl2sol completed.
<<<<< Function evaluation summary: 27 total (26 new, 1 duplicate)
<<<<< Best parameters =
3.7541004764e-01 x1
1.9358463401e+00 x2
-1.4646865611e+00 x3
1.2867533504e-02 x4
2.2122702030e-02 x5
<<<<< Best residual norm = 7.3924926090e-03; 0.5 *normˆ2 = 2.7324473487e-05
<<<<< Best residual terms =
-2.5698266189e-03
4.4759880011e-03
9.9223430643e-04
-1.0634409194e-03
...
Confidence Interval for x1 is [ 3.7116510206e-01, 3.7965499323e-01 ]
Confidence Interval for x2 is [ 1.4845485507e+00, 2.3871441295e+00 ]
Confidence Interval for x3 is [ -1.9189348458e+00, -1.0104382765e+00 ]
Confidence Interval for x4 is [ 1.1948590669e-02, 1.3786476338e-02 ]
Confidence Interval for x5 is [ 2.0289951664e-02, 2.3955452397e-02 ]
Figure 7.1: Example of confidence intervals on optimal parameters
corresponding experimental or measured value; and (5) write these residuals (differences) to an external file that
gets passed back to Dakota. Note there will be one line per residual term, specified with calibration terms
in the Dakota input file. It is the last two steps which are different from most other Dakota applications.
To simplify specifying a least squares problem, a user may specify a data file containing experimental results or
other calibration data. In the case of scalar calibration terms, this file may be specified with calibration data file.
In this case, Dakota will calculate the residuals (that is, the simulation model results minus the experimental re-
sults), and the user-provided script can omit this step: the script can just return the simulation outputs of interest.
An example of this can be found in the file named Dakota/examples/users/textbook nls datafile.in.
In this example, there are 3 residual terms. The data file of experimental results associated with this example
is textbook nls datafile.lsq.dat. These three values are subtracted from the least-squares terms to
produce residuals for the nonlinear least-squares problem. Note that the file may be annotated (specified by
annotated) or freeform (specified by freeform). The number of experiments in the calibration data file
may be specified with num experiments, with one row of data per experiment. When multiple experiments
are present, the total number of least squares terms will be the number of calibration terms times the number of
experiments.
Finally, the calibration data file may contain additional information than just the observed experimental responses.
If the observed data has measurement error associated with it, this can be specified in columns of such error data
after the response data. The type of measurement error is specified by variance type. For scalar calibration
terms, the variance type can be either none (the user does not specify a measurement variance associated
with each calibration term) or scalar (the user specifies one measurement variance per calibration term). For
field calibration terms, the variance type can also be diagonal or matrix. These are explained in more
detail in the Reference manual. Additionally, there is sometimes the need to specify configuration variables.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

152 CHAPTER 7. NONLINEAR LEAST SQUARES CAPABILITIES
These are often used in Bayesian calibration analysis. These are specified as num config variables. If the
user specifies a positive number of configuration variables, it is expected that they will occur in the text file before
the responses.
7.6 Usage Guidelines
Calibration problems can be transformed to general optimization problems where the objective is some type of
aggregated error metric. For example, the objective could be the sum of squared error terms. However, it also
could be the mean of the absolute value of the error terms, the maximum difference between the simulation
results and observational results, etc. In all of these cases, one can pose the calibration problem as an optimization
problem that can be solved by any of Dakota’s optimizers. In this situation, when applying an general optimization
solver to a calibration problem, the guidelines in Table 6.4 still apply.
In some cases, it will be better to use a nonlinear least-squares method instead of a general optimizer to determine
optimal parameter values which result in simulation responses that “best fit” the observational data. Nonlinear
least squares methods exploit the special structure of a sum of the squares objective function. They can be much
more efficient than general optimizers. However, these methods require the gradients of the function with respect
to the parameters being calibrated. If the model is not able to produce gradients, one can use finite differencing
to obtain gradients. However, the gradients must be reasonably accurate for the method to proceed. Note that
the nonlinear least-squares methods only operate on a sum of squared errors as the objective. Also, the user must
return each residual term separately to Dakota, whereas the user can return an aggregated error measure in the
case of general optimizers.
The three nonlinear least-squares methods are the Gauss-Newton method in OPT++, NLSSOL, and NL2SOL.
Any of these may be tried; they give similar performance on many problems. NL2SOL tends to be more robust
than Gauss-Newton, especially for nonlinear functions and large-residual problems where one is not able to drive
the residuals to zero at the solution. NLSSOL does require that the user has the NPSOL library. Note that all of
these methods are local in the sense that they are gradient-based and depend on an initial starting point. Often they
are used in conjunction with a multi-start method, to perform several repetitions of the optimization at different
starting points in the parameter space. Another approach is to use a general global optimizer such as a genetic
algorithm or DIRECT as mentioned above. This can be much more expensive, however, in terms of the number
of function evaluations required.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
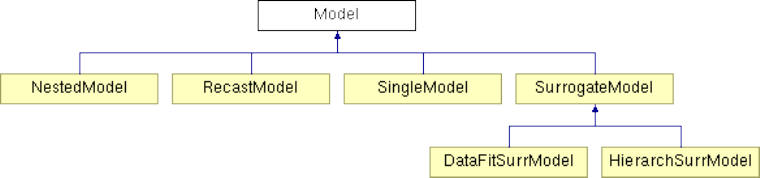
Chapter 8
Models
8.1 Overview
Chapters 3through 7presented the different “iterators” (or methods) available in Dakota. An iterator iterates on
a model in order to map a set of variables into a set of responses. This model may involve a simple mapping
involving a single interface, or it may involve recursions using sub-iterators and sub-models. These recursion
capabilities were developed in order to provide mechanisms for “nesting,” “layering,” and “recasting” of software
components, which allows the use of these components as building blocks to accomplish more sophisticated
studies, such as surrogate-based optimization or optimization under uncertainty. In a nested relationship, a sub-
iterator is executed using its sub-model for every evaluation of the nested model. In a layered relationship, on
the other hand, sub-iterators and sub-models are used only for periodic updates and verifications. And in a recast
relationship, the input variable and output response definitions in a sub-model are reformulated in order to support
new problem definitions. In each of these cases, the sub-model is of arbitrary type, such that model recursions
can be chained together in as long of a sequence as needed (e.g., layered containing nested contained layered
containing single in Section 15.2.2). Figure 8.1 displays the model class hierarchy from the Dakota Developers
Manual [2], with derived classes for single models, nested models, recast models, and two types of surrogate
models: data fit and hierarchical/multifidelity. A third type of derived surrogate model supporting reduced-order
models (ROM) is planned for future releases.
Section 8.2 describes single models, Section 8.3 describes recast models, Section 8.4 describes surrogate models
of various types, Section 8.5 describes nested models, Section 8.6 describes random field models, and Section
8.7 describes active subspace models. Finally, Chapter 15 presents a number of advanced examples demonstrating
these model recursions.
Figure 8.1: The Dakota model class hierarchy.

154 CHAPTER 8. MODELS
8.2 Single Models
The single model is the simplest model type. It uses a single interface instance (see Chapter 10) to map variables
(see Chapter 9) into responses (see Chapter 11). There is no recursion in this case. Refer to the Models chapter in
the Dakota Reference Manual [3] for additional information on the single model specification.
8.3 Recast Models
The recast model is not directly visible to the user within the input specification. Rather, it is used “behind the
scenes” to recast the inputs and outputs of a sub-model for the purposes of reformulating the problem posed to
an iterator. Examples include variable and response scaling (see Section 6.3.2), transformations of uncertain vari-
ables and associated response derivatives to employ standardized random variables (see Sections 5.3 and 5.4),
multiobjective optimization (see Section 6.3.1), merit functions (see Section 14.6.1), and expected improvemen-
t/feasibility (see Sections 6.2.3 and 5.3.2). Refer to the Dakota Developers Manual [2] for additional details on
the mechanics of recasting problem formulations.
8.4 Surrogate Models
Surrogate models are inexpensive approximate models that are intended to capture the salient features of an
expensive high-fidelity model. They can be used to explore the variations in response quantities over regions
of the parameter space, or they can serve as inexpensive stand-ins for optimization or uncertainty quantification
studies (see, for example, the surrogate-based optimization methods in Section 14.6). Surrogate models supported
in Dakota can be categorized into three types: data fits, multifidelity, and reduced-order model surrogates. An
overview and discussion of surrogate correction is provided here, with details following.
8.4.1 Overview of Surrogate Types
Data fitting methods involve construction of an approximation or surrogate model using data (response values,
gradients, and Hessians) generated from the original truth model. Data fit methods can be further categorized
as local, multipoint, and global approximation techniques, based on the number of points used in generating the
data fit. Local methods involve response data from a single point in parameter space. Available local techniques
currently include:
Known Issue: When using discrete variables, there have been sometimes significant differences in data fit surro-
gate behavior observed across computing platforms in some cases. The cause has not yet been fully diagnosed
and is currently under investigation. In addition, guidance on appropriate construction and use of surrogates with
discrete variables is under development. In the meantime, users should therefore be aware that there is a risk of
inaccurate results when using surrogates with discrete variables.
Taylor Series Expansion: This is a local first-order or second-order expansion centered at a single point in the
parameter space.
Multipoint approximations involve response data from two or more points in parameter space, often involving the
current and previous iterates of a minimization algorithm. Available techniques currently include:
TANA-3: This multipoint approximation uses a two-point exponential approximation [153,46] built with re-
sponse value and gradient information from the current and previous iterates.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8.4. SURROGATE MODELS 155
Global methods, often referred to as response surface methods, involve many points spread over the parameter
ranges of interest. These surface fitting methods work in conjunction with the sampling methods and design of
experiments methods described in Sections 5.2 and 4.2.
Polynomial Regression: First-order (linear), second-order (quadratic), and third-order (cubic) polynomial re-
sponse surfaces computed using linear least squares regression methods. Note: there is currently no use of
forward- or backward-stepping regression methods to eliminate unnecessary terms from the polynomial model.
Gaussian Process (GP) or Kriging Interpolation Dakota contains two implementations of Gaussian process,
also known as Kriging [63], spatial interpolation. One of these resides in the Surfpack sub-package of Dakota,
the other resides in Dakota itself. Both versions use the Gaussian correlation function with parameters that are
selected by Maximum Likelihood Estimation (MLE). This correlation function results in a response surface that
is C∞-continuous. Prior to Dakota 5.2, the Surfpack GP was referred to as the “Kriging” model and the Dakota
version was labeled as the “Gaussian Process.” These terms are now used interchangeably. As of Dakota 5.2,the
Surfpack GP is used by default. For now the user still has the option to select the Dakota GP, but the Dakota GP
is deprecated and will be removed in a future release.
•Surfpack GP: Ill-conditioning due to a poorly spaced sample design is handled by discarding points that
contribute the least unique information to the correlation matrix. Therefore, the points that are discarded
are the ones that are easiest to predict. The resulting surface will exactly interpolate the data values at the
retained points but is not guaranteed to interpolate the discarded points.
•Dakota GP: Ill-conditioning is handled by adding a jitter term or “nugget” to diagonal elements of the
correlation matrix. When this happens, the Dakota GP may not exactly interpolate the data values.
Artificial Neural Networks: An implementation of the stochastic layered perceptron neural network developed
by Prof. D. C. Zimmerman of the University of Houston [154]. This neural network method is intended to have a
lower training (fitting) cost than typical back-propagation neural networks.
Multivariate Adaptive Regression Splines (MARS): Software developed by Prof. J. H. Friedman of Stanford
University [50]. The MARS method creates a C2-continuous patchwork of splines in the parameter space.
Radial Basis Functions (RBF): Radial basis functions are functions whose value typically depends on the dis-
tance from a center point, called the centroid. The surrogate model approximation is constructed as the weighted
sum of individual radial basis functions.
Moving Least Squares (MLS): Moving Least Squares can be considered a more specialized version of linear
regression models. MLS is a weighted least squares approach where the weighting is “moved” or recalculated for
every new point where a prediction is desired. [106]
Piecewise Decomposition Option for Global Surrogates: Typically, the previous regression techniques use all
available sample points to approximate the underlying function anywhere in the domain. An alternative option
is to use piecewise decomposition to locally approximate the function at some point using a few sample points
from its neighborhood. This option currently supports Polynomial Regression, Gaussian Process (GP) Interpo-
lation, and Radial Basis Functions (RBF) Regression. It requires a decomposition cell type (currently set to be
Voronoi cells), an optional number of support layers of neighbors, and optional discontinuity detection parameters
(jump/gradient).
In addition to data fit surrogates, Dakota supports multifidelity and reduced-order model approximations:
Multifidelity Surrogates: Multifidelity modeling involves the use of a low-fidelity physics-based model as a
surrogate for the original high-fidelity model. The low-fidelity model typically involves a coarser mesh, looser
convergence tolerances, reduced element order, or omitted physics. It is a separate model in its own right and
does not require data from the high-fidelity model for construction. Rather, the primary need for high-fidelity
Dakota Version 6.7 User’s Manual generated on November 13, 2017

156 CHAPTER 8. MODELS
evaluations is for defining correction functions that are applied to the low-fidelity results.
Reduced Order Models: A reduced-order model (ROM) is mathematically derived from a high-fidelity model
using the technique of Galerkin projection. By computing a set of basis functions (e.g., eigenmodes, left singular
vectors) that capture the principal dynamics of a system, the original high-order system can be projected to a much
smaller system, of the size of the number of retained basis functions.
8.4.2 Correction Approaches
Each of the surrogate model types supports the use of correction factors that improve the local accuracy of the
surrogate models. The correction factors force the surrogate models to match the true function values and possibly
true function derivatives at the center point of each trust region. Currently, Dakota supports either zeroth-, first-, or
second-order accurate correction methods, each of which can be applied using either an additive, multiplicative, or
combined correction function. For each of these correction approaches, the correction is applied to the surrogate
model and the corrected model is then interfaced with whatever algorithm is being employed. The default behavior
is that no correction factor is applied.
The simplest correction approaches are those that enforce consistency in function values between the surrogate
and original models at a single point in parameter space through use of a simple scalar offset or scaling applied
to the surrogate model. First-order corrections such as the first-order multiplicative correction (also known as
beta correction [16]) and the first-order additive correction [96] also enforce consistency in the gradients and
provide a much more substantial correction capability that is sufficient for ensuring provable convergence in SBO
algorithms (see Section 14.6.1). SBO convergence rates can be further accelerated through the use of second-
order corrections which also enforce consistency in the Hessians [37], where the second-order information may
involve analytic, finite-difference, or quasi-Newton Hessians.
Correcting surrogate models with additive corrections involves
ˆ
fhiα(x) = flo(x) + α(x)(8.1)
where multifidelity notation has been adopted for clarity. For multiplicative approaches, corrections take the form
ˆ
fhiβ(x) = flo(x)β(x)(8.2)
where, for local corrections, α(x)and β(x)are first or second-order Taylor series approximations to the exact
correction functions:
α(x) = A(xc) + ∇A(xc)T(x−xc) + 1
2(x−xc)T∇2A(xc)(x−xc)(8.3)
β(x) = B(xc) + ∇B(xc)T(x−xc) + 1
2(x−xc)T∇2B(xc)(x−xc)(8.4)
where the exact correction functions are
A(x) = fhi(x)−flo(x)(8.5)
B(x) = fhi(x)
flo(x)(8.6)
Refer to [37] for additional details on the derivations.
A combination of additive and multiplicative corrections can provide for additional flexibility in minimizing the
impact of the correction away from the trust region center. In other words, both additive and multiplicative
Dakota Version 6.7 User’s Manual generated on November 13, 2017
8.4. SURROGATE MODELS 157
corrections can satisfy local consistency, but through the combination, global accuracy can be addressed as well.
This involves a convex combination of the additive and multiplicative corrections:
ˆ
fhiγ(x) = γˆ
fhiα(x) + (1 −γ)ˆ
fhiβ(x)(8.7)
where γis calculated to satisfy an additional matching condition, such as matching values at the previous design
iterate.
8.4.3 Data Fit Surrogate Models
A surrogate of the data fit type is a non-physics-based approximation typically involving interpolation or regres-
sion of a set of data generated from the original model. Data fit surrogates can be further characterized by the
number of data points used in the fit, where a local approximation (e.g., first or second-order Taylor series) uses
data from a single point, a multipoint approximation (e.g., two-point exponential approximations (TPEA) or two-
point adaptive nonlinearity approximations (TANA)) uses a small number of data points often drawn from the
previous iterates of a particular algorithm, and a global approximation (e.g., polynomial response surfaces, krig-
ing/gaussian process, neural networks, radial basis functions, splines) uses a set of data points distributed over the
domain of interest, often generated using a design of computer experiments.
Dakota contains several types of surface fitting methods that can be used with optimization and uncertainty quan-
tification methods and strategies such as surrogate-based optimization and optimization under uncertainty. These
are: polynomial models (linear, quadratic, and cubic), first-order Taylor series expansion, kriging spatial inter-
polation, artificial neural networks, multivariate adaptive regression splines, radial basis functions, and moving
least squares. With the exception of Taylor series methods, all of the above methods listed in the previous sen-
tence are accessed in Dakota through the Surfpack library. All of these surface fitting methods can be applied to
problems having an arbitrary number of design parameters. However, surface fitting methods usually are practical
only for problems where there are a small number of parameters (e.g., a maximum of somewhere in the range of
30-50 design parameters). The mathematical models created by surface fitting methods have a variety of names in
the engineering community. These include surrogate models, meta-models, approximation models, and response
surfaces. For this manual, the terms surface fit model and surrogate model are used.
The data fitting methods in Dakota include software developed by Sandia researchers and by various researchers
in the academic community.
8.4.3.1 Procedures for Surface Fitting
The surface fitting process consists of three steps: (1) selection of a set of design points, (2) evaluation of the true
response quantities (e.g., from a user-supplied simulation code) at these design points, and (3) using the response
data to solve for the unknown coefficients (e.g., polynomial coefficients, neural network weights, kriging correla-
tion factors) in the surface fit model. In cases where there is more than one response quantity (e.g., an objective
function plus one or more constraints), then a separate surface is built for each response quantity. Currently, most
surface fit models are built using only 0th-order information (function values only), although extensions to using
higher-order information (gradients and Hessians) are possible, and the Kriging model does allow construction
for gradient data. Each surface fitting method employs a different numerical method for computing its internal
coefficients. For example, the polynomial surface uses a least-squares approach that employs a singular value
decomposition to compute the polynomial coefficients, whereas the kriging surface uses Maximum Likelihood
Estimation to compute its correlation coefficients. More information on the numerical methods used in the surface
fitting codes is provided in the Dakota Developers Manual [2].
The set of design points that is used to construct a surface fit model is generated using either the DDACE software
package [137] or the LHS software package [82]. These packages provide a variety of sampling methods including
Dakota Version 6.7 User’s Manual generated on November 13, 2017

158 CHAPTER 8. MODELS
Monte Carlo (random) sampling, Latin hypercube sampling, orthogonal array sampling, central composite design
sampling, and Box-Behnken sampling. More information on these software packages is provided in Chapter 4.
Optionally, the quality of a surrogate model can be assessed with surrogate metrics or diagnostics as described in
Section 8.4.3.11.
8.4.3.2 Taylor Series
The Taylor series model is purely a local approximation method. That is, it provides local trends in the vicinity of
a single point in parameter space. The first-order Taylor series expansion is:
ˆ
f(x)≈f(x0) + ∇xf(x0)T(x−x0)(8.8)
and the second-order expansion is:
ˆ
f(x)≈f(x0) + ∇xf(x0)T(x−x0) + 1
2(x−x0)T∇2
xf(x0)(x−x0)(8.9)
where x0is the expansion point in n-dimensional parameter space and f(x0),∇xf(x0), and ∇2
xf(x0)are the
computed response value, gradient, and Hessian at the expansion point, respectively. As dictated by the responses
specification used in building the local surrogate, the gradient may be analytic or numerical and the Hessian may
be analytic, numerical, or based on quasi-Newton secant updates.
In general, the Taylor series model is accurate only in the region of parameter space that is close to x0. While the
accuracy is limited, the first-order Taylor series model reproduces the correct value and gradient at the point x0,
and the second-order Taylor series model reproduces the correct value, gradient, and Hessian. This consistency is
useful in provably-convergent surrogate-based optimization. The other surface fitting methods do not use gradient
information directly in their models, and these methods rely on an external correction procedure in order to satisfy
the consistency requirements of provably-convergent SBO.
8.4.3.3 Two Point Adaptive Nonlinearity Approximation
The TANA-3 method [153] is a multipoint approximation method based on the two point exponential approxima-
tion [46]. This approach involves a Taylor series approximation in intermediate variables where the powers used
for the intermediate variables are selected to match information at the current and previous expansion points. The
form of the TANA model is:
ˆ
f(x)≈f(x2) +
n
X
i=1
∂f
∂xi
(x2)x1−pi
i,2
pi
(xpi
i−xpi
i,2) + 1
2(x)
n
X
i=1
(xpi
i−xpi
i,2)2(8.10)
where nis the number of variables and:
pi= 1 + ln "∂f
∂xi(x1)
∂f
∂xi(x2)#ln xi,1
xi,2(8.11)
(x) = H
Pn
i=1(xpi
i−xpi
i,1)2+Pn
i=1(xpi
i−xpi
i,2)2(8.12)
H= 2 "f(x1)−f(x2)−
n
X
i=1
∂f
∂xi
(x2)x1−pi
i,2
pi
(xpi
i,1−xpi
i,2)#(8.13)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8.4. SURROGATE MODELS 159
and x2and x1are the current and previous expansion points. Prior to the availability of two expansion points, a
first-order Taylor series is used.
8.4.3.4 Linear, Quadratic, and Cubic Polynomial Models
Linear, quadratic, and cubic polynomial models are available in Dakota. The form of the linear polynomial model
is
ˆ
f(x)≈c0+
n
X
i=1
cixi(8.14)
the form of the quadratic polynomial model is:
ˆ
f(x)≈c0+
n
X
i=1
cixi+
n
X
i=1
n
X
j≥i
cij xixj(8.15)
and the form of the cubic polynomial model is:
ˆ
f(x)≈c0+
n
X
i=1
cixi+
n
X
i=1
n
X
j≥i
cij xixj+
n
X
i=1
n
X
j≥i
n
X
k≥j
cijkxixjxk(8.16)
In all of the polynomial models, ˆ
f(x)is the response of the polynomial model; the xi, xj, xkterms are the com-
ponents of the n-dimensional design parameter values; the c0,ci,cij ,cijk terms are the polynomial coefficients,
and nis the number of design parameters. The number of coefficients, nc, depends on the order of polynomial
model and the number of design parameters. For the linear polynomial:
nclinear =n+ 1 (8.17)
for the quadratic polynomial:
ncquad =(n+ 1)(n+ 2)
2(8.18)
and for the cubic polynomial:
nccubic =(n3+ 6n2+ 11n+ 6)
6(8.19)
There must be at least ncdata samples in order to form a fully determined linear system and solve for the polyno-
mial coefficients. For discrete design variables, a further requirement for a well-posed problem is for the number
of distinct values that each discrete variable can take must be greater than the order of polynomial model (by at
least one level). For the special case involving anisotropy in which the degree can be specified differently per
dimension, the number of values for each discrete variable needs to be greater than the corresponding order along
the respective dimension. In Dakota, a least-squares approach involving a singular value decomposition numerical
method is applied to solve the linear system.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
160 CHAPTER 8. MODELS
The utility of the polynomial models stems from two sources: (1) over a small portion of the parameter space, a
low-order polynomial model is often an accurate approximation to the true data trends, and (2) the least-squares
procedure provides a surface fit that smooths out noise in the data. For this reason, the surrogate-based opti-
mization approach often is successful when using polynomial models, particularly quadratic models. However, a
polynomial surface fit may not be the best choice for modeling data trends over the entire parameter space, unless
it is known a priori that the true data trends are close to linear, quadratic, or cubic. See [104] for more information
on polynomial models.
This surrogate model supports the domain decomposition option, further explained in 8.4.3.10.
8.4.3.5 Kriging/Gaussian-Process Spatial Interpolation Models
In the current release of Dakota, we have two versions of spatial interpolation models. One is located in Dakota
itself and the other in the Surfpack subpackage of Dakota which can be compiled in a stand alone mode. These
models are denoted as kriging dakota and kriging surfpack or as gaussian process dakota
and gaussian process surfpack. In Dakota releases prior to 5.2, the dakota version was referred to
as the gaussian process model while the surfpack version was referred to as the kriging model. As
of Dakota 5.2, specifying only gaussian process or kriging will default to the surfpack version in all
contexts except Bayesian calibration. For now, both versions are supported but the dakota version is deprecated
and intended to be removed in a future release. The two kriging or gaussian process models are very
similar: the differences between them are explained in more detail below.
The Kriging, also known as Gaussian process (GP), method uses techniques developed in the geostatistics and
spatial statistics communities ( [23], [89]) to produce smooth surface fit models of the response values from a set
of data points. The number of times the fitted surface is differentiable will depend on the correlation function that
is used. Currently, the Gaussian correlation function is the only option for either version included in Dakota; this
makes the GP model C∞-continuous. The form of the GP model is
ˆ
f(x)≈g(x)Tβ+r(x)TR−1(f−G β)(8.20)
where xis the current point in n-dimensional parameter space; g(x)is the vector of trend basis functions evaluated
at x;βis a vector containing the generalized least squares estimates of the trend basis function coefficients; r(x)
is the correlation vector of terms between xand the data points; Ris the correlation matrix for all of the data
points; fis the vector of response values; and Gis the matrix containing the trend basis functions evaluated at all
data points. The terms in the correlation vector and matrix are computed using a Gaussian correlation function
and are dependent on an n-dimensional vector of correlation parameters, θ={θ1, . . . , θn}T. By default, Dakota
determines the value of θusing a Maximum Likelihood Estimation (MLE) procedure. However, the user can also
opt to manually set them in the gaussian process surfpack model by specifying a vector of correlation
lengths, l={l1, . . . , ln}Twhere θi= 1/(2l2
i). This definition of correlation lengths makes their effect on the
GP model’s behavior directly analogous to the role played by the standard deviation in a normal (a.k.a. Gaussian)
distribution. In the gaussian process surpack model, we used this analogy to define a small feasible
region in which to search for correlation lengths. This region should (almost) always contain some correlation
matrices that are well conditioned and some that are optimal, or at least near optimal. More details on Kriging/GP
models may be found in [63].
Since a GP has a hyper-parametric error model, it can be used to model surfaces with slope discontinuities along
with multiple local minima and maxima. GP interpolation is useful for both SBO and OUU, as well as for studying
the global response value trends in the parameter space. This surface fitting method needs a minimum number
of design points equal to the sum of the number of basis functions and the number of dimensions, n, but it is
recommended to use at least double this amount.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8.4. SURROGATE MODELS 161
The GP model is guaranteed to pass through all of the response data values that are used to construct the model.
Generally, this is a desirable feature. However, if there is considerable numerical noise in the response data, then
a surface fitting method that provides some data smoothing (e.g., quadratic polynomial, MARS) may be a better
choice for SBO and OUU applications. Another feature of the GP model is that the predicted response values,
ˆ
f(x), decay to the trend function, g(x)Tβ, when xis far from any of the data points from which the GP model
was constructed (i.e., when the model is used for extrapolation).
As mentioned above, there are two gaussian process models in Dakota, the surfpack version and the
dakota version. More details on the gaussian process dakota model can be found in [100]. The
differences between these models are as follows:
•Trend Function: The GP models incorporate a parametric trend function whose purpose is to capture large-
scale variations. In both models, the trend function can be a constant, linear,or reduced quadratic (main
effects only, no interaction terms) polynomial. This is specified by the keyword trend followed by one of
constant,linear, or reduced quadratic (in Dakota 5.0 and earlier, the reduced quadratic option
for the dakota version was selected using the keyword, quadratic). The
gaussian process surfpack model has the additional option of a full (i.e. it includes interaction
terms) quadratic polynomial; this is accessed by following the trend keyword with quadratic.
•Correlation Parameter Determination: Both of the gaussian process models use a Maximum Likeli-
hood Estimation (MLE) approach to find the optimal values of the hyper-parameters governing the mean and
correlation functions. By default both models use the global optimization method called DIRECT, although
they search regions with different extents. For the gaussian process dakota model, DIRECT is
the only option. The gaussian process surfpack model has several options for the optimization
method used. These are specified by the optimization method keyword followed by one of these
strings:
–’global’ which uses the default DIRECT optimizer,
–’local’ which uses the CONMIN optimizer,
–’sampling’ which generates several random guesses and picks the candidate with greatest likeli-
hood, and
–’none’
The ’none’ option, and the starting location of the ’local’ optimization, default to the center, in
log(correlation length) scale, of the small feasible region. However, these can also be user specified with
the correlation lengths keyword followed by a list of nreal numbers. The total number of evalu-
ations of the gaussian process surfpack model’s likelihood function can be controlled using the
max trials keyword followed by a positive integer. Note that we have found the ’global’ optimiza-
tion method to be the most robust.
•Ill-conditioning. One of the major problems in determining the governing values for a Gaussian process
or Kriging model is the fact that the correlation matrix can easily become ill-conditioned when there
are too many input points close together. Since the predictions from the Gaussian process model in-
volve inverting the correlation matrix, ill-conditioning can lead to poor predictive capability and should
be avoided. The gaussian process surfpack model defines a small feasible search region for cor-
relation lengths, which should (almost) always contain some well conditioned correlation matrices. In
Dakota 5.1, the kriging (now gaussian process surfpack or kriging surfpack) model
avoided ill-conditioning by explicitly excluding poorly conditioned Rfrom consideration on the basis of
their having a large (estimate of) condition number; this constraint acted to decrease the size of admissible
correlation lengths. Note that a sufficiently bad sample design could require correlation lengths to be so
Dakota Version 6.7 User’s Manual generated on November 13, 2017

162 CHAPTER 8. MODELS
short that any interpolatory Kriging/GP model would become inept at extrapolation and interpolation.
The gaussian process dakota model has two features to overcome ill-conditioning. The first is
that the algorithm will add a small amount of noise to the diagonal elements of the matrix (this is often
referred to as a “nugget”) and sometimes this is enough to improve the conditioning. The second is that
the user can specify to build the GP based only on a subset of points. The algorithm chooses an “optimal”
subset of points (with respect to predictive capability on the remaining unchosen points) using a greedy
heuristic. This option is specified with the keyword point selection in the input file.
As of Dakota 5.2, the gaussian process surfpack model has a similar capability. Points are
not discarded prior to the construction of the model. Instead, within the maximum likelihood optimiza-
tion loop, when the correlation matrix violates the explicit (estimate of) condition number constraint, the
gaussian process surfpack model will perform a pivoted Cholesky factorization of the correlation
matrix. A bisection search is then used to efficiently find the last point for which the reordered correlation
matrix is not too ill-conditioned. Subsequent reordered points are excluded from the GP/Kriging model for
the current set of correlation lengths, i.e. they are not used to construct this GP model or compute its like-
lihood. When necessary, the gaussian process surfpack model will automatically decrease the
order of the polynomial trend function. Once the maximum likelihood optimization has been completed,
the subset of points that is retained will be the one associated with the most likely set of correlation lengths.
Note that a matrix being ill-conditioned means that its rows or columns contain a significant amount of
duplicate information. Since the points that were discarded were the ones that contained the least unique
information, they should be the ones that are the easiest to predict and provide maximum improvement of
the condition number. However, the gaussian process surfpack model is not guaranteed to ex-
actly interpolate the discarded points. Warning: when two very nearby points are on opposite sides of a
discontinuity, it is possible for one of them to be discarded by this approach.
Note that a pivoted Cholesky factorization can be significantly slower than the highly optimized imple-
mentation of non-pivoted Cholesky factorization in typical LAPACK distributions. A consequence of
this is that the gaussian process surfpack model can take significantly more time to build than
the gaussian process dakota version. However, tests indicate that the gaussian process
surfpack version will often be more accurate and/or require fewer evaluations of the true function than
the gaussian process dakota. For this reason, the gaussian process surfpack version is
the default option as of Dakota 5.2.
•Gradient Enhanced Kriging (GEK). As of Dakota 5.2, the use derivatives keyword will cause the
gaussian process surfpack model to be built from a combination of function value and gradient
information. The gaussian process dakota model does not have this capability. Incorporating gra-
dient information will only be beneficial if accurate and inexpensive derivative information is available, and
the derivatives are not infinite or nearly so. Here “inexpensive” means that the cost of evaluating a function
value plus gradient is comparable to the cost of evaluating only the function value, for example gradients
computed by analytical, automatic differentiation, or continuous adjoint techniques. It is not cost effective to
use derivatives computed by finite differences. In tests, GEK models built from finite difference derivatives
were also significantly less accurate than those built from analytical derivatives. Note that GEK’s corre-
lation matrix tends to have a significantly worse condition number than Kriging for the same sample design.
This issue was addressed by using a pivoted Cholesky factorization of Kriging’s correlation matrix (which
is a small sub-matrix within GEK’s correlation matrix) to rank points by how much unique information
they contain. This reordering is then applied to whole points (the function value at a point immediately
followed by gradient information at the same point) in GEK’s correlation matrix. A standard non-pivoted
Cholesky is then applied to the reordered GEK correlation matrix and a bisection search is used to find the
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8.4. SURROGATE MODELS 163
last equation that meets the constraint on the (estimate of) condition number. The cost of performing piv-
oted Cholesky on Kriging’s correlation matrix is usually negligible compared to the cost of the non-pivoted
Cholesky factorization of GEK’s correlation matrix. In tests, it also resulted in more accurate GEK models
than when pivoted Cholesky or whole-point-block pivoted Cholesky was performed on GEK’s correlation
matrix.
This surrogate model supports the domain decomposition option, further explained in 8.4.3.10.
8.4.3.6 Artificial Neural Network (ANN) Models
The ANN surface fitting method in Dakota employs a stochastic layered perceptron (SLP) artificial neural network
based on the direct training approach of Zimmerman [154]. The SLP ANN method is designed to have a lower
training cost than traditional ANNs. This is a useful feature for SBO and OUU where new ANNs are constructed
many times during the optimization process (i.e., one ANN for each response function, and new ANNs for each
optimization iteration). The form of the SLP ANN model is
ˆ
f(x)≈tanh(tanh((xA0+θ0)A1+θ1)) (8.21)
where xis the current point in n-dimensional parameter space, and the terms A0, θ0,A1, θ1are the matrices and
vectors that correspond to the neuron weights and offset values in the ANN model. These terms are computed
during the ANN training process, and are analogous to the polynomial coefficients in a quadratic surface fit. A
singular value decomposition method is used in the numerical methods that are employed to solve for the weights
and offsets.
The SLP ANN is a non parametric surface fitting method. Thus, along with kriging and MARS, it can be used
to model data trends that have slope discontinuities as well as multiple maxima and minima. However, unlike
kriging, the ANN surface is not guaranteed to exactly match the response values of the data points from which
it was constructed. This ANN can be used with SBO and OUU strategies. As with kriging, this ANN can be
constructed from fewer than ncquad data points, however, it is a good rule of thumb to use at least ncquad data
points when possible.
8.4.3.7 Multivariate Adaptive Regression Spline (MARS) Models
This surface fitting method uses multivariate adaptive regression splines from the MARS3.6 package [50] devel-
oped at Stanford University.
The form of the MARS model is based on the following expression:
ˆ
f(x) =
M
X
m=1
amBm(x)(8.22)
where the amare the coefficients of the truncated power basis functions Bm, and Mis the number of basis
functions. The MARS software partitions the parameter space into subregions, and then applies forward and
backward regression methods to create a local surface model in each subregion. The result is that each subregion
contains its own basis functions and coefficients, and the subregions are joined together to produce a smooth,
C2-continuous surface model.
MARS is a nonparametric surface fitting method and can represent complex multimodal data trends. The regres-
sion component of MARS generates a surface model that is not guaranteed to pass through all of the response
Dakota Version 6.7 User’s Manual generated on November 13, 2017

164 CHAPTER 8. MODELS
data values. Thus, like the quadratic polynomial model, it provides some smoothing of the data. The MARS ref-
erence material does not indicate the minimum number of data points that are needed to create a MARS surface
model. However, in practice it has been found that at least ncquad , and sometimes as many as 2 to 4 times ncquad ,
data points are needed to keep the MARS software from terminating. Provided that sufficient data samples can
be obtained, MARS surface models can be useful in SBO and OUU applications, as well as in the prediction of
global trends throughout the parameter space.
8.4.3.8 Radial Basis Functions
Radial basis functions are functions whose value typically depends on the distance from a center point, called the
centroid, c. The surrogate model approximation is then built up as the sum of K weighted radial basis functions:
ˆ
f(x) =
K
X
k=1
wkφ(kx−ckk)(8.23)
where the φare the individual radial basis functions. These functions can be of any form, but often a Gaussian
bell-shaped function or splines are used. Our implementation uses a Gaussian radial basis function. The weights
are determined via a linear least squares solution approach. See [110] for more details. This surrogate model
supports the domain decomposition option, further explained in 8.4.3.10.
8.4.3.9 Moving Least Squares
Moving Least Squares can be considered a more specialized version of linear regression models. In linear re-
gression, one usually attempts to minimize the sum of the squared residuals, where the residual is defined as
the difference between the surrogate model and the true model at a fixed number of points. In weighted least
squares, the residual terms are weighted so the determination of the optimal coefficients governing the polyno-
mial regression function, denoted by ˆ
f(x), are obtained by minimizing the weighted sum of squares at N data
points:
N
X
n=1
wn(kˆ
f(xn)−f(xn)k)(8.24)
Moving least squares is a further generalization of weighted least squares where the weighting is “moved” or
recalculated for every new point where a prediction is desired. [106] The implementation of moving least squares
is still under development. We have found that it works well in trust region methods where the surrogate model
is constructed in a constrained region over a few points. It does not appear to be working as well globally, at least
at this point in time.
8.4.3.10 Piecewise Decomposition Option for Global Surrogate Models
Regression techniques typically use all available sample points to approximate the underlying function anywhere
in the domain. An alternative option is to use piecewise dcomposition to locally approximate the function at
some point using a few sample points from its neighborhood. This option currently supports Polynomial Re-
gression, Gaussian Process (GP) Interpolation, and Radial Basis Functions (RBF) Regression. This option re-
quires a decomposition cell type. A valid cell type is one where any point in the domain is assigned to some
Dakota Version 6.7 User’s Manual generated on November 13, 2017
8.4. SURROGATE MODELS 165
cell(s), and each cell identifies its neighbor cells. Currently, only Voronoi cells are supported. Each cell con-
structs its own piece of the global surrogate, using the function information at its seed and a few layers of its
neighbors, parametrized by support layers. It also supports an optional discontinuity detection capability
discontinuity detection, specified by either a jump threshold value jump threshold or a gradient
threshold one gradient threshold.
The surrogate construction uses all available data, including derivatives, not only function evaluations. The user
should list the keyword use derivatives to indicate the availability of derivative information for the surro-
gate to use. If listed, the user can replace the default response parameters no gradients and no hessians
with other response options, e.g., numerical gradients or analytic hessians. More details on using
gradients and Hessians, if available, can be found in chapter 11.
The features of the current (Voronoi) piecewise decomposition choice are further explained below:
•In the Voronoi piecewise decomposition option, we decompose the high-dimensional parameter space using
the implicit Voronoi tessellation around the known function evaluations as seeds. Using this approach, any
point in the domain is assigned to a Voronoi cell using a simple nearest neighbor search, and the neighbor
cells are then identified using Spoke Darts without constructing an explicit mesh.
•The one-to-one mapping between the number of function evaluations and the number of Voronoi cells,
regardless of the number of dimensions, eliminates the curse of dimensionality associated with standard
domain decompositions. This Voronoi decomposition enables low-order piecewise polynomial approxima-
tion of the underlying function (and the associated error estimate) in the neighborhood of each function
evaluation, independently. Moreover, the tessellation is naturally updated with the addition of new function
evaluations.
Extending the piecewise decomposition option to other global surrogate models is under development.
8.4.3.11 Surrogate Diagnostic Metrics
The surrogate models provided by Dakota’s Surfpack package (polynomial, Kriging, ANN, MARS, RBF, and
MLS) include the ability to compute diagnostic metrics on the basis of (1) simple prediction error with respect
to the training data, (2) prediction error estimated by cross-validation (iteratively omitting subsets of the training
data), and (3) prediction error with respect to user-supplied hold-out or challenge data. All diagnostics are based
on differences between o(xi)the observed value, and p(xi), the surrogate model prediction for training (or omitted
or challenge) data point xi. In the simple error metric case, the points xiare those used to train the model, for
cross validation they are points selectively omitted from the build, and for challenge data, they are supplementary
points provided by the user. The basic metrics are specified via the metrics keyword, followed by one or more
of:
•sum squared:Pn
i=1 (o(xi)−p(xi))2
•mean squared:1
nPn
i=1 (o(xi)−p(xi))2
•root mean squared:q1
nPn
i=1 (o(xi)−p(xi))2
•sum abs:Pn
i=1 |o(xi)−p(xi)|
•mean abs:1
nPn
i=1 |o(xi)−p(xi)|
•max abs:maxi|o(xi)−p(xi)|
Dakota Version 6.7 User’s Manual generated on November 13, 2017

166 CHAPTER 8. MODELS
•rsquared R2=Pn
i=1 (pi−¯o)2
Pn
i=1 (oi−¯o)2
Here, nis the number of data points used to create the model, and ¯ois the mean of the true response values. R2,
developed for and most useful with polynomial regression, quantifies the amount of variability in the data that is
captured by the model. The value of R2falls on in the interval [0,1]. Values close to 1indicate that the model
matches the data closely. The remainder of the metrics measure error, so smaller values indicate better fit.
Cross-validation: With the exception of R2, the above metrics can be computed via a cross-validation process.
The class of k-fold cross-validation metrics is used to predict how well a model might generalize to unseen
data. The training data is randomly divided into kpartitions. Then kmodels are computed, each excluding the
corresponding kth partition of the data. Each model is evaluated at the points that were excluded in its generation
and any metrics specified above are computed with respect to the held out data. A special case, when kis equal to
the number of data points, is known as leave-one-out cross-validation or prediction error sum of squares (PRESS).
To specify k-fold cross-validation or PRESS, follow the list of metrics with cross validate and/or press,
respectively.
Challenge data: A user may optionally specify challenge points file, a data file in freeform or annotated
format that contains additional trial point/response data, one point per row. When specified, any of the above
metrics specified will be computed with respect to the challenge data.
Caution is advised when applying and interpreting these metrics. In general, lower errors are better, but for
interpolatory models like Kriging models, will almost always be zero. Root-mean-squared and the absolute
metrics are on the same scale as the predictions and data. R2is meaningful for polynomial models, but less so for
other model types. When possible, general 5-fold or 10-fold cross validation will provide more reliable estimates
of the true model prediction error. Goodness-of-fit metrics provide a valuable tool for analyzing and comparing
models but must not be applied blindly.
8.4.4 Multifidelity Surrogate Models
A second type of surrogate is the model hierarchy type (also called multifidelity, variable fidelity, variable com-
plexity, etc.). In this case, a model that is still physics-based but is of lower fidelity (e.g., coarser discretization,
reduced element order, looser convergence tolerances, omitted physics) is used as the surrogate in place of the
high-fidelity model. For example, an inviscid, incompressible Euler CFD model on a coarse discretization could
be used as a low-fidelity surrogate for a high-fidelity Navier-Stokes model on a fine discretization.
8.4.5 Reduced Order Models
A third type of surrogate model involves reduced-order modeling techniques such as proper orthogonal decompo-
sition (POD) in computational fluid dynamics (also known as principal components analysis or Karhunen-Loeve
in other fields) or spectral decomposition (also known as modal analysis) in structural dynamics. These surrogate
models are generated directly from a high-fidelity model through the use of a reduced basis (e.g., eigenmodes for
modal analysis or left singular vectors for POD) and projection of the original high-dimensional system down to a
small number of generalized coordinates. These surrogates are still physics-based (and may therefore have better
predictive qualities than data fits), but do not require multiple system models of varying fidelity (as required for
model hierarchy surrogates).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

8.5. NESTED MODELS 167
8.4.6 Surrogate Model Selection
This section offers some guidance on choosing from among the available surrogate model types.
•For Surrogate Based Local Optimization, i.e. the surrogate based local method, with a trust region,
either surrogate local taylor series or surrogate multipoint tana will probably work
best. If for some reason you wish or need to use a global surrogate (not recommended) then the best of these
options is likely to be either surrogate global gaussian process surfpack or surrogate
global moving least squares.
•For Efficient Global Optimization (EGO), i.e. the efficient global method, the default
gaussian process surfpack is likely to find a more optimal value and/or use fewer true function
evaluations than the alternative, gaussian process dakota. However, the surfpack version will
likely take more time to build than the dakota version. Note that currently the use derivatives
keyword is not recommended for use with EGO based methods.
•For EGO based global interval estimation (EGIE), i.e. the global interval est ego method, the de-
fault gaussian process surfpack will likely work better than the alternative gaussian process
dakota.
•For Efficient Global Reliability Analysis (EGRA), i.e. the global reliability method the surfpack
and dakota versions of the gaussian process tend to give similar answers with the dakota version tending
to use fewer true function evaluations. Since this is based on EGO, it is likely that the default surfpack
version is more accurate, although this has not been rigorously demonstrated.
•For EGO based Dempster-Shafer Theory of Evidence, i.e. the global evidence ego method, the
default gaussian process surfpack will often use significantly fewer true function evaluations than
the alternative gaussian process dakota.
•When using a global surrogate to extrapolate, either the gaussian process surfpack or polynomial
quadratic or polynomial cubic is recommended.
•When there is over roughly two or three thousand data points and you wish to interpolate (or approximately
interpolate) then a Taylor series, Radial Basis Function Network, or Moving Least Squares fit is recom-
mended. The only reason that the gaussian process surfpack model is not recommended is that it
can take a considerable amount of time to construct when the number of data points is very large. Use of
the third party MARS package included in Dakota is generally discouraged.
•In other situations that call for a global surrogate, the gaussian process surfpack is generally
recommended. The use derivatives keyword will only be useful if accurate and an inexpensive
derivatives are available. Finite difference derivatives are disqualified on both counts. However, derivatives
generated by analytical, automatic differentiation, or continuous adjoint techniques can be appropriate. Cur-
rently, first order derivatives, i.e. gradients, are the highest order derivatives that can be used to construct
the gaussian process surfpack model; Hessians will not be used even if they are available.
8.5 Nested Models
Nested models utilize a sub-iterator and a sub-model to perform a complete iterative study as part of every evalu-
ation of the model. This sub-iteration accepts variables from the outer level, performs the sub-level analysis, and
computes a set of sub-level responses which are passed back up to the outer level. As described in the Models
Dakota Version 6.7 User’s Manual generated on November 13, 2017
168 CHAPTER 8. MODELS
chapter of the Reference Manual [3], mappings are employed for both the variable inputs to the sub-model and
the response outputs from the sub-model.
In the variable mapping case, primary and secondary variable mapping specifications are used to map from the top-
level variables into the sub-model variables. These mappings support three possibilities in any combination: (1)
insertion of an active top-level variable value into an identified sub-model distribution parameter for an identified
active sub-model variable, (2) insertion of an active top-level variable value into an identified active sub-model
variable value, and (3) addition of an active top-level variable value as an inactive sub-model variable, augmenting
the active sub-model variables.
In the response mapping case, primary and secondary response mapping specifications are used to map from the
sub-model responses back to the top-level responses. These specifications provide real-valued multipliers that are
applied to the sub-iterator response results to define the outer level response set. These nested data results may be
combined with non-nested data through use of the “optional interface” component within nested models.
The nested model is used within a wide variety of multi-iterator, multi-model solution approaches. For exam-
ple, optimization within optimization (for hierarchical multidisciplinary optimization), uncertainty quantification
within uncertainty quantification (for mixed aleatory-epistemic UQ), uncertainty quantification within optimiza-
tion (for optimization under uncertainty), and optimization within uncertainty quantification (for uncertainty of
optima) are all supported, with and without surrogate model indirection. Several examples of nested model us-
age are provided in Chapter 15, most notably mixed epistemic-aleatory UQ in Section 15.1, optimization under
uncertainty (OUU) in Section 15.2, and surrogate-based UQ in Section 15.3.
8.6 Random Field Models
As of Dakota 6.4, we have a preliminary capability to generate random fields. This is an experimental capability
that is undergoing active development, so the following description and the associated syntax may change.
Our goal with a random field model is to have a fairly general capability, where we can generate a random field
representation in one of three ways: from data, from simulation runs (e.g. running an ensemble of simulations
where each one produces a field response), or from a covariance matrix defined over a mesh. Then, a random field
model (such as a Karhunen-Loeve expansion) will be built based on the data. A final step is to draw realizations
from the random field model to propagate to another simulation model. For example, the random field may
represent a pressure or temperature boundary condition for a simulation.
The random field model is currently specified with a model type of random field. The first section of
the random field specification tells Dakota what data to use to build the random field. This is specified with
build source. The source of data to build the random field may be a file with data (where the N rows of data
correspond to N samples of the random field and the M columns correspond to field values), or it may be a sim-
ulation that generates field data, or it may be specified given a mesh and a covariance matrix governing how the
field varies over the mesh. In the case of using a simulation to generate field data, the simulation is defined with
dace method pointer. In the case of using a mesh and a covariance, the form of the covariance is defined
with analytic covariance.
The next section of the random field model specifies the form of the expansion, expansion form. This can be
either a Karhunen-Loeve expansion or a Principal components analysis. These are very similar: both involve the
eigenvalues of the covariance matrix of the field data. The only difference is in the treatment of the estimation of
the coefficients of the eigenvector basis functions. In the PCA case, we have developed an approach which makes
the coefficients explicit functions of the uncertain variables used to generate the random field. The specification
of the random field can also include the number of bases to retain or a truncation tolerance, which defines the
percent variance that the expansion should capture.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
8.7. ACTIVE SUBSPACE MODELS 169
The final section of the random field model allows the user to specify a pointer to a model over which the random
field will be propagated, propagation model pointer, meaning the model which will be driven with the
random field input.
8.7 Active Subspace Models
The active subspace technique [18] seeks directions in the input space for which the response function(s) show
little variation. After a rotation to align with these directions, significant dimension reduction may be possible.
The Dakota model type subspace manages the input subspace identification and transforms the original simu-
lation model into the new coordinates. This capability is new as of Dakota 6.4 and under very active development,
so the following information may be outdated.
In Dakota 6.4, the active subspace model can be used in conjunction with the following uncertainty quantification
methods:
•polynomial chaos
•sampling
•local reliability
An error message similar to:
Error: Resizing is not yet supported in method <method name>.
will be written and Dakota will exit if the active subspace model is used with a non-compatible method. The set
of compatible methods will be expanded in future releases.
The active subspace implementation in Dakota 6.4 first transforms uncertain variables to standard normal distribu-
tions using a Nataf transformm before forming the subspace. This is a nonlinear transformation for non-normally
distributed uncertain variables and may potentially decrease sparse structure in a fullspace model. Future Dakota
releases will not use this transformation and should perform better in the general case.
The only required keyword when using a subspace model is the actual model pointer which points to
the underlying model (specified by its id model) on which to build the subspace. The subspace model
requires either analytical (preferred) or numerical gradients of the response functions. The active subspace
model first samples the gradient of the fullspace model. The number of gradient samples can be specified with
initial samples. The gradient samples are compiled into the columns of a matrix. A singular value decom-
position is performed of the derivative matrix and the resulting singular values and vectors are used to determine
the basis vectors and size of the active subspace.
Constantine [18] recommends choosing initial samples such that:
initial samples =αk log(m),
where αis an oversampling factor between 2 and 10, kis the number of singular values to approximate, and m
is the number of fullspace variables. To ensure accurate results, kshould be greater than the estimated subspace
size determined by one of the truncation methods described below.
Dakota has everal metrics to estimate the size of an active subspace:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

170 CHAPTER 8. MODELS
•constantine (default)
•bing li
•energy
•cross validation
Additionally, if the desired subspace size is known it can be explicitly selected using the input parameter dimension.
The constantine and bing li truncation methods both use bootstrap sampling of the compiled deriva-
tive matrix to estimate an active subspace size. The number of bootstrap samples used with these methods
can be specified with the keyword bootstrap samples, but typically the default value works well. The
energy method computes the number of bases so that the subspace representation accounts for all but a max-
imum percentage (specified as a decimal) of the total eigenvalue energy. This value is specified using the
truncation tolerance keyword.
For more information on active subspaces please consult the Theory Manual [4] and/or references [21,19,18].
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 9
Variables
9.1 Overview
The variables specification in a Dakota input file specifies the parameter set to be iterated by a particular
method. In the case of an optimization study, these variables are adjusted in order to locate an optimal design; in
the case of parameter studies/sensitivity analysis/design of experiments, these parameters are perturbed to explore
the parameter space; and in the case of uncertainty analysis, the variables are associated with distribution/interval
characterizations which are used to compute corresponding distribution/interval characterizations for response
functions. To accommodate these and other types of studies, Dakota supports design, uncertain, and state variable
types for continuous and discrete variable domains. Uncertain types can be further categorized as either aleatory
or epistemic, and discrete domains can include discrete range, discrete integer set, discrete string set, and discrete
real set.
This chapter will present a brief overview of the main types of variables and their uses, as well as cover some user
issues relating to file formats and the active set vector. For a detailed description of variables section syntax and
example specifications, refer to the variables keywords in the Dakota Reference Manual [3].
9.2 Design Variables
Design variables are those variables which are modified in the course of determining an optimal design. These
variables may be continuous (real-valued between bounds), discrete range (integer-valued between bounds), dis-
crete set of integers (integer-valued from finite set), discrete set of strings (string-valued from finite set), and
discrete set of reals (real-valued from finite set).
9.2.1 Continuous Design Variables
The most common type of design variables encountered in engineering applications are of the continuous type.
These variables may assume any real value (e.g., 12.34,-1.735e+07) within their bounds. All but a handful
of the optimization algorithms in Dakota support continuous design variables exclusively.

172 CHAPTER 9. VARIABLES
9.2.2 Discrete Design Variables
Engineering design problems may contain discrete variables such as material types, feature counts, stock gauge
selections, etc. These variables may assume only a fixed number of values, as compared to a continuous variable
which has an uncountable number of possible values within its range. Discrete variables may involve a range of
consecutive integers (xcan be any integer between 1and 10), a set of integer values (xcan be 101,212, or
355), a set of string values (xcan be ’direct’,’gmres’, or ’jacobi’), or a set of real values (e.g., xcan
be identically 4.2,6.4, or 8.5).
Discrete variables may be classified as either “categorical” or “noncategorical.” In the latter noncategorical case,
the discrete requirement can be relaxed during the solution process since the model can still compute meaningful
response functions for values outside the allowed discrete range or set. For example, a discrete variable repre-
senting the thickness of a structure is generally a noncategorical variable since it can assume a continuous range
of values during the algorithm iterations, even if it is desired to have a stock gauge thickness in the end. In the
former categorical case, the discrete requirement cannot be relaxed since the model cannot obtain a solution for
values outside the range or set. For example, feature counts are generally categorical discrete variables, since
most computational models will not support a non-integer value for the number of instances of some feature (e.g.,
number of support brackets). Dakota supports a categorical specification to indicate which discrete real and
discrete integer variables are restricted vs. relaxable. String variables cannot be relaxed.
Gradient-based optimization methods cannot be directly applied to problems with discrete variables since deriva-
tives only exist for a variable continuum. For problems with noncategorical variables, the experimental branch
and bound capability (branch and bound) can be used to relax the discrete requirements and apply gradient-
based methods to a series of generated subproblems. For problems with categorical variables, nongradient-based
methods (e.g., coliny ea) are commonly used; however, most of those methods do not take advantage of any
structure that may be associated with the categorical variables. The exception is mesh adaptive search. If it
is possible to define a subjective relationship between the different values a given categorical variable can take on,
the user can communicate that relationship in the form of an adjacency matrix. The mesh adaptive search
will take that relationship into consideration. Further documentation can be found in [3] under the keywords
adjacency matrix and neighbor order. Branch and bound techniques are discussed in Section 14.5 and
nongradient-based methods are further described in Chapter 6.
In addition to engineering applications, many non-engineering applications in the fields of scheduling, logistics,
and resource allocation contain discrete design parameters. Within the Department of Energy, solution techniques
for these problems impact programs in stockpile evaluation and management, production planning, nonprolifer-
ation, transportation (routing, packing, logistics), infrastructure analysis and design, energy production, environ-
mental remediation, and tools for massively parallel computing such as domain decomposition and meshing.
9.2.2.1 Discrete Design Integer Variables
There are two types of discrete design integer variables supported by Dakota.
•The discrete design range specification supports a range of consecutive integers between specified
lower bounds and upper bounds.
•The discrete design set integer specification supports a set of enumerated integer values through
the elements specification. The set of values specified is stored internally as an STL set container, which
enforces an ordered, unique representation of the integer data. Underlying this set of ordered, unique in-
tegers is a set of indices that run from 0 to one less than the number of set values. These indices are used
by some iterative algorithms (e.g., parameter studies, SCOLIB iterators) for simplicity in discrete value
Dakota Version 6.7 User’s Manual generated on November 13, 2017

9.3. UNCERTAIN VARIABLES 173
enumeration when the actual corresponding set values are immaterial. In the case of parameter studies, this
index representation is exposed through certain step and partition control specifications (see Chapter 3).
9.2.2.2 Discrete Design String Variables
There is one type of discrete design string variable supported by Dakota.
•The discrete design set string specification supports a set of enumerated string values through
the elements specification. As for the discrete integer set variables described in Section 9.2.2.1, internal
storage of the set values is ordered and unique and an underlying index representation is exposed for the
specification of some iterative algorithms.
Each string element value must be quoted in the Dakota input file and may contain alphanumeric, dash, under-
score, and colon. White space, quote characters, and backslash/meta-characters are not permitted.
9.2.2.3 Discrete Design Real Variables
There is one type of discrete design real variable supported by Dakota.
•The discrete design set real specification specification supports a set of enumerated real val-
ues through the set values specification. As for the discrete integer set variables described in Sec-
tion 9.2.2.1, internal storage of the set values is ordered and unique and an underlying index representation
is exposed for the specification of some iterative algorithms.
9.3 Uncertain Variables
Deterministic variables (i.e., those with a single known value) do not capture the behavior of the input variables in
all situations. In many cases, the exact value of a model parameter is not precisely known. An example of such an
input variable is the thickness of a heat treatment coating on a structural steel I-beam used in building construction.
Due to variability and tolerances in the coating process, the thickness of the layer is known to follow a normal
distribution with a certain mean and standard deviation as determined from experimental data. The inclusion of
the uncertainty in the coating thickness is essential to accurately represent the resulting uncertainty in the response
of the building.
9.3.1 Aleatory Uncertain Variables
Aleatory uncertainties are irreducible variabilities inherent in nature. They are characterized by having a suffi-
ciently rich set of data as to allow modeling using probability distributions, and probabilistic methods are com-
monly used for propagating input aleatory uncertainties described by probability distribution specifications. The
two following sections describe the continuous and discrete aleatory uncertain variables supported by Dakota.
For aleatory random variables, Dakota supports a user-supplied correlation matrix to provide correlations among
the input variables. By default, the correlation matrix is set to the identity matrix, i.e., no correlation among the
uncertain variables.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

174 CHAPTER 9. VARIABLES
For additional information on random variable probability distributions, refer to [73] and [132]. Refer to the
Dakota Reference Manual [3] for more detail on the uncertain variable specifications and to Chapter 5for a
description of methods available to quantify the uncertainty in the response.
9.3.1.1 Continuous Aleatory Uncertain Variables
•Normal: a probability distribution characterized by a mean and standard deviation. Also referred to as
Gaussian. Bounded normal is also supported by some methods with an additional specification of lower
and upper bounds.
•Lognormal: a probability distribution characterized by a mean and either a standard deviation or an error
factor. The natural logarithm of a lognormal variable has a normal distribution. Bounded lognormal is also
supported by some methods with an additional specification of lower and upper bounds.
•Uniform: a probability distribution characterized by a lower bound and an upper bound. Probability is
constant between the bounds.
•Loguniform: a probability distribution characterized by a lower bound and an upper bound. The natural
logarithm of a loguniform variable has a uniform distribution.
•Triangular: a probability distribution characterized by a mode, a lower bound, and an upper bound.
•Exponential: a probability distribution characterized by a beta parameter.
•Beta: a flexible probability distribution characterized by a lower bound and an upper bound and alpha and
beta parameters. The uniform distribution is a special case.
•Gamma: a flexible probability distribution characterized by alpha and beta parameters. The exponential
distribution is a special case.
•Gumbel: the Type I Largest Extreme Value probability distribution. Characterized by alpha and beta pa-
rameters.
•Frechet: the Type II Largest Extreme Value probability distribution. Characterized by alpha and beta pa-
rameters.
•Weibull: the Type III Smallest Extreme Value probability distribution. Characterized by alpha and beta
parameters.
•Histogram Bin: an empirically-based probability distribution characterized by a set of (x, y)pairs that map
out histogram bins (a continuous interval with associated bin count).
9.3.1.2 Discrete Aleatory Uncertain Variables
The following types of discrete aleatory uncertain variables are available:
•Poisson: integer-valued distribution used to predict the number of discrete events that happen in a given
time interval.
•Binomial: integer-valued distribution used to predict the number of failures in a number of independent
tests or trials.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

9.4. STATE VARIABLES 175
•Negative Binomial: integer-valued distribution used to predict the number of times to perform a test to have
a target number of successes.
•Geometric: integer-valued distribution used to model the number of successful trials that might occur before
a failure is observed.
•Hypergeometric: integer-valued distribution used to model the number of failures observed in a set of tests
that has a known proportion of failures.
•Histogram Point (integer, string, real): an empirically-based probability distribution characterized by a set
of integer-valued (i, c), string-valued (s, c), and/or real-valued r, c pairs that map out histogram points (each
a discrete point value i,s, or r, with associated count c).
9.3.2 Epistemic Uncertain Variables
Epistemic uncertainties are reducible uncertainties resulting from a lack of knowledge. For epistemic uncertain-
ties, data is generally sparse, making the use of probability theory questionable and leading to nonprobabilistic
methods based on interval or fuzzy specifications. Dakota currently supports the following epistemic uncertain
variable types.
9.3.2.1 Continuous Epistemic Uncertain Variables
•Continuous Interval: a real-valued interval-based specification characterized by sets of lower and upper
bounds and Basic Probability Assignments (BPAs) associated with each interval. The intervals may be
overlapping, contiguous, or disjoint, and a single interval (with probability = 1) per variable is an impor-
tant special case. The interval distribution is not a probability distribution, as the exact structure of the
probabilities within each interval is not known. It is commonly used with epistemic uncertainty methods.
9.3.2.2 Discrete Epistemic Uncertain Variables
•Discrete Interval: an integer-valued variant of the Continuous Interval described above ( 9.3.2.1).
•Discrete Set (integer, string, and real): Similar to discrete design set variables 9.2.2, these epistemic vari-
ables admit a finite number of values (elements) for type integer, string, or real, each with an associated
probability.
9.4 State Variables
State variables consist of “other” variables which are to be mapped through the simulation interface, in that they
are not to be used for design and they are not modeled as being uncertain. State variables provide a conve-
nient mechanism for parameterizing additional model inputs which, in the case of a numerical simulator, might
include solver convergence tolerances, time step controls, or mesh fidelity parameters. For additional model pa-
rameterizations involving strings (e.g., “mesh1.exo”), refer to the analysis components specification described in
Section 9.6.1 and in the Interface Commands chapter of the Dakota Reference Manual [3]. Similar to the design
variables discussed in Section 9.2, state variables can be specified with a continuous range (real-valued between
bounds), a discrete range (integer-valued between bounds), a discrete integer-valued set, a discrete string-valued
set, or a discrete real-valued set.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

176 CHAPTER 9. VARIABLES
State variables, as with other types of variables, are viewed differently depending on the method in use. Since
these variables are neither design nor uncertain variables, algorithms for optimization, least squares, and uncer-
tainty quantification do not iterate on these variables; i.e., they are not active and are hidden from the algorithm.
However, Dakota still maps these variables through the user’s interface where they affect the computational model
in use. This allows optimization, least squares, and uncertainty quantification studies to be executed under dif-
ferent simulation conditions (which will result, in general, in different results). Parameter studies and design of
experiments methods, on the other hand, are general-purpose iterative techniques which do not draw a distinction
between variable types. They include state variables in the set of variables to be iterated, which allows these
studies to explore the effect of state variable values on the response data of interest.
In the future, state variables might be used in direct coordination with an optimization, least squares, or uncertainty
quantification algorithm. For example, state variables could be used to enact model adaptivity through the use of
a coarse mesh or loose solver tolerances in the initial stages of an optimization with continuous model refinement
as the algorithm nears the optimal solution.
9.5 Management of Mixed Variables by Iterator
9.5.1 View
As alluded to in the previous section, the iterative method selected for use in Dakota partially determines what
subset, or view, of the variables data is active in the iteration. (Section 9.5.3 contains a discussion of how user
overrides, response function type, and method are used to determine active variable view.) The general case
of having a mixture of various different types of variables is supported within all of the Dakota methods even
though certain methods will only modify certain types of variables (e.g., optimizers and least squares methods
only modify design variables, and uncertainty quantification methods typically only utilize uncertain variables).
This implies that variables which are not under the direct control of a particular iterator will be mapped through
the interface in an unmodified state. This allows for a variety of parameterizations within the model in addition
to those which are being used by a particular iterator, which can provide the convenience of consolidating the
control over various modeling parameters in a single file (the Dakota input file). An important related point is that
the variable set that is active with a particular iterator is the same variable set for which derivatives are typically
computed (see Section 11.3).
There are certain situations where the user may want to explicitly control the subset of variables that is considered
active for a certain Dakota method. This is done by specifying the keyword active in the variables specification
block, followed by one of the following: all,design,uncertain,aleatory,epistemic, or state.
Specifying one of these subsets of variables will allow the Dakota method to operate on the specified variable
types and override the defaults. For example, the default behavior for a nondeterministic sampling method is to
sample the uncertain variables. However, if the user specified active all in the variables specification block,
the sampling would be performed over all variables (e.g. design and state variables as well as uncertain variables).
This may be desired in situations such as surrogate based optimization under uncertainty, where a surrogate may
be built over both design and uncertain variables. Another situation where one may want the fine-grained control
available by specifying one of these variable types is when one has state variables but only wants to sample over
the design variables when constructing a surrogate model. Finally, more sophisticated uncertainty studies may
involve various combinations of epistemic vs. aleatory variables being active in nested models.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
9.6. DAKOTA PARAMETERS FILE DATA FORMAT 177
9.5.2 Domain
Another control that the user can specify in the variables specification block controls the domain type. We have
two domains currently: mixed and relaxed. Both domain types can have design, uncertain, and state variables. The
domain specifies how the discrete variables are treated. If the user specifies mixed in the variable specification
block, the continuous and discrete variables are treated separately. If the user specifies relaxed in the variable
specification block, the discrete variables are relaxed and treated as continuous variables. This may be useful
in optimization problems involving both continuous and discrete variables when a user would like to use an
optimization method that is designed for continuous variable optimization. All Dakota methods have a default
value of mixed for the domain type except for the branch-and-bound method which has a default domain type of
relaxed. Note that the branch-and-bound method is experimental and still under development at this time.
9.5.3 Precedence
If the user does not specify any explicit override of the active view of the variables, Dakota then considers the
response function specification. If the user specifies objective functions or calibration terms in the response
specification block, the active variables will be the design variables. If the user specifies the more generic re-
sponse type, response functions, general response functions do not have a specific interpretation the way
objective functions or calibration terms do. In the case of generic response functions, Dakota
then tries to infer the active view from the method. If the method is a parameter study, or any of the methods
available under dace, psuade, or fsu methods, the active view is set to all variables. For uncertainty quantification
methods, if the method is sampling, then the view is set to aleatory if only aleatory variables are present, epistemic
if only epistemic variables are present, or uncertain (covering both aleatory and epistemic) if both are present. If
the uncertainty method involves interval estimation or evidence calculations, the view is set to epistemic. For other
uncertainty quantification methods not mentioned in the previous sentences (e.g., reliability methods or stochastic
expansion methods), the view is set to aleatory. Finally, for verification studies using the Richardson extrapolation
method, the active view is set to state. Note that in surrogate-based optimization, where the surrogate is built on
points defined by the method defined by the dace method pointer, the sampling used to generate the points
is performed only over the design variables as a default unless otherwise specified (e.g. state variables will not be
sampled for surrogate construction).
With respect to domain type, if the user does not specify an explicit override of mixed or relaxed, Dakota
infers the domain type from the method. As mentioned above, all methods currently use a mixed domain as a
default, except the branch-and-bound method which is under development.
9.6 Dakota Parameters File Data Format
Simulation interfaces which employ system calls and forks to create separate simulation processes must commu-
nicate with the simulation code through the file system. This is accomplished through the reading and writing of
parameters and results files. Dakota uses a particular format for this data input/output. Depending on the user’s
interface specification, Dakota will write the parameters file in either standard or APREPRO format (future XML
formats are planned). The former option uses a simple “value tag” format, whereas the latter option uses a “{
tag = value }” format for compatibility with the APREPRO utility [122] (as well as DPrePro, BPREPRO,
and JPrePost variants).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

178 CHAPTER 9. VARIABLES
<int> variables
<double> <label_cdvi> (i = 1 to ncdv)
<int> <label_ddivi> (i = 1 to nddiv)
<string> <label_ddsvi> (i = 1 to nddsv)
<double> <label_ddrvi> (i = 1 to nddrv )
<double> <label_cauvi> (i = 1 to ncauv)
<int> <label_dauivi> (i = 1 to ndauiv)
<string> <label_dausvi> (i = 1 to ndausv)
<double> <label_daurvi> (i = 1 to ndaurv )
<double> <label_ceuvi> (i = 1 to nceuv)
<int> <label_deuivi> (i = 1 to ndeuiv)
<string> <label_deusvi> (i = 1 to ndeusv)
<double> <label_deurvi> (i = 1 to ndeurv )
<double> <label_csvi> (i = 1 to ncsv)
<int> <label_dsivi> (i = 1 to ndsiv)
<string> <label_dssvi> (i = 1 to ndssv)
<double> <label_dsrvi> (i = 1 to ndsrv )
<int> functions
<int> ASV_i:label_responsei(i = 1 to m)
<int> derivative_variables
<int> DVV_i:label_cdvi(i = 1 to p)
<int> analysis_components
<string> AC_i:analysis_driver_namei(i = 1 to q)
<string> eval_id
Figure 9.1: Parameters file data format - standard option.
9.6.1 Parameters file format (standard)
Prior to invoking a simulation, Dakota creates a parameters file which contains the current parameter values and
a set of function requests. The standard format for this parameters file is shown in Figure 9.1.
Integer values are denoted by “<int>”, “<double>” denotes a double precision value, and “<string>”
denotes a string value. Each of the colored blocks (black for variables, blue for active set vector, red for derivative
variables vector, and green for analysis components) denotes an array which begins with an array length and a
descriptive tag. These array lengths are useful for dynamic memory allocation within a simulator or filter program.
The first array for variables begins with the total number of variables (n) with its identifier string “variables.”
The next nlines specify the current values and descriptors of all of the variables within the parameter set in
the following order: continuous design, discrete integer design (integer range, integer set), discrete string design
(string set), discrete real design (real set), continuous aleatory uncertain (normal, lognormal, uniform, loguni-
form, triangular, exponential, beta, gamma, gumbel, frechet, weibull, histogram bin), discrete integer aleatory
uncertain (poisson, binomial, negative binomial, geometric, hypergeometric, histogram point integer), discrete
string aleatory uncertain (histogram point string), discrete real aleatory uncertain (histogram point real), contin-
uous epistemic uncertain (real interval), discrete integer epistemic uncertain (interval, then set), discrete string
epistemic uncertain (set), discrete real epistemic uncertain (set), continuous state, discrete integer state (integer
range, integer set), discrete string state, and discrete real state (real set) variables. This ordering is consistent with
the lists in Sections 9.2.2.1,9.3.1.1 and 9.3.1.2 and the specification order in dakota.input.summary. The lengths
Dakota Version 6.7 User’s Manual generated on November 13, 2017

9.6. DAKOTA PARAMETERS FILE DATA FORMAT 179
of these vectors add to a total of n(that is, n=ncdv +nddiv +nddsv +nddrv +ncauv +ndauiv +ndausv +
ndaurv +nceuv +ndeuiv +ndeusv +ndeurv +ncsv +ndsiv +ndssv +ndsrv ). If any of the variable types are
not present in the problem, then its block is omitted entirely from the parameters file. The tags are the variable
descriptors specified in the user’s Dakota input file, or if no descriptors have been specified, default descriptors
are used.
The second array for the active set vector (ASV) begins with the total number of functions (m) and its identifier
string “functions.” The next mlines specify the request vector for each of the mfunctions in the response
data set followed by the tags “ASV i:label response”, where the label is either a user-provided response
descriptor or a default-generated one. These integer codes indicate what data is required on the current function
evaluation and are described further in Section 9.7.
The third array for the derivative variables vector (DVV) begins with the number of derivative variables (p) and its
identifier string “derivative variables.” The next plines specify integer variable identifiers followed by
the tags “DVV i:label cdv”. These integer identifiers are used to identify the subset of variables that are active
for the calculation of derivatives (gradient vectors and Hessian matrices), and correspond to the list of variables
in the first array (e.g., an identifier of 2 indicates that the second variable in the list is active for derivatives). The
labels are again taken from user-provided or default variable descriptors.
The final array for the analysis components (AC) begins with the number of analysis components (q) and its iden-
tifier string “analysis components.” The next qlines provide additional strings for use in specializing a sim-
ulation interface followed by the tags “AC i:analysis driver name”, where analysis driver name
indicates the driver associated with this component. These strings are specified in a user’s input file for a set of
analysis drivers using the analysis components specification. The subset of the analysis compo-
nents used for a particular analysis driver is the set passed in a particular parameters file.
The final entry eval id in the parameters file is the evaluation ID, by default an integer indicating interface
evaluation ID number. When hierarchical tagging is enabled as described in 10.5.2, the identifier will be a colon-
separated string, e.g., 4:9:2. Several standard-format parameters file examples are shown in Section 10.6.
9.6.2 Parameters file format (APREPRO)
For the APREPRO format option, the same data is present and the same ordering is used as in the standard
format. The only difference is that values are associated with their tags within “{tag = value }” constructs
as shown in Figure 9.2. An APREPRO-format parameters file example is shown in Section 10.6.
The use of the APREPRO format option allows direct usage of these parameters files by the APREPRO util-
ity, which is a file pre-processor that can significantly simplify model parameterization. Similar pre-processors
include DPrePro, BPREPRO, and JPrePost. [Note: APREPRO is a Sandia-developed pre-processor that is not
currently distributed with Dakota. DPrePro is a Perl script distributed with Dakota that performs many of the
same functions as APREPRO, and is optimized for use with Dakota parameters files in either format. BPREPRO
and JPrePost are additional Perl and JAVA tools, respectively, in use at other sites.] When a parameters file in
APREPRO format is included within a template file (using an include directive), the APREPRO utility recog-
nizes these constructs as variable definitions which can then be used to populate targets throughout the template
file [122]. DPrePro, conversely, does not require the use of includes since it processes the Dakota parameters file
and template simulation file separately to create a simulation input file populated with the variables data.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

180 CHAPTER 9. VARIABLES
{DAKOTA_VARS = <int> }
{<label_cdvi> = <double> }(i=1toncdv)
{<label_ddivi> = <int> }(i=1tonddiv)
{<label_ddsvi> = <string> }(i=1tonddsv)
{<label_ddrvi> = <double> }(i=1tonddrv )
{<label_cauvi> = <double> }(i=1toncauv)
{<label_dauivi> = <int> }(i=1tondauiv)
{<label_dausvi> = <string> }(i=1tondausv)
{<label_daurvi> = <double> }(i=1tondaurv )
{<label_ceuvi> = <double> }(i=1tonceuv)
{<label_deuivi> = <int> }(i=1tondeuiv)
{<label_deusvi> = <string> }(i=1tondeusv)
{<label_deurvi> = <double> }(i=1tondeurv )
{<label_csvi> = <double> }(i=1toncsv)
{<label_dsivi> = <int> }(i=1tondsiv)
{<label_dssvi> = <string> }(i=1tondssv)
{<label_dsrvi> = <double> }(i=1tondsrv )
{DAKOTA_FNS = <int> }
{ASV_i:label_responsei= <int> }(i = 1 to m)
{DAKOTA_DER_VARS = <int> }
{DVV_i:label_cdvi= <int> }(i = 1 to p)
{DAKOTA_AN_COMPS = <int> }
{AC_i:analysis_driver_namei= <string> }(i = 1 to q)
{DAKOTA_EVAL_ID = <string> }
Figure 9.2: Parameters file data format - APREPRO option.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

9.7. THE ACTIVE SET VECTOR 181
Table 9.1: Active set vector integer codes.
Integer Code Binary representation Meaning
7 111 Get Hessian, gradient, and value
6 110 Get Hessian and gradient
5 101 Get Hessian and value
4 100 Get Hessian
3 011 Get gradient and value
2 010 Get gradient
1 001 Get value
0 000 No data required, function is inactive
9.7 The Active Set Vector
The active set vector contains a set of integer codes, one per response function, which describe the data needed
on a particular execution of an interface. Integer values of 0 through 7 denote a 3-bit binary representation of all
possible combinations of value, gradient, and Hessian requests for a particular function, with the most significant
bit denoting the Hessian, the middle bit denoting the gradient, and the least significant bit denoting the value. The
specific translations are shown in Table 9.1.
The active set vector in Dakota gets its name from managing the active set, i.e., the set of functions that are active
on a particular function evaluation. However, it also manages the type of data that is needed for functions that are
active, and in that sense, has an extended meaning beyond that typically used in the optimization literature.
9.7.1 Active set vector control
Active set vector control may be turned off to allow the user to simplify the supplied interface by removing
the need to check the content of the active set vector on each evaluation. The Interface Commands chapter in the
Dakota Reference Manual [3] provides additional information on this option (deactivate active set vector).
Of course, this option trades some efficiency for simplicity and is most appropriate for those cases in which only
a relatively small penalty occurs when computing and returning more data than may be needed on a particular
function evaluation.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

182 CHAPTER 9. VARIABLES
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 10
Interfaces
10.1 Overview
The interface specification in a Dakota input file controls details of function evaluations. The mechanisms
currently in place for function evaluations involve interfacing with one or more computational simulation codes,
computing algebraic mappings (refer to Section 16.1), or a combination of the two.
This chapter will focus on mechanisms for simulation code invocation, starting with interface types in Section 10.2
and followed by a guide to constructing simulation-based interfaces in Section 10.3. This chapter also provides an
overview of simulation interface components, covers issues relating to file management, and presents a number
of example data mappings.
For a detailed description of interface specification syntax, refer to the interface commands chapter in the Dakota
Reference Manual [3].
10.2 Simulation Interfaces
The invocation of a simulation code is performed using either system calls or forks or via direct linkage. In the
system call and fork cases, a separate process is created for the simulation and communication between Dakota
and the simulation occurs through parameter and response files. For system call and fork interfaces, the interface
section must specify the details of this data transfer. In the direct case, a separate process is not created and
communication occurs in memory through a prescribed API. Sections 10.2.1 through 10.2.5 provide information
on the simulation interfacing approaches.
10.2.1 Direct Simulation Interface
The direct interface may be used to invoke simulations that are linked into the Dakota executable. This interface
eliminates overhead from process creation and file I/O and can simplify operations on massively parallel comput-
ers. These advantages are balanced with the practicality of converting an existing simulation code into a library
with a subroutine interface. Sandia codes for structural dynamics (Salinas), computational fluid dynamics (Sage),
and circuit simulation (Xyce) and external codes such as Phoenix Integration’s ModelCenter framework and The
Mathworks’ Matlab have been linked in this way, and a direct interface to Sandia’s SIERRA multiphysics frame-

184 CHAPTER 10. INTERFACES
work is under development. In the latter case, the additional effort is particularly justified since SIERRA unifies
an entire suite of physics codes. [Note: the “sandwich implementation” of combining a direct interface plug-in
with Dakota’s library mode is discussed in the Dakota Developers Manual [2]].
In addition to direct linking with simulation codes, the direct interface also provides access to internal polyno-
mial test functions that are used for algorithm performance and regression testing. The following test functions
are available: cantilever,cyl head,log ratio,rosenbrock,short column, and text book (in-
cluding text book1,text book2,text book3, and text book ouu). While these functions are also
available as external programs in the Dakota/test directory, maintaining internally linked versions allows
more rapid testing. See Chapter 20 for additional information on several of these test problems. An example input
specification for a direct interface follows:
interface,
direct
analysis_driver = ’rosenbrock’
Additional specification examples are provided in Section 2.3 and additional information on asynchronous usage
of the direct function interface is provided in Section 17.2.1.1. Guidance for usage of some particular direct
simulation interfaces is in Section 16.3 and the details of adding a simulation code to the direct interface are
provided in Section 16.2.
10.2.2 System Call Simulation Interface
Users are strongly encouraged to use the fork simulation interface if possible, though the system interface
is still supported for portability and backward compatibility. The system call approach invokes a simulation
code or simulation driver by using the system function from the standard C library [87]. In this approach, the
system call creates a new process that communicates with Dakota through parameter and response files. The
system call approach allows the simulation to be initiated via its standard invocation procedure (as a “black box”)
and then coordinated with a variety of tools for pre- and post-processing. This approach has been widely used
in previous studies [40,42,34]. The system call approach involves more process creation and file I/O overhead
than the direct function approach, but this extra overhead is usually insignificant compared with the cost of a
simulation. An example of a system call interface specification follows:
interface,
system
analysis_driver = ’text_book’
parameters_file = ’text_book.in’
results_file = ’text_book.out’
file_tag file_save
Information on asynchronous usage of the system interface is provided in Section 17.2.1.2.
10.2.3 Fork Simulation Interface
The fork simulation interface uses the fork,exec, and wait families of functions to manage simulation
codes or simulation drivers. (In a native MS Windows version of Dakota, similar Win32 functions, such as
spawnvp(), are used instead.) Calls to fork or vfork create a copy of the Dakota process, execvp replaces
this copy with the simulation code or driver process, and then Dakota uses the wait or waitpid functions to
wait for completion of the new process. Transfer of variables and response data between Dakota and the simula-
tor code or driver occurs through the file system in exactly the same manner as for the system call interface. An
example of a fork interface specification follows:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.2. SIMULATION INTERFACES 185
interface,
fork
input_filter = ’test_3pc_if’
output_filter = ’test_3pc_of’
analysis_driver = ’test_3pc_ac’
parameters_file = ’tb.in’
results_file = ’tb.out’
file_tag
More detailed examples of using the fork call interface are provided in Section 2.3.5.1 and in Section 10.3, and
information on asynchronous usage of the fork call interface is provided in Section 17.2.1.3.
10.2.4 Syntax for Filter and Driver Strings
With the fork interface, and on most systems, with the system interface as well, the string values supplied
for input filter,output filter, and analysis driver can involve simple Bourne-shell syntax for
specifying environment values that the filter or driver will see. For example,
analysis_driver = ’opfile=myspec outlev=2 mydriver’
would cause mydriver to be invoked with environment variables opfile and outlev having the values
“myspec” and “2”, respectively. If the driver is a shell script, it can access these values as $opfile and
$outlev; a compiled driver can obtain these values from a function; drivers written in C or C++ can use the
standard getenv function (e.g., invoking getenv("opfile")).
Both the values assigned to environment variables and name of the file invoked as filter or driver can contain
spaces, provided that the values in question are quoted. Within strings delimited by single quotes, you can use
double quotes for quoting, and vice versa. For instance,
analysis_driver = ’opfile="my spec" "my driver"’
and
analysis_driver = "opfile=’my spec’ ’my driver’"
both specify a driver named “my driver” and value “my spec” for $opfile.
10.2.5 Fork or System Call: Which to Use?
The primary operational difference between the fork and system call simulation interfaces is that, in the fork in-
terface, the fork/exec functions return a process identifier that the wait/waitpid functions can use to detect
the completion of a simulation for either synchronous or asynchronous operations. The system call simulation
interface, on the other hand, must use a response file detection scheme for this purpose in the asynchronous case.
Thus, an important advantage of the fork interface over the system call interface is that it avoids the potential of a
file race condition when employing asynchronous local parallelism (refer to Section 17.2.1). This condition can
occur when the responses file has been created but the writing of the response data set to this file has not been
completed (see Section 17.2.1.2). While significant care has been taken to manage this file race condition in the
system call case, the fork interface still has the potential to be more robust when performing function evaluations
asynchronously.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

186 CHAPTER 10. INTERFACES
Another advantage of the fork interface is that it has additional asynchronous capabilities when a function eval-
uation involves multiple analyses. As shown in Table 17.1, the fork interface supports asynchronous local and
hybrid parallelism modes for managing concurrent analyses within function evaluations, whereas the system call
interface does not. These additional capabilities again stem from the ability to track child processes by their
process identifiers.
The only disadvantage to the fork interface compared with the system interface is that the fork/exec/wait
functions are not part of the standard C library, whereas the system function is. As a result, support for imple-
mentations of the fork/exec/wait functions can vary from platform to platform. At one time, these commands
were not available on some of Sandia’s massively parallel computers. However, in the more mainstream UNIX
environments, availability of fork/exec/wait should not be an issue.
In summary, the system call interface has been a workhorse for many years and is well tested and proven, but
the fork interface supports additional capabilities and is recommended when managing asynchronous simulation
code executions. Having both interfaces available has proven to be useful on a number of occasions and they will
both continue to be supported for the foreseeable future.
10.3 Building a Black-Box Interface to a Simulation Code
To interface a simulation code to Dakota using one of the black-box interfaces (system call or fork), pre- and
post-processing functionality typically needs to be supplied (or developed) in order to transfer the parameters
from Dakota to the simulator input file and to extract the response values of interest from the simulator’s output
file for return to Dakota (see Figures 1.1 and 10.5). This is often managed through the use of scripting languages,
such as C-shell [6], Bourne shell [13], Perl [144], or Python [99]. While these are common and convenient
choices for simulation drivers/filters, it is important to recognize that any executable file can be used. If the user
prefers, the desired pre- and post-processing functionality may also be compiled or interpreted from any number
of programming languages (C, C++, F77, F95, JAVA, Basic, etc.).
In the Dakota/examples/script interfaces/generic directory, a simple example uses the Rosen-
brock test function as a mock engineering simulation code. Several scripts have been included to demonstrate
ways to accomplish the pre- and post-processing needs. Actual simulation codes will, of course, have different
pre- and post-processing requirements, and as such, this example serves only to demonstrate the issues associated
with interfacing a simulator. Modifications will almost surely be required for new applications.
10.3.1 Generic Script Interface Files
The Dakota/examples/script interfaces/generic directory contains four important files: dakota rosenbrock.in
(the Dakota input file), simulator script (the simulation driver script), dprepro (a pre-processing utility),
and
templatedir/ros.template (a template simulation input file).
The file dakota rosenbrock.in specifies the study that Dakota will perform and, in the interface section,
describes the components to be used in performing function evaluations. In particular, it identifies
simulator script as its analysis driver, as shown in Figure 10.1.
The simulator script listed in Figure 10.2 is a short driver shell script that Dakota executes to perform each
function evaluation. The names of the parameters and results files are passed to the script on its command line;
they are referenced in the script by $1 and $2, respectively. The simulator script is divided into three
parts: pre-processing, analysis, and post-processing.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.3. BUILDING A BLACK-BOX INTERFACE TO A SIMULATION CODE 187
# DAKOTA INPUT FILE - dakota_rosenbrock.in
# This sample Dakota input file optimizes the Rosenbrock function.
# See p. 95 in Practical Optimization by Gill, Murray, and Wright.
method,
npsol_sqp
# if NPSOL is not available, comment the above and try the following instead:
## conmin_frcg
variables,
continuous_design = 2
cdv_initial_point -1.0 1.0
cdv_lower_bounds -2.0 -2.0
cdv_upper_bounds 2.0 2.0
cdv_descriptor ’x1’ ’x2’
interface,
fork
# asynchronous
analysis_driver = ’simulator_script’
parameters_file = ’params.in’
results_file = ’results.out’
work_directory directory_tag
copy_files = ’templatedir/*’
# uncomment to leave params.in and results.out files in work_dir subdirectories
# named ’workdir’ file_save directory_save
aprepro
deactivate active_set_vector
responses,
num_objective_functions = 1
analytic_gradients
no_hessians
Figure 10.1: The dakota rosenbrock.in input file.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

188 CHAPTER 10. INTERFACES
#!/bin/sh
# Sample simulator to Dakota system call script
# See Advanced Simulation Code Interfaces chapter in Users Manual
# $1 is params.in FROM Dakota
# $2 is results.out returned to Dakota
# --------------
# PRE-PROCESSING
# --------------
# Incorporate the parameters from DAKOTA into the template, writing ros.in
# Use the following line if SNL’s APREPRO utility is used instead of DPrePro.
# ../aprepro -c ’*’ -q --nowarning ros.template ros.in
dprepro $1 ros.template ros.in
# --------
# ANALYSIS
# --------
rosenbrock_bb
# ---------------
# POST-PROCESSING
# ---------------
# extract function value from the simulation output
grep ’Function value’ ros.out | cut -c 18- > results.tmp
# extract gradients from the simulation output (in this case will be ignored
# by DAKOTA if not needed)
grep -i ’Function g’ ros.out | cut -c 21- >> results.tmp
mv results.tmp $2
Figure 10.2: The simulator script sample driver script.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.3. BUILDING A BLACK-BOX INTERFACE TO A SIMULATION CODE 189
Usage:
dprepro [options] parameters_file template_input_file new_input_file
Options:
--help
print brief help message
--man
print full manual page and exit
--left-delimiter=string, --right-delimiter=string
override the default curly brace delimiters { and }; these may need
to be quoted or escaped on the command line, e.g., require escaping
with backslash: ‘ $ # require quotes or escaping: \ ’ ( ) |
--output-format=string
use the specified C-style format specification string as the default
for numeric output in all substitutions; will be overridden by
field-specific format strings; may need to be quoted or escaped
Figure 10.3: Partial listing of the dprepro script.
In the pre-processing portion, the simulator script uses dprepro, a parsing utility, to extract the current
variable values from a parameters file ($1) and combine them with the simulator template input file (ros.template)
to create a new input file (ros.in) for the simulator. Internal to Sandia, the APREPRO utility is often used for
this purpose. For external sites where APREPRO is not available, the DPrePro utility mentioned above is an
alternative with many of the capabilities of APREPRO that is specifically tailored for use with Dakota and is
distributed with it (in
Dakota/examples/script interfaces/generic/dprepro, or Dakota/bin in a binary distribu-
tion). Additionally, the BPREPRO utility is another alternative to APREPRO (see [146]), and at Lockheed Martin
sites, the JPrePost utility is available as a JAVA pre- and post-processor [48]. The dprepro script (usage shown
in Figure 10.3) will be used here for simplicity of discussion. It can use either Dakota’s aprepro parameters file
format (see Section 9.6.2) or Dakota’s standard format (see Section 9.6.1), so either option may be selected in the
interface section of the Dakota input file. The ros.template file listed in Figure 10.4 is a template simulation
input file which contains targets for the incoming variable values, identified by the strings “{x1}” and “{x2}”.
These identifiers match the variable descriptors specified in dakota rosenbrock.in. The template input file
is contrived as Rosenbrock has nothing to do with finite element analysis; it only mimics a finite element code
to demonstrate the simulator template process. The dprepro script will search the simulator template input file
for fields marked with curly brackets and then create a new file (ros.in) by replacing these targets with the
corresponding numerical values for the variables. As noted in the usage information for dprepro and shown
in simulator script, the names for the Dakota parameters file ($1), template file (ros.template), and
generated input file (ros.in) must be specified in the dprepro command line arguments.
The second part of the script executes the rosenbrock bb simulator. The input and output file names, ros.in
and ros.out, respectively, are hard-coded into the FORTRAN 77 program rosenbrock bb.f. When the
rosenbrock bb simulator is executed, the values for x1 and x2 are read in from ros.in, the Rosenbrock
function is evaluated, and the function value is written out to ros.out.
The third part performs the post-processing and writes the response results to a file for Dakota to read. Using
Dakota Version 6.7 User’s Manual generated on November 13, 2017

190 CHAPTER 10. INTERFACES
Title of Model: Rosenbrock black box
***************************************************************************
*Description: This is an input file to the Rosenbrock black box
*Fortran simulator. This simulator is structured so
*as to resemble the input/output from an engineering
*simulation code, even though Rosenbrock’s function
*is a simple analytic function. The node, element,
*and material blocks are dummy inputs.
*
*Input: x1 and x2
*Output: objective function value
***************************************************************************
node 1 location 0.0 0.0
node 2 location 0.0 1.0
node 3 location 1.0 0.0
node 4 location 1.0 1.0
node 5 location 2.0 0.0
node 6 location 2.0 1.0
node 7 location 3.0 0.0
node 8 location 3.0 1.0
element 1 nodes 1 3 4 2
element 2 nodes 3 5 6 4
element 3 nodes 5 7 8 6
element 4 nodes 7 9 10 8
material 1 elements 1 2
material 2 elements 3 4
variable 1 {x1}
variable 2 {x2}
end
Figure 10.4: Listing of the ros.template file
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.3. BUILDING A BLACK-BOX INTERFACE TO A SIMULATION CODE 191
the UNIX “grep” utility, the particular response values of interest are extracted from the raw simulator output
and saved to a temporary file (results.tmp). When complete, this file is renamed $2, which in this example
is always “results.out”. Note that moving or renaming the completed results file avoids any problems with
read race conditions (see Section 17.2.1.2).
Because the Dakota input file dakota rosenbrock.in (Figure 10.1) specifies work directory and directory tag
in its interface section, each invocation of simulator script wakes up in its own temporary directory, which
Dakota has populated with the contents of directory templatedir. Having a separate directory for each in-
vocation of simulator script simplifies the script when the Dakota input file specifies asynchronous
(so several instances of simulator script might run simultaneously), as fixed names such as ros.in,
ros.out, and results.tmp can be used for intermediate files. If neither asynchronous nor file tag
is specified, and if there is no need (e.g., for debugging) to retain intermediate files having fixed names, then
directory tag offers no benefit and can be omitted. An alternative to directory tag is to proceed as
earlier versions of this chapter — prior to Dakota 5.0’s introduction of work directory — recommended:
add two more steps to the simulator script, an initial one to create a temporary directory explicitly and
copy templatedir to it if needed, and a final step to remove the temporary directory and any files in it.
When work directory is specified, Dakota adjusts the $PATH seen by simulator script so that sim-
ple program names (i.e., names not containing a slash) that are visible in Dakota’s directory will also be visible
in the work directory. Relative path names — involving an intermediate slash but not an initial one, such as
./rosenbrock bb or a/bc/rosenbrock bb — will only be visible in the work directory if a link files
or copy files specification (see §10.5.5) has made them visible there.
As an example of the data flow on a particular function evaluation, consider evaluation 60. The parameters file
for this evaluation consists of:
{ DAKOTA_VARS = 2 }
{ x1 = 1.638247697999295e-01 }
{ x2 = 2.197298209103481e-02 }
{ DAKOTA_FNS = 1 }
{ ASV_1 = 1 }
{ DAKOTA_DER_VARS = 2 }
{ DVV_1 = 1 }
{ DVV_2 = 2 }
{ DAKOTA_AN_COMPS = 0 }
This file is called workdir/workdir.60/params.in if the line
named ’workdir’ file_save directory_save
in Figure 10.1 is uncommented. The first portion of the file indicates that there are two variables, followed
by new values for variables x1 and x2, and one response function (an objective function), followed by an ac-
tive set vector (ASV) value of 1. The ASV indicates the need to return the value of the objective function
for these parameters (see Section 9.7). The dprepro script reads the variable values from this file, namely
1.638247697999295e-01 and 2.197298209103481e-02 for x1 and x2 respectively, and substitutes
them in the {x1}and {x2}fields of the ros.template file. The final three lines of the resulting input file
(ros.in) then appear as follows:
variable 1 1.638247697999295e-01
variable 2 2.197298209103481e-02
end
where all other lines are identical to the template file. The rosenbrock bb simulator accepts ros.in as its
input file and generates the following output to the file ros.out:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

192 CHAPTER 10. INTERFACES
Beginning execution of model: Rosenbrock black box
Set up complete.
Reading nodes.
Reading elements.
Reading materials.
Checking connectivity...OK
*****************************************************
Input value for x1 = 0.1638247697999295E+00
Input value for x2 = 0.2197298209103481E-01
Computing solution...Done
*****************************************************
Function value = 0.7015563957680092E+00
Function gradient = [ -0.1353509902591768E+01 -0.9731146217930163E+00 ]
Next, the appropriate values are extracted from the raw simulator output and returned in the results file. This
post-processing is relatively trivial in this case, and the simulator script uses the grep and cut utilities
to extract the value from the “Function value” line of the ros.out output file and save it to $2, which is
the results.out file for this evaluation. This single value provides the objective function value requested by
the ASV.
After 132 of these function evaluations, the following Dakota output shows the final solution using the
rosenbrock bb simulator:
Exit NPSOL - Optimal solution found.
Final nonlinear objective value = 0.1165704E-06
NPSOL exits with INFORM code = 0 (see "Interpretation of output" section in NPSOL manual)
NOTE: see Fortran device 9 file (fort.9 or ftn09)
for complete NPSOL iteration history.
<<<<< Iterator npsol_sqp completed.
<<<<< Function evaluation summary: 132 total (132 new, 0 duplicate)
<<<<< Best parameters =
9.9965861667e-01 x1
9.9931682203e-01 x2
<<<<< Best objective function =
1.1657044253e-07
<<<<< Best data captured at function evaluation 130
<<<<< Iterator npsol_sqp completed.
<<<<< Single Method Strategy completed.
Dakota execution time in seconds:
Total CPU = 0.12 [parent = 0.116982, child = 0.003018]
Total wall clock = 1.47497
10.3.2 Adapting These Scripts to Another Simulation
To adapt this approach for use with another simulator, several steps need to be performed:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.4. SIMULATION INTERFACE COMPONENTS 193
1. Create a template simulation input file by identifying the fields in an existing input file that correspond to
the variables of interest and then replacing them with {} identifiers (e.g. {cdv 1},{cdv 2}, etc.) which
match the Dakota variable descriptors. Copy this template input file to a templatedir that will be used to
create working directories for the simulation.
2. Modify the dprepro arguments in simulator script to reflect names of the Dakota parameters file
(previously “$1”), template file name (previously “ros.template”) and generated input file (previously
“ros.in”). Alternatively, use APREPRO, BPREPRO, or JPrePost to perform this step (and adapt the
syntax accordingly).
3. Modify the analysis section of simulator script to replace the rosenbrock bb function call with
the new simulator name and command line syntax (typically including the input and output file names).
4. Change the post-processing section in simulator script to reflect the revised extraction process. At a
minimum, this would involve changing the grep command to reflect the name of the output file, the string
to search for, and the characters to cut out of the captured output line. For more involved post-processing
tasks, invocation of additional tools may have to be added to the script.
5. Modify the dakota rosenbrock.in input file to reflect, at a minimum, updated variables and re-
sponses specifications.
These nonintrusive interfacing approaches can be used to rapidly interface with simulation codes. While generally
custom for each new application, typical interface development time is on the order of an hour or two. Thus, this
approach is scalable when dealing with many different application codes. Weaknesses of this approach include
the potential for loss of data precision (if care is not taken to preserve precision in pre- and post-processing file
I/O), a lack of robustness in post-processing (if the data capture is too simplistic), and scripting overhead (only
noticeable if the simulation time is on the order of a second or less).
If the application scope at a particular site is more focused and only a small number of simulation codes are of
interest, then more sophisticated interfaces may be warranted. For example, the economy of scale afforded by a
common simulation framework justifies additional effort in the development of a high quality Dakota interface.
In these cases, more sophisticated interfacing approaches could involve a more thoroughly developed black box
interface with robust support of a variety of inputs and outputs, or it might involve intrusive interfaces such as the
direct simulation interface discussed below in Section 16.2 or the SAND interface described in Section 1.3.
10.3.3 Additional Examples
A variety of additional examples of black-box interfaces to simulation codes are maintained in the
Dakota/examples/script interfaces directory in the source code distribution.
10.4 Simulation Interface Components
Figure 10.5 is an extension of Figure 1.1 that adds details of the components that make up each of the simulation
interfaces (system call, fork, and direct). These components include an input filter (“IFilter”), one or
more analysis drivers (“Analysis Code/Driver”), and an output filter (“OFilter”). The input and
output filters provide optional facilities for managing simulation pre- and post-processing, respectively. More
specifically, the input filter can be used to insert the Dakota parameters into the input files required by the simulator
program, and the output filter can be used to recover the raw data from the simulation results and compute the
Dakota Version 6.7 User’s Manual generated on November 13, 2017
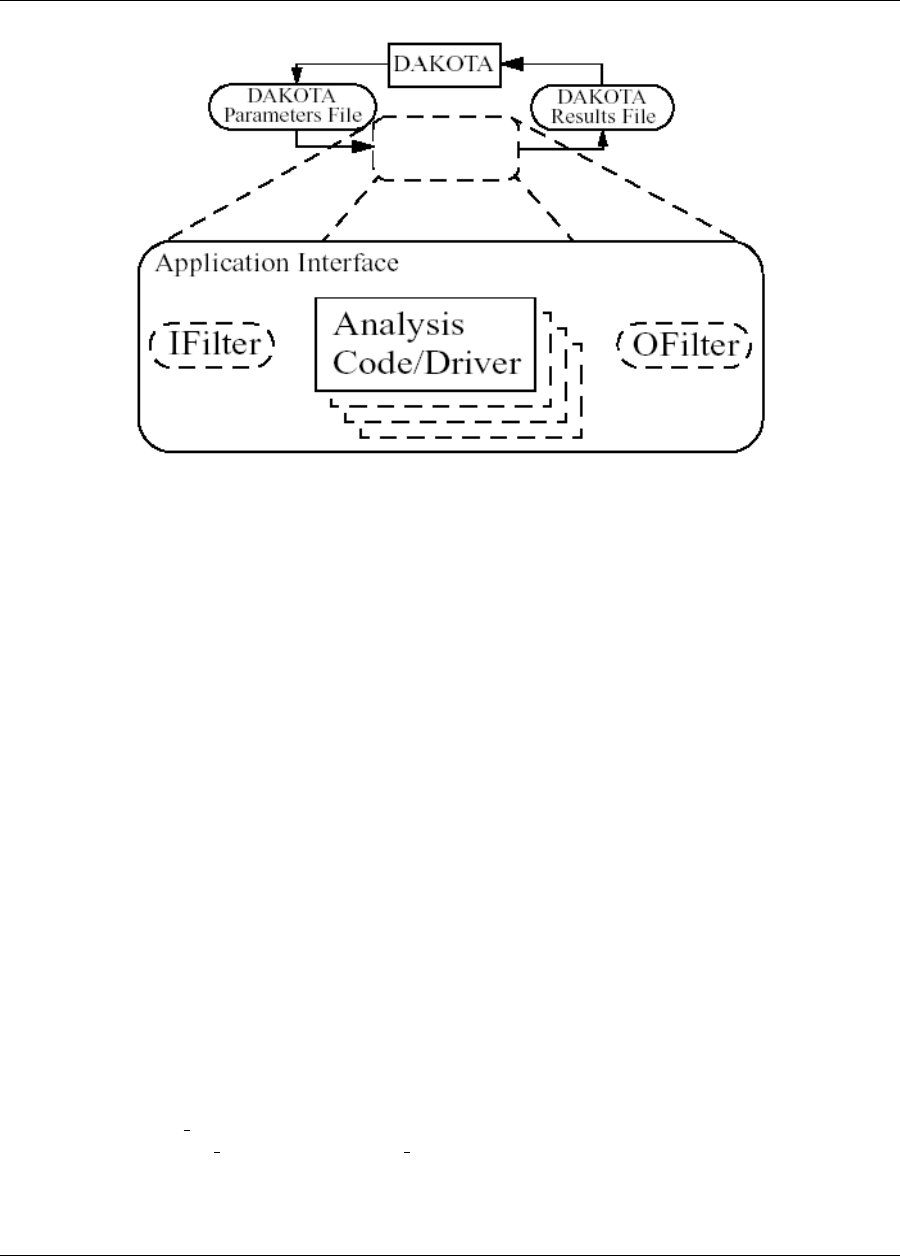
194 CHAPTER 10. INTERFACES
Figure 10.5: Components of the simulation interface
desired response data set. If there is a single analysis code, it is often convenient to combine these pre- and post-
processing functions into a single simulation driver script, and the separate input and output filter facilities are
rarely used in this case. If there are multiple analysis drivers, however, the input and output filter facilities provide
a convenient means for managing non-repeated portions of the pre- and post-processing for multiple analyses.
That is, pre- and post-processing tasks that must be performed for each analysis can be performed within the
individual analysis drivers, and shared pre- and post-processing tasks that are only performed once for the set of
analyses can be performed within the input and output filters.
When spawning function evaluations using system calls or forks, Dakota must communicate parameter and re-
sponse data with the analysis drivers and filters through use of the file system. This is accomplished by passing
the names of the parameters and results files on the command line when executing an analysis driver or filter.
The input filter or analysis driver read data from the parameters file and the output filter or analysis driver write
the appropriate data to the responses file. While not essential when the file names are fixed, the file names must
be retrieved from the command line when Dakota is changing the file names from one function evaluation to the
next (i.e., using temporary files or root names tagged with numerical identifiers). In the case of a UNIX C-shell
script, the two command line arguments are retrieved using $argv[1] and $argv[2] (see [6]). Similarly,
Bourne shell scripts retrieve the two command line arguments using $1 and $2, and Perl scripts retrieve the two
command line arguments using @ARGV[0] and @ARGV[1]. In the case of a C or C++ program, command line
arguments are retrieved using argc (argument count) and argv (argument vector) [87], and for Fortran 77, the
iargc function returns the argument count and the getarg subroutine returns command line arguments.
10.4.1 Single analysis driver without filters
If a single analysis driver is selected in the interface specification and filters are not needed (as indicated
by omission of the input filter and output filter specifications), then only one process will appear in
the execution syntax of the simulation interface. An example of this syntax in the system call case is:
driver params.in results.out
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.4. SIMULATION INTERFACE COMPONENTS 195
where “driver” is the user-specified analysis driver and “params.in” and “results.out” are the names
of the parameters and results files, respectively, passed on the command line. In this case, the user need not
retrieve the command line arguments since the same file names will be used each time.
For the same mapping, the fork simulation interface echoes the following syntax:
blocking fork: driver params.in results.out
for which only a single blocking fork is needed to perform the evaluation.
Executing the same mapping with the direct simulation interface results in an echo of the following syntax:
Direct function: invoking driver
where this analysis driver must be linked as a function within Dakota’s direct interface (see Section 16.2). Note
that no parameter or response files are involved, since such values are passed directly through the function argu-
ment lists.
Both the system call and fork interfaces support asynchronous operations. The asynchronous system call execu-
tion syntax involves executing the system call in the background:
driver params.in.1 results.out.1 &
and the asynchronous fork execution syntax involves use of a nonblocking fork:
nonblocking fork: driver params.in.1 results.out.1
where file tagging (see Section 10.5.2) has been user-specified in both cases to prevent conflicts between con-
current analysis drivers. In these cases, the user must retrieve the command line arguments since the file names
change on each evaluation. Execution of the direct interface must currently be performed synchronously since
multithreading is not yet supported (see Section 17.2.1.1).
10.4.2 Single analysis driver with filters
When filters are used, the syntax of the system call that Dakota performs is:
ifilter params.in results.out; driver params.in results.out;
ofilter params.in results.out
in which the input filter (“ifilter”), analysis driver (“driver”), and output filter (“ofilter”) processes
are combined into a single system call through the use of semi-colons (see [6]). All three portions are passed the
names of the parameters and results files on the command line.
For the same mapping, the fork simulation interface echoes the following syntax:
blocking fork: ifilter params.in results.out;
driver params.in results.out; ofilter params.in results.out
where a series of three blocking forks is used to perform the evaluation.
Executing the same mapping with the direct simulation interface results in an echo of the following syntax:
Dakota Version 6.7 User’s Manual generated on November 13, 2017
196 CHAPTER 10. INTERFACES
Direct function: invoking { ifilter driver ofilter }
where each of the three components must be linked as a function within Dakota’s direct interface. Since asyn-
chronous operations are not yet supported, execution simply involves invocation of each of the three linked func-
tions in succession. Again, no files are involved since parameter and response data are passed directly through the
function argument lists.
Asynchronous executions would appear as follows for the system call interface:
(ifilter params.in.1 results.out.1; driver params.in.1 results.out.1;
ofilter params.in.1 results.out.1) &
and, for the fork interface, as:
nonblocking fork: ifilter params.in.1 results.out.1;
driver params.in.1 results.out.1; ofilter params.in.1 results.out.1
where file tagging of evaluations has again been user-specified in both cases. For the system call simulation
interface, use of parentheses and semi-colons to bind the three processes into a single system call simplifies
asynchronous process management compared to an approach using separate system calls. The fork simulation
interface, on the other hand, does not rely on parentheses and accomplishes asynchronous operations by first
forking an intermediate process. This intermediate process is then reforked for the execution of the input filter,
analysis driver, and output filter. The intermediate process can be blocking or nonblocking (nonblocking in this
case), and the second level of forks can be blocking or nonblocking (blocking in this case). The fact that forks
can be reforked multiple times using either blocking or nonblocking approaches provides the enhanced flexibility
to support a variety of local parallelism approaches (see Chapter 17).
10.4.3 Multiple analysis drivers without filters
If a list of analysis drivers is specified and filters are not needed (i.e., neither input filter nor
output filter appears), then the system call syntax would appear as:
driver1 params.in results.out.1; driver2 params.in results.out.2;
driver3 params.in results.out.3
where “driver1”, “driver2”, and “driver3” are the user-specified analysis drivers and “params.in”
and “results.out” are the user-selected names of the parameters and results files. Note that the results files
for the different analysis drivers have been automatically tagged to prevent overwriting. This automatic tagging of
analyses (see Section 10.5.4) is a separate operation from user-selected tagging of evaluations (see Section 10.5.2).
For the same mapping, the fork simulation interface echoes the following syntax:
blocking fork: driver1 params.in results.out.1;
driver2 params.in results.out.2; driver3 params.in results.out.3
for which a series of three blocking forks is needed (no reforking of an intermediate process is required).
Executing the same mapping with the direct simulation interface results in an echo of the following syntax:
Direct function: invoking { driver1 driver2 driver3 }
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.4. SIMULATION INTERFACE COMPONENTS 197
where, again, each of these components must be linked within Dakota’s direct interface and no files are involved
for parameter and response data transfer.
Both the system call and fork interfaces support asynchronous function evaluations. The asynchronous system
call execution syntax would be reported as
(driver1 params.in.1 results.out.1.1; driver2 params.in.1 results.out.1.2;
driver3 params.in.1 results.out.1.3) &
and the nonblocking fork execution syntax would be reported as
nonblocking fork: driver1 params.in.1 results.out.1.1;
driver2 params.in.1 results.out.1.2; driver3 params.in.1 results.out.1.3
where, in both cases, file tagging of evaluations has been user-specified to prevent conflicts between concurrent
analysis drivers and file tagging of the results files for multiple analyses is automatically used. In the fork interface
case, an intermediate process is forked to allow a non-blocking function evaluation, and this intermediate process
is then reforked for the execution of each of the analysis drivers.
10.4.4 Multiple analysis drivers with filters
Finally, when combining filters with multiple analysis drivers, the syntax of the system call that Dakota
performs is:
ifilter params.in.1 results.out.1;
driver1 params.in.1 results.out.1.1;
driver2 params.in.1 results.out.1.2;
driver3 params.in.1 results.out.1.3;
ofilter params.in.1 results.out.1
in which all processes have again been combined into a single system call through the use of semi-colons and
parentheses. Note that the secondary file tagging for the results files is only used for the analysis drivers and
not for the filters. This is consistent with the filters’ defined purpose of managing the non-repeated portions of
analysis pre- and post-processing (e.g., overlay of response results from individual analyses; see Section 10.5.4
for additional information).
For the same mapping, the fork simulation interface echoes the following syntax:
blocking fork: ifilter params.in.1 results.out.1;
driver1 params.in.1 results.out.1.1;
driver2 params.in.1 results.out.1.2;
driver3 params.in.1 results.out.1.3;
ofilter params.in.1 results.out.1
for which a series of five blocking forks is used (no reforking of an intermediate process is required).
Executing the same mapping with the direct simulation interface results in an echo of the following syntax:
Direct function: invoking { ifilter driver1 driver2 driver3 ofilter }
where each of these components must be linked as a function within Dakota’s direct interface. Since asynchronous
operations are not supported, execution simply involves invocation of each of the five linked functions in succes-
sion. Again, no files are involved for parameter and response data transfer since this data is passed directly through
the function argument lists.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
198 CHAPTER 10. INTERFACES
Asynchronous executions would appear as follows for the system call interface:
(ifilter params.in.1 results.out.1;
driver1 params.in.1 results.out.1.1;
driver2 params.in.1 results.out.1.2;
driver3 params.in.1 results.out.1.3;
ofilter params.in.1 results.out.1) &
and for the fork interface:
nonblocking fork: ifilter params.in.1 results.out.1;
driver1 params.in.1 results.out.1.1;
driver2 params.in.1 results.out.1.2;
driver3 params.in.1 results.out.1.3;
ofilter params.in.1 results.out.1
where, again, user-selected file tagging of evaluations is combined with automatic file tagging of analyses. In
the fork interface case, an intermediate process is forked to allow a non-blocking function evaluation, and this
intermediate process is then reforked for the execution of the input filter, each of the analysis drivers, and the
output filter.
A complete example of these filters and multi-part drivers can be found in Dakota/test/dakota 3pc/dakota 3pc.in.
10.5 Simulation File Management
This section describes some management features used for files that transfer data between Dakota and simulation
codes (i.e., when the system call or fork interfaces are used). These features can generate unique filenames when
Dakota executes programs in parallel and can help one debug the interface between Dakota and a simulation code.
10.5.1 File Saving
Before driver execution: In Dakota 5.0 and newer, an existing results file will be removed immediately prior to
executing the analysis driver. This new behavior addresses a common user problem resulting from starting Dakota
with stale results files in the run directory. To override this default behavior and preserve any existing results files,
specify allow existing results.
After driver execution: The file save option in the interface specification allows the user to control whether
parameters and results files are retained or removed from the working directory after the analysis completes.
Dakota’s default behavior is to remove files once their use is complete to reduce clutter. If the method output
setting is verbose, a file remove notification will follow the function evaluation echo, e.g.,
driver /usr/tmp/aaaa20305 /usr/tmp/baaa20305
Removing /usr/tmp/aaaa20305 and /usr/tmp/baaa20305
However, if file save appears in the interface specification, these files will not be removed. This latter be-
havior is often useful for debugging communication between Dakota and simulator programs. An example of a
file save specification is shown in the file tagging example below.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
10.5. SIMULATION FILE MANAGEMENT 199
10.5.2 File Tagging for Evaluations
When a user provides parameters file and results file specifications, the file tag option in the
interface specification causes Dakota to make the names of these files unique by appending the function evaluation
number to the root file names. Default behavior is to not tag these files, which has the advantage of allowing the
user to ignore command line argument passing and always read to and write from the same file names. However,
it has the disadvantage that files may be overwritten from one function evaluation to the next. When file tag
appears in the interface specification, the file names are made unique by the appended evaluation number. This
uniqueness requires the user’s interface to get the names of these files from the command line. The file tagging
feature is most often used when concurrent simulations are running in a common disk space, since it can prevent
conflicts between the simulations. An example specification of file tag and file save is shown below:
interface,
system
analysis_driver = ’text_book’
parameters_file = ’text_book.in’
results_file = ’text_book.out’
file_tag file_save
Special case: When a user specifies names for the parameters and results files and file save is used without
file tag, untagged files are used in the function evaluation but are then moved to tagged files after the function
evaluation is complete, to prevent overwriting files for which a file save request has been given. If the output
control is set to verbose, then a notification similar to the following will follow the function evaluation echo:
driver params.in results.out
Files with non-unique names will be tagged to enable file_save:
Moving params.in to params.in.1
Moving results.out to results.out.1
Hierarchical tagging: When a model’s specification includes the hierarchical tagging keyword, the
tag applied to parameter and results file names of any subordinate interfaces will reflect any model hierarchy
present. This option is useful for studies involving multiple models with a nested or hierarchical relationship.
For example a nested model has a sub-method, which itself likely operates on a sub-model, or a hierarchical
approximation involves coordination of low and high fidelity models. Specifying hierarchical tagging
will yield function evaluation identifiers (“tags”) composed of the evaluation IDs of the models involved, e.g.,
outermodel.innermodel.interfaceid = 4.9.2. This communicates the outer contexts to the analysis driver when
performing a function evaluation. For an example of using hierarhical tagging in a nested model context, see
dakota/test/dakota uq timeseries *optinterf.in.
10.5.3 Temporary Files
If parameters file and results file are not specified by the user, temporary files having generated
names are used. For example, a system call to a single analysis driver might appear as:
driver /tmp/dakota_params_aaaa2035 /tmp/dakota_results_baaa2030
and a system call to an analysis driver with filter programs might appear as:
ifilter /tmp/dakota_params_aaaa2490 /tmp/dakota_results_baaa2490;
driver /tmp/dakota_params_aaaa2490 tmp/dakota_results_baaa2490;
ofilter /tmp/dakota_params_aaaa2490 /tmp/dakota_results_baa22490
Dakota Version 6.7 User’s Manual generated on November 13, 2017

200 CHAPTER 10. INTERFACES
These files have unique names created by Boost filesystem utilities. This uniqueness requires the user’s interface
to get the names of these files from the command line. File tagging with evaluation number is unnecessary with
temporary files, but can be helpful for the user workflow to identify the evaluation number. Thus file tag
requests will be honored. A file save request will be honored, but it should be used with care since the
temporary file directory could easily become cluttered without the user noticing.
10.5.4 File Tagging for Analysis Drivers
When multiple analysis drivers are involved in performing a function evaluation with either the system call or
fork simulation interface, a secondary file tagging is automatically used to distinguish the results files used for
the individual analyses. This applies to both the case of user-specified names for the parameters and results files
and the default temporary file case. Examples for the former case were shown previously in Section 10.4.3 and
Section 10.4.4. The following examples demonstrate the latter temporary file case. Even though Unix temporary
files have unique names for a particular function evaluation, tagging is still needed to manage the individual
contributions of the different analysis drivers to the response results, since the same root results filename is used
for each component. For the system call interface, the syntax would be similar to the following:
ifilter /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ;
driver1 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.1;
driver2 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.2;
driver3 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.3;
ofilter /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ
and, for the fork interface, similar to:
blocking fork:
ifilter /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ;
driver1 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.1;
driver2 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.2;
driver3 /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ.3;
ofilter /var/tmp/aaawkaOKZ /var/tmp/baaxkaOKZ
Tagging of results files with an analysis identifier is needed since each analysis driver must contribute a user-
defined subset of the total response results for the evaluation. If an output filter is not supplied, Dakota will
combine these portions through a simple overlaying of the individual contributions (i.e., summing the results in
/var/tmp/baaxkaOKZ.1,/var/tmp/baaxkaOKZ.2, and /var/tmp/baaxkaOKZ.3). If this simple
approach is inadequate, then an output filter should be supplied to perform the combination. This is the reason
why the results file for the output filter does not use analysis tagging; it is responsible for the results combination
(i.e., combining /var/tmp/baaxkaOKZ.1,/var/tmp/baaxkaOKZ.2, and /var/tmp/baaxkaOKZ.3
into /var/tmp/baaxkaOKZ). In this case, Dakota will read only the results file from the output filter (i.e.,
/var/tmp/baaxkaOKZ) and interpret it as the total response set for the evaluation.
Parameters files are not currently tagged with an analysis identifier. This reflects the fact that Dakota does not
attempt to subdivide the requests in the active set vector for different analysis portions. Rather, the total active set
vector is passed to each analysis driver and the appropriate subdivision of work must be defined by the user. This
allows the division of labor to be very flexible. In some cases, this division might occur across response functions,
with different analysis drivers managing the data requests for different response functions. And in other cases, the
subdivision might occur within response functions, with different analysis drivers contributing portions to each of
the response functions. The only restriction is that each of the analysis drivers must follow the response format
dictated by the total active set vector. For response data for which an analysis driver has no contribution, 0’s must
be used as placeholders.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.5. SIMULATION FILE MANAGEMENT 201
10.5.5 Work Directories
Sometimes it is convenient for simulators and filters to run in a directory different from the one where Dakota is
invoked. For instance, when performing concurrent evaluations and/or analyses, it is often necessary to cloister
input and output files in separate directories to avoid conflicts. A simulator script used as an analysis driver
can of course include commands to change to a different directory if desired (while still arranging to write a results
file in the original directory), but Dakota has facilities that may simplify the creation of simulator scripts. When the
work directory feature is enabled, Dakota will create a directory for each evaluation/analysis (with optional
tagging and saving as with files). To enable the work directory feature an interface specification includes the
keyword
work_directory
then Dakota will arrange for the simulator and any filters to wake up in the work directory, with $PATH adjusted
(if necessary) so programs that could be invoked without a relative path to them (i.e., by a name not involving any
slashes) from Dakota’s directory can also be invoked from the simulator’s (and filter’s) directory. On occasion, it
is convenient for the simulator to have various files, e.g., data files, available in the directory where it runs. If, say,
my/special/directory is such a directory (as seen from Dakota’s directory), the interface specification
work_directory named ’my/special/directory’
would cause Dakota to start the simulator and any filters in that directory. If the directory did not already exist,
Dakota would create it and would remove it after the simulator (or output filter, if specifed) finished, unless
instructed not to do so by the appearance of directory save (or its deprecated synonym dir save) in the
interface specification. If named ’...’does not appear, then directory save cannot appear either, and
Dakota creates a temporary directory (using the tmpnam function to determine its name) for use by the simulator
and any filters. If you specify directory tag (or the deprecated dir tag), Dakota causes each invocation of
the simulator and any filters to start in a a subdirectory of the work directory with a name composed of the work
directory’s name followed by a period and the invocation number (1, 2, ...); this might be useful in debugging.
Sometimes it can be helpful for the simulator and filters to start in a new directory populated with some files.
Adding
link_files ’templatedir/*’
to the work directory specification would cause the contents of directory templatedir to be linked into the
work directory. Linking makes sense if files are large, but when practical, it is far more reliable to have copies of
the files; adding copy files to the specification would cause the contents of the template directory to be copied
to the work directory. The linking or copying does not overwrite existing files unless replace also appears in
the specification.
Here is a summary of possibilities for a work directory specification, with [...]denoting that ... is optional:
work_directory [ named ’...’ ]
[ directory_tag ] # (or dir_tag)
[ directory_save ] # (or dir_save)
[ link_files ’...’ ’...’ ]
[ copy_files ’...’ ’...’ ]
[ replace ]
Dakota Version 6.7 User’s Manual generated on November 13, 2017

202 CHAPTER 10. INTERFACES
10.6 Parameter to Response Mapping Examples
In this section, interface mapping examples are presented through the discussion of several parameters files and
their corresponding results files. A typical input file for 2 variables (n= 2) and 3 functions (m= 3) using the
standard parameters file format (see Section 9.6.1) is as follows:
2 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
3 functions
1 ASV_1
1 ASV_2
1 ASV_3
2 derivative_variables
1 DVV_1
2 DVV_2
0 analysis_components
where numerical values are associated with their tags within “value tag” constructs. The number of design
variables (n) and the string “variables” are followed by the values of the design variables and their tags, the
number of functions (m) and the string “functions”, the active set vector (ASV) and its tags, the number of
derivative variables and the string “derivative variables”, the derivative variables vector (DVV) and its
tags, the number of analysis components and the string “analysis components”, and the analysis compo-
nents array and its tags. The descriptive tags for the variables are always present and they are either the descriptors
in the user’s variables specification, if given there, or are default descriptors. The length of the active set vector is
equal to the number of functions (m). In the case of an optimization data set with an objective function and two
nonlinear constraints (three response functions total), the first ASV value is associated with the objective function
and the remaining two are associated with the constraints (in whatever consistent constraint order has been defined
by the user). The DVV defines a subset of the variables used for computing derivatives. Its identifiers are 1-based
and correspond to the full set of variables listed in the first array. Finally, the analysis components pass additional
strings from the user’s analysis components specification in a Dakota input file through to the simulator.
They allow the development of simulation drivers that are more flexible, by allowing them to be passed additional
specifics at run time, e.g., the names of model files such as a particular mesh to use.
For the APREPRO format option (see Section 9.6.2), the same set of data appears as follows:
{ DAKOTA_VARS = 2 }
{ cdv_1 = 1.500000000000000e+00 }
{ cdv_2 = 1.500000000000000e+00 }
{ DAKOTA_FNS = 3 }
{ ASV_1 = 1 }
{ ASV_2 = 1 }
{ ASV_3 = 1 }
{ DAKOTA_DER_VARS = 2 }
{ DVV_1 = 1 }
{ DVV_2 = 2 }
{ DAKOTA_AN_COMPS = 0 }
where the numerical values are associated with their tags within “{tag = value }” constructs.
The user-supplied simulation interface, comprised of a simulator program or driver and (optionally) filter pro-
grams, is responsible for reading the parameters file and creating a results file that contains the response data
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.6. PARAMETER TO RESPONSE MAPPING EXAMPLES 203
requested in the ASV. This response data is written in the format described in Section 11.2. Since the ASV con-
tains all ones in this case, the response file corresponding to the above input file would contain values for the three
functions:
1.250000000000000e-01 f
1.500000000000000e+00 c1
1.500000000000000e+00 c2
Since function tags are optional, the following would be equally acceptable:
1.250000000000000e-01
1.500000000000000e+00
1.500000000000000e+00
For the same parameters with different ASV components,
2 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
3 functions
3 ASV_1
3 ASV_2
3 ASV_3
2 derivative_variables
1 DVV_1
2 DVV_2
0 analysis_components
the following response data is required:
1.250000000000000e-01 f
1.500000000000000e+00 c1
1.500000000000000e+00 c2
[ 5.000000000000000e-01 5.000000000000000e-01 ]
[ 3.000000000000000e+00 -5.000000000000000e-01 ]
[ -5.000000000000000e-01 3.000000000000000e+00 ]
Here, we need not only the function values, but also each of their gradients. The derivatives are computed with
respect to cdv 1 and cdv 2 as indicated by the DVV values. Another modification to the ASV components
yields the following parameters file:
2 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
3 functions
2 ASV_1
0 ASV_2
2 ASV_3
2 derivative_variables
1 DVV_1
2 DVV_2
0 analysis_components
Dakota Version 6.7 User’s Manual generated on November 13, 2017

204 CHAPTER 10. INTERFACES
for which the following results file is needed:
[ 5.000000000000000e-01 5.000000000000000e-01 ]
[ -5.000000000000000e-01 3.000000000000000e+00 ]
Here, we need gradients for functions fand c2, but not for c1, presumably since this constraint is inactive.
A full Newton optimizer might make the following request:
2 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
1 functions
7 ASV_1
2 derivative_variables
1 DVV_1
2 DVV_2
0 analysis_components
for which the following results file,
1.250000000000000e-01 f
[ 5.000000000000000e-01 5.000000000000000e-01 ]
[[ 3.000000000000000e+00 0.000000000000000e+00
0.000000000000000e+00 3.000000000000000e+00 ]]
containing the objective function, its gradient vector, and its Hessian matrix, is needed. Again, the derivatives
(gradient vector and Hessian matrix) are computed with respect to cdv 1 and cdv 2 as indicated by the DVV
values.
Lastly, a more advanced example could have multiple types of variables present; in this example, 2 continuous
design and 3 discrete design range, 2 normal uncertain, and 3 continuous state and 2 discrete state range variables.
When a mixture of variable types is present, the content of the DVV (and therefore the required length of gradient
vectors and Hessian matrices) depends upon the type of study being performed (see Section 11.3). For a reliability
analysis problem, the uncertain variables are the active continuous variables and the following parameters file
would be typical:
12 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
2 ddriv_1
2 ddriv_2
2 ddriv_3
5.000000000000000e+00 nuv_1
5.000000000000000e+00 nuv_2
3.500000000000000e+00 csv_1
3.500000000000000e+00 csv_2
3.500000000000000e+00 csv_3
4 dsriv_1
4 dsriv_2
3 functions
3 ASV_1
3 ASV_2
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.6. PARAMETER TO RESPONSE MAPPING EXAMPLES 205
3 ASV_3
2 derivative_variables
6 DVV_1
7 DVV_2
2 analysis_components
mesh1.exo AC_1
db1.xml AC_2
Gradients are requested with respect to variable entries 6 and 7, which correspond to normal uncertain variables
nuv 1 and nuv 2. The following response data would be appropriate:
7.943125000000000e+02 f
1.500000000000000e+00 c1
1.500000000000000e+00 c2
[ 2.560000000000000e+02 2.560000000000000e+02 ]
[ 0.000000000000000e+00 0.000000000000000e+00 ]
[ 0.000000000000000e+00 0.000000000000000e+00 ]
In a parameter study, however, no distinction is drawn between different types of continuous variables, and deriva-
tives would be needed with respect to all continuous variables (ndvv = 7 for the continuous design variables
cdv 1 and cdv 2, the normal uncertain variables nuv 1 and nuv 2, and the continuous state variables csv 1,
csv 2 and csv 3). The parameters file would appear as
12 variables
1.500000000000000e+00 cdv_1
1.500000000000000e+00 cdv_2
2 ddriv_1
2 ddriv_2
2 ddriv_3
5.000000000000000e+00 nuv_1
5.000000000000000e+00 nuv_2
3.500000000000000e+00 csv_1
3.500000000000000e+00 csv_2
3.500000000000000e+00 csv_3
4 dsriv_1
4 dsriv_2
3 functions
3 ASV_1
3 ASV_2
3 ASV_3
7 derivative_variables
1 DVV_1
2 DVV_2
6 DVV_3
7 DVV_4
8 DVV_5
9 DVV_6
10 DVV_7
2 analysis_components
mesh1.exo AC_1
db1.xml AC_2
and the corresponding results would appear as
Dakota Version 6.7 User’s Manual generated on November 13, 2017

206 CHAPTER 10. INTERFACES
7.943125000000000e+02 f
1.500000000000000e+00 c1
1.500000000000000e+00 c2
[ 5.000000000000000e-01 5.000000000000000e-01 2.560000000000000e+02
2.560000000000000e+02 6.250000000000000e+01 6.250000000000000e+01
6.250000000000000e+01 ]
[ 3.000000000000000e+00 -5.000000000000000e-01 0.000000000000000e+00
0.000000000000000e+00 0.000000000000000e+00 0.000000000000000e+00
0.000000000000000e+00 ]
[ -5.000000000000000e-01 3.000000000000000e+00 0.000000000000000e+00
0.000000000000000e+00 0.000000000000000e+00 0.000000000000000e+00
0.000000000000000e+00 ]
10.7 Parameters and Results Files with dakota.interfacing
The Python module dakota.interfacing first was made available with Dakota 6.6. (It was released with
Dakota 6.5 as the module dipy.) By providing a Python interface to read and write, respectively, Dakota param-
eters and results files, dakota.interfacing can greatly simplify development of black-box interfaces. The
benefit may be greatest when one or more phases of the interface (pre-processing, execution, post-processing) is
written in Python.
The following sections describe the components of dakota.interfacing. These include a Parameters
class for making variable information available, a Results class for collecting results and writing them to
file, and a convenience function read parameters file, the preferred way to construct Parameters and
Results objects from a Dakota parameters file.
10.7.1 Creating Parameters and Results objects
dakota.interfacing has one free function, read parameters file, which creates Parameters and
Results objects based on a Dakota parameters file. Its signature is:
dakota.interfacing.read parameters file(parameters file=None,results file=None,ignore asv=False)
parameters file and results file are the names of the parameters file that is to be read and the results file that
ultimately is to be written. The names can be absolute or relative filepaths or just filenames. If a parameters
file or results file is not provided, it will be obtained from the command line arguments. (The results filename is
assumed to be the last command line argument, and the parameters file the second to last.) Note that if the working
directory has changed since script invocation, filenames provided as command line arguments by Dakota’s fork
or system interfaces may be incorrect.
If results file is set to the constant dakota.interfacing.UNNAMED, the Results object is constructed
without a results file name. In this case, an output stream must be provided when Results.write() is called.
Unnamed results files are most helpful when no results file will be written, as with a script intended purely for
pre-processing.
By default, the returned Results object enforces the active set vector (see the Results class section). This
behavior can be overriden, allowing any property (function, gradient, Hessian) of a response to be set, by setting
ignore asv to True.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
10.7. PARAMETERS AND RESULTS FILES WITH DAKOTA.INTERFACING 207
10.7.2 Parameters objects
Parameters objects make the variables, analysis components, evaluation ID, and evaluation number read from
a Dakota parameters file available through a combination of key-value access and object attributes. Although
Parameters objects may be constructed directly, it is advisable to use the read parameters file function
instead.
Variable values can be accessed by Dakota descriptor or by index using [] on the object itself. Variables types
(integer, real, string) are inferred by first attempting to convert to int and then, if this fails, to float.
Analysis components are accessible by index only using the an comps attribute. Parameters objects support
iteration over the variables, yielding the index, variable descriptor, and variable value.
Parameters objects have the attributes:
•an comps List of the analysis components (strings).
•eval id Evaluation id (string).
•eval num Evaluation number (final token in eval id) (int).
•aprepro format Boolean indicating whether the parameters file was in aprepro (True) or Dakota (False)
format.
•descriptors List of the variable descriptors
•num variables Number of variables
•num an comps Number of analysis components
10.7.3 Results objects
Results objects:
•communicate response requests from Dakota (active set vector and derivative variables)
•collect response data (function values, gradients, and Hessians)
•write Dakota results files
Results objects are collections of Response objects, which are documented in the following section. Each
Response can be accessed by name (Dakota descriptor) or by index using [] on the Results object itself.
Results objects support iteration of the Responses, yielding the index, response descriptor, and Response.
Although Results objects may be constructed directly, it is advisable to use the read parameters file
function instead.
Results objects have the attributes:
•eval id Evaluation id (a string).
•eval num Evaluation number (final token in eval id) (int).
•aprepro format Boolean indicating whether the parameters file was in aprepro (True) or Dakota (False)
format.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

208 CHAPTER 10. INTERFACES
•descriptors List of the response descriptors (strings)
•num responses Number of variables (read-only)
•deriv vars List of the derivative variables (strings)
•num deriv varsNumber of derivative variables (int)
Results objects have the methods:
•fail() Set the FAIL attribute. When the results file is written, it will contain only the word FAIL, triggering
Dakota’s failure capturing behavior (See Chapter 19).
•write(stream=None,ignore asv=None) Write the results to the Dakota results file. If stream is set, it
overrides the results file name provided at construct time. It must be an open file-like object, rather than the
name of a file. If ignore asv is True, the file will be written even if information requested via the active set
vector is missing.
10.7.4 Response object
Response objects store response information. They typically are instantiated and accessed through a Results
object by index or response descriptor using [].
Responses have the attributes:
•asv acollections.namedtuple with three members, function,gradient, and hessian. Each is a
boolean indicating whether Dakota requested the associated information for the response. namedtuples
can be accessed by index or by member.
•function Function value for the response. A ResponseError is raised if Dakota did not request the
function value (and ignore asv is False).
•gradient Gradient for the response. Gradients must be a 1D iterable of values that can be converted to
floats, such as a list or 1D numpy array. A ResponseError is raised if Dakota did not request the
gradient (and ignore asv is False), or if the number of elements does not equal the number of derivative
variables.
•hessian Hessian value for the response. Hessians must be an iterable of iterables (e.g. a 2D numpy
array or list of lists). A ResponseError is raised if Dakota did not request the Hessian (and ignore asv is
False), or if the dimension does not correspond correctly with the number of derivative variables.
10.7.5 dakota.interfacing Examples
In addition to those in this section, the Dakota/examples/script interfaces/Python folder contains
two runnable examples of Python analysis drivers. In one, rosenbrock bb.py, parameters file parsing is per-
formed manually. The other, rosenbrock bb di.py, demonstrates the dakota.interfacing module.
For most applications, using dakota.interfacing is straightforward. The first example, in Figure 10.6, is a
mock analysis driver. Two variables with the descriptors x1 and x2 are read from the Dakota parameters file and
used to evaluate the fictitious user function applic module.run(). The result, stored in f, is assigned to the
Dakota Version 6.7 User’s Manual generated on November 13, 2017

10.7. PARAMETERS AND RESULTS FILES WITH DAKOTA.INTERFACING 209
import dakota.interfacing as di
import applic_module
params, results = di.read_parameters_file()
# parameters can be accessed by descriptor, as shown here, or by index
x1 = params["x1"]
x2 = params["x2"]
f = applic_module.run(x1,x2)
# Responses also can be accessed by descriptor or index
results["f"].function = f
results.write()
Figure 10.6: A simple analysis driver that uses dakota.interfacing
function value of the appropriate response. (A common error is leaving off the function attribute, which is
needed to distinguish the function value of the response from its gradient and Hessian.)
The Results object exposes the active set vector read from the parameters file. When analytic gradients or Hes-
sians are available for a response, the ASV should be queried to determine what Dakota has requested for an evalu-
ation. If an attempt is made to addunrequested information to a response, a dakota.interface.ResponseError
is raised. The same exception results if a requested piece of information is missing when Results.write() is
called. The ignore asv option to read parameters file and Results.write() overrides ASV checks.
In Figure 10.7,applic module.run() has been modified to return not only the function value of f, but also
its gradient and Hessian. The asv attribute is examined to determine which of these to add to results["f"].
Dakota Version 6.7 User’s Manual generated on November 13, 2017

210 CHAPTER 10. INTERFACES
import dakota.interfacing as di
import applic_module # fictitious application
params, results = di.read_parameters_file()
x1 = params["x1"]
x2 = params["x2"]
f, df, df2 = applic_module.run(x1,x2)
if Results.asv.function:
results["f"].function = f
if Results.asv.gradient:
results["f"].gradient = df
if Results.asv.hessian:
results["f"] = df2
results.write()
Figure 10.7: Examining the active set vector
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 11
Responses
11.1 Overview
The responses specification in a Dakota input file controls the types of data that can be returned from an inter-
face during Dakota’s execution. The specification includes the number and type of response functions (objective
functions, nonlinear constraints, calibration terms, etc.) as well as availability of first and second derivatives
(gradient vectors and Hessian matrices) for these response functions.
This chapter will present a brief overview of the response data sets and their uses, as well as cover some user
issues relating to file formats and derivative vector and matrix sizing. For a detailed description of responses
section syntax and example specifications, refer to the Responses Commands chapter in the Dakota Reference
Manual [3].
11.1.1 Response function types
The types of response functions listed in the responses specification should be consistent with the iterative tech-
nique called for in the method specification:
•an optimization data set comprised of num objective functions,
num nonlinear inequality constraints, and num nonlinear equality constraints.
This data set is appropriate for use with optimization methods (e.g., the methods in Chapter 6). When using
results files (11.2), the responses must be ordered: objectives, inequalities, then equalities.
•a calibration data set comprised of calibration terms,
num nonlinear inequality constraints, and num nonlinear equality constraints.
This data set is appropriate for use with nonlinear least squares algorithms (e.g., the methods in Chapter 7).
When using results files (11.2), the responses must be ordered: calibration terms, inequalities, then equali-
ties.
•a generic data set comprised of num response functions. This data set is appropriate for use with
uncertainty quantification methods (e.g., the methods in Section 5).
Certain general-purpose iterative techniques, such as parameter studies and design of experiments methods, can
be used with any of these data sets.

212 CHAPTER 11. RESPONSES
11.1.2 Gradient availability
Gradient availability for these response functions may be described by:
•no gradients: gradients will not be used.
•numerical gradients: gradients are needed and will be approximated by finite differences.
•analytic gradients: gradients are needed and will be supplied by the simulation code (without any
finite differencing by Dakota).
•mixed gradients: the simulation will supply some gradient components and Dakota will approximate
the others by finite differences.
The gradient specification also links back to the iterative method used. Gradients commonly are needed when
the iterative study involves gradient-based optimization, reliability analysis for uncertainty quantification, or local
sensitivity analysis.
11.1.3 Hessian availability
Hessian availability for the response functions is similar to the gradient availability specifications, with the addi-
tion of support for “quasi-Hessians”:
•no hessians: Hessians will not be used.
•numerical gradients: Hessians are needed and will be approximated by finite differences. These
finite differences may involve first-order differences of gradients (if analytic gradients are available for the
response function of interest) or second-order differences of function values (in all other cases).
•quasi hessians: Hessians are needed and will be approximated by secant updates (BFGS or SR1) from
a series of gradient evaluations.
•analytic hessians: Hessians are needed and are available directly from the simulation code.
•mixed hessians: Hessians are needed and will be obtained from a mix of numerical, analytic, and
“quasi” sources.
The Hessian specification also links back to the iterative method in use; Hessians commonly would be used
in gradient-based optimization by full Newton methods or in reliability analysis with second-order limit state
approximations or second-order probability integrations.
11.1.4 Field Data
Prior to Dakota 6.1, Dakota responses have been treated as scalar responses. That is, if the user specifies
response functions=5, Dakota treats the five responses as five separate scalar quantities. There are some
cases where responses are a “field” quantity, meaning that the responses are a function of one or more indepen-
dent variables such as time and/or spatial location. In these cases, the responses should be treated as field data.
For example, it can become extremely cumbersome to represent 5000 values from a time-temperature trace or a
Dakota Version 6.7 User’s Manual generated on November 13, 2017

11.2. DAKOTA RESULTS FILE DATA FORMAT 213
current-voltage curve in Dakota. With scalar response quantities, we ignore the independent variable(s). For ex-
ample, if we have a response Ras a function of time t, the user currently gives Dakota a set of discrete responses
at particular times and Dakota doesn’t know the times.
With the field data capability, the user can specify that they have one field response of size 5000 x 1 (for example).
Dakota will have a large set of data R=f(t), with both the response Rand independent coordinates tspecified
to Dakota. The independent variable(s) can be useful in interpolation between simulation responses and exper-
imental observations. It also can be useful in surrogate construction. We plan to handle correlation or structure
between field responses, which is currently not handled when we treat the responses as individual, separate scalar
quantities.
For all three major response types (objective functions,calibration terms, and response functions),
one can specify field responses (e.g. with field objectives,field calibration terms, and field responses).
For each type of field response, one can specify the length of the field (e.g. lengths=5000) and the number of
independent coordinates (num coordinates per field). The user can specify the independent coordinates
by specifying read field coordinates and providing the coordinates in files named response descriptor.coords.
In the case of field data from physical experiments used to calibrate field data from simulation experiments, the
specification is more involved: the user should refer to the Dakota Reference manual to get the syntax. Note that
at this time, field responses may be specified by the user as outlined above. All methods can handle field data,
but currently the calibration methods are the only methods specialized for field data, specifically they interpolate
the simulation field data to the experiment field data points to calculate the residual terms. This is applicable to
nl2sol,nlssol,optpp g newton, the MCMC Bayesian methods, as well as general optimization methods
that recast the residuals into a sum-of-squares error. The other methods simply handle the field responses as a
number of scalar responses currently. In future versions, we are planning some additional features with methods
that can handle field data, including reduction of the field data.
11.2 Dakota Results File Data Format
Simulation interfaces using system calls and forks to create separate simulation processes must communicate with
the simulation through the file system. This is done by reading and writing files of parameters and results. Dakota
uses its own format for this data input/output. For the results file, only one format is supported (versus the two
parameter-file formats described in Section 9.6). Ordering of response functions is as listed in Section 11.1.1
(e.g., objective functions or calibration terms are first, followed by nonlinear inequality constraints, followed by
nonlinear equality constraints).
After a simulation, Dakota expects to read a file containing responses reflecting the current parameters and corre-
sponding to the function requests in the active set vector. The response data must be in the format shown in Figure
11.1.
The first block of data (shown in black) conveys the requested function values and is followed by a block of
requested gradients (shown in blue), followed by a block of requested Hessians (shown in red). If the amount of
data in the file does not match the function request vector, Dakota will abort execution with an error message.
Function values have no bracket delimiters, but each may be followed by its own non-numeric label. Labels
must be separated from numeric function values by white space (one or more blanks, tabs, or newline characters)
and they must not contain any white space themselves (e.g., use “response1” or “response 1,” but not
“response 1”). Labels also must not resemble numerical values.
By default, function value labels are optional and are ignored by Dakota; they are permitted only as a convenience
to the user. However, if strict checking is activated by including the labeled keyword in the interface section
of the Dakota input file, then labels are required for every function value. Further, labels must exactly match the
Dakota Version 6.7 User’s Manual generated on November 13, 2017

214 CHAPTER 11. RESPONSES
<double> <fn_label1>
<double> <fn_label2>
...
<double> <fn_labelm>
[ <double> <double> .. <double> ]
[ <double> <double> .. <double> ]
...
[ <double> <double> .. <double> ]
[[ <double> <double> .. <double> ]]
[[ <double> <double> .. <double> ]]
...
[[ <double> <double> .. <double> ]]
Figure 11.1: Results file data format.
response descriptors of their corresponding function values. These stricter labeling requirements enable Dakota
to detect and report when function values are returned out-of-order, or when specific function values are repeated
or missing.
Gradient vectors are surrounded by single brackets [. . . ndvv -vector of doubles. . . ]. Labels are not used and must
not be present. White space separating the brackets from the data is optional.
Hessian matrices are surrounded by double brackets [[. . . ndvv ×ndvv matrix of doubles. . . ]]. Hessian components
(numeric values for second partial derivatives) are listed by rows and separated by white space; in particular, they
can be spread across multiple lines for readability. Labels are not used and must not be present. White space after
the initial double bracket and before the final one is optional, but none can appear within the double brackets.
The format of the numeric fields may be floating point or scientific notation. In the latter case, acceptable exponent
characters are “E” or “e.” A common problem when dealing with Fortran programs is that a C++ read of
a numeric field using “D” or “d” as the exponent (i.e., a double precision value from Fortran) may fail or be
truncated. In this case, the “D” exponent characters must be replaced either through modifications to the Fortran
source or compiler flags or through a separate post-processing step (e.g., using the UNIX sed utility).
11.3 Active Variables for Derivatives
An important question for proper management of both gradient and Hessian data is: if several different types of
variables are used, for which variables are response function derivatives needed? That is, how is ndvv deter-
mined? The short answer is that the derivative variables vector (DVV) specifies the set of variables to be used for
computing derivatives, and ndvv is the length of this vector.
In most cases, the DVV is defined directly from the set of active continuous variables for the iterative method in
use. Since methods operate over a subset, or view, of the variables that is active in the iteration, it is this same set
of variables for which derivatives are most commonly computed. Derivatives are never needed with respect to any
discrete variables (since these derivatives do not in general exist) and the active continuous variables depend on
view override specifications, inference by response type, and inference by method type, in that order, as described
in Section 9.5.
In a few cases, derivatives are needed with respect to the inactive continuous variables. This occurs for nested
Dakota Version 6.7 User’s Manual generated on November 13, 2017

11.3. ACTIVE VARIABLES FOR DERIVATIVES 215
iteration where a top-level iterator sets derivative requirements (with respect to its active continuous variables) on
the final solution of the lower-level iterator (for which the top-level active variables are inactive). For example, in
an uncertainty analysis within a nested design under uncertainty algorithm, derivatives of the lower-level response
functions may be needed with respect to the design variables, which are active continuous variables at the top
level but are inactive within the uncertainty quantification. These instances are the reason for the creation and
inclusion of the DVV vector — to clearly indicate the variables whose partial derivatives are needed.
In all cases, if the DVV is honored, then the correct derivative components are returned. In simple cases, such as
optimization and calibration studies that only specify design variables and for nondeterministic analyses that only
specify uncertain variables, derivative component subsets are not an issue and the exact content of the DVV may
be safely ignored.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

216 CHAPTER 11. RESPONSES
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 12
Inputs to Dakota
12.1 Overview of Inputs
Dakota supports a number of command-line arguments, as described in Section 2.4. Among these are specifica-
tions for the Dakota input file and, optionally, a restart file. The syntax of the Dakota input file is described in
detail in the Dakota Reference Manual [3], and the restart file is described in Chapter 18.
A Dakota input file may be prepared with a text editor such as Emacs, Vi, or WordPad, or with the Dakota graphical
user interface. The Dakota GUI is built on the Java-based Eclipse Framework [33] and presents the Dakota input
specification options in synchronized text-editing and graphical views. The Dakota GUI includes templates and
wizards for helping create Dakota studies and can invoke Dakota to run an analysis. The Dakota GUI for Linux,
Windows, and Mac, is available for download from the Dakota website http://dakota.sandia.gov/,
along with licensing information, separate GUI documentation, and installation tips.
12.1.1 Tabular Data Formats
The Dakota input file and/or command line may identify additional text files for tabular data import in contexts
described in Section 12.2. Examples include data from which to build a surrogate, points at which to run a list
parameter study, post-run input data, and least squares and Bayesian calibration data. Dakota writes and reads
tabular data with C++ stream operators/conversions, so most integer and floating point formats are acceptable for
imported numeric data. Dakota supports the following tabular formats:
•Annotated: In most contexts, Dakota tabular data defaults to “annotated” tabular format. An annotated
tabular file is a whitespace-separated text file with one leading header row of comments/column labels. In
most imports/exports, each subsequent row contains an evaluation ID and interface ID, followed by data
for variables, or variables followed by responses, depending on context. This example shows 5 variables,
followed by the 1 text book response:
%eval_id interface TF1ln TF1ln hpu_r1 hpu_r2 ModelForm text_book
1 I1 0.97399 1.0476 12 4.133 3 14753
2 I1 0.94468 1.0636 4.133 12 3 14753
3 I1 1.0279 1.0035 12 4.133 3 14753
Another example is shown in Figure 13.2.Note: Dakota 6.1 and newer include a column for the interface
ID. See the discussion of custom-annotated format for importing/exporting Dakota 6.0 format files.

218 CHAPTER 12. INPUTS TO DAKOTA
For scalar experiment data files, each subsequent row contains an experiment ID, followed by data for
configuration variables, observations, and/or observation errors, depending on context. This example shows
3 data points for each of two experiments.
%experiment d1 d2 d3
1 82 15.5 2.02
2 82.2 15.45 2
•Free-form: When optionally specifying freeform for a given tabular import, the data file must be pro-
vided in a free-form format, omitting the leading header row and ID column(s). The raw num rows x
num cols numeric data entries may appear separated with any whitespace including arbitrary spaces, tabs,
and newlines. In this format, vectors may therefore appear as a single row or single column (or mixture;
entries will populate the vector in order). This example shows the free-form version of the annotated data
above:
0.97399 1.0476 12 4.133 3 14753
0.94468 1.0636 4.133 12 3 14753
1.0279 1.0035 12 4.133 3 14753
•Custom-annotated: In Dakota 6.2 and newer, a custom-annotated format is supported, to allow backward-
compatibility with Dakota 6.0 tabular formats, which had a header and evaluation ID, but no interface ID.
This can be specified, for example, with
method
list_parameter_study
import_points_file = ’dakota_pstudy.3.dat’
custom_annotated header eval_id
The custom annotated keyword has options to control header row, eval id column, and interface id
column.
In tabular files, variables appear in input specification order as documented in the reference manual. As of Dakota
6.1, tabular I/O has columns for all of the variables (active and inactive), not only the active variables as in
previous versions. To import data corresponding only to the active variables, use the keyword active only
when specifying the import file.
Attention: Prior to October 2011, samples, calibration, and surrogate data files were free-form format. They now
default to annotated format, though there are freeform and custom annotated options. For both formats,
a warning will be generated if a specific number of data are expected, but extra is found and an error generated
when there is insufficient data. Some TPLs like SCOLIB and JEGA manage their own file I/O and only support
the free-form option.
12.2 Data Imports
The Dakota input file and/or command line may identify additional files used to import data into Dakota.
12.2.1 AMPL algebraic mappings: stub.nl, stub.row, and stub.col
As described in Section 16.1, an AMPL specification of algebraic input-to-output relationships may be imported
into Dakota and used to define or augment the mappings of a particular interface.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

12.2. DATA IMPORTS 219
12.2.2 Genetic algorithm population import
Genetic algorithms (GAs) from the JEGA and SCOLIB packages support a population import feature using the
keywords initialization type flat file = STRING. This is useful for warm starting GAs from
available data or previous runs. Refer to the Method Specification chapter in the Dakota Reference Manual [3]
for additional information on this specification. The flat file must be in free-form format as described in Sec-
tion 12.1.1.
12.2.3 Calibration data import
Calibration methods (deterministic least squares and Bayesian) require residuals, or differences between model
predictions q(θ)and data d:
r(θ) = q(θ)−d,(12.1)
By default, if a Dakota input file specifies responses,calibration terms, the simulation interface is
required to return a vector of residuals to Dakota. If in addition the input file includes calibration data or
calibration data file, Dakota assumes the interface will return the model predictions q(θ)themselves
and Dakota will compute residuals based on the provided data.
There are two calibration data import mechanisms:
1. Scalar responses only with calibration data file: This uses a single tabular text file to import data
values and (optionally) experiment numbers, configurations, and observation variances. Each row of the
data file expresses this information for a single experiment.
2. Field and/or scalar responses with calibration data: In order to accommodate the richer structure of
field-valued responses, this specification requires separate data files per response group (descriptor) DESC,
per experiment NUM. The files are named DESC.NUM.*and must each be in a tabular text format.
The tabular data files may be specified to be annotated (default), custom annotated, or freeform
format.
Calibration data imports include the following information:
•Configuration variables (optional): state variable values indicating the configuration at which this exper-
iment was conducted; length must agree with the number of state variables active in the study.
•Experimental observations (required): experimental data values to difference with model responses;
length equal to the total response length (number of scalars + sum(field lengths)).
•Experimental variances (optional): measurement errors (variances/covariances) associated with the ex-
perimental observations
For specifics on specifying calibration data imports, see 7.5 and the responses >calibration terms
keyword in the Dakota Reference Manual [3].
Note on variance: Field responses may optionally have scalar, diagonal, or matrix-valued error covariance infor-
mation. As an example, Figure 12.1 shows an observation vector with 5 responses; 2 scalar + 3 field (each field
of length >1). The corresponding covariance matrix has scalar variances σ2
1, σ2
2for each of the scalars s1, s2,
diagonal covariance D3for field f3, scalar covariance σ2
4for field f4, and full matrix covariance C5for field f5.
In total, Dakota supports block diagonal covariance Σacross the responses, with blocks Σi, which could be fully
dense within a given field response group. Covariance across the highest-level responses (off-diagonal blocks) is
not supported, nor is covariance between experiments.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
220 CHAPTER 12. INPUTS TO DAKOTA
Figure 12.1: An example of scalar and field response data, with associated block-diagonal observation error
covariance.
12.2.4 PCE coefficient import
Polynomial chaos expansion (PCE) methods compute coefficients for response expansions which employ a basis
of multivariate orthogonal polynomials. Normally, the polynomial chaos method calculates these coeffi-
cients based either on a spectral projection or a linear regression (see Section 5.4). However, Dakota also supports
the option of importing a set of response PCE coefficients from a file specified with
import expansion file = STRING. Each row of the free-form formatted file must be comprised of a
coefficient followed by its associated multi-index (the same format used for output described in Section 13.6).
This file import can be used to evaluate moments analytically or compute probabilities numerically from a known
response expansion. Refer to the Method Specification chapter in the Dakota Reference Manual [3] for additional
information on this specification.
12.2.5 Surrogate construction and evaluation data
Global data fit surrogates, including some stochastic expansions, may be constructed from a variety of data
sources. One of these sources is an auxiliary data file, as specified by the keyword import points file
=STRING. The file may be in annotated (default), custom annotated, or free-form format with columns corre-
sponding to variables and responses. Surfpack global surrogate models may also be evaluated at a user-provided
file containing challenge points. Refer to the Model Specification chapter in the Dakota Reference Man-
ual [3] for additional information on this specification.
12.2.6 Variables/responses import to post-run
The post-run mode (supported only for sampling, parameter study, and DACE methods) requires specification of
a file containing parameter and response data. Annotated is the default format (see Section 12.1.1), where leading
columns for evaluation and interface IDs are followed by columns for variables (active and inactive by default),
then those for responses, with an ignored header row of labels and then one row per evaluation. Typically this
file would be generated by executing dakota -i dakota.in -pre run ::variables.dat and then
adding columns of response data to variables.dat to make varsresponses.dat. The file is specified at the command
line with:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

12.2. DATA IMPORTS 221
dakota -i dakota.in -post_run varsresponses.dat::
To import post-run data in other formats, specify post run in the input file instead of at the command-line, and
provide a format option.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

222 CHAPTER 12. INPUTS TO DAKOTA
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Chapter 13
Output from Dakota
13.1 Overview of Output Formats
While Dakota primarily targets complex numerical simulation codes run on massively parallel supercomputers,
Dakota’s output focuses on succinct, text-based reporting of the iterations and function evaluations performed by
an algorithm. In a number of contexts, Dakota generates tabular output useful for data analysis and visualization
with external tools. Unix versions of Dakota have a basic graphical output capability that is useful as a monitoring
tool. The Dakota GUI is an emerging capability that will provide more advanced visualization facilities in time.
13.2 Standard Output
Dakota prints information on algorithm progress, function evaluations, and summary results to standard out and
error (screen, terminal, or console) as it runs. Detailed information for a function evaluation may include an
evaluation number, parameter values, execution syntax, the active set vector, and the response data set. This
output may be redirected to a file using the command-line options described in Section 2.4.
Here, optimization of the “container” problem (see Chapter 20) is used as an example to describe Dakota output.
The input file shown in Figure 13.1 specifies one equality constraint, and that Dakota’s finite difference algorithm
will provide central difference numerical gradients to the NPSOL optimizer.

224 CHAPTER 13. OUTPUT FROM DAKOTA
# Dakota Input File: container_opt_npsol.in
environment
graphics
tabular_data
tabular_data_file = ’container_opt_npsol.dat’
method
npsol_sqp
variables
continuous_design = 2
descriptors ’H’ ’D’
initial_point 4.5 4.5
lower_bounds 0.0 0.0
interface
analysis_drivers = ’container’
fork
parameters_file = ’container.in’
results_file = ’container.out’
file_tag
responses
objective_functions = 1
nonlinear_equality_constraints = 1
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 0.001
no_hessians
Figure 13.1: Dakota input file for the “container” test problem – see
Dakota/examples/users/container opt npsol.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

13.2. STANDARD OUTPUT 225
A partial listing of the Dakota output for the container optimization example follows:
Dakota version 5.4+ (stable) released May 2 2014.
Subversion revision 2508 built May 2 2014 15:26:14.
Running MPI Dakota executable in serial mode.
Start time: Fri May 2 15:38:11 2014
----------------------------------------------------------------
Begin DAKOTA input file
/home/briadam/dakota/build/examples/users/container_opt_npsol.in
----------------------------------------------------------------
# Dakota Input File: container_opt_npsol.in
environment
graphics
<SNIP>
---------------------
End DAKOTA input file
---------------------
Using Dakota input file ’/home/briadam/dakota/build/examples/users/container_opt_npsol.in’
Writing new restart file dakota.rst
>>>>> Executing environment.
>>>>> Running npsol_sqp iterator.
------------------------------------------
Begin Dakota derivative estimation routine
------------------------------------------
>>>>> Initial map for analytic portion of response:
---------------------
Begin Evaluation 1
---------------------
Parameters for evaluation 1:
4.5000000000e+00 H
4.5000000000e+00 D
blocking fork: container container.in.1 container.out.1
Active response data for evaluation 1:
Active set vector = { 1 1 }
1.0713145108e+02 obj_fn
8.0444076396e+00 nln_eq_con_1
>>>>> Dakota finite difference gradient evaluation for x[1] + h:
---------------------
Begin Evaluation 2
---------------------
Dakota Version 6.7 User’s Manual generated on November 13, 2017

226 CHAPTER 13. OUTPUT FROM DAKOTA
Parameters for evaluation 2:
4.5045000000e+00 H
4.5000000000e+00 D
blocking fork: container container.in.2 container.out.2
Active response data for evaluation 2:
Active set vector = { 1 1 }
1.0719761302e+02 obj_fn
8.1159770472e+00 nln_eq_con_1
>>>>> Dakota finite difference gradient evaluation for x[1] - h:
---------------------
Begin Evaluation 3
---------------------
Parameters for evaluation 3:
4.4955000000e+00 H
4.5000000000e+00 D
blocking fork: container container.in.3 container.out.3
Active response data for evaluation 3:
Active set vector = { 1 1 }
1.0706528914e+02 obj_fn
7.9728382320e+00 nln_eq_con_1
>>>>> Dakota finite difference gradient evaluation for x[2] + h:
---------------------
Begin Evaluation 4
---------------------
Parameters for evaluation 4:
4.5000000000e+00 H
4.5045000000e+00 D
blocking fork: container container.in.4 container.out.4
Active response data for evaluation 4:
Active set vector = { 1 1 }
1.0727959301e+02 obj_fn
8.1876180243e+00 nln_eq_con_1
>>>>> Dakota finite difference gradient evaluation for x[2] - h:
---------------------
Begin Evaluation 5
---------------------
Parameters for evaluation 5:
4.5000000000e+00 H
4.4955000000e+00 D
Dakota Version 6.7 User’s Manual generated on November 13, 2017

13.2. STANDARD OUTPUT 227
blocking fork: container container.in.5 container.out.5
Active response data for evaluation 5:
Active set vector = { 1 1 }
1.0698339109e+02 obj_fn
7.9013403937e+00 nln_eq_con_1
>>>>> Total response returned to iterator:
Active set vector = { 3 3 } Deriv vars vector = { 1 2 }
1.0713145108e+02 obj_fn
8.0444076396e+00 nln_eq_con_1
[ 1.4702653619e+01 3.2911324639e+01 ] obj_fn gradient
[ 1.5904312809e+01 3.1808625618e+01 ] nln_eq_con_1 gradient
<SNIP>
>>>>> Dakota finite difference gradient evaluation for x[2] - h:
---------------------
Begin Evaluation 40
---------------------
Parameters for evaluation 40:
4.9873894231e+00 H
4.0230575428e+00 D
blocking fork: container container.in.40 container.out.40
Active response data for evaluation 40:
Active set vector = { 1 1 }
9.8301287596e+01 obj_fn
-1.2698647501e-01 nln_eq_con_1
>>>>> Total response returned to iterator:
Active set vector = { 3 3 } Deriv vars vector = { 1 2 }
9.8432498116e+01 obj_fn
-9.6918029158e-12 nln_eq_con_1
[ 1.3157517860e+01 3.2590159623e+01 ] obj_fn gradient
[ 1.2737124497e+01 3.1548877601e+01 ] nln_eq_con_1 gradient
NPSOL exits with INFORM code = 0 (see "Interpretation of output" section in NPSOL manual)
NOTE: see Fortran device 9 file (fort.9 or ftn09)
for complete NPSOL iteration history.
<<<<< Function evaluation summary: 40 total (40 new, 0 duplicate)
<<<<< Best parameters =
Dakota Version 6.7 User’s Manual generated on November 13, 2017

228 CHAPTER 13. OUTPUT FROM DAKOTA
4.9873894231e+00 H
4.0270846274e+00 D
<<<<< Best objective function =
9.8432498116e+01
<<<<< Best constraint values =
-9.6918029158e-12
<<<<< Best data captured at function evaluation 36
<<<<< Iterator npsol_sqp completed.
<<<<< Environment execution completed.
DAKOTA execution time in seconds:
Total CPU = 0.03 [parent = 0.023997, child = 0.006003]
Total wall clock = 0.090703
Exit graphics window to terminate DAKOTA.
The output begins with information on the Dakota version, compilation date, and run mode. It then echos the
user input file before proceeding to execution phase. The lines following “>>>>> Running npsol sqp
iterator.” show Dakota performing function evaluations 1–5 that have been requested by NPSOL. Evalua-
tions 6 through 39 have been omitted from the listing for brevity.
Immediately following the line “Begin Function Evaluation 1”, the initial values of the design vari-
ables, the syntax of the blocking fork function evaluation, and the resulting objective and constraint function
values returned by the simulation are listed. The values of the design variables are labeled with the tags H
and D, respectively, according to the descriptors given in the input file, Figure 13.1. The values of the ob-
jective function and volume constraint are labeled with the tags obj fn and nln eq con 1, respectively.
Note that the initial design parameters are infeasible since the equality constraint is violated (6= 0). However,
by the end of the run, the optimizer finds a design that is both feasible and optimal for this example. Be-
tween the design variables and response values, the content of the system call to the simulator is displayed as
“(container container.in.1 container.out.1)”, with container being the name of the sim-
ulator and container.in.1 and container.out.1 being the names of the parameters and results files,
respectively.
Just preceding the output of the objective and constraint function values is the line “Active set vector =
{1 1}”. The active set vector indicates the types of data that are required from the simulator for the objective and
constraint functions, and values of “1” indicate that the simulator must return values for these functions (gradient
and Hessian data are not required). For more information on the active set vector, see Section 9.7.
Since finite difference gradients have been specified, Dakota computes their values by making additional function
evaluation requests to the simulator at perturbed parameter values. Examples of the gradient-related function eval-
uations have been included in the sample output, beginning with the line that reads “>>>>> Dakota finite
difference evaluation for x[1] + h:”. The resulting finite difference gradients are listed after
function evaluation 5 beginning with the line “>>>>> Total response returned to iterator:”.
Here, another active set vector is displayed in the Dakota output file. The line “Active set vector = {3
3}” indicates that the total response resulting from the finite differencing contains function values and gradients.
The final lines of the Dakota output, beginning with the line “<<<<< Function evaluation summary:”,
summarize the results of the optimization study. The best values of the optimization parameters, objective func-
tion, and volume constraint are presented along with the function evaluation number where they occurred, total
function evaluation counts, and a timing summary. In the end, the objective function has been minimized and the
equality constraint has been satisfied (driven to zero within the constraint tolerance).
The Dakota results may be intermixed with iteration information from the NPSOL library. For example lines with
Dakota Version 6.7 User’s Manual generated on November 13, 2017
13.3. TABULAR OUTPUT DATA 229
%eval_id interface H D obj_fn nln_eq_con_1
1 NO_ID 4.5 4.5 107.1314511 8.04440764
2 NO_ID 5.801246882 3.596476363 94.33737399 -4.59103645
3 NO_ID 5.197920019 3.923577479 97.7797214 -0.6780884711
4 NO_ID 4.932877133 4.044776216 98.28930566 -0.1410680284
5 NO_ID 4.989328733 4.026133158 98.4270019 -0.005324671422
6 NO_ID 4.987494493 4.027041977 98.43249058 -7.307058453e-06
7 NO_ID 4.987391669 4.02708372 98.43249809 -2.032538049e-08
8 NO_ID 4.987389423 4.027084627 98.43249812 -9.691802916e-12
Figure 13.2: Dakota’s tabular output file showing the iteration history of the “container” optimization problem.
the heading “Majr Minr Step Fun Merit function Norm gZ Violtn nZ Penalty Conv” come
from Fortran write statements within NPSOL. The output is mixed since both Dakota and NPSOL are writing to
the same standard output stream. The relative locations of these output contributions can vary depending on the
specifics of output buffering and flushing on a particular platform and depending on whether or not the standard
output is being redirected to a file. In some cases, output from the optimization library may appear on each it-
eration (as in this example), and in other cases, it may appear at the end of the Dakota output. Finally, a more
detailed summary of the NPSOL iterations is written to the Fortran device 9 file (e.g., fort.9 or ftn09).
13.3 Tabular Output Data
In a number of contexts, Dakota can output information in a whitespace-separated columnar data file, a tabular
data file. The most common usage, to capture the iteration history in a tabular file, is enabled by including the
keyword tabular data in the environment specification (see Figure 13.1). This output format facilitates
the transfer of Dakota’s iteration history data to external mathematical analysis and/or graphics plotting packages
(e.g., MATLAB, TECplot, Excel, S-plus, Minitab).
The default file name for the top-level tabular output data is “dakota tabular.dat,” though tabular data file
allows specification of an alternate name. Example tabular output from the “container” optimization problem is
shown in Figure 13.2. This annotated tabular format (see Section 12.1.1) file contains the complete history of data
requests from NPSOL (8 requests map into a total of 40 function evaluations when including the central finite
differencing). The first column is the data request number, the second column is the interface ID (which is NO ID
if the user does not specify a name for the interface), the third and fourth columns are the design parameter values
(labeled in the example as “H” and “D”), the fifth column is the objective function (labeled “obj fn”), and the
sixth column is the nonlinear equality constraint (labeled “nln eq con 1”).
Attention: The second column labeled “interface” is new as of Dakota 6.1. It identifies which interface
was used to map the variables to responses on each line of the tabular file (recall that the interface defines which
simulation is being run though the analysis driver specification). Disambiguating the interface is important
when using hybrid methods, multi-fidelity methods, or nested models. In more common, simpler analyses, users
typically ignore the first two columns and only focus on the columns of inputs (variables) and outputs (responses).
To generate tabular output in Dakota 6.0 format, use the custom-annotated format described in Section 12.1.1.
Attention: As of Dakota 6.1, the tabular file will include columns for all of the variables (both active and inactive)
present in a given interface. Previously, Dakota only wrote the “active” variables. Recall that some variables may
be inactive if they are not operated on by a particular method (e.g. uncertain variables might not be active in an
optimization, design variables may not be active in a sampling study). The order of the variables printed out will
Dakota Version 6.7 User’s Manual generated on November 13, 2017

230 CHAPTER 13. OUTPUT FROM DAKOTA
Figure 13.3: Dakota 2D graphics for “container” problem showing history of an objective function, an equality
constraint, and two variables.
be in Dakota’s standard variable ordering, which is indicated by the input specification order, and summarized in
the Dakota Reference Manual.
Any evaluations from Dakota’s internal finite differencing are suppressed, to facilitate rapid plotting of the most
critical data. This suppression of lower level data is consistent with the data that is sent to the graphics windows,
as described in Section 13.4. If this data suppression is undesirable, Section 18.2.3 describes an approach where
every function evaluation, even the ones from finite differencing, can be saved to a file in tabular format by using
the Dakota restart utility.
13.4 Graphics Output
Graphics capabilities are available for monitoring the progress of an iterative study. The graphics option is invoked
by adding the graphics flag in the environment specification of the Dakota input file (see Figure 13.1). The
graphics display the values of each response function (e.g., objective and constraint functions) and each parameter
for the function evaluations in the study. As for the tabular output described in Section 13.3, internal finite
difference evaluations are suppressed in order to omit this clutter from the graphics. Figure 13.3 shows the
optimization iteration history for the container example.
If Dakota is executed on a remote machine, the DISPLAY variable in the user’s UNIX environment [58] may need
to be set to the local machine in order to display the graphics window.
The scroll bars which are located on each graph below and to the right of each plot may be operated by dragging
on the bars or pressing the arrows, both of which result in expansion/contraction of the axis scale. Clicking on the
“Options” button results in the window shown in Figure 13.4, which allows the user to include min/max markers
on the vertical axis, vertical and horizontal axis labels, and a plot legend within the corresponding graphics plot.
In addition, the values of either or both axes may be plotted using a logarithmic scale (so long as all plot values
are greater than zero) and an encapsulated postscript (EPS) file, named dakota graphic i.eps where iis
the plot window number, can be created using the “Print” button.
13.5 Error Messages Output
A variety of error messages are printed by Dakota in the event that an error is detected in the input specification.
Some of the more common input errors, and the associated error messages, are described below. See also the
Common Specification Mistakes section in the Dakota Reference Manual [3].
Dakota Version 6.7 User’s Manual generated on November 13, 2017

13.5. ERROR MESSAGES OUTPUT 231
Figure 13.4: Options for Dakota 2D graphics.
Incorrectly spelled specifications, such as ‘‘numericl gradients’’, will result in error messages of the
form:
Input line 31: unrecognized identifier ’numericl_gradients’.
Input line 31: unrecognized identifier ’method_source’.
Input line 31: unrecognized identifier ’dakota’.
Input line 31: unrecognized identifier ’interval_type’.
Input line 31: unrecognized identifier ’central’.
Input line 31: unrecognized identifier ’fd_gradient_step_size’.
Input line 31: One of the following 4 entities
must be specified for responses...
analytic_gradients
mixed_gradients
no_gradients
numerical_gradients
In this example the line numbers given are approximate, as all input following an errant keywords is considered a
single line through the end of the block.
The input parser catches syntax errors, but not logic errors. The fact that certain input combinations are erroneous
must be detected after parsing, at object construction time. For example, if a no gradients specification for
a response data set is combined with selection of a gradient-based optimization method, then this error must be
detected during set-up of the optimizer (see last line of listing):
Error: gradient-based minimizers require a gradient specification.
Many such errors can be detected earlier by running dakota -check.
Another common mistake involves a mismatch between the amount of data expected on a function evaluation and
the data returned by the user’s simulation code or driver. The available response data is specified in the responses
keyword block, and the subset of this data needed for a particular evaluation is managed by the active set vector.
For example, if Dakota expects function values and gradients to be returned (as indicated by an active set vector
containing 3’s), but the user’s simulation code only returns function values, then the following error message is
generated:
At EOF: insufficient data for functionGradient 1
Dakota Version 6.7 User’s Manual generated on November 13, 2017
232 CHAPTER 13. OUTPUT FROM DAKOTA
Unfortunately, descriptive error messages are not available for all possible failure modes of Dakota. If you en-
counter core dumps, segmentation faults, or other failures, please request help using the support mechanisms
described on the Dakota website.
13.6 Stochastic expansion exports
Polynomial chaos expansion (PCE) methods compute coefficients for response expansions which employ a basis
of multivariate orthogonal polynomials. The polynomial chaos method calculates these coefficients based
on a number of approaches described in Section 5.4). One may output the PCE coefficients to a file using the
keyword export expansion file = STRING. Each row of the exported file will contain a coefficient,
followed by the multi-index indicating which basis terms correspond to it. Only free-form format (Section 12.1.1)
is supported for this file.
When using numerical integration schemes with structured rules, Dakota can also output the integration points
and corresponding weights to a tabular file. This output is generated when method output is verbose
or higher. Weights and points are printed to a file dakota quadrature tabular.dat (tensor product
quadrature), dakota sparse tabular.dat (sparse grids), or dakota cubature tabular.dat (cu-
bature methods), with one line per integration point.
13.7 Surrogate Model Exports
Most Dakota surrogate models, including all those implemented in Surfpack and some stochastic expansion ap-
proaches support the keyword export approx points file = STRING. When specified, any approxi-
mate evaluations performed on the surrogate model will be output to the specified data file. The data file can be
exported in any of the tabular formats described in Section 12.1.1 (default annotated). This facilitates plotting or
external diagnostics of the surrogate model.
In addition, the Surfpack family of global surrogate models supports export to a human-readable and self-
documenting algebraic form, suitable for reuse in user-developed tools, and to non-human readable model files,
which are intended for use with the surfpack executable or library API. The export model keyword group
is used to specify model export filenames and formats. It is fully described in the Dakota Reference Manual [3].
13.8 Variables Output from Pre-run
The pre-run mode (supported only for select methods) permits specification of an output file to which Dakota will
write parameter (variables) data in any supported tabular format (default annotated; see Section 12.1.1) with data
columns corresponding to each variable. This file can be generated with sampling, parameter study, and DACE
methods by invoking
dakota -i dakota.in -pre_run ::variables.dat
for example, to output the variables (samples) in an LHS study. If a user adds the corresponding response values
to this file, it may then be imported using Dakota’s post-run mode. Command line pre-run will always export
in annotated format. To export pre-run data in other formats, specify pre run in the input file instead of at the
command-line, and provide a format option.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 14
Advanced Methods
14.1 Overview
A variety of “meta-algorithm” capabilities have been developed in order to provide a mechanism for employing
individual iterators and models as reusable components within higher-level solution approaches. This capability
allows the use of existing iterative algorithm and computational model software components as building blocks
to accomplish more sophisticated studies, such as hybrid, multistart, Pareto, or surrogate-based minimization.
Further multi-component capabilities are enabled by the model recursion capabilities described in Chapter 8with
specific examples in Chapter 15.
14.2 Hybrid Minimization
In the hybrid minimization method (keyword: hybrid), a sequence of minimization methods are applied to find
an optimal design point. The goal of this method is to exploit the strengths of different minimization algorithms
through different stages of the minimization process. Global/local optimization hybrids (e.g., genetic algorithms
combined with nonlinear programming) are a common example in which the desire for a global optimum is
balanced with the need for efficient navigation to a local optimum. An important related feature is that the
sequence of minimization algorithms can employ models of varying fidelity. In the global/local case, for example,
it would often be advantageous to use a low-fidelity model in the global search phase, followed by use of a more
refined model in the local search phase.
The specification for hybrid minimization involves a list of method identifier strings, and each of the corresponding
method specifications has the responsibility for identifying the model specification (which may in turn identify
variables, interface, and responses specifications) that each method will use (see the Dakota Reference Manual [3]
and the example discussed below). Currently, only the sequential hybrid approach is available. The embedded
and collaborative approaches are not fully functional at this time.
In the sequential hybrid minimization approach, a sequence of minimization methods is invoked in the order
specified in the Dakota input file. After each method completes execution, the best solution or solutions from
that method are used as the starting point(s) for the following method. The number of solutions transferred is
defined by how many that method can generate and how many the user specifies with the individual method
keyword final solutions. For example, currently only a few of the global optimization methods such as
genetic algorithms (e.g. moga and coliny ea) and sampling methods return multiple solutions. In this case,

234 CHAPTER 14. ADVANCED METHODS
the specified number of solutions from the previous method will be used to initialize the subsequent method. If
the subsequent method cannot accept multiple input points (currently only a few methods such as the genetic
algorithms in JEGA allow multiple input points), then multiple instances of the subsequent method are generated,
each one initialized by one of the optimal solutions from the previous method. For example, if LHS sampling
were run as the first method and the number of final solutions was 10 and the DOT conjugate gradient was the
second method, there would be 10 instances of dot frcg started, each with a separate LHS sample solution
as its initial point. Method switching is governed by the separate convergence controls of each method; that is,
each method is allowed to run to its own internal definition of completion without interference. Individual method
completion may be determined by convergence criteria (e.g., convergence tolerance) or iteration limits
(e.g., max iterations).
Figure 14.1 shows a Dakota input file that specifies a sequential hybrid optimization method to solve the “text-
book” optimization test problem. The textbook hybrid strat.in file provided in Dakota/examples/users
starts with a coliny ea solution which feeds its best point into a coliny pattern search optimization
which feeds its best point into optpp newton. While this approach is overkill for such a simple problem, it is
useful for demonstrating the coordination between multiple sub-methods in the hybrid minimization algorithm.
The three optimization methods are identified using the method list specification in the hybrid method sec-
tion of the input file. The identifier strings listed in the specification are ‘GA’ for genetic algorithm, ‘PS’ for
pattern search, and ‘NLP’ for nonlinear programming. Following the hybrid method keyword block are the three
corresponding method keyword blocks. Note that each method has a tag following the id method keyword that
corresponds to one of the method names listed in the hybrid method keyword block. By following the identifier
tags from method to model and from model to variables,interface, and responses, it is easy to see
the specification linkages for this problem. The GA optimizer runs first and uses model ‘M1’ which includes vari-
ables ‘V1’, interface ‘I1’, and responses ‘R1’. Note that in the specification, final solutions=1, so only
one (the best) solution is returned from the GA. However, it is possible to change this to final solutions=5
and get five solutions passed from the GA to the Pattern Search (for example). Once the GA is complete, the PS
optimizer starts from the best GA result and again uses model ‘M1’. Since both GA and PS are nongradient-based
optimization methods, there is no need for gradient or Hessian information in the ‘R1’ response keyword block.
The NLP optimizer runs last, using the best result from the PS method as its starting point. It uses model ‘M2’
which includes the same ‘V1’ and ‘I1’ keyword blocks, but uses the responses keyword block ‘R2’ since the full
Newton optimizer used in this example (optpp newton) needs analytic gradient and Hessian data to perform
its search.
14.3 Multistart Local Minimization
A simple, heuristic, global minimization technique is to use many local minimization runs, each of which is
started from a different initial point in the parameter space. This is known as multistart local minimization. This
is an attractive method in situations where multiple local optima are known or expected to exist in the parameter
space. However, there is no theoretical guarantee that the global optimum will be found. This approach com-
bines the efficiency of local minimization methods with a user-specified global stratification (using a specified
starting points list, a number of specified random starts, or both; see the Dakota Reference Man-
ual [3] for additional specification details). Since solutions for different starting points are independent, parallel
computing may be used to concurrently run the local minimizations.
An example input file for multistart local optimization on the “quasi sine” test function (see quasi sine fcn.C
in Dakota Source/test) is shown in Figure 14.2. The method keyword block in the input file contains the
keyword multi start, along with the set of starting points (3 random and 5 listed) that will be used for the
optimization runs. The other keyword blocks in the input file are similar to what would be used in a single
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14.3. MULTISTART LOCAL MINIMIZATION 235
# Dakota Input File: textbook_hybrid_strat.in
environment
top_method_pointer = ’HS’
graphics
method
id_method = ’HS’
hybrid sequential
method_pointer_list = ’GA’ ’PS’ ’NLP’
method
id_method = ’GA’
coliny_ea
seed = 1234
population_size = 5
model_pointer = ’M1’
final_solutions = 1
output verbose
method
id_method = ’PS’
coliny_pattern_search stochastic
seed = 1234
initial_delta = 0.1
threshold_delta = 1.e-4
solution_target = 1.e-10
exploratory_moves basic_pattern
model_pointer = ’M1’
output verbose
method
id_method = ’NLP’
optpp_newton
gradient_tolerance = 1.e-12
convergence_tolerance = 1.e-15
model_pointer = ’M2’
output verbose
model
id_model = ’M1’
single
interface_pointer = ’I1’
variables_pointer = ’V1’
responses_pointer = ’R1’
model
id_model = ’M2’
single
interface_pointer = ’I1’
variables_pointer = ’V1’
responses_pointer = ’R2’
variables
id_variables = ’V1’
continuous_design = 2
initial_point 0.6 0.7
upper_bounds 5.8 2.9
lower_bounds 0.5 -2.9
descriptors ’x1’ ’x2’
interface
id_interface = ’I1’
analysis_drivers = ’text_book’
direct
responses
id_responses = ’R1’
objective_functions = 1
no_gradients
no_hessians
responses
id_responses = ’R2’
objective_functions = 1
analytic_gradients
analytic_hessians
Figure 14.1: Dakota input file for a sequential hybrid optimization method – see
Dakota/examples/users/textbook hybrid strat.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
236 CHAPTER 14. ADVANCED METHODS
optimization run.
The quasi sine test function has multiple local minima, but there is an overall trend in the function that tends
toward the global minimum at (x1, x2) = (0.177,0.177). See [61] for more information on this test function.
Figure 14.3 shows the results summary for the eight local optimizations performed. From the five specified starting
points and the 3 random starting points (as identified by the x1,x2 headers), the eight local optima (as identified
by the x1*,x2*headers) are all different and only one of the local optimizations finds the global minimum.
14.4 Pareto Optimization
The Pareto optimization method (keyword: pareto set) is one of three multiobjective optimization capabilities
discussed in Section 6.3.1. In the Pareto optimization method, multiple sets of multiobjective weightings are eval-
uated. The user can specify these weighting sets in the method keyword block using a multi objective weight sets
list, a number of random weight sets, or both (see the Dakota Reference Manual [3] for additional specifi-
cation details).
Dakota performs one multiobjective optimization problem for each set of multiobjective weights. The collection
of computed optimal solutions form a Pareto set, which can be useful in making trade-off decisions in engineering
design. Since solutions for different multiobjective weights are independent, parallel computing may be used to
concurrently execute the multiobjective optimization problems.
Figure 14.5 shows the results summary for the Pareto-set optimization method. For the four multiobjective
weighting sets (as identified by the w1,w2,w3 headers), the local optima (as identified by the x1,x2 head-
ers) are all different and correspond to individual objective function values of (f1, f2, f3) = (0.0,0.5,0.5), (13.1,-
1.2,8.16), (532.,33.6,-2.9), and (0.125,0.0,0.0) (note: the composite objective function is tabulated under the
obj fn header). The first three solutions reflect exclusive optimization of each of the individual objective func-
tions in turn, whereas the final solution reflects a balanced weighting and the lowest sum of the three objectives.
Plotting these (f1, f2, f3) triplets on a 3-dimensional plot results in a Pareto surface (not shown), which is useful
for visualizing the trade-offs in the competing objectives.
14.5 Mixed Integer Nonlinear Programming (MINLP)
Many nonlinear optimization problems involve a combination of discrete and continuous variables. These are
known as mixed integer nonlinear programming (MINLP) problems. A typical MINLP optimization problem is
formulated as follows:
minimize: f(x,d)
subject to: gL≤g(x,d)≤gU
h(x,d) = ht(14.1)
xL≤x≤xU
d∈ {−2,−1,0,1,2}
where dis a vector whose elements are integer values. In situations where the discrete variables can be tem-
porarily relaxed (i.e., noncategorical discrete variables, see Section 9.2.2), the branch-and-bound algorithm can
be applied. Categorical variables (e.g., true/false variables, feature counts, etc.) that are not relaxable cannot be
used with the branch and bound method. During the branch and bound process, the discrete variables are treated
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14.5. MIXED INTEGER NONLINEAR PROGRAMMING (MINLP) 237
# Dakota Input File: qsf_multistart_strat.in
environment
top_method_pointer = ’MS’
graphics
method
id_method = ’MS’
multi_start
method_pointer = ’NLP’
random_starts = 3 seed = 123
starting_points = -0.8 -0.8
-0.8 0.8
0.8 -0.8
0.8 0.8
0.0 0.0
method
id_method = ’NLP’
dot_bfgs
variables
continuous_design = 2
lower_bounds -1.0 -1.0
upper_bounds 1.0 1.0
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’quasi_sine_fcn’
fork #asynchronous
responses
objective_functions = 1
analytic_gradients
no_hessians
Figure 14.2: Dakota input file for a multistart local optimization method – see
Dakota/examples/users/qsf multistart strat.in
<<<<< Results summary:
set_id x1 x2 x1*x2*obj_fn
1 -0.8 -0.8 -0.8543728666 -0.8543728666 0.5584096919
2 -0.8 0.8 -0.9998398719 0.177092822 0.291406596
3 0.8 -0.8 0.177092822 -0.9998398719 0.291406596
4 0.8 0.8 0.1770928217 0.1770928217 0.0602471946
5 0 0 0.03572926375 0.03572926375 0.08730499239
6 -0.7767971993 0.01810943539 -0.7024118387 0.03572951143 0.3165522387
7 -0.3291571008 -0.7697378755 0.3167607374 -0.4009188363 0.2471403213
8 0.8704730469 0.7720679005 0.177092899 0.3167611757 0.08256082751
Figure 14.3: Dakota results summary for a multistart local optimization method.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

238 CHAPTER 14. ADVANCED METHODS
# Dakota Input File: textbook_pareto_strat.in
environment
top_method_pointer = ’PS’
graphics
method
id_method = ’PS’
pareto_set
method_pointer = ’NLP’
weight_sets =
1.0 0.0 0.0
0.0 1.0 0.0
0.0 0.0 1.0
0.333 0.333 0.333
method
id_method = ’NLP’
dot_bfgs
model
single
variables
continuous_design = 2
initial_point 0.9 1.1
upper_bounds 5.8 2.9
lower_bounds 0.5 -2.9
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’text_book’
direct
responses
objective_functions = 3
analytic_gradients
no_hessians
Figure 14.4: Dakota input file for the Pareto optimization method – see
Dakota/examples/users/textbook pareto strat.in
<<<<< Results summary:
set_id w1 w2 w3 x1 x2 obj_fn
1 1 0 0 0.9996554048 0.997046351 7.612301561e-11
2 0 1 0 0.5 2.9 -1.2
3 0 0 1 5.8 1.12747589e-11 -2.9
4 0.333 0.333 0.333 0.5 0.5000000041 0.041625
Figure 14.5: Dakota results summary for the Pareto-set optimization method.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
14.5. MIXED INTEGER NONLINEAR PROGRAMMING (MINLP) 239
as continuous variables and the integrality conditions on these variables are incrementally enforced through a se-
quence of optimization subproblems. By the end of this process, an optimal solution that is feasible with respect
to the integrality conditions is computed.
Dakota’s branch and bound method (keyword: branch and bound) can solve optimization problems having
either discrete or mixed continuous/discrete variables. This method uses the parallel branch-and-bound algorithm
from the PEBBL software package [32] to generate a series of optimization subproblems (“branches”). These
subproblems are solved as continuous variable problems using any of Dakota’s nonlinear optimization algorithms
(e.g., DOT, NPSOL). When a solution to a branch is feasible with respect to the integrality constraints, it provides
an upper bound on the optimal objective function, which can be used to prune branches with higher objective
functions that are not yet feasible. Since solutions for different branches are independent, parallel computing may
be used to concurrently execute the optimization subproblems.
PEBBL, by itself, targets the solution of mixed integer linear programming (MILP) problems, and through cou-
pling with Dakota’s nonlinear optimizers, is extended to solution of MINLP problems. In the case of MILP
problems, the upper bound obtained with a feasible solution is an exact bound and the branch and bound process
is provably convergent to the global minimum. For nonlinear problems which may exhibit nonconvexity or multi-
modality, the process is heuristic in general, since there may be good solutions that are missed during the solution
of a particular branch. However, the process still computes a series of locally optimal solutions, and is therefore
a natural extension of the results from local optimization techniques for continuous domains. Only with rigorous
global optimization of each branch can a global minimum be guaranteed when performing branch and bound on
nonlinear problems of unknown structure.
In cases where there are only a few discrete variables and when the discrete values are drawn from a small set,
then it may be reasonable to perform a separate optimization problem for all of the possible combinations of the
discrete variables. However, this brute force approach becomes computationally intractable if these conditions
are not met. The branch-and-bound algorithm will generally require solution of fewer subproblems than the
brute force method, although it will still be significantly more expensive than solving a purely continuous design
problem.
14.5.1 Example MINLP Problem
As an example, consider the following MINLP problem [43]:
minimize: f(x) =
6
X
i=1
(xi−1.4)4
g1=x2
1−x2
2≤0
g2=x2
2−x1
2≤0(14.2)
−10 ≤x1, x2, x3, x4≤10
x5, x6∈ {0,1,2,3,4}
This problem is a variant of the textbook test problem described in Section 20.1. In addition to the introduction
of two integer variables, a modified value of 1.4is used inside the quartic sum to render the continuous solution a
non-integral solution.
Figure 14.6 shows the sequence of branches generated for this problem. The first optimization subproblem relaxes
the integrality constraint on parameters x5and x6, so that 0≤x5≤4and 0≤x6≤4. The values for x5and x6
Dakota Version 6.7 User’s Manual generated on November 13, 2017
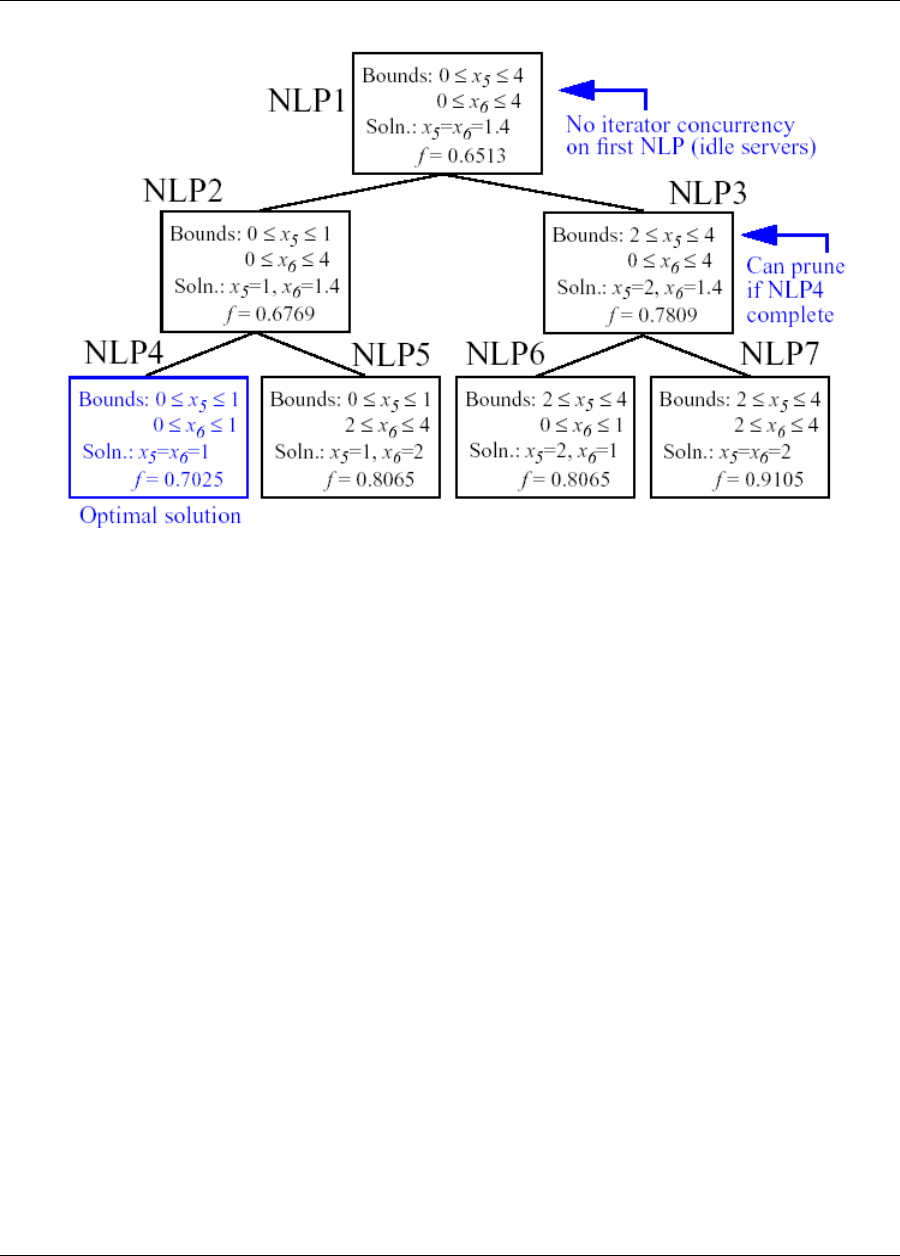
240 CHAPTER 14. ADVANCED METHODS
Figure 14.6: Branching history for example MINLP optimization problem.
at the solution to this first subproblem are x5=x6= 1.4. Since x5and x6must be integers, the next step in the
solution process “branches” on parameter x5to create two new optimization subproblems; one with 0≤x5≤1
and the other with 2≤x5≤4. Note that, at this first branching, the bounds on x6are still 0≤x6≤4.
Next, the two new optimization subproblems are solved. Since they are independent, they can be performed in
parallel. The branch-and-bound process continues, operating on both x5and x6, until a optimization subproblem
is solved where x5and x6are integer-valued. At the solution to this problem, the optimal values for x5and x6
are x5=x6= 1.
In this example problem, the branch-and-bound algorithm executes as few as five and no more than seven opti-
mization subproblems to reach the solution. For comparison, the brute force approach would require 25 optimiza-
tion problems to be solved (i.e., five possible values for each of x5and x6).
In the example given above, the discrete variables are integer-valued. In some cases, the discrete variables may
be real-valued, such as x∈ {0.0,0.5,1.0,1.5,2.0}. The branch-and-bound algorithm is restricted to work with
integer values. Therefore, it is up to the user to perform a transformation between the discrete integer values from
Dakota and the discrete real values that are passed to the simulation code (see Section 9.2.2). When integrality
is not being relaxed, a common mapping is to use the integer value from Dakota as the index into a vector of
discrete real values. However, when integrality is relaxed, additional logic for interpolating between the discrete
real values is needed.
14.6 Surrogate-Based Minimization
Surrogate models approximate an original, high fidelity “truth” model, typically at reduced computational cost. In
Dakota, several surrogate model selections are possible, which are categorized as data fits, multifidelity models,
Dakota Version 6.7 User’s Manual generated on November 13, 2017
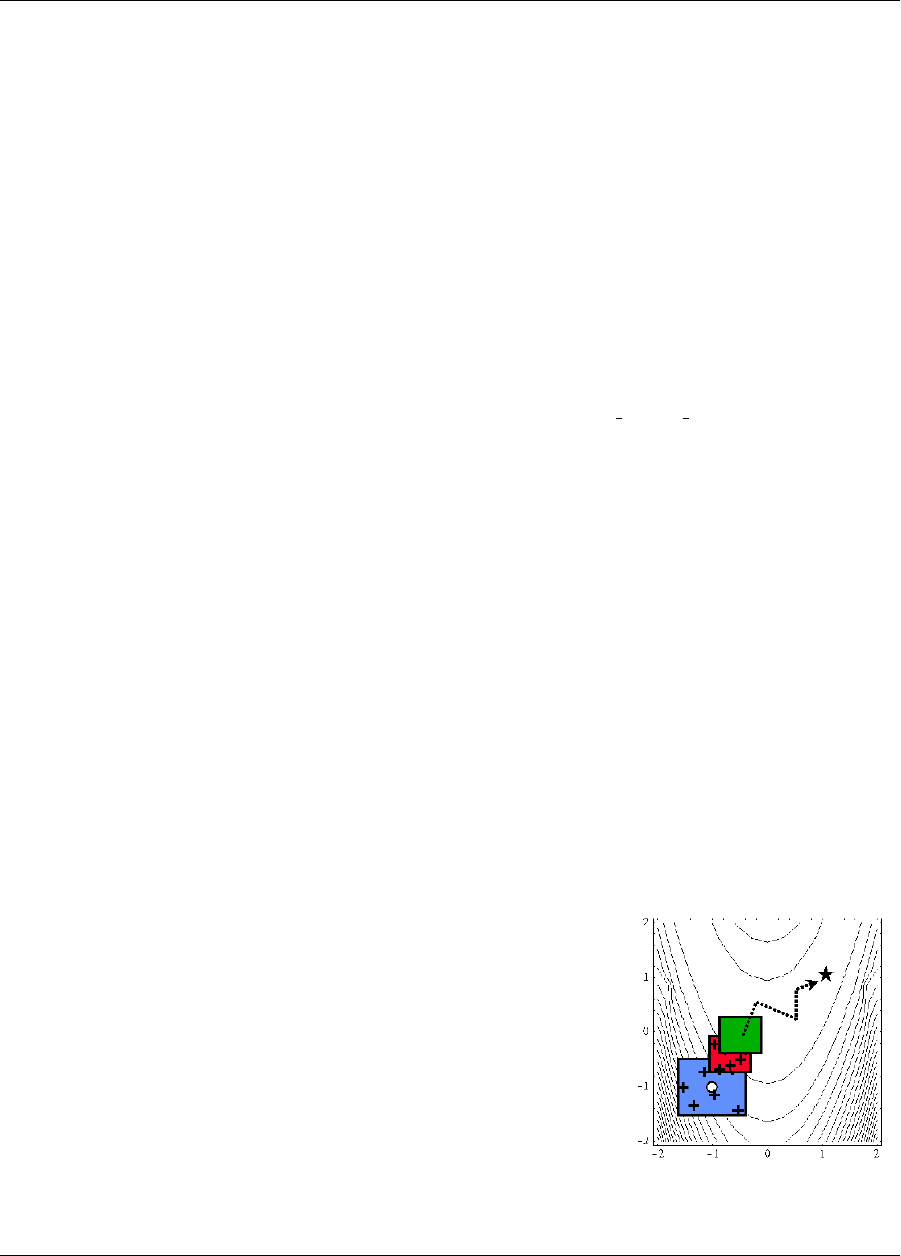
14.6. SURROGATE-BASED MINIMIZATION 241
and reduced-order models, as described in Section 8.4. In the context of minimization (optimization or calibra-
tion), surrogate models can speed convergence by reducing function evaluation cost or smoothing noisy response
functions. Three categories of surrogate-based minimization are discussed in this chapter:
•Trust region-managed surrogate-based local minimization, with data fit surrogate, multifidelity models, or
reduced-order models.
•Surrogate-based global minimization, where a single surrogate is built (and optionally iteratively updated)
over the whole design space.
•Efficient global minimization: nongradient-based constrained and unconstrained optimization and nonlinear
least squares based on Gaussian process models, guided by an expected improvement function.
14.6.1 Surrogate-Based Local Minimization
In the surrogate-based local minimization method (keyword: surrogate based local) the minimization
algorithm operates on a surrogate model instead of directly operating on the computationally expensive simulation
model. The surrogate model can be based on data fits, multifidelity models, or reduced-order models, as described
in Section 8.4. Since the surrogate will generally have a limited range of accuracy, the surrogate-based local
algorithm periodically checks the accuracy of the surrogate model against the original simulation model and
adaptively manages the extent of the approximate optimization cycles using a trust region approach.
Refer to the Dakota Theory Manual [4] for algorithmic details on iterate acceptance, merit function formulations,
convergence assessment, and constraint relaxation.
14.6.1.1 SBO with Data Fits
When performing SBO with local, multipoint, and global data fit surrogates, it is necessary to regenerate or
update the data fit for each new trust region. In the global data fit case, this can mean performing a new design
of experiments on the original high-fidelity model for each trust region, which can effectively limit the approach
to use on problems with, at most, tens of variables. Figure 14.7 displays this case. However, an important benefit
of the global sampling is that the global data fits can tame poorly-behaved, nonsmooth, discontinuous response
variations within the original model into smooth, differentiable, easily navigated surrogates. This allows SBO
with global data fits to extract the relevant global design trends from noisy simulation data.
Figure 14.7: SBO iteration pro-
gression for global data fits.
When enforcing local consistency between a global data fit surrogate and a
high-fidelity model at a point, care must be taken to balance this local con-
sistency requirement with the global accuracy of the surrogate. In particular,
performing a correction on an existing global data fit in order to enforce lo-
cal consistency can skew the data fit and destroy its global accuracy. One
approach for achieving this balance is to include the consistency requirement
within the data fit process by constraining the global data fit calculation (e.g.,
using constrained linear least squares). This allows the data fit to satisfy the
consistency requirement while still addressing global accuracy with its re-
maining degrees of freedom. Embedding the consistency within the data fit
also reduces the sampling requirements. For example, a quadratic polyno-
mial normally requires at least (n+ 1)(n+ 2)/2samples for nvariables
to perform the fit. However, with an embedded first-order consistency con-
straint at a single point, the minimum number of samples is reduced by n+ 1
to (n2+n)/2.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

242 CHAPTER 14. ADVANCED METHODS
In the local and multipoint data fit cases, the iteration progression will appear
as in Fig. 14.9. Both cases involve a single new evaluation of the original
high-fidelity model per trust region, with the distinction that multipoint approximations reuse information from
previous SBO iterates. Like model hierarchy surrogates, these techniques scale to larger numbers of design vari-
ables. Unlike model hierarchy surrogates, they generally do not require surrogate corrections, since the matching
conditions are embedded in the surrogate form (as discussed for the global Taylor series approach above). The
primary disadvantage to these surrogates is that the region of accuracy tends to be smaller than for global data
fits and multifidelity surrogates, requiring more SBO cycles with smaller trust regions. More information on the
design of experiments methods is available in Chapter 4, and the data fit surrogates are described in Section 8.4.3.
Figure 14.8 shows a Dakota input file that implements surrogate-based optimization on Rosenbrock’s function.
The first method keyword block contains the SBO keyword surrogate based local, plus the commands
for specifying the trust region size and scaling factors. The optimization portion of SBO, using the CONMIN
Fletcher-Reeves conjugate gradient method, is specified in the following keyword blocks for method,model,
variables, and responses. The model used by the optimization method specifies that a global surrogate will
be used to map variables into responses (no interface specification is used by the surrogate model). The global
surrogate is constructed using a DACE method which is identified with the ‘SAMPLING’ identifier. This data
sampling portion of SBO is specified in the final set of keyword blocks for method,model,interface, and
responses (the earlier variables specification is reused). This example problem uses the Latin hypercube
sampling method in the LHS software to select 10 design points in each trust region. A single surrogate model
is constructed for the objective function using a quadratic polynomial. The initial trust region is centered at the
design point (x1, x2) = (−1.2,1.0), and extends ±0.4(10% of the global bounds) from this point in the x1and
x2coordinate directions.
If this input file is executed in Dakota, it will converge to the optimal design point at (x1, x2) = (1,1) in ap-
proximately 800 function evaluations. While this solution is correct, it is obtained at a much higher cost than a
traditional gradient-based optimizer (e.g., see the results obtained in Section 2.3.3). This demonstrates that the
SBO method with global data fits is not really intended for use with smooth continuous optimization problems;
direct gradient-based optimization can be more efficient for such applications. Rather, SBO with global data fits
is best-suited for the types of problems that occur in engineering design where the response quantities may be dis-
continuous, nonsmooth, or may have multiple local optima [60]. In these types of engineering design problems,
traditional gradient-based optimizers often are ineffective, whereas global data fits can extract the global trends of
interest despite the presence of local nonsmoothness (for an example problem with multiple local optima, look in
Dakota/test for the file dakota sbo sine fcn.in [61]).
The surrogate-based local minimizer is only mathematically guaranteed to find a local minimum. However, in
practice, SBO can often find the global minimum. Due to the random sampling method used within the SBO
algorithm, the SBO method will solve a given problem a little differently each time it is run (unless the user
specifies a particular random number seed in the dakota input file as is shown in Figure 14.8). Our experience on
the quasi-sine function mentioned above is that if you run this problem 10 times with the same starting conditions
but different seeds, then you will find the global minimum in about 70-80% of the trials. This is good performance
for what is mathematically only a local optimization method.
14.6.1.2 SBO with Multifidelity Models
When performing SBO with model hierarchies, the low-fidelity model is normally fixed, requiring only a single
high-fidelity evaluation to compute a new correction for each new trust region. Figure 14.9 displays this case. This
renders the multifidelity SBO technique more scalable to larger numbers of design variables since the number of
high-fidelity evaluations per iteration (assuming no finite differencing for derivatives) is independent of the scale
of the design problem. However, the ability to smooth poorly-behaved response variations in the high-fidelity
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14.6. SURROGATE-BASED MINIMIZATION 243
# Dakota Input File: rosen_opt_sbo.in
environment
tabular_data
tabular_data_file = ’rosen_opt_sbo.dat’
top_method_pointer = ’SBLO’
method
id_method = ’SBLO’
surrogate_based_local
model_pointer = ’SURROGATE’
method_pointer = ’NLP’
max_iterations = 500
trust_region
initial_size = 0.10
minimum_size = 1.0e-6
contract_threshold = 0.25
expand_threshold = 0.75
contraction_factor = 0.50
expansion_factor = 1.50
method
id_method = ’NLP’
conmin_frcg
max_iterations = 50
convergence_tolerance = 1e-8
model
id_model = ’SURROGATE’
surrogate global
correction additive zeroth_order
polynomial quadratic
dace_method_pointer = ’SAMPLING’
responses_pointer = ’SURROGATE_RESP’
variables
continuous_design = 2
initial_point -1.2 1.0
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ ’x2’
responses
id_responses = ’SURROGATE_RESP’
objective_functions = 1
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 1.e-6
no_hessians
method
id_method = ’SAMPLING’
sampling
samples = 10
seed = 531
sample_type lhs
model_pointer = ’TRUTH’
model
id_model = ’TRUTH’
single
interface_pointer = ’TRUE_FN’
responses_pointer = ’TRUE_RESP’
interface
id_interface = ’TRUE_FN’
analysis_drivers = ’rosenbrock’
direct
deactivate evaluation_cache restart_file
responses
id_responses = ’TRUE_RESP’
objective_functions = 1
no_gradients
no_hessians
Figure 14.8: Dakota input file for the surrogate-based local optimization example – see
Dakota/examples/users/rosen opt sbo.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

244 CHAPTER 14. ADVANCED METHODS
model is lost, and the technique becomes dependent on having a well-behaved low-fidelity model1. In addition, the
parameterizations for the low and high-fidelity models may differ, requiring the use of a mapping between these
parameterizations. Space mapping, corrected space mapping, POD mapping, and hybrid POD space mapping are
being explored for this purpose [112,113].
Figure 14.9: SBO iteration pro-
gression for model hierarchies.
When applying corrections to the low-fidelity model, there is no concern for
balancing global accuracy with the local consistency requirements. However,
with only a single high-fidelity model evaluation at the center of each trust
region, it is critical to use the best correction possible on the low-fidelity
model in order to achieve rapid convergence rates to the optimum of the high-
fidelity model [37].
A multifidelity test problem named dakota sbo hierarchical.in
is available in Dakota/test to demonstrate this SBO approach.
This test problem uses the Rosenbrock function as the high fidelity
model and a function named “lf rosenbrock” as the low fidelity model.
Here, lf rosenbrock is a variant of the Rosenbrock function (see
Dakota Source/test/lf rosenbrock.C for formulation) with the
minimum point at (x1, x2) = (0.80,0.44), whereas the minimum of the orig-
inal Rosenbrock function is (x1, x2) = (1,1). Multifidelity SBO locates the
high-fidelity minimum in 11 high fidelity evaluations for additive second-
order corrections and in 208 high fidelity evaluations for additive first-order
corrections, but fails for zeroth-order additive corrections by converging to
the low-fidelity minimum.
14.6.1.3 SBO with Reduced Order Models
When performing SBO with reduced-order models (ROMs), the ROM is mathematically generated from the high-
fidelity model. A critical issue in this ROM generation is the ability to capture the effect of parametric changes
within the ROM. Two approaches to parametric ROM are extended ROM (E-ROM) and spanning ROM (S-ROM)
techniques [147]. Closely related techniques include tensor singular value decomposition (SVD) methods [92].
In the single-point and multipoint E-ROM cases, the SBO iteration can appear as in Fig. 14.9, whereas in the
S-ROM, global E-ROM, and tensor SVD cases, the SBO iteration will appear as in Fig. 14.7. In addition to the
high-fidelity model analysis requirements, procedures for updating the system matrices and basis vectors are also
required.
Relative to data fits and multifidelity models, ROMs have some attractive advantages. Compared to data fits such
as regression-based polynomial models, they are more physics-based and would be expected to be more predictive
(e.g., in extrapolating away from the immediate data). Compared to multifidelity models, ROMS may be more
practical in that they do not require multiple computational models or meshes which are not always available. The
primary disadvantage is potential invasiveness to the simulation code for projecting the system using the reduced
basis.
14.6.2 Surrogate-Based Global Minimization
Surrogate-based global minimization differs from the surrogate-based local minimization approach discussed in
the previous section in several ways: it is not a trust-region approach; initially there is one global surrogate
1It is also possible to use a hybrid data fit/multifidelity approach in which a smooth data fit of a noisy low fidelity model is used in
combination with a high fidelity model
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14.6. SURROGATE-BASED MINIMIZATION 245
constructed over a set of sample points and the optimizer operates on that surrogate (as opposed to adaptively
selecting points and re-building a surrogate in each trust region); and there is no guarantee of convergence.
The surrogate based global method was developed to address two needs. The first is the case where a
user wishes to use existing function evaluations or a fixed sample size (perhaps based on computational cost and
allocation of resources) to build a surrogate once and optimize on it. In this case (a single global optimization on
a surrogate model), the set of surrogate building points is determined in advance as opposed to the trust-region
local surrogate optimization in which the number of “true” function evaluations depends on the location and size
of the trust region, the goodness of the surrogate within the trust-region, and problem characteristics.
In the second surrogate based global use case, we want to update the surrogate, but globally. That is, we
add points to the sample set used to create the surrogate, rebuild the surrogate, and then perform another global
optimization on the new surrogate. Thus, surrogate-based global optimization can be used in an iterative scheme.
In one iteration, minimizers of the surrogate model are found, and a selected subset of these are passed to the
next iteration. In the next iteration, these surrogate points are evaluated with the “truth” model, and then added
to the set of points upon which the next surrogate is constructed. This presents a more accurate surrogate to the
minimizer at each subsequent iteration, presumably driving to optimality quickly. Note that a global surrogate is
constructed using the same bounds in each iteration. This approach has no guarantee of convergence.
The surrogate-based global method was originally designed for MOGA (a multi-objective genetic algorithm).
Since genetic algorithms often need thousands or tens of thousands of points to produce optimal or near-optimal
solutions, surrogates can help by reducing the necessary truth model evaluations. Instead of creating one set of
surrogates for the individual objectives and running the optimization algorithm on the surrogate once, the idea is
to select points along the (surrogate) Pareto frontier, which can be used to supplement the existing points. In this
way, one does not need to use many points initially to get a very accurate surrogate. The surrogate becomes more
accurate as the iterations progress.
Most single objective optimization methods will return only a single optimal point. In that case, only one point
from the surrogate model will be evaluated with the “true” function and added to the pointset upon which the
surrogate is based. In this case, it will take many iterations of the surrogate-based global optimization for the
approach to converge, and its utility may not be as great as for the multi-objective case when multiple optimal
solutions are passed from one iteration to the next to supplement the surrogate. Note that the user has the option of
appending the optimal points from the surrogate model to the current set of truth points or using the optimal points
from the surrogate model to replace the optimal set of points from the previous iteration. Although appending to
the set is the default behavior, at this time we strongly recommend using the option replace points because
it appears to be more accurate and robust.
When using the surrogate-based global method, we first recommend running one optimization on a single sur-
rogate model. That is, set max iterations to 1. This will allow one to get a sense of where the optima are
located and also what surrogate types are the most accurate to use for the problem. Note that by fixing the seed of
the sample on which the surrogate is built, one can take a Dakota input file, change the surrogate type, and re-run
the problem without any additional function evaluations by specifying the use of the dakota restart file which will
pick up the existing function evaluations, create the new surrogate type, and run the optimization on that new
surrogate. Also note that one can specify that surrogates be built for all primary functions and constraints or for
only a subset of these functions and constraints. This allows one to use a ”truth” model directly for some of the
response functions, perhaps due to them being much less expensive than other functions. Finally, a diagnostic
threshold can be used to stop the method if the surrogate is so poor that it is unlikely to provide useful points. If
the goodness-of-fit has an R-squared value less than 0.5, meaning that less than half the variance of the output can
be explained or accounted for by the surrogate model, the surrogate-based global optimization stops and outputs
an error message. This is an arbitrary threshold, but generally one would want to have an R-squared value as close
to 1.0 as possible, and an R-squared value below 0.5 indicates a very poor fit.
For the surrogate-based global method, we initially recommend a small number of maximum iterations, such as
Dakota Version 6.7 User’s Manual generated on November 13, 2017

246 CHAPTER 14. ADVANCED METHODS
3–5, to get a sense of how the optimization is evolving as the surrogate gets updated globally. If it appears to be
changing significantly, then a larger number (used in combination with restart) may be needed.
Figure 14.10 shows a Dakota input file that implements surrogate-based global optimization on a multi-objective
test function. The first method keyword block contains the keyword surrogate based global, plus the
commands for specifying five as the maximum iterations and the option to replace points in the global surrogate
construction. The method block identified as MOGA specifies a multi-objective genetic algorithm optimizer and
its controls. The model keyword block specifies a surrogate model. In this case, a gaussian process model
is used as a surrogate. The dace method pointer specifies that the surrogate will be build on 100 Latin
Hypercube samples with a seed = 531. The remainder of the input specification deals with the interface to the
actual analysis driver and the 2 responses being returned as objective functions from that driver.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

14.6. SURROGATE-BASED MINIMIZATION 247
# Dakota Input File: mogatest1_opt_sbo.in
environment
tabular_data
tabular_data_file = ’mogatest1_opt_sbo.dat’
top_method_pointer = ’SBGO’
method
id_method = ’SBGO’
surrogate_based_global
model_pointer = ’SURROGATE’
method_pointer = ’MOGA’
max_iterations = 5
replace_points
output verbose
method
id_method = ’MOGA’
moga
seed = 10983
population_size = 300
max_function_evaluations = 5000
initialization_type unique_random
crossover_type shuffle_random
num_offspring = 2 num_parents = 2
crossover_rate = 0.8
mutation_type replace_uniform
mutation_rate = 0.1
fitness_type domination_count
replacement_type below_limit = 6
shrinkage_percentage = 0.9
niching_type distance 0.05 0.05
postprocessor_type
orthogonal_distance 0.05 0.05
convergence_type metric_tracker
percent_change = 0.05 num_generations = 10
output silent
model
id_model = ’SURROGATE’
surrogate global
dace_method_pointer = ’SAMPLING’
correction additive zeroth_order
gaussian_process dakota
method
id_method = ’SAMPLING’
sampling
samples = 100
seed = 531
sample_type lhs
model_pointer = ’TRUTH’
model
id_model = ’TRUTH’
single
interface_pointer = ’TRUE_FN’
variables
continuous_design = 3
initial_point 0 0 0
upper_bounds 4 4 4
lower_bounds -4 -4 -4
descriptors ’x1’ ’x2’ ’x3’
interface
id_interface = ’TRUE_FN’
analysis_drivers = ’mogatest1’
direct
responses
objective_functions = 2
no_gradients
no_hessians
Figure 14.10: MOGA example – see Dakota/examples/users/mogatest1 opt sbo.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

248 CHAPTER 14. ADVANCED METHODS
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 15
Advanced Model Recursions
The surrogate and nested model constructs admit a wide variety of multi-iterator, multi-model solution ap-
proaches. For example, optimization within optimization (for hierarchical multidisciplinary optimization), uncer-
tainty quantification within uncertainty quantification (for interval-valued probability, second-order probability,
or Dempster-Shafer approaches to mixed aleatory-epistemic UQ), uncertainty quantification within optimization
(for optimization under uncertainty), and optimization within uncertainty quantification (for uncertainty of op-
tima) are all supported, with and without surrogate model indirection. Three important examples are highlighted:
mixed aleatory-epistemic UQ, optimization under uncertainty, and surrogate-based UQ.
Starting with Dakota version 6.1, concurrency can now be exploited across sub-iteration instances. For exam-
ple, multiple inner loop UQ assessments can be performed simultaneously within optimization under uncertainty
or mixed aleatory-epistemic UQ studies, provided the outer loop algorithm supports concurrency in its evalua-
tions. Both meta-iterators and nested models support iterator servers,processors per iterator,
and iterator scheduling specifications which can be used to define a parallel configuration that partitions
servers for supporting sub-iteration concurrency. Refer to Chapter 17 for additional information on parallel con-
figurations, and to the Methods and Models chapters of the Reference Manual [3] for additional information on
these specifications.
15.1 Mixed Aleatory-Epistemic UQ
Mixed UQ approaches employ nested models to embed one uncertainty quantification (UQ) within another. The
outer level UQ is commonly linked to epistemic uncertainties (also known as reducible uncertainties) resulting
from a lack of knowledge, and the inner UQ is commonly linked to aleatory uncertainties (also known as irre-
ducible uncertainties) that are inherent in nature. The outer level generates sets of realizations of the epistemic
parameters, and each set of these epistemic parameters in used within a separate inner loop probabilistic analysis
over the aleatory random variables. In this manner, ensembles of aleatory statistics are generated, one set for each
realization of the epistemic parameters.
In Dakota, we support interval-valued probability (IVP), second-order probability (SOP), and Dempster-Shafer
theory of evidence (DSTE) approaches to mixed uncertainty. These three approaches differ in how they treat
the epistemic variables in the outer loop: they are treated as intervals in IVP, as belief structures in DSTE, and
as subjective probability distributions in SOP. This set of techniques provides a spectrum of assumed epistemic
structure, from strongest assumptions in SOP to weakest in IVP.
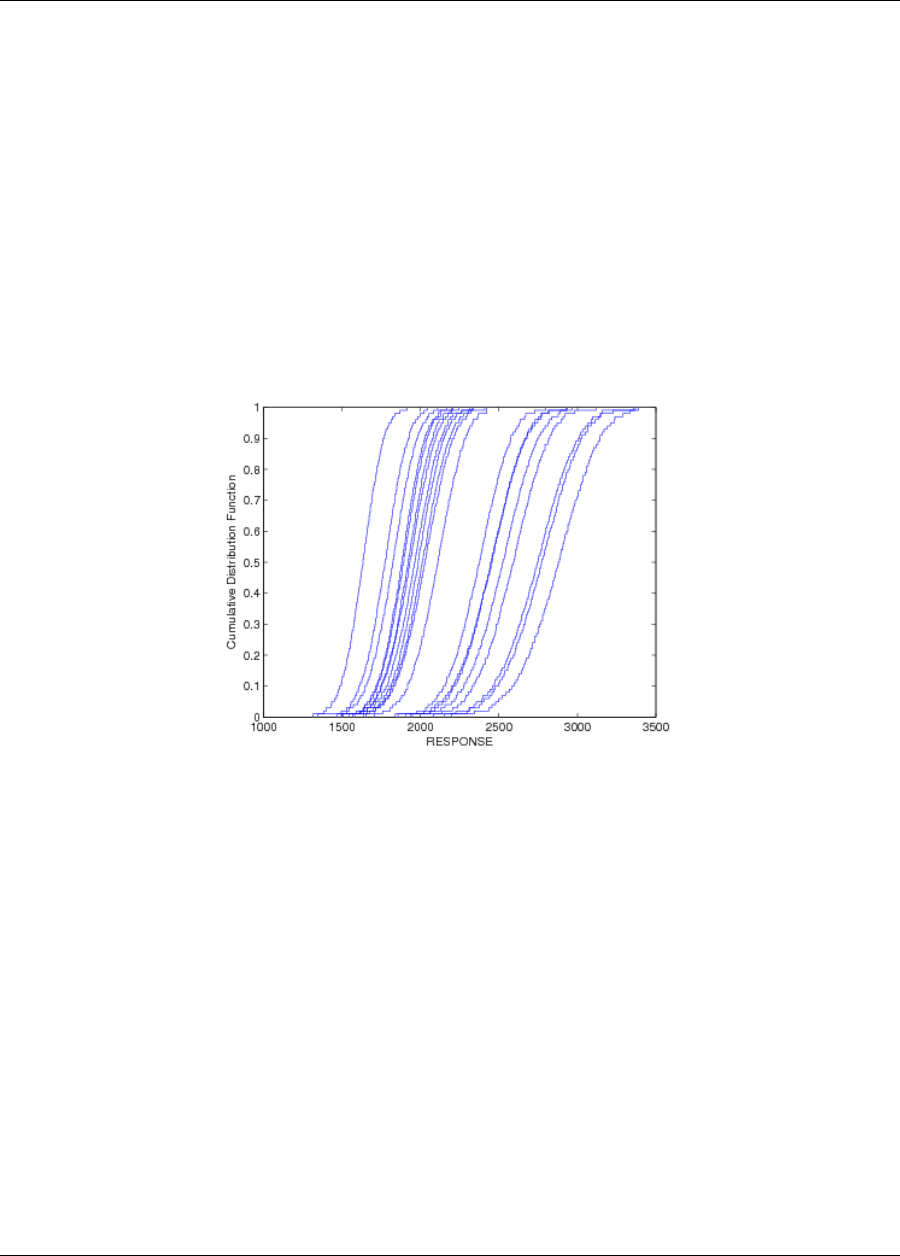
250 CHAPTER 15. ADVANCED MODEL RECURSIONS
15.1.1 Interval-valued probability (IVP)
In IVP (also known as probability bounds analysis [47,85,9]), we employ an outer loop of interval estimation
in combination with an aleatory inner loop. In interval analysis, it is assumed that nothing is known about the
uncertain input variables except that they lie within certain intervals. The problem of uncertainty propagation then
becomes an interval analysis problem: given inputs that are defined within intervals, what are the corresponding
intervals on the outputs?
Starting from a specification of intervals and probability distributions on the inputs, the intervals may augment
the probability distributions, insert into the probability distributions, or some combination (refer to Section 8.5
and to the Models chapter of the Reference Manual [3]). We generate an ensemble of cumulative distribution
functions (CDF) or Complementary Cumulative Distribution Functions (CCDF), one CDF/CCDF result for each
aleatory analysis. Plotting an entire ensemble of CDFs or CCDFs in a “horsetail” plot allows one to visualize
the upper and lower bounds on the family of distributions (see Figure 15.1). Given that the ensemble stems
Figure 15.1: Example CDF ensemble. Commonly referred to as a “horsetail” plot.
from multiple realizations of the epistemic uncertainties, the interpretation is that each CDF/CCDF instance has
no relative probability of occurrence, only that each instance is possible. For prescribed response levels on the
CDF/CCDF, an interval on the probability is computed based on the bounds of the ensemble at that level, and vice
versa for prescribed probability levels. This interval on a statistic is interpreted simply as a possible range, where
the statistic could take any of the possible values in the range.
A sample input file is shown in Figure 15.2, in which the outer epistemic level variables are defined as intervals.
Samples will be generated from these intervals to select means for Xand Ythat are employed in an inner level
reliability analysis of the cantilever problem (see Section 20.7). Figure 15.3 shows excerpts from the resulting
output. In this particular example, the outer loop generates 50 possible realizations of epistemic variables, which
are then sent to the inner loop to calculate statistics such as the mean weight, and cumulative distribution function
for the stress and displacement reliability indices. Thus, the outer loop has 50 possible values for the mean
weight, but since there is no distribution structure on these observations, only the minimum and maximum value
are reported. Similarly, the minimum and maximum values of the CCDF for the stress and displacement reliability
indices are reported.
When performing a mixed aleatory-epistemic analysis, response levels and probability levels should only be
Dakota Version 6.7 User’s Manual generated on November 13, 2017

15.1. MIXED ALEATORY-EPISTEMIC UQ 251
defined in the (inner) aleatory loop. For example, if one wants to generate an interval around possible CDFs
or CCDFS, we suggest defining a number of probability levels in the inner loop (0.1, 0.2, 0.3, etc). For each
epistemic instance, these will be calculated during the inner loop and reported back to the outer loop. In this
way, there will be an ensemble of CDF percentiles (for example) and one will have interval bounds for each of
these percentile levels defined. Finally, although the epistemic variables are often values defining distribution
parameters for the inner loop, they are not required to be: they can just be separate uncertain variables in the
problem.
As compared to aleatory quantities of interest (e.g., mean, variance, probability) that must be integrated over a full
probability domain, we observe that the desired minima and maxima of the output ranges are local point solutions
in the epistemic parameter space, such that we may employ directed optimization techniques to compute these
extrema and potentially avoid the cost of sampling the full epistemic space.
In dakota/test, test input files such as dakota uq cantilever ivp exp.in and
dakota uq short column ivp exp.in replace the outer loop sampling with the local and global interval
optimization methods described in Section 5.7.1. In these cases, we no longer generate horse tails and infer
intervals, but rather compute the desired intervals directly.
15.1.2 Second-order probability (SOP)
SOP is similar to IVP in its segregation of aleatory and epistemic uncertainties and its use of nested iteration.
However, rather than modeling epistemic uncertainty with a single interval per variable and computing interval-
valued statistics, we instead employ subjective probability distributions and compute epistemic statistics on the
aleatory statistics (for example, probabilities on probabilities – the source of the “second-order” terminology [66]).
Now the different hairs of the horsetail shown in Figure 15.1 have a relative probability of occurrence and stronger
inferences may be drawn. In particular, mean, 5th percentile, and 95th percentile probability values are a common
example. Second-order probability is sometimes referred to as probability of frequency (PoF) analysis, referring
to a probabilistic interpretation of the epistemic variables and a frequency interpretation of the aleatory variables.
The PoF terminology is used in a recent National Academy of Sciences report on the Quantification of Margins
and Uncertainties (QMU) [105].
Rather than employing interval estimation techniques at the outer loop in SOP, we instead apply probabilistic
methods, potentially the same ones as used for the aleatory propagation on the inner loop. The previous example
in Figure 15.2 can be modified to define the epistemic outer loop using uniform variables instead of interval
variables (annotated test #1 in dakota/test/dakota uq cantilever sop rel.in). The process of
generating the epistemic values is essentially the same in both cases; however, the interpretation of results is
quite different. In IVP, each “hair” or individual CDF in the horsetail plot in Figure 15.1 would be interpreted as a
possible realization of aleatory uncertainty conditional on a particular epistemic sample realization. The ensemble
then indicates the influence of the epistemic variables (e.g. by how widespread the ensemble is). However, if the
outer loop variables are defined to be uniformly distributed in SOP, then the outer loop results will be reported as
statistics (such as mean and standard deviation) and not merely intervals. It is important to emphasize that these
outer level output statistics are only meaningful to the extent that the outer level input probability specifications
are meaningful (i.e., to the extent that uniform distributions are believed to be representative of the epistemic
variables).
In dakota/test, additional test input files such as dakota uq cantilever sop exp.in and
dakota uq short column sop exp.in explore other outer/inner loop probabilistic analysis combinations,
particulary using stochastic expansion methods.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

252 CHAPTER 15. ADVANCED MODEL RECURSIONS
# Dakota Input File: cantilever_uq_sop_rel.in
environment
top_method_pointer = ’EPISTEMIC’
method
id_method = ’EPISTEMIC’
sampling
samples = 50 seed = 12347
model_pointer = ’EPIST_M’
model
id_model = ’EPIST_M’
nested
sub_method_pointer = ’ALEATORY’
primary_variable_mapping = ’X’ ’Y’
secondary_variable_mapping = ’mean’ ’mean’
primary_response_mapping = 1. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 1. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 1.
variables_pointer = ’EPIST_V’
responses_pointer = ’EPIST_R’
variables
id_variables = ’EPIST_V’
continuous_interval_uncertain = 2
num_intervals = 1 1
interval_probabilities = 1.0 1.0
lower_bounds = 400.0 800.0
upper_bounds = 600.0 1200.0
descriptors ’X_mean’ ’Y_mean’
responses
id_responses = ’EPIST_R’
response_functions = 3
descriptors = ’mean_wt’ ’ccdf_beta_s’ ’ccdf_beta_d’
no_gradients
no_hessians
method
id_method = ’ALEATORY’
local_reliability
mpp_search no_approx
response_levels = 0.0 0.0
num_response_levels = 0 1 1
compute reliabilities
distribution complementary
model_pointer = ’ALEAT_M’
model
id_model = ’ALEAT_M’
single
interface_pointer = ’ALEAT_I’
variables_pointer = ’ALEAT_V’
responses_pointer = ’ALEAT_R’
variables
id_variables = ’ALEAT_V’
continuous_design = 2
initial_point 2.4522 3.8826
descriptors ’w’ ’t’
normal_uncertain = 4
means = 40000. 29.E+6 500. 1000.
std_deviations = 2000. 1.45E+6 100. 100.
descriptors = ’R’ ’E’ ’X’ ’Y’
interface
id_interface = ’ALEAT_I’
analysis_drivers = ’cantilever’
direct
deactivate evaluation_cache restart_file
responses
id_responses = ’ALEAT_R’
response_functions = 3
descriptors = ’weight’ ’stress’ ’displ’
analytic_gradients
no_hessians
Figure 15.2: Dakota input file for the interval-valued probability example – see
Dakota/examples/users/cantilever uq sop rel.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017

15.2. OPTIMIZATION UNDER UNCERTAINTY (OUU) 253
Statistics based on 50 samples:
Min and Max values for each response function:
mean_wt: Min = 9.5209117200e+00 Max = 9.5209117200e+00
ccdf_beta_s: Min = 1.7627715524e+00 Max = 4.2949468386e+00
ccdf_beta_d: Min = 2.0125192955e+00 Max = 3.9385559339e+00
Figure 15.3: Interval-valued statistics for cantilever beam reliability indices.
15.1.3 Dempster-Shafer Theory of Evidence
In IVP, we estimate a single epistemic output interval for each aleatory statistic. This same nested analysis
procedure may be employed within the cell computations of a DSTE approach. Instead of a single interval, we
now compute multiple output intervals, one for each combination of the input basic probability assignments, in
order to define epistemic belief and plausibility functions on the aleatory statistics computed in the inner loop.
While this can significantly increase the computational requirements, belief and plausibility functions provide a
more finely resolved epistemic characterization than a basic output interval.
The single-level DSTE approach for propagating epistemic uncertainties is described in Section 5.7.2 and in the
Dakota Theory Manual [4]. An example of nested DSTE for propagating mixed uncertainties can be seen in
dakota/test in the input file dakota uq ishigami dste exp.in.
15.2 Optimization Under Uncertainty (OUU)
Optimization under uncertainty (OUU) approaches incorporate an uncertainty quantification method within the
optimization process. This is often needed in engineering design problems when one must include the effect of
input parameter uncertainties on the response functions of interest. A typical engineering example of OUU would
minimize the probability of failure of a structure for a set of applied loads, where there is uncertainty in the loads
and/or material properties of the structural components.
In OUU, a nondeterministic method is used to evaluate the effect of uncertain variable distributions on response
functions of interest (refer to Chapter 5for additional information on nondeterministic analysis). Statistics on
these response functions are then included in the objective and constraint functions of an optimization process.
Different UQ methods can have very different features from an optimization perspective, leading to the tailoring
of optimization under uncertainty approaches to particular underlying UQ methodologies.
If the UQ method is sampling based, then three approaches are currently supported: nested OUU, surrogate-based
OUU, and trust-region surrogate-based OUU. Additional details and computational results are provided in [38].
Another class of OUU algorithms is called reliability-based design optimization (RBDO). RBDO methods are
used to perform design optimization accounting for reliability metrics. The reliability analysis capabilities de-
scribed in Section 5.3 provide a rich foundation for exploring a variety of RBDO formulations. [35] investigated
bi-level, fully-analytic bi-level, and first-order sequential RBDO approaches employing underlying first-order
reliability assessments. [36] investigated fully-analytic bi-level and second-order sequential RBDO approaches
employing underlying second-order reliability assessments.
When using stochastic expansions for UQ, analytic moments and analytic design sensitivities can be exploited
as described in [45]. Several approaches for obtaining design sensitivities of statistical metrics are discussed in
Section 15.2.5.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

254 CHAPTER 15. ADVANCED MODEL RECURSIONS
Figure 15.4: Formulation 1: Nested OUU.
Finally, when employing epistemic methods for UQ, the set of statistics available for use within optimization are
interval-based. Robustness metrics typically involve the width of the intervals, and reliability metrics typically
involve the worst case upper or lower bound of the interval.
Each of these OUU methods is overviewed in the following sections.
15.2.1 Nested OUU
In the case of a nested approach, the optimization loop is the outer loop which seeks to optimize a nondeterministic
quantity (e.g., minimize probability of failure). The uncertainty quantification (UQ) inner loop evaluates this
nondeterministic quantity (e.g., computes the probability of failure) for each optimization function evaluation.
Figure 15.4 depicts the nested OUU iteration where dare the design variables, uare the uncertain variables
characterized by probability distributions, ru(d,u)are the response functions from the simulation, and su(d)are
the statistics generated from the uncertainty quantification on these response functions.
Figure 15.5 shows a Dakota input file for a nested OUU example problem that is based on the textbook test
problem. In this example, the objective function contains two probability of failure estimates, and an inequality
constraint contains another probability of failure estimate. For this example, failure is defined to occur when one
of the textbook response functions exceeds its threshold value. The environment keyword block at the top of the
input file identifies this as an OUU problem. The environment keyword block is followed by the optimization
specification, consisting of the optimization method, the continuous design variables, and the response quantities
that will be used by the optimizer. The mapping matrices used for incorporating UQ statistics into the optimization
response data are described in the Dakota Reference Manual [3]. The uncertainty quantification specification
includes the UQ method, the uncertain variable probability distributions, the interface to the simulation code,
and the UQ response attributes. As with other complex Dakota input files, the identification tags given in each
keyword block can be used to follow the relationships among the different keyword blocks.
Latin hypercube sampling is used as the UQ method in this example problem. Thus, each evaluation of the
response functions by the optimizer entails 50 Latin hypercube samples. In general, nested OUU studies can
easily generate several thousand function evaluations and gradient-based optimizers may not perform well due
to noisy or insensitive statistics resulting from under-resolved sampling. These observations motivate the use of
surrogate-based approaches to OUU.
Other nested OUU examples in the dakota/test directory include dakota ouu1 tbch.in, which adds an
additional interface for including deterministic data in the textbook OUU problem, and
dakota ouu1 cantilever.in, which solves the cantilever OUU problem (see Section 20.7) with a nested
approach. For each of these files, the “1” identifies formulation 1, which is short-hand for the nested approach.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

15.2. OPTIMIZATION UNDER UNCERTAINTY (OUU) 255
# Dakota Input File: textbook_opt_ouu1.in
environment
top_method_pointer = ’OPTIM’
method
id_method = ’OPTIM’
npsol_sqp
convergence_tolerance = 1.e-10
model_pointer = ’OPTIM_M’
model
id_model = ’OPTIM_M’
nested
sub_method_pointer = ’UQ’
primary_response_mapping = 0. 0. 1. 0. 0. 1. 0. 0. 0.
secondary_response_mapping = 0. 0. 0. 0. 0. 0. 0. 0. 1.
variables_pointer = ’OPTIM_V’
responses_pointer = ’OPTIM_R’
variables
id_variables = ’OPTIM_V’
continuous_design = 2
initial_point 1.8 1.0
upper_bounds 2.164 4.0
lower_bounds 1.5 0.0
descriptors ’d1’ ’d2’
responses
id_responses = ’OPTIM_R’
objective_functions = 1
nonlinear_inequality_constraints = 1
upper_bounds = .1
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 1.e-1
no_hessians
method
id_method = ’UQ’
sampling
model_pointer = ’UQ_M’
samples = 50 sample_type lhs
seed = 1
response_levels = 3.6e+11 1.2e+05 3.5e+05
distribution complementary
model
id_model = ’UQ_M’
single
interface_pointer = ’UQ_I’
variables_pointer = ’UQ_V’
responses_pointer = ’UQ_R’
variables
id_variables = ’UQ_V’
continuous_design = 2
normal_uncertain = 2
means = 248.89 593.33
std_deviations = 12.4 29.7
descriptors = ’nuv1’ ’nuv2’
uniform_uncertain = 2
lower_bounds = 199.3 474.63
upper_bounds = 298.5 712.
descriptors = ’uuv1’ ’uuv2’
weibull_uncertain = 2
alphas = 12. 30.
betas = 250. 590.
descriptors = ’wuv1’ ’wuv2’
interface
id_interface = ’UQ_I’
analysis_drivers = ’text_book_ouu’
direct
# fork asynch evaluation_concurrency = 5
responses
id_responses = ’UQ_R’
response_functions = 3
no_gradients
no_hessians
Figure 15.5: Dakota input file for the nested OUU example – see
Dakota/examples/users/textbook opt ouu1.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
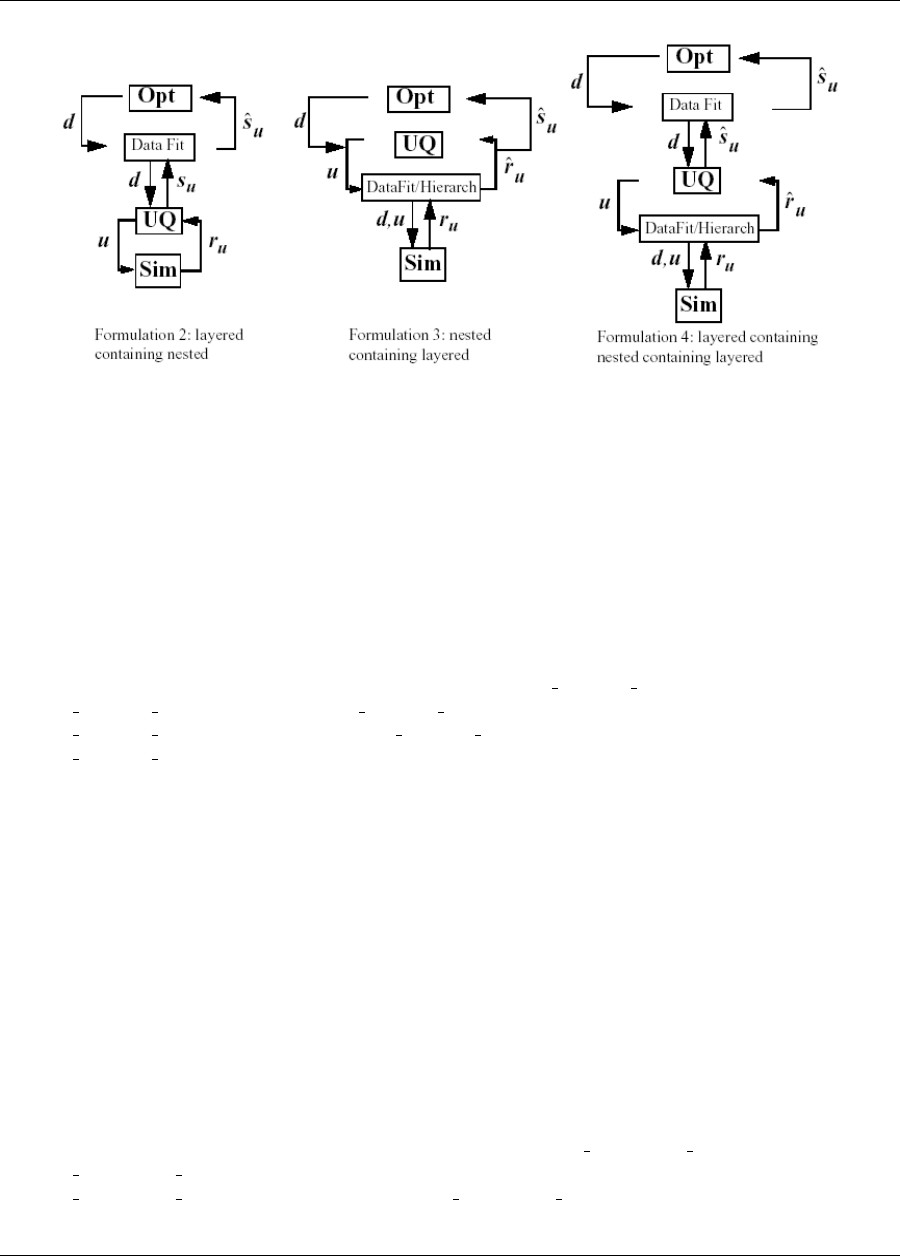
256 CHAPTER 15. ADVANCED MODEL RECURSIONS
Figure 15.6: Formulations 2, 3, and 4 for Surrogate-based OUU.
15.2.2 Surrogate-Based OUU (SBOUU)
Surrogate-based optimization under uncertainty strategies can be effective in reducing the expense of OUU stud-
ies. Possible formulations include use of a surrogate model at the optimization level, at the uncertainty quantifica-
tion level, or at both levels. These surrogate models encompass both data fit surrogates (at the optimization or UQ
level) and model hierarchy surrogates (at the UQ level only). Figure 15.6 depicts the different surrogate-based for-
mulations where ˆruand ˆsuare approximate response functions and approximate response statistics, respectively,
generated from the surrogate models.
SBOUU examples in the dakota/test directory include dakota sbouu2 tbch.in,
dakota sbouu3 tbch.in, and dakota sbouu4 tbch.in, which solve the textbook OUU problem, and
dakota sbouu2 cantilever.in,dakota sbouu3 cantilever.in, and
dakota sbouu4 cantilever.in, which solve the cantilever OUU problem (see Section 20.7). For each
of these files, the “2,” “3,” and “4” identify formulations 2, 3, and 4, which are short-hand for the “layered
containing nested,” “nested containing layered,” and “layered containing nested containing layered” surrogate-
based formulations, respectively. In general, the use of surrogates greatly reduces the computational expense of
these OUU study. However, without restricting and verifying the steps in the approximate optimization cycles,
weaknesses in the data fits can be exploited and poor solutions may be obtained. The need to maintain accuracy
of results leads to the use of trust-region surrogate-based approaches.
15.2.3 Trust-Region Surrogate-Based OUU (TR-SBOUU)
The TR-SBOUU approach applies the trust region logic of deterministic SBO (see Section 14.6.1) to SBOUU.
Trust-region verifications are applicable when surrogates are used at the optimization level, i.e., formulations 2
and 4. As a result of periodic verifications and surrogate rebuilds, these techniques are more expensive than
SBOUU; however they are more reliable in that they maintain the accuracy of results. Relative to nested OUU
(formulation 1), TR-SBOUU tends to be less expensive and less sensitive to initial seed and starting point.
TR-SBOUU examples in the dakota/test directory include dakota trsbouu2 tbch.in and
dakota trsbouu4 tbch.in, which solve the textbook OUU problem, and
dakota trsbouu2 cantilever.in and dakota trsbouu4 cantilever.in, which solve the can-
tilever OUU problem (see Section 20.7).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

15.2. OPTIMIZATION UNDER UNCERTAINTY (OUU) 257
Computational results for several example problems are available in [38].
15.2.4 RBDO
Bi-level and sequential approaches to reliability-based design optimization (RBDO) and their associated sensi-
tivity analysis requirements are described in the Optimization Under Uncertainty chapter of the Dakota Theory
Manual [4].
A number of bi-level RBDO examples are provided in dakota/test. The dakota rbdo cantilever.in,
dakota rbdo short column.in, and dakota rbdo steel column.in input files solve the cantilever
(see Section 20.7), short column (see Section 20.10.4), and steel column (see Section 20.10.5) OUU problems us-
ing a bi-level RBDO approach employing numerical design gradients. The dakota rbdo cantilever analytic.in
and dakota rbdo short column analytic.in input files solve the cantilever and short column OUU
problems using a bi-level RBDO approach with analytic design gradients and first-order limit state approxima-
tions. The dakota rbdo cantilever analytic2.in,dakota rbdo short column analytic2.in,
and dakota rbdo steel column analytic2.in input files also employ analytic design gradients, but are
extended to employ second-order limit state approximations and integrations.
Sequential RBDO examples are also provided in dakota/test. The dakota rbdo cantilever trsb.in
and dakota rbdo short column trsb.in input files solve the cantilever and short column OUU problems
using a first-order sequential RBDO approach with analytic design gradients and first-order limit state approxi-
mations. The dakota rbdo cantilever trsb2.in,dakota rbdo short column trsb2.in, and
dakota rbdo steel column trsb2.in input files utilize second-order sequential RBDO approaches that
employ second-order limit state approximations and integrations (from analytic limit state Hessians with respect
to the uncertain variables) and quasi-Newton approximations to the reliability metric Hessians with respect to
design variables.
15.2.5 Stochastic Expansion-Based Design Optimization
For stochastic expansion-based approaches to optimization under uncertainty, bi-level, sequential, and multifi-
delity approaches and their associated sensitivity analysis requirements are described in the Optimization Under
Uncertainty chapter of the Dakota Theory Manual [4].
In dakota/test, the dakota pcbdo cantilever.in,dakota pcbdo rosenbrock.in,
dakota pcbdo short column.in, and dakota pcbdo steel column.in input files solve cantilever
(see Section 20.7), Rosenbrock, short column (see Section 20.10.4), and steel column (see Section 20.10.5) OUU
problems using a bi-level polynomial chaos-based approach, where the statistical design metrics are reliability
indices based on moment projection (see Mean Value section in Reliability Methods Chapter of Dakota Theory
Manual [4]). The test matrix in the former three input files evaluate design gradients of these reliability indices
using several different approaches: analytic design gradients based on a PCE formed over only over the random
variables, analytic design gradients based on a PCE formed over all variables, numerical design gradients based
on a PCE formed only over the random variables, and numerical design gradients based on a PCE formed over all
variables. In the cases where the expansion is formed over all variables, only a single PCE construction is required
for the complete PCBDO process, whereas the expansions only over the random variables must be recomputed
for each change in design variables. Sensitivities for “augmented” design variables (which are separate from
and augment the random variables) may be handled using either analytic approach; however, sensitivities for
“inserted” design variables (which define distribution parameters for the random variables) must be computed
using dR
dx
dx
ds (refer to Stochastic Sensitivity Analysis section in Optimization Under Uncertainty chapter of Dakota
Theory Manual [4]). Additional test input files include:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

258 CHAPTER 15. ADVANCED MODEL RECURSIONS
•dakota scbdo cantilever.in,dakota scbdo rosenbrock.in,
dakota scbdo short column.in, and dakota scbdo steel column.in input files solve can-
tilever, Rosenbrock, short column, and steel column OUU problems using a bi-level stochastic collocation-
based approach.
•dakota pcbdo cantilever trsb.in,dakota pcbdo rosenbrock trsb.in,
dakota pcbdo short column trsb.in,dakota pcbdo steel column trsb.in,
dakota scbdo cantilever trsb.in,dakota scbdo rosenbrock trsb.in,
dakota scbdo short column trsb.in, and dakota scbdo steel column trsb.in input
files solve cantilever, Rosenbrock, short column, and steel column OUU problems using sequential polyno-
mial chaos-based and stochastic collocation-based approaches.
•dakota pcbdo cantilever mf.in,dakota pcbdo rosenbrock mf.in,
dakota pcbdo short column mf.in,dakota scbdo cantilever mf.in,
dakota scbdo rosenbrock mf.in, and dakota scbdo short column mf.in input files solve
cantilever, Rosenbrock, and short column OUU problems using multifidelity polynomial chaos-based and
stochastic collocation-based approaches.
15.2.6 Epistemic OUU
An emerging capability is optimization under epistemic uncertainty. As described in the Nested Model section of
the Reference Manual [3], epistemic and mixed aleatory/epistemic uncertainty quantification methods generate
lower and upper interval bounds for all requested response, probability, reliability, and generalized reliability level
mappings. Design for robustness in the presence of epistemic uncertainty could simply involve minimizing the
range of these intervals (subtracting lower from upper using the nested model response mappings), and design for
reliability in the presence of epistemic uncertainty could involve controlling the worst case upper or lower bound
of the interval.
We now have the capability to perform epistemic analysis by using interval optimization on the “outer loop” to
calculate bounding statistics of the aleatory uncertainty on the “inner loop.” Preliminary studies [44] have shown
this approach is more efficient and accurate than nested sampling (which was described in Section 15.1.2). This
approach uses an efficient global optimization method for the outer loop and stochastic expansion methods (e.g.
polynomial chaos or stochastic collocation on the inner loop). The interval optimization is described in Sec-
tion 5.7.1. Example input files demonstrating the use of interval estimation for epistemic analysis, specifically in
epistemic-aleatory nesting, are: dakota uq cantilever sop exp.in, and dakota short column sop exp.in.
Both files are in Dakota/test.
15.3 Surrogate-Based Uncertainty Quantification
Many uncertainty quantification (UQ) methods are computationally costly. For example, sampling often requires
many function evaluations to obtain accurate estimates of moments or percentile values of an output distribution.
One approach to overcome the computational cost of sampling is to evaluate the true function (e.g. run the analysis
driver) on a fixed, small set of samples, use these sample evaluations to create a response surface approximation
(e.g. a surrogate model or meta-model) of the underlying “true” function, then perform random sampling (using
thousands or millions of samples) on the approximation to obtain estimates of the mean, variance, and percentiles
of the response.
This approach, called “surrogate-based uncertainty quantification” is easy to do in Dakota, and one can set up
input files to compare the results using no approximation (e.g. determine the mean, variance, and percentiles
Dakota Version 6.7 User’s Manual generated on November 13, 2017

15.3. SURROGATE-BASED UNCERTAINTY QUANTIFICATION 259
of the output directly based on the initial sample values) with the results obtained by sampling a variety of
surrogate approximations. Example input files of a standard UQ analysis based on sampling alone vs. sam-
pling a surrogate are shown in the textbook uq sampling.in and textbook uq surrogate.in in the
Dakota/examples/users directory.
Note that one must exercise some caution when using surrogate-based methods for uncertainty quantification.
In general, there is not a single, straightforward approach to incorporate the error of the surrogate fit into the
uncertainty estimates of the output produced by sampling the surrogate. Two references which discuss some of the
related issues are [62] and [130]. The first reference shows that statistics of a response based on a surrogate model
were less accurate, and sometimes biased, for surrogates constructed on very small sample sizes. In many cases,
however, [62] shows that surrogate-based UQ performs well and sometimes generates more accurate estimates
of statistical quantities on the output. The second reference goes into more detail about the interaction between
sample type and response surface type (e.g., are some response surfaces more accurate when constructed on a
particular sample type such as LHS vs. an orthogonal array?) In general, there is not a strong dependence of the
surrogate performance with respect to sample type, but some sample types perform better with respect to some
metrics and not others (for example, a Hammersley sample may do well at lowering root mean square error of the
surrogate fit but perform poorly at lowering the maximum absolute deviation of the error). Much of this work is
empirical and application dependent. If you choose to use surrogates in uncertainty quantification, we strongly
recommend trying a variety of surrogates and examining diagnostic goodness-of-fit metrics.
Known Issue: When using discrete variables, there have been sometimes significant differences in data fit surro-
gate behavior observed across computing platforms in some cases. The cause has not yet been fully diagnosed
and is currently under investigation. In addition, guidance on appropriate construction and use of surrogates with
discrete variables is under development. In the meantime, users should therefore be aware that there is a risk of
inaccurate results when using surrogates with discrete variables.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

260 CHAPTER 15. ADVANCED MODEL RECURSIONS
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 16
Advanced Simulation Code Interfaces
This chapter extends the interface discussion in Chapter 10 and its discussion of generic black-box interfaces to
simulations (Section 10.3). It describes specialized, tightly integrated, and advanced interfaces through which
Dakota can perform function evaluation mappings. It describes AMPL-based algebraic mappings (Section 16.1),
tight integration of a simulation code into Dakota (Section 16.2), and specialized interfaces to Matlab, Python,
and Scilab (Sections 16.3 and 16.4).
16.1 Algebraic Mappings
If desired, one can define algebraic input-output mappings using the AMPL code [49] and save these mappings
in 3 files: stub.nl,stub.col, and stub.row, where stub is a particular root name describing a particular
problem. These files names can be communicated to Dakota using the algebraic mappings input.
Dakota will use stub.col and stub.row to obtain input and output identifier strings, respectively, and will
use the AMPL solver library [52] to evaluate expressions conveyed in stub.nl, and, if needed, their first and
second derivatives.
As a simple example (from Dakota/test/dakota ampl*), consider algebraic mappings based on Newton’s
law F=ma. The following is an AMPL input file of variable and expression declarations and output commands:
var mass;
var a;
var v;
minimize force: mass*a;
minimize energy: 0.5 *mass *vˆ2;
option auxfiles rc; # request stub.row and stub.col
write gfma; # write stub.nl, stub.row, stub.col
When processed by an AMPL processor, three files are created (as requested by the “option auxfiles” command).
The first is the dakota ampl fma.nl file containing problem statistics, expression graphs, bounds, etc.:

262 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
g3 0 1 0 # problem fma
3 0 2 0 0 # vars, constraints, objectives, ranges, eqns
0 2 # nonlinear constraints, objectives
0 0 # network constraints: nonlinear, linear
0 3 0 # nonlinear vars in constraints, objectives, both
0 0 0 1 # linear network variables; functions; arith, flags
0 0 0 0 0 # discrete variables: binary, integer, nonlinear (b,c,o)
0 4 # nonzeros in Jacobian, gradients
6 4 # max name lengths: constraints, variables
0 0 0 0 0 # common exprs: b,c,o,c1,o1
O0 0
o2
v0
v1
O1 0
o2
o2
n0.5
v0
o5
v2
n2
b
3
3
3
k2
0
0
G0 2
0 0
1 0
G1 2
0 0
2 0
Next, the dakota ampl fma.col file contains the set of variable descriptor strings:
mass
a
v
and the dakota ampl fma.row file contains the set of response descriptor strings:
force
energy
The variable and objective function names declared within AMPL should be a subset of the variable descriptors
and response descriptors used by Dakota (see the Dakota Reference Manual [3] for information on Dakota variable
and response descriptors). Ordering of the inputs and outputs within the AMPL declaration is not important, as
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16.1. ALGEBRAIC MAPPINGS 263
Dakota will reorder data as needed. The following listing shows an excerpt from Dakota/test/dakota ampl fma.in,
which demonstrates a combined algebraic/simulation-based mapping in which algebraic mappings from the fma
definition are overlaid with simulation-based mappings from text book:
variables,
continuous_design = 5
descriptor ’x1’ ’mass’ ’a’ ’x4’ ’v’
initial_point 0.0 2.0 1.0 0.0 3.0
lower_bounds -3.0 0.0 -5.0 -3.0 -5.0
upper_bounds 3.0 10.0 5.0 3.0 5.0
interface,
algebraic_mappings = ’dakota_ampl_fma.nl’
system
analysis_driver = ’text_book’
parameters_file = ’tb.in’
results_file = ’tb.out’
file_tag
responses,
response_descriptors = ’force’ ’ineq1’ ’energy’
num_objective_functions = 1
num_nonlinear_inequality_constraints = 1
num_nonlinear_equality_constraints = 1
nonlinear_equality_targets = 20.0
analytic_gradients
no_hessians
Note that the algebraic inputs and outputs are a subset of the total inputs and outputs and that Dakota will track
the algebraic contributions to the total response set using the order of the descriptor strings. In the case where
both the algebraic and simulation-based components contribute to the same function, they are added together.
To solve text book algebraically (refer to Section 20.1 for definition), the following AMPL model file could
be used
Dakota Version 6.7 User’s Manual generated on November 13, 2017

264 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
# Problem : Textbook problem used in DAKOTA testing
# Constrained quartic, 2 continuous variables
# Solution: x=(0.5, 0.5), obj = .125, c1 = 0, c2 = 0
#
# continuous variables
var x1 >= 0.5 <= 5.8 := 0.9;
var x2 >= -2.9 <= 2.9 := 1.1;
# objective function
minimize obj: (x1 - 1)ˆ4 + (x2 - 1)ˆ4;
# constraints (current required syntax for DAKOTA/AMPL interface)
minimize c1: x1ˆ2 - 0.5*x2;
minimize c2: x2ˆ2 - 0.5*x1;
# required for output of *.row and *.col files
option auxfiles rc;
Note that the nonlinear constraints should not currently be declared as constraints within AMPL. Since the Dakota
variable bounds and constraint bounds/targets currently take precedence over any AMPL specification, the current
approach is to declare all AMPL outputs as objective functions and then map them into the appropriate response
function type (objectives, least squares terms, nonlinear inequality/equality constraints, or generic response func-
tions) within the Dakota input specification.
16.2 Developing a Direct Simulation Interface
If a more efficient interface to a simulation is desired (e.g., to eliminate process creation and file I/O overhead) or
if a targeted computer architecture cannot accommodate separate optimization and simulation processes (e.g., due
to lightweight operating systems on compute nodes of large parallel computers), then linking a simulation code
directly with Dakota may be desirable. This is an advanced capability of Dakota, and it requires a user to have
access to (and knowledge of) the Dakota source code, as well as the source code of the simulation code.
Three approaches are outlined below for developing direct linking between Dakota and a simulation: extension,
derivation, and sandwich. For additional information, refer to “Interfacing with Dakota as a Library” in the Dakota
Developers Manual [2].
Once performed, Dakota can bind with the new direct simulation interface using the direct interface specifi-
cation in combination with an analysis driver,input filter or output filter specification that
corresponds to the name of the new subroutine.
16.2.1 Extension
The first approach to using the direct function capability with a new simulation (or new internal test function)
involves extension of the existing DirectFnApplicInterface class to include new simulation member functions.
In this case, the following steps are performed:
1. The functions to be invoked (analysis programs, input and output filters, internal testers) must have their
main programs changed into callable functions/subroutines.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16.2. DEVELOPING A DIRECT SIMULATION INTERFACE 265
2. The resulting callable function can then be added directly to the private member functions in DirectF-
nApplicInterface if this function will directly access the Dakota data structures (variables, active set, and
response attributes of the class). It is more common to add a wrapper function to DirectFnApplicInter-
face which manages the Dakota data structures, but allows the simulator subroutine to retain a level of
independence from Dakota (see Salinas, ModelCenter, and Matlab wrappers as examples).
3. The if-else blocks in the derived map if(),derived map ac(), and derived map of() member functions of
the DirectFnApplicInterface class must be extended to include the new function names as options. If the
new functions are class member functions, then Dakota data access may be performed through the existing
class member attributes and data objects do not need to be passed through the function parameter list. In
this case, the following function prototype is appropriate:
int function_name();
If, however, the new function names are not members of the DirectFnApplicInterface class, then an
extern declaration may additionally be needed and the function prototype should include passing of
the Variables, ActiveSet, and Response data members:
int function_name(const Dakota::Variables& vars,
const Dakota::ActiveSet& set, Dakota::Response& response);
4. The Dakota system must be recompiled and linked with the new function object files or libraries.
Various header files may have to be included, particularly within the DirectFnApplicInterface class, in order
to recognize new external functions and compile successfully. Refer to the Dakota Developers Manual [2] for
additional information on the DirectFnApplicInterface class and the Dakota data types.
16.2.2 Derivation
As described in “Interfacing with Dakota as a Library” in the Dakota Developers Manual [2], a derivation approach
can be employed to further increase the level of independence between Dakota and the host application. In
this case, rather than adding a new function to the existing DirectFnApplicInterface class, a new interface
class is derived from DirectFnApplicInterface which redefines the derived map if(),derived map ac(), and
derived map of() virtual functions.
In the approach of Section 16.2.3 below, the class derivation approach avoids the need to recompile the Dakota
library when the simulation or its direct interface class is modified.
16.2.3 Sandwich
In a “sandwich” implementation, a simulator provides both the “front end” and “back end” with Dakota sand-
wiched in the middle. To accomplish this approach, the simulation code is responsible for interacting with the
user (the front end), links Dakota in as a library (refer to “Interfacing with Dakota as a Library” in the Dakota
Developers Manual [2]), and plugs in a derived direct interface class to provide a closely-coupled mechanism for
performing function evaluations (the back end). This approach makes Dakota services available to other codes
and frameworks and is currently used by Sandia codes such as Xyce (electrical simulation), Sage (CFD), and
SIERRA (multiphysics).
Dakota Version 6.7 User’s Manual generated on November 13, 2017
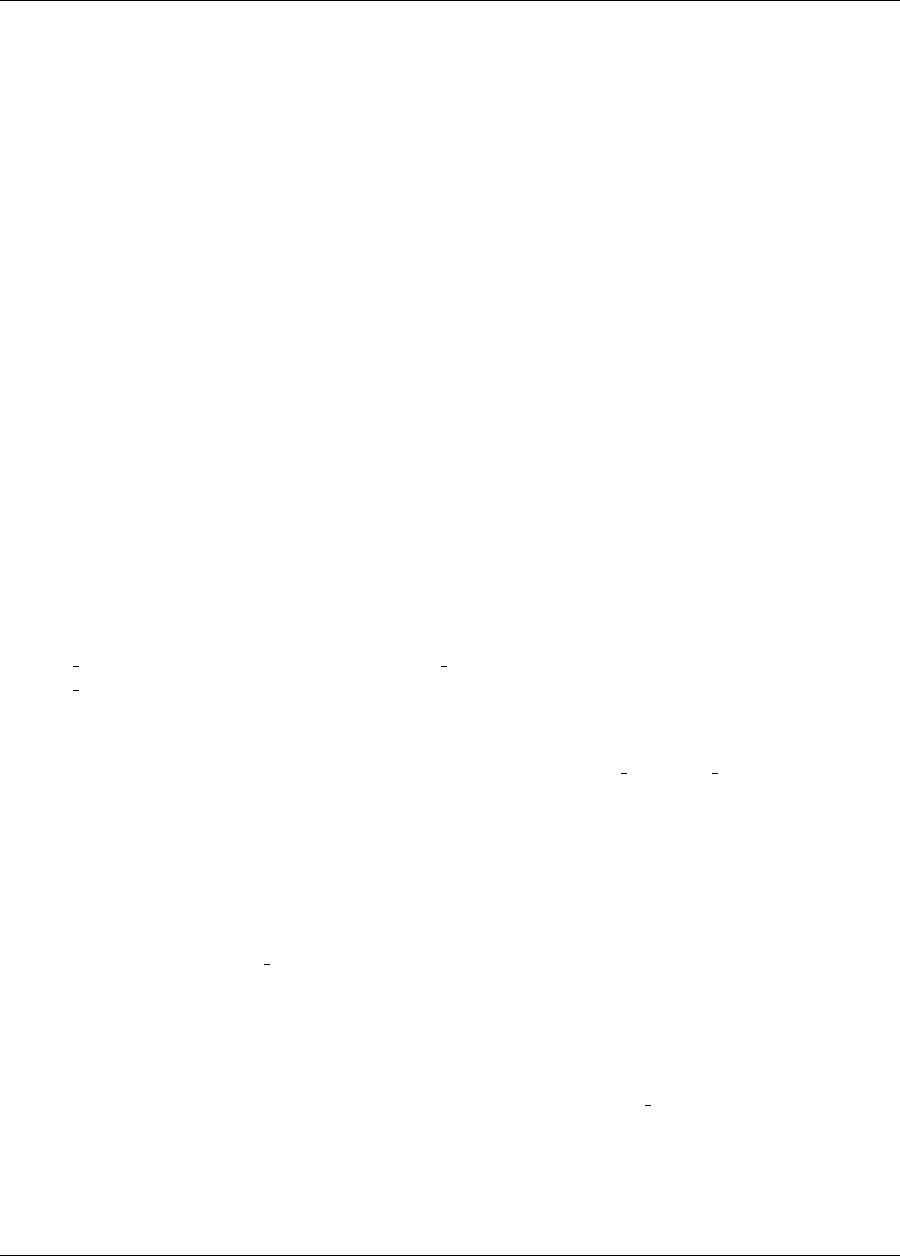
266 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
16.3 Existing Direct Interfaces to External Simulators
In addition to built-in polynomial test functions described in Section 10.2.1, Dakota includes direct interfaces to
Sandia’s Salinas code for structural dynamics, Phoenix Integration’s ModelCenter framework, The Mathworks’
Matlab scientific computing environment, Scilab (as described in Section 16.4), and Python. While these can be
interfaced to with a script-based approach, some usability and efficiency gains may be realized by re-compiling
Dakota with these direct interfaces enabled. Some details on Matlab and Python interfaces are provided here.
Note that these capabilities permit using Matlab or Python to evaluate a parameter to response mapping; they do
not make Dakota algorithms available as a service, i.e., as a Matlab toolbox or Python module.
16.3.1 Matlab
Dakota’s direct function interface includes the capability to invoke Matlab for function evaluations, using the
Matlab engine API. When using this close-coupling, the Matlab engine is started once when Dakota initializes,
and then during analysis function evaluations are performed exchanging parameters and results through the Matlab
C API. This eliminates the need to use the file system and the expense of initializing the Matlab engine for each
function evaluation.
The Dakota/Matlab interface has been built and tested on 32-bit Linux with Matlab 7.0 (R14) and on 64-bit Linux
with Matlab 7.1 (R14SP3). Configuration support for other platforms is included, but is untested. Builds on other
platforms or with other versions of Matlab may require modifications to Dakota including its build system
To use the Dakota/Matlab interface, Dakota must be configured and compiled with the Matlab feature enabled.
The Mathworks only provides shared object libraries for its engine API, so Dakota must be dynamically linked
to at least the Matlab libraries. To compile Dakota with the Matlab interface enabled, set the CMake variable
DAKOTA MATLAB:BOOL=ON, possibly with MATLAB DIR:FILEPATH=/path/to/matlab, where
MATLAB DIR is the root of your Matlab installation (it should be a directory containing directories bin/YOUR-
PLATFORM and extern/include).
Since the Matlab libraries are linked dynamically, they must be accessible at compile time and at run time. Make
sure the path to the appropriate Matlab shared object libraries is on your LD LIBRARY PATH. For example to
accomplish this in BASH on 32-bit Linux, one might type
export LD_LIBRARY_PATH=/usr/local/matlab/bin/glnx86:$LD_LIBRARY_PATH
or add such a command to the .bashrc file. Then proceed with compiling as usual.
Example files corresponding to the following tutorial are available in
Dakota/examples/linked interfaces/Matlab.
16.3.1.1 Dakota/Matlab input file specification
The Matlab direct interface is specified with direct, matlab keywords in an interface specification. The
Matlab m-file which performs the analysis is specified through the analysis drivers keyword. Here is a
sample Dakota interface specification:
interface,
matlab
analysis_drivers = ’myanalysis.m’
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16.3. EXISTING DIRECT INTERFACES TO EXTERNAL SIMULATORS 267
Dakota.
numFns number of functions (responses, constraints)
numVars total number of variables
numACV number active continuous variables
numADIV number active discrete integer variables
numADRV number active discrete real variables
numDerivVars number of derivative variables specified in directFnDVV
xC continuous variable values ([1 x numACV])
xDI discrete integer variable values ([1 x numADIV])
xDR discrete real variable values ([1 x numADRV])
xCLabels continuous var labels (cell array of numACV strings)
xDILabels discrete integer var labels (cell array of numADIV strings)
xDRLabels discrete real var labels (cell array of numADIV strings)
directFnASV active set vector ([1 x numFns])
directFnDVV derivative variables vector ([1 x numDerivVars])
fnFlag nonzero if function values requested
gradFlag nonzero if gradients requested
hessFlag nonzero if hessians requested
currEvalId current evaluation ID
Figure 16.1: Dakota/Matlab parameter data structure.
Multiple Matlab analysis drivers are supported. Multiple analysis components are supported as for other interfaces
as described in Section 10.4. The .m extension in the analysis drivers specification is optional and will be
stripped by the interface before invoking the function. So myanalysis and myanalysis.m will both cause
the interface to attempt to execute a Matlab function myanalysis for the evaluation.
16.3.1.2 Matlab .m file specification
The Matlab analysis file myanalysis.m must define a Matlab function that accepts a Matlab structure as its
sole argument and returns the same structure in a variable called Dakota. A manual execution of the call to the
analysis in Matlab should therefore look like:
>> Dakota = myanalysis(Dakota)
Note that the structure named Dakota will be pushed into the Matlab workspace before the analysis function is
called. The structure passed from Dakota to the analysis m-function contains essentially the same information that
would be passed to a Dakota direct function included in DirectApplicInterface.C, with fields shown in
Figure 16.1.
The structure Dakota returned from the analysis must contain a subset of the fields shown in Figure 16.2. It
may contain additional fields and in fact is permitted to be the structure passed in, augmented with any required
outputs.
An example Matlab analysis driver rosenbrock.m for the Rosenbrock function is shown in Figure 16.3.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

268 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
Dakota.
fnVals ([1 x numFns], required if function values requested)
fnGrads ([numFns x numDerivVars], required if gradients requested)
fnHessians ([numFns x numDerivVars x numDerivVars],
required if hessians requested)
fnLabels (cell array of numFns strings, optional)
failure (optional: zero indicates success, nonzero failure
Figure 16.2: Dakota/Matlab response data structure.
16.3.2 Python
Dakota’s Python direct interface has been tested on Linux with Python 2.x. When enabled, it allows Dakota to
make function evaluation calls directly to an analysis function in a user-provided Python module. Data may flow
between Dakota and Python either in multiply-subscripted lists or NumPy arrays.
The Python direct interface must be enabled when compiling Dakota. Set the CMake variable
DAKOTA PYTHON:BOOL=ON, and optionally DAKOTA PYTHON NUMPY:BOOL=ON (default is ON) to use Dakota’s
NumPy array interface (requires NumPy installation providing arrayobject.h). If NumPy is not enabled, Dakota
will use multiply-subscripted lists for data flow.
An example of using the Python direct interface with both lists and arrays is included in
Dakota/examples/linked interfaces/Python. The Python direct driver is selected with, for exam-
ple,
interface,
python
# numpy
analysis_drivers = ’python_module:analysis_function’
where python module denotes the module (file python module.py) Dakota will attempt to import into the
Python environment and analysis function denotes the function to call when evaluating a parameter set. If
the Python module is not in the directory from which Dakota is started, setting the PYTHONPATH environment
variable to include its location can help the Python engine find it. The optional numpy keyword indicates Dakota
will communicate with the Python analysis function using numarray data structures instead of the default lists.
Whether using the list or array interface, data from Dakota is passed (via kwargs) into the user function in a
dictionary containing the entries shown in Table 16.1. The analysis function must return a dictionary
containing the data specified by the active set vector with fields “fns”, “fnGrads”, and “fnHessians”, corresponding
to function values, gradients, and Hessians, respectively. The function may optionally include a failure code in
“failure” (zero indicates success, nonzero failure) and function labels in “fnLabels”. See the linked interfaces
example referenced above for more details.
16.4 Scilab Script and Direct Interfaces
Scilab is open source computation software which can be used to perform function evaluations during Dakota
studies, for example to calculate the objective function in optimization. Dakota includes three Scilab interface
variants: scripted, linked, and compiled. In each mode, Dakota calls Scilab to perform a function evaluation and
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16.4. SCILAB SCRIPT AND DIRECT INTERFACES 269
function Dakota = rosenbrock(Dakota)
Dakota.failure = 0;
if ( Dakota.numVars ˜= 2 | Dakota.numADV | ...
( ˜isempty( find(Dakota.directFnASM(2,:)) | ...
find(Dakota.directFnASM(3,:)) ) & Dakota.numDerivVars ˜= 2 ) )
sprintf(’Error: Bad number of variables in rosenbrock.m fn.\n’);
Dakota.failure = 1;
elseif (Dakota.numFns > 2)
% 1 fn -> opt, 2 fns -> least sq
sprintf(’Error: Bad number of functions in rosenbrock.m fn.\n’);
Dakota.failure = 1;
else
if Dakota.numFns > 1
least_sq_flag = true;
else
least_sq_flag = false;
end
f0 = Dakota.xC(2)-Dakota.xC(1)*Dakota.xC(1);
f1 = 1.-Dakota.xC(1);
%**** f:
if (least_sq_flag)
if Dakota.directFnASM(1,1)
Dakota.fnVals(1) = 10*f0;
end
if Dakota.directFnASM(1,2)
Dakota.fnVals(2) = f1;
end
else
if Dakota.directFnASM(1,1)
Dakota.fnVals(1) = 100.*f0*f0+f1*f1;
end
end
%**** df/dx:
if (least_sq_flag)
if Dakota.directFnASM(2,1)
Dakota.fnGrads(1,1) = -20.*Dakota.xC(1);
Dakota.fnGrads(1,2) = 10.;
end
if Dakota.directFnASM(2,2)
Dakota.fnGrads(2,1) = -1.;
Dakota.fnGrads(2,2) = 0.;
end
else
if Dakota.directFnASM(2,1)
Dakota.fnGrads(1,1) = -400.*f0*Dakota.xC(1) - 2.*f1;
Dakota.fnGrads(1,2) = 200.*f0;
end
end
%**** dˆ2f/dxˆ2:
if (least_sq_flag)
if Dakota.directFnASM(3,1)
Dakota.fnHessians(1,1,1) = -20.;
Dakota.fnHessians(1,1,2) = 0.;
Dakota.fnHessians(1,2,1) = 0.;
Dakota.fnHessians(1,2,2) = 0.;
end
if Dakota.directFnASM(3,2)
Dakota.fnHessians(2,1:2,1:2) = 0.;
end
else
if Dakota.directFnASM(3,1)
fx = Dakota.xC(2) - 3.*Dakota.xC(1)*Dakota.xC(1);
Dakota.fnHessians(1,1,1) = -400.*fx + 2.0;
Dakota.fnHessians(1,1,2) = -400.*Dakota.xC(1);
Dakota.fnHessians(1,2,1) = -400.*Dakota.xC(1);
Dakota.fnHessians(1,2,2) = 200.;
end
end
Dakota.fnLabels = {’f1’};
end
Figure 16.3: Sample Matlab implementation of the Rosenbrock test function for the Dakota/Matlab interface.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
270 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
Table 16.1: Data dictionary passed to Python direct interface.
Entry Name Description
functions number of functions (responses, constraints)
variables total number of variables
cv list/array of continuous variable values
div list/array of discrete integer variable values
drv list/array of discrete real variable values
av single list/array of all variable values
cv labels continuous variable labels
div labels discrete integer variable labels
drv labels discrete real variable labels
av labels all variable labels
asv active set vector
dvv derivative variables vector
analysis components list of analysis components as strings
currEvalId current evaluation ID number
then retrieves the Scilab results. Dakota’s Scilab interface was contributed in 2011 by Yann Collette and Yann
Chapalain. The Dakota/Scilab interface variants are described next.
16.4.1 Scilab Script Interface
Dakota distributions include a directory Dakota/examples/script interfaces/Scilab which demon-
strates script-based interfacing to Scilab. The Rosenbrock subdirectory contains four notable files:
•dakota scilab rosenbrock.in (the Dakota input file),
•rosenbrock.sci (the Scilab computation code),
•scilab rosen bb simulator.sh (the analysis driver), and
•scilab rosen wrapper.sci (Scilab script).
The dakota scilab rosenbrock.in file specifies the Dakota study to perform. The interface type is ex-
ternal (fork) and the shell script scilab rosen bb simulator.sh is the analysis driver used to perform
function evaluations.
The Scilab file rosenbrock.sci accepts variable values and computes the objective, gradient, and Hessian
values of the Rosenbrock function as requested by Dakota.
The scilab rosen bb simulator.sh is a short shell driver script, like that described in Section 10.3, that
Dakota executes to perform each function evaluation. Dakota passes the names of the parameters and results
files to this script as $argv[1] and $argv[2], respectively. The scilab rosen bb simulator.sh is
divided into three parts: pre-processing, analysis, and post-processing.
In the analysis portion, the scilab rosen bb simulator.sh uses scilab rosen wrapper.sci to
extract the current variable values from the input parameters file ($argv[1]) and communicate them to the
computation code in rosenbrock.sci. The resulting objective function is transmitted to Dakota via the output
result file ($argv[1]), and the driver script cleans up any temporary files.
The directory also includes PID and FemTRUSS examples, which are run in a similar way.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

16.4. SCILAB SCRIPT AND DIRECT INTERFACES 271
16.4.2 Scilab Linked Interface
The Dakota/Scilab linked interface allows Dakota to communicate directly with Scilab through in-memory data
structures, typically resulting in faster communication, as it does not rely on files or pipes. In this mode, Dakota
publishes a data structure into the Scilab workspace, and then invokes the specified Scilab analysis driver directly.
In Scilab, this structure is an mlist (http://help.scilab.org/docs/5.3.2/en_US/mlist.html),
with the same fields as in the Matlab interface 16.1, with the addition of a field dakota type, which is used to
validate the names of fields in the data structure.
The linked interface is implemented in source files src/ScilabInterface.[CH] directory, and must be
enabled at compile time when building Dakota from source by setting DAKOTA SCILAB:BOOL=ON, and setting
appropriate environment variables at compile and run time as described in README.Scilab in
Dakota/examples/linked interfaces/Scilab/. This directory also contains examples for the Rosen-
brock and PID problems.
These examples are similar to those in Dakota/examples/script interfaces, with a few notable ex-
ceptions:
1. There is no shell driver script
2. The Dakota input file specifies the interface as ’scilab’, indicating a direct, internal interface to Scilab using
the Dakota data structure described above:
interface,
scilab
analysis_driver = ’rosenbrock.sci’
16.4.3 Scilab Compiled Interface
In “compiled interface” mode, the Dakota analysis driver is a lightweight shim, which communicates with the run-
ning application code such as Scilab via named pipes. It is similar to that for Matlab in Dakota/examples/compiled interfaces/Matlab,
whose README is likely instructive. An example of a Scilab compiled interface is included in
Dakota/examples/compiled interfaces/Scilab/Rosenbrock.
As with the other Scilab examples, there are computation code and Dakota input files. Note the difference in
the Dakota input file rosenbrock.in, where the analysis driver starts the dakscilab shim program and always
evaluates functions, gradients, and Hessians.
interface,
fork
analysis_driver = ’../dakscilab -d -fp "exec fp.sci" -fpp "exec fpp.sci"’
parameters_file = ’r.in’
results_file = ’r.out’
deactivate active_set_vector
The dakscilab executable results from compiling dakscilab.c and has the following behavior and options.
The driver dakscilab launches a server. This server then facilitates communication between Dakota and Scilab via
named pipes communication. The user can also use the first named pipe (${DAKSCILAB PIPE}1) to commu-
nicate with the server:
echo dbg scilab_script.sce > ${DAKSCILAB_PIPE}1
echo quit > ${DAKSCILAB_PIPE}1
Dakota Version 6.7 User’s Manual generated on November 13, 2017

272 CHAPTER 16. ADVANCED SIMULATION CODE INTERFACES
The first command, with the keyword ’dbg’, launches the script scilab script.sci for evaluation in Scilab. It permits
to give instructions to Scilab. The second command ’quit’ stops the server.
The dakscilab shim supports the following options for the driver call:
1. -s to start the server
2. -si to run an init script
3. -sf to run a final script
4. -f -fp -fpp to specify names of objective function, gradient and hessian, then load them.
For the included PID example, the driver call is
analysis_driver = ’../dakscilab -d -si "exec init_test_automatic.sce;"
-sf "exec visualize_solution.sce;" -f "exec f_pid.sci"’
Here there is an initialization script (init test automatic.sce;) which is launched before the main com-
putation. It initializes a specific Scilab module called xcos. A finalization script to visualize the xcos solution
is also specified (visualize solution.sce). Finally, the objective function is given with the computation
code called f pid.sci.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 17
Parallel Computing
17.1 Overview
This chapter describes the various parallel computing capabilities provided by Dakota. We begin with a high-level
summary.
Dakota has been designed to exploit a wide range of parallel computing resources such as those found in a desktop
multiprocessor workstation, a network of workstations, or a massively parallel computing platform. This parallel
computing capability is a critical technology for rendering real-world engineering design problems computation-
ally tractable. Dakota employs the concept of multilevel parallelism, which takes simultaneous advantage of
opportunities for parallel execution from multiple sources:
Parallel Simulation Codes: Dakota works equally well with both serial and parallel simulation codes.
Concurrent Execution of Analyses within a Function Evaluation: Some engineering design applications call
for the use of multiple simulation code executions (different disciplinary codes, the same code for different load
cases or environments, etc.) in order to evaluate a single response data set1(e.g., objective functions and con-
straints) for a single set of parameters. If these simulation code executions are independent (or if coupling is
enforced at a higher level), Dakota can perform them concurrently.
Concurrent Execution of Function Evaluations within an Iterator: With very few exceptions, the iterative
algorithms described in Chapters 3–7all provide opportunities for the concurrent evaluation of response data sets
for different parameter sets. Whenever there exists a set of function evaluations that are independent, Dakota can
perform them in parallel.
Concurrent Execution of Sub-Iterators within a Meta-iterator or Nested Model: The advanced methods
described in Chapter 14 are examples of meta-iterators, and the advanced model recursions described in Sec-
tions 15.1–15.2 all utilize nested models. Both of these cases generate sets of iterator subproblems that can
be executed concurrently. For example, the Pareto-set and multi-start strategies generate sets of optimization
subproblems. Similarly, optimization under uncertainty (15.2) generates sets of uncertainty quantification sub-
problems. Whenever these subproblems are independent, Dakota can perform them in parallel.
It is important to recognize that these four parallelism sources can be combined recursively. For example, a meta-
iterator can schedule and manage concurrent iterators, each of which may manage concurrent function evaluations,
each of which may manage concurrent analyses, each of which may execute on multiple processors. Moreover,
1the term “function evaluation” is used broadly to mean any individual data request from an iterative algorithm

274 CHAPTER 17. PARALLEL COMPUTING
more than one source of sub-iteration concurrency can be exploited when combining meta-iteration and nested
model sources. In an extreme example, defining the Pareto frontier for mixed-integer nonlinear programming
under mixed aleatory-epistemic uncertainty might exploit up to four levels of nested sub-iterator concurrency in
addition to available levels from function evaluation concurrency, analysis concurrency, and simulation paral-
lelism. The majority of application scenarios, however, will employ one to two levels of parallelism.
Navigating the body of this chapter: The range of capabilities is extensive and can be daunting at first; therefore,
this chapter takes an incremental approach in first describing the simplest single-level parallel computing models
(Section 17.2) using asynchronous local, message passing, and hybrid approaches. More advanced uses of Dakota
can build on this foundation to exploit multiple levels of parallelism, as described in Section 17.3.
The chapter concludes with a discussion of using Dakota with applications that run as independent MPI processes
(parallel application tiling, for example on a large compute cluster). This last section is a good quick start for
interfacing Dakota to your parallel (or serial) application on a cluster.
17.1.1 Categorization of parallelism
To understand the parallel computing possibilities, it is instructive to first categorize the opportunities for exploit-
ing parallelism into four main areas [39], consisting of coarse-grained and fine-grained parallelism opportunities
within algorithms and their function evaluations:
1. Algorithmic coarse-grained parallelism: This parallelism involves the concurrent execution of independent
function evaluations, where a “function evaluation” is defined as a data request from an algorithm (which
may involve value, gradient, and Hessian data from multiple objective and constraint functions). This
concept can also be extended to the concurrent execution of multiple “iterators” within a “meta-iterator.”
Examples of algorithms containing coarse-grained parallelism include:
•Gradient-based algorithms: finite difference gradient evaluations, speculative optimization, parallel
line search.
•Nongradient-based algorithms: genetic algorithms (GAs), pattern search (PS), Monte Carlo sampling.
•Approximate methods: design of computer experiments for building surrogate models.
•Concurrent sub-iteration: optimization under uncertainty, branch and bound, multi-start local search,
Pareto set optimization, island-model GAs.
2. Algorithmic fine-grained parallelism: This involves computing the basic computational steps of an opti-
mization algorithm (i.e., the internal linear algebra) in parallel. This is primarily of interest in large-scale
optimization problems and simultaneous analysis and design (SAND).
3. Function evaluation coarse-grained parallelism: This involves concurrent computation of separable parts
of a single function evaluation. This parallelism can be exploited when the evaluation of the response data
set requires multiple independent simulations (e.g. multiple loading cases or operational environments) or
multiple dependent analyses where the coupling is applied at the optimizer level (e.g., multiple disciplines
in the individual discipline feasible formulation [26]).
4. Function evaluation fine-grained parallelism: This involves parallelization of the solution steps within a
single analysis code. Support for massively parallel simulation continues to grow in areas of nonlinear
mechanics, structural dynamics, heat transfer, computational fluid dynamics, shock physics, and many
others.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.1. OVERVIEW 275
By definition, coarse-grained parallelism requires very little inter-processor communication and is therefore “em-
barrassingly parallel,” meaning that there is little loss in parallel efficiency due to communication as the number
of processors increases. However, it is often the case that there are not enough separable computations on each
algorithm cycle to utilize the thousands of processors available on massively parallel machines. For example,
a thermal safety application [40] demonstrated this limitation with a pattern search optimization in which the
maximum speedup exploiting only coarse-grained algorithmic parallelism was shown to be limited by the size
of the design problem (coordinate pattern search has at most 2nindependent evaluations per cycle for ndesign
variables).
Fine-grained parallelism, on the other hand, involves much more communication among processors and care must
be taken to avoid the case of inefficient machine utilization in which the communication demands among proces-
sors outstrip the amount of actual computational work to be performed. For example, a chemically-reacting flow
application [39] illustrated this limitation for a simulation of fixed size in which it was shown that, while simu-
lation run time did monotonically decrease with increasing number of processors, the relative parallel efficiency
ˆ
Eof the computation for fixed model size decreased rapidly (from ˆ
E≈0.8at 64 processors to ˆ
E≈0.4at 512
processors). This was due to the fact that the total amount of computation was approximately fixed, whereas the
communication demands were increasing rapidly with increasing numbers of processors. Therefore, there is a
practical limit on the number of processors that can be employed for fine-grained parallel simulation of a partic-
ular model size, and only for extreme model sizes can thousands of processors be efficiently utilized in studies
exploiting fine-grained parallelism alone.
These limitations point us to the exploitation of multiple levels of parallelism, in particular the combination of
coarse-grained and fine-grained approaches. This will allow us to execute fine-grained parallel simulations on sets
of processors where they are most efficient and then replicate this efficiency with many coarse-grained instances
involving one or more levels of nested job scheduling.
17.1.2 Parallel Dakota algorithms
In Dakota, the following parallel algorithms, comprised of iterators and meta-iterators, provide support for coarse-
grained algorithmic parallelism. Note that, even if a particular algorithm is serial in terms of its data request
concurrency, other concurrency sources (e.g., function evaluation coarse-grained and fine-grained parallelism)
may still be available.
17.1.2.1 Parallel iterators
•Gradient-based optimizers: CONMIN, DOT, NLPQL, NPSOL, and OPT++ can all exploit parallelism
through the use of Dakota’s native finite differencing routine (selected with method source dakota
in the responses specification), which will perform concurrent evaluations for each of the parameter offsets.
For nvariables, forward differences result in an n+ 1 concurrency and central differences result in a 2n+ 1
concurrency. In addition, CONMIN, DOT, and OPT++ can use speculative gradient techniques [15] to
obtain better parallel load balancing. By speculating that the gradient information associated with a given
line search point will be used later and computing the gradient information in parallel at the same time as
the function values, the concurrency during the gradient evaluation and line search phases can be balanced.
NPSOL does not use speculative gradients since this approach is superseded by NPSOL’s gradient-based
line search in user-supplied derivative mode. NLPQL also supports a distributed line search capability for
generating concurrency [117]. Finally, finite-difference Newton algorithms can exploit additional concur-
rency in numerically evaluating Hessian matrices.
•Nongradient-based optimizers: HOPSPACK, JEGA methods, and most SCOLIB methods support paral-
Dakota Version 6.7 User’s Manual generated on November 13, 2017

276 CHAPTER 17. PARALLEL COMPUTING
lelism. HOPSPACK and SCOLIB methods exploit parallelism through the use of Dakota’s concurrent func-
tion evaluations; however, there are some limitations on the levels of concurrency and asynchrony that can
be exploited. These are detailed in the Dakota Reference Manual. Serial SCOLIB methods include Solis-
Wets (coliny solis wets) and certain exploratory moves options (adaptive pattern and
multi step) in pattern search (coliny pattern search). OPT++ PDS (optpp pds) and NCSU
DIRECT (ncsu direct) are also currently serial due to incompatibilities in Dakota and OPT++/NCSU
parallelism models. Finally, coliny pattern search and asynch pattern search support dy-
namic job queues managed with nonblocking synchronization.
•Least squares methods: in an identical manner to the gradient-based optimizers, NL2SOL, NLSSOL, and
Gauss-Newton can exploit parallelism through the use of Dakota’s native finite differencing routine. In
addition, NL2SOL and Gauss-Newton can use speculative gradient techniques to obtain better parallel load
balancing. NLSSOL does not use speculative gradients since this approach is superseded by NLSSOL’s
gradient-based line search in user-supplied derivative mode.
•Surrogate-based minimizers: surrogate based local,surrogate based global, and efficient global
all support parallelism in the initial surrogate construction, but subsequent concurrency varies. In the case
of efficient global, only a single point is generated for evaluation for each subsequent cycle and
there is no derivatove concurrency for this point. In the case of surrogate based local, only a sin-
gle point is generated per subsequent cycle, but derivative concurrency for numerical gradient or Hessian
evaluations may be available. And in the case of surrogate based global, multiple points may be
generated on each subsequent cycle, depending on the multipoint return capability of specific minimizers.
•Parameter studies: all parameter study methods (vector,list,centered, and multidim) support
parallelism. These methods avoid internal synchronization points, so all evaluations are available for con-
current execution.
•Design of experiments: all dace (grid,random,oas,lhs,oa lhs,box behnken, and central composite),
fsu quasi mc (halton and hammersley), fsu cvt, and psuade moat methods support paral-
lelism.
•Uncertainty quantification: all nondeterministic methods (sampling, reliability, stochastic expansion, and
epistemic) support parallelism. In the case of gradient-based methods (local reliability, local interval es-
timation), parallelism can be exploited through the use of Dakota’s native finite differencing routine for
computing gradients. In the case of many global methods (e.g., global reliability, global interval estimation,
polynomial chaos), initial surrogate construction is highly parallel, but any subsequent (adaptive) refinement
may have greater concurrency restrictions (including a single point per refinement cycle in some cases).
17.1.2.2 Advanced methods
Certain advanced methods support concurrency in multiple iterator executions. Currently, the methods which can
exploit this level of parallelism are:
•Hybrid minimization: when the sequential hybrid transfers multiple solution points between methods,
single-point minimizers will be executed concurrently using each of the transferred solution points.
•Pareto-set optimization: a meta-iterator for multiobjective optimization using the simple weighted-sum
approach for computing sets of points on the Pareto front of nondominated solutions.
•Multi-start iteration: a meta-iterator for executing multiple instances of an iterator from different starting
points.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 277
The hybrid minimization case will display varying levels of iterator concurrency based on differing support of
multipoint solution input/output between iterators; however, the use of multiple parallel configurations among the
iterator sequence should prevent parallel inefficiencies. On the other hand, pareto-set and multi-start have a fixed
set of jobs to perform and should exhibit good load balancing.
17.1.2.3 Parallel models
Parallelism support in model classes (see Chapter 8) is an important issue for advanced model recursions such as
surrogate-based minimization, optimization under uncertainty, and mixed aleatory-epistemic UQ (see Chapters 14
and 15). Support is as follows:
•Single model: parallelism is managed as specified in the model’s associated interface instance.
•Recast model: most parallelism is forwarded on to the sub-model. An exception to this is finite differencing
in the presence of variable scaling. Since it is desirable to perform offsets in the scaled space (and avoid
minimum step size tolerances), this parallelism is not forwarded to the sub-model, instead being enacted at
the recast level.
•Data fit surrogate model: parallelism is supported in the construction of global surrogate models via the
concurrent evaluation of points generated by design of experiments methods. Local and multipoint ap-
proximations evaluate only a single point at a time, so concurrency is available only from any numerical
differencing required for gradient and Hessian data. Since the top-level iterator is interfaced only with the
(inexpensive) surrogate, no parallelism is exploited there. Load balancing can be an important issue when
performing evaluations to (adaptively) update existing surrogate models.
•Hierarchical surrogate model: parallelism is supported for the low or the high fidelity models, and in some
contexts, for both models at the same time. In the multifidelity optimization context, the optimizer is
interfaced only with the low-fidelity model, and the high-fidelity model is used only for verifications and
correction updating. For this case, the algorithmic coarse-grained parallelism supported by the optimizer is
enacted on the low fidelity model and the only parallelism available for high fidelity executions arises from
any numerical differencing required for high-fidelity gradient and Hessian data. In contexts that compute
model discrepancies, such as multifidelity UQ, the algorithmic concurrency involves evaluation of both low
and high fidelity models, so parallel schedulers can exploit simultaneous concurrency for both models.
•Nested model: concurrent executions of the optional interface and concurrent executions of the sub-iterator
are supported and are synchronized in succession. Currently, synchronization is blocking (all concurrent
evaluations are completed before new batches are scheduled); nonblocking schedulers (see 17.2) may be
supported in time. Nested model concurrency and meta-iterator concurrency (Section 17.1.2.2) may be
combined within an arbitrary number of levels of recursion. Primary clients for this capability include
optimization under uncertainty and mixed aleatory-epistemic UQ (see Section 8.5).
17.2 Single-level parallelism
Dakota’s parallel facilities support a broad range of computing hardware, from custom massively parallel super-
computers on the high end, to clusters and networks of workstations in the middle range, to desktop multipro-
cessors on the low end. Given the reduced scale in the middle to low ranges, it is more common to exploit only
one of the levels of parallelism; however, this can still be quite effective in reducing the time to obtain a solution.
Three single-level parallelism models will be discussed, and are depicted in Figure 17.1:
Dakota Version 6.7 User’s Manual generated on November 13, 2017
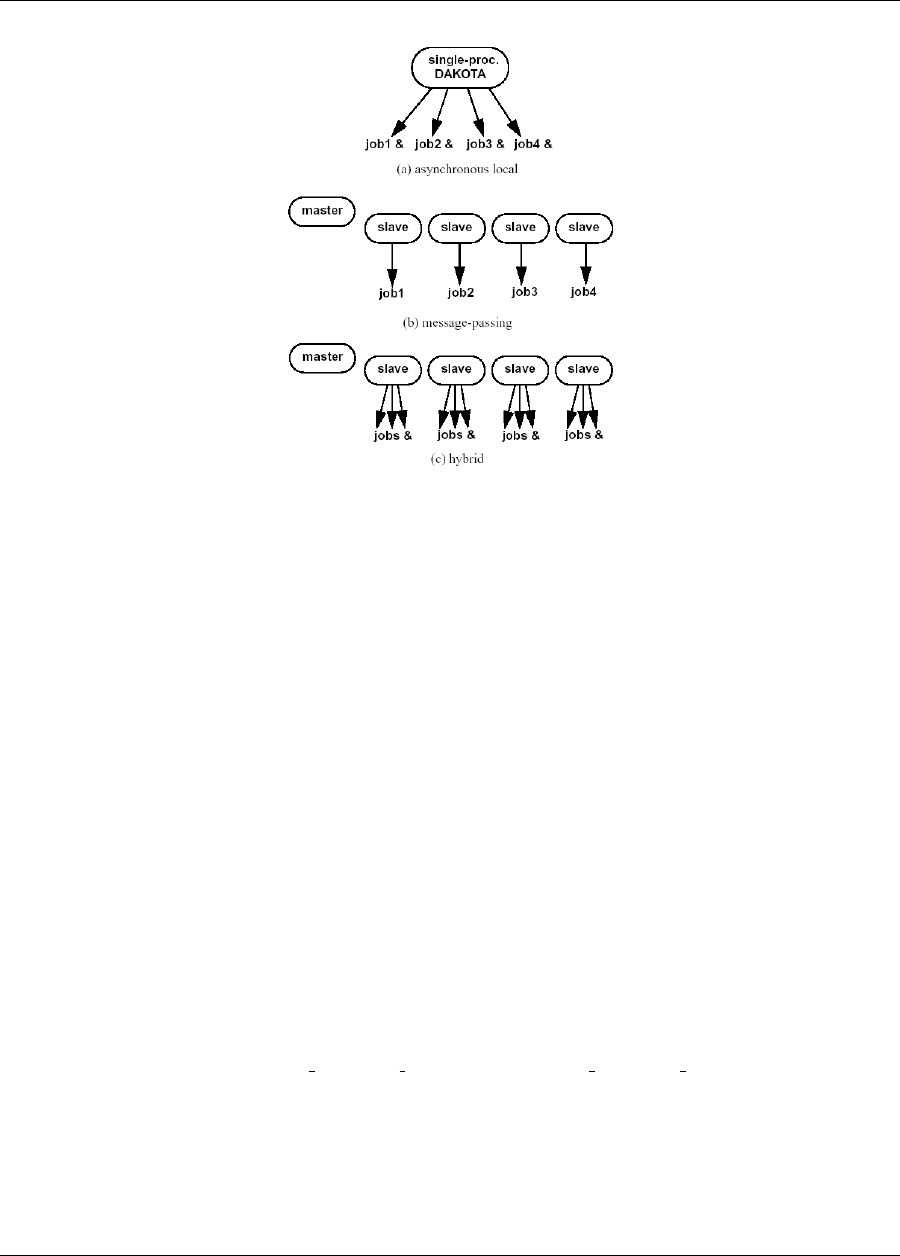
278 CHAPTER 17. PARALLEL COMPUTING
Figure 17.1: External, internal, and hybrid job management.
•asynchronous local: Dakota executes on a single processor, but launches multiple jobs concurrently using
asynchronous job launching techniques.
•message passing: Dakota executes in parallel using message passing to communicate between processors.
A single job is launched per processor using synchronous job launching techniques.
•hybrid: a combination of message passing and asynchronous local. Dakota executes in parallel across
multiple processors and launches concurrent jobs on each processor.
In each of these cases, jobs are executing concurrently and must be collected in some manner for return to an
algorithm. Blocking and nonblocking approaches are provided for this, where the blocking approach is used in
most cases:
•blocking synchronization: all jobs in the queue are completed before exiting the scheduler and returning
the set of results to the algorithm. The job queue fills and then empties completely, which provides a
synchronization point for the algorithm.
•nonblocking synchronization: the job queue is dynamic, with jobs entering and leaving continuously. There
are no defined synchronization points for the algorithm, which requires specialized algorithm logic (only
currently supported by coliny pattern search and asynch pattern search, which are some-
times referred to as “fully asynchronous” algorithms).
Given these job management capabilities, it is worth noting that the popular term “asynchronous” can be ambigu-
ous when used in isolation. In particular, it can be important to qualify whether one is referring to “asynchronous
job launch” (synonymous with any of the three concurrent job launch approaches described above) or “asyn-
chronous job recovery” (synonymous with the latter nonblocking job synchronization approach).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 279
17.2.1 Asynchronous Local Parallelism
This section describes software components which manage simulation invocations local to a processor. These
invocations may be either synchronous (i.e., blocking) or asynchronous (i.e., nonblocking). Synchronous eval-
uations proceed one at a time with the evaluation running to completion before control is returned to Dakota.
Asynchronous evaluations are initiated such that control is returned to Dakota immediately, prior to evaluation
completion, thereby allowing the initiation of additional evaluations which will execute concurrently.
The synchronous local invocation capabilities are used in two contexts: (1) by themselves to provide serial execu-
tion on a single processor, and (2) in combination with Dakota’s message-passing schedulers to provide function
evaluations local to each processor. Similarly, the asynchronous local invocation capabilities are used in two
contexts: (1) by themselves to launch concurrent jobs from a single processor that rely on external means (e.g.,
operating system, job queues) for assignment to other processors, and (2) in combination with Dakota’s message-
passing schedulers to provide a hybrid parallelism (see Section 17.2.3). Thus, Dakota supports any of the four
combinations of synchronous or asynchronous local combined with message passing or without.
Asynchronous local schedulers may be used for managing concurrent function evaluations requested by an iterator
or for managing concurrent analyses within each function evaluation. The former iterator/evaluation concurrency
supports either blocking (all jobs in the queue must be completed by the scheduler) or nonblocking (dynamic
job queue may shrink or expand) synchronization, where blocking synchronization is used by most iterators and
nonblocking synchronization is used by fully asynchronous algorithms such as asynch pattern search and
coliny pattern search. The latter evaluation/analysis concurrency is restricted to blocking synchroniza-
tion. The “Asynchronous Local” column in Table 17.1 summarizes these capabilities.
Dakota supports three local simulation invocation approaches based on the direct function, system call, and fork
simulation interfaces. For each of these cases, an input filter, one or more analysis drivers, and an output filter
make up the interface, as described in Section 10.4.
17.2.1.1 Direct function synchronization
The direct function capability may be used synchronously. Synchronous operation of the direct function simu-
lation interface involves a standard procedure call to the input filter, if present, followed by calls to one or more
simulations, followed by a call to the output filter, if present (refer to Sections 10.2-10.4 for additional details and
examples). Each of these components must be linked as functions within Dakota. Control does not return to the
calling code until the evaluation is completed and the response object has been populated.
Asynchronous operation will be supported in the future and will involve the use of multithreading (e.g., POSIX
threads) to accomplish multiple simultaneous simulations. When spawning a thread (e.g., using pthread create),
control returns to the calling code after the simulation is initiated. In this way, multiple threads can be created
simultaneously. An array of responses corresponding to the multiple threads of execution would then be recovered
in a synchronize operation (e.g., using pthread join).
17.2.1.2 System call synchronization
The system call capability may be used synchronously or asynchronously. In both cases, the system utility from
the standard C library is used. Synchronous operation of the system call simulation interface involves spawning
the system call (containing the filters and analysis drivers bound together with parentheses and semi-colons) in
the foreground. Control does not return to the calling code until the simulation is completed and the response file
has been written. In this case, the possibility of a race condition (see below) does not exist and any errors during
response recovery will cause an immediate abort of the Dakota process (note: detection of the string “fail” is not
Dakota Version 6.7 User’s Manual generated on November 13, 2017

280 CHAPTER 17. PARALLEL COMPUTING
a response recovery error; see Chapter 19).
Asynchronous operation involves spawning the system call in the background, continuing with other tasks (e.g.,
spawning other system calls), periodically checking for process completion, and finally retrieving the results. An
array of responses corresponding to the multiple system calls is recovered in a synchronize operation.
In this synchronize operation, completion of a function evaluation is detected by testing for the existence of the
evaluation’s results file using the stat utility [87]. Care must be taken when using asynchronous system calls
since they are prone to the race condition in which the results file passes the existence test but the recording of the
function evaluation results in the file is incomplete. In this case, the read operation performed by Dakota will result
in an error due to an incomplete data set. In order to address this problem, Dakota contains exception handling
which allows for a fixed number of response read failures per asynchronous system call evaluation. The number
of allowed failures must have a limit, so that an actual response format error (unrelated to the race condition) will
eventually abort the system. Therefore, to reduce the possibility of exceeding the limit on allowable read failures,
the user’s interface should minimize the amount of time an incomplete results file exists in the directory where its
status is being tested. This can be accomplished through two approaches: (1) delay the creation of the results file
until the simulation computations are complete and all of the response data is ready to be written to the results
file, or (2) perform the simulation computations in a subdirectory, and as a last step, move the completed results
file into the main working directory where its existence is being queried.
If concurrent simulations are executing in a shared disk space, then care must be taken to maintain independence
of the simulations. In particular, the parameters and results files used to communicate between Dakota and the
simulation, as well as any other files used by this simulation, must be protected from other files of the same name
used by the other concurrent simulations. With respect to the parameters and results files, these files may be
made unique through the use of the file tag option (e.g., params.in.1,results.out.1, etc.) or the
default temporary file option (e.g., /var/tmp/aaa0b2Mfv, etc.). However, if additional simulation files must
be protected (e.g., model.i,model.o,model.g,model.e, etc.), then an effective approach is to create a
tagged working subdirectory for each simulation instance. Section 10.3 provides an example system call interface
that demonstrates both the use of tagged working directories and the relocation of completed results files to avoid
the race condition.
17.2.1.3 Fork synchronization
The fork capability is quite similar to the system call; however, it has the advantage that asynchronous fork invoca-
tions can avoid the results file race condition that may occur with asynchronous system calls (see Section 10.2.5).
The fork interface invokes the filters and analysis drivers using the fork and exec family of functions, and
completion of these processes is detected using the wait family of functions. Since wait is based on a process
id handle rather than a file existence test, an incomplete results file is not an issue.
Depending on the platform, the fork simulation interface executes either a vfork or a fork call. These calls
generate a new child process with its own UNIX process identification number, which functions as a copy of the
parent process (dakota). The execvp function is then called by the child process, causing it to be replaced by
the analysis driver or filter. For synchronous operation, the parent dakota process then awaits completion of the
forked child process through a blocking call to waitpid. On most platforms, the fork/exec procedure is
efficient since it operates in a copy-on-write mode, and no copy of the parent is actually created. Instead, the
parents address space is borrowed until the exec function is called.
The fork/exec behavior for asynchronous operation is similar to that for synchronous operation, the only
difference being that dakota invokes multiple simulations through the fork/exec procedure prior to recovering
response results for these jobs using the wait function. The combined use of fork/exec and wait functions
in asynchronous mode allows the scheduling of a specified number of concurrent function evaluations and/or
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 281
concurrent analyses.
17.2.1.4 Asynchronous Local Example
The test file Dakota/test/dakota dace.in computes 49 orthogonal array samples, which may be evalu-
ated concurrently using parallel computing. When executing Dakota with this input file on a single processor, the
following execution syntax may be used:
dakota -i dakota_dace.in
For serial execution (the default), the interface specification within dakota dace.in would appear similar to
interface,
system
analysis_driver = ’text_book’
which results in function evaluation output similar to the following (for output set to quiet mode):
>>>>> Running dace iterator.
DACE method = 12 Samples = 49 Symbols = 7 Seed (user-specified) = 5
------------------------------
Begin I1 Evaluation 1
------------------------------
text_book /tmp/fileia6gVb /tmp/filedDo5MH
------------------------------
Begin I1 Evaluation 2
------------------------------
text_book /tmp/fileyfkQGd /tmp/fileAbmBAJ
<snip>
<<<<< Iterator dace completed.
where it is evident that each function evaluation is being performed sequentially.
For parallel execution using asynchronous local approaches, the Dakota execution syntax is unchanged as Dakota
is still launched on a single processor. However, the interface specification is augmented to include the asynchronous
keyword with optional concurrency limiter to indicate that multiple analysis driver instances will be exe-
cuted concurrently:
interface,
system asynchronous evaluation_concurrency = 4
analysis_driver = ’text_book’
which results in output excerpts similar to the following:
>>>>> Running dace iterator.
DACE method = 12 Samples = 49 Symbols = 7 Seed (user-specified) = 5
Dakota Version 6.7 User’s Manual generated on November 13, 2017

282 CHAPTER 17. PARALLEL COMPUTING
------------------------------
Begin I1 Evaluation 1
------------------------------
(Asynchronous job 1 added to I1 queue)
------------------------------
Begin I1 Evaluation 2
------------------------------
(Asynchronous job 2 added to I1 queue)
<snip>
------------------------------
Begin I1 Evaluation 49
------------------------------
(Asynchronous job 49 added to I1 queue)
Blocking synchronize of 49 asynchronous evaluations
First pass: initiating 4 local asynchronous jobs
Initiating I1 evaluation 1
text_book /tmp/fileuLcfBp /tmp/file6XIhpm &
Initiating I1 evaluation 2
text_book /tmp/fileeC29dj /tmp/fileIdA22f &
Initiating I1 evaluation 3
text_book /tmp/fileuhCESc /tmp/fileajLgI9 &
Initiating I1 evaluation 4
text_book /tmp/filevJHMy6 /tmp/fileHFKip3 &
Second pass: scheduling 45 remaining local asynchronous jobs
Waiting on completed jobs
I1 evaluation 1 has completed
I1 evaluation 2 has completed
I1 evaluation 3 has completed
Initiating I1 evaluation 5
text_book /tmp/fileISsjh0 /tmp/fileSaek9W &
Initiating I1 evaluation 6
text_book /tmp/filefN271T /tmp/fileSNYVUQ &
Initiating I1 evaluation 7
text_book /tmp/filebAQaON /tmp/fileaMPpHK &
I1 evaluation 49 has completed
<snip>
<<<<< Iterator dace completed.
where it is evident that each of the 49 jobs is first queued and then a blocking synchronization is performed. This
synchronization uses a simple scheduler that initiates 4 jobs and then replaces completing jobs with new ones
until all 49 are complete.
The default job concurrency for asynchronous local parallelism is all that is available from the algorithm (49 in
this case), which could be too many for the computational resources or their usage policies. The concurrency
level specification (4 in this case) instructs the scheduler to keep 4 jobs running concurrently, which would be
appropriate for, e.g., a dual-processor dual-core workstation. In this case, it is the operating system’s responsibility
to assign the concurrent text book jobs to available processors/cores. Specifying greater concurrency than that
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 283
supported by the hardware will result in additional context switching within a multitasking operating system and
will generally degrade performance. Note however that, in this example, there are a total of 5 processes running,
one for Dakota and four for the concurrent function evaluations. Since the Dakota process checks periodically
for job completion and sleeps in between checks, it is relatively lightweight and does not require a dedicated
processor.
17.2.1.5 Local evaluation scheduling options
The default behavior for asynchronous local parallelism is for Dakota to dispatch the next evaluation the local
queue when one completes (and can optionally be specified by local evaluation scheduling dynamic.
In some cases, the simulation code interface benefits from knowing which job number will replace a com-
pleted job. This includes some modes of application tiling with certain MPI implementations, where send-
ing a job to the correct subset of available processors is done with relative node scheduling. The keywords
local evaluation scheduling static forces this behavior, so a completed evaluation will be replaced
with one congruent modulo the evaluation concurrency. For example, with 6 concurrent jobs, eval number 2 will
be replaced with eval number 8. Examples of this usage can be seen in Dakota/examples/parallelism.
17.2.2 Message Passing Parallelism
Dakota uses a “single program-multiple data” (SPMD) parallel programming model. It uses message-passing
routines from the Message Passing Interface (MPI) standard [70], [125] to communicate data between processors.
The SPMD designation simply denotes that the same Dakota executable is loaded on all processors during the
parallel invocation. This differs from the MPMD model (“multiple program-multiple data”) which would have
the Dakota executable on one or more processors communicating directly with simulator executables on other
processors. The MPMD model has some advantages, but heterogeneous executable loads are not supported by
all parallel environments. Moreover, the MPMD model requires simulation code intrusion on the same order
as conversion to a subroutine, so subroutine conversion (see Section 16.2) in a direct-linked SPMD model is
preferred.
17.2.2.1 Partitioning
A level of message passing parallelism can use either of two processor partitioning models:
•Dedicated master: a single processor is dedicated to scheduling operations and the remaining processors
are split into server partitions.
•Peer partition: all processors are allocated to server partitions and the loss of a processor to scheduling is
avoided.
These models are depicted in Figure 17.2. The peer partition is desirable since it utilizes all processors for
computation; however, it requires either the use of sophisticated mechanisms for distributed scheduling or a
problem for which static scheduling of concurrent work performs well (see Scheduling below). If neither of these
characteristics is present, then use of the dedicated master partition supports a dynamic scheduling which assures
that server idleness is minimized.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
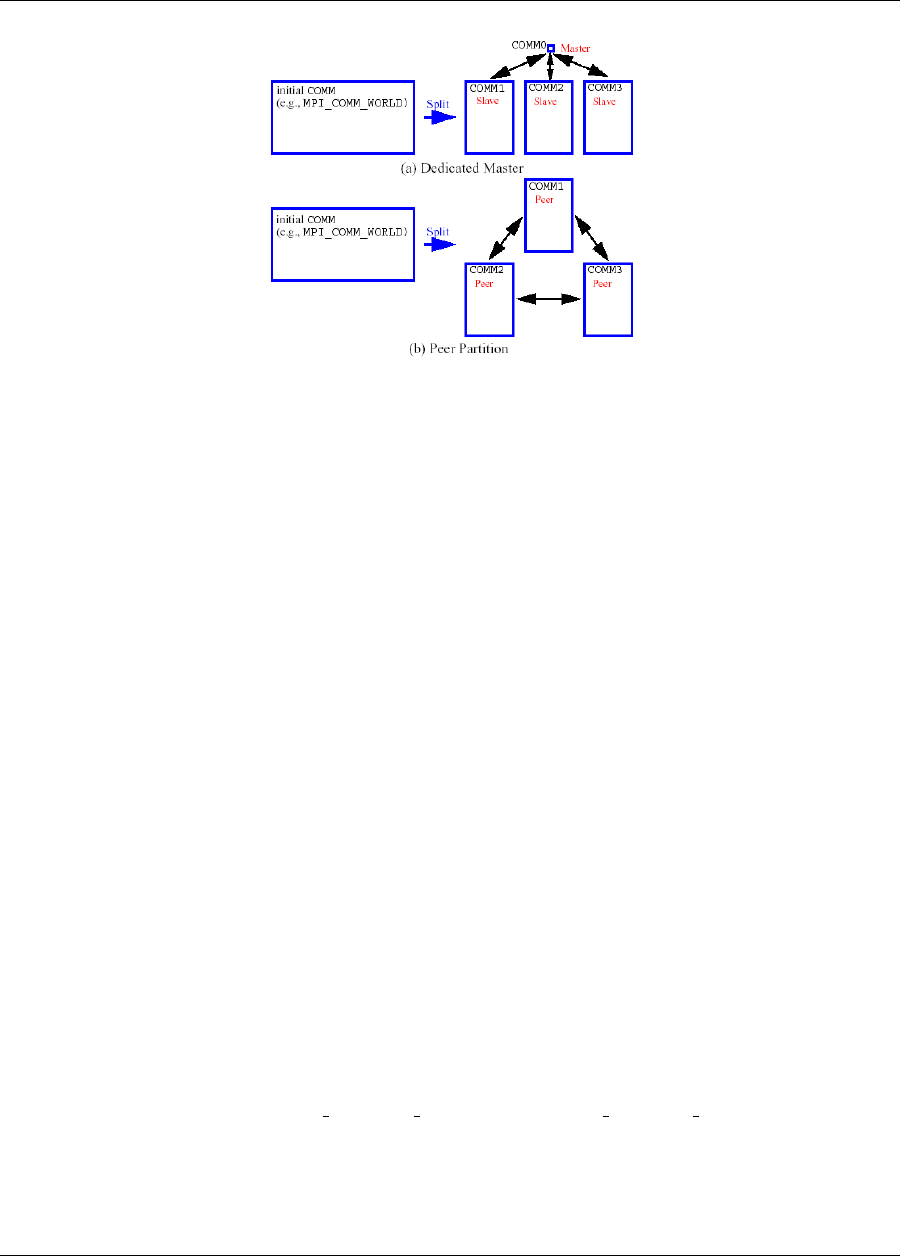
284 CHAPTER 17. PARALLEL COMPUTING
Figure 17.2: Communicator partitioning models.
17.2.2.2 Scheduling
The following scheduling approaches are available within a level of message passing parallelism:
•Dynamic scheduling: in the dedicated master model, the master processor manages a single processing
queue and maintains a prescribed number of jobs (usually one) active on each slave. Once a slave server
has completed a job and returned its results, the master assigns the next job to this slave. Thus, the job
assignment on the master adapts to the job completion speed on the slaves. This provides a simple dynamic
scheduler in that heterogeneous processor speeds and/or job durations are naturally handled, provided there
are sufficient instances scheduled through the servers to balance the variation. In the case of a peer partition,
dynamic schedulers can also be employed, provided that peer 1 can employ nonblocking synchronization
of its local evaluations. This allows it to balance its local work with servicing job assignments and returns
from the other peers.
•Static scheduling: if scheduling is statically determined at start-up, then no master processor is needed
to direct traffic and a peer partitioning approach is applicable. If the static schedule is a good one (ideal
conditions), then this approach will have superior performance. However, heterogeneity, when not known
a priori, can very quickly degrade performance since there is no mechanism to adapt.
Message passing schedulers may be used for managing concurrent sub-iterator executions within a meta-iterator,
concurrent evaluations within an iterator, or concurrent analyses within an evaluation. In the former and latter
cases, the message passing scheduler is currently restricted to blocking synchronization, in that all jobs in the
queue are completed before exiting the scheduler and returning the set of results to the algorithm. Nonblock-
ing message-passing scheduling is supported for the iterator–evaluation concurrency level in support of fully
asynchronous algorithms (e.g., asynch pattern search and coliny pattern search) that avoid syn-
chronization points that can harm scaling.
Message passing is also used within a fine-grained parallel simulation code, although this is separate from
Dakota’s capabilities (Dakota may, at most, pass a communicator partition to the simulation). The “Message
Passing” column in Table 17.1 summarizes these capabilities.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 285
17.2.2.3 Message Passing Example
Revisiting the test file dakota dace.in, Dakota will now compute the 49 orthogonal array samples using
a message passing approach. In this case, a parallel launch utility is used to execute Dakota across multiple
processors using syntax similar to the following:
mpirun -np 5 -machinefile machines dakota -i dakota_dace.in
Since the asynchronous local parallelism will not be used, the interface specification does not include the asynchronous
keyword and would appear similar to:
interface,
system
analysis_driver = ’text_book’
The relevant excerpts from the Dakota output for a dedicated master partition and dynamic schedule, the default
when the maximum concurrency (49) exceeds the available capacity (5), would appear similar to the following:
Running MPI Dakota executable in parallel on 5 processors.
-----------------------------------------------------------------------------
DAKOTA parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 5 1 peer
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1 (1 dakota, 0 analysis)
-----------------------------------------------------------------------------
>>>>> Executing environment.
>>>>> Running dace iterator.
DACE method = 12 Samples = 49 Symbols = 7 Seed (user-specified) = 5
------------------------------
Begin I1 Evaluation 1
------------------------------
(Asynchronous job 1 added to I1 queue)
------------------------------
Begin I1 Evaluation 2
------------------------------
(Asynchronous job 2 added to I1 queue)
<snip>
------------------------------
Begin I1 Evaluation 49
------------------------------
(Asynchronous job 49 added to I1 queue)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

286 CHAPTER 17. PARALLEL COMPUTING
Blocking synchronize of 49 asynchronous evaluations
Peer dynamic schedule: first pass assigning 4 jobs among 4 remote peers
Peer 1 assigning I1 evaluation 1 to peer 2
Peer 1 assigning I1 evaluation 2 to peer 3
Peer 1 assigning I1 evaluation 3 to peer 4
Peer 1 assigning I1 evaluation 4 to peer 5
Peer dynamic schedule: first pass launching 1 local jobs
Initiating I1 evaluation 5
text_book /tmp/file5LRsBu /tmp/fileT2mS65 &
Peer dynamic schedule: second pass scheduling 44 remaining jobs
Initiating I1 evaluation 5
text_book /tmp/file5LRsBu /tmp/fileT2mS65 &
Peer dynamic schedule: second pass scheduling 44 remaining jobs
I1 evaluation 5 has completed
Initiating I1 evaluation 6
text_book /tmp/fileZJaODH /tmp/filewoUJaj &
I1 evaluation 2 has returned from peer server 3
Peer 1 assigning I1 evaluation 7 to peer 3
I1 evaluation 4 has returned from peer server 5
<snip>
I1 evaluation 46 has returned from peer server 2
I1 evaluation 49 has returned from peer server 5
<<<<< Function evaluation summary (I1): 49 total (49 new, 0 duplicate)
<<<<< Iterator dace completed.
where it is evident that each of the 49 jobs is first queued and then a blocking synchronization is performed. This
synchronization uses a dynamic scheduler that initiates five jobs, one on each of five evaluation servers, and then
replaces completing jobs with new ones until all 49 are complete. It is important to note that job execution local
to each of the four servers is synchronous.
17.2.3 Hybrid Parallelism
The asynchronous local approaches described in Section 17.2.1 can be considered to rely on external scheduling
mechanisms, since it is generally the operating system or some external queue/load sharing software that allocates
jobs to processors. Conversely, the message-passing approaches described in Section 17.2.2 rely on internal
scheduling mechanisms to distribute work among processors. These two approaches provide building blocks
which can be combined in a variety of ways to manage parallelism at multiple levels. At one extreme, Dakota
can execute on a single processor and rely completely on external means to map all jobs to processors (i.e., using
asynchronous local approaches). At the other extreme, Dakota can execute on many processors and manage all
levels of parallelism, including the parallel simulations, using completely internal approaches (i.e., using message
passing at all levels as in Figure 17.4). While all-internal or all-external approaches are common cases, many
additional approaches exist between the two extremes in which some parallelism is managed internally and some
is managed externally.
These combined approaches are referred to as hybrid parallelism, since the internal distribution of work based on
message-passing is being combined with external allocation using asynchronous local approaches2. Figure 17.1
2The term “hybrid parallelism” is often used to describe the combination of MPI message passing and OpenMP shared memory parallelism
models. This can be considered to be a special case of the meaning here, as OpenMP is based on threads, which is analagous to asynchronous
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.2. SINGLE-LEVEL PARALLELISM 287
depicts the asynchronous local, message-passing, and hybrid approaches for a dedicated-master partition. Ap-
proaches (b) and (c) both use MPI message-passing to distribute work from the master to the slaves, and ap-
proaches (a) and (c) both manage asynchronous jobs local to a processor. The hybrid approach (c) can be seen
to be a combination of (a) and (b) since jobs are being internally distributed to slave servers through message-
passing and each slave server is managing multiple concurrent jobs using an asynchronous local approach. From
a different perspective, one could consider (a) and (b) to be special cases within the range of configurations sup-
ported by (c). The hybrid approach is useful for supercomputers that maintain a service/compute node distinction
and for supercomputers or networks of workstations that involve clusters of symmetric multiprocessors (SMPs).
In the service/compute node case, concurrent multiprocessor simulations are launched into the compute nodes
from the service node partition. While an asynchronous local approach from a single service node would be
sufficient, spreading the application load by running Dakota in parallel across multiple service nodes results in
better performance [41]. If the number of concurrent jobs to be managed in the compute partition exceeds the
number of available service nodes, then hybrid parallelism is the preferred approach. In the case of a cluster of
SMPs (or network of multiprocessor workstations), message-passing can be used to communicate between SMPs,
and asynchronous local approaches can be used within an SMP. Hybrid parallelism can again result in improved
performance, since the total number of Dakota MPI processes is reduced in comparison to a pure message-passing
approach over all processors.
Hybrid schedulers may be used for managing concurrent evaluations within an iterator or concurrent analyses
within an evaluation. In the former case, blocking or nonblocking synchronization can be used, whereas the latter
case is restricted to blocking synchronization. The “Hybrid” column in Table 17.1 summarizes these capabilities.
17.2.3.1 Hybrid Example
Revisiting the test file dakota dace.in, Dakota will now compute the 49 orthogonal array samples using a
hybrid approach. As for the message passing case, a parallel launch utility is used to execute Dakota across
multiple processors:
mpirun -np 5 -machinefile machines dakota -i dakota_dace.in
Since the asynchronous local parallelism will also be used, the interface specification includes the asynchronous
keyword and appears similar to
interface,
system asynchronous evaluation_concurrency = 2
analysis_driver = ’text_book’
In the hybrid case, the specification of the desired concurrency level must be included, since the default is no
longer all available (as it is for asynchronous local parallelism). Rather the default is to employ message passing
parallelism, and hybrid parallelism is only available through the specification of asynchronous concurrency greater
than one.
The relevant excerpts of the Dakota output for a peer partition and dynamic schedule , the default when the
maximum concurrency (49) exceeds the maximum available capacity (10), would appear similar to the following:
Running MPI Dakota executable in parallel on 5 processors.
-----------------------------------------------------------------------------
DAKOTA parallel configuration:
local usage of the direct simulation interface.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

288 CHAPTER 17. PARALLEL COMPUTING
Level num_servers procs_per_server partition
---------------- ---------------- ---------
concurrent evaluations 5 1 peer
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1 (1 dakota, 0 analysis)
-----------------------------------------------------------------------------
>>>>> Executing environment.
>>>>> Running dace iterator.
DACE method = 12 Samples = 49 Symbols = 7 Seed (user-specified) = 5
------------------------------
Begin I1 Evaluation 1
------------------------------
(Asynchronous job 1 added to I1 queue)
------------------------------
Begin I1 Evaluation 2
------------------------------
(Asynchronous job 2 added to I1 queue)
<snip>
Blocking synchronize of 49 asynchronous evaluations
Peer dynamic schedule: first pass assigning 8 jobs among 4 remote peers
Peer 1 assigning I1 evaluation 1 to peer 2
Peer 1 assigning I1 evaluation 2 to peer 3
Peer 1 assigning I1 evaluation 3 to peer 4
Peer 1 assigning I1 evaluation 4 to peer 5
Peer 1 assigning I1 evaluation 6 to peer 2
Peer 1 assigning I1 evaluation 7 to peer 3
Peer 1 assigning I1 evaluation 8 to peer 4
Peer 1 assigning I1 evaluation 9 to peer 5
Peer dynamic schedule: first pass launching 2 local jobs
Initiating I1 evaluation 5
text_book /tmp/fileJU1Ez2 /tmp/fileVGZzEX &
Initiating I1 evaluation 10
text_book /tmp/fileKfUgKS /tmp/fileMgZXPN &
Peer dynamic schedule: second pass scheduling 39 remaining jobs
<snip>
I1 evaluation 49 has completed
I1 evaluation 43 has returned from peer server 2
I1 evaluation 44 has returned from peer server 3
I1 evaluation 48 has returned from peer server 4
I1 evaluation 47 has returned from peer server 2
I1 evaluation 45 has returned from peer server 3
<<<<< Function evaluation summary (I1): 49 total (49 new, 0 duplicate)
Dakota Version 6.7 User’s Manual generated on November 13, 2017
17.3. MULTILEVEL PARALLELISM 289
<<<<< Iterator dace completed.
where it is evident that each of the 49 jobs is first queued and then a blocking synchronization is performed. This
synchronization uses a dynamic scheduler that initiates ten jobs, two on each of five evaluation servers, and then
replaces completing jobs with new ones until all 49 are complete. It is important to note that job execution local
to each of the four servers is asynchronous.
17.3 Multilevel parallelism
Parallel computers within the Department of Energy national laboratories have achieved nearly 20 quadrillion
(1015) floating point operations per second (20 petaFLOPS) in Linpack benchmarks. Planning for ”exascale”
systems, rated at 1000 petaFLOPS, is well underway. This performance is achieved through the use of massively
parallel (MP) processing using O[105−106]processors. In order to harness the power of these machines for
performing design, uncertainty quantification, and other systems analyses, parallel algorithms are needed which
are scalable to thousands of processors.
Dakota supports an open-ended number of levels of nested parallelism which, as described in Section 17.1, can
be categorized into three types of concurrent job scheduling and four types of parallelism: (a) concurrent iterators
within a meta-iterator (scheduled by Dakota), (b) concurrent function evaluations within each iterator (scheduled
by Dakota), (c) concurrent analyses within each function evaluation (scheduled by Dakota), and (d) multiprocessor
analyses (work distributed by a parallel analysis code). In combination, these parallelism levels can minimize
efficiency losses and achieve near linear scaling on MP computers. Types (a) and (b) are classified as algorithmic
coarse-grained parallelism, type (c) is function evaluation coarse-grained parallelism, and type (d) is function
evaluation fine-grained parallelism (see Section 17.1.1). Algorithmic fine-grained parallelism is not currently
supported in Dakota, although this picture is rapidly evolving.
A particular application may support one or more of these parallelism types, and Dakota provides for convenient
selection and combination of multiple levels. If multiple types of parallelism can be exploited, then the question
may arise as to how the amount of parallelism at each level should be selected so as to maximize the overall
parallel efficiency of the study. For performance analysis of multilevel parallelism formulations and detailed dis-
cussion of these issues, refer to [41]. In many cases, the user may simply employ Dakota’s automatic parallelism
configuration facilities, which implement the recommendations from the aforementioned paper.
Figure 17.3 shows typical fixed-size scaling performance using a modified version of the extended text book
problem (see Section 20.1). Three levels of parallelism (concurrent evaluations within an iterator, concurrent anal-
yses within each evaluation, and multiprocessor analyses) are exercised within a modest partition of processors
(circa year 2000). Despite the use of a fixed problem size and the presence of some idleness within the scheduling
at multiple levels, the efficiency is still reasonably high3. Greater efficiencies are obtainable for scaled speedup
studies (or for larger problems in fixed-size studies) and for problems optimized for minimal scheduler idleness
(by, e.g., managing all concurrency in as few scheduling levels as possible). Note that speedup and efficiency are
measured relative to the case of a single instance of a multiprocessor analysis, since it was desired to investigate
the effectiveness of the Dakota schedulers independent from the efficiency of the parallel analysis.
3Note that overhead is reduced in these scaling studies by deactivating the evaluation cache and restart file logging.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
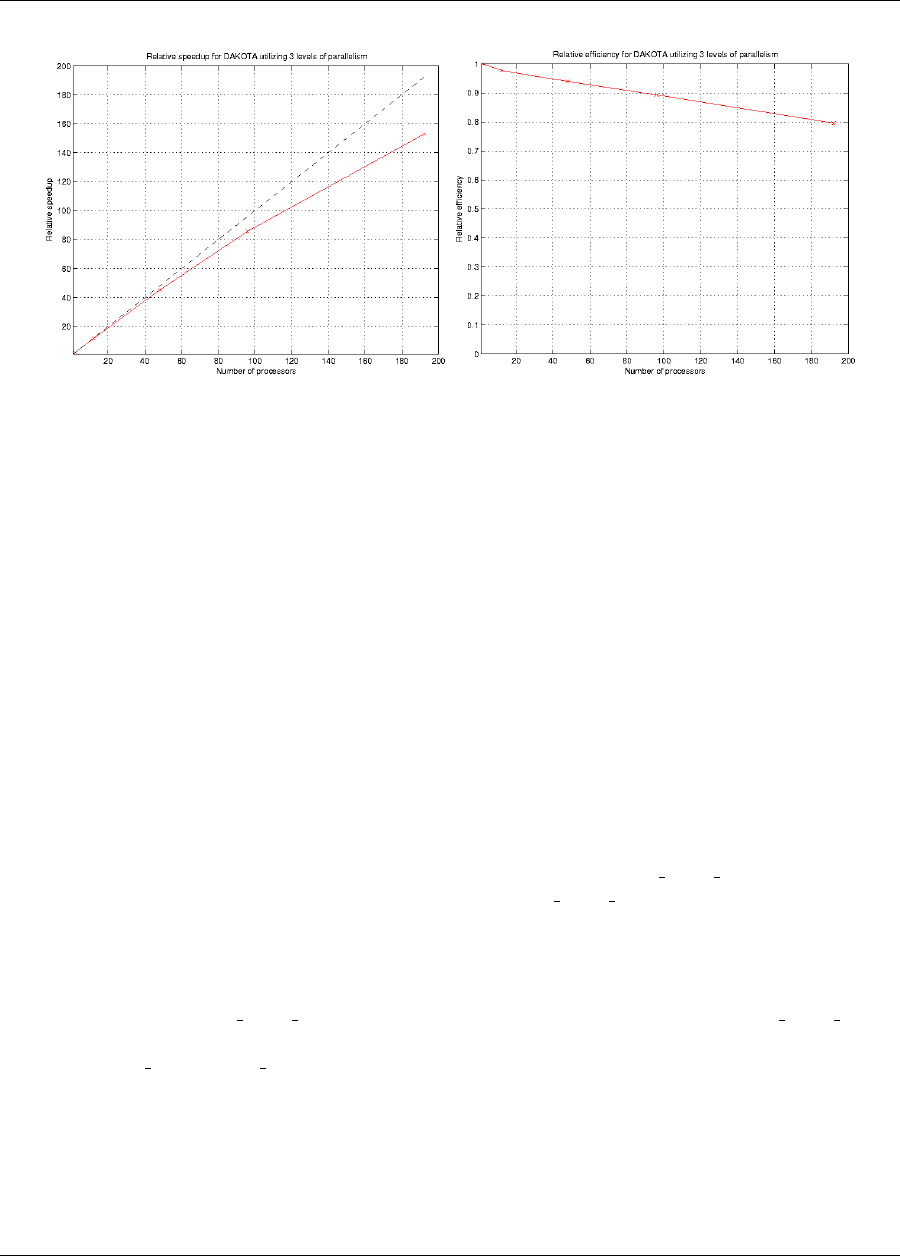
290 CHAPTER 17. PARALLEL COMPUTING
(a) Relative speedup. (b) Relative efficiency.
Figure 17.3: Fixed-size scaling results for three levels of parallelism.
17.3.1 Asynchronous Local Parallelism
In most cases, the use of asynchronous local parallelism is the termination point for multilevel parallelism, in that
any level of parallelism lower than an asynchronous local level will be serialized (see discussion in Section 17.3.3).
The exception to this rule is reforking of forked processes for concurrent analyses within forked evaluations. In
this case, a new process is created using fork for one of several concurrent evaluations; however, the new process
is not replaced immediately using exec. Rather, the new process is reforked to create additional child processes
for executing concurrent analyses within each concurrent evaluation process. This capability is not supported by
system calls and provides one of the key advantages to using fork over system (see Section 10.2.5).
17.3.2 Message Passing Parallelism
17.3.2.1 Partitioning of levels
Dakota uses MPI communicators to identify groups of processors. The global MPI COMM WORLD communicator
provides the total set of processors allocated to the Dakota run. MPI COMM WORLD can be partitioned into new
intra-communicators which each define a set of processors to be used for a multiprocessor server. Each of these
servers may be further partitioned to nest one level of parallelism within the next. At the lowest parallelism level,
these intra-communicators can be passed into a simulation for use as the simulation’s computational context, pro-
vided that the simulation has been designed, or can be modified, to be modular on a communicator (i.e., it does
not assume ownership of MPI COMM WORLD). New intra-communicators are created with the MPI Comm split
routine, and in order to send messages between these intra-communicators, new inter-communicators are created
with calls to MPI Intercomm create. Multiple parallel configurations (containing a set of communicator
partitions) are allocated for use in studies with multiple iterators and models (e.g., 16 servers of 64 processors
each could be used for iteration on a lower fidelity model, followed by two servers of 512 processors each for sub-
sequent iteration on a higher fidelity model), and can be alternated at run time. Each of the parallel configurations
are allocated at object construction time and are reported at the beginning of the Dakota output.
Each tier within Dakota’s nested parallelism hierarchy can use the dedicated master and peer partition approaches
described in Section 17.2.2.1. To recursively partition the subcommunicators of Figure 17.2,COMM1/2/3 in the
Dakota Version 6.7 User’s Manual generated on November 13, 2017
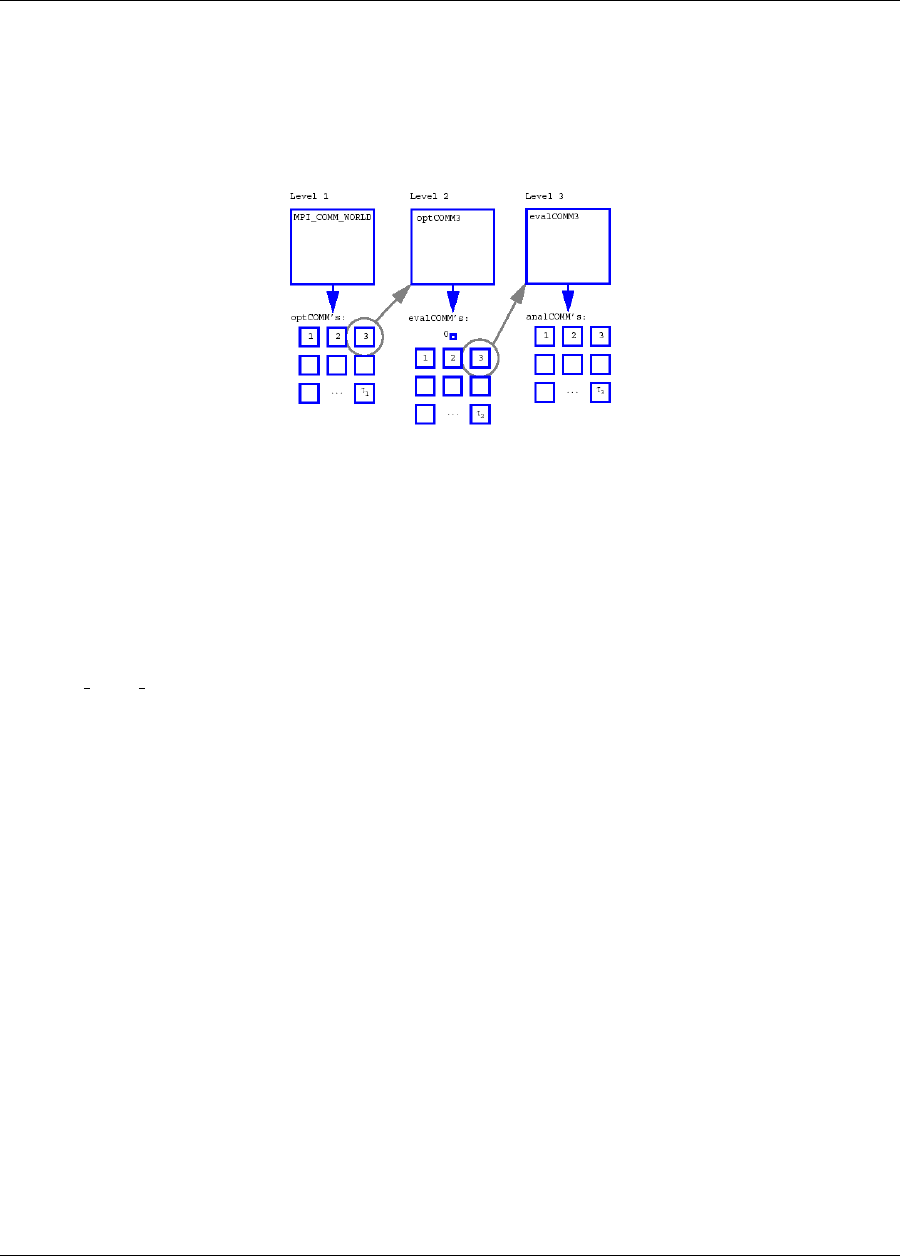
17.3. MULTILEVEL PARALLELISM 291
dedicated master or peer partition case would be further subdivided using the appropriate partitioning model for
the next lower level of parallelism.
17.3.2.2 Scheduling within levels
Figure 17.4: Recursive partitioning for nested parallelism.
Dakota is designed to allow the freedom to configure each parallelism level with either the dedicated master
partition/dynamic scheduling combination or the peer partition/static scheduling combination. In addition, the
iterator-evaluation level supports a peer partition/dynamic scheduling option, and certain external libraries may
provide custom options. As an example, Figure 17.4 shows a case in which a branch and bound meta-iterator
employs peer partition/distributed scheduling at level 1, each optimizer partition employs concurrent function
evaluations in a dedicated master partition/dynamic scheduling model at level 2, and each function evaluation
partition employs concurrent multiprocessor analyses in a peer partition/static scheduling model at level 3. In this
case, MPI COMM WORLD is subdivided into optCOMM1/2/3/.../τ1, each optCOMM is further subdivided
into evalCOMM0 (master) and evalCOMM1/2/3/.../τ2(slaves), and each slave evalCOMM is further sub-
divided into analCOMM1/2/3/.../τ3. Logic for selecting the τithat maximize overall efficiency is discussed
in [41].
17.3.3 Hybrid Parallelism
Hybrid parallelism approaches can take several forms when used in the multilevel parallel context. A concep-
tual boundary can be considered to exist for which all parallelism above the boundary is managed internally
using message-passing and all parallelism below the boundary is managed externally using asynchronous local
approaches. Hybrid parallelism approaches can then be categorized based on whether this boundary between
internal and external management occurs within a parallelism level (intra-level) or between two parallelism levels
(inter-level). In the intra-level case, the jobs for the parallelism level containing the boundary are scheduled using
a hybrid scheduler, in which a capacity multiplier is used for the number of jobs to assign to each server. Each
server is then responsible for concurrently executing its capacity of jobs using an asynchronous local approach. In
the inter-level case, one level of parallelism manages its parallelism internally using a message-passing approach
and the next lower level of parallelism manages its parallelism externally using an asynchronous local approach.
That is, the jobs for the higher level of parallelism are scheduled using a standard message-passing scheduler,
in which a single job is assigned to each server. However, each of these jobs has multiple components, as man-
aged by the next lower level of parallelism, and each server is responsible for executing these sub-components
concurrently using an asynchronous local approach.
For example, consider a multiprocessor Dakota run which involves an iterator scheduling a set of concurrent
Dakota Version 6.7 User’s Manual generated on November 13, 2017

292 CHAPTER 17. PARALLEL COMPUTING
Table 17.1: Support of job management approaches within parallelism levels. Shown in parentheses are supported
simulation interfaces and supported synchronization approaches.
Parallelism Level Asynchronous Local Message Passing Hybrid
concurrent iterators within a X
meta-iterator or nested model (blocking synch)
concurrent function evaluations XXX
within an iterator (system, fork) (system, fork, direct) (system, fork)
(blocking, nonblocking) (blocking, nonblocking) (blocking, nonblocking)
concurrent analyses XXX
within a function evaluation (fork only) (system, fork, direct) (fork only)
(blocking synch) (blocking synch) (blocking synch)
fine-grained parallel analysis X
function evaluations across a cluster of SMPs. A hybrid parallelism approach will be applied in which message-
passing parallelism is used between SMPs and asynchronous local parallelism is used within each SMP. In the
hybrid intra-level case, multiple function evaluations would be scheduled to each SMP, as dictated by the capacity
of the SMPs, and each SMP would manage its own set of concurrent function evaluations using an asynchronous
local approach. Any lower levels of parallelism would be serialized. In the hybrid inter-level case, the function
evaluations would be scheduled one per SMP, and the analysis components within each of these evaluations
would be executed concurrently using asynchronous local approaches within the SMP. Thus, the distinction can
be viewed as whether the concurrent jobs on each server in Figure 17.1c reflect the same level of parallelism
as that being scheduled by the master (intra-level) or one level of parallelism below that being scheduled by the
master (inter-level).
17.4 Capability Summary
Table 17.1 shows a matrix of the supported job management approaches for each of the parallelism levels, with
supported simulation interfaces and synchronization approaches shown in parentheses. The concurrent iterator
and multiprocessor analysis parallelism levels can only be managed with message-passing approaches. In the
former case, this is due to the fact that a separate process or thread for an iterator is not currently supported.
The latter case reflects a finer point on the definition of external parallelism management. While a multiprocessor
analysis can most certainly be launched (e.g., using mpirun/yod) from one of Dakota’s analysis drivers, resulting
in a parallel analysis external to Dakota (which is consistent with asynchronous local and hybrid approaches),
this parallelism is not visible to Dakota and therefore does not qualify as parallelism that Dakota manages (and
therefore is not included in Table 17.1). The concurrent evaluation and analysis levels can be managed either
with message-passing, asynchronous local, or hybrid techniques, with the exceptions that the direct interface does
not support asynchronous operations (asynchronous local or hybrid) at either of these levels and the system call
interface does not support asynchronous operations (asynchronous local or hybrid) at the concurrent analysis level.
The direct interface restrictions are present since multithreading in not yet supported and the system call interface
restrictions result from the inability to manage concurrent analyses within a nonblocking function evaluation
system call. Finally, nonblocking synchronization is only supported at the concurrent function evaluation level,
although it spans asynchronous local, message passing, and hybrid parallelism options.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.5. RUNNING A PARALLEL DAKOTA JOB 293
17.5 Running a Parallel Dakota Job
Section 17.2 provides a few examples of serial and parallel execution of Dakota using asynchronous local, mes-
sage passing, and hybrid approaches to single-level parallelism. The following sections provides a more complete
discussion of the parallel execution syntax and available specification controls.
17.5.1 Single-processor execution
The command for running Dakota on a single-processor and exploiting asynchronous local parallelism is the same
as for running Dakota on a single-processor for a serial study, e.g.:
dakota -i dakota.in > dakota.out
See Section 2.4 for additional information on single-processor command syntax.
17.5.2 Multiprocessor execution
Running a Dakota job on multiple processors requires the use of an executable loading facility such as mpirun,
mpiexec,poe, or yod. On a network of workstations, the mpirun script is commonly used to initiate a parallel
Dakota job, e.g.:
mpirun -np 12 dakota -i dakota.in > dakota.out
mpirun -machinefile machines -np 12 dakota -i dakota.in > dakota.out
where both examples specify the use of 12 processors, the former selecting them from a default system resources
file and the latter specifying particular machines in a machine file (see [69] for details).
On a massively parallel computer, the familiar mpirun/mpiexec options may be replaced with other launch scripts
as dictated by the particular software stack, e.g.:
yod -sz 512 dakota -i dakota.in > dakota.out
In each of these cases, MPI command line arguments are used by MPI (extracted first in the call to MPI Init)
and Dakota command line arguments are used by Dakota (extracted second by Dakota’s command line handler).
Finally, when running on computer resources that employ NQS/PBS batch schedulers, the single-processor
dakota command syntax or the multiprocessor mpirun command syntax might be contained within an ex-
ecutable script file which is submitted to the batch queue. For example, a command
qsub -l size=512 run_dakota
could be submitted to a PBS queue for execution. The NQS syntax is similar:
qsub -q snl -lP 512 -lT 6:00:00 run_dakota
These commands allocate 512 compute nodes for the study, and execute the run dakota script on a service
node. If this script contains a single-processor dakota command, then Dakota will execute on a single service
node from which it can launch parallel simulations into the compute nodes using analysis drivers that contain yod
commands (any yod executions occurring at any level underneath the run dakota script are mapped to the 512
Dakota Version 6.7 User’s Manual generated on November 13, 2017

294 CHAPTER 17. PARALLEL COMPUTING
compute node allocation). If the script submitted to qsub contains a multiprocessor mpirun command, then
Dakota will execute across multiple service nodes so that it can spread the application load in either a message-
passing or hybrid parallelism approach. Again, analysis drivers containing yod commands would be responsible
for utilizing the 512 compute nodes. And, finally, if the script submitted to qsub contains a yod of the dakota
executable, then Dakota will execute directly on the compute nodes and manage all of the parallelism internally
(note that a yod of this type without a qsub would be mapped to the interactive partition, rather than to the batch
partition).
Not all supercomputers employ the same model for service/compute partitions or provide the same support for
tiling of concurrent multiprocessor simulations within a single NQS/PBS allocation. For this reason, templates
for parallel job configuration are being catalogued within Dakota/examples/script interfaces and
Dakota/examples/parallelism (in the software distributions) that are intended to provide guidance for
individual machine idiosyncrasies.
Dakota relies on hints from the runtime environment and command line arguments to detect when it has been
launched in parallel. Due to the large number of HPC vendors and MPI implementations, parallel launch is not
always detected properly. A parallel launch is indicated by the status message
Running MPI Dakota executable in parallel on N processors.
which is written to the console near the beginning of the Dakota run.
Beginning with release 6.5, if Dakota incorrectly detects a parallel launch, automatic detection can be overriden
by setting the environment variable DAKOTA RUN PARALLEL. If the first character is set to 1,t, or T, Dakota
will configure itself to run in parallel. If the variable exists but is set to anything else, Dakota will configure itself
to run in serial mode.
17.6 Specifying Parallelism
Given an allotment of processors, Dakota contains logic based on the theoretical work in [41] to automatically
determine an efficient parallel configuration, consisting of partitioning and scheduling selections for each of the
parallelism levels. This logic accounts for problem size, the concurrency supported by particular iterative algo-
rithms, and any user inputs or overrides.
Concurrency is pushed up for most parallelism levels. That is, available processors will be assigned to concurrency
at the higher parallelism levels first as we partition from the top down. If more processors are available than
needed for concurrency at a level, then the server size is increased to support concurrency in the next lower level
of parallelism. This process is continued until all available processors have been assigned. These assignments
can be overridden by the user by specifying a number of servers, processors per server, or both, for the concurrent
iterator, evaluation, and analysis parallelism levels. For example, if it is desired to parallelize concurrent analyses
within each function evaluation, then an evaluation servers = 1 override would serialize the concurrent
function evaluations level and ensure processor availability for concurrent analyses.
The exception to this push up of concurrency occurs for concurrent-iterator parallelism levels, since iterator ex-
ecutions tend to have high variability in duration whenever they utilize feedback of results. For these levels,
concurrency is pushed down since it is generally best to serialize the levels with the highest job variation and
exploit concurrency elsewhere.
Partition type (master or peer) may also be specified for each level, and peer scheduling type (dynamic or static)
may be specified at the level of evaluation concurrency. However, these selections may be overridden by Dakota
if they are inconsistent with the number of user-requested servers, processors per server, and available processors.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
17.6. SPECIFYING PARALLELISM 295
In the following sections, the user inputs and overrides are described, followed by specification examples for
single and multi-processor Dakota executions.
17.6.1 The interface specification
Specifying parallelism within an interface can involve the use of the asynchronous,evaluation concurrency,
and analysis concurrency keywords to specify concurrency local to a processor (i.e., asynchronous local
parallelism). This asynchronous specification has dual uses:
•When running Dakota on a single-processor, the asynchronous keyword specifies the use of asyn-
chronous invocations local to the processor (these jobs then rely on external means to be allocated to other
processors). The default behavior is to simultaneously launch all function evaluations available from the
iterator as well as all available analyses within each function evaluation. In some cases, the default behavior
can overload a machine or violate a usage policy, resulting in the need to limit the number of concurrent
jobs using the evaluation concurrency and analysis concurrency specifications.
•When executing Dakota across multiple processors and managing jobs with a message-passing scheduler,
the asynchronous keyword specifies the use of asynchronous invocations local to each server processor,
resulting in a hybrid parallelism approach (see Section 17.2.3). In this case, the default behavior is one
job per server, which must be overridden with an evaluation concurrency specification and/or an
analysis concurrency specification. When a hybrid parallelism approach is specified, the capacity
of the servers (used in the automatic configuration logic) is defined as the number of servers times the
number of asynchronous jobs per server.
In both cases, the scheduling of local evaluations is dynamic by default, but may be explicitly selected or overriden
using local evaluation scheduling dynamic or static.
In addition, evaluation servers,processors per evaluation, and evaluation scheduling
keywords can be used to override the automatic parallel configuration for concurrent function evaluations. Eval-
uation scheduling may be selected to be master or peer, where the latter must be further specified to be
dynamic or static.
To override the automatic parallelism configuration for concurrent analyses, the analysis servers and
analysis scheduling keywords may be specified, and the processors per analysis keyword can
be used to override the automatic parallelism configuration for the size of multiprocessor analyses used in a direct
function simulation interface. Scheduling options for this level include master or peer, where the latter is
static (no dynamic peer option supported). Each of these keywords appears as part of the interface commands
specification in the Dakota Reference Manual [3].
17.6.2 The meta-iterator and nested model specifications
To specify concurrency in sub-iterator executions within meta-iterators and nested models, the iterator servers,
processors per iterator, and iterator scheduling keywords are used to override the automatic
parallelism configuration. For this level, the available scheduling options are master or peer, where the latter
is static (no dynamic peer option supported). See the method and model commands specification in the Dakota
Reference Manual [3] for additional details.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

296 CHAPTER 17. PARALLEL COMPUTING
17.6.3 Single-processor Dakota specification
Specifying a single-processor Dakota job that exploits parallelism through asynchronous local approaches (see
Figure 17.1a) requires inclusion of the asynchronous keyword in the interface specification. Once the input
file is defined, single-processor Dakota jobs are executed using the command syntax described previously in
Section 17.5.1.
17.6.3.1 Example 1
For example, the following specification runs an NPSOL optimization which will perform asynchronous finite
differencing:
method,
npsol_sqp
variables,
continuous_design = 5
initial_point 0.2 0.05 0.08 0.2 0.2
lower_bounds 0.15 0.02 0.05 0.1 0.1
upper_bounds 2.0 2.0 2.0 2.0 2.0
interface,
system,
asynchronous
analysis_drivers = ’text_book’
responses,
num_objective_functions = 1
num_nonlinear_inequality_constraints = 2
numerical_gradients
interval_type central
method_source dakota
fd_gradient_step_size = 1.e-4
no_hessians
Note that method source dakota selects Dakota’s internal finite differencing routine so that the concurrency
in finite difference offsets can be exploited. In this case, central differencing has been selected and 11 function
evaluations (one at the current point plus two offsets in each of five variables) can be performed simultaneously
for each NPSOL response request. These 11 evaluations will be launched with system calls in the background and
presumably assigned to additional processors through the operating system of a multiprocessor compute server or
other comparable method. The concurrency specification may be included if it is necessary to limit the maximum
number of simultaneous evaluations. For example, if a maximum of six compute processors were available, the
command
evaluation_concurrency = 6
could be added to the asynchronous specification within the interface keyword from the preceding ex-
ample.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
17.6. SPECIFYING PARALLELISM 297
17.6.3.2 Example 2
If, in addition, multiple analyses can be executed concurrently within a function evaluation (e.g., from multi-
ple load cases or disciplinary analyses that must be evaluated to compute the response data set), then an input
specification similar to the following could be used:
method,
npsol_sqp
variables,
continuous_design = 5
initial_point 0.2 0.05 0.08 0.2 0.2
lower_bounds 0.15 0.02 0.05 0.1 0.1
upper_bounds 2.0 2.0 2.0 2.0 2.0
interface,
fork
asynchronous
evaluation_concurrency = 6
analysis_concurrency = 3
analysis_drivers = ’text_book1’ ’text_book2’ ’text_book3’
responses,
num_objective_functions = 1
num_nonlinear_inequality_constraints = 2
numerical_gradients
method_source dakota
interval_type central
fd_gradient_step_size = 1.e-4
no_hessians
In this case, the default concurrency with just an asynchronous specification would be all 11 function evalua-
tions and all 3 analyses, which can be limited by the evaluation concurrency and analysis concurrency
specifications. The input file above limits the function evaluation concurrency, but not the analysis concurrency (a
specification of 3 is the default in this case and could be omitted). Changing the input to evaluation concurrency
= 1 would serialize the function evaluations, and changing the input to analysis concurrency = 1 would
serialize the analyses.
17.6.4 Multiprocessor Dakota specification
In multiprocessor executions, server evaluations are synchronous (Figure 17.1b) by default and the asynchronous
keyword is only used if a hybrid parallelism approach (Figure 17.1c) is desired. Multiprocessor Dakota jobs are
executed using the command syntax described previously in Section 17.5.2.
17.6.4.1 Example 3
To run Example 1 using a message-passing approach, the asynchronous keyword would be removed (since
the servers will execute their evaluations synchronously), resulting in the following interface specification:
interface,
Dakota Version 6.7 User’s Manual generated on November 13, 2017

298 CHAPTER 17. PARALLEL COMPUTING
system,
analysis_drivers = ’text_book’
Running Dakota on 4 processors (syntax: mpirun -np 4 dakota -i dakota.in) would result in the
following parallel configuration report from the Dakota output:
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 4 1 peer
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1 (1 dakota, 0 analysis)
-----------------------------------------------------------------------------
In this case, a peer partition and dynamic scheduling algorithm are automatically selected for the concurrent evalu-
ations. If a dedicated master is desired instead, then this logic could be overriden by adding evaluation scheduling
master:
interface,
system,
evaluation_scheduling master
analysis_drivers = ’text_book’
Running Dakota again on 4 processors (syntax: mpirun -np 4 dakota -i dakota.in) would now re-
sult in this parallel configuration report:
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 3 1 ded. master
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1 (1 dakota, 0 analysis)
-----------------------------------------------------------------------------
Now the 11 jobs will be dynamically distributed among 3 slave servers, under the control of 1 dedicated master.
As a related example, consider the case where each of the workstations used in the parallel execution has multiple
processors. In this case, a hybrid parallelism approach which combines message-passing parallelism with asyn-
chronous local parallelism (see Figure 17.1c) would be a good choice. To specify hybrid parallelism, one uses the
same asynchronous specification as was used for the single-processor examples, e.g.:
interface,
system
asynchronous evaluation_concurrency = 3
analysis_drivers = ‘text_book’
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.6. SPECIFYING PARALLELISM 299
With 3 function evaluations concurrent on each server, the capacity of a 4 processor Dakota execution (syntax:
mpirun -np 4 dakota -i dakota.in) has increased to 12 evaluations. Since all 11 jobs can now be
scheduled in a single pass, a peer static scheduler is sufficient.
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 4 1 peer
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1
-----------------------------------------------------------------------------
17.6.4.2 Example 4
To run Example 2 using a message-passing approach, the asynchronous specification is again removed:
interface,
fork
analysis_drivers = ‘text_book1’ ‘text_book2’ ‘text_book3’
Running this example on 6 processors (syntax: mpirun -np 6 dakota -i dakota.in) would result in
the following parallel configuration report:
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 6 1 peer
concurrent analyses 1 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 1
-----------------------------------------------------------------------------
in which all of the processors have been assigned to support evaluation concurrency due to the “push up” automatic
configuration logic. To assign some of the available processors to the concurrent analysis level, the following input
could be used:
interface,
fork
analysis_drivers = ‘text_book1’ ‘text_book2’ ‘text_book3’
evaluation_scheduling peer static
evaluation_servers = 2
which results in the following 2-level parallel configuration:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

300 CHAPTER 17. PARALLEL COMPUTING
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 2 3 peer
concurrent analyses 3 1 peer
multiprocessor analysis 1 N/A N/A
Total parallelism levels = 2
-----------------------------------------------------------------------------
The six processors available have been split into two evaluation servers of three processors each, where the
three processors in each evaluation server manage the three analyses, one per processor. Note that without the
scheduling override, a dedicated master partition at the evaluation level would have been chosen automatically,
dividing the six available processors into one evaluation server with three processors and another with two.
Next, consider the following 3-level parallel case, in which text book1,text book2, and text book3
from the previous examples now execute on two processors each. In this case, the processors per analysis
keyword is added and the fork interface is changed to a direct interface since the fine-grained parallelism of
the three simulations is managed internally:
interface,
direct
analysis_drivers = ‘text_book1’ ‘text_book2’ ‘text_book3’
evaluation_scheduling peer static
evaluation_servers = 2
processors_per_analysis = 2
This results in the following parallel configuration for a 12 processor Dakota run
(syntax: mpirun -np 12 dakota -i dakota.in):
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent evaluations 2 6 peer
concurrent analyses 3 2 peer
multiprocessor analysis 2 N/A N/A
Total parallelism levels = 3 (2 dakota, 1 analysis)
-----------------------------------------------------------------------------
An important point to recognize is that, since each of the parallel configuration inputs has been tied to the inter-
face specification up to this point, these parallel configurations can be reallocated for each interface in a multi-
iterator/multi-model study. For example, a Dakota execution on 40 processors might involve the following two
interface specifications:
interface,
direct,
id_interface = ’COARSE’
analysis_driver = ’sim1’
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.6. SPECIFYING PARALLELISM 301
evaluation_scheduling peer dynamic
processors_per_analysis = 5
interface,
direct,
id_interface = ’FINE’
analysis_driver = ’sim2’
evaluation_scheduling peer dynamic
processors_per_analysis = 10
for which the coarse model would employ 8 evaluation servers of 5 processors each and the fine model would
employ 4 evaluation servers of 10 processors each.
Next, consider the following 4-level parallel case that employs the Pareto set optimization meta-iterator. In this
case, iterator servers and iterator scheduling peer requests are included in the method specifi-
cation:
method,
pareto_set
iterator_servers = 2
iterator_scheduling peer
opt_method_pointer = ’NLP’
random_weight_sets = 4
Adding this pareto set method specification to the input file from the previous 12 processor example results
in the following parallel configuration for a 24 processor Dakota run
(syntax: mpirun -np 24 dakota -i dakota.in):
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent iterators 2 12 peer
concurrent evaluations 2 6 peer
concurrent analyses 3 2 peer
multiprocessor analysis 2 N/A N/A
Total parallelism levels = 4 (3 dakota, 1 analysis)
-----------------------------------------------------------------------------
Note that for this example, the parallel configuration is written to the file dakota.out.1 because of the use of
concurrent iterators.
17.6.4.3 Example 5
As a final example, consider a multi-start optimization conducted on 384 processors. A job of this size must be
submitted to the batch queue, using syntax similar to:
qsub -q snl -lP 384 -lT 6:00:00 run_dakota
where the run dakota script appears as
Dakota Version 6.7 User’s Manual generated on November 13, 2017

302 CHAPTER 17. PARALLEL COMPUTING
#!/bin/sh
cd /scratch/<some_workdir>
yod -sz 384 dakota -i dakota.in > dakota.out
the interface specifications from the dakota.in input file appears as
interface,
direct,
analysis_drivers = ’text_book1’ ’text_book2’ ’text_book3’
evaluation_servers = 8
evaluation_scheduling peer dynamic
processors_per_analysis = 2
and finally, an additional method section is added
method,
multi_start
method_pointer = ’CPS’
iterator_servers = 8
random_starts = 8
The resulting parallel configuration is reported as
-----------------------------------------------------------------------------
Dakota parallel configuration:
Level num_servers procs_per_server partition
----- ----------- ---------------- ---------
concurrent iterators 8 48 peer
concurrent evaluations 8 6 peer
concurrent analyses 3 2 peer
multiprocessor analysis 2 N/A N/A
Total parallelism levels = 4 (3 dakota, 1 analysis)
-----------------------------------------------------------------------------
Since the concurrency at each of the nested levels has a multiplicative effect on the number of processors that can
be utilized, it is easy to see how large numbers of processors can be put to effective use in reducing the time to
reach a solution, even when, as in this example, the concurrency per level is relatively low.
17.7 Application Parallelism Use Cases
This section describes several common use cases for running Dakota on parallel computing clusters with various
combinations of Dakota and application parallelism. In three of the four cases addressed, the application launched
by Dakota is assumed MPI-enabled and run as an independent parallel process.
The examples/parallelism folder in the Dakota installation includes examples of the use cases. In all four,
Dakota performs a vector parameter on the ”textbook” test function described in Section 20.1. The application
executed for serial demonstration is the text book example driver, and for parallel execution, a modified version
named text book simple par. Both are located in Dakota’s test folder. Dakota uses its fork interface to
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.7. APPLICATION PARALLELISM USE CASES 303
Table 17.2: Cases for Dakota and application-level parallelism with Mavailable processors and each application
job requiring Nprocessors. Cases 1–3 assume that Dakota and any application runs will execute wholly within a
single scheduled job, whereas Case 4 is relevant when analysis jobs must be individually submitted to a scheduler.
Case Name Dakota Application Notes
1Massively
Serial parallel serial Msimultaneous application instances, each N= 1
processor
2Sequential
Parallel serial parallel 1 simultaneous application instance on Nprocessors
3Evaluation
Tiling serial parallel M/N simultaneous Nprocessor jobs
4Evaluation
Submission serial parallel submit expensive Nprocessor application jobs to a
scheduler (e.g., qsub)
launch interface scripts written either in Bash or Python, which include mock pre-processing to prepare application
input, application execution in serial or parallel, and post-processing of application results to return to Dakota.
The combinations of Dakota and application parallelism are summarized in Table 17.2. In each case, Mdenotes
the total number of processors (or MPI tasks) allocated and Ndenotes the number of processors used by a single
application analysis. For most scenarios, Cases 1–3, where Dakota and the application jobs run within a single
cluster processor allocation (queued job), are preferred. However for particularly long-running or large jobs, or
platforms that not supporting the first scheduling modes, Case 4 may be most appropriate.
Relevant example files for each case are included in directories Dakota/examples/parallelism/ with
the Dakota distribution. These typically include a PBS or SLURM job submission script to launch the Dakota
study, a Dakota input file, and a driver script.
17.7.1 Case 1: Massively Serial — Multiple serial analysis jobs
In this case, Dakota will launch multiple simultaneous single processor application runs (an embarrassingly par-
allel model). Dakota is run in parallel, making this example an elaboration of the message-passing single-level
parallel mode described in Section 17.2. Specifically in this example, Dakota is run in parallel with M= 6
processors (pbs submission):
mpiexec -n 6 dakota dakota_pstudy.in
and will launch Msimultaneous analysis jobs, and as each job completes, another will be launched, until all jobs
are complete.
•If the analysis is extremely fast, performance may be improved by launching multiple evaluation jobs local
to each Dakota MPI process, specifying
asynchronous evaluation_concurrency = [2 or more]
As discussed in Section 17.2.3, combining MPI and local (asynchronous) parallelism in this way is an
example of hybrid parallelism.
•Conversely, if the analysis has large memory requirements, Dakota may be launched on fewer than the total
number of available cores, which has the effect of increasing the memory available to each MPI task. This is
Dakota Version 6.7 User’s Manual generated on November 13, 2017

304 CHAPTER 17. PARALLEL COMPUTING
known as undersubscription. In this case, the simulation may still be able to take advantage of thread-based
parallelism technologies such as OpenMP. Users are advised to consult their HPC’s documentation or user
support to determine how to control the number of MPI tasks launched per compute node.
•Hybrid parallelism is another way to reduce Dakota’s memory footprint. Dakota may be launched in parallel
using one MPI task per node and configured to run multiple evaluations concurrently on each node using
local parallelism. Suppose it is desired to run 160 concurrent evaluations, and the compute nodes each have
16 processors. The job script should reserve 10 nodes, assign one MPI task per node, and to run Dakota
using 10 tasks. The interface section of the Dakota input file should contain:
asynchronous evaluation_concurrency = 16
Note: The MPI standard does not support nested calls to MPI Init. Although some MPI implementations are
tolerant of nested calls and work as naively expected, it is not possible generally to launch an MPI-enabled user
simulation in parallel beneath Dakota running in parallel. This restriction includes launching parallelized user
simulations on one core (i.e. mpiexec -n 1).
17.7.2 Case 2: Sequential Parallel — One parallel analysis job at a time
This case is relevant for multi-processor analysis jobs, typically where the analysis is expensive (i.e., is long-
running or sufficient processors are not available to run more than one simultaneous analysis). Note that for
extremely long-running parallel jobs, Case 4 (Evaluation Submission) below may be more appropriate.
In this case, Dakota runs in serial
dakota dakota_pstudy.in
and the driver script launches the application with mpiexec -n K, where K≤M, to launch the application
code within the processor allocation:
mpiexec -n 6 text_book_par application.in application.out
17.7.3 Case 3: Evaluation Tiling — Multiple simultaneous parallel analysis jobs
In this case, the nodes or processors (or MPI tasks) of a single job are partitioned into equally-sized tiles. The
number of MPI tasks in each tile is N, the number needed to run the parallel application, and so there are a total
of M/N tiles, where Mis the total number of MPI tasks in the allocation. Dakota, which is run serially by the
job script, asynchronously launches evaluations, each of which runs a parallel application on an available tile.
It is up to the user to ensure consistency among the number of nodes in the allocation, the number of processors (or
MPI tasks) per node, Dakota’s evaluation concurrency, and the number of processors (or MPI tasks) per
parallel application run. For instance, suppose it is desired to perform 10 concurrent runs of a parallel application,
each requiring 32 processors. The compute nodes each have 16 processors. The job script must reserve 2 nodes
per application run (32/16) for a total of 2·10 = 20 nodes. Dakota’s evaluation concurrency must be
set to 10.
Under ideal circumstances, as Dakota concurrently launches evaluations of the user’s parallel application, the
cluster workload manager (e.g. SLURM, PBS) performs load balancing and ensures that the runs ”land” on idle
resources. In this situation, the Dakota-application interface script is relatively simple; in the execution phase, the
application is run using the appropriate parallel launcher (e.g. srun), specifying the number of MPI tasks to use.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

17.7. APPLICATION PARALLELISM USE CASES 305
However, if load balancing is not automatically handled by the workload manager, and the user does nothing to
manage tiling, then all the evaluations may land on the first few nodes, leaving the rest idle and severly degrading
performance. Clearly, care must be taken to ensure that evaluations are tiled correctly.
Whether correct evaluation tiling occurs automatically can depend intimately on how the HPC adminstrators
configured the workload manager and MPI. Users are advised to perform small-scale experiments to determine
whether performance is as expected, and/or to contact their system administrator for guidance.
Dakota provides a few examples and tools to help users orchestrate placement of parallel applications on available
resources when the resource manager does not. They are explained in the following sections.
A related consideration is the memory usage of Dakota itself. If the user’s application is memory intensive, it may
be desirable to reserve a node or a portion of a node for Dakota to prevent it from degrading the performance of
evaluations. It is necessary in this case to determine where the job script, and hence Dakota, is run. Consulting
the workload manager’s documenation or the HPC’s system administrator is advised.
17.7.3.1 Mpiexec server mode
Mpiexec (http://www.osc.edu/ pw/mpiexec/) works in concert with MPICH implementations, extending mpirun
to run jobs in a PBS environment with additional features. It offers a background server option which can be used
to tile multiple MPI jobs within a single parallel resource allocation. (Note that with MPICH, there is a difference
between mpirun and mpiexec, unlike with OpenMPI, where both are typically aliases for orterun.) See the
example in Case3-EvaluationTiling/MPICH.
In this case, an mpiexec server process is started and backgrounded to service application requests for proces-
sors; Dakota runs in serial (pbs submission):
mpiexec -server &
dakota dakota_pstudy.in
and asynchronously launches M/N = 3 evaluations (dakota pstudy.in):
interface
fork
asynchronous evaluation_concurrency = 3
analysis_driver = ’text_book_par_driver’
The simulator script calls mpiexec -n 2 to run the analysis in parallel and the mpiexec server assigns a subset
of the available processors to the particular MPI task (text book par):
mpiexec -n 2 text_book_simple_par application.in application.out
An error will result if more application tasks are launched than the processor allocation permits. An error may
result if the application does not exit cleanly. At present similar capability is not supported by OpenMPI, although
a daemon mode similar to Mpiexec has been proposed.
17.7.3.2 Relative node scheduling
This Evaluation Tiling variant uses OpenMPI 1.3.3 or newer. It leverages Dakota’s local evaluation scheduling
static option together with integer arithmetic to schedule each evaluation on the right subset of the processor al-
Dakota Version 6.7 User’s Manual generated on November 13, 2017
306 CHAPTER 17. PARALLEL COMPUTING
location. A Bash-based example is provided in Case3-EvaluationTiling/OpenMPI. Similar approaches
work with some AIX/POE installations as well.
The mpitile utility, released with Dakota 6.6, transparently manages construction of relative node lists when
using the OpenMPI command mpirun and the SLURM workload manager. mpitile resides in the Dakota
bin/ folder and is a wrapper for mpirun. It uses a file locking mechanism to support dynamic scheduling of
evaluations but also has a --static option. Using the --dedicated-master option, either an entire NODE
or a TILE can be reserved for Dakota. Running mpitile with the --help option provides a basic description
of its options. The script text book mpitile dynamic.sh in the OpenMPI example folder demonstrates
usage of mpitile.
mpitile is based on the Python module dakota.interfacing.parallel, also released with Dakota
6.6. Interface scripts written in Python may benefit from using its API directly. An example is located at
Case3-EvaluationTiling/OpenMPI/text book di dynamic.py. The dakota Python package is
located in share/dakota/Python/, which users should add to the environment variable PYTHONPATH.
17.7.3.3 Machinefile management
This Evaluation Tiling variant applies when the application must be compiled with OpenMPI or another MPI
implementation that does not support a server mode for job tiling, but does support the use of machine files spec-
ifying the resources on which to run the application job. A set of scripts are used to manage the partitioning
of the Mprocessor allocation into tiles contain Nprocessors. Each tile has an associated machines file con-
sisting of a unique subset of the assigned resources. Note that this will not work with early OpenMPI versions
with some resource managers (e.g., OpenMPI 1.2 with Torque), where machinefiles, even if a proper subset of
$PBS NODEFILE, are ignored. This will however work with OpenMPI 1.3 and newer. See the example in
Case3-EvaluationTiling/MachinefileMgmt.
In this case the pbs submission script defines variables specifying how to create a separate node file for each
job and sets up a set of nodefiles for use by each evaluation. As when using relative node lists, Dakota runs in serial
and uses asynchronous evaluation concurrency to launch the jobs. The interface script text book par driver
contains logic to lock a node file for the application run and return it when complete. As each job completes, the
next is scheduled.
17.7.4 Case 4: Evaluation Submission — Parallel analysis jobs submitted to a queue
This case describes running Dakota to submit parallel jobs to a batch queue. This option is likely only useful when
the cost of an individual analysis evaluation is high (such that the job requires far too many processors or hours to
run all the evaluations) and there is no feedback to Dakota required to generate subsequent evaluation points. So
this scenario is likely more relevant for sensitivity analysis and uncertainty quantification than optimization.
In the first pass, Dakota runs (likely interactively) in serial on a login node or other node capable of job submission:
dakota dakota_pstudy.in
For each evaluation, the simulator script (text book par driver) will generate a pbs submission script
and submit it to the scheduler. Dummy results are returned to Dakota which will exit when all jobs have been
scheduled.
In the second pass, when analysis is complete, the analysis driver is changed to post process and Dakota is
executed on a login node to collect the results of the study.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 18
Restart Capabilities and Utilities
18.1 Restart Management
Dakota was developed for solving problems that require multiple calls to computationally expensive simulation
codes. In some cases you may want to conduct the same optimization, but to a tighter final convergence tolerance.
This would be costly if the entire optimization analysis had to be repeated. Interruptions imposed by computer
usage policies, power outages, and system failures could also result in costly delays. However, Dakota automat-
ically records the variable and response data from all function evaluations so that new executions of Dakota can
pick up where previous executions left off.
The Dakota restart file (e.g., dakota.rst) is written in a binary format, leveraging the Boost.Serialization
library. While the cross-platform portability may NOT be as general as, say, the XDR standard, experience has
shown it to be a sufficiently portable format to meet most users needs. Caution should be exercised to ensure
consistent endianness of the computer architectures involved when attempting to leverage the restart capability
in a multi-host environment. For example, if a little endian host is used to create the restart file, it can only be
reliably ported and read on a host that is also little endian. As shown in Section 2.4, the primary restart commands
for Dakota are -read restart,-write restart, and -stop restart.
To write a restart file using a particular name, the -write restart command line input (may be abbreviated
as -w) is used:
dakota -i dakota.in -write_restart my_restart_file
If no -write restart specification is used, then Dakota will still write a restart file, but using the default name
dakota.rst instead of a user-specified name. To turn restart recording off, the user may select deactivate
restart file in the interface specification (refer to the Interface Commands chapter in the Dakota Ref-
erence Manual [3] for additional information). This can increase execution speed and reduce disk storage re-
quirements, but at the expense of a loss in the ability to recover and continue a run that terminates prematurely.
Obviously, this option is not recommended when function evaluations are costly or prone to failure. Please note
that using the deactivate restart file specification will result in a zero length restart file with the de-
fault name dakota.rst.
To restart Dakota from a restart file, the -read restart command line input (may be abbreviated as -r) is
used:
dakota -i dakota.in -read_restart my_restart_file

308 CHAPTER 18. RESTART CAPABILITIES AND UTILITIES
If no -read restart specification is used, then Dakota will not read restart information from any file (i.e., the
default is no restart processing).
A new Dakota feature (as of version 6.0) is an input file specification block providing users with additional
control in the management of the function evaluation cache, duplicate evaluation detection, and restart data file
entries. In the interfaces analysis driver definition, it is possible to provide additional deactivate parameters in
the specification block (e.g., deactivate strict cache equality. It should be noted that, by default,
Dakota’s evaluation cache and restart capabilities are based on strict binary equality. This provides a performance
advantage, as it permits a hash-based data structure to be used to search the evaluation cache. The use of the
deactivate strict cache equality keywords may prevent cache misses, which can occur when at-
tempting to use a restart file on a machine different from the one on which it was generated. Specifying those
keywords in the Dakota input file when performing a restart analysis should be considered judiciously, on a case-
by-case basis, since there will be a performance penalty for the non-hashed evaluation cache lookups for detection
of duplicates. That said, there are situations in which it is desirable to accept the performance hit of the slower
cache lookups (for example a computationally expensive analysis driver).
If the -write restart and -read restart specifications identify the same file (including the case where
-write restart is not specified and -read restart identifies dakota.rst), then new evaluations will
be appended to the existing restart file. If the -write restart and -read restart specifications identify
different files, then the evaluations read from the file identified by -read restart are first written to the
-write restart file. Any new evaluations are then appended to the -write restart file. In this way,
restart operations can be chained together indefinitely with the assurance that all of the relevant evaluations are
present in the latest restart file.
To read in only a portion of a restart file, the -stop restart control (may be abbreviated as -s) is used
to specify the number of entries to be read from the database. Note that this integer value corresponds to the
restart record processing counter (as can be seen when using the print utility; see Section 18.2.1 below), which
may differ from the evaluation numbers used in the previous run if, for example, any duplicates were detected
(since these duplicates are not recorded in the restart file). In the case of a -stop restart specification, it is
usually desirable to specify a new restart file using -write restart so as to remove the records of erroneous
or corrupted function evaluations. For example, to read in the first 50 evaluations from dakota.rst:
dakota -i dakota.in -r dakota.rst -s 50 -w dakota_new.rst
The dakota new.rst file will contain the 50 processed evaluations from dakota.rst as well as any new
evaluations. All evaluations following the 50th in dakota.rst have been removed from the latest restart record.
Dakota’s restart algorithm relies on its duplicate detection capabilities. Processing a restart file populates the
list of function evaluations that have been performed. Then, when the study is restarted, it is started from the
beginning (not a “warm” start) and many of the function evaluations requested by the iterator are intercepted
by the duplicate detection code. This approach has the primary advantage of restoring the complete state of the
iteration (including the ability to correctly detect subsequent duplicates) for all iterators and multi-iterator methods
without the need for iterator-specific restart code. However, the possibility exists for numerical round-off error
to cause a divergence between the evaluations performed in the previous and restarted studies. This has been
extremely rare to date.
18.2 The Dakota Restart Utility
The Dakota restart utility program provides a variety of facilities for managing restart files from Dakota execu-
tions. The executable program name is dakota restart util and it has the following options, as shown by
the usage message returned when executing the utility without any options:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

18.2. THE DAKOTA RESTART UTILITY 309
Usage:
dakota_restart_util command <arg1> [<arg2> <arg3> ...] --options
dakota_restart_util print <restart_file>
dakota_restart_util to_neutral <restart_file> <neutral_file>
dakota_restart_util from_neutral <neutral_file> <restart_file>
dakota_restart_util to_tabular <restart_file> <text_file>
[--custom_annotated [header] [eval_id] [interface_id]]
[--output_precision <int>]
dakota_restart_util remove <double> <old_restart_file> <new_restart_file>
dakota_restart_util remove_ids <int_1> ... <int_n> <old_restart_file> <new_restart_file>
dakota_restart_util cat <restart_file_1> ... <restart_file_n> <new_restart_file>
options:
--help show dakota_restart_util help message
--custom_annotated arg tabular file options: header, eval_id,
interface_id
--freeform tabular file: freeform format
--output_precision arg (=10) set tabular output precision
Several of these functions involve format conversions. In particular, the binary format used for restart files can be
converted to ASCII text and printed to the screen, converted to and from a neutral file format, or converted to a
tabular format for importing into 3rd-party graphics programs. In addition, a restart file with corrupted data can
be repaired by value or id, and multiple restart files can be combined to create a master database.
18.2.1 Print
The print option outputs the contents of a particular restart file in human-readable format, since the binary
format is not convenient for direct inspection. The restart data is printed in full precision, so that (near-)exact
matching of points is possible for restarted runs or corrupted data removals. For example, the following command
dakota_restart_util print dakota.rst
results in output similar to the following (from the example in Section 20.5):
------------------------------------------
Restart record 1 (evaluation id 1):
------------------------------------------
Parameters:
1.8000000000000000e+00 intake_dia
1.0000000000000000e+00 flatness
Active response data:
Active set vector = { 3 3 3 3 }
-2.4355973813420619e+00 obj_fn
-4.7428486677140930e-01 nln_ineq_con_1
-4.5000000000000001e-01 nln_ineq_con_2
1.3971143170299741e-01 nln_ineq_con_3
[ -4.3644298963447897e-01 1.4999999999999999e-01 ] obj_fn gradient
[ 1.3855136437818300e-01 0.0000000000000000e+00 ] nln_ineq_con_1 gradient
[ 0.0000000000000000e+00 1.4999999999999999e-01 ] nln_ineq_con_2 gradient
[ 0.0000000000000000e+00 -1.9485571585149869e-01 ] nln_ineq_con_3 gradient
------------------------------------------
Restart record 2 (evaluation id 2):
------------------------------------------
Dakota Version 6.7 User’s Manual generated on November 13, 2017

310 CHAPTER 18. RESTART CAPABILITIES AND UTILITIES
Parameters:
2.1640000000000001e+00 intake_dia
1.7169994018008317e+00 flatness
Active response data:
Active set vector = { 3 3 3 3 }
-2.4869127192988878e+00 obj_fn
6.9256958799989843e-01 nln_ineq_con_1
-3.4245008972987528e-01 nln_ineq_con_2
8.7142207937157910e-03 nln_ineq_con_3
[ -4.3644298963447897e-01 1.4999999999999999e-01 ] obj_fn gradient
[ 2.9814239699997572e+01 0.0000000000000000e+00 ] nln_ineq_con_1 gradient
[ 0.0000000000000000e+00 1.4999999999999999e-01 ] nln_ineq_con_2 gradient
[ 0.0000000000000000e+00 -1.6998301774282701e-01 ] nln_ineq_con_3 gradient
...<snip>...
Restart file processing completed: 11 evaluations retrieved.
18.2.2 To/From Neutral File Format
A Dakota restart file can be converted to a neutral file format using a command like the following:
dakota_restart_util to_neutral dakota.rst dakota.neu
which results in a report similar to the following:
Writing neutral file dakota.neu
Restart file processing completed: 11 evaluations retrieved.
Similarly, a neutral file can be returned to binary format using a command like the following:
dakota_restart_util from_neutral dakota.neu dakota.rst
which results in a report similar to the following:
Reading neutral file dakota.neu
Writing new restart file dakota.rst
Neutral file processing completed: 11 evaluations retrieved.
The contents of the generated neutral file are similar to the following (from the first two records for the example
in Section 20.5):
6 7 2 1.8000000000000000e+00 intake_dia 1.0000000000000000e+00 flatness 0 0 0 0
NULL 4 2 1 0 3 3 3 3 1 2 obj_fn nln_ineq_con_1 nln_ineq_con_2 nln_ineq_con_3
-2.4355973813420619e+00 -4.7428486677140930e-01 -4.5000000000000001e-01
1.3971143170299741e-01 -4.3644298963447897e-01 1.4999999999999999e-01
1.3855136437818300e-01 0.0000000000000000e+00 0.0000000000000000e+00
1.4999999999999999e-01 0.0000000000000000e+00 -1.9485571585149869e-01 1
6 7 2 2.1640000000000001e+00 intake_dia 1.7169994018008317e+00 flatness 0 0 0 0
NULL 4 2 1 0 3 3 3 3 1 2 obj_fn nln_ineq_con_1 nln_ineq_con_2 nln_ineq_con_3
Dakota Version 6.7 User’s Manual generated on November 13, 2017

18.2. THE DAKOTA RESTART UTILITY 311
-2.4869127192988878e+00 6.9256958799989843e-01 -3.4245008972987528e-01
8.7142207937157910e-03 -4.3644298963447897e-01 1.4999999999999999e-01
2.9814239699997572e+01 0.0000000000000000e+00 0.0000000000000000e+00
1.4999999999999999e-01 0.0000000000000000e+00 -1.6998301774282701e-01 2
This format is not intended for direct viewing (print should be used for this purpose). Rather, the neutral
file capability has been used in the past for managing portability of restart data across platforms of dissimilar
endianness of the computer architectures (e.g. creator of the file was little endian but the need exists to run dakota
with restart on a big endian host. The neutral file format has also been shown to be useful for for advanced repair
of restart records (in cases where the techniques of Section 18.2.5 were insufficient).
18.2.3 To Tabular Format
Conversion of a binary restart file to a tabular format enables convenient import of this data into 3rd-party post-
processing tools such as Matlab, TECplot, Excel, etc. This facility is similar to the tabular data option in the
Dakota input file specification (described in Section 13.3), but with two important differences:
1. No function evaluations are suppressed as they are with tabular data (i.e., any internal finite difference
evaluations are included).
2. The conversion can be performed after Dakota completion, i.e., for Dakota runs executed previously.
An example command for converting a restart file to tabular format is:
dakota_restart_util to_tabular dakota.rst dakota.m
which results in a report similar to the following:
Writing tabular text file dakota.m
Restart file processing completed: 10 evaluations tabulated.
The contents of the generated tabular file are similar to the following (from the example in Section 20.1.1).
Note that while evaluations resulting from numerical derivative offsets would be reported (as described above),
derivatives returned as part of the evaluations are not reported (since they do not readily fit within a compact
tabular format):
%eval_id interface x1 x2 obj_fn nln_ineq_con_1 nln_ineq_con_2
1 NO_ID 0.9 1.1 0.0002 0.26 0.76
2 NO_ID 0.58256179 0.4772224441 0.1050555937 0.1007670171 -0.06353963386
3 NO_ID 0.5 0.4318131566 0.1667232695 0.03409342169 -0.06353739777
4 NO_ID 0.5 0.3695495062 0.2204806721 0.06522524692 -0.1134331625
5 NO_ID 0.5 0.3757758727 0.2143316122 0.06211206365 -0.1087924935
6 NO_ID 0.5 0.3695495062 0.2204806721 0.06522524692 -0.1134331625
7 NO_ID 0.5005468682 -0.5204065326 5.405888123 0.5107504335 0.02054952507
8 NO_ID 0.5000092554 0.4156974409 0.1790558059 0.04216053506 -0.07720026537
9 NO_ID 0.500000919 0.4302129149 0.1679019175 0.0348944616 -0.0649173074
10 NO_ID 0.50037519 -0.2214765079 2.288391116 0.3611135847 -0.2011357515
...
Controlling tabular format: The command-line options --freeform and --custom annotated give con-
trol of headers in the resulting tabular file. give control of headers in the resulting tabular file. Freeform will
generate a tabular file with no leading row nor columns (variable and response values only). Custom annotated
format accepts any or all of the options:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

312 CHAPTER 18. RESTART CAPABILITIES AND UTILITIES
•header: include %-commented header row with labels
•eval id: include leading column with evaluation ID
•interface id: include leading column with interface ID
For example, to recover Dakota 6.0 tabular format, which contained a header row, leading column with evaluation
ID, but no interface ID:
dakota_restart_util to_tabular dakota.rst dakota.m --custom_annotated header eval_id
Resulting in
%eval_id x1 x2 obj_fn nln_ineq_con_1 nln_ineq_con_2
1 0.9 1.1 0.0002 0.26 0.76
2 0.90009 1.1 0.0001996404857 0.2601620081 0.759955
3 0.89991 1.1 0.0002003604863 0.2598380081 0.760045
...
Finally, --output precision <int> will generate tabular output with the specified integer digits of preci-
sion.
18.2.4 Concatenation of Multiple Restart Files
In some instances, it is useful to combine restart files into a single master function evaluation database. For
example, when constructing a data fit surrogate model, data from previous studies can be pulled in and reused to
create a combined data set for the surrogate fit. An example command for concatenating multiple restart files is:
dakota_restart_util cat dakota.rst.1 dakota.rst.2 dakota.rst.3 dakota.rst.all
which results in a report similar to the following:
Writing new restart file dakota.rst.all
dakota.rst.1 processing completed: 10 evaluations retrieved.
dakota.rst.2 processing completed: 110 evaluations retrieved.
dakota.rst.3 processing completed: 65 evaluations retrieved.
The dakota.rst.all database now contains 185 evaluations and can be read in for use in a subsequent Dakota
study using the -read restart option to the dakota executable (see Section 18.1).
18.2.5 Removal of Corrupted Data
On occasion, a simulation or computer system failure may cause a corruption of the Dakota restart file. For
example, a simulation crash may result in failure of a post-processor to retrieve meaningful data. If 0’s (or other
erroneous data) are returned from the user’s analysis driver, then this bad data will get recorded in the
restart file. If there is a clear demarcation of where corruption initiated (typical in a process with feedback, such
as gradient-based optimization), then use of the -stop restart option for the dakota executable can be
effective in continuing the study from the point immediately prior to the introduction of bad data. If, however,
there are interspersed corruptions throughout the restart database (typical in a process without feedback, such as
sampling), then the remove and remove ids options of dakota restart util can be useful.
An example of the command syntax for the remove option is:
Dakota Version 6.7 User’s Manual generated on November 13, 2017

18.2. THE DAKOTA RESTART UTILITY 313
dakota_restart_util remove 2.e-04 dakota.rst dakota.rst.repaired
which results in a report similar to the following:
Writing new restart file dakota.rst.repaired
Restart repair completed: 65 evaluations retrieved, 2 removed, 63 saved.
where any evaluations in dakota.rst having an active response function value that matches 2.e-04 within
machine precision are discarded when creating dakota.rst.repaired.
An example of the command syntax for the remove ids option is:
dakota_restart_util remove_ids 12 15 23 44 57 dakota.rst dakota.rst.repaired
which results in a report similar to the following:
Writing new restart file dakota.rst.repaired
Restart repair completed: 65 evaluations retrieved, 5 removed, 60 saved.
where evaluation ids 12,15,23,44, and 57 have been discarded when creating dakota.rst.repaired.
An important detail is that, unlike the -stop restart option which operates on restart record numbers (see
Section 18.1)), the remove ids option operates on evaluation ids. Thus, removal is not necessarily based on the
order of appearance in the restart file. This distinction is important when removing restart records for a run that
contained either asynchronous or duplicate evaluations, since the restart insertion order and evaluation ids may not
correspond in these cases (asynchronous evaluations have ids assigned in the order of job creation but are inserted
in the restart file in the order of job completion, and duplicate evaluations are not recorded which introduces offsets
between evaluation id and record number). This can also be important if removing records from a concatenated
restart file, since the same evaluation id could appear more than once. In this case, all evaluation records with ids
matching the remove ids list will be removed.
If neither of these removal options is sufficient to handle a particular restart repair need, then the fallback position
is to resort to direct editing of a neutral file (refer to Section 18.2.2) to perform the necessary modifications.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

314 CHAPTER 18. RESTART CAPABILITIES AND UTILITIES
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 19
Simulation Failure Capturing
Dakota provides the capability to manage failures in simulation codes within its system call, fork, and direct
simulation interfaces (see Section 10.2 for simulation interface descriptions). Failure capturing consists of three
operations: failure detection, failure communication, and failure mitigation.
19.1 Failure detection
Since the symptoms of a simulation failure are highly code and application dependent, it is the user’s responsi-
bility to detect failures within their analysis driver,input filter, or output filter. One popular
example of simulation monitoring is to rely on a simulation’s internal detection of errors. In this case, the UNIX
grep utility can be used within a user’s driver/filter script to detect strings in output files which indicate analysis
failure. For example, the following simple C shell script excerpt
grep ERROR analysis.out > /dev/null
if ( $status == 0 )
echo "FAIL" > results.out
endif
will pass the if test and communicate simulation failure to Dakota if the grep command finds the string ERROR
anywhere in the analysis.out file. The /dev/null device file is called the “bit bucket” and the grep
command output is discarded by redirecting it to this destination. The $status shell variable contains the exit
status of the last command executed [6], which is the exit status of grep in this case (0 if successful in finding
the error string, nonzero otherwise). For Bourne shells [13], the $? shell variable serves the same purpose as
$status for C shells. In a related approach, if the return code from a simulation can be used directly for failure
detection purposes, then $status or $? could be queried immediately following the simulation execution using
an if test like that shown above.
If the simulation code is not returning error codes or providing direct error diagnostic information, then failure
detection may require monitoring of simulation results for sanity (e.g., is the mesh distorting excessively?) or
potentially monitoring for continued process existence to detect a simulation segmentation fault or core dump.
While this can get complicated, the flexibility of Dakota’s interfaces allows for a wide variety of user-defined
monitoring approaches.

316 CHAPTER 19. SIMULATION FAILURE CAPTURING
19.2 Failure communication
Once a failure is detected, it must be communicated so that Dakota can take the appropriate corrective action. The
form of this communication depends on the type of simulation interface in use.
In the system call and fork simulation interfaces, a detected simulation failure is communicated to Dakota through
the results file. Instead of returning the standard results file data, the string “fail” should appear at the beginning
of the results file. Any data appearing after the fail string will be ignored. Also, Dakota’s detection of this string
is case insensitive, so “FAIL”, “Fail”, etc., are equally valid.
In the direct simulation interface case, a detected simulation failure is communicated to Dakota through the
return code provided by the user’s analysis driver,input filter, or output filter. As shown in
Section 16.2.1, the prototype for simulations linked within the direct interface includes an integer return code.
This code has the following meanings: zero (false) indicates that all is normal and nonzero (true) indicates an
exception (i.e., a simulation failure).
19.3 Failure mitigation
Once the analysis failure has been communicated, Dakota will attempt to recover from the failure using one of
the following four mechanisms, as governed by the interface specification in the user’s input file (see the Interface
Commands chapter in the Dakota Reference Manual [3] for additional information).
19.3.1 Abort (default)
If the abort option is active (the default), then Dakota will terminate upon detecting a failure. Note that if the
problem causing the failure can be corrected, Dakota’s restart capability (see Chapter 18) can be used to continue
the study.
19.3.2 Retry
If the retry option is specified, then Dakota will re-invoke the failed simulation up to the specified number of
retries. If the simulation continues to fail on each of these retries, Dakota will terminate. The retry option is
appropriate for those cases in which simulation failures may be resulting from transient computing environment
issues, such as shared disk space, software license access, or networking problems.
19.3.3 Recover
If the recover option is specified, then Dakota will not attempt the failed simulation again. Rather, it will return
a “dummy” set of function values as the results of the function evaluation. The dummy function values to be
returned are specified by the user. Any gradient or Hessian data requested in the active set vector will be zero.
This option is appropriate for those cases in which a failed simulation may indicate a region of the design space
to be avoided and the dummy values can be used to return a large objective function or constraint violation which
will discourage an optimizer from further investigating the region.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

19.4. SPECIAL VALUES 317
19.3.4 Continuation
If the continuation option is specified, then Dakota will attempt to step towards the failing “target” simulation
from a nearby “source” simulation through the use of a continuation algorithm. This option is appropriate for those
cases in which a failed simulation may be caused by an inadequate initial guess. If the “distance” between the
source and target can be divided into smaller steps in which information from one step provides an adequate initial
guess for the next step, then the continuation method can step towards the target in increments sufficiently small
to allow for convergence of the simulations.
When the failure occurs, the interval between the last successful evaluation (the source point) and the current
target point is halved and the evaluation is retried. This halving is repeated until a successful evaluation occurs.
The algorithm then marches towards the target point using the last interval as a step size. If a failure occurs while
marching forward, the interval will be halved again. Each invocation of the continuation algorithm is allowed
a total of ten failures (ten halvings result in up to 1024 evaluations from source to target) prior to aborting the
Dakota process.
While Dakota manages the interval halving and function evaluation invocations, the user is responsible for man-
aging the initial guess for the simulation program. For example, in a GOMA input file [118], the user specifies
the files to be used for reading initial guess data and writing solution data. When using the last successful eval-
uation in the continuation algorithm, the translation of initial guess data can be accomplished by simply copying
the solution data file leftover from the last evaluation to the initial guess file for the current evaluation (and in
fact this is useful for all evaluations, not just continuation). However, a more general approach would use the
closest successful evaluation (rather than the last successful evaluation) as the source point in the continuation
algorithm. This will be especially important for nonlocal methods (e.g., genetic algorithms) in which the last
successful evaluation may not necessarily be in the vicinity of the current evaluation. This approach will require
the user to save and manipulate previous solutions (likely tagged with evaluation number) so that the results from
a particular simulation (specified by Dakota after internal identification of the closest point) can be used as the
current simulation’s initial guess. This more general approach is not yet supported in Dakota.
19.4 Special values
In IEEE arithmetic, “NaN” indicates “not a number” and ±“Inf” or ±“Infinity” indicates positive or negative
infinity. These special values may be returned directly in function evaluation results from a simulation interface
or they may be specified in a user’s input file within the recover specification described in Section 19.3.3. There
is a key difference between these two cases. In the former case of direct simulation return, failure mitigation can
be managed on a per response function basis. When using recover, however, the failure applies to the complete
set of simulation results.
In both of these cases, the handling of NaN or Inf is managed using iterator-specific approaches. Currently,
nondeterministic sampling methods (see Section 5.2), polynomial chaos expansions using either regression ap-
proaches or spectral projection with random sampling (see Section 5.4), and the NL2SOL method for nonlinear
least squares (see §7.4.3) are the only methods with special numerical exception handling: the sampling methods
simply omit any samples that are not finite from the statistics generation, the polynomial chaos methods omit any
samples that are not finite from the coefficient estimation, and NL2SOL treats NaN or Infinity in a residual vector
(i.e., values in a results file for a function evaluation) computed for a trial step as an indication that the trial step
was too long and violates an unstated constraint; NL2SOL responds by trying a shorter step.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

318 CHAPTER 19. SIMULATION FAILURE CAPTURING
Dakota Version 6.7 User’s Manual generated on November 13, 2017

Chapter 20
Additional Examples
This chapter contains additional examples of available methods being applied to several test problems. The
examples are organized by the test problem being used. See Section 1.5 for help in finding the files referenced
here.
Many of these examples are also used as code verification tests. The examples are run periodically and the results
are checked against known solutions. This ensures that the algorithms are correctly implemented.
20.1 Textbook
The two-variable version of the “textbook” test problem provides a nonlinearly constrained optimization test case.
It is formulated as:
minimize f= (x1−1)4+ (x2−1)4
subject to g1=x2
1−x2
2≤0
g2=x2
2−x1
2≤0(20.1)
0.5≤x1≤5.8
−2.9≤x2≤2.9
Contours of this test problem are illustrated in Figure 20.1(a), with a close-up view of the feasible region given in
Figure 20.1(b).
For the textbook test problem, the unconstrained minimum occurs at (x1, x2) = (1,1). However, the inclusion of
the constraints moves the minimum to (x1, x2) = (0.5,0.5). Equation 20.1 presents the 2-dimensional form of
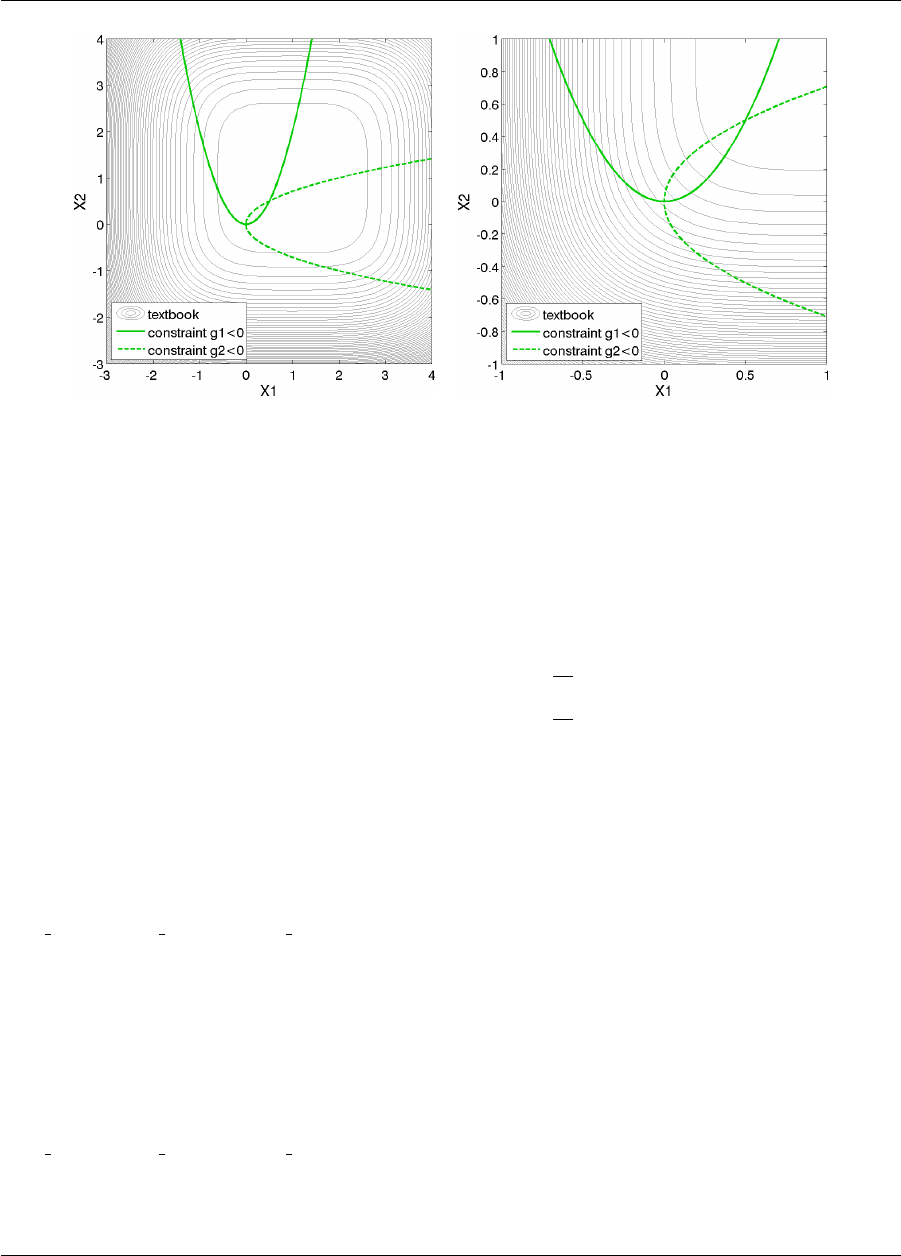
320 CHAPTER 20. ADDITIONAL EXAMPLES
(a) (b)
Figure 20.1: Contours of the textbook problem (a) on the [−3,4] ×[−3,4] domain and (b) zoomed into an area
containing the constrained optimum point (x1, x2) = (0.5,0.5). The feasible region lies at the intersection of the
two constraints g1(solid) and g2(dashed).
the textbook problem. An extended formulation is stated as
minimize f=
n
X
i=1
(xi−1)4
subject to g1=x2
1−x2
2≤0(20.2)
g2=x2
2−x1
2≤0
0.5≤x1≤5.8
−2.9≤x2≤2.9
where nis the number of design variables. The objective function is designed to accommodate an arbitrary
number of design variables in order to allow flexible testing of a variety of data sets. Contour plots for the n= 2
case have been shown previously in Figure 20.1.
For the optimization problem given in Equation 20.2, the unconstrained solution
(num nonlinear inequality constraints set to zero) for two design variables is:
x1= 1.0
x2= 1.0
with
f∗= 0.0
The solution for the optimization problem constrained by g1
(num nonlinear inequality constraints set to one) is:
x1= 0.763
x2= 1.16
Dakota Version 6.7 User’s Manual generated on November 13, 2017
20.1. TEXTBOOK 321
with
f∗= 0.00388
g∗
1= 0.0 (active)
The solution for the optimization problem constrained by g1and g2
(num nonlinear inequality constraints set to two) is:
x1= 0.500
x2= 0.500
with
f∗= 0.125
g∗
1= 0.0 (active)
g∗
2= 0.0 (active)
Note that as constraints are added, the design freedom is restricted (the additional constraints are active at the
solution) and an increase in the optimal objective function is observed.
20.1.1 Gradient-based Constrained Optimization
This example demonstrates the use of a gradient-based optimization algorithm on a nonlinearly constrained prob-
lem. The Dakota input file for this example is shown in Figure 20.2. This input file is similar to the input file for
the unconstrained gradient-based optimization example involving the Rosenbrock function, seen in Section 2.3.3.
Note the addition of commands in the responses block of the input file that identify the number and type of con-
straints, along with the upper bounds on these constraints. The commands direct and analysis driver =
’text book’ specify that Dakota will use its internal version of the textbook problem.
The conmin mfd keyword in Figure 20.2 tells Dakota to use the CONMIN package’s implementation of the
Method of Feasible Directions (see Section 6.2.1.1 for more details).
A significantly faster alternative is the DOT package’s Modified Method of Feasible Directions, i.e. dot mmfd
(see Section 6.2.1.1 for more details). However, DOT is licensed software that may not be available on a particular
system. If it is installed on your system and Dakota has been compiled without the --without-dot flag, you
may use it by commenting out the line with conmin mfd and uncommenting the line with dot mmfd.
The results of the optimization example are listed at the end of the output file (see Section 2.1.3. This information
shows that the optimizer stopped at the point (x1, x2) = (0.5,0.5), where both constraints are approximately
satisfied, and where the objective function value is 0.128. The progress of the optimization algorithm is shown in
Figure 20.3(b) where the dots correspond to the end points of each iteration in the algorithm. The starting point
is (x1, x2) = (0.9,1.1), where both constraints are violated. The optimizer takes a sequence of steps to minimize
the objective function while reducing the infeasibility of the constraints. The optimization graphics are also shown
in Figure 20.3(a).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

322 CHAPTER 20. ADDITIONAL EXAMPLES
# Dakota Input File: textbook_opt_conmin.in
environment
graphics
tabular_data
tabular_data_file = ’textbook_opt_conmin.dat’
method
# dot_mmfd #DOT performs better but may not be available
conmin_mfd
max_iterations = 50
convergence_tolerance = 1e-4
variables
continuous_design = 2
initial_point 0.9 1.1
upper_bounds 5.8 2.9
lower_bounds 0.5 -2.9
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’text_book’
direct
responses
objective_functions = 1
nonlinear_inequality_constraints = 2
descriptors ’f’ ’c1’ ’c2’
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 1.e-4
no_hessians
Figure 20.2: Textbook gradient-based constrained optimization example: the Dakota input file – see
Dakota/examples/users/textbook opt conmin.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
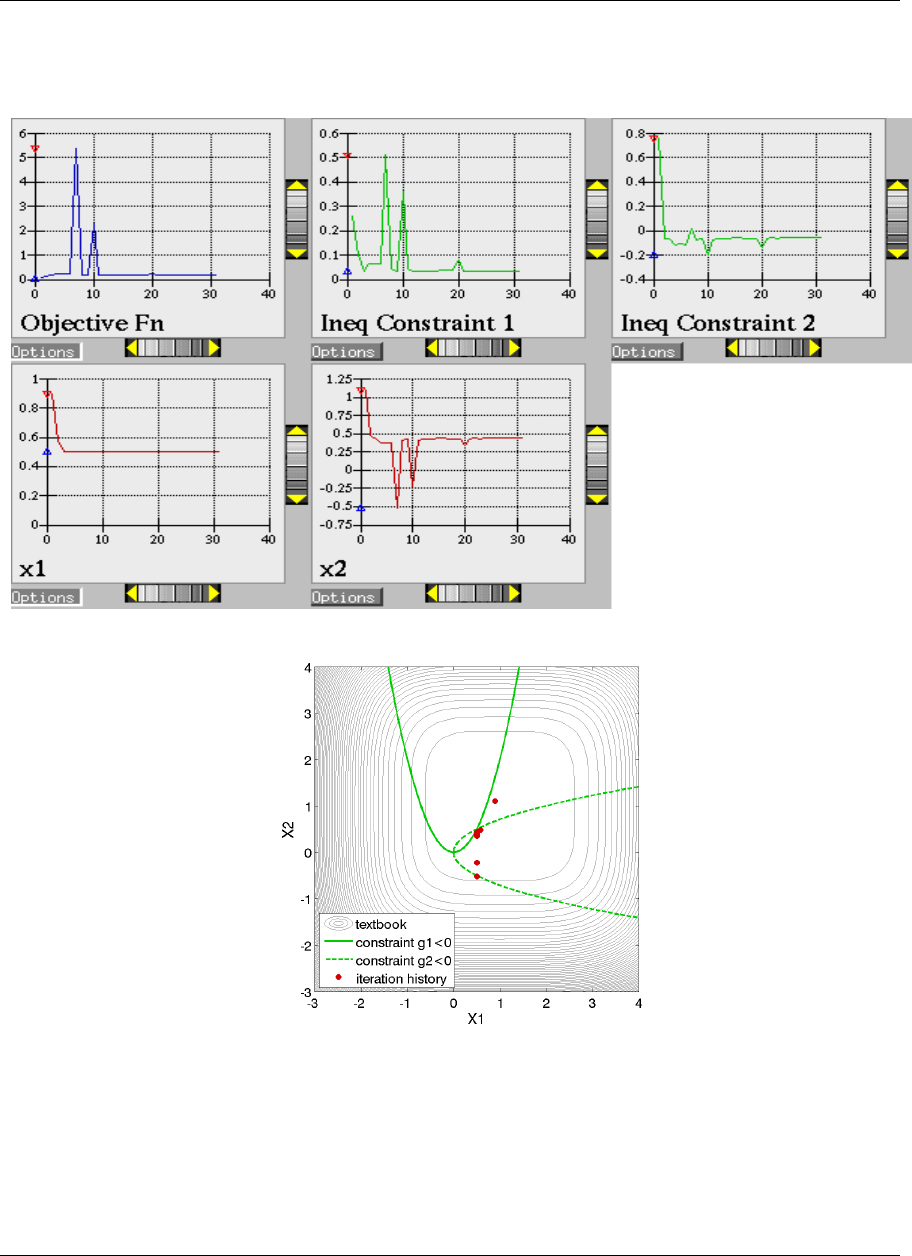
20.1. TEXTBOOK 323
(a)
(b)
Figure 20.3: Textbook gradient-based constrained optimization example: (a) screen capture of the Dakota graphics
shows how the objective function was reduced during the search for a feasible design point and (b) iteration history
(iterations marked by solid dots).
Dakota Version 6.7 User’s Manual generated on November 13, 2017

324 CHAPTER 20. ADDITIONAL EXAMPLES
20.2 Rosenbrock
The Rosenbrock function [57] is a well known test problem for optimization algorithms. The standard formulation
includes two design variables, and computes a single objective function. This problem can also be posed as a
least-squares optimization problem with two residuals to be minimzed because the objective function is the sum
of squared terms.
Standard Formulation
The standard two-dimensional formulation can be stated as
minimize f= 100(x2−x2
1)2+ (1 −x1)2(20.3)
Surface and contour plots for this function have been shown previously in Figure 2.5.
The optimal solution is:
x1= 1.0
x2= 1.0
with
f∗= 0.0
A discussion of gradient based optimization to minimize this function is in Section 2.3.3.
A Least-Squares Optimization Formulation
This test problem may also be used to exercise least-squares solution methods by recasting the standard problem
formulation into:
minimize f= (f1)2+ (f2)2(20.4)
where
f1= 10(x2−x2
1)(20.5)
and
f2= 1 −x1(20.6)
are residual terms.
The included analysis driver can handle both formulations. In the Dakota/test directory, the rosenbrock
executable (compiled from Dakota Source/test/rosenbrock.cpp) checks the number of response func-
tions passed in the parameters file and returns either an objective function (as computed from Equation 20.3) for
use with optimization methods or two least squares terms (as computed from Equations 20.5-20.6) for use with
least squares methods. Both cases support analytic gradients of the function set with respect to the design vari-
ables. See Figure 2.7 (std formulation) and Figure 20.4 (least squares formulation) for examples of each usage.
20.2.1 Least-Squares Optimization
Least squares methods are often used for calibration or parameter estimation, that is, to seek parameters maxi-
mizing agreement of models with experimental data. The least-squares formulation was described in the previous
section.
When using a least-squares approach to minimize a function, each of the least-squares terms f1, f2, . . . is driven
toward zero. This formulation permits the use of specialized algorithms that can be more efficient than general
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.2. ROSENBROCK 325
purpose optimization algorithms. See Chapter 7for more detail on the algorithms used for least-squares mini-
mization, as well as a discussion on the types of engineering design problems (e.g., parameter estimation) that can
make use of the least-squares approach.
Figure 20.4 is a listing of the Dakota input file rosen opt nls.in. This differs from the input file shown in
Figure 2.7 in several key areas. The responses block of the input file uses the keyword calibration terms
= 2 instead of objective functions = 1. The method block of the input file shows that the NL2SOL
algorithm [25] (nl2sol) is used in this example. (The Gauss-Newton, NL2SOL, and NLSSOL SQP algorithms
are currently available for exploiting the special mathematical structure of least squares minimization problems).
# Dakota Input File: rosen_opt_nls.in
environment
graphics
tabular_data
tabular_data_file = ’rosen_opt_nls.dat’
method
nl2sol
convergence_tolerance = 1e-4
max_iterations = 100
model
single
variables
continuous_design = 2
initial_point -1.2 1.0
lower_bounds -2.0 -2.0
upper_bounds 2.0 2.0
descriptors ’x1’ "x2"
interface
analysis_drivers = ’rosenbrock’
direct
responses
calibration_terms = 2
analytic_gradients
no_hessians
Figure 20.4: Rosenbrock nonlinear least squares example: the Dakota input file – see
Dakota/examples/users/rosen opt nls.in
The optimization results at the end of the output file show that the least squares minimization approach has
found the same optimum design point, (x1, x2) = (1.0,1.0), as was found using the conventional gradient-based
optimization approach. The iteration history of the least squares minimization is given in Figure 20.5, and shows
that 14 function evaluations were needed for convergence. In this example the least squares approach required
about half the number of function evaluations as did conventional gradient-based optimization. In many cases a
good least squares algorithm will converge more rapidly in the vicinity of the solution.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
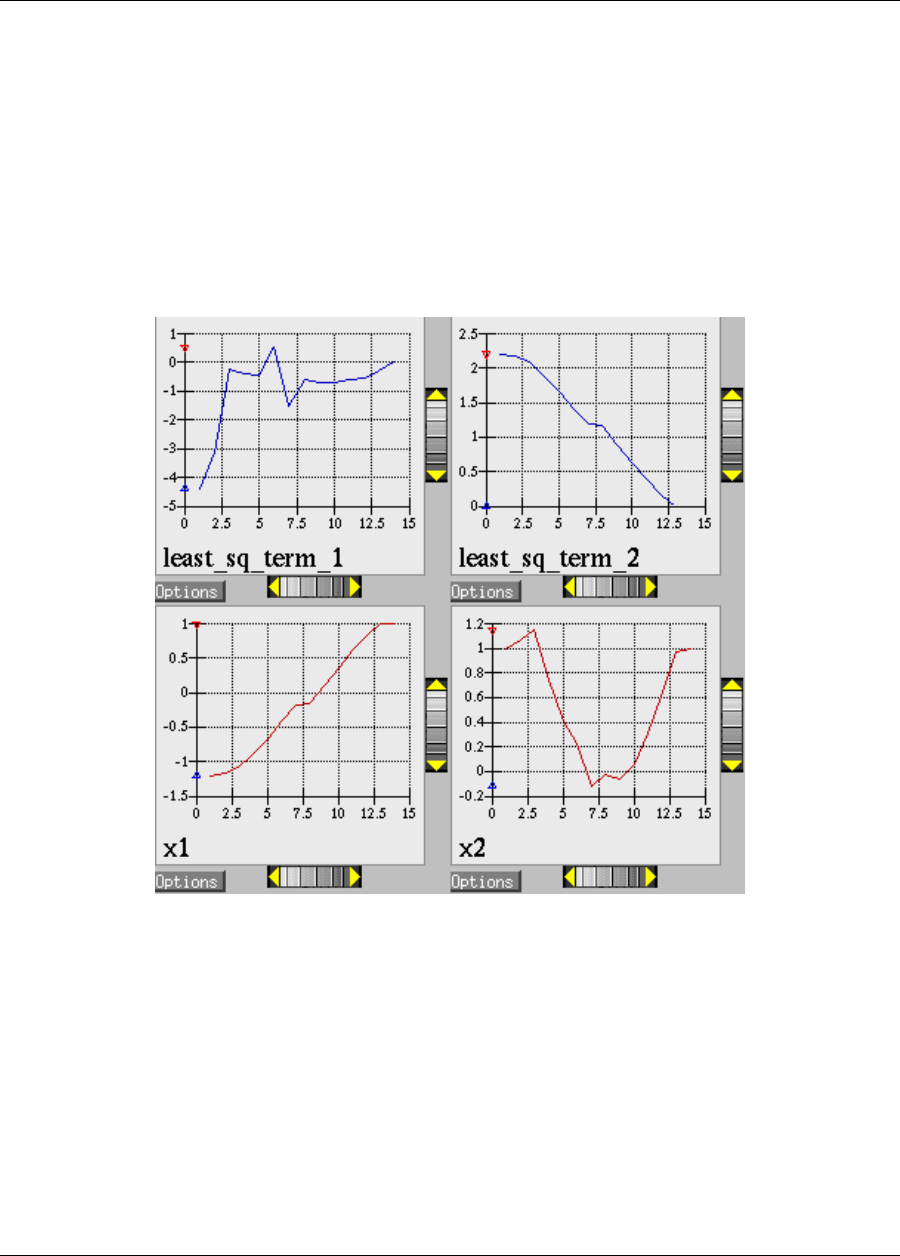
326 CHAPTER 20. ADDITIONAL EXAMPLES
Figure 20.5: Rosenbrock nonlinear least squares example: iteration history for least squares terms f1and f2.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
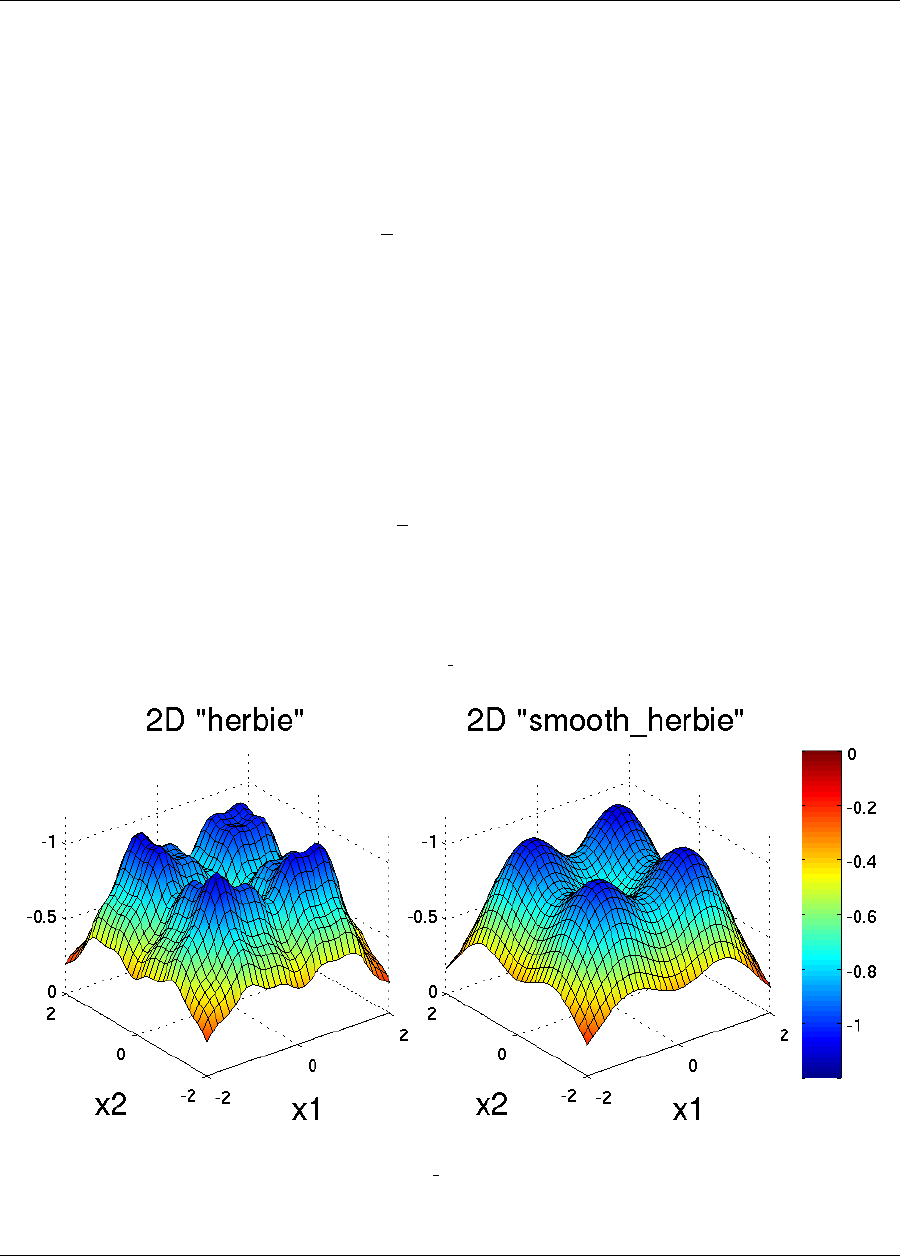
20.3. HERBIE, SMOOTH HERBIE, AND SHUBERT 327
20.3 Herbie, Smooth Herbie, and Shubert
Lee, et al. [94] developed the Herbie function as a 2D test problem for surrogate-based optimization. However,
since it is separable and each dimension is identical it is easily generalized to an arbitrary number of dimensions.
The generalized (to Mdimensions) Herbie function is
herb(x) = −
M
Y
k=1
wherb (xk)
where
wherb (xk) = exp(−(xk−1)2) + exp(−0.8(xk+ 1)2)−0.05 sin (8 (xk+ 0.1)) .
The Herbie function’s high frequency sine component creates a large number of local minima and maxima, making
it a significantly more challenging test problem. However, when testing a method’s ability to exploit smoothness
in the true response, it is desirable to have a less oscillatory function. For this reason, the “smooth Herbie” test
function omits the high frequency sine term but is otherwise identical to the Herbie function. The formula for
smooth Herbie is
herbsm(x) = −
M
Y
k=1
wsm (xk)
where
wsm (xk) = exp(−(xk−1)2) + exp(−0.8(xk+ 1)2).
Two dimensional versions of the herbie and smooth herbie test functions are plotted in Figure 20.6.
Figure 20.6: Plots of the herbie (left) and smooth herbie (right) test functions in 2 dimensions. They can
accept an arbitrary number of inputs. The direction of the z-axis has been reversed (negative is up) to better view
the functions’ minima.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

328 CHAPTER 20. ADDITIONAL EXAMPLES
Shubert is another separable (and therefore arbitrary dimensional) test function. Its analytical formula is
shu(x) =
M
Y
k=1
wshu (xk)
wshu (xk) =
5
X
i=1
icos((i+ 1)xk+i)
The 2D version of the shubert function is shown in Figure 20.8.
20.3.1 Efficient Global Optimization
The Dakota input file herbie shubert opt ego.in shows how to use efficient global optimization (ego) to
minimize the 5D version of any of these 3 separable functions. The input file is shown in Figure 20.7. Note that
in the variables section the 5*preceding the values -2.0 and 2.0 for the lower bounds and upper bounds,
respectively, tells Dakota to repeat them 5 times. The “interesting” region for each of these functions is −2≤
xk≤2for all dimensions.
20.4 Sobol and Ishigami Functions
These functions are often used to test sensitivity analysis methods. These are documented in [127]. The first is
the Sobol rational function, given by the equation:
f(x) = (x2+ 0.5)4
(x1+ 0.5)4(20.7)
This function is monotonic across each of the inputs. However, there is substantial interaction between x1and x2
which makes sensitivity analysis difficult. This function in shown in Figure 20.9.
The Ishigami test problem [127] is a smooth C∞function:
f(x) = sin(2πx1−π) + 7 sin2(2πx2−π)+0.1(2πx3−π)4sin(2πx1−π)(20.8)
where the distributions for x1,x2, and x3are iid uniform on [0,1]. This function was created as a test for global
sensitivity analysis methods, but is challenging for any method based on low-order structured grids (e.g., due to
term cancellation at midpoints and bounds). This function in shown in Figure 20.10.
At the opposite end of the smoothness spectrum, Sobol’s g-function [127] is C0with the absolute value contribut-
ing a slope discontinuity at the center of the domain:
f(x)=2
5
Y
j=1
|4xj−2|+aj
1 + aj
;a= [0,1,2,4,8] (20.9)
The distributions for xjfor j= 1,2,3,4,5are iid uniform on [0,1]. This function in shown in Figure 20.11.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.5. CYLINDER HEAD 329
# Dakota Input File: herbie_shubert_opt_ego.in
# Example of using EGO to find the minumum of the 5 dimensional version
# of the abitrary-dimensional/separable ’herbie’ OR ’smooth_herbie’ OR
# ’shubert’ test functions
environment
tabular_data
tabular_data_file = ’herbie_shubert_opt_ego.dat’
method
efficient_global # EGO Efficient Global Optimization
initial_samples 50
seed = 123456
variables
continuous_design = 5 # 5 dimensions
lower_bounds 5*-2.0 # use 5 copies of -2.0 for bound
upper_bounds 5*2.0 # use 5 copies of 2.0 for bound
interface
# analysis_drivers = ’herbie’ # use this for herbie
analysis_drivers = ’smooth_herbie’ # use this for smooth_herbie
# analysis_drivers = ’shubert’ # use this for shubert
direct
responses
objective_functions = 1
no_gradients
no_hessians
Figure 20.7: Herbie/Shubert examples: the Dakota input file – see
Dakota/examples/users/herbie shubert opt ego.in
20.5 Cylinder Head
The cylinder head test problem is stated as:
minimize f=−1horsepower
250 +warranty
100000
subject to σmax ≤0.5σyield (20.10)
warranty ≥100000
timecycle ≤60
1.5≤dintake ≤2.164
0.0≤flatness ≤4.0
This formulation seeks to simultaneously maximize normalized engine horsepower and engine warranty over
variables of valve intake diameter (dintake) in inches and overall head flatness (flatness) in thousandths of an
inch subject to inequality constraints that the maximum stress cannot exceed half of yield, that warranty must
be at least 100000 miles, and that manufacturing cycle time must be less than 60 seconds. Since the constraints
Dakota Version 6.7 User’s Manual generated on November 13, 2017
330 CHAPTER 20. ADDITIONAL EXAMPLES
Figure 20.8: Plot of the shubert test function in 2 dimensions. It can accept an arbitrary number of inputs.
Figure 20.9: Plot of the sobol rational test function in 2 dimensions.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
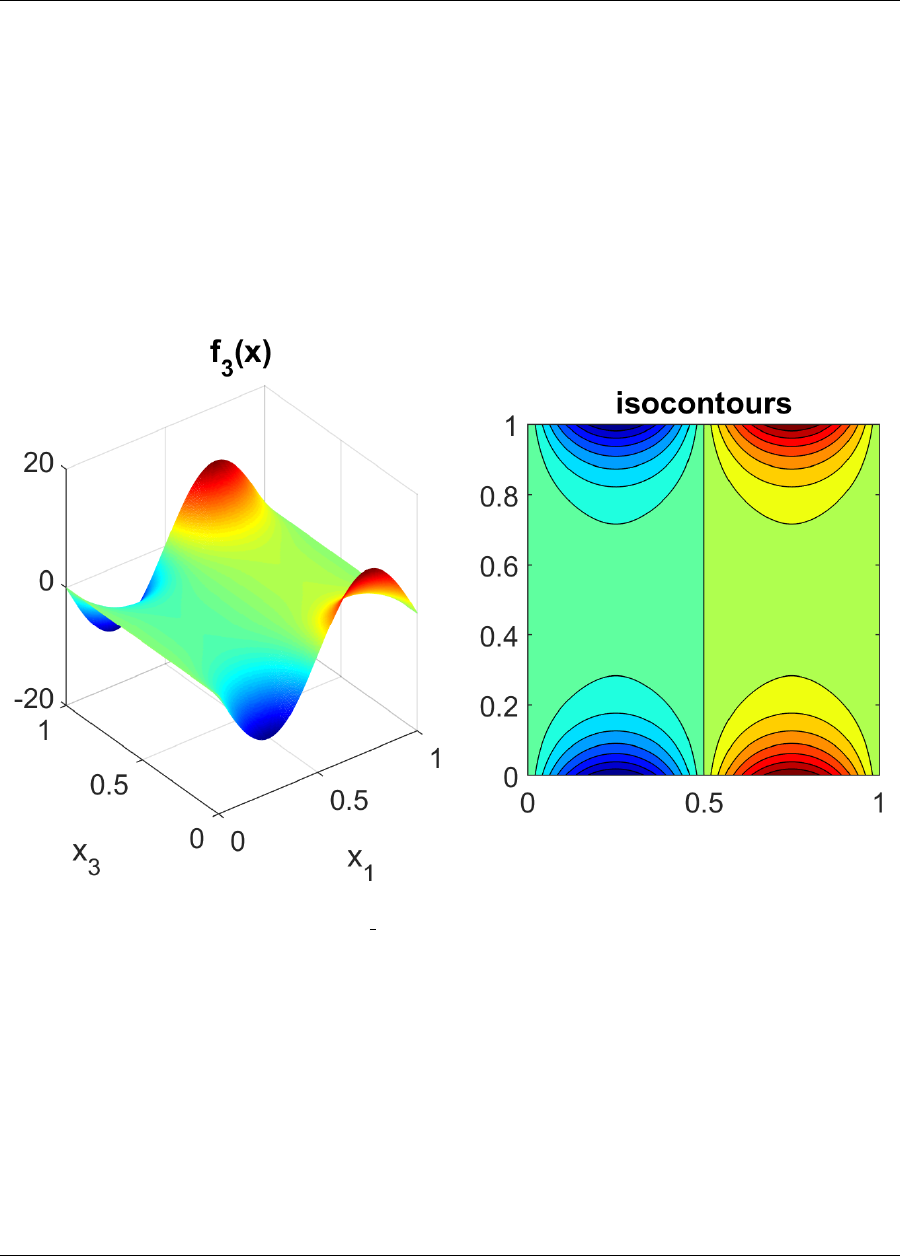
20.5. CYLINDER HEAD 331
Figure 20.10: Plot of the sobol ishigami test function as a function of x1 and x3.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
332 CHAPTER 20. ADDITIONAL EXAMPLES
Figure 20.11: Plot of the sobol g function test function.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.5. CYLINDER HEAD 333
involve different scales, they should be nondimensionalized (note: the nonlinear constraint scaling described in
Section 6.3.2 can now do this automatically). In addition, they can be converted to the standard 1-sided form
g(x)≤0as follows:
g1=2σmax
σyield −1≤0
g2= 1 −warranty
100000 ≤0(20.11)
g3=timecycle
60 −1≤0
The objective function and constraints are related analytically to the design variables according to the following
simple expressions:
warranty = 100000 + 15000(4 −flatness)
timecycle = 45 + 4.5(4 −flatness)1.5
horsepower = 250 + 200dintake
1.833 −1(20.12)
σmax = 750 + 1
(twall)2.5
twall =offsetintake −offsetexhaust −(dintake +dexhaust)
2
where the constants in Equation 20.11 and Equation 20.12 assume the following values: σyield = 3000,offsetintake =
3.25,offsetexhaust = 1.34, and dexhaust = 1.556.
20.5.1 Constrained Gradient Based Optimization
An example using the cylinder head test problem is shown below:
The interface keyword specifies use of the cyl head executable (compiled from Dakota Source/test/cyl head.cpp)
as the simulator. The variables and responses keywords specify the data sets to be used in the iteration by pro-
viding the initial point, descriptors, and upper and lower bounds for two continuous design variables and by
specifying the use of one objective function, three inequality constraints, and numerical gradients in the problem.
The method keyword specifies the use of the npsol sqp method to solve this constrained optimization problem.
No environment keyword is specified, so the default single method approach is used.
The solution for the constrained optimization problem is:
intake dia = 2.122
flatness = 1.769
with
f∗=−2.461
g∗
1= 0.0 (active)
g∗
2=−0.3347 (inactive)
g∗
3= 0.0 (active)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

334 CHAPTER 20. ADDITIONAL EXAMPLES
# Dakota Input File: cylhead_opt_npsol.in
method
npsol_sqp
convergence_tolerance = 1.e-8
variables
continuous_design = 2
initial_point 1.8 1.0
upper_bounds 2.164 4.0
lower_bounds 1.5 0.0
descriptors ’intake_dia’ ’flatness’
interface
analysis_drivers = ’cyl_head’
fork asynchronous
responses
objective_functions = 1
nonlinear_inequality_constraints = 3
numerical_gradients
method_source dakota
interval_type central
fd_step_size = 1.e-4
no_hessians
Figure 20.12: Cylinder Head Example: the Dakota input file – see
Dakota/examples/users/cylhead opt npsol.in
which corresponds to the following optimal response quantities:
warranty = 133472
cycle time = 60
wall thickness = 0.0707906
horse power = 281.579
max stress = 1500
The final report from the Dakota output is as follows:
<<<<< Iterator npsol_sqp completed.
<<<<< Function evaluation summary: 55 total (55 new, 0 duplicate)
<<<<< Best parameters =
2.1224188322e+00 intake_dia
1.7685568331e+00 flatness
<<<<< Best objective function =
-2.4610312954e+00
<<<<< Best constraint values =
1.8407497748e-13
-3.3471647504e-01
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.5. CYLINDER HEAD 335
0.0000000000e+00
<<<<< Best data captured at function evaluation 51
<<<<< Environment execution completed.
Dakota execution time in seconds:
Total CPU = 0.04 [parent = 0.031995, child = 0.008005]
Total wall clock = 0.232134
Dakota Version 6.7 User’s Manual generated on November 13, 2017
336 CHAPTER 20. ADDITIONAL EXAMPLES
20.6 Container
For this example, suppose that a high-volume manufacturer of light weight steel containers wants to minimize
the amount of raw sheet material that must be used to manufacture a 1.1 quart cylindrical-shaped can, including
waste material. Material for the container walls and end caps is stamped from stock sheet material of constant
thickness. The seal between the end caps and container wall is manufactured by a press forming operation on the
end caps. The end caps can then be attached to the container wall forming a seal through a crimping operation.
Figure 20.13: Container wall-to-end-cap seal
For preliminary design purposes, the extra material that would normally go into the container end cap seals is
approximated by increasing the cut dimensions of the end cap diameters by 12% and the height of the container
wall by 5%, and waste associated with stamping the end caps in a specialized pattern from sheet stock is estimated
as 15% of the cap area. The equation for the area of the container materials including waste is
A= 2 ×
end cap
waste
material
factor
×
end cap
seal
material
factor
×
nominal
end cap
area
+
container
wall seal
material
factor
×
nominal
container
wall area
or
A= 2(1.15)(1.12)πD2
4+ (1.05)πDH (20.13)
where Dand Hare the diameter and height of the finished product in units of inches, respectively. The volume
of the finished product is specified to be
V=πD2H
4= (1.1qt)(57.75in3/qt)(20.14)
The equation for area is the objective function for this problem; it is to be minimized. The equation for volume is
an equality constraint; it must be satisfied at the conclusion of the optimization problem. Any combination of D
and Hthat satisfies the volume constraint is a feasible solution (although not necessarily the optimal solution) to
the area minimization problem, and any combination that does not satisfy the volume constraint is an infeasible
solution. The area that is a minimum subject to the volume constraint is the optimal area, and the corresponding
values for the parameters Dand Hare the optimal parameter values.
It is important that the equations supplied to a numerical optimization code be limited to generating only phys-
ically realizable values, since an optimizer will not have the capability to differentiate between meaningful and
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.6. CONTAINER 337
Figure 20.14: A graphical representation of the container optimization problem.
nonphysical parameter values. It is often up to the engineer to supply these limits, usually in the form of param-
eter bound constraints. For example, by observing the equations for the area objective function and the volume
constraint, it can be seen that by allowing the diameter, D, to become negative, it is algebraically possible to
generate relatively small values for the area that also satisfy the volume constraint. Negative values for Dare of
course physically meaningless. Therefore, to ensure that the numerically-solved optimization problem remains
meaningful, a bound constraint of −D≤0must be included in the optimization problem statement. A positive
value for His implied since the volume constraint could never be satisfied if Hwere negative. However, a bound
constraint of −H≤0can be added to the optimization problem if desired. The optimization problem can then
be stated in a standardized form as
minimize 2(1.15)(1.12)πD2
4+ (1.05)2πDH
subject to πD2H
4= (1.1qt)(57.75in3/qt)(20.15)
−D≤0,−H≤0
A graphical view of the container optimization test problem appears in Figure 20.14. The 3-D surface defines the
area, A, as a function of diameter and height. The curved line that extends across the surface defines the areas
that satisfy the volume equality constraint, V. Graphically, the container optimization problem can be viewed as
one of finding the point along the constraint line with the smallest 3-D surface height in Figure 20.14. This point
corresponds to the optimal values for diameter and height of the final product.
20.6.1 Constrained Gradient Based Optimization
The input file for this example is named container opt npsol.in. The solution to this example problem is
(H, D) = (4.99,4.03), with a minimum area of 98.43 in2.
The final report from the Dakota output is as follows:
<<<<< Iterator npsol_sqp completed.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
338 CHAPTER 20. ADDITIONAL EXAMPLES
<<<<< Function evaluation summary: 40 total (40 new, 0 duplicate)
<<<<< Best parameters =
4.9873894231e+00 H
4.0270846274e+00 D
<<<<< Best objective function =
9.8432498116e+01
<<<<< Best constraint values =
-9.6301439045e-12
<<<<< Best data captured at function evaluation 36
<<<<< Environment execution completed.
Dakota execution time in seconds:
Total CPU = 0.18 [parent = 0.18, child = 0]
Total wall clock = 0.809126
20.7 Cantilever
This test problem is adapted from the reliability-based design optimization literature [129], [150] and involves a
simple uniform cantilever beam as shown in Figure 20.15.
Figure 20.15: Cantilever beam test problem.
The design problem is to minimize the weight (or, equivalently, the cross-sectional area) of the beam subject to a
displacement constraint and a stress constraint. Random variables in the problem include the yield stress Rof the
beam material, the Young’s modulus Eof the material, and the horizontal and vertical loads, Xand Y, which are
modeled with normal distributions using N(40000,2000),N(2.9E7,1.45E6),N(500,100), and N(1000,100),
respectively. Problem constants include L= 100in and D0= 2.2535in. The constraints have the following
analytic form:
stress =600
wt2Y+600
w2tX≤R(20.16)
displacement =4L3
EwtsY
t22
+X
w22
≤D0
or when scaled:
gS=stress
R−1≤0(20.17)
gD=displacement
D0−1≤0
(20.18)
Deterministic Formulation
If the random variables E,R,X, and Yare fixed at their means, the resulting deterministic design problem can
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.7. CANTILEVER 339
be formulated as
minimize f=wt
subject to gS≤0(20.19)
gD≤0
1.0≤w≤4.0
1.0≤t≤4.0
Stochastic Formulation
If the normal distributions for the random variables E,R,X, and Yare included, a stochastic design problem can
be formulated as
minimize f=wt
subject to βD≥3(20.20)
βS≥3
1.0≤w≤4.0
1.0≤t≤4.0
where a 3-sigma reliability level (probability of failure = 0.00135 if responses are normally-distributed) is being
sought on the scaled constraints.
20.7.1 Constrained Gradient Based Optimization
The test problem is solved using cantilever opt npsol.in:
The deterministic solution is (w, t) = (2.35,3.33) with an objective function of 7.82. The final report from the
Dakota output is as follows:
<<<<< Iterator npsol_sqp completed.
<<<<< Function evaluation summary: 33 total (33 new, 0 duplicate)
<<<<< Best parameters =
2.3520341271e+00 beam_width
3.3262784077e+00 beam_thickness
4.0000000000e+04 R
2.9000000000e+07 E
5.0000000000e+02 X
1.0000000000e+03 Y
<<<<< Best objective function =
7.8235203313e+00
<<<<< Best constraint values =
-1.6009000260e-02
-3.7083558446e-11
<<<<< Best data captured at function evaluation 31
<<<<< Environment execution completed.
Dakota execution time in seconds:
Total CPU = 0.03 [parent = 0.027995, child = 0.002005]
Total wall clock = 0.281375
Dakota Version 6.7 User’s Manual generated on November 13, 2017
340 CHAPTER 20. ADDITIONAL EXAMPLES
# Dakota Input File: cantilever_opt_npsol.in
method
npsol_sqp
convergence_tolerance = 1.e-8
variables
continuous_design = 2
initial_point 4.0 4.0
upper_bounds 10.0 10.0
lower_bounds 1.0 1.0
descriptors ’w’ ’t’
continuous_state = 4
initial_state 40000. 29.E+6 500. 1000.
descriptors ’R’ ’E’ ’X’ ’Y’
interface
analysis_drivers = ’cantilever’
fork
asynchronous evaluation_concurrency = 2
responses
objective_functions = 1
nonlinear_inequality_constraints = 2
numerical_gradients
method_source dakota
interval_type forward
fd_step_size = 1.e-4
no_hessians
Figure 20.16: Cantilever Example: the Dakota input file – see Dakota/examples/users/cantilever opt npsol.in
20.7.2 Optimization Under Uncertainty
Optimization under uncertainty solutions to the stochastic problem are described in [38,35,36], for which the
solution is (w, t) = (2.45,3.88) with an objective function of 9.52. This demonstrates that a more conservative
design is needed to satisfy the probabilistic constraints.
20.8 Multiobjective Test Problems
Multiobjective optimization means that there are two or more objective functions that you wish to optimize simul-
taneously. Often these are conflicting objectives, such as cost and performance. The answer to a multi-objective
problem is usually not a single point. Rather, it is a set of points called the Pareto front. Each point on the Pareto
front satisfies the Pareto optimality criterion, i.e., locally there exists no other feasible vector that would improve
some objective without causing a simultaneous worsening in at least one other objective. Thus a feasible point X0
from which small moves improve one or more objectives without worsening any others is not Pareto optimal: it
is said to be “dominated” and the points along the Pareto front are said to be “non-dominated”.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.8. MULTIOBJECTIVE TEST PROBLEMS 341
Often multi-objective problems are addressed by simply assigning weights to the individual objectives, summing
the weighted objectives, and turning the problem into a single-objective one which can be solved with a variety
of optimization techniques. While this approach provides a useful “first cut” analysis (and is supported within
Dakota—see Section 6.3.1), this approach has many limitations. The major limitation is that a local solver with
a weighted sum objective will only find one point on the Pareto front; if one wants to understand the effects of
changing weights, this method can be computationally expensive. Since each optimization of a single weighted
objective will find only one point on the Pareto front, many optimizations must be performed to get a good
parametric understanding of the influence of the weights and to achieve a good sampling of the entire Pareto
frontier.
There are three examples that are taken from a multiobjective evolutionary algorithm (MOEA) test suite described
by Van Veldhuizen et. al. in [17]. These three examples illustrate the different forms that the Pareto set may take.
For each problem, we describe the Dakota input and show a graph of the Pareto front. These problems are all
solved with the moga method. The first example is discussed in Section 6.3.1. The next two are discussed below.
Section 6.3.1 provide more information on multiobjective optimization.
20.8.1 Multiobjective Test Problem 2
The second test problem is a case where both Ptrue and PFtrue are disconnected. PFtrue has four separate Pareto
curves. The problem is to simultaneously optimize f1and f2given two input variables, x1and x2, where the
inputs are bounded by 0≤xi≤1, and:
f1(x) = x1
f2(x) = (1 + 10x2)×"1−x1
1 + 10x22
−x1
1 + 10x2
sin(8πx1)#
The input file for this example is shown in Figure 20.17, which references the mogatest2 executable (compiled
from Dakota Source/test/mogatest2.cpp) as the simulator. The Pareto front is shown in Figure 20.18.
Note the discontinuous nature of the front in this example.
20.8.2 Multiobjective Test Problem 3
The third test problem is a case where Ptrue is disconnected but PFtrue is connected. This problem also has two
nonlinear constraints. The problem is to simultaneously optimize f1and f2given two input variables, x1and x2,
where the inputs are bounded by −20 ≤xi≤20, and:
f1(x)=(x1−2)2+ (x2−1)2+ 2
f2(x)=9x1−(x2−1)2
The constraints are:
0≤x2
1+x2
2−225
0≤x1−3x2+ 10
The input file for this example is shown in Figure 20.19. It differs from Figure 20.17 in the variables and responses
specifications, in the use of the mogatest3 executable (compiled from Dakota Source/test/mogatest3.cpp)
as the simulator, and in the max function evaluations and mutation type MOGA controls. The
Pareto set is shown in Figure 20.20. Note the discontinuous nature of the Pareto set (in the design space) in this
example. The Pareto front is shown in Figure 20.21.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

342 CHAPTER 20. ADDITIONAL EXAMPLES
# Dakota Input File: mogatest2.in
environment
graphics
tabular_data
tabular_data_file = ’mogatest2.dat’
method
moga
seed = 10983
max_function_evaluations = 3000
initialization_type unique_random
crossover_type
multi_point_parameterized_binary = 2
crossover_rate = 0.8
mutation_type replace_uniform
mutation_rate = 0.1
fitness_type domination_count
replacement_type below_limit = 6
shrinkage_fraction = 0.9
convergence_type metric_tracker
percent_change = 0.05 num_generations = 10
final_solutions = 3
output silent
variables
continuous_design = 2
initial_point 0.5 0.5
upper_bounds 1 1
lower_bounds 0 0
descriptors ’x1’ ’x2’
interface
analysis_drivers = ’mogatest2’
direct
responses
objective_functions = 2
no_gradients
no_hessians
Figure 20.17: Dakota input file specifying the use of MOGA on mogatest2 – see
Dakota/examples/users/mogatest2.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
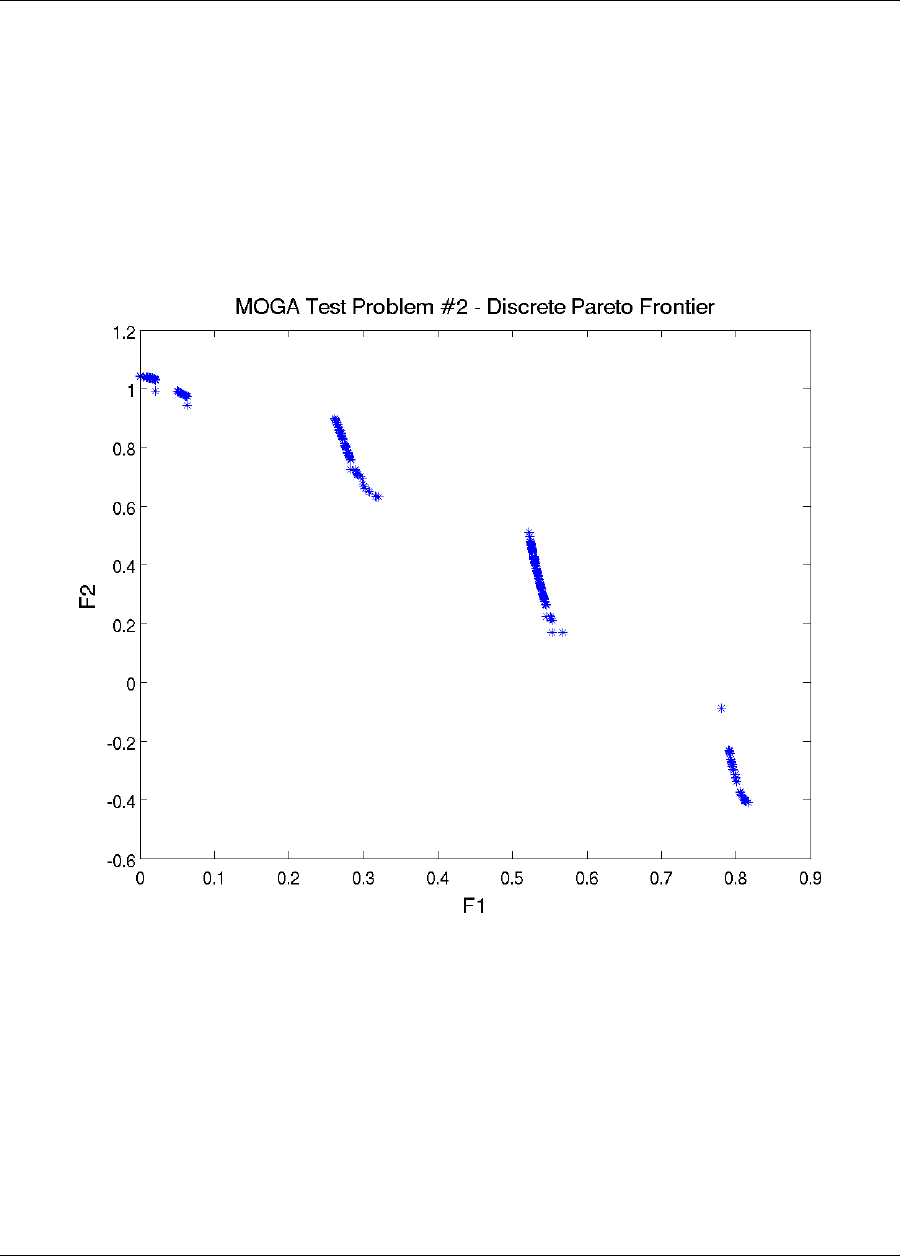
20.8. MULTIOBJECTIVE TEST PROBLEMS 343
Figure 20.18: Pareto Front showing Tradeoffs between Function F1 and Function F2 for mogatest2
Dakota Version 6.7 User’s Manual generated on November 13, 2017

344 CHAPTER 20. ADDITIONAL EXAMPLES
# Dakota Input File: mogatest3.in
environment
graphics
tabular_data
tabular_data_file = ’mogatest3.dat’
method
moga
seed = 10983
max_function_evaluations = 2000
initialization_type unique_random
crossover_type
multi_point_parameterized_binary = 2
crossover_rate = 0.8
mutation_type offset_normal
mutation_scale = 0.1
fitness_type domination_count
replacement_type below_limit = 6
shrinkage_fraction = 0.9
convergence_type metric_tracker
percent_change = 0.05 num_generations = 10
final_solutions = 3
output silent
variables
continuous_design = 2
descriptors ’x1’ ’x2’
initial_point 0 0
upper_bounds 20 20
lower_bounds -20 -20
interface
analysis_drivers = ’mogatest3’
direct
responses
objective_functions = 2
nonlinear_inequality_constraints = 2
upper_bounds = 0.0 0.0
no_gradients
no_hessians
Figure 20.19: Dakota input file specifying the use of MOGA on mogatest3 – see
Dakota/examples/users/mogatest3.in
Dakota Version 6.7 User’s Manual generated on November 13, 2017
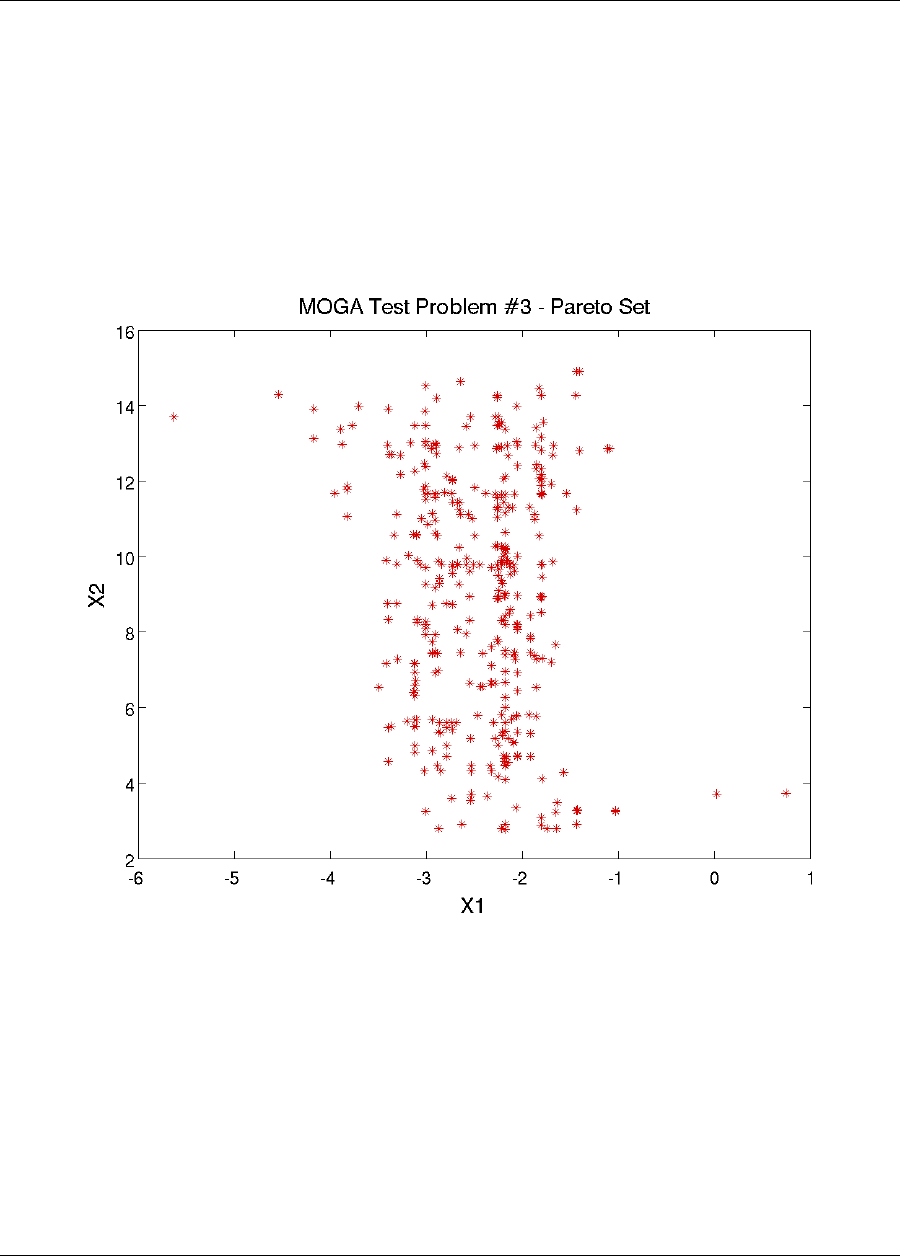
20.8. MULTIOBJECTIVE TEST PROBLEMS 345
Figure 20.20: Pareto Set of Design Variables corresponding to the Pareto front for mogatest3
Dakota Version 6.7 User’s Manual generated on November 13, 2017
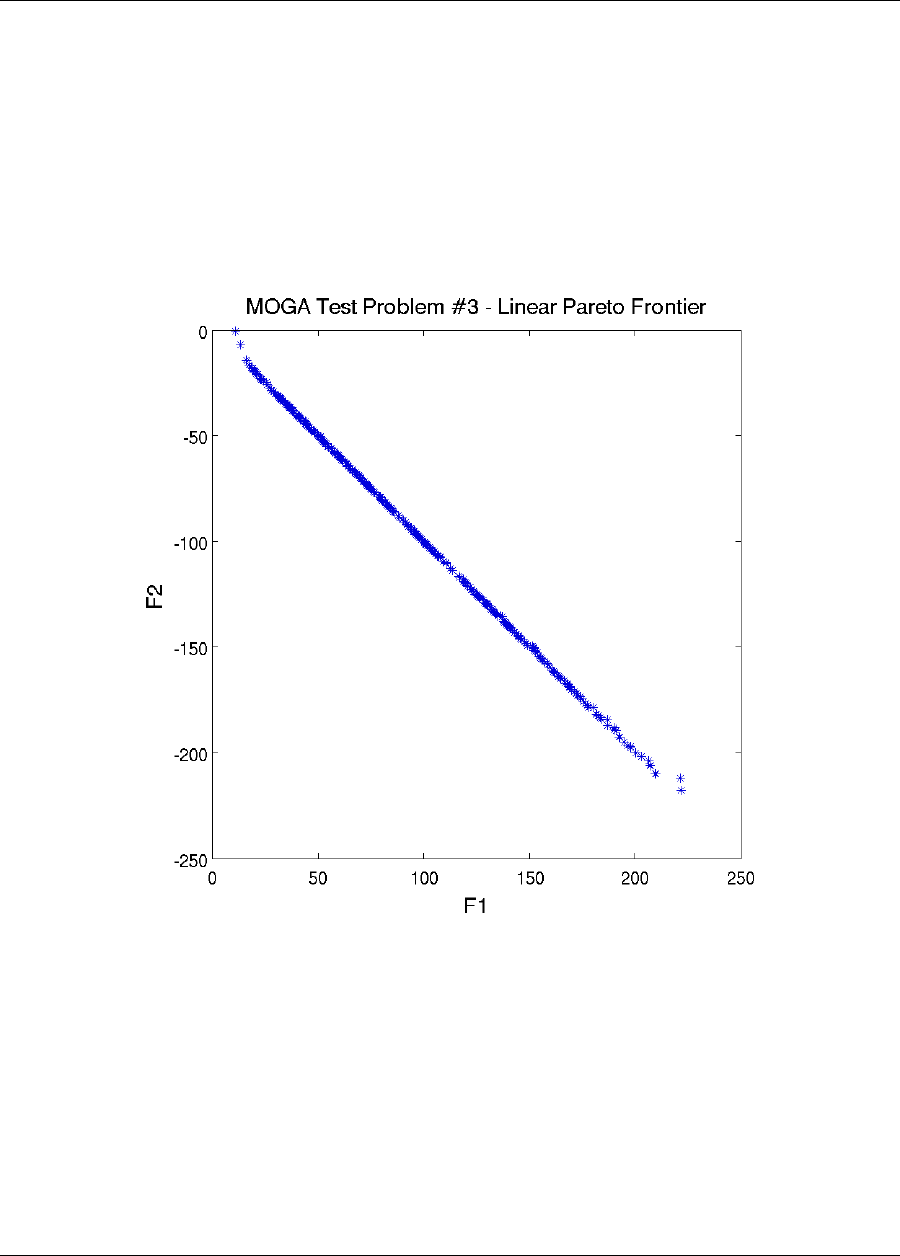
346 CHAPTER 20. ADDITIONAL EXAMPLES
Figure 20.21: Pareto Front showing Tradeoffs between Function F1 and Function F2 for mogatest3
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.9. MORRIS 347
20.9 Morris
Morris [103] includes a screening design test problem with a single-output analytical test function. The output
depends on 20 inputs with first- through fourth-order interaction terms, some having large fixed coefficients and
others small random coefficients. Thus the function values generated depend on the random number generator
employed in the function evaluator. The computational model is:
y=β0+
20
X
i=1
βiwi+
20
X
i<j
βi,j wiwj+
20
X
i<j<l
βi,j,lwiwjwl
+
20
X
i<j<l<s
βi,j,l,swiwjwlws,
where wi= 2(xi−0.5) except for i= 3,5,and 7, where wi= 2(1.1xi/(xi+ 0.1) −0.5). Large-valued
coefficients are assigned as
βi= +20 i= 1,...,10; βi,j =−15 i, j = 1,...,6;
βi,j,l =−10 i, j, l = 1,...,5; βi,j,l,s = +5 i, j, l, s = 1,...,4.
The remaining first- and second-order coefficients βiand βi,j , respectively, are independently generated from
a standard normal distribution (zero mean and unit standard deviation); the remaining third- and fourth-order
coefficients are set to zero.
Examination of the test function reveals that one should be able to conclude the following (stated and verified
computationally in [116]) for this test problem:
1. the first ten factors are important;
2. of these, the first seven have significant effects involving either interactions or curvatures; and
3. the other three are important mainly because of their first-order effect.
20.9.1 Morris One-at-a-Time Sensitivity Study
The dakota input morris ps moat.in exercises the MOAT algorithm described in Section 4.5 on the Morris
problem. The Dakota output obtained is shown in Figures 20.22 and 20.23. The MOAT analysis output reveals
that each of the desired observations can be made for the test problem. These are also reflected in Figure 20.24.
The modified mean (based on averaging absolute values of elementary effects) shows a clear difference in inputs
1–10 as compared to inputs 11–20. The standard deviation of the (signed) elementary effects indicates correctly
that inputs 1–7 have substantial interaction-based or nonlinear effect on the output, while the others have less.
While some of inputs 11–20 have nontrivial values of σ, their relatively small modified means µ∗indicate they
have little overall influence.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

348 CHAPTER 20. ADDITIONAL EXAMPLES
Running MPI executable in serial mode.
Dakota version 6.0 release.
Subversion revision xxxx built May ...
Writing new restart file dakota.rst
gradientType = none
hessianType = none
>>>>> Executing environment.
>>>>> Running psuade_moat iterator.
PSUADE DACE method = psuade_moat Samples = 84 Seed (user-specified) = 500
Partitions = 3 (Levels = 4)
Figure 20.22: Dakota initialization output for the PSUADE MOAT method on the Morris test problem showing
the study parameters.
>>>>>> PSUADE MOAT output for function 0:
*************************************************************
*********************** MOAT Analysis ***********************
-------------------------------------------------------------
Input 1 (mod. mean & std) = 9.5329e+01 9.0823e+01
Input 2 (mod. mean & std) = 6.7297e+01 9.5242e+01
Input 3 (mod. mean & std) = 1.0648e+02 1.5479e+02
Input 4 (mod. mean & std) = 6.6231e+01 7.5895e+01
Input 5 (mod. mean & std) = 9.5717e+01 1.2733e+02
Input 6 (mod. mean & std) = 8.0394e+01 9.9959e+01
Input 7 (mod. mean & std) = 3.2722e+01 2.7947e+01
Input 8 (mod. mean & std) = 4.2013e+01 7.6090e+00
Input 9 (mod. mean & std) = 4.1965e+01 7.8535e+00
Input 10 (mod. mean & std) = 3.6809e+01 3.6151e+00
Input 11 (mod. mean & std) = 8.2655e+00 1.0311e+01
Input 12 (mod. mean & std) = 4.9299e+00 7.0591e+00
Input 13 (mod. mean & std) = 3.5455e+00 4.4025e+00
Input 14 (mod. mean & std) = 3.4151e+00 2.4905e+00
Input 15 (mod. mean & std) = 2.5143e+00 5.5168e-01
Input 16 (mod. mean & std) = 9.0344e+00 1.0115e+01
Input 17 (mod. mean & std) = 6.4357e+00 8.3820e+00
Input 18 (mod. mean & std) = 9.1886e+00 2.5373e+00
Input 19 (mod. mean & std) = 2.4105e+00 3.1102e+00
Input 20 (mod. mean & std) = 5.8234e+00 7.2403e+00
<<<<< Function evaluation summary: 84 total (84 new, 0 duplicate)
Figure 20.23: Dakota analysis output for the PSUADE MOAT method on the Morris problem showing the
modified mean and standard deviation of the elementary effect corresponding to each input factor.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
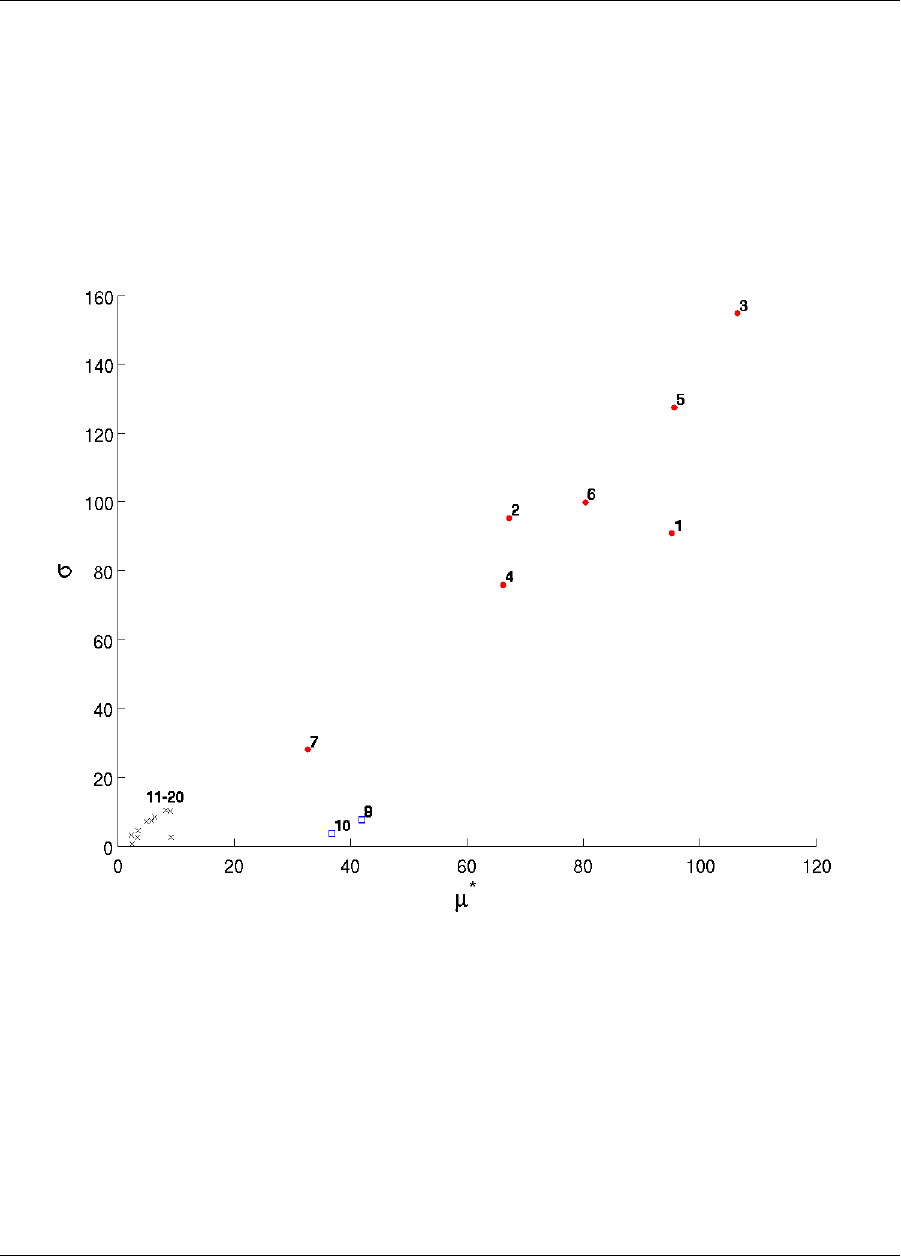
20.9. MORRIS 349
Figure 20.24: Standard deviation of elementary effects plotted against modified mean for Morris for each of 20
inputs. Red circles 1–7 correspond to inputs having interactions or nonlinear effects, blue squares 8–10 indicate
those with mainly linear effects, and black Xs denote insignificant inputs.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
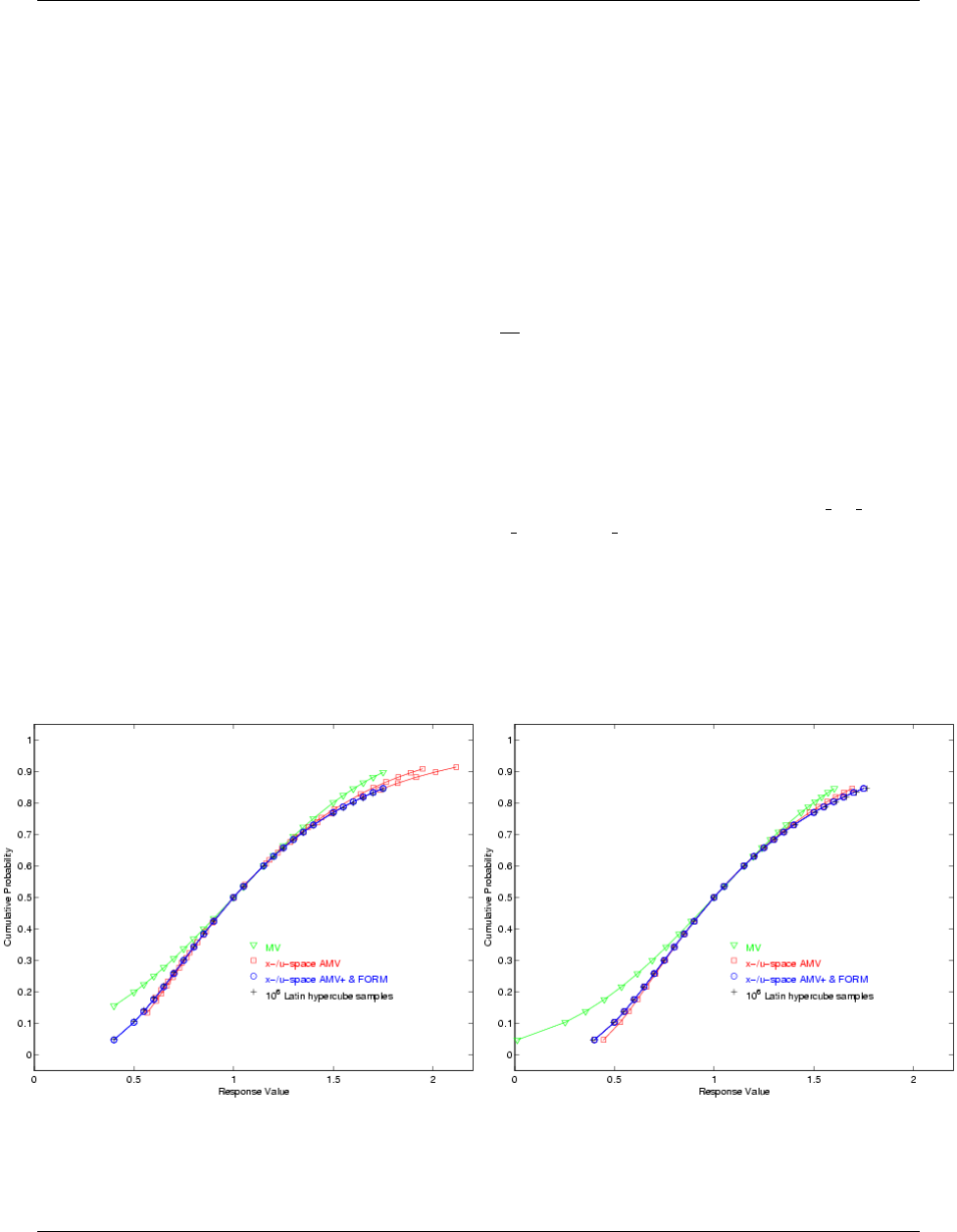
350 CHAPTER 20. ADDITIONAL EXAMPLES
20.10 Test Problems for Reliability Analyses
This section includes several test problems and examples related to reliability analyses. These are NOT included
in the Dakota/examples/users directory, but are in the Dakota/test directory.
20.10.1 Log Ratio
This test problem, mentioned previously in Section 5.3.3, has a limit state function defined by the ratio of two
lognormally-distributed random variables.
g(x) = x1
x2
(20.21)
The distributions for both x1and x2are Lognormal(1, 0.5) with a correlation coefficient between the two variables
of 0.3.
Reliability Analyses
First-order and second-order reliability analysis (FORM and SORM) are performed in the logratio uq reliability.in
in the Dakota/examples/users directory and dakota logratio taylor2.in in directory Dakota/test.
For the reliability index approach (RIA), 24 response levels (.4, .5, .55, .6, .65, .7, .75, .8, .85, .9, 1, 1.05, 1.15, 1.2,
1.25, 1.3, 1.35, 1.4, 1.5, 1.55, 1.6, 1.65, 1.7, and 1.75) are mapped into the corresponding cumulative probability
levels. For performance measure approach (PMA), these 24 probability levels (the fully converged results from
RIA FORM) are mapped back into the original response levels. Figure 20.25 overlays the computed CDF values
for a number of first-order reliability method variants as well as a Latin Hypercube reference solution of 106
samples.
(a) RIA methods (b) PMA methods
Figure 20.25: Lognormal ratio cumulative distribution function, RIA/PMA methods.
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.10. TEST PROBLEMS FOR RELIABILITY ANALYSES 351
20.10.2 Steel Section
This test problem is used extensively in [73]. It involves a W16x31 steel block of A36 steel that must carry an
applied deterministic bending moment of 1140 kip-in. For Dakota, it has been used as a code verification test for
second-order integrations in reliability methods. The limit state function is defined as:
g(x) = FyZ−1140 (20.22)
where Fyis Lognormal(38., 3.8), Zis Normal(54., 2.7), and the variables are uncorrelated.
The Dakota/test/dakota steel section.in input file computes a first-order CDF probability of p(g≤
0.)= 1.297e-07 and a second-order CDF probability of p(g≤0.)= 1.375e-07. This second-order result differs
from that reported in [73], since Dakota uses the Nataf nonlinear transformation to u-space (see MPP Search
Methods block in Reliability Methods chapter of Dakota Theory Manual [4]) and [73] uses a linearized transfor-
mation.
20.10.3 Portal Frame
This test problem is taken from [138,80]. It involves a plastic collapse mechanism of a simple portal frame. It also
has been used as a verification test for second-order integrations in reliability methods. The limit state function is
defined as:
g(x) = x1+ 2x2+ 2x3+x4−5x5−5x6(20.23)
where x1−x4are Lognormal(120., 12.), x5is Lognormal(50., 15.), x6is Lognormal(40., 12.), and the variables
are uncorrelated.
While the limit state is linear in x-space, the nonlinear transformation of lognormals to u-space induces curvature.
The Dakota/test/dakota portal frame.in input file computes a first-order CDF probability of p(g≤
0.)= 9.433e-03 and a second-order CDF probability of p(g≤0.)= 1.201e-02. These results agree with the
published results from the literature.
20.10.4 Short Column
This test problem involves the plastic analysis and design of a short column with rectangular cross section (width b
and depth h) having uncertain material properties (yield stress Y) and subject to uncertain loads (bending moment
Mand axial force P) [91]. The limit state function is defined as:
g(x)=1−4M
bh2Y−P2
b2h2Y2(20.24)
The distributions for P,M, and Yare Normal(500, 100), Normal(2000, 400), and Lognormal(5, 0.5), respec-
tively, with a correlation coefficient of 0.5 between Pand M(uncorrelated otherwise). The nominal values for b
and hare 5 and 15, respectively.
Reliability Analyses
First-order and second-order reliability analysis are performed in the dakota short column.in and
dakota short column taylor2.in input files in Dakota/test. For RIA, 43 response levels (-9.0, -
8.75, -8.5, -8.0, -7.75, -7.5, -7.25, -7.0, -6.5, -6.0, -5.5, -5.0, -4.5, -4.0, -3.5, -3.0, -2.5, -2.0, -1.9, -1.8, -1.7, -1.6,
-1.5, -1.4, -1.3, -1.2, -1.1, -1.0, -0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, -0.2, -0.1, 0.0, 0.05, 0.1, 0.15, 0.2, 0.25)
Dakota Version 6.7 User’s Manual generated on November 13, 2017
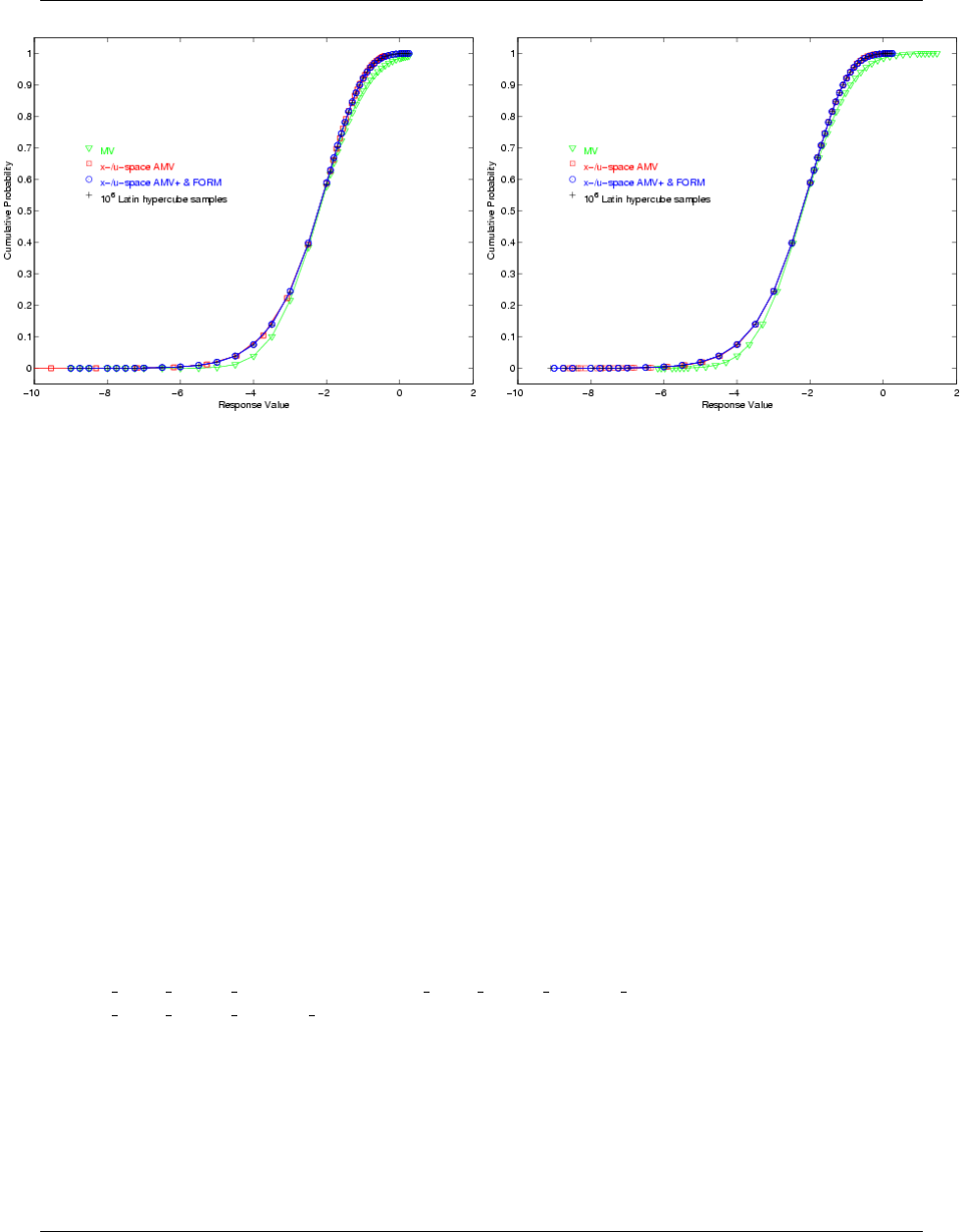
352 CHAPTER 20. ADDITIONAL EXAMPLES
(a) RIA methods (b) PMA methods
Figure 20.26: Short column cumulative distribution function, RIA/PMA methods.
are mapped into the corresponding cumulative probability levels. For PMA, these 43 probability levels (the fully
converged results from RIA FORM) are mapped back into the original response levels. Figure 20.26 overlays the
computed CDF values for several first-order reliability method variants as well as a Latin Hypercube reference
solution of 106samples.
Reliability-Based Design Optimization
The short column test problem is also amenable to Reliability-Based Design Optimization (RBDO). An objective
function of cross-sectional area and a target reliability index of 2.5 (cumulative failure probability p(g≤0) ≤
0.00621) are used in the design problem:
min bh
s.t. β ≥2.5
5.0≤b≤15.0
15.0≤h≤25.0(20.25)
As is evident from the UQ results shown in Figure 20.26, the initial design of (b, h) = (5,15) is infeasible and the
optimization must add material to obtain the target reliability at the optimal design (b, h) = (8.68,25.0). Simple
bi-level, fully analytic bi-level, and sequential RBDO methods are explored in inputs files
dakota rbdo short column.in,dakota rbdo short column analytic.in, and
dakota rbdo short column trsb.in, with results as described in [35,36]. These files are located in
Dakota/test.
20.10.5 Steel Column
This test problem involves the trade-off between cost and reliability for a steel column [91]. The cost is defined
as
Cost =bd + 5h(20.26)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.11. TEST PROBLEMS FOR FORWARD UNCERTAINTY QUANTIFICATION 353
where b,d, and hare the means of the flange breadth, flange thickness, and profile height, respectively. Nine uncor-
related random variables are used in the problem to define the yield stress Fs(lognormal with µ/σ = 400/35 MPa),
dead weight load P1(normal with µ/σ = 500000/50000 N), variable load P2(gumbel with µ/σ = 600000/90000
N), variable load P3(gumbel with µ/σ = 600000/90000 N), flange breadth B(lognormal with µ/σ =b/3 mm),
flange thickness D(lognormal with µ/σ =d/2 mm), profile height H(lognormal with µ/σ =h/5 mm), initial
deflection F0(normal with µ/σ = 30/10 mm), and Young’s modulus E(Weibull with µ/σ = 21000/4200 MPa).
The limit state has the following analytic form:
g=Fs−P1
2BD +F0
BDH
Eb
Eb−P(20.27)
where
P=P1+P2+P3(20.28)
Eb=π2EBDH2
2L2(20.29)
and the column length Lis 7500 mm.
This design problem (dakota rbdo steel column.in in Dakota/test) demonstrates design variable
insertion into random variable distribution parameters through the design of the mean flange breadth, flange
thickness, and profile height. The RBDO formulation maximizes the reliability subject to a cost constraint:
maximize β
subjectto Cost ≤4000.
200.0≤b≤400.0(20.30)
10.0≤d≤30.0
100.0≤h≤500.0
which has the solution (b,d,h) = (200.0, 17.50, 100.0) with a maximal reliability of 3.132.
20.11 Test Problems for Forward Uncertainty Quantification
This section includes several test problems and examples related to forward uncertainty quantification. These are
NOT included in the Dakota/examples/users directory, but are in the Dakota/test directory.
20.11.1 Genz functions
The Genz functions have traditionally been used to test quadrature methods, however more recently they hav
also been used to test forward UQ methdos. Here we consider the oscilatory and corner-peak test functions,
respectively given by
fOS(ξ) = cos −
d
X
i=1
ciξi!,ξ∈[0,1]d
fCP(ξ) = 1 +
d
X
i=1
ciξi!−(d+1)
,ξ∈[0,1]d
Dakota Version 6.7 User’s Manual generated on November 13, 2017
354 CHAPTER 20. ADDITIONAL EXAMPLES
The coefficients ckcan be used to control the effective dimensionality and the variability of these functions. In
dakota we support three choices of =(c1, . . . , cd)T, specifically
c(1)
k=k−1
2
d, c(2)
k=1
k2and c(3)
k= exp klog(10−8)
d, k = 1, . . . , d
normalizing such that for the oscillatory function Pd
k=1 ck= 4.5and for the corner peak function Pd
k=1 ck=
0.25. The different decay rates of the coefficients represent increasing levels of anisotropy and decreasing effective
dimensionality. Anisotropy refers to the dependence of the function variability.
In Dakota the genz function can be set by specifying analysis driver=’genz’. The type of coefficients
decay can be set by sepcifying os1, cp1 which uses c(1),os2, cp2 which uses c(2), and os3, cp3 which
uses c(3), where os is to be used with the oscillatory function and cp for the corner peak function
20.11.2 Elliptic Partial differential equation with uncertain coefficients
Consider the following problem with d≥1random dimensions:
−d
dx a(x, ξ)du
dx(x, ξ)= 10,(x, ξ)∈(0,1) ×Iξ(20.31)
subject to the physical boundary conditions
u(0,ξ)=0, u(1,ξ) = 0.(20.32)
We are interested in quantifying the uncertainty in the solution uat a number of locations x∈[0,1] which can be
specified by the user. This function can be run using dakota by specifying
analysis driver=’steady state diffusion 1d’.
We represent the random diffusivity field ausing two types of expansions. The first option is to use represent the
logarithm of the diffusivity field as Karhunen Lo´
eve expansion
log(a(x, ξ)) = ¯a+σa
d
X
k=1 pλkφk(x)ξk(20.33)
where {λk}d
k=1 and {φk(x)}d
k=1 are, respectively, the eigenvalues and eigenfunctions of the covariance kernel
Ca(x1, x2) = exp −(x1−x2)p
lc.(20.34)
for some power p= 1,2. The variability of the diffusivity field (20.33) is controlled by σaand the correlation
length lcwhich determines the decay of the eigenvalues λk. Dakota sets σa= 1.but allows the number of random
variables d, the order of the kernel pand the correlation length lcto vary. The random variables can be bounded
or unbounded.
The second expansion option is to represent the diffusivity by
a(x, ξ) = 1 + σ
d
X
k=1
1
k2π2cos(2πkx)ξk(20.35)
where ξk∈[−1,1],k= 1, . . . , d are bounded random variables. The form of (20.35) is similar to that obtained
from a Karhunen-Lo`
eve expansion. If the variables are i.i.d. uniform in [-1,1] the the diffusivity satisfies satisfies
the auxiliary properties
E[a(x, ξ)] = 1 and 1−σ
6< a(x, ξ)<1 + σ
6.(20.36)
This is the same test case used in [151].
Dakota Version 6.7 User’s Manual generated on November 13, 2017

20.11. TEST PROBLEMS FOR FORWARD UNCERTAINTY QUANTIFICATION 355
20.11.3 Damped Oscillator
Consider a damped linear oscillator subject to external forcing with six unknown parameters ξ= (γ, k, f, ω, x0, x1)
d2x
dt2(t, ξ) + γdx
dt +kx =fcos(ωt),(20.37)
subject to the initial conditions
x(0) = x0,˙x(0) = x1,(20.38)
Here we assume the damping coefficient γ, spring constant k, forcing amplitude fand frequency ω, and the initial
conditions x0and x1are all uncertain.
This test function can be specified with analysis driver=’damped oscillator’. This function only
works with the uncertain variables defined over certain ranges. These ranges are
γk∈[0.08,0.12], k ∈[0.03,0.04], f ∈[0.08,0.12], ω ∈[0.8,1.2], x0∈[0.45,0.55], x1∈[−0.05,0.05].
Do not use this function with unbounded variables, however any bounded variables such as Beta and trucated
Normal variables that satisfy the aforementioned variable bounds are fine.
20.11.4 Non-linear coupled system of ODEs
Consider the non-linear system of ordinary differential equations governing a competitive LotkaVolterra model of
the population dynamics of species competing for some common resource. The model is given by
(dui
dt =riui1−P3
j=1 αij uj, t ∈(0,10],
ui(0) = ui,0
,(20.39)
for i= 1,2,3. The initial condition, ui,0, and the self-interacting terms, αii, are given, but the remaining
interaction parameters, αij with i6=jas well as the re-productivity parameters, ri, are unknown. We approximate
the solution to (20.39) in time using a Backward Euler method.
This test function can be specified with analysis driver=’predator prey’.
We assume that these parameters are bounded. We have tested this model with all 9 parameters ξi∈[0.3,0.7].
However larger bounds are probably valid. When using the aforemetioned ranges and 1000 time steps with
∆t= 0.01 the average (over the random parameters) deterministic error is approximately 1.00 ×10−4.
Dakota returns the population of each species ui(T)at the final time T. The final time and the number of time-
steps can be changed.
20.11.5 Experimental Design
This example tests the Bayesian experimental design algorithm described in Section 5.8.9, in which a low-fidelity
model is calibrated to optimally-selected data points of a high-fidelity model. The analysis driver for the
the low and high-fidelity models implement the steady state heat example given in [95]. The high-fidelity model
is the analytic solution to the example described therein,
T(x) = c1exp(−γx) + c2exp(γx) + Tamb,(20.40)
Dakota Version 6.7 User’s Manual generated on November 13, 2017

356 CHAPTER 20. ADDITIONAL EXAMPLES
where
c1=−Φ
Kγ exp(γL)(h+Kγ)
exp(−γL)(h−Kγ) + exp(γL)(h+Kγ),
c2=Φ
Kγ +c1,
γ=r2(a+b)h
abK .
The ambient room temperature Tamb, thermal conductivity coefficient K, convective heat transfer coefficient h,
source heat flux Φ, and system dimenions a,b, and Lare all set to constant values. The experimental design
variable x∈[10,70], is called a configuration variable in Dakota and is the only variable that also appears in the
low-fidelity model,
y=Ax2+Bx +C. (20.41)
The goal of this example is to calibrate the low-fidelity model parameters A, B, and Cwith the Bayesian exper-
imental design algorithm. Refer to Section 5.8.9 for further details regarding the Dakota implementation of this
example.
20.11.6 Bayes linear
This is a simple model that is only available by using the direct interface with the analysis driver=’bayes linear’.
The model is discussed extensively in [5] both on pages 93–102 and in Appendix A. The model is simply the
sum of the d input parameters:
y=
d
X
i=1
xi(20.42)
where the input varaibles xican be any uncertain variable type but are typically considered as uniform or normal
uncertain inputs.
Dakota Version 6.7 User’s Manual generated on November 13, 2017
Bibliography
[1] M.A. Abramson, C. Audet, G. Couture, J.E. Dennis, Jr., S. Le Digabel, and C. Tribes. The NOMAD
project. Software available at http://www.gerad.ca/nomad.125
[2] B. M. Adams, W. J. Bohnhoff, K. R. Dalbey, J. P. Eddy, M. S. Ebeida, M. S. Eldred, J. R. Frye, G Ger-
arci, R. W. Hooper, P. D. Hough, K. T. Hu, J. D. Jakeman, M. Khalil, K. A. Maupin, J. A. Monschke,
E. M. Ridgway, A. Rushdi, J. A. Stephens, L. P. Swiler, D. M. Vigil, and T. M. Wildey. Dakota, a
multilevel parallel object-oriented framework for design optimization, parameter estimation, uncertainty
quantification, and sensitivity analysis: Version 6.7 developers manual. Technical Report SAND2014-
5014, Sandia National Laboratories, Albuquerque, NM, Updated May 2017. Available online from
http://dakota.sandia.gov/documentation.html.23,153,154,157,184,264,265
[3] B. M. Adams, W. J. Bohnhoff, K. R. Dalbey, J. P. Eddy, M. S. Ebeida, M. S. Eldred, J. R. Frye, G Ger-
arci, R. W. Hooper, P. D. Hough, K. T. Hu, J. D. Jakeman, M. Khalil, K. A. Maupin, J. A. Monschke,
E. M. Ridgway, A. Rushdi, J. A. Stephens, L. P. Swiler, D. M. Vigil, and T. M. Wildey. Dakota, a
multilevel parallel object-oriented framework for design optimization, parameter estimation, uncertainty
quantification, and sensitivity analysis: Version 6.7 reference manual. Technical Report SAND2014-
5015, Sandia National Laboratories, Albuquerque, NM, Updated May 2017. Available online from
http://dakota.sandia.gov/documentation.html.31,44,48,72,81,89,108,114,126,
131,137,149,150,154,168,171,172,174,175,181,183,211,217,219,220,230,232,233,234,236,
249,250,254,258,262,295,307,316
[4] B. M. Adams, W. J. Bohnhoff, K. R. Dalbey, J. P. Eddy, M. S. Ebeida, M. S. Eldred, J. R. Frye, G Ger-
arci, R. W. Hooper, P. D. Hough, K. T. Hu, J. D. Jakeman, M. Khalil, K. A. Maupin, J. A. Monschke,
E. M. Ridgway, A. Rushdi, J. A. Stephens, L. P. Swiler, D. M. Vigil, and T. M. Wildey. Dakota,
a multilevel parallel object-oriented framework for design optimization, parameter estimation, uncer-
tainty quantification, and sensitivity analysis: Version 6.7 theory manual. Technical Report SAND2014-
4253, Sandia National Laboratories, Albuquerque, NM, Updated May 2017. Available online from
http://dakota.sandia.gov/documentation.html.81,84,85,89,90,93,107,108,113,
117,129,170,241,253,257,351
[5] B. M. Adams, R. W. Hooper, A. Lewis, J. A. McMahan, R. C. Smith, L. P. Swiler, and B. J. Williams. User
guidelines and best practices for casl vuq analysis using dakota. Technical Report CASL-U-2014-0038-
000, 2014. 356
[6] G. Anderson and P. Anderson. The UNIX C Shell Field Guide. Prentice-Hall, Englewood Cliffs, NJ, 1986.
43,186,194,195,315
[7] J. S. Arora. Introduction to Optimum Design. McGraw-Hill, New York, 1989. 121
[8] C. Audet, S. Le Digabel, and C. Tribes. NOMAD user guide. Technical Report G-2009-37, Les cahiers du
GERAD, 2009. 125

358 BIBLIOGRAPHY
[9] J. M. Aughenbaugh and C. J. J. Paredis. Probability bounds analysis as a general approach to sensitivity
analysis in decision making under uncertainty. In SAE World Congress and Exposition, number SAE-2007-
01-1480, Detroit, MI, 2007. SAE. 250
[10] F. Augustin and Y. M. Marzouk. NOWPAC: A provably convergent derivative-free nonlinear optimizer
with path-augmented constraints. arXiv, math.OC:1403.1931, 2014. 126
[11] J.-P. Berrut and L. N. Trefethen. Barycentric lagrange interpolation. SIAM Review, 46(3):501–517, 2004.
70
[12] B. J. Bichon, M. S. Eldred, L. P. Swiler, S. Mahadevan, and J. M. McFarland. Efficient global reliability
analysis for nonlinear implicit performance functions. AIAA Journal, 46(10):2459–2468, 2008. 82,83
[13] B. Blinn. Portable Shell Programming: An Extensive Collection of Bourne Shell Examples. Prentice Hall
PTR, New Jersey, 1996. 186,315
[14] T. Butler, J. D. Jakeman, and T. M. Wildey. A consistent bayesian formulation for stochastic inverse
problems based on push-forward measures. arXiv, math.NA:1704.00680, 2017. 108
[15] R. H. Byrd, R. B. Schnabel, and G. A. Schultz. Parallel quasi-newton methods for unconstrained optimiza-
tion. Mathematical Programming, 42:273–306, 1988. 275
[16] K. J. Chang, R. T. Haftka, G. L. Giles, and P.-J. Kao. Sensitivity-based scaling for approximating structural
response. J. Aircraft, 30:283–288, 1993. 156
[17] C. A. Coello, D. A. Van Veldhuizen, and G. B. Lamont. Evolutionary Algorithms for Solving Multi-
Objective Problems. Kluwer Academic/Plenum Publishers, New York, 2002. 137,341
[18] P. G. Constantine. Active subspaces: Emerging ideas for dimension reduction in parameter studies, vol-
ume 2. SIAM, 2015. 169,170
[19] P. G. Constantine, E. Dow, and Q. Wang. Active subspace methods in theory and practice: applications to
kriging surfaces. SIAM Journal on Scientific Computing, 36(4):A1500–A1524, 2014. 170
[20] P. G. Constantine, M. S. Eldred, and E. T. Phipps. Sparse pseudospectral approximation method. Computer
Methods in Applied Mechanics and Engineering, 229–232:1–12, July 2012. 90
[21] P. G. Constantine and D. F. Gleich. Computing active subspaces. arXiv, math.NA:1408.0545, 2014. 170
[22] P. G. Constantine, D. F. Gleich, and G. Iaccarino. Spectral methods for parameterized matrix equations.
SIAM Journal on Matrix Analysis and Applications, 31(5):2681–2699, 2010. 90
[23] N. Cressie. Statistics of Spatial Data. John Wiley and Sons, New York, 1991. 160
[24] K. Dalbey and L. P. Swiler. Gaussian Process Adaptive Importance Sampling. International Journal for
Uncertainty Quantification, 4(2):133–149, 2014. 96
[25] J. E. Dennis, D. M. Gay, and R. E. Welsch. ALGORITHM 573: NL2SOL–an adaptive nonlinear least-
squares algorithm. ACM Trans. Math. Software, 7:369–383, 1981. 150,325
[26] J. E. Dennis and R. M. Lewis. Problem formulations and other optimization issues in multidisciplinary
optimization. In Proc. AIAA Symposium on Fluid Dynamics, number AIAA-94-2196, Colorado Springs,
Colordao, June 1994. 274
[27] J. E. Dennis and V. J. Torczon. Derivative-free pattern search methods for multidisciplinary design prob-
lems. In Proc. 5th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization,
number AIAA-94-4349, pages 922–932, Panama City, FL, September 7–9 1994. 126
Dakota Version 6.7 User’s Manual generated on November 13, 2017

BIBLIOGRAPHY 359
[28] A. Der Kiureghian and P. L. Liu. Structural reliability under incomplete information. J. Eng. Mech., ASCE,
112(EM-1):85–104, 1986. 80
[29] A. Dey and S. Mahadevan. Ductile structural system reliability analysis using adaptive importance sam-
pling. Structural Safety, 20:137–154, 1998. 83
[30] Q. Du, V. Faber, and M. Gunzburger. Centroidal voronoi tessellations: Applications and algorithms. SIAM
Review, 41:637–676, 1999. 63
[31] Mohamed S Ebeida, Scott A Mitchell, Laura P Swiler, Vicente J Romero, and Ahmad A Rushdi. Pof-
darts: Geometric adaptive sampling for probability of failure. Reliability Engineering & System Safety,
155:64–77, 2016. 98
[32] J. Eckstein, C. A. Phillips, and W. E. Hart. PEBBL 1.0 user guide. Technical report, October 2009. http:
//www.researchgate.net/publication/266173679_PEBBL_1.0_User_Guide.239
[33] Eclipse.org home. http://www.eclipse.org/. Last accessed: July 6, 2009. 217
[34] M. S. Eldred. Optimization strategies for complex engineering applications. Technical Report SAND98-
0340, Sandia National Laboratories, Albuquerque, NM, 1998. 19,184
[35] M. S. Eldred, H. Agarwal, V. M. Perez, S. F. Wojtkiewicz, Jr., and J. E. Renaud. Investigation of reliability
method formulations in DAKOTA/UQ. Structure & Infrastructure Engineering: Maintenance, Manage-
ment, Life-Cycle Design & Performance, 3(3):199–213, 2007. 69,253,340,352
[36] M. S. Eldred and B. J. Bichon. Second-order reliability formulations in DAKOTA/UQ. In Proceedings of
the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, number
AIAA-2006-1828, Newport, RI, May 1–4 2006. 85,253,340,352
[37] M. S. Eldred, A. A. Giunta, and S. S. Collis. Second-order corrections for surrogate-based optimization
with model hierarchies. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimiza-
tion Conference, Albany, NY,, Aug. 30–Sept. 1, 2004. AIAA Paper 2004-4457. 156,244
[38] M. S. Eldred, A. A. Giunta, S. F. Wojtkiewicz, Jr., and T. G. Trucano. Formulations for surrogate-based
optimization under uncertainty. In Proc. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and
Optimization, number AIAA-2002-5585, Atlanta, GA, September 4–6, 2002. 253,257,340
[39] M. S. Eldred and W. E. Hart. Design and implementation of multilevel parallel optimization on the Intel
TeraFLOPS. In Proc. 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Opti-
mization, number AIAA-98-4707, pages 44–54, St. Louis, MO, September 2–4 1998. 274,275
[40] M. S. Eldred, W. E. Hart, W. J. Bohnhoff, V. J. Romero, S. A. Hutchinson, and A. G. Salinger. Utilizing
object-oriented design to build advanced optimization strategies with generic implementation. In Proc. 6th
AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, number AIAA-96-
4164, pages 1568–1582, Bellevue, WA, September 4–6 1996. 184,275
[41] M. S. Eldred, W. E. Hart, B. D. Schimel, and B. G. van Bloemen Waanders. Multilevel parallelism for op-
timization on MP computers: Theory and experiment. In Proc. 8th AIAA/USAF/NASA/ISSMO Symposium
on Multidisciplinary Analysis and Optimization, number AIAA-2000-4818, Long Beach, CA, 2000. 287,
289,291,294
[42] M. S. Eldred, D. E. Outka, W. J. Bohnhoff, W. R. Witkowski, V. J. Romero, E. R. Ponslet, and K. S. Chen.
Optimization of complex mechanics simulations with object-oriented software design. Computer Modeling
and Simulation in Engineering, 1(3), August 1996. 184
Dakota Version 6.7 User’s Manual generated on November 13, 2017

360 BIBLIOGRAPHY
[43] M. S. Eldred and B. D. Schimel. Extended parallelism models for optimization on massively parallel
computers. In Proc. 3rd World Congress of Structural and Multidisciplinary Optimization (WCSMO-3),
number 16-POM-2, Amherst, NY, May 17–21 1999. 239
[44] M. S Eldred and L. P. Swiler. Efficient algorithms for mixed aleatory-epistemic uncertainty quantification
with application to radiation-hardened electronics. part 1: Algorithms and benchmark results. Technical
Report SAND2009-5805, Sandia National Laboratories, Albuquerque, NM, 2009. 258
[45] M. S. Eldred, C. G. Webster, and P. Constantine. Evaluation of non-intrusive approaches for wiener-
askey generalized polynomial chaos. In Proceedings of the 10th AIAA Non-Deterministic Approaches
Conference, number AIAA-2008-1892, Schaumburg, IL, April 7–10 2008. 253
[46] G. M. Fadel, M. F. Riley, and J.-F. M. Barthelemy. Two point exponential approximation method for
structural optimization. Structural Optimization, 2(2):117–124, 1990. 154,158
[47] S. Ferson and W. T. Tucker. Sensitivity analysis using probability bounding. Reliability Engineering and
System Safety, 91:1435–1442, 2006. 250
[48] D. Flaggs. JPrePost user’s manual. In preparation. 189
[49] R. Fourer, D. M. Gay, and B. W. Kernighan. AMPL: A Modeling Language for Mathematical Programming,
2nd ed. Duxbury Press/Brooks/Cole Publishing Co., Pacific Grove, CA, 2003. For small examples, e.g., at
most 300 variables, a student version of AMPL suffices; see http://www.ampl.com/DOWNLOADS.
261
[50] J. H. Friedman. Multivariate adaptive regression splines. Annals of Statistics, 19(1):1–141, March 1991.
155,163
[51] J. Gablonsky. Direct version 2.0 userguide technical report. Technical Report CRSC-TR01-08, North
Carolina State University, Center for Research in Scientific Computation, Raleigh, NC, 2001. 129
[52] D. M. Gay. Hooking your solver to AMPL. Technical Report Technical Report 97-4-06, Bell Labo-
ratories, Murray Hill, NJ, 1997. Available online as http://www.ampl.com/REFS/HOOKING/
index.html and http://www.ampl.com/REFS/hooking2.pdf and http://www.ampl.
com/REFS/hooking2.ps.gz.261
[53] R. Ghanem and J. R. Red-Horse. Propagation of probabilistic uncertainty in complex physical systems
using a stochastic finite element technique. Physica D, 133:137–144, 1999. 69,70,89
[54] R. G. Ghanem and P. D. Spanos. Stochastic Finite Elements: A Spectral Approach. Springer-Verlag, New
York, 1991. 69,70,89
[55] W.R. Gilks, S. Richardson, and D.J. Spiegelhalter. Markov chain Monte Carlo in practice. Chapman &
Hall, 1998. 106
[56] P. E. Gill, W. Murray, M. A. Saunders, and M. H. Wright. User’s guide for NPSOL (Version 4.0): A Fortran
package for nonlinear programming. Technical Report TR SOL-86-2, System Optimization Laboratory,
Stanford University, Stanford, CA, 1986. 124
[57] P. E. Gill, W. Murray, and M. H. Wright. Practical Optimization. Academic Press, San Diego, CA, 1981.
32,121,147,324
[58] D. Gilly. UNIX in a Nutshell. O’Reilly and Associates, Inc., Sebastopol, CA, 1992. 230
Dakota Version 6.7 User’s Manual generated on November 13, 2017

BIBLIOGRAPHY 361
[59] David Ginsbourger, Rodolphe Riche, and Laurent Carraro. Kriging is well-suited to parallelize optimiza-
tion. In Yoel Tenne and Chi-Keong Goh, editors, Computational Intelligence in Expensive Optimization
Problems, volume 2 of Adaptation, Learning, and Optimization, pages 131–162. Springer Berlin Heidel-
berg, 2010. 98
[60] A. A. Giunta. Use of data sampling, surrogate models, and numerical optimization in engineering design.
In Proc. 40th AIAA Aerospace Science Meeting and Exhibit, number AIAA-2002-0538, Reno, NV, January
2002. 242
[61] A. A. Giunta and M. S. Eldred. Implementation of a trust region model management strategy in the
DAKOTA optimization toolkit. In Proc. 8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary
Analysis and Optimization, number AIAA-2000-4935, Long Beach, CA, September 6–8, 2000. 236,242
[62] A. A. Giunta, J. M. McFarland, L. P. Swiler, and M. S. Eldred. The promise and peril of uncertainty quan-
tification using respone surface approximations. Structure and Infrastructure Engineering, 2(3-4):175–189,
September-December 2006. 259
[63] A. A. Giunta and L. T. Watson. A comparison of approximation modeling techniques: Polynomial versus
interpolating models. In Proc. 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis
and Optimization, number AIAA-98-4758, pages 392–404, St. Louis, MO, 1998. 155,160
[64] D. E. Goldberg. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wessley
Publishing Co., Inc., Reading, MA, 1989. 129
[65] G. H.. Golub and J. H. Welsch. Caclulation of gauss quadrature rules. Mathematics of Computation,
23(106):221–230, 1969. 90
[66] I. R. Goodman and H. T. Nguyen. Probability updating using second order probabilities and conditional
event algebra. Information Sciences, 121:295–347, 1999. 251
[67] G. A. Gray and T. G. Kolda. Algorithm 856: APPSPACK 4.0: Asynchronous parallel pattern search for
derivative-free optimization. ACM Transactions on Mathematical Software, 32(3):485–507, September
2006. 125
[68] J. D Griffin and T. G. Kolda. Nonlinearly-constrained optimization using asynchronous parallel generating
set search. Technical Report SAND2007-3257, Sandia National Laboratories, Livermore, CA, 2007. 125
[69] W. Gropp and E. Lusk. User’s guide for mpich, a portable implementation of MPI. Technical Report
ANL/MCS-TM-ANL-96/6, Argonne National Laboratory, Mathematics and Computer Science Division,
1996. 293
[70] W. Gropp, E. Lusk, and A. Skjellum. Using MPI, Portable Parallel Programing with the Message-Passing
Interface. The MIT Press, Cambridge, MA, 1994. 283
[71] Heikki Haario, Marko Laine, Antonietta Mira, and Eero Saksman. Dram: Efficient adaptive mcmc. Statis-
tics and Computing, 16:339–354, 2006. 106
[72] R. T. Haftka and Z. Gurdal. Elements of Structural Optimization. Kluwer, Boston, 1992. 121,129
[73] A. Haldar and S. Mahadevan. Probability, Reliability, and Statistical Methods in Engineering Design.
Wiley, New York, 2000. 69,70,174,351
[74] W. E. Hart. The coliny project. Web site, 2007. http://software.sandia.gov/Acro/Coliny/.
126,131
Dakota Version 6.7 User’s Manual generated on November 13, 2017

362 BIBLIOGRAPHY
[75] A. S. Hedayat, N. J. A. Sloane, and J. Stufken. Orthogonal Arrays: Theory and Applications. Springer-
Verlag, New York, 1999. 61
[76] J. C. Helton and F. J. Davis. Sampling-based methods for uncertainty and sensitivity analysis. Technical
Report SAND99-2240, Sandia National Laboratories, Albuquerque, NM, 2000. 72
[77] J. C. Helton, J. D. Johnson, W. L. Oberkampf, and C. B Storlie. A sampling-based computational strategy
for the representation of epistemic uncertainty in model predictions with evidence theory. Comp. Methods
in Applied Mechanics and Engineering, 196:3980–3998, 2007. 99,102
[78] D. Higdon, J. Gattiker, B. Williams, and M. Rightley. Computer model calibration using high-dimensional
output. Journal of the American Statistical Association, 103(482):570–583, 2008. 108
[79] N. J. Higham. The numerical stability of barycentric lagrange interpolation. IMA Journal of Numerical
Analysis, 24(4):547–556, 2004. 70
[80] H.P. Hong. Simple approximations for improving second-order reliability estimates. J. Eng. Mech., ASCE,
125(5):592–595, 1999. 351
[81] D. Huang, T. T. Allen, W. I. Notz, and N. Zeng. Global optimization of stochastic black-box systems via
sequential kriging meta-models. Journal of Global Optimization, 34:441–466, 2006. 82,129
[82] R. L. Iman and M. J Shortencarier. A Fortran 77 program and user’s guide for the generation of latin
hypercube samples for use with computer models. Technical Report NUREG/CR-3624, SAND83-2365,
Sandia National Laboratories, Albuquerque, NM, 1984. 70,72,157
[83] E. T. Jaynes and G. Larry. Bretthorst. Probability theory : the logic of science. Cambridge University
Press, Cambridge, UK; New York, NY, 2003. 105
[84] D. Jones, M. Schonlau, and W. Welch. Efficient global optimization of expensive black-box functions.
Journal of Global Optimization, 13:455–492, 1998. 82,129
[85] D. R. Karanki, H. S. Kishwaha, A. K. Verma, and S. Ajit. Uncertainty analysis based on probability bounds
(p-box) approach in probabilistic safety assessment. Risk Analysis, 29:662–675, 2009. 250
[86] M. C. Kennedy and A. O’Hagan. Bayesian calibration of computer models. Journal of the Royal Statistical
Society, 63:425–464, 2001. 105,108,111
[87] B. W. Kernighan and D. M. Ritchie. The C Programming Language. Prentice Hall PTR, Englewood Cliffs,
NJ, 2nd edition, 1988. 184,194,280
[88] W. A. Klimke. Uncertainty Modeling using Fuzzy Arithmetic and Sparse Grids. PhD thesis, Universit¨
at
Stuttgart, Stuttgart, Germany, 2005. 70
[89] J. R. Koehler and A. B. Owen. Computer experiments. In S. Ghosh and C. R. Rao, editors, Handbook of
Statistics, volume 13. Elsevier Science, New York, 1996. 59,160
[90] Alexander Kraskov, Harald St¨
ogbauer, and Peter Grassberger. Estimating mutual information. Physical
review E, 69(6):066138, 2004. 117
[91] N. Kuschel and R. Rackwitz. Two basic problems in reliability-based structural optimization. Math. Method
Oper. Res., 46:309–333, 1997. 351,352
[92] L. D. Lathauwer, B. D. Moor, and J. Vandewalle. A multilinear singular value decomposition. SIAM
Journal on Matrix Analysis and Applications, 21(4):1253–1278, 2000. 244
Dakota Version 6.7 User’s Manual generated on November 13, 2017

BIBLIOGRAPHY 363
[93] S. Le Digabel. Algorithm 909: NOMAD: Nonlinear optimization with the MADS algorithm. ACM Trans-
actions on Mathematical Software, 37(4):1–15, 2011. 125
[94] H. Lee, R. Gramacy, C. Linkletter, and G. Gray. Optimization Subject to Hidden Constraints via Statistical
Emulation. Pacific Journal of Optimization, to appear. 327
[95] Allison Lewis, Ralph Smith, Brian Williams, and Victor Figueroa. An information theoretic approach to
use high-fidelity codes to calibrate low-fidelity codes. Journal of Computational Physics, 324:24 – 43,
2016. 117,355
[96] R. M. Lewis and S. N. Nash. A multigrid approach to the optimization of systems governed by differential
equations. In Proceedings of the 8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis
and Optimization, number AIAA-2000-4890, Long Beach, CA, Sep 2000. 156
[97] David J. C. MacKay. Information-based objective functions for active data selection. Neural Computation,
4:590–604, 1992. 97
[98] Daniel P. Maljovec, Bei Wang, Ana Kupresanin, Gardar Johannesson, Valerio Pascucci, and Peer-Timo
Bremer. Adaptive sampling with topological scores. International Journal for Uncertainty Quantification,
1(1), 2012. 98
[99] A. Martelli. Python in a Nutshell. O’Reilly and Associates, Cambridge, MA, 2003. 186
[100] J. M. McFarland. Uncertainty Analysis for Computer Simulations through Validation and Calibra-
tion. PhD thesis, Vanderbilt University, Nashville, Tennesssee, 2008. available for download at
http://etd.library.vanderbilt.edu/ETD-db/available/etd-03282008-125137/. 161
[101] M. D. McKay, R. J. Beckman, and W. J. Conover. A comparison of three methods for selecting values of
input variables in the analysis of output from a computer code. Technometrics, 21(2):239–245, 1979. 72
[102] J. C. Meza, R. A. Oliva, P. D. Hough, and P. J. Williams. OPT++: an object oriented toolkit for nonlinear
optimization. ACM Transactions on Mathematical Software, 33(2), 2007. 149
[103] M. D. Morris. Factorial sampling plans for preliminary computational experiments. Technometrics,
33(2):161–174, 1991. 63,347
[104] R. H. Myers and D. C. Montgomery. Response Surface Methodology: Process and Product Optimization
Using Designed Experiments. John Wiley & Sons, Inc., New York, 1995. 66,160
[105] National Research Council of the National Academies. Evaluation of Quantification of Margins and Un-
certainties Methodology for Assessing and Certifying the Reliability of the Nuclear Stockpile. National
Academy Press, Washington D.C., 2008. 251
[106] A. Nealen. A short-as-possible introduction to the least squares, weighted least squares, and moving least
squares methods for scattered data approximation and interpolation. Technical report, Discrete Geometric
Modeling Group, Technishe Universitaet, Berlin, Germany, 2004. 155,164
[107] J. Nocedal and Wright S. J. Numerical Optimization. Springer Series in Operations Research. Springer,
New York, 1999. 121
[108] W.T. Nutt and G.B. Wallis. Evaluation of nuclear safety from the outputs of computer codes in the presence
of uncertainties. Reliability Engineering and System Safety, 83:57–77, 2004. 79
[109] W. .L. Oberkampf and J. C. Helton. Evidence theory for engineering applications. Technical Report
SAND2003-3559P, Sandia National Laboratories, Albuquerque, NM, 2003. 99,100
Dakota Version 6.7 User’s Manual generated on November 13, 2017

364 BIBLIOGRAPHY
[110] M. J. L. Orr. Introduction to radial basis function networks. Technical report, University of Edinburgh,
Edinburgh, Scotland, 1996. 164
[111] A. B. Owen. Orthogonal arrays for computer experiments, integration, and visualization. Statistica Sinica,
2(2):439–452, 1992. 62
[112] T. D. Robinson, M. S. Eldred, K. E. Willcox, and R. Haimes. Strategies for multifidelity optimization with
variable dimensional hierarchical models. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Struc-
tures, Structural Dynamics, and Materials Conference (2nd AIAA Multidisciplinary Design Optimization
Specialist Conference), Newport, RI, May 1–4, 2006. AIAA Paper 2006-1819. 244
[113] T. D. Robinson, K. E. Willcox, M. S. Eldred, and R. Haimes. Multifidelity optimization for variable-
complexity design. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization
Conference, Portsmouth, VA, September 6–8, 2006. AIAA Paper 2006-7114. 244
[114] M. Rosenblatt. Remarks on a multivariate transformation. Annals of Mathematical Statistics, 23(3):470–
472, 1952. 80
[115] H. H. Rosenbrock. An automatic method for finding the greatest or least value of a function. Computer
Journal, 3:175–184, 1960. 32
[116] A. Saltelli, S. Tarantola, F. Campolongo, and M. Ratto. Sensitivity Analysis in Practice: A Guide to
Assessing Scientific Models. John Wiley & Sons, 2004. 64,66,67,347
[117] K. Schittkowski. NLPQLP: A fortran implementation of a sequential quadratic programming algorithm
with distributed and non-monotone line search – user’s guide. Technical report, Department of Mathemat-
ics, University of Bayreuth, Bayreuth, Germany, 2004. 124,275
[118] P. R. Schunk, P. A. Sackinger, R. R. Rao, K. S. Chen, and R. A. Cairncross. GOMA – a full-newton finite
element program for free and moving boundary problems with coupled fluid/solid momentum, energy,
mass, and chemical species transport: User’s guide. Technical Report SAND95-2937, Sandia National
Laboratories, Albuquerque, NM, 1995. 317
[119] G. A. F. Seber and C. J. Wild. Nonlinear Regression. Wiley, New Jersey, 2003. 150
[120] Sambu Seo, Marko Wallat, Thore Graepel, and Klaus Obermayer. Gaussian process regression: Active
data selection and test point rejection. In In Proceedings of the International Joint Conference on Neural
Networks (IJCNN), pages 241–246. IEEE, 2000. 97
[121] I.C. Simpson. Numerical integration over a semi-infinite interval, using the lognormal distibution. Nu-
merische Mathematik, 31:71–76, 1978. 90
[122] G. D. Sjaardema. APREPRO: An algebraic preprocessor for parameterizing finite element analyses. Tech-
nical Report SAND92-2291, Sandia National Laboratories, Albuquerque, NM, 1992. 177,179
[123] R.C. Smith. Uncertainty Quantification: Theory, Implementation, and Applications. Computational Sci-
ence and Engineering. SIAM, 2013. 107
[124] S.A. Smolyak. Quadrature and interpolation formulas for tensor products of certain classes of functions.
Dokl. Akad. Nauk SSSR, 4:240–243, 1963. 89
[125] M. Snir, S. Otto, S. Huss-Lederman, D. Walker, and J. Dongarra. MPI: The Complete Reference. MIT
Press, Cambridge, MA, 1996. 283
[126] R. Srinivasan. Importance Sampling. Springer-Verlag, 2002. 95
Dakota Version 6.7 User’s Manual generated on November 13, 2017

BIBLIOGRAPHY 365
[127] C. B. Storlie, L. P. Swiler, J. C. Helton, and C. J. Sallaberry. Implementation and evaluation of nonpara-
metric regression procedures for s ensitivity analysis of computationally demanding models. Reliability
Engineering and System Safety, 94:1735–1763, 2009. 328
[128] A. Stroud. Approximate Calculation of Multiple Integrals. Prentice Hall, 1971. 89
[129] R. Sues, M. Aminpour, and Y. Shin. Reliability-based multidisciplinary optimization for aerospace systems.
In Proc. 42rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference,
number AIAA-2001-1521, Seattle, WA, April 16-19 2001. 338
[130] L. P Swiler, R. Slepoy, and A. A. Giunta. Evaluation of sampling methods in constructing response sur-
face approximations. In Proc. 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and
Materials Conference, number AIAA-2006-1827, Newport, RI, May 1-4 2006. 259
[131] L. P. Swiler and N. J. West. Importance sampling: Promises and limitations. In Proceedings of the 12th
AIAA Non-Deterministic Approaches Conference, number AIAA-2010-2850, 2010. 95
[132] L. P. Swiler and G. D. Wyss. A user’s guide to Sandia’s latin hypercube sampling software: LHS UNIX
library and standalone version. Technical Report SAND04-2439, Sandia National Laboratories, Albu-
querque, NM, July 2004. 57,73,174
[133] G. Tang, G. Iaccarino, and M. S Eldred. Global sensitivity analysis for stochastic collocation expansion.
In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials
Conference (12th AIAA Non-Deterministic Approaches conference), Orlando, FL, April 12-15, 2010. AIAA
Paper 2010-XXXX. 105
[134] G. Tang, L. P. Swiler, and M. S Eldred. Using stochastic expansion methods in evidence theory for mixed
aleatory-epistemic uncertainty quantification. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC
Structures, Structural Dynamics, and Materials Conference (12th AIAA Non-Deterministic Approaches
conference), Orlando, FL, April 12-15, 2010. AIAA Paper 2010-XXXX. 69
[135] M.A. Tatang. Direct incorporation of uncertainty in chemical and environmental engineering systems. PhD
thesis, MIT, 1995. 89
[136] C. H. Tong. The PSUADE software library. Web site, 2005. http://www.llnl.gov/CASC/
uncertainty_quantification/#psuade.57,63
[137] C. H. Tong and J. C. Meza. DDACE: A distributed object-oriented software with multiple samplings for the
design and analysis of computer experiments. Draft as yet unpublished, see also http://www.sandia.
gov/csit/research/computation/ddace.php.57,59,157
[138] L. Tvedt. Distribution of quadratic forms in normal space – applications to structural reliability. J. Eng.
Mech., ASCE, 116(6):1183–1197, 1990. 351
[139] G. N. Vanderplaats. CONMIN – a FORTRAN program for constrained function minimization. Technical
Report TM X-62282, NASA, 1973. See also Addendum to Technical Memorandum, 1978. 34,125
[140] G. N. Vanderplaats. Numerical Optimization Techniques for Engineering Design: With Applications.
McGraw-Hill, New York, 1984. 121
[141] Vanderplaats Research and Development, Inc., Colorado Springs, CO. DOT Users Manual, Version 4.20,
1995. 124
[142] J. A. Vrugt, C. J. F. ter Braak, C. G. H. Diks, B. A. Robinson, J. M. Hyman, and D. Higdon. Accelerating
Markov chain Monte Carlo simulation by self-adaptive differential evolution with randomized subspace
sampling. International Journal of Nonlinear Scientific Numerical Simulation, 10(3), 2009. 106,108
Dakota Version 6.7 User’s Manual generated on November 13, 2017

366 BIBLIOGRAPHY
[143] K. W. Vugrin, L. P. Swiler, R. M. Roberts, N. J. Stuckey-Mack, and S. P Sullivan. Confidence region
estimation techniques for nonlinear regression in groundwater flow: Three case studies. Water Resources
Research, 43, 2007. 150
[144] L. Wall, T. Christiansen, and R. L. Schwartz. Programming Perl. O’Reilly & Associates, Cambridge, 2nd
edition, 1996. 186
[145] R. W. Walters. Towards stochastic fluid mechanics via polynomial chaos. In Proceedings of the 41st AIAA
Aerospace Sciences Meeting and Exhibit, number AIAA-2003-0413, Reno, NV, January 6–9, 2003. 89
[146] B. Walton. BPREPRO preprocessor documentation. Online document http://bwalton.com/
bprepro.html.189
[147] G. Weickum, M. S. Eldred, and K. Maute. Multi-point extended reduced order modeling for design op-
timization and uncertainty analysis. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures,
Structural Dynamics, and Materials Conference (2nd AIAA Multidisciplinary Design Optimization Spe-
cialist Conference), Newport, RI, May 1–4, 2006. AIAA Paper 2006-2145. 244
[148] V. G. Weirs, J. R. Kamm, L. P. Swiler, M. Ratto, S. Tarantola, B. M. Adams, W. J. Rider, and M. S Eldred.
Sensitivity analysis techniques applied to a system of hyperbolic conservation laws. Reliability Engineering
and System Safety, 107:157–170, 2012. 67
[149] S. S. Wilks. Determination of sample sizes for setting tolerance limits. Ann. Math. Stat., 12(1):91–96,
1941. 79
[150] Y.-T. Wu, Y. Shin, R. Sues, and M. Cesare. Safety-factor based approach for probability-based design
optimization. In Proc. 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials
Conference, number AIAA-2001-1522, Seattle, WA, April 16–19 2001. 338
[151] D. Xiu and J.S. Hesthaven. High-order collocation methods for differential equations with random inputs.
SIAM J. Sci. Comput., 27(3):1118–1139 (electronic), 2005. 354
[152] D. Xiu and G. M. Karniadakis. The wiener-askey polynomial chaos for stochastic differential equations.
SIAM J. Sci. Comput., 24(2):619–644, 2002. 89
[153] S. Xu and R. V. Grandhi. Effective two-point function approximation for design optimization. AIAA J.,
36(12):2269–2275, 1998. 154,158
[154] D. C. Zimmerman. Genetic algorithms for navigating expensive and complex design spaces, September
1996. Final Report for Sandia National Laboratories contract AO-7736 CA 02. 155,163
Dakota Version 6.7 User’s Manual generated on November 13, 2017