Octave Manual
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 1004 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface
- A Brief Introduction to Octave
- Getting Started
- Data Types
- Numeric Data Types
- Strings
- Data Containers
- Variables
- Expressions
- Evaluation
- Statements
- Functions and Scripts
- Introduction to Function and Script Files
- Defining Functions
- Multiple Return Values
- Variable-length Argument Lists
- Ignoring Arguments
- Variable-length Return Lists
- Returning from a Function
- Default Arguments
- Function Files
- Script Files
- Function Handles, Anonymous Functions, Inline Functions
- Commands
- Organization of Functions Distributed with Octave
- Errors and Warnings
- Debugging
- Input and Output
- Basic Input and Output
- C-Style I/O Functions
- Opening and Closing Files
- Simple Output
- Line-Oriented Input
- Formatted Output
- Output Conversion for Matrices
- Output Conversion Syntax
- Table of Output Conversions
- Integer Conversions
- Floating-Point Conversions
- Other Output Conversions
- Formatted Input
- Input Conversion Syntax
- Table of Input Conversions
- Numeric Input Conversions
- String Input Conversions
- Binary I/O
- Temporary Files
- End of File and Errors
- File Positioning
- Plotting
- Introduction to Plotting
- High-Level Plotting
- Graphics Data Structures
- Introduction to Graphics Structures
- Graphics Objects
- Graphics Object Properties
- Root Figure Properties
- Figure Properties
- Axes Properties
- Line Properties
- Text Properties
- Image Properties
- Patch Properties
- Surface Properties
- Light Properties
- Uimenu Properties
- Uibuttongroup Properties
- Uicontextmenu Properties
- Uipanel Properties
- Uicontrol Properties
- Uitoolbar Properties
- Uipushtool Properties
- Uitoggletool Properties
- Searching Properties
- Managing Default Properties
- Advanced Plotting
- Matrix Manipulation
- Arithmetic
- Linear Algebra
- Vectorization and Faster Code Execution
- Nonlinear Equations
- Diagonal and Permutation Matrices
- Sparse Matrices
- Numerical Integration
- Differential Equations
- Optimization
- Statistics
- Sets
- Polynomial Manipulations
- Interpolation
- Geometry
- Signal Processing
- Image Processing
- Audio Processing
- Object Oriented Programming
- GUI Development
- System Utilities
- Packages
- External Code Interface
- Oct-Files
- Getting Started with Oct-Files
- Matrices and Arrays in Oct-Files
- Character Strings in Oct-Files
- Cell Arrays in Oct-Files
- Structures in Oct-Files
- Sparse Matrices in Oct-Files
- Accessing Global Variables in Oct-Files
- Calling Octave Functions from Oct-Files
- Calling External Code from Oct-Files
- Allocating Local Memory in Oct-Files
- Input Parameter Checking in Oct-Files
- Exception and Error Handling in Oct-Files
- Documentation and Testing of Oct-Files
- Mex-Files
- Standalone Programs
- Java Interface
- Oct-Files
- Test and Demo Functions
- Obsolete Functions
- Known Causes of Trouble
- Installing Octave
- Grammar and Parser
- GNU GENERAL PUBLIC LICENSE
- Concept Index
- Function Index
- Operator Index

GNU Octave
A high-level interactive language for numerical computations
Edition 4 for Octave version 4.2.1
February 2017
Free Your Numbers
John W. Eaton
David Bateman
Søren Hauberg
Rik Wehbring
Copyright c
1996, 1997, 1999, 2000, 2001, 2002, 2005, 2006, 2007, 2011, 2013, 2015, 2016,
2017 John W. Eaton.
This is the fourth edition of the Octave documentation, and is consistent with version 4.2.1
of Octave.
Permission is granted to make and distribute verbatim copies of this manual provided the
copyright notice and this permission notice are preserved on all copies.
Permission is granted to copy and distribute modified versions of this manual under the con-
ditions for verbatim copying, provided that the entire resulting derived work is distributed
under the terms of a permission notice identical to this one.
Permission is granted to copy and distribute translations of this manual into another lan-
guage, under the same conditions as for modified versions.
Portions of this document have been adapted from the gawk,readline,gcc, and C library
manuals, published by the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor,
Boston, MA 02110-1301–1307, USA.
i
Table of Contents
Preface .......................................................... 1
Acknowledgements ................................................................. 1
Citing Octave in Publications ....................................................... 5
How You Can Contribute to Octave.................................................5
Distribution ........................................................................ 6
1 A Brief Introduction to Octave ............................ 7
1.1 Running Octave ............................................................... 7
1.2 Simple Examples .............................................................. 7
1.2.1 Elementary Calculations .................................................. 7
1.2.2 Creating a Matrix ........................................................ 8
1.2.3 Matrix Arithmetic ........................................................ 8
1.2.4 Solving Systems of Linear Equations ...................................... 8
1.2.5 Integrating Differential Equations ......................................... 9
1.2.6 Producing Graphical Output ............................................ 10
1.2.7 Help and Documentation ................................................ 10
1.2.8 Editing What You Have Typed .......................................... 11
1.3 Conventions .................................................................. 11
1.3.1 Fonts....................................................................11
1.3.2 Evaluation Notation ..................................................... 11
1.3.3 Printing Notation ....................................................... 12
1.3.4 Error Messages .......................................................... 12
1.3.5 Format of Descriptions .................................................. 12
1.3.5.1 A Sample Function Description ..................................... 12
1.3.5.2 A Sample Command Description ....................................13
2 Getting Started ............................................ 15
2.1 Invoking Octave from the Command Line .....................................15
2.1.1 Command Line Options ................................................. 15
2.1.2 Startup Files ............................................................ 19
2.2 Quitting Octave .............................................................. 19
2.3 Commands for Getting Help .................................................. 20
2.4 Command Line Editing.......................................................25
2.4.1 Cursor Motion...........................................................25
2.4.2 Killing and Yanking ..................................................... 26
2.4.3 Commands for Changing Text ........................................... 27
2.4.4 Letting Readline Type for You...........................................27
2.4.5 Commands for Manipulating the History .................................28
2.4.6 Customizing readline...................................................32
2.4.7 Customizing the Prompt.................................................32
2.4.8 Diary and Echo Commands ..............................................34
2.5 How Octave Reports Errors .................................................. 35
ii GNU Octave
2.6 Executable Octave Programs ................................................. 36
2.7 Comments in Octave Programs ............................................... 37
2.7.1 Single Line Comments ................................................... 37
2.7.2 Block Comments ........................................................ 38
2.7.3 Comments and the Help System ......................................... 38
3 Data Types.................................................39
3.1 Built-in Data Types .......................................................... 39
3.1.1 Numeric Objects ........................................................ 42
3.1.2 Missing Data ............................................................ 43
3.1.3 String Objects...........................................................43
3.1.4 Data Structure Objects .................................................. 43
3.1.5 Cell Array Objects ...................................................... 44
3.2 User-defined Data Types ..................................................... 44
3.3 Object Sizes..................................................................44
4 Numeric Data Types ...................................... 47
4.1 Matrices ..................................................................... 48
4.1.1 Empty Matrices ......................................................... 51
4.2 Ranges ....................................................................... 52
4.3 Single Precision Data Types .................................................. 54
4.4 Integer Data Types...........................................................54
4.4.1 Integer Arithmetic.......................................................57
4.5 Bit Manipulations ............................................................ 58
4.6 Logical Values................................................................60
4.7 Promotion and Demotion of Data Types ...................................... 61
4.8 Predicates for Numeric Objects ............................................... 62
5 Strings......................................................67
5.1 Escape Sequences in String Constants ........................................ 67
5.2 Character Arrays .............................................................68
5.3 Creating Strings..............................................................69
5.3.1 Concatenating Strings ................................................... 70
5.3.2 Converting Numerical Data to Strings ................................... 73
5.4 Comparing Strings ........................................................... 76
5.5 Manipulating Strings ......................................................... 77
5.6 String Conversions ........................................................... 91
5.7 Character Class Functions .................................................... 96
6 Data Containers ........................................... 99
6.1 Structures....................................................................99
6.1.1 Basic Usage and Examples...............................................99
6.1.2 Structure Arrays ....................................................... 103
6.1.3 Creating Structures .................................................... 104
6.1.4 Manipulating Structures ................................................107
6.1.5 Processing Data in Structures .......................................... 111

iii
6.2 Cell Arrays ................................................................. 112
6.2.1 Basic Usage of Cell Arrays..............................................112
6.2.2 Creating Cell Arrays ................................................... 114
6.2.3 Indexing Cell Arrays ................................................... 116
6.2.4 Cell Arrays of Strings .................................................. 118
6.2.5 Processing Data in Cell Arrays ......................................... 119
6.3 Comma Separated Lists ..................................................... 120
6.3.1 Comma Separated Lists Generated from Cell Arrays .................... 121
6.3.2 Comma Separated Lists Generated from Structure Arrays ...............122
7 Variables .................................................. 123
7.1 Global Variables ............................................................ 124
7.2 Persistent Variables ......................................................... 126
7.3 Status of Variables .......................................................... 127
8 Expressions ............................................... 135
8.1 Index Expressions ........................................................... 135
8.1.1 Advanced Indexing ..................................................... 136
8.2 Calling Functions ........................................................... 140
8.2.1 Call by Value .......................................................... 141
8.2.2 Recursion .............................................................. 142
8.3 Arithmetic Operators ....................................................... 142
8.4 Comparison Operators ...................................................... 146
8.5 Boolean Expressions.........................................................147
8.5.1 Element-by-element Boolean Operators ................................. 147
8.5.2 Short-circuit Boolean Operators ........................................ 149
8.6 Assignment Expressions ..................................................... 151
8.7 Increment Operators ........................................................ 153
8.8 Operator Precedence ........................................................ 154
9 Evaluation ................................................ 157
9.1 Calling a Function by its Name ..............................................158
9.2 Evaluation in a Different Context............................................159
10 Statements .............................................. 161
10.1 The if Statement ........................................................... 161
10.2 The switch Statement ...................................................... 163
10.2.1 Notes for the C Programmer .......................................... 164
10.3 The while Statement ....................................................... 165
10.4 The do-until Statement .................................................... 166
10.5 The for Statement ......................................................... 166
10.5.1 Looping Over Structure Elements......................................167
10.6 The break Statement.......................................................168
10.7 The continue Statement .................................................... 169
10.8 The unwind protect Statement ............................................. 170
10.9 The try Statement ......................................................... 170
10.10 Continuation Lines........................................................171
iv GNU Octave
11 Functions and Scripts...................................173
11.1 Introduction to Function and Script Files ...................................173
11.2 Defining Functions ......................................................... 173
11.3 Multiple Return Values .................................................... 176
11.4 Variable-length Argument Lists ............................................ 184
11.5 Ignoring Arguments ........................................................ 186
11.6 Variable-length Return Lists ............................................... 187
11.7 Returning from a Function ................................................. 188
11.8 Default Arguments .........................................................189
11.9 Function Files..............................................................189
11.9.1 Manipulating the Load Path...........................................192
11.9.2 Subfunctions .......................................................... 195
11.9.3 Private Functions ..................................................... 195
11.9.4 Nested Functions ......................................................196
11.9.5 Overloading and Autoloading..........................................198
11.9.6 Function Locking......................................................199
11.9.7 Function Precedence .................................................. 201
11.10 Script Files ............................................................... 201
11.10.1 Publish Octave Script Files...........................................203
11.10.2 Publishing Markup...................................................205
11.10.2.1 Using Publishing Markup in Script Files ......................... 205
11.10.2.2 Text Formatting ................................................ 206
11.10.2.3 Sections .........................................................206
11.10.2.4 Preformatted Code .............................................. 207
11.10.2.5 Preformatted Text .............................................. 207
11.10.2.6 Bulleted Lists ................................................... 207
11.10.2.7 Numbered Lists ................................................. 207
11.10.2.8 Including File Content .......................................... 208
11.10.2.9 Including Graphics .............................................. 208
11.10.2.10 Including URLs ................................................ 208
11.10.2.11 Mathematical Equations ....................................... 209
11.10.2.12 HTML Markup ................................................ 209
11.10.2.13 LaTeX Markup ................................................ 209
11.11 Function Handles, Anonymous Functions, Inline Functions .................209
11.11.1 Function Handles .................................................... 209
11.11.2 Anonymous Functions ................................................211
11.11.3 Inline Functions ......................................................212
11.12 Commands ............................................................... 213
11.13 Organization of Functions Distributed with Octave ........................ 213
12 Errors and Warnings ................................... 215
12.1 Handling Errors............................................................215
12.1.1 Raising Errors ........................................................ 215
12.1.2 Catching Errors ....................................................... 218
12.1.3 Recovering From Errors ............................................... 221
12.2 Handling Warnings.........................................................221
12.2.1 Issuing Warnings ...................................................... 222
12.2.2 Enabling and Disabling Warnings......................................228
v
13 Debugging ............................................... 229
13.1 Entering Debug Mode ......................................................229
13.2 Leaving Debug Mode.......................................................230
13.3 Breakpoints ................................................................230
13.4 Debug Mode ............................................................... 234
13.5 Call Stack ................................................................. 235
13.6 Profiling ................................................................... 236
13.7 Profiler Example ........................................................... 238
14 Input and Output ....................................... 243
14.1 Basic Input and Output ....................................................243
14.1.1 Terminal Output ...................................................... 243
14.1.1.1 Paging Screen Output ............................................ 246
14.1.2 Terminal Input ........................................................248
14.1.3 Simple File I/O ....................................................... 250
14.1.3.1 Saving Data on Unexpected Exits.................................262
14.2 C-Style I/O Functions......................................................264
14.2.1 Opening and Closing Files.............................................265
14.2.2 Simple Output ........................................................ 267
14.2.3 Line-Oriented Input ................................................... 267
14.2.4 Formatted Output .................................................... 268
14.2.5 Output Conversion for Matrices ....................................... 270
14.2.6 Output Conversion Syntax ............................................ 270
14.2.7 Table of Output Conversions .......................................... 271
14.2.8 Integer Conversions ................................................... 272
14.2.9 Floating-Point Conversions ............................................ 273
14.2.10 Other Output Conversions ........................................... 273
14.2.11 Formatted Input ..................................................... 274
14.2.12 Input Conversion Syntax ............................................. 275
14.2.13 Table of Input Conversions ........................................... 276
14.2.14 Numeric Input Conversions...........................................277
14.2.15 String Input Conversions ............................................. 277
14.2.16 Binary I/O .......................................................... 277
14.2.17 Temporary Files ..................................................... 280
14.2.18 End of File and Errors ............................................... 282
14.2.19 File Positioning ...................................................... 283
15 Plotting .................................................. 285
15.1 Introduction to Plotting ....................................................285
15.2 High-Level Plotting ........................................................ 285
15.2.1 Two-Dimensional Plots ................................................285
15.2.1.1 Axis Configuration ............................................... 313
15.2.1.2 Two-dimensional Function Plotting ............................... 316
15.2.1.3 Two-dimensional Geometric Shapes ...............................319
15.2.2 Three-Dimensional Plots .............................................. 320
15.2.2.1 Aspect Ratio ..................................................... 342
15.2.2.2 Three-dimensional Function Plotting..............................343
vi GNU Octave
15.2.2.3 Three-dimensional Geometric Shapes ............................. 346
15.2.3 Plot Annotations ......................................................347
15.2.4 Multiple Plots on One Page ........................................... 354
15.2.5 Multiple Plot Windows ................................................355
15.2.6 Manipulation of Plot Objects ..........................................356
15.2.7 Manipulation of Plot Windows ........................................ 357
15.2.8 Use of the interpreter Property ..................................... 361
15.2.9 Printing and Saving Plots ............................................. 364
15.2.10 Interacting with Plots ................................................ 371
15.2.11 Test Plotting Functions .............................................. 372
15.3 Graphics Data Structures .................................................. 373
15.3.1 Introduction to Graphics Structures ................................... 373
15.3.2 Graphics Objects......................................................375
15.3.2.1 Creating Graphics Objects........................................375
15.3.2.2 Handle Functions.................................................378
15.3.3 Graphics Object Properties............................................383
15.3.3.1 Root Figure Properties ........................................... 383
15.3.3.2 Figure Properties.................................................385
15.3.3.3 Axes Properties .................................................. 390
15.3.3.4 Line Properties ...................................................397
15.3.3.5 Text Properties...................................................399
15.3.3.6 Image Properties ................................................. 401
15.3.3.7 Patch Properties ................................................. 402
15.3.3.8 Surface Properties ................................................ 405
15.3.3.9 Light Properties .................................................. 408
15.3.3.10 Uimenu Properties .............................................. 409
15.3.3.11 Uibuttongroup Properties ....................................... 410
15.3.3.12 Uicontextmenu Properties ....................................... 412
15.3.3.13 Uipanel Properties .............................................. 413
15.3.3.14 Uicontrol Properties ............................................. 414
15.3.3.15 Uitoolbar Properties.............................................416
15.3.3.16 Uipushtool Properties ........................................... 417
15.3.3.17 Uitoggletool Properties .......................................... 418
15.3.4 Searching Properties .................................................. 419
15.3.5 Managing Default Properties .......................................... 421
15.4 Advanced Plotting ......................................................... 422
15.4.1 Colors ................................................................ 422
15.4.2 Line Styles ............................................................ 422
15.4.3 Marker Styles ......................................................... 422
15.4.4 Callbacks ............................................................. 423
15.4.5 Application-defined Data .............................................. 424
15.4.6 Object Groups ........................................................ 425
15.4.6.1 Data Sources in Object Groups ................................... 430
15.4.6.2 Area Series ....................................................... 430
15.4.6.3 Bar Series ........................................................ 431
15.4.6.4 Contour Groups .................................................. 432
15.4.6.5 Error Bar Series .................................................. 433
15.4.6.6 Line Series ....................................................... 433
vii
15.4.6.7 Quiver Group .................................................... 434
15.4.6.8 Scatter Group .................................................... 435
15.4.6.9 Stair Group ...................................................... 435
15.4.6.10 Stem Series ..................................................... 436
15.4.6.11 Surface Group...................................................437
15.4.7 Graphics Toolkits ..................................................... 437
15.4.7.1 Customizing Toolkit Behavior .................................... 438
16 Matrix Manipulation ................................... 439
16.1 Finding Elements and Checking Conditions .................................439
16.2 Rearranging Matrices ...................................................... 443
16.3 Special Utility Matrices .................................................... 453
16.4 Famous Matrices ........................................................... 461
17 Arithmetic ............................................... 471
17.1 Exponents and Logarithms ................................................. 471
17.2 Complex Arithmetic ....................................................... 473
17.3 Trigonometry .............................................................. 474
17.4 Sums and Products ........................................................ 478
17.5 Utility Functions ........................................................... 480
17.6 Special Functions .......................................................... 488
17.7 Rational Approximations ...................................................496
17.8 Coordinate Transformations ................................................ 496
17.9 Mathematical Constants ................................................... 498
18 Linear Algebra .......................................... 503
18.1 Techniques Used for Linear Algebra ........................................ 503
18.2 Basic Matrix Functions.....................................................503
18.3 Matrix Factorizations ...................................................... 511
18.4 Functions of a Matrix ...................................................... 523
18.5 Specialized Solvers ......................................................... 524
19 Vectorization and Faster Code Execution ............. 529
19.1 Basic Vectorization.........................................................529
19.2 Broadcasting ...............................................................531
19.2.1 Broadcasting and Legacy Code ........................................ 534
19.3 Function Application .......................................................534
19.4 Accumulation .............................................................. 539
19.5 JIT Compiler .............................................................. 541
19.6 Miscellaneous Techniques...................................................542
19.7 Examples .................................................................. 544
20 Nonlinear Equations .................................... 545
20.1 Solvers.....................................................................545
20.2 Minimizers .................................................................548
viii GNU Octave
21 Diagonal and Permutation Matrices...................551
21.1 Creating and Manipulating Diagonal/Permutation Matrices.................551
21.1.1 Creating Diagonal Matrices............................................552
21.1.2 Creating Permutation Matrices ........................................ 552
21.1.3 Explicit and Implicit Conversions ......................................553
21.2 Linear Algebra with Diagonal/Permutation Matrices........................554
21.2.1 Expressions Involving Diagonal Matrices ...............................554
21.2.2 Expressions Involving Permutation Matrices ........................... 555
21.3 Functions That Are Aware of These Matrices ............................... 556
21.3.1 Diagonal Matrix Functions ............................................ 556
21.3.2 Permutation Matrix Functions.........................................556
21.4 Examples of Usage ......................................................... 556
21.5 Differences in Treatment of Zero Elements .................................. 557
22 Sparse Matrices ......................................... 559
22.1 Creation and Manipulation of Sparse Matrices .............................. 559
22.1.1 Storage of Sparse Matrices ............................................ 559
22.1.2 Creating Sparse Matrices .............................................. 560
22.1.3 Finding Information about Sparse Matrices ............................ 566
22.1.4 Basic Operators and Functions on Sparse Matrices .....................569
22.1.4.1 Sparse Functions ................................................. 570
22.1.4.2 Return Types of Operators and Functions ........................ 570
22.1.4.3 Mathematical Considerations ..................................... 572
22.2 Linear Algebra on Sparse Matrices ......................................... 580
22.3 Iterative Techniques Applied to Sparse Matrices ............................ 589
22.4 Real Life Example using Sparse Matrices ................................... 597
23 Numerical Integration .................................. 601
23.1 Functions of One Variable .................................................. 601
23.2 Orthogonal Collocation .................................................... 608
23.3 Functions of Multiple Variables.............................................609
24 Differential Equations .................................. 613
24.1 Ordinary Differential Equations ............................................ 613
24.1.1 Matlab-compatible solvers ............................................. 615
24.2 Differential-Algebraic Equations ............................................ 620
25 Optimization ............................................ 629
25.1 Linear Programming ....................................................... 629
25.2 Quadratic Programming....................................................635
25.3 Nonlinear Programming .................................................... 637
25.4 Linear Least Squares ....................................................... 639
ix
26 Statistics ................................................. 643
26.1 Descriptive Statistics ....................................................... 643
26.2 Basic Statistical Functions ................................................. 649
26.3 Statistical Plots ............................................................ 653
26.4 Correlation and Regression Analysis ........................................ 654
26.5 Distributions...............................................................656
26.6 Tests ...................................................................... 664
26.7 Random Number Generation ............................................... 671
27 Sets ...................................................... 679
27.1 Set Operations ............................................................. 679
28 Polynomial Manipulations..............................683
28.1 Evaluating Polynomials .................................................... 683
28.2 Finding Roots ............................................................. 684
28.3 Products of Polynomials ................................................... 685
28.4 Derivatives / Integrals / Transforms ........................................ 688
28.5 Polynomial Interpolation ................................................... 689
28.6 Miscellaneous Functions .................................................... 698
29 Interpolation ............................................ 701
29.1 One-dimensional Interpolation..............................................701
29.2 Multi-dimensional Interpolation ............................................ 705
30 Geometry ................................................ 711
30.1 Delaunay Triangulation .................................................... 711
30.1.1 Plotting the Triangulation .............................................713
30.1.2 Identifying Points in Triangulation .................................... 716
30.2 Voronoi Diagrams .......................................................... 718
30.3 Convex Hull ............................................................... 721
30.4 Interpolation on Scattered Data ............................................ 723
31 Signal Processing ....................................... 727
32 Image Processing ....................................... 741
32.1 Loading and Saving Images ................................................ 741
32.2 Displaying Images..........................................................747
32.3 Representing Images ....................................................... 749
32.4 Plotting on top of Images .................................................. 759
32.5 Color Conversion...........................................................759
x GNU Octave
33 Audio Processing ....................................... 761
33.1 Audio File Utilities.........................................................761
33.2 Audio Device Information .................................................. 762
33.3 Audio Player...............................................................762
33.3.1 Playback .............................................................. 763
33.3.2 Properties.............................................................763
33.4 Audio Recorder ............................................................ 764
33.4.1 Recording ............................................................. 764
33.4.2 Data Retrieval ........................................................ 765
33.4.3 Properties.............................................................765
33.5 Audio Data Processing ..................................................... 765
34 Object Oriented Programming.........................769
34.1 Creating a Class ........................................................... 769
34.2 Class Methods ............................................................. 771
34.3 Indexing Objects ...........................................................775
34.3.1 Defining Indexing And Indexed Assignment............................775
34.3.2 Indexed Assignment Optimization ..................................... 778
34.4 Overloading Objects ....................................................... 779
34.4.1 Function Overloading ................................................. 779
34.4.2 Operator Overloading ................................................. 780
34.4.3 Precedence of Objects ................................................. 781
34.5 Inheritance and Aggregation ............................................... 783
35 GUI Development.......................................789
35.1 I/O Dialogs ................................................................ 789
35.2 Progress Bar ............................................................... 796
35.3 UI Elements ............................................................... 796
35.4 GUI Utility Functions ...................................................... 802
35.5 User-Defined Preferences ................................................... 804
36 System Utilities ......................................... 807
36.1 Timing Utilities ............................................................ 807
36.2 Filesystem Utilities.........................................................818
36.3 File Archiving Utilities ..................................................... 827
36.4 Networking Utilities ........................................................830
36.4.1 FTP Objects .......................................................... 830
36.4.2 URL Manipulation .................................................... 832
36.4.3 Base64 and Binary Data Transmission ................................. 833
36.5 Controlling Subprocesses ................................................... 833
36.6 Process, Group, and User IDs .............................................. 841
36.7 Environment Variables ..................................................... 842
36.8 Current Working Directory .................................................842
36.9 Password Database Functions .............................................. 844
36.10 Group Database Functions ................................................ 845
36.11 System Information ....................................................... 846
36.12 Hashing Functions ........................................................ 850

xi
37 Packages ................................................. 853
37.1 Installing and Removing Packages .......................................... 853
37.2 Using Packages ............................................................ 856
37.3 Administrating Packages ................................................... 857
37.4 Creating Packages..........................................................857
37.4.1 The DESCRIPTION File..............................................859
37.4.2 The INDEX File ...................................................... 861
37.4.3 PKG ADD and PKG DEL Directives ................................. 862
37.4.4 Missing Components .................................................. 862
Appendix A External Code Interface ..................... 863
A.1 Oct-Files ................................................................... 864
A.1.1 Getting Started with Oct-Files ......................................... 864
A.1.2 Matrices and Arrays in Oct-Files .......................................867
A.1.3 Character Strings in Oct-Files..........................................870
A.1.4 Cell Arrays in Oct-Files ................................................871
A.1.5 Structures in Oct-Files ................................................. 872
A.1.6 Sparse Matrices in Oct-Files ........................................... 873
A.1.6.1 Array and Sparse Class Differences ................................ 874
A.1.6.2 Creating Sparse Matrices in Oct-Files ............................. 875
A.1.6.3 Using Sparse Matrices in Oct-Files ................................ 878
A.1.7 Accessing Global Variables in Oct-Files ................................ 878
A.1.8 Calling Octave Functions from Oct-Files ............................... 879
A.1.9 Calling External Code from Oct-Files .................................. 881
A.1.10 Allocating Local Memory in Oct-Files.................................883
A.1.11 Input Parameter Checking in Oct-Files................................883
A.1.12 Exception and Error Handling in Oct-Files ............................ 884
A.1.13 Documentation and Testing of Oct-Files .............................. 886
A.2 Mex-Files...................................................................887
A.2.1 Getting Started with Mex-Files ........................................ 887
A.2.2 Working with Matrices and Arrays in Mex-Files ........................ 889
A.2.3 Character Strings in Mex-Files ......................................... 891
A.2.4 Cell Arrays with Mex-Files.............................................892
A.2.5 Structures with Mex-Files..............................................893
A.2.6 Sparse Matrices with Mex-Files ........................................ 894
A.2.7 Calling Other Functions in Mex-Files...................................898
A.3 Standalone Programs ....................................................... 899
A.4 Java Interface .............................................................. 901
A.4.1 Making Java Classes Available ......................................... 902
A.4.2 How to use Java from within Octave ................................... 903
A.4.3 Passing parameters to the JVM ........................................ 905
A.4.4 Java Interface Functions ............................................... 906
Appendix B Test and Demo Functions ................... 913
B.1 Test Functions ..............................................................913
B.2 Demonstration Functions ................................................... 920
xii GNU Octave
Appendix C Obsolete Functions ........................... 925
Appendix D Known Causes of Trouble ................... 929
D.1 Actual Bugs We Haven’t Fixed Yet ......................................... 929
D.2 Reporting Bugs.............................................................929
D.2.1 Have You Found a Bug? ............................................... 929
D.2.2 Where to Report Bugs ................................................. 930
D.2.3 How to Report Bugs ................................................... 930
D.2.4 Sending Patches for Octave ............................................ 931
D.3 How To Get Help with Octave .............................................. 932
D.4 How to Distinguish Between Octave and Matlab ............................ 932
Appendix E Installing Octave ............................. 935
E.1 Build Dependencies ......................................................... 935
E.1.1 Obtaining the Dependencies Automatically ............................. 935
E.1.2 Build Tools ............................................................ 935
E.1.3 External Packages ..................................................... 936
E.2 Running Configure and Make ............................................... 938
E.3 Compiling Octave with 64-bit Indexing ......................................942
E.4 Installation Problems ....................................................... 945
Appendix F Grammar and Parser ........................ 949
F.1 Keywords ...................................................................949
F.2 Parser ...................................................................... 949
Appendix G GNU GENERAL PUBLIC LICENSE . . . . . . 951
Concept Index................................................963
Function Index ............................................... 975
Operator Index ............................................... 989
1
Preface
Octave was originally intended to be companion software for an undergraduate-level text-
book on chemical reactor design being written by James B. Rawlings of the University of
Wisconsin-Madison and John G. Ekerdt of the University of Texas.
Clearly, Octave is now much more than just another ‘courseware’ package with limited
utility beyond the classroom. Although our initial goals were somewhat vague, we knew
that we wanted to create something that would enable students to solve realistic problems,
and that they could use for many things other than chemical reactor design problems. We
find that most students pick up the basics of Octave quickly, and are using it confidently in
just a few hours.
Although it was originally intended to be used to teach reactor design, it has been used in
several other undergraduate and graduate courses in the Chemical Engineering Department
at the University of Texas, and the math department at the University of Texas has been
using it for teaching differential equations and linear algebra as well. More recently, Octave
has been used as the primary computational tool for teaching Stanford’s online Machine
Learning class (ml-class . org) taught by Andrew Ng. Tens of thousands of students
participated in the course.
If you find Octave useful, please let us know. We are always interested to find out how
Octave is being used.
Virtually everyone thinks that the name Octave has something to do with music, but
it is actually the name of one of John W. Eaton’s former professors who wrote a famous
textbook on chemical reaction engineering, and who was also well known for his ability
to do quick ‘back of the envelope’ calculations. We hope that this software will make it
possible for many people to do more ambitious computations just as easily.
Everyone is encouraged to share this software with others under the terms of the GNU
General Public License (see Appendix G [Copying], page 951). You are also encouraged to
help make Octave more useful by writing and contributing additional functions for it, and
by reporting any problems you may have.
Acknowledgements
Many people have contributed to Octave’s development. The following people have helped
code parts of Octave or aided in various other ways (listed alphabetically).
Ben Abbott Drew Abbot Andy Adler
Adam H. Aitkenhead Joakim And´en Giles Anderson
Joel Andersson Lachlan Andrew Pedro Angelo
Damjan Angelovski Muthiah Annamalai Markus Appel
Branden Archer Willem Atsma Marco Atzeri
Ander Aurrekoetxea Shai Ayal Roger Banks
Ben Barrowes Alexander Barth David Bateman
Heinz Bauschke Julien Bect Stefan Beller
Roman Belov Markus Bergholz Karl Berry
Atri Bhattacharya Ethan Biery David Billinghurst
Don Bindner Jakub Bogusz Moritz Borgmann
Paul Boven Richard Bovey John Bradshaw
2 GNU Octave
Marcus Brinkmann Max Brister Remy Bruno
Clemens Buchacher Ansgar Burchard Marco Caliari
Daniel Calvelo John C. Campbell Juan Pablo Carbajal
Jean-Francois Cardoso Joao Cardoso Larrie Carr
David Castelow Vincent Cautaerts Clinton Chee
Albert Chin-A-Young Carsten Clark Catalin Codreanu
J. D. Cole Jacopo Corno Martin Costabel
Michael Creel Richard Crozier Jeff Cunningham
Martin Dalecki Jacob Dawid Jorge Barros de Abreu
Carlo de Falco Thomas D. Dean Philippe Defert
Bill Denney Fabian Deutsch Christos Dimitrakakis
Pantxo Diribarne Vivek Dogra John Donoghue
David M. Doolin Carn¨e Draug Pascal A. Dupuis
John W. Eaton Dirk Eddelbuettel Pieter Eendebak
Paul Eggert Stephen Eglen Peter Ekberg
Garrett Euler Edmund Grimley Evans Rolf Fabian
Gunnar Farneb¨ack Massimiliano Fasi Stephen Fegan
Ramon Garcia Fernandez Torsten Finke Colin Foster
Jose Daniel Munoz Frias Brad Froehle Castor Fu
Eduardo Gallestey Walter Gautschi Klaus Gebhardt
Driss Ghaddab Eugenio Gianniti Hartmut Gimpel
Nicolo Giorgetti Arun Giridhar Michael D. Godfrey
Michael Goffioul Glenn Golden Tomislav Goles
Keith Goodman Brian Gough Michael C. Grant
Steffen Groot Etienne Grossmann David Grundberg
Kyle Guinn Vaibhav Gupta Peter Gustafson
Kai Habel Patrick H¨acker William P. Y. Hadisoeseno
Jaroslav Hajek Benjamin Hall Kim Hansen
Søren Hauberg Dave Hawthorne Oliver Heimlich
Daniel Heiserer Piotr Held Martin Helm
Stefan Hepp Martin Hepperle Jordi Guti´errez Hermoso
Yozo Hida Ryan Hinton Roman Hodek
A. Scottedward Hodel Richard Allan Holcombe Tom Holroyd
David Hoover Kurt Hornik Christopher Hulbert
Cyril Humbert John Hunt Teemu Ikonen
Alan W. Irwin Allan Jacobs Geoff Jacobsen
Vytautas Janˇcauskas Nicholas R. Jankowski Mats Jansson
Robert Jenssen Cai Jianming Steven G. Johnson
Heikki Junes Matthias J¨uschke Atsushi Kajita
Jarkko Kaleva Avinoam Kalma Mohamed Kamoun
Lute Kamstra Fotios Kasolis Thomas Kasper
Joel Keay Mumit Khan Paul Kienzle
Lars Kindermann Aaron A. King Erik Kjellson
Arno J. Klaassen Alexander Klein Geoffrey Knauth
Heine Kolltveit Ken Kouno Kacper Kowalik
Daniel Kraft Nir Krakauer Aravindh Krishnamoorthy
Oyvind Kristiansen Artem Krosheninnikov Piotr Krzyzanowski
Preface 3
Volker Kuhlmann Ilya Kurdyukov Tetsuro Kurita
Philipp Kutin Miroslaw Kwasniak Rafael Laboissiere
Kai Labusch Claude Lacoursiere Walter Landry
Bill Lash Dirk Laurie Maurice LeBrun
Friedrich Leisch Johannes Leuschner Thorsten Liebig
Jyh-miin Lin Timo Lindfors Benjamin Lindner
Ross Lippert Yu Liu David Livings
Barbara Locsi Sebastien Loisel Erik de Castro Lopo
Massimo Lorenzin Emil Lucretiu Yi-Hong Lyu
Hoxide Ma Colin Macdonald James Macnicol
Jens-Uwe Mager Stefan Mahr Rob Mahurin
Alexander Mamonov Ricardo Marranita Orestes Mas
Axel Math´ei Makoto Matsumoto Tatsuro Matsuoka
Christoph Mayer Laurent Mazet G. D. McBain
Ronald van der Meer J´ulio Hoffimann Mendes Ed Meyer
Thorsten Meyer Stefan Miereis Petr Mikulik
Mike Miller Serviscope Minor Stefan Monnier
Rafael Monteiro Antoine Moreau Kai P. Mueller
Armin M¨uller Hannes M¨uller Victor Munoz
PrasannaKumar
Muralidharan
Iain Murray Markus M¨utzel
Carmen Navarrete Todd Neal Philip Nienhuis
Al Niessner Felipe G. Nievinski Rick Niles
Takuji Nishimura Akira Noda Kai Noda
Patrick Noffke Eric Norum Krzesimir Nowak
Michael O’Brien Cillian O’Driscoll Peter O’Gorman
Thorsten Ohl Kai T. Ohlhus Arno Onken
Valentin Ortega-Clavero Luis F. Ortiz Carl Osterwisch
Janne Olavi Paanaj¨arvi Scott Pakin Jos´e Luis Garc´ıa Pallero
Jason Alan Palmer Gabriele Pannocchia Sylvain Pelissier
Rolando Pereira Per Persson Primozz Peterlin
Jim Peterson Danilo Piazzalunga Nicholas Piper
Elias Pipping Robert Platt Hans Ekkehard Plesser
Sergey Plotnikov Tom Poage Nathan Podlich
Orion Poplawski Ondrej Popp Jef Poskanzer
Francesco Potort`ı Konstantinos Poulios Jarno Rajahalme
Eduardo Ramos Pooja Rao James B. Rawlings
Eric S. Raymond Balint Reczey Joshua Redstone
Lukas Reichlin Michael Reifenberger Ernst Reissner
Jens Restemeier Anthony Richardson Jason Riedy
E. Joshua Rigler Sander van Rijn Petter Risholm
Matthew W. Roberts Dmitry Roshchin Peter Rosin
Andrew Ross Fabio Rossi Mark van Rossum
Joe Rothweiler David R¨orich Kevin Ruland
Kristian Rumberg Ryan Rusaw Olli Saarela
Toni Saarela Juhani Saastamoinen Radek Salac
4 GNU Octave
Mike Sander Ben Sapp Aleksej Saushev
Alois Schl¨ogl Michel D. Schmid Julian Schnidder
Sebastian Sch¨ops Nicol N. Schraudolph Sebastian Schubert
Lasse Schuirmann Ludwig Schwardt Thomas L. Scofield
Daniel J. Sebald Dmitri A. Sergatskov Vanya Sergeev
Marko Seric Ahsan Ali Shahid Baylis Shanks
Andriy Shinkarchuck Robert T. Short Joseph P. Skudlarek
John Smith Julius Smith Shan G. Smith
Peter L. Sondergaard Joerg Specht Quentin H. Spencer
Christoph Spiel David Spies Richard Stallman
Russell Standish Brett Stewart Doug Stewart
Jonathan Stickel Judd Storrs Thomas Stuart
Bernardo Sulzbach Ivan Sutoris John Swensen
Daisuke Takago Ariel Tankus Falk Tannh¨auser
Duncan Temple Lang Matthew Tenny Kris Thielemans
Georg Thimm Corey Thomasson Andrew Thornton
Olaf Till Christophe Tournery Thomas Treichl
Karsten Trulsen David Turner Frederick Umminger
Utkarsh Upadhyay Stefan van der Walt Peter Van Wieren
James R. Van Zandt Risto Vanhanen Gregory Vanuxem
Mihas Varantsou Ivana Varekova S´ebastien Villemot
Marco Vitetta Daniel Wagenaar Thomas Walter
Andreas Weber Olaf Weber Thomas Weber
Rik Wehbring Bob Weigel Andreas Weingessel
Martin Weiser Michael Weitzel David Wells
Joachim Wiesemann Fook Fah Yap Sean Young
Michele Zaffalon Johannes Zarl Michael Zeising
Federico Zenith Alex Zvoleff
Special thanks to the following people and organizations for supporting the development
of Octave:
•The United States Department of Energy, through grant number DE-FG02-04ER25635.
•Ashok Krishnamurthy, David Hudak, Juan Carlos Chaves, and Stanley C. Ahalt of the
Ohio Supercomputer Center.
•The National Science Foundation, through grant numbers CTS-0105360, CTS-9708497,
CTS-9311420, CTS-8957123, and CNS-0540147.
•The industrial members of the Texas-Wisconsin Modeling and Control Consortium
(TWMCC).
•The Paul A. Elfers Endowed Chair in Chemical Engineering at the University of
Wisconsin-Madison.
•Digital Equipment Corporation, for an equipment grant as part of their External Re-
search Program.
•Sun Microsystems, Inc., for an Academic Equipment grant.
•International Business Machines, Inc., for providing equipment as part of a grant to
the University of Texas College of Engineering.
Preface 5
•Texaco Chemical Company, for providing funding to continue the development of this
software.
•The University of Texas College of Engineering, for providing a Challenge for Excellence
Research Supplement, and for providing an Academic Development Funds grant.
•The State of Texas, for providing funding through the Texas Advanced Technology
Program under Grant No. 003658-078.
•Noel Bell, Senior Engineer, Texaco Chemical Company, Austin Texas.
•John A. Turner, Group Leader, Continuum Dynamics (CCS-2), Los Alamos National
Laboratory, for registering the octave.org domain name.
•James B. Rawlings, Professor, University of Wisconsin-Madison, Department of Chem-
ical and Biological Engineering.
•Richard Stallman, for writing GNU.
This project would not have been possible without the GNU software used in and to
produce Octave.
Citing Octave in Publications
In view of the many contributions made by numerous developers over many years it is
common courtesy to cite Octave in publications when it has been used during the course of
research or the preparation of figures. The citation function can automatically generate
a recommended citation text for Octave or any of its packages. See the help text below on
how to use citation.
citation
citation package
Display instructions for citing GNU Octave or its packages in publications.
When called without an argument, display information on how to cite the core GNU
Octave system.
When given a package name package, display information on citing the specific named
package. Note that some packages may not yet have instructions on how to cite them.
The GNU Octave developers and its active community of package authors have in-
vested a lot of time and effort in creating GNU Octave as it is today. Please give
credit where credit is due and cite GNU Octave and its packages when you use them.
How You Can Contribute to Octave
There are a number of ways that you can contribute to help make Octave a better system.
Perhaps the most important way to contribute is to write high-quality code for solving
new problems, and to make your code freely available for others to use. See http://www.
octave.org/get-involved.html for detailed information.
If you find Octave useful, consider providing additional funding to continue its develop-
ment. Even a modest amount of additional funding could make a significant difference in
the amount of time that is available for development and support.
Donations supporting Octave development may be made on the web at https://my.
fsf.org/donate/working-together/octave. These donations also help to support the
Free Software Foundation
6 GNU Octave
If you’d prefer to pay by check or money order, you can do so by sending a check to the
FSF at the following address:
Free Software Foundation
51 Franklin Street, Suite 500
Boston, MA 02110-1335
USA
If you pay by check, please be sure to write “GNU Octave” in the memo field of your check.
If you cannot provide funding or contribute code, you can still help make Octave better
and more reliable by reporting any bugs you find and by offering suggestions for ways to
improve Octave. See Appendix D [Trouble], page 929, for tips on how to write useful bug
reports.
Distribution
Octave is free software. This means that everyone is free to use it and free to redistribute
it on certain conditions. Octave is not, however, in the public domain. It is copyrighted
and there are restrictions on its distribution, but the restrictions are designed to ensure
that others will have the same freedom to use and redistribute Octave that you have. The
precise conditions can be found in the GNU General Public License that comes with Octave
and that also appears in Appendix G [Copying], page 951.
To download a copy of Octave, please visit http://www.octave.org/download.html.
7
1 A Brief Introduction to Octave
GNU Octave is a high-level language primarily intended for numerical computations. It is
typically used for such problems as solving linear and nonlinear equations, numerical linear
algebra, statistical analysis, and for performing other numerical experiments. It may also
be used as a batch-oriented language for automated data processing.
The current version of Octave executes in a graphical user interface (GUI). The GUI
hosts an Integrated Development Environment (IDE) which includes a code editor with
syntax highlighting, built-in debugger, documentation browser, as well as the interpreter
for the language itself. A command-line interface for Octave is also available.
GNU Octave is freely redistributable software. You may redistribute it and/or modify
it under the terms of the GNU General Public License as published by the Free Software
Foundation. The GPL is included in this manual, see Appendix G [Copying], page 951.
This manual provides comprehensive documentation on how to install, run, use, and
extend GNU Octave. Additional chapters describe how to report bugs and help contribute
code.
This document corresponds to Octave version 4.2.1.
1.1 Running Octave
On most systems, Octave is started with the shell command ‘octave’. This starts the
graphical user interface. The central window in the GUI is the Octave command-line inter-
face. In this window Octave displays an initial message and then a prompt indicating it is
ready to accept input. If you have chosen the traditional command-line interface then only
the command prompt appears in the same window that was running a shell. In either case,
you can immediately begin typing Octave commands.
If you get into trouble, you can usually interrupt Octave by typing Control-C (written
C-c for short). C-c gets its name from the fact that you type it by holding down CTRL and
then pressing c. Doing this will normally return you to Octave’s prompt.
To exit Octave, type quit or exit at the Octave prompt.
On systems that support job control, you can suspend Octave by sending it a SIGTSTP
signal, usually by typing C-z.
1.2 Simple Examples
The following chapters describe all of Octave’s features in detail, but before doing that, it
might be helpful to give a sampling of some of its capabilities.
If you are new to Octave, we recommend that you try these examples to begin learning
Octave by using it. Lines marked like so, ‘octave:13>’, are lines you type, ending each
with a carriage return. Octave will respond with an answer, or by displaying a graph.
1.2.1 Elementary Calculations
Octave can easily be used for basic numerical calculations. Octave knows about arithmetic
operations (+,-,*,/), exponentiation (^), natural logarithms/exponents (log, exp), and the
trigonometric functions (sin, cos, . . . ). Moreover, Octave calculations work on real or
imaginary numbers (i,j). In addition, some mathematical constants such as the base of
8 GNU Octave
the natural logarithm (e) and the ratio of a circle’s circumference to its diameter (pi) are
pre-defined.
For example, to verify Euler’s Identity,
eıπ =−1
type the following which will evaluate to -1 within the tolerance of the calculation.
octave:1> exp (i*pi)
1.2.2 Creating a Matrix
Vectors and matrices are the basic building blocks for numerical analysis. To create a new
matrix and store it in a variable so that you can refer to it later, type the command
octave:1> A = [ 1, 1, 2; 3, 5, 8; 13, 21, 34 ]
Octave will respond by printing the matrix in neatly aligned columns. Octave uses a comma
or space to separate entries in a row, and a semicolon or carriage return to separate one row
from the next. Ending a command with a semicolon tells Octave not to print the result of
the command. For example,
octave:2> B = rand (3, 2);
will create a 3 row, 2 column matrix with each element set to a random value between zero
and one.
To display the value of a variable, simply type the name of the variable at the prompt.
For example, to display the value stored in the matrix B, type the command
octave:3> B
1.2.3 Matrix Arithmetic
Octave uses standard mathematical notation with the advantage over low-level languages
that operators may act on scalars, vector, matrices, or N-dimensional arrays. For example,
to multiply the matrix Aby a scalar value, type the command
octave:4> 2 * A
To multiply the two matrices Aand B, type the command
octave:5> A * B
and to form the matrix product ATA, type the command
octave:6> A’ * A
1.2.4 Solving Systems of Linear Equations
Systems of linear equations are ubiquitous in numerical analysis. To solve the set of linear
equations Ax= b, use the left division operator, ‘\’:
x=A\b
This is conceptually equivalent to A−1b, but avoids computing the inverse of a matrix
directly.
If the coefficient matrix is singular, Octave will print a warning message and compute a
minimum norm solution.

Chapter 1: A Brief Introduction to Octave 9
A simple example comes from chemistry and the need to obtain balanced chemical
equations. Consider the burning of hydrogen and oxygen to produce water.
H2+ O2→H2O
The equation above is not accurate. The Law of Conservation of Mass requires that the num-
ber of molecules of each type balance on the left- and right-hand sides of the equation. Writ-
ing the variable overall reaction with individual equations for hydrogen and oxygen one finds:
x1H2+x2O2→H2O
H : 2x1+ 0x2→2
O : 0x1+ 2x2→1
The solution in Octave is found in just three steps.
octave:1> A = [ 2, 0; 0, 2 ];
octave:2> b = [ 2; 1 ];
octave:3> x = A \ b
1.2.5 Integrating Differential Equations
Octave has built-in functions for solving nonlinear differential equations of the form
dx
dt =f(x, t), x(t=t0) = x0
For Octave to integrate equations of this form, you must first provide a definition of the
function f(x, t). This is straightforward, and may be accomplished by entering the function
body directly on the command line. For example, the following commands define the right-
hand side function for an interesting pair of nonlinear differential equations. Note that
while you are entering a function, Octave responds with a different prompt, to indicate that
it is waiting for you to complete your input.
octave:1> function xdot = f (x, t)
>
> r = 0.25;
> k = 1.4;
> a = 1.5;
> b = 0.16;
> c = 0.9;
> d = 0.8;
>
> xdot(1) = r*x(1)*(1 - x(1)/k) - a*x(1)*x(2)/(1 + b*x(1));
> xdot(2) = c*a*x(1)*x(2)/(1 + b*x(1)) - d*x(2);
>
> endfunction
Given the initial condition
octave:2> x0 = [1; 2];
and the set of output times as a column vector (note that the first output time corresponds
to the initial condition given above)
octave:3> t = linspace (0, 50, 200)’;
10 GNU Octave
it is easy to integrate the set of differential equations:
octave:4> x = lsode ("f", x0, t);
The function lsode uses the Livermore Solver for Ordinary Differential Equations, described
in A. C. Hindmarsh, ODEPACK, a Systematized Collection of ODE Solvers, in: Scientific
Computing, R. S. Stepleman et al. (Eds.), North-Holland, Amsterdam, 1983, pages 55–64.
1.2.6 Producing Graphical Output
To display the solution of the previous example graphically, use the command
octave:1> plot (t, x)
Octave will automatically create a separate window to display the plot.
To save a plot once it has been displayed on the screen, use the print command. For
example,
print -dpdf foo.pdf
will create a file called foo.pdf that contains a rendering of the current plot in Portable
Document Format. The command
help print
explains more options for the print command and provides a list of additional output file
formats.
1.2.7 Help and Documentation
Octave has an extensive help facility. The same documentation that is available in printed
form is also available from the Octave prompt, because both forms of the documentation
are created from the same input file.
In order to get good help you first need to know the name of the command that you want
to use. The name of this function may not always be obvious, but a good place to start is to
type help --list. This will show you all the operators, keywords, built-in functions, and
loadable functions available in the current session of Octave. An alternative is to search
the documentation using the lookfor function (described in Section 2.3 [Getting Help],
page 20).
Once you know the name of the function you wish to use, you can get more help on the
function by simply including the name as an argument to help. For example,
help plot
will display the help text for the plot function.
Octave sends output that is too long to fit on one screen through a pager like less or
more. Type a RET to advance one line, a SPC to advance one page, and qto quit the pager.
The part of Octave’s help facility that allows you to read the complete text of the printed
manual from within Octave normally uses a separate program called Info. When you invoke
Info you will be put into a menu driven program that contains the entire Octave manual.
Help for using Info is provided in this manual, see Section 2.3 [Getting Help], page 20.
Chapter 1: A Brief Introduction to Octave 11
1.2.8 Editing What You Have Typed
At the Octave prompt, you can recall, edit, and reissue previous commands using Emacs-
or vi-style editing commands. The default keybindings use Emacs-style commands. For
example, to recall the previous command, press Control-p (written C-p for short). Doing
this will normally bring back the previous line of input. C-n will bring up the next line of
input, C-b will move the cursor backward on the line, C-f will move the cursor forward on
the line, etc.
A complete description of the command line editing capability is given in this manual,
see Section 2.4 [Command Line Editing], page 25.
1.3 Conventions
This section explains the notation conventions that are used in this manual. You may want
to skip this section and refer back to it later.
1.3.1 Fonts
Examples of Octave code appear in this font or form: svd (a). Names that represent
variables or function arguments appear in this font or form: first-number. Commands
that you type at the shell prompt appear in this font or form: ‘octave --no-init-file’.
Commands that you type at the Octave prompt sometimes appear in this font or form:
foo --bar --baz. Specific keys on your keyboard appear in this font or form: RET.
1.3.2 Evaluation Notation
In the examples in this manual, results from expressions that you evaluate are indicated
with ‘⇒’. For example:
sqrt (2)
⇒1.4142
You can read this as “sqrt (2) evaluates to 1.4142”.
In some cases, matrix values that are returned by expressions are displayed like this
[1, 2; 3, 4] == [1, 3; 2, 4]
⇒[1,0;0,1]
and in other cases, they are displayed like this
eye (3)
⇒100
010
001
in order to clearly show the structure of the result.
Sometimes to help describe one expression, another expression is shown that produces
identical results. The exact equivalence of expressions is indicated with ‘ ≡’. For example:
rot90 ([1, 2; 3, 4], -1)
≡
rot90 ([1, 2; 3, 4], 3)
≡
rot90 ([1, 2; 3, 4], 7)
12 GNU Octave
1.3.3 Printing Notation
Many of the examples in this manual print text when they are evaluated. In this manual
the printed text resulting from an example is indicated by ‘ a’. The value that is returned
by evaluating the expression is displayed with ‘⇒’ (1in the next example) and follows on
a separate line.
printf ("foo %s\n", "bar")
afoo bar
⇒1
1.3.4 Error Messages
Some examples signal errors. This normally displays an error message on your terminal.
Error messages are shown on a line beginning with error:.
fieldnames ([1, 2; 3, 4])
error: fieldnames: Invalid input argument
1.3.5 Format of Descriptions
Functions and commands are described in this manual in a uniform format. The first line
of a description contains the name of the item followed by its arguments, if any. If there
are multiple ways to invoke the function then each allowable form is listed.
The description follows on succeeding lines, sometimes with examples.
1.3.5.1 A Sample Function Description
In a function description, the name of the function being described appears first. It is
followed on the same line by a list of parameters. The names used for the parameters are
also used in the body of the description.
After all of the calling forms have been enumerated, the next line is a concise one-sentence
summary of the function.
After the summary there may be documentation on the inputs and outputs, examples
of function usage, notes about the algorithm used, and references to related functions.
Here is a description of an imaginary function foo:

Chapter 1: A Brief Introduction to Octave 13
foo (x)
foo (x,y)
foo (x,y, . . .)
Subtract xfrom y, then add any remaining arguments to the result.
The input xmust be a numeric scalar, vector, or array.
The optional input ydefaults to 19 if it is not supplied.
Example:
foo (1, [3, 5], 3, 9)
⇒[ 14, 16 ]
foo (5)
⇒14
More generally,
foo (w,x,y, ...)
≡
x-w+y+ ...
See also: bar
Any parameter whose name contains the name of a type (e.g., integer or matrix) is
expected to be of that type. Parameters named object may be of any type. Parameters
with other sorts of names (e.g., new file) are discussed specifically in the description of
the function. In some sections, features common to parameters of several functions are
described at the beginning.
1.3.5.2 A Sample Command Description
Commands are functions that may be called without surrounding their arguments in paren-
theses. Command descriptions have a format similar to function descriptions. For example,
here is the description for Octave’s diary command:
14 GNU Octave
diary
diary on
diary off
diary filename
Record a list of all commands and the output they produce, mixed together just as
they appear on the terminal.
Valid options are:
on Start recording a session in a file called diary in the current working
directory.
off Stop recording the session in the diary file.
filename Record the session in the file named filename.
With no arguments, diary toggles the current diary state.
See also: history, evalc.
15
2 Getting Started
This chapter explains some of Octave’s basic features, including how to start an Octave ses-
sion, get help at the command prompt, edit the command line, and write Octave programs
that can be executed as commands from your shell.
2.1 Invoking Octave from the Command Line
Normally, Octave is used interactively by running the program ‘octave’ without any ar-
guments. Once started, Octave reads commands from the terminal until you tell it to
exit.
You can also specify the name of a file on the command line, and Octave will read and
execute the commands from the named file and then exit when it is finished.
You can further control how Octave starts by using the command-line options described
in the next section, and Octave itself can remind you of the options available. Type ‘octave
--help’ to display all available options and briefly describe their use (‘octave -h’ is a shorter
equivalent).
2.1.1 Command Line Options
Here is a complete list of the command line options that Octave accepts.
--built-in-docstrings-file filename
Specify the name of the file containing documentation strings for the built-in
functions of Octave. This value is normally correct and should only need to
specified in extraordinary situations.
--debug
-d Enter parser debugging mode. Using this option will cause Octave’s parser to
print a lot of information about the commands it reads, and is probably only
useful if you are actually trying to debug the parser.
--debug-jit
Enable JIT compiler debugging and tracing.
--doc-cache-file filename
Specify the name of the doc cache file to use. The value of filename specified
on the command line will override any value of OCTAVE_DOC_CACHE_FILE found
in the environment, but not any commands in the system or user startup files
that use the doc_cache_file function.
--echo-commands
-x Echo commands as they are executed.
--eval code
Evaluate code and exit when finished unless --persist is also specified.
--exec-path path
Specify the path to search for programs to run. The value of path specified on
the command line will override any value of OCTAVE_EXEC_PATH found in the
environment, but not any commands in the system or user startup files that set
the built-in variable EXEC_PATH.
16 GNU Octave
--force-gui
Force the graphical user interface (GUI) to start.
--help
-h
-? Print short help message and exit.
--image-path path
Add path to the head of the search path for images. The value of path specified
on the command line will override any value of OCTAVE_IMAGE_PATH found in
the environment, but not any commands in the system or user startup files that
set the built-in variable IMAGE_PATH.
--info-file filename
Specify the name of the info file to use. The value of filename specified on
the command line will override any value of OCTAVE_INFO_FILE found in the
environment, but not any commands in the system or user startup files that
use the info_file function.
--info-program program
Specify the name of the info program to use. The value of program specified
on the command line will override any value of OCTAVE_INFO_PROGRAM found
in the environment, but not any commands in the system or user startup files
that use the info_program function.
--interactive
-i Force interactive behavior. This can be useful for running Octave via a remote
shell command or inside an Emacs shell buffer.
--jit-compiler
Enable the JIT compiler used for accelerating loops.
--line-editing
Force readline use for command-line editing.
--no-gui Disable the graphical user interface (GUI) and use the command line interface
(CLI) instead.
--no-history
-H Disable recording of command-line history.
--no-init-file
Don’t read the initialization files ~/.octaverc and .octaverc.
--no-init-path
Don’t initialize the search path for function files to include default locations.
--no-line-editing
Disable command-line editing.
--no-site-file
Don’t read the site-wide octaverc initialization files.
--no-window-system
-W Disable use of a windowing system including graphics. This forces a strictly
terminal-only environment.

Chapter 2: Getting Started 17
--norc
-f Don’t read any of the system or user initialization files at startup. This is
equivalent to using both of the options --no-init-file and --no-site-file.
--path path
-p path Add path to the head of the search path for function files. The value of path
specified on the command line will override any value of OCTAVE_PATH found
in the environment, but not any commands in the system or user startup files
that set the internal load path through one of the path functions.
--persist
Go to interactive mode after --eval or reading from a file named on the com-
mand line.
--silent
--quiet
-q Don’t print the usual greeting and version message at startup.
--texi-macros-file filename
Specify the name of the file containing Texinfo macros for use by makeinfo.
--traditional
--braindead
For compatibility with matlab, set initial values for user preferences to the
following values
PS1 = ">> "
PS2 = ""
beep_on_error = true
confirm_recursive_rmdir = false
crash_dumps_octave_core = false
disable_diagonal_matrix = true
disable_permutation_matrix = true
disable_range = true
fixed_point_format = true
history_timestamp_format_string = "%%-- %D %I:%M %p --%%"
page_screen_output = false
print_empty_dimensions = false
save_default_options = "-mat-binary"
struct_levels_to_print = 0
and disable the following warnings
Octave:abbreviated-property-match
Octave:fopen-file-in-path
Octave:function-name-clash
Octave:load-file-in-path
Octave:possible-matlab-short-circuit-operator
Note that this does not enable the Octave:language-extension warning,
which you might want if you want to be told about writing code that works in
Octave but not matlab (see [warning], page 222,[warning ids], page 223).

18 GNU Octave
--verbose
-V Turn on verbose output.
--version
-v Print the program version number and exit.
file Execute commands from file. Exit when done unless --persist is also specified.
Octave also includes several functions which return information about the command line,
including the number of arguments and all of the options.
argv ()
Return the command line arguments passed to Octave.
For example, if you invoked Octave using the command
octave --no-line-editing --silent
argv would return a cell array of strings with the elements --no-line-editing and
--silent.
If you write an executable Octave script, argv will return the list of arguments passed
to the script. See Section 2.6 [Executable Octave Programs], page 36, for an example
of how to create an executable Octave script.
program_name ()
Return the last component of the value returned by program_invocation_name.
See also: [program invocation name], page 18.
program_invocation_name ()
Return the name that was typed at the shell prompt to run Octave.
If executing a script from the command line (e.g., octave foo.m) or using an ex-
ecutable Octave script, the program name is set to the name of the script. See
Section 2.6 [Executable Octave Programs], page 36, for an example of how to create
an executable Octave script.
See also: [program name], page 18.
Here is an example of using these functions to reproduce the command line which invoked
Octave.
printf ("%s", program_name ());
arg_list = argv ();
for i = 1:nargin
printf (" %s", arg_list{i});
endfor
printf ("\n");
See Section 6.2.3 [Indexing Cell Arrays], page 116, for an explanation of how to retrieve
objects from cell arrays, and Section 11.2 [Defining Functions], page 173, for information
about the variable nargin.
Chapter 2: Getting Started 19
2.1.2 Startup Files
When Octave starts, it looks for commands to execute from the files in the following list.
These files may contain any valid Octave commands, including function definitions.
octave-home/share/octave/site/m/startup/octaverc
where octave-home is the directory in which Octave is installed (the default
is /usr/local). This file is provided so that changes to the default Octave
environment can be made globally for all users at your site for all versions of
Octave you have installed. Care should be taken when making changes to this
file since all users of Octave at your site will be affected. The default file may
be overridden by the environment variable OCTAVE_SITE_INITFILE.
octave-home/share/octave/version/m/startup/octaverc
where octave-home is the directory in which Octave is installed (the default
is /usr/local), and version is the version number of Octave. This file is pro-
vided so that changes to the default Octave environment can be made glob-
ally for all users of a particular version of Octave. Care should be taken
when making changes to this file since all users of Octave at your site will
be affected. The default file may be overridden by the environment variable
OCTAVE_VERSION_INITFILE.
~/.octaverc
This file is used to make personal changes to the default Octave environment.
.octaverc
This file can be used to make changes to the default Octave environment for a
particular project. Octave searches for this file in the current directory after it
reads ~/.octaverc. Any use of the cd command in the ~/.octaverc file will
affect the directory where Octave searches for .octaverc.
If you start Octave in your home directory, commands from the file
~/.octaverc will only be executed once.
startup.m
This file is used to make personal changes to the default Octave environment. It
is executed for matlab compatibility, but ~/.octaverc is the preferred location
for configuration changes.
A message will be displayed as each of the startup files is read if you invoke Octave with
the --verbose option but without the --silent option.
2.2 Quitting Octave
Shutdown is initiated with the exit or quit commands (they are equivalent). Similar
to startup, Octave has a shutdown process that can be customized by user script files.
During shutdown Octave will search for the script file finish.m in the function load path.
Commands to save all workspace variables or cleanup temporary files may be placed there.
Additional functions to execute on shutdown may be registered with atexit.
exit
exit (status)
20 GNU Octave
quit
quit (status)
Exit the current Octave session.
If the optional integer value status is supplied, pass that value to the operating system
as Octave’s exit status. The default value is zero.
When exiting, Octave will attempt to run the m-file finish.m if it exists. User
commands to save the workspace or clean up temporary files may be placed in that
file. Alternatively, another m-file may be scheduled to run using atexit.
See also: [atexit], page 20.
atexit (fcn)
atexit (fcn,flag)
Register a function to be called when Octave exits.
For example,
function last_words ()
disp ("Bye bye");
endfunction
atexit ("last_words");
will print the message "Bye bye" when Octave exits.
The additional argument flag will register or unregister fcn from the list of functions
to be called when Octave exits. If flag is true, the function is registered, and if flag
is false, it is unregistered. For example, after registering the function last_words
above,
atexit ("last_words", false);
will remove the function from the list and Octave will not call last_words when it
exits.
Note that atexit only removes the first occurrence of a function from the list, so if a
function was placed in the list multiple times with atexit, it must also be removed
from the list multiple times.
See also: [quit], page 19.
2.3 Commands for Getting Help
The entire text of this manual is available from the Octave prompt via the command doc.
In addition, the documentation for individual user-written functions and variables is also
available via the help command. This section describes the commands used for reading
the manual and the documentation strings for user-supplied functions and variables. See
Section 11.9 [Function Files], page 189, for more information about how to document the
functions you write.
help name
help –list
help .
help
Display the help text for name.

Chapter 2: Getting Started 21
For example, the command help help prints a short message describing the help
command.
Given the single argument --list, list all operators, keywords, built-in functions,
and loadable functions available in the current session of Octave.
Given the single argument ., list all operators available in the current session of
Octave.
If invoked without any arguments, help displays instructions on how to access help
from the command line.
The help command can provide information about most operators, but name must
be enclosed by single or double quotes to prevent the Octave interpreter from acting
on name. For example, help "+" displays help on the addition operator.
See also: [doc], page 21,[lookfor], page 21,[which], page 132,[info], page 22.
doc function_name
doc
Display documentation for the function function name directly from an online version
of the printed manual, using the GNU Info browser.
If invoked without an argument, the manual is shown from the beginning.
For example, the command doc rand starts the GNU Info browser at the rand node
in the online version of the manual.
Once the GNU Info browser is running, help for using it is available using the com-
mand C-h.
See also: [help], page 20.
lookfor str
lookfor -all str
[fcn,help1str] = lookfor (str)
[fcn,help1str] = lookfor ("-all",str)
Search for the string str in the documentation of all functions in the current function
search path.
By default, lookfor looks for str in just the first sentence of the help string for each
function found. The entire help text of each function can be searched by using the
"-all" argument. All searches are case insensitive.
When called with no output arguments, lookfor prints the list of matching functions
to the terminal. Otherwise, the output argument fcns contains the function names
and help1str contains the first sentence from the help string of each function.
Programming Note: The ability of lookfor to correctly identify the first sentence
of the help text is dependent on the format of the function’s help. All Octave core
functions are correctly formatted, but the same can not be guaranteed for external
packages and user-supplied functions. Therefore, the use of the "-all" argument
may be necessary to find related functions that are not a part of Octave.
The speed of lookup is greatly enhanced by having a cached documentation file. See
doc_cache_create for more information.
See also: [help], page 20,[doc], page 21,[which], page 132,[path], page 193,
[doc cache create], page 24.

22 GNU Octave
To see what is new in the current release of Octave, use the news function.
news
news package
Display the current NEWS file for Octave or an installed package.
When called without an argument, display the NEWS file for Octave.
When given a package name package, display the current NEWS file for that package.
See also: [ver], page 848,[pkg], page 853.
info ()
Display contact information for the GNU Octave community.
warranty ()
Describe the conditions for copying and distributing Octave.
The following functions can be used to change which programs are used for displaying
the documentation, and where the documentation can be found.
val = info_file ()
old_val = info_file (new_val)
info_file (new_val,"local")
Query or set the internal variable that specifies the name of the Octave info file.
The default value is octave-home/info/octave.info, in which octave-home is the
root directory of the Octave installation. The default value may be overridden by the
environment variable OCTAVE_INFO_FILE, or the command line argument --info-
file FNAME.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [info program], page 22,[doc], page 21,[help], page 20,[makeinfo program],
page 23.
val = info_program ()
old_val = info_program (new_val)
info_program (new_val,"local")
Query or set the internal variable that specifies the name of the info program to run.
The default value is octave-home/libexec/octave/version/exec/arch/info
in which octave-home is the root directory of the Octave installation, version
is the Octave version number, and arch is the system type (for example,
i686-pc-linux-gnu). The default value may be overridden by the environment
variable OCTAVE_INFO_PROGRAM, or the command line argument --info-program
NAME.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [info file], page 22,[doc], page 21,[help], page 20,[makeinfo program],
page 23.

Chapter 2: Getting Started 23
val = makeinfo_program ()
old_val = makeinfo_program (new_val)
makeinfo_program (new_val,"local")
Query or set the internal variable that specifies the name of the program that Octave
runs to format help text containing Texinfo markup commands.
The default value is makeinfo.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [texi macros file], page 23,[info file], page 22,[info program], page 22,[doc],
page 21,[help], page 20.
val = texi_macros_file ()
old_val = texi_macros_file (new_val)
texi_macros_file (new_val,"local")
Query or set the internal variable that specifies the name of the file containing Tex-
info macros that are prepended to documentation strings before they are passed to
makeinfo.
The default value is octave-home/share/octave/version/etc/macros.texi, in
which octave-home is the root directory of the Octave installation, and version
is the Octave version number. The default value may be overridden by the
environment variable OCTAVE_TEXI_MACROS_FILE, or the command line argument
--texi-macros-file FNAME.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [makeinfo program], page 23.
val = doc_cache_file ()
old_val = doc_cache_file (new_val)
doc_cache_file (new_val,"local")
Query or set the internal variable that specifies the name of the Octave documentation
cache file.
A cache file significantly improves the performance of the lookfor command. The
default value is octave-home/share/octave/version/etc/doc-cache, in which
octave-home is the root directory of the Octave installation, and version is the Octave
version number. The default value may be overridden by the environment variable
OCTAVE_DOC_CACHE_FILE, or the command line argument --doc-cache-file FNAME.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [doc cache create], page 24,[lookfor], page 21,[info program], page 22,
[doc], page 21,[help], page 20,[makeinfo program], page 23.
See also: [lookfor], page 21.

24 GNU Octave
val = built_in_docstrings_file ()
old_val = built_in_docstrings_file (new_val)
built_in_docstrings_file (new_val,"local")
Query or set the internal variable that specifies the name of the file containing doc-
strings for built-in Octave functions.
The default value is octave-home/share/octave/version/etc/built-in-
docstrings, in which octave-home is the root directory of the Octave installation,
and version is the Octave version number. The default value may be overridden by
the environment variable OCTAVE_BUILT_IN_DOCSTRINGS_FILE, or the command
line argument --built-in-docstrings-file FNAME.
Note: This variable is only used when Octave is initializing itself. Modifying it during
a running session of Octave will have no effect.
val = suppress_verbose_help_message ()
old_val = suppress_verbose_help_message (new_val)
suppress_verbose_help_message (new_val,"local")
Query or set the internal variable that controls whether Octave will add additional
help information to the end of the output from the help command and usage messages
for built-in commands.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
The following functions are principally used internally by Octave for generating the docu-
mentation. They are documented here for completeness and because they may occasionally
be useful for users.
doc_cache_create (out_file,directory)
doc_cache_create (out_file)
doc_cache_create ()
Generate documentation cache for all functions in directory.
A documentation cache is generated for all functions in directory which may be a
single string or a cell array of strings. The cache is used to speed up the function
lookfor.
The cache is saved in the file out file which defaults to the value doc-cache if not
given.
If no directory is given (or it is the empty matrix), a cache for built-in functions,
operators, and keywords is generated.
See also: [doc cache file], page 23,[lookfor], page 21,[path], page 193.
[text,format] = get_help_text (name)
Return the raw help text of function name.
The raw help text is returned in text and the format in format The format is a string
which is one of "texinfo","html", or "plain text".
See also: [get help text from file], page 25.

Chapter 2: Getting Started 25
[text,format] = get_help_text_from_file (fname)
Return the raw help text from the file fname.
The raw help text is returned in text and the format in format The format is a string
which is one of "texinfo","html", or "plain text".
See also: [get help text], page 24.
text = get_first_help_sentence (name)
text = get_first_help_sentence (name,max_len)
[text,status] = get_first_help_sentence (. . . )
Return the first sentence of a function’s help text.
The first sentence is defined as the text after the function declaration until either the
first period (".") or the first appearance of two consecutive newlines ("\n\n"). The
text is truncated to a maximum length of max len, which defaults to 80.
The optional output argument status returns the status reported by makeinfo. If
only one output argument is requested, and status is nonzero, a warning is displayed.
As an example, the first sentence of this help text is
get_first_help_sentence ("get_first_help_sentence")
aans = Return the first sentence of a function’s help text.
2.4 Command Line Editing
Octave uses the GNU Readline library to provide an extensive set of command-line editing
and history features. Only the most common features are described in this manual. In
addition, all of the editing functions can be bound to different key strokes at the user’s
discretion. This manual assumes no changes from the default Emacs bindings. See the
GNU Readline Library manual for more information on customizing Readline and for a
complete feature list.
To insert printing characters (letters, digits, symbols, etc.), simply type the character.
Octave will insert the character at the cursor and advance the cursor forward.
Many of the command-line editing functions operate using control characters. For ex-
ample, the character Control-a moves the cursor to the beginning of the line. To type
C-a, hold down CTRL and then press a. In the following sections, control characters such as
Control-a are written as C-a.
Another set of command-line editing functions use Meta characters. To type M-u, hold
down the META key and press u. Depending on the keyboard, the META key may be labeled
ALT or even WINDOWS. If your terminal does not have a META key, you can still type Meta
characters using two-character sequences starting with ESC. Thus, to enter M-u, you would
type ESC u. The ESC character sequences are also allowed on terminals with real Meta keys.
In the following sections, Meta characters such as Meta-u are written as M-u.
2.4.1 Cursor Motion
The following commands allow you to position the cursor.
C-b Move back one character.
C-f Move forward one character.
26 GNU Octave
BACKSPACE
Delete the character to the left of the cursor.
DEL Delete the character underneath the cursor.
C-d Delete the character underneath the cursor.
M-f Move forward a word.
M-b Move backward a word.
C-a Move to the start of the line.
C-e Move to the end of the line.
C-l Clear the screen, reprinting the current line at the top.
C-_
C-/ Undo the last action. You can undo all the way back to an empty line.
M-r Undo all changes made to this line. This is like typing the ‘undo’ command
enough times to get back to the beginning.
The above table describes the most basic possible keystrokes that you need in order to
do editing of the input line. On most terminals, you can also use the left and right arrow
keys in place of C-f and C-b to move forward and backward.
Notice how C-f moves forward a character, while M-f moves forward a word. It is a loose
convention that control keystrokes operate on characters while meta keystrokes operate on
words.
The function clc will allow you to clear the screen from within Octave programs.
clc ()
home ()
Clear the terminal screen and move the cursor to the upper left corner.
2.4.2 Killing and Yanking
Killing text means to delete the text from the line, but to save it away for later use, usually
by yanking it back into the line. If the description for a command says that it ‘kills’ text,
then you can be sure that you can get the text back in a different (or the same) place later.
Here is the list of commands for killing text.
C-k Kill the text from the current cursor position to the end of the line.
M-d Kill from the cursor to the end of the current word, or if between words, to the
end of the next word.
M-DEL Kill from the cursor to the start of the previous word, or if between words, to
the start of the previous word.
C-w Kill from the cursor to the previous whitespace. This is different than M-DEL
because the word boundaries differ.
And, here is how to yank the text back into the line. Yanking means to copy the
most-recently-killed text from the kill buffer.
C-y Yank the most recently killed text back into the buffer at the cursor.
Chapter 2: Getting Started 27
M-y Rotate the kill-ring, and yank the new top. You can only do this if the prior
command is C-y or M-y.
When you use a kill command, the text is saved in a kill-ring. Any number of consecutive
kills save all of the killed text together, so that when you yank it back, you get it in one
clean sweep. The kill ring is not line specific; the text that you killed on a previously typed
line is available to be yanked back later, when you are typing another line.
2.4.3 Commands for Changing Text
The following commands can be used for entering characters that would otherwise have a
special meaning (e.g., TAB,C-q, etc.), or for quickly correcting typing mistakes.
C-q
C-v Add the next character that you type to the line verbatim. This is how to insert
things like C-q for example.
M-TAB Insert a tab character.
C-t Drag the character before the cursor forward over the character at the cursor,
also moving the cursor forward. If the cursor is at the end of the line, then
transpose the two characters before it.
M-t Drag the word behind the cursor past the word in front of the cursor moving
the cursor over that word as well.
M-u Uppercase the characters following the cursor to the end of the current (or
following) word, moving the cursor to the end of the word.
M-l Lowercase the characters following the cursor to the end of the current (or
following) word, moving the cursor to the end of the word.
M-c Uppercase the character following the cursor (or the beginning of the next word
if the cursor is between words), moving the cursor to the end of the word.
2.4.4 Letting Readline Type for You
The following commands allow Octave to complete command and variable names for you.
TAB Attempt to do completion on the text before the cursor. Octave can complete
the names of commands and variables.
M-? List the possible completions of the text before the cursor.
val = completion_append_char ()
old_val = completion_append_char (new_val)
completion_append_char (new_val,"local")
Query or set the internal character variable that is appended to successful command-
line completion attempts.
The default value is " " (a single space).
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
28 GNU Octave
completion_matches (hint)
Generate possible completions given hint.
This function is provided for the benefit of programs like Emacs which might be
controlling Octave and handling user input. The current command number is not
incremented when this function is called. This is a feature, not a bug.
2.4.5 Commands for Manipulating the History
Octave normally keeps track of the commands you type so that you can recall previous
commands to edit or execute them again. When you exit Octave, the most recent commands
you have typed, up to the number specified by the variable history_size, are saved in a
file. When Octave starts, it loads an initial list of commands from the file named by the
variable history_file.
Here are the commands for simple browsing and searching the history list.
LFD
RET Accept the current line regardless of where the cursor is. If the line is non-
empty, add it to the history list. If the line was a history line, then restore the
history line to its original state.
C-p Move ‘up’ through the history list.
C-n Move ‘down’ through the history list.
M-<Move to the first line in the history.
M->Move to the end of the input history, i.e., the line you are entering!
C-r Search backward starting at the current line and moving ‘up’ through the his-
tory as necessary. This is an incremental search.
C-s Search forward starting at the current line and moving ‘down’ through the
history as necessary.
On most terminals, you can also use the up and down arrow keys in place of C-p and
C-n to move through the history list.
In addition to the keyboard commands for moving through the history list, Octave
provides three functions for viewing, editing, and re-running chunks of commands from the
history list.
history
history opt1 . . .
h= history ()
h= history (opt1, . . . )
If invoked with no arguments, history displays a list of commands that you have
executed.
Valid options are:
n
-nDisplay only the most recent nlines of history.
-c Clear the history list.

Chapter 2: Getting Started 29
-q Don’t number the displayed lines of history. This is useful for cutting and
pasting commands using the X Window System.
-r file Read the file file, appending its contents to the current history list. If the
name is omitted, use the default history file (normally ~/.octave_hist).
-w file Write the current history to the file file. If the name is omitted, use the
default history file (normally ~/.octave_hist).
For example, to display the five most recent commands that you have typed without
displaying line numbers, use the command history -q 5.
If invoked with a single output argument, the history will be saved to that argument
as a cell string and will not be output to screen.
See also: [edit history], page 29,[run history], page 29.
edit_history
edit_history cmd_number
edit_history first last
Edit the history list using the editor named by the variable EDITOR.
The commands to be edited are first copied to a temporary file. When you exit
the editor, Octave executes the commands that remain in the file. It is often more
convenient to use edit_history to define functions rather than attempting to enter
them directly on the command line. The block of commands is executed as soon as
you exit the editor. To avoid executing any commands, simply delete all the lines
from the buffer before leaving the editor.
When invoked with no arguments, edit the previously executed command; With one
argument, edit the specified command cmd number; With two arguments, edit the
list of commands between first and last. Command number specifiers may also be
negative where -1 refers to the most recently executed command. The following are
equivalent and edit the most recently executed command.
edit_history
edit_history -1
When using ranges, specifying a larger number for the first command than the last
command reverses the list of commands before they are placed in the buffer to be
edited.
See also: [run history], page 29,[history], page 28.
run_history
run_history cmd_number
run_history first last
Run commands from the history list.
When invoked with no arguments, run the previously executed command;
With one argument, run the specified command cmd number;
With two arguments, run the list of commands between first and last. Command
number specifiers may also be negative where -1 refers to the most recently executed
command. For example, the command

30 GNU Octave
run_history
OR
run_history -1
executes the most recent command again. The command
run_history 13 169
executes commands 13 through 169.
Specifying a larger number for the first command than the last command reverses the
list of commands before executing them. For example:
disp (1)
disp (2)
run_history -1 -2
⇒
2
1
See also: [edit history], page 29,[history], page 28.
Octave also allows you customize the details of when, where, and how history is saved.
val = history_save ()
old_val = history_save (new_val)
history_save (new_val,"local")
Query or set the internal variable that controls whether commands entered on the
command line are saved in the history file.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [history control], page 30,[history file], page 31,[history size], page 31,
[history timestamp format string], page 31.
val = history_control ()
old_val = history_control (new_val)
Query or set the internal variable that specifies how commands are saved to the
history list.
The default value is an empty character string, but may be overridden by the envi-
ronment variable OCTAVE_HISTCONTROL.
The value of history_control is a colon-separated list of values controlling how
commands are saved on the history list. If the list of values includes ignorespace,
lines which begin with a space character are not saved in the history list. A value of
ignoredups causes lines matching the previous history entry to not be saved. A value
of ignoreboth is shorthand for ignorespace and ignoredups. A value of erasedups
causes all previous lines matching the current line to be removed from the history list
before that line is saved. Any value not in the above list is ignored. If history_
control is the empty string, all commands are saved on the history list, subject to
the value of history_save.
See also: [history file], page 31,[history size], page 31,[history timestamp format string],
page 31,[history save], page 30.
Chapter 2: Getting Started 31
val = history_file ()
old_val = history_file (new_val)
Query or set the internal variable that specifies the name of the file used to store
command history.
The default value is ~/.octave_hist, but may be overridden by the environment
variable OCTAVE_HISTFILE.
See also: [history size], page 31,[history save], page 30,[history timestamp format string],
page 31.
val = history_size ()
old_val = history_size (new_val)
Query or set the internal variable that specifies how many entries to store in the
history file.
The default value is 1000, but may be overridden by the environment variable
OCTAVE_HISTSIZE.
See also: [history file], page 31,[history timestamp format string], page 31,
[history save], page 30.
val = history_timestamp_format_string ()
old_val = history_timestamp_format_string (new_val)
history_timestamp_format_string (new_val,"local")
Query or set the internal variable that specifies the format string for the comment
line that is written to the history file when Octave exits.
The format string is passed to strftime. The default value is
"# Octave VERSION, %a %b %d %H:%M:%S %Y %Z <USER@HOST>"
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [strftime], page 809,[history file], page 31,[history size], page 31,
[history save], page 30.
val = EDITOR ()
old_val = EDITOR (new_val)
EDITOR (new_val,"local")
Query or set the internal variable that specifies the default text editor.
The default value is taken from the environment variable EDITOR when Octave starts.
If the environment variable is not initialized, EDITOR will be set to "emacs".
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [edit], page 190,[edit history], page 29.

32 GNU Octave
2.4.6 Customizing readline
Octave uses the GNU Readline library for command-line editing and history features. Read-
line is very flexible and can be modified through a configuration file of commands (See the
GNU Readline library for the exact command syntax). The default configuration file is
normally ~/.inputrc.
Octave provides two commands for initializing Readline and thereby changing the com-
mand line behavior.
readline_read_init_file (file)
Read the readline library initialization file file.
If file is omitted, read the default initialization file (normally ~/.inputrc).
See Section “Readline Init File” in GNU Readline Library, for details.
See also: [readline re read init file], page 32.
readline_re_read_init_file ()
Re-read the last readline library initialization file that was read.
See Section “Readline Init File” in GNU Readline Library, for details.
See also: [readline read init file], page 32.
2.4.7 Customizing the Prompt
The following variables are available for customizing the appearance of the command-line
prompts. Octave allows the prompt to be customized by inserting a number of backslash-
escaped special characters that are decoded as follows:
‘\t’ The time.
‘\d’ The date.
‘\n’ Begins a new line by printing the equivalent of a carriage return followed by a
line feed.
‘\s’ The name of the program (usually just ‘octave’).
‘\w’ The current working directory.
‘\W’ The basename of the current working directory.
‘\u’ The username of the current user.
‘\h’ The hostname, up to the first ‘.’.
‘\H’ The hostname.
‘\#’ The command number of this command, counting from when Octave starts.
‘\!’ The history number of this command. This differs from ‘\#’ by the number of
commands in the history list when Octave starts.
‘\$’ If the effective UID is 0, a ‘#’, otherwise a ‘$’.
‘\nnn’ The character whose character code in octal is nnn.
‘\\’ A backslash.
Chapter 2: Getting Started 33
val = PS1 ()
old_val = PS1 (new_val)
PS1 (new_val,"local")
Query or set the primary prompt string.
When executing interactively, Octave displays the primary prompt when it is ready
to read a command.
The default value of the primary prompt string is "octave:\#> ". To change it, use
a command like
PS1 ("\\u@\\H> ")
which will result in the prompt ‘boris@kremvax> ’ for the user ‘boris’ logged in
on the host ‘kremvax.kgb.su’. Note that two backslashes are required to enter a
backslash into a double-quoted character string. See Chapter 5 [Strings], page 67.
You can also use ANSI escape sequences if your terminal supports them. This can be
useful for coloring the prompt. For example,
PS1 (’\[\033[01;31m\]\s:\#> \[\033[0m\]’)
will give the default Octave prompt a red coloring.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [PS2], page 33,[PS4], page 33.
val = PS2 ()
old_val = PS2 (new_val)
PS2 (new_val,"local")
Query or set the secondary prompt string.
The secondary prompt is printed when Octave is expecting additional input to com-
plete a command. For example, if you are typing a for loop that spans several lines,
Octave will print the secondary prompt at the beginning of each line after the first.
The default value of the secondary prompt string is "> ".
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [PS1], page 32,[PS4], page 33.
val = PS4 ()
old_val = PS4 (new_val)
PS4 (new_val,"local")
Query or set the character string used to prefix output produced when echoing com-
mands is enabled.
The default value is "+ ". See Section 2.4.8 [Diary and Echo Commands], page 34,
for a description of echoing commands.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.

34 GNU Octave
See also: [echo], page 34,[echo executing commands], page 34,[PS1], page 32,[PS2],
page 33.
2.4.8 Diary and Echo Commands
Octave’s diary feature allows you to keep a log of all or part of an interactive session by
recording the input you type and the output that Octave produces in a separate file.
diary
diary on
diary off
diary filename
Record a list of all commands and the output they produce, mixed together just as
they appear on the terminal.
Valid options are:
on Start recording a session in a file called diary in the current working
directory.
off Stop recording the session in the diary file.
filename Record the session in the file named filename.
With no arguments, diary toggles the current diary state.
See also: [history], page 28,[evalc], page 157.
Sometimes it is useful to see the commands in a function or script as they are being
evaluated. This can be especially helpful for debugging some kinds of problems.
echo
echo on
echo off
echo on all
echo off all
Control whether commands are displayed as they are executed.
Valid options are:
on Enable echoing of commands as they are executed in script files.
off Disable echoing of commands as they are executed in script files.
on all Enable echoing of commands as they are executed in script files and
functions.
off all Disable echoing of commands as they are executed in script files and
functions.
With no arguments, echo toggles the current echo state.
See also: [echo executing commands], page 34.
val = echo_executing_commands ()
old_val = echo_executing_commands (new_val)
Chapter 2: Getting Started 35
echo_executing_commands (new_val,"local")
Query or set the internal variable that controls the echo state.
It may be the sum of the following values:
1 Echo commands read from script files.
2 Echo commands from functions.
4 Echo commands read from command line.
More than one state can be active at once. For example, a value of 3 is equivalent to
the command echo on all.
The value of echo_executing_commands may be set by the echo command or the
command line option --echo-commands.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [echo], page 34.
2.5 How Octave Reports Errors
Octave reports two kinds of errors for invalid programs.
Aparse error occurs if Octave cannot understand something you have typed. For exam-
ple, if you misspell a keyword,
octave:13> function y = f (x) y = x***2; endfunction
Octave will respond immediately with a message like this:
parse error:
syntax error
>>> function y = f (x) y = x***2; endfunction
^
For most parse errors, Octave uses a caret (‘^’) to mark the point on the line where it was
unable to make sense of your input. In this case, Octave generated an error message because
the keyword for exponentiation (**) was misspelled. It marked the error at the third ‘*’
because the code leading up to this was correct but the final ‘*’ was not understood.
Another class of error message occurs at evaluation time. These errors are called run-time
errors, or sometimes evaluation errors, because they occur when your program is being run,
or evaluated. For example, if after correcting the mistake in the previous function definition,
you type
octave:13> f ()
Octave will respond with
error: ‘x’ undefined near line 1 column 24
error: called from:
error: f at line 1, column 22

36 GNU Octave
This error message has several parts, and gives quite a bit of information to help you locate
the source of the error. The messages are generated from the point of the innermost error,
and provide a traceback of enclosing expressions and function calls.
In the example above, the first line indicates that a variable named ‘x’ was found to be
undefined near line 1 and column 24 of some function or expression. For errors occurring
within functions, lines are counted from the beginning of the file containing the function
definition. For errors occurring outside of an enclosing function, the line number indicates
the input line number, which is usually displayed in the primary prompt string.
The second and third lines of the error message indicate that the error occurred within
the function f. If the function fhad been called from within another function, for example,
g, the list of errors would have ended with one more line:
error: g at line 1, column 17
These lists of function calls make it fairly easy to trace the path your program took
before the error occurred, and to correct the error before trying again.
2.6 Executable Octave Programs
Once you have learned Octave, you may want to write self-contained Octave scripts, using
the ‘#!’ script mechanism. You can do this on GNU systems and on many Unix systems1.
Self-contained Octave scripts are useful when you want to write a program which users
can invoke without knowing that the program is written in the Octave language. Octave
scripts are also used for batch processing of data files. Once an algorithm has been developed
and tested in the interactive portion of Octave, it can be committed to an executable script
and used again and again on new data files.
As a trivial example of an executable Octave script, you might create a text file named
hello, containing the following lines:
#! octave-interpreter-name -qf
# a sample Octave program
printf ("Hello, world!\n");
(where octave-interpreter-name should be replaced with the full path and name of your
Octave binary). Note that this will only work if ‘#!’ appears at the very beginning of the
file. After making the file executable (with the chmod command on Unix systems), you can
simply type:
hello
at the shell, and the system will arrange to run Octave as if you had typed:
octave hello
The line beginning with ‘#!’ lists the full path and filename of an interpreter to be run,
and an optional initial command line argument to pass to that interpreter. The operating
system then runs the interpreter with the given argument and the full argument list of
the executed program. The first argument in the list is the full filename of the Octave
executable. The rest of the argument list will either be options to Octave, or data files, or
both. The ‘-qf’ options are usually specified in stand-alone Octave programs to prevent
1The ‘#!’ mechanism works on Unix systems derived from Berkeley Unix, System V Release 4, and some
System V Release 3 systems.
Chapter 2: Getting Started 37
them from printing the normal startup message, and to keep them from behaving differently
depending on the contents of a particular user’s ~/.octaverc file. See Section 2.1 [Invoking
Octave from the Command Line], page 15.
Note that some operating systems may place a limit on the number of characters that
are recognized after ‘#!’. Also, the arguments appearing in a ‘#!’ line are parsed differently
by various shells/systems. The majority of them group all the arguments together in one
string and pass it to the interpreter as a single argument. In this case, the following script:
#! octave-interpreter-name -q -f # comment
is equivalent to typing at the command line:
octave "-q -f # comment"
which will produce an error message. Unfortunately, it is not possible for Octave to deter-
mine whether it has been called from the command line or from a ‘#!’ script, so some care
is needed when using the ‘#!’ mechanism.
Note that when Octave is started from an executable script, the built-in function argv
returns a cell array containing the command line arguments passed to the executable Octave
script, not the arguments passed to the Octave interpreter on the ‘#!’ line of the script. For
example, the following program will reproduce the command line that was used to execute
the script, not ‘-qf’.
#! /bin/octave -qf
printf ("%s", program_name ());
arg_list = argv ();
for i = 1:nargin
printf (" %s", arg_list{i});
endfor
printf ("\n");
2.7 Comments in Octave Programs
Acomment is some text that is included in a program for the sake of human readers, and
which is NOT an executable part of the program. Comments can explain what the program
does, and how it works. Nearly all programming languages have provisions for comments,
because programs are typically hard to understand without them.
2.7.1 Single Line Comments
In the Octave language, a comment starts with either the sharp sign character, ‘#’, or the
percent symbol ‘%’ and continues to the end of the line. Any text following the sharp sign
or percent symbol is ignored by the Octave interpreter and not executed. The following
example shows whole line and partial line comments.
function countdown
# Count down for main rocket engines
disp (3);
disp (2);
disp (1);
disp ("Blast Off!"); # Rocket leaves pad
endfunction
38 GNU Octave
2.7.2 Block Comments
Entire blocks of code can be commented by enclosing the code between matching ‘#{’ and
‘#}’ or ‘%{’ and ‘%}’ markers. For example,
function quick_countdown
# Count down for main rocket engines
disp (3);
#{
disp (2);
disp (1);
#}
disp ("Blast Off!"); # Rocket leaves pad
endfunction
will produce a very quick countdown from ’3’ to "Blast Off" as the lines "disp (2);"
and "disp (1);" won’t be executed.
The block comment markers must appear alone as the only characters on a line (excepting
whitespace) in order to be parsed correctly.
2.7.3 Comments and the Help System
The help command (see Section 2.3 [Getting Help], page 20) is able to find the first block
of comments in a function and return those as a documentation string. This means that the
same commands used to get help on built-in functions are available for properly formatted
user-defined functions. For example, after defining the function fbelow,
function xdot = f (x, t)
# usage: f (x, t)
#
# This function defines the right-hand
# side functions for a set of nonlinear
# differential equations.
r = 0.25;
...
endfunction
the command help f produces the output
usage: f (x, t)
This function defines the right-hand
side functions for a set of nonlinear
differential equations.
Although it is possible to put comment lines into keyboard-composed, throw-away Oc-
tave programs, it usually isn’t very useful because the purpose of a comment is to help you
or another person understand the program at a later time.
The help parser currently only recognizes single line comments (see Section 2.7.1 [Single
Line Comments], page 37) and not block comments for the initial help text.
39
3 Data Types
All versions of Octave include a number of built-in data types, including real and complex
scalars and matrices, character strings, a data structure type, and an array that can contain
all data types.
It is also possible to define new specialized data types by writing a small amount of C++
code. On some systems, new data types can be loaded dynamically while Octave is running,
so it is not necessary to recompile all of Octave just to add a new type. See Appendix A
[External Code Interface], page 863, for more information about Octave’s dynamic linking
capabilities. Section 3.2 [User-defined Data Types], page 44, describes what you must do
to define a new data type for Octave.
typeinfo ()
typeinfo (expr)
Return the type of the expression expr, as a string.
If expr is omitted, return a cell array of strings containing all the currently installed
data types.
See also: [class], page 39,[isa], page 39.
3.1 Built-in Data Types
The standard built-in data types are real and complex scalars and matrices, ranges, char-
acter strings, a data structure type, and cell arrays. Additional built-in data types may
be added in future versions. If you need a specialized data type that is not currently pro-
vided as a built-in type, you are encouraged to write your own user-defined data type and
contribute it for distribution in a future release of Octave.
The data type of a variable can be determined and changed through the use of the
following functions.
classname = class (obj)
class (s,id)
class (s,id,p, . . .)
Return the class of the object obj, or create a class with fields from structure sand
name (string) id.
Additional arguments name a list of parent classes from which the new class is derived.
See also: [typeinfo], page 39,[isa], page 39.
isa (obj,classname)
Return true if obj is an object from the class classname.
classname may also be one of the following class categories:
"float" Floating point value comprising classes "double" and "single".
"integer"
Integer value comprising classes (u)int8, (u)int16, (u)int32, (u)int64.
"numeric"
Numeric value comprising either a floating point or integer value.
40 GNU Octave
If classname is a cell array of string, a logical array of the same size is returned,
containing true for each class to which obj belongs to.
See also: [class], page 39,[typeinfo], page 39.
cast (val,"type")
Convert val to data type type.
Both val and type are typically one of the following built-in classes:
"double"
"single"
"logical"
"char"
"int8"
"int16"
"int32"
"int64"
"uint8"
"uint16"
"uint32"
"uint64"
The value val may be modified to fit within the range of the new type.
Examples:
cast (-5, "uint8")
⇒0
cast (300, "int8")
⇒127
Programming Note: This function relies on the object val having a conversion method
named type. User-defined classes may implement only a subset of the full list of types
shown above. In that case, it may be necessary to call cast twice in order to reach the
desired type. For example, the conversion to double is nearly always implemented,
but the conversion to uint8 might not be. In that case, the following code will work
cast (cast (user_defined_val, "double"), "uint8")
See also: [typecast], page 40,[int8], page 55,[uint8], page 55,[int16], page 55,[uint16],
page 55,[int32], page 55,[uint32], page 55,[int64], page 55,[uint64], page 55,[double],
page 47,[single], page 54,[logical], page 60,[char], page 71,[class], page 39,[typeinfo],
page 39.
y= typecast (x,"class")
Return a new array yresulting from interpreting the data of xin memory as data of
the numeric class class.
Both the class of xand class must be one of the built-in numeric classes:
Chapter 3: Data Types 41
"logical"
"char"
"int8"
"int16"
"int32"
"int64"
"uint8"
"uint16"
"uint32"
"uint64"
"double"
"single"
"double complex"
"single complex"
the last two are only used with class; they indicate that a complex-valued result is
requested. Complex arrays are stored in memory as consecutive pairs of real numbers.
The sizes of integer types are given by their bit counts. Both logical and char are
typically one byte wide; however, this is not guaranteed by C++. If your system is
IEEE conformant, single and double will be 4 bytes and 8 bytes wide, respectively.
"logical" is not allowed for class.
If the input is a row vector, the return value is a row vector, otherwise it is a column
vector.
If the bit length of xis not divisible by that of class, an error occurs.
An example of the use of typecast on a little-endian machine is
x= uint16 ([1, 65535]);
typecast (x, "uint8")
⇒[ 1, 0, 255, 255]
See also: [cast], page 40,[bitpack], page 41,[bitunpack], page 42,[swapbytes],
page 41.
swapbytes (x)
Swap the byte order on values, converting from little endian to big endian and vice
versa.
For example:
swapbytes (uint16 (1:4))
⇒[ 256 512 768 1024]
See also: [typecast], page 40,[cast], page 40.
y= bitpack (x,class)
Return a new array yresulting from interpreting the logical array xas raw bit patterns
for data of the numeric class class.
class must be one of the built-in numeric classes:
42 GNU Octave
"double"
"single"
"double complex"
"single complex"
"char"
"int8"
"int16"
"int32"
"int64"
"uint8"
"uint16"
"uint32"
"uint64"
The number of elements of xshould be divisible by the bit length of class. If it is
not, excess bits are discarded. Bits come in increasing order of significance, i.e., x(1)
is bit 0, x(2) is bit 1, etc.
The result is a row vector if xis a row vector, otherwise it is a column vector.
See also: [bitunpack], page 42,[typecast], page 40.
y= bitunpack (x)
Return a logical array ycorresponding to the raw bit patterns of x.
xmust belong to one of the built-in numeric classes:
"double"
"single"
"char"
"int8"
"int16"
"int32"
"int64"
"uint8"
"uint16"
"uint32"
"uint64"
The result is a row vector if xis a row vector; otherwise, it is a column vector.
See also: [bitpack], page 41,[typecast], page 40.
3.1.1 Numeric Objects
Octave’s built-in numeric objects include real, complex, and integer scalars and matrices.
All built-in floating point numeric data is currently stored as double precision numbers.
On systems that use the IEEE floating point format, values in the range of approximately
2.2251 ×10−308 to 1.7977 ×10308 can be stored, and the relative precision is approximately
2.2204 ×10−16. The exact values are given by the variables realmin,realmax, and eps,
respectively.
Matrix objects can be of any size, and can be dynamically reshaped and resized. It is
easy to extract individual rows, columns, or submatrices using a variety of powerful indexing
features. See Section 8.1 [Index Expressions], page 135.
Chapter 3: Data Types 43
See Chapter 4 [Numeric Data Types], page 47, for more information.
3.1.2 Missing Data
It is possible to represent missing data explicitly in Octave using NA (short for “Not Avail-
able”). Missing data can only be represented when data is represented as floating point
numbers. In this case missing data is represented as a special case of the representation of
NaN.
NA
NA (n)
NA (n,m)
NA (n,m,k, . . .)
NA (. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
special constant used to designate missing values.
Note that NA always compares not equal to NA (NA != NA). To find NA values, use
the isna function.
When called with no arguments, return a scalar with the value ‘NA’.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [isna], page 43.
isna (x)
Return a logical array which is true where the elements of xare NA (missing) values
and false where they are not.
For example:
isna ([13, Inf, NA, NaN])
⇒[0,0,1,0]
See also: [isnan], page 440,[isinf], page 440,[isfinite], page 441.
3.1.3 String Objects
A character string in Octave consists of a sequence of characters enclosed in either double-
quote or single-quote marks. Internally, Octave currently stores strings as matrices of
characters. All the indexing operations that work for matrix objects also work for strings.
See Chapter 5 [Strings], page 67, for more information.
3.1.4 Data Structure Objects
Octave’s data structure type can help you to organize related objects of different types.
The current implementation uses an associative array with indices limited to strings, but
the syntax is more like C-style structures.
See Section 6.1 [Structures], page 99, for more information.
44 GNU Octave
3.1.5 Cell Array Objects
A Cell Array in Octave is general array that can hold any number of different data types.
See Section 6.2 [Cell Arrays], page 112, for more information.
3.2 User-defined Data Types
Someday I hope to expand this to include a complete description of Octave’s mechanism
for managing user-defined data types. Until this feature is documented here, you will have
to make do by reading the code in the ov.h,ops.h, and related files from Octave’s src
directory.
3.3 Object Sizes
The following functions allow you to determine the size of a variable or expression. These
functions are defined for all objects. They return −1 when the operation doesn’t make
sense. For example, Octave’s data structure type doesn’t have rows or columns, so the
rows and columns functions return −1 for structure arguments.
ndims (a)
Return the number of dimensions of a.
For any array, the result will always be greater than or equal to 2. Trailing singleton
dimensions are not counted.
ndims (ones (4, 1, 2, 1))
⇒3
See also: [size], page 45.
columns (a)
Return the number of columns of a.
See also: [rows], page 44,[size], page 45,[length], page 45,[numel], page 44,[isscalar],
page 63,[isvector], page 63,[ismatrix], page 63.
rows (a)
Return the number of rows of a.
See also: [columns], page 44,[size], page 45,[length], page 45,[numel], page 44,
[isscalar], page 63,[isvector], page 63,[ismatrix], page 63.
numel (a)
numel (a,idx1,idx2, . . .)
Return the number of elements in the object a.
Optionally, if indices idx1,idx2, . . . are supplied, return the number of elements that
would result from the indexing
a(idx1,idx2, ...)
Note that the indices do not have to be scalar numbers. For example,
a= 1;
b= ones (2, 3);
numel (a,b)

Chapter 3: Data Types 45
will return 6, as this is the number of ways to index with b. Or the index could be
the string ":" which represents the colon operator. For example,
a= ones (5, 3);
numel (a, 2, ":")
will return 3 as the second row has three column entries.
This method is also called when an object appears as lvalue with cs-list indexing, i.e.,
object{...} or object(...).field.
See also: [size], page 45,[length], page 45,[ndims], page 44.
length (a)
Return the length of the object a.
The length is 0 for empty objects, 1 for scalars, and the number of elements for
vectors. For matrix or N-dimensional objects, the length is the number of elements
along the largest dimension (equivalent to max (size (a))).
See also: [numel], page 44,[size], page 45.
sz = size (a)
dim_sz = size (a,dim)
[rows,cols, ..., dim_N_sz] = size (. . . )
Return a row vector with the size (number of elements) of each dimension for the
object a.
When given a second argument, dim, return the size of the corresponding dimension.
With a single output argument, size returns a row vector. When called with multiple
output arguments, size returns the size of dimension N in the Nth argument. The
number of rows, dimension 1, is returned in the first argument, the number of columns,
dimension 2, is returned in the second argument, etc. If there are more dimensions
in athen there are output arguments, size returns the total number of elements in
the remaining dimensions in the final output argument.
Example 1: single row vector output
size ([1, 2; 3, 4; 5, 6])
⇒[3,2]
Example 2: number of elements in 2nd dimension (columns)
size ([1, 2; 3, 4; 5, 6], 2)
⇒2
Example 3: number of output arguments == number of dimensions
[nr, nc] = size ([1, 2; 3, 4; 5, 6])
⇒nr = 3
⇒nc = 2
Example 4: number of output arguments != number of dimensions
[nr, remainder] = size (ones (2, 3, 4, 5))
⇒nr = 2
⇒remainder = 60
See also: [numel], page 44,[ndims], page 44,[length], page 45,[rows], page 44,
[columns], page 44,[size equal], page 46,[common size], page 441.

46 GNU Octave
isempty (a)
Return true if ais an empty matrix (any one of its dimensions is zero).
See also: [isnull], page 46,[isa], page 39.
isnull (x)
Return true if xis a special null matrix, string, or single quoted string.
Indexed assignment with such a value on the right-hand side should delete array
elements. This function should be used when overloading indexed assignment for
user-defined classes instead of isempty, to distinguish the cases:
A(I) = [] This should delete elements if Iis nonempty.
X = []; A(I) = X
This should give an error if Iis nonempty.
See also: [isempty], page 46,[isindex], page 139.
sizeof (val)
Return the size of val in bytes.
See also: [whos], page 128.
size_equal (a,b, . . .)
Return true if the dimensions of all arguments agree.
Trailing singleton dimensions are ignored. When called with a single argument, or no
argument, size_equal returns true.
See also: [size], page 45,[numel], page 44,[ndims], page 44,[common size], page 441.
squeeze (x)
Remove singleton dimensions from xand return the result.
Note that for compatibility with matlab, all objects have a minimum of two dimen-
sions and row vectors are left unchanged.
See also: [reshape], page 446.

47
4 Numeric Data Types
Anumeric constant may be a scalar, a vector, or a matrix, and it may contain complex
values.
The simplest form of a numeric constant, a scalar, is a single number. Note that by
default numeric constants are represented within Octave by IEEE 754 double precision
(binary64) floating-point format (complex constants are stored as pairs of binary64 values).
It is, however, possible to represent real integers as described in Section 4.4 [Integer Data
Types], page 54.
If the numeric constant is a real integer, it can be defined in decimal, hexadecimal,
or binary notation. Hexadecimal notation starts with ‘0x’ or ‘0X’, binary notation starts
with ‘0b’ or ‘0B’, otherwise decimal notation is assumed. As a consequence, ‘0b’ is not a
hexadecimal number, in fact, it is not a valid number at all.
For better readability, digits may be partitioned by the underscore separator ‘_’, which is
ignored by the Octave interpreter. Here are some examples of real-valued integer constants,
which all represent the same value and are internally stored as binary64:
42 # decimal notation
0x2A # hexadecimal notation
0b101010 # binary notation
0b10_1010 # underscore notation
round (42.1) # also binary64
In decimal notation, the numeric constant may be denoted as decimal fraction or even
in scientific (exponential) notation. Note that this is not possible for hexadecimal or binary
notation. Again, in the following example all numeric constants represent the same value:
.105
1.05e-1
.00105e+2
Unlike most programming languages, complex numeric constants are denoted as the
sum of real and imaginary parts. The imaginary part is denoted by a real-valued numeric
constant followed immediately by a complex value indicator (‘i’, ‘j’, ‘I’, or ‘J’ which rep-
resents √−1). No spaces are allowed between the numeric constant and the complex value
indicator. Some examples of complex numeric constants that all represent the same value:
3 + 42i
3 + 42j
3 + 42I
3 + 42J
3.0 + 42.0i
3.0 + 0x2Ai
3.0 + 0b10_1010i
0.3e1 + 420e-1i
double (x)
Convert xto double precision type.
See also: [single], page 54.
48 GNU Octave
complex (x)
complex (re,im)
Return a complex value from real arguments.
With 1 real argument x, return the complex result x+ 0i.
With 2 real arguments, return the complex result re +im.complex can often be
more convenient than expressions such as a + i*b. For example:
complex ([1, 2], [3, 4])
⇒[1+3i 2+4i]
See also: [real], page 474,[imag], page 473,[iscomplex], page 63,[abs], page 473,[arg],
page 473.
4.1 Matrices
It is easy to define a matrix of values in Octave. The size of the matrix is determined
automatically, so it is not necessary to explicitly state the dimensions. The expression
a = [1, 2; 3, 4]
results in the matrix
a=1 2
3 4
Elements of a matrix may be arbitrary expressions, provided that the dimensions all
make sense when combining the various pieces. For example, given the above matrix, the
expression
[a,a]
produces the matrix
ans =
1212
3434
but the expression
[a,1]
produces the error
error: number of rows must match (1 != 2) near line 13, column 6
(assuming that this expression was entered as the first thing on line 13, of course).
Inside the square brackets that delimit a matrix expression, Octave looks at the sur-
rounding context to determine whether spaces and newline characters should be converted
into element and row separators, or simply ignored, so an expression like
a=[12
34]
will work. However, some possible sources of confusion remain. For example, in the expres-
sion
[1-1]
the ‘-’ is treated as a binary operator and the result is the scalar 0, but in the expression
[1-1]
Chapter 4: Numeric Data Types 49
the ‘-’ is treated as a unary operator and the result is the vector [ 1, -1 ]. Similarly, the
expression
[ sin (pi) ]
will be parsed as
[ sin, (pi) ]
and will result in an error since the sin function will be called with no arguments. To get
around this, you must omit the space between sin and the opening parenthesis, or enclose
the expression in a set of parentheses:
[ (sin (pi)) ]
Whitespace surrounding the single quote character (‘’’, used as a transpose operator
and for delimiting character strings) can also cause confusion. Given a = 1, the expression
[1a’]
results in the single quote character being treated as a transpose operator and the result is
the vector [ 1, 1 ], but the expression
[1a’]
produces the error message
parse error:
syntax error
>>>[1a’]
^
because not doing so would cause trouble when parsing the valid expression
[ a ’foo’ ]
For clarity, it is probably best to always use commas and semicolons to separate matrix
elements and rows.
The maximum number of elements in a matrix is fixed when Octave is compiled. The
allowable number can be queried with the function sizemax. Note that other factors, such as
the amount of memory available on your machine, may limit the maximum size of matrices
to something smaller.
sizemax ()
Return the largest value allowed for the size of an array.
If Octave is compiled with 64-bit indexing, the result is of class int64, otherwise it is
of class int32. The maximum array size is slightly smaller than the maximum value
allowable for the relevant class as reported by intmax.
See also: [intmax], page 56.
When you type a matrix or the name of a variable whose value is a matrix, Octave
responds by printing the matrix in with neatly aligned rows and columns. If the rows of
the matrix are too large to fit on the screen, Octave splits the matrix and displays a header
before each section to indicate which columns are being displayed. You can use the following
variables to control the format of the output.

50 GNU Octave
val = output_max_field_width ()
old_val = output_max_field_width (new_val)
output_max_field_width (new_val,"local")
Query or set the internal variable that specifies the maximum width of a numeric
output field.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [format], page 244,[fixed point format], page 51,[output precision],
page 50.
val = output_precision ()
old_val = output_precision (new_val)
output_precision (new_val,"local")
Query or set the internal variable that specifies the minimum number of significant
figures to display for numeric output.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [format], page 244,[fixed point format], page 51,[output max field width],
page 49.
It is possible to achieve a wide range of output styles by using different values of output_
precision and output_max_field_width. Reasonable combinations can be set using the
format function. See Section 14.1 [Basic Input and Output], page 243.
val = split_long_rows ()
old_val = split_long_rows (new_val)
split_long_rows (new_val,"local")
Query or set the internal variable that controls whether rows of a matrix may be split
when displayed to a terminal window.
If the rows are split, Octave will display the matrix in a series of smaller pieces, each
of which can fit within the limits of your terminal width and each set of rows is labeled
so that you can easily see which columns are currently being displayed. For example:
octave:13> rand (2,10)
ans =
Columns 1 through 6:
0.75883 0.93290 0.40064 0.43818 0.94958 0.16467
0.75697 0.51942 0.40031 0.61784 0.92309 0.40201
Columns 7 through 10:
0.90174 0.11854 0.72313 0.73326
0.44672 0.94303 0.56564 0.82150

Chapter 4: Numeric Data Types 51
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [format], page 244.
Octave automatically switches to scientific notation when values become very large or
very small. This guarantees that you will see several significant figures for every value in
a matrix. If you would prefer to see all values in a matrix printed in a fixed point format,
you can set the built-in variable fixed_point_format to a nonzero value. But doing so is
not recommended, because it can produce output that can easily be misinterpreted.
val = fixed_point_format ()
old_val = fixed_point_format (new_val)
fixed_point_format (new_val,"local")
Query or set the internal variable that controls whether Octave will use a scaled
format to print matrix values.
The scaled format prints a scaling factor on the first line of output chosen such that
the largest matrix element can be written with a single leading digit. For example:
logspace (1, 7, 5)’
ans =
1.0e+07 *
0.00000
0.00003
0.00100
0.03162
1.00000
Notice that the first value appears to be 0 when it is actually 1. Because of the
possibility for confusion you should be careful about enabling fixed_point_format.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [format], page 244,[output max field width], page 49,[output precision],
page 50.
4.1.1 Empty Matrices
A matrix may have one or both dimensions zero, and operations on empty matrices are
handled as described by Carl de Boor in An Empty Exercise, SIGNUM, Volume 25, pages
2-6, 1990 and C. N. Nett and W. M. Haddad, in A System-Theoretic Appropriate Realiza-
tion of the Empty Matrix Concept, IEEE Transactions on Automatic Control, Volume 38,
Number 5, May 1993. Briefly, given a scalar s, an m×nmatrix Mm×n, and an m×nempty
52 GNU Octave
matrix [ ]m×n(with either one or both dimensions equal to zero), the following are true:
s·[ ]m×n= [ ]m×n·s= [ ]m×n
[ ]m×n+ [ ]m×n= [ ]m×n
[ ]0×m·Mm×n= [ ]0×n
Mm×n·[ ]n×0= [ ]m×0
[ ]m×0·[ ]0×n= 0m×n
By default, dimensions of the empty matrix are printed along with the empty matrix
symbol, ‘[]’. The built-in variable print_empty_dimensions controls this behavior.
val = print_empty_dimensions ()
old_val = print_empty_dimensions (new_val)
print_empty_dimensions (new_val,"local")
Query or set the internal variable that controls whether the dimensions of empty
matrices are printed along with the empty matrix symbol, ‘[]’.
For example, the expression
zeros (3, 0)
will print
ans = [](3x0)
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [format], page 244.
Empty matrices may also be used in assignment statements as a convenient way to delete
rows or columns of matrices. See Section 8.6 [Assignment Expressions], page 151.
When Octave parses a matrix expression, it examines the elements of the list to determine
whether they are all constants. If they are, it replaces the list with a single matrix constant.
4.2 Ranges
Arange is a convenient way to write a row vector with evenly spaced elements. A range
expression is defined by the value of the first element in the range, an optional value for the
increment between elements, and a maximum value which the elements of the range will
not exceed. The base, increment, and limit are separated by colons (the ‘:’ character) and
may contain any arithmetic expressions and function calls. If the increment is omitted, it
is assumed to be 1. For example, the range
1:5
defines the set of values [ 1, 2, 3, 4, 5 ], and the range
1:3:5
defines the set of values [ 1, 4 ].
Although a range constant specifies a row vector, Octave does not normally convert range
constants to vectors unless it is necessary to do so. This allows you to write a constant like
1 : 10000 without using 80,000 bytes of storage on a typical 32-bit workstation.

Chapter 4: Numeric Data Types 53
A common example of when it does become necessary to convert ranges into vectors
occurs when they appear within a vector (i.e., inside square brackets). For instance, whereas
x=0:0.1:1;
defines xto be a variable of type range and occupies 24 bytes of memory, the expression
y=[0:0.1:1];
defines yto be of type matrix and occupies 88 bytes of memory.
This space saving optimization may be disabled using the function disable range.
val = disable_range ()
old_val = disable_range (new_val)
disable_range (new_val,"local")
Query or set the internal variable that controls whether ranges are stored in a special
space-efficient format.
The default value is true. If this option is disabled Octave will store ranges as full
matrices.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [disable diagonal matrix], page 551,[disable permutation matrix],
page 551.
Note that the upper (or lower, if the increment is negative) bound on the range is not
always included in the set of values, and that ranges defined by floating point values can
produce surprising results because Octave uses floating point arithmetic to compute the
values in the range. If it is important to include the endpoints of a range and the number of
elements is known, you should use the linspace function instead (see Section 16.3 [Special
Utility Matrices], page 453).
When adding a scalar to a range, subtracting a scalar from it (or subtracting a range
from a scalar) and multiplying by scalar, Octave will attempt to avoid unpacking the range
and keep the result as a range, too, if it can determine that it is safe to do so. For instance,
doing
a = 2*(1:1e7) - 1;
will produce the same result as 1:2:2e7-1, but without ever forming a vector with ten
million elements.
Using zero as an increment in the colon notation, as 1:0:1 is not allowed, because a
division by zero would occur in determining the number of range elements. However, ranges
with zero increment (i.e., all elements equal) are useful, especially in indexing, and Octave
allows them to be constructed using the built-in function ones. Note that because a range
must be a row vector, ones (1, 10) produces a range, while ones (10, 1) does not.
When Octave parses a range expression, it examines the elements of the expression to
determine whether they are all constants. If they are, it replaces the range expression with
a single range constant.
54 GNU Octave
4.3 Single Precision Data Types
Octave includes support for single precision data types, and most of the functions in Octave
accept single precision values and return single precision answers. A single precision variable
is created with the single function.
single (x)
Convert xto single precision type.
See also: [double], page 47.
for example:
sngl = single (rand (2, 2))
⇒sngl =
0.37569 0.92982
0.11962 0.50876
class (sngl)
⇒single
Many functions can also return single precision values directly. For example
ones (2, 2, "single")
zeros (2, 2, "single")
eye (2, 2, "single")
rand (2, 2, "single")
NaN (2, 2, "single")
NA (2, 2, "single")
Inf (2, 2, "single")
will all return single precision matrices.
4.4 Integer Data Types
Octave supports integer matrices as an alternative to using double precision. It is possible
to use both signed and unsigned integers represented by 8, 16, 32, or 64 bits. It should be
noted that most computations require floating point data, meaning that integers will often
change type when involved in numeric computations. For this reason integers are most
often used to store data, and not for calculations.
In general most integer matrices are created by casting existing matrices to integers.
The following example shows how to cast a matrix into 32 bit integers.
float = rand (2, 2)
⇒float = 0.37569 0.92982
0.11962 0.50876
integer = int32 (float)
⇒integer = 0 1
0 1
As can be seen, floating point values are rounded to the nearest integer when converted.
isinteger (x)
Return true if xis an integer object (int8, uint8, int16, etc.).
Chapter 4: Numeric Data Types 55
Note that isinteger (14) is false because numeric constants in Octave are double
precision floating point values.
See also: [isfloat], page 62,[ischar], page 68,[islogical], page 62,[isnumeric], page 62,
[isa], page 39.
int8 (x)
Convert xto 8-bit integer type.
See also: [uint8], page 55,[int16], page 55,[uint16], page 55,[int32], page 55,[uint32],
page 55,[int64], page 55,[uint64], page 55.
uint8 (x)
Convert xto unsigned 8-bit integer type.
See also: [int8], page 55,[int16], page 55,[uint16], page 55,[int32], page 55,[uint32],
page 55,[int64], page 55,[uint64], page 55.
int16 (x)
Convert xto 16-bit integer type.
See also: [int8], page 55,[uint8], page 55,[uint16], page 55,[int32], page 55,[uint32],
page 55,[int64], page 55,[uint64], page 55.
uint16 (x)
Convert xto unsigned 16-bit integer type.
See also: [int8], page 55,[uint8], page 55,[int16], page 55,[int32], page 55,[uint32],
page 55,[int64], page 55,[uint64], page 55.
int32 (x)
Convert xto 32-bit integer type.
See also: [int8], page 55,[uint8], page 55,[int16], page 55,[uint16], page 55,[uint32],
page 55,[int64], page 55,[uint64], page 55.
uint32 (x)
Convert xto unsigned 32-bit integer type.
See also: [int8], page 55,[uint8], page 55,[int16], page 55,[uint16], page 55,[int32],
page 55,[int64], page 55,[uint64], page 55.
int64 (x)
Convert xto 64-bit integer type.
See also: [int8], page 55,[uint8], page 55,[int16], page 55,[uint16], page 55,[int32],
page 55,[uint32], page 55,[uint64], page 55.
uint64 (x)
Convert xto unsigned 64-bit integer type.
See also: [int8], page 55,[uint8], page 55,[int16], page 55,[uint16], page 55,[int32],
page 55,[uint32], page 55,[int64], page 55.
56 GNU Octave
intmax (type)
Return the largest integer that can be represented in an integer type.
The variable type can be
int8 signed 8-bit integer.
int16 signed 16-bit integer.
int32 signed 32-bit integer.
int64 signed 64-bit integer.
uint8 unsigned 8-bit integer.
uint16 unsigned 16-bit integer.
uint32 unsigned 32-bit integer.
uint64 unsigned 64-bit integer.
The default for type is int32.
See also: [intmin], page 56,[flintmax], page 56.
intmin (type)
Return the smallest integer that can be represented in an integer type.
The variable type can be
int8 signed 8-bit integer.
int16 signed 16-bit integer.
int32 signed 32-bit integer.
int64 signed 64-bit integer.
uint8 unsigned 8-bit integer.
uint16 unsigned 16-bit integer.
uint32 unsigned 32-bit integer.
uint64 unsigned 64-bit integer.
The default for type is int32.
See also: [intmax], page 56,[flintmax], page 56.
flintmax ()
flintmax ("double")
flintmax ("single")
Return the largest integer that can be represented consecutively in a floating point
value.
The default class is "double", but "single" is a valid option. On IEEE 754 com-
patible systems, flintmax is 253 for "double" and 224 for "single".
See also: [intmax], page 56,[realmax], page 500,[realmin], page 501.
Chapter 4: Numeric Data Types 57
4.4.1 Integer Arithmetic
While many numerical computations can’t be carried out in integers, Octave does support
basic operations like addition and multiplication on integers. The operators +,-,.*, and
./ work on integers of the same type. So, it is possible to add two 32 bit integers, but not
to add a 32 bit integer and a 16 bit integer.
When doing integer arithmetic one should consider the possibility of underflow and
overflow. This happens when the result of the computation can’t be represented using the
chosen integer type. As an example it is not possible to represent the result of 10 −20
when using unsigned integers. Octave makes sure that the result of integer computations is
the integer that is closest to the true result. So, the result of 10 −20 when using unsigned
integers is zero.
When doing integer division Octave will round the result to the nearest integer. This is
different from most programming languages, where the result is often floored to the nearest
integer. So, the result of int32 (5) ./ int32 (8) is 1.
idivide (x,y,op)
Integer division with different rounding rules.
The standard behavior of integer division such as a./ bis to round the result to
the nearest integer. This is not always the desired behavior and idivide permits
integer element-by-element division to be performed with different treatment for the
fractional part of the division as determined by the op flag. op is a string with one
of the values:
"fix" Calculate a./ bwith the fractional part rounded towards zero.
"round" Calculate a./ bwith the fractional part rounded towards the nearest
integer.
"floor" Calculate a./ bwith the fractional part rounded towards negative infin-
ity.
"ceil" Calculate a./ bwith the fractional part rounded towards positive infin-
ity.
If op is not given it defaults to "fix". An example demonstrating these rounding
rules is
idivide (int8 ([-3, 3]), int8 (4), "fix")
⇒int8 ([0, 0])
idivide (int8 ([-3, 3]), int8 (4), "round")
⇒int8 ([-1, 1])
idivide (int8 ([-3, 3]), int8 (4), "floor")
⇒int8 ([-1, 0])
idivide (int8 ([-3, 3]), int8 (4), "ceil")
⇒int8 ([0, 1])
See also: [ldivide], page 144,[rdivide], page 145.
58 GNU Octave
4.5 Bit Manipulations
Octave provides a number of functions for the manipulation of numeric values on a bit by
bit basis. The basic functions to set and obtain the values of individual bits are bitset
and bitget.
C= bitset (A,n)
C= bitset (A,n,val)
Set or reset bit(s) nof the unsigned integers in A.
val = 0 resets and val = 1 sets the bits. The least significant bit is n= 1. All variables
must be the same size or scalars.
dec2bin (bitset (10, 1))
⇒1011
See also: [bitand], page 58,[bitor], page 59,[bitxor], page 59,[bitget], page 58,
[bitcmp], page 59,[bitshift], page 59,[intmax], page 56,[flintmax], page 56.
c= bitget (A,n)
Return the status of bit(s) nof the unsigned integers in A.
The least significant bit is n= 1.
bitget (100, 8:-1:1)
⇒01100100
See also: [bitand], page 58,[bitor], page 59,[bitxor], page 59,[bitset], page 58,
[bitcmp], page 59,[bitshift], page 59,[intmax], page 56,[flintmax], page 56.
The arguments to all of Octave’s bitwise operations can be scalar or arrays, except for
bitcmp, whose kargument must a scalar. In the case where more than one argument is an
array, then all arguments must have the same shape, and the bitwise operator is applied to
each of the elements of the argument individually. If at least one argument is a scalar and
one an array, then the scalar argument is duplicated. Therefore
bitget (100, 8:-1:1)
is the same as
bitget (100 * ones (1, 8), 8:-1:1)
It should be noted that all values passed to the bit manipulation functions of Octave
are treated as integers. Therefore, even though the example for bitset above passes the
floating point value 10, it is treated as the bits [1, 0, 1, 0] rather than the bits of the
native floating point format representation of 10.
As the maximum value that can be represented by a number is important for bit manip-
ulation, particularly when forming masks, Octave supplies two utility functions: flintmax
for floating point integers, and intmax for integer objects (uint8,int64, etc.).
Octave also includes the basic bitwise ’and’, ’or’, and ’exclusive or’ operators.
bitand (x,y)
Return the bitwise AND of non-negative integers.
x,ymust be in the range [0,intmax]
See also: [bitor], page 59,[bitxor], page 59,[bitset], page 58,[bitget], page 58,
[bitcmp], page 59,[bitshift], page 59,[intmax], page 56,[flintmax], page 56.
Chapter 4: Numeric Data Types 59
bitor (x,y)
Return the bitwise OR of non-negative integers xand y.
See also: [bitor], page 59,[bitxor], page 59,[bitset], page 58,[bitget], page 58,
[bitcmp], page 59,[bitshift], page 59,[intmax], page 56,[flintmax], page 56.
bitxor (x,y)
Return the bitwise XOR of non-negative integers xand y.
See also: [bitand], page 58,[bitor], page 59,[bitset], page 58,[bitget], page 58,
[bitcmp], page 59,[bitshift], page 59,[intmax], page 56,[flintmax], page 56.
The bitwise ’not’ operator is a unary operator that performs a logical negation of each
of the bits of the value. For this to make sense, the mask against which the value is negated
must be defined. Octave’s bitwise ’not’ operator is bitcmp.
bitcmp (A,k)
Return the k-bit complement of integers in A.
If kis omitted k = log2 (flintmax) + 1 is assumed.
bitcmp (7,4)
⇒8
dec2bin (11)
⇒1011
dec2bin (bitcmp (11, 6))
⇒110100
See also: [bitand], page 58,[bitor], page 59,[bitxor], page 59,[bitset], page 58,[bitget],
page 58,[bitcmp], page 59,[bitshift], page 59,[flintmax], page 56.
Octave also includes the ability to left-shift and right-shift values bitwise.
bitshift (a,k)
bitshift (a,k,n)
Return a kbit shift of n-digit unsigned integers in a.
A positive kleads to a left shift; A negative value to a right shift.
If nis omitted it defaults to 64. nmust be in the range [1,64].
bitshift (eye (3), 1)
⇒
200
020
002
bitshift (10, [-2, -1, 0, 1, 2])
⇒2 5 10 20 40
See also: [bitand], page 58,[bitor], page 59,[bitxor], page 59,[bitset], page 58,[bitget],
page 58,[bitcmp], page 59,[intmax], page 56,[flintmax], page 56.
60 GNU Octave
Bits that are shifted out of either end of the value are lost. Octave also uses arithmetic
shifts, where the sign bit of the value is kept during a right shift. For example:
bitshift (-10, -1)
⇒-5
bitshift (int8 (-1), -1)
⇒-1
Note that bitshift (int8 (-1), -1) is -1 since the bit representation of -1 in the int8
data type is [1, 1, 1, 1, 1, 1, 1, 1].
4.6 Logical Values
Octave has built-in support for logical values, i.e., variables that are either true or false.
When comparing two variables, the result will be a logical value whose value depends on
whether or not the comparison is true.
The basic logical operations are &,|, and !, which correspond to “Logical And”, “Logical
Or”, and “Logical Negation”. These operations all follow the usual rules of logic.
It is also possible to use logical values as part of standard numerical calculations. In
this case true is converted to 1, and false to 0, both represented using double precision
floating point numbers. So, the result of true*22 - false/6 is 22.
Logical values can also be used to index matrices and cell arrays. When indexing with
a logical array the result will be a vector containing the values corresponding to true parts
of the logical array. The following example illustrates this.
data = [ 1, 2; 3, 4 ];
idx = (data <= 2);
data(idx)
⇒ans=[1;2]
Instead of creating the idx array it is possible to replace data(idx) with data( data <= 2 )
in the above code.
Logical values can also be constructed by casting numeric objects to logical values, or
by using the true or false functions.
logical (x)
Convert the numeric object xto logical type.
Any nonzero values will be converted to true (1) while zero values will be converted
to false (0). The non-numeric value NaN cannot be converted and will produce an
error.
Compatibility Note: Octave accepts complex values as input, whereas matlab issues
an error.
See also: [double], page 47,[single], page 54,[char], page 71.
true (x)
true (n,m)
true (n,m,k, . . .)
Return a matrix or N-dimensional array whose elements are all logical 1.
Chapter 4: Numeric Data Types 61
If invoked with a single scalar integer argument, return a square matrix of the specified
size.
If invoked with two or more scalar integer arguments, or a vector of integer values,
return an array with given dimensions.
See also: [false], page 61.
false (x)
false (n,m)
false (n,m,k, . . .)
Return a matrix or N-dimensional array whose elements are all logical 0.
If invoked with a single scalar integer argument, return a square matrix of the specified
size.
If invoked with two or more scalar integer arguments, or a vector of integer values,
return an array with given dimensions.
See also: [true], page 60.
4.7 Promotion and Demotion of Data Types
Many operators and functions can work with mixed data types. For example,
uint8 (1) + 1
⇒2
where the above operator works with an 8-bit integer and a double precision value and
returns an 8-bit integer value. Note that the type is demoted to an 8-bit integer, rather
than promoted to a double precision value as might be expected. The reason is that if
Octave promoted values in expressions like the above with all numerical constants would
need to be explicitly cast to the appropriate data type like
uint8 (1) + uint8 (1)
⇒2
which becomes difficult for the user to apply uniformly and might allow hard to find bugs
to be introduced. The same applies to single precision values where a mixed operation such
as
single (1) + 1
⇒2
returns a single precision value. The mixed operations that are valid and their returned
data types are
Mixed Operation Result
double OP single single
double OP integer integer
double OP char double
double OP logical double
single OP integer integer
single OP char single
single OP logical single
62 GNU Octave
The same logic applies to functions with mixed arguments such as
min (single (1), 0)
⇒0
where the returned value is single precision.
In the case of mixed type indexed assignments, the type is not changed. For example,
x = ones (2, 2);
x(1, 1) = single (2)
⇒x = 2 1
1 1
where xremains of the double precision type.
4.8 Predicates for Numeric Objects
Since the type of a variable may change during the execution of a program, it can be
necessary to do type checking at run-time. Doing this also allows you to change the behavior
of a function depending on the type of the input. As an example, this naive implementation
of abs returns the absolute value of the input if it is a real number, and the length of the
input if it is a complex number.
function a = abs (x)
if (isreal (x))
a = sign (x) .* x;
elseif (iscomplex (x))
a = sqrt (real(x).^2 + imag(x).^2);
endif
endfunction
The following functions are available for determining the type of a variable.
isnumeric (x)
Return true if xis a numeric object, i.e., an integer, real, or complex array.
Logical and character arrays are not considered to be numeric.
See also: [isinteger], page 54,[isfloat], page 62,[isreal], page 63,[iscomplex], page 63,
[islogical], page 62,[ischar], page 68,[iscell], page 113,[isstruct], page 107,[isa],
page 39.
islogical (x)
isbool (x)
Return true if xis a logical object.
See also: [isfloat], page 62,[isinteger], page 54,[ischar], page 68,[isnumeric], page 62,
[isa], page 39.
isfloat (x)
Return true if xis a floating-point numeric object.
Objects of class double or single are floating-point objects.
See also: [isinteger], page 54,[ischar], page 68,[islogical], page 62,[isnumeric], page 62,
[isa], page 39.
Chapter 4: Numeric Data Types 63
isreal (x)
Return true if xis a non-complex matrix or scalar.
For compatibility with matlab, this includes logical and character matrices.
See also: [iscomplex], page 63,[isnumeric], page 62,[isa], page 39.
iscomplex (x)
Return true if xis a complex-valued numeric object.
See also: [isreal], page 63,[isnumeric], page 62,[islogical], page 62,[ischar], page 68,
[isfloat], page 62,[isa], page 39.
ismatrix (a)
Return true if ais a 2-D array.
See also: [isscalar], page 63,[isvector], page 63,[iscell], page 113,[isstruct], page 107,
[issparse], page 566,[isa], page 39.
isvector (x)
Return true if xis a vector.
A vector is a 2-D array where one of the dimensions is equal to 1. As a consequence
a 1x1 array, or scalar, is also a vector.
See also: [isscalar], page 63,[ismatrix], page 63,[size], page 45,[rows], page 44,
[columns], page 44,[length], page 45.
isrow (x)
Return true if xis a row vector 1xN with non-negative N.
See also: [iscolumn], page 63,[isscalar], page 63,[isvector], page 63,[ismatrix],
page 63.
iscolumn (x)
Return true if xis a column vector Nx1 with non-negative N.
See also: [isrow], page 63,[isscalar], page 63,[isvector], page 63,[ismatrix], page 63.
isscalar (x)
Return true if xis a scalar.
See also: [isvector], page 63,[ismatrix], page 63.
issquare (x)
Return true if xis a square matrix.
See also: [isscalar], page 63,[isvector], page 63,[ismatrix], page 63,[size], page 45.
issymmetric (A)
issymmetric (A,tol)
Return true if Ais a symmetric matrix within the tolerance specified by tol.
The default tolerance is zero (uses faster code).
Matrix Ais considered symmetric if norm (A-A.’, Inf) / norm (A, Inf) < tol.
See also: [ishermitian], page 64,[isdefinite], page 64.
64 GNU Octave
ishermitian (A)
ishermitian (A,tol)
Return true if Ais Hermitian within the tolerance specified by tol.
The default tolerance is zero (uses faster code).
Matrix Ais considered symmetric if norm (A-A’, Inf) / norm (A, Inf) < tol.
See also: [issymmetric], page 63,[isdefinite], page 64.
isdefinite (A)
isdefinite (A,tol)
Return 1 if Ais symmetric positive definite within the tolerance specified by tol or 0
if Ais symmetric positive semidefinite. Otherwise, return -1.
If tol is omitted, use a tolerance of 100 * eps * norm (A, "fro")
See also: [issymmetric], page 63,[ishermitian], page 64.
isbanded (A,lower,upper)
Return true if Ais a matrix with entries confined between lower diagonals below the
main diagonal and upper diagonals above the main diagonal.
lower and upper must be non-negative integers.
See also: [isdiag], page 64,[istril], page 64,[istriu], page 64,[bandwidth], page 504.
isdiag (A)
Return true if Ais a diagonal matrix.
See also: [isbanded], page 64,[istril], page 64,[istriu], page 64,[diag], page 452,
[bandwidth], page 504.
istril (A)
Return true if Ais a lower triangular matrix.
A lower triangular matrix has nonzero entries only on the main diagonal and below.
See also: [istriu], page 64,[isbanded], page 64,[isdiag], page 64,[tril], page 450,
[bandwidth], page 504.
istriu (A)
Return true if Ais an upper triangular matrix.
An upper triangular matrix has nonzero entries only on the main diagonal and above.
See also: [isdiag], page 64,[isbanded], page 64,[istril], page 64,[triu], page 450,
[bandwidth], page 504.
isprime (x)
Return a logical array which is true where the elements of xare prime numbers and
false where they are not.
A prime number is conventionally defined as a positive integer greater than 1 (e.g.,
2, 3, . . . ) which is divisible only by itself and 1. Octave extends this definition to
include both negative integers and complex values. A negative integer is prime if its
positive counterpart is prime. This is equivalent to isprime (abs (x)).
Chapter 4: Numeric Data Types 65
If class (x)is complex, then primality is tested in the domain of Gaussian integers
(http://en.wikipedia.org/wiki/Gaussian_integer). Some non-complex integers
are prime in the ordinary sense, but not in the domain of Gaussian integers. For
example, 5 = (1 + 2i)∗(1 −2i) shows that 5 is not prime because it has a factor other
than itself and 1. Exercise caution when testing complex and real values together in
the same matrix.
Examples:
isprime (1:6)
⇒[0, 1, 1, 0, 1, 0]
isprime ([i, 2, 3, 5])
⇒[0, 0, 1, 0]
Programming Note: isprime is appropriate if the maximum value in xis not too
large (<1e15). For larger values special purpose factorization code should be used.
Compatibility Note: matlab does not extend the definition of prime numbers and will
produce an error if given negative or complex inputs.
See also: [primes], page 487,[factor], page 486,[gcd], page 486,[lcm], page 486.
If instead of knowing properties of variables, you wish to know which variables are
defined and to gather other information about the workspace itself, see Section 7.3 [Status
of Variables], page 127.
67
5 Strings
Astring constant consists of a sequence of characters enclosed in either double-quote or
single-quote marks. For example, both of the following expressions
"parrot"
’parrot’
represent the string whose contents are ‘parrot’. Strings in Octave can be of any length.
Since the single-quote mark is also used for the transpose operator (see Section 8.3
[Arithmetic Ops], page 142) but double-quote marks have no other purpose in Octave, it is
best to use double-quote marks to denote strings.
Strings can be concatenated using the notation for defining matrices. For example, the
expression
[ "foo" , "bar" , "baz" ]
produces the string whose contents are ‘foobarbaz’. See Chapter 4 [Numeric Data Types],
page 47, for more information about creating matrices.
5.1 Escape Sequences in String Constants
In double-quoted strings, the backslash character is used to introduce escape sequences that
represent other characters. For example, ‘\n’ embeds a newline character in a double-quoted
string and ‘\"’ embeds a double quote character. In single-quoted strings, backslash is not
a special character. Here is an example showing the difference:
toascii ("\n")
⇒10
toascii (’\n’)
⇒[ 92 110 ]
Here is a table of all the escape sequences used in Octave (within double quoted strings).
They are the same as those used in the C programming language.
\\ Represents a literal backslash, ‘\’.
\" Represents a literal double-quote character, ‘"’.
\’ Represents a literal single-quote character, ‘’’.
\0 Represents the null character, control-@, ASCII code 0.
\a Represents the “alert” character, control-g, ASCII code 7.
\b Represents a backspace, control-h, ASCII code 8.
\f Represents a formfeed, control-l, ASCII code 12.
\n Represents a newline, control-j, ASCII code 10.
\r Represents a carriage return, control-m, ASCII code 13.
\t Represents a horizontal tab, control-i, ASCII code 9.
\v Represents a vertical tab, control-k, ASCII code 11.
\nnn Represents the octal value nnn, where nnn are one to three digits between 0
and 7. For example, the code for the ASCII ESC (escape) character is ‘\033’.

68 GNU Octave
\xhh... Represents the hexadecimal value hh, where hh are hexadecimal digits (‘0’
through ‘9’ and either ‘A’ through ‘F’ or ‘a’ through ‘f’). Like the same construct
in ansi C, the escape sequence continues until the first non-hexadecimal digit
is seen. However, using more than two hexadecimal digits produces undefined
results.
In a single-quoted string there is only one escape sequence: you may insert a single quote
character using two single quote characters in succession. For example,
’I can’’t escape’
⇒I can’t escape
In scripts the two different string types can be distinguished if necessary by using is_
dq_string and is_sq_string.
is_dq_string (x)
Return true if xis a double-quoted character string.
See also: [is sq string], page 68,[ischar], page 68.
is_sq_string (x)
Return true if xis a single-quoted character string.
See also: [is dq string], page 68,[ischar], page 68.
5.2 Character Arrays
The string representation used by Octave is an array of characters, so internally the string
"dddddddddd" is actually a row vector of length 10 containing the value 100 in all places
(100 is the ASCII code of "d"). This lends itself to the obvious generalization to character
matrices. Using a matrix of characters, it is possible to represent a collection of same-length
strings in one variable. The convention used in Octave is that each row in a character matrix
is a separate string, but letting each column represent a string is equally possible.
The easiest way to create a character matrix is to put several strings together into a
matrix.
collection = [ "String #1"; "String #2" ];
This creates a 2-by-9 character matrix.
The function ischar can be used to test if an object is a character matrix.
ischar (x)
Return true if xis a character array.
See also: [isfloat], page 62,[isinteger], page 54,[islogical], page 62,[isnumeric], page 62,
[iscellstr], page 119,[isa], page 39.
To test if an object is a string (i.e., a character vector and not a character matrix) you
can use the ischar function in combination with the isvector function as in the following
example:
Chapter 5: Strings 69
ischar (collection)
⇒1
ischar (collection) && isvector (collection)
⇒0
ischar ("my string") && isvector ("my string")
⇒1
One relevant question is, what happens when a character matrix is created from strings
of different length. The answer is that Octave puts blank characters at the end of strings
shorter than the longest string. It is possible to use a different character than the blank
character using the string_fill_char function.
val = string_fill_char ()
old_val = string_fill_char (new_val)
string_fill_char (new_val,"local")
Query or set the internal variable used to pad all rows of a character matrix to the
same length.
The value must be a single character and the default is " " (a single space). For
example:
string_fill_char ("X");
[ "these"; "are"; "strings" ]
⇒"theseXX"
"areXXXX"
"strings"
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
This shows a problem with character matrices. It simply isn’t possible to represent
strings of different lengths. The solution is to use a cell array of strings, which is described
in Section 6.2.4 [Cell Arrays of Strings], page 118.
5.3 Creating Strings
The easiest way to create a string is, as illustrated in the introduction, to enclose a text
in double-quotes or single-quotes. It is however possible to create a string without actually
writing a text. The function blanks creates a string of a given length consisting only of
blank characters (ASCII code 32).
blanks (n)
Return a string of nblanks.
For example:
70 GNU Octave
blanks (10);
whos ans
⇒
Attr Name Size Bytes Class
==== ==== ==== ===== =====
ans 1x10 10 char
See also: [repmat], page 454.
5.3.1 Concatenating Strings
Strings can be concatenated using matrix notation (see Chapter 5 [Strings], page 67,
Section 5.2 [Character Arrays], page 68) which is often the most natural method. For
example:
fullname = [fname ".txt"];
email = ["<" user "@" domain ">"];
In each case it is easy to see what the final string will look like. This method is also the
most efficient. When using matrix concatenation the parser immediately begins joining the
strings without having to process the overhead of a function call and the input validation
of the associated function.
Nevertheless, there are several other functions for concatenating string objects which
can be useful in specific circumstances: char,strvcat,strcat, and cstrcat. Finally,
the general purpose concatenation functions can be used: see [cat], page 445,[horzcat],
page 445, and [vertcat], page 445.
•All string concatenation functions except cstrcat convert numerical input into char-
acter data by taking the corresponding ASCII character for each element, as in the
following example:
char ([98, 97, 110, 97, 110, 97])
⇒banana
•char and strvcat concatenate vertically, while strcat and cstrcat concatenate hor-
izontally. For example:
char ("an apple", "two pears")
⇒an apple
two pears
strcat ("oc", "tave", " is", " good", " for you")
⇒octave is good for you
•char generates an empty row in the output for each empty string in the input. strvcat,
on the other hand, eliminates empty strings.
char ("orange", "green", "", "red")
⇒orange
green
red
Chapter 5: Strings 71
strvcat ("orange", "green", "", "red")
⇒orange
green
red
•All string concatenation functions except cstrcat also accept cell array data (see
Section 6.2 [Cell Arrays], page 112). char and strvcat convert cell arrays into char-
acter arrays, while strcat concatenates within the cells of the cell arrays:
char ({"red", "green", "", "blue"})
⇒red
green
blue
strcat ({"abc"; "ghi"}, {"def"; "jkl"})
⇒{
[1,1] = abcdef
[2,1] = ghijkl
}
•strcat removes trailing white space in the arguments (except within cell arrays), while
cstrcat leaves white space untouched. Both kinds of behavior can be useful as can be
seen in the examples:
strcat (["dir1";"directory2"], ["/";"/"], ["file1";"file2"])
⇒dir1/file1
directory2/file2
cstrcat (["thirteen apples"; "a banana"], [" 5$";" 1$"])
⇒thirteen apples 5$
a banana 1$
Note that in the above example for cstrcat, the white space originates from the inter-
nal representation of the strings in a string array (see Section 5.2 [Character Arrays],
page 68).
char (x)
char (x, . . .)
char (s1,s2, . . .)
char (cell_array)
Create a string array from one or more numeric matrices, character matrices, or cell
arrays.
Arguments are concatenated vertically. The returned values are padded with blanks
as needed to make each row of the string array have the same length. Empty input
strings are significant and will concatenated in the output.
For numerical input, each element is converted to the corresponding ASCII character.
A range error results if an input is outside the ASCII range (0-255).
For cell arrays, each element is concatenated separately. Cell arrays converted through
char can mostly be converted back with cellstr. For example:
72 GNU Octave
char ([97, 98, 99], "", {"98", "99", 100}, "str1", ["ha", "lf"])
⇒["abc "
" "
"98 "
"99 "
"d "
"str1 "
"half "]
See also: [strvcat], page 72,[cellstr], page 119.
strvcat (x)
strvcat (x, . . .)
strvcat (s1,s2, . . .)
strvcat (cell_array)
Create a character array from one or more numeric matrices, character matrices, or
cell arrays.
Arguments are concatenated vertically. The returned values are padded with blanks
as needed to make each row of the string array have the same length. Unlike char,
empty strings are removed and will not appear in the output.
For numerical input, each element is converted to the corresponding ASCII character.
A range error results if an input is outside the ASCII range (0-255).
For cell arrays, each element is concatenated separately. Cell arrays converted through
strvcat can mostly be converted back with cellstr. For example:
strvcat ([97, 98, 99], "", {"98", "99", 100}, "str1", ["ha", "lf"])
⇒["abc "
"98 "
"99 "
"d "
"str1 "
"half "]
See also: [char], page 71,[strcat], page 72,[cstrcat], page 73.
strcat (s1,s2, . . .)
Return a string containing all the arguments concatenated horizontally.
If the arguments are cell strings, strcat returns a cell string with the individual cells
concatenated. For numerical input, each element is converted to the corresponding
ASCII character. Trailing white space for any character string input is eliminated be-
fore the strings are concatenated. Note that cell string values do not have whitespace
trimmed.
For example:
strcat ("|", " leading space is preserved", "|")
⇒| leading space is preserved|
strcat ("|", "trailing space is eliminated ", "|")
⇒|trailing space is eliminated|
Chapter 5: Strings 73
strcat ("homogeneous space |", " ", "| is also eliminated")
⇒homogeneous space || is also eliminated
s = [ "ab"; "cde" ];
strcat (s, s, s)
⇒"ababab "
"cdecdecde"
s = { "ab"; "cd " };
strcat (s, s, s)
⇒{
[1,1] = ababab
[2,1] = cd cd cd
}
See also: [cstrcat], page 73,[char], page 71,[strvcat], page 72.
cstrcat (s1,s2, . . .)
Return a string containing all the arguments concatenated horizontally with trailing
white space preserved.
For example:
cstrcat ("ab ", "cd")
⇒"ab cd"
s = [ "ab"; "cde" ];
cstrcat (s, s, s)
⇒"ab ab ab "
"cdecdecde"
See also: [strcat], page 72,[char], page 71,[strvcat], page 72.
5.3.2 Converting Numerical Data to Strings
Apart from the string concatenation functions (see Section 5.3.1 [Concatenating Strings],
page 70) which cast numerical data to the corresponding ASCII characters, there are several
functions that format numerical data as strings. mat2str and num2str convert real or
complex matrices, while int2str converts integer matrices. int2str takes the real part
of complex values and round fractional values to integer. A more flexible way to format
numerical data as strings is the sprintf function (see Section 14.2.4 [Formatted Output],
page 268,[sprintf], page 269).
s= mat2str (x,n)
s= mat2str (x,n,"class")
Format real, complex, and logical matrices as strings.
The returned string may be used to reconstruct the original matrix by using the eval
function.
The precision of the values is given by n. If nis a scalar then both real and imaginary
parts of the matrix are printed to the same precision. Otherwise n(1) defines the
74 GNU Octave
precision of the real part and n(2) defines the precision of the imaginary part. The
default for nis 15.
If the argument "class" is given then the class of xis included in the string in such
a way that eval will result in the construction of a matrix of the same class.
mat2str ([ -1/3 + i/7; 1/3 - i/7 ], [4 2])
⇒"[-0.3333+0.14i;0.3333-0.14i]"
mat2str ([ -1/3 +i/7; 1/3 -i/7 ], [4 2])
⇒"[-0.3333+0i 0+0.14i;0.3333+0i -0-0.14i]"
mat2str (int16 ([1 -1]), "class")
⇒"int16([1 -1])"
mat2str (logical (eye (2)))
⇒"[true false;false true]"
isequal (x, eval (mat2str (x)))
⇒1
See also: [sprintf], page 269,[num2str], page 74,[int2str], page 75.
num2str (x)
num2str (x,precision)
num2str (x,format)
Convert a number (or array) to a string (or a character array).
The optional second argument may either give the number of significant digits (pre-
cision) to be used in the output or a format template string (format) as in sprintf
(see Section 14.2.4 [Formatted Output], page 268). num2str can also process complex
numbers.
Examples:
Chapter 5: Strings 75
num2str (123.456)
⇒"123.46"
num2str (123.456, 4)
⇒"123.5"
s = num2str ([1, 1.34; 3, 3.56], "%5.1f")
⇒s =
1.0 1.3
3.0 3.6
whos s
⇒
Attr Name Size Bytes Class
==== ==== ==== ===== =====
s 2x8 16 char
num2str (1.234 + 27.3i)
⇒"1.234+27.3i"
The num2str function is not very flexible. For better control over the results, use
sprintf (see Section 14.2.4 [Formatted Output], page 268).
Programming Notes:
For matlab compatibility, leading spaces are stripped before returning the string.
Integers larger than flintmax may not be displayed correctly.
For complex x, the format string may only contain one output conversion specification
and nothing else. Otherwise, results will be unpredictable.
Any optional format specified by the programmer is used without modification. This
is in contrast to matlab which tampers with the format based on internal heuristics.
See also: [sprintf], page 269,[int2str], page 75,[mat2str], page 73.
int2str (n)
Convert an integer (or array of integers) to a string (or a character array).
int2str (123)
⇒"123"
s = int2str ([1, 2, 3; 4, 5, 6])
⇒s =
123
456
whos s
⇒
Attr Name Size Bytes Class
==== ==== ==== ===== =====
s 2x7 14 char
This function is not very flexible. For better control over the results, use sprintf
(see Section 14.2.4 [Formatted Output], page 268).
76 GNU Octave
Programming Notes:
Non-integers are rounded to integers before display. Only the real part of complex
numbers is displayed.
See also: [sprintf], page 269,[num2str], page 74,[mat2str], page 73.
5.4 Comparing Strings
Since a string is a character array, comparisons between strings work element by element
as the following example shows:
GNU = "GNU’s Not UNIX";
spaces = (GNU == " ")
⇒spaces =
00000100010000
To determine if two strings are identical it is necessary to use the strcmp function. It com-
pares complete strings and is case sensitive. strncmp compares only the first Ncharacters
(with Ngiven as a parameter). strcmpi and strncmpi are the corresponding functions for
case-insensitive comparison.
strcmp (s1,s2)
Return 1 if the character strings s1 and s2 are the same, and 0 otherwise.
If either s1 or s2 is a cell array of strings, then an array of the same size is returned,
containing the values described above for every member of the cell array. The other
argument may also be a cell array of strings (of the same size or with only one
element), char matrix or character string.
Caution: For compatibility with matlab, Octave’s strcmp function returns 1 if the
character strings are equal, and 0 otherwise. This is just the opposite of the corre-
sponding C library function.
See also: [strcmpi], page 77,[strncmp], page 76,[strncmpi], page 77.
strncmp (s1,s2,n)
Return 1 if the first ncharacters of strings s1 and s2 are the same, and 0 otherwise.
strncmp ("abce", "abcd", 3)
⇒1
If either s1 or s2 is a cell array of strings, then an array of the same size is returned,
containing the values described above for every member of the cell array. The other
argument may also be a cell array of strings (of the same size or with only one
element), char matrix or character string.
strncmp ("abce", {"abcd", "bca", "abc"}, 3)
⇒[1, 0, 1]
Caution: For compatibility with matlab, Octave’s strncmp function returns 1 if
the character strings are equal, and 0 otherwise. This is just the opposite of the
corresponding C library function.
See also: [strncmpi], page 77,[strcmp], page 76,[strcmpi], page 77.
Chapter 5: Strings 77
strcmpi (s1,s2)
Return 1 if the character strings s1 and s2 are the same, disregarding case of alpha-
betic characters, and 0 otherwise.
If either s1 or s2 is a cell array of strings, then an array of the same size is returned,
containing the values described above for every member of the cell array. The other
argument may also be a cell array of strings (of the same size or with only one
element), char matrix or character string.
Caution: For compatibility with matlab, Octave’s strcmp function returns 1 if the
character strings are equal, and 0 otherwise. This is just the opposite of the corre-
sponding C library function.
Caution: National alphabets are not supported.
See also: [strcmp], page 76,[strncmp], page 76,[strncmpi], page 77.
strncmpi (s1,s2,n)
Return 1 if the first ncharacter of s1 and s2 are the same, disregarding case of
alphabetic characters, and 0 otherwise.
If either s1 or s2 is a cell array of strings, then an array of the same size is returned,
containing the values described above for every member of the cell array. The other
argument may also be a cell array of strings (of the same size or with only one
element), char matrix or character string.
Caution: For compatibility with matlab, Octave’s strncmpi function returns 1 if
the character strings are equal, and 0 otherwise. This is just the opposite of the
corresponding C library function.
Caution: National alphabets are not supported.
See also: [strncmp], page 76,[strcmp], page 76,[strcmpi], page 77.
5.5 Manipulating Strings
Octave supports a wide range of functions for manipulating strings. Since a string is just a
matrix, simple manipulations can be accomplished using standard operators. The following
example shows how to replace all blank characters with underscores.
quote = ...
"First things first, but not necessarily in that order";
quote( quote == " " ) = "_"
⇒quote =
First_things_first,_but_not_necessarily_in_that_order
For more complex manipulations, such as searching, replacing, and general regular ex-
pressions, the following functions come with Octave.
deblank (s)
Remove trailing whitespace and nulls from s.
If sis a matrix, deblank trims each row to the length of longest string. If sis a cell
array of strings, operate recursively on each string element.
78 GNU Octave
Examples:
deblank (" abc ")
⇒" abc"
deblank ([" abc "; " def "])
⇒[" abc " ; " def"]
See also: [strtrim], page 78.
strtrim (s)
Remove leading and trailing whitespace from s.
If sis a matrix, strtrim trims each row to the length of longest string. If sis a cell
array of strings, operate recursively on each string element.
For example:
strtrim (" abc ")
⇒"abc"
strtrim ([" abc "; " def "])
⇒["abc " ; " def"]
See also: [deblank], page 77.
strtrunc (s,n)
Truncate the character string sto length n.
If sis a character matrix, then the number of columns is adjusted.
If sis a cell array of strings, then the operation is performed on each cell element and
the new cell array is returned.
findstr (s,t)
findstr (s,t,overlap)
Return the vector of all positions in the longer of the two strings sand twhere an
occurrence of the shorter of the two starts.
If the optional argument overlap is true (default), the returned vector can include
overlapping positions. For example:
findstr ("ababab", "a")
⇒[1, 3, 5];
findstr ("abababa", "aba", 0)
⇒[1, 5]
Caution: findstr is scheduled for deprecation. Use strfind in all new code.
See also: [strfind], page 79,[strmatch], page 80,[strcmp], page 76,[strncmp], page 76,
[strcmpi], page 77,[strncmpi], page 77,[find], page 441.
idx = strchr (str,chars)
idx = strchr (str,chars,n)
idx = strchr (str,chars,n,direction)
[i,j] = strchr (. . . )
Search for the string str for occurrences of characters from the set chars.
Chapter 5: Strings 79
The return value(s), as well as the nand direction arguments behave identically as in
find.
This will be faster than using regexp in most cases.
See also: [find], page 441.
index (s,t)
index (s,t,direction)
Return the position of the first occurrence of the string tin the string s, or 0 if no
occurrence is found.
smay also be a string array or cell array of strings.
For example:
index ("Teststring", "t")
⇒4
If direction is "first", return the first element found. If direction is "last", return
the last element found.
See also: [find], page 441,[rindex], page 79.
rindex (s,t)
Return the position of the last occurrence of the character string tin the character
string s, or 0 if no occurrence is found.
smay also be a string array or cell array of strings.
For example:
rindex ("Teststring", "t")
⇒6
The rindex function is equivalent to index with direction set to "last".
See also: [find], page 441,[index], page 79.
idx = strfind (str,pattern)
idx = strfind (cellstr,pattern)
idx = strfind (. . . , "overlaps",val)
Search for pattern in the string str and return the starting index of every such occur-
rence in the vector idx.
If there is no such occurrence, or if pattern is longer than str, or if pattern itself is
empty, then idx is the empty array [].
The optional argument "overlaps" determines whether the pattern can match at
every position in str (true), or only for unique occurrences of the complete pattern
(false). The default is true.
If a cell array of strings cellstr is specified then idx is a cell array of vectors, as
specified above.
Examples:
80 GNU Octave
strfind ("abababa", "aba")
⇒[1, 3, 5]
strfind ("abababa", "aba", "overlaps", false)
⇒[1, 5]
strfind ({"abababa", "bebebe", "ab"}, "aba")
⇒{
[1,1] =
135
[1,2] = [](1x0)
[1,3] = [](1x0)
}
See also: [findstr], page 78,[strmatch], page 80,[regexp], page 87,[regexpi], page 89,
[find], page 441.
str = strjoin (cstr)
str = strjoin (cstr,delimiter)
Join the elements of the cell string array, cstr, into a single string.
If no delimiter is specified, the elements of cstr are separated by a space.
If delimiter is specified as a string, the cell string array is joined using the string.
Escape sequences are supported.
If delimiter is a cell string array whose length is one less than cstr, then the elements of
cstr are joined by interleaving the cell string elements of delimiter. Escape sequences
are not supported.
strjoin ({’Octave’,’Scilab’,’Lush’,’Yorick’}, ’*’)
⇒’Octave*Scilab*Lush*Yorick’
See also: [strsplit], page 81.
strmatch (s,A)
strmatch (s,A,"exact")
Return indices of entries of Awhich begin with the string s.
The second argument Amust be a string, character matrix, or a cell array of strings.
If the third argument "exact" is not given, then sonly needs to match Aup to the
length of s. Trailing spaces and nulls in sand Aare ignored when matching.
For example:
Chapter 5: Strings 81
strmatch ("apple", "apple juice")
⇒1
strmatch ("apple", ["apple "; "apple juice"; "an apple"])
⇒[1; 2]
strmatch ("apple", ["apple "; "apple juice"; "an apple"], "exact")
⇒[1]
Caution: strmatch is scheduled for deprecation. Use strncmp (normal case), or
strcmp ("exact" case), or regexp in all new code.
See also: [strfind], page 79,[findstr], page 78,[strcmp], page 76,[strncmp], page 76,
[strcmpi], page 77,[strncmpi], page 77,[find], page 441.
[tok,rem] = strtok (str)
[tok,rem] = strtok (str,delim)
Find all characters in the string str up to, but not including, the first character which
is in the string delim.
str may also be a cell array of strings in which case the function executes on every
individual string and returns a cell array of tokens and remainders.
Leading delimiters are ignored. If delim is not specified, whitespace is assumed.
If rem is requested, it contains the remainder of the string, starting at the first de-
limiter.
Examples:
strtok ("this is the life")
⇒"this"
[tok, rem] = strtok ("14*27+31", "+-*/")
⇒tok = 14
rem = *27+31
See also: [index], page 79,[strsplit], page 81,[strchr], page 78,[isspace], page 97.
[cstr] = strsplit (str)
[cstr] = strsplit (str,del)
[cstr] = strsplit (. . . , name,value)
[cstr,matches] = strsplit (. . . )
Split the string str using the delimiters specified by del and return a cell string array
of substrings.
If a delimiter is not specified the string is split at whitespace {" ", "\f", "\n",
"\r", "\t", "\v"}. Otherwise, the delimiter, del must be a string or cell array of
strings. By default, consecutive delimiters in the input string sare collapsed into one
resulting in a single split.
Supported name/value pair arguments are:
•collapsedelimiters which may take the value of true (default) or false.
82 GNU Octave
•delimitertype which may take the value of "simple" (default) or
"regularexpression". A simple delimiter matches the text exactly as written.
Otherwise, the syntax for regular expressions outlined in regexp is used.
The optional second output, matches, returns the delimiters which were matched in
the original string.
Examples with simple delimiters:
strsplit ("a b c")
⇒{
[1,1] = a
[1,2] = b
[1,3] = c
}
strsplit ("a,b,c", ",")
⇒{
[1,1] = a
[1,2] = b
[1,3] = c
}
strsplit ("a foo b,bar c", {" ", ",", "foo", "bar"})
⇒{
[1,1] = a
[1,2] = b
[1,3] = c
}
strsplit ("a,,b, c", {",", " "}, "collapsedelimiters", false)
⇒{
[1,1] = a
[1,2] =
[1,3] = b
[1,4] =
[1,5] = c
}
Examples with regularexpression delimiters:
strsplit ("a foo b,bar c", ’,|\s|foo|bar’, "delimitertype", "regularexpression")
⇒
{
[1,1] = a
[1,2] = b
[1,3] = c

Chapter 5: Strings 83
}
strsplit ("a,,b, c", ’[, ]’, "collapsedelimiters", false, "delimitertype", "regularexpression")
⇒
{
[1,1] = a
[1,2] =
[1,3] = b
[1,4] =
[1,5] = c
}
strsplit ("a,\t,b, c", {’,’, ’\s’}, "delimitertype", "regularexpression")
⇒
{
[1,1] = a
[1,2] = b
[1,3] = c
}
strsplit ("a,\t,b, c", {’,’, ’ ’, ’\t’}, "collapsedelimiters", false)
⇒
{
[1,1] = a
[1,2] =
[1,3] =
[1,4] = b
[1,5] =
[1,6] = c
}
See also: [ostrsplit], page 83,[strjoin], page 80,[strtok], page 81,[regexp], page 87.
[cstr] = ostrsplit (s,sep)
[cstr] = ostrsplit (s,sep,strip_empty)
Split the string susing one or more separators sep and return a cell array of strings.
Consecutive separators and separators at boundaries result in empty strings, unless
strip empty is true. The default value of strip empty is false.
2-D character arrays are split at separators and at the original column boundaries.
Example:
84 GNU Octave
ostrsplit ("a,b,c", ",")
⇒{
[1,1] = a
[1,2] = b
[1,3] = c
}
ostrsplit (["a,b" ; "cde"], ",")
⇒{
[1,1] = a
[1,2] = b
[1,3] = cde
}
See also: [strsplit], page 81,[strtok], page 81.
[a, ...] = strread (str)
[a, ...] = strread (str,format)
[a, ...] = strread (str,format,format_repeat)
[a, ...] = strread (str,format,prop1,value1, . . .)
[a, ...] = strread (str,format,format_repeat,prop1,value1, . . .)
Read data from a string.
The string str is split into words that are repeatedly matched to the specifiers in
format. The first word is matched to the first specifier, the second to the second
specifier and so forth. If there are more words than specifiers, the process is repeated
until all words have been processed.
The string format describes how the words in str should be parsed. It may contain
any combination of the following specifiers:
%s The word is parsed as a string.
%f
%n The word is parsed as a number and converted to double.
%d
%u The word is parsed as a number and converted to int32.
%*’, ’%*f’, ’%*s
The word is skipped.
For %s and %d, %f, %n, %u and the associated %*s . . . specifiers an
optional width can be specified as %Ns, etc. where N is an integer >1.
For %f, format specifiers like %N.Mf are allowed.
literals In addition the format may contain literal character strings; these will be
skipped during reading.
Parsed word corresponding to the first specifier are returned in the first output argu-
ment and likewise for the rest of the specifiers.

Chapter 5: Strings 85
By default, format is "%f", meaning that numbers are read from str. This will do if
str contains only numeric fields.
For example, the string
str = "\
Bunny Bugs 5.5\n\
Duck Daffy -7.5e-5\n\
Penguin Tux 6"
can be read using
[a,b,c] = strread (str, "%s %s %f");
Optional numeric argument format repeat can be used for limiting the number of
items read:
-1 (default) read all of the string until the end.
N Read N times nargout items. 0 (zero) is an acceptable value for for-
mat repeat.
The behavior of strread can be changed via property-value pairs. The following
properties are recognized:
"commentstyle"
Parts of str are considered comments and will be skipped. value is the
comment style and can be any of the following.
•"shell" Everything from #characters to the nearest end-of-line is
skipped.
•"c" Everything between /* and */ is skipped.
•"c++" Everything from // characters to the nearest end-of-line is
skipped.
•"matlab" Everything from %characters to the nearest end-of-line is
skipped.
•user-supplied. Two options: (1) One string, or 1x1 cell string: Skip
everything to the right of it; (2) 2x1 cell string array: Everything
between the left and right strings is skipped.
"delimiter"
Any character in value will be used to split str into words (default value
= any whitespace). Note that whitespace is implicitly added to the set
of delimiter characters unless a "%s" format conversion specifier is sup-
plied; see "whitespace" parameter below. The set of delimiter characters
cannot be empty; if needed Octave substitutes a space as delimiter.
"emptyvalue"
Value to return for empty numeric values in non-whitespace delimited
data. The default is NaN. When the data type does not support NaN
(int32 for example), then default is zero.
"multipledelimsasone"
Treat a series of consecutive delimiters, without whitespace in between,
as a single delimiter. Consecutive delimiter series need not be vertically
"aligned".
86 GNU Octave
"treatasempty"
Treat single occurrences (surrounded by delimiters or whitespace) of the
string(s) in value as missing values.
"returnonerror"
If value true (1, default), ignore read errors and return normally. If false
(0), return an error.
"whitespace"
Any character in value will be interpreted as whitespace and trimmed; the
string defining whitespace must be enclosed in double quotes for proper
processing of special characters like "\t". In each data field, multiple
consecutive whitespace characters are collapsed into one space and leading
and trailing whitespace is removed. The default value for whitespace is
" \b\r\n\t" (note the space). Whitespace is always added to the set of
delimiter characters unless at least one "%s" format conversion specifier is
supplied; in that case only whitespace explicitly specified in "delimiter"
is retained as delimiter and removed from the set of whitespace characters.
If whitespace characters are to be kept as-is (in e.g., strings), specify an
empty value (i.e., "") for "whitespace"; obviously, whitespace cannot be
a delimiter then.
When the number of words in str doesn’t match an exact multiple of the number of
format conversion specifiers, strread’s behavior depends on the last character of str:
last character = "\n"
Data columns are padded with empty fields or Nan so that all columns
have equal length
last character is not "\n"
Data columns are not padded; strread returns columns of unequal length
See also: [textscan], page 258,[textread], page 256,[load], page 253,[dlmread],
page 256,[fscanf], page 274.
newstr = strrep (str,ptn,rep)
newstr = strrep (cellstr,ptn,rep)
newstr = strrep (. . . , "overlaps",val)
Replace all occurrences of the pattern ptn in the string str with the string rep and
return the result.
The optional argument "overlaps" determines whether the pattern can match at
every position in str (true), or only for unique occurrences of the complete pattern
(false). The default is true.
smay also be a cell array of strings, in which case the replacement is done for each
element and a cell array is returned.
Example:
strrep ("This is a test string", "is", "&%$")
⇒"Th&%$ &%$ a test string"
See also: [regexprep], page 90,[strfind], page 79,[findstr], page 78.
Chapter 5: Strings 87
substr (s,offset)
substr (s,offset,len)
Return the substring of swhich starts at character number offset and is len characters
long.
Position numbering for offsets begins with 1. If offset is negative, extraction starts
that far from the end of the string.
If len is omitted, the substring extends to the end of s. A negative value for len
extracts to within len characters of the end of the string
Examples:
substr ("This is a test string", 6, 9)
⇒"is a test"
substr ("This is a test string", -11)
⇒"test string"
substr ("This is a test string", -11, -7)
⇒"test"
This function is patterned after the equivalent function in Perl.
[s,e,te,m,t,nm,sp] = regexp (str,pat)
[...] = regexp (str,pat,"opt1", . . .)
Regular expression string matching.
Search for pat in str and return the positions and substrings of any matches, or empty
values if there are none.
The matched pattern pat can include any of the standard regex operators, including:
.Match any character
* + ? {} Repetition operators, representing
*Match zero or more times
+Match one or more times
?Match zero or one times
{n}Match exactly ntimes
{n,} Match nor more times
{m,n}Match between mand ntimes
[...] [^...]
List operators. The pattern will match any character listed between "["
and "]". If the first character is "^" then the pattern is inverted and any
character except those listed between brackets will match.
Escape sequences defined below can also be used inside list operators.
For example, a template for a floating point number might be [-+.\d]+.
() (?:) Grouping operator. The first form, parentheses only, also creates a token.
|Alternation operator. Match one of a choice of regular expressions. The
alternatives must be delimited by the grouping operator () above.
88 GNU Octave
^ $ Anchoring operators. Requires pattern to occur at the start (^) or end
($) of the string.
In addition, the following escaped characters have special meaning.
\d Match any digit
\D Match any non-digit
\s Match any whitespace character
\S Match any non-whitespace character
\w Match any word character
\W Match any non-word character
\< Match the beginning of a word
\> Match the end of a word
\B Match within a word
Implementation Note: For compatibility with matlab, escape sequences in pat (e.g.,
"\n" =>newline) are expanded even when pat has been defined with single quotes.
To disable expansion use a second backslash before the escape sequence (e.g., "\\n")
or use the regexptranslate function.
The outputs of regexp default to the order given below
sThe start indices of each matching substring
eThe end indices of each matching substring
te The extents of each matched token surrounded by (...) in pat
mA cell array of the text of each match
tA cell array of the text of each token matched
nm A structure containing the text of each matched named token, with
the name being used as the fieldname. A named token is denoted by
(?<name>...).
sp A cell array of the text not returned by match, i.e., what remains if you
split the string based on pat.
Particular output arguments, or the order of the output arguments, can be selected
by additional opt arguments. These are strings and the correspondence between the
output arguments and the optional argument are
’start’ s
’end’ e
’tokenExtents’ te
’match’ m
’tokens’ t
’names’ nm
’split’ sp
Additional arguments are summarized below.
‘once’ Return only the first occurrence of the pattern.
Chapter 5: Strings 89
‘matchcase’
Make the matching case sensitive. (default)
Alternatively, use (?-i) in the pattern.
‘ignorecase’
Ignore case when matching the pattern to the string.
Alternatively, use (?i) in the pattern.
‘stringanchors’
Match the anchor characters at the beginning and end of the string.
(default)
Alternatively, use (?-m) in the pattern.
‘lineanchors’
Match the anchor characters at the beginning and end of the line.
Alternatively, use (?m) in the pattern.
‘dotall’ The pattern .matches all characters including the newline character.
(default)
Alternatively, use (?s) in the pattern.
‘dotexceptnewline’
The pattern .matches all characters except the newline character.
Alternatively, use (?-s) in the pattern.
‘literalspacing’
All characters in the pattern, including whitespace, are significant and
are used in pattern matching. (default)
Alternatively, use (?-x) in the pattern.
‘freespacing’
The pattern may include arbitrary whitespace and also comments begin-
ning with the character ‘#’.
Alternatively, use (?x) in the pattern.
‘noemptymatch’
Zero-length matches are not returned. (default)
‘emptymatch’
Return zero-length matches.
regexp (’a’, ’b*’, ’emptymatch’) returns [1 2] because there are
zero or more ’b’ characters at positions 1 and end-of-string.
See also: [regexpi], page 89,[strfind], page 79,[regexprep], page 90.
[s,e,te,m,t,nm,sp] = regexpi (str,pat)
[...] = regexpi (str,pat,"opt1", . . .)
Case insensitive regular expression string matching.
Search for pat in str and return the positions and substrings of any matches, or empty
values if there are none. See [regexp], page 87, for details on the syntax of the search
pattern.
See also: [regexp], page 87.
90 GNU Octave
outstr = regexprep (string,pat,repstr)
outstr = regexprep (string,pat,repstr,"opt1", . . . )
Replace occurrences of pattern pat in string with repstr.
The pattern is a regular expression as documented for regexp. See [regexp], page 87.
The replacement string may contain $i, which substitutes for the ith set of parentheses
in the match string. For example,
regexprep ("Bill Dunn", ’(\w+) (\w+)’, ’$2, $1’)
returns "Dunn, Bill"
Options in addition to those of regexp are
‘once’ Replace only the first occurrence of pat in the result.
‘warnings’
This option is present for compatibility but is ignored.
Implementation Note: For compatibility with matlab, escape sequences in pat (e.g.,
"\n" =>newline) are expanded even when pat has been defined with single quotes.
To disable expansion use a second backslash before the escape sequence (e.g., "\\n")
or use the regexptranslate function.
See also: [regexp], page 87,[regexpi], page 89,[strrep], page 86.
regexptranslate (op,s)
Translate a string for use in a regular expression.
This may include either wildcard replacement or special character escaping.
The behavior is controlled by op which can take the following values
"wildcard"
The wildcard characters .,*, and ?are replaced with wildcards that are
appropriate for a regular expression. For example:
regexptranslate ("wildcard", "*.m")
⇒".*\.m"
"escape" The characters $.?[], that have special meaning for regular expressions
are escaped so that they are treated literally. For example:
regexptranslate ("escape", "12.5")
⇒"12\.5"
See also: [regexp], page 87,[regexpi], page 89,[regexprep], page 90.
untabify (t)
untabify (t,tw)
untabify (t,tw,deblank)
Replace TAB characters in twith spaces.
The input, t, may be either a 2-D character array, or a cell array of character strings.
The output is the same class as the input.
The tab width is specified by tw, and defaults to eight.
If the optional argument deblank is true, then the spaces will be removed from the
end of the character data.
Chapter 5: Strings 91
The following example reads a file and writes an untabified version of the same file
with trailing spaces stripped.
fid = fopen ("tabbed_script.m");
text = char (fread (fid, "uchar")’);
fclose (fid);
fid = fopen ("untabified_script.m", "w");
text = untabify (strsplit (text, "\n"), 8, true);
fprintf (fid, "%s\n", text{:});
fclose (fid);
See also: [strjust], page 94,[strsplit], page 81,[deblank], page 77.
5.6 String Conversions
Octave supports various kinds of conversions between strings and numbers. As an example,
it is possible to convert a string containing a hexadecimal number to a floating point number.
hex2dec ("FF")
⇒255
bin2dec (s)
Return the decimal number corresponding to the binary number represented by the
string s.
For example:
bin2dec ("1110")
⇒14
Spaces are ignored during conversion and may be used to make the binary number
more readable.
bin2dec ("1000 0001")
⇒129
If sis a string matrix, return a column vector with one converted number per row of
s; Invalid rows evaluate to NaN.
If sis a cell array of strings, return a column vector with one converted number per
cell element in s.
See also: [dec2bin], page 91,[base2dec], page 92,[hex2dec], page 92.
dec2bin (d,len)
Return a binary number corresponding to the non-negative integer d, as a string of
ones and zeros.
For example:
dec2bin (14)
⇒"1110"
If dis a matrix or cell array, return a string matrix with one row per element in d,
padded with leading zeros to the width of the largest value.
The optional second argument, len, specifies the minimum number of digits in the
result.
See also: [bin2dec], page 91,[dec2base], page 92,[dec2hex], page 92.
92 GNU Octave
dec2hex (d,len)
Return the hexadecimal string corresponding to the non-negative integer d.
For example:
dec2hex (2748)
⇒"ABC"
If dis a matrix or cell array, return a string matrix with one row per element in d,
padded with leading zeros to the width of the largest value.
The optional second argument, len, specifies the minimum number of digits in the
result.
See also: [hex2dec], page 92,[dec2base], page 92,[dec2bin], page 91.
hex2dec (s)
Return the integer corresponding to the hexadecimal number represented by the string
s.
For example:
hex2dec ("12B")
⇒299
hex2dec ("12b")
⇒299
If sis a string matrix, return a column vector with one converted number per row of
s; Invalid rows evaluate to NaN.
If sis a cell array of strings, return a column vector with one converted number per
cell element in s.
See also: [dec2hex], page 92,[base2dec], page 92,[bin2dec], page 91.
dec2base (d,base)
dec2base (d,base,len)
Return a string of symbols in base base corresponding to the non-negative integer d.
dec2base (123, 3)
⇒"11120"
If dis a matrix or cell array, return a string matrix with one row per element in d,
padded with leading zeros to the width of the largest value.
If base is a string then the characters of base are used as the symbols for the digits
of d. Space (’ ’) may not be used as a symbol.
dec2base (123, "aei")
⇒"eeeia"
The optional third argument, len, specifies the minimum number of digits in the
result.
See also: [base2dec], page 92,[dec2bin], page 91,[dec2hex], page 92.
base2dec (s,base)
Convert sfrom a string of digits in base base to a decimal integer (base 10).
base2dec ("11120", 3)
⇒123
Chapter 5: Strings 93
If sis a string matrix, return a column vector with one value per row of s. If a row
contains invalid symbols then the corresponding value will be NaN.
If sis a cell array of strings, return a column vector with one value per cell element
in s.
If base is a string, the characters of base are used as the symbols for the digits of s.
Space (’ ’) may not be used as a symbol.
base2dec ("yyyzx", "xyz")
⇒123
See also: [dec2base], page 92,[bin2dec], page 91,[hex2dec], page 92.
s= num2hex (n)
Typecast a double or single precision number or vector to a 8 or 16 character hex-
adecimal string of the IEEE 754 representation of the number.
For example:
num2hex ([-1, 1, e, Inf])
⇒"bff0000000000000
3ff0000000000000
4005bf0a8b145769
7ff0000000000000"
If the argument nis a single precision number or vector, the returned string has a
length of 8. For example:
num2hex (single ([-1, 1, e, Inf]))
⇒"bf800000
3f800000
402df854
7f800000"
See also: [hex2num], page 93,[hex2dec], page 92,[dec2hex], page 92.
n= hex2num (s)
n= hex2num (s,class)
Typecast the 16 character hexadecimal character string to an IEEE 754 double pre-
cision number.
If fewer than 16 characters are given the strings are right padded with ’0’ characters.
Given a string matrix, hex2num treats each row as a separate number.
hex2num (["4005bf0a8b145769"; "4024000000000000"])
⇒[2.7183; 10.000]
The optional argument class can be passed as the string "single" to specify that the
given string should be interpreted as a single precision number. In this case, sshould
be an 8 character hexadecimal string. For example:
hex2num (["402df854"; "41200000"], "single")
⇒[2.7183; 10.000]
See also: [num2hex], page 93,[hex2dec], page 92,[dec2hex], page 92.
94 GNU Octave
str2double (s)
Convert a string to a real or complex number.
The string must be in one of the following formats where a and b are real numbers
and the complex unit is ’i’ or ’j’:
•a+bi
•a+b*i
•a+i*b
•bi +a
•b*i +a
•i*b +a
If present, a and/or b are of the form [+-]d[,.]d[[eE][+-]d] where the brackets indicate
optional arguments and ’d’ indicates zero or more digits. The special input values
Inf,NaN, and NA are also accepted.
smay be a character string, character matrix, or cell array. For character arrays
the conversion is repeated for every row, and a double or complex array is returned.
Empty rows in sare deleted and not returned in the numeric array. For cell arrays
each character string element is processed and a double or complex array of the same
dimensions as sis returned.
For unconvertible scalar or character string input str2double returns a NaN. Simi-
larly, for character array input str2double returns a NaN for any row of sthat could
not be converted. For a cell array, str2double returns a NaN for any element of s
for which conversion fails. Note that numeric elements in a mixed string/numeric cell
array are not strings and the conversion will fail for these elements and return NaN.
str2double can replace str2num, and it avoids the security risk of using eval on
unknown data.
See also: [str2num], page 95.
strjust (s)
strjust (s,pos)
Return the text, s, justified according to pos, which may be "left","center", or
"right".
If pos is omitted it defaults to "right".
Null characters are replaced by spaces. All other character data are treated as non-
white space.
Example:
strjust (["a"; "ab"; "abc"; "abcd"])
⇒" a"
" ab"
" abc"
"abcd"
See also: [deblank], page 77,[strrep], page 86,[strtrim], page 78,[untabify], page 90.
Chapter 5: Strings 95
x= str2num (s)
[x,state] = str2num (s)
Convert the string (or character array) sto a number (or an array).
Examples:
str2num ("3.141596")
⇒3.141596
str2num (["1, 2, 3"; "4, 5, 6"])
⇒123
456
The optional second output, state, is logically true when the conversion is successful.
If the conversion fails the numeric output, x, is empty and state is false.
Caution: As str2num uses the eval function to do the conversion, str2num will
execute any code contained in the string s. Use str2double for a safer and faster
conversion.
For cell array of strings use str2double.
See also: [str2double], page 94,[eval], page 157.
toascii (s)
Return ASCII representation of sin a matrix.
For example:
toascii ("ASCII")
⇒[ 65, 83, 67, 73, 73 ]
See also: [char], page 71.
tolower (s)
lower (s)
Return a copy of the string or cell string s, with each uppercase character replaced
by the corresponding lowercase one; non-alphabetic characters are left unchanged.
For example:
tolower ("MiXeD cAsE 123")
⇒"mixed case 123"
See also: [toupper], page 95.
toupper (s)
upper (s)
Return a copy of the string or cell string s, with each lowercase character replaced by
the corresponding uppercase one; non-alphabetic characters are left unchanged.
For example:
toupper ("MiXeD cAsE 123")
⇒"MIXED CASE 123"
See also: [tolower], page 95.

96 GNU Octave
do_string_escapes (string)
Convert escape sequences in string to the characters they represent.
Escape sequences begin with a leading backslash (’\’) followed by 1–3 characters
(.e.g., "\n" =>newline).
See also: [undo string escapes], page 96.
undo_string_escapes (s)
Convert special characters in strings back to their escaped forms.
For example, the expression
bell = "\a";
assigns the value of the alert character (control-g, ASCII code 7) to the string variable
bell. If this string is printed, the system will ring the terminal bell (if it is possible).
This is normally the desired outcome. However, sometimes it is useful to be able to
print the original representation of the string, with the special characters replaced by
their escape sequences. For example,
octave:13> undo_string_escapes (bell)
ans = \a
replaces the unprintable alert character with its printable representation.
See also: [do string escapes], page 96.
5.7 Character Class Functions
Octave also provides the following character class test functions patterned after the functions
in the standard C library. They all operate on string arrays and return matrices of zeros and
ones. Elements that are nonzero indicate that the condition was true for the corresponding
character in the string array. For example:
isalpha ("!Q@WERT^Y&")
⇒[0,1,0,1,1,1,1,0,1,0]
isalnum (s)
Return a logical array which is true where the elements of sare letters or digits and
false where they are not.
This is equivalent to (isalpha (s) | isdigit (s)).
See also: [isalpha], page 96,[isdigit], page 97,[ispunct], page 97,[isspace], page 97,
[iscntrl], page 97.
isalpha (s)
Return a logical array which is true where the elements of sare letters and false where
they are not.
This is equivalent to (islower (s) | isupper (s)).
See also: [isdigit], page 97,[ispunct], page 97,[isspace], page 97,[iscntrl], page 97,
[isalnum], page 96,[islower], page 97,[isupper], page 97.
Chapter 5: Strings 97
isletter (s)
Return a logical array which is true where the elements of sare letters and false where
they are not.
This is an alias for the isalpha function.
See also: [isalpha], page 96,[isdigit], page 97,[ispunct], page 97,[isspace], page 97,
[iscntrl], page 97,[isalnum], page 96.
islower (s)
Return a logical array which is true where the elements of sare lowercase letters and
false where they are not.
See also: [isupper], page 97,[isalpha], page 96,[isletter], page 97,[isalnum], page 96.
isupper (s)
Return a logical array which is true where the elements of sare uppercase letters and
false where they are not.
See also: [islower], page 97,[isalpha], page 96,[isletter], page 97,[isalnum], page 96.
isdigit (s)
Return a logical array which is true where the elements of sare decimal digits (0-9)
and false where they are not.
See also: [isxdigit], page 97,[isalpha], page 96,[isletter], page 97,[ispunct], page 97,
[isspace], page 97,[iscntrl], page 97.
isxdigit (s)
Return a logical array which is true where the elements of sare hexadecimal digits
(0-9 and a-fA-F).
See also: [isdigit], page 97.
ispunct (s)
Return a logical array which is true where the elements of sare punctuation characters
and false where they are not.
See also: [isalpha], page 96,[isdigit], page 97,[isspace], page 97,[iscntrl], page 97.
isspace (s)
Return a logical array which is true where the elements of sare whitespace characters
(space, formfeed, newline, carriage return, tab, and vertical tab) and false where they
are not.
See also: [iscntrl], page 97,[ispunct], page 97,[isalpha], page 96,[isdigit], page 97.
iscntrl (s)
Return a logical array which is true where the elements of sare control characters
and false where they are not.
See also: [ispunct], page 97,[isspace], page 97,[isalpha], page 96,[isdigit], page 97.
isgraph (s)
Return a logical array which is true where the elements of sare printable characters
(but not the space character) and false where they are not.
See also: [isprint], page 98.
98 GNU Octave
isprint (s)
Return a logical array which is true where the elements of sare printable characters
(including the space character) and false where they are not.
See also: [isgraph], page 97.
isascii (s)
Return a logical array which is true where the elements of sare ASCII characters (in
the range 0 to 127 decimal) and false where they are not.
isstrprop (str,prop)
Test character string properties.
For example:
isstrprop ("abc123", "alpha")
⇒[1, 1, 1, 0, 0, 0]
If str is a cell array, isstrpop is applied recursively to each element of the cell array.
Numeric arrays are converted to character strings.
The second argument prop must be one of
"alpha" True for characters that are alphabetic (letters).
"alnum"
"alphanum"
True for characters that are alphabetic or digits.
"lower" True for lowercase letters.
"upper" True for uppercase letters.
"digit" True for decimal digits (0-9).
"xdigit" True for hexadecimal digits (a-fA-F0-9).
"space"
"wspace" True for whitespace characters (space, formfeed, newline, carriage return,
tab, vertical tab).
"punct" True for punctuation characters (printing characters except space or letter
or digit).
"cntrl" True for control characters.
"graph"
"graphic"
True for printing characters except space.
"print" True for printing characters including space.
"ascii" True for characters that are in the range of ASCII encoding.
See also: [isalpha], page 96,[isalnum], page 96,[islower], page 97,[isupper], page 97,
[isdigit], page 97,[isxdigit], page 97,[isspace], page 97,[ispunct], page 97,[iscntrl],
page 97,[isgraph], page 97,[isprint], page 98,[isascii], page 98.
99
6 Data Containers
Octave includes support for two different mechanisms to contain arbitrary data types in
the same variable. Structures, which are C-like, and are indexed with named fields, and
cell arrays, where each element of the array can have a different data type and or shape.
Multiple input arguments and return values of functions are organized as another data
container, the comma separated list.
6.1 Structures
Octave includes support for organizing data in structures. The current implementation
uses an associative array with indices limited to strings, but the syntax is more like C-style
structures.
6.1.1 Basic Usage and Examples
Here are some examples of using data structures in Octave.
Elements of structures can be of any value type. For example, the three expressions
x.a = 1;
x.b = [1, 2; 3, 4];
x.c = "string";
create a structure with three elements. The ‘.’ character separates the structure name from
the field name and indicates to Octave that this variable is a structure. To print the value
of the structure you can type its name, just as for any other variable:
x
⇒x =
{
a=1
b =
1 2
3 4
c = string
}
Note that Octave may print the elements in any order.
Structures may be copied just like any other variable:
100 GNU Octave
y=x
⇒y =
{
a=1
b =
1 2
3 4
c = string
}
Since structures are themselves values, structure elements may reference other structures.
The following statements change the value of the element bof the structure xto be a data
structure containing the single element d, which has a value of 3.
x.b.d = 3;
x.b
⇒ans =
{
d=3
}
x
⇒x =
{
a=1
b =
{
d=3
}
c = string
}
Note that when Octave prints the value of a structure that contains other structures,
only a few levels are displayed. For example:

Chapter 6: Data Containers 101
a.b.c.d.e = 1;
a
⇒a =
{
b =
{
c =
{
1x1 struct array containing the fields:
d: 1x1 struct
}
}
}
This prevents long and confusing output from large deeply nested structures. The number
of levels to print for nested structures may be set with the function struct_levels_to_
print, and the function print_struct_array_contents may be used to enable printing
of the contents of structure arrays.
val = struct_levels_to_print ()
old_val = struct_levels_to_print (new_val)
struct_levels_to_print (new_val,"local")
Query or set the internal variable that specifies the number of structure levels to
display.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [print struct array contents], page 101.
val = print_struct_array_contents ()
old_val = print_struct_array_contents (new_val)
print_struct_array_contents (new_val,"local")
Query or set the internal variable that specifies whether to print struct array contents.
If true, values of struct array elements are printed. This variable does not affect scalar
structures whose elements are always printed. In both cases, however, printing will
be limited to the number of levels specified by struct levels to print.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [struct levels to print], page 101.
Functions can return structures. For example, the following function separates the real
and complex parts of a matrix and stores them in two elements of the same structure
variable.
102 GNU Octave
function y = f (x)
y.re = real (x);
y.im = imag (x);
endfunction
When called with a complex-valued argument, freturns the data structure containing
the real and imaginary parts of the original function argument.
f (rand (2) + rand (2) * I)
⇒ans =
{
im =
0.26475 0.14828
0.18436 0.83669
re =
0.040239 0.242160
0.238081 0.402523
}
Function return lists can include structure elements, and they may be indexed like any
other variable. For example:
[ x.u, x.s(2:3,2:3), x.v ] = svd ([1, 2; 3, 4]);
x
⇒x =
{
u =
-0.40455 -0.91451
-0.91451 0.40455
s =
0.00000 0.00000 0.00000
0.00000 5.46499 0.00000
0.00000 0.00000 0.36597
v =
-0.57605 0.81742
-0.81742 -0.57605
}
It is also possible to cycle through all the elements of a structure in a loop, using a
special form of the for statement (see Section 10.5.1 [Looping Over Structure Elements],
page 167).
Chapter 6: Data Containers 103
6.1.2 Structure Arrays
A structure array is a particular instance of a structure, where each of the fields of the
structure is represented by a cell array. Each of these cell arrays has the same dimensions.
Conceptually, a structure array can also be seen as an array of structures with identical
fields. An example of the creation of a structure array is
x(1).a = "string1";
x(2).a = "string2";
x(1).b = 1;
x(2).b = 2;
which creates a 2-by-1 structure array with two fields. Another way to create a structure
array is with the struct function (see Section 6.1.3 [Creating Structures], page 104). As
previously, to print the value of the structure array, you can type its name:
x
⇒x =
{
1x2 struct array containing the fields:
a
b
}
Individual elements of the structure array can be returned by indexing the variable like
x(1), which returns a structure with two fields:
x(1)
⇒ans =
{
a = string1
b = 1
}
Furthermore, the structure array can return a comma separated list of field values (see
Section 6.3 [Comma Separated Lists], page 120), if indexed by one of its own field names.
For example:
x.a
⇒ans = string1
ans = string2
Here is another example, using this comma separated list on the left-hand side of an
assignment:
[x.a] = deal ("new string1", "new string2");
x(1).a
⇒ans = new string1
x(2).a
⇒ans = new string2
Just as for numerical arrays, it is possible to use vectors as indices (see Section 8.1 [Index
Expressions], page 135):
104 GNU Octave
x(3:4) = x(1:2);
[x([1,3]).a] = deal ("other string1", "other string2");
x.a
⇒ans = other string1
ans = new string2
ans = other string2
ans = new string2
The function size will return the size of the structure. For the example above
size (x)
⇒ans =
1 4
Elements can be deleted from a structure array in a similar manner to a numerical array,
by assigning the elements to an empty matrix. For example
in = struct ("call1", {x, Inf, "last"},
"call2", {x, Inf, "first"})
⇒in =
{
1x3 struct array containing the fields:
call1
call2
}
in(1) = [];
in.call1
⇒ans = Inf
ans = last
6.1.3 Creating Structures
Besides the index operator ".", Octave can use dynamic naming "(var)" or the struct
function to create structures. Dynamic naming uses the string value of a variable as the
field name. For example:
a = "field2";
x.a = 1;
x.(a) = 2;
x
⇒x =
{
a = 1
field2 = 2
}
Dynamic indexing also allows you to use arbitrary strings, not merely valid Octave identifiers
(note that this does not work on matlab):

Chapter 6: Data Containers 105
a = "long field with spaces (and funny char$)";
x.a = 1;
x.(a) = 2;
x
⇒x =
{
a = 1
long field with spaces (and funny char$) = 2
}
The warning id Octave:language-extension can be enabled to warn about this usage.
See [warning ids], page 223.
More realistically, all of the functions that operate on strings can be used to build the
correct field name before it is entered into the data structure.
names = ["Bill"; "Mary"; "John"];
ages = [37; 26; 31];
for i = 1:rows (names)
database.(names(i,:)) = ages(i);
endfor
database
⇒database =
{
Bill = 37
Mary = 26
John = 31
}
The third way to create structures is the struct command. struct takes pairs of
arguments, where the first argument in the pair is the fieldname to include in the structure
and the second is a scalar or cell array, representing the values to include in the structure
or structure array. For example:
struct ("field1", 1, "field2", 2)
⇒ans =
{
field1 = 1
field2 = 2
}
If the values passed to struct are a mix of scalar and cell arrays, then the scalar argu-
ments are expanded to create a structure array with a consistent dimension. For example:
106 GNU Octave
s = struct ("field1", {1, "one"}, "field2", {2, "two"},
"field3", 3);
s.field1
⇒ans = 1
ans = one
s.field2
⇒ans = 2
ans = two
s.field3
⇒ans = 3
ans = 3
If you want to create a struct which contains a cell array as an individual field, you must
wrap it in another cell array as shown in the following example:
struct ("field1", {{1, "one"}}, "field2", 2)
⇒ans =
{
field1 =
{
[1,1] = 1
[1,2] = one
}
field2 = 2
}
s= struct ()
s= struct (field1,value1,field2,value2, . . . )
s= struct (obj)
Create a scalar or array structure and initialize its values.
The field1,field2, . . . variables are strings specifying the names of the fields and the
value1,value2, . . . variables can be of any type.
If the values are cell arrays, create a structure array and initialize its values. The
dimensions of each cell array of values must match. Singleton cells and non-cell values
are repeated so that they fill the entire array. If the cells are empty, create an empty
structure array with the specified field names.
If the argument is an object, return the underlying struct.
Observe that the syntax is optimized for struct arrays. Consider the following exam-
ples:
Chapter 6: Data Containers 107
struct ("foo", 1)
⇒scalar structure containing the fields:
foo = 1
struct ("foo", {})
⇒0x0 struct array containing the fields:
foo
struct ("foo", { {} })
⇒scalar structure containing the fields:
foo = {}(0x0)
struct ("foo", {1, 2, 3})
⇒1x3 struct array containing the fields:
foo
The first case is an ordinary scalar struct—one field, one value. The second produces
an empty struct array with one field and no values, since being passed an empty cell
array of struct array values. When the value is a cell array containing a single entry,
this becomes a scalar struct with that single entry as the value of the field. That
single entry happens to be an empty cell array.
Finally, if the value is a non-scalar cell array, then struct produces a struct array.
See also: [cell2struct], page 120,[fieldnames], page 107,[getfield], page 109,[setfield],
page 108,[rmfield], page 109,[isfield], page 108,[orderfields], page 109,[isstruct],
page 107,[structfun], page 538.
The function isstruct can be used to test if an object is a structure or a structure
array.
isstruct (x)
Return true if xis a structure or a structure array.
See also: [ismatrix], page 63,[iscell], page 113,[isa], page 39.
6.1.4 Manipulating Structures
Other functions that can manipulate the fields of a structure are given below.
numfields (s)
Return the number of fields of the structure s.
See also: [fieldnames], page 107.
names = fieldnames (struct)
names = fieldnames (obj)
names = fieldnames (javaobj)
names = fieldnames ("javaclassname")
Return a cell array of strings with the names of the fields in the specified input.
When the input is a structure struct, the names are the elements of the structure.

108 GNU Octave
When the input is an Octave object obj, the names are the public properties of the
object.
When the input is a Java object javaobj or a string containing the name of a Java
class javaclassname, the names are the public fields (data members) of the object or
class.
See also: [numfields], page 107,[isfield], page 108,[orderfields], page 109,[struct],
page 106,[methods], page 771.
isfield (x,"name")
isfield (x,name)
Return true if the xis a structure and it includes an element named name.
If name is a cell array of strings then a logical array of equal dimension is returned.
See also: [fieldnames], page 107.
sout = setfield (s,field,val)
sout = setfield (s,sidx1,field1,fidx1,sidx2,field2,fidx2, . . . , val)
Return a copy of the structure swith the field member field set to the value val.
For example:
s= struct ();
s= setfield (s, "foo bar", 42);
This is equivalent to
s.("foo bar") = 42;
Note that ordinary structure syntax s.foo bar = 42 cannot be used here, as the
field name is not a valid Octave identifier because of the space character. Using
arbitrary strings for field names is incompatible with matlab, and this usage will
emit a warning if the warning ID Octave:language-extension is enabled. See
[XREFwarning ids], page 223.
With the second calling form, set a field of a structure array. The input sidx selects
an element of the structure array, field specifies the field name of the selected element,
and fidx selects which element of the field (in the case of an array or cell array). The
sidx,field, and fidx inputs can be repeated to address nested structure array elements.
The structure array index and field element index must be cell arrays while the field
name must be a string.
For example:
s= struct ("baz", 42);
setfield (s, {1}, "foo", {1}, "bar", 54)
⇒ans =
scalar structure containing the fields:
baz = 42
foo =
scalar structure containing the fields:
bar = 54
The example begins with an ordinary scalar structure to which a nested scalar struc-
ture is added. In all cases, if the structure index sidx is not specified it defaults to
Chapter 6: Data Containers 109
1 (scalar structure). Thus, the example above could be written more concisely as
setfield (s, "foo", "bar", 54)
Finally, an example with nested structure arrays:
sa.foo = 1;
sa = setfield (sa, {2}, "bar", {3}, "baz", {1, 4}, 5);
sa(2).bar(3)
⇒ans =
scalar structure containing the fields:
baz = 0 0 0 5
Here sa is a structure array whose field at elements 1 and 2 is in turn another structure
array whose third element is a simple scalar structure. The terminal scalar structure
has a field which contains a matrix value.
Note that the same result as in the above example could be achieved by:
sa.foo = 1;
sa(2).bar(3).baz(1,4) = 5
See also: [getfield], page 109,[rmfield], page 109,[orderfields], page 109,[isfield],
page 108,[fieldnames], page 107,[isstruct], page 107,[struct], page 106.
val = getfield (s,field)
val = getfield (s,sidx1,field1,fidx1, . . . )
Get the value of the field named field from a structure or nested structure s.
If sis a structure array then sidx selects an element of the structure array, field
specifies the field name of the selected element, and fidx selects which element of
the field (in the case of an array or cell array). See setfield for a more complete
description of the syntax.
See also: [setfield], page 108,[rmfield], page 109,[orderfields], page 109,[isfield],
page 108,[fieldnames], page 107,[isstruct], page 107,[struct], page 106.
sout = rmfield (s,"f")
sout = rmfield (s,f)
Return a copy of the structure (array) swith the field fremoved.
If fis a cell array of strings or a character array, remove each of the named fields.
See also: [orderfields], page 109,[fieldnames], page 107,[isfield], page 108.
sout = orderfields (s1)
sout = orderfields (s1,s2)
sout = orderfields (s1,{cellstr})
sout = orderfields (s1,p)
[sout,p] = orderfields (. . . )
Return a copy of s1 with fields arranged alphabetically, or as specified by the second
input.
Given one input struct s1, arrange field names alphabetically.
If a second struct argument is given, arrange field names in s1 as they appear in s2.
The second argument may also specify the order in a cell array of strings cellstr. The
second argument may also be a permutation vector.
110 GNU Octave
The optional second output argument pis the permutation vector which converts the
original name order to the new name order.
Examples:
s = struct ("d", 4, "b", 2, "a", 1, "c", 3);
t1 = orderfields (s)
⇒t1 =
{
a = 1
b = 2
c = 3
d = 4
}
t = struct ("d", {}, "c", {}, "b", {}, "a", {});
t2 = orderfields (s, t)
⇒t2 =
{
d = 4
c = 3
b = 2
a = 1
}
t3 = orderfields (s, [3, 2, 4, 1])
⇒t3 =
{
a = 1
b = 2
c = 3
d = 4
}
[t4, p] = orderfields (s, {"d", "c", "b", "a"})
⇒t4 =
{
d = 4
c = 3
b = 2
a = 1
}
p =
1
4
2
3
See also: [fieldnames], page 107,[getfield], page 109,[setfield], page 108,[rmfield],
page 109,[isfield], page 108,[isstruct], page 107,[struct], page 106.
Chapter 6: Data Containers 111
substruct (type,subs, . . .)
Create a subscript structure for use with subsref or subsasgn.
For example:
idx = substruct ("()", {3, ":"})
⇒idx =
{
type = ()
subs =
{
[1,1] = 3
[1,2] = :
}
}
x = [1, 2, 3;
4, 5, 6;
7, 8, 9];
subsref (x, idx)
⇒789
See also: [subsref], page 775,[subsasgn], page 776.
6.1.5 Processing Data in Structures
The simplest way to process data in a structure is within a for loop (see Section 10.5.1
[Looping Over Structure Elements], page 167). A similar effect can be achieved with the
structfun function, where a user defined function is applied to each field of the structure.
See [structfun], page 538.
Alternatively, to process the data in a structure, the structure might be converted to
another type of container before being treated.
c= struct2cell (s)
Create a new cell array from the objects stored in the struct object.
If fis the number of fields in the structure, the resulting cell array will have a
dimension vector corresponding to [fsize(s)]. For example:
112 GNU Octave
s = struct ("name", {"Peter", "Hannah", "Robert"},
"age", {23, 16, 3});
c = struct2cell (s)
⇒c = {2x1x3 Cell Array}
c(1,1,:)(:)
⇒{
[1,1] = Peter
[2,1] = Hannah
[3,1] = Robert
}
c(2,1,:)(:)
⇒{
[1,1] = 23
[2,1] = 16
[3,1] = 3
}
See also: [cell2struct], page 120,[fieldnames], page 107.
6.2 Cell Arrays
It can be both necessary and convenient to store several variables of different size or type
in one variable. A cell array is a container class able to do just that. In general cell arrays
work just like N-dimensional arrays with the exception of the use of ‘{’ and ‘}’ as allocation
and indexing operators.
6.2.1 Basic Usage of Cell Arrays
As an example, the following code creates a cell array containing a string and a 2-by-2
random matrix
c = {"a string", rand(2, 2)};
To access the elements of a cell array, it can be indexed with the {and }operators. Thus,
the variable created in the previous example can be indexed like this:
c{1}
⇒ans = a string
As with numerical arrays several elements of a cell array can be extracted by indexing with
a vector of indexes
c{1:2}
⇒ans = a string
⇒ans =
0.593993 0.627732
0.377037 0.033643
The indexing operators can also be used to insert or overwrite elements of a cell array.
The following code inserts the scalar 3 on the third place of the previously created cell array
Chapter 6: Data Containers 113
c{3} = 3
⇒c =
{
[1,1] = a string
[1,2] =
0.593993 0.627732
0.377037 0.033643
[1,3] = 3
}
Details on indexing cell arrays are explained in Section 6.2.3 [Indexing Cell Arrays],
page 116.
In general nested cell arrays are displayed hierarchically as in the previous example.
In some circumstances it makes sense to reference them by their index, and this can be
performed by the celldisp function.
celldisp (c)
celldisp (c,name)
Recursively display the contents of a cell array.
By default the values are displayed with the name of the variable c. However, this
name can be replaced with the variable name. For example:
c = {1, 2, {31, 32}};
celldisp (c, "b")
⇒b{1} =
1
b{2} =
2
b{3}{1} =
31
b{3}{2} =
32
See also: [disp], page 243.
To test if an object is a cell array, use the iscell function. For example:
iscell (c)
⇒ans = 1
iscell (3)
⇒ans = 0
iscell (x)
Return true if xis a cell array object.
See also: [ismatrix], page 63,[isstruct], page 107,[iscellstr], page 119,[isa], page 39.
114 GNU Octave
6.2.2 Creating Cell Arrays
The introductory example (see Section 6.2.1 [Basic Usage of Cell Arrays], page 112) showed
how to create a cell array containing currently available variables. In many situations,
however, it is useful to create a cell array and then fill it with data.
The cell function returns a cell array of a given size, containing empty matrices. This
function is similar to the zeros function for creating new numerical arrays. The following
example creates a 2-by-2 cell array containing empty matrices
c = cell (2,2)
⇒c =
{
[1,1] = [](0x0)
[2,1] = [](0x0)
[1,2] = [](0x0)
[2,2] = [](0x0)
}
Just like numerical arrays, cell arrays can be multi-dimensional. The cell function
accepts any number of positive integers to describe the size of the returned cell array. It is
also possible to set the size of the cell array through a vector of positive integers. In the
following example two cell arrays of equal size are created, and the size of the first one is
displayed
c1 = cell (3, 4, 5);
c2 = cell ( [3, 4, 5] );
size (c1)
⇒ans =
345
As can be seen, the [size], page 45, function also works for cell arrays. As do other functions
describing the size of an object, such as [length], page 45,[numel], page 44,[rows], page 44,
and [columns], page 44.
cell (n)
cell (m,n)
cell (m,n,k, . . .)
cell ([m n . . .])
Create a new cell array object.
If invoked with a single scalar integer argument, return a square NxN cell array. If
invoked with two or more scalar integer arguments, or a vector of integer values,
return an array with the given dimensions.
See also: [cellstr], page 119,[mat2cell], page 115,[num2cell], page 114,[struct2cell],
page 111.
As an alternative to creating empty cell arrays, and then filling them, it is possible to
convert numerical arrays into cell arrays using the num2cell,mat2cell and cellslices
functions.
Chapter 6: Data Containers 115
C= num2cell (A)
C= num2cell (A,dim)
Convert the numeric matrix Ato a cell array.
If dim is defined, the value Cis of dimension 1 in this dimension and the elements of
Aare placed into Cin slices. For example:
num2cell ([1,2;3,4])
⇒{
[1,1] = 1
[2,1] = 3
[1,2] = 2
[2,2] = 4
}
num2cell ([1,2;3,4],1)
⇒{
[1,1] =
1
3
[1,2] =
2
4
}
See also: [mat2cell], page 115.
C= mat2cell (A,m,n)
C= mat2cell (A,d1,d2, . . . )
C= mat2cell (A,r)
Convert the matrix Ato a cell array.
If Ais 2-D, then it is required that sum (m) == size (A, 1) and sum (n) == size (A,
2). Similarly, if Ais multi-dimensional and the number of dimensional arguments is
equal to the dimensions of A, then it is required that sum (di) == size (A, i).
Given a single dimensional argument r, the other dimensional arguments are assumed
to equal size (A,i).
An example of the use of mat2cell is
mat2cell (reshape (1:16,4,4), [3,1], [3,1])
⇒
{
[1,1] =
159
2 6 10
3 7 11
[2,1] =
116 GNU Octave
4 8 12
[1,2] =
13
14
15
[2,2] = 16
}
See also: [num2cell], page 114,[cell2mat], page 119.
sl = cellslices (x,lb,ub,dim)
Given an array x, this function produces a cell array of slices from the array deter-
mined by the index vectors lb,ub, for lower and upper bounds, respectively.
In other words, it is equivalent to the following code:
n = length (lb);
sl = cell (1, n);
for i = 1:length (lb)
sl{i} = x(:,...,lb(i):ub(i),...,:);
endfor
The position of the index is determined by dim. If not specified, slicing is done along
the first non-singleton dimension.
See also: [cell2mat], page 119,[cellindexmat], page 118,[cellfun], page 536.
6.2.3 Indexing Cell Arrays
As shown in see Section 6.2.1 [Basic Usage of Cell Arrays], page 112, elements can be
extracted from cell arrays using the ‘{’ and ‘}’ operators. If you want to extract or access
subarrays which are still cell arrays, you need to use the ‘(’ and ‘)’ operators. The following
example illustrates the difference:
c = {"1", "2", "3"; "x", "y", "z"; "4", "5", "6"};
c{2,3}
⇒ans = z
c(2,3)
⇒ans =
{
[1,1] = z
}
So with ‘{}’ you access elements of a cell array, while with ‘()’ you access a sub array of a
cell array.
Using the ‘(’ and ‘)’ operators, indexing works for cell arrays like for multi-dimensional
arrays. As an example, all the rows of the first and third column of a cell array can be set
to 0with the following command:
Chapter 6: Data Containers 117
c(:, [1, 3]) = {0}
⇒=
{
[1,1] = 0
[2,1] = 0
[3,1] = 0
[1,2] = 2
[2,2] = y
[3,2] = 5
[1,3] = 0
[2,3] = 0
[3,3] = 0
}
Note, that the above can also be achieved like this:
c(:, [1, 3]) = 0;
Here, the scalar ‘0’ is automatically promoted to cell array ‘{0}’ and then assigned to the
subarray of c.
To give another example for indexing cell arrays with ‘()’, you can exchange the first
and the second row of a cell array as in the following command:
c = {1, 2, 3; 4, 5, 6};
c([1, 2], :) = c([2, 1], :)
⇒=
{
[1,1] = 4
[2,1] = 1
[1,2] = 5
[2,2] = 2
[1,3] = 6
[2,3] = 3
}
Accessing multiple elements of a cell array with the ‘{’ and ‘}’ operators will result in
a comma-separated list of all the requested elements (see Section 6.3 [Comma Separated
Lists], page 120). Using the ‘{’ and ‘}’ operators the first two rows in the above example
can be swapped back like this:
[c{[1,2], :}] = deal (c{[2, 1], :})
⇒=
{
[1,1] = 1
[2,1] = 4
[1,2] = 2
[2,2] = 5
[1,3] = 3
[2,3] = 6
}
118 GNU Octave
As for struct arrays and numerical arrays, the empty matrix ‘[]’ can be used to delete
elements from a cell array:
x = {"1", "2"; "3", "4"};
x(1, :) = []
⇒x =
{
[1,1] = 3
[1,2] = 4
}
The following example shows how to just remove the contents of cell array elements but
not delete the space for them:
x = {"1", "2"; "3", "4"};
x(1, :) = {[]}
⇒x =
{
[1,1] = [](0x0)
[2,1] = 3
[1,2] = [](0x0)
[2,2] = 4
}
The indexing operations operate on the cell array and not on the objects within the cell
array. By contrast, cellindexmat applies matrix indexing to the objects within each cell
array entry and returns the requested values.
y= cellindexmat (x,varargin)
Perform indexing of matrices in a cell array.
Given a cell array of matrices x, this function computes
Y = cell (size (X));
for i = 1:numel (X)
Y{i} = X{i}(varargin{1}, varargin{2}, ..., varargin{N});
endfor
The indexing arguments may be scalar (2), arrays ([1, 3]), ranges (1:3), or the colon
operator (":"). However, the indexing keyword end is not available.
See also: [cellslices], page 116,[cellfun], page 536.
6.2.4 Cell Arrays of Strings
One common use of cell arrays is to store multiple strings in the same variable. It is also
possible to store multiple strings in a character matrix by letting each row be a string. This,
however, introduces the problem that all strings must be of equal length. Therefore, it is
recommended to use cell arrays to store multiple strings. For cases, where the character
matrix representation is required for an operation, there are several functions that convert
a cell array of strings to a character array and back. char and strvcat convert cell arrays
to a character array (see Section 5.3.1 [Concatenating Strings], page 70), while the function
cellstr converts a character array to a cell array of strings:
Chapter 6: Data Containers 119
a = ["hello"; "world"];
c = cellstr (a)
⇒c =
{
[1,1] = hello
[2,1] = world
}
cstr = cellstr (strmat)
Create a new cell array object from the elements of the string array strmat.
Each row of strmat becomes an element of cstr. Any trailing spaces in a row are
deleted before conversion.
To convert back from a cellstr to a character array use char.
See also: [cell], page 114,[char], page 71.
One further advantage of using cell arrays to store multiple strings is that most functions
for string manipulations included with Octave support this representation. As an example,
it is possible to compare one string with many others using the strcmp function. If one
of the arguments to this function is a string and the other is a cell array of strings, each
element of the cell array will be compared to the string argument:
c = {"hello", "world"};
strcmp ("hello", c)
⇒ans =
1 0
The following string functions support cell arrays of strings: char,strvcat,strcat (see
Section 5.3.1 [Concatenating Strings], page 70), strcmp,strncmp,strcmpi,strncmpi (see
Section 5.4 [Comparing Strings], page 76), str2double,deblank,strtrim,strtrunc,
strfind,strmatch, , regexp,regexpi (see Section 5.5 [Manipulating Strings], page 77)
and str2double (see Section 5.6 [String Conversions], page 91).
The function iscellstr can be used to test if an object is a cell array of strings.
iscellstr (cell)
Return true if every element of the cell array cell is a character string.
See also: [ischar], page 68.
6.2.5 Processing Data in Cell Arrays
Data that is stored in a cell array can be processed in several ways depending on the actual
data. The simplest way to process that data is to iterate through it using one or more
for loops. The same idea can be implemented more easily through the use of the cellfun
function that calls a user-specified function on all elements of a cell array. See [cellfun],
page 536.
An alternative is to convert the data to a different container, such as a matrix or a data
structure. Depending on the data this is possible using the cell2mat and cell2struct
functions.

120 GNU Octave
m= cell2mat (c)
Convert the cell array cinto a matrix by concatenating all elements of cinto a
hyperrectangle.
Elements of cmust be numeric, logical, or char matrices; or cell arrays; or structs;
and cat must be able to concatenate them together.
See also: [mat2cell], page 115,[num2cell], page 114.
cell2struct (cell,fields)
cell2struct (cell,fields,dim)
Convert cell to a structure.
The number of fields in fields must match the number of elements in cell along dimen-
sion dim, that is numel (fields) == size (cell,dim). If dim is omitted, a value of
1 is assumed.
A = cell2struct ({"Peter", "Hannah", "Robert";
185, 170, 168},
{"Name","Height"}, 1);
A(1)
⇒{
Name = Peter
Height = 185
}
See also: [struct2cell], page 111,[cell2mat], page 119,[struct], page 106.
6.3 Comma Separated Lists
Comma separated lists1are the basic argument type to all Octave functions - both for input
and return arguments. In the example
max (a,b)
‘a,b’ is a comma separated list. Comma separated lists can appear on both the right and
left hand side of an assignment. For example
x=[1010011;0000007];
[i,j] = find (x, 2, "last");
Here, ‘x, 2, "last"’ is a comma separated list constituting the input arguments of find.
find returns a comma separated list of output arguments which is assigned element by
element to the comma separated list ‘i,j’.
Another example of where comma separated lists are used is in the creation of a new
array with [] (see Section 4.1 [Matrices], page 48) or the creation of a cell array with {}
(see Section 6.2.1 [Basic Usage of Cell Arrays], page 112). In the expressions
a = [1, 2, 3, 4];
c = {4, 5, 6, 7};
both ‘1, 2, 3, 4’ and ‘4, 5, 6, 7’ are comma separated lists.
1Comma-separated lists are also sometimes informally referred to as cs-lists.
Chapter 6: Data Containers 121
Comma separated lists cannot be directly manipulated by the user. However, both
structure arrays and cell arrays can be converted into comma separated lists, and thus used
in place of explicitly written comma separated lists. This feature is useful in many ways,
as will be shown in the following subsections.
6.3.1 Comma Separated Lists Generated from Cell Arrays
As has been mentioned above (see Section 6.2.3 [Indexing Cell Arrays], page 116), elements
of a cell array can be extracted into a comma separated list with the {and }operators. By
surrounding this list with [and ], it can be concatenated into an array. For example:
a = {1, [2, 3], 4, 5, 6};
b = [a{1:4}]
⇒b =
12345
Similarly, it is possible to create a new cell array containing cell elements selected with
{}. By surrounding the list with ‘{’ and ‘}’ a new cell array will be created, as the following
example illustrates:
a = {1, rand(2, 2), "three"};
b={a{[1,3]}}
⇒b =
{
[1,1] = 1
[1,2] = three
}
Furthermore, cell elements (accessed by {}) can be passed directly to a function. The
list of elements from the cell array will be passed as an argument list to a given function
as if it is called with the elements as individual arguments. The two calls to printf in the
following example are identical but the latter is simpler and can handle cell arrays of an
arbitrary size:
c = {"GNU", "Octave", "is", "Free", "Software"};
printf ("%s ", c{1}, c{2}, c{3}, c{4}, c{5});
aGNU Octave is Free Software
printf ("%s ", c{:});
aGNU Octave is Free Software
If used on the left-hand side of an assignment, a comma separated list generated with
{} can be assigned to. An example is
122 GNU Octave
in{1} = [10, 20, 30];
in{2} = inf;
in{3} = "last";
in{4} = "first";
out = cell (4, 1);
[out{1:3}] = in{1 : 3};
[out{4:6}] = in{[1, 2, 4]})
⇒out =
{
[1,1] =
10 20 30
[2,1] = Inf
[3,1] = last
[4,1] =
10 20 30
[5,1] = Inf
[6,1] = first
}
6.3.2 Comma Separated Lists Generated from Structure Arrays
Structure arrays can equally be used to create comma separated lists. This is done by
addressing one of the fields of a structure array. For example:
x = ceil (randn (10, 1));
in = struct ("call1", {x, 3, "last"},
"call2", {x, inf, "first"});
out = struct ("call1", cell (2, 1), "call2", cell (2, 1));
[out.call1] = find (in.call1);
[out.call2] = find (in.call2);
123
7 Variables
Variables let you give names to values and refer to them later. You have already seen
variables in many of the examples. The name of a variable must be a sequence of letters,
digits and underscores, but it may not begin with a digit. Octave does not enforce a limit
on the length of variable names, but it is seldom useful to have variables with names longer
than about 30 characters. The following are all valid variable names
x
x15
__foo_bar_baz__
fucnrdthsucngtagdjb
However, names like __foo_bar_baz__ that begin and end with two underscores are under-
stood to be reserved for internal use by Octave. You should not use them in code you write,
except to access Octave’s documented internal variables and built-in symbolic constants.
Case is significant in variable names. The symbols aand Aare distinct variables.
A variable name is a valid expression by itself. It represents the variable’s current value.
Variables are given new values with assignment operators and increment operators. See
Section 8.6 [Assignment Expressions], page 151.
There is one built-in variable with a special meaning. The ans variable always contains
the result of the last computation, where the output wasn’t assigned to any variable. The
code a = cos (pi) will assign the value -1 to the variable a, but will not change the value
of ans. However, the code cos (pi) will set the value of ans to -1.
Variables in Octave do not have fixed types, so it is possible to first store a numeric
value in a variable and then to later use the same name to hold a string value in the same
program. Variables may not be used before they have been given a value. Doing so results
in an error.
[Automatic Variable]ans
The most recently computed result that was not explicitly assigned to a variable.
For example, after the expression
3^2 + 4^2
is evaluated, the value returned by ans is 25.
isvarname (name)
Return true if name is a valid variable name.
See also: [iskeyword], page 949,[exist], page 130,[who], page 128.
varname = genvarname (str)
varname = genvarname (str,exclusions)
Create valid unique variable name(s) from str.
If str is a cellstr, then a unique variable is created for each cell in str.
genvarname ({"foo", "foo"})
⇒{
[1,1] = foo
[1,2] = foo1
}
124 GNU Octave
If exclusions is given, then the variable(s) will be unique to each other and to exclu-
sions (exclusions may be either a string or a cellstr).
x = 3.141;
genvarname ("x", who ())
⇒x1
Note that the result is a char array or cell array of strings, not the variables themselves.
To define a variable, eval() can be used. The following trivial example sets xto 42.
name = genvarname ("x");
eval ([name " = 42"]);
⇒x = 42
This can be useful for creating unique struct field names.
x = struct ();
for i = 1:3
x.(genvarname ("a", fieldnames (x))) = i;
endfor
⇒x =
{
a = 1
a1 = 2
a2 = 3
}
Since variable names may only contain letters, digits, and underscores, genvarname
will replace any sequence of disallowed characters with an underscore. Also, variables
may not begin with a digit; in this case an ‘x’ is added before the variable name.
Variable names beginning and ending with two underscores "__" are valid, but they
are used internally by Octave and should generally be avoided; therefore, genvarname
will not generate such names.
genvarname will also ensure that returned names do not clash with keywords such as
"for" and "if". A number will be appended if necessary. Note, however, that this
does not include function names such as "sin". Such names should be included in
exclusions if necessary.
See also: [isvarname], page 123,[iskeyword], page 949,[exist], page 130,[who],
page 128,[tempname], page 281,[eval], page 157.
namelengthmax ()
Return the matlab compatible maximum variable name length.
Octave is capable of storing strings up to 231 −1 in length. However for matlab
compatibility all variable, function, and structure field names should be shorter than
the length returned by namelengthmax. In particular, variables stored to a matlab
file format (*.mat) will have their names truncated to this length.
7.1 Global Variables
A variable that has been declared global may be accessed from within a function body
without having to pass it as a formal parameter.
Chapter 7: Variables 125
A variable may be declared global using a global declaration statement. The following
statements are all global declarations.
global a
global a b
global c = 2
globald=3ef=5
A global variable may only be initialized once in a global statement. For example, after
executing the following code
global gvar = 1
global gvar = 2
the value of the global variable gvar is 1, not 2. Issuing a ‘clear gvar’ command does not
change the above behavior, but ‘clear all’ does.
It is necessary declare a variable as global within a function body in order to access it.
For example,
global x
function f ()
x = 1;
endfunction
f ()
does not set the value of the global variable xto 1. In order to change the value of the
global variable x, you must also declare it to be global within the function body, like this
function f ()
global x;
x = 1;
endfunction
Passing a global variable in a function parameter list will make a local copy and not
modify the global value. For example, given the function
function f (x)
x=0
endfunction
and the definition of xas a global variable at the top level,
global x = 13
the expression
f (x)
will display the value of xfrom inside the function as 0, but the value of xat the top level
remains unchanged, because the function works with a copy of its argument.
isglobal (name)
Return true if name is a globally visible variable.
For example:
global x
isglobal ("x")
⇒1
See also: [isvarname], page 123,[exist], page 130.
126 GNU Octave
7.2 Persistent Variables
A variable that has been declared persistent within a function will retain its contents in
memory between subsequent calls to the same function. The difference between persistent
variables and global variables is that persistent variables are local in scope to a particular
function and are not visible elsewhere.
The following example uses a persistent variable to create a function that prints the
number of times it has been called.
function count_calls ()
persistent calls = 0;
printf ("’count_calls’ has been called %d times\n",
++calls);
endfunction
for i = 1:3
count_calls ();
endfor
a’count_calls’ has been called 1 times
a’count_calls’ has been called 2 times
a’count_calls’ has been called 3 times
As the example shows, a variable may be declared persistent using a persistent decla-
ration statement. The following statements are all persistent declarations.
persistent a
persistent a b
persistent c = 2
persistent d = 3 e f = 5
The behavior of persistent variables is equivalent to the behavior of static variables in
C.
Like global variables, a persistent variable may only be initialized once. For example,
after executing the following code
persistent pvar = 1
persistent pvar = 2
the value of the persistent variable pvar is 1, not 2.
If a persistent variable is declared but not initialized to a specific value, it will contain an
empty matrix. So, it is also possible to initialize a persistent variable by checking whether
it is empty, as the following example illustrates.
function count_calls ()
persistent calls;
if (isempty (calls))
calls = 0;
endif
printf ("’count_calls’ has been called %d times\n",
++calls);
endfunction
Chapter 7: Variables 127
This implementation behaves in exactly the same way as the previous implementation of
count_calls.
The value of a persistent variable is kept in memory until it is explicitly cleared. As-
suming that the implementation of count_calls is saved on disk, we get the following
behavior.
for i = 1:2
count_calls ();
endfor
a’count_calls’ has been called 1 times
a’count_calls’ has been called 2 times
clear
for i = 1:2
count_calls ();
endfor
a’count_calls’ has been called 3 times
a’count_calls’ has been called 4 times
clear all
for i = 1:2
count_calls ();
endfor
a’count_calls’ has been called 1 times
a’count_calls’ has been called 2 times
clear count_calls
for i = 1:2
count_calls ();
endfor
a’count_calls’ has been called 1 times
a’count_calls’ has been called 2 times
That is, the persistent variable is only removed from memory when the function containing
the variable is removed. Note that if the function definition is typed directly into the Octave
prompt, the persistent variable will be cleared by a simple clear command as the entire
function definition will be removed from memory. If you do not want a persistent variable to
be removed from memory even if the function is cleared, you should use the mlock function
(see Section 11.9.6 [Function Locking], page 199).
7.3 Status of Variables
When creating simple one-shot programs it can be very convenient to see which variables
are available at the prompt. The function who and its siblings whos and whos_line_format
will show different information about what is in memory, as the following shows.
128 GNU Octave
str = "A random string";
who -variables
a*** local user variables:
a
a__nargin__ str
who
who pattern . . .
who option pattern . . .
C = who ("pattern", . . . )
List currently defined variables matching the given patterns.
Valid pattern syntax is the same as described for the clear command. If no patterns
are supplied, all variables are listed.
By default, only variables visible in the local scope are displayed.
The following are valid options, but may not be combined.
global List variables in the global scope rather than the current scope.
-regexp The patterns are considered to be regular expressions when matching the
variables to display. The same pattern syntax accepted by the regexp
function is used.
-file The next argument is treated as a filename. All variables found within the
specified file are listed. No patterns are accepted when reading variables
from a file.
If called as a function, return a cell array of defined variable names matching the
given patterns.
See also: [whos], page 128,[isglobal], page 125,[isvarname], page 123,[exist], page 130,
[regexp], page 87.
whos
whos pattern . . .
whos option pattern . . .
S = whos ("pattern", . . . )
Provide detailed information on currently defined variables matching the given pat-
terns.
Options and pattern syntax are the same as for the who command.
Extended information about each variable is summarized in a table with the following
default entries.
Attr Attributes of the listed variable. Possible attributes are:
blank Variable in local scope
aAutomatic variable. An automatic variable is one created by
the interpreter, for example argn.
cVariable of complex type.
fFormal parameter (function argument).

Chapter 7: Variables 129
gVariable with global scope.
pPersistent variable.
Name The name of the variable.
Size The logical size of the variable. A scalar is 1x1, a vector is 1xN or Nx1,
a 2-D matrix is MxN.
Bytes The amount of memory currently used to store the variable.
Class The class of the variable. Examples include double, single, char, uint16,
cell, and struct.
The table can be customized to display more or less information through the function
whos_line_format.
If whos is called as a function, return a struct array of defined variable names matching
the given patterns. Fields in the structure describing each variable are: name, size,
bytes, class, global, sparse, complex, nesting, persistent.
See also: [who], page 128,[whos line format], page 129.
val = whos_line_format ()
old_val = whos_line_format (new_val)
whos_line_format (new_val,"local")
Query or set the format string used by the command whos.
A full format string is:
%[modifier]<command>[:width[:left-min[:balance]]];
The following command sequences are available:
%a Prints attributes of variables (g=global, p=persistent, f=formal parame-
ter, a=automatic variable).
%b Prints number of bytes occupied by variables.
%c Prints class names of variables.
%e Prints elements held by variables.
%n Prints variable names.
%s Prints dimensions of variables.
%t Prints type names of variables.
Every command may also have an alignment modifier:
lLeft alignment.
rRight alignment (default).
cColumn-aligned (only applicable to command %s).
The width parameter is a positive integer specifying the minimum number of columns
used for printing. No maximum is needed as the field will auto-expand as required.
The parameters left-min and balance are only available when the column-aligned
modifier is used with the command ‘%s’. balance specifies the column number within
130 GNU Octave
the field width which will be aligned between entries. Numbering starts from 0 which
indicates the leftmost column. left-min specifies the minimum field width to the
left of the specified balance column.
The default format is:
" %a:4; %ln:6; %cs:16:6:1; %rb:12; %lc:-1;\n"
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [whos], page 128.
Instead of displaying which variables are in memory, it is possible to determine if a given
variable is available. That way it is possible to alter the behavior of a program depending
on the existence of a variable. The following example illustrates this.
if (! exist ("meaning", "var"))
disp ("The program has no ’meaning’");
endif
c= exist (name)
c= exist (name,type)
Check for the existence of name as a variable, function, file, directory, or class.
The return code cis one of
1name is a variable.
2name is an absolute filename, an ordinary file in Octave’s path, or (after
appending ‘.m’) a function file in Octave’s path.
3name is a ‘.oct’ or ‘.mex’ file in Octave’s path.
5name is a built-in function.
7name is a directory.
103 name is a function not associated with a file (entered on the command
line).
0name does not exist.
If the optional argument type is supplied, check only for symbols of the specified type.
Valid types are
"var" Check only for variables.
"builtin"
Check only for built-in functions.
"dir" Check only for directories.
"file" Check only for files and directories.
"class" Check only for classes. (Note: This option is accepted, but not currently
implemented)

Chapter 7: Variables 131
If no type is given, and there are multiple possible matches for name, exist will
return a code according to the following priority list: variable, built-in function, oct-
file, directory, file, class.
exist returns 2 if a regular file called name is present in Octave’s search path. If you
want information about other types of files not on the search path you should use
some combination of the functions file_in_path and stat instead.
Programming Note: If name is implemented by a buggy .oct/.mex file, calling exist
may cause Octave to crash. To maintain high performance, Octave trusts .oct/.mex
files instead of sandboxing them.
See also: [file in loadpath], page 194,[file in path], page 824,[dir in loadpath],
page 194,[stat], page 821.
Usually Octave will manage the memory, but sometimes it can be practical to remove
variables from memory manually. This is usually needed when working with large variables
that fill a substantial part of the memory. On a computer that uses the IEEE floating point
format, the following program allocates a matrix that requires around 128 MB memory.
large_matrix = zeros (4000, 4000);
Since having this variable in memory might slow down other computations, it can be nec-
essary to remove it manually from memory. The clear function allows this.
clear [options]pattern . . .
Delete the names matching the given patterns from the symbol table.
The pattern may contain the following special characters:
?Match any single character.
*Match zero or more characters.
[list ]Match the list of characters specified by list. If the first character is
!or ^, match all characters except those specified by list. For example,
the pattern ‘[a-zA-Z]’ will match all lowercase and uppercase alphabetic
characters.
For example, the command
clear foo b*r
clears the name foo and all names that begin with the letter band end with the letter
r.
If clear is called without any arguments, all user-defined variables (local and global)
are cleared from the symbol table.
If clear is called with at least one argument, only the visible names matching the ar-
guments are cleared. For example, suppose you have defined a function foo, and then
hidden it by performing the assignment foo = 2. Executing the command clear foo
once will clear the variable definition and restore the definition of foo as a function.
Executing clear foo a second time will clear the function definition.
The following options are available in both long and short form
-all, -a Clear all local and global user-defined variables and all functions from
the symbol table.
132 GNU Octave
-exclusive, -x
Clear the variables that don’t match the following pattern.
-functions, -f
Clear the function names and the built-in symbols names.
-global, -g
Clear global symbol names.
-variables, -v
Clear local variable names.
-classes, -c
Clears the class structure table and clears all objects.
-regexp, -r
The arguments are treated as regular expressions as any variables that
match will be cleared.
With the exception of exclusive, all long options can be used without the dash as
well.
See also: [who], page 128,[whos], page 128,[exist], page 130.
pack ()
Consolidate workspace memory in matlab.
This function is provided for compatibility, but does nothing in Octave.
See also: [clear], page 131.
Information about a function or variable such as its location in the file system can also be
acquired from within Octave. This is usually only useful during development of programs,
and not within a program.
type name . . .
type -q name . . .
text = type ("name", . . . )
Display the contents of name which may be a file, function (m-file), variable, operator,
or keyword.
type normally prepends a header line describing the category of name such as function
or variable; The -q option suppresses this behavior.
If no output variable is used the contents are displayed on screen. Otherwise, a cell
array of strings is returned, where each element corresponds to the contents of each
requested function.
which name . . .
Display the type of each name.
If name is defined from a function file, the full name of the file is also displayed.
See also: [help], page 20,[lookfor], page 21.
Chapter 7: Variables 133
what
what dir
w = what (dir)
List the Octave specific files in directory dir.
If dir is not specified then the current directory is used.
If a return argument is requested, the files found are returned in the structure w. The
structure contains the following fields:
path Full path to directory dir
m Cell array of m-files
mat Cell array of mat files
mex Cell array of mex files
oct Cell array of oct files
mdl Cell array of mdl files
slx Cell array of slx files
p Cell array of p-files
classes Cell array of class directories (@classname/)
packages Cell array of package directories (+pkgname/)
Compatibility Note: Octave does not support mdl, slx, and p files; nor does it support
package directories. what will always return an empty list for these categories.
See also: [which], page 132,[ls], page 843,[exist], page 130.
135
8 Expressions
Expressions are the basic building block of statements in Octave. An expression evaluates
to a value, which you can print, test, store in a variable, pass to a function, or assign a new
value to a variable with an assignment operator.
An expression can serve as a statement on its own. Most other kinds of statements
contain one or more expressions which specify data to be operated on. As in other languages,
expressions in Octave include variables, array references, constants, and function calls, as
well as combinations of these with various operators.
8.1 Index Expressions
An index expression allows you to reference or extract selected elements of a matrix or
vector.
Indices may be scalars, vectors, ranges, or the special operator ‘:’, which may be used
to select entire rows or columns.
Vectors are indexed using a single index expression. Matrices (2-D) and higher multi-
dimensional arrays are indexed using either one index or Nindices where Nis the dimension
of the array. When using a single index expression to index 2-D or higher data the elements
of the array are taken in column-first order (like Fortran).
The output from indexing assumes the dimensions of the index expression. For example:
a(2) # result is a scalar
a(1:2) # result is a row vector
a([1; 2]) # result is a column vector
As a special case, when a colon is used as a single index, the output is a column vector
containing all the elements of the vector or matrix. For example:
a(:) # result is a column vector
a(:)’ # result is a row vector
The above two code idioms are often used in place of reshape when a simple vector,
rather than an arbitrarily sized array, is needed.
Given the matrix
a = [1, 2; 3, 4]
all of the following expressions are equivalent and select the first row of the matrix.
a(1, [1, 2]) # row 1, columns 1 and 2
a(1, 1:2) # row 1, columns in range 1-2
a(1, :) # row 1, all columns
In index expressions the keyword end automatically refers to the last entry for a partic-
ular dimension. This magic index can also be used in ranges and typically eliminates the
needs to call size or length to gather array bounds before indexing. For example:
136 GNU Octave
a = [1, 2, 3, 4];
a(1:end/2) # first half of a => [1, 2]
a(end + 1) = 5; # append element
a(end) = []; # delete element
a(1:2:end) # odd elements of a => [1, 3]
a(2:2:end) # even elements of a => [2, 4]
a(end:-1:1) # reversal of a => [4, 3, 2 , 1]
8.1.1 Advanced Indexing
An array with ‘n’ dimensions can be indexed using ‘m’ indices. More generally, the set of
index tuples determining the result is formed by the Cartesian product of the index vectors
(or ranges or scalars).
For the ordinary and most common case, m == n, and each index corresponds to its
respective dimension. If m < n and every index is less than the size of the array in the
ith dimension, m(i) < n(i), then the index expression is padded with trailing singleton
dimensions ([ones (m-n, 1)]). If m < n but one of the indices m(i) is outside the size of
the current array, then the last n-m+1 dimensions are folded into a single dimension with
an extent equal to the product of extents of the original dimensions. This is easiest to
understand with an example.
a = reshape (1:8, 2, 2, 2) # Create 3-D array
a =
ans(:,:,1) =
1 3
2 4
ans(:,:,2) =
5 7
6 8
a(2,1,2); # Case (m == n): ans = 6
a(2,1); # Case (m < n), idx within array:
# equivalent to a(2,1,1), ans = 2
a(2,4); # Case (m < n), idx outside array:
# Dimension 2 & 3 folded into new dimension of size 2x2 = 4
# Select 2nd row, 4th element of [2, 4, 6, 8], ans = 8
One advanced use of indexing is to create arrays filled with a single value. This can be
done by using an index of ones on a scalar value. The result is an object with the dimensions
of the index expression and every element equal to the original scalar. For example, the
following statements
a = 13;
a(ones (1, 4))
produce a vector whose four elements are all equal to 13.

Chapter 8: Expressions 137
Similarly, by indexing a scalar with two vectors of ones it is possible to create a matrix.
The following statements
a = 13;
a(ones (1, 2), ones (1, 3))
create a 2x3 matrix with all elements equal to 13.
The last example could also be written as
13(ones (2, 3))
It is more efficient to use indexing rather than the code construction scalar * ones (N,
M, ...) because it avoids the unnecessary multiplication operation. Moreover, multiplica-
tion may not be defined for the object to be replicated whereas indexing an array is always
defined. The following code shows how to create a 2x3 cell array from a base unit which is
not itself a scalar.
{"Hello"}(ones (2, 3))
It should be, noted that ones (1, n) (a row vector of ones) results in a range (with zero
increment). A range is stored internally as a starting value, increment, end value, and total
number of values; hence, it is more efficient for storage than a vector or matrix of ones
whenever the number of elements is greater than 4. In particular, when ‘r’ is a row vector,
the expressions
r(ones (1, n), :)
r(ones (n, 1), :)
will produce identical results, but the first one will be significantly faster, at least for ‘r’
and ‘n’ large enough. In the first case the index is held in compressed form as a range which
allows Octave to choose a more efficient algorithm to handle the expression.
A general recommendation, for a user unaware of these subtleties, is to use the function
repmat for replicating smaller arrays into bigger ones.
A second use of indexing is to speed up code. Indexing is a fast operation and judicious
use of it can reduce the requirement for looping over individual array elements which is a
slow operation.
Consider the following example which creates a 10-element row vector acontaining the
values ai=√i.
for i = 1:10
a(i) = sqrt (i);
endfor
It is quite inefficient to create a vector using a loop like this. In this case, it would have
been much more efficient to use the expression
a = sqrt (1:10);
which avoids the loop entirely.
In cases where a loop cannot be avoided, or a number of values must be combined to
form a larger matrix, it is generally faster to set the size of the matrix first (pre-allocate
storage), and then insert elements using indexing commands. For example, given a matrix
a,
138 GNU Octave
[nr, nc] = size (a);
x = zeros (nr, n * nc);
for i = 1:n
x(:,(i-1)*nc+1:i*nc) = a;
endfor
is considerably faster than
x = a;
for i = 1:n-1
x = [x, a];
endfor
because Octave does not have to repeatedly resize the intermediate result.
ind = sub2ind (dims,i,j)
ind = sub2ind (dims,s1,s2, . . . , sN)
Convert subscripts to linear indices.
The input dims is a dimension vector where each element is the size of the array in
the respective dimension (see [size], page 45). The remaining inputs are scalars or
vectors of subscripts to be converted.
The output vector ind contains the converted linear indices.
Background: Array elements can be specified either by a linear index which starts
at 1 and runs through the number of elements in the array, or they may be specified
with subscripts for the row, column, page, etc. The functions ind2sub and sub2ind
interconvert between the two forms.
The linear index traverses dimension 1 (rows), then dimension 2 (columns), then
dimension 3 (pages), etc. until it has numbered all of the elements. Consider the
following 3-by-3 matrices:
[(1,1), (1,2), (1,3)] [1, 4, 7]
[(2,1), (2,2), (2,3)] ==> [2, 5, 8]
[(3,1), (3,2), (3,3)] [3, 6, 9]
The left matrix contains the subscript tuples for each matrix element. The right
matrix shows the linear indices for the same matrix.
The following example shows how to convert the two-dimensional indices (2,1) and
(2,3) of a 3-by-3 matrix to linear indices with a single call to sub2ind.
s1 = [2, 2];
s2 = [1, 3];
ind = sub2ind ([3, 3], s1, s2)
⇒ind = 2 8
See also: [ind2sub], page 138,[size], page 45.
[s1,s2, ..., sN] = ind2sub (dims,ind)
Convert linear indices to subscripts.
The input dims is a dimension vector where each element is the size of the array in
the respective dimension (see [size], page 45). The second input ind contains linear
indies to be converted.
Chapter 8: Expressions 139
The outputs s1, . . ., sN contain the converted subscripts.
Background: Array elements can be specified either by a linear index which starts
at 1 and runs through the number of elements in the array, or they may be specified
with subscripts for the row, column, page, etc. The functions ind2sub and sub2ind
interconvert between the two forms.
The linear index traverses dimension 1 (rows), then dimension 2 (columns), then
dimension 3 (pages), etc. until it has numbered all of the elements. Consider the
following 3-by-3 matrices:
[1, 4, 7] [(1,1), (1,2), (1,3)]
[2, 5, 8] ==> [(2,1), (2,2), (2,3)]
[3, 6, 9] [(3,1), (3,2), (3,3)]
The left matrix contains the linear indices for each matrix element. The right matrix
shows the subscript tuples for the same matrix.
The following example shows how to convert the two-dimensional indices (2,1) and
(2,3) of a 3-by-3 matrix to linear indices with a single call to sub2ind.
The following example shows how to convert the linear indices 2and 8in a 3-by-3
matrix into subscripts.
ind = [2, 8];
[r, c] = ind2sub ([3, 3], ind)
⇒r = 2 2
⇒c = 1 3
If the number of output subscripts exceeds the number of dimensions, the exceeded
dimensions are set to 1. On the other hand, if fewer subscripts than dimensions are
provided, the exceeding dimensions are merged into the final requested dimension.
For clarity, consider the following examples:
ind = [2, 8];
dims = [3, 3];
## same as dims = [3, 3, 1]
[r, c, s] = ind2sub (dims, ind)
⇒r = 2 2
⇒c = 1 3
⇒s = 1 1
## same as dims = [9]
r = ind2sub (dims, ind)
⇒r = 2 8
See also: [ind2sub], page 138,[size], page 45.
isindex (ind)
isindex (ind,n)
Return true if ind is a valid index.
Valid indices are either positive integers (although possibly of real data type), or
logical arrays.
If present, nspecifies the maximum extent of the dimension to be indexed. When
possible the internal result is cached so that subsequent indexing using ind will not
perform the check again.
140 GNU Octave
Implementation Note: Strings are first converted to double values before the checks
for valid indices are made. Unless a string contains the NULL character "\0", it will
always be a valid index.
val = allow_noninteger_range_as_index ()
old_val = allow_noninteger_range_as_index (new_val)
allow_noninteger_range_as_index (new_val,"local")
Query or set the internal variable that controls whether non-integer ranges are allowed
as indices.
This might be useful for matlab compatibility; however, it is still not entirely com-
patible because matlab treats the range expression differently in different contexts.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
8.2 Calling Functions
Afunction is a name for a particular calculation. Because it has a name, you can ask for it
by name at any point in the program. For example, the function sqrt computes the square
root of a number.
A fixed set of functions are built-in, which means they are available in every Octave
program. The sqrt function is one of these. In addition, you can define your own functions.
See Chapter 11 [Functions and Scripts], page 173, for information about how to do this.
The way to use a function is with a function call expression, which consists of the function
name followed by a list of arguments in parentheses. The arguments are expressions which
give the raw materials for the calculation that the function will do. When there is more
than one argument, they are separated by commas. If there are no arguments, you can
omit the parentheses, but it is a good idea to include them anyway, to clearly indicate that
a function call was intended. Here are some examples:
sqrt (x^2 + y^2) # One argument
ones (n, m) # Two arguments
rand () # No arguments
Each function expects a particular number of arguments. For example, the sqrt function
must be called with a single argument, the number to take the square root of:
sqrt (argument)
Some of the built-in functions take a variable number of arguments, depending on the
particular usage, and their behavior is different depending on the number of arguments
supplied.
Like every other expression, the function call has a value, which is computed by the
function based on the arguments you give it. In this example, the value of sqrt (argument)
is the square root of the argument. A function can also have side effects, such as assigning
the values of certain variables or doing input or output operations.
Unlike most languages, functions in Octave may return multiple values. For example,
the following statement
[u, s, v] = svd (a)
Chapter 8: Expressions 141
computes the singular value decomposition of the matrix aand assigns the three result
matrices to u,s, and v.
The left side of a multiple assignment expression is itself a list of expressions, and is
allowed to be a list of variable names or index expressions. See also Section 8.1 [Index
Expressions], page 135, and Section 8.6 [Assignment Ops], page 151.
8.2.1 Call by Value
In Octave, unlike Fortran, function arguments are passed by value, which means that each
argument in a function call is evaluated and assigned to a temporary location in memory
before being passed to the function. There is currently no way to specify that a function
parameter should be passed by reference instead of by value. This means that it is impossible
to directly alter the value of a function parameter in the calling function. It can only change
the local copy within the function body. For example, the function
function f (x, n)
while (n-- > 0)
disp (x);
endwhile
endfunction
displays the value of the first argument ntimes. In this function, the variable nis used as a
temporary variable without having to worry that its value might also change in the calling
function. Call by value is also useful because it is always possible to pass constants for any
function parameter without first having to determine that the function will not attempt to
modify the parameter.
The caller may use a variable as the expression for the argument, but the called function
does not know this: it only knows what value the argument had. For example, given a
function called as
foo = "bar";
fcn (foo)
you should not think of the argument as being “the variable foo.” Instead, think of the
argument as the string value, "bar".
Even though Octave uses pass-by-value semantics for function arguments, values are not
copied unnecessarily. For example,
x = rand (1000);
f (x);
does not actually force two 1000 by 1000 element matrices to exist unless the function f
modifies the value of its argument. Then Octave must create a copy to avoid changing the
value outside the scope of the function f, or attempting (and probably failing!) to modify
the value of a constant or the value of a temporary result.

142 GNU Octave
8.2.2 Recursion
With some restrictions1, recursive function calls are allowed. A recursive function is one
which calls itself, either directly or indirectly. For example, here is an inefficient2way to
compute the factorial of a given integer:
function retval = fact (n)
if (n > 0)
retval = n * fact (n-1);
else
retval = 1;
endif
endfunction
This function is recursive because it calls itself directly. It eventually terminates because
each time it calls itself, it uses an argument that is one less than was used for the previous
call. Once the argument is no longer greater than zero, it does not call itself, and the
recursion ends.
The built-in variable max_recursion_depth specifies a limit to the recursion depth and
prevents Octave from recursing infinitely.
val = max_recursion_depth ()
old_val = max_recursion_depth (new_val)
max_recursion_depth (new_val,"local")
Query or set the internal limit on the number of times a function may be called
recursively.
If the limit is exceeded, an error message is printed and control returns to the top
level.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
8.3 Arithmetic Operators
The following arithmetic operators are available, and work on scalars and matrices. The
element-by-element operators and functions broadcast (see Section 19.2 [Broadcasting],
page 531).
x+yAddition. If both operands are matrices, the number of rows and columns must
both agree, or they must be broadcastable to the same shape.
x.+yElement-by-element addition. This operator is equivalent to +.
x-ySubtraction. If both operands are matrices, the number of rows and columns
of both must agree, or they must be broadcastable to the same shape.
1Some of Octave’s functions are implemented in terms of functions that cannot be called recursively. For
example, the ODE solver lsode is ultimately implemented in a Fortran subroutine that cannot be called
recursively, so lsode should not be called either directly or indirectly from within the user-supplied
function that lsode requires. Doing so will result in an error.
2It would be much better to use prod (1:n), or gamma (n+1) instead, after first checking to ensure that
the value nis actually a positive integer.
Chapter 8: Expressions 143
x.- yElement-by-element subtraction. This operator is equivalent to -.
x*yMatrix multiplication. The number of columns of xmust agree with the number
of rows of y, or they must be broadcastable to the same shape.
x.* yElement-by-element multiplication. If both operands are matrices, the number
of rows and columns must both agree, or they must be broadcastable to the
same shape.
x/yRight division. This is conceptually equivalent to the expression
(inverse (y’) * x’)’
but it is computed without forming the inverse of y’.
If the system is not square, or if the coefficient matrix is singular, a minimum
norm solution is computed.
x./ yElement-by-element right division.
x\yLeft division. This is conceptually equivalent to the expression
inverse (x) * y
but it is computed without forming the inverse of x.
If the system is not square, or if the coefficient matrix is singular, a minimum
norm solution is computed.
x.\yElement-by-element left division. Each element of yis divided by each corre-
sponding element of x.
x^y
x** yPower operator. If xand yare both scalars, this operator returns xraised to
the power y. If xis a scalar and yis a square matrix, the result is computed
using an eigenvalue expansion. If xis a square matrix, the result is computed
by repeated multiplication if yis an integer, and by an eigenvalue expansion if
yis not an integer. An error results if both xand yare matrices.
The implementation of this operator needs to be improved.
x.^y
x.** yElement-by-element power operator. If both operands are matrices, the number
of rows and columns must both agree, or they must be broadcastable to the
same shape. If several complex results are possible, the one with smallest non-
negative argument (angle) is taken. This rule may return a complex root even
when a real root is also possible. Use realpow,realsqrt,cbrt, or nthroot if
a real result is preferred.
-xNegation.
+xUnary plus. This operator has no effect on the operand.
x’ Complex conjugate transpose. For real arguments, this operator is the same as
the transpose operator. For complex arguments, this operator is equivalent to
the expression
conj (x.’)
x.’ Transpose.
144 GNU Octave
Note that because Octave’s element-by-element operators begin with a ‘.’, there is a
possible ambiguity for statements like
1./m
because the period could be interpreted either as part of the constant or as part of the
operator. To resolve this conflict, Octave treats the expression as if you had typed
(1) ./ m
and not
(1.) / m
Although this is inconsistent with the normal behavior of Octave’s lexer, which usually
prefers to break the input into tokens by preferring the longest possible match at any given
point, it is more useful in this case.
ctranspose (x)
Return the complex conjugate transpose of x.
This function and x’ are equivalent.
See also: [transpose], page 145.
ldivide (x,y)
Return the element-by-element left division of xand y.
This function and x .\ y are equivalent.
See also: [rdivide], page 145,[mldivide], page 144,[times], page 145,[plus], page 145.
minus (x,y)
This function and x - y are equivalent.
See also: [plus], page 145,[uminus], page 146.
mldivide (x,y)
Return the matrix left division of xand y.
This function and x \ y are equivalent.
See also: [mrdivide], page 144,[ldivide], page 144,[rdivide], page 145.
mpower (x,y)
Return the matrix power operation of xraised to the ypower.
This function and x ^ y are equivalent.
See also: [power], page 145,[mtimes], page 145,[plus], page 145,[minus], page 144.
mrdivide (x,y)
Return the matrix right division of xand y.
This function and x / y are equivalent.
See also: [mldivide], page 144,[rdivide], page 145,[plus], page 145,[minus], page 144.
Chapter 8: Expressions 145
mtimes (x,y)
mtimes (x1,x2, . . . )
Return the matrix multiplication product of inputs.
This function and x * y are equivalent. If more arguments are given, the multiplica-
tion is applied cumulatively from left to right:
(...((x1 * x2) * x3) * ...)
At least one argument is required.
See also: [times], page 145,[plus], page 145,[minus], page 144,[rdivide], page 145,
[mrdivide], page 144,[mldivide], page 144,[mpower], page 144.
plus (x,y)
plus (x1,x2, . . . )
This function and x + y are equivalent.
If more arguments are given, the summation is applied cumulatively from left to right:
(...((x1 + x2) + x3) + ...)
At least one argument is required.
See also: [minus], page 144,[uplus], page 146.
power (x,y)
Return the element-by-element operation of xraised to the ypower.
This function and x .^ y are equivalent.
If several complex results are possible, returns the one with smallest non-negative
argument (angle). Use realpow,realsqrt,cbrt, or nthroot if a real result is pre-
ferred.
See also: [mpower], page 144,[realpow], page 472,[realsqrt], page 472,[cbrt],
page 472,[nthroot], page 472.
rdivide (x,y)
Return the element-by-element right division of xand y.
This function and x ./ y are equivalent.
See also: [ldivide], page 144,[mrdivide], page 144,[times], page 145,[plus], page 145.
times (x,y)
times (x1,x2, . . . )
Return the element-by-element multiplication product of inputs.
This function and x .* y are equivalent. If more arguments are given, the multipli-
cation is applied cumulatively from left to right:
(...((x1 .* x2) .* x3) .* ...)
At least one argument is required.
See also: [mtimes], page 145,[rdivide], page 145.
transpose (x)
Return the transpose of x.
This function and x.’ are equivalent.
See also: [ctranspose], page 144.
146 GNU Octave
uminus (x)
This function and - x are equivalent.
See also: [uplus], page 146,[minus], page 144.
uplus (x)
This function and + x are equivalent.
See also: [uminus], page 146,[plus], page 145,[minus], page 144.
8.4 Comparison Operators
Comparison operators compare numeric values for relationships such as equality. They are
written using relational operators.
All of Octave’s comparison operators return a value of 1 if the comparison is true, or 0
if it is false. For matrix values, they all work on an element-by-element basis. Broadcasting
rules apply. See Section 19.2 [Broadcasting], page 531. For example:
[1, 2; 3, 4] == [1, 3; 2, 4]
⇒1 0
0 1
According to broadcasting rules, if one operand is a scalar and the other is a matrix, the
scalar is compared to each element of the matrix in turn, and the result is the same size as
the matrix.
x<yTrue if xis less than y.
x<= yTrue if xis less than or equal to y.
x== yTrue if xis equal to y.
x>= yTrue if xis greater than or equal to y.
x>yTrue if xis greater than y.
x!= y
x~= yTrue if xis not equal to y.
For complex numbers, the following ordering is defined: z1 <z2 if and only if
abs (z1) < abs (z2)
|| (abs (z1) == abs (z2) && arg (z1) < arg (z2))
This is consistent with the ordering used by max,min and sort, but is not consistent
with matlab, which only compares the real parts.
String comparisons may also be performed with the strcmp function, not with the com-
parison operators listed above. See Chapter 5 [Strings], page 67.
eq (x,y)
Return true if the two inputs are equal.
This function is equivalent to x == y.
See also: [ne], page 147,[isequal], page 147,[le], page 147,[ge], page 147,[gt], page 147,
[ne], page 147,[lt], page 147.
Chapter 8: Expressions 147
ge (x,y)
This function is equivalent to x >= y.
See also: [le], page 147,[eq], page 146,[gt], page 147,[ne], page 147,[lt], page 147.
gt (x,y)
This function is equivalent to x > y.
See also: [le], page 147,[eq], page 146,[ge], page 147,[ne], page 147,[lt], page 147.
isequal (x1,x2, . . . )
Return true if all of x1,x2, . . . are equal.
See also: [isequaln], page 147.
isequaln (x1,x2, . . . )
Return true if all of x1,x2, . . . are equal under the additional assumption that NaN
== NaN (no comparison of NaN placeholders in dataset).
See also: [isequal], page 147.
le (x,y)
This function is equivalent to x <= y.
See also: [eq], page 146,[ge], page 147,[gt], page 147,[ne], page 147,[lt], page 147.
lt (x,y)
This function is equivalent to x < y.
See also: [le], page 147,[eq], page 146,[ge], page 147,[gt], page 147,[ne], page 147.
ne (x,y)
Return true if the two inputs are not equal.
This function is equivalent to x != y.
See also: [eq], page 146,[isequal], page 147,[le], page 147,[ge], page 147,[lt],
page 147.
8.5 Boolean Expressions
8.5.1 Element-by-element Boolean Operators
An element-by-element boolean expression is a combination of comparison expressions using
the boolean operators “or” (‘|’), “and” (‘&’), and “not” (‘!’), along with parentheses to
control nesting. The truth of the boolean expression is computed by combining the truth
values of the corresponding elements of the component expressions. A value is considered
to be false if it is zero, and true otherwise.
Element-by-element boolean expressions can be used wherever comparison expressions
can be used. They can be used in if and while statements. However, a matrix value used
as the condition in an if or while statement is only true if all of its elements are nonzero.
Like comparison operations, each element of an element-by-element boolean expression
also has a numeric value (1 if true, 0 if false) that comes into play if the result of the boolean
expression is stored in a variable, or used in arithmetic.
148 GNU Octave
Here are descriptions of the three element-by-element boolean operators.
boolean1 &boolean2
Elements of the result are true if both corresponding elements of boolean1 and
boolean2 are true.
boolean1 |boolean2
Elements of the result are true if either of the corresponding elements of
boolean1 or boolean2 is true.
!boolean
~boolean Each element of the result is true if the corresponding element of boolean is
false.
These operators work on an element-by-element basis. For example, the expression
[1, 0; 0, 1] & [1, 0; 2, 3]
returns a two by two identity matrix.
For the binary operators, broadcasting rules apply. See Section 19.2 [Broadcasting],
page 531. In particular, if one of the operands is a scalar and the other a matrix, the
operator is applied to the scalar and each element of the matrix.
For the binary element-by-element boolean operators, both subexpressions boolean1 and
boolean2 are evaluated before computing the result. This can make a difference when the
expressions have side effects. For example, in the expression
a & b++
the value of the variable bis incremented even if the variable ais zero.
This behavior is necessary for the boolean operators to work as described for matrix-
valued operands.
z= and (x,y)
z= and (x1,x2, . . . )
Return the logical AND of xand y.
This function is equivalent to the operator syntax x & y. If more than two arguments
are given, the logical AND is applied cumulatively from left to right:
(...((x1 & x2) & x3) & ...)
At least one argument is required.
See also: [or], page 148,[not], page 148,[xor], page 439.
z= not (x)
Return the logical NOT of x.
This function is equivalent to the operator syntax ! x.
See also: [and], page 148,[or], page 148,[xor], page 439.
z= or (x,y)
z= or (x1,x2, . . . )
Return the logical OR of xand y.
Chapter 8: Expressions 149
This function is equivalent to the operator syntax x | y. If more than two arguments
are given, the logical OR is applied cumulatively from left to right:
(...((x1 | x2) | x3) | ...)
At least one argument is required.
See also: [and], page 148,[not], page 148,[xor], page 439.
8.5.2 Short-circuit Boolean Operators
Combined with the implicit conversion to scalar values in if and while conditions, Oc-
tave’s element-by-element boolean operators are often sufficient for performing most logical
operations. However, it is sometimes desirable to stop evaluating a boolean expression as
soon as the overall truth value can be determined. Octave’s short-circuit boolean operators
work this way.
boolean1 && boolean2
The expression boolean1 is evaluated and converted to a scalar using the equiv-
alent of the operation all (boolean1(:)). If it is false, the result of the overall
expression is 0. If it is true, the expression boolean2 is evaluated and converted
to a scalar using the equivalent of the operation all (boolean2(:)). If it is
true, the result of the overall expression is 1. Otherwise, the result of the overall
expression is 0.
Warning: there is one exception to the rule of evaluating all (boolean1(:)),
which is when boolean1 is the empty matrix. The truth value of an empty
matrix is always false so [] && true evaluates to false even though all
([]) is true.
boolean1 || boolean2
The expression boolean1 is evaluated and converted to a scalar using the equiv-
alent of the operation all (boolean1(:)). If it is true, the result of the overall
expression is 1. If it is false, the expression boolean2 is evaluated and converted
to a scalar using the equivalent of the operation all (boolean2(:)). If it is
true, the result of the overall expression is 1. Otherwise, the result of the overall
expression is 0.
Warning: the truth value of an empty matrix is always false, see the previous
list item for details.
The fact that both operands may not be evaluated before determining the overall truth
value of the expression can be important. For example, in the expression
a && b++
the value of the variable bis only incremented if the variable ais nonzero.
This can be used to write somewhat more concise code. For example, it is possible write
function f (a, b, c)
if (nargin > 2 && ischar (c))
...
instead of having to use two if statements to avoid attempting to evaluate an argument
that doesn’t exist. For example, without the short-circuit feature, it would be necessary to
write

150 GNU Octave
function f (a, b, c)
if (nargin > 2)
if (ischar (c))
...
Writing
function f (a, b, c)
if (nargin > 2 & ischar (c))
...
would result in an error if fwere called with one or two arguments because Octave would
be forced to try to evaluate both of the operands for the operator ‘&’.
matlab has special behavior that allows the operators ‘&’ and ‘|’ to short-circuit when
used in the truth expression for if and while statements. Octave also behaves the same way
by default, though the use of the ‘&’ and ‘|’ operators in this way is strongly discouraged.
Instead, you should use the ‘&&’ and ‘||’ operators that always have short-circuit behavior.
val = do_braindead_shortcircuit_evaluation ()
old_val = do_braindead_shortcircuit_evaluation (new_val)
do_braindead_shortcircuit_evaluation (new_val,"local")
Query or set the internal variable that controls whether Octave will do short-circuit
evaluation of ‘|’ and ‘&’ operators inside the conditions of if or while statements.
This feature is only provided for compatibility with matlab and should not be used
unless you are porting old code that relies on this feature.
To obtain short-circuit behavior for logical expressions in new programs, you should
always use the ‘&&’ and ‘||’ operators.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
Finally, the ternary operator (?:) is not supported in Octave. If short-circuiting is not
important, it can be replaced by the ifelse function.
merge (mask,tval,fval)
ifelse (mask,tval,fval)
Merge elements of true val and false val, depending on the value of mask.
If mask is a logical scalar, the other two arguments can be arbitrary values. Otherwise,
mask must be a logical array, and tval,fval should be arrays of matching class, or
cell arrays. In the scalar mask case, tval is returned if mask is true, otherwise fval is
returned.
In the array mask case, both tval and fval must be either scalars or arrays with
dimensions equal to mask. The result is constructed as follows:
result(mask) = tval(mask);
result(! mask) = fval(! mask);
mask can also be arbitrary numeric type, in which case it is first converted to logical.
See also: [logical], page 60,[diff], page 440.
Chapter 8: Expressions 151
8.6 Assignment Expressions
An assignment is an expression that stores a new value into a variable. For example, the
following expression assigns the value 1 to the variable z:
z=1
After this expression is executed, the variable zhas the value 1. Whatever old value zhad
before the assignment is forgotten. The ‘=’ sign is called an assignment operator.
Assignments can store string values also. For example, the following expression would
store the value "this food is good" in the variable message:
thing = "food"
predicate = "good"
message = [ "this " , thing , " is " , predicate ]
(This also illustrates concatenation of strings.)
Most operators (addition, concatenation, and so on) have no effect except to compute
a value. If you ignore the value, you might as well not use the operator. An assignment
operator is different. It does produce a value, but even if you ignore the value, the assignment
still makes itself felt through the alteration of the variable. We call this a side effect.
The left-hand operand of an assignment need not be a variable (see Chapter 7 [Variables],
page 123). It can also be an element of a matrix (see Section 8.1 [Index Expressions],
page 135) or a list of return values (see Section 8.2 [Calling Functions], page 140). These
are all called lvalues, which means they can appear on the left-hand side of an assignment
operator. The right-hand operand may be any expression. It produces the new value which
the assignment stores in the specified variable, matrix element, or list of return values.
It is important to note that variables do not have permanent types. The type of a
variable is simply the type of whatever value it happens to hold at the moment. In the
following program fragment, the variable foo has a numeric value at first, and a string value
later on:
octave:13> foo = 1
foo = 1
octave:13> foo = "bar"
foo = bar
When the second assignment gives foo a string value, the fact that it previously had a
numeric value is forgotten.
Assignment of a scalar to an indexed matrix sets all of the elements that are referenced
by the indices to the scalar value. For example, if ais a matrix with at least two columns,
a(:, 2) = 5
sets all the elements in the second column of ato 5.
Assigning an empty matrix ‘[]’ works in most cases to allow you to delete rows or
columns of matrices and vectors. See Section 4.1.1 [Empty Matrices], page 51. For example,
given a 4 by 5 matrix A, the assignment
A (3, :) = []
deletes the third row of A, and the assignment
A (:, 1:2:5) = []
152 GNU Octave
deletes the first, third, and fifth columns.
An assignment is an expression, so it has a value. Thus, z = 1 as an expression has the
value 1. One consequence of this is that you can write multiple assignments together:
x=y=z=0
stores the value 0 in all three variables. It does this because the value of z = 0, which is 0,
is stored into y, and then the value of y=z=0, which is 0, is stored into x.
This is also true of assignments to lists of values, so the following is a valid expression
[a, b, c] = [u, s, v] = svd (a)
that is exactly equivalent to
[u, s, v] = svd (a)
a=u
b=s
c=v
In expressions like this, the number of values in each part of the expression need not
match. For example, the expression
[a, b] = [u, s, v] = svd (a)
is equivalent to
[u, s, v] = svd (a)
a=u
b=s
The number of values on the left side of the expression can, however, not exceed the number
of values on the right side. For example, the following will produce an error.
[a, b, c, d] = [u, s, v] = svd (a);
aerror: element number 4 undefined in return list
The symbol ~may be used as a placeholder in the list of lvalues, indicating that the
corresponding return value should be ignored and not stored anywhere:
[~, s, v] = svd (a);
This is cleaner and more memory efficient than using a dummy variable. The nargout
value for the right-hand side expression is not affected. If the assignment is used as an
expression, the return value is a comma-separated list with the ignored values dropped.
A very common programming pattern is to increment an existing variable with a given
value, like this
a=a+2;
This can be written in a clearer and more condensed form using the += operator
a += 2;
Similar operators also exist for subtraction (-=), multiplication (*=), and division (/=). An
expression of the form
expr1 op=expr2
is evaluated as
expr1 = (expr1)op (expr2)
Chapter 8: Expressions 153
where op can be either +,-,*, or /, as long as expr2 is a simple expression with no side
effects. If expr2 also contains an assignment operator, then this expression is evaluated as
temp =expr2
expr1 = (expr1)op temp
where temp is a placeholder temporary value storing the computed result of evaluating
expr2. So, the expression
a *= b+1
is evaluated as
a = a * (b+1)
and not
a=a*b+1
You can use an assignment anywhere an expression is called for. For example, it is valid
to write x != (y = 1) to set yto 1 and then test whether xequals 1. But this style tends
to make programs hard to read. Except in a one-shot program, you should rewrite it to get
rid of such nesting of assignments. This is never very hard.
8.7 Increment Operators
Increment operators increase or decrease the value of a variable by 1. The operator to
increment a variable is written as ‘++’. It may be used to increment a variable either before
or after taking its value.
For example, to pre-increment the variable x, you would write ++x. This would add one
to xand then return the new value of xas the result of the expression. It is exactly the
same as the expression x=x+ 1.
To post-increment a variable x, you would write x++. This adds one to the variable x,
but returns the value that xhad prior to incrementing it. For example, if xis equal to 2,
the result of the expression x++ is 2, and the new value of xis 3.
For matrix and vector arguments, the increment and decrement operators work on each
element of the operand.
Here is a list of all the increment and decrement expressions.
++xThis expression increments the variable x. The value of the expression is the
new value of x. It is equivalent to the expression x=x+ 1.
--xThis expression decrements the variable x. The value of the expression is the
new value of x. It is equivalent to the expression x=x- 1.
x++ This expression causes the variable xto be incremented. The value of the
expression is the old value of x.
x-- This expression causes the variable xto be decremented. The value of the
expression is the old value of x.
154 GNU Octave
8.8 Operator Precedence
Operator precedence determines how operators are grouped, when different operators ap-
pear close by in one expression. For example, ‘*’ has higher precedence than ‘+’. Thus, the
expression a+b*cmeans to multiply band c, and then add ato the product (i.e., a + (b
* c)).
You can overrule the precedence of the operators by using parentheses. You can think
of the precedence rules as saying where the parentheses are assumed if you do not write
parentheses yourself. In fact, it is wise to use parentheses whenever you have an unusual
combination of operators, because other people who read the program may not remember
what the precedence is in this case. You might forget as well, and then you too could make
a mistake. Explicit parentheses will help prevent any such mistake.
When operators of equal precedence are used together, the leftmost operator groups
first, except for the assignment operators, which group in the opposite order. Thus, the
expression a-b+cgroups as (a - b) + c, but the expression a=b=cgroups as a = (b =
c).
The precedence of prefix unary operators is important when another operator follows
the operand. For example, -x^2 means -(x^2), because ‘-’ has lower precedence than ‘^’.
Here is a table of the operators in Octave, in order of decreasing precedence. Unless
noted, all operators group left to right.
function call and array indexing, cell array indexing, and structure element
indexing
‘()’ ‘{}’ ‘.’
postfix increment, and postfix decrement
‘++’ ‘--’
These operators group right to left.
transpose and exponentiation
‘’’ ‘.’’ ‘^’ ‘**’ ‘.^’ ‘.**’
unary plus, unary minus, prefix increment, prefix decrement, and logical "not"
‘+’ ‘-’ ‘++’ ‘--’ ‘~’ ‘!’
multiply and divide
‘*’ ‘/’ ‘\’ ‘.\’ ‘.*’ ‘./’
add, subtract
‘+’ ‘-’
colon ‘:’
relational
‘<’ ‘<=’ ‘==’ ‘>=’ ‘>’ ‘!=’ ‘~=’
element-wise "and"
‘&’
element-wise "or"
‘|’
155
logical "and"
‘&&’
logical "or"
‘||’
assignment
‘=’ ‘+=’ ‘-=’ ‘*=’ ‘/=’ ‘\=’ ‘^=’ ‘.*=’ ‘./=’ ‘.\=’ ‘.^=’ ‘|=’ ‘&=’
These operators group right to left.

157
9 Evaluation
Normally, you evaluate expressions simply by typing them at the Octave prompt, or by
asking Octave to interpret commands that you have saved in a file.
Sometimes, you may find it necessary to evaluate an expression that has been computed
and stored in a string, which is exactly what the eval function lets you do.
eval (try)
eval (try,catch)
Parse the string try and evaluate it as if it were an Octave program.
If execution fails, evaluate the optional string catch.
The string try is evaluated in the current context, so any results remain available
after eval returns.
The following example creates the variable Awith the approximate value of 3.1416
in the current workspace.
eval ("A = acos(-1);");
If an error occurs during the evaluation of try then the catch string is evaluated, as
the following example shows:
eval (’error ("This is a bad example");’,
’printf ("This error occurred:\n%s\n", lasterr ());’);
aThis error occurred:
This is a bad example
Programming Note: if you are only using eval as an error-capturing mechanism,
rather than for the execution of arbitrary code strings, Consider using try/catch
blocks or unwind protect/unwind protect cleanup blocks instead. These techniques
have higher performance and don’t introduce the security considerations that the
evaluation of arbitrary code does.
See also: [evalin], page 160,[evalc], page 157,[assignin], page 160,[feval], page 158.
The evalc function additionally captures any console output produced by the evaluated
expression.
s= evalc (try)
s= evalc (try,catch)
Parse and evaluate the string try as if it were an Octave program, while capturing
the output into the return variable s.
If execution fails, evaluate the optional string catch.
This function behaves like eval, but any output or warning messages which would
normally be written to the console are captured and returned in the string s.
The diary is disabled during the execution of this function. When system is used,
any output produced by external programs is not captured, unless their output is
captured by the system function itself.
s = evalc ("t = 42"), t
⇒s = t = 42
⇒t = 42
158 GNU Octave
See also: [eval], page 157,[diary], page 34.
9.1 Calling a Function by its Name
The feval function allows you to call a function from a string containing its name. This
is useful when writing a function that needs to call user-supplied functions. The feval
function takes the name of the function to call as its first argument, and the remaining
arguments are given to the function.
The following example is a simple-minded function using feval that finds the root of a
user-supplied function of one variable using Newton’s method.
function result = newtroot (fname, x)
# usage: newtroot (fname, x)
#
# fname : a string naming a function f(x).
# x : initial guess
delta = tol = sqrt (eps);
maxit = 200;
fx = feval (fname, x);
for i = 1:maxit
if (abs (fx) < tol)
result = x;
return;
else
fx_new = feval (fname, x + delta);
deriv = (fx_new - fx) / delta;
x = x - fx / deriv;
fx = fx_new;
endif
endfor
result = x;
endfunction
Note that this is only meant to be an example of calling user-supplied functions and
should not be taken too seriously. In addition to using a more robust algorithm, any serious
code would check the number and type of all the arguments, ensure that the supplied func-
tion really was a function, etc. See Section 4.8 [Predicates for Numeric Objects], page 62, for
a list of predicates for numeric objects, and see Section 7.3 [Status of Variables], page 127,
for a description of the exist function.
feval (name, . . . )
Evaluate the function named name.
Any arguments after the first are passed as inputs to the named function. For example,
feval ("acos", -1)
⇒3.1416
Chapter 9: Evaluation 159
calls the function acos with the argument ‘-1’.
The function feval can also be used with function handles of any sort (see
Section 11.11.1 [Function Handles], page 209). Historically, feval was the only way
to call user-supplied functions in strings, but function handles are now preferred due
to the cleaner syntax they offer. For example,
f= @exp;
feval (f, 1)
⇒2.7183
f(1)
⇒2.7183
are equivalent ways to call the function referred to by f. If it cannot be predicted
beforehand whether fis a function handle, function name in a string, or inline function
then feval can be used instead.
A similar function run exists for calling user script files, that are not necessarily on the
user path
run script
run ("script")
Run script in the current workspace.
Scripts which reside in directories specified in Octave’s load path, and which end with
the extension ".m", can be run simply by typing their name. For scripts not located
on the load path, use run.
The filename script can be a bare, fully qualified, or relative filename and with or
without a file extension. If no extension is specified, Octave will first search for a script
with the ".m" extension before falling back to the script name without an extension.
Implementation Note: If script includes a path component, then run first changes the
working directory to the directory where script is found. Next, the script is executed.
Finally, run returns to the original working directory unless script has specifically
changed directories.
See also: [path], page 193,[addpath], page 192,[source], page 202.
9.2 Evaluation in a Different Context
Before you evaluate an expression you need to substitute the values of the variables used in
the expression. These are stored in the symbol table. Whenever the interpreter starts a new
function it saves the current symbol table and creates a new one, initializing it with the list
of function parameters and a couple of predefined variables such as nargin. Expressions
inside the function use the new symbol table.
Sometimes you want to write a function so that when you call it, it modifies variables in
your own context. This allows you to use a pass-by-name style of function, which is similar
to using a pointer in programming languages such as C.
Consider how you might write save and load as m-files. For example:
160 GNU Octave
function create_data
x = linspace (0, 10, 10);
y = sin (x);
save mydata x y
endfunction
With evalin, you could write save as follows:
function save (file, name1, name2)
f = open_save_file (file);
save_var (f, name1, evalin ("caller", name1));
save_var (f, name2, evalin ("caller", name2));
endfunction
Here, ‘caller’ is the create_data function and name1 is the string "x", which evaluates
simply as the value of x.
You later want to load the values back from mydata in a different context:
function process_data
load mydata
... do work ...
endfunction
With assignin, you could write load as follows:
function load (file)
f = open_load_file (file);
[name, val] = load_var (f);
assignin ("caller", name, val);
[name, val] = load_var (f);
assignin ("caller", name, val);
endfunction
Here, ‘caller’ is the process_data function.
You can set and use variables at the command prompt using the context ‘base’ rather
than ‘caller’.
These functions are rarely used in practice. One example is the fail (‘code’,
‘pattern’) function which evaluates ‘code’ in the caller’s context and checks that the
error message it produces matches the given pattern. Other examples such as save and
load are written in C++ where all Octave variables are in the ‘caller’ context and evalin
is not needed.
evalin (context,try)
evalin (context,try,catch)
Like eval, except that the expressions are evaluated in the context context, which
may be either "caller" or "base".
See also: [eval], page 157,[assignin], page 160.
assignin (context,varname,value)
Assign value to varname in context context, which may be either "base" or "caller".
See also: [evalin], page 160.
161
10 Statements
Statements may be a simple constant expression or a complicated list of nested loops and
conditional statements.
Control statements such as if,while, and so on control the flow of execution in Octave
programs. All the control statements start with special keywords such as if and while,
to distinguish them from simple expressions. Many control statements contain other state-
ments; for example, the if statement contains another statement which may or may not be
executed.
Each control statement has a corresponding end statement that marks the end of the
control statement. For example, the keyword endif marks the end of an if statement, and
endwhile marks the end of a while statement. You can use the keyword end anywhere a
more specific end keyword is expected, but using the more specific keywords is preferred
because if you use them, Octave is able to provide better diagnostics for mismatched or
missing end tokens.
The list of statements contained between keywords like if or while and the correspond-
ing end statement is called the body of a control statement.
10.1 The if Statement
The if statement is Octave’s decision-making statement. There are three basic forms of an
if statement. In its simplest form, it looks like this:
if (condition)
then-body
endif
condition is an expression that controls what the rest of the statement will do. The then-
body is executed only if condition is true.
The condition in an if statement is considered true if its value is nonzero, and false if
its value is zero. If the value of the conditional expression in an if statement is a vector or
a matrix, it is considered true only if it is non-empty and all of the elements are nonzero.
The conceptually equivalent code when condition is a matrix is shown below.
if (matrix)≡if (all (matrix(:)))
The second form of an if statement looks like this:
if (condition)
then-body
else
else-body
endif
If condition is true, then-body is executed; otherwise, else-body is executed.
Here is an example:
if (rem (x, 2) == 0)
printf ("x is even\n");
else
printf ("x is odd\n");
endif
162 GNU Octave
In this example, if the expression rem (x, 2) == 0 is true (that is, the value of xis
divisible by 2), then the first printf statement is evaluated, otherwise the second printf
statement is evaluated.
The third and most general form of the if statement allows multiple decisions to be
combined in a single statement. It looks like this:
if (condition)
then-body
elseif (condition)
elseif-body
else
else-body
endif
Any number of elseif clauses may appear. Each condition is tested in turn, and if one is
found to be true, its corresponding body is executed. If none of the conditions are true and
the else clause is present, its body is executed. Only one else clause may appear, and it
must be the last part of the statement.
In the following example, if the first condition is true (that is, the value of xis divisible
by 2), then the first printf statement is executed. If it is false, then the second condition
is tested, and if it is true (that is, the value of xis divisible by 3), then the second printf
statement is executed. Otherwise, the third printf statement is performed.
if (rem (x, 2) == 0)
printf ("x is even\n");
elseif (rem (x, 3) == 0)
printf ("x is odd and divisible by 3\n");
else
printf ("x is odd\n");
endif
Note that the elseif keyword must not be spelled else if, as is allowed in Fortran. If
it is, the space between the else and if will tell Octave to treat this as a new if statement
within another if statement’s else clause. For example, if you write
if (c1)
body-1
else if (c2)
body-2
endif
Octave will expect additional input to complete the first if statement. If you are using
Octave interactively, it will continue to prompt you for additional input. If Octave is reading
this input from a file, it may complain about missing or mismatched end statements, or, if
you have not used the more specific end statements (endif,endfor, etc.), it may simply
produce incorrect results, without producing any warning messages.
It is much easier to see the error if we rewrite the statements above like this,
Chapter 10: Statements 163
if (c1)
body-1
else
if (c2)
body-2
endif
using the indentation to show how Octave groups the statements. See Chapter 11 [Functions
and Scripts], page 173.
10.2 The switch Statement
It is very common to take different actions depending on the value of one variable. This is
possible using the if statement in the following way
if (X == 1)
do_something ();
elseif (X == 2)
do_something_else ();
else
do_something_completely_different ();
endif
This kind of code can however be very cumbersome to both write and maintain. To overcome
this problem Octave supports the switch statement. Using this statement, the above
example becomes
switch (X)
case 1
do_something ();
case 2
do_something_else ();
otherwise
do_something_completely_different ();
endswitch
This code makes the repetitive structure of the problem more explicit, making the code
easier to read, and hence maintain. Also, if the variable Xshould change its name, only one
line would need changing compared to one line per case when if statements are used.
The general form of the switch statement is
switch (expression)
case label
command_list
case label
command_list
...
otherwise
command_list
endswitch

164 GNU Octave
where label can be any expression. However, duplicate label values are not detected, and
only the command list corresponding to the first match will be executed. For the switch
statement to be meaningful at least one case label command_list clause must be present,
while the otherwise command_list clause is optional.
If label is a cell array the corresponding command list is executed if any of the elements of
the cell array match expression. As an example, the following program will print ‘Variable
is either 6 or 7’.
A = 7;
switch (A)
case { 6, 7 }
printf ("variable is either 6 or 7\n");
otherwise
printf ("variable is neither 6 nor 7\n");
endswitch
As with all other specific end keywords, endswitch may be replaced by end, but you
can get better diagnostics if you use the specific forms.
One advantage of using the switch statement compared to using if statements is that
the labels can be strings. If an if statement is used it is not possible to write
if (X == "a string") # This is NOT valid
since a character-to-character comparison between Xand the string will be made instead of
evaluating if the strings are equal. This special-case is handled by the switch statement,
and it is possible to write programs that look like this
switch (X)
case "a string"
do_something
...
endswitch
10.2.1 Notes for the C Programmer
The switch statement is also available in the widely used C programming language. There
are, however, some differences between the statement in Octave and C
•Cases are exclusive, so they don’t ‘fall through’ as do the cases in the switch statement
of the C language.
•The command list elements are not optional. Making the list optional would have
meant requiring a separator between the label and the command list. Otherwise,
things like
switch (foo)
case (1) -2
...
would produce surprising results, as would
switch (foo)
case (1)
case (2)
doit ();
...
Chapter 10: Statements 165
particularly for C programmers. If doit() should be executed if foo is either 1or 2,
the above code should be written with a cell array like this
switch (foo)
case { 1, 2 }
doit ();
...
10.3 The while Statement
In programming, a loop means a part of a program that is (or at least can be) executed
two or more times in succession.
The while statement is the simplest looping statement in Octave. It repeatedly executes
a statement as long as a condition is true. As with the condition in an if statement, the
condition in a while statement is considered true if its value is nonzero, and false if its
value is zero. If the value of the conditional expression in a while statement is a vector or
a matrix, it is considered true only if it is non-empty and all of the elements are nonzero.
Octave’s while statement looks like this:
while (condition)
body
endwhile
Here body is a statement or list of statements that we call the body of the loop, and
condition is an expression that controls how long the loop keeps running.
The first thing the while statement does is test condition. If condition is true, it executes
the statement body. After body has been executed, condition is tested again, and if it is
still true, body is executed again. This process repeats until condition is no longer true. If
condition is initially false, the body of the loop is never executed.
This example creates a variable fib that contains the first ten elements of the Fibonacci
sequence.
fib = ones (1, 10);
i = 3;
while (i <= 10)
fib (i) = fib (i-1) + fib (i-2);
i++;
endwhile
Here the body of the loop contains two statements.
The loop works like this: first, the value of iis set to 3. Then, the while tests whether
iis less than or equal to 10. This is the case when iequals 3, so the value of the i-th
element of fib is set to the sum of the previous two values in the sequence. Then the i++
increments the value of iand the loop repeats. The loop terminates when ireaches 11.
A newline is not required between the condition and the body; but using one makes the
program clearer unless the body is very simple.
166 GNU Octave
10.4 The do-until Statement
The do-until statement is similar to the while statement, except that it repeatedly ex-
ecutes a statement until a condition becomes true, and the test of the condition is at the
end of the loop, so the body of the loop is always executed at least once. As with the
condition in an if statement, the condition in a do-until statement is considered true if
its value is nonzero, and false if its value is zero. If the value of the conditional expression
in a do-until statement is a vector or a matrix, it is considered true only if it is non-empty
and all of the elements are nonzero.
Octave’s do-until statement looks like this:
do
body
until (condition)
Here body is a statement or list of statements that we call the body of the loop, and
condition is an expression that controls how long the loop keeps running.
This example creates a variable fib that contains the first ten elements of the Fibonacci
sequence.
fib = ones (1, 10);
i = 2;
do
i++;
fib (i) = fib (i-1) + fib (i-2);
until (i == 10)
A newline is not required between the do keyword and the body; but using one makes
the program clearer unless the body is very simple.
10.5 The for Statement
The for statement makes it more convenient to count iterations of a loop. The general
form of the for statement looks like this:
for var =expression
body
endfor
where body stands for any statement or list of statements, expression is any valid expression,
and var may take several forms. Usually it is a simple variable name or an indexed variable.
If the value of expression is a structure, var may also be a vector with two elements. See
Section 10.5.1 [Looping Over Structure Elements], page 167, below.
The assignment expression in the for statement works a bit differently than Octave’s
normal assignment statement. Instead of assigning the complete result of the expression, it
assigns each column of the expression to var in turn. If expression is a range, a row vector,
or a scalar, the value of var will be a scalar each time the loop body is executed. If var is a
column vector or a matrix, var will be a column vector each time the loop body is executed.
The following example shows another way to create a vector containing the first ten
elements of the Fibonacci sequence, this time using the for statement:
Chapter 10: Statements 167
fib = ones (1, 10);
for i = 3:10
fib(i) = fib(i-1) + fib(i-2);
endfor
This code works by first evaluating the expression 3:10, to produce a range of values from 3
to 10 inclusive. Then the variable iis assigned the first element of the range and the body
of the loop is executed once. When the end of the loop body is reached, the next value in
the range is assigned to the variable i, and the loop body is executed again. This process
continues until there are no more elements to assign.
Within Octave is it also possible to iterate over matrices or cell arrays using the for
statement. For example consider
disp ("Loop over a matrix")
for i = [1,3;2,4]
i
endfor
disp ("Loop over a cell array")
for i = {1,"two";"three",4}
i
endfor
In this case the variable itakes on the value of the columns of the matrix or cell matrix.
So the first loop iterates twice, producing two column vectors [1;2], followed by [3;4],
and likewise for the loop over the cell array. This can be extended to loops over multi-
dimensional arrays. For example:
a = [1,3;2,4]; c = cat (3, a, 2*a);
for i = c
i
endfor
In the above case, the multi-dimensional matrix cis reshaped to a two-dimensional matrix as
reshape (c, rows (c), prod (size (c)(2:end))) and then the same behavior as a loop
over a two-dimensional matrix is produced.
Although it is possible to rewrite all for loops as while loops, the Octave language has
both statements because often a for loop is both less work to type and more natural to
think of. Counting the number of iterations is very common in loops and it can be easier
to think of this counting as part of looping rather than as something to do inside the loop.
10.5.1 Looping Over Structure Elements
A special form of the for statement allows you to loop over all the elements of a structure:
for [ val,key ] = expression
body
endfor
In this form of the for statement, the value of expression must be a structure. If it is, key
and val are set to the name of the element and the corresponding value in turn, until there
are no more elements. For example:
168 GNU Octave
x.a = 1
x.b = [1, 2; 3, 4]
x.c = "string"
for [val, key] = x
key
val
endfor
akey = a
aval = 1
akey = b
aval =
a
a1 2
a3 4
a
akey = c
aval = string
The elements are not accessed in any particular order. If you need to cycle through
the list in a particular way, you will have to use the function fieldnames and sort the list
yourself.
10.6 The break Statement
The break statement jumps out of the innermost while,do-until, or for loop that encloses
it. The break statement may only be used within the body of a loop. The following example
finds the smallest divisor of a given integer, and also identifies prime numbers:
num = 103;
div = 2;
while (div*div <= num)
if (rem (num, div) == 0)
break;
endif
div++;
endwhile
if (rem (num, div) == 0)
printf ("Smallest divisor of %d is %d\n", num, div)
else
printf ("%d is prime\n", num);
endif
When the remainder is zero in the first while statement, Octave immediately breaks
out of the loop. This means that Octave proceeds immediately to the statement following
the loop and continues processing. (This is very different from the exit statement which
stops the entire Octave program.)
Here is another program equivalent to the previous one. It illustrates how the condition
of a while statement could just as well be replaced with a break inside an if:
Chapter 10: Statements 169
num = 103;
div = 2;
while (1)
if (rem (num, div) == 0)
printf ("Smallest divisor of %d is %d\n", num, div);
break;
endif
div++;
if (div*div > num)
printf ("%d is prime\n", num);
break;
endif
endwhile
10.7 The continue Statement
The continue statement, like break, is used only inside while,do-until, or for loops.
It skips over the rest of the loop body, causing the next cycle around the loop to begin
immediately. Contrast this with break, which jumps out of the loop altogether. Here is an
example:
# print elements of a vector of random
# integers that are even.
# first, create a row vector of 10 random
# integers with values between 0 and 100:
vec = round (rand (1, 10) * 100);
# print what we’re interested in:
for x = vec
if (rem (x, 2) != 0)
continue;
endif
printf ("%d\n", x);
endfor
If one of the elements of vec is an odd number, this example skips the print statement
for that element, and continues back to the first statement in the loop.
This is not a practical example of the continue statement, but it should give you a clear
understanding of how it works. Normally, one would probably write the loop like this:
for x = vec
if (rem (x, 2) == 0)
printf ("%d\n", x);
endif
endfor

170 GNU Octave
10.8 The unwind protect Statement
Octave supports a limited form of exception handling modeled after the unwind-protect
form of Lisp.
The general form of an unwind_protect block looks like this:
unwind_protect
body
unwind_protect_cleanup
cleanup
end_unwind_protect
where body and cleanup are both optional and may contain any Octave expressions or
commands. The statements in cleanup are guaranteed to be executed regardless of how
control exits body.
This is useful to protect temporary changes to global variables from possible errors. For
example, the following code will always restore the original value of the global variable
frobnosticate even if an error occurs in the first part of the unwind_protect block.
save_frobnosticate = frobnosticate;
unwind_protect
frobnosticate = true;
...
unwind_protect_cleanup
frobnosticate = save_frobnosticate;
end_unwind_protect
Without unwind_protect, the value of frobnosticate would not be restored if an error occurs
while evaluating the first part of the unwind_protect block because evaluation would stop
at the point of the error and the statement to restore the value would not be executed.
In addition to unwind protect, Octave supports another form of exception handling, the
try block.
10.9 The try Statement
The original form of a try block looks like this:
try
body
catch
cleanup
end_try_catch
where body and cleanup are both optional and may contain any Octave expressions or
commands. The statements in cleanup are only executed if an error occurs in body.
No warnings or error messages are printed while body is executing. If an error does
occur during the execution of body,cleanup can use the functions lasterr or lasterror
to access the text of the message that would have been printed, as well as its identifier. The
alternative form,
Chapter 10: Statements 171
try
body
catch err
cleanup
end_try_catch
will automatically store the output of lasterror in the structure err. See Chapter 12
[Errors and Warnings], page 215, for more information about the lasterr and lasterror
functions.
10.10 Continuation Lines
In the Octave language, most statements end with a newline character and you must tell
Octave to ignore the newline character in order to continue a statement from one line to
the next. Lines that end with the characters ... are joined with the following line before
they are divided into tokens by Octave’s parser. For example, the lines
x = long_variable_name ...
+ longer_variable_name ...
- 42
form a single statement.
Any text between the continuation marker and the newline character is ignored. For
example, the statement
x = long_variable_name ... # comment one
+ longer_variable_name ...comment two
- 42 # last comment
is equivalent to the one shown above.
Inside double-quoted string constants, the character \has to be used as continuation
marker. The \must appear at the end of the line just before the newline character:
s = "This text starts in the first line \
and is continued in the second line."
Input that occurs inside parentheses can be continued to the next line without having to
use a continuation marker. For example, it is possible to write statements like
if (fine_dining_destination == on_a_boat
|| fine_dining_destination == on_a_train)
seuss (i, will, not, eat, them, sam, i, am, i,
will, not, eat, green, eggs, and, ham);
endif
without having to add to the clutter with continuation markers.
173
11 Functions and Scripts
Complicated Octave programs can often be simplified by defining functions. Functions can
be defined directly on the command line during interactive Octave sessions, or in external
files, and can be called just like built-in functions.
11.1 Introduction to Function and Script Files
There are seven different things covered in this section.
1. Typing in a function at the command prompt.
2. Storing a group of commands in a file — called a script file.
3. Storing a function in a file—called a function file.
4. Subfunctions in function files.
5. Multiple functions in one script file.
6. Private functions.
7. Nested functions.
Both function files and script files end with an extension of .m, for matlab compatibility.
If you want more than one independent functions in a file, it must be a script file (see
Section 11.10 [Script Files], page 201), and to use these functions you must execute the
script file before you can use the functions that are in the script file.
11.2 Defining Functions
In its simplest form, the definition of a function named name looks like this:
function name
body
endfunction
A valid function name is like a valid variable name: a sequence of letters, digits and under-
scores, not starting with a digit. Functions share the same pool of names as variables.
The function body consists of Octave statements. It is the most important part of the
definition, because it says what the function should actually do.
For example, here is a function that, when executed, will ring the bell on your terminal
(assuming that it is possible to do so):
function wakeup
printf ("\a");
endfunction
The printf statement (see Chapter 14 [Input and Output], page 243) simply tells Octave
to print the string "\a". The special character ‘\a’ stands for the alert character (ASCII
7). See Chapter 5 [Strings], page 67.
Once this function is defined, you can ask Octave to evaluate it by typing the name of
the function.
Normally, you will want to pass some information to the functions you define. The
syntax for passing parameters to a function in Octave is
174 GNU Octave
function name (arg-list)
body
endfunction
where arg-list is a comma-separated list of the function’s arguments. When the function is
called, the argument names are used to hold the argument values given in the call. The list
of arguments may be empty, in which case this form is equivalent to the one shown above.
To print a message along with ringing the bell, you might modify the wakeup to look
like this:
function wakeup (message)
printf ("\a%s\n", message);
endfunction
Calling this function using a statement like this
wakeup ("Rise and shine!");
will cause Octave to ring your terminal’s bell and print the message ‘Rise and shine!’,
followed by a newline character (the ‘\n’ in the first argument to the printf statement).
In most cases, you will also want to get some information back from the functions you
define. Here is the syntax for writing a function that returns a single value:
function ret-var =name (arg-list)
body
endfunction
The symbol ret-var is the name of the variable that will hold the value to be returned by
the function. This variable must be defined before the end of the function body in order
for the function to return a value.
Variables used in the body of a function are local to the function. Variables named
in arg-list and ret-var are also local to the function. See Section 7.1 [Global Variables],
page 124, for information about how to access global variables inside a function.
For example, here is a function that computes the average of the elements of a vector:
function retval = avg (v)
retval = sum (v) / length (v);
endfunction
If we had written avg like this instead,
function retval = avg (v)
if (isvector (v))
retval = sum (v) / length (v);
endif
endfunction
and then called the function with a matrix instead of a vector as the argument, Octave
would have printed an error message like this:
error: value on right hand side of assignment is undefined
because the body of the if statement was never executed, and retval was never defined.
To prevent obscure errors like this, it is a good idea to always make sure that the return
Chapter 11: Functions and Scripts 175
variables will always have values, and to produce meaningful error messages when problems
are encountered. For example, avg could have been written like this:
function retval = avg (v)
retval = 0;
if (isvector (v))
retval = sum (v) / length (v);
else
error ("avg: expecting vector argument");
endif
endfunction
There is still one additional problem with this function. What if it is called without an
argument? Without additional error checking, Octave will probably print an error message
that won’t really help you track down the source of the error. To allow you to catch errors
like this, Octave provides each function with an automatic variable called nargin. Each
time a function is called, nargin is automatically initialized to the number of arguments
that have actually been passed to the function. For example, we might rewrite the avg
function like this:
function retval = avg (v)
retval = 0;
if (nargin != 1)
usage ("avg (vector)");
endif
if (isvector (v))
retval = sum (v) / length (v);
else
error ("avg: expecting vector argument");
endif
endfunction
Although Octave does not automatically report an error if you call a function with more
arguments than expected, doing so probably indicates that something is wrong. Octave
also does not automatically report an error if a function is called with too few arguments,
but any attempt to use a variable that has not been given a value will result in an error.
To avoid such problems and to provide useful messages, we check for both possibilities and
issue our own error message.
nargin ()
nargin (fcn)
Report the number of input arguments to a function.
Called from within a function, return the number of arguments passed to the function.
At the top level, return the number of command line arguments passed to Octave.
If called with the optional argument fcn—a function name or handle—return the
declared number of arguments that the function can accept.
If the last argument to fcn is varargin the returned value is negative. For example,
the function union for sets is declared as
176 GNU Octave
function [y, ia, ib] = union (a, b, varargin)
and
nargin ("union")
⇒-3
Programming Note: nargin does not work on compiled functions (.oct files) such as
built-in or dynamically loaded functions.
See also: [nargout], page 178,[narginchk], page 179,[varargin], page 184,[inputname],
page 176.
inputname (n)
Return the name of the n-th argument to the calling function.
If the argument is not a simple variable name, return an empty string. As an example,
a reference to a field in a structure such as s.field is not a simple name and will
return "".
inputname is only useful within a function. When used at the command line it always
returns an empty string.
See also: [nargin], page 175,[nthargout], page 177.
val = silent_functions ()
old_val = silent_functions (new_val)
silent_functions (new_val,"local")
Query or set the internal variable that controls whether internal output from a func-
tion is suppressed.
If this option is disabled, Octave will display the results produced by evaluating
expressions within a function body that are not terminated with a semicolon.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
11.3 Multiple Return Values
Unlike many other computer languages, Octave allows you to define functions that return
more than one value. The syntax for defining functions that return multiple values is
function [ret-list] = name (arg-list)
body
endfunction
where name,arg-list, and body have the same meaning as before, and ret-list is a comma-
separated list of variable names that will hold the values returned from the function. The
list of return values must have at least one element. If ret-list has only one element, this
form of the function statement is equivalent to the form described in the previous section.
Here is an example of a function that returns two values, the maximum element of a
vector and the index of its first occurrence in the vector.
Chapter 11: Functions and Scripts 177
function [max, idx] = vmax (v)
idx = 1;
max = v (idx);
for i = 2:length (v)
if (v (i) > max)
max = v (i);
idx = i;
endif
endfor
endfunction
In this particular case, the two values could have been returned as elements of a single
array, but that is not always possible or convenient. The values to be returned may not
have compatible dimensions, and it is often desirable to give the individual return values
distinct names.
It is possible to use the nthargout function to obtain only some of the return values or
several at once in a cell array. See Section 3.1.5 [Cell Array Objects], page 44.
nthargout (n,func, . . . )
nthargout (n,ntot,func, . . . )
Return the nth output argument of the function specified by the function handle or
string func.
Any additional arguments are passed directly to func. The total number of arguments
to call func with can be passed in ntot; by default ntot is n. The input ncan also be
a vector of indices of the output, in which case the output will be a cell array of the
requested output arguments.
The intended use nthargout is to avoid intermediate variables. For example, when
finding the indices of the maximum entry of a matrix, the following two compositions
of nthargout
m= magic (5);
cell2mat (nthargout ([1, 2], @ind2sub, size (m),
nthargout (2, @max, m(:))))
⇒5 3
are completely equivalent to the following lines:
m= magic (5);
[~, idx] = max (M(:));
[i, j] = ind2sub (size (m), idx);
[i, j]
⇒5 3
It can also be helpful to have all output arguments in a single cell in the following
manner:
USV = nthargout ([1:3], @svd, hilb (5));
See also: [nargin], page 175,[nargout], page 178,[varargin], page 184,[varargout],
page 184,[isargout], page 187.
178 GNU Octave
In addition to setting nargin each time a function is called, Octave also automatically
initializes nargout to the number of values that are expected to be returned. This allows
you to write functions that behave differently depending on the number of values that the
user of the function has requested. The implicit assignment to the built-in variable ans
does not figure in the count of output arguments, so the value of nargout may be zero.
The svd and lu functions are examples of built-in functions that behave differently
depending on the value of nargout.
It is possible to write functions that only set some return values. For example, calling
the function
function [x, y, z] = f ()
x = 1;
z = 2;
endfunction
as
[a, b, c] = f ()
produces:
a=1
b = [](0x0)
c=2
along with a warning.
nargout ()
nargout (fcn)
Report the number of output arguments from a function.
Called from within a function, return the number of values the caller expects to
receive. At the top level, nargout with no argument is undefined and will produce
an error.
If called with the optional argument fcn—a function name or handle—return the
number of declared output values that the function can produce.
If the final output argument is varargout the returned value is negative.
For example,
f ()
will cause nargout to return 0 inside the function fand
[s, t] = f ()
will cause nargout to return 2 inside the function f.
In the second usage,
nargout (@histc) # or nargout ("histc") using a string input
will return 2, because histc has two outputs, whereas
nargout (@imread)
will return -2, because imread has two outputs and the second is varargout.
Chapter 11: Functions and Scripts 179
Programming Note. nargout does not work for built-in functions and returns -1 for
all anonymous functions.
See also: [nargin], page 175,[varargout], page 184,[isargout], page 187,[nthargout],
page 177.
It is good practice at the head of a function to verify that it has been called correctly.
In Octave the following idiom is seen frequently
if (nargin < min_#_inputs || nargin > max_#_inputs)
print_usage ();
endif
which stops the function execution and prints a message about the correct way to call the
function whenever the number of inputs is wrong.
For compatibility with matlab,narginchk and nargoutchk are available which provide
similar error checking.
narginchk (minargs,maxargs)
Check for correct number of input arguments.
Generate an error message if the number of arguments in the calling function is outside
the range minargs and maxargs. Otherwise, do nothing.
Both minargs and maxargs must be scalar numeric values. Zero, Inf, and negative
values are all allowed, and minargs and maxargs may be equal.
Note that this function evaluates nargin on the caller.
See also: [nargoutchk], page 179,[error], page 215,[nargout], page 178,[nargin],
page 175.
nargoutchk (minargs,maxargs)
msgstr = nargoutchk (minargs,maxargs,nargs)
msgstr = nargoutchk (minargs,maxargs,nargs,"string")
msgstruct = nargoutchk (minargs,maxargs,nargs,"struct")
Check for correct number of output arguments.
In the first form, return an error if the number of arguments is not between minargs
and maxargs. Otherwise, do nothing. Note that this function evaluates the value of
nargout on the caller so its value must have not been tampered with.
Both minargs and maxargs must be numeric scalars. Zero, Inf, and negative are all
valid, and they can have the same value.
For backwards compatibility, the other forms return an appropriate error message
string (or structure) if the number of outputs requested is invalid.
This is useful for checking to that the number of output arguments supplied to a
function is within an acceptable range.
See also: [narginchk], page 179,[error], page 215,[nargout], page 178,[nargin],
page 175.
Besides the number of arguments, inputs can be checked for various properties.
validatestring is used for string arguments and validateattributes for numeric
arguments.

180 GNU Octave
validstr = validatestring (str,strarray)
validstr = validatestring (str,strarray,funcname)
validstr = validatestring (str,strarray,funcname,varname)
validstr = validatestring (. . . , position)
Verify that str is an element, or substring of an element, in strarray.
When str is a character string to be tested, and strarray is a cellstr of valid values,
then validstr will be the validated form of str where validation is defined as str being
a member or substring of validstr. This is useful for both verifying and expanding
short options, such as "r", to their longer forms, such as "red". If str is a substring
of validstr, and there are multiple matches, the shortest match will be returned if all
matches are substrings of each other. Otherwise, an error will be raised because the
expansion of str is ambiguous. All comparisons are case insensitive.
The additional inputs funcname,varname, and position are optional and will make
any generated validation error message more specific.
Examples:
validatestring ("r", {"red", "green", "blue"})
⇒"red"
validatestring ("b", {"red", "green", "blue", "black"})
⇒error: validatestring: multiple unique matches were found for ’b’:
blue, black
See also: [strcmp], page 76,[strcmpi], page 77,[validateattributes], page 180,
[inputParser], page 182.
validateattributes (A,classes,attributes)
validateattributes (A,classes,attributes,arg_idx)
validateattributes (A,classes,attributes,func_name)
validateattributes (A,classes,attributes,func_name,arg_name)
validateattributes (A,classes,attributes,func_name,arg_name,
arg_idx)
Check validity of input argument.
Confirms that the argument Ais valid by belonging to one of classes, and holding
all of the attributes. If it does not, an error is thrown, with a message formatted
accordingly. The error message can be made further complete by the function name
fun name, the argument name arg name, and its position in the input arg idx.
classes must be a cell array of strings (an empty cell array is allowed) with the name
of classes (remember that a class name is case sensitive). In addition to the class
name, the following categories names are also valid:
"float" Floating point value comprising classes "double" and "single".
"integer"
Integer value comprising classes (u)int8, (u)int16, (u)int32, (u)int64.
"numeric"
Numeric value comprising either a floating point or integer value.
attributes must be a cell array with names of checks for A. Some of them require an
additional value to be supplied right after the name (see details for each below).
"<=" All values are less than or equal to the following value in attributes.
Chapter 11: Functions and Scripts 181
"<" All values are less than the following value in attributes.
">=" All values are greater than or equal to the following value in attributes.
">" All values are greater than the following value in attributes.
"2d" A 2-dimensional matrix. Note that vectors and empty matrices have 2
dimensions, one of them being of length 1, or both length 0.
"3d" Has no more than 3 dimensions. A 2-dimensional matrix is a 3-D matrix
whose 3rd dimension is of length 1.
"binary" All values are either 1 or 0.
"column" Values are arranged in a single column.
"decreasing"
No value is NaN, and each is less than the preceding one.
"diag" Value is a diagonal matrix.
"even" All values are even numbers.
"finite" All values are finite.
"increasing"
No value is NaN, and each is greater than the preceding one.
"integer"
All values are integer. This is different than using isinteger which only
checks its an integer type. This checks that each value in Ais an integer
value, i.e., it has no decimal part.
"ncols" Has exactly as many columns as the next value in attributes.
"ndims" Has exactly as many dimensions as the next value in attributes.
"nondecreasing"
No value is NaN, and each is greater than or equal to the preceding one.
"nonempty"
It is not empty.
"nonincreasing"
No value is NaN, and each is less than or equal to the preceding one.
"nonnan" No value is a NaN.
"nonnegative"
All values are non negative.
"nonsparse"
It is not a sparse matrix.
"nonzero"
No value is zero.
"nrows" Has exactly as many rows as the next value in attributes.
"numel" Has exactly as many elements as the next value in attributes.
182 GNU Octave
"odd" All values are odd numbers.
"positive"
All values are positive.
"real" It is a non-complex matrix.
"row" Values are arranged in a single row.
"scalar" It is a scalar.
"size" Its size has length equal to the values of the next in attributes. The next
value must is an array with the length for each dimension. To ignore the
check for a certain dimension, the value of NaN can be used.
"square" Is a square matrix.
"vector" Values are arranged in a single vector (column or vector).
See also: [isa], page 39,[validatestring], page 179,[inputParser], page 182.
If none of the preceding functions is sufficient there is also the class inputParser which
can perform extremely complex input checking for functions.
p= inputParser ()
Create object pof the inputParser class.
This class is designed to allow easy parsing of function arguments. The class supports
four types of arguments:
1. mandatory (see addRequired);
2. optional (see addOptional);
3. named (see addParameter);
4. switch (see addSwitch).
After defining the function API with these methods, the supplied arguments can be
parsed with the parse method and the parsing results accessed with the Results
accessor.
inputParser.Parameters
Return list of parameter names already defined.
inputParser.Results
Return structure with argument names as fieldnames and corresponding values.
inputParser.Unmatched
Return structure similar to Results, but for unmatched parameters. See the
KeepUnmatched property.
inputParser.UsingDefaults
Return cell array with the names of arguments that are using default values.
inputParser.CaseSensitive =boolean
Set whether matching of argument names should be case sensitive. Defaults to false.
Chapter 11: Functions and Scripts 183
inputParser.FunctionName =name
Set function name to be used in error messages; Defaults to empty string.
inputParser.KeepUnmatched =boolean
Set whether an error should be given for non-defined arguments. Defaults to false. If
set to true, the extra arguments can be accessed through Unmatched after the parse
method. Note that since Switch and Parameter arguments can be mixed, it is not
possible to know the unmatched type. If argument is found unmatched it is assumed
to be of the Parameter type and it is expected to be followed by a value.
inputParser.StructExpand =boolean
Set whether a structure can be passed to the function instead of parameter/value
pairs. Defaults to true.
The following example shows how to use this class:
function check (varargin)
p = inputParser (); # create object
p.FunctionName = "check"; # set function name
p.addRequired ("pack", @ischar); # mandatory argument
p.addOptional ("path", pwd(), @ischar); # optional argument
## create a function handle to anonymous functions for validators
val_mat = @(x) isvector (x) && all (x <= 1) && all (x >= 0);
p.addOptional ("mat", [0 0], val_mat);
## create two arguments of type "Parameter"
val_type = @(x) any (strcmp (x, {"linear", "quadratic"}));
p.addParameter ("type", "linear", val_type);
val_verb = @(x) any (strcmp (x, {"low", "medium", "high"}));
p.addParameter ("tolerance", "low", val_verb);
## create a switch type of argument
p.addSwitch ("verbose");
p.parse (varargin{:}); # Run created parser on inputs
## the rest of the function can access inputs by using p.Results.
## for example, get the tolerance input with p.Results.tolerance
endfunction
184 GNU Octave
check ("mech"); # valid, use defaults for other arguments
check (); # error, one argument is mandatory
check (1); # error, since ! ischar
check ("mech", "~/dev"); # valid, use defaults for other arguments
check ("mech", "~/dev", [0 1 0 0], "type", "linear"); # valid
## following is also valid. Note how the Switch argument type can
## be mixed into or before the Parameter argument type (but it
## must still appear after any Optional argument).
check ("mech", "~/dev", [0 1 0 0], "verbose", "tolerance", "high");
## following returns an error since not all optional arguments,
## ‘path’ and ‘mat’, were given before the named argument ‘type’.
check ("mech", "~/dev", "type", "linear");
Note 1 : A function can have any mixture of the four API types but they must appear
in a specific order. Required arguments must be first and can be followed by any
Optional arguments. Only the Parameter and Switch arguments may be mixed
together and they must appear at the end.
Note 2 : If both Optional and Parameter arguments are mixed in a function API
then once a string Optional argument fails to validate it will be considered the end
of the Optional arguments. The remaining arguments will be compared against any
Parameter or Switch arguments.
See also: [nargin], page 175,[validateattributes], page 180,[validatestring], page 179,
[varargin], page 184.
11.4 Variable-length Argument Lists
Sometimes the number of input arguments is not known when the function is defined. As
an example think of a function that returns the smallest of all its input arguments. For
example:
a = smallest (1, 2, 3);
b = smallest (1, 2, 3, 4);
In this example both aand bwould be 1. One way to write the smallest function is
function val = smallest (arg1, arg2, arg3, arg4, arg5)
body
endfunction
and then use the value of nargin to determine which of the input arguments should be
considered. The problem with this approach is that it can only handle a limited number of
input arguments.
If the special parameter name varargin appears at the end of a function parameter list
it indicates that the function takes a variable number of input arguments. Using varargin
the function looks like this
function val = smallest (varargin)
body
endfunction
Chapter 11: Functions and Scripts 185
In the function body the input arguments can be accessed through the variable varargin.
This variable is a cell array containing all the input arguments. See Section 6.2 [Cell Arrays],
page 112, for details on working with cell arrays. The smallest function can now be defined
like this
function val = smallest (varargin)
val = min ([varargin{:}]);
endfunction
This implementation handles any number of input arguments, but it’s also a very simple
solution to the problem.
A slightly more complex example of varargin is a function print_arguments that prints
all input arguments. Such a function can be defined like this
function print_arguments (varargin)
for i = 1:length (varargin)
printf ("Input argument %d: ", i);
disp (varargin{i});
endfor
endfunction
This function produces output like this
print_arguments (1, "two", 3);
aInput argument 1: 1
aInput argument 2: two
aInput argument 3: 3
[reg,prop] = parseparams (params)
[reg,var1, ...] = parseparams (params,name1,default1, . . . )
Return in reg the cell elements of param up to the first string element and in prop
all remaining elements beginning with the first string element.
For example:
[reg, prop] = parseparams ({1, 2, "linewidth", 10})
reg =
{
[1,1] = 1
[1,2] = 2
}
prop =
{
[1,1] = linewidth
[1,2] = 10
}
The parseparams function may be used to separate regular numeric arguments from
additional arguments given as property/value pairs of the varargin cell array.
In the second form of the call, available options are specified directly with their default
values given as name-value pairs. If params do not form name-value pairs, or if an
option occurs that does not match any of the available options, an error occurs.
186 GNU Octave
When called from an m-file function, the error is prefixed with the name of the caller
function.
The matching of options is case-insensitive.
See also: [varargin], page 184,[inputParser], page 182.
11.5 Ignoring Arguments
In the formal argument list, it is possible to use the dummy placeholder ~instead of a name.
This indicates that the corresponding argument value should be ignored and not stored to
any variable.
function val = pick2nd (~, arg2)
val = arg2;
endfunction
The value of nargin is not affected by using this declaration.
Return arguments can also be ignored using the same syntax. For example, the sort
function returns both the sorted values, and an index vector for the original input which
will result in a sorted output. Ignoring the second output is simple—don’t request more
than one output. But ignoring the first, and calculating just the second output, requires
the use of the ~placeholder.
x = [2, 3, 1];
[s, i] = sort (x)
⇒
s =
123
i =
312
[~, i] = sort (x)
⇒
i =
312
When using the ~placeholder, commas—not whitespace—must be used to separate
output arguments. Otherwise, the interpreter will view ~as the logical not operator.
[~ i] = sort (x)
parse error:
invalid left hand side of assignment
Functions may take advantage of ignored outputs to reduce the number of calculations
performed. To do so, use the isargout function to query whether the output argument is
wanted. For example:
Chapter 11: Functions and Scripts 187
function [out1, out2] = long_function (x, y, z)
if (isargout (1))
## Long calculation
...
out1 = result;
endif
...
endfunction
isargout (k)
Within a function, return a logical value indicating whether the argument kwill be
assigned to a variable on output.
If the result is false, the argument has been ignored during the function call through
the use of the tilde (~) special output argument. Functions can use isargout to avoid
performing unnecessary calculations for outputs which are unwanted.
If kis outside the range 1:max (nargout), the function returns false. kcan also be
an array, in which case the function works element-by-element and a logical array is
returned. At the top level, isargout returns an error.
See also: [nargout], page 178,[varargout], page 184,[nthargout], page 177.
11.6 Variable-length Return Lists
It is possible to return a variable number of output arguments from a function using a
syntax that’s similar to the one used with the special varargin parameter name. To let a
function return a variable number of output arguments the special output parameter name
varargout is used. As with varargin,varargout is a cell array that will contain the
requested output arguments.
As an example the following function sets the first output argument to 1, the second to
2, and so on.
function varargout = one_to_n ()
for i = 1:nargout
varargout{i} = i;
endfor
endfunction
When called this function returns values like this
[a, b, c] = one_to_n ()
⇒a = 1
⇒b = 2
⇒c = 3
If varargin (varargout) does not appear as the last element of the input (output)
parameter list, then it is not special, and is handled the same as any other parameter name.
[r1,r2, ..., rn] = deal (a)
[r1,r2, ..., rn] = deal (a1,a2, . . . , an)
Copy the input parameters into the corresponding output parameters.
If only a single input parameter is supplied, its value is copied to each of the outputs.
188 GNU Octave
For example,
[a, b, c] = deal (x, y, z);
is equivalent to
a = x;
b = y;
c = z;
and
[a, b, c] = deal (x);
is equivalent to
a=b=c=x;
Programming Note: deal is often used with comma separated lists derived from cell
arrays or structures. This is unnecessary as the interpreter can perform the same
action without the overhead of a function call. For example:
c = {[1 2], "Three", 4};
[x, y, z] = c{:}
⇒x =
1 2
y = Three
z = 4
See also: [cell2struct], page 120,[struct2cell], page 111,[repmat], page 454.
11.7 Returning from a Function
The body of a user-defined function can contain a return statement. This statement returns
control to the rest of the Octave program. It looks like this:
return
Unlike the return statement in C, Octave’s return statement cannot be used to return
a value from a function. Instead, you must assign values to the list of return variables that
are part of the function statement. The return statement simply makes it easier to exit
a function from a deeply nested loop or conditional statement.
Here is an example of a function that checks to see if any elements of a vector are nonzero.
function retval = any_nonzero (v)
retval = 0;
for i = 1:length (v)
if (v (i) != 0)
retval = 1;
return;
endif
endfor
printf ("no nonzero elements found\n");
endfunction
Chapter 11: Functions and Scripts 189
Note that this function could not have been written using the break statement to exit
the loop once a nonzero value is found without adding extra logic to avoid printing the
message if the vector does contain a nonzero element.
[Keyword]return
When Octave encounters the keyword return inside a function or script, it returns
control to the caller immediately. At the top level, the return statement is ignored.
Areturn statement is assumed at the end of every function definition.
11.8 Default Arguments
Since Octave supports variable number of input arguments, it is very useful to assign default
values to some input arguments. When an input argument is declared in the argument list
it is possible to assign a default value to the argument like this
function name (arg1 =val1, ...)
body
endfunction
If no value is assigned to arg1 by the user, it will have the value val1.
As an example, the following function implements a variant of the classic “Hello, World”
program.
function hello (who = "World")
printf ("Hello, %s!\n", who);
endfunction
When called without an input argument the function prints the following
hello ();
aHello, World!
and when it’s called with an input argument it prints the following
hello ("Beautiful World of Free Software");
aHello, Beautiful World of Free Software!
Sometimes it is useful to explicitly tell Octave to use the default value of an input
argument. This can be done writing a ‘:’ as the value of the input argument when calling
the function.
hello (:);
aHello, World!
11.9 Function Files
Except for simple one-shot programs, it is not practical to have to define all the functions
you need each time you need them. Instead, you will normally want to save them in a file
so that you can easily edit them, and save them for use at a later time.
Octave does not require you to load function definitions from files before using them.
You simply need to put the function definitions in a place where Octave can find them.
When Octave encounters an identifier that is undefined, it first looks for variables or
functions that are already compiled and currently listed in its symbol table. If it fails to
find a definition there, it searches a list of directories (the path) for files ending in .m that

190 GNU Octave
have the same base name as the undefined identifier.1Once Octave finds a file with a name
that matches, the contents of the file are read. If it defines a single function, it is compiled
and executed. See Section 11.10 [Script Files], page 201, for more information about how
you can define more than one function in a single file.
When Octave defines a function from a function file, it saves the full name of the file it
read and the time stamp on the file. If the time stamp on the file changes, Octave may reload
the file. When Octave is running interactively, time stamp checking normally happens at
most once each time Octave prints the prompt. Searching for new function definitions also
occurs if the current working directory changes.
Checking the time stamp allows you to edit the definition of a function while Octave is
running, and automatically use the new function definition without having to restart your
Octave session.
To avoid degrading performance unnecessarily by checking the time stamps on functions
that are not likely to change, Octave assumes that function files in the directory tree octave-
home/share/octave/version/m will not change, so it doesn’t have to check their time
stamps every time the functions defined in those files are used. This is normally a very
good assumption and provides a significant improvement in performance for the function
files that are distributed with Octave.
If you know that your own function files will not change while you are running Octave,
you can improve performance by calling ignore_function_time_stamp ("all"), so that
Octave will ignore the time stamps for all function files. Passing "system" to this function
resets the default behavior.
edit name
edit field value
value = edit ("get",field)
value = edit ("get","all")
Edit the named function, or change editor settings.
If edit is called with the name of a file or function as its argument it will be opened
in the text editor defined by EDITOR.
•If the function name is available in a file on your path and that file is modifiable,
then it will be edited in place. If it is a system function, then it will first be
copied to the directory HOME (see below) and then edited. If no file is found, then
the m-file variant, ending with ".m", will be considered. If still no file is found,
then variants with a leading "@" and then with both a leading "@" and trailing
".m" will be considered.
•If name is the name of a function defined in the interpreter but not in an m-file,
then an m-file will be created in HOME to contain that function along with its
current definition.
•If name.cc is specified, then it will search for name.cc in the path and try to
modify it, otherwise it will create a new .cc file in the current directory. If name
happens to be an m-file or interpreter defined function, then the text of that
function will be inserted into the .cc file as a comment.
1The ‘.m’ suffix was chosen for compatibility with matlab.
Chapter 11: Functions and Scripts 191
•If name.ext is on your path then it will be edited, otherwise the editor will be
started with name.ext in the current directory as the filename. If name.ext is
not modifiable, it will be copied to HOME before editing.
Warning: You may need to clear name before the new definition is available. If
you are editing a .cc file, you will need to execute mkoctfile name.cc before the
definition will be available.
If edit is called with field and value variables, the value of the control field field will
be set to value.
If an output argument is requested and the first input argument is get then edit
will return the value of the control field field. If the control field does not exist, edit
will return a structure containing all fields and values. Thus, edit ("get", "all")
returns a complete control structure.
The following control fields are used:
‘home’ This is the location of user local m-files. Be sure it is in your path. The
default is ~/octave.
‘author’ This is the name to put after the "## Author:"field of new functions.
By default it guesses from the gecos field of the password database.
‘email’ This is the e-mail address to list after the name in the author field. By
default it guesses <$LOGNAME@$HOSTNAME>, and if $HOSTNAME is not de-
fined it uses uname -n. You probably want to override this. Be sure to
use the format user@host.
‘license’
‘gpl’ GNU General Public License (default).
‘bsd’ BSD-style license without advertising clause.
‘pd’ Public domain.
‘"text"’ Your own default copyright and license.
Unless you specify ‘pd’, edit will prepend the copyright statement with
"Copyright (C) YYYY Author".
‘mode’ This value determines whether the editor should be started in async mode
(editor is started in the background and Octave continues) or sync mode
(Octave waits until the editor exits). Set it to "sync" to start the editor
in sync mode. The default is "async" (see [system], page 833).
‘editinplace’
Determines whether files should be edited in place, without regard to
whether they are modifiable or not. The default is false.
mfilename ()
mfilename ("fullpath")
mfilename ("fullpathext")
Return the name of the currently executing file.
When called from outside an m-file return the empty string.
192 GNU Octave
Given the argument "fullpath", include the directory part of the filename, but not
the extension.
Given the argument "fullpathext", include the directory part of the filename and
the extension.
val = ignore_function_time_stamp ()
old_val = ignore_function_time_stamp (new_val)
Query or set the internal variable that controls whether Octave checks the time stamp
on files each time it looks up functions defined in function files.
If the internal variable is set to "system", Octave will not automatically recompile
function files in subdirectories of octave-home/lib/version if they have changed
since they were last compiled, but will recompile other function files in the search
path if they change.
If set to "all", Octave will not recompile any function files unless their definitions
are removed with clear.
If set to "none", Octave will always check time stamps on files to determine whether
functions defined in function files need to recompiled.
11.9.1 Manipulating the Load Path
When a function is called, Octave searches a list of directories for a file that contains the
function declaration. This list of directories is known as the load path. By default the
load path contains a list of directories distributed with Octave plus the current working
directory. To see your current load path call the path function without any input or output
arguments.
It is possible to add or remove directories to or from the load path using addpath and
rmpath. As an example, the following code adds ‘~/Octave’ to the load path.
addpath ("~/Octave")
After this the directory ‘~/Octave’ will be searched for functions.
addpath (dir1, . . . )
addpath (dir1, . . . , option)
Add named directories to the function search path.
If option is "-begin" or 0 (the default), prepend the directory name to the current
path. If option is "-end" or 1, append the directory name to the current path.
Directories added to the path must exist.
In addition to accepting individual directory arguments, lists of directory names sep-
arated by pathsep are also accepted. For example:
addpath ("dir1:/dir2:~/dir3")
For each directory that is added, and that was not already in the path, addpath
checks for the existence of a file named PKG_ADD (note lack of .m extension) and runs
it if it exists.
See also: [path], page 193,[rmpath], page 193,[genpath], page 193,[pathdef],
page 194,[savepath], page 193,[pathsep], page 194.
Chapter 11: Functions and Scripts 193
genpath (dir)
genpath (dir,skip, . . . )
Return a path constructed from dir and all its subdirectories.
If additional string parameters are given, the resulting path will exclude directories
with those names.
rmpath (dir1, . . . )
Remove dir1, . . . from the current function search path.
In addition to accepting individual directory arguments, lists of directory names sep-
arated by pathsep are also accepted. For example:
rmpath ("dir1:/dir2:~/dir3")
For each directory that is removed, rmpath checks for the existence of a file named
PKG_DEL (note lack of .m extension) and runs it if it exists.
See also: [path], page 193,[addpath], page 192,[genpath], page 193,[pathdef],
page 194,[savepath], page 193,[pathsep], page 194.
savepath ()
savepath (file)
status = savepath (. . . )
Save the unique portion of the current function search path that is not set during
Octave’s initialization process to file.
If file is omitted, Octave looks in the current directory for a project-specific .octaverc
file in which to save the path information. If no such file is present then the user’s
configuration file ~/.octaverc is used.
If successful, savepath returns 0.
The savepath function makes it simple to customize a user’s configuration file to
restore the working paths necessary for a particular instance of Octave. Assuming no
filename is specified, Octave will automatically restore the saved directory paths from
the appropriate .octaverc file when starting up. If a filename has been specified
then the paths may be restored manually by calling source file.
See also: [path], page 193,[addpath], page 192,[rmpath], page 193,[genpath],
page 193,[pathdef], page 194.
path ()
str = path ()
str = path (path1, . . . )
Modify or display Octave’s load path.
If nargin and nargout are zero, display the elements of Octave’s load path in an easy
to read format.
If nargin is zero and nargout is greater than zero, return the current load path.
If nargin is greater than zero, concatenate the arguments, separating them with
pathsep. Set the internal search path to the result and return it.
No checks are made for duplicate elements.
See also: [addpath], page 192,[rmpath], page 193,[genpath], page 193,[pathdef],
page 194,[savepath], page 193,[pathsep], page 194.

194 GNU Octave
val = pathdef ()
Return the default path for Octave.
The path information is extracted from one of four sources. The possible sources, in
order of preference, are:
1. .octaverc
2. ~/.octaverc
3. <OCTAVE_HOME>/.../<version>/m/startup/octaverc
4. Octave’s path prior to changes by any octaverc file.
See also: [path], page 193,[addpath], page 192,[rmpath], page 193,[genpath],
page 193,[savepath], page 193.
val = pathsep ()
old_val = pathsep (new_val)
Query or set the character used to separate directories in a path.
See also: [filesep], page 825.
rehash ()
Reinitialize Octave’s load path directory cache.
file_in_loadpath (file)
file_in_loadpath (file,"all")
Return the absolute name of file if it can be found in the list of directories specified
by path.
If no file is found, return an empty character string.
If the first argument is a cell array of strings, search each directory of the loadpath
for element of the cell array and return the first that matches.
If the second optional argument "all" is supplied, return a cell array containing the
list of all files that have the same name in the path. If no files are found, return an
empty cell array.
See also: [file in path], page 824,[dir in loadpath], page 194,[path], page 193.
restoredefaultpath (. . .)
Restore Octave’s path to its initial state at startup.
See also: [path], page 193,[addpath], page 192,[rmpath], page 193,[genpath],
page 193,[pathdef], page 194,[savepath], page 193,[pathsep], page 194.
command_line_path (. . .)
Return the command line path variable.
See also: [path], page 193,[addpath], page 192,[rmpath], page 193,[genpath],
page 193,[pathdef], page 194,[savepath], page 193,[pathsep], page 194.
dir_in_loadpath (dir)
dir_in_loadpath (dir,"all")
Return the full name of the path element matching dir.

Chapter 11: Functions and Scripts 195
The match is performed at the end of each path element. For example, if dir
is "foo/bar", it matches the path element "/some/dir/foo/bar", but not
"/some/dir/foo/bar/baz" "/some/dir/allfoo/bar".
If the optional second argument is supplied, return a cell array containing all name
matches rather than just the first.
See also: [file in path], page 824,[file in loadpath], page 194,[path], page 193.
11.9.2 Subfunctions
A function file may contain secondary functions called subfunctions. These secondary func-
tions are only visible to the other functions in the same function file. For example, a file
f.m containing
function f ()
printf ("in f, calling g\n");
g ()
endfunction
function g ()
printf ("in g, calling h\n");
h ()
endfunction
function h ()
printf ("in h\n")
endfunction
defines a main function fand two subfunctions. The subfunctions gand hmay only be
called from the main function for from the other subfunctions, but not from outside the
file f.m.
localfunctions ()
Return a list of all local functions, i.e., subfunctions, within the current file.
The return value is a column cell array of function handles to all local functions
accessible from the function from which localfunctions is called. Nested functions
are not included in the list.
If the call is from the command line, an anonymous function, or a script, the return
value is an empty cell array.
Compatibility Note: Subfunctions which contain nested functions are not included in
the list. This is a known issue.
11.9.3 Private Functions
In many cases one function needs to access one or more helper functions. If the helper
function is limited to the scope of a single function, then subfunctions as discussed above
might be used. However, if a single helper function is used by more than one function,
then this is no longer possible. In this case the helper functions might be placed in a
subdirectory, called "private", of the directory in which the functions needing access to this
helper function are found.
As a simple example, consider a function func1, that calls a helper function func2 to
do much of the work. For example:
196 GNU Octave
function y = func1 (x)
y = func2 (x);
endfunction
Then if the path to func1 is <directory>/func1.m, and if func2 is found in the directory
<directory>/private/func2.m, then func2 is only available for use of the functions, like
func1, that are found in <directory>.
11.9.4 Nested Functions
Nested functions are similar to subfunctions in that only the main function is visible outside
the file. However, they also allow for child functions to access the local variables in their
parent function. This shared access mimics using a global variable to share information —
but a global variable which is not visible to the rest of Octave. As a programming strategy,
sharing data this way can create code which is difficult to maintain. It is recommended to
use subfunctions in place of nested functions when possible.
As a simple example, consider a parent function foo, that calls a nested child function
bar, with a shared variable x.
function y = foo ()
x = 10;
bar ();
y = x;
function bar ()
x = 20;
endfunction
endfunction
foo ()
⇒20
Notice that there is no special syntax for sharing x. This can lead to problems with acci-
dental variable sharing between a parent function and its child. While normally variables
are inherited, child function parameters and return values are local to the child function.
Now consider the function foobar that uses variables xand y.foobar calls a nested
function foo which takes xas a parameter and returns y.foo then calls bat which does
some computation.
Chapter 11: Functions and Scripts 197
function z = foobar ()
x = 0;
y = 0;
z = foo (5);
z+=x+y;
function y = foo (x)
y = x + bat ();
function z = bat ()
z = x;
endfunction
endfunction
endfunction
foobar ()
⇒10
It is important to note that the xand yin foobar remain zero, as in foo they are a return
value and parameter respectively. The xin bat refers to the xin foo.
Variable inheritance leads to a problem for eval and scripts. If a new variable is created
in a parent function, it is not clear what should happen in nested child functions. For
example, consider a parent function foo with a nested child function bar:
function y = foo (to_eval)
bar ();
eval (to_eval);
function bar ()
eval ("x = 100;");
eval ("y = x;");
endfunction
endfunction
foo ("x = 5;")
⇒error: can not add variable "x" to a static workspace
foo ("y = 10;")
⇒10
foo ("")
⇒100
The parent function foo is unable to create a new variable x, but the child function bar
was successful. Furthermore, even in an eval statement yin bar is the same yas in its
parent function foo. The use of eval in conjunction with nested functions is best avoided.
As with subfunctions, only the first nested function in a file may be called from the
outside. Inside a function the rules are more complicated. In general a nested function may
call:
198 GNU Octave
0. Globally visible functions
1. Any function that the nested function’s parent can call
2. Sibling functions (functions that have the same parents)
3. Direct children
As a complex example consider a parent function ex_top with two child functions, ex_a
and ex_b. In addition, ex_a has two more child functions, ex_aa and ex_ab. For example:
function ex_top ()
## Can call: ex_top, ex_a, and ex_b
## Can NOT call: ex_aa and ex_ab
function ex_a ()
## Call call everything
function ex_aa ()
## Can call everything
endfunction
function ex_ab ()
## Can call everything
endfunction
endfunction
function ex_b ()
## Can call: ex_top, ex_a, and ex_b
## Can NOT call: ex_aa and ex_ab
endfunction
endfunction
11.9.5 Overloading and Autoloading
Functions can be overloaded to work with different input arguments. For example, the oper-
ator ’+’ has been overloaded in Octave to work with single, double, uint8, int32, and many
other arguments. The preferred way to overload functions is through classes and object
oriented programming (see Section 34.4.1 [Function Overloading], page 779). Occasionally,
however, one needs to undo user overloading and call the default function associated with
a specific type. The builtin function exists for this purpose.
[...] = builtin (f, . . . )
Call the base function feven if fis overloaded to another function for the given type
signature.
This is normally useful when doing object-oriented programming and there is a re-
quirement to call one of Octave’s base functions rather than the overloaded one of a
new class.
A trivial example which redefines the sin function to be the cos function shows how
builtin works.

Chapter 11: Functions and Scripts 199
sin (0)
⇒0
function y = sin (x), y = cos (x); endfunction
sin (0)
⇒1
builtin ("sin", 0)
⇒0
A single dynamically linked file might define several functions. However, as Octave
searches for functions based on the functions filename, Octave needs a manner in which to
find each of the functions in the dynamically linked file. On operating systems that support
symbolic links, it is possible to create a symbolic link to the original file for each of the
functions which it contains.
However, there is at least one well known operating system that doesn’t support symbolic
links. Making copies of the original file for each of the functions is undesirable as it increases
the amount of disk space used by Octave. Instead Octave supplies the autoload function,
that permits the user to define in which file a certain function will be found.
autoload_map = autoload ()
autoload (function,file)
autoload (. . ., "remove")
Define function to autoload from file.
The second argument, file, should be an absolute filename or a file name in the same
directory as the function or script from which the autoload command was run. file
should not depend on the Octave load path.
Normally, calls to autoload appear in PKG ADD script files that are evaluated when
a directory is added to Octave’s load path. To avoid having to hardcode directory
names in file, if file is in the same directory as the PKG ADD script then
autoload ("foo", "bar.oct");
will load the function foo from the file bar.oct. The above usage when bar.oct is
not in the same directory, or usages such as
autoload ("foo", file_in_loadpath ("bar.oct"))
are strongly discouraged, as their behavior may be unpredictable.
With no arguments, return a structure containing the current autoload map.
If a third argument "remove" is given, the function is cleared and not loaded anymore
during the current Octave session.
See also: [PKG ADD], page 858.
11.9.6 Function Locking
It is sometime desirable to lock a function into memory with the mlock function. This is
typically used for dynamically linked functions in Oct-files or mex-files that contain some
initialization, and it is desirable that calling clear does not remove this initialization.
As an example,
function my_function ()
mlock ();
...
200 GNU Octave
prevents my_function from being removed from memory after it is called, even if clear is
called. It is possible to determine if a function is locked into memory with the mislocked,
and to unlock a function with munlock, which the following illustrates.
my_function ();
mislocked ("my_function")
⇒ans = 1
munlock ("my_function");
mislocked ("my_function")
⇒ans = 0
A common use of mlock is to prevent persistent variables from being removed from
memory, as the following example shows:
function count_calls ()
mlock ();
persistent calls = 0;
printf ("’count_calls’ has been called %d times\n",
++calls);
endfunction
count_calls ();
a’count_calls’ has been called 1 times
clear count_calls
count_calls ();
a’count_calls’ has been called 2 times
mlock might equally be used to prevent changes to a function from having effect in
Octave, though a similar effect can be had with the ignore_function_time_stamp function.
mlock ()
Lock the current function into memory so that it can’t be cleared.
See also: [munlock], page 200,[mislocked], page 200,[persistent], page 126.
munlock ()
munlock (fcn)
Unlock the named function fcn.
If no function is named then unlock the current function.
See also: [mlock], page 200,[mislocked], page 200,[persistent], page 126.
mislocked ()
mislocked (fcn)
Return true if the named function fcn is locked.
If no function is named then return true if the current function is locked.
See also: [mlock], page 200,[munlock], page 200,[persistent], page 126.
Chapter 11: Functions and Scripts 201
11.9.7 Function Precedence
Given the numerous different ways that Octave can define a function, it is possible and even
likely that multiple versions of a function, might be defined within a particular scope. The
precedence of which function will be used within a particular scope is given by
1. Subfunction A subfunction with the required function name in the given scope.
2. Private function A function defined within a private directory of the directory which
contains the current function.
3. Class constructor A function that constructs a user class as defined in chapter
Chapter 34 [Object Oriented Programming], page 769.
4. Class method An overloaded function of a class as in chapter Chapter 34 [Object
Oriented Programming], page 769.
5. Command-line Function A function that has been defined on the command-line.
6. Autoload function A function that is marked as autoloaded with See [autoload],
page 199.
7. A Function on the Path A function that can be found on the users load-path. There can
also be Oct-file, mex-file or m-file versions of this function and the precedence between
these versions are in that order.
8. Built-in function A function that is a part of core Octave such as numel,size, etc.
11.10 Script Files
A script file is a file containing (almost) any sequence of Octave commands. It is read and
evaluated just as if you had typed each command at the Octave prompt, and provides a
convenient way to perform a sequence of commands that do not logically belong inside a
function.
Unlike a function file, a script file must not begin with the keyword function. If it does,
Octave will assume that it is a function file, and that it defines a single function that should
be evaluated as soon as it is defined.
A script file also differs from a function file in that the variables named in a script file
are not local variables, but are in the same scope as the other variables that are visible on
the command line.
Even though a script file may not begin with the function keyword, it is possible to
define more than one function in a single script file and load (but not execute) all of them
at once. To do this, the first token in the file (ignoring comments and other white space)
must be something other than function. If you have no other statements to evaluate, you
can use a statement that has no effect, like this:
# Prevent Octave from thinking that this
# is a function file:
1;
# Define function one:
function one ()
...
202 GNU Octave
To have Octave read and compile these functions into an internal form, you need to
make sure that the file is in Octave’s load path (accessible through the path function), then
simply type the base name of the file that contains the commands. (Octave uses the same
rules to search for script files as it does to search for function files.)
If the first token in a file (ignoring comments) is function, Octave will compile the func-
tion and try to execute it, printing a message warning about any non-whitespace characters
that appear after the function definition.
Note that Octave does not try to look up the definition of any identifier until it needs
to evaluate it. This means that Octave will compile the following statements if they appear
in a script file, or are typed at the command line,
# not a function file:
1;
function foo ()
do_something ();
endfunction
function do_something ()
do_something_else ();
endfunction
even though the function do_something is not defined before it is referenced in the function
foo. This is not an error because Octave does not need to resolve all symbols that are
referenced by a function until the function is actually evaluated.
Since Octave doesn’t look for definitions until they are needed, the following code will
always print ‘bar = 3’ whether it is typed directly on the command line, read from a script
file, or is part of a function body, even if there is a function or script file called bar.m in
Octave’s path.
eval ("bar = 3");
bar
Code like this appearing within a function body could fool Octave if definitions were
resolved as the function was being compiled. It would be virtually impossible to make
Octave clever enough to evaluate this code in a consistent fashion. The parser would have
to be able to perform the call to eval at compile time, and that would be impossible unless
all the references in the string to be evaluated could also be resolved, and requiring that
would be too restrictive (the string might come from user input, or depend on things that
are not known until the function is evaluated).
Although Octave normally executes commands from script files that have the name
file.m, you can use the function source to execute commands from any file.
source (file)
source (file,context)
Parse and execute the contents of file.
Without specifying context, this is equivalent to executing commands from a script
file, but without requiring the file to be named file.m or to be on the execution path.
Instead of the current context, the script may be executed in either the context of
the function that called the present function ("caller"), or the top-level context
("base").
Chapter 11: Functions and Scripts 203
See also: [run], page 159.
11.10.1 Publish Octave Script Files
The function publish provides a dynamic possibility to document your script file. Unlike
static documentation, publish runs the script file, saves any figures and output while
running the script, and presents them alongside static documentation in a desired output
format. The static documentation can make use of Section 11.10.2 [Publishing Markup],
page 205, to enhance and customize the output.
publish (filename)
publish (filename,output_format)
publish (filename,option1,value1, . . . )
publish (filename,options)
output_file = publish (filename, . . . )
Generate reports from Octave script files in several output formats.
The generated reports consider Publishing Markup in comments, which is explained
in detail in the GNU Octave manual. Assume the following example, using some
Publishing Markup, to be the content of a script file named ‘example.m’:
%% Headline title
%
% Some *bold*, _italic_, or |monospaced| Text with
% a <http://www.octave.org link to *GNU Octave*>.
%%
# "Real" Octave commands to be evaluated
sombrero ()
## Octave comment style supported as well
#
# * Bulleted list item 1
# * Bulleted list item 2
#
# # Numbered list item 1
# # Numbered list item 2
To publish this script file, type publish ("example.m").
With only filename given, a HTML report is generated in a subdirectory ‘html’ rel-
ative to the current working directory. The Octave commands are evaluated in a
separate context and any figures created while executing the script file are included
in the report. All formatting syntax of filename is treated according to the specified
output format and included in the report.
Using publish (filename,output_format)is equivalent to the function call using
a structure
options.format = output_format;
publish (filename,options)
which is described below. The same holds for using option-value-pairs
204 GNU Octave
options.option1 =value1;
publish (filename,options)
The structure options can have the following field names. If a field name is not
specified, the default value is considered:
•‘format’ — Output format of the published script file, one of
‘html’ (default), ‘doc’, ‘latex’, ‘ppt’, ‘xml’, or ‘pdf’.
The output formats ‘doc’, ‘ppt’, and ‘xml’ are currently not supported. To
generate a ‘doc’ report, open a generated ‘html’ report with your office suite.
•‘outputDir’ — Full path string of a directory, where the generated report will be
located. If no directory is given, the report is generated in a subdirectory ‘html’
relative to the current working directory.
•‘stylesheet’ — Not supported, only for matlab compatibility.
•‘createThumbnail’ — Not supported, only for matlab compatibility.
•‘figureSnapMethod’ — Not supported, only for matlab compatibility.
•‘imageFormat’ — Desired format for images produced, while evaluating the code.
The allowed image formats depend on the output format:
•‘html’ and ‘xml’—‘png’ (default), any other image format supported by
Octave
•‘latex’ — ‘epsc2’ (default), any other image format supported by Octave
•‘pdf’ — ‘jpg’ (default) or ‘bmp’, note matlab uses ‘bmp’ as default
•‘doc’ or ‘ppt’ — ‘png’ (default), ‘jpg’, ‘bmp’, or ‘tiff’
•‘maxHeight’ and ‘maxWidth’ — Maximum height (width) of the produced images
in pixels. An empty value means no restriction. Both values have to be set, to
work properly.
‘[]’ (default), integer value ≥0
•‘useNewFigure’ — Use a new figure window for figures created by the evaluated
code. This avoids side effects with already opened figure windows.
‘true’ (default) or ‘false’
•‘evalCode’ — Evaluate code of the Octave source file
‘true’ (default) or ‘false’
•‘catchError’ — Catch errors while code evaluation and continue
‘true’ (default) or ‘false’
•‘codeToEvaluate’ — Octave commands that should be evaluated prior to pub-
lishing the script file. These Octave commands do not appear in the generated
report.
•‘maxOutputLines’ — Maximum number of shown output lines of the code eval-
uation
‘Inf’ (default) or integer value >0
•‘showCode’ — Show the evaluated Octave commands in the generated report
‘true’ (default) or ‘false’

Chapter 11: Functions and Scripts 205
The returned output file is a string with the path and file name of the generated
report.
See also: [grabcode], page 205.
The counterpart to publish is grabcode:
grabcode (url)
code_str = grabcode (url)
Grab by the publish function generated HTML reports from Octave script files.
The input parameter url must point to a local or remote HTML file with extension
‘.htm’ or ‘.html’ which was generated by the publish function. With any other
HTML file this will not work!
If no return value is given, the grabbed code is saved to a temporary file and opened
in the default editor.
NOTE: You have to save the file at another location with arbitrary name, otherwise
any grabbed code will be lost!
With a return value given, the grabbed code will be returned as string code str.
An example:
publish ("my_script.m");
grabcode ("html/my_script.html");
The example above publishes ‘my_script.m’ by default to ‘html/my_script.html’.
Afterwards this published Octave script is grabbed to edit its content in a new tem-
porary file.
See also: [publish], page 203.
11.10.2 Publishing Markup
11.10.2.1 Using Publishing Markup in Script Files
To use Publishing Markup, start by typing ‘##’ or ‘%%’ at the beginning of a new line. For
matlab compatibility ‘%%’ is treated the same way as ‘##’.
The lines following ‘##’ or ‘%%’ start with one of either ‘#’ or ‘%’ followed by at least one
space. These lines are interpreted as section. A section ends at the first line not starting
with ‘#’ or ‘%’, or when the end of the document is reached.
A section starting in the first line of the document, followed by another start of a section
that might be empty, is interpreted as a document title and introduction text.
See the example below for clarity:
206 GNU Octave
%% Headline title
%
% Some *bold*, _italic_, or |monospaced| Text with
% a <http://www.octave.org link to GNU Octave>.
%%
# "Real" Octave commands to be evaluated
sombrero ()
## Octave comment style supported as well
#
# * Bulleted list item 1
# * Bulleted list item 2
#
# # Numbered list item 1
# # Numbered list item 2
11.10.2.2 Text Formatting
Basic text formatting is supported inside sections, see the example given below:
##
#*bold*,_italic_, or |monospaced| Text
Additionally two trademark symbols are supported, just embrace the letters ‘TM’ or ‘R’.
##
# (TM) or (R)
11.10.2.3 Sections
A section is started by typing ‘##’ or ‘%%’ at the beginning of a new line. A section title can
be provided by writing it, separated by a space, in the first line after ‘##’ or ‘%%’. Without
a section title, the section is interpreted as a continuation of the previous section. For
matlab compatibility ‘%%’ is treated the same way as ‘%%’.
some_code ();
## Section 1
#
## Section 2
some_code ();
##
# Still in section 2
some_code ();
### Section 3
#
#
Chapter 11: Functions and Scripts 207
11.10.2.4 Preformatted Code
To write preformatted code inside a section, indent the code by three spaces after ‘#’ at the
beginning of each line and leave the lines above and below the code blank, except for ‘#’ at
the beginning of those lines.
##
# This is a syntax highlighted for-loop:
#
# for i = 1:5
# disp (i);
# endfor
#
# And more usual text.
11.10.2.5 Preformatted Text
To write preformatted text inside a section, indent the code by two spaces after ‘#’ at the
beginning of each line and leave the lines above and below the preformatted text blank,
except for ‘#’ at the beginning of those lines.
##
# This following text is preformatted:
#
# "To be, or not to be: that is the question:
# Whether ’tis nobler in the mind to suffer
# The slings and arrows of outrageous fortune,
# Or to take arms against a sea of troubles,
# And by opposing end them? To die: to sleep;"
#
# --"Hamlet" by W. Shakespeare
11.10.2.6 Bulleted Lists
To create a bulleted list, type
##
#
# * Bulleted list item 1
# * Bulleted list item 2
#
to get output like
•Bulleted list item 1
•Bulleted list item 2
Notice the blank lines, except for the ‘#’ or ‘%’ before and after the bulleted list!
11.10.2.7 Numbered Lists
To create a numbered list, type
208 GNU Octave
##
#
# # Numbered list item 1
# # Numbered list item 2
#
to get output like
1. Numbered list item 1
2. Numbered list item 2
Notice the blank lines, except for the ‘#’ or ‘%’ before and after the numbered list!
11.10.2.8 Including File Content
To include the content of an external file, e.g., a file called ‘my_function.m’ at the same
location as the published Octave script, use the following syntax to include it with Octave
syntax highlighting.
Alternatively, you can write the full or relative path to the file.
##
#
# <include>my_function.m</include>
#
# <include>/full/path/to/my_function.m</include>
#
# <include>../relative/path/to/my_function.m</include>
#
11.10.2.9 Including Graphics
To include external graphics, e.g., a graphic called ‘my_graphic.png’ at the same location
as the published Octave script, use the following syntax.
Alternatively, you can write the full path to the graphic.
##
#
# <<my_graphic.png>>
#
# <</full/path/to/my_graphic.png>>
#
# <<../relative/path/to/my_graphic.png>>
#
11.10.2.10 Including URLs
Basically, a URL is written between an opening ‘<’ and a closing ‘>’ angle.
##
# <http://www.octave.org>
Text that is within these angles and separated by at least one space from the URL is a
displayed text for the link.
##
# <http://www.octave.org GNU Octave>
Chapter 11: Functions and Scripts 209
A link starting with ‘<octave:’ followed by the name of a GNU Octave function, op-
tionally with a displayed text, results in a link to the online GNU Octave documentations
function index.
##
# <octave:DISP The display function>
11.10.2.11 Mathematical Equations
One can insert L
A
T
E
X inline math, surrounded by single ‘$’ signs, or displayed math, sur-
rounded by double ‘$$’ signs, directly inside sections.
##
# Some shorter inline equation $e^{ix} = \cos x + i\sin x$.
#
# Or more complicated formulas as displayed math:
# $$e^x = \lim_{n\rightarrow\infty}\left(1+\dfrac{x}{n}\right)^{n}.$$
11.10.2.12 HTML Markup
If the published output is a HTML report, you can insert HTML markup, that is only
visible in this kind of output.
##
# <html>
# <table style="border:1px solid black;">
# <tr><td>1</td><td>2</td></tr>
# <tr><td>3</td><td>3</td></tr>
# </html>
11.10.2.13 LaTeX Markup
If the published output is a L
A
T
E
X or PDF report, you can insert L
A
T
E
X markup, that is
only visible in this kind of output.
##
# <latex>
# Some output only visible in LaTeX or PDF reports.
# \begin{equation}
# e^x = \lim\limits_{n\rightarrow\infty}\left(1+\dfrac{x}{n}\right)^{n}
# \end{equation}
# </latex>
11.11 Function Handles, Anonymous Functions, Inline
Functions
It can be very convenient store a function in a variable so that it can be passed to a different
function. For example, a function that performs numerical minimization needs access to
the function that should be minimized.
11.11.1 Function Handles
A function handle is a pointer to another function and is defined with the syntax
@function-name

210 GNU Octave
For example,
f = @sin;
creates a function handle called fthat refers to the function sin.
Function handles are used to call other functions indirectly, or to pass a function as an
argument to another function like quad or fsolve. For example:
f = @sin;
quad (f, 0, pi)
⇒2
You may use feval to call a function using function handle, or simply write the name
of the function handle followed by an argument list. If there are no arguments, you must
use an empty argument list ‘()’. For example:
f = @sin;
feval (f, pi/4)
⇒0.70711
f (pi/4)
⇒0.70711
is_function_handle (x)
Return true if xis a function handle.
See also: [isa], page 39,[typeinfo], page 39,[class], page 39,[functions], page 210.
s= functions (fcn_handle)
Return a structure containing information about the function handle fcn handle.
The structure salways contains these three fields:
function The function name. For an anonymous function (no name) this will be
the actual function definition.
type Type of the function.
anonymous
The function is anonymous.
private The function is private.
overloaded
The function overloads an existing function.
simple The function is a built-in or m-file function.
subfunction
The function is a subfunction within an m-file.
file The m-file that will be called to perform the function. This field is empty
for anonymous and built-in functions.
In addition, some function types may return more information in additional fields.
Warning: functions is provided for debugging purposes only. Its behavior may
change in the future and programs should not depend on any particular output format.
See also: [func2str], page 211,[str2func], page 211.

Chapter 11: Functions and Scripts 211
func2str (fcn_handle)
Return a string containing the name of the function referenced by the function handle
fcn handle.
See also: [str2func], page 211,[functions], page 210.
str2func (fcn_name)
str2func (fcn_name,"global")
Return a function handle constructed from the string fcn name.
If the optional "global" argument is passed, locally visible functions are ignored in
the lookup.
See also: [func2str], page 211,[inline], page 212,[functions], page 210.
11.11.2 Anonymous Functions
Anonymous functions are defined using the syntax
@(argument-list)expression
Any variables that are not found in the argument list are inherited from the enclosing scope.
Anonymous functions are useful for creating simple unnamed functions from expressions or
for wrapping calls to other functions to adapt them for use by functions like quad. For
example,
f = @(x) x.^2;
quad (f, 0, 10)
⇒333.33
creates a simple unnamed function from the expression x.^2 and passes it to quad,
quad (@(x) sin (x), 0, pi)
⇒2
wraps another function, and
a = 1;
b = 2;
quad (@(x) betainc (x, a, b), 0, 0.4)
⇒0.13867
adapts a function with several parameters to the form required by quad. In this example,
the values of aand bthat are passed to betainc are inherited from the current environment.
Note that for performance reasons it is better to use handles to existing Octave functions,
rather than to define anonymous functions which wrap an existing function. The integration
of sin (x) is 5X faster if the code is written as
quad (@sin, 0, pi)
rather than using the anonymous function @(x) sin (x). There are many operators which
have functional equivalents that may be better choices than an anonymous function. Instead
of writing
f=@(x,y)x+y
this should be coded as
f = @plus
See Section 34.4.2 [Operator Overloading], page 780, for a list of operators which also
have a functional form.
212 GNU Octave
11.11.3 Inline Functions
An inline function is created from a string containing the function body using the inline
function. The following code defines the function f(x) = x2+ 2.
f = inline ("x^2 + 2");
After this it is possible to evaluate fat any xby writing f(x).
Caution:matlab has begun the process of deprecating inline functions. At some point
in the future support will be dropped and eventually Octave will follow matlab and also
remove inline functions. Use anonymous functions in all new code.
inline (str)
inline (str,arg1, . . . )
inline (str,n)
Create an inline function from the character string str.
If called with a single argument, the arguments of the generated function are extracted
from the function itself. The generated function arguments will then be in alphabetical
order. It should be noted that i and j are ignored as arguments due to the ambiguity
between their use as a variable or their use as an built-in constant. All arguments
followed by a parenthesis are considered to be functions. If no arguments are found,
a function taking a single argument named xwill be created.
If the second and subsequent arguments are character strings, they are the names of
the arguments of the function.
If the second argument is an integer n, the arguments are "x","P1", . . . , "PN".
Programming Note: The use of inline is discouraged and it may be removed from
a future version of Octave. The preferred way to create functions from strings is
through the use of anonymous functions (see Section 11.11.2 [Anonymous Functions],
page 211) or str2func.
See also: [argnames], page 212,[formula], page 212,[vectorize], page 530,[str2func],
page 211.
argnames (fun)
Return a cell array of character strings containing the names of the arguments of the
inline function fun.
See also: [inline], page 212,[formula], page 212,[vectorize], page 530.
formula (fun)
Return a character string representing the inline function fun.
Note that char (fun)is equivalent to formula (fun).
See also: [char], page 71,[argnames], page 212,[inline], page 212,[vectorize],
page 530.
vars = symvar (str)
Identify the symbolic variable names in the string str.
Common constant names such as i,j,pi,Inf and Octave functions such as sin or
plot are ignored.
Chapter 11: Functions and Scripts 213
Any names identified are returned in a cell array of strings. The array is empty if no
variables were found.
Example:
symvar ("x^2 + y^2 == 4")
⇒{
[1,1] = x
[2,1] = y
}
11.12 Commands
Commands are a special class of functions that only accept string input arguments. A
command can be called as an ordinary function, but it can also be called without the
parentheses. For example,
my_command hello world
is equivalent to
my_command ("hello", "world")
The general form of a command call is
cmdname arg1 arg2 ...
which translates directly to
cmdname ("arg1", "arg2", ...)
Any regular function can be used as a command if it accepts string input arguments.
For example:
toupper lower_case_arg
⇒ans = LOWER_CASE_ARG
One difficulty of commands occurs when one of the string input arguments is stored in a
variable. Because Octave can’t tell the difference between a variable name and an ordinary
string, it is not possible to pass a variable as input to a command. In such a situation a
command must be called as a function. For example:
strvar = "hello world";
toupper strvar
⇒ans = STRVAR
toupper (strvar)
⇒ans = HELLO WORLD
11.13 Organization of Functions Distributed with Octave
Many of Octave’s standard functions are distributed as function files. They are loosely
organized by topic, in subdirectories of octave-home/lib/octave/version/m, to make it
easier to find them.
The following is a list of all the function file subdirectories, and the types of functions
you will find there.
audio Functions for playing and recording sounds.
214 GNU Octave
deprecated
Out-of-date functions which will eventually be removed from Octave.
elfun Elementary functions, principally trigonometric.
@ftp Class functions for the FTP object.
general Miscellaneous matrix manipulations, like flipud,rot90, and triu, as well as
other basic functions, like ismatrix,narginchk, etc.
geometry Functions related to Delaunay triangulation.
help Functions for Octave’s built-in help system.
image Image processing tools. These functions require the X Window System.
io Input-output functions.
linear-algebra
Functions for linear algebra.
miscellaneous
Functions that don’t really belong anywhere else.
optimization
Functions related to minimization, optimization, and root finding.
path Functions to manage the directory path Octave uses to find functions.
pkg Package manager for installing external packages of functions in Octave.
plot Functions for displaying and printing two- and three-dimensional graphs.
polynomial
Functions for manipulating polynomials.
prefs Functions implementing user-defined preferences.
set Functions for creating and manipulating sets of unique values.
signal Functions for signal processing applications.
sparse Functions for handling sparse matrices.
specfun Special functions such as bessel or factor.
special-matrix
Functions that create special matrix forms such as Hilbert or Vandermonde
matrices.
startup Octave’s system-wide startup file.
statistics
Statistical functions.
strings Miscellaneous string-handling functions.
testfun Functions for performing unit tests on other functions.
time Functions related to time and date processing.
215
12 Errors and Warnings
Octave includes several functions for printing error and warning messages. When you write
functions that need to take special action when they encounter abnormal conditions, you
should print the error messages using the functions described in this chapter.
Since many of Octave’s functions use these functions, it is also useful to understand
them, so that errors and warnings can be handled.
12.1 Handling Errors
An error is something that occurs when a program is in a state where it doesn’t make sense
to continue. An example is when a function is called with too few input arguments. In this
situation the function should abort with an error message informing the user of the lacking
input arguments.
Since an error can occur during the evaluation of a program, it is very convenient to be
able to detect that an error occurred, so that the error can be fixed. This is possible with
the try statement described in Section 10.9 [The try Statement], page 170.
12.1.1 Raising Errors
The most common use of errors is for checking input arguments to functions. The following
example calls the error function if the function fis called without any input arguments.
function f (arg1)
if (nargin == 0)
error ("not enough input arguments");
endif
endfunction
When the error function is called, it prints the given message and returns to the Octave
prompt. This means that no code following a call to error will be executed.
It is also possible to assign an identification string to an error. If an error has such
an ID the user can catch this error as will be described in the next section. To assign
an ID to an error, simply call error with two string arguments, where the first is the
identification string, and the second is the actual error. Note that error IDs are in the format
"NAMESPACE:ERROR-NAME". The namespace "Octave" is used for Octave’s own errors. Any
other string is available as a namespace for user’s own errors.
error (template, . . . )
error (id,template, . . . )
Display an error message and stop m-file execution.
Format the optional arguments under the control of the template string template
using the same rules as the printf family of functions (see Section 14.2.4 [Formatted
Output], page 268) and print the resulting message on the stderr stream. The
message is prefixed by the character string ‘error: ’.
Calling error also sets Octave’s internal error state such that control will return to
the top level without evaluating any further commands. This is useful for aborting
from functions or scripts.
216 GNU Octave
If the error message does not end with a newline character, Octave will print a trace-
back of all the function calls leading to the error. For example, given the following
function definitions:
function f () g (); end
function g () h (); end
function h () nargin == 1 || error ("nargin != 1"); end
calling the function fwill result in a list of messages that can help you to quickly find
the exact location of the error:
f ()
error: nargin != 1
error: called from:
error: h at line 1, column 27
error: g at line 1, column 15
error: f at line 1, column 15
If the error message ends in a newline character, Octave will print the message but
will not display any traceback messages as it returns control to the top level. For
example, modifying the error message in the previous example to end in a newline
causes Octave to only print a single message:
function h () nargin == 1 || error ("nargin != 1\n"); end
f ()
error: nargin != 1
A null string ("") input to error will be ignored and the code will continue running
as if the statement were a NOP. This is for compatibility with matlab. It also makes
it possible to write code such as
err_msg = "";
if (CONDITION 1)
err_msg = "CONDITION 1 found";
elseif (CONDITION2)
err_msg = "CONDITION 2 found";
...
endif
error (err_msg);
which will only stop execution if an error has been found.
Implementation Note: For compatibility with matlab, escape sequences in template
(e.g., "\n" =>newline) are processed regardless of whether template has been defined
with single quotes, as long as there are two or more input arguments. To disable escape
sequence expansion use a second backslash before the sequence (e.g., "\\n") or use
the regexptranslate function.
See also: [warning], page 222,[lasterror], page 218.
Since it is common to use errors when there is something wrong with the input to a
function, Octave supports functions to simplify such code. When the print_usage function
is called, it reads the help text of the function calling print_usage, and presents a useful
error. If the help text is written in Texinfo it is possible to present an error message that
only contains the function prototypes as described by the @deftypefn parts of the help
Chapter 12: Errors and Warnings 217
text. When the help text isn’t written in Texinfo, the error message contains the entire
help message.
Consider the following function.
## -*- texinfo -*-
## @deftypefn {} f (@var{arg1})
## Function help text goes here...
## @end deftypefn
function f (arg1)
if (nargin == 0)
print_usage ();
endif
endfunction
When it is called with no input arguments it produces the following error.
f ()
aerror: Invalid call to f. Correct usage is:
a
a-- f (ARG1)
a
a
aAdditional help for built-in functions and operators is
aavailable in the online version of the manual. Use the command
a’doc <topic>’ to search the manual index.
a
aHelp and information about Octave is also available on the WWW
aat http://www.octave.org and via the help@octave.org
amailing list.
print_usage ()
print_usage (name)
Print the usage message for the function name.
When called with no input arguments the print_usage function displays the usage
message of the currently executing function.
See also: [help], page 20.
beep ()
Produce a beep from the speaker (or visual bell).
This function sends the alarm character "\a" to the terminal. Depending on the
user’s configuration this may produce an audible beep, a visual bell, or nothing at all.
See also: [puts], page 267,[fputs], page 267,[printf], page 268,[fprintf], page 269.
val = beep_on_error ()
old_val = beep_on_error (new_val)
beep_on_error (new_val,"local")
Query or set the internal variable that controls whether Octave will try to ring the
terminal bell before printing an error message.
218 GNU Octave
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
12.1.2 Catching Errors
When an error occurs, it can be detected and handled using the try statement as described
in Section 10.9 [The try Statement], page 170. As an example, the following piece of code
counts the number of errors that occurs during a for loop.
number_of_errors = 0;
for n = 1:100
try
...
catch
number_of_errors++;
end_try_catch
endfor
The above example treats all errors the same. In many situations it can however be
necessary to discriminate between errors, and take different actions depending on the error.
The lasterror function returns a structure containing information about the last error
that occurred. As an example, the code above could be changed to count the number of
errors related to the ‘*’ operator.
number_of_errors = 0;
for n = 1:100
try
...
catch
msg = lasterror.message;
if (strfind (msg, "operator *"))
number_of_errors++;
endif
end_try_catch
endfor
Alternatively, the output of the lasterror function can be found in a variable indicated
immediately after the catch keyword, as in the example below showing how to redirect an
error as a warning:
try
...
catch err
warning(err.identifier, err.message);
...
end_try_catch
lasterr = lasterror ()
lasterror (err)
lasterror ("reset")
Query or set the last error message structure.
Chapter 12: Errors and Warnings 219
When called without arguments, return a structure containing the last error message
and other information related to this error. The elements of the structure are:
message The text of the last error message
identifier
The message identifier of this error message
stack A structure containing information on where the message occurred. This
may be an empty structure if the information cannot be obtained. The
fields of the structure are:
file The name of the file where the error occurred
name The name of function in which the error occurred
line The line number at which the error occurred
column An optional field with the column number at which the error
occurred
The last error structure may be set by passing a scalar structure, err, as input. Any
fields of err that match those above are set while any unspecified fields are initialized
with default values.
If lasterror is called with the argument "reset", all fields are set to their default
values.
See also: [lasterr], page 219,[error], page 215,[lastwarn], page 223.
[msg,msgid] = lasterr ()
lasterr (msg)
lasterr (msg,msgid)
Query or set the last error message.
When called without input arguments, return the last error message and message
identifier.
With one argument, set the last error message to msg.
With two arguments, also set the last message identifier.
See also: [lasterror], page 218,[error], page 215,[lastwarn], page 223.
The next example counts indexing errors. The errors are caught using the field identifier
of the structure returned by the function lasterror.
number_of_errors = 0;
for n = 1:100
try
...
catch
id = lasterror.identifier;
if (strcmp (id, "Octave:invalid-indexing"))
number_of_errors++;
endif
end_try_catch
endfor
220 GNU Octave
The functions distributed with Octave can issue one of the following errors.
Octave:invalid-context
Indicates the error was generated by an operation that cannot be executed in
the scope from which it was called. For example, the function print_usage ()
when called from the Octave prompt raises this error.
Octave:invalid-input-arg
Indicates that a function was called with invalid input arguments.
Octave:invalid-fun-call
Indicates that a function was called in an incorrect way, e.g., wrong number of
input arguments.
Octave:invalid-indexing
Indicates that a data-type was indexed incorrectly, e.g., real-value index for
arrays, nonexistent field of a structure.
Octave:bad-alloc
Indicates that memory couldn’t be allocated.
Octave:undefined-function
Indicates a call to a function that is not defined. The function may exist but
Octave is unable to find it in the search path.
When an error has been handled it is possible to raise it again. This can be useful when
an error needs to be detected, but the program should still abort. This is possible using
the rethrow function. The previous example can now be changed to count the number of
errors related to the ‘*’ operator, but still abort if another kind of error occurs.
number_of_errors = 0;
for n = 1:100
try
...
catch
msg = lasterror.message;
if (strfind (msg, "operator *"))
number_of_errors++;
else
rethrow (lasterror);
endif
end_try_catch
endfor
rethrow (err)
Reissue a previous error as defined by err.
err is a structure that must contain at least the "message" and "identifier" fields.
err can also contain a field "stack" that gives information on the assumed location
of the error. Typically err is returned from lasterror.
See also: [lasterror], page 218,[lasterr], page 219,[error], page 215.

Chapter 12: Errors and Warnings 221
err = errno ()
err = errno (val)
err = errno (name)
Return the current value of the system-dependent variable errno, set its value to
val and return the previous value, or return the named error code given name as a
character string, or -1 if name is not found.
See also: [errno list], page 221.
errno_list ()
Return a structure containing the system-dependent errno values.
See also: [errno], page 221.
12.1.3 Recovering From Errors
Octave provides several ways of recovering from errors. There are try/catch blocks,
unwind_protect/unwind_protect_cleanup blocks, and finally the onCleanup command.
The onCleanup command associates an ordinary Octave variable (the trigger) with an
arbitrary function (the action). Whenever the Octave variable ceases to exist—whether
due to a function return, an error, or simply because the variable has been removed with
clear—then the assigned function is executed.
The function can do anything necessary for cleanup such as closing open file handles,
printing an error message, or restoring global variables to their initial values. The last
example is a very convenient idiom for Octave code. For example:
function rand42
old_state = rand ("state");
restore_state = onCleanup (@() rand ("state", old_state));
rand ("state", 42);
...
endfunction # rand generator state restored by onCleanup
obj = onCleanup (function)
Create a special object that executes a given function upon destruction.
If the object is copied to multiple variables (or cell or struct array elements) or
returned from a function, function will be executed after clearing the last copy of
the object. Note that if multiple local onCleanup variables are created, the order in
which they are called is unspecified. For similar functionality See Section 10.8 [The
unwind protect Statement], page 170.
12.2 Handling Warnings
Like an error, a warning is issued when something unexpected happens. Unlike an error,
a warning doesn’t abort the currently running program. A simple example of a warning is
when a number is divided by zero. In this case Octave will issue a warning and assign the
value Inf to the result.
a = 1/0
awarning: division by zero
⇒a = Inf

222 GNU Octave
12.2.1 Issuing Warnings
It is possible to issue warnings from any code using the warning function. In its most simple
form, the warning function takes a string describing the warning as its input argument. As
an example, the following code controls if the variable ‘a’ is non-negative, and if not issues
a warning and sets ‘a’ to zero.
a = -1;
if (a < 0)
warning ("’a’ must be non-negative. Setting ’a’ to zero.");
a = 0;
endif
a’a’ must be non-negative. Setting ’a’ to zero.
Since warnings aren’t fatal to a running program, it is not possible to catch a warning
using the try statement or something similar. It is however possible to access the last
warning as a string using the lastwarn function.
It is also possible to assign an identification string to a warning. If a warning has such an
ID the user can enable and disable this warning as will be described in the next section. To
assign an ID to a warning, simply call warning with two string arguments, where the first
is the identification string, and the second is the actual warning. Note that warning IDs are
in the format "NAMESPACE:WARNING-NAME". The namespace "Octave" is used for Octave’s
own warnings. Any other string is available as a namespace for user’s own warnings.
warning (template, . . . )
warning (id,template, . . . )
warning ("on",id)
warning ("off",id)
warning ("query",id)
warning ("error",id)
warning (state,"backtrace")
warning (state,id,"local")
Display a warning message or control the behavior of Octave’s warning system.
Format the optional arguments under the control of the template string template
using the same rules as the printf family of functions (see Section 14.2.4 [Formatted
Output], page 268) and print the resulting message on the stderr stream. The
message is prefixed by the character string ‘warning: ’. You should use this function
when you want to notify the user of an unusual condition, but only when it makes
sense for your program to go on.
The optional message identifier allows users to enable or disable warnings tagged by
id. A message identifier is of the form "NAMESPACE:WARNING-NAME". Octave’s
own warnings use the "Octave" namespace (see [XREFwarning ids], page 223). The
special identifier "all" may be used to set the state of all warnings.
If the first argument is "on" or "off", set the state of a particular warning using
the identifier id. If the first argument is "query", query the state of this warning
instead. If the identifier is omitted, a value of "all" is assumed. If you set the state
of a warning to "error", the warning named by id is handled as if it were an error
instead. So, for example, the following handles all warnings as errors:
warning ("error");

Chapter 12: Errors and Warnings 223
If the state is "on" or "off" and the third argument is "backtrace", then a stack
trace is printed along with the warning message when warnings occur inside function
calls. This option is enabled by default.
If the state is "on","off", or "error" and the third argument is "local", then the
warning state will be set temporarily, until the end of the current function. Changes to
warning states that are set locally affect the current function and all functions called
from the current scope. The previous warning state is restored on return from the
current function. The "local" option is ignored if used in the top-level workspace.
Implementation Note: For compatibility with matlab, escape sequences in template
(e.g., "\n" =>newline) are processed regardless of whether template has been defined
with single quotes, as long as there are two or more input arguments. To disable escape
sequence expansion use a second backslash before the sequence (e.g., "\\n") or use
the regexptranslate function.
See also: [warning ids], page 223,[lastwarn], page 223,[error], page 215.
[msg,msgid] = lastwarn ()
lastwarn (msg)
lastwarn (msg,msgid)
Query or set the last warning message.
When called without input arguments, return the last warning message and message
identifier.
With one argument, set the last warning message to msg.
With two arguments, also set the last message identifier.
See also: [warning], page 222,[lasterror], page 218,[lasterr], page 219.
The functions distributed with Octave can issue one of the following warnings.
Octave:abbreviated-property-match
By default, the Octave:abbreviated-property-match warning is enabled.
Octave:array-as-logical
If the Octave:array-as-logical warning is enabled, Octave will warn when
an array of size greater than 1x1 is used as a truth value in an if, while or until
statement. By default, the Octave:array-as-logical warning is disabled.
Octave:array-to-scalar
If the Octave:array-to-scalar warning is enabled, Octave will warn when an
implicit conversion from an array to a scalar value is attempted. By default,
the Octave:array-to-scalar warning is disabled.
Octave:array-to-vector
If the Octave:array-to-vector warning is enabled, Octave will warn when an
implicit conversion from an array to a vector value is attempted. By default,
the Octave:array-to-vector warning is disabled.
Octave:assign-as-truth-value
If the Octave:assign-as-truth-value warning is enabled, a warning is issued
for statements like
if (s = t)
...

224 GNU Octave
since such statements are not common, and it is likely that the intent was to
write
if (s == t)
...
instead.
There are times when it is useful to write code that contains assignments within
the condition of a while or if statement. For example, statements like
while (c = getc ())
...
are common in C programming.
It is possible to avoid all warnings about such statements by disabling the
Octave:assign-as-truth-value warning, but that may also let real errors
like
if (x = 1) # intended to test (x == 1)!
...
slip by.
In such cases, it is possible suppress errors for specific statements by writing
them with an extra set of parentheses. For example, writing the previous ex-
ample as
while ((c = getc ()))
...
will prevent the warning from being printed for this statement, while allowing
Octave to warn about other assignments used in conditional contexts.
By default, the Octave:assign-as-truth-value warning is enabled.
Octave:associativity-change
If the Octave:associativity-change warning is enabled, Octave will warn
about possible changes in the meaning of some code due to changes in associa-
tivity for some operators. Associativity changes have typically been made for
matlab compatibility. By default, the Octave:associativity-change warn-
ing is enabled.
Octave:autoload-relative-file-name
If the Octave:autoload-relative-file-name is enabled, Octave will warn
when parsing autoload() function calls with relative paths to function files.
This usually happens when using autoload() calls in PKG ADD files, when the
PKG ADD file is not in the same directory as the .oct file referred to by the
autoload() command. By default, the Octave:autoload-relative-file-name
warning is enabled.
Octave:built-in-variable-assignment
By default, the Octave:built-in-variable-assignment warning is enabled.
Octave:deprecated-function
If the Octave:deprecated-function warning is enabled, a warning is issued
when Octave encounters a function that is obsolete and scheduled for removal
Chapter 12: Errors and Warnings 225
from Octave. By default, the Octave:deprecated-function warning is en-
abled.
Octave:deprecated-keyword
If the Octave:deprecated-keyword warning is enabled, a warning is issued
when Octave encounters a keyword that is obsolete and scheduled for removal
from Octave. By default, the Octave:deprecated-keyword warning is enabled.
Octave:deprecated-property
If the Octave:deprecated-property warning is enabled, a warning is issued
when Octave encounters a graphics property that is obsolete and scheduled for
removal from Octave. By default, the Octave:deprecated-property warning
is enabled.
Octave:divide-by-zero
If the Octave:divide-by-zero warning is enabled, a warning is issued when
Octave encounters a division by zero. By default, the Octave:divide-by-zero
warning is enabled.
Octave:fopen-file-in-path
By default, the Octave:fopen-file-in-path warning is enabled.
Octave:function-name-clash
If the Octave:function-name-clash warning is enabled, a warning is issued
when Octave finds that the name of a function defined in a function file differs
from the name of the file. (If the names disagree, the name declared inside
the file is ignored.) By default, the Octave:function-name-clash warning is
enabled.
Octave:future-time-stamp
If the Octave:future-time-stamp warning is enabled, Octave will print a
warning if it finds a function file with a time stamp that is in the future. By
default, the Octave:future-time-stamp warning is enabled.
Octave:glyph-render
By default, the Octave:glyph-render warning is enabled.
Octave:imag-to-real
If the Octave:imag-to-real warning is enabled, a warning is printed for
implicit conversions of complex numbers to real numbers. By default, the
Octave:imag-to-real warning is disabled.
Octave:language-extension
Print warnings when using features that are unique to the Octave
language and that may still be missing in matlab. By default, the
Octave:language-extension warning is disabled. The --traditional or
--braindead startup options for Octave may also be of use, see Section 2.1.1
[Command Line Options], page 15.
Octave:load-file-in-path
By default, the Octave:load-file-in-path warning is enabled.
Octave:logical-conversion
By default, the Octave:logical-conversion warning is enabled.
226 GNU Octave
Octave:missing-glyph
By default, the Octave:missing-glyph warning is enabled.
Octave:missing-semicolon
If the Octave:missing-semicolon warning is enabled, Octave will warn when
statements in function definitions don’t end in semicolons. By default the
Octave:missing-semicolon warning is disabled.
Octave:mixed-string-concat
If the Octave:mixed-string-concat warning is enabled, print a warning when
concatenating a mixture of double and single quoted strings. By default, the
Octave:mixed-string-concat warning is disabled.
Octave:neg-dim-as-zero
If the Octave:neg-dim-as-zero warning is enabled, print a warning for ex-
pressions like
eye (-1)
By default, the Octave:neg-dim-as-zero warning is disabled.
Octave:nested-functions-coerced
By default, the Octave:nested-functions-coerced warning is enabled.
Octave:noninteger-range-as-index
By default, the Octave:noninteger-range-as-index warning is enabled.
Octave:num-to-str
If the Octave:num-to-str warning is enable, a warning is printed for implicit
conversions of numbers to their ASCII character equivalents when strings are
constructed using a mixture of strings and numbers in matrix notation. For
example,
[ "f", 111, 111 ]
⇒"foo"
elicits a warning if the Octave:num-to-str warning is enabled. By default, the
Octave:num-to-str warning is enabled.
Octave:possible-matlab-short-circuit-operator
If the Octave:possible-matlab-short-circuit-operator warning is
enabled, Octave will warn about using the not short circuiting operators &
and |inside if or while conditions. They normally never short circuit, but
matlab always short circuits if any logical operators are used in a condition.
You can turn on the option
do_braindead_shortcircuit_evaluation (1)
if you would like to enable this short-circuit evaluation in Octave. Note that
the && and || operators always short circuit in both Octave and matlab,
so it’s only necessary to enable matlab-style short-circuiting if it’s too ar-
duous to modify existing code that relies on this behavior. By default, the
Octave:possible-matlab-short-circuit-operator warning is enabled.
Octave:precedence-change
If the Octave:precedence-change warning is enabled, Octave will warn about
possible changes in the meaning of some code due to changes in precedence

Chapter 12: Errors and Warnings 227
for some operators. Precedence changes have typically been made for matlab
compatibility. By default, the Octave:precedence-change warning is enabled.
Octave:recursive-path-search
By default, the Octave:recursive-path-search warning is enabled.
Octave:remove-init-dir
The path function changes the search path that Octave uses to find functions.
It is possible to set the path to a value which excludes Octave’s own built-in
functions. If the Octave:remove-init-dir warning is enabled then Octave will
warn when the path function has been used in a way that may render Octave
unworkable. By default, the Octave:remove-init-dir warning is enabled.
Octave:reload-forces-clear
If several functions have been loaded from the same file, Octave must
clear all the functions before any one of them can be reloaded. If the
Octave:reload-forces-clear warning is enabled, Octave will warn you
when this happens, and print a list of the additional functions that it is forced
to clear. By default, the Octave:reload-forces-clear warning is enabled.
Octave:resize-on-range-error
If the Octave:resize-on-range-error warning is enabled, print a warning
when a matrix is resized by an indexed assignment with indices outside the
current bounds. By default, the Octave:resize-on-range-error warning is
disabled.
Octave:separator-insert
Print warning if commas or semicolons might be inserted automatically in literal
matrices. By default, the Octave:separator-insert warning is disabled.
Octave:shadowed-function
By default, the Octave:shadowed-function warning is enabled.
Octave:single-quote-string
Print warning if a single quote character is used to introduce a string constant.
By default, the Octave:single-quote-string warning is disabled.
Octave:nearly-singular-matrix
Octave:singular-matrix
By default, the Octave:nearly-singular-matrix and Octave:singular-matrix
warnings are enabled.
Octave:sqrtm:SingularMatrix
By default, the Octave:sqrtm:SingularMatrix warning is enabled.
Octave:str-to-num
If the Octave:str-to-num warning is enabled, a warning is printed for implicit
conversions of strings to their numeric ASCII equivalents. For example,
"abc" + 0
⇒97 98 99
elicits a warning if the Octave:str-to-num warning is enabled. By default, the
Octave:str-to-num warning is disabled.
228 GNU Octave
Octave:undefined-return-values
If the Octave:undefined-return-values warning is disabled, print a warning
if a function does not define all the values in the return list which are expected.
By default, the Octave:undefined-return-values warning is enabled.
Octave:variable-switch-label
If the Octave:variable-switch-label warning is enabled, Octave will print a
warning if a switch label is not a constant or constant expression. By default,
the Octave:variable-switch-label warning is disabled.
12.2.2 Enabling and Disabling Warnings
The warning function also allows you to control which warnings are actually printed to
the screen. If the warning function is called with a string argument that is either "on" or
"off" all warnings will be enabled or disabled.
It is also possible to enable and disable individual warnings through their string identi-
fications. The following code will issue a warning
warning ("example:non-negative-variable",
"’a’ must be non-negative. Setting ’a’ to zero.");
while the following won’t issue a warning
warning ("off", "example:non-negative-variable");
warning ("example:non-negative-variable",
"’a’ must be non-negative. Setting ’a’ to zero.");

229
13 Debugging
Octave includes a built-in debugger to aid in the development of scripts. This can be used
to interrupt the execution of an Octave script at a certain point, or when certain conditions
are met. Once execution has stopped, and debug mode is entered, the symbol table at the
point where execution has stopped can be examined and modified to check for errors.
The normal command-line editing and history functions are available in debug mode.
13.1 Entering Debug Mode
There are two basic means of interrupting the execution of an Octave script. These are
breakpoints (see Section 13.3 [Breakpoints], page 230), discussed in the next section, and
interruption based on some condition.
Octave supports three means to stop execution based on the values set in the functions
debug_on_interrupt,debug_on_warning, and debug_on_error.
val = debug_on_interrupt ()
old_val = debug_on_interrupt (new_val)
debug_on_interrupt (new_val,"local")
Query or set the internal variable that controls whether Octave will try to enter
debugging mode when it receives an interrupt signal (typically generated with C-c).
If a second interrupt signal is received before reaching the debugging mode, a normal
interrupt will occur.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [debug on error], page 229,[debug on warning], page 229.
val = debug_on_warning ()
old_val = debug_on_warning (new_val)
debug_on_warning (new_val,"local")
Query or set the internal variable that controls whether Octave will try to enter the
debugger when a warning is encountered.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [debug on error], page 229,[debug on interrupt], page 229.
val = debug_on_error ()
old_val = debug_on_error (new_val)
debug_on_error (new_val,"local")
Query or set the internal variable that controls whether Octave will try to enter the
debugger when an error is encountered.
This will also inhibit printing of the normal traceback message (you will only see the
top-level error message).

230 GNU Octave
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [debug on warning], page 229,[debug on interrupt], page 229.
13.2 Leaving Debug Mode
Use either dbcont or return to leave the debug mode and continue the normal execution
of the script.
dbcont
Leave command-line debugging mode and continue code execution normally.
See also: [dbstep], page 235,[dbquit], page 230.
To quit debug mode and return directly to the prompt without executing any additional
code use dbquit.
dbquit
Quit debugging mode immediately without further code execution and return to the
Octave prompt.
See also: [dbcont], page 230,[dbstep], page 235.
Finally, typing exit or quit at the debug prompt will result in Octave terminating
normally.
13.3 Breakpoints
Breakpoints can be set in any m-file function by using the dbstop function.
dbstop func
dbstop func line
dbstop func line1 line2 . . .
dbstop line1 . . .
dbstop in func
dbstop in func at line
dbstop in func at line if "condition"
dbstop if event
dbstop if event ID
dbstop (bp_struct)
rline = dbstop . . .
Set breakpoints for the built-in debugger.
func is the name of a function on the current path. When already in debug mode the
func argument can be omitted and the current function will be used. Breakpoints
at subfunctions are set with the scope operator ‘>’. For example, If file.m has a
subfunction func2, then a breakpoint in func2 can be specified by file>func2.
line is the line number at which to break. If line is not specified, it defaults to the
first executable line in the file func.m. Multiple lines can be specified in a single

Chapter 13: Debugging 231
command; when function syntax is used, the lines may also be passed as a single
vector argument ([line1,line2, ...]).
condition is any Octave expression that can be evaluated in the code context that
exists at the breakpoint. When the breakpoint is encountered, condition will be eval-
uated, and execution will stop if condition is true. If condition cannot be evaluated,
for example because it refers to an undefined variable, an error will be thrown. Ex-
pressions with side effects (such as y++ > 1) will alter variables, and should generally
be avoided. Conditions containing quotes (‘"’, ‘’’) or comment characters (‘#’, ‘%’)
must be enclosed in quotes. (This does not apply to conditions entered from the
editor’s context menu.) For example:
dbstop in strread at 209 if ’any (format == "%f")’
The form specifying event does not cause a specific breakpoint at a given function and
line number. Instead it causes debug mode to be entered when certain unexpected
events are encountered. Possible values are
error Stop when an error is reported. This is equivalent to specifying both
debug_on_error (true) and debug_on_interrupt (true).
caught error
Stop when an error is caught by a try-catch block (not yet implemented).
interrupt
Stop when an interrupt (Ctrl-C) occurs.
naninf Stop when code returns a non-finite value (not yet implemented).
warning Stop when a warning is reported. This is equivalent to specifying debug_
on_warning (true).
The events error,caught error, and warning can all be followed by a string speci-
fying an error ID or warning ID. If that is done, only errors with the specified ID will
cause execution to stop. To stop on one of a set of IDs, multiple dbstop commands
must be issued.
Breakpoints and events can be removed using the dbclear command with the same
syntax.
It is possible to save all breakpoints and restore them at once by issuing the commands
bp_state = dbstatus; ...; dbstop (bp_state).
The optional output rline is the real line number where the breakpoint was set. This
can differ from the specified line if the line is not executable. For example, if a
breakpoint attempted on a blank line then Octave will set the real breakpoint at the
next executable line.
When a file is re-parsed, such as when it is modified outside the GUI, all breakpoints
within the file are cleared.
See also: [dbclear], page 232,[dbstatus], page 232,[dbstep], page 235,
[debug on error], page 229,[debug on warning], page 229,[debug on interrupt],
page 229.

232 GNU Octave
Breakpoints in class methods are also supported (e.g., dbstop ("@class/method")). How-
ever, breakpoints cannot be set in built-in functions (e.g., sin, etc.) or dynamically loaded
functions (i.e., oct-files).
To set a breakpoint immediately upon entering a function use line number 1, or omit
the line number entirely and just give the function name. When setting the breakpoint
Octave will ignore the leading comment block, and the breakpoint will be set on the first
executable statement in the function. For example:
dbstop ("asind", 1)
⇒29
Note that the return value of 29 means that the breakpoint was effectively set to line 29.
The status of breakpoints in a function can be queried with dbstatus.
dbstatus
dbstatus func
bp_list = dbstatus . . .
Report the location of active breakpoints.
When called with no input or output arguments, print the list of all functions with
breakpoints and the line numbers where those breakpoints are set.
If a function name func is specified then only report breakpoints for the named func-
tion and its subfunctions.
The optional return argument bp list is a struct array with the following fields.
name The name of the function with a breakpoint. A subfunction, say func2
within an m-file, say file.m, is specified as file>func2.
file The name of the m-file where the function code is located.
line The line number with the breakpoint.
cond The condition that must be satisfied for the breakpoint to be active, or
the empty string for unconditional breakpoints.
If dbstop if error is true but no explicit IDs are specified, the return value will have
an empty field called "errs". If IDs are specified, the errs field will have one row
per ID. If dbstop if error is false, there is no "errs" field. The "warn" field is set
similarly by dbstop if warning.
See also: [dbstop], page 230,[dbclear], page 232,[dbwhere], page 234,[dblist],
page 234,[dbstack], page 235.
Reusing the previous example, dbstatus ("asind") will return 29. The breakpoints listed
can then be cleared with the dbclear function.
dbclear func
dbclear func line
dbclear func line1 line2 . . .
dbclear line . . .
dbclear all
dbclear in func
dbclear in func at line
Chapter 13: Debugging 233
dbclear if event
dbclear ("func")
dbclear ("func",line)
dbclear ("func",line1,line2, . . . )
dbclear ("func",line1, . . . )
dbclear (line, . . . )
dbclear ("all")
Delete a breakpoint at line number line in the function func.
Arguments are
func Function name as a string variable. When already in debug mode this
argument can be omitted and the current function will be used.
line Line number from which to remove a breakpoint. Multiple lines may be
given as separate arguments or as a vector.
event An event such as error,interrupt, or warning (see [dbstop], page 230,
for details).
When called without a line number specification all breakpoints in the named function
are cleared.
If the requested line is not a breakpoint no action is performed.
The special keyword "all" will clear all breakpoints from all files.
See also: [dbstop], page 230,[dbstatus], page 232,[dbwhere], page 234.
A breakpoint may also be set in a subfunction. For example, if a file contains the
functions
function y = func1 (x)
y = func2 (x);
endfunction
function y = func2 (x)
y=x+1;
endfunction
then a breakpoint can be set at the start of the subfunction directly with
dbstop (["func1", filemarker(), "func2"])
⇒5
Note that filemarker returns the character that marks subfunctions from the file con-
taining them. Unless the default has been changed this character is ‘>’. Thus, a quicker
and more normal way to set the breakpoint would be
dbstop func1>func2
Another simple way of setting a breakpoint in an Octave script is the use of the keyboard
function.
keyboard ()
keyboard ("prompt")
Stop m-file execution and enter debug mode.
234 GNU Octave
When the keyboard function is executed, Octave prints a prompt and waits for user
input. The input strings are then evaluated and the results are printed. This makes it
possible to examine the values of variables within a function, and to assign new values
if necessary. To leave the prompt and return to normal execution type ‘return’ or
‘dbcont’. The keyboard function does not return an exit status.
If keyboard is invoked without arguments, a default prompt of ‘debug> ’ is used.
See also: [dbstop], page 230,[dbcont], page 230,[dbquit], page 230.
The keyboard function is placed in a script at the point where the user desires that the
execution be stopped. It automatically sets the running script into the debug mode.
13.4 Debug Mode
There are three additional support functions that allow the user to find out where in the
execution of a script Octave entered the debug mode, and to print the code in the script
surrounding the point where Octave entered debug mode.
dbwhere
In debugging mode, report the current file and line number where execution is
stopped.
See also: [dbstack], page 235,[dblist], page 234,[dbstatus], page 232,[dbcont],
page 230,[dbstep], page 235,[dbup], page 236,[dbdown], page 236.
dbtype
dbtype lineno
dbtype startl:endl
dbtype startl:end
dbtype func
dbtype func lineno
dbtype func startl:endl
dbtype func startl:end
Display a script file with line numbers.
When called with no arguments in debugging mode, display the script file currently
being debugged.
An optional range specification can be used to list only a portion of the file. The
special keyword "end" is a valid line number specification for the last line of the file.
When called with the name of a function, list that script file with line numbers.
See also: [dblist], page 234,[dbwhere], page 234,[dbstatus], page 232,[dbstop],
page 230.
dblist
dblist n
In debugging mode, list nlines of the function being debugged centered around the
current line to be executed.
If unspecified ndefaults to 10 (+/- 5 lines)
See also: [dbwhere], page 234,[dbtype], page 234,[dbstack], page 235.
Chapter 13: Debugging 235
You may also use isdebugmode to determine whether the debugger is currently active.
isdebugmode ()
Return true if in debugging mode, otherwise false.
See also: [dbwhere], page 234,[dbstack], page 235,[dbstatus], page 232.
Debug mode also allows single line stepping through a function using the command
dbstep.
dbstep
dbstep n
dbstep in
dbstep out
dbnext . . .
In debugging mode, execute the next nlines of code.
If nis omitted, execute the next single line of code. If the next line of code is itself
defined in terms of an m-file remain in the existing function.
Using dbstep in will cause execution of the next line to step into any m-files defined
on the next line.
Using dbstep out will cause execution to continue until the current function returns.
dbnext is an alias for dbstep.
See also: [dbcont], page 230,[dbquit], page 230.
When in debug mode the RETURN key will execute the last entered command. This is
useful, for example, after hitting a breakpoint and entering dbstep once. After that, one
can advance line by line through the code with only a single key stroke.
13.5 Call Stack
The function being debugged may be the leaf node of a series of function calls. After
examining values in the current subroutine it may turn out that the problem occurred in
earlier pieces of code. Use dbup and dbdown to move up and down through the series of
function calls to locate where variables first took on the wrong values. dbstack shows the
entire series of function calls and at what level debugging is currently taking place.
dbstack
dbstack n
dbstack -completenames
[stack,idx] = dbstack (. . . )
Display or return current debugging function stack information.
With optional argument n, omit the ninnermost stack frames.
Although accepted, the argument -completenames is silently ignored. Octave always
returns absolute filenames.
The arguments nand -completenames can be both specified in any order.
The optional return argument stack is a struct array with the following fields:
file The name of the m-file where the function code is located.
236 GNU Octave
name The name of the function with a breakpoint.
line The line number of an active breakpoint.
column The column number of the line where the breakpoint begins.
scope Undocumented.
context Undocumented.
The return argument idx specifies which element of the stack struct array is currently
active.
See also: [dbup], page 236,[dbdown], page 236,[dbwhere], page 234,[dblist], page 234,
[dbstatus], page 232.
dbup
dbup n
In debugging mode, move up the execution stack nframes.
If nis omitted, move up one frame.
See also: [dbstack], page 235,[dbdown], page 236.
dbdown
dbdown n
In debugging mode, move down the execution stack nframes.
If nis omitted, move down one frame.
See also: [dbstack], page 235,[dbup], page 236.
13.6 Profiling
Octave supports profiling of code execution on a per-function level. If profiling is enabled,
each call to a function (supporting built-ins, operators, functions in oct- and mex-files, user-
defined functions in Octave code and anonymous functions) is recorded while running Octave
code. After that, this data can aid in analyzing the code behavior, and is in particular helpful
for finding “hot spots” in the code which use up a lot of computation time and are the best
targets to spend optimization efforts on.
The main command for profiling is profile, which can be used to start or stop the
profiler and also to query collected data afterwards. The data is returned in an Octave data
structure which can then be examined or further processed by other routines or tools.
profile on
profile off
profile resume
profile clear
S= profile ("status")
T= profile ("info")
Control the built-in profiler.
profile on
Start the profiler, clearing all previously collected data if there is any.
Chapter 13: Debugging 237
profile off
Stop profiling. The collected data can later be retrieved and examined
with T = profile ("info").
profile clear
Clear all collected profiler data.
profile resume
Restart profiling without clearing the old data. All newly collected statis-
tics are added to the existing ones.
S= profile ("status")
Return a structure with information about the current status of the pro-
filer. At the moment, the only field is ProfilerStatus which is either
"on" or "off".
T= profile ("info")
Return the collected profiling statistics in the structure T. The flat profile
is returned in the field FunctionTable which is an array of structures,
each entry corresponding to a function which was called and for which pro-
filing statistics are present. In addition, the field Hierarchical contains
the hierarchical call tree. Each node has an index into the FunctionTable
identifying the function it corresponds to as well as data fields for number
of calls and time spent at this level in the call tree.
See also: [profshow], page 237,[profexplore], page 238.
An easy way to get an overview over the collected data is profshow. This function takes
the profiler data returned by profile as input and prints a flat profile, for instance:
Function Attr Time (s) Calls
----------------------------------------
>myfib R 2.195 13529
binary <= 0.061 13529
binary - 0.050 13528
binary + 0.026 6764
This shows that most of the run time was spent executing the function ‘myfib’, and
some minor proportion evaluating the listed binary operators. Furthermore, it is shown
how often the function was called and the profiler also records that it is recursive.
profshow (data)
profshow (data,n)
profshow ()
profshow (n)
Display flat per-function profiler results.
Print out profiler data (execution time, number of calls) for the most critical nfunc-
tions. The results are sorted in descending order by the total time spent in each
function. If nis unspecified it defaults to 20.
The input data is the structure returned by profile ("info"). If unspecified,
profshow will use the current profile dataset.
238 GNU Octave
The attribute column displays ‘R’ for recursive functions, and is blank for all other
function types.
See also: [profexplore], page 238,[profile], page 236.
profexport (dir)
profexport (dir,data)
profexport (dir,name)
profexport (dir,name,data)
Export profiler data as HTML.
Export the profiling data in data into a series of HTML files in the folder dir. The
initial file will be data/index.html.
If name is specified, it must be a string that contains a “name” for the profile being
exported. This name is included in the HTML.
The input data is the structure returned by profile ("info"). If unspecified,
profexport will use the current profile dataset.
See also: [profshow], page 237,[profexplore], page 238,[profile], page 236.
profexplore ()
profexplore (data)
Interactively explore hierarchical profiler output.
Assuming data is the structure with profile data returned by profile ("info"),
this command opens an interactive prompt that can be used to explore the call-tree.
Type help to get a list of possible commands. If data is omitted, profile ("info")
is called and used in its place.
See also: [profile], page 236,[profshow], page 237.
13.7 Profiler Example
Below, we will give a short example of a profiler session. See Section 13.6 [Profiling],
page 236, for the documentation of the profiler functions in detail. Consider the code:
global N A;
N = 300;
A = rand (N, N);
function xt = timesteps (steps, x0, expM)
global N;
if (steps == 0)
xt = NA (N, 0);
else
xt = NA (N, steps);
x1 = expM * x0;
xt(:, 1) = x1;
xt(:, 2 : end) = timesteps (steps - 1, x1, expM);
endif
Chapter 13: Debugging 239
endfunction
function foo ()
global N A;
initial = @(x) sin (x);
x0 = (initial (linspace (0, 2 * pi, N)))’;
expA = expm (A);
xt = timesteps (100, x0, expA);
endfunction
function fib = bar (N)
if (N <= 2)
fib = 1;
else
fib = bar (N - 1) + bar (N - 2);
endif
endfunction
If we execute the two main functions, we get:
tic; foo; toc;
⇒Elapsed time is 2.37338 seconds.
tic; bar (20); toc;
⇒Elapsed time is 2.04952 seconds.
But this does not give much information about where this time is spent; for instance,
whether the single call to expm is more expensive or the recursive time-stepping itself. To
get a more detailed picture, we can use the profiler.
profile on;
foo;
profile off;
data = profile ("info");
profshow (data, 10);
This prints a table like:

240 GNU Octave
# Function Attr Time (s) Calls
---------------------------------------------
7 expm 1.034 1
3 binary * 0.823 117
41 binary \ 0.188 1
38 binary ^ 0.126 2
43 timesteps R 0.111 101
44 NA 0.029 101
39 binary + 0.024 8
34 norm 0.011 1
40 binary - 0.004 101
33 balance 0.003 1
The entries are the individual functions which have been executed (only the 10 most
important ones), together with some information for each of them. The entries like ‘binary
*’ denote operators, while other entries are ordinary functions. They include both built-
ins like expm and our own routines (for instance timesteps). From this profile, we can
immediately deduce that expm uses up the largest proportion of the processing time, even
though it is only called once. The second expensive operation is the matrix-vector product
in the routine timesteps.1
Timing, however, is not the only information available from the profile. The attribute
column shows us that timesteps calls itself recursively. This may not be that remarkable
in this example (since it’s clear anyway), but could be helpful in a more complex setting.
As to the question of why is there a ‘binary \’ in the output, we can easily shed some
light on that too. Note that data is a structure array (Section 6.1.2 [Structure Arrays],
page 103) which contains the field FunctionTable. This stores the raw data for the profile
shown. The number in the first column of the table gives the index under which the shown
function can be found there. Looking up data.FunctionTable(41) gives:
scalar structure containing the fields:
FunctionName = binary \
TotalTime = 0.18765
NumCalls = 1
IsRecursive = 0
Parents = 7
Children = [](1x0)
Here we see the information from the table again, but have additional fields Parents
and Children. Those are both arrays, which contain the indices of functions which have
directly called the function in question (which is entry 7, expm, in this case) or been called
by it (no functions). Hence, the backslash operator has been used internally by expm.
Now let’s take a look at bar. For this, we start a fresh profiling session (profile on
does this; the old data is removed before the profiler is restarted):
1We only know it is the binary multiplication operator, but fortunately this operator appears only at one
place in the code and thus we know which occurrence takes so much time. If there were multiple places,
we would have to use the hierarchical profile to find out the exact place which uses up the time which is
not covered in this example.
241
profile on;
bar (20);
profile off;
profshow (profile ("info"));
This gives:
# Function Attr Time (s) Calls
-------------------------------------------------------
1 bar R 2.091 13529
2 binary <= 0.062 13529
3 binary - 0.042 13528
4 binary + 0.023 6764
5 profile 0.000 1
8 false 0.000 1
6 nargin 0.000 1
7 binary != 0.000 1
9 __profiler_enable__ 0.000 1
Unsurprisingly, bar is also recursive. It has been called 13,529 times in the course of
recursively calculating the Fibonacci number in a suboptimal way, and most of the time
was spent in bar itself.
Finally, let’s say we want to profile the execution of both foo and bar together. Since
we already have the run-time data collected for bar, we can restart the profiler without
clearing the existing data and collect the missing statistics about foo. This is done by:
profile resume;
foo;
profile off;
profshow (profile ("info"), 10);
As you can see in the table below, now we have both profiles mixed together.
# Function Attr Time (s) Calls
---------------------------------------------
1 bar R 2.091 13529
16 expm 1.122 1
12 binary * 0.798 117
46 binary \ 0.185 1
45 binary ^ 0.124 2
48 timesteps R 0.115 101
2 binary <= 0.062 13529
3 binary - 0.045 13629
4 binary + 0.041 6772
49 NA 0.036 101
243
14 Input and Output
Octave supports several ways of reading and writing data to or from the prompt or a file.
The simplest functions for data Input and Output (I/O) are easy to use, but only provide
limited control of how data is processed. For more control, a set of functions modeled after
the C standard library are also provided by Octave.
14.1 Basic Input and Output
14.1.1 Terminal Output
Since Octave normally prints the value of an expression as soon as it has been evaluated, the
simplest of all I/O functions is a simple expression. For example, the following expression
will display the value of ‘pi’
pi
api = 3.1416
This works well as long as it is acceptable to have the name of the variable (or ‘ans’)
printed along with the value. To print the value of a variable without printing its name,
use the function disp.
The format command offers some control over the way Octave prints values with disp
and through the normal echoing mechanism.
disp (x)
Display the value of x.
For example:
disp ("The value of pi is:"), disp (pi)
athe value of pi is:
a3.1416
Note that the output from disp always ends with a newline.
If an output value is requested, disp prints nothing and returns the formatted output
in a string.
See also: [fdisp], page 254.
list_in_columns (arg,width,prefix)
Return a string containing the elements of arg listed in columns with an overall
maximum width of width and optional prefix prefix.
The argument arg must be a cell array of character strings or a character array.
If width is not specified or is an empty matrix, or less than or equal to zero, the width
of the terminal screen is used. Newline characters are used to break the lines in the
output string. For example:

244 GNU Octave
list_in_columns ({"abc", "def", "ghijkl", "mnop", "qrs", "tuv"}, 20)
⇒abc mnop
def qrs
ghijkl tuv
whos ans
⇒
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
ans 1x37 37 char
Total is 37 elements using 37 bytes
See also: [terminal size], page 244.
terminal_size ()
Return a two-element row vector containing the current size of the terminal window
in characters (rows and columns).
See also: [list in columns], page 243.
format
format options
Reset or specify the format of the output produced by disp and Octave’s normal
echoing mechanism.
This command only affects the display of numbers but not how they are stored or
computed. To change the internal representation from the default double use one of
the conversion functions such as single,uint8,int64, etc.
By default, Octave displays 5 significant digits in a human readable form (option
‘short’ paired with ‘loose’ format for matrices). If format is invoked without any
options, this default format is restored.
Valid formats for floating point numbers are listed in the following table.
short Fixed point format with 5 significant figures in a field that is a maximum
of 10 characters wide. (default).
If Octave is unable to format a matrix so that columns line up on the
decimal point and all numbers fit within the maximum field width then
it switches to an exponential ‘e’ format.
long Fixed point format with 15 significant figures in a field that is a maximum
of 20 characters wide.
As with the ‘short’ format, Octave will switch to an exponential ‘e’
format if it is unable to format a matrix properly using the current format.
short e
long e Exponential format. The number to be represented is split between a
mantissa and an exponent (power of 10). The mantissa has 5 significant
digits in the short format and 15 digits in the long format. For example,
with the ‘short e’ format, pi is displayed as 3.1416e+00.
Chapter 14: Input and Output 245
short E
long E Identical to ‘short e’ or ‘long e’ but displays an uppercase ‘E’ to indicate
the exponent. For example, with the ‘long E’ format, pi is displayed as
3.14159265358979E+00.
short g
long g Optimally choose between fixed point and exponential format based on
the magnitude of the number. For example, with the ‘short g’ format,
pi .^ [2; 4; 8; 16; 32] is displayed as
ans =
9.8696
97.409
9488.5
9.0032e+07
8.1058e+15
short eng
long eng Identical to ‘short e’ or ‘long e’ but displays the value using an engi-
neering format, where the exponent is divisible by 3. For example, with
the ‘short eng’ format, 10 * pi is displayed as 31.4159e+00.
long G
short G Identical to ‘short g’ or ‘long g’ but displays an uppercase ‘E’ to indicate
the exponent.
free
none Print output in free format, without trying to line up columns of matrices
on the decimal point. This also causes complex numbers to be format-
ted as numeric pairs like this ‘(0.60419, 0.60709)’ instead of like this
‘0.60419 + 0.60709i’.
The following formats affect all numeric output (floating point and integer types).
"+"
"+" chars
plus
plus chars
Print a ‘+’ symbol for matrix elements greater than zero, a ‘-’ symbol for
elements less than zero and a space for zero matrix elements. This format
can be very useful for examining the structure of a large sparse matrix.
The optional argument chars specifies a list of 3 characters to use for
printing values greater than zero, less than zero and equal to zero. For
example, with the ‘"+" "+-."’ format, [1, 0, -1; -1, 0, 1] is displayed
as
ans =
+.-
-.+
bank Print in a fixed format with two digits to the right of the decimal point.

246 GNU Octave
native-hex
Print the hexadecimal representation of numbers as they are stored in
memory. For example, on a workstation which stores 8 byte real values
in IEEE format with the least significant byte first, the value of pi when
printed in native-hex format is 400921fb54442d18.
hex The same as native-hex, but always print the most significant byte first.
native-bit
Print the bit representation of numbers as stored in memory. For example,
the value of pi is
01000000000010010010000111111011
01010100010001000010110100011000
(shown here in two 32 bit sections for typesetting purposes) when printed
in native-bit format on a workstation which stores 8 byte real values in
IEEE format with the least significant byte first.
bit The same as native-bit, but always print the most significant bits first.
rat Print a rational approximation, i.e., values are approximated as the ratio
of small integers. For example, with the ‘rat’ format, pi is displayed as
355/113.
The following two options affect the display of all matrices.
compact Remove blank lines around column number labels and between matrices
producing more compact output with more data per page.
loose Insert blank lines above and below column number labels and between
matrices to produce a more readable output with less data per page.
(default).
See also: [fixed point format], page 51,[output max field width], page 49,
[output precision], page 50,[split long rows], page 50,[print empty dimensions],
page 52,[rats], page 496.
14.1.1.1 Paging Screen Output
When running interactively, Octave normally sends any output intended for your terminal
that is more than one screen long to a paging program, such as less or more. This avoids
the problem of having a large volume of output stream by before you can read it. With
less (and some versions of more) you can also scan forward and backward, and search for
specific items.
Normally, no output is displayed by the pager until just before Octave is ready to print
the top level prompt, or read from the standard input (for example, by using the fscanf or
scanf functions). This means that there may be some delay before any output appears on
your screen if you have asked Octave to perform a significant amount of work with a single
command statement. The function fflush may be used to force output to be sent to the
pager (or any other stream) immediately.
You can select the program to run as the pager using the PAGER function, and you can
turn paging off by using the function more.

Chapter 14: Input and Output 247
more
more on
more off
Turn output pagination on or off.
Without an argument, more toggles the current state.
The current state can be determined via page_screen_output.
See also: [page screen output], page 247,[page output immediately], page 248,
[PAGER], page 247,[PAGER FLAGS], page 247.
val = PAGER ()
old_val = PAGER (new_val)
PAGER (new_val,"local")
Query or set the internal variable that specifies the program to use to display terminal
output on your system.
The default value is normally "less","more", or "pg", depending on what programs
are installed on your system. See Appendix E [Installation], page 935.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [PAGER FLAGS], page 247,[page output immediately], page 248,[more],
page 246,[page screen output], page 247.
val = PAGER_FLAGS ()
old_val = PAGER_FLAGS (new_val)
PAGER_FLAGS (new_val,"local")
Query or set the internal variable that specifies the options to pass to the pager.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [PAGER], page 247,[more], page 246,[page screen output], page 247,
[page output immediately], page 248.
val = page_screen_output ()
old_val = page_screen_output (new_val)
page_screen_output (new_val,"local")
Query or set the internal variable that controls whether output intended for the
terminal window that is longer than one page is sent through a pager.
This allows you to view one screenful at a time. Some pagers (such as less—see
Appendix E [Installation], page 935) are also capable of moving backward on the
output.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [more], page 246,[page output immediately], page 248,[PAGER], page 247,
[PAGER FLAGS], page 247.

248 GNU Octave
val = page_output_immediately ()
old_val = page_output_immediately (new_val)
page_output_immediately (new_val,"local")
Query or set the internal variable that controls whether Octave sends output to the
pager as soon as it is available.
Otherwise, Octave buffers its output and waits until just before the prompt is printed
to flush it to the pager.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [page screen output], page 247,[more], page 246,[PAGER], page 247,
[PAGER FLAGS], page 247.
fflush (fid)
Flush output to file descriptor fid.
fflush returns 0 on success and an OS dependent error value (−1 on Unix) on error.
Programming Note: Flushing is useful for ensuring that all pending output makes it
to the screen before some other event occurs. For example, it is always a good idea
to flush the standard output stream before calling input.
See also: [fopen], page 265,[fclose], page 266.
14.1.2 Terminal Input
Octave has three functions that make it easy to prompt users for input. The input and
menu functions are normally used for managing an interactive dialog with a user, and the
keyboard function is normally used for doing simple debugging.
ans = input (prompt)
ans = input (prompt,"s")
Print prompt and wait for user input.
For example,
input ("Pick a number, any number! ")
prints the prompt
Pick a number, any number!
and waits for the user to enter a value. The string entered by the user is evaluated
as an expression, so it may be a literal constant, a variable name, or any other valid
Octave code.
The number of return arguments, their size, and their class depend on the expression
entered.
If you are only interested in getting a literal string value, you can call input with the
character string "s" as the second argument. This tells Octave to return the string
entered by the user directly, without evaluating it first.
Because there may be output waiting to be displayed by the pager, it is a good idea to
always call fflush (stdout) before calling input. This will ensure that all pending
output is written to the screen before your prompt.

Chapter 14: Input and Output 249
See also: [yes or no], page 249,[kbhit], page 249,[pause], page 813,[menu], page 249,
[listdlg], page 792.
choice = menu (title,opt1, . . . )
choice = menu (title,{opt1, . . . })
Display a menu with heading title and options opt1, . . ., and wait for user input.
If the GUI is running, the menu is displayed graphically using listdlg. Otherwise,
the title and menu options are printed on the console.
title is a string and the options may be input as individual strings or as a cell array
of strings.
The return value choice is the number of the option selected by the user counting
from 1. If the user aborts the dialog or makes an invalid selection then 0 is returned.
This function is useful for interactive programs. There is no limit to the number of
options that may be passed in, but it may be confusing to present more than will fit
easily on one screen.
See also: [input], page 248,[listdlg], page 792.
ans = yes_or_no ("prompt")
Ask the user a yes-or-no question.
Return logical true if the answer is yes or false if the answer is no.
Takes one argument, prompt, which is the string to display when asking the question.
prompt should end in a space; yes-or-no adds the string ‘(yes or no) ’ to it. The
user must confirm the answer with RET and can edit it until it has been confirmed.
See also: [input], page 248.
For input, the normal command line history and editing functions are available at the
prompt.
Octave also has a function that makes it possible to get a single character from the
keyboard without requiring the user to type a carriage return.
kbhit ()
kbhit (1)
Read a single keystroke from the keyboard.
If called with an argument, don’t wait for a keypress.
For example,
x = kbhit ();
will set xto the next character typed at the keyboard as soon as it is typed.
x = kbhit (1);
is identical to the above example, but doesn’t wait for a keypress, returning the empty
string if no key is available.
See also: [input], page 248,[pause], page 813.
250 GNU Octave
14.1.3 Simple File I/O
The save and load commands allow data to be written to and read from disk files in various
formats. The default format of files written by the save command can be controlled using
the functions save_default_options and save_precision.
As an example the following code creates a 3-by-3 matrix and saves it to the file
‘myfile.mat’.
A = [ 1:3; 4:6; 7:9 ];
save myfile.mat A
Once one or more variables have been saved to a file, they can be read into memory
using the load command.
load myfile.mat
A
aA =
a
a123
a456
a789
save file
save options file
save options file v1 v2 . . .
save options file -struct STRUCT f1 f2 . . .
save -v1 v2 . . .
str = save ("-","v1","v2", . . . )
Save the named variables v1,v2, . . ., in the file file.
The special filename ‘-’ may be used to return the content of the variables as a string.
If no variable names are listed, Octave saves all the variables in the current scope.
Otherwise, full variable names or pattern syntax can be used to specify the variables to
save. If the -struct modifier is used, fields f1 f2 . . . of the scalar structure STRUCT
are saved as if they were variables with corresponding names. Valid options for the
save command are listed in the following table. Options that modify the output
format override the format specified by save_default_options.
If save is invoked using the functional form
save ("-option1", ..., "file", "v1", ...)
then the options,file, and variable name arguments (v1, . . . ) must be specified as
character strings.
If called with a filename of "-", write the output to stdout if nargout is 0, otherwise
return the output in a character string.
-append Append to the destination instead of overwriting.
-ascii Save a single matrix in a text file without header or any other information.
-binary Save the data in Octave’s binary data format.
Chapter 14: Input and Output 251
-float-binary
Save the data in Octave’s binary data format but only using single pre-
cision. Only use this format if you know that all the values to be saved
can be represented in single precision.
-hdf5 Save the data in hdf5 format. (HDF5 is a free, portable binary format
developed by the National Center for Supercomputing Applications at
the University of Illinois.) This format is only available if Octave was
built with a link to the hdf5 libraries.
-float-hdf5
Save the data in hdf5 format but only using single precision. Only use
this format if you know that all the values to be saved can be represented
in single precision.
-V7
-v7
-7
-mat7-binary
Save the data in matlab’s v7 binary data format.
-V6
-v6
-6
-mat
-mat-binary
Save the data in matlab’s v6 binary data format.
-V4
-v4
-4
-mat4-binary
Save the data in the binary format written by matlab version 4.
-text Save the data in Octave’s text data format. (default).
-zip
-z Use the gzip algorithm to compress the file. This works equally on files
that are compressed with gzip outside of octave, and gzip can equally be
used to convert the files for backward compatibility. This option is only
available if Octave was built with a link to the zlib libraries.
The list of variables to save may use wildcard patterns containing the following special
characters:
?Match any single character.
*Match zero or more characters.
[list ]Match the list of characters specified by list. If the first character is !or
^, match all characters except those specified by list. For example, the
pattern [a-zA-Z] will match all lower and uppercase alphabetic charac-
ters.

252 GNU Octave
Wildcards may also be used in the field name specifications when using
the -struct modifier (but not in the struct name itself).
Except when using the matlab binary data file format or the ‘-ascii’ format, saving
global variables also saves the global status of the variable. If the variable is restored
at a later time using ‘load’, it will be restored as a global variable.
The command
save -binary data a b*
saves the variable ‘a’ and all variables beginning with ‘b’ to the file data in Octave’s
binary format.
See also: [load], page 253,[save default options], page 252,[save header format string],
page 252,[dlmread], page 256,[csvread], page 256,[fread], page 277.
There are three functions that modify the behavior of save.
val = save_default_options ()
old_val = save_default_options (new_val)
save_default_options (new_val,"local")
Query or set the internal variable that specifies the default options for the save
command, and defines the default format.
Typical values include "-ascii","-text -zip". The default value is -text.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [save], page 250.
val = save_precision ()
old_val = save_precision (new_val)
save_precision (new_val,"local")
Query or set the internal variable that specifies the number of digits to keep when
saving data in text format.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
val = save_header_format_string ()
old_val = save_header_format_string (new_val)
save_header_format_string (new_val,"local")
Query or set the internal variable that specifies the format string used for the comment
line written at the beginning of text-format data files saved by Octave.
The format string is passed to strftime and should begin with the character ‘#’ and
contain no newline characters. If the value of save_header_format_string is the
empty string, the header comment is omitted from text-format data files. The default
value is
"# Created by Octave VERSION, %a %b %d %H:%M:%S %Y %Z <USER@HOST>"
Chapter 14: Input and Output 253
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [strftime], page 809,[save], page 250.
load file
load options file
load options file v1 v2 . . .
S = load ("options","file","v1","v2", . . . )
load file options
load file options v1 v2 . . .
S = load ("file","options","v1","v2", . . . )
Load the named variables v1,v2, . . ., from the file file.
If no variables are specified then all variables found in the file will be loaded. As with
save, the list of variables to extract can be full names or use a pattern syntax. The
format of the file is automatically detected but may be overridden by supplying the
appropriate option.
If load is invoked using the functional form
load ("-option1", ..., "file", "v1", ...)
then the options,file, and variable name arguments (v1, . . . ) must be specified as
character strings.
If a variable that is not marked as global is loaded from a file when a global symbol
with the same name already exists, it is loaded in the global symbol table. Also, if
a variable is marked as global in a file and a local symbol exists, the local symbol is
moved to the global symbol table and given the value from the file.
If invoked with a single output argument, Octave returns data instead of insert-
ing variables in the symbol table. If the data file contains only numbers (TAB- or
space-delimited columns), a matrix of values is returned. Otherwise, load returns a
structure with members corresponding to the names of the variables in the file.
The load command can read data stored in Octave’s text and binary formats,
and matlab’s binary format. If compiled with zlib support, it can also load
gzip-compressed files. It will automatically detect the type of file and do conversion
from different floating point formats (currently only IEEE big and little endian,
though other formats may be added in the future).
Valid options for load are listed in the following table.
-force This option is accepted for backward compatibility but is ignored. Octave
now overwrites variables currently in memory with those of the same name
found in the file.
-ascii Force Octave to assume the file contains columns of numbers in text
format without any header or other information. Data in the file will be
loaded as a single numeric matrix with the name of the variable derived
from the name of the file.
-binary Force Octave to assume the file is in Octave’s binary format.
254 GNU Octave
-hdf5 Force Octave to assume the file is in hdf5 format. (hdf5 is a free,
portable binary format developed by the National Center for Supercom-
puting Applications at the University of Illinois.) Note that Octave can
read hdf5 files not created by itself, but may skip some datasets in for-
mats that it cannot support. This format is only available if Octave was
built with a link to the hdf5 libraries.
-import This option is accepted for backward compatibility but is ignored. Octave
can now support multi-dimensional HDF data and automatically modifies
variable names if they are invalid Octave identifiers.
-mat
-mat-binary
-6
-v6
-7
-v7 Force Octave to assume the file is in matlab’s version 6 or 7 binary
format.
-mat4-binary
-4
-v4
-V4 Force Octave to assume the file is in the binary format written by matlab
version 4.
-text Force Octave to assume the file is in Octave’s text format.
See also: [save], page 250,[dlmwrite], page 255,[csvwrite], page 256,[fwrite],
page 280.
str = fileread (filename)
Read the contents of filename and return it as a string.
See also: [fread], page 277,[textread], page 256,[sscanf], page 275.
native_float_format ()
Return the native floating point format as a string.
It is possible to write data to a file in a similar way to the disp function for writing data
to the screen. The fdisp works just like disp except its first argument is a file pointer as
created by fopen. As an example, the following code writes to data ‘myfile.txt’.
fid = fopen ("myfile.txt", "w");
fdisp (fid, "3/8 is ");
fdisp (fid, 3/8);
fclose (fid);
See Section 14.2.1 [Opening and Closing Files], page 265, for details on how to use fopen
and fclose.
fdisp (fid,x)
Display the value of xon the stream fid.
Chapter 14: Input and Output 255
For example:
fdisp (stdout, "The value of pi is:"), fdisp (stdout, pi)
athe value of pi is:
a3.1416
Note that the output from fdisp always ends with a newline.
See also: [disp], page 243.
Octave can also read and write matrices text files such as comma separated lists.
dlmwrite (file,M)
dlmwrite (file,M,delim,r,c)
dlmwrite (file,M,key,val . . .)
dlmwrite (file,M,"-append", . . . )
dlmwrite (fid, . . . )
Write the numeric matrix Mto the text file file using a delimiter.
file should be a filename or a writable file ID given by fopen.
The parameter delim specifies the delimiter to use to separate values on a row. If no
delimiter is specified the comma character ‘,’ is used.
The value of rspecifies the number of delimiter-only lines to add to the start of the
file.
The value of cspecifies the number of delimiters to prepend to each line of data.
If the argument "-append" is given, append to the end of file.
In addition, the following keyword value pairs may appear at the end of the argument
list:
"append" Either "on" or "off". See "-append" above.
"delimiter"
See delim above.
"newline"
The character(s) to separate each row. Three special cases exist for this
option. "unix" is changed into "\n","pc" is changed into "\r\n", and
"mac" is changed into "\r". Any other value is used directly as the
newline separator.
"roffset"
See rabove.
"coffset"
See cabove.
"precision"
The precision to use when writing the file. It can either be a format string
(as used by fprintf) or a number of significant digits.
dlmwrite ("file.csv", reshape (1:16, 4, 4));
dlmwrite ("file.tex", a, "delimiter", "&", "newline", "\n")
See also: [dlmread], page 256,[csvread], page 256,[csvwrite], page 256.
256 GNU Octave
data = dlmread (file)
data = dlmread (file,sep)
data = dlmread (file,sep,r0,c0)
data = dlmread (file,sep,range)
data = dlmread (. . . , "emptyvalue",EMPTYVAL)
Read numeric data from the text file file which uses the delimiter sep between data
values.
If sep is not defined the separator between fields is determined from the file itself.
The optional scalar arguments r0 and c0 define the starting row and column of the
data to be read. These values are indexed from zero, i.e., the first data row corresponds
to an index of zero.
The range parameter specifies exactly which data elements are read. The first form of
the parameter is a 4-element vector containing the upper left and lower right corners
[R0,C0,R1,C1]where the indices are zero-based. Alternatively, a spreadsheet style
form such as "A2..Q15" or "T1:AA5" can be used. The lowest alphabetical index ’A’
refers to the first column. The lowest row index is 1.
file should be a filename or a file id given by fopen. In the latter case, the file is read
until end of file is reached.
The "emptyvalue" option may be used to specify the value used to fill empty fields.
The default is zero. Note that any non-numeric values, such as text, are also replaced
by the "emptyvalue".
See also: [csvread], page 256,[textscan], page 258,[textread], page 256,[dlmwrite],
page 255.
csvwrite (filename,x)
csvwrite (filename,x,dlm_opt1, . . . )
Write the numeric matrix xto the file filename in comma-separated-value (CSV)
format.
This function is equivalent to
dlmwrite (filename,x, ",", dlm_opt1, ...)
Any optional arguments are passed directly to dlmwrite (see [dlmwrite], page 255).
See also: [csvread], page 256,[dlmwrite], page 255,[dlmread], page 256.
x= csvread (filename)
x= csvread (filename,dlm_opt1, . . . )
Read the comma-separated-value (CSV) file filename into the matrix x.
Note: only CSV files containing numeric data can be read.
This function is equivalent to
x= dlmread (filename, "," , dlm_opt1, ...)
Any optional arguments are passed directly to dlmread (see [dlmread], page 256).
See also: [dlmread], page 256,[textread], page 256,[textscan], page 258,[csvwrite],
page 256,[dlmwrite], page 255.
Formatted data from can be read from, or written to, text files as well.
Chapter 14: Input and Output 257
[a, ...] = textread (filename)
[a, ...] = textread (filename,format)
[a, ...] = textread (filename,format,n)
[a, ...] = textread (filename,format,prop1,value1, . . . )
[a, ...] = textread (filename,format,n,prop1,value1, . . . )
Read data from a text file.
The file filename is read and parsed according to format. The function behaves like
strread except it works by parsing a file instead of a string. See the documentation
of strread for details.
In addition to the options supported by strread, this function supports two more:
•"headerlines": The first value number of lines of filename are skipped.
•"endofline": Specify a single character or "\r\n". If no value is given, it will be
inferred from the file. If set to "" (empty string) EOLs are ignored as delimiters.
The optional input n(format repeat count) specifies the number of times the format
string is to be used or the number of lines to be read, whichever happens first while
reading. The former is equivalent to requesting that the data output vectors should
be of length N. Note that when reading files with format strings referring to multiple
lines, nshould rather be the number of lines to be read than the number of format
string uses.
If the format string is empty (not just omitted) and the file contains only numeric data
(excluding headerlines), textread will return a rectangular matrix with the number
of columns matching the number of numeric fields on the first data line of the file.
Empty fields are returned as zero values.
Examples:
Assume a data file like:
1a2b
3c4d
5 e
[a, b] = textread (f, "%f %s")
returns two columns of data, one with doubles, the other a
cellstr array:
a = [1; 2; 3; 4; 5]
b = {"a"; "b"; "c"; "d"; "e"}
[a, b] = textread (f, "%f %s", 3)
(read data into two culumns, try to use the format string
three times)
returns
a = [1; 2; 3]
b = {"a"; "b"; "c"}
258 GNU Octave
With a data file like:
1
a
2
b
[a, b] = textread (f, "%f %s", 2)
returns a = 1 and b = {"a"}; i.e., the format string is used
only once because the format string refers to 2 lines of the
data file. To obtain 2x1 data output columns, specify N = 4
(number of data lines containing all requested data) rather
than 2.
See also: [strread], page 84,[load], page 253,[dlmread], page 256,[fscanf], page 274,
[textscan], page 258.
C= textscan (fid,format)
C= textscan (fid,format,repeat)
C= textscan (fid,format,param,value, . . . )
C= textscan (fid,format,repeat,param,value, . . . )
C= textscan (str, . . . )
[C,position,errmsg] = textscan (. . . )
Read data from a text file or string.
The string str or file associated with fid is read from and parsed according to format.
The function is an extension of strread and textread. Differences include: the
ability to read from either a file or a string, additional options, and additional format
specifiers.
The input is interpreted as a sequence of words, delimiters (such as whitespace), and
literals. The characters that form delimiters and whitespace are determined by the
options. The format consists of format specifiers interspersed between literals. In the
format, whitespace forms a delimiter between consecutive literals, but is otherwise
ignored.
The output Cis a cell array where the number of columns is determined by the
number of format specifiers.
The first word of the input is matched to the first specifier of the format and placed
in the first column of the output; the second is matched to the second specifier and
placed in the second column and so forth. If there are more words than specifiers
then the process is repeated until all words have been processed or the limit imposed
by repeat has been met (see below).
The string format describes how the words in str should be parsed. As in fscanf, any
(non-whitespace) text in the format that is not one of these specifiers is considered a
literal. If there is a literal between two format specifiers then that same literal must
appear in the input stream between the matching words.
The following specifiers are valid:
%f
%f64
%n The word is parsed as a number and converted to double.
Chapter 14: Input and Output 259
%f32 The word is parsed as a number and converted to single (float).
%d
%d8
%d16
%d32
%d64 The word is parsed as a number and converted to int8, int16, int32, or
int64. If no size is specified then int32 is used.
%u
%u8
%u16
%u32
%u64 The word is parsed as a number and converted to uint8, uint16, uint32,
or uint64. If no size is specified then uint32 is used.
%s The word is parsed as a string ending at the last character before white-
space, an end-of-line, or a delimiter specified in the options.
%q The word is parsed as a "quoted string". If the first character of the
string is a double quote (") then the string includes everything until a
matching double quote—including whitespace, delimiters, and end-of-line
characters. If a pair of consecutive double quotes appears in the input,
it is replaced in the output by a single double quote. For examples, the
input "He said ""Hello""" would return the value ’He said "Hello"’.
%c The next character of the input is read. This includes delimiters, white-
space, and end-of-line characters.
%[...]
%[^...] In the first form, the word consists of the longest run consisting of only
characters between the brackets. Ranges of characters can be specified
by a hyphen; for example, %[0-9a-zA-Z] matches all alphanumeric char-
acters (if the underlying character set is ASCII). Since matlab treats
hyphens literally, this expansion only applies to alphanumeric characters.
To include ’-’ in the set, it should appear first or last in the brackets; to
include ’]’, it should be the first character. If the first character is ’^’ then
the word consists of characters not listed.
%N... For %s, %c %d, %f, %n, %u, an optional width can be specified as %Ns,
etc. where N is an integer >1. For %c, this causes exactly N characters
to be read instead of a single character. For the other specifiers, it is
an upper bound on the number of characters read; normal delimiters can
cause fewer characters to be read. For complex numbers, this limit applies
to the real and imaginary components individually. For %f and %n,
format specifiers like %N.Mf are allowed, where M is an upper bound on
number of characters after the decimal point to be considered; subsequent
digits are skipped. For example, the specifier %8.2f would read 12.345e6
as 1.234e7.
%*... The word specified by the remainder of the conversion specifier is skipped.
260 GNU Octave
literals In addition the format may contain literal character strings; these will be
skipped during reading. If the input string does not match this literal,
the processing terminates.
Parsed words corresponding to the first specifier are returned in the first output
argument and likewise for the rest of the specifiers.
By default, if there is only one input argument, format is "%f". This means that
numbers are read from the input into a single column vector. If format is explicitly
empty ("") then textscan will return data in a number of columns matching the
number of fields on the first data line of the input. Either of these is suitable only
when the input is exclusively numeric.
For example, the string
str = "\
Bunny Bugs 5.5\n\
Duck Daffy -7.5e-5\n\
Penguin Tux 6"
can be read using
a= textscan (str, "%s %s %f");
The optional numeric argument repeat can be used for limiting the number of items
read:
-1 Read all of the string or file until the end (default).
N Read until the first of two conditions occurs: 1) the format has been
processed N times, or 2) N lines of the input have been processed. Zero
(0) is an acceptable value for repeat. Currently, end-of-line characters
inside %q, %c, and %[. . . ]$ conversions do not contribute to the line
count. This is incompatible with matlab and may change in future.
The behavior of textscan can be changed via property/value pairs. The following
properties are recognized:
"BufSize"
This specifies the number of bytes to use for the internal buffer. A modest
speed improvement may be obtained by setting this to a large value when
reading a large file, especially if the input contains long strings. The
default is 4096, or a value dependent on nif that is specified.
"CollectOutput"
A value of 1 or true instructs textscan to concatenate consecutive
columns of the same class in the output cell array. A value of 0 or false
(default) leaves output in distinct columns.
"CommentStyle"
Specify parts of the input which are considered comments and will be
skipped. value is the comment style and can be either (1) A string or
1x1 cell string, to skip everything to the right of it; (2) A cell array
of two strings, to skip everything between the first and second strings.
Comments are only parsed where whitespace is accepted and do not act
as delimiters.
Chapter 14: Input and Output 261
"Delimiter"
If value is a string, any character in value will be used to split the input
into words. If value is a cell array of strings, any string in the array will
be used to split the input into words. (default value = any whitespace.)
"EmptyValue"
Value to return for empty numeric values in non-whitespace delimited
data. The default is NaN. When the data type does not support NaN
(int32 for example), then the default is zero.
"EndOfLine"
value can be either an emtpy or one character specifying the end-of-line
character, or the pair "\r\n" (CRLF). In the latter case, any of "\r",
"\n" or "\r\n" is counted as a (single) newline. If no value is given,
"\r\n" is used.
"HeaderLines"
The first value number of lines of fid are skipped. Note that this does
not refer to the first non-comment lines, but the first lines of any type.
"MultipleDelimsAsOne"
If value is nonzero, treat a series of consecutive delimiters, without white-
space in between, as a single delimiter. Consecutive delimiter series need
not be vertically aligned. Without this option, a single delimiter before
the end of the line does not cause the line to be considered to end with
an empty value, but a single delimiter at the start of a line causes the
line to be considered to start with an empty value.
"TreatAsEmpty"
Treat single occurrences (surrounded by delimiters or whitespace) of the
string(s) in value as missing values.
"ReturnOnError"
If set to numerical 1 or true, return normally as soon as an error is
encountered, such as trying to read a string using %f. If set to 0 or false,
return an error and no data.
"Whitespace"
Any character in value will be interpreted as whitespace and trimmed;
The default value for whitespace is " \b\r\n\t" (note the space). Unless
whitespace is set to "" (empty) AND at least one "%s" format conversion
specifier is supplied, a space is always part of whitespace.
When the number of words in str or fid doesn’t match an exact multiple of the
number of format conversion specifiers, textscan’s behavior depends on whether the
last character of the string or file is an end-of-line as specified by the EndOfLine
option:
last character = end-of-line
Data columns are padded with empty fields, NaN or 0 (for integer fields)
so that all columns have equal length

262 GNU Octave
last character is not end-of-line
Data columns are not padded; textscan returns columns of unequal
length
The second output position provides the location, in characters from the beginning
of the file or string, where processing stopped.
See also: [dlmread], page 256,[fscanf], page 274,[load], page 253,[strread], page 84,
[textread], page 256.
The importdata function has the ability to work with a wide variety of data.
A= importdata (fname)
A= importdata (fname,delimiter)
A= importdata (fname,delimiter,header_rows)
[A,delimiter] = importdata (. . . )
[A,delimiter,header_rows] = importdata (. . . )
Import data from the file fname.
Input parameters:
•fname The name of the file containing data.
•delimiter The character separating columns of data. Use \t for tab. (Only valid
for ASCII files)
•header rows The number of header rows before the data begins. (Only valid for
ASCII files)
Different file types are supported:
•ASCII table
Import ASCII table using the specified number of header rows and the specified
delimiter.
•Image file
•matlab file
•Spreadsheet files (depending on external software)
•WAV file
See also: [textscan], page 258,[dlmread], page 256,[csvread], page 256,[load],
page 253.
14.1.3.1 Saving Data on Unexpected Exits
If Octave for some reason exits unexpectedly it will by default save the variables avail-
able in the workspace to a file in the current directory. By default this file is named
‘octave-workspace’ and can be loaded into memory with the load command. While the
default behavior most often is reasonable it can be changed through the following functions.
val = crash_dumps_octave_core ()
old_val = crash_dumps_octave_core (new_val)
crash_dumps_octave_core (new_val,"local")
Query or set the internal variable that controls whether Octave tries to save all current
variables to the file octave-workspace if it crashes or receives a hangup, terminate
or similar signal.

Chapter 14: Input and Output 263
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [octave core file limit], page 263,[octave core file name], page 264,
[octave core file options], page 263.
val = sighup_dumps_octave_core ()
old_val = sighup_dumps_octave_core (new_val)
sighup_dumps_octave_core (new_val,"local")
Query or set the internal variable that controls whether Octave tries to save all current
variables to the file octave-workspace if it receives a hangup signal.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
val = sigterm_dumps_octave_core ()
old_val = sigterm_dumps_octave_core (new_val)
sigterm_dumps_octave_core (new_val,"local")
Query or set the internal variable that controls whether Octave tries to save all current
variables to the file octave-workspace if it receives a terminate signal.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
val = octave_core_file_options ()
old_val = octave_core_file_options (new_val)
octave_core_file_options (new_val,"local")
Query or set the internal variable that specifies the options used for saving the
workspace data if Octave aborts.
The value of octave_core_file_options should follow the same format as the op-
tions for the save function. The default value is Octave’s binary format.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [crash dumps octave core], page 262,[octave core file name], page 264,
[octave core file limit], page 263.
val = octave_core_file_limit ()
old_val = octave_core_file_limit (new_val)
octave_core_file_limit (new_val,"local")
Query or set the internal variable that specifies the maximum amount of memory (in
kilobytes) of the top-level workspace that Octave will attempt to save when writing
data to the crash dump file (the name of the file is specified by octave core file name).
If octave core file options flags specify a binary format, then octave core file limit
will be approximately the maximum size of the file. If a text file format is used, then
the file could be much larger than the limit. The default value is -1 (unlimited)

264 GNU Octave
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [crash dumps octave core], page 262,[octave core file name], page 264,
[octave core file options], page 263.
val = octave_core_file_name ()
old_val = octave_core_file_name (new_val)
octave_core_file_name (new_val,"local")
Query or set the internal variable that specifies the name of the file used for saving
data from the top-level workspace if Octave aborts.
The default value is "octave-workspace"
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [crash dumps octave core], page 262,[octave core file name], page 264,
[octave core file options], page 263.
14.2 C-Style I/O Functions
Octave’s C-style input and output functions provide most of the functionality of the C
programming language’s standard I/O library. The argument lists for some of the input
functions are slightly different, however, because Octave has no way of passing arguments
by reference.
In the following, file refers to a filename and fid refers to an integer file number, as
returned by fopen.
There are three files that are always available. Although these files can be accessed using
their corresponding numeric file ids, you should always use the symbolic names given in the
table below, since it will make your programs easier to understand.
stdin ()
Return the numeric value corresponding to the standard input stream.
When Octave is used interactively, stdin is filtered through the command line editing
functions.
See also: [stdout], page 264,[stderr], page 264.
stdout ()
Return the numeric value corresponding to the standard output stream.
Data written to the standard output is normally filtered through the pager.
See also: [stdin], page 264,[stderr], page 264.
stderr ()
Return the numeric value corresponding to the standard error stream.
Even if paging is turned on, the standard error is not sent to the pager. It is useful
for error messages and prompts.
See also: [stdin], page 264,[stdout], page 264.
Chapter 14: Input and Output 265
14.2.1 Opening and Closing Files
When reading data from a file it must be opened for reading first, and likewise when writing
to a file. The fopen function returns a pointer to an open file that is ready to be read or
written. Once all data has been read from or written to the opened file it should be closed.
The fclose function does this. The following code illustrates the basic pattern for writing
to a file, but a very similar pattern is used when reading a file.
filename = "myfile.txt";
fid = fopen (filename, "w");
# Do the actual I/O here...
fclose (fid);
fid = fopen (name)
fid = fopen (name,mode)
fid = fopen (name,mode,arch)
[fid,msg] = fopen (. . . )
fid_list = fopen ("all")
[file,mode,arch] = fopen (fid)
Open a file for low-level I/O or query open files and file descriptors.
The first form of the fopen function opens the named file with the specified mode
(read-write, read-only, etc.) and architecture interpretation (IEEE big endian, IEEE
little endian, etc.), and returns an integer value that may be used to refer to the file
later. If an error occurs, fid is set to −1 and msg contains the corresponding system
error message. The mode is a one or two character string that specifies whether the
file is to be opened for reading, writing, or both.
The second form of the fopen function returns a vector of file ids corresponding to
all the currently open files, excluding the stdin,stdout, and stderr streams.
The third form of the fopen function returns information about the open file given
its file id.
For example,
myfile = fopen ("splat.dat", "r", "ieee-le");
opens the file splat.dat for reading. If necessary, binary numeric values will be read
assuming they are stored in IEEE format with the least significant bit first, and then
converted to the native representation.
Opening a file that is already open simply opens it again and returns a separate file
id. It is not an error to open a file several times, though writing to the same file
through several different file ids may produce unexpected results.
The possible values ‘mode’ may have are
‘r’ (default)
Open a file for reading.
‘w’ Open a file for writing. The previous contents are discarded.
‘a’ Open or create a file for writing at the end of the file.
‘r+’ Open an existing file for reading and writing.
‘w+’ Open a file for reading or writing. The previous contents are discarded.
266 GNU Octave
‘a+’ Open or create a file for reading or writing at the end of the file.
Append a "t" to the mode string to open the file in text mode or a "b" to open in
binary mode. On Windows and Macintosh systems, text mode reading and writing
automatically converts linefeeds to the appropriate line end character for the system
(carriage-return linefeed on Windows, carriage-return on Macintosh). The default
when no mode is specified is binary mode.
Additionally, you may append a "z" to the mode string to open a gzipped file for
reading or writing. For this to be successful, you must also open the file in binary
mode.
The parameter arch is a string specifying the default data format for the file. Valid
values for arch are:
"native" or "n" (default)
The format of the current machine.
"ieee-be" or "b"
IEEE big endian format.
"ieee-le" or "l"
IEEE little endian format.
However, conversions are currently only supported for ‘native’, ‘ieee-be’, and
‘ieee-le’ formats.
When opening a new file that does not yet exist, permissions will be set to 0666 -
umask.
See also: [fclose], page 266,[fgets], page 268,[fgetl], page 267,[fscanf], page 274,
[fread], page 277,[fputs], page 267,[fdisp], page 254,[fprintf], page 269,[fwrite],
page 280,[fskipl], page 268,[fseek], page 283,[frewind], page 283,[ftell], page 283,
[feof], page 282,[ferror], page 282,[fclear], page 282,[fflush], page 248,[freport],
page 282,[umask], page 820.
fclose (fid)
fclose ("all")
status = fclose ("all")
Close the file specified by the file descriptor fid.
If successful, fclose returns 0, otherwise, it returns -1. The second form of the fclose
call closes all open files except stdin,stdout,stderr, and any FIDs associated with
gnuplot.
See also: [fopen], page 265,[fflush], page 248,[freport], page 282.
is_valid_file_id (fid)
Return true if fid refers to an open file.
See also: [freport], page 282,[fopen], page 265.
Chapter 14: Input and Output 267
14.2.2 Simple Output
Once a file has been opened for writing a string can be written to the file using the fputs
function. The following example shows how to write the string ‘Free Software is needed
for Free Science’ to the file ‘free.txt’.
filename = "free.txt";
fid = fopen (filename, "w");
fputs (fid, "Free Software is needed for Free Science");
fclose (fid);
fputs (fid,string)
status = fputs (fid,string)
Write the string string to the file with file descriptor fid.
The string is written to the file with no additional formatting. Use fdisp instead to
automatically append a newline character appropriate for the local machine.
Return a non-negative number on success or EOF on error.
See also: [fdisp], page 254,[fprintf], page 269,[fwrite], page 280,[fopen], page 265.
A function much similar to fputs is available for writing data to the screen. The puts
function works just like fputs except it doesn’t take a file pointer as its input.
puts (string)
status = puts (string)
Write a string to the standard output with no formatting.
The string is written verbatim to the standard output. Use disp to automatically
append a newline character appropriate for the local machine.
Return a non-negative number on success and EOF on error.
See also: [fputs], page 267,[disp], page 243.
14.2.3 Line-Oriented Input
To read from a file it must be opened for reading using fopen. Then a line can be read
from the file using fgetl as the following code illustrates
fid = fopen ("free.txt");
txt = fgetl (fid)
aFree Software is needed for Free Science
fclose (fid);
This of course assumes that the file ‘free.txt’ exists and contains the line ‘Free Software
is needed for Free Science’.
str = fgetl (fid)
str = fgetl (fid,len)
Read characters from a file, stopping after a newline, or EOF, or len characters have
been read.
The characters read, excluding the possible trailing newline, are returned as a string.
If len is omitted, fgetl reads until the next newline character.
If there are no more characters to read, fgetl returns −1.
268 GNU Octave
To read a line and return the terminating newline see fgets.
See also: [fgets], page 268,[fscanf], page 274,[fread], page 277,[fopen], page 265.
str = fgets (fid)
str = fgets (fid,len)
Read characters from a file, stopping after a newline, or EOF, or len characters have
been read.
The characters read, including the possible trailing newline, are returned as a string.
If len is omitted, fgets reads until the next newline character.
If there are no more characters to read, fgets returns −1.
To read a line and discard the terminating newline see fgetl.
See also: [fputs], page 267,[fgetl], page 267,[fscanf], page 274,[fread], page 277,
[fopen], page 265.
nlines = fskipl (fid)
nlines = fskipl (fid,count)
nlines = fskipl (fid, Inf)
Read and skip count lines from the file specified by the file descriptor fid.
fskipl discards characters until an end-of-line is encountered exactly count-times, or
until the end-of-file marker is found.
If count is omitted, it defaults to 1. count may also be Inf, in which case lines are
skipped until the end of the file. This form is suitable for counting the number of
lines in a file.
Returns the number of lines skipped (end-of-line sequences encountered).
See also: [fgetl], page 267,[fgets], page 268,[fscanf], page 274,[fopen], page 265.
14.2.4 Formatted Output
This section describes how to call printf and related functions.
The following functions are available for formatted output. They are modeled after the
C language functions of the same name, but they interpret the format template differently
in order to improve the performance of printing vector and matrix values.
Implementation Note: For compatibility with matlab, escape sequences in the template
string (e.g., "\n" =>newline) are expanded even when the template string is defined with
single quotes.
printf (template, . . . )
Print optional arguments under the control of the template string template to the
stream stdout and return the number of characters printed.
See the Formatted Output section of the GNU Octave manual for a complete descrip-
tion of the syntax of the template string.
Implementation Note: For compatibility with matlab, escape sequences in the tem-
plate string (e.g., "\n" =>newline) are expanded even when the template string is
defined with single quotes.
See also: [fprintf], page 269,[sprintf], page 269,[scanf], page 275.
Chapter 14: Input and Output 269
fprintf (fid,template, . . . )
fprintf (template, . . . )
numbytes = fprintf (. . . )
This function is equivalent to printf, except that the output is written to the file
descriptor fid instead of stdout.
If fid is omitted, the output is written to stdout making the function exactly equiv-
alent to printf.
The optional output returns the number of bytes written to the file.
Implementation Note: For compatibility with matlab, escape sequences in the tem-
plate string (e.g., "\n" =>newline) are expanded even when the template string is
defined with single quotes.
See also: [fputs], page 267,[fdisp], page 254,[fwrite], page 280,[fscanf], page 274,
[printf], page 268,[sprintf], page 269,[fopen], page 265.
sprintf (template, . . . )
This is like printf, except that the output is returned as a string.
Unlike the C library function, which requires you to provide a suitably sized string
as an argument, Octave’s sprintf function returns the string, automatically sized to
hold all of the items converted.
Implementation Note: For compatibility with matlab, escape sequences in the tem-
plate string (e.g., "\n" =>newline) are expanded even when the template string is
defined with single quotes.
See also: [printf], page 268,[fprintf], page 269,[sscanf], page 275.
The printf function can be used to print any number of arguments. The template
string argument you supply in a call provides information not only about the number of
additional arguments, but also about their types and what style should be used for printing
them.
Ordinary characters in the template string are simply written to the output stream
as-is, while conversion specifications introduced by a ‘%’ character in the template cause
subsequent arguments to be formatted and written to the output stream. For example,
pct = 37;
filename = "foo.txt";
printf ("Processed %d%% of ’%s’.\nPlease be patient.\n",
pct, filename);
produces output like
Processed 37% of ’foo.txt’.
Please be patient.
This example shows the use of the ‘%d’ conversion to specify that a scalar argument
should be printed in decimal notation, the ‘%s’ conversion to specify printing of a string
argument, and the ‘%%’ conversion to print a literal ‘%’ character.
There are also conversions for printing an integer argument as an unsigned value in
octal, decimal, or hexadecimal radix (‘%o’, ‘%u’, or ‘%x’, respectively); or as a character
value (‘%c’).
270 GNU Octave
Floating-point numbers can be printed in normal, fixed-point notation using the ‘%f’
conversion or in exponential notation using the ‘%e’ conversion. The ‘%g’ conversion uses
either ‘%e’ or ‘%f’ format, depending on what is more appropriate for the magnitude of the
particular number.
You can control formatting more precisely by writing modifiers between the ‘%’ and
the character that indicates which conversion to apply. These slightly alter the ordinary
behavior of the conversion. For example, most conversion specifications permit you to
specify a minimum field width and a flag indicating whether you want the result left- or
right-justified within the field.
The specific flags and modifiers that are permitted and their interpretation vary de-
pending on the particular conversion. They’re all described in more detail in the following
sections.
14.2.5 Output Conversion for Matrices
When given a matrix value, Octave’s formatted output functions cycle through the format
template until all the values in the matrix have been printed. For example:
printf ("%4.2f %10.2e %8.4g\n", hilb (3));
a1.00 5.00e-01 0.3333
a0.50 3.33e-01 0.25
a0.33 2.50e-01 0.2
If more than one value is to be printed in a single call, the output functions do not
return to the beginning of the format template when moving on from one value to the next.
This can lead to confusing output if the number of elements in the matrices are not exact
multiples of the number of conversions in the format template. For example:
printf ("%4.2f %10.2e %8.4g\n", [1, 2], [3, 4]);
a1.00 2.00e+00 3
a4.00
If this is not what you want, use a series of calls instead of just one.
14.2.6 Output Conversion Syntax
This section provides details about the precise syntax of conversion specifications that can
appear in a printf template string.
Characters in the template string that are not part of a conversion specification are
printed as-is to the output stream.
The conversion specifications in a printf template string have the general form:
%flags width [.precision ]type conversion
For example, in the conversion specifier ‘%-10.8ld’, the ‘-’ is a flag, ‘10’ specifies the field
width, the precision is ‘8’, the letter ‘l’ is a type modifier, and ‘d’ specifies the conversion
style. (This particular type specifier says to print a numeric argument in decimal notation,
with a minimum of 8 digits left-justified in a field at least 10 characters wide.)
In more detail, output conversion specifications consist of an initial ‘%’ character followed
in sequence by:
Chapter 14: Input and Output 271
•Zero or more flag characters that modify the normal behavior of the conversion speci-
fication.
•An optional decimal integer specifying the minimum field width. If the normal conver-
sion produces fewer characters than this, the field is padded with spaces to the specified
width. This is a minimum value; if the normal conversion produces more characters
than this, the field is not truncated. Normally, the output is right-justified within the
field.
You can also specify a field width of ‘*’. This means that the next argument in the
argument list (before the actual value to be printed) is used as the field width. The
value is rounded to the nearest integer. If the value is negative, this means to set the
‘-’ flag (see below) and to use the absolute value as the field width.
•An optional precision to specify the number of digits to be written for the numeric
conversions. If the precision is specified, it consists of a period (‘.’) followed optionally
by a decimal integer (which defaults to zero if omitted).
You can also specify a precision of ‘*’. This means that the next argument in the
argument list (before the actual value to be printed) is used as the precision. The value
must be an integer, and is ignored if it is negative.
•An optional type modifier character. This character is ignored by Octave’s printf
function, but is recognized to provide compatibility with the C language printf.
•A character that specifies the conversion to be applied.
The exact options that are permitted and how they are interpreted vary between the
different conversion specifiers. See the descriptions of the individual conversions for infor-
mation about the particular options that they use.
14.2.7 Table of Output Conversions
Here is a table summarizing what all the different conversions do:
‘%d’, ‘%i’ Print an integer as a signed decimal number. See Section 14.2.8 [Integer Con-
versions], page 272, for details. ‘%d’ and ‘%i’ are synonymous for output, but are
different when used with scanf for input (see Section 14.2.13 [Table of Input
Conversions], page 276).
‘%o’ Print an integer as an unsigned octal number. See Section 14.2.8 [Integer Con-
versions], page 272, for details.
‘%u’ Print an integer as an unsigned decimal number. See Section 14.2.8 [Integer
Conversions], page 272, for details.
‘%x’, ‘%X’ Print an integer as an unsigned hexadecimal number. ‘%x’ uses lowercase letters
and ‘%X’ uses uppercase. See Section 14.2.8 [Integer Conversions], page 272, for
details.
‘%f’ Print a floating-point number in normal (fixed-point) notation. See
Section 14.2.9 [Floating-Point Conversions], page 273, for details.
‘%e’, ‘%E’ Print a floating-point number in exponential notation. ‘%e’ uses lowercase
letters and ‘%E’ uses uppercase. See Section 14.2.9 [Floating-Point Conversions],
page 273, for details.
272 GNU Octave
‘%g’, ‘%G’ Print a floating-point number in either normal (fixed-point) or exponential
notation, whichever is more appropriate for its magnitude. ‘%g’ uses lowercase
letters and ‘%G’ uses uppercase. See Section 14.2.9 [Floating-Point Conversions],
page 273, for details.
‘%c’ Print a single character. See Section 14.2.10 [Other Output Conversions],
page 273.
‘%s’ Print a string. See Section 14.2.10 [Other Output Conversions], page 273.
‘%%’ Print a literal ‘%’ character. See Section 14.2.10 [Other Output Conversions],
page 273.
If the syntax of a conversion specification is invalid, unpredictable things will happen, so
don’t do this. In particular, matlab allows a bare percentage sign ‘%’ with no subsequent
conversion character. Octave will emit an error and stop if it sees such code. When the
string variable to be processed cannot be guaranteed to be free of potential format codes it
is better to use the two argument form of any of the printf functions and set the format
string to %s. Alternatively, for code which is not required to be backwards-compatible with
matlab the Octave function puts or disp can be used.
printf (strvar); # Unsafe if strvar contains format codes
printf ("%s", strvar); # Safe
puts (strvar); # Safe
If there aren’t enough function arguments provided to supply values for all the conversion
specifications in the template string, or if the arguments are not of the correct types, the
results are unpredictable. If you supply more arguments than conversion specifications, the
extra argument values are simply ignored; this is sometimes useful.
14.2.8 Integer Conversions
This section describes the options for the ‘%d’, ‘%i’, ‘%o’, ‘%u’, ‘%x’, and ‘%X’ conversion
specifications. These conversions print integers in various formats.
The ‘%d’ and ‘%i’ conversion specifications both print an numeric argument as a signed
decimal number; while ‘%o’, ‘%u’, and ‘%x’ print the argument as an unsigned octal, decimal,
or hexadecimal number (respectively). The ‘%X’ conversion specification is just like ‘%x’
except that it uses the characters ‘ABCDEF’ as digits instead of ‘abcdef’.
The following flags are meaningful:
‘-’ Left-justify the result in the field (instead of the normal right-justification).
‘+’ For the signed ‘%d’ and ‘%i’ conversions, print a plus sign if the value is positive.
‘ ’ For the signed ‘%d’ and ‘%i’ conversions, if the result doesn’t start with a plus
or minus sign, prefix it with a space character instead. Since the ‘+’ flag ensures
that the result includes a sign, this flag is ignored if you supply both of them.
‘#’ For the ‘%o’ conversion, this forces the leading digit to be ‘0’, as if by increasing
the precision. For ‘%x’ or ‘%X’, this prefixes a leading ‘0x’ or ‘0X’ (respectively) to
the result. This doesn’t do anything useful for the ‘%d’, ‘%i’, or ‘%u’ conversions.
‘0’ Pad the field with zeros instead of spaces. The zeros are placed after any
indication of sign or base. This flag is ignored if the ‘-’ flag is also specified, or
if a precision is specified.
Chapter 14: Input and Output 273
If a precision is supplied, it specifies the minimum number of digits to appear; leading
zeros are produced if necessary. If you don’t specify a precision, the number is printed with
as many digits as it needs. If you convert a value of zero with an explicit precision of zero,
then no characters at all are produced.
14.2.9 Floating-Point Conversions
This section discusses the conversion specifications for floating-point numbers: the ‘%f’,
‘%e’, ‘%E’, ‘%g’, and ‘%G’ conversions.
The ‘%f’ conversion prints its argument in fixed-point notation, producing output of the
form [-]ddd.ddd, where the number of digits following the decimal point is controlled by
the precision you specify.
The ‘%e’ conversion prints its argument in exponential notation, producing output of
the form [-]d.ddde[+|-]dd. Again, the number of digits following the decimal point is
controlled by the precision. The exponent always contains at least two digits. The ‘%E’
conversion is similar but the exponent is marked with the letter ‘E’ instead of ‘e’.
The ‘%g’ and ‘%G’ conversions print the argument in the style of ‘%e’ or ‘%E’ (respectively)
if the exponent would be less than -4 or greater than or equal to the precision; otherwise
they use the ‘%f’ style. Trailing zeros are removed from the fractional portion of the result
and a decimal-point character appears only if it is followed by a digit.
The following flags can be used to modify the behavior:
‘-’ Left-justify the result in the field. Normally the result is right-justified.
‘+’ Always include a plus or minus sign in the result.
‘ ’ If the result doesn’t start with a plus or minus sign, prefix it with a space
instead. Since the ‘+’ flag ensures that the result includes a sign, this flag is
ignored if you supply both of them.
‘#’ Specifies that the result should always include a decimal point, even if no digits
follow it. For the ‘%g’ and ‘%G’ conversions, this also forces trailing zeros after
the decimal point to be left in place where they would otherwise be removed.
‘0’ Pad the field with zeros instead of spaces; the zeros are placed after any sign.
This flag is ignored if the ‘-’ flag is also specified.
The precision specifies how many digits follow the decimal-point character for the ‘%f’,
‘%e’, and ‘%E’ conversions. For these conversions, the default precision is 6. If the precision
is explicitly 0, this suppresses the decimal point character entirely. For the ‘%g’ and ‘%G’
conversions, the precision specifies how many significant digits to print. Significant digits
are the first digit before the decimal point, and all the digits after it. If the precision is 0
or not specified for ‘%g’ or ‘%G’, it is treated like a value of 1. If the value being printed
cannot be expressed precisely in the specified number of digits, the value is rounded to the
nearest number that fits.
14.2.10 Other Output Conversions
This section describes miscellaneous conversions for printf.
274 GNU Octave
The ‘%c’ conversion prints a single character. The ‘-’ flag can be used to specify left-
justification in the field, but no other flags are defined, and no precision or type modifier
can be given. For example:
printf ("%c%c%c%c%c", "h", "e", "l", "l", "o");
prints ‘hello’.
The ‘%s’ conversion prints a string. The corresponding argument must be a string. A
precision can be specified to indicate the maximum number of characters to write; otherwise
characters in the string up to but not including the terminating null character are written
to the output stream. The ‘-’ flag can be used to specify left-justification in the field, but
no other flags or type modifiers are defined for this conversion. For example:
printf ("%3s%-6s", "no", "where");
prints ‘ nowhere ’ (note the leading and trailing spaces).
14.2.11 Formatted Input
Octave provides the scanf,fscanf, and sscanf functions to read formatted input. There
are two forms of each of these functions. One can be used to extract vectors of data from
a file, and the other is more ‘C-like’.
[val,count,errmsg] = fscanf (fid,template,size)
[v1,v2, ..., count,errmsg] = fscanf (fid,template,"C")
In the first form, read from fid according to template, returning the result in the
matrix val.
The optional argument size specifies the amount of data to read and may be one of
Inf Read as much as possible, returning a column vector.
nr Read up to nr elements, returning a column vector.
[nr, Inf] Read as much as possible, returning a matrix with nr rows. If the number
of elements read is not an exact multiple of nr, the last column is padded
with zeros.
[nr,nc]Read up to nr *nc elements, returning a matrix with nr rows. If the
number of elements read is not an exact multiple of nr, the last column
is padded with zeros.
If size is omitted, a value of Inf is assumed.
A string is returned if template specifies only character conversions.
The number of items successfully read is returned in count.
If an error occurs, errmsg contains a system-dependent error message.
In the second form, read from fid according to template, with each conversion specifier
in template corresponding to a single scalar return value. This form is more “C-like”,
and also compatible with previous versions of Octave. The number of successful
conversions is returned in count
See the Formatted Input section of the GNU Octave manual for a complete description
of the syntax of the template string.
See also: [fgets], page 268,[fgetl], page 267,[fread], page 277,[scanf], page 275,
[sscanf], page 275,[fopen], page 265.
Chapter 14: Input and Output 275
[val,count,errmsg] = scanf (template,size)
[v1,v2, ..., count,errmsg]] = scanf (template,"C")
This is equivalent to calling fscanf with fid =stdin.
It is currently not useful to call scanf in interactive programs.
See also: [fscanf], page 274,[sscanf], page 275,[printf], page 268.
[val,count,errmsg,pos] = sscanf (string,template,size)
[v1,v2, ..., count,errmsg] = sscanf (string,template,"C")
This is like fscanf, except that the characters are taken from the string string instead
of from a stream.
Reaching the end of the string is treated as an end-of-file condition. In addition to
the values returned by fscanf, the index of the next character to be read is returned
in pos.
See also: [fscanf], page 274,[scanf], page 275,[sprintf], page 269.
Calls to scanf are superficially similar to calls to printf in that arbitrary arguments are
read under the control of a template string. While the syntax of the conversion specifications
in the template is very similar to that for printf, the interpretation of the template is
oriented more towards free-format input and simple pattern matching, rather than fixed-
field formatting. For example, most scanf conversions skip over any amount of “white
space” (including spaces, tabs, and newlines) in the input file, and there is no concept
of precision for the numeric input conversions as there is for the corresponding output
conversions. Ordinarily, non-whitespace characters in the template are expected to match
characters in the input stream exactly.
When a matching failure occurs, scanf returns immediately, leaving the first non-
matching character as the next character to be read from the stream, and scanf returns all
the items that were successfully converted.
The formatted input functions are not used as frequently as the formatted output func-
tions. Partly, this is because it takes some care to use them properly. Another reason is
that it is difficult to recover from a matching error.
14.2.12 Input Conversion Syntax
Ascanf template string is a string that contains ordinary multibyte characters interspersed
with conversion specifications that start with ‘%’.
Any whitespace character in the template causes any number of whitespace characters
in the input stream to be read and discarded. The whitespace characters that are matched
need not be exactly the same whitespace characters that appear in the template string. For
example, write ‘ ,’ in the template to recognize a comma with optional whitespace before
and after.
Other characters in the template string that are not part of conversion specifications
must match characters in the input stream exactly; if this is not the case, a matching
failure occurs.
The conversion specifications in a scanf template string have the general form:
%flags width type conversion
276 GNU Octave
In more detail, an input conversion specification consists of an initial ‘%’ character fol-
lowed in sequence by:
•An optional flag character ‘*’, which says to ignore the text read for this specification.
When scanf finds a conversion specification that uses this flag, it reads input as directed
by the rest of the conversion specification, but it discards this input, does not return
any value, and does not increment the count of successful assignments.
•An optional decimal integer that specifies the maximum field width. Reading of char-
acters from the input stream stops either when this maximum is reached or when a
non-matching character is found, whichever happens first. Most conversions discard
initial whitespace characters, and these discarded characters don’t count towards the
maximum field width. Conversions that do not discard initial whitespace are explicitly
documented.
•An optional type modifier character. This character is ignored by Octave’s scanf
function, but is recognized to provide compatibility with the C language scanf.
•A character that specifies the conversion to be applied.
The exact options that are permitted and how they are interpreted vary between the
different conversion specifiers. See the descriptions of the individual conversions for infor-
mation about the particular options that they allow.
14.2.13 Table of Input Conversions
Here is a table that summarizes the various conversion specifications:
‘%d’ Matches an optionally signed integer written in decimal. See Section 14.2.14
[Numeric Input Conversions], page 277.
‘%i’ Matches an optionally signed integer in any of the formats that the C language
defines for specifying an integer constant. See Section 14.2.14 [Numeric Input
Conversions], page 277.
‘%o’ Matches an unsigned integer written in octal radix. See Section 14.2.14 [Nu-
meric Input Conversions], page 277.
‘%u’ Matches an unsigned integer written in decimal radix. See Section 14.2.14
[Numeric Input Conversions], page 277.
‘%x’, ‘%X’ Matches an unsigned integer written in hexadecimal radix. See Section 14.2.14
[Numeric Input Conversions], page 277.
‘%e’, ‘%f’, ‘%g’, ‘%E’, ‘%G’
Matches an optionally signed floating-point number. See Section 14.2.14 [Nu-
meric Input Conversions], page 277.
‘%s’ Matches a string containing only non-whitespace characters. See Section 14.2.15
[String Input Conversions], page 277.
‘%c’ Matches a string of one or more characters; the number of characters read is con-
trolled by the maximum field width given for the conversion. See Section 14.2.15
[String Input Conversions], page 277.
‘%%’ This matches a literal ‘%’ character in the input stream. No corresponding
argument is used.
Chapter 14: Input and Output 277
If the syntax of a conversion specification is invalid, the behavior is undefined. If there
aren’t enough function arguments provided to supply addresses for all the conversion spec-
ifications in the template strings that perform assignments, or if the arguments are not of
the correct types, the behavior is also undefined. On the other hand, extra arguments are
simply ignored.
14.2.14 Numeric Input Conversions
This section describes the scanf conversions for reading numeric values.
The ‘%d’ conversion matches an optionally signed integer in decimal radix.
The ‘%i’ conversion matches an optionally signed integer in any of the formats that the
C language defines for specifying an integer constant.
For example, any of the strings ‘10’, ‘0xa’, or ‘012’ could be read in as integers under
the ‘%i’ conversion. Each of these specifies a number with decimal value 10.
The ‘%o’, ‘%u’, and ‘%x’ conversions match unsigned integers in octal, decimal, and hex-
adecimal radices, respectively.
The ‘%X’ conversion is identical to the ‘%x’ conversion. They both permit either uppercase
or lowercase letters to be used as digits.
Unlike the C language scanf, Octave ignores the ‘h’, ‘l’, and ‘L’ modifiers.
14.2.15 String Input Conversions
This section describes the scanf input conversions for reading string and character values:
‘%s’ and ‘%c’.
The ‘%c’ conversion is the simplest: it matches a fixed number of characters, always. The
maximum field with says how many characters to read; if you don’t specify the maximum,
the default is 1. This conversion does not skip over initial whitespace characters. It reads
precisely the next ncharacters, and fails if it cannot get that many.
The ‘%s’ conversion matches a string of non-whitespace characters. It skips and dis-
cards initial whitespace, but stops when it encounters more whitespace after having read
something.
For example, reading the input:
hello, world
with the conversion ‘%10c’ produces " hello, wo", but reading the same input with the
conversion ‘%10s’ produces "hello,".
14.2.16 Binary I/O
Octave can read and write binary data using the functions fread and fwrite, which are
patterned after the standard C functions with the same names. They are able to automat-
ically swap the byte order of integer data and convert among the supported floating point
formats as the data are read.
val = fread (fid)
val = fread (fid,size)
val = fread (fid,size,precision)
val = fread (fid,size,precision,skip)
278 GNU Octave
val = fread (fid,size,precision,skip,arch)
[val,count] = fread (. . . )
Read binary data from the file specified by the file descriptor fid.
The optional argument size specifies the amount of data to read and may be one of
Inf Read as much as possible, returning a column vector.
nr Read up to nr elements, returning a column vector.
[nr, Inf] Read as much as possible, returning a matrix with nr rows. If the number
of elements read is not an exact multiple of nr, the last column is padded
with zeros.
[nr,nc]Read up to nr *nc elements, returning a matrix with nr rows. If the
number of elements read is not an exact multiple of nr, the last column
is padded with zeros.
If size is omitted, a value of Inf is assumed.
The optional argument precision is a string specifying the type of data to read and
may be one of
"schar"
"signed char"
Signed character.
"uchar"
"unsigned char"
Unsigned character.
"int8"
"integer*1"
8-bit signed integer.
"int16"
"integer*2"
16-bit signed integer.
"int32"
"integer*4"
32-bit signed integer.
"int64"
"integer*8"
64-bit signed integer.
"uint8" 8-bit unsigned integer.
"uint16" 16-bit unsigned integer.
"uint32" 32-bit unsigned integer.
"uint64" 64-bit unsigned integer.
"single"
"float32"
"real*4" 32-bit floating point number.
Chapter 14: Input and Output 279
"double"
"float64"
"real*8" 64-bit floating point number.
"char"
"char*1" Single character.
"short" Short integer (size is platform dependent).
"int" Integer (size is platform dependent).
"long" Long integer (size is platform dependent).
"ushort"
"unsigned short"
Unsigned short integer (size is platform dependent).
"uint"
"unsigned int"
Unsigned integer (size is platform dependent).
"ulong"
"unsigned long"
Unsigned long integer (size is platform dependent).
"float" Single precision floating point number (size is platform dependent).
The default precision is "uchar".
The precision argument may also specify an optional repeat count. For example,
‘32*single’ causes fread to read a block of 32 single precision floating point numbers.
Reading in blocks is useful in combination with the skip argument.
The precision argument may also specify a type conversion. For example,
‘int16=>int32’ causes fread to read 16-bit integer values and return an array of
32-bit integer values. By default, fread returns a double precision array. The special
form ‘*TYPE’ is shorthand for ‘TYPE=>TYPE’.
The conversion and repeat counts may be combined. For example, the specification
‘32*single=>single’ causes fread to read blocks of single precision floating point
values and return an array of single precision values instead of the default array of
double precision values.
The optional argument skip specifies the number of bytes to skip after each element
(or block of elements) is read. If it is not specified, a value of 0 is assumed. If the
final block read is not complete, the final skip is omitted. For example,
fread (f, 10, "3*single=>single", 8)
will omit the final 8-byte skip because the last read will not be a complete block of 3
values.
The optional argument arch is a string specifying the data format for the file. Valid
values are
"native" or "n"
The format of the current machine.
280 GNU Octave
"ieee-be" or "b"
IEEE big endian.
"ieee-le" or "l"
IEEE little endian.
If no arch is given the value used in the call to fopen which created the file descrip-
tor is used. Otherwise, the value specified with fread overrides that of fopen and
determines the data format.
The output argument val contains the data read from the file.
The optional return value count contains the number of elements read.
See also: [fwrite], page 280,[fgets], page 268,[fgetl], page 267,[fscanf], page 274,
[fopen], page 265.
fwrite (fid,data)
fwrite (fid,data,precision)
fwrite (fid,data,precision,skip)
fwrite (fid,data,precision,skip,arch)
count = fwrite (. . . )
Write data in binary form to the file specified by the file descriptor fid, returning the
number of values count successfully written to the file.
The argument data is a matrix of values that are to be written to the file. The values
are extracted in column-major order.
The remaining arguments precision,skip, and arch are optional, and are interpreted
as described for fread.
The behavior of fwrite is undefined if the values in data are too large to fit in the
specified precision.
See also: [fread], page 277,[fputs], page 267,[fprintf], page 269,[fopen], page 265.
14.2.17 Temporary Files
Sometimes one needs to write data to a file that is only temporary. This is most commonly
used when an external program launched from within Octave needs to access data. When
Octave exits all temporary files will be deleted, so this step need not be executed manually.
[fid,name,msg] = mkstemp ("template")
[fid,name,msg] = mkstemp ("template",delete)
Return the file descriptor fid corresponding to a new temporary file with a unique
name created from template.
The last six characters of template must be "XXXXXX" and these are replaced with a
string that makes the filename unique. The file is then created with mode read/write
and permissions that are system dependent (on GNU/Linux systems, the permissions
will be 0600 for versions of glibc 2.0.7 and later). The file is opened in binary mode
and with the O_EXCL flag.
If the optional argument delete is supplied and is true, the file will be deleted auto-
matically when Octave exits.
Chapter 14: Input and Output 281
If successful, fid is a valid file ID, name is the name of the file, and msg is an empty
string. Otherwise, fid is -1, name is empty, and msg contains a system-dependent
error message.
See also: [tempname], page 281,[tempdir], page 281,[P tmpdir], page 281,[tmpfile],
page 281,[fopen], page 265.
[fid,msg] = tmpfile ()
Return the file ID corresponding to a new temporary file with a unique name.
The file is opened in binary read/write ("w+b") mode and will be deleted automatically
when it is closed or when Octave exits.
If successful, fid is a valid file ID and msg is an empty string. Otherwise, fid is -1
and msg contains a system-dependent error message.
See also: [tempname], page 281,[mkstemp], page 280,[tempdir], page 281,
[P tmpdir], page 281.
fname = tempname ()
fname = tempname (dir)
fname = tempname (dir,prefix)
Return a unique temporary filename as a string.
If prefix is omitted, a value of "oct-" is used.
If dir is also omitted, the default directory for temporary files (P_tmpdir) is used. If
dir is provided, it must exist, otherwise the default directory for temporary files is
used.
Programming Note: Because the named file is not opened by tempname, it is possible,
though relatively unlikely, that it will not be available by the time your program
attempts to open it. If this is a concern, see tmpfile.
See also: [mkstemp], page 280,[tempdir], page 281,[P tmpdir], page 281,[tmpfile],
page 281.
dir = tempdir ()
Return the name of the host system’s directory for temporary files.
The directory name is taken first from the environment variable TMPDIR. If that does
not exist the system default returned by P_tmpdir is used.
See also: [P tmpdir], page 281,[tempname], page 281,[mkstemp], page 280,[tmpfile],
page 281.
P_tmpdir ()
Return the name of the host system’s default directory for temporary files.
Programming Note: The value returned by P_tmpdir is always the default location.
This value may not agree with that returned from tempdir if the user has overridden
the default with the TMPDIR environment variable.
See also: [tempdir], page 281,[tempname], page 281,[mkstemp], page 280,[tmpfile],
page 281.
282 GNU Octave
14.2.18 End of File and Errors
Once a file has been opened its status can be acquired. As an example the feof functions
determines if the end of the file has been reached. This can be very useful when reading
small parts of a file at a time. The following example shows how to read one line at a time
from a file until the end has been reached.
filename = "myfile.txt";
fid = fopen (filename, "r");
while (! feof (fid) )
text_line = fgetl (fid);
endwhile
fclose (fid);
Note that in some situations it is more efficient to read the entire contents of a file and then
process it, than it is to read it line by line. This has the potential advantage of removing
the loop in the above code.
status = feof (fid)
Return 1 if an end-of-file condition has been encountered for the file specified by file
descriptor fid and 0 otherwise.
Note that feof will only return 1 if the end of the file has already been encountered,
not if the next read operation will result in an end-of-file condition.
See also: [fread], page 277,[frewind], page 283,[fseek], page 283,[fclear], page 282,
[fopen], page 265.
msg = ferror (fid)
[msg,err] = ferror (fid)
[...] = ferror (fid,"clear")
Query the error status of the stream specified by file descriptor fid
If an error condition exists then return a string msg describing the error. Otherwise,
return an empty string "".
The second input "clear" is optional. If supplied, the error state on the stream will
be cleared.
The optional second output is a numeric indication of the error status. err is 1 if an
error condition has been encountered and 0 otherwise.
Note that ferror indicates if an error has already occurred, not whether the next
operation will result in an error condition.
See also: [fclear], page 282,[fopen], page 265.
fclear (fid)
Clear the stream state for the file specified by the file descriptor fid.
See also: [ferror], page 282,[fopen], page 265.
freport ()
Print a list of which files have been opened, and whether they are open for reading,
writing, or both.

Chapter 14: Input and Output 283
For example:
freport ()
anumber mode arch name
a------ ---- ---- ----
a0 r ieee-le stdin
a1 w ieee-le stdout
a2 w ieee-le stderr
a3 r ieee-le myfile
See also: [fopen], page 265,[fclose], page 266,[is valid file id], page 266.
14.2.19 File Positioning
Three functions are available for setting and determining the position of the file pointer for
a given file.
pos = ftell (fid)
Return the position of the file pointer as the number of characters from the beginning
of the file specified by file descriptor fid.
See also: [fseek], page 283,[frewind], page 283,[feof], page 282,[fopen], page 265.
fseek (fid,offset)
fseek (fid,offset,origin)
status = fseek (. . . )
Set the file pointer to the location offset within the file fid.
The pointer is positioned offset characters from the origin, which may be one of the
predefined variables SEEK_CUR (current position), SEEK_SET (beginning), or SEEK_END
(end of file) or strings "cof","bof" or "eof". If origin is omitted, SEEK_SET is
assumed. offset may be positive, negative, or zero but not all combinations of origin
and offset can be realized.
fseek returns 0 on success and -1 on error.
See also: [fskipl], page 268,[frewind], page 283,[ftell], page 283,[fopen], page 265.
SEEK_SET ()
SEEK_CUR ()
SEEK_END ()
Return the numerical value to pass to fseek to perform one of the following actions:
SEEK_SET Position file relative to the beginning.
SEEK_CUR Position file relative to the current position.
SEEK_END Position file relative to the end.
See also: [fseek], page 283.
frewind (fid)
status = frewind (fid)
Move the file pointer to the beginning of the file specified by file descriptor fid.
284 GNU Octave
frewind returns 0 for success, and -1 if an error is encountered. It is equivalent to
fseek (fid, 0, SEEK_SET).
See also: [fseek], page 283,[ftell], page 283,[fopen], page 265.
The following example stores the current file position in the variable marker, moves the
pointer to the beginning of the file, reads four characters, and then returns to the original
position.
marker = ftell (myfile);
frewind (myfile);
fourch = fgets (myfile, 4);
fseek (myfile, marker, SEEK_SET);
285
15 Plotting
15.1 Introduction to Plotting
Earlier versions of Octave provided plotting through the use of gnuplot. This capability is
still available. But, a newer plotting capability is provided by access to OpenGL. Which
plotting system is used is controlled by the graphics_toolkit function. See Section 15.4.7
[Graphics Toolkits], page 437.
The function call graphics_toolkit ("qt") selects the Qt/OpenGL system,
graphics_toolkit ("fltk") selects the FLTK/OpenGL system, and graphics_toolkit
("gnuplot") selects the gnuplot system. The three systems may be used selectively
through the use of the graphics_toolkit property of the graphics handle for each figure.
This is explained in Section 15.3 [Graphics Data Structures], page 373.Caution: The
OpenGL-based toolkits use single precision variables internally which limits the maximum
value that can be displayed to approximately 1038. If your data contains larger values you
must use the gnuplot toolkit which supports values up to 10308.
15.2 High-Level Plotting
Octave provides simple means to create many different types of two- and three-dimensional
plots using high-level functions.
If you need more detailed control, see Section 15.3 [Graphics Data Structures], page 373,
and Section 15.4 [Advanced Plotting], page 422.
15.2.1 Two-Dimensional Plots
The plot function allows you to create simple x-y plots with linear axes. For example,
x = -10:0.1:10;
plot (x, sin (x));
xlabel ("x");
ylabel ("sin (x)");
title ("Simple 2-D Plot");
displays a sine wave shown in Figure 15.1. On most systems, this command will open a
separate plot window to display the graph.
286 GNU Octave
-10 -5 0 5 10
-1
-0.5
0
0.5
1
x
sin (x)
Simple 2-D Plot
Figure 15.1: Simple Two-Dimensional Plot.
plot (y)
plot (x,y)
plot (x,y,fmt)
plot (. . ., property,value, . . .)
plot (x1,y1, . . . , xn,yn)
plot (hax, . . . )
h= plot (. . . )
Produce 2-D plots.
Many different combinations of arguments are possible. The simplest form is
plot (y)
where the argument is taken as the set of ycoordinates and the xcoordinates are
taken to be the range 1:numel (y).
If more than one argument is given, they are interpreted as
plot (y,property,value, ...)
or
plot (x,y,property,value, ...)
or
plot (x,y,fmt, ...)
and so on. Any number of argument sets may appear. The xand yvalues are
interpreted as follows:
•If a single data argument is supplied, it is taken as the set of ycoordinates and
the xcoordinates are taken to be the indices of the elements, starting with 1.
•If xand yare scalars, a single point is plotted.
•squeeze() is applied to arguments with more than two dimensions, but no more
than two singleton dimensions.
Chapter 15: Plotting 287
•If both arguments are vectors, the elements of yare plotted versus the elements
of x.
•If xis a vector and yis a matrix, then the columns (or rows) of yare plotted
versus x. (using whichever combination matches, with columns tried first.)
•If the xis a matrix and yis a vector, yis plotted versus the columns (or rows)
of x. (using whichever combination matches, with columns tried first.)
•If both arguments are matrices, the columns of yare plotted versus the columns
of x. In this case, both matrices must have the same number of rows and columns
and no attempt is made to transpose the arguments to make the number of rows
match.
Multiple property-value pairs may be specified, but they must appear in pairs.
These arguments are applied to the line objects drawn by plot. Useful properties
to modify are "linestyle","linewidth","color","marker","markersize",
"markeredgecolor","markerfacecolor". See Section 15.3.3.4 [Line Properties],
page 397.
The fmt format argument can also be used to control the plot style. It is a string com-
posed of four optional parts: "<linestyle><marker><color><;displayname;>". When a
marker is specified, but no linestyle, only the markers are plotted. Similarly, if a
linestyle is specified, but no marker, then only lines are drawn. If both are speci-
fied then lines and markers will be plotted. If no fmt and no property/value pairs
are given, then the default plot style is solid lines with no markers and the color
determined by the "colororder" property of the current axes.
Format arguments:
linestyle
‘-’ Use solid lines (default).
‘--’ Use dashed lines.
‘:’ Use dotted lines.
‘-.’ Use dash-dotted lines.
marker
‘+’ crosshair
‘o’ circle
‘*’ star
‘.’ point
‘x’ cross
‘s’ square
‘d’ diamond
‘^’ upward-facing triangle
‘v’ downward-facing triangle
‘>’ right-facing triangle
‘<’ left-facing triangle
‘p’ pentagram
‘h’ hexagram
color
288 GNU Octave
‘k’ blacK
‘r’ Red
‘g’ Green
‘b’ Blue
‘y’ Yellow
‘m’ Magenta
‘c’ Cyan
‘w’ White
";displayname;"
Here "displayname" is the label to use for the plot legend.
The fmt argument may also be used to assign legend labels. To do so, include the
desired label between semicolons after the formatting sequence described above, e.g.,
"+b;Key Title;". Note that the last semicolon is required and Octave will generate
an error if it is left out.
Here are some plot examples:
plot (x, y, "or", x, y2, x, y3, "m", x, y4, "+")
This command will plot ywith red circles, y2 with solid lines, y3 with solid magenta
lines, and y4 with points displayed as ‘+’.
plot (b, "*", "markersize", 10)
This command will plot the data in the variable b, with points displayed as ‘*’ and a
marker size of 10.
t = 0:0.1:6.3;
plot (t, cos(t), "-;cos(t);", t, sin(t), "-b;sin(t);");
This will plot the cosine and sine functions and label them accordingly in the legend.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the created line objects.
To save a plot, in one of several image formats such as PostScript or PNG, use the
print command.
See also: [axis], page 313,[box], page 350,[grid], page 351,[hold], page 359,[legend],
page 348,[title], page 348,[xlabel], page 349,[ylabel], page 349,[xlim], page 315,
[ylim], page 315,[ezplot], page 317,[errorbar], page 303,[fplot], page 316,[line],
page 376,[plot3], page 337,[polar], page 307,[loglog], page 290,[semilogx], page 289,
[semilogy], page 289,[subplot], page 354.
The plotyy function may be used to create a plot with two independent y axes.
plotyy (x1,y1,x2,y2)
plotyy (. . ., fun)
plotyy (. . ., fun1,fun2)
plotyy (hax, . . . )
[ax,h1,h2] = plotyy (. . . )
Plot two sets of data with independent y-axes and a common x-axis.
Chapter 15: Plotting 289
The arguments x1 and y1 define the arguments for the first plot and x1 and y2 for
the second.
By default the arguments are evaluated with feval (@plot, x,y). However the type
of plot can be modified with the fun argument, in which case the plots are generated
by feval (fun,x,y).fun can be a function handle, an inline function, or a string
of a function name.
The function to use for each of the plots can be independently defined with fun1 and
fun2.
If the first argument hax is an axes handle, then it defines the principal axis in which
to plot the x1 and y1 data.
The return value ax is a vector with the axis handles of the two y-axes. h1 and h2
are handles to the objects generated by the plot commands.
x = 0:0.1:2*pi;
y1 = sin (x);
y2 = exp (x - 1);
ax = plotyy (x, y1, x - 1, y2, @plot, @semilogy);
xlabel ("X");
ylabel (ax(1), "Axis 1");
ylabel (ax(2), "Axis 2");
See also: [plot], page 286.
The functions semilogx,semilogy, and loglog are similar to the plot function, but
produce plots in which one or both of the axes use log scales.
semilogx (y)
semilogx (x,y)
semilogx (x,y,property,value, . . . )
semilogx (x,y,fmt)
semilogx (hax, . . . )
h= semilogx (. . . )
Produce a 2-D plot using a logarithmic scale for the x-axis.
See the documentation of plot for a description of the arguments that semilogx will
accept.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
See also: [plot], page 286,[semilogy], page 289,[loglog], page 290.
semilogy (y)
semilogy (x,y)
semilogy (x,y,property,value, . . . )
semilogy (x,y,fmt)
semilogy (h, . . . )
h= semilogy (. . . )
Produce a 2-D plot using a logarithmic scale for the y-axis.
290 GNU Octave
See the documentation of plot for a description of the arguments that semilogy will
accept.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
See also: [plot], page 286,[semilogx], page 289,[loglog], page 290.
loglog (y)
loglog (x,y)
loglog (x,y,prop,value, . . . )
loglog (x,y,fmt)
loglog (hax, . . . )
h= loglog (. . . )
Produce a 2-D plot using logarithmic scales for both axes.
See the documentation of plot for a description of the arguments that loglog will
accept.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
See also: [plot], page 286,[semilogx], page 289,[semilogy], page 289.
The functions bar,barh,stairs, and stem are useful for displaying discrete data. For
example,
randn ("state", 1);
hist (randn (10000, 1), 30);
xlabel ("Value");
ylabel ("Count");
title ("Histogram of 10,000 normally distributed random numbers");
produces the histogram of 10,000 normally distributed random numbers shown in
Figure 15.2. Note that, randn ("state", 1);, initializes the random number generator
for randn to a known value so that the returned values are reproducible; This guarantees
that the figure produced is identical to the one in this manual.
Chapter 15: Plotting 291
-4 -2 0 2 4
0
200
400
600
800
1000
Value
Count
Histogram of 10,000 normally distributed random numbers
Figure 15.2: Histogram.
bar (y)
bar (x,y)
bar (. . ., w)
bar (. . ., style)
bar (. . ., prop,val, . . .)
bar (hax, . . . )
h= bar (. . . , prop,val, . . . )
Produce a bar graph from two vectors of X-Y data.
If only one argument is given, y, it is taken as a vector of Y values and the X
coordinates are the range 1:numel (y).
The optional input wcontrols the width of the bars. A value of 1.0 will cause each
bar to exactly touch any adjacent bars. The default width is 0.8.
If yis a matrix, then each column of yis taken to be a separate bar graph plotted
on the same graph. By default the columns are plotted side-by-side. This behavior
can be changed by the style argument which can take the following values:
"grouped" (default)
Side-by-side bars with a gap between bars and centered over the X-
coordinate.
"stacked"
Bars are stacked so that each X value has a single bar composed of mul-
tiple segments.
"hist" Side-by-side bars with no gap between bars and centered over the X-
coordinate.
"histc" Side-by-side bars with no gap between bars and left-aligned to the X-
coordinate.
292 GNU Octave
Optional property/value pairs are passed directly to the underlying patch objects.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of handles to the created "bar series"hggroups
with one handle per column of the variable y. This series makes it possible to change
a common element in one bar series object and have the change reflected in the other
"bar series". For example,
h = bar (rand (5, 10));
set (h(1), "basevalue", 0.5);
changes the position on the base of all of the bar series.
The following example modifies the face and edge colors using property/value pairs.
bar (randn (1, 100), "facecolor", "r", "edgecolor", "b");
The color of the bars is taken from the figure’s colormap, such that
bar (rand (10, 3));
colormap (summer (64));
will change the colors used for the bars. The color of bars can also be set manually
using the "facecolor" property as shown below.
h = bar (rand (10, 3));
set (h(1), "facecolor", "r")
set (h(2), "facecolor", "g")
set (h(3), "facecolor", "b")
See also: [barh], page 292,[hist], page 293,[pie], page 307,[plot], page 286,[patch],
page 376.
barh (y)
barh (x,y)
barh (. . ., w)
barh (. . ., style)
barh (. . ., prop,val, . . .)
barh (hax, . . . )
h= barh (. . . , prop,val, . . . )
Produce a horizontal bar graph from two vectors of X-Y data.
If only one argument is given, it is taken as a vector of Y values and the X coordinates
are the range 1:numel (y).
The optional input wcontrols the width of the bars. A value of 1.0 will cause each
bar to exactly touch any adjacent bars. The default width is 0.8.
If yis a matrix, then each column of yis taken to be a separate bar graph plotted
on the same graph. By default the columns are plotted side-by-side. This behavior
can be changed by the style argument which can take the following values:
"grouped" (default)
Side-by-side bars with a gap between bars and centered over the Y-
coordinate.
Chapter 15: Plotting 293
"stacked"
Bars are stacked so that each Y value has a single bar composed of mul-
tiple segments.
"hist" Side-by-side bars with no gap between bars and centered over the Y-
coordinate.
"histc" Side-by-side bars with no gap between bars and left-aligned to the Y-
coordinate.
Optional property/value pairs are passed directly to the underlying patch objects.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created bar series hggroup.
For a description of the use of the bar series, see [bar], page 291.
See also: [bar], page 291,[hist], page 293,[pie], page 307,[plot], page 286,[patch],
page 376.
hist (y)
hist (y,x)
hist (y,nbins)
hist (y,x,norm)
hist (. . ., prop,val, . . .)
hist (hax, . . . )
[nn,xx] = hist (. . . )
Produce histogram counts or plots.
With one vector input argument, y, plot a histogram of the values with 10 bins. The
range of the histogram bins is determined by the range of the data. With one matrix
input argument, y, plot a histogram where each bin contains a bar per input column.
Given a second vector argument, x, use that as the centers of the bins, with the width
of the bins determined from the adjacent values in the vector.
If scalar, the second argument, nbins, defines the number of bins.
If a third argument is provided, the histogram is normalized such that the sum of the
bars is equal to norm.
Extreme values are lumped into the first and last bins.
The histogram’s appearance may be modified by specifying property/value pairs. For
example the face and edge color may be modified.
hist (randn (1, 100), 25, "facecolor", "r", "edgecolor", "b");
The histogram’s colors also depend upon the current colormap.
hist (rand (10, 3));
colormap (summer ());
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
With two output arguments, produce the values nn (numbers of elements) and xx
(bin centers) such that bar (xx,nn)will plot the histogram.
See also: [histc], page 650,[bar], page 291,[pie], page 307,[rose], page 299.

294 GNU Octave
stemleaf (x,caption)
stemleaf (x,caption,stem_sz)
plotstr = stemleaf (. . . )
Compute and display a stem and leaf plot of the vector x.
The input xshould be a vector of integers. Any non-integer values will be converted
to integer by x= fix (x). By default each element of xwill be plotted with the last
digit of the element as a leaf value and the remaining digits as the stem. For example,
123 will be plotted with the stem ‘12’ and the leaf ‘3’. The second argument, caption,
should be a character array which provides a description of the data. It is included
as a heading for the output.
The optional input stem sz sets the width of each stem. The stem width is determined
by 10^(stem_sz + 1). The default stem width is 10.
The output of stemleaf is composed of two parts: a "Fenced Letter Display,"followed
by the stem-and-leaf plot itself. The Fenced Letter Display is described in Exploratory
Data Analysis. Briefly, the entries are as shown:
Fenced Letter Display
#% nx|___________________ nx = numel (x)
M% mi| md | mi median index, md median
H% hi|hl hu| hs hi lower hinge index, hl,hu hinges,
1 |x(1) x(nx)| hs h_spreadx(1), x(nx) first
_______ and last data value.
______|step |_______ step 1.5*h_spread
f|ifl ifh| inner fence, lower and higher
|nfl nfh| no.\ of data points within fences
F|ofl ofh| outer fence, lower and higher
|nFl nFh| no.\ of data points outside outer
fences
The stem-and-leaf plot shows on each line the stem value followed by the string made
up of the leaf digits. If the stem sz is not 1 the successive leaf values are separated
by ",".
With no return argument, the plot is immediately displayed. If an output argument
is provided, the plot is returned as an array of strings.
The leaf digits are not sorted. If sorted leaf values are desired, use xs = sort (x)
before calling stemleaf (xs).
The stem and leaf plot and associated displays are described in: Chapter 3, Ex-
ploratory Data Analysis by J. W. Tukey, Addison-Wesley, 1977.
See also: [hist], page 293,[printd], page 294.
printd (obj,filename)
out_file = printd (. . . )
Convert any object acceptable to disp into the format selected by the suffix of
filename.
If the return argument out file is given, the name of the created file is returned.
Chapter 15: Plotting 295
This function is intended to facilitate manipulation of the output of functions such
as stemleaf.
See also: [stemleaf], page 294.
stairs (y)
stairs (x,y)
stairs (. . ., style)
stairs (. . ., prop,val, . . .)
stairs (hax, . . . )
h= stairs (. . . )
[xstep,ystep] = stairs (. . . )
Produce a stairstep plot.
The arguments xand ymay be vectors or matrices. If only one argument is given, it
is taken as a vector of Y values and the X coordinates are taken to be the indices of
the elements.
The style to use for the plot can be defined with a line style style of the same format
as the plot command.
Multiple property/value pairs may be specified, but they must appear in pairs.
If the first argument hax is an axis handle, then plot into this axis, rather than the
current axis handle returned by gca.
If one output argument is requested, return a graphics handle to the created plot.
If two output arguments are specified, the data are generated but not plotted. For
example,
stairs (x, y);
and
[xs, ys] = stairs (x, y);
plot (xs, ys);
are equivalent.
See also: [bar], page 291,[hist], page 293,[plot], page 286,[stem], page 295.
stem (y)
stem (x,y)
stem (. . ., linespec)
stem (. . ., "filled")
stem (. . ., prop,val, . . .)
stem (hax, . . . )
h= stem (. . . )
Plot a 2-D stem graph.
If only one argument is given, it is taken as the y-values and the x-coordinates are
taken from the indices of the elements.
If yis a matrix, then each column of the matrix is plotted as a separate stem graph.
In this case xcan either be a vector, the same length as the number of rows in y, or
it can be a matrix of the same size as y.
296 GNU Octave
The default color is "b" (blue), the default line style is "-", and the default marker
is "o". The line style can be altered by the linespec argument in the same manner
as the plot command. If the "filled" argument is present the markers at the top
of the stems will be filled in. For example,
x = 1:10;
y = 2*x;
stem (x, y, "r");
plots 10 stems with heights from 2 to 20 in red;
Optional property/value pairs may be specified to control the appearance of the plot.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a handle to a "stem series"hggroup. The single
hggroup handle has all of the graphical elements comprising the plot as its children;
This allows the properties of multiple graphics objects to be changed by modifying
just a single property of the "stem series"hggroup.
For example,
x = [0:10]’;
y = [sin(x), cos(x)]
h = stem (x, y);
set (h(2), "color", "g");
set (h(1), "basevalue", -1)
changes the color of the second "stem series"and moves the base line of the first.
Stem Series Properties
linestyle The linestyle of the stem. (Default: "-")
linewidth The width of the stem. (Default: 0.5)
color The color of the stem, and if not separately specified, the marker. (De-
fault: "b" [blue])
marker The marker symbol to use at the top of each stem. (Default: "o")
markeredgecolor
The edge color of the marker. (Default: "color" property)
markerfacecolor
The color to use for "filling"the marker. (Default: "none" [unfilled])
markersize
The size of the marker. (Default: 6)
baseline The handle of the line object which implements the baseline. Use set
with the returned handle to change graphic properties of the baseline.
basevalue The y-value where the baseline is drawn. (Default: 0)
See also: [stem3], page 297,[bar], page 291,[hist], page 293,[plot], page 286,[stairs],
page 295.
Chapter 15: Plotting 297
stem3 (x,y,z)
stem3 (. . ., linespec)
stem3 (. . ., "filled")
stem3 (. . ., prop,val, . . .)
stem3 (hax, . . . )
h= stem3 (. . . )
Plot a 3-D stem graph.
Stems are drawn from the height zto the location in the x-y plane determined by x
and y. The default color is "b" (blue), the default line style is "-", and the default
marker is "o".
The line style can be altered by the linespec argument in the same manner as the
plot command. If the "filled" argument is present the markers at the top of the
stems will be filled in.
Optional property/value pairs may be specified to control the appearance of the plot.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a handle to the "stem series"hggroup containing the
line and marker objects used for the plot. See [stem], page 295, for a description of
the "stem series"object.
Example:
theta = 0:0.2:6;
stem3 (cos (theta), sin (theta), theta);
plots 31 stems with heights from 0 to 6 lying on a circle.
Implementation Note: Color definitions with RGB-triples are not valid.
See also: [stem], page 295,[bar], page 291,[hist], page 293,[plot], page 286.
scatter (x,y)
scatter (x,y,s)
scatter (x,y,s,c)
scatter (. . ., style)
scatter (. . ., "filled")
scatter (. . ., prop,val, . . .)
scatter (hax, . . . )
h= scatter (. . . )
Draw a 2-D scatter plot.
A marker is plotted at each point defined by the coordinates in the vectors xand y.
The size of the markers is determined by s, which can be a scalar or a vector of the
same length as xand y. If sis not given, or is an empty matrix, then a default value
of 36 square points is used (The marker size itself is sqrt (s)).
The color of the markers is determined by c, which can be a string defining a fixed
color; a 3-element vector giving the red, green, and blue components of the color; a
vector of the same length as xthat gives a scaled index into the current colormap; or
an Nx3 matrix defining the RGB color of each marker individually.
298 GNU Octave
The marker to use can be changed with the style argument; it is a string defining a
marker in the same manner as the plot command. If no marker is specified it defaults
to "o" or circles. If the argument "filled" is given then the markers are filled.
Additional property/value pairs are passed directly to the underlying patch object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created scatter object.
Example:
x = randn (100, 1);
y = randn (100, 1);
scatter (x, y, [], sqrt (x.^2 + y.^2));
See also: [scatter3], page 340,[patch], page 376,[plot], page 286.
plotmatrix (x,y)
plotmatrix (x)
plotmatrix (. . ., style)
plotmatrix (hax, . . . )
[h,ax,bigax,p,pax] = plotmatrix (. . . )
Scatter plot of the columns of one matrix against another.
Given the arguments xand ythat have a matching number of rows, plotmatrix
plots a set of axes corresponding to
plot (x(:, i), y(:, j))
When called with a single argument xthis is equivalent to
plotmatrix (x,x)
except that the diagonal of the set of axes will be replaced with the histogram hist
(x(:, i)).
The marker to use can be changed with the style argument, that is a string defining
a marker in the same manner as the plot command.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value hprovides handles to the individual graphics objects in the
scatter plots, whereas ax returns the handles to the scatter plot axis objects.
bigax is a hidden axis object that surrounds the other axes, such that the commands
xlabel,title, etc., will be associated with this hidden axis.
Finally, preturns the graphics objects associated with the histogram and pax the
corresponding axes objects.
Example:
plotmatrix (randn (100, 3), "g+")
See also: [scatter], page 297,[plot], page 286.
pareto (y)
pareto (y,x)
pareto (hax, . . . )
Chapter 15: Plotting 299
h= pareto (. . . )
Draw a Pareto chart.
A Pareto chart is a bar graph that arranges information in such a way that priorities
for process improvement can be established; It organizes and displays information to
show the relative importance of data. The chart is similar to the histogram or bar
chart, except that the bars are arranged in decreasing magnitude from left to right
along the x-axis.
The fundamental idea (Pareto principle) behind the use of Pareto diagrams is that the
majority of an effect is due to a small subset of the causes. For quality improvement,
the first few contributing causes (leftmost bars as presented on the diagram) to a
problem usually account for the majority of the result. Thus, targeting these "major
causes"for elimination results in the most cost-effective improvement scheme.
Typically only the magnitude data yis present in which case xis taken to be the
range 1 : length (y). If xis given it may be a string array, a cell array of strings,
or a numerical vector.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a 2-element vector with a graphics handle for the
created bar plot and a second handle for the created line plot.
An example of the use of pareto is
Cheese = {"Cheddar", "Swiss", "Camembert", ...
"Munster", "Stilton", "Blue"};
Sold = [105, 30, 70, 10, 15, 20];
pareto (Sold, Cheese);
See also: [bar], page 291,[barh], page 292,[hist], page 293,[pie], page 307,[plot],
page 286.
rose (th)
rose (th,nbins)
rose (th,bins)
rose (hax, . . . )
h= rose (. . . )
[thout rout] = rose (. . . )
Plot an angular histogram.
With one vector argument, th, plot the histogram with 20 angular bins. If th is a
matrix then each column of th produces a separate histogram.
If nbins is given and is a scalar, then the histogram is produced with nbin bins. If
bins is a vector, then the center of each bin is defined by the values in bins and the
number of bins is given by the number of elements in bins.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the line objects repre-
senting each histogram.
If two output arguments are requested then no plot is made and the polar vectors
necessary to plot the histogram are returned instead.
300 GNU Octave
Example
[th, r] = rose ([2*randn(1e5,1), pi + 2*randn(1e5,1)]);
polar (th, r);
Programming Note: When specifying bin centers with the bins input, the edges for
bins 2 to N-1 are spaced so that bins(i) is centered between the edges. The final
edge is drawn halfway between bin N and bin 1. This guarantees that all input th
will be placed into one of the bins, but also means that for some combinations bin 1
and bin N may not be centered on the user’s given values.
See also: [hist], page 293,[polar], page 307.
The contour,contourf and contourc functions produce two-dimensional contour plots
from three-dimensional data.
contour (z)
contour (z,vn)
contour (x,y,z)
contour (x,y,z,vn)
contour (. . ., style)
contour (hax, . . . )
[c,h] = contour (. . . )
Create a 2-D contour plot.
Plot level curves (contour lines) of the matrix z, using the contour matrix ccomputed
by contourc from the same arguments; see the latter for their interpretation.
The appearance of contour lines can be defined with a line style style in the same
manner as plot. Only line style and color are used; Any markers defined by style are
ignored.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional output ccontains the contour levels in contourc format.
The optional return value his a graphics handle to the hggroup comprising the contour
lines.
Example:
x = 0:2;
y = x;
z=x’*y;
contour (x, y, z, 2:3)
See also: [ezcontour], page 318,[contourc], page 301,[contourf], page 300,[contour3],
page 302,[clabel], page 350,[meshc], page 322,[surfc], page 324,[caxis], page 315,
[colormap], page 751,[plot], page 286.
contourf (z)
contourf (z,vn)
contourf (x,y,z)
contourf (x,y,z,vn)
contourf (. . ., style)
Chapter 15: Plotting 301
contourf (hax, . . . )
[c,h] = contourf (. . . )
Create a 2-D contour plot with filled intervals.
Plot level curves (contour lines) of the matrix zand fill the region between lines with
colors from the current colormap.
The level curves are taken from the contour matrix ccomputed by contourc for the
same arguments; see the latter for their interpretation.
The appearance of contour lines can be defined with a line style style in the same
manner as plot. Only line style and color are used; Any markers defined by style are
ignored.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional output ccontains the contour levels in contourc format.
The optional return value his a graphics handle to the hggroup comprising the contour
lines.
The following example plots filled contours of the peaks function.
[x, y, z] = peaks (50);
contourf (x, y, z, -7:9)
See also: [ezcontourf], page 318,[contour], page 300,[contourc], page 301,[contour3],
page 302,[clabel], page 350,[meshc], page 322,[surfc], page 324,[caxis], page 315,
[colormap], page 751,[plot], page 286.
[c,lev] = contourc (z)
[c,lev] = contourc (z,vn)
[c,lev] = contourc (x,y,z)
[c,lev] = contourc (x,y,z,vn)
Compute contour lines (isolines of constant Z value).
The matrix zcontains height values above the rectangular grid determined by xand
y. If only a single input zis provided then xis taken to be 1:rows (z)and yis taken
to be 1:columns (z).
The optional input vn is either a scalar denoting the number of contour lines to
compute or a vector containing the Z values where lines will be computed. When vn
is a vector the number of contour lines is numel (vn). However, to compute a single
contour line at a given value use vn = [val, val]. If vn is omitted it defaults to 10.
The return value cis a 2xnmatrix containing the contour lines in the following format
c= [lev1, x1, x2, ..., levn, x1, x2, ...
len1, y1, y2, ..., lenn, y1, y2, ...]
in which contour line nhas a level (height) of levn and length of lenn.
The optional return value lev is a vector with the Z values of the contour levels.
Example:
302 GNU Octave
x = 0:2;
y = x;
z=x’*y;
contourc (x, y, z, 2:3)
⇒2.0000 2.0000 1.0000 3.0000 1.5000 2.0000
2.0000 1.0000 2.0000 2.0000 2.0000 1.5000
See also: [contour], page 300,[contourf], page 300,[contour3], page 302,[clabel],
page 350.
contour3 (z)
contour3 (z,vn)
contour3 (x,y,z)
contour3 (x,y,z,vn)
contour3 (. . ., style)
contour3 (hax, . . . )
[c,h] = contour3 (. . . )
Create a 3-D contour plot.
contour3 plots level curves (contour lines) of the matrix zat a Z level corresponding
to each contour. This is in contrast to contour which plots all of the contour lines at
the same Z level and produces a 2-D plot.
The level curves are taken from the contour matrix ccomputed by contourc for the
same arguments; see the latter for their interpretation.
The appearance of contour lines can be defined with a line style style in the same
manner as plot. Only line style and color are used; Any markers defined by style are
ignored.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional output care the contour levels in contourc format.
The optional return value his a graphics handle to the hggroup comprising the contour
lines.
Example:
contour3 (peaks (19));
colormap cool;
hold on;
surf (peaks (19), "facecolor", "none", "edgecolor", "black");
See also: [contour], page 300,[contourc], page 301,[contourf], page 300,[clabel],
page 350,[meshc], page 322,[surfc], page 324,[caxis], page 315,[colormap], page 751,
[plot], page 286.
The errorbar,semilogxerr,semilogyerr, and loglogerr functions produce plots
with error bar markers. For example,
Chapter 15: Plotting 303
rand ("state", 2);
x = 0:0.1:10;
y = sin (x);
lerr = 0.1 .* rand (size (x));
uerr = 0.1 .* rand (size (x));
errorbar (x, y, lerr, uerr);
axis ([0, 10, -1.1, 1.1]);
xlabel ("x");
ylabel ("sin (x)");
title ("Errorbar plot of sin (x)");
produces the figure shown in Figure 15.3.
0246810
-1
-0.5
0
0.5
1
x
sin (x)
Errorbar plot of sin (x)
Figure 15.3: Errorbar plot.
errorbar (y,ey)
errorbar (y, . . . , fmt)
errorbar (x,y,ey)
errorbar (x,y,err,fmt)
errorbar (x,y,lerr,uerr,fmt)
errorbar (x,y,ex,ey,fmt)
errorbar (x,y,lx,ux,ly,uy,fmt)
errorbar (x1,y1, . . . , fmt,xn,yn, . . .)
errorbar (hax, . . . )
h= errorbar (. . . )
Create a 2-D plot with errorbars.
Many different combinations of arguments are possible. The simplest form is
errorbar (y,ey)
304 GNU Octave
where the first argument is taken as the set of ycoordinates, the second argument ey
are the errors around the yvalues, and the xcoordinates are taken to be the indices
of the elements (1:numel (y)).
The general form of the function is
errorbar (x,y,err1, ..., fmt, ...)
After the xand yarguments there can be 1, 2, or 4 parameters specifying the error
values depending on the nature of the error values and the plot format fmt.
err (scalar)
When the error is a scalar all points share the same error value. The
errorbars are symmetric and are drawn from data-err to data+err. The
fmt argument determines whether err is in the x-direction, y-direction
(default), or both.
err (vector or matrix)
Each data point has a particular error value. The errorbars are symmetric
and are drawn from data(n)-err(n) to data(n)+err(n).
lerr,uerr (scalar)
The errors have a single low-side value and a single upper-side value. The
errorbars are not symmetric and are drawn from data-lerr to data+uerr.
lerr,uerr (vector or matrix)
Each data point has a low-side error and an upper-side error. The
errorbars are not symmetric and are drawn from data(n)-lerr(n) to
data(n)+uerr(n).
Any number of data sets (x1,y1,x2,y2, . . .) may appear as long as they are separated
by a format string fmt.
If yis a matrix, xand the error parameters must also be matrices having the same
dimensions. The columns of yare plotted versus the corresponding columns of xand
errorbars are taken from the corresponding columns of the error parameters.
If fmt is missing, the yerrorbars ("~") plot style is assumed.
If the fmt argument is supplied then it is interpreted, as in normal plots, to specify
the line style, marker, and color. In addition, fmt may include an errorbar style which
must precede the ordinary format codes. The following errorbar styles are supported:
‘~’ Set yerrorbars plot style (default).
‘>’ Set xerrorbars plot style.
‘~>’ Set xyerrorbars plot style.
‘#~’ Set yboxes plot style.
‘#’ Set xboxes plot style.
‘#~>’ Set xyboxes plot style.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
Chapter 15: Plotting 305
The optional return value his a handle to the hggroup object representing the data
plot and errorbars.
Note: For compatibility with matlab a line is drawn through all data points. How-
ever, most scientific errorbar plots are a scatter plot of points with errorbars. To
accomplish this, add a marker style to the fmt argument such as ".". Alternatively, re-
move the line by modifying the returned graphic handle with set (h, "linestyle",
"none").
Examples:
errorbar (x,y,ex, ">.r")
produces an xerrorbar plot of yversus xwith xerrorbars drawn from x-ex to x+ex.
The marker "." is used so no connecting line is drawn and the errorbars appear in
red.
errorbar (x,y1,ey, "~",
x,y2,ly,uy)
produces yerrorbar plots with y1 and y2 versus x. Errorbars for y1 are drawn from
y1-ey to y1+ey, errorbars for y2 from y2-ly to y2+uy.
errorbar (x,y,lx,ux,
ly,uy, "~>")
produces an xyerrorbar plot of yversus xin which xerrorbars are drawn from x-lx
to x+ux and yerrorbars from y-ly to y+uy.
See also: [semilogxerr], page 305,[semilogyerr], page 306,[loglogerr], page 306,[plot],
page 286.
semilogxerr (y,ey)
semilogxerr (y, . . . , fmt)
semilogxerr (x,y,ey)
semilogxerr (x,y,err,fmt)
semilogxerr (x,y,lerr,uerr,fmt)
semilogxerr (x,y,ex,ey,fmt)
semilogxerr (x,y,lx,ux,ly,uy,fmt)
semilogxerr (x1,y1, . . . , fmt,xn,yn, . . .)
semilogxerr (hax, . . . )
h= semilogxerr (. . . )
Produce 2-D plots using a logarithmic scale for the x-axis and errorbars at each data
point.
Many different combinations of arguments are possible. The most common form is
semilogxerr (x,y,ey,fmt)
which produces a semi-logarithmic plot of yversus xwith errors in the y-scale defined
by ey and the plot format defined by fmt. See [errorbar], page 303, for available
formats and additional information.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [errorbar], page 303,[semilogyerr], page 306,[loglogerr], page 306.
306 GNU Octave
semilogyerr (y,ey)
semilogyerr (y, . . . , fmt)
semilogyerr (x,y,ey)
semilogyerr (x,y,err,fmt)
semilogyerr (x,y,lerr,uerr,fmt)
semilogyerr (x,y,ex,ey,fmt)
semilogyerr (x,y,lx,ux,ly,uy,fmt)
semilogyerr (x1,y1, . . . , fmt,xn,yn, . . .)
semilogyerr (hax, . . . )
h= semilogyerr (. . . )
Produce 2-D plots using a logarithmic scale for the y-axis and errorbars at each data
point.
Many different combinations of arguments are possible. The most common form is
semilogyerr (x,y,ey,fmt)
which produces a semi-logarithmic plot of yversus xwith errors in the y-scale defined
by ey and the plot format defined by fmt. See [errorbar], page 303, for available
formats and additional information.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [errorbar], page 303,[semilogxerr], page 305,[loglogerr], page 306.
loglogerr (y,ey)
loglogerr (y, . . . , fmt)
loglogerr (x,y,ey)
loglogerr (x,y,err,fmt)
loglogerr (x,y,lerr,uerr,fmt)
loglogerr (x,y,ex,ey,fmt)
loglogerr (x,y,lx,ux,ly,uy,fmt)
loglogerr (x1,y1, . . . , fmt,xn,yn, . . .)
loglogerr (hax, . . . )
h= loglogerr (. . . )
Produce 2-D plots on a double logarithm axis with errorbars.
Many different combinations of arguments are possible. The most common form is
loglogerr (x,y,ey,fmt)
which produces a double logarithm plot of yversus xwith errors in the y-scale defined
by ey and the plot format defined by fmt. See [errorbar], page 303, for available
formats and additional information.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [errorbar], page 303,[semilogxerr], page 305,[semilogyerr], page 306.
Finally, the polar function allows you to easily plot data in polar coordinates. However,
the display coordinates remain rectangular and linear. For example,
polar (0:0.1:10*pi, 0:0.1:10*pi);
title ("Example polar plot from 0 to 10*pi");
Chapter 15: Plotting 307
produces the spiral plot shown in Figure 15.4.
10
20
30
40
0
30
60
90
120
150
180
210
240
270
300
330
Example polar plot from 0 to 10*pi
Figure 15.4: Polar plot.
polar (theta,rho)
polar (theta,rho,fmt)
polar (cplx)
polar (cplx,fmt)
polar (hax, . . . )
h= polar (. . . )
Create a 2-D plot from polar coordinates theta and rho.
If a single complex input cplx is given then the real part is used for theta and the
imaginary part is used for rho.
The optional argument fmt specifies the line format in the same way as plot.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
Implementation Note: The polar axis is drawn using line and text objects encapsu-
lated in an hggroup. The hggroup properties are linked to the original axes object
such that altering an appearance property, for example fontname, will update the
polar axis. Two new properties are added to the original axes–rtick,ttick–which
replace xtick,ytick. The first is a list of tick locations in the radial (rho) direc-
tion; The second is a list of tick locations in the angular (theta) direction specified in
degrees, i.e., in the range 0–359.
See also: [rose], page 299,[compass], page 310,[plot], page 286.
pie (x)
pie (. . ., explode)
pie (. . ., labels)
308 GNU Octave
pie (hax, . . . );
h= pie (. . . );
Plot a 2-D pie chart.
When called with a single vector argument, produce a pie chart of the elements in x.
The size of the ith slice is the percentage that the element xi represents of the total
sum of x:pct = x(i) / sum (x).
The optional input explode is a vector of the same length as xthat, if nonzero,
"explodes"the slice from the pie chart.
The optional input labels is a cell array of strings of the same length as xspecifying
the label for each slice.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a list of handles to the patch and text objects generating
the plot.
Note: If sum (x)≤1then the elements of xare interpreted as percentages directly
and are not normalized by sum (x). Furthermore, if the sum is less than 1 then there
will be a missing slice in the pie plot to represent the missing, unspecified percentage.
See also: [pie3], page 308,[bar], page 291,[hist], page 293,[rose], page 299.
pie3 (x)
pie3 (. . ., explode)
pie3 (. . ., labels)
pie3 (hax, . . . );
h= pie3 (. . . );
Plot a 3-D pie chart.
Called with a single vector argument, produces a 3-D pie chart of the elements in x.
The size of the ith slice is the percentage that the element xi represents of the total
sum of x:pct = x(i) / sum (x).
The optional input explode is a vector of the same length as xthat, if nonzero,
"explodes"the slice from the pie chart.
The optional input labels is a cell array of strings of the same length as xspecifying
the label for each slice.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a list of graphics handles to the patch, surface, and
text objects generating the plot.
Note: If sum (x)≤1then the elements of xare interpreted as percentages directly
and are not normalized by sum (x). Furthermore, if the sum is less than 1 then there
will be a missing slice in the pie plot to represent the missing, unspecified percentage.
See also: [pie], page 307,[bar], page 291,[hist], page 293,[rose], page 299.
quiver (u,v)
quiver (x,y,u,v)
quiver (. . ., s)
Chapter 15: Plotting 309
quiver (. . ., style)
quiver (. . ., "filled")
quiver (hax, . . . )
h= quiver (. . . )
Plot a 2-D vector field with arrows.
Plot the (u,v) components of a vector field in an (x,y) meshgrid. If the grid is
uniform then xand ycan be specified as vectors.
If xand yare undefined they are assumed to be (1:m, 1:n)where [m,n] = size
(u).
The variable sis a scalar defining a scaling factor to use for the arrows of the field
relative to the mesh spacing. A value of 0 disables all scaling. The default value is
0.9.
The style to use for the plot can be defined with a line style style of the same format
as the plot command. If a marker is specified then markers at the grid points of the
vectors are drawn rather than arrows. If the argument "filled" is given then the
markers are filled.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to a quiver object. A quiver object
regroups the components of the quiver plot (body, arrow, and marker), and allows
them to be changed together.
Example:
[x, y] = meshgrid (1:2:20);
h = quiver (x, y, sin (2*pi*x/10), sin (2*pi*y/10));
set (h, "maxheadsize", 0.33);
See also: [quiver3], page 309,[compass], page 310,[feather], page 310,[plot],
page 286.
quiver3 (u,v,w)
quiver3 (x,y,z,u,v,w)
quiver3 (. . ., s)
quiver3 (. . ., style)
quiver3 (. . ., "filled")
quiver3 (hax, . . . )
h= quiver3 (. . . )
Plot a 3-D vector field with arrows.
Plot the (u,v,w) components of a vector field in an (x,y,z) meshgrid. If the grid is
uniform then x,y, and zcan be specified as vectors.
If x,y, and zare undefined they are assumed to be (1:m, 1:n, 1:p)where [m,n] =
size (u)and p= max (size (w)).
The variable sis a scalar defining a scaling factor to use for the arrows of the field
relative to the mesh spacing. A value of 0 disables all scaling. The default value is
0.9.
The style to use for the plot can be defined with a line style style of the same format
as the plot command. If a marker is specified then markers at the grid points of the
310 GNU Octave
vectors are drawn rather than arrows. If the argument "filled" is given then the
markers are filled.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to a quiver object. A quiver object
regroups the components of the quiver plot (body, arrow, and marker), and allows
them to be changed together.
[x, y, z] = peaks (25);
surf (x, y, z);
hold on;
[u, v, w] = surfnorm (x, y, z / 10);
h = quiver3 (x, y, z, u, v, w);
set (h, "maxheadsize", 0.33);
See also: [quiver], page 308,[compass], page 310,[feather], page 310,[plot], page 286.
compass (u,v)
compass (z)
compass (. . ., style)
compass (hax, . . . )
h= compass (. . . )
Plot the (u,v)components of a vector field emanating from the origin of a polar
plot.
The arrow representing each vector has one end at the origin and the tip at [u(i),
v(i)]. If a single complex argument zis given, then u= real (z)and v= imag (z).
The style to use for the plot can be defined with a line style style of the same format
as the plot command.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the line objects repre-
senting the drawn vectors.
a = toeplitz ([1;randn(9,1)], [1,randn(1,9)]);
compass (eig (a));
See also: [polar], page 307,[feather], page 310,[quiver], page 308,[rose], page 299,
[plot], page 286.
feather (u,v)
feather (z)
feather (. . ., style)
feather (hax, . . . )
h= feather (. . . )
Plot the (u,v)components of a vector field emanating from equidistant points on
the x-axis.
If a single complex argument zis given, then u= real (z)and v= imag (z).
The style to use for the plot can be defined with a line style style of the same format
as the plot command.
Chapter 15: Plotting 311
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the line objects repre-
senting the drawn vectors.
phi = [0 : 15 : 360] * pi/180;
feather (sin (phi), cos (phi));
See also: [plot], page 286,[quiver], page 308,[compass], page 310.
pcolor (x,y,c)
pcolor (c)
pcolor (hax, . . . )
h= pcolor (. . . )
Produce a 2-D density plot.
Apcolor plot draws rectangles with colors from the matrix cover the two-dimensional
region represented by the matrices xand y.xand yare the coordinates of the mesh’s
vertices and are typically the output of meshgrid. If xand yare vectors, then a typical
vertex is (x(j), y(i), c(i,j)). Thus, columns of ccorrespond to different xvalues and
rows of ccorrespond to different yvalues.
The values in care scaled to span the range of the current colormap. Limits may be
placed on the color axis by the command caxis, or by setting the clim property of
the parent axis.
The face color of each cell of the mesh is determined by interpolating the values of c
for each of the cell’s vertices; Contrast this with imagesc which renders one cell for
each element of c.
shading modifies an attribute determining the manner by which the face color of
each cell is interpolated from the values of c, and the visibility of the cells’ edges. By
default the attribute is "faceted", which renders a single color for each cell’s face
with the edge visible.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
See also: [caxis], page 315,[shading], page 340,[meshgrid], page 337,[contour],
page 300,[imagesc], page 748.
area (y)
area (x,y)
area (. . ., lvl)
area (. . ., prop,val, . . .)
area (hax, . . . )
h= area (. . . )
Area plot of the columns of y.
This plot shows the contributions of each column value to the row sum. It is func-
tionally similar to plot (x, cumsum (y, 2)), except that the area under the curve is
shaded.
312 GNU Octave
If the xargument is omitted it defaults to 1:rows (y). A value lvl can be defined
that determines where the base level of the shading under the curve should be defined.
The default level is 0.
Additional property/value pairs are passed directly to the underlying patch object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the hggroup object comprising
the area patch objects. The "BaseValue" property of the hggroup can be used to
adjust the level where shading begins.
Example: Verify identity sin^2+cos^2 = 1
t = linspace (0, 2*pi, 100)’;
y = [sin(t).^2, cos(t).^2];
area (t, y);
legend ("sin^2", "cos^2", "location", "NorthEastOutside");
See also: [plot], page 286,[patch], page 376.
fill (x,y,c)
fill (x1,y1,c1,x2,y2,c2)
fill (. . ., prop,val)
fill (hax, . . . )
h= fill (. . . )
Create one or more filled 2-D polygons.
The inputs xand yare the coordinates of the polygon vertices. If the inputs are ma-
trices then the rows represent different vertices and each column produces a different
polygon. fill will close any open polygons before plotting.
The input cdetermines the color of the polygon. The simplest form is a single color
specification such as a plot format or an RGB-triple. In this case the polygon(s) will
have one unique color. If cis a vector or matrix then the color data is first scaled
using caxis and then indexed into the current colormap. A row vector will color each
polygon (a column from matrices xand y) with a single computed color. A matrix c
of the same size as xand ywill compute the color of each vertex and then interpolate
the face color between the vertices.
Multiple property/value pairs for the underlying patch object may be specified, but
they must appear in pairs.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the created patch
objects.
Example: red square
Chapter 15: Plotting 313
vertices = [0 0
1 0
1 1
0 1];
fill (vertices(:,1), vertices(:,2), "r");
axis ([-0.5 1.5, -0.5 1.5])
axis equal
See also: [patch], page 376,[caxis], page 315,[colormap], page 751.
comet (y)
comet (x,y)
comet (x,y,p)
comet (hax, . . . )
Produce a simple comet style animation along the trajectory provided by the input
coordinate vectors (x,y).
If xis not specified it defaults to the indices of y.
The speed of the comet may be controlled by p, which represents the time each point
is displayed before moving to the next one. The default for pis 0.1 seconds.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [comet3], page 313.
comet3 (z)
comet3 (x,y,z)
comet3 (x,y,z,p)
comet3 (hax, . . . )
Produce a simple comet style animation along the trajectory provided by the input
coordinate vectors (x,y,z).
If only zis specified then x,ydefault to the indices of z.
The speed of the comet may be controlled by p, which represents the time each point
is displayed before moving to the next one. The default for pis 0.1 seconds.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [comet], page 313.
15.2.1.1 Axis Configuration
The axis function may be used to change the axis limits of an existing plot and various
other axis properties, such as the aspect ratio and the appearance of tic marks.
axis ()
axis ([x_lo x_hi])
axis ([x_lo x_hi y_lo y_hi])
axis ([x_lo x_hi y_lo y_hi z_lo z_hi])
axis ([x_lo x_hi y_lo y_hi z_lo z_hi c_lo c_hi])
axis (option)
314 GNU Octave
axis (option1,option2, . . . )
axis (hax, . . . )
limits = axis ()
Set axis limits and appearance.
The argument limits should be a 2-, 4-, 6-, or 8-element vector. The first and second
elements specify the lower and upper limits for the x-axis. The third and fourth
specify the limits for the y-axis, the fifth and sixth specify the limits for the z-axis,
and the seventh and eighth specify the limits for the color axis. The special values
-Inf and Inf may be used to indicate that the limit should be automatically computed
based on the data in the axis.
Without any arguments, axis turns autoscaling on.
With one output argument, limits = axis returns the current axis limits.
The vector argument specifying limits is optional, and additional string arguments
may be used to specify various axis properties.
The following options control the aspect ratio of the axes.
"square" Force a square axis aspect ratio.
"equal" Force x-axis unit distance to equal y-axis (and z-axis) unit distance.
"normal" Restore default aspect ratio.
The following options control the way axis limits are interpreted.
"auto"
"auto[xyz]"
Set the specified axes to have nice limits around the data or all if no axes
are specified.
"manual" Fix the current axes limits.
"tight" Fix axes to the limits of the data.
"image" Equivalent to "tight" and "equal".
The following options affect the appearance of tick marks.
"tic[xyz]"
Turn tick marks on for all axes, or turn them on for the specified axes
and off for the remainder.
"label[xyz]"
Turn tick labels on for all axes, or turn them on for the specified axes
and off for the remainder.
"nolabel"
Turn tick labels off for all axes.
Note: If there are no tick marks for an axis then there can be no labels.
The following options affect the direction of increasing values on the axes.
"xy" Default y-axis, larger values are near the top.
"ij" Reverse y-axis, smaller values are near the top.
Chapter 15: Plotting 315
The following options affects the visibility of the axes.
"on" Make the axes visible.
"off" Hide the axes.
If the first argument hax is an axes handle, then operate on this axes rather than the
current axes returned by gca.
Example 1: set X/Y limits and force a square aspect ratio
axis ([1, 2, 3, 4], "square");
Example 2: enable tick marks on all axes, enable tick mark labels only on the y-axis
axis ("tic", "labely");
See also: [xlim], page 315,[ylim], page 315,[zlim], page 315,[caxis], page 315,
[daspect], page 342,[pbaspect], page 342,[box], page 350,[grid], page 351.
Similarly the axis limits of the colormap can be changed with the caxis function.
caxis ([cmin cmax])
caxis ("auto")
caxis ("manual")
caxis (hax, . . . )
limits = caxis ()
Query or set color axis limits for plots.
The limits argument should be a 2-element vector specifying the lower and upper
limits to assign to the first and last value in the colormap. Data values outside this
range are clamped to the first and last colormap entries.
If the "auto" option is given then automatic colormap limits are applied. The au-
tomatic algorithm sets cmin to the minimum data value and cmax to the maximum
data value. If "manual" is specified then the "climmode" property is set to "manual"
and the numeric values in the "clim" property are used for limits.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
Called without arguments the current color axis limits are returned.
Programming Note: The color axis affects the display of image, patch, and sur-
face graphics objects, but only if the "cdata" property has indexed data and the
"cdatamapping" property is set to "scaled". Graphic objects with true color cdata,
or "direct" cdatamapping are not affected.
See also: [colormap], page 751,[axis], page 313.
The xlim,ylim, and zlim functions may be used to get or set individual axis limits.
Each has the same form.
xlimits = xlim ()
xmode = xlim ("mode")
xlim ([x_lo x_hi])
xlim ("auto")
xlim ("manual")

316 GNU Octave
xlim (hax, . . . )
Query or set the limits of the x-axis for the current plot.
Called without arguments xlim returns the x-axis limits of the current plot.
With the input query "mode", return the current x-limit calculation mode which is
either "auto" or "manual".
If passed a 2-element vector [x lo x hi], the limits of the x-axis are set to these values
and the mode is set to "manual". The special values -Inf and Inf can be used to
indicate that either the lower axis limit or upper axis limit should be automatically
calculated.
The current plotting mode can be changed by using either "auto" or "manual" as
the argument.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
Programming Note: The xlim function operates by modifying the "xlim" and
"xlimmode" properties of an axes object. These properties can be be directly
inspected and altered with get/set.
See also: [ylim], page 315,[zlim], page 315,[axis], page 313,[set], page 381,[get],
page 381,[gca], page 379.
15.2.1.2 Two-dimensional Function Plotting
Octave can plot a function from a function handle, inline function, or string defining the
function without the user needing to explicitly create the data to be plotted. The function
fplot also generates two-dimensional plots with linear axes using a function name and
limits for the range of the x-coordinate instead of the x and y data. For example,
fplot (@sin, [-10, 10], 201);
produces a plot that is equivalent to the one above, but also includes a legend displaying
the name of the plotted function.
fplot (fn,limits)
fplot (. . ., tol)
fplot (. . ., n)
fplot (. . ., fmt)
[x,y] = fplot (. . . )
Plot a function fn within the range defined by limits.
fn is a function handle, inline function, or string containing the name of the function
to evaluate.
The limits of the plot are of the form [xlo,xhi]or [xlo,xhi,ylo,yhi].
The next three arguments are all optional and any number of them may be given in
any order.
tol is the relative tolerance to use for the plot and defaults to 2e-3 (.2%).
nis the minimum number of points to use. When nis specified, the maximum
stepsize will be xhi -xlo /n. More than npoints may still be used in order to meet
the relative tolerance requirement.
The fmt argument specifies the linestyle to be used by the plot command.
Chapter 15: Plotting 317
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
With no output arguments the results are immediately plotted. With two output
arguments the 2-D plot data is returned. The data can subsequently be plotted
manually with plot (x,y).
Example:
fplot (@cos, [0, 2*pi])
fplot ("[cos(x), sin(x)]", [0, 2*pi])
Programming Notes:
fplot works best with continuous functions. Functions with discontinuities are un-
likely to plot well. This restriction may be removed in the future.
fplot requires that the function accept and return a vector argument. Consider this
when writing user-defined functions and use .*,./, etc. See the function vectorize
for potentially converting inline or anonymous functions to vectorized versions.
See also: [ezplot], page 317,[plot], page 286,[vectorize], page 530.
Other functions that can create two-dimensional plots directly from a function include
ezplot,ezcontour,ezcontourf and ezpolar.
ezplot (f)
ezplot (f2v)
ezplot (fx,fy)
ezplot (. . ., dom)
ezplot (. . ., n)
ezplot (hax, . . . )
h= ezplot (. . . )
Plot the 2-D curve defined by the function f.
The function fmay be a string, inline function, or function handle and can have
either one or two variables. If fhas one variable, then the function is plotted over
the domain -2*pi < x< 2*pi with 500 points.
If f2v is a function of two variables then the implicit function f(x,y) = 0 is calculated
over the meshed domain -2*pi <= x|y<= 2*pi with 60 points in each dimension.
For example:
ezplot (@(x,y)x.^2 - y.^2 - 1)
If two functions are passed as inputs then the parametric function
x=fx (t)
y=fy (t)
is plotted over the domain -2*pi <= t<= 2*pi with 500 points.
If dom is a two element vector, it represents the minimum and maximum values of
both xand y, or tfor a parametric plot. If dom is a four element vector, then the
minimum and maximum values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in plotting the function.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
318 GNU Octave
The optional return value his a vector of graphics handles to the created line objects.
See also: [plot], page 286,[ezplot3], page 343,[ezpolar], page 319,[ezcontour],
page 318,[ezcontourf], page 318,[ezmesh], page 343,[ezmeshc], page 344,[ezsurf],
page 345,[ezsurfc], page 345.
ezcontour (f)
ezcontour (. . ., dom)
ezcontour (. . ., n)
ezcontour (hax, . . . )
h= ezcontour (. . . )
Plot the contour lines of a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
Example:
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezcontour (f, [-3, 3]);
See also: [contour], page 300,[ezcontourf], page 318,[ezplot], page 317,[ezmeshc],
page 344,[ezsurfc], page 345.
ezcontourf (f)
ezcontourf (. . ., dom)
ezcontourf (. . ., n)
ezcontourf (hax, . . . )
h= ezcontourf (. . . )
Plot the filled contour lines of a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
Chapter 15: Plotting 319
Example:
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezcontourf (f, [-3, 3]);
See also: [contourf], page 300,[ezcontour], page 318,[ezplot], page 317,[ezmeshc],
page 344,[ezsurfc], page 345.
ezpolar (f)
ezpolar (. . ., dom)
ezpolar (. . ., n)
ezpolar (hax, . . . )
h= ezpolar (. . . )
Plot a 2-D function in polar coordinates.
The function fis a string, inline function, or function handle with a single argument.
The expected form of the function is rho =f(theta). By default the plot is over the
domain 0 <= theta <= 2*pi with 500 points.
If dom is a two element vector, it represents the minimum and maximum values of
theta.
nis a scalar defining the number of points to use in plotting the function.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
Example:
ezpolar (@(t) sin (5/4 * t), [0, 8*pi]);
See also: [polar], page 307,[ezplot], page 317.
15.2.1.3 Two-dimensional Geometric Shapes
rectangle ()
rectangle (. . ., "Position",pos)
rectangle (. . ., "Curvature",curv)
rectangle (. . ., "EdgeColor",ec)
rectangle (. . ., "FaceColor",fc)
rectangle (hax, . . . )
h= rectangle (. . . )
Draw a rectangular patch defined by pos and curv.
The variable pos(1:2) defines the lower left-hand corner of the patch and pos(3:4)
defines its width and height. By default, the value of pos is [0, 0, 1, 1].
The variable curv defines the curvature of the sides of the rectangle and may be a
scalar or two-element vector with values between 0 and 1. A value of 0 represents
no curvature of the side, whereas a value of 1 means that the side is entirely curved
into the arc of a circle. If curv is a two-element vector, then the first element is the
curvature along the x-axis of the patch and the second along y-axis.
If curv is a scalar, it represents the curvature of the shorter of the two sides of the
rectangle and the curvature of the other side is defined by
min (pos(1:2)) / max (pos(1:2)) * curv
320 GNU Octave
Additional property/value pairs are passed to the underlying patch command.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created rectangle object.
See also: [patch], page 376,[line], page 376,[cylinder], page 346,[ellipsoid], page 347,
[sphere], page 347.
15.2.2 Three-Dimensional Plots
The function mesh produces mesh surface plots. For example,
tx = ty = linspace (-8, 8, 41)’;
[xx, yy] = meshgrid (tx, ty);
r = sqrt (xx .^ 2 + yy .^ 2) + eps;
tz = sin (r) ./ r;
mesh (tx, ty, tz);
xlabel ("tx");
ylabel ("ty");
zlabel ("tz");
title ("3-D Sombrero plot");
produces the familiar “sombrero” plot shown in Figure 15.5. Note the use of the function
meshgrid to create matrices of X and Y coordinates to use for plotting the Z data. The
ndgrid function is similar to meshgrid, but works for N-dimensional matrices.
-5
ty 0
5
10
-10 -10
-0.4
tx
-0.2
0
tz
0.2
0.4
0.6
0.8
1
-5 0510
3-D Sombrero plot
Figure 15.5: Mesh plot.
The meshc function is similar to mesh, but also produces a plot of contours for the
surface.
The plot3 function displays arbitrary three-dimensional data, without requiring it to
form a surface. For example,
Chapter 15: Plotting 321
t = 0:0.1:10*pi;
r = linspace (0, 1, numel (t));
z = linspace (0, 1, numel (t));
plot3 (r.*sin (t), r.*cos (t), z);
xlabel ("r.*sin (t)");
ylabel ("r.*cos (t)");
zlabel ("z");
title ("plot3 display of 3-D helix");
displays the spiral in three dimensions shown in Figure 15.6.
r.*cos (t) r.*sin (t)
-0.5
0
0.5
1
-1 -1
0
0.2
-0.5
0.4
z
0.6
0.8
1
plot3 display of 3-D helix
00.5 1
Figure 15.6: Three-dimensional spiral.
Finally, the view function changes the viewpoint for three-dimensional plots.
mesh (x,y,z)
mesh (z)
mesh (. . ., c)
mesh (. . ., prop,val, . . .)
mesh (hax, . . . )
h= mesh (. . . )
Plot a 3-D wireframe mesh.
The wireframe mesh is plotted using rectangles. The vertices of the rectangles [x,
y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the mesh is computed by linearly scaling the zvalues to fit the range of the
current colormap. Use caxis and/or change the colormap to control the appearance.
322 GNU Octave
Optionally, the color of the mesh can be specified independently of zby supplying a
color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
See also: [ezmesh], page 343,[meshc], page 322,[meshz], page 322,[trimesh],
page 713,[contour], page 300,[surf], page 323,[surface], page 377,[meshgrid],
page 337,[hidden], page 323,[shading], page 340,[colormap], page 751,[caxis],
page 315.
meshc (x,y,z)
meshc (z)
meshc (. . ., c)
meshc (. . ., prop,val, . . .)
meshc (hax, . . . )
h= meshc (. . . )
Plot a 3-D wireframe mesh with underlying contour lines.
The wireframe mesh is plotted using rectangles. The vertices of the rectangles [x,
y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the mesh is computed by linearly scaling the zvalues to fit the range of the
current colormap. Use caxis and/or change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of zby supplying a
color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a 2-element vector with a graphics handle to the created
surface object and to the created contour plot.
See also: [ezmeshc], page 344,[mesh], page 321,[meshz], page 322,[contour],
page 300,[surfc], page 324,[surface], page 377,[meshgrid], page 337,[hidden],
page 323,[shading], page 340,[colormap], page 751,[caxis], page 315.
meshz (x,y,z)
meshz (z)
meshz (. . ., c)
meshz (. . ., prop,val, . . .)
meshz (hax, . . . )
h= meshz (. . . )
Plot a 3-D wireframe mesh with a surrounding curtain.
Chapter 15: Plotting 323
The wireframe mesh is plotted using rectangles. The vertices of the rectangles [x,y]
are typically the output of meshgrid. over a 2-D rectangular region in the x-y plane.
zdetermines the height above the plane of each vertex. If only a single zmatrix is
given, then it is plotted over the meshgrid x= 0:columns (z) - 1, y= 0:rows (z)
- 1. Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the mesh is computed by linearly scaling the zvalues to fit the range of the
current colormap. Use caxis and/or change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of zby supplying a
color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
See also: [mesh], page 321,[meshc], page 322,[contour], page 300,[surf], page 323,
[surface], page 377,[waterfall], page 341,[meshgrid], page 337,[hidden], page 323,
[shading], page 340,[colormap], page 751,[caxis], page 315.
hidden
hidden on
hidden off
mode = hidden (. . . )
Control mesh hidden line removal.
When called with no argument the hidden line removal state is toggled.
When called with one of the modes "on" or "off" the state is set accordingly.
The optional output argument mode is the current state.
Hidden Line Removal determines what graphic objects behind a mesh plot are visible.
The default is for the mesh to be opaque and lines behind the mesh are not visible. If
hidden line removal is turned off then objects behind the mesh can be seen through
the faces (openings) of the mesh, although the mesh grid lines are still opaque.
See also: [mesh], page 321,[meshc], page 322,[meshz], page 322,[ezmesh], page 343,
[ezmeshc], page 344,[trimesh], page 713,[waterfall], page 341.
surf (x,y,z)
surf (z)
surf (. . ., c)
surf (. . ., prop,val, . . .)
surf (hax, . . . )
h= surf (. . . )
Plot a 3-D surface mesh.
The surface mesh is plotted using shaded rectangles. The vertices of the rectangles
[x,y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
324 GNU Octave
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the surface is computed by linearly scaling the zvalues to fit the range
of the current colormap. Use caxis and/or change the colormap to control the
appearance.
Optionally, the color of the surface can be specified independently of zby supplying
a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Note: The exact appearance of the surface can be controlled with the shading com-
mand or by using set to control surface object properties.
See also: [ezsurf], page 345,[surfc], page 324,[surfl], page 325,[surfnorm], page 325,
[trisurf], page 714,[contour], page 300,[mesh], page 321,[surface], page 377,
[meshgrid], page 337,[hidden], page 323,[shading], page 340,[colormap], page 751,
[caxis], page 315.
surfc (x,y,z)
surfc (z)
surfc (. . ., c)
surfc (. . ., prop,val, . . .)
surfc (hax, . . . )
h= surfc (. . . )
Plot a 3-D surface mesh with underlying contour lines.
The surface mesh is plotted using shaded rectangles. The vertices of the rectangles
[x,y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the surface is computed by linearly scaling the zvalues to fit the range
of the current colormap. Use caxis and/or change the colormap to control the
appearance.
Optionally, the color of the surface can be specified independently of zby supplying
a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Note: The exact appearance of the surface can be controlled with the shading com-
mand or by using set to control surface object properties.
See also: [ezsurfc], page 345,[surf], page 323,[surfl], page 325,[surfnorm], page 325,
[trisurf], page 714,[contour], page 300,[mesh], page 321,[surface], page 377,
Chapter 15: Plotting 325
[meshgrid], page 337,[hidden], page 323,[shading], page 340,[colormap], page 751,
[caxis], page 315.
surfl (z)
surfl (x,y,z)
surfl (. . ., lsrc)
surfl (x,y,z,lsrc,P)
surfl (. . ., "cdata")
surfl (. . ., "light")
surfl (hax, . . . )
h= surfl (. . . )
Plot a 3-D surface using shading based on various lighting models.
The surface mesh is plotted using shaded rectangles. The vertices of the rectangles
[x,y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The default lighting mode "cdata", changes the cdata property of the surface object
to give the impression of a lighted surface. Warning: The alternative mode "light"
mode which creates a light object to illuminate the surface is not implemented (yet).
The light source location can be specified using lsrc. It can be given as a 2-element
vector [azimuth, elevation] in degrees, or as a 3-element vector [lx, ly, lz]. The default
value is rotated 45 degrees counterclockwise to the current view.
The material properties of the surface can specified using a 4-element vector P=
[AM D SP exp] which defaults to p= [0.55 0.6 0.4 10].
"AM" strength of ambient light
"D" strength of diffuse reflection
"SP" strength of specular reflection
"EXP" specular exponent
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Example:
colormap (bone (64));
surfl (peaks);
shading interp;
See also: [diffuse], page 334,[specular], page 334,[surf], page 323,[shading], page 340,
[colormap], page 751,[caxis], page 315.
surfnorm (x,y,z)
surfnorm (z)
surfnorm (. . ., prop,val, . . .)
surfnorm (hax, . . . )
326 GNU Octave
[nx,ny,nz] = surfnorm (. . . )
Find the vectors normal to a meshgridded surface.
If xand yare vectors, then a typical vertex is (x(j), y(i), z(i,j)). Thus, columns of
zcorrespond to different xvalues and rows of zcorrespond to different yvalues. If
only a single input zis given then xis taken to be 1:rows (z)and yis 1:columns
(z).
If no return arguments are requested, a surface plot with the normal vectors to the
surface is plotted.
Any property/value input pairs are assigned to the surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
If output arguments are requested then the components of the normal vectors are
returned in nx,ny, and nz and no plot is made. The normal vectors are unnormalized
(magnitude != 1). To normalize, use
mag = sqrt (nx.^2 + ny.^2 + nz.^2);
nx ./= len; ny ./= len; nz ./= len;
An example of the use of surfnorm is
surfnorm (peaks (25));
Algorithm: The normal vectors are calculated by taking the cross product of the
diagonals of each of the quadrilateral faces in the meshgrid to find the normal vectors
at the center of each face. Next, for each meshgrid point the four nearest normal
vectors are averaged to obtain the final normal to the surface at the meshgrid point.
For surface objects, the "VertexNormals" property contains equivalent information,
except possibly near the boundary of the surface where different interpolation schemes
may yield slightly different values.
See also: [isonormals], page 328,[quiver3], page 309,[surf], page 323,[meshgrid],
page 337.
fv = isosurface (v,isoval)
fv = isosurface (v)
fv = isosurface (x,y,z,v,isoval)
fv = isosurface (x,y,z,v)
fvc = isosurface (. . . , col)
fv = isosurface (. . . , "noshare")
fv = isosurface (. . . , "verbose")
[f,v] = isosurface (. . . )
[f,v,c] = isosurface (. . . )
isosurface (. . .)
Calculate isosurface of 3-D volume data.
An isosurface connects points with the same value and is analogous to a contour plot,
but in three dimensions.
The input argument vis a three-dimensional array that contains data sampled over
a volume.
Chapter 15: Plotting 327
The input isoval is a scalar that specifies the value for the isosurface. If isoval is
omitted or empty, a "good"value for an isosurface is determined from v.
When called with a single output argument isosurface returns a structure array
fv that contains the fields faces and vertices computed at the points [x,y,z] =
meshgrid (1:l, 1:m, 1:n) where [l, m, n] = size (v). The output fv can be used
directly as input to the patch function.
If called with additional input arguments x,y, and zthat are three-dimensional arrays
with the same size as vor vectors with lengths corresponding to the dimensions of v,
then the volume data is taken at the specified points. If x,y, or zare empty, the grid
corresponds to the indices (1:n) in the respective direction (see [meshgrid], page 337).
The optional input argument col, which is a three-dimensional array of the same size
as v, specifies coloring of the isosurface. The color data is interpolated, as necessary,
to match isoval. The output structure array, in this case, has the additional field
facevertexcdata.
If given the string input argument "noshare", vertices may be returned multiple times
for different faces. The default behavior is to eliminate vertices shared by adjacent
faces with unique which may be time consuming.
The string input argument "verbose" is supported for matlab compatibility, but
has no effect.
Any string arguments must be passed after the other arguments.
If called with two or three output arguments, return the information about the faces
f, vertices v, and color data cas separate arrays instead of a single structure array.
If called with no output argument, the isosurface geometry is directly plotted with
the patch command and a light object is added to the axes if not yet present.
For example,
[x, y, z] = meshgrid (1:5, 1:5, 1:5);
v = rand (5, 5, 5);
isosurface (x, y, z, v, .5);
will directly draw a random isosurface geometry in a graphics window.
An example of an isosurface geometry with different additional coloring:
N = 15; # Increase number of vertices in each direction
iso = .4; # Change isovalue to .1 to display a sphere
lin = linspace (0, 2, N);
[x, y, z] = meshgrid (lin, lin, lin);
v = abs ((x-.5).^2 + (y-.5).^2 + (z-.5).^2);
figure ();
subplot (2,2,1); view (-38, 20);
[f, vert] = isosurface (x, y, z, v, iso);
p = patch ("Faces", f, "Vertices", vert, "EdgeColor", "none");
pbaspect ([1 1 1]);
isonormals (x, y, z, v, p)
set (p, "FaceColor", "green", "FaceLighting", "gouraud");
light ("Position", [1 1 5]);
subplot (2,2,2); view (-38, 20);
p = patch ("Faces", f, "Vertices", vert, "EdgeColor", "blue");
pbaspect ([1 1 1]);
328 GNU Octave
isonormals (x, y, z, v, p)
set (p, "FaceColor", "none", "EdgeLighting", "gouraud");
light ("Position", [1 1 5]);
subplot (2,2,3); view (-38, 20);
[f, vert, c] = isosurface (x, y, z, v, iso, y);
p = patch ("Faces", f, "Vertices", vert, "FaceVertexCData", c, ...
"FaceColor", "interp", "EdgeColor", "none");
pbaspect ([1 1 1]);
isonormals (x, y, z, v, p)
set (p, "FaceLighting", "gouraud");
light ("Position", [1 1 5]);
subplot (2,2,4); view (-38, 20);
p = patch ("Faces", f, "Vertices", vert, "FaceVertexCData", c, ...
"FaceColor", "interp", "EdgeColor", "blue");
pbaspect ([1 1 1]);
isonormals (x, y, z, v, p)
set (p, "FaceLighting", "gouraud");
light ("Position", [1 1 5]);
See also: [isonormals], page 328,[isocolors], page 330,[isocaps], page 329,[smooth3],
page 331,[reducevolume], page 332,[reducepatch], page 332,[patch], page 376.
[vn] = isonormals (val,vert)
[vn] = isonormals (val,hp)
[vn] = isonormals (x,y,z,val,vert)
[vn] = isonormals (x,y,z,val,hp)
[vn] = isonormals (. . . , "negate")
isonormals (val,hp)
isonormals (x,y,z,val,hp)
isonormals (. . ., "negate")
Calculate normals to an isosurface.
The vertex normals vn are calculated from the gradient of the 3-dimensional array val
(size: lxmxn) with the data for an isosurface geometry. The normals point towards
lower values in val.
If called with one output argument vn and the second input argument vert holds
the vertices of an isosurface, the normals vn are calculated at the vertices vert on a
grid given by [x, y, z] = meshgrid (1:l, 1:m, 1:n). The output argument vn has
the same size as vert and can be used to set the "VertexNormals" property of the
corresponding patch.
If called with further input arguments x,y, and zwhich are 3-dimensional arrays
with the same size as val, the volume data is taken at these points. Instead of the
vertex data vert, a patch handle hp can be passed to this function.
If the last input argument is the string "negate", compute the reverse vector normals
of an isosurface geometry (i.e., pointed towards higher values in val).
If no output argument is given, the property "VertexNormals" of the patch associated
with the patch handle hp is changed directly.
See also: [isosurface], page 326,[isocolors], page 330,[smooth3], page 331.

Chapter 15: Plotting 329
fvc = isocaps (v,isoval)
fvc = isocaps (v)
fvc = isocaps (x,y,z,v,isoval)
fvc = isocaps (x,y,z,v)
fvc = isocaps (. . . , which_caps)
fvc = isocaps (. . . , which_plane)
fvc = isocaps (. . . , "verbose")
[faces,vertices,fvcdata] = isocaps (. . . )
isocaps (. . .)
Create end-caps for isosurfaces of 3-D data.
This function places caps at the open ends of isosurfaces.
The input argument vis a three-dimensional array that contains data sampled over
a volume.
The input isoval is a scalar that specifies the value for the isosurface. If isoval is
omitted or empty, a "good"value for an isosurface is determined from v.
When called with a single output argument, isocaps returns a structure array fvc
with the fields: faces,vertices, and facevertexcdata. The results are computed
at the points [x,y,z] = meshgrid (1:l, 1:m, 1:n) where [l, m, n] = size (v).
The output fvc can be used directly as input to the patch function.
If called with additional input arguments x,y, and zthat are three-dimensional arrays
with the same size as vor vectors with lengths corresponding to the dimensions of v,
then the volume data is taken at the specified points. If x,y, or zare empty, the grid
corresponds to the indices (1:n) in the respective direction (see [meshgrid], page 337).
The optional parameter which caps can have one of the following string values which
defines how the data will be enclosed:
"above","a" (default)
for end-caps that enclose the data above isoval.
"below","b"
for end-caps that enclose the data below isoval.
The optional parameter which plane can have one of the following string values to
define which end-cap should be drawn:
"all" (default)
for all of the end-caps.
"xmin" for end-caps at the lower x-plane of the data.
"xmax" for end-caps at the upper x-plane of the data.
"ymin" for end-caps at the lower y-plane of the data.
"ymax" for end-caps at the upper y-plane of the data.
"zmin" for end-caps at the lower z-plane of the data.
"zmax" for end-caps at the upper z-plane of the data.
330 GNU Octave
The string input argument "verbose" is supported for matlab compatibility, but
has no effect.
If called with two or three output arguments, the data for faces faces, vertices vertices,
and the color data facevertexcdata are returned in separate arrays instead of a single
structure.
If called with no output argument, the end-caps are drawn directly in the current
figure with the patch command.
See also: [isosurface], page 326,[isonormals], page 328,[patch], page 376.
[cd] = isocolors (c,v)
[cd] = isocolors (x,y,z,c,v)
[cd] = isocolors (x,y,z,r,g,b,v)
[cd] = isocolors (r,g,b,v)
[cd] = isocolors (. . . , p)
isocolors (. . .)
Compute isosurface colors.
If called with one output argument and the first input argument cis a
three-dimensional array that contains color values and the second input argument v
keeps the vertices of a geometry then return a matrix cd with color data information
for the geometry at computed points [x, y, z] = meshgrid (1:l, 1:m, 1:n). The
output argument cd can be taken to manually set FaceVertexCData of a patch.
If called with further input arguments x,yand zwhich are three–dimensional arrays
of the same size than cthen the color data is taken at those given points. Instead
of the color data cthis function can also be called with RGB values r,g,b. If input
argumnets x,y,zare not given then again meshgrid computed values are taken.
Optionally, the patch handle pcan be given as the last input argument to all variations
of function calls instead of the vertices data v. Finally, if no output argument is given
then directly change the colors of a patch that is given by the patch handle p.
For example:
function isofinish (p)
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
set (p, "FaceColor", "interp");
## set (p, "FaceLighting", "flat");
## light ("Position", [1 1 5]); # Available with JHandles
endfunction
N = 15; # Increase number of vertices in each direction
iso = .4; # Change isovalue to .1 to display a sphere
lin = linspace (0, 2, N);
[x, y, z] = meshgrid (lin, lin, lin);
c = abs ((x-.5).^2 + (y-.5).^2 + (z-.5).^2);
figure (); # Open another figure window
subplot (2,2,1); view (-38, 20);

Chapter 15: Plotting 331
[f, v] = isosurface (x, y, z, c, iso);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
cdat = rand (size (c)); # Compute random patch color data
isocolors (x, y, z, cdat, p); # Directly set colors of patch
isofinish (p); # Call user function isofinish
subplot (2,2,2); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
[r, g, b] = meshgrid (lin, 2-lin, 2-lin);
cdat = isocolors (x, y, z, c, v); # Compute color data vertices
set (p, "FaceVertexCData", cdat); # Set color data manually
isofinish (p);
subplot (2,2,3); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
cdat = isocolors (r, g, b, c, p); # Compute color data patch
set (p, "FaceVertexCData", cdat); # Set color data manually
isofinish (p);
subplot (2,2,4); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
r = g = b = repmat ([1:N] / N, [N, 1, N]); # Black to white
cdat = isocolors (x, y, z, r, g, b, v);
set (p, "FaceVertexCData", cdat);
isofinish (p);
See also: [isosurface], page 326,[isonormals], page 328.
smoothed_data = smooth3 (data)
smoothed_data = smooth3 (data,method)
smoothed_data = smooth3 (data,method,sz)
smoothed_data = smooth3 (data,method,sz,std_dev)
Smooth values of 3-dimensional matrix data.
This function can be used, for example, to reduce the impact of noise in data before
calculating isosurfaces.
data must be a non-singleton 3-dimensional matrix. The smoothed data from this
matrix is returned in smoothed data which is of the same size as data.
The option input method determines which convolution kernel is used for the smooth-
ing process. Possible choices:
"box","b" (default)
to use a convolution kernel with sharp edges.
"gaussian","g"
to use a convolution kernel that is represented by a non-correlated trivari-
ate normal distribution function.

332 GNU Octave
sz is either a vector of 3 elements representing the size of the convolution kernel in
x-, y- and z-direction or a scalar, in which case the same size is used in all three
dimensions. The default value is 3.
When method is "gaussian",std dev defines the standard deviation of the trivariate
normal distribution function. std dev is either a vector of 3 elements representing
the standard deviation of the Gaussian convolution kernel in x-, y- and z-directions
or a scalar, in which case the same value is used in all three dimensions. The default
value is 0.65.
See also: [isosurface], page 326,[isonormals], page 328,[patch], page 376.
[nx,ny,nz,nv] = reducevolume (v,r)
[nx,ny,nz,nv] = reducevolume (x,y,z,v,r)
nv = reducevolume (. . . )
Reduce the volume of the dataset in vaccording to the values in r.
vis a matrix that is non-singleton in the first 3 dimensions.
rcan either be a vector of 3 elements representing the reduction factors in the x-,
y-, and z-directions or a scalar, in which case the same reduction factor is used in all
three dimensions.
reducevolume reduces the number of elements of vby taking only every r-th element
in the respective dimension.
Optionally, x,y, and zcan be supplied to represent the set of coordinates of v.
They can either be matrices of the same size as vor vectors with sizes according to
the dimensions of v, in which case they are expanded to matrices (see [meshgrid],
page 337).
If reducevolume is called with two arguments then x,y, and zare assumed to match
the respective indices of v.
The reduced matrix is returned in nv.
Optionally, the reduced set of coordinates are returned in nx,ny, and nz, respectively.
Examples:
v= reshape (1:6*8*4, [6 8 4]);
nv = reducevolume (v, [4 3 2]);
v= reshape (1:6*8*4, [6 8 4]);
x= 1:3:24; y= -14:5:11; z= linspace (16, 18, 4);
[nx,ny,nz,nv] = reducevolume (x,y,z,v, [4 3 2]);
See also: [isosurface], page 326,[isonormals], page 328.
reduced_fv = reducepatch (fv)
reduced_fv = reducepatch (faces,vertices)
reduced_fv = reducepatch (patch_handle)
reducepatch (patch_handle)
reduced_fv = reducepatch (. . . , reduction_factor)
reduced_fv = reducepatch (. . . , "fast")
reduced_fv = reducepatch (. . . , "verbose")
Chapter 15: Plotting 333
[reduced_faces,reduces_vertices] = reducepatch (. . . )
Reduce the number of faces and vertices in a patch object while retaining the overall
shape of the patch.
The input patch can be represented by a structure fv with the fields faces and
vertices, by two matrices faces and vertices (see, e.g., the result of isosurface), or
by a handle to a patch object patch handle (see [patch], page 376).
The number of faces and vertices in the patch is reduced by iteratively collapsing the
shortest edge of the patch to its midpoint (as discussed, e.g., here: http://libigl.
github.io/libigl/tutorial/tutorial.html#meshdecimation).
Currently, only patches consisting of triangles are supported. The resulting patch
also consists only of triangles.
If reducepatch is called with a handle to a valid patch patch handle, and without
any output arguments, then the given patch is updated immediately.
If the reduction factor is omitted, the resulting structure reduced fv includes ap-
proximately 50% of the faces of the original patch. If reduction factor is a fraction
between 0 (excluded) and 1 (excluded), a patch with approximately the corresponding
fraction of faces is determined. If reduction factor is an integer greater than or equal
to 1, the resulting patch has approximately reduction factor faces. Depending on the
geometry of the patch, the resulting number of faces can differ from the given value
of reduction factor. This is especially true when many shared vertices are detected.
For the reduction, it is necessary that vertices of touching faces are shared. Shared
vertices are detected automatically. This detection can be skipped by passing the
optional string argument "fast".
With the optional string arguments "verbose", additional status messages are printed
to the command window.
Any string input arguments must be passed after all other arguments.
If called with one output argument, the reduced faces and vertices are returned in a
structure reduced fv with the fields faces and vertices (see the one output option
of isosurface).
If called with two output arguments, the reduced faces and vertices are returned in
two separate matrices reduced faces and reduced vertices.
See also: [isosurface], page 326,[isonormals], page 328,[reducevolume], page 332,
[patch], page 376.
shrinkfaces (p,sf)
nfv = shrinkfaces (p,sf)
nfv = shrinkfaces (fv,sf)
nfv = shrinkfaces (f,v,sf)
[nf,nv] = shrinkfaces (. . . )
Reduce the size of faces in a patch by the shrink factor sf.
The patch object can be specified by a graphics handle (p), a patch structure (fv)
with the fields "faces" and "vertices", or as two separate matrices (f,v) of faces
and vertices.
The shrink factor sf is a positive number specifying the percentage of the original
area the new face will occupy. If no factor is given the default is 0.3 (a reduction to
334 GNU Octave
30% of the original size). A factor greater than 1.0 will result in the expansion of
faces.
Given a patch handle as the first input argument and no output parameters, perform
the shrinking of the patch faces in place and redraw the patch.
If called with one output argument, return a structure with fields "faces",
"vertices", and "facevertexcdata" containing the data after shrinking. This
structure can be used directly as an input argument to the patch function.
Caution:: Performing the shrink operation on faces which are not convex can lead to
undesirable results.
Example: a triangulated 3/4 circle and the corresponding shrunken version.
[phi r] = meshgrid (linspace (0, 1.5*pi, 16), linspace (1, 2, 4));
tri = delaunay (phi(:), r(:));
v = [r(:).*sin(phi(:)) r(:).*cos(phi(:))];
clf ()
p = patch ("Faces", tri, "Vertices", v, "FaceColor", "none");
fv = shrinkfaces (p);
patch (fv)
axis equal
grid on
See also: [patch], page 376.
diffuse (sx,sy,sz,lv)
Calculate the diffuse reflection strength of a surface defined by the normal vector
elements sx,sy,sz.
The light source location vector lv can be given as a 2-element vector [azimuth,
elevation] in degrees or as a 3-element vector [x, y, z].
See also: [specular], page 334,[surfl], page 325.
specular (sx,sy,sz,lv,vv)
specular (sx,sy,sz,lv,vv,se)
Calculate the specular reflection strength of a surface defined by the normal vector
elements sx,sy,sz using Phong’s approximation.
The light source location and viewer location vectors are specified using parameters
lv and vv respectively. The location vectors can given as 2-element vectors [azimuth,
elevation] in degrees or as 3-element vectors [x, y, z].
An optional sixth argument specifies the specular exponent (spread) se. If not given,
se defaults to 10.
See also: [diffuse], page 334,[surfl], page 325.
lighting (type)
lighting (hax,type)
Set the lighting of patch or surface graphic objects.
Valid arguments for type are
"flat" Draw objects with faceted lighting effects.

Chapter 15: Plotting 335
"gouraud"
Draw objects with linear interpolation of the lighting effects between the
vertices.
"none" Draw objects without light and shadow effects.
If the first argument hax is an axes handle, then change the lighting effects of objects
in this axis, rather than the current axes returned by gca.
The lighting effects are only visible if at least one light object is present and visible
in the same axes.
See also: [light], page 377,[fill], page 312,[mesh], page 321,[patch], page 376,[pcolor],
page 311,[surf], page 323,[surface], page 377,[shading], page 340.
material shiny
material dull
material metal
material default
material ([as,ds,ss])
material ([as,ds,ss,se])
material ([as,ds,ss,se,scr])
material (hlist, . . . )
mtypes = material ()
refl_props = material (mtype_string)
Set reflectance properties for the lighting of surfaces and patches.
This function changes the ambient, diffuse, and specular strengths, as well as the
specular exponent and specular color reflectance, of all patch and surface objects
in the current axes. This can be used to simulate, to some extent, the reflectance
properties of certain materials when used with light.
When called with a string, the aforementioned properties are set according to the
values in the following table:
mtype ambient-
strength
diffuse-
strength
specular-
strength
specular-
exponent
specular-
color-
reflectance
"shiny" 0.3 0.6 0.9 20 1.0
"dull" 0.3 0.8 0.0 10 1.0
"metal" 0.3 0.3 1.0 25 0.5
"default" "default" "default" "default" "default" "default"
When called with a vector of three elements, the ambient, diffuse, and specular
strengths of all patch and surface objects in the current axes are updated. An
optional fourth vector element updates the specular exponent, and an optional fifth
vector element updates the specular color reflectance.
A list of graphic handles can also be passed as the first argument. In this case, the
properties of these handles and all child patch and surface objects will be updated.
Additionally, material can be called with a single output argument. If called without
input arguments, a column cell vector mtypes with the strings for all available mate-
rials is returned. If the one input argument mtype string is the name of a material, a

336 GNU Octave
1x5 cell vector refl props with the reflectance properties of that material is returned.
In both cases, no graphic properties are changed.
See also: [light], page 377,[fill], page 312,[mesh], page 321,[patch], page 376,[pcolor],
page 311,[surf], page 323,[surface], page 377.
camlight
camlight right
camlight left
camlight headlight
camlight (az,el)
camlight (. . ., style)
camlight (hl, . . . )
h= camlight (. . . )
Add a light object to a figure using a simple interface.
When called with no arguments, a light object is added to the current plot and is
placed slightly above and to the right of the camera’s current position: this is equiv-
alent to camlight right. The commands camlight left and camlight headlight
behave similarly with the placement being either left of the camera position or cen-
tered on the camera position.
For more control, the light position can be specified by an azimuthal rotation az and
an elevation angle el, both in degrees, relative to the current properties of the camera.
The optional string style specifies whether the light is a local point source ("local",
the default) or placed at infinite distance ("infinite").
If the first argument hl is a handle to a light object, then act on this light object
rather than creating a new object.
The optional return value his a graphics handle to the light object. This can be used
to move or further change properties of the light object.
Examples:
Add a light object to a plot
sphere (36);
camlight
Position the light source exactly
camlight (45, 30);
Here the light is first pitched upwards from the camera position by 30 degrees. It is
then yawed by 45 degrees to the right. Both rotations are centered around the camera
target.
Return a handle to further manipulate the light object
clf
sphere (36);
hl = camlight ("left");
set (hl, "color", "r");
See also: [light], page 377.
Chapter 15: Plotting 337
[xx,yy] = meshgrid (x,y)
[xx,yy,zz] = meshgrid (x,y,z)
[xx,yy] = meshgrid (x)
[xx,yy,zz] = meshgrid (x)
Given vectors of xand ycoordinates, return matrices xx and yy corresponding to a
full 2-D grid.
The rows of xx are copies of x, and the columns of yy are copies of y. If yis omitted,
then it is assumed to be the same as x.
If the optional zinput is given, or zz is requested, then the output will be a full 3-D
grid.
meshgrid is most frequently used to produce input for a 2-D or 3-D function that will
be plotted. The following example creates a surface plot of the “sombrero” function.
f = @(x,y) sin (sqrt (x.^2 + y.^2)) ./ sqrt (x.^2 + y.^2);
range = linspace (-8, 8, 41);
[X,Y] = meshgrid (range, range);
Z = f (X, Y);
surf (X, Y, Z);
Programming Note: meshgrid is restricted to 2-D or 3-D grid generation. The ndgrid
function will generate 1-D through N-D grids. However, the functions are not com-
pletely equivalent. If xis a vector of length M and yis a vector of length N, then
meshgrid will produce an output grid which is NxM. ndgrid will produce an output
which is MxN (transpose) for the same input. Some core functions expect meshgrid
input and others expect ndgrid input. Check the documentation for the function in
question to determine the proper input format.
See also: [ndgrid], page 337,[mesh], page 321,[contour], page 300,[surf], page 323.
[y1,y2, ..., yn] = ndgrid (x1,x2, . . . , xn)
[y1,y2, ..., yn] = ndgrid (x)
Given n vectors x1, . . ., xn, ndgrid returns n arrays of dimension n.
The elements of the i-th output argument contains the elements of the vector xi
repeated over all dimensions different from the i-th dimension. Calling ndgrid with
only one input argument xis equivalent to calling ndgrid with all n input arguments
equal to x:
[y1,y2, . . ., yn] = ndgrid (x, . . ., x)
Programming Note: ndgrid is very similar to the function meshgrid except that the
first two dimensions are transposed in comparison to meshgrid. Some core functions
expect meshgrid input and others expect ndgrid input. Check the documentation
for the function in question to determine the proper input format.
See also: [meshgrid], page 337.
plot3 (x,y,z)
plot3 (x,y,z,prop,value, . . . )
plot3 (x,y,z,fmt)
plot3 (x,cplx)
plot3 (cplx)
338 GNU Octave
plot3 (hax, . . . )
h= plot3 (. . . )
Produce 3-D plots.
Many different combinations of arguments are possible. The simplest form is
plot3 (x,y,z)
in which the arguments are taken to be the vertices of the points to be plotted in three
dimensions. If all arguments are vectors of the same length, then a single continuous
line is drawn. If all arguments are matrices, then each column of is treated as a
separate line. No attempt is made to transpose the arguments to make the number
of rows match.
If only two arguments are given, as
plot3 (x,cplx)
the real and imaginary parts of the second argument are used as the yand zcoordi-
nates, respectively.
If only one argument is given, as
plot3 (cplx)
the real and imaginary parts of the argument are used as the yand zvalues, and
they are plotted versus their index.
Arguments may also be given in groups of three as
plot3 (x1,y1,z1,x2,y2,z2, ...)
in which each set of three arguments is treated as a separate line or set of lines in
three dimensions.
To plot multiple one- or two-argument groups, separate each group with an empty
format string, as
plot3 (x1,c1, "", c2, "", ...)
Multiple property-value pairs may be specified which will affect the line objects drawn
by plot3. If the fmt argument is supplied it will format the line objects in the same
manner as plot.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
Example:
z = [0:0.05:5];
plot3 (cos (2*pi*z), sin (2*pi*z), z, ";helix;");
plot3 (z, exp (2i*pi*z), ";complex sinusoid;");
See also: [ezplot3], page 343,[plot], page 286.
view (azimuth,elevation)
view ([azimuth elevation])
view ([x y z])
view (2)
view (3)
view (hax, . . . )
Chapter 15: Plotting 339
[azimuth,elevation] = view ()
Query or set the viewpoint for the current axes.
The parameters azimuth and elevation can be given as two arguments or as 2-element
vector. The viewpoint can also be specified with Cartesian coordinates x,y, and z.
The call view (2) sets the viewpoint to azimuth = 0 and elevation = 90, which is the
default for 2-D graphs.
The call view (3) sets the viewpoint to azimuth = -37.5 and elevation = 30, which
is the default for 3-D graphs.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
If no inputs are given, return the current azimuth and elevation.
slice (x,y,z,v,sx,sy,sz)
slice (x,y,z,v,xi,yi,zi)
slice (v,sx,sy,sz)
slice (v,xi,yi,zi)
slice (. . ., method)
slice (hax, . . . )
h= slice (. . . )
Plot slices of 3-D data/scalar fields.
Each element of the 3-dimensional array vrepresents a scalar value at a location given
by the parameters x,y, and z. The parameters x,x, and zare either 3-dimensional
arrays of the same size as the array vin the "meshgrid" format or vectors. The
parameters xi, etc. respect a similar format to x, etc., and they represent the points
at which the array vi is interpolated using interp3. The vectors sx,sy, and sz contain
points of orthogonal slices of the respective axes.
If x,y,zare omitted, they are assumed to be x = 1:size (v, 2),y = 1:size (v, 1)
and z = 1:size (v, 3).
method is one of:
"nearest"
Return the nearest neighbor.
"linear" Linear interpolation from nearest neighbors.
"cubic" Cubic interpolation from four nearest neighbors (not implemented yet).
"spline" Cubic spline interpolation—smooth first and second derivatives through-
out the curve.
The default method is "linear".
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Examples:
340 GNU Octave
[x, y, z] = meshgrid (linspace (-8, 8, 32));
v = sin (sqrt (x.^2 + y.^2 + z.^2)) ./ (sqrt (x.^2 + y.^2 + z.^2));
slice (x, y, z, v, [], 0, []);
[xi, yi] = meshgrid (linspace (-7, 7));
zi = xi + yi;
slice (x, y, z, v, xi, yi, zi);
See also: [interp3], page 706,[surface], page 377,[pcolor], page 311.
ribbon (y)
ribbon (x,y)
ribbon (x,y,width)
ribbon (hax, . . . )
h= ribbon (. . . )
Draw a ribbon plot for the columns of yvs. x.
If xis omitted, a vector containing the row numbers is assumed (1:rows (Y)). Alter-
natively, xcan also be a vector with same number of elements as rows of yin which
case the same xis used for each column of y.
The optional parameter width specifies the width of a single ribbon (default is 0.75).
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a vector of graphics handles to the surface objects
representing each ribbon.
See also: [surface], page 377,[waterfall], page 341.
shading (type)
shading (hax,type)
Set the shading of patch or surface graphic objects.
Valid arguments for type are
"flat" Single colored patches with invisible edges.
"faceted"
Single colored patches with black edges.
"interp" Colors between patch vertices are interpolated and the patch edges are
invisible.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
See also: [fill], page 312,[mesh], page 321,[patch], page 376,[pcolor], page 311,[surf],
page 323,[surface], page 377,[hidden], page 323,[lighting], page 334.
scatter3 (x,y,z)
scatter3 (x,y,z,s)
scatter3 (x,y,z,s,c)
scatter3 (. . ., style)
scatter3 (. . ., "filled")
Chapter 15: Plotting 341
scatter3 (. . ., prop,val)
scatter3 (hax, . . . )
h= scatter3 (. . . )
Draw a 3-D scatter plot.
A marker is plotted at each point defined by the coordinates in the vectors x,y, and
z.
The size of the markers is determined by s, which can be a scalar or a vector of the
same length as x,y, and z. If sis not given, or is an empty matrix, then a default
value of 8 points is used.
The color of the markers is determined by c, which can be a string defining a fixed
color; a 3-element vector giving the red, green, and blue components of the color; a
vector of the same length as xthat gives a scaled index into the current colormap; or
an Nx3 matrix defining the RGB color of each marker individually.
The marker to use can be changed with the style argument, that is a string defining a
marker in the same manner as the plot command. If no marker is specified it defaults
to "o" or circles. If the argument "filled" is given then the markers are filled.
Additional property/value pairs are passed directly to the underlying patch object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the hggroup object representing
the points.
[x, y, z] = peaks (20);
scatter3 (x(:), y(:), z(:), [], z(:));
See also: [scatter], page 297,[patch], page 376,[plot], page 286.
waterfall (x,y,z)
waterfall (z)
waterfall (. . ., c)
waterfall (. . ., prop,val, . . .)
waterfall (hax, . . . )
h= waterfall (. . . )
Plot a 3-D waterfall plot.
A waterfall plot is similar to a meshz plot except only mesh lines for the rows of z
(x-values) are shown.
The wireframe mesh is plotted using rectangles. The vertices of the rectangles [x,
y] are typically the output of meshgrid. over a 2-D rectangular region in the x-y
plane. zdetermines the height above the plane of each vertex. If only a single z
matrix is given, then it is plotted over the meshgrid x= 1:columns (z), y= 1:rows
(z). Thus, columns of zcorrespond to different xvalues and rows of zcorrespond to
different yvalues.
The color of the mesh is computed by linearly scaling the zvalues to fit the range of the
current colormap. Use caxis and/or change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of zby supplying a
color matrix, c.
342 GNU Octave
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
See also: [meshz], page 322,[mesh], page 321,[meshc], page 322,[contour], page 300,
[surf], page 323,[surface], page 377,[ribbon], page 340,[meshgrid], page 337,[hidden],
page 323,[shading], page 340,[colormap], page 751,[caxis], page 315.
15.2.2.1 Aspect Ratio
For three-dimensional plots the aspect ratio can be set for data with daspect and for the
plot box with pbaspect. See Section 15.2.1.1 [Axis Configuration], page 313, for controlling
the x-, y-, and z-limits for plotting.
data_aspect_ratio = daspect ()
daspect (data_aspect_ratio)
daspect (mode)
data_aspect_ratio_mode = daspect ("mode")
daspect (hax, . . . )
Query or set the data aspect ratio of the current axes.
The aspect ratio is a normalized 3-element vector representing the span of the x, y,
and z-axis limits.
daspect (mode)
Set the data aspect ratio mode of the current axes. mode is either "auto" or
"manual".
daspect ("mode")
Return the data aspect ratio mode of the current axes.
daspect (hax, ...)
Operate on the axes in handle hax instead of the current axes.
See also: [axis], page 313,[pbaspect], page 342,[xlim], page 315,[ylim], page 315,
[zlim], page 315.
plot_box_aspect_ratio = pbaspect ( )
pbaspect (plot_box_aspect_ratio)
pbaspect (mode)
plot_box_aspect_ratio_mode = pbaspect ("mode")
pbaspect (hax, . . . )
Query or set the plot box aspect ratio of the current axes.
The aspect ratio is a normalized 3-element vector representing the rendered lengths
of the x, y, and z axes.
pbaspect(mode)
Set the plot box aspect ratio mode of the current axes. mode is either "auto" or
"manual".
pbaspect ("mode")
Return the plot box aspect ratio mode of the current axes.
Chapter 15: Plotting 343
pbaspect (hax, ...)
Operate on the axes in handle hax instead of the current axes.
See also: [axis], page 313,[daspect], page 342,[xlim], page 315,[ylim], page 315,
[zlim], page 315.
15.2.2.2 Three-dimensional Function Plotting
ezplot3 (fx,fy,fz)
ezplot3 (. . ., dom)
ezplot3 (. . ., n)
ezplot3 (. . ., "animate")
ezplot3 (hax, . . . )
h= ezplot3 (. . . )
Plot a parametrically defined curve in three dimensions.
fx,fy, and fz are strings, inline functions, or function handles with one argument
defining the function. By default the plot is over the domain 0 <= t<= 2*pi with 500
points.
If dom is a two element vector, it represents the minimum and maximum values of t.
nis a scalar defining the number of points to use in plotting the function.
If the "animate" option is given then the plotting is animated in the style of comet3.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created plot.
fx = @(t) cos (t);
fy = @(t) sin (t);
fz = @(t) t;
ezplot3 (fx, fy, fz, [0, 10*pi], 100);
See also: [plot3], page 337,[comet3], page 313,[ezplot], page 317,[ezmesh], page 343,
[ezsurf], page 345.
ezmesh (f)
ezmesh (fx,fy,fz)
ezmesh (. . ., dom)
ezmesh (. . ., n)
ezmesh (. . ., "circ")
ezmesh (hax, . . . )
h= ezmesh (. . . )
Plot the mesh defined by a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If three functions are passed, then plot the parametrically defined function [fx (s,
t), fy (s,t), fz (s,t)].
344 GNU Octave
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the argument "circ" is given, then the function is plotted over a disk centered on
the middle of the domain dom.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Example 1: 2-argument function
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezmesh (f, [-3, 3]);
Example 2: parametrically defined function
fx = @(s,t) cos (s) .* cos (t);
fy = @(s,t) sin (s) .* cos (t);
fz = @(s,t) sin (t);
ezmesh (fx, fy, fz, [-pi, pi, -pi/2, pi/2], 20);
See also: [mesh], page 321,[ezmeshc], page 344,[ezplot], page 317,[ezsurf], page 345,
[ezsurfc], page 345,[hidden], page 323.
ezmeshc (f)
ezmeshc (fx,fy,fz)
ezmeshc (. . ., dom)
ezmeshc (. . ., n)
ezmeshc (. . ., "circ")
ezmeshc (hax, . . . )
h= ezmeshc (. . . )
Plot the mesh and contour lines defined by a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If three functions are passed, then plot the parametrically defined function [fx (s,
t), fy (s,t), fz (s,t)].
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the argument "circ" is given, then the function is plotted over a disk centered on
the middle of the domain dom.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a 2-element vector with a graphics handle for the
created mesh plot and a second handle for the created contour plot.
Chapter 15: Plotting 345
Example: 2-argument function
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezmeshc (f, [-3, 3]);
See also: [meshc], page 322,[ezmesh], page 343,[ezplot], page 317,[ezsurf], page 345,
[ezsurfc], page 345,[hidden], page 323.
ezsurf (f)
ezsurf (fx,fy,fz)
ezsurf (. . ., dom)
ezsurf (. . ., n)
ezsurf (. . ., "circ")
ezsurf (hax, . . . )
h= ezsurf (. . . )
Plot the surface defined by a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If three functions are passed, then plot the parametrically defined function [fx (s,
t), fy (s,t), fz (s,t)].
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the argument "circ" is given, then the function is plotted over a disk centered on
the middle of the domain dom.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
Example 1: 2-argument function
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezsurf (f, [-3, 3]);
Example 2: parametrically defined function
fx = @(s,t) cos (s) .* cos (t);
fy = @(s,t) sin (s) .* cos (t);
fz = @(s,t) sin (t);
ezsurf (fx, fy, fz, [-pi, pi, -pi/2, pi/2], 20);
See also: [surf], page 323,[ezsurfc], page 345,[ezplot], page 317,[ezmesh], page 343,
[ezmeshc], page 344,[shading], page 340.
ezsurfc (f)
ezsurfc (fx,fy,fz)
ezsurfc (. . ., dom)
ezsurfc (. . ., n)
ezsurfc (. . ., "circ")
346 GNU Octave
ezsurfc (hax, . . . )
h= ezsurfc (. . . )
Plot the surface and contour lines defined by a function.
fis a string, inline function, or function handle with two arguments defining the
function. By default the plot is over the meshed domain -2*pi <= x|y<= 2*pi
with 60 points in each dimension.
If three functions are passed, then plot the parametrically defined function [fx (s,
t), fy (s,t), fz (s,t)].
If dom is a two element vector, it represents the minimum and maximum values of
both xand y. If dom is a four element vector, then the minimum and maximum
values are [xmin xmax ymin ymax].
nis a scalar defining the number of points to use in each dimension.
If the argument "circ" is given, then the function is plotted over a disk centered on
the middle of the domain dom.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a 2-element vector with a graphics handle for the
created surface plot and a second handle for the created contour plot.
Example:
f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
ezsurfc (f, [-3, 3]);
See also: [surfc], page 324,[ezsurf], page 345,[ezplot], page 317,[ezmesh], page 343,
[ezmeshc], page 344,[shading], page 340.
15.2.2.3 Three-dimensional Geometric Shapes
cylinder
cylinder (r)
cylinder (r,n)
cylinder (hax, . . . )
[x,y,z] = cylinder (. . . )
Plot a 3-D unit cylinder.
The optional input ris a vector specifying the radius along the unit z-axis. The
default is [1 1] indicating radius 1 at Z == 0 and at Z == 1.
The optional input ndetermines the number of faces around the circumference of the
cylinder. The default value is 20.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
If outputs are requested cylinder returns three matrices in meshgrid format, such
that surf (x,y,z)generates a unit cylinder.
Example:
[x, y, z] = cylinder (10:-1:0, 50);
surf (x, y, z);
title ("a cone");
Chapter 15: Plotting 347
See also: [ellipsoid], page 347,[rectangle], page 319,[sphere], page 347.
sphere ()
sphere (n)
sphere (hax, . . . )
[x,y,z] = sphere (. . . )
Plot a 3-D unit sphere.
The optional input ndetermines the number of faces around the circumference of the
sphere. The default value is 20.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
If outputs are requested sphere returns three matrices in meshgrid format such that
surf (x,y,z)generates a unit sphere.
Example:
[x, y, z] = sphere (40);
surf (3*x, 3*y, 3*z);
axis equal;
title ("sphere of radius 3");
See also: [cylinder], page 346,[ellipsoid], page 347,[rectangle], page 319.
ellipsoid (xc,yc,zc,xr,yr,zr,n)
ellipsoid (. . ., n)
ellipsoid (hax, . . . )
[x,y,z] = ellipsoid (. . . )
Plot a 3-D ellipsoid.
The inputs xc,yc,zc specify the center of the ellipsoid. The inputs xr,yr,zr specify
the semi-major axis lengths.
The optional input ndetermines the number of faces around the circumference of the
cylinder. The default value is 20.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
If outputs are requested ellipsoid returns three matrices in meshgrid format, such
that surf (x,y,z)generates the ellipsoid.
See also: [cylinder], page 346,[rectangle], page 319,[sphere], page 347.
15.2.3 Plot Annotations
You can add titles, axis labels, legends, and arbitrary text to an existing plot. For example:
x = -10:0.1:10;
plot (x, sin (x));
title ("sin(x) for x = -10:0.1:10");
xlabel ("x");
ylabel ("sin (x)");
text (pi, 0.7, "arbitrary text");
legend ("sin (x)");
348 GNU Octave
The functions grid and box may also be used to add grid and border lines to the plot.
By default, the grid is off and the border lines are on.
Finally, arrows, text and rectangular or elliptic boxes can be added to highlight parts of
a plot using the annotation function. Those objects are drawn in an invisible axes, on top
of every other axes.
title (string)
title (string,prop,val, . . . )
title (hax, . . . )
h= title (. . . )
Specify the string used as a title for the current axis.
An optional list of property/value pairs can be used to change the appearance of the
created title text object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created text object.
See also: [xlabel], page 349,[ylabel], page 349,[zlabel], page 349,[text], page 349.
legend (str1,str2, . . . )
legend (matstr)
legend (cellstr)
legend (. . ., "location",pos)
legend (. . ., "orientation",orient)
legend (hax, . . . )
legend (hobjs, . . . )
legend (hax,hobjs, . . . )
legend ("option")
[hleg,hleg_obj,hplot,labels] = legend (. . . )
Display a legend for the current axes using the specified strings as labels.
Legend entries may be specified as individual character string arguments, a character
array, or a cell array of character strings.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca. If the handles, hobjs, are not specified then the legend’s
strings will be associated with the axes’ descendants. legend works on line graphs,
bar graphs, etc. A plot must exist before legend is called.
The optional parameter pos specifies the location of the legend as follows:
pos location of the legend
north center top
south center bottom
east right center
west left center
northeast right top (default)
northwest left top
southeast right bottom

Chapter 15: Plotting 349
southwest left bottom
outside can be appended to any location string
The optional parameter orient determines if the key elements are placed vertically or
horizontally. The allowed values are "vertical" (default) or "horizontal".
The following customizations are available using option:
"show" Show legend on the plot
"hide" Hide legend on the plot
"toggle" Toggles between "hide" and "show"
"boxon" Show a box around legend (default)
"boxoff" Hide the box around legend
"right" Place label text to the right of the keys (default)
"left" Place label text to the left of the keys
"off" Delete the legend object
The optional output values are
hleg The graphics handle of the legend object.
hleg obj Graphics handles to the text and line objects which make up the legend.
hplot Graphics handles to the plot objects which were used in making the leg-
end.
labels A cell array of strings of the labels in the legend.
The legend label text is either provided in the call to legend or is taken from the
DisplayName property of graphics objects. If no labels or DisplayNames are available,
then the label text is simply "data1","data2", . . ., "dataN".
Implementation Note: A legend is implemented as an additional axes object of the
current figure with the "tag" set to "legend". Properties of the legend object may
be manipulated directly by using set.
text (x,y,string)
text (x,y,z,string)
text (. . ., prop,val, . . .)
h= text (. . . )
Create a text object with text string at position x,y, (z) on the current axes.
Multiple locations can be specified if x,y, (z) are vectors. Multiple strings can be
specified with a character matrix or a cell array of strings.
Optional property/value pairs may be used to control the appearance of the text.
The optional return value his a vector of graphics handles to the created text objects.
See also: [gtext], page 372,[title], page 348,[xlabel], page 349,[ylabel], page 349,
[zlabel], page 349.
See Section 15.3.3.5 [Text Properties], page 399, for the properties that you can set.
350 GNU Octave
xlabel (string)
xlabel (string,property,val, . . . )
xlabel (hax, . . . )
h= xlabel (. . . )
Specify the string used to label the x-axis of the current axis.
An optional list of property/value pairs can be used to change the properties of the
created text label.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created text object.
See also: [ylabel], page 349,[zlabel], page 349,[datetick], page 817,[title], page 348,
[text], page 349.
clabel (c,h)
clabel (c,h,v)
clabel (c,h,"manual")
clabel (c)
clabel (. . ., prop,val, . . .)
h= clabel (. . . )
Add labels to the contours of a contour plot.
The contour levels are specified by the contour matrix cwhich is returned by contour,
contourc,contourf, and contour3. Contour labels are rotated to match the local
line orientation and centered on the line. The position of labels along the contour
line is chosen randomly.
If the argument his a handle to a contour group object, then label this plot rather
than the one in the current axes returned by gca.
By default, all contours are labeled. However, the contours to label can be specified
by the vector v. If the "manual" argument is given then the contours to label can be
selected with the mouse.
Additional property/value pairs that are valid properties of text objects can be given
and are passed to the underlying text objects. Moreover, the contour group prop-
erty "LabelSpacing" is available which determines the spacing between labels on a
contour to be specified. The default is 144 points, or 2 inches.
The optional return value his a vector of graphics handles to the text objects repre-
senting each label. The "userdata" property of the text objects contains the numer-
ical value of the contour label.
An example of the use of clabel is
[c, h] = contour (peaks (), -4 : 6);
clabel (c, h, -4:2:6, "fontsize", 12);
See also: [contour], page 300,[contourf], page 300,[contour3], page 302,[meshc],
page 322,[surfc], page 324,[text], page 349.
box
box on
box off
Chapter 15: Plotting 351
box (hax, . . . )
Control display of the axis border.
The argument may be either "on" or "off". If it is omitted, the current box state is
toggled.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
See also: [axis], page 313,[grid], page 351.
grid
grid on
grid off
grid minor
grid minor on
grid minor off
grid (hax, . . . )
Control the display of plot grid lines.
The function state input may be either "on" or "off". If it is omitted, the current
grid state is toggled.
When the first argument is "minor" all subsequent commands modify the minor grid
rather than the major grid.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
To control the grid lines for an individual axis use the set function. For example:
set (gca, "ygrid", "on");
See also: [axis], page 313,[box], page 350.
colorbar
colorbar (loc)
colorbar (delete_option)
colorbar (hcb, . . . )
colorbar (hax, . . . )
colorbar (. . ., "peer",hax, . . .)
colorbar (. . ., "location",loc, . . .)
colorbar (. . ., prop,val, . . .)
h= colorbar (. . . )
Add a colorbar to the current axes.
A colorbar displays the current colormap along with numerical rulings so that the
color scale can be interpreted.
The optional input loc determines the location of the colorbar. Valid values for loc
are
"EastOutside"
Place the colorbar outside the plot to the right. This is the default.
"East" Place the colorbar inside the plot to the right.

352 GNU Octave
"WestOutside"
Place the colorbar outside the plot to the left.
"West" Place the colorbar inside the plot to the left.
"NorthOutside"
Place the colorbar above the plot.
"North" Place the colorbar at the top of the plot.
"SouthOutside"
Place the colorbar under the plot.
"South" Place the colorbar at the bottom of the plot.
To remove a colorbar from a plot use any one of the following keywords for the
delete option:"delete","hide","off".
If the argument "peer" is given, then the following argument is treated as the axes
handle in which to add the colorbar. Alternatively, If the first argument hax is an
axes handle, then the colorbar is added to this axis, rather than the current axes
returned by gca.
If the first argument hcb is a handle to a colorbar object, then operate on this colorbar
directly.
Additional property/value pairs are passed directly to the underlying axes object.
The optional return value his a graphics handle to the created colorbar object.
Implementation Note: A colorbar is created as an additional axes to the current figure
with the "tag" property set to "colorbar". The created axes object has the extra
property "location" which controls the positioning of the colorbar.
See also: [colormap], page 751.
annotation (type)
annotation ("line",x,y)
annotation ("arrow",x,y)
annotation ("doublearrow",x,y)
annotation ("textarrow",x,y)
annotation ("textbox",pos)
annotation ("rectangle",pos)
annotation ("ellipse",pos)
annotation (. . ., prop,val)
annotation (hf, . . . )
h= annotation (. . . )
Draw annotations to emphasize parts of a figure.
You may build a default annotation by specifying only the type of the annotation.
Otherwise you can select the type of annotation and then set its position using either
xand ycoordinates for line-based annotations or a position vector pos for others. In
either case, coordinates are interpreted using the "units" property of the annotation
object. The default is "normalized", which means the lower left hand corner of the
figure has coordinates ‘[0 0]’ and the upper right hand corner ‘[1 1]’.
Chapter 15: Plotting 353
If the first argument hf is a figure handle, then plot into this figure, rather than the
current figure returned by gcf.
Further arguments can be provided in the form of prop/val pairs to customize the
annotation appearance.
The optional return value his a graphics handle to the created annotation object.
This can be used with the set function to customize an existing annotation object.
All annotation objects share two properties:
•"units": the units in which coordinates are interpreted.
Its value may be one of "centimeters" | "characters" | "inches" |
"{normalized}" | "pixels" | "points".
•"position": a four-element vector [x0 y0 width height].
The vector specifies the coordinates (x0,y0) of the origin of the annotation object,
its width, and its height. The width and height may be negative, depending on
the orientation of the object.
Valid annotation types and their specific properties are described below:
"line" Constructs a line. xand ymust be two-element vectors specifying the x
and y coordinates of the two ends of the line.
The line can be customized using "linewidth","linestyle", and
"color" properties the same way as for line objects.
"arrow" Construct an arrow. The second point in vectors xand yspecifies the
arrowhead coordinates.
Besides line properties, the arrowhead can be customized using
"headlength","headwidth", and "headstyle" properties. Supported
values for "headstyle" property are: ["diamond" | "ellipse" |
"plain" | "rectangle" | "vback1" | "{vback2}" | "vback3"]
"doublearrow"
Construct a double arrow. Vectors xand yspecify the arrowhead coor-
dinates.
The line and the arrowhead can be customized as for ar-
row annotations, but some property names are duplicated:
"head1length"/"head2length","head1width"/"head2width", etc.
The index 1 marks the properties of the arrowhead at the first point in
xand ycoordinates.
"textarrow"
Construct an arrow with a text label at the opposite end from the arrow-
head.
Use the "string" property to change the text string. The line and the
arrowhead can be customized as for arrow annotations, and the text
can be customized using the same properties as text graphics objects.
Note, however, that some text property names are prefixed with "text"
to distinguish them from arrow properties: "textbackgroundcolor",
"textcolor","textedgecolor","textlinewidth","textmargin",
"textrotation".
354 GNU Octave
"textbox"
Construct a box with text inside. pos specifies the "position" property
of the annotation.
Use the "string" property to change the text string. You may use
"backgroundcolor","edgecolor","linestyle", and "linewidth"
properties to customize the box background color and edge appearance.
A limited set of text objects properties are also available; Besides
"font..." properties, you may also use "horizontalalignment" and
"verticalalignment" to position the text inside the box.
Finally, the "fitboxtotext" property controls the actual extent of the
box. If "on" (the default) the box limits are fitted to the text extent.
"rectangle"
Construct a rectangle. pos specifies the "position" property of the an-
notation.
You may use "facecolor","color","linestyle", and "linewidth"
properties to customize the rectangle background color and edge appear-
ance.
"ellipse"
Construct an ellipse. pos specifies the "position" property of the anno-
tation.
See "rectangle" annotations for customization.
See also: [xlabel], page 349,[ylabel], page 349,[zlabel], page 349,[title], page 348,
[text], page 349,[gtext], page 372,[legend], page 348,[colorbar], page 351.
15.2.4 Multiple Plots on One Page
Octave can display more than one plot in a single figure. The simplest way to do this is to
use the subplot function to divide the plot area into a series of subplot windows that are
indexed by an integer. For example,
subplot (2, 1, 1)
fplot (@sin, [-10, 10]);
subplot (2, 1, 2)
fplot (@cos, [-10, 10]);
creates a figure with two separate axes, one displaying a sine wave and the other a cosine
wave. The first call to subplot divides the figure into two plotting areas (two rows and one
column) and makes the first plot area active. The grid of plot areas created by subplot is
numbered in row-major order (left to right, top to bottom). After plotting a sine wave, the
next call to subplot activates the second subplot area, but does not re-partition the figure.
subplot (rows,cols,index)
subplot (rcn)
subplot (hax)
subplot (. . ., "align")
subplot (. . ., "replace")
subplot (. . ., "position",pos)

Chapter 15: Plotting 355
subplot (. . ., prop,val, . . .)
hax = subplot (. . . )
Set up a plot grid with rows by cols subwindows and set the current axes for plotting
(gca) to the location given by index.
If only one numeric argument is supplied, then it must be a three digit value specifying
the number of rows in digit 1, the number of columns in digit 2, and the plot index
in digit 3.
The plot index runs row-wise; First, all columns in a row are numbered and then the
next row is filled.
For example, a plot with 2x3 grid will have plot indices running as follows:
1 2 3
4 5 6
index may also be a vector. In this case, the new axis will enclose the grid locations
specified. The first demo illustrates this:
demo ("subplot", 1)
The index of the subplot to make active may also be specified by its axes handle, hax,
returned from a previous subplot command.
If the option "align" is given then the plot boxes of the subwindows will align, but
this may leave no room for axis tick marks or labels.
If the option "replace" is given then the subplot axis will be reset, rather than just
switching the current axis for plotting to the requested subplot.
The "position" property can be used to exactly position the subplot axes within
the current figure. The option pos is a 4-element vector [x, y, width, height] that
determines the location and size of the axes. The values in pos are normalized in the
range [0,1].
Any property/value pairs are passed directly to the underlying axes object.
If the output hax is requested, subplot returns the axis handle for the subplot. This
is useful for modifying the properties of a subplot using set.
See also: [axes], page 375,[plot], page 286,[gca], page 379,[set], page 381.
15.2.5 Multiple Plot Windows
You can open multiple plot windows using the figure function. For example,
figure (1);
fplot (@sin, [-10, 10]);
figure (2);
fplot (@cos, [-10, 10]);
creates two figures, with the first displaying a sine wave and the second a cosine wave.
Figure numbers must be positive integers.
356 GNU Octave
figure
figure n
figure (n)
figure (. . ., "property",value, . . .)
h= figure (. . . )
Create a new figure window for plotting.
If no arguments are specified, a new figure with the next available number is created.
If called with an integer n, and no such numbered figure exists, then a new figure with
the specified number is created. If the figure already exists then it is made visible
and becomes the current figure for plotting.
Multiple property-value pairs may be specified for the figure object, but they must
appear in pairs.
The optional return value his a graphics handle to the created figure object.
See also: [axes], page 375,[gcf], page 379,[clf], page 360,[close], page 361.
15.2.6 Manipulation of Plot Objects
pan
pan on
pan off
pan xon
pan yon
pan (hfig,option)
Control the interactive panning mode of a figure in the GUI.
Given the option "on" or "off", set the interactive pan mode on or off.
With no arguments, toggle the current pan mode on or off.
Given the option "xon" or "yon", enable pan mode for the x or y axis only.
If the first argument hfig is a figure, then operate on the given figure rather than the
current figure as returned by gcf.
See also: [rotate3d], page 356,[zoom], page 357.
rotate (h,dir,alpha)
rotate (. . ., origin)
Rotate the plot object hthrough alpha degrees around the line with direction dir and
origin origin.
The default value of origin is the center of the axes object that is the parent of h.
If his a vector of handles, they must all have the same parent axes object.
Graphics objects that may be rotated are lines, surfaces, patches, and images.
rotate3d
rotate3d on
rotate3d off
rotate3d (hfig,option)
Control the interactive 3-D rotation mode of a figure in the GUI.
Given the option "on" or "off", set the interactive rotate mode on or off.
Chapter 15: Plotting 357
With no arguments, toggle the current rotate mode on or off.
If the first argument hfig is a figure, then operate on the given figure rather than the
current figure as returned by gcf.
See also: [pan], page 356,[zoom], page 357.
zoom
zoom (factor)
zoom on
zoom off
zoom xon
zoom yon
zoom out
zoom reset
zoom (hfig,option)
Zoom the current axes object or control the interactive zoom mode of a figure in the
GUI.
Given a numeric argument greater than zero, zoom by the given factor. If the zoom
factor is greater than one, zoom in on the plot. If the factor is less than one, zoom
out. If the zoom factor is a two- or three-element vector, then the elements specify
the zoom factors for the x, y, and z axes respectively.
Given the option "on" or "off", set the interactive zoom mode on or off.
With no arguments, toggle the current zoom mode on or off.
Given the option "xon" or "yon", enable zoom mode for the x or y-axis only.
Given the option "out", zoom to the initial zoom setting.
Given the option "reset", store the current zoom setting so that zoom out will return
to this zoom level.
If the first argument hfig is a figure, then operate on the given figure rather than the
current figure as returned by gcf.
See also: [pan], page 356,[rotate3d], page 356.
15.2.7 Manipulation of Plot Windows
By default, Octave refreshes the plot window when a prompt is printed, or when waiting
for input. The drawnow function is used to cause a plot window to be updated.
drawnow ()
drawnow ("expose")
drawnow (term,file,debug_file)
Update figure windows and their children.
The event queue is flushed and any callbacks generated are executed.
With the optional argument "expose", only graphic objects are updated and no other
events or callbacks are processed.
The third calling form of drawnow is for debugging and is undocumented.
See also: [refresh], page 358.
358 GNU Octave
Only figures that are modified will be updated. The refresh function can also be used
to cause an update of the current figure, even if it is not modified.
refresh ()
refresh (h)
Refresh a figure, forcing it to be redrawn.
When called without an argument the current figure is redrawn. Otherwise, the figure
with graphic handle his redrawn.
See also: [drawnow], page 357.
Normally, high-level plot functions like plot or mesh call newplot to initialize the state
of the current axes so that the next plot is drawn in a blank window with default property
settings. To have two plots superimposed over one another, use the hold function. For
example,
hold on;
x = -10:0.1:10;
plot (x, sin (x));
plot (x, cos (x));
hold off;
displays sine and cosine waves on the same axes. If the hold state is off, consecutive plotting
commands like this will only display the last plot.
newplot ()
newplot (hfig)
newplot (hax)
hax = newplot (. . . )
Prepare graphics engine to produce a new plot.
This function is called at the beginning of all high-level plotting functions. It is not
normally required in user programs. newplot queries the "NextPlot" field of the
current figure and axis to determine what to do.
Figure NextPlot Action
"new" Create a new figure and make it the current figure.
"add" (default) Add new graphic objects to the current figure.
"replacechildren" Delete child objects whose HandleVisibility is set to "on". Set
NextPlot property to "add". This typically clears a figure, but
leaves in place hidden objects such as menubars. This is equivalent
to clf.
"replace" Delete all child objects of the figure and reset all figure properties
to their defaults. However, the following four properties are not
reset: Position, Units, PaperPosition, PaperUnits. This is equiva-
lent to clf reset.
Chapter 15: Plotting 359
Axis NextPlot Action
"add" Add new graphic objects to the current axes. This is equivalent
to hold on.
"replacechildren" Delete child objects whose HandleVisibility is set to "on", but
leave axis properties unmodified. This typically clears a plot, but
preserves special settings such as log scaling for axes. This is
equivalent to cla.
"replace" (default) Delete all child objects of the axis and reset all axis properties
to their defaults. However, the following properties are not reset:
Position, Units. This is equivalent to cla reset.
If the optional input hfig or hax is given then prepare the specified figure or axes
rather than the current figure and axes.
The optional return value hax is a graphics handle to the created axes object (not
figure).
Caution: Calling newplot may change the current figure and current axis.
hold
hold on
hold off
hold (hax, . . . )
Toggle or set the "hold" state of the plotting engine which determines whether new
graphic objects are added to the plot or replace the existing objects.
hold on Retain plot data and settings so that subsequent plot commands are
displayed on a single graph. Line color and line style are advanced for
each new plot added.
hold all (deprecated)
Equivalent to hold on.
hold off Restore default graphics settings which clear the graph and reset axis
properties before each new plot command. (default).
hold Toggle the current hold state.
When given the additional argument hax, the hold state is modified for this axis
rather than the current axes returned by gca.
To query the current hold state use the ishold function.
See also: [ishold], page 359,[cla], page 360,[clf], page 360,[newplot], page 358.
ishold
ishold (hax)
ishold (hfig)
Return true if the next plot will be added to the current plot, or false if the plot
device will be cleared before drawing the next plot.
If the first argument is an axes handle hax or figure handle hfig then operate on this
plot rather than the current one.
See also: [hold], page 359,[newplot], page 358.
360 GNU Octave
To clear the current figure, call the clf function. To clear the current axis, call the cla
function. To bring the current figure to the top of the window stack, call the shg function.
To delete a graphics object, call delete on its index. To close the figure window, call the
close function.
clf
clf reset
clf (hfig)
clf (hfig,"reset")
h= clf (. . . )
Clear the current figure window.
clf operates by deleting child graphics objects with visible handles (HandleVisibility
="on").
If the optional argument "reset" is specified, delete all child objects including those
with hidden handles and reset all figure properties to their defaults. However, the
following properties are not reset: Position, Units, PaperPosition, PaperUnits.
If the first argument hfig is a figure handle, then operate on this figure rather than
the current figure returned by gcf.
The optional return value his the graphics handle of the figure window that was
cleared.
See also: [cla], page 360,[close], page 361,[delete], page 360,[reset], page 421.
cla
cla reset
cla (hax)
cla (hax,"reset")
Clear the current axes.
cla operates by deleting child graphic objects with visible handles (HandleVisibility
="on").
If the optional argument "reset" is specified, delete all child objects including those
with hidden handles and reset all axis properties to their defaults. However, the
following properties are not reset: Position, Units.
If the first argument hax is an axes handle, then operate on this axis rather than the
current axes returned by gca.
See also: [clf], page 360,[delete], page 360,[reset], page 421.
shg
Show the graph window.
Currently, this is the same as executing drawnow.
See also: [drawnow], page 357,[figure], page 355.
delete (file)
delete (file1,file2, . . . )
delete (handle)
Delete the named file or graphics handle.
Chapter 15: Plotting 361
file may contain globbing patterns such as ‘*’. Multiple files to be deleted may be
specified in the same function call.
handle may be a scalar or vector of graphic handles to delete.
Programming Note: Deleting graphics objects is the proper way to remove features
from a plot without clearing the entire figure.
See also: [clf], page 360,[cla], page 360,[unlink], page 819,[rmdir], page 820.
close
close h
close (h)
close (h,"force")
close all
close all hidden
close all force
Close figure window(s).
When called with no arguments, close the current figure. This is equivalent to close
(gcf). If the input his a graphic handle, or vector of graphics handles, then close
each figure in h.
If the argument "all" is given then all figures with visible handles (HandleVisibility
="on") are closed.
If the argument "all hidden" is given then all figures, including hidden ones, are
closed.
If the argument "force" is given then figures are closed even when
"closerequestfcn" has been altered to prevent closing the window.
Implementation Note: close operates by calling the function specified by the
"closerequestfcn" property for each figure. By default, the function closereq is
used. It is possible that the function invoked will delay or abort removing the figure.
To remove a figure without executing any callback functions use delete. When
writing a callback function to close a window do not use close to avoid recursion.
See also: [closereq], page 361,[delete], page 360.
closereq ()
Close the current figure and delete all graphics objects associated with it.
By default, the "closerequestfcn" property of a new plot figure points to this
function.
See also: [close], page 361,[delete], page 360.
15.2.8 Use of the interpreter Property
All text objects—such as titles, labels, legends, and text—include the property
"interpreter" that determines the manner in which special control sequences in the text
are rendered.
The interpreter property can take three values: "none","tex","latex". If the inter-
preter is set to "none" then no special rendering occurs—the displayed text is a verbatim
copy of the specified text. Currently, the "latex" interpreter is not implemented and is
equivalent to "none".
362 GNU Octave
The "tex" option implements a subset of T
E
X functionality when rendering text. This
allows the insertion of special glyphs such as Greek characters or mathematical symbols.
Special characters are inserted by using a backslash (\) character followed by a code, as
shown in Table 15.1.
Besides special glyphs, the formatting of the text can be changed within the string by
using the codes
\bf Bold font
\it Italic font
\sl Oblique Font
\rm Normal font
These codes may be used in conjunction with the {and }characters to limit the change
to a part of the string. For example,
xlabel (’{\bf H} = a {\bf V}’)
where the character ’a’ will not appear in bold font. Note that to avoid having Octave
interpret the backslash character in the strings, the strings themselves should be in single
quotes.
It is also possible to change the fontname and size within the text
\fontname{fontname}Specify the font to use
\fontsize{size}Specify the size of the font to use
The color of the text may also be changed inline using either a string (e.g., "red") or
numerically with a Red-Green-Blue (RGB) specification (.e.g., [1 0 0], also red).
\color{color}Specify the color as a string
\color[rgb]{R G B}Specify the color numerically
Finally, superscripting and subscripting can be controlled with the ’^’ and ’_’ charac-
ters. If the ’^’ or ’_’ is followed by a {character, then all of the block surrounded by the {
}pair is superscripted or subscripted. Without the { } pair, only the character immediately
following the ’^’ or ’_’ is changed.
Chapter 15: Plotting 363
Greek Lowercase Letters
Code Sym Code Sym Code Sym
\alpha α\beta β\gamma γ
\delta δ\epsilon \zeta ζ
\eta η\theta θ\vartheta ϑ
\iota ι\kappa κ\lambda λ
\mu µ\nu ν\xi ξ
\oo\pi π\varpi $
\rho ρ\sigma σ\varsigma ς
\tau τ\upsilon υ\phi φ
\chi χ\psi ψ\omega ω
Greek Uppercase Letters
Code Sym Code Sym Code Sym
\Gamma Γ \Delta Δ \Theta Θ
\Lambda Λ \Xi Ξ \Pi Π
\Sigma Σ \Upsilon ϒ \Phi Φ
\Psi Ψ \Omega Ω
Misc Symbols Type Ord
Code Sym Code Sym Code Sym
\aleph ℵ \wp ℘\Re <
\Im = \partial ∂\infty ∞
\prime 0 \nabla ∇ \surd √
\angle 6\forall ∀ \exists ∃
\neg ¬ \clubsuit ♣ \diamondsuit ♦
\heartsuit ♥ \spadesuit ♠
“Large” Operators
Code Sym Code Sym Code Sym
\int R
Binary operators
Code Sym Code Sym Code Sym
\pm ± \cdot · \times ×
\ast ∗ \circ ◦ \bullet •
\div ÷ \cap ∩ \cup ∪
\vee ∨ \wedge ∧ \oplus ⊕
\otimes ⊗ \oslash
Table 15.1: Available special characters in T
E
X mode

364 GNU Octave
Relations
Code Sym Code Sym Code Sym
\leq ≤ \subset ⊂ \subseteq ⊆
\in ∈ \geq ≥ \supset ⊃
\supseteq ⊇ \ni 3 \mid |
\equiv ≡ \sim ∼ \approx ≈
\cong ∼
=\propto ∝ \perp ⊥
Arrows
Code Sym Code Sym Code Sym
\leftarrow ← \Leftarrow ⇐ \rightarrow →
\Rightarrow ⇒ \leftrightarrow ↔ \uparrow ↑
\downarrow ↓
Openings and Closings
Code Sym Code Sym Code Sym
\lfloor b \langle h \lceil d
\rfloor c \rangle i \rceil e
Alternate Names
Code Sym Code Sym Code Sym
\neq 6=
Other (not in Appendix F Tables)
Code Sym Code Sym Code Sym
\ldots . . . \0 \copyright c
\deg ◦
Table 15.1: Available special characters in T
E
X mode (cont.)
15.2.9 Printing and Saving Plots
The print command allows you to send plots to you printer and to save plots in a variety
of formats. For example,
print -dpsc
prints the current figure to a color PostScript printer. And,
print -deps foo.eps
saves the current figure to an encapsulated PostScript file called foo.eps.
The current graphic toolkits produce very similar graphic displays but differ in their
capability to display text and in print capabilities. In particular, the OpenGL based toolkits
such as fltk and qt do not support the "interpreter" property of text objects. This
means that when using OpenGL toolkits special symbols drawn with the "tex" interpreter
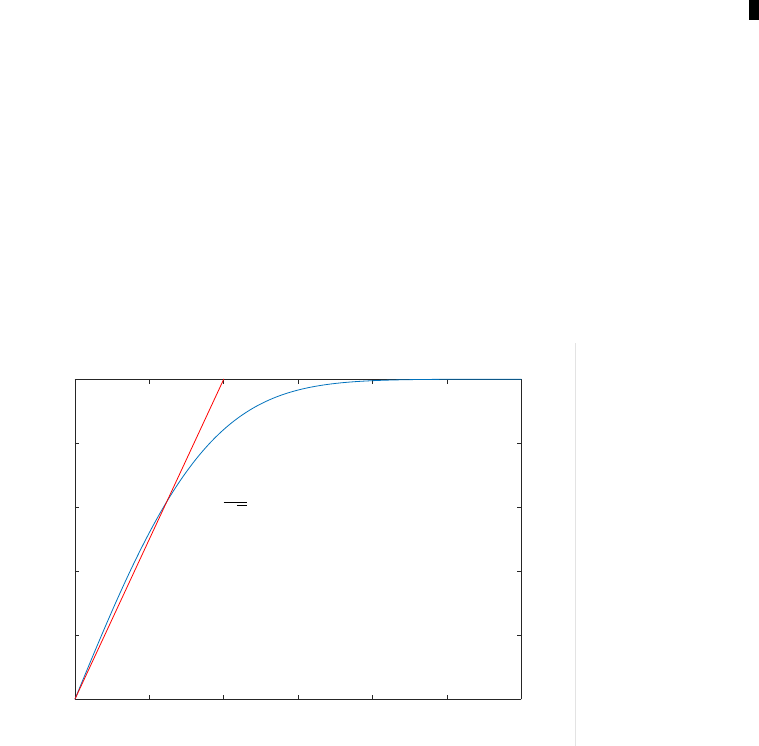
Chapter 15: Plotting 365
will appear correctly on-screen but will be rendered with interpreter "none" when printing
unless one of the standalone (see below) modes is used. These modes provide access to
the pdflatex processor and therefore allow full use of L
A
T
E
X commands.
A complete example showing the capabilities of text printing using the
-dpdflatexstandalone option is:
x = 0:0.01:3;
hf = figure ();
plot (x, erf (x));
hold on;
plot (x, x, "r");
axis ([0, 3, 0, 1]);
text (0.65, 0.6175, [’$\displaystyle\leftarrow x = {2\over\sqrt{\pi}}’...
’\int_{0}^{x}e^{-t^2} dt = 0.6175$’]);
xlabel ("x");
ylabel ("erf (x)");
title ("erf (x) with text annotation");
set (hf, "visible", "off");
print (hf, "plot15_7.pdf", "-dpdflatexstandalone");
set (hf, "visible", "on");
system ("pdflatex plot15_7");
open ("plot15_7.pdf");
The result of this example can be seen in Figure 15.7
0 0.5 1 1.5 2 2.5 3
0
0.2
0.4
0.6
0.8
1
x
erf (x)
←x=2
√πZx
0
e−t2dt = 0.6175
erf (x) with text annotation
Figure 15.7: Example of inclusion of text with use of -dpdflatexstandalone
print ()
print (options)
print (filename,options)
366 GNU Octave
print (h,filename,options)
Print a plot, or save it to a file.
Both output formatted for printing (PDF and PostScript), and many bitmapped and
vector image formats are supported.
filename defines the name of the output file. If the filename has no suffix, one is
inferred from the specified device and appended to the filename. If no filename is
specified, the output is sent to the printer.
hspecifies the handle of the figure to print. If no handle is specified the current figure
is used.
For output to a printer, PostScript file, or PDF file, the paper size is specified by
the figure’s papersize property. The location and size of the image on the page
are specified by the figure’s paperposition property. The orientation of the page is
specified by the figure’s paperorientation property.
The width and height of images are specified by the figure’s paperpositon(3:4)
property values.
The print command supports many options:
-fhSpecify the handle, h, of the figure to be printed. The default is the
current figure.
-Pprinter
Set the printer name to which the plot is sent if no filename is specified.
-Gghostscript_command
Specify the command for calling Ghostscript. For Unix and Windows the
defaults are "gs" and "gswin32c", respectively.
-color
-mono Color or monochrome output.
-solid
-dashed Force all lines to be solid or dashed, respectively.
-portrait
-landscape
Specify the orientation of the plot for printed output. For non-printed
output the aspect ratio of the output corresponds to the plot area defined
by the "paperposition" property in the orientation specified. This op-
tion is equivalent to changing the figure’s "paperorientation" property.
-TextAlphaBits=n
-GraphicsAlphaBits=n
Octave is able to produce output for various printers, bitmaps, and vector
formats by using Ghostscript. For bitmap and printer output anti-aliasing
is applied using Ghostscript’s TextAlphaBits and GraphicsAlphaBits op-
tions. The default number of bits are 4 and 1 respectively. Allowed values
for Nare 1, 2, or 4.
-ddevice The available output format is specified by the option device, and is one
of:
Chapter 15: Plotting 367
ps
ps2
psc
psc2 PostScript (level 1 and 2, mono and color). The FLTK graph-
ics toolkit generates PostScript level 3.0.
eps
eps2
epsc
epsc2 Encapsulated PostScript (level 1 and 2, mono and color). The
FLTK graphic toolkit generates PostScript level 3.0.
pslatex
epslatex
pdflatex
pslatexstandalone
epslatexstandalone
pdflatexstandalone
Generate a L
A
T
E
X file filename.tex for the text portions of
a plot and a file filename.(ps|eps|pdf) for the remaining
graphics. The graphics file suffix .ps|eps|pdf is determined
by the specified device type. The L
A
T
E
X file produced by the
‘standalone’ option can be processed directly by L
A
T
E
X. The
file generated without the ‘standalone’ option is intended to
be included from another L
A
T
E
X document. In either case, the
L
A
T
E
X file contains an \includegraphics command so that
the generated graphics file is automatically included when
the L
A
T
E
X file is processed. The text that is written to the
L
A
T
E
X file contains the strings exactly as they were speci-
fied in the plot. If any special characters of the T
E
X mode
interpreter were used, the file must be edited before L
A
T
E
X
processing. Specifically, the special characters must be en-
closed with dollar signs ($ ... $), and other characters that
are recognized by L
A
T
E
X may also need editing (.e.g., braces).
The ‘pdflatex’ device, and any of the ‘standalone’ formats,
are not available with the Gnuplot toolkit.
epscairo
pdfcairo
epscairolatex
pdfcairolatex
epscairolatexstandalone
pdfcairolatexstandalone
Generate Cairo based output when using the Gnuplot graph-
ics toolkit. The ‘epscairo’ and ‘pdfcairo’ devices are syn-
onymous with the ‘epsc’ device. The L
A
T
E
X variants gen-
erate a L
A
T
E
X file, filename.tex, for the text portions of a
plot, and an image file, filename.(eps|pdf), for the graph
368 GNU Octave
portion of the plot. The ‘standalone’ variants behave as
described for ‘epslatexstandalone’ above.
ill
aifm Adobe Illustrator (Obsolete for Gnuplot versions >4.2)
canvas Javascript-based drawing on HTML5 canvas viewable in a
web browser (only available for the Gnuplot graphics toolkit).
cdr
corel CorelDraw
dxf AutoCAD
emf
meta Microsoft Enhanced Metafile
fig XFig. For the Gnuplot graphics toolkit, the additional op-
tions -textspecial or -textnormal can be used to control
whether the special flag should be set for the text in the fig-
ure. (default is -textnormal)
gif GIF image (only available for the Gnuplot graphics toolkit)
hpgl HP plotter language
jpg
jpeg JPEG image
latex L
A
T
E
X picture environment (only available for the Gnuplot
graphics toolkit).
mf Metafont
png Portable network graphics
pbm PBMplus
pdf Portable document format
svg Scalable vector graphics
tikz
tikzstandalone
Generate a L
A
T
E
X file using PGF/TikZ. For the FLTK toolkit the result
is PGF. The ‘tikzstandalone’ device produces a L
A
T
E
X document which
includes the TikZ file (‘tikzstandalone’ is only available for the Gnuplot
graphics toolkit).
If the device is omitted, it is inferred from the file extension, or if there
is no filename it is sent to the printer as PostScript.
-dghostscript_device
Additional devices are supported by Ghostscript. Some examples are;
pdfwrite Produces pdf output from eps
ljet2p HP LaserJet IIP
Chapter 15: Plotting 369
pcx24b 24-bit color PCX file format
ppm Portable Pixel Map file format
For a complete list, type system ("gs -h") to see what formats and
devices are available.
When Ghostscript output is sent to a printer the size is determined by the
figure’s "papersize" property. When the output is sent to a file the size
is determined by the plot box defined by the figure’s "paperposition"
property.
-append Append PostScript or PDF output to a pre-existing file of the same type.
-rNUM Resolution of bitmaps in pixels per inch. For both metafiles and SVG the
default is the screen resolution; for other formats it is 150 dpi. To specify
screen resolution, use "-r0".
-loose
-tight Force a tight or loose bounding box for eps files. The default is loose.
-preview Add a preview to eps files. Supported formats are:
-interchange
Provide an interchange preview.
-metafile
Provide a metafile preview.
-pict Provide pict preview.
-tiff Provide a tiff preview.
-Sxsize,ysize
Plot size in pixels for EMF, GIF, JPEG, PBM, PNG, and SVG. For
PS, EPS, PDF, and other vector formats the plot size is in points. This
option is equivalent to changing the size of the plot box associated with
the "paperposition" property. When using the command form of the
print function you must quote the xsize,ysize option. For example, by
writing "-S640,480".
-Ffontname
-Ffontname:size
-F:size Use fontname and/or fontsize for all text. fontname is ignored for some
devices: dxf, fig, hpgl, etc.
The filename and options can be given in any order.
Example: Print to a file using the pdf device.
figure (1);
clf ();
surf (peaks);
print figure1.pdf
Example: Print to a file using jpg device.
clf ();
surf (peaks);
print -djpg figure2.jpg

370 GNU Octave
Example: Print to printer named PS printer using ps format.
clf ();
surf (peaks);
print -dpswrite -PPS_printer
See also: [saveas], page 370,[hgsave], page 371,[orient], page 370,[figure], page 355.
saveas (h,filename)
saveas (h,filename,fmt)
Save graphic object hto the file filename in graphic format fmt.
fmt should be one of the following formats:
ps PostScript
eps Encapsulated PostScript
jpg JPEG Image
png PNG Image
emf Enhanced Meta File
pdf Portable Document Format
All device formats specified in print may also be used. If fmt is omitted it is extracted
from the extension of filename. The default format is "pdf".
clf ();
surf (peaks);
saveas (1, "figure1.png");
See also: [print], page 365,[hgsave], page 371,[orient], page 370.
orient (orientation)
orient (hfig,orientation)
orientation = orient ()
orientation = orient (hfig)
Query or set the print orientation for figure hfig.
Valid values for orientation are "portrait","landscape", and "tall".
The "landscape" option changes the orientation so the plot width is larger than the
plot height. The "paperposition" is also modified so that the plot fills the page,
while leaving a 0.25 inch border.
The "tall" option sets the orientation to "portrait" and fills the page with the
plot, while leaving a 0.25 inch border.
The "portrait" option (default) changes the orientation so the plot height is larger
than the plot width. It also restores the default "paperposition" property.
When called with no arguments, return the current print orientation.
If the argument hfig is omitted, then operate on the current figure returned by gcf.
See also: [print], page 365,[saveas], page 370.
Chapter 15: Plotting 371
print and saveas are used when work on a plot has finished and the output must be in a
publication-ready format. During intermediate stages it is often better to save the graphics
object and all of its associated information so that changes—to colors, axis limits, marker
styles, etc.—can be made easily from within Octave. The hgsave/hgload commands can
be used to save and re-create a graphics object.
hgsave (filename)
hgsave (h,filename)
hgsave (h,filename,fmt)
Save the graphics handle hto the file filename in the format fmt.
If unspecified, his the current figure as returned by gcf.
When filename does not have an extension the default filename extension .ofig will
be appended.
If present, fmt should be one of the following:
•-binary,-float-binary
•-hdf5,-float-hdf5
•-V7,-v7,-7,-mat7-binary
•-V6,-v6,-6,-mat6-binary
•-text
•-zip,-z
When producing graphics for final publication use print or saveas. When it is impor-
tant to be able to continue to edit a figure as an Octave object, use hgsave/hgload.
See also: [hgload], page 371,[hdl2struct], page 382,[saveas], page 370,[print],
page 365.
h= hgload (filename)
Load the graphics object in filename into the graphics handle h.
If filename has no extension, Octave will try to find the file with and without the
standard extension of .ofig.
See also: [hgsave], page 371,[struct2hdl], page 383.
15.2.10 Interacting with Plots
The user can select points on a plot with the ginput function or select the position at which
to place text on the plot with the gtext function using the mouse.
[x,y,buttons] = ginput (n)
[x,y,buttons] = ginput ()
Return the position and type of mouse button clicks and/or key strokes in the current
figure window.
If nis defined, then capture nevents before returning. When nis not defined ginput
will loop until the return key RET is pressed.
The return values x,yare the coordinates where the mouse was clicked in the units
of the current axes. The return value button is 1, 2, or 3 for the left, middle, or right
button. If a key is pressed the ASCII value is returned in button.

372 GNU Octave
Implementation Note: ginput is intenteded for 2-D plots. For 3-D plots see the
currentpoint property of the current axes which can be transformed with knowledge
of the current view into data units.
See also: [gtext], page 372,[waitforbuttonpress], page 372.
waitforbuttonpress ()
b= waitforbuttonpress ()
Wait for mouse click or key press over the current figure window.
The return value of bis 0 if a mouse button was pressed or 1 if a key was pressed.
See also: [waitfor], page 803,[ginput], page 371,[kbhit], page 249.
gtext (s)
gtext ({s1,s2, . . . })
gtext ({s1;s2; . . . })
gtext (. . ., prop,val, . . .)
h= gtext (. . . )
Place text on the current figure using the mouse.
The text is defined by the string s. If sis a cell string organized as a row vector then
each string of the cell array is written to a separate line. If sis organized as a column
vector then one string element of the cell array is placed for every mouse click.
Optional property/value pairs are passed directly to the underlying text objects.
The optional return value his a graphics handle to the created text object(s).
See also: [ginput], page 371,[text], page 349.
More sophisticated user interaction mechanisms can be obtained using the ui* family of
functions, see Section 35.3 [UI Elements], page 796.
15.2.11 Test Plotting Functions
The functions sombrero and peaks provide a way to check that plotting is working. Typing
either sombrero or peaks at the Octave prompt should display a three-dimensional plot.
sombrero ()
sombrero (n)
z= sombrero (. . . )
[x,y,z] = sombrero (. . . )
Plot the familiar 3-D sombrero function.
The function plotted is
z=sin(p(x2+ y2))
p(x2+ y2)
Called without a return argument, sombrero plots the surface of the above function
over the meshgrid [-8,8] using surf.
If nis a scalar the plot is made with ngrid lines. The default value for nis 41.
When called with output arguments, return the data for the function evaluated over
the meshgrid. This can subsequently be plotted with surf (x,y,z).
See also: [peaks], page 373,[meshgrid], page 337,[mesh], page 321,[surf], page 323.

Chapter 15: Plotting 373
peaks ()
peaks (n)
peaks (x,y)
z= peaks (. . . )
[x,y,z] = peaks (. . . )
Plot a function with lots of local maxima and minima.
The function has the form
f(x, y) = 3(1 −x)2e(−x2−(y+1)2)−10 x
5−x3−y5−1
3e(−(x+1)2−y2)
Called without a return argument, peaks plots the surface of the above function using
surf.
If nis a scalar, peaks plots the value of the above function on an n-by-nmesh over
the range [-3,3]. The default value for nis 49.
If nis a vector, then it represents the grid values over which to calculate the function.
If xand yare specified then the function value is calculated over the specified grid
of vertices.
When called with output arguments, return the data for the function evaluated over
the meshgrid. This can subsequently be plotted with surf (x,y,z).
See also: [sombrero], page 372,[meshgrid], page 337,[mesh], page 321,[surf],
page 323.
15.3 Graphics Data Structures
15.3.1 Introduction to Graphics Structures
The graphics functions use pointers, which are of class graphics handle, in order to address
the data structures which control visual display. A graphics handle may point to any one of
a number of different base object types and these objects are the graphics data structures
themselves. The primitive graphic object types are: figure,axes,line,text,patch,
surface,text,image, and light.
Each of these objects has a function by the same name, and, each of these functions
returns a graphics handle pointing to an object of the corresponding type. In addition
there are several functions which operate on properties of the graphics objects and which
also return handles: the functions plot and plot3 return a handle pointing to an object
of type line, the function subplot returns a handle pointing to an object of type axes, the
function fill returns a handle pointing to an object of type patch, the functions area,
bar,barh,contour,contourf,contour3,surf,mesh,surfc,meshc,errorbar,quiver,
quiver3,scatter,scatter3,stair,stem,stem3 each return a handle to a complex data
structure as documented in [Data Sources], page 430.
The graphics objects are arranged in a hierarchy:
1. The root is at 0. In other words, get (0) returns the properties of the root object.
2. Below the root are figure objects.
3. Below the figure objects are axes objects.

374 GNU Octave
4. Below the axes objects are line,text,patch,surface,image, and light objects.
Graphics handles may be distinguished from function handles (see Section 11.11.1 [Func-
tion Handles], page 209) by means of the function ishandle.ishandle returns true if its
argument is a handle of a graphics object. In addition, a figure or axes object may be tested
using isfigure or isaxes respectively. The test functions return true only if the argument
is both a handle and of the correct type (figure or axes).
The whos function can be used to show the object type of each currently defined graphics
handle. (Note: this is not true today, but it is, I hope, considered an error in whos. It may
be better to have whos just show graphics handle as the class, and provide a new function
which, given a graphics handle, returns its object type. This could generalize the ishandle()
functions and, in fact, replace them.)
The get and set commands are used to obtain and set the values of properties of graphics
objects. In addition, the get command may be used to obtain property names.
For example, the property "type" of the graphics object pointed to by the graphics
handle h may be displayed by:
get (h, "type")
The properties and their current values are returned by get (h) where h is a handle
of a graphics object. If only the names of the allowed properties are wanted they may be
displayed by: get (h, "").
Thus, for example:
h = figure ();
get (h, "type")
ans = figure
get (h, "");
error: get: ambiguous figure property name ; possible matches:
__enhanced__ hittest resize
__graphics_toolkit__ integerhandle resizefcn
__guidata__ interruptible selected
__modified__ inverthardcopy selectionhighlight
__myhandle__ keypressfcn selectiontype
__plot_stream__ keyreleasefcn tag
alphamap menubar toolbar
beingdeleted mincolormap type
busyaction name uicontextmenu
buttondownfcn nextplot units
children numbertitle userdata
clipping outerposition visible
closerequestfcn paperorientation windowbuttondownfcn
color paperposition windowbuttonmotionfcn
colormap paperpositionmode windowbuttonupfcn
createfcn papersize windowkeypressfcn
currentaxes papertype windowkeyreleasefcn
currentcharacter paperunits windowscrollwheelfcn
currentobject parent windowstyle
currentpoint pointer wvisual
deletefcn pointershapecdata wvisualmode
dockcontrols pointershapehotspot xdisplay
doublebuffer position xvisual
filename renderer xvisualmode
handlevisibility renderermode
Chapter 15: Plotting 375
The root figure has index 0. Its properties may be displayed by: get (0, "").
The uses of get and set are further explained in [get], page 381,[set], page 381.
res = isprop (obj,"prop")
Return true if prop is a property of the object obj.
obj may also be an array of objects in which case res will be a logical array indicating
whether each handle has the property prop.
For plotting, obj is a handle to a graphics object. Otherwise, obj should be an
instance of a class.
See also: [get], page 381,[set], page 381,[ismethod], page 771,[isobject], page 770.
15.3.2 Graphics Objects
The hierarchy of graphics objects was explained above. See Section 15.3.1 [Introduction to
Graphics Structures], page 373. Here the specific objects are described, and the properties
contained in these objects are discussed. Keep in mind that graphics objects are always
referenced by handle.
root figure the top level of the hierarchy and the parent of all figure objects. The handle
index of the root figure is 0.
figure A figure window.
axes A set of axes. This object is a child of a figure object and may be a parent of
line, text, image, patch, surface, or light objects.
line A line in two or three dimensions.
text Text annotations.
image A bitmap image.
patch A filled polygon, currently limited to two dimensions.
surface A three-dimensional surface.
light A light object used for lighting effects on patches and surfaces.
15.3.2.1 Creating Graphics Objects
You can create any graphics object primitive by calling the function of the same name as
the object; In other words, figure,axes,line,text,image,patch,surface, and light
functions. These fundamental graphic objects automatically become children of the current
axes object as if hold on was in place. Separately, axes will automatically become children
of the current figure object and figures will become children of the root object 0.
If this auto-joining feature is not desired then it is important to call newplot first to
prepare a new figure and axes for plotting. Alternatively, the easier way is to call a high-
level graphics routine which will both create the plot and then populate it with low-level
graphics objects. Instead of calling line, use plot. Or use surf instead of surface. Or
use fill instead of patch.
376 GNU Octave
axes ()
axes (property,value, . . . )
axes (hax)
h= axes (. . . )
Create an axes object and return a handle to it, or set the current axes to hax.
Called without any arguments, or with property/value pairs, construct a new axes.
For accepted properties and corresponding values, see [set], page 381.
Called with a single axes handle argument hax, the function makes hax the current
axis. It also restacks the axes in the corresponding figure so that hax is the first
entry in the list of children. This causes hax to be displayed on top of any other axes
objects (Z-order stacking).
See also: [gca], page 379,[set], page 381,[get], page 381.
line ()
line (x,y)
line (x,y,property,value, . . . )
line (x,y,z)
line (x,y,z,property,value, . . . )
line (property,value, . . . )
line (hax, . . . )
h= line (. . . )
Create line object from xand y(and possibly z) and insert in the current axes.
Multiple property-value pairs may be specified for the line object, but they must
appear in pairs.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle (or vector of handles) to the line
objects created.
See also: [image], page 748,[patch], page 376,[rectangle], page 319,[surface],
page 377,[text], page 349.
patch ()
patch (x,y,c)
patch (x,y,z,c)
patch ("Faces",faces,"Vertices",verts, . . . )
patch (. . ., prop,val, . . .)
patch (. . ., propstruct, . . .)
patch (hax, . . . )
h= patch (. . . )
Create patch object in the current axes with vertices at locations (x,y) and of color
c.
If the vertices are matrices of size MxN then each polygon patch has M vertices and a
total of N polygons will be created. If some polygons do not have M vertices use NaN
to represent "no vertex". If the zinput is present then 3-D patches will be created.
The color argument ccan take many forms. To create polygons which all share a
single color use a string value (e.g., "r" for red), a scalar value which is scaled by
Chapter 15: Plotting 377
caxis and indexed into the current colormap, or a 3-element RGB vector with the
precise TrueColor.
If cis a vector of length N then the ith polygon will have a color determined by scaling
entry c(i) according to caxis and then indexing into the current colormap. More
complicated coloring situations require directly manipulating patch property/value
pairs.
Instead of specifying polygons by matrices xand y, it is possible to present a unique
list of vertices and then a list of polygon faces created from those vertices. In this case
the "Vertices" matrix will be an Nx2 (2-D patch) or Nx3 (3-D patch). The MxN
"Faces" matrix describes M polygons having N vertices—each row describes a single
polygon and each column entry is an index into the "Vertices" matrix to identify a
vertex. The patch object can be created by directly passing the property/value pairs
"Vertices"/verts,"Faces"/faces as inputs.
Instead of using property/value pairs, any property can be set by passing a structure
propstruct with the respective field names.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created patch object.
Implementation Note: Patches are highly configurable objects. To truly customize
them requires setting patch properties directly. Useful patch properties are: "cdata",
"edgecolor","facecolor","faces","facevertexcdata".
See also: [fill], page 312,[get], page 381,[set], page 381.
surface (x,y,z,c)
surface (x,y,z)
surface (z,c)
surface (z)
surface (. . ., prop,val, . . .)
surface (hax, . . . )
h= surface (. . . )
Create a surface graphic object given matrices xand yfrom meshgrid and a matrix
of values zcorresponding to the xand ycoordinates of the surface.
If xand yare vectors, then a typical vertex is (x(j), y(i), z(i,j)). Thus, columns of
zcorrespond to different xvalues and rows of zcorrespond to different yvalues. If
only a single input zis given then xis taken to be 1:rows (z)and yis 1:columns
(z).
Any property/value input pairs are assigned to the surface object.
If the first argument hax is an axes handle, then plot into this axis, rather than the
current axes returned by gca.
The optional return value his a graphics handle to the created surface object.
See also: [surf], page 323,[mesh], page 321,[patch], page 376,[line], page 376.
light ()
light (. . ., "prop",val, . . .)
light (hax, . . . )
378 GNU Octave
h= light (. . . )
Create a light object in the current axes or for axes hax.
When a light object is present in an axes object, and the properties "EdgeLighting"
or "FaceLighting" of a patch or surface object are set to a value other than "none",
these objects are drawn with light and shadow effects. Supported values for Lighting
properties are "none" (no lighting effects), "flat" (faceted look of the objects), and
"gouraud" (linear interpolation of the lighting effects between the vertices). For
patch objects, the normals must be set manually (property "VertexNormals").
Up to eight light objects are supported per axes.
Lighting is only supported for OpenGL graphic toolkits (i.e., "fltk" and "qt").
A light object has the following properties which alter the appearance of the plot.
"Color": The color of the light can be passed as an
RGB-vector (e.g., [1 0 0] for red) or as a string (e.g., "r" for red). The
default color is white ([1 1 1]).
"Position": The direction from which the light emanates as a
1x3-vector. The default direction is [1 0 1].
"Style": This string defines whether the light emanates from a
light source at infinite distance ("infinite") or from a local point source
("local"). The default is "infinite".
If the first argument hax is an axes handle, then add the light object to this axes,
rather than the current axes returned by gca.
The optional return value his a graphics handle to the created light object.
See also: [lighting], page 334,[material], page 335,[patch], page 376,[surface],
page 377.
15.3.2.2 Handle Functions
To determine whether a variable is a graphics object index, or an index to an axes or figure,
use the functions ishandle,isaxes, and isfigure.
ishandle (h)
Return true if his a graphics handle and false otherwise.
hmay also be a matrix of handles in which case a logical array is returned that is
true where the elements of hare graphics handles and false where they are not.
See also: [isaxes], page 379,[isfigure], page 379.
ishghandle (h)
ishghandle (h,type)
Return true if his a graphics handle (of type type) and false otherwise.
When no type is specified the function is equivalent to ishandle.
See also: [ishandle], page 378.
Chapter 15: Plotting 379
isaxes (h)
Return true if his an axes graphics handle and false otherwise.
If his a matrix then return a logical array which is true where the elements of hare
axes graphics handles and false where they are not.
See also: [isaxes], page 379,[ishandle], page 378.
isfigure (h)
Return true if his a figure graphics handle and false otherwise.
If his a matrix then return a logical array which is true where the elements of hare
figure graphics handles and false where they are not.
See also: [isaxes], page 379,[ishandle], page 378.
The function gcf returns an index to the current figure object, or creates one if none
exists. Similarly, gca returns the current axes object, or creates one (and its parent figure
object) if none exists.
h= gcf ()
Return a handle to the current figure.
The current figure is the default target for graphics output. If multiple figures exist,
gcf returns the last created figure or the last figure that was clicked on with the
mouse.
If a current figure does not exist, create one and return its handle. The handle may
then be used to examine or set properties of the figure. For example,
fplot (@sin, [-10, 10]);
fig = gcf ();
set (fig, "numbertitle", "off", "name", "sin plot")
plots a sine wave, finds the handle of the current figure, and then renames the figure
window to describe the contents.
Note: To find the current figure without creating a new one if it does not exist, query
the "CurrentFigure" property of the root graphics object.
get (0, "currentfigure");
See also: [gca], page 379,[gco], page 380,[gcbf], page 424,[gcbo], page 424,[get],
page 381,[set], page 381.
h= gca ()
Return a handle to the current axis object.
The current axis is the default target for graphics output. In the case of a figure with
multiple axes, gca returns the last created axes or the last axes that was clicked on
with the mouse.
If no current axes object exists, create one and return its handle. The handle may
then be used to examine or set properties of the axes. For example,
ax = gca ();
set (ax, "position", [0.5, 0.5, 0.5, 0.5]);
creates an empty axes object and then changes its location and size in the figure
window.
380 GNU Octave
Note: To find the current axis without creating a new axes object if it does not exist,
query the "CurrentAxes" property of a figure.
get (gcf, "currentaxes");
See also: [gcf], page 379,[gco], page 380,[gcbf], page 424,[gcbo], page 424,[get],
page 381,[set], page 381.
h= gco ()
h= gco (fig)
Return a handle to the current object of the current figure, or a handle to the current
object of the figure with handle fig.
The current object of a figure is the object that was last clicked on. It is stored in
the "CurrentObject" property of the target figure.
If the last mouse click did not occur on any child object of the figure, then the current
object is the figure itself.
If no mouse click occurred in the target figure, this function returns an empty matrix.
Programming Note: The value returned by this function is not necessarily the same
as the one returned by gcbo during callback execution. An executing callback can be
interrupted by another callback and the current object may be changed.
See also: [gcbo], page 424,[gca], page 379,[gcf], page 379,[gcbf], page 424,[get],
page 381,[set], page 381.
The get and set functions may be used to examine and set properties for graphics
objects. For example,
get (0)
⇒ans =
{
type = root
currentfigure = [](0x0)
children = [](0x0)
visible = on
...
}
returns a structure containing all the properties of the root figure. As with all functions
in Octave, the structure is returned by value, so modifying it will not modify the internal
root figure plot object. To do that, you must use the set function. Also, note that in this
case, the currentfigure property is empty, which indicates that there is no current figure
window.
The get function may also be used to find the value of a single property. For example,
get (gca (), "xlim")
⇒[01]
returns the range of the x-axis for the current axes object in the current figure.
To set graphics object properties, use the set function. For example,
set (gca (), "xlim", [-10, 10]);
sets the range of the x-axis for the current axes object in the current figure to ‘[-10, 10]’.
Chapter 15: Plotting 381
Default property values can also be queried if the set function is called without a value
argument. When only one argument is given (a graphic handle) then a structure with
defaults for all properties of the given object type is returned. For example,
set (gca ())
returns a structure containing the default property values for axes objects. If set is called
with two arguments (a graphic handle and a property name) then only the defaults for the
requested property are returned.
val = get (h)
val = get (h,p)
Return the value of the named property pfrom the graphics handle h.
If pis omitted, return the complete property list for h.
If his a vector, return a cell array including the property values or lists respectively.
See also: [set], page 381.
set (h,property,value, . . . )
set (h,properties,values)
set (h,pv)
value_list = set (h,property)
all_value_list = set (h)
Set named property values for the graphics handle (or vector of graphics handles) h.
There are three ways to give the property names and values:
•as a comma separated list of property,value pairs
Here, each property is a string containing the property name, each value is a
value of the appropriate type for the property.
•as a cell array of strings properties containing property names and a cell array
values containing property values.
In this case, the number of columns of values must match the number of elements
in properties. The first column of values contains values for the first entry in
properties, etc. The number of rows of values must be 1 or match the number
of elements of h. In the first case, each handle in hwill be assigned the same
values. In the latter case, the first handle in hwill be assigned the values from
the first row of values and so on.
•as a structure array pv
Here, the field names of pv represent the property names, and the field values
give the property values. In contrast to the previous case, all elements of pv will
be set in all handles in hindependent of the dimensions of pv.
set is also used to query the list of values a named property will take. clist = set
(h, "property") will return the list of possible values for "property" in the cell list
clist. If no output variable is used then the list is formatted and printed to the screen.
If no property is specified (slist = set (h)) then a structure slist is returned where
the fieldnames are the properties of the object hand the fields are the list of possible
values for each property. If no output variable is used then the list is formatted and
printed to the screen.
382 GNU Octave
For example,
hf = figure ();
set (hf, "paperorientation")
⇒paperorientation: [ landscape | {portrait} | rotated ]
shows the paperorientation property can take three values with the default being
"portrait".
See also: [get], page 381.
parent = ancestor (h,type)
parent = ancestor (h,type,"toplevel")
Return the first ancestor of handle object hwhose type matches type, where type is
a character string.
If type is a cell array of strings, return the first parent whose type matches any of the
given type strings.
If the handle object hitself is of type type, return h.
If "toplevel" is given as a third argument, return the highest parent in the object
hierarchy that matches the condition, instead of the first (nearest) one.
See also: [findobj], page 419,[findall], page 420,[allchild], page 382.
h= allchild (handles)
Find all children, including hidden children, of a graphics object.
This function is similar to get (h, "children"), but also returns hidden objects
(HandleVisibility = "off").
If handles is a scalar, hwill be a vector. Otherwise, hwill be a cell matrix of the
same size as handles and each cell will contain a vector of handles.
See also: [findall], page 420,[findobj], page 419,[get], page 381,[set], page 381.
findfigs ()
Find all visible figures that are currently off the screen and move them onto the screen.
See also: [allchild], page 382,[figure], page 355,[get], page 381,[set], page 381.
Figures can be printed or saved in many graphics formats with print and saveas.
Occasionally, however, it may be useful to save the original Octave handle graphic directly
so that further modifications can be made such as modifying a title or legend.
This can be accomplished with the following functions by
fig_struct = hdl2struct (gcf);
save myplot.fig -struct fig_struct;
...
fig_struct = load ("myplot.fig");
struct2hdl (fig_struct);
s= hdl2struct (h)
Return a structure, s, whose fields describe the properties of the object, and its
children, associated with the handle, h.
Chapter 15: Plotting 383
The fields of the structure sare "type","handle","properties","children", and
"special".
See also: [struct2hdl], page 383,[hgsave], page 371,[findobj], page 419.
h= struct2hdl (s)
h= struct2hdl (s,p)
h= struct2hdl (s,p,hilev)
Construct a graphics handle object hfrom the structure s.
The structure must contain the fields "handle","type","children","properties",
and "special".
If the handle of an existing figure or axes is specified, p, the new object will be created
as a child of that object. If no parent handle is provided then a new figure and the
necessary children will be constructed using the default values from the root figure.
A third boolean argument hilev can be passed to specify whether the function should
preserve listeners/callbacks, e.g., for legends or hggroups. The default is false.
See also: [hdl2struct], page 382,[hgload], page 371,[findobj], page 419.
hnew = copyobj (horig)
hnew = copyobj (horig,hparent)
Construct a copy of the graphic objects associated with the handles horig and return
new handles hnew to the new objects.
If a parent handle hparent (root, figure, axes, or hggroup) is specified, the copied
object will be created as a child of hparent.
If horig is a vector of handles, and hparent is a scalar, then each handle in the vector
hnew has its "Parent" property set to hparent. Conversely, if horig is a scalar and
hparent a vector, then each parent object will receive a copy of horig. If horig and
hparent are both vectors with the same number of elements then hnew(i) will have
parent hparent(i).
See also: [struct2hdl], page 383,[hdl2struct], page 382,[findobj], page 419.
15.3.3 Graphics Object Properties
In this Section the graphics object properties are discussed in detail, starting with the root
figure properties and continuing through the objects hierarchy. The documentation about a
specific graphics object can be displayed using doc function, e.g., doc ("axes properties")
will show Section 15.3.3.3 [Axes Properties], page 390.
The allowed values for radio (string) properties can be retrieved programmatically or
displayed using the one or two arguments call to set function. See [set], page 381.
In the following documentation, default values are enclosed in { }.
15.3.3.1 Root Figure Properties
The root figure properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
beingdeleted is unused.
384 GNU Octave
busyaction:"cancel" | {"queue"}
busyaction is unused.
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
callbackobject (read-only): graphics handle, def. [](0x0)
Graphics handle of the current object whose callback is executing.
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the root’s children.
clipping:"off" | {"on"}
clipping is unused.
commandwindowsize (read-only): def. [0 0]
createfcn: string |function handle, def. [](0x0)
createfcn is unused.
currentfigure: graphics handle, def. [](0x0)
Graphics handle of the current figure.
deletefcn: string |function handle, def. [](0x0)
deletefcn is unused.
fixedwidthfontname: string, def. "Courier"
handlevisibility:"callback" | "off" | {"on"}
handlevisibility is unused.
hittest:"off" | {"on"}
hittest is unused.
interruptible:"off" | {"on"}
interruptible is unused.
monitorpositions (read-only):
monitorpositions is unused.
parent: graphics handle, def. [](0x0)
Root figure has no parent graphics object. parent is always empty.
pointerlocation: two-element vector, def. [0 0]
pointerlocation is unused.
pointerwindow (read-only): graphics handle, def. 0
pointerwindow is unused.
screendepth (read-only): double
screenpixelsperinch (read-only): double
screensize (read-only): four-element vector
selected:{"off"}| "on"
selected is unused.
selectionhighlight:"off" | {"on"}
selectionhighlight is unused.
Chapter 15: Plotting 385
showhiddenhandles:{"off"}| "on"
If showhiddenhandles is "on", all graphics objects handles are visible in their
parents’ children list, regardless of the value of their handlevisibility prop-
erty.
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "root"
uicontextmenu: graphics handle, def. [](0x0)
uicontextmenu is unused.
units:"centimeters" | "inches" | "normalized" | {"pixels"}| "points"
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
visible is unused.
15.3.3.2 Figure Properties
The figure properties are:
__modified__:"off" | {"on"}
alphamap: def. 64-by-1 double
Transparency is not yet implemented for figure objects. alphamap is unused.
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the figure’s children.
clipping:"off" | {"on"}
clipping is unused.
closerequestfcn: string |function handle, def. "closereq"
Function that is executed when a figure is deleted. See [closereq function],
page 361.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
color: colorspec, def. [1 1 1]
Color of the figure background. See Section 15.4.1 [colorspec], page 422.
colormap: N-by-3 matrix, def. 64-by-3 double
A matrix containing the RGB color map for the current axes.
386 GNU Octave
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after figure has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultfigurecreatefcn", ’disp ("figure created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
currentaxes: graphics handle, def. [](0x0)
Handle to the graphics object of the current axes.
currentcharacter (read-only): def. ""
currentcharacter is unused.
currentobject (read-only): graphics handle, def. [](0x0)
currentpoint (read-only): two-element vector, def. [0; 0]
A 1-by-2 matrix which holds the coordinates of the point over which the mouse
pointer was when a mouse event occurred. The X and Y coordinates are in
units defined by the figure’s units property and their origin is the lower left
corner of the plotting area.
Events which set currentpoint are
A mouse button was pressed
always
A mouse button was released
only if the figure’s callback windowbuttonupfcn is defined
The pointer was moved while pressing the mouse button (drag)
only if the figure’s callback windowbuttonmotionfcn is defined
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before figure is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
dockcontrols:{"off"}| "on"
dockcontrols is unused.
filename: string, def. ""
The filename used when saving the plot figure.
graphicssmoothing:"off" | {"on"}
Use smoothing techniques to reduce the appearance of jagged lines.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the figure’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
integerhandle:"off" | {"on"}
Assign the next lowest unused integer as the Figure number.
interruptible:"off" | {"on"}
inverthardcopy:"off" | {"on"}
Replace the figure and axes background color with white when printing.
Chapter 15: Plotting 387
keypressfcn: string |function handle, def. [](0x0)
Callback function executed when a keystroke event happens while the figure
has focus. The actual key that was pressed can be retrieved using the second
argument ’evt’ of the function. For information on how to write graphics listener
functions see Section 15.4.4 [Callbacks section], page 423.
keyreleasefcn: string |function handle, def. [](0x0)
With keypressfcn, the keyboard callback functions. These callback functions
are called when a key is pressed/released respectively. The functions are called
with two input arguments. The first argument holds the handle of the calling
figure. The second argument holds an event structure which has the following
members:
Character:
The ASCII value of the key
Key: Lowercase value of the key
Modifier:
A cell array containing strings representing the modifiers pressed
with the key.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
menubar:{"figure"}| "none"
Control the display of the figure menu bar at the top of the figure.
name: string, def. ""
Name to be displayed in the figure title bar. The name is displayed to the right
of any title determined by the numbertitle property.
nextplot:{"add"}| "new" | "replace" | "replacechildren"
nextplot is used by high level plotting functions to decide what to do with
axes already present in the figure. See [newplot function], page 358.
numbertitle:"off" | {"on"}
Display "Figure"followed by the numerical figure handle value in the figure
title bar.
outerposition: four-element vector, def. [-1 -1 -1 -1]
Specify the position and size of the figure including the top menubar and the
bottom status bar. The four elements of the vector are the coordinates of
the lower left corner and width and height of the figure. See [units property],
page 389.
paperorientation:"landscape" | {"portrait"}
The value for the papersize, and paperposition properties depends upon
paperorientation. The horizontal and vertical values for papersize and
paperposition reverse order when paperorientation is switched between
"portrait" and "landscape".
paperposition: four-element vector, def. [0.25000 2.50000 8.00000 6.00000]
Vector [left bottom width height] defining the position and size of the figure
(in paperunits units) on the printed page. The position [left bottom] defines
388 GNU Octave
the lower left corner of the figure on the page, and the size is defined by [width
height]. For output formats not implicitly rendered on paper, width and
height define the size of the image and the position information is ignored.
Setting paperposition also forces the paperpositionmode property to be set
to "manual".
paperpositionmode:"auto" | {"manual"}
If paperpositionmode is set to "auto", the paperposition property is auto-
matically computed: the printed figure will have the same size as the on-screen
figure and will be centered on the output page. Setting the paperpositionmode
to "auto" does not modify the value of the paperposition property.
papersize: two-element vector, def. [8.5000 11.0000]
Vector [width height] defining the size of the paper for printing. Setting
the papersize property to a value, not associated with one of the defined
papertypes and consistent with the setting for paperorientation, forces
the papertype property to the value "<custom>". If papersize is set to
a value associated with a supported papertype and consistent with the
paperorientation, the papertype value is modified to the associated value.
papertype:"<custom>" | "a" | "a0" | "a1" | "a2" | "a3" | "a4" | "a5" | "arch-a" |
"arch-b" | "arch-c" | "arch-d" | "arch-e" | "b" | "b0" | "b1" | "b2" | "b3" | "b4"
| "b5" | "c" | "d" | "e" | "tabloid" | "uslegal" | {"usletter"}
Name of the paper used for printed output. Setting papertype also changes
papersize, while maintaining consistency with the paperorientation prop-
erty.
paperunits:"centimeters" | {"inches"}| "normalized" | "points"
The unit used to compute the paperposition property. For paperunits set to
"pixels", the conversion between physical units (ex: "inches") and "pixels"
is dependent on the screenpixelsperinch property of the root object.
parent: graphics handle, def. 0
Handle of the parent graphics object.
pointer:{"arrow"}| "botl" | "botr" | "bottom" | "circle" | "cross" |
"crosshair" | "custom" | "fleur" | "fullcrosshair" | "hand" | "ibeam" | "left" |
"right" | "top" | "topl" | "topr" | "watch"
pointer is unused.
pointershapecdata: def. 16-by-16 double
pointershapecdata is unused.
pointershapehotspot: def. [0 0]
pointershapehotspot is unused.
position: four-element vector, def. [300 200 560 420]
Specify the position and size of the figure canvas. The four elements of the
vector are the coordinates of the lower left corner and width and height of the
figure. See [units property], page 389.
renderer:{"opengl"}| "painters"
renderer is unused.
Chapter 15: Plotting 389
renderermode:{"auto"}| "manual"
renderermode is unused.
resize:"off" | {"on"}
resize is unused.
resizefcn: string |function handle, def. [](0x0)
resizefcn is deprecated. Use sizechangedfcn instead.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
selectiontype:"alt" | "extend" | {"normal"}| "open"
sizechangedfcn: string |function handle, def. [](0x0)
Callback triggered when the figure window size is changed.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
tag: string, def. ""
A user-defined string to label the graphics object.
toolbar:{"auto"}| "figure" | "none"
Control the display of the toolbar (along the bottom of the menubar) and the
status bar. When set to "auto", the display is based on the value of the menubar
property.
type (read-only): string
Class name of the graphics object. type is always "figure"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this figure object.
units:"centimeters" | "characters" | "inches" | "normalized" | {"pixels"}|
"points"
The unit used to compute the position and outerposition properties.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the figure is not rendered on screen.
windowbuttondownfcn: string |function handle, def. [](0x0)
See [windowbuttonupfcn property], page 389.
windowbuttonmotionfcn: string |function handle, def. [](0x0)
See [windowbuttonupfcn property], page 389.
windowbuttonupfcn: string |function handle, def. [](0x0)
With windowbuttondownfcn and windowbuttonmotionfcn, the mouse callback
functions. These callback functions are called when a mouse button is pressed,
dragged, or released respectively. When these callback functions are executed,
the currentpoint property holds the current coordinates of the cursor.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
390 GNU Octave
windowkeypressfcn: string |function handle, def. [](0x0)
Function that is executed when a key is pressed and the figure has focus.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
windowkeyreleasefcn: string |function handle, def. [](0x0)
Function that is executed when a key is released and the figure has focus.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
windowscrollwheelfcn: string |function handle, def. [](0x0)
windowscrollwheelfcn is unused.
windowstyle:"docked" | "modal" | {"normal"}
The window style of a figure. One of the following values:
normal Set the window style as non modal.
modal Set the window as modal so that it will stay on top of all normal
figures.
docked Setting the window style as docked currently does not dock the
window.
Changing modes of a visible figure may cause the figure to close and reopen.
15.3.3.3 Axes Properties
The axes properties are:
__modified__:"off" | {"on"}
activepositionproperty:{"outerposition"}| "position"
Specify which of "position" or "outerposition" properties takes precedence
when axes annotations extent changes. See [position property], page 393, and
[outerposition property], page 393.
alim: def. [0 1]
Transparency is not yet implemented for axes objects. alim is unused.
alimmode:{"auto"}| "manual"
ambientlightcolor: def. [1 1 1]
ambientlightcolor is unused.
beingdeleted:{"off"}| "on"
box:{"off"}| "on"
Control whether the axes has a surrounding box.
boxstyle:{"back"}| "full"
For 3-D axes, control whether the "full" box is drawn or only the 3 "back"
axes
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
Chapter 15: Plotting 391
cameraposition: three-element vector, def. [0.50000 0.50000 9.16025]
camerapositionmode:{"auto"}| "manual"
cameratarget: three-element vector, def. [0.50000 0.50000 0.50000]
cameratargetmode:{"auto"}| "manual"
cameraupvector: three-element vector, def. [-0 1 0]
cameraupvectormode:{"auto"}| "manual"
cameraviewangle: scalar, def. 6.6086
cameraviewanglemode:{"auto"}| "manual"
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the axes’s children.
clim: two-element vector, def. [0 1]
Define the limits for the color axis of image children. Setting clim also forces
the climmode property to be set to "manual". See [pcolor function], page 311.
climmode:{"auto"}| "manual"
clipping:"off" | {"on"}
clipping is unused.
clippingstyle:{"3dbox"}| "rectangle"
clippingstyle is unused.
color: colorspec, def. [1 1 1]
Color of the axes background. See Section 15.4.1 [colorspec], page 422.
colororder: N-by-3 RGB matrix, def. 7-by-3 double
RGB values used by plot function for automatic line coloring.
colororderindex: def. 1
colororderindex is unused.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after axes has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultaxescreatefcn", ’disp ("axes created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
currentpoint: 2-by-3 matrix, def. 2-by-3 double
Matrix [xf, yf, zf; xb, yb, zb] which holds the coordinates (in axes data
units) of the point over which the mouse pointer was when the mouse button
was pressed. If a mouse callback function is defined, currentpoint holds the
pointer coordinates at the time the mouse button was pressed. For 3-D plots,
the first row of the returned matrix specifies the point nearest to the current
camera position and the second row the furthest point. The two points forms
a line which is perpendicular to the screen.
dataaspectratio: three-element vector, def. [1 1 1]
Specify the relative height and width of the data displayed in the axes. Setting
dataaspectratio to [1, 2] causes the length of one unit as displayed on the x-
axis to be the same as the length of 2 units on the y-axis. See [daspect function],
392 GNU Octave
page 342. Setting dataaspectratio also forces the dataaspectratiomode
property to be set to "manual".
dataaspectratiomode:{"auto"}| "manual"
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before axes is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
drawmode:"fast" | {"normal"}
fontangle:"italic" | {"normal"}
Control whether the font is italic or normal.
fontname: string, def. "*"
Name of the font used for axes annotations.
fontsize: scalar, def. 10
Size of the font used for axes annotations. See [fontunits property], page 392.
fontsmoothing:"off" | {"on"}
fontsmoothing is unused.
fontunits:"centimeters" | "inches" | "normalized" | "pixels" | {"points"}
Unit used to interpret fontsize property.
fontweight:"bold" | {"normal"}
Control variant of base font used: bold, demi, light, normal.
gridalpha: def. 0.15000
Transparency is not yet implemented for axes objects. gridalpha is unused.
gridalphamode:{"auto"}| "manual"
gridalphamode is unused.
gridcolor: def. [0.15000 0.15000 0.15000]
gridcolor is unused.
gridcolormode:{"auto"}| "manual"
gridcolormode is unused.
gridlinestyle:{"-"}| "--" | "-." | ":" | "none"
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the axes’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
labelfontsizemultiplier: def. 1.1000
Ratio between the x/y/zlabel fontsize and the tick label fontsize
layer:{"bottom"}| "top"
Control whether the axes is drawn below child graphics objects (ticks, labels,
etc. covered by plotted objects) or above.
linestyleorder: def. "-"
linestyleorder is unused.
Chapter 15: Plotting 393
linestyleorderindex: def. 1
linestyleorderindex is unused.
linewidth: def. 0.50000
Width of the main axes lines
minorgridalpha: def. 0.25000
Transparency is not yet implemented for axes objects. minorgridalpha is
unused.
minorgridalphamode:{"auto"}| "manual"
minorgridalphamode is unused.
minorgridcolor: def. [0.10000 0.10000 0.10000]
minorgridcolor is unused.
minorgridcolormode:{"auto"}| "manual"
minorgridcolormode is unused.
minorgridlinestyle:"-" | "--" | "-." | {":"}| "none"
mousewheelzoom: scalar in the range (0, 1), def. 0.50000
Fraction of axes limits to zoom for each wheel movement.
nextplot:"add" | {"replace"}| "replacechildren"
nextplot is used by high level plotting functions to decide what to do with
graphics objects already present in the axes. See [newplot function], page 358.
The state of nextplot is typically controlled using the hold function. See
[hold function], page 359.
outerposition: four-element vector, def. [0 0 1 1]
Specify the position of the plot including titles, axes, and legend. The four
elements of the vector are the coordinates of the lower left corner and width
and height of the plot, in units normalized to the width and height of the plot
window. For example, [0.2, 0.3, 0.4, 0.5] sets the lower left corner of the
axes at (0.2,0.3) and the width and height to be 0.4 and 0.5 respectively. See
[position property], page 393.
parent: graphics handle
Handle of the parent graphics object.
pickableparts:"all" | "none" | {"visible"}
pickableparts is unused.
plotboxaspectratio: def. [1 1 1]
See [pbaspect function], page 342. Setting plotboxaspectratio also forces the
plotboxaspectratiomode property to be set to "manual".
plotboxaspectratiomode:{"auto"}| "manual"
position: four-element vector, def. [0.13000 0.11000 0.77500 0.81500]
Specify the position of the plot excluding titles, axes, and legend. The four
elements of the vector are the coordinates of the lower left corner and width
and height of the plot, in units normalized to the width and height of the plot
window. For example, [0.2, 0.3, 0.4, 0.5] sets the lower left corner of the
axes at (0.2,0.3) and the width and height to be 0.4 and 0.5 respectively. See
[outerposition property], page 393.
394 GNU Octave
projection:{"orthographic"}| "perspective"
projection is unused.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
sortmethod:"childorder" | {"depth"}
sortmethod is unused.
tag: string, def. ""
A user-defined string to label the graphics object.
tickdir:{"in"}| "out"
Control whether axes tick marks project "in"to the plot box or "out". Setting
tickdir also forces the tickdirmode property to be set to "manual".
tickdirmode:{"auto"}| "manual"
ticklabelinterpreter:"latex" | "none" | {"tex"}
Control the way x/y/zticklabel properties are interpreted. See
[Use of the interpreter property], page 361.
ticklength: two-element vector, def. [0.010000 0.025000]
Two-element vector [2Dlen 3Dlen] specifying the length of the tickmarks rel-
ative to the longest visible axis.
tightinset (read-only): four-element vector, def. [0.044643 0.038106 0.000000
0.023810]
Size of the [left bottom right top] margins around the axes that enclose
labels and title annotations.
title: graphics handle
Graphics handle of the title text object.
titlefontsizemultiplier: positive scalar, def. 1.1000
Ratio between the title fontsize and the tick label fontsize
titlefontweight:{"bold"}| "normal"
Control variant of base font used for the axes title.
type (read-only): string
Class name of the graphics object. type is always "axes"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this axes object.
units:"centimeters" | "characters" | "inches" | {"normalized"}| "pixels" |
"points"
Units used to interpret the "position","outerposition", and "tightinset"
properties.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
view: two-element vector, def. [0 90]
Two-element vector [azimuth elevation] specifying the viewpoint for three-
dimensional plots
Chapter 15: Plotting 395
visible:"off" | {"on"}
If visible is "off", the axes is not rendered on screen.
xaxislocation:{"bottom"}| "origin" | "top" | "zero"
Control the x axis location.
xcolor:{colorspec}| "none", def. [0.15000 0.15000 0.15000]
Color of the x-axis. See Section 15.4.1 [colorspec], page 422. Setting xcolor
also forces the xcolormode property to be set to "manual".
xcolormode:{"auto"}| "manual"
xdir:{"normal"}| "reverse"
Direction of the x axis: "normal" is left to right.
xgrid:{"off"}| "on"
Control whether major x grid lines are displayed.
xlabel: graphics handle
Graphics handle of the x label text object.
xlim: two-element vector, def. [0 1]
Two-element vector [xmin xmax] specifying the limits for the x-axis. Set-
ting xlim also forces the xlimmode property to be set to "manual". See
[xlim function], page 315.
xlimmode:{"auto"}| "manual"
xminorgrid:{"off"}| "on"
Control whether minor x grid lines are displayed.
xminortick:{"off"}| "on"
xscale:{"linear"}| "log"
xtick: vector
Position of x tick marks. Setting xtick also forces the xtickmode property to
be set to "manual".
xticklabel: string |cell array of strings, def. 1-by-6 cell
Labels of x tick marks. Setting xticklabel also forces the xticklabelmode
property to be set to "manual".
xticklabelmode:{"auto"}| "manual"
xticklabelrotation: def. 0
xticklabelrotation is unused.
xtickmode:{"auto"}| "manual"
yaxislocation:{"left"}| "origin" | "right" | "zero"
Control the y-axis location.
ycolor:{colorspec}| "none", def. [0.15000 0.15000 0.15000]
Color of the y-axis. See Section 15.4.1 [colorspec], page 422.
ycolormode:{"auto"}| "manual"
ydir:{"normal"}| "reverse"
Direction of the y-axis: "normal" is bottom to top.
396 GNU Octave
ygrid:{"off"}| "on"
Control whether major y grid lines are displayed.
ylabel: graphics handle
Graphics handle of the y label text object.
ylim: two-element vector, def. [0 1]
Two-element vector [ymin ymax] specifying the limits for the y-axis. Set-
ting ylim also forces the ylimmode property to be set to "manual". See
[ylim function], page 315.
ylimmode:{"auto"}| "manual"
yminorgrid:{"off"}| "on"
Control whether minor y grid lines are displayed.
yminortick:{"off"}| "on"
yscale:{"linear"}| "log"
ytick: vector
Position of y tick marks. Setting ytick also forces the ytickmode property to
be set to "manual".
yticklabel: string |cell array of strings, def. 1-by-6 cell
Labels of y tick marks. Setting yticklabel also forces the yticklabelmode
property to be set to "manual".
yticklabelmode:{"auto"}| "manual"
yticklabelrotation: def. 0
yticklabelrotation is unused.
ytickmode:{"auto"}| "manual"
zcolor:{colorspec}| "none", def. [0.15000 0.15000 0.15000]
Color of the z-axis. See Section 15.4.1 [colorspec], page 422.
zcolormode:{"auto"}| "manual"
zdir:{"normal"}| "reverse"
zgrid:{"off"}| "on"
Control whether major z grid lines are displayed.
zlabel: graphics handle
Graphics handle of the z label text object.
zlim: two-element vector, def. [0 1]
Two-element vector [zmin zmaz] specifying the limits for the z-axis. Set-
ting zlim also forces the zlimmode property to be set to "manual". See
[zlim function], page 315.
zlimmode:{"auto"}| "manual"
zminorgrid:{"off"}| "on"
Control whether minor z grid lines are displayed.
zminortick:{"off"}| "on"
zscale:{"linear"}| "log"
ztick: vector
Position of z tick marks. Setting ztick also forces the ztickmode property to
be set to "manual".
Chapter 15: Plotting 397
zticklabel: string |cell array of strings, def. 1-by-6 cell
Labels of z tick marks. Setting zticklabel also forces the zticklabelmode
property to be set to "manual".
zticklabelmode:{"auto"}| "manual"
zticklabelrotation: def. 0
zticklabelrotation is unused.
ztickmode:{"auto"}| "manual"
15.3.3.4 Line Properties
The line properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the line is clipped in its parent axes limits.
color: colorspec, def. [0 0 0]
Color of the line object. See Section 15.4.1 [colorspec], page 422.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after line has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultlinecreatefcn", ’disp ("line created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before line is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
displayname: string |cell array of strings, def. ""
Text for the legend entry corresponding to this line.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the line’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
interpreter:"latex" | "none" | {"tex"}
interruptible:"off" | {"on"}
linestyle:{"-"}| "--" | "-." | ":" | "none"
See Section 15.4.2 [Line Styles], page 422.
398 GNU Octave
linewidth: def. 0.50000
Width of the line object measured in points.
marker:"*" | "+" | "." | "<" | ">" | "^" | "d" | "diamond" | "h" | "hexagram" |
{"none"}| "o" | "p" | "pentagram" | "s" | "square" | "v" | "x"
Shape of the marker for each data point. See Section 15.4.3 [Marker Styles],
page 422.
markeredgecolor:{"auto"}| "none"
Color of the edge of the markers. When set to "auto", the marker edges have
the same color as the line. If set to "none", no marker edges are displayed. This
property can also be set to any color. See Section 15.4.1 [colorspec], page 422.
markerfacecolor:"auto" | {"none"}
Color of the face of the markers. When set to "auto", the marker faces have the
same color as the line. If set to "none", the marker faces are not displayed. This
property can also be set to any color. See Section 15.4.1 [colorspec], page 422.
markersize: scalar, def. 6
Size of the markers measured in points.
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "line"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this line object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the line is not rendered on screen.
xdata: vector, def. [0 1]
Vector of x data to be plotted.
xdatasource: string, def. ""
Name of a vector in the current base workspace to use as x data.
ydata: vector, def. [0 1]
Vector of y data to be plotted.
ydatasource: string, def. ""
Name of a vector in the current base workspace to use as y data.
zdata: vector, def. [](0x0)
Vector of z data to be plotted.
Chapter 15: Plotting 399
zdatasource: string, def. ""
Name of a vector in the current base workspace to use as z data.
15.3.3.5 Text Properties
The text properties are:
__modified__:"off" | {"on"}
backgroundcolor: colorspec, def. "none"
Background area is not yet implemented for text objects. backgroundcolor is
unused.
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the text is clipped in its parent axes limits.
color: colorspec, def. [0 0 0]
Color of the text. See Section 15.4.1 [colorspec], page 422.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after text has been created.
Function is set by using default property on root object, e.g., set (0,
"defaulttextcreatefcn", ’disp ("text created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before text is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
displayname: def. ""
edgecolor: colorspec, def. "none"
Background area is not yet implemented for text objects. edgecolor is unused.
editing:{"off"}| "on"
editing is unused.
extent (read-only): four-element vector, def. [0.000000 -0.005843 0.000000 0.032136]
Vector [x0 y0 width height] indicating the size and location of the text string.
fontangle:"italic" | {"normal"}| "oblique"
Control whether the font is italic or normal. fontangle is currently unused.
fontname: string, def. "*"
The font used for the text.
400 GNU Octave
fontsize: scalar, def. 10
The font size of the text as measured in fontunits.
fontunits:"centimeters" | "inches" | "normalized" | "pixels" | {"points"}
The units used to interpret fontsize property.
fontweight:"bold" | "demi" | "light" | {"normal"}
Control variant of base font used: bold, light, normal, etc.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the text’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
horizontalalignment:"center" | {"left"}| "right"
interpreter:"latex" | "none" | {"tex"}
Control the way the "string" property is interpreted. See
[Use of the interpreter property], page 361.
interruptible:"off" | {"on"}
linestyle:{"-"}| "--" | "-." | ":" | "none"
Background area is not yet implemented for text objects. linestyle is unused.
linewidth: scalar, def. 0.50000
Background area is not yet implemented for text objects. linewidth is unused.
margin: scalar, def. 2
Background area is not yet implemented for text objects. margin is unused.
parent: graphics handle
Handle of the parent graphics object.
position: four-element vector, def. [0 0 0]
Vector [X0 Y0 Z0] where X0, Y0 and Z0 indicate the position of the text anchor
as defined by verticalalignment and horizontalalignment.
rotation: scalar, def. 0
The angle of rotation for the displayed text, measured in degrees.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
string: string, def. ""
The text object string content.
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "text"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this text object.
Chapter 15: Plotting 401
units:"centimeters" | {"data"}| "inches" | "normalized" | "pixels" | "points"
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
verticalalignment:"baseline" | "bottom" | "cap" | {"middle"}| "top"
visible:"off" | {"on"}
If visible is "off", the text is not rendered on screen.
15.3.3.6 Image Properties
The image properties are:
__modified__:"off" | {"on"}
alphadata: scalar |matrix, def. 1
Transparency is not yet implemented for image objects. alphadata is unused.
alphadatamapping:"direct" | {"none"}| "scaled"
Transparency is not yet implemented for image objects. alphadatamapping is
unused.
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
cdata: matrix, def. 64-by-64 double
cdatamapping:{"direct"}| "scaled"
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the image is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after image has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultimagecreatefcn", ’disp ("image created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before image is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
displayname: string |cell array of strings, def. ""
Text for the legend entry corresponding to this image.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the image’s handle is not visible in its parent’s
"children"property.
402 GNU Octave
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "image"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this image object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the image is not rendered on screen.
xdata: two-element vector, def. [1 64]
Two-element vector [xmin xmax] specifying the x coordinates of the first and
last columns of the image.
Setting xdata to the empty matrix ([]) will restore the default value of [1
columns(image)].
ydata: two-element vector, def. [1 64]
Two-element vector [ymin ymax] specifying the y coordinates of the first and
last rows of the image.
Setting ydata to the empty matrix ([]) will restore the default value of [1
rows(image)].
15.3.3.7 Patch Properties
The patch properties are:
__modified__:"off" | {"on"}
alphadatamapping:"direct" | "none" | {"scaled"}
Transparency is not yet implemented for patch objects. alphadatamapping is
unused.
ambientstrength: scalar, def. 0.30000
Strength of the ambient light. Value between 0.0 and 1.0
backfacelighting:"lit" | {"reverselit"}| "unlit"
"lit": The normals are used as is for lighting. "reverselit": The normals
are always oriented towards the point of view. "unlit": Faces with normals
pointing away from the point of view are unlit.
Chapter 15: Plotting 403
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
cdata: scalar |matrix, def. [](0x0)
Data defining the patch object color. Patch color can be defined for faces or
for vertices.
If cdata is a scalar index into the current colormap or a RGB triplet, it defines
the color of all faces.
If cdata is an N-by-1 vector of indices or an N-by-3 (RGB) matrix, it defines
the color of each one of the N faces.
If cdata is an N-by-M or an N-by-M-by-3 (RGB) matrix, it defines the color at
each vertex.
cdatamapping:"direct" | {"scaled"}
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the patch is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after patch has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultpatchcreatefcn", ’disp ("patch created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before patch is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
diffusestrength: scalar, def. 0.60000
Strength of the diffuse reflex. Value between 0.0 (no diffuse reflex) and 1.0 (full
diffuse reflex).
displayname: def. ""
Text of the legend entry corresponding to this patch.
edgealpha: scalar |matrix, def. 1
Transparency is not yet implemented for patch objects. edgealpha is unused.
edgecolor: def. [0 0 0]
edgelighting:"flat" | "gouraud" | {"none"}| "phong"
When set to a value other than "none", the edges of the object are drawn with
light and shadow effects. Supported values are "none" (no lighting effects),
"flat" (facetted look) and "gouraud" (linear interpolation of the lighting ef-
fects between the vertices). "phong" is deprecated and has the same effect as
"gouraud".
404 GNU Octave
facealpha: scalar |matrix, def. 1
Transparency is not yet implemented for patch objects. facealpha is unused.
facecolor:{colorspec}| "none" | "flat" | "interp", def. [0 0 0]
facelighting:{"flat"}| "gouraud" | "none" | "phong"
When set to a value other than "none", the faces of the object are drawn with
light and shadow effects. Supported values are "none" (no lighting effects),
"flat" (facetted look) and "gouraud" (linear interpolation of the lighting ef-
fects between the vertices). "phong" is deprecated and has the same effect as
"gouraud".
facenormals: def. [](0x0)
facenormalsmode:{"auto"}| "manual"
faces: def. [1 2 3]
facevertexalphadata: scalar |matrix, def. [](0x0)
Transparency is not yet implemented for patch objects. facevertexalphadata
is unused.
facevertexcdata: def. [](0x0)
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the patch’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
interpreter:"latex" | "none" | {"tex"}
interpreter is unused.
interruptible:"off" | {"on"}
linestyle:{"-"}| "--" | "-." | ":" | "none"
linewidth: def. 0.50000
marker:"*" | "+" | "." | "<" | ">" | "^" | "d" | "diamond" | "h" | "hexagram" |
{"none"}| "o" | "p" | "pentagram" | "s" | "square" | "v" | "x"
See [line marker property], page 398.
markeredgecolor:{"auto"}| "flat" | "none"
See [line markeredgecolor property], page 398.
markerfacecolor:"auto" | "flat" | {"none"}
See [line markerfacecolor property], page 398.
markersize: scalar, def. 6
See [line markersize property], page 398.
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
specularcolorreflectance: scalar, def. 1
Reflectance for specular color. Value between 0.0 (color of underlying face) and
1.0 (color of light source).
Chapter 15: Plotting 405
specularexponent: scalar, def. 10
Exponent for the specular reflex. The lower the value, the more the reflex is
spread out.
specularstrength: scalar, def. 0.90000
Strength of the specular reflex. Value between 0.0 (no specular reflex) and 1.0
(full specular reflex).
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "patch"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this patch object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
vertexnormals: def. [](0x0)
vertexnormalsmode:{"auto"}| "manual"
vertices: vector |matrix, def. 3-by-2 double
visible:"off" | {"on"}
If visible is "off", the patch is not rendered on screen.
xdata: vector |matrix, def. [0; 1; 0]
ydata: vector |matrix, def. [1; 1; 0]
zdata: vector |matrix, def. [](0x0)
15.3.3.8 Surface Properties
The surface properties are:
__modified__:"off" | {"on"}
alphadata: scalar |matrix, def. 1
Transparency is not yet implemented for surface objects. alphadata is unused.
alphadatamapping:"direct" | "none" | {"scaled"}
Transparency is not yet implemented for surface objects. alphadatamapping
is unused.
ambientstrength: scalar, def. 0.30000
Strength of the ambient light. Value between 0.0 and 1.0
backfacelighting:"lit" | {"reverselit"}| "unlit"
"lit": The normals are used as is for lighting. "reverselit": The normals
are always oriented towards the point of view. "unlit": Faces with normals
pointing away from the point of view are unlit.
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
406 GNU Octave
cdata: matrix, def. 3-by-3 double
cdatamapping:"direct" | {"scaled"}
cdatasource: def. ""
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the surface is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after surface has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultsurfacecreatefcn", ’disp ("surface created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before surface is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
diffusestrength: scalar, def. 0.60000
Strength of the diffuse reflex. Value between 0.0 (no diffuse reflex) and 1.0 (full
diffuse reflex).
displayname: def. ""
Text for the legend entry corresponding to this surface.
edgealpha: scalar, def. 1
Transparency is not yet implemented for surface objects. edgealpha is unused.
edgecolor: def. [0 0 0]
edgelighting:"flat" | "gouraud" | {"none"}| "phong"
When set to a value other than "none", the edges of the object are drawn with
light and shadow effects. Supported values are "none" (no lighting effects),
"flat" (facetted look) and "gouraud" (linear interpolation of the lighting ef-
fects between the vertices). "phong" is deprecated and has the same effect as
"gouraud".
facealpha: scalar |matrix, def. 1
Transparency is not yet implemented for surface objects. facealpha is unused.
facecolor:{"flat"}| "interp" | "none" | "texturemap"
facelighting:{"flat"}| "gouraud" | "none" | "phong"
When set to a value other than "none", the faces of the object are drawn with
light and shadow effects. Supported values are "none" (no lighting effects),
"flat" (facetted look) and "gouraud" (linear interpolation of the lighting ef-
fects between the vertices). "phong" is deprecated and has the same effect as
"gouraud".
Chapter 15: Plotting 407
facenormals: def. [](0x0)
facenormalsmode:{"auto"}| "manual"
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the surface’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
interpreter:"latex" | "none" | {"tex"}
interruptible:"off" | {"on"}
linestyle:{"-"}| "--" | "-." | ":" | "none"
See Section 15.4.2 [Line Styles], page 422.
linewidth: def. 0.50000
See [line linewidth property], page 397.
marker:"*" | "+" | "." | "<" | ">" | "^" | "d" | "diamond" | "h" | "hexagram" |
{"none"}| "o" | "p" | "pentagram" | "s" | "square" | "v" | "x"
See Section 15.4.3 [Marker Styles], page 422.
markeredgecolor:{"auto"}| "flat" | "none"
See [line markeredgecolor property], page 398.
markerfacecolor:"auto" | "flat" | {"none"}
See [line markerfacecolor property], page 398.
markersize: scalar, def. 6
See [line markersize property], page 398.
meshstyle:{"both"}| "column" | "row"
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
specularcolorreflectance: scalar, def. 1
Reflectance for specular color. Value between 0.0 (color of underlying face) and
1.0 (color of light source).
specularexponent: scalar, def. 10
Exponent for the specular reflex. The lower the value, the more the reflex is
spread out.
specularstrength: scalar, def. 0.90000
Strength of the specular reflex. Value between 0.0 (no specular reflex) and 1.0
(full specular reflex).
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "surface"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this surface object.
408 GNU Octave
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
vertexnormals: def. 3-by-3-by-3 double
vertexnormalsmode:{"auto"}| "manual"
visible:"off" | {"on"}
If visible is "off", the surface is not rendered on screen.
xdata: matrix, def. [1 2 3]
xdatasource: def. ""
ydata: matrix, def. [1; 2; 3]
ydatasource: def. ""
zdata: matrix, def. 3-by-3 double
zdatasource: def. ""
15.3.3.9 Light Properties
The light properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
children (read-only): vector of graphics handles, def. [](0x1)
children is unused.
clipping:"off" | {"on"}
If clipping is "on", the light is clipped in its parent axes limits.
color: colorspec, def. [1 1 1]
Color of the light source. See Section 15.4.1 [colorspec], page 422.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after light has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultlightcreatefcn", ’disp ("light created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before light is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the light’s handle is not visible in its parent’s
"children"property.
Chapter 15: Plotting 409
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
position: def. [1 0 1]
Position of the light source.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
style:{"infinite"}| "local"
This string defines whether the light emanates from a light source at infinite
distance ("infinite") or from a local point source ("local").
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "light"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this light object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the light is not rendered on screen.
15.3.3.10 Uimenu Properties
The uimenu properties are:
__modified__:"off" | {"on"}
accelerator: def. ""
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
callback: def. [](0x0)
checked:{"off"}| "on"
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uimenu’s children.
clipping:"off" | {"on"}
If clipping is "on", the uimenu is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uimenu has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuimenucreatefcn", ’disp ("uimenu created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
410 GNU Octave
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uimenu is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
enable:"off" | {"on"}
foregroundcolor: def. [0 0 0]
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uimenu’s handle is not visible in its parent’s
"children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
label: def. ""
parent: graphics handle
Handle of the parent graphics object.
position: def. 1
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
separator:{"off"}| "on"
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "uimenu"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uimenu object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uimenu is not rendered on screen.
15.3.3.11 Uibuttongroup Properties
The uibuttongroup properties are:
__modified__:"off" | {"on"}
backgroundcolor: def. [0.90980 0.90980 0.90588]
beingdeleted:{"off"}| "on"
bordertype:"beveledin" | "beveledout" | {"etchedin"}| "etchedout" | "line" |
"none"
borderwidth: def. 1
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
Chapter 15: Plotting 411
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uibuttongroup’s children.
clipping:"off" | {"on"}
If clipping is "on", the uibuttongroup is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uibuttongroup has been
created. Function is set by using default property on root object, e.g.,
set (0, "defaultuibuttongroupcreatefcn", ’disp ("uibuttongroup
created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uibuttongroup is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
fontangle:"italic" | {"normal"}| "oblique"
fontname: def. "*"
fontsize: def. 10
fontunits:"centimeters" | "inches" | "normalized" | "pixels" | {"points"}
fontweight:"bold" | "demi" | "light" | {"normal"}
foregroundcolor: def. [0.18039 0.20392 0.21176]
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uibuttongroup’s handle is not visible in its
parent’s "children"property.
highlightcolor: def. [1 1 1]
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
position: def. [0 0 1 1]
resizefcn: def. [](0x0)
selected:{"off"}| "on"
selectedobject: def. [](0x0)
selectionchangedfcn: def. [](0x0)
selectionhighlight:"off" | {"on"}
shadowcolor: def. [0.75816 0.75816 0.75489]
sizechangedfcn: def. [](0x0)
tag: string, def. ""
A user-defined string to label the graphics object.
title: def. ""
titleposition:"centerbottom" | "centertop" | "leftbottom" | {"lefttop"}|
"rightbottom" | "righttop"
type (read-only): string
Class name of the graphics object. type is always "uibuttongroup"
412 GNU Octave
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uibuttongroup object.
units:"centimeters" | "characters" | "inches" | {"normalized"}| "pixels" |
"points"
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uibuttongroup is not rendered on screen.
15.3.3.12 Uicontextmenu Properties
The uicontextmenu properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
callback: def. [](0x0)
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uicontextmenu’s children.
clipping:"off" | {"on"}
If clipping is "on", the uicontextmenu is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uicontextmenu has been
created. Function is set by using default property on root object, e.g.,
set (0, "defaultuicontextmenucreatefcn", ’disp ("uicontextmenu
created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uicontextmenu is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uicontextmenu’s handle is not visible in its
parent’s "children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
Chapter 15: Plotting 413
position: def. [0 0]
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "uicontextmenu"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uicontextmenu object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uicontextmenu is not rendered on screen.
15.3.3.13 Uipanel Properties
The uipanel properties are:
__modified__:"off" | {"on"}
backgroundcolor: def. [0.90980 0.90980 0.90588]
beingdeleted:{"off"}| "on"
bordertype:"beveledin" | "beveledout" | {"etchedin"}| "etchedout" | "line" |
"none"
borderwidth: def. 1
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uipanel’s children.
clipping:"off" | {"on"}
If clipping is "on", the uipanel is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uipanel has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuipanelcreatefcn", ’disp ("uipanel created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uipanel is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
414 GNU Octave
fontangle:"italic" | {"normal"}| "oblique"
fontname: def. "*"
fontsize: def. 10
fontunits:"centimeters" | "inches" | "normalized" | "pixels" | {"points"}
fontweight:"bold" | "demi" | "light" | {"normal"}
foregroundcolor: def. [0.18039 0.20392 0.21176]
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uipanel’s handle is not visible in its parent’s
"children"property.
highlightcolor: def. [1 1 1]
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
position: def. [0 0 1 1]
resizefcn: def. [](0x0)
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
shadowcolor: def. [0.75816 0.75816 0.75489]
tag: string, def. ""
A user-defined string to label the graphics object.
title: def. ""
titleposition:"centerbottom" | "centertop" | "leftbottom" | {"lefttop"}|
"rightbottom" | "righttop"
type (read-only): string
Class name of the graphics object. type is always "uipanel"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uipanel object.
units:"centimeters" | "characters" | "inches" | {"normalized"}| "pixels" |
"points"
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uipanel is not rendered on screen.
15.3.3.14 Uicontrol Properties
The uicontrol properties are:
Chapter 15: Plotting 415
__modified__:"off" | {"on"}
backgroundcolor: def. [0.90980 0.90980 0.90588]
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
callback: def. [](0x0)
cdata: def. [](0x0)
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uicontrol’s children.
clipping:"off" | {"on"}
If clipping is "on", the uicontrol is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uicontrol has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuicontrolcreatefcn", ’disp ("uicontrol created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uicontrol is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
enable:"inactive" | "off" | {"on"}
extent (read-only): def. [0 0 0 0]
fontangle:"italic" | {"normal"}| "oblique"
fontname: def. "*"
fontsize: def. 10
fontunits:"centimeters" | "inches" | "normalized" | "pixels" | {"points"}
fontweight:"bold" | "demi" | "light" | {"normal"}
foregroundcolor: def. [0.18039 0.20392 0.21176]
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uicontrol’s handle is not visible in its par-
ent’s "children"property.
hittest:"off" | {"on"}
horizontalalignment:{"center"}| "left" | "right"
interruptible:"off" | {"on"}
keypressfcn: def. [](0x0)
listboxtop: def. 1
max: def. 1
min: def. 0
parent: graphics handle
Handle of the parent graphics object.
416 GNU Octave
position: def. [0 0 80 30]
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
sliderstep: def. [0.010000 0.100000]
string: def. ""
style:"checkbox" | "edit" | "frame" | "listbox" | "popupmenu" | {"pushbutton"}
| "radiobutton" | "slider" | "text" | "togglebutton"
tag: string, def. ""
A user-defined string to label the graphics object.
tooltipstring: def. ""
type (read-only): string
Class name of the graphics object. type is always "uicontrol"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uicontrol object.
units:"centimeters" | "characters" | "inches" | "normalized" | {"pixels"}|
"points"
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
value: def. 0
verticalalignment:"bottom" | {"middle"}| "top"
visible:"off" | {"on"}
If visible is "off", the uicontrol is not rendered on screen.
15.3.3.15 Uitoolbar Properties
The uitoolbar properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uitoolbar’s children.
clipping:"off" | {"on"}
If clipping is "on", the uitoolbar is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uitoolbar has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuitoolbarcreatefcn", ’disp ("uitoolbar created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uitoolbar is deleted.
Chapter 15: Plotting 417
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uitoolbar’s handle is not visible in its par-
ent’s "children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
tag: string, def. ""
A user-defined string to label the graphics object.
type (read-only): string
Class name of the graphics object. type is always "uitoolbar"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uitoolbar object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uitoolbar is not rendered on screen.
15.3.3.16 Uipushtool Properties
The uipushtool properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
cdata: def. [](0x0)
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uipushtool’s children.
clickedcallback: def. [](0x0)
clipping:"off" | {"on"}
If clipping is "on", the uipushtool is clipped in its parent axes limits.
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uipushtool has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuipushtoolcreatefcn", ’disp ("uipushtool created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
418 GNU Octave
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uipushtool is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
enable:"off" | {"on"}
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uipushtool’s handle is not visible in its
parent’s "children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
separator:{"off"}| "on"
tag: string, def. ""
A user-defined string to label the graphics object.
tooltipstring: def. ""
type (read-only): string
Class name of the graphics object. type is always "uipushtool"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uipushtool object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uipushtool is not rendered on screen.
15.3.3.17 Uitoggletool Properties
The uitoggletool properties are:
__modified__:"off" | {"on"}
beingdeleted:{"off"}| "on"
busyaction:"cancel" | {"queue"}
buttondownfcn: string |function handle, def. [](0x0)
buttondownfcn is unused.
cdata: def. [](0x0)
children (read-only): vector of graphics handles, def. [](0x1)
Graphics handles of the uitoggletool’s children.
clickedcallback: def. [](0x0)
clipping:"off" | {"on"}
If clipping is "on", the uitoggletool is clipped in its parent axes limits.
Chapter 15: Plotting 419
createfcn: string |function handle, def. [](0x0)
Callback function executed immediately after uitoggletool has been created.
Function is set by using default property on root object, e.g., set (0,
"defaultuitoggletoolcreatefcn", ’disp ("uitoggletool created!")’).
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
deletefcn: string |function handle, def. [](0x0)
Callback function executed immediately before uitoggletool is deleted.
For information on how to write graphics listener functions see Section 15.4.4
[Callbacks section], page 423.
enable:"off" | {"on"}
handlevisibility:"callback" | "off" | {"on"}
If handlevisibility is "off", the uitoggletool’s handle is not visible in its
parent’s "children"property.
hittest:"off" | {"on"}
interruptible:"off" | {"on"}
offcallback: def. [](0x0)
oncallback: def. [](0x0)
parent: graphics handle
Handle of the parent graphics object.
selected:{"off"}| "on"
selectionhighlight:"off" | {"on"}
separator:{"off"}| "on"
state:{"off"}| "on"
tag: string, def. ""
A user-defined string to label the graphics object.
tooltipstring: def. ""
type (read-only): string
Class name of the graphics object. type is always "uitoggletool"
uicontextmenu: graphics handle, def. [](0x0)
Graphics handle of the uicontextmenu object that is currently associated to
this uitoggletool object.
userdata: Any Octave data, def. [](0x0)
User-defined data to associate with the graphics object.
visible:"off" | {"on"}
If visible is "off", the uitoggletool is not rendered on screen.
15.3.4 Searching Properties
h= findobj ()
h= findobj (prop_name,prop_value, . . . )
h= findobj (prop_name,prop_value,"-logical_op",prop_name,
prop_value)

420 GNU Octave
h= findobj ("-property",prop_name)
h= findobj ("-regexp",prop_name,pattern)
h= findobj (hlist, . . . )
h= findobj (hlist,"flat", . . . )
h= findobj (hlist,"-depth",d, . . . )
Find graphics object with specified property values.
The simplest form is
findobj (prop_name,prop_value)
which returns the handles of all objects which have a property named prop name
that has the value prop value. If multiple property/value pairs are specified then
only objects meeting all of the conditions are returned.
The search can be limited to a particular set of objects and their descendants, by
passing a handle or set of handles hlist as the first argument.
The depth of the object hierarchy to search can be limited with the "-depth" argu-
ment. An example of searching only three generations of children is:
findobj (hlist, "-depth", 3, prop_name,prop_value)
Specifying a depth dof 0, limits the search to the set of objects passed in hlist. A
depth dof 0 is equivalent to the "flat" argument.
A specified logical operator may be applied to the pairs of prop name and prop value.
The supported logical operators are: "-and","-or","-xor","-not".
Objects may also be matched by comparing a regular expression to the property val-
ues, where property values that match regexp (prop_value,pattern)are returned.
Finally, objects may be matched by property name only by using the "-property"
option.
Implementation Note: The search only includes objects with visible handles (Handle-
Visibility = "on"). See [findall], page 420, to search for all objects including hidden
ones.
See also: [findall], page 420,[allchild], page 382,[get], page 381,[set], page 381.
h= findall ()
h= findall (prop_name,prop_value, . . . )
h= findall (prop_name,prop_value,"-logical_op",prop_name,
prop_value)
h= findall ("-property",prop_name)
h= findall ("-regexp",prop_name,pattern)
h= findall (hlist, . . . )
h= findall (hlist,"flat", . . . )
h= findall (hlist,"-depth",d, . . . )
Find graphics object, including hidden ones, with specified property values.
The return value his a list of handles to the found graphic objects.
findall performs the same search as findobj, but it includes hidden objects (Han-
dleVisibility = "off"). For full documentation, see [findobj], page 419.
See also: [findobj], page 419,[allchild], page 382,[get], page 381,[set], page 381.
Chapter 15: Plotting 421
15.3.5 Managing Default Properties
Object properties have two classes of default values, factory defaults (the initial values) and
user-defined defaults, which may override the factory defaults.
Although default values may be set for any object, they are set in parent objects and
apply to child objects, of the specified object type. For example, setting the default color
property of line objects to "green", for the root object, will result in all line objects
inheriting the color "green" as the default value.
set (0, "defaultlinecolor", "green");
sets the default line color for all objects. The rule for constructing the property name to
set a default value is
default + object-type +property-name
This rule can lead to some strange looking names, for example defaultlinelinewidth"
specifies the default linewidth property for line objects.
The example above used the root figure object, 0, so the default property value will
apply to all line objects. However, default values are hierarchical, so defaults set in a figure
objects override those set in the root figure object. Likewise, defaults set in axes objects
override those set in figure or root figure objects. For example,
subplot (2, 1, 1);
set (0, "defaultlinecolor", "red");
set (1, "defaultlinecolor", "green");
set (gca (), "defaultlinecolor", "blue");
line (1:10, rand (1, 10));
subplot (2, 1, 2);
line (1:10, rand (1, 10));
figure (2)
line (1:10, rand (1, 10));
produces two figures. The line in first subplot window of the first figure is blue because it
inherits its color from its parent axes object. The line in the second subplot window of the
first figure is green because it inherits its color from its parent figure object. The line in the
second figure window is red because it inherits its color from the global root figure parent
object.
To remove a user-defined default setting, set the default property to the value "remove".
For example,
set (gca (), "defaultlinecolor", "remove");
removes the user-defined default line color setting from the current axes object. To quickly
remove all user-defined defaults use the reset function.
reset (h)
Reset the properties of the graphic object hto their default values.
For figures, the properties "position","units","windowstyle", and "paperunits"
are not affected. For axes, the properties "position" and "units" are not affected.
The input hmay also be a vector of graphic handles in which case each individual
object will be reset.
See also: [cla], page 360,[clf], page 360,[newplot], page 358.
422 GNU Octave
Getting the "default" property of an object returns a list of user-defined defaults set
for the object. For example,
get (gca (), "default");
returns a list of user-defined default values for the current axes object.
Factory default values are stored in the root figure object. The command
get (0, "factory");
returns a list of factory defaults.
15.4 Advanced Plotting
15.4.1 Colors
Colors may be specified as RGB triplets with values ranging from zero to one, or by name.
Recognized color names include "blue","black","cyan","green","magenta","red",
"white", and "yellow".
15.4.2 Line Styles
Line styles are specified by the following properties:
linestyle
May be one of
"-" Solid line. [default]
"--" Dashed line.
":" Dotted line.
"-." A dash-dot line.
"none" No line. Points will still be marked using the current Marker Style.
linewidth
A number specifying the width of the line. The default is 1. A value of 2 is
twice as wide as the default, etc.
15.4.3 Marker Styles
Marker styles are specified by the following properties:
marker A character indicating a plot marker to be place at each data point, or "none",
meaning no markers should be displayed.
markeredgecolor
The color of the edge around the marker, or "auto", meaning that the edge
color is the same as the face color. See Section 15.4.1 [Colors], page 422.
markerfacecolor
The color of the marker, or "none" to indicate that the marker should not be
filled. See Section 15.4.1 [Colors], page 422.
markersize
A number specifying the size of the marker. The default is 1. A value of 2 is
twice as large as the default, etc.
Chapter 15: Plotting 423
The colstyle function will parse a plot-style specification and will return the color,
line, and marker values that would result.
[style,color,marker,msg] = colstyle (linespec)
Parse linespec and return the line style, color, and markers given.
In the case of an error, the string msg will return the text of the error.
15.4.4 Callbacks
Callback functions can be associated with graphics objects and triggered after certain events
occur. The basic structure of all callback function is
function mycallback (hsrc, evt)
...
endfunction
where hsrc is a handle to the source of the callback, and evt gives some event specific data.
The function can be provided as a function handle to a plain Octave function, as an
anonymous function or as a string representing an Octvae command. The latter syntax
is not recommended since syntax errors will only occur when the string is evaluated. See
Section 11.11 [Function Handles section], page 209.
This can then be associated with an object either at the objects creation or later with
the set function. For example,
plot (x, "DeleteFcn", @(h, e) disp ("Window Deleted"))
where at the moment that the plot is deleted, the message "Window Deleted"will be
displayed.
Additional user arguments can be passed to callback functions, and will be passed after
the 2 default arguments. For example:
plot (x, "DeleteFcn", {@mycallback, "1"})
...
function mycallback (h, e, a1)
fprintf ("Closing plot %d\n", a1);
endfunction
The basic callback functions that are available for all graphics objects are
•CreateFcn: called at the moment of the objects creation. It is not called if the object
is altered in any way, and so it only makes sense to define this callback in the function
call that defines the object. Callbacks that are added to CreateFcn later with the set
function will never be executed.
•DeleteFcn: called at the moment an object is deleted.
•ButtonDownFcn: called if a mouse button is pressed while the pointer is over this
object. Note, that the gnuplot interface does not respect this callback.
Caution: the second evt argument in callback functions is only loosely implemented in
the Qt graphics toolkit:
•Mouse click events: evt is a class double value, 1 for left, 2 for middle and 3 for right
click.
•Key press events: evt is a structure with fields Key (string), Character (string) and
Modifier (cell array of strings).
424 GNU Octave
•Other events: evt is a class double empty matrix.
The object and figure that the event occurred in that resulted in the callback being
called can be found with the gcbo and gcbf functions.
h= gcbo ()
[h,fig] = gcbo ()
Return a handle to the object whose callback is currently executing.
If no callback is executing, this function returns the empty matrix. This handle is
obtained from the root object property "CallbackObject".
When called with a second output argument, return the handle of the figure containing
the object whose callback is currently executing. If no callback is executing the second
output is also set to the empty matrix.
See also: [gcbf], page 424,[gco], page 380,[gca], page 379,[gcf], page 379,[get],
page 381,[set], page 381.
fig = gcbf ()
Return a handle to the figure containing the object whose callback is currently exe-
cuting.
If no callback is executing, this function returns the empty matrix. The handle
returned by this function is the same as the second output argument of gcbo.
See also: [gcbo], page 424,[gcf], page 379,[gco], page 380,[gca], page 379,[get],
page 381,[set], page 381.
Callbacks can equally be added to properties with the addlistener function described
below.
15.4.5 Application-defined Data
Octave has a provision for attaching application-defined data to a graphics handle. The
data can be anything which is meaningful to the application, and will be completely ignored
by Octave.
setappdata (h,name,value)
setappdata (h,name1,value1,name2,value3, . . . )
Set the application data name to value for the graphics object with handle h.
hmay also be a vector of graphics handles. If the application data with the specified
name does not exist, it is created. Multiple name/value pairs can be specified at a
time.
See also: [getappdata], page 424,[isappdata], page 425,[rmappdata], page 425,
[guidata], page 802,[get], page 381,[set], page 381,[getpref], page 804,[setpref],
page 804.
value = getappdata (h,name)
appdata = getappdata (h)
Return the value of the application data name for the graphics object with handle h.
hmay also be a vector of graphics handles. If no second argument name is given then
getappdata returns a structure, appdata, whose fields correspond to the appdata
properties.
Chapter 15: Plotting 425
See also: [setappdata], page 424,[isappdata], page 425,[rmappdata], page 425,
[guidata], page 802,[get], page 381,[set], page 381,[getpref], page 804,[setpref],
page 804.
rmappdata (h,name)
rmappdata (h,name1,name2, . . . )
Delete the application data name from the graphics object with handle h.
hmay also be a vector of graphics handles. Multiple application data names may be
supplied to delete several properties at once.
See also: [setappdata], page 424,[getappdata], page 424,[isappdata], page 425.
valid = isappdata (h,name)
Return true if the named application data, name, exists for the graphics object with
handle h.
hmay also be a vector of graphics handles.
See also: [getappdata], page 424,[setappdata], page 424,[rmappdata], page 425,
[guidata], page 802,[get], page 381,[set], page 381,[getpref], page 804,[setpref],
page 804.
15.4.6 Object Groups
A number of Octave high level plot functions return groups of other graphics objects or
they return graphics objects that have their properties linked in such a way that changes to
one of the properties results in changes in the others. A graphic object that groups other
objects is an hggroup
hggroup ()
hggroup (hax)
hggroup (. . ., property,value, . . .)
h= hggroup (. . . )
Create handle graphics group object with axes parent hax.
If no parent is specified, the group is created in the current axes.
Multiple property/value pairs may be specified for the hggroup, but they must appear
in pairs.
The optional return value his a graphics handle to the created hggroup object.
Programming Note: An hggroup is a way to group base graphics objects such as line
objects or patch objects into a single unit which can react appropriately. For example,
the individual lines of a contour plot are collected into a single hggroup so that they
can be made visible/invisible with a single command, set (hg_handle, "visible",
"off").
See also: [addproperty], page 426,[addlistener], page 427.
For example a simple use of a hggroup might be
426 GNU Octave
x = 0:0.1:10;
hg = hggroup ();
plot (x, sin (x), "color", [1, 0, 0], "parent", hg);
hold on
plot (x, cos (x), "color", [0, 1, 0], "parent", hg);
set (hg, "visible", "off");
which groups the two plots into a single object and controls their visibility directly. The
default properties of an hggroup are the same as the set of common properties for the other
graphics objects. Additional properties can be added with the addproperty function.
addproperty (name,h,type)
addproperty (name,h,type,arg, . . . )
Create a new property named name in graphics object h.
type determines the type of the property to create. args usually contains the default
value of the property, but additional arguments might be given, depending on the
type of the property.
The supported property types are:
string A string property. arg contains the default string value.
any An un-typed property. This kind of property can hold any octave value.
args contains the default value.
radio A string property with a limited set of accepted values. The first argu-
ment must be a string with all accepted values separated by a vertical
bar (’|’). The default value can be marked by enclosing it with a ’{’ ’}’
pair. The default value may also be given as an optional second string
argument.
boolean A boolean property. This property type is equivalent to a radio property
with "on|off"as accepted values. arg contains the default property value.
double A scalar double property. arg contains the default value.
handle A handle property. This kind of property holds the handle of a graphics
object. arg contains the default handle value. When no default value is
given, the property is initialized to the empty matrix.
data A data (matrix) property. arg contains the default data value. When no
default value is given, the data is initialized to the empty matrix.
color A color property. arg contains the default color value. When no default
color is given, the property is set to black. An optional second string
argument may be given to specify an additional set of accepted string
values (like a radio property).
type may also be the concatenation of a core object type and a valid property name
for that object type. The property created then has the same characteristics as the
referenced property (type, possible values, hidden state. . . ). This allows one to clone
an existing property into the graphics object h.
Chapter 15: Plotting 427
Examples:
addproperty ("my_property", gcf, "string", "a string value");
addproperty ("my_radio", gcf, "radio", "val_1|val_2|{val_3}");
addproperty ("my_style", gcf, "linelinestyle", "--");
See also: [addlistener], page 427,[hggroup], page 425.
Once a property in added to an hggroup, it is not linked to any other property of either
the children of the group, or any other graphics object. Add so to control the way in which
this newly added property is used, the addlistener function is used to define a callback
function that is executed when the property is altered.
addlistener (h,prop,fcn)
Register fcn as listener for the property prop of the graphics object h.
Property listeners are executed (in order of registration) when the property is set.
The new value is already available when the listeners are executed.
prop must be a string naming a valid property in h.
fcn can be a function handle, a string or a cell array whose first element is a function
handle. If fcn is a function handle, the corresponding function should accept at least
2 arguments, that will be set to the object handle and the empty matrix respectively.
If fcn is a string, it must be any valid octave expression. If fcn is a cell array, the first
element must be a function handle with the same signature as described above. The
next elements of the cell array are passed as additional arguments to the function.
Example:
function my_listener (h, dummy, p1)
fprintf ("my_listener called with p1=%s\n", p1);
endfunction
addlistener (gcf, "position", {@my_listener, "my string"})
See also: [addproperty], page 426,[hggroup], page 425.
dellistener (h,prop,fcn)
Remove the registration of fcn as a listener for the property prop of the graphics
object h.
The function fcn must be the same variable (not just the same value), as was passed
to the original call to addlistener.
If fcn is not defined then all listener functions of prop are removed.
Example:
function my_listener (h, dummy, p1)
fprintf ("my_listener called with p1=%s\n", p1);
endfunction
c = {@my_listener, "my string"};
addlistener (gcf, "position", c);
dellistener (gcf, "position", c);
428 GNU Octave
An example of the use of these two functions might be
x = 0:0.1:10;
hg = hggroup ();
h = plot (x, sin (x), "color", [1, 0, 0], "parent", hg);
addproperty ("linestyle", hg, "linelinestyle", get (h, "linestyle"));
addlistener (hg, "linestyle", @update_props);
hold on
plot (x, cos (x), "color", [0, 1, 0], "parent", hg);
function update_props (h, d)
set (get (h, "children"), "linestyle", get (h, "linestyle"));
endfunction
that adds a linestyle property to the hggroup and propagating any changes its value to
the children of the group. The linkprop function can be used to simplify the above to be
x = 0:0.1:10;
hg = hggroup ();
h1 = plot (x, sin (x), "color", [1, 0, 0], "parent", hg);
addproperty ("linestyle", hg, "linelinestyle", get (h, "linestyle"));
hold on
h2 = plot (x, cos (x), "color", [0, 1, 0], "parent", hg);
hlink = linkprop ([hg, h1, h2], "color");
hlink = linkprop (h,"prop")
hlink = linkprop (h,{"prop1","prop2", . . . })
Link graphic object properties, such that a change in one is propagated to the others.
The input his a vector of graphic handles to link.
prop may be a string when linking a single property, or a cell array of strings for
multiple properties. During the linking process all properties in prop will initially be
set to the values that exist on the first object in the list h.
The function returns hlink which is a special object describing the link. As long as
the reference hlink exists the link between graphic objects will be active. This means
that hlink must be preserved in a workspace variable, a global variable, or otherwise
stored using a function such as setappdata,guidata. To unlink properties, execute
clear hlink.
An example of the use of linkprop is
x = 0:0.1:10;
subplot (1,2,1);
h1 = plot (x, sin (x));
subplot (1,2,2);
h2 = plot (x, cos (x));
hlink = linkprop ([h1, h2], {"color","linestyle"});
set (h1, "color", "green");
set (h2, "linestyle", "--");
See also: [linkaxes], page 429.
Chapter 15: Plotting 429
linkaxes (hax)
linkaxes (hax,optstr)
Link the axis limits of 2-D plots such that a change in one is propagated to the others.
The axes handles to be linked are passed as the first argument hax.
The optional second argument is a string which defines which axis limits will be linked.
The possible values for optstr are:
"x" Link x-axes
"y" Link y-axes
"xy" (default)
Link both axes
"off" Turn off linking
If unspecified the default is to link both X and Y axes.
When linking, the limits from the first axes in hax are applied to the other axes in
the list. Subsequent changes to any one of the axes will be propagated to the others.
See also: [linkprop], page 428,[addproperty], page 426.
These capabilities are used in a number of basic graphics objects. The hggroup objects
created by the functions of Octave contain one or more graphics object and are used to:
•group together multiple graphics objects,
•create linked properties between different graphics objects, and
•to hide the nominal user data, from the actual data of the objects.
For example the stem function creates a stem series where each hggroup of the stem series
contains two line objects representing the body and head of the stem. The ydata property
of the hggroup of the stem series represents the head of the stem, whereas the body of the
stem is between the baseline and this value. For example
h = stem (1:4)
get (h, "xdata")
⇒[ 1 2 3 4]’
get (get (h, "children")(1), "xdata")
⇒[ 1 1 NaN 2 2 NaN 3 3 NaN 4 4 NaN]’
shows the difference between the xdata of the hggroup of a stem series object and the
underlying line.
The basic properties of such group objects is that they consist of one or more linked
hggroup, and that changes in certain properties of these groups are propagated to other
members of the group. Whereas, certain properties of the members of the group only apply
to the current member.
In addition the members of the group can also be linked to other graphics objects through
callback functions. For example the baseline of the bar or stem functions is a line object,
whose length and position are automatically adjusted, based on changes to the correspond-
ing hggroup elements.
430 GNU Octave
15.4.6.1 Data Sources in Object Groups
All of the group objects contain data source parameters. There are string parameters that
contain an expression that is evaluated to update the relevant data property of the group
when the refreshdata function is called.
refreshdata ()
refreshdata (h)
refreshdata (h,workspace)
Evaluate any ‘datasource’ properties of the current figure and update the plot if the
corresponding data has changed.
If the first argument his a list of graphic handles, then operate on these objects rather
than the current figure returned by gcf.
The optional second argument workspace can take the following values:
"base" Evaluate the datasource properties in the base workspace. (default).
"caller" Evaluate the datasource properties in the workspace of the function that
called refreshdata.
An example of the use of refreshdata is:
x = 0:0.1:10;
y = sin (x);
plot (x, y, "ydatasource", "y");
for i = 1 : 100
pause (0.1);
y = sin (x + 0.1*i);
refreshdata ();
endfor
15.4.6.2 Area Series
Area series objects are created by the area function. Each of the hggroup elements contains
a single patch object. The properties of the area series are
basevalue
The value where the base of the area plot is drawn.
linewidth
linestyle
The line width and style of the edge of the patch objects making up the areas.
See Section 15.4.2 [Line Styles], page 422.
edgecolor
facecolor
The line and fill color of the patch objects making up the areas. See
Section 15.4.1 [Colors], page 422.
xdata
ydata The x and y coordinates of the original columns of the data passed to area
prior to the cumulative summation used in the area function.
Chapter 15: Plotting 431
xdatasource
ydatasource
Data source variables.
15.4.6.3 Bar Series
Bar series objects are created by the bar or barh functions. Each hggroup element contains
a single patch object. The properties of the bar series are
showbaseline
baseline
basevalue
The property showbaseline flags whether the baseline of the bar series is dis-
played (default is "on"). The handle of the graphics object representing the
baseline is given by the baseline property and the y-value of the baseline by
the basevalue property.
Changes to any of these properties are propagated to the other members of the
bar series and to the baseline itself. Equally, changes in the properties of the
base line itself are propagated to the members of the corresponding bar series.
barwidth
barlayout
horizontal
The property barwidth is the width of the bar corresponding to the width vari-
able passed to bar or barh. Whether the bar series is "grouped" or "stacked"
is determined by the barlayout property and whether the bars are horizontal
or vertical by the horizontal property.
Changes to any of these property are propagated to the other members of the
bar series.
linewidth
linestyle
The line width and style of the edge of the patch objects making up the bars.
See Section 15.4.2 [Line Styles], page 422.
edgecolor
facecolor
The line and fill color of the patch objects making up the bars. See Section 15.4.1
[Colors], page 422.
xdata The nominal x positions of the bars. Changes in this property and propagated
to the other members of the bar series.
ydata The y value of the bars in the hggroup.
xdatasource
ydatasource
Data source variables.
432 GNU Octave
15.4.6.4 Contour Groups
Contour group objects are created by the contour,contourf and contour3 functions. The
are equally one of the handles returned by the surfc and meshc functions. The properties
of the contour group are
contourmatrix
A read only property that contains the data return by contourc used to create
the contours of the plot.
fill A radio property that can have the values "on" or "off" that flags whether the
contours to plot are to be filled.
zlevelmode
zlevel The radio property zlevelmode can have the values "none","auto", or
"manual". When its value is "none" there is no z component to the plotted
contours. When its value is "auto" the z value of the plotted contours is at
the same value as the contour itself. If the value is "manual", then the z value
at which to plot the contour is determined by the zlevel property.
levellistmode
levellist
levelstepmode
levelstep
If levellistmode is "manual", then the levels at which to plot the contours
is determined by levellist. If levellistmode is set to "auto", then the
distance between contours is determined by levelstep. If both levellistmode
and levelstepmode are set to "auto", then there are assumed to be 10 equal
spaced contours.
textlistmode
textlist
textstepmode
textstep If textlistmode is "manual", then the labeled contours is determined by
textlist. If textlistmode is set to "auto", then the distance between labeled
contours is determined by textstep. If both textlistmode and textstepmode
are set to "auto", then there are assumed to be 10 equal spaced labeled con-
tours.
showtext Flag whether the contour labels are shown or not.
labelspacing
The distance between labels on a single contour in points.
linewidth
linestyle
linecolor
The properties of the contour lines. The properties linewidth and linestyle
are similar to the corresponding properties for lines. The property linecolor
is a color property (see Section 15.4.1 [Colors], page 422), that can also have
the values of "none" or "auto". If linecolor is "none", then no contour line
is drawn. If linecolor is "auto" then the line color is determined by the
colormap.
Chapter 15: Plotting 433
xdata
ydata
zdata The original x, y, and z data of the contour lines.
xdatasource
ydatasource
zdatasource
Data source variables.
15.4.6.5 Error Bar Series
Error bar series are created by the errorbar function. Each hggroup element contains two
line objects representing the data and the errorbars separately. The properties of the error
bar series are
color The RGB color or color name of the line objects of the error bars. See
Section 15.4.1 [Colors], page 422.
linewidth
linestyle
The line width and style of the line objects of the error bars. See Section 15.4.2
[Line Styles], page 422.
marker
markeredgecolor
markerfacecolor
markersize
The line and fill color of the markers on the error bars. See Section 15.4.1
[Colors], page 422.
xdata
ydata
ldata
udata
xldata
xudata The original x, y, l, u, xl, xu data of the error bars.
xdatasource
ydatasource
ldatasource
udatasource
xldatasource
xudatasource
Data source variables.
15.4.6.6 Line Series
Line series objects are created by the plot and plot3 functions and are of the type line.
The properties of the line series with the ability to add data sources.
color The RGB color or color name of the line objects. See Section 15.4.1 [Colors],
page 422.
434 GNU Octave
linewidth
linestyle
The line width and style of the line objects. See Section 15.4.2 [Line Styles],
page 422.
marker
markeredgecolor
markerfacecolor
markersize
The line and fill color of the markers. See Section 15.4.1 [Colors], page 422.
xdata
ydata
zdata The original x, y and z data.
xdatasource
ydatasource
zdatasource
Data source variables.
15.4.6.7 Quiver Group
Quiver series objects are created by the quiver or quiver3 functions. Each hggroup element
of the series contains three line objects as children representing the body and head of the
arrow, together with a marker as the point of origin of the arrows. The properties of the
quiver series are
autoscale
autoscalefactor
Flag whether the length of the arrows is scaled or defined directly from
the u,vand wdata. If the arrow length is flagged as being scaled by the
autoscale property, then the length of the autoscaled arrow is controlled by
the autoscalefactor.
maxheadsize
This property controls the size of the head of the arrows in the quiver series.
The default value is 0.2.
showarrowhead
Flag whether the arrow heads are displayed in the quiver plot.
color The RGB color or color name of the line objects of the quiver. See Section 15.4.1
[Colors], page 422.
linewidth
linestyle
The line width and style of the line objects of the quiver. See Section 15.4.2
[Line Styles], page 422.
marker
markerfacecolor
markersize
The line and fill color of the marker objects at the original of the arrows. See
Section 15.4.1 [Colors], page 422.
Chapter 15: Plotting 435
xdata
ydata
zdata The origins of the values of the vector field.
udata
vdata
wdata The values of the vector field to plot.
xdatasource
ydatasource
zdatasource
udatasource
vdatasource
wdatasource
Data source variables.
15.4.6.8 Scatter Group
Scatter series objects are created by the scatter or scatter3 functions. A single hggroup
element contains as many children as there are points in the scatter plot, with each child
representing one of the points. The properties of the stem series are
linewidth
The line width of the line objects of the points. See Section 15.4.2 [Line Styles],
page 422.
marker
markeredgecolor
markerfacecolor
The line and fill color of the markers of the points. See Section 15.4.1 [Colors],
page 422.
xdata
ydata
zdata The original x, y and z data of the stems.
cdata The color data for the points of the plot. Each point can have a separate color,
or a unique color can be specified.
sizedata The size data for the points of the plot. Each point can its own size or a unique
size can be specified.
xdatasource
ydatasource
zdatasource
cdatasource
sizedatasource
Data source variables.
15.4.6.9 Stair Group
Stair series objects are created by the stair function. Each hggroup element of the series
contains a single line object as a child representing the stair. The properties of the stair
series are
436 GNU Octave
color The RGB color or color name of the line objects of the stairs. See Section 15.4.1
[Colors], page 422.
linewidth
linestyle
The line width and style of the line objects of the stairs. See Section 15.4.2
[Line Styles], page 422.
marker
markeredgecolor
markerfacecolor
markersize
The line and fill color of the markers on the stairs. See Section 15.4.1 [Colors],
page 422.
xdata
ydata The original x and y data of the stairs.
xdatasource
ydatasource
Data source variables.
15.4.6.10 Stem Series
Stem series objects are created by the stem or stem3 functions. Each hggroup element
contains a single line object as a child representing the stems. The properties of the stem
series are
showbaseline
baseline
basevalue
The property showbaseline flags whether the baseline of the stem series is
displayed (default is "on"). The handle of the graphics object representing
the baseline is given by the baseline property and the y-value (or z-value for
stem3) of the baseline by the basevalue property.
Changes to any of these property are propagated to the other members of the
stem series and to the baseline itself. Equally changes in the properties of the
base line itself are propagated to the members of the corresponding stem series.
color The RGB color or color name of the line objects of the stems. See Section 15.4.1
[Colors], page 422.
linewidth
linestyle
The line width and style of the line objects of the stems. See Section 15.4.2
[Line Styles], page 422.
marker
markeredgecolor
markerfacecolor
markersize
The line and fill color of the markers on the stems. See Section 15.4.1 [Colors],
page 422.
Chapter 15: Plotting 437
xdata
ydata
zdata The original x, y and z data of the stems.
xdatasource
ydatasource
zdatasource
Data source variables.
15.4.6.11 Surface Group
Surface group objects are created by the surf or mesh functions, but are equally one of
the handles returned by the surfc or meshc functions. The surface group is of the type
surface.
The properties of the surface group are
edgecolor
facecolor
The RGB color or color name of the edges or faces of the surface. See
Section 15.4.1 [Colors], page 422.
linewidth
linestyle
The line width and style of the lines on the surface. See Section 15.4.2 [Line
Styles], page 422.
marker
markeredgecolor
markerfacecolor
markersize
The line and fill color of the markers on the surface. See Section 15.4.1 [Colors],
page 422.
xdata
ydata
zdata
cdata The original x, y, z and c data.
xdatasource
ydatasource
zdatasource
cdatasource
Data source variables.
15.4.7 Graphics Toolkits
name = graphics_toolkit ()
name = graphics_toolkit (hlist)
graphics_toolkit (name)
graphics_toolkit (hlist,name)
Query or set the default graphics toolkit which is assigned to new figures.

438 GNU Octave
With no inputs, return the current default graphics toolkit. If the input is a list of
figure graphic handles, hlist, then return the name of the graphics toolkit in use for
each figure.
When called with a single input name set the default graphics toolkit to name. If the
toolkit is not already loaded, it is initialized by calling the function __init_name__.
If the first input is a list of figure handles, hlist, then the graphics toolkit is set to
name for these figures only.
See also: [available graphics toolkits], page 438.
available_graphics_toolkits ()
Return a cell array of registered graphics toolkits.
See also: [graphics toolkit], page 437,[register graphics toolkit], page 438.
loaded_graphics_toolkits ()
Return a cell array of the currently loaded graphics toolkits.
See also: [available graphics toolkits], page 438.
register_graphics_toolkit (toolkit)
List toolkit as an available graphics toolkit.
See also: [available graphics toolkits], page 438.
15.4.7.1 Customizing Toolkit Behavior
The specific behavior of the backend toolkit may be modified using the following utility
functions. Note: Not all functions apply to every graphics toolkit.
[prog,args] = gnuplot_binary ()
[old_prog,old_args] = gnuplot_binary (new_prog,arg1, . . . )
Query or set the name of the program invoked by the plot command when the graphics
toolkit is set to "gnuplot".
Additional arguments to pass to the external plotting program may also be given.
The default value is "gnuplot" with no additional arguments. See Appendix E [In-
stallation], page 935.
See also: [graphics toolkit], page 437.
439
16 Matrix Manipulation
There are a number of functions available for checking to see if the elements of a matrix
meet some condition, and for rearranging the elements of a matrix. For example, Octave
can easily tell you if all the elements of a matrix are finite, or are less than some specified
value. Octave can also rotate the elements, extract the upper- or lower-triangular parts, or
sort the columns of a matrix.
16.1 Finding Elements and Checking Conditions
The functions any and all are useful for determining whether any or all of the elements
of a matrix satisfy some condition. The find function is also useful in determining which
elements of a matrix meet a specified condition.
any (x)
any (x,dim)
For a vector argument, return true (logical 1) if any element of the vector is nonzero.
For a matrix argument, return a row vector of logical ones and zeros with each element
indicating whether any of the elements of the corresponding column of the matrix are
nonzero. For example:
any (eye (2, 4))
⇒[1,1,0,0]
If the optional argument dim is supplied, work along dimension dim. For example:
any (eye (2, 4), 2)
⇒[1;1]
See also: [all], page 439.
all (x)
all (x,dim)
For a vector argument, return true (logical 1) if all elements of the vector are nonzero.
For a matrix argument, return a row vector of logical ones and zeros with each element
indicating whether all of the elements of the corresponding column of the matrix are
nonzero. For example:
all ([2, 3; 1, 0])
⇒[1,0]
If the optional argument dim is supplied, work along dimension dim.
See also: [any], page 439.
Since the comparison operators (see Section 8.4 [Comparison Ops], page 146) return
matrices of ones and zeros, it is easy to test a matrix for many things, not just whether the
elements are nonzero. For example,
all (all (rand (5) < 0.9))
⇒0
tests a random 5 by 5 matrix to see if all of its elements are less than 0.9.
Note that in conditional contexts (like the test clause of if and while statements) Octave
treats the test as if you had typed all (all (condition)).
440 GNU Octave
z= xor (x,y)
z= xor (x1,x2, . . . )
Return the exclusive or of xand y.
For boolean expressions xand y,xor (x,y)is true if and only if one of xor yis
true. Otherwise, if xand yare both true or both false, xor returns false.
The truth table for the xor operation is
x y z
- - -
0 0 0
1 0 1
0 1 1
1 1 0
If more than two arguments are given the xor operation is applied cumulatively from
left to right:
(...((x1 XOR x2) XOR x3) XOR ...)
See also: [and], page 148,[or], page 148,[not], page 148.
diff (x)
diff (x,k)
diff (x,k,dim)
If xis a vector of length n,diff (x)is the vector of first differences x2−x1, . . . , xn−
xn−1.
If xis a matrix, diff (x)is the matrix of column differences along the first non-
singleton dimension.
The second argument is optional. If supplied, diff (x,k), where kis a non-negative
integer, returns the k-th differences. It is possible that kis larger than the first non-
singleton dimension of the matrix. In this case, diff continues to take the differences
along the next non-singleton dimension.
The dimension along which to take the difference can be explicitly stated with the
optional variable dim. In this case the k-th order differences are calculated along this
dimension. In the case where kexceeds size (x,dim)an empty matrix is returned.
See also: [sort], page 448,[merge], page 150.
isinf (x)
Return a logical array which is true where the elements of xare infinite and false
where they are not.
For example:
isinf ([13, Inf, NA, NaN])
⇒[0,1,0,0]
See also: [isfinite], page 441,[isnan], page 440,[isna], page 43.
isnan (x)
Return a logical array which is true where the elements of xare NaN values and false
where they are not.

Chapter 16: Matrix Manipulation 441
NA values are also considered NaN values. For example:
isnan ([13, Inf, NA, NaN])
⇒[0,0,1,1]
See also: [isna], page 43,[isinf], page 440,[isfinite], page 441.
isfinite (x)
Return a logical array which is true where the elements of xare finite values and false
where they are not.
For example:
isfinite ([13, Inf, NA, NaN])
⇒[1,0,0,0]
See also: [isinf], page 440,[isnan], page 440,[isna], page 43.
[err,yi, ...] = common_size (xi, . . . )
Determine if all input arguments are either scalar or of common size.
If true, err is zero, and yi is a matrix of the common size with all entries equal to xi
if this is a scalar or xi otherwise. If the inputs cannot be brought to a common size,
err is 1, and yi is xi. For example:
[err, a, b] = common_size ([1 2; 3 4], 5)
⇒err = 0
⇒a=[1,2;3,4]
⇒b=[5,5;5,5]
This is useful for implementing functions where arguments can either be scalars or of
common size.
See also: [size], page 45,[size equal], page 46,[numel], page 44,[ndims], page 44.
idx = find (x)
idx = find (x,n)
idx = find (x,n,direction)
[i, j] = find (. . . )
[i, j, v] = find (. . . )
Return a vector of indices of nonzero elements of a matrix, as a row if xis a row
vector or as a column otherwise.
To obtain a single index for each matrix element, Octave pretends that the columns
of a matrix form one long vector (like Fortran arrays are stored). For example:
find (eye (2))
⇒[1;4]
If two inputs are given, nindicates the maximum number of elements to find from
the beginning of the matrix or vector.
If three inputs are given, direction should be one of "first" or "last", requesting
only the first or last nindices, respectively. However, the indices are always returned
in ascending order.
442 GNU Octave
If two outputs are requested, find returns the row and column indices of nonzero
elements of a matrix. For example:
[i, j] = find (2 * eye (2))
⇒i=[1;2]
⇒j=[1;2]
If three outputs are requested, find also returns a vector containing the nonzero
values. For example:
[i, j, v] = find (3 * eye (2))
⇒i=[1;2]
⇒j=[1;2]
⇒v=[3;3]
Note that this function is particularly useful for sparse matrices, as it extracts the
nonzero elements as vectors, which can then be used to create the original matrix.
For example:
sz = size (a);
[i, j, v] = find (a);
b = sparse (i, j, v, sz(1), sz(2));
See also: [nonzeros], page 566.
idx = lookup (table,y)
idx = lookup (table,y,opt)
Lookup values in a sorted table.
This function is usually used as a prelude to interpolation.
If table is increasing and idx = lookup (table, y), then table(idx(i)) <= y(i) <
table(idx(i+1)) for all y(i) within the table. If y(i) < table(1) then idx(i) is
0. If y(i) >= table(end) or isnan (y(i)) then idx(i) is n.
If the table is decreasing, then the tests are reversed. For non-strictly monotonic
tables, empty intervals are always skipped. The result is undefined if table is not
monotonic, or if table contains a NaN.
The complexity of the lookup is O(M*log(N)) where N is the size of table and
M is the size of y. In the special case when yis also sorted, the complexity is
O(min(M*log(N),M+N)).
table and ycan also be cell arrays of strings (or ycan be a single string). In this
case, string lookup is performed using lexicographical comparison.
If opts is specified, it must be a string with letters indicating additional options.
m table(idx(i)) == val(i) if val(i) occurs in table; otherwise, idx(i)
is zero.
b idx(i) is a logical 1 or 0, indicating whether val(i) is contained in table
or not.
lFor numeric lookups the leftmost subinterval shall be extended to infinity
(i.e., all indices at least 1)
rFor numeric lookups the rightmost subinterval shall be extended to infin-
ity (i.e., all indices at most n-1).
Chapter 16: Matrix Manipulation 443
If you wish to check if a variable exists at all, instead of properties its elements may
have, consult Section 7.3 [Status of Variables], page 127.
16.2 Rearranging Matrices
fliplr (x)
Flip array left to right.
Return a copy of xwith the order of the columns reversed. In other words, xis
flipped left-to-right about a vertical axis. For example:
fliplr ([1, 2; 3, 4])
⇒2 1
4 3
See also: [flipud], page 443,[flip], page 443,[rot90], page 444,[rotdim], page 444.
flipud (x)
Flip array upside down.
Return a copy of xwith the order of the rows reversed. In other words, xis flipped
upside-down about a horizontal axis. For example:
flipud ([1, 2; 3, 4])
⇒3 4
1 2
See also: [fliplr], page 443,[flip], page 443,[rot90], page 444,[rotdim], page 444.
flip (x)
flip (x,dim)
Flip array across dimension dim.
Return a copy of xflipped about the dimension dim.dim defaults to the first non-
singleton dimension. For example:
flip ([1 2 3 4])
⇒4321
flip ([1; 2; 3; 4])
⇒4
3
2
1
flip ([1 2; 3 4])
⇒3 4
1 2
flip ([1 2; 3 4], 2)
⇒2 1
4 3
See also: [fliplr], page 443,[flipud], page 443,[rot90], page 444,[rotdim], page 444,
[permute], page 445,[transpose], page 145.
444 GNU Octave
rot90 (A)
rot90 (A,k)
Rotate array by 90 degree increments.
Return a copy of Awith the elements rotated counterclockwise in 90-degree incre-
ments.
The second argument is optional, and specifies how many 90-degree rotations are
to be applied (the default value is 1). Negative values of krotate the matrix in a
clockwise direction. For example,
rot90 ([1, 2; 3, 4], -1)
⇒3 1
4 2
rotates the given matrix clockwise by 90 degrees. The following are all equivalent
statements:
rot90 ([1, 2; 3, 4], -1)
rot90 ([1, 2; 3, 4], 3)
rot90 ([1, 2; 3, 4], 7)
The rotation is always performed on the plane of the first two dimensions, i.e., rows
and columns. To perform a rotation on any other plane, use rotdim.
See also: [rotdim], page 444,[fliplr], page 443,[flipud], page 443,[flip], page 443.
rotdim (x)
rotdim (x,n)
rotdim (x,n,plane)
Return a copy of xwith the elements rotated counterclockwise in 90-degree incre-
ments.
The second argument nis optional, and specifies how many 90-degree rotations are
to be applied (the default value is 1). Negative values of nrotate the matrix in a
clockwise direction.
The third argument is also optional and defines the plane of the rotation. If present,
plane is a two element vector containing two different valid dimensions of the matrix.
When plane is not given the first two non-singleton dimensions are used.
For example,
rotdim ([1, 2; 3, 4], -1, [1, 2])
⇒3 1
4 2
rotates the given matrix clockwise by 90 degrees. The following are all equivalent
statements:
rotdim ([1, 2; 3, 4], -1, [1, 2])
rotdim ([1, 2; 3, 4], 3, [1, 2])
rotdim ([1, 2; 3, 4], 7, [1, 2])
See also: [rot90], page 444,[fliplr], page 443,[flipud], page 443,[flip], page 443.
Chapter 16: Matrix Manipulation 445
cat (dim,array1,array2, . . . , arrayN)
Return the concatenation of N-D array objects, array1,array2, . . ., arrayN along
dimension dim.
A = ones (2, 2);
B = zeros (2, 2);
cat (2, A, B)
⇒1100
1100
Alternatively, we can concatenate Aand Balong the second dimension in the following
way:
[A, B]
dim can be larger than the dimensions of the N-D array objects and the result will
thus have dim dimensions as the following example shows:
cat (4, ones (2, 2), zeros (2, 2))
⇒ans(:,:,1,1) =
1 1
1 1
ans(:,:,1,2) =
0 0
0 0
See also: [horzcat], page 445,[vertcat], page 445.
horzcat (array1,array2, . . . , arrayN)
Return the horizontal concatenation of N-D array objects, array1,array2, . . . , arrayN
along dimension 2.
Arrays may also be concatenated horizontally using the syntax for creating new ma-
trices. For example:
hcat = [ array1,array2, ... ]
See also: [cat], page 445,[vertcat], page 445.
vertcat (array1,array2, . . . , arrayN)
Return the vertical concatenation of N-D array objects, array1,array2, . . . , arrayN
along dimension 1.
Arrays may also be concatenated vertically using the syntax for creating new matrices.
For example:
vcat = [ array1;array2; ... ]
See also: [cat], page 445,[horzcat], page 445.
permute (A,perm)
Return the generalized transpose for an N-D array object A.
446 GNU Octave
The permutation vector perm must contain the elements 1:ndims (A) (in any order,
but each element must appear only once). The Nth dimension of Agets remapped
to dimension PERM(N). For example:
x= zeros ([2, 3, 5, 7]);
size (x)
⇒2357
size (permute (x, [2, 1, 3, 4]))
⇒3257
size (permute (x, [1, 3, 4, 2]))
⇒2573
## The identity permutation
size (permute (x, [1, 2, 3, 4]))
⇒2357
See also: [ipermute], page 446.
ipermute (A,iperm)
The inverse of the permute function.
The expression
ipermute (permute (A, perm), perm)
returns the original array A.
See also: [permute], page 445.
reshape (A,m,n, . . . )
reshape (A,[m n . . . ])
reshape (A, . . . , [], . . .)
reshape (A,size)
Return a matrix with the specified dimensions (m,n, . . . ) whose elements are taken
from the matrix A.
The elements of the matrix are accessed in column-major order (like Fortran arrays
are stored).
The following code demonstrates reshaping a 1x4 row vector into a 2x2 square matrix.
reshape ([1, 2, 3, 4], 2, 2)
⇒1 3
2 4
Note that the total number of elements in the original matrix (prod (size (A)))
must match the total number of elements in the new matrix (prod ([m n ...])).
A single dimension of the return matrix may be left unspecified and Octave will
determine its size automatically. An empty matrix ([]) is used to flag the unspecified
dimension.
See also: [resize], page 447,[vec], page 451,[postpad], page 452,[cat], page 445,
[squeeze], page 46.
Chapter 16: Matrix Manipulation 447
resize (x,m)
resize (x,m,n, . . . )
resize (x,[m n . . . ])
Resize xcutting off elements as necessary.
In the result, element with certain indices is equal to the corresponding element of x
if the indices are within the bounds of x; otherwise, the element is set to zero.
In other words, the statement
y = resize (x, dv)
is equivalent to the following code:
y = zeros (dv, class (x));
sz = min (dv, size (x));
for i = 1:length (sz)
idx{i} = 1:sz(i);
endfor
y(idx{:}) = x(idx{:});
but is performed more efficiently.
If only mis supplied, and it is a scalar, the dimension of the result is m-by-m. If m,
n, . . . are all scalars, then the dimensions of the result are m-by-n-by-. . . . If given a
vector as input, then the dimensions of the result are given by the elements of that
vector.
An object can be resized to more dimensions than it has; in such case the missing
dimensions are assumed to be 1. Resizing an object to fewer dimensions is not possible.
See also: [reshape], page 446,[postpad], page 452,[prepad], page 451,[cat], page 445.
y= circshift (x,n)
y= circshift (x,n,dim)
Circularly shift the values of the array x.
nmust be a vector of integers no longer than the number of dimensions in x. The
values of ncan be either positive or negative, which determines the direction in which
the values of xare shifted. If an element of nis zero, then the corresponding dimension
of xwill not be shifted.
If a scalar dim is given then operate along the specified dimension. In this case n
must be a scalar as well.
Examples:
448 GNU Octave
x = [1, 2, 3; 4, 5, 6; 7, 8, 9];
circshift (x, 1)
⇒7, 8, 9
1, 2, 3
4, 5, 6
circshift (x, -2)
⇒7, 8, 9
1, 2, 3
4, 5, 6
circshift (x, [0,1])
⇒3, 1, 2
6, 4, 5
9, 7, 8
See also: [permute], page 445,[ipermute], page 446,[shiftdim], page 448.
shift (x,b)
shift (x,b,dim)
If xis a vector, perform a circular shift of length bof the elements of x.
If xis a matrix, do the same for each column of x.
If the optional dim argument is given, operate along this dimension.
y= shiftdim (x,n)
[y,ns] = shiftdim (x)
Shift the dimensions of xby n, where nmust be an integer scalar.
When nis positive, the dimensions of xare shifted to the left, with the leading
dimensions circulated to the end. If nis negative, then the dimensions of xare
shifted to the right, with nleading singleton dimensions added.
Called with a single argument, shiftdim, removes the leading singleton dimensions,
returning the number of dimensions removed in the second output argument ns.
For example:
x = ones (1, 2, 3);
size (shiftdim (x, -1))
⇒[1, 1, 2, 3]
size (shiftdim (x, 1))
⇒[2, 3]
[b, ns] = shiftdim (x)
⇒b = [1, 1, 1; 1, 1, 1]
⇒ns = 1
See also: [reshape], page 446,[permute], page 445,[ipermute], page 446,[circshift],
page 447,[squeeze], page 46.
[s,i] = sort (x)
[s,i] = sort (x,dim)
[s,i] = sort (x,mode)
[s,i] = sort (x,dim,mode)
Return a copy of xwith the elements arranged in increasing order.
Chapter 16: Matrix Manipulation 449
For matrices, sort orders the elements within columns
For example:
sort ([1, 2; 2, 3; 3, 1])
⇒1 1
2 2
3 3
If the optional argument dim is given, then the matrix is sorted along the dimension
defined by dim. The optional argument mode defines the order in which the values
will be sorted. Valid values of mode are "ascend" or "descend".
The sort function may also be used to produce a matrix containing the original row
indices of the elements in the sorted matrix. For example:
[s, i] = sort ([1, 2; 2, 3; 3, 1])
⇒s = 1 1
2 2
3 3
⇒i = 1 3
2 1
3 2
For equal elements, the indices are such that equal elements are listed in the order in
which they appeared in the original list.
Sorting of complex entries is done first by magnitude (abs (z)) and for any ties by
phase angle (angle (z)). For example:
sort ([1+i; 1; 1-i])
⇒1 + 0i
1 - 1i
1 + 1i
NaN values are treated as being greater than any other value and are sorted to the
end of the list.
The sort function may also be used to sort strings and cell arrays of strings, in which
case ASCII dictionary order (uppercase ’A’ precedes lowercase ’a’) of the strings is
used.
The algorithm used in sort is optimized for the sorting of partially ordered lists.
See also: [sortrows], page 449,[issorted], page 450.
[s,i] = sortrows (A)
[s,i] = sortrows (A,c)
Sort the rows of the matrix Aaccording to the order of the columns specified in c.
By default (comitted, or a particular column unspecified in c) an ascending sort
order is used. However, if elements of care negative then the corresponding column
is sorted in descending order. If the elements of Aare strings then a lexicographical
sort is used.
Example: sort by column 2 in descending order, then 3 in ascending order

450 GNU Octave
x=[7,1,4;
8, 3, 5;
9, 3, 6 ];
sortrows (x, [-2, 3])
⇒835
936
714
See also: [sort], page 448.
issorted (a)
issorted (a,mode)
issorted (a,"rows",mode)
Return true if the array is sorted according to mode, which may be either
"ascending","descending", or "either".
By default, mode is "ascending". NaNs are treated in the same manner as sort.
If the optional argument "rows" is supplied, check whether the array is sorted by
rows as output by the function sortrows (with no options).
This function does not support sparse matrices.
See also: [sort], page 448,[sortrows], page 449.
nth_element (x,n)
nth_element (x,n,dim)
Select the n-th smallest element of a vector, using the ordering defined by sort.
The result is equivalent to sort(x)(n).
ncan also be a contiguous range, either ascending l:u or descending u:-1:l, in which
case a range of elements is returned.
If xis an array, nth_element operates along the dimension defined by dim, or the
first non-singleton dimension if dim is not given.
Programming Note: nth element encapsulates the C++ standard library algorithms
nth element and partial sort. On average, the complexity of the operation is
O(M*log(K)), where M = size (x,dim)and K = length (n). This function is
intended for cases where the ratio K/M is small; otherwise, it may be better to use
sort.
See also: [sort], page 448,[min], page 481,[max], page 481.
tril (A)
tril (A,k)
tril (A,k,pack)
triu (A)
triu (A,k)
triu (A,k,pack)
Return a new matrix formed by extracting the lower (tril) or upper (triu) triangular
part of the matrix A, and setting all other elements to zero.
The second argument is optional, and specifies how many diagonals above or below
the main diagonal should also be set to zero.
Chapter 16: Matrix Manipulation 451
The default value of kis zero, so that triu and tril normally include the main
diagonal as part of the result.
If the value of kis nonzero integer, the selection of elements starts at an offset of
kdiagonals above or below the main diagonal; above for positive kand below for
negative k.
The absolute value of kmust not be greater than the number of subdiagonals or
superdiagonals.
For example:
tril (ones (3), -1)
⇒000
100
110
and
tril (ones (3), 1)
⇒110
111
111
If the option "pack" is given as third argument, the extracted elements are not
inserted into a matrix, but rather stacked column-wise one above other.
See also: [diag], page 452.
v= vec (x)
v= vec (x,dim)
Return the vector obtained by stacking the columns of the matrix xone above the
other.
Without dim this is equivalent to x(:).
If dim is supplied, the dimensions of vare set to dim with all elements along the last
dimension. This is equivalent to shiftdim (x(:), 1-dim).
See also: [vech], page 451,[resize], page 447,[cat], page 445.
vech (x)
Return the vector obtained by eliminating all superdiagonal elements of the square
matrix xand stacking the result one column above the other.
This has uses in matrix calculus where the underlying matrix is symmetric and it
would be pointless to keep values above the main diagonal.
See also: [vec], page 451.
prepad (x,l)
prepad (x,l,c)
prepad (x,l,c,dim)
Prepend the scalar value cto the vector xuntil it is of length l. If cis not given, a
value of 0 is used.
If length (x) > l, elements from the beginning of xare removed until a vector of
length lis obtained.
452 GNU Octave
If xis a matrix, elements are prepended or removed from each row.
If the optional argument dim is given, operate along this dimension.
If dim is larger than the dimensions of x, the result will have dim dimensions.
See also: [postpad], page 452,[cat], page 445,[resize], page 447.
postpad (x,l)
postpad (x,l,c)
postpad (x,l,c,dim)
Append the scalar value cto the vector xuntil it is of length l. If cis not given, a
value of 0 is used.
If length (x) > l, elements from the end of xare removed until a vector of length l
is obtained.
If xis a matrix, elements are appended or removed from each row.
If the optional argument dim is given, operate along this dimension.
If dim is larger than the dimensions of x, the result will have dim dimensions.
See also: [prepad], page 451,[cat], page 445,[resize], page 447.
M= diag (v)
M= diag (v,k)
M= diag (v,m,n)
v= diag (M)
v= diag (M,k)
Return a diagonal matrix with vector von diagonal k.
The second argument is optional. If it is positive, the vector is placed on the k-th
superdiagonal. If it is negative, it is placed on the -k-th subdiagonal. The default
value of kis 0, and the vector is placed on the main diagonal. For example:
diag ([1, 2, 3], 1)
⇒0100
0020
0003
0000
The 3-input form returns a diagonal matrix with vector von the main diagonal and
the resulting matrix being of size mrows x ncolumns.
Given a matrix argument, instead of a vector, diag extracts the k-th diagonal of the
matrix.
blkdiag (A,B,C, . . . )
Build a block diagonal matrix from A,B,C, . . .
All arguments must be numeric and either two-dimensional matrices or scalars. If
any argument is of type sparse, the output will also be sparse.
See also: [diag], page 452,[horzcat], page 445,[vertcat], page 445,[sparse], page 564.
Chapter 16: Matrix Manipulation 453
16.3 Special Utility Matrices
eye (n)
eye (m,n)
eye ([m n])
eye (. . ., class)
Return an identity matrix.
If invoked with a single scalar argument n, return a square NxN identity matrix.
If supplied two scalar arguments (m,n), eye takes them to be the number of rows
and columns. If given a vector with two elements, eye uses the values of the elements
as the number of rows and columns, respectively. For example:
eye (3)
⇒100
010
001
The following expressions all produce the same result:
eye (2)
≡
eye (2, 2)
≡
eye (size ([1, 2; 3, 4]))
The optional argument class, allows eye to return an array of the specified type, like
val = zeros (n,m, "uint8")
Calling eye with no arguments is equivalent to calling it with an argument of 1. Any
negative dimensions are treated as zero. These odd definitions are for compatibility
with matlab.
See also: [speye], page 562,[ones], page 453,[zeros], page 454.
ones (n)
ones (m,n)
ones (m,n,k, . . . )
ones ([m n . . . ])
ones (. . ., class)
Return a matrix or N-dimensional array whose elements are all 1.
If invoked with a single scalar integer argument n, return a square NxN matrix.
If invoked with two or more scalar integer arguments, or a vector of integer values,
return an array with the given dimensions.
To create a constant matrix whose values are all the same use an expression such as
val_matrix = val * ones (m, n)
The optional argument class specifies the class of the return array and defaults to
double. For example:
val = ones (m,n, "uint8")
See also: [zeros], page 454.
454 GNU Octave
zeros (n)
zeros (m,n)
zeros (m,n,k, . . . )
zeros ([m n . . . ])
zeros (. . ., class)
Return a matrix or N-dimensional array whose elements are all 0.
If invoked with a single scalar integer argument, return a square NxN matrix.
If invoked with two or more scalar integer arguments, or a vector of integer values,
return an array with the given dimensions.
The optional argument class specifies the class of the return array and defaults to
double. For example:
val = zeros (m,n, "uint8")
See also: [ones], page 453.
repmat (A,m)
repmat (A,m,n)
repmat (A,m,n,p. . .)
repmat (A,[m n])
repmat (A,[m n p . . . ])
Repeat matrix or N-D array.
Form a block matrix of size mby n, with a copy of matrix Aas each element.
If nis not specified, form an mby mblock matrix. For copying along more than two
dimensions, specify the number of times to copy across each dimension m,n,p, . . .,
in a vector in the second argument.
See also: [bsxfun], page 532,[kron], page 523,[repelems], page 454.
repelems (x,r)
Construct a vector of repeated elements from x.
ris a 2xNinteger matrix specifying which elements to repeat and how often to
repeat each element. Entries in the first row, r(1,j), select an element to repeat. The
corresponding entry in the second row, r(2,j), specifies the repeat count. If xis a
matrix then the columns of xare imagined to be stacked on top of each other for
purposes of the selection index. A row vector is always returned.
Conceptually the result is calculated as follows:
y = [];
for i = 1:columns (r)
y = [y, x(r(1,i)*ones(1, r(2,i)))];
endfor
See also: [repmat], page 454,[cat], page 445.
The functions linspace and logspace make it very easy to create vectors with evenly
or logarithmically spaced elements. See Section 4.2 [Ranges], page 52.
Chapter 16: Matrix Manipulation 455
linspace (base,limit)
linspace (base,limit,n)
Return a row vector with nlinearly spaced elements between base and limit.
If the number of elements is greater than one, then the endpoints base and limit are
always included in the range. If base is greater than limit, the elements are stored in
decreasing order. If the number of points is not specified, a value of 100 is used.
The linspace function returns a row vector when both base and limit are scalars.
If one, or both, inputs are vectors, then linspace transforms them to column
vectors and returns a matrix where each row is an independent sequence between
base(row_n), limit(row_n).
For compatibility with matlab, return the second argument (limit) if fewer than two
values are requested.
See also: [logspace], page 455.
logspace (a,b)
logspace (a,b,n)
logspace (a, pi, n)
Return a row vector with nelements logarithmically spaced from 10ato 10b.
If nis unspecified it defaults to 50.
If bis equal to π, the points are between 10aand π,not 10aand 10π, in order to be
compatible with the corresponding matlab function.
Also for compatibility with matlab, return the second argument bif fewer than two
values are requested.
See also: [linspace], page 454.
rand (n)
rand (m,n, . . . )
rand ([m n . . . ])
v= rand ("state")
rand ("state",v)
rand ("state","reset")
v= rand ("seed")
rand ("seed",v)
rand ("seed","reset")
rand (. . ., "single")
rand (. . ., "double")
Return a matrix with random elements uniformly distributed on the interval (0, 1).
The arguments are handled the same as the arguments for eye.
You can query the state of the random number generator using the form
v = rand ("state")
This returns a column vector vof length 625. Later, you can restore the random
number generator to the state vusing the form
rand ("state", v)
456 GNU Octave
You may also initialize the state vector from an arbitrary vector of length ≤625 for
v. This new state will be a hash based on the value of v, not vitself.
By default, the generator is initialized from /dev/urandom if it is available, otherwise
from CPU time, wall clock time, and the current fraction of a second. Note that this
differs from matlab, which always initializes the state to the same state at startup.
To obtain behavior comparable to matlab, initialize with a deterministic state vector
in Octave’s startup files (see Section 2.1.2 [Startup Files], page 19).
To compute the pseudo-random sequence, rand uses the Mersenne Twister with a
period of 219937 −1 (See M. Matsumoto and T. Nishimura, Mersenne Twister: A
623-dimensionally equidistributed uniform pseudorandom number generator, ACM
Trans. on Modeling and Computer Simulation Vol. 8, No. 1, pp. 3–30, January
1998, http://www .math.sci.hiroshima-u .ac.jp/~m-mat /MT/emt.html). Do
not use for cryptography without securely hashing several returned values together,
otherwise the generator state can be learned after reading 624 consecutive values.
Older versions of Octave used a different random number generator. The new genera-
tor is used by default as it is significantly faster than the old generator, and produces
random numbers with a significantly longer cycle time. However, in some circum-
stances it might be desirable to obtain the same random sequences as produced by
the old generators. To do this the keyword "seed" is used to specify that the old
generators should be used, as in
rand ("seed", val)
which sets the seed of the generator to val. The seed of the generator can be queried
with
s = rand ("seed")
However, it should be noted that querying the seed will not cause rand to use the
old generators, only setting the seed will. To cause rand to once again use the new
generators, the keyword "state" should be used to reset the state of the rand.
The state or seed of the generator can be reset to a new random value using the
"reset" keyword.
The class of the value returned can be controlled by a trailing "double" or "single"
argument. These are the only valid classes.
See also: [randn], page 457,[rande], page 457,[randg], page 459,[randp], page 458.
randi (imax)
randi (imax,n)
randi (imax,m,n, . . . )
randi ([imin imax], . . . )
randi (. . ., "class")
Return random integers in the range 1:imax.
Additional arguments determine the shape of the return matrix. When no arguments
are specified a single random integer is returned. If one argument nis specified then
a square matrix (nxn) is returned. Two or more arguments will return a multi-
dimensional matrix (mxnx . . .).
Chapter 16: Matrix Manipulation 457
The integer range may optionally be described by a two element matrix with a
lower and upper bound in which case the returned integers will be on the interval
[imin,imax].
The optional argument class will return a matrix of the requested type. The default
is "double".
The following example returns 150 integers in the range 1–10.
ri = randi (10, 150, 1)
Implementation Note: randi relies internally on rand which uses class "double" to
represent numbers. This limits the maximum integer (imax) and range (imax -imin)
to the value returned by the flintmax function. For IEEE floating point numbers
this value is 253 −1.
See also: [rand], page 455.
randn (n)
randn (m,n, . . . )
randn ([m n . . . ])
v= randn ("state")
randn ("state",v)
randn ("state","reset")
v= randn ("seed")
randn ("seed",v)
randn ("seed","reset")
randn (. . ., "single")
randn (. . ., "double")
Return a matrix with normally distributed random elements having zero mean and
variance one.
The arguments are handled the same as the arguments for rand.
By default, randn uses the Marsaglia and Tsang “Ziggurat technique” to transform
from a uniform to a normal distribution.
The class of the value returned can be controlled by a trailing "double" or "single"
argument. These are the only valid classes.
Reference: G. Marsaglia and W.W. Tsang, Ziggurat Method for Generating Random
Variables, J. Statistical Software, vol 5, 2000, http://www.jstatsoft.org/v05/
i08/
See also: [rand], page 455,[rande], page 457,[randg], page 459,[randp], page 458.
rande (n)
rande (m,n, . . . )
rande ([m n . . . ])
v= rande ("state")
rande ("state",v)
rande ("state","reset")
v= rande ("seed")
rande ("seed",v)
rande ("seed","reset")
458 GNU Octave
rande (. . ., "single")
rande (. . ., "double")
Return a matrix with exponentially distributed random elements.
The arguments are handled the same as the arguments for rand.
By default, rande uses the Marsaglia and Tsang “Ziggurat technique” to transform
from a uniform to an exponential distribution.
The class of the value returned can be controlled by a trailing "double" or "single"
argument. These are the only valid classes.
Reference: G. Marsaglia and W.W. Tsang, Ziggurat Method for Generating Random
Variables, J. Statistical Software, vol 5, 2000, http://www.jstatsoft.org/v05/
i08/
See also: [rand], page 455,[randn], page 457,[randg], page 459,[randp], page 458.
randp (l,n)
randp (l,m,n, . . . )
randp (l,[m n . . . ])
v= randp ("state")
randp ("state",v)
randp ("state","reset")
v= randp ("seed")
randp ("seed",v)
randp ("seed","reset")
randp (. . ., "single")
randp (. . ., "double")
Return a matrix with Poisson distributed random elements with mean value param-
eter given by the first argument, l.
The arguments are handled the same as the arguments for rand, except for the argu-
ment l.
Five different algorithms are used depending on the range of land whether or not l
is a scalar or a matrix.
For scalar l≤12, use direct method.
W.H. Press, et al., Numerical Recipes in C, Cambridge University Press,
1992.
For scalar l>12, use rejection method.[1]
W.H. Press, et al., Numerical Recipes in C, Cambridge University Press,
1992.
For matrix l≤10, use inversion method.[2]
E. Stadlober, et al., WinRand source code, available via FTP.
For matrix l>10, use patchwork rejection method.
E. Stadlober, et al., WinRand source code, available via FTP, or H. Zech-
ner, Efficient sampling from continuous and discrete unimodal distribu-
tions, Doctoral Dissertation, 156pp., Technical University Graz, Austria,
1994.
Chapter 16: Matrix Manipulation 459
For l>1e8, use normal approximation.
L. Montanet, et al., Review of Particle Properties, Physical Review D 50
p1284, 1994.
The class of the value returned can be controlled by a trailing "double" or "single"
argument. These are the only valid classes.
See also: [rand], page 455,[randn], page 457,[rande], page 457,[randg], page 459.
randg (n)
randg (m,n, . . . )
randg ([m n . . . ])
v= randg ("state")
randg ("state",v)
randg ("state","reset")
v= randg ("seed")
randg ("seed",v)
randg ("seed","reset")
randg (. . ., "single")
randg (. . ., "double")
Return a matrix with gamma (a,1) distributed random elements.
The arguments are handled the same as the arguments for rand, except for the argu-
ment a.
This can be used to generate many distributions:
gamma (a, b) for a > -1,b > 0
r = b * randg (a)
beta (a, b) for a > -1,b > -1
r1 = randg (a, 1)
r = r1 / (r1 + randg (b, 1))
Erlang (a, n)
r = a * randg (n)
chisq (df) for df > 0
r = 2 * randg (df / 2)
t (df) for 0 < df < inf (use randn if df is infinite)
r = randn () / sqrt (2 * randg (df / 2) / df)
F (n1, n2) for 0 < n1,0 < n2
## r1 equals 1 if n1 is infinite
r1 = 2 * randg (n1 / 2) / n1
## r2 equals 1 if n2 is infinite
r2 = 2 * randg (n2 / 2) / n2
r=r1/r2
negative binomial (n, p) for n > 0,0 < p <= 1
r = randp ((1 - p) / p * randg (n))

460 GNU Octave
non-central chisq (df, L), for df >= 0 and L > 0
(use chisq if L = 0)
r = randp (L / 2)
r(r > 0) = 2 * randg (r(r > 0))
r(df > 0) += 2 * randg (df(df > 0)/2)
Dirichlet (a1, ... ak)
r = (randg (a1), ..., randg (ak))
r = r / sum (r)
The class of the value returned can be controlled by a trailing "double" or "single"
argument. These are the only valid classes.
See also: [rand], page 455,[randn], page 457,[rande], page 457,[randp], page 458.
The generators operate in the new or old style together, it is not possible to mix the
two. Initializing any generator with "state" or "seed" causes the others to switch to the
same style for future calls.
The state of each generator is independent and calls to different generators can be
interleaved without affecting the final result. For example,
rand ("state", [11, 22, 33]);
randn ("state", [44, 55, 66]);
u = rand (100, 1);
n = randn (100, 1);
and
rand ("state", [11, 22, 33]);
randn ("state", [44, 55, 66]);
u = zeros (100, 1);
n = zeros (100, 1);
for i = 1:100
u(i) = rand ();
n(i) = randn ();
end
produce equivalent results. When the generators are initialized in the old style with "seed"
only rand and randn are independent, because the old rande,randg and randp generators
make calls to rand and randn.
The generators are initialized with random states at start-up, so that the sequences of
random numbers are not the same each time you run Octave.1If you really do need to
reproduce a sequence of numbers exactly, you can set the state or seed to a specific value.
If invoked without arguments, rand and randn return a single element of a random
sequence.
The original rand and randn functions use Fortran code from ranlib, a library of Fortran
routines for random number generation, compiled by Barry W. Brown and James Lovato
of the Department of Biomathematics at The University of Texas, M.D. Anderson Cancer
Center, Houston, TX 77030.
1The old versions of rand and randn obtain their initial seeds from the system clock.
Chapter 16: Matrix Manipulation 461
randperm (n)
randperm (n,m)
Return a row vector containing a random permutation of 1:n.
If mis supplied, return munique entries, sampled without replacement from 1:n.
The complexity is O(n) in memory and O(m) in time, unless m<n/5, in which case
O(m) memory is used as well. The randomization is performed using rand(). All
permutations are equally likely.
See also: [perms], page 651.
16.4 Famous Matrices
The following functions return famous matrix forms.
gallery (name)
gallery (name,args)
Create interesting matrices for testing.
c= gallery ("cauchy",x)
c= gallery ("cauchy",x,y)
Create a Cauchy matrix.
c= gallery ("chebspec",n)
c= gallery ("chebspec",n,k)
Create a Chebyshev spectral differentiation matrix.
c= gallery ("chebvand",p)
c= gallery ("chebvand",m,p)
Create a Vandermonde-like matrix for the Chebyshev polynomials.
a= gallery ("chow",n)
a= gallery ("chow",n,alpha)
a= gallery ("chow",n,alpha,delta)
Create a Chow matrix – a singular Toeplitz lower Hessenberg matrix.
c= gallery ("circul",v)
Create a circulant matrix.
a= gallery ("clement",n)
a= gallery ("clement",n,k)
Create a tridiagonal matrix with zero diagonal entries.
c= gallery ("compar",a)
c= gallery ("compar",a,k)
Create a comparison matrix.
a= gallery ("condex",n)
a= gallery ("condex",n,k)
a= gallery ("condex",n,k,theta)
Create a ‘counterexample’ matrix to a condition estimator.
462 GNU Octave
a= gallery ("cycol",[m n])
a= gallery ("cycol",n)
a= gallery (. . . , k)
Create a matrix whose columns repeat cyclically.
[c,d,e] = gallery ("dorr",n)
[c,d,e] = gallery ("dorr",n,theta)
a= gallery ("dorr", . . . )
Create a diagonally dominant, ill-conditioned, tridiagonal matrix.
a= gallery ("dramadah",n)
a= gallery ("dramadah",n,k)
Create a (0, 1) matrix whose inverse has large integer entries.
a= gallery ("fiedler",c)
Create a symmetric Fiedler matrix.
a= gallery ("forsythe",n)
a= gallery ("forsythe",n,alpha)
a= gallery ("forsythe",n,alpha,lambda)
Create a Forsythe matrix (a perturbed Jordan block).
f= gallery ("frank",n)
f= gallery ("frank",n,k)
Create a Frank matrix (ill-conditioned eigenvalues).
c= gallery ("gcdmat",n)
Create a greatest common divisor matrix.
cis an n-by-nmatrix whose values correspond to the greatest common divisor of its
coordinate values, i.e., c(i,j) correspond gcd (i, j).
a= gallery ("gearmat",n)
a= gallery ("gearmat",n,i)
a= gallery ("gearmat",n,i,j)
Create a Gear matrix.
g= gallery ("grcar",n)
g= gallery ("grcar",n,k)
Create a Toeplitz matrix with sensitive eigenvalues.
a= gallery ("hanowa",n)
a= gallery ("hanowa",n,d)
Create a matrix whose eigenvalues lie on a vertical line in the complex plane.
v= gallery ("house",x)
[v,beta] = gallery ("house",x)
Create a householder matrix.
Chapter 16: Matrix Manipulation 463
a= gallery ("integerdata",imax,[M N . . . ],j)
a= gallery ("integerdata",imax,M,N, . . . , j)
a= gallery ("integerdata",[imin,imax],[M N . . . ],j)
a= gallery ("integerdata",[imin,imax],M,N, . . . , j)
a= gallery ("integerdata", . . . , "class")
Create a matrix with random integers in the range [1, imax]. If imin is given then
the integers are in the range [imin,imax].
The second input is a matrix of dimensions describing the size of the output. The
dimensions can also be input as comma-separated arguments.
The input jis an integer index in the range [0, 2^32-1]. The values of the output
matrix are always exactly the same (reproducibility) for a given size input and jindex.
The final optional argument determines the class of the resulting matrix. Possible
values for class:"uint8","uint16","uint32","int8","int16", int32","single",
"double". The default is "double".
a= gallery ("invhess",x)
a= gallery ("invhess",x,y)
Create the inverse of an upper Hessenberg matrix.
a= gallery ("invol",n)
Create an involutory matrix.
a= gallery ("ipjfact",n)
a= gallery ("ipjfact",n,k)
Create a Hankel matrix with factorial elements.
a= gallery ("jordbloc",n)
a= gallery ("jordbloc",n,lambda)
Create a Jordan block.
u= gallery ("kahan",n)
u= gallery ("kahan",n,theta)
u= gallery ("kahan",n,theta,pert)
Create a Kahan matrix (upper trapezoidal).
a= gallery ("kms",n)
a= gallery ("kms",n,rho)
Create a Kac-Murdock-Szego Toeplitz matrix.
b= gallery ("krylov",a)
b= gallery ("krylov",a,x)
b= gallery ("krylov",a,x,j)
Create a Krylov matrix.
a= gallery ("lauchli",n)
a= gallery ("lauchli",n,mu)
Create a Lauchli matrix (rectangular).
a= gallery ("lehmer",n)
Create a Lehmer matrix (symmetric positive definite).
464 GNU Octave
t= gallery ("lesp",n)
Create a tridiagonal matrix with real, sensitive eigenvalues.
a= gallery ("lotkin",n)
Create a Lotkin matrix.
a= gallery ("minij",n)
Create a symmetric positive definite matrix MIN(i,j).
a= gallery ("moler",n)
a= gallery ("moler",n,alpha)
Create a Moler matrix (symmetric positive definite).
[a,t] = gallery ("neumann",n)
Create a singular matrix from the discrete Neumann problem (sparse).
a= gallery ("normaldata",[M N . . . ],j)
a= gallery ("normaldata",M,N, . . . , j)
a= gallery ("normaldata", . . . , "class")
Create a matrix with random samples from the standard normal distribution (mean
= 0, std = 1).
The first input is a matrix of dimensions describing the size of the output. The
dimensions can also be input as comma-separated arguments.
The input jis an integer index in the range [0, 2^32-1]. The values of the output
matrix are always exactly the same (reproducibility) for a given size input and jindex.
The final optional argument determines the class of the resulting matrix. Possible
values for class:"single","double". The default is "double".
q= gallery ("orthog",n)
q= gallery ("orthog",n,k)
Create orthogonal and nearly orthogonal matrices.
a= gallery ("parter",n)
Create a Parter matrix (a Toeplitz matrix with singular values near pi).
p= gallery ("pei",n)
p= gallery ("pei",n,alpha)
Create a Pei matrix.
a= gallery ("Poisson",n)
Create a block tridiagonal matrix from Poisson’s equation (sparse).
a= gallery ("prolate",n)
a= gallery ("prolate",n,w)
Create a prolate matrix (symmetric, ill-conditioned Toeplitz matrix).
h= gallery ("randhess",x)
Create a random, orthogonal upper Hessenberg matrix.
Chapter 16: Matrix Manipulation 465
a= gallery ("rando",n)
a= gallery ("rando",n,k)
Create a random matrix with elements -1, 0 or 1.
a= gallery ("randsvd",n)
a= gallery ("randsvd",n,kappa)
a= gallery ("randsvd",n,kappa,mode)
a= gallery ("randsvd",n,kappa,mode,kl)
a= gallery ("randsvd",n,kappa,mode,kl,ku)
Create a random matrix with pre-assigned singular values.
a= gallery ("redheff",n)
Create a zero and ones matrix of Redheffer associated with the Riemann hypothesis.
a= gallery ("riemann",n)
Create a matrix associated with the Riemann hypothesis.
a= gallery ("ris",n)
Create a symmetric Hankel matrix.
a= gallery ("smoke",n)
a= gallery ("smoke",n,k)
Create a complex matrix, with a ‘smoke ring’ pseudospectrum.
t= gallery ("toeppd",n)
t= gallery ("toeppd",n,m)
t= gallery ("toeppd",n,m,w)
t= gallery ("toeppd",n,m,w,theta)
Create a symmetric positive definite Toeplitz matrix.
p= gallery ("toeppen",n)
p= gallery ("toeppen",n,a)
p= gallery ("toeppen",n,a,b)
p= gallery ("toeppen",n,a,b,c)
p= gallery ("toeppen",n,a,b,c,d)
p= gallery ("toeppen",n,a,b,c,d,e)
Create a pentadiagonal Toeplitz matrix (sparse).
a= gallery ("tridiag",x,y,z)
a= gallery ("tridiag",n)
a= gallery ("tridiag",n,c,d,e)
Create a tridiagonal matrix (sparse).
t= gallery ("triw",n)
t= gallery ("triw",n,alpha)
t= gallery ("triw",n,alpha,k)
Create an upper triangular matrix discussed by Kahan, Golub, and Wilkinson.
a= gallery ("uniformdata",[M N . . . ],j)
a= gallery ("uniformdata",M,N, . . . , j)
466 GNU Octave
a= gallery ("uniformdata", . . . , "class")
Create a matrix with random samples from the standard uniform distribution (range
[0,1]).
The first input is a matrix of dimensions describing the size of the output. The
dimensions can also be input as comma-separated arguments.
The input jis an integer index in the range [0, 2^32-1]. The values of the output
matrix are always exactly the same (reproducibility) for a given size input and jindex.
The final optional argument determines the class of the resulting matrix. Possible
values for class:"single","double". The default is "double".
a= gallery ("wathen",nx,ny)
a= gallery ("wathen",nx,ny,k)
Create the Wathen matrix.
[a,b] = gallery ("wilk",n)
Create various specific matrices devised/discussed by Wilkinson.
hadamard (n)
Construct a Hadamard matrix (Hn) of size n-by-n.
The size nmust be of the form 2k∗pin which p is one of 1, 12, 20 or 28. The returned
matrix is normalized, meaning Hn(:,1) == 1 and Hn(1,:) == 1.
Some of the properties of Hadamard matrices are:
•kron (Hm, Hn) is a Hadamard matrix of size m-by-n.
•Hn * Hn’ = n* eye (n).
•The rows of Hn are orthogonal.
•det (A) <= abs (det (Hn)) for all Awith abs (A(i, j)) <= 1.
•Multiplying any row or column by -1 and the matrix will remain a Hadamard
matrix.
See also: [compan], page 684,[hankel], page 466,[toeplitz], page 468.
hankel (c)
hankel (c,r)
Return the Hankel matrix constructed from the first column c, and (optionally) the
last row r.
If the last element of cis not the same as the first element of r, the last element of c
is used. If the second argument is omitted, it is assumed to be a vector of zeros with
the same size as c.
A Hankel matrix formed from an m-vector c, and an n-vector r, has the elements
H(i, j) = ci+j−1, i +j−1≤m;
ri+j−m,otherwise.
See also: [hadamard], page 466,[toeplitz], page 468.

Chapter 16: Matrix Manipulation 467
hilb (n)
Return the Hilbert matrix of order n.
The i, j element of a Hilbert matrix is defined as
H(i, j) = 1
(i+j−1)
Hilbert matrices are close to being singular which make them difficult to invert with
numerical routines. Comparing the condition number of a random matrix 5x5 matrix
with that of a Hilbert matrix of order 5 reveals just how difficult the problem is.
cond (rand (5))
⇒14.392
cond (hilb (5))
⇒4.7661e+05
See also: [invhilb], page 467.
invhilb (n)
Return the inverse of the Hilbert matrix of order n.
This can be computed exactly using
Aij =−1i+j(i+j−1) n+i−1
n−jn+j−1
n−ii+j−2
i−22
=p(i)p(j)
(i+j−1)
where
p(k) = −1kk+n−1
k−1n
k
The validity of this formula can easily be checked by expanding the binomial coeffi-
cients in both formulas as factorials. It can be derived more directly via the theory
of Cauchy matrices. See J. W. Demmel, Applied Numerical Linear Algebra, p. 92.
Compare this with the numerical calculation of inverse (hilb (n)), which suffers
from the ill-conditioning of the Hilbert matrix, and the finite precision of your com-
puter’s floating point arithmetic.
See also: [hilb], page 467.
magic (n)
Create an n-by-nmagic square.
A magic square is an arrangement of the integers 1:n^2 such that the row sums,
column sums, and diagonal sums are all equal to the same value.
Note: nmust be a scalar greater than or equal to 3. If you supply nless than 3,
magic returns either a nonmagic square, or else the degenerate magic squares 1 and
[].
468 GNU Octave
pascal (n)
pascal (n,t)
Return the Pascal matrix of order nif t= 0.
The default value of tis 0.
When t= 1, return the pseudo-lower triangular Cholesky factor of the Pascal matrix
(The sign of some columns may be negative). This matrix is its own inverse, that is
pascal (n, 1) ^ 2 == eye (n).
If t= -1, return the true Cholesky factor with strictly positive values on the diagonal.
If t= 2, return a transposed and permuted version of pascal (n, 1), which is the
cube root of the identity matrix. That is, pascal (n, 2) ^ 3 == eye (n).
See also: [chol], page 511.
rosser ()
Return the Rosser matrix.
This is a difficult test case used to evaluate eigenvalue algorithms.
See also: [wilkinson], page 469,[eig], page 505.
toeplitz (c)
toeplitz (c,r)
Return the Toeplitz matrix constructed from the first column c, and (optionally) the
first row r.
If the first element of ris not the same as the first element of c, the first element of
cis used. If the second argument is omitted, the first row is taken to be the same as
the first column.
A square Toeplitz matrix has the form:
c0r1r2··· rn
c1c0r1··· rn−1
c2c1c0··· rn−2
.
.
..
.
..
.
.....
.
.
cncn−1cn−2. . . c0
See also: [hankel], page 466.
vander (c)
vander (c,n)
Return the Vandermonde matrix whose next to last column is c.
If nis specified, it determines the number of columns; otherwise, nis taken to be
equal to the length of c.
A Vandermonde matrix has the form:
cn−1
1··· c2
1c11
cn−1
2··· c2
2c21
.
.
.....
.
..
.
..
.
.
cn−1
n··· c2
ncn1
See also: [polyfit], page 689.
Chapter 16: Matrix Manipulation 469
wilkinson (n)
Return the Wilkinson matrix of order n.
Wilkinson matrices are symmetric and tridiagonal with pairs of nearly, but not ex-
actly, equal eigenvalues. They are useful in testing the behavior and performance of
eigenvalue solvers.
See also: [rosser], page 468,[eig], page 505.

471
17 Arithmetic
Unless otherwise noted, all of the functions described in this chapter will work for real and
complex scalar, vector, or matrix arguments. Functions described as mapping functions
apply the given operation individually to each element when given a matrix argument. For
example:
sin ([1, 2; 3, 4])
⇒0.84147 0.90930
0.14112 -0.75680
17.1 Exponents and Logarithms
exp (x)
Compute exfor each element of x.
To compute the matrix exponential, see Chapter 18 [Linear Algebra], page 503.
See also: [log], page 471.
expm1 (x)
Compute ex−1 accurately in the neighborhood of zero.
See also: [exp], page 471.
log (x)
Compute the natural logarithm, ln (x),for each element of x.
To compute the matrix logarithm, see Chapter 18 [Linear Algebra], page 503.
See also: [exp], page 471,[log1p], page 471,[log2], page 471,[log10], page 471,
[logspace], page 455.
reallog (x)
Return the real-valued natural logarithm of each element of x.
If any element results in a complex return value reallog aborts and issues an error.
See also: [log], page 471,[realpow], page 472,[realsqrt], page 472.
log1p (x)
Compute ln (1 + x) accurately in the neighborhood of zero.
See also: [log], page 471,[exp], page 471,[expm1], page 471.
log10 (x)
Compute the base-10 logarithm of each element of x.
See also: [log], page 471,[log2], page 471,[logspace], page 455,[exp], page 471.
log2 (x)
[f,e] = log2 (x)
Compute the base-2 logarithm of each element of x.
If called with two output arguments, split xinto binary mantissa and exponent so
that 1
2≤ |f|<1 and eis an integer. If x= 0, f=e= 0.
See also: [pow2], page 472,[log], page 471,[log10], page 471,[exp], page 471.
472 GNU Octave
pow2 (x)
pow2 (f,e)
With one input argument, compute 2xfor each element of x.
With two input arguments, return f·2e.
See also: [log2], page 471,[nextpow2], page 472,[power], page 145.
nextpow2 (x)
Compute the exponent for the smallest power of two larger than the input.
For each element in the input array x, return the first integer nsuch that 2n≥ |x|.
See also: [pow2], page 472,[log2], page 471.
realpow (x,y)
Compute the real-valued, element-by-element power operator.
This is equivalent to x.^ y, except that realpow reports an error if any return value
is complex.
See also: [power], page 145,[reallog], page 471,[realsqrt], page 472.
sqrt (x)
Compute the square root of each element of x.
If xis negative, a complex result is returned.
To compute the matrix square root, see Chapter 18 [Linear Algebra], page 503.
See also: [realsqrt], page 472,[nthroot], page 472.
realsqrt (x)
Return the real-valued square root of each element of x.
If any element results in a complex return value realsqrt aborts and issues an error.
See also: [sqrt], page 472,[realpow], page 472,[reallog], page 471.
cbrt (x)
Compute the real cube root of each element of x.
Unlike x^(1/3), the result will be negative if xis negative.
See also: [nthroot], page 472.
nthroot (x,n)
Compute the real (non-complex) n-th root of x.
xmust have all real entries and nmust be a scalar. If nis an even integer and xhas
negative entries then nthroot aborts and issues an error.
Example:
nthroot (-1, 3)
⇒-1
(-1) ^ (1 / 3)
⇒0.50000 - 0.86603i
See also: [realsqrt], page 472,[sqrt], page 472,[cbrt], page 472.

Chapter 17: Arithmetic 473
17.2 Complex Arithmetic
In the descriptions of the following functions, zis the complex number x+iy, where iis
defined as √−1.
abs (z)
Compute the magnitude of z.
The magnitude is defined as |z|=√x2+y2.
For example:
abs (3 + 4i)
⇒5
See also: [arg], page 473.
arg (z)
angle (z)
Compute the argument, i.e., angle of z.
This is defined as, θ=atan2(y, x),in radians.
For example:
arg (3 + 4i)
⇒0.92730
See also: [abs], page 473.
conj (z)
Return the complex conjugate of z.
The complex conjugate is defined as ¯z=x−iy.
See also: [real], page 474,[imag], page 473.
cplxpair (z)
cplxpair (z,tol)
cplxpair (z,tol,dim)
Sort the numbers zinto complex conjugate pairs ordered by increasing real part.
The negative imaginary complex numbers are placed first within each pair. All real
numbers (those with abs (imag (z) / z) < tol) are placed after the complex pairs.
tol is a weighting factor which determines the tolerance of matching. The default
value is 100 and the resulting tolerance for a given complex pair is 100 * eps (abs
(z(i))).
By default the complex pairs are sorted along the first non-singleton dimension of z.
If dim is specified, then the complex pairs are sorted along this dimension.
Signal an error if some complex numbers could not be paired. Signal an error if all
complex numbers are not exact conjugates (to within tol). Note that there is no
defined order for pairs with identical real parts but differing imaginary parts.
cplxpair (exp (2i*pi*[0:4]’/5)) == exp (2i*pi*[3; 2; 4; 1; 0]/5)
imag (z)
Return the imaginary part of zas a real number.
See also: [real], page 474,[conj], page 473.
474 GNU Octave
real (z)
Return the real part of z.
See also: [imag], page 473,[conj], page 473.
17.3 Trigonometry
Octave provides the following trigonometric functions where angles are specified in radians.
To convert from degrees to radians multiply by π/180 or use the deg2rad function. For
example, sin (30 * pi/180) returns the sine of 30 degrees. As an alternative, Octave
provides a number of trigonometric functions which work directly on an argument specified
in degrees. These functions are named after the base trigonometric function with a ‘d’ suffix.
As an example, sin expects an angle in radians while sind expects an angle in degrees.
Octave uses the C library trigonometric functions. It is expected that these functions
are defined by the ISO/IEC 9899 Standard. This Standard is available at: http://www.
open-std.org /jtc1/ sc22/wg14/ www/docs/ n1124.pdf. Section F.9.1 deals with the
trigonometric functions. The behavior of most of the functions is relatively straightforward.
However, there are some exceptions to the standard behavior. Many of the exceptions
involve the behavior for -0. The most complex case is atan2. Octave exactly implements
the behavior given in the Standard. Including atan2(±0,−0) returns ±π.
It should be noted that matlab uses different definitions which apparently do not dis-
tinguish -0.
rad = deg2rad (deg)
Convert degrees to radians.
The input deg must be a scalar, vector, or N-dimensional array of double or single
floating point values. deg may be complex in which case the real and imaginary
components are converted separately.
The output rad is the same size and shape as deg with degrees converted to radians
using the conversion constant pi/180.
Example:
deg2rad ([0, 90, 180, 270, 360])
⇒0.00000 1.57080 3.14159 4.71239 6.28319
See also: [rad2deg], page 474.
deg = rad2deg (rad)
Convert radians to degrees.
The input rad must be a scalar, vector, or N-dimensional array of double or single
floating point values. rad may be complex in which case the real and imaginary
components are converted separately.
The output deg is the same size and shape as rad with radians converted to degrees
using the conversion constant 180/pi.
Example:
rad2deg ([0, pi/2, pi, 3/2*pi, 2*pi])
⇒0 90 180 270 360
See also: [deg2rad], page 474.
Chapter 17: Arithmetic 475
sin (x)
Compute the sine for each element of xin radians.
See also: [asin], page 475,[sind], page 477,[sinh], page 476.
cos (x)
Compute the cosine for each element of xin radians.
See also: [acos], page 475,[cosd], page 477,[cosh], page 476.
tan (z)
Compute the tangent for each element of xin radians.
See also: [atan], page 475,[tand], page 477,[tanh], page 476.
sec (x)
Compute the secant for each element of xin radians.
See also: [asec], page 475,[secd], page 477,[sech], page 476.
csc (x)
Compute the cosecant for each element of xin radians.
See also: [acsc], page 475,[cscd], page 477,[csch], page 476.
cot (x)
Compute the cotangent for each element of xin radians.
See also: [acot], page 475,[cotd], page 477,[coth], page 476.
asin (x)
Compute the inverse sine in radians for each element of x.
See also: [sin], page 475,[asind], page 477.
acos (x)
Compute the inverse cosine in radians for each element of x.
See also: [cos], page 475,[acosd], page 478.
atan (x)
Compute the inverse tangent in radians for each element of x.
See also: [tan], page 475,[atand], page 478.
asec (x)
Compute the inverse secant in radians for each element of x.
See also: [sec], page 475,[asecd], page 478.
acsc (x)
Compute the inverse cosecant in radians for each element of x.
See also: [csc], page 475,[acscd], page 478.
acot (x)
Compute the inverse cotangent in radians for each element of x.
See also: [cot], page 475,[acotd], page 478.
476 GNU Octave
sinh (x)
Compute the hyperbolic sine for each element of x.
See also: [asinh], page 476,[cosh], page 476,[tanh], page 476.
cosh (x)
Compute the hyperbolic cosine for each element of x.
See also: [acosh], page 476,[sinh], page 476,[tanh], page 476.
tanh (x)
Compute hyperbolic tangent for each element of x.
See also: [atanh], page 476,[sinh], page 476,[cosh], page 476.
sech (x)
Compute the hyperbolic secant of each element of x.
See also: [asech], page 476.
csch (x)
Compute the hyperbolic cosecant of each element of x.
See also: [acsch], page 476.
coth (x)
Compute the hyperbolic cotangent of each element of x.
See also: [acoth], page 476.
asinh (x)
Compute the inverse hyperbolic sine for each element of x.
See also: [sinh], page 476.
acosh (x)
Compute the inverse hyperbolic cosine for each element of x.
See also: [cosh], page 476.
atanh (x)
Compute the inverse hyperbolic tangent for each element of x.
See also: [tanh], page 476.
asech (x)
Compute the inverse hyperbolic secant of each element of x.
See also: [sech], page 476.
acsch (x)
Compute the inverse hyperbolic cosecant of each element of x.
See also: [csch], page 476.
acoth (x)
Compute the inverse hyperbolic cotangent of each element of x.
See also: [coth], page 476.
Chapter 17: Arithmetic 477
atan2 (y,x)
Compute atan (y/x) for corresponding elements of yand x.
yand xmust match in size and orientation. The signs of elements of yand xare
used to determine the quadrants of each resulting value.
This function is equivalent to arg (complex (x,y)).
See also: [tan], page 475,[tand], page 477,[tanh], page 476,[atanh], page 476.
Octave provides the following trigonometric functions where angles are specified in de-
grees. These functions produce true zeros at the appropriate intervals rather than the small
round-off error that occurs when using radians. For example:
cosd (90)
⇒0
cos (pi/2)
⇒6.1230e-17
sind (x)
Compute the sine for each element of xin degrees.
Returns zero for elements where x/180 is an integer.
See also: [asind], page 477,[sin], page 475.
cosd (x)
Compute the cosine for each element of xin degrees.
Returns zero for elements where (x-90)/180 is an integer.
See also: [acosd], page 478,[cos], page 475.
tand (x)
Compute the tangent for each element of xin degrees.
Returns zero for elements where x/180 is an integer and Inf for elements where
(x-90)/180 is an integer.
See also: [atand], page 478,[tan], page 475.
secd (x)
Compute the secant for each element of xin degrees.
See also: [asecd], page 478,[sec], page 475.
cscd (x)
Compute the cosecant for each element of xin degrees.
See also: [acscd], page 478,[csc], page 475.
cotd (x)
Compute the cotangent for each element of xin degrees.
See also: [acotd], page 478,[cot], page 475.
asind (x)
Compute the inverse sine in degrees for each element of x.
See also: [sind], page 477,[asin], page 475.
478 GNU Octave
acosd (x)
Compute the inverse cosine in degrees for each element of x.
See also: [cosd], page 477,[acos], page 475.
atand (x)
Compute the inverse tangent in degrees for each element of x.
See also: [tand], page 477,[atan], page 475.
atan2d (y,x)
Compute atan2 (y/x) in degrees for corresponding elements from yand x.
See also: [tand], page 477,[atan2], page 477.
asecd (x)
Compute the inverse secant in degrees for each element of x.
See also: [secd], page 477,[asec], page 475.
acscd (x)
Compute the inverse cosecant in degrees for each element of x.
See also: [cscd], page 477,[acsc], page 475.
acotd (x)
Compute the inverse cotangent in degrees for each element of x.
See also: [cotd], page 477,[acot], page 475.
17.4 Sums and Products
sum (x)
sum (x,dim)
sum (. . ., "native")
sum (. . ., "double")
sum (. . ., "extra")
Sum of elements along dimension dim.
If dim is omitted, it defaults to the first non-singleton dimension.
The optional "type" input determines the class of the variable used for calculations.
If the argument "native" is given, then the operation is performed in the same type
as the original argument, rather than the default double type.
For example:
sum ([true, true])
⇒2
sum ([true, true], "native")
⇒true
On the contrary, if "double" is given, the sum is performed in double precision even
for single precision inputs.
For double precision inputs, the "extra" option will use a more accurate algorithm
than straightforward summation. For single precision inputs, "extra" is the same as
"double". Otherwise, "extra" has no effect.
Chapter 17: Arithmetic 479
See also: [cumsum], page 479,[sumsq], page 480,[prod], page 479.
prod (x)
prod (x,dim)
prod (. . ., "native")
prod (. . ., "double")
Product of elements along dimension dim.
If dim is omitted, it defaults to the first non-singleton dimension.
The optional "type" input determines the class of the variable used for calculations.
If the argument "native" is given, then the operation is performed in the same type
as the original argument, rather than the default double type.
For example:
prod ([true, true])
⇒1
prod ([true, true], "native")
⇒true
On the contrary, if "double" is given, the operation is performed in double precision
even for single precision inputs.
See also: [cumprod], page 479,[sum], page 478.
cumsum (x)
cumsum (x,dim)
cumsum (. . ., "native")
cumsum (. . ., "double")
cumsum (. . ., "extra")
Cumulative sum of elements along dimension dim.
If dim is omitted, it defaults to the first non-singleton dimension. For example:
cumsum ([1, 2; 3, 4; 5, 6])
⇒1 2
4 6
9 12
See sum for an explanation of the optional parameters "native","double", and
"extra".
See also: [sum], page 478,[cumprod], page 479.
cumprod (x)
cumprod (x,dim)
Cumulative product of elements along dimension dim.
If dim is omitted, it defaults to the first non-singleton dimension. For example:
cumprod ([1, 2; 3, 4; 5, 6])
⇒1 2
3 8
15 48
See also: [prod], page 479,[cumsum], page 479.
480 GNU Octave
sumsq (x)
sumsq (x,dim)
Sum of squares of elements along dimension dim.
If dim is omitted, it defaults to the first non-singleton dimension.
This function is conceptually equivalent to computing
sum (x .* conj (x), dim)
but it uses less memory and avoids calling conj if xis real.
See also: [sum], page 478,[prod], page 479.
17.5 Utility Functions
ceil (x)
Return the smallest integer not less than x.
This is equivalent to rounding towards positive infinity.
If xis complex, return ceil (real (x)) + ceil (imag (x)) * I.
ceil ([-2.7, 2.7])
⇒-2 3
See also: [floor], page 480,[round], page 480,[fix], page 480.
fix (x)
Truncate fractional portion of xand return the integer portion.
This is equivalent to rounding towards zero. If xis complex, return fix (real (x))
+ fix (imag (x)) * I.
fix ([-2.7, 2.7])
⇒-2 2
See also: [ceil], page 480,[floor], page 480,[round], page 480.
floor (x)
Return the largest integer not greater than x.
This is equivalent to rounding towards negative infinity. If xis complex, return floor
(real (x)) + floor (imag (x)) * I.
floor ([-2.7, 2.7])
⇒-3 2
See also: [ceil], page 480,[round], page 480,[fix], page 480.
round (x)
Return the integer nearest to x.
If xis complex, return round (real (x)) + round (imag (x)) * I. If there are two
nearest integers, return the one further away from zero.
round ([-2.7, 2.7])
⇒-3 3
See also: [ceil], page 480,[floor], page 480,[fix], page 480,[roundb], page 481.
Chapter 17: Arithmetic 481
roundb (x)
Return the integer nearest to x. If there are two nearest integers, return the even one
(banker’s rounding).
If xis complex, return roundb (real (x)) + roundb (imag (x)) * I.
See also: [round], page 480.
max (x)
max (x,[],dim)
[w,iw] = max (x)
max (x,y)
Find maximum values in the array x.
For a vector argument, return the maximum value. For a matrix argument, return a
row vector with the maximum value of each column. For a multi-dimensional array,
max operates along the first non-singleton dimension.
If the optional third argument dim is present then operate along this dimension. In
this case the second argument is ignored and should be set to the empty matrix.
For two matrices (or a matrix and a scalar), return the pairwise maximum.
Thus,
max (max (x))
returns the largest element of the 2-D matrix x, and
max (2:5, pi)
⇒3.1416 3.1416 4.0000 5.0000
compares each element of the range 2:5 with pi, and returns a row vector of the
maximum values.
For complex arguments, the magnitude of the elements are used for comparison. If
the magnitudes are identical, then the results are ordered by phase angle in the range
(-pi, pi]. Hence,
max ([-1 i 1 -i])
⇒-1
because all entries have magnitude 1, but -1 has the largest phase angle with value
pi.
If called with one input and two output arguments, max also returns the first index
of the maximum value(s). Thus,
[x, ix] = max ([1, 3, 5, 2, 5])
⇒x=5
ix = 3
See also: [min], page 481,[cummax], page 482,[cummin], page 483.
min (x)
min (x,[],dim)
[w,iw] = min (x)
min (x,y)
Find minimum values in the array x.
482 GNU Octave
For a vector argument, return the minimum value. For a matrix argument, return a
row vector with the minimum value of each column. For a multi-dimensional array,
min operates along the first non-singleton dimension.
If the optional third argument dim is present then operate along this dimension. In
this case the second argument is ignored and should be set to the empty matrix.
For two matrices (or a matrix and a scalar), return the pairwise minimum.
Thus,
min (min (x))
returns the smallest element of the 2-D matrix x, and
min (2:5, pi)
⇒2.0000 3.0000 3.1416 3.1416
compares each element of the range 2:5 with pi, and returns a row vector of the
minimum values.
For complex arguments, the magnitude of the elements are used for comparison. If
the magnitudes are identical, then the results are ordered by phase angle in the range
(-pi, pi]. Hence,
min ([-1 i 1 -i])
⇒-i
because all entries have magnitude 1, but -i has the smallest phase angle with value
-pi/2.
If called with one input and two output arguments, min also returns the first index
of the minimum value(s). Thus,
[x, ix] = min ([1, 3, 0, 2, 0])
⇒x=0
ix = 3
See also: [max], page 481,[cummin], page 483,[cummax], page 482.
cummax (x)
cummax (x,dim)
[w,iw] = cummax (. . . )
Return the cumulative maximum values along dimension dim.
If dim is unspecified it defaults to column-wise operation. For example:
cummax ([1 3 2 6 4 5])
⇒133666
If called with two output arguments the index of the maximum value is also returned.
[w, iw] = cummax ([1 3 2 6 4 5])
⇒
w=133666
iw=122444
See also: [cummin], page 483,[max], page 481,[min], page 481.
Chapter 17: Arithmetic 483
cummin (x)
cummin (x,dim)
[w,iw] = cummin (x)
Return the cumulative minimum values along dimension dim.
If dim is unspecified it defaults to column-wise operation. For example:
cummin ([5 4 6 2 3 1])
⇒544221
If called with two output arguments the index of the minimum value is also returned.
[w, iw] = cummin ([5 4 6 2 3 1])
⇒
w=544221
iw=122446
See also: [cummax], page 482,[min], page 481,[max], page 481.
hypot (x,y)
hypot (x,y,z, . . . )
Compute the element-by-element square root of the sum of the squares of xand y.
This is equivalent to sqrt (x.^2 + y.^2), but is calculated in a manner that avoids
overflows for large values of xor y.
hypot can also be called with more than 2 arguments; in this case, the arguments are
accumulated from left to right:
hypot (hypot (x,y), z)
hypot (hypot (hypot (x,y), z), w), etc.
dx = gradient (m)
[dx,dy,dz, ...] = gradient (m)
[...] = gradient (m,s)
[...] = gradient (m,x,y,z, . . . )
[...] = gradient (f,x0)
[...] = gradient (f,x0,s)
[...] = gradient (f,x0,x,y, . . . )
Calculate the gradient of sampled data or a function.
If mis a vector, calculate the one-dimensional gradient of m. If mis a matrix the
gradient is calculated for each dimension.
[dx,dy] = gradient (m)calculates the one-dimensional gradient for xand ydirec-
tion if mis a matrix. Additional return arguments can be use for multi-dimensional
matrices.
A constant spacing between two points can be provided by the sparameter. If sis a
scalar, it is assumed to be the spacing for all dimensions. Otherwise, separate values
of the spacing can be supplied by the x, . . . arguments. Scalar values specify an
equidistant spacing. Vector values for the x, . . . arguments specify the coordinate for
that dimension. The length must match their respective dimension of m.
At boundary points a linear extrapolation is applied. Interior points are calculated
with the first approximation of the numerical gradient
y’(i) = 1/(x(i+1)-x(i-1)) * (y(i-1)-y(i+1)).
484 GNU Octave
If the first argument fis a function handle, the gradient of the function at the points
in x0 is approximated using central difference. For example, gradient (@cos, 0)
approximates the gradient of the cosine function in the point x0 = 0. As with sampled
data, the spacing values between the points from which the gradient is estimated can
be set via the sor dx,dy, . . . arguments. By default a spacing of 1 is used.
See also: [diff], page 440,[del2], page 485.
dot (x,y,dim)
Compute the dot product of two vectors.
If xand yare matrices, calculate the dot products along the first non-singleton
dimension.
If the optional argument dim is given, calculate the dot products along this dimension.
This is equivalent to sum (conj (X) .* Y,dim), but avoids forming a temporary
array and is faster. When Xand Yare column vectors, the result is equivalent to X’
*Y.
See also: [cross], page 484,[divergence], page 484.
cross (x,y)
cross (x,y,dim)
Compute the vector cross product of two 3-dimensional vectors xand y.
If xand yare matrices, the cross product is applied along the first dimension with
three elements.
The optional argument dim forces the cross product to be calculated along the spec-
ified dimension.
Example Code:
cross ([1,1,0], [0,1,1])
⇒[ 1; -1; 1 ]
See also: [dot], page 484,[curl], page 484,[divergence], page 484.
div = divergence (x,y,z,fx,fy,fz)
div = divergence (fx,fy,fz)
div = divergence (x,y,fx,fy)
div = divergence (fx,fy)
Calculate divergence of a vector field given by the arrays fx,fy, and fz or fx,fy
respectively.
divF (x, y, z) = ∂xF+∂yF+∂zF
The coordinates of the vector field can be given by the arguments x,y,zor x,y
respectively.
See also: [curl], page 484,[gradient], page 483,[del2], page 485,[dot], page 484.
[cx,cy,cz,v] = curl (x,y,z,fx,fy,fz)
[cz,v] = curl (x,y,fx,fy)
[...] = curl (fx,fy,fz)

Chapter 17: Arithmetic 485
[...] = curl (fx,fy)
v= curl (. . . )
Calculate curl of vector field given by the arrays fx,fy, and fz or fx,fy respectively.
curlF (x, y, z) = ∂d
∂y Fz−∂d
∂z Fy,∂d
∂z Fx−∂d
∂xFz,∂d
∂xFy−∂d
∂y Fx
The coordinates of the vector field can be given by the arguments x,y,zor x,y
respectively. vcalculates the scalar component of the angular velocity vector in
direction of the z-axis for two-dimensional input. For three-dimensional input the
scalar rotation is calculated at each grid point in direction of the vector field at that
point.
See also: [divergence], page 484,[gradient], page 483,[del2], page 485,[cross],
page 484.
d= del2 (M)
d= del2 (M,h)
d= del2 (M,dx,dy, . . . )
Calculate the discrete Laplace operator (∇2).
For a 2-dimensional matrix Mthis is defined as
d=1
4d2
dx2M(x, y) + d2
dy2M(x, y)
For N-dimensional arrays the sum in parentheses is expanded to include second deriva-
tives over the additional higher dimensions.
The spacing between evaluation points may be defined by h, which is a scalar defining
the equidistant spacing in all dimensions. Alternatively, the spacing in each dimen-
sion may be defined separately by dx,dy, etc. A scalar spacing argument defines
equidistant spacing, whereas a vector argument can be used to specify variable spac-
ing. The length of the spacing vectors must match the respective dimension of M.
The default spacing value is 1.
At least 3 data points are needed for each dimension. Boundary points are calculated
from the linear extrapolation of interior points.
See also: [gradient], page 483,[diff], page 440.
factorial (n)
Return the factorial of nwhere nis a real non-negative integer.
If nis a scalar, this is equivalent to prod (1:n). For vector or matrix arguments,
return the factorial of each element in the array.
For non-integers see the generalized factorial function gamma. Note that the factorial
function grows large quite quickly, and even with double precision values overflow will
occur if n>171. For such cases consider gammaln.
See also: [prod], page 479,[gamma], page 494,[gammaln], page 495.
486 GNU Octave
pf = factor (q)
[pf,n] = factor (q)
Return the prime factorization of q.
The prime factorization is defined as prod (pf) == qwhere every element of pf is a
prime number. If q== 1, return 1.
With two output arguments, return the unique prime factors pf and their multiplic-
ities. That is, prod (pf .^ n) == q.
Implementation Note: The input qmust be less than flintmax (9.0072e+15) in order
to factor correctly.
See also: [gcd], page 486,[lcm], page 486,[isprime], page 64,[primes], page 487.
g= gcd (a1,a2, . . . )
[g,v1, ...] = gcd (a1,a2, . . . )
Compute the greatest common divisor of a1,a2, . . ..
If more than one argument is given then all arguments must be the same size or scalar.
In this case the greatest common divisor is calculated for each element individually.
All elements must be ordinary or Gaussian (complex) integers. Note that for Gaussian
integers, the gcd is only unique up to a phase factor (multiplication by 1, -1, i, or -i),
so an arbitrary greatest common divisor among the four possible is returned.
Optional return arguments v1, . . ., contain integer vectors such that,
g=v1a1+v2a2+···
Example code:
gcd ([15, 9], [20, 18])
⇒5 9
See also: [lcm], page 486,[factor], page 486,[isprime], page 64.
lcm (x,y)
lcm (x,y, . . . )
Compute the least common multiple of xand y, or of the list of all arguments.
All elements must be numeric and of the same size or scalar.
See also: [factor], page 486,[gcd], page 486,[isprime], page 64.
chop (x,ndigits,base)
Truncate elements of xto a length of ndigits such that the resulting numbers are
exactly divisible by base.
If base is not specified it defaults to 10.
format long
chop (-pi, 5, 10)
⇒-3.14200000000000
chop (-pi, 5, 5)
⇒-3.14150000000000
rem (x,y)
Return the remainder of the division x/y.

Chapter 17: Arithmetic 487
The remainder is computed using the expression
x - y .* fix (x ./ y)
An error message is printed if the dimensions of the arguments do not agree, or if
either argument is complex.
Programming Notes: Floating point numbers within a few eps of an integer will be
rounded to an integer before computation for compatibility with matlab.
By convention,
rem (x, 0) = NaN if xis a floating point variable
rem (x, 0) = 0 if xis an integer variable
rem (x,y) returns a value with the signbit from x
For the opposite conventions see the mod function. In general, rem is best when com-
puting the remainder after division of two positive numbers. For negative numbers,
or when the values are periodic, mod is a better choice.
See also: [mod], page 487.
mod (x,y)
Compute the modulo of xand y.
Conceptually this is given by
x - y .* floor (x ./ y)
and is written such that the correct modulus is returned for integer types. This
function handles negative values correctly. That is, mod (-1, 3) is 2, not -1, as
rem (-1, 3) returns.
An error results if the dimensions of the arguments do not agree, or if either of the
arguments is complex.
Programming Notes: Floating point numbers within a few eps of an integer will be
rounded to an integer before computation for compatibility with matlab.
By convention,
mod (x, 0) = x
mod (x,y) returns a value with the signbit from y
For the opposite conventions see the rem function. In general, mod is a better choice
than rem when any of the inputs are negative numbers or when the values are periodic.
See also: [rem], page 486.
primes (n)
Return all primes up to n.
The output data class (double, single, uint32, etc.) is the same as the input class of
n. The algorithm used is the Sieve of Eratosthenes.
Notes: If you need a specific number of primes you can use the fact that the distance
from one prime to the next is, on average, proportional to the logarithm of the prime.
Integrating, one finds that there are about kprimes less than klog(5k).
See also list_primes if you need a specific number nof primes.
See also: [list primes], page 488,[isprime], page 64.
488 GNU Octave
list_primes ()
list_primes (n)
List the first nprimes.
If nis unspecified, the first 25 primes are listed.
See also: [primes], page 487,[isprime], page 64.
sign (x)
Compute the signum function.
This is defined as
sign(x) =
1, x > 0;
0, x = 0;
−1, x < 0.
For complex arguments, sign returns x ./ abs (x).
Note that sign (-0.0) is 0. Although IEEE 754 floating point allows zero to be
signed, 0.0 and -0.0 compare equal. If you must test whether zero is signed, use the
signbit function.
See also: [signbit], page 488.
signbit (x)
Return logical true if the value of xhas its sign bit set and false otherwise.
This behavior is consistent with the other logical functions. See Section 4.6 [Logical
Values], page 60. The behavior differs from the C language function which returns
nonzero if the sign bit is set.
This is not the same as x < 0.0, because IEEE 754 floating point allows zero to
be signed. The comparison -0.0 < 0.0 is false, but signbit (-0.0) will return a
nonzero value.
See also: [sign], page 488.
17.6 Special Functions
[a,ierr] = airy (k,z,opt)
Compute Airy functions of the first and second kind, and their derivatives.
K Function Scale factor (if "opt" is supplied)
--- -------- ---------------------------------------
0 Ai (Z) exp ((2/3) * Z * sqrt (Z))
1 dAi(Z)/dZ exp ((2/3) * Z * sqrt (Z))
2 Bi (Z) exp (-abs (real ((2/3) * Z * sqrt (Z))))
3 dBi(Z)/dZ exp (-abs (real ((2/3) * Z * sqrt (Z))))
The function call airy (z)is equivalent to airy (0, z).
The result is the same size as z.
If requested, ierr contains the following status information and is the same size as the
result.
0. Normal return.
1. Input error, return NaN.
Chapter 17: Arithmetic 489
2. Overflow, return Inf.
3. Loss of significance by argument reduction results in less than half of machine
accuracy.
4. Complete loss of significance by argument reduction, return NaN.
5. Error—no computation, algorithm termination condition not met, return NaN.
[j,ierr] = besselj (alpha,x,opt)
[y,ierr] = bessely (alpha,x,opt)
[i,ierr] = besseli (alpha,x,opt)
[k,ierr] = besselk (alpha,x,opt)
[h,ierr] = besselh (alpha,k,x,opt)
Compute Bessel or Hankel functions of various kinds:
besselj Bessel functions of the first kind. If the argument opt is 1 or true, the
result is multiplied by exp (-abs (imag (x))).
bessely Bessel functions of the second kind. If the argument opt is 1 or true, the
result is multiplied by exp (-abs (imag (x))).
besseli
Modified Bessel functions of the first kind. If the argument opt is 1 or
true, the result is multiplied by exp (-abs (real (x))).
besselk
Modified Bessel functions of the second kind. If the argument opt is 1 or
true, the result is multiplied by exp (x).
besselh Compute Hankel functions of the first (k= 1) or second (k= 2) kind. If
the argument opt is 1 or true, the result is multiplied by exp (-I*x)for
k= 1 or exp (I*x)for k= 2.
If alpha is a scalar, the result is the same size as x. If xis a scalar, the result is the
same size as alpha. If alpha is a row vector and xis a column vector, the result is a
matrix with length (x)rows and length (alpha)columns. Otherwise, alpha and x
must conform and the result will be the same size.
The value of alpha must be real. The value of xmay be complex.
If requested, ierr contains the following status information and is the same size as the
result.
0. Normal return.
1. Input error, return NaN.
2. Overflow, return Inf.
3. Loss of significance by argument reduction results in less than half of machine
accuracy.
4. Complete loss of significance by argument reduction, return NaN.
5. Error—no computation, algorithm termination condition not met, return NaN.

490 GNU Octave
beta (a,b)
Compute the Beta function for real inputs aand b.
The Beta function definition is
B(a, b) = Γ(a)Γ(b)
Γ(a+b).
The Beta function can grow quite large and it is often more useful to work with the
logarithm of the output rather than the function directly. See [betaln], page 490, for
computing the logarithm of the Beta function in an efficient manner.
See also: [betaln], page 490,[betainc], page 490,[betaincinv], page 490.
betainc (x,a,b)
Compute the regularized incomplete Beta function.
The regularized incomplete Beta function is defined by
I(x, a, b) = 1
B(a, b)Zx
0
t(a−z)(1 −t)(b−1)dt.
If xhas more than one component, both aand bmust be scalars. If xis a scalar, a
and bmust be of compatible dimensions.
See also: [betaincinv], page 490,[beta], page 490,[betaln], page 490.
betaincinv (y,a,b)
Compute the inverse of the incomplete Beta function.
The inverse is the value xsuch that
y== betainc (x,a,b)
See also: [betainc], page 490,[beta], page 490,[betaln], page 490.
betaln (a,b)
Compute the natural logarithm of the Beta function for real inputs aand b.
betaln is defined as
betaln(a, b) = ln(B(a, b)) ≡ln(Γ(a)Γ(b)
Γ(a+b)).
and is calculated in a way to reduce the occurrence of underflow.
The Beta function can grow quite large and it is often more useful to work with the
logarithm of the output rather than the function directly.
See also: [beta], page 490,[betainc], page 490,[betaincinv], page 490,[gammaln],
page 495.
bincoeff (n,k)
Return the binomial coefficient of nand k, defined as
n
k!=n(n−1)(n−2) ···(n−k+ 1)
k!

Chapter 17: Arithmetic 491
For example:
bincoeff (5, 2)
⇒10
In most cases, the nchoosek function is faster for small scalar integer arguments. It
also warns about loss of precision for big arguments.
See also: [nchoosek], page 651.
commutation_matrix (m,n)
Return the commutation matrix Km,n which is the unique mn ×mn matrix such that
Km,n ·vec(A) = vec(AT) for all m×nmatrices A.
If only one argument mis given, Km,m is returned.
See Magnus and Neudecker (1988), Matrix Differential Calculus with Applications in
Statistics and Econometrics.
duplication_matrix (n)
Return the duplication matrix Dnwhich is the unique n2×n(n+ 1)/2 matrix such
that Dn∗vech(A) = vec(A) for all symmetric n×nmatrices A.
See Magnus and Neudecker (1988), Matrix Differential Calculus with Applications in
Statistics and Econometrics.
dawson (z)
Compute the Dawson (scaled imaginary error) function.
The Dawson function is defined as
√π
2e−z2erfi(z)≡ −i√π
2e−z2erf(iz)
See also: [erfc], page 492,[erf], page 492,[erfcx], page 493,[erfi], page 493,[erfinv],
page 493,[erfcinv], page 493.
[sn,cn,dn,err] = ellipj (u,m)
[sn,cn,dn,err] = ellipj (u,m,tol)
Compute the Jacobi elliptic functions sn,cn, and dn of complex argument uand real
parameter m.
If mis a scalar, the results are the same size as u. If uis a scalar, the results are the
same size as m. If uis a column vector and mis a row vector, the results are matrices
with length (u)rows and length (m)columns. Otherwise, uand mmust conform
in size and the results will be the same size as the inputs.
The value of umay be complex. The value of mmust be 0 ≤m≤1.
The optional input tol is currently ignored (matlab uses this to allow faster, less
accurate approximation).
If requested, err contains the following status information and is the same size as the
result.
0. Normal return.
1. Error—no computation, algorithm termination condition not met, return NaN.

492 GNU Octave
Reference: Milton Abramowitz and Irene A Stegun, Handbook of Mathematical Func-
tions, Chapter 16 (Sections 16.4, 16.13, and 16.15), Dover, 1965.
See also: [ellipke], page 492.
k= ellipke (m)
k= ellipke (m,tol)
[k,e] = ellipke (. . . )
Compute complete elliptic integrals of the first K(m) and second E(m) kind.
mmust be a scalar or real array with -Inf ≤m≤1.
The optional input tol controls the stopping tolerance of the algorithm and defaults to
eps (class (m)). The tolerance can be increased to compute a faster, less accurate
approximation.
When called with one output only elliptic integrals of the first kind are returned.
Mathematical Note:
Elliptic integrals of the first kind are defined as
K(m) = Z1
0
dt
p(1 −t2)(1 −mt2)
Elliptic integrals of the second kind are defined as
E(m) = Z1
0
√1−mt2
√1−t2dt
Reference: Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical
Functions, Chapter 17, Dover, 1965.
See also: [ellipj], page 491.
erf (z)
Compute the error function.
The error function is defined as
erf(z) = 2
√πZz
0
e−t2dt
See also: [erfc], page 492,[erfcx], page 493,[erfi], page 493,[dawson], page 491,
[erfinv], page 493,[erfcinv], page 493.
erfc (z)
Compute the complementary error function.
The complementary error function is defined as 1 −erf(z).
See also: [erfcinv], page 493,[erfcx], page 493,[erfi], page 493,[dawson], page 491,
[erf], page 492,[erfinv], page 493.

Chapter 17: Arithmetic 493
erfcx (z)
Compute the scaled complementary error function.
The scaled complementary error function is defined as
ez2erfc(z)≡ez2(1 −erf(z))
See also: [erfc], page 492,[erf], page 492,[erfi], page 493,[dawson], page 491,[erfinv],
page 493,[erfcinv], page 493.
erfi (z)
Compute the imaginary error function.
The imaginary error function is defined as
−ierf(iz)
See also: [erfc], page 492,[erf], page 492,[erfcx], page 493,[dawson], page 491,[erfinv],
page 493,[erfcinv], page 493.
erfinv (x)
Compute the inverse error function.
The inverse error function is defined such that
erf (y) == x
See also: [erf], page 492,[erfc], page 492,[erfcx], page 493,[erfi], page 493,[dawson],
page 491,[erfcinv], page 493.
erfcinv (x)
Compute the inverse complementary error function.
The inverse complementary error function is defined such that
erfc (y) == x
See also: [erfc], page 492,[erf], page 492,[erfcx], page 493,[erfi], page 493,[dawson],
page 491,[erfinv], page 493.
expint (x)
Compute the exponential integral:
E1(x) = Z∞
x
e−t
tdt
Note: For compatibility, this functions uses the matlab definition of the exponential
integral. Most other sources refer to this particular value as E1(x), and the exponen-
tial integral as
Ei(x) = −Z∞
−x
e−t
tdt.
The two definitions are related, for positive real values of x, by E1(−x) = −Ei(x)−iπ.

494 GNU Octave
gamma (z)
Compute the Gamma function.
The Gamma function is defined as
Γ(z) = Z∞
0
tz−1e−tdt.
Programming Note: The gamma function can grow quite large even for small input
values. In many cases it may be preferable to use the natural logarithm of the gamma
function (gammaln) in calculations to minimize loss of precision. The final result is
then exp (result_using_gammaln).
See also: [gammainc], page 494,[gammaln], page 495,[factorial], page 485.
gammainc (x,a)
gammainc (x,a,"lower")
gammainc (x,a,"upper")
Compute the normalized incomplete gamma function.
This is defined as
γ(x, a) = 1
Γ(a)Zx
0
ta−1e−tdt
with the limiting value of 1 as xapproaches infinity. The standard notation is P(a, x),
e.g., Abramowitz and Stegun (6.5.1).
If ais scalar, then gammainc (x,a)is returned for each element of xand vice versa.
If neither xnor ais scalar, the sizes of xand amust agree, and gammainc is applied
element-by-element.
By default the incomplete gamma function integrated from 0 to xis computed. If
"upper" is given then the complementary function integrated from xto infinity is
calculated. It should be noted that
gammainc (x,a)≡1 - gammainc (x,a, "upper")
See also: [gamma], page 494,[gammaln], page 495.
l= legendre (n,x)
l= legendre (n,x,normalization)
Compute the associated Legendre function of degree nand order m= 0 . . . n.
The value nmust be a real non-negative integer.
xis a vector with real-valued elements in the range [-1, 1].
The optional argument normalization may be one of "unnorm","sch", or "norm".
The default if no normalization is given is "unnorm".
When the optional argument normalization is "unnorm", compute the associated Leg-
endre function of degree nand order mand return all values for m= 0 . . . n. The
return value has one dimension more than x.
The associated Legendre function of degree nand order m:
Pm
n(x)=(−1)m(1 −x2)m/2dm
dxmPn(x)

Chapter 17: Arithmetic 495
with Legendre polynomial of degree n:
P(x) = 1
2nn!dn
dxn(x2−1)n
legendre (3, [-1.0, -0.9, -0.8]) returns the matrix:
x | -1.0 | -0.9 | -0.8
------------------------------------
m=0 | -1.00000 | -0.47250 | -0.08000
m=1 | 0.00000 | -1.99420 | -1.98000
m=2 | 0.00000 | -2.56500 | -4.32000
m=3 | 0.00000 | -1.24229 | -3.24000
When the optional argument normalization is "sch", compute the Schmidt semi-
normalized associated Legendre function. The Schmidt semi-normalized associated
Legendre function is related to the unnormalized Legendre functions by the following:
For Legendre functions of degree nand order 0:
SP 0
n(x) = P0
n(x)
For Legendre functions of degree n and order m:
SP m
n(x) = Pm
n(x)(−1)m2(n−m)!
(n+m)! 0.5
When the optional argument normalization is "norm", compute the fully normalized
associated Legendre function. The fully normalized associated Legendre function is
related to the unnormalized associated Legendre functions by the following:
For Legendre functions of degree nand order m
NP m
n(x) = Pm
n(x)(−1)m(n+ 0.5)(n−m)!
(n+m)! 0.5
gammaln (x)
lgamma (x)
Return the natural logarithm of the gamma function of x.
See also: [gamma], page 494,[gammainc], page 494.
psi (z)
psi (k,z)
Compute the psi (polygamma) function.
The polygamma functions are the kth derivative of the logarithm of the gamma
function. If unspecified, kdefaults to zero. A value of zero computes the digamma
function, a value of 1, the trigamma function, and so on.
The digamma function is defined:
Ψ(z) = d(log(Γ(z)))
dx
496 GNU Octave
When computing the digamma function (when kequals zero), zcan have any value
real or complex value. However, for polygamma functions (khigher than 0), zmust
be real and non-negative.
See also: [gamma], page 494,[gammainc], page 494,[gammaln], page 495.
17.7 Rational Approximations
s= rat (x,tol)
[n,d] = rat (x,tol)
Find a rational approximation to xwithin the tolerance defined by tol using a con-
tinued fraction expansion.
For example:
rat (pi) = 3 + 1/(7 + 1/16) = 355/113
rat (e) = 3 + 1/(-4 + 1/(2 + 1/(5 + 1/(-2 + 1/(-7)))))
= 1457/536
When called with two output arguments return the numerator and denominator sep-
arately as two matrices.
See also: [rats], page 496.
rats (x,len)
Convert xinto a rational approximation represented as a string.
The string can be converted back into a matrix as follows:
r = rats (hilb (4));
x = str2num (r)
The optional second argument defines the maximum length of the string representing
the elements of x. By default len is 9.
If the length of the smallest possible rational approximation exceeds len, an asterisk
(*) padded with spaces will be returned instead.
See also: [format], page 244,[rat], page 496.
17.8 Coordinate Transformations
[theta,r] = cart2pol (x,y)
[theta,r,z] = cart2pol (x,y,z)
[theta,r] = cart2pol (C)
[theta,r,z] = cart2pol (C)
P= cart2pol (. . . )
Transform Cartesian coordinates to polar or cylindrical coordinates.
The inputs x,y(, and z) must be the same shape, or scalar. If called with a single
matrix argument then each row of Crepresents the Cartesian coordinate (x,y(, z)).
theta describes the angle relative to the positive x-axis.
ris the distance to the z-axis (0, 0, z).
If only a single return argument is requested then return a matrix Pwhere each row
represents one polar/(cylindrical) coordinate (theta,phi (, z)).
See also: [pol2cart], page 497,[cart2sph], page 497,[sph2cart], page 497.
Chapter 17: Arithmetic 497
[x,y] = pol2cart (theta,r)
[x,y,z] = pol2cart (theta,r,z)
[x,y] = pol2cart (P)
[x,y,z] = pol2cart (P)
C= pol2cart (. . . )
Transform polar or cylindrical coordinates to Cartesian coordinates.
The inputs theta,r, (and z) must be the same shape, or scalar. If called with a single
matrix argument then each row of Prepresents the polar/(cylindrical) coordinate
(theta,r(, z)).
theta describes the angle relative to the positive x-axis.
ris the distance to the z-axis (0, 0, z).
If only a single return argument is requested then return a matrix Cwhere each row
represents one Cartesian coordinate (x,y(, z)).
See also: [cart2pol], page 496,[sph2cart], page 497,[cart2sph], page 497.
[theta,phi,r] = cart2sph (x,y,z)
[theta,phi,r] = cart2sph (C)
S= cart2sph (. . . )
Transform Cartesian coordinates to spherical coordinates.
The inputs x,y, and zmust be the same shape, or scalar. If called with a single
matrix argument then each row of Crepresents the Cartesian coordinate (x,y,z).
theta describes the angle relative to the positive x-axis.
phi is the angle relative to the xy-plane.
ris the distance to the origin (0, 0, 0).
If only a single return argument is requested then return a matrix Swhere each row
represents one spherical coordinate (theta,phi,r).
See also: [sph2cart], page 497,[cart2pol], page 496,[pol2cart], page 497.
[x,y,z] = sph2cart (theta,phi,r)
[x,y,z] = sph2cart (S)
C= sph2cart (. . . )
Transform spherical coordinates to Cartesian coordinates.
The inputs theta,phi, and rmust be the same shape, or scalar. If called with a single
matrix argument then each row of Srepresents the spherical coordinate (theta,phi,
r).
theta describes the angle relative to the positive x-axis.
phi is the angle relative to the xy-plane.
ris the distance to the origin (0, 0, 0).
If only a single return argument is requested then return a matrix Cwhere each row
represents one Cartesian coordinate (x,y,z).
See also: [cart2sph], page 497,[pol2cart], page 497,[cart2pol], page 496.

498 GNU Octave
17.9 Mathematical Constants
e
e(n)
e(n,m)
e(n,m,k, . . . )
e(. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
base of natural logarithms.
The constant esatisfies the equation log(e) = 1.
When called with no arguments, return a scalar with the value e.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [log], page 471,[exp], page 471,[pi], page 498,[I], page 498.
pi
pi (n)
pi (n,m)
pi (n,m,k, . . . )
pi (. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
ratio of the circumference of a circle to its diameter(π).
Internally, pi is computed as ‘4.0 * atan (1.0)’.
When called with no arguments, return a scalar with the value of π.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [e], page 498,[I], page 498.
I
I(n)
I(n,m)
I(n,m,k, . . . )
I(. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
pure imaginary unit, defined as √−1.
Chapter 17: Arithmetic 499
I, and its equivalents i, j, and J, are functions so any of the names may be reused for
other purposes (such as i for a counter variable).
When called with no arguments, return a scalar with the value i.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [e], page 498,[pi], page 498,[log], page 471,[exp], page 471.
Inf
Inf (n)
Inf (n,m)
Inf (n,m,k, . . . )
Inf (. . ., class)
Return a scalar, matrix or N-dimensional array whose elements are all equal to the
IEEE representation for positive infinity.
Infinity is produced when results are too large to be represented using the IEEE
floating point format for numbers. Two common examples which produce infinity are
division by zero and overflow.
[ 1/0 e^800 ]
⇒Inf Inf
When called with no arguments, return a scalar with the value ‘Inf’.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [isinf], page 440,[NaN], page 499.
NaN
NaN (n)
NaN (n,m)
NaN (n,m,k, . . . )
NaN (. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
IEEE symbol NaN (Not a Number).
NaN is the result of operations which do not produce a well defined numerical result.
Common operations which produce a NaN are arithmetic with infinity (∞−∞), zero
divided by zero (0/0), and any operation involving another NaN value (5 +NaN).
500 GNU Octave
Note that NaN always compares not equal to NaN (NaN != NaN). This behavior is
specified by the IEEE standard for floating point arithmetic. To find NaN values, use
the isnan function.
When called with no arguments, return a scalar with the value ‘NaN’.
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [isnan], page 440,[Inf], page 499.
eps
eps (x)
eps (n,m)
eps (n,m,k, . . . )
eps (. . ., class)
Return a scalar, matrix or N-dimensional array whose elements are all eps, the ma-
chine precision.
More precisely, eps is the relative spacing between any two adjacent numbers in the
machine’s floating point system. This number is obviously system dependent. On
machines that support IEEE floating point arithmetic, eps is approximately 2.2204 ×
10−16 for double precision and 1.1921 ×10−7for single precision.
When called with no arguments, return a scalar with the value eps (1.0).
Given a single argument x, return the distance between xand the next largest value.
When called with more than one argument the first two arguments are taken as the
number of rows and columns and any further arguments specify additional matrix
dimensions. The optional argument class specifies the return type and may be either
"double" or "single".
See also: [realmax], page 500,[realmin], page 501,[intmax], page 56,[flintmax],
page 56.
realmax
realmax (n)
realmax (n,m)
realmax (n,m,k, . . . )
realmax (. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
largest floating point number that is representable.
The actual value is system dependent. On machines that support IEEE floating
point arithmetic, realmax is approximately 1.7977 ×10308 for double precision and
3.4028 ×1038 for single precision.
When called with no arguments, return a scalar with the value realmax ("double").
Chapter 17: Arithmetic 501
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [realmin], page 501,[intmax], page 56,[flintmax], page 56,[eps], page 500.
realmin
realmin (n)
realmin (n,m)
realmin (n,m,k, . . . )
realmin (. . ., class)
Return a scalar, matrix, or N-dimensional array whose elements are all equal to the
smallest normalized floating point number that is representable.
The actual value is system dependent. On machines that support IEEE floating
point arithmetic, realmin is approximately 2.2251 ×10−308 for double precision and
1.1755 ×10−38 for single precision.
When called with no arguments, return a scalar with the value realmin ("double").
When called with a single argument, return a square matrix with the dimension
specified.
When called with more than one scalar argument the first two arguments are taken as
the number of rows and columns and any further arguments specify additional matrix
dimensions.
The optional argument class specifies the return type and may be either "double" or
"single".
See also: [realmax], page 500,[intmin], page 56,[eps], page 500.
503
18 Linear Algebra
This chapter documents the linear algebra functions provided in Octave. Reference material
for many of these functions may be found in Golub and Van Loan, Matrix Computations,
2nd Ed., Johns Hopkins, 1989, and in the lapack Users’ Guide, SIAM, 1992. The lapack
Users’ Guide is available at: http://www.netlib.org/lapack/lug/
A common text for engineering courses is G. Strang, Linear Algebra and Its Applications,
4th Edition. It has become a widespread reference for linear algebra. An alternative is
P. Lax Linear Algebra and Its Applications, and also is a good choice. It claims to be
suitable for high school students with substantial mathematical interests as well as first-
year undergraduates.
18.1 Techniques Used for Linear Algebra
Octave includes a polymorphic solver that selects an appropriate matrix factorization de-
pending on the properties of the matrix itself. Generally, the cost of determining the matrix
type is small relative to the cost of factorizing the matrix itself. In any case the matrix type
is cached once it is calculated so that it is not re-determined each time it is used in a linear
equation.
The selection tree for how the linear equation is solved or a matrix inverse is formed is
given by:
1. If the matrix is upper or lower triangular sparse use a forward or backward substitution
using the lapack xTRTRS function, and goto 4.
2. If the matrix is square, Hermitian with a real positive diagonal, attempt Cholesky fac-
torization using the lapack xPOTRF function.
3. If the Cholesky factorization failed or the matrix is not Hermitian with a real positive
diagonal, and the matrix is square, factorize using the lapack xGETRF function.
4. If the matrix is not square, or any of the previous solvers flags a singular or near
singular matrix, find a least squares solution using the lapack xGELSD function.
The user can force the type of the matrix with the matrix_type function. This overcomes
the cost of discovering the type of the matrix. However, it should be noted that identifying
the type of the matrix incorrectly will lead to unpredictable results, and so matrix_type
should be used with care.
It should be noted that the test for whether a matrix is a candidate for Cholesky fac-
torization, performed above, and by the matrix_type function, does not make certain that
the matrix is Hermitian. However, the attempt to factorize the matrix will quickly detect
a non-Hermitian matrix.
18.2 Basic Matrix Functions
AA = balance (A)
AA = balance (A,opt)
[DD,AA] = balance (A,opt)
[D,P,AA] = balance (A,opt)
504 GNU Octave
[CC,DD,AA,BB] = balance (A,B,opt)
Balance the matrix Ato reduce numerical errors in future calculations.
Compute AA =DD \A*DD in which AA is a matrix whose row and column norms
are roughly equal in magnitude, and DD =P*D, in which Pis a permutation matrix
and Dis a diagonal matrix of powers of two. This allows the equilibration to be
computed without round-off. Results of eigenvalue calculation are typically improved
by balancing first.
If two output values are requested, balance returns the diagonal Dand the permu-
tation Pseparately as vectors. In this case, DD = eye(n)(:,P) * diag (D), where n
is the matrix size.
If four output values are requested, compute AA =CC*A*DD and BB =CC*B*DD, in
which AA and BB have nonzero elements of approximately the same magnitude and
CC and DD are permuted diagonal matrices as in DD for the algebraic eigenvalue
problem.
The eigenvalue balancing option opt may be one of:
"noperm","S"
Scale only; do not permute.
"noscal","P"
Permute only; do not scale.
Algebraic eigenvalue balancing uses standard lapack routines.
Generalized eigenvalue problem balancing uses Ward’s algorithm (SIAM Journal on
Scientific and Statistical Computing, 1981).
bw = bandwidth (A,type)
[lower,upper] = bandwidth (A)
Compute the bandwidth of A.
The type argument is the string "lower" for the lower bandwidth and "upper" for the
upper bandwidth. If no type is specified return both the lower and upper bandwidth
of A.
The lower/upper bandwidth of a matrix is the number of subdiagonals/superdiagonals
with nonzero entries.
See also: [isbanded], page 64,[isdiag], page 64,[istril], page 64,[istriu], page 64.
cond (A)
cond (A,p)
Compute the p-norm condition number of a matrix with respect to inversion.
cond (A)is defined as kAkp∗ k A−1kp.
By default, p= 2 is used which implies a (relatively slow) singular value decomposi-
tion. Other possible selections are p= 1, Inf, "fro" which are generally faster. See
norm for a full discussion of possible pvalues.
The condition number of a matrix quantifies the sensitivity of the matrix inversion
operation when small changes are made to matrix elements. Ideally the condition
number will be close to 1. When the number is large this indicates small changes
(such as underflow or round-off error) will produce large changes in the resulting
Chapter 18: Linear Algebra 505
output. In such cases the solution results from numerical computing are not likely to
be accurate.
See also: [condest], page 582,[rcond], page 511,[condeig], page 505,[norm], page 509,
[svd], page 521.
c= condeig (a)
[v,lambda,c] = condeig (a)
Compute condition numbers of a matrix with respect to eigenvalues.
The condition numbers are the reciprocals of the cosines of the angles between the
left and right eigenvectors; Large values indicate that the matrix has multiple distinct
eigenvalues.
The input amust be a square numeric matrix.
The outputs are:
•cis a vector of condition numbers for the eigenvalues of a.
•vis the matrix of right eigenvectors of a. The result is equivalent to calling [v,
lambda] = eig (a).
•lambda is the diagonal matrix of eigenvalues of a. The result is equivalent to
calling [v,lambda] = eig (a).
Example
a = [1, 2; 3, 4];
c = condeig (a)
⇒[1.0150; 1.0150]
See also: [eig], page 505,[cond], page 504,[balance], page 503.
det (A)
[d,rcond] = det (A)
Compute the determinant of A.
Return an estimate of the reciprocal condition number if requested.
Programming Notes: Routines from lapack are used for full matrices and code from
umfpack is used for sparse matrices.
The determinant should not be used to check a matrix for singularity. For that, use
any of the condition number functions: cond,condest,rcond.
See also: [cond], page 504,[condest], page 582,[rcond], page 511.
lambda = eig (A)
lambda = eig (A,B)
[V,lambda] = eig (A)
[V,lambda] = eig (A,B)
[V,lambda,W] = eig (A)
[V,lambda,W] = eig (A,B)
[...] = eig (A,balanceOption)
[...] = eig (A,B,algorithm)
[...] = eig (. . . , eigvalOption)
Compute the right eigenvalues(V) and optionally the eigenvectors(lambda) and the
left eigenvalues(W) of a matrix or a pair of matrices.
506 GNU Octave
The flag balanceOption can be one of:
"balance"
Preliminary balancing is on. (default)
"nobalance"
Disables preliminary balancing.
The flag eigvalOption can be one of:
"matrix" Return the eigenvalues in a diagonal matrix. (default if 2 or 3 outputs
are specified)
"vector" Return the eigenvalues in a column vector. (default if 1 output is speci-
fied, e.g. lambda = eig (A))
The flag algorithm can be one of:
"chol" Uses the Cholesky factorization of B. (default if A is symmetric (Hermi-
tian) and B is symmetric (Hermitian) positive definite)
"qz" Uses the QZ algorithm. (When A or B are not symmetric always the QZ
algorithm will be used)
no flag chol qz
both are symmetric "chol" "chol" "qz"
at least one is not symmetric "qz" "qz" "qz"
The eigenvalues returned by eig are not ordered.
See also: [eigs], page 586,[svd], page 521.
G= givens (x,y)
[c,s] = givens (x,y)
Compute the Givens rotation matrix G.
The Givens matrix is a 2 ×2 orthogonal matrix
G=c s
−s0c
such that
Gx
y=∗
0
with xand yscalars.
If two output arguments are requested, return the factors cand srather than the
Givens rotation matrix.
For example:
givens (1, 1)
⇒0.70711 0.70711
-0.70711 0.70711
See also: [planerot], page 507.

Chapter 18: Linear Algebra 507
[G,y] = planerot (x)
Given a two-element column vector, return the 2 ×2 orthogonal matrix Gsuch that
y=g*xand y(2) = 0.
See also: [givens], page 506.
x= inv (A)
[x,rcond] = inv (A)
Compute the inverse of the square matrix A.
Return an estimate of the reciprocal condition number if requested, otherwise warn
of an ill-conditioned matrix if the reciprocal condition number is small.
In general it is best to avoid calculating the inverse of a matrix directly. For example,
it is both faster and more accurate to solve systems of equations (A*x=b) with y=
A\b, rather than y= inv (A) * b.
If called with a sparse matrix, then in general xwill be a full matrix requiring signif-
icantly more storage. Avoid forming the inverse of a sparse matrix if possible.
See also: [ldivide], page 144,[rdivide], page 145.
x= linsolve (A,b)
x= linsolve (A,b,opts)
[x,R] = linsolve (. . . )
Solve the linear system A*x = b.
With no options, this function is equivalent to the left division operator (x=A\b)
or the matrix-left-divide function (x = mldivide (A, b)).
Octave ordinarily examines the properties of the matrix Aand chooses a solver that
best matches the matrix. By passing a structure opts to linsolve you can inform Oc-
tave directly about the matrix A. In this case Octave will skip the matrix examination
and proceed directly to solving the linear system.
Warning: If the matrix Adoes not have the properties listed in the opts structure
then the result will not be accurate AND no warning will be given. When in doubt,
let Octave examine the matrix and choose the appropriate solver as this step takes
little time and the result is cached so that it is only done once per linear system.
Possible opts fields (set value to true/false):
LT Ais lower triangular
UT Ais upper triangular
UHESS Ais upper Hessenberg (currently makes no difference)
SYM Ais symmetric or complex Hermitian (currently makes no difference)
POSDEF Ais positive definite
RECT Ais general rectangular (currently makes no difference)
TRANSA Solve A’*x = b by transpose (A) \ b
The optional second output Ris the inverse condition number of A(zero if matrix is
singular).
See also: [mldivide], page 144,[matrix type], page 508,[rcond], page 511.
508 GNU Octave
type = matrix_type (A)
type = matrix_type (A,"nocompute")
A= matrix_type (A,type)
A= matrix_type (A,"upper",perm)
A= matrix_type (A,"lower",perm)
A= matrix_type (A,"banded",nl,nu)
Identify the matrix type or mark a matrix as a particular type.
This allows more rapid solutions of linear equations involving Ato be performed.
Called with a single argument, matrix_type returns the type of the matrix and caches
it for future use.
Called with more than one argument, matrix_type allows the type of the matrix to
be defined.
If the option "nocompute" is given, the function will not attempt to guess the type
if it is still unknown. This is useful for debugging purposes.
The possible matrix types depend on whether the matrix is full or sparse, and can be
one of the following
"unknown"
Remove any previously cached matrix type, and mark type as unknown.
"full" Mark the matrix as full.
"positive definite"
Probable full positive definite matrix.
"diagonal"
Diagonal matrix. (Sparse matrices only)
"permuted diagonal"
Permuted Diagonal matrix. The permutation does not need to be specifi-
cally indicated, as the structure of the matrix explicitly gives this. (Sparse
matrices only)
"upper" Upper triangular. If the optional third argument perm is given, the ma-
trix is assumed to be a permuted upper triangular with the permutations
defined by the vector perm.
"lower" Lower triangular. If the optional third argument perm is given, the matrix
is assumed to be a permuted lower triangular with the permutations
defined by the vector perm.
"banded"
"banded positive definite"
Banded matrix with the band size of nl below the diagonal and nu above
it. If nl and nu are 1, then the matrix is tridiagonal and treated with
specialized code. In addition the matrix can be marked as probably a
positive definite. (Sparse matrices only)
"singular"
The matrix is assumed to be singular and will be treated with a minimum
norm solution.
Chapter 18: Linear Algebra 509
Note that the matrix type will be discovered automatically on the first attempt to
solve a linear equation involving A. Therefore matrix_type is only useful to give
Octave hints of the matrix type. Incorrectly defining the matrix type will result in
incorrect results from solutions of linear equations; it is entirely the responsibility of
the user to correctly identify the matrix type.
Also, the test for positive definiteness is a low-cost test for a Hermitian matrix with
a real positive diagonal. This does not guarantee that the matrix is positive defi-
nite, but only that it is a probable candidate. When such a matrix is factorized, a
Cholesky factorization is first attempted, and if that fails the matrix is then treated
with an LU factorization. Once the matrix has been factorized, matrix_type will
return the correct classification of the matrix.
norm (A)
norm (A,p)
norm (A,p,opt)
Compute the p-norm of the matrix A.
If the second argument is not given, p = 2 is used.
If Ais a matrix (or sparse matrix):
p=11-norm, the largest column sum of the absolute values of A.
p=2Largest singular value of A.
p=Inf or "inf"
Infinity norm, the largest row sum of the absolute values of A.
p="fro"
Frobenius norm of A,sqrt (sum (diag (A’ * A))).
other p,p> 1
maximum norm (A*x, p) such that norm (x, p) == 1
If Ais a vector or a scalar:
p=Inf or "inf"
max (abs (A)).
p=-Inf min (abs (A)).
p="fro"
Frobenius norm of A,sqrt (sumsq (abs (A))).
p= 0 Hamming norm—the number of nonzero elements.
other p,p> 1
p-norm of A,(sum (abs (A) .^ p)) ^ (1/p).
other pp< 1
the p-pseudonorm defined as above.
If opt is the value "rows", treat each row as a vector and compute its norm. The
result is returned as a column vector. Similarly, if opt is "columns" or "cols" then
compute the norms of each column and return a row vector.
See also: [normest], page 581,[normest1], page 581,[cond], page 504,[svd], page 521.
510 GNU Octave
null (A)
null (A,tol)
Return an orthonormal basis of the null space of A.
The dimension of the null space is taken as the number of singular values of Anot
greater than tol. If the argument tol is missing, it is computed as
max (size (A)) * max (svd (A)) * eps
See also: [orth], page 510.
orth (A)
orth (A,tol)
Return an orthonormal basis of the range space of A.
The dimension of the range space is taken as the number of singular values of A
greater than tol. If the argument tol is missing, it is computed as
max (size (A)) * max (svd (A)) * eps
See also: [null], page 510.
[y,h] = mgorth (x,v)
Orthogonalize a given column vector xwith respect to a set of orthonormal vectors
comprising the columns of vusing the modified Gram-Schmidt method.
On exit, yis a unit vector such that:
norm (y)=1
v’ * y= 0
x= [v,y]*h’
pinv (x)
pinv (x,tol)
Return the pseudoinverse of x.
Singular values less than tol are ignored.
If the second argument is omitted, it is taken to be
tol = max (size (x)) * sigma_max (x) * eps,
where sigma_max (x)is the maximal singular value of x.
rank (A)
rank (A,tol)
Compute the rank of matrix A, using the singular value decomposition.
The rank is taken to be the number of singular values of Athat are greater than the
specified tolerance tol. If the second argument is omitted, it is taken to be
tol = max (size (A)) * sigma(1) * eps;
where eps is machine precision and sigma(1) is the largest singular value of A.
The rank of a matrix is the number of linearly independent rows or columns and
determines how many particular solutions exist to a system of equations. Use null
for finding the remaining homogenous solutions.
Chapter 18: Linear Algebra 511
Example:
x=[123
456
7 8 9];
rank (x)
⇒2
The number of linearly independent rows is only 2 because the final row is a linear
combination of -1*row1 +2*row2.
See also: [null], page 510,[sprank], page 584,[svd], page 521.
c= rcond (A)
Compute the 1-norm estimate of the reciprocal condition number as returned by
lapack.
If the matrix is well-conditioned then cwill be near 1 and if the matrix is poorly
conditioned it will be close to 0.
The matrix Amust not be sparse. If the matrix is sparse then condest (A)or rcond
(full (A)) should be used instead.
See also: [cond], page 504,[condest], page 582.
trace (A)
Compute the trace of A, the sum of the elements along the main diagonal.
The implementation is straightforward: sum (diag (A)).
See also: [eig], page 505.
rref (A)
rref (A,tol)
[r,k] = rref (. . . )
Return the reduced row echelon form of A.
tol defaults to eps * max (size (A)) * norm (A, inf).
The optional return argument kcontains the vector of "bound variables", which are
those columns on which elimination has been performed.
18.3 Matrix Factorizations
R= chol (A)
[R,p] = chol (A)
[R,p,Q] = chol (A)
[R,p,Q] = chol (A,"vector")
[L, ...] = chol (. . . , "lower")
[R, ...] = chol (. . . , "upper")
Compute the upper Cholesky factor, R, of the real symmetric or complex Hermitian
positive definite matrix A.
The upper Cholesky factor Ris computed by using the upper triangular part of matrix
Aand is defined by RTR=A.
512 GNU Octave
Calling chol using the optional "upper" flag has the same behavior. In contrast, using
the optional "lower" flag, chol returns the lower triangular factorization, computed
by using the lower triangular part of matrix A, such that LLT=A.
Called with one output argument chol fails if matrix Ais not positive definite. Note
that if matrix Ais not real symmetric or complex Hermitian then the lower triangular
part is considered to be the (complex conjugate) transpose of the upper triangular
part, or vice versa, given the "lower" flag.
Called with two or more output arguments pflags whether the matrix Awas positive
definite and chol does not fail. A zero value of pindicates that matrix Ais positive
definite and Rgives the factorization. Otherwise, pwill have a positive value.
If called with three output arguments matrix Amust be sparse and a sparsity pre-
serving row/column permutation is applied to matrix Aprior to the factorization.
That is Ris the factorization of A(Q,Q)such that RTR=QTAQ.
The sparsity preserving permutation is generally returned as a matrix. However, given
the optional flag "vector",Qwill be returned as a vector such that RTR=A(Q, Q).
In general the lower triangular factorization is significantly faster for sparse matrices.
See also: [hess], page 513,[lu], page 514,[qr], page 515,[qz], page 518,[schur],
page 519,[svd], page 521,[ichol], page 593,[cholinv], page 512,[chol2inv], page 512,
[cholupdate], page 512,[cholinsert], page 513,[choldelete], page 513,[cholshift],
page 513.
cholinv (A)
Compute the inverse of the symmetric positive definite matrix Ausing the
Cholesky factorization.
See also: [chol], page 511,[chol2inv], page 512,[inv], page 507.
chol2inv (U)
Invert a symmetric, positive definite square matrix from its Cholesky decomposition,
U.
Note that Ushould be an upper-triangular matrix with positive diagonal elements.
chol2inv (U)provides inv (U’*U)but it is much faster than using inv.
See also: [chol], page 511,[cholinv], page 512,[inv], page 507.
[R1,info] = cholupdate (R,u,op)
Update or downdate a Cholesky factorization.
Given an upper triangular matrix Rand a column vector u, attempt to determine
another upper triangular matrix R1 such that
•R1’*R1 =R’*R+u*u’ if op is "+"
•R1’*R1 =R’*R-u*u’ if op is "-"
If op is "-",info is set to
•0 if the downdate was successful,
•1 if R’*R-u*u’ is not positive definite,
•2 if Ris singular.
Chapter 18: Linear Algebra 513
If info is not present, an error message is printed in cases 1 and 2.
See also: [chol], page 511,[cholinsert], page 513,[choldelete], page 513,[cholshift],
page 513.
R1 = cholinsert (R,j,u)
[R1,info] = cholinsert (R,j,u)
Given a Cholesky factorization of a real symmetric or complex Hermitian positive
definite matrix A=R’*R,Rupper triangular, return the Cholesky factorization of
A1, where A1(p,p) = A, A1(:,j) = A1(j,:)’ = u and p = [1:j-1,j+1:n+1]. u(j) should
be positive.
On return, info is set to
•0 if the insertion was successful,
•1 if A1 is not positive definite,
•2 if Ris singular.
If info is not present, an error message is printed in cases 1 and 2.
See also: [chol], page 511,[cholupdate], page 512,[choldelete], page 513,[cholshift],
page 513.
R1 = choldelete (R,j)
Given a Cholesky factorization of a real symmetric or complex Hermitian positive
definite matrix A=R’*R,Rupper triangular, return the Cholesky factorization of
A(p,p), where p = [1:j-1,j+1:n+1].
See also: [chol], page 511,[cholupdate], page 512,[cholinsert], page 513,[cholshift],
page 513.
R1 = cholshift (R,i,j)
Given a Cholesky factorization of a real symmetric or complex Hermitian positive
definite matrix A=R’*R,Rupper triangular, return the Cholesky factorization of
A(p,p), where p is the permutation
p = [1:i-1, shift(i:j, 1), j+1:n] if i<j
or
p = [1:j-1, shift(j:i,-1), i+1:n] if j<i.
See also: [chol], page 511,[cholupdate], page 512,[cholinsert], page 513,[choldelete],
page 513.
H= hess (A)
[P,H] = hess (A)
Compute the Hessenberg decomposition of the matrix A.
The Hessenberg decomposition is
A=P HP T
where Pis a square unitary matrix (PTP=I), and His upper Hessenberg (Hi,j =
0,∀i>j+ 1).
514 GNU Octave
The Hessenberg decomposition is usually used as the first step in an eigenvalue com-
putation, but has other applications as well (see Golub, Nash, and Van Loan, IEEE
Transactions on Automatic Control, 1979).
See also: [eig], page 505,[chol], page 511,[lu], page 514,[qr], page 515,[qz], page 518,
[schur], page 519,[svd], page 521.
[L,U] = lu (A)
[L,U,P] = lu (A)
[L,U,P,Q] = lu (S)
[L,U,P,Q,R] = lu (S)
[...] = lu (S,thres)
y= lu (. . . )
[...] = lu (. . . , "vector")
Compute the LU decomposition of A.
If Ais full then subroutines from lapack are used, and if Ais sparse then umfpack
is used.
The result is returned in a permuted form, according to the optional return value P.
For example, given the matrix a = [1, 2; 3, 4],
[l, u, p] = lu (a)
returns
l =
1.00000 0.00000
0.33333 1.00000
u =
3.00000 4.00000
0.00000 0.66667
p =
0 1
1 0
The matrix is not required to be square.
When called with two or three output arguments and a sparse input matrix, lu does
not attempt to perform sparsity preserving column permutations. Called with a fourth
output argument, the sparsity preserving column transformation Qis returned, such
that P*A*Q=L*U.
Called with a fifth output argument and a sparse input matrix, lu attempts to use a
scaling factor Ron the input matrix such that P* (R\A) * Q=L*U. This typically
leads to a sparser and more stable factorization.
An additional input argument thres, that defines the pivoting threshold can be given.
thres can be a scalar, in which case it defines the umfpack pivoting tolerance for
both symmetric and unsymmetric cases. If thres is a 2-element vector, then the
Chapter 18: Linear Algebra 515
first element defines the pivoting tolerance for the unsymmetric umfpack pivoting
strategy and the second for the symmetric strategy. By default, the values defined by
spparms are used ([0.1, 0.001]).
Given the string argument "vector",lu returns the values of Pand Qas vector
values, such that for full matrix, A(P,:) = L*U, and R(P,:) * A(:,Q) = L*U.
With two output arguments, returns the permuted forms of the upper and lower
triangular matrices, such that A=L*U. With one output argument y, then the
matrix returned by the lapack routines is returned. If the input matrix is sparse
then the matrix Lis embedded into Uto give a return value similar to the full case.
For both full and sparse matrices, lu loses the permutation information.
See also: [luupdate], page 515,[ilu], page 595,[chol], page 511,[hess], page 513,[qr],
page 515,[qz], page 518,[schur], page 519,[svd], page 521.
[L,U] = luupdate (L,U,x,y)
[L,U,P] = luupdate (L,U,P,x,y)
Given an LU factorization of a real or complex matrix A=L*U,Llower unit trape-
zoidal and Uupper trapezoidal, return the LU factorization of A+x*y.’, where x
and yare column vectors (rank-1 update) or matrices with equal number of columns
(rank-k update).
Optionally, row-pivoted updating can be used by supplying a row permutation (piv-
oting) matrix P; in that case, an updated permutation matrix is returned. Note that
if L,U,Pis a pivoted LU factorization as obtained by lu:
[L,U,P]=lu(A);
then a factorization of A+x*y.’ can be obtained either as
[L1,U1]=lu(L,U,P*x,y)
or
[L1,U1,P1]=lu(L,U,P,x,y)
The first form uses the unpivoted algorithm, which is faster, but less stable. The
second form uses a slower pivoted algorithm, which is more stable.
The matrix case is done as a sequence of rank-1 updates; thus, for large enough k, it
will be both faster and more accurate to recompute the factorization from scratch.
See also: [lu], page 514,[cholupdate], page 512,[qrupdate], page 517.
[Q,R] = qr (A)
[Q,R,P] = qr (A)# non-sparse A
X= qr (A)
R= qr (A)# sparse A
[C,R] = qr (A,B)
[...] = qr (. . . , 0)
[...] = qr (. . . , ’vector’)
[...] = qr (. . . , ’matrix’)
Compute the QR factorization of A, using standard lapack subroutines. The QR fac-
torization is QR =Awhere Qis an orthogonal matrix and Ris upper triangular.
For example, given the matrix A= [1, 2; 3, 4],
[Q,R]=qr(A)
516 GNU Octave
returns
Q=
-0.31623 -0.94868
-0.94868 0.31623
R=
-3.16228 -4.42719
0.00000 -0.63246
The qr factorization has applications in the solution of least squares problems
min
xkAx −bk2
for overdetermined systems of equations (i.e., Ais a tall, thin matrix).
If only a single return value is requested, then it is either Rif Ais sparse, or Xsuch
that R= triu (X)if Ais full. (Note: Unlike most commands, the single return value
is not the first return value when multiple are requested.)
If the matrix Ais full, the permuted QR factorization [Q,R,P] = qr (A)forms the
QR factorization such that the diagonal entries of Rare decreasing in magnitude
order. For example, given the matrix a = [1, 2; 3, 4],
[Q,R,P]=qr(A)
returns
Q=
-0.44721 -0.89443
-0.89443 0.44721
R=
-4.47214 -3.13050
0.00000 0.44721
P=
0 1
1 0
The permuted qr factorization [Q,R,P] = qr (A)factorization allows the construc-
tion of an orthogonal basis of span (A).
If the matrix Ais sparse, then the sparse QR factorization of Ais computed using
CSparse. As the matrix Qis in general a full matrix, it is recommended to request
only one return value, which is the Q-less factorization Rof A, such that R= chol
(A’ * A).
Chapter 18: Linear Algebra 517
If an additional matrix Bis supplied and two return values are requested, then qr
returns C, where C=Q’ * B. This allows the least squares approximation of A\Bto
be calculated as
[C,R]=qr(A,B)
x = R\C
If the final argument is the scalar 0 and the number of rows is larger than the number
of columns, then an "economy" factorization is returned, omitting zeroes of Rand
the corresponding columns of Q. That is, Rwill have only size (A,1) rows. In this
case, Pis a vector rather than a matrix.
If the final argument is the string "vector" then Pis a permutation vector instead
of a permutation matrix.
See also: [chol], page 511,[hess], page 513,[lu], page 514,[qz], page 518,[schur],
page 519,[svd], page 521,[qrupdate], page 517,[qrinsert], page 517,[qrdelete],
page 517,[qrshift], page 518.
[Q1,R1] = qrupdate (Q,R,u,v)
Given a QR factorization of a real or complex matrix A=Q*R,Qunitary and
Rupper trapezoidal, return the QR factorization of A+u*v’, where uand vare
column vectors (rank-1 update) or matrices with equal number of columns (rank-k
update). Notice that the latter case is done as a sequence of rank-1 updates; thus, for
k large enough, it will be both faster and more accurate to recompute the factorization
from scratch.
The QR factorization supplied may be either full (Q is square) or economized (R is
square).
See also: [qr], page 515,[qrinsert], page 517,[qrdelete], page 517,[qrshift], page 518.
[Q1,R1] = qrinsert (Q,R,j,x,orient)
Given a QR factorization of a real or complex matrix A=Q*R,Qunitary and
Rupper trapezoidal, return the QR factorization of [A(:,1:j-1) x A(:,j:n)], where uis
a column vector to be inserted into A(if orient is "col"), or the QR factorization
of [A(1:j-1,:);x;A(:,j:n)], where xis a row vector to be inserted into A(if orient is
"row").
The default value of orient is "col". If orient is "col",umay be a matrix and
jan index vector resulting in the QR factorization of a matrix Bsuch that B(:,j)
gives uand B(:,j) = [] gives A. Notice that the latter case is done as a sequence of
k insertions; thus, for k large enough, it will be both faster and more accurate to
recompute the factorization from scratch.
If orient is "col", the QR factorization supplied may be either full (Q is square) or
economized (R is square).
If orient is "row", full factorization is needed.
See also: [qr], page 515,[qrupdate], page 517,[qrdelete], page 517,[qrshift], page 518.
[Q1,R1] = qrdelete (Q,R,j,orient)
Given a QR factorization of a real or complex matrix A=Q*R,Qunitary and
Rupper trapezoidal, return the QR factorization of [A(:,1:j-1), U, A(:,j:n)], where u
518 GNU Octave
is a column vector to be inserted into A(if orient is "col"), or the QR factorization
of [A(1:j-1,:);X;A(:,j:n)], where xis a row orient is "row"). The default value of orient
is "col".
If orient is "col",jmay be an index vector resulting in the QR factorization of
a matrix Bsuch that A(:,j) = [] gives B. Notice that the latter case is done as a
sequence of k deletions; thus, for k large enough, it will be both faster and more
accurate to recompute the factorization from scratch.
If orient is "col", the QR factorization supplied may be either full (Q is square) or
economized (R is square).
If orient is "row", full factorization is needed.
See also: [qr], page 515,[qrupdate], page 517,[qrinsert], page 517,[qrshift], page 518.
[Q1,R1] = qrshift (Q,R,i,j)
Given a QR factorization of a real or complex matrix A=Q*R,Qunitary and
Rupper trapezoidal, return the QR factorization of A(:,p), where p is the permutation
p = [1:i-1, shift(i:j, 1), j+1:n] if i<j
or
p = [1:j-1, shift(j:i,-1), i+1:n] if j<i.
See also: [qr], page 515,[qrupdate], page 517,[qrinsert], page 517,[qrdelete],
page 517.
lambda = qz (A,B)
lambda = qz (A,B,opt)
QZ decomposition of the generalized eigenvalue problem (Ax =sBx).
There are three ways to call this function:
1. lambda = qz (A,B)
Computes the generalized eigenvalues λof (A−sB).
2. [AA, BB, Q, Z, V, W, lambda] = qz (A,B)
Computes QZ decomposition, generalized eigenvectors, and generalized eigenval-
ues of (A−sB)
AV =BV diag(λ)
WTA= diag(λ)WTB
AA =QTAZ, BB =QTBZ
with Qand Zorthogonal (unitary)= I
3. [AA,BB,Z{, lambda}] = qz (A,B,opt)
As in form [2], but allows ordering of generalized eigenpairs for, e.g., solution
of discrete time algebraic Riccati equations. Form 3 is not available for com-
plex matrices, and does not compute the generalized eigenvectors V,W, nor the
orthogonal matrix Q.
opt for ordering eigenvalues of the GEP pencil. The leading block of the
revised pencil contains all eigenvalues that satisfy:
"N" = unordered (default)
Chapter 18: Linear Algebra 519
"S" = small: leading block has all |lambda|≤1
"B" = big: leading block has all |lambda|≥1
"-" = negative real part: leading block has all eigenvalues in
the open left half-plane
"+" = non-negative real part: leading block has all eigenval-
ues in the closed right half-plane
Note: qz performs permutation balancing, but not scaling (see [XREFbalance],
page 503). The order of output arguments was selected for compatibility with
matlab.
See also: [eig], page 505,[balance], page 503,[lu], page 514,[chol], page 511,[hess],
page 513,[qr], page 515,[qzhess], page 519,[schur], page 519,[svd], page 521.
[aa,bb,q,z] = qzhess (A,B)
Compute the Hessenberg-triangular decomposition of the matrix pencil (A,B), re-
turning aa =q*A*z,bb =q*B*z, with qand zorthogonal.
For example:
[aa, bb, q, z] = qzhess ([1, 2; 3, 4], [5, 6; 7, 8])
⇒aa = [ -3.02244, -4.41741; 0.92998, 0.69749 ]
⇒bb = [ -8.60233, -9.99730; 0.00000, -0.23250 ]
⇒q = [ -0.58124, -0.81373; -0.81373, 0.58124 ]
⇒z=[1,0;0,1]
The Hessenberg-triangular decomposition is the first step in Moler and Stewart’s
QZ decomposition algorithm.
Algorithm taken from Golub and Van Loan, Matrix Computations, 2nd edition.
See also: [lu], page 514,[chol], page 511,[hess], page 513,[qr], page 515,[qz], page 518,
[schur], page 519,[svd], page 521.
S= schur (A)
S= schur (A,"real")
S= schur (A,"complex")
S= schur (A,opt)
[U,S] = schur (. . . )
Compute the Schur decomposition of A.
The Schur decomposition is defined as
S=UTAU
where Uis a unitary matrix (UTUis identity) and Sis upper triangular. The eigen-
values of A(and S) are the diagonal elements of S. If the matrix Ais real, then the
real Schur decomposition is computed, in which the matrix Uis orthogonal and S
is block upper triangular with blocks of size at most 2 ×2 along the diagonal. The
diagonal elements of S(or the eigenvalues of the 2 ×2 blocks, when appropriate) are
the eigenvalues of Aand S.
The default for real matrices is a real Schur decomposition. A complex decomposition
may be forced by passing the flag "complex".
520 GNU Octave
The eigenvalues are optionally ordered along the diagonal according to the value of
opt.opt = "a" indicates that all eigenvalues with negative real parts should be moved
to the leading block of S(used in are), opt = "d" indicates that all eigenvalues with
magnitude less than one should be moved to the leading block of S(used in dare),
and opt = "u", the default, indicates that no ordering of eigenvalues should occur.
The leading kcolumns of Ualways span the A-invariant subspace corresponding to
the kleading eigenvalues of S.
The Schur decomposition is used to compute eigenvalues of a square matrix, and has
applications in the solution of algebraic Riccati equations in control (see are and
dare).
See also: [rsf2csf], page 520,[ordschur], page 520,[lu], page 514,[chol], page 511,
[hess], page 513,[qr], page 515,[qz], page 518,[svd], page 521.
[U,T] = rsf2csf (UR,TR)
Convert a real, upper quasi-triangular Schur form TR to a complex, upper triangular
Schur form T.
Note that the following relations hold:
UR ·T R ·URT=UT U †and U†Uis the identity matrix I.
Note also that Uand Tare not unique.
See also: [schur], page 519.
[UR,SR] = ordschur (U,S,select)
Reorders the real Schur factorization (U,S) obtained with the schur function, so that
selected eigenvalues appear in the upper left diagonal blocks of the quasi triangular
Schur matrix.
The logical vector select specifies the selected eigenvalues as they appear along S’s
diagonal.
For example, given the matrix A= [1, 2; 3, 4], and its Schur decomposition
[U,S] = schur (A)
which returns
U=
-0.82456 -0.56577
0.56577 -0.82456
S=
-0.37228 -1.00000
0.00000 5.37228
It is possible to reorder the decomposition so that the positive eigenvalue is in the
upper left corner, by doing:
[U,S] = ordschur (U,S, [0,1])
See also: [schur], page 519.

Chapter 18: Linear Algebra 521
angle = subspace (A,B)
Determine the largest principal angle between two subspaces spanned by the columns
of matrices Aand B.
s= svd (A)
[U,S,V] = svd (A)
[U,S,V] = svd (A,econ)
Compute the singular value decomposition of A
A=USV †
The function svd normally returns only the vector of singular values. When called
with three return values, it computes U,S, and V. For example,
svd (hilb (3))
returns
ans =
1.4083189
0.1223271
0.0026873
and
[u, s, v] = svd (hilb (3))
returns
u =
-0.82704 0.54745 0.12766
-0.45986 -0.52829 -0.71375
-0.32330 -0.64901 0.68867
s =
1.40832 0.00000 0.00000
0.00000 0.12233 0.00000
0.00000 0.00000 0.00269
v =
-0.82704 0.54745 0.12766
-0.45986 -0.52829 -0.71375
-0.32330 -0.64901 0.68867
If given a second argument, svd returns an economy-sized decomposition, eliminating
the unnecessary rows or columns of Uor V.
See also: [svd driver], page 522,[svds], page 588,[eig], page 505,[lu], page 514,[chol],
page 511,[hess], page 513,[qr], page 515,[qz], page 518.
522 GNU Octave
val = svd_driver ()
old_val = svd_driver (new_val)
svd_driver (new_val,"local")
Query or set the underlying lapack driver used by svd.
Currently recognized values are "gesvd" and "gesdd". The default is "gesvd".
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [svd], page 521.
[housv,beta,zer] = housh (x,j,z)
Compute Householder reflection vector housv to reflect xto be the j-th column of
identity, i.e.,
(I - beta*housv*housv’)x = norm (x)*e(j) if x(j) < 0,
(I - beta*housv*housv’)x = -norm (x)*e(j) if x(j) >= 0
Inputs
xvector
jindex into vector
zthreshold for zero (usually should be the number 0)
Outputs (see Golub and Van Loan):
beta If beta = 0, then no reflection need be applied (zer set to 0)
housv householder vector
[u,h,nu] = krylov (A,V,k,eps1,pflg)
Construct an orthogonal basis uof block Krylov subspace
[v a*v a^2*v ... a^(k+1)*v]
using Householder reflections to guard against loss of orthogonality.
If Vis a vector, then hcontains the Hessenberg matrix such that a*u == u*h+rk*ek’,
in which rk = a*u(:,k)-u*h(:,k), and ek’ is the vector [0, 0, ..., 1] of length
k. Otherwise, his meaningless.
If Vis a vector and kis greater than length (A) - 1, then hcontains the Hessenberg
matrix such that a*u == u*h.
The value of nu is the dimension of the span of the Krylov subspace (based on eps1).
If bis a vector and kis greater than m-1, then hcontains the Hessenberg decompo-
sition of A.
The optional parameter eps1 is the threshold for zero. The default value is 1e-12.
If the optional parameter pflg is nonzero, row pivoting is used to improve numerical
behavior. The default value is 0.
Reference: A. Hodel, P. Misra, Partial Pivoting in the Computation of Krylov Sub-
spaces of Large Sparse Systems, Proceedings of the 42nd IEEE Conference on Decision
and Control, December 2003.

Chapter 18: Linear Algebra 523
18.4 Functions of a Matrix
expm (A)
Return the exponential of a matrix.
The matrix exponential is defined as the infinite Taylor series
exp(A) = I+A+A2
2! +A3
3! +···
However, the Taylor series is not the way to compute the matrix exponential; see
Moler and Van Loan, Nineteen Dubious Ways to Compute the Exponential of a
Matrix, SIAM Review, 1978. This routine uses Ward’s diagonal Pad´e approximation
method with three step preconditioning (SIAM Journal on Numerical Analysis, 1977).
Diagonal Pad´e approximations are rational polynomials of matrices Dq(A)−1Nq(A)
whose Taylor series matches the first 2q+ 1 terms of the Taylor series above; direct
evaluation of the Taylor series (with the same preconditioning steps) may be desirable
in lieu of the Pad´e approximation when Dq(A) is ill-conditioned.
See also: [logm], page 523,[sqrtm], page 523.
s= logm (A)
s= logm (A,opt_iters)
[s,iters] = logm (. . . )
Compute the matrix logarithm of the square matrix A.
The implementation utilizes a Pad´e approximant and the identity
logm (A) = 2^k * logm (A^(1 / 2^k))
The optional input opt iters is the maximum number of square roots to compute and
defaults to 100.
The optional output iters is the number of square roots actually computed.
See also: [expm], page 523,[sqrtm], page 523.
s= sqrtm (A)
[s,error_estimate] = sqrtm (A)
Compute the matrix square root of the square matrix A.
Ref: N.J. Higham. A New sqrtm for matlab. Numerical Analysis Report No. 336,
Manchester Centre for Computational Mathematics, Manchester, England, January
1999.
See also: [expm], page 523,[logm], page 523.
kron (A,B)
kron (A1,A2, . . . )
Form the Kronecker product of two or more matrices.
This is defined block by block as
x = [ a(i,j)*b ]
For example:
kron (1:4, ones (3, 1))
⇒1234
1234
1234
524 GNU Octave
If there are more than two input arguments A1,A2, . . . , An the Kronecker product
is computed as
kron (kron (A1,A2), ..., An)
Since the Kronecker product is associative, this is well-defined.
blkmm (A,B)
Compute products of matrix blocks.
The blocks are given as 2-dimensional subarrays of the arrays A,B. The size of A
must have the form [m,k,...] and size of Bmust be [k,n,...]. The result is then
of size [m,n,...] and is computed as follows:
for i = 1:prod (size (A)(3:end))
C(:,:,i) = A(:,:,i) * B(:,:,i)
endfor
X= sylvester (A,B,C)
Solve the Sylvester equation
AX +XB =C
using standard lapack subroutines.
For example:
sylvester ([1, 2; 3, 4], [5, 6; 7, 8], [9, 10; 11, 12])
⇒[ 0.50000, 0.66667; 0.66667, 0.50000 ]
18.5 Specialized Solvers
x= bicg (A,b,rtol,maxit,M1,M2,x0)
x= bicg (A,b,rtol,maxit,P)
[x,flag,relres,iter,resvec] = bicg (A,b, . . . )
Solve A x = b using the Bi-conjugate gradient iterative method.
−rtol is the relative tolerance, if not given or set to [] the default value 1e-6 is used.
−maxit the maximum number of outer iterations, if not given or set to [] the default
value min (20, numel (b)) is used.
−x0 the initial guess, if not given or set to [] the default value zeros (size (b))
is used.
Acan be passed as a matrix or as a function handle or inline function fsuch that
f(x, "notransp") = A*x and f(x, "transp") = A’*x.
The preconditioner Pis given as P = M1 * M2. Both M1 and M2 can be passed as a
matrix or as a function handle or inline function gsuch that g(x, "notransp") = M1 \
xor g(x, "notransp") = M2 \ x and g(x, "transp") = M1’ \ x or g(x, "transp")
= M2’ \ x.
If called with more than one output parameter
−flag indicates the exit status:
−0: iteration converged to the within the chosen tolerance
Chapter 18: Linear Algebra 525
−1: the maximum number of iterations was reached before convergence
−3: the algorithm reached stagnation
(the value 2 is unused but skipped for compatibility).
−relres is the final value of the relative residual.
−iter is the number of iterations performed.
−resvec is a vector containing the relative residual at each iteration.
See also: [bicgstab], page 525,[cgs], page 525,[gmres], page 526,[pcg], page 589,
[qmr], page 527.
x= bicgstab (A,b,rtol,maxit,M1,M2,x0)
x= bicgstab (A,b,rtol,maxit,P)
[x,flag,relres,iter,resvec] = bicgstab (A,b, . . . )
Solve A x = b using the stabilizied Bi-conjugate gradient iterative method.
−rtol is the relative tolerance, if not given or set to [] the default value 1e-6 is used.
−maxit the maximum number of outer iterations, if not given or set to [] the default
value min (20, numel (b)) is used.
−x0 the initial guess, if not given or set to [] the default value zeros (size (b))
is used.
Acan be passed as a matrix or as a function handle or inline function fsuch that
f(x) = A*x.
The preconditioner Pis given as P = M1 * M2. Both M1 and M2 can be passed as a
matrix or as a function handle or inline function gsuch that g(x) = M1 \ x or g(x)
= M2 \ x.
If called with more than one output parameter
−flag indicates the exit status:
−0: iteration converged to the within the chosen tolerance
−1: the maximum number of iterations was reached before convergence
−3: the algorithm reached stagnation
(the value 2 is unused but skipped for compatibility).
−relres is the final value of the relative residual.
−iter is the number of iterations performed.
−resvec is a vector containing the relative residual at each iteration.
See also: [bicg], page 524,[cgs], page 525,[gmres], page 526,[pcg], page 589,[qmr],
page 527.
x= cgs (A,b,rtol,maxit,M1,M2,x0)
x= cgs (A,b,rtol,maxit,P)
[x,flag,relres,iter,resvec] = cgs (A,b, . . . )
Solve A x = b, where Ais a square matrix, using the Conjugate Gradients Squared
method.
−rtol is the relative tolerance, if not given or set to [] the default value 1e-6 is used.
526 GNU Octave
−maxit the maximum number of outer iterations, if not given or set to [] the default
value min (20, numel (b)) is used.
−x0 the initial guess, if not given or set to [] the default value zeros (size (b))
is used.
Acan be passed as a matrix or as a function handle or inline function fsuch that
f(x) = A*x.
The preconditioner Pis given as P = M1 * M2. Both M1 and M2 can be passed as a
matrix or as a function handle or inline function gsuch that g(x) = M1 \ x or g(x)
= M2 \ x.
If called with more than one output parameter
−flag indicates the exit status:
−0: iteration converged to the within the chosen tolerance
−1: the maximum number of iterations was reached before convergence
−3: the algorithm reached stagnation
(the value 2 is unused but skipped for compatibility).
−relres is the final value of the relative residual.
−iter is the number of iterations performed.
−resvec is a vector containing the relative residual at each iteration.
See also: [pcg], page 589,[bicgstab], page 525,[bicg], page 524,[gmres], page 526,
[qmr], page 527.
x= gmres (A,b,m,rtol,maxit,M1,M2,x0)
x= gmres (A,b,m,rtol,maxit,P)
[x,flag,relres,iter,resvec] = gmres (. . . )
Solve A x = b using the Preconditioned GMRES iterative method with restart, a.k.a.
PGMRES(m).
−rtol is the relative tolerance, if not given or set to [] the default value 1e-6 is used.
−maxit is the maximum number of outer iterations, if not given or set to [] the
default value min (10, numel (b) / restart) is used.
−x0 is the initial guess, if not given or set to [] the default value zeros (size (b))
is used.
−mis the restart parameter, if not given or set to [] the default value numel (b)
is used.
Argument Acan be passed as a matrix, function handle, or inline function fsuch
that f(x) = A*x.
The preconditioner Pis given as P = M1 * M2. Both M1 and M2 can be passed as a
matrix, function handle, or inline function gsuch that g(x) = M1\x or g(x) = M2\x.
Besides the vector x, additional outputs are:
−flag indicates the exit status:
Chapter 18: Linear Algebra 527
0 : iteration converged to within the specified tolerance
1 : maximum number of iterations exceeded
2 : unused, but skipped for compatibility
3 : algorithm reached stagnation (no change between iterations)
−relres is the final value of the relative residual.
−iter is a vector containing the number of outer iterations and total iterations
performed.
−resvec is a vector containing the relative residual at each iteration.
See also: [bicg], page 524,[bicgstab], page 525,[cgs], page 525,[pcg], page 589,[pcr],
page 591,[qmr], page 527.
x= qmr (A,b,rtol,maxit,M1,M2,x0)
x= qmr (A,b,rtol,maxit,P)
[x,flag,relres,iter,resvec] = qmr (A,b, . . . )
Solve A x = b using the Quasi-Minimal Residual iterative method (without look-
ahead).
−rtol is the relative tolerance, if not given or set to [] the default value 1e-6 is used.
−maxit the maximum number of outer iterations, if not given or set to [] the default
value min (20, numel (b)) is used.
−x0 the initial guess, if not given or set to [] the default value zeros (size (b))
is used.
Acan be passed as a matrix or as a function handle or inline function fsuch that
f(x, "notransp") = A*x and f(x, "transp") = A’*x.
The preconditioner Pis given as P = M1 * M2. Both M1 and M2 can be passed as a
matrix or as a function handle or inline function gsuch that g(x, "notransp") = M1 \
xor g(x, "notransp") = M2 \ x and g(x, "transp") = M1’ \ x or g(x, "transp")
= M2’ \ x.
If called with more than one output parameter
−flag indicates the exit status:
−0: iteration converged to the within the chosen tolerance
−1: the maximum number of iterations was reached before convergence
−3: the algorithm reached stagnation
(the value 2 is unused but skipped for compatibility).
−relres is the final value of the relative residual.
−iter is the number of iterations performed.
−resvec is a vector containing the residual norms at each iteration.
References:
1. R. Freund and N. Nachtigal, QMR: a quasi-minimal residual method for non-
Hermitian linear systems, Numerische Mathematik, 1991, 60, pp. 315-339.
2. R. Barrett, M. Berry, T. Chan, J. Demmel, J. Donato, J. Dongarra, V. Eijkhour,
R. Pozo, C. Romine, and H. van der Vorst, Templates for the solution of linear
systems: Building blocks for iterative methods, SIAM, 2nd ed., 1994.
529
19 Vectorization and Faster Code Execution
Vectorization is a programming technique that uses vector operations instead of element-by-
element loop-based operations. Besides frequently producing more succinct Octave code,
vectorization also allows for better optimization in the subsequent implementation. The
optimizations may occur either in Octave’s own Fortran, C, or C++ internal implementation,
or even at a lower level depending on the compiler and external numerical libraries used to
build Octave. The ultimate goal is to make use of your hardware’s vector instructions if
possible or to perform other optimizations in software.
Vectorization is not a concept unique to Octave, but it is particularly important because
Octave is a matrix-oriented language. Vectorized Octave code will see a dramatic speed up
(10X–100X) in most cases.
This chapter discusses vectorization and other techniques for writing faster code.
19.1 Basic Vectorization
To a very good first approximation, the goal in vectorization is to write code that avoids
loops and uses whole-array operations. As a trivial example, consider
for i = 1:n
for j = 1:m
c(i,j) = a(i,j) + b(i,j);
endfor
endfor
compared to the much simpler
c=a+b;
This isn’t merely easier to write; it is also internally much easier to optimize. Octave del-
egates this operation to an underlying implementation which, among other optimizations,
may use special vector hardware instructions or could conceivably even perform the addi-
tions in parallel. In general, if the code is vectorized, the underlying implementation has
more freedom about the assumptions it can make in order to achieve faster execution.
This is especially important for loops with "cheap"bodies. Often it suffices to vectorize
just the innermost loop to get acceptable performance. A general rule of thumb is that the
"order"of the vectorized body should be greater or equal to the "order"of the enclosing
loop.
As a less trivial example, instead of
for i = 1:n-1
a(i) = b(i+1) - b(i);
endfor
write
a = b(2:n) - b(1:n-1);
This shows an important general concept about using arrays for indexing instead of
looping over an index variable. See Section 8.1 [Index Expressions], page 135. Also use
530 GNU Octave
boolean indexing generously. If a condition needs to be tested, this condition can also be
written as a boolean index. For instance, instead of
for i = 1:n
if (a(i) > 5)
a(i) -= 20
endif
endfor
write
a(a>5) -= 20;
which exploits the fact that a > 5 produces a boolean index.
Use elementwise vector operators whenever possible to avoid looping (operators like .*
and .^). See Section 8.3 [Arithmetic Ops], page 142. For simple inline functions, the
vectorize function can do this automatically.
vectorize (fun)
Create a vectorized version of the inline function fun by replacing all occurrences of
*,/, etc., with .*,./, etc.
This may be useful, for example, when using inline functions with numerical integra-
tion or optimization where a vector-valued function is expected.
fcn = vectorize (inline ("x^2 - 1"))
⇒fcn = f(x) = x.^2 - 1
quadv (fcn, 0, 3)
⇒6
See also: [inline], page 212,[formula], page 212,[argnames], page 212.
Also exploit broadcasting in these elementwise operators both to avoid looping and
unnecessary intermediate memory allocations. See Section 19.2 [Broadcasting], page 531.
Use built-in and library functions if possible. Built-in and compiled functions are very
fast. Even with an m-file library function, chances are good that it is already optimized, or
will be optimized more in a future release.
For instance, even better than
a = b(2:n) - b(1:n-1);
is
a = diff (b);
Most Octave functions are written with vector and array arguments in mind. If you
find yourself writing a loop with a very simple operation, chances are that such a function
already exists. The following functions occur frequently in vectorized code:
•Index manipulation
•find
•sub2ind
•ind2sub
•sort
•unique
Chapter 19: Vectorization and Faster Code Execution 531
•lookup
•ifelse / merge
•Repetition
•repmat
•repelems
•Vectorized arithmetic
•sum
•prod
•cumsum
•cumprod
•sumsq
•diff
•dot
•cummax
•cummin
•Shape of higher dimensional arrays
•reshape
•resize
•permute
•squeeze
•deal
19.2 Broadcasting
Broadcasting refers to how Octave binary operators and functions behave when their matrix
or array operands or arguments differ in size. Since version 3.6.0, Octave now automati-
cally broadcasts vectors, matrices, and arrays when using elementwise binary operators and
functions. Broadly speaking, smaller arrays are “broadcast” across the larger one, until
they have a compatible shape. The rule is that corresponding array dimensions must either
1. be equal, or
2. one of them must be 1.
In case all dimensions are equal, no broadcasting occurs and ordinary element-by-element
arithmetic takes place. For arrays of higher dimensions, if the number of dimensions isn’t
the same, then missing trailing dimensions are treated as 1. When one of the dimensions is
1, the array with that singleton dimension gets copied along that dimension until it matches
the dimension of the other array. For example, consider
x=[123;
4 5 6;
7 8 9];
y = [10 20 30];
x+y
532 GNU Octave
Without broadcasting, x + y would be an error because the dimensions do not agree. How-
ever, with broadcasting it is as if the following operation were performed:
x=[123
456
7 8 9];
y = [10 20 30
10 20 30
10 20 30];
x+y
⇒11 22 33
14 25 36
17 28 39
That is, the smaller array of size [1 3] gets copied along the singleton dimension (the
number of rows) until it is [3 3]. No actual copying takes place, however. The internal im-
plementation reuses elements along the necessary dimension in order to achieve the desired
effect without copying in memory.
Both arrays can be broadcast across each other, for example, all pairwise differences of
the elements of a vector with itself:
y - y’
⇒0 10 20
-10 0 10
-20 -10 0
Here the vectors of size [1 3] and [3 1] both get broadcast into matrices of size [3 3]
before ordinary matrix subtraction takes place.
A special case of broadcasting that may be familiar is when all dimensions of the array
being broadcast are 1, i.e., the array is a scalar. Thus for example, operations like x - 42
and max (x, 2) are basic examples of broadcasting.
For a higher-dimensional example, suppose img is an RGB image of size [m n 3] and we
wish to multiply each color by a different scalar. The following code accomplishes this with
broadcasting,
img .*= permute ([0.8, 0.9, 1.2], [1, 3, 2]);
Note the usage of permute to match the dimensions of the [0.8, 0.9, 1.2] vector with
img.
For functions that are not written with broadcasting semantics, bsxfun can be useful
for coercing them to broadcast.
bsxfun (f,A,B)
The binary singleton expansion function performs broadcasting, that is, it applies a
binary function felement-by-element to two array arguments Aand B, and expands
as necessary singleton dimensions in either input argument.
fis a function handle, inline function, or string containing the name of the function to
evaluate. The function fmust be capable of accepting two column-vector arguments
of equal length, or one column vector argument and a scalar.
Chapter 19: Vectorization and Faster Code Execution 533
The dimensions of Aand Bmust be equal or singleton. The singleton dimensions of
the arrays will be expanded to the same dimensionality as the other array.
See also: [arrayfun], page 534,[cellfun], page 536.
Broadcasting is only applied if either of the two broadcasting conditions hold. As usual,
however, broadcasting does not apply when two dimensions differ and neither is 1:
x=[123
4 5 6];
y = [10 20
30 40];
x+y
This will produce an error about nonconformant arguments.
Besides common arithmetic operations, several functions of two arguments also broad-
cast. The full list of functions and operators that broadcast is
plus + .+
minus - .-
times .*
rdivide ./
ldivide .\
power .^ .**
lt <
le <=
eq ==
gt >
ge >=
ne != ~=
and &
or |
atan2
hypot
max
min
mod
rem
xor
+= -= .+= .-= .*= ./= .\= .^= .**= &= |=
Beware of resorting to broadcasting if a simpler operation will suffice. For matrices a
and b, consider the following:
c= sum (permute (a, [1, 3, 2]) .* permute (b, [3, 2, 1]), 3);
This operation broadcasts the two matrices with permuted dimensions across each other
during elementwise multiplication in order to obtain a larger 3-D array, and this array is
then summed along the third dimension. A moment of thought will prove that this operation
is simply the much faster ordinary matrix multiplication, c=a*b;.
534 GNU Octave
A note on terminology: “broadcasting” is the term popularized by the Numpy numerical
environment in the Python programming language. In other programming languages and
environments, broadcasting may also be known as binary singleton expansion (BSX, in
matlab, and the origin of the name of the bsxfun function), recycling (R programming
language), single-instruction multiple data (SIMD), or replication.
19.2.1 Broadcasting and Legacy Code
The new broadcasting semantics almost never affect code that worked in previous versions
of Octave. Consequently, all code inherited from matlab that worked in previous versions
of Octave should still work without change in Octave. The only exception is code such as
try
c = a.*b;
catch
c = a.*a;
end_try_catch
that may have relied on matrices of different size producing an error. Because such operation
is now valid Octave syntax, this will no longer produce an error. Instead, the following code
should be used:
if (isequal (size (a), size (b)))
c=a.*b;
else
c=a.*a;
endif
19.3 Function Application
As a general rule, functions should already be written with matrix arguments in mind
and should consider whole matrix operations in a vectorized manner. Sometimes, writing
functions in this way appears difficult or impossible for various reasons. For those situations,
Octave provides facilities for applying a function to each element of an array, cell, or struct.
arrayfun (func,A)
x= arrayfun (func,A)
x= arrayfun (func,A,b, . . . )
[x,y, ...] = arrayfun (func,A, . . . )
arrayfun (. . ., "UniformOutput",val)
arrayfun (. . ., "ErrorHandler",errfunc)
Execute a function on each element of an array.
This is useful for functions that do not accept array arguments. If the function does
accept array arguments it is better to call the function directly.
The first input argument func can be a string, a function handle, an inline function, or
an anonymous function. The input argument Acan be a logic array, a numeric array,
a string array, a structure array, or a cell array. By a call of the function arrayfun
all elements of Aare passed on to the named function func individually.
The named function can also take more than two input arguments, with the input
arguments given as third input argument b, fourth input argument c, . . . If given
Chapter 19: Vectorization and Faster Code Execution 535
more than one array input argument then all input arguments must have the same
sizes, for example:
arrayfun (@atan2, [1, 0], [0, 1])
⇒[ 1.57080 0.00000 ]
If the parameter val after a further string input argument "UniformOutput" is set
true (the default), then the named function func must return a single element which
then will be concatenated into the return value and is of type matrix. Otherwise, if
that parameter is set to false, then the outputs are concatenated in a cell array. For
example:
arrayfun (@(x,y) x:y, "abc", "def", "UniformOutput", false)
⇒{
[1,1] = abcd
[1,2] = bcde
[1,3] = cdef
}
If more than one output arguments are given then the named function must return
the number of return values that also are expected, for example:
[A, B, C] = arrayfun (@find, [10; 0], "UniformOutput", false)
⇒
A =
{
[1,1] = 1
[2,1] = [](0x0)
}
B =
{
[1,1] = 1
[2,1] = [](0x0)
}
C =
{
[1,1] = 10
[2,1] = [](0x0)
}
If the parameter errfunc after a further string input argument "ErrorHandler" is
another string, a function handle, an inline function, or an anonymous function,
then errfunc defines a function to call in the case that func generates an error. The
definition of the function must be of the form
function [...] = errfunc (s, ...)
where there is an additional input argument to errfunc relative to func, given by
s. This is a structure with the elements "identifier","message", and "index"
giving, respectively, the error identifier, the error message, and the index of the array
elements that caused the error. The size of the output argument of errfunc must have
536 GNU Octave
the same size as the output argument of func, otherwise a real error is thrown. For
example:
function y = ferr (s, x), y = "MyString"; endfunction
arrayfun (@str2num, [1234],
"UniformOutput", false, "ErrorHandler", @ferr)
⇒{
[1,1] = MyString
}
See also: [spfun], page 536,[cellfun], page 536,[structfun], page 538.
y= spfun (f,S)
Compute f(S)for the nonzero values of S.
This results in a sparse matrix with the same structure as S. The function fcan be
passed as a string, a function handle, or an inline function.
See also: [arrayfun], page 534,[cellfun], page 536,[structfun], page 538.
cellfun (name,C)
cellfun ("size",C,k)
cellfun ("isclass",C,class)
cellfun (func,C)
cellfun (func,C,D)
[a, ...] = cellfun (. . . )
cellfun (. . ., "ErrorHandler",errfunc)
cellfun (. . ., "UniformOutput",val)
Evaluate the function named name on the elements of the cell array C.
Elements in Care passed on to the named function individually. The function name
can be one of the functions
isempty Return 1 for empty elements.
islogical
Return 1 for logical elements.
isnumeric
Return 1 for numeric elements.
isreal Return 1 for real elements.
length Return a vector of the lengths of cell elements.
ndims Return the number of dimensions of each element.
numel
prodofsize
Return the number of elements contained within each cell element. The
number is the product of the dimensions of the object at each cell element.
size Return the size along the k-th dimension.
isclass Return 1 for elements of class.
Chapter 19: Vectorization and Faster Code Execution 537
Additionally, cellfun accepts an arbitrary function func in the form of an inline
function, function handle, or the name of a function (in a character string). The
function can take one or more arguments, with the inputs arguments given by C,D,
etc. Equally the function can return one or more output arguments. For example:
cellfun ("atan2", {1, 0}, {0, 1})
⇒[ 1.57080 0.00000 ]
The number of output arguments of cellfun matches the number of output argu-
ments of the function. The outputs of the function will be collected into the output
arguments of cellfun like this:
function [a, b] = twoouts (x)
a = x;
b = x*x;
endfunction
[aa, bb] = cellfun (@twoouts, {1, 2, 3})
⇒aa =
123
bb =
149
Note that per default the output argument(s) are arrays of the same size as the input
arguments. Input arguments that are singleton (1x1) cells will be automatically
expanded to the size of the other arguments.
If the parameter "UniformOutput" is set to true (the default), then the function
must return scalars which will be concatenated into the return array(s). If
"UniformOutput" is false, the outputs are concatenated into a cell array (or cell
arrays). For example:
cellfun ("tolower", {"Foo", "Bar", "FooBar"},
"UniformOutput", false)
⇒{"foo", "bar", "foobar"}
Given the parameter "ErrorHandler", then errfunc defines a function to call in case
func generates an error. The form of the function is
function [...] = errfunc (s, ...)
where there is an additional input argument to errfunc relative to func, given by
s. This is a structure with the elements "identifier","message", and "index"
giving respectively the error identifier, the error message, and the index into the
input arguments of the element that caused the error. For example:
function y = foo (s, x), y = NaN; endfunction
cellfun ("factorial", {-1,2}, "ErrorHandler", @foo)
⇒[NaN 2]
Use cellfun intelligently. The cellfun function is a useful tool for avoiding loops.
It is often used with anonymous function handles; however, calling an anonymous
function involves an overhead quite comparable to the overhead of an m-file function.
Passing a handle to a built-in function is faster, because the interpreter is not involved
in the internal loop. For example:
538 GNU Octave
a = {...}
v = cellfun (@(x) det (x), a); # compute determinants
v = cellfun (@det, a); # faster
See also: [arrayfun], page 534,[structfun], page 538,[spfun], page 536.
structfun (func,S)
[A, ...] = structfun (. . . )
structfun (. . ., "ErrorHandler",errfunc)
structfun (. . ., "UniformOutput",val)
Evaluate the function named name on the fields of the structure S. The fields of S
are passed to the function func individually.
structfun accepts an arbitrary function func in the form of an inline function, func-
tion handle, or the name of a function (in a character string). In the case of a
character string argument, the function must accept a single argument named x, and
it must return a string value. If the function returns more than one argument, they
are returned as separate output variables.
If the parameter "UniformOutput" is set to true (the default), then the function
must return a single element which will be concatenated into the return value. If
"UniformOutput" is false, the outputs are placed into a structure with the same
fieldnames as the input structure.
s.name1 = "John Smith";
s.name2 = "Jill Jones";
structfun (@(x) regexp (x, ’(\w+)$’, "matches"){1}, s,
"UniformOutput", false)
⇒{
name1 = Smith
name2 = Jones
}
Given the parameter "ErrorHandler",errfunc defines a function to call in case func
generates an error. The form of the function is
function [...] = errfunc (se, ...)
where there is an additional input argument to errfunc relative to func, given by
se. This is a structure with the elements "identifier","message" and "index",
giving respectively the error identifier, the error message, and the index into the input
arguments of the element that caused the error. For an example on how to use an
error handler, see [cellfun], page 536.
See also: [cellfun], page 536,[arrayfun], page 534,[spfun], page 536.
Consistent with earlier advice, seek to use Octave built-in functions whenever possible
for the best performance. This advice applies especially to the four functions above. For
example, when adding two arrays together element-by-element one could use a handle to
the built-in addition function @plus or define an anonymous function @(x,y) x + y. But,
the anonymous function is 60% slower than the first method. See Section 34.4.2 [Opera-
tor Overloading], page 780, for a list of basic functions which might be used in place of
anonymous ones.
Chapter 19: Vectorization and Faster Code Execution 539
19.4 Accumulation
Whenever it’s possible to categorize according to indices the elements of an array when
performing a computation, accumulation functions can be useful.
accumarray (subs,vals,sz,func,fillval,issparse)
accumarray (subs,vals, . . . )
Create an array by accumulating the elements of a vector into the positions defined
by their subscripts.
The subscripts are defined by the rows of the matrix subs and the values by vals.
Each row of subs corresponds to one of the values in vals. If vals is a scalar, it will
be used for each of the row of subs. If subs is a cell array of vectors, all vectors must
be of the same length, and the subscripts in the kth vector must correspond to the
kth dimension of the result.
The size of the matrix will be determined by the subscripts themselves. However, if
sz is defined it determines the matrix size. The length of sz must correspond to the
number of columns in subs. An exception is if subs has only one column, in which
case sz may be the dimensions of a vector and the subscripts of subs are taken as the
indices into it.
The default action of accumarray is to sum the elements with the same subscripts.
This behavior can be modified by defining the func function. This should be a function
or function handle that accepts a column vector and returns a scalar. The result of
the function should not depend on the order of the subscripts.
The elements of the returned array that have no subscripts associated with them are
set to zero. Defining fillval to some other value allows these values to be defined. This
behavior changes, however, for certain values of func. If func is min (respectively, max)
then the result will be filled with the minimum (respectively, maximum) integer if
vals is of integral type, logical false (respectively, logical true) if vals is of logical type,
zero if fillval is zero and all values are non-positive (respectively, non-negative), and
NaN otherwise.
By default accumarray returns a full matrix. If issparse is logically true, then a sparse
matrix is returned instead.
The following accumarray example constructs a frequency table that in the first
column counts how many occurrences each number in the second column has, taken
from the vector x. Note the usage of unique for assigning to all repeated elements of
xthe same index (see [unique], page 679).
x= [91, 92, 90, 92, 90, 89, 91, 89, 90, 100, 100, 100];
[u, ~, j] = unique (x);
[accumarray(j’, 1), u’]
⇒2 89
3 90
2 91
2 92
3 100
Another example, where the result is a multi-dimensional 3-D array and the default
value (zero) appears in the output:
540 GNU Octave
accumarray ([1, 1, 1;
2, 1, 2;
2, 3, 2;
2, 1, 2;
2, 3, 2], 101:105)
⇒ans(:,:,1) = [101, 0, 0; 0, 0, 0]
⇒ans(:,:,2) = [0, 0, 0; 206, 0, 208]
The sparse option can be used as an alternative to the sparse constructor (see [sparse],
page 564). Thus
sparse (i,j,sv)
can be written with accumarray as
accumarray ([i,j], sv’, [], [], 0, true)
For repeated indices, sparse adds the corresponding value. To take the minimum
instead, use min as an accumulator function:
accumarray ([i,j], sv’, [], @min, 0, true)
The complexity of accumarray in general for the non-sparse case is generally O(M+N),
where N is the number of subscripts and M is the maximum subscript (linearized in
multi-dimensional case). If func is one of @sum (default), @max,@min or @(x) {x}, an
optimized code path is used. Note that for general reduction function the interpreter
overhead can play a major part and it may be more efficient to do multiple accumarray
calls and compute the results in a vectorized manner.
See also: [accumdim], page 540,[unique], page 679,[sparse], page 564.
accumdim (subs,vals,dim,n,func,fillval)
Create an array by accumulating the slices of an array into the positions defined by
their subscripts along a specified dimension.
The subscripts are defined by the index vector subs. The dimension is specified by
dim. If not given, it defaults to the first non-singleton dimension. The length of subs
must be equal to size (vals,dim).
The extent of the result matrix in the working dimension will be determined by the
subscripts themselves. However, if nis defined it determines this extent.
The default action of accumdim is to sum the subarrays with the same subscripts. This
behavior can be modified by defining the func function. This should be a function or
function handle that accepts an array and a dimension, and reduces the array along
this dimension. As a special exception, the built-in min and max functions can be
used directly, and accumdim accounts for the middle empty argument that is used in
their calling.
The slices of the returned array that have no subscripts associated with them are set
to zero. Defining fillval to some other value allows these values to be defined.
An example of the use of accumdim is:

Chapter 19: Vectorization and Faster Code Execution 541
accumdim ([1, 2, 1, 2, 1], [ 7, -10, 4;
-5, -12, 8;
-12, 2, 8;
-10, 9, -3;
-5, -3, -13])
⇒[-10,-11,-1;-15,-3,5]
See also: [accumarray], page 539.
19.5 JIT Compiler
Vectorization is the preferred technique for eliminating loops and speeding up code. Nev-
ertheless, it is not always possible to replace every loop. In such situations it may be worth
trying Octave’s experimental Just-In-Time (JIT) compiler.
A JIT compiler works by analyzing the body of a loop, translating the Octave statements
into another language, compiling the new code segment into an executable, and then running
the executable and collecting any results. The process is not simple and there is a significant
amount of work to perform for each step. It can still make sense, however, if the number
of loop iterations is large. Because Octave is an interpreted language every time through
a loop Octave must parse the statements in the loop body before executing them. With a
JIT compiler this is done just once when the body is translated to another language.
The JIT compiler is a very new feature in Octave and not all valid Octave statements
can currently be accelerated. However, if no other technique is available it may be worth
benchmarking the code with JIT enabled. The function jit_enable is used to turn compi-
lation on or off. The function jit_startcnt sets the threshold for acceleration. Loops with
iteration counts above jit_startcnt will be accelerated. The functions jit_failcnt and
debug_jit are not likely to be of use to anyone not working directly on the implementation
of the JIT compiler.
val = jit_enable ()
old_val = jit_enable (new_val)
jit_enable (new_val,"local")
Query or set the internal variable that enables Octave’s JIT compiler.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [jit startcnt], page 541,[debug jit], page 542.
val = jit_startcnt ()
old_val = jit_startcnt (new_val)
jit_startcnt (new_val,"local")
Query or set the internal variable that determines whether JIT compilation will take
place for a specific loop.
Because compilation is a costly operation it does not make sense to employ JIT when
the loop count is low. By default only loops with greater than 1000 iterations will be
accelerated.
542 GNU Octave
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [jit enable], page 541,[jit failcnt], page 542,[debug jit], page 542.
val = jit_failcnt ()
old_val = jit_failcnt (new_val)
jit_failcnt (new_val,"local")
Query or set the internal variable that counts the number of JIT fail exceptions for
Octave’s JIT compiler.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [jit enable], page 541,[jit startcnt], page 541,[debug jit], page 542.
val = debug_jit ()
old_val = debug_jit (new_val)
debug_jit (new_val,"local")
Query or set the internal variable that determines whether debugging/tracing is en-
abled for Octave’s JIT compiler.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [jit enable], page 541,[jit startcnt], page 541.
19.6 Miscellaneous Techniques
Here are some other ways of improving the execution speed of Octave programs.
•Avoid computing costly intermediate results multiple times. Octave currently does
not eliminate common subexpressions. Also, certain internal computation results are
cached for variables. For instance, if a matrix variable is used multiple times as an
index, checking the indices (and internal conversion to integers) is only done once.
•Be aware of lazy copies (copy-on-write). When a copy of an object is created, the data
is not immediately copied, but rather shared. The actual copying is postponed until
the copied data needs to be modified. For example:
a = zeros (1000); # create a 1000x1000 matrix
b = a; # no copying done here
b(1) = 1; # copying done here
Lazy copying applies to whole Octave objects such as matrices, cells, struct, and also
individual cell or struct elements (not array elements).
Additionally, index expressions also use lazy copying when Octave can determine that
the indexed portion is contiguous in memory. For example:
a = zeros (1000); # create a 1000x1000 matrix
b = a(:,10:100); # no copying done here
b = a(10:100,:); # copying done here
Chapter 19: Vectorization and Faster Code Execution 543
This applies to arrays (matrices), cell arrays, and structs indexed using ‘()’. Index
expressions generating comma-separated lists can also benefit from shallow copying in
some cases. In particular, when ais a struct array, expressions like {a.x}, {a(:,2).x}
will use lazy copying, so that data can be shared between a struct array and a cell array.
Most indexing expressions do not live longer than their parent objects. In rare cases,
however, a lazily copied slice outlasts its parent, in which case it becomes orphaned,
still occupying unnecessarily more memory than needed. To provide a remedy working
in most real cases, Octave checks for orphaned lazy slices at certain situations, when a
value is stored into a "permanent"location, such as a named variable or cell or struct
element, and possibly economizes them. For example:
a = zeros (1000); # create a 1000x1000 matrix
b = a(:,10:100); # lazy slice
a = []; # the original "a" array is still allocated
c{1} = b; # b is reallocated at this point
•Avoid deep recursion. Function calls to m-file functions carry a relatively significant
overhead, so rewriting a recursion as a loop often helps. Also, note that the maximum
level of recursion is limited.
•Avoid resizing matrices unnecessarily. When building a single result matrix from a
series of calculations, set the size of the result matrix first, then insert values into it.
Write
result = zeros (big_n, big_m)
for i = over:and_over
ridx = ...
cidx = ...
result(ridx, cidx) = new_value ();
endfor
instead of
result = [];
for i = ever:and_ever
result = [ result, new_value() ];
endfor
Sometimes the number of items can not be computed in advance, and stack-like oper-
ations are needed. When elements are being repeatedly inserted or removed from the
end of an array, Octave detects it as stack usage and attempts to use a smarter memory
management strategy by pre-allocating the array in bigger chunks. This strategy is also
applied to cell and struct arrays.
a = [];
while (condition)
...
a(end+1) = value; # "push" operation
...
a(end) = []; # "pop" operation
...
endwhile
544 GNU Octave
•Avoid calling eval or feval excessively. Parsing input or looking up the name of a
function in the symbol table are relatively expensive operations.
If you are using eval merely as an exception handling mechanism, and not because you
need to execute some arbitrary text, use the try statement instead. See Section 10.9
[The try Statement], page 170.
•Use ignore_function_time_stamp when appropriate. If you are calling lots of func-
tions, and none of them will need to change during your run, set the variable ignore_
function_time_stamp to "all". This will stop Octave from checking the time stamp
of a function file to see if it has been updated while the program is being run.
19.7 Examples
The following are examples of vectorization questions asked by actual users of Octave and
their solutions.
•For a vector A, the following loop
n = length (A);
B = zeros (n, 2);
for i = 1:length (A)
## this will be two columns, the first is the difference and
## the second the mean of the two elements used for the diff.
B(i,:) = [A(i+1)-A(i), (A(i+1) + A(i))/2];
endfor
can be turned into the following one-liner:
B = [diff(A)(:), 0.5*(A(1:end-1)+A(2:end))(:)]
Note the usage of colon indexing to flatten an intermediate result into a column vector.
This is a common vectorization trick.
545
20 Nonlinear Equations
20.1 Solvers
Octave can solve sets of nonlinear equations of the form
f(x)=0
using the function fsolve, which is based on the minpack subroutine hybrd. This is an
iterative technique so a starting point must be provided. This also has the consequence
that convergence is not guaranteed even if a solution exists.
fsolve (fcn,x0,options)
[x,fvec,info,output,fjac] = fsolve (fcn, . . . )
Solve a system of nonlinear equations defined by the function fcn.
fcn should accept a vector (array) defining the unknown variables, and return a vector
of left-hand sides of the equations. Right-hand sides are defined to be zeros. In
other words, this function attempts to determine a vector xsuch that fcn (x)gives
(approximately) all zeros.
x0 determines a starting guess. The shape of x0 is preserved in all calls to fcn, but
otherwise it is treated as a column vector.
options is a structure specifying additional options. Currently, fsolve
recognizes these options: "FunValCheck","OutputFcn","TolX","TolFun",
"MaxIter","MaxFunEvals","Jacobian","Updating","ComplexEqn" "TypicalX",
"AutoScaling" and "FinDiffType".
If "Jacobian" is "on", it specifies that fcn, called with 2 output arguments also re-
turns the Jacobian matrix of right-hand sides at the requested point. "TolX" specifies
the termination tolerance in the unknown variables, while "TolFun" is a tolerance for
equations. Default is 1e-7 for both "TolX" and "TolFun".
If "AutoScaling" is on, the variables will be automatically scaled according to the
column norms of the (estimated) Jacobian. As a result, TolF becomes scaling-
independent. By default, this option is off because it may sometimes deliver un-
expected (though mathematically correct) results.
If "Updating" is "on", the function will attempt to use Broyden updates to update
the Jacobian, in order to reduce the amount of Jacobian calculations. If your user
function always calculates the Jacobian (regardless of number of output arguments)
then this option provides no advantage and should be set to false.
"ComplexEqn" is "on",fsolve will attempt to solve complex equations in complex
variables, assuming that the equations possess a complex derivative (i.e., are holo-
morphic). If this is not what you want, you should unpack the real and imaginary
parts of the system to get a real system.
For description of the other options, see optimset.
On return, fval contains the value of the function fcn evaluated at x.
info may be one of the following values:
1 Converged to a solution point. Relative residual error is less than specified
by TolFun.
546 GNU Octave
2 Last relative step size was less that TolX.
3 Last relative decrease in residual was less than TolF.
0 Iteration limit exceeded.
-3 The trust region radius became excessively small.
Note: If you only have a single nonlinear equation of one variable, using fzero is
usually a much better idea.
Note about user-supplied Jacobians: As an inherent property of the algorithm, a
Jacobian is always requested for a solution vector whose residual vector is already
known, and it is the last accepted successful step. Often this will be one of the last
two calls, but not always. If the savings by reusing intermediate results from residual
calculation in Jacobian calculation are significant, the best strategy is to employ
OutputFcn: After a vector is evaluated for residuals, if OutputFcn is called with that
vector, then the intermediate results should be saved for future Jacobian evaluation,
and should be kept until a Jacobian evaluation is requested or until OutputFcn is
called with a different vector, in which case they should be dropped in favor of this
most recent vector. A short example how this can be achieved follows:
function [fvec, fjac] = user_func (x, optimvalues, state)
persistent sav = [], sav0 = [];
if (nargin == 1)
## evaluation call
if (nargout == 1)
sav0.x = x; # mark saved vector
## calculate fvec, save results to sav0.
elseif (nargout == 2)
## calculate fjac using sav.
endif
else
## outputfcn call.
if (all (x == sav0.x))
sav = sav0;
endif
## maybe output iteration status, etc.
endif
endfunction
## ...
fsolve (@user_func, x0, optimset ("OutputFcn", @user_func, ...))
See also: [fzero], page 547,[optimset], page 641.
The following is a complete example. To solve the set of equations
−2x2+ 3xy + 4 sin(y)−6=0
3x2−2xy2+ 3 cos(x) + 4 = 0

Chapter 20: Nonlinear Equations 547
you first need to write a function to compute the value of the given function. For example:
function y = f (x)
y = zeros (2, 1);
y(1) = -2*x(1)^2 + 3*x(1)*x(2) + 4*sin(x(2)) - 6;
y(2) = 3*x(1)^2 - 2*x(1)*x(2)^2 + 3*cos(x(1)) + 4;
endfunction
Then, call fsolve with a specified initial condition to find the roots of the system of
equations. For example, given the function fdefined above,
[x, fval, info] = fsolve (@f, [1; 2])
results in the solution
x =
0.57983
2.54621
fval =
-5.7184e-10
5.5460e-10
info = 1
A value of info = 1 indicates that the solution has converged.
When no Jacobian is supplied (as in the example above) it is approximated numerically.
This requires more function evaluations, and hence is less efficient. In the example above
we could compute the Jacobian analytically as
∂f1
∂x1
∂f1
∂x2
∂f2
∂x1
∂f2
∂x2=3x2−4x14 cos(x2)+3x1
−2x2
2−3 sin(x1)+6x1−4x1x2
and compute it with the following Octave function
function [y, jac] = f (x)
y = zeros (2, 1);
y(1) = -2*x(1)^2 + 3*x(1)*x(2) + 4*sin(x(2)) - 6;
y(2) = 3*x(1)^2 - 2*x(1)*x(2)^2 + 3*cos(x(1)) + 4;
if (nargout == 2)
jac = zeros (2, 2);
jac(1,1) = 3*x(2) - 4*x(1);
jac(1,2) = 4*cos(x(2)) + 3*x(1);
jac(2,1) = -2*x(2)^2 - 3*sin(x(1)) + 6*x(1);
jac(2,2) = -4*x(1)*x(2);
endif
endfunction
The Jacobian can then be used with the following call to fsolve:
[x, fval, info] = fsolve (@f, [1; 2], optimset ("jacobian", "on"));
which gives the same solution as before.
548 GNU Octave
fzero (fun,x0)
fzero (fun,x0,options)
[x,fval,info,output] = fzero (. . . )
Find a zero of a univariate function.
fun is a function handle, inline function, or string containing the name of the function
to evaluate.
x0 should be a two-element vector specifying two points which bracket a zero. In
other words, there must be a change in sign of the function between x0(1) and x0(2).
More mathematically, the following must hold
sign (fun(x0(1))) * sign (fun(x0(2))) <= 0
If x0 is a single scalar then several nearby and distant values are probed in an attempt
to obtain a valid bracketing. If this is not successful, the function fails.
options is a structure specifying additional options. Currently, fzero recognizes these
options: "FunValCheck","OutputFcn","TolX","MaxIter","MaxFunEvals". For a
description of these options, see [optimset], page 641.
On exit, the function returns x, the approximate zero point and fval, the function
value thereof.
info is an exit flag that can have these values:
•1 The algorithm converged to a solution.
•0 Maximum number of iterations or function evaluations has been reached.
•-1 The algorithm has been terminated from user output function.
•-5 The algorithm may have converged to a singular point.
output is a structure containing runtime information about the fzero algorithm.
Fields in the structure are:
•iterations Number of iterations through loop.
•nfev Number of function evaluations.
•bracketx A two-element vector with the final bracketing of the zero along the
x-axis.
•brackety A two-element vector with the final bracketing of the zero along the
y-axis.
See also: [optimset], page 641,[fsolve], page 545.
20.2 Minimizers
Often it is useful to find the minimum value of a function rather than just the zeroes
where it crosses the x-axis. fminbnd is designed for the simpler, but very common, case of a
univariate function where the interval to search is bounded. For unbounded minimization of
a function with potentially many variables use fminunc or fminsearch. The two functions
use different internal algorithms and some knowledge of the objective function is required.
For functions which can be differentiated, fminunc is appropriate. For functions with
discontinuities, or for which a gradient search would fail, use fminsearch. See Chapter 25
[Optimization], page 629, for minimization with the presence of constraint functions. Note
that searches can be made for maxima by simply inverting the objective function (Fmax =
−Fmin).
Chapter 20: Nonlinear Equations 549
[x,fval,info,output] = fminbnd (fun,a,b,options)
Find a minimum point of a univariate function.
fun should be a function handle or name. a,bspecify a starting interval. options
is a structure specifying additional options. Currently, fminbnd recognizes these
options: "FunValCheck","OutputFcn","TolX","MaxIter","MaxFunEvals". For a
description of these options, see [optimset], page 641.
On exit, the function returns x, the approximate minimum point and fval, the function
value thereof.
info is an exit flag that can have these values:
•1 The algorithm converged to a solution.
•0 Maximum number of iterations or function evaluations has been exhausted.
•-1 The algorithm has been terminated from user output function.
Notes: The search for a minimum is restricted to be in the interval bound by aand
b. If you only have an initial point to begin searching from you will need to use
an unconstrained minimization algorithm such as fminunc or fminsearch.fminbnd
internally uses a Golden Section search strategy.
See also: [fzero], page 547,[fminunc], page 549,[fminsearch], page 550,[optimset],
page 641.
fminunc (fcn,x0)
fminunc (fcn,x0,options)
[x,fval,info,output,grad,hess] = fminunc (fcn, . . . )
Solve an unconstrained optimization problem defined by the function fcn.
fcn should accept a vector (array) defining the unknown variables, and return the
objective function value, optionally with gradient. fminunc attempts to determine a
vector xsuch that fcn (x)is a local minimum.
x0 determines a starting guess. The shape of x0 is preserved in all calls to fcn, but
otherwise is treated as a column vector.
options is a structure specifying additional options. Currently, fminunc recognizes
these options: "FunValCheck","OutputFcn","TolX","TolFun","MaxIter",
"MaxFunEvals","GradObj","FinDiffType","TypicalX","AutoScaling".
If "GradObj" is "on", it specifies that fcn, when called with two output arguments,
also returns the Jacobian matrix of partial first derivatives at the requested point.
TolX specifies the termination tolerance for the unknown variables x, while TolFun is
a tolerance for the objective function value fval. The default is 1e-7 for both options.
For a description of the other options, see optimset.
On return, xis the location of the minimum and fval contains the value of the objective
function at x.
info may be one of the following values:
1 Converged to a solution point. Relative gradient error is less than speci-
fied by TolFun.
2 Last relative step size was less than TolX.
550 GNU Octave
3 Last relative change in function value was less than TolFun.
0 Iteration limit exceeded—either maximum number of algorithm iterations
MaxIter or maximum number of function evaluations MaxFunEvals.
-1 Algorithm terminated by OutputFcn.
-3 The trust region radius became excessively small.
Optionally, fminunc can return a structure with convergence statistics (output), the
output gradient (grad) at the solution x, and approximate Hessian (hess) at the
solution x.
Application Notes: If the objective function is a single nonlinear equation of one
variable then using fminbnd is usually a better choice.
The algorithm used by fminunc is a gradient search which depends on the objective
function being differentiable. If the function has discontinuities it may be better to
use a derivative-free algorithm such as fminsearch.
See also: [fminbnd], page 548,[fminsearch], page 550,[optimset], page 641.
x= fminsearch (fun,x0)
x= fminsearch (fun,x0,options)
[x,fval] = fminsearch (. . . )
Find a value of xwhich minimizes the function fun.
The search begins at the point x0 and iterates using the Nelder & Mead Simplex
algorithm (a derivative-free method). This algorithm is better-suited to functions
which have discontinuities or for which a gradient-based search such as fminunc fails.
Options for the search are provided in the parameter options using the function
optimset. Currently, fminsearch accepts the options: "TolX","MaxFunEvals",
"MaxIter","Display". For a description of these options, see optimset.
On exit, the function returns x, the minimum point, and fval, the function value
thereof.
Example usages:
fminsearch (@(x) (x(1)-5).^2+(x(2)-8).^4, [0;0])
fminsearch (inline ("(x(1)-5).^2+(x(2)-8).^4", "x"), [0;0])
See also: [fminbnd], page 548,[fminunc], page 549,[optimset], page 641.

551
21 Diagonal and Permutation Matrices
21.1 Creating and Manipulating Diagonal/Permutation
Matrices
A diagonal matrix is defined as a matrix that has zero entries outside the main diagonal;
that is, Dij = 0 if i6=jMost often, square diagonal matrices are considered; however, the
definition can equally be applied to non-square matrices, in which case we usually speak of
a rectangular diagonal matrix.
A permutation matrix is defined as a square matrix that has a single element equal to
unity in each row and each column; all other elements are zero. That is, there exists a
permutation (vector) psuch that Pij = 1 if j=piand Pij = 0 otherwise.
Octave provides special treatment of real and complex rectangular diagonal matrices,
as well as permutation matrices. They are stored as special objects, using efficient storage
and algorithms, facilitating writing both readable and efficient matrix algebra expressions
in the Octave language. The special treatment may be disabled by using the functions
disable diagonal matrix and disable permutation matrix.
val = disable_diagonal_matrix ()
old_val = disable_diagonal_matrix (new_val)
disable_diagonal_matrix (new_val,"local")
Query or set the internal variable that controls whether diagonal matrices are stored
in a special space-efficient format.
The default value is true. If this option is disabled Octave will store diagonal matrices
as full matrices.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [disable range], page 53,[disable permutation matrix], page 551.
val = disable_permutation_matrix ()
old_val = disable_permutation_matrix (new_val)
disable_permutation_matrix (new_val,"local")
Query or set the internal variable that controls whether permutation matrices are
stored in a special space-efficient format.
The default value is true. If this option is disabled Octave will store permutation
matrices as full matrices.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [disable range], page 53,[disable diagonal matrix], page 551.
The space savings are significant as demonstrated by the following code.
552 GNU Octave
x = diag (rand (10, 1));
xf = full (x);
sizeof (x)
⇒80
sizeof (xf)
⇒800
21.1.1 Creating Diagonal Matrices
The most common and easiest way to create a diagonal matrix is using the built-in function
diag. The expression diag (v), with va vector, will create a square diagonal matrix with
elements on the main diagonal given by the elements of v, and size equal to the length of v.
diag (v, m, n) can be used to construct a rectangular diagonal matrix. The result of these
expressions will be a special diagonal matrix object, rather than a general matrix object.
Diagonal matrix with unit elements can be created using eye. Some other built-in func-
tions can also return diagonal matrices. Examples include balance or inv.
Example:
diag (1:4)
⇒
Diagonal Matrix
1000
0200
0030
0004
diag (1:3,5,3)
⇒
Diagonal Matrix
100
020
003
000
000
21.1.2 Creating Permutation Matrices
For creating permutation matrices, Octave does not introduce a new function, but rather
overrides an existing syntax: permutation matrices can be conveniently created by indexing
an identity matrix by permutation vectors. That is, if qis a permutation vector of length
n, the expression
P = eye (n) (:, q);
will create a permutation matrix - a special matrix object.
eye (n) (q, :)
will also work (and create a row permutation matrix), as well as
Chapter 21: Diagonal and Permutation Matrices 553
eye (n) (q1, q2).
For example:
eye (4) ([1,3,2,4],:)
⇒
Permutation Matrix
1000
0010
0100
0001
eye (4) (:,[1,3,2,4])
⇒
Permutation Matrix
1000
0010
0100
0001
Mathematically, an identity matrix is both diagonal and permutation matrix. In Oc-
tave, eye (n) returns a diagonal matrix, because a matrix can only have one class. You
can convert this diagonal matrix to a permutation matrix by indexing it by an identity
permutation, as shown below. This is a special property of the identity matrix; indexing
other diagonal matrices generally produces a full matrix.
eye (3)
⇒
Diagonal Matrix
100
010
001
eye(3)(1:3,:)
⇒
Permutation Matrix
100
010
001
Some other built-in functions can also return permutation matrices. Examples include
inv or lu.
21.1.3 Explicit and Implicit Conversions
The diagonal and permutation matrices are special objects in their own right. A number of
operations and built-in functions are defined for these matrices to use special, more efficient
554 GNU Octave
code than would be used for a full matrix in the same place. Examples are given in further
sections.
To facilitate smooth mixing with full matrices, backward compatibility, and compatibility
with matlab, the diagonal and permutation matrices should allow any operation that works
on full matrices, and will either treat it specially, or implicitly convert themselves to full
matrices.
Instances include matrix indexing, except for extracting a single element or a leading
submatrix, indexed assignment, or applying most mapper functions, such as exp.
An explicit conversion to a full matrix can be requested using the built-in function full.
It should also be noted that the diagonal and permutation matrix objects will cache the
result of the conversion after it is first requested (explicitly or implicitly), so that subsequent
conversions will be very cheap.
21.2 Linear Algebra with Diagonal/Permutation Matrices
As has been already said, diagonal and permutation matrices make it possible to use efficient
algorithms while preserving natural linear algebra syntax. This section describes in detail
the operations that are treated specially when performed on these special matrix objects.
21.2.1 Expressions Involving Diagonal Matrices
Assume Dis a diagonal matrix. If Mis a full matrix, then D*M will scale the rows of M.
That means, if S = D*M, then for each pair of indices i,j it holds
Sij =DiiMij
Similarly, M*D will do a column scaling.
The matrix Dmay also be rectangular, m-by-n where m != n. If m < n, then the expres-
sion D*M is equivalent to
D(:,1:m) * M(1:m,:),
i.e., trailing n-m rows of Mare ignored. If m > n, then D*M is equivalent to
[D(1:n,n) * M; zeros(m-n, columns (M))],
i.e., null rows are appended to the result. The situation for right-multiplication M*D is
analogous.
The expressions D \ M and M / D perform inverse scaling. They are equivalent to solv-
ing a diagonal (or rectangular diagonal) in a least-squares minimum-norm sense. In exact
arithmetic, this is equivalent to multiplying by a pseudoinverse. The pseudoinverse of a rec-
tangular diagonal matrix is again a rectangular diagonal matrix with swapped dimensions,
where each nonzero diagonal element is replaced by its reciprocal. The matrix division
algorithms do, in fact, use division rather than multiplication by reciprocals for better nu-
merical accuracy; otherwise, they honor the above definition. Note that a diagonal matrix
is never truncated due to ill-conditioning; otherwise, it would not be of much use for scaling.
This is typically consistent with linear algebra needs. A full matrix that only happens to
be diagonal (and is thus not a special object) is of course treated normally.
Multiplication and division by diagonal matrices work efficiently also when combined
with sparse matrices, i.e., D*S, where Dis a diagonal matrix and Sis a sparse matrix scales
Chapter 21: Diagonal and Permutation Matrices 555
the rows of the sparse matrix and returns a sparse matrix. The expressions S*D,D\S,S/D
work analogically.
If D1 and D2 are both diagonal matrices, then the expressions
D1 + D2
D1 - D2
D1 * D2
D1 / D2
D1 \ D2
again produce diagonal matrices, provided that normal dimension matching rules are
obeyed. The relations used are same as described above.
Also, a diagonal matrix Dcan be multiplied or divided by a scalar, or raised to a scalar
power if it is square, producing diagonal matrix result in all cases.
A diagonal matrix can also be transposed or conjugate-transposed, giving the expected
result. Extracting a leading submatrix of a diagonal matrix, i.e., D(1:m,1:n), will produce
a diagonal matrix, other indexing expressions will implicitly convert to full matrix.
Adding a diagonal matrix to a full matrix only operates on the diagonal elements. Thus,
A = A + eps * eye (n)
is an efficient method of augmenting the diagonal of a matrix. Subtraction works analogi-
cally.
When involved in expressions with other element-by-element operators, .*,./,.\ or .^,
an implicit conversion to full matrix will take place. This is not always strictly necessary
but chosen to facilitate better consistency with matlab.
21.2.2 Expressions Involving Permutation Matrices
If Pis a permutation matrix and Ma matrix, the expression P*M will permute the rows of
M. Similarly, M*P will yield a column permutation. Matrix division P\M and M/P can be
used to do inverse permutation.
The previously described syntax for creating permutation matrices can actually help an
user to understand the connection between a permutation matrix and a permuting vector.
Namely, the following holds, where I = eye (n) is an identity matrix:
I(p,:) * M = (I*M) (p,:) = M(p,:)
Similarly,
M * I(:,p) = (M*I) (:,p) = M(:,p)
The expressions I(p,:) and I(:,p) are permutation matrices.
A permutation matrix can be transposed (or conjugate-transposed, which is the same,
because a permutation matrix is never complex), inverting the permutation, or equivalently,
turning a row-permutation matrix into a column-permutation one. For permutation ma-
trices, transpose is equivalent to inversion, thus P\M is equivalent to P’*M. Transpose of a
permutation matrix (or inverse) is a constant-time operation, flipping only a flag internally,
and thus the choice between the two above equivalent expressions for inverse permuting is
completely up to the user’s taste.
Multiplication and division by permutation matrices works efficiently also when com-
bined with sparse matrices, i.e., P*S, where Pis a permutation matrix and Sis a sparse
556 GNU Octave
matrix permutes the rows of the sparse matrix and returns a sparse matrix. The expressions
S*P,P\S,S/P work analogically.
Two permutation matrices can be multiplied or divided (if their sizes match), performing
a composition of permutations. Also a permutation matrix can be indexed by a permutation
vector (or two vectors), giving again a permutation matrix. Any other operations do not
generally yield a permutation matrix and will thus trigger the implicit conversion.
21.3 Functions That Are Aware of These Matrices
This section lists the built-in functions that are aware of diagonal and permutation matrices
on input, or can return them as output. Passed to other functions, these matrices will in
general trigger an implicit conversion. (Of course, user-defined dynamically linked functions
may also work with diagonal or permutation matrices).
21.3.1 Diagonal Matrix Functions
inv and pinv can be applied to a diagonal matrix, yielding again a diagonal matrix. det will
use an efficient straightforward calculation when given a diagonal matrix, as well as cond.
The following mapper functions can be applied to a diagonal matrix without converting it
to a full one: abs,real,imag,conj,sqrt. A diagonal matrix can also be returned from the
balance and svd functions. The sparse function will convert a diagonal matrix efficiently
to a sparse matrix.
21.3.2 Permutation Matrix Functions
inv and pinv will invert a permutation matrix, preserving its specialness. det can be applied
to a permutation matrix, efficiently calculating the sign of the permutation (which is equal
to the determinant).
A permutation matrix can also be returned from the built-in functions lu and qr, if a
pivoted factorization is requested.
The sparse function will convert a permutation matrix efficiently to a sparse matrix.
The find function will also work efficiently with a permutation matrix, making it possible
to conveniently obtain the permutation indices.
21.4 Examples of Usage
The following can be used to solve a linear system A*x = b using the pivoted LU factoriza-
tion:
[L, U, P] = lu (A); ## now L*U = P*A
x=U\L\P*b;
This is one way to normalize columns of a matrix Xto unit norm:
s = norm (X, "columns");
X /= diag (s);
The same can also be accomplished with broadcasting (see Section 19.2 [Broadcasting],
page 531):
s = norm (X, "columns");
X ./= s;
Chapter 21: Diagonal and Permutation Matrices 557
The following expression is a way to efficiently calculate the sign of a permutation, given
by a permutation vector p. It will also work in earlier versions of Octave, but slowly.
det (eye (length (p))(p, :))
Finally, here’s how to solve a linear system A*x = b with Tikhonov regularization (ridge
regression) using SVD (a skeleton only):
m = rows (A); n = columns (A);
[U, S, V] = svd (A);
## determine the regularization factor alpha
## alpha = ...
## transform to orthogonal basis
b = U’*b;
## Use the standard formula, replacing A with S.
## S is diagonal, so the following will be very fast and accurate.
x = (S’*S + alpha^2 * eye (n)) \ (S’ * b);
## transform to solution basis
x = V*x;
21.5 Differences in Treatment of Zero Elements
Making diagonal and permutation matrices special matrix objects in their own right and
the consequent usage of smarter algorithms for certain operations implies, as a side effect,
small differences in treating zeros. The contents of this section apply also to sparse matrices,
discussed in the following chapter. (see Chapter 22 [Sparse Matrices], page 559)
The IEEE floating point standard defines the result of the expressions 0*Inf and 0*NaN
as NaN. This is widely agreed to be a good compromise. Numerical software dealing with
structured and sparse matrices (including Octave) however, almost always makes a distinc-
tion between a "numerical zero"and an "assumed zero". A "numerical zero"is a zero
value occurring in a place where any floating-point value could occur. It is normally stored
somewhere in memory as an explicit value. An "assumed zero", on the contrary, is a zero
matrix element implied by the matrix structure (diagonal, triangular) or a sparsity pattern;
its value is usually not stored explicitly anywhere, but is implied by the underlying data
structure.
The primary distinction is that an assumed zero, when multiplied by any number, or
divided by any nonzero number, yields *always* a zero, even when, e.g., multiplied by Inf
or divided by NaN. The reason for this behavior is that the numerical multiplication is not
actually performed anywhere by the underlying algorithm; the result is just assumed to be
zero. Equivalently, one can say that the part of the computation involving assumed zeros
is performed symbolically, not numerically.
This behavior not only facilitates the most straightforward and efficient implementation
of algorithms, but also preserves certain useful invariants, like:
•scalar * diagonal matrix is a diagonal matrix
•sparse matrix / scalar preserves the sparsity pattern
•permutation matrix * matrix is equivalent to permuting rows
all of these natural mathematical truths would be invalidated by treating assumed zeros
as numerical ones.
558 GNU Octave
Note that matlab does not strictly follow this principle and converts assumed zeros to
numerical zeros in certain cases, while not doing so in other cases. As of today, there are
no intentions to mimic such behavior in Octave.
Examples of effects of assumed zeros vs. numerical zeros:
Inf * eye (3)
⇒Inf 0 0
0 Inf 0
0 0 Inf
Inf * speye (3)
⇒
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])
(1, 1) -> Inf
(2, 2) -> Inf
(3, 3) -> Inf
Inf * full (eye (3))
⇒Inf NaN NaN
NaN Inf NaN
NaN NaN Inf
diag (1:3) * [NaN; 1; 1]
⇒NaN
2
3
sparse (1:3,1:3,1:3) * [NaN; 1; 1]
⇒NaN
2
3
[1,0,0;0,2,0;0,0,3] * [NaN; 1; 1]
⇒NaN
NaN
NaN

559
22 Sparse Matrices
22.1 Creation and Manipulation of Sparse Matrices
The size of mathematical problems that can be treated at any particular time is generally
limited by the available computing resources. Both, the speed of the computer and its
available memory place limitation on the problem size.
There are many classes of mathematical problems which give rise to matrices, where a
large number of the elements are zero. In this case it makes sense to have a special matrix
type to handle this class of problems where only the nonzero elements of the matrix are
stored. Not only does this reduce the amount of memory to store the matrix, but it also
means that operations on this type of matrix can take advantage of the a priori knowledge
of the positions of the nonzero elements to accelerate their calculations.
A matrix type that stores only the nonzero elements is generally called sparse. It is the
purpose of this document to discuss the basics of the storage and creation of sparse matrices
and the fundamental operations on them.
22.1.1 Storage of Sparse Matrices
It is not strictly speaking necessary for the user to understand how sparse matrices are
stored. However, such an understanding will help to get an understanding of the size of
sparse matrices. Understanding the storage technique is also necessary for those users
wishing to create their own oct-files.
There are many different means of storing sparse matrix data. What all of the methods
have in common is that they attempt to reduce the complexity and storage given a priori
knowledge of the particular class of problems that will be solved. A good summary of
the available techniques for storing sparse matrix is given by Saad1. With full matrices,
knowledge of the point of an element of the matrix within the matrix is implied by its
position in the computers memory. However, this is not the case for sparse matrices, and
so the positions of the nonzero elements of the matrix must equally be stored.
An obvious way to do this is by storing the elements of the matrix as triplets, with two
elements being their position in the array (rows and column) and the third being the data
itself. This is conceptually easy to grasp, but requires more storage than is strictly needed.
The storage technique used within Octave is the compressed column format. It is similar
to the Yale format.2In this format the position of each element in a row and the data are
stored as previously. However, if we assume that all elements in the same column are stored
adjacent in the computers memory, then we only need to store information on the number
of nonzero elements in each column, rather than their positions. Thus assuming that the
matrix has more nonzero elements than there are columns in the matrix, we win in terms
of the amount of memory used.
In fact, the column index contains one more element than the number of columns, with
the first element always being zero. The advantage of this is a simplification in the code, in
1Y. Saad "SPARSKIT: A basic toolkit for sparse matrix computation", 1994, http://www-users.cs.
umn.edu/~saad/software/SPARSKIT/paper.ps
2http://en.wikipedia.org/wiki/Sparse_matrix#Yale_format
560 GNU Octave
that there is no special case for the first or last columns. A short example, demonstrating
this in C is.
for (j = 0; j < nc; j++)
for (i = cidx(j); i < cidx(j+1); i++)
printf ("nonzero element (%i,%i) is %d\n",
ridx(i), j, data(i));
A clear understanding might be had by considering an example of how the above applies
to an example matrix. Consider the matrix
1 2 0 0
0 0 0 3
0 0 0 4
The nonzero elements of this matrix are
(1, 1) ⇒1
(1, 2) ⇒2
(2, 4) ⇒3
(3, 4) ⇒4
This will be stored as three vectors cidx,ridx and data, representing the column indexing,
row indexing and data respectively. The contents of these three vectors for the above matrix
will be
cidx = [0, 1, 2, 2, 4]
ridx = [0, 0, 1, 2]
data = [1, 2, 3, 4]
Note that this is the representation of these elements with the first row and column
assumed to start at zero, while in Octave itself the row and column indexing starts at one.
Thus the number of elements in the i-th column is given by cidx (i+ 1) - cidx (i).
Although Octave uses a compressed column format, it should be noted that compressed
row formats are equally possible. However, in the context of mixed operations between
mixed sparse and dense matrices, it makes sense that the elements of the sparse matrices
are in the same order as the dense matrices. Octave stores dense matrices in column major
ordering, and so sparse matrices are equally stored in this manner.
A further constraint on the sparse matrix storage used by Octave is that all elements in
the rows are stored in increasing order of their row index, which makes certain operations
faster. However, it imposes the need to sort the elements on the creation of sparse matrices.
Having disordered elements is potentially an advantage in that it makes operations such as
concatenating two sparse matrices together easier and faster, however it adds complexity
and speed problems elsewhere.
22.1.2 Creating Sparse Matrices
There are several means to create sparse matrix.
Returned from a function
There are many functions that directly return sparse matrices. These include
speye,sprand,diag, etc.
Chapter 22: Sparse Matrices 561
Constructed from matrices or vectors
The function sparse allows a sparse matrix to be constructed from three vectors
representing the row, column and data. Alternatively, the function spconvert
uses a three column matrix format to allow easy importation of data from
elsewhere.
Created and then filled
The function sparse or spalloc can be used to create an empty matrix that is
then filled by the user
From a user binary program
The user can directly create the sparse matrix within an oct-file.
There are several basic functions to return specific sparse matrices. For example the
sparse identity matrix, is a matrix that is often needed. It therefore has its own function to
create it as speye (n)or speye (r,c), which creates an n-by-nor r-by-csparse identity
matrix.
Another typical sparse matrix that is often needed is a random distribution of random
elements. The functions sprand and sprandn perform this for uniform and normal random
distributions of elements. They have exactly the same calling convention, where sprand
(r,c,d), creates an r-by-csparse matrix with a density of filled elements of d.
Other functions of interest that directly create sparse matrices, are diag or its general-
ization spdiags, that can take the definition of the diagonals of the matrix and create the
sparse matrix that corresponds to this. For example,
s = diag (sparse (randn (1,n)), -1);
creates a sparse (n+1)-by-(n+1) sparse matrix with a single diagonal defined.
B= spdiags (A)
[B,d] = spdiags (A)
B= spdiags (A,d)
A= spdiags (v,d,A)
A= spdiags (v,d,m,n)
A generalization of the function diag.
Called with a single input argument, the nonzero diagonals dof Aare extracted.
With two arguments the diagonals to extract are given by the vector d.
The other two forms of spdiags modify the input matrix by replacing the diagonals.
They use the columns of vto replace the diagonals represented by the vector d. If the
sparse matrix Ais defined then the diagonals of this matrix are replaced. Otherwise
a matrix of mby nis created with the diagonals given by the columns of v.
Negative values of drepresent diagonals below the main diagonal, and positive values
of ddiagonals above the main diagonal.
For example:
spdiags (reshape (1:12, 4, 3), [-1 0 1], 5, 4)
⇒5 10 0 0
1 6 11 0
0 2 7 12
0038
0004
562 GNU Octave
See also: [diag], page 452.
s= speye (m,n)
s= speye (m)
s= speye (sz)
Return a sparse identity matrix of size mxn.
The implementation is significantly more efficient than sparse (eye (m)) as the full
matrix is not constructed.
Called with a single argument a square matrix of size m-by-mis created. If called
with a single vector argument sz, this argument is taken to be the size of the matrix
to create.
See also: [sparse], page 564,[spdiags], page 561,[eye], page 453.
r= spones (S)
Replace the nonzero entries of Swith ones.
This creates a sparse matrix with the same structure as S.
See also: [sparse], page 564,[sprand], page 562,[sprandn], page 562,[sprandsym],
page 563,[spfun], page 536,[spy], page 568.
sprand (m,n,d)
sprand (m,n,d,rc)
sprand (s)
Generate a sparse matrix with uniformly distributed random values.
The size of the matrix is mxnwith a density of values d.dmust be between 0 and 1.
Values will be uniformly distributed on the interval (0, 1).
If called with a single matrix argument, a sparse matrix is generated with random
values wherever the matrix sis nonzero.
If called with a scalar fourth argument rc, a random sparse matrix with reciprocal
condition number rc is generated. If rc is a vector, then it specifies the first singular
values of the generated matrix (length (rc) <= min (m,n)).
See also: [sprandn], page 562,[sprandsym], page 563,[rand], page 455.
sprandn (m,n,d)
sprandn (m,n,d,rc)
sprandn (s)
Generate a sparse matrix with normally distributed random values.
The size of the matrix is mxnwith a density of values d.dmust be between 0 and 1.
Values will be normally distributed with a mean of 0 and a variance of 1.
If called with a single matrix argument, a sparse matrix is generated with random
values wherever the matrix sis nonzero.
If called with a scalar fourth argument rc, a random sparse matrix with reciprocal
condition number rc is generated. If rc is a vector, then it specifies the first singular
values of the generated matrix (length (rc) <= min (m,n)).
See also: [sprand], page 562,[sprandsym], page 563,[randn], page 457.
Chapter 22: Sparse Matrices 563
sprandsym (n,d)
sprandsym (s)
Generate a symmetric random sparse matrix.
The size of the matrix will be nxn, with a density of values given by d.dmust be
between 0 and 1 inclusive. Values will be normally distributed with a mean of zero
and a variance of 1.
If called with a single matrix argument, a random sparse matrix is generated wherever
the matrix sis nonzero in its lower triangular part.
See also: [sprand], page 562,[sprandn], page 562,[spones], page 562,[sparse],
page 564.
The recommended way for the user to create a sparse matrix, is to create two vectors
containing the row and column index of the data and a third vector of the same size
containing the data to be stored. For example,
ri=ci=d=[];
for j = 1:c
ri = [ri; randperm(r,n)’];
ci = [ci; j*ones(n,1)];
d = [d; rand(n,1)];
endfor
s = sparse (ri, ci, d, r, c);
creates an r-by-csparse matrix with a random distribution of n(<r) elements per column.
The elements of the vectors do not need to be sorted in any particular order as Octave will
sort them prior to storing the data. However, pre-sorting the data will make the creation
of the sparse matrix faster.
The function spconvert takes a three or four column real matrix. The first two columns
represent the row and column index respectively and the third and four columns, the real
and imaginary parts of the sparse matrix. The matrix can contain zero elements and the
elements can be sorted in any order. Adding zero elements is a convenient way to define
the size of the sparse matrix. For example:
s = spconvert ([1 2 3 4; 1 3 4 4; 1 2 3 0]’)
⇒Compressed Column Sparse (rows=4, cols=4, nnz=3)
(1 , 1) -> 1
(2 , 3) -> 2
(3 , 4) -> 3
An example of creating and filling a matrix might be
k = 5;
nz=r*k;
s = spalloc (r, c, nz)
for j = 1:c
idx = randperm (r);
s (:, j) = [zeros(r - k, 1); ...
rand(k, 1)] (idx);
endfor
564 GNU Octave
It should be noted, that due to the way that the Octave assignment functions are written
that the assignment will reallocate the memory used by the sparse matrix at each iteration
of the above loop. Therefore the spalloc function ignores the nz argument and does not
pre-assign the memory for the matrix. Therefore, it is vitally important that code using
to above structure should be vectorized as much as possible to minimize the number of
assignments and reduce the number of memory allocations.
FM = full (SM)
Return a full storage matrix from a sparse, diagonal, or permutation matrix, or a
range.
See also: [sparse], page 564,[issparse], page 566.
s= spalloc (m,n,nz)
Create an m-by-nsparse matrix with pre-allocated space for at most nz nonzero
elements.
This is useful for building a matrix incrementally by a sequence of indexed assign-
ments. Subsequent indexed assignments after spalloc will reuse the pre-allocated
memory, provided they are of one of the simple forms
•s(I:J) = x
•s(:,I:J) = x
•s(K:L,I:J) = x
and that the following conditions are met:
•the assignment does not decrease nnz (S).
•after the assignment, nnz (S) does not exceed nz.
•no index is out of bounds.
Partial movement of data may still occur, but in general the assignment will be more
memory and time efficient under these circumstances. In particular, it is possible to
efficiently build a pre-allocated sparse matrix from a contiguous block of columns.
The amount of pre-allocated memory for a given matrix may be queried using the
function nzmax.
See also: [nzmax], page 566,[sparse], page 564.
s= sparse (a)
s= sparse (i,j,sv,m,n)
s= sparse (i,j,sv)
s= sparse (m,n)
s= sparse (i,j,s,m,n,"unique")
s= sparse (i,j,sv,m,n,nzmax)
Create a sparse matrix from a full matrix, or row, column, value triplets.
If ais a full matrix, convert it to a sparse matrix representation, removing all zero
values in the process.
Given the integer index vectors iand j, and a 1-by-nnz vector of real or complex values
sv, construct the sparse matrix S(i(k),j(k)) = sv(k)with overall dimensions mand
n. If any of sv,ior jare scalars, they are expanded to have a common size.
Chapter 22: Sparse Matrices 565
If mor nare not specified their values are derived from the maximum index in the
vectors iand jas given by m= max (i),n= max (j).
Note: if multiple values are specified with the same i,jindices, the corresponding
value in swill be the sum of the values at the repeated location. See accumarray
for an example of how to produce different behavior, such as taking the minimum
instead.
If the option "unique" is given, and more than one value is specified at the same i,j
indices, then the last specified value will be used.
sparse (m,n)will create an empty mxnsparse matrix and is equivalent to sparse
([], [], [], m,n)
The argument nzmax is ignored but accepted for compatibility with matlab.
Example 1 (sum at repeated indices):
i= [1 1 2]; j= [1 1 2]; sv = [3 4 5];
sparse (i,j,sv, 3, 4)
⇒
Compressed Column Sparse (rows = 3, cols = 4, nnz = 2 [17%])
(1, 1) -> 7
(2, 2) -> 5
Example 2 ("unique"option):
i= [1 1 2]; j= [1 1 2]; sv = [3 4 5];
sparse (i,j,sv, 3, 4, "unique")
⇒
Compressed Column Sparse (rows = 3, cols = 4, nnz = 2 [17%])
(1, 1) -> 4
(2, 2) -> 5
See also: [full], page 564,[accumarray], page 539,[spalloc], page 564,[spdiags],
page 561,[speye], page 562,[spones], page 562,[sprand], page 562,[sprandn],
page 562,[sprandsym], page 563,[spconvert], page 565,[spfun], page 536.
x= spconvert (m)
Convert a simple sparse matrix format easily generated by other programs into Oc-
tave’s internal sparse format.
The input mis either a 3 or 4 column real matrix, containing the row, column, real,
and imaginary parts of the elements of the sparse matrix. An element with a zero
real and imaginary part can be used to force a particular matrix size.
See also: [sparse], page 564.
The above problem of memory reallocation can be avoided in oct-files. However, the
construction of a sparse matrix from an oct-file is more complex than can be discussed
here. See Appendix A [External Code Interface], page 863, for a full description of the
techniques involved.

566 GNU Octave
22.1.3 Finding Information about Sparse Matrices
There are a number of functions that allow information concerning sparse matrices to be
obtained. The most basic of these is issparse that identifies whether a particular Octave
object is in fact a sparse matrix.
Another very basic function is nnz that returns the number of nonzero entries there are
in a sparse matrix, while the function nzmax returns the amount of storage allocated to the
sparse matrix. Note that Octave tends to crop unused memory at the first opportunity for
sparse objects. There are some cases of user created sparse objects where the value returned
by nzmax will not be the same as nnz, but in general they will give the same result. The
function spstats returns some basic statistics on the columns of a sparse matrix including
the number of elements, the mean and the variance of each column.
issparse (x)
Return true if xis a sparse matrix.
See also: [ismatrix], page 63.
n= nnz (a)
Return the number of nonzero elements in a.
See also: [nzmax], page 566,[nonzeros], page 566,[find], page 441.
nonzeros (s)
Return a vector of the nonzero values of the sparse matrix s.
See also: [find], page 441,[nnz], page 566.
n= nzmax (SM)
Return the amount of storage allocated to the sparse matrix SM.
Note that Octave tends to crop unused memory at the first opportunity for sparse
objects. Thus, in general the value of nzmax will be the same as nnz except for some
cases of user-created sparse objects.
See also: [nnz], page 566,[spalloc], page 564,[sparse], page 564.
[count,mean,var] = spstats (S)
[count,mean,var] = spstats (S,j)
Return the stats for the nonzero elements of the sparse matrix S.
count is the number of nonzeros in each column, mean is the mean of the nonzeros in
each column, and var is the variance of the nonzeros in each column.
Called with two input arguments, if Sis the data and jis the bin number for the
data, compute the stats for each bin. In this case, bins can contain data values of
zero, whereas with spstats (S)the zeros may disappear.
When solving linear equations involving sparse matrices Octave determines the means to
solve the equation based on the type of the matrix (see Section 22.2 [Sparse Linear Algebra],
page 580). Octave probes the matrix type when the div (/) or ldiv (\) operator is first used
with the matrix and then caches the type. However the matrix type function can be used
Chapter 22: Sparse Matrices 567
to determine the type of the sparse matrix prior to use of the div or ldiv operators. For
example,
a = tril (sprandn (1024, 1024, 0.02), -1) ...
+ speye (1024);
matrix_type (a);
ans = Lower
shows that Octave correctly determines the matrix type for lower triangular matrices. ma-
trix type can also be used to force the type of a matrix to be a particular type. For
example:
a = matrix_type (tril (sprandn (1024, ...
1024, 0.02), -1) + speye (1024), "Lower");
This allows the cost of determining the matrix type to be avoided. However, incorrectly
defining the matrix type will result in incorrect results from solutions of linear equations,
and so it is entirely the responsibility of the user to correctly identify the matrix type
There are several graphical means of finding out information about sparse matrices. The
first is the spy command, which displays the structure of the nonzero elements of the matrix.
See Figure 22.1, for an example of the use of spy. More advanced graphical information can
be obtained with the treeplot,etreeplot and gplot commands.
0 50 100 150 200
0
50
100
150
200
Figure 22.1: Structure of simple sparse matrix.
One use of sparse matrices is in graph theory, where the interconnections between nodes
are represented as an adjacency matrix. That is, if the i-th node in a graph is connected to
the j-th node. Then the ij-th node (and in the case of undirected graphs the ji-th node) of the
sparse adjacency matrix is nonzero. If each node is then associated with a set of coordinates,
then the gplot command can be used to graphically display the interconnections between
nodes.
As a trivial example of the use of gplot consider the example,

568 GNU Octave
A = sparse ([2,6,1,3,2,4,3,5,4,6,1,5],
[1,1,2,2,3,3,4,4,5,5,6,6],1,6,6);
xy = [0,4,8,6,4,2;5,0,5,7,5,7]’;
gplot (A,xy)
which creates an adjacency matrix Awhere node 1 is connected to nodes 2 and 6, node 2
with nodes 1 and 3, etc. The coordinates of the nodes are given in the n-by-2 matrix xy.
See Figure 22.2.
02468
0
1
2
3
4
5
6
7
Figure 22.2: Simple use of the gplot command.
The dependencies between the nodes of a Cholesky factorization can be calculated in
linear time without explicitly needing to calculate the Cholesky factorization by the etree
command. This command returns the elimination tree of the matrix and can be displayed
graphically by the command treeplot (etree (A)) if Ais symmetric or treeplot (etree
(A+A’)) otherwise.
spy (x)
spy (. . ., markersize)
spy (. . ., line_spec)
Plot the sparsity pattern of the sparse matrix x.
If the argument markersize is given as a scalar value, it is used to determine the point
size in the plot.
If the string line spec is given it is passed to plot and determines the appearance of
the plot.
See also: [plot], page 286,[gplot], page 569.
p= etree (S)
p= etree (S,typ)
[p,q] = etree (S,typ)
Return the elimination tree for the matrix S.
Chapter 22: Sparse Matrices 569
By default Sis assumed to be symmetric and the symmetric elimination tree is re-
turned. The argument typ controls whether a symmetric or column elimination tree is
returned. Valid values of typ are "sym" or "col", for symmetric or column elimination
tree respectively.
Called with a second argument, etree also returns the postorder permutations on
the tree.
etreeplot (A)
etreeplot (A,node_style,edge_style)
Plot the elimination tree of the matrix Aor A+A’if Ain not symmetric.
The optional parameters node style and edge style define the output style.
See also: [treeplot], page 569,[gplot], page 569.
gplot (A,xy)
gplot (A,xy,line_style)
[x,y] = gplot (A,xy)
Plot a graph defined by Aand xy in the graph theory sense.
Ais the adjacency matrix of the array to be plotted and xy is an n-by-2 matrix
containing the coordinates of the nodes of the graph.
The optional parameter line style defines the output style for the plot. Called with
no output arguments the graph is plotted directly. Otherwise, return the coordinates
of the plot in xand y.
See also: [treeplot], page 569,[etreeplot], page 569,[spy], page 568.
treeplot (tree)
treeplot (tree,node_style,edge_style)
Produce a graph of tree or forest.
The first argument is vector of predecessors.
The optional parameters node style and edge style define the output plot style.
The complexity of the algorithm is O(n) in terms of is time and memory requirements.
See also: [etreeplot], page 569,[gplot], page 569.
treelayout (tree)
treelayout (tree,permutation)
treelayout lays out a tree or a forest.
The first argument tree is a vector of predecessors.
The parameter permutation is an optional postorder permutation.
The complexity of the algorithm is O(n) in terms of time and memory requirements.
See also: [etreeplot], page 569,[gplot], page 569,[treeplot], page 569.
22.1.4 Basic Operators and Functions on Sparse Matrices

570 GNU Octave
22.1.4.1 Sparse Functions
Many Octave functions have been overloaded to work with either sparse or full matrices.
There is no difference in calling convention when using an overloaded function with a sparse
matrix, however, there is also no access to potentially sparse-specific features. At any time
the sparse matrix specific version of a function can be used by explicitly calling its function
name.
The table below lists all of the sparse functions of Octave. Note that the names of the
specific sparse forms of the functions are typically the same as the general versions with a
sp prefix. In the table below, and in the rest of this article, the specific sparse versions of
functions are used.
Generate sparse matrices:
spalloc,spdiags,speye,sprand,sprandn,sprandsym
Sparse matrix conversion:
full,sparse,spconvert
Manipulate sparse matrices
issparse,nnz,nonzeros,nzmax,spfun,spones,spy
Graph Theory:
etree,etreeplot,gplot,treeplot
Sparse matrix reordering:
amd,ccolamd,colamd,colperm,csymamd,dmperm,symamd,randperm,sym-
rcm
Linear algebra:
condest,eigs,matrix type,normest,normest1,sprank,spaugment,svds
Iterative techniques:
ichol,ilu,pcg,pcr
Miscellaneous:
spparms,symbfact,spstats
In addition all of the standard Octave mapper functions (i.e., basic math functions that
take a single argument) such as abs, etc. can accept sparse matrices. The reader is referred
to the documentation supplied with these functions within Octave itself for further details.
22.1.4.2 Return Types of Operators and Functions
The two basic reasons to use sparse matrices are to reduce the memory usage and to not have
to do calculations on zero elements. The two are closely related in that the computation
time on a sparse matrix operator or function is roughly linear with the number of nonzero
elements.
Therefore, there is a certain density of nonzero elements of a matrix where it no longer
makes sense to store it as a sparse matrix, but rather as a full matrix. For this reason
operators and functions that have a high probability of returning a full matrix will always
return one. For example adding a scalar constant to a sparse matrix will almost always
make it a full matrix, and so the example,
Chapter 22: Sparse Matrices 571
speye (3) + 0
⇒100
010
001
returns a full matrix as can be seen.
Additionally, if sparse_auto_mutate is true, all sparse functions test the amount of
memory occupied by the sparse matrix to see if the amount of storage used is larger than
the amount used by the full equivalent. Therefore speye (2) * 1 will return a full matrix
as the memory used is smaller for the full version than the sparse version.
As all of the mixed operators and functions between full and sparse matrices exist, in
general this does not cause any problems. However, one area where it does cause a problem
is where a sparse matrix is promoted to a full matrix, where subsequent operations would
resparsify the matrix. Such cases are rare, but can be artificially created, for example
(fliplr (speye (3)) + speye (3)) - speye (3) gives a full matrix when it should give a
sparse one. In general, where such cases occur, they impose only a small memory penalty.
There is however one known case where this behavior of Octave’s sparse matrices will
cause a problem. That is in the handling of the diag function. Whether diag returns a
sparse or full matrix depending on the type of its input arguments. So
a = diag (sparse ([1,2,3]), -1);
should return a sparse matrix. To ensure this actually happens, the sparse function, and
other functions based on it like speye, always returns a sparse matrix, even if the memory
used will be larger than its full representation.
val = sparse_auto_mutate ()
old_val = sparse_auto_mutate (new_val)
sparse_auto_mutate (new_val,"local")
Query or set the internal variable that controls whether Octave will automatically
mutate sparse matrices to full matrices to save memory.
For example:
s = speye (3);
sparse_auto_mutate (false);
s(:, 1) = 1;
typeinfo (s)
⇒sparse matrix
sparse_auto_mutate (true);
s(1, :) = 1;
typeinfo (s)
⇒matrix
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
Note that the sparse_auto_mutate option is incompatible with matlab, and so it is
off by default.
572 GNU Octave
22.1.4.3 Mathematical Considerations
The attempt has been made to make sparse matrices behave in exactly the same manner
as there full counterparts. However, there are certain differences and especially differences
with other products sparse implementations.
First, the "./" and ".^" operators must be used with care. Consider what the examples
s = speye (4);
a1 = s .^ 2;
a2 = s .^ s;
a3 = s .^ -2;
a4 = s ./ 2;
a5 = 2 ./ s;
a6 = s ./ s;
will give. The first example of sraised to the power of 2 causes no problems. However s
raised element-wise to itself involves a large number of terms 0 .^ 0 which is 1. There s.^
sis a full matrix.
Likewise s.^ -2 involves terms like 0 .^ -2 which is infinity, and so s.^ -2 is equally
a full matrix.
For the "./"operator s./ 2 has no problems, but 2 ./ sinvolves a large number of
infinity terms as well and is equally a full matrix. The case of s./ sinvolves terms like 0
./ 0 which is a NaN and so this is equally a full matrix with the zero elements of sfilled
with NaN values.
The above behavior is consistent with full matrices, but is not consistent with sparse
implementations in other products.
A particular problem of sparse matrices comes about due to the fact that as the zeros
are not stored, the sign-bit of these zeros is equally not stored. In certain cases the sign-bit
of zero is important. For example:
a = 0 ./ [-1, 1; 1, -1];
b=1./a
⇒-Inf Inf
Inf -Inf
c = 1 ./ sparse (a)
⇒Inf Inf
Inf Inf
To correct this behavior would mean that zero elements with a negative sign-bit would
need to be stored in the matrix to ensure that their sign-bit was respected. This is not done
at this time, for reasons of efficiency, and so the user is warned that calculations where the
sign-bit of zero is important must not be done using sparse matrices.
In general any function or operator used on a sparse matrix will result in a sparse
matrix with the same or a larger number of nonzero elements than the original matrix.
This is particularly true for the important case of sparse matrix factorizations. The usual
way to address this is to reorder the matrix, such that its factorization is sparser than
the factorization of the original matrix. That is the factorization of L*U=P*S*Qhas
sparser terms Land Uthan the equivalent factorization L*U=S.
Chapter 22: Sparse Matrices 573
Several functions are available to reorder depending on the type of the matrix to be
factorized. If the matrix is symmetric positive-definite, then symamd or csymamd should be
used. Otherwise amd,colamd or ccolamd should be used. For completeness the reordering
functions colperm and randperm are also available.
See Figure 22.3, for an example of the structure of a simple positive definite matrix.
0 50 100 150 200
0
50
100
150
200
Figure 22.3: Structure of simple sparse matrix.
The standard Cholesky factorization of this matrix can be obtained by the same com-
mand that would be used for a full matrix. This can be visualized with the command r =
chol (A); spy (r);. See Figure 22.4. The original matrix had 598 nonzero terms, while
this Cholesky factorization has 10200, with only half of the symmetric matrix being stored.
This is a significant level of fill in, and although not an issue for such a small test case, can
represents a large overhead in working with other sparse matrices.
The appropriate sparsity preserving permutation of the original matrix is given by
symamd and the factorization using this reordering can be visualized using the command
q = symamd (A); r = chol (A(q,q)); spy (r). This gives 399 nonzero terms which is a
significant improvement.
The Cholesky factorization itself can be used to determine the appropriate sparsity
preserving reordering of the matrix during the factorization, In that case this might be
obtained with three return arguments as [r, p, q] = chol (A); spy (r).
574 GNU Octave
0 50 100 150 200
0
50
100
150
200
Figure 22.4: Structure of the unpermuted Cholesky factorization of the above matrix.
0 50 100 150 200
0
50
100
150
200
Figure 22.5: Structure of the permuted Cholesky factorization of the above matrix.
In the case of an asymmetric matrix, the appropriate sparsity preserving permutation is
colamd and the factorization using this reordering can be visualized using the command q
= colamd (A); [l, u, p] = lu (A(:,q)); spy (l+u).
Finally, Octave implicitly reorders the matrix when using the div (/) and ldiv (\) op-
erators, and so no the user does not need to explicitly reorder the matrix to maximize
performance.
Chapter 22: Sparse Matrices 575
p= amd (S)
p= amd (S,opts)
Return the approximate minimum degree permutation of a matrix.
This is a permutation such that the Cholesky factorization of S(p,p)tends to be
sparser than the Cholesky factorization of Sitself. amd is typically faster than symamd
but serves a similar purpose.
The optional parameter opts is a structure that controls the behavior of amd. The
fields of the structure are
opts.dense Determines what amd considers to be a dense row or column of the input
matrix. Rows or columns with more than max (16, (dense * sqrt (n)))
entries, where nis the order of the matrix S, are ignored by amd during
the calculation of the permutation. The value of dense must be a positive
scalar and the default value is 10.0
opts.aggressive
If this value is a nonzero scalar, then amd performs aggressive absorption.
The default is not to perform aggressive absorption.
The author of the code itself is Timothy A. Davis davis@cise.ufl.edu, University
of Florida (see http://www.cise.ufl.edu/research/sparse/amd).
See also: [symamd], page 578,[colamd], page 576.
p= ccolamd (S)
p= ccolamd (S,knobs)
p= ccolamd (S,knobs,cmember)
[p,stats] = ccolamd (. . . )
Constrained column approximate minimum degree permutation.
p= ccolamd (S)returns the column approximate minimum degree permutation vec-
tor for the sparse matrix S. For a non-symmetric matrix S,S(:, p)tends to have
sparser LU factors than S.chol (S(:, p)’ * S(:, p)) also tends to be sparser than
chol (S’ * S).p= ccolamd (S, 1) optimizes the ordering for lu (S(:, p)). The
ordering is followed by a column elimination tree post-ordering.
knobs is an optional 1-element to 5-element input vector, with a default value of [0
10 10 1 0] if not present or empty. Entries not present are set to their defaults.
knobs(1) if nonzero, the ordering is optimized for lu (S(:, p)). It will be a poor
ordering for chol (S(:, p)’ * S(:, p)). This is the most important
knob for ccolamd.
knobs(2) if Sis m-by-n, rows with more than max (16, knobs(2) * sqrt (n)) en-
tries are ignored.
knobs(3) columns with more than max (16, knobs(3) * sqrt (min (m,n))) en-
tries are ignored and ordered last in the output permutation (subject to
the cmember constraints).
knobs(4) if nonzero, aggressive absorption is performed.
knobs(5) if nonzero, statistics and knobs are printed.
576 GNU Octave
cmember is an optional vector of length n. It defines the constraints on the column
ordering. If cmember(j) = c, then column jis in constraint set c(cmust be in the
range 1 to n). In the output permutation p, all columns in set 1 appear first, followed
by all columns in set 2, and so on. cmember = ones (1,n) if not present or empty.
ccolamd (S, [], 1 : n) returns 1 : n
p= ccolamd (S)is about the same as p= colamd (S).knobs and its default values
differ. colamd always does aggressive absorption, and it finds an ordering suitable for
both lu (S(:, p)) and chol (S(:, p)’ * S(:, p)); it cannot optimize its ordering
for lu (S(:, p)) to the extent that ccolamd (S, 1) can.
stats is an optional 20-element output vector that provides data about the ordering
and the validity of the input matrix S. Ordering statistics are in stats(1 : 3).
stats(1) and stats(2) are the number of dense or empty rows and columns ignored
by ccolamd and stats(3) is the number of garbage collections performed on the
internal data structure used by ccolamd (roughly of size 2.2 * nnz (S) + 4 * m+ 7
*nintegers).
stats(4 : 7) provide information if CCOLAMD was able to continue. The matrix is
OK if stats(4) is zero, or 1 if invalid. stats(5) is the rightmost column index that
is unsorted or contains duplicate entries, or zero if no such column exists. stats(6)
is the last seen duplicate or out-of-order row index in the column index given by
stats(5), or zero if no such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8 : 20) is always zero in the current version of
ccolamd (reserved for future use).
The authors of the code itself are S. Larimore, T. Davis (Univ. of Florida) and
S. Rajamanickam in collaboration with J. Bilbert and E. Ng. Supported by the
National Science Foundation (DMS-9504974, DMS-9803599, CCR-0203270), and a
grant from Sandia National Lab. See http://www.cise.ufl.edu/research/sparse
for ccolamd, csymamd, amd, colamd, symamd, and other related orderings.
See also: [colamd], page 576,[csymamd], page 577.
p= colamd (S)
p= colamd (S,knobs)
[p,stats] = colamd (S)
[p,stats] = colamd (S,knobs)
Compute the column approximate minimum degree permutation.
p= colamd (S)returns the column approximate minimum degree permutation vector
for the sparse matrix S. For a non-symmetric matrix S,S(:,p)tends to have sparser
LU factors than S. The Cholesky factorization of S(:,p)’ * S(:,p)also tends to be
sparser than that of S’ * S.
knobs is an optional one- to three-element input vector. If Sis m-by-n, then rows
with more than max(16,knobs(1)*sqrt(n)) entries are ignored. Columns with more
than max (16,knobs(2)*sqrt(min(m,n))) entries are removed prior to ordering, and
ordered last in the output permutation p. Only completely dense rows or columns
are removed if knobs(1) and knobs(2) are <0, respectively. If knobs(3) is nonzero,
stats and knobs are printed. The default is knobs = [10 10 0]. Note that knobs
differs from earlier versions of colamd.
Chapter 22: Sparse Matrices 577
stats is an optional 20-element output vector that provides data about the order-
ing and the validity of the input matrix S. Ordering statistics are in stats(1:3).
stats(1) and stats(2) are the number of dense or empty rows and columns ignored
by colamd and stats(3) is the number of garbage collections performed on the
internal data structure used by colamd (roughly of size 2.2 * nnz(S) + 4 * m+ 7 *
nintegers).
Octave built-in functions are intended to generate valid sparse matrices, with no
duplicate entries, with ascending row indices of the nonzeros in each column, with a
non-negative number of entries in each column (!) and so on. If a matrix is invalid,
then colamd may or may not be able to continue. If there are duplicate entries (a
row index appears two or more times in the same column) or if the row indices in
a column are out of order, then colamd can correct these errors by ignoring the
duplicate entries and sorting each column of its internal copy of the matrix S(the
input matrix Sis not repaired, however). If a matrix is invalid in other ways then
colamd cannot continue, an error message is printed, and no output arguments (p
or stats) are returned. colamd is thus a simple way to check a sparse matrix to see
if it’s valid.
stats(4:7) provide information if colamd was able to continue. The matrix is OK
if stats(4) is zero, or 1 if invalid. stats(5) is the rightmost column index that is
unsorted or contains duplicate entries, or zero if no such column exists. stats(6)
is the last seen duplicate or out-of-order row index in the column index given by
stats(5), or zero if no such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8:20) is always zero in the current version of
colamd (reserved for future use).
The ordering is followed by a column elimination tree post-ordering.
The authors of the code itself are Stefan I. Larimore and Timothy A. Davis
davis@cise.ufl.edu, University of Florida. The algorithm was developed in
collaboration with John Gilbert, Xerox PARC, and Esmond Ng, Oak Ridge National
Laboratory. (see http://www.cise.ufl.edu/research/sparse/colamd)
See also: [colperm], page 577,[symamd], page 578,[ccolamd], page 575.
p= colperm (s)
Return the column permutations such that the columns of s(:, p)are ordered in
terms of increasing number of nonzero elements.
If sis symmetric, then pis chosen such that s(p,p)orders the rows and columns
with increasing number of nonzeros elements.
p= csymamd (S)
p= csymamd (S,knobs)
p= csymamd (S,knobs,cmember)
[p,stats] = csymamd (. . . )
For a symmetric positive definite matrix S, return the permutation vector psuch that
S(p,p)tends to have a sparser Cholesky factor than S.
Sometimes csymamd works well for symmetric indefinite matrices too. The matrix S
is assumed to be symmetric; only the strictly lower triangular part is referenced. S
must be square. The ordering is followed by an elimination tree post-ordering.
578 GNU Octave
knobs is an optional 1-element to 3-element input vector, with a default value of [10
1 0]. Entries not present are set to their defaults.
knobs(1) If Sis n-by-n, then rows and columns with more than
max(16,knobs(1)*sqrt(n)) entries are ignored, and ordered
last in the output permutation (subject to the cmember constraints).
knobs(2) If nonzero, aggressive absorption is performed.
knobs(3) If nonzero, statistics and knobs are printed.
cmember is an optional vector of length n. It defines the constraints on the ordering.
If cmember(j) = S, then row/column j is in constraint set c(cmust be in the range
1 to n). In the output permutation p, rows/columns in set 1 appear first, followed by
all rows/columns in set 2, and so on. cmember = ones (1,n) if not present or empty.
csymamd (S,[],1:n) returns 1:n.
p= csymamd (S)is about the same as p= symamd (S).knobs and its default values
differ.
stats(4:7) provide information if CCOLAMD was able to continue. The matrix is
OK if stats(4) is zero, or 1 if invalid. stats(5) is the rightmost column index that
is unsorted or contains duplicate entries, or zero if no such column exists. stats(6)
is the last seen duplicate or out-of-order row index in the column index given by
stats(5), or zero if no such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8:20) is always zero in the current version of
ccolamd (reserved for future use).
The authors of the code itself are S. Larimore, T. Davis (Univ. of Florida) and
S. Rajamanickam in collaboration with J. Bilbert and E. Ng. Supported by the
National Science Foundation (DMS-9504974, DMS-9803599, CCR-0203270), and a
grant from Sandia National Lab. See http://www.cise.ufl.edu/research/sparse
for ccolamd, csymamd, amd, colamd, symamd, and other related orderings.
See also: [symamd], page 578,[ccolamd], page 575.
p= dmperm (S)
[p,q,r,S] = dmperm (S)
Perform a Dulmage-Mendelsohn permutation of the sparse matrix S.
With a single output argument dmperm performs the row permutations psuch that
S(p,:) has no zero elements on the diagonal.
Called with two or more output arguments, returns the row and column permutations,
such that S(p,q)is in block triangular form. The values of rand Sdefine the
boundaries of the blocks. If Sis square then r== S.
The method used is described in: A. Pothen & C.-J. Fan. Computing the Block
Triangular Form of a Sparse Matrix. ACM Trans. Math. Software, 16(4):303-324,
1990.
See also: [colamd], page 576,[ccolamd], page 575.
p= symamd (S)
p= symamd (S,knobs)
[p,stats] = symamd (S)
Chapter 22: Sparse Matrices 579
[p,stats] = symamd (S,knobs)
For a symmetric positive definite matrix S, returns the permutation vector p such
that S(p,p)tends to have a sparser Cholesky factor than S.
Sometimes symamd works well for symmetric indefinite matrices too. The matrix S
is assumed to be symmetric; only the strictly lower triangular part is referenced. S
must be square.
knobs is an optional one- to two-element input vector. If Sis n-by-n, then rows
and columns with more than max (16,knobs(1)*sqrt(n)) entries are removed prior
to ordering, and ordered last in the output permutation p. No rows/columns are
removed if knobs(1) < 0. If knobs (2) is nonzero, stats and knobs are printed. The
default is knobs = [10 0]. Note that knobs differs from earlier versions of symamd.
stats is an optional 20-element output vector that provides data about the order-
ing and the validity of the input matrix S. Ordering statistics are in stats(1:3).
stats(1) = stats(2) is the number of dense or empty rows and columns ignored by
SYMAMD and stats(3) is the number of garbage collections performed on the in-
ternal data structure used by SYMAMD (roughly of size 8.4 * nnz (tril (S, -1))
+ 9 * nintegers).
Octave built-in functions are intended to generate valid sparse matrices, with no
duplicate entries, with ascending row indices of the nonzeros in each column, with a
non-negative number of entries in each column (!) and so on. If a matrix is invalid,
then SYMAMD may or may not be able to continue. If there are duplicate entries
(a row index appears two or more times in the same column) or if the row indices in
a column are out of order, then SYMAMD can correct these errors by ignoring the
duplicate entries and sorting each column of its internal copy of the matrix S (the
input matrix S is not repaired, however). If a matrix is invalid in other ways then
SYMAMD cannot continue, an error message is printed, and no output arguments (p
or stats) are returned. SYMAMD is thus a simple way to check a sparse matrix to
see if it’s valid.
stats(4:7) provide information if SYMAMD was able to continue. The matrix is
OK if stats (4) is zero, or 1 if invalid. stats(5) is the rightmost column index that
is unsorted or contains duplicate entries, or zero if no such column exists. stats(6)
is the last seen duplicate or out-of-order row index in the column index given by
stats(5), or zero if no such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8:20) is always zero in the current version of
SYMAMD (reserved for future use).
The ordering is followed by a column elimination tree post-ordering.
The authors of the code itself are Stefan I. Larimore and Timothy A. Davis
davis@cise.ufl.edu, University of Florida. The algorithm was developed in
collaboration with John Gilbert, Xerox PARC, and Esmond Ng, Oak Ridge National
Laboratory. (see http://www.cise.ufl.edu/research/sparse/colamd)
See also: [colperm], page 577,[colamd], page 576.
p= symrcm (S)
Return the symmetric reverse Cuthill-McKee permutation of S.
580 GNU Octave
pis a permutation vector such that S(p,p)tends to have its diagonal elements closer
to the diagonal than S. This is a good preordering for LU or Cholesky factorization
of matrices that come from “long, skinny” problems. It works for both symmetric
and asymmetric S.
The algorithm represents a heuristic approach to the NP-complete bandwidth mini-
mization problem. The implementation is based in the descriptions found in
E. Cuthill, J. McKee. Reducing the Bandwidth of Sparse Symmetric Matrices. Pro-
ceedings of the 24th ACM National Conference, 157–172 1969, Brandon Press, New
Jersey.
A. George, J.W.H. Liu. Computer Solution of Large Sparse Positive Definite Systems,
Prentice Hall Series in Computational Mathematics, ISBN 0-13-165274-5, 1981.
See also: [colperm], page 577,[colamd], page 576,[symamd], page 578.
22.2 Linear Algebra on Sparse Matrices
Octave includes a polymorphic solver for sparse matrices, where the exact solver used to
factorize the matrix, depends on the properties of the sparse matrix itself. Generally, the
cost of determining the matrix type is small relative to the cost of factorizing the matrix
itself, but in any case the matrix type is cached once it is calculated, so that it is not
re-determined each time it is used in a linear equation.
The selection tree for how the linear equation is solve is
1. If the matrix is diagonal, solve directly and goto 8
2. If the matrix is a permuted diagonal, solve directly taking into account the permuta-
tions. Goto 8
3. If the matrix is square, banded and if the band density is less than that given by
spparms ("bandden") continue, else goto 4.
a. If the matrix is tridiagonal and the right-hand side is not sparse continue, else goto
3b.
1. If the matrix is Hermitian, with a positive real diagonal, attempt Cholesky fac-
torization using lapack xPTSV.
2. If the above failed or the matrix is not Hermitian with a positive real diagonal
use Gaussian elimination with pivoting using lapack xGTSV, and goto 8.
b. If the matrix is Hermitian with a positive real diagonal, attempt Cholesky factor-
ization using lapack xPBTRF.
c. if the above failed or the matrix is not Hermitian with a positive real diagonal use
Gaussian elimination with pivoting using lapack xGBTRF, and goto 8.
4. If the matrix is upper or lower triangular perform a sparse forward or backward sub-
stitution, and goto 8
5. If the matrix is an upper triangular matrix with column permutations or lower triangu-
lar matrix with row permutations, perform a sparse forward or backward substitution,
and goto 8
6. If the matrix is square, Hermitian with a real positive diagonal, attempt sparse
Cholesky factorization using cholmod.

Chapter 22: Sparse Matrices 581
7. If the sparse Cholesky factorization failed or the matrix is not Hermitian with a real
positive diagonal, and the matrix is square, factorize using umfpack.
8. If the matrix is not square, or any of the previous solvers flags a singular or near
singular matrix, find a minimum norm solution using cxsparse3.
The band density is defined as the number of nonzero values in the band divided by the
total number of values in the full band. The banded matrix solvers can be entirely disabled
by using spparms to set bandden to 1 (i.e., spparms ("bandden", 1)).
The QR solver factorizes the problem with a Dulmage-Mendelsohn decomposition, to
separate the problem into blocks that can be treated as over-determined, multiple well
determined blocks, and a final over-determined block. For matrices with blocks of strongly
connected nodes this is a big win as LU decomposition can be used for many blocks. It also
significantly improves the chance of finding a solution to over-determined problems rather
than just returning a vector of NaN’s.
All of the solvers above, can calculate an estimate of the condition number. This can
be used to detect numerical stability problems in the solution and force a minimum norm
solution to be used. However, for narrow banded, triangular or diagonal matrices, the cost
of calculating the condition number is significant, and can in fact exceed the cost of factoring
the matrix. Therefore the condition number is not calculated in these cases, and Octave
relies on simpler techniques to detect singular matrices or the underlying lapack code in
the case of banded matrices.
The user can force the type of the matrix with the matrix_type function. This overcomes
the cost of discovering the type of the matrix. However, it should be noted that identifying
the type of the matrix incorrectly will lead to unpredictable results, and so matrix_type
should be used with care.
nest = normest (A)
nest = normest (A,tol)
[nest,iter] = normest (. . . )
Estimate the 2-norm of the matrix Ausing a power series analysis.
This is typically used for large matrices, where the cost of calculating norm (A)is
prohibitive and an approximation to the 2-norm is acceptable.
tol is the tolerance to which the 2-norm is calculated. By default tol is 1e-6.
The optional output iter returns the number of iterations that were required for
normest to converge.
See also: [normest1], page 581,[norm], page 509,[cond], page 504,[condest],
page 582.
nest = normest1 (A)
nest = normest1 (A,t)
nest = normest1 (A,t,x0)
nest = normest1 (Afun,t,x0,p1,p2, . . . )
[nest,v] = normest1 (A, . . . )
[nest,v,w] = normest1 (A, . . . )
3The cholmod,umfpack and cxsparse packages were written by Tim Davis and are available at http://
www.cise.ufl.edu/research/sparse/
582 GNU Octave
[nest,v,w,iter] = normest1 (A, . . . )
Estimate the 1-norm of the matrix Ausing a block algorithm.
normest1 is best for large sparse matrices where only an estimate of the norm is
required. For small to medium sized matrices, consider using norm (A, 1). In ad-
dition, normest1 can be used for the estimate of the 1-norm of a linear operator A
when matrix-vector products A*xand A’ * xcan be cheaply computed. In this case,
instead of the matrix A, a function Afun (flag,x)is used; it must return:
•the dimension nof A, if flag is "dim"
•true if Ais a real operator, if flag is "real"
•the result A*x, if flag is "notransp"
•the result A’ * x, if flag is "transp"
A typical case is Adefined by b^m, in which the result A*xcan be computed
without even forming explicitly b^mby:
y=x;
for i= 1:m
y=b*y;
endfor
The parameters p1,p2, . . . are arguments of Afun (flag,x,p1,p2, ...).
The default value for tis 2. The algorithm requires matrix-matrix products with sizes
nxnand nxt.
The initial matrix x0 should have columns of unit 1-norm. The default initial matrix
x0 has the first column ones (n, 1) / nand, if t>1, the remaining columns with
random elements -1 / n,1 / n, divided by n.
On output, nest is the desired estimate, vand ware vectors such that w=A*v, with
norm (w, 1) =c* norm (v, 1).iter contains in iter(1) the number of iterations
(the maximum is hardcoded to 5) and in iter(2) the total number of products A*
xor A’ * xperformed by the algorithm.
Algorithm Note: normest1 uses random numbers during evaluation. Therefore, if
consistent results are required, the "state" of the random generator should be fixed
before invoking normest1.
Reference: N. J. Higham and F. Tisseur, A block algorithm for matrix 1-norm esti-
mation, with and application to 1-norm pseudospectra, SIAM J. Matrix Anal. Appl.,
pp. 1185–1201, Vol 21, No. 4, 2000.
See also: [normest], page 581,[norm], page 509,[cond], page 504,[condest], page 582.
cest = condest (A)
cest = condest (A,t)
cest = condest (A,solvefun,t,p1,p2, . . . )
cest = condest (Afcn,solvefun,t,p1,p2, . . . )
[cest,v] = condest (. . . )
Estimate the 1-norm condition number of a square matrix Ausing ttest vectors and
a randomized 1-norm estimator.
The optional input tspecifies the number of test vectors (default 5).
Chapter 22: Sparse Matrices 583
If the matrix is not explicit, e.g., when estimating the condition number of Agiven
an LU factorization, condest uses the following functions:
−Afcn which must return
•the dimension nof a, if flag is "dim"
•true if ais a real operator, if flag is "real"
•the result a*x, if flag is "notransp"
•the result a’ * x, if flag is "transp"
−solvefun which must return
•the dimension nof a, if flag is "dim"
•true if ais a real operator, if flag is "real"
•the result a\x, if flag is "notransp"
•the result a’ \ x, if flag is "transp"
The parameters p1,p2, . . . are arguments of Afcn (flag,x,p1,p2, ...) and
solvefcn (flag,x,p1,p2, ...).
The principal output is the 1-norm condition number estimate cest.
The optional second output is an approximate null vector when cest is large; it satisfies
the equation norm (A*v, 1) == norm (A, 1) * norm (v, 1) / est.
Algorithm Note: condest uses a randomized algorithm to approximate the 1-norms.
Therefore, if consistent results are required, the "state" of the random generator
should be fixed before invoking condest.
References:
•N.J. Higham and F. Tisseur, A Block Algorithm for Matrix 1-Norm Estimation,
with an Application to 1-Norm Pseudospectra. SIMAX vol 21, no 4, pp 1185-
1201. http://dx.doi.org/10.1137/S0895479899356080
•N.J. Higham and F. Tisseur, A Block Algorithm for Matrix 1-Norm Estimation,
with an Application to 1-Norm Pseudospectra.http://citeseer.ist.psu.
edu/223007.html
See also: [cond], page 504,[norm], page 509,[normest1], page 581,[normest],
page 581.
spparms ()
vals = spparms ()
[keys,vals] = spparms ()
val = spparms (key)
spparms (vals)
spparms ("default")
spparms ("tight")
spparms (key,val)
Query or set the parameters used by the sparse solvers and factorization functions.
The first four calls above get information about the current settings, while the others
change the current settings. The parameters are stored as pairs of keys and values,
where the values are all floats and the keys are one of the following strings:
‘spumoni’ Printing level of debugging information of the solvers (default 0)
584 GNU Octave
‘ths_rel’ Included for compatibility. Not used. (default 1)
‘ths_abs’ Included for compatibility. Not used. (default 1)
‘exact_d’ Included for compatibility. Not used. (default 0)
‘supernd’ Included for compatibility. Not used. (default 3)
‘rreduce’ Included for compatibility. Not used. (default 3)
‘wh_frac’ Included for compatibility. Not used. (default 0.5)
‘autommd’ Flag whether the LU/QR and the ’\’ and ’/’ operators will automatically
use the sparsity preserving mmd functions (default 1)
‘autoamd’ Flag whether the LU and the ’\’ and ’/’ operators will automatically use
the sparsity preserving amd functions (default 1)
‘piv_tol’ The pivot tolerance of the umfpack solvers (default 0.1)
‘sym_tol’ The pivot tolerance of the umfpack symmetric solvers (default 0.001)
‘bandden’ The density of nonzero elements in a banded matrix before it is treated
by the lapack banded solvers (default 0.5)
‘umfpack’ Flag whether the umfpack or mmd solvers are used for the LU, ’\’ and
’/’ operations (default 1)
The value of individual keys can be set with spparms (key,val). The default values
can be restored with the special keyword "default". The special keyword "tight"
can be used to set the mmd solvers to attempt a sparser solution at the potential cost
of longer running time.
See also: [chol], page 511,[colamd], page 576,[lu], page 514,[qr], page 515,[symamd],
page 578.
p= sprank (S)
Calculate the structural rank of the sparse matrix S.
Note that only the structure of the matrix is used in this calculation based on a
Dulmage-Mendelsohn permutation to block triangular form. As such the numerical
rank of the matrix Sis bounded by sprank (S) >= rank (S). Ignoring floating point
errors sprank (S) == rank (S).
See also: [dmperm], page 578.
[count,h,parent,post,R] = symbfact (S)
[...] = symbfact (S,typ)
[...] = symbfact (S,typ,mode)
Perform a symbolic factorization analysis of the sparse matrix S.
The input variables are
S S is a real or complex sparse matrix.
typ Is the type of the factorization and can be one of
"sym" (default)
Factorize S. Assumes Sis symmetric and uses the upper
triangular portion of the matrix.
Chapter 22: Sparse Matrices 585
"col" Factorize S’ * S.
"row" Factorize S*S’.
"lo" Factorize S’. Assumes Sis symmetric and uses the lower
triangular portion of the matrix.
mode When mode is unspecified return the Cholesky factorization for R. If
mode is "lower" or "L" then return the conjugate transpose R’which is
a lower triangular factor. The conjugate transpose version is faster and
uses less memory, but still returns the same values for all other outputs:
count,h,parent, and post.
The output variables are:
count The row counts of the Cholesky factorization as determined by typ. The
computational difficulty of performing the true factorization using chol
is sum (count .^ 2).
hThe height of the elimination tree.
parent The elimination tree itself.
post A sparse boolean matrix whose structure is that of the Cholesky factor-
ization as determined by typ.
See also: [chol], page 511,[etree], page 568,[treelayout], page 569.
For non square matrices, the user can also utilize the spaugment function to find a least
squares solution to a linear equation.
s= spaugment (A,c)
Create the augmented matrix of A.
This is given by
[c* eye(m,m), A;
A’, zeros(n,n)]
This is related to the least squares solution of A\b, by
s* [ r/c;x]=[b, zeros(n, columns(b)) ]
where ris the residual error
r=b-A*x
As the matrix sis symmetric indefinite it can be factorized with lu, and the minimum
norm solution can therefore be found without the need for a qr factorization. As the
residual error will be zeros (m,m)for underdetermined problems, and example can
be
m = 11; n = 10; mn = max (m, n);
A = spdiags ([ones(mn,1), 10*ones(mn,1), -ones(mn,1)],
[-1, 0, 1], m, n);
x0 = A \ ones (m,1);
s = spaugment (A);
[L, U, P, Q] = lu (s);
x1 = Q * (U \ (L \ (P * [ones(m,1); zeros(n,1)])));
x1 = x1(end - n + 1 : end);
586 GNU Octave
To find the solution of an overdetermined problem needs an estimate of the residual
error rand so it is more complex to formulate a minimum norm solution using the
spaugment function.
In general the left division operator is more stable and faster than using the spaugment
function.
See also: [mldivide], page 144.
Finally, the function eigs can be used to calculate a limited number of eigenvalues and
eigenvectors based on a selection criteria and likewise for svds which calculates a limited
number of singular values and vectors.
d= eigs (A)
d= eigs (A,k)
d= eigs (A,k,sigma)
d= eigs (A,k,sigma,opts)
d= eigs (A,B)
d= eigs (A,B,k)
d= eigs (A,B,k,sigma)
d= eigs (A,B,k,sigma,opts)
d= eigs (af,n)
d= eigs (af,n,B)
d= eigs (af,n,k)
d= eigs (af,n,B,k)
d= eigs (af,n,k,sigma)
d= eigs (af,n,B,k,sigma)
d= eigs (af,n,k,sigma,opts)
d= eigs (af,n,B,k,sigma,opts)
[V,d] = eigs (A, . . . )
[V,d] = eigs (af,n, . . . )
[V,d,flag] = eigs (A, . . . )
[V,d,flag] = eigs (af,n, . . . )
Calculate a limited number of eigenvalues and eigenvectors of A, based on a selection
criteria.
The number of eigenvalues and eigenvectors to calculate is given by kand defaults to
6.
By default, eigs solve the equation Aν =λν, where λis a scalar representing one of
the eigenvalues, and νis the corresponding eigenvector. If given the positive definite
matrix Bthen eigs solves the general eigenvalue equation Aν =λBν.
The argument sigma determines which eigenvalues are returned. sigma can be either
a scalar or a string. When sigma is a scalar, the keigenvalues closest to sigma are
returned. If sigma is a string, it must have one of the following values.
"lm" Largest Magnitude (default).
"sm" Smallest Magnitude.
"la" Largest Algebraic (valid only for real symmetric problems).
"sa" Smallest Algebraic (valid only for real symmetric problems).
Chapter 22: Sparse Matrices 587
"be" Both Ends, with one more from the high-end if kis odd (valid only for
real symmetric problems).
"lr" Largest Real part (valid only for complex or unsymmetric problems).
"sr" Smallest Real part (valid only for complex or unsymmetric problems).
"li" Largest Imaginary part (valid only for complex or unsymmetric prob-
lems).
"si" Smallest Imaginary part (valid only for complex or unsymmetric prob-
lems).
If opts is given, it is a structure defining possible options that eigs should use. The
fields of the opts structure are:
issym If af is given, then flags whether the function af defines a symmetric
problem. It is ignored if Ais given. The default is false.
isreal If af is given, then flags whether the function af defines a real problem.
It is ignored if Ais given. The default is true.
tol Defines the required convergence tolerance, calculated as tol * norm (A).
The default is eps.
maxit The maximum number of iterations. The default is 300.
pThe number of Lanzcos basis vectors to use. More vectors will result in
faster convergence, but a greater use of memory. The optimal value of
pis problem dependent and should be in the range kto n. The default
value is 2 * k.
v0 The starting vector for the algorithm. An initial vector close to the final
vector will speed up convergence. The default is for arpack to randomly
generate a starting vector. If specified, v0 must be an n-by-1 vector where
n= rows (A)
disp The level of diagnostic printout (0|1|2). If disp is 0 then diagnostics are
disabled. The default value is 0.
cholB Flag if chol (B)is passed rather than B. The default is false.
permB The permutation vector of the Cholesky factorization of Bif cholB is
true. That is chol (B(permB, permB)). The default is 1:n.
It is also possible to represent Aby a function denoted af.af must be followed by a
scalar argument ndefining the length of the vector argument accepted by af.af can
be a function handle, an inline function, or a string. When af is a string it holds the
name of the function to use.
af is a function of the form y = af (x) where the required return value of af is
determined by the value of sigma. The four possible forms are
A * x if sigma is not given or is a string other than "sm".
A \ x if sigma is 0 or "sm".
588 GNU Octave
(A - sigma * I) \ x
for the standard eigenvalue problem, where Iis the identity matrix of the
same size as A.
(A - sigma * B) \ x
for the general eigenvalue problem.
The return arguments of eigs depend on the number of return arguments requested.
With a single return argument, a vector dof length kis returned containing the k
eigenvalues that have been found. With two return arguments, Vis a n-by-kmatrix
whose columns are the keigenvectors corresponding to the returned eigenvalues. The
eigenvalues themselves are returned in din the form of a n-by-kmatrix, where the
elements on the diagonal are the eigenvalues.
Given a third return argument flag,eigs returns the status of the convergence. If
flag is 0 then all eigenvalues have converged. Any other value indicates a failure to
converge.
This function is based on the arpack package, written by R. Lehoucq, K. Maschhoff,
D. Sorensen, and C. Yang. For more information see http://www.caam.rice.edu/
software/ARPACK/.
See also: [eig], page 505,[svds], page 588.
s= svds (A)
s= svds (A,k)
s= svds (A,k,sigma)
s= svds (A,k,sigma,opts)
[u,s,v] = svds (. . . )
[u,s,v,flag] = svds (. . . )
Find a few singular values of the matrix A.
The singular values are calculated using
[m,n] = size (A);
s= eigs ([sparse(m,m), A;
A’, sparse(n,n)])
The eigenvalues returned by eigs correspond to the singular values of A. The number
of singular values to calculate is given by kand defaults to 6.
The argument sigma specifies which singular values to find. When sigma is the string
’L’, the default, the largest singular values of Aare found. Otherwise, sigma must be
a real scalar and the singular values closest to sigma are found. As a corollary, sigma
= 0 finds the smallest singular values. Note that for relatively small values of sigma,
there is a chance that the requested number of singular values will not be found. In
that case sigma should be increased.
opts is a structure defining options that svds will pass to eigs. The possible fields
of this structure are documented in eigs. By default, svds sets the following three
fields:
tol The required convergence tolerance for the singular values. The default
value is 1e-10. eigs is passed tol / sqrt(2).
maxit The maximum number of iterations. The default is 300.

Chapter 22: Sparse Matrices 589
disp The level of diagnostic printout (0|1|2). If disp is 0 then diagnostics are
disabled. The default value is 0.
If more than one output is requested then svds will return an approximation of the
singular value decomposition of A
A_approx = u*s*v’
where Aapprox is a matrix of size Abut only rank k.
flag returns 0 if the algorithm has succesfully converged, and 1 otherwise. The test
for convergence is
norm (A*v-u*s, 1) <= tol * norm (A, 1)
svds is best for finding only a few singular values from a large sparse matrix. Other-
wise, svd (full (A)) will likely be more efficient.
See also: [svd], page 521,[eigs], page 586.
22.3 Iterative Techniques Applied to Sparse Matrices
The left division \and right division /operators, discussed in the previous section, use
direct solvers to resolve a linear equation of the form x=A\bor x=b/A. Octave also
includes a number of functions to solve sparse linear equations using iterative techniques.
x= pcg (A,b,tol,maxit,m1,m2,x0, . . . )
[x,flag,relres,iter,resvec,eigest] = pcg (. . . )
Solve the linear system of equations A*x=bby means of the Preconditioned Con-
jugate Gradient iterative method.
The input arguments are
•Acan be either a square (preferably sparse) matrix or a function handle, inline
function or string containing the name of a function which computes A*x. In
principle, Ashould be symmetric and positive definite; if pcg finds Anot to be
positive definite, a warning is printed and the flag output will be set.
•bis the right-hand side vector.
•tol is the required relative tolerance for the residual error, b-A*x. The iteration
stops if norm (b-A*x)≤tol * norm (b). If tol is omitted or empty then a
tolerance of 1e-6 is used.
•maxit is the maximum allowable number of iterations; if maxit is omitted or
empty then a value of 20 is used.
•m=m1 *m2 is the (left) preconditioning matrix, so that the iteration is (the-
oretically) equivalent to solving by pcg P*x=m\b, with P=m\A. Note that
a proper choice of the preconditioner may dramatically improve the overall per-
formance of the method. Instead of matrices m1 and m2, the user may pass two
functions which return the results of applying the inverse of m1 and m2 to a
vector (usually this is the preferred way of using the preconditioner). If m1 is
omitted or empty [] then no preconditioning is applied. If m2 is omitted, m=
m1 will be used as a preconditioner.
•x0 is the initial guess. If x0 is omitted or empty then the function sets x0 to a
zero vector by default.
590 GNU Octave
The arguments which follow x0 are treated as parameters, and passed in a proper
way to any of the functions (Aor m) which are passed to pcg. See the examples
below for further details. The output arguments are
•xis the computed approximation to the solution of A*x=b.
•flag reports on the convergence. A value of 0 means the solution converged and
the tolerance criterion given by tol is satisfied. A value of 1 means that the
maxit limit for the iteration count was reached. A value of 3 indicates that the
(preconditioned) matrix was found not to be positive definite.
•relres is the ratio of the final residual to its initial value, measured in the Eu-
clidean norm.
•iter is the actual number of iterations performed.
•resvec describes the convergence history of the method. resvec(i,1) is the
Euclidean norm of the residual, and resvec(i,2) is the preconditioned residual
norm, after the (i-1)-th iteration, i= 1, 2, ..., iter+1. The preconditioned
residual norm is defined as norm (r) ^ 2 = r’ * (m\r)where r=b-A*x, see
also the description of m. If eigest is not required, only resvec(:,1) is returned.
•eigest returns the estimate for the smallest eigest(1) and largest eigest(2)
eigenvalues of the preconditioned matrix P=m\A. In particular, if no pre-
conditioning is used, the estimates for the extreme eigenvalues of Aare re-
turned. eigest(1) is an overestimate and eigest(2) is an underestimate, so
that eigest(2) / eigest(1) is a lower bound for cond (P, 2), which neverthe-
less in the limit should theoretically be equal to the actual value of the condition
number. The method which computes eigest works only for symmetric positive
definite Aand m, and the user is responsible for verifying this assumption.
Let us consider a trivial problem with a diagonal matrix (we exploit the sparsity of
A)
n = 10;
A = diag (sparse (1:n));
b = rand (n, 1);
[l, u, p] = ilu (A, struct ("droptol", 1.e-3));
Example 1: Simplest use of pcg
x = pcg (A, b)
Example 2: pcg with a function which computes A*x
function y = apply_a (x)
y = [1:N]’ .* x;
endfunction
x = pcg ("apply_a", b)
Example 3: pcg with a preconditioner: l*u
x = pcg (A, b, 1.e-6, 500, l*u)
Example 4: pcg with a preconditioner: l*u. Faster than Example 3 since lower
and upper triangular matrices are easier to invert
x = pcg (A, b, 1.e-6, 500, l, u)
Chapter 22: Sparse Matrices 591
Example 5: Preconditioned iteration, with full diagnostics. The preconditioner
(quite strange, because even the original matrix Ais trivial) is defined as a function
function y = apply_m (x)
k = floor (length (x) - 2);
y = x;
y(1:k) = x(1:k) ./ [1:k]’;
endfunction
[x, flag, relres, iter, resvec, eigest] = ...
pcg (A, b, [], [], "apply_m");
semilogy (1:iter+1, resvec);
Example 6: Finally, a preconditioner which depends on a parameter k.
function y = apply_M (x, varargin)
K = varargin{1};
y = x;
y(1:K) = x(1:K) ./ [1:K]’;
endfunction
[x, flag, relres, iter, resvec, eigest] = ...
pcg (A, b, [], [], "apply_m", [], [], 3)
References:
1. C.T. Kelley, Iterative Methods for Linear and Nonlinear Equations, SIAM, 1995.
(the base PCG algorithm)
2. Y. Saad, Iterative Methods for Sparse Linear Systems, PWS 1996. (condition
number estimate from PCG) Revised version of this book is available online at
http://www-users.cs.umn.edu/~saad/books.html
See also: [sparse], page 564,[pcr], page 591.
x= pcr (A,b,tol,maxit,m,x0, . . . )
[x,flag,relres,iter,resvec] = pcr (. . . )
Solve the linear system of equations A*x=bby means of the Preconditioned Con-
jugate Residuals iterative method.
The input arguments are
•Acan be either a square (preferably sparse) matrix or a function handle, inline
function or string containing the name of a function which computes A*x. In
principle Ashould be symmetric and non-singular; if pcr finds Ato be numeri-
cally singular, you will get a warning message and the flag output parameter will
be set.
•bis the right hand side vector.
•tol is the required relative tolerance for the residual error, b-A*x. The itera-
tion stops if norm (b-A*x) <= tol * norm (b-A*x0). If tol is empty or is
omitted, the function sets tol = 1e-6 by default.
•maxit is the maximum allowable number of iterations; if [] is supplied for maxit,
or pcr has less arguments, a default value equal to 20 is used.
592 GNU Octave
•mis the (left) preconditioning matrix, so that the iteration is (theoretically)
equivalent to solving by pcr P*x=m\b, with P=m\A. Note that a proper
choice of the preconditioner may dramatically improve the overall performance
of the method. Instead of matrix m, the user may pass a function which returns
the results of applying the inverse of mto a vector (usually this is the preferred
way of using the preconditioner). If [] is supplied for m, or mis omitted, no
preconditioning is applied.
•x0 is the initial guess. If x0 is empty or omitted, the function sets x0 to a zero
vector by default.
The arguments which follow x0 are treated as parameters, and passed in a proper
way to any of the functions (Aor m) which are passed to pcr. See the examples
below for further details.
The output arguments are
•xis the computed approximation to the solution of A*x=b.
•flag reports on the convergence. flag = 0 means the solution converged and the
tolerance criterion given by tol is satisfied. flag = 1 means that the maxit limit
for the iteration count was reached. flag = 3 reports a pcr breakdown, see [1]
for details.
•relres is the ratio of the final residual to its initial value, measured in the Eu-
clidean norm.
•iter is the actual number of iterations performed.
•resvec describes the convergence history of the method, so that resvec (i) con-
tains the Euclidean norms of the residual after the (i-1)-th iteration, i= 1,2,
..., iter+1.
Let us consider a trivial problem with a diagonal matrix (we exploit the sparsity of
A)
n = 10;
A = sparse (diag (1:n));
b = rand (N, 1);
Example 1: Simplest use of pcr
x = pcr (A, b)
Example 2: pcr with a function which computes A*x.
function y = apply_a (x)
y = [1:10]’ .* x;
endfunction
x = pcr ("apply_a", b)
Example 3: Preconditioned iteration, with full diagnostics. The preconditioner
(quite strange, because even the original matrix Ais trivial) is defined as a function
Chapter 22: Sparse Matrices 593
function y = apply_m (x)
k = floor (length (x) - 2);
y = x;
y(1:k) = x(1:k) ./ [1:k]’;
endfunction
[x, flag, relres, iter, resvec] = ...
pcr (A, b, [], [], "apply_m")
semilogy ([1:iter+1], resvec);
Example 4: Finally, a preconditioner which depends on a parameter k.
function y = apply_m (x, varargin)
k = varargin{1};
y = x;
y(1:k) = x(1:k) ./ [1:k]’;
endfunction
[x, flag, relres, iter, resvec] = ...
pcr (A, b, [], [], "apply_m"’, [], 3)
References:
[1] W. Hackbusch, Iterative Solution of Large Sparse Systems of Equations, section
9.5.4; Springer, 1994
See also: [sparse], page 564,[pcg], page 589.
The speed with which an iterative solver converges to a solution can be accelerated with
the use of a pre-conditioning matrix M. In this case the linear equation M^-1 * x=M^-1 *
A\bis solved instead. Typical pre-conditioning matrices are partial factorizations of the
original matrix.
L= ichol (A)
L= ichol (A,opts)
Compute the incomplete Cholesky factorization of the sparse square matrix A.
By default, ichol uses only the lower triangle of Aand produces a lower triangular
factor Lsuch that L*L’ approximates A.
The factor given by this routine may be useful as a preconditioner for a system
of linear equations being solved by iterative methods such as PCG (Preconditioned
Conjugate Gradient).
The factorization may be modified by passing options in a structure opts. The option
name is a field of the structure and the setting is the value of field. Names and
specifiers are case sensitive.
type Type of factorization.
"nofill" (default)
Incomplete Cholesky factorization with no fill-in (IC(0)).
"ict" Incomplete Cholesky factorization with threshold dropping
(ICT).
594 GNU Octave
diagcomp A non-negative scalar alpha for incomplete Cholesky factorization of A+
alpha * diag (diag (A)) instead of A. This can be useful when Ais not
positive definite. The default value is 0.
droptol A non-negative scalar specifying the drop tolerance for factorization if
performing ICT. The default value is 0 which produces the complete
Cholesky factorization.
Non-diagonal entries of Lare set to 0 unless
abs (L(i,j)) >= droptol * norm (A(j:end, j), 1).
michol Modified incomplete Cholesky factorization:
"off" (default)
Row and column sums are not necessarily preserved.
"on" The diagonal of Lis modified so that row (and column) sums
are preserved even when elements have been dropped during
the factorization. The relationship preserved is: A* e = L*
L’ * e, where e is a vector of ones.
shape
"lower" (default)
Use only the lower triangle of Aand return a lower triangular
factor Lsuch that L*L’ approximates A.
"upper" Use only the upper triangle of Aand return an upper trian-
gular factor Usuch that U’*U approximates A.
EXAMPLES
The following problem demonstrates how to factorize a sample symmetric positive
definite matrix with the full Cholesky decomposition and with the incomplete one.
A = [ 0.37, -0.05, -0.05, -0.07;
-0.05, 0.116, 0.0, -0.05;
-0.05, 0.0, 0.116, -0.05;
-0.07, -0.05, -0.05, 0.202];
A = sparse (A);
nnz (tril (A))
ans = 9
L = chol (A, "lower");
nnz (L)
ans = 10
norm (A - L * L’, "fro") / norm (A, "fro")
ans = 1.1993e-16
opts.type = "nofill";
L = ichol (A, opts);
nnz (L)
ans = 9
norm (A - L * L’, "fro") / norm (A, "fro")
ans = 0.019736
Chapter 22: Sparse Matrices 595
Another example for decomposition is a finite difference matrix used to solve a bound-
ary value problem on the unit square.
nx = 400; ny = 200;
hx=1/(nx+1);hy=1/(ny+1);
Dxx = spdiags ([ones(nx, 1), -2*ones(nx, 1), ones(nx, 1)],
[-1 0 1 ], nx, nx) / (hx ^ 2);
Dyy = spdiags ([ones(ny, 1), -2*ones(ny, 1), ones(ny, 1)],
[-1 0 1 ], ny, ny) / (hy ^ 2);
A = -kron (Dxx, speye (ny)) - kron (speye (nx), Dyy);
nnz (tril (A))
ans = 239400
opts.type = "nofill";
L = ichol (A, opts);
nnz (tril (A))
ans = 239400
norm (A - L * L’, "fro") / norm (A, "fro")
ans = 0.062327
References for implemented algorithms:
[1] Y. Saad. "Preconditioning Techniques."Iterative Methods for Sparse Linear Sys-
tems, PWS Publishing Company, 1996.
[2] M. Jones, P. Plassmann: An Improved Incomplete Cholesky Factorization, 1992.
See also: [chol], page 511,[ilu], page 595,[pcg], page 589.
ilu (A)
ilu (A,opts)
[L,U] = ilu (. . . )
[L,U,P] = ilu (. . . )
Compute the incomplete LU factorization of the sparse square matrix A.
ilu returns a unit lower triangular matrix L, an upper triangular matrix U, and
optionally a permutation matrix P, such that L*Uapproximates P*A.
The factors given by this routine may be useful as preconditioners for a system of linear
equations being solved by iterative methods such as BICG (BiConjugate Gradients)
or GMRES (Generalized Minimum Residual Method).
The factorization may be modified by passing options in a structure opts. The option
name is a field of the structure and the setting is the value of field. Names and
specifiers are case sensitive.
type Type of factorization.
"nofill" ILU factorization with no fill-in (ILU(0)).
Additional supported options: milu.
"crout" Crout version of ILU factorization (ILUC).
Additional supported options: milu,droptol.
"ilutp" (default)
ILU factorization with threshold and pivoting.
596 GNU Octave
Additional supported options: milu,droptol,udiag,
thresh.
droptol A non-negative scalar specifying the drop tolerance for factorization. The
default value is 0 which produces the complete LU factorization.
Non-diagonal entries of Uare set to 0 unless
abs (U(i,j)) >= droptol * norm (A(:,j)).
Non-diagonal entries of Lare set to 0 unless
abs (L(i,j)) >= droptol * norm (A(:,j))/U(j,j).
milu Modified incomplete LU factorization:
"row" Row-sum modified incomplete LU factorization. The factor-
ization preserves row sums: A* e = L*U* e, where e is a
vector of ones.
"col" Column-sum modified incomplete LU factorization. The fac-
torization preserves column sums: e’ * A= e’ * L*U.
"off" (default)
Row and column sums are not necessarily preserved.
udiag If true, any zeros on the diagonal of the upper triangular factor are re-
placed by the local drop tolerance droptol * norm (A(:,j))/U(j,j).
The default is false.
thresh Pivot threshold for factorization. It can range between 0 (diagonal pivot-
ing) and 1 (default), where the maximum magnitude entry in the column
is chosen to be the pivot.
If ilu is called with just one output, the returned matrix is L+U- speye (size
(A)), where Lis unit lower triangular and Uis upper triangular.
With two outputs, ilu returns a unit lower triangular matrix Land an upper trian-
gular matrix U. For opts.type == "ilutp", one of the factors is permuted based on
the value of opts.milu. When opts.milu == "row",Uis a column permuted upper
triangular factor. Otherwise, Lis a row-permuted unit lower triangular factor.
If there are three named outputs and opts.milu != "row",Pis returned such that L
and Uare incomplete factors of P*A. When opts.milu == "row",Pis returned such
that Land Uare incomplete factors of A*P.
EXAMPLES
A = gallery ("neumann", 1600) + speye (1600);
opts.type = "nofill";
nnz (A)
ans = 7840
nnz (lu (A))
ans = 126478
nnz (ilu (A, opts))
ans = 7840

Chapter 22: Sparse Matrices 597
This shows that Ahas 7,840 nonzeros, the complete LU factorization
has 126,478 nonzeros, and the incomplete LU factorization, with 0
level of fill-in, has 7,840 nonzeros, the same amount as A. Taken from:
http://www.mathworks.com/help/matlab/ref/ilu.html
A = gallery ("wathen", 10, 10);
b = sum (A, 2);
tol = 1e-8;
maxit = 50;
opts.type = "crout";
opts.droptol = 1e-4;
[L, U] = ilu (A, opts);
x = bicg (A, b, tol, maxit, L, U);
norm (A * x - b, inf)
This example uses ILU as preconditioner for a random FEM-Matrix, which has a
large condition number. Without Land UBICG would not converge.
See also: [lu], page 514,[ichol], page 593,[bicg], page 524,[gmres], page 526.
22.4 Real Life Example using Sparse Matrices
A common application for sparse matrices is in the solution of Finite Element Models.
Finite element models allow numerical solution of partial differential equations that do not
have closed form solutions, typically because of the complex shape of the domain.
In order to motivate this application, we consider the boundary value Laplace equation.
This system can model scalar potential fields, such as heat or electrical potential. Given
a medium Ω with boundary ∂Ω. At all points on the ∂Ω the boundary conditions are
known, and we wish to calculate the potential in Ω. Boundary conditions may specify the
potential (Dirichlet boundary condition), its normal derivative across the boundary (Neu-
mann boundary condition), or a weighted sum of the potential and its derivative (Cauchy
boundary condition).
In a thermal model, we want to calculate the temperature in Ω and know the boundary
temperature (Dirichlet condition) or heat flux (from which we can calculate the Neumann
condition by dividing by the thermal conductivity at the boundary). Similarly, in an electri-
cal model, we want to calculate the voltage in Ω and know the boundary voltage (Dirichlet)
or current (Neumann condition after diving by the electrical conductivity). In an electrical
model, it is common for much of the boundary to be electrically isolated; this is a Neumann
boundary condition with the current equal to zero.
The simplest finite element models will divide Ω into simplexes (triangles in 2D, pyramids
in 3D). We take as a 3-D example a cylindrical liquid filled tank with a small non-conductive
ball from the EIDORS project4. This is model is designed to reflect an application of
electrical impedance tomography, where current patterns are applied to such a tank in order
to image the internal conductivity distribution. In order to describe the FEM geometry, we
have a matrix of vertices nodes and simplices elems.
4EIDORS - Electrical Impedance Tomography and Diffuse optical Tomography Reconstruction Software
http://eidors3d.sourceforge.net
598 GNU Octave
The following example creates a simple rectangular 2-D electrically conductive medium
with 10 V and 20 V imposed on opposite sides (Dirichlet boundary conditions). All other
edges are electrically isolated.
node_y = [1;1.2;1.5;1.8;2]*ones(1,11);
node_x = ones(5,1)*[1,1.05,1.1,1.2, ...
1.3,1.5,1.7,1.8,1.9,1.95,2];
nodes = [node_x(:), node_y(:)];
[h,w] = size (node_x);
elems = [];
for idx = 1:w-1
widx = (idx-1)*h;
elems = [elems; ...
widx+[(1:h-1);(2:h);h+(1:h-1)]’; ...
widx+[(2:h);h+(2:h);h+(1:h-1)]’ ];
endfor
E = size (elems,1); # No. of simplices
N = size (nodes,1); # No. of vertices
D = size (elems,2); # dimensions+1
This creates a N-by-2 matrix nodes and a E-by-3 matrix elems with values, which define
finite element triangles:
nodes(1:7,:)’
1.00 1.00 1.00 1.00 1.00 1.05 1.05 ...
1.00 1.20 1.50 1.80 2.00 1.00 1.20 ...
elems(1:7,:)’
1234234...
2345789...
6789678...
Using a first order FEM, we approximate the electrical conductivity distribution in Ω
as constant on each simplex (represented by the vector conductivity). Based on the
finite element geometry, we first calculate a system (or stiffness) matrix for each simplex
(represented as 3-by-3 elements on the diagonal of the element-wise system matrix SE).
Based on SE and a N-by-DE connectivity matrix C, representing the connections between
simplices and vertices, the global connectivity matrix Sis calculated.
## Element conductivity
conductivity = [1*ones(1,16), ...
2*ones(1,48), 1*ones(1,16)];
## Connectivity matrix
C = sparse ((1:D*E), reshape (elems’, ...
D*E, 1), 1, D*E, N);
## Calculate system matrix
Siidx = floor ([0:D*E-1]’/D) * D * ...
Chapter 22: Sparse Matrices 599
ones(1,D) + ones(D*E,1)*(1:D) ;
Sjidx = [1:D*E]’*ones (1,D);
Sdata = zeros (D*E,D);
dfact = factorial (D-1);
for j = 1:E
a = inv ([ones(D,1), ...
nodes(elems(j,:), :)]);
const = conductivity(j) * 2 / ...
dfact / abs (det (a));
Sdata(D*(j-1)+(1:D),:) = const * ...
a(2:D,:)’ * a(2:D,:);
endfor
## Element-wise system matrix
SE = sparse(Siidx,Sjidx,Sdata);
## Global system matrix
S = C’* SE *C;
The system matrix acts like the conductivity Sin Ohm’s law SV =I. Based on the
Dirichlet and Neumann boundary conditions, we are able to solve for the voltages at each
vertex V.
## Dirichlet boundary conditions
D_nodes = [1:5, 51:55];
D_value = [10*ones(1,5), 20*ones(1,5)];
V = zeros (N,1);
V(D_nodes) = D_value;
idx = 1:N; # vertices without Dirichlet
# boundary condns
idx(D_nodes) = [];
## Neumann boundary conditions. Note that
## N_value must be normalized by the
## boundary length and element conductivity
N_nodes = [];
N_value = [];
Q = zeros (N,1);
Q(N_nodes) = N_value;
V(idx) = S(idx,idx) \ ( Q(idx) - ...
S(idx,D_nodes) * V(D_nodes));
Finally, in order to display the solution, we show each solved voltage value in the z-axis
for each simplex vertex. See Figure 22.6.
600 GNU Octave
elemx = elems(:,[1,2,3,1])’;
xelems = reshape (nodes(elemx, 1), 4, E);
yelems = reshape (nodes(elemx, 2), 4, E);
velems = reshape (V(elemx), 4, E);
plot3 (xelems,yelems,velems,"k");
print "grid.eps";
11.2 1.4 1.6 1.8 2
2
1.8
1.6
1.4
1.2
1
10
12
14
16
18
20
Figure 22.6: Example finite element model the showing triangular elements. The height
of each vertex corresponds to the solution value.

601
23 Numerical Integration
Octave comes with several built-in functions for computing the integral of a function numer-
ically (termed quadrature). These functions all solve 1-dimensional integration problems.
23.1 Functions of One Variable
Octave supports five different algorithms for computing the integral
Zb
a
f(x)dx
of a function fover the interval from ato b. These are
quad Numerical integration based on Gaussian quadrature.
quadv Numerical integration using an adaptive vectorized Simpson’s rule.
quadl Numerical integration using an adaptive Lobatto rule.
quadgk Numerical integration using an adaptive Gauss-Konrod rule.
quadcc Numerical integration using adaptive Clenshaw-Curtis rules.
trapz, cumtrapz
Numerical integration of data using the trapezoidal method.
The best quadrature algorithm to use depends on the integrand. If you have empirical data,
rather than a function, the choice is trapz or cumtrapz. If you are uncertain about the
characteristics of the integrand, quadcc will be the most robust as it can handle discon-
tinuities, singularities, oscillatory functions, and infinite intervals. When the integrand is
smooth quadgk may be the fastest of the algorithms.
Function Characteristics
quad Low accuracy with nonsmooth integrands
quadv Medium accuracy with smooth integrands
quadl Medium accuracy with smooth integrands. Slower than quadgk.
quadgk Medium accuracy (1e−6–1e−9) with smooth integrands.
Handles oscillatory functions and infinite bounds
quadcc Low to High accuracy with nonsmooth/smooth integrands
Handles oscillatory functions, singularities, and infinite bounds
Here is an example of using quad to integrate the function
f(x) = xsin(1/x)q|1−x|
from x= 0 to x= 3.
This is a fairly difficult integration (plot the function over the range of integration to see
why).
The first step is to define the function:
function y = f (x)
y = x .* sin (1./x) .* sqrt (abs (1 - x));
endfunction
602 GNU Octave
Note the use of the ‘dot’ forms of the operators. This is not necessary for the quad
integrator, but is required by the other integrators. In any case, it makes it much easier to
generate a set of points for plotting because it is possible to call the function with a vector
argument to produce a vector result.
The second step is to call quad with the limits of integration:
[q, ier, nfun, err] = quad ("f", 0, 3)
⇒1.9819
⇒1
⇒5061
⇒1.1522e-07
Although quad returns a nonzero value for ier, the result is reasonably accurate (to see
why, examine what happens to the result if you move the lower bound to 0.1, then 0.01,
then 0.001, etc.).
The function "f" can be the string name of a function, a function handle, or an inline
function. These options make it quite easy to do integration without having to fully define
a function in an m-file. For example:
# Verify integral (x^3) = x^4/4
f = inline ("x.^3");
quadgk (f, 0, 1)
⇒0.25000
# Verify gamma function = (n-1)! for n = 4
f = @(x) x.^3 .* exp (-x);
quadcc (f, 0, Inf)
⇒6.0000
q= quad (f,a,b)
q= quad (f,a,b,tol)
q= quad (f,a,b,tol,sing)
[q,ier,nfun,err] = quad (. . . )
Numerically evaluate the integral of ffrom ato busing Fortran routines from
quadpack.
fis a function handle, inline function, or a string containing the name of the function
to evaluate. The function must have the form y = f (x) where yand xare scalars.
aand bare the lower and upper limits of integration. Either or both may be infinite.
The optional argument tol is a vector that specifies the desired accuracy of the result.
The first element of the vector is the desired absolute tolerance, and the second
element is the desired relative tolerance. To choose a relative test only, set the absolute
tolerance to zero. To choose an absolute test only, set the relative tolerance to zero.
Both tolerances default to sqrt (eps) or approximately 1.5e−8.
The optional argument sing is a vector of values at which the integrand is known to
be singular.
The result of the integration is returned in q.
ier contains an integer error code (0 indicates a successful integration).
nfun indicates the number of function evaluations that were made.

Chapter 23: Numerical Integration 603
err contains an estimate of the error in the solution.
The function quad_options can set other optional parameters for quad.
Note: because quad is written in Fortran it cannot be called recursively. This pre-
vents its use in integrating over more than one variable by routines dblquad and
triplequad.
See also: [quad options], page 603,[quadv], page 603,[quadl], page 604,[quadgk],
page 604,[quadcc], page 606,[trapz], page 607,[dblquad], page 609,[triplequad],
page 610.
quad_options ()
val = quad_options (opt)
quad_options (opt,val)
Query or set options for the function quad.
When called with no arguments, the names of all available options and their current
values are displayed.
Given one argument, return the value of the option opt.
When called with two arguments, quad_options sets the option opt to value val.
Options include
"absolute tolerance"
Absolute tolerance; may be zero for pure relative error test.
"relative tolerance"
Non-negative relative tolerance. If the absolute tolerance is zero, the rel-
ative tolerance must be greater than or equal to max (50*eps, 0.5e-28).
"single precision absolute tolerance"
Absolute tolerance for single precision; may be zero for pure relative error
test.
"single precision relative tolerance"
Non-negative relative tolerance for single precision. If the absolute tol-
erance is zero, the relative tolerance must be greater than or equal to
max (50*eps, 0.5e-28).
q= quadv (f,a,b)
q= quadv (f,a,b,tol)
q= quadv (f,a,b,tol,trace)
q= quadv (f,a,b,tol,trace,p1,p2, . . . )
[q,nfun] = quadv (. . . )
Numerically evaluate the integral of ffrom ato busing an adaptive Simpson’s rule.
fis a function handle, inline function, or string containing the name of the function
to evaluate. quadv is a vectorized version of quad and the function defined by fmust
accept a scalar or vector as input and return a scalar, vector, or array as output.
aand bare the lower and upper limits of integration. Both limits must be finite.
The optional argument tol defines the absolute tolerance used to stop the adaptation
procedure. The default value is 1e-6.
604 GNU Octave
The algorithm used by quadv involves recursively subdividing the integration interval
and applying Simpson’s rule on each subinterval. If trace is true then after computing
each of these partial integrals display: (1) the total number of function evaluations, (2)
the left end of the subinterval, (3) the length of the subinterval, (4) the approximation
of the integral over the subinterval.
Additional arguments p1, etc., are passed directly to the function f. To use default
values for tol and trace, one may pass empty matrices ([]).
The result of the integration is returned in q.
The optional output nfun indicates the total number of function evaluations per-
formed.
Note: quadv is written in Octave’s scripting language and can be used recursively in
dblquad and triplequad, unlike the quad function.
See also: [quad], page 602,[quadl], page 604,[quadgk], page 604,[quadcc], page 606,
[trapz], page 607,[dblquad], page 609,[triplequad], page 610.
q= quadl (f,a,b)
q= quadl (f,a,b,tol)
q= quadl (f,a,b,tol,trace)
q= quadl (f,a,b,tol,trace,p1,p2, . . . )
[q,nfun] = quadl (. . . )
Numerically evaluate the integral of ffrom ato busing an adaptive Lobatto rule.
fis a function handle, inline function, or string containing the name of the function
to evaluate. The function fmust be vectorized and return a vector of output values
when given a vector of input values.
aand bare the lower and upper limits of integration. Both limits must be finite.
The optional argument tol defines the absolute tolerance with which to perform the
integration. The default value is 1e−6.
The algorithm used by quadl involves recursively subdividing the integration interval.
If trace is defined then for each subinterval display: (1) the total number of function
evaluations, (2) the left end of the subinterval, (3) the length of the subinterval, (4)
the approximation of the integral over the subinterval.
Additional arguments p1, etc., are passed directly to the function f. To use default
values for tol and trace, one may pass empty matrices ([]).
The result of the integration is returned in q.
The optional output nfun indicates the total number of function evaluations per-
formed.
Reference: W. Gander and W. Gautschi, Adaptive Quadrature - Revisited, BIT Vol.
40, No. 1, March 2000, pp. 84–101. http://www.inf.ethz.ch/personal/gander/
See also: [quad], page 602,[quadv], page 603,[quadgk], page 604,[quadcc], page 606,
[trapz], page 607,[dblquad], page 609,[triplequad], page 610.
q= quadgk (f,a,b)
q= quadgk (f,a,b,abstol)
q= quadgk (f,a,b,abstol,trace)
Chapter 23: Numerical Integration 605
q= quadgk (f,a,b,prop,val, . . . )
[q,err] = quadgk (. . . )
Numerically evaluate the integral of ffrom ato busing adaptive Gauss-Konrod
quadrature.
fis a function handle, inline function, or string containing the name of the function
to evaluate. The function fmust be vectorized and return a vector of output values
when given a vector of input values.
aand bare the lower and upper limits of integration. Either or both limits may be
infinite or contain weak end singularities. Variable transformation will be used to
treat any infinite intervals and weaken the singularities. For example:
quadgk (@(x) 1 ./ (sqrt (x) .* (x + 1)), 0, Inf)
Note that the formulation of the integrand uses the element-by-element operator ./
and all user functions to quadgk should do the same.
The optional argument tol defines the absolute tolerance used to stop the integration
procedure. The default value is 1e-10.
The algorithm used by quadgk involves subdividing the integration interval and eval-
uating each subinterval. If trace is true then after computing each of these partial
integrals display: (1) the number of subintervals at this step, (2) the current estimate
of the error err, (3) the current estimate for the integral q.
Alternatively, properties of quadgk can be passed to the function as pairs "prop",
val. Valid properties are
AbsTol Define the absolute error tolerance for the quadrature. The default ab-
solute tolerance is 1e-10 (1e-5 for single).
RelTol Define the relative error tolerance for the quadrature. The default relative
tolerance is 1e-6 (1e-4 for single).
MaxIntervalCount
quadgk initially subdivides the interval on which to perform the
quadrature into 10 intervals. Subintervals that have an unacceptable
error are subdivided and re-evaluated. If the number of subintervals
exceeds 650 subintervals at any point then a poor convergence is signaled
and the current estimate of the integral is returned. The property
"MaxIntervalCount" can be used to alter the number of subintervals
that can exist before exiting.
WayPoints
Discontinuities in the first derivative of the function to integrate can be
flagged with the "WayPoints" property. This forces the ends of a subin-
terval to fall on the breakpoints of the function and can result in signif-
icantly improved estimation of the error in the integral, faster computa-
tion, or both. For example,
quadgk (@(x) abs (1 - x.^2), 0, 2, "Waypoints", 1)
signals the breakpoint in the integrand at x= 1.
Trace If logically true quadgk prints information on the convergence of the
quadrature at each iteration.

606 GNU Octave
If any of a,b, or waypoints is complex then the quadrature is treated as a contour
integral along a piecewise continuous path defined by the above. In this case the
integral is assumed to have no edge singularities. For example,
quadgk (@(z) log (z), 1+1i, 1+1i, "WayPoints",
[1-1i, -1,-1i, -1+1i])
integrates log (z) along the square defined by [1+1i, 1-1i, -1-1i, -1+1i].
The result of the integration is returned in q.
err is an approximate bound on the error in the integral abs (q-I), where Iis the
exact value of the integral.
Reference: L.F. Shampine, "Vectorized adaptive quadrature in matlab", Journal of
Computational and Applied Mathematics, pp. 131–140, Vol 211, Issue 2, Feb 2008.
See also: [quad], page 602,[quadv], page 603,[quadl], page 604,[quadcc], page 606,
[trapz], page 607,[dblquad], page 609,[triplequad], page 610.
q= quadcc (f,a,b)
q= quadcc (f,a,b,tol)
q= quadcc (f,a,b,tol,sing)
[q,err,nr_points] = quadcc (. . . )
Numerically evaluate the integral of ffrom ato busing doubly-adaptive Clenshaw-
Curtis quadrature.
fis a function handle, inline function, or string containing the name of the function
to evaluate. The function fmust be vectorized and must return a vector of output
values if given a vector of input values. For example,
f = @(x) x .* sin (1./x) .* sqrt (abs (1 - x));
which uses the element-by-element “dot” form for all operators.
aand bare the lower and upper limits of integration. Either or both limits may be
infinite. quadcc handles an inifinite limit by substituting the variable of integration
with x = tan (pi/2*u).
The optional argument tol defines the relative tolerance used to stop the integration
procedure. The default value is 1e−6.
The optional argument sing contains a list of points where the integrand has known
singularities, or discontinuities in any of its derivatives, inside the integration interval.
For the example above, which has a discontinuity at x=1, the call to quadcc would
be as follows
int = quadcc (f, a, b, 1.0e-6, [ 1 ]);
The result of the integration is returned in q.
err is an estimate of the absolute integration error.
nr points is the number of points at which the integrand was evaluated.
If the adaptive integration did not converge, the value of err will be larger than the
requested tolerance. Therefore, it is recommended to verify this value for difficult
integrands.
quadcc is capable of dealing with non-numeric values of the integrand such as NaN or
Inf. If the integral diverges, and quadcc detects this, then a warning is issued and
Inf or -Inf is returned.
Chapter 23: Numerical Integration 607
Note: quadcc is a general purpose quadrature algorithm and, as such, may be less
efficient for a smooth or otherwise well-behaved integrand than other methods such
as quadgk.
The algorithm uses Clenshaw-Curtis quadrature rules of increasing degree in each
interval and bisects the interval if either the function does not appear to be smooth
or a rule of maximum degree has been reached. The error estimate is computed from
the L2-norm of the difference between two successive interpolations of the integrand
over the nodes of the respective quadrature rules.
Reference: P. Gonnet, Increasing the Reliability of Adaptive Quadrature Using Ex-
plicit Interpolants, ACM Transactions on Mathematical Software, Vol. 37, Issue 3,
Article No. 3, 2010.
See also: [quad], page 602,[quadv], page 603,[quadl], page 604,[quadgk], page 604,
[trapz], page 607,[dblquad], page 609,[triplequad], page 610.
Sometimes one does not have the function, but only the raw (x, y) points from which to
perform an integration. This can occur when collecting data in an experiment. The trapz
function can integrate these values as shown in the following example where "data"has
been collected on the cosine function over the range [0, pi/2).
x = 0:0.1:pi/2; # Uniformly spaced points
y = cos (x);
trapz (x, y)
⇒0.99666
The answer is reasonably close to the exact value of 1. Ordinary quadrature is sensitive
to the characteristics of the integrand. Empirical integration depends not just on the
integrand, but also on the particular points chosen to represent the function. Repeating the
example above with the sine function over the range [0, pi/2) produces far inferior results.
x = 0:0.1:pi/2; # Uniformly spaced points
y = sin (x);
trapz (x, y)
⇒0.92849
However, a slightly different choice of data points can change the result significantly.
The same integration, with the same number of points, but spaced differently produces a
more accurate answer.
x = linspace (0, pi/2, 16); # Uniformly spaced, but including endpoint
y = sin (x);
trapz (x, y)
⇒0.99909
In general there may be no way of knowing the best distribution of points ahead of time.
Or the points may come from an experiment where there is no freedom to select the best
distribution. In any case, one must remain aware of this issue when using trapz.
q= trapz (y)
q= trapz (x,y)
q= trapz (. . . , dim)
Numerically evaluate the integral of points yusing the trapezoidal method.
608 GNU Octave
trapz (y)computes the integral of yalong the first non-singleton dimension. When
the argument xis omitted an equally spaced xvector with unit spacing (1) is assumed.
trapz (x,y)evaluates the integral with respect to the spacing in xand the values
in y. This is useful if the points in yhave been sampled unevenly.
If the optional dim argument is given, operate along this dimension.
Application Note: If xis not specified then unit spacing will be used. To scale the
integral to the correct value you must multiply by the actual spacing value (deltaX).
As an example, the integral of x3over the range [0, 1] is x4/4 or 0.25. The following
code uses trapz to calculate the integral in three different ways.
x = 0:0.1:1;
y = x.^3;
q = trapz (y)
⇒q = 2.525 # No scaling
q * 0.1
⇒q = 0.2525 # Approximation to integral by scaling
trapz (x, y)
⇒q = 0.2525 # Same result by specifying x
See also: [cumtrapz], page 608.
q= cumtrapz (y)
q= cumtrapz (x,y)
q= cumtrapz (. . . , dim)
Cumulative numerical integration of points yusing the trapezoidal method.
cumtrapz (y)computes the cumulative integral of yalong the first non-singleton
dimension. Where trapz reports only the overall integral sum, cumtrapz reports the
current partial sum value at each point of y.
When the argument xis omitted an equally spaced xvector with unit spacing (1)
is assumed. cumtrapz (x,y)evaluates the integral with respect to the spacing in x
and the values in y. This is useful if the points in yhave been sampled unevenly.
If the optional dim argument is given, operate along this dimension.
Application Note: If xis not specified then unit spacing will be used. To scale the
integral to the correct value you must multiply by the actual spacing value (deltaX).
See also: [trapz], page 607,[cumsum], page 479.
23.2 Orthogonal Collocation
[r,amat,bmat,q] = colloc (n,"left","right")
Compute derivative and integral weight matrices for orthogonal collocation.
Reference: J. Villadsen, M. L. Michelsen, Solution of Differential Equation Models
by Polynomial Approximation.
Here is an example of using colloc to generate weight matrices for solving the second
order differential equation u0−αu00 = 0 with the boundary conditions u(0) = 0 and u(1) = 1.

Chapter 23: Numerical Integration 609
First, we can generate the weight matrices for npoints (including the endpoints of the
interval), and incorporate the boundary conditions in the right hand side (for a specific
value of α).
n = 7;
alpha = 0.1;
[r, a, b] = colloc (n-2, "left", "right");
at = a(2:n-1,2:n-1);
bt = b(2:n-1,2:n-1);
rhs = alpha * b(2:n-1,n) - a(2:n-1,n);
Then the solution at the roots ris
u = [ 0; (at - alpha * bt) \ rhs; 1]
⇒[ 0.00; 0.004; 0.01 0.00; 0.12; 0.62; 1.00 ]
23.3 Functions of Multiple Variables
Octave does not have built-in functions for computing the integral of functions of multiple
variables directly. It is possible, however, to compute the integral of a function of multiple
variables using the existing functions for one-dimensional integrals.
To illustrate how the integration can be performed, we will integrate the function
f(x, y) = sin(πxy)√xy
for xand ybetween 0 and 1.
The first approach creates a function that integrates fwith respect to x, and then
integrates that function with respect to y. Because quad is written in Fortran it cannot
be called recursively. This means that quad cannot integrate a function that calls quad,
and hence cannot be used to perform the double integration. Any of the other integrators,
however, can be used which is what the following code demonstrates.
function q = g(y)
q = ones (size (y));
for i = 1:length (y)
f = @(x) sin (pi*x.*y(i)) .* sqrt (x.*y(i));
q(i) = quadgk (f, 0, 1);
endfor
endfunction
I = quadgk ("g", 0, 1)
⇒0.30022
The above process can be simplified with the dblquad and triplequad functions for
integrals over two and three variables. For example:
I = dblquad (@(x, y) sin (pi*x.*y) .* sqrt (x.*y), 0, 1, 0, 1)
⇒0.30022
dblquad (f,xa,xb,ya,yb)
dblquad (f,xa,xb,ya,yb,tol)
dblquad (f,xa,xb,ya,yb,tol,quadf)
610 GNU Octave
dblquad (f,xa,xb,ya,yb,tol,quadf, . . . )
Numerically evaluate the double integral of f.
fis a function handle, inline function, or string containing the name of the function
to evaluate. The function fmust have the form z=f(x, y) where xis a vector and
yis a scalar. It should return a vector of the same length and orientation as x.
xa,ya and xb,yb are the lower and upper limits of integration for x and y respectively.
The underlying integrator determines whether infinite bounds are accepted.
The optional argument tol defines the absolute tolerance used to integrate each sub-
integral. The default value is 1e−6.
The optional argument quadf specifies which underlying integrator function to use.
Any choice but quad is available and the default is quadcc.
Additional arguments, are passed directly to f. To use the default value for tol or
quadf one may pass ’:’ or an empty matrix ([]).
See also: [triplequad], page 610,[quad], page 602,[quadv], page 603,[quadl], page 604,
[quadgk], page 604,[quadcc], page 606,[trapz], page 607.
triplequad (f,xa,xb,ya,yb,za,zb)
triplequad (f,xa,xb,ya,yb,za,zb,tol)
triplequad (f,xa,xb,ya,yb,za,zb,tol,quadf)
triplequad (f,xa,xb,ya,yb,za,zb,tol,quadf, . . . )
Numerically evaluate the triple integral of f.
fis a function handle, inline function, or string containing the name of the function
to evaluate. The function fmust have the form w=f(x, y, z) where either xor yis
a vector and the remaining inputs are scalars. It should return a vector of the same
length and orientation as xor y.
xa,ya,za and xb,yb,zb are the lower and upper limits of integration for x, y,
and z respectively. The underlying integrator determines whether infinite bounds are
accepted.
The optional argument tol defines the absolute tolerance used to integrate each sub-
integral. The default value is 1e-6.
The optional argument quadf specifies which underlying integrator function to use.
Any choice but quad is available and the default is quadcc.
Additional arguments, are passed directly to f. To use the default value for tol or
quadf one may pass ’:’ or an empty matrix ([]).
See also: [dblquad], page 609,[quad], page 602,[quadv], page 603,[quadl], page 604,
[quadgk], page 604,[quadcc], page 606,[trapz], page 607.
The above mentioned approach works, but is fairly slow, and that problem increases
exponentially with the dimensionality of the integral. Another possible solution is to use
Orthogonal Collocation as described in the previous section (see Section 23.2 [Orthogonal
Collocation], page 608). The integral of a function f(x, y) for xand ybetween 0 and 1 can
be approximated using npoints by
Z1
0Z1
0
f(x, y)dxdy ≈
n
X
i=1
n
X
j=1
qiqjf(ri, rj),
611
where qand ris as returned by colloc (n). The generalization to more than two variables
is straight forward. The following code computes the studied integral using n= 8 points.
f = @(x,y) sin (pi*x*y’) .* sqrt (x*y’);
n = 8;
[t, ~, ~, q] = colloc (n);
I = q’*f(t,t)*q;
⇒0.30022
It should be noted that the number of points determines the quality of the approximation.
If the integration needs to be performed between aand b, instead of 0 and 1, then a change
of variables is needed.
613
24 Differential Equations
Octave has built-in functions for solving ordinary differential equations, and differential-
algebraic equations. All solvers are based on reliable ODE routines written in Fortran.
24.1 Ordinary Differential Equations
The function lsode can be used to solve ODEs of the form
dx
dt =f(x, t)
using Hindmarsh’s ODE solver lsode.
[x,istate,msg] = lsode (fcn,x_0,t)
[x,istate,msg] = lsode (fcn,x_0,t,t_crit)
Ordinary Differential Equation (ODE) solver.
The set of differential equations to solve is
dx
dt =f(x, t)
with
x(t0) = x0
The solution is returned in the matrix x, with each row corresponding to an element
of the vector t. The first element of tshould be t0and should correspond to the initial
state of the system x 0, so that the first row of the output is x 0.
The first argument, fcn, is a string, inline, or function handle that names the function
fto call to compute the vector of right hand sides for the set of equations. The
function must have the form
xdot =f(x,t)
in which xdot and xare vectors and tis a scalar.
If fcn is a two-element string array or a two-element cell array of strings, inline
functions, or function handles, the first element names the function fdescribed above,
and the second element names a function to compute the Jacobian of f. The Jacobian
function must have the form
jac =j(x,t)
in which jac is the matrix of partial derivatives
J=∂fi
∂xj
=
∂f1
∂x1
∂f1
∂x2··· ∂f1
∂xN
∂f2
∂x1
∂f2
∂x2··· ∂f2
∂xN
.
.
..
.
.....
.
.
∂f3
∂x1
∂f3
∂x2··· ∂f3
∂xN
The second and third arguments specify the initial state of the system, x0, and the
initial value of the independent variable t0.
614 GNU Octave
The fourth argument is optional, and may be used to specify a set of times that
the ODE solver should not integrate past. It is useful for avoiding difficulties with
singularities and points where there is a discontinuity in the derivative.
After a successful computation, the value of istate will be 2 (consistent with the
Fortran version of lsode).
If the computation is not successful, istate will be something other than 2 and msg
will contain additional information.
You can use the function lsode_options to set optional parameters for lsode.
See also: [daspk], page 620,[dassl], page 624,[dasrt], page 626.
lsode_options ()
val = lsode_options (opt)
lsode_options (opt,val)
Query or set options for the function lsode.
When called with no arguments, the names of all available options and their current
values are displayed.
Given one argument, return the value of the option opt.
When called with two arguments, lsode_options sets the option opt to value val.
Options include
"absolute tolerance"
Absolute tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector.
"relative tolerance"
Relative tolerance parameter. Unlike the absolute tolerance, this param-
eter may only be a scalar.
The local error test applied at each integration step is
abs (local error in x(i)) <= ...
rtol * abs (y(i)) + atol(i)
"integration method"
A string specifying the method of integration to use to solve the ODE
system. Valid values are
"adams"
"non-stiff"
No Jacobian used (even if it is available).
"bdf"
"stiff" Use stiff backward differentiation formula (BDF) method. If
a function to compute the Jacobian is not supplied, lsode
will compute a finite difference approximation of the Jacobian
matrix.
"initial step size"
The step size to be attempted on the first step (default is determined
automatically).
Chapter 24: Differential Equations 615
"maximum order"
Restrict the maximum order of the solution method. If using the Adams
method, this option must be between 1 and 12. Otherwise, it must be
between 1 and 5, inclusive.
"maximum step size"
Setting the maximum stepsize will avoid passing over very large regions
(default is not specified).
"minimum step size"
The minimum absolute step size allowed (default is 0).
"step limit"
Maximum number of steps allowed (default is 100000).
Here is an example of solving a set of three differential equations using lsode. Given
the function
## oregonator differential equation
function xdot = f (x, t)
xdot = zeros (3,1);
xdot(1) = 77.27 * (x(2) - x(1)*x(2) + x(1) \
- 8.375e-06*x(1)^2);
xdot(2) = (x(3) - x(1)*x(2) - x(2)) / 77.27;
xdot(3) = 0.161*(x(1) - x(3));
endfunction
and the initial condition x0 = [ 4; 1.1; 4 ], the set of equations can be integrated using
the command
t = linspace (0, 500, 1000);
y = lsode ("f", x0, t);
If you try this, you will see that the value of the result changes dramatically between t
= 0 and 5, and again around t= 305. A more efficient set of output points might be
t = [0, logspace(-1, log10(303), 150), \
logspace(log10(304), log10(500), 150)];
See Alan C. Hindmarsh, ODEPACK, A Systematized Collection of ODE Solvers, in
Scientific Computing, R. S. Stepleman, editor, (1983) for more information about the inner
workings of lsode.
An m-file for the differential equation used above is included with the Octave distribution
in the examples directory under the name oregonator.m.
24.1.1 Matlab-compatible solvers
Octave also provides a set of solvers for initial value problems for Ordinary Differential
Equations that have a matlab-compatible interface. The options for this class of methods
are set using the functions.
•odeset

616 GNU Octave
•odeget
Currently implemented solvers are:
•Runge-Kutta methods
•ode45 Integrates a system of non–stiff ordinary differential equations (non–stiff
ODEs and DAEs) using second order Dormand-Prince method. This is a fourth–
order accurate integrator therefore the local error normally expected is O(h5). This
solver requires six function evaluations per integration step.
•ode23 Integrates a system of non–stiff ordinary differential equations (non-stiff
ODEs and DAEs) using second order Bogacki-Shampine method. This is a second-
order accurate integrator therefore the local error normally expected is O(h3). This
solver requires three function evaluations per integration step.
[t,y] = ode45 (fun,trange,init)
[t,y] = ode45 (fun,trange,init,ode_opt)
[t,y,te,ye,ie] = ode45 (. . . )
solution = ode45 (. . . )
ode45 (. . .)
Solve a set of non-stiff Ordinary Differential Equations (non-stiff ODEs) with the well
known explicit Dormand-Prince method of order 4.
fun is a function handle, inline function, or string containing the name of the function
that defines the ODE: y’ = f(t,y). The function must accept two inputs where the
first is time tand the second is a column vector of unknowns y.
trange specifies the time interval over which the ODE will be evaluated. Typically,
it is a two-element vector specifying the initial and final times ([tinit, tfinal]).
If there are more than two elements then the solution will also be evaluated at these
intermediate time instances.
By default, ode45 uses an adaptive timestep with the integrate_adaptive algo-
rithm. The tolerance for the timestep computation may be changed by using the
options "RelTol" and "AbsTol".
init contains the initial value for the unknowns. If it is a row vector then the solution
ywill be a matrix in which each column is the solution for the corresponding initial
value in init.
The optional fourth argument ode opt specifies non-default options to the ODE
solver. It is a structure generated by odeset.
The function typically returns two outputs. Variable tis a column vector and contains
the times where the solution was found. The output yis a matrix in which each
column refers to a different unknown of the problem and each row corresponds to a
time in t.
The output can also be returned as a structure solution which has a field xcontaining
a row vector of times where the solution was evaluated and a field ycontaining the
solution matrix such that each column corresponds to a time in x. Use fieldnames
(solution)to see the other fields and additional information returned.
If no output arguments are requested, and no OutputFcn is specified in ode opt, then
the OutputFcn is set to odeplot and the results of the solver are plotted immediately.

Chapter 24: Differential Equations 617
If using the "Events" option then three additional outputs may be returned. te holds
the time when an Event function returned a zero. ye holds the value of the solution
at time te.ie contains an index indicating which Event function was triggered in the
case of multiple Event functions.
Example: Solve the Van der Pol equation
fvdp = @(t,y) [y(2); (1 - y(1)^2) * y(2) - y(1)];
[t,y] = ode45 (fvdp, [0, 20], [2, 0]);
See also: [odeset], page 618,[odeget], page 620,[ode23], page 617.
[t,y] = ode23 (fun,trange,init)
[t,y] = ode23 (fun,trange,init,ode_opt)
[t,y,te,ye,ie] = ode23 (. . . )
solution = ode23 (. . . )
ode23 (. . .)
Solve a set of non-stiff Ordinary Differential Equations (non-stiff ODEs) with the well
known explicit Bogacki-Shampine method of order 3. For the definition of this method
see http://en.wikipedia.org/wiki/List_of_Runge%E2%80%93Kutta_methods.
fun is a function handle, inline function, or string containing the name of the function
that defines the ODE: y’ = f(t,y). The function must accept two inputs where the
first is time tand the second is a column vector of unknowns y.
trange specifies the time interval over which the ODE will be evaluated. Typically,
it is a two-element vector specifying the initial and final times ([tinit, tfinal]).
If there are more than two elements then the solution will also be evaluated at these
intermediate time instances.
By default, ode23 uses an adaptive timestep with the integrate_adaptive algo-
rithm. The tolerance for the timestep computation may be changed by using the
options "RelTol" and "AbsTol".
init contains the initial value for the unknowns. If it is a row vector then the solution
ywill be a matrix in which each column is the solution for the corresponding initial
value in init.
The optional fourth argument ode opt specifies non-default options to the ODE
solver. It is a structure generated by odeset.
The function typically returns two outputs. Variable tis a column vector and contains
the times where the solution was found. The output yis a matrix in which each
column refers to a different unknown of the problem and each row corresponds to a
time in t.
The output can also be returned as a structure solution which has a field xcontaining
a row vector of times where the solution was evaluated and a field ycontaining the
solution matrix such that each column corresponds to a time in x. Use fieldnames
(solution)to see the other fields and additional information returned.
If no output arguments are requested, and no OutputFcn is specified in ode opt, then
the OutputFcn is set to odeplot and the results of the solver are plotted immediately.
If using the "Events" option then three additional outputs may be returned. te holds
the time when an Event function returned a zero. ye holds the value of the solution
618 GNU Octave
at time te.ie contains an index indicating which Event function was triggered in the
case of multiple Event functions.
Example: Solve the Van der Pol equation
fvdp = @(t,y) [y(2); (1 - y(1)^2) * y(2) - y(1)];
[t,y] = ode23 (fvdp, [0, 20], [2, 0]);
See also: [odeset], page 618,[odeget], page 620,[ode45], page 616.
odestruct = odeset ()
odestruct = odeset ("field1",value1,"field2",value2, . . . )
odestruct = odeset (oldstruct,"field1",value1,"field2",value2, . . . )
odestruct = odeset (oldstruct,newstruct)
odeset ()
Create or modify an ODE options structure.
When called with no input argument and one output argument, return a new ODE
options structure that contains all possible fields initialized to their default values. If
no output argument is requested, display a list of the common ODE solver options
along with their default value.
If called with name-value input argument pairs "field1","value1","field2","value2",
. . . return a new ODE options structure with all the most common option fields
initialized, and set the values of the fields "field1","field2", . . . to the values value1,
value2, . . ..
If called with an input structure oldstruct then overwrite the values of the options
"field1","field2", . . . with new values value1,value2, . . . and return the modified
structure.
When called with two input ODE options structures oldstruct and newstruct over-
write all values from the structure oldstruct with new values from the structure
newstruct. Empty values in newstruct will not overwrite values in oldstruct.
The most commonly used ODE options, which are always assigned a value by odeset,
are the following:
AbsTol Absolute error tolerance.
BDF Use BDF formulas in implicit multistep methods. Note: This option is
not yet implemented.
Events Event function. An event function must have the form [value,
isterminal, direction] = my_events_f (t, y)
InitialSlope
Consistent initial slope vector for DAE solvers.
InitialStep Initial time step size.
Jacobian Jacobian matrix, specified as a constant matrix or a function of time and
state.
JConstant Specify whether the Jacobian is a constant matrix or depends on the
state.
Chapter 24: Differential Equations 619
JPattern If the Jacobian matrix is sparse and non-constant but maintains a con-
stant sparsity pattern, specify the sparsity pattern.
Mass Mass matrix, specified as a constant matrix or a function of time and
state.
MassSingular
Specify whether the mass matrix is singular. Accepted values include
"yes","no","maybe".
MaxOrder Maximum order of formula.
MaxStep Maximum time step value.
MStateDependence
Specify whether the mass matrix depends on the state or only on time.
MvPattern
If the mass matrix is sparse and non-constant but maintains a constant
sparsity pattern, specify the sparsity pattern. Note: This option is not
yet implemented.
NonNegative
Specify elements of the state vector that are expected to remain nonneg-
ative during the simulation.
NormControl
Control error relative to the 2-norm of the solution, rather than its abso-
lute value.
OutputFcn
Function to monitor the state during the simulation. For the form of the
function to use see odeplot.
OutputSel Indices of elements of the state vector to be passed to the output moni-
toring function.
Refine Specify whether output should be returned only at the end of each time
step or also at intermediate time instances. The value should be a scalar
indicating the number of equally spaced time points to use within each
timestep at which to return output. Note: This option is not yet imple-
mented.
RelTol Relative error tolerance.
Stats Print solver statistics after simulation.
Vectorized Specify whether odefun can be passed multiple values of the state at
once.
Field names that are not in the above list are also accepted and added to the result
structure.
See also: [odeget], page 620.

620 GNU Octave
val = odeget (ode_opt,field)
val = odeget (ode_opt,field,default)
Query the value of the property field in the ODE options structure ode opt.
If called with two input arguments and the first input argument ode opt is an ODE
option structure and the second input argument field is a string specifying an option
name, then return the option value val corresponding to field from ode opt.
If called with an optional third input argument, and field is not set in the structure
ode opt, then return the default value default instead.
See also: [odeset], page 618.
stop_solve = odeplot (t,y,flag)
Open a new figure window and plot the solution of an ode problem at each time step
during the integration.
The types and values of the input parameters tand ydepend on the input flag that
is of type string. Valid values of flag are:
"init" The input tmust be a column vector of length 2 with the first and last
time step ([tfirst tlast]. The input ycontains the initial conditions
for the ode problem (y0).
"" The input tmust be a scalar double specifying the time for which the
solution in input ywas calculated.
"done" The inputs should be empty, but are ignored if they are present.
odeplot always returns false, i.e., don’t stop the ode solver.
Example: solve an anonymous implementation of the "Van der Pol" equation and
display the results while solving.
fvdp = @(t,y) [y(2); (1 - y(1)^2) * y(2) - y(1)];
opt = odeset ("OutputFcn", @odeplot, "RelTol", 1e-6);
sol = ode45 (fvdp, [0 20], [2 0], opt);
Background Information: This function is called by an ode solver function if it was
specified in the "OutputFcn" property of an options structure created with odeset.
The ode solver will initially call the function with the syntax odeplot ([tfirst,
tlast], y0, "init"). The function initializes internal variables, creates a new figure
window, and sets the x limits of the plot. Subsequently, at each time step during the
integration the ode solver calls odeplot (t,y, []). At the end of the solution the
ode solver calls odeplot ([], [], "done") so that odeplot can perform any clean-up
actions required.
See also: [odeset], page 618,[odeget], page 620,[ode23], page 617,[ode45], page 616.
24.2 Differential-Algebraic Equations
The function daspk can be used to solve DAEs of the form
0 = f( ˙x, x, t), x(t= 0) = x0,˙x(t= 0) = ˙x0
where ˙x=dx
dt is the derivative of x. The equation is solved using Petzold’s DAE solver
daspk.

Chapter 24: Differential Equations 621
[x,xdot,istate,msg] = daspk (fcn,x_0,xdot_0,t,t_crit)
Solve the set of differential-algebraic equations
0 = f(x, ˙x, t)
with
x(t0) = x0,˙x(t0) = ˙x0
The solution is returned in the matrices xand xdot, with each row in the result
matrices corresponding to one of the elements in the vector t. The first element of t
should be t0and correspond to the initial state of the system x 0 and its derivative
xdot 0, so that the first row of the output xis x 0 and the first row of the output
xdot is xdot 0.
The first argument, fcn, is a string, inline, or function handle that names the function
fto call to compute the vector of residuals for the set of equations. It must have the
form
res =f(x,xdot,t)
in which x,xdot, and res are vectors, and tis a scalar.
If fcn is a two-element string array or a two-element cell array of strings, inline
functions, or function handles, the first element names the function fdescribed above,
and the second element names a function to compute the modified Jacobian
J=∂f
∂x +c∂f
∂˙x
The modified Jacobian function must have the form
jac =j(x,xdot,t,c)
The second and third arguments to daspk specify the initial condition of the states
and their derivatives, and the fourth argument specifies a vector of output times at
which the solution is desired, including the time corresponding to the initial condition.
The set of initial states and derivatives are not strictly required to be consistent.
If they are not consistent, you must use the daspk_options function to provide
additional information so that daspk can compute a consistent starting point.
The fifth argument is optional, and may be used to specify a set of times that the DAE
solver should not integrate past. It is useful for avoiding difficulties with singularities
and points where there is a discontinuity in the derivative.
After a successful computation, the value of istate will be greater than zero (consistent
with the Fortran version of daspk).
If the computation is not successful, the value of istate will be less than zero and msg
will contain additional information.
You can use the function daspk_options to set optional parameters for daspk.
See also: [dassl], page 624.

622 GNU Octave
daspk_options ()
val = daspk_options (opt)
daspk_options (opt,val)
Query or set options for the function daspk.
When called with no arguments, the names of all available options and their current
values are displayed.
Given one argument, return the value of the option opt.
When called with two arguments, daspk_options sets the option opt to value val.
Options include
"absolute tolerance"
Absolute tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the relative tolerance must
also be a vector of the same length.
"relative tolerance"
Relative tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the absolute tolerance must
also be a vector of the same length.
The local error test applied at each integration step is
abs (local error in x(i))
<= rtol(i) * abs (Y(i)) + atol(i)
"compute consistent initial condition"
Denoting the differential variables in the state vector by ‘Y_d’ and the
algebraic variables by ‘Y_a’, ddaspk can solve one of two initialization
problems:
1. Given Y d, calculate Y a and Y’ d
2. Given Y’, calculate Y.
In either case, initial values for the given components are input, and
initial guesses for the unknown components must also be provided as
input. Set this option to 1 to solve the first problem, or 2 to solve the
second (the default is 0, so you must provide a set of initial conditions
that are consistent).
If this option is set to a nonzero value, you must also set the "algebraic
variables" option to declare which variables in the problem are alge-
braic.
"use initial condition heuristics"
Set to a nonzero value to use the initial condition heuristics options de-
scribed below.
"initial condition heuristics"
A vector of the following parameters that can be used to control the initial
condition calculation.
MXNIT Maximum number of Newton iterations (default is 5).
MXNJ Maximum number of Jacobian evaluations (default is 6).
Chapter 24: Differential Equations 623
MXNH Maximum number of values of the artificial stepsize
parameter to be tried if the "compute consistent initial
condition" option has been set to 1 (default is 5).
Note that the maximum total number of Newton iterations
allowed is MXNIT*MXNJ*MXNH if the "compute consistent
initial condition" option has been set to 1 and
MXNIT*MXNJ if it is set to 2.
LSOFF Set to a nonzero value to disable the linesearch algorithm
(default is 0).
STPTOL Minimum scaled step in linesearch algorithm (default is
eps^(2/3)).
EPINIT Swing factor in the Newton iteration convergence test. The
test is applied to the residual vector, premultiplied by the
approximate Jacobian. For convergence, the weighted RMS
norm of this vector (scaled by the error weights) must be less
than EPINIT*EPCON, where EPCON = 0.33 is the analogous
test constant used in the time steps. The default is EPINIT
= 0.01.
"print initial condition info"
Set this option to a nonzero value to display detailed information about
the initial condition calculation (default is 0).
"exclude algebraic variables from error test"
Set to a nonzero value to exclude algebraic variables from the error test.
You must also set the "algebraic variables" option to declare which
variables in the problem are algebraic (default is 0).
"algebraic variables"
A vector of the same length as the state vector. A nonzero element
indicates that the corresponding element of the state vector is an algebraic
variable (i.e., its derivative does not appear explicitly in the equation set).
This option is required by the "compute consistent initial
condition" and "exclude algebraic variables from error test"
options.
"enforce inequality constraints"
Set to one of the following values to enforce the inequality constraints
specified by the "inequality constraint types" option (default is 0).
1. To have constraint checking only in the initial condition calculation.
2. To enforce constraint checking during the integration.
3. To enforce both options 1 and 2.
"inequality constraint types"
A vector of the same length as the state specifying the type of inequality
constraint. Each element of the vector corresponds to an element of the
state and should be assigned one of the following codes
-2 Less than zero.

624 GNU Octave
-1 Less than or equal to zero.
0 Not constrained.
1 Greater than or equal to zero.
2 Greater than zero.
This option only has an effect if the "enforce inequality constraints"
option is nonzero.
"initial step size"
Differential-algebraic problems may occasionally suffer from severe scaling
difficulties on the first step. If you know a great deal about the scaling
of your problem, you can help to alleviate this problem by specifying an
initial stepsize (default is computed automatically).
"maximum order"
Restrict the maximum order of the solution method. This option must
be between 1 and 5, inclusive (default is 5).
"maximum step size"
Setting the maximum stepsize will avoid passing over very large regions
(default is not specified).
Octave also includes dassl, an earlier version of daspk, and dasrt, which can be used
to solve DAEs with constraints (stopping conditions).
[x,xdot,istate,msg] = dassl (fcn,x_0,xdot_0,t,t_crit)
Solve the set of differential-algebraic equations
0 = f(x, ˙x, t)
with
x(t0) = x0,˙x(t0) = ˙x0
The solution is returned in the matrices xand xdot, with each row in the result
matrices corresponding to one of the elements in the vector t. The first element of t
should be t0and correspond to the initial state of the system x 0 and its derivative
xdot 0, so that the first row of the output xis x 0 and the first row of the output
xdot is xdot 0.
The first argument, fcn, is a string, inline, or function handle that names the function
fto call to compute the vector of residuals for the set of equations. It must have the
form
res =f(x,xdot,t)
in which x,xdot, and res are vectors, and tis a scalar.
If fcn is a two-element string array or a two-element cell array of strings, inline
functions, or function handles, the first element names the function fdescribed above,
and the second element names a function to compute the modified Jacobian
J=∂f
∂x +c∂f
∂˙x
Chapter 24: Differential Equations 625
The modified Jacobian function must have the form
jac =j(x,xdot,t,c)
The second and third arguments to dassl specify the initial condition of the states
and their derivatives, and the fourth argument specifies a vector of output times at
which the solution is desired, including the time corresponding to the initial condition.
The set of initial states and derivatives are not strictly required to be consistent. In
practice, however, dassl is not very good at determining a consistent set for you, so
it is best if you ensure that the initial values result in the function evaluating to zero.
The fifth argument is optional, and may be used to specify a set of times that the DAE
solver should not integrate past. It is useful for avoiding difficulties with singularities
and points where there is a discontinuity in the derivative.
After a successful computation, the value of istate will be greater than zero (consistent
with the Fortran version of dassl).
If the computation is not successful, the value of istate will be less than zero and msg
will contain additional information.
You can use the function dassl_options to set optional parameters for dassl.
See also: [daspk], page 620,[dasrt], page 626,[lsode], page 613.
dassl_options ()
val = dassl_options (opt)
dassl_options (opt,val)
Query or set options for the function dassl.
When called with no arguments, the names of all available options and their current
values are displayed.
Given one argument, return the value of the option opt.
When called with two arguments, dassl_options sets the option opt to value val.
Options include
"absolute tolerance"
Absolute tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the relative tolerance must
also be a vector of the same length.
"relative tolerance"
Relative tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the absolute tolerance must
also be a vector of the same length.
The local error test applied at each integration step is
abs (local error in x(i))
<= rtol(i) * abs (Y(i)) + atol(i)
"compute consistent initial condition"
If nonzero, dassl will attempt to compute a consistent set of initial con-
ditions. This is generally not reliable, so it is best to provide a consistent
set and leave this option set to zero.

626 GNU Octave
"enforce nonnegativity constraints"
If you know that the solutions to your equations will always be non-
negative, it may help to set this parameter to a nonzero value. However,
it is probably best to try leaving this option set to zero first, and only
setting it to a nonzero value if that doesn’t work very well.
"initial step size"
Differential-algebraic problems may occasionally suffer from severe scaling
difficulties on the first step. If you know a great deal about the scaling
of your problem, you can help to alleviate this problem by specifying an
initial stepsize.
"maximum order"
Restrict the maximum order of the solution method. This option must
be between 1 and 5, inclusive.
"maximum step size"
Setting the maximum stepsize will avoid passing over very large regions
(default is not specified).
"step limit"
Maximum number of integration steps to attempt on a single call to the
underlying Fortran code.
[x,xdot,t_out,istat,msg] = dasrt (fcn,[],x_0,xdot_0,t)
... = dasrt (fcn,g,x_0,xdot_0,t)
... = dasrt (fcn,[],x_0,xdot_0,t,t_crit)
... = dasrt (fcn,g,x_0,xdot_0,t,t_crit)
Solve the set of differential-algebraic equations
0 = f(x, ˙x, t)
with
x(t0) = x0,˙x(t0) = ˙x0
with functional stopping criteria (root solving).
The solution is returned in the matrices xand xdot, with each row in the result
matrices corresponding to one of the elements in the vector t out. The first element
of tshould be t0and correspond to the initial state of the system x 0 and its derivative
xdot 0, so that the first row of the output xis x 0 and the first row of the output
xdot is xdot 0.
The vector tprovides an upper limit on the length of the integration. If the stopping
condition is met, the vector t out will be shorter than t, and the final element of t out
will be the point at which the stopping condition was met, and may not correspond
to any element of the vector t.
The first argument, fcn, is a string, inline, or function handle that names the function
fto call to compute the vector of residuals for the set of equations. It must have the
form
res =f(x,xdot,t)

Chapter 24: Differential Equations 627
in which x,xdot, and res are vectors, and tis a scalar.
If fcn is a two-element string array or a two-element cell array of strings, inline
functions, or function handles, the first element names the function fdescribed above,
and the second element names a function to compute the modified Jacobian
J=∂f
∂x +c∂f
∂˙x
The modified Jacobian function must have the form
jac =j(x,xdot,t,c)
The optional second argument names a function that defines the constraint functions
whose roots are desired during the integration. This function must have the form
g_out =g(x,t)
and return a vector of the constraint function values. If the value of any of the
constraint functions changes sign, dasrt will attempt to stop the integration at the
point of the sign change.
If the name of the constraint function is omitted, dasrt solves the same problem as
daspk or dassl.
Note that because of numerical errors in the constraint functions due to round-off
and integration error, dasrt may return false roots, or return the same root at two
or more nearly equal values of T. If such false roots are suspected, the user should
consider smaller error tolerances or higher precision in the evaluation of the constraint
functions.
If a root of some constraint function defines the end of the problem, the input to
dasrt should nevertheless allow integration to a point slightly past that root, so that
dasrt can locate the root by interpolation.
The third and fourth arguments to dasrt specify the initial condition of the states
and their derivatives, and the fourth argument specifies a vector of output times at
which the solution is desired, including the time corresponding to the initial condition.
The set of initial states and derivatives are not strictly required to be consistent. In
practice, however, dassl is not very good at determining a consistent set for you, so
it is best if you ensure that the initial values result in the function evaluating to zero.
The sixth argument is optional, and may be used to specify a set of times that the DAE
solver should not integrate past. It is useful for avoiding difficulties with singularities
and points where there is a discontinuity in the derivative.
After a successful computation, the value of istate will be greater than zero (consistent
with the Fortran version of dassl).
If the computation is not successful, the value of istate will be less than zero and msg
will contain additional information.
You can use the function dasrt_options to set optional parameters for dasrt.
See also: [dasrt options], page 628,[daspk], page 620,[dasrt], page 626,[lsode],
page 613.
628 GNU Octave
dasrt_options ()
val = dasrt_options (opt)
dasrt_options (opt,val)
Query or set options for the function dasrt.
When called with no arguments, the names of all available options and their current
values are displayed.
Given one argument, return the value of the option opt.
When called with two arguments, dasrt_options sets the option opt to value val.
Options include
"absolute tolerance"
Absolute tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the relative tolerance must
also be a vector of the same length.
"relative tolerance"
Relative tolerance. May be either vector or scalar. If a vector, it must
match the dimension of the state vector, and the absolute tolerance must
also be a vector of the same length.
The local error test applied at each integration step is
abs (local error in x(i)) <= ...
rtol(i) * abs (Y(i)) + atol(i)
"initial step size"
Differential-algebraic problems may occasionally suffer from severe scaling
difficulties on the first step. If you know a great deal about the scaling
of your problem, you can help to alleviate this problem by specifying an
initial stepsize.
"maximum order"
Restrict the maximum order of the solution method. This option must
be between 1 and 5, inclusive.
"maximum step size"
Setting the maximum stepsize will avoid passing over very large regions.
"step limit"
Maximum number of integration steps to attempt on a single call to the
underlying Fortran code.
See K. E. Brenan, et al., Numerical Solution of Initial-Value Problems in Differential-
Algebraic Equations, North-Holland (1989) for more information about the implementation
of dassl.
629
25 Optimization
Octave comes with support for solving various kinds of optimization problems. Specifically
Octave can solve problems in Linear Programming, Quadratic Programming, Nonlinear
Programming, and Linear Least Squares Minimization.
25.1 Linear Programming
Octave can solve Linear Programming problems using the glpk function. That is, Octave
can solve
min
xcTx
subject to the linear constraints Ax =bwhere x≥0.
The glpk function also supports variations of this problem.
[xopt,fmin,errnum,extra] = glpk (c,A,b,lb,ub,ctype,vartype,
sense,param)
Solve a linear program using the GNU glpk library.
Given three arguments, glpk solves the following standard LP:
min
xCTx
subject to
Ax =b x ≥0
but may also solve problems of the form
[min
x|max
x]CTx
subject to
Ax[= | ≤ | ≥]b LB ≤x≤UB
Input arguments:
cA column array containing the objective function coefficients.
AA matrix containing the constraints coefficients.
bA column array containing the right-hand side value for each constraint
in the constraint matrix.
lb An array containing the lower bound on each of the variables. If lb is not
supplied, the default lower bound for the variables is zero.
ub An array containing the upper bound on each of the variables. If ub is
not supplied, the default upper bound is assumed to be infinite.
ctype An array of characters containing the sense of each constraint in the
constraint matrix. Each element of the array may be one of the following
values
"F" A free (unbounded) constraint (the constraint is ignored).
630 GNU Octave
"U" An inequality constraint with an upper bound (A(i,:)*x <=
b(i)).
"S" An equality constraint (A(i,:)*x = b(i)).
"L" An inequality with a lower bound (A(i,:)*x >= b(i)).
"D" An inequality constraint with both upper and lower bounds
(A(i,:)*x >= -b(i))and (A(i,:)*x <= b(i)).
vartype A column array containing the types of the variables.
"C" A continuous variable.
"I" An integer variable.
sense If sense is 1, the problem is a minimization. If sense is -1, the problem is
a maximization. The default value is 1.
param A structure containing the following parameters used to define the be-
havior of solver. Missing elements in the structure take on default values,
so you only need to set the elements that you wish to change from the
default.
Integer parameters:
msglev (default: 1)
Level of messages output by solver routines:
0 (GLP_MSG_OFF)
No output.
1 (GLP_MSG_ERR)
Error and warning messages only.
2 (GLP_MSG_ON)
Normal output.
3 (GLP_MSG_ALL)
Full output (includes informational messages).
scale (default: 16)
Scaling option. The values can be combined with the bitwise
OR operator and may be the following:
1 (GLP_SF_GM)
Geometric mean scaling.
16 (GLP_SF_EQ)
Equilibration scaling.
32 (GLP_SF_2N)
Round scale factors to power of two.
64 (GLP_SF_SKIP)
Skip if problem is well scaled.
Chapter 25: Optimization 631
Alternatively, a value of 128 (GLP_SF_AUTO) may be also spec-
ified, in which case the routine chooses the scaling options
automatically.
dual (default: 1)
Simplex method option:
1 (GLP_PRIMAL)
Use two-phase primal simplex.
2 (GLP_DUALP)
Use two-phase dual simplex, and if it fails, switch
to the primal simplex.
3 (GLP_DUAL)
Use two-phase dual simplex.
price (default: 34)
Pricing option (for both primal and dual simplex):
17 (GLP_PT_STD)
Textbook pricing.
34 (GLP_PT_PSE)
Steepest edge pricing.
itlim (default: intmax)
Simplex iterations limit. It is decreased by one each time
when one simplex iteration has been performed, and reaching
zero value signals the solver to stop the search.
outfrq (default: 200)
Output frequency, in iterations. This parameter specifies how
frequently the solver sends information about the solution to
the standard output.
branch (default: 4)
Branching technique option (for MIP only):
1 (GLP_BR_FFV)
First fractional variable.
2 (GLP_BR_LFV)
Last fractional variable.
3 (GLP_BR_MFV)
Most fractional variable.
4 (GLP_BR_DTH)
Heuristic by Driebeck and Tomlin.
5 (GLP_BR_PCH)
Hybrid pseudocost heuristic.
632 GNU Octave
btrack (default: 4)
Backtracking technique option (for MIP only):
1 (GLP_BT_DFS)
Depth first search.
2 (GLP_BT_BFS)
Breadth first search.
3 (GLP_BT_BLB)
Best local bound.
4 (GLP_BT_BPH)
Best projection heuristic.
presol (default: 1)
If this flag is set, the simplex solver uses the built-in LP
presolver. Otherwise the LP presolver is not used.
lpsolver (default: 1)
Select which solver to use. If the problem is a MIP problem
this flag will be ignored.
1 Revised simplex method.
2 Interior point method.
rtest (default: 34)
Ratio test technique:
17 (GLP_RT_STD)
Standard ("textbook").
34 (GLP_RT_HAR)
Harris’ two-pass ratio test.
tmlim (default: intmax)
Searching time limit, in milliseconds.
outdly (default: 0)
Output delay, in seconds. This parameter specifies how long
the solver should delay sending information about the solu-
tion to the standard output.
save (default: 0)
If this parameter is nonzero, save a copy of the problem in
CPLEX LP format to the file "outpb.lp". There is currently
no way to change the name of the output file.
Real parameters:
tolbnd (default: 1e-7)
Relative tolerance used to check if the current basic solution
is primal feasible. It is not recommended that you change
this parameter unless you have a detailed understanding of
its purpose.
Chapter 25: Optimization 633
toldj (default: 1e-7)
Absolute tolerance used to check if the current basic solution
is dual feasible. It is not recommended that you change this
parameter unless you have a detailed understanding of its
purpose.
tolpiv (default: 1e-10)
Relative tolerance used to choose eligible pivotal elements of
the simplex table. It is not recommended that you change
this parameter unless you have a detailed understanding of
its purpose.
objll (default: -DBL_MAX)
Lower limit of the objective function. If the objective func-
tion reaches this limit and continues decreasing, the solver
stops the search. This parameter is used in the dual simplex
method only.
objul (default: +DBL_MAX)
Upper limit of the objective function. If the objective func-
tion reaches this limit and continues increasing, the solver
stops the search. This parameter is used in the dual simplex
only.
tolint (default: 1e-5)
Relative tolerance used to check if the current basic solution
is integer feasible. It is not recommended that you change
this parameter unless you have a detailed understanding of
its purpose.
tolobj (default: 1e-7)
Relative tolerance used to check if the value of the objective
function is not better than in the best known integer feasible
solution. It is not recommended that you change this param-
eter unless you have a detailed understanding of its purpose.
Output values:
xopt The optimizer (the value of the decision variables at the optimum).
fopt The optimum value of the objective function.
errnum Error code.
0 No error.
1 (GLP_EBADB)
Invalid basis.
2 (GLP_ESING)
Singular matrix.
3 (GLP_ECOND)
Ill-conditioned matrix.
634 GNU Octave
4 (GLP_EBOUND)
Invalid bounds.
5 (GLP_EFAIL)
Solver failed.
6 (GLP_EOBJLL)
Objective function lower limit reached.
7 (GLP_EOBJUL)
Objective function upper limit reached.
8 (GLP_EITLIM)
Iterations limit exhausted.
9 (GLP_ETMLIM)
Time limit exhausted.
10 (GLP_ENOPFS)
No primal feasible solution.
11 (GLP_ENODFS)
No dual feasible solution.
12 (GLP_EROOT)
Root LP optimum not provided.
13 (GLP_ESTOP)
Search terminated by application.
14 (GLP_EMIPGAP)
Relative MIP gap tolerance reached.
15 (GLP_ENOFEAS)
No primal/dual feasible solution.
16 (GLP_ENOCVG)
No convergence.
17 (GLP_EINSTAB)
Numerical instability.
18 (GLP_EDATA)
Invalid data.
19 (GLP_ERANGE)
Result out of range.
extra A data structure containing the following fields:
lambda Dual variables.
redcosts Reduced Costs.
time Time (in seconds) used for solving LP/MIP problem.
status Status of the optimization.
1 (GLP_UNDEF)
Solution status is undefined.

Chapter 25: Optimization 635
2 (GLP_FEAS)
Solution is feasible.
3 (GLP_INFEAS)
Solution is infeasible.
4 (GLP_NOFEAS)
Problem has no feasible solution.
5 (GLP_OPT)
Solution is optimal.
6 (GLP_UNBND)
Problem has no unbounded solution.
Example:
c = [10, 6, 4]’;
A=[1,1,1;
10, 4, 5;
2, 2, 6];
b = [100, 600, 300]’;
lb = [0, 0, 0]’;
ub = [];
ctype = "UUU";
vartype = "CCC";
s = -1;
param.msglev = 1;
param.itlim = 100;
[xmin, fmin, status, extra] = ...
glpk (c, A, b, lb, ub, ctype, vartype, s, param);
25.2 Quadratic Programming
Octave can also solve Quadratic Programming problems, this is
min
x
1
2xTHx +xTq
subject to
Ax =b lb ≤x≤ub Alb ≤Ain ≤Aub
[x,obj,info,lambda] = qp (x0,H)
[x,obj,info,lambda] = qp (x0,H,q)
[x,obj,info,lambda] = qp (x0,H,q,A,b)
[x,obj,info,lambda] = qp (x0,H,q,A,b,lb,ub)
[x,obj,info,lambda] = qp (x0,H,q,A,b,lb,ub,A_lb,A_in,A_ub)
[x,obj,info,lambda] = qp (. . . , options)
Solve a quadratic program (QP).

636 GNU Octave
Solve the quadratic program defined by
min
x
1
2xTHx +xTq
subject to
Ax =b lb ≤x≤ub Alb ≤Ain ≤Aub
using a null-space active-set method.
Any bound (A,b,lb,ub,A lb,A ub) may be set to the empty matrix ([]) if not
present. If the initial guess is feasible the algorithm is faster.
options An optional structure containing the following parameter(s) used to define
the behavior of the solver. Missing elements in the structure take on
default values, so you only need to set the elements that you wish to
change from the default.
MaxIter (default: 200)
Maximum number of iterations.
info Structure containing run-time information about the algorithm. The fol-
lowing fields are defined:
solveiter
The number of iterations required to find the solution.
info An integer indicating the status of the solution.
0 The problem is feasible and convex. Global solu-
tion found.
1 The problem is not convex. Local solution found.
2 The problem is not convex and unbounded.
3 Maximum number of iterations reached.
6 The problem is infeasible.
x= pqpnonneg (c,d)
x= pqpnonneg (c,d,x0)
[x,minval] = pqpnonneg (. . . )
[x,minval,exitflag] = pqpnonneg (. . . )
[x,minval,exitflag,output] = pqpnonneg (. . . )
[x,minval,exitflag,output,lambda] = pqpnonneg (. . . )
Minimize 1/2*x’*c*x + d’*x subject to x>= 0.
cand dmust be real, and cmust be symmetric and positive definite.
x0 is an optional initial guess for x.
Outputs:
•minval
The minimum attained model value, 1/2*xmin’*c*xmin +d’*xmin
Chapter 25: Optimization 637
•exitflag
An indicator of convergence. 0 indicates that the iteration count was exceeded,
and therefore convergence was not reached; >0 indicates that the algorithm con-
verged. (The algorithm is stable and will converge given enough iterations.)
•output
A structure with two fields:
•"algorithm": The algorithm used ("nnls")
•"iterations": The number of iterations taken.
•lambda
Not implemented.
See also: [optimset], page 641,[lsqnonneg], page 640,[qp], page 635.
25.3 Nonlinear Programming
Octave can also perform general nonlinear minimization using a successive quadratic pro-
gramming solver.
[x,obj,info,iter,nf,lambda] = sqp (x0,phi)
[...] = sqp (x0,phi,g)
[...] = sqp (x0,phi,g,h)
[...] = sqp (x0,phi,g,h,lb,ub)
[...] = sqp (x0,phi,g,h,lb,ub,maxiter)
[...] = sqp (x0,phi,g,h,lb,ub,maxiter,tol)
Minimize an objective function using sequential quadratic programming (SQP).
Solve the nonlinear program
min
xφ(x)
subject to
g(x)=0 h(x)≥0lb ≤x≤ub
using a sequential quadratic programming method.
The first argument is the initial guess for the vector x0.
The second argument is a function handle pointing to the objective function phi. The
objective function must accept one vector argument and return a scalar.
The second argument may also be a 2- or 3-element cell array of function handles.
The first element should point to the objective function, the second should point
to a function that computes the gradient of the objective function, and the third
should point to a function that computes the Hessian of the objective function. If the
gradient function is not supplied, the gradient is computed by finite differences. If
the Hessian function is not supplied, a BFGS update formula is used to approximate
the Hessian.
When supplied, the gradient function phi{2} must accept one vector argument and
return a vector. When supplied, the Hessian function phi{3} must accept one vector
argument and return a matrix.

638 GNU Octave
The third and fourth arguments gand hare function handles pointing to functions
that compute the equality constraints and the inequality constraints, respectively. If
the problem does not have equality (or inequality) constraints, then use an empty
matrix ([]) for g(or h). When supplied, these equality and inequality constraint
functions must accept one vector argument and return a vector.
The third and fourth arguments may also be 2-element cell arrays of function handles.
The first element should point to the constraint function and the second should point
to a function that computes the gradient of the constraint function:
∂f(x)
∂x1
,∂f(x)
∂x2
,...,∂f(x)
∂xN!T
The fifth and sixth arguments, lb and ub, contain lower and upper bounds on x.
These must be consistent with the equality and inequality constraints gand h. If the
arguments are vectors then x(i) is bound by lb(i) and ub(i). A bound can also be a
scalar in which case all elements of xwill share the same bound. If only one bound
(lb, ub) is specified then the other will default to (-realmax,+realmax).
The seventh argument maxiter specifies the maximum number of iterations. The
default value is 100.
The eighth argument tol specifies the tolerance for the stopping criteria. The default
value is sqrt (eps).
The value returned in info may be one of the following:
101 The algorithm terminated normally. All constraints meet the specified
tolerance.
102 The BFGS update failed.
103 The maximum number of iterations was reached.
104 The stepsize has become too small, i.e., Δx, is less than tol * norm (x).
An example of calling sqp:
function r = g (x)
r = [ sumsq(x)-10;
x(2)*x(3)-5*x(4)*x(5);
x(1)^3+x(2)^3+1 ];
endfunction
function obj = phi (x)
obj = exp (prod (x)) - 0.5*(x(1)^3+x(2)^3+1)^2;
endfunction
x0 = [-1.8; 1.7; 1.9; -0.8; -0.8];
[x, obj, info, iter, nf, lambda] = sqp (x0, @phi, @g, [])
x =
Chapter 25: Optimization 639
-1.71714
1.59571
1.82725
-0.76364
-0.76364
obj = 0.053950
info = 101
iter = 8
nf = 10
lambda =
-0.0401627
0.0379578
-0.0052227
See also: [qp], page 635.
25.4 Linear Least Squares
Octave also supports linear least squares minimization. That is, Octave can find the param-
eter bsuch that the model y=xb fits data (x, y) as well as possible, assuming zero-mean
Gaussian noise. If the noise is assumed to be isotropic the problem can be solved using the
‘\’ or ‘/’ operators, or the ols function. In the general case where the noise is assumed to
be anisotropic the gls is needed.
[beta,sigma,r] = ols (y,x)
Ordinary least squares estimation.
OLS applies to the multivariate model y=xb +ewith ¯e= 0, and cov(vec(e)) = kron
(s, I) where yis a t×pmatrix, xis a t×kmatrix, bis a k×pmatrix, and eis a
t×pmatrix.
Each row of yand xis an observation and each column a variable.
The return values beta,sigma, and rare defined as follows.
beta The OLS estimator for b.beta is calculated directly via (xTx)−1xTyif the
matrix xTxis of full rank. Otherwise, beta = pinv (x) * ywhere pinv
(x)denotes the pseudoinverse of x.
sigma The OLS estimator for the matrix s,
sigma = (y-x*beta)’
* (y-x*beta)
/ (t-rank(x))
rThe matrix of OLS residuals, r=y-x*beta.
See also: [gls], page 639,[pinv], page 510.
[beta,v,r] = gls (y,x,o)
Generalized least squares model.
640 GNU Octave
Perform a generalized least squares estimation for the multivariate model y=xb +e
with ¯e= 0 and cov(vec(e)) = (s2)o, where yis a t×pmatrix, xis a t×kmatrix, b
is a k×pmatrix, eis a t×pmatrix, and ois a tp ×tp matrix.
Each row of yand xis an observation and each column a variable. The return values
beta,v, and rare defined as follows.
beta The GLS estimator for b.
vThe GLS estimator for s2.
rThe matrix of GLS residuals, r=y−x∗beta.
See also: [ols], page 639.
x= lsqnonneg (c,d)
x= lsqnonneg (c,d,x0)
x= lsqnonneg (c,d,x0,options)
[x,resnorm] = lsqnonneg (. . . )
[x,resnorm,residual] = lsqnonneg (. . . )
[x,resnorm,residual,exitflag] = lsqnonneg (. . . )
[x,resnorm,residual,exitflag,output] = lsqnonneg (. . . )
[x,resnorm,residual,exitflag,output,lambda] = lsqnonneg (. . . )
Minimize norm (c*x- d) subject to x>= 0.
cand dmust be real.
x0 is an optional initial guess for x.
Currently, lsqnonneg recognizes these options: "MaxIter","TolX". For a description
of these options, see [optimset], page 641.
Outputs:
•resnorm
The squared 2-norm of the residual: norm (c*x-d)^2
•residual
The residual: d-c*x
•exitflag
An indicator of convergence. 0 indicates that the iteration count was exceeded,
and therefore convergence was not reached; >0 indicates that the algorithm con-
verged. (The algorithm is stable and will converge given enough iterations.)
•output
A structure with two fields:
•"algorithm": The algorithm used ("nnls")
•"iterations": The number of iterations taken.
•lambda
Not implemented.
See also: [optimset], page 641,[pqpnonneg], page 636,[lscov], page 641.
Chapter 25: Optimization 641
x= lscov (A,b)
x= lscov (A,b,V)
x= lscov (A,b,V,alg)
[x,stdx,mse,S] = lscov (. . . )
Compute a generalized linear least squares fit.
Estimate xunder the model b=Ax +w, where the noise wis assumed to follow a
normal distribution with covariance matrix σ2V.
If the size of the coefficient matrix Ais n-by-p, the size of the vector/array of constant
terms bmust be n-by-k.
The optional input argument Vmay be a n-by-1 vector of positive weights (inverse
variances), or a n-by-n symmetric positive semidefinite matrix representing the co-
variance of b. If Vis not supplied, the ordinary least squares solution is returned.
The alg input argument, a guidance on solution method to use, is currently ignored.
Besides the least-squares estimate matrix x(p-by-k), the function also returns stdx
(p-by-k), the error standard deviation of estimated x;mse (k-by-1), the estimated
data error covariance scale factors (σ2); and S(p-by-p, or p-by-p-by-k if k >1), the
error covariance of x.
Reference: Golub and Van Loan (1996), Matrix Computations (3rd Ed.), Johns Hop-
kins, Section 5.6.3
See also: [ols], page 639,[gls], page 639,[lsqnonneg], page 640.
optimset ()
options = optimset ()
options = optimset (par,val, . . . )
options = optimset (old,par,val, . . . )
options = optimset (old,new)
Create options structure for optimization functions.
When called without any input or output arguments, optimset prints a list of all
valid optimization parameters.
When called with one output and no inputs, return an options structure with all valid
option parameters initialized to [].
When called with a list of parameter/value pairs, return an options structure with
only the named parameters initialized.
When the first input is an existing options structure old, the values are updated from
either the par/val list or from the options structure new.
Valid parameters are:
AutoScaling
ComplexEqn
Display Request verbose display of results from optimizations. Values are:
"off" [default]
No display.
"iter" Display intermediate results for every loop iteration.
"final" Display the result of the final loop iteration.
642 GNU Octave
"notify" Display the result of the final loop iteration if the function
has failed to converge.
FinDiffType
FunValCheck
When enabled, display an error if the objective function returns an invalid
value (a complex number, NaN, or Inf). Must be set to "on" or "off"
[default]. Note: the functions fzero and fminbnd correctly handle Inf
values and only complex values or NaN will cause an error in this case.
GradObj When set to "on", the function to be minimized must return a second
argument which is the gradient, or first derivative, of the function at the
point x. If set to "off" [default], the gradient is computed via finite
differences.
Jacobian When set to "on", the function to be minimized must return a second
argument which is the Jacobian, or first derivative, of the function at the
point x. If set to "off" [default], the Jacobian is computed via finite
differences.
MaxFunEvals
Maximum number of function evaluations before optimization stops.
Must be a positive integer.
MaxIter Maximum number of algorithm iterations before optimization stops.
Must be a positive integer.
OutputFcn
A user-defined function executed once per algorithm iteration.
TolFun Termination criterion for the function output. If the difference in the
calculated objective function between one algorithm iteration and the
next is less than TolFun the optimization stops. Must be a positive
scalar.
TolX Termination criterion for the function input. If the difference in x, the
current search point, between one algorithm iteration and the next is less
than TolX the optimization stops. Must be a positive scalar.
TypicalX
Updating
See also: [optimget], page 642.
optimget (options,parname)
optimget (options,parname,default)
Return the specific option parname from the optimization options structure options
created by optimset.
If parname is not defined then return default if supplied, otherwise return an empty
matrix.
See also: [optimset], page 641.

643
26 Statistics
Octave has support for various statistical methods. This includes basic descriptive statistics,
probability distributions, statistical tests, random number generation, and much more.
The functions that analyze data all assume that multi-dimensional data is arranged in a
matrix where each row is an observation, and each column is a variable. Thus, the matrix
defined by
a = [ 0.9, 0.7;
0.1, 0.1;
0.5, 0.4 ];
contains three observations from a two-dimensional distribution. While this is the default
data arrangement, most functions support different arrangements.
It should be noted that the statistics functions don’t test for data containing NaN, NA,
or Inf. These values need to be detected and dealt with explicitly. See [isnan], page 440,
[isna], page 43,[isinf], page 440,[isfinite], page 441.
26.1 Descriptive Statistics
One principal goal of descriptive statistics is to represent the essence of a large data set
concisely. Octave provides the mean, median, and mode functions which all summarize a
data set with just a single number corresponding to the central tendency of the data.
mean (x)
mean (x,dim)
mean (x,opt)
mean (x,dim,opt)
Compute the mean of the elements of the vector x.
The mean is defined as
mean(x) = ¯x=1
N
N
X
i=1
xi
If xis a matrix, compute the mean for each column and return them in a row vector.
If the optional argument dim is given, operate along this dimension.
The optional argument opt selects the type of mean to compute. The following options
are recognized:
"a" Compute the (ordinary) arithmetic mean. [default]
"g" Compute the geometric mean.
"h" Compute the harmonic mean.
Both dim and opt are optional. If both are supplied, either may appear first.
See also: [median], page 644,[mode], page 644.
644 GNU Octave
median (x)
median (x,dim)
Compute the median value of the elements of the vector x.
When the elements of xare sorted, the median is defined as
median(x) = x(dN/2e), N odd;
(x(N/2) + x(N/2 + 1))/2, N even.
If xis of a discrete type such as integer or logical, then the case of even N rounds up
(or toward true).
If xis a matrix, compute the median value for each column and return them in a row
vector.
If the optional dim argument is given, operate along this dimension.
See also: [mean], page 643,[mode], page 644.
mode (x)
mode (x,dim)
[m,f,c] = mode (. . . )
Compute the most frequently occurring value in a dataset (mode).
mode determines the frequency of values along the first non-singleton dimension and
returns the value with the highest frequency. If two, or more, values have the same
frequency mode returns the smallest.
If the optional argument dim is given, operate along this dimension.
The return variable fis the number of occurrences of the mode in the dataset.
The cell array ccontains all of the elements with the maximum frequency.
See also: [mean], page 643,[median], page 644.
Using just one number, such as the mean, to represent an entire data set may not give
an accurate picture of the data. One way to characterize the fit is to measure the dispersion
of the data. Octave provides several functions for measuring dispersion.
range (x)
range (x,dim)
Return the range, i.e., the difference between the maximum and the minimum of the
input data.
If xis a vector, the range is calculated over the elements of x. If xis a matrix, the
range is calculated over each column of x.
If the optional argument dim is given, operate along this dimension.
The range is a quickly computed measure of the dispersion of a data set, but is less
accurate than iqr if there are outlying data points.
See also: [iqr], page 644,[std], page 645.
iqr (x)
iqr (x,dim)
Return the interquartile range, i.e., the difference between the upper and lower quar-
tile of the input data.

Chapter 26: Statistics 645
If xis a matrix, do the above for first non-singleton dimension of x.
If the optional argument dim is given, operate along this dimension.
As a measure of dispersion, the interquartile range is less affected by outliers than
either range or std.
See also: [range], page 644,[std], page 645.
meansq (x)
meansq (x,dim)
Compute the mean square of the elements of the vector x.
The mean square is defined as
meansq(x) = PN
i=1 xi2
N
where ¯xis the mean value of x. For matrix arguments, return a row vector containing
the mean square of each column.
If the optional argument dim is given, operate along this dimension.
See also: [var], page 645,[std], page 645,[moment], page 647.
std (x)
std (x,opt)
std (x,opt,dim)
Compute the standard deviation of the elements of the vector x.
The standard deviation is defined as
std(x) = σ=sPN
i=1(xi−¯x)2
N−1
where ¯xis the mean value of xand Nis the number of elements.
If xis a matrix, compute the standard deviation for each column and return them in
a row vector.
The argument opt determines the type of normalization to use. Valid values are
0: normalize with N−1, provides the square root of the best unbiased
estimator of the variance [default]
1: normalize with N, this provides the square root of the second moment
around the mean
If the optional argument dim is given, operate along this dimension.
See also: [var], page 645,[range], page 644,[iqr], page 644,[mean], page 643,[median],
page 644.
In addition to knowing the size of a dispersion it is useful to know the shape of the data
set. For example, are data points massed to the left or right of the mean? Octave provides
several common measures to describe the shape of the data set. Octave can also calculate
moments allowing arbitrary shape measures to be developed.

646 GNU Octave
var (x)
var (x,opt)
var (x,opt,dim)
Compute the variance of the elements of the vector x.
The variance is defined as
var(x) = σ2=PN
i=1(xi−¯x)2
N−1
where ¯xis the mean value of x. If xis a matrix, compute the variance for each column
and return them in a row vector.
The argument opt determines the type of normalization to use. Valid values are
0: normalize with N−1, provides the best unbiased estimator of the variance
[default]
1: normalizes with N, this provides the second moment around the mean
If N== 1 the value of opt is ignored and normalization by Nis used.
If the optional argument dim is given, operate along this dimension.
See also: [cov], page 654,[std], page 645,[skewness], page 646,[kurtosis], page 647,
[moment], page 647.
skewness (x)
skewness (x,flag)
skewness (x,flag,dim)
Compute the sample skewness of the elements of x.
The sample skewness is defined as
skewness(x) =
1
NPN
i=1(xi−¯x)3
σ3,
where Nis the length of x, ¯xits mean and σits (uncorrected) standard deviation.
The optional argument flag controls which normalization is used. If flag is equal to
1 (default value, used when flag is omitted or empty), return the sample skewness as
defined above. If flag is equal to 0, return the adjusted skewness coefficient instead:
skewness(x) = pN(N−1)
N−2×
1
NPN
i=1(xi−¯x)3
σ3
The adjusted skewness coefficient is obtained by replacing the sample second and
third central moments by their bias-corrected versions.
If xis a matrix, or more generally a multi-dimensional array, return the skewness along
the first non-singleton dimension. If the optional dim argument is given, operate along
this dimension.
See also: [var], page 645,[kurtosis], page 647,[moment], page 647.

Chapter 26: Statistics 647
kurtosis (x)
kurtosis (x,flag)
kurtosis (x,flag,dim)
Compute the sample kurtosis of the elements of x.
The sample kurtosis is defined as
κ1=
1
NPN
i=1(xi−¯x)4
σ4,
where Nis the length of x, ¯xits mean, and σits (uncorrected) standard deviation.
The optional argument flag controls which normalization is used. If flag is equal to
1 (default value, used when flag is omitted or empty), return the sample kurtosis as
defined above. If flag is equal to 0, return the "bias-corrected"kurtosis coefficient
instead:
κ0= 3 + N−1
(N−2)(N−3) ((N+ 1) κ1−3(N−1))
The bias-corrected kurtosis coefficient is obtained by replacing the sample second and
fourth central moments by their unbiased versions. It is an unbiased estimate of the
population kurtosis for normal populations.
If xis a matrix, or more generally a multi-dimensional array, return the kurtosis along
the first non-singleton dimension. If the optional dim argument is given, operate along
this dimension.
See also: [var], page 645,[skewness], page 646,[moment], page 647.
moment (x,p)
moment (x,p,type)
moment (x,p,dim)
moment (x,p,type,dim)
moment (x,p,dim,type)
Compute the p-th central moment of the vector x.
PN
i=1(xi−¯x)p
N
If xis a matrix, return the row vector containing the p-th central moment of each
column.
If the optional argument dim is given, operate along this dimension.
The optional string type specifies the type of moment to be computed. Valid options
are:
"c" Central Moment (default).
"a"
"ac" Absolute Central Moment. The moment about the mean ignoring sign
defined as
PN
i=1 |xi−¯x|p
N
"r" Raw Moment. The moment about zero defined as

648 GNU Octave
moment(x) = PN
i=1 xip
N
"ar" Absolute Raw Moment. The moment about zero ignoring sign defined as
PN
i=1 |xi|p
N
If both type and dim are given they may appear in any order.
See also: [var], page 645,[skewness], page 646,[kurtosis], page 647.
q= quantile (x)
q= quantile (x,p)
q= quantile (x,p,dim)
q= quantile (x,p,dim,method)
For a sample, x, calculate the quantiles, q, corresponding to the cumulative probability
values in p. All non-numeric values (NaNs) of xare ignored.
If xis a matrix, compute the quantiles for each column and return them in a matrix,
such that the i-th row of qcontains the p(i)th quantiles of each column of x.
If pis unspecified, return the quantiles for [0.00 0.25 0.50 0.75 1.00]. The op-
tional argument dim determines the dimension along which the quantiles are calcu-
lated. If dim is omitted it defaults to the first non-singleton dimension.
The methods available to calculate sample quantiles are the nine methods used by R
(http://www.r-project.org/). The default value is METHOD = 5.
Discontinuous sample quantile methods 1, 2, and 3
1. Method 1: Inverse of empirical distribution function.
2. Method 2: Similar to method 1 but with averaging at discontinuities.
3. Method 3: SAS definition: nearest even order statistic.
Continuous sample quantile methods 4 through 9, where p(k) is the linear interpola-
tion function respecting each methods’ representative cdf.
4. Method 4: p(k) = k / n. That is, linear interpolation of the empirical cdf.
5. Method 5: p(k) = (k - 0.5) / n. That is a piecewise linear function where the
knots are the values midway through the steps of the empirical cdf.
6. Method 6: p(k) = k / (n +1).
7. Method 7: p(k) = (k - 1) / (n - 1).
8. Method 8: p(k) = (k - 1/3) / (n +1/3). The resulting quantile estimates are
approximately median-unbiased regardless of the distribution of x.
9. Method 9: p(k) = (k - 3/8) / (n +1/4). The resulting quantile estimates are
approximately unbiased for the expected order statistics if xis normally dis-
tributed.
Hyndman and Fan (1996) recommend method 8. Maxima, S, and R (versions prior to
2.0.0) use 7 as their default. Minitab and SPSS use method 6. matlab uses method
5.
Chapter 26: Statistics 649
References:
•Becker, R. A., Chambers, J. M. and Wilks, A. R. (1988) The New S Language.
Wadsworth & Brooks/Cole.
•Hyndman, R. J. and Fan, Y. (1996) Sample quantiles in statistical packages,
American Statistician, 50, 361–365.
•R: A Language and Environment for Statistical Computing; http: / / cran .
r-project.org/doc/manuals/fullrefman.pdf.
Examples:
x = randi (1000, [10, 1]); # Create empirical data in range 1-1000
q = quantile (x, [0, 1]); # Return minimum, maximum of distribution
q = quantile (x, [0.25 0.5 0.75]); # Return quartiles of distribution
See also: [prctile], page 649.
q= prctile (x)
q= prctile (x,p)
q= prctile (x,p,dim)
For a sample x, compute the quantiles, q, corresponding to the cumulative probability
values, p, in percent.
If xis a matrix, compute the percentiles for each column and return them in a matrix,
such that the i-th row of ycontains the p(i)th percentiles of each column of x.
If pis unspecified, return the quantiles for [0 25 50 75 100].
The optional argument dim determines the dimension along which the percentiles are
calculated. If dim is omitted it defaults to the first non-singleton dimension.
Programming Note: All non-numeric values (NaNs) of xare ignored.
See also: [quantile], page 648.
A summary view of a data set can be generated quickly with the statistics function.
statistics (x)
statistics (x,dim)
Return a vector with the minimum, first quartile, median, third quartile, maximum,
mean, standard deviation, skewness, and kurtosis of the elements of the vector x.
If xis a matrix, calculate statistics over the first non-singleton dimension.
If the optional argument dim is given, operate along this dimension.
See also: [min], page 481,[max], page 481,[median], page 644,[mean], page 643,
[std], page 645,[skewness], page 646,[kurtosis], page 647.
26.2 Basic Statistical Functions
Octave supports various helpful statistical functions. Many are useful as initial steps to
prepare a data set for further analysis. Others provide different measures from those of the
basic descriptive statistics.
650 GNU Octave
center (x)
center (x,dim)
Center data by subtracting its mean.
If xis a vector, subtract its mean.
If xis a matrix, do the above for each column.
If the optional argument dim is given, operate along this dimension.
Programming Note: center has obvious application for normalizing statistical data.
It is also useful for improving the precision of general numerical calculations. When-
ever there is a large value that is common to a batch of data, the mean can be
subtracted off, the calculation performed, and then the mean added back to obtain
the final answer.
See also: [zscore], page 650.
z= zscore (x)
z= zscore (x,opt)
z= zscore (x,opt,dim)
[z,mu,sigma] = zscore (. . . )
Compute the Z score of x
If xis a vector, subtract its mean and divide by its standard deviation. If the standard
deviation is zero, divide by 1 instead.
The optional parameter opt determines the normalization to use when computing the
standard deviation and has the same definition as the corresponding parameter for
std.
If xis a matrix, calculate along the first non-singleton dimension. If the third optional
argument dim is given, operate along this dimension.
The optional outputs mu and sigma contain the mean and standard deviation.
See also: [mean], page 643,[std], page 645,[center], page 649.
n= histc (x,edges)
n= histc (x,edges,dim)
[n,idx] = histc (. . . )
Compute histogram counts.
When xis a vector, the function counts the number of elements of xthat fall in the
histogram bins defined by edges. This must be a vector of monotonically increasing
values that define the edges of the histogram bins. n(k) contains the number of
elements in xfor which edges(k) <= x<edges(k+1). The final element of ncontains
the number of elements of xexactly equal to the last element of edges.
When xis an N-dimensional array, the computation is carried out along dimension
dim. If not specified dim defaults to the first non-singleton dimension.
When a second output argument is requested an index matrix is also returned. The
idx matrix has the same size as x. Each element of idx contains the index of the
histogram bin in which the corresponding element of xwas counted.
See also: [hist], page 293.

Chapter 26: Statistics 651
unique function documented at [unique], page 679, is often useful for statistics.
c= nchoosek (n,k)
c= nchoosek (set,k)
Compute the binomial coefficient of nor list all possible combinations of a set of
items.
If nis a scalar then calculate the binomial coefficient of nand kwhich is defined as
n
k!=n(n−1)(n−2) ···(n−k+ 1)
k!=n!
k!(n−k)!
This is the number of combinations of nitems taken in groups of size k.
If the first argument is a vector, set, then generate all combinations of the elements
of set, taken kat a time, with one row per combination. The result chas kcolumns
and nchoosek (length (set), k)rows.
For example:
How many ways can three items be grouped into pairs?
nchoosek (3, 2)
⇒3
What are the possible pairs?
nchoosek (1:3, 2)
⇒1 2
1 3
2 3
Programming Note: When calculating the binomial coefficient nchoosek works only
for non-negative, integer arguments. Use bincoeff for non-integer and negative scalar
arguments, or for computing many binomial coefficients at once with vector inputs
for nor k.
See also: [bincoeff], page 490,[perms], page 651.
perms (v)
Generate all permutations of vwith one row per permutation.
The result has size factorial (n) * n, where nis the length of v.
Example
perms ([1, 2, 3])
⇒123
213
132
231
312
321
Programming Note: The maximum length of vshould be less than or equal to 10 to
limit memory consumption.
See also: [permute], page 445,[randperm], page 460,[nchoosek], page 651.

652 GNU Octave
ranks (x,dim)
Return the ranks of xalong the first non-singleton dimension adjusted for ties.
If the optional argument dim is given, operate along this dimension.
See also: [spearman], page 654,[kendall], page 655.
run_count (x,n)
run_count (x,n,dim)
Count the upward runs along the first non-singleton dimension of xof length 1, 2,
. . ., n-1 and greater than or equal to n.
If the optional argument dim is given then operate along this dimension.
See also: [runlength], page 652.
count = runlength (x)
[count, value] = runlength (x)
Find the lengths of all sequences of common values.
count is a vector with the lengths of each repeated value.
The optional output value contains the value that was repeated in the sequence.
runlength ([2, 2, 0, 4, 4, 4, 0, 1, 1, 1, 1])
⇒[2, 1, 3, 1, 4]
See also: [run count], page 652.
probit (p)
Return the probit (the quantile of the standard normal distribution) for each element
of p.
See also: [logit], page 652.
logit (p)
Compute the logit for each value of p
The logit is defined as
logit(p) = log p
1−p
See also: [probit], page 652,[logistic cdf], page 660.
cloglog (x)
Return the complementary log-log function of x.
The complementary log-log function is defined as
cloglog(x) = −log(−log(x))
[t,l_x] = table (x)
[t,l_x,l_y] = table (x,y)
Create a contingency table tfrom data vectors.
The l x and l y vectors are the corresponding levels.
Currently, only 1- and 2-dimensional tables are supported.

Chapter 26: Statistics 653
26.3 Statistical Plots
Octave can create Quantile Plots (QQ-Plots), and Probability Plots (PP-Plots). These are
simple graphical tests for determining if a data set comes from a certain distribution.
Note that Octave can also show histograms of data using the hist function as described
in Section 15.2.1 [Two-Dimensional Plots], page 285.
[q,s] = qqplot (x)
[q,s] = qqplot (x,y)
[q,s] = qqplot (x,dist)
[q,s] = qqplot (x,y,params)
qqplot (. . .)
Perform a QQ-plot (quantile plot).
If F is the CDF of the distribution dist with parameters params and G its inverse,
and xa sample vector of length n, the QQ-plot graphs ordinate s(i) = i-th largest
element of x versus abscissa q(if) = G((i- 0.5)/n).
If the sample comes from F, except for a transformation of location and scale, the
pairs will approximately follow a straight line.
If the second argument is a vector ythe empirical CDF of yis used as dist.
The default for dist is the standard normal distribution. The optional argument
params contains a list of parameters of dist. For example, for a quantile plot of the
uniform distribution on [2,4] and x, use
qqplot (x, "unif", 2, 4)
dist can be any string for which a function distinv or dist inv exists that calculates
the inverse CDF of distribution dist.
If no output arguments are given, the data are plotted directly.
[p,y] = ppplot (x,dist,params)
Perform a PP-plot (probability plot).
If F is the CDF of the distribution dist with parameters params and xa sample vector
of length n, the PP-plot graphs ordinate y(i) = F (i-th largest element of x) versus
abscissa p(i)=(i- 0.5)/n. If the sample comes from F, the pairs will approximately
follow a straight line.
The default for dist is the standard normal distribution.
The optional argument params contains a list of parameters of dist.
For example, for a probability plot of the uniform distribution on [2,4] and x, use
ppplot (x, "uniform", 2, 4)
dist can be any string for which a function dist cdf that calculates the CDF of
distribution dist exists.
If no output is requested then the data are plotted immediately.

654 GNU Octave
26.4 Correlation and Regression Analysis
cov (x)
cov (x,opt)
cov (x,y)
cov (x,y,opt)
Compute the covariance matrix.
If each row of xand yis an observation, and each column is a variable, then the
(i,j)-th entry of cov (x,y)is the covariance between the i-th variable in xand the
j-th variable in y.
σij =1
N−1
N
X
i=1
(xi−¯x)(yi−¯y)
where ¯xand ¯yare the mean values of xand y.
If called with one argument, compute cov (x,x), the covariance between the columns
of x.
The argument opt determines the type of normalization to use. Valid values are
0: normalize with N−1, provides the best unbiased estimator of the covari-
ance [default]
1: normalize with N, this provides the second moment around the mean
Compatibility Note:: Octave always treats rows of xand yas multivariate random
variables. For two inputs, however, matlab treats xand yas two univariate distri-
butions regardless of their shapes, and will calculate cov ([x(:), y(:)]) whenever
the number of elements in xand yare equal. This will result in a 2x2 matrix. Code
relying on matlab’s definition will need to be changed when running in Octave.
See also: [corr], page 654.
corr (x)
corr (x,y)
Compute matrix of correlation coefficients.
If each row of xand yis an observation and each column is a variable, then the
(i,j)-th entry of corr (x,y)is the correlation between the i-th variable in xand the
j-th variable in y.
corr(x, y) = cov(x, y)
std(x)std(y)
If called with one argument, compute corr (x,x), the correlation between the
columns of x.
See also: [cov], page 654.
spearman (x)
spearman (x,y)
Compute Spearman’s rank correlation coefficient rho.
For two data vectors xand y, Spearman’s rho is the correlation coefficient of the
ranks of xand y.

Chapter 26: Statistics 655
If xand yare drawn from independent distributions, rho has zero mean and variance
1 / (n - 1), and is asymptotically normally distributed.
spearman (x)is equivalent to spearman (x,x).
See also: [ranks], page 652,[kendall], page 655.
kendall (x)
kendall (x,y)
Compute Kendall’s tau.
For two data vectors x,yof common length n, Kendall’s tau is the correlation of the
signs of all rank differences of xand y; i.e., if both xand yhave distinct entries, then
τ=1
n(n−1) X
i,j
sign(qi−qj)sign(ri−rj)
in which the qiand riare the ranks of xand y, respectively.
If xand yare drawn from independent distributions, Kendall’s tau is asymptotically
normal with mean 0 and variance 2(2n+5)
9n(n−1) .
kendall (x)is equivalent to kendall (x,x).
See also: [ranks], page 652,[spearman], page 654.
[theta,beta,dev,dl,d2l,p] = logistic_regression (y,x,print,
theta,beta)
Perform ordinal logistic regression.
Suppose ytakes values in kordered categories, and let gamma_i (x)be the cumulative
probability that yfalls in one of the first icategories given the covariate x. Then
[theta, beta] = logistic_regression (y, x)
fits the model
logit (gamma_i (x)) = theta_i - beta’ * x, i = 1 ... k-1
The number of ordinal categories, k, is taken to be the number of distinct values of
round (y). If kequals 2, yis binary and the model is ordinary logistic regression.
The matrix xis assumed to have full column rank.
Given yonly, theta = logistic_regression (y) fits the model with baseline logit
odds only.
The full form is
[theta, beta, dev, dl, d2l, gamma]
= logistic_regression (y, x, print, theta, beta)
in which all output arguments and all input arguments except yare optional.
Setting print to 1 requests summary information about the fitted model to be dis-
played. Setting print to 2 requests information about convergence at each iteration.
Other values request no information to be displayed. The input arguments theta and
beta give initial estimates for theta and beta.
The returned value dev holds minus twice the log-likelihood.
The returned values dl and d2l are the vector of first and the matrix of second
derivatives of the log-likelihood with respect to theta and beta.
pholds estimates for the conditional distribution of ygiven x.

656 GNU Octave
26.5 Distributions
Octave has functions for computing the Probability Density Function (PDF), the Cumu-
lative Distribution function (CDF), and the quantile (the inverse of the CDF) for a large
number of distributions.
The following table summarizes the supported distributions (in alphabetical order).
Distribution PDF CDF Quantile
Beta betapdf betacdf betainv
Binomial binopdf binocdf binoinv
Cauchy cauchy pdf cauchy cdf cauchy inv
Chi-Square chi2pdf chi2cdf chi2inv
Univariate Discrete discrete pdf discrete cdf discrete inv
Empirical empirical pdf empirical cdf empirical inv
Exponential exppdf expcdf expinv
F fpdf fcdf finv
Gamma gampdf gamcdf gaminv
Geometric geopdf geocdf geoinv
Hypergeometric hygepdf hygecdf hygeinv
Kolmogorov Smirnov Not Available kolmogorov Not Available
smirnov cdf
Laplace laplace pdf laplace cdf laplace inv
Logistic logistic pdf logistic cdf logistic inv
Log-Normal lognpdf logncdf logninv
Univariate Normal normpdf normcdf norminv
Pascal nbinpdf nbincdf nbininv
Poisson poisspdf poisscdf poissinv
Standard Normal stdnormal pdf stdnormal cdf stdnormal inv
t (Student) tpdf tcdf tinv
Uniform Discrete unidpdf unidcdf unidinv
Uniform unifpdf unifcdf unifinv
Weibull wblpdf wblcdf wblinv
betapdf (x,a,b)
For each element of x, compute the probability density function (PDF) at xof the
Beta distribution with parameters aand b.
betacdf (x,a,b)
For each element of x, compute the cumulative distribution function (CDF) at xof
the Beta distribution with parameters aand b.
betainv (x,a,b)
For each element of x, compute the quantile (the inverse of the CDF) at xof the Beta
distribution with parameters aand b.
Chapter 26: Statistics 657
binopdf (x,n,p)
For each element of x, compute the probability density function (PDF) at xof the
binomial distribution with parameters nand p, where nis the number of trials and
pis the probability of success.
binocdf (x,n,p)
For each element of x, compute the cumulative distribution function (CDF) at xof
the binomial distribution with parameters nand p, where nis the number of trials
and pis the probability of success.
binoinv (x,n,p)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
binomial distribution with parameters nand p, where nis the number of trials and
pis the probability of success.
cauchy_pdf (x)
cauchy_pdf (x,location,scale)
For each element of x, compute the probability density function (PDF) at xof the
Cauchy distribution with location parameter location and scale parameter scale >0.
Default values are location = 0, scale = 1.
cauchy_cdf (x)
cauchy_cdf (x,location,scale)
For each element of x, compute the cumulative distribution function (CDF) at xof
the Cauchy distribution with location parameter location and scale parameter scale.
Default values are location = 0, scale = 1.
cauchy_inv (x)
cauchy_inv (x,location,scale)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
Cauchy distribution with location parameter location and scale parameter scale.
Default values are location = 0, scale = 1.
chi2pdf (x,n)
For each element of x, compute the probability density function (PDF) at xof the
chi-square distribution with ndegrees of freedom.
chi2cdf (x,n)
For each element of x, compute the cumulative distribution function (CDF) at xof
the chi-square distribution with ndegrees of freedom.
chi2inv (x,n)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
chi-square distribution with ndegrees of freedom.
discrete_pdf (x,v,p)
For each element of x, compute the probability density function (PDF) at xof a
univariate discrete distribution which assumes the values in vwith probabilities p.
658 GNU Octave
discrete_cdf (x,v,p)
For each element of x, compute the cumulative distribution function (CDF) at xof a
univariate discrete distribution which assumes the values in vwith probabilities p.
discrete_inv (x,v,p)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
univariate distribution which assumes the values in vwith probabilities p.
empirical_pdf (x,data)
For each element of x, compute the probability density function (PDF) at xof the
empirical distribution obtained from the univariate sample data.
empirical_cdf (x,data)
For each element of x, compute the cumulative distribution function (CDF) at xof
the empirical distribution obtained from the univariate sample data.
empirical_inv (x,data)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
empirical distribution obtained from the univariate sample data.
exppdf (x,lambda)
For each element of x, compute the probability density function (PDF) at xof the
exponential distribution with mean lambda.
expcdf (x,lambda)
For each element of x, compute the cumulative distribution function (CDF) at xof
the exponential distribution with mean lambda.
The arguments can be of common size or scalars.
expinv (x,lambda)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
exponential distribution with mean lambda.
fpdf (x,m,n)
For each element of x, compute the probability density function (PDF) at xof the F
distribution with mand ndegrees of freedom.
fcdf (x,m,n)
For each element of x, compute the cumulative distribution function (CDF) at xof
the F distribution with mand ndegrees of freedom.
finv (x,m,n)
For each element of x, compute the quantile (the inverse of the CDF) at xof the F
distribution with mand ndegrees of freedom.
gampdf (x,a,b)
For each element of x, return the probability density function (PDF) at xof the
Gamma distribution with shape parameter aand scale b.
gamcdf (x,a,b)
For each element of x, compute the cumulative distribution function (CDF) at xof
the Gamma distribution with shape parameter aand scale b.
Chapter 26: Statistics 659
gaminv (x,a,b)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
Gamma distribution with shape parameter aand scale b.
geopdf (x,p)
For each element of x, compute the probability density function (PDF) at xof the
geometric distribution with parameter p.
The geometric distribution models the number of failures (x-1) of a Bernoulli trial
with probability pbefore the first success (x).
geocdf (x,p)
For each element of x, compute the cumulative distribution function (CDF) at xof
the geometric distribution with parameter p.
The geometric distribution models the number of failures (x-1) of a Bernoulli trial
with probability pbefore the first success (x).
geoinv (x,p)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
geometric distribution with parameter p.
The geometric distribution models the number of failures (x-1) of a Bernoulli trial
with probability pbefore the first success (x).
hygepdf (x,t,m,n)
Compute the probability density function (PDF) at xof the hypergeometric distri-
bution with parameters t,m, and n.
This is the probability of obtaining xmarked items when randomly drawing a sample
of size nwithout replacement from a population of total size tcontaining mmarked
items.
The parameters t,m, and nmust be positive integers with mand nnot greater than
t.
hygecdf (x,t,m,n)
Compute the cumulative distribution function (CDF) at xof the hypergeometric
distribution with parameters t,m, and n.
This is the probability of obtaining not more than xmarked items when randomly
drawing a sample of size nwithout replacement from a population of total size t
containing mmarked items.
The parameters t,m, and nmust be positive integers with mand nnot greater than
t.
hygeinv (x,t,m,n)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
hypergeometric distribution with parameters t,m, and n.
This is the probability of obtaining xmarked items when randomly drawing a sample
of size nwithout replacement from a population of total size tcontaining mmarked
items.
The parameters t,m, and nmust be positive integers with mand nnot greater than
t.
660 GNU Octave
kolmogorov_smirnov_cdf (x,tol)
Return the cumulative distribution function (CDF) at xof the Kolmogorov-Smirnov
distribution.
This is defined as
Q(x) =
∞
X
k=−∞
(−1)kexp(−2k2x2)
for x>0.
The optional parameter tol specifies the precision up to which the series should be
evaluated; the default is tol =eps.
laplace_pdf (x)
For each element of x, compute the probability density function (PDF) at xof the
Laplace distribution.
laplace_cdf (x)
For each element of x, compute the cumulative distribution function (CDF) at xof
the Laplace distribution.
laplace_inv (x)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
Laplace distribution.
logistic_pdf (x)
For each element of x, compute the PDF at xof the logistic distribution.
logistic_cdf (x)
For each element of x, compute the cumulative distribution function (CDF) at xof
the logistic distribution.
logistic_inv (x)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
logistic distribution.
lognpdf (x)
lognpdf (x,mu,sigma)
For each element of x, compute the probability density function (PDF) at xof the
lognormal distribution with parameters mu and sigma.
If a random variable follows this distribution, its logarithm is normally distributed
with mean mu and standard deviation sigma.
Default values are mu = 0, sigma = 1.
logncdf (x)
logncdf (x,mu,sigma)
For each element of x, compute the cumulative distribution function (CDF) at xof
the lognormal distribution with parameters mu and sigma.
If a random variable follows this distribution, its logarithm is normally distributed
with mean mu and standard deviation sigma.
Default values are mu = 0, sigma = 1.
Chapter 26: Statistics 661
logninv (x)
logninv (x,mu,sigma)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
lognormal distribution with parameters mu and sigma.
If a random variable follows this distribution, its logarithm is normally distributed
with mean mu and standard deviation sigma.
Default values are mu = 0, sigma = 1.
nbinpdf (x,n,p)
For each element of x, compute the probability density function (PDF) at xof the
negative binomial distribution with parameters nand p.
When nis integer this is the Pascal distribution. When nis extended to real numbers
this is the Polya distribution.
The number of failures in a Bernoulli experiment with success probability pbefore
the n-th success follows this distribution.
nbincdf (x,n,p)
For each element of x, compute the cumulative distribution function (CDF) at xof
the negative binomial distribution with parameters nand p.
When nis integer this is the Pascal distribution. When nis extended to real numbers
this is the Polya distribution.
The number of failures in a Bernoulli experiment with success probability pbefore
the n-th success follows this distribution.
nbininv (x,n,p)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
negative binomial distribution with parameters nand p.
When nis integer this is the Pascal distribution. When nis extended to real numbers
this is the Polya distribution.
The number of failures in a Bernoulli experiment with success probability pbefore
the n-th success follows this distribution.
normpdf (x)
normpdf (x,mu,sigma)
For each element of x, compute the probability density function (PDF) at xof the
normal distribution with mean mu and standard deviation sigma.
Default values are mu = 0, sigma = 1.
normcdf (x)
normcdf (x,mu,sigma)
For each element of x, compute the cumulative distribution function (CDF) at xof
the normal distribution with mean mu and standard deviation sigma.
Default values are mu = 0, sigma = 1.
norminv (x)
norminv (x,mu,sigma)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
normal distribution with mean mu and standard deviation sigma.
662 GNU Octave
Default values are mu = 0, sigma = 1.
poisspdf (x,lambda)
For each element of x, compute the probability density function (PDF) at xof the
Poisson distribution with parameter lambda.
poisscdf (x,lambda)
For each element of x, compute the cumulative distribution function (CDF) at xof
the Poisson distribution with parameter lambda.
poissinv (x,lambda)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
Poisson distribution with parameter lambda.
stdnormal_pdf (x)
For each element of x, compute the probability density function (PDF) at xof the
standard normal distribution (mean = 0, standard deviation = 1).
stdnormal_cdf (x)
For each element of x, compute the cumulative distribution function (CDF) at xof
the standard normal distribution (mean = 0, standard deviation = 1).
stdnormal_inv (x)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
standard normal distribution (mean = 0, standard deviation = 1).
tpdf (x,n)
For each element of x, compute the probability density function (PDF) at xof the t
(Student) distribution with ndegrees of freedom.
tcdf (x,n)
For each element of x, compute the cumulative distribution function (CDF) at xof
the t (Student) distribution with ndegrees of freedom.
tinv (x,n)
For each element of x, compute the quantile (the inverse of the CDF) at xof the t
(Student) distribution with ndegrees of freedom.
This function is analogous to looking in a table for the t-value of a single-tailed
distribution.
unidpdf (x,n)
For each element of x, compute the probability density function (PDF) at xof a
discrete uniform distribution which assumes the integer values 1–nwith equal prob-
ability.
Warning: The underlying implementation uses the double class and will only be
accurate for n< flintmax (253 on IEEE 754 compatible systems).
unidcdf (x,n)
For each element of x, compute the cumulative distribution function (CDF) at x
of a discrete uniform distribution which assumes the integer values 1–nwith equal
probability.

Chapter 26: Statistics 663
unidinv (x,n)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
discrete uniform distribution which assumes the integer values 1–nwith equal prob-
ability.
unifpdf (x)
unifpdf (x,a,b)
For each element of x, compute the probability density function (PDF) at xof the
uniform distribution on the interval [a,b].
Default values are a= 0, b= 1.
unifcdf (x)
unifcdf (x,a,b)
For each element of x, compute the cumulative distribution function (CDF) at xof
the uniform distribution on the interval [a,b].
Default values are a= 0, b= 1.
unifinv (x)
unifinv (x,a,b)
For each element of x, compute the quantile (the inverse of the CDF) at xof the
uniform distribution on the interval [a,b].
Default values are a= 0, b= 1.
wblpdf (x)
wblpdf (x,scale)
wblpdf (x,scale,shape)
Compute the probability density function (PDF) at xof the Weibull distribution with
scale parameter scale and shape parameter shape.
This is given by shape
scaleshape ·xshape−1·e−(x
scale )shape
for x≥0.
Default values are scale = 1, shape = 1.
wblcdf (x)
wblcdf (x,scale)
wblcdf (x,scale,shape)
Compute the cumulative distribution function (CDF) at xof the Weibull distribution
with scale parameter scale and shape parameter shape.
This is defined as
1−e−(x
scale )shape
for x≥0.
wblinv (x)
wblinv (x,scale)
wblinv (x,scale,shape)
Compute the quantile (the inverse of the CDF) at xof the Weibull distribution with
scale parameter scale and shape parameter shape.
Default values are scale = 1, shape = 1.

664 GNU Octave
26.6 Tests
Octave can perform many different statistical tests. The following table summarizes the
available tests.
Hypothesis Test Functions
Equal mean values anova, hotelling test2, t test 2,
welch test, wilcoxon test, z test 2
Equal medians kruskal wallis test, sign test
Equal variances bartlett test, manova, var test
Equal distributions chisquare test homogeneity,
kolmogorov smirnov test 2, u test
Equal marginal frequencies mcnemar test
Equal success probabilities prop test 2
Independent observations chisquare test independence,
run test
Uncorrelated observations cor test
Given mean value hotelling test, t test, z test
Observations from distribution kolmogorov smirnov test
Regression f test regression, t test regression
The tests return a p-value that describes the outcome of the test. Assuming that the
test hypothesis is true, the p-value is the probability of obtaining a worse result than the
observed one. So large p-values corresponds to a successful test. Usually a test hypothesis
is accepted if the p-value exceeds 0.05.
[pval,f,df_b,df_w] = anova (y,g)
Perform a one-way analysis of variance (ANOVA).
The goal is to test whether the population means of data taken from kdifferent groups
are all equal.
Data may be given in a single vector ywith groups specified by a corresponding
vector of group labels g(e.g., numbers from 1 to k). This is the general form which
does not impose any restriction on the number of data in each group or the group
labels.
If yis a matrix and gis omitted, each column of yis treated as a group. This form
is only appropriate for balanced ANOVA in which the numbers of samples from each
group are all equal.
Under the null of constant means, the statistic ffollows an F distribution with df b
and df w degrees of freedom.
The p-value (1 minus the CDF of this distribution at f) is returned in pval.
If no output argument is given, the standard one-way ANOVA table is printed.
See also: [manova], page 667.
[pval,chisq,df] = bartlett_test (x1, . . . )
Perform a Bartlett test for the homogeneity of variances in the data vectors x1,x2,
. . ., xk, where k>1.
Chapter 26: Statistics 665
Under the null of equal variances, the test statistic chisq approximately follows a
chi-square distribution with df degrees of freedom.
The p-value (1 minus the CDF of this distribution at chisq) is returned in pval.
If no output argument is given, the p-value is displayed.
[pval,chisq,df] = chisquare_test_homogeneity (x,y,c)
Given two samples xand y, perform a chisquare test for homogeneity of the null
hypothesis that xand ycome from the same distribution, based on the partition
induced by the (strictly increasing) entries of c.
For large samples, the test statistic chisq approximately follows a chisquare distribu-
tion with df =length (c)degrees of freedom.
The p-value (1 minus the CDF of this distribution at chisq) is returned in pval.
If no output argument is given, the p-value is displayed.
[pval,chisq,df] = chisquare_test_independence (x)
Perform a chi-square test for independence based on the contingency table x.
Under the null hypothesis of independence, chisq approximately has a chi-square
distribution with df degrees of freedom.
The p-value (1 minus the CDF of this distribution at chisq) of the test is returned in
pval.
If no output argument is given, the p-value is displayed.
cor_test (x,y,alt,method)
Test whether two samples xand ycome from uncorrelated populations.
The optional argument string alt describes the alternative hypothesis, and can be
"!=" or "<>" (nonzero), ">" (greater than 0), or "<" (less than 0). The default is the
two-sided case.
The optional argument string method specifies which correlation coefficient to use
for testing. If method is "pearson" (default), the (usual) Pearson’s product moment
correlation coefficient is used. In this case, the data should come from a bivariate
normal distribution. Otherwise, the other two methods offer nonparametric alterna-
tives. If method is "kendall", then Kendall’s rank correlation tau is used. If method
is "spearman", then Spearman’s rank correlation rho is used. Only the first character
is necessary.
The output is a structure with the following elements:
pval The p-value of the test.
stat The value of the test statistic.
dist The distribution of the test statistic.
params The parameters of the null distribution of the test statistic.
alternative
The alternative hypothesis.
method The method used for testing.
If no output argument is given, the p-value is displayed.

666 GNU Octave
[pval,f,df_num,df_den] = f_test_regression (y,x,rr,r)
Perform an F test for the null hypothesis rr * b = r in a classical normal regression
model y = X * b +e.
Under the null, the test statistic ffollows an F distribution with df num and df den
degrees of freedom.
The p-value (1 minus the CDF of this distribution at f) is returned in pval.
If not given explicitly, r= 0.
If no output argument is given, the p-value is displayed.
[pval,tsq] = hotelling_test (x,m)
For a sample xfrom a multivariate normal distribution with unknown mean and
covariance matrix, test the null hypothesis that mean (x) == m.
Hotelling’s T2is returned in tsq. Under the null, (n−p)T2/(p(n−1)) has an F
distribution with pand n−pdegrees of freedom, where nand pare the numbers of
samples and variables, respectively.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,tsq] = hotelling_test_2 (x,y)
For two samples xfrom multivariate normal distributions with the same number of
variables (columns), unknown means and unknown equal covariance matrices, test
the null hypothesis mean (x) == mean (y).
Hotelling’s two-sample T2is returned in tsq. Under the null,
(nx+ny−p−1)T2
p(nx+ny−2)
has an F distribution with pand nx+ny−p−1 degrees of freedom, where nxand
nyare the sample sizes and pis the number of variables.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,ks] = kolmogorov_smirnov_test (x,dist,params,alt)
Perform a Kolmogorov-Smirnov test of the null hypothesis that the sample xcomes
from the (continuous) distribution dist.
if F and G are the CDFs corresponding to the sample and dist, respectively, then the
null is that F == G.
The optional argument params contains a list of parameters of dist. For example, to
test whether a sample xcomes from a uniform distribution on [2,4], use
kolmogorov_smirnov_test (x, "unif", 2, 4)
dist can be any string for which a function distcdf that calculates the CDF of distri-
bution dist exists.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative F != G. In
this case, the test statistic ks follows a two-sided Kolmogorov-Smirnov distribution.

Chapter 26: Statistics 667
If alt is ">", the one-sided alternative F >G is considered. Similarly for "<", the
one-sided alternative F >G is considered. In this case, the test statistic ks has a
one-sided Kolmogorov-Smirnov distribution. The default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value is displayed.
[pval,ks,d] = kolmogorov_smirnov_test_2 (x,y,alt)
Perform a 2-sample Kolmogorov-Smirnov test of the null hypothesis that the samples
xand ycome from the same (continuous) distribution.
If F and G are the CDFs corresponding to the xand ysamples, respectively, then
the null is that F == G.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative F != G. In
this case, the test statistic ks follows a two-sided Kolmogorov-Smirnov distribution.
If alt is ">", the one-sided alternative F >G is considered. Similarly for "<", the
one-sided alternative F <G is considered. In this case, the test statistic ks has a
one-sided Kolmogorov-Smirnov distribution. The default is the two-sided case.
The p-value of the test is returned in pval.
The third returned value, d, is the test statistic, the maximum vertical distance
between the two cumulative distribution functions.
If no output argument is given, the p-value is displayed.
[pval,k,df] = kruskal_wallis_test (x1, . . . )
Perform a Kruskal-Wallis one-factor analysis of variance.
Suppose a variable is observed for k>1 different groups, and let x1, . . . , xk be the
corresponding data vectors.
Under the null hypothesis that the ranks in the pooled sample are not affected by the
group memberships, the test statistic kis approximately chi-square with df =k- 1
degrees of freedom.
If the data contains ties (some value appears more than once) kis divided by
1 - sum ties / (n^3 - n)
where sum ties is the sum of t^2 - tover each group of ties where tis the number
of ties in the group and nis the total number of values in the input data. For more
info on this adjustment see William H. Kruskal and W. Allen Wallis, Use of Ranks
in One-Criterion Variance Analysis, Journal of the American Statistical Association,
Vol. 47, No. 260 (Dec 1952).
The p-value (1 minus the CDF of this distribution at k) is returned in pval.
If no output argument is given, the p-value is displayed.
manova (x,g)
Perform a one-way multivariate analysis of variance (MANOVA).
The goal is to test whether the p-dimensional population means of data taken from
kdifferent groups are all equal. All data are assumed drawn independently from
p-dimensional normal distributions with the same covariance matrix.
668 GNU Octave
The data matrix is given by x. As usual, rows are observations and columns are
variables. The vector gspecifies the corresponding group labels (e.g., numbers from
1 to k).
The LR test statistic (Wilks’ Lambda) and approximate p-values are computed and
displayed.
See also: [anova], page 664.
[pval,chisq,df] = mcnemar_test (x)
For a square contingency table xof data cross-classified on the row and column
variables, McNemar’s test can be used for testing the null hypothesis of symmetry of
the classification probabilities.
Under the null, chisq is approximately distributed as chisquare with df degrees of
freedom.
The p-value (1 minus the CDF of this distribution at chisq) is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,z] = prop_test_2 (x1,n1,x2,n2,alt)
If x1 and n1 are the counts of successes and trials in one sample, and x2 and n2 those
in a second one, test the null hypothesis that the success probabilities p1 and p2 are
the same.
Under the null, the test statistic zapproximately follows a standard normal distribu-
tion.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative p1 != p2. If
alt is ">", the one-sided alternative p1 >p2 is used. Similarly for "<", the one-sided
alternative p1 <p2 is used. The default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,chisq] = run_test (x)
Perform a chi-square test with 6 degrees of freedom based on the upward runs in the
columns of x.
run_test can be used to decide whether xcontains independent data.
The p-value of the test is returned in pval.
If no output argument is given, the p-value is displayed.
[pval,b,n] = sign_test (x,y,alt)
For two matched-pair samples xand y, perform a sign test of the null hypothesis
PROB (x>y) == PROB (x<y) == 1/2.
Under the null, the test statistic broughly follows a binomial distribution with pa-
rameters n= sum (x!= y)and p= 1/2.
With the optional argument alt, the alternative of interest can be selected. If alt is
"!=" or "<>", the null hypothesis is tested against the two-sided alternative PROB
(x<y) != 1/2. If alt is ">", the one-sided alternative PROB (x>y)>1/2 ("x
is stochastically greater than y") is considered. Similarly for "<", the one-sided
Chapter 26: Statistics 669
alternative PROB (x>y)<1/2 ("x is stochastically less than y") is considered. The
default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,t,df] = t_test (x,m,alt)
For a sample xfrom a normal distribution with unknown mean and variance, perform
a t-test of the null hypothesis mean (x) == m.
Under the null, the test statistic tfollows a Student distribution with df = length
(x) - 1 degrees of freedom.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative mean (x) != m.
If alt is ">", the one-sided alternative mean (x) > mis considered. Similarly for "<",
the one-sided alternative mean (x) < mis considered. The default is the two-sided
case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,t,df] = t_test_2 (x,y,alt)
For two samples x and y from normal distributions with unknown means and unknown
equal variances, perform a two-sample t-test of the null hypothesis of equal means.
Under the null, the test statistic tfollows a Student distribution with df degrees of
freedom.
With the optional argument string alt, the alternative of interest can be selected.
If alt is "!=" or "<>", the null is tested against the two-sided alternative mean (x)
!= mean (y). If alt is ">", the one-sided alternative mean (x) > mean (y)is used.
Similarly for "<", the one-sided alternative mean (x) < mean (y)is used. The default
is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,t,df] = t_test_regression (y,x,rr,r,alt)
Perform a t test for the null hypothesis rr *b=rin a classical normal regression
model y=x*b+e.
Under the null, the test statistic tfollows a tdistribution with df degrees of freedom.
If ris omitted, a value of 0 is assumed.
With the optional argument string alt, the alternative of interest can be selected.
If alt is "!=" or "<>", the null is tested against the two-sided alternative rr *b!=
r. If alt is ">", the one-sided alternative rr *b>ris used. Similarly for "<", the
one-sided alternative rr *b<ris used. The default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.

670 GNU Octave
[pval,z] = u_test (x,y,alt)
For two samples xand y, perform a Mann-Whitney U-test of the null hypothesis
PROB (x>y) == 1/2 == PROB (x<y).
Under the null, the test statistic zapproximately follows a standard normal distribu-
tion. Note that this test is equivalent to the Wilcoxon rank-sum test.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative PROB (x>
y) != 1/2. If alt is ">", the one-sided alternative PROB (x>y)>1/2 is considered.
Similarly for "<", the one-sided alternative PROB (x>y)<1/2 is considered. The
default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,f,df_num,df_den] = var_test (x,y,alt)
For two samples xand yfrom normal distributions with unknown means and unknown
variances, perform an F-test of the null hypothesis of equal variances.
Under the null, the test statistic ffollows an F-distribution with df num and df den
degrees of freedom.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative var (x) != var
(y). If alt is ">", the one-sided alternative var (x) > var (y)is used. Similarly for
"<", the one-sided alternative var (x) > var (y)is used. The default is the two-sided
case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,t,df] = welch_test (x,y,alt)
For two samples xand yfrom normal distributions with unknown means and unknown
and not necessarily equal variances, perform a Welch test of the null hypothesis of
equal means.
Under the null, the test statistic tapproximately follows a Student distribution with
df degrees of freedom.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative mean (x) != m.
If alt is ">", the one-sided alternative mean(x) >mis considered. Similarly for "<",
the one-sided alternative mean(x) <mis considered. The default is the two-sided
case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,z] = wilcoxon_test (x,y,alt)
For two matched-pair sample vectors xand y, perform a Wilcoxon signed-rank test
of the null hypothesis PROB (x>y) == 1/2.
Under the null, the test statistic zapproximately follows a standard normal distribu-
tion when n>25.

Chapter 26: Statistics 671
Caution: This function assumes a normal distribution for zand thus is invalid for n
≤25.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative PROB (x>
y) != 1/2. If alt is ">", the one-sided alternative PROB (x>y)>1/2 is considered.
Similarly for "<", the one-sided alternative PROB (x>y)<1/2 is considered. The
default is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed.
[pval,z] = z_test (x,m,v,alt)
Perform a Z-test of the null hypothesis mean (x) == mfor a sample xfrom a normal
distribution with unknown mean and known variance v.
Under the null, the test statistic zfollows a standard normal distribution.
With the optional argument string alt, the alternative of interest can be selected. If
alt is "!=" or "<>", the null is tested against the two-sided alternative mean (x) != m.
If alt is ">", the one-sided alternative mean (x) > mis considered. Similarly for "<",
the one-sided alternative mean (x) < mis considered. The default is the two-sided
case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed along with some
information.
[pval,z] = z_test_2 (x,y,v_x,v_y,alt)
For two samples xand yfrom normal distributions with unknown means and known
variances v x and v y, perform a Z-test of the hypothesis of equal means.
Under the null, the test statistic zfollows a standard normal distribution.
With the optional argument string alt, the alternative of interest can be selected.
If alt is "!=" or "<>", the null is tested against the two-sided alternative mean (x)
!= mean (y). If alt is ">", the one-sided alternative mean (x) > mean (y)is used.
Similarly for "<", the one-sided alternative mean (x) < mean (y)is used. The default
is the two-sided case.
The p-value of the test is returned in pval.
If no output argument is given, the p-value of the test is displayed along with some
information.
26.7 Random Number Generation
Octave can generate random numbers from a large number of distributions. The random
number generators are based on the random number generators described in Section 16.3
[Special Utility Matrices], page 453.
The following table summarizes the available random number generators (in alphabetical
order).
672 GNU Octave
Distribution Function
Beta Distribution betarnd
Binomial Distribution binornd
Cauchy Distribution cauchy rnd
Chi-Square Distribution chi2rnd
Univariate Discrete Distribution discrete rnd
Empirical Distribution empirical rnd
Exponential Distribution exprnd
F Distribution frnd
Gamma Distribution gamrnd
Geometric Distribution geornd
Hypergeometric Distribution hygernd
Laplace Distribution laplace rnd
Logistic Distribution logistic rnd
Log-Normal Distribution lognrnd
Pascal Distribution nbinrnd
Univariate Normal Distribution normrnd
Poisson Distribution poissrnd
Standard Normal Distribution stdnormal rnd
t (Student) Distribution trnd
Univariate Discrete Distribution unidrnd
Uniform Distribution unifrnd
Weibull Distribution wblrnd
Wiener Process wienrnd
betarnd (a,b)
betarnd (a,b,r)
betarnd (a,b,r,c, . . . )
betarnd (a,b,[sz])
Return a matrix of random samples from the Beta distribution with parameters a
and b.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of aand b.
binornd (n,p)
binornd (n,p,r)
binornd (n,p,r,c, . . . )
binornd (n,p,[sz])
Return a matrix of random samples from the binomial distribution with parameters
nand p, where nis the number of trials and pis the probability of success.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
Chapter 26: Statistics 673
If no size arguments are given then the result matrix is the common size of nand p.
cauchy_rnd (location,scale)
cauchy_rnd (location,scale,r)
cauchy_rnd (location,scale,r,c, . . . )
cauchy_rnd (location,scale,[sz])
Return a matrix of random samples from the Cauchy distribution with parameters
location and scale.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of location
and scale.
chi2rnd (n)
chi2rnd (n,r)
chi2rnd (n,r,c, . . . )
chi2rnd (n,[sz])
Return a matrix of random samples from the chi-square distribution with ndegrees
of freedom.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of n.
discrete_rnd (v,p)
discrete_rnd (v,p,r)
discrete_rnd (v,p,r,c, . . . )
discrete_rnd (v,p,[sz])
Return a matrix of random samples from the univariate distribution which assumes
the values in vwith probabilities p.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of vand p.
empirical_rnd (data)
empirical_rnd (data,r)
empirical_rnd (data,r,c, . . . )
empirical_rnd (data,[sz])
Return a matrix of random samples from the empirical distribution obtained from
the univariate sample data.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
674 GNU Octave
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is a random ordering of the
sample data.
exprnd (lambda)
exprnd (lambda,r)
exprnd (lambda,r,c, . . . )
exprnd (lambda,[sz])
Return a matrix of random samples from the exponential distribution with mean
lambda.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of lambda.
frnd (m,n)
frnd (m,n,r)
frnd (m,n,r,c, . . . )
frnd (m,n,[sz])
Return a matrix of random samples from the F distribution with mand ndegrees of
freedom.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of mand n.
gamrnd (a,b)
gamrnd (a,b,r)
gamrnd (a,b,r,c, . . . )
gamrnd (a,b,[sz])
Return a matrix of random samples from the Gamma distribution with shape param-
eter aand scale b.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of aand b.
geornd (p)
geornd (p,r)
geornd (p,r,c, . . . )
geornd (p,[sz])
Return a matrix of random samples from the geometric distribution with parameter
p.
Chapter 26: Statistics 675
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of p.
The geometric distribution models the number of failures (x-1) of a Bernoulli trial
with probability pbefore the first success (x).
hygernd (t,m,n)
hygernd (t,m,n,r)
hygernd (t,m,n,r,c, . . . )
hygernd (t,m,n,[sz])
Return a matrix of random samples from the hypergeometric distribution with pa-
rameters t,m, and n.
The parameters t,m, and nmust be positive integers with mand nnot greater than
t.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of t,m, and
n.
laplace_rnd (r)
laplace_rnd (r,c, . . . )
laplace_rnd ([sz])
Return a matrix of random samples from the Laplace distribution.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
logistic_rnd (r)
logistic_rnd (r,c, . . . )
logistic_rnd ([sz])
Return a matrix of random samples from the logistic distribution.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
lognrnd (mu,sigma)
lognrnd (mu,sigma,r)
lognrnd (mu,sigma,r,c, . . . )
lognrnd (mu,sigma,[sz])
Return a matrix of random samples from the lognormal distribution with parameters
mu and sigma.
676 GNU Octave
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of mu and
sigma.
nbinrnd (n,p)
nbinrnd (n,p,r)
nbinrnd (n,p,r,c, . . . )
nbinrnd (n,p,[sz])
Return a matrix of random samples from the negative binomial distribution with
parameters nand p.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of nand p.
normrnd (mu,sigma)
normrnd (mu,sigma,r)
normrnd (mu,sigma,r,c, . . . )
normrnd (mu,sigma,[sz])
Return a matrix of random samples from the normal distribution with parameters
mean mu and standard deviation sigma.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of mu and
sigma.
poissrnd (lambda)
poissrnd (lambda,r)
poissrnd (lambda,r,c, . . . )
poissrnd (lambda,[sz])
Return a matrix of random samples from the Poisson distribution with parameter
lambda.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of lambda.
stdnormal_rnd (r)
stdnormal_rnd (r,c, . . . )
Chapter 26: Statistics 677
stdnormal_rnd ([sz])
Return a matrix of random samples from the standard normal distribution (mean =
0, standard deviation = 1).
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
trnd (n)
trnd (n,r)
trnd (n,r,c, . . . )
trnd (n,[sz])
Return a matrix of random samples from the t (Student) distribution with ndegrees
of freedom.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of n.
unidrnd (n)
unidrnd (n,r)
unidrnd (n,r,c, . . . )
unidrnd (n,[sz])
Return a matrix of random samples from the discrete uniform distribution which
assumes the integer values 1–nwith equal probability.
nmay be a scalar or a multi-dimensional array.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the size of n.
unifrnd (a,b)
unifrnd (a,b,r)
unifrnd (a,b,r,c, . . . )
unifrnd (a,b,[sz])
Return a matrix of random samples from the uniform distribution on [a,b].
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of aand b.
wblrnd (scale,shape)
wblrnd (scale,shape,r)
678 GNU Octave
wblrnd (scale,shape,r,c, . . . )
wblrnd (scale,shape,[sz])
Return a matrix of random samples from the Weibull distribution with parameters
scale and shape.
When called with a single size argument, return a square matrix with the dimension
specified. When called with more than one scalar argument the first two arguments are
taken as the number of rows and columns and any further arguments specify additional
matrix dimensions. The size may also be specified with a vector of dimensions sz.
If no size arguments are given then the result matrix is the common size of scale and
shape.
wienrnd (t,d,n)
Return a simulated realization of the d-dimensional Wiener Process on the interval
[0, t].
If dis omitted, d= 1 is used. The first column of the return matrix contains time,
the remaining columns contain the Wiener process.
The optional parameter ndefines the number of summands used for simulating the
process over an interval of length 1. If nis omitted, n= 1000 is used.
679
27 Sets
Octave has a number of functions for managing sets of data. A set is defined as a collection
of unique elements and is typically represented by a vector of numbers sorted in ascending
order. Any vector or matrix can be converted to a set by removing duplicates through the
use of the unique function. However, it isn’t necessary to explicitly create a set as all of
the functions which operate on sets will convert their input to a set before proceeding.
unique (x)
unique (x,"rows")
[y,i,j] = unique (. . . )
[y,i,j] = unique (. . . , "first")
[y,i,j] = unique (. . . , "last")
Return the unique elements of xsorted in ascending order.
If the input xis a column vector then return a column vector; Otherwise, return a
row vector. xmay also be a cell array of strings.
If the optional argument "rows" is given then return the unique rows of xsorted in
ascending order. The input must be a 2-D matrix to use this option.
If requested, return index vectors iand jsuch that y=x(i)and x=y(j).
Additionally, if iis a requested output then one of "first" or "last" may be given
as an input. If "last" is specified, return the highest possible indices in i, otherwise,
if "first" is specified, return the lowest. The default is "last".
See also: [union], page 680,[intersect], page 679,[setdiff], page 680,[setxor], page 680,
[ismember], page 680.
27.1 Set Operations
Octave supports several basic set operations. Octave can compute the union, intersection,
and difference of two sets. Octave also supports the Exclusive Or set operation.
The functions for set operations all work in the same way by accepting two input sets
and returning a third set. As an example, assume that aand bcontains two sets, then
union (a, b)
computes the union of the two sets.
Finally, determining whether elements belong to a set can be done with the ismember
function. Because sets are ordered this operation is very efficient and is of order O(log2(n))
which is preferable to the find function which is of order O(n).
c= intersect (a,b)
c= intersect (a,b,"rows")
[c,ia,ib] = intersect (. . . )
Return the unique elements common to both aand bsorted in ascending order.
If aand bare both row vectors then return a row vector; Otherwise, return a column
vector. The inputs may also be cell arrays of strings.
If the optional input "rows" is given then return the common rows of aand b. The
inputs must be 2-D matrices to use this option.
If requested, return index vectors ia and ib such that c=a(ia)and c=b(ib).
680 GNU Octave
See also: [unique], page 679,[union], page 680,[setdiff], page 680,[setxor], page 680,
[ismember], page 680.
c= union (a,b)
c= union (a,b,"rows")
[c,ia,ib] = union (. . . )
Return the unique elements that are in either aor bsorted in ascending order.
If aand bare both row vectors then return a row vector; Otherwise, return a column
vector. The inputs may also be cell arrays of strings.
If the optional input "rows" is given then return rows that are in either aor b. The
inputs must be 2-D matrices to use this option.
The optional outputs ia and ib are index vectors such that a(ia)and b(ib)are
disjoint sets whose union is c.
See also: [unique], page 679,[intersect], page 679,[setdiff], page 680,[setxor],
page 680,[ismember], page 680.
c= setdiff (a,b)
c= setdiff (a,b,"rows")
[c,ia] = setdiff (. . . )
Return the unique elements in athat are not in bsorted in ascending order.
If ais a row vector return a column vector; Otherwise, return a column vector. The
inputs may also be cell arrays of strings.
If the optional input "rows" is given then return the rows in athat are not in b. The
inputs must be 2-D matrices to use this option.
If requested, return the index vector ia such that c=a(ia).
See also: [unique], page 679,[union], page 680,[intersect], page 679,[setxor], page 680,
[ismember], page 680.
c= setxor (a,b)
c= setxor (a,b,"rows")
[c,ia,ib] = setxor (. . . )
Return the unique elements exclusive to sets aor bsorted in ascending order.
If aand bare both row vectors then return a row vector; Otherwise, return a column
vector. The inputs may also be cell arrays of strings.
If the optional input "rows" is given then return the rows exclusive to sets aand b.
The inputs must be 2-D matrices to use this option.
If requested, return index vectors ia and ib such that a(ia)and b(ib)are disjoint
sets whose union is c.
See also: [unique], page 679,[union], page 680,[intersect], page 679,[setdiff], page 680,
[ismember], page 680.
tf = ismember (a,s)
tf = ismember (a,s,"rows")
[tf,s_idx] = ismember (. . . )
Return a logical matrix tf with the same shape as awhich is true (1) if the element
in ais found in sand false (0) if it is not.
Chapter 27: Sets 681
If a second output argument is requested then the index into sof each matching
element is also returned.
a = [3, 10, 1];
s = [0:9];
[tf, s_idx] = ismember (a, s)
⇒tf = [1, 0, 1]
⇒s_idx = [4, 0, 2]
The inputs aand smay also be cell arrays.
a = {"abc"};
s = {"abc", "def"};
[tf, s_idx] = ismember (a, s)
⇒tf = [1, 0]
⇒s_idx = [1, 0]
If the optional third argument "rows" is given then compare rows in awith rows in
s. The inputs must be 2-D matrices with the same number of columns to use this
option.
a = [1:3; 5:7; 4:6];
s = [0:2; 1:3; 2:4; 3:5; 4:6];
[tf, s_idx] = ismember (a, s, "rows")
⇒tf = logical ([1; 0; 1])
⇒s_idx = [2; 0; 5];
See also: [lookup], page 442,[unique], page 679,[union], page 680,[intersect],
page 679,[setdiff], page 680,[setxor], page 680.
powerset (a)
powerset (a,"rows")
Compute the powerset (all subsets) of the set a.
The set amust be a numerical matrix or a cell array of strings. The output will
always be a cell array of either vectors or strings.
With the optional argument "rows", each row of the set ais considered one element
of the set. The input must be a 2-D numeric matrix to use this argument.
See also: [unique], page 679,[union], page 680,[intersect], page 679,[setdiff], page 680,
[setxor], page 680,[ismember], page 680.
683
28 Polynomial Manipulations
In Octave, a polynomial is represented by its coefficients (arranged in descending order).
For example, a vector cof length N+ 1 corresponds to the following polynomial of order N
p(x) = c1xN+. . . +cNx+cN+1.
28.1 Evaluating Polynomials
The value of a polynomial represented by the vector ccan be evaluated at the point xvery
easily, as the following example shows:
N = length (c) - 1;
val = dot (x.^(N:-1:0), c);
While the above example shows how easy it is to compute the value of a polynomial, it isn’t
the most stable algorithm. With larger polynomials you should use more elegant algorithms,
such as Horner’s Method, which is exactly what the Octave function polyval does.
In the case where xis a square matrix, the polynomial given by cis still well-defined.
As when xis a scalar the obvious implementation is easily expressed in Octave, but also in
this case more elegant algorithms perform better. The polyvalm function provides such an
algorithm.
y= polyval (p,x)
y= polyval (p,x,[],mu)
[y,dy] = polyval (p,x,s)
[y,dy] = polyval (p,x,s,mu)
Evaluate the polynomial pat the specified values of x.
If xis a vector or matrix, the polynomial is evaluated for each of the elements of x.
When mu is present, evaluate the polynomial for (x-mu(1))/mu(2).
In addition to evaluating the polynomial, the second output represents the prediction
interval, y+/- dy, which contains at least 50% of the future predictions. To calculate
the prediction interval, the structured variable s, originating from polyfit, must be
supplied.
See also: [polyvalm], page 683,[polyaffine], page 689,[polyfit], page 689,[roots],
page 684,[poly], page 698.
polyvalm (c,x)
Evaluate a polynomial in the matrix sense.
polyvalm (c,x)will evaluate the polynomial in the matrix sense, i.e., matrix mul-
tiplication is used instead of element by element multiplication as used in polyval.
The argument xmust be a square matrix.
See also: [polyval], page 683,[roots], page 684,[poly], page 698.

684 GNU Octave
28.2 Finding Roots
Octave can find the roots of a given polynomial. This is done by computing the companion
matrix of the polynomial (see the compan function for a definition), and then finding its
eigenvalues.
roots (c)
Compute the roots of the polynomial c.
For a vector cwith Ncomponents, return the roots of the polynomial
c1xN−1+··· +cN−1x+cN.
As an example, the following code finds the roots of the quadratic polynomial
p(x) = x2−5.
c = [1, 0, -5];
roots (c)
⇒2.2361
⇒-2.2361
Note that the true result is ±√5 which is roughly ±2.2361.
See also: [poly], page 698,[compan], page 684,[fzero], page 547.
z= polyeig (C0,C1, . . . , Cl)
[v,z] = polyeig (C0,C1, . . . , Cl)
Solve the polynomial eigenvalue problem of degree l.
Given an n*n matrix polynomial
C(s) = C0 +C1 s + ... + Cl s^l
polyeig solves the eigenvalue problem
(C0 +C1 + ... + Cl)v = 0.
Note that the eigenvalues zare the zeros of the matrix polynomial. zis a row vector
with n*l elements. vis a matrix (nxn*l) with columns that correspond to the
eigenvectors.
See also: [eig], page 505,[eigs], page 586,[compan], page 684.
compan (c)
Compute the companion matrix corresponding to polynomial coefficient vector c.
The companion matrix is
A=
−c2/c1−c3/c1··· −cN/c1−cN+1/c1
1 0 ··· 0 0
0 1 ··· 0 0
.
.
..
.
.....
.
..
.
.
0 0 ··· 1 0
.
The eigenvalues of the companion matrix are equal to the roots of the polynomial.
See also: [roots], page 684,[poly], page 698,[eig], page 505.
Chapter 28: Polynomial Manipulations 685
[multp,idxp] = mpoles (p)
[multp,idxp] = mpoles (p,tol)
[multp,idxp] = mpoles (p,tol,reorder)
Identify unique poles in pand their associated multiplicity.
The output is ordered from largest pole to smallest pole.
If the relative difference of two poles is less than tol then they are considered to be
multiples. The default value for tol is 0.001.
If the optional parameter reorder is zero, poles are not sorted.
The output multp is a vector specifying the multiplicity of the poles. multp(n) refers
to the multiplicity of the Nth pole p(idxp(n)).
For example:
p=[23112];
[m, n] = mpoles (p)
⇒m = [1; 1; 2; 1; 2]
⇒n = [2; 5; 1; 4; 3]
⇒p(n) = [3, 2, 2, 1, 1]
See also: [residue], page 687,[poly], page 698,[roots], page 684,[conv], page 685,
[deconv], page 686.
28.3 Products of Polynomials
conv (a,b)
conv (a,b,shape)
Convolve two vectors aand b.
The output convolution is a vector with length equal to length (a) + length (b)
- 1. When aand bare the coefficient vectors of two polynomials, the convolution
represents the coefficient vector of the product polynomial.
The optional shape argument may be
shape ="full"
Return the full convolution. (default)
shape ="same"
Return the central part of the convolution with the same size as a.
See also: [deconv], page 686,[conv2], page 686,[convn], page 685,[fftconv], page 730.
C= convn (A,B)
C= convn (A,B,shape)
Return the n-D convolution of Aand B.
The size of the result is determined by the optional shape argument which takes the
following values
shape ="full"
Return the full convolution. (default)
686 GNU Octave
shape ="same"
Return central part of the convolution with the same size as A. The
central part of the convolution begins at the indices floor ([size(B)/2]
+ 1).
shape ="valid"
Return only the parts which do not include zero-padded edges. The size
of the result is max (size (A) - size (B) + 1, 0).
See also: [conv2], page 686,[conv], page 685.
deconv (y,a)
Deconvolve two vectors.
[b, r] = deconv (y, a) solves for band rsuch that y = conv (a, b) + r.
If yand aare polynomial coefficient vectors, bwill contain the coefficients of the
polynomial quotient and rwill be a remainder polynomial of lowest order.
See also: [conv], page 685,[residue], page 687.
conv2 (A,B)
conv2 (v1,v2,m)
conv2 (. . ., shape)
Return the 2-D convolution of Aand B.
The size of the result is determined by the optional shape argument which takes the
following values
shape ="full"
Return the full convolution. (default)
shape ="same"
Return the central part of the convolution with the same size as A. The
central part of the convolution begins at the indices floor ([size(B)/2]
+ 1).
shape ="valid"
Return only the parts which do not include zero-padded edges. The size
of the result is max (size (A) - size (B) + 1, 0).
When the third argument is a matrix, return the convolution of the matrix mby the
vector v1 in the column direction and by the vector v2 in the row direction.
See also: [conv], page 685,[convn], page 685.
q= polygcd (b,a)
q= polygcd (b,a,tol)
Find the greatest common divisor of two polynomials.
This is equivalent to the polynomial found by multiplying together all the common
roots. Together with deconv, you can reduce a ratio of two polynomials.
The tolerance tol defaults to sqrt (eps).
Caution: This is a numerically unstable algorithm and should not be used on large
polynomials.

Chapter 28: Polynomial Manipulations 687
Example code:
polygcd (poly (1:8), poly (3:12)) - poly (3:8)
⇒[0,0,0,0,0,0,0]
deconv (poly (1:8), polygcd (poly (1:8), poly (3:12))) - poly (1:2)
⇒[0,0,0]
See also: [poly], page 698,[roots], page 684,[conv], page 685,[deconv], page 686,
[residue], page 687.
[r,p,k,e] = residue (b,a)
[b,a] = residue (r,p,k)
[b,a] = residue (r,p,k,e)
The first calling form computes the partial fraction expansion for the quotient of the
polynomials, band a.
The quotient is defined as
B(s)
A(s)=
M
X
m=1
rm
(s−pm)e
m
+
N
X
i=1
kisN−i.
where Mis the number of poles (the length of the r,p, and e), the kvector is a
polynomial of order N−1 representing the direct contribution, and the evector
specifies the multiplicity of the m-th residue’s pole.
For example,
b = [1, 1, 1];
a = [1, -5, 8, -4];
[r, p, k, e] = residue (b, a)
⇒r = [-2; 7; 3]
⇒p = [2; 2; 1]
⇒k = [](0x0)
⇒e = [1; 2; 1]
which represents the following partial fraction expansion
s2+s+ 1
s3−5s2+ 8s−4=−2
s−2+7
(s−2)2+3
s−1
The second calling form performs the inverse operation and computes the reconsti-
tuted quotient of polynomials, b(s)/a(s), from the partial fraction expansion; repre-
sented by the residues, poles, and a direct polynomial specified by r,pand k, and the
pole multiplicity e.
If the multiplicity, e, is not explicitly specified the multiplicity is determined by the
function mpoles.
For example:

688 GNU Octave
r = [-2; 7; 3];
p = [2; 2; 1];
k = [1, 0];
[b, a] = residue (r, p, k)
⇒b = [1, -5, 9, -3, 1]
⇒a = [1, -5, 8, -4]
where mpoles is used to determine e = [1; 2; 1]
Alternatively the multiplicity may be defined explicitly, for example,
r = [7; 3; -2];
p = [2; 1; 2];
k = [1, 0];
e = [2; 1; 1];
[b, a] = residue (r, p, k, e)
⇒b = [1, -5, 9, -3, 1]
⇒a = [1, -5, 8, -4]
which represents the following partial fraction expansion
−2
s−2+7
(s−2)2+3
s−1+s=s4−5s3+ 9s2−3s+ 1
s3−5s2+ 8s−4
See also: [mpoles], page 685,[poly], page 698,[roots], page 684,[conv], page 685,
[deconv], page 686.
28.4 Derivatives / Integrals / Transforms
Octave comes with functions for computing the derivative and the integral of a polynomial.
The functions polyder and polyint both return new polynomials describing the result. As
an example we’ll compute the definite integral of p(x) = x2+ 1 from 0 to 3.
c = [1, 0, 1];
integral = polyint (c);
area = polyval (integral, 3) - polyval (integral, 0)
⇒12
polyder (p)
[k] = polyder (a,b)
[q,d] = polyder (b,a)
Return the coefficients of the derivative of the polynomial whose coefficients are given
by the vector p.
If a pair of polynomials is given, return the derivative of the product a∗b.
If two inputs and two outputs are given, return the derivative of the polynomial
quotient b/a. The quotient numerator is in qand the denominator in d.
See also: [polyint], page 688,[polyval], page 683,[polyreduce], page 699.
polyint (p)
polyint (p,k)
Return the coefficients of the integral of the polynomial whose coefficients are repre-
sented by the vector p.
Chapter 28: Polynomial Manipulations 689
The variable kis the constant of integration, which by default is set to zero.
See also: [polyder], page 688,[polyval], page 683.
polyaffine (f,mu)
Return the coefficients of the polynomial vector fafter an affine transformation.
If fis the vector representing the polynomial f(x), then g= polyaffine (f,mu)is
the vector representing:
g(x) = f( (x - mu(1)) / mu(2) )
See also: [polyval], page 683,[polyfit], page 689.
28.5 Polynomial Interpolation
Octave comes with good support for various kinds of interpolation, most of which are de-
scribed in Chapter 29 [Interpolation], page 701. One simple alternative to the functions
described in the aforementioned chapter, is to fit a single polynomial, or a piecewise poly-
nomial (spline) to some given data points. To avoid a highly fluctuating polynomial, one
most often wants to fit a low-order polynomial to data. This usually means that it is neces-
sary to fit the polynomial in a least-squares sense, which just is what the polyfit function
does.
p= polyfit (x,y,n)
[p,s] = polyfit (x,y,n)
[p,s,mu] = polyfit (x,y,n)
Return the coefficients of a polynomial p(x) of degree nthat minimizes the least-
squares-error of the fit to the points [x,y].
If nis a logical vector, it is used as a mask to selectively force the corresponding
polynomial coefficients to be used or ignored.
The polynomial coefficients are returned in a row vector.
The optional output sis a structure containing the following fields:
‘R’ Triangular factor R from the QR decomposition.
‘X’ The Vandermonde matrix used to compute the polynomial coefficients.
‘C’ The unscaled covariance matrix, formally equal to the inverse of x’*x,
but computed in a way minimizing roundoff error propagation.
‘df’ The degrees of freedom.
‘normr’ The norm of the residuals.
‘yf’ The values of the polynomial for each value of x.
The second output may be used by polyval to calculate the statistical error limits of
the predicted values. In particular, the standard deviation of pcoefficients is given
by
sqrt (diag (s.C)/s.df)*s.normr.
When the third output, mu, is present the coefficients, p, are associated with a poly-
nomial in
690 GNU Octave
xhat = (x-mu(1)) / mu(2)
where mu(1) = mean (x), and mu(2) = std (x).
This linear transformation of ximproves the numerical stability of the fit.
See also: [polyval], page 683,[polyaffine], page 689,[roots], page 684,[vander],
page 468,[zscore], page 650.
In situations where a single polynomial isn’t good enough, a solution is to use several
polynomials pieced together. The function splinefit fits a piecewise polynomial (spline)
to a set of data.
pp = splinefit (x,y,breaks)
pp = splinefit (x,y,p)
pp = splinefit (. . . , "periodic",periodic)
pp = splinefit (. . . , "robust",robust)
pp = splinefit (. . . , "beta",beta)
pp = splinefit (. . . , "order",order)
pp = splinefit (. . . , "constraints",constraints)
Fit a piecewise cubic spline with breaks (knots) breaks to the noisy data, xand y.
xis a vector, and yis a vector or N-D array. If yis an N-D array, then x(j) is matched
to y(:,. . .,:,j).
pis a positive integer defining the number of intervals along x, and p+1 is the number
of breaks. The number of points in each interval differ by no more than 1.
The optional property periodic is a logical value which specifies whether a periodic
boundary condition is applied to the spline. The length of the period is max (breaks)
- min (breaks). The default value is false.
The optional property robust is a logical value which specifies if robust fitting is to be
applied to reduce the influence of outlying data points. Three iterations of weighted
least squares are performed. Weights are computed from previous residuals. The
sensitivity of outlier identification is controlled by the property beta. The value of
beta is restricted to the range, 0 <beta <1. The default value is beta = 1/2. Values
close to 0 give all data equal weighting. Increasing values of beta reduce the influence
of outlying data. Values close to unity may cause instability or rank deficiency.
The fitted spline is returned as a piecewise polynomial, pp, and may be evaluated
using ppval.
The splines are constructed of polynomials with degree order. The default is a cubic,
order=3. A spline with P pieces has P+order degrees of freedom. With periodic
boundary conditions the degrees of freedom are reduced to P.
The optional property, constaints, is a structure specifying linear constraints on the
fit. The structure has three fields, "xc","yc", and "cc".
"xc" Vector of the x-locations of the constraints.
"yc" Constraining values at the locations xc. The default is an array of zeros.
"cc" Coefficients (matrix). The default is an array of ones. The number of
rows is limited to the order of the piecewise polynomials, order.
Chapter 28: Polynomial Manipulations 691
Constraints are linear combinations of derivatives of order 0 to order-1 according to
cc(1, j)·y(xc(j)) + cc(2, j)·y0(xc(j)) + ... =yc(:,...,:, j).
See also: [interp1], page 701,[unmkpp], page 697,[ppval], page 698,[spline], page 705,
[pchip], page 736,[ppder], page 698,[ppint], page 698,[ppjumps], page 698.
The number of breaks (or knots) used to construct the piecewise polynomial is a signifi-
cant factor in suppressing the noise present in the input data, xand y. This is demonstrated
by the example below.
x = 2 * pi * rand (1, 200);
y = sin (x) + sin (2 * x) + 0.2 * randn (size (x));
## Uniform breaks
breaks = linspace (0, 2 * pi, 41); % 41 breaks, 40 pieces
pp1 = splinefit (x, y, breaks);
## Breaks interpolated from data
pp2 = splinefit (x, y, 10); % 11 breaks, 10 pieces
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "41 breaks, 40 pieces", "11 breaks, 10 pieces"})
The result of which can be seen in Figure 28.1.
692 GNU Octave
0 1 2 3 4 5 6
-2
-1
0
1
2
data
41 breaks, 40 pieces
11 breaks, 10 pieces
Figure 28.1: Comparison of a fitting a piecewise polynomial with 41 breaks to one with
11 breaks. The fit with the large number of breaks exhibits a fast ripple that is not present
in the underlying function.
The piecewise polynomial fit, provided by splinefit, has continuous derivatives up to
the order-1. For example, a cubic fit has continuous first and second derivatives. This is
demonstrated by the code
## Data (200 points)
x = 2 * pi * rand (1, 200);
y = sin (x) + sin (2 * x) + 0.1 * randn (size (x));
## Piecewise constant
pp1 = splinefit (x, y, 8, "order", 0);
## Piecewise linear
pp2 = splinefit (x, y, 8, "order", 1);
## Piecewise quadratic
pp3 = splinefit (x, y, 8, "order", 2);
## Piecewise cubic
pp4 = splinefit (x, y, 8, "order", 3);
## Piecewise quartic
pp5 = splinefit (x, y, 8, "order", 4);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
y3 = ppval (pp3, xx);
y4 = ppval (pp4, xx);
y5 = ppval (pp5, xx);
plot (x, y, ".", xx, [y1; y2; y3; y4; y5])
Chapter 28: Polynomial Manipulations 693
axis tight
ylim auto
legend ({"data", "order 0", "order 1", "order 2", "order 3", "order 4"})
The result of which can be seen in Figure 28.2.
0 1 2 3 4 5 6
-2
-1
0
1
2
data
order 0
order 1
order 2
order 3
order 4
Figure 28.2: Comparison of a piecewise constant, linear, quadratic, cubic, and quar-
tic polynomials with 8 breaks to noisy data. The higher order solutions more accurately
represent the underlying function, but come with the expense of computational complexity.
When the underlying function to provide a fit to is periodic, splinefit is able to apply
the boundary conditions needed to manifest a periodic fit. This is demonstrated by the
code below.
## Data (100 points)
x = 2 * pi * [0, (rand (1, 98)), 1];
y = sin (x) - cos (2 * x) + 0.2 * randn (size (x));
## No constraints
pp1 = splinefit (x, y, 10, "order", 5);
## Periodic boundaries
pp2 = splinefit (x, y, 10, "order", 5, "periodic", true);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "no constraints", "periodic"})
The result of which can be seen in Figure 28.3.
694 GNU Octave
0 1 2 3 4 5 6
-2
-1
0
1
2
3data
no constraints
periodic
Figure 28.3: Comparison of piecewise polynomial fits to a noisy periodic function with,
and without, periodic boundary conditions.
More complex constraints may be added as well. For example, the code below illustrates
a periodic fit with values that have been clamped at the endpoints, and a second periodic
fit which is hinged at the endpoints.
## Data (200 points)
x = 2 * pi * rand (1, 200);
y = sin (2 * x) + 0.1 * randn (size (x));
## Breaks
breaks = linspace (0, 2 * pi, 10);
## Clamped endpoints, y = y’ = 0
xc = [0, 0, 2*pi, 2*pi];
cc = [(eye (2)), (eye (2))];
con = struct ("xc", xc, "cc", cc);
pp1 = splinefit (x, y, breaks, "constraints", con);
## Hinged periodic endpoints, y = 0
con = struct ("xc", 0);
pp2 = splinefit (x, y, breaks, "constraints", con, "periodic", true);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "clamped", "hinged periodic"})
The result of which can be seen in Figure 28.4.
Chapter 28: Polynomial Manipulations 695
0 1 2 3 4 5 6
-1.5
-1
-0.5
0
0.5
1
1.5 data
clamped
hinged periodic
Figure 28.4: Comparison of two periodic piecewise cubic fits to a noisy periodic signal.
One fit has its endpoints clamped and the second has its endpoints hinged.
The splinefit function also provides the convenience of a robust fitting, where the effect
of outlying data is reduced. In the example below, three different fits are provided. Two
with differing levels of outlier suppression and a third illustrating the non-robust solution.
## Data
x = linspace (0, 2*pi, 200);
y = sin (x) + sin (2 * x) + 0.05 * randn (size (x));
## Add outliers
x = [x, linspace(0,2*pi,60)];
y = [y, -ones(1,60)];
## Fit splines with hinged conditions
con = struct ("xc", [0, 2*pi]);
## Robust fitting, beta = 0.25
pp1 = splinefit (x, y, 8, "constraints", con, "beta", 0.25);
## Robust fitting, beta = 0.75
pp2 = splinefit (x, y, 8, "constraints", con, "beta", 0.75);
## No robust fitting
pp3 = splinefit (x, y, 8, "constraints", con);
## Plot
xx = linspace (0, 2*pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
y3 = ppval (pp3, xx);
plot (x, y, ".", xx, [y1; y2; y3])
legend ({"data with outliers","robust, beta = 0.25", ...
"robust, beta = 0.75", "no robust fitting"})
696 GNU Octave
axis tight
ylim auto
The result of which can be seen in Figure 28.5.
0 1 2 3 4 5 6
-2
-1
0
1
2data with outliers
robust, beta = 0.25
robust, beta = 0.75
no robust fitting
Figure 28.5: Comparison of two different levels of robust fitting (beta = 0.25 and 0.75)
to noisy data combined with outlying data. A conventional fit, without robust fitting (beta
= 0) is also included.
A very specific form of polynomial interpretation is the Pad´e approximant. For control
systems, a continuous-time delay can be modeled very simply with the approximant.
[num,den] = padecoef (T)
[num,den] = padecoef (T,N)
Compute the Nth-order Pad´e approximant of the continuous-time delay Tin transfer
function form.
The Pad´e approximant of e−sT is defined by the following equation
e−sT ≈Pn(s)
Qn(s)
where both Pn(s) and Qn(s) are Nth-order rational functions defined by the following
expressions
Pn(s) =
N
X
k=0
(2N−k)!N!
(2N)!k!(N−k)!(−sT )k
Qn(s) = Pn(−s)
The inputs Tand Nmust be non-negative numeric scalars. If Nis unspecified it
defaults to 1.
Chapter 28: Polynomial Manipulations 697
The output row vectors num and den contain the numerator and denominator coef-
ficients in descending powers of s. Both are Nth-order polynomials.
For example:
t = 0.1;
n = 4;
[num, den] = padecoef (t, n)
⇒num =
1.0000e-04 -2.0000e-02 1.8000e+00 -8.4000e+01 1.6800e+03
⇒den =
1.0000e-04 2.0000e-02 1.8000e+00 8.4000e+01 1.6800e+03
The function, ppval, evaluates the piecewise polynomials, created by mkpp or other
means, and unmkpp returns detailed information about the piecewise polynomial.
The following example shows how to combine two linear functions and a quadratic into
one function. Each of these functions is expressed on adjoined intervals.
x = [-2, -1, 1, 2];
p = [ 0, 1, 0;
1, -2, 1;
0, -1, 1 ];
pp = mkpp (x, p);
xi = linspace (-2, 2, 50);
yi = ppval (pp, xi);
plot (xi, yi);
pp = mkpp (breaks,coefs)
pp = mkpp (breaks,coefs,d)
Construct a piecewise polynomial (pp) structure from sample points breaks and co-
efficients coefs.
breaks must be a vector of strictly increasing values. The number of intervals is given
by ni = length (breaks) - 1.
When mis the polynomial order coefs must be of size: ni xm+1.
The i-th row of coefs,coefs (i,:), contains the coefficients for the polynomial over
the i-th interval, ordered from highest (m) to lowest (0).
coefs may also be a multi-dimensional array, specifying a vector-valued or array-valued
polynomial. In that case the polynomial order is defined by the length of the last
dimension of coefs. The size of first dimension(s) are given by the scalar or vector d.
If dis not given it is set to 1. In any case coefs is reshaped to a 2-D matrix of size
[ni*prod(d m)].
See also: [unmkpp], page 697,[ppval], page 698,[spline], page 705,[pchip], page 736,
[ppder], page 698,[ppint], page 698,[ppjumps], page 698.
[x,p,n,k,d] = unmkpp (pp)
Extract the components of a piecewise polynomial structure pp.
The components are:
xSample points.
698 GNU Octave
pPolynomial coefficients for points in sample interval. p(i, :) contains
the coefficients for the polynomial over interval iordered from highest to
lowest. If d> 1,p(r,i, :) contains the coefficients for the r-th polyno-
mial defined on interval i.
nNumber of polynomial pieces.
kOrder of the polynomial plus 1.
dNumber of polynomials defined for each interval.
See also: [mkpp], page 697,[ppval], page 698,[spline], page 705,[pchip], page 736.
yi = ppval (pp,xi)
Evaluate the piecewise polynomial structure pp at the points xi.
If pp describes a scalar polynomial function, the result is an array of the same shape
as xi. Otherwise, the size of the result is [pp.dim, length(xi)] if xi is a vector, or
[pp.dim, size(xi)] if it is a multi-dimensional array.
See also: [mkpp], page 697,[unmkpp], page 697,[spline], page 705,[pchip], page 736.
ppd = ppder (pp)
ppd = ppder (pp, m)
Compute the piecewise m-th derivative of a piecewise polynomial struct pp.
If mis omitted the first derivative is calculated.
See also: [mkpp], page 697,[ppval], page 698,[ppint], page 698.
ppi = ppint (pp)
ppi = ppint (pp,c)
Compute the integral of the piecewise polynomial struct pp.
c, if given, is the constant of integration.
See also: [mkpp], page 697,[ppval], page 698,[ppder], page 698.
jumps = ppjumps (pp)
Evaluate the boundary jumps of a piecewise polynomial.
If there are nintervals, and the dimensionality of pp is d, the resulting array has
dimensions [d, n-1].
See also: [mkpp], page 697.
28.6 Miscellaneous Functions
poly (A)
poly (x)
If Ais a square N-by-Nmatrix, poly (A)is the row vector of the coefficients of det
(z * eye (N) - A), the characteristic polynomial of A.
For example, the following code finds the eigenvalues of Awhich are the roots of poly
(A).
roots (poly (eye (3)))
⇒1.00001 + 0.00001i
1.00001 - 0.00001i
0.99999 + 0.00000i
Chapter 28: Polynomial Manipulations 699
In fact, all three eigenvalues are exactly 1 which emphasizes that for numerical per-
formance the eig function should be used to compute eigenvalues.
If xis a vector, poly (x)is a vector of the coefficients of the polynomial whose roots
are the elements of x. That is, if cis a polynomial, then the elements of d= roots
(poly (c)) are contained in c. The vectors cand dare not identical, however, due
to sorting and numerical errors.
See also: [roots], page 684,[eig], page 505.
polyout (c)
polyout (c,x)
str = polyout (. . . )
Display a formatted version of the polynomial c.
The formatted polynomial
c(x) = c1xn+. . . +cnx+cn+1
is returned as a string or written to the screen if nargout is zero.
The second argument xspecifies the variable name to use for each term and defaults
to the string "s".
See also: [polyreduce], page 699.
polyreduce (c)
Reduce a polynomial coefficient vector to a minimum number of terms by stripping
off any leading zeros.
See also: [polyout], page 699.
701
29 Interpolation
29.1 One-dimensional Interpolation
Octave supports several methods for one-dimensional interpolation, most of which are de-
scribed in this section. Section 28.5 [Polynomial Interpolation], page 689, and Section 30.4
[Interpolation on Scattered Data], page 723, describe additional methods.
yi = interp1 (x,y,xi)
yi = interp1 (y,xi)
yi = interp1 (. . . , method)
yi = interp1 (. . . , extrap)
yi = interp1 (. . . , "left")
yi = interp1 (. . . , "right")
pp = interp1 (. . . , "pp")
One-dimensional interpolation.
Interpolate input data to determine the value of yi at the points xi. If not specified, x
is taken to be the indices of y(1:length (y)). If yis a matrix or an N-dimensional
array, the interpolation is performed on each column of y.
The interpolation method is one of:
"nearest"
Return the nearest neighbor.
"previous"
Return the previous neighbor.
"next" Return the next neighbor.
"linear" (default)
Linear interpolation from nearest neighbors.
"pchip" Piecewise cubic Hermite interpolating polynomial—shape-preserving in-
terpolation with smooth first derivative.
"cubic" Cubic interpolation (same as "pchip").
"spline" Cubic spline interpolation—smooth first and second derivatives through-
out the curve.
Adding ’*’ to the start of any method above forces interp1 to assume that xis
uniformly spaced, and only x(1) and x(2) are referenced. This is usually faster, and
is never slower. The default method is "linear".
If extrap is the string "extrap", then extrapolate values beyond the endpoints using
the current method. If extrap is a number, then replace values beyond the endpoints
with that number. When unspecified, extrap defaults to NA.
If the string argument "pp" is specified, then xi should not be supplied and interp1
returns a piecewise polynomial object. This object can later be used with ppval to
evaluate the interpolation. There is an equivalence, such that ppval (interp1 (x,
y,method, "pp"), xi) == interp1 (x,y,xi,method, "extrap").
702 GNU Octave
Duplicate points in xspecify a discontinuous interpolant. There may be at most 2
consecutive points with the same value. If xis increasing, the default discontinuous in-
terpolant is right-continuous. If xis decreasing, the default discontinuous interpolant
is left-continuous. The continuity condition of the interpolant may be specified by
using the options "left" or "right" to select a left-continuous or right-continuous
interpolant, respectively. Discontinuous interpolation is only allowed for "nearest"
and "linear" methods; in all other cases, the x-values must be unique.
An example of the use of interp1 is
xf = [0:0.05:10];
yf = sin (2*pi*xf/5);
xp = [0:10];
yp = sin (2*pi*xp/5);
lin = interp1 (xp, yp, xf);
near = interp1 (xp, yp, xf, "nearest");
pch = interp1 (xp, yp, xf, "pchip");
spl = interp1 (xp, yp, xf, "spline");
plot (xf,yf,"r", xf,near,"g", xf,lin,"b", xf,pch,"c", xf,spl,"m",
xp,yp,"r*");
legend ("original", "nearest", "linear", "pchip", "spline");
See also: [pchip], page 736,[spline], page 705,[interpft], page 703,[interp2], page 705,
[interp3], page 706,[interpn], page 707.
There are some important differences between the various interpolation methods. The
"spline" method enforces that both the first and second derivatives of the interpolated
values have a continuous derivative, whereas the other methods do not. This means that the
results of the "spline" method are generally smoother. If the function to be interpolated
is in fact smooth, then "spline" will give excellent results. However, if the function to be
evaluated is in some manner discontinuous, then "pchip" interpolation might give better
results.
This can be demonstrated by the code
t = -2:2;
dt = 1;
ti =-2:0.025:2;
dti = 0.025;
y = sign (t);
ys = interp1 (t,y,ti,"spline");
yp = interp1 (t,y,ti,"pchip");
ddys = diff (diff (ys)./dti) ./ dti;
ddyp = diff (diff (yp)./dti) ./ dti;
figure (1);
plot (ti,ys,"r-", ti,yp,"g-");
legend ("spline", "pchip", 4);
figure (2);
plot (ti,ddys,"r+", ti,ddyp,"g*");
legend ("spline", "pchip");
The result of which can be seen in Figure 29.1 and Figure 29.2.
Chapter 29: Interpolation 703
-2 -1 0 1 2
-1.5
-1
-0.5
0
0.5
1
1.5
spline
pchip
Figure 29.1: Comparison of "pchip" and "spline" interpolation methods for a step
function
-2 -1 0 1 2
-4
-2
0
2
4spline
pchip
Figure 29.2: Comparison of the second derivative of the "pchip" and "spline" inter-
polation methods for a step function
Fourier interpolation, is a resampling technique where a signal is converted to the fre-
quency domain, padded with zeros and then reconverted to the time domain.
704 GNU Octave
interpft (x,n)
interpft (x,n,dim)
Fourier interpolation.
If xis a vector then xis resampled with npoints. The data in xis assumed to be
equispaced. If xis a matrix or an N-dimensional array, the interpolation is performed
on each column of x.
If dim is specified, then interpolate along the dimension dim.
interpft assumes that the interpolated function is periodic, and so assumptions are
made about the endpoints of the interpolation.
See also: [interp1], page 701.
There are two significant limitations on Fourier interpolation. First, the function signal is
assumed to be periodic, and so non-periodic signals will be poorly represented at the edges.
Second, both the signal and its interpolation are required to be sampled at equispaced
points. An example of the use of interpft is
t = 0 : 0.3 : pi; dt = t(2)-t(1);
n = length (t); k = 100;
ti = t(1) + [0 : k-1]*dt*n/k;
y = sin (4*t + 0.3) .* cos (3*t - 0.1);
yp = sin (4*ti + 0.3) .* cos (3*ti - 0.1);
plot (ti, yp, "g", ti, interp1 (t, y, ti, "spline"), "b", ...
ti, interpft (y, k), "c", t, y, "r+");
legend ("sin(4t+0.3)cos(3t-0.1)", "spline", "interpft", "data");
which demonstrates the poor behavior of Fourier interpolation for non-periodic functions,
as can be seen in Figure 29.3.
0 0.5 1 1.5 2 2.5 3 3.5
-1
-0.5
0
0.5
1
1.5 sin(4t+0.3)cos(3t-0.1)
spline
interpft
data
Figure 29.3: Comparison of interp1 and interpft for non-periodic data
Chapter 29: Interpolation 705
In addition, the support functions spline and lookup that underlie the interp1 function
can be called directly.
pp = spline (x,y)
yi = spline (x,y,xi)
Return the cubic spline interpolant of points xand y.
When called with two arguments, return the piecewise polynomial pp that may be
used with ppval to evaluate the polynomial at specific points.
When called with a third input argument, spline evaluates the spline at the points
xi. The third calling form spline (x,y,xi)is equivalent to ppval (spline (x,
y), xi).
The variable xmust be a vector of length n.
ycan be either a vector or array. If yis a vector it must have a length of either nor
n+ 2. If the length of yis n, then the "not-a-knot" end condition is used. If the
length of yis n+ 2, then the first and last values of the vector yare the values of the
first derivative of the cubic spline at the endpoints.
If yis an array, then the size of ymust have the form
[s1, s2,···, sk, n]
or
[s1, s2,···, sk, n + 2].
The array is reshaped internally to a matrix where the leading dimension is given by
s1s2···sk
and each row of this matrix is then treated separately. Note that this is exactly the
opposite of interp1 but is done for matlab compatibility.
See also: [pchip], page 736,[ppval], page 698,[mkpp], page 697,[unmkpp], page 697.
29.2 Multi-dimensional Interpolation
There are three multi-dimensional interpolation functions in Octave, with similar capabil-
ities. Methods using Delaunay tessellation are described in Section 30.4 [Interpolation on
Scattered Data], page 723.
zi = interp2 (x,y,z,xi,yi)
zi = interp2 (z,xi,yi)
zi = interp2 (z,n)
zi = interp2 (z)
zi = interp2 (. . . , method)
zi = interp2 (. . . , method,extrap)
Two-dimensional interpolation.
Interpolate reference data x,y,zto determine zi at the coordinates xi,yi. The
reference data x,ycan be matrices, as returned by meshgrid, in which case the sizes
of x,y, and zmust be equal. If x,yare vectors describing a grid then length (x)
706 GNU Octave
== columns (z)and length (y) == rows (z). In either case the input data must be
strictly monotonic.
If called without x,y, and just a single reference data matrix z, the 2-D region x=
1:columns (z), y= 1:rows (z)is assumed. This saves memory if the grid is regular
and the distance between points is not important.
If called with a single reference data matrix zand a refinement value n, then perform
interpolation over a grid where each original interval has been recursively subdivided
ntimes. This results in 2^n-1 additional points for every interval in the original grid.
If nis omitted a value of 1 is used. As an example, the interval [0,1] with n==2 results
in a refined interval with points at [0, 1/4, 1/2, 3/4, 1].
The interpolation method is one of:
"nearest"
Return the nearest neighbor.
"linear" (default)
Linear interpolation from nearest neighbors.
"pchip" Piecewise cubic Hermite interpolating polynomial—shape-preserving in-
terpolation with smooth first derivative.
"cubic" Cubic interpolation (same as "pchip").
"spline" Cubic spline interpolation—smooth first and second derivatives through-
out the curve.
extrap is a scalar number. It replaces values beyond the endpoints with extrap. Note
that if extrapval is used, method must be specified as well. If extrap is omitted
and the method is "spline", then the extrapolated values of the "spline" are used.
Otherwise the default extrap value for any other method is "NA".
See also: [interp1], page 701,[interp3], page 706,[interpn], page 707,[meshgrid],
page 337.
vi = interp3 (x,y,z,v,xi,yi,zi)
vi = interp3 (v,xi,yi,zi)
vi = interp3 (v,n)
vi = interp3 (v)
vi = interp3 (. . . , method)
vi = interp3 (. . . , method,extrapval)
Three-dimensional interpolation.
Interpolate reference data x,y,z,vto determine vi at the coordinates xi,yi,zi. The
reference data x,y,zcan be matrices, as returned by meshgrid, in which case the
sizes of x,y,z, and vmust be equal. If x,y,zare vectors describing a cubic grid then
length (x) == columns (v),length (y) == rows (v), and length (z) == size (v,
3). In either case the input data must be strictly monotonic.
If called without x,y,z, and just a single reference data matrix v, the 3-D region x=
1:columns (v), y= 1:rows (v), z= 1:size (v, 3) is assumed. This saves memory
if the grid is regular and the distance between points is not important.
Chapter 29: Interpolation 707
If called with a single reference data matrix vand a refinement value n, then per-
form interpolation over a 3-D grid where each original interval has been recursively
subdivided ntimes. This results in 2^n-1 additional points for every interval in the
original grid. If nis omitted a value of 1 is used. As an example, the interval [0,1]
with n==2 results in a refined interval with points at [0, 1/4, 1/2, 3/4, 1].
The interpolation method is one of:
"nearest"
Return the nearest neighbor.
"linear" (default)
Linear interpolation from nearest neighbors.
"cubic" Piecewise cubic Hermite interpolating polynomial—shape-preserving in-
terpolation with smooth first derivative (not implemented yet).
"spline" Cubic spline interpolation—smooth first and second derivatives through-
out the curve.
extrapval is a scalar number. It replaces values beyond the endpoints with extrapval.
Note that if extrapval is used, method must be specified as well. If extrapval is
omitted and the method is "spline", then the extrapolated values of the "spline"
are used. Otherwise the default extrapval value for any other method is "NA".
See also: [interp1], page 701,[interp2], page 705,[interpn], page 707,[meshgrid],
page 337.
vi = interpn (x1,x2, . . . , v,y1,y2, . . . )
vi = interpn (v,y1,y2, . . . )
vi = interpn (v,m)
vi = interpn (v)
vi = interpn (. . . , method)
vi = interpn (. . . , method,extrapval)
Perform n-dimensional interpolation, where nis at least two.
Each element of the n-dimensional array vrepresents a value at a location given
by the parameters x1,x2, . . . , xn. The parameters x1,x2, . . ., xn are either n-
dimensional arrays of the same size as the array vin the "ndgrid" format or vectors.
The parameters y1, etc. respect a similar format to x1, etc., and they represent the
points at which the array vi is interpolated.
If x1, . . . , xn are omitted, they are assumed to be x1 = 1 : size (v, 1), etc. If
mis specified, then the interpolation adds a point half way between each of the
interpolation points. This process is performed mtimes. If only vis specified, then
mis assumed to be 1.
The interpolation method is one of:
"nearest"
Return the nearest neighbor.
"linear" (default)
Linear interpolation from nearest neighbors.
708 GNU Octave
"pchip" Piecewise cubic Hermite interpolating polynomial—shape-preserving in-
terpolation with smooth first derivative (not implemented yet).
"cubic" Cubic interpolation (same as "pchip" [not implemented yet]).
"spline" Cubic spline interpolation—smooth first and second derivatives through-
out the curve.
The default method is "linear".
extrapval is a scalar number. It replaces values beyond the endpoints with extrapval.
Note that if extrapval is used, method must be specified as well. If extrapval is
omitted and the method is "spline", then the extrapolated values of the "spline"
are used. Otherwise the default extrapval value for any other method is "NA".
See also: [interp1], page 701,[interp2], page 705,[interp3], page 706,[spline], page 705,
[ndgrid], page 337.
A significant difference between interpn and the other two multi-dimensional interpola-
tion functions is the fashion in which the dimensions are treated. For interp2 and interp3,
the y-axis is considered to be the columns of the matrix, whereas the x-axis corresponds to
the rows of the array. As Octave indexes arrays in column major order, the first dimension
of any array is the columns, and so interpn effectively reverses the ’x’ and ’y’ dimensions.
Consider the example,
x=y=z=-1:1;
f = @(x,y,z) x.^2 - y - z.^2;
[xx, yy, zz] = meshgrid (x, y, z);
v = f (xx,yy,zz);
xi = yi = zi = -1:0.1:1;
[xxi, yyi, zzi] = meshgrid (xi, yi, zi);
vi = interp3 (x, y, z, v, xxi, yyi, zzi, "spline");
[xxi, yyi, zzi] = ndgrid (xi, yi, zi);
vi2 = interpn (x, y, z, v, xxi, yyi, zzi, "spline");
mesh (zi, yi, squeeze (vi2(1,:,:)));
where vi and vi2 are identical. The reversal of the dimensions is treated in the meshgrid
and ndgrid functions respectively. The result of this code can be seen in Figure 29.4.
709
-0.5
0
0.5
1
-1 -1
0
0.5
1
1.5
2
-0.5
0
0.5
1
Figure 29.4: Demonstration of the use of interpn

711
30 Geometry
Much of the geometry code in Octave is based on the Qhull library1. Some of the docu-
mentation for Qhull, particularly for the options that can be passed to delaunay,voronoi
and convhull, etc., is relevant to Octave users.
30.1 Delaunay Triangulation
The Delaunay triangulation is constructed from a set of circum-circles. These circum-circles
are chosen so that there are at least three of the points in the set to triangulation on the
circumference of the circum-circle. None of the points in the set of points falls within any
of the circum-circles.
In general there are only three points on the circumference of any circum-circle. However,
in some cases, and in particular for the case of a regular grid, 4 or more points can be on a
single circum-circle. In this case the Delaunay triangulation is not unique.
tri = delaunay (x,y)
tetr = delaunay (x,y,z)
tri = delaunay (x)
tri = delaunay (. . . , options)
Compute the Delaunay triangulation for a 2-D or 3-D set of points.
For 2-D sets, the return value tri is a set of triangles which satisfies the Delaunay
circum-circle criterion, i.e., only a single data point from [x,y] is within the circum-
circle of the defining triangle. The set of triangles tri is a matrix of size [n, 3]. Each
row defines a triangle and the three columns are the three vertices of the triangle.
The value of tri(i,j) is an index into xand yfor the location of the j-th vertex of
the i-th triangle.
For 3-D sets, the return value tetr is a set of tetrahedrons which satisfies the Delaunay
circum-circle criterion, i.e., only a single data point from [x,y,z] is within the circum-
circle of the defining tetrahedron. The set of tetrahedrons is a matrix of size [n, 4].
Each row defines a tetrahedron and the four columns are the four vertices of the
tetrahedron. The value of tetr(i,j) is an index into x,y,zfor the location of the
j-th vertex of the i-th tetrahedron.
The input xmay also be a matrix with two or three columns where the first column
contains x-data, the second y-data, and the optional third column contains z-data.
The optional last argument, which must be a string or cell array of strings, contains
options passed to the underlying qhull command. See the documentation for the
Qhull library for details http://www.qhull.org/html/qh-quick.htm#options.
The default options are {"Qt", "Qbb", "Qc", "Qz"}.
If options is not present or [] then the default arguments are used. Otherwise,
options replaces the default argument list. To append user options to the defaults it
is necessary to repeat the default arguments in options. Use a null string to pass no
arguments.
1Barber, C.B., Dobkin, D.P., and Huhdanpaa, H.T., The Quickhull Algorithm for Convex Hulls, ACM
Trans. on Mathematical Software, 22(4):469–483, Dec 1996, http://www.qhull.org
712 GNU Octave
x = rand (1, 10);
y = rand (1, 10);
tri = delaunay (x, y);
triplot (tri, x, y);
hold on;
plot (x, y, "r*");
axis ([0,1,0,1]);
See also: [delaunayn], page 712,[convhull], page 721,[voronoi], page 718,[triplot],
page 713,[trimesh], page 713,[tetramesh], page 714,[trisurf], page 714.
For 3-D inputs delaunay returns a set of tetrahedra that satisfy the Delaunay circum-
circle criteria. Similarly, delaunayn returns the N-dimensional simplex satisfying the De-
launay circum-circle criteria. The N-dimensional extension of a triangulation is called a
tessellation.
T= delaunayn (pts)
T= delaunayn (pts,options)
Compute the Delaunay triangulation for an N-dimensional set of points.
The Delaunay triangulation is a tessellation of the convex hull of a set of points such
that no N-sphere defined by the N-triangles contains any other points from the set.
The input matrix pts of size [n, dim] contains n points in a space of dimension dim.
The return matrix Thas size [m, dim+1]. Each row of Tcontains a set of indices
back into the original set of points pts which describes a simplex of dimension dim.
For example, a 2-D simplex is a triangle and 3-D simplex is a tetrahedron.
An optional second argument, which must be a string or cell array of strings, contains
options passed to the underlying qhull command. See the documentation for the
Qhull library for details http://www.qhull.org/html/qh-quick.htm#options.
The default options depend on the dimension of the input:
•2-D and 3-D: options ={"Qt", "Qbb", "Qc", "Qz"}
•4-D and higher: options ={"Qt", "Qbb", "Qc", "Qx"}
If options is not present or [] then the default arguments are used. Otherwise,
options replaces the default argument list. To append user options to the defaults it
is necessary to repeat the default arguments in options. Use a null string to pass no
arguments.
See also: [delaunay], page 711,[convhulln], page 722,[voronoin], page 718,[trimesh],
page 713,[tetramesh], page 714.
An example of a Delaunay triangulation of a set of points is
rand ("state", 2);
x = rand (10, 1);
y = rand (10, 1);
T = delaunay (x, y);
X = [ x(T(:,1)); x(T(:,2)); x(T(:,3)); x(T(:,1)) ];
Y = [ y(T(:,1)); y(T(:,2)); y(T(:,3)); y(T(:,1)) ];
axis ([0, 1, 0, 1]);
plot (X, Y, "b", x, y, "r*");
Chapter 30: Geometry 713
The result of which can be seen in Figure 30.1.
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Figure 30.1: Delaunay triangulation of a random set of points
30.1.1 Plotting the Triangulation
Octave has the functions triplot,trimesh, and trisurf to plot the Delaunay triangulation
of a 2-dimensional set of points. tetramesh will plot the triangulation of a 3-dimensional
set of points.
triplot (tri,x,y)
triplot (tri,x,y,linespec)
h= triplot (. . . )
Plot a 2-D triangular mesh.
tri is typically the output of a Delaunay triangulation over the grid of x,y. Every
row of tri represents one triangle and contains three indices into [x,y] which are the
vertices of the triangles in the x-y plane.
The linestyle to use for the plot can be defined with the argument linespec of the
same format as the plot command.
The optional return value his a graphics handle to the created patch object.
See also: [plot], page 286,[trimesh], page 713,[trisurf], page 714,[delaunay],
page 711.
trimesh (tri,x,y,z,c)
trimesh (tri,x,y,z)
trimesh (tri,x,y)
trimesh (. . ., prop,val, . . .)
h= trimesh (. . . )
Plot a 3-D triangular wireframe mesh.
714 GNU Octave
In contrast to mesh, which plots a mesh using rectangles, trimesh plots the mesh
using triangles.
tri is typically the output of a Delaunay triangulation over the grid of x,y. Every
row of tri represents one triangle and contains three indices into [x,y] which are the
vertices of the triangles in the x-y plane. zdetermines the height above the plane of
each vertex. If no zinput is given then the triangles are plotted as a 2-D figure.
The color of the trimesh is computed by linearly scaling the zvalues to fit the range
of the current colormap. Use caxis and/or change the colormap to control the
appearance.
Optionally, the color of the mesh can be specified independently of zby supplying a
color matrix, c. If zhas N elements, then cshould be an Nx1 vector for colormap
data or an Nx3 matrix for RGB data.
Any property/value pairs are passed directly to the underlying patch object.
The optional return value his a graphics handle to the created patch object.
See also: [mesh], page 321,[tetramesh], page 714,[triplot], page 713,[trisurf],
page 714,[delaunay], page 711,[patch], page 376,[hidden], page 323.
trisurf (tri,x,y,z,c)
trisurf (tri,x,y,z)
trisurf (. . ., prop,val, . . .)
h= trisurf (. . . )
Plot a 3-D triangular surface.
In contrast to surf, which plots a surface mesh using rectangles, trisurf plots the
mesh using triangles.
tri is typically the output of a Delaunay triangulation over the grid of x,y. Every
row of tri represents one triangle and contains three indices into [x,y] which are the
vertices of the triangles in the x-y plane. zdetermines the height above the plane of
each vertex.
The color of the trimesh is computed by linearly scaling the zvalues to fit the range
of the current colormap. Use caxis and/or change the colormap to control the
appearance.
Optionally, the color of the mesh can be specified independently of zby supplying a
color matrix, c. If zhas N elements, then cshould be an Nx1 vector for colormap
data or an Nx3 matrix for RGB data.
Any property/value pairs are passed directly to the underlying patch object.
The optional return value his a graphics handle to the created patch object.
See also: [surf], page 323,[triplot], page 713,[trimesh], page 713,[delaunay], page 711,
[patch], page 376,[shading], page 340.
tetramesh (T,X)
tetramesh (T,X,C)
tetramesh (. . ., property,val, . . .)
h= tetramesh (. . . )
Display the tetrahedrons defined in the m-by-4 matrix Tas 3-D patches.
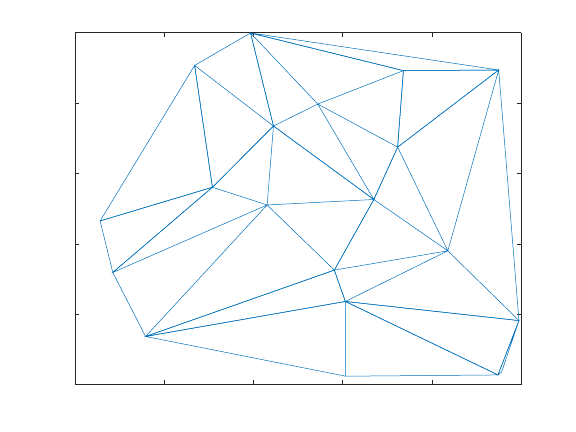
Chapter 30: Geometry 715
Tis typically the output of a Delaunay triangulation of a 3-D set of points. Every row
of Tcontains four indices into the n-by-3 matrix Xof the vertices of a tetrahedron.
Every row in Xrepresents one point in 3-D space.
The vector Cspecifies the color of each tetrahedron as an index into the current
colormap. The default value is 1:m where m is the number of tetrahedrons; the indices
are scaled to map to the full range of the colormap. If there are more tetrahedrons
than colors in the colormap then the values in Care cyclically repeated.
Calling tetramesh (..., "property", "value", ...) passes all property/value
pairs directly to the patch function as additional arguments.
The optional return value his a vector of patch handles where each handle represents
one tetrahedron in the order given by T. A typical use case for his to turn the
respective patch "visible" property "on" or "off".
Type demo tetramesh to see examples on using tetramesh.
See also: [trimesh], page 713,[delaunay], page 711,[delaunayn], page 712,[patch],
page 376.
The difference between triplot, and trimesh or triplot, is that the former only plots
the 2-dimensional triangulation itself, whereas the second two plot the value of a function
f (x,y). An example of the use of the triplot function is
rand ("state", 2)
x = rand (20, 1);
y = rand (20, 1);
tri = delaunay (x, y);
triplot (tri, x, y);
which plots the Delaunay triangulation of a set of random points in 2-dimensions. The
output of the above can be seen in Figure 30.2.
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Figure 30.2: Delaunay triangulation of a random set of points
716 GNU Octave
30.1.2 Identifying Points in Triangulation
It is often necessary to identify whether a particular point in the N-dimensional space
is within the Delaunay tessellation of a set of points in this N-dimensional space, and if
so which N-simplex contains the point and which point in the tessellation is closest to the
desired point. The functions tsearch and dsearch perform this function in a triangulation,
and tsearchn and dsearchn in an N-dimensional tessellation.
To identify whether a particular point represented by a vector pfalls within one of the
simplices of an N-simplex, we can write the Cartesian coordinates of the point in a para-
metric form with respect to the N-simplex. This parametric form is called the Barycentric
Coordinates of the point. If the points defining the N-simplex are given by N+ 1 vectors
t(i,:), then the Barycentric coordinates defining the point pare given by
p= sum (beta(1:N+1) * t(1:N+1),:)
where there are N+ 1 values beta(i)that together as a vector represent the Barycentric
coordinates of the point p. To ensure a unique solution for the values of beta(i)an
additional criteria of
sum (beta(1:N+1)) == 1
is imposed, and we can therefore write the above as
p-t(end, :) = beta(1:end-1) * (t(1:end-1, :)
- ones (N, 1) * t(end, :)
Solving for beta we can then write
beta(1:end-1) = (p-t(end, :)) / (t(1:end-1, :)
- ones (N, 1) * t(end, :))
beta(end) = sum (beta(1:end-1))
which gives the formula for the conversion of the Cartesian coordinates of the point pto
the Barycentric coordinates beta. An important property of the Barycentric coordinates is
that for all points in the N-simplex
0 <= beta(i) <= 1
Therefore, the test in tsearch and tsearchn essentially only needs to express each point in
terms of the Barycentric coordinates of each of the simplices of the N-simplex and test the
values of beta. This is exactly the implementation used in tsearchn.tsearch is optimized
for 2-dimensions and the Barycentric coordinates are not explicitly formed.
idx = tsearch (x,y,t,xi,yi)
Search for the enclosing Delaunay convex hull.
For t= delaunay (x,y), finds the index in tcontaining the points (xi,yi). For
points outside the convex hull, idx is NaN.
See also: [delaunay], page 711,[delaunayn], page 712.
idx = tsearchn (x,t,xi)
[idx,p] = tsearchn (x,t,xi)
Search for the enclosing Delaunay convex hull.
For t= delaunayn (x), finds the index in tcontaining the points xi. For points
outside the convex hull, idx is NaN.
Chapter 30: Geometry 717
If requested tsearchn also returns the Barycentric coordinates pof the enclosing
triangles.
See also: [delaunay], page 711,[delaunayn], page 712.
An example of the use of tsearch can be seen with the simple triangulation
x= [-1; -1; 1; 1];
y= [-1; 1; -1; 1];
tri = [1, 2, 3; 2, 3, 1];
consisting of two triangles defined by tri. We can then identify which triangle a point falls
in like
tsearch (x,y,tri, -0.5, -0.5)
⇒1
tsearch (x,y,tri, 0.5, 0.5)
⇒2
and we can confirm that a point doesn’t lie within one of the triangles like
tsearch (x,y,tri, 2, 2)
⇒NaN
The dsearch and dsearchn find the closest point in a tessellation to the desired point.
The desired point does not necessarily have to be in the tessellation, and even if it the
returned point of the tessellation does not have to be one of the vertexes of the N-simplex
within which the desired point is found.
idx = dsearch (x,y,tri,xi,yi)
idx = dsearch (x,y,tri,xi,yi,s)
Return the index idx of the closest point in x,yto the elements [xi(:), yi(:)].
The variable sis accepted for compatibility but is ignored.
See also: [dsearchn], page 717,[tsearch], page 716.
idx = dsearchn (x,tri,xi)
idx = dsearchn (x,tri,xi,outval)
idx = dsearchn (x,xi)
[idx,d] = dsearchn (. . . )
Return the index idx of the closest point in xto the elements xi.
If outval is supplied, then the values of xi that are not contained within one of the
simplices tri are set to outval. Generally, tri is returned from delaunayn (x).
See also: [dsearch], page 717,[tsearch], page 716.
An example of the use of dsearch, using the above values of x,yand tri is
dsearch (x,y,tri, -2, -2)
⇒1
If you wish the points that are outside the tessellation to be flagged, then dsearchn can
be used as
dsearchn ([x,y], tri, [-2, -2], NaN)
⇒NaN
dsearchn ([x,y], tri, [-0.5, -0.5], NaN)
⇒1
718 GNU Octave
where the point outside the tessellation are then flagged with NaN.
30.2 Voronoi Diagrams
A Voronoi diagram or Voronoi tessellation of a set of points sin an N-dimensional space,
is the tessellation of the N-dimensional space such that all points in v(p), a partitions of
the tessellation where pis a member of s, are closer to pthan any other point in s. The
Voronoi diagram is related to the Delaunay triangulation of a set of points, in that the
vertexes of the Voronoi tessellation are the centers of the circum-circles of the simplices of
the Delaunay tessellation.
voronoi (x,y)
voronoi (x,y,options)
voronoi (. . ., "linespec")
voronoi (hax, . . . )
h= voronoi (. . . )
[vx,vy] = voronoi (. . . )
Plot the Voronoi diagram of points (x,y).
The Voronoi facets with points at infinity are not drawn.
The options argument, which must be a string or cell array of strings, contains options
passed to the underlying qhull command. See the documentation for the Qhull library
for details http://www.qhull.org/html/qh-quick.htm#options.
If "linespec" is given it is used to set the color and line style of the plot.
If an axis graphics handle hax is supplied then the Voronoi diagram is drawn on the
specified axis rather than in a new figure.
If a single output argument is requested then the Voronoi diagram will be plotted and
a graphics handle hto the plot is returned.
[vx,vy] = voronoi (. . . ) returns the Voronoi vertices instead of plotting the diagram.
x = rand (10, 1);
y = rand (size (x));
h = convhull (x, y);
[vx, vy] = voronoi (x, y);
plot (vx, vy, "-b", x, y, "o", x(h), y(h), "-g");
legend ("", "points", "hull");
See also: [voronoin], page 718,[delaunay], page 711,[convhull], page 721.
[C,F] = voronoin (pts)
[C,F] = voronoin (pts,options)
Compute N-dimensional Voronoi facets.
The input matrix pts of size [n, dim] contains n points in a space of dimension dim.
Ccontains the points of the Voronoi facets. The list Fcontains, for each facet, the
indices of the Voronoi points.
An optional second argument, which must be a string or cell array of strings, contains
options passed to the underlying qhull command. See the documentation for the Qhull
library for details http://www.qhull.org/html/qh-quick.htm#options.
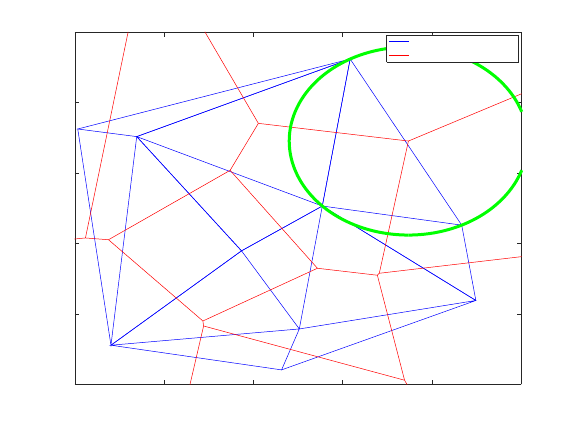
Chapter 30: Geometry 719
The default options depend on the dimension of the input:
•2-D and 3-D: options ={"Qbb"}
•4-D and higher: options ={"Qbb", "Qx"}
If options is not present or [] then the default arguments are used. Otherwise,
options replaces the default argument list. To append user options to the defaults it
is necessary to repeat the default arguments in options. Use a null string to pass no
arguments.
See also: [voronoi], page 718,[convhulln], page 722,[delaunayn], page 712.
An example of the use of voronoi is
rand ("state",9);
x = rand (10,1);
y = rand (10,1);
tri = delaunay (x, y);
[vx, vy] = voronoi (x, y, tri);
triplot (tri, x, y, "b");
hold on;
plot (vx, vy, "r");
The result of which can be seen in Figure 30.3. Note that the circum-circle of one of the
triangles has been added to this figure, to make the relationship between the Delaunay
tessellation and the Voronoi diagram clearer.
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1Delaunay Triangulation
Voronoi Diagram
Figure 30.3: Delaunay triangulation and Voronoi diagram of a random set of points
Additional information about the size of the facets of a Voronoi diagram, and which
points of a set of points is in a polygon can be had with the polyarea and inpolygon
functions respectively.
720 GNU Octave
polyarea (x,y)
polyarea (x,y,dim)
Determine area of a polygon by triangle method.
The variables xand ydefine the vertex pairs, and must therefore have the same
shape. They can be either vectors or arrays. If they are arrays then the columns of
xand yare treated separately and an area returned for each.
If the optional dim argument is given, then polyarea works along this dimension of
the arrays xand y.
An example of the use of polyarea might be
rand ("state", 2);
x = rand (10, 1);
y = rand (10, 1);
[c, f] = voronoin ([x, y]);
af = zeros (size (f));
for i = 1 : length (f)
af(i) = polyarea (c (f {i, :}, 1), c (f {i, :}, 2));
endfor
Facets of the Voronoi diagram with a vertex at infinity have infinity area. A simplified
version of polyarea for rectangles is available with rectint
area = rectint (a,b)
Compute area or volume of intersection of rectangles or N-D boxes.
Compute the area of intersection of rectangles in aand rectangles in b. N-dimensional
boxes are supported in which case the volume, or hypervolume is computed according
to the number of dimensions.
2-dimensional rectangles are defined as [xpos ypos width height] where xpos and
ypos are the position of the bottom left corner. Higher dimensions are supported
where the coordinates for the minimum value of each dimension follow the length
of the box in that dimension, e.g., [xpos ypos zpos kpos ... width height depth
k_length ...].
Each row of aand bdefine a rectangle, and if both define multiple rectangles, then
the output, area, is a matrix where the i-th row corresponds to the i-th row of a and
the j-th column corresponds to the j-th row of b.
See also: [polyarea], page 719.
in = inpolygon (x,y,xv,yv)
[in,on] = inpolygon (x,y,xv,yv)
For a polygon defined by vertex points (xv,yv), return true if the points (x,y)are
inside (or on the boundary) of the polygon; Otherwise, return false.
The input variables xand y, must have the same dimension.
The optional output on returns true if the points are exactly on the polygon edge,
and false otherwise.
See also: [delaunay], page 711.
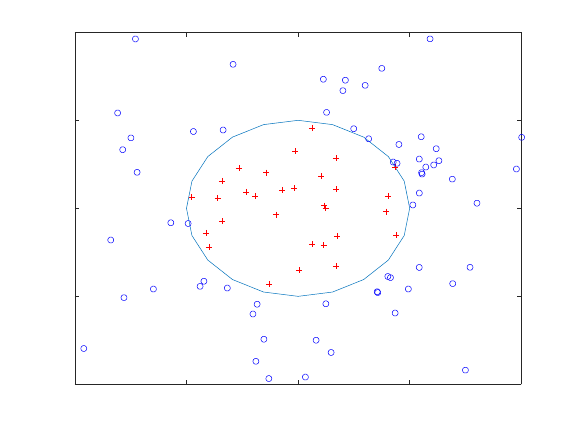
Chapter 30: Geometry 721
An example of the use of inpolygon might be
randn ("state", 2);
x = randn (100, 1);
y = randn (100, 1);
vx = cos (pi * [-1 : 0.1: 1]);
vy = sin (pi * [-1 : 0.1 : 1]);
in = inpolygon (x, y, vx, vy);
plot (vx, vy, x(in), y(in), "r+", x(!in), y(!in), "bo");
axis ([-2, 2, -2, 2]);
The result of which can be seen in Figure 30.4.
-2 -1 0 1 2
-2
-1
0
1
2
Figure 30.4: Demonstration of the inpolygon function to determine the points inside a
polygon
30.3 Convex Hull
The convex hull of a set of points is the minimum convex envelope containing all of the
points. Octave has the functions convhull and convhulln to calculate the convex hull of
2-dimensional and N-dimensional sets of points.
H= convhull (x,y)
H= convhull (x,y,options)
Compute the convex hull of the set of points defined by the arrays xand y. The
hull His an index vector into the set of points and specifies which points form the
enclosing hull.
An optional third argument, which must be a string or cell array of strings, contains
options passed to the underlying qhull command. See the documentation for the
Qhull library for details http://www.qhull.org/html/qh-quick.htm#options.
The default option is {"Qt"}.
722 GNU Octave
If options is not present or [] then the default arguments are used. Otherwise,
options replaces the default argument list. To append user options to the defaults it
is necessary to repeat the default arguments in options. Use a null string to pass no
arguments.
See also: [convhulln], page 722,[delaunay], page 711,[voronoi], page 718.
h= convhulln (pts)
h= convhulln (pts,options)
[h,v] = convhulln (. . . )
Compute the convex hull of the set of points pts.
pts is a matrix of size [n, dim] containing n points in a space of dimension dim.
The hull his an index vector into the set of points and specifies which points form
the enclosing hull.
An optional second argument, which must be a string or cell array of strings, contains
options passed to the underlying qhull command. See the documentation for the
Qhull library for details http://www.qhull.org/html/qh-quick.htm#options.
The default options depend on the dimension of the input:
•2D, 3D, 4D: options ={"Qt"}
•5D and higher: options ={"Qt", "Qx"}
If options is not present or [] then the default arguments are used. Otherwise,
options replaces the default argument list. To append user options to the defaults it
is necessary to repeat the default arguments in options. Use a null string to pass no
arguments.
If the second output vis requested the volume of the enclosing convex hull is calcu-
lated.
See also: [convhull], page 721,[delaunayn], page 712,[voronoin], page 718.
An example of the use of convhull is
x = -3:0.05:3;
y = abs (sin (x));
k = convhull (x, y);
plot (x(k), y(k), "r-", x, y, "b+");
axis ([-3.05, 3.05, -0.05, 1.05]);
The output of the above can be seen in Figure 30.5.
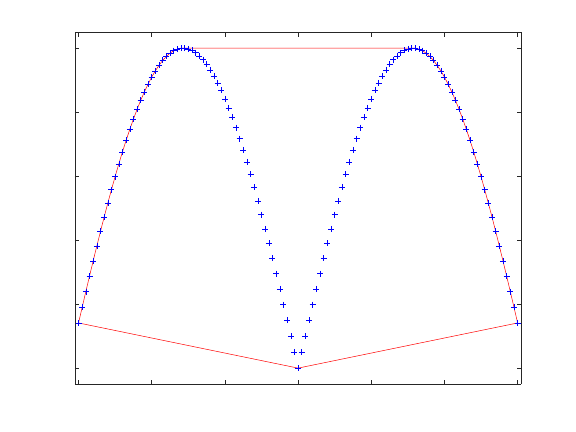
Chapter 30: Geometry 723
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Figure 30.5: The convex hull of a simple set of points
30.4 Interpolation on Scattered Data
An important use of the Delaunay tessellation is that it can be used to interpolate from
scattered data to an arbitrary set of points. To do this the N-simplex of the known set of
points is calculated with delaunay or delaunayn. Then the simplices in to which the desired
points are found are identified. Finally the vertices of the simplices are used to interpolate to
the desired points. The functions that perform this interpolation are griddata,griddata3
and griddatan.
zi = griddata (x,y,z,xi,yi)
zi = griddata (x,y,z,xi,yi,method)
[xi,yi,zi] = griddata (. . . )
Generate a regular mesh from irregular data using interpolation.
The function is defined by z= f (x,y). Inputs x,y,zare vectors of the same length
or x,yare vectors and zis matrix.
The interpolation points are all (xi,yi). If xi,yi are vectors then they are made
into a 2-D mesh.
The interpolation method can be "nearest","cubic" or "linear". If method is
omitted it defaults to "linear".
See also: [griddata3], page 723,[griddatan], page 724,[delaunay], page 711.
vi = griddata3 (x,y,z,v,xi,yi,zi)
vi = griddata3 (x,y,z,v,xi,yi,zi,method)
vi = griddata3 (x,y,z,v,xi,yi,zi,method,options)
Generate a regular mesh from irregular data using interpolation.
724 GNU Octave
The function is defined by v= f (x,y,z). The interpolation points are specified by
xi,yi,zi.
The interpolation method can be "nearest" or "linear". If method is omitted it
defaults to "linear".
The optional argument options is passed directly to Qhull when computing the De-
launay triangulation used for interpolation. See delaunayn for information on the
defaults and how to pass different values.
See also: [griddata], page 723,[griddatan], page 724,[delaunayn], page 712.
yi = griddatan (x,y,xi)
yi = griddatan (x,y,xi,method)
yi = griddatan (x,y,xi,method,options)
Generate a regular mesh from irregular data using interpolation.
The function is defined by y= f (x). The interpolation points are all xi.
The interpolation method can be "nearest" or "linear". If method is omitted it
defaults to "linear".
The optional argument options is passed directly to Qhull when computing the De-
launay triangulation used for interpolation. See delaunayn for information on the
defaults and how to pass different values.
See also: [griddata], page 723,[griddata3], page 723,[delaunayn], page 712.
An example of the use of the griddata function is
rand ("state", 1);
x = 2*rand (1000,1) - 1;
y = 2*rand (size (x)) - 1;
z = sin (2*(x.^2+y.^2));
[xx,yy] = meshgrid (linspace (-1,1,32));
zz = griddata (x, y, z, xx, yy);
mesh (xx, yy, zz);
that interpolates from a random scattering of points, to a uniform grid. The output of the
above can be seen in Figure 30.6.
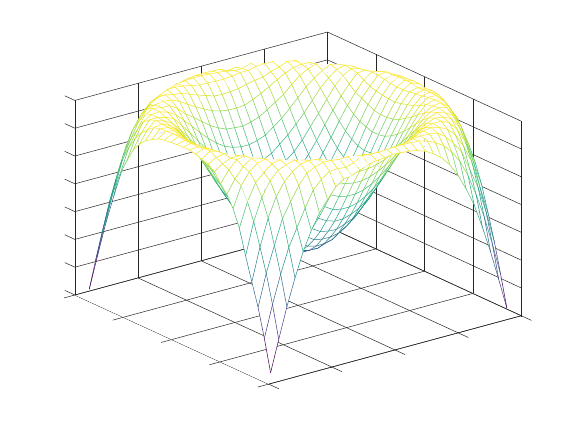
725
-0.5
0
0.5
1
-1 -1
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1
0.5
-0.5
0
Figure 30.6: Interpolation from a scattered data to a regular grid
727
31 Signal Processing
This chapter describes the signal processing and fast Fourier transform functions available
in Octave. Fast Fourier transforms are computed with the fftw or fftpack libraries
depending on how Octave is built.
fft (x)
fft (x,n)
fft (x,n,dim)
Compute the discrete Fourier transform of Ausing a Fast Fourier Transform (FFT)
algorithm.
The FFT is calculated along the first non-singleton dimension of the array. Thus if x
is a matrix, fft (x)computes the FFT for each column of x.
If called with two arguments, nis expected to be an integer specifying the number of
elements of xto use, or an empty matrix to specify that its value should be ignored.
If nis larger than the dimension along which the FFT is calculated, then xis resized
and padded with zeros. Otherwise, if nis smaller than the dimension along which the
FFT is calculated, then xis truncated.
If called with three arguments, dim is an integer specifying the dimension of the
matrix along which the FFT is performed
See also: [ifft], page 727,[fft2], page 727,[fftn], page 728,[fftw], page 728.
ifft (x)
ifft (x,n)
ifft (x,n,dim)
Compute the inverse discrete Fourier transform of Ausing a Fast Fourier Transform
(FFT) algorithm.
The inverse FFT is calculated along the first non-singleton dimension of the array.
Thus if xis a matrix, fft (x)computes the inverse FFT for each column of x.
If called with two arguments, nis expected to be an integer specifying the number of
elements of xto use, or an empty matrix to specify that its value should be ignored.
If nis larger than the dimension along which the inverse FFT is calculated, then xis
resized and padded with zeros. Otherwise, if nis smaller than the dimension along
which the inverse FFT is calculated, then xis truncated.
If called with three arguments, dim is an integer specifying the dimension of the
matrix along which the inverse FFT is performed
See also: [fft], page 727,[ifft2], page 728,[ifftn], page 728,[fftw], page 728.
fft2 (A)
fft2 (A,m,n)
Compute the two-dimensional discrete Fourier transform of Ausing a Fast Fourier
Transform (FFT) algorithm.
The optional arguments mand nmay be used specify the number of rows and columns
of Ato use. If either of these is larger than the size of A,Ais resized and padded
with zeros.
728 GNU Octave
If Ais a multi-dimensional matrix, each two-dimensional sub-matrix of Ais treated
separately.
See also: [ifft2], page 728,[fft], page 727,[fftn], page 728,[fftw], page 728.
ifft2 (A)
ifft2 (A,m,n)
Compute the inverse two-dimensional discrete Fourier transform of Ausing a Fast
Fourier Transform (FFT) algorithm.
The optional arguments mand nmay be used specify the number of rows and columns
of Ato use. If either of these is larger than the size of A,Ais resized and padded
with zeros.
If Ais a multi-dimensional matrix, each two-dimensional sub-matrix of Ais treated
separately
See also: [fft2], page 727,[ifft], page 727,[ifftn], page 728,[fftw], page 728.
fftn (A)
fftn (A,size)
Compute the N-dimensional discrete Fourier transform of Ausing a Fast Fourier
Transform (FFT) algorithm.
The optional vector argument size may be used specify the dimensions of the array
to be used. If an element of size is smaller than the corresponding dimension of A,
then the dimension of Ais truncated prior to performing the FFT. Otherwise, if
an element of size is larger than the corresponding dimension then Ais resized and
padded with zeros.
See also: [ifftn], page 728,[fft], page 727,[fft2], page 727,[fftw], page 728.
ifftn (A)
ifftn (A,size)
Compute the inverse N-dimensional discrete Fourier transform of Ausing a Fast
Fourier Transform (FFT) algorithm.
The optional vector argument size may be used specify the dimensions of the array to
be used. If an element of size is smaller than the corresponding dimension of A, then
the dimension of Ais truncated prior to performing the inverse FFT. Otherwise, if
an element of size is larger than the corresponding dimension then Ais resized and
padded with zeros.
See also: [fftn], page 728,[ifft], page 727,[ifft2], page 728,[fftw], page 728.
Octave uses the fftw libraries to perform FFT computations. When Octave starts up
and initializes the fftw libraries, they read a system wide file (on a Unix system, it is typi-
cally /etc/fftw/wisdom) that contains information useful to speed up FFT computations.
This information is called the wisdom. The system-wide file allows wisdom to be shared
between all applications using the fftw libraries.
Use the fftw function to generate and save wisdom. Using the utilities provided to-
gether with the fftw libraries (fftw-wisdom on Unix systems), you can even add wisdom
generated by Octave to the system-wide wisdom file.
Chapter 31: Signal Processing 729
method = fftw ("planner")
fftw ("planner",method)
wisdom = fftw ("dwisdom")
fftw ("dwisdom",wisdom)
fftw ("threads",nthreads)
nthreads = fftw ("threads")
Manage fftw wisdom data.
Wisdom data can be used to significantly accelerate the calculation of the FFTs, but
implies an initial cost in its calculation. When the fftw libraries are initialized, they
read a system wide wisdom file (typically in /etc/fftw/wisdom), allowing wisdom to
be shared between applications other than Octave. Alternatively, the fftw function
can be used to import wisdom. For example,
wisdom = fftw ("dwisdom")
will save the existing wisdom used by Octave to the string wisdom. This string can
then be saved to a file and restored using the save and load commands respectively.
This existing wisdom can be re-imported as follows
fftw ("dwisdom", wisdom)
If wisdom is an empty string, then the wisdom used is cleared.
During the calculation of Fourier transforms further wisdom is generated. The fashion
in which this wisdom is generated is also controlled by the fftw function. There are
five different manners in which the wisdom can be treated:
"estimate"
Specifies that no run-time measurement of the optimal means of calcu-
lating a particular is performed, and a simple heuristic is used to pick a
(probably sub-optimal) plan. The advantage of this method is that there
is little or no overhead in the generation of the plan, which is appropriate
for a Fourier transform that will be calculated once.
"measure"
In this case a range of algorithms to perform the transform is considered
and the best is selected based on their execution time.
"patient"
Similar to "measure", but a wider range of algorithms is considered.
"exhaustive"
Like "measure", but all possible algorithms that may be used to treat
the transform are considered.
"hybrid" As run-time measurement of the algorithm can be expensive, this is a
compromise where "measure" is used for transforms up to the size of
8192 and beyond that the "estimate" method is used.
The default method is "estimate". The current method can be queried with
method = fftw ("planner")
or set by using
fftw ("planner", method)
730 GNU Octave
Note that calculated wisdom will be lost when restarting Octave. However, the wis-
dom data can be reloaded if it is saved to a file as described above. Saved wisdom
files should not be used on different platforms since they will not be efficient and the
point of calculating the wisdom is lost.
The number of threads used for computing the plans and executing the transforms
can be set with
fftw ("threads", NTHREADS)
Note that octave must be compiled with multi-threaded fftw support for this feature.
The number of processors available to the current process is used per default.
See also: [fft], page 727,[ifft], page 727,[fft2], page 727,[ifft2], page 728,[fftn],
page 728,[ifftn], page 728.
fftconv (x,y)
fftconv (x,y,n)
Convolve two vectors using the FFT for computation.
c = fftconv (x,y)returns a vector of length equal to length (x) + length (y) -
1. If xand yare the coefficient vectors of two polynomials, the returned value is the
coefficient vector of the product polynomial.
The computation uses the FFT by calling the function fftfilt. If the optional
argument nis specified, an N-point FFT is used.
See also: [deconv], page 686,[conv], page 685,[conv2], page 686.
fftfilt (b,x)
fftfilt (b,x,n)
Filter xwith the FIR filter busing the FFT.
If xis a matrix, filter each column of the matrix.
Given the optional third argument, n,fftfilt uses the overlap-add method to filter
xwith busing an N-point FFT. The FFT size must be an even power of 2 and must
be greater than or equal to the length of b. If the specified ndoes not meet these
criteria, it is automatically adjusted to the nearest value that does.
See also: [filter], page 730,[filter2], page 731.
y= filter (b,a,x)
[y,sf] = filter (b,a,x,si)
[y,sf] = filter (b,a,x,[],dim)
[y,sf] = filter (b,a,x,si,dim)
Apply a 1-D digital filter to the data x.
filter returns the solution to the following linear, time-invariant difference equation:
N
X
k=0
ak+1yn−k=
M
X
k=0
bk+1xn−k,1≤n≤P
where a∈ <N−1,b∈ <M−1, and x∈ <P. The result is calculated over the first
non-singleton dimension of xor over dim if supplied.

Chapter 31: Signal Processing 731
An equivalent form of the equation is:
yn=−
N
X
k=1
ck+1yn−k+
M
X
k=0
dk+1xn−k,1≤n≤P
where c=a/a1and d=b/a1.
If the fourth argument si is provided, it is taken as the initial state of the system and
the final state is returned as sf. The state vector is a column vector whose length is
equal to the length of the longest coefficient vector minus one. If si is not supplied,
the initial state vector is set to all zeros.
In terms of the Z Transform, yis the result of passing the discrete-time signal x
through a system characterized by the following rational system function:
H(z) =
M
X
k=0
dk+1z−k
1 +
N
X
k+1
ck+1z−k
See also: [filter2], page 731,[fftfilt], page 730,[freqz], page 731.
y= filter2 (b,x)
y= filter2 (b,x,shape)
Apply the 2-D FIR filter bto x.
If the argument shape is specified, return an array of the desired shape. Possible
values are:
"full" pad xwith zeros on all sides before filtering.
"same" unpadded x(default)
"valid" trim xafter filtering so edge effects are no included.
Note this is just a variation on convolution, with the parameters reversed and b
rotated 180 degrees.
See also: [conv2], page 686.
[h,w] = freqz (b,a,n,"whole")
[h,w] = freqz (b)
[h,w] = freqz (b,a)
[h,w] = freqz (b,a,n)
h= freqz (b,a,w)
[h,w] = freqz (. . . , Fs)
freqz (. . .)
Return the complex frequency response hof the rational IIR filter whose numerator
and denominator coefficients are band a, respectively.
The response is evaluated at nangular frequencies between 0 and 2π.
The output value wis a vector of the frequencies.

732 GNU Octave
If ais omitted, the denominator is assumed to be 1 (this corresponds to a simple FIR
filter).
If nis omitted, a value of 512 is assumed. For fastest computation, nshould factor
into a small number of small primes.
If the fourth argument, "whole", is omitted the response is evaluated at frequencies
between 0 and π.
freqz (b,a,w)
Evaluate the response at the specific frequencies in the vector w. The values for w
are measured in radians.
[...] = freqz (..., Fs)
Return frequencies in Hz instead of radians assuming a sampling rate Fs. If you
are evaluating the response at specific frequencies w, those frequencies should be
requested in Hz rather than radians.
freqz (...)
Plot the magnitude and phase response of hrather than returning them.
See also: [freqz plot], page 732.
freqz_plot (w,h)
freqz_plot (w,h,freq_norm)
Plot the magnitude and phase response of h.
If the optional freq norm argument is true, the frequency vector wis in units of
normalized radians. If freq norm is false, or not given, then wis measured in Hertz.
See also: [freqz], page 731.
sinc (x)
Compute the sinc function.
Return sin(πx)/(πx).
b= unwrap (x)
b= unwrap (x,tol)
b= unwrap (x,tol,dim)
Unwrap radian phases by adding or subtracting multiples of 2*pi as appropriate to
remove jumps greater than tol.
tol defaults to pi.
Unwrap will work along the dimension dim. If dim is unspecified it defaults to the
first non-singleton dimension.
[a,b] = arch_fit (y,x,p,iter,gamma,a0,b0)
Fit an ARCH regression model to the time series yusing the scoring algorithm in
Engle’s original ARCH paper.
The model is
y(t) = b(1) * x(t,1) + ... + b(k) * x(t,k) + e(t),
h(t) = a(1) + a(2) * e(t-1)^2 + ... + a(p+1) * e(t-p)^2
Chapter 31: Signal Processing 733
in which e(t) is N(0, h(t)), given a time-series vector yup to time t−1 and a matrix
of (ordinary) regressors xup to t. The order of the regression of the residual variance
is specified by p.
If invoked as arch_fit (y,k,p)with a positive integer k, fit an ARCH(k,p) process,
i.e., do the above with the t-th row of xgiven by
[1, y(t-1), ..., y(t-k)]
Optionally, one can specify the number of iterations iter, the updating factor gamma,
and initial values a0 and b0 for the scoring algorithm.
arch_rnd (a,b,t)
Simulate an ARCH sequence of length twith AR coefficients band CH coefficients
a.
The result y(t) follows the model
y(t) = b(1) + b(2) * y(t-1) + ... + b(lb) * y(t-lb+1) + e(t),
where e(t), given yup to time t−1, is N(0, h(t)), with
h(t) = a(1) + a(2) * e(t-1)^2 + ... + a(la) * e(t-la+1)^2
[pval,lm] = arch_test (y,x,p)
For a linear regression model
y=x*b+e
perform a Lagrange Multiplier (LM) test of the null hypothesis of no conditional
heteroscedascity against the alternative of CH(p).
I.e., the model is
y(t) = b(1) * x(t,1) + ... + b(k) * x(t,k) + e(t),
given yup to t−1 and xup to t,e(t) is N(0, h(t)) with
h(t) = v + a(1) * e(t-1)^2 + ... + a(p) * e(t-p)^2,
and the null is a(1) == . . . == a(p) == 0.
If the second argument is a scalar integer, k, perform the same test in a linear au-
toregression model of order k, i.e., with
[1, y(t-1), ..., y(t-k)]
as the t-th row of x.
Under the null, LM approximately has a chisquare distribution with pdegrees of
freedom and pval is the p-value (1 minus the CDF of this distribution at LM) of the
test.
If no output argument is given, the p-value is displayed.
arma_rnd (a,b,v,t,n)
Return a simulation of the ARMA model.
The ARMA model is defined by
x(n) = a(1) * x(n-1) + ... + a(k) * x(n-k)
+ e(n) + b(1) * e(n-1) + ... + b(l) * e(n-l)
in which kis the length of vector a,lis the length of vector band eis Gaussian white
noise with variance v. The function returns a vector of length t.
734 GNU Octave
The optional parameter ngives the number of dummy x(i) used for initialization, i.e.,
a sequence of length t+nis generated and x(n+1:t+n) is returned. If nis omitted, n
= 100 is used.
autoreg_matrix (y,k)
Given a time series (vector) y, return a matrix with ones in the first column and the
first klagged values of yin the other columns.
In other words, for t>k,[1, y(t-1), ..., y(t-k)] is the t-th row of the result.
The resulting matrix may be used as a regressor matrix in autoregressions.
bartlett (m)
Return the filter coefficients of a Bartlett (triangular) window of length m.
For a definition of the Bartlett window see, e.g., A.V. Oppenheim & R. W. Schafer,
Discrete-Time Signal Processing.
blackman (m)
blackman (m,"periodic")
blackman (m,"symmetric")
Return the filter coefficients of a Blackman window of length m.
If the optional argument "periodic" is given, the periodic form of the window is
returned. This is equivalent to the window of length m+1 with the last coefficient
removed. The optional argument "symmetric" is equivalent to not specifying a second
argument.
For a definition of the Blackman window, see, e.g., A.V. Oppenheim & R. W. Schafer,
Discrete-Time Signal Processing.
detrend (x,p)
If xis a vector, detrend (x,p)removes the best fit of a polynomial of order pfrom
the data x.
If xis a matrix, detrend (x,p)does the same for each column in x.
The second argument pis optional. If it is not specified, a value of 1 is assumed. This
corresponds to removing a linear trend.
The order of the polynomial can also be given as a string, in which case pmust be
either "constant" (corresponds to p=0) or "linear" (corresponds to p=1).
See also: [polyfit], page 689.
[d,dd] = diffpara (x,a,b)
Return the estimator dfor the differencing parameter of an integrated time series.
The frequencies from [2 ∗pi ∗a/t, 2∗pi ∗b/T ] are used for the estimation. If bis
omitted, the interval [2 ∗pi/T, 2∗pi ∗a/T ] is used. If both band aare omitted then
a= 0.5∗sqrt(T) and b= 1.5∗sqrt(T) is used, where Tis the sample size. If xis a
matrix, the differencing parameter of each column is estimated.
The estimators for all frequencies in the intervals described above is returned in dd.
The value of dis simply the mean of dd.
Reference: P.J. Brockwell & R.A. Davis. Time Series: Theory and Methods. Springer
1987.
Chapter 31: Signal Processing 735
durbinlevinson (c,oldphi,oldv)
Perform one step of the Durbin-Levinson algorithm.
The vector cspecifies the autocovariances [gamma_0, ..., gamma_t] from lag 0 to t,
oldphi specifies the coefficients based on c(t-1) and oldv specifies the corresponding
error.
If oldphi and oldv are omitted, all steps from 1 to tof the algorithm are performed.
fftshift (x)
fftshift (x,dim)
Perform a shift of the vector x, for use with the fft and ifft functions, in order to
move the frequency 0 to the center of the vector or matrix.
If xis a vector of Nelements corresponding to Ntime samples spaced by dt, then
fftshift (fft (x)) corresponds to frequencies
f = [ -(ceil((N-1)/2):-1:1), 0, (1:floor((N-1)/2)) ] * df
where df = 1/(N∗dt).
If xis a matrix, the same holds for rows and columns. If xis an array, then the same
holds along each dimension.
The optional dim argument can be used to limit the dimension along which the
permutation occurs.
See also: [ifftshift], page 735.
ifftshift (x)
ifftshift (x,dim)
Undo the action of the fftshift function.
For even length x,fftshift is its own inverse, but odd lengths differ slightly.
See also: [fftshift], page 735.
fractdiff (x,d)
Compute the fractional differences (1 −L)dxwhere Ldenotes the lag-operator and d
is greater than -1.
hamming (m)
hamming (m,"periodic")
hamming (m,"symmetric")
Return the filter coefficients of a Hamming window of length m.
If the optional argument "periodic" is given, the periodic form of the window is
returned. This is equivalent to the window of length m+1 with the last coefficient
removed. The optional argument "symmetric" is equivalent to not specifying a second
argument.
For a definition of the Hamming window see, e.g., A.V. Oppenheim & R. W. Schafer,
Discrete-Time Signal Processing.
hanning (m)
hanning (m,"periodic")
hanning (m,"symmetric")
Return the filter coefficients of a Hanning window of length m.
736 GNU Octave
If the optional argument "periodic" is given, the periodic form of the window is
returned. This is equivalent to the window of length m+1 with the last coefficient
removed. The optional argument "symmetric" is equivalent to not specifying a second
argument.
For a definition of the Hanning window see, e.g., A.V. Oppenheim & R. W. Schafer,
Discrete-Time Signal Processing.
hurst (x)
Estimate the Hurst parameter of sample xvia the rescaled range statistic.
If xis a matrix, the parameter is estimated for every column.
pp = pchip (x,y)
yi = pchip (x,y,xi)
Return the Piecewise Cubic Hermite Interpolating Polynomial (pchip) of points x
and y.
If called with two arguments, return the piecewise polynomial pp that may be used
with ppval to evaluate the polynomial at specific points.
When called with a third input argument, pchip evaluates the pchip polynomial at
the points xi. The third calling form is equivalent to ppval (pchip (x,y), xi).
The variable xmust be a strictly monotonic vector (either increasing or decreasing)
of length n.
ycan be either a vector or array. If yis a vector then it must be the same length n
as x. If yis an array then the size of ymust have the form
[s1, s2,···, sk, n]
The array is reshaped internally to a matrix where the leading dimension is given by
s1s2···sk
and each row of this matrix is then treated separately. Note that this is exactly
opposite to interp1 but is done for matlab compatibility.
See also: [spline], page 705,[ppval], page 698,[mkpp], page 697,[unmkpp], page 697.
[Pxx,w] = periodogram (x)
[Pxx,w] = periodogram (x,win)
[Pxx,w] = periodogram (x,win,nfft)
[Pxx,f] = periodogram (x,win,nfft,Fs)
[Pxx,f] = periodogram (. . . , "range")
periodogram (. . .)
Return the periodogram (Power Spectral Density) of x.
The possible inputs are:
x
data vector. If xis real-valued a one-sided spectrum is estimated. If x
is complex-valued, or "range"specifies "twosided", the full spectrum is
estimated.

Chapter 31: Signal Processing 737
win window weight data. If window is empty or unspecified a default rectan-
gular window is used. Otherwise, the window is applied to the signal (x
.* win) before computing the periodogram. The window data must be a
vector of the same length as x.
nfft number of frequency bins. The default is 256 or the next higher power of
2 greater than the length of x(max (256, 2.^nextpow2 (length (x)))).
If nfft is greater than the length of the input then xwill be zero-padded
to the length of nfft.
Fs sampling rate. The default is 1.
range range of spectrum. "onesided" computes spectrum from [0..nfft/2+1].
"twosided" computes spectrum from [0..nfft-1].
The optional second output ware the normalized angular frequencies. For a one-sided
calculation wis in the range [0, pi] if nfft is even and [0, pi) if nfft is odd. Similarly,
for a two-sided calculation wis in the range [0, 2*pi] or [0, 2*pi) depending on nfft.
If a sampling frequency is specified, Fs, then the output frequencies fwill be in the
range [0, Fs/2] or [0, Fs/2) for one-sided calculations. For two-sided calculations the
range will be [0, Fs).
When called with no outputs the periodogram is immediately plotted in the current
figure window.
See also: [fft], page 727.
sinetone (freq,rate,sec,ampl)
Return a sinetone of frequency freq with a length of sec seconds at sampling rate rate
and with amplitude ampl.
The arguments freq and ampl may be vectors of common size.
The defaults are rate = 8000, sec = 1, and ampl = 64.
See also: [sinewave], page 737.
sinewave (m,n,d)
Return an m-element vector with i-th element given by sin (2 * pi * (i+d-1) / n).
The default value for dis 0 and the default value for nis m.
See also: [sinetone], page 737.
spectral_adf (c)
spectral_adf (c,win)
spectral_adf (c,win,b)
Return the spectral density estimator given a vector of autocovariances c, window
name win, and bandwidth, b.
The window name, e.g., "triangle" or "rectangle" is used to search for a function
called win_lw.
If win is omitted, the triangle window is used.
If bis omitted, 1 / sqrt (length (x)) is used.
See also: [spectral xdf], page 738.
738 GNU Octave
spectral_xdf (x)
spectral_xdf (x,win)
spectral_xdf (x,win,b)
Return the spectral density estimator given a data vector x, window name win, and
bandwidth, b.
The window name, e.g., "triangle" or "rectangle" is used to search for a function
called win_sw.
If win is omitted, the triangle window is used.
If bis omitted, 1 / sqrt (length (x)) is used.
See also: [spectral adf], page 737.
spencer (x)
Return Spencer’s 15 point moving average of each column of x.
y= stft (x)
y= stft (x,win_size)
y= stft (x,win_size,inc)
y= stft (x,win_size,inc,num_coef)
y= stft (x,win_size,inc,num_coef,win_type)
[y,c] = stft (. . . )
Compute the short-time Fourier transform of the vector xwith num coef coefficients
by applying a window of win size data points and an increment of inc points.
Before computing the Fourier transform, one of the following windows is applied:
"hanning"
win type = 1
"hamming"
win type = 2
"rectangle"
win type = 3
The window names can be passed as strings or by the win type number.
The following defaults are used for unspecified arguments: win size = 80, inc = 24,
num coef = 64, and win type = 1.
y= stft (x, ...) returns the absolute values of the Fourier coefficients according to
the num coef positive frequencies.
[y,c] = stft (x, ...) returns the entire STFT-matrix yand a 3-element vector
ccontaining the window size, increment, and window type, which is needed by the
synthesis function.
See also: [synthesis], page 738.
x= synthesis (y,c)
Compute a signal from its short-time Fourier transform yand a 3-element vector c
specifying window size, increment, and window type.
The values yand ccan be derived by
[y,c] = stft (x, ...)
See also: [stft], page 738.
739
[a,v] = yulewalker (c)
Fit an AR (p)-model with Yule-Walker estimates given a vector cof autocovariances
[gamma_0, ..., gamma_p].
Returns the AR coefficients, a, and the variance of white noise, v.
741
32 Image Processing
Since an image is basically a matrix, Octave is a very powerful environment for processing
and analyzing images. To illustrate how easy it is to do image processing in Octave, the
following example will load an image, smooth it by a 5-by-5 averaging filter, and compute
the gradient of the smoothed image.
I = imread ("myimage.jpg");
S = conv2 (I, ones (5, 5) / 25, "same");
[Dx, Dy] = gradient (S);
In this example Scontains the smoothed image, and Dx and Dy contains the partial spatial
derivatives of the image.
32.1 Loading and Saving Images
The first step in most image processing tasks is to load an image into Octave which is done
with the imread function. The imwrite function is the corresponding function for writing
images to the disk.
In summary, most image processing code will follow the structure of this code
I = imread ("my_input_image.img");
J = process_my_image (I);
imwrite (J, "my_output_image.img");
[img,map,alpha] = imread (filename)
[...] = imread (url)
[...] = imread (. . . , ext)
[...] = imread (. . . , idx)
[...] = imread (. . . , param1,value1, . . . )
Read images from various file formats.
Read an image as a matrix from the file filename or from the online resource url. If
neither is given, but ext was specified, look for a file with the extension ext.
The size and class of the output depends on the format of the image. A color image
is returned as an MxNx3 matrix. Grayscale and black-and-white images are of size
MxN. Multipage images will have an additional 4th dimension.
The bit depth of the image determines the class of the output: "uint8","uint16",
or "single" for grayscale and color, and "logical" for black-and-white. Note that
indexed images always return the indexes for a colormap, independent of whether
map is a requested output. To obtain the actual RGB image, use ind2rgb. When
more than one indexed image is being read, map is obtained from the first. In some
rare cases this may be incorrect and imfinfo can be used to obtain the colormap of
each image.
See the Octave manual for more information in representing images.
Some file formats, such as TIFF and GIF, are able to store multiple images in a
single file. idx can be a scalar or vector specifying the index of the images to read.
By default, Octave will read only the first page.

742 GNU Octave
Depending on the file format, it is possible to configure the reading of images with
parameter,value pairs. The following options are supported:
"Frames" or "Index"
This is an alternative method to specify idx. When specifying it in this
way, its value can also be the string "all".
"Info" This option exists for matlab compatibility, but has no effect. For max-
imum performance when reading multiple images from a single file, use
the "Index" option.
"PixelRegion"
Controls the image region that is read. The value must be a cell array with
two arrays of 3 elements {[rows], [cols]}. The elements in the array
are the start, increment, and end pixel to be read. If the increment value
is omitted it defaults to 1. For example, the following are all equivalent:
imread (filename, "PixelRegion", {[200 600], [300 700]});
imread (filename, "PixelRegion", {[200 1 600], [300 1 700]});
imread (filename)(200:600, 300:700);
See also: [imwrite], page 742,[imfinfo], page 744,[imformats], page 746.
imwrite (img,filename)
imwrite (img,filename,ext)
imwrite (img,map,filename)
imwrite (. . ., param1,val1, . . .)
Write images in various file formats.
The image img can be a binary, grayscale, RGB, or multi-dimensional image. The
size and class of img should be the same as what should be expected when reading it
with imread: the 3rd and 4th dimensions reserved for color space, and multiple pages
respectively. If it’s an indexed image, the colormap map must also be specified.
If ext is not supplied, the file extension of filename is used to determine the format.
The actual supported formats are dependent on options made during the build of
Octave. Use imformats to check the support of the different image formats.
Depending on the file format, it is possible to configure the writing of images with
param,val pairs. The following options are supported:
‘Alpha’ Alpha (transparency) channel for the image. This must be a matrix
with same class, and number of rows and columns of img. In case of a
multipage image, the size of the 4th dimension must also match and the
third dimension must be a singleton. By default, image will be completely
opaque.
‘Compression’
Compression to use one the image. Can be one of the following: "none"
(default), "bzip","fax3","fax4","jpeg","lzw","rle", or "deflate". Note
that not all compression types are available for all image formats in which
it defaults to your Magick library.

Chapter 32: Image Processing 743
‘DelayTime’
For formats that accept animations (such as GIF), controls for how long
a frame is displayed until it moves to the next one. The value must be
scalar (which will applied to all frames in img), or a vector of length equal
to the number of frames in im. The value is in seconds, must be between
0 and 655.35, and defaults to 0.5.
‘DisposalMethod’
For formats that accept animations (such as GIF), controls what happens
to a frame before drawing the next one. Its value can be one of the fol-
lowing strings: "doNotSpecify"(default); "leaveInPlace";"restoreBG";
and "restorePrevious", or a cell array of those string with length equal
to the number of frames in img.
‘LoopCount’
For formats that accept animations (such as GIF), controls how many
times the sequence is repeated. A value of Inf means an infinite loop
(default), a value of 0 or 1 that the sequence is played only once (loops zero
times), while a value of 2 or above loops that number of times (looping
twice means it plays the complete sequence 3 times). This option is
ignored when there is only a single image at the end of writing the file.
‘Quality’ Set the quality of the compression. The value should be an integer be-
tween 0 and 100, with larger values indicating higher visual quality and
lower compression. Defaults to 75.
‘WriteMode’
Some file formats, such as TIFF and GIF, are able to store multiple
images in a single file. This option specifies if img should be appended
to the file (if it exists) or if a new file should be created for it (possibly
overwriting an existing file). The value should be the string "Overwrite"
(default), or "Append".
Despite this option, the most efficient method of writing a multipage
image is to pass a 4 dimensional img to imwrite, the same matrix that
could be expected when using imread with the option "Index" set to
"all".
See also: [imread], page 741,[imfinfo], page 744,[imformats], page 746.
val = IMAGE_PATH ()
old_val = IMAGE_PATH (new_val)
IMAGE_PATH (new_val,"local")
Query or set the internal variable that specifies a colon separated list of directories in
which to search for image files.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [EXEC PATH], page 837,[OCTAVE HOME], page 847.
744 GNU Octave
It is possible to get information about an image file on disk, without actually reading it
into Octave. This is done using the imfinfo function which provides read access to many
of the parameters stored in the header of the image file.
info = imfinfo (filename)
info = imfinfo (url)
info = imfinfo (. . . , ext)
Read image information from a file.
imfinfo returns a structure containing information about the image stored in the
file filename. If there is no file filename, and ext was specified, it will look for a file
named filename and extension ext, i.e., a file named filename.ext.
The output structure info contains the following fields:
‘Filename’
The full name of the image file.
‘FileModDate’
Date of last modification to the file.
‘FileSize’
Number of bytes of the image on disk
‘Format’ Image format (e.g., "jpeg").
‘Height’ Image height in pixels.
‘Width’ Image Width in pixels.
‘BitDepth’
Number of bits per channel per pixel.
‘ColorType’
Image type. Value is "grayscale","indexed","truecolor","CMYK",
or "undefined".
‘XResolution’
X resolution of the image.
‘YResolution’
Y resolution of the image.
‘ResolutionUnit’
Units of image resolution. Value is "Inch","Centimeter", or
"undefined".
‘DelayTime’
Time in 1/100ths of a second (0 to 65535) which must expire before
displaying the next image in an animated sequence.
‘LoopCount’
Number of iterations to loop an animation.
‘ByteOrder’
Endian option for formats that support it. Value is "little-endian",
"big-endian", or "undefined".
Chapter 32: Image Processing 745
‘Gamma’ Gamma level of the image. The same color image displayed on two dif-
ferent workstations may look different due to differences in the display
monitor.
‘Quality’ JPEG/MIFF/PNG compression level. Value is an integer in the range [0
100].
‘DisposalMethod’
Only valid for GIF images, control how successive frames are rendered
(how the preceding frame is disposed of) when creating a GIF anima-
tion. Values can be "doNotSpecify","leaveInPlace","restoreBG",
or "restorePrevious". For non-GIF files, value is an empty string.
‘Chromaticities’
Value is a 1x8 Matrix with the x,y chromaticity values for white, red,
green, and blue points, in that order.
‘Comment’ Image comment.
‘Compression’
Compression type. Value can be "none","bzip","fax3","fax4",
"jpeg","lzw","rle","deflate","lzma","jpeg2000","jbig2",
"jbig2", or "undefined".
‘Colormap’
Colormap for each image.
‘Orientation’
The orientation of the image with respect to the rows and columns. Value
is an integer between 1 and 8 as defined in the TIFF 6 specifications, and
for matlab compatibility.
‘Software’
Name and version of the software or firmware of the camera or image
input device used to generate the image.
‘Make’ The manufacturer of the recording equipment. This is the manufacture
of the DSC, scanner, video digitizer or other equipment that generated
the image.
‘Model’ The model name or model number of the recording equipment as men-
tioned on the field "Make".
‘DateTime’
The date and time of image creation as defined by the Exif standard, i.e.,
it is the date and time the file was changed.
‘ImageDescription’
The title of the image as defined by the Exif standard.
‘Artist’ Name of the camera owner, photographer or image creator.
‘Copyright’
Copyright notice of the person or organization claiming rights to the
image.
746 GNU Octave
‘DigitalCamera’
A struct with information retrieved from the Exif tag.
‘GPSInfo’ A struct with geotagging information retrieved from the Exif tag.
See also: [imread], page 741,[imwrite], page 742,[imshow], page 747,[imformats],
page 746.
By default, Octave’s image IO functions (imread,imwrite, and imfinfo) use the
GraphicsMagick library for their operations. This means a vast number of image formats is
supported but considering the large amount of image formats in science and its commonly
closed nature, it is impossible to have a library capable of reading them all. Because of
this, the function imformats keeps a configurable list of available formats, their extensions,
and what functions should the image IO functions use. This allows one to expand Octave’s
image IO capabilities by creating functions aimed at acting on specific file formats.
While it would be possible to call the extra functions directly, properly configuring
Octave with imformats allows one to keep a consistent code that is abstracted from file
formats.
It is important to note that a file format is not actually defined by its file extension and
that GraphicsMagick is capable to read and write more file formats than the ones listed by
imformats. What this means is that even with an incorrect or missing extension the image
may still be read correctly, and that even unlisted formats are not necessarily unsupported.
imformats ()
formats = imformats (ext)
formats = imformats (format)
formats = imformats ("add",format)
formats = imformats ("remove",ext)
formats = imformats ("update",ext,format)
formats = imformats ("factory")
Manage supported image formats.
formats is a structure with information about each supported file format, or from a
specific format ext, the value displayed on the field ext. It contains the following
fields:
ext The name of the file format. This may match the file extension but
Octave will automatically detect the file format.
description
A long description of the file format.
isa A function handle to confirm if a file is of the specified format.
write A function handle to write if a file is of the specified format.
read A function handle to open files the specified format.
info A function handle to obtain image information of the specified format.
alpha Logical value if format supports alpha channel (transparency or matte).
multipage Logical value if format supports multipage (multiple images per file).

Chapter 32: Image Processing 747
It is possible to change the way Octave manages file formats with the options "add",
"remove", and "update", and supplying a structure format with the required fields.
The option "factory" resets the configuration to the default.
This can be used by Octave packages to extend the image reading capabilities Octave,
through use of the PKG ADD and PKG DEL commands.
See also: [imfinfo], page 744,[imread], page 741,[imwrite], page 742.
32.2 Displaying Images
A natural part of image processing is visualization of an image. The most basic function
for this is the imshow function that shows the image given in the first input argument.
imshow (im)
imshow (im,limits)
imshow (im,map)
imshow (rgb, . . . )
imshow (filename)
imshow (. . ., string_param1,value1, . . .)
h= imshow (. . . )
Display the image im, where im can be a 2-dimensional (grayscale image) or a 3-
dimensional (RGB image) matrix.
If limits is a 2-element vector [low,high], the image is shown using a display range
between low and high. If an empty matrix is passed for limits, the display range is
computed as the range between the minimal and the maximal value in the image.
If map is a valid color map, the image will be shown as an indexed image using the
supplied color map.
If a filename is given instead of an image, the file will be read and shown.
If given, the parameter string param1 has value value1.string param1 can be any
of the following:
"displayrange"
value1 is the display range as described above.
"colormap"
value1 is the colormap to use when displaying an indexed image.
"xdata" If value1 is a two element vector, it must contain horizontal axis limits in
the form [xmin xmax]; Otherwise value1 must be a vector and only the
first and last elements will be used for xmin and xmax respectively.
"ydata" If value1 is a two element vector, it must contain vertical axis limits in
the form [ymin ymax]; Otherwise value1 must be a vector and only the
first and last elements will be used for ymin and ymax respectively.
The optional return value his a graphics handle to the image.
See also: [image], page 748,[imagesc], page 748,[colormap], page 751,[gray2ind],
page 750,[rgb2ind], page 750.
748 GNU Octave
image (img)
image (x,y,img)
image (. . ., "prop",val, . . .)
image ("prop1",val1, . . . )
h= image (. . . )
Display a matrix as an indexed color image.
The elements of img are indices into the current colormap.
xand yare optional 2-element vectors, [min, max], which specify the range for the
axis labels. If a range is specified as [max, min] then the image will be reversed along
that axis. For convenience, xand ymay be specified as N-element vectors matching
the length of the data in img. However, only the first and last elements will be used
to determine the axis limits.
Multiple property/value pairs may be specified for the image object, but they must
appear in pairs.
The optional return value his a graphics handle to the image.
Implementation Note: The origin (0, 0) for images is located in the upper left. For
ordinary plots, the origin is located in the lower left. Octave handles this inversion by
plotting the data normally, and then reversing the direction of the y-axis by setting
the ydir property to "reverse". This has implications whenever an image and an
ordinary plot need to be overlaid. The recommended solution is to display the image
and then plot the reversed ydata using, for example, flipud (ydata).
Calling Forms: The image function can be called in two forms: High-Level and Low-
Level. When invoked with normal options, the High-Level form is used which first
calls newplot to prepare the graphic figure and axes. When the only inputs to image
are property/value pairs the Low-Level form is used which creates a new instance of
an image object and inserts it in the current axes.
See also: [imshow], page 747,[imagesc], page 748,[colormap], page 751.
imagesc (img)
imagesc (x,y,img)
imagesc (. . ., climits)
imagesc (. . ., "prop",val, . . .)
imagesc ("prop1",val1, . . . )
imagesc (hax, . . . )
h= imagesc (. . . )
Display a scaled version of the matrix img as a color image.
The colormap is scaled so that the entries of the matrix occupy the entire colormap.
If climits = [lo,hi]is given, then that range is set to the "clim" of the current
axes.
The axis values corresponding to the matrix elements are specified in xand y, either
as pairs giving the minimum and maximum values for the respective axes, or as values
for each row and column of the matrix img.
The optional return value his a graphics handle to the image.
Calling Forms: The imagesc function can be called in two forms: High-Level and
Low-Level. When invoked with normal options, the High-Level form is used which
Chapter 32: Image Processing 749
first calls newplot to prepare the graphic figure and axes. When the only inputs
to image are property/value pairs the Low-Level form is used which creates a new
instance of an image object and inserts it in the current axes.
See also: [image], page 748,[imshow], page 747,[caxis], page 315.
32.3 Representing Images
In general Octave supports four different kinds of images, grayscale images, RGB images,
binary images, and indexed images. A grayscale image is represented with an M-by-N
matrix in which each element corresponds to the intensity of a pixel. An RGB image is
represented with an M-by-N-by-3 array where each 3-vector corresponds to the red, green,
and blue intensities of each pixel.
The actual meaning of the value of a pixel in a grayscale or RGB image depends on the
class of the matrix. If the matrix is of class double pixel intensities are between 0 and 1, if
it is of class uint8 intensities are between 0 and 255, and if it is of class uint16 intensities
are between 0 and 65535.
A binary image is an M-by-N matrix of class logical. A pixel in a binary image is black
if it is false and white if it is true.
An indexed image consists of an M-by-N matrix of integers and a C-by-3 color map.
Each integer corresponds to an index in the color map, and each row in the color map
corresponds to an RGB color. The color map must be of class double with values between
0 and 1.
im2double (img)
im2double (img,"indexed")
Convert image to double precision.
The conversion of img to double precision, is dependent on the type of input image.
The following input classes are supported:
‘uint8, uint16, and int16’
The range of values from the class is scaled to the interval [0 1].
‘logical’ True and false values are assigned a value of 0 and 1 respectively.
‘single’ Values are cast to double.
‘double’ Returns the same image.
If img is an indexed image, then the second argument should be the string "indexed".
If so, then img must either be of floating point class, or unsigned integer class and it
will simply be cast to double. If it is an integer class, a +1 offset is applied.
See also: [double], page 47.
iscolormap (cmap)
Return true if cmap is a colormap.
A colormap is a real matrix, of class single or double, with 3 columns. Each row
represents a single color. The 3 columns contain red, green, and blue intensities
respectively.
750 GNU Octave
All values in a colormap should be in the [0 1] range but this is not enforced. Each
function must decide what to do for values outside this range.
See also: [colormap], page 751,[rgbplot], page 752.
img = gray2ind (I)
img = gray2ind (I,n)
img = gray2ind (BW)
img = gray2ind (BW,n)
[img,map] = gray2ind (. . . )
Convert a grayscale or binary intensity image to an indexed image.
The indexed image will consist of ndifferent intensity values. If not given ndefaults
to 64 for grayscale images or 2 for binary black and white images.
The output img is of class uint8 if nis less than or equal to 256; Otherwise the return
class is uint16.
See also: [ind2gray], page 750,[rgb2ind], page 750.
I= ind2gray (x,map)
Convert a color indexed image to a grayscale intensity image.
The image xmust be an indexed image which will be converted using the colormap
cmap. If cmap does not contain enough colors for the image, pixels in xoutside the
range are mapped to the last color in the map before conversion to grayscale.
The output Iis of the same class as the input xand may be one of uint8,uint16,
single, or double.
Implementation Note: There are several ways of converting colors to grayscale inten-
sities. This functions uses the luminance value obtained from rgb2ntsc which is I =
0.299*R + 0.587*G + 0.114*B. Other possibilities include the value component from
rgb2hsv or using a single color channel from ind2rgb.
See also: [gray2ind], page 750,[ind2rgb], page 751.
[x,map] = rgb2ind (rgb)
[x,map] = rgb2ind (R,G,B)
Convert an image in red-green-blue (RGB) color space to an indexed image.
The input image rgb can be specified as a single matrix of size MxNx3, or as three
separate variables, R,G, and B, its three color channels, red, green, and blue.
It outputs an indexed image xand a colormap map to interpret an image exactly
the same as the input. No dithering or other form of color quantization is performed.
The output class of the indexed image xcan be uint8, uint16 or double, whichever is
required to specify the number of unique colors in the image (which will be equal to
the number of rows in map) in order
Multi-dimensional indexed images (of size MxNx3xK) are also supported, both via a
single input (rgb) or its three color channels as separate variables.
See also: [ind2rgb], page 751,[rgb2hsv], page 759,[rgb2ntsc], page 760.
Chapter 32: Image Processing 751
rgb = ind2rgb (x,map)
[R,G,B] = ind2rgb (x,map)
Convert an indexed image to red, green, and blue color components.
The image xmust be an indexed image which will be converted using the colormap
map. If map does not contain enough colors for the image, pixels in xoutside the
range are mapped to the last color in the map.
The output may be a single RGB image (MxNx3 matrix where M and N are the
original image xdimensions, one for each of the red, green and blue channels). Al-
ternatively, the individual red, green, and blue color matrices of size MxN may be
returned.
Multi-dimensional indexed images (of size MxNx1xK) are also supported.
See also: [rgb2ind], page 750,[ind2gray], page 750,[hsv2rgb], page 759,[ntsc2rgb],
page 760.
[x,map] = frame2im (f)
Convert movie frame to indexed image.
A movie frame is simply a struct with the fields "cdata" and "colormap".
Support for N-dimensional images or movies is given when fis a struct array. In such
cases, xwill be a MxNx1xK or MxNx3xK for indexed and RGB movies respectively,
with each frame concatenated along the 4th dimension.
See also: [im2frame], page 751.
im2frame (rgb)
im2frame (x,map)
Convert image to movie frame.
A movie frame is simply a struct with the fields "cdata" and "colormap".
Support for N-dimensional images is given when each image projection, matrix sizes
of MxN and MxNx3 for RGB images, is concatenated along the fourth dimension. In
such cases, the returned value is a struct array.
See also: [frame2im], page 751.
cmap = colormap ()
cmap = colormap (map)
cmap = colormap ("default")
cmap = colormap (map_name)
cmap = colormap (hax, . . . )
colormap map_name
Query or set the current colormap.
With no input arguments, colormap returns the current color map.
colormap (map)sets the current colormap to map. The colormap should be an nrow
by 3 column matrix. The columns contain red, green, and blue intensities respectively.
All entries must be between 0 and 1 inclusive. The new colormap is returned.
colormap ("default") restores the default colormap (the viridis map with 64 en-
tries). The default colormap is returned.

752 GNU Octave
The map may also be specified by a string, map name, which is the name of a function
that returns a colormap.
If the first argument hax is an axes handle, then the colormap for the parent figure
of hax is queried or set.
For convenience, it is also possible to use this function with the command form,
colormap map_name.
The list of built-in colormaps is:
Map Description
viridis default
jet colormap traversing blue, cyan, green, yellow, red.
cubehelix colormap traversing black, blue, green, red, white with increasing intensity.
hsv cyclic colormap traversing Hue, Saturation, Value space.
rainbow colormap traversing red, yellow, blue, green, violet.
————- ———————————————————————————————
hot colormap traversing black, red, orange, yellow, white.
cool colormap traversing cyan, purple, magenta.
spring colormap traversing magenta to yellow.
summer colormap traversing green to yellow.
autumn colormap traversing red, orange, yellow.
winter colormap traversing blue to green.
————- ———————————————————————————————
gray colormap traversing black to white in shades of gray.
bone colormap traversing black, gray-blue, white.
copper colormap traversing black to light copper.
pink colormap traversing black, gray-pink, white.
ocean colormap traversing black, dark-blue, white.
————- ———————————————————————————————
colorcube equally spaced colors in RGB color space.
flag cyclic 4-color map of red, white, blue, black.
lines cyclic colormap with colors from axes "ColorOrder" property.
prism cyclic 6-color map of red, orange, yellow, green, blue, violet.
————- ———————————————————————————————
white all white colormap (no colors).
See also: [viridis], page 756,[jet], page 755,[cubehelix], page 754,[hsv], page 755,
[rainbow], page 756,[hot], page 754,[cool], page 753,[spring], page 756,[summer],
page 756,[autumn], page 753,[winter], page 757,[gray], page 754,[bone], page 753,
[copper], page 754,[pink], page 755,[ocean], page 755,[colorcube], page 753,[flag],
page 754,[lines], page 755,[prism], page 756,[white], page 756.
rgbplot (cmap)
rgbplot (cmap,style)
h= rgbplot (. . . )
Plot the components of a colormap.
Two different styles are available for displaying the cmap:
Chapter 32: Image Processing 753
profile (default)
Plot the RGB line profile of the colormap for each of the channels (red,
green and blue) with the plot lines colored appropriately. Each line rep-
resents the intensity of an RGB component across the colormap.
composite Draw the colormap across the X-axis so that the actual index colors are
visible rather than the individual color components.
The optional return value his a graphics handle to the created plot.
Run demo rgbplot to see an example of rgbplot and each style option.
See also: [colormap], page 751.
map = autumn ()
map = autumn (n)
Create color colormap. This colormap ranges from red through orange to yellow.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = bone ()
map = bone (n)
Create color colormap. This colormap varies from black to white with gray-blue
shades.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = colorcube ()
map = colorcube (n)
Create color colormap. This colormap is composed of as many equally spaced colors
(not grays) in the RGB color space as possible.
If there are not a perfect number nof regularly spaced colors then the remaining
entries in the colormap are gradients of pure red, green, blue, and gray.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = cool ()
map = cool (n)
Create color colormap. The colormap varies from cyan to magenta.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
754 GNU Octave
map = copper ()
map = copper (n)
Create color colormap. This colormap varies from black to a light copper tone.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = cubehelix ()
map = cubehelix (n)
Create cubehelix colormap.
This colormap varies from black to white going though blue, green, and red tones while
maintaining a monotonically increasing perception of intensity. This is achieved by
traversing a color cube from black to white through a helix, hence the name cubehelix,
while taking into account the perceived brightness of each channel according to the
NTSC specifications from 1953.
rgbplot (cubehelix (256))
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
Reference: Green, D. A., 2011, "A colour scheme for the display of astronomical
intensity images", Bulletin of the Astronomical Society of India, 39, 289.
See also: [colormap], page 751.
map = flag ()
map = flag (n)
Create color colormap. This colormap cycles through red, white, blue, and black with
each index change.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = gray ()
map = gray (n)
Create gray colormap. This colormap varies from black to white with shades of gray.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = hot ()
map = hot (n)
Create color colormap. This colormap ranges from black through dark red, red,
orange, yellow, to white.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
Chapter 32: Image Processing 755
hsv (n)
Create color colormap. This colormap begins with red, changes through yellow, green,
cyan, blue, and magenta, before returning to red.
It is useful for displaying periodic functions. The map is obtained by linearly varying
the hue through all possible values while keeping constant maximum saturation and
value. The equivalent code is hsv2rgb ([(0:N-1)’/N, ones(N,2)]).
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = jet ()
map = jet (n)
Create color colormap. This colormap ranges from dark blue through blue, cyan,
green, yellow, red, to dark red.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = lines ()
map = lines (n)
Create color colormap. This colormap is composed of the list of colors in the current
axes "ColorOrder" property. The default is blue, orange, yellow, purple, green, light
blue, and dark red.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = ocean ()
map = ocean (n)
Create color colormap. This colormap varies from black to white with shades of blue.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = pink ()
map = pink (n)
Create color colormap. This colormap varies from black to white with shades of
gray-pink.
This colormap gives a sepia tone when used on grayscale images.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
756 GNU Octave
map = prism ()
map = prism (n)
Create color colormap. This colormap cycles through red, orange, yellow, green, blue
and violet with each index change.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = rainbow ()
map = rainbow (n)
Create color colormap. This colormap ranges from red through orange, yellow, green,
blue, to violet.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = spring ()
map = spring (n)
Create color colormap. This colormap varies from magenta to yellow.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = summer ()
map = summer (n)
Create color colormap. This colormap varies from green to yellow.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = viridis ()
map = viridis (n)
Create color colormap. This colormap ranges from dark purplish-blue through blue,
green, to yellow.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
map = white ()
map = white (n)
Create color colormap. This colormap is completely white.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
Chapter 32: Image Processing 757
map = winter ()
map = winter (n)
Create color colormap. This colormap varies from blue to green.
The argument nmust be a scalar. If unspecified, the length of the current colormap,
or 64, is used.
See also: [colormap], page 751.
cmap = contrast (x)
cmap = contrast (x,n)
Return a gray colormap that maximizes the contrast in an image.
The returned colormap will have nrows. If nis not defined then the size of the current
colormap is used.
See also: [colormap], page 751,[brighten], page 757.
The following three functions modify the existing colormap rather than replace it.
map_out = brighten (beta)
map_out = brighten (map,beta)
map_out = brighten (h,beta)
brighten (. . .)
Brighten or darken a colormap.
The argument beta must be a scalar between -1 and 1, where a negative value darkens
and a positive value brightens the colormap.
If the map argument is omitted, the function is applied to the current colormap.
The first argument can also be a valid graphics handle h, in which case brighten is
applied to the colormap associated with this handle.
If no output is specified then the result is written to the current colormap.
See also: [colormap], page 751,[contrast], page 757.
spinmap ()
spinmap (t)
spinmap (t,inc)
spinmap ("inf")
Cycle the colormap for tseconds with a color increment of inc.
Both parameters are optional. The default cycle time is 5 seconds and the default
increment is 2. If the option "inf" is given then cycle continuously until Control-C
is pressed.
When rotating, the original color 1 becomes color 2, color 2 becomes color 3, etc. A
positive or negative increment is allowed and a higher value of inc will cause faster
cycling through the colormap.
See also: [colormap], page 751.
whitebg ()
whitebg (color)
whitebg ("none")
758 GNU Octave
whitebg (hfig, . . . )
Invert the colors in the current color scheme.
The root properties are also inverted such that all subsequent plot use the new color
scheme.
If the optional argument color is present then the background color is set to color
rather than inverted. color may be a string representing one of the eight known
colors or an RGB triplet. The special string argument "none" restores the plot to
the default colors.
If the first argument hfig is a figure handle, then operate on this figure rather than
the current figure returned by gcf. The root properties will not be changed.
See also: [reset], page 421,[get], page 381,[set], page 381.
The following functions can be used to manipulate colormaps.
[Y,newmap] = cmunique (X,map)
[Y,newmap] = cmunique (RGB)
[Y,newmap] = cmunique (I)
Convert an input image Xto an ouput indexed image Ywhich uses the smallest
colormap possible newmap.
When the input is an indexed image (Xwith colormap map) the output is a colormap
newmap from which any repeated rows have been eliminated. The output image, Y, is
the original input image with the indices adjusted to match the new, possibly smaller,
colormap.
When the input is an RGB image (an MxNx3 array), the output colormap will contain
one entry for every unique color in the original image. In the worst case the new map
could have as many rows as the number of pixels in the original image.
When the input is a grayscale image I, the output colormap will contain one entry
for every unique intensity value in the original image. In the worst case the new map
could have as many rows as the number of pixels in the original image.
Implementation Details:
newmap is always an Mx3 matrix, even if the input image is an intensity grayscale
image I(all three RGB planes are assigned the same value).
The output image is of class uint8 if the size of the new colormap is less than or equal
to 256. Otherwise, the output image is of class double.
See also: [rgb2ind], page 750,[gray2ind], page 750.
[Y,newmap] = cmpermute (X,map)
[Y,newmap] = cmpermute (X,map,index)
Reorder colors in a colormap.
When called with only two arguments, cmpermute randomly rearranges the colormap
map and returns a new colormap newmap. It also returns the indexed image Ywhich
is the equivalent of the original input image Xwhen displayed using newmap.
When called with an optional third argument the order of colors in the new colormap
is defined by index.
Caution: index should not have repeated elements or the function will fail.
Chapter 32: Image Processing 759
32.4 Plotting on top of Images
If gnuplot is being used to display images it is possible to plot on top of images. Since an
image is a matrix it is indexed by row and column values. The plotting system is, however,
based on the traditional (x, y) system. To minimize the difference between the two systems
Octave places the origin of the coordinate system in the point corresponding to the pixel
at (1,1). So, to plot points given by row and column values on top of an image, one should
simply call plot with the column values as the first argument and the row values as the
second. As an example the following code generates an image with random intensities
between 0 and 1, and shows the image with red circles over pixels with an intensity above
0.99.
I = rand (100, 100);
[row, col] = find (I > 0.99);
hold ("on");
imshow (I);
plot (col, row, "ro");
hold ("off");
32.5 Color Conversion
Octave supports conversion from the RGB color system to NTSC and HSV and vice versa.
hsv_map = rgb2hsv (rgb_map)
hsv_img = rgb2hsv (rgb_img)
Transform a colormap or image from RGB to HSV color space.
A color in the RGB space consists of red, green, and blue intensities.
A color in HSV space is represented by hue, saturation and value (brightness) levels
in a cylindrical coordinate system. Hue is the azimuth and describes the dominant
color. Saturation is the radial distance and gives the amount of hue mixed into the
color. Value is the height and is the amount of light in the color.
Output class and size will be the same as input.
See also: [hsv2rgb], page 759,[rgb2ind], page 750,[rgb2ntsc], page 760.
rgb_map = hsv2rgb (hsv_map)
rgb_img = hsv2rgb (hsv_img)
Transform a colormap or image from HSV to RGB color space.
A color in HSV space is represented by hue, saturation and value (brightness) levels
in a cylindrical coordinate system. Hue is the azimuth and describes the dominant
color. Saturation is the radial distance and gives the amount of hue mixed into the
color. Value is the height and is the amount of light in the color.
The input can be both a colormap or RGB image. In the case of floating point input,
values are expected to be on the [0 1] range. In the case of hue (azimuth), since the
value corresponds to an angle, mod (h, 1) is used.
760 GNU Octave
>> hsv2rgb ([0.5 1 1])
⇒ans=011
>> hsv2rgb ([2.5 1 1])
⇒ans=011
>> hsv2rgb ([3.5 1 1])
⇒ans=011
Output class and size will be the same as input.
See also: [rgb2hsv], page 759,[ind2rgb], page 751,[ntsc2rgb], page 760.
yiq_map = rgb2ntsc (rgb_map)
yiq_img = rgb2ntsc (rgb_img)
Transform a colormap or image from red-green-blue (RGB) color space to luminance-
chrominance (NTSC) space. The input may be of class uint8, uint16, single, or double.
The output is of class double.
Implementation Note: The reference matrix for the transformation is
/Y\ 0.299 0.587 0.114 /R\
|I| = 0.596 -0.274 -0.322 |G|
\Q/ 0.211 -0.523 0.312 \B/
as documented in http://en.wikipedia.org/wiki/YIQ and truncated to 3 signif-
icant figures. Note: The FCC version of NTSC uses only 2 significant digits and is
slightly different.
See also: [ntsc2rgb], page 760,[rgb2hsv], page 759,[rgb2ind], page 750.
rgb_map = ntsc2rgb (yiq_map)
rgb_img = ntsc2rgb (yiq_img)
Transform a colormap or image from luminance-chrominance (NTSC) space to red-
green-blue (RGB) color space.
Implementation Note: The conversion matrix is chosen to be the inverse of the matrix
used for rgb2ntsc such that
x == ntsc2rgb (rgb2ntsc (x))
matlab uses a slightly different matrix where rounding means the equality above
does not hold.
See also: [rgb2ntsc], page 760,[hsv2rgb], page 759,[ind2rgb], page 751.
761
33 Audio Processing
33.1 Audio File Utilities
The following functions allow you to read, write and retrieve information about audio files.
Various formats are supported including wav, flac and ogg vorbis.
info = audioinfo (filename)
Return information about an audio file specified by filename.
[y,fs] = audioread (filename)
[y,fs] = audioread (filename,samples)
[y,fs] = audioread (filename,datatype)
[y,fs] = audioread (filename,samples,datatype)
Read the audio file filename and return the audio data yand sampling rate fs.
The audio data is stored as matrix with rows corresponding to audio frames and
columns corresponding to channels.
The optional two-element vector argument samples specifies starting and ending
frames.
The optional argument datatype specifies the datatype to return. If it is "native",
then the type of data depends on how the data is stored in the audio file.
audiowrite (filename,y,fs)
audiowrite (filename,y,fs,name,value, . . . )
Write audio data from the matrix yto filename at sampling rate fs with the file
format determined by the file extension.
Additional name/value argument pairs may be used to specify the following options:
‘BitsPerSample’
Number of bits per sample. Valid values are 8, 16, 24, and 32. Default is
16.
‘BitRate’ Valid argument name, but ignored. Left for compatibility with matlab.
‘Quality’ Quality setting for the Ogg Vorbis compressor. Values can range between
0 and 100 with 100 being the highest quality setting. Default is 75.
‘Title’ Title for the audio file.
‘Artist’ Artist name.
‘Comment’ Comment.
audioformats ()
audioformats (format)
Display information about all supported audio formats.
If the optional argument format is given, then display only formats with names that
start with format.
762 GNU Octave
33.2 Audio Device Information
devinfo = audiodevinfo ()
devs = audiodevinfo (io)
name = audiodevinfo (io,id)
id = audiodevinfo (io,name)
id = audiodevinfo (io,rate,bits,chans)
supports = audiodevinfo (io,id,rate,bits,chans)
Return a structure describing the available audio input and output devices.
The devinfo structure has two fields "input" and "output". The value of each field
is a structure array with fields "Name","DriverVersion"and "ID" describing an audio
device.
If the optional argument io is 1, return information about input devices only. If it is
0, return information about output devices only.
If the optional argument id is provided, return information about the corresponding
device.
If the optional argument name is provided, return the id of the named device.
Given a sampling rate, bits per sample, and number of channels for an input or output
device, return the ID of the first device that supports playback or recording using the
specified parameters.
If also given a device ID, return true if the device supports playback or recording
using those parameters.
33.3 Audio Player
The following methods are used to create and use audioplayer objects. These objects can be
used to play back audio data stored in Octave matrices and arrays. The audioplayer object
supports playback from various devices available to the system, blocking and non-blocking
playback, convenient pausing and resuming and much more.
player = audioplayer (y,fs)
player = audioplayer (y,fs,nbits)
player = audioplayer (y,fs,nbits,id)
player = audioplayer (recorder)
player = audioplayer (recorder,id)
Create an audioplayer object that will play back data yat sample rate fs.
The optional arguments nbits, and id specify the bit depth and player device id,
respectively. Device IDs may be found using the audiodevinfo function. Given an
audioplayer object, use the data from the object to initialize the player.
The signal ycan be a vector or a two-dimensional array.
The following example will create an audioplayer object that will play back one second
of white noise at 44100 sample rate using 8 bits per sample.
y = 0.25 * randn (2, 44100);
player = audioplayer (y, 44100, 8);
play (player);
Chapter 33: Audio Processing 763
33.3.1 Playback
The following methods are used to control player playback.
play (player)
play (player,start)
play (player,limits)
Play audio stored in the audioplayer object player without blocking.
Given optional argument start, begin playing at start seconds in the recording. Given
a two-element vector limits, begin and end playing at the number of seconds specified
by the elements of the vector.
playblocking (player)
playblocking (player,start)
playblocking (player,limits)
Play audio stored in the audioplayer object player with blocking.
Given optional argument start, begin playing at start seconds in the recording. Given
a two-element vector limits, begin and end playing at the number of seconds specified
by the elements of the vector.
pause (player)
Pause the audioplayer player.
resume (player)
Resume playback for the paused audioplayer object player.
stop (player)
Stop the playback for the audioplayer player and reset the relevant variables to their
starting values.
isplaying (player)
Return true if the audioplayer object player is currently playing back audio and false
otherwise.
33.3.2 Properties
The remaining couple of methods are used to get and set various properties of the audio-
player object.
value = get (player,name)
values = get (player)
Return the value of the property identified by name.
If name is a cell array return the values of the properties identified by the elements
of the cell array. Given only the player object, return a scalar structure with values
of all properties of player. The field names of the structure correspond to property
names.
set (player,name,value)
set (player,properties)
properties = set (player)
Set the value of property specified by name to a given value.
764 GNU Octave
If name and value are cell arrays, set each property to the corresponding value. Given
a structure of properties with fields corresponding to property names, set the value
of those properties to the field values. Given only the audioplayer object, return a
structure of settable properties.
33.4 Audio Recorder
The following methods are used to create and use audiorecorder objects. These objects can
be used to record audio data from various devices available to the system. You can use
convenient methods to retrieve that data or audioplayer objects created from that data.
Methods for blocking and non-blocking recording, pausing and resuming recording and
much more is available.
recorder = audiorecorder ()
recorder = audiorecorder (fs,nbits,channels)
recorder = audiorecorder (fs,nbits,channels,id)
Create an audiorecorder object recording 8 bit mono audio at 8000 Hz sample rate.
The optional arguments fs,nbits,channels, and id specify the sample rate, bit depth,
number of channels and recording device id, respectively. Device IDs may be found
using the audiodevinfo function.
33.4.1 Recording
The following methods control the recording process.
record (recorder)
record (recorder,length)
Record audio without blocking using the audiorecorder object recorder until stopped
or paused by the stop or pause method.
Given the optional argument length, record for length seconds.
recordblocking (recorder,length)
Record audio with blocking (synchronous I/O).
The length of the recording in seconds (length) must be specified.
pause (recorder)
Pause recording with audiorecorder object recorder.
resume (recorder)
Resume recording with the paused audiorecorder object recorder.
stop (recorder)
Stop the audiorecorder object recorder and clean up any audio streams.
isrecording (recorder)
Return true if the audiorecorder object recorder is currently recording audio and false
otherwise.
Chapter 33: Audio Processing 765
33.4.2 Data Retrieval
The following methods allow you to retrieve recorded audio data in various ways.
data = getaudiodata (recorder)
data = getaudiodata (recorder,datatype)
Return recorder audio data as a matrix with values between -1.0 and 1.0 and with as
many columns as there are channels in the recorder.
Given the optional argument datatype, convert the recorded data to the specified
type, which may be one of "double","single","int16","int8" or "uint8".
player = getplayer (recorder)
Return an audioplayer object with data recorded by the audiorecorder object recorder.
player = play (recorder)
player = play (recorder,start)
player = play (recorder,[start,end])
Play the audio recorded in recorder and return a corresponding audioplayer object.
If the optional argument start is provided, begin playing start seconds in to the
recording.
If the optional argument end is provided, stop playing at end seconds in the recording.
33.4.3 Properties
The remaining two methods allow you to read or alter the properties of audiorecorder
objects.
value = get (recorder,name)
values = get (recorder)
Return the value of the property identified by name.
If name is a cell array, return the values of the properties corresponding to the ele-
ments of the cell array. Given only the recorder object, return a scalar structure with
values of all properties of recorder. The field names of the structure correspond to
property names.
set (recorder,name,value)
set (recorder,properties)
properties = set (recorder)
Set the value of property specified by name to a given value.
If name and value are cell arrays of the same size, set each property to a corresponding
value. Given a structure with fields corresponding to property names, set the value
of those properties to the corresponding field values. Given only the recorder object,
return a structure of settable properties.
33.5 Audio Data Processing
Octave provides a few functions for dealing with audio data. An audio ‘sample’ is a single
output value from an A/D converter, i.e., a small integer number (usually 8 or 16 bits), and
audio data is just a series of such samples. It can be characterized by three parameters: the
766 GNU Octave
sampling rate (measured in samples per second or Hz, e.g., 8000 or 44100), the number of
bits per sample (e.g., 8 or 16), and the number of channels (1 for mono, 2 for stereo, etc.).
There are many different formats for representing such data. Currently, only the two
most popular, linear encoding and mu-law encoding, are supported by Octave. There is an
excellent FAQ on audio formats by Guido van Rossum guido@cwi.nl which can be found at
any FAQ ftp site, in particular in the directory /pub/usenet/news.answers/audio-fmts
of the archive site rtfm.mit.edu.
Octave simply treats audio data as vectors of samples (non-mono data are not supported
yet). It is assumed that audio files using linear encoding have one of the extensions lin or
raw, and that files holding data in mu-law encoding end in au,mu, or snd.
lin2mu (x,n)
Convert audio data from linear to mu-law.
Mu-law values use 8-bit unsigned integers. Linear values use n-bit signed integers or
floating point values in the range -1 ≤x≤1 if nis 0.
If nis not specified it defaults to 0, 8, or 16 depending on the range of values in x.
See also: [mu2lin], page 766.
mu2lin (x,n)
Convert audio data from mu-law to linear.
Mu-law values are 8-bit unsigned integers. Linear values use n-bit signed integers or
floating point values in the range -1≤y≤1 if nis 0.
If nis not specified it defaults to 0.
See also: [lin2mu], page 766.
record (sec)
record (sec,fs)
Record sec seconds of audio from the system’s default audio input at a sampling rate
of 8000 samples per second.
If the optional argument fs is given, it specifies the sampling rate for recording.
For more control over audio recording, use the audiorecorder class.
See also: [sound], page 766,[soundsc], page 767.
sound (y)
sound (y,fs)
sound (y,fs,nbits)
Play audio data yat sample rate fs to the default audio device.
The audio signal ycan be a vector or a two-column array, representing mono or stereo
audio, respectively.
If fs is not given, a default sample rate of 8000 samples per second is used.
The optional argument nbits specifies the bit depth to play to the audio device and
defaults to 8 bits.
For more control over audio playback, use the audioplayer class.
See also: [soundsc], page 767,[record], page 766.
Chapter 33: Audio Processing 767
soundsc (y)
soundsc (y,fs)
soundsc (y,fs,nbits)
soundsc (. . ., [ymin,ymax])
Scale the audio data yand play it at sample rate fs to the default audio device.
The audio signal ycan be a vector or a two-column array, representing mono or stereo
audio, respectively.
If fs is not given, a default sample rate of 8000 samples per second is used.
The optional argument nbits specifies the bit depth to play to the audio device and
defaults to 8 bits.
By default, yis automatically normalized to the range [-1, 1]. If the range [ymin,
ymax] is given, then elements of ythat fall within the range ymin ≤y≤ymax are
scaled to the range [-1, 1] instead.
For more control over audio playback, use the audioplayer class.
See also: [sound], page 766,[record], page 766.
769
34 Object Oriented Programming
Octave has the ability to create user-defined classes—including the capabilities of operator
and function overloading. Classes can protect internal properties so that they may not be
altered accidentally which facilitates data encapsulation. In addition, rules can be created
to address the issue of class precedence in mixed class operations.
This chapter discusses the means of constructing a user class, how to query and set the
properties of a class, and how to overload operators and functions. Throughout this chapter
real code examples are given using a class designed for polynomials.
34.1 Creating a Class
This chapter illustrates user-defined classes and object oriented programming through a
custom class designed for polynomials. This class was chosen for its simplicity which does
not distract unnecessarily from the discussion of the programming features of Octave. Even
so, a bit of background on the goals of the polynomial class is necessary before the syntax
and techniques of Octave object oriented programming are introduced.
The polynomial class is used to represent polynomials of the form
a0+a1x+a2x2+. . . anxn
where a0,a1, etc. are elements of <. Thus the polynomial can be represented by a vector
a = [a0, a1, a2, ..., an];
This is a sufficient specification to begin writing the constructor for the polynomial class.
All object oriented classes in Octave must be located in a directory that is the name of the
class prepended with the ‘@’ symbol. For example, the polynomial class will have all of its
methods defined in the @polynomial directory.
The constructor for the class must be the name of the class itself; in this example
the constructor resides in the file @polynomial/polynomial.m. Ideally, even when the
constructor is called with no arguments it should return a valid object. A constructor for
the polynomial class might look like
## -*- texinfo -*-
## @deftypefn {} {} polynomial ()
## @deftypefnx {} {} polynomial (@var{a})
## Create a polynomial object representing the polynomial
##
## @example
## a0 + a1 * x + a2 * x^2 + @dots{} + an * x^n
## @end example
##
## @noindent
## from a vector of coefficients [a0 a1 a2 @dots{} an].
## @end deftypefn
function p = polynomial (a)
770 GNU Octave
if (nargin > 1)
print_usage ();
endif
if (nargin == 0)
p.poly = [0];
p = class (p, "polynomial");
else
if (strcmp (class (a), "polynomial"))
p = a;
elseif (isreal (a) && isvector (a))
p.poly = a(:).’; # force row vector
p = class (p, "polynomial");
else
error ("@polynomial: A must be a real vector");
endif
endif
endfunction
Note that the return value of the constructor must be the output of the class function.
The first argument to the class function is a structure and the second is the name of the
class itself. An example of calling the class constructor to create an instance is
p = polynomial ([1, 0, 1]);
Methods are defined by m-files in the class directory and can have embedded docu-
mentation the same as any other m-file. The help for the constructor can be obtained by
using the constructor name alone, that is, for the polynomial constructor help polynomial
will return the help string. Help can be restricted to a particular class by using the class
directory name followed by the method. For example, help @polynomial/polynomial is
another way of displaying the help string for the polynomial constructor. This second means
is the only way to obtain help for the overloaded methods and functions of a class.
The same specification mechanism can be used wherever Octave expects a function name.
For example type @polynomial/display will print the code of the display method of the
polynomial class to the screen, and dbstop @polynomial/display will set a breakpoint at
the first executable line of the display method of the polynomial class.
To check whether a variable belongs to a user class, the isobject and isa functions can
be used. For example:
p = polynomial ([1, 0, 1]);
isobject (p)
⇒1
isa (p, "polynomial")
⇒1
isobject (x)
Return true if xis a class object.
See also: [class], page 39,[typeinfo], page 39,[isa], page 39,[ismethod], page 771,
[isprop], page 375.
Chapter 34: Object Oriented Programming 771
The available methods of a class can be displayed with the methods function.
methods (obj)
methods ("classname")
mtds = methods (. . . )
List the names of the public methods for the object obj or the named class classname.
obj may be an Octave class object or a Java object. classname may be the name of
an Octave class or a Java class.
When called with no output arguments, methods prints the list of method names to
the screen. Otherwise, the output argument mtds contains the list in a cell array of
strings.
See also: [fieldnames], page 107.
To inquire whether a particular method exists for a user class, the ismethod function can
be used.
ismethod (obj,method)
ismethod (clsname,method)
Return true if the string method is a valid method of the object obj or of the class
clsname.
See also: [isprop], page 375,[isobject], page 770.
For example:
p = polynomial ([1, 0, 1]);
ismethod (p, "roots")
⇒1
34.2 Class Methods
There are a number of basic class methods that can (and should) be defined to allow the
contents of the classes to be queried and set. The most basic of these is the display method.
The display method is used by Octave whenever a class should be displayed on the screen.
Usually this is the result of an Octave expression that doesn’t end with a semicolon. If this
method is not defined, then Octave won’t print anything when displaying the contents of a
class which can be confusing.
display (obj)
Display the contents of the object obj.
The Octave interpreter calls the display function whenever it needs to present a class
on-screen. Typically, this would be a statement which does not end in a semicolon to
suppress output. For example:
myobj = myclass (...)
User-defined classes should overload the display method so that something useful is
printed for a class object. Otherwise, Octave will report only that the object is an
instance of its class.
myobj = myclass (...)
⇒myobj = <class myclass>
See also: [class], page 39,[subsref], page 775,[subsasgn], page 776.
772 GNU Octave
An example of a display method for the polynomial class might be
function display (p)
printf ("%s =", inputname (1));
a = p.poly;
first = true;
for i = 1 : length (a);
if (a(i) != 0)
if (first)
first = false;
elseif (a(i) > 0 || isnan (a(i)))
printf (" +");
endif
if (a(i) < 0)
printf (" -");
endif
if (i == 1)
printf (" %.5g", abs (a(i)));
elseif (abs (a(i)) != 1)
printf (" %.5g *", abs (a(i)));
endif
if (i > 1)
printf (" X");
endif
if (i > 2)
printf (" ^ %d", i - 1);
endif
endif
endfor
if (first)
printf (" 0");
endif
printf ("\n");
endfunction
Note that in the display method it makes sense to start the method with the line
printf ("%s =", inputname (1)) to be consistent with the rest of Octave which prints
the variable name to be displayed followed by the value.
To be consistent with the Octave graphic handle classes, a class should also define the
get and set methods. The get method accepts one or two arguments. The first argument
is an object of the appropriate class. If no second argument is given then the method should
return a structure with all the properties of the class. If the optional second argument is
given it should be a property name and the specified property should be retrieved.
function val = get (p, prop)
Chapter 34: Object Oriented Programming 773
if (nargin < 1 || nargin > 2)
print_usage ();
endif
if (nargin == 1)
val.poly = p.poly;
else
if (! ischar (prop))
error ("@polynomial/get: PROPERTY must be a string");
endif
switch (prop)
case "poly"
val = p.poly;
otherwise
error (’@polynomial/get: invalid PROPERTY "%s"’, prop);
endswitch
endif
endfunction
Similarly, the first argument to the set method should be an object and any additional
arguments should be property/value pairs.
function pout = set (p, varargin)
if (numel (varargin) < 2 || rem (numel (varargin), 2) != 0)
error ("@polynomial/set: expecting PROPERTY/VALUE pairs");
endif
pout = p;
while (numel (varargin) > 1)
prop = varargin{1};
val = varargin{2};
varargin(1:2) = [];
if (! ischar (prop) || ! strcmp (prop, "poly"))
error ("@polynomial/set: invalid PROPERTY for polynomial class");
elseif (! (isreal (val) && isvector (val)))
error ("@polynomial/set: VALUE must be a real vector");
endif
pout.poly = val(:).’; # force row vector
endwhile
endfunction
Note that Octave does not implement pass by reference; Therefore, to modify an object
requires an assignment statement using the return value from the set method.
774 GNU Octave
p = set (p, "poly", [1, 0, 0, 0, 1]);
The set method makes use of the subsasgn method of the class, and therefore this method
must also be defined. The subsasgn method is discussed more thoroughly in the next
section (see Section 34.3 [Indexing Objects], page 775).
Finally, user classes can be considered to be a special type of a structure, and they can
be saved to a file in the same manner as a structure. For example:
p = polynomial ([1, 0, 1]);
save userclass.mat p
clear p
load userclass.mat
All of the file formats supported by save and load are supported. In certain circumstances
a user class might contain a field that it doesn’t make sense to save, or a field that needs
to be initialized before it is saved. This can be done with the saveobj method of the class.
b= saveobj (a)
Method of a class to manipulate an object prior to saving it to a file.
The function saveobj is called when the object ais saved using the save function.
An example of the use of saveobj might be to remove fields of the object that don’t
make sense to be saved or it might be used to ensure that certain fields of the object
are initialized before the object is saved. For example:
function b = saveobj (a)
b = a;
if (isempty (b.field))
b.field = initfield (b);
endif
endfunction
See also: [loadobj], page 774,[class], page 39.
saveobj is called just prior to saving the class to a file. Similarly, the loadobj method is
called just after a class is loaded from a file, and can be used to ensure that any removed
fields are reinserted into the user object.
b= loadobj (a)
Method of a class to manipulate an object after loading it from a file.
The function loadobj is called when the object ais loaded using the load function.
An example of the use of saveobj might be to add fields to an object that don’t make
sense to be saved. For example:
function b = loadobj (a)
b = a;
b.addmissingfield = addfield (b);
endfunction
See also: [saveobj], page 774,[class], page 39.
Chapter 34: Object Oriented Programming 775
34.3 Indexing Objects
34.3.1 Defining Indexing And Indexed Assignment
Objects can be indexed with parentheses or braces, either like obj(idx)or like obj{idx},
or even like obj(idx).field. However, it is up to the programmer to decide what this
indexing actually means. In the case of the polynomial class p(n)might mean either
the coefficient of the n-th power of the polynomial, or it might be the evaluation of the
polynomial at n. The meaning of this subscripted referencing is determined by the subsref
method.
subsref (val,idx)
Perform the subscripted element selection operation on val according to the subscript
specified by idx.
The subscript idx must be a structure array with fields ‘type’ and ‘subs’. Valid
values for ‘type’ are "()","{}", and ".". The ‘subs’ field may be either ":" or a
cell array of index values.
The following example shows how to extract the first two columns of a matrix
val = magic (3)
⇒val = [ 8 1 6
357
4 9 2 ]
idx.type = "()";
idx.subs = {":", 1:2};
subsref (val, idx)
⇒[ 8 1
3 5
4 9 ]
Note that this is the same as writing val(:, 1:2).
If idx is an empty structure array with fields ‘type’ and ‘subs’, return val.
See also: [subsasgn], page 776,[substruct], page 111.
For example, this class uses the convention that indexing with "()" evaluates the poly-
nomial and indexing with "{}" returns the n-th coefficient (of the n-th power). The code
for the subsref method looks like
function r = subsref (p, s)
if (isempty (s))
error ("@polynomial/subsref: missing index");
endif
switch (s(1).type)
case "()"
idx = s(1).subs;
if (numel (idx) != 1)
776 GNU Octave
error ("@polynomial/subsref: need exactly one index");
endif
r = polyval (fliplr (p.poly), idx{1});
case "{}"
idx = s(1).subs;
if (numel (idx) != 1)
error ("@polynomial/subsref: need exactly one index");
endif
if (isnumeric (idx{1}))
r = p.poly(idx{1}+1);
else
r = p.poly(idx{1});
endif
case "."
fld = s.subs;
if (! strcmp (fld, "poly"))
error (’@polynomial/subsref: invalid property "%s"’, fld);
endif
r = p.poly;
otherwise
error ("@polynomial/subsref: invalid subscript type");
endswitch
if (numel (s) > 1)
r = subsref (r, s(2:end));
endif
endfunction
The equivalent functionality for subscripted assignments uses the subsasgn method.
subsasgn (val,idx,rhs)
Perform the subscripted assignment operation according to the subscript specified by
idx.
The subscript idx must be a structure array with fields ‘type’ and ‘subs’. Valid
values for ‘type’ are "()","{}", and ".". The ‘subs’ field may be either ":" or a
cell array of index values.
The following example shows how to set the two first columns of a 3-by-3 matrix to
zero.

Chapter 34: Object Oriented Programming 777
val = magic (3);
idx.type = "()";
idx.subs = {":", 1:2};
subsasgn (val, idx, 0)
⇒[ 0 0 6
007
0 0 2 ]
Note that this is the same as writing val(:, 1:2) = 0.
If idx is an empty structure array with fields ‘type’ and ‘subs’, return rhs.
See also: [subsref], page 775,[substruct], page 111,[optimize subsasgn calls],
page 777.
val = optimize_subsasgn_calls ()
old_val = optimize_subsasgn_calls (new_val)
optimize_subsasgn_calls (new_val,"local")
Query or set the internal flag for subsasgn method call optimizations.
If true, Octave will attempt to eliminate the redundant copying when calling the
subsasgn method of a user-defined class.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [subsasgn], page 776.
Note that the subsref and subsasgn methods always receive the whole index chain,
while they usually handle only the first element. It is the responsibility of these methods
to handle the rest of the chain (if needed), usually by forwarding it again to subsref or
subsasgn.
If you wish to use the end keyword in subscripted expressions of an object, then there
must be an end method defined. For example, the end method for the polynomial class
might look like
function r = end (obj, index_pos, num_indices)
if (num_indices != 1)
error ("polynomial object may only have one index");
endif
r = length (obj.poly) - 1;
endfunction
which is a fairly generic end method that has a behavior similar to the end keyword for
Octave Array classes. An example using the polynomial class is then
p = polynomial ([1,2,3,4]);
p{end-1}
⇒3
Objects can also be used themselves as the index in a subscripted expression and this is
controlled by the subsindex function.
778 GNU Octave
idx = subsindex (obj)
Convert an object to an index vector.
When obj is a class object defined with a class constructor, then subsindex is the
overloading method that allows the conversion of this class object to a valid indexing
vector. It is important to note that subsindex must return a zero-based real integer
vector of the class "double". For example, if the class constructor were
function obj = myclass (a)
obj = class (struct ("a", a), "myclass");
endfunction
then the subsindex function
function idx = subsindex (obj)
idx = double (obj.a) - 1.0;
endfunction
could be used as follows
a = myclass (1:4);
b = 1:10;
b(a)
⇒1234
See also: [class], page 39,[subsref], page 775,[subsasgn], page 776.
Finally, objects can be used like ranges by providing a colon method.
r= colon (base,limit)
r= colon (base,increment,limit)
Return the result of the colon expression corresponding to base,limit, and optionally,
increment.
This function is equivalent to the operator syntax base : limit or
base : increment : limit.
34.3.2 Indexed Assignment Optimization
Octave’s ubiquitous lazily-copied pass-by-value semantics implies a problem for performance
of user-defined subsasgn methods. Imagine the following call to subsasgn
ss = substruct ("()", {1});
x = subsasgn (x, ss, 1);
where the corresponding method looking like this:
function x = subsasgn (x, ss, val)
...
x.myfield (ss.subs{1}) = val;
endfunction
The problem is that on entry to the subsasgn method, xis still referenced from the
caller’s scope, which means that the method will first need to unshare (copy) xand
x.myfield before performing the assignment. Upon completing the call, unless an error
occurs, the result is immediately assigned to xin the caller’s scope, so that the previous
value of x.myfield is forgotten. Hence, the Octave language implies a copy of N elements
Chapter 34: Object Oriented Programming 779
(N being the size of x.myfield), where modifying just a single element would actually
suffice. In other words, a constant-time operation is degraded to linear-time one. This
may be a real problem for user classes that intrinsically store large arrays.
To partially solve the problem Octave uses a special optimization for user-defined
subsasgn methods coded as m-files. When the method gets called as a result of the
built-in assignment syntax (not a direct subsasgn call as shown above), i.e., x(1) = 1,
AND if the subsasgn method is declared with identical input and output arguments,
as in the example above, then Octave will ignore the copy of xinside the caller’s scope;
therefore, any changes made to xduring the method execution will directly affect the
caller’s copy as well. This allows, for instance, defining a polynomial class where modifying
a single element takes constant time.
It is important to understand the implications that this optimization brings. Since no
extra copy of xwill exist in the caller’s scope, it is solely the callee’s responsibility to not
leave xin an invalid state if an error occurs during the execution. Also, if the method
partially changes xand then errors out, the changes will affect xin the caller’s scope.
Deleting or completely replacing xinside subsasgn will not do anything, however, only
indexed assignments matter.
Since this optimization may change the way code works (especially if badly written), a
built-in variable optimize_subsasgn_calls is provided to control it. It is on by default.
Another way to avoid the optimization is to declare subsasgn methods with different output
and input arguments like this:
function y = subsasgn (x, ss, val)
...
endfunction
34.4 Overloading Objects
34.4.1 Function Overloading
Any Octave function can be overloaded, and this allows an object-specific version of a
function to be called as needed. A pertinent example for the polynomial class might be to
overload the polyval function.
function [y, dy] = polyval (p, varargin)
if (nargout > 1)
[y, dy] = polyval (fliplr (p.poly), varargin{:});
else
y = polyval (fliplr (p.poly), varargin{:});
endif
endfunction
This function just hands off the work to the normal Octave polyval function. Another
interesting example of an overloaded function for the polynomial class is the plot function.
780 GNU Octave
function h = plot (p, varargin)
n = 128;
rmax = max (abs (roots (p.poly)));
x = [0 : (n - 1)] / (n - 1) * 2.2 * rmax - 1.1 * rmax;
if (nargout > 0)
h = plot (x, polyval (p, x), varargin{:});
else
plot (x, polyval (p, x), varargin{:});
endif
endfunction
which allows polynomials to be plotted in the domain near the region of the roots of the
polynomial.
Functions that are of particular interest for overloading are the class conversion functions
such as double. Overloading these functions allows the cast function to work with a user
class. It can also can aid in the use of a class object with methods and functions from other
classes since the object can be transformed to the requisite input form for the new function.
An example double function for the polynomial class might look like
function a = double (p)
a = p.poly;
endfunction
34.4.2 Operator Overloading
The following table shows, for each built-in numerical operation, the corresponding function
name to use when providing an overloaded method for a user class.
Chapter 34: Object Oriented Programming 781
Operation Method Description
a + b plus (a, b) Binary addition
a - b minus (a, b) Binary subtraction
+a uplus (a) Unary addition
-a uminus (a) Unary subtraction
a .* b times (a, b) Element-wise multiplication
a * b mtimes (a, b) Matrix multiplication
a ./ b rdivide (a, b) Element-wise right division
a / b mrdivide (a, b) Matrix right division
a .\ b ldivide (a, b) Element-wise left division
a \ b mldivide (a, b) Matrix left division
a .^ b power (a, b) Element-wise power
a ^ b mpower (a, b) Matrix power
a < b lt (a, b) Less than
a <= b le (a, b) Less than or equal to
a > b gt (a, b) Greater than
a >= b ge (a, b) Greater than or equal to
a == b eq (a, b) Equal to
a != b ne (a, b) Not equal to
a & b and (a, b) Logical and
a | b or (a, b) Logical or
!a not (a) Logical not
a’ ctranspose (a) Complex conjugate transpose
a.’ transpose (a) Transpose
a:b colon (a, b) Two element range
a:b:c colon (a, b, c) Three element range
[a, b] horzcat (a, b) Horizontal concatenation
[a; b] vertcat (a, b) Vertical concatenation
a(s1,...,sn) subsref (a, s) Subscripted reference
a(s1,...,sn) = b subsasgn (a, s, b) Subscripted assignment
b(a) subsindex (a) Convert object to index
display display (a) Object display
Table 34.1: Available overloaded operators and their corresponding class method
An example mtimes method for the polynomial class might look like
function p = mtimes (a, b)
p = polynomial (conv (double (a), double (b)));
endfunction
34.4.3 Precedence of Objects
Many functions and operators take two or more arguments and the situation can easily arise
where these functions are called with objects of different classes. It is therefore necessary
to determine the precedence of which method from which class to call when there are
mixed objects given to a function or operator. To do this the superiorto and inferiorto
functions can be used

782 GNU Octave
superiorto (class_name, . . . )
When called from a class constructor, mark the object currently constructed as having
a higher precedence than class name.
More that one such class can be specified in a single call. This function may only be
called from a class constructor.
See also: [inferiorto], page 782.
inferiorto (class_name, . . . )
When called from a class constructor, mark the object currently constructed as having
a lower precedence than class name.
More that one such class can be specified in a single call. This function may only be
called from a class constructor.
See also: [superiorto], page 781.
With the polynomial class, consider the case
2 * polynomial ([1, 0, 1]);
that mixes an object of the class "double" with an object of the class "polynomial". In
this case the return type should be "polynomial" and so the superiorto function is used
in the class constructor. In particular the polynomial class constructor would be modified
to
## -*- texinfo -*-
## @deftypefn {} {} polynomial ()
## @deftypefnx {} {} polynomial (@var{a})
## Create a polynomial object representing the polynomial
##
## @example
## a0 + a1 * x + a2 * x^2 + @dots{} + an * x^n
## @end example
##
## @noindent
## from a vector of coefficients [a0 a1 a2 @dots{} an].
## @end deftypefn
function p = polynomial (a)
if (nargin > 1)
print_usage ();
endif
if (nargin == 0)
p.poly = [0];
p = class (p, "polynomial");
else
if (strcmp (class (a), "polynomial"))
p = a;
elseif (isreal (a) && isvector (a))
Chapter 34: Object Oriented Programming 783
p.poly = a(:).’; # force row vector
p = class (p, "polynomial");
else
error ("@polynomial: A must be a real vector");
endif
endif
superiorto ("double");
endfunction
Note that user classes always have higher precedence than built-in Octave types. Thus,
marking the polynomial class higher than the "double" class is not actually necessary.
When confronted with two objects of equal precedence, Octave will use the method of
the object that appears first in the list of arguments.
34.5 Inheritance and Aggregation
Using classes to build new classes is supported by Octave through the use of both inheritance
and aggregation.
Class inheritance is provided by Octave using the class function in the class constructor.
As in the case of the polynomial class, the Octave programmer will create a structure that
contains the data fields required by the class, and then call the class function to indicate
that an object is to be created from the structure. Creating a child of an existing object
is done by creating an object of the parent class and providing that object as the third
argument of the class function.
This is most easily demonstrated by example. Suppose the programmer needs a FIR
filter, i.e., a filter with a numerator polynomial but a denominator of 1. In traditional
Octave programming this would be performed as follows.
octave:1> x = [some data vector];
octave:2> n = [some coefficient vector];
octave:3> y = filter (n, 1, x);
The equivalent behavior can be implemented as a class @FIRfilter. The constructor for
this class is the file FIRfilter.m in the class directory @FIRfilter.
## -*- texinfo -*-
## @deftypefn {} {} FIRfilter ()
## @deftypefnx {} {} FIRfilter (@var{p})
## Create a FIR filter with polynomial @var{p} as coefficient vector.
## @end deftypefn
function f = FIRfilter (p)
if (nargin > 1)
print_usage ();
endif
if (nargin == 0)
784 GNU Octave
p = @polynomial ([1]);
elseif (! isa (p, "polynomial"))
error ("@FIRfilter: P must be a polynomial object");
endif
f.polynomial = [];
f = class (f, "FIRfilter", p);
endfunction
As before, the leading comments provide documentation for the class constructor. This
constructor is very similar to the polynomial class constructor, except that a polynomial ob-
ject is passed as the third argument to the class function, telling Octave that the FIRfilter
class will be derived from the polynomial class. The FIR filter class itself does not have any
data fields, but it must provide a struct to the class function. Given that the @polynomial
constructor will add an element named polynomial to the object struct, the @FIRfilter just
initializes a struct with a dummy field polynomial which will later be overwritten.
Note that the sample code always provides for the case in which no arguments are
supplied. This is important because Octave will call a constructor with no arguments when
loading objects from saved files in order to determine the inheritance structure.
A class may be a child of more than one class (see [class], page 39), and inheritance may
be nested. There is no limitation to the number of parents or the level of nesting other than
memory or other physical issues.
As before, a class requires a display method. A simple example might be
function display (f)
printf ("%s.polynomial", inputname (1));
display (f.polynomial);
endfunction
Note that the FIRfilter’s display method relies on the display method from the polyno-
mial class to actually display the filter coefficients.
Once a constructor and display method exist, it is possible to create an instance of the
class. It is also possible to check the class type and examine the underlying structure.
octave:1> f = FIRfilter (polynomial ([1 1 1]/3))
f.polynomial = 0.33333 + 0.33333 * X + 0.33333 * X ^ 2
octave:2> class (f)
ans = FIRfilter
octave:3> isa (f, "FIRfilter")
ans = 1
octave:4> isa (f, "polynomial")
ans = 1
octave:5> struct (f)
ans =
scalar structure containing the fields:
polynomial = 0.33333 + 0.33333 * X + 0.33333 * X ^ 2

Chapter 34: Object Oriented Programming 785
The only thing remaining to make this class usable is a method for processing data. But
before that, it is usually desirable to also have a way of changing the data stored in a class.
Since the fields in the underlying struct are private by default, it is necessary to provide a
mechanism to access the fields. The subsref method may be used for both tasks.
function r = subsref (f, x)
switch (x.type)
case "()"
n = f.polynomial;
r = filter (n.poly, 1, x.subs{1});
case "."
fld = x.subs;
if (! strcmp (fld, "polynomial"))
error (’@FIRfilter/subsref: invalid property "%s"’, fld);
endif
r = f.polynomial;
otherwise
error ("@FIRfilter/subsref: invalid subscript type for FIR filter");
endswitch
endfunction
The "()" case allows us to filter data using the polynomial provided to the constructor.
octave:2> f = FIRfilter (polynomial ([1 1 1]/3));
octave:3> x = ones (5,1);
octave:4> y = f(x)
y =
0.33333
0.66667
1.00000
1.00000
1.00000
The "." case allows us to view the contents of the polynomial field.
octave:1> f = FIRfilter (polynomial ([1 1 1]/3));
octave:2> f.polynomial
ans = 0.33333 + 0.33333 * X + 0.33333 * X ^ 2
In order to change the contents of the object a subsasgn method is needed. For example,
the following code makes the polynomial field publicly writable
786 GNU Octave
function fout = subsasgn (f, index, val)
switch (index.type)
case "."
fld = index.subs;
if (! strcmp (fld, "polynomial"))
error (’@FIRfilter/subsasgn: invalid property "%s"’, fld);
endif
fout = f;
fout.polynomial = val;
otherwise
error ("@FIRfilter/subsasgn: Invalid index type")
endswitch
endfunction
so that
octave:1> f = FIRfilter ();
octave:2> f.polynomial = polynomial ([1 2 3])
f.polynomial = 1 + 2 * X + 3 * X ^ 2
Defining the FIRfilter class as a child of the polynomial class implies that a FIRfilter
object may be used any place that a polynomial object may be used. This is not a normal
use of a filter. It may be a more sensible design approach to use aggregation rather than
inheritance. In this case, the polynomial is simply a field in the class structure. A class
constructor for the aggregation case might be
## -*- texinfo -*-
## @deftypefn {} {} FIRfilter ()
## @deftypefnx {} {} FIRfilter (@var{p})
## Create a FIR filter with polynomial @var{p} as coefficient vector.
## @end deftypefn
function f = FIRfilter (p)
if (nargin > 1)
print_usage ();
endif
if (nargin == 0)
f.polynomial = @polynomial ([1]);
else
if (! isa (p, "polynomial"))
error ("@FIRfilter: P must be a polynomial object");
endif
f.polynomial = p;
endif
787
f = class (f, "FIRfilter");
endfunction
For this example only the constructor needs changing, and all other class methods stay
the same.

789
35 GUI Development
Octave is principally a batch or command-line language. However, it does offer some features
for constructing graphical interfaces that interact with users.
The GUI elements available are I/O dialogs, a progress bar, and UI elements for plot
windows. For example, rather than hardcoding a filename for output results a script can
open a dialog box and allow the user to choose a file. Similarly, if a calculation is expected
to take a long time a script can display a progress bar. The various UI elements can be
used to fully customize the plot window with menubars, context menus,
Several utility functions make it possible to store private data for use with a GUI which
will not pollute the user’s variable space.
Finally, a program written in Octave might want to have long term storage of preferences
or state variables. This can be done with user-defined preferences.
35.1 I/O Dialogs
Simple dialog menus are available for choosing directories or files. They return a string
variable which can then be used with any command requiring a filename.
dirname = uigetdir ()
dirname = uigetdir (init_path)
dirname = uigetdir (init_path,dialog_name)
Open a GUI dialog for selecting a directory.
If init path is not given the current working directory is used.
dialog name may be used to customize the dialog title.
See also: [uigetfile], page 789,[uiputfile], page 790.
[fname,fpath,fltidx] = uigetfile ()
[...] = uigetfile (flt)
[...] = uigetfile (flt,dialog_name)
[...] = uigetfile (flt,dialog_name,default_file)
[...] = uigetfile (. . . , "Position",[px py])
[...] = uigetfile (. . . , "MultiSelect",mode)
Open a GUI dialog for selecting a file and return the filename fname, the path to this
file fpath, and the filter index fltidx.
flt contains a (list of) file filter string(s) in one of the following formats:
"/path/to/filename.ext"
If a filename is given then the file extension is extracted and used as
filter. In addition, the path is selected as current path and the filename
is selected as default file. Example: uigetfile ("myfun.m")
A single file extension "*.ext"
Example: uigetfile ("*.ext")
A 2-column cell array
containing a file extension in the first column and a brief description
in the second column. Example: uigetfile ({"*.ext", "My
Description";"*.xyz", "XYZ-Format"})

790 GNU Octave
The filter string can also contain a semicolon separated list of filter ex-
tensions. Example: uigetfile ({"*.gif;*.png;*.jpg", "Supported
Picture Formats"})
A directory name or path name
If the folder name of path name contains a trailing file separator, the
contents of that folder will be displayed. If no trailing file separator is
present the parent directory is listed. The substring to the right of the
rightmost file separator (if any) will be interpreted as a file or directory
name and if that file or directory exists it will be highlighted. If the
path name or directory name is wholly or partly nonexistent, the current
working directory will be displayed. No filter will be active.
dialog name can be used to customize the dialog title.
If default file is given then it will be selected in the GUI dialog. If, in addition, a
path is given it is also used as current path.
The screen position of the GUI dialog can be set using the "Position" key and a
2-element vector containing the pixel coordinates. Two or more files can be selected
when setting the "MultiSelect" key to "on". In that case fname is a cell array
containing the files.
See also: [uiputfile], page 790,[uigetdir], page 789.
[fname,fpath,fltidx] = uiputfile ()
[fname,fpath,fltidx] = uiputfile (flt)
[fname,fpath,fltidx] = uiputfile (flt,dialog_name)
[fname,fpath,fltidx] = uiputfile (flt,dialog_name,default_file)
Open a GUI dialog for selecting a file.
flt contains a (list of) file filter string(s) in one of the following formats:
"/path/to/filename.ext"
If a filename is given the file extension is extracted and used as filter. In
addition the path is selected as current path and the filename is selected
as default file. Example: uiputfile ("myfun.m")
"*.ext" A single file extension. Example: uiputfile ("*.ext")
{"*.ext", "My Description"}
A 2-column cell array containing the file extension in the 1st column
and a brief description in the 2nd column. Example: uiputfile
({"*.ext","My Description";"*.xyz", "XYZ-Format"})
The filter string can also contain a semicolon separated list of filter extensions. Ex-
ample: uiputfile ({"*.gif;*.png;*.jpg", "Supported Picture Formats"})
dialog name can be used to customize the dialog title. If default file is given it is
preselected in the GUI dialog. If, in addition, a path is given it is also used as current
path.
See also: [uigetfile], page 789,[uigetdir], page 789.
Additionally, there are dialog boxes for printing further help, warnings or errors and to
get textual input from the user.
Chapter 35: GUI Development 791
h= errordlg ()
h= errordlg (msg)
h= errordlg (msg,title)
h= errordlg (msg,title,createmode)
Display an error dialog box with error message msg and caption title.
The default error message is "This is the default error string." and the default
caption is "Error Dialog".
The error message may have multiple lines separated by newline characters ("\n"),
or it may be a cellstr array with one element for each line.
The return value his always 1.
Compatibility Note: The optional argument createmode is accepted for matlab com-
patibility, but is not implemented. See msgbox for details.
Examples:
errordlg ("Some fancy error occurred.");
errordlg ("Some fancy error\nwith two lines.");
errordlg ({"Some fancy error", "with two lines."});
errordlg ("Some fancy error occurred.", "Fancy caption");
See also: [helpdlg], page 791,[inputdlg], page 791,[listdlg], page 792,[msgbox],
page 793,[questdlg], page 794,[warndlg], page 794.
h= helpdlg ()
h= helpdlg (msg)
h= helpdlg (msg,title)
Display a help dialog box with help message msg and caption title.
The default help message is "This is the default help string." and the default
caption is "Help Dialog".
The help message may have multiple lines separated by newline characters ("\n"), or
it may be a cellstr array with one element for each line.
The return value his always 1.
Examples:
helpdlg ("Some helpful text for the user.");
helpdlg ("Some helpful text\nwith two lines.");
helpdlg ({"Some helpful text", "with two lines."});
helpdlg ("Some helpful text for the user.", "Fancy caption");
See also: [errordlg], page 790,[inputdlg], page 791,[listdlg], page 792,[msgbox],
page 793,[questdlg], page 794,[warndlg], page 794.
cstr = inputdlg (prompt)
cstr = inputdlg (prompt,title)
cstr = inputdlg (prompt,title,rowscols)
cstr = inputdlg (prompt,title,rowscols,defaults)
cstr = inputdlg (prompt,title,rowscols,defaults,options)
Return user input from a multi-textfield dialog box in a cell array of strings, or an
empty cell array if the dialog is closed by the Cancel button.

792 GNU Octave
Inputs:
prompt A cell array with strings labeling each text field. This input is required.
title String to use for the caption of the dialog. The default is "Input Dialog".
rowscols Specifies the size of the text fields and can take three forms:
1. a scalar value which defines the number of rows used for each text
field.
2. a vector which defines the individual number of rows used for each
text field.
3. a matrix which defines the individual number of rows and columns
used for each text field. In the matrix each row describes a single
text field. The first column specifies the number of input rows to use
and the second column specifies the text field width.
defaults A list of default values to place in each text fields. It must be a cell array
of strings with the same size as prompt.
options Not supported, only for matlab compatibility.
Example:
prompt = {"Width", "Height", "Depth"};
defaults = {"1.10", "2.20", "3.30"};
rowscols = [1,10; 2,20; 3,30];
dims = inputdlg (prompt, "Enter Box Dimensions", rowscols, defaults);
See also: [errordlg], page 790,[helpdlg], page 791,[listdlg], page 792,[msgbox],
page 793,[questdlg], page 794,[warndlg], page 794.
[sel,ok] = listdlg (key,value, . . . )
Return user inputs from a list dialog box in a vector of selection indices (sel) and a
flag indicating how the user closed the dialog box (ok).
The indices in sel are 1-based.
The value of ok is 1 if the user closed the box with the OK button, otherwise it is 0
and sel is empty.
Input arguments are specified in form of key,value pairs. The "ListString" argu-
ment pair must be specified.
Valid key and value pairs are:
"ListString"
a cell array of strings with the contents of the list.
"SelectionMode"
can be either "Single" or "Multiple" (default).
"ListSize"
a vector with two elements width and height defining the size of the list
field in pixels. Default is [160 300].
"InitialValue"
a vector containing 1-based indices of preselected elements. Default is 1
(first item).
Chapter 35: GUI Development 793
"Name" a string to be used as the dialog caption. Default is "".
"PromptString"
a cell array of strings to be displayed above the list field. Default is {}.
"OKString"
a string used to label the OK button. Default is "OK".
"CancelString"
a string used to label the Cancel button. Default is "Cancel".
Example:
my_options = {"An item", "another", "yet another"};
[sel, ok] = listdlg ("ListString", my_options,
"SelectionMode", "Multiple");
if (ok == 1)
disp ("You selected:");
for i = 1:numel (sel)
disp (sprintf ("\t%s", my_options{sel(i)}));
endfor
else
disp ("You cancelled.");
endif
See also: [menu], page 249,[errordlg], page 790,[helpdlg], page 791,[inputdlg],
page 791,[msgbox], page 793,[questdlg], page 794,[warndlg], page 794.
h= msgbox (msg)
h= msgbox (msg,title)
h= msgbox (msg,title,icon)
h= msgbox (. . . , createmode)
Display msg using a message dialog box.
The message may have multiple lines separated by newline characters ("\n"), or it
may be a cellstr array with one element for each line.
The optional input title (character string) can be used to decorate the dialog caption.
The optional argument icon selects a dialog icon. It can be one of "none" (default),
"error","help", or "warn".
The return value is always 1.
Compatibility Note: The optional argument createmode is accepted for matlab com-
patibility, but is not implemented. A valid createmode is either one of the charac-
ter strings "nonmodal","modal", or "replace", or a structure containing a field
"WindowStyle" with one of the three character strings.
Examples:

794 GNU Octave
msgbox ("Some message for the user.");
msgbox ("Some message\nwith two lines.");
msgbox ({"Some message", "with two lines."});
msgbox ("Some message for the user.", "Fancy caption");
% A message dialog box with error icon
msgbox ("Some message for the user.", "Fancy caption", "error");
See also: [errordlg], page 790,[helpdlg], page 791,[inputdlg], page 791,[listdlg],
page 792,[questdlg], page 794,[warndlg], page 794.
btn = questdlg (msg)
btn = questdlg (msg,title)
btn = questdlg (msg,title,default)
btn = questdlg (msg,title,btn1,btn2,default)
btn = questdlg (msg,title,btn1,btn2,btn3,default)
Display msg using a question dialog box and return the caption of the activated
button.
The message may have multiple lines separated by newline characters ("\n"), or it
may be a cellstr array with one element for each line.
The optional title (character string) can be used to specify the dialog caption. It
defaults to "Question Dialog".
The dialog may contain two or three buttons which will all close the dialog.
The string default identifies the default button, which is activated by pressing the
ENTER key. It must match one of the strings given in btn1,btn2, or btn3.
If only msg and title are specified, three buttons with the default captions "Yes",
"No", and "Cancel" are used.
If only two button captions, btn1 and btn2, are specified the dialog will have only
these two buttons.
Examples:
btn = questdlg ("Close Octave?", "Some fancy title", "Yes", "No", "No");
if (strcmp (btn, "Yes"))
exit ();
endif
See also: [errordlg], page 790,[helpdlg], page 791,[inputdlg], page 791,[listdlg],
page 792,[msgbox], page 793,[warndlg], page 794.
h= warndlg ()
h= warndlg (msg)
h= warndlg (msg,title)
h= warndlg (msg,title,createmode)
Display a warning dialog box with warning message msg and caption title.
The default warning message is "This is the default warning string." and the
default caption is "Warning Dialog".
The warning message may have multiple lines separated by newline characters ("\n"),
or it may be a cellstr array with one element for each line.
Chapter 35: GUI Development 795
The return value his always 1.
Compatibility Note: The optional argument createmode is accepted for matlab com-
patibility, but is not implemented. See msgbox for details.
Examples:
warndlg ("Some warning text for the user.");
warndlg ("Some warning text\nwith two lines.");
warndlg ({"Some warning text", "with two lines."});
warndlg ("Some warning text for the user.", "Fancy caption");
See also: [errordlg], page 790,[helpdlg], page 791,[inputdlg], page 791,[listdlg],
page 792,[msgbox], page 793,[questdlg], page 794.
For creating new dialog types, there is a dialog function.
h= dialog (. . . , "property",value, . . . )
Create an empty modal dialog window that other uicontrols can be added to.
The dialog box is a figure object with properties as recommended for a dialog box.
The default properties differing from a figure are:
buttondownfcn
if isempty(allchild(gcbf)), close(gcbf), end
colormap []
color defaultuicontrolbackgroundcolor
dockcontrols
off
handlevisibility
callback
integerhandle
off
inverthardcopy
off
menubar none
numbertitle
off
paperpositionmode
auto
resize off
visible on
windowstyle
modal
796 GNU Octave
Multiple property-value pairs may be specified for the dialog object, but they must
appear in pairs.
The return value his a graphics handle to the created figure. object.
Examples:
% create an empty dialog window titled ’Dialog Example’
h = dialog ("name", "Dialog Example");
% create a button (default style)
b = uicontrol (h, "string", "OK", "position",[10 10 150 40], "callback","delete(gcf)");
% wait for dialog to resume or close
uiwait (h);
See also: [figure], page 355,[uiwait], page 803.
35.2 Progress Bar
h= waitbar (frac)
h= waitbar (frac,msg)
h= waitbar (. . . , "createcancelbtn",fcn, . . . )
h= waitbar (. . . , prop,val, . . . )
waitbar (frac)
waitbar (frac,h)
waitbar (frac,h,msg)
Return a handle hto a new progress indicator ("waitbar") object.
The waitbar is filled to fraction frac which must be in the range [0, 1].
The optional message msg is centered and displayed above the waitbar.
A cancel button can be added to the bottom of the waitbar using the
"createcancelbtn" property of waitbar figures. The action to be executed when
the user presses the button is specified using a string or function handle fcn.
The appearance of the waitbar figure window can be configured by passing prop/val
pairs to the function.
When called with a single input the current waitbar, if it exists, is updated to the
new value frac. If there are multiple outstanding waitbars they can be updated
individually by passing the handle hof the specific waitbar to modify.
See also: [delete], page 360.
35.3 UI Elements
The ui* series of functions work best with the qt graphics toolkit, although some function-
ality is available with the fltk toolkit. There is no support for the gnuplot toolkit.
hui = uimenu (property,value, . . . )
hui = uimenu (h,property,value, . . . )
Create a uimenu object and return a handle to it.
Chapter 35: GUI Development 797
If his omitted then a top-level menu for the current figure is created. If his given
then a submenu relative to his created.
uimenu objects have the following specific properties:
"accelerator"
A string containing the key combination together with CTRL to execute
this menu entry (e.g., "x" for CTRL+x).
"callback"
Is the function called when this menu entry is executed. It can be either
a function string (e.g., "myfun"), a function handle (e.g., @myfun) or a
cell array containing the function handle and arguments for the callback
function (e.g., {@myfun, arg1, arg2}).
"checked"
Can be set "on" or "off". Sets a mark at this menu entry.
"enable" Can be set "on" or "off". If disabled the menu entry cannot be selected
and it is grayed out.
"foregroundcolor"
A color value setting the text color for this menu entry.
"label" A string containing the label for this menu entry. A "&"-symbol can be
used to mark the "accelerator" character (e.g., "E&xit")
"position"
An scalar value containing the relative menu position. The entry with
the lowest value is at the first position starting from left or top.
"separator"
Can be set "on" or "off". If enabled it draws a separator line above the
current position. It is ignored for top level entries.
Examples:
f = uimenu ("label", "&File", "accelerator", "f");
e = uimenu ("label", "&Edit", "accelerator", "e");
uimenu (f, "label", "Close", "accelerator", "q", ...
"callback", "close (gcf)");
uimenu (e, "label", "Toggle &Grid", "accelerator", "g", ...
"callback", "grid (gca)");
See also: [figure], page 355.
hui = uibuttongroup (property,value, . . . )
hui = uibuttongroup (parent,property,value, . . . )
uibuttongroup (h)
Create a uibuttongroup object and return a handle to it.
uibuttongroups are used to create group uicontrols.
If parent is omitted then a uibuttongroup for the current figure is created. If no figure
is available, a new figure is created first.
If parent is given then a uibuttongroup relative to parent is created.

798 GNU Octave
Any provided property value pairs will override the default values of the created
uibuttongroup object.
Uibuttongroup properties are documented at Section 15.3.3.11 [Uibuttongroup Prop-
erties], page 410.
Examples:
% create figure and panel on it
f = figure;
% create a button group
gp = uibuttongroup (f, "Position", [ 0 0.5 1 1])
% create a buttons in the group
b1 = uicontrol (gp, "style", "radiobutton", ...
"string", "Choice 1", ...
"Position", [ 10 150 100 50 ]);
b2 = uicontrol (gp, "style", "radiobutton", ...
"string", "Choice 2", ...
"Position", [ 10 50 100 30 ]);
% create a button not in the group
b3 = uicontrol (f, "style", "radiobutton", ...
"string", "Not in the group", ...
"Position", [ 10 50 100 50 ]);
See also: [figure], page 355,[uipanel], page 800.
hui = uicontextmenu (property,value, . . . )
hui = uicontextmenu (h,property,value, . . . )
Create a uicontextmenu object and return a handle to it.
If his omitted then a uicontextmenu for the current figure is created. If no figure is
available, a new figure is created first.
If his given then a uicontextmenu relative to his created.
Any provided property value pairs will override the default values of the created
uicontextmenu object.
Uicontextmenu properties are documented at Section 15.3.3.12 [Uicontextmenu Prop-
erties], page 412.
Examples:
% create figure and uicontextmenu
f = figure;
c = uicontextmenu (f);
% create menus in the context menu
m1 = uimenu ("parent",c,"label","Menu item 1","callback","disp(’menu item 1’)");
m2 = uimenu ("parent",c,"label","Menu item 2","callback","disp(’menu item 2’)");
% set the context menu for the figure
set (f, "uicontextmenu", c);
See also: [figure], page 355,[uimenu], page 796.
Chapter 35: GUI Development 799
hui = uicontrol (property,value, . . . )
hui = uicontrol (parent,property,value, . . . )
uicontrol (h)
Create a uicontrol object and return a handle to it.
uicontrols are used to create simple interactive controls such as push buttons, check-
boxes, edit and list controls.
If parent is omitted then a uicontrol for the current figure is created. If no figure is
available, a new figure is created first.
If parent is given then a uicontrol relative to parent is created.
Any provided property value pairs will override the default values of the created
uicontrol object.
Uicontrol properties are documented at Section 15.3.3.14 [Uicontrol Properties],
page 414.
Control of the type of uicontrol created is through the use of the style property. If
no style property is provided, a push button will be created.
Valid styles for uicontrol are:
"checkbox"
Create a checkbox control that allows user on/off selection.
"edit" Create an edit control that allows user input of single or multiple lines of
text.
"listbox"
Create a listbox control that displays a list of items and allows user se-
lection of single or multiple items.
"popupmenu"
Create a popupmenu control that displays a list of options that can be
selected when the user clicks on the control.
"pushbutton"
Create a push button control that allows user to press to cause an action.
"radiobutton"
Create a radio button control intended to be used for mutually exclusive
input in a group of radiobutton controls.
"slider" Create a slider control that allows user selection from a range of values
by sliding knob on the control.
"text" Create a static text control to display single or multiple lines of text.
"togglebutton"
Create a toggle button control that appears like a push button but allows
the user to select between two states.
Examples:

800 GNU Octave
% create figure and panel on it
f = figure;
% create a button (default style)
b1 = uicontrol (f, "string", "A Button", "position",[10 10 150 40]);
% create an edit control
e1 = uicontrol (f, "style", "edit", "string", "editable text", "position",[10 60 300 40]);
% create a checkbox
c1 = uicontrol (f, "style", "checkbox", "string", "a checkbox", "position",[10 120 150 40]);
See also: [figure], page 355,[uipanel], page 800.
hui = uipanel (property,value, . . . )
hui = uipanel (parent,"property,value, . . . )
Create a uipanel object and return a handle to it.
uipanels are used as containers to group other uicontrol objects.
If parent is omitted then a uipanel for the current figure is created. If no figure is
available, a new figure is created first.
If parent is given then a uipanel relative to parent is created.
Any provided property value pairs will override the default values of the created
uipanel object.
Uipanel properties are documented at Section 15.3.3.13 [Uipanel Properties], page 413.
Examples:
% create figure and panel on it
f = figure;
p = uipanel ("title", "Panel Title", "position", [.25 .25 .5 .5]);
% add two buttons to the panel
b1 = uicontrol ("parent", p, "string", "A Button", "position",[18 10 150 36]);
b2 = uicontrol ("parent", p, "string", "Another Button", "position",[18 60 150 36]);
See also: [figure], page 355,[uicontrol], page 799.
hui = uipushtool (property,value, . . . )
hui = uipushtool (parent,property,value, . . . )
Create a uipushtool object and return a handle to it.
uipushtools are buttons that appear on a figure toolbar. The button is created with
a border that is shown when the user hovers over the button. An image can be set
using the cdata property.
If parent is omitted then a uipushtool for the current figure is created. If no figure is
available, a new figure is created first. If a figure is available, but does not contain a
uitoolbar, a uitoolbar will be created.
If parent is given then an uipushtools is created on the parent uitoolbar.
Any provided property value pairs will override the default values of the created
uipushtool object.
Chapter 35: GUI Development 801
Uipushtool properties are documented at Section 15.3.3.16 [Uipushtool Properties],
page 417.
Examples:
% create figure without a default toolbar
f = figure ("toolbar", "none");
% create empty toolbar
t = uitoolbar (f);
% create a 19x19x3 black square
img=zeros(19,19,3);
% add pushtool button to toolbar
b = uipushtool (t, "cdata", img);
See also: [figure], page 355,[uitoolbar], page 801,[uitoggletool], page 801.
hui = uitoggletool (property,value, . . . )
hui = uitoggletool (parent,property,value, . . . )
Create a uitoggletool object and return a handle to it.
uitoggletool are togglebuttons that appear on a figure toolbar. The button is created
with a border that is shown when the user hovers over the button. An image can be
set using the cdata property.
If parent is omitted then a uitoggletool for the current figure is created. If no figure
is available, a new figure is created first. If a figure is available, but does not contain
a uitoolbar, a uitoolbar will be created.
If parent is given then a uitoggletool is created on the parent uitoolbar.
Any provided property value pairs will override the default values of the created
uitoggletool object.
Uitoggletool properties are documented at Section 15.3.3.17 [Uitoggletool Properties],
page 418.
Examples:
% create figure without a default toolbar
f = figure ("toolbar", "none");
% create empty toolbar
t = uitoolbar (f);
% create a 19x19x3 black square
img=zeros(19,19,3);
% add uitoggletool button to toolbar
b = uitoggletool (t, "cdata", img);
See also: [figure], page 355,[uitoolbar], page 801,[uipushtool], page 800.
hui = uitoolbar (property,value, . . . )
hui = uitoolbar (parent,property,value, . . . )
Create a uitoolbar object and return a handle to it. A uitoolbar displays uitoggletool
and uipushtool buttons.
If parent is omitted then a uitoolbar for the current figure is created. If no figure is
available, a new figure is created first.
802 GNU Octave
If parent is given then a uitoolbar relative to parent is created.
Any provided property value pairs will override the default values of the created
uitoolbar object.
Uitoolbar properties are documented at Section 15.3.3.15 [Uitoolbar Properties],
page 416.
Examples:
% create figure without a default toolbar
f = figure ("toolbar", "none");
% create empty toolbar
t = uitoolbar (f);
See also: [figure], page 355,[uitoggletool], page 801,[uipushtool], page 800.
35.4 GUI Utility Functions
These functions do not implement a GUI element but are useful when developing programs
that do. The functions uiwait,uiresume, and waitfor are only available with the qt or
fltk toolkits.
used = desktop ("-inuse")
Return true if the desktop (GUI) is currently in use.
See also: [isguirunning], page 803.
data = guidata (h)
guidata (h,data)
Query or set user-custom GUI data.
The GUI data is stored in the figure handle h. If his not a figure handle then it’s
parent figure will be used for storage.
data must be a single object which means it is usually preferable for it to be a data
container such as a cell array or struct so that additional data items can be added
easily.
See also: [getappdata], page 424,[setappdata], page 424,[get], page 381,[set],
page 381,[getpref], page 804,[setpref], page 804.
hdata = guihandles (h)
hdata = guihandles
Return a structure of object handles for the figure associated with handle h.
If no handle is specified the current figure returned by gcf is used.
The fieldname for each entry of hdata is taken from the "tag" property of the
graphic object. If the tag is empty then the handle is not returned. If there are
multiple graphic objects with the same tag then the entry in hdata will be a vec-
tor of handles. guihandles includes all possible handles, including those for which
"HandleVisibility" is "off".
See also: [guidata], page 802,[findobj], page 419,[findall], page 420,[allchild],
page 382.

Chapter 35: GUI Development 803
have_window_system ()
Return true if a window system is available (X11, Windows, or Apple OS X) and false
otherwise.
See also: [isguirunning], page 803.
isguirunning ()
Return true if Octave is running in GUI mode and false otherwise.
See also: [have window system], page 803.
uiwait
uiwait (h)
uiwait (h,timeout)
Suspend program execution until the figure with handle his deleted or uiresume is
called.
When no figure handle is specified this function uses the current figure. If the figure
handle is invalid or there is no current figure, this functions returns immediately.
When specified, timeout defines the number of seconds to wait for the figure deletion
or the uiresume call. The timeout value must be at least 1. If a smaller value is
specified, a warning is issued and a timeout value of 1 is used instead. If a non-
integer value is specified, it is truncated towards 0. If timeout is not specified, the
program execution is suspended indefinitely.
See also: [uiresume], page 803,[waitfor], page 803.
uiresume (h)
Resume program execution suspended with uiwait.
The handle hmust be the same as the on specified in uiwait. If the handle is invalid
or there is no uiwait call pending for the figure with handle h, this function does
nothing.
See also: [uiwait], page 803.
waitfor (h)
waitfor (h,prop)
waitfor (h,prop,value)
waitfor (. . ., "timeout",timeout)
Suspend the execution of the current program until a condition is satisfied on the
graphics handle h.
While the program is suspended graphics events are still processed normally, allowing
callbacks to modify the state of graphics objects. This function is reentrant and can
be called from a callback, while another waitfor call is pending at the top-level.
In the first form, program execution is suspended until the graphics object his de-
stroyed. If the graphics handle is invalid, the function returns immediately.
In the second form, execution is suspended until the graphics object is destroyed or
the property named prop is modified. If the graphics handle is invalid or the property
does not exist, the function returns immediately.
In the third form, execution is suspended until the graphics object is destroyed or
the property named prop is set to value. The function isequal is used to compare
804 GNU Octave
property values. If the graphics handle is invalid, the property does not exist or the
property is already set to value, the function returns immediately.
An optional timeout can be specified using the property timeout. This timeout value
is the number of seconds to wait for the condition to be true. timeout must be at
least 1. If a smaller value is specified, a warning is issued and a value of 1 is used
instead. If the timeout value is not an integer, it is truncated towards 0.
To define a condition on a property named timeout, use the string \timeout instead.
In all cases, typing CTRL-C stops program execution immediately.
See also: [waitforbuttonpress], page 372,[isequal], page 147.
35.5 User-Defined Preferences
val = getpref ("group","pref")
val = getpref ("group","pref",default)
{val1,val2, ...} = getpref ("group",{"pref1","pref2", . . . })
prefstruct = getpref ("group")
prefstruct = getpref ()
Return the preference value corresponding to the named preference pref in the pref-
erence group group.
The named preference group must be a string.
If pref does not exist in group and default is specified, create the preference with
value default and return default.
The preference pref may be a string or cell array of strings. If it is a cell array of
strings then a cell array of preferences is returned.
The corresponding default value default may be any Octave value, .e.g., double, struct,
cell array, object, etc. Or, if pref is a cell array of strings then default must be a cell
array of values with the same size as pref.
If neither pref nor default are specified, return a structure of preferences for the
preference group group.
If no arguments are specified, return a structure containing all groups of preferences
and their values.
See also: [addpref], page 805,[setpref], page 804,[ispref], page 805,[rmpref],
page 805.
setpref ("group","pref",val)
setpref ("group",{"pref1","pref2", . . . },{val1,val2, . . . })
Set the preference pref to the given val in the named preference group group.
The named preference group must be a string.
The preference pref may be a string or a cell array of strings.
The corresponding value val may be any Octave value, .e.g., double, struct, cell array,
object, etc. Or, if pref is a cell array of strings then val must be a cell array of values
with the same size as pref.
If the named preference or group does not exist, it is added.
Chapter 35: GUI Development 805
See also: [addpref], page 805,[getpref], page 804,[ispref], page 805,[rmpref],
page 805.
addpref ("group","pref",val)
addpref ("group",{"pref1","pref2", . . . },{val1,val2, . . . })
Add the preference pref and associated value val to the named preference group
group.
The named preference group must be a string.
The preference pref may be a string or a cell array of strings. An error will be issued
if the preference already exists.
The corresponding value val may be any Octave value, .e.g., double, struct, cell array,
object, etc. Or, if pref is a cell array of strings then val must be a cell array of values
with the same size as pref.
See also: [setpref], page 804,[getpref], page 804,[ispref], page 805,[rmpref],
page 805.
rmpref ("group","pref")
rmpref ("group",{"pref1","pref2", . . . })
rmpref ("group")
Remove the named preference pref from the preference group group.
The named preference group must be a string.
The preference pref may be a string or cell array of strings.
If pref is not specified, remove the preference group group.
It is an error to remove a nonexistent preference or group.
See also: [addpref], page 805,[ispref], page 805,[setpref], page 804,[getpref],
page 804.
ispref ("group","pref")
ispref ("group",{"pref1","pref2", . . . })
ispref ("group")
Return true if the named preference pref exists in the preference group group.
The named preference group must be a string.
The preference pref may be a string or a cell array of strings.
If pref is not specified, return true if the preference group group exists.
See also: [getpref], page 804,[addpref], page 805,[setpref], page 804,[rmpref],
page 805.
prefdir
prefdir (1)
dir = prefdir
Return the directory that holds the preferences for Octave.
Examples:
Display the preferences directory
prefdir
806 GNU Octave
Change to the preferences folder
cd (prefdir)
If called with an argument, the preferences directory is created if it doesn’t already
exist.
See also: [getpref], page 804,[setpref], page 804,[addpref], page 805,[rmpref],
page 805,[ispref], page 805.
preferences
Display the GUI preferences dialog window for Octave.

807
36 System Utilities
This chapter describes the functions that are available to allow you to get information about
what is happening outside of Octave, while it is still running, and use this information in
your program. For example, you can get information about environment variables, the
current time, and even start other programs from the Octave prompt.
36.1 Timing Utilities
Octave’s core set of functions for manipulating time values are patterned after the cor-
responding functions from the standard C library. Several of these functions use a data
structure for time that includes the following elements:
usec Microseconds after the second (0-999999).
sec Seconds after the minute (0-60). This number can be 60 to account for leap
seconds.
min Minutes after the hour (0-59).
hour Hours since midnight (0-23).
mday Day of the month (1-31).
mon Months since January (0-11).
year Years since 1900.
wday Days since Sunday (0-6).
yday Days since January 1 (0-365).
isdst Daylight Savings Time flag.
gmtoff Seconds offset from UTC.
zone Time zone.
In the descriptions of the following functions, this structure is referred to as a tm struct.
seconds = time ()
Return the current time as the number of seconds since the epoch.
The epoch is referenced to 00:00:00 CUT (Coordinated Universal Time) 1 Jan 1970.
For example, on Monday February 17, 1997 at 07:15:06 CUT, the value returned by
time was 856163706.
See also: [strftime], page 809,[strptime], page 811,[localtime], page 808,[gmtime],
page 808,[mktime], page 809,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
t = now ()
Return the current local date/time as a serial day number (see datenum).
The integral part, floor (now) corresponds to the number of days between today
and Jan 1, 0000.
The fractional part, rem (now, 1) corresponds to the current time.
See also: [clock], page 811,[date], page 812,[datenum], page 813.
808 GNU Octave
ctime (t)
Convert a value returned from time (or any other non-negative integer), to the local
time and return a string of the same form as asctime.
The function ctime (time) is equivalent to asctime (localtime (time)). For ex-
ample:
ctime (time ())
⇒"Mon Feb 17 01:15:06 1997\n"
See also: [asctime], page 809,[time], page 807,[localtime], page 808.
tm_struct = gmtime (t)
Given a value returned from time, or any non-negative integer, return a time structure
corresponding to CUT (Coordinated Universal Time).
For example:
gmtime (time ())
⇒{
usec = 0
sec = 6
min = 15
hour = 7
mday = 17
mon = 1
year = 97
wday = 1
yday = 47
isdst = 0
gmtoff = 0
zone = GMT
}
See also: [strftime], page 809,[strptime], page 811,[localtime], page 808,[mktime],
page 809,[time], page 807,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
tm_struct = localtime (t)
Given a value returned from time, or any non-negative integer, return a time structure
corresponding to the local time zone.

Chapter 36: System Utilities 809
localtime (time ())
⇒{
usec = 0
sec = 6
min = 15
hour = 1
mday = 17
mon = 1
year = 97
wday = 1
yday = 47
isdst = 0
gmtoff = -21600
zone = CST
}
See also: [strftime], page 809,[strptime], page 811,[gmtime], page 808,[mktime],
page 809,[time], page 807,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
seconds = mktime (tm_struct)
Convert a time structure corresponding to the local time to the number of seconds
since the epoch.
For example:
mktime (localtime (time ()))
⇒856163706
See also: [strftime], page 809,[strptime], page 811,[localtime], page 808,[gmtime],
page 808,[time], page 807,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
asctime (tm_struct)
Convert a time structure to a string using the following format: "ddd mmm mm
HH:MM:SS yyyy\n".
For example:
asctime (localtime (time ()))
⇒"Mon Feb 17 01:15:06 1997\n"
This is equivalent to ctime (time ()).
See also: [ctime], page 808,[localtime], page 808,[time], page 807.
strftime (fmt,tm_struct)
Format the time structure tm struct in a flexible way using the format string fmt
that contains ‘%’ substitutions similar to those in printf.
Except where noted, substituted fields have a fixed size; numeric fields are padded if
necessary. Padding is with zeros by default; for fields that display a single number,
810 GNU Octave
padding can be changed or inhibited by following the ‘%’ with one of the modifiers
described below. Unknown field specifiers are copied as normal characters. All other
characters are copied to the output without change. For example:
strftime ("%r (%Z) %A %e %B %Y", localtime (time ()))
⇒"01:15:06 AM (CST) Monday 17 February 1997"
Octave’s strftime function supports a superset of the ANSI C field specifiers.
Literal character fields:
%% % character.
%n Newline character.
%t Tab character.
Numeric modifiers (a nonstandard extension):
- (dash) Do not pad the field.
_ (underscore)
Pad the field with spaces.
Time fields:
%H Hour (00-23).
%I Hour (01-12).
%k Hour (0-23).
%l Hour (1-12).
%M Minute (00-59).
%p Locale’s AM or PM.
%r Time, 12-hour (hh:mm:ss [AP]M).
%R Time, 24-hour (hh:mm).
%s Time in seconds since 00:00:00, Jan 1, 1970 (a nonstandard extension).
%S Second (00-61).
%T Time, 24-hour (hh:mm:ss).
%X Locale’s time representation (%H:%M:%S).
%z Offset from UTC (±hhmm), or nothing if no time zone is determinable.
%Z Time zone (EDT), or nothing if no time zone is determinable.
Date fields:
%a Locale’s abbreviated weekday name (Sun-Sat).
%A Locale’s full weekday name, variable length (Sunday-Saturday).
%b Locale’s abbreviated month name (Jan-Dec).
%B Locale’s full month name, variable length (January-December).

Chapter 36: System Utilities 811
%c Locale’s date and time (Sat Nov 04 12:02:33 EST 1989).
%C Century (00-99).
%d Day of month (01-31).
%e Day of month ( 1-31).
%D Date (mm/dd/yy).
%h Same as %b.
%j Day of year (001-366).
%m Month (01-12).
%U Week number of year with Sunday as first day of week (00-53).
%w Day of week (0-6).
%W Week number of year with Monday as first day of week (00-53).
%x Locale’s date representation (mm/dd/yy).
%y Last two digits of year (00-99).
%Y Year (1970-).
See also: [strptime], page 811,[localtime], page 808,[gmtime], page 808,[mktime],
page 809,[time], page 807,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
[tm_struct,nchars] = strptime (str,fmt)
Convert the string str to the time structure tm struct under the control of the format
string fmt.
If fmt fails to match, nchars is 0; otherwise, it is set to the position of last matched
character plus 1. Always check for this unless you’re absolutely sure the date string
will be parsed correctly.
See also: [strftime], page 809,[localtime], page 808,[gmtime], page 808,[mktime],
page 809,[time], page 807,[now], page 807,[date], page 812,[clock], page 811,
[datenum], page 813,[datestr], page 814,[datevec], page 816,[calendar], page 817,
[weekday], page 817.
Most of the remaining functions described in this section are not patterned after the
standard C library. Some are available for compatibility with matlab and others are
provided because they are useful.
clock ()
Return the current local date and time as a date vector.
The date vector contains the following fields: current year, month (1-12), day (1-31),
hour (0-23), minute (0-59), and second (0-61). The seconds field has a fractional part
after the decimal point for extended accuracy.
812 GNU Octave
For example:
fix (clock ())
⇒[ 1993, 8, 20, 4, 56, 1 ]
clock is more accurate on systems that have the gettimeofday function.
See also: [now], page 807,[date], page 812,[datevec], page 816.
date ()
Return the current date as a character string in the form DD-MMM-YYYY.
For example:
date ()
⇒"20-Aug-1993"
See also: [now], page 807,[clock], page 811,[datestr], page 814,[localtime], page 808.
etime (t2,t1)
Return the difference in seconds between two time values returned from clock (t2 −
t1).
For example:
t0 = clock ();
# many computations later...
elapsed_time = etime (clock (), t0);
will set the variable elapsed_time to the number of seconds since the variable t0
was set.
See also: [tic], page 813,[toc], page 813,[clock], page 811,[cputime], page 812,
[addtodate], page 816.
[total,user,system] = cputime ();
Return the CPU time used by your Octave session.
The first output is the total time spent executing your process and is equal to the sum
of second and third outputs, which are the number of CPU seconds spent executing
in user mode and the number of CPU seconds spent executing in system mode,
respectively.
If your system does not have a way to report CPU time usage, cputime returns 0 for
each of its output values.
Note that because Octave used some CPU time to start, it is reasonable to check to
see if cputime works by checking to see if the total CPU time used is nonzero.
See also: [tic], page 813,[toc], page 813.
is_leap_year ()
is_leap_year (year)
Return true if year is a leap year and false otherwise.
If no year is specified, is_leap_year uses the current year.
For example:
is_leap_year (2000)
⇒1
See also: [weekday], page 817,[eomday], page 817,[calendar], page 817.
Chapter 36: System Utilities 813
tic ()
id = tic ()
toc ()
toc (id)
val = toc (. . . )
Set or check a wall-clock timer.
Calling tic without an output argument sets the internal timer state. Subsequent
calls to toc return the number of seconds since the timer was set. For example,
tic ();
# many computations later...
elapsed_time = toc ();
will set the variable elapsed_time to the number of seconds since the most recent
call to the function tic.
If called with one output argument, tic returns a scalar of type uint64 that may be
later passed to toc.
id = tic; pause (5); toc (id)
⇒5.0010
Calling tic and toc this way allows nested timing calls.
If you are more interested in the CPU time that your process used, you should use
the cputime function instead. The tic and toc functions report the actual wall clock
time that elapsed between the calls. This may include time spent processing other
jobs or doing nothing at all.
See also: [toc], page 813,[cputime], page 812.
pause ()
pause (n)
Suspend the execution of the program for nseconds.
If invoked without an input arguments then the program is suspended until a character
is typed.
nis a positive real value and may be a fraction of a second, for example:
tic; pause (0.05); toc
aElapsed time is 0.05039 seconds.
The following example prints a message and then waits 5 seconds before clearing the
screen.
disp ("wait please...");
pause (5);
clc;
See also: [kbhit], page 249.
days = datenum (datevec)
days = datenum (year,month,day)
days = datenum (year,month,day,hour)
days = datenum (year,month,day,hour,minute)
days = datenum (year,month,day,hour,minute,second)
814 GNU Octave
days = datenum ("datestr")
days = datenum ("datestr",f)
days = datenum ("datestr",p)
[days,secs] = datenum (. . . )
Return the date/time input as a serial day number, with Jan 1, 0000 defined as day
1.
The integer part, floor (days)counts the number of complete days in the date input.
The fractional part, rem (days, 1) corresponds to the time on the given day.
The input may be a date vector (see datevec), datestr (see datestr), or directly
specified as input.
When processing input datestrings, fis the format string used to interpret date strings
(see datestr). If no format fis specified, then a relatively slow search is performed
through various formats. It is always preferable to specify the format string fif it
is known. Formats which do not specify a particular time component will have the
value set to zero. Formats which do not specify a date will default to January 1st of
the current year.
pis the year at the start of the century to which two-digit years will be referenced.
If not specified, it defaults to the current year minus 50.
The optional output secs holds the time on the specified day with greater precision
than days.
Notes:
•Years can be negative and/or fractional.
•Months below 1 are considered to be January.
•Days of the month start at 1.
•Days beyond the end of the month go into subsequent months.
•Days before the beginning of the month go to the previous month.
•Days can be fractional.
Caution: this function does not attempt to handle Julian calendars so dates before
October 15, 1582 are wrong by as much as eleven days. Also, be aware that only
Roman Catholic countries adopted the calendar in 1582. It took until 1924 for it to
be adopted everywhere. See the Wikipedia entry on the Gregorian calendar for more
details.
Warning: leap seconds are ignored. A table of leap seconds is available on the
Wikipedia entry for leap seconds.
See also: [datestr], page 814,[datevec], page 816,[now], page 807,[clock], page 811,
[date], page 812.
str = datestr (date)
str = datestr (date,f)
str = datestr (date,f,p)
Format the given date/time according to the format fand return the result in str.
date is a serial date number (see datenum) or a date vector (see datevec). The value
of date may also be a string or cell array of strings.
Chapter 36: System Utilities 815
fcan be an integer which corresponds to one of the codes in the table below, or a
date format string.
pis the year at the start of the century in which two-digit years are to be interpreted
in. If not specified, it defaults to the current year minus 50.
For example, the date 730736.65149 (2000-09-07 15:38:09.0934) would be formatted
as follows:
Code Format Example
0 dd-mmm-yyyy HH:MM:SS 07-Sep-2000 15:38:09
1 dd-mmm-yyyy 07-Sep-2000
2 mm/dd/yy 09/07/00
3 mmm Sep
4 m S
5 mm 09
6 mm/dd 09/07
7 dd 07
8 ddd Thu
9 d T
10 yyyy 2000
11 yy 00
12 mmmyy Sep00
13 HH:MM:SS 15:38:09
14 HH:MM:SS PM 3:38:09 PM
15 HH:MM 15:38
16 HH:MM PM 3:38 PM
17 QQ-YY Q3-00
18 QQ Q3
19 dd/mm 07/09
20 dd/mm/yy 07/09/00
21 mmm.dd,yyyy HH:MM:SS Sep.07,2000 15:38:08
22 mmm.dd,yyyy Sep.07,2000
23 mm/dd/yyyy 09/07/2000
24 dd/mm/yyyy 07/09/2000
25 yy/mm/dd 00/09/07
26 yyyy/mm/dd 2000/09/07
27 QQ-YYYY Q3-2000
28 mmmyyyy Sep2000
29 yyyy-mm-dd 2000-09-07
30 yyyymmddTHHMMSS 20000907T153808
31 yyyy-mm-dd HH:MM:SS 2000-09-07 15:38:08
If fis a format string, the following symbols are recognized:
Symbol Meaning Example
yyyy Full year 2005
yy Two-digit year 05
mmmm Full month name December
816 GNU Octave
mmm Abbreviated month name Dec
mm Numeric month number (padded with zeros) 01, 08, 12
m First letter of month name (capitalized) D
dddd Full weekday name Sunday
ddd Abbreviated weekday name Sun
dd Numeric day of month (padded with zeros) 11
d First letter of weekday name (capitalized) S
HH Hour of day, padded with zeros, 09:00
or padded with spaces if PM is set 9:00 AM
MM Minute of hour (padded with zeros) 10:05
SS Second of minute (padded with zeros) 10:05:03
FFF Milliseconds of second (padded with zeros) 10:05:03.012
AM Use 12-hour time format 11:30 AM
PM Use 12-hour time format 11:30 PM
If fis not specified or is -1, then use 0, 1 or 16, depending on whether the date
portion or the time portion of date is empty.
If pis nor specified, it defaults to the current year minus 50.
If a matrix or cell array of dates is given, a column vector of date strings is returned.
See also: [datenum], page 813,[datevec], page 816,[date], page 812,[now], page 807,
[clock], page 811.
v= datevec (date)
v= datevec (date,f)
v= datevec (date,p)
v= datevec (date,f,p)
[y,m,d,h,mi,s] = datevec (. . . )
Convert a serial date number (see datenum) or date string (see datestr) into a date
vector.
A date vector is a row vector with six members, representing the year, month, day,
hour, minute, and seconds respectively.
fis the format string used to interpret date strings (see datestr). If date is a string,
but no format is specified, then a relatively slow search is performed through various
formats. It is always preferable to specify the format string fif it is known. Formats
which do not specify a particular time component will have the value set to zero.
Formats which do not specify a date will default to January 1st of the current year.
pis the year at the start of the century to which two-digit years will be referenced.
If not specified, it defaults to the current year minus 50.
See also: [datenum], page 813,[datestr], page 814,[clock], page 811,[now], page 807,
[date], page 812.
d= addtodate (d,q,f)
Add qamount of time (with units f) to the serial datenum, d.
fmust be one of "year","month","day","hour","minute","second", or
"millisecond".
See also: [datenum], page 813,[datevec], page 816,[etime], page 812.

Chapter 36: System Utilities 817
c= calendar ()
c= calendar (d)
c= calendar (y,m)
calendar (. . .)
Return the current monthly calendar in a 6x7 matrix.
If dis specified, return the calendar for the month containing the date d, which must
be a serial date number or a date string.
If yand mare specified, return the calendar for year yand month m.
If no output arguments are specified, print the calendar on the screen instead of
returning a matrix.
See also: [datenum], page 813,[datestr], page 814.
[n,s] = weekday (d)
[n,s] = weekday (d,format)
Return the day of the week as a number in nand as a string in s.
The days of the week are numbered 1–7 with the first day being Sunday.
dis a serial date number or a date string.
If the string format is not present or is equal to "short" then swill contain the
abbreviated name of the weekday. If format is "long" then swill contain the full
name.
Table of return values based on format:
n"short" "long"
1 Sun Sunday
2 Mon Monday
3 Tue Tuesday
4 Wed Wednesday
5 Thu Thursday
6 Fri Friday
7 Sat Saturday
See also: [eomday], page 817,[is leap year], page 812,[calendar], page 817,[datenum],
page 813,[datevec], page 816.
e= eomday (y,m)
Return the last day of the month mfor the year y.
See also: [weekday], page 817,[datenum], page 813,[datevec], page 816,[is leap year],
page 812,[calendar], page 817.
datetick ()
datetick (date_format)
datetick (axis_str,date_format)
datetick (. . ., "keeplimits")
datetick (. . ., "keepticks")
datetick (hax, . . . )
Add date formatted tick labels to an axis.

818 GNU Octave
The axis to apply the ticks to is determined by axis str which can take the values
"x","y", or "z". The default value is "x".
The formatting of the labels is determined by the variable date format, which can
either be a string or positive integer that datestr accepts.
See also: [datenum], page 813,[datestr], page 814.
36.2 Filesystem Utilities
Octave includes many utility functions for copying, moving, renaming, and deleting files;
for creating, reading, and deleting directories; for retrieving status information on files; and
for manipulating file and path names.
movefile (f1)
movefile (f1,f2)
movefile (f1,f2, ’f’)
[status,msg,msgid] = movefile (. . . )
Move the source files or directories f1 to the destination f2.
The name f1 may contain globbing patterns. If f1 expands to multiple filenames,
f2 must be a directory. If no destination f2 is specified then the destination is the
present working directory. If f2 is a filename then f1 is renamed to f2.
When the force flag ’f’ is given any existing files will be overwritten without prompt-
ing.
If successful, status is 1, and msg,msgid are empty character strings (""). Otherwise,
status is 0, msg contains a system-dependent error message, and msgid contains a
unique message identifier. Note that the status code is exactly opposite that of the
system command.
See also: [rename], page 818,[copyfile], page 818,[unlink], page 819,[delete], page 360,
[glob], page 824.
rename old new
[err,msg] = rename (old,new)
Change the name of file old to new.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [movefile], page 818,[copyfile], page 818,[ls], page 843,[dir], page 843.
[status,msg,msgid] = copyfile (f1,f2)
[status,msg,msgid] = copyfile (f1,f2, ’f’)
Copy the source files or directories f1 to the destination f2.
The name f1 may contain globbing patterns. If f1 expands to multiple filenames, f2
must be a directory.
When the force flag ’f’ is given any existing files will be overwritten without prompt-
ing.
If successful, status is 1, and msg,msgid are empty character strings (""). Otherwise,
status is 0, msg contains a system-dependent error message, and msgid contains a
Chapter 36: System Utilities 819
unique message identifier. Note that the status code is exactly opposite that of the
system command.
See also: [movefile], page 818,[rename], page 818,[unlink], page 819,[delete],
page 360,[glob], page 824.
[err,msg] = unlink (file)
Delete the file named file.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [delete], page 360,[rmdir], page 820.
link old new
[err,msg] = link (old,new)
Create a new link (also known as a hard link) to an existing file.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [symlink], page 819,[unlink], page 819,[readlink], page 819,[lstat],
page 821.
symlink old new
[err,msg] = symlink (old,new)
Create a symbolic link new which contains the string old.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [link], page 819,[unlink], page 819,[readlink], page 819,[lstat], page 821.
readlink symlink
[result,err,msg] = readlink (symlink)
Read the value of the symbolic link symlink.
If successful, result contains the contents of the symbolic link symlink,err is 0, and
msg is an empty string. Otherwise, err is nonzero and msg contains a system-
dependent error message.
See also: [lstat], page 821,[symlink], page 819,[link], page 819,[unlink], page 819,
[delete], page 360.
mkdir dir
mkdir (parent,dir)
[status,msg,msgid] = mkdir (. . . )
Create a directory named dir in the directory parent, creating any intermediate di-
rectories if necessary.
If dir is a relative path and no parent directory is specified then the present working
directory is used.
If successful, status is 1, and msg and msgid are empty strings (""). Otherwise,
status is 0, msg contains a system-dependent error message, and msgid contains a
unique message identifier.

820 GNU Octave
When creating a directory permissions will be set to 0777 - UMASK.
See also: [rmdir], page 820,[pwd], page 844,[cd], page 842,[umask], page 820.
rmdir dir
rmdir (dir,"s")
[status,msg,msgid] = rmdir (. . . )
Remove the directory named dir.
If the optional second parameter is supplied with value "s", recursively remove all
subdirectories as well.
If successful, status is 1, and msg,msgid are empty character strings (""). Otherwise,
status is 0, msg contains a system-dependent error message, and msgid contains a
unique message identifier.
See also: [mkdir], page 819,[confirm recursive rmdir], page 820,[pwd], page 844.
val = confirm_recursive_rmdir ()
old_val = confirm_recursive_rmdir (new_val)
confirm_recursive_rmdir (new_val,"local")
Query or set the internal variable that controls whether Octave will ask for confirma-
tion before recursively removing a directory tree.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [rmdir], page 820.
err = mkfifo (name,mode)
[err,msg] = mkfifo (name,mode)
Create a FIFO special file named name with file mode mode.
mode is interpreted as an octal number and is subject to umask processing. The final
calculated mode is mode -umask.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [pipe], page 837,[umask], page 820.
umask (mask)
Set the permission mask for file creation.
The parameter mask is an integer, interpreted as an octal number.
If successful, returns the previous value of the mask (as an integer to be interpreted
as an octal number); otherwise an error message is printed.
The permission mask is a UNIX concept used when creating new objects on a file
system such as files, directories, or named FIFOs. The object to be created has base
permissions in an octal number mode which are modified according to the octal value
of mask. The final permissions for the new object are mode -mask.
See also: [fopen], page 265,[mkdir], page 819,[mkfifo], page 820.
Chapter 36: System Utilities 821
[info,err,msg] = stat (file)
[info,err,msg] = stat (fid)
[info,err,msg] = lstat (file)
[info,err,msg] = lstat (fid)
Return a structure info containing the following information about file or file identifier
fid.
dev ID of device containing a directory entry for this file.
ino File number of the file.
mode File mode, as an integer. Use the functions S_ISREG,S_ISDIR,S_ISCHR,
S_ISBLK,S_ISFIFO,S_ISLNK, or S_ISSOCK to extract information from
this value.
modestr File mode, as a string of ten letters or dashes as would be returned by ls
-l.
nlink Number of links.
uid User ID of file’s owner.
gid Group ID of file’s group.
rdev ID of device for block or character special files.
size Size in bytes.
atime Time of last access in the same form as time values returned from time.
See Section 36.1 [Timing Utilities], page 807.
mtime Time of last modification in the same form as time values returned from
time. See Section 36.1 [Timing Utilities], page 807.
ctime Time of last file status change in the same form as time values returned
from time. See Section 36.1 [Timing Utilities], page 807.
blksize Size of blocks in the file.
blocks Number of blocks allocated for file.
If the call is successful err is 0 and msg is an empty string. If the file does not exist,
or some other error occurs, info is an empty matrix, err is −1, and msg contains the
corresponding system error message.
If file is a symbolic link, stat will return information about the actual file that is
referenced by the link. Use lstat if you want information about the symbolic link
itself.
For example:
[info, err, msg] = stat ("/vmlinuz")
⇒info =
{
atime = 855399756
rdev = 0
ctime = 847219094
uid = 0
822 GNU Octave
size = 389218
blksize = 4096
mtime = 847219094
gid = 6
nlink = 1
blocks = 768
mode = -rw-r--r--
modestr = -rw-r--r--
ino = 9316
dev = 2049
}
⇒err = 0
⇒msg =
See also: [lstat], page 821,[ls], page 843,[dir], page 843.
S_ISBLK (mode)
Return true if mode corresponds to a block device.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
S_ISCHR (mode)
Return true if mode corresponds to a character device.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
S_ISDIR (mode)
Return true if mode corresponds to a directory.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
S_ISFIFO (mode)
Return true if mode corresponds to a fifo.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
S_ISLNK (mode)
Return true if mode corresponds to a symbolic link.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
S_ISREG (mode)
Return true if mode corresponds to a regular file.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
Chapter 36: System Utilities 823
S_ISSOCK (mode)
Return true if mode corresponds to a socket.
The value of mode is assumed to be returned from a call to stat.
See also: [stat], page 821,[lstat], page 821.
fileattrib (file)
fileattrib ()
[status,msg,msgid] = fileattrib (. . . )
Return information about file.
If successful, status is 1 and msg is a structure with the following fields:
Name Full name of file.
archive True if file is an archive (Windows).
system True if file is a system file (Windows).
hidden True if file is a hidden file (Windows).
directory
True if file is a directory.
UserRead
GroupRead
OtherRead
True if the user (group; other users) has read permission for file.
UserWrite
GroupWrite
OtherWrite
True if the user (group; other users) has write permission for file.
UserExecute
GroupExecute
OtherExecute
True if the user (group; other users) has execute permission for file.
If an attribute does not apply (i.e., archive on a Unix system) then the field is set to
NaN.
If attrib fails, msg is a non-empty string containing an error message and msg id is
the non-empty string "fileattrib".
With no input arguments, return information about the current directory.
If file contains globbing characters, return information about all the matching files.
See also: [glob], page 824.
isdir (f)
Return true if fis a directory.
See also: [exist], page 130,[stat], page 821,[is absolute filename], page 827,
[is rooted relative filename], page 827.
824 GNU Octave
files = readdir (dir)
[files,err,msg] = readdir (dir)
Return the names of files in the directory dir as a cell array of strings.
If an error occurs, return an empty cell array in files. If successful, err is 0 and msg
is an empty string. Otherwise, err is nonzero and msg contains a system-dependent
error message.
See also: [ls], page 843,[dir], page 843,[glob], page 824,[what], page 133.
glob (pattern)
Given an array of pattern strings (as a char array or a cell array) in pattern, return a
cell array of filenames that match any of them, or an empty cell array if no patterns
match.
The pattern strings are interpreted as filename globbing patterns (as they are used
by Unix shells).
Within a pattern
*matches any string, including the null string,
?matches any single character, and
[...] matches any of the enclosed characters.
Tilde expansion is performed on each of the patterns before looking for matching
filenames. For example:
ls
⇒file1 file2 file3 myfile1 myfile1b
glob ("*file1")
⇒{
[1,1] = file1
[2,1] = myfile1
}
glob ("myfile?")
⇒{
[1,1] = myfile1
}
glob ("file[12]")
⇒{
[1,1] = file1
[2,1] = file2
}
See also: [ls], page 843,[dir], page 843,[readdir], page 824,[what], page 133.
file_in_path (path,file)
file_in_path (path,file,"all")
Return the absolute name of file if it can be found in path.

Chapter 36: System Utilities 825
The value of path should be a colon-separated list of directories in the format described
for path. If no file is found, return an empty character string. For example:
file_in_path (EXEC_PATH, "sh")
⇒"/bin/sh"
If the second argument is a cell array of strings, search each directory of the path for
element of the cell array and return the first that matches.
If the third optional argument "all" is supplied, return a cell array containing the
list of all files that have the same name in the path. If no files are found, return an
empty cell array.
See also: [file in loadpath], page 194,[dir in loadpath], page 194,[path], page 193.
filesep ()
filesep ("all")
Return the system-dependent character used to separate directory names.
If "all" is given, the function returns all valid file separators in the form of a string.
The list of file separators is system-dependent. It is ‘/’ (forward slash) under UNIX
or Mac OS X, ‘/’ and ‘\’ (forward and backward slashes) under Windows.
See also: [pathsep], page 194.
val = filemarker ()
old_val = filemarker (new_val)
filemarker (new_val,"local")
Query or set the character used to separate the filename from the subfunction names
contained within the file.
By default this is the character ‘>’. This can be used in a generic manner to interact
with subfunctions. For example,
help (["myfunc", filemarker, "mysubfunc"])
returns the help string associated with the subfunction mysubfunc located in the file
myfunc.m.
filemarker is also useful during debugging for placing breakpoints within subfunc-
tions or nested functions. For example,
dbstop (["myfunc", filemarker, "mysubfunc"])
will set a breakpoint at the first line of the subfunction mysubfunc.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
[dir,name,ext] = fileparts (filename)
Return the directory, name, and extension components of filename.
The input filename is a string which is parsed. There is no attempt to check whether
the filename or directory specified actually exists.
See also: [fullfile], page 826,[filesep], page 825.

826 GNU Octave
filename = fullfile (dir1,dir2, . . . , file)
filenames = fullfile (. . . , files)
Build complete filename from separate parts.
Joins any number of path components intelligently. The return value is the concate-
nation of each component with exactly one file separator between each non empty
part and at most one leading and/or trailing file separator.
If the last component part is a cell array, returns a cell array of filepaths, one for each
element in the last component, e.g.:
fullfile ("/home/username", "data", {"f1.csv", "f2.csv", "f3.csv"})
⇒/home/username/data/f1.csv
/home/username/data/f2.csv
/home/username/data/f3.csv
On Windows systems, while forward slash file separators do work, they are replaced by
backslashes; in addition drive letters are stripped of leading file separators to obtain
a valid file path.
Note: fullfile does not perform any validation of the resulting full filename.
See also: [fileparts], page 825,[filesep], page 825.
tilde_expand (string)
tilde_expand (cellstr)
Perform tilde expansion on string.
If string begins with a tilde character, (‘~’), all of the characters preceding the first
slash (or all characters, if there is no slash) are treated as a possible user name,
and the tilde and the following characters up to the slash are replaced by the home
directory of the named user. If the tilde is followed immediately by a slash, the tilde
is replaced by the home directory of the user running Octave.
If the input is a cell array of strings cellstr then tilde expansion is performed on each
string element.
Examples:
tilde_expand ("~joeuser/bin")
⇒"/home/joeuser/bin"
tilde_expand ("~/bin")
⇒"/home/jwe/bin"
[cname,status,msg] = canonicalize_file_name (fname)
Return the canonical name of file fname.
If the file does not exist the empty string ("") is returned.
See also: [make absolute filename], page 826,[is absolute filename], page 827,
[is rooted relative filename], page 827.
make_absolute_filename (file)
Return the full name of file beginning from the root of the file system.
No check is done for the existence of file.
See also: [canonicalize file name], page 826,[is absolute filename], page 827,
[is rooted relative filename], page 827,[isdir], page 823.

Chapter 36: System Utilities 827
is_absolute_filename (file)
Return true if file is an absolute filename.
See also: [is rooted relative filename], page 827,[make absolute filename], page 826,
[isdir], page 823.
is_rooted_relative_filename (file)
Return true if file is a rooted-relative filename.
See also: [is absolute filename], page 827,[make absolute filename], page 826,[isdir],
page 823.
current_state = recycle ()
old_state = recycle (new_state)
Query or set the preference for recycling deleted files.
When recycling is enabled, commands which would permanently erase files instead
move them to a temporary location (such as the directory labeled Trash).
Programming Note: This function is provided for matlab compatibility, but recycling
is not implemented in Octave. To help avoid accidental data loss an error will be raised
if an attempt is made to enable file recycling.
See also: [delete], page 360,[rmdir], page 820.
36.3 File Archiving Utilities
filelist = bunzip2 (bzfile)
filelist = bunzip2 (bzfile,dir)
Unpack the bzip2 archive bzfile.
If dir is specified the files are unpacked in this directory rather than the one where
bzfile is located.
The optional output filelist is a list of the uncompressed files.
See also: [bzip2], page 829,[unpack], page 829,[gunzip], page 828,[unzip], page 829,
[untar], page 828.
filelist = gzip (files)
filelist = gzip (files,dir)
Compress the list of files and directories specified in files.
files is a character array or cell array of strings. Shell wildcards in the filename such
as ‘*’ or ‘?’ are accepted and expanded. Each file is compressed separately and a
new file with a ".gz" extension is created. The original files are not modified, but
existing compressed files will be silently overwritten. If a directory is specified then
gzip recursively compresses all files in the directory.
If dir is defined the compressed files are placed in this directory, rather than the orig-
inal directory where the uncompressed file resides. Note that this does not replicate
a directory tree in dir which may lead to files overwriting each other if there are
multiple files with the same name.
If dir does not exist it is created.
The optional output filelist is a list of the compressed files.
828 GNU Octave
See also: [gunzip], page 828,[unpack], page 829,[bzip2], page 829,[zip], page 828,
[tar], page 828.
filelist = gunzip (gzfile)
filelist = gunzip (gzfile,dir)
Unpack the gzip archive gzfile.
If gzfile is a directory, all gzfiles in the directory will be recursively unpacked.
If dir is specified the files are unpacked in this directory rather than the one where
gzfile is located.
The optional output filelist is a list of the uncompressed files.
See also: [gzip], page 827,[unpack], page 829,[bunzip2], page 827,[unzip], page 829,
[untar], page 828.
filelist = tar (tarfile,files)
filelist = tar (tarfile,files,rootdir)
Pack the list of files and directories specified in files into the TAR archive tarfile.
files is a character array or cell array of strings. Shell wildcards in the filename such
as ‘*’ or ‘?’ are accepted and expanded. Directories are recursively traversed and all
files are added to the archive.
If rootdir is defined then any files without absolute pathnames are located relative to
rootdir rather than the current directory.
The optional output filelist is a list of the files that were included in the archive.
See also: [untar], page 828,[unpack], page 829,[bzip2], page 829,[gzip], page 827,
[zip], page 828.
untar (tarfile)
untar (tarfile,dir)
Unpack the TAR archive tarfile.
If dir is specified the files are unpacked in this directory rather than the one where
tarfile is located.
The optional output filelist is a list of the uncompressed files.
See also: [tar], page 828,[unpack], page 829,[bunzip2], page 827,[gunzip], page 828,
[unzip], page 829.
filelist = zip (zipfile,files)
filelist = zip (zipfile,files,rootdir)
Compress the list of files and directories specified in files into the ZIP archive zipfile.
files is a character array or cell array of strings. Shell wildcards in the filename such
as ‘*’ or ‘?’ are accepted and expanded. Directories are recursively traversed and all
files are compressed and added to the archive.
If rootdir is defined then any files without absolute pathnames are located relative to
rootdir rather than the current directory.
The optional output filelist is a list of the files that were included in the archive.
See also: [unzip], page 829,[unpack], page 829,[bzip2], page 829,[gzip], page 827,
[tar], page 828.
Chapter 36: System Utilities 829
filelist = unzip (zipfile)
filelist = unzip (zipfile,dir)
Unpack the ZIP archive zipfile.
If dir is specified the files are unpacked in this directory rather than the one where
zipfile is located.
The optional output filelist is a list of the uncompressed files.
See also: [zip], page 828,[unpack], page 829,[bunzip2], page 827,[gunzip], page 828,
[untar], page 828.
files = unpack (file)
files = unpack (file,dir)
files = unpack (file,dir,filetype)
Unpack the archive file based on its extension to the directory dir.
If file is a list of strings, then each file is unpacked individually. Shell wildcards in
the filename such as ‘*’ or ‘?’ are accepted and expanded.
If dir is not specified or is empty ([]), it defaults to the current directory. If a
directory is in the file list, then filetype must also be specified.
The specific archive filetype is inferred from the extension of the file. The filetype
may also be specified directly using a string which corresponds to a known extension.
Valid filetype extensions:
bz
bz2 bzip archive
gz gzip archive
tar tar archive
tarbz
tarbz2
tbz
tbz2 tar +bzip archive
targz
tgz tar +gzip archive
zcompress archive
zip zip archive
The optional return value is a list of files unpacked.
See also: [bunzip2], page 827,[gunzip], page 828,[unzip], page 829,[untar], page 828,
[bzip2], page 829,[gzip], page 827,[zip], page 828,[tar], page 828.
filelist = bzip2 (files)
filelist = bzip2 (files,dir)
Compress the list of files specified in files.
files is a character array or cell array of strings. Shell wildcards in the filename such
as ‘*’ or ‘?’ are accepted and expanded. Each file is compressed separately and a
830 GNU Octave
new file with a ".bz2" extension is created. The original files are not modified, but
existing compressed files will be silently overwritten.
If dir is defined the compressed files are placed in this directory, rather than the orig-
inal directory where the uncompressed file resides. Note that this does not replicate
a directory tree in dir which may lead to files overwriting each other if there are
multiple files with the same name.
If dir does not exist it is created.
The optional output filelist is a list of the compressed files.
See also: [bunzip2], page 827,[unpack], page 829,[gzip], page 827,[zip], page 828,
[tar], page 828.
36.4 Networking Utilities
gethostname ()
Return the hostname of the system where Octave is running.
36.4.1 FTP Objects
Octave supports the FTP protocol through an object-oriented interface. Use the function
ftp to create an FTP object which represents the connection. All FTP functions take an
FTP object as the first argument.
f= ftp (host)
f= ftp (host,username,password)
Connect to the FTP server host with username and password.
If username and password are not specified, user "anonymous" with no password is
used. The returned FTP object frepresents the established FTP connection.
The list of actions for an FTP object are shown below. All functions require an FTP
object as the first argument.
Method Description
ascii Set transfer type to ascii
binary Set transfer type to binary
cd Change remote working directory
close Close FTP connection
delete Delete remote file
dir List remote directory contents
mget Download remote files
mkdir Create remote directory
mput Upload local files
rename Rename remote file or directory
rmdir Remove remote directory
close (f)
Close the FTP connection represented by the FTP object f.
fis an FTP object returned by the ftp function.
Chapter 36: System Utilities 831
mget (f,file)
mget (f,dir)
mget (f,remote_name,target)
Download a remote file file or directory dir to the local directory on the FTP con-
nection f.
fis an FTP object returned by the ftp function.
The arguments file and dir can include wildcards and any files or directories on the
remote server that match will be downloaded.
If a third string argument target is given, then it must indicate the path to the local
destination directory. target may be a relative or absolute path.
mput (f,file)
Upload the local file file into the current remote directory on the FTP connection f.
fis an FTP object returned by the ftp function.
The argument file is passed through the glob function and any files that match the
wildcards in file will be uploaded.
cd (f)
cd (f,path)
Get or set the remote directory on the FTP connection f.
fis an FTP object returned by the ftp function.
If path is not specified, return the remote current working directory. Otherwise, set
the remote directory to path and return the new remote working directory.
If the directory does not exist, an error message is printed and the working directory
is not changed.
lst = dir (f)
List the current directory in verbose form for the FTP connection f.
fis an FTP object returned by the ftp function.
ascii (f)
Set the FTP connection fto use ASCII mode for transfers.
ASCII mode is only appropriate for text files as it will convert the remote host’s
newline representation to the local host’s newline representation.
fis an FTP object returned by the ftp function.
binary (f)
Set the FTP connection fto use binary mode for transfers.
In binary mode there is no conversion of newlines from the remote representation to
the local representation.
fis an FTP object returned by the ftp function.
delete (f,file)
Delete the remote file file over the FTP connection f.
fis an FTP object returned by the ftp function.
832 GNU Octave
rename (f,oldname,newname)
Rename or move the remote file or directory oldname to newname, over the FTP
connection f.
fis an FTP object returned by the ftp function.
mkdir (f,path)
Create the remote directory path, over the FTP connection f.
fis an FTP object returned by the ftp function.
rmdir (f,path)
Remove the remote directory path, over the FTP connection f.
fis an FTP object returned by the ftp function.
36.4.2 URL Manipulation
s= urlread (url)
[s,success] = urlread (url)
[s,success,message] = urlread (url)
[...] = urlread (url,method,param)
Download a remote file specified by its url and return its content in string s.
For example:
s = urlread ("ftp://ftp.octave.org/pub/README");
The variable success is 1 if the download was successful, otherwise it is 0 in which
case message contains an error message.
If no output argument is specified and an error occurs, then the error is signaled
through Octave’s error handling mechanism.
This function uses libcurl. Curl supports, among others, the HTTP, FTP, and FILE
protocols. Username and password may be specified in the URL. For example:
s = urlread ("http://user:password@example.com/file.txt");
GET and POST requests can be specified by method and param. The parameter
method is either ‘get’ or ‘post’ and param is a cell array of parameter and value
pairs. For example:
s = urlread ("http://www.google.com/search", "get",
{"query", "octave"});
See also: [urlwrite], page 832.
urlwrite (url,localfile)
f= urlwrite (url,localfile)
[f,success] = urlwrite (url,localfile)
[f,success,message] = urlwrite (url,localfile)
Download a remote file specified by its url and save it as localfile.
For example:
urlwrite ("ftp://ftp.octave.org/pub/README",
"README.txt");
The full path of the downloaded file is returned in f.

Chapter 36: System Utilities 833
The variable success is 1 if the download was successful, otherwise it is 0 in which
case message contains an error message.
If no output argument is specified and an error occurs, then the error is signaled
through Octave’s error handling mechanism.
This function uses libcurl. Curl supports, among others, the HTTP, FTP, and FILE
protocols. Username and password may be specified in the URL, for example:
urlwrite ("http://username:password@example.com/file.txt",
"file.txt");
GET and POST requests can be specified by method and param. The parameter
method is either ‘get’ or ‘post’ and param is a cell array of parameter and value
pairs. For example:
urlwrite ("http://www.google.com/search", "search.html",
"get", {"query", "octave"});
See also: [urlread], page 832.
36.4.3 Base64 and Binary Data Transmission
Some transmission channels can not accept binary data. It is customary to encode binary
data in Base64 for transmission and to decode the data upon reception.
s= base64_encode (x)
Encode a double matrix or array xinto the base64 format string s.
See also: [base64 decode], page 833.
x= base64_decode (s)
x= base64_decode (s,dims)
Decode the double matrix or array xfrom the base64 encoded string s.
The optional input parameter dims should be a vector containing the dimensions of
the decoded array.
See also: [base64 encode], page 833.
36.5 Controlling Subprocesses
Octave includes some high-level commands like system and popen for starting subprocesses.
If you want to run another program to perform some task and then look at its output, you
will probably want to use these functions.
Octave also provides several very low-level Unix-like functions which can also be used
for starting subprocesses, but you should probably only use them if you can’t find any way
to do what you need with the higher-level functions.
system ("string")
system ("string",return_output)
system ("string",return_output,type)
[status,output] = system (. . . )
Execute a shell command specified by string.
If the optional argument type is "async", the process is started in the background
and the process ID of the child process is returned immediately. Otherwise, the child

834 GNU Octave
process is started and Octave waits until it exits. If the type argument is omitted, it
defaults to the value "sync".
If system is called with one or more output arguments, or if the optional argument
return output is true and the subprocess is started synchronously, then the output
from the command is returned as a variable. Otherwise, if the subprocess is executed
synchronously, its output is sent to the standard output. To send the output of a
command executed with system through the pager, use a command like
[~, text] = system ("cmd");
disp (text);
or
printf ("%s\n", nthargout (2, "system", "cmd"));
The system function can return two values. The first is the exit status of the command
and the second is any output from the command that was written to the standard
output stream. For example,
[status, output] = system ("echo foo; exit 2");
will set the variable output to the string ‘foo’, and the variable status to the integer
‘2’.
For commands run asynchronously, status is the process id of the command shell that
is started to run the command.
See also: [unix], page 834,[dos], page 834.
unix ("command")
status = unix ("command")
[status,text] = unix ("command")
[...] = unix ("command","-echo")
Execute a system command if running under a Unix-like operating system, otherwise
do nothing.
Octave waits for the external command to finish before returning the exit status of
the program in status and any output in text.
When called with no output argument, or the "-echo" argument is given, then text
is also sent to standard output.
See also: [dos], page 834,[system], page 833,[isunix], page 847,[ismac], page 847,
[ispc], page 847.
dos ("command")
status = dos ("command")
[status,text] = dos ("command")
[...] = dos ("command","-echo")
Execute a system command if running under a Windows-like operating system, oth-
erwise do nothing.
Octave waits for the external command to finish before returning the exit status of
the program in status and any output in text.
When called with no output argument, or the "-echo" argument is given, then text
is also sent to standard output.
Chapter 36: System Utilities 835
See also: [unix], page 834,[system], page 833,[isunix], page 847,[ismac], page 847,
[ispc], page 847.
open file
output = open (file)
Open the file file in Octave or in an external application based on the file type as
determined by the filename extension.
Recognized file types are
.m Open file in the editor.
.mat Load the file in the base workspace.
.exe Execute the program (on Windows systems only).
Other file types are opened in the appropriate external application.
output = perl (scriptfile)
output = perl (scriptfile,argument1,argument2, . . . )
[output,status] = perl (. . . )
Invoke Perl script scriptfile, possibly with a list of command line arguments.
Return output in output and optional status in status. If scriptfile is not an absolute
filename it is searched for in the current directory and then in the Octave loadpath.
See also: [system], page 833,[python], page 835.
output = python (scriptfile)
output = python (scriptfile,argument1,argument2, . . . )
[output,status] = python (. . . )
Invoke Python script scriptfile, possibly with a list of command line arguments.
Return output in output and optional status in status. If scriptfile is not an absolute
filename it is searched for in the current directory and then in the Octave loadpath.
See also: [system], page 833,[perl], page 835.
fid = popen (command,mode)
Start a process and create a pipe.
The name of the command to run is given by command. The argument mode may
be
"r" The pipe will be connected to the standard output of the process, and
open for reading.
"w" The pipe will be connected to the standard input of the process, and open
for writing.
The file identifier corresponding to the input or output stream of the process is re-
turned in fid.
For example:
836 GNU Octave
fid = popen ("ls -ltr / | tail -3", "r");
while (ischar (s = fgets (fid)))
fputs (stdout, s);
endwhile
adrwxr-xr-x 33 root root 3072 Feb 15 13:28 etc
adrwxr-xr-x 3 root root 1024 Feb 15 13:28 lib
adrwxrwxrwt 15 root root 2048 Feb 17 14:53 tmp
See also: [popen2], page 836.
pclose (fid)
Close a file identifier that was opened by popen.
The function fclose may also be used for the same purpose.
See also: [fclose], page 266,[popen], page 835.
[in,out,pid] = popen2 (command,args)
Start a subprocess with two-way communication.
The name of the process is given by command, and args is an array or cell array of
strings containing options for the command.
The file identifiers for the input and output streams of the subprocess are returned
in in and out. If execution of the command is successful, pid contains the process ID
of the subprocess. Otherwise, pid is −1.
For example:
[in, out, pid] = popen2 ("sort", "-r");
fputs (in, "these\nare\nsome\nstrings\n");
fclose (in);
EAGAIN = errno ("EAGAIN");
done = false;
do
s = fgets (out);
if (ischar (s))
fputs (stdout, s);
elseif (errno () == EAGAIN)
pause (0.1);
fclear (out);
else
done = true;
endif
until (done)
fclose (out);
waitpid (pid);
athese
astrings
asome
aare

Chapter 36: System Utilities 837
Note that popen2, unlike popen, will not "reap"the child process. If you don’t use
waitpid to check the child’s exit status, it will linger until Octave exits.
See also: [popen], page 835,[waitpid], page 838.
val = EXEC_PATH ()
old_val = EXEC_PATH (new_val)
EXEC_PATH (new_val,"local")
Query or set the internal variable that specifies a colon separated list of directories
to append to the shell PATH when executing external programs.
The initial value of is taken from the environment variable OCTAVE_EXEC_PATH, but
that value can be overridden by the command line argument --exec-path PATH.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [IMAGE PATH], page 743,[OCTAVE HOME], page 847.
In most cases, the following functions simply decode their arguments and make the
corresponding Unix system calls. For a complete example of how they can be used, look at
the definition of the function popen2.
[pid,msg] = fork ()
Create a copy of the current process.
Fork can return one of the following values:
>0 You are in the parent process. The value returned from fork is the
process id of the child process. You should probably arrange to wait for
any child processes to exit.
0 You are in the child process. You can call exec to start another process.
If that fails, you should probably call exit.
<0 The call to fork failed for some reason. You must take evasive action. A
system dependent error message will be waiting in msg.
[err,msg] = exec (file,args)
Replace current process with a new process.
Calling exec without first calling fork will terminate your current Octave process
and replace it with the program named by file. For example,
exec ("ls", "-l")
will run ls and return you to your shell prompt.
If successful, exec does not return. If exec does return, err will be nonzero, and msg
will contain a system-dependent error message.
[read_fd,write_fd,err,msg] = pipe ()
Create a pipe and return the reading and writing ends of the pipe into read fd and
write fd respectively.
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [mkfifo], page 820.
838 GNU Octave
[fid,msg] = dup2 (old,new)
Duplicate a file descriptor.
If successful, fid is greater than zero and contains the new file ID. Otherwise, fid is
negative and msg contains a system-dependent error message.
See also: [fopen], page 265,[fclose], page 266,[fcntl], page 840.
[pid,status,msg] = waitpid (pid,options)
Wait for process pid to terminate.
The pid argument can be:
−1 Wait for any child process.
0 Wait for any child process whose process group ID is equal to that of the
Octave interpreter process.
>0 Wait for termination of the child process with ID pid.
The options argument can be a bitwise OR of zero or more of the following constants:
0Wait until signal is received or a child process exits (this is the default if
the options argument is missing).
WNOHANG Do not hang if status is not immediately available.
WUNTRACED
Report the status of any child processes that are stopped, and whose
status has not yet been reported since they stopped.
WCONTINUE
Return if a stopped child has been resumed by delivery of SIGCONT. This
value may not be meaningful on all systems.
If the returned value of pid is greater than 0, it is the process ID of the child process
that exited. If an error occurs, pid will be less than zero and msg will contain a
system-dependent error message. The value of status contains additional system-
dependent information about the subprocess that exited.
See also: [WCONTINUE], page 838,[WCOREDUMP], page 838,[WEXITSTATUS],
page 839,[WIFCONTINUED], page 839,[WIFSIGNALED], page 839,
[WIFSTOPPED], page 839,[WNOHANG], page 839,[WSTOPSIG], page 840,
[WTERMSIG], page 840,[WUNTRACED], page 840.
WCONTINUE ()
Return the numerical value of the option argument that may be passed to waitpid
to indicate that it should also return if a stopped child has been resumed by delivery
of a SIGCONT signal.
See also: [waitpid], page 838,[WNOHANG], page 839,[WUNTRACED], page 840.
WCOREDUMP (status)
Given status from a call to waitpid, return true if the child produced a core dump.
This function should only be employed if WIFSIGNALED returned true. The macro
used to implement this function is not specified in POSIX.1-2001 and is not available
on some Unix implementations (e.g., AIX, SunOS).
Chapter 36: System Utilities 839
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WIFSIGNALED], page 839,[WTERMSIG], page 840,[WIFSTOPPED], page 839,
[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WEXITSTATUS (status)
Given status from a call to waitpid, return the exit status of the child.
This function should only be employed if WIFEXITED returned true.
See also: [waitpid], page 838,[WIFEXITED], page 839,[WIFSIGNALED], page 839,
[WTERMSIG], page 840,[WCOREDUMP], page 838,[WIFSTOPPED], page 839,
[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WIFCONTINUED (status)
Given status from a call to waitpid, return true if the child process was resumed by
delivery of SIGCONT.
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WIFSIGNALED], page 839,[WTERMSIG], page 840,[WCOREDUMP], page 838,
[WIFSTOPPED], page 839,[WSTOPSIG], page 840.
WIFSIGNALED (status)
Given status from a call to waitpid, return true if the child process was terminated
by a signal.
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WTERMSIG], page 840,[WCOREDUMP], page 838,[WIFSTOPPED], page 839,
[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WIFSTOPPED (status)
Given status from a call to waitpid, return true if the child process was stopped by
delivery of a signal.
This is only possible if the call was done using WUNTRACED or when the child is being
traced (see ptrace(2)).
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WIFSIGNALED], page 839,[WTERMSIG], page 840,[WCOREDUMP], page 838,
[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WIFEXITED (status)
Given status from a call to waitpid, return true if the child terminated normally.
See also: [waitpid], page 838,[WEXITSTATUS], page 839,[WIFSIGNALED],
page 839,[WTERMSIG], page 840,[WCOREDUMP], page 838,[WIFSTOPPED],
page 839,[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WNOHANG ()
Return the numerical value of the option argument that may be passed to waitpid to
indicate that it should return its status immediately instead of waiting for a process
to exit.
See also: [waitpid], page 838,[WUNTRACED], page 840,[WCONTINUE], page 838.
840 GNU Octave
WSTOPSIG (status)
Given status from a call to waitpid, return the number of the signal which caused
the child to stop.
This function should only be employed if WIFSTOPPED returned true.
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WIFSIGNALED], page 839,[WTERMSIG], page 840,[WCOREDUMP], page 838,
[WIFSTOPPED], page 839,[WIFCONTINUED], page 839.
WTERMSIG (status)
Given status from a call to waitpid, return the number of the signal that caused the
child process to terminate.
This function should only be employed if WIFSIGNALED returned true.
See also: [waitpid], page 838,[WIFEXITED], page 839,[WEXITSTATUS], page 839,
[WIFSIGNALED], page 839,[WCOREDUMP], page 838,[WIFSTOPPED], page 839,
[WSTOPSIG], page 840,[WIFCONTINUED], page 839.
WUNTRACED ()
Return the numerical value of the option argument that may be passed to waitpid
to indicate that it should also return if the child process has stopped but is not traced
via the ptrace system call
See also: [waitpid], page 838,[WNOHANG], page 839,[WCONTINUE], page 838.
[err,msg] = fcntl (fid,request,arg)
Change the properties of the open file fid.
The following values may be passed as request:
F_DUPFD Return a duplicate file descriptor.
F_GETFD Return the file descriptor flags for fid.
F_SETFD Set the file descriptor flags for fid.
F_GETFL Return the file status flags for fid. The following codes may be returned
(some of the flags may be undefined on some systems).
O_RDONLY Open for reading only.
O_WRONLY Open for writing only.
O_RDWR Open for reading and writing.
O_APPEND Append on each write.
O_CREAT Create the file if it does not exist.
O_NONBLOCK
Non-blocking mode.
O_SYNC Wait for writes to complete.
O_ASYNC Asynchronous I/O.
F_SETFL Set the file status flags for fid to the value specified by arg. The only
flags that can be changed are O_APPEND and O_NONBLOCK.
Chapter 36: System Utilities 841
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
See also: [fopen], page 265,[dup2], page 838.
[err,msg] = kill (pid,sig)
Send signal sig to process pid.
If pid is positive, then signal sig is sent to pid.
If pid is 0, then signal sig is sent to every process in the process group of the current
process.
If pid is -1, then signal sig is sent to every process except process 1.
If pid is less than -1, then signal sig is sent to every process in the process group -pid.
If sig is 0, then no signal is sent, but error checking is still performed.
Return 0 if successful, otherwise return -1.
SIG ()
Return a structure containing Unix signal names and their defined values.
36.6 Process, Group, and User IDs
pgid = getpgrp ()
Return the process group id of the current process.
pid = getpid ()
Return the process id of the current process.
See also: [getppid], page 841.
pid = getppid ()
Return the process id of the parent process.
See also: [getpid], page 841.
euid = geteuid ()
Return the effective user id of the current process.
See also: [getuid], page 841.
uid = getuid ()
Return the real user id of the current process.
See also: [geteuid], page 841.
egid = getegid ()
Return the effective group id of the current process.
See also: [getgid], page 841.
gid = getgid ()
Return the real group id of the current process.
See also: [getegid], page 841.
842 GNU Octave
36.7 Environment Variables
getenv (var)
Return the value of the environment variable var.
For example,
getenv ("PATH")
returns a string containing the value of your path.
See also: [setenv], page 842,[unsetenv], page 842.
setenv (var,value)
setenv (var)
putenv (. . .)
Set the value of the environment variable var to value.
If no value is specified then the variable will be assigned the null string.
See also: [unsetenv], page 842,[getenv], page 842.
status = unsetenv (var)
Delete the environment variable var.
Return 0 if the variable was deleted, or did not exist, and -1 if an error occurred.
See also: [setenv], page 842,[getenv], page 842.
homedir = get_home_directory ()
Return the current home directory.
On most systems, this is equivalent to getenv ("HOME"). On Windows systems, if
the environment variable HOME is not set then it is equivalent to fullfile (getenv
("HOMEDRIVE"), getenv ("HOMEPATH"))
See also: [getenv], page 842.
36.8 Current Working Directory
cd dir
cd
old_dir = cd (dir)
chdir . . .
Change the current working directory to dir.
If dir is omitted, the current directory is changed to the user’s home directory ("~").
For example,
cd ~/octave
changes the current working directory to ~/octave. If the directory does not exist,
an error message is printed and the working directory is not changed.
chdir is an alias for cd and can be used in all of the same calling formats.
Compatibility Note: When called with no arguments, matlab prints the present
working directory rather than changing to the user’s home directory.
See also: [pwd], page 844,[mkdir], page 819,[rmdir], page 820,[dir], page 843,[ls],
page 843.

Chapter 36: System Utilities 843
ls
ls filenames
ls options
ls options filenames
list = ls (. . . )
List directory contents.
The ls command is implemented by calling the native operating system’s directory
listing command—available options will vary from system to system.
Filenames are subject to shell expansion if they contain any wildcard characters ‘*’,
‘?’, ‘[]’. To find a literal example of a wildcard character the wildcard must be
escaped using the backslash operator ‘\’.
If the optional output list is requested then ls returns a character array with one row
for each file/directory name.
Example usage on a UNIX-like system:
ls -l
atotal 12
a-rw-r--r-- 1 jwe users 4488 Aug 19 04:02 foo.m
a-rw-r--r-- 1 jwe users 1315 Aug 17 23:14 bar.m
See also: [dir], page 843,[readdir], page 824,[glob], page 824,[what], page 133,[stat],
page 821,[filesep], page 825,[ls command], page 843.
val = ls_command ()
old_val = ls_command (new_val)
Query or set the shell command used by Octave’s ls command.
See also: [ls], page 843.
dir
dir (directory)
[list] = dir (directory)
Display file listing for directory directory.
If directory is not specified then list the present working directory.
If a return value is requested, return a structure array with the fields
name File or directory name.
date Timestamp of file modification (string value).
bytes File size in bytes.
isdir True if name is a directory.
datenum Timestamp of file modification as serial date number (double).
statinfo Information structure returned from stat.
If directory is a filename, rather than a directory, then return information about the
named file. directory may also be a list rather than a single directory or file.
directory is subject to shell expansion if it contains any wildcard characters ‘*’, ‘?’,
‘[]’. To find a literal example of a wildcard character the wildcard must be escaped
using the backslash operator ‘\’.

844 GNU Octave
Note that for symbolic links, dir returns information about the file that the symbolic
link points to rather than the link itself. However, if the link points to a nonexistent
file, dir returns information about the link.
See also: [ls], page 843,[readdir], page 824,[glob], page 824,[what], page 133,[stat],
page 821,[lstat], page 821.
pwd ()
dir = pwd ()
Return the current working directory.
See also: [cd], page 842,[dir], page 843,[ls], page 843,[mkdir], page 819,[rmdir],
page 820.
36.9 Password Database Functions
Octave’s password database functions return information in a structure with the following
fields.
name The user name.
passwd The encrypted password, if available.
uid The numeric user id.
gid The numeric group id.
gecos The GECOS field.
dir The home directory.
shell The initial shell.
In the descriptions of the following functions, this data structure is referred to as a
pw struct.
pw_struct = getpwent ()
Return a structure containing an entry from the password database, opening it if
necessary.
Once the end of the data has been reached, getpwent returns 0.
See also: [setpwent], page 845,[endpwent], page 845.
pw_struct = getpwuid (uid).
Return a structure containing the first entry from the password database with the
user ID uid.
If the user ID does not exist in the database, getpwuid returns 0.
See also: [getpwnam], page 844.
pw_struct = getpwnam (name)
Return a structure containing the first entry from the password database with the
user name name.
If the user name does not exist in the database, getpwname returns 0.
See also: [getpwuid], page 844.

Chapter 36: System Utilities 845
setpwent ()
Return the internal pointer to the beginning of the password database.
See also: [getpwent], page 844,[endpwent], page 845.
endpwent ()
Close the password database.
See also: [getpwent], page 844,[setpwent], page 845.
36.10 Group Database Functions
Octave’s group database functions return information in a structure with the following
fields.
name The user name.
passwd The encrypted password, if available.
gid The numeric group id.
mem The members of the group.
In the descriptions of the following functions, this data structure is referred to as a
grp struct.
grp_struct = getgrent ()
Return an entry from the group database, opening it if necessary.
Once the end of data has been reached, getgrent returns 0.
See also: [setgrent], page 845,[endgrent], page 845.
grp_struct = getgrgid (gid).
Return the first entry from the group database with the group ID gid.
If the group ID does not exist in the database, getgrgid returns 0.
See also: [getgrnam], page 845.
grp_struct = getgrnam (name)
Return the first entry from the group database with the group name name.
If the group name does not exist in the database, getgrnam returns 0.
See also: [getgrgid], page 845.
setgrent ()
Return the internal pointer to the beginning of the group database.
See also: [getgrent], page 845,[endgrent], page 845.
endgrent ()
Close the group database.
See also: [getgrent], page 845,[setgrent], page 845.
846 GNU Octave
36.11 System Information
computer ()
c= computer ()
[c,maxsize] = computer ()
[c,maxsize,endian] = computer ()
arch = computer ("arch")
Print or return a string of the form cpu-vendor-os that identifies the type of computer
that Octave is running on.
If invoked with an output argument, the value is returned instead of printed. For
example:
computer ()
ai586-pc-linux-gnu
mycomp = computer ()
⇒mycomp = "i586-pc-linux-gnu"
If two output arguments are requested, also return the maximum number of elements
for an array. This will depend on whether Octave has been compiled with 32-bit or
64-bit index vectors.
If three output arguments are requested, also return the byte order of the current
system as a character ("B" for big-endian or "L" for little-endian).
If the argument "arch" is specified, return a string indicating the architecture of the
computer on which Octave is running.
See also: [isunix], page 847,[ismac], page 847,[ispc], page 847.
[uts,err,msg] = uname ()
Return system information in the structure.
For example:
uname ()
⇒{
sysname = x86_64
nodename = segfault
release = 2.6.15-1-amd64-k8-smp
version = Linux
machine = #2 SMP Thu Feb 23 04:57:49 UTC 2006
}
If successful, err is 0 and msg is an empty string. Otherwise, err is nonzero and msg
contains a system-dependent error message.
nproc ()
nproc (query)
Return the current number of available processors.
If called with the optional argument query, modify how processors are counted as
follows:
all total number of processors.

Chapter 36: System Utilities 847
current processors available to the current process.
overridable
same as current, but overridable through the OMP_NUM_THREADS envi-
ronment variable.
ispc ()
Return true if Octave is running on a Windows system and false otherwise.
See also: [isunix], page 847,[ismac], page 847.
isunix ()
Return true if Octave is running on a Unix-like system and false otherwise.
See also: [ismac], page 847,[ispc], page 847.
ismac ()
Return true if Octave is running on a Mac OS X system and false otherwise.
See also: [isunix], page 847,[ispc], page 847.
isieee ()
Return true if your computer claims to conform to the IEEE standard for floating
point calculations.
No actual tests are performed.
isdeployed ()
Return true if the current program has been compiled and is running separately from
the Octave interpreter and false if it is running in the Octave interpreter.
Currently, this function always returns false in Octave.
isstudent ()
Return true if running in the student edition of matlab.
isstudent always returns false in Octave.
See also: [false], page 61.
OCTAVE_HOME ()
Return the name of the top-level Octave installation directory.
See also: [EXEC PATH], page 837,[IMAGE PATH], page 743.
matlabroot ()
Return the name of the top-level Octave installation directory.
This is an alias for the function OCTAVE_HOME provided for compatibility.
See also: [OCTAVE HOME], page 847.
OCTAVE_VERSION ()
Return the version number of Octave as a string.
See also: [ver], page 848,[version], page 848.

848 GNU Octave
v= version ()
[v,d] = version ()
v= version (feature)
Get version information for Octave.
If called without input argument, the first return value vgives the version number of
Octave as a string. The second return value dholds the release date as a string.
The following options can be passed for feature:
"-date" for the release date of the running build,
"-description"
for a description of the release (always an empty string),
"-release"
for the name of the running build (always an empty string),
"-java" for version information of the Java VM,
"-fftw" for version information for the linked fftw,
"-blas" for version information for the linked blas (not implemented),
"-lapack"
for version information for the linked lapack (not implemented).
The variant with no input and output argument is an alias for the function
OCTAVE_VERSION provided for compatibility.
See also: [OCTAVE VERSION], page 847,[ver], page 848.
ver
ver Octave
ver package
v = ver (. . . )
Display a header containing the current Octave version number, license string, and
operating system. The header is followed by a list of installed packages, versions, and
installation directories.
Use the package name package or Octave to limit the listing to a desired component.
When called with an output argument, return a vector of structures describing Octave
and each installed package. The structure includes the following fields.
Name Package name.
Version Version of the package.
Revision Revision of the package.
Date Date of the version/revision.
See also: [version], page 848,[usejava], page 910,[pkg], page 853.
compare_versions (v1,v2,operator)
Compare two version strings using the given operator.
Chapter 36: System Utilities 849
This function assumes that versions v1 and v2 are arbitrarily long strings made of
numeric and period characters possibly followed by an arbitrary string (e.g., "1.2.3",
"0.3","0.1.2+", or "1.2.3.4-test1").
The version is first split into numeric and character portions and then the parts are
padded to be the same length (i.e., "1.1" would be padded to be "1.1.0" when being
compared with "1.1.1", and separately, the character parts of the strings are padded
with nulls).
The operator can be any logical operator from the set
•"==" equal
•"<" less than
•"<=" less than or equal to
•">" greater than
•">=" greater than or equal to
•"!=" not equal
•"~=" not equal
Note that version "1.1-test2" will compare as greater than "1.1-test10". Also,
since the numeric part is compared first, "a" compares less than "1a" because the
second string starts with a numeric part even though double ("a") is greater than
double ("1").
license
license inuse
license inuse feature
license ("inuse")
retval = license ("inuse")
retval = license ("test",feature)
retval = license ("checkout",feature)
[retval,errmsg] = license ("checkout",feature)
Get license information for Octave and Octave packages.
GNU Octave is free software distributed under the GNU General Public License
(GPL), and a license manager makes no sense. This function is provided only for
matlab compatibility.
When called with no extra input arguments, it returns the Octave license, otherwise
the first input defines the operation mode and must be one of the following strings:
inuse,test, and checkout. The optional feature argument can either be "octave"
(core), or an Octave package.
"inuse" Returns a list of loaded features, i.e., octave and the list of loaded pack-
ages. If an output is requested, it returns a struct array with the fields
"feature", and "user".
"test" Return true if the specified feature is installed, false otherwise.
An optional third argument "enable" or "disable" is accepted but ig-
nored.
850 GNU Octave
"checkout"
Return true if the specified feature is installed, false otherwise. An op-
tional second output will have an error message if a package is not in-
stalled.
See also: [pkg], page 853,[ver], page 848,[version], page 848.
getrusage ()
Return a structure containing a number of statistics about the current Octave process.
Not all fields are available on all systems. If it is not possible to get CPU time
statistics, the CPU time slots are set to zero. Other missing data are replaced by
NaN. The list of possible fields is:
idrss Unshared data size.
inblock Number of block input operations.
isrss Unshared stack size.
ixrss Shared memory size.
majflt Number of major page faults.
maxrss Maximum data size.
minflt Number of minor page faults.
msgrcv Number of messages received.
msgsnd Number of messages sent.
nivcsw Number of involuntary context switches.
nsignals Number of signals received.
nswap Number of swaps.
nvcsw Number of voluntary context switches.
oublock Number of block output operations.
stime A structure containing the system CPU time used. The structure has the
elements sec (seconds) usec (microseconds).
utime A structure containing the user CPU time used. The structure has the
elements sec (seconds) usec (microseconds).
36.12 Hashing Functions
It is often necessary to find if two strings or files are identical. This might be done by
comparing them character by character and looking for differences. However, this can be
slow, and so comparing a hash of the string or file can be a rapid way of finding if the files
differ.
Another use of the hashing function is to check for file integrity. The user can check the
hash of the file against a known value and find if the file they have is the same as the one
that the original hash was produced with.
Octave supplies the hash function to calculate hash values of strings and files, the latter
in combination with the fileread function. The hash function supports the most common
used cryptographic hash functions, namely MD5 and SHA-1.
851
hash (hfun,str)
Calculate the hash value of the string str using the hash function hfun.
The available hash functions are given in the table below.
‘MD2’ Message-Digest Algorithm 2 (RFC 1319).
‘MD4’ Message-Digest Algorithm 4 (RFC 1320).
‘MD5’ Message-Digest Algorithm 5 (RFC 1321).
‘SHA1’ Secure Hash Algorithm 1 (RFC 3174)
‘SHA224’ Secure Hash Algorithm 2 (224 Bits, RFC 3874)
‘SHA256’ Secure Hash Algorithm 2 (256 Bits, RFC 6234)
‘SHA384’ Secure Hash Algorithm 2 (384 Bits, RFC 6234)
‘SHA512’ Secure Hash Algorithm 2 (512 Bits, RFC 6234)
To calculate for example the MD5 hash value of the string "abc" the hash function
is called as follows:
hash ("md5", "abc")
aans = 900150983cd24fb0d6963f7d28e17f72
For the same string, the SHA-1 hash value is calculated with:
hash ("sha1", "abc")
aans = a9993e364706816aba3e25717850c26c9cd0d89d
And to compute the hash value of a file, e.g., file = "file.txt", call hash in com-
bination with the fileread:
hash ("md5", fileread (file));
853
37 Packages
Since Octave is Free Software users are encouraged to share their programs amongst each
other. To aid this sharing Octave supports the installation of extra packages. The ‘Octave-
Forge’ project is a community-maintained set of packages that can be downloaded and
installed in Octave. At the time of writing the ‘Octave-Forge’ project can be found online
at http://octave.sourceforge.net, but since the Internet is an ever-changing place this
may not be true at the time of reading. Therefore it is recommended to see the Octave
website for an updated reference.
37.1 Installing and Removing Packages
Assuming a package is available in the file image-1.0.0.tar.gz it can be installed from
the Octave prompt with the command
pkg install image-1.0.0.tar.gz
If the package is installed successfully nothing will be printed on the prompt, but if an error
occurred during installation it will be reported. It is possible to install several packages
at once by writing several package files after the pkg install command. If a different
version of the package is already installed it will be removed prior to installing the new
package. This makes it easy to upgrade and downgrade the version of a package, but makes
it impossible to have several versions of the same package installed at once.
To see which packages are installed type
pkg list
aPackage Name | Version | Installation directory
a--------------+---------+-----------------------
aimage *| 1.0.0 | /home/jwe/octave/image-1.0.0
In this case only version 1.0.0 of the image package is installed. The ’*’ character next to
the package name shows that the image package is loaded and ready for use.
It is possible to remove a package from the system using the pkg uninstall command
like this
pkg uninstall image
If the package is removed successfully nothing will be printed in the prompt, but if an error
occurred it will be reported. It should be noted that the package file used for installation is
not needed for removal, and that only the package name as reported by pkg list should be
used when removing a package. It is possible to remove several packages at once by writing
several package names after the pkg uninstall command.
To minimize the amount of code duplication between packages it is possible that one
package depends on another one. If a package depends on another, it will check if that
package is installed during installation. If it is not, an error will be reported and the
package will not be installed. This behavior can be disabled by passing the -nodeps flag to
the pkg install command
pkg install -nodeps my_package_with_dependencies.tar.gz
Since the installed package expects its dependencies to be installed it may not function
correctly. Because of this it is not recommended to disable dependency checking.
854 GNU Octave
pkg command pkg_name
pkg command option pkg_name
[out1, ...] = pkg (command, . . . )
Manage or query packages (groups of add-on functions) for Octave.
Different actions are available depending on the value of command and on return
arguments.
Available commands:
‘install’ Install named packages. For example,
pkg install image-1.0.0.tar.gz
installs the package found in the file image-1.0.0.tar.gz.
The option variable can contain options that affect the manner in which
a package is installed. These options can be one or more of
-nodeps The package manager will disable dependency checking.
With this option it is possible to install a package even when
it depends on another package which is not installed on the
system. Use this option with care.
-local A local installation (package available only to current user)
is forced, even if the user has system privileges.
-global A global installation (package available to all users) is forced,
even if the user doesn’t normally have system privileges.
-forge Install a package directly from the Octave-Forge repository.
This requires an internet connection and the cURL library.
Security risk: no verification of the package is performed be-
fore the installation. There are no signature for packages,
or checksums to confirm the correct file was downloaded. It
has the same security issues as manually downloading the
package from the Octave Forge repository and installing it.
-verbose The package manager will print the output of all commands
as they are performed.
‘update’ Check installed Octave-Forge packages against repository and update any
outdated items. This requires an internet connection and the cURL li-
brary. Usage:
pkg update
‘uninstall’
Uninstall named packages. For example,
pkg uninstall image
removes the image package from the system. If another installed package
depends on the image package an error will be issued. The package can
be uninstalled anyway by using the -nodeps option.
‘load’ Add named packages to the path. After loading a package it is possible
to use the functions provided by the package. For example,
pkg load image

Chapter 37: Packages 855
adds the image package to the path.
‘unload’ Remove named packages from the path. After unloading a package it is
no longer possible to use the functions provided by the package.
‘list’ Show the list of currently installed packages. For example,
pkg list
will produce a short report with the package name, version, and installa-
tion directory for each installed package. Supply a package name to limit
reporting to a particular package. For example:
pkg list image
If a single return argument is requested then pkg returns a cell array
where each element is a structure with information on a single package.
installed_packages = pkg ("list")
If two output arguments are requested pkg splits the list of installed
packages into those which were installed by the current user, and those
which were installed by the system administrator.
[user_packages, system_packages] = pkg ("list")
The "-forge" option lists packages available at the Octave-Forge repos-
itory. This requires an internet connection and the cURL library. For
example:
oct_forge_pkgs = pkg ("list", "-forge")
‘describe’
Show a short description of installed packages. With the option
"-verbose" also list functions provided by the package. For example,
pkg describe -verbose
will describe all installed packages and the functions they provide. Display
can be limited to a set of packages:
pkg describe control signal # describe control and signal packages
If one output is requested a cell of structure containing the description
and list of functions of each package is returned as output rather than
printed on screen:
desc = pkg ("describe", "secs1d", "image")
If any of the requested packages is not installed, pkg returns an error,
unless a second output is requested:
[desc, flag] = pkg ("describe", "secs1d", "image")
flag will take one of the values "Not installed","Loaded", or "Not
loaded" for each of the named packages.
‘prefix’ Set the installation prefix directory. For example,
pkg prefix ~/my_octave_packages
sets the installation prefix to ~/my_octave_packages. Packages will be
installed in this directory.

856 GNU Octave
It is possible to get the current installation prefix by requesting an output
argument. For example:
pfx = pkg ("prefix")
The location in which to install the architecture dependent files can be
independently specified with an addition argument. For example:
pkg prefix ~/my_octave_packages ~/my_arch_dep_pkgs
‘local_list’
Set the file in which to look for information on locally installed packages.
Locally installed packages are those that are available only to the current
user. For example:
pkg local_list ~/.octave_packages
It is possible to get the current value of local list with the following
pkg local_list
‘global_list’
Set the file in which to look for information on globally installed packages.
Globally installed packages are those that are available to all users. For
example:
pkg global_list /usr/share/octave/octave_packages
It is possible to get the current value of global list with the following
pkg global_list
‘build’ Build a binary form of a package or packages. The binary file produced
will itself be an Octave package that can be installed normally with pkg.
The form of the command to build a binary package is
pkg build builddir image-1.0.0.tar.gz ...
where builddir is the name of a directory where the temporary installa-
tion will be produced and the binary packages will be found. The options
-verbose and -nodeps are respected, while all other options are ignored.
‘rebuild’ Rebuild the package database from the installed directories. This can be
used in cases where the package database has been corrupted.
See also: [ver], page 848,[news], page 22.
37.2 Using Packages
By default installed packages are not available from the Octave prompt, but it is possible to
control this using the pkg load and pkg unload commands. The functions from a package
can be added to the Octave path by typing
pkg load package_name
where package_name is the name of the package to be added to the path.
In much the same way a package can be removed from the Octave path by typing
pkg unload package_name
Chapter 37: Packages 857
37.3 Administrating Packages
On UNIX-like systems it is possible to make both per-user and system-wide installations of
a package. If the user performing the installation is root the packages will be installed in
a system-wide directory that defaults to OCTAVE_HOME/share/octave/packages/. If the
user is not root the default installation directory is ~/octave/. Packages will be installed
in a subdirectory of the installation directory that will be named after the package. It is
possible to change the installation directory by using the pkg prefix command
pkg prefix new_installation_directory
The current installation directory can be retrieved by typing
current_installation_directory = pkg prefix
To function properly the package manager needs to keep some information about
the installed packages. For per-user packages this information is by default stored
in the file ~/.octave_packages and for system-wide installations it is stored in
OCTAVE_HOME/share/octave/octave_packages. The path to the per-user file can be
changed with the pkg local_list command
pkg local_list /path/to/new_file
For system-wide installations this can be changed in the same way using the pkg global_
list command. If these commands are called without a new path, the current path will be
returned.
37.4 Creating Packages
Internally a package is simply a gzipped tar file that contains a top level directory of any
given name. This directory will in the following be referred to as package and may contain
the following files:
package/CITATION
This is am optional file describing instructions on how to cite the package for
publication. It will be displayed verbatim by the function citation.
package/COPYING
This is a required file containing the license of the package. No restrictions is
made on the license in general. If however the package contains dynamically
linked functions the license must be compatible with the GNU General Public
License.
package/DESCRIPTION
This is a required file containing information about the package. See
Section 37.4.1 [The DESCRIPTION File], page 859, for details on this file.
package/ChangeLog
This is an optional file describing all the changes made to the package source
files.
package/INDEX
This is an optional file describing the functions provided by the package. If
this file is not given then one with be created automatically from the functions
in the package and the Categories keyword in the DESCRIPTION file. See
Section 37.4.2 [The INDEX File], page 861, for details on this file.

858 GNU Octave
package/NEWS
This is an optional file describing all user-visible changes worth mentioning. As
this file increases on size, old entries can be moved into package/ONEWS.
package/ONEWS
This is an optional file describing old entries from the NEWS file.
package/PKG_ADD
An optional file that includes commands that are run when the package is
added to the users path. Note that PKG_ADD directives in the source code of the
package will also be added to this file by the Octave package manager. Note
that symbolic links are to be avoided in packages, as symbolic links do not exist
on some file systems, and so a typical use for this file is the replacement of the
symbolic link
ln -s foo.oct bar.oct
with an autoload directive like
autoload (’bar’, which (’foo’));
See Section 37.4.3 [PKG ADD and PKG DEL Directives], page 862, for details
on PKG_ADD directives.
package/PKG_DEL
An optional file that includes commands that are run when the package is
removed from the users path. Note that PKG_DEL directives in the source code
of the package will also be added to this file by the Octave package manager.
See Section 37.4.3 [PKG ADD and PKG DEL Directives], page 862, for details
on PKG_DEL directives.
package/pre_install.m
This is an optional function that is run prior to the installation of a package.
This function is called with a single argument, a struct with fields names after
the data in the DESCRIPTION, and the paths where the package functions will
be installed.
package/post_install.m
This is an optional function that is run after the installation of a package.
This function is called with a single argument, a struct with fields names after
the data in the DESCRIPTION, and the paths where the package functions were
installed.
package/on_uninstall.m
This is an optional function that is run prior to the removal of a package. This
function is called with a single argument, a struct with fields names after the
data in the DESCRIPTION, the paths where the package functions are installed,
and whether the package is currently loaded.
Besides the above mentioned files, a package can also contain one or more of the following
directories:
package/inst
An optional directory containing any files that are directly installed by the
package. Typically this will include any m-files.
Chapter 37: Packages 859
package/src
An optional directory containing code that must be built prior to the packages
installation. The Octave package manager will execute ./configure in this
directory if this script exists, and will then call make if a file Makefile exists
in this directory. make install will however not be called. The environment
variables MKOCTFILE,OCTAVE_CONFIG, and OCTAVE will be set to the full paths
of the programs mkoctfile,octave-config, and octave, respectively, of the
correct version when configure and make are called. If a file called FILES exists
all files listed there will be copied to the inst directory, so they also will be
installed. If the FILES file doesn’t exist, src/*.m and src/*.oct will be copied
to the inst directory.
package/doc
An optional directory containing documentation for the package. The files in
this directory will be directly installed in a sub-directory of the installed package
for future reference.
package/bin
An optional directory containing files that will be added to the Octave
EXEC_PATH when the package is loaded. This might contain external scripts,
etc., called by functions within the package.
37.4.1 The DESCRIPTION File
The DESCRIPTION file contains various information about the package, such as its name,
author, and version. This file has a very simple format
•Lines starting with ‘#’ are comments.
•Lines starting with a blank character are continuations from the previous line.
•Everything else is of the form NameOfOption: ValueOfOption.
The following is a simple example of a DESCRIPTION file
Name: The name of my package
Version: 1.0.0
Date: 2007-18-04
Author: The name (and possibly email) of the package author.
Maintainer: The name (and possibly email) of the current
package maintainer.
Title: The title of the package
Description: A short description of the package. If this
description gets too long for one line it can continue
on the next by adding a space to the beginning of the
following lines.
License: GPLv3+
The package manager currently recognizes the following keywords
Name Name of the package.
Version Version of the package. A package version must be 3 numbers separated by
dots.
860 GNU Octave
Date Date of last update.
Author Original author of the package.
Maintainer
Maintainer of the package.
Title A one line description of the package.
Description
A one paragraph description of the package.
Categories
Optional keyword describing the package (if no INDEX file is given this is manda-
tory).
Problems Optional list of known problems.
Url Optional list of homepages related to the package.
Depends A list of other Octave packages that this package depends on. This can include
dependencies on particular versions, with a format
Depends: package (>= 1.0.0)
Possible operators are <,<=,==,>= or >. If the part of the dependency in ()
is missing, any version of the package is acceptable. Multiple dependencies can
be defined either as a comma separated list or on separate Depends lines.
License An optional short description of the used license (e.g., GPL version 3 or newer).
This is optional since the file COPYING is mandatory.
SystemRequirements
These are the external install dependencies of the package and are not checked
by the package manager. This is here as a hint to the distribution packager.
They follow the same conventions as the Depends keyword.
BuildRequires
These are the external build dependencies of the package and are not checked by
the package manager. This is here as a hint to the distribution packager. They
follow the same conventions as the Depends keyword. Note that in general,
packaging systems such as rpm or deb and autoprobe the install dependencies
from the build dependencies, and therefore the often a BuildRequires depen-
dency removes the need for a SystemRequirements dependency.
The developer is free to add additional arguments to the DESCRIPTION file for their own
purposes. One further detail to aid the packager is that the SystemRequirements and
BuildRequires keywords can have a distribution dependent section, and the automatic
build process will use these. An example of the format of this is
BuildRequires: libtermcap-devel [Mandriva] libtermcap2-devel
where the first package name will be used as a default and if the RPMs are built on a
Mandriva distribution, then the second package name will be used instead.
Chapter 37: Packages 861
37.4.2 The INDEX File
The optional INDEX file provides a categorical view of the functions in the package. This
file has a very simple format
•Lines beginning with ‘#’ are comments.
•The first non-comment line should look like this
toolbox >> Toolbox name
•Lines beginning with an alphabetical character indicates a new category of functions.
•Lines starting with a white space character indicate that the function names on the
line belong to the last mentioned category.
The format can be summarized with the following example:
# A comment
toolbox >> Toolbox name
Category Name 1
function1 function2 function3
function4
Category Name 2
function2 function5
If you wish to refer to a function that users might expect to find in your package but is
not there, providing a work around or pointing out that the function is available elsewhere,
you can use:
fn = workaround description
This workaround description will not appear when listing functions in the package with
pkg describe but they will be published in the HTML documentation online. Workaround
descriptions can use any HTML markup, but keep in mind that it will be enclosed in a
bold-italic environment. For the special case of:
fn = use <code>alternate expression</code>
the bold-italic is automatically suppressed. You will need to use <code> even in references:
fn = use <a href="someothersite.html"><code>fn</code></a>
Sometimes functions are only partially compatible, in which case you can list the non-
compatible cases separately. To refer to another function in the package, use <f>fn</f>.
For example:
eig (a, b) = use <f>qz</f>
Since sites may have many missing functions, you can define a macro rather than typing
the same link over and again.
$id = expansion
defines the macro id. You can use $id anywhere in the description and it will be expanded.
For example:
$TSA = see <a href="link_to_spctools">SPC Tools</a>
arcov = $TSA <code>armcv</code>
id is any string of letters, numbers and _.

862 GNU Octave
37.4.3 PKG ADD and PKG DEL Directives
If the package contains files called PKG_ADD or PKG_DEL the commands in these files will be
executed when the package is added or removed from the users path. In some situations
such files are a bit cumbersome to maintain, so the package manager supports automatic
creation of such files. If a source file in the package contains a PKG_ADD or PKG_DEL directive
they will be added to either the PKG_ADD or PKG_DEL files.
In m-files a PKG_ADD directive looks like this
## PKG_ADD: some_octave_command
Such lines should be added before the function keyword. In C++ files a PKG_ADD directive
looks like this
// PKG_ADD: some_octave_command
In both cases some_octave_command should be replaced by the command that should be
placed in the PKG_ADD file. PKG_DEL directives work in the same way, except the PKG_ADD
keyword is replaced with PKG_DEL and the commands get added to the PKG_DEL file.
37.4.4 Missing Components
If a package relies on a component, such as another Octave package, that may not be
present it may be useful to install a function which informs users what to do when a
particular component is missing. The function must be written by the package maintainer
and registered with Octave using missing_component_hook.
val = missing_component_hook ()
old_val = missing_component_hook (new_val)
missing_component_hook (new_val,"local")
Query or set the internal variable that specifies the function to call when a component
of Octave is missing.
This can be useful for packagers that may split the Octave installation into multiple
sub-packages, for example, to provide a hint to users for how to install the missing
components.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
The hook function is expected to be of the form
fcn (component)
Octave will call fcn with the name of the function that requires the component and a
string describing the missing component. The hook function should return an error
message to be displayed.
See also: [missing function hook], page 950.
863
Appendix A External Code Interface
"The sum of human wisdom is not contained in any one language"
— Ezra Pound
Octave is a fantastic language for solving many problems in science and engineering.
However, it is not the only computer language and there are times when you may want to
use code written in other languages. Good reasons for doing so include: 1) not re-inventing
the wheel; existing function libraries which have been thoroughly tested and debugged or
large scale simulation codebases are a good example, 2) accessing unique capabilities of a
different language; for example the well-known regular expression functions of Perl (but
don’t do that because regexp already exists in Octave).
Performance should generally not be a reason for using compiled extensions. Although
compiled extensions can run faster, particularly if they replace a loop in Octave code,
this is almost never the best path to take. First, there are many techniques to speed
up Octave performance while remaining within the language. Second, Octave is a high-
level language that makes it easy to perform common mathematical tasks. Giving that up
means shifting the focus from solving the real problem to solving a computer programming
problem. It means returning to low-level constructs such as pointers, memory management,
mathematical overflow/underflow, etc. Because of the low level nature, and the fact that
the compiled code is executed outside of Octave, there is the very real possibility of crashing
the interpreter and losing work.
Before going further, you should first determine if you really need to bother writing code
outside of Octave.
•Can I get the same functionality using the Octave scripting language alone?
Even when a function already exists outside the language, it may be better to simply
reproduce the behavior in an m-file rather than attempt to interface to the outside
code.
•Is the code thoroughly optimized for Octave?
If performance is an issue you should always start with the in-language techniques
for getting better performance. Chief among these is vectorization (see Chapter 19
[Vectorization and Faster Code Execution], page 529) which not only makes the code
concise and more understandable but improves performance (10X-100X). If loops must
be used, make sure that the allocation of space for variables takes place outside the
loops using an assignment to a matrix of the right size, or zeros.
•Does the code make as much use as possible of existing built-in library routines?
These routines are highly optimized and many do not carry the overhead of being
interpreted.
•Does writing a dynamically linked function represent a useful investment of your time,
relative to staying in Octave?
It will take time to learn Octave’s interface for external code and there will inevitably
be issues with tools such as compilers.
With that said, Octave offers a versatile interface for including chunks of compiled code
as dynamically linked extensions. These dynamically linked functions can be called from the
interpreter in the same manner as any ordinary function. The interface is bi-directional and
864 GNU Octave
external code can call Octave functions (like plot) which otherwise might be very difficult
to develop.
The interface is centered around supporting the languages C++, C, and Fortran. Octave
itself is written in C++ and can call external C++/C code through its native oct-file interface.
The C language is also supported through the mex-file interface for compatibility with
matlab. Fortran code is easiest to reach through the oct-file interface.
Because many other languages provide C or C++ APIs it is relatively simple to build
bridges between Octave and other languages. This is also a way to bridge to hardware
resources which often have device drivers written in C.
A.1 Oct-Files
A.1.1 Getting Started with Oct-Files
Oct-files are pieces of C++ code that have been compiled with the Octave API into a
dynamically loadable object. They take their name from the file which contains the object
which has the extension .oct.
Finding a C++ compiler, using the correct switches, adding the right include paths for
header files, etc. is a difficult task. Octave automates this by providing the mkoctfile
command with which to build oct-files. The command is available from within Octave or
at the shell command line.
mkoctfile [-options]file . . .
[output,status] = mkoctfile (. . . )
The mkoctfile function compiles source code written in C, C++, or Fortran. De-
pending on the options used with mkoctfile, the compiled code can be called within
Octave or can be used as a stand-alone application.
mkoctfile can be called from the shell prompt or from the Octave prompt. Calling
it from the Octave prompt simply delegates the call to the shell prompt. The output
is stored in the output variable and the exit status in the status variable.
mkoctfile accepts the following options, all of which are optional except for the
filename of the code you wish to compile:
‘-I DIR’ Add the include directory DIR to compile commands.
‘-D DEF’ Add the definition DEF to the compiler call.
‘-l LIB’ Add the library LIB to the link command.
‘-L DIR’ Add the library directory DIR to the link command.
‘-M’
‘--depend’
Generate dependency files (.d) for C and C++ source files.
‘-R DIR’ Add the run-time path to the link command.
‘-Wl,...’ Pass flags though the linker like "-Wl,-rpath=. . .". The quotes are
needed since commas are interpreted as command separators.
‘-W...’ Pass flags though the compiler like "-Wa,OPTION".
Appendix A: External Code Interface 865
‘-c’ Compile but do not link.
‘-g’ Enable debugging options for compilers.
‘-o FILE’
‘--output FILE’
Output filename. Default extension is .oct (or .mex if ‘--mex’ is specified)
unless linking a stand-alone executable.
‘-p VAR’
‘--print VAR’
Print the configuration variable VAR. Recognized variables are:
ALL_CFLAGS INCFLAGS
ALL_CXXFLAGS INCLUDEDIR
ALL_FFLAGS LAPACK_LIBS
ALL_LDFLAGS LD_CXX
AR LDFLAGS
BLAS_LIBS LD_STATIC_FLAG
CC LFLAGS
CFLAGS LIBDIR
CPICFLAG LIBOCTAVE
CPPFLAGS LIBOCTINTERP
CXX LIBS
CXXFLAGS OCTAVE_HOME
CXXPICFLAG OCTAVE_LIBS
DEPEND_EXTRA_SED_PATTERN OCTAVE_LINK_DEPS
DEPEND_FLAGS OCTAVE_LINK_OPTS
DL_LD OCTAVE_PREFIX
DL_LDFLAGS OCTINCLUDEDIR
F77 OCTLIBDIR
F77_INTEGER8_FLAG OCT_LINK_DEPS
FFLAGS OCT_LINK_OPTS
FFTW3F_LDFLAGS RANLIB
FFTW3F_LIBS RDYNAMIC_FLAG
FFTW3_LDFLAGS READLINE_LIBS
FFTW3_LIBS SED
FFTW_LIBS SPECIAL_MATH_LIB
FLIBS XTRA_CFLAGS
FPICFLAG XTRA_CXXFLAGS
‘--link-stand-alone’
Link a stand-alone executable file.
‘--mex’ Assume we are creating a MEX file. Set the default output extension to
".mex".
‘-s’
‘--strip’ Strip the output file.
866 GNU Octave
‘-v’
‘--verbose’
Echo commands as they are executed.
‘file’ The file to compile or link. Recognized file types are
.c C source
.cc C++ source
.C C++ source
.cpp C++ source
.f Fortran source (fixed form)
.F Fortran source (fixed form)
.f90 Fortran source (free form)
.F90 Fortran source (free form)
.o object file
.a library file
Consider the following short example which introduces the basics of writing a C++ func-
tion that can be linked to Octave.
#include <octave/oct.h>
DEFUN_DLD (helloworld, args, nargout,
"Hello World Help String")
{
octave_stdout << "Hello World has "
<< args.length () << " input arguments and "
<< nargout << " output arguments.\n";
return octave_value_list ();
}
The first critical line is #include <octave/oct.h> which makes available most of the
definitions necessary for a C++ oct-file. Note that octave/oct.h is a C++ header and cannot
be directly #include’ed in a C source file, nor any other language.
Included by oct.h is a definition for the macro DEFUN_DLD which creates a dynamically
loaded function. This macro takes four arguments:
1. The function name as it will be seen in Octave,
2. The list of arguments to the function of type octave_value_list,
3. The number of output arguments, which can be—and often is—omitted if not used,
and
4. The string to use for the help text of the function.
The return type of functions defined with DEFUN_DLD is always octave_value_list.
There are a couple of important considerations in the choice of function name. First,
it must be a valid Octave function name and so must be a sequence of letters, digits, and
underscores not starting with a digit. Second, as Octave uses the function name to define
the filename it attempts to find the function in, the function name in the DEFUN_DLD macro
Appendix A: External Code Interface 867
must match the filename of the oct-file. Therefore, the above function should be in a file
helloworld.cc, and would be compiled to an oct-file using the command
mkoctfile helloworld.cc
This will create a file called helloworld.oct that is the compiled version of the function.
It should be noted that it is perfectly acceptable to have more than one DEFUN_DLD function
in a source file. However, there must either be a symbolic link to the oct-file for each
of the functions defined in the source code with the DEFUN_DLD macro or the autoload
(Section 11.9 [Function Files], page 189) function should be used.
The rest of the function shows how to find the number of input arguments, how to
print through the Octave pager, and how to return from the function. After compiling this
function as above, an example of its use is
helloworld (1, 2, 3)
aHello World has 3 input arguments and 0 output arguments.
Subsequent sections show how to use specific classes from Octave’s core internals. Base
classes like dMatrix (a matrix of double values) are found in the directory liboctave/array.
The definitive reference for how to use a particular class is the header file itself. However,
it is often enough simply to study the examples in the manual in order to be able to use a
class.
A.1.2 Matrices and Arrays in Oct-Files
Octave supports a number of different array and matrix classes, the majority of which are
based on the Array class. The exception are the sparse matrix types discussed separately
below. There are three basic matrix types:
Matrix A double precision matrix class defined in dMatrix.h
ComplexMatrix
A complex matrix class defined in CMatrix.h
BoolMatrix
A boolean matrix class defined in boolMatrix.h
These are the basic two-dimensional matrix types of Octave. In addition there are a
number of multi-dimensional array types including
NDArray A double precision array class defined in dNDArray.h
ComplexNDarray
A complex array class defined in CNDArray.h
boolNDArray
A boolean array class defined in boolNDArray.h
int8NDArray
int16NDArray
int32NDArray
int64NDArray
8, 16, 32, and 64-bit signed array classes defined in int8NDArray.h,
int16NDArray.h, etc.

868 GNU Octave
uint8NDArray
uint16NDArray
uint32NDArray
uint64NDArray
8, 16, 32, and 64-bit unsigned array classes defined in uint8NDArray.h,
uint16NDArray.h, etc.
There are several basic ways of constructing matrices or multi-dimensional arrays. Using
the class Matrix as an example one can
•Create an empty matrix or array with the empty constructor. For example:
Matrix a;
This can be used for all matrix and array types.
•Define the dimensions of the matrix or array with a dim vector which has the same
characteristics as the vector returned from size. For example:
dim_vector dv (2, 3); // 2 rows, 3 columns
Matrix a (dv);
This can be used for all matrix and array types.
•Define the number of rows and columns in the matrix. For example:
Matrix a (2, 2)
This constructor can only be used with matrix types.
These types all share a number of basic methods and operators. Many bear a resemblance
to functions that exist in the interpreter. A selection of useful methods include
[Method]T& operator () (octave idx type)
[Method]T& elem (octave idx type)
The () operator or elem method allow the values of the matrix or array to be read
or set. These methods take a single argument, which is of type octave_idx_type,
that is the index into the matrix or array. Additionally, the matrix type allows two
argument versions of the () operator and elem method, giving the row and column
index of the value to get or set.
Note that these functions do significant error checking and so in some circumstances the
user might prefer to access the data of the array or matrix directly through the fortran_vec
method discussed below.
[Method]octave_idx_type numel (void)const
The total number of elements in the matrix or array.
[Method]size_t byte_size (void)const
The number of bytes used to store the matrix or array.
[Method]dim_vector dims (void)const
The dimensions of the matrix or array in value of type dim_vector.
[Method]int ndims (void)const
The number of dimensions of the matrix or array. Matrices are always 2-D, but arrays
can be N-dimensional.

Appendix A: External Code Interface 869
[Method]void resize (const dim vector&)
[Method]void resize (nrows, ncols)
A method taking either an argument of type dim_vector, or, in the case of a matrix,
two arguments of type octave_idx_type defining the number of rows and columns
in the matrix.
[Method]T* fortran_vec (void)
This method returns a pointer to the underlying data of the matrix or array so that
it can be manipulated directly, either within Octave or by an external library.
Operators such as +,-, or *can be used on the majority of the matrix and array types.
In addition there are a number of methods that are of interest only for matrices such as
transpose,hermitian,solve, etc.
The typical way to extract a matrix or array from the input arguments of DEFUN_DLD
function is as follows
#include <octave/oct.h>
DEFUN_DLD (addtwomatrices, args, , "Add A to B")
{
if (args.length () != 2)
print_usage ();
NDArray A = args(0).array_value ();
NDArray B = args(1).array_value ();
return octave_value (A + B);
}
To avoid segmentation faults causing Octave to abort, this function explicitly checks
that there are sufficient arguments available before accessing these arguments. It then
obtains two multi-dimensional arrays of type NDArray and adds these together. Note that
the array_value method is called without using the is_matrix_type method. If an error
occurs when attempting to extract the value, Octave will print a message and throw an
exception. The reason to prefer this coding structure is that the arguments might be a type
which is not an NDArray, but for which it would make sense to convert them to one. The
array_value method allows this conversion to be performed transparently when possible.
If you need to catch errors like this, and perform some kind of cleanup or other operation,
you can catch the octave_execution_error exception.
A + B, operating on two NDArray objects returns an NDArray, which is cast to an octave_
value on the return from the function. An example of the use of this demonstration function
is
addtwomatrices (ones (2, 2), eye (2, 2))
⇒2 1
1 2
A list of the basic Matrix and Array types, the methods to extract these from an
octave_value, and the associated header file is listed below.
870 GNU Octave
Type Function Source Code
RowVector row_vector_value dRowVector.h
ComplexRowVector complex_row_vector_value CRowVector.h
ColumnVector column_vector_value dColVector.h
ComplexColumnVector complex_column_vector_value CColVector.h
Matrix matrix_value dMatrix.h
ComplexMatrix complex_matrix_value CMatrix.h
boolMatrix bool_matrix_value boolMatrix.h
charMatrix char_matrix_value chMatrix.h
NDArray array_value dNDArray.h
ComplexNDArray complex_array_value CNDArray.h
boolNDArray bool_array_value boolNDArray.h
charNDArray char_array_value charNDArray.h
int8NDArray int8_array_value int8NDArray.h
int16NDArray int16_array_value int16NDArray.h
int32NDArray int32_array_value int32NDArray.h
int64NDArray int64_array_value int64NDArray.h
uint8NDArray uint8_array_value uint8NDArray.h
uint16NDArray uint16_array_value uint16NDArray.h
uint32NDArray uint32_array_value uint32NDArray.h
uint64NDArray uint64_array_value uint64NDArray.h
A.1.3 Character Strings in Oct-Files
A character string in Octave is just a special Array class. Consider the example:
#include <octave/oct.h>
DEFUN_DLD (stringdemo, args, , "String Demo")
{
if (args.length () != 1)
print_usage ();
octave_value_list retval;
charMatrix ch = args(0).char_matrix_value ();
retval(1) = octave_value (ch, ’\’’); // Single Quote String
octave_idx_type nr = ch.rows ();
for (octave_idx_type i = 0; i < nr / 2; i++)
{
std::string tmp = ch.row_as_string (i);
ch.insert (ch.row_as_string (nr-i-1).c_str (), i, 0);
ch.insert (tmp.c_str (), nr-i-1, 0);
}
Appendix A: External Code Interface 871
retval(0) = octave_value (ch, ’"’); // Double Quote String
return retval;
}
An example of the use of this function is
s0 = ["First String"; "Second String"];
[s1,s2] = stringdemo (s0)
⇒s1 = Second String
First String
⇒s2 = First String
Second String
typeinfo (s2)
⇒sq_string
typeinfo (s1)
⇒string
One additional complication of strings in Octave is the difference between single quoted
and double quoted strings. To find out if an octave_value contains a single or double
quoted string use one of the predicate tests shown below.
if (args(0).is_sq_string ())
octave_stdout << "First argument is a single quoted string\n";
else if (args(0).is_dq_string ())
octave_stdout << "First argument is a double quoted string\n";
Note, however, that both types of strings are represented by the charNDArray type, and
so when assigning to an octave_value, the type of string should be specified. For example:
octave_value_list retval;
charNDArray ch;
...
// Create single quoted string
retval(1) = octave_value (ch); // default constructor is sq_string
OR
retval(1) = octave_value (ch, ’\’’); // explicitly create sq_string
// Create a double quoted string
retval(0) = octave_value (ch, ’"’);
A.1.4 Cell Arrays in Oct-Files
Octave’s cell type is also available from within oct-files. A cell array is just an Array
of octave_values, and thus each element of the cell array can be treated like any other
octave_value. A simple example is
#include <octave/oct.h>
#include <octave/Cell.h>
872 GNU Octave
DEFUN_DLD (celldemo, args, , "Cell Demo")
{
if (args.length () != 1)
print_usage ();
Cell c = args(0).cell_value ();
octave_value_list retval;
retval.resize (c.numel ()); // faster code by pre-declaring size
for (octave_idx_type i = 0; i < c.numel (); i++)
{
retval(i) = c(i); // using operator syntax
//retval(i) = c.elem (i); // using method syntax
}
return retval;
}
Note that cell arrays are used less often in standard oct-files and so the Cell.h header
file must be explicitly included. The rest of the example extracts the octave_values one
by one from the cell array and returns them as individual output arguments. For example:
[b1, b2, b3] = celldemo ({1, [1, 2], "test"})
⇒
b1 = 1
b2 =
1 2
b3 = test
A.1.5 Structures in Oct-Files
A structure in Octave is a map between a number of fields represented and their values. The
Standard Template Library map class is used, with the pair consisting of a std::string
and an Octave Cell variable.
A simple example demonstrating the use of structures within oct-files is
#include <octave/oct.h>
#include <octave/ov-struct.h>
DEFUN_DLD (structdemo, args, , "Struct Demo")
{
if (args.length () != 2)
print_usage ();
if (! args(0).is_map ())
error ("structdemo: ARG1 must be a struct");
Appendix A: External Code Interface 873
octave_scalar_map arg0 = args(0).scalar_map_value ();
//octave_map arg0 = args(0).map_value ();
if (! args(1).is_string ())
error ("structdemo: ARG2 must be a character string");
std::string arg1 = args(1).string_value ();
octave_value tmp = arg0.contents (arg1);
//octave_value tmp = arg0.contents (arg1)(0);
if (! tmp.is_defined ())
error ("structdemo: struct does not have a field named ’%s’\n",
arg1.c_str ());
octave_scalar_map st;
st.assign ("selected", tmp);
return octave_value (st);
}
An example of its use is
x.a = 1; x.b = "test"; x.c = [1, 2];
structdemo (x, "b")
⇒selected = test
The example above specifically uses the octave_scalar_map class which is for repre-
senting a single struct. For structure arrays, the octave_map class is used instead. The
commented code shows how the demo could be modified to handle a structure array. In
that case, the contents method returns a Cell which may have more than one element.
Therefore, to obtain the underlying octave_value in the single struct example we would
write
octave_value tmp = arg0.contents (arg1)(0);
where the trailing (0) is the () operator on the Cell object. If this were a true structure
array with multiple elements we could iterate over the elements using the () operator.
Structures are a relatively complex data container and there are more functions available
in oct-map.h which make coding with them easier than relying on just contents.
A.1.6 Sparse Matrices in Oct-Files
There are three classes of sparse objects that are of interest to the user.
SparseMatrix
A double precision sparse matrix class
SparseComplexMatrix
A complex sparse matrix class
SparseBoolMatrix
A boolean sparse matrix class
874 GNU Octave
All of these classes inherit from the Sparse<T> template class, and so all have similar
capabilities and usage. The Sparse<T> class was based on Octave’s Array<T> class and
users familiar with Octave’s Array classes will be comfortable with the use of the sparse
classes.
The sparse classes will not be entirely described in this section, due to their similarity
with the existing Array classes. However, there are a few differences due the nature of
sparse objects, and these will be described. First, although it is fundamentally possible to
have N-dimensional sparse objects, the Octave sparse classes do not allow them at this time;
All instances of the sparse classes must be 2-dimensional. This means that SparseMatrix
is actually more similar to Octave’s Matrix class than it is to the NDArray class.
A.1.6.1 Array and Sparse Class Differences
The number of elements in a sparse matrix is considered to be the number of nonzero
elements, rather than the product of the dimensions. Therefore,
SparseMatrix sm;
...
int nnz = sm.nelem ();
returns the number of nonzero elements (like the interpreter function nnz). If the user really
requires the number of elements in the matrix, including the nonzero elements, they should
use numel rather than nelem. Note that for very large matrices, where the product of the
two dimensions is larger than the representation of an unsigned int, numel can overflow. An
example is speye (1e6) which will create a matrix with a million rows and columns, but
only a million nonzero elements. In this case, the number of rows multiplied by the number
of columns is more than two hundred times the maximum value that can be represented by
an unsigned 32-bit int. The use of numel should, therefore, be avoided unless it is known
that it will not overflow.
Extreme care is also required when using the elem method or the () operator which
perform essentially the same function. The reason is that if a sparse object is non-const,
then Octave will assume that a request for a zero element in a sparse matrix is in fact a
request to create this element so it can be filled. Therefore, a piece of code like
SparseMatrix sm;
...
for (int j = 0; j < nc; j++)
for (int i = 0; i < nr; i++)
std::cerr << " (" << i << "," << j << "): " << sm(i,j) << "\n";
is a great way of turning a sparse matrix into a dense one, and a very slow way at that
since it reallocates the sparse object for each zero element in the matrix.
A simple way of preventing the above from happening is to create a temporary constant
version of the sparse matrix. Note that only the container for the sparse matrix will be
copied, while the actual representation of the data will be shared between the two versions
of the sparse matrix; This is not a costly operation. The example above, re-written to
prevent sparse-to-dense conversion, is
Appendix A: External Code Interface 875
SparseMatrix sm;
...
const SparseMatrix tmp (sm);
for (int j = 0; j < nc; j++)
for (int i = 0; i < nr; i++)
std::cerr << " (" << i << "," << j << "): " << tmp(i,j) << "\n";
Finally, because the sparse types aren’t represented by a contiguous block of memory,
the fortran_vec method of Array<T> is not available. It is, however, replaced by three
separate methods ridx,cidx, and data, that access the raw compressed column format
that Octave sparse matrices are stored in. These methods can be used in a manner similar
to elem to allow the matrix to be accessed or filled. However, it is up to the user to respect
the sparse matrix compressed column format or the matrix will become corrupted.
A.1.6.2 Creating Sparse Matrices in Oct-Files
There are two useful strategies for creating a sparse matrix. The first is to create three
vectors representing the row index, column index, and data values, and from these create the
matrix. The second alternative is to create a sparse matrix with the appropriate amount of
space, and then fill in the values. Both techniques have their advantages and disadvantages.
Below is an example of creating a small sparse matrix using the first technique
int nz, nr, nc;
nz=4,nr=3,nc=4;
ColumnVector ridx (nz);
ColumnVector cidx (nz);
ColumnVector data (nz);
ridx(0) = 1; cidx(0) = 1; data(0) = 1;
ridx(1) = 2; cidx(1) = 2; data(1) = 2;
ridx(2) = 2; cidx(2) = 4; data(2) = 3;
ridx(3) = 3; cidx(3) = 4; data(3) = 4;
SparseMatrix sm (data, ridx, cidx, nr, nc);
which creates the matrix given in section Section 22.1.1 [Storage of Sparse Matrices],
page 559. Note that the compressed matrix format is not used at the time of the cre-
ation of the matrix itself, but is used internally.
As discussed in the chapter on Sparse Matrices, the values of the sparse matrix are
stored in increasing column-major ordering. Although the data passed by the user need
not respect this requirement, pre-sorting the data will significantly speed up creation of the
sparse matrix.
The disadvantage of this technique for creating a sparse matrix is that there is a brief
time when two copies of the data exist. For extremely memory constrained problems this
may not be the best technique for creating a sparse matrix.
The alternative is to first create a sparse matrix with the desired number of nonzero
elements and then later fill those elements in. Sample code:
876 GNU Octave
int nz, nr, nc;
nz=4,nr=3,nc=4;
SparseMatrix sm (nr, nc, nz);
sm(0,0) = 1; sm(0,1) = 2; sm(1,3) = 3; sm(2,3) = 4;
This creates the same matrix as previously. Again, although not strictly necessary, it is
significantly faster if the sparse matrix is created and the elements are added in column-
major ordering. The reason for this is that when elements are inserted at the end of the
current list of known elements then no element in the matrix needs to be moved to allow
the new element to be inserted; Only the column indices need to be updated.
There are a few further points to note about this method of creating a sparse matrix.
First, it is possible to create a sparse matrix with fewer elements than are actually inserted
in the matrix. Therefore,
int nr, nc;
nr = 3, nc = 4;
SparseMatrix sm (nr, nc, 0);
sm(0,0) = 1; sm(0,1) = 2; sm(1,3) = 3; sm(2,3) = 4;
is perfectly valid. However, it is a very bad idea because as each new element is added to
the sparse matrix the matrix needs to request more space and reallocate memory. This is
an expensive operation that will significantly slow this means of creating a sparse matrix.
It is possible to create a sparse matrix with excess storage, so having nz greater than 4 in
this example is also valid. The disadvantage is that the matrix occupies more memory than
strictly needed.
Of course, it is not always possible to know the number of nonzero elements prior to filling
a matrix. For this reason the additional unused storage of a sparse matrix can be removed
after its creation with the maybe_compress function. In addition to deallocating unused
storage, maybe_compress can also remove zero elements from the matrix. The removal of
zero elements from the matrix is controlled by setting the argument of the maybe_compress
function to be true. However, the cost of removing the zeros is high because it implies
re-sorting the elements. If possible, it is better for the user to avoid adding the unnecessary
zeros in the first place. An example of the use of maybe_compress is
int nz, nr, nc;
nz=6,nr=3,nc=4;
SparseMatrix sm1 (nr, nc, nz);
sm1(0,0) = 1; sm1(0,1) = 2; sm1(1,3) = 3; sm1(2,3) = 4;
sm1.maybe_compress (); // No zero elements were added
SparseMatrix sm2 (nr, nc, nz);
sm2(0,0) = 1; sm2(0,1) = 2; sm(0,2) = 0; sm(1,2) = 0;
sm1(1,3) = 3; sm1(2,3) = 4;
sm2.maybe_compress (true); // Zero elements were added
The use of the maybe_compress function should be avoided if possible as it will slow the
creation of the matrix.
A third means of creating a sparse matrix is to work directly with the data in compressed
row format. An example of this advanced technique might be
Appendix A: External Code Interface 877
octave_value arg;
...
int nz, nr, nc;
nz = 6, nr = 3, nc = 4; // Assume we know the max # nz
SparseMatrix sm (nr, nc, nz);
Matrix m = arg.matrix_value ();
int ii = 0;
sm.cidx (0) = 0;
for (int j = 1; j < nc; j++)
{
for (int i = 0; i < nr; i++)
{
double tmp = m(i,j);
if (tmp != 0.)
{
sm.data(ii) = tmp;
sm.ridx(ii) = i;
ii++;
}
}
sm.cidx(j+1) = ii;
}
sm.maybe_compress (); // If don’t know a priori the final # of nz.
which is probably the most efficient means of creating a sparse matrix.
Finally, it may sometimes arise that the amount of storage initially created is insufficient
to completely store the sparse matrix. Therefore, the method change_capacity exists to
reallocate the sparse memory. The above example would then be modified as
octave_value arg;
...
int nz, nr, nc;
nz = 6, nr = 3, nc = 4; // Guess the number of nz elements
SparseMatrix sm (nr, nc, nz);
Matrix m = arg.matrix_value ();
int ii = 0;
sm.cidx (0) = 0;
for (int j = 1; j < nc; j++)
{
for (int i = 0; i < nr; i++)
{
double tmp = m(i,j);
if (tmp != 0.)
{
if (ii == nz)
{
878 GNU Octave
nz += 2; // Add 2 more elements
sm.change_capacity (nz);
}
sm.data(ii) = tmp;
sm.ridx(ii) = i;
ii++;
}
}
sm.cidx(j+1) = ii;
}
sm.maybe_compress (); // If don’t know a priori the final # of nz.
Note that both increasing and decreasing the number of nonzero elements in a sparse
matrix is expensive as it involves memory reallocation. Also because parts of the matrix,
though not its entirety, exist as old and new copies at the same time, additional memory is
needed. Therefore, if possible avoid changing capacity.
A.1.6.3 Using Sparse Matrices in Oct-Files
Most of the same operators and functions for sparse matrices that are available from the
Octave interpeter are also available within oct-files. The basic means of extracting a sparse
matrix from an octave_value, and returning it as an octave_value, can be seen in the
following example.
octave_value_list retval;
SparseMatrix sm = args(0).sparse_matrix_value ();
SparseComplexMatrix scm = args(1).sparse_complex_matrix_value ();
SparseBoolMatrix sbm = args(2).sparse_bool_matrix_value ();
...
retval(2) = sbm;
retval(1) = scm;
retval(0) = sm;
The conversion to an octave_value is handled by the sparse octave_value constructors,
and so no special care is needed.
A.1.7 Accessing Global Variables in Oct-Files
Global variables allow variables in the global scope to be accessed. Global variables
can be accessed within oct-files by using the support functions get_global_value
and set_global_value.get_global_value takes two arguments, the first is a string
representing the variable name to obtain. The second argument is a boolean argument
specifying what to do if no global variable of the desired name is found. An example of
the use of these two functions is
#include <octave/oct.h>
DEFUN_DLD (globaldemo, args, , "Global Demo")
{
if (args.length () != 1)
print_usage ();
Appendix A: External Code Interface 879
octave_value retval;
std::string s = args(0).string_value ();
octave_value tmp = get_global_value (s, true);
if (tmp.is_defined ())
retval = tmp;
else
retval = "Global variable not found";
set_global_value ("a", 42.0);
return retval;
}
An example of its use is
global a b
b = 10;
globaldemo ("b")
⇒10
globaldemo ("c")
⇒"Global variable not found"
num2str (a)
⇒42
A.1.8 Calling Octave Functions from Oct-Files
There is often a need to be able to call another Octave function from within an oct-file, and
there are many examples of such within Octave itself. For example, the quad function is an
oct-file that calculates the definite integral by quadrature over a user-supplied function.
There are also many ways in which a function could be given as input. It might be
passed as one of
1. Function Handle
2. Anonymous Function Handle
3. Inline Function
4. String
The code below demonstrates all four methods of passing a function to an oct-file.
#include <octave/oct.h>
#include <octave/parse.h>
DEFUN_DLD (funcdemo, args, nargout, "Function Demo")
{
int nargin = args.length ();

880 GNU Octave
if (nargin < 2)
print_usage ();
octave_value_list newargs;
for (octave_idx_type i = nargin - 1; i > 0; i--)
newargs(i-1) = args(i);
octave_value_list retval;
if (args(0).is_function_handle () || args(0).is_inline_function ())
{
octave_function *fcn = args(0).function_value ();
retval = feval (fcn, newargs, nargout);
}
else if (args(0).is_string ())
{
std::string fcn = args(0).string_value ();
retval = feval (fcn, newargs, nargout);
}
else
error ("funcdemo: INPUT must be string, inline, or function handle");
return retval;
}
The first input to the demonstration code is a user-supplied function and the remaining
arguments are all passed to the function.
funcdemo (@sin, 1)
⇒0.84147
funcdemo (@(x) sin (x), 1)
⇒0.84147
funcdemo (inline ("sin (x)"), 1)
⇒0.84147
funcdemo ("sin", 1)
⇒0.84147
funcdemo (@atan2, 1, 1)
⇒0.78540
When the user function is passed as a string the treatment of the function is different.
In some cases it is necessary to have the user supplied function as an octave_function
object. In that case the string argument can be used to create a temporary function as
demonstrated below.
Appendix A: External Code Interface 881
std::octave fcn_name = unique_symbol_name ("__fcn__");
std::string fcode = "function y = ";
fcode.append (fcn_name);
fcode.append ("(x) y = ");
fcn = extract_function (args(0), "funcdemo", fcn_name,
fcode, "; endfunction");
...
if (fcn_name.length ())
clear_function (fcn_name);
There are two important things to know in this case. First, the number of input argu-
ments to the user function is fixed, and in the above example is a single argument. Second,
to avoid leaving the temporary function in the Octave symbol table it should be cleared
after use. Also, by convention all internal function names begin and end with the character
sequence ‘__’.
A.1.9 Calling External Code from Oct-Files
Linking external C code to Octave is relatively simple, as the C functions can easily be called
directly from C++. One possible issue is that the declarations of the external C functions
may need to be explicitly defined as C functions to the compiler. If the declarations of
the external C functions are in the header foo.h, then the tactic to ensure that the C++
compiler treats these declarations as C code is
#ifdef __cplusplus
extern "C"
{
#endif
#include "foo.h"
#ifdef __cplusplus
} /* end extern "C" */
#endif
Calling Fortran code, however, can pose more difficulties. This is due to differences in
the manner in which compilers treat the linking of Fortran code with C or C++ code. Octave
supplies several macros that allow consistent behavior across a number of compilers.
The underlying Fortran code should use the XSTOPX function to replace the Fortran STOP
function. XSTOPX uses the Octave exception handler to treat failing cases in the Fortran
code explicitly. Note that Octave supplies its own replacement blas XERBLA function, which
uses XSTOPX.
If the code calls XSTOPX, then the F77_XFCN macro should be used to call the underlying
Fortran function. The Fortran exception state can then be checked with the global variable
f77_exception_encountered. If XSTOPX will not be called, then the F77_FCN macro should
be used instead to call the Fortran code.
There is no great harm in using F77_XFCN in all cases, except that for Fortran code that
is short running and executes a large number of times, there is potentially an overhead in
doing so. However, if F77_FCN is used with code that calls XSTOP, Octave can generate a
segmentation fault.

882 GNU Octave
An example of the inclusion of a Fortran function in an oct-file is given in the following
example, where the C++ wrapper is
#include <octave/oct.h>
#include <octave/f77-fcn.h>
extern "C"
{
F77_RET_T
F77_FUNC (fortransub, FORTSUB)
(const F77_INT&, F77_DBLE*, F77_CHAR_ARG_DECL F77_CHAR_ARG_LEN_DECL);
}
DEFUN_DLD (fortrandemo, args, , "Fortran Demo")
{
if (args.length () != 1)
print_usage ();
NDArray a = args(0).array_value ();
double *av = a.fortran_vec ();
octave_idx_type na = a.numel ();
OCTAVE_LOCAL_BUFFER (char, ctmp, 128);
F77_XFCN (fortransub, FORTSUB,
(na, av, ctmp F77_CHAR_ARG_LEN (128)));
return ovl (a, std::string (ctmp));
}
and the Fortran function is
subroutine fortransub (n, a, s)
implicit none
character*(*) s
real*8 a(*)
integer*4 i, n, ioerr
doi=1,n
if (a(i) .eq. 0d0) then
call xstopx (’fortransub: divide by zero’)
else
a(i) = 1d0 / a(i)
endif
enddo
write (unit = s, fmt = ’(a,i3,a,a)’, iostat = ioerr)
$ ’There are ’, n,
$ ’ values in the input vector’, char(0)
if (ioerr .ne. 0) then
Appendix A: External Code Interface 883
call xstopx (’fortransub: error writing string’)
endif
return
end
This example demonstrates most of the features needed to link to an external Fortran
function, including passing arrays and strings, as well as exception handling. Both the
Fortran and C++ files need to be compiled in order for the example to work.
mkoctfile fortrandemo.cc fortransub.f
[b, s] = fortrandemo (1:3)
⇒b = 1.00000 0.50000 0.33333
s = There are 3 values in the input vector
[b, s] = fortrandemo (0:3)
error: fortrandemo: fortransub: divide by zero
A.1.10 Allocating Local Memory in Oct-Files
Allocating memory within an oct-file might seem easy, as the C++ new/delete opera-
tors can be used. However, in that case great care must be taken to avoid memory
leaks. The preferred manner in which to allocate memory for use locally is to use the
OCTAVE_LOCAL_BUFFER macro. An example of its use is
OCTAVE_LOCAL_BUFFER (double, tmp, len)
that returns a pointer tmp of type double * of length len.
In this case, Octave itself will worry about reference counting and variable scope and
will properly free memory without programmer intervention.
A.1.11 Input Parameter Checking in Oct-Files
Because oct-files are compiled functions they open up the possibility of crashing Octave
through careless function calls or memory faults. It is quite important that each and every
function have a sufficient level of parameter checking to ensure that Octave behaves well.
The minimum requirement, as previously discussed, is to check the number of input
arguments before using them to avoid referencing a nonexistent argument. However, in
some cases this might not be sufficient as the underlying code imposes further constraints.
For example, an external function call might be undefined if the input arguments are not
integers, or if one of the arguments is zero, or if the input is complex and a real value was
expected. Therefore, oct-files often need additional input parameter checking.
There are several functions within Octave that can be useful for the purposes of param-
eter checking. These include the methods of the octave_value class like is_real_matrix,
is_numeric_type, etc. (See ov.h). Often, with a knowledge of the Octave m-file language,
you can guess at what the corresponding C++ routine will. In addition there are some more
specialized input validation functions of which a few are demonstrated below.
#include <octave/oct.h>
DEFUN_DLD (paramdemo, args, nargout, "Parameter Check Demo")
{
if (args.length () != 1)
884 GNU Octave
print_usage ();
NDArray m = args(0).array_value ();
double min_val = -10.0;
double max_val = 10.0;
octave_stdout << "Properties of input array:\n";
if (m.any_element_is_negative ())
octave_stdout << " includes negative values\n";
if (m.any_element_is_inf_or_nan ())
octave_stdout << " includes Inf or NaN values\n";
if (m.any_element_not_one_or_zero ())
octave_stdout << " includes other values than 1 and 0\n";
if (m.all_elements_are_int_or_inf_or_nan ())
octave_stdout << " includes only int, Inf or NaN values\n";
if (m.all_integers (min_val, max_val))
octave_stdout << " includes only integers in [-10,10]\n";
return octave_value_list ();
}
An example of its use is:
paramdemo ([1, 2, NaN, Inf])
⇒Properties of input array:
includes Inf or NaN values
includes other values than 1 and 0
includes only int, Inf or NaN values
A.1.12 Exception and Error Handling in Oct-Files
Another important feature of Octave is its ability to react to the user typing Control-C
during extended calculations. This ability is based on the C++ exception handler, where
memory allocated by the C++ new/delete methods is automatically released when the ex-
ception is treated. When writing an oct-file which may run for a long time the programmer
must periodically use the macro OCTAVE_QUIT, in order to allow Octave to check and pos-
sibly respond to a user typing Control-C. For example:
for (octave_idx_type i = 0; i < a.nelem (); i++)
{
OCTAVE_QUIT;
b.elem (i) = 2. * a.elem (i);
}

Appendix A: External Code Interface 885
The presence of the OCTAVE_QUIT macro in the inner loop allows Octave to detect and
acknowledge a Control-C key sequence. Without this macro, the user must either wait
for the oct-file function to return before the interrupt is processed, or the user must press
Control-C three times which will force Octave to exit completely.
The OCTAVE_QUIT macro does impose a very small performance penalty; For loops that
are known to be small it may not make sense to include OCTAVE_QUIT.
When creating an oct-file that uses an external library, the function might spend a
significant portion of its time in the external library. It is not generally possible to use the
OCTAVE_QUIT macro in this case. The alternative code in this case is
BEGIN_INTERRUPT_IMMEDIATELY_IN_FOREIGN_CODE;
... some code that calls a "foreign" function ...
END_INTERRUPT_IMMEDIATELY_IN_FOREIGN_CODE;
The disadvantage of this is that if the foreign code allocates any memory internally,
then this memory might be lost during an interrupt, without being deallocated. Therefore,
ideally Octave itself should allocate any memory that is needed by the foreign code, with
either the fortran_vec method or the OCTAVE_LOCAL_BUFFER macro.
The Octave unwind_protect mechanism (Section 10.8 [The unwind protect Statement],
page 170) can also be used in oct-files. In conjunction with the exception handling of Octave,
it ensures that certain recovery code is always run even if an exception occurs. An example
of the use of this mechanism is
#include <octave/oct.h>
#include <octave/unwind-prot.h>
void
my_err_handler (const char *fmt, ...)
{
// Do nothing!!
}
void
my_err_with_id_handler (const char *id, const char *fmt, ...)
{
// Do nothing!!
}
DEFUN_DLD (unwinddemo, args, nargout, "Unwind Demo")
{
if (args.length () < 2)
print_usage ();
NDArray a = args(0).array_value ();
NDArray b = args(1).array_value ();
// Declare unwind_protect frame which lasts as long as
// the variable frame has scope.
886 GNU Octave
octave::unwind_protect frame;
frame.add_fcn (set_liboctave_warning_handler,
current_liboctave_warning_handler);
frame.add_fcn (set_liboctave_warning_with_id_handler,
current_liboctave_warning_with_id_handler);
set_liboctave_warning_handler (my_err_handler);
set_liboctave_warning_with_id_handler (my_err_with_id_handler);
return octave_value (quotient (a, b));
}
As can be seen in the example:
unwinddemo (1, 0)
⇒Inf
1/0
⇒warning: division by zero
Inf
The warning for division by zero (and in fact all warnings) are disabled in the unwinddemo
function.
A.1.13 Documentation and Testing of Oct-Files
The documentation for an oct-file is contained in the fourth string parameter of the
DEFUN_DLD macro. This string can be formatted in the same manner as the help strings
for user functions, however there are some issues that are particular to the formatting of
help strings within oct-files.
The major issue is that the help string will typically be longer than a single line of text,
and so the formatting of long multi-line help strings needs to be taken into account. There
are several possible solutions, but the most common is illustrated in the following example,
DEFUN_DLD (do_what_i_want, args, nargout,
"-*- texinfo -*-\n\
@deftypefn {} {} do_what_i_say (@var{n})\n\
A function that does what the user actually wants rather\n\
than what they requested.\n\
@end deftypefn")
{
...
}
where each line of text is terminated by \n\ which is an embedded newline in the string
together with a C++ string continuation character. Note that the final \must be the last
character on the line.
Octave also includes the ability to embed test and demonstration code for a function
within the code itself (see Appendix B [Test and Demo Functions], page 913). This can
be used from within oct-files (or in fact any file) with certain provisos. First, the test and
demo functions of Octave look for %! as the first two characters of a line to identify test
Appendix A: External Code Interface 887
and demonstration code. This is a requirement for oct-files as well. In addition, the test
and demonstration code must be wrapped in a comment block to avoid it being interpreted
by the compiler. Finally, the Octave test and demonstration code must have access to the
original source code of the oct-file—not just the compiled code—as the tests are stripped
from the compiled code. An example in an oct-file might be
/*
%!assert (sin ([1,2]), [sin(1),sin(2)])
%!error (sin ())
%!error (sin (1,1))
*/
A.2 Mex-Files
Octave includes an interface to allow legacy mex-files to be compiled and used with Octave.
This interface can also be used to share compiled code between Octave and matlab users.
However, as mex-files expose matlab’s internal API, and the internal structure of Octave
is different, a mex-file can never have the same performance in Octave as the equivalent oct-
file. In particular, to support the manner in which variables are passed to mex functions
there are a significant number of additional copies of memory blocks when invoking or
returning from a mex-file function. For this reason, it is recommended that any new code
be written with the oct-file interface previously discussed.
A.2.1 Getting Started with Mex-Files
The basic command to build a mex-file is either mkoctfile --mex or mex. The first com-
mand can be used either from within Octave or from the command line. To avoid issues
with matlab’s own mex command, the use of the command mex is limited to within Octave.
Compiled mex-files have the extension .mex.
mex [options]file . . .
Compile source code written in C, C++, or Fortran, to a MEX file.
This is equivalent to mkoctfile --mex [options] file.
See also: [mkoctfile], page 864,[mexext], page 887.
mexext ()
Return the filename extension used for MEX files.
See also: [mex], page 887.
Consider the following short example:
#include "mex.h"
void
mexFunction (int nlhs, mxArray *plhs[],
int nrhs, const mxArray *prhs[])
{
mexPrintf ("Hello, World!\n");
mexPrintf ("I have %d inputs and %d outputs\n", nrhs, nlhs);
}
888 GNU Octave
The first line #include "mex.h" makes available all of the definitions necessary for a
mex-file. One important difference between Octave and matlab is that the header file
"matrix.h" is implicitly included through the inclusion of "mex.h". This is necessary to
avoid a conflict with the Octave file "Matrix.h" for operating systems and compilers that
don’t distinguish between filenames in upper and lower case.
The entry point into the mex-file is defined by mexFunction. The function takes four
arguments:
1. The number of return arguments (# of left-hand side args).
2. An array of pointers to return arguments.
3. The number of input arguments (# of right-hand side args).
4. An array of pointers to input arguments.
Note that the function name definition is not explicitly included in mexFunction and
so there can only be a single mexFunction entry point per file. Instead, the name of
the function as seen in Octave is determined by the name of the mex-file itself minus the
extension. If the above function is in the file myhello.c, it can be compiled with
mkoctfile --mex myhello.c
which creates a file myhello.mex. The function can then be run from Octave as
myhello (1,2,3)
⇒Hello, World!
⇒I have 3 inputs and 0 outputs
It should be noted that the mex-file contains no help string. To document mex-files,
there should exist an m-file in the same directory as the mex-file itself. Taking the above
as an example, there would need to be a file myhello.m which might contain the text
%MYHELLO Simple test of the functionality of a mex-file.
In this case, the function that will be executed within Octave will be given by the mex-
file, while the help string will come from the m-file. This can also be useful to allow a sample
implementation of the mex-file within the Octave language itself for testing purposes.
Although there cannot be multiple entry points in a single mex-file, one can use the
mexFunctionName function to determine what name the mex-file was called with. This can
be used to alter the behavior of the mex-file based on the function name. For example, if
Appendix A: External Code Interface 889
#include "mex.h"
void
mexFunction (int nlhs, mxArray *plhs[],
int nrhs, const mxArray *prhs[])
{
const char *nm;
nm = mexFunctionName ();
mexPrintf ("You called function: %s\n", nm);
if (strcmp (nm, "myfunc") == 0)
mexPrintf ("This is the principal function\n", nm);
return;
}
is in the file myfunc.c, and is compiled with
mkoctfile --mex myfunc.c
ln -s myfunc.mex myfunc2.mex
then as can be seen by
myfunc ()
⇒You called function: myfunc
This is the principal function
myfunc2 ()
⇒You called function: myfunc2
the behavior of the mex-file can be altered depending on the function’s name.
Although the user should only include mex.h in their code, Octave declares additional
functions, typedefs, etc., available to the user to write mex-files in the headers mexproto.h
and mxarray.h.
A.2.2 Working with Matrices and Arrays in Mex-Files
The basic mex type of all variables is mxArray. Any object, such as a matrix, cell array,
or structure, is stored in this basic type. mxArray serves essentially the same purpose as
the octave_value class in oct-files in that it acts as a container for all the more specialized
types.
The mxArray structure contains at a minimum, the name of the variable it represents, its
dimensions, its type, and whether the variable is real or complex. It can also contain a num-
ber of additional fields depending on the type of the mxArray. There are a number of func-
tions to create mxArray structures, including mxCreateDoubleMatrix,mxCreateCellArray,
mxCreateSparse, and the generic mxCreateNumericArray.
The basic function to access the data in an array is mxGetPr. Because the mex interface
assumes that real and imaginary parts of a complex array are stored separately, there is
an equivalent function mxGetPi that gets the imaginary part. Both of these functions
are only for use with double precision matrices. The generic functions mxGetData and
mxGetImagData perform the same operation for all matrix types. For example:
890 GNU Octave
mxArray *m;
mwSize *dims;
UINT32_T *pr;
dims = (mwSize *) mxMalloc (2 * sizeof (mwSize));
dims[0] = 2; dims[1] = 2;
m = mxCreateNumericArray (2, dims, mxUINT32_CLASS, mxREAL);
pr = (UINT32_T *) mxGetData (m);
There are also the functions mxSetPr, etc., that perform the inverse, and set the data of
an array to use the block of memory pointed to by the argument of mxSetPr.
Note the type mwSize used above, and also mwIndex, are defined as the native precision
of the indexing in Octave on the platform on which the mex-file is built. This allows both
32- and 64-bit platforms to support mex-files. mwSize is used to define array dimensions
and the maximum number or elements, while mwIndex is used to define indexing into arrays.
An example that demonstrates how to work with arbitrary real or complex double pre-
cision arrays is given by the file mypow2.c shown below.
#include "mex.h"
void
mexFunction (int nlhs, mxArray* plhs[],
int nrhs, const mxArray* prhs[])
{
mwSize n;
mwIndex i;
double *vri, *vro;
if (nrhs != 1 || ! mxIsDouble (prhs[0]))
mexErrMsgTxt ("ARG1 must be a double matrix");
n = mxGetNumberOfElements (prhs[0]);
plhs[0] = mxCreateNumericArray (mxGetNumberOfDimensions (prhs[0]),
mxGetDimensions (prhs[0]),
mxGetClassID (prhs[0]),
mxIsComplex (prhs[0]));
vri = mxGetPr (prhs[0]);
vro = mxGetPr (plhs[0]);
if (mxIsComplex (prhs[0]))
{
double *vii, *vio;
vii = mxGetPi (prhs[0]);
vio = mxGetPi (plhs[0]);
for (i = 0; i < n; i++)
{
vro[i] = vri[i] * vri[i] - vii[i] * vii[i];
Appendix A: External Code Interface 891
vio[i] = 2 * vri[i] * vii[i];
}
}
else
{
for (i = 0; i < n; i++)
vro[i] = vri[i] * vri[i];
}
}
An example of its use is
b = randn (4,1) + 1i * randn (4,1);
all (b.^2 == mypow2 (b))
⇒1
The example above uses the functions mxGetDimensions,mxGetNumberOfElements, and
mxGetNumberOfDimensions to work with the dimensions of multi-dimensional arrays. The
functions mxGetM, and mxGetN are also available to find the number of rows and columns in
a 2-D matrix (MxN matrix).
A.2.3 Character Strings in Mex-Files
As mex-files do not make the distinction between single and double quoted strings that
Octave does, there is perhaps less complexity in the use of strings and character matrices.
An example of their use that parallels the demo in stringdemo.cc is given in the file
mystring.c, as shown below.
#include <string.h>
#include "mex.h"
void
mexFunction (int nlhs, mxArray *plhs[],
int nrhs, const mxArray *prhs[])
{
mwSize m, n;
mwIndex i, j;
mxChar *pi, *po;
if (nrhs != 1 || ! mxIsChar (prhs[0])
|| mxGetNumberOfDimensions (prhs[0]) > 2)
mexErrMsgTxt ("ARG1 must be a char matrix");
m = mxGetM (prhs[0]);
n = mxGetN (prhs[0]);
pi = mxGetChars (prhs[0]);
plhs[0] = mxCreateNumericMatrix (m, n, mxCHAR_CLASS, mxREAL);
po = mxGetChars (plhs[0]);
for (j = 0; j < n; j++)
for (i = 0; i < m; i++)
892 GNU Octave
po[j*m + m - 1 - i] = pi[j*m + i];
}
An example of its expected output is
mystring (["First String"; "Second String"])
⇒Second String
First String
Other functions in the mex interface for handling character strings are mxCreateString,
mxArrayToString, and mxCreateCharMatrixFromStrings. In a mex-file, a character string
is considered to be a vector rather than a matrix. This is perhaps an arbitrary distinction
as the data in the mxArray for the matrix is consecutive in any case.
A.2.4 Cell Arrays with Mex-Files
One can perform exactly the same operations on Cell arrays in mex-files as in oct-files. An
example that duplicates the function of the celldemo.cc oct-file in a mex-file is given by
mycell.c as shown below.
#include "mex.h"
void
mexFunction (int nlhs, mxArray* plhs[],
int nrhs, const mxArray* prhs[])
{
mwSize n;
mwIndex i;
if (nrhs != 1 || ! mxIsCell (prhs[0]))
mexErrMsgTxt ("ARG1 must be a cell");
n = mxGetNumberOfElements (prhs[0]);
n = (n > nlhs ? nlhs : n);
for (i = 0; i < n; i++)
plhs[i] = mxDuplicateArray (mxGetCell (prhs[0], i));
}
The output is identical to the oct-file version as well.
[b1, b2, b3] = mycell ({1, [1, 2], "test"})
⇒
b1 = 1
b2 =
1 2
b3 = test
Note in the example the use of the mxDuplicateArray function. This is needed as the
mxArray pointer returned by mxGetCell might be deallocated. The inverse function to
mxGetCell, used for setting Cell values, is mxSetCell and is defined as
Appendix A: External Code Interface 893
void mxSetCell (mxArray *ptr, int idx, mxArray *val);
Finally, to create a cell array or matrix, the appropriate functions are
mxArray *mxCreateCellArray (int ndims, const int *dims);
mxArray *mxCreateCellMatrix (int m, int n);
A.2.5 Structures with Mex-Files
The basic function to create a structure in a mex-file is mxCreateStructMatrix which
creates a structure array with a two dimensional matrix, or mxCreateStructArray.
mxArray *mxCreateStructArray (int ndims, int *dims,
int num_keys,
const char **keys);
mxArray *mxCreateStructMatrix (int rows, int cols,
int num_keys,
const char **keys);
Accessing the fields of the structure can then be performed with mxGetField and
mxSetField or alternatively with the mxGetFieldByNumber and mxSetFieldByNumber
functions.
mxArray *mxGetField (const mxArray *ptr, mwIndex index,
const char *key);
mxArray *mxGetFieldByNumber (const mxArray *ptr,
mwIndex index, int key_num);
void mxSetField (mxArray *ptr, mwIndex index,
const char *key, mxArray *val);
void mxSetFieldByNumber (mxArray *ptr, mwIndex index,
int key_num, mxArray *val);
A difference between the oct-file interface to structures and the mex-file version is that
the functions to operate on structures in mex-files directly include an index over the ele-
ments of the arrays of elements per field; Whereas, the oct-file structure includes a Cell
Array per field of the structure.
An example that demonstrates the use of structures in a mex-file can be found in the
file mystruct.c shown below.
#include "mex.h"
void
mexFunction (int nlhs, mxArray* plhs[],
int nrhs, const mxArray* prhs[])
{
int i;
mwIndex j;
mxArray *v;
const char *keys[] = { "this", "that" };
if (nrhs != 1 || ! mxIsStruct (prhs[0]))
mexErrMsgTxt ("ARG1 must be a struct");

894 GNU Octave
for (i = 0; i < mxGetNumberOfFields (prhs[0]); i++)
for (j = 0; j < mxGetNumberOfElements (prhs[0]); j++)
{
mexPrintf ("field %s(%d) = ", mxGetFieldNameByNumber (prhs[0], i), j);
v = mxGetFieldByNumber (prhs[0], j, i);
mexCallMATLAB (0, NULL, 1, &v, "disp");
}
v = mxCreateStructMatrix (2, 2, 2, keys);
mxSetFieldByNumber (v, 0, 0, mxCreateString ("this1"));
mxSetFieldByNumber (v, 0, 1, mxCreateString ("that1"));
mxSetFieldByNumber (v, 1, 0, mxCreateString ("this2"));
mxSetFieldByNumber (v, 1, 1, mxCreateString ("that2"));
mxSetFieldByNumber (v, 2, 0, mxCreateString ("this3"));
mxSetFieldByNumber (v, 2, 1, mxCreateString ("that3"));
mxSetFieldByNumber (v, 3, 0, mxCreateString ("this4"));
mxSetFieldByNumber (v, 3, 1, mxCreateString ("that4"));
if (nlhs)
plhs[0] = v;
}
An example of the behavior of this function within Octave is then
a(1).f1 = "f11"; a(1).f2 = "f12";
a(2).f1 = "f21"; a(2).f2 = "f22";
b = mystruct (a);
⇒field f1(0) = f11
field f1(1) = f21
field f2(0) = f12
field f2(1) = f22
b
⇒2x2 struct array containing the fields:
this
that
b(3)
⇒scalar structure containing the fields:
this = this3
that = that3
A.2.6 Sparse Matrices with Mex-Files
The Octave format for sparse matrices is identical to the mex format in that it is a com-
pressed column sparse format. Also, in both implementations sparse matrices are required
Appendix A: External Code Interface 895
to be two-dimensional. The only difference of importance to the programmer is that the
real and imaginary parts of the matrix are stored separately.
The mex-file interface, in addition to using mxGetM,mxGetN,mxSetM,mxSetN,mxGetPr,
mxGetPi,mxSetPr, and mxSetPi, also supplies the following functions.
mwIndex *mxGetIr (const mxArray *ptr);
mwIndex *mxGetJc (const mxArray *ptr);
mwSize mxGetNzmax (const mxArray *ptr);
void mxSetIr (mxArray *ptr, mwIndex *ir);
void mxSetJc (mxArray *ptr, mwIndex *jc);
void mxSetNzmax (mxArray *ptr, mwSize nzmax);
mxGetNzmax gets the maximum number of elements that can be stored in the sparse matrix.
This is not necessarily the number of nonzero elements in the sparse matrix. mxGetJc returns
an array with one additional value than the number of columns in the sparse matrix. The
difference between consecutive values of the array returned by mxGetJc define the number
of nonzero elements in each column of the sparse matrix. Therefore,
mwSize nz, n;
mwIndex *Jc;
mxArray *m;
...
n = mxGetN (m);
Jc = mxGetJc (m);
nz = Jc[n];
returns the actual number of nonzero elements stored in the matrix in nz. As the arrays
returned by mxGetPr and mxGetPi only contain the nonzero values of the matrix, we also
need a pointer to the rows of the nonzero elements, and this is given by mxGetIr. A complete
example of the use of sparse matrices in mex-files is given by the file mysparse.c shown
below.
#include "mex.h"
void
mexFunction (int nlhs, mxArray *plhs[],
int nrhs, const mxArray *prhs[])
{
mwSize m, n, nz;
mxArray *v;
mwIndex i;
double *pr, *pi;
double *pr2, *pi2;
mwIndex *ir, *jc;
mwIndex *ir2, *jc2;
if (nrhs != 1 || ! mxIsSparse (prhs[0]))
mexErrMsgTxt ("ARG1 must be a sparse matrix");
896 GNU Octave
m = mxGetM (prhs[0]);
n = mxGetN (prhs[0]);
nz = mxGetNzmax (prhs[0]);
if (mxIsComplex (prhs[0]))
{
mexPrintf ("Matrix is %d-by-%d complex sparse matrix", m, n);
mexPrintf (" with %d elements\n", nz);
pr = mxGetPr (prhs[0]);
pi = mxGetPi (prhs[0]);
ir = mxGetIr (prhs[0]);
jc = mxGetJc (prhs[0]);
i = n;
while (jc[i] == jc[i-1] && i != 0) i--;
mexPrintf ("last nonzero element (%d, %d) = (%g, %g)\n",
ir[nz-1]+ 1, i, pr[nz-1], pi[nz-1]);
v = mxCreateSparse (m, n, nz, mxCOMPLEX);
pr2 = mxGetPr (v);
pi2 = mxGetPi (v);
ir2 = mxGetIr (v);
jc2 = mxGetJc (v);
for (i = 0; i < nz; i++)
{
pr2[i] = 2 * pr[i];
pi2[i] = 2 * pi[i];
ir2[i] = ir[i];
}
for (i = 0; i < n + 1; i++)
jc2[i] = jc[i];
if (nlhs > 0)
plhs[0] = v;
}
else if (mxIsLogical (prhs[0]))
{
mxLogical *pbr, *pbr2;
mexPrintf ("Matrix is %d-by-%d logical sparse matrix", m, n);
mexPrintf (" with %d elements\n", nz);
pbr = mxGetLogicals (prhs[0]);
ir = mxGetIr (prhs[0]);
jc = mxGetJc (prhs[0]);
Appendix A: External Code Interface 897
i = n;
while (jc[i] == jc[i-1] && i != 0) i--;
mexPrintf ("last nonzero element (%d, %d) = %d\n",
ir[nz-1]+ 1, i, pbr[nz-1]);
v = mxCreateSparseLogicalMatrix (m, n, nz);
pbr2 = mxGetLogicals (v);
ir2 = mxGetIr (v);
jc2 = mxGetJc (v);
for (i = 0; i < nz; i++)
{
pbr2[i] = pbr[i];
ir2[i] = ir[i];
}
for (i = 0; i < n + 1; i++)
jc2[i] = jc[i];
if (nlhs > 0)
plhs[0] = v;
}
else
{
mexPrintf ("Matrix is %d-by-%d real sparse matrix", m, n);
mexPrintf (" with %d elements\n", nz);
pr = mxGetPr (prhs[0]);
ir = mxGetIr (prhs[0]);
jc = mxGetJc (prhs[0]);
i = n;
while (jc[i] == jc[i-1] && i != 0) i--;
mexPrintf ("last nonzero element (%d, %d) = %g\n",
ir[nz-1]+ 1, i, pr[nz-1]);
v = mxCreateSparse (m, n, nz, mxREAL);
pr2 = mxGetPr (v);
ir2 = mxGetIr (v);
jc2 = mxGetJc (v);
for (i = 0; i < nz; i++)
{
pr2[i] = 2 * pr[i];
ir2[i] = ir[i];
}
for (i = 0; i < n + 1; i++)

898 GNU Octave
jc2[i] = jc[i];
if (nlhs > 0)
plhs[0] = v;
}
}
A sample usage of mysparse is
sm = sparse ([1, 0; 0, pi]);
mysparse (sm)
⇒
Matrix is 2-by-2 real sparse matrix with 2 elements
last nonzero element (2, 2) = 3.14159
A.2.7 Calling Other Functions in Mex-Files
It is possible to call other Octave functions from within a mex-file using mexCallMATLAB.
An example of the use of mexCallMATLAB can be see in the example below.
#include "mex.h"
void
mexFunction (int nlhs, mxArray* plhs[],
int nrhs, const mxArray* prhs[])
{
char *str;
mexPrintf ("Starting file myfeval.mex\n");
mexPrintf ("I have %d inputs and %d outputs\n", nrhs, nlhs);
if (nrhs < 1 || ! mxIsChar (prhs[0]))
mexErrMsgTxt ("ARG1 must be a function name");
str = mxArrayToString (prhs[0]);
mexPrintf ("I’m going to call the function %s\n", str);
if (nlhs == 0)
nlhs = 1; // Octave’s automatic ’ans’ variable
/* Cast prhs just to get rid of ’const’ qualifier and stop compile warning */
mexCallMATLAB (nlhs, plhs, nrhs-1, (mxArray**)prhs+1, str);
mxFree (str);
}
If this code is in the file myfeval.c, and is compiled to myfeval.mex, then an example
of its use is
Appendix A: External Code Interface 899
a = myfeval ("sin", 1)
⇒Starting file myfeval.mex
I have 2 inputs and 1 outputs
I’m going to call the interpreter function sin
a = 0.84147
Note that it is not possible to use function handles or inline functions within a mex-file.
A.3 Standalone Programs
The libraries Octave uses itself can be utilized in standalone applications. These applications
then have access, for example, to the array and matrix classes, as well as to all of the
Octave algorithms. The following C++ program, uses class Matrix from liboctave.a or
liboctave.so.
#include <iostream>
#include <octave/oct.h>
int
main (void)
{
std::cout << "Hello Octave world!\n";
int n = 2;
Matrix a_matrix = Matrix (n, n);
for (octave_idx_type i = 0; i < n; i++)
for (octave_idx_type j = 0; j < n; j++)
a_matrix(i,j) = (i + 1) * 10 + (j + 1);
std::cout << a_matrix;
return 0;
}
mkoctfile can be used to build a standalone application with a command like
$ mkoctfile --link-stand-alone standalone.cc -o standalone
$ ./standalone
Hello Octave world!
11 12
21 22
$
Note that the application standalone will be dynamically linked against the Octave
libraries and any Octave support libraries. The above allows the Octave math libraries to
be used by an application. It does not, however, allow the script files, oct-files, or built-in
functions of Octave to be used by the application. To do that, the Octave interpreter needs
to be initialized first. An example of how to do this can then be seen in the code
#include <iostream>
#include <octave/oct.h>
900 GNU Octave
#include <octave/octave.h>
#include <octave/parse.h>
#include <octave/interpreter.h>
int
main (void)
{
string_vector argv (2);
argv(0) = "embedded";
argv(1) = "-q";
octave_main (2, argv.c_str_vec (), 1);
octave_idx_type n = 2;
octave_value_list in;
for (octave_idx_type i = 0; i < n; i++)
in(i) = octave_value (5 * (i + 2));
octave_value_list out = feval ("gcd", in, 1);
if (out.length () > 0)
std::cout << "GCD of ["
<< in(0).int_value ()
<< ", "
<< in(1).int_value ()
<< "] is " << out(0).int_value ()
<< std::endl;
else
std::cout << "invalid\n";
clean_up_and_exit (0);
}
which, as before, is compiled and run as a standalone application with
$ mkoctfile --link-stand-alone embedded.cc -o embedded
$ ./embedded
GCD of [10, 15] is 5
$
It is worth re-iterating that, if only built-in functions are to be called from a C++ stand-
alone program then it does not need to initialize the interpreter. The general rule is that for
a built-in function named function_name in the interpreter, there will be a C++ function
named Ffunction_name (note the prepended capital F) accessible in the C++ API. The dec-
larations for all built-in functions are collected in the header file builtin-defun-decls.h.
This feature should be used with care as the list of built-in functions can change. No guar-
antees can be made that a function that is currently a built-in won’t be implemented as a
Appendix A: External Code Interface 901
.m file or as a dynamically linked function in the future. An example of how to call built-in
functions from C++ can be seen in the code
#include <iostream>
#include <octave/oct.h>
#include <octave/builtin-defun-decls.h>
int
main (void)
{
int n = 2;
Matrix a_matrix = Matrix (n, n);
for (octave_idx_type i = 0; i < n; i++)
for (octave_idx_type j = 0; j < n; j++)
a_matrix(i,j) = (i + 1) * 10 + (j + 1);
std::cout << "This is a matrix:" << std::endl
<< a_matrix << std::endl;
octave_value_list in;
in(0) = a_matrix;
octave_value_list out = Fnorm (in, 1);
double norm_of_the_matrix = out(0).double_value ();
std::cout << "This is the norm of the matrix:" << std::endl
<< norm_of_the_matrix << std::endl;
return 0;
}
which is compiled and run as a standalone application with
$ mkoctfile --link-stand-alone standalonebuiltin.cc -o standalonebuiltin
$ ./standalonebuiltin
This is a matrix:
11 12
21 22
This is the norm of the matrix:
34.4952
$
A.4 Java Interface
The Java Interface is designed for calling Java functions from within Octave. If you want to
do the reverse, and call Octave from within Java, try a library like javaOctave (https://
kenai.com/projects/javaoctave/pages/Home) or joPas (http://jopas.sourceforge.
net/).
902 GNU Octave
A.4.1 Making Java Classes Available
Java finds classes by searching a classpath which is a list of Java archive files and/or direc-
tories containing class files. In Octave the classpath is composed of two parts:
•the static classpath is initialized once at startup of the JVM, and
•the dynamic classpath which can be modified at runtime.
Octave searches the static classpath first, and then the dynamic classpath. Classes
appearing in the static classpath, as well as in the dynamic classpath, will therefore be found
in the static classpath and loaded from this location. Classes which will be used frequently,
or must be available to all users, should be added to the static classpath. The static
classpath is populated once from the contents of a plain text file named javaclasspath.txt
(or classpath.txt historically) when the Java Virtual Machine starts. This file contains
one line for each individual classpath to be added to the static classpath. These lines can
identify directories containing class files, or Java archives with complete class file hierarchies.
Comment lines starting with a ‘#’ or a ‘%’ character are ignored.
The search rules for the file javaclasspath.txt (or classpath.txt) are:
•First, Octave tries to locate it in the current directory (where Octave was started
from). If such a file is found, it is read and defines the initial static classpath. Thus, it
is possible to define a static classpath on a ’per Octave invocation’ basis.
•Next, Octave searches in the user’s home directory. If a file javaclasspath.txt exists
here, its contents are appended to the static classpath (if any). Thus, it is possible to
build an initial static classpath on a ’per user’ basis.
•Finally, Octave looks for a javaclasspath.txt in the m-file directory where Octave
Java functions live. This is where the function javaclasspath.m resides, usually some-
thing like OCTAVE_HOME/share/octave/OCTAVE_VERSION/m/java/. You can find this
directory by executing the command
which javaclasspath
If this file exists here, its contents are also appended to the static classpath. Note that
the archives and class directories defined in this last step will affect all users.
Classes which are used only by a specific script should be placed in the dynamic classpath.
This portion of the classpath can be modified at runtime using the javaaddpath and
javarmpath functions.
Example:
octave> base_path = "C:/Octave/java_files";
octave> # add two JAR archives to the dynamic classpath
octave> javaaddpath ([base_path, "/someclasses.jar"]);
octave> javaaddpath ([base_path, "/moreclasses.jar"]);
octave> # check the dynamic classpath
octave> p = javaclasspath;
octave> disp (p{1});
C:/Octave/java_files/someclasses.jar
octave> disp (p{2});
Appendix A: External Code Interface 903
C:/Octave/java_files/moreclasses.jar
octave> # remove the first element from the classpath
octave> javarmpath ([base_path, "/someclasses.jar"]);
octave> p = javaclasspath;
octave> disp (p{1});
C:/Octave/java_files/moreclasses.jar
octave> # provoke an error
octave> disp (p{2});
error: A(I): Index exceeds matrix dimension.
Another way to add files to the dynamic classpath exclusively for your user account is
to use the file .octaverc which is stored in your home directory. All Octave commands in
this file are executed each time you start a new instance of Octave. The following example
adds the directory octave to Octave’s search path and the archive myclasses.jar in this
directory to the Java search path.
# contents of .octaverc:
addpath ("~/octave");
javaaddpath ("~/octave/myclasses.jar");
A.4.2 How to use Java from within Octave
The function [javaObject], page 906, creates Java objects. In fact it invokes the public
constructor of the class with the given name and with the given parameters.
The following example shows how to invoke the constructors BigDecimal(double) and
BigDecimal(String) of the builtin Java class java.math.BigDecimal.
javaObject ("java.math.BigDecimal", 1.001 );
javaObject ("java.math.BigDecimal", "1.001");
Note that parameters of the Octave type double are implicitly converted into the Java
type double and the Octave type (array of) char is converted into the java type String.
A Java object created by [javaObject], page 906, is never automatically converted into an
Octave type but remains a Java object. It can be assigned to an Octave variable.
a = 1.001;
b = javaObject ("java.math.BigDecimal", a);
Using [isjava], page 906, it is possible to check whether a variable is a Java object and
its class can be determined as well. In addition to the previous example:
isjava (a)
⇒ans = 0
class (a)
⇒ans = double
isjava (b)
⇒ans = 1
class (b)
⇒ans = java.math.BigDecimal
The example above can be carried out using only Java objects:
a = javaObject ("java.lang.Double", 1.001);

904 GNU Octave
b = javaObject ("java.math.BigDecimal", a);
isjava (a)
⇒ans = 1
class (a)
⇒ans = java.lang.Double
isjava (b)
⇒ans = 1
class (b)
⇒ans = java.math.BigDecimal
One can see, that even a java.lang.Double is not converted to an Octave double,
when created by [javaObject], page 906. But ambiguities might arise, if the Java classes
java.lang.Double or double are parameters of a method (or a constructor). In this case
they can be converted into one another, depending on the context.
Via [javaObject], page 906, one may create all kinds of Java objects but arrays. The
latter are created through [javaArray], page 906.
It is possible to invoke public member methods on Java objects in Java syntax:
a.toString
⇒ans = 1.001
b.toString
⇒ans = 1.000999999999999889865...
The second result may be surprising, but simply comes from the fact, that 1.001 cannot
exactly be represented as double, due to rounding. Note that unlike in Java, in Octave
methods without arguments can be invoked with and without parentheses ().
Currently it is not possible to invoke static methods with a Java like syntax from within
Octave. Instead, one has to use the function [javaMethod], page 908, as in the following
example:
java.math.BigDecimal.valueOf(1.001); # does not work
javaMethod ("valueOf", "java.math.BigDecimal", 1.001); # workaround
As mentioned before, method and constructor parameters are converted automatically
between Octave and Java types, if appropriate. For functions this is also true with return
values, whereas for constructors this is not.
It is also possible to access public fields of Java objects from within Octave using Java
syntax, with the limitation of static fields:
java.math.BigDecimal.ONE; # does not work
java_get ("java.math.BigDecimal", "ONE"); # workaround
Accordingly, with [java set], page 907, the value of a field can be set. Note that only
public Java fields are accessible from within Octave.
The following example indicates that in Octave empty brackets [] represent Java’s null
value and how Java exceptions are represented.
javaObject ("java.math.BigDecimal", []);
⇒error: [java] java.lang.NullPointerException
It is not recommended to represent Java’s null value by empty brackets [], because
null has no type whereas [] has type double.

Appendix A: External Code Interface 905
In Octave it is possible to provide limited Java reflection by listing the public fields and
methods of a Java object, both static or not.
fieldnames (<Java object>)
methods (<Java object>)
Finally, an examples is shown how to access the stack trace from within Octave, where
the function [debug java], page 911, is used to set and to get the current debug state. In
debug mode, the Java error and the stack trace are displayed.
debug_java (true) # use "false" to omit display of stack trace
debug_java ()
⇒ans = 1
javaObject ("java.math.BigDecimal", "1") ...
.divide (javaObject ("java.math.BigDecimal", "0"))
A.4.3 Passing parameters to the JVM
In order to execute Java code Octave creates a Java Virtual Machine (JVM). Such a JVM
allocates a fixed amount of initial memory and may expand this pool up to a fixed maximum
memory limit. The default values depend on the Java version (see [javamem], page 910).
The memory pool is shared by all Java objects running in the JVM. This strict memory limit
is intended mainly to avoid runaway applications inside web browsers or in enterprise servers
which can consume all memory and crash the system. When the maximum memory limit
is hit, Java code will throw exceptions so that applications will fail or behave unexpectedly.
You can specify options for the creation of the JVM inside a file named java.opts. This
is a text file where enter you enter lines containing -X and -D options that are then passed
to the JVM during initialization.
The directory where the Java options file is located is specified by the environment
variable OCTAVE_JAVA_DIR. If unset the directory where javaclasspath.m resides is used
instead (typically OCTAVE_HOME/share/octave/OCTAVE_VERSION/m/java/). You can find
this directory by executing
which javaclasspath
The -X options allow you to increase the maximum amount of memory available to the
JVM. The following example allows up to 256 Megabytes to be used by adding the following
line to the java.opts file:
-Xmx256m
The maximum possible amount of memory depends on your system. On a Windows
system with 2 Gigabytes main memory you should be able to set this maximum to about 1
Gigabyte.
If your application requires a large amount of memory from the beginning, you can also
specify the initial amount of memory allocated to the JVM. Adding the following line to
the java.opts file starts the JVM with 64 Megabytes of initial memory:
-Xms64m
For more details on the available -X options of your Java Virtual Machine issue the
command ‘java -X’ at the operating system command prompt and consult the Java docu-
mentation.
906 GNU Octave
The -D options can be used to define system properties which can then be used by Java
classes inside Octave. System properties can be retrieved by using the getProperty()
methods of the java.lang.System class. The following example line defines the property
MyProperty and assigns it the string 12.34.
-DMyProperty=12.34
The value of this property can then be retrieved as a string by a Java object or in Octave:
octave> javaMethod ("getProperty", "java.lang.System", "MyProperty");
ans = 12.34
See also: javamem.
A.4.4 Java Interface Functions
The following functions are the core of the Java Interface. They provide a way to create
a Java object, get and set its data fields, and call Java methods which return results to
Octave.
jobj = javaObject (classname)
jobj = javaObject (classname,arg1, . . . )
Create a Java object of class classsname, by calling the class constructor with the
arguments arg1, . . .
The first example below creates an uninitialized object, while the second example
supplies an initial argument to the constructor.
x = javaObject ("java.lang.StringBuffer")
x = javaObject ("java.lang.StringBuffer", "Initial string")
See also: [javaMethod], page 908,[javaArray], page 906.
jary = javaArray (classname,sz)
jary = javaArray (classname,m,n, . . . )
Create a Java array of size sz with elements of class classname.
classname may be a Java object representing a class or a string containing the fully
qualified class name. The size of the object may also be specified with individual
integer arguments m,n, etc.
The generated array is uninitialized. All elements are set to null if classname is a
reference type, or to a default value (usually 0) if classname is a primitive type.
Sample code:
jary = javaArray ("java.lang.String", 2, 2);
jary(1,1) = "Hello";
See also: [javaObject], page 906.
There are many different variable types in Octave, but only ones created through
javaObject can use Java functions. Before using Java with an unknown object the type
can be checked with isjava.
isjava (x)
Return true if xis a Java object.
See also: [class], page 39,[typeinfo], page 39,[isa], page 39,[javaObject], page 906.

Appendix A: External Code Interface 907
Once an object has been created it is natural to find out what fields the object has, and
to read (get) and write (set) them.
In Octave the fieldnames function for structures has been overloaded to return the
fields of a Java object. For example:
dobj = javaObject ("java.lang.Double", pi);
fieldnames (dobj)
⇒
{
[1,1] = public static final double java.lang.Double.POSITIVE_INFINITY
[1,2] = public static final double java.lang.Double.NEGATIVE_INFINITY
[1,3] = public static final double java.lang.Double.NaN
[1,4] = public static final double java.lang.Double.MAX_VALUE
[1,5] = public static final double java.lang.Double.MIN_NORMAL
[1,6] = public static final double java.lang.Double.MIN_VALUE
[1,7] = public static final int java.lang.Double.MAX_EXPONENT
[1,8] = public static final int java.lang.Double.MIN_EXPONENT
[1,9] = public static final int java.lang.Double.SIZE
[1,10] = public static final java.lang.Class java.lang.Double.TYPE
}
The analogy of objects with structures is carried over into reading and writing object
fields. To read a field the object is indexed with the ‘.’ operator from structures. This
is the preferred method for reading fields, but Octave also provides a function interface to
read fields with java_get. An example of both styles is shown below.
dobj = javaObject ("java.lang.Double", pi);
dobj.MAX_VALUE
⇒1.7977e+308
java_get ("java.lang.Float", "MAX_VALUE")
⇒3.4028e+38
val = java_get (obj,name)
Get the value of the field name of the Java object obj.
For static fields, obj can be a string representing the fully qualified name of the
corresponding class.
When obj is a regular Java object, structure-like indexing can be used as a shortcut
syntax. For instance, the following two statements are equivalent
java_get (x, "field1")
x.field1
See also: [java set], page 907,[javaMethod], page 908,[javaObject], page 906.
obj = java_set (obj,name,val)
Set the value of the field name of the Java object obj to val.
For static fields, obj can be a string representing the fully qualified named of the
corresponding Java class.
When obj is a regular Java object, structure-like indexing can be used as a shortcut
syntax. For instance, the following two statements are equivalent

908 GNU Octave
java_set (x, "field1", val)
x.field1 = val
See also: [java get], page 907,[javaMethod], page 908,[javaObject], page 906.
To see what functions can be called with an object use methods. For example, using the
previously created dobj:
methods (dobj)
⇒
Methods for class java.lang.Double:
boolean equals(java.lang.Object)
java.lang.String toString(double)
java.lang.String toString()
...
To call a method of an object the same structure indexing operator ‘.’ is used. Octave
also provides a functional interface to calling the methods of an object through javaMethod.
An example showing both styles is shown below.
dobj = javaObject ("java.lang.Double", pi);
dobj.equals (3)
⇒0
javaMethod ("equals", dobj, pi)
⇒1
ret = javaMethod (methodname,obj)
ret = javaMethod (methodname,obj,arg1, . . . )
Invoke the method methodname on the Java object obj with the arguments arg1,
. . ..
For static methods, obj can be a string representing the fully qualified name of the
corresponding class.
When obj is a regular Java object, structure-like indexing can be used as a shortcut
syntax. For instance, the two following statements are equivalent
ret = javaMethod ("method1", x, 1.0, "a string")
ret = x.method1 (1.0, "a string")
javaMethod returns the result of the method invocation.
See also: [methods], page 771,[javaObject], page 906.
The following three functions are used to display and modify the class path used by the
Java Virtual Machine. This is entirely separate from Octave’s PATH variable and is used by
the JVM to find the correct code to execute.
javaclasspath ()
dpath = javaclasspath ()
[dpath,spath] = javaclasspath ()
clspath = javaclasspath (what)
Return the class path of the Java virtual machine in the form of a cell array of strings.
If called with no inputs:
•If no output is requested, the dynamic and static classpaths are printed to the
standard output.
Appendix A: External Code Interface 909
•If one output value dpath is requested, the result is the dynamic classpath.
•If two output valuesdpath and spath are requested, the first variable will contain
the dynamic classpath and the second will contain the static classpath.
If called with a single input parameter what:
"-dynamic"
Return the dynamic classpath.
"-static"
Return the static classpath.
"-all" Return both the static and dynamic classpath in a single cellstr.
See also: [javaaddpath], page 909,[javarmpath], page 909.
javaaddpath (clspath)
javaaddpath (clspath1, . . . )
Add clspath to the dynamic class path of the Java virtual machine.
clspath may either be a directory where .class files are found, or a .jar file con-
taining Java classes. Multiple paths may be added at once by specifying additional
arguments.
See also: [javarmpath], page 909,[javaclasspath], page 908.
javarmpath (clspath)
javarmpath (clspath1, . . . )
Remove clspath from the dynamic class path of the Java virtual machine.
clspath may either be a directory where .class files are found, or a .jar file con-
taining Java classes. Multiple paths may be removed at once by specifying additional
arguments.
See also: [javaaddpath], page 909,[javaclasspath], page 908.
The following functions provide information and control over the interface between Oc-
tave and the Java Virtual Machine.
javachk (feature)
javachk (feature,component)
msg = javachk (. . . )
Check for the presence of the Java feature in the current session and print or return
an error message if it is not.
Possible features are:
"awt" Abstract Window Toolkit for GUIs.
"desktop"
Interactive desktop is running.
"jvm" Java Virtual Machine.
"swing" Swing components for lightweight GUIs.
910 GNU Octave
If feature is supported and
•no output argument is requested:
Return an empty string
•an output argument is requested:
Return a struct with fields "feature" and "identifier" both empty
If feature is not supported and
•no output argument is requested:
Emit an error message
•an output argument is requested:
Return a struct with field "feature" set to feature and field "identifier" set
to component
The optional input component will be used in place of feature in any error messages
for greater specificity.
javachk determines if specific Java features are available in an Octave session. This
function is provided for scripts which may alter their behavior based on the availability
of Java. The feature "desktop" is never available as Octave has no Java-based desk-
top. Other features may be available if Octave was compiled with the Java Interface
and Java is installed.
See also: [usejava], page 910,[error], page 215.
usejava (feature)
Return true if the Java element feature is available.
Possible features are:
"awt" Abstract Window Toolkit for GUIs.
"desktop"
Interactive desktop is running.
"jvm" Java Virtual Machine.
"swing" Swing components for lightweight GUIs.
usejava determines if specific Java features are available in an Octave session. This
function is provided for scripts which may alter their behavior based on the availability
of Java. The feature "desktop" always returns false as Octave has no Java-based
desktop. Other features may be available if Octave was compiled with the Java
Interface and Java is installed.
See also: [javachk], page 909.
javamem ()
jmem = javamem ()
Show the current memory usage of the Java virtual machine (JVM) and run the
garbage collector.
When no return argument is given the info is printed to the screen. Otherwise, the
output cell array jmem contains Maximum, Total, and Free memory (in bytes).

Appendix A: External Code Interface 911
All Java-based routines are run in the JVM’s shared memory pool, a dedicated and
separate part of memory claimed by the JVM from your computer’s total memory
(which comprises physical RAM and virtual memory / swap space on hard disk).
The maximum allowable memory usage can be configured using the file java.opts.
The directory where this file resides is determined by the environment variable
OCTAVE_JAVA_DIR. If unset, the directory where javaaddpath.m resides is used
instead (typically OCTAVE_HOME/share/octave/OCTAVE_VERSION/m/java/).
java.opts is a plain text file with one option per line. The default initial memory
size and default maximum memory size (which are both system dependent) can be
overridden like so:
-Xms64m
-Xmx512m
(in megabytes in this example). You can adapt these values to your own requirements
if your system has limited available physical memory or if you get Java memory errors.
"Total memory" is what the operating system has currently assigned to the JVM
and depends on actual and active memory usage. "Free memory" is self-explanatory.
During operation of Java-based Octave functions the amount of Total and Free mem-
ory will vary, due to Java’s own cleaning up and your operating system’s memory
management.
val = java_matrix_autoconversion ()
old_val = java_matrix_autoconversion (new_val)
java_matrix_autoconversion (new_val,"local")
Query or set the internal variable that controls whether Java arrays are automatically
converted to Octave matrices.
The default value is false.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [java unsigned autoconversion], page 911,[debug java], page 911.
val = java_unsigned_autoconversion ()
old_val = java_unsigned_autoconversion (new_val)
java_unsigned_autoconversion (new_val,"local")
Query or set the internal variable that controls how integer classes are converted when
java_matrix_autoconversion is enabled.
When enabled, Java arrays of class Byte or Integer are converted to matrices of class
uint8 or uint32 respectively. The default value is true.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [java matrix autoconversion], page 911,[debug java], page 911.
val = debug_java ()
old_val = debug_java (new_val)

912 GNU Octave
debug_java (new_val,"local")
Query or set the internal variable that determines whether extra debugging informa-
tion regarding the initialization of the JVM and any Java exceptions is printed.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [java matrix autoconversion], page 911,[java unsigned autoconversion],
page 911.
913
Appendix B Test and Demo Functions
Octave includes a number of functions to allow the integration of testing and demonstration
code in the source code of the functions themselves.
B.1 Test Functions
test name
test name quiet|normal|verbose
test ("name","quiet|normal|verbose",fid)
test ("name","quiet|normal|verbose",fname)
success = test (. . . )
[n,nmax,nxfail,nskip] = test (. . . )
[code,idx] = test ("name","grabdemo")
test ([],"explain",fid)
test ([],"explain",fname)
Perform built-in self-tests from the first file in the loadpath matching name.
test can be called in either command or functional form. The exact operation of
test is determined by a combination of mode (interactive or batch), reporting level
("quiet","normal","verbose"), and whether a logfile or summary output variable
is used.
The default mode when test is called from the command line is interactive. In
this mode, tests will be run until the first error is encountered, or all tests complete
successfully. In batch mode, all tests are run regardless of any failures, and the results
are collected for reporting. Tests which require user interaction, i.e., demo blocks, are
never run in batch mode.
Batch mode is enabled by either 1) specifying a logfile using the third argument fname
or fid, or 2) requesting an output argument such as success,n, etc.
The optional second argument determines the amount of output to generate and
which types of tests to run. The default value is "normal". Requesting an output
argument will suppress printing the final summary message and any intermediate
warnings, unless verbose reporting is enabled.
"quiet" Print a summary message when all tests pass, or print an error with the
results of the first bad test when a failure occurs. Don’t run tests which
require user interaction.
"normal" Display warning messages about skipped tests or failing xtests during
test execution. Print a summary message when all tests pass, or print an
error with the results of the first bad test when a failure occurs. Don’t
run tests which require user interaction.
"verbose"
Display tests before execution. Print all warning messages. In interactive
mode, run all tests including those which require user interaction.
The optional third input argument specifies a logfile where results of the tests should
be written. The logfile may be a character string (fname) or an open file descriptor
914 GNU Octave
ID (fid). To enable batch processing, but still print the results to the screen, use
stdout for fid.
When called with just a single output argument success,test returns true if all of the
tests were successful. If called with more than one output argument then the number
of successful tests (n), the total number of tests in the file (nmax), the number of
xtest failures (nxfail), and the number of skipped tests (nskip) are returned.
Example
test sind
⇒
PASSES 5 out of 5 tests
[n, nmax] = test ("sind")
⇒
n = 5
nmax = 5
Additional Calling Syntaxes
If the second argument is the string "grabdemo", the contents of any built-in demo
blocks are extracted but not executed. The text for all code blocks is concatenated
and returned as code with idx being a vector of positions of the ends of each demo
block. For an easier way to extract demo blocks from files, See [example], page 921.
If the second argument is "explain" then name is ignored and an explanation of the
line markers used in test output reports is written to the file specified by fname or
fid.
See also: [assert], page 919,[fail], page 920,[demo], page 920,[example], page 921,
[error], page 215.
test scans the named script file looking for lines which start with the identifier ‘%!’. The
prefix is stripped off and the rest of the line is processed through the Octave interpreter. If
the code generates an error, then the test is said to fail.
Since eval() will stop at the first error it encounters, you must divide your tests up
into blocks, with anything in a separate block evaluated separately. Blocks are introduced
by valid keywords like test,function, or assert immediately following ‘%!’. A block is
defined by indentation as in Python. Lines beginning with ‘%!<whitespace>’ are part of
the preceeding block.
For example:
%!test error ("this test fails!")
%!test "test doesn’t fail. it doesn’t generate an error"
When a test fails, you will see something like:
***** test error ("this test fails!")
!!!!! test failed
this test fails!
Generally, to test if something works, you want to assert that it produces a correct value.
A real test might look something like
Appendix B: Test and Demo Functions 915
%!test
%! a= [1, 2, 3; 4, 5, 6]; B = [1; 2];
%! expect = [ a; 2*a];
%! get = kron (b,a);
%! if (any (size (expect) != size (get)))
%! error ("wrong size: expected %d,%d but got %d,%d",
%! size (expect), size (get));
%! elseif (any (any (expect != get)))
%! error ("didn’t get what was expected.");
%! endif
To make the process easier, use the assert function. For example, with assert the
previous test is reduced to:
%!test
%! a= [1, 2, 3; 4, 5, 6]; b= [1; 2];
%! assert (kron (b,a), [ a; 2*a]);
assert can accept a tolerance so that you can compare results absolutely or relatively.
For example, the following all succeed:
%!test assert (1+eps, 1, 2*eps) # absolute error
%!test assert (100+100*eps, 100, -2*eps) # relative error
You can also do the comparison yourself, but still have assert generate the error:
%!test assert (isempty ([]))
%!test assert ([1, 2; 3, 4] > 0)
Because assert is so frequently used alone in a test block, there is a shorthand form:
%!assert (...)
which is equivalent to:
%!test assert (...)
Occasionally a block of tests will depend on having optional functionality in Octave.
Before testing such blocks the availability of the required functionality must be checked.
A%!testif HAVE_XXX block will only be run if Octave was compiled with functionality
‘HAVE_XXX’. For example, the sparse single value decomposition, svds(), depends on having
the arpack library. All of the tests for svds begin with
%!testif HAVE_ARPACK
Review config.h or __octave_config_info__ ("build_features") to see some of the
possible values to check.
Sometimes during development there is a test that should work but is known to fail.
You still want to leave the test in because when the final code is ready the test should pass,
but you may not be able to fix it immediately. To avoid unnecessary bug reports for these
known failures, mark the block with xtest rather than test:
%!xtest assert (1==0)
%!xtest fail ("success=1", "error")
In this case, the test will run and any failure will be reported. However, testing is not
aborted and subsequent test blocks will be processed normally. Another use of xtest is for
statistical tests which should pass most of the time but are known to fail occasionally.
916 GNU Octave
Each block is evaluated in its own function environment, which means that variables
defined in one block are not automatically shared with other blocks. If you do want to
share variables, then you must declare them as shared before you use them. For example,
the following declares the variable a, gives it an initial value (default is empty), and then
uses it in several subsequent tests.
%!shared a
%! a= [1, 2, 3; 4, 5, 6];
%!assert (kron ([1; 2], a), [ a; 2*a])
%!assert (kron ([1, 2], a), [ a, 2*a])
%!assert (kron ([1,2; 3,4], a), [ a,2*a; 3*a,4*a])
You can share several variables at the same time:
%!shared a,b
You can also share test functions:
%!function a= fn (b)
%! a= 2*b;
%!endfunction
%!assert (fn(2), 4)
Note that all previous variables and values are lost when a new shared block is declared.
Remember that %!function begins a new block and that %!endfunction ends this
block. Be aware that until a new block is started, lines starting with ‘%!<space>’ will be
discarded as comments. The following is nearly identical to the example above, but does
nothing.
%!function a= fn (b)
%! a= 2*b;
%!endfunction
%!assert (fn(2), 4)
Because there is a space after ‘%!’ the assert statement does not begin a new block and
this line is treated as a comment.
Error and warning blocks are like test blocks, but they only succeed if the code generates
an error. You can check the text of the error is correct using an optional regular expression
<pattern>. For example:
%!error <passes!> error ("this test passes!")
If the code doesn’t generate an error, the test fails. For example:
%!error "this is an error because it succeeds."
produces
***** error "this is an error because it succeeds."
!!!!! test failed: no error
It is important to automate the tests as much as possible, however some tests require
user interaction. These can be isolated into demo blocks, which if you are in batch mode,
are only run when called with demo or the verbose option to test. The code is displayed
before it is executed. For example,
Appendix B: Test and Demo Functions 917
%!demo
%! t= [0:0.01:2*pi]; x= sin (t);
%! plot (t,x);
%! # you should now see a sine wave in your figure window
produces
funcname example 1:
t= [0:0.01:2*pi]; x= sin (t);
plot (t,x);
# you should now see a sine wave in your figure window
Press <enter> to continue:
Note that demo blocks cannot use any shared variables. This is so that they can be
executed by themselves, ignoring all other tests.
If you want to temporarily disable a test block, put #in place of the block type. This
creates a comment block which is echoed in the log file but not executed. For example:
%!#demo
%! t= [0:0.01:2*pi]; x= sin (t);
%! plot (t,x);
%! # you should now see a sine wave in your figure window
The following trivial code snippet provides examples for the use of fail, assert, error, and
xtest:
function output = must_be_zero (input)
if (input != 0)
error ("Nonzero input!")
endif
output = input;
endfunction
%!fail ("must_be_zero (1)")
%!assert (must_be_zero (0), 0)
%!error <Nonzero> must_be_zero (1)
%!xtest error ("This code generates an error")
When putting this in a file must_be_zero.m, and running the test, we see
test must_be_zero verbose
⇒
>>>>> /path/to/must_be_zero.m
***** fail ("must_be_zero (1)")
***** assert (must_be_zero (0), 0)
***** error <Nonzero> must_be_zero (1)
***** xtest error ("This code generates an error")
!!!!! known failure
This code generates an error
PASSES 3 out of 4 tests (1 expected failure)

918 GNU Octave
Block type summary:
%!test
%!test <MESSAGE>
Check that entire block is correct. If <MESSAGE> is present, the test block is
interpreted as for xtest.
%!testif HAVE_XXX
%!testif HAVE_XXX, HAVE_YYY, ...
%!testif ... <MESSAGE>
Check block only if Octave was compiled with feature HAVE XXX. If
<MESSAGE> is present, the test block is interpreted as for xtest.
%!xtest
%!xtest <MESSAGE>
Check block, report a test failure but do not abort testing. If <MESSAGE> is
present, then the text of the message is displayed if the test fails, like this:
!!!!! Known bug: MESSAGE
If the message is an integer, it is interpreted as a bug ID for the Octave bug
tracker and reported as
!!!!! Known bug: http://octave.org/testfailure/?BUG-ID
in which BUG-ID is the integer bug number. The intent is to allow clearer
documentation of known problems.
%!error
%!error <MESSAGE>
%!warning
%!warning <MESSAGE>
Check for correct error or warning message. If <MESSAGE> is supplied it is
interpreted as a regular expression pattern that is expected to match the error
or warning message.
%!demo Demo only executes in interactive mode.
%!# Comment. Ignore everything within the block
%!shared x,y,z
Declare variables for use in multiple tests.
%!function
Define a function for use in multiple tests.
%!endfunction
Close a function definition.
%!assert (x, y, tol)
%!assert <MESSAGE> (x, y, tol)
%!fail (CODE, PATTERN)
%!fail <MESSAGE> (CODE, PATTERN)
Shorthand for %!test assert (x, y, tol) or %!test fail (CODE, PATTERN).
If <MESSAGE> is present, the test block is interpreted as for xtest.
Appendix B: Test and Demo Functions 919
When coding tests the Octave convention is that lines that begin with a block type do
not have a semicolon at the end. Any code that is within a block, however, is normal Octave
code and usually will have a trailing semicolon. For example,
## bare block instantiation
%!assert (sin (0), 0)
but
## test block with normal Octave code
%!test
%! assert (sin (0), 0);
You can also create test scripts for built-in functions and your own C++ functions. To
do so, put a file with the bare function name (no .m extension) in a directory in the load
path and it will be discovered by the test function. Alternatively, you can embed tests
directly in your C++ code:
/*
%!test disp ("this is a test")
*/
or
#if 0
%!test disp ("this is a test")
#endif
However, in this case the raw source code will need to be on the load path and the user will
have to remember to type test ("funcname.cc").
assert (cond)
assert (cond,errmsg)
assert (cond,errmsg, . . . )
assert (cond,msg_id,errmsg, . . . )
assert (observed,expected)
assert (observed,expected,tol)
Produce an error if the specified condition is not met.
assert can be called in three different ways.
assert (cond)
assert (cond,errmsg)
assert (cond,errmsg, ...)
assert (cond,msg_id,errmsg, ...)
Called with a single argument cond,assert produces an error if cond is
false (numeric zero).
Any additional arguments are passed to the error function for processing.
assert (observed,expected)
Produce an error if observed is not the same as expected.
Note that observed and expected can be scalars, vectors, matrices,
strings, cell arrays, or structures.
920 GNU Octave
assert (observed,expected,tol)
Produce an error if observed is not the same as expected but equality
comparison for numeric data uses a tolerance tol.
If tol is positive then it is an absolute tolerance which will produce an
error if abs (observed -expected) > abs (tol).
If tol is negative then it is a relative tolerance which will produce an error
if abs (observed -expected) > abs (tol *expected).
If expected is zero tol will always be interpreted as an absolute tolerance.
If tol is not scalar its dimensions must agree with those of observed and
expected and tests are performed on an element-by-element basis.
See also: [fail], page 920,[test], page 913,[error], page 215,[isequal], page 147.
fail (code)
fail (code,pattern)
fail (code,"warning")
fail (code,"warning",pattern)
Return true if code fails with an error message matching pattern, otherwise produce
an error.
code must be in the form of a string that is passed to the Octave interpreter via the
evalin function, i.e., a (quoted) string constant or a string variable.
Note that if code runs successfully, rather than failing, the error printed is:
expected error <.> but got none
If called with two arguments, the return value will be true only if code fails with an
error message containing pattern (case sensitive). If the code fails with a different
error than the one specified in pattern then the message produced is:
expected <pattern>
but got <text of actual error>
The angle brackets are not part of the output.
When called with the "warning" option fail will produce an error if executing the
code produces no warning.
See also: [assert], page 919,[error], page 215.
B.2 Demonstration Functions
demo name
demo name n
demo ("name")
demo ("name",n)
Run example code block nassociated with the function name.
If nis not specified, all examples are run.
The preferred location for example code blocks is embedded within the script m-file
immediately following the code that it exercises. Alternatively, the examples may be
stored in a file with the same name but no extension located on Octave’s load path.
Appendix B: Test and Demo Functions 921
To separate examples from regular script code all lines are prefixed by %!. Each
example must also be introduced by the keyword "demo" flush left to the prefix with
no intervening spaces. The remainder of the example can contain arbitrary Octave
code. For example:
%!demo
%! t = 0:0.01:2*pi;
%! x = sin (t);
%! plot (t, x);
%! title ("one cycle of a sine wave");
%! #-------------------------------------------------
%! # the figure window shows one cycle of a sine wave
Note that the code is displayed before it is executed so that a simple comment at the
end suffices for labeling what is being shown. For plots, labeling can also be done
with title or text. It is generally not necessary to use disp or printf within the
demo.
Demos are run in a stand-alone function environment with no access to external
variables. This means that every demo must have separate initialization code. Alter-
natively, all demos can be combined into a single large demo with the code
%! input ("Press <enter> to continue: ", "s");
between the sections, but this usage is discouraged. Other techniques to avoid multiple
initialization blocks include using multiple plots with a new figure command between
each plot, or using subplot to put multiple plots in the same window.
Finally, because demo evaluates within a function context it is not possible to de-
fine new functions within the code. Anonymous functions make a good substitute
in most instances. If function blocks must be used then the code eval (example
("function", n)) will allow Octave to see them. This has its own problems, how-
ever, as eval only evaluates one line or statement at a time. In this case the function
declaration must be wrapped with "if 1 <demo stuff> endif" where "if" is on the
same line as "demo". For example:
%!demo if 1
%! function y = f(x)
%! y = x;
%! endfunction
%! f(3)
%! endif
See also: [rundemos], page 922,[example], page 921,[test], page 913.
example name
example name n
example ("name")
example ("name",n)
[s,idx] = example (. . . )
Display the code for example nassociated with the function name, but do not run it.
If nis not specified, all examples are displayed.

922 GNU Octave
When called with output arguments, the examples are returned in the form of a string
s, with idx indicating the ending position of the various examples.
See demo for a complete explanation.
See also: [demo], page 920,[test], page 913.
rundemos ()
rundemos (directory)
Execute built-in demos for all m-files in the specified directory.
Demo blocks in any C++ source files (*.cc) will also be executed for use with dynam-
ically linked oct-file functions.
If no directory is specified, operate on all directories in Octave’s search path for
functions.
See also: [demo], page 920,[runtests], page 922,[path], page 193.
runtests ()
runtests (directory)
Execute built-in tests for all m-files in the specified directory.
Test blocks in any C++ source files (*.cc) will also be executed for use with dynami-
cally linked oct-file functions.
If no directory is specified, operate on all directories in Octave’s search path for
functions.
See also: [rundemos], page 922,[test], page 913,[path], page 193.
speed (f,init,max_n,f2,tol)
[order,n,T_f,T_f2] = speed (. . . )
Determine the execution time of an expression (f) for various input values (n).
The nare log-spaced from 1 to max n. For each n, an initialization expression (init)
is computed to create any data needed for the test. If a second expression (f2) is given
then the execution times of the two expressions are compared. When called without
output arguments the results are printed to stdout and displayed graphically.
fThe code expression to evaluate.
max_n The maximum test length to run. The default value is 100. Alternatively,
use [min_n, max_n] or specify the nexactly with [n1, n2, ..., nk].
init Initialization expression for function argument values. Use kfor the test
number and nfor the size of the test. This should compute values for
all variables used by f. Note that init will be evaluated first for k= 0,
so things which are constant throughout the test series can be computed
once. The default value is x= randn (n, 1).
f2 An alternative expression to evaluate, so that the speed of two expressions
can be directly compared. The default is [].
tol Tolerance used to compare the results of expression fand expression f2.
If tol is positive, the tolerance is an absolute one. If tol is negative, the
tolerance is a relative one. The default is eps. If tol is Inf, then no
comparison will be made.

923
order The time complexity of the expression O(a∗np). This is a structure with
fields aand p.
nThe values nfor which the expression was calculated AND the execution
time was greater than zero.
T_f The nonzero execution times recorded for the expression fin seconds.
T_f2 The nonzero execution times recorded for the expression f2 in seconds. If
required, the mean time ratio is simply mean (T_f ./ T_f2).
The slope of the execution time graph shows the approximate power of the asymptotic
running time O(np). This power is plotted for the region over which it is approximated
(the latter half of the graph). The estimated power is not very accurate, but should
be sufficient to determine the general order of an algorithm. It should indicate if,
for example, the implementation is unexpectedly O(n2) rather than O(n) because it
extends a vector each time through the loop rather than pre-allocating storage. In
the current version of Octave, the following is not the expected O(n).
speed ("for i = 1:n, y{i} = x(i); endfor", "", [1000, 10000])
But it is if you preallocate the cell array y:
speed ("for i = 1:n, y{i} = x(i); endfor", ...
"x = rand (n, 1); y = cell (size (x));", [1000, 10000])
An attempt is made to approximate the cost of individual operations, but it is wildly
inaccurate. You can improve the stability somewhat by doing more work for each n.
For example:
speed ("airy(x)", "x = rand (n, 10)", [10000, 100000])
When comparing two different expressions (f,f2), the slope of the line on the speedup
ratio graph should be larger than 1 if the new expression is faster. Better algorithms
have a shallow slope. Generally, vectorizing an algorithm will not change the slope of
the execution time graph, but will shift it relative to the original. For example:
speed ("sum (x)", "", [10000, 100000], ...
"v = 0; for i = 1:length (x), v += x(i); endfor")
The following is a more complex example. If there was an original version of xcorr
using for loops and a second version using an FFT, then one could compare the run
speed for various lags as follows, or for a fixed lag with varying vector lengths as
follows:
speed ("xcorr (x, n)", "x = rand (128, 1);", 100,
"xcorr_orig (x, n)", -100*eps)
speed ("xcorr (x, 15)", "x = rand (20+n, 1);", 100,
"xcorr_orig (x, n)", -100*eps)
Assuming one of the two versions is in xcorr orig, this would compare their speed and
their output values. Note that the FFT version is not exact, so one must specify an
acceptable tolerance on the comparison 100*eps. In this case, the comparison should
be computed relatively, as abs ((x-y) ./ y)rather than absolutely as abs (x-y).
Type example ("speed")to see some real examples or demo ("speed")to run them.
925
Appendix C Obsolete Functions
After being marked as deprecated for two major releases, the following functions have
been removed from Octave. The third column of the table shows the version of Octave in
which the function was removed. Prior to removal, each function in the list was marked
as deprecated for at least two major releases. All deprecated functions issue warnings
explaining that they will be removed in a future version of Octave, and which function
should be used instead.
Replacement functions do not always accept precisely the same arguments as the obsolete
function, but should provide equivalent functionality.
Obsolete Function Replacement Version
beta_cdf betacdf 3.4.0
beta_inv betainv 3.4.0
beta_pdf betapdf 3.4.0
beta_rnd betarnd 3.4.0
binomial_cdf binocdf 3.4.0
binomial_inv binoinv 3.4.0
binomial_pdf binopdf 3.4.0
binomial_rnd binornd 3.4.0
chisquare_cdf chi2cdf 3.4.0
chisquare_inv chi2inv 3.4.0
chisquare_pdf chi2pdf 3.4.0
chisquare_rnd chi2rnd 3.4.0
clearplot clf 3.4.0
com2str num2str 3.4.0
exponential_cdf expcdf 3.4.0
exponential_inv expinv 3.4.0
exponential_pdf exppdf 3.4.0
exponential_rnd exprnd 3.4.0
f_cdf fcdf 3.4.0
f_inv finv 3.4.0
f_pdf fpdf 3.4.0
f_rnd frnd 3.4.0
gamma_cdf gamcdf 3.4.0
gamma_inv gaminv 3.4.0
gamma_pdf gampdf 3.4.0
gamma_rnd gamrnd 3.4.0
geometric_cdf geocdf 3.4.0
geometric_inv geoinv 3.4.0
geometric_pdf geopdf 3.4.0
geometric_rnd geornd 3.4.0
hypergeometric_cdf hygecdf 3.4.0
hypergeometric_inv hygeinv 3.4.0
hypergeometric_pdf hygepdf 3.4.0
hypergeometric_rnd hygernd 3.4.0
926 GNU Octave
intersection intersect 3.4.0
is_bool isbool 3.4.0
is_complex iscomplex 3.4.0
is_list islist 3.4.0
is_matrix ismatrix 3.4.0
is_scalar isscalar 3.4.0
is_square issquare 3.4.0
is_stream isstream 3.4.0
is_struct isstruct 3.4.0
is_symmetric issymmetric 3.4.0
is_vector isvector 3.4.0
lognormal_cdf logncdf 3.4.0
lognormal_inv logninv 3.4.0
lognormal_pdf lognpdf 3.4.0
lognormal_rnd lognrnd 3.4.0
meshdom meshgrid 3.4.0
normal_cdf normcdf 3.4.0
normal_inv norminv 3.4.0
normal_pdf normpdf 3.4.0
normal_rnd normrnd 3.4.0
pascal_cdf nbincdf 3.4.0
pascal_inv nbininv 3.4.0
pascal_pdf nbinpdf 3.4.0
pascal_rnd nbinrnd 3.4.0
poisson_cdf poisscdf 3.4.0
poisson_inv poissinv 3.4.0
poisson_pdf poisspdf 3.4.0
poisson_rnd poissrnd 3.4.0
polyinteg polyint 3.4.0
struct_contains isfield 3.4.0
struct_elements fieldnames 3.4.0
t_cdf tcdf 3.4.0
t_inv tinv 3.4.0
t_pdf tpdf 3.4.0
t_rnd trnd 3.4.0
uniform_cdf unifcdf 3.4.0
uniform_inv unifinv 3.4.0
uniform_pdf unifpdf 3.4.0
uniform_rnd unifrnd 3.4.0
weibull_cdf wblcdf 3.4.0
weibull_inv wblinv 3.4.0
weibull_pdf wblpdf 3.4.0
weibull_rnd wblrnd 3.4.0
wiener_rnd wienrnd 3.4.0
create_set unique 3.6.0
dmult diag (A) * B 3.6.0
iscommand None 3.6.0
Appendix C: Obsolete Functions 927
israwcommand None 3.6.0
lchol chol (..., "lower") 3.6.0
loadimage load or imread 3.6.0
mark_as_command None 3.6.0
mark_as_rawcommand None 3.6.0
spatan2 atan2 3.6.0
spchol chol 3.6.0
spchol2inv chol2inv 3.6.0
spcholinv cholinv 3.6.0
spcumprod cumprod 3.6.0
spcumsum cumsum 3.6.0
spdet det 3.6.0
spdiag sparse (diag (...)) 3.6.0
spfind find 3.6.0
sphcat horzcat 3.6.0
spinv inv 3.6.0
spkron kron 3.6.0
splchol chol (..., "lower") 3.6.0
split char (strsplit (s,
t))
3.6.0
splu lu 3.6.0
spmax max 3.6.0
spmin min 3.6.0
spprod prod 3.6.0
spqr qr 3.6.0
spsum sum 3.6.0
spsumsq sumsq 3.6.0
spvcat vertcat 3.6.0
str2mat char 3.6.0
unmark_command None 3.6.0
unmark_rawcommand None 3.6.0
autocor Octave-Forge signal pkg,
xcor
3.8.0
autocov Octave-Forge signal pkg,
xcov
3.8.0
betai betainc 3.8.0
cellidx ismember 3.8.0
cquad quadcc 3.8.0
dispatch None 3.8.0
fstat stat 3.8.0
gammai gammainc 3.8.0
glpkmex glpk 3.8.0
is_duplicate_entry unique 3.8.0
is_global isglobal 3.8.0
krylovb [Uret, ~, Ucols] =
krylov (...)
3.8.0
928 GNU Octave
perror None 3.8.0
replot refresh 3.8.0
saveimage imwrite 3.8.0
setstr char 3.8.0
strerror None 3.8.0
values unique 3.8.0
cut histc 4.0.0
cor corr 4.0.0
corrcoef corr 4.0.0
__error_text__ lasterr 4.0.0
error_text lasterr 4.0.0
polyderiv polyder 4.0.0
shell_cmd system 4.0.0
studentize zscore 4.0.0
sylvester_matrix hadamard (2^k) 4.0.0
929
Appendix D Known Causes of Trouble
This section describes known problems that affect users of Octave. Most of these are not
Octave bugs per se—if they were, we would fix them. But the result for a user may be like
the result of a bug.
Some of these problems are due to bugs in other software, some are missing features that
are too much work to add, and some are places where people’s opinions differ as to what is
best.
D.1 Actual Bugs We Haven’t Fixed Yet
•Output that comes directly from Fortran functions is not sent through the pager and
may appear out of sequence with other output that is sent through the pager. One way
to avoid this is to force pending output to be flushed before calling a function that will
produce output from within Fortran functions. To do this, use the command
fflush (stdout)
Another possible workaround is to use the command
page_screen_output (false);
to turn the pager off.
A list of ideas for future enhancements is distributed with Octave. See the file PROJECTS
in the top level directory in the source distribution.
D.2 Reporting Bugs
Your bug reports play an essential role in making Octave reliable.
When you encounter a problem, the first thing to do is to see if it is already known. See
Appendix D [Trouble], page 929. If it isn’t known, then you should report the problem.
Reporting a bug may help you by bringing a solution to your problem, or it may not.
In any case, the principal function of a bug report is to help the entire community by
making the next version of Octave work better. Bug reports are your contribution to the
maintenance of Octave.
In order for a bug report to serve its purpose, you must include the information that
makes it possible to fix the bug.
D.2.1 Have You Found a Bug?
If you are not sure whether you have found a bug, here are some guidelines:
•If Octave gets a fatal signal, for any input whatever, that is a bug. Reliable interpreters
never crash.
•If Octave produces incorrect results, for any input whatever, that is a bug.
•Some output may appear to be incorrect when it is in fact due to a program whose
behavior is undefined, which happened by chance to give the desired results on another
system. For example, the range operator may produce different results because of
differences in the way floating point arithmetic is handled on various systems.
•If Octave produces an error message for valid input, that is a bug.
930 GNU Octave
•If Octave does not produce an error message for invalid input, that is a bug. However,
you should note that your idea of “invalid input” might be my idea of “an extension”
or “support for traditional practice”.
•If you are an experienced user of programs like Octave, your suggestions for improve-
ment are welcome in any case.
D.2.2 Where to Report Bugs
To report a bug in Octave, submit a bug report to the Octave bug tracker http://bugs.
octave.org.
Do not send bug reports to ‘help-octave’. Most users of Octave do not want to receive
bug reports.
D.2.3 How to Report Bugs
Submit bug reports for Octave to the Octave bug tracker http://bugs.octave.org.
The fundamental principle of reporting bugs usefully is this: report all the facts. If you
are not sure whether to state a fact or leave it out, state it!
Often people omit facts because they think they know what causes the problem and
they conclude that some details don’t matter. Thus, you might assume that the name of
the variable you use in an example does not matter. Well, probably it doesn’t, but one
cannot be sure. Perhaps the bug is a stray memory reference which happens to fetch from
the location where that name is stored in memory; perhaps, if the name were different, the
contents of that location would fool the interpreter into doing the right thing despite the
bug. Play it safe and give a specific, complete example.
Keep in mind that the purpose of a bug report is to enable someone to fix the bug if it
is not known. Always write your bug reports on the assumption that the bug is not known.
Sometimes people give a few sketchy facts and ask, “Does this ring a bell?” This cannot
help us fix a bug. It is better to send a complete bug report to begin with.
Try to make your bug report self-contained. If we have to ask you for more information, it
is best if you include all the previous information in your response, as well as the information
that was missing.
To enable someone to investigate the bug, you should include all these things:
•The version of Octave. You can get this by noting the version number that is printed
when Octave starts, or running it with the ‘-v’ option.
•A complete input file that will reproduce the bug.
A single statement may not be enough of an example—the bug might depend on other
details that are missing from the single statement where the error finally occurs.
•The command arguments you gave Octave to execute that example and observe the
bug. To guarantee you won’t omit something important, list all the options.
If we were to try to guess the arguments, we would probably guess wrong and then we
would not encounter the bug.
•The type of machine you are using, and the operating system name and version number.
•The command-line arguments you gave to the configure command when you installed
the interpreter.
Appendix D: Known Causes of Trouble 931
•A complete list of any modifications you have made to the interpreter source.
Be precise about these changes—show a context diff for them.
•Details of any other deviations from the standard procedure for installing Octave.
•A description of what behavior you observe that you believe is incorrect. For example,
"The interpreter gets a fatal signal,"or, "The output produced at line 208 is incorrect."
Of course, if the bug is that the interpreter gets a fatal signal, then one can’t miss it.
But if the bug is incorrect output, we might not notice unless it is glaringly wrong.
Even if the problem you experience is a fatal signal, you should still say so explicitly.
Suppose something strange is going on, such as, your copy of the interpreter is out
of sync, or you have encountered a bug in the C library on your system. Your copy
might crash and the copy here would not. If you said to expect a crash, then when the
interpreter here fails to crash, we would know that the bug was not happening. If you
don’t say to expect a crash, then we would not know whether the bug was happening.
We would not be able to draw any conclusion from our observations.
Often the observed symptom is incorrect output when your program is run. Unfortu-
nately, this is not enough information unless the program is short and simple. It is very
helpful if you can include an explanation of the expected output, and why the actual
output is incorrect.
•If you wish to suggest changes to the Octave source, send them as context diffs. If you
even discuss something in the Octave source, refer to it by context, not by line number,
because the line numbers in the development sources probably won’t match those in
your sources.
Here are some things that are not necessary:
•A description of the envelope of the bug.
Often people who encounter a bug spend a lot of time investigating which changes to
the input file will make the bug go away and which changes will not affect it. Such
information is usually not necessary to enable us to fix bugs in Octave, but if you can
find a simpler example to report instead of the original one, that is a convenience.
Errors in the output will be easier to spot, running under the debugger will take less
time, etc. Most Octave bugs involve just one function, so the most straightforward way
to simplify an example is to delete all the function definitions except the one in which
the bug occurs.
However, simplification is not vital; if you don’t want to do this, report the bug anyway
and send the entire test case you used.
•A patch for the bug. Patches can be helpful, but if you find a bug, you should report
it, even if you cannot send a fix for the problem.
D.2.4 Sending Patches for Octave
If you would like to write bug fixes or improvements for Octave, that is very helpful. When
you send your changes, please follow these guidelines to avoid causing extra work for us in
studying the patches.
If you don’t follow these guidelines, your information might still be useful, but using it
will take extra work. Maintaining Octave is a lot of work in the best of circumstances, and
we can’t keep up unless you do your best to help.
932 GNU Octave
•Send an explanation with your changes of what problem they fix or what improvement
they bring about. For a bug fix, just include a copy of the bug report, and explain why
the change fixes the bug.
•Always include a proper bug report for the problem you think you have fixed. We need
to convince ourselves that the change is right before installing it. Even if it is right, we
might have trouble judging it if we don’t have a way to reproduce the problem.
•Include all the comments that are appropriate to help people reading the source in the
future understand why this change was needed.
•Don’t mix together changes made for different reasons. Send them individually.
If you make two changes for separate reasons, then we might not want to install them
both. We might want to install just one.
•Use ‘diff -c’ to make your diffs. Diffs without context are hard for us to install
reliably. More than that, they make it hard for us to study the diffs to decide whether
we want to install them. Unified diff format is better than contextless diffs, but not as
easy to read as ‘-c’ format.
If you have GNU diff, use ‘diff -cp’, which shows the name of the function that each
change occurs in.
•Write the change log entries for your changes.
Read the ChangeLog file to see what sorts of information to put in, and to learn the
style that we use. The purpose of the change log is to show people where to find what
was changed. So you need to be specific about what functions you changed; in large
functions, it’s often helpful to indicate where within the function the change was made.
On the other hand, once you have shown people where to find the change, you need
not explain its purpose. Thus, if you add a new function, all you need to say about it
is that it is new. If you feel that the purpose needs explaining, it probably does—but
the explanation will be much more useful if you put it in comments in the code.
If you would like your name to appear in the header line for who made the change,
send us the header line.
D.3 How To Get Help with Octave
The mailing list help@octave.org exists for the discussion of matters related to using
and installing Octave. If would like to join the discussion, please send a short note to
help-request@octave.org.
Please do not send requests to be added or removed from the mailing list, or other
administrative trivia to the list itself.
If you think you have found a bug in Octave or in the installation procedure, however,
you should submit a complete bug report to the Octave bug tracker at http:// bugs.
octave.org. But before you submit a bug report, please read http://www.octave.org/
bugs.html to learn how to submit a useful bug report.
D.4 How to Distinguish Between Octave and Matlab
Octave and matlab are very similar, but handle Java slightly different. Therefore it may
be necessary to detect the environment and use the appropriate functions. The following
933
function can be used to detect the environment. Due to the persistent variable it can be
called repeatedly without a heavy performance hit.
Example:
%%
%% Return: true if the environment is Octave.
%%
function retval = isOctave
persistent cacheval; % speeds up repeated calls
if isempty (cacheval)
cacheval = (exist ("OCTAVE_VERSION", "builtin") > 0);
end
retval = cacheval;
end
935
Appendix E Installing Octave
The procedure for installing Octave from source on a Unix-like system is described next.
Building on other platforms will follow similar steps. Note that this description applies
to Octave releases. Building the development sources from the Mercurial archive requires
additional steps as described in the development source itself.
E.1 Build Dependencies
Octave is a fairly large program with many build dependencies. You may be able to find
pre-packaged versions of the dependencies distributed as part of your system, or you may
have to build some or all of them yourself.
E.1.1 Obtaining the Dependencies Automatically
On some systems you can obtain many of Octave’s build dependencies automatically. The
commands for doing this vary by system. Similarly, the names of pre-compiled packages
vary by system and do not always match exactly the names listed in Section E.1.2 [Build
Tools], page 935, and Section E.1.3 [External Packages], page 936.
You will usually need the development version of an external dependency so that you get
the libraries and header files for building software, not just for running already compiled
programs. These packages typically have names that end with the suffix -dev or -devel.
On systems with apt-get (Debian, Ubuntu, etc.), you may be able to install most of
the tools and external packages using a command similar to
apt-get build-dep octave
The specific package name may be octave3.2 or octave3.4. The set of required tools and
external dependencies does not change frequently, so it is not important that the version
match exactly, but you should use the most recent one available.
On systems with yum (Fedora, Red Hat, etc.), you may be able to install most of the
tools and external packages using a command similar to
yum-builddep octave
The yum-builddep utility is part of the yum-utils package.
For either type of system, the package name may include a version number. The set of
required tools and external dependencies does not change frequently, so it is not important
that the version exactly match the version you are installing, but you should use the most
recent one available.
E.1.2 Build Tools
The following tools are required:
C++, C, and Fortran compilers
The Octave sources are primarily written in C++, but some portions are also
written in C and Fortran. The Octave sources are intended to be portable.
Recent versions of the GNU compiler collection (GCC) should work (http://
gcc.gnu.org). If you use GCC, you should avoid mixing versions. For example,
be sure that you are not using the obsolete g77 Fortran compiler with modern
versions of gcc and g++.
936 GNU Octave
GNU Make
Tool for building software (http://www.gnu.org/software/make). Octave’s
build system requires GNU Make. Other versions of Make will not work. For-
tunately, GNU Make is highly portable and easy to install.
AWK, sed, and other Unix utilities
Basic Unix system utilities are required for building Octave. All will be available
with any modern Unix system and also on Windows with either Cygwin or
MinGW and MSYS.
Additionally, the following tools may be needed:
Bison Parser generator (http:/ /www.gnu.org/ software/bison). You will need
Bison if you modify the oct-parse.yy source file or if you delete the files that
are generated from it.
Flex Lexer analyzer (http://www.gnu.org/software/flex). You will need Flex if
you modify the lex.ll source file or if you delete the files that are generated
from it.
Autoconf Package for software configuration (http: / / www . gnu . org / software /
autoconf). Autoconf is required if you modify Octave’s configure.ac file or
other files that it requires.
Automake Package for Makefile generation (http://www.gnu.org/software/automake).
Automake is required if you modify Octave’s Makefile.am files or other files
that they depend on.
Libtool Package for building software libraries (http: / / www . gnu . org / software /
libtool). Libtool is required by Automake.
gperf Perfect hash function generator (http://www.gnu.org/software/gperf). You
will need gperf if you modify the octave.gperf file or if you delete the file that
is generated from it.
Texinfo Package for generating online and print documentation (http://www.gnu.org/
software/texinfo). You will need Texinfo to build Octave’s documentation
or if you modify the documentation source files or the docstring of any Octave
function.
E.1.3 External Packages
The following external packages are required:
BLAS Basic Linear Algebra Subroutine library. Accelerated blas libraries such as
OpenBLAS (http://www.openblas.net/) or ATLAS (http://math-atlas.
sourceforge.net) are recommended for best performance. The reference im-
plementation (http: / / www . netlib . org / blas) is slow, unmaintained, and
suffers from certain bugs in corner case inputs.
LAPACK Linear Algebra Package (http://www.netlib.org/lapack).
PCRE The Perl Compatible Regular Expression library (http://www.pcre.org).
Appendix E: Installing Octave 937
The following external package is optional but strongly recommended:
GNU Readline
Command-line editing library (www.gnu.org/s/readline).
If you wish to build Octave without GNU readline installed, you must use the
--disable-readline option when running the configure script.
The following external software packages are optional but recommended:
ARPACK Library for the solution of large-scale eigenvalue problems (http:/ /forge.
scilab.org/index.php/p/arpack-ng). arpack is required to provide the
functions eigs and svds.
cURL Library for transferring data with URL syntax (http://curl.haxx.se). cURL
is required to provide the urlread and urlwrite functions and the ftp class.
FFTW3 Library for computing discrete Fourier transforms (http://www.fftw.org).
FFTW3 is used to provide better performance for functions that compute dis-
crete Fourier transforms (fft,ifft,fft2, etc.)
FLTK Portable GUI toolkit (http://www.fltk .org). FLTK is currently used to
provide windows for Octave’s OpenGL-based graphics functions.
fontconfig Library for configuring and customizing font access (http: / / www .
freedesktop . org / wiki / Software / fontconfig). Fontconfig is used to
manage fonts for Octave’s OpenGL-based graphics functions.
FreeType Portable font engine (http://www.freetype.org). FreeType is used to per-
form font rendering for Octave’s OpenGL-based graphics functions.
GLPK GNU Linear Programming Kit (http: / / www . gnu . org / software / glpk).
GPLK is required for the function glpk.
gl2ps OpenGL to PostScript printing library (http://www.geuz.org/gl2ps/). gl2ps
is required for printing when using OpenGL-based graphics toolkits (currently
either FLTK or Qt).
gnuplot Interactive graphics program (http://www.gnuplot.info). gnuplot is cur-
rently the default graphics renderer for Octave.
GraphicsMagick++
Image processing library (http://www.graphicsmagick.org). GraphicsMag-
ick++ is used to provide the imread and imwrite functions.
HDF5 Library for manipulating portable data files (http: / / www . hdfgroup . org /
HDF5). hdf5 is required for Octave’s load and save commands to read and
write HDF data files.
Java Development Kit
Java programming language compiler and libraries. The OpenJDK free soft-
ware implementation is recommended (http://openjdk.java.net/), although
other JDK implementations may work. Java is required to be able to call Java
functions from within Octave.
LLVM Compiler framework, (http://www.llvm.org). LLVM is required for Octave’s
experimental just-in-time (JIT) compilation for speeding up the interpreter.
938 GNU Octave
OpenGL API for portable 2-D and 3-D graphics (http: / / www . opengl . org). An
OpenGL implementation is required to provide Octave’s OpenGL-based graph-
ics functions. Octave’s OpenGL-based graphics functions usually outperform
the gnuplot-based graphics functions because plot data can be rendered di-
rectly instead of sending data and commands to gnuplot for interpretation and
rendering.
Qhull Computational geometry library (http://www.qhull.org). Qhull is required
to provide the functions convhull,convhulln,delaunay,delaunayn,voronoi,
and voronoin.
QRUPDATE
QR factorization updating library (http: / / sourceforge . net / projects /
qrupdate). QRUPDATE is used to provide improved performance for the func-
tions qrdelete,qrinsert,qrshift, and qrupdate.
QScintilla Source code highlighter and manipulator; a Qt port of Scintilla (http://www.
riverbankcomputing.co.uk/software/qscintilla). QScintilla is used for
syntax highlighting and code completion in the GUI.
Qt GUI and utility libraries (). Qt is required for building the GUI. It is a large
framework, but the only components required are the GUI, core, and network
modules.
SuiteSparse
Sparse matrix factorization library (http://www.cise.ufl.edu/research/
sparse/SuiteSparse). SuiteSparse is required to provide sparse matrix fac-
torizations and solution of linear equations for sparse systems.
zlib Data compression library (http:// zlib.net). The zlib library is required
for Octave’s load and save commands to handle compressed data, including
matlab v5 MAT files.
E.2 Running Configure and Make
•Run the shell script configure. This will determine the features your system has
(or doesn’t have) and create a file named Makefile from each of the files named
Makefile.in.
Here is a summary of the configure options that are most frequently used when building
Octave:
--help Print a summary of the options recognized by the configure script.
--prefix=prefix
Install Octave in subdirectories below prefix. The default value of prefix is
/usr/local.
--srcdir=dir
Look for Octave sources in the directory dir.
--enable-64
This is an experimental option to enable Octave to use 64-bit integers for
array dimensions and indexing on 64-bit platforms. You probably don’t
Appendix E: Installing Octave 939
want to use this option unless you know what you are doing. See Section E.3
[Compiling Octave with 64-bit Indexing], page 942, for more details about
building Octave with this option.
--enable-bounds-check
Enable bounds checking for indexing operators in the internal array classes.
This option is primarily used for debugging Octave. Building Octave with
this option has a negative impact on performance and is not recommended
for general use.
--disable-docs
Disable building all forms of the documentation (Info, PDF, HTML). The
default is to build documentation, but your system will need functioning
Texinfo and T
E
X installs for this to succeed.
--enable-float-truncate
This option allows for truncation of intermediate floating point results in
calculations. It is only necessary for certain platforms.
--enable-readline
Use the readline library to provide for editing of the command line in
terminal environments. This option is on by default.
--enable-shared
Create shared libraries (this is the default). If you are planning to use
the dynamic loading features, you will probably want to use this option.
It will make your .oct files much smaller and on some systems it may
be necessary to build shared libraries in order to use dynamically linked
functions.
You may also want to build a shared version of libstdc++, if your system
doesn’t already have one.
--enable-dl
Use dlopen and friends to make Octave capable of dynamically linking
externally compiled functions (this is the default if --enable-shared is
specified). This option only works on systems that actually have these
functions. If you plan on using this feature, you should probably also use
--enable-shared to reduce the size of your .oct files.
--with-blas=<lib>
By default, configure looks for the best blas matrix libraries on your sys-
tem, including optimized implementations such as the free ATLAS 3.0, as
well as vendor-tuned libraries. (The use of an optimized blas will gener-
ally result in several-times faster matrix operations.) Use this option to
specify a particular blas library that Octave should use.
--with-lapack=<lib>
By default, configure looks for the best lapack matrix libraries on your
system, including optimized implementations such as the free ATLAS 3.0,
as well as vendor-tuned libraries. (The use of an optimized lapack will
generally result in several-times faster matrix operations.) Use this option
to specify a particular lapack library that Octave should use.
940 GNU Octave
--with-magick=<lib>
Select the library to use for image I/O. The two possible values are
"GraphicsMagick" (default) or "ImageMagick".
--with-sepchar=<char>
Use <char>as the path separation character. This option can help when
running Octave on non-Unix systems.
--without-amd
Don’t use amd, disable some sparse matrix functionality.
--without-camd
Don’t use camd, disable some sparse matrix functionality.
--without-colamd
Don’t use colamd, disable some sparse matrix functionality.
--without-ccolamd
Don’t use ccolamd, disable some sparse matrix functionality.
--without-cholmod
Don’t use cholmod, disable some sparse matrix functionality.
--without-curl
Don’t use the cURL library, disable the ftp objects, urlread and urlwrite
functions.
--without-cxsparse
Don’t use cxsparse, disable some sparse matrix functionality.
--without-fftw3
Use the included fftpack library for computing Fast Fourier Transforms
instead of the fftw3 library.
--without-fftw3f
Use the included fftpack library for computing Fast Fourier Transforms
instead of the fftw3 library when operating on single precision (float)
values.
--without-glpk
Don’t use the glpk library for linear programming.
--without-hdf5
Don’t use the hdf5 library, disable reading and writing of hdf5 files.
--without-opengl
Don’t use OpenGL, disable native graphics toolkit for plotting. You will
need gnuplot installed in order to make plots.
--without-qhull
Don’t use Qhull, disable delaunay,convhull, and related functions.
--without-qrupdate
Don’t use qrupdate, disable QR and Cholesky update functions.
--without-umfpack
Don’t use umfpack, disable some sparse matrix functionality.
Appendix E: Installing Octave 941
--without-zlib
Don’t use the zlib library, disable data file compression and support for
recent MAT file formats.
--without-framework-carbon
Don’t use framework Carbon headers, libraries, or specific source code even
if the configure test succeeds (the default is to use Carbon framework if
available). This is a platform specific configure option for Mac systems.
--without-framework-opengl
Don’t use framework OpenGL headers, libraries, or specific source code
even if the configure test succeeds. If this option is given then OpenGL
headers and libraries in standard system locations are tested (the default
value is --with-framework-opengl). This is a platform specific configure
option for Mac systems.
See the file INSTALL for more general information about the command line options used
by configure. That file also contains instructions for compiling in a directory other than
the one where the source is located.
•Run make.
You will need a recent version of GNU Make as Octave relies on certain features not
generally available in all versions of make. Modifying Octave’s makefiles to work with
other make programs is probably not worth your time; instead, we simply recommend
installing GNU Make.
There are currently three options for plotting in Octave: the external program gnuplot,
the internal graphics engine using OpenGL coupled with either FLTK or Qt widgets.
Gnuplot is a command-driven interactive function plotting program.
To compile Octave, you will need a recent version of g++ or other ANSI C++ compiler.
In addition, you will need a Fortran 77 compiler or f2c. If you use f2c, you will need
a script like fort77 that works like a normal Fortran compiler by combining f2c with
your C compiler in a single script.
If you plan to modify the parser you will also need GNU bison and flex. If you modify
the documentation, you will need GNU Texinfo.
GNU Make, gcc (and libstdc++), gnuplot,bison,flex, and Texinfo are all available
from many anonymous ftp archives. The primary site is ftp.gnu.org, but it is often
very busy. A list of sites that mirror the software on ftp.gnu.org is available by
anonymous ftp from ftp://ftp.gnu.org/pub/gnu/GNUinfo/FTP.
Octave requires approximately 1.4 GB of disk storage to unpack and compile from
source (significantly less, 400 MB, if you don’t compile with debugging symbols). To
compile without debugging symbols try the command
make CFLAGS=-O CXXFLAGS=-O LDFLAGS=
instead of just make.
•If you encounter errors while compiling Octave, first see Section E.4 [Installation Prob-
lems], page 945, for a list of known problems and if there is a workaround or solution
for your problem. If not, see Appendix D [Trouble], page 929, for information about
how to report bugs.
942 GNU Octave
•Once you have successfully compiled Octave, run make install.
This will install a copy of Octave, its libraries, and its documentation in the destination
directory. As distributed, Octave is installed in the following directories. In the table
below, prefix defaults to /usr/local,version stands for the current version number
of the interpreter, and arch is the type of computer on which Octave is installed (for
example, ‘i586-unknown-gnu’).
prefix/bin
Octave and other binaries that people will want to run directly.
prefix/lib/octave-version
Libraries like liboctave.a and liboctinterp.a.
prefix/octave-version/include/octave
Include files distributed with Octave.
prefix/share
Architecture-independent data files.
prefix/share/man/man1
Unix-style man pages describing Octave.
prefix/share/info
Info files describing Octave.
prefix/share/octave/version/m
Function files distributed with Octave. This includes the Octave version,
so that multiple versions of Octave may be installed at the same time.
prefix/libexec/octave/version/exec/arch
Executables to be run by Octave rather than the user.
prefix/lib/octave/version/oct/arch
Object files that will be dynamically loaded.
prefix/share/octave/version/imagelib
Image files that are distributed with Octave.
E.3 Compiling Octave with 64-bit Indexing
Note: the following only applies to systems that have 64-bit pointers. Configuring Octave
with --enable-64 cannot magically make a 32-bit system have a 64-bit address space.
On 64-bit systems, Octave is limited to (approximately) the following array sizes when
using the default 32-bit indexing mode:
double: 16 GB
single: 8 GB
uint64, int64: 16 GB
uint32, int32: 8 GB
uint16, int16: 4 GB
uint8, int8: 2 GB
In each case, the limit is really (approximately) 231 elements because of the default type
of the value used for indexing arrays (signed 32-bit integer, corresponding to the size of a
Fortran INTEGER value).

Appendix E: Installing Octave 943
Trying to create larger arrays will produce the following error:
octave:1> a = zeros (1024*1024*1024*3, 1, ’int8’);
error: memory exhausted or requested size too large
for range of Octave’s index type --
trying to return to prompt
You will obtain this error even if your system has enough memory to create this array (4
GB in the above case).
To use arrays larger than 2 GB, Octave has to be configured with the option --enable-
64. This option is experimental and you are encouraged to submit bug reports if you find a
problem. With this option, Octave will use 64-bit integers internally for array dimensions
and indexing. However, all numerical libraries used by Octave will also need to use 64-bit
integers for array dimensions and indexing. In most cases, this means they will need to be
compiled from source since most (all?) distributions which package these libraries compile
them with the default Fortran integer size, which is normally 32-bits wide.
The following instructions were tested with the development version of Octave and GCC
4.3.4 on an x86 64 Debian system.
The versions listed below are the versions used for testing. If newer versions of these
packages are available, you should try to use them, although there may be some differences.
All libraries and header files will be installed in subdirectories of $prefix64 (you must
choose the location of this directory).
•blas and lapack (http://www.netlib.org/lapack)
Reference versions for both libraries are included in the reference lapack 3.2.1 distri-
bution from netlib.org.
−Copy the file make.inc.example and name it make.inc. The options -fdefault-
integer-8 and -fPIC (on 64-bit CPU) have to be added to the variable OPTS and
NOOPT.
−Once you have compiled this library make sure that you use it for compiling Suite
Sparse and Octave. In the following we assume that you installed the lapack
library as $prefix64/lib/liblapack.a.
•QRUPDATE (http://sourceforge.net/projects/qrupdate)
In the Makeconf file:
−Add -fdefault-integer-8 to FFLAGS.
−Adjust the blas and lapack variables as needed if your 64-bit aware blas and
lapack libraries are in a non-standard location.
−Set PREFIX to the top-level directory of your install tree.
−Run make solib to make a shared library.
−Run make install to install the library.
•SuiteSparse (http://www.cise.ufl.edu/research/sparse/SuiteSparse)
Pass the following options to make to enable 64-bit integers for blas library calls. On
64-bit Windows systems, use -DLONGBLAS="long long" instead.
CFLAGS=’-DLONGBLAS=long’
CXXFLAGS=’-DLONGBLAS=long’
944 GNU Octave
The SuiteSparse makefiles don’t generate shared libraries. On some systems, you can
generate them by doing something as simple as
top=$(pwd)
for f in *.a; do
mkdir tmp
cd tmp
ar vx ../$f
gcc -shared -o ../${f%%.a}.so *.o
cd $top
rm -rf tmp
done
Other systems may require a different solution.
•arpack (http://forge.scilab.org/index.php/p/arpack-ng/)
−Add -fdefault-integer-8 to FFLAGS when running configure.
−Run make to build the library.
−Run make install to install the library.
•ATLAS instead of reference blas and lapack
Suggestions on how to compile ATLAS would be most welcome.
•glpk
•Qhull (http://www.qhull.org)
Both glpk and Qhull use int internally so maximum problem sizes may be limited.
•Octave
Octave’s 64-bit index support is activated with the configure option --enable-64.
./configure \
LD_LIBRARY_PATH="$prefix64/lib" \
CPPFLAGS="-I$prefix64/include" LDFLAGS="-L$prefix64/lib" \
--enable-64
You must ensure that all Fortran sources except those in the liboctave/cruft/ranlib
directory are compiled such that INTEGERS are 8-bytes wide. If you are using
gfortran, the configure script should automatically set the Makefile variable
F77_INTEGER_8_FLAG to -fdefault-integer-8. If you are using another compiler,
you must set this variable yourself. You should NOT set this flag in FFLAGS, otherwise
the files in liboctave/cruft/ranlib will be miscompiled.
•Other dependencies
Probably nothing special needs to be done for the following dependencies. If you
discover that something does need to be done, please submit a bug report.
−pcre
−zlib
−hdf5
−fftw3
−cURL
−GraphicsMagick++
Appendix E: Installing Octave 945
−OpenGL
−freetype
−fontconfig
−fltk
E.4 Installation Problems
This section contains a list of problems (and some apparent problems that don’t really mean
anything is wrong) that may show up during installation of Octave.
•On some SCO systems, info fails to compile if HAVE_TERMIOS_H is defined in config.h.
Simply removing the definition from info/config.h should allow it to compile.
•If configure finds dlopen,dlsym,dlclose, and dlerror, but not the header file
dlfcn.h, you need to find the source for the header file and install it in the directory
usr/include. This is reportedly a problem with Slackware 3.1. For Linux/GNU
systems, the source for dlfcn.h is in the ldso package.
•Building .oct files doesn’t work.
You should probably have a shared version of libstdc++. A patch is needed to build
shared versions of version 2.7.2 of libstdc++ on the HP-PA architecture. You can find
the patch at ftp://ftp.cygnus.com/pub/g++/libg++-2.7.2-hppa-gcc-fix.
•On some DEC alpha systems there may be a problem with the libdxml library, result-
ing in floating point errors and/or segmentation faults in the linear algebra routines
called by Octave. If you encounter such problems, then you should modify the configure
script so that SPECIAL_MATH_LIB is not set to -ldxml.
•On FreeBSD systems Octave may hang while initializing some internal constants. The
fix appears to be to use
options GPL_MATH_EMULATE
rather than
options MATH_EMULATE
in the kernel configuration files (typically found in the directory /sys/i386/conf).
After making this change, you’ll need to rebuild the kernel, install it, and reboot.
•If you encounter errors like
passing ‘void (*)()’ as argument 2 of
‘octave_set_signal_handler(int, void (*)(int))’
or
warning: ANSI C++ prohibits conversion from ‘(int)’
to ‘(...)’
while compiling sighandlers.cc, you may need to edit some files in the gcc include
subdirectory to add proper prototypes for functions there. For example, Ultrix 4.2
needs proper declarations for the signal function and the SIG_IGN macro in the file
signal.h.
On some systems the SIG_IGN macro is defined to be something like this:
#define SIG_IGN (void (*)())1
946 GNU Octave
when it should really be something like:
#define SIG_IGN (void (*)(int))1
to match the prototype declaration for the signal function. This change should also
be made for the SIG_DFL and SIG_ERR symbols. It may be necessary to change the
definitions in sys/signal.h as well.
The gcc fixincludes and fixproto scripts should probably fix these problems when
gcc installs its modified set of header files, but I don’t think that’s been done yet.
You should not change the files in /usr/include. You can find the gcc include direc-
tory tree by running the command
gcc -print-libgcc-file-name
The directory of gcc include files normally begins in the same directory that contains
the file libgcc.a.
•Some of the Fortran subroutines may fail to compile with older versions of the Sun
Fortran compiler. If you get errors like
zgemm.f:
zgemm:
warning: unexpected parent of complex expression subtree
zgemm.f, line 245: warning: unexpected parent of complex
expression subtree
warning: unexpected parent of complex expression subtree
zgemm.f, line 304: warning: unexpected parent of complex
expression subtree
warning: unexpected parent of complex expression subtree
zgemm.f, line 327: warning: unexpected parent of complex
expression subtree
pcc_binval: missing IR_CONV in complex op
make[2]: *** [zgemm.o] Error 1
when compiling the Fortran subroutines in the liboctave/cruft subdirectory, you
should either upgrade your compiler or try compiling with optimization turned off.
•On NeXT systems, if you get errors like this:
/usr/tmp/cc007458.s:unknown:Undefined local
symbol LBB7656
/usr/tmp/cc007458.s:unknown:Undefined local
symbol LBE7656
when compiling Array.cc and Matrix.cc, try recompiling these files without -g.
•Some people have reported that calls to system() and the pager do not work on SunOS
systems. This is apparently due to having G_HAVE_SYS_WAIT defined to be 0 instead of
1 when compiling libg++.
•On systems where the reference blas library is used the following matrix-by-vector
multiplication incorrectly handles NaN values of the form NaN * 0.
947
[NaN, 1; 0, 0] * [0; 1]
⇒
[ 1
0 ]
correct result ⇒
[ NaN
0 ]
Install a different blas library such as OpenBLAS or ATLAS to correct this issue.
•On NeXT systems, linking to libsys_s.a may fail to resolve the following functions
_tcgetattr
_tcsetattr
_tcflow
which are part of libposix.a. Unfortunately, linking Octave with -posix results in
the following undefined symbols.
.destructors_used
.constructors_used
_objc_msgSend
_NXGetDefaultValue
_NXRegisterDefaults
.objc_class_name_NXStringTable
.objc_class_name_NXBundle
One kluge around this problem is to extract termios.o from libposix.a, put it in
Octave’s src directory, and add it to the list of files to link together in the makefile.
Suggestions for better ways to solve this problem are welcome!
•If Octave crashes immediately with a floating point exception, it is likely that it is
failing to initialize the IEEE floating point values for infinity and NaN.
If your system actually does support IEEE arithmetic, you should be able to fix this
problem by modifying the function octave_ieee_init in the file lo-ieee.cc to cor-
rectly initialize Octave’s internal infinity and NaN variables.
If your system does not support IEEE arithmetic but Octave’s configure script incor-
rectly determined that it does, you can work around the problem by editing the file
config.h to not define HAVE_ISINF,HAVE_FINITE, and HAVE_ISNAN.
In any case, please report this as a bug since it might be possible to modify Octave’s
configuration script to automatically determine the proper thing to do.
•If Octave is unable to find a header file because it is installed in a location that is not
normally searched by the compiler, you can add the directory to the include search
path by specifying (for example) CPPFLAGS=-I/some/nonstandard/directory as an
argument to configure. Other variables that can be specified this way are CFLAGS,
CXXFLAGS,FFLAGS, and LDFLAGS. Passing them as options to the configure script also
records them in the config.status file. By default, CPPFLAGS and LDFLAGS are empty,
CFLAGS and CXXFLAGS are set to "-g -O2" and FFLAGS is set to "-O".
949
Appendix F Grammar and Parser
This appendix will eventually contain a semi-formal description of Octave’s language.
F.1 Keywords
The following identifiers are keywords, and may not be used as variable or function names:
__FILE__ __LINE__ break
case catch classdef
continue do else
elseif end end_try_catch
end_unwind_protect endclassdef endenumeration
endevents endfor endfunction
endif endmethods endparfor
endproperties endswitch endwhile
enumeration events for
function global if
methods otherwise parfor
persistent properties return
switch try until
unwind_protect unwind_protect_cleanup while
The function iskeyword can be used to quickly check whether an identifier is reserved
by Octave.
iskeyword ()
iskeyword (name)
Return true if name is an Octave keyword.
If name is omitted, return a list of keywords.
See also: [isvarname], page 123,[exist], page 130.
F.2 Parser
The parser has a number of variables that affect its internal operation. These variables
are generally documented in the manual alongside the code that they affect. For example,
allow_noninteger_range_as_index is discussed in the section on index expressions.
In addition, there are three non-specific parser customization functions. add_input_
event_hook can be used to schedule a user function for periodic evaluation. remove_
input_event_hook will stop a user function from being evaluated periodically.
id = add_input_event_hook (fcn)
id = add_input_event_hook (fcn,data)
Add the named function or function handle fcn to the list of functions to call period-
ically when Octave is waiting for input.
The function should have the form
fcn (data)
If data is omitted, Octave calls the function without any arguments.

950 GNU Octave
The returned identifier may be used to remove the function handle from the list of
input hook functions.
See also: [remove input event hook], page 950.
remove_input_event_hook (name)
remove_input_event_hook (fcn_id)
Remove the named function or function handle with the given identifier from the list
of functions to call periodically when Octave is waiting for input.
See also: [add input event hook], page 949.
Finally, when the parser cannot identify an input token it calls a particular function to
handle this. By default, this is the internal function "__unimplemented__" which makes
suggestions about possible Octave substitutes for matlab functions.
val = missing_function_hook ()
old_val = missing_function_hook (new_val)
missing_function_hook (new_val,"local")
Query or set the internal variable that specifies the function to call when an unknown
identifier is requested.
When called from inside a function with the "local" option, the variable is changed
locally for the function and any subroutines it calls. The original variable value is
restored when exiting the function.
See also: [missing component hook], page 862.
951
Appendix G GNU GENERAL PUBLIC LICENSE
Version 3, 29 June 2007
Copyright c
2007 Free Software Foundation, Inc. http://fsf.org/
Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.
Preamble
The GNU General Public License is a free, copyleft license for software and other kinds of
works.
The licenses for most software and other practical works are designed to take away your
freedom to share and change the works. By contrast, the GNU General Public License is
intended to guarantee your freedom to share and change all versions of a program—to make
sure it remains free software for all its users. We, the Free Software Foundation, use the
GNU General Public License for most of our software; it applies also to any other work
released this way by its authors. You can apply it to your programs, too.
When we speak of free software, we are referring to freedom, not price. Our General
Public Licenses are designed to make sure that you have the freedom to distribute copies
of free software (and charge for them if you wish), that you receive source code or can get
it if you want it, that you can change the software or use pieces of it in new free programs,
and that you know you can do these things.
To protect your rights, we need to prevent others from denying you these rights or asking
you to surrender the rights. Therefore, you have certain responsibilities if you distribute
copies of the software, or if you modify it: responsibilities to respect the freedom of others.
For example, if you distribute copies of such a program, whether gratis or for a fee, you
must pass on to the recipients the same freedoms that you received. You must make sure
that they, too, receive or can get the source code. And you must show them these terms so
they know their rights.
Developers that use the GNU GPL protect your rights with two steps: (1) assert copy-
right on the software, and (2) offer you this License giving you legal permission to copy,
distribute and/or modify it.
For the developers’ and authors’ protection, the GPL clearly explains that there is no
warranty for this free software. For both users’ and authors’ sake, the GPL requires that
modified versions be marked as changed, so that their problems will not be attributed
erroneously to authors of previous versions.
Some devices are designed to deny users access to install or run modified versions of the
software inside them, although the manufacturer can do so. This is fundamentally incom-
patible with the aim of protecting users’ freedom to change the software. The systematic
pattern of such abuse occurs in the area of products for individuals to use, which is pre-
cisely where it is most unacceptable. Therefore, we have designed this version of the GPL
to prohibit the practice for those products. If such problems arise substantially in other
domains, we stand ready to extend this provision to those domains in future versions of the
GPL, as needed to protect the freedom of users.
952 GNU Octave
Finally, every program is threatened constantly by software patents. States should not
allow patents to restrict development and use of software on general-purpose computers, but
in those that do, we wish to avoid the special danger that patents applied to a free program
could make it effectively proprietary. To prevent this, the GPL assures that patents cannot
be used to render the program non-free.
The precise terms and conditions for copying, distribution and modification follow.
TERMS AND CONDITIONS
0. Definitions.
“This License” refers to version 3 of the GNU General Public License.
“Copyright” also means copyright-like laws that apply to other kinds of works, such as
semiconductor masks.
“The Program” refers to any copyrightable work licensed under this License. Each
licensee is addressed as “you”. “Licensees” and “recipients” may be individuals or
organizations.
To “modify” a work means to copy from or adapt all or part of the work in a fashion
requiring copyright permission, other than the making of an exact copy. The resulting
work is called a “modified version” of the earlier work or a work “based on” the earlier
work.
A “covered work” means either the unmodified Program or a work based on the Pro-
gram.
To “propagate” a work means to do anything with it that, without permission, would
make you directly or secondarily liable for infringement under applicable copyright law,
except executing it on a computer or modifying a private copy. Propagation includes
copying, distribution (with or without modification), making available to the public,
and in some countries other activities as well.
To “convey” a work means any kind of propagation that enables other parties to make
or receive copies. Mere interaction with a user through a computer network, with no
transfer of a copy, is not conveying.
An interactive user interface displays “Appropriate Legal Notices” to the extent that it
includes a convenient and prominently visible feature that (1) displays an appropriate
copyright notice, and (2) tells the user that there is no warranty for the work (except
to the extent that warranties are provided), that licensees may convey the work under
this License, and how to view a copy of this License. If the interface presents a list
of user commands or options, such as a menu, a prominent item in the list meets this
criterion.
1. Source Code.
The “source code” for a work means the preferred form of the work for making modi-
fications to it. “Object code” means any non-source form of a work.
A “Standard Interface” means an interface that either is an official standard defined
by a recognized standards body, or, in the case of interfaces specified for a particular
programming language, one that is widely used among developers working in that
language.
Appendix G: GNU GENERAL PUBLIC LICENSE 953
The “System Libraries” of an executable work include anything, other than the work as
a whole, that (a) is included in the normal form of packaging a Major Component, but
which is not part of that Major Component, and (b) serves only to enable use of the
work with that Major Component, or to implement a Standard Interface for which an
implementation is available to the public in source code form. A “Major Component”,
in this context, means a major essential component (kernel, window system, and so
on) of the specific operating system (if any) on which the executable work runs, or a
compiler used to produce the work, or an object code interpreter used to run it.
The “Corresponding Source” for a work in object code form means all the source code
needed to generate, install, and (for an executable work) run the object code and to
modify the work, including scripts to control those activities. However, it does not
include the work’s System Libraries, or general-purpose tools or generally available
free programs which are used unmodified in performing those activities but which are
not part of the work. For example, Corresponding Source includes interface definition
files associated with source files for the work, and the source code for shared libraries
and dynamically linked subprograms that the work is specifically designed to require,
such as by intimate data communication or control flow between those subprograms
and other parts of the work.
The Corresponding Source need not include anything that users can regenerate auto-
matically from other parts of the Corresponding Source.
The Corresponding Source for a work in source code form is that same work.
2. Basic Permissions.
All rights granted under this License are granted for the term of copyright on the
Program, and are irrevocable provided the stated conditions are met. This License ex-
plicitly affirms your unlimited permission to run the unmodified Program. The output
from running a covered work is covered by this License only if the output, given its
content, constitutes a covered work. This License acknowledges your rights of fair use
or other equivalent, as provided by copyright law.
You may make, run and propagate covered works that you do not convey, without
conditions so long as your license otherwise remains in force. You may convey covered
works to others for the sole purpose of having them make modifications exclusively
for you, or provide you with facilities for running those works, provided that you
comply with the terms of this License in conveying all material for which you do not
control copyright. Those thus making or running the covered works for you must do
so exclusively on your behalf, under your direction and control, on terms that prohibit
them from making any copies of your copyrighted material outside their relationship
with you.
Conveying under any other circumstances is permitted solely under the conditions
stated below. Sublicensing is not allowed; section 10 makes it unnecessary.
3. Protecting Users’ Legal Rights From Anti-Circumvention Law.
No covered work shall be deemed part of an effective technological measure under
any applicable law fulfilling obligations under article 11 of the WIPO copyright treaty
adopted on 20 December 1996, or similar laws prohibiting or restricting circumvention
of such measures.
954 GNU Octave
When you convey a covered work, you waive any legal power to forbid circumvention of
technological measures to the extent such circumvention is effected by exercising rights
under this License with respect to the covered work, and you disclaim any intention
to limit operation or modification of the work as a means of enforcing, against the
work’s users, your or third parties’ legal rights to forbid circumvention of technological
measures.
4. Conveying Verbatim Copies.
You may convey verbatim copies of the Program’s source code as you receive it, in any
medium, provided that you conspicuously and appropriately publish on each copy an
appropriate copyright notice; keep intact all notices stating that this License and any
non-permissive terms added in accord with section 7 apply to the code; keep intact all
notices of the absence of any warranty; and give all recipients a copy of this License
along with the Program.
You may charge any price or no price for each copy that you convey, and you may offer
support or warranty protection for a fee.
5. Conveying Modified Source Versions.
You may convey a work based on the Program, or the modifications to produce it from
the Program, in the form of source code under the terms of section 4, provided that
you also meet all of these conditions:
a. The work must carry prominent notices stating that you modified it, and giving a
relevant date.
b. The work must carry prominent notices stating that it is released under this Li-
cense and any conditions added under section 7. This requirement modifies the
requirement in section 4 to “keep intact all notices”.
c. You must license the entire work, as a whole, under this License to anyone who
comes into possession of a copy. This License will therefore apply, along with any
applicable section 7 additional terms, to the whole of the work, and all its parts,
regardless of how they are packaged. This License gives no permission to license
the work in any other way, but it does not invalidate such permission if you have
separately received it.
d. If the work has interactive user interfaces, each must display Appropriate Legal
Notices; however, if the Program has interactive interfaces that do not display
Appropriate Legal Notices, your work need not make them do so.
A compilation of a covered work with other separate and independent works, which
are not by their nature extensions of the covered work, and which are not combined
with it such as to form a larger program, in or on a volume of a storage or distribution
medium, is called an “aggregate” if the compilation and its resulting copyright are
not used to limit the access or legal rights of the compilation’s users beyond what the
individual works permit. Inclusion of a covered work in an aggregate does not cause
this License to apply to the other parts of the aggregate.
6. Conveying Non-Source Forms.
You may convey a covered work in object code form under the terms of sections 4 and
5, provided that you also convey the machine-readable Corresponding Source under
the terms of this License, in one of these ways:
Appendix G: GNU GENERAL PUBLIC LICENSE 955
a. Convey the object code in, or embodied in, a physical product (including a phys-
ical distribution medium), accompanied by the Corresponding Source fixed on a
durable physical medium customarily used for software interchange.
b. Convey the object code in, or embodied in, a physical product (including a physi-
cal distribution medium), accompanied by a written offer, valid for at least three
years and valid for as long as you offer spare parts or customer support for that
product model, to give anyone who possesses the object code either (1) a copy of
the Corresponding Source for all the software in the product that is covered by this
License, on a durable physical medium customarily used for software interchange,
for a price no more than your reasonable cost of physically performing this con-
veying of source, or (2) access to copy the Corresponding Source from a network
server at no charge.
c. Convey individual copies of the object code with a copy of the written offer to
provide the Corresponding Source. This alternative is allowed only occasionally
and noncommercially, and only if you received the object code with such an offer,
in accord with subsection 6b.
d. Convey the object code by offering access from a designated place (gratis or for
a charge), and offer equivalent access to the Corresponding Source in the same
way through the same place at no further charge. You need not require recipients
to copy the Corresponding Source along with the object code. If the place to
copy the object code is a network server, the Corresponding Source may be on
a different server (operated by you or a third party) that supports equivalent
copying facilities, provided you maintain clear directions next to the object code
saying where to find the Corresponding Source. Regardless of what server hosts
the Corresponding Source, you remain obligated to ensure that it is available for
as long as needed to satisfy these requirements.
e. Convey the object code using peer-to-peer transmission, provided you inform other
peers where the object code and Corresponding Source of the work are being offered
to the general public at no charge under subsection 6d.
A separable portion of the object code, whose source code is excluded from the Cor-
responding Source as a System Library, need not be included in conveying the object
code work.
A “User Product” is either (1) a “consumer product”, which means any tangible per-
sonal property which is normally used for personal, family, or household purposes, or
(2) anything designed or sold for incorporation into a dwelling. In determining whether
a product is a consumer product, doubtful cases shall be resolved in favor of coverage.
For a particular product received by a particular user, “normally used” refers to a
typical or common use of that class of product, regardless of the status of the par-
ticular user or of the way in which the particular user actually uses, or expects or is
expected to use, the product. A product is a consumer product regardless of whether
the product has substantial commercial, industrial or non-consumer uses, unless such
uses represent the only significant mode of use of the product.
“Installation Information” for a User Product means any methods, procedures, autho-
rization keys, or other information required to install and execute modified versions of a
covered work in that User Product from a modified version of its Corresponding Source.
956 GNU Octave
The information must suffice to ensure that the continued functioning of the modified
object code is in no case prevented or interfered with solely because modification has
been made.
If you convey an object code work under this section in, or with, or specifically for
use in, a User Product, and the conveying occurs as part of a transaction in which
the right of possession and use of the User Product is transferred to the recipient in
perpetuity or for a fixed term (regardless of how the transaction is characterized),
the Corresponding Source conveyed under this section must be accompanied by the
Installation Information. But this requirement does not apply if neither you nor any
third party retains the ability to install modified object code on the User Product (for
example, the work has been installed in ROM).
The requirement to provide Installation Information does not include a requirement
to continue to provide support service, warranty, or updates for a work that has been
modified or installed by the recipient, or for the User Product in which it has been
modified or installed. Access to a network may be denied when the modification itself
materially and adversely affects the operation of the network or violates the rules and
protocols for communication across the network.
Corresponding Source conveyed, and Installation Information provided, in accord with
this section must be in a format that is publicly documented (and with an implementa-
tion available to the public in source code form), and must require no special password
or key for unpacking, reading or copying.
7. Additional Terms.
“Additional permissions” are terms that supplement the terms of this License by mak-
ing exceptions from one or more of its conditions. Additional permissions that are
applicable to the entire Program shall be treated as though they were included in this
License, to the extent that they are valid under applicable law. If additional permis-
sions apply only to part of the Program, that part may be used separately under those
permissions, but the entire Program remains governed by this License without regard
to the additional permissions.
When you convey a copy of a covered work, you may at your option remove any
additional permissions from that copy, or from any part of it. (Additional permissions
may be written to require their own removal in certain cases when you modify the
work.) You may place additional permissions on material, added by you to a covered
work, for which you have or can give appropriate copyright permission.
Notwithstanding any other provision of this License, for material you add to a covered
work, you may (if authorized by the copyright holders of that material) supplement
the terms of this License with terms:
a. Disclaiming warranty or limiting liability differently from the terms of sections 15
and 16 of this License; or
b. Requiring preservation of specified reasonable legal notices or author attributions
in that material or in the Appropriate Legal Notices displayed by works containing
it; or
c. Prohibiting misrepresentation of the origin of that material, or requiring that mod-
ified versions of such material be marked in reasonable ways as different from the
original version; or
Appendix G: GNU GENERAL PUBLIC LICENSE 957
d. Limiting the use for publicity purposes of names of licensors or authors of the
material; or
e. Declining to grant rights under trademark law for use of some trade names, trade-
marks, or service marks; or
f. Requiring indemnification of licensors and authors of that material by anyone who
conveys the material (or modified versions of it) with contractual assumptions
of liability to the recipient, for any liability that these contractual assumptions
directly impose on those licensors and authors.
All other non-permissive additional terms are considered “further restrictions” within
the meaning of section 10. If the Program as you received it, or any part of it, con-
tains a notice stating that it is governed by this License along with a term that is a
further restriction, you may remove that term. If a license document contains a further
restriction but permits relicensing or conveying under this License, you may add to a
covered work material governed by the terms of that license document, provided that
the further restriction does not survive such relicensing or conveying.
If you add terms to a covered work in accord with this section, you must place, in the
relevant source files, a statement of the additional terms that apply to those files, or a
notice indicating where to find the applicable terms.
Additional terms, permissive or non-permissive, may be stated in the form of a sep-
arately written license, or stated as exceptions; the above requirements apply either
way.
8. Termination.
You may not propagate or modify a covered work except as expressly provided un-
der this License. Any attempt otherwise to propagate or modify it is void, and will
automatically terminate your rights under this License (including any patent licenses
granted under the third paragraph of section 11).
However, if you cease all violation of this License, then your license from a particular
copyright holder is reinstated (a) provisionally, unless and until the copyright holder
explicitly and finally terminates your license, and (b) permanently, if the copyright
holder fails to notify you of the violation by some reasonable means prior to 60 days
after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if
the copyright holder notifies you of the violation by some reasonable means, this is the
first time you have received notice of violation of this License (for any work) from that
copyright holder, and you cure the violation prior to 30 days after your receipt of the
notice.
Termination of your rights under this section does not terminate the licenses of parties
who have received copies or rights from you under this License. If your rights have
been terminated and not permanently reinstated, you do not qualify to receive new
licenses for the same material under section 10.
9. Acceptance Not Required for Having Copies.
You are not required to accept this License in order to receive or run a copy of the
Program. Ancillary propagation of a covered work occurring solely as a consequence of
using peer-to-peer transmission to receive a copy likewise does not require acceptance.
958 GNU Octave
However, nothing other than this License grants you permission to propagate or modify
any covered work. These actions infringe copyright if you do not accept this License.
Therefore, by modifying or propagating a covered work, you indicate your acceptance
of this License to do so.
10. Automatic Licensing of Downstream Recipients.
Each time you convey a covered work, the recipient automatically receives a license
from the original licensors, to run, modify and propagate that work, subject to this
License. You are not responsible for enforcing compliance by third parties with this
License.
An “entity transaction” is a transaction transferring control of an organization, or
substantially all assets of one, or subdividing an organization, or merging organizations.
If propagation of a covered work results from an entity transaction, each party to that
transaction who receives a copy of the work also receives whatever licenses to the work
the party’s predecessor in interest had or could give under the previous paragraph, plus
a right to possession of the Corresponding Source of the work from the predecessor in
interest, if the predecessor has it or can get it with reasonable efforts.
You may not impose any further restrictions on the exercise of the rights granted or
affirmed under this License. For example, you may not impose a license fee, royalty, or
other charge for exercise of rights granted under this License, and you may not initiate
litigation (including a cross-claim or counterclaim in a lawsuit) alleging that any patent
claim is infringed by making, using, selling, offering for sale, or importing the Program
or any portion of it.
11. Patents.
A “contributor” is a copyright holder who authorizes use under this License of the
Program or a work on which the Program is based. The work thus licensed is called
the contributor’s “contributor version”.
A contributor’s “essential patent claims” are all patent claims owned or controlled by
the contributor, whether already acquired or hereafter acquired, that would be infringed
by some manner, permitted by this License, of making, using, or selling its contributor
version, but do not include claims that would be infringed only as a consequence of
further modification of the contributor version. For purposes of this definition, “con-
trol” includes the right to grant patent sublicenses in a manner consistent with the
requirements of this License.
Each contributor grants you a non-exclusive, worldwide, royalty-free patent license
under the contributor’s essential patent claims, to make, use, sell, offer for sale, import
and otherwise run, modify and propagate the contents of its contributor version.
In the following three paragraphs, a “patent license” is any express agreement or com-
mitment, however denominated, not to enforce a patent (such as an express permission
to practice a patent or covenant not to sue for patent infringement). To “grant” such
a patent license to a party means to make such an agreement or commitment not to
enforce a patent against the party.
If you convey a covered work, knowingly relying on a patent license, and the Corre-
sponding Source of the work is not available for anyone to copy, free of charge and under
the terms of this License, through a publicly available network server or other readily
accessible means, then you must either (1) cause the Corresponding Source to be so
Appendix G: GNU GENERAL PUBLIC LICENSE 959
available, or (2) arrange to deprive yourself of the benefit of the patent license for this
particular work, or (3) arrange, in a manner consistent with the requirements of this
License, to extend the patent license to downstream recipients. “Knowingly relying”
means you have actual knowledge that, but for the patent license, your conveying the
covered work in a country, or your recipient’s use of the covered work in a country,
would infringe one or more identifiable patents in that country that you have reason
to believe are valid.
If, pursuant to or in connection with a single transaction or arrangement, you convey,
or propagate by procuring conveyance of, a covered work, and grant a patent license
to some of the parties receiving the covered work authorizing them to use, propagate,
modify or convey a specific copy of the covered work, then the patent license you grant
is automatically extended to all recipients of the covered work and works based on it.
A patent license is “discriminatory” if it does not include within the scope of its cover-
age, prohibits the exercise of, or is conditioned on the non-exercise of one or more of the
rights that are specifically granted under this License. You may not convey a covered
work if you are a party to an arrangement with a third party that is in the business of
distributing software, under which you make payment to the third party based on the
extent of your activity of conveying the work, and under which the third party grants,
to any of the parties who would receive the covered work from you, a discriminatory
patent license (a) in connection with copies of the covered work conveyed by you (or
copies made from those copies), or (b) primarily for and in connection with specific
products or compilations that contain the covered work, unless you entered into that
arrangement, or that patent license was granted, prior to 28 March 2007.
Nothing in this License shall be construed as excluding or limiting any implied license or
other defenses to infringement that may otherwise be available to you under applicable
patent law.
12. No Surrender of Others’ Freedom.
If conditions are imposed on you (whether by court order, agreement or otherwise) that
contradict the conditions of this License, they do not excuse you from the conditions
of this License. If you cannot convey a covered work so as to satisfy simultaneously
your obligations under this License and any other pertinent obligations, then as a
consequence you may not convey it at all. For example, if you agree to terms that
obligate you to collect a royalty for further conveying from those to whom you convey
the Program, the only way you could satisfy both those terms and this License would
be to refrain entirely from conveying the Program.
13. Use with the GNU Affero General Public License.
Notwithstanding any other provision of this License, you have permission to link or
combine any covered work with a work licensed under version 3 of the GNU Affero
General Public License into a single combined work, and to convey the resulting work.
The terms of this License will continue to apply to the part which is the covered work,
but the special requirements of the GNU Affero General Public License, section 13,
concerning interaction through a network will apply to the combination as such.
14. Revised Versions of this License.
960 GNU Octave
The Free Software Foundation may publish revised and/or new versions of the GNU
General Public License from time to time. Such new versions will be similar in spirit
to the present version, but may differ in detail to address new problems or concerns.
Each version is given a distinguishing version number. If the Program specifies that
a certain numbered version of the GNU General Public License “or any later version”
applies to it, you have the option of following the terms and conditions either of that
numbered version or of any later version published by the Free Software Foundation.
If the Program does not specify a version number of the GNU General Public License,
you may choose any version ever published by the Free Software Foundation.
If the Program specifies that a proxy can decide which future versions of the GNU
General Public License can be used, that proxy’s public statement of acceptance of a
version permanently authorizes you to choose that version for the Program.
Later license versions may give you additional or different permissions. However, no
additional obligations are imposed on any author or copyright holder as a result of your
choosing to follow a later version.
15. Disclaimer of Warranty.
THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PER-
MITTED BY APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN
WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE
THE PROGRAM “AS IS” WITHOUT WARRANTY OF ANY KIND, EITHER EX-
PRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED
WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR
PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE
OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE DEFEC-
TIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR
CORRECTION.
16. Limitation of Liability.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN
WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO
MODIFIES AND/OR CONVEYS THE PROGRAM AS PERMITTED ABOVE, BE
LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL, SPECIAL, IN-
CIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR
INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO
LOSS OF DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUS-
TAINED BY YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM
TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR
OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAM-
AGES.
17. Interpretation of Sections 15 and 16.
If the disclaimer of warranty and limitation of liability provided above cannot be given
local legal effect according to their terms, reviewing courts shall apply local law that
most closely approximates an absolute waiver of all civil liability in connection with
the Program, unless a warranty or assumption of liability accompanies a copy of the
Program in return for a fee.
Appendix G: GNU GENERAL PUBLIC LICENSE 961
END OF TERMS AND CONDITIONS
How to Apply These Terms to Your New Programs
If you develop a new program, and you want it to be of the greatest possible use to the public,
the best way to achieve this is to make it free software which everyone can redistribute and
change under these terms.
To do so, attach the following notices to the program. It is safest to attach them to the
start of each source file to most effectively state the exclusion of warranty; and each file
should have at least the “copyright” line and a pointer to where the full notice is found.
one line to give the program’s name and a brief idea of what it does.
Copyright (C) year name of author
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or (at
your option) any later version.
This program is distributed in the hope that it will be useful, but
WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see http://www.gnu.org/licenses/.
Also add information on how to contact you by electronic and paper mail.
If the program does terminal interaction, make it output a short notice like this when it
starts in an interactive mode:
program Copyright (C) year name of author
This program comes with ABSOLUTELY NO WARRANTY; for details type ‘show w’.
This is free software, and you are welcome to redistribute it
under certain conditions; type ‘show c’ for details.
The hypothetical commands ‘show w’ and ‘show c’ should show the appropriate parts of
the General Public License. Of course, your program’s commands might be different; for a
GUI interface, you would use an “about box”.
You should also get your employer (if you work as a programmer) or school, if any, to
sign a “copyright disclaimer” for the program, if necessary. For more information on this,
and how to apply and follow the GNU GPL, see http://www.gnu.org/licenses/.
The GNU General Public License does not permit incorporating your program into
proprietary programs. If your program is a subroutine library, you may consider it more
useful to permit linking proprietary applications with the library. If this is what you want
to do, use the GNU Lesser General Public License instead of this License. But first, please
read http://www.gnu.org/philosophy/why-not-lgpl.html.

963
Concept Index
#
‘#’............................................. 37
‘#!’............................................ 36
‘#{’............................................ 38
%
‘%’............................................. 37
‘%{’............................................ 38
–
--braindead ................................... 17
--built-in-docstrings-file filename........ 15
--debug ....................................... 15
--debug-jit ................................... 15
--doc-cache-file filename ................... 15
--echo-commands .............................. 15
--exec-path path ............................. 15
--force-gui ................................... 16
--help......................................... 16
--image-path path ............................ 16
--info-file filename ......................... 16
--info-program program....................... 16
--interactive ................................ 16
--jit-compiler ............................... 16
--line-editing ............................... 16
--no-gui ...................................... 16
--no-history.................................. 16
--no-init-file ............................... 16
--no-init-path ............................... 16
--no-line-editing ............................ 16
--no-site-file ............................... 16
--no-window-system ........................... 16
--norc......................................... 17
--path path ................................... 17
--persist ..................................... 17
--quiet ....................................... 17
--silent ...................................... 17
--texi-macros-file filename ................. 17
--traditional ................................ 17
--verbose ..................................... 18
--version ..................................... 18
-? ............................................. 16
-d ............................................. 15
-f ............................................. 17
-h ............................................. 16
-H ............................................. 16
-i ............................................. 16
-p path ........................................ 17
-q ............................................. 17
-v ............................................. 18
-V ............................................. 18
-x ............................................. 15
.
... continuation marker ...................... 171
.octaverc ..................................... 19
:
:end .......................................... 135
\
\continuation marker ........................ 171
~
~/.inputrc .................................... 32
~/.octaverc ................................... 19
A
acknowledgements............................... 1
addition ................................. 142,780
and operator ............................. 147,780
anonymous functions.......................... 209
ans ........................................... 123
answers, incorrect ........................ 929,931
application-defined data....................... 424
apply ......................................... 534
area series .................................... 430
arguments in function call..................... 140
arithmetic operators ..................... 142,780
array, creating a Java array ............. ...... 906
assignment expressions ........................ 151
assignment operators ......................... 151
axes modified ............................. 390
axes activepositionproperty ................... 390
axes alim ..................................... 390
axes alimmode ................................ 390
axes ambientlightcolor ........................ 390
axes beingdeleted ............................. 390
axes box ...................................... 390
axes boxstyle ................................. 390
axes busyaction ............................... 390
axes buttondownfcn........................... 390
axes cameraposition .......................... 390
axes camerapositionmode .. ................... 391
axes cameratarget ............................ 391
axes cameratargetmode ....................... 391
axes cameraupvector ................ .......... 391
axes cameraupvectormode..................... 391
axes cameraviewangle ................ ......... 391
axes cameraviewanglemode.................... 391
axes children.................................. 391
axes clim ..................................... 391
axes climmode ................................ 391
964 GNU Octave
axes clipping.. ................................ 391
axes clippingstyle ............................. 391
axes color...... ............................... 391
axes colororder ............................... 391
axes colororderindex .......................... 391
axes createfcn................................. 391
axes currentpoint ............................. 391
axes dataaspectratio .......................... 391
axes dataaspectratiomode .. ................... 392
axes deletefcn................................. 392
axes drawmode ............................... 392
axes fontangle ................................ 392
axes fontname ................................ 392
axes fontsize .................................. 392
axes fontsmoothing ........................... 392
axes fontunits................................. 392
axes fontweight ............................... 392
axes graphics object .......................... 375
axes gridalpha ................................ 392
axes gridalphamode ........................... 392
axes gridcolor ................................. 392
axes gridcolormode ........................... 392
axes gridlinestyle ............................. 392
axes handlevisibility .......................... 392
axes hittest ................................... 392
axes interruptible ............................. 392
axes labelfontsizemultiplier .................... 392
axes layer..................................... 392
axes linestyleorder ............................ 392
axes linestyleorderindex ....................... 392
axes linewidth ................................ 393
axes minorgridalpha .......................... 393
axes minorgridalphamode ..................... 393
axes minorgridcolor ........................... 393
axes minorgridcolormode...................... 393
axes minorgridlinestyle ........................ 393
axes mousewheelzoom ........................ 393
axes nextplot ................................. 393
axes outerposition ............................ 393
axes parent ................................... 393
axes pickableparts ......... ................... 393
axes plotboxaspectratio ....................... 393
axes plotboxaspectratiomode .................. 393
axes position ................................. 393
axes projection ............................... 393
axes properties ............................... 390
axes selected .................................. 394
axes selectionhighlight ........................ 394
axes sortmethod .............................. 394
axes tag ...................................... 394
axes tickdir ................................... 394
axes tickdirmode.............................. 394
axes ticklabelinterpreter............. .......... 394
axes ticklength................................ 394
axes tightinset ................................ 394
axes title ..................................... 394
axes titlefontsizemultiplier ................ .... 394
axes titlefontweight ........................... 394
axes type ..................................... 394
axes uicontextmenu ................ ........... 394
axes units .................................... 394
axes userdata ................................. 394
axes view ..................................... 394
axes visible ................................... 394
axes xaxislocation ............................ 395
axes xcolor ................................... 395
axes xcolormode .............................. 395
axes xdir ..................................... 395
axes xgrid .................................... 395
axes xlabel ................................... 395
axes xlim ..................................... 395
axes xlimmode ................................ 395
axes xminorgrid .............................. 395
axes xminortick ............................... 395
axes xscale ................................... 395
axes xtick.............................. ....... 395
axes xticklabel ................................ 395
axes xticklabelmode........................... 395
axes xticklabelrotation ........................ 395
axes xtickmode ............................... 395
axes yaxislocation........................... .. 395
axes ycolor ................................... 395
axes ycolormode .............................. 395
axes ydir ..................................... 395
axes ygrid .................................... 395
axes ylabel ................................... 396
axes ylim ..................................... 396
axes ylimmode ................................ 396
axes yminorgrid .............................. 396
axes yminortick ............................... 396
axes yscale ................................... 396
axes ytick.............................. ....... 396
axes yticklabel ................................ 396
axes yticklabelmode........................... 396
axes yticklabelrotation ........................ 396
axes ytickmode ............................... 396
axes zcolor...... .............................. 396
axes zcolormode .............................. 396
axes zdir...... ................................ 396
axes zgrid .................................... 396
axes zlabel.................................... 396
axes zlim ..................................... 396
axes zlimmode ................................ 396
axes zminorgrid ............................... 396
axes zminortick ............................... 396
axes zscale .................................... 396
axes ztick ..................................... 396
axes zticklabel ................................ 396
axes zticklabelmode ........................... 397
axes zticklabelrotation ........................ 397
axes ztickmode ............................... 397
Concept Index 965
B
bar series ..................................... 431
batch processing ............................... 36
block comments................................ 38
body of a loop ................................ 165
boolean expressions ...................... 147,780
boolean operators ........................ 147,780
break statement .............................. 168
broadcast ..................................... 531
broadcasting .................................. 531
BSX .......................................... 531
bug criteria ................................... 929
bug tracker ................ ................... 930
bugs .......................................... 929
bugs, investigating ................ ............ 931
bugs, known .................................. 929
bugs, reporting ............................... 930
built-in data types ............................. 39
C
callbacks.............................. ........ 423
calling Java from Octave ...................... 901
calling Octave from Java ...................... 901
case statement ............................... 163
catch..................................... .... 170
cell arrays................................. 44,112
character strings ........................... 43,67
Cholesky factorization ........................ 511
Citations........................................ 5
Citing Octave ................ ................... 5
classes, making available to Octave ............ 902
classpath, adding new path ................... 909
classpath, difference between
static and dynamic ......................... 902
classpath, displaying .......................... 908
classpath, dynamic ....................... 908,909
classpath, removing path...................... 909
classpath, setting ............................. 902
classpath, static .............................. 908
classpath.txt ............................... 902
clearing the screen ............................. 26
code profiling ................................. 236
colors, graphics ............................... 422
comma separated lists ........................ 120
command and output logs...................... 34
command completion .......................... 27
command descriptions ......................... 13
command echoing .............................. 34
command history .............................. 28
command options .............................. 15
command-line editing .......................... 25
comments...................................... 37
comparison expressions................... 146,780
complex-conjugate transpose ............. 142,780
containers ..................................... 99
continuation lines .................... ......... 171
continue statement........................... 169
contour series ................................. 432
contributing to Octave .......................... 5
contributors..................................... 1
conversion specifications (printf)............. 269
conversion specifications (scanf).............. 275
copy-on-write ................................. 542
copyright ..................................... 951
core dump .................................... 929
COW......................................... 542
creating graphics objects ...................... 375
cs-lists ........................................ 120
customizing readline .......................... 32
customizing the prompt ........................ 32
D
DAE ......................................... 613
data sources in object groups ................. 430
data structures ............................. 43,99
data types ..................................... 39
data types, built-in ............................ 39
data types, user-defined ........................ 44
decrement operator ........................... 153
default arguments............................. 189
default graphics properties ................ .... 421
defining functions ............................. 173
deprecated functions .......................... 925
description format ............................. 12
diagonal and permutation matrices ............ 551
diagonal matrix expressions ................... 554
dialog, displaying a dialog for
selecting directories ......................... 789
dialog, displaying a dialog for selecting files. . . . 789
dialog, displaying a dialog for storing files ..... 790
dialog, displaying a help dialog ................ 791
dialog, displaying a list dialog ................. 792
dialog, displaying a message dialog ............ 793
dialog, displaying a modal dialog .............. 795
dialog, displaying a question dialog ............ 794
dialog, displaying a warning dialog ............ 794
dialog, displaying an error dialog .............. 790
dialog, displaying an input dialog ...... ....... 791
diary of commands and output ................. 34
differential equations .......................... 613
diffs, submitting .............................. 931
distribution of Octave ........................... 6
division .................................. 142,780
do-until statement........................... 166
documentation fonts ........................... 11
documentation notation ........................ 11
documenting functions ......................... 38
documenting Octave programs ................. 37
documenting user scripts ....................... 38
Dulmage-Mendelsohn decomposition .......... 578
dynamic classpath ....................... 902,908
dynamic classpath, adding new path .......... 909
dynamic naming .............................. 104

966 GNU Octave
dynamic-linking............................... 863
Dynamically Linked Functions ................ 863
E
echoing executing commands ............. ...... 34
editing the command line .. .................... 25
element-by-element evaluation ................ 147
else statement ............................... 161
elseif statement ............................. 161
end statement ................................ 161
end, indexing ................................. 135
end_try_catch ............................... 170
end_unwind_protect.......................... 170
endfor statement ............................. 166
endfunction statement ....................... 173
endif statement .............................. 161
endswitch statement ......................... 163
endwhile statement........................... 165
equality operator......................... 146,780
equality, tests for......................... 146,780
equations, nonlinear .......................... 545
erroneous messages ........................... 929
erroneous results ......................... 929,931
error bar series .............................. . 433
error ids ...................................... 220
error message notation ......................... 12
error messages ................................. 35
error messages, incorrect ...................... 929
escape sequence notation ....................... 67
evaluation notation ................ ............ 11
executable scripts .............................. 36
execution speed ............................... 542
exiting octave ............................... 7,19
exponentiation ........................... 142,780
expression, range................ ............... 52
expressions ................................... 135
expressions, assignment ....................... 151
expressions, boolean...................... 147,780
expressions, comparison .................. 146,780
expressions, logical ....................... 147,780
F
factorial function ............................. 142
fatal signal ................................... 929
field, returning value of Java object field ...... 907
field, setting value of Java object field ......... 907
fields, displaying available fields
of a Java object ............................ 907
figure modified ............................ 385
figure alphamap .............................. 385
figure beingdeleted ............................ 385
figure busyaction.............................. 385
figure buttondownfcn ......................... 385
figure children ................................ 385
figure clipping ................................ 385
figure closerequestfcn ......................... 385
figure color ................................... 385
figure colormap ............................... 385
figure createfcn ............................... 385
figure currentaxes ............................. 386
figure currentcharacter ................ ........ 386
figure currentobject ........................... 386
figure currentpoint ............................ 386
figure deletefcn ............................... 386
figure dockcontrols ............................ 386
figure filename ................................ 386
figure graphics object ......................... 375
figure graphicssmoothing ...................... 386
figure handlevisibility ......................... 386
figure hittest.................................. 386
figure integerhandle ........................... 386
figure interruptible ............................ 386
figure inverthardcopy ......................... 386
figure keypressfcn ............................. 386
figure keyreleasefcn ........................... 387
figure menubar ............................... 387
figure name ................................... 387
figure nextplot ................................ 387
figure numbertitle............................. 387
figure outerposition ........................... 387
figure paperorientation ........................ 387
figure paperposition ........................... 387
figure paperpositionmode ..................... 388
figure papersize ............................... 388
figure papertype .............................. 388
figure paperunits.............................. 388
figure parent .................................. 388
figure pointer ................................. 388
figure pointershapecdata ...................... 388
figure pointershapehotspot .................... 388
figure position ................................ 388
figure properties .............................. 385
figure renderer ................................ 388
figure renderermode........................... 388
figure resize................................... 389
figure resizefcn ................................ 389
figure selected ................................ 389
figure selectionhighlight ....................... 389
figure selectiontype ........................... 389
figure sizechangedfcn.......................... 389
figure tag ..................................... 389
figure toolbar ................................. 389
figure type .................................... 389
figure uicontextmenu.......................... 389
figure units ................................... 389
figure userdata................................ 389
figure visible .................................. 389
figure windowbuttondownfcn ................ .. 389
figure windowbuttonmotionfcn ................ 389
figure windowbuttonupfcn..................... 389
figure windowkeypressfcn ................ ..... 389
figure windowkeyreleasefcn ................ .... 390
figure windowscrollwheelfcn ................... 390
figure windowstyle ................ ............ 390

Concept Index 967
finding minimums............................. 548
finish.m........................................ 19
flag character (printf)........................ 271
flag character (scanf)......................... 276
for statement ................................ 166
Frobenius norm ............................... 509
function application........................... 534
function descriptions ........................... 12
function file................................... 189
function statement........................... 173
functions, deprecated ......................... 925
functions, obsolete ............................ 925
functions, user-defined ........................ 173
funding Octave development .................... 5
G
general p-norm ............................... 509
global statement ............................. 124
global variables ................ ............... 124
grammar rules ................................ 949
graphics ...................................... 285
graphics colors ................................ 422
graphics data structures ...................... 373
graphics line styles ............................ 422
graphics marker styles ........................ 422
graphics object properties ..................... 383
graphics object, axes .......................... 375
graphics object, figure ........................ 375
graphics object, image ........................ 375
graphics object, light.......................... 375
graphics object, line .......................... 375
graphics object, patch......................... 375
graphics object, root figure.................... 375
graphics object, surface ....................... 375
graphics object, text .......................... 375
graphics objects .............................. 375
graphics objects, saving ....................... 382
graphics properties, default ................... 421
graphics toolkits .............................. 437
greater than operator .................... 146,780
group objects ....................... 434,435,437
H
handle functions .............................. 378
handle, function handles ...................... 209
help, online .................................... 20
help, user-defined functions .................... 38
help, where to find ............................ 932
Hermitian operator....................... 142,780
Hessenberg decomposition .................... 513
history .......................................... 1
history of commands ........................... 28
I
if statement.................... .............. 161
image modified ........................... 401
image alphadata .............................. 401
image alphadatamapping...................... 401
image beingdeleted ........................... 401
image busyaction ............................. 401
image buttondownfcn ......................... 401
image cdata .................................. 401
image cdatamapping .......................... 401
image children ................................ 401
image clipping ................................ 401
image createfcn ............................... 401
image deletefcn ............................... 401
image displayname............................ 401
image graphics object ......................... 375
image handlevisibility ......................... 401
image hittest ................................. 401
image interruptible ........................... 402
image parent ................................. 402
image properties .............................. 401
image selected ................................ 402
image selectionhighlight ....................... 402
image tag..................................... 402
image type ................................... 402
image uicontextmenu ................ ......... 402
image userdata ............................... 402
image visible.. ................................ 402
image xdata .................................. 402
image ydata .................................. 402
improving Octave ........................ 930,931
incorrect error messages....................... 929
incorrect output.......................... 929,931
incorrect results .......................... 929,931
increment operator............................ 153
infinity norm ................................. 509
initialization ................................... 19
inline, inline functions ........................ 209
input conversions, for scanf................... 276
input history.. ................................. 28
installation trouble............................ 929
installing Octave ................ .............. 935
instance, creating a Java instance ............. 906
introduction .................................... 7
introduction to graphics structures ............ 373
invalid input .................................. 929
J
Java, calling from Octave ..................... 901
Java, using with Octave....................... 901
javaclasspath.txt ........................... 902
K
Kendall’s Tau................................. 655
keywords ..................................... 949
known causes of trouble ....................... 929

968 GNU Octave
L
language definition............................ 949
less than operator ........................ 146,780
light modified ............................. 408
light beingdeleted ............................. 408
light busyaction............................... 408
light buttondownfcn .......................... 408
light children ................................. 408
light clipping ................................. 408
light color .................................... 408
light createfcn ................................ 408
light deletefcn ................................ 408
light graphics object .......................... 375
light handlevisibility .......................... 408
light hittest ................................... 408
light interruptible ............................. 409
light parent ................................... 409
light position ................................. 409
light properties ............................... 408
light selected ................................. 409
light selectionhighlight ........................ 409
light style..................................... 409
light tag ...................................... 409
light type ..................................... 409
light uicontextmenu .. ......................... 409
light userdata ................................. 409
light visible ................................... 409
line modified .............................. 397
line beingdeleted .............................. 397
line busyaction.............................. .. 397
line buttondownfcn ........................... 397
line children .................................. 397
line clipping .................................. 397
line color ..................................... 397
line createfcn ................................. 397
line deletefcn ................................. 397
line displayname .............................. 397
line graphics object ........................... 375
line handlevisibility ........................... 397
line hittest.................................... 397
line interpreter................................ 397
line interruptible .............................. 397
line linestyle .................................. 397
line linewidth ................................. 397
line marker ................................... 398
line markeredgecolor .......................... 398
line markerfacecolor........................... 398
line markersize................................ 398
line parent .................................... 398
line properties ................................ 397
line selected .................................. 398
line selectionhighlight ......................... 398
line series ..................................... 433
line styles, graphics ........................... 422
line tag ....................................... 398
line type ...................................... 398
line uicontextmenu............................ 398
line userdata.................................. 398
line visible .................................... 398
line xdata .................................... 398
line xdatasource .............................. 398
line ydata .................................... 398
line ydatasource .............................. 398
line zdata..................................... 398
line zdatasource............................... 398
linear algebra ................................. 503
linear algebra, techniques ......... ............ 503
loading data .................................. 250
local minimum................................ 548
logging commands and output.................. 34
logical expressions........................ 147,780
logical operators ......................... 147,780
loop .......................................... 165
looping over structure elements ............... 167
LP ........................................... 629
LU decomposition ............................ 514
lvalue......................................... 151
M
map .......................................... 534
marker styles, graphics........................ 422
matching failure, in scanf..................... 275
matrices ....................................... 48
matrices, diagonal and permutation ........... 551
matrix factorizations .......................... 511
matrix functions, basic ........................ 503
matrix multiplication..................... 142,780
matrix, functions of ........................... 523
matrix, permutation functions ................ 556
matrix, specialized solvers..................... 524
matrix, zero elements ......................... 557
maximum field width (scanf)................. 276
memory management ......................... 542
memory, displaying Java memory status ....... 910
memory, limitations on JVM .................. 905
messages, error ................................ 35
method, invoking a method of a Java object . . . 908
methods, displaying available methods
of a Java object ............................ 908
mex .......................................... 887
mex-files ...................................... 887
minimum field width (printf)................ 271
missing data ................................... 43
mkoctfile ..................................... 864
multi-line comments ........................... 38
multiplication ............................ 142,780

Concept Index 969
N
negation ................................. 142,780
NLP.......................................... 629
nonlinear equations ........................... 545
nonlinear programming ....................... 629
not operator ............................. 147,780
numeric constant ........................... 42,47
numeric value .............................. 42,47
O
object groups ................................. 425
object, creating a Java object ................. 906
obsolete functions ............................. 925
oct ........................................... 864
oct-files ....................................... 864
Octave and matlab, how to
distinguish between ......................... 932
Octave API .................... ............... 863
Octave command options .. .................... 15
Octave, calling from Java ..................... 901
ODE ......................................... 613
online help..................................... 20
operator precedence........................... 154
operators, arithmetic ..................... 142,780
operators, assignment ......................... 151
operators, boolean ....................... 147,780
operators, decrement.......................... 153
operators, increment .......................... 153
operators, logical ......................... 147,780
operators, relational ...................... 146,780
optimization ............................. 542,629
options, Octave command ...................... 15
or operator .............................. 147,780
oregonator .................................... 615
otherwise statement ......................... 163
output conversions, for printf ................ 271
P
parser ........................................ 949
patch modified ............................ 402
patch alphadatamapping ...................... 402
patch ambientstrength ........................ 402
patch backfacelighting ........................ 402
patch beingdeleted ............................ 402
patch busyaction.............................. 403
patch buttondownfcn ......................... 403
patch cdata ................................... 403
patch cdatamapping .......................... 403
patch children ................................ 403
patch clipping ................................ 403
patch createfcn ............................... 403
patch deletefcn ............................... 403
patch diffusestrength.......................... 403
patch displayname ............................ 403
patch edgealpha .............................. 403
patch edgecolor ............................... 403
patch edgelighting ............................ 403
patch facealpha ............................... 403
patch facecolor........................... ..... 404
patch facelighting ............................. 404
patch facenormals............................. 404
patch facenormalsmode ....................... 404
patch faces ................................... 404
patch facevertexalphadata .................... 404
patch facevertexcdata ......................... 404
patch graphics object ......................... 375
patch handlevisibility ......................... 404
patch hittest .................................. 404
patch interpreter.............................. 404
patch interruptible ............................ 404
patch linestyle ................................ 404
patch linewidth ............................... 404
patch marker ................................. 404
patch markeredgecolor ........................ 404
patch markerfacecolor......................... 404
patch markersize .............................. 404
patch parent .................................. 404
patch properties .............................. 402
patch selected ................................ 404
patch selectionhighlight ....................... 404
patch specularcolorreflectance ................. 404
patch specularexponent ....................... 404
patch specularstrength ........................ 405
patch tag ..................................... 405
patch type .................................... 405
patch uicontextmenu .. ........................ 405
patch userdata ................................ 405
patch vertexnormals .......................... 405
patch vertexnormalsmode ..................... 405
patch vertices ................................. 405
patch visible .................................. 405
patch xdata.................... ............... 405
patch ydata.................... ............... 405
patch zdata ................................... 405
patches, submitting ........................... 931
path, adding to classpath ..................... 909
path, removing from classpath ................ 909
permutation matrix functions ................. 556
persistent statement ........................ 126
persistent variables ........................... 126
personal startup file............................ 19
PKG ADD ............. ...................... 858
PKG DEL.................................... 858
plotting..................................... .. 285
plotting, high-level ............................ 285
plotting, multiple plot windows .. ............. 355
plotting, multiple plots per figure ............. 354
plotting, object manipulation ................. 356
plotting, saving and printing plots............. 364
plotting, three-dimensional .................... 320
plotting, two-dimensional functions............ 316
plotting, window manipulation ...... .......... 357
precision (printf)............................ 271
printing notation............................... 12

970 GNU Octave
printing plots ................................. 364
profiler ....................................... 236
program, self contained ........................ 36
Progress Bar.................................. 796
project startup file ............................. 19
prompt customization .......................... 32
pseudoinverse ............................ 510,554
Q
QP ........................................... 629
QR factorization .............................. 515
quadratic programming ....................... 629
quitting octave .............................. 7,19
quiver group .................................. 434
quotient ................................. 142,780
R
range expressions .............................. 52
readline customization ........................ 32
recycling...................................... 531
relational operators ...................... 146,780
reporting bugs ........................... 929,930
results, incorrect ......................... 929,931
root modified ............................. 383
root beingdeleted ............................. 383
root busyaction ............................... 383
root buttondownfcn ........................... 384
root callbackobject............................ 384
root children.................................. 384
root clipping .................................. 384
root commandwindowsize ..................... 384
root createfcn................................. 384
root currentfigure ............................. 384
root deletefcn ................................. 384
root figure graphics object .................... 375
root figure properties ......................... 383
root fixedwidthfontname ...................... 384
root handlevisibility........................... 384
root hittest ................................... 384
root interruptible ............................. 384
root monitorpositions ......................... 384
root parent ................................... 384
root pointerlocation ............. .............. 384
root pointerwindow ........................... 384
root screendepth .............................. 384
root screenpixelsperinch......... .............. 384
root screensize ................................ 384
root selected .................................. 384
root selectionhighlight ........................ 384
root showhiddenhandles....................... 384
root tag ...................................... 385
root type ..................................... 385
root uicontextmenu ........................... 385
root units..................................... 385
root userdata ................................. 385
root visible ................................... 385
S
saving data ................................... 250
saving graphics objects........................ 382
saving plots................................... 364
scatter group ................................. 435
Schur decomposition .......................... 519
script files .................................... 173
scripts ......................................... 36
self contained programs ........................ 36
series objects .............. 430,431,432,433,436
short-circuit evaluation ................ ....... 149
side effect.. ................................... 151
SIMD ........................................ 531
singular value decomposition .................. 521
site exiting file .............................. ... 19
site startup file .............................. .. 19
Spearman’s Rho .............................. 654
speedups ..................................... 542
stair group.................................... 435
startup ........................................ 19
startup files .................................... 19
statements .................................... 161
static classpath .......................... 902,908
stem series.................................... 436
strings ..................................... 43,67
structural rank ............................... 584
structure elements, looping over ............... 167
structures .................................. 43,99
submitting diffs ............................... 931
submitting patches............................ 931
subtraction .............................. 142,780
suggestions ................................... 930
surface modified .......................... 405
surface alphadata ............................. 405
surface alphadatamapping .................... 405
surface ambientstrength ................ ....... 405
surface backfacelighting ................ ....... 405
surface beingdeleted .......................... 405
surface busyaction ............................ 405
surface buttondownfcn ........................ 405
surface cdata ................................. 405
surface cdatamapping ......................... 406
surface cdatasource ........................... 406
surface children ............................... 406
surface clipping ............................... 406
surface createfcn .............................. 406
surface deletefcn .............................. 406
surface diffusestrength ........................ 406
surface displayname........................... 406
surface edgealpha ............................. 406
surface edgecolor......... ..................... 406
surface edgelighting ........................... 406
surface facealpha.............................. 406
surface facecolor .............................. 406
surface facelighting ........................... 406
surface facenormals ........................... 406
surface facenormalsmode ...................... 407
surface graphics object ........................ 375

Concept Index 971
surface group ................................. 437
surface handlevisibility ........................ 407
surface hittest ................................ 407
surface interpreter ............................ 407
surface interruptible .......................... 407
surface linestyle ............................... 407
surface linewidth...... ........................ 407
surface marker ................................ 407
surface markeredgecolor ....................... 407
surface markerfacecolor ....................... 407
surface markersize ............................ 407
surface meshstyle ............................. 407
surface parent ................................ 407
surface properties ............................. 405
surface selected ............................... 407
surface selectionhighlight...................... 407
surface specularcolorreflectance ............... 407
surface specularexponent...................... 407
surface specularstrength ...................... 407
surface tag...... .............................. 407
surface type .................................. 407
surface uicontextmenu ................ ........ 407
surface userdata .............................. 407
surface vertexnormals ......................... 408
surface vertexnormalsmode.................... 408
surface visible ................................ 408
surface xdata ................................. 408
surface xdatasource ........................... 408
surface ydata ................................. 408
surface ydatasource ........................... 408
surface zdata ................................. 408
surface zdatasource ........................... 408
switch statement ............................. 163
T
test functions ................................. 913
tests for equality ......................... 146,780
text modified ............................. 399
text backgroundcolor ......................... 399
text beingdeleted ............................. 399
text busyaction ............................... 399
text buttondownfcn ........................... 399
text children .................................. 399
text clipping .................................. 399
text color ..................................... 399
text createfcn ................................. 399
text deletefcn ................................. 399
text displayname ............................. 399
text edgecolor ................................ 399
text editing ................................... 399
text extent ................................... 399
text fontangle................................. 399
text fontname ................................ 399
text fontsize .................................. 399
text fontunits ................................. 400
text fontweight ............................... 400
text graphics object ....................... .... 375
text handlevisibility........................... 400
text hittest ................................... 400
text horizontalalignment ................ ...... 400
text interpreter ............................... 400
text interruptible ............................. 400
text linestyle.................................. 400
text linewidth ................................ 400
text margin ................................... 400
text parent ................................... 400
text position .................................. 400
text properties ................................ 399
text rotation .................................. 400
text selected .................................. 400
text selectionhighlight......................... 400
text string .................................... 400
text tag ...................................... 400
text type ..................................... 400
text uicontextmenu ................ ........... 400
text units ..................................... 400
text userdata ................................. 401
text verticalalignment......................... 401
text visible ................................... 401
toolkit customization ......................... 438
toolkits, graphics ............................. 437
transpose ................................ 142,780
transpose, complex-conjugate............. 142,780
troubleshooting ............................... 929
try statement ................................ 170
U
uibuttongroup modified ................... 410
uibuttongroup backgroundcolor ............... 410
uibuttongroup beingdeleted ................... 410
uibuttongroup bordertype ..................... 410
uibuttongroup borderwidth ................... 410
uibuttongroup busyaction ..................... 410
uibuttongroup buttondownfcn................. 410
uibuttongroup children........................ 410
uibuttongroup clipping........................ 411
uibuttongroup createfcn....................... 411
uibuttongroup deletefcn ....................... 411
uibuttongroup fontangle ...................... 411
uibuttongroup fontname ...................... 411
uibuttongroup fontsize ........................ 411
uibuttongroup fontunits....................... 411
uibuttongroup fontweight ..................... 411
uibuttongroup foregroundcolor ................ 411
uibuttongroup handlevisibility ................ 411
uibuttongroup highlightcolor .................. 411
uibuttongroup hittest ......................... 411
uibuttongroup interruptible ................... 411
uibuttongroup parent ......................... 411
uibuttongroup position........................ 411
uibuttongroup properties...................... 410
uibuttongroup resizefcn ....................... 411
uibuttongroup selected ........................ 411
uibuttongroup selectedobject .. ................ 411

972 GNU Octave
uibuttongroup selectionchangedfcn ............ 411
uibuttongroup selectionhighlight .............. 411
uibuttongroup shadowcolor............. ....... 411
uibuttongroup sizechangedfcn ................. 411
uibuttongroup tag ............................ 411
uibuttongroup title ........................... 411
uibuttongroup titleposition.................... 411
uibuttongroup type ........................... 411
uibuttongroup uicontextmenu ................ . 411
uibuttongroup units........................... 412
uibuttongroup userdata ....................... 412
uibuttongroup visible ......................... 412
uicontextmenu modified ................... 412
uicontextmenu beingdeleted ................... 412
uicontextmenu busyaction..................... 412
uicontextmenu buttondownfcn ................ 412
uicontextmenu callback ....................... 412
uicontextmenu children ....................... 412
uicontextmenu clipping .................... ... 412
uicontextmenu createfcn .................... .. 412
uicontextmenu deletefcn .................... .. 412
uicontextmenu handlevisibility ................ 412
uicontextmenu hittest .................... ..... 412
uicontextmenu interruptible ................... 412
uicontextmenu parent ......................... 412
uicontextmenu position ....................... 412
uicontextmenu properties ..................... 412
uicontextmenu selected ....................... 413
uicontextmenu selectionhighlight .............. 413
uicontextmenu tag .................... ........ 413
uicontextmenu type .................... ....... 413
uicontextmenu uicontextmenu................. 413
uicontextmenu userdata .................... ... 413
uicontextmenu visible .................... ..... 413
uicontrol modified ........................ 415
uicontrol backgroundcolor ..................... 415
uicontrol beingdeleted......................... 415
uicontrol busyaction .......................... 415
uicontrol buttondownfcn ...................... 415
uicontrol callback ............................. 415
uicontrol cdata ............................... 415
uicontrol children ............................. 415
uicontrol clipping ............................. 415
uicontrol createfcn ............................ 415
uicontrol deletefcn ............................ 415
uicontrol enable............................... 415
uicontrol extent ............................... 415
uicontrol fontangle ............................ 415
uicontrol fontname ............................ 415
uicontrol fontsize ............................. 415
uicontrol fontunits ............................ 415
uicontrol fontweight........................... 415
uicontrol foregroundcolor...................... 415
uicontrol handlevisibility ...................... 415
uicontrol hittest .............................. 415
uicontrol horizontalalignment ................. 415
uicontrol interruptible............. ............ 415
uicontrol keypressfcn .......................... 415
uicontrol listboxtop ........................... 415
uicontrol max................................. 415
uicontrol min ................................. 415
uicontrol parent...... ......................... 415
uicontrol position ............................. 415
uicontrol properties ........................... 414
uicontrol selected ............................. 416
uicontrol selectionhighlight .................... 416
uicontrol sliderstep............................ 416
uicontrol string ............................... 416
uicontrol style ................................ 416
uicontrol tag .................................. 416
uicontrol tooltipstring......................... 416
uicontrol type........................... ...... 416
uicontrol uicontextmenu ...................... 416
uicontrol units ................................ 416
uicontrol userdata ............................ 416
uicontrol value ................................ 416
uicontrol verticalalignment .................... 416
uicontrol visible............................... 416
uimenu modified .......................... 409
uimenu accelerator ............................ 409
uimenu beingdeleted .......................... 409
uimenu busyaction ............................ 409
uimenu buttondownfcn........................ 409
uimenu callback .............................. 409
uimenu checked ............................... 409
uimenu children...... ......................... 409
uimenu clipping............................... 409
uimenu createfcn........................... ... 409
uimenu deletefcn.............................. 409
uimenu enable ................................ 410
uimenu foregroundcolor ....................... 410
uimenu handlevisibility ....................... 410
uimenu hittest ................................ 410
uimenu interruptible .......................... 410
uimenu label.................................. 410
uimenu parent ................................ 410
uimenu position............................... 410
uimenu properties ............................ 409
uimenu selected ............................... 410
uimenu selectionhighlight ..................... 410
uimenu separator ............................. 410
uimenu tag ................................... 410
uimenu type .................................. 410
uimenu uicontextmenu ........................ 410
uimenu userdata .............................. 410
uimenu visible ................................ 410
uipanel modified .......................... 413
uipanel backgroundcolor ...................... 413
uipanel beingdeleted .......................... 413
uipanel bordertype ............................ 413
uipanel borderwidth .......................... 413
uipanel busyaction ............................ 413
uipanel buttondownfcn........................ 413
uipanel children............................... 413
uipanel clipping............................... 413
uipanel createfcn.............................. 413

Concept Index 973
uipanel deletefcn .............................. 413
uipanel fontangle ............................. 413
uipanel fontname ............................. 414
uipanel fontsize ............................... 414
uipanel fontunits.............................. 414
uipanel fontweight ............................ 414
uipanel foregroundcolor ....................... 414
uipanel handlevisibility ....................... 414
uipanel highlightcolor ......................... 414
uipanel hittest ................................ 414
uipanel interruptible .......................... 414
uipanel parent ................................ 414
uipanel position............................... 414
uipanel properties............................. 413
uipanel resizefcn .............................. 414
uipanel selected ............................... 414
uipanel selectionhighlight ..................... 414
uipanel shadowcolor......... .................. 414
uipanel tag ................................... 414
uipanel title .................................. 414
uipanel titleposition........................... 414
uipanel type .................................. 414
uipanel uicontextmenu ................ ........ 414
uipanel units.................................. 414
uipanel userdata .............................. 414
uipanel visible ................................ 414
uipushtool modified ....................... 417
uipushtool beingdeleted ....................... 417
uipushtool busyaction ......................... 417
uipushtool buttondownfcn..................... 417
uipushtool cdata .............................. 417
uipushtool children ........................... 417
uipushtool clickedcallback ..................... 417
uipushtool clipping............................ 417
uipushtool createfcn .......................... 417
uipushtool deletefcn................ ........... 417
uipushtool enable ............................. 418
uipushtool handlevisibility .................... 418
uipushtool hittest ............................. 418
uipushtool interruptible ....................... 418
uipushtool parent ............................. 418
uipushtool properties ......................... 417
uipushtool selected............................ 418
uipushtool selectionhighlight .................. 418
uipushtool separator .......................... 418
uipushtool tag ................................ 418
uipushtool tooltipstring ....................... 418
uipushtool type ............................... 418
uipushtool uicontextmenu ..................... 418
uipushtool userdata ........................... 418
uipushtool visible ............................. 418
uitoggletool modified ...................... 418
uitoggletool beingdeleted ............. ......... 418
uitoggletool busyaction ....................... 418
uitoggletool buttondownfcn ................... 418
uitoggletool cdata........................... .. 418
uitoggletool children .......................... 418
uitoggletool clickedcallback.................... 418
uitoggletool clipping .......................... 418
uitoggletool createfcn ......................... 418
uitoggletool deletefcn ......................... 419
uitoggletool enable ............................ 419
uitoggletool handlevisibility ................... 419
uitoggletool hittest............................ 419
uitoggletool interruptible...................... 419
uitoggletool offcallback........................ 419
uitoggletool oncallback ........................ 419
uitoggletool parent............................ 419
uitoggletool properties ........................ 418
uitoggletool selected .......................... 419
uitoggletool selectionhighlight ................. 419
uitoggletool separator ......................... 419
uitoggletool state ............................. 419
uitoggletool tag ............................... 419
uitoggletool tooltipstring ...................... 419
uitoggletool type .............................. 419
uitoggletool uicontextmenu.................... 419
uitoggletool userdata.......................... 419
uitoggletool visible ............................ 419
uitoolbar modified ........................ 416
uitoolbar beingdeleted ........................ 416
uitoolbar busyaction .......................... 416
uitoolbar buttondownfcn ...................... 416
uitoolbar children ............................. 416
uitoolbar clipping ............................. 416
uitoolbar createfcn ............................ 416
uitoolbar deletefcn ............................ 416
uitoolbar handlevisibility...................... 417
uitoolbar hittest .............................. 417
uitoolbar interruptible ........................ 417
uitoolbar parent .............................. 417
uitoolbar properties ........................... 416
uitoolbar selected ............................. 417
uitoolbar selectionhighlight.................... 417
uitoolbar tag ................................. 417
uitoolbar type ................................ 417
uitoolbar uicontextmenu ...................... 417
uitoolbar userdata ............................ 417
uitoolbar visible .............................. 417
unary minus ............................. 142,780
undefined behavior......... ................... 929
undefined function value ...................... 929
unwind_protect statement .................... 170
unwind_protect_cleanup ..................... 170
use of comments ............................... 37
user-defined data types......................... 44
user-defined functions ......................... 173
user-defined variables ................ ......... 123
using Octave with Java ...... ................. 901
974 GNU Octave
V
varargin ..................................... 184
varargout .................................... 187
variable-length argument lists ................. 184
variable-length return lists .................... 187
variables, global ................ .............. 124
variables, persistent ........................... 126
variables, user-defined......................... 123
vectorization.................................. 529
vectorize...................................... 529
version startup file ............................. 19
W
warning ids ................................... 223
warranty...................................... 951
while statement .............................. 165
wrong answers ........................... 929,931
975
Function Index
A
abs ........................................... 473
accumarray ................................... 539
accumdim ..................................... 540
acos .......................................... 475
acosd..................................... .... 478
acosh..................................... .... 476
acot .......................................... 475
acotd..................................... .... 478
acoth..................................... .... 476
acsc .......................................... 475
acscd..................................... .... 478
acsch..................................... .... 476
add_input_event_hook ....................... 949
addlistener .................................. 427
addpath ...................................... 192
addpref ...................................... 805
addproperty .................................. 426
addtodate .................................... 816
airy .......................................... 488
all ........................................... 439
allchild ..................................... 382
allow_noninteger_range_as_index ........... 140
amd ........................................... 575
ancestor ..................................... 382
and ........................................... 148
angle..................................... .... 473
annotation ................................... 352
anova..................................... .... 664
any ........................................... 439
arch_fit ..................................... 732
arch_rnd ..................................... 733
arch_test .................................... 733
area .......................................... 311
arg ........................................... 473
argnames ..................................... 212
argv ........................................... 18
arma_rnd ..................................... 733
arrayfun ..................................... 534
ascii..................................... .... 831
asctime ...................................... 809
asec .......................................... 475
asecd..................................... .... 478
asech..................................... .... 476
asin .......................................... 475
asind..................................... .... 477
asinh..................................... .... 476
assert ....................................... 919
assignin ..................................... 160
atan .......................................... 475
atan2..................................... .... 477
atan2d ....................................... 478
atand..................................... .... 478
atanh..................................... .... 476
atexit......................................... 20
audiodevinfo ................................ 762
audioformats ................................ 761
audioinfo .................................... 761
audioplayer .................................. 762
audioread .................................... 761
audiorecorder ............................... 764
audiowrite ................................... 761
autoload ..................................... 199
autoreg_matrix .............................. 734
autumn ....................................... 753
available_graphics_toolkits ............... 438
axes .......................................... 376
axis ..................................... 313,314
B
balance ...................................... 503
bandwidth .................................... 504
bar ........................................... 291
barh .......................................... 292
bartlett ..................................... 734
bartlett_test ............................... 664
base2dec ...................................... 92
base64_decode ............................... 833
base64_encode ............................... 833
beep .......................................... 217
beep_on_error ............................... 217
besselh ...................................... 489
besseli ...................................... 489
besselj ...................................... 489
besselk ...................................... 489
bessely ...................................... 489
beta .......................................... 490
betacdf ...................................... 656
betainc ...................................... 490
betaincinv ................................... 490
betainv ...................................... 656
betaln ....................................... 490
betapdf ...................................... 656
betarnd ...................................... 672
bicg .......................................... 524
bicgstab ..................................... 525
bin2dec ....................................... 91
binary ....................................... 831
bincoeff ..................................... 490
binocdf ...................................... 657
binoinv ...................................... 657
binopdf ...................................... 657
binornd ...................................... 672
bitand......................................... 58
bitcmp......................................... 59
bitget......................................... 58
bitor .......................................... 59
bitpack ....................................... 41
976 GNU Octave
bitset......................................... 58
bitshift ...................................... 59
bitunpack ..................................... 42
bitxor......................................... 59
blackman ..................................... 734
blanks......................................... 69
blkdiag ...................................... 452
blkmm..................................... .... 524
bone .......................................... 753
box ........................................... 350
brighten ..................................... 757
bsxfun ....................................... 532
built_in_docstrings_file .................... 24
builtin ...................................... 198
bunzip2 ...................................... 827
byte_size .................................... 868
bzip2..................................... .... 829
C
calendar ..................................... 817
camlight ..................................... 336
canonicalize_file_name ..................... 826
cart2pol ..................................... 496
cart2sph ..................................... 497
cast ........................................... 40
cat ........................................... 445
cauchy_cdf ................................... 657
cauchy_inv ................................... 657
cauchy_pdf ................................... 657
cauchy_rnd ................................... 673
caxis..................................... .... 315
cbrt .......................................... 472
ccolamd ...................................... 575
cd ....................................... 831,842
ceil .......................................... 480
cell .......................................... 114
cell2mat ..................................... 120
cell2struct .................................. 120
celldisp ..................................... 113
cellfun ...................................... 536
cellindexmat ................................ 118
cellslices ................................... 116
cellstr ...................................... 119
center ....................................... 650
cgs ........................................... 525
char ........................................... 71
chdir..................................... .... 842
chi2cdf ...................................... 657
chi2inv ...................................... 657
chi2pdf ...................................... 657
chi2rnd ...................................... 673
chisquare_test_homogeneity ................ 665
chisquare_test_independence ............... 665
chol .......................................... 511
chol2inv ..................................... 512
choldelete ................................... 513
cholinsert ................................... 513
cholinv ...................................... 512
cholshift .................................... 513
cholupdate ................................... 512
chop .......................................... 486
circshift .................................... 447
citation ....................................... 5
cla ........................................... 360
clabel ....................................... 350
class .......................................... 39
clc ............................................ 26
clear.................................. ....... 131
clf ........................................... 360
clock.................................. ....... 811
cloglog ...................................... 652
close .................................... 361,830
closereq ..................................... 361
cmpermute .................................... 758
cmunique ..................................... 758
colamd ....................................... 576
colloc ....................................... 608
colon.................................. ....... 778
colorbar ..................................... 351
colorcube .................................... 753
colormap ..................................... 751
colperm ...................................... 577
colstyle ..................................... 423
columns ....................................... 44
comet.................................. ....... 313
comet3 ....................................... 313
command_line_path ........................... 194
common_size .................................. 441
commutation_matrix.......................... 491
compan ....................................... 684
compare_versions ............................ 848
compass ...................................... 310
completion_append_char ...................... 27
completion_matches ........................... 28
complex ....................................... 48
computer ..................................... 846
cond .......................................... 504
condeig ...................................... 505
condest ...................................... 582
confirm_recursive_rmdir .................... 820
conj .......................................... 473
contour ...................................... 300
contour3 ..................................... 302
contourc ..................................... 301
contourf ................................ 300,301
contrast ..................................... 757
conv .......................................... 685
conv2.................................. ....... 686
convhull ..................................... 721
convhulln .................................... 722
convn.................................. ....... 685
cool .......................................... 753
copper ....................................... 754
copyfile ..................................... 818
copyobj ...................................... 383
Function Index 977
cor_test ..................................... 665
corr .......................................... 654
cos ........................................... 475
cosd .......................................... 477
cosh .......................................... 476
cot ........................................... 475
cotd .......................................... 477
coth .......................................... 476
cov ........................................... 654
cplxpair ..................................... 473
cputime ...................................... 812
crash_dumps_octave_core .................... 262
cross..................................... .... 484
csc ........................................... 475
cscd .......................................... 477
csch .......................................... 476
cstrcat ....................................... 73
csvread ...................................... 256
csvwrite ..................................... 256
csymamd ...................................... 577
ctime..................................... .... 808
ctranspose ................................... 144
cubehelix .................................... 754
cummax ....................................... 482
cummin ....................................... 483
cumprod ...................................... 479
cumsum ....................................... 479
cumtrapz ..................................... 608
curl ..................................... 484,485
cylinder ..................................... 346
D
daspect ...................................... 342
daspk..................................... .... 621
daspk_options ............................... 622
dasrt..................................... .... 626
dasrt_options ............................... 628
dassl..................................... .... 624
dassl_options ............................... 625
date .......................................... 812
datenum ................................. 813,814
datestr ...................................... 814
datetick ..................................... 817
datevec ...................................... 816
dawson ....................................... 491
dbclear ................................. 232,233
dbcont ....................................... 230
dbdown ....................................... 236
dblist ....................................... 234
dblquad ...................................... 609
dbnext ....................................... 235
dbquit ....................................... 230
dbstack ...................................... 235
dbstatus ..................................... 232
dbstep ....................................... 235
dbstop ....................................... 230
dbtype ....................................... 234
dbup .......................................... 236
dbwhere ...................................... 234
deal .......................................... 187
deblank ....................................... 77
debug_java ................................... 911
debug_jit .................................... 542
debug_on_error .............................. 229
debug_on_interrupt.......................... 229
debug_on_warning ............................ 229
dec2base ...................................... 92
dec2bin ....................................... 91
dec2hex ....................................... 92
deconv ....................................... 686
deg2rad ...................................... 474
del2 .......................................... 485
delaunay ..................................... 711
delaunayn .................................... 712
delete................................... 360,831
dellistener .................................. 427
demo .......................................... 920
desktop ...................................... 802
det ........................................... 505
detrend ...................................... 734
diag .......................................... 452
dialog ....................................... 795
diary ...................................... 14,34
diff .......................................... 440
diffpara ..................................... 734
diffuse ...................................... 334
dims .......................................... 868
dir ...................................... 831,843
dir_in_loadpath ............................. 194
disable_diagonal_matrix .................... 551
disable_permutation_matrix ................ 551
disable_range ................................ 53
discrete_cdf ................................ 658
discrete_inv ................................ 658
discrete_pdf ................................ 657
discrete_rnd ................................ 673
disp .......................................... 243
display ...................................... 771
divergence ................................... 484
dlmread ...................................... 256
dlmwrite ..................................... 255
dmperm ....................................... 578
do_braindead_shortcircuit_evaluation ..... 150
do_string_escapes ............................ 96
doc ............................................ 21
doc_cache_create ............................. 24
doc_cache_file ............................... 23
dos ........................................... 834
dot ........................................... 484
double......................................... 47
drawnow ...................................... 357
dsearch ...................................... 717
dsearchn ..................................... 717
dup2 .......................................... 838
978 GNU Octave
duplication_matrix.......................... 491
durbinlevinson .............................. 735
E
e............................................. 498
echo ........................................... 34
echo_executing_commands ..................... 34
edit .......................................... 190
edit_history.................................. 29
EDITOR......................................... 31
eig ........................................... 505
eigs .......................................... 586
elem .......................................... 868
ellipj ....................................... 491
ellipke ...................................... 492
ellipsoid .................................... 347
empirical_cdf ............................... 658
empirical_inv ............................... 658
empirical_pdf ............................... 658
empirical_rnd ............................... 673
endgrent ..................................... 845
endpwent ..................................... 845
eomday ....................................... 817
eps ........................................... 500
eq ............................................ 146
erf ........................................... 492
erfc .......................................... 492
erfcinv ...................................... 493
erfcx..................................... .... 493
erfi .......................................... 493
erfinv ....................................... 493
errno..................................... .... 221
errno_list ................................... 221
error..................................... .... 215
errorbar ..................................... 303
errordlg ..................................... 791
etime..................................... .... 812
etree..................................... .... 568
etreeplot .................................... 569
eval .......................................... 157
evalc..................................... .... 157
evalin ....................................... 160
example ...................................... 921
exec .......................................... 837
EXEC_PATH .................................... 837
exist..................................... .... 130
exit ........................................... 19
exp ........................................... 471
expcdf ....................................... 658
expint ....................................... 493
expinv ....................................... 658
expm .......................................... 523
expm1..................................... .... 471
exppdf ....................................... 658
exprnd ....................................... 674
eye ........................................... 453
ezcontour .................................... 318
ezcontourf ................................... 318
ezmesh ....................................... 343
ezmeshc ...................................... 344
ezplot ....................................... 317
ezplot3 ...................................... 343
ezpolar ...................................... 319
ezsurf ....................................... 345
ezsurfc ................................. 345,346
F
f_test_regression ........................... 666
factor ....................................... 486
factorial .................................... 485
fail .......................................... 920
false .......................................... 61
fcdf .......................................... 658
fclear ....................................... 282
fclose ....................................... 266
fcntl.................................. ....... 840
fdisp.................................. ....... 254
feather ...................................... 310
feof .......................................... 282
ferror ....................................... 282
feval.................................. ....... 158
fflush ....................................... 248
fft ........................................... 727
fft2 .......................................... 727
fftconv ...................................... 730
fftfilt ...................................... 730
fftn .......................................... 728
fftshift ..................................... 735
fftw .......................................... 729
fgetl.................................. ....... 267
fgets.................................. ....... 268
fieldnames ................................... 107
figure ....................................... 356
file_in_loadpath ............................ 194
file_in_path ................................ 824
fileattrib ................................... 823
filemarker ................................... 825
fileparts .................................... 825
fileread ..................................... 254
filesep ...................................... 825
fill .......................................... 312
filter ....................................... 730
filter2 ...................................... 731
find .......................................... 441
findall ...................................... 420
findfigs ..................................... 382
findobj ................................. 419,420
findstr ....................................... 78
finv .......................................... 658
fix ........................................... 480
fixed_point_format ........................... 51
flag .......................................... 754
flintmax ...................................... 56
flip .......................................... 443
Function Index 979
fliplr ....................................... 443
flipud ....................................... 443
floor..................................... .... 480
fminbnd ...................................... 549
fminsearch ................................... 550
fminunc ...................................... 549
foo ............................................ 13
fopen..................................... .... 265
fork .......................................... 837
format ....................................... 244
formula ...................................... 212
fortran_vec .................................. 869
fpdf .......................................... 658
fplot..................................... .... 316
fprintf ...................................... 269
fputs..................................... .... 267
fractdiff .................................... 735
frame2im ..................................... 751
fread .................................... 277,278
freport ...................................... 282
freqz..................................... .... 731
freqz_plot ................................... 732
frewind ...................................... 283
frnd .......................................... 674
fscanf ....................................... 274
fseek..................................... .... 283
fskipl ....................................... 268
fsolve ....................................... 545
ftell..................................... .... 283
ftp ........................................... 830
full .......................................... 564
fullfile ..................................... 826
func2str ..................................... 211
functions .................................... 210
fwrite ....................................... 280
fzero..................................... .... 548
G
gallery .............. 461,462,463,464,465,466
gamcdf ....................................... 658
gaminv ....................................... 659
gamma..................................... .... 494
gammainc ..................................... 494
gammaln ...................................... 495
gampdf ....................................... 658
gamrnd ....................................... 674
gca ........................................... 379
gcbf .......................................... 424
gcbo .......................................... 424
gcd ........................................... 486
gcf ........................................... 379
gco ........................................... 380
ge ............................................ 147
genpath ...................................... 193
genvarname ................................... 123
geocdf ....................................... 659
geoinv ....................................... 659
geopdf ....................................... 659
geornd ....................................... 674
get ................................. 381,763,765
get_first_help_sentence ..................... 25
get_help_text ................................ 24
get_help_text_from_file ..................... 25
get_home_directory.......................... 842
getappdata ................................... 424
getaudiodata ................................ 765
getegid ...................................... 841
getenv ....................................... 842
geteuid ...................................... 841
getfield ..................................... 109
getgid ....................................... 841
getgrent ..................................... 845
getgrgid ..................................... 845
getgrnam ..................................... 845
gethostname .................................. 830
getpgrp ...................................... 841
getpid ....................................... 841
getplayer .................................... 765
getppid ...................................... 841
getpref ...................................... 804
getpwent ..................................... 844
getpwnam ..................................... 844
getpwuid ..................................... 844
getrusage .................................... 850
getuid ....................................... 841
ginput ....................................... 371
givens ....................................... 506
glob .......................................... 824
glpk .......................................... 629
gls ........................................... 639
gmres.................................. ....... 526
gmtime ....................................... 808
gnuplot_binary .............................. 438
gplot.................................. ....... 569
grabcode ..................................... 205
gradient ..................................... 483
graphics_toolkit ............................ 437
gray .......................................... 754
gray2ind ..................................... 750
grid .......................................... 351
griddata ..................................... 723
griddata3 .................................... 723
griddatan .................................... 724
gt ............................................ 147
gtext.................................. ....... 372
guidata ...................................... 802
guihandles ................................... 802
gunzip ....................................... 828
gzip .......................................... 827
980 GNU Octave
H
hadamard ..................................... 466
hamming ...................................... 735
hankel ....................................... 466
hanning ...................................... 735
hash .......................................... 851
have_window_system.......................... 803
hdl2struct ................................... 382
help ........................................... 20
helpdlg ...................................... 791
hess .......................................... 513
hex2dec ....................................... 92
hex2num ....................................... 93
hggroup ...................................... 425
hgload ....................................... 371
hgsave ....................................... 371
hidden ....................................... 323
hilb .......................................... 467
hist .......................................... 293
histc..................................... .... 650
history ....................................... 28
history_control .............................. 30
history_file.................................. 31
history_save.................................. 30
history_size.................................. 31
history_timestamp_format_string ............ 31
hold .......................................... 359
home ........................................... 26
horzcat ...................................... 445
hot ........................................... 754
hotelling_test .............................. 666
hotelling_test_2 ............................ 666
housh..................................... .... 522
hsv ........................................... 755
hsv2rgb ...................................... 759
hurst..................................... .... 736
hygecdf ...................................... 659
hygeinv ...................................... 659
hygepdf ...................................... 659
hygernd ...................................... 675
hypot..................................... .... 483
I
i............................................. 498
ichol..................................... .... 593
idivide ....................................... 57
ifelse ....................................... 150
ifft .......................................... 727
ifft2..................................... .... 728
ifftn..................................... .... 728
ifftshift .................................... 735
ignore_function_time_stamp ................ 192
ilu ........................................... 595
im2double .................................... 749
im2frame ..................................... 751
imag .......................................... 473
image..................................... .... 748
IMAGE_PATH ................................... 743
imagesc ...................................... 748
imfinfo ...................................... 744
imformats .................................... 746
importdata ................................... 262
imread ....................................... 741
imshow ....................................... 747
imwrite ...................................... 742
ind2gray ..................................... 750
ind2rgb ...................................... 751
ind2sub ...................................... 138
index .......................................... 79
Inf ........................................... 499
inf ........................................... 499
inferiorto ................................... 782
info ........................................... 22
info_file ..................................... 22
info_program.................................. 22
inline ....................................... 212
inpolygon .................................... 720
input.................................. ....... 248
inputdlg ..................................... 791
inputname .................................... 176
inputParser .................................. 182
inputParser.CaseSensitive.................. 182
inputParser.FunctionName ................... 183
inputParser.KeepUnmatched.................. 183
inputParser.Parameters ..................... 182
inputParser.Results ........................ 182
inputParser.StructExpand ................... 183
inputParser.Unmatched ...................... 182
inputParser.UsingDefaults.................. 182
int16 .......................................... 55
int2str ....................................... 75
int32 .......................................... 55
int64 .......................................... 55
int8 ........................................... 55
interp1 ...................................... 701
interp2 ...................................... 705
interp3 ...................................... 706
interpft ..................................... 704
interpn ...................................... 707
intersect .................................... 679
intmax......................................... 56
intmin......................................... 56
inv ........................................... 507
invhilb ...................................... 467
ipermute ..................................... 446
iqr ........................................... 644
is_absolute_filename ....................... 827
is_dq_string.................................. 68
is_function_handle.......................... 210
is_leap_year ................................ 812
is_rooted_relative_filename ............... 827
is_sq_string.................................. 68
is_valid_file_id ............................ 266
isa ............................................ 39
isalnum ....................................... 96
Function Index 981
isalpha ....................................... 96
isappdata .................................... 425
isargout ..................................... 187
isascii ....................................... 98
isaxes ....................................... 379
isbanded ...................................... 64
isbool......................................... 62
iscell ....................................... 113
iscellstr .................................... 119
ischar......................................... 68
iscntrl ....................................... 97
iscolormap ................................... 749
iscolumn ...................................... 63
iscomplex ..................................... 63
isdebugmode .................................. 235
isdefinite .................................... 64
isdeployed ................................... 847
isdiag......................................... 64
isdigit ....................................... 97
isdir..................................... .... 823
isempty ....................................... 46
isequal ...................................... 147
isequaln ..................................... 147
isfield ...................................... 108
isfigure ..................................... 379
isfinite ..................................... 441
isfloat ....................................... 62
isglobal ..................................... 125
isgraph ....................................... 97
isguirunning ................................ 803
ishandle ..................................... 378
ishermitian ................................... 64
ishghandle ................................... 378
ishold ....................................... 359
isieee ....................................... 847
isindex ...................................... 139
isinf..................................... .... 440
isinteger ..................................... 54
isjava ....................................... 906
iskeyword .................................... 949
isletter ...................................... 97
islogical ..................................... 62
islower ....................................... 97
ismac..................................... .... 847
ismatrix ...................................... 63
ismember ..................................... 680
ismethod ..................................... 771
isna ........................................... 43
isnan..................................... .... 440
isnull......................................... 46
isnumeric ..................................... 62
isobject ..................................... 770
isocaps ...................................... 329
isocolors .................................... 330
isonormals ................................... 328
isosurface ................................... 326
ispc .......................................... 847
isplaying .................................... 763
ispref ....................................... 805
isprime ....................................... 64
isprint ....................................... 98
isprop ....................................... 375
ispunct ....................................... 97
isreal......................................... 63
isrecording .................................. 764
isrow .......................................... 63
isscalar ...................................... 63
issorted ..................................... 450
isspace ....................................... 97
issparse ..................................... 566
issquare ...................................... 63
isstrprop ..................................... 98
isstruct ..................................... 107
isstudent .................................... 847
issymmetric ................................... 63
istril......................................... 64
istriu......................................... 64
isunix ....................................... 847
isupper ....................................... 97
isvarname .................................... 123
isvector ...................................... 63
isxdigit ...................................... 97
I............................................. 498
J
j............................................. 498
java_get ..................................... 907
java_matrix_autoconversion ................ 911
java_set ..................................... 907
java_unsigned_autoconversion .............. 911
javaaddpath .................................. 909
javaArray .................................... 906
javachk ...................................... 909
javaclasspath ............................... 908
javamem ...................................... 910
javaMethod ................................... 908
javaObject ................................... 906
javarmpath ................................... 909
jet ........................................... 755
jit_enable ................................... 541
jit_failcnt .................................. 542
jit_startcnt ................................ 541
J............................................. 498
K
kbhit.................................. ....... 249
kendall ...................................... 655
keyboard ..................................... 233
kill .......................................... 841
kolmogorov_smirnov_cdf ..................... 660
kolmogorov_smirnov_test .................... 666
kolmogorov_smirnov_test_2.................. 667
kron .......................................... 523
kruskal_wallis_test ........................ 667
982 GNU Octave
krylov ....................................... 522
kurtosis ..................................... 647
L
laplace_cdf .................................. 660
laplace_inv .................................. 660
laplace_pdf .................................. 660
laplace_rnd .................................. 675
lasterr ...................................... 219
lasterror .................................... 218
lastwarn ..................................... 223
lcm ........................................... 486
ldivide ...................................... 144
le ............................................ 147
legend ....................................... 348
legendre ..................................... 494
length......................................... 45
lgamma ....................................... 495
license ...................................... 849
light..................................... .... 377
lighting ..................................... 334
lin2mu ....................................... 766
line .......................................... 376
lines..................................... .... 755
link .......................................... 819
linkaxes ..................................... 429
linkprop ..................................... 428
linsolve ..................................... 507
linspace ..................................... 455
list_in_columns ............................. 243
list_primes .................................. 488
listdlg ...................................... 792
load .......................................... 253
loaded_graphics_toolkits ................... 438
loadobj ...................................... 774
localfunctions .............................. 195
localtime .................................... 808
log ........................................... 471
log10..................................... .... 471
log1p..................................... .... 471
log2 .......................................... 471
logical ....................................... 60
logistic_cdf ................................ 660
logistic_inv ................................ 660
logistic_pdf ................................ 660
logistic_regression ........................ 655
logistic_rnd ................................ 675
logit..................................... .... 652
loglog ....................................... 290
loglogerr .................................... 306
logm .......................................... 523
logncdf ...................................... 660
logninv ...................................... 661
lognpdf ...................................... 660
lognrnd ...................................... 675
logspace ..................................... 455
lookfor ....................................... 21
lookup ....................................... 442
lower .......................................... 95
ls ............................................ 843
ls_command ................................... 843
lscov.................................. ....... 641
lsode.................................. ....... 613
lsode_options ............................... 614
lsqnonneg .................................... 640
lstat.................................. ....... 821
lt ............................................ 147
lu ............................................ 514
luupdate ..................................... 515
M
magic.................................. ....... 467
make_absolute_filename ..................... 826
makeinfo_program ............................. 23
manova ....................................... 667
mat2cell ..................................... 115
mat2str ....................................... 73
material ..................................... 335
matlabroot ................................... 847
matrix_type .................................. 508
max ........................................... 481
max_recursion_depth ........................ 142
mcnemar_test ................................ 668
mean .......................................... 643
meansq ....................................... 645
median ....................................... 644
menu .......................................... 249
merge.................................. ....... 150
mesh .......................................... 321
meshc.................................. ....... 322
meshgrid ..................................... 337
meshz.................................. ....... 322
methods ...................................... 771
mex ........................................... 887
mexext ....................................... 887
mfilename .................................... 191
mget .......................................... 831
mgorth ....................................... 510
min ........................................... 481
minus.................................. ....... 144
mislocked .................................... 200
missing_component_hook ..................... 862
missing_function_hook ...................... 950
mkdir .................................... 819,832
mkfifo ....................................... 820
mkoctfile .................................... 864
mkpp .......................................... 697
mkstemp ...................................... 280
mktime ....................................... 809
mldivide ..................................... 144
mlock.................................. ....... 200
mod ........................................... 487
mode .......................................... 644
moment ....................................... 647
Function Index 983
more .......................................... 247
movefile ..................................... 818
mpoles ....................................... 685
mpower ....................................... 144
mput .......................................... 831
mrdivide ..................................... 144
msgbox ....................................... 793
mtimes ....................................... 145
mu2lin ....................................... 766
munlock ...................................... 200
N
namelengthmax ............................... 124
nan ........................................... 499
NaN ........................................... 499
nargin ....................................... 175
narginchk .................................... 179
nargout ...................................... 178
nargoutchk ................................... 179
native_float_format ........................ 254
NA ............................................. 43
nbincdf ...................................... 661
nbininv ...................................... 661
nbinpdf ...................................... 661
nbinrnd ...................................... 676
nchoosek ..................................... 651
ndgrid ....................................... 337
ndims ..................................... 44,868
ne ............................................ 147
newplot ...................................... 358
news ........................................... 22
nextpow2 ..................................... 472
nnz ........................................... 566
nonzeros ..................................... 566
norm .......................................... 509
normcdf ...................................... 661
normest ...................................... 581
normest1 ..................................... 581
norminv ...................................... 661
normpdf ...................................... 661
normrnd ...................................... 676
not ........................................... 148
now ........................................... 807
nproc..................................... .... 846
nth_element .................................. 450
nthargout .................................... 177
nthroot ...................................... 472
ntsc2rgb ..................................... 760
null .......................................... 510
num2cell ..................................... 115
num2hex ....................................... 93
num2str ....................................... 74
numel ..................................... 44,868
numfields .................................... 107
nzmax..................................... .... 566
O
ocean.................................. ....... 755
octave_core_file_limit ..................... 263
octave_core_file_name ...................... 264
octave_core_file_options ................... 263
OCTAVE_HOME .................................. 847
OCTAVE_VERSION .............................. 847
ode23.................................. ....... 617
ode45.................................. ....... 616
odeget ....................................... 620
odeplot ...................................... 620
odeset ....................................... 618
ols ........................................... 639
onCleanup .................................... 221
ones .......................................... 453
open .......................................... 835
operator ..................................... 868
optimget ..................................... 642
optimize_subsasgn_calls .................... 777
optimset ..................................... 641
or ............................................ 148
orderfields .................................. 109
ordschur ..................................... 520
orient ....................................... 370
orth .......................................... 510
ostrsplit ..................................... 83
output_max_field_width ...................... 50
output_precision ............................. 50
P
P_tmpdir ..................................... 281
pack .......................................... 132
padecoef ..................................... 696
page_output_immediately .................... 248
page_screen_output.......................... 247
PAGER.................................. ....... 247
PAGER_FLAGS .................................. 247
pan ........................................... 356
pareto ....................................... 298
parseparams .................................. 185
pascal ....................................... 468
patch.................................. ....... 376
path .......................................... 193
pathdef ...................................... 194
pathsep ...................................... 194
pause ............................... 763,764,813
pbaspect ..................................... 342
pcg ........................................... 589
pchip.................................. ....... 736
pclose ....................................... 836
pcolor ....................................... 311
pcr ........................................... 591
peaks.................................. ....... 373
periodogram .................................. 736
perl .......................................... 835
perms.................................. ....... 651
permute ...................................... 445
984 GNU Octave
pi ............................................ 498
pie ...................................... 307,308
pie3 .......................................... 308
pink .......................................... 755
pinv .......................................... 510
pipe .......................................... 837
pkg ...................................... 853,854
planerot ..................................... 507
play ..................................... 763,765
playblocking ................................ 763
plot .......................................... 286
plot3 .................................... 337,338
plotmatrix ................................... 298
plotyy ....................................... 288
plus .......................................... 145
poisscdf ..................................... 662
poissinv ..................................... 662
poisspdf ..................................... 662
poissrnd ..................................... 676
pol2cart ..................................... 497
polar..................................... .... 307
poly .......................................... 698
polyaffine ................................... 689
polyarea ..................................... 720
polyder ...................................... 688
polyeig ...................................... 684
polyfit ...................................... 689
polygcd ...................................... 686
polyint ...................................... 688
polyout ...................................... 699
polyreduce ................................... 699
polyval ...................................... 683
polyvalm ..................................... 683
popen..................................... .... 835
popen2 ....................................... 836
postpad ...................................... 452
pow2 .......................................... 472
power..................................... .... 145
powerset ..................................... 681
ppder..................................... .... 698
ppint..................................... .... 698
ppjumps ...................................... 698
ppplot ....................................... 653
ppval..................................... .... 698
pqpnonneg .................................... 636
prctile ...................................... 649
prefdir ...................................... 805
preferences .................................. 806
prepad ....................................... 451
primes ....................................... 487
print..................................... .... 365
print_empty_dimensions ...................... 52
print_struct_array_contents ............... 101
print_usage .................................. 217
printd ....................................... 294
printf ....................................... 268
prism..................................... .... 756
probit ....................................... 652
prod .......................................... 479
profexplore .................................. 238
profexport ................................... 238
profile ...................................... 236
profshow ..................................... 237
program_invocation_name ..................... 18
program_name.................................. 18
prop_test_2 .................................. 668
PS1 ............................................ 33
PS2 ............................................ 33
PS4 ............................................ 33
psi ........................................... 495
publish ...................................... 203
putenv ....................................... 842
puts .......................................... 267
pwd ........................................... 844
python ....................................... 835
Q
qmr ........................................... 527
qp ............................................ 635
qqplot ....................................... 653
qr ............................................ 515
qrdelete ..................................... 517
qrinsert ..................................... 517
qrshift ...................................... 518
qrupdate ..................................... 517
quad .......................................... 602
quad_options ................................ 603
quadcc ....................................... 606
quadgk................................... 604,605
quadl.................................. ....... 604
quadv.................................. ....... 603
quantile ..................................... 648
questdlg ..................................... 794
quit ....................................... 19,20
quiver................................... 308,309
quiver3 ...................................... 309
qz ............................................ 518
qzhess ....................................... 519
R
rad2deg ...................................... 474
rainbow ...................................... 756
rand .......................................... 455
rande .................................... 457,458
randg.................................. ....... 459
randi.................................. ....... 456
randn.................................. ....... 457
randp.................................. ....... 458
randperm ..................................... 461
range.................................. ....... 644
rank .......................................... 510
ranks.................................. ....... 652
rat ........................................... 496
rats .......................................... 496
Function Index 985
rcond..................................... .... 511
rdivide ...................................... 145
readdir ...................................... 824
readline_re_read_init_file.................. 32
readline_read_init_file ..................... 32
readlink ..................................... 819
real .......................................... 474
reallog ...................................... 471
realmax ...................................... 500
realmin ...................................... 501
realpow ...................................... 472
realsqrt ..................................... 472
record................................... 764,766
recordblocking .............................. 764
rectangle .................................... 319
rectint ...................................... 720
recycle ...................................... 827
reducepatch .................................. 332
reducevolume ................................ 332
refresh ...................................... 358
refreshdata .................................. 430
regexp......................................... 87
regexpi ....................................... 89
regexprep ..................................... 90
regexptranslate .............................. 90
register_graphics_toolkit.................. 438
rehash ....................................... 194
rem ........................................... 486
remove_input_event_hook .................... 950
rename................................... 818,832
repelems ..................................... 454
repmat ....................................... 454
reset..................................... .... 421
reshape ...................................... 446
residue ...................................... 687
resize................................... 447,869
restoredefaultpath.......................... 194
resume................................... 763,764
rethrow ...................................... 220
return ....................................... 189
rgb2hsv ...................................... 759
rgb2ind ...................................... 750
rgb2ntsc ..................................... 760
rgbplot ...................................... 752
ribbon ....................................... 340
rindex......................................... 79
rmappdata .................................... 425
rmdir .................................... 820,832
rmfield ...................................... 109
rmpath ....................................... 193
rmpref ....................................... 805
roots..................................... .... 684
rose .......................................... 299
rosser ....................................... 468
rot90..................................... .... 444
rotate ....................................... 356
rotate3d ..................................... 356
rotdim ....................................... 444
round.................................. ....... 480
roundb ....................................... 481
rows ........................................... 44
rref .......................................... 511
rsf2csf ...................................... 520
run ........................................... 159
run_count .................................... 652
run_history ................................... 29
run_test ..................................... 668
rundemos ..................................... 922
runlength .................................... 652
runtests ..................................... 922
S
S_ISBLK ...................................... 822
S_ISCHR ...................................... 822
S_ISDIR ...................................... 822
S_ISFIFO ..................................... 822
S_ISLNK ...................................... 822
S_ISREG ...................................... 822
S_ISSOCK ..................................... 823
save .......................................... 250
save_default_options ....................... 252
save_header_format_string.................. 252
save_precision .............................. 252
saveas ....................................... 370
saveobj ...................................... 774
savepath ..................................... 193
scanf.................................. ....... 275
scatter ...................................... 297
scatter3 ................................ 340,341
schur.................................. ....... 519
sec ........................................... 475
secd .......................................... 477
sech .......................................... 476
SEEK_CUR ..................................... 283
SEEK_END ..................................... 283
SEEK_SET ..................................... 283
semilogx ..................................... 289
semilogxerr .................................. 305
semilogy ..................................... 289
semilogyerr .................................. 306
set ................................. 381,763,765
setappdata ................................... 424
setdiff ...................................... 680
setenv ....................................... 842
setfield ..................................... 108
setgrent ..................................... 845
setpref ...................................... 804
setpwent ..................................... 845
setxor ....................................... 680
shading ...................................... 340
shg ........................................... 360
shift.................................. ....... 448
shiftdim ..................................... 448
shrinkfaces .................................. 333
sighup_dumps_octave_core ................... 263
986 GNU Octave
sign .......................................... 488
sign_test .................................... 668
signbit ...................................... 488
sigterm_dumps_octave_core.................. 263
SIG ........................................... 841
silent_functions ............................ 176
sin ........................................... 475
sinc .......................................... 732
sind .......................................... 477
sinetone ..................................... 737
sinewave ..................................... 737
single......................................... 54
sinh .......................................... 476
size ........................................... 45
size_equal .................................... 46
sizemax ....................................... 49
sizeof......................................... 46
skewness ..................................... 646
slice..................................... .... 339
smooth3 ...................................... 331
sombrero ..................................... 372
sort .......................................... 448
sortrows ..................................... 449
sound..................................... .... 766
soundsc ...................................... 767
source ....................................... 202
spalloc ...................................... 564
sparse ....................................... 564
sparse_auto_mutate.......................... 571
spaugment .................................... 585
spconvert .................................... 565
spdiags ...................................... 561
spearman ..................................... 654
spectral_adf ................................ 737
spectral_xdf ................................ 738
specular ..................................... 334
speed..................................... .... 922
spencer ...................................... 738
speye..................................... .... 562
spfun..................................... .... 536
sph2cart ..................................... 497
sphere ....................................... 347
spinmap ...................................... 757
spline ....................................... 705
splinefit .................................... 690
split_long_rows .............................. 50
spones ....................................... 562
spparms ...................................... 583
sprand ....................................... 562
sprandn ...................................... 562
sprandsym .................................... 563
sprank ....................................... 584
spring ....................................... 756
sprintf ...................................... 269
spstats ...................................... 566
spy ........................................... 568
sqp ........................................... 637
sqrt .......................................... 472
sqrtm.................................. ....... 523
squeeze ....................................... 46
sscanf ....................................... 275
stairs ....................................... 295
stat .......................................... 821
statistics ................................... 649
std ........................................... 645
stderr ....................................... 264
stdin.................................. ....... 264
stdnormal_cdf ............................... 662
stdnormal_inv ............................... 662
stdnormal_pdf ............................... 662
stdnormal_rnd ............................... 676
stdout ....................................... 264
stem .......................................... 295
stem3.................................. ....... 297
stemleaf ..................................... 294
stft .......................................... 738
stop ..................................... 763,764
str2double .................................... 94
str2func ..................................... 211
str2num ....................................... 95
strcat......................................... 72
strchr......................................... 78
strcmp......................................... 76
strcmpi ....................................... 77
strfind ....................................... 79
strftime ..................................... 809
string_fill_char ............................. 69
strjoin ....................................... 80
strjust ....................................... 94
strmatch ...................................... 80
strncmp ....................................... 76
strncmpi ...................................... 77
strptime ..................................... 811
strread ....................................... 84
strrep......................................... 86
strsplit ...................................... 81
strtok......................................... 81
strtrim ....................................... 78
strtrunc ...................................... 78
struct ....................................... 106
struct_levels_to_print ..................... 101
struct2cell .................................. 111
struct2hdl ................................... 383
structfun .................................... 538
strvcat ....................................... 72
sub2ind ...................................... 138
subplot ................................. 354,355
subsasgn ..................................... 776
subsindex .................................... 778
subspace ..................................... 521
subsref ...................................... 775
substr......................................... 87
substruct .................................... 111
sum ........................................... 478
summer ....................................... 756
sumsq.................................. ....... 480
Function Index 987
superiorto ................................... 782
suppress_verbose_help_message .............. 24
surf .......................................... 323
surface ...................................... 377
surfc..................................... .... 324
surfl..................................... .... 325
surfnorm ..................................... 325
svd ........................................... 521
svd_driver ................................... 522
svds .......................................... 588
swapbytes ..................................... 41
sylvester .................................... 524
symamd ....................................... 578
symbfact ..................................... 584
symlink ...................................... 819
symrcm ....................................... 579
symvar ....................................... 212
synthesis .................................... 738
system ....................................... 833
T
t_test ....................................... 669
t_test_2 ..................................... 669
t_test_regression ........................... 669
table..................................... .... 652
tan ........................................... 475
tand .......................................... 477
tanh .......................................... 476
tar ........................................... 828
tcdf .......................................... 662
tempdir ...................................... 281
tempname ..................................... 281
terminal_size ............................... 244
test .......................................... 913
tetramesh .................................... 714
texi_macros_file ............................. 23
text .......................................... 349
textread ..................................... 257
textscan ..................................... 258
tic ........................................... 813
tilde_expand ................................ 826
time .......................................... 807
times..................................... .... 145
tinv .......................................... 662
title..................................... .... 348
tmpfile ...................................... 281
toascii ....................................... 95
toc ........................................... 813
toeplitz ..................................... 468
tolower ....................................... 95
toupper ....................................... 95
tpdf .......................................... 662
trace..................................... .... 511
transpose .................................... 145
trapz..................................... .... 607
treelayout ................................... 569
treeplot ..................................... 569
tril .......................................... 450
trimesh ...................................... 713
triplequad ................................... 610
triplot ...................................... 713
trisurf ...................................... 714
triu .......................................... 450
trnd .......................................... 677
true ........................................... 60
tsearch ...................................... 716
tsearchn ..................................... 716
type .......................................... 132
typecast ...................................... 40
typeinfo ...................................... 39
U
u_test ....................................... 670
uibuttongroup ............................... 797
uicontextmenu ............................... 798
uicontrol .................................... 799
uigetdir ..................................... 789
uigetfile .................................... 789
uimenu ....................................... 796
uint16......................................... 55
uint32......................................... 55
uint64......................................... 55
uint8 .......................................... 55
uipanel ...................................... 800
uipushtool ................................... 800
uiputfile .................................... 790
uiresume ..................................... 803
uitoggletool ................................ 801
uitoolbar .................................... 801
uiwait ....................................... 803
umask.................................. ....... 820
uminus ....................................... 146
uname.................................. ....... 846
undo_string_escapes......... ................. 96
unidcdf ...................................... 662
unidinv ...................................... 663
unidpdf ...................................... 662
unidrnd ...................................... 677
unifcdf ...................................... 663
unifinv ...................................... 663
unifpdf ...................................... 663
unifrnd ...................................... 677
union.................................. ....... 680
unique ....................................... 679
unix .......................................... 834
unlink ....................................... 819
unmkpp ....................................... 697
unpack ....................................... 829
unsetenv ..................................... 842
untabify ...................................... 90
untar.................................. ....... 828
unwrap ....................................... 732
unzip.................................. ....... 829
uplus.................................. ....... 146
988 GNU Octave
upper .......................................... 95
urlread ...................................... 832
urlwrite ..................................... 832
usejava ...................................... 910
V
validateattributes.......................... 180
validatestring .............................. 180
vander ....................................... 468
var ........................................... 646
var_test ..................................... 670
vec ........................................... 451
vech .......................................... 451
vectorize .................................... 530
ver ........................................... 848
version ...................................... 848
vertcat ...................................... 445
view .......................................... 338
viridis ...................................... 756
voronoi ...................................... 718
voronoin ..................................... 718
W
waitbar ...................................... 796
waitfor ...................................... 803
waitforbuttonpress.......................... 372
waitpid ...................................... 838
warndlg ...................................... 794
warning ...................................... 222
warranty ...................................... 22
waterfall .................................... 341
wblcdf ....................................... 663
wblinv ....................................... 663
wblpdf ....................................... 663
wblrnd................................... 677,678
WCONTINUE .................................... 838
WCOREDUMP .................................... 838
weekday ...................................... 817
welch_test ................................... 670
WEXITSTATUS .................................. 839
what .......................................... 133
which.................................. ....... 132
white.................................. ....... 756
whitebg ...................................... 757
who ........................................... 128
whos .......................................... 128
whos_line_format ............................ 129
wienrnd ...................................... 678
WIFCONTINUED ................................ 839
WIFEXITED .................................... 839
WIFSIGNALED .................................. 839
WIFSTOPPED ................................... 839
wilcoxon_test ............................... 670
wilkinson .................................... 469
winter ....................................... 757
WNOHANG ...................................... 839
WSTOPSIG ..................................... 840
WTERMSIG ..................................... 840
WUNTRACED .................................... 840
X
xlabel ....................................... 350
xlim .......................................... 315
xor ........................................... 440
Y
yes_or_no .................................... 249
ylim .......................................... 315
yulewalker ................................... 739
Z
z_test ....................................... 671
z_test_2 ..................................... 671
zeros.................................. ....... 454
zip ........................................... 828
zlim .......................................... 315
zoom .......................................... 357
zscore ....................................... 650
989
Operator Index
!
!......................................... 148,781
!= .................................. 146,147,781
"
"........................................... 43,67
&
&........................................ 148,781
&& ........................................... 149
’
’............................. 43,67,143,144,781
(
(............................................. 135
)
)............................................. 135
*
*.................................... 143,145,781
** ....................................... 143,144
*= ........................................... 152
+
+.......................... 142,143,145,146,781
++ ............................................ 153
+=........................................... 152
,
,............................................... 48
–
-........................... 142,143,144,146,781
-- ............................................ 153
-= ............................................ 152
.
................................................ 99
.’.................................... 143,145,781
.* ................................... 143,145,781
.**....................................... 143,145
.+............................................ 142
./ ................................... 143,145,781
.^................................... 143,145,781
.\................................... 143,144,781
/
/.................................... 143,144,781
/= ........................................... 152
:
:..................................... 52,135,781
;
;............................................... 48
<
<.................................... 146,147,781
<=.................................. 146,147,781
=
=............................................. 151
== ...................................... 146,781
>
>.................................... 146,147,781
>=.................................. 146,147,781
[
[............................................... 48
]
]............................................... 48
^
^.................................... 143,144,781
990 GNU Octave
\
\.................................... 143,144,781
{
{............................................. 112
}
}............................................. 112
|
|........................................ 148,781
|| ............................................ 149
~
~............................................. 148
~=.................................. 146,147,781