[Titel Van Rapport] SPHY Manual V6
SPHY_manualV6
SPHY_manualV6
SPHY_manualV6
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 71

FutureWater
Costerweg 1V
6702 AA Wageningen
The Netherlands
+31 (0)317 460050
info@futurewater.nl
www.futurewater.nl
SPHY v2.0: Spatial Processes in Hydrology
Model theory, installation, and data
preparation
October 2015
Author
W. Terink
A.F. Lutz
W.W. Immerzeel
Report FutureWater: 142

2
Acknowledgements
The development and publication of the SPHY model source code, its binaries, GUIs, and case-
studies has been supported through various (research) projects that were partly or completely
funded by the following organizations:
International Centre for Integrated Mountain Development (ICIMOD
1
);
European Space Agency (ESA
2
);
Asian Development Bank (ADB
3
);
World Bank
4
;
Rijksdienst voor Ondernemend Nedeland (RVO
5
)
NUFFIC
6
We are very grateful to these organizations that made the development of the SPHY model
possible. We hope to continue to collaborate with these organizations in the future in order to
further develop and improve the SPHY model and its interfaces.
1
http://www.icimod.org/
2
http://www.esa.int/ESA
3
http://www.adb.org/
4
http://www.worldbank.org/
5
http://www.rvo.nl/
6
https://www.nuffic.nl/en

3
Table of contents
Acknowledgements 2
1 Introduction 7
2 Theory 10
2.1 Background 10
2.2 Modules 12
2.3 Reference and potential evapotranspiration 13
2.4 Dynamic vegetation processes 14
2.4.1 Maximum canopy storage 14
2.4.2 Interception 15
2.5 Snow processes 16
2.5.1 Snow and rainfall 16
2.5.2 Snowmelt, refreezing, and storage 17
2.5.3 Snow runoff 18
2.6 Glacier processes 18
2.6.1 Glacier melt 18
2.6.2 Glacier runoff 19
2.6.3 Glacier percolation 19
2.7 Soil water processes 19
2.7.1 Soil water balances 19
2.7.2 Actual evapotranspiration 20
2.7.3 Surface runoff 21
2.7.4 Lateral flow 22
2.7.5 Percolation 23
2.7.6 Groundwater recharge 23
2.7.7 Baseflow 24
2.8 Routing 25
2.8.1 Runoff routing 25
2.8.2 Lake/reservoir routing 26
3 Applications 28
3.1 Irrigation management in lowland areas 28
3.2 Snow- and glacier-fed river basins 30
3.3 Flow forecasting 34
4 Installation of SPHY 38
4.1 General 38
4.2 Installing SPHY as a stand-alone application 38
4.2.1 Python 2.7.6 32-bit 38
4.2.2 Numpy 1.8.0 32-bit 40
4.2.3 PCRaster 4.0 32-bit 41
4.2.4 SPHY v2.0 source code 43
5 Build your own SPHY-model 44
5.1 Select projection extent and resolution 44
5.2 Clone map 44
5.3 DEM and Slope 45
5.4 Delineate catchment and create local drain direction map 50
5.5 Preparing stations map and sub-basins.map 51
5.6 Glacier fraction map 56

4
5.7 Other static input maps 58
5.8 Meteorological forcing map series 59
6 References 60
Copyright 70

5
Tables
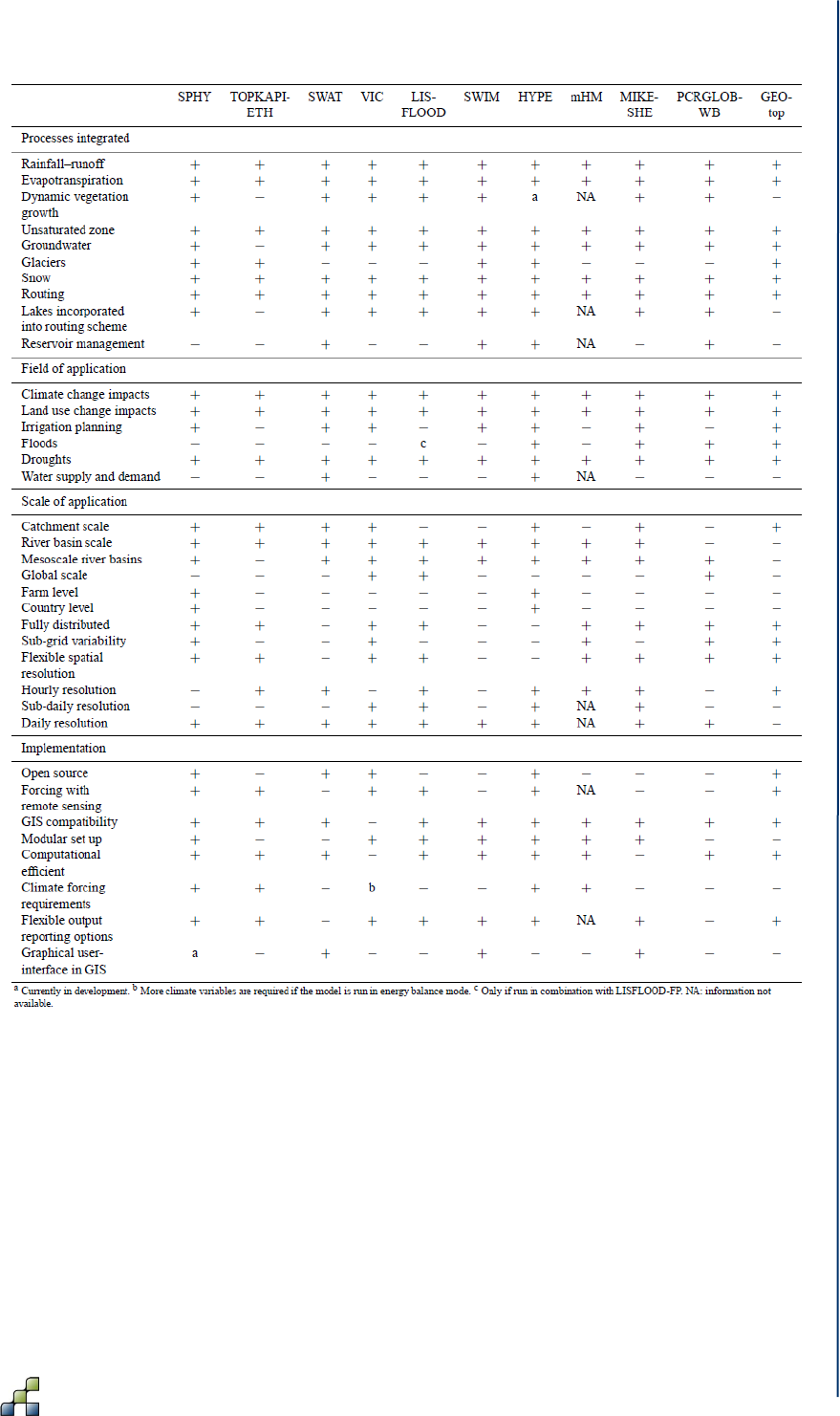
Table 1: Pros (+) and cons (-) of some well-known hydrological models, including the SPHY
model. A categorization is made between (i) processes that are integrated, (ii) field of
application, (iii) scale of application, and (iv) implementation. ...................................................... 9
Table 2: LAImax values for different vegetation types (Sellers et al., 1996). ................................ 15
Table 3: Station locations used for calibration and validation of the SPHY model in HICAP (Lutz
et al., 2014a). Three stations were used for calibration for 1998–2007. Five stations were used
for an independent validation for the same period. The Nash–Sutcliffe efficiency (NS) and bias
metrics were calculated at a monthly time step. ......................................................................... 32
Table 4: Resampling settings based on the layer data type. ...................................................... 49
Table 5: Data types used in SPHY. ............................................................................................. 59
Table 6: Overview of SPHY model parameters. The last column indicates whether the
parameter is observable, or can be determined by calibration (free). ......................................... 71
Figures
Figure 1: Illustration of SPHY sub-grid variability. A grid cell in SPHY can be (a) partially
covered with glaciers, or (b) completely covered with glaciers, or (c1) free of snow, or
(c2) completely covered with snow. In the case of (c1), the free land surface can consist of bare
soil, vegetation, or open water. ................................................................................................... 10
Figure 2: SPHY modeling concepts. The fluxes in grey are only incorporated when the
groundwater module is not used. Abbreviations are explained in the text. ................................. 11
Figure 3: Modules of the SPHY model that can be switched on/off. ........................................... 13
Figure 4: Spatial distribution of evapotranspiration (ET) deficit, as simulated by the SPHY model
for a Romanian farm on 03 April 2014. Transparency means no ET deficit. .............................. 29
Figure 5: Measured and simulated daily root-zone soil moisture content during the 2014 growing
season. Rainfallirrigation has been measured by the rain gauge that was attached to the
moisture sensor. .......................................................................................................................... 30
Figure 6: Average monthly observed and SPHY-simulated flow (1998–2007) for the Chatara
major discharge measurement location in the Ganges basin (Lutz et al. 2014a). Metrics are
calculated based on monthly time steps. .................................................................................... 31
Figure 7: The contribution of glacier melt (a), snowmelt (b), and rainfall (c) to the total flow for
major streams in the upstream basins of the Indus, Ganges, Brahmaputra, Salween and
Mekong during 1998–2007 (Lutz et al. 2014a). .......................................................................... 32
Figure 8: Observed and simulated average fractional snow cover in the upper Indus basin. The
values represent the 9-year average for 46 (8-day) periods during 2000–2007. ........................ 33
Figure 9: (a) SPHY simulated snow cover 2000–2007 and (b) MODIS observed snow cover
2000–2007. .................................................................................................................................. 33
Figure 10: Snow storage (mm) as simulated by the SPHY model on 12 August (left) and 01
October (right) during the snow melting season of 2013 in the Laja River basin. ...................... 35
Figure 11: Daily observed vs. SPHY simulated streamflow (period 2007–2008) for the
streamflow stations Canal Abanico (ID 19) and Rio Laja en Tucapel (ID 23). The Nash–Sutcliffe
(NS) and bias model performance indicators are shown as well. ............................................... 36
Figure 12: Bias between total cumulative forecasted flow and observed flow for the 23 model
runs that were executed between the end of September 2013 and March 2014. Results are
shown for the locations Canal Abanico (ID 19) and Rio Laja en Tucapel (ID 23). ...................... 36

6
Figure 13: System properties to set Environmental Variables. ................................................... 39
Figure 14: Setting the Path variable. ........................................................................................... 40
Figure 15: Adding the Python27 installation folder to the Path system variables. ...................... 40
Figure 16: Illustration of selecting the Python installation folder during installation of the Numpy
package. ...................................................................................................................................... 41
Figure 17: Adding the PCRaster bin folder to the Path system variables. .................................. 42
Figure 18: Editing or creating the PYTHONPATH variable for the PCRaster package. ............. 42
Figure 19: Command prompt view of testing a successful installation of PCRaster after entering
the pcrcalc command. ................................................................................................................. 43
Figure 20: Command line menu for clone creation ..................................................................... 45
Figure 21: Opening the “Processing Toolbox”. ........................................................................... 45
Figure 22: Selecting the “Advanced interface” in the “Processing Toolbox”. .............................. 46
Figure 23: Warp tool .................................................................................................................... 47
Figure 24: Setting the files and Source and Target SRS in the Warp Tool................................. 47
Figure 25: Selecting the Resampling tool in the Processing Toolbox. ........................................ 48
Figure 26: Setting the Resampling tool options. ......................................................................... 48
Figure 27: Translate tool (convert raster format) ......................................................................... 49
Figure 28: Setting the Translate options. .................................................................................... 50
Figure 29: Saving the translated raster as a PCRaster Raster File (*.map). .............................. 50
Figure 30: Create new shapefile layer ........................................................................................ 51
Figure 31: Setting the properties of the New Shapefile Layer. ................................................... 52
Figure 32: Toggle Editing for Shapefiles. .................................................................................... 52
Figure 33: Add Feature for Shapefiles. ....................................................................................... 53
Figure 34: Adding points to the locations Shapefile layer using the accuflux.map. .................... 53
Figure 35: Selecting the v.to.rast.attribute tool from the Processing Toolbox. ........................... 54
Figure 36: Setting the options in the v.to.rast.attribute tool. ........................................................ 54
Figure 37: Editing the command for Translation. ........................................................................ 55
Figure 38: Adding the “-ot Float32” syntax to the command for Translation. .............................. 55
Figure 39: Reclassify tool ............................................................................................................ 56
Figure 40: Reclassify tool dialog box .......................................................................................... 57
Figure 41: GRASS aggregation tool ............................................................................................ 58
Figure 42: GRASS aggregation tool dialog box .......................................................................... 58

7
1 Introduction
The number and diversity of water-related challenges are large and are expected to increase in
the future (Wagener et al. 2010; Lall 2014). Even today, the ideal condition of having the
appropriate amount of good-quality water at the desired place and time is most often not
satisfied (Biswas and Tortajada 2010; Droogers and Bouma 2014). It is likely that climate
variability and change will intensify food insecurity by water shortages (Wheeler and Braun
2013), and loss of access to drinking water (Rockström et al. 2012). Current and future water-
related challenges are location and time specific and can vary from impact of glacier dynamics
(Immerzeel et al. 2011), economic and population growth (Droogers et al. 2012), floods or
extended and more prolonged droughts (Dai 2011), amongst others.
In response to these challenges, hydrologists and water resource specialists are developing
modeling tools to analyze, understand and explore solutions to support decision makers and
operational water managers (Pechlivanidis et al. 2011). Despite difficulties in connecting the
scientific advances in hydrological modeling with the needs of decision makers and water
managers, progress has been made and there is no doubt that modeling tools are
indispensable in what is called good “water governance” (Droogers and Bouma 2014; Liu et al.
2008).
The strength of hydrological models is that they can provide output at high temporal and spatial
resolutions, and for hydrological processes that are difficult to observe on the large scale that
they are generally applied on (Bastiaanssen et al. 2007). The most important aspect of applying
models is in their use in exploring different scenarios, expressing for example, possible effects
of changes in population and climate on the water cycle (Droogers and Aerts 2005). Models are
also applied at the operational level to explore interventions (management scenarios) to be
used by water managers and policy makers. Examples of this are changes in reservoir
operation rules, water allocation between sectors, investment in infrastructure such as water
treatment or desalination plants, and agricultural and irrigation practices. In other words: models
enable hydrologists and water managers to change focus from a re-active towards a pro-active
approach.
Over the past decades, the land surface and hydrologic communities have made substantial
progress in understanding the spatial presentation of fluxes of water and energy (Abbott et al.
1986; Wigmosta et al., 1994; Van der Kwaak and Loague 2001; Rigon et al., 2006). Their efforts
have led to the development of well-known hydrological models, such as, e.g., VIC (Liang et al.
1994, 1996), SWAT (Neitsch et al. 2009), TOPKAPI-ETH (Finger et al. 2011; Ragettli and
Pellicciotti 2012; Ragettli et al. 2013; Ragettli et al. 2014), LISFLOOD (Van Der Knijff et al,
2010), SWIM (Krysanova et al. 2015; Krysanova et al. 2000; Krysanova et al., 1998), HYPE
(Lindström et al. 2010), mHM (Samaniego et al., 2010), PCR-GLOBWB (Beek and Bierkens
2008; Bierkens and Beek 2009; Wada et al. 2010; Sperna Weiland et al. 2010), MIKE-SHE
(Refshaard and Storm 1995; Oogathoo et al. 2008; Deb and Shukla 2011) and GEOtop (Rigon
et al., 2006; Endrizzi et al. 2013; Endrizzi et al. 2011), amongst others. The number of existing
hydrological models is probably in the tens of thousands (Droogers and Bouma 2014). Some
existing model reviews cover a substantial number of models: IRRISOFT (Irrisoft 2014): 114;
USGS (2014): 110; EPA (2014): 211; USACE (HEC 2014): 18.
All these hydrological models are different with respect to (i) the number and detail of
hydrological processes that are integrated, (ii) their field and (iii) scale of application, and (iv) the
way they are implemented. Whereas, for example, the SWIM (Krysanova et al. 2015;

8
Krysanova et al. 2000; Krysanova, Müller-Wohlfeil, and Becker 1998) and HYPE (Lindström et
al. 2010) models both include all major hydrological processes, the SWIM model is typically
developed for large-scale (large river basins to continental) applications, and the HYPE model
operates on the sub-basin scale. Therefore, these models contain less detail, in contrast to fully
distributed models operating at grid level, such as, e.g., GEOtop (Rigon et al., 2006; Endrizzi et
al. 2013; Endrizzi et al. 2011) and TOPKAPI-ETH (Finger et al. 2011; Ragettli and Pellicciotti
2012; Ragettli et al. 2013; Ragettli et al. 2014). Models like, e.g., MIKE-SHE (Refshaard and
Storm 1995; Oogathoo et al. 2008; Deb and Shukla 2011) and LISFLOOD (Van Der Knijff,
Younis, and De Roo 2010) have the advantage of being flexible in terms of the spatial and
temporal resolutions, but their disadvantages are that they do not include glacier processes and
that they are not open source and therefore not available to the larger community.
It is clear that all these models have their pros and cons in terms of (i) processes integrated,
(ii) field of application, (iii) scale of application, and iv) implementation. Table 1 shows the pros
and cons of some well-known hydrological models, including the Spatial Processes in
HYdrology (SPHY) model. Over the last couple of years we have developed the SPHY model,
and improved its usefulness by applying the model in various research projects. SPHY has
been developed with the explicit aim of simulating terrestrial hydrology under various
physiographical and hydroclimatic conditions by integrating key components from existing and
well-tested models: HydroS (Droogers and Immerzeel 2010), SWAT (Neitsch et al. 2009), PCR-
GLOBWB (Beek and Bierkens 2008; Bierkens and Beek 2009; Wada et al. 2010; Sperna
Weiland et al. 2010), SWAP (Dam et al. 1997) and HimSim (Immerzeel et al. 2011). Based on
Table 1it is clear that SPHY (i) integrates most hydrologic processes, including glacier
processes, (ii) has the flexibility to study a wide range of applications, including climate and land
use change impacts, irrigation planning, and droughts, (iii) can be used for catchment- and
river-basin-scale applications as well as farm- and country-level applications, and has a flexible
spatial resolution, and (iv) can easily be implemented. Implementation of SPHY is relatively
easy because (i) it is open source, (ii) input and output maps can directly be used in GIS, (iii) it
is set up modular in order to switch on/off relevant/irrelevant processes and thus decreases
model run time and data requirements, (iv) it needs only daily precipitation and temperature
data as climate forcing, (v) it can be forced with remote sensing data, and (vi) it uses a
configuration file that allows the user to change model parameters and choose the model output
that needs to be reported.
The objectives of this manual are:
Introduce and present the SPHY model (v2.0)
Present the SPHY model (v2.0) theory and demonstrate some typical applications
Provide the steps that are required to install the SPHY model as a standalone
application
Learn how-to prepare model data for a SPHY model for your own area of interest
The model source code is in the public domain (open access) and can be obtained from the
SPHY model website free of charge (www.sphy-model.org). The peer-reviewed open-access
publication of the SPHY model can be found at http://www.geosci-model-
dev.net/8/2009/2015/gmd-8-2009-2015.pdf (Terink et al., 2015).
9
Table 1: Pros (+) and cons (-) of some well-known hydrological models, including the
SPHY model. A categorization is made between (i) processes that are integrated, (ii) field
of application, (iii) scale of application, and (iv) implementation.

10
2 Theory
2.1 Background
SPHY is a spatially distributed leaky bucket type of model, and is applied on a cell-by-cell basis.
The main terrestrial hydrological processes are described in a conceptual way so that changes
in storages and fluxes can be assessed adequately over time and space. SPHY is written in the
Python programming language using the PCRaster (Karssenberg et al. 2001; Karssenberg et
al. 2010; Karssenberg 2002; Schmitz et al. 2009; Schmitz et al. 2013) dynamic modeling
framework.
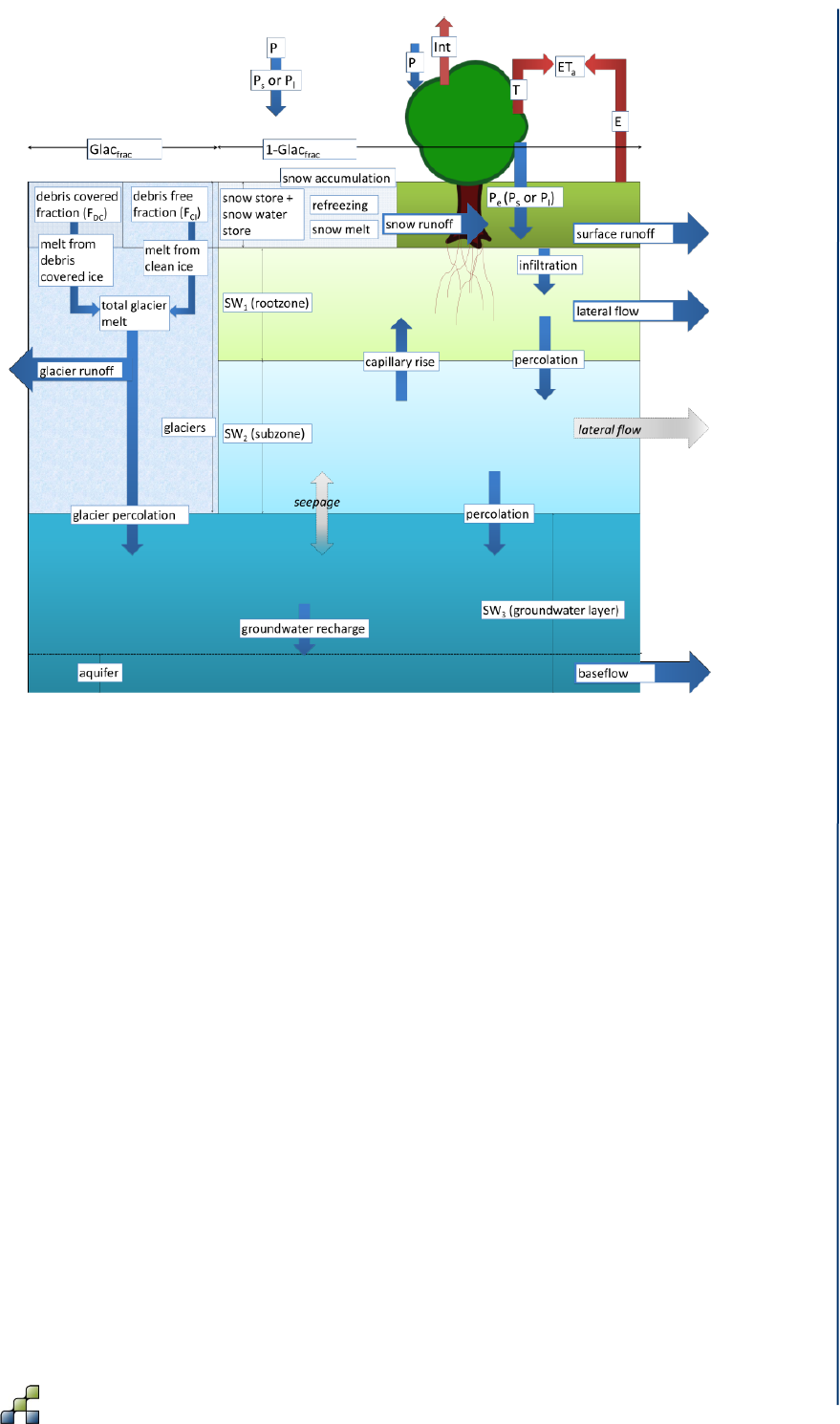
SPHY is grid based and cell values represent averages over a cell (Figure 1). For glaciers, sub-
grid variability is taken into account: a cell can be glacier free, partially glacierized, or completely
covered by glaciers. The cell fraction not covered by glaciers consists of either land covered
with snow or land that is free of snow. Land that is free of snow can consist of vegetation, bare
soil, or open water. The dynamic vegetation module accounts for a time-varying fractional
vegetation coverage, which affects processes such as interception, effective precipitation, and
potential evapotranspiration. Figure 2 provides a schematic overview of the SPHY modeling
concepts.
Figure 1: Illustration of SPHY sub-grid variability. A grid cell in SPHY can be (a) partially
covered with glaciers, or (b) completely covered with glaciers, or (c1) free of snow, or
(c2) completely covered with snow. In the case of (c1), the free land surface can consist
of bare soil, vegetation, or open water.
11
Figure 2: SPHY modeling concepts. The fluxes in grey are only incorporated when the
groundwater module is not used. Abbreviations are explained in the text.
The soil column structure is similar to VIC (Liang et al. 1994, 1996), with two upper soil storages
and a third groundwater storage. Their corresponding drainage components are surface runoff,
lateral flow and baseflow. SPHY simulates for each cell precipitation in the form of rain or snow,
depending on the temperature. Precipitation that falls on land surfaces can be intercepted by
vegetation and evaporated in part or whole. The snow storage is updated with snow
accumulation and/or snowmelt. A part of the liquid precipitation is transformed in surface runoff,
whereas the remainder infiltrates into the soil. The resulting soil moisture is subject to
evapotranspiration, depending on the soil properties and fractional vegetation cover, while the
remainder contributes to river discharge by means of lateral flow from the first soil layer, and
baseflow from the groundwater layer.
Melting of glacier ice contributes to the river discharge by means of a slow and fast component,
being (i) percolation to the groundwater layer that eventually becomes baseflow, and (ii) direct
runoff. The cell-specific runoff, which becomes available for routing, is the sum of surface runoff,
lateral flow, baseflow, snowmelt and glacier melt.
If no lakes are present, then the user can choose a simple flow accumulation routing scheme:
for each cell, the accumulated amount of water that flows out of the cell into its neighboring
downstream cell is calculated. This accumulated amount is the amount of water in the cell itself
plus the amount of water in upstream cells of the cell, and is calculated using the flow direction
network. If lakes are present, then the fractional accumulation flux routing scheme is used;

12
depending on the actual lake storage, a fraction of that storage becomes available for routing
and is extracted from the lake, while the remaining part becomes the updated actual lake
storage. The flux available for routing is routed in the same way as in the simple flow
accumulation routing scheme.
As input, SPHY requires static data as well as dynamic data. For the static data, the most
relevant are digital elevation model (DEM), land use type, glacier cover, lakes/reservoirs and
soil characteristics. The main dynamic data consist of climate data, such as precipitation,
temperature, and reference evapotranspiration. Since SPHY is grid based, optimal use of
remote sensing data and global data sources can be made. For example, the Normalized
Difference Vegetation Index (NDVI) (Tucker 1979; Carlson and Ripley 1997; Myneni and
Williams 1994) can be used to determine the leaf-area index (LAI) in order to estimate the
growth stage of land cover. For setting up the model, streamflow data are not necessary.
However, to undertake a proper calibration and validation procedure, flow data are required.
The model could also be calibrated using actual evapotranspiration, soil moisture contents,
and/or snow-covered area (SCA). Section 3.2 contains an example application in which the
SPHY model has been calibrated using MODIS snow cover images. An overview of the
adjustable SPHY model parameters is shown in Appendix 1 (Table 6).
The SPHY model provides a wealth of output variables that can be selected based on the
preference of the user. Spatial output can be presented as maps of all the available hydrological
processes, i.e., actual evapotranspiration, runoff generation (separated by its components), and
groundwater recharge. These maps can be generated on a daily basis, but can also be
aggregated at monthly or annual time periods. Time series can be generated for each cell in the
study area. Time series often used are streamflow, actual evapotranspiration and recharge to
the groundwater.
2.2 Modules
SPHY enables the user to turn on/off modules (processes) that are relevant/irrelevant for the
area of interest. This concept is very useful if the user is studying hydrological processes in
regions where not all hydrological processes are relevant. A user may for example be interested
in studying irrigation water requirements in central Africa. For this region, glacier and snow
melting processes are irrelevant, and can thus be switched off. The advantages of turning off
irrelevant modules are two-fold: (i) decrease model run time, and (ii) decrease the number of
required model input data. It should be noted, however, that the hydrologic model structure
should be specific to the catchment’s characteristics (Pomeroy et al. 2007; Clark et al. 2008; Niu
et al. 2011; Essery et al. 2013; Clark et al., 2015a, 2015b). It is therefore essential that the user
knows which catchment characteristics and processes should be included in their modeling
framework.
Figure 3 represents an overview of the six modules available: glaciers, snow, groundwater,
dynamic vegetation, simple routing, and lake/reservoir routing. All modules can run
independently of each other, except for the glacier module. If glaciers are present, then snow
processes are relevant as well (Verbunt et al. 2003; Singh and Kumar 1997). Since melting
glacier water percolates to the groundwater layer, the glacier module cannot run with the
groundwater module turned off. Two modules are available for runoff routing: (i) a simple flow
accumulation routing scheme, and (ii) a fractional flow accumulation routing scheme used when
lakes/reservoirs are present. The user has the option to turn off routing, or to choose between

13
one of these two routing modules. All hydrological processes incorporated in the SPHY model
are described in detail in the following sections.
Figure 3: Modules of the SPHY model that can be switched on/off.
2.3 Reference and potential evapotranspiration
Despite the good physical underlying theory of the Penman–Monteith equation (Allen et al.
1998) for calculating the reference evapotranspiration (ET), its major limitation is the high data
demand for energy-based methods. This brought Hargreaves and Samani (1985) to derive the
modified Hargreaves equation that is based on temperature only. For this reason, this equation
has also been implemented in the SPHY model, according to
Equation 1
with Ra () the extraterrestrial radiation, (C) the average daily air temperature, and
TD (C) the daily temperature range, defined as the difference between the daily maximum and
minimum air temperature. The constant 0.408 is required to convert the units to mm, and Ra
can be obtained from tables (Allen et al. 1998) or equations using the day of the year and the
latitude of the area of interest.
According to Allen et al. (1998), is the evapotranspiration rate from a reference surface with
access to sufficient water to allow evapotranspiration at the potential rate. The reference
surface is a hypothetical grass reference crop with specific characteristics. The potential
evapotranspiration has no limitations on crop growth or evapotranspiration from soil water
and salinity stress, crop density, pests and diseases, weed infestation or low fertility. Allen et al.
(1998) determined by the crop coefficient approach, where the effects of various weather
conditions are incorporated into and the crop characteristics in the crop coefficient (Kc),
using
Equation 2
with (mm) the potential evapotranspiration on day , (mm) the reference
evapotranspiration on day , and Kc (–) the crop coefficient. The effects of both crop
transpiration and soil evaporation are integrated into the Kc.
If the dynamic vegetation module in SPHY is not used, then the user can opt (i) to use a single
constant Kc throughout the entire simulation period or (ii) to use a pre-defined time series of
crop coefficients as model input. Plausible values for Kc can be obtained from the literature
(Allen et al. 1998; FAO 2013). However, vegetation is generally very dynamic throughout the

14
year. It is therefore more realistic to use a pre-defined time series of crop coefficients or to use
the dynamic vegetation module, instead of a single constant Kc. This can be adjusted according
to the user’s preferences.
Kc can be estimated using remotely sensed data (Rafn et al., 2008; Contreras et al., 2014). In
the dynamic vegetation module, Kc is scaled throughout the year using NDVI and the maximum
and minimum values for Kc, which are crop specific. These values for Kc can easily be obtained
from Allen et al. (1998). Then Kc is calculated using
Equation 3
with (-) and (-) the maximum and minimum values for NDVI (vegetation type
dependent). This approach shows the flexibility of SPHY in using remote sensing data (e.g.,
NDVI) as input to improve model accuracy.
2.4 Dynamic vegetation processes
2.4.1 Maximum canopy storage
SPHY allows the user to use the dynamic vegetation module in order to incorporate a time-
variable vegetation cover and corresponding rainfall interception. In order to calculate the
rainfall interception, the canopy storage needs to be calculated, using a time series of NDVI
(Carlson and Ripley 1997). The first step involves the calculation of the fraction
photosynthetically active radiation (FPAR). FPAR can be calculated using a relation between
NDVI and FPAR, which was found by Peng et al. (2012) and described by Sellers et al. (1996),
according to
Equation 4
with
Equation 5
and (-) and (–) having values of 0.95 and 0.001, respectively. An FPAR of
0.95 is equivalent to the maximum LAI for a particular class, and an FPAR of 0.001 is equivalent
to a minimum LAI. In order to calculate FPAR, an NDVI time series is required.
The second step is the calculation of the leaf-area index (LAI), which is eventually required to
calculate the maximum canopy storage (). According to Monteith (1973), LAI for
vegetation that is evenly distributed over a surface can be calculated using a logarithmic relation
between LAI and FPAR, according to

15
Equation 6
with LAI (–) the leaf-area index, and (-) the maximum leaf-area index (vegetation type
dependent). This means that the maximum and minimum LAI values are related to the
maximum and minimum of FPAR. Table 2 shows the values for a certain number of
vegetation types.
Table 2: LAImax values for different vegetation types (Sellers et al., 1996).
Vegetation type
LAImax [-]
Broadleaf evergreen trees
7
Broadleaf deciduous trees
7
Mixed trees
7.5
Needleleaf evergreen trees
8
High latitude deciduous trees
8
Grass with 10 - 40% woody cover
5
Grass with <10% woody cover
5
Shrubs and bare soil
5
Moss and lichens
5
Bare
5
Cultivated
6
For vegetation that is concentrated in clusters, the linear relation from Goward and Huemmrich
(1992) is often used. However, since SPHY is generally applied using grid-cell resolutions
between 250m and 1km, we can assume that the effect of having vegetation concentrated in
clusters is negligible. Therefore, the calculation of LAI in SPHY is done using the logarithmic
relation of Monteith (1973) (Equation 6).
The next step involves the calculation of the maximum canopy storage ( (mm)). Many
different relations between and LAI can be found in the literature, depending on the
vegetation type (Jong and Jetten 2010). The best results for crop canopies are shown by Kozak
et al. (2007) and are archived by Von Hoyningen-Huene (1981), who derived the following
relation between and LAI:
Equation 7
2.4.2 Interception
Interception is calculated on a daily basis if the dynamic vegetation module is used, and
consists of the daily precipitation plus the intercepted water remaining in the canopy storage
from the previous day. First, the canopy storage is updated with the amount of precipitation of
the current day:
Equation 8
with (mm) the canopy storage on day , (mm) the canopy storage on day ,
and (mm) the amount of precipitation on day . The portion of precipitation that cannot be
stored in the canopy storage is known as precipitation throughfall, or effective precipitation,
according to:
Equation 9

16
with (mm) the effective precipitation on day , and (mm) the canopy storage on day .
This equation shows that precipitation throughfall only occurs if the water stored in the canopy
exceeds the maximum canopy storage. After the effective precipitation has been calculated, the
canopy storage is updated as:
Equation 10
The remaining amount of water stored in the canopy is available for interception, and the
amount of water that will be intercepted depends on the atmospheric demand for open water
evaporation. A commonly used value for the atmospheric demand for open water evaporation is
1.5 (Allen et al. 1998), which is derived from the ratio between 1 and the mean pan evaporation
coefficient Kp (0.65). The interception can now be calculated using:
Equation 11
with (mm) the intercepted water on day , and (mm) the reference evapotranspiration
on day . Finally, the canopy storage is updated by subtracting the interception:
Equation 12
2.5 Snow processes
For each cell, a dynamic snow storage is simulated at a daily time step, adopted from the model
presented by Kokkonen et al. (2006). The model keeps track of a snow storage, which is fed by
precipitation and generates runoff from snowmelt. Refreezing of snowmelt and rainfall within the
snowpack are simulated as well.
2.5.1 Snow and rainfall
Depending on a temperature threshold, precipitation is defined as falling in either solid or liquid
form. Daily snow accumulation, which is defined as solid precipitation, is calculated as:
Equation 13
with (mm) the snowfall on day , (mm) the effective precipitation on day , (°C) the
mean air temperature on day , and (°C) a calibrated temperature threshold for precipitation
to fall as snow. The precipitation that falls as rain is defined as liquid precipitation, and is
calculated as:
Equation 14
with (mm) being the amount of rainfall on day .

17
2.5.2 Snowmelt, refreezing, and storage
To simulate snowmelt, the well-established and widely used degree-day melt modeling
approach is used (Hock 2003). The application of degree-day models is widespread in
cryospheric models and is based on an empirical relationship between melt and air
temperature. Degree-day models are easier to set up compared to energy-balance models, and
only require air temperature, which is mostly available and relatively easy to interpolate (Hock
2005). Using a degree-day modeling approach, the daily potential snowmelt is calculated as
follows:
Equation 15
with (mm) the potential snowmelt on day , and a calibrated degree-
day factor for snow. The actual snowmelt is limited by the snow storage at the end of the
previous day, and is calculated as:
Equation 16
with (mm) the actual snowmelt on day , and (mm) the snow storage on day .
The snow storage from day is then updated to the current day , using the actual
snowmelt () and the solid precipitation (). Part of the actual snowmelt freezes within the
snowpack and thus does not run off immediately. When temperature is below the melting point,
meltwater that has frozen in the snowpack during is added to the snow storage as:
Equation 17
with the snow storage on day , the snow storage on day , the solid
precipitation on day , the actual snowmelt on day , and the amount of frozen
meltwater on day . The units for all terms are mm.
The capacity of the snowpack to freeze snowmelt is characterized by introducing a calibrated
water storage capacity , which is the total water equivalent of snowmelt (mm)
that can freeze per mm water equivalent of snow in the snow storage. The maximum of
meltwater that can freeze ((mm)) is thus limited by the thickness of the snow storage:
Equation 18
Then the amount of meltwater stored in the snowpack, and that can freeze in the next time step,
is calculated as:
Equation 19
with the amount of meltwater in the snowpack on day , the maximum of
meltwater that can freeze on day , the amount of frozen meltwater on day , the

18
amount of rainfall on day , and the actual snowmelt on day . The units of all terms are in
mm.
The total snow storage (SST (mm)) consists of the snow storage and the meltwater that can
freeze within it, according to:
Equation 20
with (–) the grid-cell fraction not covered with glaciers. In SPHY it is therefore
assumed that snow accumulation and snowmelt can only occur on the grid-cell fraction
determined as land surface. Snow falling on glaciers is incorporated in the glacier module.
2.5.3 Snow runoff
Runoff from snow (SRo (mm)) is generated when the air temperature is above melting point and
no more meltwater can be frozen within the snowpack, according to:
Equation 21
with (mm) the change in meltwater stored in the snowpack according to:
Equation 22
2.6 Glacier processes
Since the SPHY model usually operates at a spatial resolution between 250m and 1km, the
dynamics of glaciers such as ice flow cannot be resolved explicitly. Therefore, glaciers in SPHY
are considered melting surfaces that can completely or partly cover a grid cell.
2.6.1 Glacier melt
Glacier melt is calculated with a degree-day modeling approach as well (Hock 2005). Because
glaciers that are covered with debris melt at different rates than debris-free glaciers (Reid et al.
2012), a distinction can be made between different degree-day factors for both types. The daily
melt from debris-free glaciers ( (mm)) is calculated as:
Equation 23
with a calibrated degree-day factor for debris-free glaciers and (–) the
fraction of debris-free glaciers within the fractional glacier cover (GlacF) of a grid cell. The daily
melt from debris-covered glaciers ( (mm)) is calculated in a similar way, but with a different
degree-day factor:

19
Equation 24
where is a degree-day factor for debris-covered glaciers and (–) is the
fraction of debris-covered glaciers within the fractional glacier cover of a grid cell. The total
glacier melt per grid cell ( (mm)) is then calculated by summing the melt from the debris-
covered and debris-free glacier types and multiplying by the fractional glacier cover, according
to:
Equation 25
2.6.2 Glacier runoff
In SPHY, a fraction of the glacier melt percolates to the groundwater while the remaining
fraction runs off. The distribution of both is defined by a calibrated glacier melt runoff factor
(GlacROF (–)) that can have any value ranging from 0 to 1. Thus, the generated runoff GRo
(mm) from glacier melt is defined as:
Equation 26
2.6.3 Glacier percolation
The percolation from glacier melt to the groundwater ( (mm)) is defined as:
Equation 27
The percolated glacier water is added to the water that percolates from the soil layers of the
non-glacierized part of the grid cell (Section 2.7.1 and 2.7.6), which eventually recharges the
groundwater.
2.7 Soil water processes
2.7.1 Soil water balances
The soil water processes in SPHY are modeled for three soil layers (Figure 2), being (i) the first
soil layer (root zone), (ii) second soil layer (subzone), and (iii) third soil layer (groundwater
layer). The water balance of the first soil layer is:
Equation 28
with and the water content in the first soil layer on days and , respectively,
the effective precipitation on day , the actual evapotranspiration on day , the
surface runoff on day , the lateral flow from the first soil layer on day , the

20
percolation from the first to the second soil layer on day , and the capillary rise from the
second to the first soil layer on day . The second soil layer water balance is:
Equation 29
with and the water content in the second soil layer on day and , respectively,
and percolation from the second to the third soil layer on day . The third soil layer water
balance is given as:
Equation 30
with and the water content in the third soil layer on day and , respectively,
groundwater recharge from the second to the third soil layer on day , and baseflow
on day . If the glacier module is used, then groundwater recharge consists of percolation from
the second soil layer and percolated glacier melt; otherwise, only percolation from the second
soil layer is taken into account.
The user can opt to run SPHY without the third soil layer (groundwater). This may be desirable
if the user for example is mainly interested in simulating soil moisture conditions in the root
zone, instead of evaluating for instance the contribution of baseflow to the total routed river flow.
In that case, only the two upper soil layers are used where the bottom boundary of soil layer two
is controlled by a seepage flux (positive outward), and instead of baseflow from the third soil
layer, water leaves the second soil layer through lateral flow. With the groundwater module
turned off, the water balance for the second soil layer is:
Equation 31
with lateral flow from the second soil layer, and Seep seepage in or out of the second soil
layer (positive is outgoing). The units for all water balance terms are in mm.
2.7.2 Actual evapotranspiration
Evapotranspiration refers to both the transpiration from vegetation and the evaporation from soil
or open water. As was mentioned in Section 2.3, the Kc accounts for both the crop transpiration
and soil evaporation. The additional use of the dynamic vegetation module accounts for a time-
variable vegetation cover, meaning that the role of evaporation becomes more dominant as
soon as vegetation cover decreases.
Many limiting factors (e.g., salinity stress, water shortage, water excess, diseases) can cause a
reduction in potential evapotranspiration (), resulting in the actual evapotranspiration rate
(). Since SPHY is a water-balance model, SPHY only accounts for stresses related to water
shortage or water excess. If there is too much water in the soil profile, then the plant is unable to
extract water because of oxygen stress (Bartholomeus et al. 2008). The calculation of
evapotranspiration reduction due to water excess (oxygen stress) is quite complex and requires
a substantial number of plant and soil properties (e.g., soil temperature, root dry weight, plant
respiration, and minimum gas filled soil porosity; (Bartholomeus et al. 2008)) that are generally
not available for the spatial scale that SPHY is applied on. Therefore, SPHY uses an

21
evapotranspiration reduction parameter () that has a value of 0 if the soil is saturated,
and otherwise it will have a value of 1. This parameter is used in the following equation to
calculate the actual evapotranspiration:
Equation 32
with (mm) the actual evapotranspiration on day , (mm) the potential
evapotranspiration on day , and and the reduction parameters for water
excess and water shortage conditions, respectively. is calculated using the Feddes
equation (Feddes et al., 1978), which assumes a linear decline in rootwater uptake if the water
pressure head drops below a critical value. This critical value can be determined using the soil
water retention curve (pF curve), which relates the moisture content of the soil to its binding
capacity. This relation is unique for each soil type. The binding capacity is a suction force ()
and is therefore often expressed in cm negative water column. The pF value is simply a
conversion of the suction force (), and is calculated as:
Equation 33
Soils that are at field capacity generally have a pF of 2, meaning 100cm of water column, and
soils that are at permanent wilting point have a pF of 4.2, or 16000cm of water column. The
permanent wilting point is often referred to as the point where the crop dies. In SPHY it is
assumed that the linear decline in rootwater uptake starts at a pF of 3 (1000cm water column).
Therefore, (–) is calculated as:
Equation 34
with (–) the reduction in rootwater uptake due to water shortage on day , (mm)
the actual soil water content in the first soil layer on day , and (mm) and (mm)
the soil water content in the first soil layer at pF3 and pF4.2, respectively. can
therefore have values ranging between 0 and 1, where a value of 1 represents optimal plant
growing conditions, and 0 means no rootwater uptake at all. is eventually used in
Equation 32 to calculate the .
2.7.3 Surface runoff
Since the SPHY model runs on a daily time step, the model does not account for sub-daily
variability in rainfall intensities. Therefore, the Hortonian runoff process (Beven 2004; Corradini
et al., 1998), which refers to infiltration excess overland flow, is considered less important. For
this reason, SPHY uses the saturation excess overland flow process, known as Hewlettian
runoff (Hewlett 1961), to calculate surface runoff. Surface runoff is calculated from the first soil
layer:
Equation 35

22
with RO (mm) surface runoff, (mm) the water content in the first soil layer, and (mm)
the saturated water content of the first soil layer.
2.7.4 Lateral flow
Lateral flow is substantial in catchments with steep gradients and soils with high hydraulic
conductivities (Beven 1981; Beven and Germann 1982; Sloan and Moore 1984). In SPHY, it is
assumed that only the amount of water exceeding field capacity can be used for lateral flow.
Therefore, the drainable volume of water (excess water) needs to be calculated first:
Equation 36
with (mm) the drainable volume of water from soil layer , (mm) the water content in
soil layer , and (mm) the field capacity of soil layer . According to Sloan and Moore
(1984), the lateral flow at the hillslope outlet can be calculated as:
Equation 37
with (mm) lateral flow from soil layer , (–) the drainable volume of water as a
fraction of the saturated volume, and () the flow velocity at the outlet. In SPHY, the
drainable volume as a fraction of the saturated volume is calculated as:
Equation 38
The velocity of flow at the outlet, (), depends on both the saturated hydraulic
conductivity () and the slope of the hill slp (–), and is defined as:
Equation 39
The slope (slp) in SPHY is calculated for each grid cell as the increase in elevation per unit
distance.
According to Neitsch et al. (2009), only a fraction of lateral flow will reach the main channel on
the day it is generated if the catchment of interest has a time of concentration greater than
1 day. This concept is also implemented in the SPHY model, and uses a lateral flow travel time
(d) to lag a portion of lateral flow release to the channel:
Equation 40
with (mm) the amount of lateral flow entering the channel on a given day, (mm) the
lateral flow (Equation 37) generated within the cell on a given day, and
(mm) the lateral
flow lagged from the previous day. SPHY assumes the lateral flow travel time to be dependent

23
on the field capacity (mm), saturated content (mm), and the saturated conductivity
(), according to:
Equation 41
A longer lateral flow travel time will result in a smoother streamflow hydrograph.
2.7.5 Percolation
If the groundwater module is used, then water can percolate from the first to the second soil
layer, and from the second to the third soil layer. If the user decides to run SPHY without the
groundwater module, percolation only occurs from the first to the second soil layer. In SPHY,
water can only percolate if the water content exceeds the field capacity of that layer, and the
water content of the underlying layer is not saturated. A similar approach has been used in the
SWAT model (Neitsch et al. 2009). The water volume available for percolation to the underlying
layer is calculated as:
Equation 42
with (mm) the drainable volume of water from layer , (mm) the water content in layer
, (mm) the field capacity of layer , (mm) the water content in layer , and
(mm) the saturated water content of layer . Only a certain amount of will
percolate to the underlying soil layer, depending on the percolation travel time (d). This
approach follows the storage routing methodology, which is also implemented in the SWAT
model (Neitsch et al. 2009):
Equation 43
with (mm) the amount of water percolating to the underlying soil layer. Since the speed at
which water can move through the soil is mainly dependent on the saturated hydraulic
conductivity (), the travel time for percolation is calculated the same way as the travel time
for lateral flow (Equation 41).
2.7.6 Groundwater recharge
Water that percolates from the second to the third soil layer will eventually reach the shallow
aquifer. This process is referred to as groundwater recharge hereafter. If the glacier module is
used as well, then glacier melt that percolates also contributes to the groundwater recharge.
Groundwater recharge often does not occur instantaneously, but with a time lag that depends
on the depth of the groundwater table and soil characteristics. SPHY uses the same exponential
decay weighting function as proposed by Venetis (1969) and used by Sangrey, Harrop-
Williams, and Klaiber (1984) in a precipitation groundwater response model. This approach has
also been adopted in the SWAT model (Neitsch et al. 2009), using:

24
Equation 44
with (mm) and (mm) the groundwater recharge on days and ,
respectively. (d) is the delay time and (mm) is the amount of water that percolates
from the second to the third layer on day .
2.7.7 Baseflow
After groundwater recharge has been calculated, SPHY calculates baseflow, which is defined
as the flow going from the shallow aquifer to the main channel. Baseflow only occurs when the
amount of water stored in the third soil layer exceeds a certain threshold () that can be
specified by the user. Baseflow calculation in SPHY is based on the steady-state response of
groundwater flow to recharge (Hooghoudt 1940) and the water table fluctuations that are a
result of the non-steady response of groundwater flow to periodic groundwater recharge
(Smedema and Rycroft 1983). The SWAT model (Neitsch et al. 2009) assumes a linear relation
between the variation in groundwater flow (baseflow) and the rate of change in water table
height, according to:
Equation 45
with (mm) the groundwater flow (baseflow) into the main channel on day , ( ) the
hydraulic conductivity of the shallow aquifer, (–) the specific yield of the shallow aquifer,
(m) the distance from the subbasin divide for the groundwater system to the main channel,
(mm) the amount of groundwater (Equation 44) recharge entering the shallow aquifer on
day , and (–) the baseflow recession coefficient. Equation 45 can be integrated and
rearranged to calculate baseflow, according to:
Equation 46
with (mm) the baseflow into the channel on day , and (mm) the baseflow into the
channel on day . Since this equation has proven its success in the SWAT model (Neitsch
et al. 2009) throughout many applications worldwide, this equation has been adopted in the
SPHY model as well.
The baseflow recession coefficient () is an index that relates the baseflow response to
changes in groundwater recharge. Lower values for therefore correspond to areas that
respond slowly to groundwater recharge, whereas higher values indicate areas that have a
rapid response to groundwater recharge. The baseflow recession coefficient is generally used
as a calibration parameter in the SPHY model, but a good first approximation of this coefficient
can be calculated using the number of baseflow days (Neitsch et al. 2009):
Equation 47

25
with BFD (d) the number of baseflow days, which is defined as the number of days required for
baseflow recession to decline.
2.8 Routing
After calculating the different runoff components, the cell-specific total runoff () is calculated
by adding these different runoff components. Depending on the modules being switched on, the
different runoff components are i) rainfall runoff (), (ii) snow runoff (), (iii) glacier runoff
(), and iv) baseflow (). Rainfall runoff is the sum of surface runoff (RO, Section 2.7.3) and
lateral flow from the first soil layer (, Section 2.7.4). If the groundwater module is not used,
then baseflow is calculated as being the lateral flow from the second soil layer. QTot is
eventually calculated according to:
Equation 48
with (mm) the cell-specific total runoff, (mm) rainfall runoff, (mm) snow runoff,
(mm) glacier runoff, and (mm) baseflow from the third soil layer or lateral flow from the
second soil layer. In order to obtain river discharge, needs to be routed through a flow
direction network. SPHY allows the user to opt between the use of a simple routing scheme
(Section 2.8.1) or a more complex routing scheme (Section 2.8.2) that involves the calculation
of lake outflow through relations. Both methods require a flow direction network map,
which can be obtained by delineating a river network using PCRaster or GIS software in
combination with a digital elevation model (DEM).
2.8.1 Runoff routing
In hydrology, streamflow routing is referred to as the transport of water through an open-
channel network. Since open-channel flow is unsteady, streamflow routing often involves
solving complex partial differential equations. The St. Venant equations (Brutsaert 1971; Morris
and Woolhiser 1980) are often used for this, but these have high data requirements related to
the river geometry and morphology, which are unavailable for the spatial scale SPHY is
generally applied on. Additionally, solving these equations requires the use of very small time
steps, which result in large model calculation times. The use of very small time steps in the
St. Venant equations is required to provide numerical stability. Other models, such as, e.g.,
SWAT (Neitsch et al. 2009), use the Manning equation (Manning 1989) to define the rate and
velocity of river flow in combination with the variable storage (Williams 1975) or Muskingum (Gill
1978) routing methods to obtain river streamflow. But, the Manning equation also requires river
bed dimensions, which are generally unknown on the spatial scale that SPHY generally is
applied on.
Therefore, SPHY calculates for each cell the accumulated amount of water that flows out of the
cell into its neighboring downstream cell. This can easily be obtained by using the accuflux
PCRaster built-in function, which calculates for each cell the accumulated specific runoff from its
upstream cells, including the specific runoff generated within the cell itself. If only the accuflux
function is used, then it is assumed that all the specific runoff generated within the catchment on
one day will end up at the most downstream location within one day, which is not plausible.
Therefore, SPHY implements a flow recession coefficient (kx (–)) that accounts for flow delay,
which can be a result of channel friction. Using this coefficient, river flow in SPHY is calculated
using the three equations shown below:

26
Equation 49
Equation 50
Equation 51
with () the specific runoff on day , the specific runoff in mm on day , ()
the grid-cell area, () the accumulated streamflow on day without flow delay taken
into account, () the routed streamflow on day , () the routed
streamflow on day , the flow direction network, and (–) the flow recession coefficient
has values ranging between 0 and 1, where values close to 0 correspond to a fast
responding catchment, and values approaching 1 correspond to a slow responding catchment.
The user can opt to route each of the four streamflow contributors separately, which may be
useful if one wants to evaluate, for example, the contribution of glacier melt or snowmelt to the
total routed runoff. However, this increases model run time substantially, because the accuflux
function, which is a time-consuming function, needs to be called multiple times, depending on
the number of flow contributors to be routed.
2.8.2 Lake/reservoir routing
Lakes or reservoirs act as a natural buffer, resulting in a delayed release of water from these
water bodies. SPHY allows the user to choose a more complex routing scheme if
lakes/reservoirs are located in their basin of interest. The use of this more advanced routing
scheme requires a known relation between lake outflow and lake level height ( relation) or
lake storage.
To use this routing scheme, SPHY requires a nominal map with the lake cells having a unique
ID, and the non-lake cells having a value of 0. The user can supply a Boolean map with “True”
for cells that have measured lake levels, and “False” for lake cells that do not have measured
lake levels. This specific application of SPHY is discussed in detail in Section 3.3.
Four different relations can be chosen to calculate the lake outflow from the lake level height or
lake storage, being (i) an exponential relation, (ii) a first-order polynomial function, (iii) a second-
order polynomial function, and (iv) a third-order polynomial function. The user needs to supply
maps containing the coefficients used in the different functions.
The lake/reservoir routing scheme simply keeps track of the actual lake storage, meaning that
an initial lake storage should be supplied. Instead of the simple accuflux function described in
the previous section, the lake/reservoir routing scheme uses the PCRaster functions
accufractionstate and accufractionflux. The accufractionflux calculates for each cell the amount
of water that is transported out of the cell, while the accufractionstate calculates the amount of
water that remains stored in the cell. For non-lake cells, the fraction that is transported to the
next cell is always equal to 1, while the fraction that is transported out of a lake/reservoir cell
depends on the actual lake storage. Each model time step, the lake storage is updated by inflow
from upstream. Using this updated storage, the lake level and corresponding lake outflow can

27
be calculated using one of the four relations mentioned before. The lake outflow can then be
calculated as a fraction ( (–)) of the actual lake storage. Instead of using Equation 50,
is then used in Equation 52 and Equation 53 to calculate the accumulated streamflow and
updated storage, respectively:
Equation 52
Equation 53
with and the actual storage and updated storage to be used in the next
time step, respectively, and () the accumulated streamflow on day , without flow
delay taken into account. Since is always equal to 1 for the non-lake cells, the
accufractionflux function becomes equal to the accuflux function used in the previous section.
This actually means that for the river network, the same routing function from Section 2.8.1 is
used, and that Equation 52 and Equation 53 only apply to lake/reservoir cells.
In order to account for non-linearity and slower responding catchments, the same kx coefficient
is used again. This involves applying Equation 51 as a last step after Equation 52 and
converting the units from to . Since the accufractionflux and accufraction state
functions are more complex to compute, the use of these functions increases model run time.

28
3 Applications
The SPHY model has been applied and tested in various studies, including real-time soil
moisture predictions in lowlands, operational reservoir inflow forecasting in mountainous
catchments, irrigation scenarios in the Nile basin, and climate change impact studies in the
snow–glacier–rain dominated Himalayan region. Some example applications will be
summarized in the following sections.
3.1 Irrigation management in lowland areas
As SPHY produces spatial outputs for the soil moisture content in the root zone and the
potential and actual evapotranspiration (ET), it is a useful tool for application in agricultural
water management decision support. By facilitating easy integration of remote sensing data,
crop growth stages can be spatially assessed at different moments in time. The SPHY dynamic
vegetation module ensures that all relevant soil water fluxes correspond to crop development
stages throughout the growing season. Spatially distributed maps of root water content and ET
deficit can be produced, enabling both the identification of locations where irrigation is required
and a quantitative assessment of crop water stress.
SPHY has been applied with the purpose of providing field-specific irrigation advice for a large-
scale farm in western Romania, comprising 380 individual fields and approximately ten different
crops. Contrary to the other case studies highlighted in this paper, a high spatial resolution is
very relevant for supporting decisions on variable-rate irrigation. The model has therefore been
set up using a 30m resolution, covering the 2013 and 2014 cropping seasons on a daily time
step. Optical satellite data from Landsat 8 (USGS 2013) were used as input to the dynamic
vegetation module. Soil properties were derived from the Harmonized World Soil Database
(Batjes et al. 2012), which for Romania contains data from the Soil Geographical Database for
Europe (Lambert et al. 2003). Using the Van Genuchten equation (Van Genuchten 1980), soil
saturated water content, field capacity, and wilting point were determined for the HWSD classes
occurring at the study site. Elevation data was obtained from the EU-DEM data set (EEA 2014),
and air temperature was measured by two on-farm weather stations.
In irrigation management applications like these, a model should be capable of simulating the
moisture stress experienced by the crop due to insufficient soil moisture contents, which
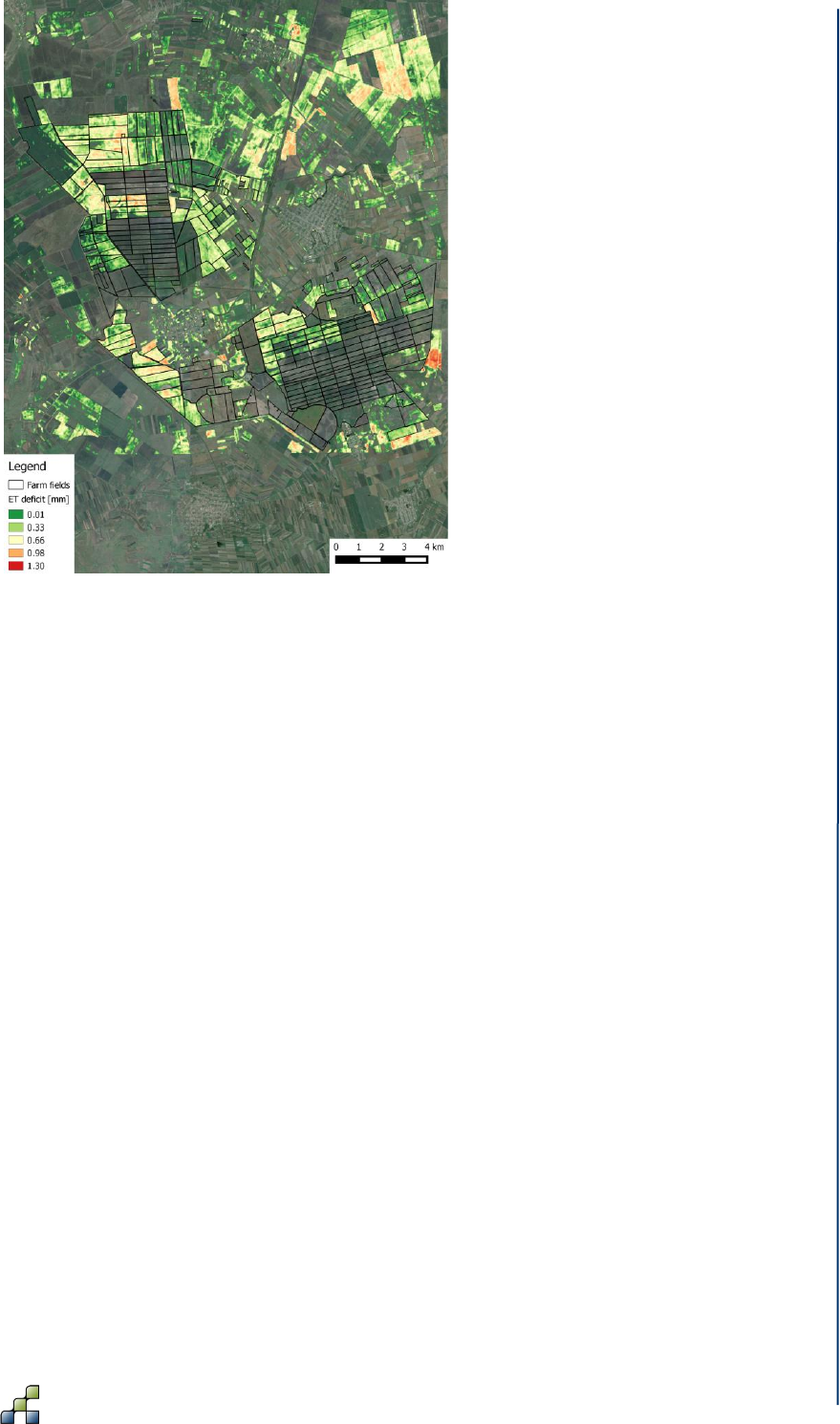
manifests itself by an evapotranspiration deficit (potential ETactual ET0). Figure 4 shows the
spatial distribution of ET deficit, as simulated by the SPHY model for the entire farm on
03 April 2014. When SPHY is run in an operational setting, this spatial information can be
included in a decision support system that aids the farmer in irrigation planning for the coming
days.
29
Figure 4: Spatial distribution of evapotranspiration (ET) deficit, as simulated by the SPHY
model for a Romanian farm on 03 April 2014. Transparency means no ET deficit.
For calibration purposes, field measurements of soil moisture and/or actual ET are desired. In
this case study, one capacitance soil moisture sensor was installed in a soybean field to monitor
root-zone water content shortly after 01 May 2014, which is the start of the soybean growing
season. The sensor measures volumetric moisture content for every 10cm of the soil profile up
to a depth of 60cm. It is also equipped with a rain gauge measuring the sum of rainfall and
applied irrigation water, which was used as an input to SPHY. Soil moisture measured over the
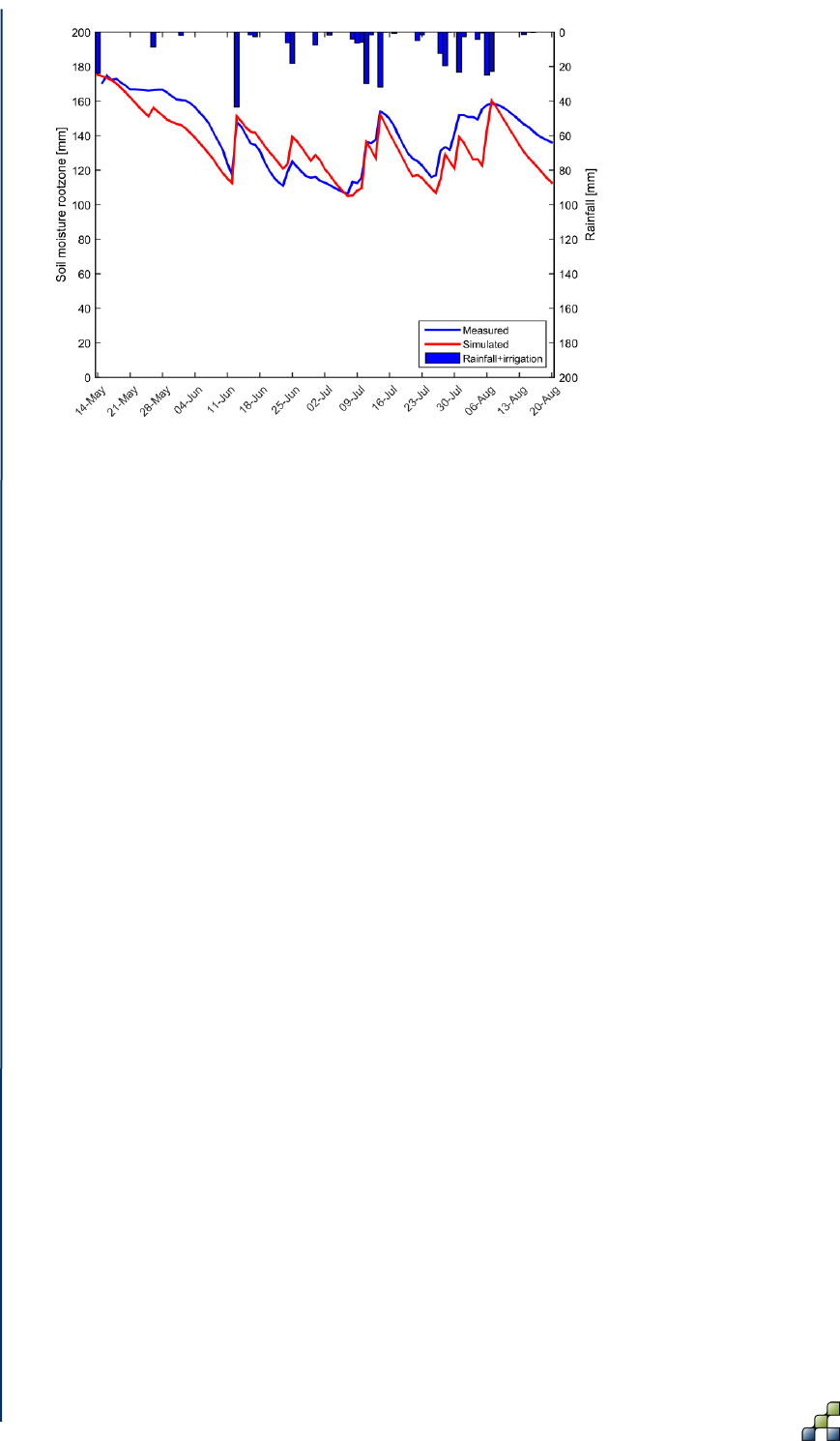
extent covered by the crop root depth was averaged and compared to simulated values (Figure
5).
Since this study was a demonstration project, only an initial model calibration was performed.
The model was in this case most sensitive for the crop coefficient (Kc), affecting the evaporative
demand for water. As can be seen in Figure 5, the temporal patterns as measured by the soil
moisture sensor are well simulated by the SPHY model. Based on daily soil moisture values, a
Nash–Sutcliffe (Nash and Sutcliffe 1970) model efficiency coefficient of 0.6 was found,
indicating that the quality of prediction of the SPHY model is “good” (Foglia et al. 2009). Soil
moisture simulations could be further improved by conducting a full model calibration, adjusting
the soil physical parameters , , , and . Remotely sensed sensed
evapotranspiration can be used in the calibration process (Immerzeel and Droogers 2008),
although such data are often not available on these small scales as ET is a very complex
variable to assess (Samain et al. 2012). It should also be noted that soil moisture content is
typically highly variable in space; a very high correlation between point measurements and grid-
cell simulations of soil moisture may therefore not always be feasible (Bramer et al., 2013).
30
Figure 5: Measured and simulated daily root-zone soil moisture content during the 2014
growing season. Rainfallirrigation has been measured by the rain gauge that was
attached to the moisture sensor.
3.2 Snow- and glacier-fed river basins
SPHY is being used in large Asian river basins with significant contribution of glacier melt and
snowmelt to the total flow (Immerzeel et al., 2012, Lutz et al., 2012, 2014a). The major goals of
these applications are two-fold:
Assess the current hydrological regimes at high resolution; e.g., assess spatial
differences in the contributions of glacier melt, snowmelt and rainfall–runoff to the total
flow.
Quantify the effects of climate change on the hydrological regimes in the future and how
these affect the water availability.
Rivers originating in the high mountains of Asia are considered to be the most meltwater-
dependent river systems on Earth (Schaner et al. 2012). In the regions surrounding the
Himalayas and the Tibetan Plateau, large human populations depend on the water supplied by
these rivers (Immerzeel et al., 2010). However, the dependency on meltwater differs strongly
between river basins as a result of differences in climate and differences in basin hypsometry
(Immerzeel and Bierkens 2012). Only by using a distributed hydrological modeling approach
that includes the simulation of key hydrological and cryospheric processes, and inclusion of
transient changes in climate, snow cover, glaciers and runoff, can appropriate adaptation and
mitigation options be developed for this region (Sorg et al. 2012). The SPHY model is very
suitable for such goals, and has therefore been widely applied in the region.
For application in this region, SPHY was set up at a 1km spatial resolution using a daily time
step, and forced with historical air temperature (, , ) and precipitation data, obtained
from global and regional data sets (e.g., APHRODITE, (Yatagai et al. 2012); Princeton,
(Sheffield, Goteti, and Wood 2006); TRMM, (Gopalan et al. 2010)) or interpolated WMO station
data from a historical reference period. For this historical reference period, SPHY was calibrated
and validated using observed streamflow. For the future period, SPHY was forced with
downscaled climate change projections obtained from general circulation models (GCMs), as
31
available through the Climate Model Intercomparison Projects (e.g., CMIP3, (Meehl et al. 2007);
CMIP5, (Taylor et al., 2012)), which were used as a basis for the Assessment Reports prepared
by the Intergovernmental Panel on Climate Change (IPCC).
In central Asia, SPHY was applied in a study (ADB 2012; Immerzeel et al., 2012; Lutz et al.,
2012) that focused on the impacts of climate change on water resources in the Amu Darya and
Syr Darya river basins. SPHY was used to quantify the hydrological regimes in both basins, and
subsequently to project the outflow from the upstream basins to the downstream areas by
forcing the model with an ensemble of five CMIP3 GCMs. The SPHY model output fed into a
water allocation model that was set up for the downstream parts of the Amu Darya and
Syr Darya river basins.
In the Himalayan Climate Change Adaptation Programme (HICAP), led by the International
Centre for Integrated Mountain Development (ICIMOD), SPHY has been successfully applied in
the upstream basins of the Indus, Ganges, Brahmaputra, Salween and Mekong rivers (Lutz et
al. 2013; Lutz et al. 2014a). In this study the hydrological regimes of these five basins have
been quantified and the calibrated and validated model (Figure 6) was forced with an ensemble
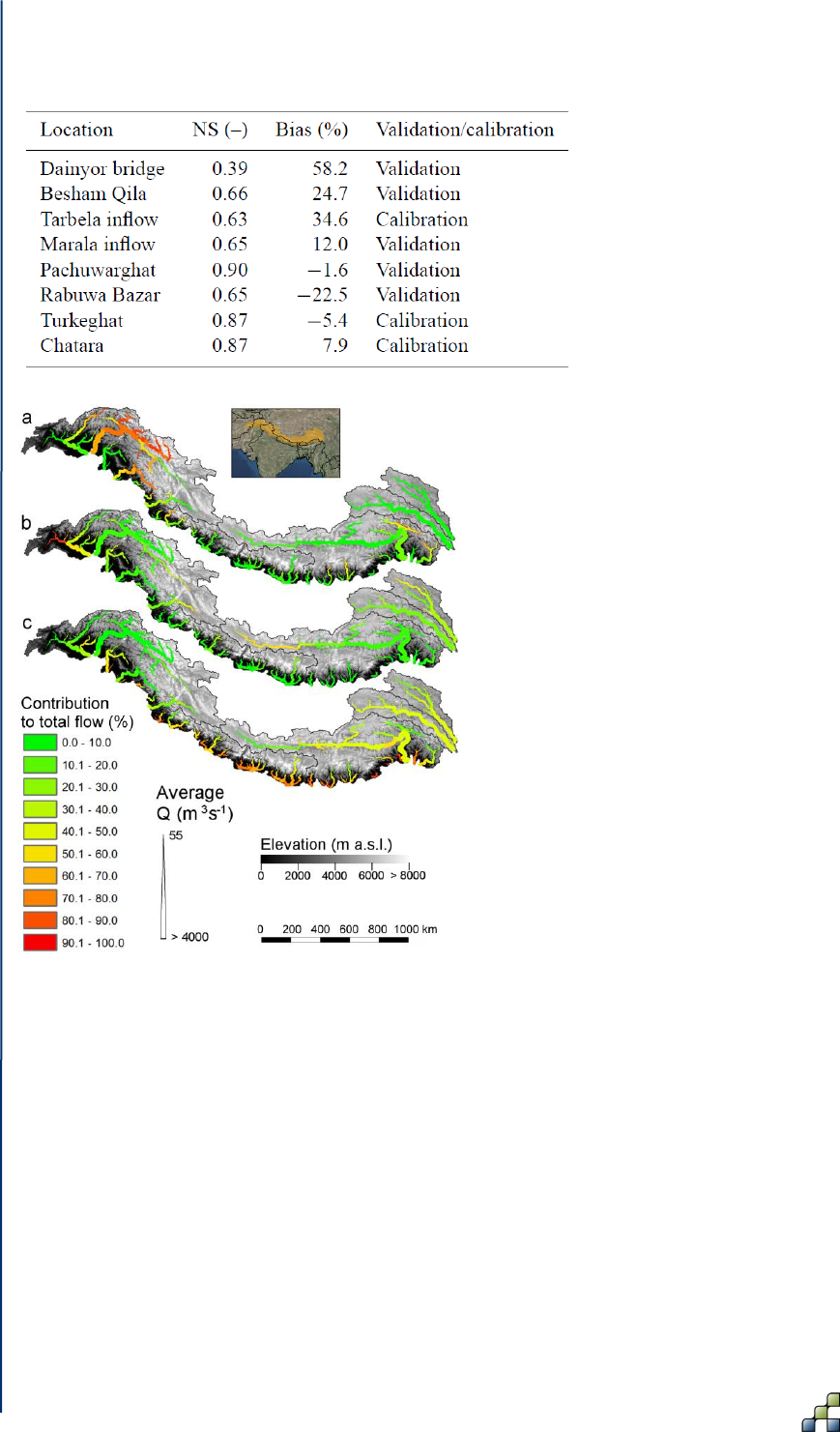
of eight GCMs to create water availability scenarios until 2050. Table 3 lists the calibration and
validation results. Based on the validation results, we concluded that the model performs
satisfactorily given the large scale, complexity and heterogeneity of the modeled region and
data scarcity (Lutz et al. 2014a). We use one parameter set for the entire domain, which
inherently means some stations perform better than others. In the particular case of the upper
Indus, another possible explanation could be uncertainty in air temperature forcing in the
highest parts of the upper Indus basin (locations Dainyor bridge, Besham Qila and Tarbela
inflow in Table 3), since especially in this area, the used forcing data sets are based on very
sparse observations. SPHY allowed the assessment of the current contribution of glacier melt
and snowmelt to total flow (Figure 7), and how total flow volumes and the intra-annual
distribution of river flow will change in the future (Lutz et al. 2014a).
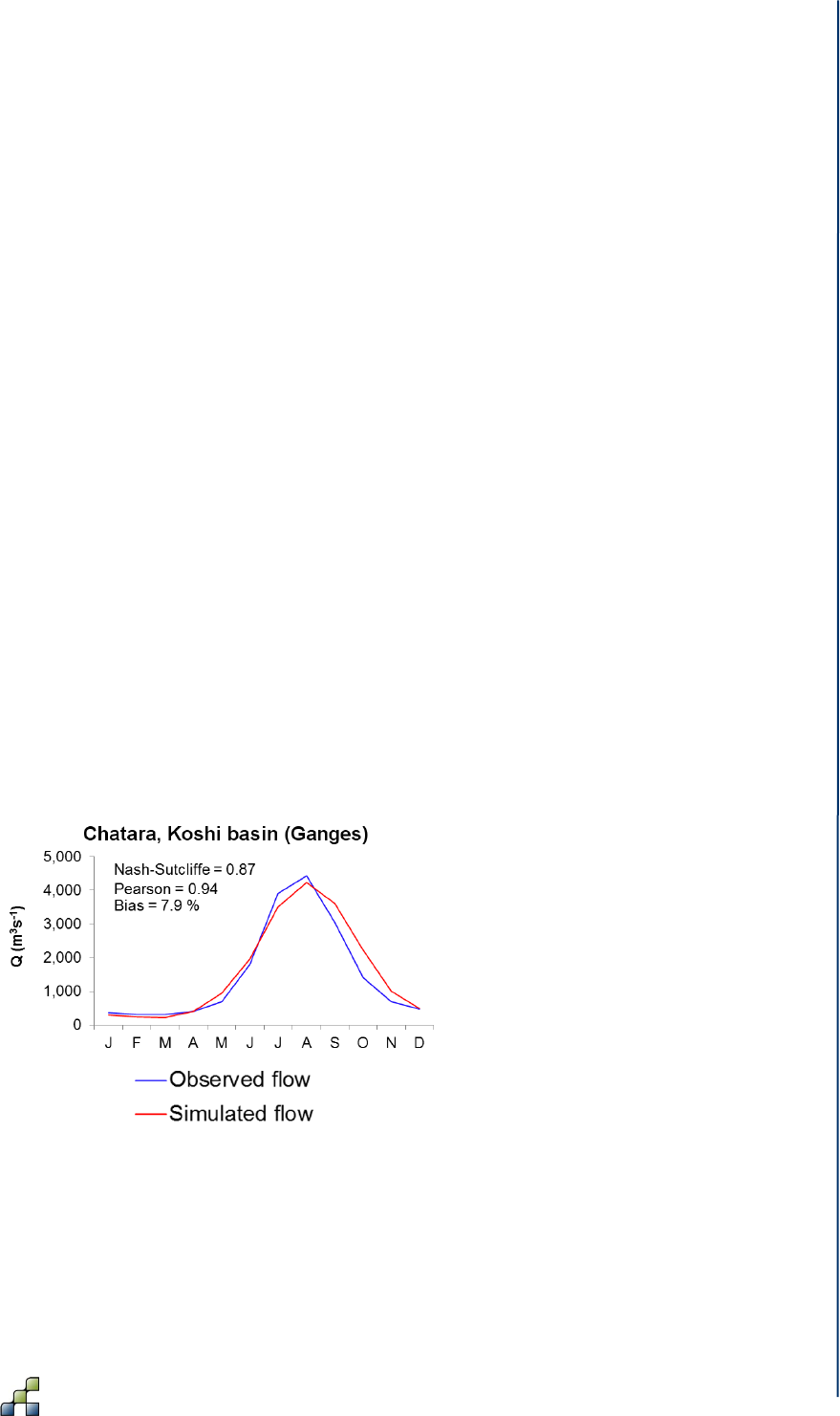
Figure 6: Average monthly observed and SPHY-simulated flow (1998–2007) for the
Chatara major discharge measurement location in the Ganges basin (Lutz et al. 2014a).
Metrics are calculated based on monthly time steps.
32
Table 3: Station locations used for calibration and validation of the SPHY model in HICAP
(Lutz et al., 2014a). Three stations were used for calibration for 1998–2007. Five stations
were used for an independent validation for the same period. The Nash–Sutcliffe
efficiency (NS) and bias metrics were calculated at a monthly time step.
Figure 7: The contribution of glacier melt (a), snowmelt (b), and rainfall (c) to the total
flow for major streams in the upstream basins of the Indus, Ganges, Brahmaputra,
Salween and Mekong during 1998–2007 (Lutz et al. 2014a).
For basins with snowmelt being an important contributor to the flow, besides calibration to
observed flow, the snow-related parameters in the SPHY model can also be calibrated to
observed snow cover. For the Upper Indus basin, the snow-related parameters degree-day
factor for snow () and snow water storage capacity (SSC) were calibrated independently
using MODIS snow cover imagery (Lutz et al., 2014b). The same MODIS data set was used as
in Immerzeel et al. (2009). From the beginning of 2000 until halfway through 2008, the snow
cover imagery was averaged for 46 different periods of 8 days (5 days for the last period) to
generate 46 different average snow cover maps. For example, period 1 is the average snow
cover for 01–08 January for 2000 until 2008, whereas period 2 is the average snow cover for
09–16 January for 2000 until 2008, etc. The SPHY model was run for 2000–2007 at a daily time
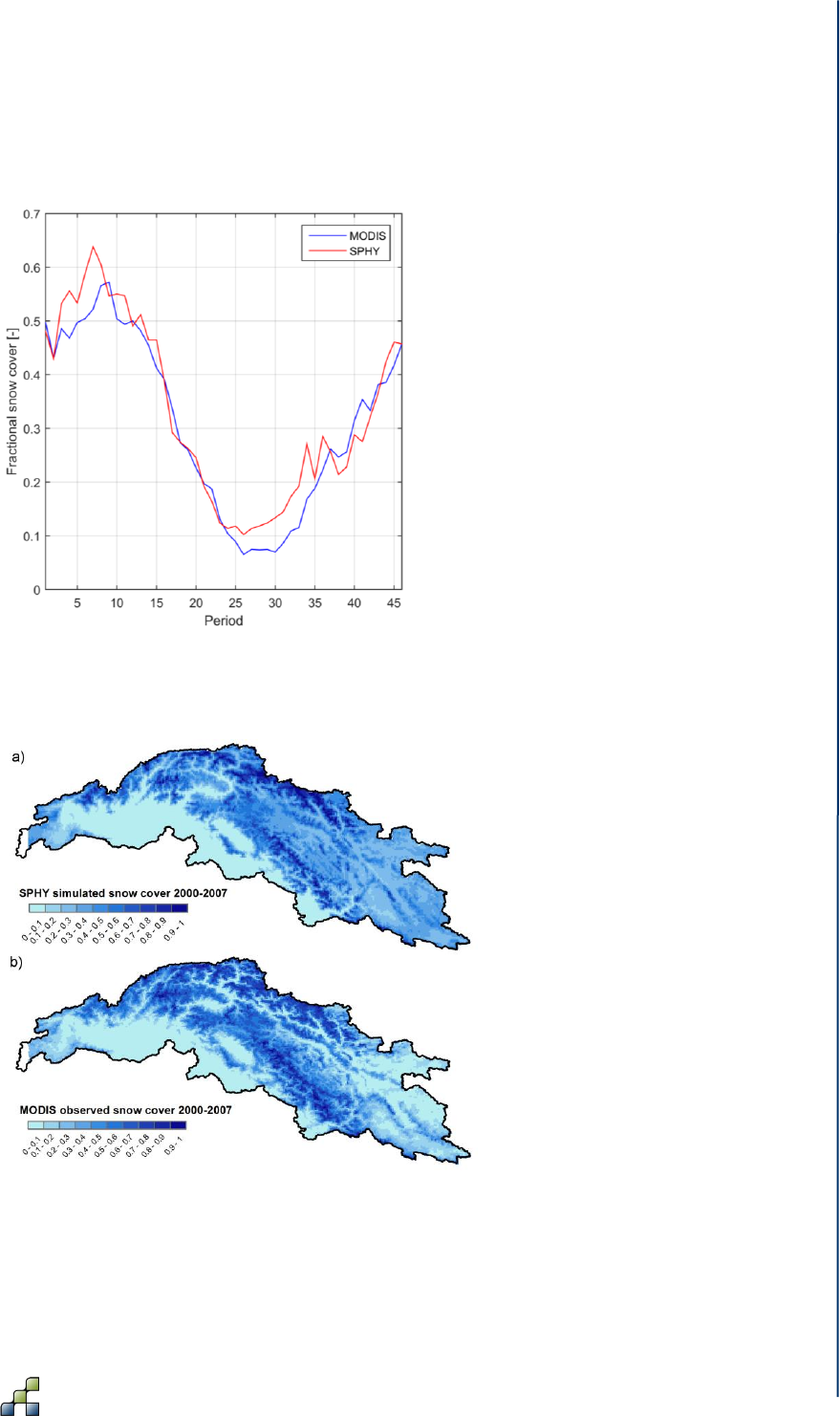
33
step and, for each km grid cell, the average snow cover was calculated for the same 46
periods as in the MODIS observed snow cover data set. Subsequently, these simulated snow
cover maps were resampled to 0.05 spatial resolution, which is the native resolution of the
MODIS product. Figure 8 shows the basin-average observed and simulated fractional snow
cover for the 46 periods during 2000–2007 and Figure 9 shows the same at the 0.05 grid-cell
level. As a final step, the baseflow recession coefficient () and routing coefficient (kx) were
calibrated to match the simulated streamflow with the observed streamflow.
Figure 8: Observed and simulated average fractional snow cover in the upper Indus
basin. The values represent the 9-year average for 46 (8-day) periods during 2000–2007.
Figure 9: (a) SPHY simulated snow cover 2000–2007 and (b) MODIS observed snow cover
2000–2007.

34
3.3 Flow forecasting
In data-scarce environments and inaccessible mountainous terrain, like in the Chilean Andes, it
is often difficult to install instrumentation and retrieve real-time physical data from these
instruments. These real-time data can be useful to capture the hydroclimatic variability in this
region, and improve the forecasting capability of hydrological models. Although statistical
models can provide skillful seasonal forecasts, using large-scale climate variables and in situ
data (Piechota and Chiew 1998; Grantz et al. 2005; Regonda et al. 2006; Bracken et al., 2010),
a particular hydropower company in Chile was mainly interested in the potential use of an
integrated system, using measurements derived from both Earth observation (EO) satellites and
in situ sensors, to force a hydrological model to forecast seasonal streamflow during the snow
melting season. The objective of the INTOGENER (INTegration of EO data and GNSS-R
signals for ENERgy applications) project was therefore to demonstrate the operational
forecasting capability of the SPHY model in data-scarce environments with large hydroclimatic
variability.
During INTOGENER, data retrieved from EO satellites consisted of a DEM and a time series of
snow cover maps. Snow cover images were retrieved on a weekly basis, using RADARSAT and
MODIS (Parajka and Blöschl 2008; Hall et al. 2002) imagery. These images were used to
update the snow storage (SS (mm)) in the model in order to initialize it for the forecasting
period. Figure 10 shows the snow storage as simulated by the SPHY model during the snow
melting season in the Laja basin. These maps clearly show the capability of SPHY to simulate
the spatial variation of snow storage, with more snow on the higher elevations, and a decrease
in snow storage throughout the melting season. Discharge, precipitation and temperature data
were collected using in situ meteorological stations. In order to calculate the lake outflow
accurately, the SPHY model was initialized with water level measurements retrieved from
reflected Global Navigation Satellite System (GNSS) signals in Laja Lake. Static data that were
used in the SPHY model consisted of soil characteristics derived from the Harmonized World
Soil Database (HWSD) (Batjes et al. 2009) and land use data obtained from the GLOBCOVER
(Bontemps et al. 2011) product. The SPHY model was set up to run at a spatial resolution of
200m.
Figure 11 shows the observed vs. simulated daily streamflow for two locations within the Laja
River basin for the historical period 2007–2008. It can be seen that model performance is quite
satisfactory for both locations, with volume errors of 4 and 9.4% for the Abanico Canal
(downstream of Lake Laja) and Rio Laja en Tucapel, respectively. The NS coefficient, which is
especially useful for assessing the simulation of high discharge peaks, is less satisfactory for
these locations. Hydropower companies, however, have more interest in expected flow volumes
for the coming weeks/months than in accurate day-to-day flow simulations, and therefore the
NS coefficient is less important in this case. If the NS coefficient is calculated for the same
period on a monthly basis, then the NS coefficients are 0.53 for the Abanico Canal and 0.81 for
Rio Laja en Tucapel. It is likely that SPHY model performance would even have been better if a
full model calibration would have been performed.
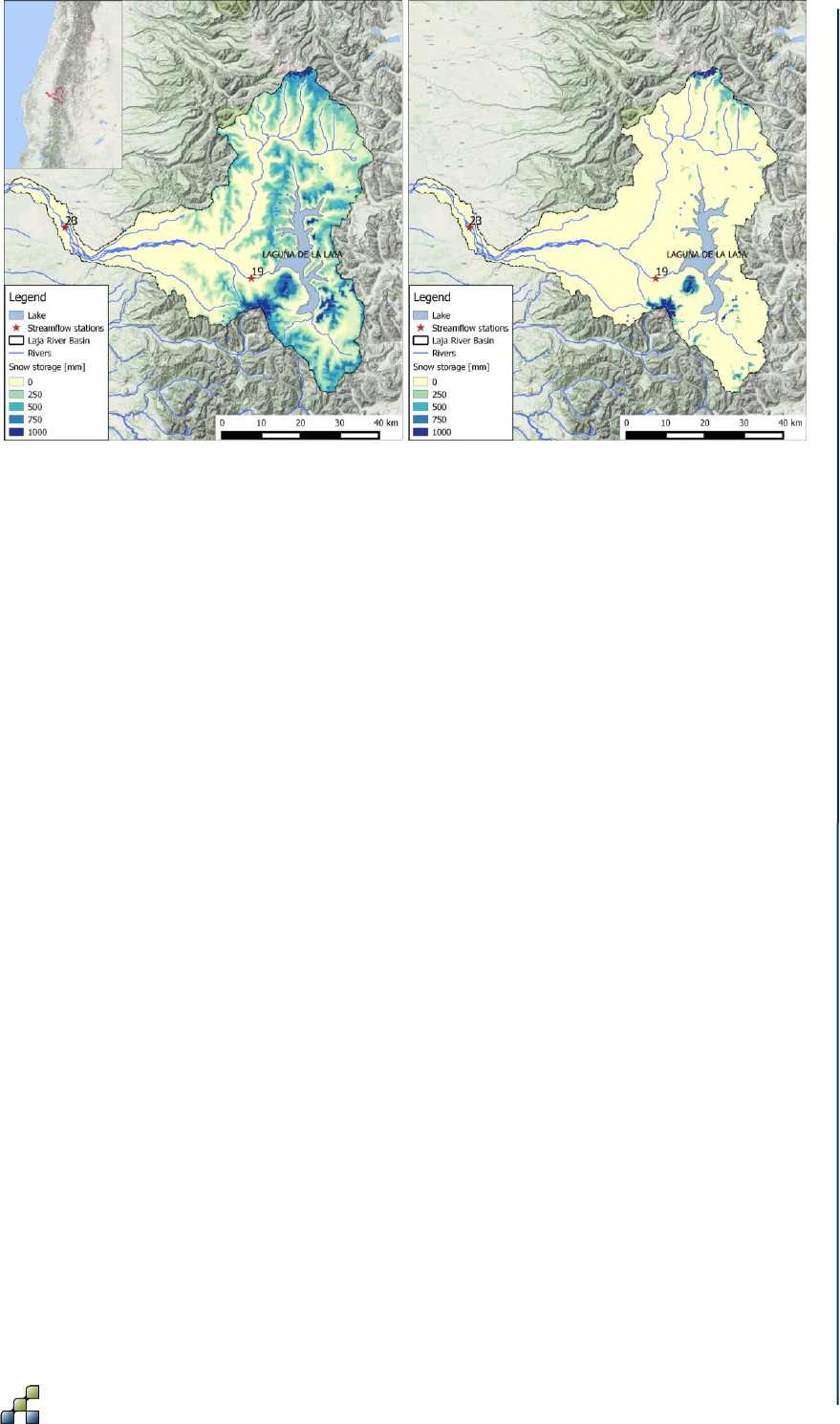
35
Figure 10: Snow storage (mm) as simulated by the SPHY model on 12 August (left) and
01 October (right) during the snow melting season of 2013 in the Laja River basin.
The hydropower company’s main interest is the model’s capacity to predict the total expected
flow for the coming weeks during the melting season (October 2013 through March 2014). To
forecast streamflow during the snow melting season, the SPHY model was forced with gridded
temperature and precipitation data from the European Centre for Medium-range Weather
Forecasts (ECMWF) Seasonal Forecasting System (SEAS) (Andersson 2013). The SEAS
model provided daily forecasts at a spatial resolution of 0.75, 7 months ahead, and was used to
forecast streamflow up till the end of the melting season. Figure 12 shows the bias between the
total cumulative forecasted flow and observed flow for the 23 model runs that were executed
during operational mode. Although there are some bias fluctuations in the Rio Laja en Tucapel
model runs, it can be concluded that the bias decreases for each next model run for both
locations, which is a logical result of a decreasing climate forcing uncertainty as the model
progresses in time. It can be seen that the SPHY model streamflow forecasts for Canal
Abanico, which is downstream of Laja Lake, are substantially better than for Rio Laja en
Tucapel (the most downstream location). The reason for this has not been investigated during
the demonstration study, but since model performance for these two locations was satisfactory
during calibration, a plausible explanation could be the larger climate forecast uncertainty in the
higher altitude areas (Hijmans et al. 2005; Rollenbeck and Bendix 2011; Vicuña et al., 2011;
McPhee et al. 2010; Mendoza et al., 2012; Ragettli and Pellicciotti 2012; Ragettli et al. 2014) in
the northeastern part of the basin that contributes to the streamflow of Rio Laja en Tucapel.
Additionally, only two in situ meteorological stations were available during operational mode,
whereas during calibration, 20 meteorological stations were available. Moreover, these
operational meteorological stations were not installed at higher altitudes, where precipitation
patterns tend to be spatially very variable (Wagner et al. 2012; Rollenbeck and Bendix 2011).
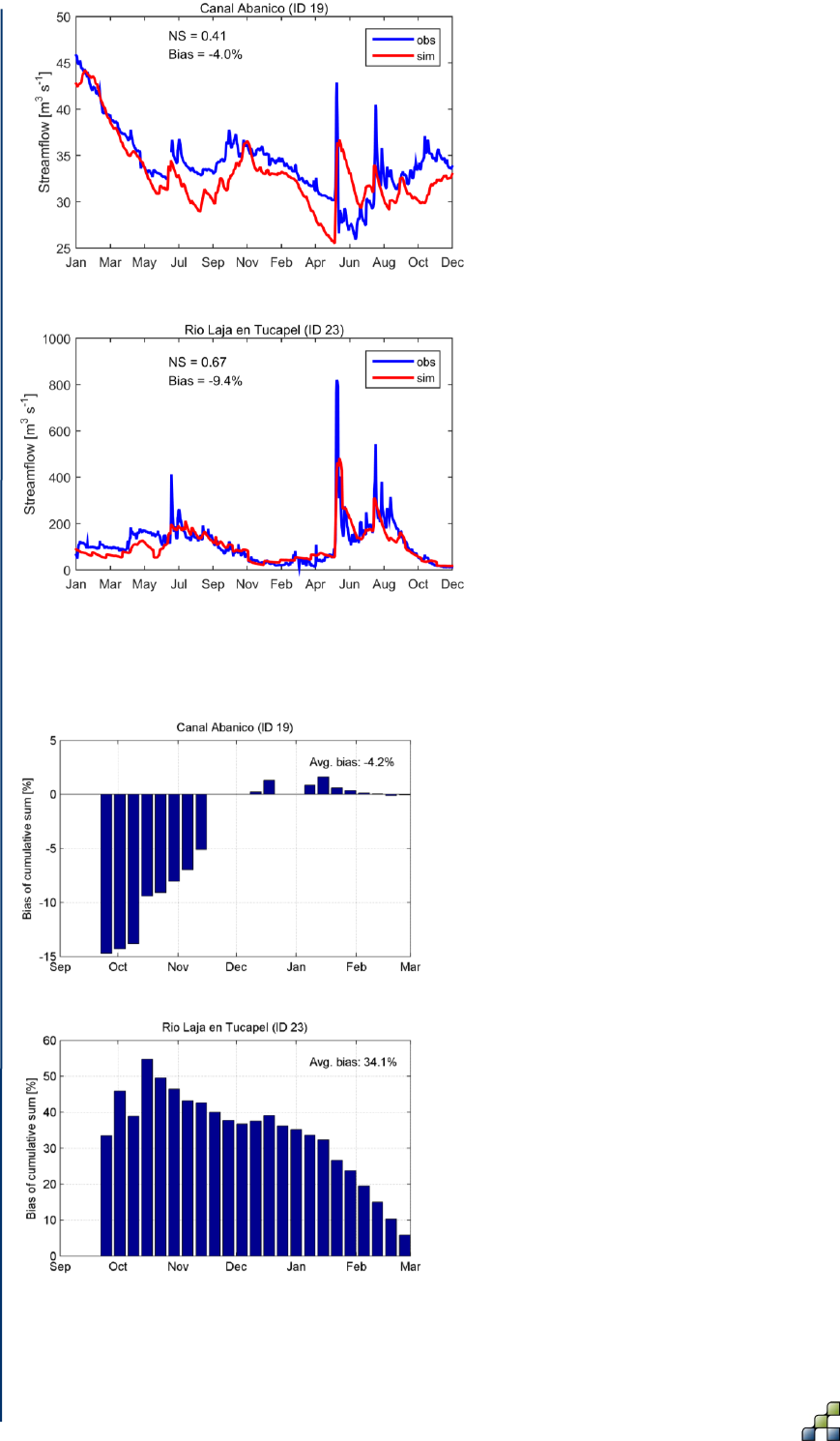
36
Figure 11: Daily observed vs. SPHY simulated streamflow (period 2007–2008) for the
streamflow stations Canal Abanico (ID 19) and Rio Laja en Tucapel (ID 23). The Nash–
Sutcliffe (NS) and bias model performance indicators are shown as well.
Figure 12: Bias between total cumulative forecasted flow and observed flow for the 23
model runs that were executed between the end of September 2013 and March 2014.

37
Results are shown for the locations Canal Abanico (ID 19) and Rio Laja en Tucapel
(ID 23).

38
4 Installation of SPHY
4.1 General
SPHY v2.0 can be either be installed as i) a stand-alone application, where the user can run the
model throughout the command prompt, or as ii) a an integrated application (plugin) in QGIS,
where the model can be run using a Graphical User-Interface (GUI). The GUI has been
developed as a plugin in QGIS
1
, and has the advantage that changing the model input and
output, as well as changing model parameters, is more clear and user-friendly. Furthermore, the
use of the plugin allows you to store and visualize your model input and output in the user-
friendly and world-wide used QGIS Geographical Information System (GIS), which is in the
public domain. The name of this SPHY model plugin is “SphyPlugin” (v1.0), and is compatible
with SPHY (v2.0). The installation of the SPHY model plugin is not part of this manual and is
described in the SPHY GUIs manual (Terink et al., 2015b).
This manual (Section 4.2) describes the installation of SPHY v2.0 as a stand-alone application.
4.2 Installing SPHY as a stand-alone application
In order to install SPHY as a stand-alone application it is required to have a PC with a windows
operating system. The software packages that are required to run the SPHY model as stand-
alone application are:
1. Python 2.7.6, 32-bit
2. NumPy 1.8.0, 32-bit
3. PCRaster 4.0, 32-bit
4. SPHY v2.0 source code
These packages need to be installed in the same order as shown above, and the installation of
the each package is described in the following sections. The Python, NumPy, and PCRaster
software packages can also be downloaded from the SPHY model website as zip-files:
Download additional software
The login credentials that are required for downloading software and data can be obtained from:
http://www.sphy.nl/software/download-sphy/
4.2.1 Python 2.7.6 32-bit
SPHY requires the installation of the Python
2
programming language. PCRaster has been
developed using the 2.7.6 version of Python. Since SPHY has been developed using the 32-bit
version of PCRaster 4.0, it is required to install the 32-bit version of Python 2.7.6, which can be
downloaded from the internet using the link below:
https://www.python.org/ftp/python/2.7.6/python-2.7.6.msi
1
http://www.qgis.org/en/site/
2
https://www.python.org/
39
After downloading Python it can be installed by double clicking the downloaded file. During
installation it will be asked where to install Python. You can choose any location that you prefer.
As an example to be used in this manual, we have installed Python in the folder:
c:\Python27\
A final installation step includes setting the environmental variables. In order to do this, follow
the steps below:
1. Go to start, then control panel, and type environment in the top-right search window.
2. Click on “Edit the system environmental variables”.
3. Click “Environmental Variables” in the bottom-right of this window (Figure 13).
4. Under system variables, select the Path variable and click “Edit” (Figure 14).
5. In order let your system know the existence of your Python installation, it is required to
add your Python installation folder to the “Path” system variable. This is shown in Figure
15 for our case, which was the c:\Python27 installation folder. It is important to have a
semicolon between the system variables.
6. Finally, click OK and OK again in order to complete the installation of Python.
Figure 13: System properties to set Environmental Variables.
40
Figure 14: Setting the Path variable.
Figure 15: Adding the Python27 installation folder to the Path system variables.
4.2.2 Numpy 1.8.0 32-bit
Numpy stands for Numerical Python, and is a fundamental package for scientific computing with
Python. It has especially been developed to work with raster data (arrays), which is also the
basis of the PCRaster dynamic modelling framework in which SPHY has been developed.
SPHY requires a Numpy version that works with the 32-bit version of Python 2.7.6, which is
Numpy 1.8.0 32-bit. This package can be downloaded using the link below:
http://sourceforge.net/projects/numpy/files/NumPy/1.8.0/numpy-1.8.0-win32-superpack-
python2.7.exe/download
After downloading the Numpy package, it can be installed by double-clicking on the downloaded
file. If Python 2.7.6 has been installed correctly in the previous step, then the Python installation
folder will be found automatically during the installation of Numpy. In our example case this
folder was c:\Python27\ (see example Figure 16).
41
Figure 16: Illustration of selecting the Python installation folder during installation of the
Numpy package.
4.2.3 PCRaster 4.0 32-bit
SPHY is written in the Python programming language using the PCRaster (Karssenberg et al.,
2001; Karssenberg, 2002; Karssenberg et al., 2010; Schmitz et al., 2009, 2013) dynamic
modelling framework. PCRaster
1
has been developed at Utrecht University. PCRaster is
targeted to the development and deployment of spatio-temporal environmental models. It allows
users to develop their own simulation models for applications in environmental sciences, such
as e.g. hydrology, ecology, geography, etc.
SPHY v2.0 is based on the 32-bit system architecture, and therefore requires the 32-bit
PCRaster 4 version. SPHY v2.0 has been built and thoroughly tested using PCRaster 4.0.0,
and it is therefore recommended to download and install this stable version of PCRaster. More
information about this version of PCRaster can be found at the link below:
http://pcraster.geo.uu.nl/pcraster-4-0-0/
In order to install PCRaster 4.0.0, it is mandatory to have successfully installed Python 2.7.6
and Numpy 1.8.0 during the previous two steps (Section 0 and 4.2.2). To install PCRaster 4.0.0
you need to perform the following steps:
1. Download the PCRaster version using this link:
http://sourceforge.net/projects/pcraster/files/PCRaster/4.0.0/pcraster-4.0.0_x86-
32.zip/download?use_mirror=heanet
2. Create a new folder on your hard disk where you prefer to install PCRaster. For
example: c:\Program Files (x86)\PCRaster40\
3. Unzip the contents of the file downloaded under 1) to this folder
4. To let your system recognize the existence of PCRaster, the Environmental Variables
need to be updated again. The steps to get to your system Environmental Variables are
shown in Section 0, steps 1-4.
1
http://pcraster.geo.uu.nl/
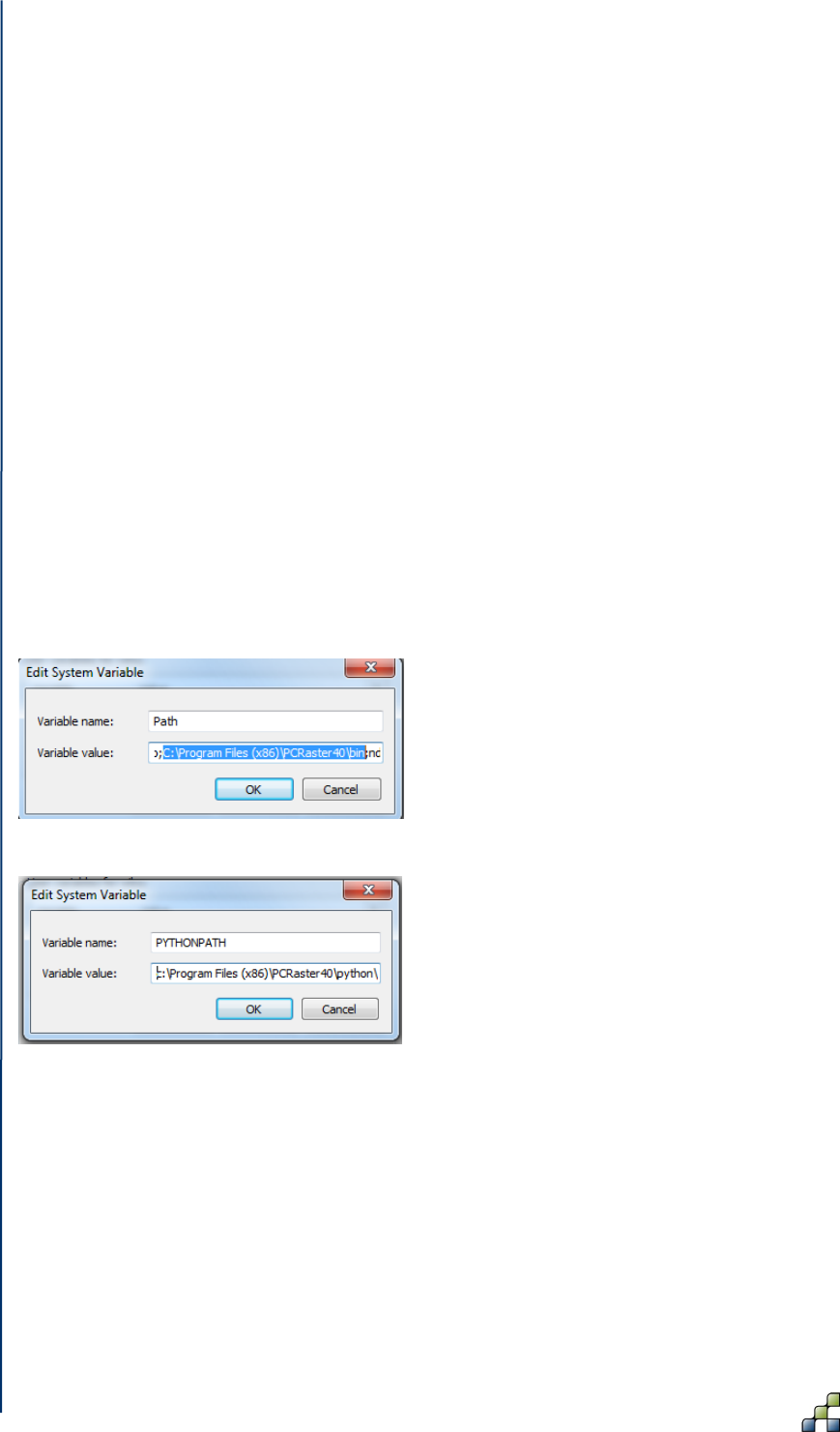
42
5. It is now required to add the “bin” directory of the extracted PCRaster package to the
“Path” system variable (Figure 17). In our example it is the folder: c:\Program Files
(x86)\PCRaster40\bin\
6. Click OK.
7. The next step involves setting the PYTHONPATH environment variable. In the same
system variables window check the existence of a PYTHONPATH variable. If it exists,
then edit the variable by adding the path (Figure 18) of the Python directory of the
extracted PCRaster package, which is in our example:
c:\Program Files (x86)\PCRaster40\python\
Otherwise click “New” to create it, and add PYTHONPATH as Variable name, and add
the Python directory folder as the Variable value.
8. Click OK and OK to complete the installation of PCRaster.
9. The successful installation of PCRaster can be tested as follows:
a. Open a command prompt
b. Type pcrcalc
c. You should see the command prompt view as is shown in Figure 19
10. To test the combination of PCRaster and Python:
a. Open a command prompt
b. Type python
c. This opens the Python interactive console
d. Type import pcraster
e. If no errors are shown, then installation has been completed successfully.
Figure 17: Adding the PCRaster bin folder to the Path system variables.
Figure 18: Editing or creating the PYTHONPATH variable for the PCRaster package.
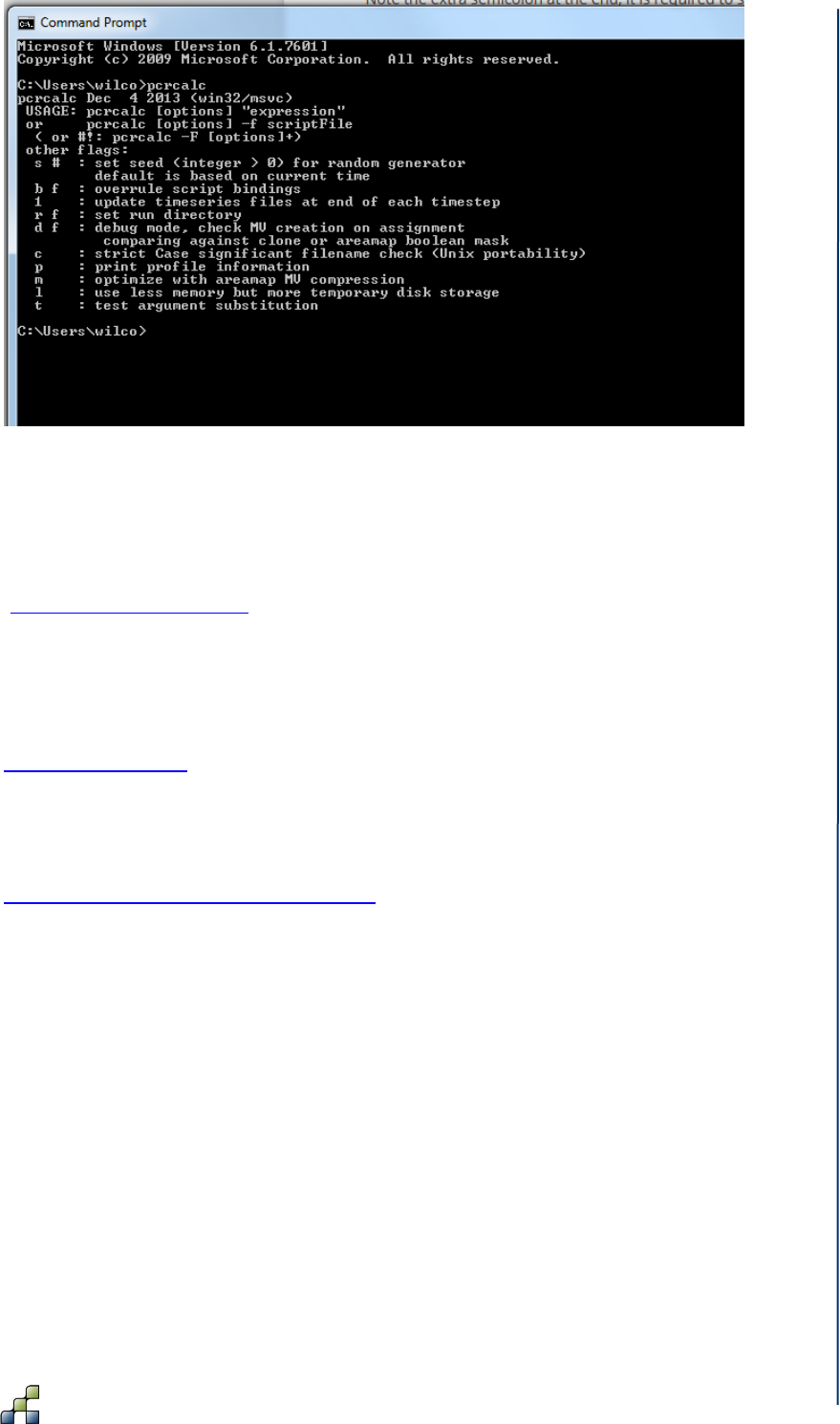
43
Figure 19: Command prompt view of testing a successful installation of PCRaster after
entering the pcrcalc command.
4.2.4 SPHY v2.0 source code
The SPHY v2.0 source code can be obtained from the SPHY model website
(http://www.sphy.nl/software/). The source code is available as a zip-file (SPHY2.0.zip) and
needs to be extracted to a folder on your hard drive. In our case we created the folder c:\SPHY
and unzipped the contents of SPHY2.0.zip to this folder. After unzipping the contents of
SPHY2.0.zip to a folder of your preference, installation has been completed successfully. The
SPHY model v2.0 source code can be downloaded directly using the link below:
Download SPHY v2.0
The login credentials that are required to download software and data from the SPHY model
website can be obtained using the link below:
http://www.sphy.nl/software/download-sphy/

44
5 Build your own SPHY-model
A SPHY model preprocessor has been developed that enables the user to automatically
generate SPHY model input data for a selected area of interest. This preprocessor has been
developed as a plugin for QGIS, and generates the input data using a database that can be
selected by the user. Currently, only one database can be used by the preprocessor: the “Hindu
Kush-Himalaya” database. The name of the SPHY model preprocessor is “SphyPreProcess”
(v1.0), and is described together with the SPHY model plugin in the SPHY GUIs manual (Terink
et al., 2015b).
If your area of interest is not covered by the extent of the database, then you can choose to
create your model input data manually (as is done in the Pungwe case-study (Terink et al.,
2015a)). You will need the PCRaster command line functions and GIS software, like the open
source QGIS. The steps that are required to do this are described in the sections below.
5.1 Select projection extent and resolution
First you need to start a new project within QGIS. Give it a useful name and save your project
regularly during the steps in the following sections. Because all calculations in SPHY are metric,
you will need to project your data in a metric coordinate system. In the example of the Pungwe
basin, we chose the WGS84 UTM Zone 36 South projection (EPSG:32736). Define the
minimum and maximum x and y values in the projection that you have chosen that cover the
entire area you want to model. Then, define the spatial resolution of your model. The choice of
resolution will be a tradeoff of the resolution of your input data, computation resources
availability, number of runs you intend to do and required detail for your modelling purpose. For
your reference, the model for the Pungwe case study has an extent of 275 x 255 km. For this
model the spatial resolution is 1000 x 1000 m, and thus the model contains ~70.000 grid cells.
Running this model at a daily time step for 5 years takes about 5 minutes.
In order to create your own model, you need to setup the directory structure. This means you
need to create a new SPHY model directory (containing the SPHY model source *.py files) and
in that directory you need to create a new input and output directory.
5.2 Clone map
You will need to define a ‘clone’ map, which is a map in PCRaster format, with the model extent
and resolution. This map is used as the ‘template’ for your model. You can create a clone map
using PCRaster’s mapattr command in the Windows Command line window. Make sure you are
in the model’s input directory. This can be done using commands as for example:
c: enter go to your c-drive
cd c:\SPHY\input enter
go to the SPHY\input directory on your c-drive
d: enter go to your d-drive
cd d:\SPHY\input enter
go to the SPHY\input directory on your d-drive
etc.
If you are in the model’s input directory, then type following in the Command line:
mapattr clone.map
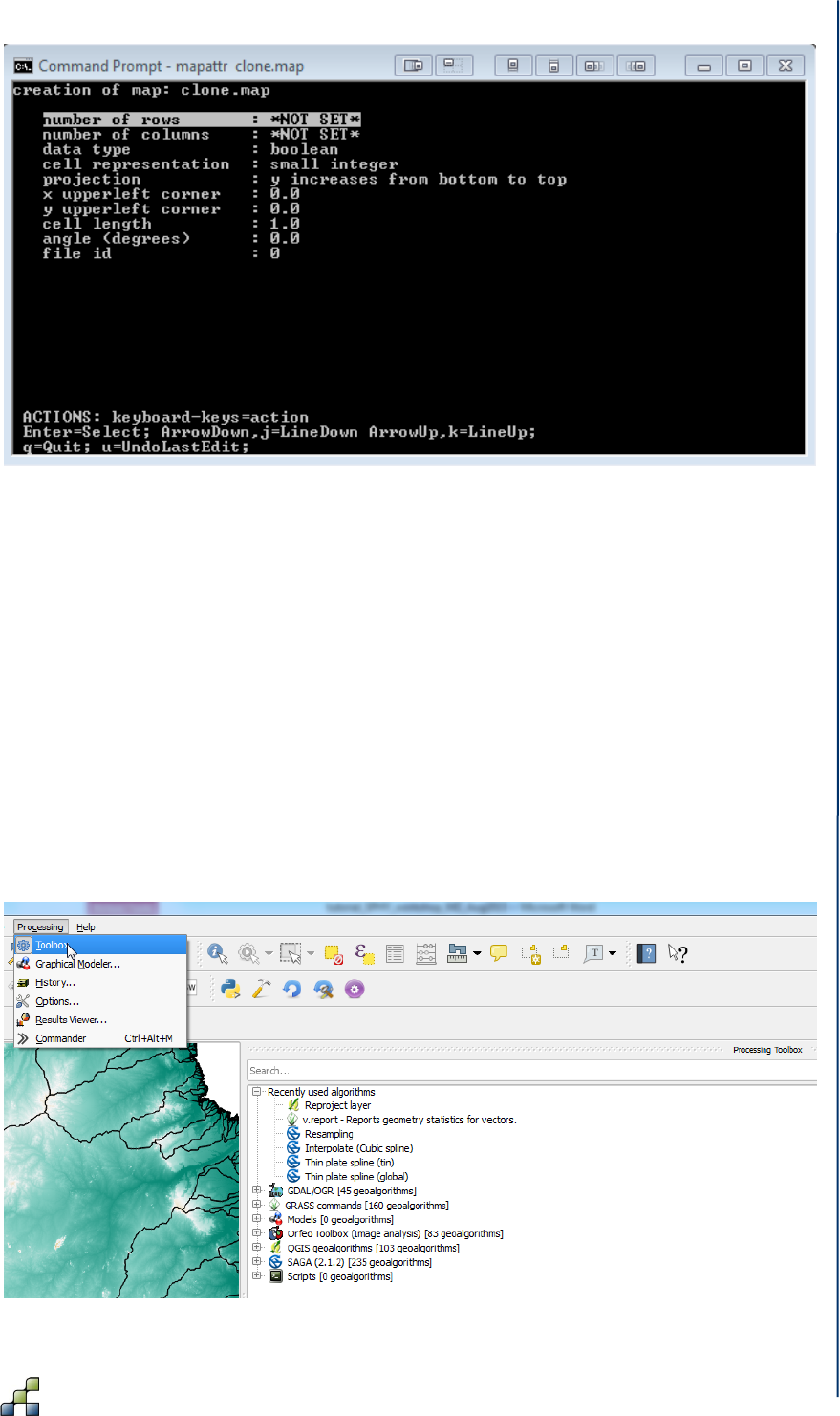
45
You will enter a menu, where you can set the clone map’s properties:
Figure 20: Command line menu for clone creation
Change the settings of the number of rows, number of columns, check if the y values in your
model projection increase from bottom to top or from top to bottom, define the x and y values of
the upperleft corner of your model’s extent, and define the cell length (spatial resolution).
When all is set, press “q” to quit and then press “y” to confirm the map creation. Then drag the
newly created map into QGIS to check if the map has the correct extent. Remember to set the
CRS of the “clone.map” after dragging the map into QGIS.
5.3 DEM and Slope
Before you continue with the next steps, make sure that you have opened the “Processing
Toolbox” in QGIS (see Figure 21). Next make sure that you select the “Advanced interface”
from the “Processing Toolbox” (see Figure 22).
Figure 21: Opening the “Processing Toolbox”.
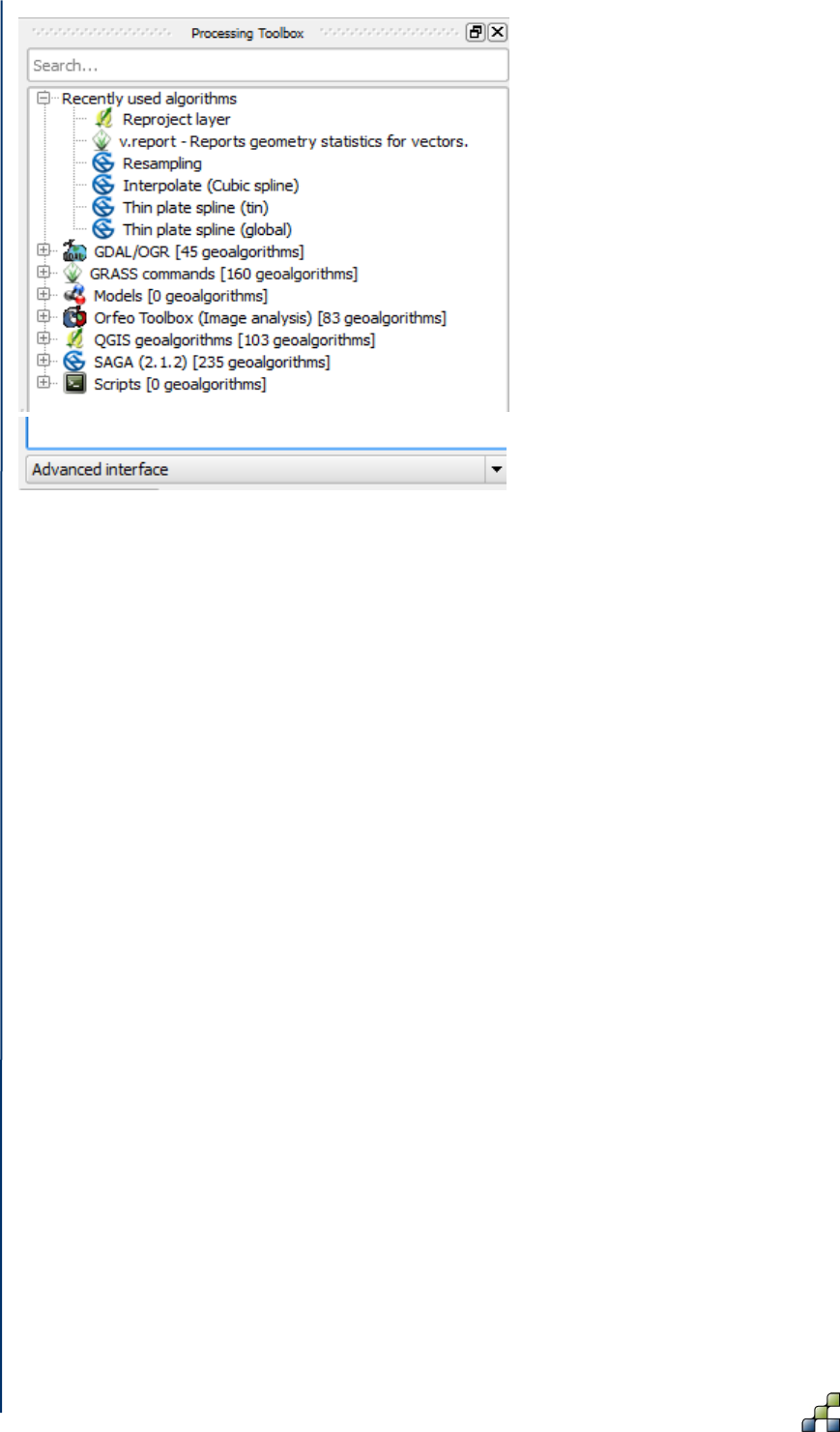
46
Figure 22: Selecting the “Advanced interface” in the “Processing Toolbox”.
Use your own DEM or otherwise the DEM provided in the database. You will need to project
your DEM in the model’s projection and resample the DEM to model resolution and extent. You
can do that using the following steps:
1. Drag the DEM inside the QGIS canvas;
2. Use the Warp tool in QGIS to reproject the DEM to the Coordinate Reference System
(CRS) of your basin (EPSG:XXXXXX). This can be found under Raster Projections
Warp (Reproject) (see Figure 23).
3. Within the Warp tool you need to select the “Input file”, the “Output file”, and the “Target
SRS”. The “Input file” is the layer that you need to reproject, which is in this case the
dem. The “Output file” is the file to which you want to save the reprojected dem in
GeoTiff format (*.tif). Give it a useful name and save it in a directory that is useful. In the
example of Figure 24, the reprojected dem is saved under the SPHY/input/ directory
with the name: dem_pr.tif. Finally, it is important that you select the correct “Target
SRS” (EPSG:XXXXX), which you defined in Section 5.1. In the example of Figure 24 it
is EPSG:32737. Then click OK to do the reprojection. After the reprojection is finished
click OK, and again OK, and finally Close.
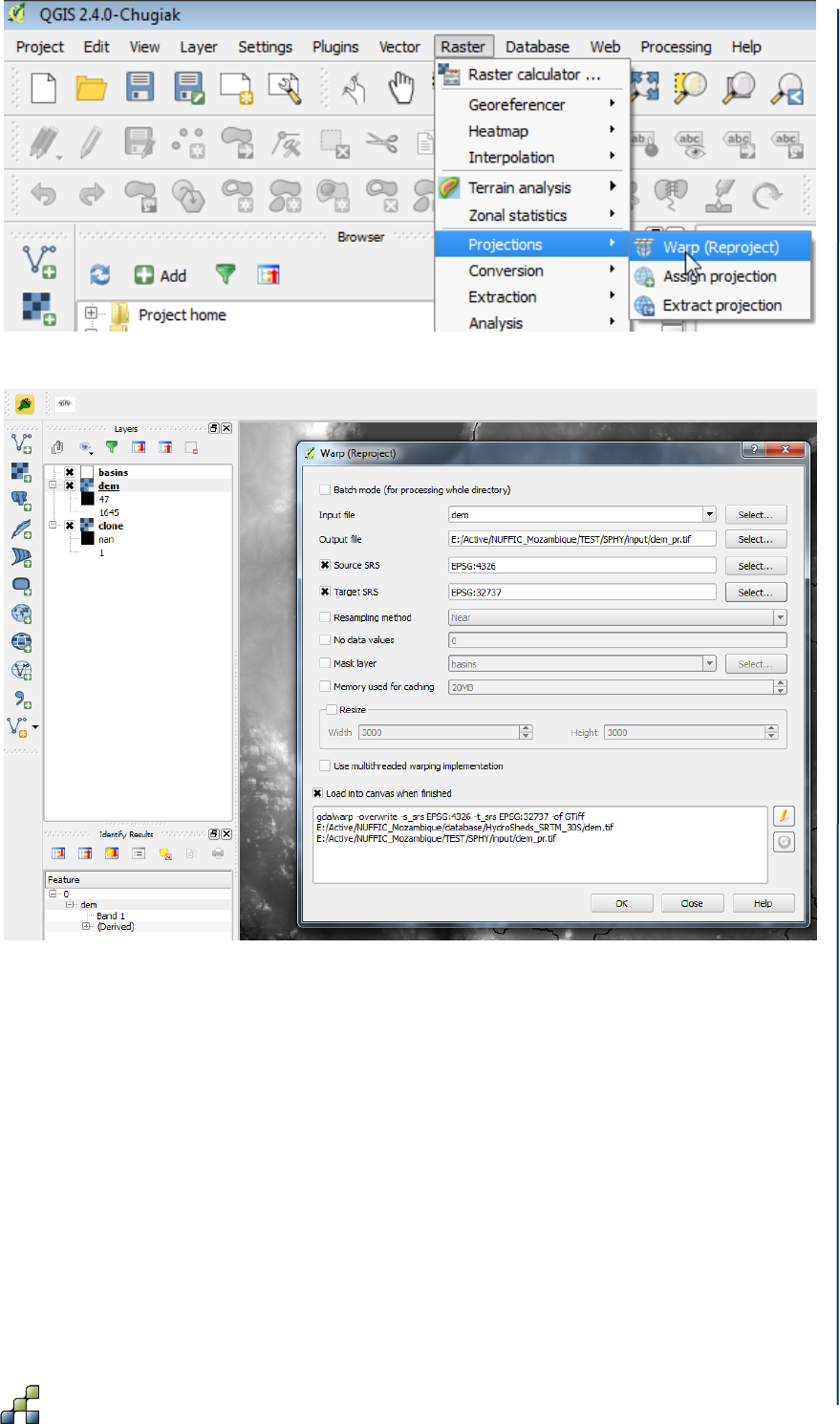
47
Figure 23: Warp tool
Figure 24: Setting the files and Source and Target SRS in the Warp Tool.
4. The next step involves resampling the projected dem from step 3) to the extent and
spatial resolution of the clone.map. For this you need to type “resampling” in the
“Processing Toolbox” search window (see Figure 25).
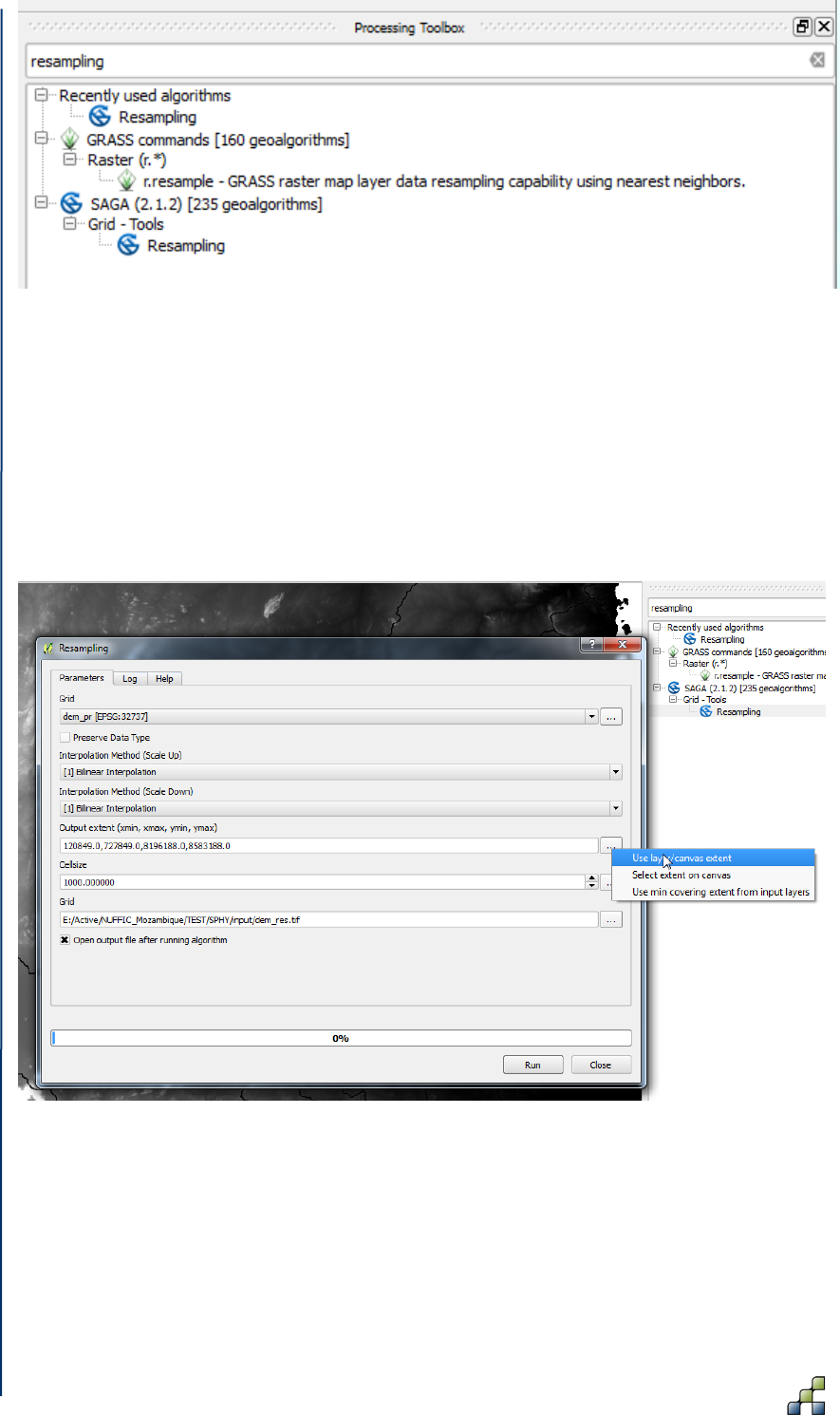
48
Figure 25: Selecting the Resampling tool in the Processing Toolbox.
5. Then double click “Resampling” under SAGA Grid – Tools to open the Resampling
tool as shown in Figure 26.
6. Within this tool you need to select the “Grid” file that you want to resample, the
“Interpolation Methods” for scaling up and for scaling down, the “Output extent”, the
“Cellsize”, and the “Grid” to which you want to save the resampled file. You also need to
check or uncheck the “Preserve Data Type” option. You can use Table 4 to determine
which options to set for the “Preserve Data Type”, and the “Interpolation Methods” for
scaling up and for scaling down.
Figure 26: Setting the Resampling tool options.
49
Table 4: Resampling settings based on the layer data type.
Layer data type
Preserve Data
Type
Interpolation
Method (scale
Up)
Interpolation
Method (scale
Down)
Example layer
Continuous
No
Bilinear
Bilinear
DEM
Classified
No
Majority
Nearest
neighbor
Landuse
7. Since the projected dem that we want to resample is continuous data, we select
“Bilinear Interpolation” for both the interpolation methods, and we uncheck the
“Preserve Data Type” option. For the “Grid” we select the projected dem from step 3).
For the “Output extent” we use the layer extent (see Figure 26) of the clone.map. For
the “Cellsize” (=cell length) you can fill in the value that you determined in Section 5.1.
Then, save the resampled Grid as GeoTiff in the “Grid” in a useful directory. In the
example of Figure 26 the file is saved as dem_res.tif under the directory SPHY/input/.
Finally, click Run to finish the resampling. If these steps are performed correctly, then
your resampled dem should have the same extent and spatial resolution as your
clone.map.
8. The final step involves converting the GeoTiff format to the PCRaster *.map format.
This can be done using the Translate function under Raster Conversion Translate
(Convert Format) (see Figure 27).
Figure 27: Translate tool (convert raster format)
9. In the “Translate” box (see Figure 28) make sure that you select the “Input Layer”
(result from step 7) and set the “Output Layer”. The “Output Layer” should be save as
PCRaster Raster File format (*.map). In the example of Figure 29 we save it in the
SPHY\input\ directory with the name dem.map. Finally click OK, and OK, and OK, and
Close to finish this step.
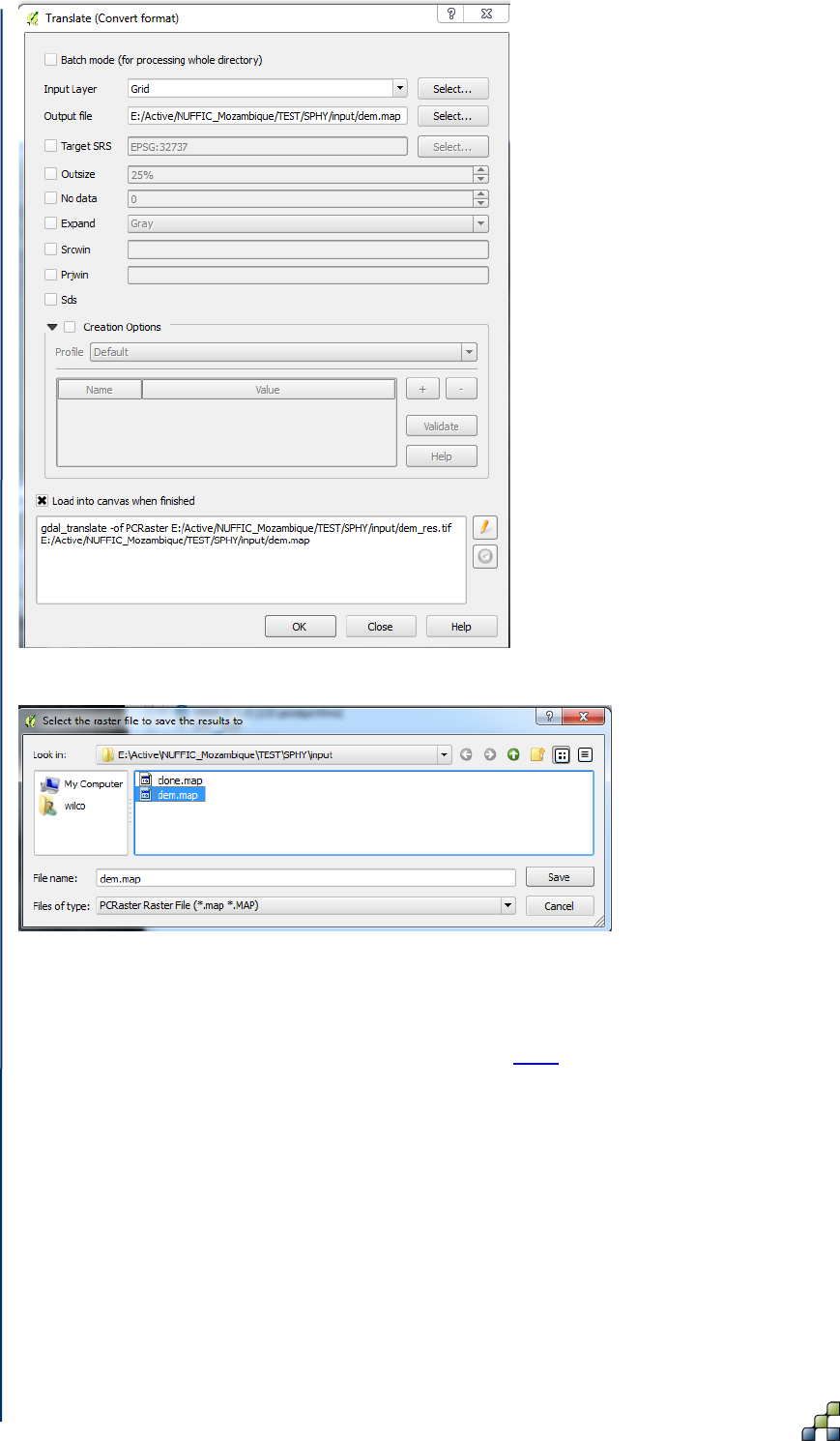
50
Figure 28: Setting the Translate options.
Figure 29: Saving the translated raster as a PCRaster Raster File (*.map).
Now you should have the DEM in the model resolution and extent and in PCRaster format.
The slope map can be derived from the DEM using the slope command. This can be done in
the Windows Command line window by typing:
pcrcalc slope.map = slope(dem.map)
5.4 Delineate catchment and create local drain direction map
You can now use the DEM you created in the previous section to generate a local drain
direction (LDD) map for your own model area.
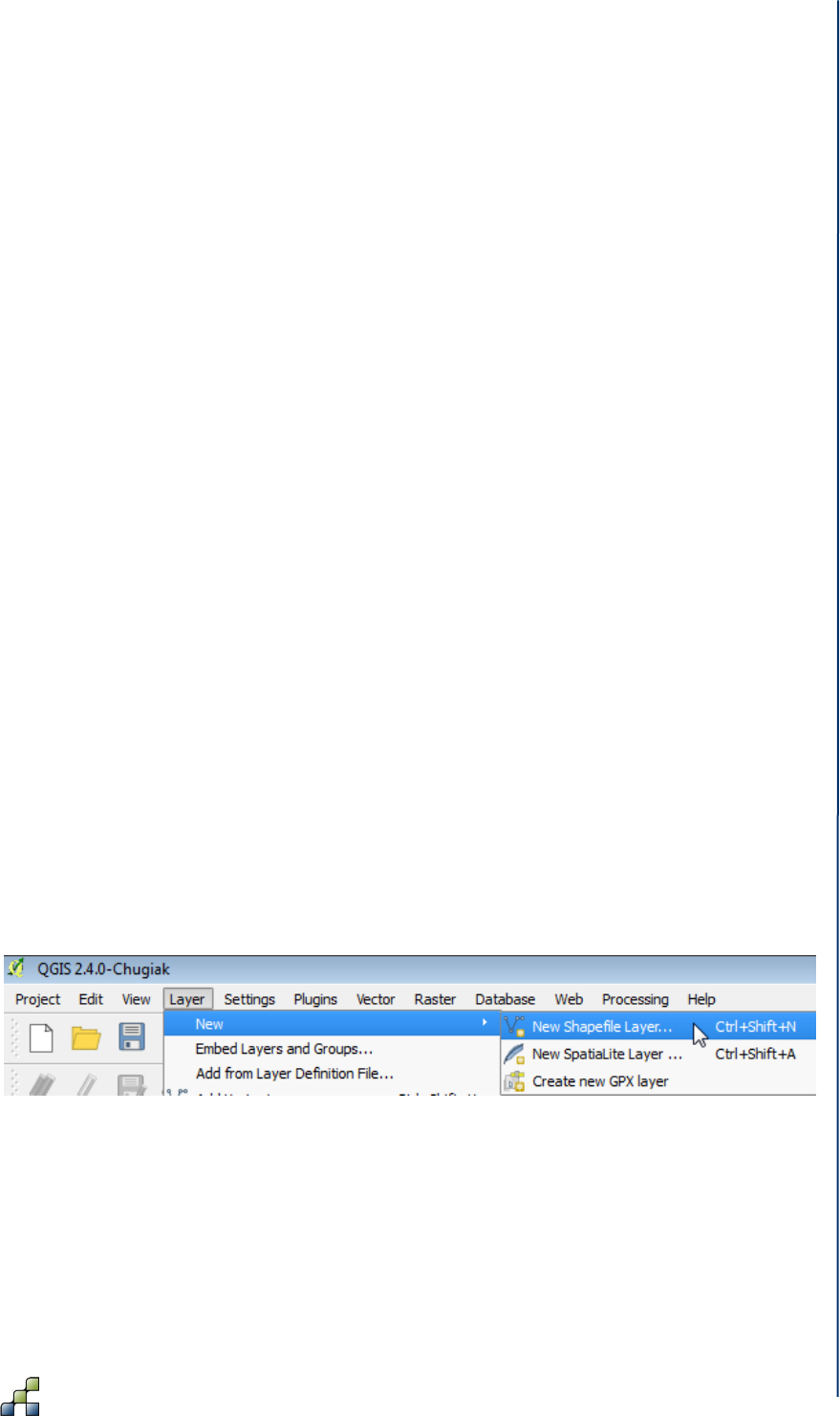
51
To create a flow direction map (or local drain direction (LDD)), you can use the pcraster
command lddcreate. Type the following command in the Windows Command line window:
pcrcalc ldd.map = lddcreate(dem.map, 1e31,1e31,1e31,1e31)
This command should also fill the sinks in the DEM to avoid that pits are generated in the
depression in the DEM, which could hamper the water to flow to the basin’s outlet. A good way
to test if the LDD map is correct is to calculate for each cell how many cells are upstream. You
can do this using the pcraster command accuflux. Type:
pcrcalc accuflux.map = accuflux(ldd.map,1)
Drag the newly generated accuflux.map to the QGIS canvas. Check if the stream network is
complete, and all branches are connected to the outlet point.
If the generated LDD is not entirely correct and not all streams are connected toward the
downstream outlet point, this happens because during the creation of the LDD map, pits have
been generated where depressions in the landscape are present. More details on the LDD
generation can be found in the PCRASTER online manual. There are multiple ways to
overcome the problem of pit generation. The first and most easy option is to try this command in
the Windows Command line window:
pcrcalc ldd.map = lddrepair(ldd.map)
If this does not solve the correct creation of the ldd.map, then you can try the following options:
Test different values for the parameters in the lddcreate command
Remove pits manually by changing the values for those cells.
Use a map with the streams present in your study area and “burn” them into the DEM to
force the other cells to drain in into them.
5.5 Preparing stations map and sub-basins.map
To prepare a stations map it is easiest to use a vector file with the point locations (for example a
shapefile), to a PCRaster grid (.map file). You can create a new shapefile with points in QGIS
under Layer New New Shapefile layer:
Figure 30: Create new shapefile layer
Make sure that you select “Point” and that the CRS corresponds (see Figure 31) with the EPSG
that you have defined in Section 5.1. Finally click OK to create the New Shapefile Layer and
save it under a useful name, for example locations.shp.
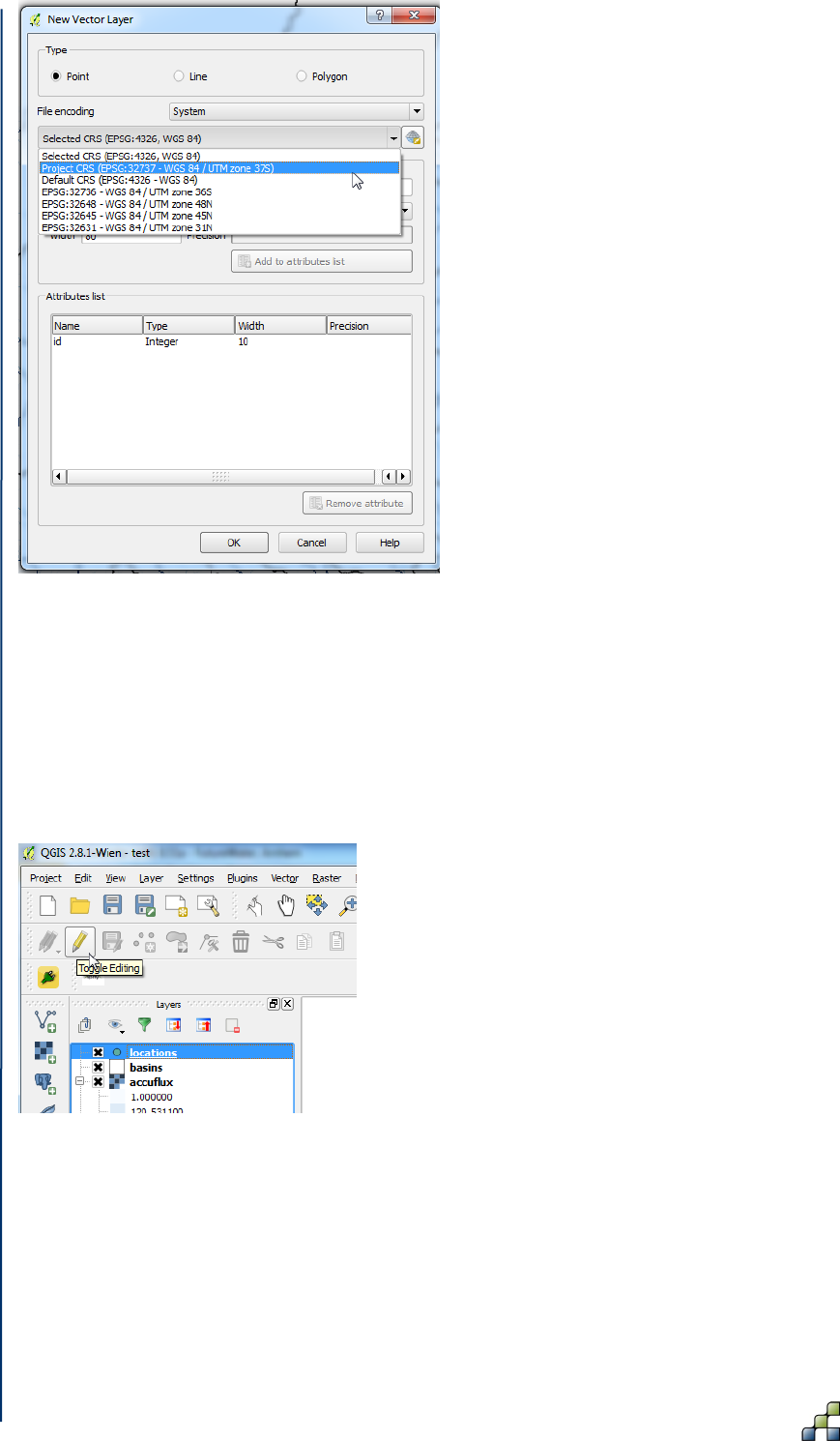
52
Figure 31: Setting the properties of the New Shapefile Layer.
The next step involves adding points to the Shapefile where you want the SPHY model to report
time-series. Often these points correspond with the locations of discharge measurement
stations. If you have an existing Shapefile of discharge measurement stations in your basin,
then you can easily drag this file into QGIS to identify these locations. Now you can start adding
points to the newly created Shapefile by following these steps:
1. Make sure the “locations” layer is selected. Then click “Toggle Editing” to change the
layer to editing mode (see Figure 32).
Figure 32: Toggle Editing for Shapefiles.
2. Then click the “Add Feature” option (see Figure 33). Now you can start adding points to
the map where you want the SPHY model to create time-series output. The
accuflux.map can help you determining if you are adding a point to the river network.
Add as many as points as you like. For each point you need to provide an ID number.
Start with ID 1, then ID 2, etc. In the example of Figure 34 we added 3 points to the
“locations” layer.

53
Figure 33: Add Feature for Shapefiles.
Figure 34: Adding points to the locations Shapefile layer using the accuflux.map.
3. If you are finished with adding the points, then you again can click the “Toggle Editing”
button and Save your edits.
4. The next step involves converting the “locations” Shapefile layer to a raster layer. This
can be done using the “v.to.rast.attribute” tool in QGIS under Processing Toolbox (see
Figure 35).
5. Within this toolbox (Figure 36) set the “locations” layer as “Input vector layer”, make
sure that the “id” column is selected, set the “GRASS region extent” by specifying the
clone.map layer, and set the “GRASS region cellsize” as determined before. Finally,
choose a “Rasterized” layer name (e.g. “locations.tif”) and click Run.
6. The final step again involves converting the resulting GeoTiff raster from step 5) to a
PCRaster *.map format. This can be done using the Raster Conversion Translate
tool (see Figure 27 and Figure 28). The only additional step required here is to click the
“Edit” button (see Figure 37) and add the following syntax: -ot Float32 (see Figure
38).
7. Finally click OK, and again OK, and again OK, and Close to finish the conversion.
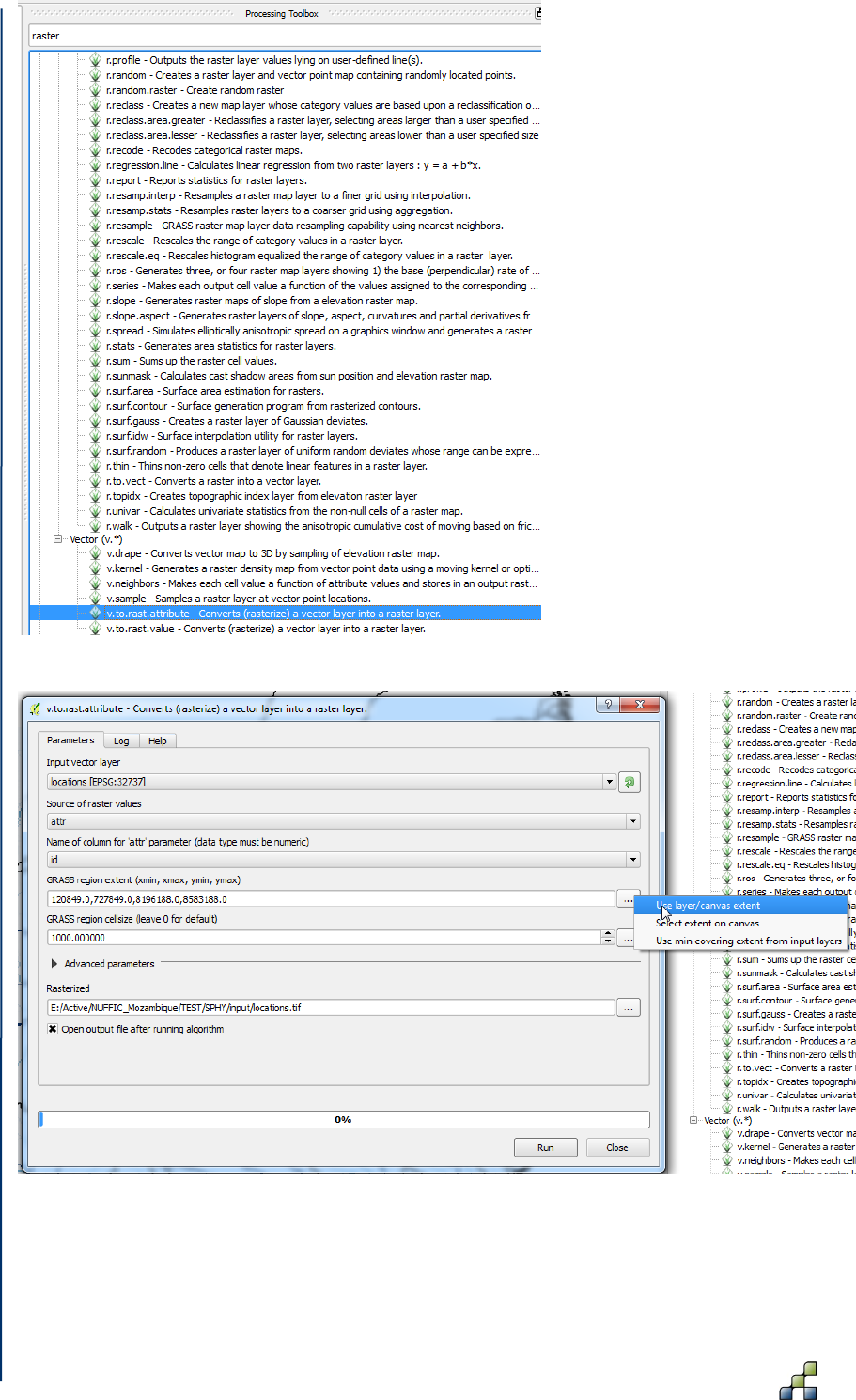
54
Figure 35: Selecting the v.to.rast.attribute tool from the Processing Toolbox.
Figure 36: Setting the options in the v.to.rast.attribute tool.
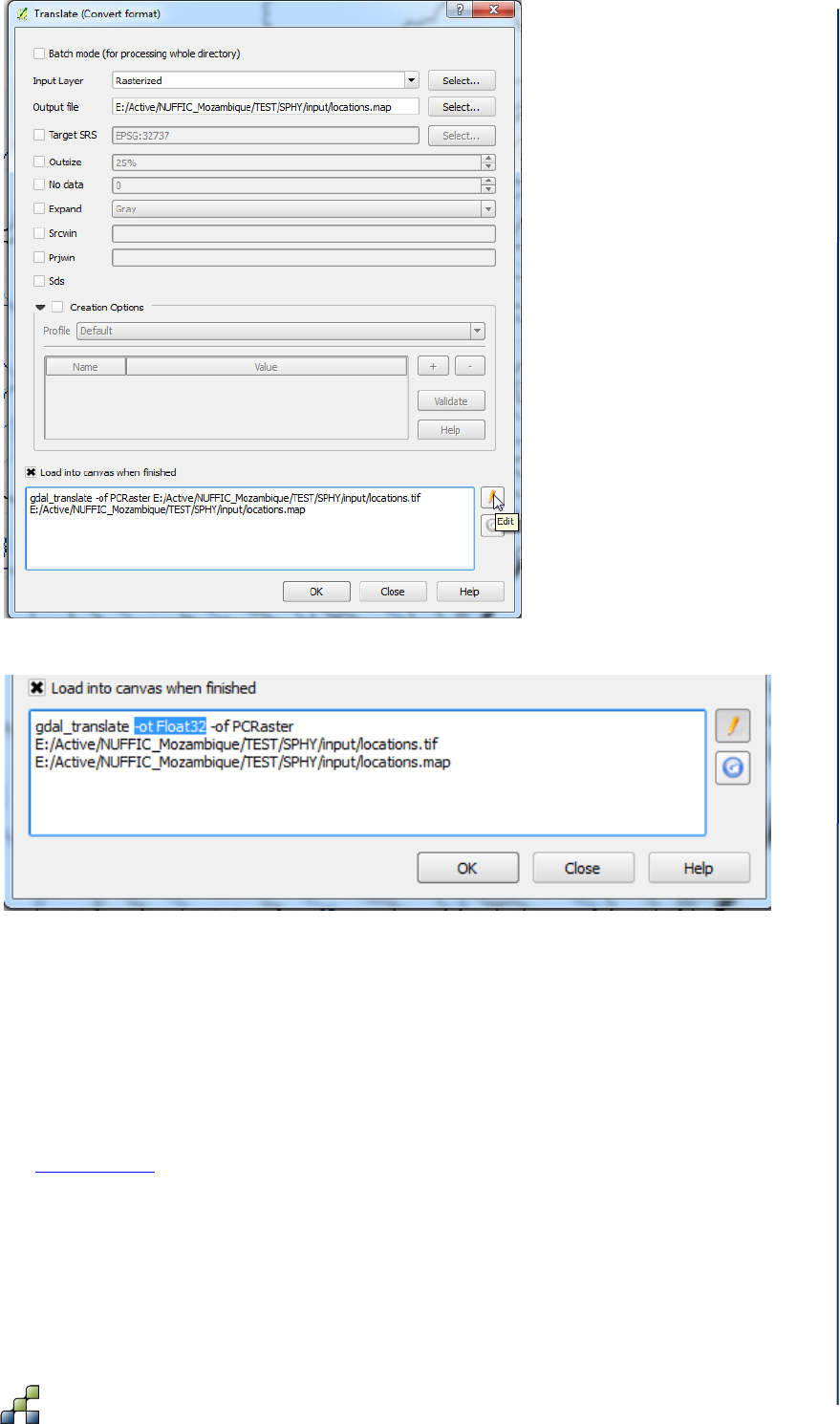
55
Figure 37: Editing the command for Translation.
Figure 38: Adding the “-ot Float32” syntax to the command for Translation.
The resulting “locations.map” is of the Float32 data format (scalar). As can be seen Table 5
from it is required to have a nominal format for station files. This can be achieved by typing the
following command in the Windows Command line:
pcrcalc locs.map = nominal(locations.map)
You can use locs.map and ldd.map to delineate the catchments of the points in locs.map. Use
the subcatchment command for that:
pcrcalc catchment.map = subcatchment(ldd.map, locs.map)
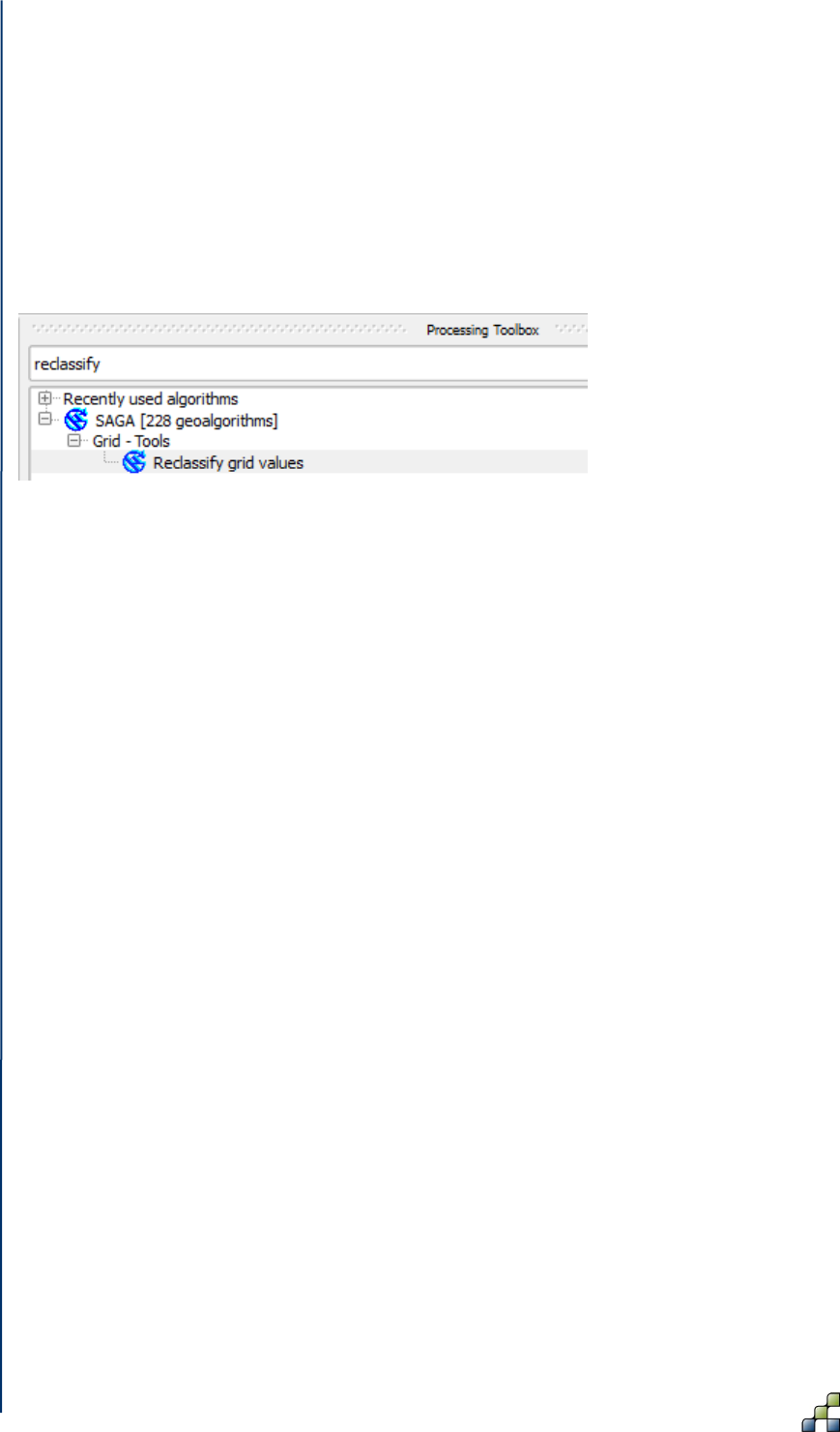
56
5.6 Glacier fraction map
The glacier fraction map can be calculated from a vector file with glacier outlines. In QGIS from
the Processing toolbox, select the “v.to.rast.value” tool like in the previous section.
Select your glacier outlines as vector input layer and convert it to raster at the same extent of
the clone map. Set the cellsize at a lower value than your model resolution. For example, if your
model cell size is 200 m, select 20 m for the converted raster.
The “nodata” values need to be reclassified to zeros. To do this use SAGA’s Reclassify tool
from the Processing toolbox. You can easily find it by typing Reclassify in the search field.
Figure 39: Reclassify tool
In the dialog box set all values to 0.0, and set “replace no data values” to “Yes”, set “new value
for no data values” to 0.0 and set “replace other values” to “No”. Select an output filename and
click “Run”.
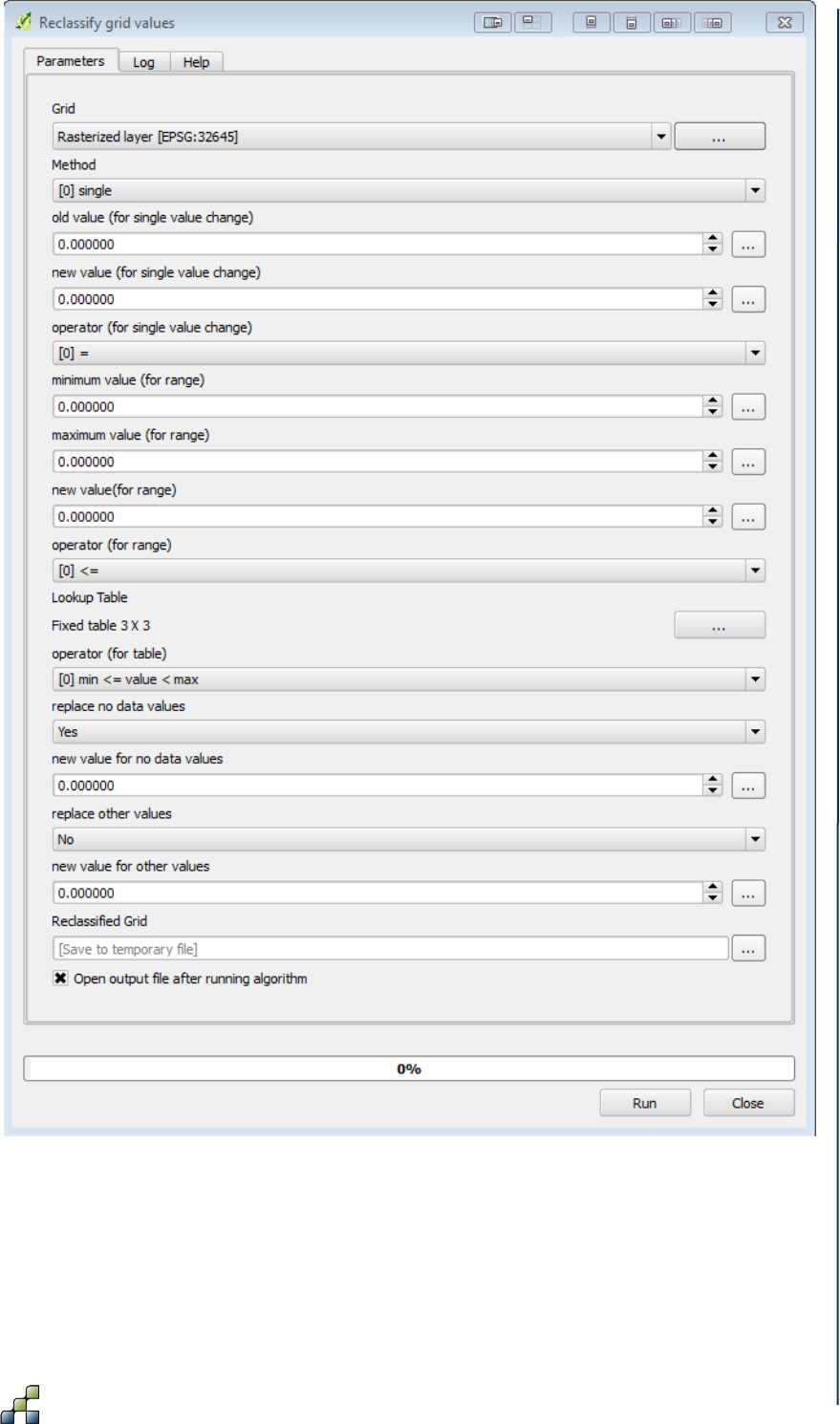
57
Figure 40: Reclassify tool dialog box
Now we aggregate the fine resolution grid with glaciers to the model resolution. This can be
done using the “r.resamp.stats” tool selected under Processing Toolbox GRASS commands
Raster r.resamp.stats.
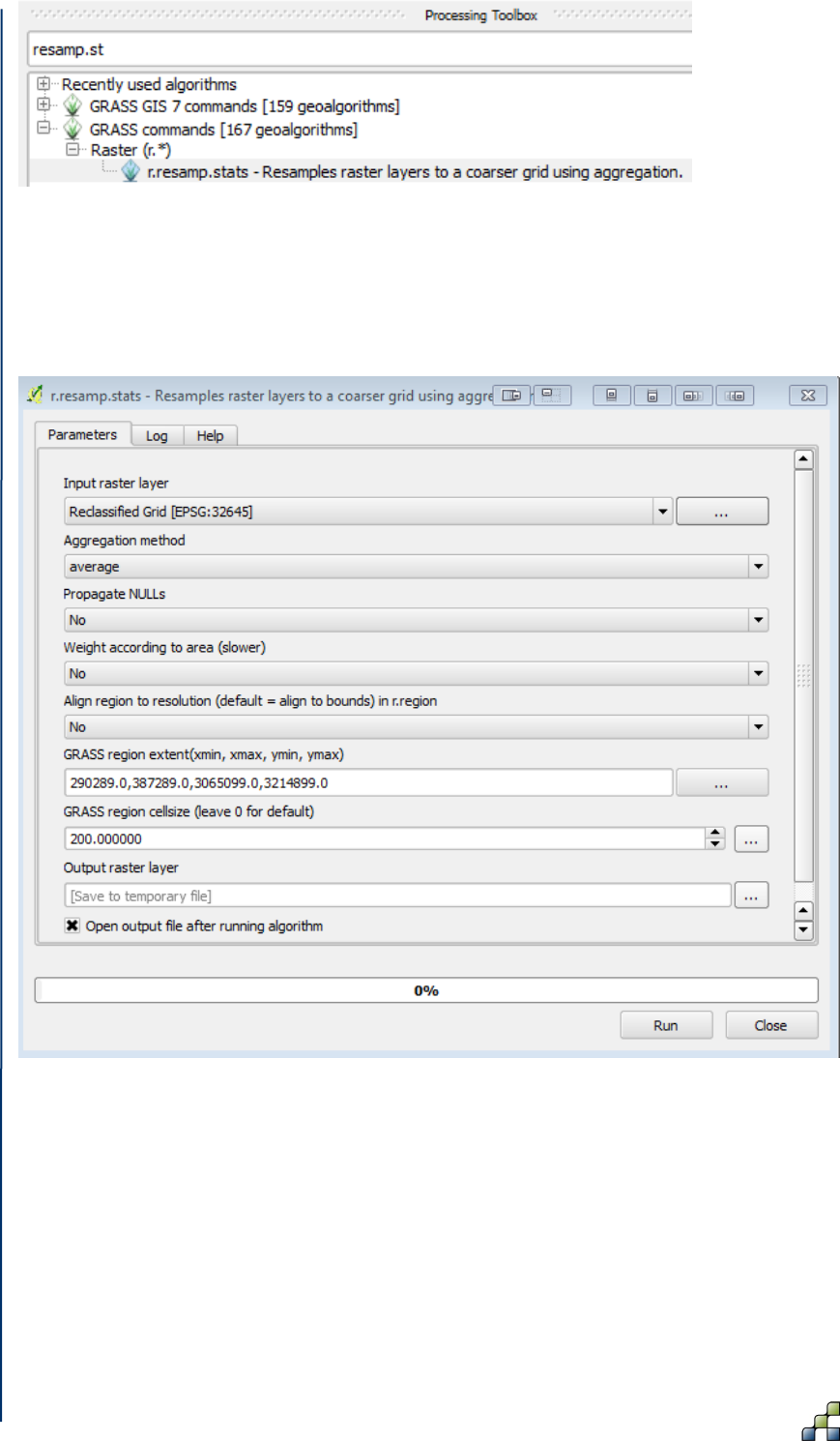
58
Figure 41: GRASS aggregation tool
In the dialog box, set the fine resolution glacier grid as input raster layer and choose
aggregation method “average”. Import the processing extent from the clone map and set the cell
size to the model resolution (in the screenshot below it is 200m as in the example of the Trisuli
case study).
Figure 42: GRASS aggregation tool dialog box
The resulting grid can be converted to a PCRaster map using step 8 from Section 5.3.
5.7 Other static input maps
Similar as the DEM, you can reproject and resample other static model input data and convert
them to PCRaster format maps using the reprojection and resampling functions in QGIS (step
1-9 from Section 5.3). Note that different data types are used for PCRaster maps. You can
convert maps from one data type to another using the command line functions boolean(),
59
nominal(), ordinal(), scalar(), directional() or ldd(). For example to convert the scalar type
landuse.map to a nominal landuse.map, type:
pcrcalc landuse_nominal.map = nominal(landuse.map)
Table 5: Data types used in SPHY.
data type
description
attributes
domain
Example
boolean
boolean
0 (false), 1 (true)
suitable/unsuitable, visible/non
visible
nominal
classified, no
order
-231 ... 231, whole values
soil classes, land use classes,
discharge stations,
administrative regions
ordinal
classified, order
-231 ... 231, whole values
succession stages, income
groups
scalar
continuous, lineair
-1037...1037, real values
elevation, temperature
directional
continuous,
directional
0 to 2 pi (radians), or to
360 (degrees), and -1 (no
direction), real values
aspect
ldd
local drain
direction to
neighbour cell
1...9 (codes of drain
directions)
drainage networks, wind
directions
5.8 Meteorological forcing map series
Meteorological forcing map-series are series of input maps with the time step indicated in each
filename. The filenames have a strict format with 8 characters before a dot (.), and three
characters behind the dot. For example the average temperature maps can have the format
tavg0000.001, tavg0000.002, etc. To generate forcing data you have two options:
1) interpolate point station data to grids at the model extent and resolution, and convert to
PCRaster grid format.
2) resample existing gridded meteorological data products to model extent and resolution
and convert to PCRaster grid format.
Depending on the number of time steps in your model you will probably need to write a script to
batch this process and repeat it automatically for multiple time steps. A script like this can be
created in any scripting language like for example Python or R. This procedure is automated in
the SPHY preprocessor plugin (Terink et al., 2015b).

60
6 References
Abbott, M., Bathurst, J., Cunge, J., O’Connell, P., and Rasmussen, J.: An introduction to the
European Hydrological System – Systeme Hydrologique Europeen, “SHE”, 2: Structure
of a physically-based, distributed modelling system, J. Hydrol., 87, 61–77, 1986.
ADB: Consultant’s Report Regional Technical Assistance: Water and Adaptation Interventions
in Central and West Asia, Tech. rep., 2012.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration – Guidelines for
computing crop water requirements, FAO Irrigation and drainage paper, 56, 1998.
Andersson, E.: User guide to ECMWF forecast products. Version 1.1, Tech. rep., ECMWF,
available at: http://old.ecmwf.int/products/forecasts/guide/user_guide.pdf (last access:
02 August 2014), 2013.
Bartholomeus, R. P., Witte, J.-P. M., van Bodegom, P. M., van Dam, J. C., and Aerts, R.:
Critical soil conditions for oxygen stress to plant roots: Substituting the Feddes function
by a process-based model, J. Hydrol., 360, 147–165, doi:10.1016/j.jhydrol.2008.07.029,
2008.
Bastiaanssen, W., Allen, R., Droogers, P., Da’Urso, G., and Steduto, P.: Twenty-five years
modeling irrigated and drained soils: State of the art, Agr. Water Managent., 92, 111–
125, doi:10.1016/j.agwat.2007.05.013, 2007.
Batjes, N., Dijkshoorn, K., van Engelen, V., Fischer, G., Jones, A., Montanarella, L., Petri, M.,
Prieler, S., Teixeira, E., Wiberg, D., and Shi, X.: Harmonized World Soil Database
(version 1.1), Tech. rep., FAO and IIASA, Rome, Italy and Laxenburg, Austria, 2009.
Batjes, N., Dijkshoorn, K., van Engelen, V., Fischer, G., Jones, A., Montanarella, L., Petri, M.,
Prieler, S., Teixeira, E., Wiberg, D., and Shi, X.: Harmonized World Soil Database
(version 1.2), Tech. rep., FAO and IIASA, Rome, Italy and Laxenburg, Austria, 2012.
Beven, K.: Kinematic subsurface stormflow,Water Resour. Res., 17, 1419–1424,
doi:10.1029/WR017i005p01419, 1981.
Beven, K.: Robert E. Horton’s perceptual model of infiltration processes, Hydrol. Process., 18,
3447–3460, doi:10.1002/hyp.5740, 2004.
Beven, K. and Germann, P.: Macropores and water flow in soils, Water Resour. Res., 18, 1311–
1325, doi:10.1029/WR018i005p01311, 1982.
Bierkens, M. F. P. and van Beek, L. P. H.: Seasonal Predictability of European Discharge: NAO
and Hydrological Response Time, J. Hydrometeorol., 10, 953–968,
doi:10.1175/2009JHM1034.1, 2009.
Biswas, A. K. and Tortajada, C.: Future Water Governance: Problems and Perspectives, Int. J.
Water Resour. D., 26, 129–139, doi:10.1080/07900627.2010.488853, 2010.
Bontemps, S., Defourny, P., van Bogaert, E., Arino, O., Kalogirou, V., and Ramos Perez, J.:
GLOBCOVER 2009. Products Description and Validation Report, Tech. rep., ESA,
2011.
Bowling, L. C., Pomeroy, J. W., and Lettenmaier, D. P.: Parameterization of Blowing-Snow
Sublimation in a Macroscale Hydrology Model, J. Hydrometeorol., 5, 745–762,
doi:10.1175/1525-7541(2004)005<0745:POBSIA>2.0.CO;2, 2004.
Bracken, C., Rajagopalan, B., and Prairie, J.: A multisite seasonal ensemble streamflow
forecasting technique, Water Resour. Res., 46, doi:10.1029/2009WR007965, 2010.
Bramer, L. M., Hornbuckle, B. K., and Caragea, P. C.: How Many Measurements of Soil
Moisture within the Footprint of a Ground-Based Microwave Radiometer Are Required
to Account for Meter-Scale Spatial Variability?, Vadose Zone J., 12, 3,
doi:10.2136/vzj2012.0100, 2013.
Brutsaert, W.: De Saint-Venant Equations Experimentally Verified, J. Hydr. Eng. Div.-ASCE, 97,
1387–1401, 1971.

61
Brutsaert, W.: Hydrology. An introduction., Cambridge University Press, Cambridge, 2005.
Carlson, T. N. and Ripley, D. A.: On the relation between NDVI, fractional vegetation cover, and
leaf area index, Remote Sens. Environ., 62, 241–252, doi:10.1016/S0034-
4257(97)00104-1, 1997.
Clark, M. P., Slater, A. G., Rupp, D. E., Woods, R. A., Vrugt, J. A., Gupta, H. V.,Wagener, T.,
and Hay, L. E.: Framework for Understanding Structural Errors (FUSE): A modular
framework to diagnose differences between hydrological models, Water Resour. Res.,
44, W00B02, doi:10.1029/2007WR006735, 2008.
Clark, M. P., Nijssen, B., Lundquist, J. D., Kavetski, D., Rupp, D. E., Woods, R. A., Freer, J. E.,
Gutmann, E. D., Wood, A. W., Brekke, L. D., Arnold, J. R., Gochis, D. J., and
Rasmussen, R. M.: A unified approach for process-based hydrologic modeling: 1.
Modeling concept, Water Resour. Res., 51, 2498–2514, doi:10.1002/2015WR017198,
2015a.
Clark, M. P., Nijssen, B., Lundquist, J. D., Kavetski, D., Rupp, D. E., Woods, R. A., Freer, J. E.,
Gutmann, E. D., Wood, A. W., Gochis, D. J., Rasmussen, R. M., Tarboton, D. G.,
Mahat, V., Flerchinger, G. N., and Marks, D. G.: A unified approach for process-based
hydrologic modeling: 2. Model implementation and case studies, Water Resour. Res.,
51, 2515–2542, doi:10.1002/2015WR017200, 2015b.
Contreras, S., Hunink, J., and Baille, A.: Building a Watershed Information System for the
Campo de Cartagena basin (Spain) integrating hydrological modeling and remote
sensing. FutureWater Report 125., Tech. rep., FutureWater, 2014.
Corradini, C., Morbidelli, R., and Melone, F.: On the interaction between infiltration and
Hortonian runoff, J. Hydrol., 204, 52–67, doi:10.1016/S0022-1694(97)00100-5, 1998.
Dai, A.: Drought under global warming: a review, Wiley Interdisciplinary Reviews: Climate
Change, 2, 45–65, doi:10.1002/wcc.81, 2011.
de Jong, S. and Jetten, V.: Distributed, quantitative assessment of canopy storage capacity by
Hyperspectral Remote Sensing, available at: http://www.geo.uu.nl/dejong/pdf-
files/Interception-by-RS.pdf (last access: 13 November 2014), 2010.
Deb, S. and Shukla, M.: Soil hydrology, land use and agriculture: measurement and modelling,
Las Cruces, doi:10.1079/9781845937973.0000, 2011.
Droogers, P. and Aerts, J.: Adaptation strategies to climate change and climate variability: A
comparative study between seven contrasting river basins, Phys. Chem. Earth Pt.
A/B/C, 30, 339–346, doi:10.1016/j.pce.2005.06.015, 2005.
Droogers, P. and Bouma, J.: Simulation modelling for water governance in basins, Int. J. Water
Resour. D., 30, 475–494, doi:10.1080/07900627.2014.903771, 2014.
Droogers, P. and Immerzeel, W. W.: Wat is het beste model?, H2O Tijdschrift voor
watervoorziening en waterbeheer, 4, 38–41, 2010.
Droogers, P., Immerzeel, W. W., Terink, W., Hoogeveen, J., Bierkens, M. F. P., van Beek, L. P.
H., and Debele, B.: Water resources trends in Middle East and North Africa towards
2050, Hydrol. Earth Syst. Sci., 16, 3101–3114, doi:10.5194/hess-16-3101-2012, 2012.
EEA: EU-DEM layers, Copernicus data and information funded by the European Union,
European Environmental Agency, Tech. rep., 2014.
Endrizzi, S., Dall’ Amico, M., Gruber, S., and Rigon, R.: GEOtop Users Manual. User Manual
Version 1.0, Tech. rep., Department of Physical Geography, University of Zurich,
Zurich, 2011.
Endrizzi, S., Gruber, S., Dall’Amico, M., and Rigon, R.: GEOtop 2.0: simulating the combined
energy and water balance at and below the land surface accounting for soil freezing,
snow cover and terrain effects, Geosci. Model Dev., 7, 2831–2857, doi:10.5194/gmd-7-
2831-2014, 2014.

62
EPA: Modeling at EPA, available at: http://www.epa.gov/epahome/models.htm (last access: 30
September 2014), 2014.
Essery, R., Morin, S., Lejeune, Y., and B Ménard, C.: A comparison of 1701 snow models using
observations from an alpine site, Adv. Water Resour., 55, 131–148,
doi:10.1016/j.advwatres.2012.07.013, 2013.
FAO: FAOWater. CropWater Information, available at: http://www.fao.org/nr/water/cropinfo.html
(last access: 09 June 2014), 2013.
Feddes, R., Kowalik, P., and Zaradny, H.: Simulation of field water use and crop yield.
Simulation Monographs, Pudoc,Wageningen University, 1978.
Finger, D., Pellicciotti, F., Konz, M., Rimkus, S., and Burlando, P.: The value of glacier mass
balance, satellite snow cover images, and hourly discharge for improving the
performance of a physically based distributed hydrological model, Water Resour. Res.,
47, W07519, doi:10.1029/2010WR009824, 2011.
Foglia, L., Hill, M. C., Mehl, S. W., and Burlando, P.: Sensitivity analysis, calibration, and testing
of a distributed hydrological model using error-based weighting and one objective
function, Water Resour. Res., 45, W06427, doi:10.1029/2008WR007255, 2009.
Gat, J. R., Bowser, C. J., and Kendall, C.: The contribution of evaporation from the Great Lakes
to the continental atmosphere: estimate based on stable isotope data, Geophys. Res.
Lett., 21, 557– 560, doi:10.1029/94GL00069, 1994.
Gill, M. A.: Flood routing by the Muskingum method, J. Hydrol., 36, 353–363, doi:10.1016/0022-
1694(78)90153-1, 1978.
Gopalan, K., Wang, N.-Y., Ferraro, R., and Liu, C.: Status of the TRMM 2A12 Land Precipitation
Algorithm, J. Atmos. Ocean. Tech., 27, 1343–1354, doi:10.1175/2010JTECHA1454.1,
2010.
Goward, S. N. and Huemmrich, K. F.: Vegetation canopy PAR absorptance and the normalized
difference vegetation index: An assessment using the SAIL model, Remote Sens.
Environ., 39, 119–140, doi:10.1016/0034-4257(92)90131-3, 1992.
Grantz, K., Rajagopalan, B., Clark, M., and Zagona, E.: A technique for incorporating large-
scale climate information in basinscale ensemble streamflow forecasts, Water Resour.
Res., 41, doi:10.1029/2004WR003467, 2005.
Groot Zwaaftink, C. D., Mott, R., and Lehning, M.: Seasonal simulation of drifting snow
sublimation in Alpine terrain, Water Resour. Res., 49, 1581–1590,
doi:10.1002/wrcr.20137, 2013.
Hall, D. K., Riggs, G. A., Salomonson, V. V., DiGirolamo, N. E., and Bayr, K. J.: MODIS snow-
cover products, Remote Sens. Environ., 83, 181–194, doi:10.1016/S0034-
4257(02)00095-0, 2002.
Hargreaves, G. H. and Samani, Z. A.: Reference Crop Evapotranspiration from Temperature,
Appl. Eng. Agric., 1, 96–99, doi:10.13031/2013.26773, 1985.
HEC: Hydrologic Engineering Center (HEC) computer software for hydrologic engineering and
planning analysis, available at: http://www.hec.usace.army.mil/software/ (last access:
03 September 2014), 2014.
Hewlett, J.: Soil moisture as a source of base flow from steep mountain watershed, Tech. rep.,
US forest Service, Southeastern Forest Experiment Station, Asheville, North Carolina,
1961.
Heynen, M., Pellicciotti, F., and Carenzo, M.: Parameter sensitivity of a distributed enhanced
temperature-index melt model, Ann. Glaciol., 54, 311–321,
doi:10.3189/2013AoG63A537, 2013.
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., and Jarvis, A.: Very high resolution
interpolated climate surfaces for global land areas, Int. J. Climatol., 25, 1965–1978,
doi:10.1002/joc.1276, 2005.

63
Hock, R.: Temperature index melt modelling in mountain areas, J. Hydrol., 282, 104–115,
doi:10.1016/S0022-1694(03)00257-9, 2003.
Hock, R.: Glacier melt: a review of processes and their modelling, Prog. Phys. Geog., 29, 362–
391, doi:10.1191/0309133305pp453ra, 2005.
Hooghoudt, S.: Bijdragen tot de kennis van eenige natuurkundige grootheden van den grond.
No. 7. Algemeene beschouwing van het probleem van de detailontwatering en de
infiltratie door middel van parallel loopende drains, greppels, slooten en kanalen, Versl.
Landbouwkd. Onderz., 46, 515–707, 1940.
Hunink, J., Niadas, I., Antonaropoulos, P., Droogers, P., and de Vente, J.: Targeting of
intervention areas to reduce reservoir sedimentation in the Tana catchment (Kenya)
using SWAT, Hydrolog. Sci. J., 58, 600–614, doi:10.1080/02626667.2013.774090,
2013.
Immerzeel, W. and Droogers, P.: Calibration of a distributed hydrological model based on
satellite evapotranspiration, J. Hydrol., 349, 411–424,
doi:10.1016/j.jhydrol.2007.11.017, 2008.
Immerzeel,W., Lutz, A., and Droogers, P.: Climate Change Impacts on the Upstream Water
Resources of the Amu and Syr Darya River Basins, Tech. rep., FutureWater,
Wageningen, 2012.
Immerzeel,W.W. and Bierkens, M. F. P.: Asia’s water balance, Nat. Geosci., 5, 841–842,
doi:10.1038/ngeo1643, 2012.
Immerzeel, W. W., Droogers, P., de Jong, S. M., and Bierkens, M. F. P.: Large-scale monitoring
of snow cover and runoff simulation in Himalayan river basins using remote sensing,
Remote Sens. Environ., 113, 40–49, doi:10.1016/j.rse.2008.08.010, 2009.
Immerzeel, W. W., van Beek, L. P. H., and Bierkens, M. F. P.: Climate change will affect the
Asian water towers, Science, 328, 1382–1385, doi:10.1126/science.1183188, 2010.
Immerzeel, W. W., Beek, L. P. H., Konz, M., Shrestha, A. B., and Bierkens, M. F. P.:
Hydrological response to climate change in a glacierized catchment in the Himalayas,
Climatic Change, 110, 721–736, doi:10.1007/s10584-011-0143-4, 2011.
Irrisoft: Database and on-line Applications in Irrigation, Drainage & Hydrology, available at:
http://www.irrisoft.org (last access: 07 May 2014), 2014.
Karssenberg, D.: The value of environmental modelling languages for building distributed
hydrological models, Hydrol. Process., 16, 2751–2766, doi:10.1002/hyp.1068, 2002.
Karssenberg, D., Burrough, P. A., Sluiter, R., and de Jong, K.: The PCRaster Software and
Course Materials for Teaching Numerical Modelling in the Environmental Sciences, T.
GIS, 5, 99–110, doi:10.1111/1467-9671.00070, 2001.
Karssenberg, D., Schmitz, O., Salamon, P., de Jong, K., and Bierkens, M. F.: A software
framework for construction of process-based stochastic spatio-temporal models and
data assimilation, Environ. Model. Softw., 25, 489–502,
doi:10.1016/j.envsoft.2009.10.004, 2010.
Kauffman, S., Droogers, P., Hunink, J., Mwaniki, B., Muchena, F., Gicheru, P., Bindraban, P.,
Onduru, D., Cleveringa, R., and Bouma, J.: Green Water Credits – exploring its
potential to enhance ecosystem services by reducing soil erosion in the Upper Tana
basin, Kenya, International Journal of Biodiversity Science, Ecosystem Services &
Management, 10, 133–143, doi:10.1080/21513732.2014.890670, 2014.
Kokkonen, T., Koivusalo, H., Jakeman, A., and Norton, J.: Construction of a Degree-Day Snow
Model in the Light of the “Ten Iterative Steps in Model Development”, in: Proceedings of
the iEMSs Third Biennial Meeting: Summit on Environmental Modelling and Software,
Environmental Modelling and Software Society, Burlington, USA, 2006.

64
Kozak, J. A., Ahuja, L. R., Green, T. R., and Ma, L.: Modelling crop canopy and residue rainfall
interception effects on soil hydrological components for semi-arid agriculture, Hydrol.
Process., 21, 229–241, doi:10.1002/hyp.6235, 2007.
Krysanova, V., Müller-Wohlfeil, D.-I., and Becker, A.: Development and test of a spatially
distributed hydrological/water quality model for mesoscale watersheds, Ecol. Model.,
106, 261–289, 1998.
Krysanova, V., Wechsung, F., Arnold, J., Srinivasan, R., and Williams, J.: PIK Report Nr. 69
“SWIM (Soil and Water Integrated Model), User Manual”, Tech. rep., Potsdam Institute
for Climate Impact Research, Potsdam, 2000.
Krysanova, V., Hattermann, F., Huang, S., Hesse, C., Vetter, T., Liersch, S., Koch, H., and
Kundzewicz, Z. W.: Modelling climate and land-use change impacts with SWIM:
lessons learnt from multiple applications, Hydrolog. Sci. J., 60, 606–635,
doi:10.1080/02626667.2014.925560, 2015.
Lall, U.: Debates – The future of hydrological sciences: A (common) path forward? One water.
One world. Many climes. Many souls, Water Resour. Res., 50, 5335–5341,
doi:10.1002/2014WR015402, 2014.
Lambert, J., Daroussin, J., Eimberck, M., Le Bas, C., Jamagne, M., King, D., and Montanarella,
L.: Soil Geographical Database for Eurasia&The Mediterranean. Instructions Guide for
Elaboration at scale 1:1,000,000 version 4.0. EUR 20422 EN., Tech. rep., JRC, Ispra,
Italy, 2003.
Lenaerts, J. T. M., van den Broeke, M. R., Déry, S. J., König-Langlo, G., Ettema, J., and
Munneke, P. K.: Modelling snowdrift sublimation on an Antarctic ice shelf, The
Cryosphere, 4, 179–190, doi:10.5194/tc-4-179-2010, 2010.
Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based
model of land surface water and energy fluxes for general circulation models, 99,
14415–14428, doi:10.1029/94JD00483, 1994.
Liang, X.,Wood, E. F., and Lettenmaier, D. P.: Surface soil moisture parameterization of the
VIC-2L model: Evaluation and modification, Global Planet. Change, 13, 195–206,
doi:10.1016/0921-8181(95)00046-1, 1996.
Lindström, G., Pers, C., Rosberg, J., Strömqvist, J., and Arheimer, B.: Development and testing
of the HYPE (Hydrological Predictions for the Environment) water quality model for
different spatial scales, Hydrol. Res., 41, 295–319, doi:10.2166/nh.2010.007, 2010.
Liu, Y., Gupta, H., Springer, E., and Wagener, T.: Linking science with environmental decision
making: Experiences from an integrated modeling approach to supporting sustainable
water resources management, Environ. Model. Softw., 23, 846–858,
doi:10.1016/j.envsoft.2007.10.007, 2008.
Lutz, A. F., Droogers, P., and Immerzeel, W.: Climate Change Impact and Adaptation on the
Water Resources in the Amu Darya and Syr Darya River Basins, Tech. rep.,
FutureWater, Wageningen, 2012.
Lutz, A. F., Immerzeel, W. W., Gobiet, A., Pellicciotti, F., and Bierkens, M. F. P.: Comparison of
climate change signals in CMIP3 and CMIP5 multi-model ensembles and implications
for Central Asian glaciers, Hydrol. Earth Syst. Sci., 17, 3661–3677, doi:10.5194/hess-
17-3661-2013, 2013.
Lutz, A. F., Immerzeel, W. W., Shrestha, A. B., and Bierkens, M. F. P.: Consistent increase in
High Asia’s runoff due to increasing glacier melt and precipitation, Nature Climate
Change, 4, 587– 592, doi:10.1038/nclimate2237, 2014a.
Lutz, A. F., Immerzeel, W., and Kraaijenbrink, P.: Gridded Meteorological Datasets and
Hydrological Modelling in the Upper Indus Basin. FutureWater Report 130, Tech. rep.,
FutureWater, Wageningen, the Netherlands, 2014b.

65
MacDonald, M. K., Pomeroy, J. W., and Pietroniro, A.: Parameterizing redistribution and
sublimation of blowing snow for hydrological models: tests in a mountainous subarctic
catchment, Hydrol. Process., 23, 2570–2583, doi:10.1002/hyp.7356, 2009.
Manning, R.: On the flow of water in open channels and pipes, Trans. Inst. Civ. Eng. Ireland, 20,
161–207, 1989.
McPhee, J., Rubio-Alvarez, E., Meza, R., Ayala, A., Vargas, X., and Vicuna, S.: An approach to
estimating hydropower impacts of climate change from a regional perspective,
Watershed Management, 2010, 13–24, doi:10.1061/41143(394)2, 2010.
Meehl, G. A., Covey, C., Taylor, K. E., Delworth, T., Stouffer, R. J., Latif, M., McAvaney, B., and
Mitchell, J. F. B.: THE WCRP CMIP3 Multimodel Dataset: A New Era in Climate
Change Research, B. Am. Meteorol. Soc., 88, 1383–1394, doi:10.1175/BAMS-88-9-
1383, 2007.
Mendoza, P. A., McPhee, J., and Vargas, X.: Uncertainty in flood forecasting: A distributed
modeling approach in a sparse data catchment, Water Resour. Res., 48, W09532,
doi:10.1029/2011WR011089, 2012.
Morris, E. M. andWoolhiser, D. A.: Unsteady one-dimensional flow over a plane: Partial
equilibrium and recession hydrographs, Water Resour. Res., 16, 355–360,
doi:10.1029/WR016i002p00355, 1980.
Myneni, R. and Williams, D.: On the relationship between FAPAR and NDVI, Remote Sens.
Environ., 49, 200–211, doi:10.1016/0034-4257(94)90016-7, 1994.
Nash, J. and Sutcliffe, J.: River flow forecasting through conceptual models part I – A discussion
of principles, J. Hydrol., 10, 282–290, doi:10.1016/0022-1694(70)90255-6, 1970.
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and Water Assessment Tool
(SWAT). Theoretical Documentation, version 2009, Tech. rep., Texas Water Resources
Institute, College Station, Texas, available at:
http://twri.tamu.edu/reports/2011/tr406.pdf (last access: 04 June 2014), 2009.
Niu, G. Y., Yang, Z. L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., Kumar, A., Manning, K.,
Niyogi, D., Rosero, E., Tewari, M., and Xia, Y.: The community Noah land surface
model with multiparameterization options (Noah-MP): 1. Model description and
evaluation with local-scale measurements, J. Geophys. Res.- Atmos., 116, D12109,
doi:10.1029/2010JD015139, 2011.
Oogathoo, S., Prasher, S., Rudra, R., and Patel, R.: Calibration and validation of the MIKE SHE
model in Canagagigue Creek watershed, in: Agricultural and biosystems engineering
for a sustainable world. International Conference on Agricultural Engineering,
Hersonissos, Crete, Greece, 2008.
Parajka, J. and Blöschl, G.: Spatio-temporal combination of MODIS images – potential for snow
cover mapping, Water Resour. Res., 44, W03406, doi:10.1029/2007WR006204, 2008.
Park, C. C.:World-wide variations in hydraulic geometry exponents of stream channels: An
analysis and some observations, J. Hydrol., 33, 133–146, doi:10.1016/0022-
1694(77)90103-2, 1977.
Pechlivanidis, I., Jackson, B., McIntyre, N., andWeather, H.: Catchment scale hydrological
modelling: a review of model types, calibration approaches and uncertainty analysis
methods in the context of recent developments in technology and applications, Global
NEST Journal, 13, 193–214, 2011.
Pellicciotti, F., Brock, B., Strasser, U., Burlando, P., Funk, M., and Corripio, J.: An enhanced
temperature-index glacier melt model including the shortwave radiation balance:
development and testing for Haut Glacier d’Arolla, Switzerland, J. Glaciol., 51, 573–587,
doi:10.3189/172756505781829124, 2005.

66
Peng, D., Zhang, B., and Liu, L.: Comparing spatiotemporal patterns in Eurasian FPAR derived
from two NDVI-based methods, International Journal of Digital Earth, 5, 283–298,
doi:10.1080/17538947.2011.598193, 2012.
Piechota, T. and Chiew, F.: Seasonal streamflow forecasting in eastern Australia and the El
Niño – Southern Oscillation, Water Resour. Res., 34, 3035–3044, 1998.
Pomeroy, J. W., Gray, D. M., Brown, T., Hedstrom, N. R., Quinton, W. L., Granger, R. J., and
Carey, S. K.: The cold regions hydrological model: A platform for basing process
representation and model structure on physical evidence, Hydrol. Process., 21, 2650–
2667, doi:10.1002/hyp.6787, 2007.
Rafn, E. B., Contor, B., and Ames, D. P.: Evaluation of a Method for Estimating Irrigated Crop-
Evapotranspiration Coefficients from Remotely Sensed Data in Idaho, J. Irrig. Drain. E.-
ASCE, 134, 722–729, doi:10.1061/(ASCE)0733-9437(2008)134:6(722), 2008.
Ragettli, S. and Pellicciotti, F.: Calibration of a physically based, spatially distributed
hydrological model in a glacierized basin: On the use of knowledge from
glaciometeorological processes to constrain model parameters,Water Resour. Res., 48,
W03509, doi:10.1029/2011WR010559, 2012.
Ragettli, S., Cortés, G., Mcphee, J., and Pellicciotti, F.: An evaluation of approaches for
modelling hydrological processes in highelevation, glacierized Andean watersheds,
Hydrol. Process., 28, 5674–5695, doi:10.1002/hyp.10055, 2014.
Ragettli, S., Pellicciotti, F., Immerzeel, W., Miles, E., Petersen, L., Heynen, M., Shea, J. M.,
Stumm, D., Joshi, S., and Shrestha, A.: Unraveling the hydrology of a Himalayan
watershed through integration of high resolution in-situ data and remote sensing with an
advanced simulation model, Adv. Water Resour., 78, 94–111,
doi:10.1016/j.advwatres.2015.01.013, 2015.
Refshaard, J. and Storm, B.: MIKE SHE, Danish Hydraulic Institute, Horsholm, 1995.
Regonda, S. K., Rajagopalan, B., Clark, M., and Zagona, E.: A multimodel ensemble forecast
framework: Application to spring seasonal flows in the Gunnison River Basin,Water
Resour. Res., 42, W09404, doi:10.1029/2005WR004653, 2006.
Reid, T. D., Carenzo, M., Pellicciotti, F., and Brock, B. W.: Including debris cover effects in a
distributed model of glacier ablation, J. Geophys. Res.-Atmos., 117, D18105,
doi:10.1029/2012JD017795, 2012.
Rigon, R., Bertoldi, G., and Over, T. M.: GEOtop: A Distributed Hydrological Model with
CoupledWater and Energy Budgets, J. Hydrometeorol., 7, 371–388,
doi:10.1175/JHM497.1, 2006.
Rockström, J., Falkenmark, M., Lannerstad, M., and Karlberg, L.: The planetary water drama:
Dual task of feeding humanity and curbing climate change, Geophys. Res. Lett., 39,
L15401, doi:10.1029/2012GL051688, 2012.
Rollenbeck, R. and Bendix, J.: Rainfall distribution in the Andes of southern Ecuador derived
from blending weather radar data and meteorological field observations, Atmos. Res.,
99, 277–289, doi:10.1016/j.atmosres.2010.10.018, 2011.
Samain, B., Simons, G. W. H., Voogt, M. P., Defloor, W., Bink, N.-J., and Pauwels, V. R. N.:
Consistency between hydrological model, large aperture scintillometer and remote
sensing based evapotranspiration estimates for a heterogeneous catchment, Hydrol.
Earth Syst. Sci., 16, 2095–2107, doi:10.5194/hess-16-2095-2012, 2012.
Samaniego, L., Kumar, R., and Attinger, S.: Multiscale parameter regionalization of a grid-based
hydrologic model at the mesoscale, Water Resour. Res., 46, W05523,
doi:10.1029/2008WR007327, 2010.
Sangrey, D. A., Harrop-Williams, K. O., and Klaiber, J. A.: Predicting Ground-Water Response
to Precipitation, J. Geotech. Eng.-ASCE, 110, 957–975, doi:10.1061/(ASCE)0733-
9410(1984)110:7(957), 1984.

67
Schaner, N., Voisin, N., Nijssen, B., and Lettenmaier, D. P.: The contribution of glacier melt to
streamflow, Environ. Res. Lett., 7, 034029, doi:10.1088/1748-9326/7/3/034029, 2012.
Schmitz, O., Karssenberg, D., van Deursen, W., and Wesseling, C.: Linking external
components to a spatiotemporal modelling framework: Coupling MODFLOW and
PCRaster, Environ. Model. Softw., 24, 1088–1099, doi:10.1016/j.envsoft.2009.02.018,
2009.
Schmitz, O., Karssenberg, D., de Jong, K., de Kok, J.-L., and de Jong, S. M.: Map algebra and
model algebra for integrated model building, Environ. Model. Softw., 48, 113–128,
doi:10.1016/j.envsoft.2013.06.009, 2013.
Sellers, P. J., Tucker, C. J., Collatz, G. J., Los, S. O., Justice, C. O., Dazlich, D. A., and Randall,
D. A.: A Revised Land Surface Parameterization (SiB2) for Atmospheric GCMS. Part II:
The Generation of Global Fields of Terrestrial Biophysical Parameters from Satellite
Data, J. Climate, 9, 706–737, doi:10.1175/1520-
0442(1996)009<0706:ARLSPF>2.0.CO;2, 1996.
Sheffield, J., Goteti, G., and Wood, E. F.: Development of a 50- Year High-Resolution Global
Dataset of Meteorological Forcings for Land Surface Modeling, J. Climate, 19, 3088–
3111, doi:10.1175/JCLI3790.1, 2006.
Singh, P. and Kumar, N.: Impact assessment of climate change on the hydrological response of
a snow and glacier melt runoff dominated Himalayan river, J. Hydrol., 193, 316–350,
doi:10.1016/S0022-1694(96)03142-3, 1997.
Sloan, P. G. and Moore, I. D.: Modeling subsurface stormflow on steeply sloping forested
watersheds, Water Resour. Res., 20, 1815–1822, doi:10.1029/WR020i012p01815,
1984.
Smedema, L. and Rycroft, D.: Land Drainage: Planning and Design of Agricultural Drainage
Systems, Cornell University Press, 1983.
Sorg, A., Bolch, T., Stoffel, M., Solomina, O., and Beniston, M.: Climate change impacts on
glaciers and runoff in Tien Shan (Central Asia), Nature Climate Change, 2, 725–731,
doi:10.1038/nclimate1592, 2012.
Sperna Weiland, F. C., van Beek, L. P. H., Kwadijk, J. C. J., and Bierkens, M. F. P.: The ability
of a GCM-forced hydrological model to reproduce global discharge variability, Hydrol.
Earth Syst. Sci., 14, 1595–1621, doi:10.5194/hess-14-1595-2010, 2010.
Strasser, U., Bernhardt, M., Weber, M., Liston, G. E., and Mauser, W.: Is snow sublimation
important in the alpine water balance?, The Cryosphere, 2, 53–66, doi:10.5194/tc-2-53-
2008, 2008.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment
Design, B. Am. Meteorol. Soc., 93, 485–498, doi:10.1175/BAMS-D-11-00094.1, 2012.
Terink, W., A.F. Lutz, G.W.H. Simons, W.W. Immerzeel, P. Droogers. 2015. SPHY v2.0: Spatial
Processes in HYdrology. Geoscientific Model Development, 8, 2009-2034,
doi:10.5194/gmd-8-2009-2015.
Terink, W., A.F. Lutz, G.W.H. Simons. 2015a. SPHY: Spatial Processes in HYdrology. Case-
studies for training. FutureWater report 144.
Terink, W., A.F. Lutz, W.W. Immerzeel. 2015b. SPHY: Spatial Processes in HYdrology.
Graphical User-Interfaces (GUIs). FutureWater report 143.
Tucker, C. J.: Red and photographic infrared linear combinations for monitoring vegetation,
Remote Sens. Environ., 8, 127–150, doi:10.1016/0034-4257(79)90013-0, 1979.
USGS: Landsat 8: U.S. Geological Survey Fact Sheet 2013–3060, Tech. rep., available at:
http://pubs.usgs.gov/fs/2013/3060/ (last access: 15 June 2014), 2013.
USGS: Water Resources Applications Software, available at:
http://water.usgs.gov/software/lists/alphabetical (last access: 30 April 2014), 2014.

68
van Beek, L. and Bierkens, M.: The Global Hydrological Model PCR-GLOBWB:
Conceptualization, Parameterization and Verification, Tech. rep., Department of
Physical Geography, Utrecht University, Utrecht, available at:
http://vanbeek.geo.uu.nl/suppinfo/vanbeekbierkens2009.pdf (last access: 24 November
2014), 2008.
van Dam, J. C., Huygen, J., Wesseling, J. G., Feddes, R. A., Kabat, P., van Walsum, P. E. V.,
Groenendijk, P., and van Diepen, C. A.: Theory of SWAP version 2.0. Simulation of
water flow, solute transport and plant growth in the Soil-Water-Atmosphere-Plant
environment, Tech. rep., DepartmentWater Resources,Wageningen Agricultural
University, 1997.
Van Der Knijff, J. M., Younis, J., and De Roo, A. P. J.: LISFLOOD: a GIS-based distributed
model for river basin scale water balance and flood simulation, Int. J. Geogr. Inf. Sci.,
24, 189–212, doi:10.1080/13658810802549154, 2010.
Van Genuchten, M.: A closed-form equation for predicting the hydraulic conductivity of
unsaturated soils, Soil Sci. Soc. Am. J., 44, 892–898, 1980.
VanderKwaak, J. E. and Loague, K.: Hydrologic-response simulations for the R-5 catchment
with a comprehensive physics-based model, Water Resour. Res., 37, 999–1013,
doi:10.1029/2000WR900272, 2001.
Venetis, C.: A STUDY ON THE RECESSION OF UNCONFINED ACQUIFERS, International
Association of Scientific Hydrology. Bulletin, 14, 119–125,
doi:10.1080/02626666909493759, 1969.
Verbunt, M., Gurtz, J., Jasper, K., Lang, H., Warmerdam, P., and Zappa, M.: The hydrological
role of snow and glaciers in alpine river basins and their distributed modeling, J.
Hydrol., 282, 36–55, doi:10.1016/S0022-1694(03)00251-8, 2003.
Vicuña, S., Garreaud, R. D., and McPhee, J.: Climate change impacts on the hydrology of a
snowmelt driven basin in semiarid Chile, Climatic Change, 105, 469–488,
doi:10.1007/s10584-010-9888-4, 2011.
Von Hoyningen-Huene, J.: Die Interzeption des Niederschlags in landwirtschaftlichen
Pflanzenbeständen, Arbeitsbericht Deutscher Verband fur Wasserwirtschaft und
Kulturbau, DWK, 1981.
Wada, Y., Van Beek, L. P. H., Van Kempen, C. M., Reckman, J. W. T. M., Vasak, S., and
Bierkens, M. F. P.: Global depletion of groundwater resources, Geophys. Res. Lett., 37,
L20402, doi:10.1029/2010GL044571, 2010.
Wagener, T., Sivapalan, M., Troch, P. A., McGlynn, B. L., Harman, C. J., Gupta, H. V., Kumar,
P., Rao, P. S. C., Basu, N. B., and Wilson, J. S.: The future of hydrology: An evolving
science for a changing world, Water Resour. Res., 46, W05301,
doi:10.1029/2009WR008906, 2010.
Wagner, P. D., Fiener, P., Wilken, F., Kumar, S., and Schneider, K.: Comparison and evaluation
of spatial interpolation schemes for daily rainfall in data scarce regions, J. Hydrol., 464–
465, 388–400, doi:10.1016/j.jhydrol.2012.07.026, 2012.
Wheeler, T. and von Braun, J.: Climate change impacts on global food security, Science, 341,
508–513, doi:10.1126/science.1239402, 2013.
Wigmosta, M. S., Vail, L. W., and Lettenmaier, D. P.: A distributed hydrology-vegetation model
for complex terrain, Water Resour. Res., 30, 1665–1680, doi:10.1029/94WR00436,
1994.
Williams, J.: HYMO flood routing, J. Hydrol., 26, 17–27, doi:10.1016/0022-1694(75)90122-5,
1975.
Yatagai, A., Kamiguchi, K., Arakawa, O., Hamada, A., Yasutomi, N., and Kitoh, A.:
APHRODITE: Constructing a Long-Term Daily Gridded Precipitation Dataset for Asia

69
Based on a Dense Network of Rain Gauges, B. Am. Meteorol. Soc., 93, 1401–1415,
doi:10.1175/BAMS-D-11-00122.1, 2012.

70
Copyright
Redistribution and use of the SPHY model source code or its binary forms, with or without
modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain this copyright notice, this list of conditions
and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice, this list of
conditions and the following disclaimer in the documentation and/or other materials
provided with the distribution.
3. Any changes, modifications, improvements and/or simplifications of the source code
should be sent to FutureWater.
4. Any redistribution of source code or binary form should be reported to FutureWater.
5. Any application, publication and/or presentation of results generated by using the
Software should be reported to FutureWater.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
"AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED
TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A
PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT
OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL,
SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED
TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF
LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING
NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
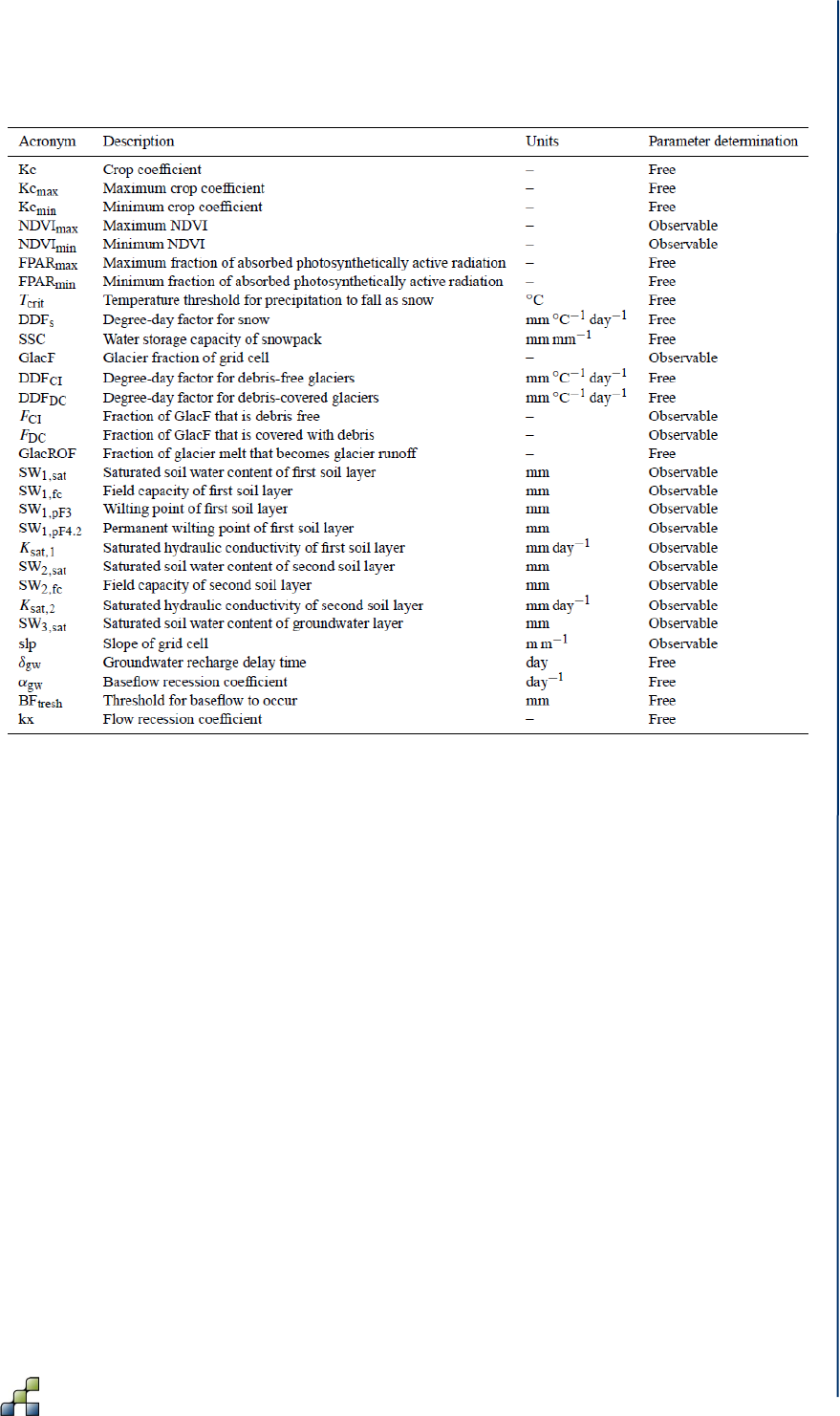
71
Appendix 1: Input and Output
Table 6: Overview of SPHY model parameters. The last column indicates whether the
parameter is observable, or can be determined by calibration (free).