I Iv PP&P C01 C04 ANS 865893 Solutions Manual
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 682 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Solutions Manual

A Glencoe Program
Student Edition
Teacher Wraparound Edition
Teacher Chapter Resources
Mini Lab Worksheets
Physics Lab Worksheets
Study Guide
Section Quizzes
Reinforcement
Enrichment
Transparency Masters
Transparency Worksheets
Chapter Assessment
Teacher Classroom Resources
Teaching Transparencies
Laboratory Manual, Student Edition
Laboratory Manual, Teacher Edition
Probeware Laboratory Manual, Student
Edition
Probeware Laboratory Manual, Teacher
Edition
Forensics Laboratory Manual, Student
Edition
Forensics Laboratory Manual, Teacher
Edition
Supplemental Problems
Additional Challenge Problems
Pre-AP/Critical Thinking Problems
Physics Test Prep: Studying for the
End-of-Course Exam, Student Edition
Physics Test Prep: Studying for the
End-of-Course Exam, Teacher Edition
Connecting Math to Physics
Solutions Manual
Technology
Answer Key Maker
ExamView® Pro
Interactive Chalkboard
McGraw-Hill Learning Network
StudentWorks™ CD-ROM
TeacherWorks™ CD-ROM
physicspp.com Web site
Copyright © by The McGraw-Hill Companies, Inc. All rights reserved. Permission is granted
to reproduce the material contained herein on the condition that such material be repro-
duced only for classroom use; be provided to students, teachers, and families without
charge; and be used solely in conjunction with the Physics: Principles and Problems
program. Any other reproduction, for use or sale, is prohibited without prior written permission
of the publisher.
Send all inquiries to:
Glencoe/McGraw-Hill
8787 Orion Place
Columbus, Ohio 43240
ISBN 0-07-865893-4
Printed in the United States of America
1 2 3 4 5 6 7 8 9 045 09 08 07 06 05 04

To the Teacher . . . . . . . . . . . . . . . . . . . . . . iv
Chapter 1
A Physics Toolkit . . . . . . . . . . . . . . . . . . . . 1
Chapter 2
Representing Motion . . . . . . . . . . . . . . . . 15
Chapter 3
Accelerated Motion . . . . . . . . . . . . . . . . . 29
Chapter 4
Forces in One Dimension . . . . . . . . . . . . 61
Chapter 5
Forces in Two Dimensions . . . . . . . . . . . 87
Chapter 6
Motion in Two Dimensions . . . . . . . . . 115
Chapter 7
Gravitation . . . . . . . . . . . . . . . . . . . . . . . 141
Chapter 8
Rotational Motion . . . . . . . . . . . . . . . . . 169
Chapter 9
Momentum and Its Conservation . . . . 193
Chapter 10
Energy, Work, and Simple Machines . . 225
Chapter 11
Energy and Its Conservation . . . . . . . . . 247
Chapter 12
Thermal Energy . . . . . . . . . . . . . . . . . . . 271
Chapter 13
States of Matter . . . . . . . . . . . . . . . . . . . 287
Chapter 14
Vibrations and Waves . . . . . . . . . . . . . . 311
Chapter 15
Sound . . . . . . . . . . . . . . . . . . . . . . . . . . . 329
Chapter 16
Fundamentals of Light . . . . . . . . . . . . . 345
Chapter 17
Reflection and Mirrors . . . . . . . . . . . . . . 357
Chapter 18
Refraction and Lenses . . . . . . . . . . . . . . 377
Chapter 19
Interference and Diffraction . . . . . . . . . 399
Chapter 20
Static Electricity . . . . . . . . . . . . . . . . . . . 413
Chapter 21
Electric Fields . . . . . . . . . . . . . . . . . . . . . 427
Chapter 22
Current Electricity . . . . . . . . . . . . . . . . . 445
Chapter 23
Series and Parallel Circuits . . . . . . . . . . 463
Chapter 24
Magnetic Fields . . . . . . . . . . . . . . . . . . . 485
Chapter 25
Electromagnetic Induction . . . . . . . . . . 501
Chapter 26
Electromagnetism . . . . . . . . . . . . . . . . . . 517
Chapter 27
Quantum Theory . . . . . . . . . . . . . . . . . . 531
Chapter 28
The Atom . . . . . . . . . . . . . . . . . . . . . . . . 545
Chapter 29
Solid-State Electronics . . . . . . . . . . . . . . 559
Chapter 30
Nuclear Physics . . . . . . . . . . . . . . . . . . . 573
Appendix B
Additional Problems . . . . . . . . . . . . . . . 591
Contents
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Physics: Principles and Problems Contents iii

iv To the Teacher Physics: Principles and Problems
To the Teacher
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The Solutions Manual is a comprehensive guide to the questions and problems in the Student Edition of
Physics: Principles and Problems. This includes the Practice Problems, Section Reviews, Chapter Assessments,
and Challenge Problems for each chapter, as well as the Additional Problems that appear in Appendix B
of the Student Edition. The Solutions Manual restates every question and problem so that you do not have
to look back at the text when reviewing problems with students.

Physics: Principles and Problems Solutions Manual 1
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1A Physics Toolkit
CHAPTER
Practice Problems
1.1 Mathematics and Physics
pages 3–10
page 5
For each problem, give the rewritten equation you
would use and the answer.
1. A lightbulb with a resistance of 50.0 ohms
is used in a circuit with a 9.0-volt battery.
What is the current through the bulb?
I
R
V
50
9
..
0
0o
vh
om
lt s
0.18 ampere
2. An object with uniform acceleration a,
starting from rest, will reach a speed of v
in time taccording to the formula vat.
What is the acceleration of a bicyclist who
accelerates from rest to 7 m/s in 4 s?
a
v
t
74
m
s
/s
1.75 m/s2
3. How long will it take a scooter accelerating
at 0.400 m/s2to go from rest to a speed of
4.00 m/s?
t
v
a
04
.4
.0
00
0m
m/
/s
s2
10.0 s
4. The pressure on a surface is equal to the
force divided by the area: PF/A.
A 53-kg woman exerts a force (weight) of
520 Newtons. If the pressure exerted on
the floor is 32,500 N/m2, what is the area
of the soles of her shoes?
A
P
F
32,5
50
20
0N
N/m2
0.016 m2
page 7
Use dimensional analysis to check your equation
before multiplying.
5. How many megahertz is 750 kilohertz?
750 kHz
10
10
k
0
H
H
zz
1,00
10M
,0H
00
zHz
0.75 MHz
6. Convert 5021 centimeters to kilometers.
5021 cm
10
1
0m
cm
11
00
k
0
m
m
5.021102km
7. How many seconds are in a leap year?
366 days
1
24
da
h
y
60
1m
hin
1
6m
0s
in
31,622,400 s
8. Convert the speed 5.30 m/s to km/h.
5.3
10
sm
1
6m
0s
in
60
1m
hin
11
00
k
0
m
m
19.08 km/h
page 8
Solve the following problems.
9. a. 6.201 cm 7.4 cm 0.68 cm
12.0 cm
6.201 cm
7.4 cm
0.68 cm
12.0 cm
26.281 cm
26.3 cm after rounding
b. 1.6 km 1.62 m 1200 cm
1.6 km 1600 m
1.62 m 1.62 m
1200 cm 12 m
1613.62 m
1600 m or 1.6 km after rounding
10. a. 10.8 g 8.264 g
10.8 g
8.264 g
2.536 g
2.5 g after rounding

b. 4.75 m 0.4168 m
4.75 m
0.4168 m
4.3332 m
4.33 m after rounding
11. a. 139 cm 2.3 cm
320 cm2or 3.2102cm2
b. 3.2145 km 4.23 km
13.6 km2
12. a. 13.78 g 11 .3 m L
1.22 g/mL
b. 18.21 g 4.4 cm3
4.1 g/cm3
Section Review
1.1 Mathematics and Physics
pages 3–10
page 10
13. Math Why are concepts in physics
described with formulas?
The formulas are concise and can be
used to predict new data.
14. Magnetism The force of a magnetic field
on a charged, moving particle is given by
FBqv, where Fis the force in kgm/s2, qis
the charge in As, and vis the speed in m/s.
Bis the strength of the magnetic field,
measured in teslas, T. What is 1 tesla
described in base units?
FBqv, so B
q
F
v
T
A
k
g
s2
1 T 1kg/As2
15. Magnetism A proton with charge
1.601019 As is moving at 2.4105m/s
through a magnetic field of 4.5 T. You want
to find the force on the proton.
a. Substitute the values into the equation
you will use. Are the units correct?
FBqv
(4.5 kg/As2)(1.601019 As)
(2.4105m/s)
Force will be measured in kgm/s2,
which is correct.
b. The values are written in scientific
notation, m10n. Calculate the 10npart
of the equation to estimate the size of
the answer.
10191051014; the answer will
be about 201014,or 21013.
c. Calculate your answer. Check it against
your estimate from part b.
1.71013 kgm/s2
d. Justify the number of significant digits
in your answer.
The least-precise value is 4.5 T, with
2 significant digits, so the answer is
rounded to 2 significant digits.
16. Magnetism Rewrite FBqv to find vin
terms of F, q, and B.
v
B
F
q
17. Critical Thinking An accepted value for
the acceleration due to gravity is 9.801 m/s2.
In an experiment with pendulums, you
calculate that the value is 9.4 m/s2. Should
the accepted value be tossed out to accom-
modate your new finding? Explain.
No. The value 9.801 m/s2has been
established by many other experiments,
and to discard the finding you would
have to explain why they were wrong.
There are probably some factors
affecting your calculation, such as
friction and how precisely you can
measure the different variables.
kgm/s2
(As)(m/s)
2Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued
Physics: Principles and Problems Solutions Manual 3
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
1.2 Measurement
pages 11–14
page 14
18. Accuracy Some wooden rulers do not start
with 0 at the edge, but have it set in a few
millimeters. How could this improve the
accuracy of the ruler?
As the edge of the ruler gets worn away
over time, the first millimeter or two of
the scale would also be worn away if
the scale started at the edge.
19. Tools You find a micrometer (a tool used
to measure objects to the nearest 0.01 mm)
that has been badly bent. How would it
compare to a new, high-quality meterstick
in terms of its precision? Its accuracy?
It would be more precise but less
accurate.
20. Parallax Does parallax affect the precision
of a measurement that you make? Explain.
No, it doesn’t change the fineness of
the divisions on its scale.
21. Error Your friend tells you that his height
is 182 cm. In your own words, explain the
range of heights implied by this statement.
His height would be between 181.5 and
182.5 cm. Precision of a measurement
is one-half the smallest division on the
instrument. The height 182 cm would
range 0.5 cm.
22. Precision A box has a length of 18.1 cm and
a width of 19.2 cm, and it is 20.3 cm tall.
a. What is its volume?
7.05103cm3
b. How precise is the measure of length?
Of volume?
nearest tenth of a cm; nearest
10 cm3
c. How tall is a stack of 12 of these boxes?
243.6 cm
d. How precise is the measure of the
height of one box? Of 12 boxes?
nearest tenth of a cm; nearest tenth
of a cm
23. Critical Thinking Your friend states in a
report that the average time required to
circle a 1.5-mi track was 65.414 s. This was
measured by timing 7 laps using a clock
with a precision of 0.1 s. How much
confidence do you have in the results of
the report? Explain.
A result can never be more precise than
the least precise measurement. The
calculated average lap time exceeds
the precision possible with the clock.
Practice Problems
1.3 Graphing Data
pages 15–19
page 18
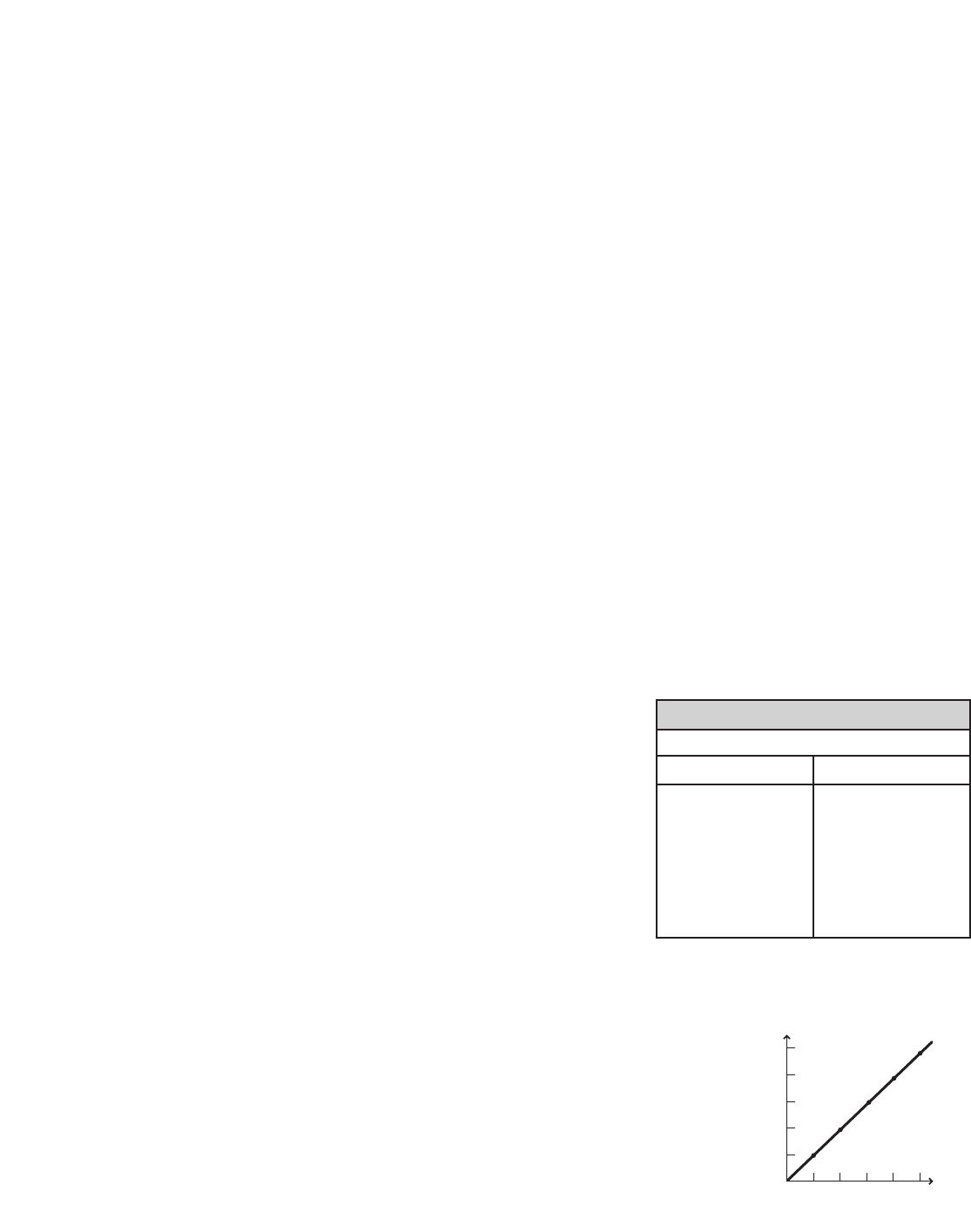
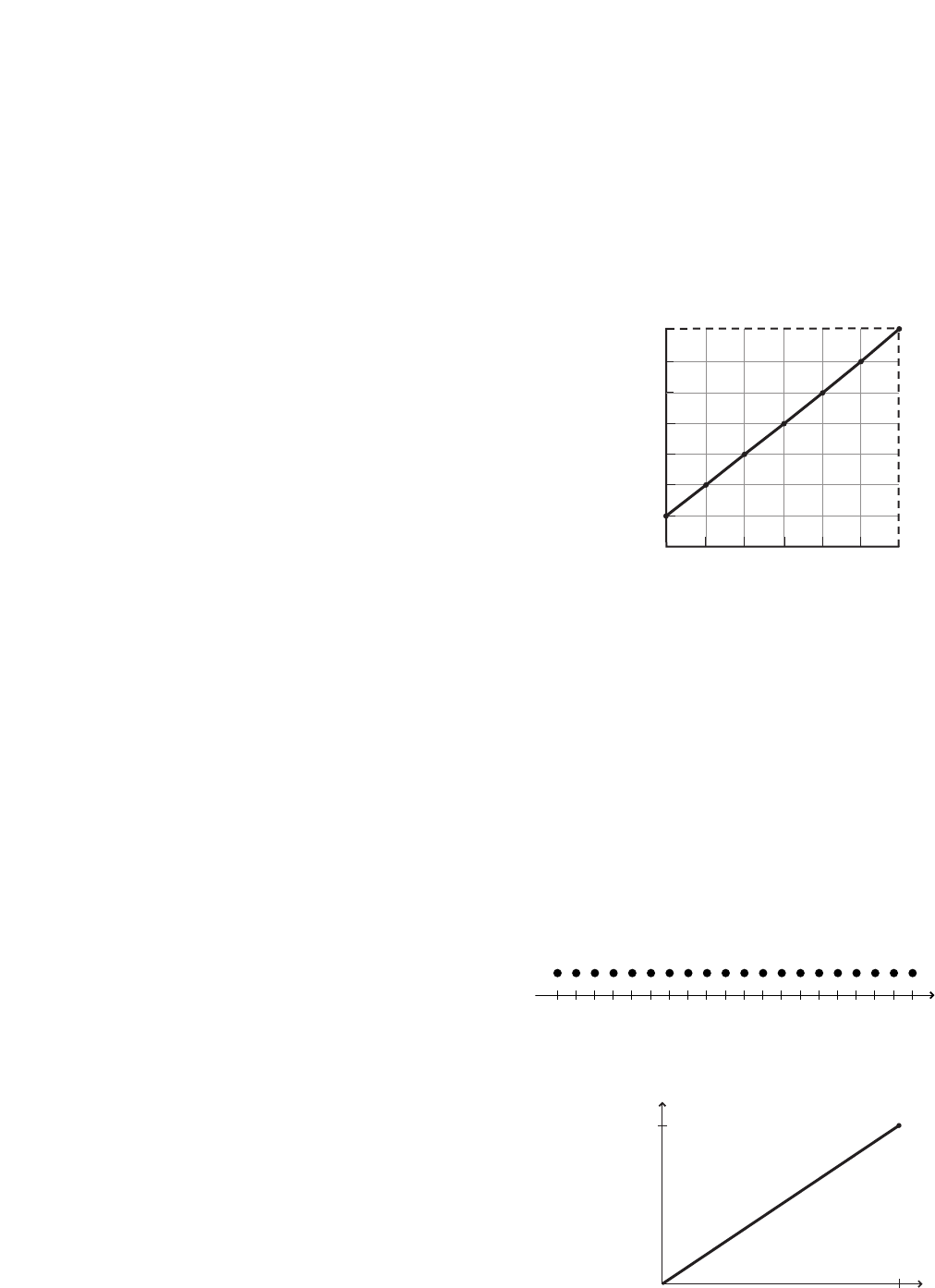
24. The mass values of specified volumes of
pure gold nuggets are given in Table 1-4.
a. Plot mass versus volume from the
values given in the table and draw
the curve that best fits all points.
123
Volume (cm3)
45
0
20
40
60
Mass (g)
80
100
Table 1-4
Mass of Pure Gold Nuggets
Volume (cm3) Mass (g)
1.0 19.4
2.0 38.6
3.0 58.1
4.0 77.4
5.0 96.5
Chapter 1 continued
b. Describe the resulting curve.
a straight line
c. According to the graph, what type of
relationship exists between the mass of
the pure gold nuggets and their volume?
The relationship is linear.
d. What is the value of the slope of this
graph? Include the proper units.
slope
y
x
19.3 g/cm3
e. Write the equation showing mass as a
function of volume for gold.
m(19.3 g/cm3)V
f. Write a word interpretation for the slope
of the line.
The mass for each cubic centimeter
of pure gold is 19.3 g.
Section Review
1.3 Graphing Data
pages 15–19
page 19
25. Make a Graph Graph the following data.
Time is the independent variable.
26. Interpret a Graph What would be the
meaning of a nonzero y-intercept to a graph
of total mass versus volume?
There is a nonzero total mass when the
volume of the material is zero.This
could happen if the mass value
includes the material’s container.
27. Predict Use the relation illustrated in
Figure 1-16 to determine the mass required
to stretch the spring 15 cm.
16 g
28. Predict Use the relation in Figure 1-18 to
predict the current when the resistance is
16 ohms.
7.5 A
29. Critical Thinking In your own words,
explain the meaning of a shallower line, or
a smaller slope than the one in Figure 1-16,
in the graph of stretch versus total mass for
a different spring.
The spring whose line has a smaller
slope is stiffer, and therefore requires
more mass to stretch it one centimeter.
Chapter Assessment
Concept Mapping
page 24
30. Complete the following concept map using
the following terms: hypothesis, graph,
mathematical model, dependent variable,
measurement.
Speed (m/s)
12
8
4
010 20
Time (s)
30
40
Time (s)
Speed (m/s)
0 5 10 15 20 25 30 35
1210864222
96.5 g 19.4 g
5.0 cm31.0 cm3
4Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued
hypothesis
experiment
measurement
independent
variable
dependent
variable
graph
mathematical
model

Physics: Principles and Problems Solutions Manual 5
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Mastering Concepts
page 24
31. Describe a scientific method. (1.1)
Identify a problem; gather information
about it by observing and experimenting;
analyze the information to arrive at an
answer.
32. Why is mathematics important to science?
(1.1)
Mathematics allows you to be quantita-
tive, to say “how fast,” not just “fast.”
33. What is the SI system? (1.1)
The International System of Units, or SI,
is a base 10 system of measurement
that is the standard in science. The base
units are the meter, kilogram, second,
kelvin, mole, ampere, and candela.
34. How are base units and derived units
related? (1.1)
The derived units are combinations of
the base units.
35. Suppose your lab partner recorded a
measurement as 100 g. (1.1)
a. Why is it difficult to tell the number of
significant digits in this measurement?
Zeros are necessary to indicate the
magnitude of the value, but there is
no way of knowing whether or not the
instrument used to measure the val-
ues actually measured the zeros.The
zeros may serve only to locate the 1.
b. How can the number of significant
digits in such a number be made clear?
Write the number in scientific
notation, including only the
significant digits.
36. Give the name for each of the following
multiples of the meter. (1.1)
a. m
centimeter
b. m
millimeter
c. 1000 m
kilometer
37. To convert 1.8 h to minutes, by what
conversion factor should you multiply? (1.1)
60
1m
hin
, because the units will cancel
correctly.
38. Solve each problem. Give the correct number
of significant digits in the answers. (1.1)
a. 4.667104g3.02105g
3.49105g
b. (1.70102J) (5.922104cm3)
2.87105J/cm3
39. What determines the precision of a
measurement? (1.2)
the precision of a measuring device,
which is limited by the finest division
on its scale
40. How does the last digit differ from the
other digits in a measurement? (1.2)
The final digit is estimated.
41. A car’s odometer measures the distance
from home to school as 3.9 km. Using
string on a map, you find the distance to be
4.2 km. Which answer do you think is more
accurate? What does accurate mean? (1.2)
The most accurate measure is the
measure closest to the actual distance.
The odometer is probably more
accurate as it actually covered the
distance. The map is a model made
from measurements, so your measure-
ments from the map are more removed
from the real distance.
42. How do you find the slope of a linear
graph? (1.3)
The slope of a linear graph is the ratio
of the vertical change to the horizontal
change, or rise over run.
1
1000
1
100
Chapter 1 continued
43. For a driver, the time between seeing a
stoplight and stepping on the brakes is
called reaction time. The distance traveled
during this time is the reaction distance.
Reaction distance for a given driver and
vehicle depends linearly on speed. (1.3)
a. Would the graph of reaction distance
versus speed have a positive or a
negative slope?
Positive. As speed increases,
reaction distance increases.
b. A driver who is distracted has a longer
reaction time than a driver who is not.
Would the graph of reaction distance
versus speed for a distracted driver have
a larger or smaller slope than for a
normal driver? Explain.
Larger.The driver who was distracted
would have a longer reaction time
and thus a greater reaction distance
at a given speed.
44. During a laboratory experiment, the
temperature of the gas in a balloon is varied
and the volume of the balloon is measured.
Which quantity is the independent
variable? Which quantity is the dependent
variable? (1.3)
Temperature is the independent vari-
able; volume is the dependent variable.
45. What type of relationship is shown in
Figure 1-20? Give the general equation for
this type of relation. (1.3)
■Figure 1-20
quadratic; yax2 bx c
46. Given the equation Fmv2/R, what
relationship exists between each of the
following? (1.3)
a. Fand R
inverse relationship
b. Fand m
linear relationship
c. Fand v
quadratic relationship
Applying Concepts
pages 25–26
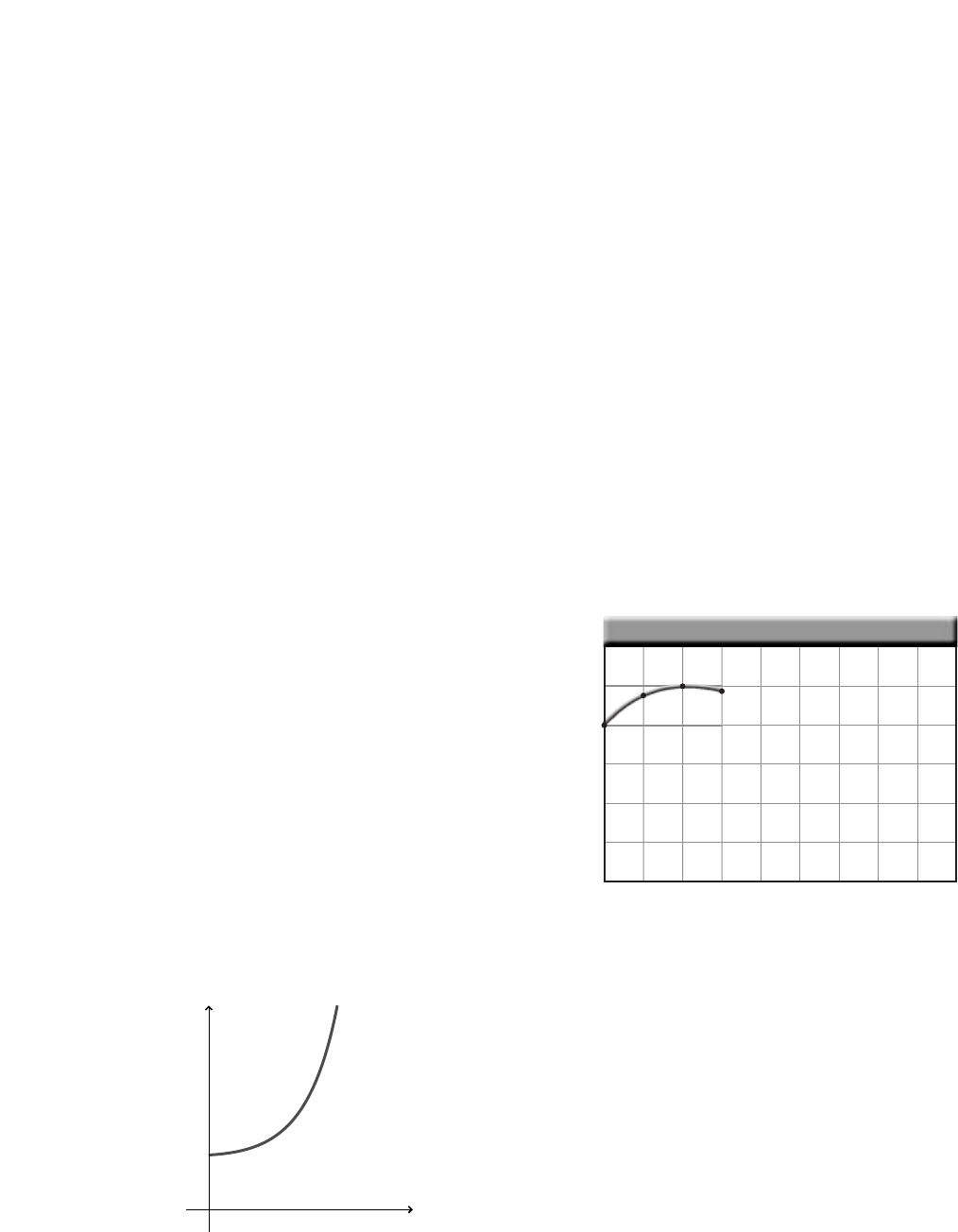
47. Figure 1-21 gives the height above the
ground of a ball that is thrown upward
from the roof of a building, for the first
1.5 s of its trajectory. What is the ball’s
height at t0? Predict the ball’s height at
t2 s and at t5 s.
■Figure 1-21
When t0 and t2, the ball’s height
will be about 20 m. When t5, the ball
will have landed on the ground so the
height will be 0 m.
48. Is a scientific method one set of clearly
defined steps? Support your answer.
There is no definite order of specific
steps. However, whatever approach
is used, it always includes close
observation, controlled experimentation,
summarizing, checking, and rechecking.
4123
0
25
20
15
10
5
Height (m)
Time (s)
Height of Ball v. Time
x
y
6Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued

Physics: Principles and Problems Solutions Manual 7
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
49. Explain the difference between a scientific
theory and a scientific law.
A scientific law is a rule of nature, where
a scientific theory is an explanation of
the scientific law based on observation.
A theory explains why something hap-
pens; a law describes what happens.
50. Density The density of a substance is its
mass per unit volume.
a. Give a possible metric unit for density.
possible answers include g/cm3or
kg/m3
b. Is the unit for density a base unit or a
derived unit?
derived unit
51. What metric unit would you use to measure
each of the following?
a. the width of your hand
cm
b. the thickness of a book cover
mm
c. the height of your classroom
m
d. the distance from your home to your
classroom
km
52. Size Make a chart of sizes of objects.
Lengths should range from less than 1 mm
to several kilometers. Samples might
include the size of a cell, the distance light
travels in 1 s, and the height of a room.
sample answer:
radius of the atom, 51011 m; virus,
107m; thickness of paper, 0.1 mm;
width of paperback book, 10.7 cm;
height of a door, 1.8 m; width of town,
7.8 km; radius of Earth, 6106m;
distance to the Moon, 4108m
53. Time Make a chart of time intervals.
Sample intervals might include the time
between heartbeats, the time between
presidential elections, the average lifetime
of a human, and the age of the United
States. Find as many very short and very
long examples as you can.
sample answer:
half-life of polonium-194, 0.7 s;
time between heartbeats, 0.8 s; time to
walk between physics class and math
class, 2.4 min; length of school year,
180 days; time between elections for
the U.S. House of Representatives,
2 years; time between U.S. presidential
elections, 4 years; age of the United
States, (about) 230 years
54. Speed of Light Two students measure
the speed of light. One obtains
(3.001 0.001)108m/s; the other obtains
(2.999 0.006)108m/s.
a. Which is more precise?
(3.001 0.001)108m/s
b. Which is more accurate?
(2.999 0.006)108m/s
55. You measure the dimensions of a desk as
132 cm, 83 cm, and 76 cm. The sum of
these measures is 291 cm, while the product
is 8.3105cm3. Explain how the significant
digits were determined in each case.
In addition and subtraction, you ask
what place the least precise measure is
known to: in this case, to the nearest
cm. So the answer is rounded to the
nearest cm. In multiplication and
division, you look at the number of
significant digits in the least precise
answer: in this case, 2. So the answer is
rounded to 2 significant digits.
56. Money Suppose you receive $5.00 at the
beginning of a week and spend $1.00 each
day for lunch. You prepare a graph of the
amount you have left at the end of each day
for one week. Would the slope of this graph
be positive, zero, or negative? Why?
negative, because the change in
vertical distance is negative for a
positive change in horizontal distance
Chapter 1 continued

57. Data are plotted on a graph, and the value
on the y-axis is the same for each value of
the independent variable. What is the
slope? Why? How does ydepend on x?
Zero.The change in vertical distance is
zero. ydoes not depend on x.
58. Driving The graph of braking distance
versus car speed is part of a parabola. Thus,
the equation is written dav2bv c.
The distance, d, has units in meters, and
velocity, v, has units in meters/second.
How could you find the units of a, b, and c?
What would they be?
The units in each term of the equation
must be in meters because distance, d,
is measured in meters.
av2a(m/s)2, so ais in s2/m;
bv b(m/s), so bis in s1.
59. How long is the leaf in Figure 1-22?
Include the uncertainty in your
measurement.
■Figure 1-22
8.3 cm 0.05 cm, or 83 mm 0.5 mm
60. The masses of two metal blocks are
measured. Block A has a mass of 8.45 g
and block B has a mass of 45.87 g.
a. How many significant digits are
expressed in these measurements?
A: three; B: four
b. What is the total mass of block A plus
block B?
54.32 g
c. What is the number of significant digits
for the total mass?
four
d. Why is the number of significant digits
different for the total mass and the
individual masses?
When adding measurements, the
precision matters: both masses are
known to the nearest hundredth of a
gram, so the total should be given to
the nearest hundredth of a gram.
Significant digits sometimes are
gained when adding.
61. History Aristotle said that the speed of a
falling object varies inversely with the density
of the medium through which it falls.
a. According to Aristotle, would a rock fall
faster in water (density 1000 kg/m3), or
in air (density 1 kg/m3)?
Lower density means faster speed,
so the rock falls faster in air.
b. How fast would a rock fall in a vacuum?
Based on this, why would Aristotle say
that there could be no such thing as a
vacuum?
Because a vacuum would have a
zero density, the rock should fall
infinitely fast. Nothing can fall that
fast.
62. Explain the difference between a hypothesis
and a scientific theory.
A scientific theory has been tested
and supported many times before it
becomes accepted. A hypothesis is an
idea about how things might work—it
has much less support.
63. Give an example of a scientific law.
Newton’s laws of motion, law of conser-
vation of energy, law of conservation of
charge, law of reflection
8Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued

Physics: Principles and Problems Solutions Manual 9
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
64. What reason might the ancient Greeks
have had not to question the hypothesis
that heavier objects fall faster than lighter
objects? Hint: Did you ever question which
falls faster?
Air resistance affects many light
objects. Without controlled experi-
ments, their everyday observations told
them that heavier objects did fall faster.
65. Mars Explain what observations led to
changes in scientists’ ideas about the surface
of Mars.
As telescopes improved and later
probes were sent into space, scientists
gained more information about the
surface. When the information did
not support old hypotheses, the
hypotheses changed.
66. A graduated cylinder is marked every mL.
How precise a measurement can you make
with this instrument?
0.5 mL
Mastering Problems
pages 26–28
1.1 Mathematics and Physics
67. Convert each of the following
measurements to meters.
a. 42.3 cm
0.423 m
b. 6.2 pm
6.21012 m
c. 21 km
2.1104m
d. 0.023 mm
2.3105m
e. 214 m
2.14104m
f. 57 nm
5.7108m
68. Add or subtract as indicated.
a. 5.80109s3.20108s
6.12109s
b. 4.87106m1.93106m
2.94106m
c. 3.14105kg 9.36105kg
1.250104kg
d. 8.12107g6.20106g
7.50107g
69. Rank the following mass measurements
from least to greatest: 11.6 mg, 1021 g,
0.000006 kg, 0.31 mg.
0.31 mg, 1021 µg, 0.000006 kg, 11.6 mg
70. State the number of significant digits in
each of the following measurements.
a. 0.00003 m
1
b. 64.01 fm
4
c. 80.001 m
5
d. 0.720 g
3
e. 2.40106kg
3
f. 6108kg
1
g. 4.071016 m
3
71. Add or subtract as indicated.
a. 16.2 m 5.008 m 13.48 m
34.7 m
b. 5.006 m 12.0077 m 8.0084 m
25.022 m
c. 78.05 cm232.046 cm2
46.00 cm2
d. 15.07 kg 12.0 kg
3.1 kg
Chapter 1 continued

72. Multiply or divide as indicated.
a. (6.21018 m)(4.71010 m)
2.9109m2
b. (5.6107m)/(2.81012 s)
2.0105m/s
c. (8.1104km)(1.6103km)
1.3106km2
d. (6.5105kg)/(3.4103m3)
1.9102kg/m3
73. Gravity The force due to gravity is Fmg
where g9.80 m/s2.
a. Find the force due to gravity on a
41.63-kg object.
408 kgm/s2
b. The force due to gravity on an object is
632 kgm/s2. What is its mass?
64.5 kg
74. Dimensional Analysis Pressure is mea-
sured in pascals, where 1 Pa 1 kg/ms2.
Will the following expression give a
pressure in the correct units?
No; it is in kg/s3
1.2 Measurement
75. A water tank has a mass of 3.64 kg when it
is empty and a mass of 51.8 kg when it is
filled to a certain level. What is the mass of
the water in the tank?
48.2 kg
76. The length of a room is 16.40 m, its width
is 4.5 m, and its height is 3.26 m. What
volume does the room enclose?
2.4102m3
77. The sides of a quadrangular plot of land
are 132.68 m, 48.3 m, 132.736 m, and
48.37 m. What is the perimeter of the plot?
362.1 m
78. How precise a measurement could you
make with the scale shown in Figure 1-23?
■Figure 1-23
0.5 g
79. Give the measure shown on the meter in
Figure 1-24 as precisely as you can. Include
the uncertainty in your answer.
■Figure 1-24
3.6 0.1 A
80. Estimate the height of the nearest door
frame in centimeters. Then measure it.
How accurate was your estimate? How
precise was your estimate? How precise
was your measurement? Why are the two
precisions different?
A standard residential doorframe height
is 80 inches, which is about 200 cm. The
precision depends on the measurement
instrument used.
0
1
2
3
4
5A
A
CLASS A
(0.55 kg)(2.1 m/s)
9.8 m/s2
10 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued

Physics: Principles and Problems Solutions Manual 11
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
81. Base Units Give six examples of quantities
you might measure in a physics lab. Include
the units you would use.
Sample: distance, cm; volume, mL;
mass, g; current, A; time, s;
temperature, °C
82. Temperature The temperature drops from
24°C to 10°C in 12 hours.
a. Find the average temperature change per
hour.
1.2°C/h
b. Predict the temperature in 2 more hours
if the trend continues.
8°C
c. Could you accurately predict the
temperature in 24 hours?
No. Temperature is unlikely to con-
tinue falling sharply and steadily
that long.
1.3 Graphing Data
83. Figure 1-25 shows the masses of three
substances for volumes between 0 and
60 cm3.
a. What is the mass of 30 cm3of each
substance?
(a) 80 g, (b) 260 g, (c) 400 g
b. If you had 100 g of each substance,
what would be their volumes?
(a) 36 cm3, (b) 11 cm3, (c) 7 cm3
c. In one or two sentences, describe the
meaning of the slopes of the lines in
this graph.
The slope represents the increased
mass of each additional cubic
centimeter of the substance.
d. What is the y-intercept of each line?
What does it mean?
The y-intercept is (0,0). It means that
when V0 cm3, there is none of the
substance present (m0 g).
■Figure 1-25
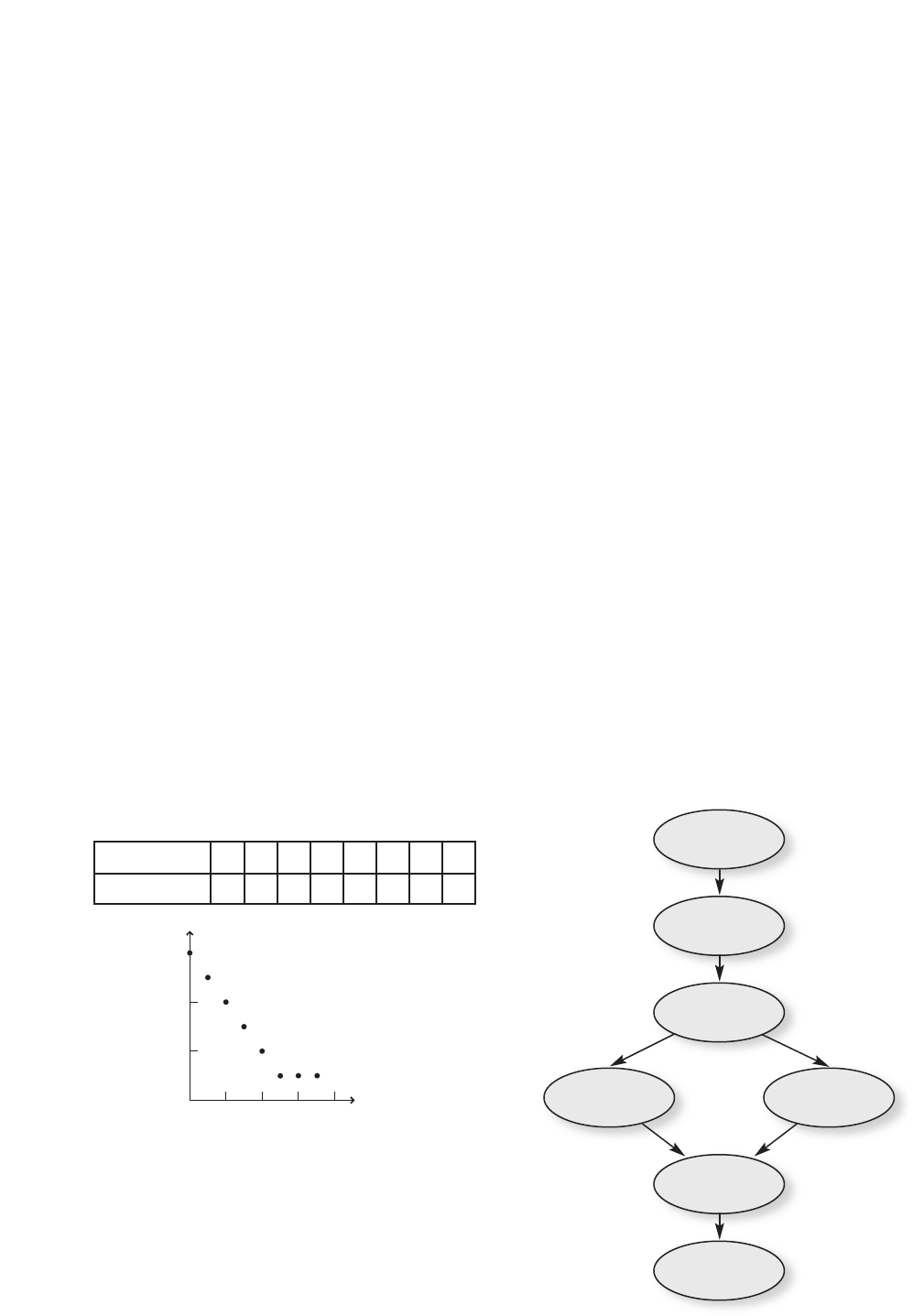
84. During a class demonstration, a physics
instructor placed a mass on a horizontal
table that was nearly frictionless. The
instructor then applied various horizontal
forces to the mass and measured the
distance it traveled in 5 seconds for each
force applied. The results of the experiment
are shown in Table 1-5.
a. Plot the values given in the table and
draw the curve that best fits all points.
0.0
40
80
120
Distance (cm)
160
Force (N)
10.0 20.0 30.0
Table 1-5
Distance Traveled with
Different Forces
Force (N) Distance (cm)
5.0 24
10.0 49
15.0 75
20.0 99
25.0 120
30.0 145
A
B
C
5020 4010 30
0
800
700
600
500
400
300
200
100
Mass (g)
Volume (cm3)
Mass of
Three Substances
Chapter 1 continued
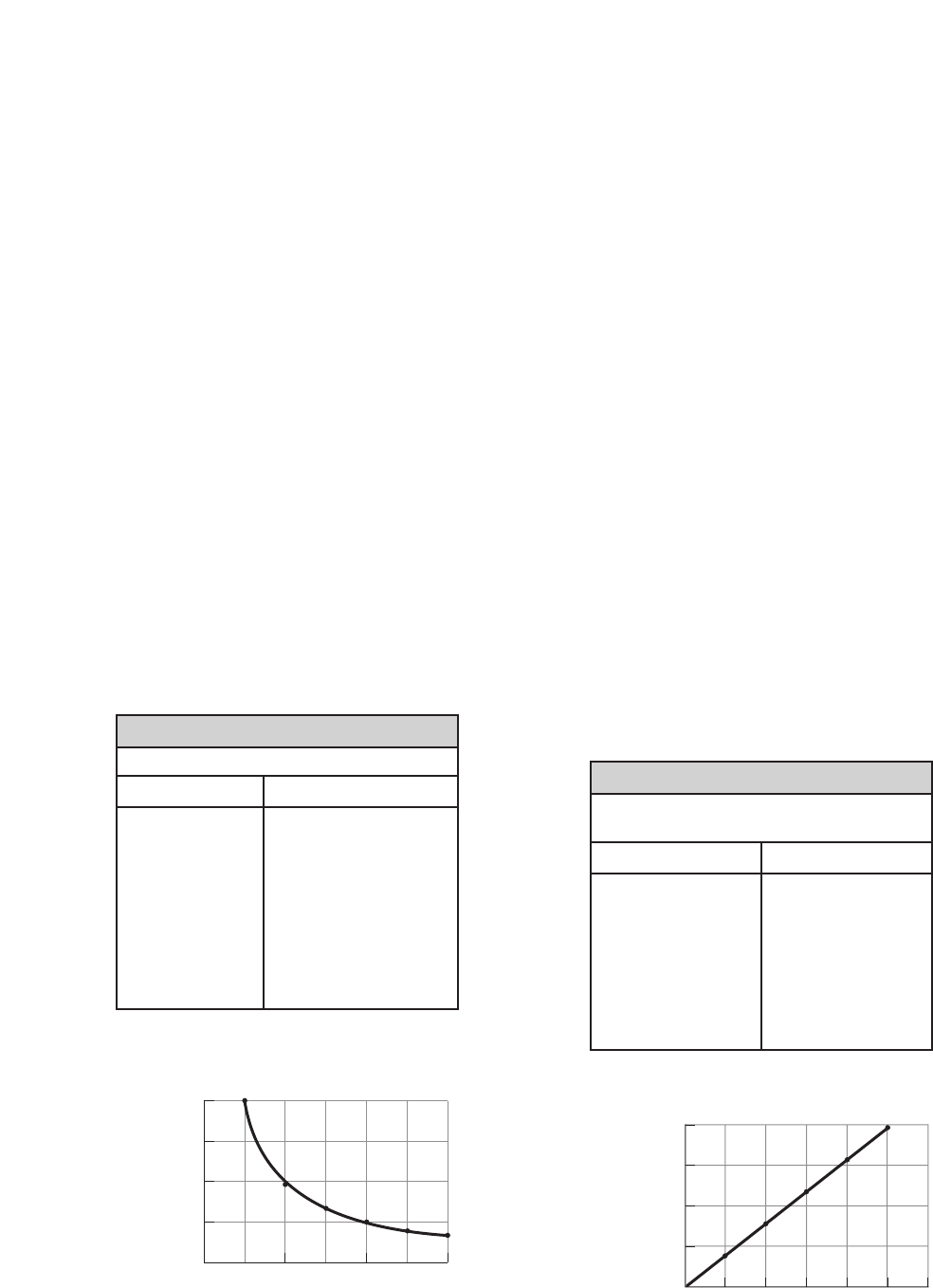
b. Describe the resulting curve.
a straight line
c. Use the graph to write an equation
relating the distance to the force.
d4.9F
d. What is the constant in the equation?
Find its units.
The constant is 4.9 and has units
cm/N.
e. Predict the distance traveled when a
22.0-N force is exerted on the object
for 5 s.
108 cm or 110 cm using 2 significant
digits
85. The physics instructor from the previous
problem changed the procedure. The mass
was varied while the force was kept con-
stant. Time and distance were measured,
and the acceleration of each mass was cal-
culated. The results of the experiment are
shown in Table 1-6.
a. Plot the values given in the table and
draw the curve that best fits all points.
b. Describe the resulting curve.
a hyperbola
c. According to the graph, what is the
relationship between mass and the
acceleration produced by a constant
force?
Acceleration varies inversely with
mass.
d. Write the equation relating acceleration
to mass given by the data in the graph.
a
1
m
2
e. Find the units of the constant in the
equation.
kgm/s2
f. Predict the acceleration of an 8.0-kg
mass.
1.5 m/s2
86. During an experiment, a student measured
the mass of 10.0 cm3of alcohol. The student
then measured the mass of 20.0 cm3of
alcohol. In this way, the data in Table 1-7
were collected.
a. Plot the values given in the table and
draw the curve that best fits all the points.
0.0
10.0
20.0
30.0
Mass (g)
40.0
Volume (cm3)
10.0 20.0 30.0 40.0 50.0 60.0
Table 1-7
The Mass Values of
Specific Volumes of Alcohol
Volume (cm3) Mass (g)
10.0 7.9
20.0 15.8
30.0 23.7
40.0 31.6
50.0 39.6
0.0
3.0
6.0
9.0
Acceleration (m/s2)
12.0
Mass (kg)
2.0 4.0 6.0
Table 1-6
Acceleration of Different Masses
Mass (kg) Acceleration (m/s2)
1.0 12.0
2.0 5.9
3.0 4.1
4.0 3.0
5.0 2.5
6.0 2.0
12 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued

Physics: Principles and Problems Solutions Manual 13
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. Describe the resulting curve.
a straight line
c. Use the graph to write an equation
relating the volume to the mass of the
alcohol.
m0.79V
d. Find the units of the slope of the graph.
What is the name given to this quantity?
g/cm3; density
e. What is the mass of 32.5 cm3of
alcohol?
25.7 g
Mixed Review
page 28
87. Arrange the following numbers from most
precise to least precise
0.0034 m 45.6 m 1234 m
0.0034 m, 45.6 m, 1234 m
88. Figure 1-26 shows the toroidal (doughnut-
shaped) interior of the now-dismantled
Tokamak Fusion Test Reactor. Explain why a
width of 80 m would be an unreasonable
value for the width of the toroid. What
would be a reasonable value?
■Figure 1-26
80 meters is equivalent to about 260 feet,
which would be very large. 10 meters
would be a more reasonable value.
89. You are cracking a code and have
discovered the following conversion
factors: 1.23 longs 23.0 mediums, and
74.5 mediums 645 shorts. How many
shorts are equal to one long?
1 long
1
2.
3
2
.3
0l
m
on
ed
g
6
74
45
.5s
m
ho
er
d
t
162 shorts
90. You are given the following measurements
of a rectangular bar: length 2.347 m,
thickness 3.452 cm, height 2.31 mm,
mass 1659 g. Determine the volume, in
cubic meters, and density, in g/cm3, of the
beam. Express your results in proper form.
volume 1.87104m3, or 187 cm3;
density 8.87 g/cm3
91. A drop of water contains 1.71021 mole-
cules. If the water evaporated at the rate of
one million molecules per second, how
many years would it take for the drop to
completely evaporate?
1.71015 s
(1.71015 s)
36
1
00
hs
1
24
da
h
y
365
1
d
y
ays
5.4107y
92. A 17.6-gram sample of metal is placed in a
graduated cylinder containing 10.0 cm3of
water. If the water level rises to 12.20 cm3,
what is the density of the metal?
density
m
V
8.00 g/cm3
Thinking Critically
page 28
93. Apply Concepts It has been said that
fools can ask more questions than the wise
can answer. In science, it is frequently the
case that one wise person is needed to ask
the right question rather than to answer it.
Explain.
The “right”question is one that points
to fruitful research and to other
questions that can be answered.
94. Apply Concepts Find the approximate mass
of water in kilograms needed to fill a con-
tainer that is 1.40 m long and 0.600 m wide
to a depth of 34.0 cm. Report your result to
one significant digit. (Use a reference source
to find the density of water.)
17.6 g
12.20 cm3 10.0 cm3
Chapter 1 continued
1.71021 molecules
1,000,000 molecules
1 s
Vw(140 cm)(60.0 cm)(34.0 cm)
285,600 cm3. Because the density of
water is 1.00 g/cm3, the mass of water
in kilograms is 286 kg.
95. Analyze and Conclude A container of gas
with a pressure of 101 kPa has a volume
of 324 cm3and a mass of 4.00 g. If the
pressure is increased to 404 kPa, what is
the density of the gas? Pressure and volume
are inversely proportional.
Pressure and volume are inversely
proportional. Since the pressure is
4 times greater, the volume will be
1
4
of the original volume.
3244
cm3
81.0 cm3
81
4
.
.
0
00
cm
g
3
0.0494 g/cm3
96. Design an Experiment How high can you
throw a ball? What variables might affect
the answer to this question?
mass of ball, footing, practice, and
conditioning
97. Calculate If the Sun suddenly ceased to
shine, how long would it take Earth to
become dark? (You will have to look up the
speed of light in a vacuum and the distance
from the Sun to Earth.) How long would it
take the surface of Jupiter to become dark?
tE
d
v
E
1
3.
.4
09
06
11
00
8
1
m
1
/
m
s
499 s 8.31 min
tJ
d
v
J
3
7
..
0
7
0
8
1
1
0
0
8
11
m
m
/s
2593 s 43.2 min
Writing in Physics
page 28
98. Research and describe a topic in the history
of physics. Explain how ideas about the
topic changed over time. Be sure to include
the contributions of scientists and to
evaluate the impact of their contributions
on scientific thought and the world outside
the laboratory.
Answers will vary.
99. Explain how improved precision in
measuring time would have led to
more accurate predictions about how
an object falls.
Answers will vary. For example, students
might suggest that improved precision
can lead to better observations.
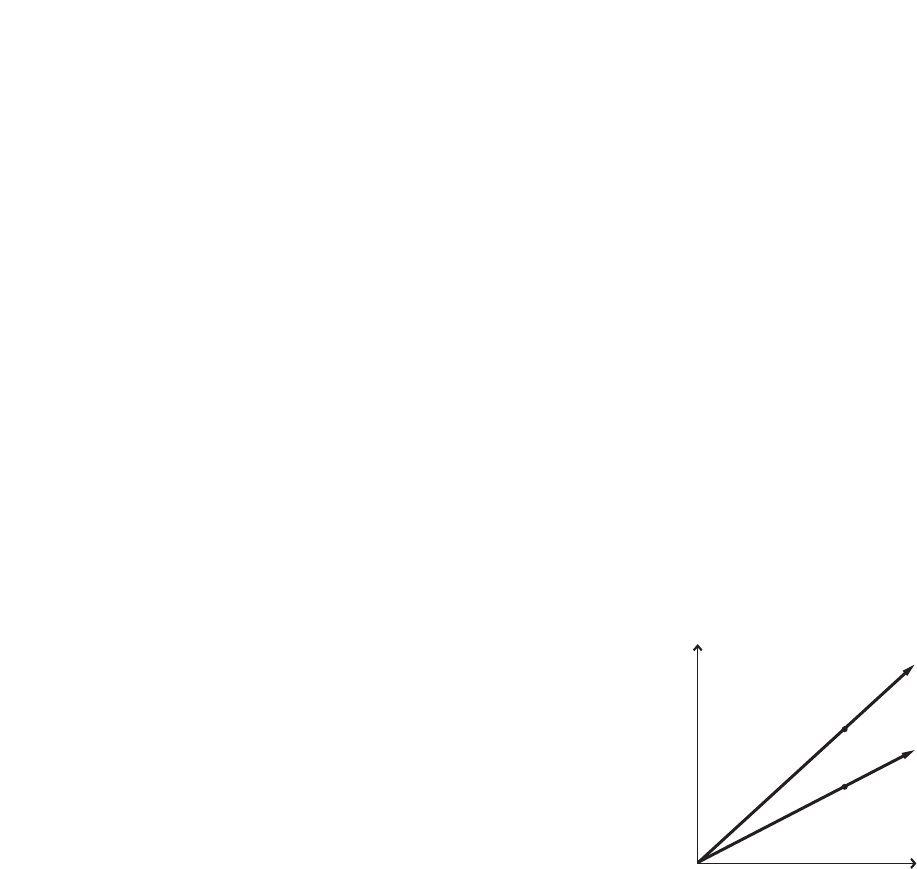
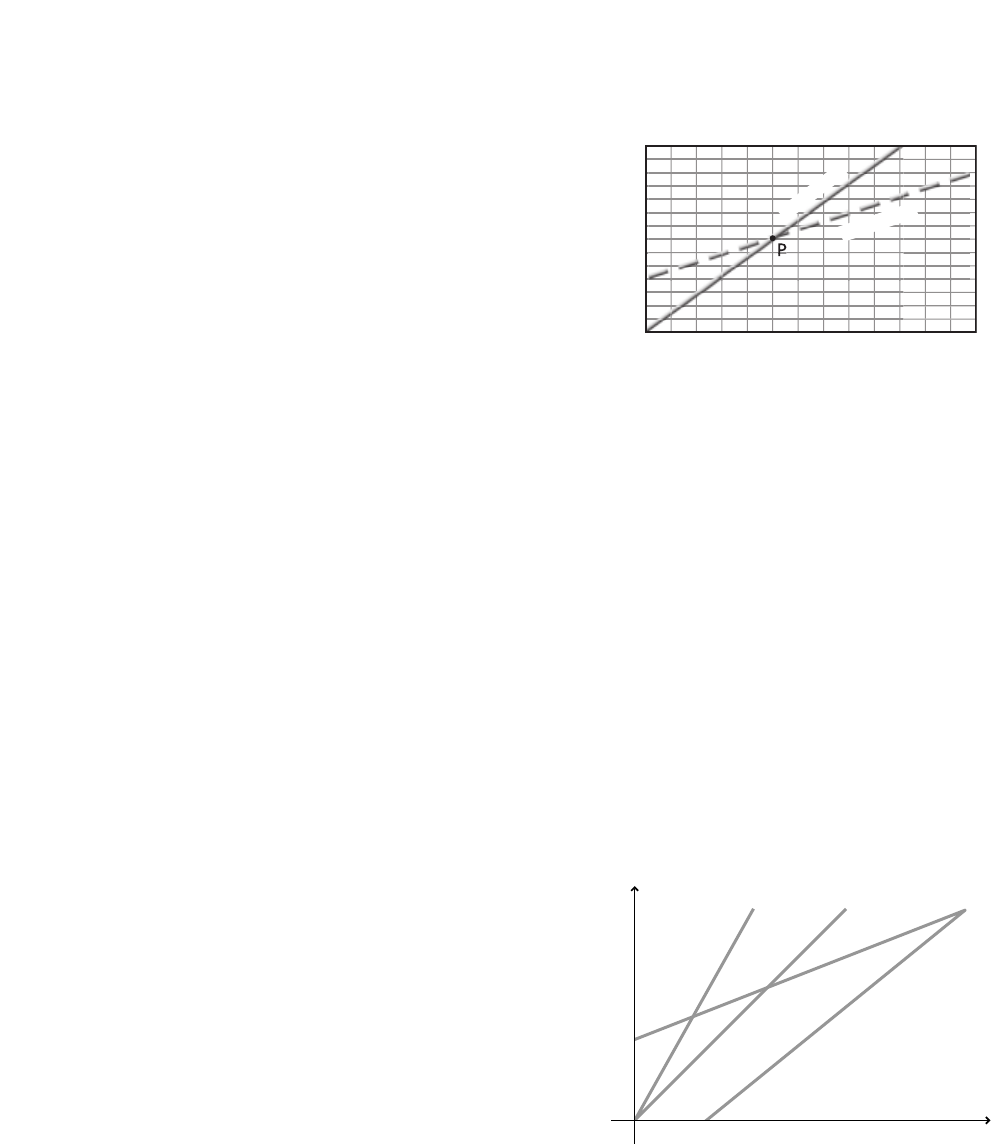
Challenge Problem
page 17
An object is suspended from spring 1, and the
spring’s elongation (the distance it stretches) is X1.
Then the same object is removed from the first
spring and suspended from a second spring. The
elongation of spring 2 is X2. X2is greater than X1.
1. On the same axes, sketch the graphs of the
mass versus elongation for both springs.
2. Is the origin included in the graph? Why or
why not?
Yes; the origin corresponds to
0 elongation when the force is 0.
3. Which slope is steeper?
The slope for X2is steeper.
4. At a given mass, X21.6 X1.
If X25.3 cm, what is X1?
X21.6X1
5.3 cm 1.6X1
3.3 cm X1
14 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued
X2
X1
X
F

Physics: Principles and Problems Solutions Manual 15
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
2Representing Motion
CHAPTER
Section Review
2.1 Picturing Motion
pages 31–33
page 33
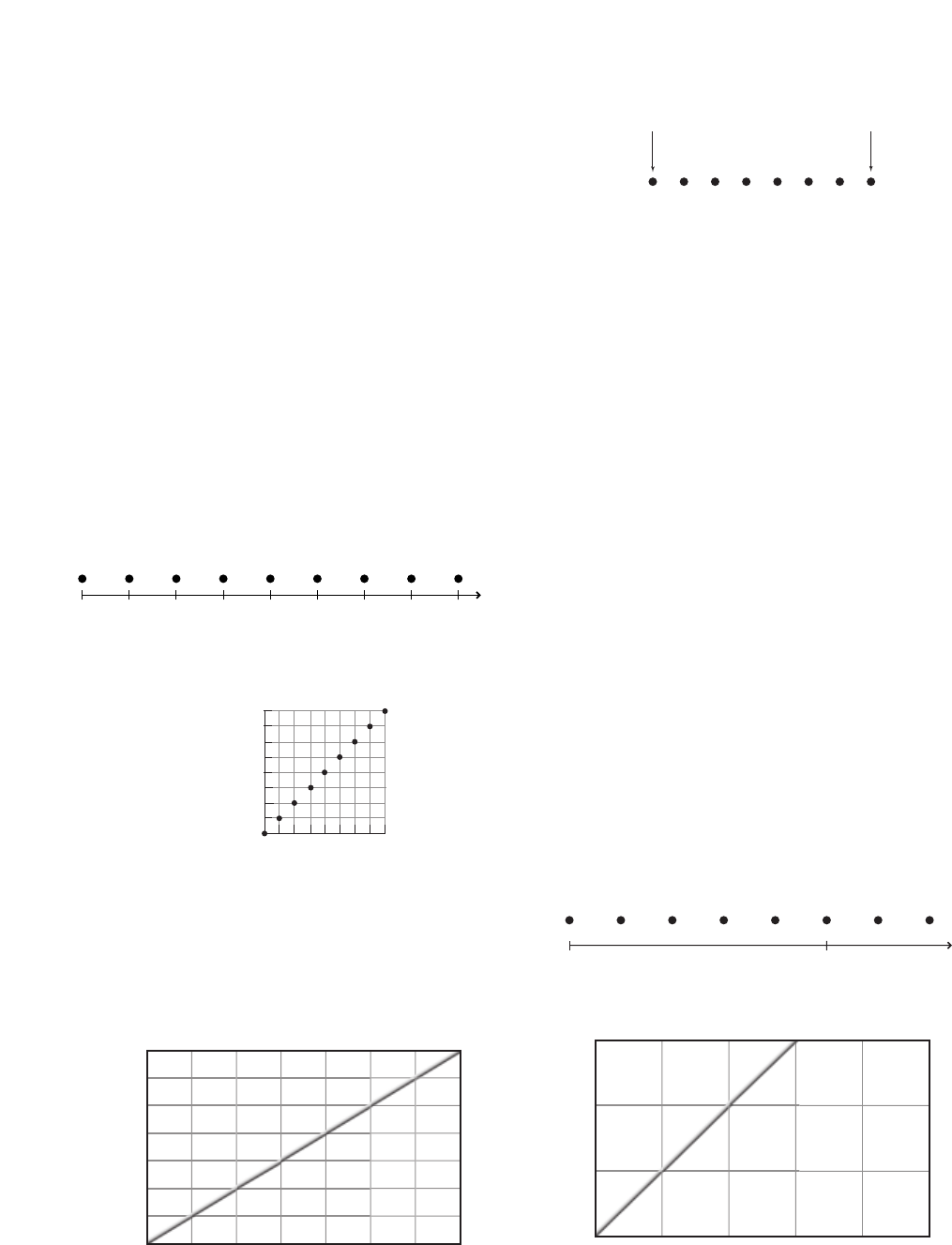
1. Motion Diagram of a Runner Use the
particle model to draw a motion diagram
for a bike rider riding at a constant pace.
2. Motion Diagram of a Bird Use the parti-
cle model to draw a simplified motion dia-
gram corresponding to the motion diagram
in Figure 2-4 for a flying bird. What point
on the bird did you choose to represent it?
■Figure 2-4
3. Motion Diagram of a Car Use the particle
model to draw a simplified motion diagram
corresponding to the motion diagram in
Figure 2-5 for a car coming to a stop at a
stop sign. What point on the car did you
use to represent it?
■Figure 2-5
4. Critical Thinking Use the particle model
to draw motion diagrams for two runners
in a race, when the first runner crosses the
finish line as the other runner is three-
fourths of the way to the finish line.
Section Review
2.2 Where and When?
pages 34–37
page 37
5. Displacement The particle model for a car
traveling on an interstate highway is shown
below. The starting point is shown.
Here There
Make a copy of the particle model, and
draw a vector to represent the displacement
of the car from the starting time to the end
of the third time interval.
6. Displacement The particle model for a boy
walking to school is shown below.
Home School
Make a copy of the particle model, and
draw vectors to represent the displacement
between each pair of dots.
SchoolHome
Here There
Runner 2
Runner 1
FinishStart
t0t1t2t3t4
t1t2t3t4
t0

7. Position Two students compared the
position vectors they each had drawn on
a motion diagram to show the position of a
moving object at the same time. They found
that their vectors did not point in the same
direction. Explain.
A position vector goes from the origin
to the object. When the origins are dif-
ferent, the position vectors are different.
On the other hand, a displacement vec-
tor has nothing to do with the origin.
8. Critical Thinking A car travels straight
along the street from the grocery store to
the post office. To represent its motion you
use a coordinate system with its origin at
the grocery store and the direction the car is
moving in as the positive direction. Your
friend uses a coordinate system with its ori-
gin at the post office and the opposite
direction as the positive direction. Would
the two of you agree on the car’s position?
Displacement? Distance? The time interval
the trip took? Explain.
The two students should agree on the
displacement, distance, and time interval
for the trip, because these three quanti-
ties are independent of where the origin
of the coordinate system is placed.The
two students would not agree on the
car’s position, because the position is
measured from the origin of the coordi-
nate system to the location of the car.
Practice Problems
2.3 Position-Time Graphs
pages 38–42
page 39
For problems 9–11, refer to Figure 2-13.
■Figure 2-13
9. Describe the motion of the car shown by
the graph.
The car begins at a position of 125.0 m
and moves toward the origin, arriving at
the origin 5.0 s after it begins moving.
The car continues beyond the origin.
10. Draw a motion diagram that corresponds to
the graph.
11. Answer the following questions about
the car’s motion. Assume that the positive
d-direction is east and the negative
d-direction is west.
a. When was the car 25.0 m east of the
origin?
at 4.0 s
b. Where was the car at 1.0 s?
100.0 m
12. Describe, in words, the motion of the
two pedestrians shown by the lines in
Figure 2-14. Assume that the positive direc-
tion is east on Broad Street and the origin is
the intersection of Broad and High Streets.
t0 0.0 s
125.0 m 0.0 m
t5 5.0 s
d
7.0
150.0
100.0
50.0
0.0
50.0
Position (m)
Time (s)
1.0 3.0 5.0
16 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued

Physics: Principles and Problems Solutions Manual 17
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
■Figure 2-14
Pedestrian A starts west of High Street
and walks east (the positive direction).
Pedestrian B begins east of High Street
and walks west (the negative direction).
Sometime after B crosses High Street,
A and B pass each other. Sometime
after they pass, Pedestrian A crosses
High Street.
13. Odina walked down the hall at school
from the cafeteria to the band room, a
distance of 100.0 m. A class of physics
students recorded and graphed her
position every 2.0 s, noting that she moved
2.6 m every 2.0 s. When was Odina in the
following positions?
a. 25.0 m from the cafeteria
19 s
b. 25.0 m from the band room
58 s
c. Create a graph showing Odina’s
motion.
page 41
For problems 14–17, refer to the figure in
Example Problem 2.
■Example Problem 2 Figure
14. What event occurred at t0.0 s?
Runner A passed the origin.
15. Which runner was ahead at t48.0 s?
runner B
16. When runner A was at 0.0 m, where was
runner B?
at 50.0 m
17. How far apart were runners A and B at
t20.0 s?
approximately 30 m
18. Juanita goes for a walk. Sometime later, her
friend Heather starts to walk after her. Their
motions are represented by the position-
time graphs in Figure 2-16.
■Figure 2-16
a. How long had Juanita been walking
when Heather started her walk?
6.0 min
0.0
Position (km)
Time (h)
1.0
2.0
3.0
4.0
5.0
6.0
1.0 2.0
1.5
Juanita
Heather
0.5
0.0 4.02.0 8.06.0 10.0 12.0
200.0
50.0
100.0
150.0
Position (m)
Time (s)
Distance from
cafeteria (m)
Time (s)
10.0 30.0 50.0 70.0
0.00
20.0
40.0
60.0
80.0
100.0
High St.
Broad St.
East
West
Position (m)
Time (s)
A
B
Chapter 2 continued
b. Will Heather catch up to Juanita? How
can you tell?
No. The lines representing Juanita’s
and Heather’s motions get farther
apart as time increases. The lines
will not intersect.
Section Review
2.3 Position-Time Graphs
pages 38–42
page 42
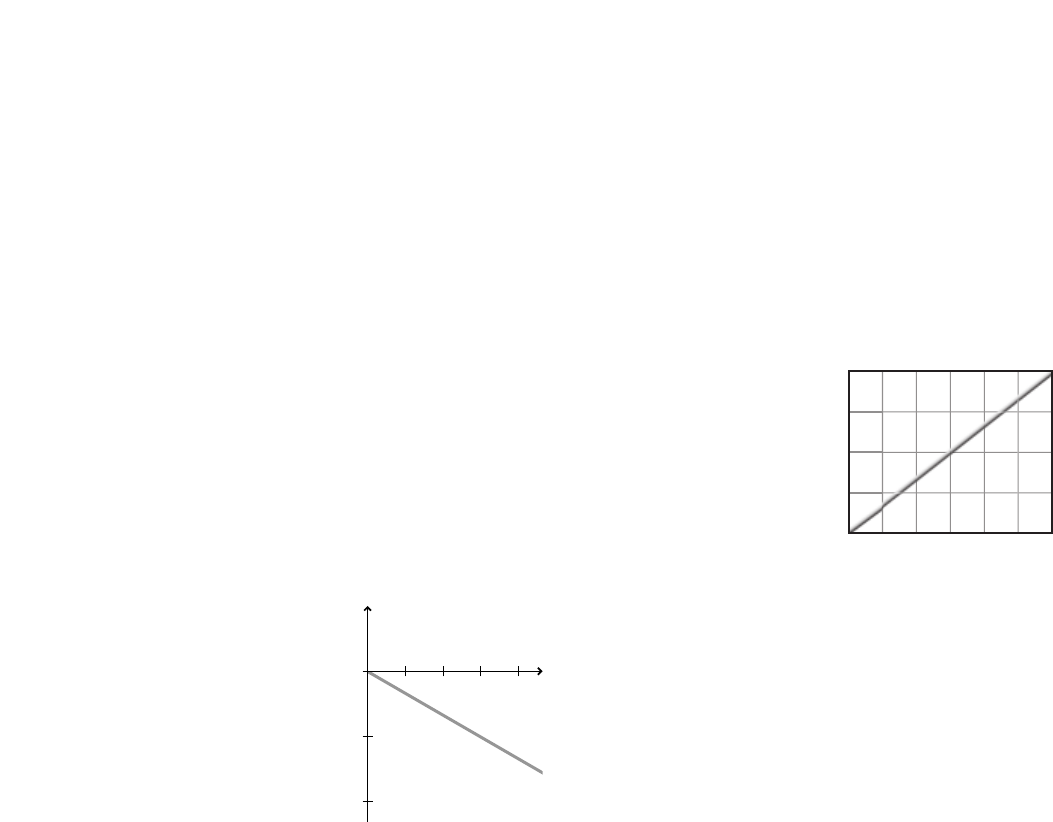
19. Position-Time Graph From the particle
model in Figure 2-17 of a baby crawling
across a kitchen floor, plot a position-time
graph to represent his motion. The time
interval between successive dots is 1 s.
■Figure 2-17
20. Motion Diagram Create a particle model
from the position-time graph of a hockey
puck gliding across a frozen pond in
Figure 2-18.
■Figure 2-18
For problems 21–23, refer to Figure 2-18.
21. Time Use the position-time graph of the
hockey puck to determine when it was
10.0 m beyond the origin.
0.5 s
22. Distance Use the position-time graph of
the hockey puck to determine how far it
moved between 0.0 s and 5.0 s.
100 m
23. Time Interval Use the position-time graph
for the hockey puck to determine how much
time it took for the puck to go from 40 m
beyond the origin to 80 m beyond the origin.
2.0 s
24. Critical Thinking Look at the particle
model and position-time graph shown in
Figure 2-19. Do they describe the same
motion? How do you know? Do not
confuse the position coordinate system in
the particle model with the horizontal axis
in the position-time graph. The time inter-
vals in the particle model are 2 s.
■Figure 2-19
0
Position (m)
Time (s)
4
8
12
12345
Position (m)
010
0 m 140 m
t0 0.0 s t7 7.0 s
0.0
Position (m)
Time (s)
20
40
60
80
100
120
140
7.0
6.05.04.03.02.01.0
Time (s)
56781234
160
140
120
100
80
60
40
20
0
Position (m)
Position (cm)
020 40 60 80 100 120 140 160
18 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
Physics: Principles and Problems Solutions Manual 19
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
No, they don’t describe the same
motion. Although both objects are trav-
eling in the positive direction, one is
moving more quickly than the other.
Students can cite a number of different
specific examples from the graph and
particle model to back this up.
Practice Problems
2.4 How Fast?
pages 43–47
page 45
25. The graph in Figure 2-22 describes the
motion of a cruise ship during its voyage
through calm waters. The positive
d-direction is defined to be south.
■Figure 2-22
a. What is the ship’s average speed?
Using the points (0.0 s, 0.0 m) and
(3.0 s, 1.0 m)
v
d
t
d
t
2
2
d
t1
1
3
1.
.0
0s
m
00
.0
.0sm
0.33 m/s
0.33 m/s
b. What is its average velocity?
The average velocity is the slope of
the line, including the sign, so it is
0.33 m/s or 0.33 m/s north.
26. Describe, in words, the motion of the cruise
ship in the previous problem.
The ship is moving to the north at a
speed of 0.33 m/s.
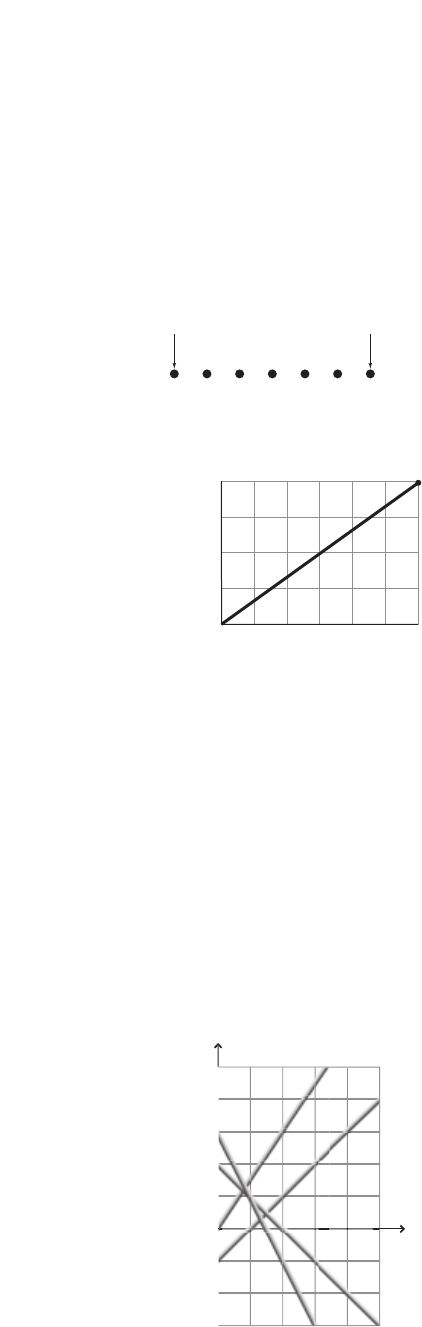
27. The graph in Figure 2-23 represents the
motion of a bicycle. Determine the bicycle’s
average speed and average velocity, and
describe its motion in words.
■Figure 2-23
Because the bicycle is moving in the
positive direction, the average speed
and average velocity are the same.
Using the points (0.0 min, 0.0 km) and
(15.0 min, 10.0 km),
v
d
t
d
t
2
2
d
t1
1
0.67 km/min
v
0.67 km/min in the positive
direction
The bicycle is moving in the positive
direction at a speed of 0.67 km/min.
10.0 km 0.0 km
15.0 min 0.0 min
Position (km)
Time (min)
20
15
10
5
030252015105
Position (m)
Time (s)
1234
2
1
0
Chapter 2 continued
28. When Marilyn takes her pet dog for a walk,
the dog walks at a very consistent pace of
0.55 m/s. Draw a motion diagram and posi-
tion-time graph to represent Marilyn’s dog
walking the 19.8-m distance from in front
of her house to the nearest fire hydrant.
Section Review
2.4 How Fast?
pages 43–47
page 47
For problems 29–31, refer to Figure 2-25.
29. Average Speed Rank the position-time
graphs according to the average speed of the
object, from greatest average speed to least
average speed. Specifically indicate any ties.
■Figure 2-25
For speed use the absolute value, there-
fore A, B, C D
SlopeA2
SlopeB
3
2
SlopeC1
SlopeD1
30. Average Velocity Rank the graphs accord-
ing to average velocity, from greatest average
velocity to least average velocity. Specifically
indicate any ties.
B, D, C, A
SlopeA2
SlopeB
3
2
SlopeC1
SlopeD1
31. Initial Position Rank the graphs according
to the object’s initial position, from most
positive position to most negative position.
Specifically indicate any ties. Would your
ranking be different if you had been asked
to do the ranking according to initial
distance from the origin?
A, C, B, D. Yes, the ranking from greatest
to least distance would be A, C, D, B.
32. Average Speed and Average Velocity
Explain how average speed and average
velocity are related to each other.
Average speed is the absolute value of
the average velocity. Speed is only a
magnitude, while velocity is a magni-
tude and a direction.
Position (m)
Time (s)
A
BD
C
t0 0 s
0.0 m 19.8 m
t6 36 s
Motion Diagram
Position-Time Graph
6 1218243036
0
5.0
10.0
15.0
Position from
house (m)
Time (s)
20.0
House Hydrant
20 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued

Physics: Principles and Problems Solutions Manual 21
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
33. Critical Thinking In solving a physics
problem, why is it important to create
pictorial and physical models before trying
to solve an equation?
Answers will vary, but here are some of
the important points. Drawing the mod-
els before writing down the equation
helps you to get the problem situation
organized in your head. It’s difficult to
write down the proper equation if you
don’t have a clear picture of how things
are situated and/or moving. Also, you
choose the coordinate system in this
step, and this is essential in making
sure you use the proper signs on the
quantities you will substitute into the
equation later.
Chapter Assessment
Concept Mapping
page 52
34. Complete the concept map below using the
following terms: words, equivalent representa-
tions, position-time graph.
Mastering Concepts
page 52
35. What is the purpose of drawing a motion
diagram? (2.1)
A motion diagram gives you a picture
of motion that helps you visualize
displacement and velocity.
36. Under what circumstances is it legitimate to
treat an object as a point particle? (2.1)
An object can be treated as a point
particle if internal motions are not
important and if the object is small in
comparison to the distance it moves.
37. The following quantities describe location
or its change: position, distance, and dis-
placement. Briefly describe the differences
among them. (2.2)
Position and displacement are different
from distance because position and dis-
placement both contain information
about the direction in which an object
has moved, while distance does not.
Distance and displacement are different
from position because they describe
how an object’s location has changed
during a time interval, where position
tells exactly where an object is located
at a precise time.
38. How can you use a clock to find a time
interval? (2.2)
Read the clock at the beginning and
end of the interval and subtract the
beginning time from the ending time.
39. In-line Skating How can you use the
position-time graphs for two in-line skaters
to determine if and when one in-line skater
will pass the other one? (2.3)
Draw the two graphs on the same set
of axes. One inline skater will pass the
other if the lines representing each of
their motions intersect. The position
coordinate of the point where the lines
intersect is the position where the
passing occurs.
40. Walking Versus Running A walker and a
runner leave your front door at the same
time. They move in the same direction at
different constant velocities. Describe the
position-time graphs of each. (2.4)
Both are straight lines that start at the
same position, but the slope of the
runner’s line is steeper.
41. What does the slope of a position-time
graph measure? (2.4)
velocity
Chapter 2 continued
words
motion
diagram
position-time
graph
data
table
equivalent
representations
42. If you know the positions of a moving
object at two points along its path, and you
also know the time it took for the object to
get from one point to the other, can you
determine the particle’s instantaneous
velocity? Its average velocity? Explain. (2.4)
It is possible to calculate the average
velocity from the information given, but
it is not possible to find the instanta-
neous velocity.
Applying Concepts
page 52
43. Test the following combinations and
explain why each does not have the proper-
ties needed to describe the concept of veloc-
ity: dt, dt, dt, t/d.
dtincreases when either term
increases. The sign of dtdepends
upon the relative sizes of dand t.
dtincreases when either increas-
es. t/ddecreases with increasing
displacement and increases with
increasing time interval, which is back-
wards from velocity.
44. Football When can a football be consid-
ered a point particle?
A football can be treated as a point
particle if its rotations are not important
and if it is small in comparison to the
distance it moves — for distances of
1 yard or more.
45. When can a football player be treated as a
point particle?
A football player can be treated as a
point particle if his or her internal
motions are not important and if he or
she is small in comparison to the dis-
tance he or she moves — for distances
of several yards or more.
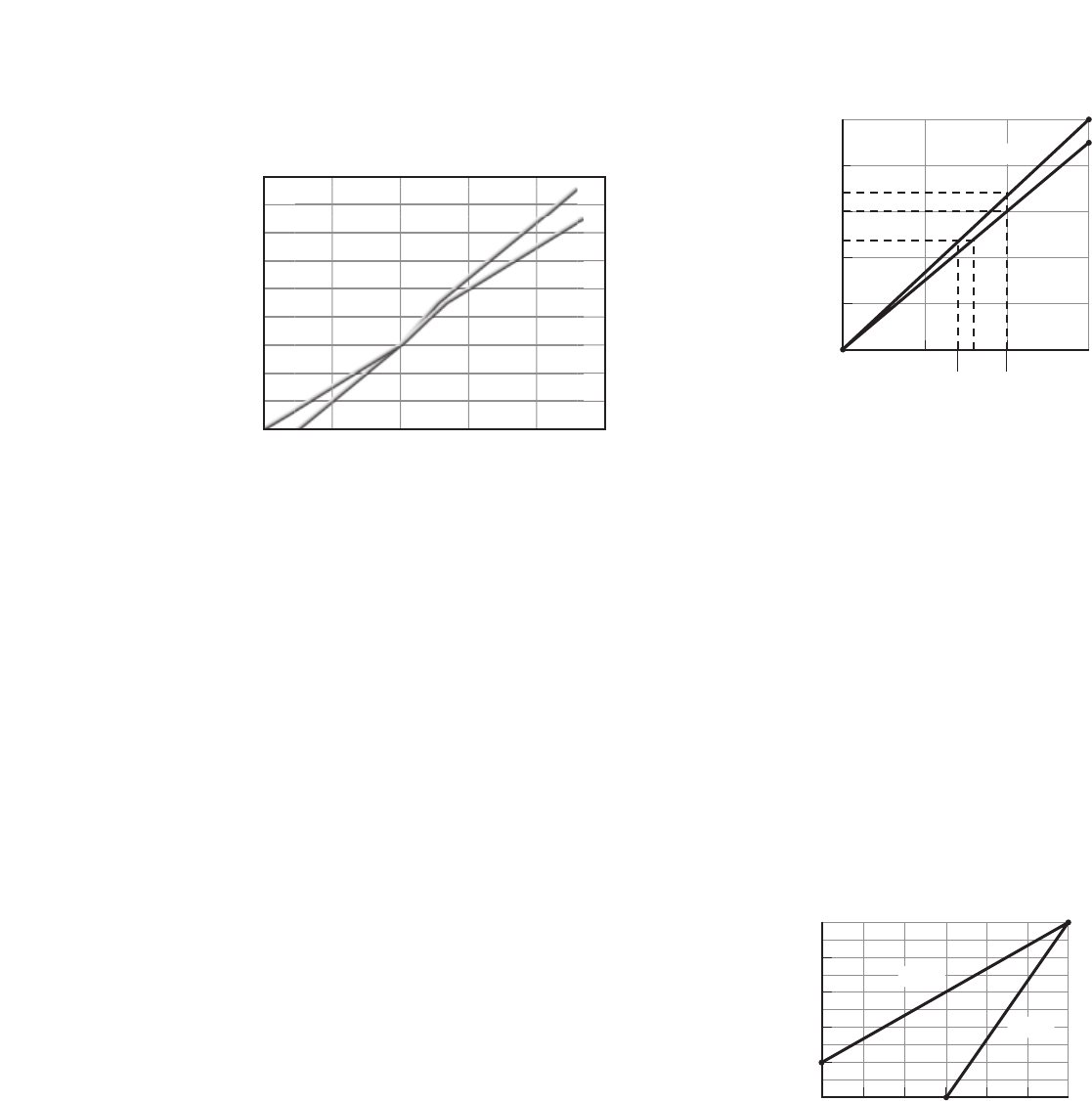
46. Figure 2-26 is a graph of two people running.
■Figure 2-26
a. Describe the position of runner A
relative to runner B at the y-intercept.
Runner A has a head start by
four units.
b. Which runner is faster?
Runner B is faster, as shown by
the steeper slope.
c. What occurs at point P and beyond?
Runner B passes runner A at point
P.
47. The position-time graph in Figure 2-27
shows the motion of four cows walking
from the pasture back to the barn. Rank the
cows according to their average velocity,
from slowest to fastest.
■Figure 2-27
Moolinda, Dolly, Bessie, Elsie
Position (m)
Time (s)
Elsie
Bessie
Dolly
Moolinda
Position (m)
Time (s)
Runner B
Runner A
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
22 Solutions Manual Physics: Principles and Problems

Physics: Principles and Problems Solutions Manual 23
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
48. Figure 2-28 is a position-time graph for a
rabbit running away from a dog.
■Figure 2-28
a. Describe how this graph would be
different if the rabbit ran twice as fast.
The only difference is that the slope
of the graph would be twice as steep.
b. Describe how this graph would be dif-
ferent if the rabbit ran in the opposite
direction.
The magnitude of the slope would be
the same, but it would be negative.
Mastering Problems
2.4 How Fast?
page 53
Level 1
49. A bike travels at a constant speed of 4.0 m/s
for 5.0 s. How far does it go?
dvt
(4.0 m/s)(5 s)
20 m
50. Astronomy Light from the Sun reaches
Earth in 8.3 min. The speed of light is
3.00108m/s. How far is Earth from
the Sun?
dvt
(3.00108m/s)(8.3 min)
1
6m
0s
in
1.51011 m
Position (m)
0
1
2
3
Time (s)
321
Chapter 2 continued
Level 2
51. A car is moving down a street at 55 km/h. A
child suddenly runs into the street. If it
takes the driver 0.75 s to react and apply
the brakes, how many meters will the car
have moved before it begins to slow down?
dvt
(55 km/h)(0.75 s)
10
10
k
0
m
m
36
1
00
hs
11 m
52. Nora jogs several times a week and always
keeps track of how much time she runs
each time she goes out. One day she forgets
to take her stopwatch with her and wonders
if there’s a way she can still have some idea
of her time. As she passes a particular bank,
she remembers that it is 4.3 km from her
house. She knows from her previous
training that she has a consistent pace of
4.0 m/s. How long has Nora been jogging
when she reaches the bank?
dvt
t
d
v
1075 s
(1075 s)
1
6m
0s
in
18 min
Level 3
53. Driving You and a friend each drive
50.0 km. You travel at 90.0 km/h; your
friend travels at 95.0 km/h. How long will
your friend have to wait for you at the end
of the trip?
dvt
t1
d
v
95
00
.0
.0kk
m
m
/h
0.556 h
t2
d
v
95
50
.0
.0kk
m
m
/h
0.526 h
t1t2(0.556 h 0.526 h)
60
1m
hin
1.8 min
Mixed Review
pages 53–54
Level 1
54. Cycling A cyclist maintains a constant
velocity of 5.0 m/s. At time t0.0 s, the
cyclist is 250 m from point A.
a. Plot a position-time graph of the
cyclist’s location from point A at 10.0-s
intervals for 60.0 s.
b. What is the cyclist’s position from point
A at 60.0 s?
550 m
c. What is the displacement from the
starting position at 60.0 s?
550 m 250 m 3.0102m
55. Figure 2-29 is a particle model for a
chicken casually walking across the road.
Time intervals are every 0.1 s. Draw the
corresponding position-time graph and
equation to describe the chicken’s motion.
■Figure 2-29
56. Figure 2-30 shows position-time graphs for
This side
The other side
1.9 s
0
t
d
This side The other side
Time intervals are 0.1 s.
200
0.0 20.010.0 40.030.0 50.0 60.0
550
250
300
350
400
450
500
Position (m)
Time (s)
(4.3 km)
11
00
k0
m
m
4.0 m/s
24 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
Physics: Principles and Problems Solutions Manual 25
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Joszi and Heike paddling canoes in a local
river.
■Figure 2-30
a. At what time(s) are Joszi and Heike in
the same place?
1.0 h
b. How much time does Joszi spend on
the river before he passes Heike?
45 min
c. Where on the river does it appear that
there might be a swift current?
from 6.0 to 9.0 km from the origin
Level 2
57. Driving Both car A and car B leave school
when a stopwatch reads zero. Car A travels
at a constant 75 km/h, and car B travels at a
constant 85 km/h.
a. Draw a position-time graph showing
the motion of both cars. How far are
the two cars from school when the stop-
watch reads 2.0 h? Calculate the dis-
tances and show them on your graph.
dAvAt
(75 km/h)(2.0 h)
150 km
dBvBt
(85 km/h)(2.0 h)
170 km
b. Both cars passed a gas station 120 km
from the school. When did each car
pass the gas station? Calculate the times
and show them on your graph.
tA
d
A
7
1
5
20
km
km
/h
1.6 h
tB
d
B
8
1
5
20
km
km
/h
1.4 h
58. Draw a position-time graph for two cars
traveling to the beach, which is 50 km from
school. At noon, Car A leaves a store that is
10 km closer to the beach than the school is
and moves at 40 km/h. Car B starts from
school at 12:30 P.M. and moves at 100 km/h.
When does each car get to the beach?
Both cars arrive at the beach at 1:00 P.M.
Level 3
59. Two cars travel along a straight road. When
a stopwatch reads t0.00 h, car A is at
dA48.0 km moving at a constant
36.0 km/h. Later, when the watch reads
t0.50 h, car B is at dB0.00 km moving
0
Noon 1220
1210 1240
1230 1250 100PM
50
10
20
30
40 Car A
Car B
Position (m)
Time
01.0 1.4
1.6 2.0 3.0
250
50
100
120
170
150
200 Car B
Car A
Position (km)
Time (h)
Position (km)
0
Time (h)
14
16
18
2
4
6
8
10
12
2.52.01.51.00.5
Heike
Joszi
Chapter 2 continued
at 48.0 km/h. Answer the following ques-
tions, first, graphically by creating a posi-
tion-time graph, and second, algebraically
by writing equations for the positions
dAand dBas a function of the stopwatch
time, t.
a. What will the watch read when car B
passes car A?
Cars pass when the distances are
equal, dAdB
dA48.0 km (36.0 km/h)t
and dB0(48.0 km/h)(t0.50 h)
so 48.0 km (36.0 km/h)t
(48.0 km/h)(t0.50 h)
(48.0 km) (36.0 km/h)t
(48.0 km/h)t24 km
72 km (12.0 km/h)t
t6.0 h
b. At what position will car B pass car A?
dA48.0 km (36.0 km/h)(6.0 h)
2.6102km
c. When the cars pass, how long will it
have been since car A was at the
reference point?
dvt
so t
d
v
3
6
4
.0
8.0
km
km
/h
1.33 h
Car A has started 1.33 h before the
clock started.
t6.0 h 1.33 h 7.3 h
60. Figure 2-31 shows the position-time graph
depicting Jim’s movement up and down the
aisle at a store. The origin is at one end of
the aisle.
■Figure 2-31
a. Write a story describing Jim’s movements
at the store that would correspond to the
motion represented by the graph.
Answers will vary.
b. When does Jim have a position of 6.0 m?
from 8.0 to 18.0 s, 53.0 to 56.0 s, and
at 43.0 s
c. How much time passes between when
Jim enters the aisle and when he gets to
a position of 12.0 m? What is Jim’s aver-
age velocity between 37.0 s and 46.0 s?
t33.0 s
Using the points (37.0 s, 12.0 m) and
(46.0 s, 3.00 m)
v
1.00 m/s
3.00 m 12.0 m
46.0 s 37.0 s
dfdi
tfti
Position (m)
Time (s)
14.0
12.0
10.0
8.0
6.0
4.0
2.0
0.00 10.0 20.0 30.0 40.0 50.0 60.0
0.00 1.00 2.00
1.00 7.003.00 4.00 5.00 6.00
300.0
50.0
100.0
150.0
150.0
200.0
Car A
Car B
Position (km)
Time (h)
26 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
Physics: Principles and Problems Solutions Manual 27
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Thinking Critically
page 54
61. Apply Calculators Members of a physics
class stood 25 m apart and used stopwatch-
es to measure the time which a car traveling
on the highway passed each person. Their
data are shown in Table 2-3.
Use a graphing calculator to fit a line to a
position-time graph of the data and to plot
this line. Be sure to set the display range of
the graph so that all the data fit on it. Find
the slope of the line. What was the speed of
the car?
The slope of the line and the speed of
the car are 19.7 m/s.
62. Apply Concepts You plan a car trip for
which you want to average 90 km/h. You
cover the first half of the distance at an
average speed of only 48 km/h. What must
your average speed be in the second half of
the trip to meet your goal? Is this reason-
able? Note that the velocities are based on
half the distance, not half the time.
720 km/h; No
Explanation:
Assume you want to travel 90 km in 1 h.
If you cover the first half of the distance
at 48 km/h, then you’ve gone 45 km in
0.9375 h (because t
d
v
). This means
you have used 93.75% of your time for
the first half of the distance leaving
6.25% of the time to go the remaining
45 km.
v
04
.0
5
62
k5
mh
720 km/h
63. Design an Experiment Every time a par-
ticular red motorcycle is driven past your
friend’s home, his father becomes angry
because he thinks the motorcycle is going
too fast for the posted 25 mph (40 km/h)
speed limit. Describe a simple experiment
you could do to determine whether or not
the motorcycle is speeding the next time it
is driven past your friend’s house.
There are actually several good possibil-
ities for answers on this one.Two that
should be among the most popular are
briefly described here. 1) Get several
people together and give everyone a
watch. Synchronize the watches and
stand along the street separated by a
consistent distance, maybe 10 m or so.
When the motorcycle passes, have each
person record the time (at least to an
accuracy of seconds) that the motorcy-
cle crossed in front of them. Plot a posi-
tion time graph, and compute the slope
of the best-fit line. If the slope is greater
than 25 mph, the motorcycle is speed-
ing. 2) Get someone with a driver’s
license to drive a car along the street at
25 mph in the same direction as you
expect the motorcycle to go. If the
motorcycle gets closer to the car (if the
distance between them decreases), the
motorcycle is speeding. If the distance
between them stays the same, the
motorcycle is driving at the speed limit.
If the distance increases, the motorcycle
is driving less than the speed limit.
64. Interpret Graphs Is it possible for an
0.0 4.02.0 8.06.0 10.0 12.0
200.0
50.0
100.0
150.0
Position (m)
Time (s)
Table 2-3
Position v. Time
Time (s) Position (m)
0.0 0.0
1.3 25.0
2.7 50.0
3.6 75.0
5.1 100.0
5.9 125.0
7.0 150.0
8.6 175.0
10.3 200.0
Chapter 2 continued

object’s position-time graph to be a hori-
zontal line? A vertical line? If you answer
yes to either situation, describe the associat-
ed motion in words.
It is possible to have a horizontal line
as a position-time graph; this would
indicate that the object’s position is not
changing, or in other words, that it is
not moving. It is not possible to have a
position-time graph that is a vertical
line, because this would mean the
object is moving at an infinite speed.
Writing in Physics
page 54
65. Physicists have determined that the speed of
light is 3.00108m/s. How did they arrive
at this number? Read about some of the
series of experiments that were done to
determine light’s speed. Describe how the
experimental techniques improved to make
the results of the experiments more accurate.
Answers will vary. Galileo attempted to
determine the speed of light but was
unsuccessful. Danish astronomer Olaus
Roemer successfully measured the
speed of light in 1676 by observing the
eclipses of the moons of Jupiter. His
estimate was 140,000 miles/s (225,308
km/s). Many others since have tried to
measure it more accurately using rotat-
ing toothed wheels, rotating mirrors and
the Kerr cell shutter.
66. Some species of animals have good
endurance, while others have the ability to
move very quickly, but for only a short
amount of time. Use reference sources to
find two examples of each quality and
describe how it is helpful to that animal.
Answers will vary. Examples of animals
with high endurance to outlast preda-
tors or prey include mules, bears, and
coyotes. Animals with the speed to
quickly escape predators or capture
prey include cheetahs, antelopes and
deer.
Cumulative Review
page 54
67. Convert each of the following time mea-
surements to its equivalent in seconds.
(Chapter 1)
a. 58 ns
5.8108s
b. 0.046 Gs
4.6107s
c. 9270 ms
9.27 s
d. 12.3 ks
1.23104s
68. State the number of significant digits in the
following measurements. (Chapter 1)
a. 3218 kg
4
b. 60.080 kg
5
c. 801 kg
3
d. 0.000534 kg
3
69. Using a calculator, Chris obtained the fol-
lowing results. Rewrite the answer to each
operation using the correct number of sig-
nificant digits. (Chapter 1)
a. 5.32 mm 2.1 mm 7.4200000 mm
7.4 mm
b. 13.597 m 3.65 m 49.62905 m2
49.6 m2
c. 83.2 kg 12.804 kg 70.3960000 kg
70.4 kg
28 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
Physics: Principles and Problems Solutions Manual 29
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
3Accelerated Motion
CHAPTER
Practice Problems
3.1 Acceleration
pages 57–64
page 61
1. A dog runs into a room and sees a cat at the
other end of the room. The dog instantly
stops running but slides along the wood
floor until he stops, by slowing down with a
constant acceleration. Sketch a motion dia-
gram for this situation, and use the velocity
vectors to find the acceleration vector.
2. Figure 3-5 is a v-t graph for Steven as he
walks along the midway at the state fair.
Sketch the corresponding motion diagram,
complete with velocity vectors.
■Figure 3-5
3. Refer to the v-t graph of the toy train
in Figure 3-6 to answer the following
questions.
■Figure 3-6
a. When is the train’s speed constant?
5.0 to 15.0 s
b. During which time interval is the train’s
acceleration positive?
0.0 to 5.0 s
c. When is the train’s acceleration most
negative?
15.0 to 20.0 s
4. Refer to Figure 3-6 to find the average
acceleration of the train during the follow-
ing time intervals.
a. 0.0 s to 5.0 s
a
2.0 m/s2
b. 15.0 s to 20.0 s
a
1.2 m/s2
c. 0.0 s to 40.0 s
a
v2v1
t2t1
4.0 m/s 10.0 m/s
20.0 s 15.0 s
v2v1
t2t1
10.0 m/s 0.0 m/s
5.0 s 0.0 s
v2v1
t2t1
30.020.010.0 40.0
0.0
6.0
4.0
2.0
12.0
10.0
8.0
Velocity (m/s)
Time (s)
Time (s) 0 1 2 3 4 56
7
8109
Velocity (m/s)
Time (s)
567894321010
StopStart
1
v1
2
v2
3
v3
Time
interval
Velocity
Position
v2
v1
a
0.0 m/s2
5. Plot a v-t graph representing the following
motion. An elevator starts at rest from the
ground floor of a three-story shopping
mall. It accelerates upward for 2.0 s at a
rate of 0.5 m/s2, continues up at a con-
stant velocity of 1.0 m/s for 12.0 s, and
then experiences a constant downward
acceleration of 0.25 m/s2for 4.0 s as it
reaches the third floor.
page 64
6. A race car’s velocity increases from 4.0 m/s
to 36 m/s over a 4.0-s time interval. What is
its average acceleration?
a
v
t
8.0 m/s2
7. The race car in the previous problem slows
from 36 m/s to 15 m/s over 3.0 s. What is
its average acceleration?
a
v
t
15 m/s
3.
0s
36 m/s
7.0 m/s2
8. A car is coasting backwards downhill at a
speed of 3.0 m/s when the driver gets the
engine started. After 2.5 s, the car is moving
uphill at 4.5 m/s. If uphill is chosen as the
positive direction, what is the car’s average
acceleration?
a
v
t
3.0 m/s2
9. A bus is moving at 25 m/s when the driver
steps on the brakes and brings the bus to a
stop in 3.0 s.
a. What is the average acceleration of the
bus while braking?
a
v
t
8.3 m/s2
b. If the bus took twice as long to stop,
how would the acceleration compare
with what you found in part a?
half as great (4.2 m/s2)
10. Rohith has been jogging to the bus stop for
2.0 min at 3.5 m/s when he looks at his
watch and sees that he has plenty of time
before the bus arrives. Over the next 10.0 s,
he slows his pace to a leisurely 0.75 m/s.
What was his average acceleration during
this 10.0 s?
a
v
t
0.28 m/s2
11. If the rate of continental drift were to
abruptly slow from 1.0 cm/yr to 0.5 cm/yr
over the time interval of a year, what would
be the average acceleration?
a
v
t
0.5 cm/yr2
Section Review
3.1 Acceleration
pages 57–64
page 64
12. Velocity-Time Graph What information
can you obtain from a velocity-time graph?
The velocity at any time, the time at
which the object had a particular
velocity, the sign of the velocity, and the
displacement.
13. Position-Time and Velocity-Time Graphs
Two joggers run at a constant velocity of
7.5 m/s toward the east. At time t0, one
0.5 cm/yr 1.0 cm/yr
1.0 yr
0.75 m/s 3.5 m/s
10.0 s
0.0 m/s 25 m/s
3.0 s
4.5 m/s (3.0 m/s)
2.5 s
36 m/s 4.0 m/s
4.0 s
Velocity (m/s)
1.0
Time (s)
15.05.00.0 10.0 20.0
0.0 m/s 0.0 m/s
40.0 s 0.0 s
30 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 31
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
is 15 m east of the origin and the other is
15 m west.
a. What would be the difference(s) in the
position-time graphs of their motion?
Both lines would have the same
slope, but they would rise from the
d-axis at different points, 15 m,
and 15 m.
b. What would be the difference(s) in their
velocity-time graphs?
Their velocity-time graphs would be
identical.
14. Velocity Explain how you would use a
velocity-time graph to find the time at
which an object had a specified velocity.
Draw or imagine a horizontal line at the
specified velocity. Find the point where
the graph intersects this line. Drop a
line straight down to the t-axis. This
would be the required time.
15. Velocity-Time Graph Sketch a velocity-time
graph for a car that goes east at 25 m/s for
100 s, then west at 25 m/s for another 100 s.
16. Average Velocity and Average Acceleration
A canoeist paddles upstream at 2 m/s and
then turns around and floats downstream at
4 m/s. The turnaround time is 8 s.
a. What is the average velocity of the canoe?
Choose a coordinate system with
the positive direction upstream.
v
1 m/s
b. What is the average acceleration of the
canoe?
a
v
t
vf
t
vi
0.8 m/s2
17. Critical Thinking A police officer clocked
a driver going 32 km/h over the speed limit
just as the driver passed a slower car. Both
drivers were issued speeding tickets. The
judge agreed with the officer that both were
guilty. The judgement was issued based on
the assumption that the cars must have
been going the same speed because they
were observed next to each other. Are the
judge and the police officer correct? Explain
with a sketch, a motion diagram, and a
position-time graph.
No, they had the same position, not
velocity. To have the same velocity, they
would have had to have the same rela-
tive position for a length of time.
(4 m/s) (2 m/s)
8 s
2 m/s (4 m/s)
2
vivf
2
25
Velocity (m/s)
25
200 Time (s)
100
Chapter 3 continued
32 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued
Practice Problems
3.2 Motion with Constant Acceleration
pages 65–71
page 65
18. A golf ball rolls up a hill toward a miniature-golf hole. Assume that the
direction toward the hole is positive.
a. If the golf ball starts with a speed of 2.0 m/s and slows at a constant rate of
0.50 m/s2, what is its velocity after 2.0 s?
vfviat
2.0 m/s (0.50 m/s2)(2.0 s)
1.0 m/s
b. What is the golf ball’s velocity if the constant acceleration continues for 6.0 s?
vfviat
2.0 m/s (0.50 m/s2)(6.0 s)
1.0 m/s
c. Describe the motion of the golf ball in words and with a motion diagram.
The ball’s velocity simply decreased in the first case. In the second
case, the ball slowed to a stop and then began rolling back down the
hill.
19. A bus that is traveling at 30.0 km/h speeds up at a constant rate of 3.5 m/s2.
What velocity does it reach 6.8 s later?
vfviat
30.0 km/h (3.5 m/s2)(6.8 s)
11
00
k
0
m
m
36
1
00
hs
120 km/h
Time interval 1 2 3
6
4
5
Velocity
Position
Velocity
Time interval
d
Time
Position
Passing
position
Position-Time Graph
t1t2t3t4
0
1
2
3
4t0t4
t3
t2
t1
t0t4
t3
t2
t1
Motion diagram
Faster car
Slower car
Sketch

Physics: Principles and Problems Solutions Manual 33
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
20. If a car accelerates from rest at a constant
5.5 m/s2, how long will it take for the car to
reach a velocity of 28 m/s?
vfviat
so t
vf
a
vi
5.1 s
21. A car slows from 22 m/s to 3.0 m/s at a
constant rate of 2.1 m/s2. How many
seconds are required before the car is
traveling at 3.0 m/s?
vfviat
so t
vf
a
vi
9.0 s
page 67
22. Use Figure 3-11 to determine the velocity
of an airplane that is speeding up at each of
the following times.
■Figure 3-11
Graph B represents constant speed. So
graph A should be used for the follow-
ing calculations.
a. 1.0 s
At 1.0 s, v74 m/s
b. 2.0 s
At 2.0 s, v78 m/s
c. 2.5 s
At 2.5 s, v80 m/s
23. Use dimensional analysis to convert an
airplane’s speed of 75 m/s to km/h.
(75 m/s)
36
1
00
hs
11
00
k
0
m
m
2.7102km/h
24. A position-time graph for a pony running
in a field is shown in Figure 3-12. Draw
the corresponding velocity-time graph using
the same time scale.
■Figure 3-12
25. A car is driven at a constant velocity of
25 m/s for 10.0 min. The car runs out of gas
and the driver walks in the same direction
at 1.5 m/s for 20.0 min to the nearest gas
station. The driver takes 2.0 min to fill a
gasoline can, then walks back to the car at
1.2 m/s and eventually drives home at
25 m/s in the direction opposite that of
the original trip.
a. Draw a v-t graph using seconds as your
time unit. Calculate the distance the dri-
ver walked to the gas station to find the
time it took him to walk back to the car.
Time (s)
Stops and
turns around
Position-time graph
Slows
down
Speeds
u
p
Speeds
up
x
y
Displacement (m)
Velocity (m/s)
Displacement (m)
Time (s) x
y
0.0 3.01.0 2.0
82
80
78
76
74
72
70
Velocity (m/s)
Time (s)
3.0 m/s 22 m/s
2.1 m/s2
28 m/s 0.0 m/s
5.5 m/s2
Chapter 3 continued
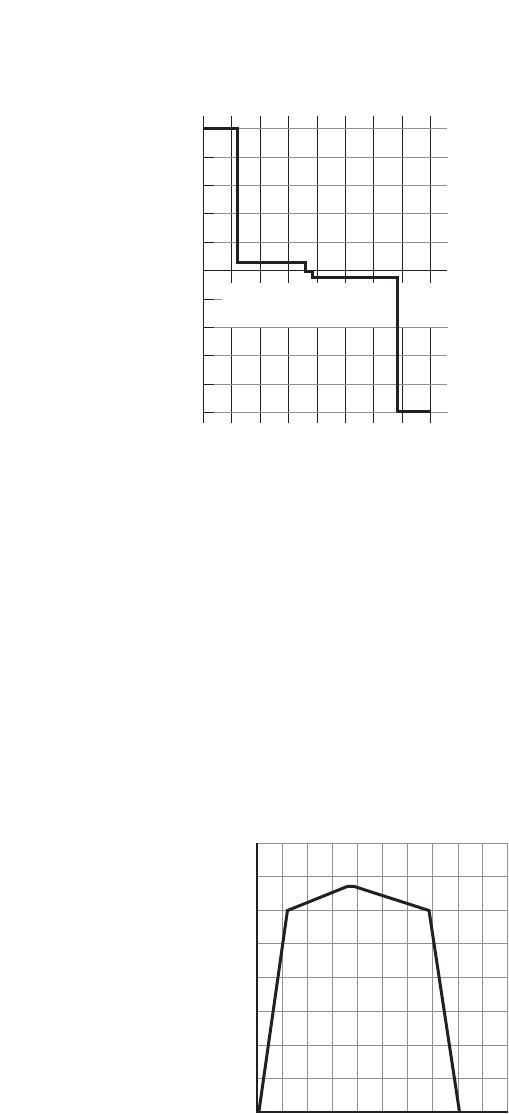
distance the driver walked to the
gas station:
dvt
(1.5 m/s)(20.0 min)(60 s/min)
1800 m
1.8 km
time to walk back to the car:
t
d
v
1
18
.2
00
mm
/s
1500 s 25 min
b. Draw a position-time graph for the
situation using the areas under the
velocity-time graph.
page 69
26. A skateboarder is moving at a constant
velocity of 1.75 m/s when she starts up an
incline that causes her to slow down with a
constant acceleration of 0.20 m/s2. How
much time passes from when she begins to
slow down until she begins to move back
down the incline?
vfviat
t
vf
a
vi
8.8 s
27. A race car travels on a racetrack at 44 m/s
and slows at a constant rate to a velocity
of 22 m/s over 11 s. How far does it move
during this time?
v
2
v
(vf
2
vi)
dv
t
(vf
2
vi)t
1.2102m
28. A car accelerates at a constant rate from
15 m/s to 25 m/s while it travels a distance
of 125 m. How long does it take to achieve
this speed?
v
2
v
(vf
2
vi)
dv
t
(vf
2
vi)t
t
25 s
29. A bike rider pedals with constant accelera-
tion to reach a velocity of 7.5 m/s over a
time of 4.5 s. During the period of accelera-
tion, the bike’s displacement is 19 m. What
was the initial velocity of the bike?
v
2
v
(vf
2
vi)
dv
t
(vf
2
vi)t
so vi
2
t
d
vf
4.5(s
2)
(19
7.m
5)
m/s
0.94 m/s
(2)(125 m)
25 m/s 15 m/s
2d
(vfvi)
(22 m/s 44 m/s)(11 s)
2
0.0 m/s 1.75 m/s
0.20 m/s2
0
5000
10,000
15,000
20,000
Position (m)
1000 2000 3000
Time (s)
4000 5000
Velocity (m/s)
Time (s)
5
10
15
20
25
0
5
15
20
25
3500
4000
3000
2500
2000
1500
1000
500
10
34 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued
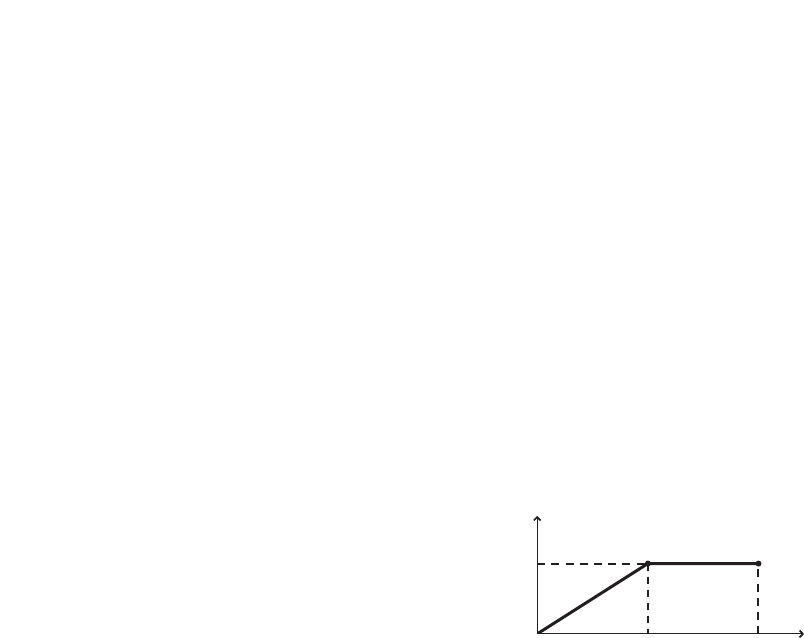
Physics: Principles and Problems Solutions Manual 35
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
page 71
30. A man runs at a velocity of 4.5 m/s for 15.0 min. When going up an increasingly
steep hill, he slows down at a constant rate of 0.05 m/s2for 90.0 s and comes to
a stop. How far did he run?
dv1t1
1
2
(v2f v2i)t2
(4.5 m/s)(15.0 min)(60 s/min)
1
2
(0.0 m/s 4.5 m/s)(90.0 s)
4.3103m
31. Sekazi is learning to ride a bike without training wheels. His father pushes him
with a constant acceleration of 0.50 m/s2for 6.0 s, and then Sekazi continues at
3.0 m/s for another 6.0 s before falling. What is Sekazi’s displacement? Solve this
problem by constructing a velocity-time graph for Sekazi’s motion and comput-
ing the area underneath the graphed line.
Part 1: Constant acceleration:
d1
1
2
(3.0 m/s)(6.0 s)
9.0 m
Part 2: Constant velocity:
d2(3.0 m/s)(12.0 s 6.0 s)
18 m
Thus dd1d29.0 m 18 m 27 m
32. You start your bicycle ride at the top of a hill. You coast down the hill at a con-
stant acceleration of 2.00 m/s2. When you get to the bottom of the hill, you are
moving at 18.0 m/s, and you pedal to maintain that speed. If you continue at this
speed for 1.00 min, how far will you have gone from the time you left the hilltop?
Part 1: Constant acceleration:
vf2vi22a(dfdi) and di0.00 m
so df
vf2
2
a
vi2
since vi0.00 m/s
df
v
2f
a
2
(2
()
1
(8
2.
.0
00
m
m
/s
/)
s
2
2)
81.0 m
Velocity (m/s)
3.0
Time (s)
6.0 12.0
12
Chapter 3 continued

Part 2: Constant velocity:
d2vt (18.0 m/s)(60.0 s) 1.08103m
Thus dd1d2
81.0 m 1.08103m
1.16103m
33. Sunee is training for an upcoming 5.0-km race. She starts out her training
run by moving at a constant pace of 4.3 m/s for 19 min. Then she accelerates
at a constant rate until she crosses the finish line, 19.4 s later. What is her
acceleration during the last portion of the training run?
Part 1: Constant velocity:
dvt
(4.3 m/s)(19 min)(60 s/min)
4902 m
Part 2: Constant acceleration:
dfdivit
1
2
at2
a
0.077 m/s2
Section Review
3.2 Motion with Constant Acceleration
pages 65–71
page 71
34. Acceleration A woman driving at a speed of 23 m/s sees a deer on the road
ahead and applies the brakes when she is 210 m from the deer. If the deer does
not move and the car stops right before it hits the deer, what is the acceleration
provided by the car’s brakes?
vf2vi22a(dfdi)
a
2
v
(f
d
2
f
v
d
i2
i)
1.3 m/s2
35. Displacement If you were given initial and final velocities and the constant
acceleration of an object, and you were asked to find the displacement, what
equation would you use?
vf2vi22adf
0.0 m/s (23 m/s)2
(2)(210 m)
(2)(5.0103m4902 m (4.3 m/s)(19.4 s))
(19.4 s)2
2(dfdivit)
t2
36 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 37
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
36. Distance An in-line skater first accelerates from 0.0 m/s to 5.0 m/s in 4.5 s, then
continues at this constant speed for another 4.5 s. What is the total distance trav-
eled by the in-line skater?
Accelerating
dfv
tf
vi
2
vf
(tf)
(4.5 s)
11.25 m
Constant speed
dfvftf
(5.0 m/s)(4.5 s)
22.5 m
total distance 11.25 m 22.5 m
34 m
37. Final Velocity A plane travels a distance of 5.0102m while being accelerated
uniformly from rest at the rate of 5.0 m/s2. What final velocity does it attain?
vf2vf22a(dfdi) and di0, so
vf2vf22adf
vf(0.0 m
/s)2
2(5.0
m/s2)(
5.01
02m)
71 m/s
38. Final Velocity An airplane accelerated uniformly from rest at the rate of 5.0
m/s2for 14 s. What final velocity did it attain?
vfviatf
0(5.0 m/s2)(14 s) 7.0101m/s
39. Distance An airplane starts from rest and accelerates at a constant 3.00 m/s2for
30.0 s before leaving the ground.
a. How far did it move?
dfvitf
1
2
atf2
(0.0 m/s)(30.0 s)2
1
2
(3.00 m/s2)(30.0 s)2
1.35103m
b. How fast was the airplane going when it took off?
vfviatf
0.0 m/s (3.00 m/s2)(30.0 s)
90.0 m/s
0.0 m/s 5.0 m/s
2
Chapter 3 continued
40. Graphs A sprinter walks up to the starting blocks at a constant speed and
positions herself for the start of the race. She waits until she hears the starting
pistol go off, and then accelerates rapidly until she attains a constant velocity.
She maintains this velocity until she crosses the finish line, and then she slows
down to a walk, taking more time to slow down than she did to speed up at
the beginning of the race. Sketch a velocity-time and a position-time graph to
represent her motion. Draw them one above the other on the same time scale.
Indicate on your p-t graph where the starting blocks and finish line are.
41. Critical Thinking Describe how you could calculate the acceleration of an auto-
mobile. Specify the measuring instruments and the procedures that you would use.
One person reads a stopwatch and calls out time intervals. Another
person reads the speedometer at each time and records it. Plot speed
versus time and find the slope.
Practice Problems
3.3 Free Fall
pages 72–75
page 74
42. A construction worker accidentally drops a brick from a high scaffold.
a. What is the velocity of the brick after 4.0 s?
Say upward is the positive direction.
vfviat,ag9.80 m/s2
vf0.0 m/s (9.80 m/s2)(4.0 s)
39 m/s when the upward direction is positive
b. How far does the brick fall during this time?
dvit
1
2
at2
0
1
2
(9.80 m/s2)(4.0 s)2
78 m
The brick falls 78 m.
43. Suppose for the previous problem you choose your coordinate system so that
the opposite direction is positive.
Starting
blocks Finish
line
Position
Time
Time
Velocity
38 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 39
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. What is the brick’s velocity after 4.0 s?
Now the positive direction is downward.
vfviat,ag9.80 m/s2
vf0.0 m/s (9.80 m/s2)(4.0 s)
39 m/s when the downward direction is positive
b. How far does the brick fall during this time?
dvit
1
2
at2,ag9.80 m/s2
(0.0 m/s)(4.0 s)
1
2
(9.80 m/s2)(4.0 s)2
78 m
The brick still falls 78 m.
44. A student drops a ball from a window 3.5 m above the sidewalk. How fast is it
moving when it hits the sidewalk?
vf2vi22ad,agand vi0
so vf2gd
(2)(9.8
0 m/s
2)(3.5
m)
8.3 m/s
45. A tennis ball is thrown straight up with an initial speed of 22.5 m/s. It is caught
at the same distance above the ground.
a. How high does the ball rise?
ag, and at the maximum height, vf0
vf2vi22ad becomes
vi22gd
d
v
2i
g
2
(2
()
2
(2
9.
.5
80
m
m
/s
/)
s
2
2)
25.8 m
b. How long does the ball remain in the air? Hint: The time it takes the ball to rise
equals the time it takes to fall.
Calculate time to rise using vfviat, with agand vf0
t
v
g
i
9
2
.2
8.
0
5m
m
//
s
s
2
2.30 s
The time to fall equals the time to rise, so the time to remain in the air is
tair 2trise (2)(2.30 s) 4.60 s
46. You decide to flip a coin to determine whether to do your physics or English
homework first. The coin is flipped straight up.
a. If the coin reaches a high point of 0.25 m above where you released it, what
was its initial speed?
Chapter 3 continued

vf2vi22ad
vivf2
2gd
where ag
and vf0 at the height of the toss, so
vi(0.0 m
/s)2
(2)(9.
80 m/
s2)(0.2
5 m)
2.2 m/s
b. If you catch it at the same height as you released it, how much time did it
spend in the air?
vfviat where ag
vi2.2 m/s and
vf2.2 m/s
t
vf
g
vi
0.45 s
Section Review
3.3 Free Fall
pages 72–75
page 75
47. Maximum Height and Flight Time Acceleration due to gravity on Mars is about
one-third that on Earth. Suppose you throw a ball upward with the same velocity
on Mars as on Earth.
a. How would the ball’s maximum height compare to that on Earth?
At maximum height, vf0,
so df
v
2i
g
2
, or three times higher.
b. How would its flight time compare?
Time is found from df
1
2
gtf2,or
tf
2
g
df
. Distance is multiplied by 3 and gis divided by 3,
so the flight time would be three times as long.
48. Velocity and Acceleration Suppose you throw a ball straight up into the air.
Describe the changes in the velocity of the ball. Describe the changes in the
acceleration of the ball.
2.2 m/s 2.2 m/s
9.80 m/s2
40 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 41
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Velocity is reduced at a constant rate as the ball travels upward. At its
highest point, velocity is zero. As the ball begins to drop, the velocity
begins to increase in the negative direction until it reaches the height
from which it was initially released. At that point, the ball has the same
speed it had upon release. The acceleration is constant throughout the
ball’s flight.
49. Final Velocity Your sister drops your house keys down to you from the second
floor window. If you catch them 4.3 m from where your sister dropped them,
what is the velocity of the keys when you catch them?
Upward is positive
v2vi22adwhere ag
vvi2
2gd
(0.0 m
/s)2
(2)(9.
80 m/
s2)(4
.3 m)
9.2 m/s
50. Initial Velocity A student trying out for the football team kicks the football
straight up in the air. The ball hits him on the way back down. If it took 3.0 s
from the time when the student punted the ball until he gets hit by the ball,
what was the football’s initial velocity?
Choose a coordinate system with up as the positive direction and the
origin at the punter. Choose the initial time at the punt and the final time
at the top of the football’s flight.
vfviatfwhere ag
vivfgtf
0.0 m/s (9.80 m/s2)(1.5 s)
15 m/s
51. Maximum Height When the student in the previous problem kicked the foot-
ball, approximately how high did the football travel?
vf2vi22a(d) where ag
d
vf2
2g
vi2
11 m
52. Critical Thinking When a ball is thrown vertically upward, it continues upward
until it reaches a certain position, and then it falls downward. At that highest
point, its velocity is instantaneously zero. Is the ball accelerating at the highest
point? Devise an experiment to prove or disprove your answer.
The ball is accelerating; its velocity is changing.Take a strobe photo to
measure its position. From photos, calculate the ball’s velocity.
(0.0 m/s)2(15 m/s)2
(2)(9.80 m/s2)
Chapter 3 continued
Chapter Assessment
Concept Mapping
page 80
53. Complete the following concept map using
the following symbols or terms: d, velocity,
m/s2, v, m, acceleration.
Mastering Concepts
page 80
54. How are velocity and acceleration related?
(3.1)
Acceleration is the change in velocity
divided by the time interval in which it
occurs: it is the rate of change of
velocity.
55. Give an example of each of the following.
(3.1)
a. an object that is slowing down, but has
a positive acceleration
if forward is the positive direction, a
car moving backward at decreasing
speed
b. an object that is speeding up, but has a
negative acceleration
in the same coordinate system, a car
moving backward at increasing
speed
56. Figure 3-16 shows the velocity-time graph
for an automobile on a test track. Describe
how the velocity changes with time. (3.1)
■Figure 3-16
The car starts from rest and increases
its speed. As the car’s speed increases,
the driver shifts gears.
57. What does the slope of the tangent to the
curve on a velocity-time graph measure?
(3.1)
instantaneous acceleration
58. Can a car traveling on an interstate highway
have a negative velocity and a positive accel-
eration at the same time? Explain. Can the
car’s velocity change signs while it is traveling
with constant acceleration? Explain. (3.1)
Yes, a car’s velocity is positive or nega-
tive with respect to its direction of
motion from some point of reference.
One direction of motion is defined as
positive, and velocities in that direction
are considered positive. The opposite
direction of motion is considered nega-
tive; all velocities in that direction are
negative. An object undergoing positive
acceleration is either increasing its
velocity in the positive direction or
reducing its velocity in the negative
direction. A car’s velocity can change
signs when experiencing constant
acceleration. For example, it can be
traveling right, while the acceleration is
to the left. The car slows down, stops,
and then starts accelerating to the left.
59. Can the velocity of an object change when
its acceleration is constant? If so, give an
example. If not, explain. (3.1)
Yes, the velocity of an object can
change when its acceleration is con-
stant. Example: dropping a book. The
5 101520253035
0
5
10
15
20
25
30
Velocity (m/s)
Time (s)
velocity
position acceleration
va
d
m/s m/s2
m
Quantities of motion
42 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 43
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
longer it drops, the faster it goes, but
the acceleration is constant at g.
60. If an object’s velocity-time graph is a straight
line parallel to the t-axis, what can you con-
clude about the object’s acceleration? (3.1)
When the velocity-time graph is a line
parallel to the t-axis, the acceleration is
zero.
61. What quantity is represented by the area
under a velocity-time graph? (3.2)
the change in displacement
62. Write a summary of the equations for
position, velocity, and time for an object
experiencing motion with uniform
acceleration. (3.2)
tf
(vf
a
vi)
vfviatf
v
2
v
vf
2
vi
dv
t
vf
2
vi
t
assuming ti0, then
ttf
d
vf
2
vi
tf
63. Explain why an aluminum ball and a steel
ball of similar size and shape, dropped
from the same height, reach the ground at
the same time. (3.3)
All objects accelerate toward the
ground at the same rate.
64. Give some examples of falling objects for
which air resistance cannot be ignored.
(3.3)
Student answers will vary. Some
examples are sheets of paper,
parachutes, leaves, and feathers.
65. Give some examples of falling objects for
which air resistance can be ignored. (3.3)
Student answers will vary. Some exam-
ples are a steel ball, a rock, and a per-
son falling through small distances.
Applying Concepts
pages 80–81
66. Does a car that is slowing down always have
a negative acceleration? Explain.
No, if the positive axis points in the
direction opposite the velocity, the
acceleration will be positive.
67. Croquet A croquet ball, after being hit by
a mallet, slows down and stops. Do the
velocity and acceleration of the ball have
the same signs?
No, they have opposite signs.
68. If an object has zero acceleration, does it
mean its velocity is zero? Give an example.
No, a0 when velocity is constant.
69. If an object has zero velocity at some
instant, is its acceleration zero? Give an
example.
No, a ball rolling uphill has zero velocity
at the instant it changes direction, but
its acceleration is nonzero.
70. If you were given a table of velocities of an
object at various times, how would you find
out whether the acceleration was constant?
Draw a velocity-time graph and see
whether the curve is a straight line or
calculate accelerations using a
v
t
and compare the answers to see if they
are the same.
71. The three notches in the graph in
Figure 3-16 occur where the driver changed
gears. Describe the changes in velocity and
acceleration of the car while in first gear. Is
the acceleration just before a gear change
larger or smaller than the acceleration just
after the change? Explain your answer.
Chapter 3 continued

Velocity increases rapidly at first, then more slowly. Acceleration is greatest
at the beginning but is reduced as velocity increases. Eventually, it is nec-
essary for the driver to shift into second gear.The acceleration is smaller
just before the gear change because the slope is less at that point on the
graph. Once the driver shifts and the gears engage, acceleration and the
slope of the curve increase.
72. Use the graph in Figure 3-16 and determine the time interval during which the
acceleration is largest and the time interval during which the acceleration is
smallest.
The acceleration is largest during an interval starting at t0 and lasting
about
1
2
s. It is smallest beyond 33 s.
73. Explain how you would walk to produce each of the position-time graphs in
Figure 3-17.
■Figure 3-17
Walk in the positive direction at a constant speed. Walk in the positive
direction at an increasing speed for a short time; keep walking at a
moderate speed for twice that amount of time; slow down over a short
time and stop; remain stopped; and turn around and repeat the procedure
until the original position is reached.
74. Draw a velocity-time graph for each of the graphs in Figure 3-18.
■Figure 3-18
Time
Velocity
Velocity
Time
Velocity
Time
Displacement
Displacement
Displacement
Time Time Time
Displacement
Displacement
Time Time
AB
CDE
F
GH
44 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 45
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
75. An object shot straight up rises for 7.0 s
before it reaches its maximum height. A sec-
ond object falling from rest takes 7.0 s to
reach the ground. Compare the
displacements of the two objects during this
time interval.
Both objects traveled the same dis-
tance. The object that is shot straight
upward rises to the same height from
which the other object fell.
76. The Moon The value of gon the Moon is
one-sixth of its value on Earth.
a. Would a ball that is dropped by an
astronaut hit the surface of the Moon
with a greater, equal, or lesser speed
than that of a ball dropped from the
same height to Earth?
The ball will hit the Moon with a
lesser speed because the accelera-
tion due to gravity is less on the
Moon.
b. Would it take the ball more, less, or
equal time to fall?
The ball will take more time to fall.
77. Jupiter The planet Jupiter has about three
times the gravitational acceleration of Earth.
Suppose a ball is thrown vertically upward
with the same initial velocity on Earth and
on Jupiter. Neglect the effects of Jupiter’s
atmospheric resistance and assume that
gravity is the only force on the ball.
a. How does the maximum height reached
by the ball on Jupiter compare to the
maximum height reached on Earth?
The relationship between dand gis
an inverse one: df
(vf2
2
g
vi2)
.
If gincreases by three times, or
df
(vf2
2
(
3g
v
)i2)
,dfchanges by
1
3
.
Therefore, a ball on Jupiter would
rise to a height of
1
3
that on Earth.
b. If the ball on Jupiter were thrown with
an initial velocity that is three times
greater, how would this affect your
answer to part a?
With vf0, the value dfis directly
proportional to the square of initial
velocity, vi. That is, dfvf2
(3
2
v
g
i)2
.
On Earth, an initial velocity three
times greater results in a ball rising
nine times higher. On Jupiter, how-
ever, the height of nine times higher
would be reduced to only three
times higher because of df’s inverse
relationship to a gthat is three
times greater.
78. Rock A is dropped from a cliff and rock B is
thrown upward from the same position.
a. When they reach the ground at the
bottom of the cliff, which rock has a
greater velocity?
Rock B hits the ground with a
greater velocity.
b. Which has a greater acceleration?
They have the same acceleration,
the acceleration due to gravity.
c. Which arrives first?
rock A
Mastering Problems
3.1 Acceleration
pages 81–82
Level 1
79. A car is driven for 2.0 h at 40.0 km/h, then
for another 2.0 h at 60.0 km/h in the same
direction.
a. What is the car’s average velocity?
Total distance:
80.0 km 120.0 km 200.0 km
total time is 4.0 hours, so,
v
d
t
204
0..0
0h
km
5.0101km/h
b. What is the car’s average velocity if it is
driven 1.0102km at each of the two
speeds?
Chapter 3 continued

Total distance is 2.03102 km;
total time
14
.0
0
.0
1k
0m
2k
/h
m
16
.0
0
.0
1k
0m
2k
/h
m
4.2 h
so v
d
t
2.0
4.
1
2
0h
2km
48 km/h
80. Find the uniform acceleration that causes a car’s velocity to change from 32 m/s
to 96 m/s in an 8.0-s period.
a
v
t
v2
t
v1
96 m/s
8.
0s
32 m/s
8.0 m/s2
81. A car with a velocity of 22 m/s is accelerated uniformly at the rate of 1.6 m/s2for
6.8 s. What is its final velocity?
vfviatf
22 m/s (1.6 m/s2)(6.8 s)
33 m/s
82. Refer to Figure 3-19 to find the acceleration of the moving object at each of the
following times.
■Figure 3-19
a. during the first 5.0 s of travel
a
v
t
6.0 m/s2
b. between 5.0 s and 10.0 s
a
v
t
0.0 m/s2
30.0 m/s 30.0 m/s
5.0 s
30.0 m/s 0.0 m/s
5.0 s
Velocity (m/s)
Time (s)
5.0 10.0 15.0 20.0 25.0 30.00.0
10.0
20.0
30.0
46 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued
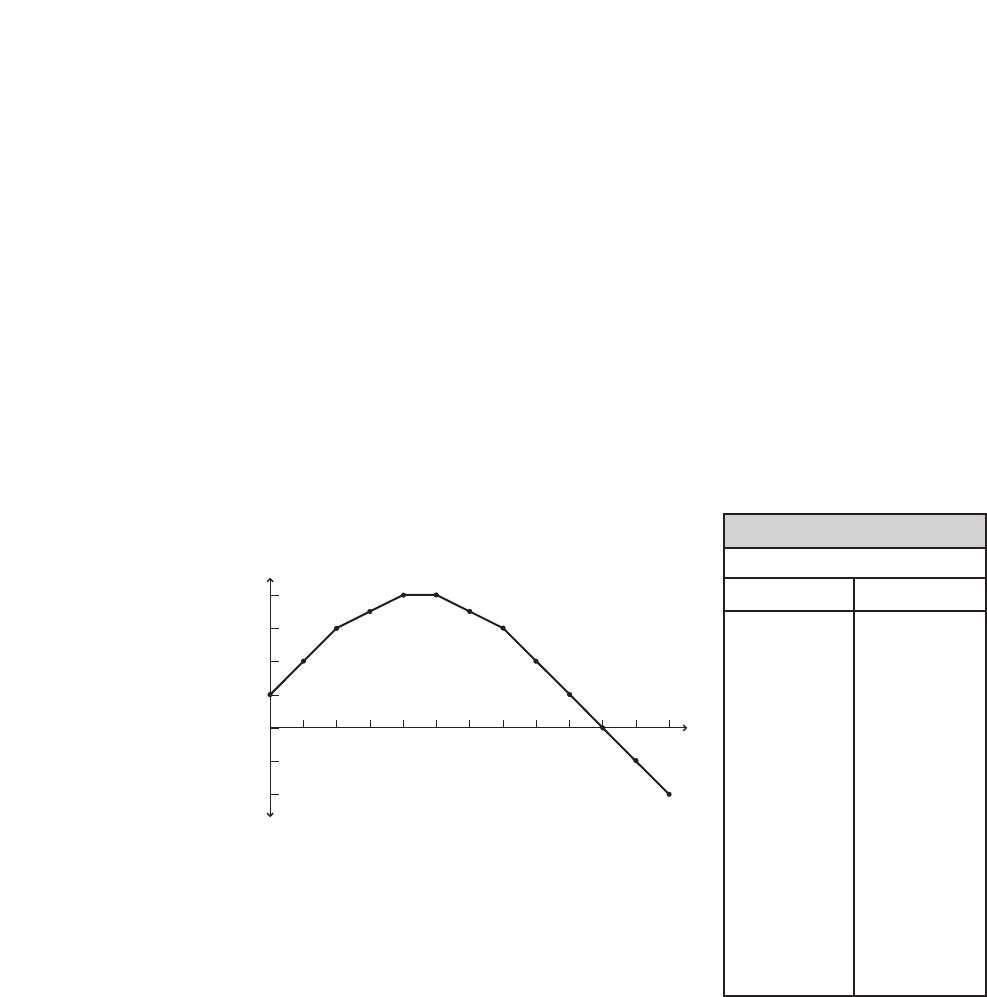
Physics: Principles and Problems Solutions Manual 47
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. between 10.0 s and 15.0 s
a
v
t
2.0 m/s2
d. between 20.0 s and 25.0 s
a
v
t
4.0 m/s2
Level 2
83. Plot a velocity-time graph using the information
in Table 3-4, and answer the following questions.
a. During what time interval is the object
speeding up? Slowing down?
speeding up from 0.0 s to 4.0 s; slowing
down from 5.0 s to 10.0 s
b. At what time does the object reverse direction?
at 10.0 s
c. How does the average acceleration of the object in the interval between 0.0 s and
2.0 s differ from the average acceleration in the interval between 7.0 s and 12.0 s?
a
v
t
between 0.0 s and 2.0 s:
a
4.0 m/s2
between 7.0 s and 12.0 s:
a
4.0 m/s2
8.0 m/s 12.0 m/s
12.0 s 7.0 s
12.0 m/s 4.0 m/s
2.0 s 0.0 s
2.00 4.00 6.00 8.00 10.0
Time (s)
8.00
4.00
0.00
4.00
8.00
12.0
16.0
Velocity (m/s)
12.0
Table 3-4
Velocity v. Time
Time (s) Velocity (m/s)
0.00 4.00
1.00 8.00
2.00 12.0
3.00 14.0
4.00 16.0
5.00 16.0
6.00 14.0
7.00 12.0
8.00 8.00
9.00 4.00
10.0 0.00
11.0 4.00
12.0 8.00
0.0 m/s 20.0 m/s
5.0 s
20.0 m/s 30.0 m/s
5.0 s
Chapter 3 continued

84. Determine the final velocity of a proton
that has an initial velocity of 2.35105m/s
and then is accelerated uniformly in an
electric field at the rate of 1.101012 m/s2
for 1.50107s.
vfviatf
2.35105m/s
(1.101012 m/s2)(1.50107s)
7.0104m/s
Level 3
85. Sports Cars Marco is looking for a used
sports car. He wants to buy the one with the
greatest acceleration. Car A can go from 0
m/s to 17.9 m/s in 4.0 s; car B can accelerate
from 0 m/s to 22.4 m/s in 3.5 s; and car C
can go from 0 to 26.8 m/s in 6.0 s. Rank the
three cars from greatest acceleration to least,
specifically indicating any ties.
Car A:
a
4.5 m/s2
Car B:
a
6.4 m/s2
Car C:
a
4.5 m/s2
Car B has the greatest acceleration of
6.4 m/s2. Using significant digits, car A
and car C tied at 4.5 m/s2.
86. Supersonic Jet A supersonic jet flying at
145 m/s experiences uniform acceleration at
the rate of 23.1 m/s2for 20.0 s.
a. What is its final velocity?
vfviatf
145 m/s (23.1 m/s2)(20.0 s)
607 m/s
b. The speed of sound in air is 331 m/s.
What is the plane’s speed in terms of
the speed of sound?
N
6
30
37
1m
m/
/s
s
1.83 times the speed of sound
3.2 Motion with Constant Acceleration
page 82
Level 1
87. Refer to Figure 3-19 to find the distance
traveled during the following time intervals.
a. t0.0 s and t5.0 s
Area I
1
2
bh
1
2
(5.0 s)(30.0 m/s)
75 m
b. t5.0 s and t10.0 s
Area II bh
(10.0 s 5.0 s)(30.0 m/s)
150 m
c. t10.0 s and t15.0 s
Area III Area IV bh
1
2
bh
(15.0 s 10.0 s)(20.0 m/s)
1
2
(15.0 s 10.0 s)(10.0 m/s)
125 m
d. t0.0 s and t25.0 s
Area I Area II
(Area III Area IV) Area V IV
75 m 150 m 125 m
bh
1
2
bh
75 m 150 m 125 m
(20.0 s 15.0 s)(20.0 m/s)
1
2
(25.0 s 20.0 s)
5.0102m
Level 2
88. A dragster starting from rest accelerates at
49 m/s2. How fast is it going when it has
traveled 325 m?
vf2vi22a(dfdi)
vfvi2
2a(df
di)
26.8 m/s 0 m/s
6.0 s 0.0 s
v
t
22.4 m/s 0 m/s
3.5 s 0.0 s
v
t
17.9 m/s 0 m/s
4.0 s 0.0 s
v
t
48 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 49
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(0.0 m
/s)2
(2)(49
m/s2)
(325 m
0.0
m)
180 m/s
89. A car moves at 12 m/s and coasts up a hill with a uniform acceleration
of 1.6 m/s2.
a. What is its displacement after 6.0 s?
dfvitf
1
2
atf2
(12 m/s)(6.0 s)
1
2
(1.6 m/s2)(6.0 s)2
43 m
b. What is its displacement after 9.0 s?
dfvitf
1
2
atf2
(12 m/s)(9.0 s)
1
2
(1.6 m/s2)(9.0 s)2
43 m
The car is on the way back down the hill. The odometer will show
that the car traveled 45 m up the hill 2 m back down 47 m.
90. Race Car A race car can be slowed with a constant acceleration of 11 m/s2.
a. If the car is going 55 m/s, how many meters will it travel before it stops?
vf2vi22adf
df
1.4102m
b. How many meters will it take to stop a car going twice as fast?
vf2vi22adf
df
550 m,
which is about 4 times longer than when going half the speed.
91. A car is traveling 20.0 m/s when the driver sees a child standing on the road. She
takes 0.80 s to react, then steps on the brakes and slows at 7.0 m/s2. How far
does the car go before it stops?
reaction displacement dr(20.0 m/s)(0.80 s) 16 m
(0.0 m/s)2(110 m/s)2
(2)(11 m/s2)
vf2vi2
2a
(0.0 m/s)2(55 m/s)2
(2)(11 m/s2)
vf2vi2
2a
Chapter 3 continued

df
braking displacement
db
29 m
total displacement is
drdb16 m 29 m 45 m
Level 3
92. Airplane Determine the displacement of a
plane that experiences uniform acceleration
from 66 m/s to 88 m/s in 12 s.
dfv
t
(vf
2
vi)t
9.2102m
93. How far does a plane fly in 15 s while its
velocity is changing from 145 m/s to
75 m/s at a uniform rate of acceleration?
dv
t
(vf
2
vi)t
1.6103m
94. Police Car A speeding car is traveling at a
constant speed of 30.0 m/s when it passes a
stopped police car. The police car acceler-
ates at 7.0 m/s2. How fast will it be going
when it catches up with the speeding car?
dspeeder vspeedert
dpolice vi policet
1
2
apolicet2
vspeedertvi policet
1
2
apolicet2
since vi police 0 then
vspeedert
1
2
apolicet2
0
1
2
apolicet2vspeedert
0t
1
2
apolicetvspeeder
therefore
t0 and
1
2
apolicetvspeeder 0
t
(2)
7
(3
.0
0.
m
0/m
s2
/s)
8.6 s
After t8.6 s, the police car’s velocity
was
vfviat
0.0 m/s (7.0 m/s2)(8.6 s)
6.0101m/s
95. Road Barrier The driver of a car going
90.0 km/h suddenly sees the lights of a bar-
rier 40.0 m ahead. It takes the driver 0.75 s
to apply the brakes, and the average acceler-
ation during braking is 10.0 m/s2.
a. Determine whether the car hits the
barrier.
The car will travel
dvt (25.0 m/s)(0.75 s)
18.8 m (Round off at the end.)
before the driver applies the brakes.
Convert km/h to m/s.
vi
25.0 m/s
vf2vi22a(dfdi)
dfdi
18.8 m
5.0101m, yes it hits the barrier
(0.0 m/s)2(25.0 m/s)2
(2)(10.0 m/s2)
vf2vi2
2a
(90.0 km/h)(1000 m/km)
3600 s/h
2vspeeder
apolice
(75 m/s 145 m/s)(15 m/s)
2
(88 m/s 66 m/s)(12 s)
2
(0.0 m/s)2(20.0 m/s)2
(2)(7.0 m/s2)
vf2vi2
2a
50 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 51
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What is the maximum speed at which
the car could be moving and not hit the
barrier 40.0 m ahead? Assume that the
acceleration doesn’t change.
dtotal dconstant ddecelerating
40.0 m
dcvt (0.75 s)v
dd
2(1
0.v
0
2
m/s2)
40 m (0.75 s)v
v2(15 m/s)v800 m2/s20
Using the quadratic equation:
v22 m/s (The sense of the prob-
lem excludes the negative value.)
3.3 Free Fall
page 82
Level 1
96. A student drops a penny from the top of a
tower and decides that she will establish a
coordinate system in which the direction of
the penny’s motion is positive. What is the
sign of the acceleration of the penny?
The direction of the velocity is positive,
and velocity is increasing. Therefore,
the acceleration is also positive.
97. Suppose an astronaut drops a feather from
1.2 m above the surface of the Moon. If the
acceleration due to gravity on the Moon is
1.62 m/s2downward, how long does it take
the feather to hit the Moon’s surface?
dfvitfatf2(0 m/s)tfatf2
tf
2
a
df
1.2 s
98. A stone that starts at rest is in free fall
for 8.0 s.
a. Calculate the stone’s velocity after 8.0 s.
vfviatfwhere ag
vigtf
0.0 m/s (9.80 m/s2)(8.0 s)
78 m/s (downward)
b. What is the stone’s displacement during
this time?
Choose the coordinate system to
have the origin where the stone is
at rest and positive to be upward.
dfvit
1
2
atf2where ag
vit
1
2
gtf2
0.0 m
1
2
(9.80 m/s2)(8.0 s)2
3.1102m
99. A bag is dropped from a hovering helicopter.
The bag has fallen for 2.0 s. What is the bag’s
velocity? How far has the bag fallen?
Velocity:
vfviatfwhere ag
vigtf
0.0 m/s (9.80 m/s2)(2.0 s)
2.0101m/s
Displacement:
dfvitf
1
2
atf2where ag
vitf
1
2
gt2
0.0 m
1
2
(9.80 m/s2)(2.0 s)2
2.0101m
Level 2
100. You throw a ball downward from a window
at a speed of 2.0 m/s. How fast will it be
moving when it hits the sidewalk 2.5 m
below?
Choose a coordinate system with the
positive direction downward and the
origin at the point where the ball
leaves your hand.
(2)(1.2 m)
(1.62 m/s2)
v2
20.0 m/s2
v2
20.0 m/s2
02v2
2a
Chapter 3 continued

vf2vi22adfwhere ag
vfvi2
2gdf
(2.0 m
/s)2
(2)(9.
80 m/
s2)(2.5
m)
7.3 m/s
101. If you throw the ball in the previous problem up instead of down, how fast will
it be moving when it hits the sidewalk?
Choose the same coordinate system.
vf2vi22adfwhere ag
vfvi2
2gdf
(2.0 m
/s)2
(2)(9.
80 m/
s2)(2.5
m)
7.3 m/s
(dfis the displacement, not the total distance traveled.)
Level 3
102. Beanbag You throw a beanbag in the air and catch it 2.2 s later.
a. How high did it go?
Choose a coordinate system with the upward direction positive and the
origin at the point where the beanbag left your hand. Assume that you
catch the beanbag at the same place where you threw it.Therefore, the
time to reach the maximum height is half of the time in the air. Choose ti
to be the time when the beanbag left your hand and tfto be the time at
the maximum height. Each formula that you know includes vi, so you
will have to
calculate that first.
vfviatfwhere ag
vivfgtf
0.0 m/s (9.80 m/s2)(1.1 s)
11 m/s
Now you can use an equation that includes the displacement.
dfdivitf
1
2
atf2where ag
divitf
1
2
gtf2
0.0 m (11 m/s)(1.1 s)
1
2
(9.80 m/s2)(1.1 s)2
6.2 m
b. What was its initial velocity?
vi11 m/s
52 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 53
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Mixed Review
pages 82–84
Level 1
103. A spaceship far from any star or planet
experiences uniform acceleration from
65.0 m/s to 162.0 m/s in 10.0 s. How far
does it move?
Choosing a coordinate system with
the origin at the point where the speed
is 65.0 m/s and given vi65.0 m/s,
vf162.0 m/s, and tf10.0 s and
needing df, we use the formula with
the average velocity.
dfdi
1
2
(vivf)tf
df0
1
2
(65.0 m/s 162.0 m/s)(10.0 s)
1.14103m
104. Figure 3-20 is a strobe photo of a
horizontally moving ball. What information
about the photo would you need and what
measurements would you make to estimate
the acceleration?
■Figure 3-20
You need to know the time between
flashes and the distance between the
first two images and the distance
between the last two. From these, you
get two velocities. Between these two
velocities, a time interval of tseconds
occurred. Divide the difference
between the two velocities by t.
105. Bicycle A bicycle accelerates from 0.0 m/s
to 4.0 m/s in 4.0 s. What distance does it
travel?
dfv
tf
vi
2
vf
tf
(4.0 s)
8.0 m
106. A weather balloon is floating at a constant
height above Earth when it releases a pack
of instruments.
a. If the pack hits the ground with a
velocity of 73.5 m/s, how far did the
pack fall?
vf2vi22adf
df
vf2
2
a
vi2
276 m
b. How long did it take for the pack to fall?
vfviatfwhere ag
tf
vf
g
vi
7.50 s
Level 2
107. Baseball A baseball pitcher throws a fast-
ball at a speed of 44 m/s. The acceleration
occurs as the pitcher holds the ball in his
hand and moves it through an almost
straight-line distance of 3.5 m. Calculate
the acceleration, assuming that it is
constant and uniform. Compare this accel-
eration to the acceleration due to gravity.
vf2vi22adf
a
(4(
4
2)
m
(3
/s
.5
)2
m
)0
2.8102m/s2
29, or 29 times g
2.8102m/s2
9.80 m/s2
vf2vi2
2df
73.5 m/s 0.00 m/s
9.80 m/s2
(73.5 m/s)2(0.00 m/s)2
(2)(9.80 m/s2)
0.0 m/s 4.0 m/s
2
Chapter 3 continued
108. The total distance a steel ball rolls down
an incline at various times is given in
Table 3-5.
a. Draw a position-time graph of the
motion of the ball. When setting up
the axes, use five divisions for each
10 m of travel on the d-axis. Use five
divisions for 1 s of time on the t-axis.
b. Calculate the distance the ball has
rolled at the end of 2.2 s.
After 2.2 seconds the ball has
rolled approximately 10 m.
109. Engineers are developing new types of
guns that might someday be used to
launch satellites as if they were bullets.
One such gun can give a small object a
velocity of 3.5 km/s while moving it
through a distance of only 2.0 cm.
a. What acceleration does the gun give
this object?
vf2vi22adf
or vf22adf
a
(3
(.
2
5
)
(0
1
.0
02
3
0
m
m
/s
))2
3.1108m/s2
b. Over what time interval does the
acceleration take place?
d
t
vf
2
df
vi
11106s
11 microseconds
110. Sleds Rocket-powered sleds are used to
test the responses of humans to accelera-
tion. Starting from rest, one sled can reach
a speed of 444 m/s in 1.80 s and can be
brought to a stop again in 2.15 s.
a. Calculate the acceleration of the sled
when starting, and compare it to the
magnitude of the acceleration due to
gravity, 9.80 m/s2.
a
v
t
v2
t
v1
247 m/s2
9
2.4
87
0m
m//s
s
2
2
25 times g
b. Find the acceleration of the sled as it is
braking and compare it to the magni-
tude of the acceleration due to gravity.
a
v
t
v2
t
v1
207 m/s2
9
2.0
87
0m
m//s
s
2
2
21 times g
0.00 m/s 444 m/s
2.15 s
444 m/s 0.00 m/s
1.80 s
(2)(0.020 m)
3.5103m/s 0.0 m/s
(vfvi)t
2
vf2
2df
1.00.0 2.0 3.0 4.0 5.0
Time (s)
Top of
incline
10.0
20.0
30.0
40.0
50.0
Position (m)
Table 3-5
Distance v. Time
Time (s) Distance (m)
0.0 0.0
1.0 2.0
2.0 8.0
3.0 18.0
4.0 32.0
5.0 50.0
54 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued
Physics: Principles and Problems Solutions Manual 55
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
111. The velocity of a car changes over an 8.0-s
time period, as shown in Table 3-6.
a. Plot the velocity-time graph of the
motion.
b. Determine the displacement of the car
during the first 2.0 s.
Find the area under the v-tcurve.
d
1
2
bh
1
2
(2.0 s)(8.0 m/s 0.0 m/s)
8.0 m
c. What displacement does the car have
during the first 4.0 s?
Find the area under the v-tcurve.
d
1
2
bh
1
2
(4.0 s)(16.0 m/s 0.0 m/s)
32 m
d. What is the displacement of the car
during the entire 8.0 s?
Find the area under the v-tcurve.
d
1
2
bh bh
1
2
(5.0 s)(20.0 m/s 0.0 m/s)
(8.0 s 5.0 s)(20.0 m/s)
110 m
e. Find the slope of the line between
t0.0 s and t4.0 s. What does this
slope represent?
a
v
t
4.0 m/s2, acceleration
f. Find the slope of the line between
t5.0 s and t7.0 s. What does this
slope indicate?
a
v
t
0.0 m/s2, constant velocity
Level 3
112. A truck is stopped at a stoplight. When the
light turns green, the truck accelerates at
2.5 m/s2. At the same instant, a car passes
the truck going 15 m/s. Where and when
does the truck catch up with the car?
Car:
dfdivtf
dcar divcartfvcartf
0(15 m/s)tf
Truck:
dfdivitf
1
2
atf2
dtruck
1
2
atrucktf2
00
1
2
(2.5 m/s2)tf2
When the truck catches up, the
displacements are equal.
vcartf
1
2
atrucktf2
0
1
2
atrucktf2vcartf
0tf
1
2
atrucktfvcar
20.0 m/s 20.0 m/s
7.0 s 5.0 s
16.0 m/s 0.00 m/s
4.0 s 0.0 s
1.00.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
Time (s)
4.0
8.0
12.0
16.0
20.0
Velocity (m/s)
Table 3-6
Velocity v. Time
Time (s) Velocity (m/s)
0.0 0.0
1.0 4.0
2.0 8.0
3.0 12.0
4.0 16.0
5.0 20.0
6.0 20.0
7.0 20.0
8.0 20.0
Chapter 3 continued

therefore
tf0 and
1
2
atrucktfvcar 0
tf
a
2
t
v
ru
c
c
a
k
r
(22
)(
.1
55
m
m
/s
/s)
12 s
df(15 m/s)tf
(15 m/s)(12 s)
180 m
113. Safety Barriers Highway safety engineers
build soft barriers, such as the one shown
in Figure 3-21, so that cars hitting them
will slow down at a safe rate. A person
wearing a safety belt can withstand an
acceleration of 3.0102m/s2. How thick
should barriers be to safely stop a car that
hits a barrier at 110 km/h?
■Figure 3-21
vi31 m/s
vf2vi22adf
with vf0 m/s, vi22adf,or
df
2
v
a
i2
1.6 m thick
114. Karate The position-time and velocity-
time graphs of George’s fist breaking a
wooden board during karate practice are
shown in Figure 3-22.
■Figure 3-22
a. Use the velocity-time graph to describe
the motion of George’s fist during the
first 10 ms.
The fist moves downward at
about 13 m/s for about 4 ms.
It then suddenly comes to a halt
(accelerates).
b. Estimate the slope of the velocity-time
graph to determine the acceleration of
his fist when it suddenly stops.
a
v
t
3.7103m/s2
c. Express the acceleration as a multiple
of the gravitational acceleration,
g9.80 m/s2.
3.8102
The acceleration is about 380g.
d. Determine the area under the velocity-
time curve to find the displacement of
the fist in the first 6 ms. Compare this
with the position-time graph.
The area can be approximated by a
rectangle:
(13 m/s)(0.006 s) 8 cm
This is in agreement with the
position-time graph where the hand
moves from 8 cm to 0 cm, for a
net displacement of 8 cm.
3.7103m/s2
9.80 m/s2
0 m/s (13 m/s)
7.5 ms 4.0 ms
Fist
5.0 10.0 15.0 20.0 25.0 30.0
15.0
10.0
5.0
0.0
5.0
0.0
5.0
10.0
Displacement (cm)Velocity (m/s)
Time (ms)
(31 m/s)2
(2)(3.0102m/s2)
(110 km/h)(1000 m/km)
3600 s/h
56 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 57
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
115. Cargo A helicopter is rising at 5.0 m/s
when a bag of its cargo is dropped. The
bag falls for 2.0 s.
a. What is the bag’s velocity?
vfviatfwhere ag
vigtf
5.0 m/s (9.80 m/s2)(2.0 s)
15 m/s
b. How far has the bag fallen?
dfvitf
1
2
atf2where ag
vitf
1
2
gtf2
(5.0 m/s)(2.0 s)
1
2
(9.80 m/s2)(2.0 s)2
1.0101m
The bag has fallen 1.0101m
c. How far below the helicopter is the
bag?
The helicopter has risen
dfvitf(5.0 m/s2)(2.0 s)
1.0101m
The bag is 1.0101m below the
origin and 2.0101m below the
helicopter.
Thinking Critically
page 84
116. Apply CBLs Design a lab to measure the
distance an accelerated object moves over
time. Use equal time intervals so that you
can plot velocity over time as well as dis-
tance. A pulley at the edge of a table with a
mass attached is a good way to achieve
uniform acceleration. Suggested materials
include a motion detector, CBL, lab cart,
string, pulley, C-clamp, and masses.
Generate distance-time and velocity-time
graphs using different masses on the
pulley. How does the change in mass affect
your graphs?
Students’labs will vary. Students
should find that a change in the mass
over the edge of the table will not
change the distance the cart moves,
because the acceleration is always
the same: g.
117. Analyze and Conclude Which has the
greater acceleration: a car that increases its
speed from 50 km/h to 60 km/h, or a bike
that goes from 0 km/h to 10 km/h in the
same time? Explain.
a
vf
t
vi
For car, a
10
km
t/h
For bike, a
10
km
t/h
The change in velocity is the same.
118. Analyze and Conclude An express train,
traveling at 36.0 m/s, is accidentally side-
tracked onto a local train track. The
express engineer spots a local train exactly
1.00102m ahead on the same track and
traveling in the same direction. The local
engineer is unaware of the situation. The
express engineer jams on the brakes and
slows the express train at a constant rate
of 3.00 m/s2. If the speed of the local
train is 11.0 m/s, will the express train
be able to stop in time, or will there be
a collision? To solve this problem, take
the position of the express train when
the engineer first sights the local train
as a point of origin. Next, keeping in
mind that the local train has exactly a
1.00102m lead, calculate how far each
train is from the origin at the end of the
12.0 s it would take the express train
to stop (accelerate at 3.00 m/s2from
36 m/s to 0 m/s).
a. On the basis of your calculations,
would you conclude that a collision
will occur?
Express:
dfvitf
1
2
atf2
(36.0 m/s)(12.0 s)
10 km/h 0 km/h
t
60 km/h 50 km/h
t
Chapter 3 continued
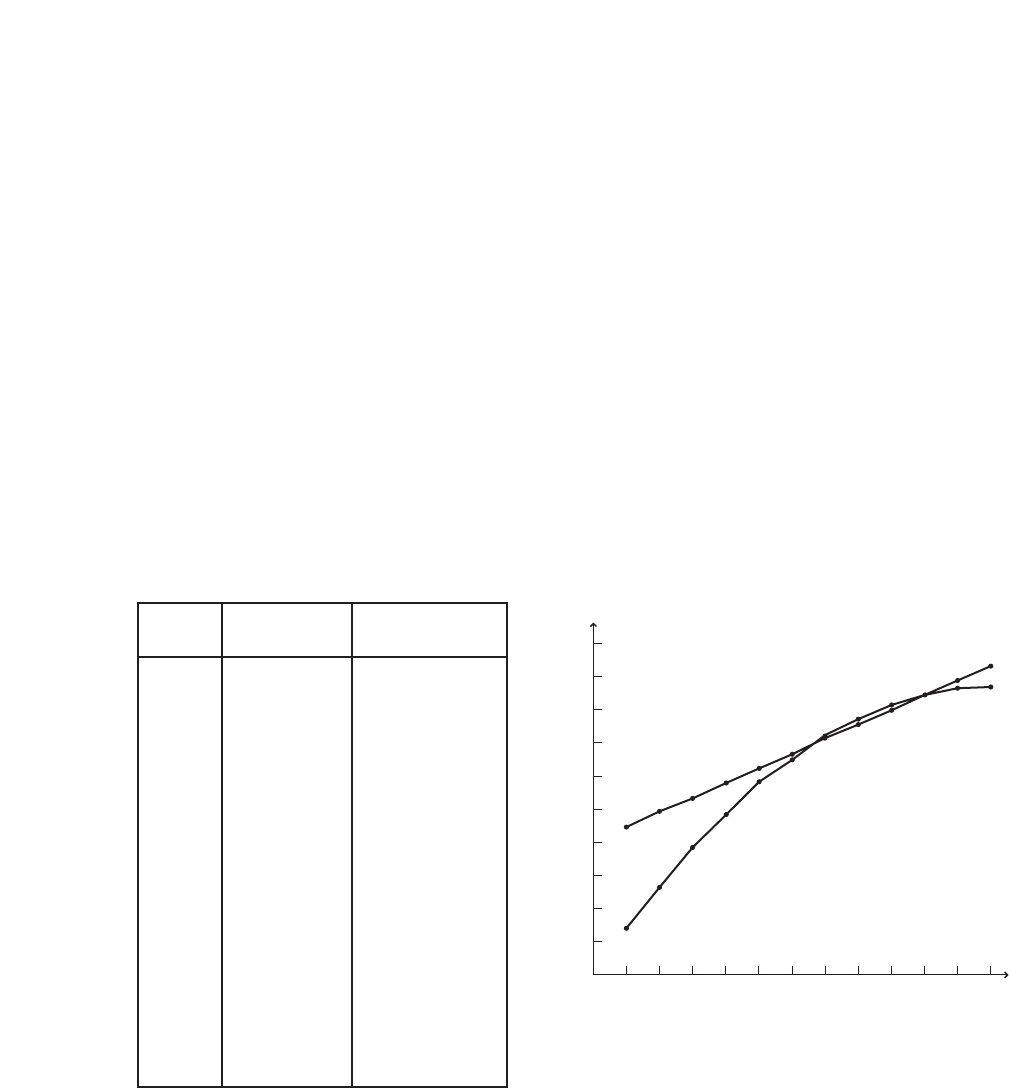
1
2
(3.00 m/s2)(12.0 s)2
432 m 216 m 216 m
Local:
dfdivitfatf2
100 m (11.0 m/s)(12.0 s) 0
232 m
On this basis, no collision will occur.
b. The calculations that you made do not allow for the possibility that a colli-
sion might take place before the end of the 12 s required for the express
train to come to a halt. To check this, take the position of the express train
when the engineer first sights the local train as the point of origin and calcu-
late the position of each train at the end of each second after the sighting.
Make a table showing the distance of each train from the origin at the end
of each second. Plot these positions on the same graph and draw two lines.
Use your graph to check your answer to part a.
They collide between 6 and 7 s.
Writing in Physics
page 84
119. Research and describe Galileo’s contributions to physics.
Student answers will vary. Answers should include Galileo’s experiments
demonstrating how objects accelerate as they fall. Answers might
include his use of a telescope to discover the moons of Jupiter and the
rings of Saturn, and his reliance on experimental results rather than
authority.
58 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued
2 4 6 8 10 12
t
Time (s)
50
100
150
200
250
Position (m)
d
Express
Local
t(s) d(Local) d(Express)
(m) (m)
1 111 35
2 122 66
3 133 95
4 144 120
5 155 145
6166 162
7177 179
8 188 192
9 199 203
10 210 210
11 221 215
12 232 216

Physics: Principles and Problems Solutions Manual 59
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
120. Research the maximum acceleration a
human body can withstand without black-
ing out. Discuss how this impacts the
design of three common entertainment or
transportation devices.
Answers will vary. Because humans
can experience negative effects, like
blackouts, the designers of roller
coasters need to structure the down-
ward slopes in such a way that the
coaster does not reach accelerations
that cause blackouts. Likewise, engi-
neers working on bullet trains, eleva-
tors, or airplanes need to design the
system in such a way that allows the
object to rapidly accelerate to high
speeds, without causing the passen-
gers to black out.
Cumulative Review
page 84
121. Solve the following problems. Express your
answers in scientific notation. (Chapter 1)
a. 6.2104m5.7103m
6.3103m
b. 8.7108km 3.4107m
8.4108km
c. (9.21105cm)(1.83108cm)
1.69104cm2
d. (2.63106m)/(4.08106s)
6.451013 m/s
122. The equation below describes the motion
of an object. Create the corresponding
position-time graph and motion diagram.
Then write a physics problem that could
be solved using that equation. Be creative.
d(35.0 m/s) t5.0 m (Chapter 2)
Graph and motion diagram indicate
constant velocity motion with a
velocity of 35.0 m/s and initial position
of 5.0 m. Answers will vary for the
create-a-problem part.
Challenge Problem
page 75
You notice a water balloon fall past your class-
room window. You estimate that it took the
balloon about tseconds to fall the length of the
window and that the window is about ymeters
high. Suppose the balloon started from rest,
approximately how high above the top of the
window was it released? Your answer should be
in terms of t, y, g, and numerical constants.
Down is positive. Work this problem in two
stages. Stage 1 is falling the distance Dto
the top of the window. Stage 2 is falling the
distance yfrom the top of the window to the
bottom of the window.
Stage 1: the origin is at the top of the fall.
vf12vi122a(df1 di1)
02g(D0)
vf1 2gD
Stage 2: the origin is at the top of the window.
df2 di1 vi1tf2
1
2
atf22
y0vf1t
1
2
gt2
02gD
(t)
1
2
gt2
2gD
y
t
g
2
t
D
2
1
g
y
t
g
2
t
2
100 428610
400
0
100
200
300
Motion Diagram
Position-Time Graph
Time (s)
Position (m)
Chapter 3 continued

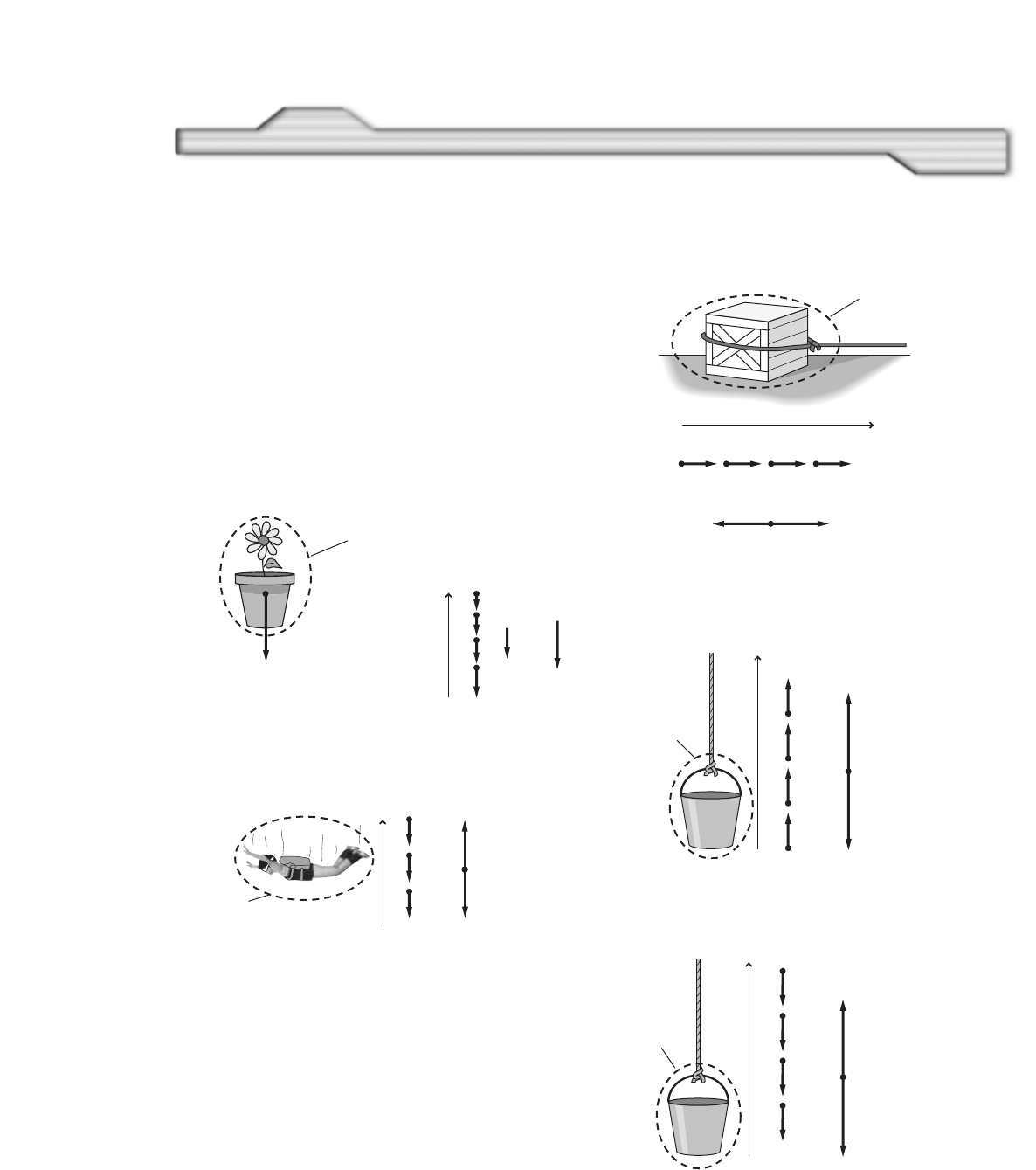
Physics: Principles and Problems Solutions Manual 61
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
4Forces in One Dimension
CHAPTER
Practice Problems
4.1 Force and Motion
pages 87–95
page 89
For each of the following situations, specify the system
and draw a motion diagram and a free-body dia-
gram. Label all forces with their agents, and indicate
the direction of the acceleration and of the net force.
Draw vectors of appropriate lengths.
1. A flowerpot falls freely from a windowsill.
(Ignore any forces due to air resistance.)
2. A sky diver falls downward through the air
at constant velocity. (The air exerts an
upward force on the person.)
3. A cable pulls a crate at a constant speed
across a horizontal surface. The surface pro-
vides a force that resists the crate’s motion.
4. A rope lifts a bucket at a constant speed.
(Ignore air resistance.)
5. A rope lowers a bucket at a constant speed.
(Ignore air resistance.)
v
v
v
v
Frope on bucket
FEarth’s mass on bucket
Fnet 0a 0
y
System
y
v
v
v
v
Frope on bucket
FEarth’s mass on bucket
Fnet 0
a 0
System
x
v
a 0
Fnet 0Fpull on crate
Ffriction
on crate
v v v
System
y
v
v
vFEarth’s mass
on diver
Fair resistance
on diver
a 0
System
Fnet 0
y
FEarth’s mass on flowerpot
va
System
Fnet

page 93
6. Two horizontal forces, 225 N and 165 N,
are exerted on a canoe. If these forces are
applied in the same direction, find the net
horizontal force on the canoe.
Fnet 225 N 165 N 3.90102N
in the direction of the two forces
7. If the same two forces as in the previous
problem are exerted on the canoe in oppo-
site directions, what is the net horizontal
force on the canoe? Be sure to indicate the
direction of the net force.
Fnet 225 N 165 N 6.0101N
in the direction of the larger force
8. Three confused sleigh dogs are trying to
pull a sled across the Alaskan snow. Alutia
pulls east with a force of 35 N, Seward also
pulls east but with a force of 42 N, and big
Kodiak pulls west with a force of 53 N.
What is the net force on the sled?
Identify east as positive and the sled as
the system.
Fnet FAlutia on sled FSeward on sled
FKodiak on sled
35 N 42 N 53 N
24 N
Fnet 24 N east
Section Review
4.1 Force and Motion
pages 87–95
page 95
9. Force Identify each of the following as
either a, b, or c: weight, mass, inertia, the
push of a hand, thrust, resistance, air resis-
tance, spring force, and acceleration.
a. a contact force
b. a field force
c. not a force
weight (b), mass (c), inertia (c), push of
a hand (a), thrust (a), resistance (a),
air resistance (a), spring force (a), accel-
eration (c)
10. Inertia Can you feel the inertia of a pencil?
Of a book? If you can, describe how.
Yes, you can feel the inertia of either
object by using your hand to give either
object an acceleration; that is, try to
change the objects velocity.
11. Free-Body Diagram Draw a free-body dia-
gram of a bag of sugar being lifted by your
hand at a constant speed. Specifically identify
the system. Label all forces with their agents
and make the arrows the correct lengths.
12. Direction of Velocity If you push a book
in the forward direction, does this mean its
velocity has to be forward?
No, it could be moving backward and
you would be reducing that velocity.
13. Free-Body Diagram Draw a free-body dia-
gram of a water bucket being lifted by a rope
at a decreasing speed. Specifically identify
the system. Label all forces with their agents
and make the arrows the correct lengths.
Frope on bucket
FEarth’s mass on bucke
t
System
a
Sugar
Fhand on bag
FEarth’s mass on bag
System
a 0
62 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 63
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
14. Critical Thinking A force of 1 N is the
only force exerted on a block, and the accel-
eration of the block is measured. When the
same force is the only force exerted on a
second block, the acceleration is three times
as large. What can you conclude about the
masses of the two blocks?
Because mF/a and the forces are the
same, the mass of the second block is
one-third the mass of the first block.
Practice Problems
4.2 Using Newton’s Laws
pages 96–101
page 97
15. You place a watermelon on a spring scale at
the supermarket. If the mass of the watermel-
on is 4.0 kg, what is the reading on the scale?
The scale reads the weight of the water-
melon:
Fgmg (4.0 kg)(9.80 m/s2) 39 N
16. Kamaria is learning how to ice-skate. She
wants her mother to pull her along so that
she has an acceleration of 0.80 m/s2. If
Kamaria’s mass is 27.2 kg, with what force
does her mother need to pull her? (Neglect
any resistance between the ice and
Kamaria’s skates.)
Fnet ma (27.2 kg)(0.80 m/s2) 22 N
17. Taru and Reiko simultaneously grab a
0.75-kg piece of rope and begin tugging on
it in opposite directions. If Taru pulls with
a force of 16.0 N and the rope accelerates
away from her at 1.25 m/s2, with what
force is Reiko pulling?
Identify Reiko’s direction as positive
and the rope as the system.
Fnet FRieko on rope FTaru on rope ma
FRieko on rope ma FTaru on rope
(0.75 kg)(1.25 m/s2)
16.0 N
17 N
18. In Figure 4-8, the block has a mass of
1.2 kg and the sphere has a mass of 3.0 kg.
What are the readings on the two scales?
(Neglect the masses of the scales.)
■Figure 4-8
Bottom scale: Identify the sphere as the
system and up as positive.
Fnet Fscale on sphere
FEarth’s mass on sphere ma 0
Fscale on sphere FEarth’s mass on sphere
msphereg
(3.0 kg)(9.80 m/s2)
29 N
Top scale: Identify the block as the sys-
tem and up as positive.
Fnet Ftop scale on block
Fbottom scale on block
FEarth’s mass on block
ma 0
Ftop scale on block Fbottom scale on block
FEarth’s mass on block
Fbottom scale on block
mblockg
29 N (1.2 kg)
(9.80 m/s2)
41 N
Chapter 4 continued

page 100
19. On Earth, a scale shows that you weigh
585 N.
a. What is your mass?
The scale reads 585 N. Since there is
no acceleration, your weight equals
the downward force of gravity:
Fgmg
so m 59.7 kg
b. What would the scale read on the Moon
(g1.60 m/s2)?
On the moon, gchanges:
FgmgMoon
(59.7 kg)(1.60 m/s2)
95.5 N
20. Use the results from Example Problem 2 to
answer questions about a scale in an eleva-
tor on Earth. What force would be exerted
by the scale on a person in the following
situations?
a. The elevator moves at constant speed.
Constant speed, so a0 and
Fnet 0.
Fscale Fg
mg (75.0 kg)(9.80 m/s2)
735 N
b. It slows at 2.00 m/s2while moving
upward.
Slowing while moving upward, so
a2.00 m/s2
Fscale Fnet Fg
ma mg
m(ag)
(75.0 kg)(2.00 m/s2
9.80 m/s2)
585 N
c. It speeds up at 2.00 m/s2while moving
downward.
Accelerating downward,
so a2.00 m/s2
Fscale Fnet Fg
ma mg
m(ag)
(75.0 kg)(2.00 m/s2
9.80 m/s2)
585 N
d. It moves downward at constant speed.
Constant speed, so
a0 and Fnet 0
Fscale Fgmg
(75.0 kg)(9.80 m/s2)
735 N
e. It slows to a stop at a constant magni-
tude of acceleration.
Constant acceleration a, though
the sign of adepends on the direc-
tion of the motion that is ending.
Fscale Fnet Fg
ma mg
(75.0 kg)(a)
(75.0 kg)(9.80 m/s2)
(75.0 kg)(a) 735 N
585 N
9.80 m/s2
Fg
g
64 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 65
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
4.2 Using Newton’s Laws
pages 96–101
page 101
21. Lunar Gravity Compare the force holding
a 10.0-kg rock on Earth and on the Moon.
The acceleration due to gravity on the
Moon is 1.62 m/s2.
To hold the rock on Earth:
Fnet FEarth on rock Fhold on rock 0
Fhold on rock FEarth on rock mgEarth
(10.0 kg)(9.80 m/s2)
98.0 N
To hold the rock on the Moon:
Fnet FMoon on rock Fhold on rock 0
Fhold on rock FMoon on rock mgMoon
(10.0 kg)(1.62 m/s2)
16.2 N
22. Real and Apparent Weight You take a ride
in a fast elevator to the top of a tall building
and ride back down while standing on a
bathroom scale. During which parts of the
ride will your apparent and real weights be
the same? During which parts will your
apparent weight be less than your real
weight? More than your real weight? Sketch
free-body diagrams to support your answers.
Apparent weight and real weight are the
same when you are traveling either up or
down at a constant velocity. Apparent
weight is less than real weight when the
elevator is slowing while rising or speed-
ing up while descending. Apparent
weight is greater when speeding up
while rising or slowing while going
down.
23. Acceleration Tecle, with a mass of 65.0 kg,
is standing by the boards at the side of an
ice-skating rink. He pushes off the boards
with a force of 9.0 N. What is his resulting
acceleration?
Identify Tecle as the system and the
direction away from the boards as
positive. The ice can be treated as a
resistance-free surface.
Fnet Fboards on Tecle ma
a
0.14 m/s2away from the boards
9.0 N
65.0 kg
Fboards on Tecle
m
Fscale
Fg
apparent weight real weight
Fscale
Fg
apparent weight real weight
Fscale
Fg
apparent wei
g
ht real wei
g
ht
Constant Velocity
Slowing While Rising/
Speeding Up While Descending
Speeding Up While Rising/
Slowing While Descending
Chapter 4 continued

24. Motion of an Elevator You are riding in
an elevator holding a spring scale with a
1-kg mass suspended from it. You look at
the scale and see that it reads 9.3 N. What,
if anything, can you conclude about the
elevator’s motion at that time?
If the elevator is stationary or moving
at a constant velocity, the scale should
read 9.80 N. Because the scale reads a
lighter weight, the elevator must be
accelerating downward. To find the
exact acceleration: identify up as posi-
tive and the 1-kg mass as the system.
Fnet Fscale on 1 kg
FEarth’s mass on 1 kg ma
a
0.5 m/s2
0.5 m/s2downward
25. Mass Marcos is playing tug-of-war with his
cat using a stuffed toy. At one instant during
the game, Marcos pulls on the toy with a
force of 22 N, the cat pulls in the opposite
direction with a force of 19.5 N, and the toy
experiences an acceleration of 6.25 m/s2.
What is the mass of the toy?
Identify the toy as the system and the
direction toward his cat as the positive
direction.
Fnet FMarcos on toy Fcat on toy ma
m
0.40 kg
26. Acceleration A sky diver falls at a constant
speed in the spread-eagle position. After he
opens his parachute, is the sky diver acceler-
ating? If so, in which direction? Explain
your answer using Newton’s laws.
Yes, for a while the diver is accelerating
upward because there is an additional
upward force due to air resistance on the
parachute. The upward acceleration
causes the driver’s downward velocity to
decrease. Newton’s second law says that
a net force in a certain direction will
result in an acceleration in that direction
(Fnet ma).
27. Critical Thinking You have a job at a meat
warehouse loading inventory onto trucks for
shipment to grocery stores. Each truck has a
weight limit of 10,000 N of cargo. You push
each crate of meat along a low-resistance
roller belt to a scale and weigh it before
moving it onto the truck. However, right
after you weigh a 1000-N crate, the scale
breaks. Describe a way in which you could
apply Newton’s laws to figure out the
approximate masses of the remaining crates.
Answers may vary. One possible answer
is the following: You can neglect resis-
tance if you do all your maneuvering on
the roller belt. Because you know the
weight of the 1000 N crate, you can use
it as your standard. Pull on the 1000 N
crate with a particular force for 1 s,
estimate its velocity, and calculate the
acceleration that your force gave to it.
Next, pull on a crate of unknown mass
with as close to the same force as you
can for 1 s. Estimate the crate’s velocity
and calculate the acceleration your
force gave to it. The force you pulled
with on each crate will be the net force
in each case.
Fnet 1000-N crate Fnet unknown crate
(1000 N)(a1000-N crate) (munk)(aunk)
munk(1000 N)(a1000-N crate)
aunk
22 N 19.5 N
6.25 m/s2
FMarcos on toy Fcat on toy
a
9.3 N 9.80 N
1 kg
Fscale on 1 kg FEarth’s mass on 1 kg
m
66 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued
Physics: Principles and Problems Solutions Manual 67
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Practice Problems
4.3 Interaction Forces
pages 102–107
page 104
28. You lift a relatively light bowling ball with
your hand, accelerating it upward. What are
the forces on the ball? What forces does the
ball exert? What objects are these forces
exerted on?
The forces on the ball are the force of
your hand and the gravitational force of
Earth’s mass. The ball exerts a force on
your hand and a gravitational force on
Earth. All these forces are exerted on
your hand, on the ball, or on Earth.
29. A brick falls from a construction scaffold.
Identify any forces acting on the brick. Also
identify any forces that the brick exerts and
the objects on which these forces are exerted.
(Air resistance may be ignored.)
The only force acting on the brick is the
gravitational attraction of Earth’s mass.
The brick exerts an equal and opposite
force on Earth.
30. You toss a ball up in the air. Draw a free-
body diagram for the ball while it is still
moving upward. Identify any forces acting
on the ball. Also identify any forces that the
ball exerts and the objects on which these
forces are exerted.
The only force acting on the ball is the
force of Earth’s mass on the ball, when
ignoring air resistance. The ball exerts
an equal and opposite force on Earth.
31. A suitcase sits on a stationary airport luggage
cart, as in Figure 4-13. Draw a free-body
diagram for each object and specifically indi-
cate any interaction pairs between the two.
■Figure 4-13
page 106
32. You are helping to repair a roof by loading
equipment into a bucket that workers hoist
to the rooftop. If the rope is guaranteed not
to break as long as the tension does not
exceed 450 N and you fill the bucket until it
has a mass of 42 kg, what is the greatest
acceleration that the workers can give the
bucket as they pull it to the roof?
Identify the bucket as the system and
up as positive.
Fnet Frope on bucket
FEarth’s mass on bucket
ma
a
0.91 m/s2
450 N (42 kg)(9.80 m/s2)
42 kg
Frope on bucket mg
m
Frope on bucket FEarth’s mass on bucket
m
Suitcase Cart
Fcart on suitcase
Fsurface on cart
FEarth’s mass
on suitcase
FEarth’s
mass
on cart Fsuitcase on cart
FEarth’s mass on ball
Chapter 4 continued

33. Diego and Mika are trying to fix a tire on
Diego’s car, but they are having trouble get-
ting the tire loose. When they pull together,
Mika with a force of 23 N and Diego with a
force of 31 N, they just barely get the tire to
budge. What is the magnitude of the strength
of the force between the tire and the wheel?
Identify the tire as the system and the
direction of pulling as positive.
Fnet Fwheel on tire FMika on tire
FDiego on tire
ma 0
Fwheel on tire FMika on tire FDiego on tire
23 N 31 N
54 N
Section Review
4.3 Interaction Forces
pages 102–107
page 107
34. Force Hold a book motionless in your
hand in the air. Identify each force and its
interaction pair on the book.
The forces on the book are downward
force of gravity due to the mass of
Earth and the upward force of the hand.
The force of the book on Earth and the
force of the book on the hand are the
other halves of the interaction pairs.
35. Force Lower the book from problem 34 at
increasing speed. Do any of the forces or their
interaction-pair partners change? Explain.
Yes, the force of the hand on the book
becomes smaller so there is a down-
ward acceleration.The force of the book
also becomes smaller; you can feel
that. The interaction pair partners
remain the same.
36. Tension A block hangs from the ceiling by
a massless rope. A second block is attached
to the first block and hangs below it on
another piece of massless rope. If each of
the two blocks has a mass of 5.0 kg, what is
the tension in each rope?
For the bottom rope with the positive
direction upward:
Fnet Fbottom rope on bottom block
FEarth’s mass on bottom block
ma 0
Fbottom rope on bottom block
FEarth’s mass on bottom block
mg
(5.0 kg)(9.80 m/s2)
49 N
For the top rope, with the positive direc-
tion upward:
Fnet Ftop rope on top block
Fbottom rope on top block
FEarth’s mass on top block
ma 0
Ftop rope on top block
FEarth’s mass on top block
Fbottom rope on top block
mg Fbottom rope on top block
(5.0 kg)(9.80 m/s2) 49 N
98 N
37. Tension If the bottom block in problem
36 has a mass of 3.0 kg and the tension in
the top rope is 63.0 N, calculate the ten-
sion in the bottom rope and the mass of
the top block.
For the bottom rope with the positive
direction upward:
Fnet Fbottom rope on bottom block
FEarth’s mass on bottom block
ma 0
Fbottom rope on bottom block
FEarth’s mass on bottom block
(3.0 kg)(9.80 m/s2)
29 N
68 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued
Physics: Principles and Problems Solutions Manual 69
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
For the top mass with the positive
direction upward:
Fnet Ftop rope on top block
Fbottom rope on top block
FEarth’s mass on top block
ma 0
FEarth’s mass on top block mg
Ftop rope on top block
Fbottom rope on top block
m
3.5 kg
38. Normal Force Poloma hands a 13-kg box
to 61-kg Stephanie, who stands on a plat-
form. What is the normal force exerted by
the platform on Stephanie?
Identify Stephanie as the system and
positive to be upward.
Fnet Fplatform on Stephanie
Fbox on Stephanie
FEarth’s mass on Stephanie
Fplatform on Stephanie
Fbox on Stephanie
FEarth’s mass on Stephanie
mboxgmStephanieg
(13 kg)(9.80 m/s2) (61 kg)(9.80 m/s2)
7.3102N
39. Critical Thinking A curtain prevents two
tug-of-war teams from seeing each other.
One team ties its end of the rope to a tree.
If the other team pulls with a 500-N force,
what is the tension? Explain.
The tension would be 500 N.The rope is
in equilibrium, so the net force on it is
zero.The team and the tree exert equal
forces in opposite directions.
Chapter Assessment
Concept Mapping
page 112
40. Complete the following concept map using
the following term and symbols: normal,
FT, Fg.
Mastering Concepts
page 112
41. A physics book is motionless on the top of
a table. If you give it a hard push with your
hand, it slides across the table and slowly
comes to a stop. Use Newton’s laws to
answer the following questions. (4.1)
a. Why does the book remain motionless
before the force of your hand is applied?
An object at rest tends to stay at
rest if no outside force acts on it.
b. Why does the book begin to move when
your hand pushes hard enough on it?
The force from your hand is greater
than any opposing force such as fric-
tion. With a net force on it, the book
slides in the direction of the net force.
c. Under what conditions would the book
remain in motion at a constant speed?
The book would remain in motion if
the net force acting on it is zero.
42. Cycling Why do you have to push harder
on the pedals of a single-speed bicycle to
start it moving than to keep it moving at a
constant velocity? (4.1)
A large force is required to accelerate the
mass of the bicycle and rider. Once the
desired constant velocity is reached, a
much smaller force is sufficient to over-
come the ever-present frictional forces.
tension normal
force
gravity
FTFNFg
63.0 N 29 N
9.80 m/s2
Ftop rope on top block Fbottom rope on top block
g
Chapter 4 continued
43. Suppose that the acceleration of an object is
zero. Does this mean that there are no
forces acting on it? Give an example sup-
porting your answer. (4.2)
No, it only means the forces acting on it
are balanced and the net force is zero.
For example, a book on a table is not
moving but the force of gravity pulls
down on it and the normal force of the
table pushes up on it and these forces
are balanced.
44. Basketball When a basketball player drib-
bles a ball, it falls to the floor and bounces
up. Is a force required to make it bounce?
Why? If a force is needed, what is the agent
involved? (4.2)
Yes, its velocity changed direction;
thus, it was accelerated and a force is
required to accelerate the basketball.
The agent is the floor.
45. Before a sky diver opens her parachute, she
may be falling at a velocity higher than the
terminal velocity that she will have after the
parachute opens. (4.2)
a. Describe what happens to her velocity
as she opens the parachute.
Because the force of air resistance
suddenly becomes larger, the
velocity of the diver drops suddenly.
b. Describe the sky diver’s velocity from
when her parachute has been open for a
time until she is about to land.
The force of air resistance and the
gravitational force are equal.Their
sum is zero, so there is no longer any
acceleration.The sky diver continues
downward at a constant velocity.
46. If your textbook is in equilibrium, what can
you say about the forces acting on it? (4.2)
If the book is in equilibrium, the net
force is zero.The forces acting on the
book are balanced.
47. A rock is dropped from a bridge into a val-
ley. Earth pulls on the rock and accelerates
it downward. According to Newton’s third
law, the rock must also be pulling on Earth,
yet Earth does not seem to accelerate.
Explain. (4.3)
The rock does pull on Earth, but Earth’s
enormous mass would undergo only a
minute acceleration as a result of such
a small force. This acceleration would
go undetected.
48. Ramon pushes on a bed that has been
pushed against a wall, as in Figure 4-17.
Draw a free-body diagram for the bed and
identify all the forces acting on it. Make a
separate list of all the forces that the bed
applies to other objects. (4.3)
■Figure 4-17
Forces that bed applies to other
objects:
Fbed on Ramon,Fbed on Earth,Fbed on floor,
Fbed on wall
Ffloor on bed
Fg
FRamon on bed
Fwall on bed
70 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued
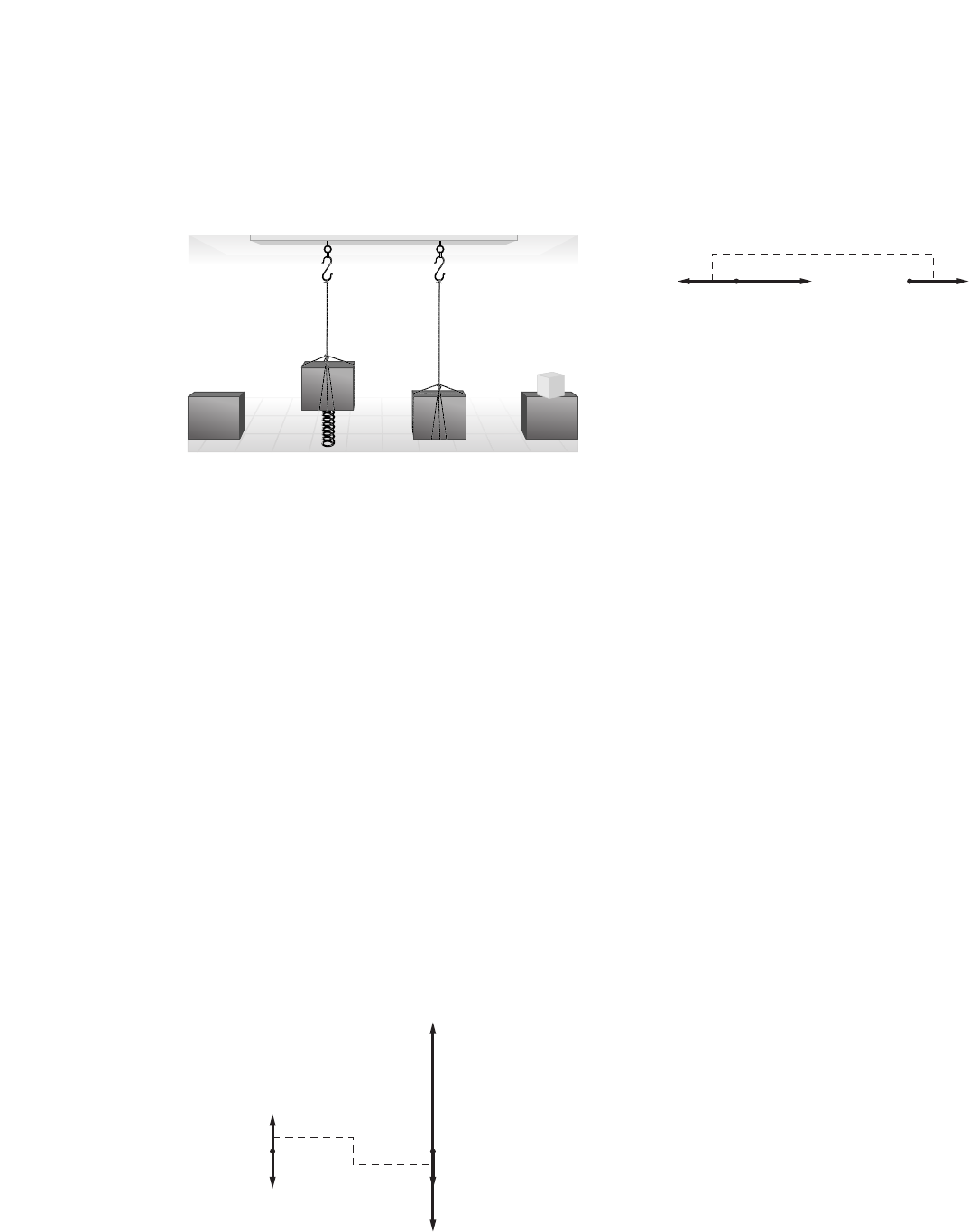
Physics: Principles and Problems Solutions Manual 71
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
49. Figure 4-18 shows a block in four different
situations. Rank them according to the mag-
nitude of the normal force between the
block and the surface, greatest to least.
Specifically indicate any ties. (4.3)
■Figure 4-18
from left to right: second > fourth >
third > first
50. Explain why the tension in a massless rope
is constant throughout it. (4.3)
If you draw a free-body diagram for any
point on the rope, there will be two ten-
sion forces acting in opposite direc-
tions. Fnet Fup Fdown ma 0
(because it is massless). Therefore,
Fup Fdown. According to Newton’s
third law, the force that the adjoining
piece of rope exerts on this point is
equal and opposite to the force that this
point exerts on it, so the force must be
constant throughout.
51. A bird sits on top of a statue of Einstein.
Draw free-body diagrams for the bird and
the statue. Specifically indicate any interac-
tion pairs between the two diagrams. (4.3)
52. Baseball A slugger swings his bat and hits
a baseball pitched to him. Draw free-body
diagrams for the baseball and the bat at
the moment of contact. Specifically indi-
cate any interaction pairs between the two
diagrams. (4.3)
Applying Concepts
pages 112–113
53. Whiplash If you are in a car that is struck
from behind, you can receive a serious neck
injury called whiplash.
a. Using Newton’s laws, explain what
happens to cause such an injury.
The car is suddenly accelerated
forward. The seat accelerates your
body, but your neck has to acceler-
ate your head. This can hurt your
neck muscles.
b. How does a headrest reduce whiplash?
The headrest pushes on your head,
accelerating it in the same direction
as the car.
54. Space Should astronauts choose pencils
with hard or soft lead for making notes in
space? Explain.
A soft lead pencil would work better
because it would require less force to
make a mark on the paper.The magni-
tude of the interaction force pair could
push the astronaut away from the paper.
Fball on bat Fbatter on bat Fbat on ball
Fstatue on bird
Fg, bird Fbird on statue
FEarth on statue
Fg, statue
Chapter 4 continued

55. When you look at the label of the product
in Figure 4-19 to get an idea of how much
the box contains, does it tell you its mass,
weight, or both? Would you need to make
any changes to this label to make it correct
for consumption on the Moon?
■Figure 4-19
The ounces tell you the weight in English
units.The grams tell you the mass in
metric units.The label would need to
read “2 oz”to be correct on the Moon.
The grams would remain unchanged.
56. From the top of a tall building, you drop
two table-tennis balls, one filled with air
and the other with water. Both experience
air resistance as they fall. Which ball reach-
es terminal velocity first? Do both hit the
ground at the same time?
The lighter, air-filled table tennis ball
reaches terminal velocity first. Its mass
is less for the same shape and size, so
the friction force of upward air resis-
tance becomes equal to the downward
force of mg sooner. Because the force
of gravity on the water-filled table-tennis
ball (more mass) is larger, its terminal
velocity is larger, and it strikes the
ground first.
57. It can be said that 1 kg equals 2.2 lb. What
does this statement mean? What would be
the proper way of making the comparison?
It means that on Earth’s surface, the
weight of 1 kg is equivalent to 2.2 lb.
You should compare masses to masses
and weights to weights. Thus 9.8 N
equals 2.2 lb.
58. You toss a ball straight up into the air.
a. Draw a free-body diagram for the ball at
three points during its motion: on the
way up, at the very top, and on the way
down. Specifically identify the forces
acting on the ball and their agents.
b. What is the velocity of the ball at the
very top of the motion?
0 m/s
c. What is the acceleration of the ball at
this same point?
Because the only force acting on it
is the gravitational attraction of
Earth, a9.80 m/s2.
Mastering Problems
4.1 Force and Motion
page 113
Level 1
59. What is the net force acting on a 1.0-kg ball
in free-fall?
Fnet Fgmg
(1.0 kg)(9.80 m/s2)
9.8 N
FEarth’s mass on ball
On the way up
FEarth’s mass on ball
At the top
FEarth’s mass on ball
On the way down
72 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 73
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
60. Skating Joyce and Efua are skating. Joyce
pushes Efua, whose mass is 40.0-kg, with a
force of 5.0 N. What is Efua’s resulting
acceleration?
Fma
a
0.12 m/s2
61. A car of mass 2300 kg slows down at a rate
of 3.0 m/s2when approaching a stop sign.
What is the magnitude of the net force
causing it to slow down?
Fma
(2300 kg)(3.0 m/s2)
6.9103N
62. Breaking the Wishbone After
Thanksgiving, Kevin and Gamal use the
turkey’s wishbone to make a wish. If Kevin
pulls on it with a force 0.17 N larger than the
force Gamal pulls with in the opposite direc-
tion, and the wishbone has a mass of 13 g,
what is the wishbone’s initial acceleration?
a
13 m/s2
4.2 Using Newton’s Laws
pages 113–114
Level 1
63. What is your weight in newtons?
Fgmg (9.80 m/s2)(m)
Answers will vary.
64. Motorcycle Your new motorcycle weighs
2450 N. What is its mass in kilograms?
Fgmg
m
2.50102N
65. Three objects are dropped simultaneously
from the top of a tall building: a shot put,
an air-filled balloon, and a basketball.
a. Rank the objects in the order in which
they will reach terminal velocity, from
first to last.
balloon, basketball, shot put
b. Rank the objects according to the order
in which they will reach the ground,
from first to last.
shot put, basketball, balloon
c. What is the relationship between your
answers to parts a and b?
They are inverses of each other.
66. What is the weight in pounds of a 100.0-N
wooden shipping case?
(100.0 N)
22 lb
67. You place a 7.50-kg television on a spring
scale. If the scale reads 78.4 N, what is the
acceleration due to gravity at that location?
Fgmg
g
10.5 m/s2
Level 2
68. Drag Racing A 873-kg (1930-lb) dragster,
starting from rest, attains a speed of
26.3 m/s (58.9 mph) in 0.59 s.
a. Find the average acceleration of the
dragster during this time interval.
a
45 m/s2
b. What is the magnitude of the average net
force on the dragster during this time?
Fma
(873 kg)(45 m/s2)
3.9104N
(26.3 m/s 0.0 m/s)
0.59 s
v
t
78.4 N
7.50 kg
Fg
m
2.2 lb
1 kg
1 kg
9.80 N
2450 N
9.80 m/s2
Fg
g
0.17 N
0.013 kg
F
m
5.0 N
40.0 kg
F
m
Chapter 4 continued

c. Assume that the driver has a mass of
68 kg. What horizontal force does the
seat exert on the driver?
Fma (68 kg)(45 m/s2)
3.1103N
69. Assume that a scale is in an elevator on
Earth. What force would the scale exert on
a 53-kg person standing on it during the
following situations?
a. The elevator moves up at a constant
speed.
Fscale Fg
mg
(53 kg)(9.80 m/s2)
5.2102N
b. It slows at 2.0 m/s2while moving
upward.
Slows while moving up or speeds
up while moving down,
Fscale FgFslowing
mg ma
m(ga)
(53 kg)(9.80 m/s2 2.0 m/s2)
4.1102N
c. It speeds up at 2.0 m/s2while moving
downward.
Slows while moving up or speeds
up while moving down,
Fscale FgFspeeding
mg ma
m(ga)
(53 kg)(9.80 m/s22.0 m/s2)
4.1102N
d. It moves downward at a constant speed.
Fscale Fg
mg
(53 kg)(9.80 m/s2)
5.2102N
e. It slows to a stop while moving down-
ward with a constant acceleration.
Depends on the magnitude of the
acceleration.
Fscale FgFslowing
mg ma
m(ga)
(53 kg)(9.80 m/s2a)
70. A grocery sack can withstand a maximum
of 230 N before it rips. Will a bag holding
15 kg of groceries that is lifted from the
checkout counter at an acceleration of
7.0 m/s2hold?
Use Newton’s second law Fnet ma.
If Fgroceries 230, then the bag rips.
Fgroceries mgroceriesagroceries
mgroceriesg
mgroceries(agroceries g)
(15 kg)(7.0 m/s29.80 m/s2)
250 N
The bag does not hold.
71. A 0.50-kg guinea pig is lifted up from the
ground. What is the smallest force needed
to lift it? Describe its resulting motion.
Flift Fg
mg
(0.50 kg)(9.80 m/s2)
4.9 N
It would move at a constant speed.
Level 3
72. Astronomy On the surface of Mercury, the
gravitational acceleration is 0.38 times its
value on Earth.
a. What would a 6.0-kg mass weigh on
Mercury?
Fgmg(0.38)
(6.0 kg)(9.80 m/s2)(0.38)
22 N
74 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 75
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. If the gravitational acceleration on the
surface of Pluto is 0.08 times that of
Mercury, what would a 7.0-kg mass
weigh on Pluto?
Fgmg(0.38)(0.08)
(7.0 kg)(9.80 m/s2)(0.38)(0.08)
2.1 N
73. A 65-kg diver jumps off of a 10.0-m tower.
a. Find the diver’s velocity when he hits
the water.
vf2vi22gd
vi0 m/s
so vf2gd
2(9.80
m/s2)
(10.0
m)
14.0 m/s
b. The diver comes to a stop 2.0 m below
the surface. Find the net force exerted by
the water.
vf2vi22ad
vf0, so a
and Fma
3.2103N
74. Car Racing A race car has a mass of 710 kg.
It starts from rest and travels 40.0 m in 3.0 s.
The car is uniformly accelerated during the
entire time. What net force is exerted on it?
dv0t
at2
Since v00,
aand Fma, so
F
6.3103N
4.3 Interaction Forces
page 114
Level 1
75. A 6.0-kg block rests on top of a 7.0-kg
block, which rests on a horizontal table.
a. What is the force (magnitude and direc-
tion) exerted by the 7.0-kg block on the
6.0-kg block?
Fnet Nmg
FNF7-kg block on 6-kg block
mg
(6.0 kg)(9.80 m/s2)
59 N; the direction is upward.
b. What is the force (magnitude and direc-
tion) exerted by the 6.0-kg block on the
7.0-kg block?
equal and opposite to that in part a;
therefore, 59 N downward
76. Rain A raindrop, with mass 2.45 mg, falls
to the ground. As it is falling, what magni-
tude of force does it exert on Earth?
Fraindrop on Earth Fg
mg
(0.00245 kg)(9.80 m/s2)
2.40102N
77. A 90.0-kg man and a 55-kg man have a
tug-of-war. The 90.0-kg man pulls on the
rope such that the 55-kg man accelerates at
0.025 m/s2. What force does the rope exert
on the 90.0-kg man?
same in magnitude as the force the
rope exerts on the 55-kg man:
Fma (55 kg)(0.025 m/s2) 1.4 N
(2)(710 kg)(40.0 m)
(3.0 s)2
2md
t2
2d
t2
1
2
(65 kg)(14.0 m/s)2
2(2.0 m)
mvi2
2d
vi2
2d
Chapter 4 continued

Level 2
78. Male lions and human sprinters can both
accelerate at about 10.0 m/s2. If a typical
lion weighs 170 kg and a typical sprinter
weighs 75 kg, what is the difference in the
force exerted on the ground during a race
between these two species?
Use Newton’s second law, Fnet ma.
The difference between
Flion and Fhuman is
Flion Fhuman
mlionalion mhumanahuman
(170 kg)(10.0 m/s2)
(75 kg)(10.0 m/s2)
9.5102N
79. A 4500-kg helicopter accelerates upward at
2.0 m/s2. What lift force is exerted by the
air on the propellers?
ma Fnet Fappl FgFappl mg
so Fappl ma mg m(ag)
(4500 kg)((2.0m/s2)
(9.8 m/s2))
5.3104N
Level 3
80. Three blocks are stacked on top of one
another, as in Figure 4-20. The top block
has a mass of 4.6 kg, the middle one has a
mass of 1.2 kg, and the bottom one has a
mass of 3.7 kg. Identify and calculate any
normal forces between the objects.
■Figure 4-20
The normal force is between the top
and middle blocks; the top block is the
system; upward is positive.
Fnet Fmiddle block on top block
FEarth’s mass on top block
ma 0
Fmiddle block on top block
FEarth’s mass on top block
mtop blockg
(4.6 kg)(9.80 m/s2)
45 N
The normal force is between the bottom
and middle block; the middle block is
the system; upward is positive.
Fnet Fbottom block on middle block
Ftop block on middle block
FEarth’s mass on middle block
ma 0
Ftop block on middle block
Fmiddle block on top block
Fbottom block on middle block
Fmiddle block on top block
FEarth’s mass on middle block
Fmiddle block on top block
mmiddle blockg
45 N (1.2 kg)(9.80 m/s2)
57 N
The normal force is between the bottom
block and the surface; the bottom block
is the system; upward is positive.
Fnet Fsurface on bottom block
Fmiddle block on bottom block
FEarth’s mass on bottom block
ma 0
76 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 77
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Fsurface on bottom block
Fmiddle block on bottom block
FEarth’s mass on bottom block
Fmiddle block on bottom block
mbottom blockg
57 N (3.7 kg)(9.80 m/s2)
93 N
Mixed Review
pages 114–115
Level 1
81. The dragster in problem 68 completed a
402.3-m (0.2500-mi) run in 4.936 s. If the
car had a constant acceleration, what was its
acceleration and final velocity?
dfdivitat2
divi0, so
a
33.02 m/s2
dfdi(vfvi)t
divi0, so
vf
163.0 m/s
Level 2
82. Jet A 2.75106-N catapult jet plane is
ready for takeoff. If the jet’s engines supply
a constant thrust of 6.35106N, how much
runway will it need to reach its minimum
takeoff speed of 285 km/h?
vf(285 km/h)(1000 m/km)
79.2 m/s
Fthrust ma, so a
Fgmg
m
vfviat and vi0, so
t
v
af
F
v
th
f
r
m
ust
dfdivitat2
divi0, so
dfat2
1
2
Fth
m
rust
F
v
th
f
r
m
ust
2
F
v
th
f2
r
m
ust
139 m
83. The dragster in problem 68 crossed the finish
line going 126.6 m/s. Does the assumption
of constant acceleration hold true? What
other piece of evidence could you use to
determine if the acceleration was constant?
126.6 m/s is slower than found in
problem 81, so the acceleration cannot
be constant. Further, the acceleration
in the first 0.59 s was 45 m/s2, not
33.02 m/s2.
(79.2 m/s)2
29
.7
.8
50
m
10
/s
6
2
N
6.35106N
1
2
vf2
F
g
g
Fthrust
1
2
1
2
1
2
1
2
vf
Fth
m
rust
Fg
g
Fthrust
m
1 h
3600s
(2)(402.3 m)
4.936 s
2df
t
1
2
(2)(402.3 m)
(4.936 s)2
2df
t2
1
2
Chapter 4 continued

84. Suppose a 65-kg boy and a 45-kg girl use a
massless rope in a tug-of-war on an icy,
resistance-free surface as in Figure 4-21.
If the acceleration of the girl toward the
boy is 3.0 m/s2, find the magnitude of the
acceleration of the boy toward the girl.
■Figure 4-21
F1,2 F1,2, so m1a1m2a2
and a1
2.1 m/s2
85. Space Station Pratish weighs 588 N and is
weightless in a space station. If she pushes
off the wall with a vertical acceleration of
3.00 m/s2, determine the force exerted by
the wall during her push off.
Use Newton’s second law to obtain
Pratish’s mass, mPratish. Use Newton’s
third law FAFBmAaAmBaB.
mPratish
Fwall on Pratish FPratish on wall
mPratishaPratish
1.80102N
86. Baseball As a baseball is being caught, its
speed goes from 30.0 m/s to 0.0 m/s in
about 0.0050 s. The mass of the baseball is
0.145 kg.
a. What is the baseball’s acceleration?
a
6.0103m/s2
b. What are the magnitude and direction
of the force acting on it?
Fma
(0.145 kg)(6.0103m/s2)
8.7102N
(opposite direction of the velocity of
the ball)
c. What are the magnitude and direction
of the force acting on the player who
caught it?
Same magnitude, opposite direction
(in direction of velocity of ball)
Level 3
87. Air Hockey An air-hockey table works by
pumping air through thousands of tiny
holes in a table to support light pucks. This
allows the pucks to move around on cush-
ions of air with very little resistance. One of
these pucks has a mass of 0.25 kg and is
pushed along by a 12.0-N force for 9.0 s.
a. What is the puck’s acceleration?
Fma
a
48 m/s2
b. What is the puck’s final velocity?
vfviat
vi0, so vfat
(48 m/s2)(9.0 s)
4.3102m/s
12.0 N
0.25 kg
F
m
0.0 m/s 30.0 m/s
0.0050 s 0.0 s
vfvi
tfti
(588 N)(3.00 m/s2)
9.80 m/s2
FgaPratish
g
Fg
g
(45 kg)(3.0 m/s2)
(65 kg)
m2a2
m1
?3.0 m/s2
78 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 79
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
88. A student stands on a bathroom scale in an
elevator at rest on the 64th floor of a build-
ing. The scale reads 836 N.
a. As the elevator moves up, the scale read-
ing increases to 936 N. Find the acceler-
ation of the elevator.
Fnet FgFelevator
Felevator Fnet Fgma
m,so
a
1.17 m/s2
b. As the elevator approaches the 74th
floor, the scale reading drops to 782 N.
What is the acceleration of the elevator?
Fnet FgFelevator
Felevator Fnet Fgma
m,so
a
0.633 m/s2
c. Using your results from parts aand b,
explain which change in velocity, start-
ing or stopping, takes the longer time.
Stopping, because the magnitude of
the acceleration is less and
t
av
89. Weather Balloon The instruments attached
to a weather balloon in Figure 4-22 have a
mass of 5.0 kg. The balloon is released and
exerts an upward force of 98 N on the
instruments.
■Figure 4-22
a. What is the acceleration of the balloon
and instruments?
Fnet Fappl Fg
Fappl mg
98 N (5.0 kg)(9.80 m/s2)
49 N (up)
a
9.8 m/s2
b. After the balloon has accelerated for
10.0 s, the instruments are released.
What is the velocity of the instruments
at the moment of their release?
vat
(9.8 m/s2)(10.0 s)
98 m/s (up)
c. What net force acts on the instruments
after their release?
just the instrument weight, 49 N
(down)
49 N
5.0 kg
Fnet
m
5.0 kg
98 N
(9.80 m/s2)(782 N 836 N)
836 N
g(Fnet Fg)
Fg
Fnet Fg
F
g
g
Fg
g
(9.80 m/s2)(963 N 836 N)
836 N
g(Fnet Fg)
Fg
Fnet Fg
F
g
g
Fg
g
Chapter 4 continued

d. When does the direction of the instru-
ments’ velocity first become downward?
The velocity becomes negative after
it passes through zero. Thus, use
vfvigt, where vf0, or
t
(
(
9
.8
9
0
8
m
m
/
/
s
s
2
)
)
1.0101s after release
90. When a horizontal force of 4.5 N acts on a
block on a resistance-free surface, it pro-
duces an acceleration of 2.5 m/s2. Suppose
a second 4.0-kg block is dropped onto the
first. What is the magnitude of the accelera-
tion of the combination if the same force
continues to act? Assume that the second
block does not slide on the first block.
Fmfirst blockainitial
mfirst block
Fmboth blocksafinal
(mfirst block msecond block)afinal
so, afinal
0.78 m/s2
91. Two blocks, masses 4.3 kg and 5.4 kg, are
pushed across a frictionless surface by a
horizontal force of 22.5 N, as shown in
Figure 4-23.
■Figure 4-23
a. What is the acceleration of the blocks?
Identify the two blocks together as
the system, and right as positive.
Fnet ma, and mm1m2
a
2.3 m/s2to the right
b. What is the force of the 4.3-kg block on
the 5.4-kg block?
Identify the 5.4-kg block as the
system and right as positive.
Fnet F4.3-kg block on 5.4-kg block
ma
(5.4 kg)(2.3 m/s2)
12 N to the right
c. What is the force of the 5.4-kg block on
the 4.3-kg block?
According to Newton’s third law, this
should be equal and opposite to the
force found in part b, so the force is
12 N to the left.
22.5 N
4.3 kg 5.4 kg
F
m1m2
4.5 N
2.4
5.5
m
N
/s2
4.0 kg
F
ain
F
itial
msecond block
F
mfirst block msecond block
F
ainitial
vi
g
80 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 81
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
92. Two blocks, one of mass 5.0 kg and the other of mass 3.0 kg, are tied together
with a massless rope as in Figure 4-24. This rope is strung over a massless, resis-
tance-free pulley. The blocks are released from rest. Find the following.
a. the tension in the rope
b. the acceleration of the blocks
Hint: you will need to solve two simultaneous equations.
■Figure 4-24
Equation 1 comes from a free-body diagram for the 5.0-kg block. Down is
positive.
Fnet FEarth’s mass on 5.0-kg block Frope on 5.0-kg block m5.0-kg blocka(1)
Equation 2 comes from a free-body diagram for the 3.0-kg block. Up is
positive.
Fnet Frope on 3.0-kg block FEarth’s mass on 3.0-kg block m3.0-kg blocka(2)
The forces of the rope on each block will have the same magnitude,
because the tension is constant throughout the rope. Call this force T.
FEarth’s mass on 5.0-kg block Tm5.0-kg blocka(1)
TFEarth’s mass on 3.0-kg block m3.0-kg blocka(2)
Solve equation 2 for Tand plug into equation 1:
m5.0-kg blockaFEarth’s mass on 5.0-kg block
FEarth’s mass on 3.0-kg block m3.0-kg blocka
a
2.4 m/s2
(5.0 kg 3.0 kg)(9.80 m/s2)
3.0 kg 5.0 kg
(m5.0-kg block m3.0-kg block)g
m3.0-kg block m5.0-kg block
FEarth’s mass on 5.0-kg block FEarth’s mass on 3.0-kg block
m5.0-kg block m3.0-kg block
3.0 kg
5.0 kg
Chapter 4 continued
Solve equation 2 for T:
TFEarth’s mass on 3.0-kg block
m3.0-kg blocka
m3.0-kg blockgm3.0-kg blocka
m3.0-kg block(ga)
(3.0 kg)(9.80 m/s22.4 m/s2)
37 N
Thinking Critically
pages 115–116
93. Formulate Models A 2.0-kg mass, mA,
and a 3.0-kg mass, mB, are connected to a
lightweight cord that passes over a friction-
less pulley. The pulley only changes the
direction of the force exerted by the rope.
The hanging masses are free to move.
Choose coordinate systems for the two
masses with the positive direction being
up for mAand down for mB.
a. Create a pictorial model.
b. Create a physical model with motion
and free-body diagrams.
c. What is the acceleration of the smaller
mass?
ma Fnet where mis the total mass
being accelerated.
For mA,mAaFTmAg
For mB,mBaFTmBg
FTmBgmBamB(ga)
Substituting into the equation for
mAgives
mAamBgmBamAg
or (mAmB)a(mBmA)g
Therefore a
g
(9.80 m/s2)
2.0 m/s2upward
94. Use Models Suppose that the masses in
problem 93 are now 1.00 kg and 4.00 kg.
Find the acceleration of the larger mass.
a
g
(9.80 m/s2)
5.88 m/s2downward
95. Infer The force exerted on a 0.145-kg
baseball by a bat changes from 0.0 N to
1.0104N in 0.0010 s, then drops back to
zero in the same amount of time. The base-
ball was going toward the bat at 25 m/s.
a. Draw a graph of force versus time. What
is the average force exerted on the ball
by the bat?
Fave Fpeak
(1.0104N)
5.0103N
1
2
1
2
0.5104
0.0 1.00.5 2.01.5
1.0104
Time (ms)
Force (N)
4.00 kg 1.00 kg
1.00 kg 4.00 kg
mBmA
mAmB
3.0 kg 2.0 kg
2.0 kg 3.0 kg
mBmA
mAmB
mA
mB
mAg
mBg
xa
FT
a
FT
mA
mB
x
82 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 83
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What is the acceleration of the ball?
a
3.4104m/s2
c. What is the final velocity of the ball,
assuming that it reverses direction?
vfviat
25 m/s (3.4104m/s2)
(0.0020 s)
43 m/s
96. Observe and Infer Three blocks that are
connected by massless strings are pulled
along a frictionless surface by a horizontal
force, as shown in Figure 4-25.
■Figure 4-25
a. What is the acceleration of each block?
Since they all move together, the
acceleration is the same for all
3 blocks.
Fma
(m1m2m3)a
a
3.0 m/s2
b. What are the tension forces in each of
the strings?
Hint: Draw a separate free-body diagram
for each block.
Fnet ma
FFT2 m3a
FT2 FT1 m2a
FT1 m1a
(2.0 kg)(3.0 m/s2)
6.0 N
FT2 m2aFT1
(4.0 kg)(3.0 m/s2) 6.0 N
18 N
97. Critique Using the Example Problems in
this chapter as models, write a solution to
the following problem. A block of mass
3.46 kg is suspended from two vertical
ropes attached to the ceiling. What is the
tension in each rope?
1 Analyze and Sketch the Problem
Draw free-body diagrams for the block
and choose upward to be positive
Solve for the Unknown
Known:
mblock 3.46 kg
Unknown:
Frope1 on block Frope2 on block ?
2 Solve for the Unknown
Use Newton’s second law to find the
tension in the ropes
Fnet 2Frope1 on block
FEarth’s mass on block
ma 0
Frope1 on block
Frope1 on block
17.0 N
(3.46 kg)(9.80 m/s2)
2
mg
2
FEarth’s mass on block
2
TT
Fg
3.46 kg
36 N
2.0 kg 4.0 kg 6.0 kg
F
m1m2m3
2.0 kg 4.0 kg 6.0 kg
FT2
FT1
m1m2m3F 36.0 N
5.0103N
0.145 kg
Fnet
m
Chapter 4 continued

3 Evaluate the Answer
•Are the units correct? N is the correct
unit for a tension, since it is a force.
•Does the sign make sense? The posi-
tive sign indicates that the tension is
pulling upwards.
•Is the magnitude realistic? We would
expect the magnitude to be on the
same order as the block’s weight.
98. Think Critically Because of your physics
knowledge, you are serving as a scientific
consultant for a new science-fiction TV
series about space exploration. In episode 3,
the heroine, Misty Moonglow, has been
asked to be the first person to ride in a new
interplanetary transport for use in our solar
system. She wants to be sure that the trans-
port actually takes her to the planet she is
supposed to be going to, so she needs to
take a testing device along with her to
measure the force of gravity when she
arrives. The script writers don’t want her to
just drop an object, because it will be hard
to depict different accelerations of falling
objects on TV. They think they’d like some-
thing involving a scale. It is your job to
design a quick experiment Misty can con-
duct involving a scale to determine which
planet in our solar system she has arrived
on. Describe the experiment and include
what the results would be for Pluto
(g0.30 m/s2), which is where she is sup-
posed to go, and Mercury (g3.70 m/s2),
which is where she actually ends up.
Answers will vary. Here is one possible
answer: She should take a known mass,
say 5.00-kg, with her and place it on the
scale. Since the gravitational force
depends upon the local acceleration
due to gravity, the scale will read a dif-
ferent number of newtons, depending
on which planet she is on.The following
analysis shows how to figure out what
the scale would read on a given planet:
Identify the mass as the system and
upward as positive.
Fnet Fscale on mass Fgma 0
Fscale on mass Fg
Fscale on mass mg
Pluto: Fscale on mass
(5.00 kg)(0.30 m/s2)
1.5 N
Mercury: Fscale on mass
(5.00 kg)(3.7 m/s2)
19 N
99. Apply Concepts Develop a CBL lab, using
a motion detector, that graphs the distance
a free-falling object moves over equal inter-
vals of time. Also graph velocity versus time.
Compare and contrast your graphs. Using
your velocity graph, determine the accelera-
tion. Does it equal g?
Student labs will vary with equipment
available and designs. p-t graphs and
v-t graphs should reflect uniform accel-
eration. The acceleration should be
close to g.
Writing in Physics
page 116
100. Research Newton’s contributions to physics
and write a one-page summary. Do you think
his three laws of motion were his greatest
accomplishments? Explain why or why not.
Answers will vary. Newton’s contribu-
tions should include his work on light
and color, telescopes, astronomy, laws
of motion, gravity, and perhaps
calculus. One argument in favor of his
three laws of motion being his greatest
accomplishments is that mechanics is
based on the foundation of these laws.
His advances in the understanding of
the concept of gravity may be suggest-
ed as his greatest accomplishment
instead of his three laws of motion.
84 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 85
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
101. Review, analyze, and critique Newton’s
first law. Can we prove this law? Explain.
Be sure to consider the role of resistance.
Answers will vary. Newton’s first law of
motion involves an object whose net
forces are zero. If the object is at rest, it
remains at rest; if it is in motion, it will
continue to move in the same direction
at a constant velocity. Only a force act-
ing on an object at rest can cause it to
move. Likewise, only a force acting on
an object in motion can cause it to
change its direction or speed.The two
cases (object at rest, object in motion)
could be viewed as two different frames
of reference. This law can be demon-
strated, but it cannot be proven.
102. Physicists classify all forces into four funda-
mental categories: gravitational, electro-
magnetic, strong nuclear, and weak nuclear.
Investigate these four forces and describe
the situations in which they are found.
Answers will vary.The strong nuclear
force has a very short range and is what
holds protons and neutrons together in
the nucleus of an atom.The weak
nuclear force is much less strong than
the strong nuclear force and is involved
in radioactive decay.The electromagnet-
ic force is involved in holding atoms
and molecules together and is based on
the attraction of opposite charges.
Gravity is a long-range force between
two or more masses.
Cumulative Review
page 116
103. Cross-Country Skiing Your friend is
training for a cross-country skiing race, and
you and some other friends have agreed to
provide him with food and water along his
training route. It is a bitterly cold day, so
none of you wants to wait outside longer
than you have to. Taro, whose house is the
stop before yours, calls you at 8:25 A.M.to
tell you that the skier just passed his house
and is planning to move at an average
speed of 8.0 km/h. If it is 5.2 km from
Taro’s house to yours, when should you
expect the skier to pass your house?
(Chapter 2)
dvt, or t
d5.2 km 5.2103m
v(8.0 km/h)
2.2 m/s
t
2.4103s
39 min
The skier should pass your house at
8:25 0:39 9:04 A.M.
104. Figure 4-26 is a position-time graph of
the motion of two cars on a road.
(Chapter 3)
■Figure 4-26
a. At what time(s) does one car pass the
other?
3 s, 8 s
b. Which car is moving faster at 7.0 s?
car A
c. At what time(s) do the cars have the
same velocity?
5 s
d. Over what time interval is car B speed-
ing up all the time?
none
e. Over what time interval is car B slow-
ing down all the time?
3 s to 10 s
02468
12
6
Distance (m)
Time (s)
Position of Two Cars
A
B
5.2103m
2.2 m/s
1h
3600 s
1000 m
1 km
d
v
Chapter 4 continued

105. Refer to Figure 4-26 to find the
instantaneous speed for the following:
(Chapter 3)
a. car B at 2.0 s
0 m/s
b. car B at 9.0 s
0 m/s
c. car A at 2.0 s
1 m/s
Challenge Problem
page 100
An air-track glider passes through a photoelectric
gate at an initial speed of 0.25 m/s. As it passes
through the gate, a constant force of 0.40 N is
applied to the glider in the same direction as its
motion. The glider has a mass of 0.50 kg.
1. What is the acceleration of the glider?
Fma
a
0.80 m/s2
2. It takes the glider 1.3 s to pass through a
second gate. What is the distance between
the two gates?
dfdivitat2
Let diposition of first gate 0.0 m
d0.0 m (0.25 m/s)(1.3 s)
(0.80 m/s2)(1.3 s)2
1.0 m
3. The 0.40-N force is applied by means of a
string attached to the glider. The other end
of the string passes over a resistance-free
pulley and is attached to a hanging mass,
m. How big is m?
Fgmmassg
mmass
F
g
g
4.1102kg
4. Derive an expression for the tension, T, in
the string as a function of the mass, M, of
the glider, the mass, m, of the hanging
mass, and g.
Tmg Ma
0.40 N
9.80 m/s2
1
2
1
2
0.40 N
0.50 kg
F
m
86 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued
Physics: Principles and Problems Solutions Manual 87
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5Forces in Two Dimensions
CHAPTER
Practice Problems
5.1 Vectors
pages 119–125
page 121
1. A car is driven 125.0 km due west, then 65.0 km due south. What is the
magnitude of its displacement? Solve this problem both graphically and
mathematically, and check your answers against each other.
R2A2B2
RA2B
2
(65.0
km)2
(12
5.0 km
)2
141 km
2. Two shoppers walk from the door of the mall to their car, which is 250.0 m down
a lane of cars, and then turn 90° to the right and walk an additional 60.0 m.
What is the magnitude of the displacement of the shoppers’ car from the mall
door? Solve this problem both graphically and mathematically, and check your
answers against each other.
R2A2B2
RA2B
2
(250.0
m)2
(60.0
m)2
257 m
3. A hiker walks 4.5 km in one direction, then makes a 45° turn to the right and
walks another 6.4 km. What is the magnitude of her displacement?
R2A2B22AB cos
RA2B
22A
Bcos
(4.5 k
m)2
(6.4 k
m)2
2(4.5
km)(6
.4 km
)(cos
135°)
1.0101km
4. An ant is crawling on the sidewalk. At one moment, it is moving south a distance
of 5.0 mm. It then turns southwest and crawls 4.0 mm. What is the magnitude of
the ant’s displacement?
R2A2B22AB cos
RA2
B2
2AB c
os
(5.0 m
m)2
(4.0 m
m)2
2(5.0
mm)(
4.0 m
m)(co
s 135
°)
8.3 mm
60.0 m
250.0 m
257 m Car
Mall
door
125.0 km
65.0 km
141 km

page 125
Solve problems 5–10 algebraically. You may also choose to solve some of them graphically to
check your answers.
5. Sudhir walks 0.40 km in a direction 60.0° west of north, then goes 0.50 km due
west. What is his displacement?
Identify north and west as the positive directions.
d1W d1sin (0.40 km)(sin 60.0°) 0.35 km
d1N d1cos (0.40 km)(cos 60.0°) 0.20 km
d2W 0.50 km d2N 0.00 km
RWd1W d2W 0.35 km 0.50 km 0.85 km
RNd1N d2N 0.20 km 0.00 km 0.20 km
RRW2
RN2
(0.85
km)2
(0.20
km)2
0.87 km
tan1
tan1
0
0.
.8
25
0k
km
m
77°
R0.87 km at 77° west of north
6. Afua and Chrissy are going to sleep
overnight in their tree house and are
using some ropes to pull up a box
containing their pillows and blankets,
which have a total mass of 3.20 kg. The
girls stand on different branches, as shown
in Figure 5-6, and pull at the angles and
with the forces indicated. Find the x- and
y-components of the net force on the box.
Hint: Draw a free-body diagram so that you do
not leave out a force.
Identify up and right as positive.
FA on box,xFA on box cos A
(20.4 N)(cos 120°)
10.2 N
FA on box,yFA on box sin A
(20.4 N)(sin 120°)
17.7 N
FC on box,xFC on box cos A
(17.7 N)(cos 55°)
RW
RN
88 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued
■Figure 5-6

Physics: Principles and Problems Solutions Manual 89
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
10.2 N
FC on box,yFC on box sin A
(17.7 N)(sin 55°)
14.5 N
Fg,x0.0 N
Fg,ymg
(3.20 kg)(9.80 m/s2)
31.4 N
Fnet on box,xFA on box,x
FC on box,xFg,x
10.2 N 10.2 N 0.0 N
0.0 N
Fnet on box,yFA on box,y
FC on box,yFg,y
17.7 N 14.5 N 31.4 N
0.8 N
The net force is 0.8 N in the upward
direction.
7. You first walk 8.0 km north from home, then
walk east until your displacement from home
is 10.0 km. How far east did you walk?
The resultant is 10.0 km. Using the
Pythagorean Theorem, the distance east
is
R2A2B2,so
BR2
A2
(10.0
km)2
(8.0
km)2
6.0 km
8. A child’s swing is held up by two ropes tied
to a tree branch that hangs 13.0° from the
vertical. If the tension in each rope is 2.28 N,
what is the combined force (magnitude and
direction) of the two ropes on the swing?
The force will be straight up. Because
the angles are equal, the horizontal
forces will be equal and opposite and
cancel out. The magnitude of this
vertical force is
Fcombined Frope1 on swing cos
Frope2 on swing cos
2Frope2 on swing cos
(2)(2.28 N)(cos 13.0°)
4.44 N upward
9. Could a vector ever be shorter than one of
its components? Equal in length to one of
its components? Explain.
It could never be shorter than one of its
components, but if it lies along either
the x- or y-axis, then one of its compo-
nents equals its length.
10. In a coordinate system in which the x-axis is
east, for what range of angles is the x-compo-
nent positive? For what range is it negative?
The x-component is positive for angles
less than 90° and for angles greater
than 270°. It’s negative for angles
greater than 90° but less than 270°.
Section Review
5.1 Vectors
pages 119–125
page 125
11. Distance v. Displacement Is the distance
that you walk equal to the magnitude of
your displacement? Give an example that
supports your conclusion.
Not necessarily. For example, you could
walk around the block (one km per
side).Your displacement would be zero,
but the distance that you walk would be
4 kilometers.
12. Vector Difference Subtract vector Kfrom
vector L, shown in Figure 5-7.
Chapter 5 continued
■Figure 5-7
6.0 (4.0) 10.0 to the right
13. Components Find the components of
vector M, shown in Figure 5-7.
Mxm cos
(5.0)(cos 37.0°)
4.0 to the right
Mymsin
(5.0)(sin 37.0°)
3.0 upward
14. Vector Sum Find the sum of the three
vectors shown in Figure 5-7.
RxKxLxMx
4.0 6.0 4.0
6.0
RyKyLyMy
0.0 0.0 3.0
3.0
RRx2
Ry2
6.02
3.02
6.7
tan1
R
Ry
x
tan1
3
6
27°
R 6.7 at 27°
15. Commutative Operations The order in
which vectors are added does not matter.
Mathematicians say that vector addition is
commutative. Which ordinary arithmetic
operations are commutative? Which are not?
Addition and multiplication are commu-
tative. Subtraction and division are not.
16. Critical Thinking A box is moved through
one displacement and then through a sec-
ond displacement. The magnitudes of the
two displacements are unequal. Could the
displacements have directions such that the
resultant displacement is zero? Suppose the
box was moved through three displace-
ments of unequal magnitude. Could the
resultant displacement be zero? Support
your conclusion with a diagram.
No, but if there are three
displacements, the sum can
be zero if the three vectors
form a triangle when they
are placed tip-to-tail. Also,
the sum of three displace-
ments can be zero without
forming a triangle if the sum of two
displacements in one direction equals
the third in the opposite direction.
Practice Problems
5.2 Friction
pages 126–130
page 128
17. A girl exerts a 36-N horizontal force as she
pulls a 52-N sled across a cement sidewalk
at constant speed. What is the coefficient of
kinetic friction between the sidewalk and
the metal sled runners? Ignore air resistance.
FNmg 52 N
Since the speed is constant, the friction
force equals the force exerted by the
girl, 36 N.
FfkFN
so k
F
F
N
f
3
56
2N
N
0.69
18. You need to move a 105-kg sofa to a differ-
ent location in the room. It takes a force of
102 N to start it moving. What is the coeffi-
cient of static friction between the sofa and
the carpet?
6.0
5.0
4.0 37.0°
K
L
M
90 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 91
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
FfsFN
s
m
F
g
f
0.0991
19. Mr. Ames is dragging a box full of books
from his office to his car. The box and
books together have a combined weight of
134 N. If the coefficient of static friction
between the pavement and the box is 0.55,
how hard must Mr. Ames push the box in
order to start it moving?
FAmes on box Ffriction
sFN
smg
(0.55)(134 N)
74 N
20. Suppose that the sled in problem 17 is
resting on packed snow. The coefficient of
kinetic friction is now only 0.12. If a person
weighing 650 N sits on the sled, what force
is needed to pull the sled across the snow at
constant speed?
At constant speed, applied force equals
friction force, so
FfkFN
(0.12)(52 N 650 N)
84 N
21. Suppose that a particular machine in a
factory has two steel pieces that must rub
against each other at a constant speed.
Before either piece of steel has been treated
to reduce friction, the force necessary to get
them to perform properly is 5.8 N. After the
pieces have been treated with oil, what will
be the required force?
Ff, before k, beforeFN
so FN
F
k
f,
,
b
b
e
e
f
f
o
o
r
r
e
e
5
0
..
8
58
N
1.0101N
Ff, after k, afterFN
(0.06)(1.0101N)
0.6 N
page 130
22. A 1.4-kg block slides across a rough surface
such that it slows down with an acceleration
of 1.25 m/s2. What is the coefficient of
kinetic friction between the block and the
surface?
Fnet kFN
ma kmg
k
g
a
1
9.
.2
85
0m
m/
/s
s
2
2
0.128
23. You help your mom move a 41-kg bookcase
to a different place in the living room. If
you push with a force of 65 N and the
bookcase accelerates at 0.12 m/s2, what is
the coefficient of kinetic friction between
the bookcase and the carpet?
Fnet FkFNFkmg ma
k
F
mg
ma
0.15
24. A shuffleboard disk is accelerated to a speed
of 5.8 m/s and released. If the coefficient of
kinetic friction between the disk and the
concrete court is 0.31, how far does the disk
go before it comes to a stop? The courts are
15.8 m long.
Identify the direction of the disk’s motion
as positive. Find the acceleration of the
disk due to the force of friction.
Fnet kFNkmg ma
akg
65 N (41 kg)(0.12 m/s2)
(41 kg)(9.80 m/s2)
102 N
(105 kg)(9.80 m/s2)
Ff
FN
Chapter 5 continued

Then use the equation vf2vi2
2a(dfdi) to find the distance.
Let di0 and solve for df.
df
vf2
2
a
vi2
5.5 m
25. Consider the force pushing the box in
Example Problem 4. How long would it
take for the velocity of the box to double to
2.0 m/s?
The initial velocity is 1.0 m/s, the final
velocity is 2.0 m/s, and the acceleration
is 2.0 m/s2,so
a
v
tf
f
v
ti
i
;let ti0 and solve for tf.
tf
vf
a
vi
0.50 s
26. Ke Min is driving along on a rainy night at
23 m/s when he sees a tree branch lying
across the road and slams on the brakes
when the branch is 60.0 m in front of him.
If the coefficient of kinetic friction between
the car’s locked tires and the road is 0.41,
will the car stop before hitting the branch?
The car has a mass of 2400 kg.
Choose positive direction as direction
of car’s movement.
Fnet kFNkmg ma
akg
Then use the equation vf2vi2
2a(dfdi) to find the distance.
Let di0 and solve for df.
df
vf2
2
a
vi2
(2
v
)
f2
(
v
k
i
g
2
)
66 m, so he hits the branch before
he can stop.
Section Review
5.2 Friction
pages 126–130
page 130
27. Friction In this section, you learned about
static and kinetic friction. How are these
two types of friction similar? What are the
differences between static and kinetic friction?
They are similar in that they both act in
a direction opposite to the motion (or
intended motion) and they both result
from two surfaces rubbing against each
other. Both are dependent on the normal
force between these two surfaces. Static
friction applies when there is no relative
motion between the two surfaces. Kinetic
friction is the type of friction when there
is relative motion.The coefficient of
static friction between two surfaces is
greater than the coefficient of kinetic fric-
tion between those same two surfaces.
28. Friction At a wedding reception, you
notice a small boy who looks like his mass
is about 25 kg, running part way across the
dance floor, then sliding on his knees until
he stops. If the kinetic coefficient of friction
between the boy’s pants and the floor is
0.15, what is the frictional force acting on
him as he slides?
Ffriction kFN
kmg
(0.15)(25 kg)(9.80 m/s2)
37 N
29. Velocity Derek is playing cards with his
friends, and it is his turn to deal. A card has
a mass of 2.3 g, and it slides 0.35 m along
the table before it stops. If the coefficient
of kinetic friction between the card and the
table is 0.24, what was the initial speed of
the card as it left Derek’s hand?
(0.0 m/s) (23 m/s)2
(2)(0.41)(9.80 m/s2)
2.0 m/s 1.0 m/s
2.0 m/s2
(0.0 m/s)2(5.8 m/s)2
(2)(0.31)(9.80 m/s2)
vf2vi2
(2)(kg)
92 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 93
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Identify the direction of the card’s
movement as positive
Fnet kFNkmg ma
akg
vfdi0 so
vi2ad
f
2(
kg)d
f
2(
0.24)(
9.80 m
/s2)(0.
35 m)
1.3 m/s
30. Force The coefficient of static friction
between a 40.0-kg picnic table and the
ground below it is 0.43 m. What is the
greatest horizontal force that could be
exerted on the table while it remains
stationary?
FfsFN
smg
(0.43)(40.0 kg)(9.80 m/s2)
1.7102N
31. Acceleration Ryan is moving to a new
apartment and puts a dresser in the back of
his pickup truck. When the truck accelerates
forward, what force accelerates the dresser?
Under what circumstances could the dresser
slide? In which direction?
Friction between the dresser and the
truck accelerates the dresser forward.
The dresser will slide backward if the
force accelerating it is greater than
smg.
32. Critical Thinking You push a 13-kg table
in the cafeteria with a horizontal force of
20 N, but it does not move. You then push
it with a horizontal force of 25 N, and it
accelerates at 0.26 m/s2. What, if anything,
can you conclude about the coefficients of
static and kinetic friction?
From the sliding portion of your experi-
ment you can determine that the coeffi-
cient of kinetic friction between the
table and the floor is
FfFon table F2
kFNFon table ma
k
Fon ta
m
ble
g
ma
0.17
All you can conclude about the coeffi-
cient of static friction is that it is
between
s
Fon
m
t
g
able
0.16
and s
Fon
m
t
g
able
0.20
Practice Problems
5.3 Force and Motion in
Two Dimensions
pages 131–135
page 133
33. An ant climbs at a steady speed up the side
of its anthill, which is inclined 30.0° from
the vertical. Sketch a free-body diagram for
the ant.
y
x
Ff
FN
Fg
FgFgx
Fgy
60.0°
25 N
(13 kg)(9.80 m/s2)
20 N
(13 kg)(9.80 m/s2)
25 N (13 kg)(0.26 m/s)
(13 kg)(9.80 m/s2)
Chapter 5 continued

34. Scott and Becca are moving a folding table
out of the sunlight. A cup of lemonade,
with a mass of 0.44 kg, is on the table. Scott
lifts his end of the table before Becca does,
and as a result, the table makes an angle of
15.0° with the horizontal. Find the compo-
nents of the cup’s weight that are parallel
and perpendicular to the plane of the table.
Fg, parallel Fgsin
(0.44 kg)(9.80 m/s2)(sin 15.0°)
1.1 N
Fg, perpendicular Fgcos
(0.44 kg)(9.80 m/s2)
(cos 15.0°)
4.2 N
35. Kohana, who has a mass of 50.0 kg, is at
the dentist’s office having her teeth cleaned,
as shown in Figure 5-14. If the component
of her weight perpendicular to the plane of
the seat of the chair is 449 N, at what angle
is the chair tilted?
■Figure 5-14
Fg, perpendicular Fgcos mg cos
cos1
cos1
23.6°
36. Fernando, who has a mass of 43.0 kg, slides
down the banister at his grandparents’ house.
If the banister makes an angle of 35.0° with
the horizontal, what is the normal force
between Fernando and the banister?
FNmg cos
(43.0 kg)(9.80 m/s2)(cos 35.0°)
345 N
37. A suitcase is on an inclined plane. At what
angle, relative to the vertical, will the com-
ponent of the suitcase’s weight parallel to
the plane be equal to half the perpendicular
component of its weight?
Fg, parallel Fgsin , when the angle is
with respect to the horizontal
Fg, perpendicular Fgcos , when the
angle is with respect to the horizontal
Fg, perpendicular 2Fg, parallel
2
ta1
n
tan1
1
2
26.6°relative to the horizontal, or
63.4°relative to the vertical
page 135
38. Consider the crate on the incline in Example
Problem 5.
a. Calculate the magnitude of the
acceleration.
a
m
F
gsin
(9.80 m/s2)(sin 30.0°)
4.90 m/s2
b. After 4.00 s, how fast will the crate be
moving?
a
v
tf
f
v
ti
i
;let viti0.
Solve for vf.
vfatf
(4.90 m/s2)(4.00 s)
19.6 m/s
mg sin
m
Fgsin
m
Fgcos
Fgsin
Fg, perpendicular
Fg, parallel
449 N
(50.0 kg)(9.80 m/s2)
Fg, perpendicular
mg
94 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 95
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
39. If the skier in Example Problem 6 were on
a 31° downhill slope, what would be the
magnitude of the acceleration?
Since ag(sin cos ),
a(9.80 m/s2)(sin 31°(0.15)(cos 31°))
3.8 m/s2
40. Stacie, who has a mass of 45 kg, starts down
a slide that is inclined at an angle of 45°
with the horizontal. If the coefficient of
kinetic friction between Stacie’s shorts and
the slide is 0.25, what is her acceleration?
FStacie’s weight parallel with slide Ffma
a
g(sin kcos )
(9.80 m/s2)[sin 45°(0.25)(cos 45°)]
5.2 m/s2
41. After the skier on the 37° hill in Example
Problem 6 had been moving for 5.0 s, the
friction of the snow suddenly increased and
made the net force on the skier zero. What
is the new coefficient of friction?
ag(sin kcos )
agsin gkcos
If a0,
0 gsin gkcos
kcos sin
k
c
so
in
s
k
c
so
in
s3
37
7°
°
0.75
Section Review
5.3 Force and Motion in
Two Dimensions
pages 131–135
page 135
42. Forces One way to get a car unstuck is to
tie one end of a strong rope to the car and
the other end to a tree, then push the rope
at its midpoint at right angles to the rope.
Draw a free-body diagram and explain why
even a small force on the rope can exert a
large force on the car.
The vectors shown in the free body
diagram indicate that even a small
force perpendicular to the rope can
increase the tension in the rope
enough to overcome the friction force.
Since F2T sin (where is the angle
between the rope’s original position and
its displaced position),
T
2s
F
in
For smaller values of , the tension, T,
will increase greatly.
Ffriction
Fcar
Fe
mg sin kmg cos
m
mg sin kFN
m
FStacie’s weight parallel with slide Ff
m
Chapter 5 continued

43. Mass A large scoreboard is suspended from the ceiling of a sports arena by
10 strong cables. Six of the cables make an angle of 8.0° with the vertical while
the other four make an angle of 10.0°. If the tension in each cable is 1300.0 N,
what is the scoreboard’s mass?
Fnet,ymay0
Fnet,yFcables on board Fg
6Fcable cos 64Fcable cos 4mg 0
m
1.31103kg
44. Acceleration A 63-kg water skier is pulled up a 14.0° incline by a rope parallel
to the incline with a tension of 512 N. The coefficient of kinetic friction is 0.27.
What are the magnitude and direction of the skier’s acceleration?
FNmg cos
Frope on skier FgFfma
Frope on skier mg sin kmg cos ma
a
3.2 m/s2, up the incline
45. Equilibrium You are hanging a painting using two lengths
of wire. The wires will break if the force is too great. Should
you hang the painting as shown in Figures 5-15a or 5-15b?
Explain.
Figure 5-15b; FT,so F
Tgets smaller as gets
larger, and is larger in 5-15b.
46. Critical Thinking Can the coefficient of friction ever have a value such that a
skier would be able to slide uphill at a constant velocity? Explain why or why
not. Assume there are no other forces acting on the skier.
No, because both the frictional force opposing the motion of the skier
and the component of Earth’s gravity parallel to the slope point downhill,
not uphill.
Fg
2 sin
512 N (63 kg)(9.80 m/s2)(sin 14.0°)(0.27)(63 kg)(9.80 m/s2)(cos 14.0°)
63 kg
Frope on skier mg sin kmg cos
m
6(1300.0 N)(cos 8.0°)4(1300.0 N)(cos 10.0°)
9.80 m/s2
6Fcable cos 64Fcable cos 4
g
96 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued
■Figure 5-15a
■Figure 5-15b
Physics: Principles and Problems Solutions Manual 97
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter Assessment
Concept Mapping
page 140
47. Complete the concept map below by label-
ing the circles with sine, cosine, or tangent to
indicate whether each function is positive
or negative in each quadrant.
Mastering Concepts
page 140
48. Describe how you would add two vectors
graphically. (5.1)
Make scale drawings of arrows represent-
ing the vector quantities. Place the
arrows for the quantities to be added tip-
to-tail. Draw an arrow from the tail of the
first to the tip of the last. Measure the
length of that arrow and find its direction.
49. Which of the following actions is permissi-
ble when you graphically add one vector to
another: moving the vector, rotating the
vector, or changing the vector’s length? (5.1)
allowed: moving the vector without
changing length or direction
50. In your own words, write a clear definition
of the resultant of two or more vectors. Do
not explain how to find it; explain what it
represents. (5.1)
The resultant is the vector sum of two
or more vectors. It represents the quan-
tity that results from adding the vectors.
51. How is the resultant displacement affected
when two displacement vectors are added
in a different order? (5.1)
It is not affected.
52. Explain the method that you would use to
subtract two vectors graphically. (5.1)
Reverse the direction of the second
vector and then add them.
53. Explain the difference between these two
symbols: Aand A. (5.1)
Ais the symbol for the vector quantity.
Ais the signed magnitude (length) of
the vector.
54. The Pythagorean theorem usually is written
c2a2b2. If this relationship is used
in vector addition, what do a, b, and c
represent? (5.1)
aand brepresent the lengths of two
vectors that are at the right angles to
one another. crepresents the length
of the sum of the two vectors.
55. When using a coordinate system, how is the
angle or direction of a vector determined
with respect to the axes of the coordinate
system? (5.1)
The angle is measured counterclock-
wise from the x-axis.
56. What is the meaning of a coefficient of
friction that is greater than 1.0? How
would you measure it? (5.2)
The frictional force is greater than the
normal force.You can pull the object
along the surface, measuring the force
needed to move it at constant speed.
Also measure the weight of the object.
57. Cars Using the model of friction described
in this textbook, would the friction between
a tire and the road be increased by a wide
rather than a narrow tire? Explain. (5.2)
It would make no difference. Friction
does not depend upon surface area.
58. Describe a coordinate system that would
be suitable for dealing with a problem in
which a ball is thrown up into the air. (5.3)
One axis is vertical, with the positive
direction either up or down.
Chapter 5 continued
Quadrant
II III IVI
sine
cosine
tangent sine cosine
tangent tangent cosine
tangent cosine sine
tangent

59. If a coordinate system is set up such that
the positive x-axis points in a direction 30°
above the horizontal, what should be the
angle between the x-axis and the y-axis?
What should be the direction of the positive
y-axis? (5.3)
The two axes must be at right angles.
The positive y-axis points 30°away
from the vertical so that it is at right
angles to the x-axis.
60. Explain how you would set up a coordinate
system for motion on a hill. (5.3)
For motion on a hill, the vertical (y) axis
is usually set up perpendicular, or nor-
mal, to the surface of the hill.
61. If your textbook is in equilibrium, what can
you say about the forces acting on it? (5.3)
The net force acting on the book is zero.
62. Can an object that is in equilibrium be
moving? Explain. (5.3)
Yes, Newton’s first law permits motion
as long as the object’s velocity is con-
stant. It cannot accelerate.
63. What is the sum of three vectors that, when
placed tip to tail, form a triangle? If these
vectors represent forces on an object, what
does this imply about the object? (5.3)
The vector sum of forces forming a
closed triangle is zero. If these are the
only forces acting on the object, the net
force on the object is zero and the
object is in equilibrium.
64. You are asked to analyze the motion of a
book placed on a sloping table. (5.3)
a. Describe the best coordinate system for
analyzing the motion.
Set up the y-axis perpendicular
to the surface of the table and the
x-axis pointing uphill and parallel to
the surface.
b. How are the components of the weight of
the book related to the angle of the table?
One component is parallel to the
inclined surface and the other is
perpendicular to it.
65. For a book on a sloping table, describe
what happens to the component of the
weight force parallel to the table and the
force of friction on the book as you
increase the angle that the table makes
with the horizontal. (5.3)
a. Which components of force(s) increase
when the angle increases?
As you increase the angle the table
makes with the horizontal, the com-
ponent of the book’s weight force
along the table increases.
b. Which components of force(s) decrease?
When the angle increases, the com-
ponent of the weight force normal to
the table decreases and the friction
force decreases.
Applying Concepts
pages 140–141
66. A vector that is 1 cm long represents a dis-
placement of 5 km. How many kilometers
are represented by a 3-cm vector drawn to
the same scale?
(3 cm)
15 km
67. Mowing the Lawn If you are pushing a
lawn mower across the grass, as shown in
Figure 5-16, can you increase the horizon-
tal component of the force that you exert
on the mower without increasing the mag-
nitude of the force? Explain.
■Figure 5-16
Fx
FyF
5 km
1 cm
98 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued
Physics: Principles and Problems Solutions Manual 99
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Yes, lower the handle to make the angle
between the handle and the horizontal
smaller.
68. A vector drawn 15 mm long represents a
velocity of 30 m/s. How long should you
draw a vector to represent a velocity of
20 m/s?
(20 m/s)
1
35
0m
mm
/s
10 mm
69. What is the largest possible displacement
resulting from two displacements with mag-
nitudes 3 m and 4 m? What is the smallest
possible resultant? Draw sketches to
demonstrate your answers.
The largest is 7 m; the smallest is 1 m.
70. How does the resultant displacement
change as the angle between two vectors
increases from 0° to 180°?
The resultant increases.
71. Aand Bare two sides of a right triangle,
where tan A/B.
a. Which side of the triangle is longer if
tan is greater than 1.0?
A is longer.
b. Which side is longer if tan is less
than 1.0?
B is longer.
c. What does it mean if tan is equal
to 1.0?
A and B are equal in length.
72. Traveling by Car A car has a velocity of
50 km/h in a direction 60° north of east. A
coordinate system with the positive x-axis
pointing east and a positive y-axis pointing
north is chosen. Which component of the
velocity vector is larger, xor y?
The northward component (y) is longer.
73. Under what conditions can the Pythagorean
theorem, rather than the law of cosines, be
used to find the magnitude of a resultant
vector?
The Pythagorean theorem can be used
only if the two vectors to be added are
at right angles to one another.
74. A problem involves a car moving up a hill,
so a coordinate system is chosen with the
positive x-axis parallel to the surface of the
hill. The problem also involves a stone that
is dropped onto the car. Sketch the problem
and show the components of the velocity
vector of the stone.
One component is in the negative
x-direction, the other in the negative
y-direction, assuming that the positive
direction points upward, perpendicular
to the hill.
75. Pulling a Cart According to legend, a horse
learned Newton’s laws. When the horse was
told to pull a cart, it refused, saying that
if it pulled the cart forward, according to
Newton’s third law, there would be an equal
force backwards; thus, there would be bal-
anced forces, and, according to Newton’s
second law, the cart would not accelerate.
How would you reason with this horse?
The equal and opposite forces referred
to in Newton’s third law are acting on
different objects.The horse would pull
on the cart, and the cart would pull
on the horse. The cart would have an
unbalanced net force on it (neglecting
friction) and would thus accelerate.
vx
v
vy
+y
+x
3 m 4 m
4 m
3 m
1 m
7 m
Chapter 5 continued

76. Tennis When stretching a tennis net
between two posts, it is relatively easy to
pull one end of the net hard enough to
remove most of the slack, but you need a
winch to take the last bit of slack out of
the net to make the top almost completely
horizontal. Why is this true?
When stretching the net between the
two posts, there is no perpendicular
component upward to balance the
weight of the net. All the force exerted
on the net is horizontal. Stretching the
net to remove the last bit of slack
requires great force in order to reduce
the flexibility of the net and to increase
the internal forces that hold it together.
77. The weight of a book on an inclined plane
can be resolved into two vector compo-
nents, one along the plane, and the other
perpendicular to it.
a. At what angle are the components
equal?
45°
b. At what angle is the parallel component
equal to zero?
0°
c. At what angle is the parallel component
equal to the weight?
90°
78. TV Towers The transmitting tower of a TV
station is held upright by guy wires that
extend from the top of the tower to the
ground. The force along the guy wires can
be resolved into two perpendicular compo-
nents. Which one is larger?
The component perpendicular to the
ground is larger if the angle between
the guy wire and horizontal is greater
than 45°.
Mastering Problems
5.1 Vectors
pages 141–142
Level 1
79. Cars A car moves 65 km due east,
then 45 km due west. What is its total
displacement?
65 km (45 km) 2.0101km
d2.0101km, east
80. Find the horizontal and vertical compo-
nents of the following vectors, as shown in
Figure 5-17.
■Figure 5-17
a. E
ExEcos
(5.0)(cos 45°)
3.5
EyEsin
(5.0)(sin 45°)
3.5
b. F
FxFcos
(5.0)(cos 225°)
3.5
FyFsin
(5.0)(sin 225°)
3.5
c. A
AxAcos
(3.0)(cos 180°)
3.0
AyAsin
(3.0)(sin 180°)
0.0
A(3.0)B(3.0)
F(5.0) C(6.0)
E(5.0)
D(4.0)
100 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 101
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
81. Graphically find the sum of the following
pairs of vectors, whose lengths and direc-
tions are shown in Figure 5-17.
a. Dand A
b. Cand D
c. Cand A
d. Eand F
Level 2
82. Graphically add the following sets of
vectors, as shown in Figure 5-17.
a. A, C,and D
b. A, B,and E
c. B, D,and F
83. You walk 30 m south and 30 m east. Find
the magnitude and direction of the resul-
tant displacement both graphically and
algebraically.
R2A2B2
R(30 m
)2(3
0 m)2
40 m
tan
3
30
0m
m
1
45°
R40 m, 45°east of south
The difference in the answers is due to
significant digits being considered in
the calculation.
84. Hiking A hiker’s trip consists of three seg-
ments. Path Ais 8.0 km long heading 60.0°
north of east. Path Bis 7.0 km long in a
direction due east. Path Cis 4.0 km long
heading 315° counterclockwise from east.
a. Graphically add the hiker’s displace-
ments in the order A, B, C.
b. Graphically add the hiker’s displace-
ments in the order C,B,A.
c. What can you conclude about the
resulting displacements?
You can add vectors in any order.
The result is always the same.
B
R
A
C
C
A
B
R
30 m E
45
30 m S R 42
F
D
B
R
A
B
R(6.5)
E
C
A
R(7.0)
D
F
E
R 0.0
A
R(3.0)
C
C
R(10.0)
D
A
R(1.0)
D
Chapter 5 continued
85. What is the net force acting on the ring in
Figure 5-18?
■Figure 5-18
R2A2B2
RA2B
2
(500.0
N)2
(400.
0 N)2
640.3 N
tan
A
B
tan1
A
B
tan1
5
40
00
0.
.0
0
51.34°from B
The net force is 640.3 N at 51.34°
86. What is the net force acting on the ring in
Figure 5-19?
■Figure 5-19
A128 N 64 N
64 N
AxA cos A
(64 N)(cos 180°)
64 N
AyA sin A
(64 N)(sin 180°)
0 N
BxBcos B
(128 N)(cos 30.0°)
111 N
ByBsin B
(128 N)(sin 30.0°)
64 N
RxAxBx
64 N 111 N
47 N
RyAyBy
0 N 64 N
64 N
RRx2
Ry2
(47 N)
2(6
4 N)2
79 N
tan1
R
Ry
x
tan1
6
44
7
54°
Level 3
87. A Ship at Sea A ship at sea is due into a
port 500.0 km due south in two days.
However, a severe storm comes in and
blows it 100.0 km due east from its original
position. How far is the ship from its desti-
nation? In what direction must it travel to
reach its destination?
R2A2B2
R(100.0
km)2
(50
0.0 km
)2
509.9 km
tan1
R
Ry
x
tan1
5
10
00
0.
.0
0
78.69°
R509.9 km, 78.69°south of west
x
y
30.0°
128 N
128 N
64 N
x
y
50.0°
40.0°
500.0 N 400.0 N
102 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 103
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
88. Space Exploration A descent vehicle land-
ing on Mars has a vertical velocity toward
the surface of Mars of 5.5 m/s. At the same
time, it has a horizontal velocity of 3.5 m/s.
a. At what speed does the vehicle move
along its descent path?
R2A2B2
R(5.5 m
/s)2
(3.5 m
/s)2
vR6.5 m/s
b. At what angle with the vertical is this
path?
tan1
R
Ry
x
tan1
5
3.
.5
5
58°from horizontal, which is 32°
from vertical
89. Navigation Alfredo leaves camp and, using
a compass, walks 4 km E, then 6 km S,
3 km E, 5 km N, 10 km W, 8 km N, and,
finally, 3 km S. At the end of three days, he
is lost. By drawing a diagram, compute how
far Alfredo is from camp and which direc-
tion he should take to get back to camp.
Take north and east to be positive
directions. North: 6 km 5 km
8 km 3 km 4 km. East: 4 km
3 km 10 km 3 km.The hiker is
4 km north and 3 km west of camp.
To return to camp, the hiker must go
3 km east and 4 km south.
R2A2B2
R(3 km
)2(4
km)2
5 km
tan1
R
Ry
x
tan1
4
3k
km
m
53°
R5 km, 53°south of east
5.2 Friction
page 142
Level 1
90. If you use a horizontal force of 30.0 N to
slide a 12.0-kg wooden crate across a floor
at a constant velocity, what is the coefficient
of kinetic friction between the crate and the
floor?
FfkFNkmg Fhorizontal
k
Fhom
riz
g
ontal
0.255
91. A 225-kg crate is pushed horizontally with a
force of 710 N. If the coefficient of friction
is 0.20, calculate the acceleration of the crate.
ma Fnet Fappl Ff
where FfkFNkmg
Therefore
a
Fappl
m
kmg
1.2 m/s2
Level 2
92. A force of 40.0 N accelerates a 5.0-kg block
at 6.0 m/s2along a horizontal surface.
a. How large is the frictional force?
ma Fnet Fappl Ff
so FfFappl ma
40.0 N (5.0 kg)(6.0 m/s2)
1.0101N
b. What is the coefficient of friction?
FfkFNkmg
so k
0.20
1.0101N
(5.0 kg)(9.80 m/s2)
Ff
mg
710 N (0.20)(225 kg)(9.80 m/s2)
225 kg
30.0 N
(12.0 kg)(9.80 m/s2)
Chapter 5 continued

93. Moving Appliances Your family just had a
new refrigerator delivered. The delivery man
has left and you realize that the refrigerator
is not quite in the right position, so you
plan to move it several centimeters. If the
refrigerator has a mass of 180 kg, the coeffi-
cient of kinetic friction between the bottom
of the refrigerator and the floor is 0.13, and
the static coefficient of friction between
these same surfaces is 0.21, how hard do
you have to push horizontally to get the
refrigerator to start moving?
Fon fridge Ffriction
sFN
smg
(0.21)(180 kg)(9.80 m/s2)
370 N
Level 3
94. Stopping at a Red Light You are driving
a 2500.0-kg car at a constant speed of
14.0 m/s along a wet, but straight, level
road. As you approach an intersection,
the traffic light turns red. You slam on the
brakes. The car’s wheels lock, the tires begin
skidding, and the car slides to a halt in a
distance of 25.0 m. What is the coefficient
of kinetic friction between your tires and
the wet road?
FfkFNma
kmg where vf 0
(The minus sign indicates the force is
acting opposite to the direction of
motion.)
k
2
v
d
i2
g
0.400
5.3 Force and Motion in Two Dimensions
pages 142–143
Level 1
95. An object in equilibrium has three forces
exerted on it. A 33.0-N force acts at 90.0°
from the x-axis and a 44.0-N force acts at
60.0° from the x-axis. What are the magni-
tude and direction of the third force?
First, find the magnitude of the sum of
these two forces. The equilibrant will
have the same magnitude but opposite
direction.
F133.0 N, 90.0°
F244.0 N, 60.0°
F3?
F1xF1cos 1
(33.0 N)(cos 90.0°)
0.0 N
F1yF1sin 1
(33.0 N)(sin 90.0°)
33.0 N
F2xF2cos 2
(44.0 N)(cos 60.0°)
22.0 N
F2yF2sin 2
(44.0 N)(sin 60.0°)
38.1 N
F3xF1xF2x
0.0 N 22.0 N
22.0 N
F3yF1yF2y
33.0 N 38.1 N
71.1 N
F3F3x2
F3y2
(22.0
N)2
(71.1
N)2
74.4 N
(14.0 m/s)2
2(25.0 m)(9.80 m/s2)
m(vf2vi2)
2d
104 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 105
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
For equilibrium, the sum of the compo-
nents must equal zero, so
tan1
180.0°
tan1
180.0°
253°
F374.4 N, 253°
Level 2
96. Five forces act on an object: (1) 60.0 N at
90.0°, (2) 40.0 N at 0.0°, (3) 80.0 N at
270.0°, (4) 40.0 N at 180.0°, and
(5) 50.0 N at 60.0°. What are the magni-
tude and direction of a sixth force that
would produce equilibrium?
Solutions by components
F160.0 N, 90.0°
F240.0 N, 0.0°
F380.0 N, 270.0°
F440.0 N, 180.0°
F550.0 N, 60.0°
F6?
F1xF1cos 1
(60.0 N)(cos 90.0°) 0.0 N
F1yF1sin 1(60.0 N)(sin 90.0°)
60.0 N
F2xF2cos 2(40.0 N)(cos 0.0°)
40.0 N
F2yF2sin 2(40.0 N)(sin 0.0°)
0.0 N
F3xF3cos 3(80.0 N)(cos 270.0°)
0.0 N
F3yF3sin 3(80.0 N)(sin 270.0°)
80.0 N
F4xF4cos 4(40.0 N)(cos 180.0°)
40.0 N
F4yF4sin 4(40.0 N)(sin 180.0°)
0.0 N
F5xF5cos 5(50.0 N)(cos 60.0°)
25.0 N
F5yF5sin 5(50.0 N)(sin 60.0°)
43.3 N
F6xF1xF2xF3xF4xF5x
0.0 N 40.0 N 0.0 N
(40.0 N) 25.0 N
25.0 N
F6yF1yF2yF3yF4yF5y
60.0 N 0.0 N (80.0 N)
0.0 N 43.3 N
23.3 N
F6F6x2
F6y2
(25.0
N)2
(23.3
N)2
34.2 N
6tan1
180.0°
tan1
180.0°
223°
F634.2 N, 223°
97. Advertising Joe wishes to hang a sign
weighing 7.50102N so that cable A,
attached to the store, makes a 30.0° angle,
as shown in Figure 5-20. Cable Bis hori-
zontal and attached to an adjoining build-
ing. What is the tension in cable B?
■Figure 5-20
30.0°A
B
23.3 N
25.0 N
F6y
F6x
71.1 N
22.0 N
F3y
F3x
Chapter 5 continued

Solution by components.The sum of
the components must equal zero, so
FAyFg0
so FAyFg
7.50102N
FAyFAsin 60.0°
so FA
866 N
Also, FBFA0, so
FBFA
FAcos 60.0°
(866 N)(cos 60.0°)
433 N, right
98. A street lamp weighs 150 N. It is supported
by two wires that form an angle of 120.0°
with each other. The tensions in the wires
are equal.
a. What is the tension in each wire sup-
porting the street lamp?
Fg2Tsin
so T
2s
F
ig
n
(2)(s
1i
5
n
03
N
0.0°)
1.5102N
b. If the angle between the wires support-
ing the street lamp is reduced to 90.0°,
what is the tension in each wire?
T
2s
F
ig
n
(2)(
1
s
5
i0
nN
45°)
1.1102N
99. A 215-N box is placed on an inclined plane
that makes a 35.0° angle with the horizon-
tal. Find the component of the weight force
parallel to the plane’s surface.
Fparallel Fgsin
(215 N)(sin 35.0°)
123 N
Level 3
100. Emergency Room You are shadowing a
nurse in the emergency room of a local
hospital. An orderly wheels in a patient
who has been in a very serious accident
and has had severe bleeding. The nurse
quickly explains to you that in a case like
this, the patient’s bed will be tilted with
the head downward to make sure the brain
gets enough blood. She tells you that, for
most patients, the largest angle that the bed
can be tilted without the patient beginning
to slide off is 32.0° from the horizontal.
a. On what factor or factors does this
angle of tilting depend?
The coefficient of static friction
between the patient and the bed’s
sheets.
b. Find the coefficient of static friction
between a typical patient and the bed’s
sheets.
Fg parallel to bed mg sin
Ff
sFN
smg cos
so s
tan
tan 32.0°
0.625
sin
cos
mg sin
mg cos
7.50102N
sin 60.0°
FAy
sin 60.0°
106 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 107
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
101. Two blocks are connected by a string over a fric-
tionless, massless pulley such that one is resting on
an inclined plane and the other is hanging over the
top edge of the plane, as shown in Figure 5-21. The
hanging block has a mass of 16.0 kg, and the one on
the plane has a mass of 8.0 kg. The coefficient of
kinetic friction between the block and the inclined
plane is 0.23. The blocks are released from rest.
■Figure 5-21
a. What is the acceleration of the blocks?
FmbothaFg hanging Fplane Ff plane
so a
4.0 m/s2
b. What is the tension in the string connecting the blocks?
FTFgFa
mg ma
m(ga)
(16.0 kg)(9.80 m/s24.0 m/s2)
93 N
102. In Figure 5-22, a block of mass Mis pushed
with such a force, F, that the smaller block of
mass mdoes not slide down the front of it.
There is no friction between the larger block
and the surface below it, but the coefficient
of static friction between the two blocks is s.
Find an expression for Fin terms of M, m, s,
and g.
Smaller block:
Ff, M on m sFN, M on m mg
FN, M on m
m
s
g
ma
a
g
s
FM
m
(9.80 ms2)(16.0 kg (8.0 kg)(sin 37.0°)(0.23)(8.0 kg)(cos 37.0°))
(16.0 kg 80 kg)
g(mhanging mplanesin kmplane cos )
mhanging mplane
mhanginggmplaneg sin kmplaneg cos
mboth
mhanginggFg plane sin kFg plane cos
mboth
37.0°
Chapter 5 continued
■Figure 5-22
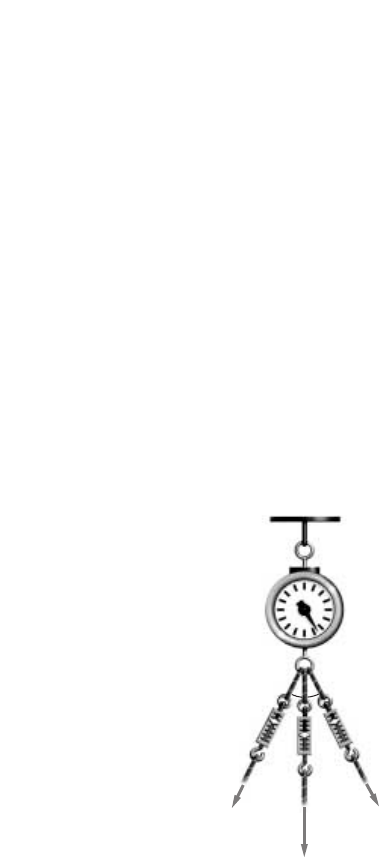
Larger block:
F– FN, m on M Ma
F
F (mM)
Mixed Review
pages 143–144
Level 1
103. The scale in Figure 5-23 is being pulled
on by three ropes. What net force does the
scale read?
■Figure 5-7
Find the y-component of the two side
ropes and then add them to the middle
rope.
FyFcos
(75.0 N)(cos 27.0°)
66.8 N
Fy, total Fy, left Fy, middle Fy, right
66.8 N 150.0 N 66.8 N
283.6 N
104. Sledding A sled with a mass of 50.0 kg is
pulled along flat, snow-covered ground.
The static friction coefficient is 0.30, and
the kinetic friction coefficient is 0.10.
a. What does the sled weigh?
Fgmg (50.0 kg)(9.80 m/s2)
4.90102N
b. What force will be needed to start the
sled moving?
FfsFN
sFg
(0.30)(4.90102N)
1.5102N
c. What force is needed to keep the sled
moving at a constant velocity?
FfsFN
sFg
(0.10)(4.90102N)
49 N, kinetic friction
d. Once moving, what total force must be
applied to the sled to accelerate it at
3.0 m/s2?
ma Fnet Fappl Ff
so Fappl ma Ff
(50.0 kg)(3.0 m/s2) 49 N
2.0102N
Level 2
105. Mythology Sisyphus was a character in
Greek mythology who was doomed in
Hades to push a boulder to the top of a
steep mountain. When he reached the top,
the boulder would slide back down the
mountain and he would have to start all
over again. Assume that Sisyphus slides the
boulder up the mountain without being
able to roll it, even though in most ver-
sions of the myth, he rolled it.
a. If the coefficient of kinetic friction
between the boulder and the mountain-
side is 0.40, the mass of the boulder is
20.0 kg, and the slope of the mountain
is a constant 30.0°, what is the force
that Sisyphus must exert on the boulder
to move it up the mountain at a con-
stant velocity?
FS on rock Fgto slope Ff
FS on rock mg sin
kmg cos ma 0
FS on rock mg sin kmg cos
150.0 N
75.0 N 75.0 N
27.0°27.0°
g
s
Mg
s
mg
s
108 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 109
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
mg(sin k cos )
(20.0 kg)(9.80 m/s2)
(sin 30.0°(0.40)(cos 30.0°))
166 N
b. If Sisyphus pushes the boulder at a velocity of 0.25 m/s and it takes him
8.0 h to reach the top of the mountain, what is the mythical mountain’s
vertical height?
hdsin
vt sin
(0.25 m/s)(8.0 h)(3600 s/h)(sin 30.0°)
3.6103m 3.6 km
Level 3
106. Landscaping A tree is being transported on a flatbed
trailer by a landscaper, as shown in Figure 5-24. If the
base of the tree slides on the tree will the trailer, fall over
and be damaged. If the coefficient of static friction
between the tree and the trailer is 0.50, what is the
minimum stopping distance of the truck, traveling
at 55 km/h, if it is to accelerate uniformly and not
have the tree slide forward and fall on the trailer?
Ftruck FfsFNsmg ma
a
m
smg
sg
(0.50)(9.80 m/s2)
4.9 m/s2
vf2vi22adwith vf0,
so d
v
2i
a
2
24 m
(55 km/h)
10
10
k
0
m
m
36
1
00
hs
2
(2)(4.9 ms2)
Chapter 5 continued
■Figure 5-24
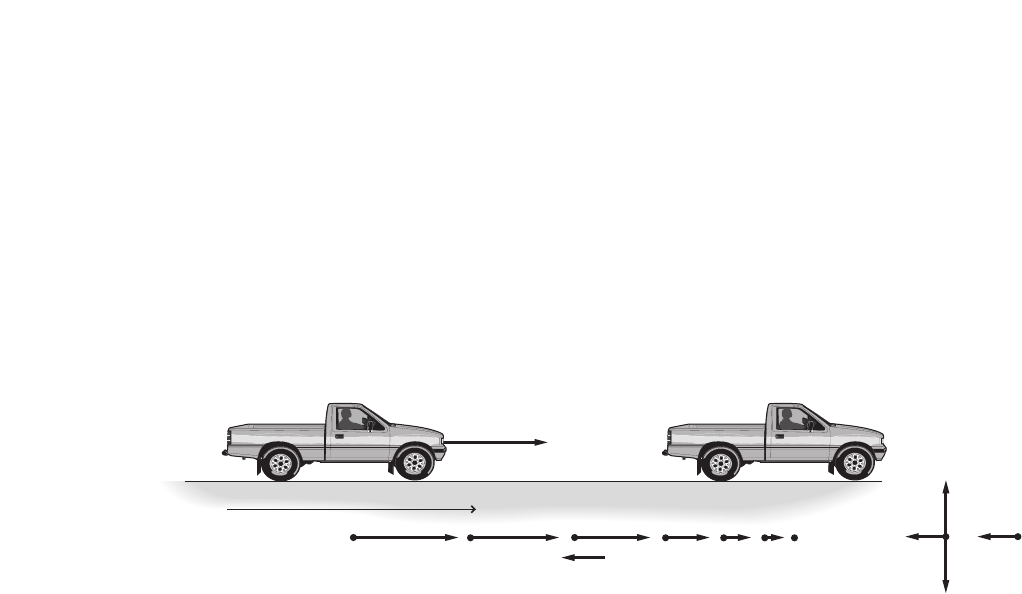
Thinking Critically
page 144
107. Use Models Using the Example Problems in this chapter as models, write an
example problem to solve the following problem. Include the following
sections: Analyze and Sketch the Problem, Solve for the Unknown (with a
complete strategy), and Evaluate the Answer. A driver of a 975-kg car traveling
25 m/s puts on the brakes. What is the shortest distance it will take for the car
to stop? Assume that the road is concrete, the force of friction of the road on the
tires is constant, and the tires do not slip.
Analyze and Sketch the Problem
•Choose a coordinate system with a positive axis in the direction
of motion.
•Draw a motion diagram.
•Label vand a.
•Draw the free-body diagram.
Known: Unknown:
di0df?
vi25 m/s
vf0
m975 kg
s0.80
Solve for the Unknown
Solve Newton’s second law for a.
Fnet ma
Ff ma Substitute Ff Fnet
FN ma Substitute Ff FN
mg ma Substitute FN mg
a g
Use the expression for acceleration to solve for distance.
vf2 vi2 2a(df di)
df di
vf2
2
a
vi2
di
(
v
2
f)
2
(
v
g
i2
)
Substitute a g
a
di
25 m/s
FN
Fg
Ff
df
+x
vFnet
110 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 111
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
0.0 m Substitute di 0.0 m, vf 0.0 m/s,
vi 25 m/s, 0.65, g 9.80 m/s2
49 m
108. Analyze and Conclude Margaret Mary, Doug, and Kako are at a local
amusement park and see an attraction called the Giant Slide, which is simply a
very long and high inclined plane. Visitors at the amusement park climb a long
flight of steps to the top of the 27° inclined plane and are given canvas sacks.
They sit on the sacks and slide down the 70-m-long plane. At the time when the
three friends walk past the slide, a 135-kg man and a 20-kg boy are each at the top
preparing to slide down. “I wonder how much less time it will take the man to
slide down than it will take the boy,” says Margaret Mary. “I think the boy will
take less time,” says Doug. “You’re both wrong,” says Kako. “They will reach the
bottom at the same time.”
a. Perform the appropriate analysis to determine who is correct.
Fnet FgFf
Fgsin kFN
mg sin kmg cos ma
ag(sin kcos ), so the acceleration is independent of the
mass. They will tie, so Kako is correct.
b. If the man and the boy do not take the same amount of time to reach the
of the slide, calculate how many seconds of difference there will be between
the two times.
They will reach the bottom at the same time.
Writing in Physics
page 144
109. Investigate some of the techniques used in industry to reduce the friction
between various parts of machines. Describe two or three of these techniques
and explain the physics of how they work.
Answers will vary and may include lubricants and reduction of the
normal force to reduce the force of friction.
110. Olympics In recent years, many Olympic athletes, such as sprinters, swimmers,
skiers, and speed skaters, have used modified equipment to reduce the effects of
friction and air or water drag. Research a piece of equipment used by one of
these types of athletes and the way it has changed over the years. Explain how
physics has impacted these changes.
Answers will vary.
(0.0 m/s)2(25 m/s)2
(2)(0.65)(9.80 m/s)2
Chapter 5 continued

Cumulative Review
page 144
111. Add or subtract as indicated and state the
answer with the correct number of signifi-
cant digits. (Chapter 1)
a. 85.26 g 4.7 g
90.0 g
b. 1.07 km 0.608 km
1.68 km
c. 186.4 kg 57.83 kg
128.6 kg
d. 60.08 s 12.2 s
47.9 s
112. You ride your bike for 1.5 h at an average
velocity of 10 km/h, then for 30 min at
15 km/h. What is your average velocity?
(Chapter 3)
Average velocity is the total displace-
ment divided by the total time.
v
d
tf
f
d
ti
i
diti0, so
v
10 km/h
113. A 45-N force is exerted in the upward
direction on a 2.0-kg briefcase. What is the
acceleration of the briefcase? (Chapter 4)
Fnet Fapplied FgFapplied mg
ma
so a
13 m/s2
Challenge Problem
page 132
Find the equilibrant for the following forces.
F161.0 N at 17.0° north of east
F238.0 N at 64.0° north of east
F354.0 N at 8.0° west of north
F493.0 N at 53.0° west of north
F565.0 N at 21.0° south of west
F6102.0 N at 15.0° west of south
F726.0 N south
F877.0 N at 22.0° east of south
F951.0 N at 33.0° east of south
F10 82.0 N at 5.0° south of east
F1x(61.0 N)(cos 17.0°) 58.3 N
F1y(61.0 N)(sin 17.0°) 17.8 N
F2x(38.0 N)(cos 64.0°) 16.7 N
F2y(38.0 N)(sin 64.0°) 34.2 N
F3x(54.0 N)(sin 8.0°) 7.52 N
F3y(54.0 N)(cos 8.0°) 53.5 N
F4x(93.0 N)(sin 53.0°) 74.3 N
F4y(93.0 N)(cos 53.0°) 56.0 N
F5x(65.0 N)(cos 21.0°) 60.7 N
F5y(65.0 N)(sin 21.0°) 23.3 N
F6x(102 N)(sin 15.0°) 26.4 N
F6y(102 N)(cos 15.0°) 98.5 N
x
y
1
2
3
4
5
6
7
8
9
10
45 N (2.0 kg)(9.80 ms2)
2.0 kg
Fapplied mg
m
(10 kmh)(1.5 h) (15 kmh)(0.5 h)
1.5 h 0.5 h
v1t1v2t2
t1t2
v1t1v2t2di
t1t2ti
112 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 113
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
F7x0.0 N
F7y26.0 N
F8x(77.0 N)(sin 22.0°) 28.8 N
F8y(77.0 N)(cos 22.0°) 71.4 N
F9x(51.0 N)(sin 33.0°) 27.8 N
F9y(51.0 N)(cos 33.0°) 42.8 N
F10x(82.0 N)(cos 5.0°) 81.7 N
F10y(82.0 N)(sin 5.0°) 7.15 N
Fx
10
i 1
Fix
44.38 N
Fy
10
i 1
Fiy
107.65 N
FR(Fx)2
(Fy)2
(44.38
N)2
(10
7.65 N
)2
116 N
Rtan1
tan1
67.6°
Fequilibrant 116 N at 112.4°
116 N at 22.4°W of N
107.65 N
44.38 N
Fy
Fx
Chapter 5 continued


Physics: Principles and Problems Solutions Manual 115
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
6Motion in Two Dimensions
CHAPTER
Practice Problems
6.1 Projectile Motion
pages 147–152
page 150
1. A stone is thrown horizontally at a speed
of 5.0 m/s from the top of a cliff that is
78.4 m high.
a. How long does it take the stone to reach
the bottom of the cliff?
Since vy0, yvyt
1
2
gt2
becomes y
1
2
gt2
or t
2
g
y
(
9
2
.
)
8
(
0
7
m
8
/
.
s
4
2m)
4.00 s
b. How far from the base of the cliff does
the stone hit the ground?
xvxt
(5.0 m/s)(4.00 s)
2.0101m
c. What are the horizontal and vertical
components of the stone’s velocity just
before it hits the ground?
vx5.0 m/s. This is the same as the
initial horizontal speed because the
acceleration of gravity influences
only the vertical motion. For the
vertical component, use vvigt
with vvyand vi, the initial vertical
component of velocity, zero.
At t4.00 s
vygt
(9.80 m/s2)(4.0 s)
39.2 m/s
2. Lucy and her friend are working at an
assembly plant making wooden toy
giraffes. At the end of the line, the giraffes
go horizontally off the edge of the conveyor
belt and fall into a box below. If the box is
0.6 m below the level of the conveyor belt
and 0.4 m away from it, what must be the
horizontal velocity of giraffes as they leave
the conveyor belt?
xvxtvx
g
2y
so vxx
g
2y
1 m/s
3. You are visiting a friend from elementary
school who now lives in a small town. One
local amusement is the ice-cream parlor,
where Stan, the short-order cook, slides his
completed ice-cream sundaes down the
counter at a constant speed of 2.0 m/s to
the servers. (The counter is kept very well
polished for this purpose.) If the servers
catch the sundaes 7.0 cm from the edge of
the counter, how far do they fall from the
edge of the counter to the point at which
the servers catch them?
xvxt;
t
v
x
x
y gt2
g
v
x
x
2
(9.80 m/s2)
0
2..0
07m
0/
m
s
2
0.0060 m or 0.60 cm
1
2
1
2
1
2
0.4 m
(
9
2
.8
)(
0
m
0.
/
6
s2
m)
page 152
4. A player kicks a football from ground
level with an initial velocity of 27.0 m/s,
30.0° above the horizontal, as shown
in Figure 6-4. Find each of the
following. Assume that air
resistance is negligible.
a. the ball’s hang time
vyvisin
When it lands, yvytgt20.
Therefore,
t2
2v
gyt
t
2
g
vy
2vis
g
in
2.76 s
b. the ball’s maximum height
Maximum height occurs at half the “hang time,” or 1.38 s. Thus,
yvyt
1
2
gt2
vi sin tgt2
(27.0 m/s)(sin 30.0°)(1.38 s) (9.80 m/s2)(1.38 s)2
9.30 m
c. the ball’s range
Distance:
vxvicos
xvxt(vicos )(t)(27.0 m/s)(cos 30.0°)(2.76 s) 64.5 m
5. The player in problem 4 then kicks the ball with the same speed, but at 60.0°
from the horizontal. What is the ball’s hang time, range, and maximum height?
Following the method of Practice Problem 4,
Hangtime:
t
2vis
g
in
4.77 s
(2)(27.0 m/s)(sin 60.0°)
9.80 m/s2
1
2
1
2
(2)(27.0 m/s)(sin 30.0°)
9.80 m/s2
1
2
116 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued
■Figure 6-4
Trajectory
25
060
y (m)
60.0°
30.0°
x (m)

Physics: Principles and Problems Solutions Manual 117
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Distance:
xvi cos t
(27.0 m/s)(cos 60.0°)(4.77 s)
64.4 m
Maximum height:
at t
1
2
(4.77 s) 2.38 s
yvi sin t
1
2
gt2
(27.0 m/s)(sin 60.0°)(2.38 s)
1
2
(9.80 m/s2)(2.38 s)2
27.9 m
6. A rock is thrown from a 50.0-m-high cliff with an initial velocity of 7.0 m/s at an
angle of 53.0° above the horizontal. Find the velocity vector for when it hits the
ground below.
vxvi cos
vyvi sin gt
vi sin g
vi sin 2yg
vvx2
vy2
(vi co
s )2
(vi sin
2yg
)2
((7.0 m/s
) cos 53
.0°)2(
7.0 m/s)
(sin 53.0
°) (2
)(50
.0 m
)(
9.80 m
/s2)
2
37 m/s
tan1
tan1
tan1
83° from horizontal
Section Review
6.1 Projectile Motion
pages 147–152
page 152
7. Projectile Motion Two baseballs are pitched horizontally from the same height,
but at different speeds. The faster ball crosses home plate within the strike zone,
but the slower ball is below the batter’s knees. Why does the faster ball not fall as
far as the slower one?
(7.0 m/s)(sin 53.0°) (2)(50
.0 m)(
9.80 m
/s2)
(7.0 m/s)(cos 53.0°)
vi sin i2yg
vi cos i
vy
vx
2y
g
Chapter 6 continued

The faster ball is in the air a shorter time, and thus gains a smaller
vertical velocity.
8. Free-Body Diagram An ice cube slides without friction across a table at a
constant velocity. It slides off the table and lands on the floor. Draw free-body
and motion diagrams of the ice cube at two points on the table and at two
points in the air.
9. Projectile Motion A softball is tossed into the air at an angle of 50.0° with the
vertical at an initial velocity of 11.0 m/s. What is its maximum height?
vf2viy22a(dfdi); ag,di0
At maximum height vf0, so
df
v
2
iy
g
2
(vic
2
o
g
s)2
2.55 m
10. Projectile Motion A tennis ball is thrown out a window 28 m above the ground
at an initial velocity of 15.0 m/s and 20.0° below the horizontal. How far does
the ball move horizontally before it hits the ground?
xv0xt, but need to find t
First, determine vyf:
vyf2vyi22gy
vyfvyi2
2gy
(vi sin
)2
2gy
((15.0
m/s)(
sin 20
.0°))2
(2)(
9.80 m
/s2)(28
m)
24.0 m/s
Now use vyfvyigt to find t.
t
vyf
g
vyi
vyf
g
visin
((11.0 m/s)(cos 50.0°))2
(2)(9.80 m/s2)
FN
Fg
FN
FgFg
Fg
On the table In the air On the table
a 0
In the air
Free-Body Diagrams Motion Diagrams
a
118 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 119
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1.92 s
xvxit
(vi cos )(t)
(15.0 m/s)(cos 20.0°)(1.92 s)
27.1 m
11. Critical Thinking Suppose that an object is thrown with the same initial
velocity and direction on Earth and on the Moon, where gis one-sixth that on
Earth. How will the following quantities change?
a. vx
will not change
b. the object’s time of flight
will be larger; t
c. ymax
will be larger
d. R
will be larger
Practice Problems
6.2 Circular Motion
pages 153–156
page 156
12. A runner moving at a speed of 8.8 m/s rounds a bend with a radius of 25 m.
What is the centripetal acceleration of the runner, and what agent exerts force on
the runner?
ac
v
r
2
(8.2
85
m
m
/s)2
3.1 m/s2, the frictional force of the track acting on
the runner’s shoes exerts the force on the runner.
13. A car racing on a flat track travels at 22 m/s around a curve with a 56-m radius.
Find the car’s centripetal acceleration. What minimum coefficient of static friction
between the tires and road is necessary for the car to round the curve without
slipping?
ac
v
r
2
(22
56
m
m
/s)2
8.6 m/s2
Recall FfFN. The friction force must supply the centripetal force so
Ffmac. The normal force is FNmg. The coefficient of friction must
be at least
F
F
N
f
m
m
a
g
c
a
g
c
0.88
8.6 m/s2
9.80 m/s2
2vy
g
2.40 m/s (15.0 m/s)(sin 20.0°)
9.80 m/s2
Chapter 6 continued

14. An airplane traveling at 201 m/s makes a
turn. What is the smallest radius of the
circular path (in km) that the pilot can
make and keep the centripetal acceleration
under 5.0 m/s2?
ac
v
r
2
, so r
v
ac
2
(2
5
0
.0
1
m
m
/
/
s
s2
)2
8.1 km
15. A 45-kg merry-go-round worker stands on
the ride’s platform 6.3 m from the center.
If her speed as she goes around the circle
is 4.1 m/s, what is the force of friction
necessary to keep her from falling off the
platform?
FfFc
mr
v2
120 N
Section Review
6.2 Circular Motion
pages 153–156
page 156
16. Uniform Circular Motion What is the
direction of the force that acts on the
clothes in the spin cycle of a washing
machine? What exerts the force?
The force is toward the center of the tub.
The walls of the tub exert the force on
the clothes. Of course, the whole point is
that some of the water in the clothes
goes out through holes in the wall of the
tub rather than moving toward the center.
17. Free-Body Diagram You are sitting in the
backseat of a car going around a curve to the
right. Sketch motion and free-body diagrams
to answer the following questions.
a. What is the direction of your
acceleration?
Your body is accelerated to the
right.
b. What is the direction of the net force
that is acting on you?
The net force acting on your body is
to the right
c. What exerts this force?
The force is exerted by the car’s
seat.
18. Centripetal Force If a 40.0-g stone is
whirled horizontally on the end of a
0.60-m string at a speed of 2.2 m/s, what is
the tension in the string?
FTmac
mr
v2
0.32 N
19. Centripetal Acceleration A newspaper
article states that when turning a corner,
a driver must be careful to balance the
centripetal and centrifugal forces to keep
from skidding. Write a letter to the editor
that critiques this article.
The letter should state that there is an
acceleration because the direction of
the velocity is changing; therefore,
there must be a net force in the direc-
tion of the center of the circle. The road
supplies that force and the friction
between the road and the tires allows
the force to be exerted on the tires. The
car’s seat exerts the force on the driver
that accelerates him or her toward the
center of the circle. The note also
should make it clear that centrifugal
force is not a real force.
20. Centripetal Force A bowling ball has a
mass of 7.3 kg. If you move it around a
circle with a radius of 0.75 m at a speed
of 2.5 m/s, what force would you have to
exert on it?
Fnet mac
mv2
r
(0.0400 kg)(22 m/s)2
0.60 m
a
Fnet
v
(45 kg)(4.1 m/s)2
6.3 m
120 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 121
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
61 N
21. Critical Thinking Because of Earth’s daily
rotation, you always move with uniform
circular motion. What is the agent that
supplies the force that accelerates you?
How does this motion affect your apparent
weight?
Earth’s gravity supplies the force that
accelerates you in circular motion.Your
uniform circular motion decreases your
apparent weight.
Practice Problems
6.3 Relative Velocity
pages 157–159
page 159
22. You are riding in a bus moving slowly
through heavy traffic at 2.0 m/s. You hurry
to the front of the bus at 4.0 m/s relative to
the bus. What is your speed relative to the
street?
vy/g vb/g vy/b
2.0 m/s 4.0 m/s
6.0 m/s relative to street
23. Rafi is pulling a toy wagon through the
neighborhood at a speed of 0.75 m/s.
A caterpillar in the wagon is crawling
toward the rear of the wagon at a rate of
2.0 cm/s. What is the caterpillar’s velocity
relative to the ground?
vc/g vw/g vc/w
0.75 m/s 0.02 m/s
0.73 m/s
24. A boat is rowed directly upriver at a speed
of 2.5 m/s relative to the water. Viewers on
the shore see that the boat is moving at
only 0.5 m/s relative to the shore. What is
the speed of the river? Is it moving with or
against the boat?
vb/g vb/w vw/g;
so, vw/g vb/g vb/w
0.5 m/s 2.5 m/s
2.0 m/s; against the boat
25. An airplane flies due north at 150 km/h relative
to the air. There is a wind blowing at 75 km/h
to the east relative to the ground. What is the
plane’s speed relative to the ground?
vvp2
vw2
(150 k
m/h)2
(75
km/h
)2
1.7102 km/h
Section Review
6.3 Relative Velocity
pages 157–159
page 159
26. Relative Velocity A fishing boat with a
maximum speed of 3 m/s relative to the
water is in a river that is flowing at 2 m/s.
What is the maximum speed the boat can
obtain relative to the shore? The minimum
speed? Give the direction of the boat, rela-
tive to the river’s current, for the maximum
speed and the minimum speed relative to
the shore.
The maximum speed relative to the
shore is when the boat moves at maxi-
mum speed in the same direction as
the river’s flow:
vb/s vb/w vw/s
3 m/s 2 m/s
5 m/s
The minimum speed relative to the
shore is when the boat moves in the
opposite direction of the river’s flow
with the same speed as the river:
vb/s vb/w vw/s
3 m/s (2 m/s)
1 m/s
(7.3 kg)(2.5 m/s)2
0.75 m
Chapter 6 continued

27. Relative Velocity of a Boat A powerboat heads due northwest at 13 m/s relative
to the water across a river that flows due north at 5.0 m/s. What is the velocity
(both magnitude and direction) of the motorboat relative to the shore?
vRvRN2
vRW2
(vbN
vrN)2
(vbW
vrW
)2
(vb sin
v
r)2(
vb cos
)2
((13 m
/s)(sin
45°)
5.0 m
/s)2
((13 m
/s)(co
s 45°)
)2
17 m/s
tan1
v
vR
R
W
N
tan1
tan1
33°
vR17 m/s, 33° west of north
28. Relative Velocity An airplane flies due south at 175 km/h relative to the air.
There is a wind blowing at 85 km/h to the east relative to the ground. What are
the plane’s speed and direction relative to the ground?
vR(175 k
m/h)2
(85
km/h
)2
190 km/h
tan1
64°
vR190 km/h, 64° south of east
29. A Plane’s Relative Velocity An airplane flies due north at 235 km/h relative to
the air. There is a wind blowing at 65 km/h to the northeast relative to the
ground. What are the plane’s speed and direction relative to the ground?
vRvRE2
vRN2
(vpE
vaE)2
(vp
Nvw
N)2
(vw co
s )2
(vp
vw si
n )2
((65 k
m/h)(c
os 45
°))2
(235
km/h
(65
km/h
)(sin 4
5°))2
280 km/h
tan1
v
vR
R
N
E
tan1
tan1
72° north of east
280 km/h, 72° north of east
235 km/h (65 km/h)(sin 45°)
(65 km/h)(cos 45°)
vpvasin
vacos
175 km/h
85 km/h
(13 m/s)(cos 45°)
(3 m/s)(sin 45°) 5.0 m/s
vbcos
vbsin vr
122 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 123
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
30. Relative Velocity An airplane has a speed of 285 km/h relative to the air. There
is a wind blowing at 95 km/h at 30.0° north of east relative to Earth. In which
direction should the plane head to land at an airport due north of its present
location? What is the plane’s speed relative to the ground?
To travel north, the east components must be equal and opposite.
cos p,so
pcos1
cos1
cos1
73° north of west
vpR vpN vwN
vp sin pvw sin w
(285 km/h)(sin 107°) (95 km/h)(sin 30.0°)
320 km/h
31. Critical Thinking You are piloting a boat across a fast-moving river. You want to
reach a pier directly opposite your starting point. Describe how you would navigate
the boat in terms of the components of your velocity relative to the water.
You should choose the component of your velocity along the direction of
the river to be equal and opposite to the velocity of the river.
Chapter Assessment
Concept Mapping
page 164
32. Use the following terms to complete the concept map below: constant speed,
horizontal part of projectile motion, constant acceleration, relative-velocity motion,
uniform circular motion.
(95 km/h)(cos 30.0°)
285 km/h
vwE cos w
vpR
vpW
vpR
vpW
vpR
Chapter 6 continued
Categories of Motion
constant
velocity constant
speed
constant
acceleration
vertical part
of projectile
motion
relative-velocity
motion
horizontal
part of projectile
motion
uniform circular
motion

Mastering Concepts
page 164
33. Consider the trajectory of the cannonball shown in Figure 6-11. (6.1)
■Figure 6-11
Up is positive, down is negative.
a. Where is the magnitude of the vertical-velocity component largest?
The greatest vertical velocity occurs at point A.
b. Where is the magnitude of the horizontal-velocity component largest?
Neglecting air resistance, the horizontal velocity at all points is the
same. Horizontal velocity is constant and independent of vertical
velocity.
c. Where is the vertical-velocity smallest?
The least vertical velocity occurs at point E.
d. Where is the magnitude of the acceleration smallest?
The magnitude of the acceleration is the same everywhere.
34. A student is playing with a radio-controlled race car on the balcony of a sixth-
floor apartment. An accidental turn sends the car through the railing and over
the edge of the balcony. Does the time it takes the car to fall depend upon the
speed it had when it left the balcony? (6.1)
No, the horizontal component of motion does not affect the vertical
component.
35. An airplane pilot flying at constant velocity and altitude drops a heavy crate.
Ignoring air resistance, where will the plane be relative to the crate when the
crate hits the ground? Draw the path of the crate as seen by an observer on the
ground. (6.1)
The plane will be directly over the crate when the crate hits the ground.
Both have the same horizontal velocity. The crate will look like it is
moving horizontally while falling vertically to an observer on the ground.
36. Can you go around a curve with the following accelerations? Explain.
a. zero acceleration
No, going around a curve causes a change in direction of velocity.
Thus, the acceleration cannot be zero.
b. constant acceleration (6.2)
No, the magnitude of the acceleration may be constant, but the
direction of the acceleration changes.
ABCD
E
124 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 125
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
37. To obtain uniform circular motion, how
must the net force depend on the speed
of the moving object? (6.2)
Circular motion results when the
direction of the force is constantly
perpendicular to the instantaneous
velocity of the object.
38. If you whirl a yo-yo about your head in a
horizontal circle, in what direction must a
force act on the yo-yo? What exerts the
force? (6.2)
The force is along the string toward the
center of the circle that the yo-yo fol-
lows.The string exerts the force.
39. Why is it that a car traveling in the opposite
direction as the car in which you are riding
on the freeway often looks like it is moving
faster than the speed limit? (6.3)
The magnitude of the relative velocity
of that car to your car can be found by
adding the magnitudes of the two cars’
velocities together. Since each car
probably is moving at close to the
speed limit, the resulting relative veloci-
ty will be larger than the posted speed
limit.
Applying Concepts
pages 164–165
40. Projectile Motion Analyze how horizontal
motion can be uniform while vertical
motion is accelerated. How will projectile
motion be affected when drag due to air
resistance is taken into consideration?
The horizontal motion is uniform
because there are no forces acting in
that direction (ignoring friction). The
vertical motion is accelerated due to
the force of gravity. The projectile
motion equations in this book do not
hold when friction is taken into
account. Projectile motion in both
directions will be impacted when
drag due to air resistance is taken
into consideration. There will be a
friction force opposing the motion.
41. Baseball A batter hits a pop-up straight
up over home plate at an initial velocity
of 20 m/s. The ball is caught by the catcher
at the same height that it was hit. At what
velocity does the ball land in the catcher’s
mitt? Neglect air resistance.
20 m/s, where the negative sign
indicates down
42. Fastball In baseball, a fastball takes about
1
2
s to reach the plate. Assuming that such a
pitch is thrown horizontally, compare the
distance the ball falls in the first
1
4
s with
the distance it falls in the second
1
4
s.
Because of the acceleration due to grav-
ity, the baseball falls a greater distance
during the second
1
4
s than during the
first
1
4
s.
43. You throw a rock horizontally. In a second
horizontal throw, you throw the rock harder
and give it even more speed.
a. How will the time it takes the rock to
hit the ground be affected? Ignore air
resistance.
The time does not change—the time it
takes to hit the ground depends only
on vertical velocities and accelera-
tion.
b. How will the increased speed affect the
distance from where the rock left your
hand to where the rock hits the ground?
A higher horizontal speed produces
a longer horizontal distance.
44. Field Biology A zoologist standing on a
cliff aims a tranquilizer gun at a monkey
hanging from a distant tree branch. The
barrel of the gun is horizontal. Just as the
zoologist pulls the trigger, the monkey lets
go and begins to fall. Will the dart hit the
monkey? Ignore air resistance.
Yes, in fact, the monkey would be safe if
it did not let go of the branch.The verti-
cal acceleration of the dart is the same
as that of the monkey. Therefore, the
dart is at the same vertical height when
Chapter 6 continued

it reaches the monkey.
45. Football A quarterback throws a football
at 24 m/s at a 45° angle. If it takes the ball
3.0 s to reach the top of its path and the
ball is caught at the same height at which it
is thrown, how long is it in the air? Ignore
air resistance.
6.0 s: 3.0 s up and 3.0 s down
46. Track and Field You are working on
improving your performance in the long
jump and believe that the information in
this chapter can help. Does the height that
you reach make any difference to your jump?
What influences the length of your jump?
Both speed and angle of launch matter,
so height does make a difference.
Maximum range is achieved when the
resultant velocity has equal vertical and
horizontal components—in other words,
a launch angle of 45°. For this reason,
height and speed affect the range.
47. Imagine that you are sitting in a car tossing
a ball straight up into the air.
a. If the car is moving at a constant velocity,
will the ball land in front of, behind, or
in your hand?
The ball will land in your hand
because you, the ball, and the car
all are moving forward with the
same speed.
b. If the car rounds a curve at a constant
speed, where will the ball land?
The ball will land beside you, toward
the outside of the curve. A top view
would show the ball moving straight
while you and the car moved out
from under the ball.
48. You swing one yo-yo around your head in a
horizontal circle. Then you swing another
yo-yo with twice the mass of the first one,
but you don’t change the length of the
string or the period. How do the tensions in
the strings differ?
The tension in the string is doubled
since FTmac.
126 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued
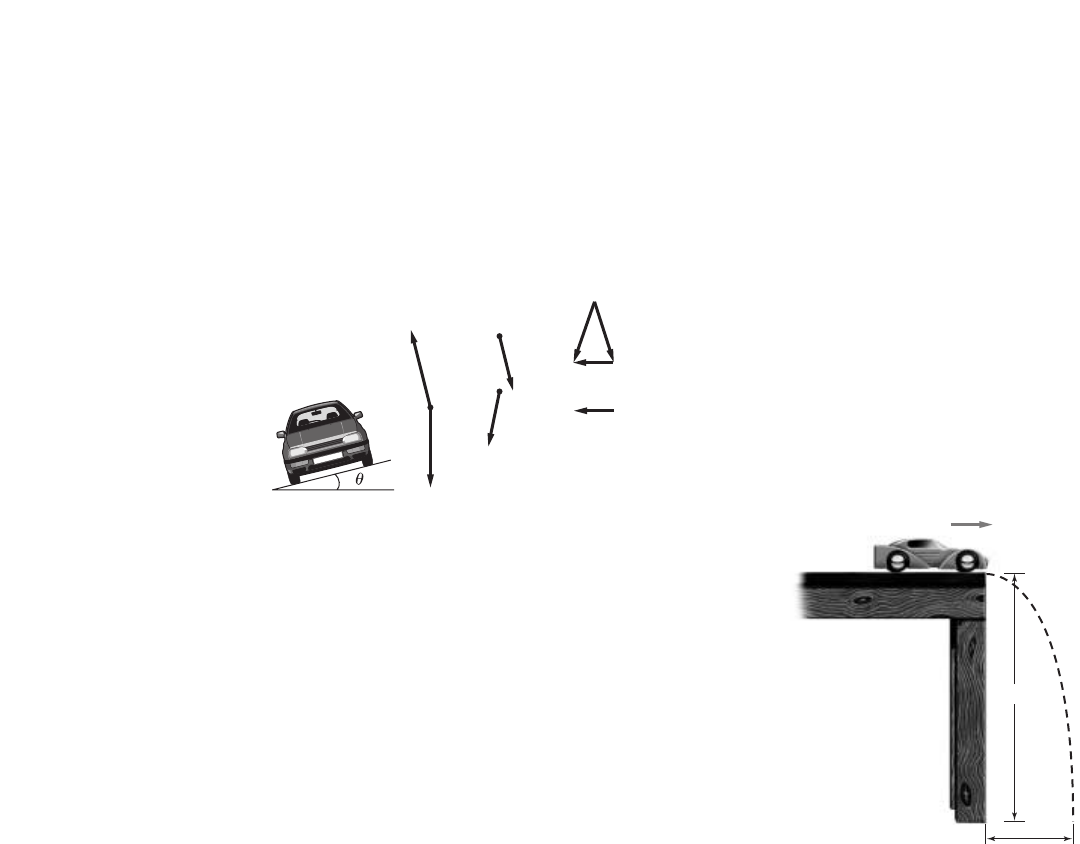
Physics: Principles and Problems Solutions Manual 127
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
49. Car Racing The curves on a race track are
banked to make it easier for cars to go
around the curves at high speeds. Draw a
free-body diagram of a car on a banked
curve. From the motion diagram, find the
direction of the acceleration.
The acceleration is directed toward the
center of the track.
a. What exerts the force in the direction of
the acceleration?
The component of the normal force
acting toward the center of the
curve, and depending on the car’s
speed, the component of the friction
force acting toward the center, both
contribute to the net force in the
direction of acceleration.
b. Can you have such a force without
friction?
Yes, the centripetal acceleration need
only be due to the normal force.
50. Driving on the Highway Explain why it is
that when you pass a car going in the same
direction as you on the freeway, it takes a
longer time than when you pass a car going
in the opposite direction.
The relative speed of two cars going in
the same direction is less than the rela-
tive speed of two cars going in the
opposite direction. Passing with the
lesser relative speed will take longer.
Mastering Problems
6.1 Projectile Motion
page 165
Level 1
51. You accidentally throw your car keys
horizontally at 8.0 m/s from a cliff 64-m
high. How far from the base of the cliff
should you look for the keys?
yvytgt2
Since initial vertical velocity is zero,
t
(
92
.8
)(
0
m
64
/sm
2
)
3.6 s
xvxt(8.0 m/s)(3.6) 28.8 m
29 m
52. The toy car in Figure 6-12 runs off the edge
of a table that is 1.225-m high. The car
lands 0.400 m from the base of the table.
■Figure 6-12
a. How long did it take the car to fall?
yvy0tgt2
Since initial vertical velocity is zero,
t
0.500 s
b. How fast was the car going on the table?
vx
0
0
..
4
5
0
0
0
0m
s
0.800 m/s
53. A dart player throws a dart horizontally at
12.4 m/s. The dart hits the board 0.32 m
below the height from which it was thrown.
How far away is the player from the board?
yvy0tgt2
and because initial velocity is zero,
t
2y
g
1
2
x
t
(2)(1.225 m)
9.80 m/s2
2y
g
1
2
v
1.225 m
0.400 m
2y
g
1
2
FN
Fg
v1
v1
v2
v2
v
a
Front View Top View
Chapter 6 continued
0.26 s
Now xvxt
(12.4 m/s)(0.26 s)
3.2 m
54. The two baseballs in Figure 6-13 were hit
with the same speed, 25 m/s. Draw separate
graphs of yversus tand xversus tfor each
ball.
■Figure 6-13
55. Swimming You took a running leap off a
high-diving platform. You were running at
2.8 m/s and hit the water 2.6 s later. How
high was the platform, and how far from
the edge of the platform did you hit the
water? Ignore air resistance.
yvyitgt2
0(2.6 s) (9.80 m/s2)(2.6 s)2
33 m, so the platform is 33 m high
xvxt(2.8 m/s)(2.6 s) 7.3 m
Level 2
56. Archery An arrow is shot at 30.0° above
the horizontal. Its velocity is 49 m/s, and it
hits the target.
a. What is the maximum height the arrow
will attain?
vy2vyi22gd
At the high point vy0, so
d
31 m
b. The target is at the height from which
the arrow was shot. How far away is it?
yvy0tgt2
but the arrow lands at the same
height, so
y0 and 0 vyigt
so t0 or
t
2v
g
yi
2vis
g
in
5.0 s
(2)(49 m/s)(sin 30.0°)
9.80 m/s2
1
2
1
2
((49 m/s)(sin 30.0°))2
(2)(9.80 m/s2)
(vi sin )2
2g
(vy0)2
2g
1
2
1
2
002143
Horizontal v. Time
5
20
60
40
60
80
002143
Vertical v. Time
5
10
5
60
30
30
15
20
25
Vertical (m)
Horizontal (m)
Time (s)
Time (s)
A
B
60°
30°
yA
xA xB
yB
(2)(0.32 m)
9.80 m/s2
Chapter 6 continued
128 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 129
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
and xvxt
(vi cos )(t)
(49 m/s)(cos 30.0°)(5.0 s)
2.1102m
57. Hitting a Home Run A pitched ball is hit
by a batter at a 45° angle and just clears the
outfield fence, 98 m away. If the fence is at
the same height as the pitch, find the velocity
of the ball when it left the bat. Ignore air
resistance.
The components of the initial velocity
are vxvicos iand vyivisin i
Now xvxt(vicos i)t,so
t
vico
xsi
And yvyitgt2,but y0, so
0vyigtt
so t0 or vyigt 0
From above
visin ig
vico
xsi
0
Multiplying by vicos igives
vi2sin icos igx 0
so vi2
thus, vi
31 m/s at 45°
Level 3
58. At-Sea Rescue An airplane traveling 1001 m
above the ocean at 125 km/h is going to
drop a box of supplies to shipwrecked
victims below.
a. How many seconds before the plane is
directly overhead should the box be
dropped?
yvyitgt2
but vyi0, so
t
14.3 s
b. What is the horizontal distance between
the plane and the victims when the box
is dropped?
xvxt
(125 km/h)
(14.3 s)
497 m
59. Diving Divers in Acapulco dive from a cliff
that is 61 m high. If the rocks below the
cliff extend outward for 23 m, what is the
minimum horizontal velocity a diver must
have to clear the rocks?
yvyitgt2
and since vyi0,
t
(
92
.8
)(
0
m
61
/sm
2
)
3.53 s
xvxt
vx
x
t
6.5 m/s
60. Jump Shot A basketball player is trying to
make a half-court jump shot and releases the
ball at the height of the basket. Assuming
that the ball is launched at 51.0°, 14.0 m
from the basket, what speed must the player
give the ball?
The components of the initial velocity
are vxivicos iand vyivisin i
Now xvxit(vicos i)t,so
23 m
3.53 s
2y
g
1
2
1000 m
1 km
1 h
3600 s
(2)(1001 m)
9.80 m/s2
2y
g
1
2
(9.80 m/s2)(98 m)
(2)(sin 45°)(cos 45°)
gx
(2)(sin i)(cos i)
gx
(2)(sin i)(cos i)
1
2
1
2
1
2
1
2
1
2
Chapter 6 continued

t
vico
xsi
And yvyitgt2,but y0, so
0vyigtt
so t0 or vyigt20
From above
v0sin ig
vico
xsi
0
Multiplying by vicos igives
vi2(sin i)(cos i) gx 0
so vi
11.8 m/s
6.2 Circular Motion
page 166
Level 1
61. Car Racing A 615-kg racing car completes
one lap in 14.3 s around a circular track
with a radius of 50.0 m. The car moves at a
constant speed.
a. What is the acceleration of the car?
ac
9.59 m/s2
b. What force must the track exert on the
tires to produce this acceleration?
Fcmac(615 kg)(9.59 m/s2)
5.90103N
42(50.0 m)
(14.3 s)2
42r
T2
v2
r
(9.80 m/s2)(14.0 m)
(2)(sin 51.0°)(cos 51.0°)
gx
(2)(sin i)(cos i)
1
2
1
2
1
2
1
2
1
2
130 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 131
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
62. Hammer Throw An athlete whirls a
7.00-kg hammer 1.8 m from the axis of
rotation in a horizontal circle, as shown in
Figure 6-14. If the hammer makes one rev-
olution in 1.0 s, what is the centripetal
acceleration of the hammer? What is the
tension in the chain?
■Figure 6-14
ac
(4
(1
2
.
)
0
(1
s
.8
)2m)
71 m/s2
Fcmac
(7.00 kg)(71 m/s2)
5.0102N
Level 2
63. A coin is placed on a vinyl stereo record
that is making 33
1
3
revolutions per minute
on a turntable.
a. In what direction is the acceleration of
the coin?
The acceleration is toward the
center of the record.
b. Find the magnitude of the acceleration
when the coin is placed 5.0, 10.0, and
15.0 cm from the center of the record.
T
(0.0300 min)
1.80 s
r5.0 cm:
ac
4T
2
2r
(4
(
2
1
)
.
(
8
0
0
.0
s
5
)
0
2m)
0.61 m/s2
r10.0 cm:
ac
4T
2
2r
(4
(
2
1
)
.
(
8
0
0
.1
s
0
)
0
2m)
1.22 m/s2
r15.0 cm:
ac
4T
2
2r
(4
(
2
1
)
.
(
8
0
0
.1
s
5
)
0
2m)
1.83 m/s2
c. What force accelerates the coin?
frictional force between coin and
record
d. At which of the three radii in part b
would the coin be most likely to fly off
the turntable? Why?
15.0 cm, the largest radius; the
friction force needed to hold it is
the greatest.
64. A rotating rod that is 15.3 cm long is spun
with its axis through one end of the rod so
that the other end of the rod has a speed of
2010 m/s (4500 mph).
a. What is the centripetal acceleration of
the end of the rod?
ac
2.64107m/s2
b. If you were to attach a 1.0-g object to
the end of the rod, what force would be
needed to hold it on the rod?
Fcmac
(0.0010 kg)(2.64107m/s2)
2.6104N
65. Friction provides the force needed for a car
to travel around a flat, circular race track.
What is the maximum speed at which a car
can safely travel if the radius of the track is
80.0 m and the coefficient of friction is 0.40?
FcFfFNmg
But Fc, thus mg.
mv2
r
mv2
r
(2010 m/s)2
0.153 m
v2
r
60 s
1 min
1
33
1
3
revmin
1
f
42r
T2
vtang
Chapter 6 continued

The mass of the car divides out to give
v2gr,so
vgr
(0.40)
(9.80
m/s2)
(80.0
m)
18 m/s
Level 3
66. A carnival clown rides a motorcycle down
a ramp and around a vertical loop. If the
loop has a radius of 18 m, what is the
slowest speed the rider can have at the top
of the loop to avoid falling? Hint: At this
slowest speed, the track exerts no force on the
motorcycle at the top of the loop.
FcmacFgmg,so
acg
v
r
2
g,so
vgr
(9.80
m/s2)
(18 m
)
13 m/s
67. A 75-kg pilot flies a plane in a loop as shown
in Figure 6-15. At the top of the loop, when
the plane is completely upside-down for an
instant, the pilot hangs freely in the seat
and does not push against the seat belt. The
airspeed indicator reads 120 m/s. What is
the radius of the plane’s loop?
■Figure 6-15
Because the net force is equal to the
weight of the pilot,
FcmacFgmg,so
acgor
v
r
2
g
so r
v
g
2
1.5103m
6.3 Relative Velocity
pages 166–167
Level 1
68. Navigating an Airplane An airplane flies
at 200.0 km/h relative to the air. What is
the velocity of the plane relative to the
ground if it flies during the following wind
conditions?
a. a 50.0-km/h tailwind
Tailwind is in the same direction as
the airplane
200.0 km/h 50.0 km/h 250.0 km/h
b. a 50.0-km/h headwind
Head wind is in the opposite direction
of the airplane
200.0 km/h 50.0 km/h 150.0 km/h
69. Odina and LaToya are sitting by a river and
decide to have a race. Odina will run down
the shore to a dock, 1.5 km away, then turn
around and run back. LaToya will also race
to the dock and back, but she will row a
boat in the river, which has a current of
2.0 m/s. If Odina’s running speed is equal
to LaToya’s rowing speed in still water,
which is 4.0 m/s, who will win the race?
Assume that they both turn instantaneously.
xvt, so t
for Odina,
t
7.5102s
For LaToya (assume against current on
the way to the dock),
t
x2
v2
x1
v1
3.0103m
4.0 m/s
x
v
(120 m/s)2
9.80 m/s2
vtang 120 m/s
132 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 133
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1.0103s
Odina wins.
Level 2
70. Crossing a River You row a boat, such as
the one in Figure 6-16, perpendicular to
the shore of a river that flows at 3.0 m/s.
The velocity of your boat is 4.0 m/s relative
to the water.
■Figure 6-16
a. What is the velocity of your boat relative
to the shore?
vb/s (vb/w)
2(v
w/s)2
(4.0 m
/s)2
(3.0 m
/s)2
5.0 m/s
tan1
tan1
53° from shore
b. What is the component of your velocity
parallel to the shore? Perpendicular
to it?
3.0 m/s; 4.0 m/s
71. Studying the Weather A weather station
releases a balloon to measure cloud condi-
tions that rises at a constant 15 m/s relative
to the air, but there is also a wind blowing
at 6.5 m/s toward the west. What are the
magnitude and direction of the velocity of
the balloon?
vb(vb/air
)2(v
air)2
(15 m
/s)2
(6.5 m
/s)2
16 m/s
tan1
tan1
67° from the horizon toward the west
Level 3
72. Boating You are boating on a river that
flows toward the east. Because of your
knowledge of physics, you head your boat
53° west of north and have a velocity of
6.0 m/s due north relative to the shore.
a. What is the velocity of the current?
tan
,so
vw/s (tan )(vb/s)
(tan 53°)(6.0 m/s)
8.0 m/s east
b. What is the speed of your boat relative
to the water?
cos
v
v
b
b
/
/
w
s
,so
vb/w
c
v
o
b
s
/s
c
6o
.0
sm
53
/s
°
1.0101m/s
73. Air Travel You are piloting a small plane,
and you want to reach an airport 450 km
due south in 3.0 h. A wind is blowing from
the west at 50.0 km/h. What heading and
airspeed should you choose to reach your
destination in time?
vs
d
ts
150 km/h
vp(150 k
m/h)2
(50
.0 km
/h)2
1.6102km/h
tan1
tan1
18° west of south
Mixed Review
50.0 km/h
150 km/h
vwind
vs
450 km
3.0 h
vw/s
vb/s
15 m/s
6.5 m/s
vb/air
vair
4.0 m/s
3.0 m/s
vb/w
vw/s
vvbb
vb
vw
1.5103m
4.0 m/s 2.0 m/s
1.5103m
4.0 m/s 2.0 m/s
Chapter 6 continued

page 167
Level 1
74. Early skeptics of the idea of a rotating Earth said that the fast spin of Earth
would throw people at the equator into space. The radius of Earth is about
6.38103km. Show why this idea is wrong by calculating the following.
a. the speed of a 97-kg person at the equator
v
d
t
464 m/s
b. the force needed to accelerate the person in the circle
Fcmac
3.3 N
c. the weight of the person
Fgmg
(97)(9.80 m/s2)
9.5102N
d. the normal force of Earth on the person, that is, the person’s apparent weight
FN9.5102N3.3 N
9.5102N
75. Firing a Missile An airplane, moving at 375 m/s relative to the ground, fires a
missile forward at a speed of 782 m/s relative to the plane. What is the speed of
the missile relative to the ground?
vm/g vp/g vm/p
375 m/s 782 m/s
1157 m/s
76. Rocketry A rocket in outer space that is moving at a speed of 1.25 km/s relative
to an observer fires its motor. Hot gases are expelled out the back at 2.75 km/s
relative to the rocket. What is the speed of the gases relative to the observer?
vg/o vr/o vg/r
1.25 km/s (2.75 km/s) 1.50 km/s
Level 2
77. Two dogs, initially separated by 500.0 m, are running towards each other, each
moving with a constant speed of 2.5 m/s. A dragonfly, moving with a constant
speed of 3.0 m/s, flies from the nose of one dog to the other, then turns around
(97 kg)(464 m/s)2
6.38106m
mv2
r
2(6.38106m)
(24 h)
36
1
00
hs
2r
T
134 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 135
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
instantaneously and flies back to the other
dog. It continues to fly back and forth until
the dogs run into each other. What distance
does the dragonfly fly during this time?
The dogs will meet in
1.0102s
The dragonfly flies
(3.0 m/s)(1.0102s) 3.0102m.
78. A 1.13-kg ball is swung vertically from a
0.50-m cord in uniform circular motion
at a speed of 2.4 m/s. What is the tension in
the cord at the bottom of the ball’s motion?
FTFgFc
mg
(1.13 kg)(9.80 m/s2)
24 N
79. Banked Roads Curves on roads often are
banked to help prevent cars from slipping
off the road. If the posted speed limit for a
particular curve of radius 36.0 m is 15.7 m/s
(35 mph), at what angle should the road be
banked so that cars will stay on a circular
path even if there were no friction between
the road and the tires? If the speed limit was
increased to 20.1 m/s (45 mph), at what
angle should the road be banked?
For 35 mph:
FcFg
cos mg sin
g
c
so
in
s
g tan
tan1
tan1
34.9°
For 45 mph:
tan1
tan1
48.9°
Level 3
80. The 1.45-kg ball in Figure 6-17 is
suspended
from a 0.80-
m string
and
swung in a
horizontal
circle at a constant
speed such that the string makes an angle
of 14.0° with the vertical.
a. What is the tension in the string?
FT cos mg
so FT
cm
os
g
14.6 N
b. What is the speed of the ball?
FcFT sin FgFT cos
mg
so
F
F
T
Tc
s
o
in
s
or tan v2
rg
mv2
rmg
mv2
r
(1.45 m/s)(9.80 m/s2)
cos 14.0°
14.0°
■Figure 6-17
(20.1 m/s)2
(9.80 m/s2)(36.0 m)
v2
gr
(15.7 m/s)2
(9.80 m/s2)(56.0 m)
v2
gr
v2
r
mv2
r
(1.13 kg)(2.4 m/s)2
0.50 m
mv2
r
500.0 m
5.0 m/s
Chapter 6 continued

so vrg tan
(0.80
m)(9.8
0 m/s
2)(tan
14.0°
)
1.4 m/s
81. A baseball is hit directly in line with an outfielder at an angle of 35.0° above the
horizontal with an initial velocity of 22.0 m/s. The outfielder starts running as soon
as the ball is hit at a constant velocity of 2.5 m/s and barely catches the ball.
Assuming that the ball is caught at the same height at which it was hit, what was the
initial separation between the hitter and outfielder? Hint: There are two possible
answers.
xvxitvptt(vxivp)
To get t,
yvyitgt2,y0
so vyitgt2,t0 or
vyigt
t
2v
gyi
2vis
g
in
so x
2vis
g
in
(vxivp)
2vis
g
in
(vi cos vp)
((22.0 m/s)(cos 35.0°)
2.5 m/s)
53 m or 4.0101m
82. A Jewel Heist You are serving as a
technical consultant for a locally produced cartoon. In one episode, two crimi-
nals, Shifty and Lefty, have stolen some jewels. Lefty has the jewels when the
police start to chase him, and he runs to the top of
a 60.0-m tall building in his attempt to escape. Meanwhile, Shifty runs to the
convenient hot-air balloon 20.0 m from the base of the building and unteth-
ers it, so it begins to rise at a constant speed. Lefty tosses the bag of jewels
horizontally with a speed of 7.3 m/s just as the balloon
(2)(22.0 m/s)(sin 35.0°)
9.80 m/s2
1
2
1
2
1
2
136 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 137
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
begins its ascent. What must the velocity of the balloon be for Shifty to easily
catch the bag?
xvxit, so t
v
x
xi
ybag vyitgt2,but vyi0
so ybag gt2
vballoon
yba
tlloon
60.0 m
t
ybag
gt
g
v
x
xi
2
g
v
x
xi
8.5 m/s
Thinking Critically
page 168
83. Apply Concepts Consider a roller-coaster loop like the one in Figure 6-18. Are
the cars traveling through the loop in uniform circular motion? Explain.
■Figure 6-18
The vertical gravitational force changes the speed of the cars, so the
motion is not uniform circular motion.
84. Use Numbers A 3-point jump shot is released 2.2 m above the ground and
6.02 m from the basket. The basket is 3.05 m above the floor. For launch angles
of 30.0° and 60.0°, find the speed the ball needs to be thrown to make the basket.
(9.80 m/s)(20.0 m)
2(7.3 m/s)
(60.0 m)(7.3 m/s)
(20.0 m)
(60.0 m)vxi
x
1
2
60.0 m
v
x
xi
1
2
60.0 m
t
60.0 m
1
2
gt2
t
1
2
1
2
Chapter 6 continued

xvixt, so t
v
x
ix
vicx
os
yviytgt2
vi sin
vicx
os
g
vicx
os
2
x tan
so vi
co
x
s
2((tan
g
)x
y)
For 30.0°
vi
co
6s
.02
3
0
m
.0°
9.5 m/s
For 60.0°
vi
co
6s
.02
6
0
m
.0°
8.6 m/s
85. Analyze For which angle in problem 84 is
it more important that the player
get the speed right? To explore this ques-
tion, vary the speed at each angle by
5 percent and find the change in the range
of the attempted shot.
Varying speed by 5 percent at 30.0°
changes Rby about 0.90 m in either
direction. At 60.0° it changes Rby only
about 0.65 m. Thus, the high launch
angle is less sensitive to speed varia-
tions.
86. Apply Computers and Calculators A base-
ball player hits a belt-high (1.0 m) fastball
down the left-field line. The ball is hit with an
initial velocity of 42.0 m/s at 26°. The left-field
wall is 96.0 m from home plate at the foul
pole and is 14-m high. Write the equation for
the height of the ball, y, as a function of its
distance from home plate, x. Use a computer
or graphing calculator to plot the path of the
ball. Trace along the path to find how high
above the ground the ball is when it is at the
wall.
a. Is the hit a home run?
Yes, the hit is a home run; the ball
clears the wall by 2.1 m.
b. What is the minimum speed at which
the ball could be hit and clear the wall?
vi
co
x
s
2((tan
)
g
x
y)
c
9
o
6s
.02
m
6°
41 m/s
c. If the initial velocity of the ball is 42.0
m/s, for what range of angles will the
ball go over the wall?
For the ball to go over the wall, the
range of angles needs to be 25°70°.
87. Analyze Albert Einstein showed that the
rule you learned for the addition of veloci-
ties does not work for objects moving near
the speed of light. For example, if a rocket
moving at velocity vAreleases a missile that
has velocity vBrelative to the rocket, then
the velocity of the missile relative to an
observer that is at rest is given by v(vA
vB)/(1 vAvB/c2), where cis the speed of
light, 3.00108m/s. This formula gives the
correct values for objects moving at slow
speeds as well. Suppose a rocket moving at
11 km/s shoots a laser beam out in front of
it. What speed would an unmoving observ-
er find for the laser light? Suppose that a
rocket moves at a speed c/2, half the speed
of light, and shoots a missile forward at a
speed of c/2 relative to the rocket. How fast
would the missile be moving relative to a
fixed observer?
vl/o
1.1104m/s 3.00108m/s
1
3.0108m/s
vm/o vr/o vm/r
1
vr/o
c
v
2m/r
(1.1104m/s)(3.00108m/s)
(3.00108m/s)2
(vr/o vl/r)
1
vr/oc
2
v1/r
9.80 m/s2
(2)((tan 26°)(96.0 m) 13 m)
9.80 m/s2
2((tan 60°(6.02 m) (3.05 m 2.2 m))
9.80 m/s2
.02 m) (3.05 m 2.2 m))
gx2
2vi2(cos )2
1
2
1
2
138 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Chapter 6 continued
c
2
c
2
1
c
88. Analyze and Conclude A ball on a light
string moves in a vertical circle. Analyze and
describe the motion of this system. Be sure
to consider the effects of gravity and ten-
sion. Is this system in uniform circular
motion? Explain your answer.
It is not uniform circular motion.
Gravity increases the speed of the ball
when it moves downward and reduces
the speed when it is moving upward.
Therefore, the centripetal acceleration
needed to keep it moving in a circle
will be larger at the bottom and small-
er at the top of the circle. At the top,
tension and gravity are in the same
direction, so the tension needed will
be even smaller. At the bottom, gravity
is outward while the tension is inward.
Thus, the tension exerted by the string
must be even larger.
Writing in Physics
page 168
89. Roller Coasters If you take a look at verti-
cal loops on roller coasters, you will notice
that most of them are not circular in shape.
Research why this is so and explain the
physics behind this decision by the coaster
engineers.
Answers will vary. Since Fc
mr
v2
,as v
decreases due to gravity when going
uphill, ris reduced to keep the force
constant.
90. Many amusement-park rides utilize cen-
tripetal acceleration to create thrills for
the park’s customers. Choose two rides
other than roller coasters that involve
circular motion and explain how the
physics of circular motion creates the
sensations for the riders.
4
5
c
2
c
2
c2
Physics: Principles and Problems Solutions Manual 139
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.


Physics: Principles and Problems Solutions Manual 141
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7Gravitation
CHAPTER
Practice Problems
7.1 Planetary Motion and Gravitation
pages 171–178
page 174
1. If Ganymede, one of Jupiter’s moons, has a period of 32 days, how many units
are there in its orbital radius? Use the information given in Example Problem 1.
T
T
G
I
2
r
r
G
I
3
rG
3(4.2 u
nits)3
2
323.4
103un
its3
29 units
2. An asteroid revolves around the Sun with a mean orbital radius twice that of
Earth’s. Predict the period of the asteroid in Earth years.
T
T
E
a
2
r
r
E
a
3with ra2rE
Ta
3TE2
3(1.0
y)2
2.8 y
3. From Table 7-1, on page 173, you can find that, on average, Mars is 1.52 times as
far from the Sun as Earth is. Predict the time required for Mars to orbit the Sun
in Earth days.
T
TM
E
2
r
rM
E
3with rM1.52rE
Thus, TM
3TE2
1.5
rE
2r
E
3(36
5 day
s)2
4.68
105da
ys2
684 days
4. The Moon has a period of 27.3 days and a mean distance of 3.90105km from
the center of Earth.
a. Use Kepler’s laws to find the period of a satellite in orbit 6.70103km from
the center of Earth.
T
T
M
s
2
r
r
M
s
3
rM
rE
2rE
rE
ra
rE
32 days
1.8 days

Ts
3TM2
6
3.
.7
90
0
1
10
0
3
5k
km
m
3(27.
3 day
s)2
3.78
103
days2
6.15102days 88.6 min
b. How far above Earth’s surface is this satellite?
hrs rE
6.70106m 6.38106m
3.2105m
3.2102km
5. Using the data in the previous problem for the period and radius of revolution
of the Moon, predict what the mean distance from Earth's center would be for an
artificial satellite that has a period of exactly 1.00 day.
T
T
M
s
2
r
r
M
s
3
rs
3rM3
T
T
M
s
2
3(3.90
105km
)3
1
2.
7
0
.
0
3d
da
ay
ys
s
2
37.96
1013 k
m3
4.30104km
Section Review
7.1 Planetary Motion and Gravitation
pages 171–178
page 178
6. Neptune’s Orbital Period Neptune orbits the Sun with
an orbital radius of 4.4951012 m, which allows gases,
such as methane, to condense and form an atmosphere,
as shown in Figure 7-8. If the mass of the Sun is
1.991030 kg, calculate the period of Neptune’s orbit.
T2
2
5.20109s6.02105days
7. Gravity If Earth began to shrink, but its mass remained the same, what would
happen to the value of gon Earth’s surface?
The value of gwould increase.
(4.4951012 m)3
(6.671011 Nm2/kg2)(1.991030 kg)
r3
GmS
■Figure 7-8
rs
rM
142 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 143
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
8. Gravitational Force What is the gravitational force between two 15-kg packages
that are 35 cm apart? What fraction is this of the weight of one package?
Fg G
m
r
E
2
m
1.2107N
Because the weight is mg 147 N, the gravitational force is 8.21010 or
0.82 parts per billion of the weight.
9. Universal Gravitational Constant Cavendish did his experiment using lead
spheres. Suppose he had replaced the lead spheres with copper spheres of equal
mass. Would his value of Gbe the same or different? Explain.
It would be the same, because the same value of Ghas been used
successfully to describe the attraction of bodies having diverse chemical
compositions: the Sun (a star), the planets, and satellites.
10. Laws or Theories? Kepler’s three statements and Newton’s equation for
gravitational attraction are called “laws.” Were they ever theories? Will they ever
become theories?
No. A scientific law is a statement of what has been observed to happen
many times. A theory explains scientific results. None of these statements
offers explanations for why the motion of planets are as they are or for
why gravitational attraction acts as it does.
11. Critical Thinking Picking up a rock requires less effort on the Moon than on
Earth.
a. How will the weaker gravitational force on the Moon’s surface affect the path
of the rock if it is thrown horizontally?
Horizontal throwing requires the same effort because the inertial
character, Fma, of the rock is involved. The mass of the rock
depends only on the amount of matter in the rock, not on its location
in the universe. The path would still be a parabola, but it could be
much wider because the rock would go farther before it hits the
ground, given the smaller acceleration rate and longer time of flight.
b. If the thrower accidentally drops the rock on her toe, will it hurt more or less
than it would on Earth? Explain.
Assume the rocks would be dropped from the same height on Earth
and on the Moon. It will hurt less because the smaller value of gon
the Moon means that the rock strikes the toe with a smaller velocity
than on Earth.
(6.671011 Nm2kg2)(15 kg)2
(0.35 m)2
Chapter 7 continued

Practice Problems
7.2 Using the Law of Universal of Gravitation
pages 179–185
page 181
For the following problems, assume a circular orbit for all calculations.
12. Suppose that the satellite in Example Problem 2 is moved to an orbit that is
24 km larger in radius than its previous orbit. What would its speed be? Is this
faster or slower than its previous speed?
r(h 2.40104m) rE
(2.25105m 2.40104m) 6.38106m6.63106m
v
Gm
rE
7.75103m/s, slower
13. Use Newton’s thought experiment on the motion of satellites to solve the following.
a. Calculate the speed that a satellite shot from a cannon must have to orbit
Earth 150 km above its surface.
v
Gm
rE
7.8103m/s
b. How long, in seconds and minutes, would it take for the satellite to complete
one orbit and return to the cannon?
T2
2
5.3103s88 min
14. Use the data for Mercury in Table 7-1 on page 173 to find the following.
a. the speed of a satellite that is in orbit 260 km above Mercury’s surface
v
Gm
rM
rrM260 km
2.44106m 0.26106m
2.70106m
v
2.86103m/s
b. the period of the satellite
T2
2
5.94103s1.65 h
(2.70106m)3
(6.671011 Nm2/kg2)(3.301023 kg)
r3
GmM
(6.671011 Nm2/kg2)(3.301023 kg)
2.70106m
(6.38106m1.5105m)3
(6.671011 Nm2/kg2)(5.971024 kg)
r3
GmE
(6.671011 Nm2/kg2)(5.971024 kg)
(6.38106m1.5105m)
(6.671011 Nm2/kg2)(5.971024 kg)
6.63106 m
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued
144 Solutions Manual Physics: Principles and Problems

Physics: Principles and Problems Solutions Manual 145
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
7.2 Using the Law of Universal of Gravitation
pages 179–185
page 185
15. Gravitational Fields The Moon is 3.9105km from Earth’s center and
1.5108km from the Sun’s center. The masses of Earth and the Sun are
6.01024 kg and 2.01030 kg, respectively.
a. Find the ratio of the gravitational fields due to Earth and the Sun at the
center of the Moon.
Gravitational field due to the Sun: gSG
r
m
S
S
2
Gravitational field due to Earth: gEG
r
m
E
E
2
g
gS
E
m
mS
E
r
rE
S
2
2
2.3
b. When the Moon is in its third quarter phase, as shown in Figure 7-17, its
direction from Earth is at right angles to the Sun’s direction. What is the net
gravitational field due to the Sun and Earth at the center of the Moon?
■Figure 7-17
Because the directions are at right angles, the net field is the square
root of the sum of the squares of the two fields.
gS
G
r
m
2S
5.9103N/kg
Similarly, gE2.6103N/kg
gnet (5.9
103
N/kg)2
(2.6
10
3N/kg
)2
6.4103N/kg
16. Gravitational Field The mass of the Moon is 7.31022 kg and its radius is
1785 km. What is the strength of the gravitational field on the surface of the Moon?
g
G
rM
2
1.5 N/kg, about one-sixth that on Earth
(6.671011 Nm2kg2)(7.31022 kg)
(1.785103m)2
(6.671011 Nm2kg2)(2.01030 kg)
(1.51011 m)2
Sun
Earth
Moon
(2.01030 kg)(3.9105km)2
(6.01024 kg)(1.5108km)2
Chapter 7 continued

17. A Satellite’s Mass When the first artificial satellite was launched into orbit by
the former Soviet Union in 1957, U.S. president Dwight D. Eisenhower asked his
scientific advisors to calculate the mass of the satellite. Would they have been
able to make this calculation? Explain.
No. Because the speed and period of the orbit don’t depend at all on the
mass of the satellite, the scientific advisors would not have been able to
calculate the mass of the satellite.
18. Orbital Period and Speed Two satellites are in circular orbits about Earth. One
is 150 km above the surface, the other 160 km.
a. Which satellite has the larger orbital period?
When the orbital radius is large, the period also will be large. Thus, the
one at 160 km will have the larger period.
b. Which one has the greater speed?
The one at 150 km, because the smaller the orbital radius, the greater
the speed.
19. Theories and Laws Why is Einstein’s description of gravity called a “theory,”
while Newton’s is a “law?”
Newton’s law describes how to calculate the force between two massive
objects. Einstein’s theory explains how an object, such as Earth, attracts
the Moon.
20. Weightlessness Chairs in an orbiting spacecraft are weightless. If you were on
board such a spacecraft and you were barefoot, would you stub your toe if you
kicked a chair? Explain.
Yes. The chairs are weightless but not massless. They still have inertia
and can exert contact forces on your toe.
21. Critical Thinking It is easier to launch a satellite from Earth into an orbit that
circles eastward than it is to launch one that circles westward. Explain.
Earth rotates toward the east, and its velocity adds to the velocity given
to the satellite by the rocket, thereby reducing the velocity that the rocket
must supply.
Chapter Assessment
Concept Mapping
page 190
22. Create a concept map using these terms: planets, stars, Newton’s law of universal
gravitation, Kepler’s first law, Kepler’s second law, Kepler’s third law, Einstein’s general
theory of relativity.
146 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued
Physics: Principles and Problems Solutions Manual 147
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Kepler’s first and second laws describe the motion of a single planet.
Kepler’s third law describes the periods versus the orbital radii of all
planets around a star. Newton’s law of universal gravitation supports
Kepler’s laws. Einstein’s theory explains Newton’s and Kepler’s laws.
Mastering Concepts
page 190
23. In 1609, Galileo looked through his telescope at Jupiter and saw four moons.
The name of one of the moons that he saw is Io. Restate Kepler’s first law for Io
and Jupiter. (7.1)
The path of Io is an ellipse, with Jupiter at one focus.
24. Earth moves more slowly in its orbit during summer in the northern hemisphere
than it does during winter. Is it closer to the Sun in summer or in winter? (7.1)
Because Earth moves more slowly in its orbit during summer, by Kepler’s
second law, it must be farther from the Sun. Therefore, Earth is closer to
the Sun in the winter months.
Einstein’s general
theory of relativity
Explains
Supports
Newton’s law of
universal gravitation
Kepler’s second
law
Describes motion of Relates periods and
radii of
moving
around
stars
planets
Kepler’s first
law
Kepler’s third
law
Chapter 7 continued

25. Is the area swept out per unit of time by
Earth moving around the Sun equal to
the area swept out per unit of time by Mars
moving around the Sun? (7.1)
No. The equality of the area swept out
per unit of time applies to each planet
individually.
26. Why did Newton think that a force must act
on the Moon? (7.1)
Newton knew that the Moon followed
a curved path; therefore, it was
accelerated. He also knew that a
force is required for acceleration.
27. How did Cavendish demonstrate that a
gravitational force of attraction exists
between two small objects? (7.1)
He carefully measured the masses, the
distance between the masses, and the
force of attraction. He then calculated
Gusing Newton’s law of universal grav-
itation.
28. What happens to the gravitational force
between two masses when the distance
between the masses is doubled? (7.1)
According to Newton, F1/r2. If the
distance is doubled, the force is cut to
one-fourth.
29. According to Newton’s version of Kepler’s
third law, how would the ratio T2/r3change
if the mass of the Sun were doubled? (7.1)
Because T2/r342/GmS, if the mass
of the Sun, mS, is doubled, the ratio will
be halved.
30. How do you answer the question, “What
keeps a satellite up?” (7.2)
Its speed; it is falling all the time.
31. A satellite is orbiting Earth. On which of
the following does its speed depend? (7.2)
a. mass of the satellite
b. distance from Earth
c. mass of Earth
Speed depends only on b, the distance
from the Earth, and c, the mass of Earth.
32. What provides the force that causes the
centripetal acceleration of a satellite in
orbit? (7.2)
gravitational attraction to the central
body
33. During space flight, astronauts often refer to
forces as multiples of the force of gravity on
Earth’s surface. What does a force of 5g
mean to an astronaut? (7.2)
A force of 5gmeans that an astronaut’s
weight is five times heavier than it is on
Earth. The force exerted on the astro-
naut is five times the force of Earth’s
gravitational force.
34. Newton assumed that a gravitational force
acts directly between Earth and the Moon.
How does Einstein’s view of the attractive
force between the two bodies differ from
Newton’s view? (7.2)
Einstein’s view is that gravity is an
effect of the curvature of space as a
result of the presence of mass, whereas
Newton’s view of gravity is that it is a
force acting directly between objects.
Thus, according to Einstein, the
attraction between Earth and the Moon
is the effect of curvature of space
caused by their combined masses.
35. Show that the dimensions of gin the
equation gF/mare in m/s2. (7.2)
The units of
m
F
are m/s2
36. If Earth were twice as massive but remained
the same size, what would happen to the
value of g? (7.2)
The value of gwould double.
Applying Concepts
pages 190–191
37. Golf Ball The force of gravity acting on an
object near Earth’s surface is proportional
to the mass of the object. Figure 7-18
shows a tennis ball and golf ball in free fall.
Why does a tennis ball not fall faster than a
golf ball?
kgm/s2
kg
N
kg
148 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued
Physics: Principles and Problems Solutions Manual 149
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
■Figure 7-18
FG
m
r
1m
22
m1Earth’s mass
a
m2object’s mass
Thus, a
G
r
m
21
The acceleration is independent of the
object’s mass. This is because more
massive objects require more force to
accelerate at the same rate.
38. What information do you need to find the
mass of Jupiter using Newton’s version of
Kepler’s third law?
You must know the period and orbital
radius of at least one of its satellites.
39. The mass of Pluto was not known until a
satellite of the planet was discovered. Why?
Orbital motion of a planet does not
depend on its mass and cannot be
used to find the mass. A satellite
orbiting the planet is necessary to
find the planet’s mass.
40. Decide whether each of the orbits shown in
Figure 7-19 is a possible orbit for a planet.
■Figure 7-19
Only d (lower right) is possible.
a (top left) and b (top right) do not
have the Sun at a focus, and in
c (lower left), the planet is not in
orbit around the Sun.
41. The Moon and Earth are attracted to each
other by gravitational force. Does the more-
massive Earth attract the Moon with a
greater force than the Moon attracts Earth?
Explain.
No. The forces constitute an action-
reaction pair, so under Newton’s third
law, they are equal and opposite.
42. What would happen to the value of Gif
Earth were twice as massive, but remained
the same size?
Nothing. Gis a universal constant, and
it is independent of Earth’s mass.
However, the force of attraction would
double.
43. Figure 7-20 shows a satellite orbiting Earth.
Examine the equation v
Gm
rE
, relating
the speed of an orbiting satellite and its
distance from the center of Earth. Does a
satellite with a large or small orbital radius
have the greater velocity?
Sun Sun
Sun
Sun
c
c
c
c
F
m2
Chapter 7 continued

■Figure 7-20 (Not to scale)
A satellite with a small radius has the
greater velocity.
44. Space Shuttle If a space shuttle goes into a
higher orbit, what happens to the shuttle’s
period?
Because T2
, if the orbital
radius increases, so will the period.
45. Mars has about one-ninth the mass of
Earth. Figure 7-21 shows satellite M, which
orbits Mars with the same orbital radius
as satellite E, which orbits Earth. Which
satellite has a smaller period?
■Figure 7-21 (Not to scale)
Because T2
, as the mass of
the planet increases, the period of the
satellite decreases. Because Earth
has a larger mass than Mars, Earth’s
satellite will have a smaller period.
46. Jupiter has about 300 times the mass of
Earth and about ten times Earth’s radius.
Estimate the size of gon the surface of
Jupiter.
g. If Jupiter has 300 times the
mass and ten times the radius of Earth,
g
3
10
00
2
3. Thus, gon Jupiter is three
times that on Earth.
47. A satellite is one Earth radius above the sur-
face of Earth. How does the acceleration
due to gravity at that location compare to
acceleration at the surface of Earth?
drErE2rE
so, ag
2g
48. If a mass in Earth’s gravitational field is
doubled, what will happen to the force
exerted by the field upon the mass?
It also will double.
49. Weight Suppose that yesterday your body
had a mass of 50.0 kg. This morning you
stepped on a scale and found that you had
gained weight.
a. What happened, if anything, to your
mass?
Your mass increased.
b. What happened, if anything, to the ratio
of your weight to your mass?
The ratio remained constant
because it is equal to the gravita-
tional field at the location, a con-
stant g.
50. As an astronaut in an orbiting space shuttle,
how would you go about “dropping” an
object down to Earth?
To “drop”an object down to Earth, you
would have to launch it backward at the
same speed at which you are traveling
in orbit. With respect to Earth, the
object’s speed perpendicular to Earth’s
gravity would be zero, and it could then
“drop”down to Earth. However, the
object is likely to burn up as a result of
friction with Earth’s atmosphere on the
way down.
51. Weather Satellites The weather pictures
that you see every day on TV come from a
spacecraft in a stationary position relative to
1
4
rE
2rE
mE
rE2
r3
Gm
Earth
ME
Mars
rMrE
r3
Gm
Satellite
Earth
r
150 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
the surface of Earth, 35,700 km above
Earth’s equator. Explain how it can stay in
exactly the same position day after day.
What would happen if it were closer?
Farther out? Hint: Draw a pictorial model.
The satellite is positioned as close to
the equator as possible so it doesn’t
appear to have much north-south move-
ment. Because it is placed at that dis-
tance, the satellite has a period of 24.0
h. If it were positioned any closer, its
period would be less than 24.0 h and it
would appear to move toward the east.
If it were positioned any farther, its peri-
od would be longer than 24.0 h.
Mastering Problems
7.1 Planetary Motion and Gravitation
pages 191–192
Level 1
52. Jupiter is 5.2 times farther from the Sun
than Earth is. Find Jupiter’s orbital period
in Earth years.
2
3
TJ
3TE2
3(1.0
y)2
141 y
2
12 y
53. Figure 7-22 shows a Cavendish apparatus
like the one used to find G. It has a large
lead sphere that is 5.9 kg in mass and a
small one with a mass of 0.047 kg. Their
centers are separated by 0.055 m. Find the
force of attraction between them.
■Figure 7-22
FG
(6.671011 Nm2/kg2)
6.1109N
54. Use Table 7-1 on p. 173 to compute the
gravitational force that the Sun exerts on
Jupiter.
FG
(6.671011 Nm2/kg2)
4.171023 N
55. Tom has a mass of 70.0 kg and Sally has a
mass of 50.0 kg. Tom and Sally are standing
20.0 m apart on the dance floor. Sally looks
up and sees Tom. She feels an attraction. If
the attraction is gravitational, find its size.
Assume that both Tom and Sally can be
replaced by spherical masses.
FG
(6.671011 Nm2/kg2)
5.841010 N
56. Two balls have their centers 2.0 m apart, as
shown in Figure 7-23. One ball has a mass
of 8.0 kg. The other has a mass of 6.0 kg.
What is the gravitational force between them?
■Figure 7-23
FG
(6.671011 Nm2/kg2)
8.01010 N
(8.0 kg)(6.0 kg)
(2.0 m)2
m1m2
r2
6.0 kg8.0 kg 2.0 m
(70.0 kg)(50.0 kg)
(20.0 m)2
mTmS
r2
(1.991030 kg)(1.901027 kg)
(7.781011 m)2
m1m2
r2
(5.9 kg)(4.7102kg)
(5.5102m)2
mSmJ
r2
0.055 m
5.9 kg
5.9 kg
0.047 kg
0.047 kg
0.055 m
5.2
1.0
rJ
rE
rJ
rE
TJ
TE
Chapter 7 continued
Physics: Principles and Problems Solutions Manual 151

57. Two bowling balls each have a mass of
6.8 kg. They are located next to each other
with their centers 21.8 cm apart. What grav-
itational force do they exert on each other?
FG
(6.671011
Nm2/kg2)
6.5108N
58. Assume that you have a mass of 50.0 kg.
Earth has a mass of 5.971024 kg and a
radius of 6.38106m.
a. What is the force of gravitational attrac-
tion between you and Earth?
Sample answer:
FG
mS
r
m
2E
(6.671011 Nm2/kg2)
489 N
b. What is your weight?
Sample answer:
Fgmg (50.0 kg)(9.80 m/s2)
4.90102N
59. The gravitational force between two electrons
that are 1.00 m apart is 5.541071 N. Find
the mass of an electron.
FG, where m1m2 me
So me
9.111031 kg
60. A 1.0-kg mass weighs 9.8 N on Earth’s sur-
face, and the radius of Earth is roughly
6.4106m.
a. Calculate the mass of Earth.
FG
mE
6.01024 kg
b. Calculate the average density of Earth.
Vr3
1.11021 m3
D
m
V
5.5103kg/m3
61. Uranus Uranus requires 84 years to circle
the Sun. Find Uranus’s orbital radius as a
multiple of Earth’s orbital radius.
T
TU
E
2
r
rU
E
3
r
rU
E
3
T
TU
E
2
3
1
8
.
4
0
y
y
2
19
So rU19rE
62. Venus Venus has a period of revolution of
225 Earth days. Find the distance between
the Sun and Venus as a multiple of Earth’s
orbital radius.
T
TV
E
2
r
rV
E
3
r
rV
E
3
T
TV
E
2
3
2
3
2
6
5
5
d
d
a
a
y
y
s
s
2
0.724
So rV0.724rE
Level 2
63. If a small planet, D, were located 8.0 times as
far from the Sun as Earth is, how many years
would it take the planet to orbit the Sun?
T
TD
E
2
r
rD
E
3
6.01024 kg
1.11021 m3
(4)(6.4106m)3
3
4
3
(9.8 N)(6.4106m)2
(6.671011 Nm2kg2)(1.0 kg)
Fr2
Gm
m1m2
r2
(5.541071 N)(1.00 m)2
6.671011 Nm2/kg2
Fr2
G
m1m2
r2
(50.0 kg)(5.971024 kg)
(6.38106m)2
(6.8 kg)(6.8 kg)
(0.218 m)2
m1m2
r2
152 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 153
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
TD
r
rD
E
3T
E2
8
1.
.0
0
3
(1.0 y
)2
23 years
64. Two spheres are placed so that their centers are 2.6 m apart. The force between the
two spheres is 2.751012 N. What is the mass of each sphere if one sphere is
twice the mass of the other sphere?
FG
m
r
1m
22
, where m22m1
FG
(m1)
r
(2
2m1)
m1
F
2r
G
2
0.3733 kg or 0.37 kg to two significant digits
m22m1(2)(0.3733 kg) 0.7466 kg or 0.75 to two significant digits
65. The Moon is 3.9105km from Earth’s center and 1.5108km from the
Sun’s center. If the masses of the Moon, Earth, and the Sun are 7.31022 kg,
6.01024 kg, and 2.01030 kg, respectively, find the ratio of the gravitational
forces exerted by Earth and the Sun on the Moon.
FG
m
r
1m
22
Earth on Moon: FE (6.671011 Nm2/kg2)
1.91020 N
Sun on Moon: FE (6.671011 Nm2/kg2)
4.31020 N
Ratio is
F
FE
S
The Sun pulls more than twice as hard on the Moon as does Earth.
66. Toy Boat A force of 40.0 N is required to pull a 10.0-kg wooden toy boat at a
constant velocity across a smooth glass surface on Earth. What force would be
required to pull the same wooden toy boat across the same glass surface on the
planet Jupiter?
F
F
N
f
m
F
b
fg
, where mbis the mass of the toy boat.
On Jupiter, the normal force is equal to the gravitational attraction
between the toy boat and Jupiter, or
FNG
m
r
b
J
m
2J
Now
F
F
N
f
, so FfJ FNG
m
r
b
J
m
2J
1.0
2.3
1.91020 N
4.31020 N
(2.01030 kg)(7.31022 kg)
(1.51011 m)2
(6.01024 kg)(7.31022 kg)
(3.9108m)2
(2.751012 N)(2.6 m)2
(2)(6.671011 Nm2kg2)
Chapter 7 continued

But
m
F
b
fg
, so FfJ
FfG
m
m
b
b
g
m
rJ
J
2
FfG
g
m
rJ
J
2
101 N
67. Mimas, one of Saturn’s moons, has an orbital radius of 1.87108m and an
orbital period of about 23.0 h. Use Newton’s version of Kepler’s third law to
find Saturn’s mass.
T2
4
G
m
2
r3
m
4
G
T
2r
2
3
5.61026 kg
Level 3
68. The Moon is 3.9108m away from Earth and has a period of 27.33 days. Use
Newton’s version of Kepler’s third law to find the mass of Earth. Compare this
mass to the mass found in problem 60.
T2
4
G
m
2
r3
m
4G
2
T
r3
2
6.31024 kg
The mass is considerably close to that found in problem 60.
69. Halley’s Comet Every 74 years, comet Halley is visible from Earth. Find the
average distance of the comet from the Sun in astronomical units (AU).
For Earth, r1.0 AU and T1.0 y
r
r
b
a
3
T
T
b
a
2
ra
3rb3
T
T
b
a
2
3(1.0 A
U)3
2
18 AU
70. Area is measured in m2, so the rate at which area is swept out by a planet or
satellite is measured in m2/s.
a. How quickly is an area swept out by Earth in its orbit about the Sun?
r1.501011 m and
T3.156107s, in 365.25 days 1.00 y
T
r2
2.241015 m2/s
(1.501011 m)2
3.156107s
74 y
1.0 y
(3.9108m)3
(2.361106s)2
42
(6.671011 Nm2/kg2)
42(1.87108m)3
(6.671011 Nm2/kg2)(8.28104s)2
(40.0 N)(6.671011 Nm2/kg2)(1.901027 kg)
(9.80 m/s2)(7.15107m)2
154 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued
Physics: Principles and Problems Solutions Manual 155
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. How quickly is an area swept out by the Moon in its orbit about Earth?
Use 3.9108m as the average distance between Earth and the Moon, and
27.33 days as the period of the Moon.
2.01011 m2/s
7.2 Using the Law of Universal Gravitation
pages 192–193
Level 1
71. Satellite A geosynchronous satellite is one that appears to remain over one spot
on Earth, as shown in Figure 7-24. Assume that a geosynchronous satellite has
an orbital radius of 4.23107m.
■Figure 7-24 (Not to scale)
a. Calculate its speed in orbit.
v
Gm
rE
3.07103m/s or 3.07 km/s
b. Calculate its period.
T2
2
21.90
108s2
8.66104s or 24.1 h
72. Asteroid The asteroid Ceres has a mass of 71020 kg and a radius of 500 km.
a. What is gon the surface of Ceres?
g
G
rm
2
0.2 m/s2
b. How much would a 90-kg astronaut weigh on Ceres?
Fg mg (90 kg)(0.2 m/s2)20 N
(6.671011 Nm2/kg2)(71020 kg)
(500103m)2
(4.23107m)3
(6.671011 Nm2/kg2)(5.971024 kg)
r3
GmE
(6.671011 Nm2/kg2)(5.97x1024 kg)
4.23107m
Satellite
Earth
r
(3.9108m)2
2.36106s
Chapter 7 continued

73. Book A 1.25-kg book in space has a weight of 8.35 N. What is the value of the
gravitational field at that location?
g
m
F
1
8
..
2
3
5
5k
N
g
6.68 N/kg
74. The Moon’s mass is 7.341022 kg, and it is 3.8108m away from Earth.
Earth’s mass is 5.971024 kg.
a. Calculate the gravitational force of attraction between Earth and the Moon.
FG
mE
r
m
2M
(6.671011 Nm2/kg2)
2.01020 N
b. Find Earth’s gravitational field at the Moon.
g 0.0028 N/kg
Note that 2.031020 N instead of 2.01020 N is used to prevent
roundoff error.
75. Two 1.00-kg masses have their centers 1.00 m apart. What is the force of
attraction between them?
FgG
m
r
1m
22
6.671011 N
Level 2
76. The radius of Earth is about 6.38103km. A 7.20103-N spacecraft travels
away from Earth. What is the weight of the spacecraft at the following distances
from Earth’s surface?
a. 6.38103km
drErE2rE
Therefore, Fg
1
4
original weight
1
4
(7.20103 N) 1.80103N
b. 1.28104km
drE2rE3rE
Fg
1
9
(7.20103N) 8.00102N
77. Rocket How high does a rocket have to go above Earth’s surface before its
weight is half of what it is on Earth?
Fg
r
1
2
So r
1
Fg
(6.671011 Nm2/kg2)(1.00 kg)(1.00 kg)
(1.00 m)2
2.031020 N
7.341022 kg
F
m
(5.981024 kg)(7.341022 kg)
(3.8108m)2
156 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 157
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
If the weight is , the distance is 2
(rE) or
r2
(6.38106m) 9.02106m
9.02106m 6.38106m2.64106m
2.64103km
78. Two satellites of equal mass are put into orbit 30.0 m apart. The gravitational force
between them is 2.0107N.
a. What is the mass of each satellite?
FG
m
r
1m
22
,m1m2m
m
F
G
r2
1.6103kg
b. What is the initial acceleration given to each satellite by gravitational force?
Fnet ma
a
F
m
net
2
1.
.0
6
1
10
0
3
7
kN
g
1.31010 m/s2
79. Two large spheres are suspended close to each other. Their centers are 4.0 m
apart, as shown in Figure 7-25. One sphere weighs 9.8102N. The other sphere
has a weight of 1.96102N. What is the gravitational force between them?
■Figure 7-25
m1
9
9
..
8
8
01
m
0/
2
sN
2
1.0102kg
m2
19
.9
.8
60
m
10
/s
2
2
N
2.00101kg
FG
m
r
1m
22
8.3109N
(6.671011 Nm2/kg2)(1.0101kg)(2.00101kg)
(4.0 m)2
Fg
g
Fg
g
4.0 m
9.8102 N 1.96102 N
(2.0107N)(30.0 m)2
6.671011 Nm2kg2
1
2
Chapter 7 continued

80. Suppose the centers of Earth and the Moon are 3.9108m apart, and the
gravitational force between them is about 1.91020 N. What is the approximate
mass of the Moon?
FG
mE
r
m
2M
mM
G
Fm
r2
E
7.31022 kg
81. On the surface of the Moon, a 91.0-kg physics teacher weighs only 145.6 N.
What is the value of the Moon’s gravitational field at its surface?
Fgmg,
So g
F
m
g
1
94
15
.0
.6
kN
g
1.60 N/kg
Level 3
82. The mass of an electron is 9.11031 kg. The mass of a proton is
1.71027 kg. An electron and a proton are about 0.591010 m apart in a
hydrogen atom. What gravitational force exists between the proton and
the electron of a hydrogen atom?
FG
m
r
em
2p
1.01047 N
83. Consider two spherical 8.0-kg objects that are 5.0 m apart.
a. What is the gravitational force between the two objects?
FG
m
r
1m
22
1.71010 N
b. What is the gravitational force between them when they are 5.0101m
apart?
FG
m
r
1m
22
1.71012 N
(6.671011 Nm2/kg2)(8.0 kg)(8.0 kg)
(5.0101m)2
(6.671011 Nm2/kg2)(8.0 kg)(8.0 kg)
(5.0 m)2
(6.671011 Nm2/kg2)(9.11031 kg)(1.71027 kg)
(1.01010 m)2
(1.91020 N)(3.9108m)2
(6.671011 Nm/kg2)(5.971024 kg)
158 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 159
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
84. If you weigh 637 N on Earth’s surface, how much would you weigh on the planet
Mars? Mars has a mass of 6.421023 kg and a radius of 3.40106m.
m
F
g
g
9.8
60
37
m
N
/s2
65.0 kg
FG
m
r
1m
22
235 N
85. Using Newton’s version of Kepler’s third law and information from Table 7-1 on
page 173, calculate the period of Earth’s Moon if the orbital radius were twice the
actual value of 3.9108m.
TM
G
4
m
2
E
(r3)
(7.8
108m
)3
6.85106s or 79 days
86. Find the value of g, acceleration due to gravity, in the following situations.
a. Earth’s mass is triple its actual value, but its radius remains the same.
g
G
(r
m
E)E
2
9.80 m/s2
2mE→2g2(9.80 m/s2)19.6 m/s2
b. Earth’s radius is tripled, but its mass remains the same.
g
G
(r
m
E)E
2
9.80 m/s2
2rE→2.45 m/s2
c. Both the mass and radius of Earth are doubled.
g
G
(r
m
E)E
2
2mEand 2rE→4.90 m/s2
87. Astronaut What would be the strength of Earth’s gravitational field at a point
where an 80.0-kg astronaut would experience a 25.0 percent reduction in weight?
Fgmg (80.0 kg)(9.80 m/s2)784 N
Fg, reduced (784 N)(0.750) 588 N
greduced
Fg, re
m
duced
8
5
0
8
.0
8k
N
g
7.35 m/s2
2(9.80 m/s2)
4
2g
4
9.80 m/s2
4
g
4
42
(6.671011 Nm2/kg2)(5.9791024 kg)
(6.671011 Nm2/kg2)(65.0 kg)(6.371023 kg)
(3.43106m)2
Chapter 7 continued

Mixed Review
pages 193–194
Level 1
88. Use the information for Earth in Table 7-1 on page 173 to calculate the mass of
the Sun, using Newton’s version of Kepler’s third law.
T2
r3,
so mT2
r3 and
m
T
r3
2
2.011030 kg
89. Earth’s gravitational field is 7.83 N/kg at the altitude of the space shuttle. At this
altitude, what is the size of the force of attraction between a student with a mass
of 45.0 kg and Earth?
g
m
F
Fmg (45.0 kg)(7.83 N/kg) 352 N
90. Use the data from Table 7-1 on page 173 to find the speed and period of a
satellite that orbits Mars 175 km above its surface.
rrM175 km 3.40106m 0.175106m
3.58106 m
v
3.46103 m/s
T2
2
6.45103s or 1.79 h
(3.58106m)3
(6.671011 Nm2/kg2)(6.421023 kg)
r3
GMM
(6.671011 Nm2/kg2)(6.421023 kg)
3.58106m
GMM
r
(1.501011 m)3
(3.156107s)2
42
6.671011 Nm2/kg2
42
G
42
G
42
Gm
160 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 161
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 2
91. Satellite A satellite is placed in orbit, as shown in Figure 7-26, with a radius
that is half the radius of the Moon’s orbit. Find the period of the satellite in units
of the period of the Moon.
■Figure 7-26
T
T
M
s
2
r
r
M
s
3
So, Ts
r
r
M
s
3
TM
0.5
rM
0r
M
3TM
2
0.125
TM2
0.35TM
92. Cannonball The Moon’s mass is 7.31022 kg and its radius is 1785 km. If
Newton’s thought experiment of firing a cannonball from a high mountain were
attempted on the Moon, how fast would the cannonball have to be fired? How
long would it take the cannonball to return to the cannon?
v
1.7103m/s
T2
2
6.8103s
93. The period of the Moon is one month. Answer the following questions
assuming that the mass of Earth is doubled.
a. What would the period of the Moon be? Express your results in months.
T2
So, if Earth’s mass were doubled, but the radius remained the same,
then the period would be reduced by a factor of , or 0.707 months.
1
2
r3
Gm
(1.785106m)3
(6.671011 Nm2/kg2)(7.31022 kg)
r3
Gm
(6.671011 Nm2/kg2)(7.31022 kg)
1.785106m
Gm
r
Earth
Satellite
Moon
rM
rM
1
2
Chapter 7 continued

b. Where would a satellite with an orbital period of one month be located?
2
r3
2(Gm)
Thus, r3would be doubled, or rwould be increased by 2 1.26 times
the present radius of the Moon.
c. How would the length of a year on Earth be affected?
The length of a year on Earth would not be affected. It does not
depend on Earth’s mass.
Level 3
94. How fast would a planet of Earth’s mass and size have to spin so that an
object at the equator would be weightless? Give the period of rotation of the
planet in minutes.
The centripetal acceleration must equal the acceleration due to gravity so
that the surface of the planet would not have to supply any force
(otherwise known as weight).
G
m
r
E
2
m
v
Gm
rE
But, v
2T
r
, so T
2
G
r
m
3
E
2
5.07103s84.5 min
95. Car Races Suppose that a Martian base has been established and car races are
being considered. A flat, circular race track has been built for the race. If a car
can achieve speeds of up to 12 m/s, what is the smallest radius of a track for
which the coefficient of friction is 0.50?
The force that causes the centripetal acceleration is the static
friction force:
Fstatic smg
The centripetal acceleration is ac
So, smg
Thus, r
v
s
2
g
Note that g
(rp
G
la
m
net)2
mv2
r
v2
r
(6.38106m)3
(6.671011 Nm2/kg2)(5.971024 kg)
2r
Gm
rE
2r
v
mv2
r
1
3
T
2
r3
Gm
T
2
162 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 163
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
To find gon Mars, the following calculation is used.
mMars 6.371023 kg, and RMars 3.43106m
So, gMars 3.61 m/s2
Therefore, R
R8.0101m
96. Apollo 11 On July 19, 1969, Apollo 11’s revolution around the Moon was adjusted
to an average orbit of 111 km. The radius of the Moon is 1785 km, and the mass
of the Moon is 7.31022 kg.
a. How many minutes did Apollo 11 take to orbit the Moon once?
rorbit 1785103m 111103m
T2
2
7.4103s
1.2102min
b. At what velocity did Apollo 11 orbit the Moon?
v
rG
or
m
bit
1.6103m/s
Thinking Critically
page 194
97. Analyze and Conclude Some people say that the tides on Earth are caused by
the pull of the Moon. Is this statement true?
a. Determine the forces that the Moon and the Sun exert on a mass, m, of water
on Earth. Your answer will be in terms of mwith units of N.
FS, m 6.671011 Nm2/kg2
(5.90103N)m
FM, m 6.671011 Nm2/kg2
(3.40105N)m
b. Which celestial body, the Sun or the Moon, has a greater pull on the waters
of Earth?
The Sun pulls approximately 100 times stronger on the waters of
Earth.
(7.361022 kg)(m)
(3.80108m)2
(1.991030 kg)(m)
(1.501011 m)2
(6.671011 Nm2/kg2)(7.31022 kg)
1896103m
(1896103m)3
(6.671011 Nm2/kg2)(7.31022 kg)
r3
Gm
(12 m/s)2
(0.50)(3.61 m/s2)
Chapter 7 continued

c. Determine the difference in force exerted by the Moon on the water at the
near surface and the water at the far surface (on the opposite side) of Earth,
as illustrated in Figure 7-27. Again, your answer will be in terms of mwith
units of N.
■Figure 7-27 (Not to scale)
Fm, mA Fm, mB (6.671011 Nm2kg2)(7.361022 kg)(m)
(2.28106N)m
d. Determine the difference in force exerted by the Sun on water at the near
surface and on water at the far surface (on the opposite side) of Earth.
FS, mA FS, mB (6.671011 Nm2kg2)(1.991030 kg)(m)
(1.00106N)m
e. Which celestial body has a greater difference in pull from one side of Earth to
the other?
the Moon
f. Why is the statement that the tides result from the pull of the Moon
misleading? Make a correct statement to explain how the Moon causes tides
on Earth.
The tides are primarily due to the difference between the pull of the
Moon on Earth’s near side and Earth’s far side.
98. Make and Use Graphs Use Newton’s law of universal gravitation to find an
equation where xis equal to an object’s distance from Earth’s center, and yis its
acceleration due to gravity. Use a graphing calculator to graph this equation,
using 6400–6600 km as the range for xand 9–10 m/s2as the range for y. The
equation should be of the form yc(1/x2). Trace along this graph and find yfor
the following locations.
a. at sea level, 6400 km
c(GmE)(106m2/km2)4.0108units
acc 9.77 m/s2
b. on top of Mt. Everest, 6410 km
9.74 m/s2
1
(1.501011 m6.37106m)2
1
(1.501011 m6.37106m)2
1
(3.80108m6.37106m)2
1
(3.80108m6.37106m)2
Earth Moon
Far tidal bulge
Near tidal bulge
164 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 165
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. in a typical satellite orbit, 6500 km
9.47 m/s2
d. in a much higher orbit, 6600 km
9.18 m/s2
Writing in Physics
page 194
99. Research and describe the historical development of the measurement of the
distance between the Sun and Earth.
One of the earliest crude measurements was made by James Bradley in
1732. The answers also should discuss measurements of the transits of
Venus done in the 1690s.
100. Explore the discovery of planets around other stars. What methods did the
astronomers use? What measurements did they take? How did they use Kepler’s
third law?
Astronomers measure the star’s tiny velocity due to the gravitational
force exerted on it by a massive planet. The velocity is calculated by
measuring the Doppler shift of the star’s light that results from that
motion. The velocity oscillates back and forth as the planets orbit the
star, allowing calculation of the planet’s period. From the size of the
velocity they can estimate the planet’s distance and mass. By comparing
the distances and periods of planets in solar systems with multiple
planets and using Kepler’s third law, astronomers can better separate
the distances and masses of stars and planets.
Cumulative Review
page 194
101. Airplanes A jet airplane took off from Pittsburgh at 2:20 P.M. and landed in
Washington, DC, at 3:15 P.M. on the same day. If the jet’s average speed while in
the air was 441.0 km/h, what is the distance between the cities? (Chapter 2)
t55 min 0.917 h
v
d
t
dv
t
(441.0 km/h)(0.917 h)
404 km
102. Carolyn wants to know how much her brother Jared weighs. He agrees to stand
on a scale for her, but only if they are riding in an elevator. If he steps on the
scale while the elevator is accelerating upward at 1.75 m/s2and the scale reads
716 N, what is Jared’s usual weight on Earth? (Chapter 4)
Identify Jared as the system and upward as positive.
Fnet Fscale on Jared FEarth’s mass on Jared
ma
Chapter 7 continued

Fscale on Jared FEarth’s mass on Jared
a
FEarth’s mass on Jared1
g
a
FEarth’s mass on Jared
608 N
103. Potato Bug A 1.0-g potato bug is walking around the outer rim of an upside-
down flying disk. If the disk has a diameter of 17.2 cm and the bug moves at a
rate of 0.63 cm/s, what is the centripetal force acting on the bug? What agent
provides this force? (Chapter 6)
Fc 5.0107N,
provided by the frictional force between the bug and the flying disk
Challenge Problem
page 176
Astronomers have detected three planets that orbit the star Upsilon Andromedae.
Planet B has an average orbital radius of 0.059 AU and a period of 4.6170 days. Planet C
has an average orbital radius of 0.829 AU and a period of 241.5 days. Planet D has an
average orbital radius of 2.53 AU and a period of 1284 days. (Distances are given in
astronomical units (AU)—Earth’s average distance from the Sun. The distance from
Earth to the Sun is 1.00 AU.)
1. Do these planets obey Kepler’s third law?
Test by calculating the following ratio
T
r3
2
.
For planet B,
T
rB
B
3
2
(4
(
.
0
6
.
1
0
7
5
0
9
d
A
a
U
y
)
s
3
)2
9.6106AU3/days2
C
BD
Upsilon
Andromedae
rC
rB
rD
(0.0010 kg)(0.0063 cm)2
0.086 m
mv2
r
716 N
1
1
9.
.7
85
0m
m/
/s
s
2
2
Fscale on Jared
1
g
a
FEarth’s mass on Jared
g
166 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 7 continued

Physics: Principles and Problems Solutions Manual 167
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
For planet C,
T
rC
C
3
2
(2
(0
4
.
1
8
.
2
5
9
d
A
a
U
ys
)3
)2
9.77106AU3/days2
For planet D,
T
rD
D
3
2
(1
(
2
2
8
.5
4
3
d
A
a
U
y
)
s
3
)2
9.82106AU3/days2
These values are quite close, so Kepler’s third law is obeyed.
2. Find the mass of the star Upsilon Andromedae in units of the Sun’s mass.
T
r3
2
For the Earth-Sun system,
T
r3
2
(1
(1
.0
.0
00
00A
y
U
)2
)3
1.000 AU3/y2
For the planet C-Upsilon system,
T
r3
2
9.77106AU3/days2
(9.77106AU3/days2)(365 days/y)21.30 AU3/y2
The ratio of the two shows the star’s slightly heavier mass to be 1.30 that
of the Sun.
Gmstar
42
Gmcentral body
42
Chapter 7 continued


Physics: Principles and Problems Solutions Manual 169
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
8Rotational Motion
CHAPTER
Practice Problems
8.1 Describing Rotational
Motion
pages 197–200
page 200
1. What is the angular displacement of each of
the following hands of a clock in 1 h? State
your answer in three significant digits.
a. the second hand
(60)(2rad)
120rad or 377 rad
b. the minute hand
2rad or 6.28 rad
c. the hour hand
(2rad)
rad or 0.524 rad
2. If a truck has a linear acceleration of
1.85 m/s2and the wheels have an angular
acceleration of 5.23 rad/s2, what is the
diameter of the truck’s wheels?
r
a
0.354 m
Thus, the diameter is 0.707 m.
3. The truck in the previous problem is towing
a trailer with wheels that have a diameter of
48 cm.
a. How does the linear acceleration of the
trailer compare with that of the truck?
The changes in velocity are the
same, so the linear accelerations
are the same.
b. How do the angular accelerations of the
wheels of the trailer and the wheels of
the truck compare?
Because the radius of the wheel is
reduced from 35.4 cm to 24 cm, the
angular acceleration will be
increased.
15.23 rad/s2
2
7.7 rad/s2
4. You want to replace the tires on your car
with tires that have a larger diameter. After
you change the tires, for trips at the same
speed and over the same distance, how will
the angular velocity and number of revolu-
tions change?
Because ,if ris increased, will
decrease. The number of revolutions
will also decrease.
Section Review
8.1 Describing Rotational
Motion
pages 197–200
page 200
5. Angular Displacement A movie lasts 2 h.
During that time, what is the angular dis-
placement of each of the following?
a. the hour hand
(2rad) rad
b. the minute hand
(2)(2rad) 4rad
6. Angular Velocity The Moon rotates
once on its axis in 27.3 days. Its radius is
1.74106m.
3
1
6
v
r
1.85 m/s2
0.24 m
a2
r
1.85 m/s2
5.23 rad/s2
6
1
12

a. What is the period of the Moon’s rota-
tion in seconds?
period (27.3 day)(24 h/day)
(3600 s/h)
2.36106s
b. What is the frequency of the Moon’s
rotation in rad/s?
rev/s, or
2.66106rad/s
c. What is the linear speed of a rock on
the Moon’s equator due only to the
Moon’s rotation
vr
(1.74106m)(2.66106rad/s)
4.63 m/s
d. Compare this speed with the speed of a
person on Earth’s equator due to Earth’s
rotation.
The speed on Earth’s equator is
464 m/s, or about 100 times faster.
7. Angular Displacement The ball in a com-
puter mouse is 2.0 cm in diameter. If you
move the mouse 12 cm, what is the angular
displacement of the ball?
dr
so 12 rad
8. Angular Displacement Do all parts of the
minute hand on a watch have the same
angular displacement? Do they move the
same linear distance? Explain.
angular displacement—yes; linear dis-
tance—no, because linear distance is a
function of the radius
9. Angular Acceleration In the spin cycle
of a clothes washer, the drum turns at
635 rev/min. If the lid of the washer is
opened, the motor is turned off. If the
drum requires 8.0 s to slow to a stop, what
is the angular acceleration of the drum?
i635 rpm 66.53 rad/s
f0.0, so 66.5 rad/s
and 8.3 rad/s2
10. Critical Thinking A CD-ROM has a spiral
track that starts 2.7 cm from the center of
the disk and ends 5.5 cm from the center.
The disk drive must turn the disk so that
the linear velocity of the track is a constant
1.4 m/s. Find the following.
a. the angular velocity of the disk (in rad/s
and rev/min) for the start of the track
52 rad/s or 5.0102rev/min
b. the disk’s angular velocity at the end of
the track
25 rad/s or 2.4102rev/min
c. the disk’s angular acceleration if the
disk is played for 76 min
5.9103rad/s2
25 rad/s 52 rad/s
(76 min)(60 s/min)
fi
t
t
1.4 m/s
0.055 m
v
r
1.4 m/s
0.027 m
v
r
66.5 rad/s
8.0 s
t
12 cm
1.0 cm
d
r
1
2.36106
1
period
170 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 171
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Practice Problems
8.2 Rotational Dynamics
pages 201–210
page 203
11. Consider the wrench in Example Problem
1. What force is needed if it is applied to
the wrench at a point perpendicular to the
wrench?
Fr sin
so F
1.4102N
12. If a torque of 55.0 Nm is required and the
largest force that can be exerted by you is
135 N, what is the length of the lever arm
that must be used?
For the shortest possible lever arm,
90.0°.
Fr sin
so r
0.407 m
13. You have a 0.234-m-long wrench. A job
requires a torque of 32.4 Nm, and you can
exert a force of 232 N. What is the smallest
angle, with respect to the vertical, at which
the force can be exerted?
Fr sin
so sin1
sin1
36.6°
14. You stand on the pedal of a bicycle. If you
have a mass of 65 kg, the pedal makes an
angle of 35° above the horizontal, and the
pedal is 18 cm from the center of the chain
ring, how much torque would you exert?
The angle between the force and the
radius is 90° 35° 55°.
Fr sin
mgr sin
(65 kg)(9.80 m/s2)(0.18 m)(sin 55°)
94 Nm
15. If the pedal in problem 14 is horizontal,
how much torque would you exert? How
much torque would you exert when the
pedal is vertical?
Horizontal 90.0°
so Fr sin
mgr sin
(65 kg)(9.80 m/s2)(0.18 m)
(sin 90.0°)
1.1102Nm
Vertical = 0.0°
So Fr sin
mgr sin
(65 kg)(9.80 m/s2)(0.18 m)
(sin 0.0°)
0.0 Nm
page 205
16. Ashok, whose mass is 43 kg, sits 1.8 m
from the center of a seesaw. Steve, whose
mass is 52 kg, wants to balance Ashok.
How far from the center of the seesaw
should Steve sit?
FArAFSrS
so rS
1.5 m
17. A bicycle-chain wheel has a radius of
7.70 cm. If the chain exerts a 35.0-N force
on the wheel in the clockwise direction,
what torque is needed to keep the wheel
from turning?
(43 kg)(1.8 m)
52 kg
mArA
mS
mAgrA
mSg
FArA
FS
32.4 Nm
(232 N)(0.234 m)
Fr
55.0 Nm
(135 N)(sin 90.0°)
Fsin
35 Nm
(0.25 m)(sin 90.0°)
rsin
Chapter 8 continued
chain Fgr
(35.0 N)(0.0770 m)
2.70 Nm
Thus, a torque of 2.70 Nm must be exerted to balance this torque.
18. Two baskets of fruit hang from strings going around
pulleys of different diameters, as shown in
Figure 8-6. What is the mass of basket A?
12
F1r1F2r2
m1gr1m2gr2
m1
0.056 kg
19. Suppose the radius of the larger pulley in problem 18 was
increased to 6.0 cm. What is the mass of basket A now?
m1
0.042 kg
20. A bicyclist, of mass 65.0 kg, stands
on the pedal of a bicycle. The crank,
which is 0.170 m long, makes a
45.0° angle with the vertical, as
shown in Figure 8-7. The crank is
attached to the chain wheel, which
has a radius of 9.70 cm. What force
must the chain exert to keep the
wheel from turning?
cr ch
Fcrrcr sin Fchrch
so Fch
789 N
(65.0 kg)(9.80 m/s2)(0.170 m)(sin 45.0°)
0.097 m
mgrcr sin
rch
Fcrrcr sin
rch
(0.23 kg)(1.1 cm)
6.0 cm
m2r2
r1
(0.23 kg)(1.1 cm)
4.5 cm
m2r2
r1
172 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
4.5 cm
0.23 kg
A
1.1 cm
0.170 m
45.0°
9.70 cm
■Figure 8-6
■Figure 8-7

Physics: Principles and Problems Solutions Manual 173
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
page 208
21. Two children of equal masses sit 0.3 m
from the center of a seesaw. Assuming that
their masses are much greater than that of
the seesaw, by how much is the moment of
inertia increased when they sit 0.6 m from
the center?
For the mass of the two children, I
mr2mr22mr2.
When ris doubled, Iis multiplied by a
factor of 4.
22. Suppose there are two balls with equal
diameters and masses. One is solid, and the
other is hollow, with all its mass distributed
at its surface. Are the moments of inertia of
the balls equal? If not, which is greater?
The more of the mass that is located far
from the center, the greater the moment
of inertia. Thus, the hollow ball has a
greater value of I.
23. Figure 8-9 shows three massive spheres on
a rod of very small mass. Consider the
moment of inertia of the system, first when
it is rotated about sphere A, and then when
it is rotated about sphere C. Are the
moments of inertia the same or different?
Explain. If the moments of inertia are
different, in which case is the moment of
inertia greater?
■Figure 8-9
The moments of inertia are different. If
the spacing between spheres is rand
each sphere has mass m, then rotation
about sphere A is
Imr2m(2r)25mr 2.
Rotation about sphere C is
Imr2mr 22mr 2.
The moment of inertia is greater when
rotating around sphere A.
24. Each sphere in the previous problem has a
mass of 0.10 kg. The distance between
spheres A and C is 0.20 m. Find the moment
of inertia in the following instances: rotation
about sphere A, rotation about sphere C.
About sphere A:
Imr2m(2r)2
5mr2
(5)(0.10 kg)(0.20 m)2
0.020 kgm2
About sphere C:
Imr2mr 2
2mr2
(2)(0.10 kg)(0.20 m)2
0.0080 kgm2
page 210
25. Consider the wheel in Example Problem 4.
If the force on the strap were twice as great,
what would be the speed of rotation of the
wheel after 15 s?
Torque is now twice as great.The angu-
lar acceleration is also twice as great,
so the change in angular velocity is
twice as great. Thus, the final angular
velocity is 32rad/s, or 16 rev/s.
26. A solid wheel accelerates at 3.25 rad/s2
when a force of 4.5 N exerts a torque on it.
If the wheel is replaced by a wheel with all
of its mass on the rim, the moment of iner-
tia is given by Imr2. If the same angular
velocity were desired, what force would
have to be exerted on the strap?
The angular acceleration has not
changed, but the moment of inertia is
twice as great. Therefore, the torque
must be twice as great.The radius of
the wheel is the same, so the force
must be twice as great, or 9.0 N.
CA
Chapter 8 continued

27. A bicycle wheel can be accelerated either by pulling on the chain that is on the
gear or by pulling on a string wrapped around the tire. The wheel’s radius is
0.38 m, while the radius of the gear is 0.14 m. If you obtained the needed
acceleration with a force of 15 N on the chain, what force would you need to
exert on the string?
The torque on the wheek comes from either the chain or the string.
chain Iwheelwheel
wheel Iwheelwheel
Thus, chain wheel
Fchainrgear Fstringrwheel
Fstring
5.5 N
28. The bicycle wheel in problem 27 is used with a smaller gear whose radius is
0.11 m. The wheel can be accelerated either by pulling on the chain that is on
thegear or by pulling string that is wrapped around the tire. If you obtained the
needed acceleration with a force of 15 N on the chain, what force would you
need to exert on the string?
Fstring
4.3 N
29. A disk with a moment of inertia of 0.26 kgm2is attached to a smaller disk
mounted on the same axle. The smaller disk has a diameter of 0.180 m and a
mass of 2.5 kg. A strap is wrapped around the smaller disk, as shown in
Figure 8-10. Find the force needed to give this system an angular acceleration
of 2.57 rad/s2.
so F
7.7 N
1
2
(2.5 kg)(0.090 m)20.26 kgm2(2.57 rad/s2)
0.090 m
1
2
msmallrsmall2Ilarge
r
(Ismall Ilarge)
r
I
r
Fr
I
I
(15 N)(0.11 m)
0.38 m
Fchainrgear
rwheel
(15 N)(0.14 m)
0.38 m
Fchainrgear
rwheel
174 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
F
■Figure 8-10

Physics: Principles and Problems Solutions Manual 175
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
8.2 Rotational Dynamics
pages 201–210
page 210
30. Torque Vijesh enters a revolving door that
is not moving. Explain where and how
Vijesh should push to produce a torque
with the least amount of force.
To produce a torque with the least
force, you should push as close to the
edge as possible and at right angles to
the door.
31. Lever Arm You try to open a door, but you
are unable to push at a right angle to the
door. So, you push the door at an angle of
55° from the perpendicular. How much
harder would you have to push to open the
door just as fast as if you were to push it at
90°?
The angle between the force and the
radius is 35°. Torque is Fr sin .
Because sin 90°1, and sin 35°0.57,
you would have to increase the
force by a ratio of 1.75 to obtain
the same torque.
32. Net Torque Two people are pulling on
ropes wrapped around the edge of a large
wheel. The wheel has a mass of 12 kg and a
diameter of 2.4 m. One person pulls in a
clockwise direction with a 43-N force, while
the other pulls in a counterclockwise direc-
tion with a 67-N force. What is the net
torque on the wheel?
net 12
F1rF2r
(F1F2)d
(43 N 67 N)
(2.4 m)
29 Nm
33. Moment of Inertia Refer to Table 8-2 on
page 206 and rank the moments of inertia
from least to greatest of the following
objects: a sphere, a wheel with almost all of
its mass at the rim, and a solid disk. All
have equal masses and diameters. Explain
the advantage of using the one with the
least moment of inertia.
from least to greatest: sphere mr2,
solid disk mr2, wheel (mr2)
The less the moment of inertia, the less
torque needed to give an object the
same angular acceleration.
34. Newton’s Second Law for Rotational
Motion A rope is wrapped around a pulley
and pulled with a force of 13.0 N. The pul-
ley’s radius is 0.150 m. The pulley’s rota-
tional speed goes from 0.0 to 14.0 rev/min
in 4.50 s. What is the moment of inertia of
the pulley?
I
5.99 kgm2
35. Critical Thinking A ball on an extremely
low-friction, tilted surface, will slide down-
hill without rotating. If the surface is rough,
however, the ball will roll. Explain why,
using a free-body diagram.
(13.0 N)(0.150 m)(4.50 s)
14.0
m
re
iv
n
0.0
m
re
iv
n
2
re
r
v
ad
6
m
0in
s
Frt
fi
Fr
t
1
2
2
5
1
2
1
2
1
0.57
Chapter 8 continued
Torque: Fr sin . The force is due to
friction, and the torque causes the ball
to rotate clockwise. If the surface is fric-
tion-free, then there is no force parallel
to the surface, no torque, and thus no
rotation. Remember, forces acting on
the pivot point (the center of the ball)
are ignored.
Practice Problems
8.3 Equilibrium
pages 211–217
page 215
36. What would be the forces exerted by the
two sawhorses if the ladder in Example
Problem 5 had a mass of 11.4 kg?
Because no distances have changed,
the equations are still valid:
FB
FB32 N
FAmg1
(11.4 kg)(9.80 m/s2)1
8.0101N
37. A 7.3-kg ladder, 1.92 m long, rests on two
sawhorses, as shown in Figure 8-15.
Sawhorse A, on the left, is located 0.30 m
from the end, and sawhorse B, on the right,
is located 0.45 m from the other end.
Choose the axis of rotation to be the center
of mass of the ladder.
■Figure 8-15
a. What are the torques acting on the
ladder?
clockwise: AFArA
FA(0.96 m – 0.30 m)
(0.66 m)FA
counterclockwise:
BFBrB
FB(0.96 m 0.45 m)
(0.51 m)FB
b. Write the equation for rotational equi-
librium.
net AB0
so BA
(0.51 m)FB((0.66 m)FA)
(0.51 m)FB(0.66 m)FA
c. Solve the equation for FAin terms of Fg.
FgFAFB
thus, FAFgFB
Fg
or FA
31 N
d. How would the forces exerted by the
two sawhorses change if A were moved
very close to, but not directly under, the
center of mass?
(7.3 kg)(9.80 m/s2)
1
0
0.
.6
56
1m
m
ma
1
0
0.
.6
56
1m
m
Fg
1
0
0.
.6
56
1m
m
(0.66 m)FA
0.51 m
AB
1.92 m
0.66 m 0.51 m 0.45 m0.30 m
0.30 m
1.05 m
rg
rB
(0.30 m)(11.4 kg)(9.80 m/s2)
1.05 m
rgmg
rB
Extremely low-friction
surface
Rough
surface
Surface
Fg
Fnormal Fnormal
Ffriction
Ffriction Surface
Fg
rr
176 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 177
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
FAwould become greater, and FB
would be less.
38. A 4.5-m-long wooden plank with a 24-kg
mass is supported in two places. One sup-
port is directly under the center of the
board, and the other is at one end. What
are the forces exerted by the two supports?
Pick the center of mass of the board as
the pivot. The unsupported end exerts
no torque, so the supported end does
not have to exert any torque. Therefore,
all the force is exerted by the center
support. That force is equal to the
weight of the board:
Fcenter Fg(24 kg)(9.80 m/s2)
2.4102N
Fend 0 N
39. A 85-kg diver walks to the end of a diving
board. The board, which is 3.5 m long with
a mass of 14 kg, is supported at the center
of mass of the board and at one end. What
are the forces on the two supports?
Choose the center of mass of the board
as the pivot. The force of Earth’s gravity
on the board is exerted totally on the
support under the center of mass.
end diver
Fendrend Fdiverrdiver
Thus, Fend
8.3102N
To find the force on the center support,
notice that because the board is not
moving,
Fend Fcenter Fdiver Fg
Thus, Fcenter Fdiver FgFend
2Fdiver Fg
2mdivergmboardg
g(2mdivergmboard)
(9.80 m/s2)
(2(85 kg) 14 kg)
1.8103N
Section Review
8.3 Equilibrium
pages 211–217
page 217
40. Center of Mass Can the center of mass of
an object be located in an area where the
object has no mass? Explain.
Yes, an object moves as if all its mass
is concentrated at the center of mass.
There is nothing in the definition that
requires any or all of the object’s mass
to be at that location.
41. Stability of an Object Why is a modified
vehicle with its body raised high on risers
less stable than a similar vehicle with its
body at normal height?
The center of mass of the vehicle will
be raised, but the size of its base will
not be increased. Therefore, it needs to
be tipped at a smaller angle to get the
center of mass outside the base of the
vehicle.
42. Conditions for Equilibrium Give an
example of an object for each of the follow-
ing conditions.
a. rotational equilibrium, but not transla-
tional equilibrium
a book that is dropped so it falls
without rotating
b. translational equilibrium, but not rota-
tional equilibrium
a seesaw that is not balanced and
rotates until one person’s feet hit the
ground
43. Center of Mass Where is the center of
mass of a roll of masking tape?
It is in the middle of the roll, in the open
space.
(85 kg)(9.80 m/s2)(1.75 m)
1.75 m
mdivergrdiver
rend
Fdiverrdiver
rend
Chapter 8 continued
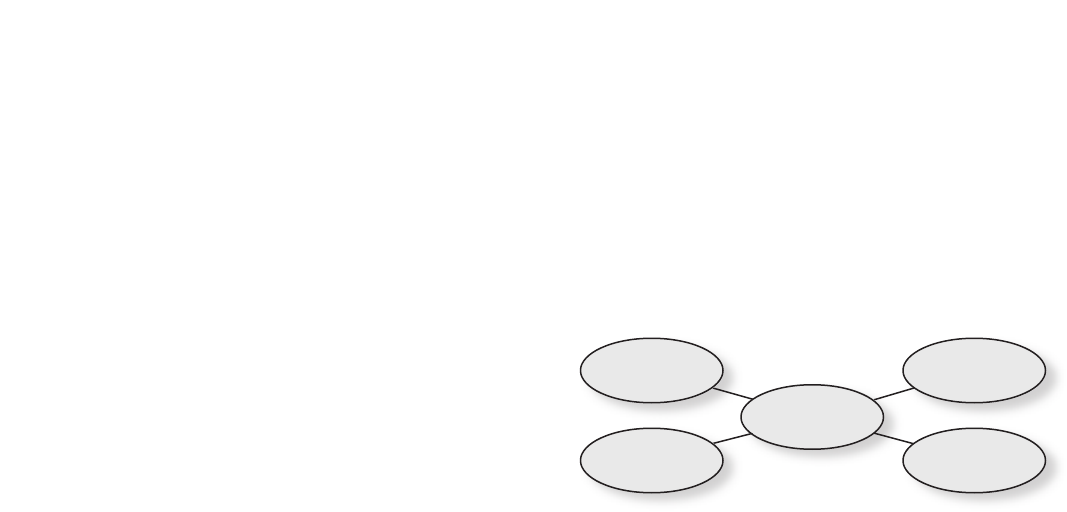
44. Locating the Center of Mass Describe
how you would find the center of mass of
this textbook.
Obtain a piece of string and attach a
small weight to it. Suspend the string
and the weight from one corner of the
book. Draw a line along the string.
Suspend the two from another corner of
the book. Again, draw a line along the
string. The point where the lines cross
is the center of mass.
45. Rotating Frames of Reference A penny is
placed on a rotating, old-fashioned record
turntable. At the highest speed, the penny
starts sliding outward. What are the forces
acting on the penny?
Earth’s mass exerts a downward force.
The turntable’s surface exerts both an
upward force to balance gravity and an
inward force due to friction that gives
the penny its centripetal acceleration.
There is no outward force. If it were not
for friction, the penny would move in a
straight line.
46. Critical Thinking You have learned why
the winds around a low-pressure area move
in a counterclockwise direction. Would the
winds move in the same or opposite direc-
tion in the southern hemisphere? Explain.
They would move in the opposite direc-
tion. Winds from the north move from
the equator, where the linear speed due
to rotation is highest, to mid-latitudes,
where it is lower. Thus, the winds bend
to the east. Winds from the south blow
from regions where the linear speed is
low to regions where it is higher; thus,
they bend to the west.These two fac-
tors result in a clockwise rotation
around a low-pressure area.
Chapter Assessment
Concept Mapping
page 222
47. Complete the following concept map using
the following terms: angular acceleration,
radius, tangential acceleration, centripetal
acceleration.
Mastering Concepts
page 222
48. A bicycle wheel rotates at a constant
25 rev/min. Is its angular velocity decreas-
ing, increasing, or constant? (8.1)
It is constant.
49. A toy rotates at a constant 5 rev/min. Is its
angular acceleration positive, negative, or
zero? (8.1)
It is zero.
50. Do all parts of Earth rotate at the same rate?
Explain. (8.1)
Yes, because all parts of a rigid body
rotate at the same rate.
51. A unicycle wheel rotates at a constant
14 rev/min. Is the total acceleration of a
point on the tire inward, outward, tangen-
tial, or zero? (8.1)
It is inward (centripetal).
52. Think about some possible rotations of
your textbook. Are the moments of inertia
about these three axes the same or differ-
ent? Explain. (8.2)
They are all different.The one with the
most mass, farthest from the axis, has
the greatest moment of inertia.
178 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
Tangential
acceleration
Angular
velocity
Angular
acceleration
Radius
Centripetal
acceleration

Physics: Principles and Problems Solutions Manual 179
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
53. Torque is important when tightening bolts.
Why is force not important? (8.2)
An angular acceleration must be pro-
duced to tighten a bolt. Different
torques can be exerted with wrenches
of different lengths.
54. Rank the torques on the five doors shown
in Figure 8-18 from least to greatest. Note
that the magnitude of all the forces is the
same. (8.2)
■Figure 8-18
0ED C B A
55. Explain how you can change an object’s
angular frequency. (8.2)
Change the amount of torque applied to
the object or change the moment of
inertia.
56. To balance a car’s wheel, it is placed on a
vertical shaft and weights are added to
make the wheel horizontal. Why is this
equivalent to moving the center of mass
until it is at the center of the wheel? (8.3)
When the wheel is balanced so it does
not tilt (rotate) in any direction, then
there is no net torque on it.This means
that the center of mass is at the pivot
point.
57. A stunt driver maneuvers a monster truck so
that it is traveling on only two wheels.
Where is the center of mass of the truck?
(8.3)
It is directly above the line between the
points where the two wheels are touch-
ing the ground.There is no net torque
on the truck, so it is momentarily stable.
58. Suppose you stand flat-footed, then you rise
and balance on tiptoe. If you stand with
your toes touching a wall, you cannot
balance on tiptoe. Explain. (8.3)
Your center of mass must be above the
point of support. But your center of
mass is roughly in the center of your
body. Thus, while you are on your toes,
about half of your body must be in front
of your toes, and half must be behind. If
your toes are against the wall, no part
of your body can be in front of your
toes.
59. Why does a gymnast appear to be floating
on air when she raises her arms above her
head in a leap? (8.3)
She moves her center of mass closer to
her head.
60. Why is a vehicle with wheels that have a
large diameter more likely to roll over than
a vehicle with wheels that have a smaller
diameter? (8.3)
The center of mass of the vehicle with
the larger wheels is located at a higher
point. Thus it does not have to be tilted
very far before it rolls over.
Applying Concepts
pages 222–223
61. Two gears are in contact and rotating. One
is larger than the other, as shown in Figure
8-19. Compare their angular velocities. Also
compare the linear velocities of two teeth
that are in contact.
■Figure 8-19
D
AB
C
E
Chapter 8 continued

The teeth have identical linear veloci-
ties. Because the radii are different
and , the angular velocities are
different.
62. Videotape When a videotape is rewound,
why does it wind up fastest towards the end?
The machine turns the spool at a con-
stant angular velocity. Towards the end,
the spool has the greatest radius.
Because vr, the velocity of the tape
is fastest when the radius is greatest.
63. Spin Cycle What does a spin cycle of a
washing machine do? Explain in terms of
the forces on the clothes and water.
In the spin cycle, the water and clothes
undergo great centripetal accelerations.
The drum can exert forces on the
clothes, but when the water reaches the
holes in the drum, no inward force can
be exerted on it and it therefore moves
in a straight line, out of the drum.
64. How can you experimentally find the
moment of inertia of an object?
You can apply a known torque and mea-
sure the resulting angular acceleration.
65. Bicycle Wheels Three bicycle wheels have
masses that are distributed in three different
ways: mostly at the rim, uniformly, and
mostly at the hub. The wheels all have the
same mass. If equal torques are applied to
them, which one will have the greatest
angular acceleration? Which one will have
the least?
The more mass there is far from the
axis, the greater the moment of inertia.
If torque is fixed, the greater the
moment of inertia, the less the angular
acceleration. Thus, the wheel with mass
mostly at the hub has the least moment
of inertia and the greatest angular
acceleration. The wheel with mass
mostly near the rim has the greatest
moment of inertia and the least angular
acceleration.
66. Bowling Ball When a bowling ball leaves a
bowler’s hand, it does not spin. After it has
gone about half the length of the lane, how-
ever, it does spin. Explain how its rotation
rate increased and why it does not continue
to increase.
Its rotation rate can be increased only if
a torque is applied to it.The frictional
force of the alley on the ball provides
this force. Once the ball is rolling so
that there is no velocity difference
between the surface of the ball and the
alley, then there is no more frictional
force and thus no more torque.
67. Flat Tire Suppose your car has a flat tire.
You get out your tools and find a lug
wrench to remove the nuts off the bolt
studs. You find it impossible to turn the
nuts. Your friend suggests ways you might
produce enough torque to turn them. What
three ways might your friend suggest?
Put an extension pipe on the end of the
wrench to increase the lever arm, exert
your force at right angles to the wrench,
or exert a greater force, perhaps by
standing on the end of the wrench.
68. Tightrope Walkers Tightrope walkers
often carry long poles that sag so that the
ends are lower than the center as shown in
Figure 8-20. How does such a pole increase
the tightrope walker’s stability? Hint:
Consider both center of mass and moment of
inertia.
■Figure 8-20
v
r
180 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 181
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The pole increases moment of inertia
because of its mass and length. The
drooping ends of the pole bring the
center of mass closer to the wire, thus
reducing the torque on the walker. The
increased moment of inertia and
decreased torque both reduce the angu-
lar acceleration if the walker becomes
unbalanced. The walker can also use
the pole to easily shift the center of
mass over the wire to compensate for
instability.
69. Merry-Go-Round While riding a merry-go-
round, you toss a key to a friend standing
on the ground. For your friend to be able to
catch the key, should you toss it a second or
two before you reach the spot where your
friend is standing or wait until your friend
is directly behind you? Explain.
You have forward tangential velocity, so
the key will leave your hand with that
velocity. Therefore, you should toss it
early.
70. Why can you ignore forces that act on the
axis of rotation of an object in static equi-
librium when determining the net torque?
The torque caused by these forces is
zero because the lever arm is zero.
71. In solving problems about static equilibri-
um, why is the axis of rotation often placed
at a point where one or more forces are act-
ing on the object?
That makes the torque caused by that
force equal to zero, reducing the num-
ber of torques that must be calculated.
Mastering Problems
8.1 Describing Rotational Motion
pages 223–224
Level 1
72. A wheel is rotated so that a point on the
edge moves through 1.50 m. The radius
of the wheel is 2.50 m, as shown in
Figure 8-21. Through what angle (in radi-
ans) is the wheel rotated?
■Figure 8-21
dr
so
0.600 rad
73. The outer edge of a truck tire that has a radius
of 45 cm has a velocity of 23 m/s. What is the
angular velocity of the tire in rad/s?
vr,
51 rad/s
74. A steering wheel is rotated through 128°, as
shown in Figure 8-22. Its radius is 22 cm.
How far would a point on the steering
wheel’s edge move?
■Figure 8-22
22 cm 128°
23 m/s
0.45 m
v
r
1.50 m
2.50 m
d
r
2.50 m
1.50 m
Chapter 8 continued

dr
(0.22 m)(128°)
0.49 m
75. Propeller A propeller spins at 1880 rev/min.
a. What is its angular velocity in rad/s?
1880
197 rad/s
b. What is the angular displacement of the
propeller in 2.50 s?
t
(197 rad/s)(2.50 s)
492 rad
76. The propeller in the previous problem
slows from 475 rev/min to 187 rev/min in
4.00 s. What is its angular acceleration?
1
6m
0s
in
7.54 rad/s2
77. An automobile wheel with a 9.00 cm
radius, as shown in Figure 8-23, rotates at
2.50 rad/s. How fast does a point 7.00 cm
from the center travel?
■Figure 8-23
vr
(7.00 cm)(2.50 rad/s)
17.5 cm/s
Level 2
78. Washing Machine A washing machine’s
two spin cycles are 328 rev/min and 542
rev/min. The diameter of the drum is 0.43 m.
a. What is the ratio of the centripetal accel-
erations for the fast and slow spin cycles?
Recall that ac
v
r
2
and vrw.
2.73
b. What is the ratio of the linear velocity of
an object at the surface of the drum for
the fast and slow spin cycles?
1.65
79. Find the maximum centripetal acceleration
in terms of gfor the washing machine in
problem 78.
ac2r
542 rev/min
2
71g
Level 3
80. A laboratory ultracentrifuge is designed
to produce a centripetal acceleration of
0.35106gat a distance of 2.50 cm from
the axis. What angular velocity in rev/min is
required?
1 g
9.80 m/s2
0.43 m
2
1 min
60 s
2rad
rev
1 g
9.80 m/s2
542 rev/min
328 rev/min
fast
slow
fastr
slowr
vfast
vslow
(542 rev/min)2
(328 rev/min)2
rfast2
rslow2
afast
aslow
2rad
rev
(187 rev/min 475 rev/min)
4.00 s
fi
t
t
min
60 s
2rad
rev
rev
min
2rad
360°
182 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
Physics: Principles and Problems Solutions Manual 183
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
ac2r
so
1
6m
0s
in
1.1105rev/min
8.2 Rotational Dynamics
page 224
Level 1
81. Wrench A bolt is to be tightened with a
torque of 8.0 Nm. If you have a wrench
that is 0.35 m long, what is the least
amount of force you must exert?
Fr sin
so F
For the least possible force, the angle is
90.0°, then
F
23 N
82. What is the torque on a bolt produced by a
15-N force exerted perpendicular to a
wrench that is 25 cm long, as shown in
Figure 8-24?
■Figure 8-24
Fr sin
(15 N)(0.25 m)(sin 90.0°)
3.8 Nm
83. A toy consisting of two balls, each 0.45 kg,
at the ends of a 0.46-m-long, thin, light-
weight rod is shown in Figure 8-25. Find
the moment of inertia of the toy. The
moment of inertia is to be found about the
center of the rod.
Imr2
(0.45 kg)(0.23 m)2(0.45 kg)(0.23 m)2
0.048 kgm2
Level 2
84. A bicycle wheel with a radius of 38 cm is
given an angular acceleration of 2.67 rad/s2
by applying a force of 0.35 N on the edge
of the wheel. What is the wheel’s moment
of inertia?
I
Fr s
in
0.050 kgm2
Level 3
85. Toy Top A toy top consists of a rod with a
diameter of 8.0-mm and a disk of mass
0.0125 kg and a diameter of 3.5 cm. The
moment of inertia of the rod can be
neglected. The top is spun by wrapping a
string around the rod and pulling it with a
velocity that increases from zero to 3.0 m/s
over 0.50 s.
(0.35 N)(0.38 m)(sin 90.0°)
2.67 rad/s2
I
0.46 m
0.45 kg 0.45 kg
■Figure 8-25
90°
F
25 cm
8.0 Nm
(0.35 m)(sin 90.0°)
rsin
rev
2rad
(0.35106)(9.80 m/s2)
0.025 m
ac
r
Chapter 8 continued

a. What is the resulting angular velocity of the top?
f
7.5102rad/s
b. What force was exerted on the string?
Frrod sin and I
Thus, Frrod sin I
F
0.72 N
8.3 Equilibrium
page 224
Level 1
86. A 12.5-kg board, 4.00 m long, is being held up on one end by Ahmed. He calls
for help, and Judi responds.
a. What is the least force that Judi could exert to lift the board to the horizontal
position? What part of the board should she lift to exert this force?
At the opposite end, she will only lift half the mass.
Fleast mg
(12.5 kg)(9.80 m/s2)
61.2 N
b. What is the greatest force that Judi could exert to lift the board to the
horizontal position? What part of the board should she lift to exert this
force?
At the board’s center of mass (middle), she will lift the entire mass.
Fgreatest mg
(12.5 kg)(9.80 m/s2)
122 N
1
2
(7.5102rad/s 0.0 rad/s)(0.0125 kg)
0.03
2
5m
2
(2)(0.50 s)
0.002
80 m
(sin 90.0°)
(fi)mrdisk2
2trrod sin
mrdisk2
2trrod sin
t
1
2
mrdisk2
rrod sin
I
rrod sin
3.0 m/s
1
2
(0.0080 m)
vf
rrod
184 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 185
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 2
87. Two people are holding up the ends of a 4.25-kg wooden
board that is 1.75 m long. A 6.00-kg box sits on the board,
0.50 m from one end, as shown in Figure 8-26. What forces
do the two people exert?
In equilibrium, the sum of all forces is zero and the
sum of the torques about an axis of rotation is zero.
Fleft Fright Fboard Fbox 0
left right board box 0
We can choose the axis of rotation at the location of one of the unknown
forces (Fleft) so that torque is eliminated, thus simplifying the calculations.
Fleftrleft Frightrright Fboardrboard Fboxrbox 0
Fleftrleft Frightrright mboardgrboard mboxgrbox 0
Fleft(0) Fright(1.25 m 0.50 m) (4.25 kg)(9.80 m/s2)
(6.00 kg)(9.80 m/s2)(1.25 m) 0
Fright 63 N
Substituting this into the force equation,
Fleft Fright Fboard Fbox 0
Fleft Fright Fboard Fbox
Fright mboardg mboxg
(63 N) (4.25 kg)(9.80 m/s2)
(6.00 kg)(9.80 m/s2)
37 N
Level 3
88. A car’s specifications state that its weight distribution is 53 percent on the front
tires and 47 percent on the rear tires. The wheel base is 2.46 m. Where is the car’s
center of mass?
Let the center of mass be xfrom the front of the car. Let the weight of the
car be Fg.
front rear
Ffrontrfront Frearrrear
(0.53 Fg)x(0.47 Fg)(2.46 m x)
x1.16 m
Mixed Review
pages 224–225
Level 1
89. A wooden door of mass, m, and length, l, is held horizontally by Dan and Ajit.
Dan suddenly drops his end.
1.25 m 0.50 m
2
6.00 kg
0.50 m
1.25 m
■Figure 8-26
Chapter 8 continued

a. What is the angular acceleration of the
door just after Dan lets go?
The torque is due to the gravitation-
al force. The force at the center of
mass is mg.
Thus,
gl
b. Is the acceleration constant? Explain.
No; the angle between the door and
the weight is changing, and there-
fore the torque is also changing.
Thus, the acceleration changes.
90. Topsoil Ten bags of topsoil, each weighing
175 N, are placed on a 2.43-m-long sheet
of wood. They are stacked 0.50 m from one
end of the sheet of wood, as shown in
Figure 8-27. Two people lift the sheet of
wood, one at each end. Ignoring the weight
of the wood, how much force must each
person exert?
■Figure 8-27
In equilibrium, the sum of the forces is
zero and the sum of the torques is zero.
Fleft Fright Fbags 0
left right bags 0
Choose the location of Fright as the axis
of rotation to make that torque zero.
Then,
left bags
Fleftrleft Fbagsrbags
Fleft
3.6102N
Substitute this into the force equation.
Fleft Fright Fbags 0
Fright Fleft Fbags
3.6102N 10(175 N)
1.4102N
91. Basketball A basketball is rolled down the
court. A regulation basketball has a diame-
ter of 24.1 cm, a mass of 0.60 kg, and a
moment of inertia of 5.8103kgm2. The
basketball’s initial velocity is 2.5 m/s.
a. What is its initial angular velocity?
21 rad/s
b. The ball rolls a total of 12 m. How
many revolutions does it make?
dr
so
2
re
r
v
ad
16 rev
c. What is its total angular displacement?
dr
so
1.0102rad
12 m
1
2
(0.241 m)
d
r
12 m
1
2
(0.241 m)
d
r
2.5 m/s
1
2
(0.241 m)
v
r
(10)(175 N)(0.50 m)
2.43 m
Fbagsrbags
rleft
0.50 m
1.93 m
3
2
mg
1
2
l(sin 90.0°)
1
3
ml2
Fr sin
1
3
ml2
I
186 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 187
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
92. The basketball in the previous problem
stops rolling after traveling 12 m.
a. If its acceleration was constant, what
was its angular acceleration?
vf2vi22ad
so a
Thus,
2.2 rad/s2
b. What torque was acting on it as it was
slowing down?
I
(5.8103kgm2)(2.2 rad/s2)
1.3102Nm
93. A cylinder with a 50 m diameter, as shown
in Figure 8-28, is at rest on a surface. A
rope is wrapped around the cylinder and
pulled. The cylinder rolls without slipping.
■Figure 8-28
a. After the rope has been pulled a dis-
tance of 2.50 m at a constant speed,
how far has the center of mass of the
cylinder moved?
The center of mass is always over
the point of contact with the surface
for a uniform cylinder. Therefore the
center of mass has moved 2.50 m.
b. If the rope was pulled a distance of
2.50 m in 1.25 s, how fast was the cen-
ter of mass of the cylinder moving?
v
2.00 m/s
c. What is the angular velocity of the
cylinder?
8102rad/s
94. Hard Drive A hard drive on a modern
computer spins at 7200 rpm (revolutions
per minute). If the drive is designed to start
from rest and reach operating speed in 1.5 s,
what is the angular acceleration of the disk?
1
6m
0s
in
5.0102rad/s2
95. Speedometers Most speedometers in auto-
mobiles measure the angular velocity of the
transmission and convert it to speed. How
will increasing the diameter of the tires
affect the reading of the speedometer?
Because increasing the diameter
decreases the angular velocity, it will
also decrease the reading of the
speedometer.
96. A box is dragged across the floor using a
rope that is a distance habove the floor.
The coefficient of friction is 0.35. The box is
0.50 m high and 0.25 m wide. Find the
force that just tips the box.
Let Mequal the mass of the box. The
center of mass of the box is 0.25 m
above the floor. The box just tips when
the torques on it are equal.
rope friction
Froperrope Ffrictionrfriction
2rad
rev
(7200 rpm 0rpm)
1.5 s
fi
t
t
2.00 m/s
1
2
(50 m)
v
r
(2.50 m)
(1.25 s)
d
t
50 m
(2.5 m/s)2
2
1
2
(0.241 m)(12 m)
vi2
2rd
a
r
vi2
2d
Chapter 8 continued

Frope
Note that when you pull the box at the
height of its center of mass, the denom-
inator becomes zero.That is, you can
pull with any amount of force and not
tip the box.
97. The second hand on a watch is 12 mm
long. What is the velocity of its tip?
vr
(0.012 m)(2rad/min)
1.3103m/s
Level 2
98. Lumber You buy a 2.44-m-long piece of
10 cm 10 cm lumber. Your friend buys a
piece of the same size and cuts it into two
lengths, each 1.22 m long, as shown in
Figure 8-29. You each carry your lumber
on your shoulders.
■Figure 8-29
a. Which load is easier to lift? Why?
The masses are the same, so the
weights are the same. Thus, the
same upward force is required to lift
each load.
b. Both you and your friend apply a
torque with your hands to keep the
lumber from rotating. Which load is
easier to keep from rotating? Why?
The longer piece of lumber would be
easier to keep from rotating because
it has a greater moment of inertia.
99. Surfboard Harris and Paul carry a surf-
board that is 2.43 m long and weighs 143 N.
Paul lifts one end with a force of 57 N.
a. What force must Harris exert?
FHFgFP
143 N 57 N
86 N
b. What part of the board should Harris lift?
Choose the point of rotation at the
end where Paul lifts.
Hg
FHrHFgrg
rH
2.0 m
Thus, Harris has to lift 2.0 m from
Paul’s end of the board.
100. A steel beam that is 6.50 m long weighs
325 N. It rests on two supports, 3.00 m
apart, with equal amounts of the beam
extending from each end. Suki, who
weighs 575 N, stands on the beam in the
center and then walks toward one end.
How close to the end can she come before
the beam begins to tip?
Each support is 1.75 m from the end of
the beam. Choose the point of rotation
to be the support at the end closer to
Suki. The center of mass of the beam
is 1.50 m from that support. The beam
will just begin to tip when Suki’s
torque (S) equals the torque of the
beam’s center of mass (cm) and the
entire weight is on the support closest
to Suki.
Scm
FSrSFcmrcm
(143 N)
2.42
3m
86 N
Fgrg
FH
2.44 m
1.22 m
1.22 m
min
60 s
(0.86 m2/s2)M
h0.25 m
(0.35)M(9.80 m/s2)(0.25 m)
h0.25 m
Mgrfriction
rrope
Ffrictionrfriction
rrope
188 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 189
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
rS
0.848 m
That is Suki can move 0.848 m from
the support or 1.75 0.848 0.90 m
from the end.
Thinking Critically
pages 225–226
101. Apply Concepts Consider a point on the
edge of a rotating wheel.
a. Under what conditions can the cen-
tripetal acceleration be zero?
when 0.0
b. Under what conditions can the tangen-
tial (linear) acceleration be zero?
when 0.0
c. Can the tangential acceleration be
nonzero while the centripetal accelera-
tion is zero? Explain.
When 0.0 instantaneously, but
is not zero, will keep changing.
d. Can the centripetal acceleration be
nonzero while the tangential accelera-
tion is zero? Explain.
Yes, as long as is constant but
not zero.
102. Apply Concepts When you apply the
brakes in a car, the front end dips. Why?
The road exerts a force on the tires
that brings the car to rest. The center
of mass is above the road. Therefore,
there is a net torque on the car, caus-
ing it to rotate in the direction that
forces the front down.
103. Analyze and Conclude A banner is sus-
pended from a horizontal, pivoted pole, as
shown in Figure 8-30. The pole is 2.10 m
long and weighs 175 N. The banner, which
weighs 105 N, is suspended 1.80 m from the
pivot point or axis of rotation. What is the
tension in the cable supporting the pole?
■Figure 8-30
We can use torques to find the vertical
component (FTy) of the tension. The
counterclockwise torques are in equi-
librium with the clockwise torques.
ccw cw
cable pole banner
FTyrcable Fpolerpole Fbannerrbanner
FTy
The total tension, then, is
FT
420 N
(175 N)(1.05 m) (105 N)(1.80 m)
(2.10 m) sin 25°
Fpolerpole Fbannerrbanner
rcable sin 25°
FTy
sin 25°
Fpolerpole Fbannerrbanner
rcable
Axis of
rotation
Center of
mass 25.0°
1.05 m
2.10 m
1.80 m
Cable
(325 N)
3.02
0m
575 N
Fcmrcm
FS
Chapter 8 continued

104. Analyze and Conclude A pivoted lamp
pole is shown in Figure 8-31. The pole
weighs 27 N, and the lamp weighs 64 N.
■Figure 8-31
a. What is the torque caused by each force?
gFgrsin
(27 N)(0.22 m)(sin 90.0°)
5.9 Nm
lamp Flamprsin
(64 N)(0.33 m)(sin 90.0°)
21 Nm
b. Determine the tension in the rope sup-
porting the lamp pole.
Use the torques to find the vertical
component (FTy) of the tension. The
counterclockwise torques are in
equilibrium with the clockwise
torques.
ccw cw
rope pole lamp
FTyrrope Fpolerpole Flamprlamp
FTy
The total tension, then, is
FT
64 N
105. Analyze and Conclude Gerald and
Evelyn carry the following objects up a
flight of stairs: a large mirror, a dresser,
and a television. Evelyn is at the front end,
and Gerald is at the bottom end. Assume
that both Evelyn and Gerald exert only
upward forces.
a. Draw a free-body diagram showing
Gerald and Evelyn exerting the same
force on the mirror.
b. Draw a free-body diagram showing
Gerald exerting more force on the bot-
tom of the dresser.
FE
Fg
rE rGE G
rE
rG
FG
cm
Dresser
FE
Fg
rE rGE G
rE
rG
FG
cm
Mirror
(27 N)
0.42
4 m
(64 N)(0.33 m)
(0.44 m)(sin 105°)
Fpolerpole Flamprlamp
rrope sin 105°
FTy
sin 105°
Fpolerpole Flamprlamp
rrope
y
x
Axis of
rotation
105.0°
0.33 m
0.44 m
Rope
Lamp
190 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
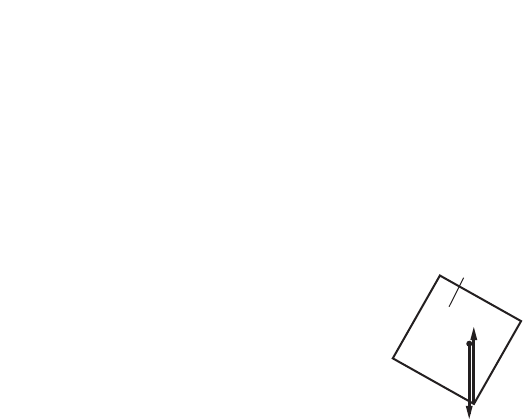
Physics: Principles and Problems Solutions Manual 191
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. Where would the center of mass of the
television have to be so that Gerald
carries all the weight?
directly above where Gerald is
lifting
Writing in Physics
page 226
106. Astronomers know that if a satellite is too
close to a planet, it will be torn apart by
tidal forces. That is, the difference in the
gravitational force on the part of the satel-
lite nearest the planet and the part farthest
from the planet is stronger than the forces
holding the satellite together. Do research
on the Roche limit and determine how
close the Moon would have to orbit Earth
to be at the Roche limit.
For a planet and a moon with identical
densities, the Roche limit is 2.446
times the radius of the planet. Earth’s
Roche limit is 18,470 km.
107. Automobile engines are rated by the
torque that they produce. Research and
explain why torque is an important quan-
tity to measure.
The force exerted by the ground on the
tire accelerates the car. This force is
produced by the engine. It creates the
force by rotating the axle. The torque is
equal to the force on the edge of the
tire multiplied by the radius of the tire.
Gears in the transmission may cause
the force to change, but they do not
change the torque. Therefore, the
amount of torque created by the
engine is delivered to the wheels.
Cumulative Review
page 226
108. Two blocks, one of mass 2.0 kg and the
other of mass 3.0 kg, are tied together with
a massless rope. This rope is strung over a
massless, resistance-free pulley. The blocks
are released from rest. Find the following.
(Chapter 4)
a. the tension in the rope
The tension on the rope is
Tm2gm2a
Tm3gm3a
Thus,
a
g
Substitute into the first equation.
T
g
(9.80 m/s2)
24 N
b. the acceleration of the blocks.
Substitute into the equation for a.
a
g
(9.80 m/s2)
1.96 m/s2
109. Eric sits on a see-saw. At what angle, rela-
tive to the vertical, will the component of
his weight parallel to the plane be equal to
one-third the perpendicular component of
his weight? (Chapter 5)
Fg, parallel Fgsin
Fg, perpendicular Fgcos
Fg, perpendicular 3Fg, parallel
3
3
ta1
n
tan1(3) 71.6°
Fgcos
Fgsin
Fg, perpendicular
Fg, parallel
3 kg 2 kg
3 kg 2 kg
m3m2
m3m2
2(2 kg)(3 kg)
2 kg 3 kg
2m2m3
m2m3
m3m2
m3m2
Fg
FG
cm
TV
Chapter 8 continued

110. The pilot of a plane wants to reach an
airport 325 km due north in 2.75 hours.
A wind is blowing from the west at
30.0 km/h. What heading and airspeed
should be chosen to reach the destination
on time? (Chapter 6)
Let gbe the distance north to the air-
port, xbe the westward deflection, and
h be the actual distance traveled. First,
find the heading as the angle traveled
eastward from the northward path.
tan
tan1
tan1
tan1
14.3°west of north
The airspeed, then, should be
vh2vx2vy2
vh(vx2vy2)
1
2
vx2
(30.0 km/h)2
122 km/h
111. A 60.0-kg speed skater with a velocity of
18.0 m/s comes into a curve of 20.0-m
radius. How much friction must be exerted
between the skates and ice to negotiate the
curve? (Chapter 6)
FfFnet
972 N
Challenge Problem
page 208
Rank the objects shown in the diagram according
to their moments of inertia about the indicated
axes. All spheres have equal masses and all sepa-
rations are the same.
bc d a
A
B
C
D
(60.0 kg)(18.0 m/s)2
20.0 m
mv2
r
1
2
(325 km)2
(2.75 h)2
1
2
dy2
ty2
(30.0 km/h)(2.75 h)
325 km
vxty
dy
vx
vy
vx
vy
192 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued
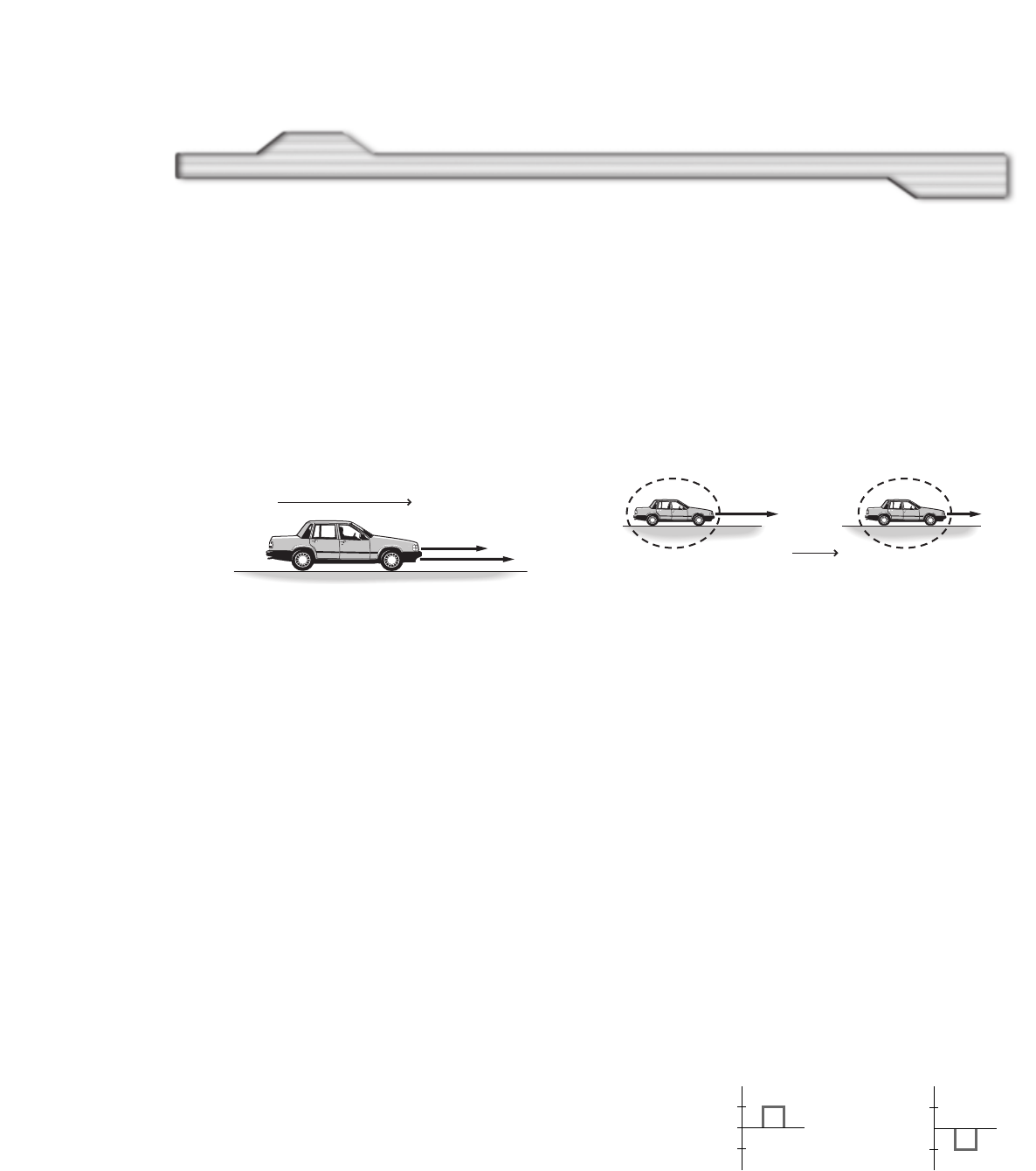
Physics: Principles and Problems Solutions Manual 193
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
9Momentum and Its
Conservation
CHAPTER
Practice Problems
9.1 Impulse and Momentum
pages 229–235
page 233
1. A compact car, with mass 725 kg, is moving
at 115 km/h toward the east. Sketch the
moving car.
a. Find the magnitude and direction of its
momentum. Draw an arrow on your
sketch showing the momentum.
pmv
(725 kg)(115 km/h)
2.32104kgm/s eastward
b. A second car, with a mass of 2175 kg,
has the same momentum. What is its
velocity?
v
38.4 km/h eastward
2. The driver of the compact car in the previ-
ous problem suddenly applies the brakes
hard for 2.0 s. As a result, an average force
of 5.0103N is exerted on the car to slow it
down.
t2.0 s
F5.0103N
a. What is the change in momentum; that
is, the magnitude and direction of the
impulse, on the car?
impulse Ft
(5.0103N)(2.0 s)
1.0104Ns
The impulse is directed westward
and has a magnitude of 1.0104Ns.
b. Complete the “before” and “after”
sketches, and determine the momentum
and the velocity of the car now.
pi2.32104kgm/s eastward
Ftppfpi
pfFtpi
1.0104kgm/s
2.32104kgm/s
1.3104kgm/s eastward
pfmvf
vf
18 m/s
65 km/h eastward
3. A 7.0-kg bowling ball is rolling down the
alley with a velocity of 2.0 m/s. For each
impulse, shown in Figures 9-3a and 9-3b,
find the resulting speed and direction of
motion of the bowling ball.
a. b.
12
Time (s)
5
5
Force (N)
0
12
5
5
Force (N)
Time (s)
0
1.3104kgm/s
725 kg
pf
m
pi
Before After
E
pf
(2.32104kgm/s)
36
1
00
hs
11
00
k
0
m
m
2175 kg
p
m
1 h
3600 s
1000 m
1 km
E
v
p
■Figure 9-3

a.Ftpfpimvfmvi
vf
2.7 m/s in the same direction
as the original velocity
b.vf
1.3 m/s in the same direction
as the original velocity
4. The driver accelerates a 240.0-kg snowmo-
bile, which results in a force being exerted
that speeds up the snowmobile from
6.00 m/s to 28.0 m/s over a time interval
of 60.0 s.
a. Sketch the event, showing the initial
and final situations.
b. What is the snowmobile’s change in
momentum? What is the impulse on
the snowmobile?
pFt
m(vfvi)
(240.0 kg)(28.0 m/s 6.00 m/s)
5.28103kgm/s
c. What is the magnitude of the average
force that is exerted on the snowmobile?
F
88.0 N
5. Suppose a 60.0-kg person was in the vehicle
that hit the concrete wall in Example
Problem 1. The velocity of the person equals
that of the car both before and after the
crash, and the velocity changes in 0.20 s.
Sketch the problem.
a. What is the average force exerted on the
person?
Ftppfpi
F
F
7.8103N opposite to the
direction of motion
b. Some people think that they can stop
their bodies from lurching forward in a
vehicle that is suddenly braking by
putting their hands on the dashboard.
Find the mass of an object that has a
weight equal to the force you just calcu-
lated. Could you lift such a mass? Are
you strong enough to stop your body
with your arms?
Fgmg
m 8.0102kg
Such a mass is too heavy to lift.You
cannot safely stop yourself with
your arms.
Section Review
9.1 Impulse and Momentum
pages 229–235
page 235
6. Momentum Is the momentum of a car
traveling south different from that of the
same car when it travels north at the same
speed? Draw the momentum vectors to sup-
port your answer.
Yes, momentum is a vector quantity,
and the momenta of the two cars are in
opposite directions.
7.8103N
9.80 m/s2
Fg
g
1 h
3600 s
1000 m
1 km
(0.0 kgm/s) (60.0 kg)(94 km/h)
0.20 s
pfmvi
t
pfpi
t
125.0 km
65.0 km
141 km
5.28103kgm/s
60.0 s
p
t
vi
Before After
x
vf
(5.0 N)(1.0 s) (7.0 kg)(2.0 m/s)
7.0 kg
Ftmvf
m
(5.0 N)(1.0 s) (7.0 kg)(2.0 m/s)
7.0 kg
Ftmvf
m
194 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 195
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. Impulse and Momentum When you jump
from a height to the ground, you let your
legs bend at the knees as your feet hit the
floor. Explain why you do this in terms of
the physics concepts introduced in this
chapter.
You reduce the force by increasing the
length of time it takes to stop the
motion of your body.
8. Momentum Which has more momentum,
a supertanker tied to a dock or a falling
raindrop?
The raindrop has more momentum,
because a supertanker at rest has zero
momentum.
9. Impulse and Momentum A 0.174-kg soft-
ball is pitched horizontally at 26.0 m/s. The
ball moves in the opposite direction at
38.0 m/s after it is hit by the bat.
a. Draw arrows showing the ball’s momen-
tum before and after the bat hits it.
b. What is the change in momentum of
the ball?
pm(vfvi)
(0.174 kg)
(38.0 m/s (26.0 m/s))
11.1 kgm/s
c. What is the impulse delivered by the bat?
Ftpfpi
p
11.1 kgm/s
11.1 Ns
d. If the bat and softball are in contact for
0.80 ms, what is the average force that
the bat exerts on the ball?
Ftm(vfvi)
F
1.4104N
10. Momentum The speed of a basketball as it
is dribbled is the same when the ball is
going toward the floor as it is when the ball
rises from the floor. Is the basketball’s
change in momentum equal to zero when it
hits the floor? If not, in which direction is
the change in momentum? Draw the bas-
ketball’s momentum vectors before and
after it hits the floor.
No, the change in momentum is
upward. Before the ball hits the floor, its
momentum vector is downward. After
the ball hits the floor, its momentum
vector is upward.
11. Angular Momentum An ice-skater spins
with his arms outstretched. When he pulls
his arms in and raises them above his head,
he spins much faster than before. Did a
torque act on the ice-skater? If not, how
could his angular velocity have increased?
No torque acted on him. By drawing his
arms in and keeping them close to the
axis of rotation, he decreased his
moment of inertia. Because the angular
momentum did not change, the skater’s
angular velocity increased.
vi
vf
Before After
y
p
p
(0.174 kg)(38.0 m/s (26.0 m/s))
(0.80 ms)
100
1
0s
ms
m(vfvi)
t
vivf
Before After
x
p
pN
S
EW
Chapter 9 continued

12. Critical Thinking An archer shoots arrows
at a target. Some of the arrows stick in the
target, while others bounce off. Assuming
that the masses of the arrows and the veloc-
ities of the arrows are the same, which
arrows produce a bigger impulse on the tar-
get? Hint: Draw a diagram to show the
momentum of the arrows before and after hit-
ting the target for the two instances.
The ones that bounce off give more
impulse because they end up with
some momentum in the reverse direc-
tion, meaning they have a larger change
in momentum.
Practice Problems
9.2 Conservation of
Momentum
pages 236–245
page 238
13. Two freight cars, each with a mass of
3.0105kg, collide and stick together. One
was initially moving at 2.2 m/s, and the
other was at rest. What is their final speed?
pipf
mvAi mvBi 2mvf
vf
1.1 m/s
14. A 0.105-kg hockey puck moving at 24 m/s
is caught and held by a 75-kg goalie at rest.
With what speed does the goalie slide on
the ice?
pPi pGi pPf pGf
mPvPi mGvGi mPvPf mGvGf
Because vGi 0.0 kgm/s,
mPvPi (mPmG)vf
where vfvPf vGf is the common
final speed of the goalie and the puck.
vf
0.034 m/s
15. A 35.0-g bullet strikes a 5.0-kg stationary
piece of lumber and embeds itself in the
wood. The piece of lumber and bullet fly
off together at 8.6 m/s. What was the origi-
nal speed of the bullet?
mbvbi mwvwi (mbmw)vf
where vfis the common final speed of
the bullet and piece of lumber.
Because vwi 0.0 m/s,
vbi
1.2103m/s
16. A 35.0-g bullet moving at 475 m/s strikes a
2.5-kg bag of flour that is on ice, at rest. The
bullet passes through the bag, as shown in
Figure 9-7, and exits it at 275 m/s. How fast
is the bag moving when the bullet exits?
■Figure 9-7
mBvBi mFvFi mBvBf mFvFf
where vFi 0.0 m/s
vFf
vFf mB(vBi vBf)
mF
(mBvBi mBvBf)
mF
275 m/s
(0.0350 kg 5.0 kg)(8.6 m/s)
0.0350 kg
(mbmw)vf
mb
(0.105 kg)(24 m/s)
(0.105 kg 75 kg)
mPvPi
(mPmG)
2.2 m/s 0.0 m/s
2
vAi vBi
2
196 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 197
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
2.8 m/s
17. The bullet in the previous problem strikes a 2.5-kg steel ball that is at rest.
The bullet bounces backward after its collision at a speed of 5.0 m/s. How fast
is the ball moving when the bullet bounces backward?
The system is the bullet and the ball.
mbulletvbullet, i mballvball, i mbulletvbullet, f mballvball, f
vball, i 0.0 m/s and vbullet, f 5.0 m/s
so vball, f
6.7 m/s
18. A 0.50-kg ball that is traveling at 6.0 m/s collides head-on with a 1.00-kg ball
moving in the opposite direction at a speed of 12.0 m/s. The 0.50-kg ball
bounces backward at 14 m/s after the collision. Find the speed of the second
ball after the collision.
Say that the first ball (ball C) is initially moving in the positive (forward)
direction.
mCvCi mDvDi mCvCf mDvDf
so vDf
2.0 m/s, or 2.0 m/s in the opposite direction
page 240
19. A 4.00-kg model rocket is launched, expelling 50.0 g of burned fuel from its
exhaust at a speed of 625 m/s. What is the velocity of the rocket after the fuel has
burned? Hint: Ignore the external forces of gravity and air resistance.
pri pfuel, i prf pfuel, f
where prf pfuel, f 0.0 kgm/s
If the initial mass of the rocket (including fuel) is mr4.00 kg, then the
final mass of the rocket is
mrf 4.00 kg 0.0500 kg 3.95 kg
0.0 kgm/s mrfvrf mfuelvfuel, f
vrf
7.91 m/s
(0.0500 kg)(625 m/s)
3.95 kg
mfuelvfuel, f
mrf
(0.50 kg)(6.0 m/s) (1.00 kg)(12.0 m/s) (0.50 kg)(14 m/s)
1.00 kg
mCvCi mDvDi mCvCf
mD
(0.0350 kg)(475 m/s (5.0 m/s))
2.5 kg
mbullet(vbullet, i vbullet, f)
mball
(0.0350 kg)(475 m/s 275 m/s)
2.5 kg
Chapter 9 continued

20. A thread holds a 1.5-kg cart and a 4.5-kg cart together. After the thread is burned, a
compressed spring pushes the carts apart, giving the 1.5-kg cart a speed of 27 cm/s
to the left. What is the velocity of the 4.5-kg cart?
Let the 1.5-kg cart be represented by “C” and the 4.5-kg cart be
represented by “D”.
pCi pDi pCf pDf
where pCi pDi 0.0 kgm/s
mDvDf mCvCf
so vDf
9.0 cm/s to the right
21. Carmen and Judi dock a canoe. 80.0-kg Carmen moves forward at 4.0 m/s as she
leaves the canoe. At what speed and in what direction do the canoe and Judi
move if their combined mass is 115 kg?
pCi pJi pCf pJf
where pCi pJi 0.0 kgm/s
mCvCf mJvJf
so vJf
2.8 m/s in the opposite direction
page 243
22. A 925-kg car moving north at 20.1 m/s collides with a 1865-kg car moving west
at 13.4 m/s. The two cars are stuck together. In what direction and at what speed
do they move after the collision?
Before:
pi, ymyvi, y
(925 kg)(20.1 m/s)
1.86104kgm/s
pi, xmxvi, x
(1865 kg)(13.4 m/s)
2.50104kgm/s
pf, ypi, y
pf, xpi, x
pfpi
(pf, x)2
(pf
,y)2
(80.0 kg)(4.0 m/s)
115 kg
mCvCf
mJ
(1.5 kg)(27 cm/s)
4.5 kg
mCvCf
mD
198 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 199
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(2.5
010
4kgm
/s)2
(1.86
104
kgm/
s)2
3.12104kgm/s
vf
11.2 m/s
tan1
tan1
36.6° north of west
23. A 1383-kg car moving south at 11.2 m/s is struck by a 1732-kg car moving east at
31.3 m/s. The cars are stuck together. How fast and in what direction do they
move immediately after the collision?
Before:
pi, xp1, xp2, x
0 m2v2i
pi, yp1, yp2, y
m1v1i 0
pfpi
p1, x2
pi, y
2
(m2v2
i)2 (
m1v1i
)2
vf
18.1 m/s
tan1
tan1
tan1
15.9°
south of east
24. A stationary billiard ball, with a mass of 0.17 kg, is struck by an identical ball
moving at 4.0 m/s. After the collision, the second ball moves 60.0° to the left of
its original direction. The stationary ball moves 30.0° to the right of the moving
ball’s original direction. What is the velocity of each ball after the collision?
pCi pDi pCf pDf
where pCi 0.0 kgm/s
mCmDm0.17 kg
(1383 kg)(11.2 m/s)
(1732 kg)(31.3 m/s)
m1v1i
m2v2i
pi, y
pi, x
((1732
kg)(3
1.3 m
/s))2
((138
3 kg)(
11.2
m/s))
2
1383 kg 1782 kg
(m2v2
i)2(
m1v1i
)2
m1m2
pf
m1m2
1.86104kgm/s
2.50104kgm/s
pf, y
pf, x
3.12104kgm/s
(925 kg 1865 kg)
pf
m1m2
Chapter 9 continued
The vector diagram provides final momentum equations for the ball that
is initially stationary, C, and the ball that is initially moving, D.
pCf pDi sin 60.0°
pDf pDi cos 60.0°
We can use the momentum equation for the stationary ball to find its
final velocity.
pCf pDi sin 60.0°
mvCf mvDi sin 60.0°
vCf vDi sin 60.0°
(4.0 m/s)(sin 60.0°)
3.5 m/s, 30.0° to the right
We can use the momentum equation for the moving ball to find its velocity.
pDf pDi cos 60.0°
mvDf mvDi cos 60.0°
vDf vDi cos 60.0°
(4.0 m/s)(cos 60.0°)
2.0 m/s, 60.0° to the left
25. A 1345-kg car moving east at 15.7 m/s is struck by a 1923-kg car moving north.
They are stuck together and move with an initial velocity of 14.5 m/s at
63.5°. Was the north-moving car exceeding the 20.1 m/s speed limit?
Before:
pi, xm1v1, i
(1345 kg)(15.7 m/s)
2.11104kgm/s
pfpi
(m1m2)vf
(1345 kg 1923 kg)(14.5 m/s)
4.74104kgm/s
pf, ypfsin
(4.74104kgm/s)(sin 63.5°)
4.24104kgm/s
vDi
vCf
pDi
pCf pDf
vDf
DiCi60.0
60.0
30.030.0
Cf
DfVector Diagram
200 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 201
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
pf, ypi, ym2v2, i
v2, i
22.1 m/s
Yes, it was exceeding the speed limit.
Section Review
9.2 Conservation of
Momentum
pages 236–245
page 245
26. Angular Momentum The outer rim of a
plastic disk is thick and heavy. Besides mak-
ing it easier to catch, how does this affect
the rotational properties of the plastic disk?
Most of the mass of the disk is located
at the rim, thereby increasing its
moment of inertia. Therefore, when the
disk is spinning, its angular momentum
is larger than it would be if more mass
were near the center. With a larger
angular momentum, the disk flies
through the air with more stability.
27. Speed A cart, weighing 24.5 N, is released
from rest on a 1.00-m ramp, inclined at an
angle of 30.0° as shown in Figure 9-14.
The cart rolls down the incline and strikes a
second cart weighing 36.8 N.
a. Calculate the speed of the first cart at
the bottom of the incline.
The force parallel to the surface of
the ramp is
FFgsin
where
aand m
so, agsin
The velocity and acceleration of the
cart are related by the motion equa-
tion, v2vi22a(ddi) with
vi0 and di0. Thus,
v22ad
v2ad
(2)(gs
in )(d
)
(2)(9.8
0 m/s
2)(sin
30.0°)
(1.00 m
)
3.13 m/s
b. If the two carts stick together, with what
initial speed will they move along?
mCvCi (mCmC)vf
so, vf
1.25 m/s
28. Conservation of Momentum During a
tennis serve, the racket of a tennis player
continues forward after it hits the ball. Is
momentum conserved in the collision?
Explain, making sure that you define the
system.
No, because the mass of the racket is
much larger than that of the ball, only a
small change in its velocity is required.
In addition, it is being held by a mas-
sive, moving arm that is attached to a
body in contact with Earth. Thus, the
racket and ball do not comprise an
isolated system.
29. Momentum A pole-vaulter runs toward the
(24.5 N)(3.13 m/s)
24.5 N 36.8 N
FCvCi
FCFD
F
g
C
vCi
F
g
C
F
g
D
mCvCi
mCmD
Fgsin
Fg/g
Fg
g
F
m
30.0°
1.00 m
24.5 N
36.8 N
■Figure 9-14
4.24104kgm/s
1923 kg
pf, y
m2
Chapter 9 continued
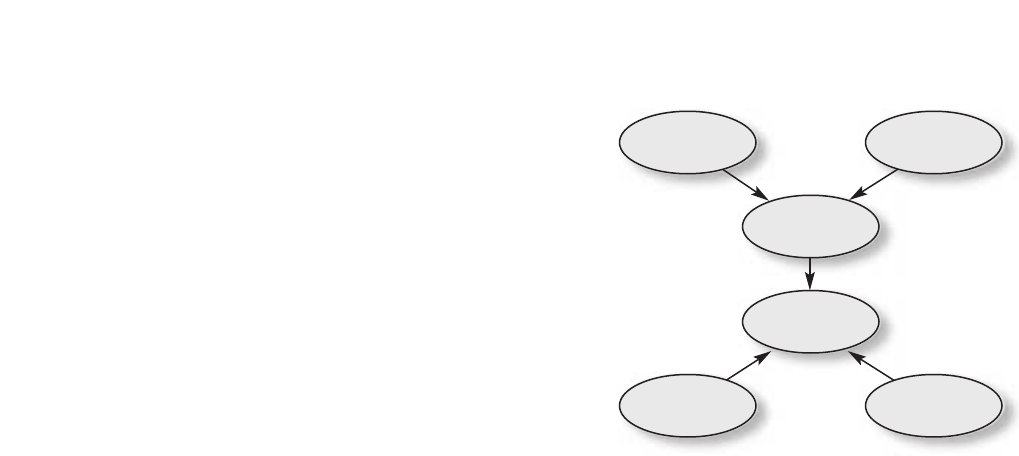
launch point with horizontal momentum.
Where does the vertical momentum come
from as the athlete vaults over the crossbar?
The vertical momentum comes from
the impulsive force of Earth against
the pole. Earth acquires an equal and
opposite vertical momentum.
30. Initial Momentum During a soccer game,
two players come from opposite directions
and collide when trying to head the ball.
They come to rest in midair and fall to the
ground. Describe their initial momenta.
Because their final momenta are zero,
their initial momenta were equal and
opposite.
31. Critical Thinking You catch a heavy ball
while you are standing on a skateboard,
and then you roll backward. If you were
standing on the ground, however, you
would be able to avoid moving while catch-
ing the ball. Explain both situations using
the law of conservation of momentum.
Explain which system you use in each case.
In the case of the skateboard, the ball,
the skateboard, and you are an isolated
system, and the momentum of the ball
is shared. In the second case, unless
Earth is included, there is an external
force, so momentum is not conserved.
If Earth’s large mass is included in the
system, the change in its velocity is
negligible.
Chapter Assessment
Concept Mapping
page 250
32. Complete the following concept map using
the following terms: mass, momentum, aver-
age force, time over which the force is exerted.
Mastering Concepts
page 250
33. Can a bullet have the same momentum as a
truck? Explain. (9.1)
Yes, for a bullet to have the same
momentum as a truck, it must have a
higher velocity because the two masses
are not the same.
mbulletvbullet mtruckvtruck
34. A pitcher throws a curve ball to the catcher.
Assume that the speed of the ball doesn’t
change in flight. (9.1)
a. Which player exerts the larger impulse
on the ball?
The pitcher and the catcher exert
the same amount of impulse on the
ball, but the two impulses are in
opposite directions.
b. Which player exerts the larger force on
the ball?
The catcher exerts the larger force
on the ball because the time interval
over which the force is exerted is
smaller.
35. Newton’s second law of motion states that
if no net force is exerted on a system, no
acceleration is possible. Does it follow that
no change in momentum can occur? (9.1)
No net force on the system means no
net impulse on the system and no net
change in momentum. However, individ-
ual parts of the system may have a
average force
impulse
momentum
Produces a change in
time over which the
force is exerted
mass velocity
Product is the
Product is the
202 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 203
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
change in momentum as long as the
net change in momentum is zero.
36. Why are cars made with bumpers that can
be pushed in during a crash? (9.1)
Cars are made with bumpers that com-
press during a crash to increase the
time of a collision, thereby reducing the
force.
37. An ice-skater is doing a spin. (9.1)
a. How can the skater’s angular momen-
tum be changed?
by applying an external torque
b. How can the skater’s angular velocity be
changed without changing the angular
momentum?
by changing the moment of inertia
38. What is meant by “an isolated system?”
(9.2)
An isolated system has no external
forces acting on it.
39. A spacecraft in outer space increases its
velocity by firing its rockets. How can hot
gases escaping from its rocket engine
change the velocity of the craft when there
is nothing in space for the gases to push
against? (9.2)
Momentum is conserved. The change in
momentum of gases in one direction
must be balanced by an equal change
in momentum of the spacecraft in the
opposite direction.
40. A cue ball travels across a pool table and
collides with the stationary eight ball. The
two balls have equal masses. After the colli-
sion, the cue ball is at rest. What must be
true regarding the speed of the eight ball?
(9.2)
The eight ball must be moving with the
same velocity that the cue ball had just
before the collision.
41. Consider a ball falling toward Earth. (9.2)
a. Why is the momentum of the ball not
conserved?
The momentum of a falling ball is
not conserved because a net exter-
nal force, gravity, is acting on it.
b. In what system that includes the falling
ball is the momentum conserved?
One such system in which total
momentum is conserved includes
the ball plus Earth.
42. A falling basketball hits the floor. Just
before it hits, the momentum is in the
downward direction, and after it hits the
floor, the momentum is in the upward
direction. (9.2)
a. Why isn’t the momentum of the basket-
ball conserved even though the bounce
is a collision?
The floor is outside the system, so it
exerts an external force, and there-
fore, an impulse on the ball.
b. In what system is the momentum con-
served?
Momentum is conserved in the sys-
tem of ball plus Earth.
43. Only an external force can change the
momentum of a system. Explain how the
internal force of a car’s brakes brings the car
to a stop. (9.2)
The external force of a car’s brakes can
bring the car to a stop by stopping the
wheels and allowing the external fric-
tional force of the road against the tires
to stop the car. If there is no friction—
for example, if the road is icy—then
there is no external force and the car
does not stop.
44. Children’s playgrounds often have circular-
motion rides. How could a child change the
angular momentum of such a ride as it is
turning? (9.2)
The child would have to exert a torque
on it. He or she could stand next to it
and exert a force tangential to the circle
on the handles as they go past. He or
she also could run at the ride and jump
onboard.
Chapter 9 continued
Applying Concepts
pages 250–251
45. Explain the concept of impulse using physi-
cal ideas rather than mathematics.
A force, F, exerted on an object over a
time, t, causes the momentum of the
object to change by the quantity Ft.
46. Is it possible for an object to obtain a larger
impulse from a smaller force than it does
from a larger force? Explain.
Yes, if the smaller force acts for a long
enough time, it can provide a larger
impulse.
47. Foul Ball You are sitting at a baseball game
when a foul ball comes in your direction.
You prepare to catch it bare-handed. To
catch it safely, should you move your hands
toward the ball, hold them still, or move
them in the same direction as the moving
ball? Explain.
You should move your hands in the
same direction the ball is traveling
to increase the time of the collision,
thereby reducing the force.
48. A 0.11-g bullet leaves a pistol at 323 m/s,
while a similar bullet leaves a rifle at 396
m/s. Explain the difference in exit speeds of
the two bullets, assuming that the forces
exerted on the bullets by the expanding
gases have the same magnitude.
The bullet is in the rifle a longer time,
so the momentum it gains is larger.
49. An object initially at rest experiences
the impulses described by the graph in
Figure 9-15. Describe the object’s
motion after impulses A, B, and C.
■Figure 9-15
After time A, the object moves with a
constant, positive velocity. After time B,
the object is at rest. After time C, the
object moves with a constant, negative
velocity.
50. During a space walk, the tether connecting
an astronaut to the spaceship breaks. Using a
gas pistol, the astronaut manages to get back
to the ship. Use the language of the impulse-
momentum theorem and a diagram to
explain why this method was effective.
When the gas pistol is fired in the oppo-
site direction, it provides the impulse
needed to move the astronaut toward
the spaceship.
51. Tennis Ball As a tennis ball bounces off a
wall, its momentum is reversed. Explain this
action in terms of the law of conservation of
momentum. Define the system and draw a
diagram as a part of your explanation.
Consider the system to be the ball, the
wall, and Earth. The wall and Earth gain
some momentum in the collision.
52. Imagine that you command spaceship
Zeldon, which is moving through interplan-
etary space at high speed. How could you
Before After
vi
+x
vf
pp
pEarth and wall
24
6 8 10 11
0
A
BC
Time (s)
2
2
Force (N)
204 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued
p
p

Physics: Principles and Problems Solutions Manual 205
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
slow your ship by applying the law of con-
servation of momentum?
By shooting mass in the form of
exhaust gas, at high velocity in the
same direction in which you are mov-
ing, its momentum would cause the
ship’s momentum to decrease.
53. Two trucks that appear to be identical col-
lide on an icy road. One was originally at
rest. The trucks are stuck together and move
at more than half the original speed of the
moving truck. What can you conclude
about the contents of the two trucks?
If the two trucks had equal masses,
they would have moved off at half the
speed of the moving truck. Thus, the
moving truck must have had a more
massive load.
54. Explain, in terms of impulse and momen-
tum, why it is advisable to place the butt of
a rifle against your shoulder when first
learning to shoot.
When held loosely, the recoil momen-
tum of the rifle works against only the
mass of the rifle, thereby producing a
larger velocity and striking your shoul-
der. The recoil momentum must work
against the mass of the rifle and you,
resulting in a smaller velocity.
55. Bullets Two bullets of equal mass are shot
at equal speeds at blocks of wood on a
smooth ice rink. One bullet, made of rub-
ber, bounces off of the wood. The other
bullet, made of aluminum, burrows into
the wood. In which case does the block of
wood move faster? Explain.
Momentum is conserved, so the
momentum of the block and bullet after
the collision equals the momentum of
the bullet before the collision. The rub-
ber bullet has a negative momentum
after impact, with respect to the block,
so the block’s momentum must be
greater in this case.
Mastering Problems
9.1 Impulse and Momentum
pages 251–252
Level 1
56. Golf Rocío strikes a 0.058-kg golf ball with
a force of 272 N and gives it a velocity of
62.0 m/s. How long was Rocío’s club in
contact with the ball?
t
0.013 s
57. A 0.145-kg baseball is pitched at 42 m/s.
The batter hits it horizontally to the pitcher
at 58 m/s.
a. Find the change in momentum of the
ball.
Take the direction of the pitch to be
positive.
pmvfmvim(vfvi)
(0.145 kg)(58 m/s (42 m/s))
14 kgm/s
b. If the ball and bat are in contact for
4.6104s, what is the average force
during contact?
Ftp
F
m(vf
t
vi)
3.2104N
58. Bowling A force of 186 N acts on a 7.3-kg
bowling ball for 0.40 s. What is the bowling
ball’s change in momentum? What is its
change in velocity?
pFt
(186 N)(0.40 s)
74 Ns
74 kgm/s
v
Ft
m
p
m
(0.145 kg)(58 m/s (42 m/s))
4.6104s
p
t
(0.058 kg)(62.0 m/s)
272 N
mv
F
Chapter 9 continued

1.0101m/s
59. A 5500-kg freight truck accelerates
from 4.2 m/s to 7.8 m/s in 15.0 s by
the application of a constant force.
a. What change in momentum occurs?
pmvm(vfvi)
(5500 kg)(7.8 m/s 4.2 m/s)
2.0104kgm/s
b. How large of a force is exerted?
F
1.3103N
60. In a ballistics test at the police department,
Officer Rios fires a 6.0-g bullet at 350 m/s
into a container that stops it in 1.8 ms. What
is the average force that stops the bullet?
F
1.2103N
61. Volleyball A 0.24-kg volleyball approaches
Tina with a velocity of 3.8 m/s. Tina bumps
the ball, giving it a speed of 2.4 m/s but in
the opposite direction. What average force
did she apply if the interaction time between
her hands and the ball was 0.025 s?
F
6.0101N
62. Hockey A hockey player makes a slap shot,
exerting a constant force of 30.0 N on the
hockey puck for 0.16 s. What is the magni-
tude of the impulse given to the puck?
Ft(30.0 N)(0.16 s)
4.8 Ns
63. Skateboarding Your brother’s mass is
35.6 kg, and he has a 1.3-kg skateboard.
What is the combined momentum of your
brother and his skateboard if they are mov-
ing at 9.50 m/s?
pmv
(mboy mboard)v
(35.6 kg 1.3 kg)(9.50 m/s)
3.5102kgm/s
64. A hockey puck has a mass of 0.115 kg and
is at rest. A hockey player makes a shot,
exerting a constant force of 30.0 N on the
puck for 0.16 s. With what speed does it
head toward the goal?
Ftmvm(vfvi)
where vi0
Thus vf
42 m/s
65. Before a collision, a 25-kg object was mov-
ing at 12 m/s. Find the impulse that acted
on the object if, after the collision, it moved
at the following velocities.
a. 8.0 m/s
Ftmvm(vfvi)
(25 kg)(8.0 m/s 12 m/s)
1.0102kgm/s
b. 8.0 m/s
Ftmvm(vfvi)
(25 kg)(8.0 m/s 12 m/s)
5.0102kgm/s
(30.0 N)(0.16 s)
0.115 kg
Ft
m
(0.24 kg)(2.4 m/s 3.8 m/s)
0.025 s
mv
t
(0.0060 kg)(0.0 m/s 350 m/s)
1.8103s
m(vfvi)
t
p
t
(5500 kg)(7.8 m/s 4.2 m/s)
15.0 s
m(vfvi)
t
p
t
(186 N)(0.40 s)
7.3 kg
206 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 207
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 2
66. A 0.150-kg ball, moving in the positive direction
at 12 m/s, is acted on by the impulse shown in
the graph in Figure 9-16. What is the ball’s
speed at 4.0 s?
Ftmv
Area of graph mv
(2.0 N)(2.0 s) m(vfvi)
2.0 Ns (0.150 kg)(vf12 m/s)
vf12 m/s
25 m/s
67. Baseball A 0.145-kg baseball is moving at 35 m/s when it is caught by a player.
a. Find the change in momentum of the ball.
pm(vfvi)
(0.145 kg)(0.0 m/s 35 m/s)
5.1 kgm/s
b. If the ball is caught with the mitt held in a stationary position so that the ball
stops in 0.050 s, what is the average force exerted on the ball?
pFaveraget
so, Faverage
1.0102N
c. If, instead, the mitt is moving backward so that the ball takes 0.500 s to stop,
what is the average force exerted by the mitt on the ball?
pFaveraget
so, Faverage
1.0101N
68. Hockey A hockey puck has a mass of 0.115 kg and strikes
the pole of the net at 37 m/s. It bounces off in the opposite
direction at 25 m/s, as shown in Figure 9-17.
a. What is the impulse on the puck?
Ftm(vfvi)
(0.115 kg)(25 m/s 37 m/s)
7.1 kgm/s
(0.145 kg)(0.0 m/s 35 m/s)
0.500 s
m(vfvi)
t
p
t
(0.145 kg)(0.0 m/s 35 m/s)
0.500 s
m(vfvi)
t
p
t
2.0 kgm/s
0.150 kg
1
2
Chapter 9 continued
123
Time (s)
4
2
2
Force (N)
0
■Figure 9-16
25 m/s
0.115 kg
■Figure 9-17

b. If the collision takes 5.0104s, what is the average force on the puck?
Ftm(vfvi)
F
1.4104N
69. A nitrogen molecule with a mass of 4.71026 kg, moving at 550 m/s, strikes
the wall of a container and bounces back at the same speed.
a. What is the impulse the molecule delivers to the wall?
Ftm(vfvi)
(4.71026 kg)(550 m/s 550 m/s)
5.21023 kgm/s
The impulse the wall delivers to the molecule is 5.21023 kgm/s.
The impulse the molecule delivers to the wall is 5.21023 kgm/s.
b. If there are 1.51023 collisions each second, what is the average force
on the wall?
Ftm(vfvi)
F
For all the collisions, the force is
Ftotal (1.51023)
(1.51023)
7.8 N
Level 3
70. Rockets Small rockets are used to make tiny adjustments in the speeds of
satellites. One such rocket has a thrust of 35 N. If it is fired to change the velocity
of a 72,000-kg spacecraft by 63 cm/s, how long should it be fired?
Ftmv
so, t
1.3103s, or 22 min
(72,000 kg)(0.63 m/s)
35 N
mt
F
(4.71026 kg)(550 m/s 550 m/s)
1.0 s
m(vfvi)
t
m(vfvi)
t
(0.115 kg)(25 m/s 37 m/s)
5.0104s
m(vfvi)
t
208 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 209
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
71. An animal rescue plane flying due east at 36.0 m/s drops a bale
of hay from an altitude of 60.0 m, as shown in Figure 9-18.
If the bale of hay weighs 175 N, what is the momentum of the
bale the moment before it strikes the ground? Give both magni-
tude and direction.
First use projectile motion to find the velocity of the bale.
pmv
To find v, consider the horizontal and vertical
components.
vx36.0 m/s
vy2viy22dg 2dg
Thus,
vvx2
vy2
vx2
2dg
The momentum, then, is
p
888 kgm/s
The angle from the horizontal is
tan
43.6°
72. Accident A car moving at 10.0 m/s crashes into a barrier and stops in 0.050 s.
There is a 20.0-kg child in the car. Assume that the child’s velocity is changed by
the same amount as that of the car, and in the same time period.
a. What is the impulse needed to stop the child?
Ftmvm(vfvi)
(20.0 kg)(0.0 m/s 10.0 m/s)
2.00102kgm/s
b. What is the average force on the child?
Ftmvm(vfvi)
so, F
4.0103N
(20.0 kg)(0.0 m/s 10.0 m/s)
0.050 s
m(vfvi)
t
(2)(60
.0 m)(
9.80 m
/s2)
36.0 m/s
2dg
vx
vy
vx
(175 N)(36.0
m/s)2
(2)(
60.0 m
)(9.80
m/s2)
9.80 m/s2
Fgvx2
2dg
g
Fgv
g
36.0 m/s
175 N
60.0 m
■Figure 9-18
Chapter 9 continued
c. What is the approximate mass of an
object whose weight equals the force in
part b?
Fgmg
so, m
4.1102kg
d. Could you lift such a weight with your
arm?
No.
e. Why is it advisable to use a proper
restraining seat rather than hold a child
on your lap?
You would not be able to protect a
child on your lap in the event of a
collision.
9.2 Conservation of Momentum
pages 252–253
Level 1
73. Football A 95-kg fullback, running at
8.2 m/s, collides in midair with a 128-kg
defensive tackle moving in the opposite
direction. Both players end up with zero
speed.
a. Identify the “before” and “after” situa-
tions and draw a diagram of both.
Before: mFB 95 kg
vFB 8.2 m/s
mDT 128 kg
vDT ?
After: m223 kg
vf0 m/s
b. What was the fullback’s momentum
before the collision?
pFB mFBvFB (95 kg)(8.2 m/s)
7.8102kgm/s
c. What was the change in the fullback’s
momentum?
pFB pfpFB
0 pFB 7.8102kgm/s
d. What was the change in the defensive
tackle’s momentum?
7.8102kgm/s
e. What was the defensive tackle’s original
momentum?
7.8102kgm/s
f. How fast was the defensive tackle mov-
ing originally?
mDTvDT 7.8102kgm/s
so, vDT
6.1 m/s
7.8102kgm/s
128 kg
Before
After
vFB
vFB vDT 0
vDT
+x
+x
4.0103N
9.80 m/s2
Fg
g
210 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued
Physics: Principles and Problems Solutions Manual 211
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
74. Marble C, with mass 5.0 g, moves at a
speed of 20.0 cm/s. It collides with a sec-
ond marble, D, with mass 10.0 g, moving at
10.0 cm/s in the same direction. After the
collision, marble C continues with a speed
of 8.0 cm/s in the same direction.
a. Sketch the situation and identify the sys-
tem. Identify the “before” and “after” sit-
uations and set up a coordinate system.
Before: mC5.0 g
mD10.0 g
vCi 20.0 cm/s
vDi 10.0 cm/s
After: mC5.0 g
mD10.0 g
vCf 8.0 cm/s
vDf ?
b. Calculate the marbles’ momenta before
the collision.
mCvCi (5.0103kg)(0.200 m/s)
1.0103kgm/s
mDvDi (1.00102kg)(0.100 m/s)
1.0103kgm/s
c. Calculate the momentum of marble C
after the collision.
mCvCf (5.0103kg)(0.080 m/s)
4.0104kgm/s
d. Calculate the momentum of marble D
after the collision.
pCi pDi pCf pDf
pDf pCi pDi pCf
1.00103kgm/s
1.00103kgm/s
4.0104kgm/s
1.6103kgm/s
e. What is the speed of marble D after the
collision?
pDf mDvDf
so, vDf
1.6101m/s 0.16 m/s
16 cm/s
75. Two lab carts are pushed together with a
spring mechanism compressed between
them. Upon release, the 5.0-kg cart repels
one way with a velocity of 0.12 m/s, while
the 2.0-kg cart goes in the opposite direc-
tion. What is the velocity of the 2.0-kg cart?
m1vim2vf
vf
m
m
1v
2
i
0.30 m/s
76. A 50.0-g projectile is launched with a hori-
zontal velocity of 647 m/s from a 4.65-kg
launcher moving in the same direction at
2.00 m/s. What is the launcher’s velocity
after the launch?
pCi pDi pCf pDf
mCvCi mDvDi mCvCf mDvDf
so, vDf
Assuming that the projectile, C, is
launched in the direction of the
launcher, D, motion,
mCvCi mDvDi mCvCf
mD
(5.0 kg)(0.12 m/s)
(2.0 kg)
1.6103kgm/s
1.00102kg
pDf
mD
Before
vCi
+x
vDi
CD
Chapter 9 continued
After
vDf
vCf
CD
+x

vDf
4.94 m/s, or 4.94 m/s backwards
Level 2
77. A 12.0-g rubber bullet travels at a velocity of
150 m/s, hits a stationary 8.5-kg concrete
block resting on a frictionless surface, and
ricochets in the opposite direction with a
velocity of 1.0102m/s, as shown in
Figure 9-19. How fast will the concrete
block be moving?
mCvCi mDvDi mCvCf mDvDf
vDf
since the block is initially at rest, this becomes
vDf
0.35 m/s
78. Skateboarding Kofi, with mass 42.00 kg, is riding a skateboard with a mass of
2.00 kg and traveling at 1.20 m/s. Kofi jumps off and the skateboard stops dead
in its tracks. In what direction and with what velocity did he jump?
(mLvLi msvsi)vimLvLf msvsf
where vsf 0 and vLi vsi vi
Thus vLf
1.26 m/s in the same direction as she was riding
79. Billiards A cue ball, with mass 0.16 kg, rolling at 4.0 m/s, hits a stationary
eight ball of similar mass. If the cue ball travels 45° above its original path and
the eight ball travels 45° below the horizontal, as shown in Figure 9-20, what
is the velocity of each ball after the collision?
(42.00 kg 2.00 kg)(1.20 m/s)
42.00 kg
(mLms)vi
mL
(0.0120 kg)(150 m/s (1.0102m/s))
8.5 kg
mC(vCi vCf)
mD
mCvCi mDvDi mCvCf
mD
(0.0500 kg)(2.00 m/s) (4.65 kg)(2.00 m/s) (0.0500 kg)(647 m/s)
4.65 kg
1.0102 m/s
12.0 g
8.5 kg
■Figure 9-19
212 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued
Physics: Principles and Problems Solutions Manual 213
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
We can get momentum equations from
the vector diagram.
pCf pCi sin 45°
mCvCf mCvCi sin 45°
vCf vCi sin 45°
(4.0 m/s)(sin 45°)
2.8 m/s
For the eight ball,
p8f pci cos 45°
m8v8f mCvCi(cos 45°)
where m8mC. Thus,
v8f vCi cos 45°
(4.0 m/s)(cos 45°)
2.8 m/s
80. A 2575-kg van runs into the back of an
825-kg compact car at rest. They move off
together at 8.5 m/s. Assuming that the fric-
tion with the road is negligible, calculate
the initial speed of the van.
pCi pDi pCf pDf
mCvCi (mCmD)vf
so, vCi
vf
11 m/s
Level 3
81. In-line Skating Diego and Keshia are on
in-line skates and stand face-to-face, then
push each other away with their hands.
Diego has a mass of 90.0 kg and Keshia has
a mass of 60.0 kg.
a. Sketch the event, identifying the
“before” and “after” situations, and set
up a coordinate axis.
Before: mK60.0 kg
mD90.0 kg
vi0.0 m/s
After: mK60.0 kg
mD90.0 kg
vKf ?
vDf ?
(2575 kg 825 kg)(8.5 m/s)
2575 kg
mCmD
mC
pCi
p8f pCf
45
45°
45°
■Figure 9-20
Chapter 9 continued
b. Find the ratio of the skaters’ velocities just after their hands lose contact.
pKi pDi 0.0 kgm/s pKf pDf
so, mKvKf mDvDf 0.0 kgm/s
and mKvKf mDvDf
Thus, the ratios of the velocities are
1.50
The negative sign shows that the velocities are in opposite directions.
c. Which skater has the greater speed?
Keshia, who has the smaller mass, has the greater speed.
d. Which skater pushed harder?
The forces were equal and opposite.
82. A 0.200-kg plastic ball moves with a velocity of 0.30 m/s. It collides with a
second plastic ball of mass 0.100 kg, which is moving along the same line at a
speed of 0.10 m/s. After the collision, both balls continue moving in the same,
original direction. The speed of the 0.100-kg ball is 0.26 m/s. What is the new
velocity of the 0.200-kg ball?
mCvCi mDvDi mCvCf mDvDf
so, vCf mCvCi mDvDi mDvDf
mC
90.0 kg
60.0 kg
mD
mK
vKf
vDf
Before
After
vKi vDi 0
vKf vDf
+x
+x
214 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 215
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
0.22 m/s in the original direction
Mixed Review
pages 253–254
Level 1
83. A constant force of 6.00 N acts on a 3.00-kg object for 10.0 s. What are the
changes in the object’s momentum and velocity?
The change in momentum is
pFt
(6.00 N)(10.0 s)
60.0 Ns 60.0 kgm/s
The change in velocity is found from the impulse.
Ftmv
v
20.0 m/s
84. The velocity of a 625-kg car is changed from 10.0 m/s to 44.0 m/s in 68.0 s by
an external, constant force.
a. What is the resulting change in momentum of the car?
pmvm(vfvi)
(625 kg)(44.0 m/s 10.0 m/s)
2.12104kgm/s
b. What is the magnitude of the force?
Ftmv
so, F
313 N
85. Dragster An 845-kg dragster accelerates on a race track from rest to 100.0 km/h
in 0.90 s.
a. What is the change in momentum of the dragster?
pm(vfvi)
(845 kg)(100.0 km/h 0.0 km/h)
2.35104kgm/s
1 h
3600 s
1000 m
1 km
(625 kg)(44.0 m/s 10.0 m/s)
68.0 s
m(vfvi)
t
mv
t
(6.00 N)(10.0 s)
3.00 kg
Ft
m
(0.200 kg)(0.30 m/s) (0.100 kg)(0.10 m/s) (0.100 kg)(0.26 m/s)
0.200 kg
Chapter 9 continued

b. What is the average force exerted on the dragster?
F
2.6104N
c. What exerts that force?
The force is exerted by the track through friction.
Level 2
86. Ice Hockey A 0.115-kg hockey puck, moving at 35.0 m/s, strikes a 0.365-kg
jacket that is thrown onto the ice by a fan of a certain hockey team. The puck
and jacket slide off together. Find their velocity.
mPvPi (mPmJ)vf
vf
8.39 m/s
87. A 50.0-kg woman, riding on a 10.0-kg cart, is moving east at 5.0 m/s. The woman
jumps off the front of the cart and lands on the ground at 7.0 m/s eastward, rela-
tive to the ground.
a. Sketch the “before” and “after” situations and assign a coordinate axis to
them.
Before: mw50.0 kg
mc10.0 kg
vi5.0 m/s
After: mw50.0 kg
mc10.0 kg
vwf 7.0 m/s
vcf ?
Before After
vCf
vi
+x
vwf
(0.115 kg)(35.0 m/s)
(0.115 kg 0.365 kg)
mPmPi
mPmJ
1 h
3600 s
1000 m
1 km
(845 kg)(100.0 km/h 0.0 km/h)
0.90 s
m(vfvi)
t
216 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 217
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. Find the cart’s velocity after the woman jumps off.
(mwmc)vimwvwf mcvcf
so, vcf
5.0 m/s, or 5.0 m/s west
88. Gymnastics Figure 9-21 shows a gymnast performing a routine. First, she does
giant swings on the high bar, holding her body straight and pivoting around her
hands. Then, she lets go of the high bar and grabs her knees with her hands in
the tuck position. Finally, she straightens up and lands on her feet.
a. In the second and final parts of the gymnast’s routine, around what axis does
she spin?
She spins around the center of mass of her body, first in the tuck posi-
tion and then also as she straightens out.
b. Rank in order, from greatest to least, her moments of inertia for the three
positions.
giant swing (greatest), straight, tuck (least)
c. Rank in order, from greatest to least, her angular velocities in the three
positions.
tuck (greatest), straight, giant swing (least)
■Figure 9-21
Level 3
89. A 60.0-kg male dancer leaps 0.32 m high.
a. With what momentum does he reach the ground?
vv022dg
Thus, the velocity of the dancer is
v2dg
(50.0 kg 10.0 kg)(5.0 m/s) (50.0 kg)(7.0 m/s)
10.0 kg
(mwmc)vimwvwf
mc
Chapter 9 continued

and his momentum is
pmv m2dg
(60.0 kg)(2)(0.3
2 m)(9
.80 m
/s2)
1.5102kgm/s down
b. What impulse is needed to stop the dancer?
Ftmvm(vfvi)
To stop the dancer, vf0. Thus,
Ftmvfp 1.5102kgm/s up
c. As the dancer lands, his knees bend, lengthening the stopping time to
0.050 s. Find the average force exerted on the dancer’s body.
Ftmvm2dg
so, F
3.0103N
d. Compare the stopping force with his weight.
Fgmg (60.0 kg)(9.80 m/s2) 5.98102N
The force is about five times the weight.
Thinking Critically
page 254
90. Apply Concepts A 92-kg fullback, running at 5.0 m/s, attempts to dive directly
across the goal line for a touchdown. Just as he reaches the line, he is met head-on
in midair by two 75-kg linebackers, both moving in the direction opposite the full-
back. One is moving at 2.0 m/s and the other at 4.0 m/s. They all become entan-
gled as one mass.
a. Sketch the event, identifying the “before” and “after” situations.
Before: mA92 kg
mB75 kg
mC75 kg
vAi 5.0 m/s
vBi 2.0 m/s
vCi 4.0 m/s
After: mA92 kg
mB75 kg
mC75 kg
vf?
(60.0 kg)(2)(0.3
2 m)(9
.80 m
/s2)
0.050 s
m2dg
t
218 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued
Physics: Principles and Problems Solutions Manual 219
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What is the velocity of the football players after the collision?
pAi pBi pCi pAf pBf pCf
mAvAi mBvBi mCvCi mAvAf mBvBf mCvCf
(mAmBmC)vf
vf
0.041 m/s
c. Does the fullback score a touchdown?
Yes. The velocity is positive, so the football crosses the goal line for
a touchdown.
91. Analyze and Conclude A student, holding a bicycle wheel with its axis vertical,
sits on a stool that can rotate without friction. She uses her hand to get the wheel
spinning. Would you expect the student and stool to turn? If so, in which
direction? Explain.
The student and the stool would spin slowly in the direction opposite to
that of the wheel. Without friction there are no external torques.Thus, the
angular momentum of the system is not changed. The angular momentum
of the student and stool must be equal and opposite to the angular
momentum of the spinning wheel.
92. Analyze and Conclude Two balls during a collision are
shown in Figure 9-22, which is drawn to scale. The balls
enter from the left, collide, and then bounce away. The heavier
ball, at the bottom of the diagram, has a mass of 0.600 kg,
and the other has a mass of 0.400 kg. Using a vector diagram,
determine whether momentum is conserved in this collision.
Explain any difference in the momentum of the system before
and after the collision.
Dotted lines show that the changes of momentum for each
ball are equal and opposite: (mAvA) (mBvB). Because the masses
have a 3:2 ratio, a 2:3 ratio of velocity changes will compensate.
■Figure 9-22
(92 kg)(5.0 m/s) (75 kg)(2.0 m/s) (75 kg)(4.0 m/s)
92 kg 75 kg 75 kg
mAvAi mBvBi mCivCi
mAmBmC
Before After
vAi vCi vf
vBi
+x
Chapter 9 continued

Writing in Physics
page 254
93. How can highway barriers be designed to
be more effective in saving people’s lives?
Research this issue and describe how
impulse and change in momentum can be
used to analyze barrier designs.
The change in a car’s momentum does
not depend on how it is brought to a
stop. Thus, the impulse also does not
change. To reduce the force, the time
over which a car is stopped must be
increased. Using barriers that can
extend the time it takes to stop a car
will reduce the force. Flexible, plastic
containers filled with sand often are
used.
94. While air bags save many lives, they also
have caused injuries and even death.
Research the arguments and responses of
automobile makers to this statement.
Determine whether the problems involve
impulse and momentum or other issues.
There are two ways an air bag reduces
injury. First, an air bag extends the time
over which the impulse acts, thereby
reducing the force. Second, an air bag
spreads the force over a larger area,
thereby reducing the pressure. Thus,
the injuries due to forces from small
objects are reduced. The dangers of air
bags mostly center on the fact that air
bags must be inflated very rapidly. The
surface of an air bag can approach the
passenger at speeds of up to 322 km/h
(200 mph). Injuries can occur when the
moving bag collides with the person.
Systems are being developed that will
adjust the rate at which gases fill the air
bags to match the size of the person.
Cumulative Review
page 254
95. A 0.72-kg ball is swung vertically from a
0.60-m string in uniform circular motion at
a speed of 3.3 m/s. What is the tension in
the cord at the top of the ball’s motion?
(Chapter 6)
The tension is the gravitational force
minus the centripetal force.
FTFgFc
mg mg
(0.72 kg)(9.80 m/s2)
6.0 N
96. You wish to launch a satellite that will
remain above the same spot on Earth’s sur-
face. This means the satellite must have a
period of exactly one day. Calculate the
radius of the circular orbit this satellite
must have. Hint: The Moon also circles Earth
and both the Moon and the satellite will obey
Kepler’s third law. The Moon is 3.9108m
from Earth and its period is 27.33 days.
(Chapter 7)
2
3
so rs
T
T
m
s
2rm3
2
1
7
.0
.3
0
3
0d
d
a
a
y
y
s
2(3.9108m)3
4.3107m
97. A rope is wrapped around a drum that is
0.600 m in diameter. A machine pulls with
a constant 40.0 N force for a total of 2.00 s.
In that time, 5.00 m of rope is unwound.
Find ,at 2.00 s, and I. (Chapter 8)
The angular acceleration is the ratio of
the linear acceleration of the drum’s
edge and drum’s radius.
1
3
1
3
rs
rm
Ts
Tm
(3.3 m/s)2
0.60 m
v2
r
mv2
r
vB1 vB2
vB
vA
vA1 vA2
vA1
vB1
mB 0.400 kg
mA 0.600 kg
220 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 221
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a
r
The linear acceleration is found from the equation of motion.
xat2
a
Thus, the angular acceleration is
a
r
8.33 rad/s2
At the end of 2.00 s, the angular velocity is
t
2
rx
t
16.7 rad/s
The moment of inertia is
I
1.44 kgm2
Challenge Problem
page 244
Your friend was driving her 1265-kg car north on Oak Street when she was hit by a
925-kg compact car going west on Maple Street. The cars stuck together and slid
23.1 m at 42° north of west. The speed limit on both streets is 22 m/s (50 mph).
Assume that momentum was conserved during the collision and that acceleration
was constant during the skid. The coefficient of kinetic friction between the tires
and the pavement is 0.65.
(40.0 N)
0.60
2
0 m
2(2.00 s)2(sin 90.0°)
(2)(5.00 m)
Fr2t2sin
2x
Fr sin
r
2
tx
2
(2)(5.00 m)
0.602
0m
(2.00 s)
2xt
rt2
(2)(5.00 m)
0.602
0m
(2.00 s)2
2x
rt2
2x
t2
1
2
Chapter 9 continued
1. Your friend claims that she wasn’t speeding, but that the driver of other car was.
How fast was your friend driving before the crash?
The vector diagram provides a momentum equation for the friend’s car.
pCi pfsin 42°
The friend’s initial velocity, then, is
vCi
We can find vffirst by finding the acceleration and time of the skid.The
acceleration is
a g
The time can be derived from the distance equation.
dat2
t
2
a
d
2d
g
The final velocity, then, is
vfat g
2d
g
2dg
Using this, we now can find the friend’s initial velocity.
vCi
2.0101m/s
(1265 kg 925 kg)(2)(23
.1 m)(
0.65)(
9.80 m
/s2)
(sin 42°)
1265 kg
(mCmD)2dg
sin 42°
mC
(mCmD)vfsin 42°
mC
1
2
(mCmD)g
mCmD
Fg
m
F
m
(mCmD)vfsin 42°
mC
pCi
mC
42°
925 kg
1265 kg
x
y
222 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 223
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
2. How fast was the other car moving before the crash? Can you support your
friend’s case in court?
From the vector diagram, the momentum equation for the other car is
pDi pfcos 42°
(mCmD)vfcos 42°
(mCmD)2dg
(cos 42°)
The other car’s initial velocity, then, is,
vDi
3.0101m/s
The friend was not exceeding the 22 m/s speed limit.The other car was
exceeding the speed limit.
(1265 kg 925 kg)(2)(23
.1 m)(
0.65)(
9.80 m
/s2)
(cos 42°)
925 kg
(mCmD)2dg
(sin 42°)
mD
pDi
mD
Chapter 9 continued


Physics: Principles and Problems Solutions Manual 225
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
10 Energy, Work, and
Simple Machines
CHAPTER
Practice Problems
10.1 Energy and Work
pages 257–265
page 261
1. Refer to Example Problem 1 to solve the
following problem.
a. If the hockey player exerted twice as
much force, 9.00 N, on the puck, how
would the puck’s change in kinetic
energy be affected?
Because WFd and KE W,
doubling the force would double
the work, which would double the
change in kinetic energy to 1.35 J.
b. If the player exerted a 9.00 N-force, but
the stick was in contact with the puck
for only half the distance, 0.075 m,
what would be the change in kinetic
energy?
Because WFd, halving the
distance would cut the work in half,
which also would cut the change in
kinetic energy in half, to 0.68 J.
2. Together, two students exert a force of 825 N
in pushing a car a distance of 35 m.
a. How much work do the students do on
the car?
WFd (825 N)(35 m)
2.9104J
b. If the force was doubled, how much
work would they do pushing the car the
same distance?
WFd
(2)(825 N)(35 m)
5.8104J which is twice as
much work
3. A rock climber wears a 7.5-kg backpack
while scaling a cliff. After 30.0 min, the
climber is 8.2 m above the starting point.
a. How much work does the climber do
on the backpack?
WFd
mgd
(7.5 kg)(9.80 m/s2)(8.2 m)
6.0102J
b. If the climber weighs 645 N, how much
work does she do lifting herself and the
backpack?
WFd 6.0102J
(645 N)(8.2 m) 6.0102J
5.9103J
c. What is the average power developed by
the climber?
P
W
t
5
3
.9
0
.01
m
03
in
J
1
6m
0s
in
3.3 W
page 262
4. If the sailor in Example Problem 2 pulled
with the same force, and along the same
distance, but at an angle of 50.0°, how
much work would he do?
WFd cos
(255 N)(30.0 m)(cos 50.0°)
4.92103J
5. Two people lift a heavy box a distance of
15 m. They use ropes, each of which makes
an angle of 15° with the vertical. Each
person exerts a force of 225 N. How much
work do they do?
WFd cos
(2)(225 N)(15 m)(cos 15°)
6.5103J

6. An airplane passenger carries a 215-N suit-
case up the stairs, a displacement of 4.20 m
vertically, and 4.60 m horizontally.
a. How much work does the passenger do?
Since gravity acts vertically, only the
vertical displacement needs to be
considered.
WFd (215 N)(4.20 m) 903 J
b. The same passenger carries the same
suitcase back down the same set of
stairs. How much work does the
passenger do now?
Force is upward, but vertical
displacement is downward, so
WFd cos
(215 N)(4.20 m)(cos 180.0°)
903 J
7. A rope is used to pull a metal box a distance
of 15.0 m across the floor. The rope is held
at an angle of 46.0° with the floor, and a
force of 628 N is applied to the rope. How
much work does the force on the rope do?
WFd cos
(628 N)(15.0 m)(cos 46.0°)
6.54103J
8. A bicycle rider pushes a bicycle that has a
mass of 13 kg up a steep hill. The incline is
25° and the road is 275 m long, as shown
in Figure 10-4. The rider pushes the bike
parallel to the road with a force of 25 N.
■Figure 10-4 (Not to scale)
a. How much work does the rider do on
the bike?
Force and displacement are in the
same direction.
WFd
(25 N)(275 m)
6.9103J
b. How much work is done by the force of
gravity on the bike?
The force is downward (90°), and
the displacement is 25° above the
horizontal or 115° from the force.
WFd cos
mgd cos
(13 kg)(9.80 m/s2)(275 m)
(cos 115°)
1.5104J
page 264
9. A box that weighs 575 N is lifted a distance
of 20.0 m straight up by a cable attached to a
motor. The job is done in 10.0 s. What power
is developed by the motor in W and kW?
P
W
t
F
t
d
(575
1
N
0
)
.
(
0
20
s
.0 m)
1.15103W1.15 kW
10. You push a wheelbarrow a distance of
60.0 m at a constant speed for 25.0 s, by
exerting a 145-N force horizontally.
a. What power do you develop?
P
W
t
F
t
d
(145
2
N
5
)
.
(
0
60
s
.0 m)
348 W
b. If you move the wheelbarrow twice as
fast, how much power is developed?
tis halved, so Pis doubled to 696 W.
11. What power does a pump develop to lift
35 L of water per minute from a depth of
110 m? (1 L of water has a mass of 1.00 kg.)
P
W
t
mg
t
d
m
t
gd
where
m
t
(35 L/min)(1.00 kg/L)
Thus,
P
m
t
gd
(35 L/min)(1.00 kg/L)(9.80 m/s2)
(110 m)(1 min/60s)
0.63 kW
25°
275 m
25 N
226 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 227
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
12. An electric motor develops 65 kW of power
as it lifts a loaded elevator 17.5 m in 35 s.
How much force does the motor exert?
P
W
t
F
t
d
F
P
dt
1.3105N
13. A winch designed to be mounted on a
truck, as shown in Figure 10-7, is adver-
tised as being able to exert a 6.8103-N
force and to develop a power of 0.30 kW.
How long would it take the truck and the
winch to pull an object 15 m?
■Figure 10-7
P
W
t
F
t
d
t
F
P
d
340 s
5.7 min
14. Your car has stalled and you need to push
it. You notice as the car gets going that you
need less and less force to keep it going.
Suppose that for the first 15 m, your force
decreased at a constant rate from 210.0 N to
40.0 N. How much work did you do on the
car? Draw a force-displacement graph to
represent the work done during this period.
The work done is the area of the
trapezoid under the solid line:
W
1
2
d(F1F2)
1
2
(15 m)(210.0 N 40.0 N)
1.9103J
Section Review
10.1 Energy and Work
pages 257–265
page 265
15. Work Murimi pushes a 20-kg mass 10 m
across a floor with a horizontal force of
80 N. Calculate the amount of work done
by Murimi.
WFd (80 N)(10 m) 8102J
The mass is not important to this
problem.
16. Work A mover loads a 185-kg refrigerator
into a moving van by pushing it up a
10.0-m, friction-free ramp at an angle of
inclination of 11.0°. How much work is
done by the mover?
y(10.0 m)(sin 11.0°)
1.91 m
WFd mgd sin
(185 kg)(9.80 m/s2)(10.0 m)(sin 11.0°)
3.46103J
17. Work and Power Does the work required
to lift a book to a high shelf depend on
how fast you raise it? Does the power
required to lift the book depend on how
fast you raise it? Explain.
No, work is not a function of time.
However, power is a function of time, so
the power required to lift the book does
depend on how fast you raise it.
Displacement (m)
210.0
40.0
015
Force (N)
(6.8103N)(15 m)
(0.30103W)
(65103W)(35 s)
17.5 m
Chapter 10 continued

18. Power An elevator lifts a total mass of
1.1103kg a distance of 40.0 m in 12.5 s.
How much power does the elevator generate?
P
W
t
F
t
d
mg
t
d
3.4104W
19. Work A 0.180-kg ball falls 2.5 m. How
much work does the force of gravity do on
the ball?
WFgdmgd
(0.180 kg)(9.80 m/s2)(2.5 m)
4.4 J
20. Mass A forklift raises a box 1.2 m and
does 7.0 kJ of work on it. What is the mass
of the box?
WFd mgd
so m
g
W
d
6.0102kg
21. Work You and a friend each carry identical
boxes from the first floor of a building to a
room located on the second floor, farther
down the hall. You choose to carry the box
first up the stairs, and then down the hall to
the room. Your friend carries it down the hall
on the first floor, then up a different stairwell
to the second floor. Who does more work?
Both do the same amount of work.
Only the height lifted and the vertical
force exerted count.
22. Work and Kinetic Energy If the work
done on an object doubles its kinetic
energy, does it double its velocity? If not,
by what ratio does it change the velocity?
Kinetic energy is proportional to the
square of the velocity, so doubling the
energy doubles the square of the veloc-
ity. The velocity increases by a factor of
the square root of 2, or 1.4.
23. Critical Thinking Explain how to find the
change in energy of a system if three agents
exert forces on the system at once.
Since work is the change in kinetic
energy, calculate the work done by each
force. The work can be positive, nega-
tive, or zero, depending on the relative
angles of the force and displacement of
the object. The sum of the three works
is the change in energy of the system.
Practice Problems
10.2 Machines
pages 266–273
page 272
24. If the gear radius in the bicycle in Example
Problem 4 is doubled, while the force exerted
on the chain and the distance the wheel rim
moves remain the same, what quantities
change, and by how much?
IMA
r
r
e
r
8
3.
5
0
.0
6c
cm
m
0.225 (doubled)
MA
1e
00
IMA
9
15
0.0
0
(0.225)
0.214 (doubled)
MA
F
F
e
r
so Fr(MA)(Fe)
(0.214)(155 N)
33.2 N
IMA
d
d
e
r
so de(IMA)(dr)
(0.225)(14.0 cm)
3.15 cm
25. A sledgehammer is used to drive a wedge
into a log to split it. When the wedge is dri-
ven 0.20 m into the log, the log is separated
a distance of 5.0 cm. A force of 1.7104N
is needed to split the log, and the sledge-
hammer exerts a force of 1.1104N.
a. What is the IMA of the wedge?
IMA
d
d
e
r
(
(
0
0
.0
.2
5
0
0
m
m
)
)
4.0
7.0103J
(9.80 m/s2)(1.2 m)
(1.1103kg)(9.80 m/s2)(40.0 m)
12.5 s
228 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued
Physics: Principles and Problems Solutions Manual 229
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What is the MA of the wedge?
MA
F
F
e
r
1.5
c. Calculate the efficiency of the wedge as
a machine.
e
IM
MA
A
100
1
4.
.5
0
100 38%
26. A worker uses a pulley system to raise
a 24.0-kg carton 16.5 m, as shown in
Figure 10-14. A force of 129 N is exerted,
and the rope is pulled 33.0 m.
■Figure 10-14
a. What is the MA of the pulley system?
MA
F
F
e
r
m
Fe
g
1.82
b. What is the efficiency of the system?
efficiency
IM
MA
A
100
91.0%
27. You exert a force of 225 N on a lever to
raise a 1.25103-N rock a distance of
13 cm. If the efficiency of the lever is
88.7 percent, how far did you move your
end of the lever?
efficiency
W
W
o
i
100
F
F
e
rd
d
r
e
100
So de
0.81 m
28. A winch has a crank with a 45-cm radius.
A rope is wrapped around a drum with a
7.5-cm radius. One revolution of the crank
turns the drum one revolution.
a. What is the ideal mechanical advantage
of this machine?
Compare effort and resistance
distances for 1 rev:
IMA
d
d
e
r
(
(
2
2
)
)
7
4
.
5
5
c
c
m
m
6.0
b. If, due to friction, the machine is only
75 percent efficient, how much force
would have to be exerted on the handle
of the crank to exert 750 N of force on
the rope?
efficiency
IM
MA
A
100
(Fe)
F
(I
r
MA)
100
so Fe
(75
(7
0
5
N
)(
)
6
(
.
1
0
0
)
0)
1.7102N
(Fr)(100)
(efficiency)(IMA)
(1.25103N)(0.13 m)(100)
(225 N)(88.7)
Frdr(100)
Fe(efficiency)
(1.82)(16.5 m)(100)
33.0 m
(MA)(dr)(100)
de
(MA)(100)
d
de
r
(24.0 kg)(9.80 m/s2)
129 N
129 N
33.0 m
16.5 m
24.0 kg
(1.7104N)
(1.1104N)
Chapter 10 continued

Section Review
10.2 Machines
pages 266–273
page 273
29. Simple Machines Classify the tools below
as a lever, a wheel and axle, an inclined
plane, a wedge, or a pulley.
a. screwdriver
wheel and axle
b. pliers
lever
c. chisel
wedge
d. nail puller
lever
30. IMA A worker is testing a multiple pulley
system to estimate the heaviest object that
he could lift. The largest downward force he
could exert is equal to his weight, 875 N.
When the worker moves the rope 1.5 m, the
object moves 0.25 m. What is the heaviest
object that he could lift?
MA
F
F
e
r
so Fr(MA)(Fe)
Assuming the efficiency is 100%,
MA IMA
d
d
e
r
(Fe)
(
(
0
1
.2
.5
5
m
m
)
)
(875 N)
5.2103N
31. Compound Machines A winch has a crank
on a 45-cm arm that turns a drum with a
7.5-cm radius through a set of gears. It takes
three revolutions of the crank to rotate the
drum through one revolution. What is the
IMA of this compound machine?
The IMA of the system is the product of
the IMA of each machine. For the crank
and drum, the ratio of distances is
2
2
(
(
7
4
.
5
5
c
c
m
m
)
)
6.0.
IMA
d
d
e
r
(3)
2
(
2
r
r)
18
32. Efficiency Suppose you increase the effi-
ciency of a simple machine. Do the MA and
IMA increase, decrease, or remain the same?
Either MA increases while IMA remains
the same, or IMA decreases while MA
remains the same, or MA increases
while IMA decreases.
33. Critical Thinking The mechanical advan-
tage of a multi-gear bicycle is changed by
moving the chain to a suitable rear gear.
a. To start out, you must accelerate the
bicycle, so you want to have the bicycle
exert the greatest possible force. Should
you choose a small or large gear?
large, to increase IMA
r
r
w
g
h
e
e
a
e
r
l
b. As you reach your traveling speed, you
want to rotate the pedals as few times as
possible. Should you choose a small or
large gear?
Small, because less chain travel,
hence few pedal revolutions, will be
required per wheel revolution.
c. Many bicycles also let you choose the
size of the front gear. If you want even
more force to accelerate while climbing
a hill, would you move to a larger or
smaller front gear?
smaller, to increase pedal-front gear
IMA because
IMA
rfr
r
o
p
n
e
t
d
g
a
e
l
ar
(3)(2)(45 cm)
(2)(7.5 cm)
230 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued
Physics: Principles and Problems Solutions Manual 231
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter Assessment
Concept Mapping
page 278
34. Create a concept map using the following
terms: force, displacement, direction of motion,
work, change in kinetic energy.
Mastering Concepts
page 278
35. In what units is work measured? (10.1)
joules
36. Suppose a satellite revolves around Earth in
a circular orbit. Does Earth’s gravity do any
work on the satellite? (10.1)
No, the force of gravity is directed
toward Earth and is perpendicular to the
direction of displacement of the satellite.
37. An object slides at constant speed on a
frictionless surface. What forces act on the
object? What work is done by each force?
(10.1)
Only gravity and an upward, normal
force act on the object. No work is
done because the displacement is
perpendicular to these forces. There
is no force in the direction of displace-
ment because the object is sliding at a
constant speed.
38. Define work and power. (10.1)
Work is the product of force and the
distance over which an object is moved
in the direction of the force. Power is
the time rate at which work is done.
39. What is a watt equivalent to in terms of
kilograms, meters, and seconds? (10.1)
WJ/s
Nm/s
(kgm/s2)m/s
kgm2/s3
40. Is it possible to get more work out of a
machine than you put into it? (10.2)
no, e100%
41. Explain how the pedals of a bicycle are a
simple machine. (10.2)
Pedals transfer force from the rider to
the bike through a wheel and axle.
Applying Concepts
page 278
42. Which requires more work, carrying
a 420-N backpack up a 200-m-high hill
or carrying a 210-N backpack up a
400-m-high hill? Why?
Each requires the same amount of
work because force times distance is
the same.
43. Lifting You slowly lift a box of books from
the floor and put it on a table. Earth’s gravity
exerts a force, magnitude mg, downward, and
you exert a force, magnitude mg, upward.
The two forces have equal magnitudes and
opposite directions. It appears that no work
is done, but you know that you did work.
Explain what work was done.
You do positive work on the box
because the force and motion are in the
same direction. Gravity does negative
work on the box because the force of
gravity is opposite to the direction of
motion. The work done by you and by
gravity are separate and do not cancel
each other.
44. You have an after-school job carrying car-
tons of new copy paper up a flight of stairs,
and then carrying recycled paper back down
the stairs. The mass of the paper does not
Chapter 10 continued
Displacement Direction
of motion
Force
Work
Change in
kinetic energy

change. Your physics teacher says that you
do not work all day, so you should not be
paid. In what sense is the physics teacher
correct? What arrangement of payments
might you make to ensure that you are
properly compensated?
The net work is zero. Carrying the carton
upstairs requires positive work; carrying
it back down is negative work. The work
done in both cases is equal and oppo-
site because the distances are equal and
opposite. The student might arrange the
payments on the basis of the time it
takes to carry paper, whether up or
down, not on the basis of work done.
45. You carry the cartons of copy paper down
the stairs, and then along a 15-m-long
hallway. Are you working now? Explain.
No, the force on the box is up and the
displacement is down the hall.They are
perpendicular and no work is done.
46. Climbing Stairs Two people of the same
mass climb the same flight of stairs. The
first person climbs the stairs in 25 s; the
second person does so in 35 s.
a. Which person does more work? Explain
your answer.
Both people are doing the same
amount of work because they both
are climbing the same flight of stairs
and they have the same mass.
b. Which person produces more power?
Explain your answer.
The person who climbs in 25 s
expends more power, as less time is
needed to cover the distance.
47. Show that power delivered can be written as
PFv cos .
P
W
t
,but WFd cos
so, P
Fd c
tos
because v
d
t
,
PFv cos
48. How can you increase the ideal mechanical
advantage of a machine?
Increase the ratio of de/drto increase
the IMA of a machine.
49. Wedge How can you increase the mechani-
cal advantage of a wedge without changing
its ideal mechanical advantage?
Reduce friction as much as possible to
reduce the resistance force.
50. Orbits Explain why a planet orbiting the Sun
does not violate the work-energy theorem.
Assuming a circular orbit, the force
due to gravity is perpendicular to the
direction of motion. This means the
work done is zero. Hence, there is no
change in kinetic energy of the planet,
so it does not speed up or slow down.
This is true for a circular orbit.
51. Claw Hammer A claw hammer is used to
pull a nail from a piece of wood, as shown
in Figure 10-16. Where should you place
your hand on the handle and where should
the nail be located in the claw to make the
effort force as small as possible?
■Figure 10-16
Your hand should be as far from the
head as possible to make deas large as
possible. The nail should be as close to
the head as possible to make dras
small as possible.
232 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 233
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Mastering Problems
10.1 Energy and Work
pages 278–280
Level 1
52. The third floor of a house is 8 m above street
level. How much work is needed to move a
150-kg refrigerator to the third floor?
WFd mgd
(150 kg)(9.80 m/s2)(8 m)
1104J
53. Haloke does 176 J of work lifting himself
0.300 m. What is Haloke’s mass?
WFd mgd; therefore,
m
g
W
d
59.9 kg
54. Football After scoring a touchdown, an
84.0-kg wide receiver celebrates by leaping
1.20 m off the ground. How much work
was done by the wide receiver in the
celebration?
WFd mgd
(84.0 kg)(9.80 m/s2)(1.20 m)
988 J
55. Tug-of-War During a tug-of-war, team A
does 2.20105J of work in pulling team B
8.00 m. What force was team A exerting?
WFd,so
F
W
d
2.2
8
0
.0
0
1m
05J
2.75104N
56. To keep a car traveling at a constant velocity,
a 551-N force is needed to balance frictional
forces. How much work is done against fric-
tion by the car as it travels from Columbus to
Cincinnati, a distance of 161 km?
WFd (551 N)(1.61105m)
8.87107J
57. Cycling A cyclist exerts a force of 15.0 N as
he rides a bike 251 m in 30.0 s. How much
power does the cyclist develop?
P
W
t
F
t
d
(15.0
3
N
0
)
.
(
0
2.
s
51 m)
126 W
58. A student librarian lifts a 2.2-kg book from
the floor to a height of 1.25 m. He carries the
book 8.0 m to the stacks and places the book
on a shelf that is 0.35 m above the floor.
How much work does he do on the book?
Only the net vertical displacement
counts.
WFd mgd
(2.2 kg)(9.80 m/s2)(0.35 m)
7.5 J
59. A force of 300.0 N is used to push a
145-kg mass 30.0 m horizontally in 3.00 s.
a. Calculate the work done on the mass.
WFd (300.0 N)(30.0 m)
9.00103J
9.00 kJ
b. Calculate the power developed.
P
W
t
9.0
3
0
.
00
10
s
3J
3.00103W
3.00 kW
Level 2
60. Wagon A wagon is pulled by a force of
38.0 N exerted on the handle at an angle of
42.0° with the horizontal. If the wagon is
pulled in a circle of radius 25.0 m, how
much work is done?
WFd cos
(F)(2r) cos
(38.0 N)(2)(25.0 m)(cos 42.0°)
4.44103J
61. Lawn Mower Shani is pushing a lawn
mower with a force of 88.0 N along a han-
dle that makes an angle of 41.0° with the
horizontal. How much work is done by
176 J
(9.80 m/s2)(0.300 m)
Chapter 10 continued

Shani in moving the lawn mower 1.2 km
to mow the yard?
WFd cos
(88.0 N)(1.2103m)(cos 41.0°)
8.0104J
62. A 17.0-kg crate is to be pulled a distance of
20.0 m, requiring 1210 J of work to be
done. If the job is done by attaching a rope
and pulling with a force of 75.0 N, at what
angle is the rope held?
WFd cos
cos1
F
W
d
cos1
(75.01N
21
)(0
20
J
.0 m)
36.2°
63. Lawn Tractor A 120-kg lawn tractor,
shown in Figure 10-17, goes up a 21°
incline that is 12.0 m long in 2.5 s.
Calculate the power that is developed
by the tractor.
■Figure 10-17
P
W
t
Fd s
tin
mgd
t
sin
2.0103W2.0 kW
64. You slide a crate up a ramp at an angle of
30.0° by exerting a 225-N force parallel to
the ramp. The crate moves at a constant
speed. The coefficient of friction is 0.28.
How much work did you do on the crate as
it was raised a vertical distance of 1.15 m?
Fand dare parallel so
WFd F
sin
h
518 J
65. Piano A 4.2103-N piano is to be slid up a
3.5-m frictionless plank at a constant speed.
The plank makes an angle of 30.0° with the
horizontal. Calculate the work done by the
person sliding the piano up the plank.
The force parallel to the plane is given by
FFsin
so WFdFd sin
W(4200 N)(3.5 m)(sin 30.0°)
7.4103J
66. Sled Diego pulls a 4.5-kg sled across level
snow with a force of 225 N on a rope that
is 35.0° above the horizontal, as shown in
Figure 10-18. If the sled moves a distance
of 65.3 m, how much work does Diego do?
■Figure 10-18
WFd cos
(225 N)(65.3 m)(cos 35.0°)
1.20104J
67. Escalator Sau-Lan has a mass of 52 kg.
She rides up the escalator at Ocean Park in
Hong Kong. This is the world’s longest
escalator, with a length of 227 m and an
average inclination of 31°. How much work
does the escalator do on Sau-Lan?
WFd sin mgd sin
(52 kg)(9.80 m/s2)(227 m)(sin 31°)
6.0104J
68. Lawn Roller A lawn roller is pushed
across a lawn by a force of 115 N along
the direction of the handle, which is 22.5°
35.0°
225 N
4.5 kg
(225 N)(1.15 m)
sin 30.0°
(120 kg)(9.80 m/s2)(12.0 m)(sin 21°)
2.5 s
21°
12.0 m
120.0 kg
234 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued
Physics: Principles and Problems Solutions Manual 235
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
above the horizontal. If 64.6 W of power
is developed for 90.0 s, what distance is
the roller pushed?
P
W
t
Fd c
tos
so,
d
Fc
P
o
ts
54.7 m
69. John pushes a crate across the floor of a
factory with a horizontal force. The rough-
ness of the floor changes, and John must
exert a force of 20 N for 5 m, then 35 N for
12 m, and then 10 N for 8 m.
a. Draw a graph of force as a function of
distance.
b. Find the work John does pushing the
crate.
WF1d1F2d2F3d3
(20 N)(5 m) (35 N)(12 m)
(10 N)(8 m)
600 J
70. Maricruz slides a 60.0-kg crate up an
inclined ramp that is 2.0-m long and
attached to a platform 1.0 m above floor
level, as shown in Figure 10-19. A 400.0-N
force, parallel to the ramp, is needed to
slide the crate up the ramp at a constant
speed.
■Figure 10-19
a. How much work does Maricruz do in
sliding the crate up the ramp?
WFd (400.0 N)(2.0 m) 8.0102J
b. How much work would be done if
Maricruz simply lifted the crate straight
up from the floor to the platform?
WFd mgd
(60.0 kg)(9.80 m/s2)(1.0 m)
5.9102J
71. Boat Engine An engine moves a boat
through the water at a constant speed of
15 m/s. The engine must exert a force
of 6.0 kN to balance the force that the
water exerts against the hull. What power
does the engine develop?
P
W
t
F
t
d
Fv
(6.0103N)(15 m/s)
9.0104W9.0101kW
Level 3
72. In Figure 10-20, the magnitude of the force
necessary to stretch a spring is plotted
against the distance the spring is stretched.
■Figure 10-20
0.10 0.20 0.30
0.00
8.00
6.00
4.00
2.00
Force (N)
400.0 N
60.0 kg
2.0 m
1.0 m
Dis
p
lacement (m)
Force (N)
25
5
0
30
20
10
10 15 20
40
(64.6 W)(90.0 s)
(115 N)(cos 22.5°)
Chapter 10 continued

a. Calculate the slope of the graph, k, and
show that Fkd, where k25 N/m.
k
y
x
0
5
..
2
0
0
0m
N
0
0.
.0
00
0N
m
F1kd1
Let d10.20 m
From the graph, F1is 5.00 N.
So k
F
d
1
1
0
5.
.2
00
0m
N
25 N/m
b. Find the amount of work done in
stretching the spring from 0.00 m to
0.20 m by calculating the area under
the graph from 0.00 m to 0.20 m.
A
1
2
(base)(height)
1
2
(0.20 m)(5.00 N)
0.50 J
c. Show that the answer to part b
can be calculated using the formula
W
1
2
kd2, where Wis the work,
k25 N/m (the slope of the graph),
and dis the distance the spring is
stretched (0.20 m).
W
1
2
kd2
1
2
(25 N/m)(0.20 m)2
0.50 J
73. Use the graph in Figure 10-20 to find the
work needed to stretch the spring from
0.12 m to 0.28 m.
Add the areas of the triangle and
rectangle. The area of the triangle is:
1
2
bh
1
2
(0.28 m 0.12 m)(7.00 N 3.00 N)
0.32 J
The area of the rectangle is:
bh (0.28 m 0.12 m)(3.00 N 0.00 N)
0.48 J
Total work is 0.32 J 0.48 J 0.80 J
74. A worker pushes a crate weighing 93 N up
an inclined plane. The worker pushes the
crate horizontally, parallel to the ground, as
illustrated in Figure 10-21.
■Figure 10-21
a. The worker exerts a force of 85 N.
How much work does he do?
Displacement in direction of force
is 4.0 m,
so WFd (85 N)(4.0 m)
3.4102J
b. How much work is done by gravity?
(Be careful with the signs you use.)
Displacement in direction of force
is 3.0 m,
so WFd (93 N)(3.0 m)
2.8102J
c. The coefficient of friction is 0.20.
How much work is done by friction?
(Be careful with the signs you use.)
WFNd(Fyou, Fg, )d
0.20(85 N)(sin )
(93 N)(cos )(5.0 m)
0.20(85 N)
3
5.
.0
0
(93 N)
4
5.
.0
0
(5.0 m)
1.3102J (work done against
friction)
75. Oil Pump In 35.0 s, a pump delivers
0.550 m3of oil into barrels on a platform
25.0 m above the intake pipe. The oil’s
density is 0.820 g/cm3.
5.0 m
3.0 m
4.0 m
93 N
85 N
236 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 237
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. Calculate the work done by the pump.
The work done is
WFgdmgh
(volume)(density)gh
(0.550 m3)(0.820 g/cm3)
1
1
00
k
0
g
g
(1.00106cm3/m3)(9.80 m/s2)
(25.0 m)
1.10105J
b. Calculate the power produced by the
pump.
P
W
t
1.1
3
0
5
.0
10
s
5J
3.14103W3.14 kW
76. Conveyor Belt A 12.0-m-long conveyor
belt, inclined at 30.0°, is used to
transport bundles of newspapers from the
mail room up to the cargo bay to be
loaded onto delivery trucks. Each newspa-
per has a mass of 1.0 kg, and there are
25 newspapers per bundle. Determine the
power that the conveyor develops if it
delivers 15 bundles per minute.
P
W
t
F
t
d
mg
t
d
(25 newspapers)(15 bundles/min)
(1.0 kg/newspaper)(9.80 m/s2)
(12.0 m)(sin 30.0°)(1 min/60 s)
3.7102W
77. A car is driven at a constant speed of
76 km/h down a road. The car’s engine
delivers 48 kW of power. Calculate the
average force that is resisting the motion
of the car.
P
W
t
F
t
d
Fv
so F
P
v
2.3103N
78. The graph in Figure 10-22 shows the force
and displacement of an object being
pulled.
a. Calculate the work done to pull the
object 7.0 m.
Find the area under the curve (see
graph):
0.0 to 2.0 m:
1
2
(20.0 N)(2.0 m) 2.0101J
2.0 m to 3.0 m:
1
2
(30.0 N)(1.0 m) (20 N)(1.0 m) 35 J
3.0 m to 7.0 m:
(50.0 N)(4.0 m) 2.0102J
Total work:
2.0101J35 J 2.0102J
2.6102J
b. Calculate the power that would be
developed if the work was done in 2.0 s.
P
W
t
2.6
2
.0
10
s
2J
1.3102W
■Figure 10-22
20.0
Force (N)
Displacement (m)
6.04.02.0
40.0
0.0
48,000 W
76
1k
h
m
10
10
k
0
m
m
36
1
00
hs
Chapter 10 continued

10.2 Machines
pages 280–281
Level 1
79. Piano Takeshi raises a 1200-N piano a
distance of 5.00 m using a set of pulleys.
He pulls in 20.0 m of rope.
a. How much effort force would Takeshi
apply if this were an ideal machine?
F
F
e
r
d
d
e
r
so Fe
F
d
rd
e
r
(1200
20
N
.
)
0
(5
m
.00 m)
3.0102N
b. What force is used to balance the friction
force if the actual effort is 340 N?
FeFfFe,ideal
FfFeFe,ideal 340 N 3.0102N
40 N
c. What is the output work?
WoFrdr(1200 N)(5.00 m)
6.0103J
d. What is the input work?
WiFede(340 N)(20.0 m)
6.8103J
e. What is the mechanical advantage?
MA
F
F
e
r
1
3
2
4
0
0
0N
N
3.5
80. Lever Because there is very little friction,
the lever is an extremely efficient simple
machine. Using a 90.0-percent-efficient
lever, what input work is required to lift an
18.0-kg mass through a distance of 0.50 m?
efficiency
W
W
o
i
100
Wi
e
(W
ffio
c
)
i
(
e
1
n
0
c
0
y
)
(mg
9
d
0
)
.
(
0
100)
98 J
81. A pulley system lifts a 1345-N weight a
distance of 0.975 m. Paul pulls the rope a
distance of 3.90 m, exerting a force of 375 N.
a. What is the ideal mechanical advantage
of the system?
IMA
d
d
e
r
0
3
.9
.9
7
0
5m
m
4.00
b. What is the mechanical advantage?
MA
1
3
3
7
4
5
5N
N
3.59
c. How efficient is the system?
efficiency
IM
MA
A
100
3
4.
.5
09
0
100
89.8%
82. A force of 1.4 N is exerted through a
distance of 40.0 cm on a rope in a pulley
system to lift a 0.50-kg mass 10.0 cm.
Calculate the following.
a. the MA
MA
F
F
e
r
m
Fe
g
3.5
b. the IMA
IMA
d
d
e
r
4
10
0.
.0
0c
cm
m
4.00
c. the efficiency
efficiency
IM
MA
A
100
4
3
.0
.5
0
100 88%
83. A student exerts a force of 250 N on a lever,
through a distance of 1.6 m, as he lifts a
150-kg crate. If the efficiency of the lever is
90.0 percent, how far is the crate lifted?
e90
IM
MA
A
100 100
F
F
e
rd
d
r
e
100
F
F
e
r
d
de
r
(0.50 kg)(9.80 m/s2)
1.4 N
Fr
Fe
(18.0 kg)(9.80 m/s2)(0.50 m)(100)
90.0
238 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 239
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
so, dr
e
1
F
00
ed
F
e
r
1
e
0
F
0
e
m
de
g
0.24 m
Level 2
84. What work is required to lift a 215-kg mass
a distance of 5.65 m, using a machine that
is 72.5 percent efficient?
e
W
W
o
i
100
F
W
rd
i
r
100
m
W
gd
i
r
100
Wi
mg
e
dr
100
1.64104J
85. The ramp in Figure 10-23 is 18 m long and
4.5 m high.
■Figure 10-23
a. What force, parallel to the ramp (FA), is
required to slide a 25-kg box at constant
speed to the top of the ramp if friction
is disregarded?
WFgdmgh
so FFg
m
d
gh
61 N
b. What is the IMA of the ramp?
IMA
d
d
e
f
4
1.8
5m
m
4.0
c. What are the real MA and the efficiency
of the ramp if a parallel force of 75 N is
actually required?
MA
F
F
e
r
m
Fe
g
3.3
efficiency
IM
MA
A
100
3
4.
.3
0
100 82%
86. Bicycle Luisa pedals a bicycle with a gear
radius of 5.00 cm and a wheel radius of
38.6 cm, as shown in Figure 10-24. If the
wheel revolves once, what is the length of
the chain that was used?
■Figure 10-24
d2r2(5.00 cm) 31.4 cm
Level 3
87. Crane A motor with an efficiency of
88 percent operates a crane with an
efficiency of 42 percent. If the power
supplied to the motor is 5.5 kW, with
what constant speed does the crane lift
a 410-kg crate of machine parts?
Total efficiency (88%)(42%) 37%
Useful Power (5.5 kW)(37%)
2.0 kW
2.0103W
38.6 cm
5.00 cm
(25 kg)(9.80 m/s2)
75 N
(25 kg)(9.80 m/s2)(4.5 m)
18 m
Fg
FA
4.5 m
18 m
(215 kg)(9.80 m/s2)(5.65 m)(100)
72.5
(90.0)(250 N)(1.6 m)
(100)(150 kg)(9.80 m/s2)
Chapter 10 continued

P
W
t
F
t
d
F
d
t
Fv
v
F
P
g
m
P
g
0.50 m/s
88. A compound machine is constructed by
attaching a lever to a pulley system.
Consider an ideal compound machine con-
sisting of a lever with an IMA of 3.0 and a
pulley system with an IMA of 2.0.
a. Show that the IMA of this compound
machine is 6.0.
Wi1 Wo1 Wi2 Wo2
Wi1 Wo2
Fe1de1 Fr2dr2
For the compound machine
IMAc
d
d
e
r2
1
d
d
e
r1
1
IMA1and
d
d
e
r2
2
IMA2
dr1 de2
IM
de
A
1
1
dr1 de2 (IMA2)(dr2)
de1 (IMA1)(IMA2)(dr2)
d
d
e
r2
1
IMAc(IMA1)(IMA2)
(3.0)(2.0) 6.0
b. If the compound machine is 60.0 percent
efficient, how much effort must be
applied to the lever to lift a 540-N box?
e
IM
MA
A
100 100
(
(
F
F
e
r)
)
(
(
I
1
M
0
A
0)
)
so Fe
(
(
F
e
r
)
)
(
(
I
1
M
0
A
0
)
)
(5
(6
4
0
0
.0
N
)
)
(
(
6
1
.
0
0
0
)
)
150 N
c. If you move the effort side of the lever
12.0 cm, how far is the box lifted?
d
d
e
r2
1
IMAc
dr2
IM
de
A
1
c
12.
6
0
.0
cm
2.0 cm
Mixed Review
pages 281–282
Level 1
89. Ramps Isra has to get a piano onto a
2.0-m-high platform. She can use a
3.0-m-long frictionless ramp or a 4.0-m-long
frictionless ramp. Which ramp should Isra use
if she wants to do the least amount of work?
Either ramp: only the vertical distance
is important. If Isra used a longer ramp,
she would require less force. The work
done would be the same.
90. Brutus, a champion weightlifter, raises
240 kg of weights a distance of 2.35 m.
a. How much work is done by Brutus
lifting the weights?
WFd mgd
(240 kg)(9.80 m/s2)(2.35 m)
5.5103J
b. How much work is done by Brutus
holding the weights above his head?
d0, so no work
c. How much work is done by Brutus
lowering them back to the ground?
dis opposite of motion in part a, so
Wis also the opposite, 5.5103J.
d. Does Brutus do work if he lets go of the
weights and they fall back to the ground?
No. He exerts no force, so he does
no work, positive or negative.
e. If Brutus completes the lift in 2.5 s, how
much power is developed?
P
W
t
5.5
2
.5
10
s
3J
2.2 kW
F
F
e
r
IMA
2.0103W
(410 kg)(9.80 m/s2)
240 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 241
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 2
91. A horizontal force of 805 N is needed to
drag a crate across a horizontal floor with a
constant speed. You drag the crate using a
rope held at an angle of 32°.
a. What force do you exert on the rope?
FxFcos
so F
co
F
s
x
c8
o
0
s
53
N
2°
9.5102N
b. How much work do you do on the crate
if you move it 22 m?
WFxd(805 N)(22 m)
1.8104J
c. If you complete the job in 8.0 s, what
power is developed?
P
W
t
1.8
8
.0
10
s
4J
2.2 kW
92. Dolly and Ramp A mover’s dolly is used
to transport a refrigerator up a ramp into
a house. The refrigerator has a mass of
115 kg. The ramp is 2.10 m long and rises
0.850 m. The mover pulls the dolly with a
force of 496 N up the ramp. The dolly and
ramp constitute a machine.
a. What work does the mover do?
WiFd (496 N)(2.10 m)
1.04103J
b. What is the work done on the
refrigerator by the machine?
dheight raised 0.850 m
WoFgdmgd
(115 kg)(9.80 m/s2)(0.850 m)
958 J
c. What is the efficiency of the machine?
efficiency
W
W
o
i
100
1.09
45
8
1J
03J
100
92.1%
93. Sally does 11.4 kJ of work dragging a wooden
crate 25.0 m across a floor at a constant
speed. The rope makes an angle of 48.0°
with the horizontal.
a. How much force does the rope exert on
the crate?
WFd cos
so F
dc
W
os
681 N
b. What is the force of friction acting on
the crate?
The crate moves with constant
speed, so the force of friction equals
the horizontal component of the
force of the rope.
FfFxFcos
(681 N)(cos 48.0°)
456 N, opposite to the direction
of motion
c. What work is done by the floor through
the force of friction between the floor
and the crate?
Force and displacement are in
opposite directions, so
WFd (456 N)(25.0 m)
1.14104J
(Because no net forces act on the
crate, the work done on the crate
must be equal in magnitude but
opposite in sign to the energy Sally
expands: 1.14104J)
94. Sledding An 845-N sled is pulled a
distance of 185 m. The task requires
1.20104J of work and is done by pulling
on a rope with a force of 125 N. At what
angle is the rope held?
WFd cos ,so
cos1
F
W
d
cos1
58.7°
1.20104J
(125 N)(185 m)
11,400 J
(25.0 m)(cos 48.0°)
Chapter 10 continued

Level 3
95. An electric winch pulls a 875-N crate up a
15° incline at 0.25 m/s. The coefficient of
friction between the crate and incline is 0.45.
a. What power does the winch develop?
Work is done on the crate by the
winch, gravity, and friction. Because
the kinetic energy of the crate does
not change, the sum of the three
works is equal to zero.
Therefore,
Wwinch Wfriction Wgravity
or, Pwinch Pfriction Pgravity
F
t
Nd
Fg
t
d
FN
d
t
Fg
d
t
FNvFgv
(Fg)(cos )(v)Fgv
(0.45)(875 N)(cos 15°)
(0.25 m/s)
(875 N)(0.25 m/s)
3.1102W
b. If the winch is 85 percent efficient,
what is the electrical power that must
be delivered to the winch?
e
W
W
o
i
P
P
o
i
so, Pi
P
e
o
3.1
0.1
80
5
2W
3.6102W
Thinking Critically
page 282
96. Analyze and Conclude You work at a store,
carrying boxes to a storage loft that is 12 m
above the ground. You have 30 boxes with a
total mass of 150 kg that must be moved as
quickly as possible, so you consider carrying
more than one up at a time. If you try to
move too many at once, you know that you
will go very slowly, resting often. If you carry
only one box at a time, most of the energy
will go into raising your own body. The
power (in watts) that your body can develop
over a long time depends on the mass that
you carry, as shown in Figure 10-25. This is
an example of a power curve that applies to
machines as well as to people. Find the
number of boxes to carry on each trip that
would minimize the time required. What
time would you spend doing the job? Ignore
the time needed to go back down the stairs
and to lift and lower each box.
■Figure 10-25
The work has to be done the same,
WFgdmgd
(150 kg)(9.80 m/s2)(12 m)
1.76104J.
From the graph, the maximum power is
25 W at 15 kg. Since the mass per box is
30
15
b
0
o
k
x
g
es
5 kg, this represents three
boxes.
P
W
t
so t
W
t
1.76
2
51
W
04J
7.0102s
12 min
97. Apply Concepts A sprinter of mass 75 kg
runs the 50.0-m dash in 8.50 s. Assume that
the sprinter’s acceleration is constant
throughout the race.
a. What is the average power of the
sprinter over the 50.0 m?
5
10
15
20
25
Power (W)
Mass (kg)
030
252015105
Power v. Mass
242 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 243
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Assume constant acceleration,
therefore constant force
ddivit
1
2
at2
but divi0
P
W
t
F
t
d
mt
ad
6.1102W
b. What is the maximum power generated
by the sprinter?
Power increases linearly from zero,
since the velocity increases linearly
as shown by
P
W
t
F
t
d
F
d
t
Fv.
Therefore
Pmax 2Pave 1.2103W
c. Make a quantitative graph of power
versus time for the entire race.
98. Apply Concepts The sprinter in the
previous problem runs the 50.0-m dash
in the same time, 8.50 s. However, this
time the sprinter accelerates in the first
second and runs the rest of the race at a
constant velocity.
a. Calculate the average power produced
for that first second.
Distance first second
Distance rest of race 50.0 m
dfdivit
1
2
at2
divi0 so
df
1
2
a(t1)2vf(t2)50.0 m
Final velocity:
vfviat
vi0 so
vfat a(t1)
Therefore,
df
1
2
at12at1t2
a
1
2
t12t1t2
a
6.25 m/s2
For the first second:
d
1
2
at2
1
2
(6.25 m/s2)(1.00 s)2
3.12 m
From Problem 97,
P
mt
ad
Pave
1.5103W
b. What is the maximum power that the
sprinter now generates?
Pmax 2Pave 3.0103W
Writing in Physics
page 282
99. Just as a bicycle is a compound machine, so
is an automobile. Find the efficiencies of
the component parts of the power train
(engine, transmission, wheels, and tires).
Explore possible improvements in each of
these efficiencies.
The overall efficiency is 15–30 percent.
The transmission’s efficiency is about
90 percent. Rolling friction in the tires is
about 1 percent (ratio of pushing force
to weight moved).The largest gain is
possible in the engine.
(75 kg)(6.25 m/s2)(3.12 m)
1.00 s
50.0 m
1
2
(1.00 s)2(1.00 s)(7.50 s)
df
1
2
t12t1t2
Time (s)
Power (W)
8.50
1.2x103
0
(2)(75 kg)(50.0 m)
(8.50 s)3
2md2
t3
m
2
td
2
d
t
Chapter 10 continued

100. The terms force, work, power, and energy
often mean the same thing in everyday
use. Obtain examples from advertisements,
print media, radio, and television that
illustrate meanings for these terms that dif-
fer from those used in physics.
Answers will vary. Some examples
include, the company Consumers’
Power changed its name to
Consumers’Energy without changing
its product, natural gas. “It’s not just
energy, it’s power!”has appeared in
the popular press.
Cumulative Review
page 282
101. You are helping your grandmother with
some gardening and have filled a garbage
can with weeds and soil. Now you have to
move the garbage can across the yard and
realize it is so heavy that you will need to
push it, rather than lift it. If the can has a
mass of 24 kg, the coefficient of kinetic
friction between the can’s bottom and the
muddy grass is 0.27, and the static coeffi-
cient of friction between those same sur-
faces is 0.35, how hard do you have to
push horizontally to get the can to just
start moving? (Chapter 5)
Fyou on can Ffriction sFNsmg
(0.35)(24 kg)(9.80 m/s2)
82 N
102. Baseball If a major league pitcher throws a
fastball horizontally at a speed of 40.3 m/s
(90 mph) and it travels 18.4 m (60 ft, 6 in),
how far has it dropped by the time it crosses
home plate? (Chapter 6)
dfxdixvxt
so t
dfxv
x
dix
18.4
40
m
.3
m
0
/s
.0 m
0.457 s
dfydiyviyt
1
2
gt2
diyviy0
so dfy
1
2
gt2
1
2
(9.80 m/s2)(0.457 s)2
1.02 m
103. People sometimes say that the Moon stays
in its orbit because the “centrifugal force
just balances the centripetal force, giving
no net force.” Explain why this idea is
wrong. (Chapter 8)
There is only one force on the moon,
the gravitational force of Earth’s mass
on it. This net force gives it an acceler-
ation which is its centripetal accelera-
tion toward Earth’s center.
Challenge Problem
page 268
An electric pump pulls water at a rate of 0.25
m3/s from a well that is 25 m deep. The water
leaves the pump at a speed of 8.5 m/s.
25 m
8.5 m/s
244 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 10 continued

Physics: Principles and Problems Solutions Manual 245
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1. What power is needed to lift the water to the surface?
The work done in lifting is Fgdmgd. Therefore,
the power is
Plift
W
t
Fg
t
d
mg
t
d
6.1104W
61 kW
2. What power is needed to increase the pump’s kinetic energy?
The work done in increasing the pump’s kinetic energy is
1
2
mv2.
Therefore, P
W
t
K
tE
9.0103W9.0 kW
3. If the pump’s efficiency is 80 percent, how much power must be delivered
to the pump?
e
W
W
o
i
100 100
P
P
o
i
100 so,
Pi
P
e
o
100 100
1.1104W
11 kW
9.0103W
80
W
to
W
ti
(0.25 m3)(1.00103kg/m3)(8.5 m/s)2
(2)(1.0 s)
mv2
2t
1
2
mv2
t
(0.25 m3)(1.00103kg/m3)(9.80 m/s2)(25 m)
1.0 s
Chapter 10 continued


Physics: Principles and Problems Solutions Manual 247
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
11 Energy and Its Conservation
CHAPTER
Practice Problems
11.1 The Many Forms of Energy
pages 285–292
page 287
1. A skater with a mass of 52.0 kg moving at
2.5 m/s glides to a stop over a distance of
24.0 m. How much work did the friction of
the ice do to bring the skater to a stop?
How much work would the skater have to
do to speed up to 2.5 m/s again?
To bring the skater to a stop:
WKEfKEi
mvf2mvi2
(52.0 kg)(0.00 m/s)2
(52.0 kg)(2.5 m/s)2
160 J
To speed up again:
This is the reverse of the first question.
WKEfKEi
mvf2mvi2
(52.0 kg)(2.5 m/s)2
(52.0 kg)(0.00 m/s)2
160 J
2. An 875.0-kg compact car speeds up from
22.0 m/s to 44.0 m/s while passing another
car. What are its initial and final energies,
and how much work is done on the car to
increase its speed?
The initial kinetic energy of the car is
KEimv2(875.0 kg)(22.0 m/s)2
2.12105J
The final kinetic energy is
KEfmv2(875.0 kg)(44.0 m/s)2
8.47105J
The work done is
KEf KEi8.47105J 2.12105J
6.35105J
3. A comet with a mass of 7.851011 kg
strikes Earth at a speed of 25.0 km/s. Find
the kinetic energy of the comet in joules,
and compare the work that is done by Earth
in stopping the comet to the 4.21015 J of
energy that was released by the largest
nuclear weapon ever built.
KE mv2
(7.851011 kg)(2.50104m/s)2
2.451020 J
K
K
E
Ec
b
o
o
m
m
e
b
t
5.8104
5.8104bombs would be required to
produce the same amount of energy
used by Earth in stopping the comet.
page 291
4. In Example Problem 1, what is the poten-
tial energy of the bowling ball relative to
the rack when it is on the floor?
PE mgh
(7.30 kg)(9.80 m/s2)(0.610 m)
43.6 J
5. If you slowly lower a 20.0-kg bag of sand
1.20 m from the trunk of a car to the drive-
way, how much work do you do?
WFd
mg(hfhi)
(20.0 kg)(9.80 m/s2)(0.00 m 1.20 m)
2.35102J
2.451020 J
4.21015 J
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2

6. A boy lifts a 2.2-kg book from his desk,
which is 0.80 m high, to a bookshelf that is
2.10 m high. What is the potential energy of
the book relative to the desk?
PE mg(hf hi)
(2.2 kg)(9.80 m/s2)(2.10 m 0.80 m)
28 J
7. If a 1.8-kg brick falls to the ground from a
chimney that is 6.7 m high, what is the
change in its potential energy?
Choose the ground as the reference
level.
PE mg(hfhi)
(1.8 kg)(9.80 m/s2)(0.0 m 6.7 m)
1.2102J
8. A warehouse worker picks up a 10.1-kg
box from the floor and sets it on a long,
1.1-m-high table. He slides the box 5.0 m
along the table and then lowers it back to
the floor. What were the changes in the
energy of the box, and how did the total
energy of the box change? (Ignore friction.)
To lift the box to the table:
WFd
mg(hfhi)
PE
(10.1 kg)(9.80 m/s2)(1.1 m 0.0 m)
1.1102J
To slide the box across the table,
W0.0 because the height did not
change and we ignored friction.
To lower the box to the floor:
WFd
mg(hfhi)
PE
(10.1 kg)(9.80 m/s2)(0.0 m 1.1 m)
1.1102J
The sum of the three energy changes is
1.1102J 0.0 J (1.1102J) 0.0 J
Section Review
11.1 The Many Forms of Energy
pages 285–292
page 292
9. Elastic Potential Energy You get a spring-
loaded toy pistol ready to fire by compress-
ing the spring. The elastic potential energy
of the spring pushes the rubber dart out of
the pistol. You use the toy pistol to shoot
the dart straight up. Draw bar graphs that
describe the forms of energy present in the
following instances.
a. The dart is pushed into the gun barrel,
thereby compressing the spring.
There should be three bars: one for
the spring’s potential energy, one for
gravitational potential energy, and
one for kinetic energy. The spring’s
potential energy is at the maximum
level, and the other two are zero.
b. The spring expands and the dart leaves
the gun barrel after the trigger is pulled.
The kinetic energy is at the maxi-
mum level, and the other two are
zero.
Spring
elastic
potential
energy
Dart
gravitational
potential
energy
Dart
kinetic
energy
Spring
elastic
potential
energy
Dart
gravitational
potential
energy
Dart
kinetic
energy
248 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 249
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. The dart reaches the top of its flight.
The gravitational potential energy is
at the maximum level, and the other
two are zero.
10. Potential Energy A 25.0-kg shell is shot
from a cannon at Earth’s surface. The refer-
ence level is Earth’s surface. What is the
gravitational potential energy of the system
when the shell is at 425 m? What is the
change in potential energy when the shell
falls to a height of 225 m?
a. PE mgh
(25.0 kg)(9.80 m/s2)(425 m)
1.04105J
b. PE mgh
(25.0 kg)(9.80 m/s2)(225 m)
5.51104J
The change in energy is
(1.04105J) (5.51104J)
4.89104J
11. Rotational Kinetic Energy Suppose some
children push a merry-go-round so that it
turns twice as fast as it did before they pushed
it. What are the relative changes in angular
momentum and rotational kinetic energy?
The angular momentum is doubled
because it is proportional to the angular
velocity. The rotational kinetic energy is
quadrupled because it is proportional
to the square of the angular velocity.
The children did work in rotating the
merry-go-round.
12. Work-Energy Theorem How can you
apply the work-energy theorem to lifting a
bowling ball from a storage rack to your
shoulder?
The bowling ball has zero kinetic energy
when it is resting on the rack or when it
is held near your shoulder. Therefore,
the total work done on the ball by you
and by gravity must equal zero.
13. Potential Energy A 90.0-kg rock climber
first climbs 45.0 m up to the top of a quarry,
then descends 85.0 m from the top to the
bottom of the quarry. If the initial height is
the reference level, find the potential energy
of the system (the climber and Earth) at the
top and at the bottom. Draw bar graphs for
both situations.
PE mgh
At the top,
PE (90.0 kg)(9.80 m/s2)(45.0 m)
3.97104J
At the bottom,
PE (90.0 kg)(9.80 m/s2)
(45.0 m 85.0 m)
3.53104J
14. Critical Thinking Karl uses an air hose to
exert a constant horizontal force on a puck,
which is on a frictionless air table. He keeps
the hose aimed at the puck, thereby creating
a constant force as the puck moves a fixed
distance.
a. Explain what happens in terms of work
and energy. Draw bar graphs.
Karl exerted a constant force Fover
a distance dand did an amount of
work WFd on the puck.This work
changed the kinetic energy of the
puck.
KEinitial KEfinal
W
3.97104 J
At the
top
At the bottom
3.53104 J
Spring
elastic
potential
energy
Dart
gravitational
potential
energy
Dart
kinetic
energy
Chapter 11 continued

W(KEfKEi)
mvf2mvi2
mvf2
b. Suppose Karl uses a different puck with
half the mass of the first one. All other
conditions remain the same. How will
the kinetic energy and work differ from
those in the first situation?
If the puck has half the mass, it still
receives the same amount of work
and has the same change in kinetic
energy. However, the smaller mass
will move faster by a factor of 1.414.
c. Explain what happened in parts aand b
in terms of impulse and momentum.
The two pucks do not have the same
final momentum.
Momentum of the first puck:
p1m1v1
Momentum of the second puck:
p2m2v2
1
2
m1(1.414v1)
0.707 p1
Thus, the second puck has less
momentum than the first puck does.
Because the change in momentum
is equal to the impulse provided by
the air hose, the second puck
receives a smaller impulse.
Practice Problems
11.2 Conservation of Energy
pages 293–301
page 297
15. A bike rider approaches a hill at a speed of
8.5 m/s. The combined mass of the bike
and the rider is 85.0 kg. Choose a suitable
system. Find the initial kinetic energy of the
system. The rider coasts up the hill.
Assuming there is no friction, at what
height will the bike come to rest?
The system is the bike rider Earth.
There are no external forces, so total
energy is conserved.
KE mv2
(85.0 kg)(8.5 m/s)2
3.1103J
KEiPEiKEfPEf
mv20 0 mgh
h
3.7 m
16. Suppose that the bike rider in problem 15
pedaled up the hill and never came to a
stop. In what system is energy conserved?
From what form of energy did the bike gain
mechanical energy?
The system of Earth, bike, and rider
remains the same, but now the energy
involved is not mechanical energy
alone. The rider must be considered as
having stored energy, some of which is
converted to mechanical energy.
Energy came from the chemical poten-
tial energy stored in the rider’s body.
17. A skier starts from rest at the top of a
45.0-m-high hill, skis down a 30° incline
into a valley, and continues up a 40.0-m-
high hill. The heights of both hills are mea-
sured from the valley floor. Assume that
you can neglect friction and the effect of the
ski poles. How fast is the skier moving at
the bottom of the valley? What is the skier’s
speed at the top of the next hill? Do the
angles of the hills affect your answers?
Bottom of valley:
KEiPEiKEfPEf
0 mgh mv20
v22gh
v2gh
(2)(9.8
0 m/s
2)(45.0
m)
1
2
(8.5 m/s)2
(2)(9.80 m/s2)
v2
2g
1
2
1
2
1
2
1
2
1
2
1
2
250 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 251
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
29.7 m/s
Top of next hill:
KEiPEiKEfPEf
0 mghimv2mghf
v22g(hihf)
2g(hi
hf)
(2)(9.8
0 ms
2)(45.0
m
40.0 m
)
9.90 m/s
No, the angles do not have any impact.
18. In a belly-flop diving contest, the winner is
the diver who makes the biggest splash upon
hitting the water. The size of the splash
depends not only on the diver’s style, but
also on the amount of kinetic energy that the
diver has. Consider a contest in which each
diver jumps from a 3.00-m platform. One
diver has a mass of 136 kg and simply steps
off the platform. Another diver has a mass of
102 kg and leaps upward from the platform.
How high would the second diver have to
leap to make a competitive splash?
Using the water as a reference level, the
kinetic energy on entry is equal to the
potential energy of the diver at the top
of his flight.The large diver has PE
mgh (136 kg)(9.80 m/s2)(3.00 m)
4.00103J
To equal this, the smaller diver would
have to jump to
h4.00 m
Thus, the smaller diver would have to
leap 1.00 m above the platform.
page 300
19. An 8.00-g bullet is fired horizontally into a
9.00-kg block of wood on an air table and
is embedded in it. After the collision, the
block and bullet slide along the frictionless
surface together with a speed of 10.0 cm/s.
What was the initial speed of the bullet?
Conservation of momentum:
mv (mM)V,or
v
1.13102m/s
20. A 0.73-kg magnetic target is suspended on a
string. A 0.025-kg magnetic dart, shot hori-
zontally, strikes the target head-on. The dart
and the target together, acting like a pendu-
lum, swing 12.0 cm above the initial level
before instantaneously coming to rest.
a. Sketch the situation and choose a system.
The system includes the suspended
target and the dart.
b. Decide what is conserved in each part
and explain your decision.
Only momentum is conserved in the
inelastic dart-target collision, so
mviMVi(mM)Vf
where Vi0 since the target is ini-
tially at rest and Vfis the common
velocity just after impact. As the
dart-target combination swings
upward, energy is conserved, so
PE KE or, at the top of the swing,
(mM)ghf(mM)(Vf)2
1
2
12 cm
System
PE 0
(0.00800 kg 9.00 kg)(0.100 m/s)
0.00800 kg
(mM)V
m
4.00103J
(102 kg)(9.80 m/s2)
1
2
Chapter 11 continued

c. What was the initial velocity of the dart?
Solve for Vf.
Vf2ghf
Substitute vfinto the momentum equation and solve for vi.
vi
mm
M
2ghf
(2)(9.8
0m/s
2)(0.12
0m)
46 m/s
21. A 91.0-kg hockey player is skating on ice at 5.50 m/s. Another hockey player of
equal mass, moving at 8.1 m/s in the same direction, hits him from behind.
They slide off together.
a. What are the total energy and momentum in the system before the collision?
KEim1v12m2v22
(91.0 kg)(5.50 m/s)2(91.0 kg)(8.1 m/s)2
4.4103J
pim1v1m2v2
(91.0 kg)(5.5 m/s) (91.0 kg)(8.1 m/s)
1.2103kgm/s
b. What is the velocity of the two hockey players after the collision?
After the collision:
pipf
m1v1m2v2(m1m2)vf
vf
6.8 m/s
c. How much energy was lost in the collision?
The final kinetic energy is
KEf(mimf)vf2
(91.0 kg 91.0 kg)(6.8 m/s)2
4.2103J
Thus, the energy lost in the collision is
KEiKEf4.4103J 4.2103J
2102J
1
2
1
2
(91.0 kg)(5.50 ms) (91.0 kg)(8.1 ms)
91.0 kg 91.0 kg
m1v1m2v2
m1m2
1
2
1
2
1
2
1
2
0.025 kg 0.73 kg
0.025 kg
252 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued
Physics: Principles and Problems Solutions Manual 253
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
11.2 Conservation of Energy
pages 293–301
page 301
22. Closed Systems Is Earth a closed, isolated
system? Support your answer.
To simplify problems that take place
over a short time, Earth is considered a
closed system. It is not actually isolated,
however, because it is acted upon by the
gravitational forces from the planets, the
Sun, and other stars. In addition, Earth is
the recipient of continuous electromag-
netic energy, primarily from the Sun.
23. Energy A child jumps on a trampoline.
Draw bar graphs to show the forms of
energy present in the following situations.
a. The child is at the highest point.
b. The child is at the lowest point.
24. Kinetic Energy Suppose a glob of chew-
ing gum and a small, rubber ball collide
head-on in midair and then rebound apart.
Would you expect kinetic energy to be con-
served? If not, what happens to the energy?
Even though the rubber ball rebounds
with little energy loss, kinetic energy
would not be conserved in this case
because the glob of chewing gum prob-
ably was deformed in the collision.
25. Kinetic Energy In table tennis, a very light
but hard ball is hit with a hard rubber or
wooden paddle. In tennis, a much softer
ball is hit with a racket. Why are the two
sets of equipment designed in this way?
Can you think of other ball-paddle pairs in
sports? How are they designed?
The balls and the paddle and racket are
designed to match so that the maximum
amount of kinetic energy is passed from
the paddle or racket to the ball. A softer
ball receives energy with less loss from a
softer paddle or racket. Other combina-
tions are a golf ball and club (both hard)
and a baseball and bat (also both hard).
26. Potential Energy A rubber ball is dropped
from a height of 8.0 m onto a hard concrete
floor. It hits the floor and bounces repeat-
edly. Each time it hits the floor, it loses
1
5
of its total energy. How many times will it
bounce before it bounces back up to a
height of only about 4 m?
Etotal mgh
Since the rebound height is proportional
to energy, each bounce will rebound to
the height of the previous bounce.
After one bounce: h
(8 m) 6.4 m
After two bounces: h
(6.4 m)
5.12 m
After three bounces: h
(5.12 m)
4.1 m
4
5
4
5
4
5
4
5
Trampoline
elastic
potential
energy
Child
gravitational
potential
energy
Child
kinetic
energy
Trampoline
elastic
potential
energy
Child
gravitational
potential
energy
Child
kinetic
energy
Chapter 11 continued
27. Energy As shown in Figure 11-15, a
36.0-kg child slides down a playground slide
that is 2.5 m high. At the bottom of the
slide, she is moving at 3.0 m/s. How much
energy was lost as she slid down the slide?
■Figure 11-15
Eimgh
(36.0 kg)(9.80 m/s2)(2.5 m)
880 J
Efmv2
(36.0 kg)(3.0 m/s)2
160 J
Energy loss 880 J – 160 J
720 J
28. Critical Thinking A ball drops 20 m.
When it has fallen half the distance, or
10 m, half of its energy is potential and half
is kinetic. When the ball has fallen for half
the amount of time it takes to fall, will
more, less, or exactly half of its energy be
potential energy?
The ball falls more slowly during the
beginning part of its drop. Therefore, in
the first half of the time that it falls, it
will not have traveled half of the dis-
tance that it will fall. Therefore, the ball
will have more potential energy than
kinetic energy.
Chapter Assessment
Concept Mapping
page 306
29. Complete the concept map using the fol-
lowing terms: gravitational potential energy,
elastic potential energy, kinetic energy.
Mastering Concepts
page 306
Unless otherwise directed, assume that air resis-
tance is negligible.
30. Explain how work and a change in energy
are related. (11.1)
The work done on an object causes a
change in the object’s energy. This is
the work-energy theorem.
31. What form of energy does a wound-up
watch spring have? What form of energy
does a functioning mechanical watch have?
When a watch runs down, what has hap-
pened to the energy? (11.1)
The wound-up watch spring has elastic
potential energy. The functioning watch
has elastic potential energy and rota-
tional kinetic energy. The watch runs
down when all of the energy has been
converted to heat by friction in the
gears and bearings.
32. Explain how energy change and force are
related. (11.1)
A force exerted over a distance does
work, which produces a change in energy.
33. A ball is dropped from the top of a build-
ing. You choose the top of the building to
be the reference level, while your friend
chooses the bottom. Explain whether the
1
2
1
2
2.5 m
36.0 kg
254 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued
kinetic
Energy
rotational
linear
potential
elasticgravitational
Physics: Principles and Problems Solutions Manual 255
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
energy calculated using these two reference
levels is the same or different for the fol-
lowing situations. (11.1)
a. the ball’s potential energy at any point
The potential energies are different
due to the different reference levels.
b. the change in the ball’s potential energy
as a result of the fall
The changes in the potential ener-
gies as a result of the fall are equal
because the change in his the same
for both reference levels.
c. the kinetic energy of the ball at any point
The kinetic energies of the ball at
any point are equal because the
velocities are the same.
34. Can the kinetic energy of a baseball ever be
negative? (11.1)
The kinetic energy of a baseball can
never be negative because the kinetic
energy depends on the square of the
velocity, which is always positive.
35. Can the gravitational potential energy of a
baseball ever be negative? Explain without
using a formula. (11.1)
The gravitational potential energy of a
baseball can be negative if the height of
the ball is lower than the reference level.
36. If a sprinter’s velocity increases to three
times the original velocity, by what factor
does the kinetic energy increase? (11.1)
The sprinter’s kinetic energy increases
by a factor of 9, because the velocity is
squared.
37. What energy transformations take place
when an athlete is pole-vaulting? (11.2)
The pole-vaulter runs (kinetic energy)
and bends the pole, thereby adding
elastic potential energy to the pole. As
he/she lifts his/her body, that kinetic
and elastic potential energy is trans-
ferred into kinetic and gravitational
potential energy. When he/she releases
the pole, all of his/her energy is kinetic
and gravitational potential energy.
38. The sport of pole-vaulting was drastically
changed when the stiff, wooden poles were
replaced by flexible, fiberglass poles.
Explain why. (11.2)
A flexible, fiberglass pole can store elas-
tic potential energy because it can be
bent easily.This energy can be released
to push the pole-vaulter higher vertically.
By contrast, the wooden pole does not
store elastic potential energy, and the
pole-vaulter’s maximum height is limited
by the direct conversion of kinetic energy
to gravitational potential energy.
39. You throw a clay ball at a hockey puck on
ice. The smashed clay ball and the hockey
puck stick together and move slowly. (11.2)
a. Is momentum conserved in the collision?
Explain.
The total momentum of the ball and
the puck together is conserved in
the collision because there are no
unbalanced forces on this system.
b. Is kinetic energy conserved? Explain.
The total kinetic energy is not
conserved. Part of it is lost in the
smashing of the clay ball and the
adhesion of the ball to the puck.
40. Draw energy bar graphs for the following
processes. (11.2)
a. An ice cube, initially at rest, slides down
a frictionless slope.
b. An ice cube, initially moving, slides up a
frictionless slope and instantaneously
comes to rest.
PEiKEiPEfKEf
PEiKEiPEfKEf
Chapter 11 continued

41. Describe the transformations from kinetic
energy to potential energy and vice versa for
a roller-coaster ride. (11.2)
On a roller-coaster ride, the car has
mostly potential energy at the tops of
the hills and mostly kinetic energy at
the bottoms of the hills.
42. Describe how the kinetic energy and elastic
potential energy are lost in a bouncing
rubber ball. Describe what happens to the
motion of the ball. (11.2)
On each bounce, some, but not all, of the
ball’s kinetic energy is stored as elastic
potential energy; the ball’s deformation
dissipates the rest of the energy as ther-
mal energy and sound. After the bounce,
the stored elastic potential energy is
released as kinetic energy. Due to the
energy losses in the deformation, each
subsequent bounce begins with a smaller
amount of kinetic energy, and results in
the ball reaching a lower height.
Eventually, all of the ball’s energy is dissi-
pated, and the ball comes to rest.
Applying Concepts
pages 306–307
43. The driver of a speeding car applies the
brakes and the car comes to a stop. The
system includes the car but not the road.
Apply the work-energy theorem to the fol-
lowing situations.
a. The car’s wheels do not skid.
If the car wheels do not skid, the
brake surfaces rub against each
other and do work that stops the car.
The work that the brakes do is equal
to the change in kinetic energy of
the car. The brake surfaces heat up
because the kinetic energy is trans-
formed to thermal energy.
b. The brakes lock and the car’s wheels skid.
If the brakes lock and the car wheels
skid, the wheels rubbing on the road
are doing the work that stops the car.
The tire surfaces heat up, not the
brakes. This is not an efficient way to
stop a car, and it ruins the tires.
44. A compact car and a trailer truck are both
traveling at the same velocity. Did the car
engine or the truck engine do more work in
accelerating its vehicle?
The trailer truck has more kinetic energy,
KE mv2, because it has greater mass
than the compact car. Thus, according
to the work-energy theorem, the truck’s
engine must have done more work.
45. Catapults Medieval warriors used catapults
to assault castles. Some catapults worked
by using a tightly wound rope to turn the
catapult arm. What forms of energy are
involved in catapulting a rock to the castle
wall?
Elastic potential energy is stored in the
wound rope, which does work on the
rock. The rock has kinetic and potential
energy as it flies through the air. When
it hits the wall, the inelastic collision
causes most of the mechanical energy
to be converted to thermal and sound
energy and to do work breaking apart
the wall structure. Some of the mechan-
ical energy appears in the fragments
thrown from the collision.
46. Two cars collide and come to a complete
stop. Where did all of their energy go?
The energy went into bending sheet
metal on the cars. Energy also was lost
due to frictional forces between the
cars and the tires, and in the form of
thermal energy and sound.
47. During a process, positive work is done on a
system, and the potential energy decreases.
Can you determine anything about the change
in kinetic energy of the system? Explain.
The work equals the change in the total
mechanical energy, W(KE PE). If W
is positive and PE is negative, then KE
must be positive and greater than W.
48. During a process, positive work is done on a
system, and the potential energy increases. Can
you tell whether the kinetic energy increased,
decreased, or remained the same? Explain.
1
2
256 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 257
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The work equals the change in the total
mechanical energy, W(KE PE ). If
Wis positive and PE is positive, then
you cannot say anything conclusive
about KE.
49. Skating Two skaters of unequal mass have
the same speed and are moving in the same
direction. If the ice exerts the same frictional
force on each skater, how will the stopping
distances of their bodies compare?
The larger skater will have more kinetic
energy. The kinetic energy of each
skater will be dissipated by the negative
work, WFd, done by the friction of
the ice. Since the frictional forces are
equal, the larger skater will go farther
before stopping.
50. You swing a 55-g mass on the end of a
0.75-m string around your head in a nearly
horizontal circle at constant speed, as
shown in Figure 11-16.
■Figure 11-16
a. How much work is done on the mass
by the tension of the string in one
revolution?
No work is done by the tension force
on the mass because the tension is
pulling perpendicular to the motion
of the mass.
b. Is your answer to part ain agreement
with the work-energy theorem? Explain.
This does not violate the work-
energy theorem because the kinetic
energy of the mass is constant; it is
moving at a constant speed.
51. Give specific examples that illustrate the
following processes.
a. Work is done on a system, thereby
increasing kinetic energy with no
change in potential energy.
pushing a hockey puck horizontally
across ice; system consists of
hockey puck only
b. Potential energy is changed to kinetic
energy with no work done on the system.
dropping a ball; system consists of
ball and Earth
c. Work is done on a system, increasing
potential energy with no change in
kinetic energy.
compressing the spring in a toy pis-
tol; system consists of spring only
d. Kinetic energy is reduced, but potential
energy is unchanged. Work is done by
the system.
A car, speeding on a level track,
brakes and reduces its speed.
52. Roller Coaster You have been hired to
make a roller coaster more exciting. The
owners want the speed at the bottom of the
first hill doubled. How much higher must
the first hill be built?
The hill must be made higher by a
factor of 4.
53. Two identical balls are thrown from the top
of a cliff, each with the same speed. One is
thrown straight up, the other straight down.
How do the kinetic energies and speeds of
the balls compare as they strike the ground?
Even though the balls are moving in
opposite directions, they have the same
kinetic energy and potential energy
when they are thrown.Therefore, they
will have the same mechanical energy
and speed when they hit the ground.
0.75 m
55 g
Chapter 11 continued

Mastering Problems
Unless otherwise directed, assume that air resistance
is negligible.
11.1 The Many Forms of Energy
pages 307–308
Level 1
54. A 1600-kg car travels at a speed of 12.5 m/s.
What is its kinetic energy?
KE mv2(1600 kg)(12.5 m/s)2
1.3105J
55. A racing car has a mass of 1525 kg. What is
its kinetic energy if it has a speed of
108 km/h?
KE mv2
(1525 kg)
2
6.86105J
56. Shawn and his bike have a combined mass
of 45.0 kg. Shawn rides his bike 1.80 km in
10.0 min at a constant velocity. What is
Shawn’s kinetic energy?
KE mv2m
2
(45 kg)
2
203 J
57. Tony has a mass of 45 kg and is moving
with a speed of 10.0 m/s.
a. Find Tony’s kinetic energy.
KE mv2(45 kg)(10.0 m/s)2
2.3103J
b. Tony’s speed changes to 5.0 m/s. Now
what is his kinetic energy?
KE mv2(45 kg)( 5.0 m/s)2
5.6102J
c. What is the ratio of the kinetic energies
in parts aand b? Explain.
Twice the velocity gives four times
the kinetic energy.The kinetic energy
is proportional to the square of the
velocity.
58. Katia and Angela each have a mass of 45 kg,
and they are moving together with a speed
of 10.0 m/s.
a. What is their combined kinetic energy?
KEcmv2(mKmA)v2
(45 kg 45 kg)(10.0 m/s)2
4.5103J
b. What is the ratio of their combined
mass to Katia’s mass?
2
1
c. What is the ratio of their combined
kinetic energy to Katia’s kinetic energy?
Explain.
KEKmKv2(45 kg)(10.0 m/s)2
2.3103J
The ratio of their combined kinetic
energy to Katia’s kinetic energy is
the same as the ratio of their com-
bined mass to Katia’s mass. Kinetic
energy is proportional to mass.
2
1
mKmA
mK
1
2
(mKmA)v2
1
2
mKv2
KEC
KEK
1
2
1
2
45 kg 45 kg
45 kg
mKmA
mK
1
2
1
2
1
2
4
1
(10.0)2
(5.0)2
v12
v22
1
2
(mv12)
1
2
(mv22)
1
2
1
2
1
2
1
2
(1.80 km)(1000 mkm)
(10.0 min)(60 smin)
1
2
d
t
1
2
1
2
(108 kmh)(1000 mkm)
3600 sh
1
2
1
2
1
2
1
2
258 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 259
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
59. Train In the 1950s, an experimental train,
which had a mass of 2.50104kg, was
powered across a level track by a jet engine
that produced a thrust of 5.00105N for a
distance of 509 m.
a. Find the work done on the train.
WFd (5.00105N)(509 m)
2.55108J
b. Find the change in kinetic energy.
KE W2.55108J
c. Find the final kinetic energy of the train
if it started from rest.
KE KEfKEi
so KEfKE KEi
2.55108J 0.00 J
2.55108J
d. Find the final speed of the train if there
had been no friction.
KEfmvf2
So vf2
So vf2.04
104m
2/s2
143 m/s
60. Car Brakes A 14,700-N car is traveling at
25 m/s. The brakes are applied suddenly,
and the car slides to a stop, as shown in
Figure 11-17. The average braking force
between the tires and the road is 7100 N.
How far will the car slide once the brakes
are applied?
■Figure 11-17
WFd mv2
Now m
F
g
g
So d
66 m
61. A 15.0-kg cart is moving with a velocity of
7.50 m/s down a level hallway. A constant
force of 10.0 N acts on the cart, and its
velocity becomes 3.20 m/s.
a. What is the change in kinetic energy of
the cart?
KE KEfKEim(vf2vi2)
(15.0 kg)((3.20 m/s)2
(7.50 m/s)2)
345 J
b. How much work was done on the cart?
WKE 345 J
c. How far did the cart move while the
force acted?
WFd
so d 34.5 m
62. How much potential energy does DeAnna
with a mass of 60.0 kg, gain when she
climbs a gymnasium rope a distance of
3.5 m?
PE mgh
(60.0 kg)(9.80 m/s2)(3.5 m)
2.1103J
63. Bowling A 6.4-kg bowling ball is lifted
2.1 m into a storage rack. Calculate the
increase in the ball’s potential energy.
PE mgh
(6.4 kg)(9.80 m/s2)(2.1 m)
1.3102J
345 J
10.0 N
W
F
1
2
1
2
1
2
9
1
.4
8,
0
70
m
0/s
N
2
(25.0 m/s)2
7100 N
1
2
F
g
g
v2
F
1
2
mv2
F
1
2
Before
(initial)
After
(final)
v 0.0 m/sv 25 m/s
m 14,700 N
2.55108J
1
2
(2.50104kg)
KEf
1
2
m
1
2
Chapter 11 continued

64. Mary weighs 505 N. She walks down a
flight of stairs to a level 5.50 m below her
starting point. What is the change in Mary’s
potential energy?
PE mghFgh
(505 N)(5.50 m)
2.78103J
65. Weightlifting A weightlifter raises a 180-kg
barbell to a height of 1.95 m. What is the
increase in the potential energy of the
barbell?
PE mgh
(180 kg)(9.80 m/s2)(1.95 m)
3.4103J
66. A 10.0-kg test rocket is fired vertically from
Cape Canaveral. Its fuel gives it a kinetic
energy of 1960 J by the time the rocket
engine burns all of the fuel. What additional
height will the rocket rise?
PE mgh KE
h
20.0 m
67. Antwan raised a 12.0-N physics book from
a table 75 cm above the floor to a shelf
2.15 m above the floor. What was the
change in the potential energy of the
system?
PE mghFghFg(hfhi)
(12.0 N)(2.15 m 0.75 m)
17 J
68. A hallway display of energy is constructed
in which several people pull on a rope that
lifts a block 1.00 m. The display indicates
that 1.00 J of work is done. What is the
mass of the block?
WPE mgh
m
0.102 kg
Level 2
69. Tennis It is not uncommon during the serve
of a professional tennis player for the racket
to exert an average force of 150.0 N on the
ball. If the ball has a mass of 0.060 kg and is
in contact with the strings of the racket, as
shown in Figure 11-18, for 0.030 s, what is
the kinetic energy of the ball as it leaves the
racket? Assume that the ball starts from rest.
■Figure 11-18
Ft mvmvfmviand vi0
so vf
75 m/s
KE mv2
(6.0102kg)(75 m/s)2
1.7102J
70. Pam, wearing a rocket pack, stands on fric-
tionless ice. She has a mass of 45 kg. The
rocket supplies a constant force for 22.0 m,
and Pam acquires a speed of 62.0 m/s.
a. What is the magnitude of the force?
KEfmvf2
(45 kg)(62.0 ms)2
8.6104J
b. What is Pam’s final kinetic energy?
Work done on Pam equals her
change in kinetic energy.
WFd KE KEfKEi
KEi0 J
So, F
3.9103N
8.6104J
22.0 m
KEf
d
1
2
1
2
1
2
1
2
(150.0 N)(3.0102s)
6.0102kg
Ft
m
150.0 N
1.00 J
(9.80 m/s2)(1.00 m)
W
gh
1960
(10.0 kg)(9.80 m/s2)
KE
mg
260 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 261
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
71. Collision A 2.00103-kg car has a speed of
12.0 m/s. The car then hits a tree. The tree
doesn’t move, and the car comes to rest, as
shown in Figure 11-19.
■Figure 11-19
a. Find the change in kinetic energy of
the car.
KE KEf KEim(vf2vi2)
(2.00103kg)((0.0 m/s)2
(12.0 m/s)2)
1.44105J
b. Find the amount of work done as the
front of the car crashes into the tree.
WKE 1.44105J
c. Find the size of the force that pushed in
the front of the car by 50.0 cm.
WFd
so F
2.88105N
72. A constant net force of 410 N is applied
upward to a stone that weighs 32 N. The
upward force is applied through a distance
of 2.0 m, and the stone is then released. To
what height, from the point of release, will
the stone rise?
WFd (410 N)(2.0 m) 8.2102J
But WPE mgh,so
h 26 m
11.2 Conservation of Energy
pages 308–309
Level 1
73. A 98.0-N sack of grain is hoisted to a stor-
age room 50.0 m above the ground floor of
a grain elevator.
a. How much work was done?
WPE mgh Fgh
(98.0 N)(50.0 m)
4.90103J
b. What is the increase in potential energy
of the sack of grain at this height?
PE W4.90103J
c. The rope being used to lift the sack of
grain breaks just as the sack reaches the
storage room. What kinetic energy does
the sack have just before it strikes the
ground floor?
KE PE 4.90103J
74. A 20-kg rock is on the edge of a 100-m cliff,
as shown in Figure 11-20.
■Figure 11-20
a. What potential energy does the rock
possess relative to the base of the cliff?
PE mgh (20 kg)(9.80 m/s2)(100 m)
2104J
b. The rock falls from the cliff. What is its
kinetic energy just before it strikes the
ground?
KE PE 2104J
c. What speed does the rock have as it
strikes the ground?
KE mv2
v
40 m/s
(2)(2104 J)
20 kg
2KE
m
1
2
100 m
20 kg
8.2102J
32 N
W
mg
1.44105J
0.500 m
W
d
1
2
1
2
After
(final)
Before
(initial)
m 2.00103 kg
vi 12.0 m/s vf 0.0 m/s
Chapter 11 continued

75. Archery An archer puts a 0.30-kg arrow to
the bowstring. An average force of 201 N is
exerted to draw the string back 1.3 m.
a. Assuming that all the energy goes into
the arrow, with what speed does the
arrow leave the bow?
Work done on the string increases
the string’s elastic potential energy.
WPE Fd
All of the stored potential energy is
transformed to the arrow’s kinetic
energy.
KE mv2PE Fd
v2
v
42 m/s
b. If the arrow is shot straight up, how
high does it rise?
The change in the arrow’s potential
energy equals the work done to pull
the string.
PE mghFd
h
89 m
76. A 2.0-kg rock that is initially at rest loses
407 J of potential energy while falling to
the ground. Calculate the kinetic energy
that the rock gains while falling. What is
the rock’s speed just before it strikes the
ground?
PEiKEiPEfKEf
KEi0
So,
KEfPEiPEf407 J
KEfmvf2
vf2
vf
2.0101m/s
77. A physics book of unknown mass is
dropped 4.50 m. What speed does the book
have just before it hits the ground?
KE PE
mv2mgh
The mass of the book divides out, so
v2gh
v2gh
2(9.80
m/s2)
(4.50
m)
9.39 m/s
78. Railroad Car A railroad car with a mass of
5.0105 kg collides with a stationary rail-
road car of equal mass. After the collision,
the two cars lock together and move off at
4.0 m/s, as shown in Figure 11-21.
■Figure 11-21
a. Before the collision, the first railroad car
was moving at 8.0 m/s. What was its
momentum?
mv (5.0105kg)(8.0 m/s)
4.0106kgm/s
b. What was the total momentum of the
two cars after the collision?
Because momentum is conserved, it
must be 4.0106kgm/s
c. What were the kinetic energies of the
two cars before and after the collision?
Before the collision:
KEimv2
(5.0105kg)(8.0 m/s)2
1.6107J
After the collision:
KEfmv2
1
2
1
2
1
2
m 5.0105 kg
v 4.0 m/s
1
2
1
2
(2)(407 J)
(2.0 kg)
2KEf
m
2KEf
m
1
2
(201 N)(1.3 m)
(0.30 kg)(9.80 ms2)
Fd
mg
(2)(201 N)(1.3 m)
0.30 kg
2Fd
m
2Fd
m
1
2
262 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 263
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(5.0105kg 5.0105kg)
(4.0 m/s)2
8.0106J
d. Account for the loss of kinetic energy.
While momentum was conserved
during the collision, kinetic energy
was not. The amount not conserved
was turned into thermal energy and
sound energy.
79. From what height would a compact car
have to be dropped to have the same
kinetic energy that it has when being driven
at 1.00102km/h?
v 1.00102
27.8 m/s
KE PE
mv2mgh
v2gh
h
2
((
2
9
7
.8
.8
0m
m
/s
/s
)2
2
)
39.4 m
Level 2
80. Kelli weighs 420 N, and she is sitting on a
playground swing that hangs 0.40 m above
the ground. Her mom pulls the swing back
and releases it when the seat is 1.00 m
above the ground.
a. How fast is Kelli moving when the swing
passes through its lowest position?
PE mghmg(hfhi)
KE m(vf2vi2)mvf2
By conservation of mechanical energy:
PE KE 0
mg(hfhi)mvf20
vf2g(hi
hf)
(2)(9.8
0 ms
2)(1.00
m0
.40 m
)
3.4 m/s
b. If Kelli moves through the lowest point
at 2.0 m/s, how much work was done
on the swing by friction?
The work done by friction equals the
change in mechanical energy.
WPE KE
mg(hfhi)mvf2
(420 N)(0.40 m 1.00 m)
(2.0 ms)2
1.7102J
81. Hakeem throws a 10.0-g ball straight down
from a height of 2.0 m. The ball strikes the
floor at a speed of 7.5 m/s. What was the
initial speed of the ball?
KEfKEiPEi
mvf2mvi2mgh
the mass of the ball divides out, so
vi2vf22gh,
vivf2
2gh
(7.5 m
/s)2
(2)(9.
80 m/
s2)(2.0
m)
4.1 m/s
82. Slide Lorena’s mass is 28 kg. She climbs the
4.8-m ladder of a slide and reaches a velocity
of 3.2 m/s at the bottom of the slide. How
much work was done by friction on Lorena?
The work done by friction on Lorena
equals the change in her mechanical
energy.
WPE KE
mg(hfhi)m(vf2vi2)
(28 kg)(9.80 ms2)(0.0 m 4.8 m)
(28 kg)((3.2 ms)2(0.0 ms)2)
1.2103J
83. A person weighing 635 N climbs up a
ladder to a height of 5.0 m. Use the person
and Earth as the system.
1
2
1
2
1
2
1
2
420 N
9.80 ms2
1
2
1
2
1
2
1
2
1
2
v2
2g
1
2
1
2
1 h
3600 s
1000 m
1 km
km
h
1
2
Chapter 11 continued
a. Draw energy bar graphs of the system
before the person starts to climb the
ladder and after the person stops at the
top. Has the mechanical energy
changed? If so, by how much?
Yes. The mechanical energy has
changed, increase in potential
energy of (635 N)(5.0 m) 3200 J.
b. Where did this energy come from?
from the internal energy of the person
Mixed Review
pages 309–310
Level 1
84. Suppose a chimpanzee swings through the
jungle on vines. If it swings from a tree on a
13-m-long vine that starts at an angle of
45°, what is the chimp’s velocity when it
reaches the ground?
The chimpanzee’s initial height is
h(13 m)(1 cos 45°) 3.8 m
Conservation of mechanical energy:
PE KE 0
mg(hfhi)m(vf2vi2)0
mghimvf20
vf2ghi
2(9.80
m/s2)
(3.8 m
)
8.6 m/s
85. An 0.80-kg cart rolls down a frictionless hill
of height 0.32 m. At the bottom of the hill,
the cart rolls on a flat surface, which exerts
a frictional force of 2.0 N on the cart. How
far does the cart roll on the flat surface
before it comes to a stop?
Emgh WFd
d
1.3 m
86. High Jump The world record for the men’s
high jump is about 2.45 m. To reach that
height, what is the minimum amount of
work that a 73.0-kg jumper must exert in
pushing off the ground?
WEmgh
(73.0 kg)(9.80 m/s2)(2.45 m)
1.75 kJ
87. A stuntwoman finds that she can safely
break her fall from a one-story building by
landing in a box filled to a 1-m depth with
foam peanuts. In her next movie, the script
calls for her to jump from a five-story build-
ing. How deep a box of foam peanuts
should she prepare?
Assume that the foam peanuts exert
a constant force to slow him down,
WFd Emgh. If the height is
increased five times, then the depth of
the foam peanuts also should be
increased five times to 5 m.
Level 2
88. Football A 110-kg football linebacker has a
head-on collision with a 150-kg defensive
end. After they collide, they come to a
complete stop. Before the collision, which
player had the greater momentum and
which player had the greater kinetic energy?
The momentum after the collision is
zero; therefore, the two players had
equal and opposite momenta before
the collision. That is,
plinebacker mlinebackervlinebacker pend
mendvend. After the collision, each had
zero energy. The energy loss for each
player was mv2
.
Because the momenta were equal but
mlinebacker mend the linebacker lost
more energy.
89. A 2.0-kg lab cart and a 1.0-kg lab cart are
held together by a compressed spring. The
lab carts move at 2.1 m/s in one direction.
The spring suddenly becomes uncompressed
and pushes the two lab carts apart. The 2-kg
p2
2m
m2v2
m
1
2
1
2
(0.80 kg)(9.80 m/s2)(0.32 m)
2.0 N
mgh
F
1
2
1
2
3200 J
KEiPEiKEfPEf
264 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 265
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
lab cart comes to a stop, and the 1.0-kg lab
cart moves ahead. How much energy did the
spring add to the lab carts?
Eimv2(2.0 kg 1.0 kg)(2.1 m/s)2
6.6 J
pimv (2.0 kg 1.0 kg)(2.1 m/s)
6.3 kgm/s pf(1.0 kg)vf
so, vf6.3 m/s
Efmvf2(1.0 kg)(6.3 m/s)219.8 J
E19.8 J 6.6 J 13.2 J
13.2 J was added by the spring.
90. A 55.0-kg scientist roping through the top of
a tree in the jungle sees a lion about to
attack a tiny antelope. She quickly swings
down from her 12.0-m-high perch and grabs
the antelope (21.0 kg) as she swings. They
barely swing back up to a tree limb out of
reach of the lion. How high is this tree limb?
EimBgh
The velocity of the botanist when she
reaches the ground is
EimBv2mBgh
v
2gh
Momentum is conserved when the
botanist grabs the antelope.
mBv(mBmA)vf
so, vf
2gh
The final energy of the two is
Ef(mBmA)vf2
(mBmA)
2(2gh)
(mBmA)ghf
So, hf
2h
2(12.0 m)
6.28 m
91. An 0.80-kg cart rolls down a 30.0° hill from
a vertical height of 0.50 m as shown in
Figure 11-22. The distance that the cart
must roll to the bottom of the hill is
0.50 m/sin 30.0° 1.0 m. The surface of the
hill exerts a frictional force of 5.0 N on the cart.
Does the cart roll to the bottom of the hill?
■Figure 11-22
Eimgh (0.80 kg)(9.80 m/s2)(0.50 m)
3.9 J
The work done by friction over 1.0 m
would be
WFd (5.0 N)(1.0 m) 5.0 J.
The work done by friction is greater
than the energy of the cart. The cart
would not reach the bottom of the hill.
Level 3
92. Object A, sliding on a frictionless surface at
3.2 m/s, hits a 2.0-kg object, B, which is
motionless. The collision of A and B is com-
pletely elastic. After the collision, A and B
move away from each other at equal and
opposite speeds. What is the mass of object A?
pimAv10
pfmA(v2) mBv2
pipf(conservation of momentum)
therefore, mAv1mA(v2) mBv2
(mBmA)v2mAv1
v2
EimAv12
EfmAv22mBv22
1
2
1
2
1
2
(mAv1)
(mBmA)
30.0°
0.50 m
m 0.80 kg
F 5.0 N
55.0 kg
55.0 kg 21.0 kg
mB
mBmA
mB
mBmA
1
2
1
2
mB
mBmA
mBv
(mBmA)
2mBgh
mB
2Ei
m
1
2
1
2
1
2
1
2
1
2
Chapter 11 continued

Ef(mAmB)v22
(mAmB)
2
EiEf(conservation of energy in
elastic collision)
therefore,
mAv12(mAmB)
2
After cancelling out common factors,
(mAmB)mA(mBmA)2
mB22mAmBmA2
mA 0.67 kg
93. Hockey A 90.0-kg hockey player moving at
5.0 m/s collides head-on with a 110-kg
hockey player moving at 3.0 m/s in the
opposite direction. After the collision, they
move off together at 1.0 m/s. How much
energy was lost in the collision?
Before: Emv12mv22
(90.0 kg)(5.0 m/s)2
(110 kg)(3.0 m/s)2
1.6103J
After: E(mm)vf2
(200.0 kg)(1.0 m/s)2
1.0102J
Energy loss 1.6103J 1.0102J
1.5103J
Thinking Critically
page 310
94. Apply Concepts A golf ball with a mass of
0.046 kg rests on a tee. It is struck by a golf
club with an effective mass of 0.220 kg and
a speed of 44 m/s. Assuming that the colli-
sion is elastic, find the speed of the ball
when it leaves the tee.
From the conservation of momentum,
mcvc1 mcvc2 mbvb2
Solve for vc2,vc2 vc1
From conservation of energy,
mcvc12mcvc22mbvb22
Multiply by two and substitute to get:
mcvc12mcvc1 2mbvb22
or mcvc12mcvc122mbvc2vc1
mbvb22
Simplify and factor:
0 (mbvb2)2vc1
mb
m
2v
c
b2
vb2
mbvb2 0 or
2vc1 1vb2 0
Ignoring the solution vb2 0, then
vb2
73 m/s
95. Apply Concepts A fly hitting the wind-
shield of a moving pickup truck is an exam-
ple of a collision in which the mass of one
of the objects is many times larger than the
other. On the other hand, the collision of
two billiard balls is one in which the masses
of both objects are the same. How is energy
transferred in these collisions? Consider an
elastic collision in which billiard ball m1has
velocity v1 and ball m2is motionless.
a. If m1m2, what fraction of the initial
energy is transferred to m2?
If m1m2, we know that m1will be
at rest after the collision and m2will
move with velocity v1. All of the
energy will be transferred to m2.
2(44 m/s)
0
0.
.0
24
26
0k
kg
g
1
2vc1
m
mb
c
1
mb
mc
mb2vb22
mc
mbvb2
mc
1
2
1
2
1
2
mbvb2
mc
1
2
1
2
1
2
1
2
1
2
1
2
2.00 kg
3
mB
3
(mAv1)
(mBmA)
1
2
1
2
(mAv1)
(mBmA)
1
2
1
2
266 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 267
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. If m1 m2, what fraction of the initial energy is transferred to m2?
If m1 m2, we know that the motion of m1will be unaffected by the
collision and that the energy transfer to m2will be minimal.
c. In a nuclear reactor, neutrons must be slowed down by causing them to collide
with atoms. (A neutron is about as massive as a proton.) Would hydrogen,
carbon, or iron atoms be more desirable to use for this purpose?
The best way to stop a neutron is to have it hit a hydrogen atom, which
has about the same mass as the neutron.
96. Analyze and Conclude In a perfectly elastic collision, both momentum and
mechanical energy are conserved. Two balls, with masses mAand mB, are moving
toward each other with speeds vAand vB, respectively. Solve the appropriate
equations to find the speeds of the two balls after the collision.
conservation of momentum
(1) mAvA1 mBvB1 mAvA2 mBvB2
mAvA1 mAvA2 mBvB1 mBvB2
(2) mA(vA1 vA2) mB(vB1 vB2)
conservation of energy
mAvA12mBvB12mAvA22mBvB22
mAvA12mAvA22mBvB12mBvB22
mA(vA12vA22) mB(vB12vB22)
(3) mA(vA1 vA2)(vA1 vA2) mB(vB1 vB2)(vB1 vB2)
Divide equation (3) by (2) to obtain
(4) vA1 vA2 vB1 vB2
Solve equation (1) for vA2 and vB2
vA2 vA1 (vB1 vB2)
vB2 vB1
m
mA
B
(vA1 vA2)
Substitute into (4) and solve for vB2 and vA2
vA1 vA1 (vB1 vB2) vB1 vB2
2mAvA1 mBvB1 mBvB2 mAvB1 mAvB2
vB2
vA1
vB1
vA1 vA2 vB1 vB1
m
mA
B
(vA1 vA2)
mBvA1 mBvA2 2mBvB1 mAvA1 mAvA2
vA2
vA1
vB1
2mB
mAmB
mAmB
mAmB
mBmA
mAmB
2mA
mAmB
mB
mA
mB
mA
1
2
1
2
1
2
1
2
Chapter 11 continued

97. Analyze and Conclude A 25-g ball is fired with an initial speed of v1toward
a 125-g ball that is hanging motionless from a 1.25-m string. The balls have a
perfectly elastic collision. As a result, the 125-g ball swings out until the string
makes an angle of 37.0° with the vertical. What is v1?
Object 1 is the incoming ball. Object 2 is the one attached to the string.
In the collision, momentum is conserved.
p1i p1f p2f or
m1v1i m1v1f m2v2f
In the collision, kinetic energy is conserved.
m1v1i2 m1v1f2 m2v2f2
m1v1i2m1v1f2m2v2f2
(m1v1i2)
(m1v1f2)
(m2v2f2)
m1
m
2v
1
1f2
m2
m
2v
2
2f2
p
m
1f
1
2
p
m
2f
2
2
p1i2p1f2
m
m1
2
p2f2
We don’t care about v1f, so get rid of p1f using p1f p1i p2f
p1i2(p1i p2f)2p2f2
p1i2p1i22p1ip2f p2f2p2f2
2p1ip2f 1p2f2
p1i
1
2
1p2f
m1v1i
1
2
(m2m1)v2f
v1i
1
2
1v2f
Now consider the pendulum.
m2v2f2m2gh
or v2f 2gh
where hL(1 cos )
Thus, v2f 2gL(1
co
s )
v2f (2)(9.8
0m/s
2
)(1.25
m)(1
cos 3
7.0°)
2.22 m/s
1
2
m2
m1
m1
m2
m1
m2
m1
m2
m1
m2
p1i2
m1
m12v1i2
m1
m2
m2
m1
m1
m1
m1
1
2
1
2
1
2
268 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 269
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
v1i 1(2.22 m/s)
6.7 m/s
Writing in Physics
page 310
98. All energy comes from the Sun. In what forms
has this solar energy come to us to allow us to
live and to operate our society? Research the
ways that the Sun’s energy is turned into a
form that we can use. After we use the Sun’s
energy, where does it go? Explain.
The Sun produces energy through
nuclear fusion and releases that energy
in the form of electromagnetic radiation,
which is transferred through the vacu-
um of space to Earth. Earth absorbs
that electromagnetic radiation in its
atmosphere, land, and oceans in the
form of thermal energy or heat. Part of
the visible radiation also is converted
by plants into chemical energy through
photosynthesis. There are several other
chemical reactions mediated by sun-
light, such as ozone production. The
energy then is transferred into various
forms, some of which are the chemical
processes that allow us to digest food
and turn it into chemical energy to build
tissues, to move, and to think. In the
end, after we have used the energy, the
remainder is dispersed as electromag-
netic radiation back into the universe.
99. All forms of energy can be classified as
either kinetic or potential energy. How
would you describe nuclear, electric, chemi-
cal, biological, solar, and light energy, and
why? For each of these types of energy,
research what objects are moving and how
energy is stored in those objects.
Potential energy is stored in the binding
of the protons and neutrons in the nucle-
us.The energy is released when a heavy
nucleus is broken into smaller pieces (fis-
sion) or when very small nuclei are com-
bined to make bigger nuclei (fusion). In
the same way, chemical potential energy
is stored when atoms are combined to
make molecules and released when the
molecules are broken up or rearranged.
Separation of electric charges produces
electric potential energy, as in a battery.
Electric potential energy is converted to
kinetic energy in the motion of electric
charges in an electric current when a con-
ductive path, or circuit, is provided.
Biological processes are all chemical, and
thus, biological energy is just a form of
chemical energy. Solar energy is fusion
energy converted to to electromagnetic
radiation. (See the answer to the previous
question.) Light is a wave form of electro-
magnetic energy whose frequency is in a
range detectible by the human eye.
Cumulative Review
page 310
100. A satellite is placed in a circular orbit with
a radius of 1.0107m and a period of
9.9103s. Calculate the mass of Earth.
Hint: Gravity is the net force on such a satel-
lite. Scientists have actually measured the
mass of Earth this way. (Chapter 7)
Fnet
Since, v
2T
r
4
T
2
2
r2
me
6.01024 kg
101. A 5.00-g bullet is fired with a velocity of
100.0 m/s toward a 10.00-kg stationary
solid block resting on a frictionless surface.
(Chapter 9)
a. What is the change in momentum of
the bullet if it is embedded in the
block?
mbvb1 mbv2mwv2
(mbmw)v2
42(1.0107m)3
(6.671011 Nm2/kg2)(9.910 s)2
42r2
GT2
Gmsme
r2
ms
r
Gmsme
r2
msv2
r
125 g
25 g
1
2
Chapter 11 continued

so v2
Then,
pv mb(v2vb1)
mbvb1
mbvb11
vb1
(100.0 ms)
0.500 kgm/s
b. What is the change in momentum of
the bullet if it ricochets in the opposite
direction with a speed of 99 m/s?
pv mb(v2vb1)
(5.00103kg)
(99.0 m/s 100.0 m/s)
0.995 kgm/s
c. In which case does the block end up
with a greater speed?
When the bullet ricochets, its
change in momentum is larger in
magnitude, and so is the block’s
change in momentum, so the block
ends up with a greater speed.
102. An automobile jack must exert a lifting
force of at least 15 kN.
a. If you want to limit the effort force to
0.10 kN, what mechanical advantage is
needed?
MA
01
.1
50kk
N
N
150
b. If the jack is 75% efficient, over what
distance must the effort force be exerted
in order to raise the auto 33 cm?
IMA
M
e
A
2.0102.
Since IMA,
de(2.0102)(33 cm)
66 m
Challenge Problem
page 300
A bullet of mass m, moving at speed v1, goes
through a motionless wooden block and exits
with speed v2. After the collision, the block,
which has mass mB, is moving.
1. What is the final speed vB, of the block?
Conservation of momentum:
mv1mv2mBvB
mBvBm(v1v2)
vB
2. How much energy was lost to the bullet?
For the bullet alone:
KE1mv12
KE2mv22
KE m(v12v22)
3. How much energy was lost to friction inside
the block?
Energy lost to friction KE1
KE2KEblock
Elost mv12mv22mBvB2
1
2
1
2
1
2
1
2
1
2
1
2
m(v1v2)
mB
v1v2
vB
Initial Final
IMA
dr
de
dr
(5.00103kg)(10.00 kg)
5.00103kg 10.00 kg
mbmw
mbmw
mb
mbmw
mbvb1
mbmw
mbvb1
mbmw
270 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued

Physics: Principles and Problems Solutions Manual 271
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
12 Thermal Energy
CHAPTER
Practice Problems
12.1 Temperature and
Thermal Energy
pages 313–322
page 317
1. Convert the following Kelvin temperatures
to Celsius temperatures.
a. 115 K
TCTK273 115 273
158°C
b. 172 K
TCTK273 172 273 101°C
c. 125 K
TCTK273 125 273 148°C
d. 402 K
TCTK273 402 273 129°C
e. 425 K
TCTK273 425 273 152°C
f. 212 K
TCTK273 212 273 61°C
2. Find the Celsius and Kelvin temperatures
for the following.
a. room temperature
Room temperature is about 72°F,
22°C.
TKTC273 22 273 295 K
b. a typical refrigerator
A refrigerator is kept at about 4°C.
TKTC273 4273 277 K
c. a hot summer day in North Carolina
A hot summer day is about 95°F,
35°C.
TKTC273 35 273 308 K
d. a winter night in Minnesota
A typical winter night in Minnesota
is about 14°F, 10°C.
TKTC273 10 273 263 K
page 319
3. When you turn on the hot water to wash
dishes, the water pipes have to heat up.
How much heat is absorbed by a copper
water pipe with a mass of 2.3 kg when its
temperature is raised from 20.0°C to
80.0°C?
QmCT
(2.3 kg)(385 J/kgK)
(80.0°C 20.0°C)
5.3104J
4. The cooling system of a car engine contains
20.0 L of water (1 L of water has a mass of
1 kg).
a. What is the change in the temperature
of the water if the engine operates until
836.0 kJ of heat is added?
QmCT
T
m
Q
C
10.0 K
b. Suppose that it is winter, and the car’s
cooling system is filled with methanol.
The density of methanol is 0.80 g/cm3.
What would be the increase in tempera-
ture of the methanol if it absorbed
836.0 kJ of heat?
The mass of methanol would be
0.80 times the mass of 20.0 L of
water, or 16 kg.
QmCT
T
m
Q
C
21 K
c. Which is the better coolant, water or
methanol? Explain.
For temperatures above 0°C, water
is the better coolant because it can
absorb heat without changing its tem-
perature as much as methanol does.
8.36105J
(16 kg)(2450 J/kgK)
(8.36105J)
(20.0 kg)(4180 J/kgK)

5. Electric power companies sell electricity by the kWh, where 1 kWh 3.6106J.
Suppose that it costs $0.08 per kWh to run an electric water heater in your neigh-
borhood. How much does it cost to heat 75 kg of water from 15°C to 43°C to
fill a bathtub?
QmCT
(75 kg)(4180 J/kgK)(43°C 15°C)
8.8106J
2.4 kWh
(2.4 kWh)($0.15 per kWh) $0.36
page 321
6. A 2.00102-g sample of water at 80.0°C is mixed with 2.00102g of water at
10.0°C. Assume that there is no heat loss to the surroundings. What is the final
temperature of the mixture?
mACA(TfTAi)mBCB(TfTBi)0
Since mAmBand CACB,
there is cancellation in this particular case so that
Tf
TAi
2
TBi
45.0°C
7. A 4.00102-g sample of methanol at 16.0°C is mixed with 4.00102g of water
at 85.0°C. Assume that there is no heat loss to the surroundings. What is the
final temperature of the mixture?
mACA(TfTAi)mWCW(TfTWi) 0
Since in this particular case, mAmW, the masses cancel and
Tf
59.5°C
8. Three lead fishing weights, each with a mass of 1.00102g and at a temperature
of 100.0°C, are placed in 1.00102g of water at 35.0°C. The final temperature of
the mixture is 45.0°C. What is the specific heat of the lead in the weights?
Heat gained by the water:
QmCT(0.100 kg)(4180 J/kg°C)(10.0°C) 4.18 kJ
Thus, heat lost by the weights 4.18 kJ mweightsCweightsT
hence, Cweights
2.53102J/kg°C
(4.184 kJ)(1000 J/kJ)
(0.100 kg)(55.0°C)
(2450 J/kgK)(16.0°C) (4180 J/kgK)(85.0°C)
2450 J/kgK4180 J/kgK
CATAi CWTWi
CACW
80.0°C 10.0°C
2
8.8106J
3.6106J/kWh
272 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 273
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
9. A 1.00102-g aluminum block at 100.0°C
is placed in 1.00102g of water at 10.0°C.
The final temperature of the mixture is
25.0°C. What is the specific heat of the
aluminum?
Heat gained by the water:
QmCT
(0.100 kg)(4180 J/kg°C)(15.0°C)
6.27 kJ
Thus, heat lost by the aluminum block
6.27 kJ mAluminumCAluminumT
hence, CAluminum
mAlum
Q
inumT
8.36102J/kg°C
Section Review
12.1 Temperature and
Thermal Energy
pages 313–322
page 322
10. Temperature Make the following
conversions.
a. 5°C to kelvins
278 K
b. 34 K to degrees Celsius
239°C
c. 212°C to kelvins
485 K
d. 316 K to degrees Celsius
43°C
11. Conversions Convert the following
Celsius temperatures to Kelvin
temperatures.
a. 28°C
301 K
b. 154°C
427 K
c. 568°C
841 K
d. 55°C
218 K
e. 184°C
89 K
12. Thermal Energy Could the thermal energy
of a bowl of hot water equal that of a bowl
of cold water? Explain your answer.
Thermal energy is the measure of the
total energy of all the molecules in an
object. The temperature (hot or cold)
measures the amount of energy per
molecule. If the bowls are identical and
contain the same amount of water, they
have the same number of molecules,
but the bowl of hot water has more
total thermal energy. However, if the
cold water mass is slightly more than
that of the hot water, the two energies
could be equal.
13. Heat Flow On a dinner plate, a baked
potato always stays hot longer than any
other food. Why?
A potato has a large specific heat and
conducts heat poorly, so it loses its
heat energy slowly.
14. Heat The hard tile floor of a bathroom
always feels cold to bare feet even though
the rest of the room is warm. Is the floor
colder than the rest of the room?
The floor is usually at the same tempera-
ture as the rest of the room, but the tile
conducts heat more efficiently than most
materials, so it conducts heat from a
person’s feet, making them feel cold.
15. Specific Heat If you take a plastic spoon
out of a cup of hot cocoa and put it in your
mouth, you are not likely to burn your
tongue. However, you could very easily
burn your tongue if you put the hot cocoa
in your mouth. Why?
The plastic spoon has a lower specific
heat than the cocoa, so it does not
transmit much heat to your tongue as
it cools.
6.27 kJ
(0.100 kg)(75.0°C)
Chapter 12 continued

16. Heat Chefs often use cooking pans made of thick aluminum. Why is thick alu-
minum better than thin aluminum for cooking?
Thick aluminum conducts heat better and does not have any “hot spots.”
17. Heat and Food It takes much longer to bake a whole potato than to cook french
fries. Why?
Potatoes do not conduct heat well. Increasing surface area by cutting a
potato into small parts increases heat flow into the potato. Heat flow from
hot oil to the potato is also more efficient than from hot air.
18. Critical Thinking As water heats in a pot on a stove, the water might produce
some mist above its surface right before the water begins to roll. What is happen-
ing, and where is the coolest part of the water in the pot?
The heat flows from the burner (the hottest part) to the top surface of the
water (coldest). The water first transfers heat from bottom to top through
conduction, and then convection begins to move hot water in currents to
the top.
Practice Problems
12.2 Changes of State and the Laws of
Thermodynamics
pages 323–331
page 325
19. How much heat is absorbed by 1.00102g of ice at 20.0°C to become water at
0.0°C?
QmCT mHf
(0.100 kg)(2060 J/kg°C)(20.0°C) (0.100 kg)(3.34105J/kg)
3.75104J
20. A 2.00102-g sample of water at 60.0°C is heated to steam at 140.0°C. How
much heat is absorbed?
QmCwaterT mHv mCsteamT
(0.200 kg)(4180 J/kg°C)(100.0°C 60.0°C) (0.200 kg)(2.26106J/kg)
(0.200 kg)(2020 J/kg°C)(140.0°C 100.0°C)
502 kJ
21. How much heat is needed to change 3.00102g of ice at 30.0°C to steam at
130.0°C?
QmCiceTmHfmCwaterTmHvmCsteamT
(0.300 kg)(2060 J/kg°C)(0.0°C (30.0°C)) (0.300 kg)
(3.34105J/kg) (0.300 kg)(4180 J/kg°C)(100.0°C 0.0°C)
(0.300 kg)(2.26106J/kg) (0.300 kg)(2020 J/kg°C)(130.0°C 100.0°C)
9.40102kJ
274 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 275
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
page 328
22. A gas balloon absorbs 75 J of heat. The bal-
loon expands but stays at the same temper-
ature. How much work did the balloon do
in expanding?
UQW
Since the balloon did not change
temperature, U0.
Therefore, QW.
Thus, the balloon did 75 J of work in
expanding.
23. A drill bores a small hole in a 0.40-kg block
of aluminum and heats the aluminum by
5.0°C. How much work did the drill do in
boring the hole?
UQWblock; since Wdrill Wblock
and assume no heat added to drill:
0Wdrill mCT
(0.40 kg)(897 J/kg°C)(5.0°C)
1.8103J
24. How many times would you have to drop a
0.50-kg bag of lead shot from a height of
1.5 m to heat the shot by 1.0°C?
UmCT
(0.50 kg)(130 J/kg°C)(1.0°C)
65 J
Each time the bag is raised its potential
energy is
PE mgh
(0.50 kg)(9.80 m/s2)(1.5 m)
7.4 J
When the bag hits the ground this
energy is (mostly) transmitted as work
on the lead shot. The number of drops
is
7
6.5
4J
J
9 drops
25. When you stir a cup of tea, you do about
0.050 J of work each time you circle the
spoon in the cup. How many times would
you have to stir the spoon to heat a 0.15-kg
cup of tea by 2.0°C?
UmCT
(0.15 kg)(4180 J/kg°C)(2.0°C)
1.3103J.
The number of stirs is
1.
0
3
.
05
1
0
03
JJ
2.6104stirs
26. How can the first law of thermodynamics
be used to explain how to reduce the
temperature of an object?
Since UQW, it is possible to
have a negative Uand therefore, cool
an object if Q0 and the object does
work, for instance, by expanding.
Alternatively, have W0 and Q
negative by having it transfer heat to
its surroundings. Any combination of
these will work well.
Section Review
12.2 Changes of State and the
Laws of Thermodynamics
pages 323–331
page 331
27. Heat of Vaporization Old-fashioned heat-
ing systems sent steam into radiators in each
room of a house. In the radiators, the steam
condensed back to water. Analyze this
process and explain how it heated a room.
The condensing steam released its heat
of vaporization into the room and was
then circulated back to the boiler to
receive the heat of vaporization again.
28. Heat of Vaporization How much heat is
needed to change 50.0 g of water at 80.0°C
to steam at 110.0°C?
QmCwaterTmHvmCsteamT
(0.500 kg)(4180 J/kg°C)(100.0°C
80.0°C) (0.500 kg)
(2.26106J/kg) (0.500 kg)
(2020 J/kg°C)(110.0°C 100.0°C)
1.18105J
Chapter 12 continued

29. Heat of Vaporization The specific heat
of mercury is 140 J/kg°C. Its heat of vapor-
ization is 3.06105J/kg. How much energy
is needed to heat 1.0 kg of mercury metal
from 10.0°C to its boiling point and
vaporize it completely? The boiling point
of mercury is 357°C.
QmCHgTmHv
(1.0 kg)(140 J/kg°C)
(357°C 10.0°C)
(1.0 kg)(3.06105J/kg)
3.5105J
30. Mechanical Energy and Thermal Energy
James Joule carefully measured the differ-
ence in temperature of water at the top and
bottom of a waterfall. Why did he expect a
difference?
The water at the top has gravitational
potential energy that is dissipated into
thermal energy when the water splash-
es at the bottom. The water should be
hotter at the bottom, but not by much.
31. Mechanical Energy and Thermal Energy
A man uses a 320-kg hammer moving at
5.0 m/s to smash a 3.0-kg block of lead
against a 450-kg rock. When he measured
the temperature he found that it had
increased by 5.0°C. Explain how this
happened.
Part of the kinetic energy of the hammer
is absorbed as thermal energy by the
lead block.The hammer’s energy is
1
2
mv2
1
2
(320 kg)(5.0 m/s)24.0 kJ.
The change in thermal energy of the
block is
UmCT
(3.0 kg)(130 J/kgK)(5.0°C)
2.0 kJ
Hence, about half of the hammer’s
energy went to the lead block.
32. Mechanical Energy and Thermal Energy
Water flows over a fall that is 125.0 m high,
as shown in Figure 12-17. If the potential
energy of the water is all converted to ther-
mal energy, calculate the temperature differ-
ence between the water at the top and the
bottom of the fall.
■Figure 12-17
PEgravity Qabsorbed by water
mgh mCT
T
g
C
h
0.293°C rise in temperature at the
bottom
33. Entropy Evaluate why heating a home
with natural gas results in an increased
amount of disorder.
The gas releases heat, Q, at its combus-
tion temperature, T.The natural gas
molecules break up and combust with
oxygen.The heat is distributed in many
new ways, and the natural gas molecules
cannot readily be reassembled.
34. Critical Thinking A new deck of cards has
all the suits (clubs, diamonds, hearts, and
spades) in order, and the cards are ordered
by number within the suits. If you shuffle
the cards many times, are you likely to
return the cards to their original order?
Explain. Of what physical law is this an
example?
The cards are very unlikely to return to
their original order. This is an example
of the second law of thermodynamics,
in which disorder increases.
(9.80 m/s2)(125.0 m)
4180 J/kg°C
125.0 m
276 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued
Physics: Principles and Problems Solutions Manual 277
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter Assessment
Concept Mapping
page 336
35. Complete the following concept map using
the following terms: heat, work, internal energy.
Mastering Concepts
page 336
36. Explain the differences among the mechani-
cal energy of a ball, its thermal energy, and
its temperature. (12.1)
The mechanical energy is the sum of
the potential and kinetic energies of the
ball considered as one mass. The ther-
mal energy is the sum of the potential
and kinetic energies of the individual
particles that make up the mass of the
ball. The temperature is a measure of
the internal energy of the ball.
37. Can temperature be assigned to a vacuum?
Explain. (12.1)
No, because there are no particles that
have energy in a vacuum.
38. Do all of the molecules or atoms in a liquid
have the same speed? (12.1)
No. There is a distribution of velocities
of the atoms or molecules.
39. Is your body a good judge of temperature?
On a cold winter day, a metal doorknob feels
much colder to your hand than a wooden
door does. Explain why this is true. (12.1)
Your skin measures heat flow to or from
itself.The metal doorknob absorbs heat
from your skin faster than the wooden
door, so it feels colder.
40. When heat flows from a warmer object in
contact with a colder object, do the two
have the same temperature changes? (12.1)
The two objects will change tempera-
tures depending on their masses and
specific heats.The temperature changes
are not necessarily the same for each.
41. Can you add thermal energy to an object
without increasing its temperature? Explain.
(12.2)
When you melt a solid or boil a
liquid, you add thermal energy
without changing the temperature.
42. When wax freezes, does it absorb or release
energy? (12.2)
When wax freezes, it releases energy.
43. Explain why water in a canteen that is sur-
rounded by dry air stays cooler if it has a
canvas cover that is kept wet. (12.2)
When the water in the cover evaporates
into the dry air, it must absorb an
amount of energy proportional to its
heat of fusion. In doing so, it cools off
the canteen. This works only if the air
is dry; if the air is humid, then the water
will not evaporate.
44. Which process occurs at the coils of a run-
ning air conditioner inside a house, vapor-
ization or condensation? Explain. (12.2)
Inside the house, the coolant is evapo-
rating in the coils to absorb energy
from the rooms.
Applying Concepts
page 336
45. Cooking Sally is cooking pasta in a pot of
boiling water. Will the pasta cook faster if
the water is boiling vigorously or if it is
boiling gently?
It should make no difference. Either way,
the water is at the same temperature.
First law of
thermodynamics
temperatureentropy external
forces
internal
energy
heat work
Chapter 12 continued

46. Which liquid would an ice cube cool faster,
water or methanol? Explain.
Methanol, because it has a lower
specific heat; for a given mass and heat
transfer, it generates a bigger Tsince
QmCT.
47. Equal masses of aluminum and lead are
heated to the same temperature. The pieces
of metal are placed on a block of ice. Which
metal melts more ice? Explain.
The specific heat of aluminum is much
greater than that of lead; therefore, it
melts more ice.
48. Why do easily vaporized liquids, such as
acetone and methanol, feel cool to the skin?
As they evaporate, they absorb their
heat of vaporization from the skin.
49. Explain why fruit growers spray their trees
with water when frost is expected to protect
the fruit from freezing.
The water on the leaves will not freeze
until it can release its heat of fusion.
This process keeps the leaves warmer
longer. The heat capacity of the ice
slows down the cooling below 0°C.
50. Two blocks of lead have the same tempera-
ture. Block A has twice the mass of block B.
They are dropped into identical cups of
water of equal temperatures. Will the two
cups of water have equal temperatures after
equilibrium is achieved? Explain.
The cup with block A will be hotter
because block A contains more thermal
energy.
51. Windows Often, architects design most of
the windows of a house on the north side.
How does putting windows on the south side
affect the heating and cooling of the house?
In the northern hemisphere, the sun-
light comes from the south.The Sun’s
light would help heat the house in the
winter but also would also heat the
house in the summer.
Mastering Problems
12.1 Temperature and Thermal Energy
pages 336–337
Level 1
52. How much heat is needed to raise the
temperature of 50.0 g of water from
4.5°C to 83.0°C?
QmCT
(0.0500 kg)(4180 J/kg°C)
(83.0°C 4.5°C)
1.64104J
53. A 5.00102-g block of metal absorbs 5016 J
of heat when its temperature changes from
20.0°C to 30.0°C. Calculate the specific
heat of the metal.
QmCT
so C
m
Q
T
1.00103J/kg°C
1.00103J/kgK
54. Coffee Cup A 4.00102-g glass coffee cup
is 20.0°C at room temperature. It is then
plunged into hot dishwater at a tempera-
ture of 80.0°C, as shown in Figure 12-18.
If the temperature of the cup reaches that of
the dishwater, how much heat does the cup
absorb? Assume that the mass of the dish-
water is large enough so that its tempera-
ture does not change appreciably.
■Figure 12-18
QmCT
(4.00101kg)(840 J/kg°C)
(80.0°C 20.0°C)
2.02104J
4.00102 g
20.0°C80.0°C
5016 J
(5.00101kg)(30.0°C 20.0°C)
278 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 279
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
55. A 1.00102-g mass of tungsten at 100.0°C is placed in 2.00102g of water
at 20.0°C. The mixture reaches equilibrium at 21.6°C. Calculate the specific heat
of tungsten.
QTQW0
or mTCTTTmWCWTW
CT
m
m
W
T
C
W
T
T
TW
171 J/kgK
56. A 6.0102-g sample of water at 90.0°C is mixed with 4.00102g of water at
22.0°C. Assume that there is no heat loss to the surroundings. What is the final
temperature of the mixture?
Tf
but CACBbecause both liquids are water, and the C’s will divide out.
Tf
63°C
57. A 10.0-kg piece of zinc at 71.0°C is
placed in a container of water, as
shown in Figure 12-19. The water
has a mass of 20.0 kg and a
temperature of 10.0°C before the
zinc is added. What is the final
temperature of the water and
the zinc?
Tf
12.7°C
Level 2
58. The kinetic energy of a compact car moving at 100 km/h is 2.9105J. To get a
feeling for the amount of energy needed to heat water, what volume of water
(in liters) would 2.9105J of energy warm from room temperature (20.0°C) to
boiling (100.0°C)?
QmCTVCTwhere is the density of the material
so, V
C
Q
T
0.87 L
2.9105J
(1.00 kg/L)(4180 J/kg°C)(100.0°C 20.0°C)
(10.0 kg)(388 J/kgK)(71.0°C) (20.0 kg)(4180 J/kgK)(10.0°C)
(10.0 kg)(388 J/kgK) (20.0 kg)(4180 J/kgK)
mACATAi mBCBTBi
mACAmBCB
20.0 kg
10.0°C
10.0 kg
■Figure 12-19
(6.0102g)(90.0°C) (4.00102g)(22.0°C)
6.0102g4.00102g
mATAi mBTBi
mAmB
mACATAi mBCBTBi
mACAmBCB
(0.200 kg)(4180 J/kgK)(21.6°C20.0°C)
(0.100 kg)(21.6°C100.0°C)
Chapter 12 continued

59. Water Heater A 3.0102-W electric
immersion heater is used to heat a cup
of water, as shown in Figure 12-20. The
cup is made of glass, and its mass is
3.00102g. It contains 250 g of water at
15°C. How much time is needed to bring
the water to the boiling point? Assume
that the temperature of the cup is the
same as the temperature of the water at
all times and that no heat is lost to the air.
QmGCGTGmWCWTW
but TGTW,so
Q(mGCGmWCW)T
((0.300 kg)(840 J/kg°C) (0.250 kg)(4180 J/kg°C))(100.0°C15°C)
1.1105J
Now P
E
t
Q
t
,so
t
Q
P
3.1
0.0
1
1
10
02
5
J
J/s
370 s 6.1 min
60. Car Engine A 2.50102-kg cast-iron car engine contains water as a coolant.
Suppose that the engine’s temperature is 35.0°C when it is shut off, and the air
temperature is 10.0°C. The heat given off by the engine and water in it as they cool
to air temperature is 4.40106J. What mass of water is used to cool the engine?
QmWCWTmiCiT
mW
Q
CW
m
iC
T
iT
15 kg
12.2 Changes of State and the Laws of Thermodynamics
page 337
Level 1
61. Years ago, a block of ice with a mass of about 20.0 kg was used daily in a home
icebox. The temperature of the ice was 0.0°C when it was delivered. As it melted,
how much heat did the block of ice absorb?
QmHf(20.0 kg)(3.34105J/kg) 6.68106J
62. A 40.0-g sample of chloroform is condensed from a vapor at 61.6°C to a liquid at
61.6°C. It liberates 9870 J of heat. What is the heat of vaporization of chloroform?
QmHv
Hv 2.47105J/kg
9870 J
0.0400 kg
Q
m
(4.4106J) ((2.50102kg)(450 J/kg°C)(35.0°C10.0°C))
(4180 J/kg°C)(35.0°C10.0°C)
280 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued
15°C
250 g
3.00102 W
3.00102 g
■Figure 12-20

Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
63. A 750-kg car moving at 23 m/s brakes to a
stop. The brakes contain about 15 kg of iron,
which absorbs the energy. What is the
increase in temperature of the brakes?
During braking, the kinetic energy of
the car is converted into heat
energy. So,
KECQB0.0, and KEC
mBCBT0.0 so,
T
m
B
K
C
E
B
C
29°C
Level 2
64. How much heat is added to 10.0 g of ice at
20.0°C to convert it to steam at 120.0°C?
Amount of heat needed to heat ice to
0.0°C:
QmCT
(0.0100 kg)(2060 J/kg°C)
(0.0°C (20.0°C))
412 J
Amount of heat to melt ice:
QmHf
(0.0100 kg)(3.34105J/kg)
3.34103J
Amount of heat to heat water to
100.0°C:
QmCT
(0.0100 kg)(4180 J/kg°C)
(100.0°C0.0°C)
4.18103J
Amount of heat to boil water:
QmHv
(0.0100 kg)(2.26106J/kg)
2.26104J
Amount of heat to heat steam to
120.0°C:
QmCT
(0.0100 kg)(2060 J/kg°C)
(120.0°C100.0°C)
404 J
The total heat is
412 J 3.34103J 4.18103J
2.26104J 404 J 3.09104J
65. A 4.2-g lead bullet moving at 275 m/s
strikes a steel plate and comes to a stop. If
all its kinetic energy is converted to thermal
energy and none leaves the bullet, what is
its temperature change?
Because the kinetic energy is converted
to thermal energy, KE Q0. So
KE mBCBTand
T
m
B
K
C
E
B
and the mass of the bullet divides out so
T
290°C
66. Soft Drink A soft drink from Australia is
labeled “Low-Joule Cola.” The label says
“100 mL yields 1.7 kJ.” The can contains
375 mL of cola. Chandra drinks the cola
and then wants to offset this input of food
energy by climbing stairs. How high would
Chandra have to climb if she has a mass of
65.0 kg?
Chandra gained (3.75)(1.7 kJ) 6.4103J
of energy from the drink.
To conserve energy, EPE 0 or
6.4103Jmghso,
h
6.4
m
10
g
3J
1.0101m, or about three flights
of stairs
6.4103J
(65.0 kg)(9.80 m/s2)
1
2
((0.0 m/s)2(275 m/s)2)
130 J/kg°C
1
2
(vf2vi2)
CB
1
2
mB(vf2vi2)
mBCB
1
2
(750 kg)(0.02(23 m/s)2)
(15 kg)(450 J/kg°C)
1
2
mC(vf2vi2)
mBCB
Chapter 12 continued
Physics: Principles and Problems Solutions Manual 281

Mixed Review
pages 337–338
Level 1
67. What is the efficiency of an engine that pro-
duces 2200 J/s while burning enough gaso-
line to produce 5300 J/s? How much waste
heat does the engine produce per second?
Efficiency 100
2
52
30
00
0J
J
100
42%
The heat loss is
5300 J 2200 J 2900 J
68. Stamping Press A metal stamping machine
in a factory does 2100 J of work each time it
stamps out a piece of metal. Each stamped
piece is then dipped in a 32.0-kg vat of water
for cooling. By how many degrees does the
vat heat up each time a piece of stamped
metal is dipped into it?
If we assume the 2100 J of work from
the machine is absorbed as thermal
energy in the stamped piece, then the
vat must absorb 2100 J in the form of
heat from each piece. No work is done
on the water, only heat is transferred.
The change in temperature of the water
is given by
UmCT,
therefore T
m
U
C
0.016°C.
69. A 1500-kg automobile comes to a stop
from 25 m/s. All of the energy of the
automobile is deposited in the brakes.
Assuming that the brakes are about 45 kg
of aluminum, what would be the change
in temperature of the brakes?
The energy change in the car is
KE
1
2
(1500 kg)(25 m/s)24.7105J.
If all of this energy is transferred
as work to the brakes, then
UKE mCT.
Therefore, T
m
K
C
E
12°C
70. Iced Tea To make iced tea, you start by
brewing the tea with hot water. Then you
add ice. If you start with 1.0 L of 90°C tea,
what is the minimum amount of ice needed
to cool it to 0°C? Would it be better to let
the tea cool to room temperature before
adding the ice?
Heat lost by the tea
QmCT
(1.0 kg)(4180 J/kgK)(90°C)
376 kJ
Amount of ice melted
m
1.1 kg
Thus, you need slightly more ice than
tea, but this ratio would make watery
tea. Let the tea cool to room tempera-
ture before adding the ice.
Level 2
71. A block of copper at 100.0°C comes in con-
tact with a block of aluminum at 20.0°C, as
shown in Figure 12-21. The final tempera-
ture of the blocks is 60.0°C. What are the
relative masses of the blocks?
■Figure 12-21
Copper Aluminum
Copper Aluminum
60.0°C60.0°C
20.0°C
100.0°C
376 kJ
334 kJ
Q
Hf
4.7105J
(45 kg)(897 J/kg°C)
2100 J
(32.0 kg)(4180 J/kg°C)
W
QH
282 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 283
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The heat lost from the copper equals
the heat gained by the aluminum. The
Tfor the copper is 40.0°C and the
aluminum heats by 40.0°C.
therefore,
mcopperCcopper maluminumCaluminum
and
2.3
The copper block has 2.3 times as
much mass as the aluminum block.
72. A 0.35-kg block of copper sliding on the
floor hits an identical block moving at the
same speed from the opposite direction.
The two blocks come to a stop together
after the collision. Their temperatures
increase by 0.20°C as a result of the colli-
sion. What was their velocity before the
collision?
The change in internal energy of the
blocks is
UmCT
(0.70 kg)(385 J/kg°C)(0.20°C)
54 J
Therefore, 54 J equals the kinetic
energy of the blocks before the
collision. 54 J (2)
1
2
mv2
v
0.5
34
5J
k
g
12 m/s
Level 3
73. A 2.2-kg block of ice slides across a rough
floor. Its initial velocity is 2.5 m/s and its
final velocity is 0.50 m/s. How much of the
ice block melted as a result of the work
done by friction?
The work done by friction equals the
negative of the change in kinetic energy
of the block, assuming not too much of
the block melted.
KE
1
2
(2.2 kg)(0.50 m/s)2
1
2
(2.2 kg)(2.5 m/s)26.6 J
Therefore, 6.6 J is added to the ice.
The amount of ice melted is given by
m
3.34
6.
1
6
05
JJ/kg
2.0105kg
Thinking Critically
page 338
74. Analyze and Conclude A certain heat
engine removes 50.0 J of thermal energy
from a hot reservoir at temperature
TH545 K and expels 40.0 J of heat to a
colder reservoir at temperature TL 325 K.
In the process, it also transfers entropy from
one reservoir to the other.
a. How does the operation of the engine
change the total entropy of the reservoirs?
As the engine operates, it removes
energy from the hot reservoir.
Therefore, SH
Q
TH
H
so that the
entropy of the hot reservoir
decreases.
The entropy of the cold reservoir
SL
Q
TL
L
increases. The net
increase in entropy of the reservoirs
together is
STSLSH
Q
TL
L
Q
TH
H
ST
4
30
2.
5
0K
J
5
50
4.
5
0K
J
0.0313 J/K
b. What would be the total entropy change
in the reservoirs if TL205 K?
ST
4
20
0.
5
0K
J
5
50
4.
5
0K
J
0.103 J/K
The total entropy change in the
reservoirs, and in the universe, has
increased approximately by a factor
of three.
KE
Hf
897 J/kgK
385 J/kgK
Caluminum
Ccopper
mcopper
maluminum
Chapter 12 continued

75. Analyze and Conclude During a game,
the metabolism of basketball players often
increases by as much as 30.0 W. How much
perspiration must a player vaporize per
hour to dissipate this extra thermal energy?
The amount of thermal energy to
be dissipated in 1.00 h is
U(30.0 J/s)(3600 s/h) 1.08105J.
The amount of water this energy,
transmitted as heat, would vaporize is
m
0.0478 kg
76. Analyze and Conclude Chemists use
calorimeters to measure the heat produced
by chemical reactions. For instance, a
chemist dissolves 1.01022 molecules of a
powdered substance into a calorimeter con-
taining 0.50 kg of water. The molecules
break up and release their binding energy to
the water. The water temperature increases
by 2.3°C. What is the binding energy per
molecule for this substance?
The amount of energy added to the
water is
UmCT
(0.50 kg)(4180 J/kg°C)(2.3°C)
4.8 kJ
The energy per molecule is therefore,
4.81019 J/molecule
77. Apply Concepts All of the energy on Earth
comes from the Sun. The surface tempera-
ture of the Sun is approximately 104K.
What would be the effect on our world if
the Sun’s surface temperature were 103K?
Student answers will vary. Answers
should reflect changing average
temperature on Earth, different weather
patterns, plant and animal species
dying out, etc.
Writing in Physics
page 338
78. Our understanding of the relationship
between heat and energy was influenced by a
soldier named Benjamin Thompson, Count
Rumford; and a brewer named James Prescott
Joule. Both relied on experimental results to
develop their ideas. Investigate what experi-
ments they did and evaluate whether or not
it is fair that the unit of energy is called the
Joule and not the Thompson.
In 1799, heat was thought to be a liquid
that flowed from one object to another.
However, Count Rumford thought that
heat was caused by the motion of parti-
cles in the metal cannon. He did not do
any quantitative measurements and his
ideas were not widely accepted. In 1843,
Joule, doing careful measurements,
measured the change in temperature
caused by adding heat or doing work
on a quantity of water. He proved that
heat is a flavor of energy and that ener-
gy is conserved. Joule deserves the
credit and the eponymic unit.
79. Water has an unusually large specific heat
and large heats of fusion and vaporization.
Our weather and ecosystems depend upon
water in all three states. How would our
world be different if water’s thermodynamic
properties were like other materials, such as
methanol?
The large specific heat and large heats
of fusion and vaporization mean that
water, ice, and water vapor can store a
lot of thermal energy without changing
their temperatures too much. The impli-
cations are many. The oceans and large
lakes moderate the temperature
changes in nearby regions on a daily
and seasonal basis. The day-to-night
temperature variation near a lake is
much smaller than the day-to-night
temperature variation in the desert. The
large heat of fusion of water controls
the change of seasons in the far north
and south. The absorption of energy by
freezing water in the fall and its release
4.8 kJ
1022 molecules
1.08105J
2.26106J/kg
Q
HV
284 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 285
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
in the spring slows the temperature
changes in the atmosphere. Water
absorbs and stores a lot of energy as it
vaporizes.This energy can be used to
drive meteorological events, such as
thunderstorms and hurricanes.
Cumulative Review
page 338
80. A rope is wound around a drum with a
radius of 0.250 m and a moment of inertia
of 2.25 kg m2. The rope is connected to a
4.00-kg block. (Chapter 8)
a. Find the linear acceleration of the block.
Solve Newton’s second law for the
block: mg FTma, where the pos-
itive direction is downward and
where FTis the force of the rope on
the drum. Newton’s second law for
the drum is FTrIor FTrIa/r.
That is, FTIa/r2. Therefore,
mg (I/r2)ama. That is,
amg/(mI/r2)g/10.0
0.980 m/s2.
b. Find the angular acceleration of the
drum.
a
r
0.
0
9
.8
20
50
m
m
/s2
3.92 rad/s2
c. Find the tension, FT, in the rope.
FT
Ir
35.3 N
d. Find the angular velocity of the drum
after the block has fallen 5.00 m.
x
1
2
at2, so t
2
a
x
3.19 s
Therefore, t
(3.92 rad/s2)(3.19 s)
12.5 rad/s
81. A weight lifter raises a 180-kg barbell to a
height of 1.95 m. How much work is done
by the weight lifter in lifting the barbell?
(Chapter 10)
Wmgh
(180 kg)(9.80 m/s2)(1.95 m)
3.4103J
82. In a Greek myth, the man Sisyphus is
condemned by the gods to forever roll an
enormous rock up a hill. Each time he
reaches the top, the rock rolls back down
to the bottom. If the rock has a mass of
215 kg, the hill is 33 m in height, and
Sisyphus can produce an average power
of 0.2 kW, how many times in 1 h can
he roll the rock up the hill? (Chapter 11)
The amount of work needed to roll the
rock up once is
W mgh (215 kg)(9.80 m/s2)(33 m)
70,000 J
In one hour Sisyphus does an amount
of work
(0.2103J)(3600 s) 720,000 J
He pushes the rock up the hill
(720,000)/(70,000) 10 times in one hour
Challenge Problem
page 329
Entropy has some interesting properties.
Compare the following situations. Explain how
and why these changes in entropy are different.
1. Heating 1.0 kg of water from 273 K to 274 K.
S
Q
T
mC
T
T
15 J/K
(1.0 kg)(4180 J/kgK)(274 K 273 K)
273 K
Tf
Ti
1 kg1 kg
Q
(2.25 kg m2)(3.92 rad/s2)
0.250 m
Chapter 12 continued

2. Heating 1.0 kg of water from 353 K to 354 K.
S
Q
T
mC
T
T
12 J/K
3. Completely melting 1.0 kg of ice at 273 K.
S
Q
T
m
T
Hf
1.2103J/K
4. Heating 1.0 kg of lead from 273 K to 274 K.
S
Q
T
mC
T
T
0.48 J/K
(1.0 kg)(130 J/kgK)(274 K 273 K)
273 K
(1.0 kg)(3.34105J/kg)
273 K
(1.0 kg)(4180 J/kgK)(354 K 353 K)
353 K
286 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 287
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
13 States of Matter
CHAPTER
Practice Problems
13.1 Properties of Fluids
pages 341–348
page 344
1. The atmospheric pressure at sea level is
about 1.0105Pa. What is the force at sea
level that air exerts on the top of a desk that
is 152 cm long and 76 cm wide?
FPA Plw
(1.0105Pa)(1.52 m)(0.76 m)
1.2105N
2. A car tire makes contact with the ground on
a rectangular area of 12 cm by 18 cm. If the
car’s mass is 925 kg, what pressure does the
car exert on the ground as it rests on all
four tires?
P
A
F
1.0102kPa
3. A lead brick, 5.0 cm 10.0 cm 20.0 cm,
rests on the ground on its smallest face.
Lead has a density of 11.8 g/cm3. What
pressure does the brick exert on the ground?
mbrick Vlwh
(11.8 g/cm3)(5.0 cm)
(10.0 cm)(20.0 cm)
1.18104g 11.8 kg
P
hg
(11.8 g/cm3)(20.0 cm)
(9.80 m/s2)
23 kPa
4. In a tornado, the pressure can be 15 percent
below normal atmospheric pressure.
Suppose that a tornado occurred outside a
door that is 195 cm high and 91 cm wide.
What net force would be exerted on the
door by a sudden 15 percent drop in
normal atmospheric pressure? In what
direction would the force be exerted?
The pressure difference across the door
is
Pdiff (15%)(Patm)
(0.15)(1.0105Pa) 1.5104Pa
FPdiffAPdifflw
(1.5104Pa)(1.95 m)(0.91 m)
2.7104N directed from the inside
of the house outward
5. In industrial buildings, large pieces of equip-
ment must be placed on wide steel plates
that spread the weight of the equipment over
larger areas. If an engineer plans to install a
454-kg device on a floor that is rated to
withstand additional pressure of 5.0104Pa,
how large should the steel support plate be?
The maximum pressure P
Therefore, A
8.9102m2
6. A tank of helium gas used to inflate toy
balloons is at a pressure of 15.5106Pa
and a temperature of 293 K. The tank’s
volume is 0.020 m3. How large a balloon
would it fill at 1.00 atmosphere and 323 K?
P
T
1V
1
1
P
T
2V
2
2
, so V2
T
P
2P
2T
1V
1
1
1.00 atm 1.013105Pa
(454 kg)(9.80 m/s2)
5.0104Pa
mg
P
mg
A
Fg
A
(100 cm)2
(1 m)2
1 kg
1000 g
lwhg
lw
Vg
lw
mbrickg
lw
Fg, brick
A
(925 kg)(9.80 m/s2)
(4)(0.12 m)(0.18 m)
mcarg
4lw
Fg, car
A

V2
3.4 m3
7. What is the mass of the helium gas in the
previous problem? The molar mass of
helium gas is 4.00 g/mol.
PV nRT
n
127.3 mol
m(127.3 mol)(4.00 g/mol) 5.1102g
8. A tank containing 200.0 L of hydrogen gas
at 0.0°C is kept at 156 kPa. The tempera-
ture is raised to 95°C, and the volume is
decreased to 175 L. What is the new
pressure of the gas?
with T1273 K and
T295°C 273°C 368 K
P2
2.4102kPa
9. The average molar mass of the components
of air (mainly diatomic oxygen gas and
diatomic nitrogen gas) is about 29 g/mol.
What is the volume of 1.0 kg of air at
atmospheric pressure and 20.0°C?
PV nRT
V
where n
m
M
and T20.0°C 273 293 K
V
0.83 m3
Section Review
13.1 Properties of Fluids
pages 341–348
page 348
10. Pressure and Force Suppose that you have
two boxes. One is 20 cm 20 cm 20 cm.
The other is 20 cm 20 cm 40 cm.
a. How does the pressure of the air on the
outside of the two boxes compare?
The pressure of the air is the same
on the two boxes.
b. How does the magnitude of the total
force of the air on the two boxes
compare?
Because FPA the total force of
the air is greater on the box with the
greater area. The second box has
twice the surface area, so it has
twice the total force of the first box.
11. Meteorology A weather balloon used by
meteorologists is made of a flexible bag that
allows the gas inside to freely expand. If a
weather balloon containing 25.0 m3of
helium gas is released from sea level, what
is the volume of gas when the balloon
reaches a height of 2100 m, where the
pressure is 0.82105Pa? Assume that
the temperature is unchanged.
P1V1P2V2
V2
3.1101m3
12. Gas Compression In a certain internal-
combustion engine, 0.0021 m3of air at
atmospheric pressure and 303 K is rapidly
compressed to a pressure of 20.1105Pa
and a volume of 0.0003 m3. What is the
final temperature of the compressed gas?
T2T1P2V2
P1V1
P2V2
T2
P1V1
T1
(1.013105Pa)(25.0 m3)
0.82105Pa
P1V1
P2
1
2
.0
9
g/
1
m
03
ol
g
(8.31 Pam3/molK)(293 K)
(1.013105Pa)
1.0103g
29 g/mol
nRT
P
(368 K)(156 kPa)(200.0 L)
(175 L)(273 K)
T2P1V1
V2T1
P2V2
T2
P1V1
T1
(15.5106Pa)(0.020 m3)
(8.31 Pam3/molK)(293 K)
PV
RT
(323 K)(15.5106Pa)(0.020 m3)
(1.013105Pa)(293 K)
288 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 289
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
9102K
13. Density and Temperature Starting at 0°C,
how will the density of water change if it is
heated to 4°C? To 8°C?
As the water is heated from 0°C, the
density will increase until it reaches a
maximum at 4°C. On further heating to
8°C, the density of the water will
decrease.
14. The Standard Molar Volume What is the
volume of 1.00 mol of a gas at atmospheric
pressure and a temperature of 273 K?
V
nR
PT
0.0224 m3
15. The Air in a Refrigerator How many
moles of air are in a refrigerator with a vol-
ume of 0.635 m3 at a temperature of
2.00°C? If the average molar mass of air is
29 g/mol, what is the mass of the air in the
refrigerator?
n
28.1 mol
mnM
(28.1 mol)(29 g/mol)
0.81 kg
16. Critical Thinking Compared to the parti-
cles that make up carbon dioxide gas, the
particles that make up helium gas are very
small. What can you conclude about the
number of particles in a 2.0-L sample of
carbon dioxide gas compared to the num-
ber of particles in a 2.0-L sample of helium
gas if both samples are at the same temper-
ature and pressure?
There are an equal number of particles
in the two samples. In an ideal gas, the
size of the particles is not relevant to
the volume of the gas or the pressure
exerted by the gas.
Section Review
13.2 Forces Within Liquids
pages 349–351
page 351
17. Evaporation and Cooling In the past,
when a baby had a high fever, the doctor
might have suggested gently sponging off
the baby with rubbing alcohol. Why would
this help?
Since alcohol evaporates easily, there is
a very noticeable evaporative cooling
effect.
18. Surface Tension A paper clip, which has a
density greater than that of water, can be
made to stay on the surface of water. What
procedures must you follow for this to
happen? Explain.
The paper clip should be placed care-
fully and flatly onto the surface of the
water. This will reduce the weight per
unit area of water surface on which it
will rest. The surface tension of the
water then is sufficient to support the
reduced weight per unit area of the
paper clip.
19. Language and Physics The English lan-
guage includes the terms adhesive tape and
working as a cohesive group. In these terms,
are adhesive and cohesive being used in the
same context as their meanings in physics?
Yes, adhesive tape is sticking to some-
thing different than tape. A cohesive
group is a collection of people working
together.
20. Adhesion and Cohesion In terms of
adhesion and cohesion, explain why
alcohol clings to the surface of a glass rod
but mercury does not.
(1.013105Pa)(0.635 m3)
(8.31 Pam3molK)(275 K)
PV
RT
(1.00 mol)(8.31 Pam3/molK)(273 K)
1.013105Pa
(303 K)(20.1105Pa)(0.0003 m3)
(1.013105Pa)(0.0021 m3)
Chapter 13 continued

Adhesion is the force between unlike
materials. Alcohol has a greater
adhesive attraction to glass than mer-
cury has. The cohesive forces of mer-
cury are strong enough to overcome its
adhesive force with glass.
21. Floating How can you tell that the paper
clip in problem 18 was not floating?
If the paper clip broke through the sur-
face of the water, it sank. An object that
floats would simply bob back to the
surface.
22. Critical Thinking On a hot, humid day,
Beth sat on the patio with a glass of cold
water. The outside of the glass was coated
with water. Her younger sister, Jo, suggested
that the water had leaked through the glass
from the inside to the outside. Suggest an
experiment that Beth could do to show Jo
where the water came from.
Beth could weigh the glass before
putting it in the refrigerator for a while
to cool it down.Then she could remove
it from the refrigerator and allow mois-
ture to collect on the outside. Finally,
she would weigh the glass a second
time. If water simply leaks from the
inside to the outside, the mass of the
glass and water will be unchanged.
However, if the moisture is condensa-
tion, there will be an increase in the
mass at the second weighing.
Practice Problems
13.3 Fluids at Rest and
in Motion
pages 352–358
page 353
23. Dentists’ chairs are examples of hydraulic-
lift systems. If a chair weighs 1600 N and
rests on a piston with a cross-sectional area
of 1440 cm2, what force must be applied to
the smaller piston, with a cross-sectional
area of 72 cm2, to lift the chair?
F2
8.0101N
24. A mechanic exerts a force of 55 N on a
0.015 m2hydraulic piston to lift a small
automobile. The piston that the automobile
sits on has an area of 2.4 m2. What is the
weight of the automobile?
F2 8.8103N
25. By multiplying a force, a hydraulic system
serves the same purpose as a lever or
seesaw. If a 400-N child standing on one
piston is balanced by a 1100-N adult
standing on another piston, what is the
ratio of the areas of their pistons?
F2
0.4
The adult stands on the larger piston.
26. In a machine shop, a hydraulic lift is used
to raise heavy equipment for repairs. The
system has a small piston with a cross-
sectional area of 7.0102 m2 and a large
piston with a cross-sectional area of
2.1101m2. An engine weighing
2.7103N rests on the large piston.
a. What force must be applied to the small
piston to lift the engine?
F2
9.0102N
b. If the engine rises 0.20 m, how far does
the smaller piston move?
V1V2and A1h1A2h2
h2
0.60 m
(2.1101m2)(0.20 m)
7.0102m2
A1h1
A2
(2.7103N)(7.0102m2)
2.1101m2
F1A2
A1
400 N
1100 N
F2
F1
A2
A1
F1A2
A1
(55 N)(2.4 m2)
(0.015 m2)
F1A2
A1
(1600 N)(72 cm2)
1440 cm2
F1A2
A1
290 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 291
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
page 356
27. Common brick is about 1.8 times denser
than water. What is the apparent weight of
a 0.20 m3block of bricks under water?
Fapparent Fg Fbuoyant
brickVg waterVg
(brick water)Vg
(1.8103kg/m3
1.00103kg/m3)
(0.20 m3)(9.80 m/s2)
1.6103N
28. A girl is floating in a freshwater lake with
her head just above the water. If she weighs
610 N, what is the volume of the submerged
part of her body?
She is floating so she displaces a
volume of water that weighs as much
as she does.
FgFbuoyant waterVg
V
6.2102m3
29. What is the tension in a wire supporting a
1250-N camera submerged in water? The
volume of the camera is 16.5103m3.
To hold the camera in place the tension
in the wire must equal the apparent
weight of the camera.
TFapparent
Fg Fbuoyant
Fg waterVg
1250 N (1.00103kg/m3)
(16.5103m3)(9.80 m/s2)
1.09103N
30. Plastic foam is about 0.10 times as dense
as water. What weight of bricks could you
stack on a 1.0 m 1.0 m 0.10 m slab
of foam so that the slab of foam floats in
water and is barely submerged, leaving the
bricks dry?
The foam would displace
V(1.0 m)(1.0 m)(0.10 m) 0.10 m3
of water. The weight of the foam is
Fg, foam foamVg
(1.0102kg/m3)(0.10 m3)
(9.80 m/s2)
98 N
The buoyant force is
Fbuoyant waterVg
(1.00103kg/m3)
(0.10 m3)(9.80 m/s2)
980 N
The weight of brick that you could stack
is
Fg, brick Fbuoyant Fg foam
980 N 98 N
8.8102N
31. Canoes often have plastic foam blocks
mounted under the seats for flotation in
case the canoe fills with water. What is the
approximate minimum volume of foam
needed for flotation for a 480-N canoe?
The buoyant force on the foam must
equal 480 N. We are assuming the
canoe is made of dense material.
Fbuoyant waterVg
V
4.9102m3
Section Review
13.3 Fluids at Rest and
in Motion
pages 352–358
page 358
32. Floating and Sinking Does a full soda pop
can float or sink in water? Try it. Does it mat-
ter whether or not the drink is diet? All soda
480 N
(1.00103kg/m3)(9.80 m/s2)
Fbuoyant
waterg
610 N
(1.00103kg/m3)(9.80 m/s2)
Fg
waterg
Chapter 13 continued

pop cans contain the same volume of liquid, 354 mL, and displace the same vol-
ume of water. What is the difference between a can that sinks and one that floats?
The difference is a lot of sugar. About one-fourth cup of sugar is dissolved
in the regular drink, making it denser than water. The diet drink has a small
amount of an artificial sweetener. The diet drink is less dense than the
sugar-laden regular soft drink.
33. Floating and Density A fishing bobber made of cork floats with one-tenth of
its volume below the water’s surface. What is the density of cork?
The weight of the water displaced equals the weight of the bobber.
FgwaterVwatergcorkVcork g
Therefore,
w
co
a
r
te
k
r
V
V
w
c
a
o
t
r
e
k
r
1
1
0
The cork is about one-tenth as dense as water.
34. Floating in Air A helium balloon rises because of the buoyant force of the
air lifting it. The density of helium is 0.18 kg/m3, and the density of air is
1.3 kg/m3. How large a volume would a helium balloon need to lift a 10-N
lead brick?
Fapparent must equal 10 N to counteract the weight of the lead brick.
Fapparent Fg Fbuoyant
heliumVballoongairVballoong
(helium air)Vballoong
Thus,
Vballoon
0.9 m3
35. Transmission of Pressure A toy rocket launcher is designed so that a child
stomps on a rubber cylinder, which increases the air pressure in a launching tube
and pushes a foam rocket into the sky. If the child stomps with a force of 150 N
on a 2.5103m2area piston, what is the additional force transmitted to the
4.0104 m2launch tube?
F2
24 N
(150 N)(4.0104m2)
2.5103m2
F1A2
A1
10 N
(0.18 kg/m3 1.3 kgm3)(9.80 ms2)
Fapparent
(helium air)g
292 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 293
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
36. Pressure and Force An automobile weigh-
ing 2.3104N is lifted by a hydraulic cylin-
der with an area of 0.15 m2.
a. What is the pressure in the hydraulic
cylinder?
P
A
F
1.5105Pa
b. The pressure in the lifting cylinder is
produced by pushing on a 0.0082 m2
cylinder. What force must be exerted on
this small cylinder to lift the automobile?
F2
1.3103N
37. Displacement Which of the following
displaces more water when it is placed in
an aquarium?
a. A 1.0-kg block of aluminum or a 1.0-kg
block of lead?
Both aluminum and iron will sink to
the bottom of the aquarium. Because
aluminum is less dense than iron,
1 kg of aluminum has a greater vol-
ume than 1 kg of iron.Therefore, the
block of aluminum will displace
more water.
b. A 10-cm3block of aluminum or a 10-cm3
block of lead?
Both blocks will sink, and each will
displace the same volume of water,
10 cm3.
38. Critical Thinking As you discovered in
Practice Problem 4, a tornado passing over a
house sometimes makes the house explode
from the inside out. How might Bernoulli’s
principle explain this phenomenon? What
could be done to reduce the danger of a
door or window exploding outward?
The fast-moving air of the tornado has a
lower pressure than the still air inside
the house. Therefore, the air inside the
house is at a higher pressure and pro-
duces an enormous force on the win-
dows, doors, and walls of the house.
This pressure difference is reduced by
opening doors and windows to let the
air flow freely to the outside.
Practice Problems
13.4 Solids
pages 359–363
page 362
39. A piece of aluminum house siding is 3.66 m
long on a cold winter day of 28°C. How
much longer is it on a very hot summer day
at 39°C?
L2L1L1(T2T1), so
LL1(T2T1)
(25106°C1)(3.66 m)
(39°C (28°C))
6.1103m 6.1 mm
40. A piece of steel is 11.5 cm long at 22°C. It is
heated to 1221°C, close to its melting tem-
perature. How long is it?
L2L1 L1(T2 T1)
(0.115 m) (12106°C1)
(0.115 m)(1221°C 22°C)
1.2101m 12 cm
41. A 400-mL glass beaker at room temperature
is filled to the brim with cold water at 4.4°C.
When the water warms up to 30.0°C, how
much water will spill from the beaker?
At the beginning, 400 mL of 4.4°C water
is in the beaker. Find the change in
volume at 30.0°C.
VVT
(210106°C1)(400106m3)
(30.0°C 4.4°C)
2106m32 mL
(2.3104N)(0.0082 m2)
0.15 m2
F1A2
A1
2.3104N
0.15 m2
Chapter 13 continued

42. A tank truck takes on a load of 45,725 L of
gasoline in Houston, where the temperature
is 28.0°C. The truck delivers its load in
Minneapolis, where the temperature is
12.0°C.
a. How many liters of gasoline does the
truck deliver?
V
1
VT
V2V1TV1
(950106°C1)(45,725 L)
(12.0°C 28.0°C) 45,725 L
4.4104L
b. What happened to the gasoline?
The gasoline volume decreased
because the temperature decreased.
The mass of the gasoline remained
the same.
43. A hole with a diameter of 0.85 cm is drilled
into a steel plate. At 30.0°C, the hole exactly
accommodates an aluminum rod of the
same diameter. What is the spacing between
the plate and the rod when they are cooled
to 0.0°C?
The aluminum shrinks more than the
steel. Let Lbe the diameter of the rod.
Laluminum LT
(25106°C1)
(0.85 cm)(0.0°C 30.0°C)
6.38104cm
For the steel, the diameter of the hole
shrinks by
Lsteel LT
(12106°C1)
(0.85 cm)(0.0°C 30.0°C)
3.06104cm
The spacing between the rod and the
hole will be
1
2
(6.4104cm 3.1104cm)
1.6104cm
44. A steel ruler is marked in millimeters so
that the ruler is absolutely correct at 30.0°C.
By what percentage would the ruler be
incorrect at 30.0°C?
Because the steel shrinks, the distances
between the millimeter marks decrease
when cooled.
% incorrect (100)
L
L
(100)(TfTi)
(100)(12106°C1)
(30.0°C 30.0°C)
0.072%
Section Review
13.4 Solids
pages 359–363
page 363
45. Relative Thermal Contraction On a hot
day, you are installing an aluminum screen
door in a concrete door frame. You want
the door to fit well on a cold winter day.
Should you make the door fit tightly in the
frame or leave extra room?
Fit the door tightly. Aluminum shrinks
when cooled much more than concrete
does.
46. States of Matter Why could candle wax be
considered a solid? Why might it also be
considered a viscous liquid?
The wax could be considered a solid
because it has a definite volume and
shape. It could be considered a viscous
liquid because the particles do not form
a fixed crystalline pattern.
47. Thermal Expansion Can you heat a piece
of copper enough to double its length?
The thermal expansion coefficient for
copper is 16106/°C.To double its
length LLLT, which means that
T1
T
1
63,000°C
1
16106°C1
V2V1
V1T
294 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued
Physics: Principles and Problems Solutions Manual 295
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The copper would be vaporized at that
temperature.
48. States of Matter Does Table 13-2 provide a
way to distinguish between solids and liquids?
The coefficients of volume expansion are
much greater for liquids than for solids.
49. Solids and Liquids A solid can be defined
as a material that can be bent and will resist
bending. Explain how these properties
relate to the binding of atoms in a solid,
but do not apply to a liquid.
Particles in a solid are closer and, there-
fore, more tightly bound.They vibrate
about a fixed position.This allows the
solid to be bent, but it also resists
bending. Particles in a liquid are farther
apart and less tightly bound. Because
the particles are free to flow past one
another, a liquid cannot be bent.
50. Critical Thinking The iron ring in
Figure 13-23 was made by cutting a small
piece from a solid ring. If the ring in the
figure is heated, will the gap become wider
or narrower? Explain your answer.
■Figure 13-23
The gap will become wider. All of the
measurements of the ring increase
when heated.
Chapter Assessment
Concept Mapping
page 368
51. Complete the concept map below using the
following terms: density, viscosity, elasticity,
pressure. A term may be used more than once.
Mastering Concepts
page 368
52. How are force and pressure different? (13.1)
Force depends only on the push or pull
on an object. Pressure depends on the
force as well as the area over which the
force is applied.
53. A gas is placed in a sealed container, and
some liquid is placed in a container of the
same size. The gas and liquid both have
definite volume. How do they differ? (13.1)
The liquid’s volume will remain
unchanged. The gas will expand to fill
the volume of the container.
54. In what way are gases and plasmas similar?
In what way are they different? (13.1)
Both gases and plasmas have no defi-
nite volume and no definite shape. A gas
is made of atoms. A plasma is made of
positively charged ions and negatively
charged electrons.The particles of a
plasma are more energetic than the
particles of a gas. Plasmas can conduct
electricity. Gases cannot.
55. The Sun is made of plasma. How is this
plasma different from the plasmas on
Earth? (13.1)
The Sun’s plasma is extremely hot, but
more importantly, it is very dense—
denser than most solids on Earth.
56. Lakes A frozen lake melts in the spring.
What effect does this have on the tempera-
ture of the air above the lake? (13.2)
Chapter 13 continued
fluids
viscosity densitydensity
pressure
solids
elasticity
States of Matter

To melt, the ice must absorb energy in
the amount of its heat of fusion from
the air and water. It will cool the air
above it.
57. Hiking Canteens used by hikers often are
covered with canvas bags. If you wet the
canvas bag covering a canteen, the water in
the canteen will be cooled. Explain. (13.2)
The water evaporates into the air,
absorbing energy from the canteen and
the water inside.
58. What do the equilibrium tubes in
Figure 13-24 tell you about the pressure
exerted by a liquid? (13.3)
■Figure 13-24
The equilibrium tubes illustrate that
pressure is independent of the shape of
the container.
59. According to Pascal’s principle, what hap-
pens to the pressure at the top of a container
if the pressure at the bottom is increased?
(13.3)
Changes in pressure are distributed
equally to all parts of the container. The
pressure at the top increases.
60. How does the water pressure 1 m below the
surface of a small pond compare with the
water pressure the same distance below the
surface of a lake? (13.3)
Size or shape of the body of water does
not matter, only the depth. The pressure
is the same in each case.
61. Does Archimedes’ principle apply to an
object inside a flask that is inside a space-
ship in orbit? (13.3)
No, it does not.The apparent weight of
the displaced fluid is zero because the
fluid is in free-fall. Thus, there is no
buoyant force.
62. A stream of water goes through a garden
hose into a nozzle. As the water speeds up,
what happens to the water pressure? (13.3)
The water pressure decreases because
of Bernoulli’s principle.
63. How does the arrangement of atoms in a
crystalline substance differ from that in an
amorphous substance? (13.4)
The atoms in a crystalline substance
are arranged in an ordered pattern. In
the amorphous substance, the atoms
are randomly arranged.
64. Does the coefficient of linear expansion
depend on the unit of length used? Explain.
(13.4)
No. The coefficient is a measure of the
expansion of an object relative to its
total length. Units and total length do
not change the coefficient of linear
expansion.
Applying Concepts
page 368–369
65. A rectangular box with its largest surface
resting on a table is rotated so that its
smallest surface is now on the table. Has
the pressure on the table increased,
decreased, or remained the same?
The pressure increased. The weight
stayed the same, but the weight per
area increased.
66. Show that a pascal is equivalent to a
kg/ms2.
Pa N/m2(kgm/s2)/m2
kg/ms2
296 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 297
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
67. Shipping Cargo Compared to an identical
empty ship, would a ship filled with table-
tennis balls sink deeper into the water or
rise in the water? Explain.
It would sink deeper into the water
because it would have a greater weight.
68. Drops of mercury, water, ethanol, and
acetone are placed on a smooth, flat
surface, as shown in Figure 13-25. From
this figure, what can you conclude about
the cohesive forces in these liquids?
■Figure 13-25
The cohesive forces are strongest in
mercury and weakest in acetone. The
stronger the cohesive force, the more
spherical the drop will be.
69. How deep would a water container have to
be to have the same pressure at the bottom
as that found at the bottom of a 10.0-cm
deep beaker of mercury, which is 13.55
times as dense as water?
Pwater Pmercury
waterhwatergmercuryhmercuryg
hwater
hmercury
(13.55)(10.0 cm)
136 cm
70. Alcohol evaporates more quickly than water
does at the same temperature. What does this
observation allow you to conclude about the
properties of the particles in the two liquids?
The cohesive forces of water are
greater than those of alcohol.
71. Suppose you use a hole punch to make a
circular hole in aluminum foil. If you heat
the foil, will the size of the hole decrease or
increase? Explain.
As you heat the foil, the hole becomes
larger. Heating transfers more energy to
particles of the aluminum, causing the
volume of the aluminum to increase.
72. Equal volumes of water are heated in two
narrow tubes that are identical, except that
tube A is made of soft glass and tube B is
made of ovenproof glass. As the temperature
increases, the water level rises higher in tube B
than in tube A. Give a possible explanation.
The ovenproof glass expands less than
the soft glass when heated. The water
does not rise as high in A because the
soft glass tube is expanding in volume.
73. A platinum wire easily can be sealed in a
glass tube, but a copper wire does not form
a tight seal with the glass. Explain.
Platinum’s coefficient of thermal expan-
sion is similar to that of glass, so it
expands and contracts as the glass
does. Copper has a much larger coeffi-
cient than glass.
74. Five objects with the following densities are
put into a tank of water.
a. 0.85 g/cm3d. 1.15 g/cm3
b. 0.95 g/cm3e. 1.25 g/cm3
c. 1.05 g/cm3
The density of water is 1.00 g/cm3. The
diagram in Figure 13-26 shows six possible
positions of these objects. Select a position,
from 1 to 6, for each of the five objects. Not
all positions need to be selected.
■Figure 13-26
The positions of the objects should be
a–1, b–2, c–6, d–6, e–6
1234
5
6
mercury
water
Chapter 13 continued
298 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued
Mastering Problems
13.1 Properties of Fluids
pages 369–370
Level 1
75. Textbooks A 0.85-kg physics book with
dimensions of 24.0 cm 20.0 cm is at rest
on a table.
a. What force does the book apply to the
table?
The force on the table is the weight
of the book.
Wmg (0.85 kg)(9.80 m/s2)
8.3 N
b. What pressure does the book apply?
The pressure applied by the book is
P
A
F
m
lw
g
1.7102Pa
76. A 75-kg solid cylinder that is 2.5 m long
and has an end radius of 7.0 cm stands on
one end. How much pressure does it exert?
P
A
F
4.8104Pa
77. What is the total downward force of the
atmosphere on the top of your head right
now? Assume that the top of your head has
an area of about 0.025 m2.
FPA (1.01105Pa)(0.025 m2)
2.5103N
78. Soft Drinks Sodas are made fizzy by the
carbon dioxide (CO2) dissolved in the
liquid. An amount of carbon dioxide equal
to about 8.0 L of carbon dioxide gas at
atmospheric pressure and 300.0 K can be
dissolved in a 2-L bottle of soda. The molar
mass of CO2is 44 g/mol.
a. How many moles of carbon dioxide are
in the 2-L bottle? (1 L 0.001 m3)
From the ideal gas law
n
P
RV
T
0.32 moles
b. What is the mass of the carbon dioxide
in the 2-L bottle of soda?
The molecular weight of carbon
dioxide is
M12 2(16)
44 g/mol
Therefore, the mass is
mnM
(0.32 mol)(44 g/mol)
14 g
79. As shown in Figure 13-27, a constant-
pressure thermometer is made with a
cylinder containing a piston that can move
freely inside the cylinder. The pressure and
the amount of gas enclosed in the cylinder
are kept constant. As the temperature
increases or decreases, the piston moves up
or down in the cylinder. At 0°C, the height
of the piston is 20 cm. What is the height of
the piston at 100°C?
■Figure 13-27
Because the pressure is kept constant,
V1/T1V2/T2. The height of the piston
is directly proportional to the volume of
the cylinder.Therefore,
h2
T2
h1
T1
Cylinder
20 cm
Gas
Piston
(1.01105Pa)(0.0080 m3)
(8.31 Pam3molK)(300.0 K)
(75 kg)(9.80 ms2)
(0.070 m)2
mg
r2
(0.85 kg)(9.80 ms2)
(2.40101m)(2.00101m)
Physics: Principles and Problems Solutions Manual 299
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
h2
3101cm
Level 2
80. A piston with an area of 0.015 m2encloses
a constant amount of gas in a cylinder with
a volume of 0.23 m3. The initial pressure of
the gas is 1.5105Pa. A 150-kg mass is
then placed on the piston, and the piston
moves downward to a new position, as
shown in Figure 13-28. If the temperature
is constant, what is the new volume of the
gas in the cylinder?
■Figure 13-28
P1V1P2V2
V2
P
P
1V
2
1
(1.5105Pa)(0.23 m3)
1.5105Pa
0.14 m3
Level 3
81. Automobiles A certain automobile tire is
specified to be used at a gauge pressure of
30.0 psi, or 30.0 pounds per square inch.
(One pound per square inch equals
6.90103Pa.) The term gauge pressure
means the pressure above atmospheric pres-
sure. Thus, the actual pressure in the tire is
1.01105Pa (30.0 psi)(6.90103Pa/psi)
3.08105Pa. As the car is driven, the
tire’s temperature increases, and the volume
and pressure increase. Suppose you filled a
car’s tire to a volume of 0.55 m3at a tem-
perature of 280 K. The initial pressure was
30.0 psi, but during the drive, the tire’s
temperature increased to 310 K and the
tire’s volume increased to 0.58 m3.
a. What is the new pressure in the tire?
P
T
1V
1
1
P
T
2V
2
2
P2
P
T
1V
1V
1T
2
2
3.2105Pa
b. What is the new gauge pressure?
Pgauge
31 psi
13.3 Fluids at Rest and in Motion
page 370
Level 1
82. Reservoirs A reservoir behind a dam is
17-m deep. What is the pressure of the
water at the following locations?
a. the base of the dam
Phg
(1.00103kg/m3)(17 m)
(9.80 m/s2)
1.7105Pa
b. 4.0 m from the top of the dam
Phg
(1.00103kg/m3)(4.0 m)
(9.80 m/s2)
3.9104Pa
(30.0 psi)(0.55 m3)(310 K)
(280 K)(0.58 m3)
(3.08105Pa)(0.55 m3)(310 K)
(280 K)(0.58 m3)
(150 kg)(9.80 m/s2)
0.015 m2
P1V1
P1
m
A
g
Volume 0.23 m3
Piston area 0.015 m2Volume ?
Gas
Gas
150 kg
(20 cm)(373 K)
273 K
h1T2
T1
Chapter 13 continued

83. A test tube standing vertically in a test-tube
rack contains 2.5 cm of oil (0.81 g/cm3)
and 6.5 cm of water. What is the pressure
exerted by the two liquids on the bottom of
the test tube?
PPoil Pwater
oilhoilgwaterhwaterg
(810 kg/m3)(0.025 m)(9.80 m/s2)
(1.00103kg/m3)(0.065 m)
(9.80 m/s2)
8.4102Pa
84. Antiques An antique yellow metal statuette
of a bird is suspended from a spring scale.
The scale reads 11.81 N when the statuette
is suspended in air, and it reads 11.19 N
when the statuette is completely submerged
in water.
a. Find the volume of the statuette.
Fbuoyant waterVg FgFapparent
Thus,
V
6.33105m3
b. Is the bird made of gold
(19.3103kg/m3) or gold-plated
aluminum (2.7103kg/m3)?
m
V
19.0103kg/m3
The statuette is made of gold.
85. During an ecology experiment, an aquarium
half-filled with water is placed on a scale.
The scale shows a weight of 195 N.
a. A rock weighing 8 N is added to the
aquarium. If the rock sinks to the bottom
of the aquarium, what will the scale read?
Fg195 N 8 N 203 N
b. The rock is removed from the aquarium,
and the amount of water is adjusted
until the scale again reads 195 N. A fish
weighing 2 N is added to the aquarium.
What is the scale reading with the fish
in the aquarium?
Fg195 N 2 N 197 N
In each case the buoyant force is
equal to the weight of the water
displaced.
86. What is the size of the buoyant force on a
26.0-N ball that is floating in fresh water?
If the ball is floating
Fbuoyant Fg26.0 N
87. What is the apparent weight of a rock sub-
merged in water if the rock weighs 45 N in
air and has a volume of 2.1103m3?
Fapparent FgFbuoyant
FgwaterVg
45 N (1.00103kg/m3)
(2.1103m3)(9.80 m/s2)
24 N
88. What is the maximum weight that a balloon
filled with 1.00 m3of helium can lift in air?
Assume that the density of air is 1.20 kg/m3
and that of helium is 0.177 kg/m3. Neglect
the mass of the balloon.
Fapparent FgFbuoyant
heliumVg airVg
(helium air)Vg
(0.177 kg/m31.20 kg/m3)
(1.00 m3)(9.80 m/s2)
10.0 N
Level 2
89. If a rock weighs 54 N in air and has an
apparent weight of 46 N when submerged
in a liquid with a density twice that of
water, what will be its apparent weight
when it is submerged in water?
11.81 N
(6.33105m3)(9.80 ms2)
Fg
Vg
11.81 N 11.19 N
(1.00103kgm3)(9.80 ms2)
FgFapparent
waterg
300 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 301
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Fapparent, water FgwaterVg
and Fapparent, liquid Fg2waterVg
or V
Substitute this into the first equation.
Fapparent, water Fgwaterg
Fg
1
2
(FgFapparent, liquid)
1
2
(FgFapparent, liquid)
1
2
(54 N 46 N)
5.0101N
Level 3
90. Oceanography As shown in
Figure 13-29, a large buoy used to
support an oceanographic research
instrument is made of a cylindrical,
hollow iron tank. The tank is 2.1 m
in height and 0.33 m in diameter.
The total mass of the buoy and the
research instrument is about 120 kg.
The buoy must float so that one end
is above the water to support a radio
transmitter. Assuming that the mass
of the buoy is evenly distributed, how
much of the buoy will be above the
waterline when it is floating?
The height of the buoy above water is
labove 1
V
Vw
bu
a
o
te
y
r
ltotal
1ltotal
1ltotal
1(2.1 m)
0.70 m
120 kg
1
2
(0.33 m)2(2.1 m)(1.00103 kgm3)
m
r2hwater
w
m
ater
r2h
0.33 m
? m
2.1 m
■Figure 13-29
FgFapparent, liquid
2waterg
FgFapparent, liquid
2waterg
Chapter 13 continued

13.4 Solids
pages 370–371
Level 1
91. A bar of an unknown metal has a length of
0.975 m at 45°C and a length of 0.972 m at
23°C. What is its coefficient of linear
expansion?
1.4104°C1
92. An inventor constructs a thermometer from
an aluminum bar that is 0.500 m in length
at 273 K. He measures the temperature by
measuring the length of the aluminum bar.
If the inventor wants to measure a 1.0-K
change in temperature, how precisely must
he measure the length of the bar?
T1.0 K 1.0°C
LL1T
(25106°C1)(0.500 m)(1.0°C)
1.3105m
93. Bridges How much longer will a 300-m
steel bridge be on a 30°C day in August
than on a 10°C night in January?
LL1TL1(T2T1)
(12106°C1)(300 m)
(30°C (10°C))
0.1 m
94. What is the change in length of a 2.00-m
copper pipe if its temperature is raised from
23°C to 978°C?
LL1TL1(T2T1)
(16106°C1)(2.00 m)
(978°C 23°C)
3.1102m
95. What is the change in volume of a 1.0-m3
concrete block if its temperature is raised
45°C?
VV1T
(36106°C1)(1.0 m3)(45°C)
1.6103m3
96. Bridges Bridge builders often use rivets
that are larger than the rivet hole to make
the joint tighter. The rivet is cooled before it
is put into the hole. Suppose that a builder
drills a hole 1.2230 cm in diameter for a
steel rivet 1.2250 cm in diameter. To what
temperature must the rivet be cooled if it is
to fit into the rivet hole, which is at 20.0°C?
L2L1L1(T2T1)
T2T1
20.0°C
1.2102°C
Level 2
97. A steel tank filled with methanol is 2.000 m
in diameter and 5.000 m in height. It is
completely filled at 10.0°C. If the tempera-
ture rises to 40.0°C, how much methanol
(in liters) will flow out of the tank, given
that both the tank and the methanol will
expand?
VV1T
(methanol steel)(r2h)(T2T1)
(1200106°C135106°C1)
()(1.000 m)2(5.000 m)
(40.0°C 10.0°C)
0.55 m3
98. An aluminum sphere is heated from 11°C to
580°C. If the volume of the sphere is 1.78
cm3at 11°C, what is the increase in volume
of the sphere at 580°C?
VV1T
(75106°C1)(1.78 cm3)
(580°C 11°C)
7.6102cm3
1.2230 cm 1.2250 cm
(12106°C1)(1.2250 cm)
(L2L1)
L1
0.972 m 0.975 m
(0.975 m)(23°C45°C)
L2L1
L1(T2T1)
302 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 303
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
99. The volume of a copper sphere is 2.56 cm3after being heated from 12°C to
984°C. What was the volume of the copper sphere at 12°C?
V2V1V1TV1(1 T)
V1
2.4 cm3
Level 3
100. A square of iron plate that is 0.3300 m on each side is heated from 0°C to 95°C.
a. What is the change in the length of the sides of the square?
LL1TL1(T2T1)
(12106°C1)(0.3300 m)(95°C 0°C)
3.8104m
b. What is the relative change in area of the square?
relative change
A2A
1
A1
2.3103
101. An aluminum cube with a volume of 0.350 m3at 350.0 K is cooled to 270.0 K.
a. What is its volume at 270.0 K?
V2V1V1T
V1(1 T)
V1(1 (T2T1))
(0.350 m3)(1 (75106°C1)(270.0 K 350.0 K))
0.348 m3
b. What is the length of a side of the cube at 270.0 K?
L (V2)
1
3
(0.348 m3)
1
3
0.703 m
(0.3300 m 3.8104m)2(0.3300 m)2
(0.3300 m)2
(L1L)2L12
L12
L22 L12
L12
A
A1
2.56 cm3
(1 (48106°C1)(984°C12°C))
V2
1T
Chapter 13 continued

102. Industry A machinist builds a rectangular mechanical part for a special refrig-
erator system from two rectangular pieces of steel and two rectangular pieces of
aluminum. At 293 K, the part is a perfect square, but at 170 K, the part becomes
warped, as shown in Figure 13-30. Which parts were made of steel and which
were made of aluminum?
Parts 1 and 2 experienced a greater reduction in length than parts 3 and
4; therefore, parts 1 and 2 must have been made of aluminum, which has
a larger coefficient of expansion than steel.
Mixed Review
page 371
Level 1
103. What is the pressure on the hull of a submarine at a depth of 65 m?
PPatmosphere watergh
(1.01105Pa) (1.00103kg/m3)(9.80 m/s2)(65 m)
7.4105Pa
104. Scuba Diving A scuba diver swimming at a depth of 5.0 m under water exhales
a 4.2106m3bubble of air. What is the volume of that bubble just before it
reaches the surface of the water?
P1V1P2V2
V2
6.2106m3
105. An 18-N bowling ball floats with about half of the ball submerged.
a. What is the diameter of the bowling ball?
FgVwaterg
g,
where Vball
4
3
r3
4
3
d
2
3
6
d3
Then Fg
1
2
g,
d3
6
Vball
2
(1.01105Pa (1.00103kgm3)(9.80 ms2)(5.0 m))(4.2106m3)
1.01105Pa
(Patmosphere watergh)V1
Patmosphere
P1V1
P2
T 293 K1133
T 170 K
2
4
2
4
■Figure 13-30
304 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 305
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
so that d
3
3
0.19 m
b. What would be the approximate apparent weight of a 36-N bowling ball?
Half the ball sank when the weight was 18 N. The apparent weight of
the 36-N ball should be near zero.
Level 2
106. An aluminum bar is floating in a bowl of mercury. When the temperature is
increased, does the aluminum float higher or sink deeper into the mercury?
The volume coefficient of expansion of mercury is greater than the
volume coefficient of expansion of aluminum. Therefore, as they are
heated, the aluminum becomes denser relative to the mercury and would
sink deeper into the mercury.
107. There is 100.0 mL of water in an 800.0-mL soft-glass beaker at 15.0°C. How
much will the water level have dropped or risen when the bottle and water are
heated to 50.0°C?
The water expands:
VVT
(210106°C1)(100.0 mL)(35.0°C)
0.735 mL
The bottle expands:
VVT
(27106°C1)(800.0 mL)(35.0°C)
0.756 mL
The water level will go down slightly, but not enough to notice.
108. Auto Maintenance A hydraulic jack used to lift cars for repairs is called a
three-ton jack. The large piston is 22 mm in diameter, and the small one is
6.3 mm in diameter. Assume that a force of 3 tons is 3.0104N.
a. What force must be exerted on the small piston to lift a 3-ton weight?
F2
F1
(3.0104N)
2
2.5103N
6.3 mm
22 mm
d22
d12
F1r22
r12
F1A2
A1
(12)(18 N)
(1.00103kgm3)(9.80 ms2)
12Fg
g
Chapter 13 continued

b. Most jacks use a lever to reduce the
force needed on the small piston. If
the resistance arm is 3.0 cm, how long
must the effort arm of an ideal lever be
to reduce the force to 100.0 N?
FrLrFeLe
Le
75 cm
109. Ballooning A hot-air balloon contains a
fixed volume of gas. When the gas is heat-
ed, it expands and pushes some gas out at
the lower, open end. As a result, the mass
of the gas in the balloon is reduced. Why
would the air in a balloon have to be hot-
ter to lift the same number of people above
Vail, Colorado, which has an altitude of
2400 m, than above the tidewater flats of
Virginia, which have an altitude of 6 m?
Atmospheric pressure is lower at high-
er altitudes. Therefore, the mass of the
volume of fluid displaced by a balloon
of the same volume is less at higher
altitudes. To obtain the same buoyant
force at higher altitudes, a balloon
must expel more gas, requiring higher
temperatures.
110. The Living World Some plants and ani-
mals are able to live in conditions of
extreme pressure.
a. What is the pressure exerted by the
water on the skin of a fish or worm
that lives near the bottom of the
Puerto Rico Trench, 8600 m below the
surface of the Atlantic Ocean? Use
1030 kg/m3for the density of seawater.
The pressure is
Pgh
(1030 kg/m3)(9.80 m/s2)(8600 m)
8.7107Pa
b. What would be the density of air at
that pressure, relative to its density
above the surface of the ocean?
The pressure in the water is
(8.7107Pa)/(1.01105Pa)
860 times greater than standard air
pressure. Therefore, the density of air
would be 860 times greater than the
density of the air on the surface of
the ocean.
Thinking Critically
page 372
111. Apply Concepts You are washing dishes
in the sink. A serving bowl has been float-
ing in the sink. You fill the bowl with water
from the sink, and it sinks to the bottom.
Did the water level in the sink go up or
down when the bowl was submerged?
When it was floating, the bowl dis-
placed a volume of water that weighed
as much as it did. When it sank, it dis-
placed a volume of water that weighed
less than the bowl, because the buoy-
ancy force is the weight of the water
displaced. In the second case, the
bowl displaces less water and the level
in the sink goes down.
112. Apply Concepts Persons confined to bed
are less likely to develop bedsores if they
use a waterbed rather than an ordinary
mattress. Explain.
The surface of the waterbed conforms
more than the surface of a mattress to
the contours of your body. One “sinks”
more easily into a waterbed. Because
H2Omattress, the buoyant force from
a waterbed is less.
113. Analyze and Conclude One method of
measuring the percentage of body fat is
based on the fact that fatty tissue is less
dense than muscle tissue. How can a per-
son’s average density be assessed with a
scale and a swimming pool? What mea-
surements does a physician need to record
to find a person’s average percentage of
body fat?
The physician weighs the person nor-
mally and then weighs the person
totally submerged. Weight has to be
(2.5103N)(3.0 cm)
100.0 N
FrLr
Fe
306 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 307
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
added to the weighing device because the density of a human is normal-
ly less than the density of water. The volume of water displaced by the
person also should be measured.The average density of the person can
be calculated from the balance of forces that hold the person in equilibri-
um underwater.
114. Analyze and Conclude A downward force of 700 N is required to fully submerge
a plastic foam sphere, as shown in Figure 13-31. The density of the foam is
95 kg/m3.
a. What percentage of the sphere would be
submerged if the sphere were released to
float freely?
The density of the foam relative to the
water is 0.095, so
9.5 percent of the floating sphere would be
submerged.
b. What is the weight of the sphere in air?
The weight of water displaced by 9.5 percent
of the sphere’s volume balances the entire weight
of the sphere, Fg. An additional 700 N is needed to submerge the
remaining 90.5 percent of the sphere’s volume. Thus,
7
00
.9
0
0N
5
Fg7101N
c. What is the volume of the sphere?
Fbuoyant FgFdown
waterVg foamVg Fdown
V
8102m3
115. Apply Concepts Tropical fish for aquariums are often transported home from
pet shops in transparent plastic bags filled mostly with water. If you placed a
fish in its unopened transport bag in a home aquarium, which of the cases in
Figure 13-32 best represents what would happen? Explain your reasoning.
■Figure 13-32
Bag
water
level
Bag
water
level Bag
water
level
Aquarium
water level
Aquarium
water level
Aquarium
water level
700 N
(1.00103kgm395 kgm3)(9.80 ms2)
Fdown
(water down)g
Fg
0.095
95 kgm3
1.00103kgm3
700 N
Chapter 13 continued
■Figure 13-31

The density of the water in the bag, the
fish, and the plastic are all near the
density of the water in the aquarium.
Therefore, the bag should float with
the water level in the bag at the same
height as the water level in the
aquarium.
Writing in Physics
page 372
116. Some solid materials expand when they
are cooled. Water between 4° and 0°C is
the most common example, but rubber
bands also expand in length when cooled.
Research what causes this expansion.
Rubber bands are made of long rubber
molecules called polymers that act like
chains with many long links. The prop-
erties of rubber come from the ability
of the chain links to twist and turn.
When the rubber is colder, the polymer
links are stretched out in a straight
line, like the links in a steel chain that
you hold at one end and let hang
freely. Because the links are ordered
that way, the polymers have relatively
little disorder, or entropy. Adding heat
to the polymers increases their ther-
mal motion. The links begin to shake
about and their disorder increases. If
you shake a chain like this, you will
see that its average length becomes
less than if the chain were hanging
motionless.
117. Research Joseph Louis Gay-Lussac and his
contributions to the gas laws. How did
Gay-Lussac’s work contribute to the discov-
ery of the formula for water?
Gay-Lussac was a French scientist
who also was interested in high-
altitude balloon ascents. He discov-
ered that when gases are at the same
temperature and pressure, their vol-
umes react in ratios of small, whole
numbers. Gay-Lussac’s work con-
tributed to the discovery of water’s
formula by showing that two volumes
of hydrogen gas react with one volume
of oxygen gas. Avogadro built on
Gay-Lussac’s work to develop the
relationship between moles of a gas
and volume.
Cumulative Review
page 372
118. Two blocks are connected by a string over
a frictionless, massless pulley such
that one is resting on an inclined plane
and the other is hanging over the top edge
of the plane, as shown in Figure 13-33.
The hanging block has a mass of 3.0 kg
and the block on the plane has a mass of
2.0 kg. The coefficient of kinetic friction
between the block and the inclined plane
is 0.19. Answer the following questions
assuming the blocks are released from rest.
(Chapter 5)
a. What is the acceleration of the blocks?
For the 2-kg block,
TkFNmg sin ma
where FNmg cos is the normal
force.
Thus,
Tkmg cos mg sin ma
T(mg)(k cos sin ) ma
For the 3-kg block,
Mg TMa
or, TMg Ma
Substitute this for Tin the 2-kg
block equation.
Mg Ma (mg)(k cos sin )
ma
2.0 kg
3.0 kg
45°
■Figure 13-33
308 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued
Physics: Principles and Problems Solutions Manual 309
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Solve for acceleration.
a
2.6 m/s2
b. What is the tension in the string connecting the blocks?
To find T, use the equation for the 3-kg block.
TMg Ma
M(ga)
(3.0 kg)(9.80 m/s22.6 m/s2)
22 N
119. A compact car with a mass of 875 kg, moving south at 15 m/s, is struck by a
full-sized car with a mass of 1584 kg, moving east at 12 m/s. The two cars stick
together, and momentum is conserved. (Chapter 9)
a. Sketch the situation, assigning coordinate axes and identifying “before”
and “after.”
b. Find the direction and speed of the wreck immediately after the collision,
remembering that momentum is a vector quantity.
pA1 mAvA(875 kg)(15 m/s)
1.31104kgm/s south
pB1 mBvB(1584 kg)(12 m/s)
1.90104kgm/s east
p2pA12
pB12
(1.31
104kg
m/s
)2(1
.901
04kg
m/s)
2
2.3104kgm/s
tan pB1
pA1
Before
(State 1)
After
(State 2)
A
B
v2 ?
p2 ?
mA 875 kg
vA 15 m/s
mB 1584 kg
vB 12 m/s
m2 2459 kg
y-axis
x
-axis
(3.0 kg)(9.80 ms2)(2.0 kg)(9.80 ms2)((0.19)(cos 45°)sin 45°)
2.0 kg 3.0 kg
Mg (mg)(kcos sin )
mM
Chapter 13 continued

tan1
tan1
55°east of south
v2
9.4 m/s
c. The wreck skids along the ground and
comes to a stop. The coefficient of
kinetic friction while the wreck is skid-
ding is 0.55. Assume that the accelera-
tion is constant. How far does the
wreck skid after impact?
To find the distance, use the equa-
tion of motion:
v2vi22a(ddi)
where the final velocity is zero and
di0. Solve for d:
d
To find acceleration, notice that the
force that slows the cars equals the
frictional force.
(mamb)ak(mamb)g
akg
The distance is then
d
8.2 m
120. A 188-W motor will lift a load at the rate
(speed) of 6.50 cm/s. How great a load can
the motor lift at this rate? (Chapter 10)
v6.50 cm/s 0.0650 m/s
P
W
t
F
t
d
F
d
t
Fv
PFgv
Fg
P
v
0.0
1
6
8
5
8
0W
m/s
2.89103N
Challenge Problem
page 363
You need to make a 1.00-m-long bar that
expands with temperature in the same way as a
1.00-m-long bar of copper would. As shown in
the figure at the right, your bar must be made
from a bar of iron and a bar of aluminum
attached end to end. How long should each of
them be?
Lcopper Laluminum Liron
and
copperLcopperT
(aluminumLaluminum ironLiron)T
Substituting Laluminum
Lcopper Liron, this gives
Liron
0.69 m
Laluminum Lcopper Liron
1.00 m 0.69 m
0.31 m
(16106°C125106°C1)(1.00 m)
12106°C125106°C1
(copper aluminum)Lcopper
iron aluminum
(9.4 ms)2
(2)(0.55)(9.80 ms2)
v02
2kg
vi2
2a
2.3104kgm/s
2459 kg
p2
m2
1.90104kgm/s
1.31104kgm/s
pB1
pA1
310 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 311
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
14 Vibrations and Waves
CHAPTER
Practice Problems
14.1 Periodic Motion
pages 375–380
page 378
1. How much force is necessary to stretch a
spring 0.25 m when the spring constant
is 95 N/m?
Fkx
(95 N/m)(0.25 m)
24 N
2. A spring has a spring constant of 56 N/m.
How far will it stretch when a block
weighing 18 N is hung from its end?
Fkx
x
F
k
56
18
NN
/m
0.32 m
3. What is the spring constant of a spring that
stretches 12 cm when an object weighing
24 N is hung from it?
Fkx
k
02
.1
4
2N
m
2.0102N/m
4. A spring with a spring constant of 144 N/m
is compressed by a distance of 16.5 cm.
How much elastic potential energy is stored
in the spring?
PEsp
1
2
kx2
1
2
(144 N/m)(0.165 m)2 1.96 J
5. A spring has a spring constant of 256 N/m.
How far must it be stretched to give it an
elastic potential energy of 48 J?
PEsp
1
2
kx2
x
2P
k
Esp
0.61 m
page 379
6. What is the period on Earth of a pendulum
with a length of 1.0 m?
T 2
g
l
2
9.8
10
.0m
m
/s2
2.0 s
7. How long must a pendulum be on the
Moon, where g1.6 m/s2, to have a
period of 2.0 s?
T 2
g
l
l g
2
T
2 (1.6 m/s2)
22
.0
s
2 0.16 m
8. On a planet with an unknown value of g,
the period of a 0.75-m-long pendulum
is 1.8 s. What is gfor this planet?
T 2
g
l
g l
2
T
2 (0.75 m)
12
.8
s
2 9.1 m/s2
Section Review
14.1 Periodic Motion
pages 375–380
page 380
9. Hooke’s Law Two springs look alike but
have different spring constants. How could
you determine which one has the greater
spring constant?
Hang the same object from both
springs. The one that stretches less
has the greater spring constant.
10. Hooke’s Law Objects of various weights
are hung from a rubber band that is sus-
pended from a hook. The weights of the
objects are plotted on a graph against the
(2)(48 J)
256 N/m
F
x

stretch of the rubber band. How can you
tell from the graph whether or not the
rubber band obeys Hooke’s law?
If the graph is a straight line, the rubber
band obeys Hooke’s law. If the graph is
curved, it does not.
11. Pendulum How must the length of a pen-
dulum be changed to double its period?
How must the length be changed to halve
the period?
PEsp kx2,so
P
P
E
E1
2
x
x1
2
2
2
4.0
The energy of the first spring is
4.0 times greater than the energy of
the second spring.
12. Energy of a Spring What is the difference
between the energy stored in a spring that is
stretched 0.40 m and the energy stored in
the same spring when it is stretched 0.20 m?
T2
g
l
, so
T
T2
1
l
l2
1
To double the period:
T
T2
1
l
l2
1
2, so
l
l2
1
4
The length must be quadrupled.
To halve the period:
T
T2
1
l
l2
1
, so
l
l2
1
The length is reduced to one-fourth its
original length.
13. Resonance If a car’s wheel is out of bal-
ance, the car will shake strongly at a specific
speed, but not when it is moving faster or
slower than that speed. Explain.
At that speed, the tire’s rotation
frequency matches the resonant
frequency of the car.
14. Critical Thinking How is uniform circular
motion similar to simple harmonic
motion? How are they different?
Both are periodic motions. In uniform
circular motion, the accelerating force
is not proportional to the displacement.
Also, simple harmonic motion is one-
dimensional and uniform circular
motion is two-dimensional.
Practice Problems
14.2 Wave Properties
pages 381–386
page 386
15. A sound wave produced by a clock chime is
heard 515 m away 1.50 s later.
a. What is the speed of sound of the
clock’s chime in air?
v
d
t
5
11
.5
5
0m
s
343 m/s
b. The sound wave has a frequency of
436 Hz. What is the period of the wave?
T
1
f
2.29103s
c. What is the wave’s wavelength?
v
f
0.787 m
16. A hiker shouts toward a vertical cliff 465 m
away. The echo is heard 2.75 s later.
a. What is the speed of sound of the
hiker’s voice in air?
v
d
t
338 m/s
(2)(465 m)
2.75 s
343 m/s
436 Hz
1
436 Hz
1
4
1
2
(0.40 m)2
(0.20 m)2
1
2
312 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 313
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. The wavelength of the sound is 0.750 m.
What is its frequency?
v f, so f
v
3
03
.7
8
50
mm
/s
451 Hz
c. What is the period of the wave?
T
1
f
451
1Hz
2.22103s
17. If you want to increase the wavelength of
waves in a rope, should you shake it at a
higher or lower frequency?
at a lower frequency, because wave-
length varies inversely with frequency
18. What is the speed of a periodic wave distur-
bance that has a frequency of 3.50 Hz and a
wavelength of 0.700 m?
v f (0.700 m)(3.50 Hz) 2.45 m/s
19. The speed of a transverse wave in a string is
15.0 m/s. If a source produces a disturbance
that has a frequency of 6.00 Hz, what is its
wavelength?
v f, so
v
f
1
6
5
.0
.0
0m
H/
z
s
2.50 m
20. Five pulses are generated every 0.100 s in a
tank of water. What is the speed of propaga-
tion of the wave if the wavelength of the
surface wave is 1.20 cm?
5
0p
.1
u
0
l0
se
s
s
0.0200 s/pulse, so
T0.0200 s
vT,so
v
T
0
1.
.0
22
00c
0m
s
60.0 cm/s 0.600 m/s
21. A periodic longitudinal wave that has a
frequency of 20.0 Hz travels along a coil
spring. If the distance between successive
compressions is 0.600 m, what is the speed
of the wave?
v f (0.600 m)(20.0 Hz) 12.0 m/s
Section Review
14.2 Wave Properties
pages 381–386
page 386
22. Speed in Different Media If you pull on
one end of a coiled-spring toy, does the
pulse reach the other end instantaneously?
What happens if you pull on a rope? What
happens if you hit the end of a metal rod?
Compare and contrast the pulses traveling
through these three materials.
It takes time for the pulse to reach the
other end in each case. It travels faster
on the rope than on the spring, and
fastest in the metal rod.
23. Wave Characteristics You are creating
transverse waves in a rope by shaking your
hand from side to side. Without changing
the distance that your hand moves, you
begin to shake it faster and faster. What
happens to the amplitude, wavelength,
frequency, period, and velocity of the wave?
The amplitude and velocity remain
unchanged, but the frequency increases
while the period and the wavelength
decrease.
24. Waves Moving Energy Suppose that
you and your lab partner are asked to
demonstrate that a transverse wave trans-
ports energy without transferring matter.
How could you do it?
Tie a piece of yarn somewhere near the
middle of a rope. With your partner
holding one end of the rope, shake the
other end up and down to create a
transverse wave. Note that while the
wave moves down the rope, the yarn
moves up and down but stays in the
same place on the rope.
25. Longitudinal Waves Describe longitudinal
waves. What types of media transmit
longitudinal waves?
In longitudinal waves, the particles of
the medium vibrate in a direction
parallel to the motion of the wave.
Chapter 14 continued
Nearly all media—solids, liquids, and
gases—transmit longitudinal waves.
26. Critical Thinking If a raindrop falls into a
pool, it creates waves with small amplitudes.
If a swimmer jumps into a pool, waves with
large amplitudes are produced. Why doesn’t
the heavy rain in a thunderstorm produce
large waves?
The energy of the swimmer is trans-
ferred to the wave in a small space
over a short time, whereas the energy
of the raindrops is spread out in
area and time.
Section Review
14.3 Wave Behavior
pages 387–391
page 391
27. Waves at Boundaries Which of the
following wave characteristics remain
unchanged when a wave crosses a boundary
into a different medium: frequency, ampli-
tude, wavelength, velocity, and/or direction?
Frequency remains unchanged. In
general, amplitude, wavelength, and
velocity will change when a wave enters
a new medium. Direction may or may
not change, depending on the original
direction of the wave.
28. Refraction of Waves Notice in
Figure 14-17a how the wave changes
direction as it passes from one medium to
another. Can two-dimensional waves cross
a boundary between two media without
changing direction? Explain.
Yes, if they strike the boundary while
traveling normal to its surface, or if they
have the same speed in both media.
29. Standing Waves In a standing wave on a
string fixed at both ends, how is the number
of nodes related to the number of antinodes?
The number of nodes is always one
greater than the number of antinodes.
30. Critical Thinking As another way to
understand wave reflection, cover the right-
hand side of each drawing in Figure 14-13a
with a piece of paper. The edge of the paper
should be at point N, the node. Now, con-
centrate on the resultant wave, shown in
darker blue. Note that it acts like a wave
reflected from a boundary. Is the boundary a
rigid wall, or is it open-ended? Repeat this
exercise for Figure 14-13b.
Figure 14-14a behaves like a rigid wall
because the reflected wave is inverted;
14-14b behaves like an open end
because the boundary is an antinode
and the reflected wave is not inverted.
Chapter Assessment
Concept Mapping
page 396
31. Complete the concept map using the fol-
lowing terms and symbols: amplitude,
frequency, v, ,T.
Mastering Concepts
page 396
32. What is periodic motion? Give three exam-
ples of periodic motion. (14.1)
Periodic motion is motion that repeats
in a regular cycle. Examples include
oscillation of a spring, swing of a simple
pendulum, and uniform circular motion.
33. What is the difference between frequency
and period? How are they related? (14.1)
Frequency is the number of cycles or
repetitions per second, and period is the
time required for one cycle. Frequency is
the inverse of the period.
Chapter 14 continued
Waves
speed amplitude period frequency wavelength
vATf
314 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 315
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
34. What is simple harmonic motion? Give an
example of simple harmonic motion.
(14.1)
Simple harmonic motion is periodic
motion that results when the restoring
force on an object is directly propor-
tional to its displacement. A block
bouncing on the end of a spring is one
example.
35. If a spring obeys Hooke’s law, how does it
behave? (14.1)
The spring stretches a distance that is
directly proportional to the force
applied to it.
36. How can the spring constant of a spring be
determined from a graph of force versus
displacement? (14.1)
The spring constant is the slope of the
graph of Fversus x.
37. How can the potential energy in a spring be
determined from the graph of force versus
displacement? (14.1)
The potential energy is the area under
the curve of the graph of Fversus x.
38. Does the period of a pendulum depend on
the mass of the bob? The length of the
string? Upon what else does the period
depend? (14.1)
no; yes; the acceleration of gravity, g
39. What conditions are necessary for
resonance to occur? (14.1)
Resonance will occur when a force is
applied to an oscillating system at the
same frequency as the natural frequency
of the system.
40. How many general methods of energy
transfer are there? Give two examples
of each. (14.2)
Two. Energy is transferred by particle
transfer and by waves.There are many
examples that can be given of each: a
baseball and a bullet for particle transfer;
sound waves and light waves.
41. What is the primary difference between a
mechanical wave and an electromagnetic
wave? (14.2)
The primary difference is that mechani-
cal waves require a medium to travel
through and electromagnetic waves do
not need a medium.
42. What are the differences among transverse,
longitudinal, and surface waves? (14.2)
A transverse wave causes the particles
of the medium to vibrate in a direction
that is perpendicular to the direction in
which the wave is moving. A longitudi-
nal wave causes the particles of the
medium to vibrate in a direction parallel
with the direction of the wave. Surface
waves have characteristics of both.
43. Waves are sent along a spring of fixed
length. (14.2)
a. Can the speed of the waves in the spring
be changed? Explain.
Speed of the waves depends only
on the medium and cannot be
changed.
b. Can the frequency of a wave in the
spring be changed? Explain.
Frequency can be changed by
changing the frequency at which the
waves are generated.
44. What is the wavelength of a wave? (14.2)
Wavelength is the distance between two
adjacent points on a wave that are in
phase.
45. Suppose you send a pulse along a rope.
How does the position of a point on the
rope before the pulse arrives compare to the
point’s position after the pulse has passed?
(14.2)
Once the pulse has passed, the point is
exactly as it was prior to the advent of
the pulse.
Chapter 14 continued

46. What is the difference between a wave pulse
and a periodic wave? (14.2)
A pulse is a single disturbance in a
medium, whereas a periodic wave con-
sists of several adjacent disturbances.
47. Describe the difference between wave
frequency and wave velocity. (14.2)
Frequency is the number of vibrations
per second of a part of the medium.
Velocity describes the motion of the
wave through the medium.
48. Suppose you produce a transverse wave by
shaking one end of a spring from side to
side. How does the frequency of your hand
compare with the frequency of the wave?
(14.2)
They are the same.
49. When are points on a wave in phase with
each other? When are they out of phase?
Give an example of each. (14.2)
Points are in phase when they have
the same displacement and the same
velocity. Otherwise, the points are out
of phase. Two crests are in phase with
each other. A crest and a trough are out
of phase with each other.
50. What is the amplitude of a wave and what
does it represent? (14.2)
Amplitude is the maximum displace-
ment of a wave from the rest or equilib-
rium position. The amplitude of the
wave represents the amount of energy
transferred.
51. Describe the relationship between the
amplitude of a wave and the energy it
carries. (14.2)
The energy carried by a wave is propor-
tional to the square of its amplitude.
52. When a wave reaches the boundary of a
new medium, what happens to it? (14.3)
Part of the wave can be reflected and
part of the wave can be transmitted into
the new medium.
53. When a wave crosses a boundary between
a thin and a thick rope, as shown in
Figure 14-18, its wavelength and speed
change, but its frequency does not. Explain
why the frequency is constant. (14.3)
■Figure 14-18
The frequency depends only on the rate
at which the thin rope is shaken and the
thin rope causes the vibrations in the
thick rope.
54. How does a spring pulse reflected from a
rigid wall differ from the incident pulse?
(14.3)
The reflected pulse will be inverted.
55. Describe interference. Is interference a prop-
erty of only some types of waves or all types
of waves? (14.3)
The superposition of two or more
waves is interference. The superposi-
tion of two waves with equal but oppo-
site amplitudes results in destructive
interference. The superposition of two
waves with amplitudes in the same
direction results in constructive inter-
ference; all waves; it is a prime test for
wave nature.
56. What happens to a spring at the nodes of a
standing wave? (14.3)
Nothing, the spring does not move.
57. Violins A metal plate is held fixed in the
center and sprinkled with sugar. With a
violin bow, the plate is stroked along one
edge and made to vibrate. The sugar begins
to collect in certain areas and move away
from others. Describe these regions in terms
of standing waves. (14.3)
Bare areas are antinodal regions where
there is maximum vibration. Sugar-
covered areas are nodal regions where
there is no vibration.
316 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 317
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
58. If a string is vibrating in four parts, there are
points where it can be touched without
disturbing its motion. Explain. How many
of these points exist? (14.3)
A standing wave exists and the string
can be touched at any of its five nodal
points.
59. Wave fronts pass at an angle from one
medium into a second medium, where they
travel with a different speed. Describe two
changes in the wave fronts. What does not
change? (14.3)
The wavelength and direction of the
wave fronts change. The frequency
does not change.
Applying Concepts
page 397
60. A ball bounces up and down on the end of
a spring. Describe the energy changes that
take place during one complete cycle. Does
the total mechanical energy change?
At the bottom of the motion, the elastic
potential energy is at a maximum, while
gravitational potential energy is at a
minimum and the kinetic energy is zero.
At the equilibrium position, the KE is at
a maximum and the elastic potential
energy is zero. At the top of the bounce,
the KE is zero, the gravitational potential
energy is at a maximum, and the elastic
potential energy is at a maximum.The
total mechanical energy is conserved.
61. Can a pendulum clock be used in the orbit-
ing International Space Station? Explain.
No, the space station is in free-fall, and
therefore, the apparent value of gis
zero.The pendulum will not swing.
62. Suppose you hold a 1-m metal bar in your
hand and hit its end with a hammer, first,
in a direction parallel to its length, and
second, in a direction at right angles to its
length. Describe the waves produced in the
two cases.
In the first case, longitudinal waves; in
the second case, transverse waves.
63. Suppose you repeatedly dip your finger into
a sink full of water to make circular waves.
What happens to the wavelength as you
move your finger faster?
The frequency of the waves will
increase; the speed will remain the
same; the wavelength will decrease.
64. What happens to the period of a wave as
the frequency increases?
As the frequency increases, the period
decreases.
65. What happens to the wavelength of a wave
as the frequency increases?
As the frequency increases, the wave-
length decreases.
66. Suppose you make a single pulse on a
stretched spring. How much energy is
required to make a pulse with twice the
amplitude?
approximately two squared, or four
times the energy
67. You can make water slosh back and forth in
a shallow pan only if you shake the pan
with the correct frequency. Explain.
The period of the vibration must equal
the time for the wave to go back and
forth across the pan to create construc-
tive interference.
Chapter 14 continued
68. In each of the four waves in Figure 14-19,
the pulse on the left is the original pulse
moving toward the right. The center pulse is
a reflected pulse; the pulse on the right is a
transmitted pulse. Describe the rigidity of
the boundaries at A, B, C, and D.
■Figure 14-19
Boundary A is more rigid; boundary B
is less rigid; boundary C is less rigid;
boundary D is more rigid.
Mastering Problems
14.1 Periodic Motion
pages 397–398
Level 1
69. A spring stretches by 0.12 m when some
apples weighing 3.2 N are suspended from
it, as shown in Figure 14-20. What is the
spring constant of the spring?
■Figure 14-20
Fkx,
so k 27 N/m
70. Car Shocks Each of the coil springs of a
car has a spring constant of 25,000 N/m.
How much is each spring compressed if it
supports one-fourth of the car’s 12,000-N
weight?
Fkx,
so x
0.12 m
71. How much potential energy is stored in a
spring with a spring constant of 27 N/m if
it is stretched by 16 cm?
PEsp kx2
(27 N/m)(0.16 m)2 0.35 J
Level 2
72. Rocket Launcher A toy rocket-launcher
contains a spring with a spring constant of
35 N/m. How far must the spring be
compressed to store 1.5 J of energy?
PEsp kx2,
so x
0.29 m
Level 3
73. Force-versus-length data for a spring are
plotted on the graph in Figure 14-21.
■Figure 14-21
0.20
0.0 0.600.40
4.0
12.0
8.0
Force (N)
Length (m)
(2)(1.5 J)
35 N/m
2PEsp
k
1
2
1
2
1
2
1
4
(12,000 N)
25,000 N/m
F
k
3.2 N
0.12 m
F
x
3.2 N
A
B
C
D
318 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 319
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. What is the spring constant of the
spring?
k slope
F
x
1
02
.6
.0m
N
0
4
.2
.0m
N
20 N/m
b. What is the energy stored in the spring
when it is stretched to a length of
50.0 cm?
PEsp area bh
(0.500 m)(10.0 N) 2.50 J
74. How long must a pendulum be to have a
period of 2.3 s on the Moon, where
g1.6 m/s2?
T 2
, so l
0.21 m
14.2 Wave Properties
page 398
Level 1
75. Building Motion The Sears Tower in
Chicago, shown in Figure 14-22, sways
back and forth in the wind with a frequency
of about 0.12 Hz. What is its period of
vibration?
■Figure 14-22
f
T
1
T
1
f
8.3 s
76. Ocean Waves An ocean wave has a length
of 12.0 m. A wave passes a fixed location
every 3.0 s. What is the speed of the wave?
v f
(12.0 m)
3.0
1s
4.0 m/s
77. Water waves in a shallow dish are 6.0-cm
long. At one point, the water moves up and
down at a rate of 4.8 oscillations/s.
a. What is the speed of the water waves?
v f
(0.060 m)(4.8 Hz) 0.29 m/s
b. What is the period of the water waves?
T
1
f
0.21 s
78. Water waves in a lake travel 3.4 m in 1.8 s.
The period of oscillation is 1.1 s.
a. What is the speed of the water waves?
v
3
1
..
4
8m
s
1.9 m/s
b. What is their wavelength?
v
f
vT
(1.9 m/s)(1.1 s)
2.1 m
Level 2
79. Sonar A sonar signal of frequency
1.00106 Hz has a wavelength of 1.50 mm
in water.
a. What is the speed of the signal in water?
v f
(1.50103m)(1.00106Hz)
1.50103m/s
b. What is its period in water?
T
1
f
1.00
1
106Hz
1.00106s
d
t
1
4.8 Hz
1
T
1
0.12 Hz
(2.3 s)2(1.6 m/s2)
42
T2g
42
l
g
1
2
1
2
Chapter 14 continued

c. What is its period in air?
1.00106s
The period and frequency remain
unchanged.
80. A sound wave of wavelength 0.60 m and a
velocity of 330 m/s is produced for 0.50 s.
a. What is the frequency of the wave?
v f
f
v
3
0
3
.6
00
m
m
/s
550 Hz
b. How many complete waves are emitted
in this time interval?
ft (550 Hz)(0.50 s)
280 complete waves
c. After 0.50 s, how far is the front of the
wave from the source of the sound?
d vt
(330 m/s)(0.50 s)
1.6102m
81. The speed of sound in water is 1498 m/s. A
sonar signal is sent straight down from a
ship at a point just below the water surface,
and 1.80 s later, the reflected signal is
detected. How deep is the water?
The time for the wave to travel down
and back up is 1.80 s.The time one way
is half 1.80 s or 0.900 s.
d vt
(1498 m/s)(0.900 s)
1350 m
Level 3
82. Pepe and Alfredo are resting on an offshore
raft after a swim. They estimate that 3.0 m
separates a trough and an adjacent crest of
each surface wave on the lake. They count
12 crests that pass by the raft in 20.0 s.
Calculate how fast the waves are moving.
(2)(3.0 m) 6.0 m
f
12
20
w
.a
0v
s
es
0.60 Hz
v f
(6.0 m)(0.60 Hz)
3.6 m/s
83. Earthquakes The velocity of the trans-
verse waves produced by an earthquake is
8.9 km/s, and that of the longitudinal
waves is 5.1 km/s. A seismograph records
the arrival of the transverse waves 68 s
before the arrival of the longitudinal
waves. How far away is the earthquake?
dvt. We do not know t, only the
difference in time, t.The transverse
distance, dTvTt, is the same as the
longitudinal distance, dL vL(tt).
Use vTt vL(tt), and solve for t:
t
t 91 s
Then putting tback into
dT vTt (8.9 km/s)(91 s)
8.1102km
14.3 Wave Behavior
pages 398–399
Level 1
84. Sketch the result for each of the three cases
shown in Figure 14-23, when the centers
of the two approaching wave pulses lie on
the dashed line so that the pulses exactly
overlap.
■Figure 14-23
1
2
3
(5.1 km/s)(68 s)
8.9 km/s 5.1 km/s
vLt
vTvL
320 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued
Physics: Principles and Problems Solutions Manual 321
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1. The amplitude is doubled.
2. The amplitudes cancel each other.
3. If the amplitude of the first pulse is
one-half of the second, the resultant
pulse is one-half the amplitude of the
second.
85. If you slosh the water in a bathtub at the
correct frequency, the water rises first at one
end and then at the other. Suppose you can
make a standing wave in a 150-cm-long tub
with a frequency of 0.30 Hz. What is the
velocity of the water wave?
2(1.5 m) 3.0 m
v f
(3.0 m)(0.30 Hz)
0.90 m/s
Level 2
86. Guitars The wave speed in a guitar string is
265 m/s. The length of the string is 63 cm. You
pluck the center of the string by pulling it up
and letting go. Pulses move in both directions
and are reflected off the ends of the string.
a. How long does it take for the pulse to
move to the string end and return to the
center?
d
(2)(6
2
3cm)
63 cm
so t
d
v
2.4103s
b. When the pulses return, is the string
above or below its resting location?
Pulses are inverted when reflected
from a more dense medium, so
returning pulse is down (below).
c. If you plucked the string 15 cm from
one end of the string, where would the
two pulses meet?
15 cm from the other end, where the
distances traveled are the same.
87. Sketch the result for each of the four cases
shown in Figure 14-24, when the centers of
each of the two wave pulses lie on the dashed
line so that the pulses exactly overlap.
■Figure 14-24
Mixed Review
page 399–400
Level 1
88. What is the period of a pendulum with a
length of 1.4 m?
T2
g
l
2
2.4 s
89. The frequency of yellow light is 5.11014 Hz.
Find the wavelength of yellow light. The
speed of light is 3.00108 m/s.
1.4 m
9.80 m/s2
1
2
3
4
0.63 m
265 m/s
Chapter 14 continued
2
3
4
1

c
f
3
5
.0
.1
0
1
1
0
0
1
8
4m
H/
z
s
5.9107m
90. Radio Wave AM-radio signals are broad-
cast at frequencies between 550 kHz
(kilohertz) and 1600 kHz and travel
3.0108 m/s.
a. What is the range of wavelengths for
these signals?
v f
1
f
v
1
550 m
2
f
v
2
190 m
Range is 190 m to 550 m.
b. FM frequencies range between 88 MHz
(megahertz) and 108 MHz and travel
at the same speed. What is the range of
FM wavelengths?
v
f
3.4 m
v
f
2.8 m
Range is 2.8 m to 3.4 m.
91. You are floating just offshore at the beach.
Even though the waves are steadily
moving in toward the beach, you don’t
move any closer to the beach.
a. What type of wave are you experiencing
as you float in the water?
transverse waves
b. Explain why the energy in the wave
does not move you closer to shore.
The displacement is perpendicular
to the direction of the wave—in
this case, up and down.
c. In the course of 15 s you count ten
waves that pass you. What is the period
of the waves?
T 1.5 s
d. What is the frequency of the waves?
f
T
1
1.5
1s
0.67 Hz
e. You estimate that the wave crests are 3 m
apart. What is the velocity of the waves?
v f (3 m)(0.67 Hz) 2 m/s
f. After returning to the beach, you learn
that the waves are moving at 1.8 m/s.
What is the actual wavelength of the
waves?
v
f
0
1.
.6
87
m
H
/s
z
2.7 m
Level 2
92. Bungee Jumper A high-altitude bungee
jumper jumps from a hot-air balloon using
a 540-m-bungee cord. When the jump is
complete and the jumper is just suspended
from the cord, it is stretched 1710 m. What
is the spring constant of the bungee cord if
the jumper has a mass of 68 kg?
k
F
x
m
xg
0.57 N/m
93. The time needed for a water wave to change
from the equilibrium level to the crest is
0.18 s.
a. What fraction of a wavelength is this?
wavelength
b. What is the period of the wave?
T (4)(0.18 s) 0.72 s
c. What is the frequency of the wave?
f
T
1
1.4 Hz
94. When a 225-g mass is hung from a spring,
the spring stretches 9.4 cm. The spring and
mass then are pulled 8.0 cm from this new
equilibrium position and released. Find the
spring constant of the spring and the maxi-
mum speed of the mass.
1
0.72 s
1
4
(68 kg)(9.80 m/s2)
1710 m 540 m
15 s
10 waves
3.0108m/s
1.08108Hz
3.0108m/s
8.8107Hz
3.0108m/s
1.6106Hz
3.0108m/s
5.5105Hz
322 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 323
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
k
F
x
23 N/m
Maximum velocity occurs when the mass
passes through the equilibrium point,
where all the energy is kinetic energy.
Using the conservation of energy:
PEsp KEmass
1
2
kx2
1
2
mv2
v2
v
0.81 m/s
95. Amusement Ride You notice that your
favorite amusement-park ride seems bigger.
The ride consists of a carriage that is
attached to a structure so it swings like a
pendulum. You remember that the carriage
used to swing from one position to another
and back again eight times in exactly 1 min.
Now it only swings six times in 1 min. Give
your answers to the following questions to
two significant digits.
a. What was the original period of the ride?
T
1
f
7.5 s
b. What is the new period of the ride?
T
1
f
1.0101s
c. What is the new frequency?
f
T
1
0.10 Hz
d. How much longer is the arm supporting
the carriage on the larger ride?
Original:
l g
4
T
2
2
(9.80 m/s2)
14 m
New:
l g
4
T
2
2
(9.80 m/s2)
25 m
The arm on the new structure is
11 m longer.
e. If the park owners wanted to double the
period of the ride, what percentage
increase would need to be made to the
length of the pendulum?
Because of the square relationship,
there would need to be a 4 times
increase in the length of the pendu-
lum, or a 300% increase.
96. Clocks The speed at which a grandfather
clock runs is controlled by a swinging
pendulum.
a. If you find that the clock loses time
each day, what adjustment would you
need to make to the pendulum so it will
keep better time?
The clock must be made to run
faster. The period of the pendulum
can be shortened, thus increasing
the speed of the clock, by shorten-
ing the length of the pendulum.
b. If the pendulum currently is 15.0 cm,
by how much would you need to
change the length to make the period
lessen by 0.0400 s?
T 2
l
g
2
2
l
g
1
2
T
l
g
2
l
g
1
2
T
g
1
l2
g
1
l1
2
T
1
g
l2
1
g
l1
T
2
g
l2
l1
(1.0101s)2
42
(7.5 s)2
42
1
1.0101s
1
6
6
s
0
w
.0
in
s
gs
1
8
6
s
0
w
.0
in
s
gs
(23 N/m)(0.080 m)2
0.225 kg
kx2
m
kx2
m
(0.225 kg)(9.80 m/s2)
0.094 m
mg
x
Chapter 14 continued

l2
T
2
g
l1
l2
T
2
g
l1
2
0.150
m
2
0.135 m
The length would need to shorten by
l1l2 0.150 m 0.135 m 0.015 m
97. Bridge Swinging In the summer over the New River in West Virginia, several
teens swing from bridges with ropes, then drop into the river after a few swings
back and forth.
a. If Pam is using a 10.0-m length of rope, how long will it take her to reach the
peak of her swing at the other end of the bridge?
swing to peak T
g
l
3.17 s
b. If Mike has a mass that is 20 kg more than Pam, how would you expect the
period of his swing to differ from Pam’s?
There should be no difference. Tis not affected by mass.
c. At what point in the swing is KE at a maximum?
At the bottom of the swing, KE is at a maximum.
d. At what point in the swing is PE at a maximum?
At the top of the swing, PE is at a maximum.
e. At what point in the swing is KE at a minimum?
At the top of the swing, KE is at a minimum.
f. At what point in the swing is PE at a minimum?
At the bottom of the swing, PE is at a minimum.
98. You have a mechanical fish scale that is made with a spring that compresses
when weight is added to a hook attached below the scale. Unfortunately, the
calibrations have completely worn off of the scale. However, you have one
known mass of 500.0 g that displaces the spring 2.0 cm.
a. What is the spring constant for the spring?
F mg kx
k
2.4102N/m
b. If a fish displaces the spring 4.5 cm, what is the mass of the fish?
F mg kx
(0.5000 kg)(9.80 m/s2)
0.020 m
mg
x
10.0 m
9.80 m/s2
1
2
(0.0400 s)9.80 m
/s2
2
324 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued
Physics: Principles and Problems Solutions Manual 325
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
m
k
g
x
1.1 kg
99. Car Springs When you add a 45-kg load
to the trunk of a new small car, the two rear
springs compress an additional 1.0 cm.
a. What is the spring constant for each of
the springs?
F mg (45 kg)(9.80 m/s2) 440 N
force per spring 220 N
F kx, so k
F
x
k
02
.0
2
1
0
0N
m
22,000 N/m
b. How much additional potential energy
is stored in each of the car springs
after loading the trunk?
PE kx2
(22,000 N/m)(0.010 m)2
1.1 J
Level 3
100. The velocity of a wave on a string depends
on how tightly the string is stretched, and
on the mass per unit length of the string. If
FTis the tension in the string, and is the
mass/unit length, then the velocity, v, can
be determined by the following equation.
v
F
T
A piece of string 5.30-m long has a mass
of 15.0 g. What must the tension in
the string be to make the wavelength of a
125-Hz wave 120.0 cm?
v f (1.200 m)(125 Hz)
1.50102m/s
and
m
L
2.83103kg/m
Now v
F
T
,so
FT v2
(1.50102m/s)2(2.83103kg/m)
63.7 N
Thinking Critically
page 400
101. Analyze and Conclude A 20-N force is
required to stretch a spring by 0.5 m.
a. What is the spring constant?
F kx, so k
F
x
0
2
.0
5N
m
40 N/m
b. How much energy is stored in the
spring?
PEsp kx2
(40 N/m)(0.5 m)2 5 J
c. Why isn’t the work done to stretch the
spring equal to the force times the
distance, or 10 J?
The force is not constant as the
spring is stretched.The average
force, 10 N, times the distance
does give the correct work.
102. Make and Use Graphs Several weights
were suspended from a spring, and the
resulting extensions of the spring were
measured. Table 14-1 shows the
collected data.
Table 14-1
Weights on a Spring
Force, F(N) Extension, x (m)
2.5 0.12
5.0 0.26
7.5 0.35
10.0 0.50
12.5 0.60
15.0 0.71
1
2
1
2
1.50102kg
5.30 m
1
2
1
2
(2.4102N/m)(4.5102m)
9.80 m/s2
Chapter 14 continued

a. Make a graph of the force applied to the spring versus the spring length. Plot
the force on the y-axis.
b. Determine the spring constant from the graph.
The spring constant is the slope.
k slope
F
x
01
.7
5
1
.0m
N
0
2
.1
.5
2N
m
21 N/m
c. Using the graph, find the elastic potential energy stored in the spring when
it is stretched to 0.50 m.
The potential energy is the area under the graph.
PEsp area
1
2
bh
1
2
(0.50 m)(10.0 N)
2.5 J
103. Apply Concepts Gravel roads often develop regularly spaced ridges that
are perpendicular to the road, as shown in Figure 14-25. This effect, called
washboarding, occurs because most cars travel at about the same speed and
the springs that connect the wheels to the cars oscillate at about the same
frequency. If the ridges on a road are 1.5 m apart and cars travel on it at
about 5 m/s, what is the frequency of the springs’ oscillation?
■Figure 14-25
vf
f
v
5
1.5
mm
/s
3 Hz
0.0
5.0
10.0
15.0
Force (N)
20.0
Stretch (m)
0.20 0.40 0.60 0.80
326 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 327
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Writing in Physics
page 400
104. Research Christiaan Huygens’ work on
waves and the controversy between him
and Newton over the nature of light.
Compare and contrast their explanations
of such phenomena as reflection and refrac-
tion. Whose model would you choose as
the best explanation? Explain why.
Huygens proposed the wave theory
of light and Newton proposed the
particle theory of light. The law of
reflection can be explained using
both theories. Huygen’s principle and
Newton’s particle theory are opposed,
however, in their explanation of the
law of refraction.
Cumulative Review
page 400
105. A 1400-kg drag racer automobile can
complete a one-quarter mile (402 m)
course in 9.8 s. The final speed of the
automobile is 250 mi/h (112 m/s).
(Chapter 11)
a. What is the kinetic energy of the
automobile?
KE mv2
(1400 kg)(112 m/s)2
8.8106J
b. What is the minimum amount of work
that was done by its engine? Why can’t
you calculate the total amount of work
done?
The minimum amount of work
must equal KE,or 8.8106J. The
engine had to do more work than
was dissipated in work done
against friction.
c. What was the average acceleration of
the automobile?
a
v
t
11
9
2
.8
m
s/s
11 m/s2
106. How much water would a steam engine
have to evaporate in 1 s to produce 1 kW
of power? Assume that the engine is
20 percent efficient. (Chapter 12)
W
t
1000 J/s
If the engine is only 20 percent
efficient it must use five times more
heat to produce the 1000 J/s.
Q
t
5000 J/s
m
t
Hv
Therefore,
m
t
500
H
0
v
J/s
2.25
60
0
1
0
06
J/J
s/kg
2103kg/s
Challenge Problem
page 380
A car of mass mrests at the top of a hill of
height hbefore rolling without friction into a
crash barrier located at the bottom of the hill.
The crash barrier contains a spring with a spring
constant, k, which is designed to bring the car to
rest with minimum damage.
1. Determine, in terms of m, h, k, and g, the
maximum distance, x, that the spring will
be compressed when the car hits it.
Conservation of energy implies that the
gravitational potential energy of the car
at the top of the hill will be equal to the
elastic potential energy in the spring
when it has brought the car to rest.The
equations for these energies can be set
equal and solved for x.
PEg PEsp, so mgh
1
2
kx2
x
2mgh
k
1
2
1
2
Chapter 14 continued

2. If the car rolls down a hill that is twice as
high, how much farther will the spring be
compressed?
The height is doubled and xis propor-
tional to the square root of the height,
so xwill increase by 2
.
3. What will happen after the car has been
brought to rest?
In the case of an ideal spring, the
spring will propel the car back to the
top of the hill.
328 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 14 continued

Physics: Principles and Problems Solutions Manual 329
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
15 Sound
CHAPTER
Practice Problems
15.1 Properties and Detection
of Sound
pages 403–410
page 405
1. Find the wavelength in air at 20°C of an
18-Hz sound wave, which is one of the
lowest frequencies that is detectable by the
human ear.
v
f
31
48
3H
m
z
/s
19 m
2. What is the wavelength of an 18-Hz sound
wave in seawater at 25°C?
v
f
15
1
3
8
3H
m
z/s
85 m
3. Find the frequency of a sound wave moving
through iron at 25°C with a wavelength of
1.25 m.
f
v
51
13
.2
0
5m
m
/s
4.10103Hz
4. If you shout across a canyon and hear the
echo 0.80 s later, how wide is the canyon?
v
d
t
so dvt (343 m/s)(0.40 s) 140 m
5. A 2280-Hz sound wave has a wavelength of
0.655 m in an unknown medium. Identify
the medium.
v
f
so vf(0.655 m)(2280 Hz)
1490 m/s
This speed corresponds to water at
25°C.
page 409
6. Repeat Example Problem 1, but with the car
moving away from you. What frequency
would you hear?
vs24.6 m/s
fd524 Hz
489 Hz
7. You are in an auto traveling at 25.0 m/s
toward a pole-mounted warning siren. If
the siren’s frequency is 365 Hz, what
frequency do you hear? Use 343 m/s as the
speed of sound.
v343 m/s, fs365 Hz, vs0,
vd25.0 m/s
fdfs
v
v
v
vd
s
(365 Hz)
392 Hz
8. You are in an auto traveling at 55 mph
(24.6 m/s). A second auto is moving toward
you at the same speed. Its horn is sounding
at 475 Hz. What frequency do you hear?
Use 343 m/s as the speed of sound.
v343 m/s, fs475 Hz, vs24.6 m/s,
vd24.6 m/s
fdfs
v
v
v
vd
s
(475 Hz)
548 Hz
9. A submarine is moving toward another
submarine at 9.20 m/s. It emits a 3.50-MHz
ultrasound. What frequency would the
second sub, at rest, detect? The speed of
sound in water is 1482 m/s.
v1482 m/s, fs3.50 MHz,
vs9.20 m/s, vd0 m/s
fdfs
v
v
v
vd
s
343 m/s 24.6 m/s
343 m/s 24.6 m/s
343 m/s 25.0 m/s
343 m/s
1
1
(
3
2
4
4
3
.6
m
m
/s
/s)

(3.50 MHz)
3.52 MHz
10. A sound source plays middle C (262 Hz).
How fast would the source have to go to
raise the pitch to C sharp (271 Hz)? Use
343 m/s as the speed of sound.
v343 m/s, fs262 Hz, fd271 Hz,
vd0 m/s, vsis unknown
fdfs
v
v
v
vd
s
Solve this equation for vs.
vsv
f
f
d
s
(vvd)
343 m/s
2
26
72
1H
Hz
z
(343 m/s 0 m/s)
11.4 m/s
Section Review
15.1 Properties and Detection
of Sound
pages 403–410
page 410
11. Graph The eardrum moves back and forth
in response to the pressure variations of a
sound wave. Sketch a graph of the displace-
ment of the eardrum versus time for two
cycles of a 1.0-kHz tone and for two cycles
of a 2.0-kHz tone.
12. Effect of Medium List two sound charac-
teristics that are affected by the medium
through which the sound passes and two
characteristics that are not affected.
affected: speed and wavelength;
unaffected: period and frequency
13. Sound Properties What physical charac-
teristic of a sound wave should be changed
to change the pitch of the sound? To
change the loudness?
frequency; amplitude
14. Decibel Scale How much greater is the
sound pressure level of a typical rock band’s
music (110 dB) than a normal conversation
(50 dB)?
The sound pressure level increases by
a factor of 10 for every 20-dB increase
in sound level.Therefore, 60 dB corre-
sponds to a 1000-fold increase in SPL.
15. Early Detection In the nineteenth century,
people put their ears to a railroad track to
get an early warning of an approaching
train. Why did this work?
The velocity of sound is greater in
solids than in gases. Therefore, sound
travels faster in steel rails than in air,
and the rails help focus the sound so it
does not die out as quickly as in air.
16. Bats A bat emits short pulses of high-
frequency sound and detects the echoes.
a. In what way would the echoes from
large and small insects compare if they
were the same distance from the bat?
They would differ in intensity. Larger
insects would reflect more of the
sound energy back to the bat.
b. In what way would the echo from an
insect flying toward the bat differ from
that of an insect flying away from the
bat?
An insect flying toward the bat
would return an echo of higher fre-
quency (Doppler shift). An insect fly-
ing away from the bat would return
an echo of lower frequency.
17. Critical Thinking Can a trooper using a
radar detector at the side of the road
determine the speed of a car at the instant
the car passes the trooper? Explain.
No. The car must be approaching or
1482 m/s
1482 m/s 9.20 m/s
330 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued
0.5 1.0 1.5 2.0 Time (ms)
Displacement
1.0 kHz
2.0 kHz

Physics: Principles and Problems Solutions Manual 331
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
receding from the detector for the
Doppler effect to be observed.
Transverse motion produces no
Doppler effect.
Practice Problems
15.2 The Physics of Music
pages 411–419
page 416
18. A 440-Hz tuning fork is held above a closed
pipe. Find the spacing between the reso-
nances when the air temperature is 20°C.
Resonance spacing
2
so using
v
f
the resonance spacing is
2
2
v
f
(2
3
)(
4
4
3
40
mH
/sz)
0.39 m
19. A 440-Hz tuning fork is used with a
resonating column to determine the
velocity of sound in helium gas. If the
spacings between resonances are 110 cm,
what is the velocity of sound in helium gas?
Resonance spacing
2
1.1 m
so 2.2 m
vf(2.2 m)(440 Hz) 970 m/s
20. The frequency of a tuning fork is unknown.
A student uses an air column at 27°C and
finds resonances spaced by 20.2 cm. What
is the frequency of the tuning fork? Use the
speed calculated in Example Problem 2 for
the speed of sound in air at 27°C.
v347 m/s at 27°C
Resonance spacing gives
2
0.202 m,
or 0.404 m
f
v
3
04
.4
7
04
mm
/s
859 Hz
21. A bugle can be thought of as an open pipe.
If a bugle were straightened out, it would be
2.65-m long.
a. If the speed of sound is 343 m/s, find
the lowest frequency that is resonant for
a bugle (ignoring end corrections).
12L(2)(2.65 m) 5.30 m
The lowest frequency is
f1
v
1
3
5
4
.3
30
m
m
/s
64.7 Hz
b. Find the next two resonant frequencies
for the bugle.
f2
v
2
L
v
3
2
4
.6
35
m
m
/s
129 Hz
f3
v
3
2
3L
v
(
(
3
2
)
)
(
(
3
2
4
.6
3
5
m
m
/s
)
)
194 Hz
Section Review
15.2 The Physics of Music
pages 411–419
page 419
22. Origins of Sound What is the vibrating
object that produces sounds in each of the
following?
a. a human voice
vocal cords
b. a clarinet
a reed
c. a tuba
the player’s lips
d. a violin
a string
23. Resonance in Air Columns Why is the
tube from which a tuba is made much
longer than that of a cornet?
The longer the tube, the lower the
resonant frequency it will produce.
24. Resonance in Open Tubes How must the
length of an open tube compare to the
wavelength of the sound to produce the
strongest resonance?
The length of the tube should be
one-half the wavelength.
25. Resonance on Strings A violin sounds a
note of F sharp, with a pitch of 370 Hz.
What are the frequencies of the next three
harmonics produced with this note?
A string’s harmonics are whole number
multiples of the fundamental, so the fre-
quencies are:
Chapter 15 continued
f22f1(2)(370 Hz) 740 Hz
f33f1(3)(370 Hz) 1110 Hz
1100 Hz
f44f1(4)(370 Hz) 1480 Hz
1500 Hz
26. Resonance in Closed Pipes One closed
organ pipe has a length of 2.40 m.
a. What is the frequency of the note
played by this pipe?
4L(4)(2.40 m) 9.60 m
v
f
f
v
3
9
4
.6
30
m
m
/s
35.7 Hz
b. When a second pipe is played at the
same time, a 1.40-Hz beat note is heard.
By how much is the second pipe too
long?
f35.7 Hz 1.40 Hz 34.3 Hz
v
f
3
34
43
.3m
H
/z
s
10.0 m
4L
L
4
10.4
0m
2.50 m
The difference in lengths is
2.50 m 2.40 m 0.10 m
27. Timbre Why do various instruments sound
different even when they play the same note?
Each instrument produces its own set
of fundamental and harmonic frequen-
cies, so they have different timbres.
28. Beats A tuning fork produces three beats
per second with a second, 392-Hz tuning
fork. What is the frequency of the first
tuning fork?
It is either 389 Hz or 395 Hz.You can’t
tell which without more information.
29. Critical Thinking Strike a tuning fork with
a rubber hammer and hold it at arm’s
length. Then press its handle against a desk,
a door, a filing cabinet, and other objects.
What do you hear? Why?
The tuning fork’s sound is amplified
greatly when it is pressed against other
objects because they resonate like a
sounding board.They sound different
because they resonate with different
harmonics; therefore, they have different
timbres.
Chapter Assessment
Concept Mapping
page 424
30. Complete the concept map below using the
following terms: amplitude, perception, pitch,
speed.
Mastering Concepts
page 424
31. What are the physical characteristics of
sound waves? (15.1)
Sound waves can be described by
frequency, wavelength, amplitude,
and speed.
32. When timing the 100-m run, officials at the
finish line are instructed to start their stop-
watches at the sight of smoke from the
starter’s pistol and not at the sound of its
firing. Explain. What would happen to the
times for the runners if the timing started
when sound was heard? (15.1)
Light travels at 3.00108m/s, while
sound travels at 343 m/s. Officials
would see the smoke before they would
hear the pistol fire. The times would be
less than actual if sound were used.
332 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued
Sound
properties
frequency
speed amplitude
perception
loudness
pitch
Physics: Principles and Problems Solutions Manual 333
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
33. Name two types of perception of sound and
the physical characteristics of sound waves
that correspond to them. (15.1)
pitch—frequency, loudness—amplitude
34. Does the Doppler shift occur for only some
types of waves or for all types of waves?
(15.1)
all types of waves
35. Sound waves with frequencies higher than
can be heard by humans, called ultrasound,
can be transmitted through the human body.
How could ultrasound be used to measure
the speed of blood flowing in veins or arter-
ies? Explain how the waves change to make
this measurement possible. (15.1)
Doctors can measure the Doppler shift
from sound reflected by the moving
blood cells. Because the blood is mov-
ing, sound gets Doppler shifted, the
compressions either get piled up or
spaced apart. This alters the frequency
of the wave.
36. What is necessary for the production and
transmission of sound? (15.2)
a vibrating object and a material medium
37. Singing How can a certain note sung by an
opera singer cause a crystal glass to shatter?
(15.2)
The frequency of the note is the same
as the natural resonance of the crystal,
causing its molecules to increase their
amplitude of vibration as energy from
the sound is accepted.
38. Marching In the military, as marching
soldiers approach a bridge, the command
“route step” is given. The soldiers then walk
out-of-step with each other as they cross the
bridge. Explain. (15.2)
While marching in step, a certain
frequency is established that could
resonate the bridge into destructive
oscillation. No single frequency is main-
tained under “route step.”
39. Musical Instruments Why don’t most
musical instruments sound like tuning
forks? (15.2)
Tuning forks produce simple, single-
frequency waves. Musical instruments
produce complex waves containing
many different frequencies. This gives
them their timbres.
40. Musical Instruments What property dis-
tinguishes notes played on both a trumpet
and a clarinet if they have the same pitch
and loudness? (15.2)
the sound quality or timbre
41. Trombones Explain how the slide of a
trombone, shown in Figure 15-21, changes
the pitch of the sound in terms of a trom-
bone being a resonance tube. (15.2)
■Figure 15-21
The slide of a trombone varies pitch by
changing the length of the resonating
column of vibrating air.
Applying Concepts
pages 424–425
42. Estimation To estimate the distance in
kilometers between you and a lightning
flash, count the seconds between the flash
and the thunder and divide by 3. Explain
how this rule works. Devise a similar rule
for miles.
The speed of sound 343 m/s
0.343 km/s (1/2.92) km/s; or, sound
travels approximately 1 km in 3 s.
Therefore, divide the number of sec-
onds by three. For miles, sound travels
approximately 1 mile in 5 s.Therefore,
divide the number of seconds by five.
Chapter 15 continued

43. The speed of sound increases by about
0.6 m/s for each degree Celsius when the
air temperature rises. For a given sound, as
the temperature increases, what happens to
the following?
a. the frequency
There is no change in frequency.
b. the wavelength
The wavelength increases.
44. Movies In a science-fiction movie, a satellite
blows up. The crew of a nearby ship immedi-
ately hears and sees the explosion. If you had
been hired as an advisor, what two physics
errors would you have noticed and corrected?
First, if you had heard a sound, you
would have heard it after you saw the
explosion. Sound waves travel much
more slowly than electromagnetic
waves. Second, in space the density of
matter is so small that the sound waves
do not propagate. Consequently, no
sound should have been heard.
45. The Redshift Astronomers have observed
that the light coming from distant galaxies
appears redder than light coming from
nearer galaxies. With the help of Figure
15-22, which shows the visible spectrum,
explain why astronomers conclude that dis-
tant galaxies are moving away from Earth.
■Figure 15-23
Red light has a longer wavelength and
therefore, a lower frequency than other
colors.The Doppler shift of their light to
lower frequencies indicates that distant
galaxies are moving away from us.
46. Does a sound of 40 dB have a factor of 100
(102) times greater pressure variation than
the threshold of hearing, or a factor of 40
times greater?
A 40-dB sound has sound pressures
100 times greater.
47. If the pitch of sound is increased, what are
the changes in the following?
a. the frequency
Frequency will increase.
b. the wavelength
Wavelength will decrease.
c. the wave velocity
Wave velocity will remain the same.
d. the amplitude of the wave
Amplitude will remain the same.
48. The speed of sound increases with tempera-
ture. Would the pitch of a closed pipe
increase or decrease when the temperature
of the air rises? Assume that the length of
the pipe does not change.
4land vfso v4fl.If v
increases and lremains unchanged, f
increases and pitch increases.
49. Marching Bands Two flutists are tuning up.
If the conductor hears the beat frequency
increasing, are the two flute frequencies get-
ting closer together or farther apart?
The frequencies are getting farther
apart.
50. Musical Instruments A covered organ
pipe plays a certain note. If the cover is
removed to make it an open pipe, is the
pitch increased or decreased?
The pitch is increased; the frequency is
twice as high for an open pipe as for a
closed pipe.
51. Stringed Instruments On a harp,
Figure 15-23a, long strings produce low
notes and short strings produce high notes.
On a guitar, Figure 15-23b, the strings are
all the same length. How can they produce
notes of different pitches?
4107 m5107 m6107 m7107 m
334 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued

Physics: Principles and Problems Solutions Manual 335
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
■Figure 15-23
The strings have different tensions and
masses per unit length. Thinner, tighter
strings produce higher notes than do
thicker, looser strings.
Mastering Problems
15.1 Properties and Detection of Sound
pages 425–426
Level 1
52. You hear the sound of the firing of a distant
cannon 5.0 s after seeing the flash. How far
are you from the cannon?
dvt (343 m/s)(5.0 s) 1.7 km
53. If you shout across a canyon and hear an
echo 3.0 s later, how wide is the canyon?
dvt (343 m/s)(3.0 s) is the total dis-
tance traveled.The distance to the wall
is
1
2
(343 m/s)(3.0 s) 5.1102m
54. A sound wave has a frequency of 4700 Hz
and travels along a steel rod. If the distance
between compressions, or regions of high
pressure, is 1.1 m, what is the speed of the
wave?
vf(1.1 m)(4700 Hz) 5200 m/s
55. Bats The sound emitted by bats has a
wavelength of 3.5 mm. What is the sound’s
frequency in air?
f
v
0
3
.0
40
33
m
5/m
s
9.8104Hz
56. Photography As shown in Figure 15-24,
some cameras determine the distance to the
subject by sending out a sound wave and
measuring the time needed for the echo to
return to the camera. How long would it
take the sound wave to return to such a
camera if the subject were 3.00 m away?
■Figure 15-24
The total distance the sound must
travel is 6.00 m.
v
d
t
so t
d
v
3
6
4
.0
30
m
m
/s
0.0175 s
57. Sound with a frequency of 261.6 Hz travels
through water at 25°C. Find the sound’s
wavelength in water. Do not confuse sound
waves moving through water with surface
waves moving through water.
v
f
1
24
69
13
.6m
H
/z
s
5.707 m
58. If the wavelength of a 4.40102-Hz sound
in freshwater is 3.30 m, what is the speed of
sound in freshwater?
vf(3.30 m)(4.40102Hz)
1.45103m/s
59. Sound with a frequency of 442 Hz travels
through an iron beam. Find the wavelength
of the sound in iron.
v
f
54
14
32
0H
m
z
/s
11.6 m
60. Aircraft Adam, an airport employee, is
working near a jet plane taking off. He
experiences a sound level of 150 dB.
a. If Adam wears ear protectors that reduce
the sound level to that of a typical
rock concert, what decrease in dB is
provided?
A typical rock concert is 110 dB, so
40 dB reduction is needed.
b. If Adam then hears something that
sounds like a barely audible whisper,
what will a person not wearing the ear
protectors hear?
A barely audible whisper is 10 dB,
so the actual level would be 50 dB,
or that of an average classroom.
61. Rock Music A rock band plays at an 80-dB
sound level. How many times greater is the
sound pressure from another rock band play-
ing at each of the following sound levels?
3.00 m
Chapter 15 continued

a. 100 dB
Each 20 dB increases pressure by a
factor of 10, so 10 times greater
pressure.
b. 120 dB
(10)(10) 100 times greater pressure
62. A coiled-spring toy is shaken at a frequency
of 4.0 Hz such that standing waves are
observed with a wavelength of 0.50 m. What
is the speed of propagation of the wave?
vf(0.50 m)(4.0 s1) 2.0 m/s
63. A baseball fan on a warm summer day
(30°C) sits in the bleachers 152 m away
from home plate.
a. What is the speed of sound in air at
30°C?
The speed increases 0.6 m/s per °C,
so the increase from 20°C to 30°C is
6 m/s. Thus, the speed is 343 6
349 m/s.
b. How long after seeing the ball hit the
bat does the fan hear the crack of the
bat?
t
d
v
1
35
42
9m
m
0.436 s
64. On a day when the temperature is 15°C, a
person stands some distance, d, as shown in
Figure 15-25, from a cliff and claps his
hands. The echo returns in 2.0 s. How far
away is the cliff?
■Figure 15-25
At 15°C, the speed of sound is 3 m/s
slower than at 20°C.Thus, the speed of
sound is 340 m/s.
v340 m/s and 2t2.0 s
dvt (340 m/s)(1.0 s) 3.4102m
Level 2
65. Medical Imaging Ultrasound with a
frequency of 4.25 MHz can be used to
produce images of the human body. If the
speed of sound in the body is the same as
in salt water, 1.50 km/s, what is the length
of a 4.25-MHz pressure wave in the body?
v
f
1
4
..
5
2
0
5
1
1
0
0
3
6m
H/
z
s
3.53104m
0.353 mm
66. Sonar A ship surveying the ocean bottom
sends sonar waves straight down into the
seawater from the surface. As illustrated in
Figure 15-26, the first reflection, off of the
mud at the sea floor, is received 1.74 s after
it was sent. The second reflection, from the
bedrock beneath the mud, returns after
2.36 s. The seawater is at a temperature of
25°C, and the speed of sound in mud is
1875 m/s.
■Figure 15-26
a. How deep is the water?
The speed of sound in the seawater
is 1533 m/s and the time for a one-
way trip is 0.87 s, so
dwvtw(1533 m/s)(0.87 s)
1300 m
b. How thick is the mud?
The round-trip time in the mud is
2.36 s 1.74 s 0.62 s
The one-way time in the mud is 0.31 s,
so dmvtm(1875 m/s)(0.31 s)
580 m
t 1.74 s
Mud
Seawater
Bedrock
t 2.36 s
d
336 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued

Physics: Principles and Problems Solutions Manual 337
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
67. Determine the variation in sound pressure
of a conversation being held at a sound
level of 60 dB.
The pressure variation at 0 dB is
2105Pa. For every 20-dB increase, the
pressure variation increases by a factor
of 10.Therefore, 60 dB has a pressure
variation amplitude of 2102Pa.
68. A fire truck is moving at 35 m/s, and a car
in front of the truck is moving in the same
direction at 15 m/s. If a 327-Hz siren blares
from the truck, what frequency is heard by
the driver of the car?
vs35 m/s, v343 m/s, vd15 m/s,
fs327 Hz
fd fs
v
v
v
vd
s
(327 Hz)
3
34
43
3
1
35
5
350 Hz
Level 3
69. A train moving toward a sound detector
at 31.0 m/s blows a 305-Hz whistle. What
frequency is detected on each of the
following?
a. a stationary train
fd fs
v
v
v
vd
s
335 Hz
b. a train moving toward the first train at
21.0 m/s
fd fs
v
v
v
vd
s
356 Hz
70. The train in the previous problem is mov-
ing away from the detector. What frequency
is now detected on each of the following?
a. a stationary train
fd fs
v
v
v
vd
s
2.80102Hz
b. a train moving away from the first train
at a speed of 21.0 m/s
fd fs
v
v
v
vd
s
2.63102Hz
15.2 The Physics of Music
pages 426–427
Level 1
71. A vertical tube with a tap at the base is
filled with water, and a tuning fork vibrates
over its mouth. As the water level is lowered
in the tube, resonance is heard when the
water level has dropped 17 cm, and again
after 49 cm of distance exists from the water
to the top of the tube. What is the frequency
of the tuning fork?
49 cm 17 cm 32 cm or 0.32 m
1
2
exists between points of resonance
1
2
0.32 m
0.64 m
f
v
3
0
4
.6
34
m
m
/s
540 Hz
72. Human Hearing The auditory canal lead-
ing to the eardrum is a closed pipe that is
3.0 cm long. Find the approximate value
(ignoring end correction) of the lowest
resonance frequency.
L
4
v
f
f
4
v
L
(4)
3
(4
03
.0m
30
/s
m)
2.9 kHz
73. If you hold a 1.2-m aluminum rod in the
center and hit one end with a hammer, it
will oscillate like an open pipe. Antinodes
of pressure correspond to nodes of molecu-
lar motion, so there is a pressure antinode
in the center of the bar. The speed of sound
(305 Hz)(343 m/s 21.0 m/s)
343 m/s (31.0 m/s)
(305 Hz)(343 m/s 0)
343 m/s (31.0 m/s)
(305 Hz)(343 m/s (21.0 m/s))
343 m/s 31.0 m/s
(305 Hz)(343 m/s 0)
343 m/s 31.0 m/s
Chapter 15 continued

in aluminum is 5150 m/s. What would be
the bar’s lowest frequency of oscillation?
The rod length is
1
2
, so 2.4 m
f
v
51
2
5
.4
0m
m/s
2.1 kHz
74. One tuning fork has a 445-Hz pitch. When
a second fork is struck, beat notes occur
with a frequency of 3 Hz. What are the two
possible frequencies of the second fork?
445 Hz 3 Hz 442 Hz
and 445 Hz 3 Hz 448 Hz
75. Flutes A flute acts as an open pipe. If a
flute sounds a note with a 370-Hz pitch,
what are the frequencies of the second,
third, and fourth harmonics of this pitch?
f22f1(2)(370 Hz) 740 Hz
f33f1(3)(370 Hz) 1110 Hz
1100 Hz
f44f1(4)(370 Hz) 1480 Hz
1500 Hz
76. Clarinets A clarinet sounds the same note,
with a pitch of 370 Hz, as in the previous
problem. The clarinet, however, acts as a
closed pipe. What are the frequencies of the
lowest three harmonics produced by this
instrument?
3f1(3)(370 Hz) 1110 Hz 1100 Hz
5f1(5)(370 Hz) 1850 Hz 1800 Hz
7f1(7)(370 Hz) 2590 Hz 2600 Hz
77. String Instruments A guitar string is
65.0 cm long and is tuned to produce a
lowest frequency of 196 Hz.
a. What is the speed of the wave on the
string?
12L(2)(0.650 m) 1.30 m
vf(1.30 m)(196 Hz) 255 m/s
b. What are the next two higher resonant
frequencies for this string?
f22f1(2)(196 Hz) 392 Hz
f33f1(3)(196 Hz) 588 Hz
78. Musical Instruments The lowest note on
an organ is 16.4 Hz.
a. What is the shortest open organ pipe
that will resonate at this frequency?
v
f
3
14
63
.4m
H
/z
s
20.9 m and
L
2
,so
L
2
v
f
(2
3
)(
4
1
3
6m
.4H
/sz)
10.5 m
b. What is the pitch if the same organ pipe
is closed?
Since a closed pipe produces a fun-
damental with a wavelength twice as
long as that of an open pipe of the
same length, the frequency would be
1
2
(16.4 Hz) 8.20 Hz.
79. Musical Instruments Two instruments are
playing musical A (440.0 Hz). A beat note
with a frequency of 2.5 Hz is heard.
Assuming that one instrument is playing
the correct pitch, what is the frequency of
the pitch played by the second instrument?
It could be either 440.0 2.5 442.5 Hz
or 440.0 2.5 437.5 Hz.
80. A flexible, corrugated, plastic tube, shown
in Figure 15-27, is 0.85 m long. When it is
swung around, it creates a tone that is the
lowest pitch for an open pipe of this length.
What is the frequency?
■Figure 15-27
L0.85 m
2
, so 1.7 m
f
v
34
13
.7m
m
/s
2.0102Hz
81. The tube from the previous problem is
swung faster, producing a higher pitch.
What is the new frequency?
f22f1(2)(2.0102Hz) 4.0102Hz
Level 2
82. During normal conversation, the amplitude
of a pressure wave is 0.020 Pa.
0.85 m
338 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued

Physics: Principles and Problems Solutions Manual 339
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. If the area of an eardrum is 0.52 cm2,
what is the force on the eardrum?
FPA
(0.020 N/m2)(0.52104m2)
1.0106N
b. The mechanical advantage of the three
bones in the middle ear is 1.5. If the force
in part ais transmitted undiminished to
the bones, what force do the bones exert
on the oval window, the membrane to
which the third bone is attached?
MA
F
F
e
r
so Fr(MA)(Fe)
Fr(1.5)(1.0106N) 1.5106N
c. The area of the oval window is
0.026 cm2. What is the pressure increase
transmitted to the liquid in the cochlea?
P
A
F
0.58 Pa
83. Musical Instruments One open organ
pipe has a length of 836 mm. A second
open pipe should have a pitch that is one
major third higher. How long should the
second pipe be?
L
2
, so 2Land
v
f
f
2
v
L
(2)
3
(4
03
.8m
36
/s
m)
205 Hz
The ratio of a frequency one major third
higher is 5:4, so (205 Hz)
5
4
256 Hz.
The length of the second pipe is
L
2
v
f
(2
3
)(
4
2
3
56
mH
/sz)
6.70102mm
84. As shown in Figure 15-28, a music box
contains a set of steel fingers clamped at
one end and plucked on the other end by
pins on a rotating drum. What is the speed
of a wave on a finger that is 2.4 cm long
and plays a note of 1760 Hz?
■Figure 15-28
The length of the steel finger clamped
at one end and free to vibrate at the
other is
1
4
wavelength. Therefore,
4L4(0.024 m) 0.096 m, and
vf(1760 Hz)(0.096 m)
1.7102m/s
Mixed Review
pages 427–428
Level 1
85. An open organ pipe is 1.65 m long. What
fundamental frequency note will it produce
if it is played in helium at 0°C?
An open pipe has a length equal to
one-half its fundamental wavelength.
Therefore, 3.30 m.The speed of
sound in helium is 972 m/s. Therefore,
f
v
9
3
7
.3
20
m
m
/s
295 Hz
86. If you drop a stone into a well that is
122.5 m deep, as illustrated in Figure
15-29, how soon after you drop the stone
will you hear it hit the bottom of the well?
■Figure 15-29
First find the time it takes the stone to
fall down the shaft by d
1
2
gt2,so
t
5.00 s
The time it takes the sound to comes
back up is found with dvst,so
t
v
d
s
1
32
42
3.5
mm
/s
0.357 s
The total time is 5.00 s 0.357 s
5.36 s.
122.5 m
1
2
(9.80 m/s2)
d
1
2
g
122.5 m
Steel fingers
1.5106N
0.026104m2
Chapter 15 continued

87. A bird on a newly discovered planet flies
toward a surprised astronaut at a speed of
19.5 m/s while singing at a pitch of 945 Hz.
The astronaut hears a tone of 985 Hz. What
is the speed of sound in the atmosphere of
this planet?
fd985 Hz, fs945 Hz, vs19.5 m/s,
v?
f
fd
s
v
vvs
So
v
v
s
1
f
f
d
s
,
or v
4.80102m/s
88. In North America, one of the hottest out-
door temperatures ever recorded is 57°C
and one of the coldest is 62°C. What are
the speeds of sound at those two tempera-
tures?
v(T) v(0°C) (0.6 m/s)T, where
v(0°C) 331 m/s. So, v(57°C)
(331 m/s)
0.6
°C
m/s
(57°C)
365 m/s
v(62°C) (331 m/s)
0.6
°C
m/s
(62°C)
294 m/s
Level 2
89. A ship’s sonar uses a frequency of 22.5 kHz.
The speed of sound in seawater is 1533 m/s.
What is the frequency received on the ship
that was reflected from a whale traveling at
4.15 m/s away from the ship? Assume that
the ship is at rest.
Part 1. From ship to whale:
vd4.15 m/s, v1533 m/s,
fs22.5 kHz, vs0
fd fs
v
v
v
vd
s
(22.5 kHz)
153
1
3
5
33
4.15
22.4 kHz
Part 2. From whale to ship:
vs4.15 m/s, v1533 m/s,
fs22.4 kHz, vd0
fd fs
v
v
v
vd
s
(22.4 kHz)
1533
15
33
4.15
22.3 kHz
90. When a wet finger is rubbed around the rim
of a glass, a loud tone of frequency 2100 Hz
is produced. If the glass has a diameter of
6.2 cm and the vibration contains one
wavelength around its rim, what is the
speed of the wave in the glass?
The wavelength is equal to the
circumference of the glass rim, d
Therefore, the speed is
vfdf
(0.062 m)(2100 Hz) 4.1102m/s
91. History of Science In 1845, Dutch scien-
tist Christoph Buys-Ballot developed a test
of the Doppler effect. He had a trumpet
player sound an A note at 440 Hz while
riding on a flatcar pulled by a locomotive.
At the same time, a stationary trumpeter
played the same note. Buys-Ballot heard
3.0 beats per second. How fast was the train
moving toward him?
fd440 Hz 3.0 Hz 443 Hz
fdfs
v
v
v
vd
s
so (v vs)fd(v vd)fsand
vsv
(v
fd
vd)fs
343 m/s
2.3 m/s
92. You try to repeat Buys-Ballot’s experiment
from the previous problem. You plan to
have a trumpet played in a rapidly moving
car. Rather than listening for beat notes,
however, you want to have the car move fast
enough so that the moving trumpet sounds
one major third above a stationary trumpet.
a. How fast would the car have to move?
major third ratio
5
4
(343 m/s 0)(440 Hz)
443 Hz
19.5 m/s
1
9
94
85
5H
Hz
z
vs
1
f
f
d
s
1
1
v
v
s
340 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued
Physics: Principles and Problems Solutions Manual 341
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
fdfs
v
v
v
vd
s
so (v vs)fd(v vd)fs
and vsv
(v
fd
vd)fs
343 m/s (343 m/s 0)
4
5
68.6 m/s
b. Should you try the experiment? Explain.
v(68.6 m/s)
36
1
00
hs
16
10m
9i
m
153 mph,
so the car would be moving
dangerously fast. Do not try
the experiment.
Level 3
93. Guitar Strings The equation for the speed
of a wave on a string is v
F
T
,where FTis
the tension in the string and is the mass
per unit length of the string. A guitar string
has a mass of 3.2 g and is 65 cm long.
What must be the tension in the string
to produce a note whose fundamental
frequency is 147 Hz?
0.0
0.0
63
52m
kg
4.9103kg/m
2L2(0.65 m) 1.30 m
vf(147 Hz)(1.30 m) 191 m/s
FTv2(191 m/s)2(4.9103kg/m)
180 N
94. A train speeding toward a tunnel at
37.5 m/s sounds its horn at 327 Hz. The
sound bounces off the tunnel mouth. What
is the frequency of the reflected sound
heard on the train? Hint: Solve the problem
in two parts. First, assume that the tunnel
is a stationary observer and find the
frequency. Then, assume that the tunnel is a
stationary source and find the frequency
measured on the train.
Part 1. vs37.5 m/s, v343 m/s,
fs327 Hz
fd fs
v
v
v
vd
s
(327 Hz)
3433
43
37.5
367 Hz
Part 2. vd37.5 m/s, v343 m/s,
fs367 Hz
fd fs
v
v
v
vd
s
(367 Hz)
343
3(
4
337.5)
407 Hz
Thinking Critically
page 428
95. Make and Use Graphs The wavelengths of
the sound waves produced by a set of tun-
ing forks with given frequencies are shown
in Table 15-2 below.
a. Plot a graph of the wavelength versus
the frequency (controlled variable).
What type of relationship does the
graph show?
The graph shows an inverse rela-
tionship between frequency and
wavelength.
b. Plot a graph of the wavelength versus
the inverse of the frequency (1/f). What
kind of graph is this? Determine the
1.00 180
f (Hz)
100 260
2.60
1.40
1.80
2.20
(m)
140 240
Chapter 15 continued
Table 15-2
Tuning Forks
Frequency (Hz) Wavelength (m)
131 2.62
147 2.33
165 2.08
196 1.75
220 1.56
247 1.39
speed of sound from this graph.
The graph shows a direct relationship
between period (1/f) and wavelength.
The speed of sound is represented
by the slope, ~343 m/s.
96. Make Graphs Suppose that the frequency
of a car horn is 300 Hz when it is station-
ary. What would the graph of the frequency
versus time look like as the car approached
and then moved past you? Complete a
rough sketch.
The graph should show a fairly steady
frequency above 300 Hz as it approach-
es and a fairly steady frequency below
300 Hz as it moves away.
97. Analyze and Conclude Describe how you
could use a stopwatch to estimate the speed
of sound if you were near the green on a 200-
m golf hole as another group of golfers hit
their tee shots. Would your estimate of the
speed of sound be too large or too small?
You could start the watch when you
saw the hit and stop the watch when
the sound reached you.The speed
would be calculated by dividing the dis-
tance, 200 m, by the measured time. The
measured time would be too large
because you could anticipate the
impact by sight, but you could not
anticipate the sound. The calculated
speed would be too small.
98. Apply Concepts A light wave coming from
a point on the left edge of the Sun is found
by astronomers to have a slightly higher
frequency than light from the right side.
What do these measurements tell you about
the Sun’s motion?
The Sun must be rotating on its axis in
the same manner as Earth. The Doppler
shift indicates that the left side of the
Sun is coming toward us, while the
right side is moving away.
99. Design an Experiment Design an experi-
ment that could test the formula for the
speed of a wave on a string. Explain what
measurements you would make, how you
would make them, and how you would use
them to test the formula.
Measure the mass and length of the
string to determine .Then clamp the
string to a table, hang one end over the
table edge, and stretch the string by
hanging weights on its end to obtain FT.
Calculate the speed of the wave using
the formula. Next, pluck the string in its
middle and determine the frequency by
matching it to a frequency generator,
using beats to tune the generator.
Multiply the frequency by twice the string
length, which is equal to the wavelength,
to obtain the speed from the wave equa-
tion. Compare the results. Repeat for dif-
ferent tensions and other strings with
different masses per unit length.
Consider possible causes of error.
Writing in Physics
page 428
100. Research the construction of a musical
instrument, such as a violin or French
horn. What factors must be considered
besides the length of the strings or tube?
What is the difference between a quality
instrument and a cheaper one? How are
they tested for tone quality?
Answers will vary. A report on violin
construction might include information
about the bridge as a link between the
strings and body and information
about the role of the body in causing
air molecules around the violin to
vibrate. Students also might discuss
1.00 6.0
(ms)
4.0 8.0
2.60
1.40
1.80
2.20
(m)
–
1
f
342 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued

Physics: Principles and Problems Solutions Manual 343
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
the ways in which the woods and fin-
ishes used in making violins affect the
quality of the sound produced by the
instruments.
101. Research the use of the Doppler effect in
the study of astronomy. What is its role in
the big bang theory? How is it used to
detect planets around other stars? To study
the motions of galaxies?
Students should discuss the work of
Edwin Hubble, the redshift and the
expanding universe, spectroscopy, and
the detection of wobbles in the motion
of planet-star systems.
Cumulative Review
page 428
102. Ball A, rolling west at 3.0 m/s, has a mass
of 1.0 kg. Ball B has a mass of 2.0 kg and
is stationary. After colliding with ball B,
ball A moves south at 2.0 m/s. (Chapter 9)
a. Sketch the system, showing the veloci-
ties and momenta before and after the
collision.
Westward and southward are
positive.
b. Calculate the momentum and velocity
of ball B after the collision.
Horizontal: mAvA1 mBvB2
So mBvB2 (1.0 kg)(3.0 m/s)
3.0 kgm/s
Vertical: 0 mAvA2 mBvB2
So mBvB2 (1.0 kg)(2.0 m/s)
2.0 kgm/s
The vector sum is
mv
(3.0 k
gm/s
)2 (
2.0
kgm/
s)2
3.6 kgm/s and tan
2
3.
.0
0k
kg
g
m
m/
/s
s
so 34°
Therefore, mBvB2 3.6 kgm/s at
34°north of west
vB2
3.6
2.
k
0
gk
m
g/s
1.8 m/s at 34°north of west
103. Chris carries a 10-N carton of milk along
a level hall to the kitchen, a distance of
3.5 m. How much work does Chris do?
(Chapter 10)
No work, because the force and the
displacement are perpendicular.
104. A movie stunt person jumps from a five-
story building (22 m high) onto a large
pillow at ground level. The pillow cush-
ions her fall so that she feels a deceleration
of no more than 3.0 m/s2. If she weighs
480 N, how much energy does the pillow
have to absorb? How much force does the
pillow exert on her? (Chapter 11)
The energy to be absorbed equals the
mechanical energy that she had, which
equals her initial potential energy.
U mgh (480 N)(22 m) 11 kJ.
The force on her is
Fma
F
g
g
(a)
9.8
40
80
m
N
/s2
(3.0 m/s2)
150 N
BBefore
After
A
A
A
p
B1 = 0 vA1 = 3.0 m/s west
pA1 = 3.0 kgm/s west
vB2 = ?
pB2 = ?
vA2 = 2.0 m/s south
pA2 = 2.0 kgm/s south
Chapter 15 continued

Challenge Problem
page 417
1. Determine the tension, FT, in a violin string of mass mand length Lthat will
play the fundamental note at the same frequency as a closed pipe also of
length L. Express your answer in terms of m, L, and the speed of sound in
air, v. The equation for the speed of a wave on a string is u
F
T
. where FTis
the tension string and is the mass per unit length of the string.
The wavelength of the fundamental in a closed pipe is equal to 4L, so
the frequency is f
4
v
L
. The wavelength of the fundamental on a string is
equal to 2L, so the frequency of the string is f
2
u
L
, where uis the speed
of the wave on the string, u
F
T
. The mass per unit length of the string
m/L. Squaring the frequencies and setting them equal gives
1v
6L
2
2
4
u
L
2
2
4L
F2
T
4
F
L
T
2L
m
4
F
LT
m
Finally, rearranging for the tension gives FT
m
4v
L
2
2. What is the tension in a string of mass 1.0 g and 40.0 cm long that plays the
same note as a closed pipe of the same length?
For a string of mass 1.0 g and length 0.400 m, the tension is
FT
m
4v
L
2
74 N
(0.0010 kg)(343 m/s)2
4(0.400 m)
344 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 15 continued

Physics: Principles and Problems Solutions Manual 345
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
16 Fundamentals of Light
CHAPTER
Practice Problems
16.1 Illumination
pages 431–438
page 436
1. A lamp is moved from 30 cm to 90 cm
above the pages of a book. Compare the
illumination on the book before and after
the lamp is moved.
; therefore, after
the lamp is moved the illumination is
one-ninth of the original illumination.
2. What is the illumination on a surface that is
3.0 m below a 150-W incandescent lamp
that emits a luminous flux of 2275 lm?
E 2.0101lx
3. Draw a graph of the illuminance produced
by a 150-W incandescent lamp between
0.50 m and 5.0 m.
Illuminance of a 150-W bulb
P2275, d0.50, 0.75, …, 5.0
E(d)
4. A 64-cd point source of light is 3.0 m above
the surface of a desk. What is the illumina-
tion on the desk’s surface in lux?
P4(64 cd) 256lm
so E
42
5
(3
6.
0l
m
m
)2
7.1 lx
5. A public school law requires a minimum
illuminance of 160 lx at the surface of each
student’s desk. An architect’s specifications
call for classroom lights to be located 2.0 m
above the desks. What is the minimum
luminous flux that the lights must produce?
E
P4Ed2
4(160 lm/m2)(2.0 m)2
8.0103lm
6. A screen is placed between two lamps so
that they illuminate the screen equally, as
shown in Figure 16-7. The first lamp emits
a luminous flux of 1445 lm and is 2.5 m
from the screen. What is the distance of
the second lamp from the screen if the
luminous flux is 2375 lm?
■Figure 16-7 (Not to scale)
E1E2
So
or d2d1
P
P2
1
(2.5 m)
3.2 m
2375
1445
P2
d22
P1
d12
P 1445 lm
2.5 m
Screen
P 2375 lm
P
4d2
P
4d2
E (lx)
r (m)
720
7.2 5.00.50
P 2275 lm
P
4d2
2275 lm
4(3.0 m)2
P
4d2
1
9
(30 cm)2
(90 cm)2
dbefore2
dafter2
4d
P
after2
4db
P
efore2
Eafter
Ebefore

Section Review
16.1 Illumination
pages 431–438
page 438
7. Use of Material Light Properties Why
might you choose a window shade that is
translucent? Opaque?
You would use a translucent window
shade to keep people from looking in or
out, while still allowing daylight in.You
would use an opaque window shade to
keep the daylight out.
8. Illuminance Does one lightbulb provide
more illuminance than two identical light-
bulbs at twice the distance? Explain.
One lightbulb provides an illuminance
that is four times larger than two of the
same lightbulb at twice the distance,
because E .
9. Luminous Intensity Two lamps illuminate
a screen equally—lamp A at 5.0 m, lamp B
at 3.0 m. If lamp A is rated 75 cd, what is
lamp B rated?
E
Since the illumination is equal,
E1E2
So
or I2
(75 (
c
5
d
.0
)(3
m
.0
)2m)2
27 cd
10. Distance of a Light Source Suppose that
a lightbulb illuminating your desk provides
only half the illuminance that it should. If
it is currently 1.0 m away, how far should it
be to provide the correct illuminance?
Illumination depends on 1/d2,
so
df
m
0.71 m
11. Distance of Light Travel How far does
light travel in the time it takes sound to
travel 1 cm in air at 20°C?
Sound velocity is 343 m/s, so sound
takes 3105s to travel 1 cm. In that
time, light travels 9 km.
vsound 343 m/s
tsound
3105s
vlight 3.00108m/s
dlight vlighttsound
(3.00108m/s)(3105s)
9103m9 km
12. Distance of Light Travel The distance to
the Moon can be found with the help of
mirrors left on the Moon by astronauts. A
pulse of light is sent to the Moon and
returns to Earth in 2.562 s. Using the
measured value of the speed of light to the
same precision, calculate the distance from
Earth to the Moon.
dct
(299,800,000 m/s)
(2.562 s)
3.840108m
13. Critical Thinking Use the correct time
taken for light to cross Earth’s orbit,
16.5 min, and the diameter of Earth’s orbit,
2.981011 m, to calculate the speed of light
using Roemer’s method. Does this method
appear to be accurate? Why or why not?
v
3.1108m/s
3.01011
(16 min)(60 s/min)
d
t
1
2
1102m
343 m/s
d
vsound
1
2
1
2
df2
(1.0 m)2
1
2
df2
di2
Ei
Ef
I1d22
d12
I2
d22
I1
d12
I
d2
P
d2
346 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued

Physics: Principles and Problems Solutions Manual 347
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Practice Problems
16.2 The Wave Nature
of Light
pages 439–447
page 447
14. What is the frequency of oxygen’s spectral
line if its wavelength is 513 nm?
Use and solve for f.
f
5.851014 Hz
15. A hydrogen atom in a galaxy moving with
a speed of 6.55106m/s away from
Earth emits light with a frequency of
6.161014 Hz. What frequency of light
from that hydrogen atom would be
observed by an astronomer on Earth?
The relative speed along the axis is much
less than the speed of light.Thus, you
can use the observed light frequency
equation. Because the astronomer and
the galaxy are moving away from each
other, use the negative form of the
observed light frequency equation.
fobs f1
(6.161014 Hz)1
6
3.
.5
05
0
1
10
0
6
8m
m/
/s
s
6.031014 Hz
16. A hydrogen atom in a galaxy moving with
a speed of 6.551016 m/s away from
Earth emits light with a wavelength of
4.86107m. What wavelength would be
observed on Earth from that hydrogen atom?
The relative speed along the axis is
much less than the speed of light. Thus,
you can use the observed Doppler shift
equation. Because the astronomer and
the galaxy are moving away from each
other, use the positive form of the
Doppler shift equation.
(obs )
obs 1
(4.86107m)1
6
3.
.5
05
0
1
10
0
6
8
m
m/
/s
s
4.97107m
17. An astronomer is looking at the spectrum of
a galaxy and finds that it has an oxygen
spectral line of 525 nm, while the laboratory
value is measured at 513 nm. Calculate how
fast the galaxy would be moving relative to
Earth. Explain whether the galaxy is moving
toward or away from Earth and how you
know.
Assume that the relative speed along
the axis is much less than the speed of
light. Thus, you can use the Doppler
shift equation.
(obs )
The observed (apparent) wavelength
appears to be longer than the known
(actual) wavelength of the oxygen
spectral line. This means that the
astronomer and the galaxy are moving
away from each other. So use the posi-
tive form of the Doppler shift equation.
(obs )
Solve for the unknown variable.
vc
(3.00108m/s)
7.02106m/s
(525 nm 513 nm)
513 nm
(obs )
v
c
v
c
v
c
v
c
v
c
3.00108m/s
5.13107 m
c
c
f
Chapter 16 continued

Section Review
16.2 The Wave Nature
of Light
pages 439–447
page 447
18. Addition of Light Colors What color of
light must be combined with blue light to
obtain white light?
yellow (a mixture of the other two pri-
maries, red and green)
19. Combination of Pigments What primary
pigment colors must be mixed to produce
red? Explain how red results using color
subtraction for pigment colors.
Yellow and magenta pigments are used
to produce red.Yellow pigment sub-
tracts blue and magenta pigment sub-
tracts green, neither subtracts red so
the mixture would reflect red.
20. Light and Pigment Interaction What
color will a yellow banana appear to be
when illuminated by each of the following?
a. white light
yellow
b. green and red light
yellow
c. blue light
black
21. Wave Properties of Light The speed of
red light is slower in air and water than in a
vacuum. The frequency, however, does not
change when red light enters water. Does
the wavelength change? If so, how?
Yes, because vfand v/f, when v
decreases, so does .
22. Polarization Describe a simple experiment
that you could do to determine whether
sunglasses in a store are polarizing.
See if the glasses reduce glare from the
reflective surfaces, such as windows or
roadways. Polarization of light allows
photographers to photograph objects
while eliminating glare.
23. Critical Thinking Astronomers have deter-
mined that Andromeda, a neighboring
galaxy to our own galaxy, the Milky Way, is
moving toward the Milky Way. Explain how
they determined this. Can you think of a
possible reason why Andromeda is moving
toward our galaxy?
The spectral lines of the emissions of
known atoms are blue-shifted in the
light we see coming from Andromeda.
Andromeda would be moving toward us
due to gravitational attraction.This
gravitational attraction could be due to
the mass of the Milky Way or other
objects located near the Milky Way.
Chapter Assessment
Concept Mapping
page 452
24. Complete the following concept map using
the following terms: wave, c, Doppler effect,
polarization.
348 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued
ray
Light Models
diffraction Doppler
effect
c
polarization 0 c/f
wave
straight
path

Physics: Principles and Problems Solutions Manual 349
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Mastering Concepts
page 452
25. Sound does not travel through a vacuum.
How do we know that light does? (16.1)
Light comes through the vacuum of
space from the Sun.
26. Distinguish between a luminous source and
an illuminated source. (16.1)
A luminous body emits light. An illumi-
nated body is one on which light falls
and is reflected.
27. Look carefully at an ordinary, frosted,
incandescent bulb. Is it a luminous or an
illuminated source? (16.1)
It is mainly illuminated.The filament
is luminous; the frosted glass is illumi-
nated.You barely can see the hot
filament through the frosted glass.
28. Explain how you can see ordinary, nonlu-
minous classroom objects. (16.1)
Ordinary nonluminous objects are illu-
minated by reflected light, allowing
them to be seen.
29. Distinguish among transparent, translucent,
and opaque objects. (16.1)
A transparent object is a material
through which light can pass without
distortion. A translucent object allows
light to pass but distorts the light to the
point where images are not discernable.
An opaque object does not allow light
to pass through.
30. To what is the illumination of a surface by a
light source directly proportional? To what
is it inversely proportional? (16.1)
The illumination on a surface is directly
proportional to the intensity of the
source and inversely proportional to the
square of the distance of the surface
from the source.
31. What did Galileo assume about the speed
of light? (16.1)
The speed of light is very fast, but finite.
32. Why is the diffraction of sound waves more
familiar in everyday experience than is the
diffraction of light waves? (16.2)
Diffraction is most pronounced around
obstacles approximately the same size
as the wavelength of the wave. We are
more accustomed to obstacles of the
size that diffract the much larger wave-
lengths of sound.
33. What color of light has the shortest
wavelength? (16.2)
Violet light has the shortest wave-
length.
34. What is the range of the wavelengths of
light, from shortest to longest? (16.2)
400 nm to 700 nm
35. Of what colors does white light consist?
(16.2)
White light is a combination of all the
colors, or at least the primary colors.
36. Why does an object appear to be black?
(16.2)
An object appears to be black because
little, if any, light is being reflected
from it.
37. Can longitudinal waves be polarized?
Explain. (16.2)
No. They have no vertical or horizontal
components.
38. If a distant galaxy were to emit a spectral
line in the green region of the light spec-
trum, would the observed wavelength on
Earth shift toward red light or toward blue
light? Explain. (16.2)
Because the galaxy is distant, it is most
likely moving away from Earth. The
wavelength actually would shift away
from the wavelength of green light
toward a longer red wavelength. If it
Chapter 16 continued

shifted toward the blue wavelength, the
wavelength would be shorter, not
longer. This would indicate the galaxy is
getting closer to Earth, and no galaxy
outside the Local Group has been dis-
covered moving toward us.
39. What happens to the wavelength of light as
the frequency increases? (16.2)
As the frequency increases, the wave-
length decreases.
Applying Concepts
page 452
40. A point source of light is 2.0 m from screen
A and 4.0 m from screen B, as shown in
Figure 16-21. How does the illuminance at
screen B compare with the illuminance at
screen A?
■Figure 16-21
Illumination El/r2; therefore, the illu-
mination at screen B will be one-fourth
of that at screen A because it is twice
as far from the source.
41. Reading Lamp You have a small reading
lamp that is 35 cm from the pages of a
book. You decide to double the distance.
a. Is the illuminance at the book the same?
No.
b. If not, how much more or less is it?
Distance is doubled, so the illumina-
tion of the page is one-fourth as
great.
42. Why are the insides of binoculars and
cameras painted black?
The insides are painted black because
black does not reflect any light, and
thus there is no interference while
observing or photographing objects.
43. Eye Sensitivity The eye is most sensitive to
yellow-green light. Its sensitivity to red and
blue light is less than 10 percent as great.
Based on this knowledge, what color would
you recommend that fire trucks and ambu-
lances be painted? Why?
Fire trucks should be painted yellow-
green, 550 nm, because less light has to
be reflected to the eye for the fire truck
to be seen.
44. Streetlight Color Some very efficient
streetlights contain sodium vapor under
high pressure. They produce light that is
mainly yellow with some red. Should a
community that has these lights buy dark
blue police cars? Why or why not?
Blue pigment of a police car will absorb
the red and yellow light. Dark blue
police cars would not be very visible. If
a community wants its police cars to be
visible, they should buy yellow cars.
Refer to Figure 16-22 for problems 45 and 46.
■Figure 16-22
45. What happens to the illuminance at a
book as the lamp is moved farther away
from the book?
Illuminance decreases, as described by
the inverse-square law.
46. What happens to the luminous intensity of
the lamp as it is moved farther away from
the book?
No change; distance does not affect the
luminous intensity of the lamp.
Source
Screen A
2 m 4 m
Screen B
350 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued
Physics: Principles and Problems Solutions Manual 351
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
47. Polarized Pictures Photographers often
put polarizing filters over camera lenses to
make clouds in the sky more visible. The
clouds remain white, while the sky looks
darker. Explain this based on your knowl-
edge of polarized light.
Light scattered from the atmosphere is
polarized, but light scattered from the
clouds is not. By rotating the filter, the
photographer can reduce the amount of
polarized light reaching the film.
48. An apple is red because it reflects red light
and absorbs blue and green light.
a. Why does red cellophane look red in
reflected light?
Cellophane reflects red light and
absorbs blue and green light.
b. Why does red cellophane make a white
lightbulb look red when you hold the
cellophane between your eye and the
lightbulb?
Cellophane transmits red light.
c. What happens to the blue and green
light?
Blue and green light are absorbed.
49. You put a piece of red cellophane over one
flashlight and a piece of green cellophane
over another. You shine the light beams on
a white wall. What color will you see where
the two flashlight beams overlap?
yellow
50. You now put both the red and green cello-
phane pieces over one of the flashlights in
Problem 49. If you shine the flashlight
beam on a white wall, what color will you
see? Explain.
Black; almost no light would get
through because the light transmitted
through the first filter would be
absorbed by the second.
51. If you have yellow, cyan, and magenta pig-
ments, how can you make a blue pigment?
Explain.
Mix cyan and magenta.
52. Traffic Violation Suppose that you are a
traffic officer and you stop a driver for
going through a red light. Further suppose
that the driver draws a picture for you
(Figure 16-23) and explains that the light
looked green because of the Doppler effect
when he went through it. Explain to him
using the Doppler shift equation just how
fast he would have had to be going for the
red light ( 645 nm), to appear green (
545 nm). Hint: For the purpose of this prob-
lem, assume that the Doppler shift equation is
valid at this speed.
■Figure 16-23
(3.00108m/s)
4.65107m/s
That is over 100 million mph. If he does
not get a ticket for running a red light,
he will get a ticket for speeding.
Mastering Problems
16.1 Illumination
page 453
Level 1
53. Find the illumination 4.0 m below a
405-lm lamp.
E
4
4
(0
45
.0lm
m)2
2.0 lx
54. Light takes 1.28 s to travel from the Moon to
Earth. What is the distance between them?
dvt (3.00108m/s)(1.28 s)
3.84108m
Level 2
55. A three-way bulb uses 50, 100, or 150 W
of electric power to deliver 665, 1620, or
2285 lm in its three settings. The bulb is
placed 80 cm above a sheet of paper. If an
P
4d2
645 nm 545 nm
645 nm
Chapter 16 continued

illumination of at least 175 lx is needed on
the paper, what is the minimum setting that
should be used?
E
P4Ed24(175 lx)(0.80 m)2
1.4103lm
Thus, the 100-W (1620-lm) setting is
needed.
56. Earth’s Speed Ole Roemer found that the
average increased delay in the disappear-
ance of Io from one orbit around Jupiter to
the next is 13 s.
a. How far does light travel in 13 s?
3.9109m
b. Each orbit of Io takes 42.5 h. Earth trav-
els the distance calculated in part ain
42.5 h. Find the speed of Earth in km/s.
v
25 km/s
c. Check to make sure that your answer for
part bis reasonable. Calculate Earth’s
speed in orbit using the orbital radius,
1.5108km, and the period, 1.0 yr.
v
3.0101km/s, so fairly accurate
Level 3
57. A student wants to compare the luminous
flux of a lightbulb with that of a 1750-lm
lamp. The lightbulb and the lamp illumi-
nate a sheet of paper equally. The 1750-lm
lamp is 1.25 m away from the sheet of
paper; the lightbulb is 1.08 m away. What
is the lightbulb’s luminous flux?
E
Since the illumination is equal,
E1E2
So
or P2
1.31103lm
58. Suppose that you wanted to measure the
speed of light by putting a mirror on a dis-
tant mountain, setting off a camera flash,
and measuring the time it takes the flash to
reflect off the mirror and return to you, as
shown in Figure 16-24. Without instru-
ments, a person can detect a time interval of
about 0.10 s. How many kilometers away
would the mirror have to be? Compare this
distance with that of some known distances.
■Figure 16-24
dvt
(3.00108m/s)(0.1 s)
3104km
The mirror would be half this distance,
or 15,000 km away. Earth is 40,000 km
in circumference, so this is three-
eighths of the way around Earth.
16.2 The Wave Nature of Light
pages 453–454
Level 1
59. Convert 700 nm, the wavelength of red
light, to meters.
(700 nm)
7107m
1109m
1 nm
1 km
1000 m
d
Mirror You
(1750 lm)(1.08 m)2
(1.25 m)2
P1d22
d12
P2
d22
P1
d12
P
4d2
1 h
3600 s
1 d
24 h
2(1.5108km)
365 d
d
t
1 km
1000 m
3.9109m
1.53105s
d
t
P
4d2
352 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued

Physics: Principles and Problems Solutions Manual 353
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
60. Galactic Motion How fast is a galaxy mov-
ing relative to Earth if a hydrogen spectral
line of 486 nm is red-shifted to 491 nm?
Assume that the relative speed along
the axis is much less than the speed of
light. Thus, you can use the Doppler
shift equation.
(app )
The light is red-shifted, so the astron-
omer and the galaxy are moving away
from each other. So use the positive
form of the apparent light wavelength
equation.
(app )
Solve for the unknown variable.
vc
(3.00108m/s)
3.09106m/s
The original assumption was valid.
61. Suppose that you are facing due east at sun-
rise. Sunlight is reflected off the surface of a
lake, as shown in Figure 16-25. Is the
reflected light polarized? If so, in what
direction?
■Figure 16-25
The reflected light is partially polarized
in the direction parallel to the surface of
the lake and perpendicular to the path
of travel of the light from the lake to
your eyes.
Level 2
62. Polarizing Sunglasses In which direction
should the transmission axis of polarizing
sunglasses be oriented to cut the glare from
the surface of a road: vertically or horizon-
tally? Explain.
The transmission axis should be
oriented vertically, since the light
reflecting off the road will be partially
polarized in the horizontal direction.
A vertical transmission axis will filter
horizontal waves.
63. Galactic Motion A hydrogen spectral line
that is known to be 434 nm is red-shifted
by 6.50 percent in light coming from a dis-
tant galaxy. How fast is the galaxy moving
away from Earth?
Assume that the relative speed along
the axis is much less than the speed of
light. Thus, you can use the Doppler
shift equation.
(app )
The light is red-shifted, so the astron-
omer and the galaxy are moving away
from each other. So use the positive
form of the apparent light wavelength
equation.
(app )
Solve for the unknown variable.
vc
(3.00108m/s)
1.95107m/s
The original assumption was valid.
Level 3
64. For any spectral line, what would be an
unrealistic value of the apparent wavelength
for a galaxy moving away from Earth? Why?
An unrealistic value would make the
galaxy seem to be moving away from us
at a speed close to or greater than the
speed of light, or vc. If this were the
(1.065)(434 nm) 434 nm
434 nm
(app )
v
c
v
c
491 nm 486 nm
486 nm
(app )
v
c
v
c
Chapter 16 continued

case, use of the low-speed Doppler shift
equation would give a wavelength
difference of (app ) . When
solved, this would give an apparent
wavelength of app 2. It would be
twice as large as the actual wavelength.
So any apparent wavelength close to or
greater than twice the actual wave-
length would be unrealistic.
Mixed Review
page 454
Level 1
65. Streetlight Illumination A streetlight
contains two identical bulbs that are 3.3 m
above the ground. If the community wants
to save electrical energy by removing one
bulb, how far from the ground should the
streetlight be positioned to have the same
illumination on the ground under the lamp?
E
If Pis reduced by a factor of 2, so
must d2.
Thus, dis reduced by a factor of 2
,
becoming
2.3 m
66. An octave in music is a doubling of fre-
quency. Compare the number of octaves
that correspond to the human hearing
range to the number of octaves in the
human vision range.
Humans hear over a range of about
nine or ten octaves (20 Hz to 10,240 or
20,480 Hz); however, human vision is
less than one “octave.”
Level 2
67. A 10.0-cd point-source lamp and a 60.0-cd
point-source lamp cast equal intensities on
a wall. If the 10.0-cd lamp is 6.0 m from the
wall, how far from the wall is the 60.0-cd
lamp?
Eand since the intensities on the
wall are equal, the wall is equally
illuminated and
E1E2
So
or d2d1
I
I2
1
(6.0 m)
6
10
0.
.0
0c
c
d
d
15 m
68. Thunder and Lightning Explain why it
takes 5 s to hear thunder when lightning is
1.6 km away.
The time for light to travel 1.6 km is a
small fraction of a second (5.3 s). The
sound travels about 340 m/s, which is
about one-fifth of the 1.6 km every
second, and takes about 4.7 s to travel
1.6 km.
Level 3
69. Solar Rotation Because the Sun rotates on
its axis, one edge of the Sun moves toward
Earth and the other moves away. The Sun
rotates approximately once every 25 days,
and the diameter of the Sun is 1.4109m.
Hydrogen on the Sun emits light of fre-
quency 6.161014 Hz from the two sides of
the Sun. What changes in wavelength are
observed?
Speed of rotation is equal to circumfer-
ence times period of rotation.
vrot
2.04103m/s
3
6.
.0
10
6
1
10
0
8
14
m
H
/s
z
4.87107m
(4.87107m)
3.31012 m
(2.04103m/s)
(3.00108m/s)
vrot
c
v
c
c
f
(1.4109m)
(25 days)(24 h/day)(3600 s/h)
I2
d22
I1
d12
I
d2
(3.3 m)
2
P
4d2
c
c
354 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued
Physics: Principles and Problems Solutions Manual 355
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Thinking Critically
page 454
70. Research Why did Galileo’s method for
measuring the speed of light not work?
It was not precise enough. He was not
able to measure the small time intervals
involved in a terrestrial measurement.
71. Make and Use Graphs A 110-cd light
source is 1.0 m from a screen. Determine
the illumination on the screen originally
and for every meter of increasing distance
up to 7.0 m. Graph the data.
a. What is the shape of the graph?
hyperbola
b. What is the relationship between illumi-
nance and distance shown by the graph?
inverse square
72. Analyze and Conclude If you were to
drive at sunset in a city filled with buildings
that have glass-covered walls, the setting
Sun reflected off the building’s walls might
temporarily blind you. Would polarizing
glasses solve this problem?
Yes. Light reflected off glass is partially
polarized, so polarizing sunglasses will
reduce much of the glare, if the sun-
glasses are aligned correctly.
Writing in Physics
page 454
73. Write an essay describing the history of
human understanding of the speed of light.
Include significant individuals and the con-
tribution that each individual made.
Answers will vary.
74. Look up information on the SI unit
candela, cd, and explain in your own
words the standard that is used to set
the value of 1 cd.
Answers will vary. Begin with the ele-
ment thorium. Heat it to the melting
point of platinum. At this temperature,
the thorium will glow. Surround the tho-
rium with an opaque material that can
take the high temperature. Leave an
opening that is one-sixtieth of a square
centimeter in size. The candela is
defined as the amount of steady flow of
light energy that is emitted by the
thorium through the opening under
these conditions.
Cumulative Review
page 454
75. A 2.0-kg object is attached to a 1.5-m long
string and swung in a vertical circle at a
constant speed of 12 m/s. (Chapter 7)
a. What is the tension in the string when
the object is at the bottom of its path?
Fnet
1.9101N
Fgmg (2.0 kg)(9.80 m/s2)
2.0102N
Fnet TFg
TFnet Fg
1.9102N 0.20102N
2.1102N
b. What is the tension in the string when
the object is at the top of its path?
Fnet TFg
TFnet Fg
1.9102N 0.20102N
1.7102N
(2.0 kg)(12 m/s)2
1.5 m
mv2
r
1.00.0 2.0 3.0 4.0 5.0 6.0 7.0
r (m)
E (lm)
110
100
90
80
70
60
50
40
30
20
10
P 1.4103 lm
Chapter 16 continued

76. A space probe with a mass of 7.600103kg
is traveling through space at 125 m/s.
Mission control decides that a course cor-
rection of 30.0° is needed and instructs the
probe to fire rockets perpendicular to its
present direction of motion. If the gas
expelled by the rockets has a speed of
3.200 km/s, what mass of gas should be
released? (Chapter 9)
tan 30.0°
mg
171 kg
77. When a 60.0-cm-long guitar string is
plucked in the middle, it plays a note of fre-
quency 440 Hz. What is the speed of the
waves on the string? (Chapter 14)
2L2(0.600 m) 1.20 m
vf(1.20 m)(440 Hz) 530 m/s
78. What is the wavelength of a sound wave
with a frequency of 17,000 Hz in water at
25°C? (Chapter 15)
0.0878 m 8.8 cm
Challenge Problem
page 444
You place an analyzer filter between the two
cross-polarized filters, such that its polarizing
axis is not parallel to either of the two filters, as
shown in the figure to the right.
1. You observe that some light passes
through filter 2, though no light passed
through filter 2 previous to inserting the
analyzer filter. Why does this happen?
The analyzer filter allows some light to
pass through, since its polarizing axis
is not perpendicular to the polarizing
axis of the first filter. The last polarizing
filter now can pass light from the ana-
lyzer filter, since the polarizing axis of
the analyzer filter is not perpendicular
to the polarizing axis of the last polariz-
ing filter.
2. The analyzer filter is placed at an angle of
relative to the polarizing axes of filter 1.
Derive an equation for the intensity of light
coming out of filter 2 compared to the
intensity of light coming out of filter 1.
I1is the light intensity out of the first fil-
ter, Ianalyzer is the light intensity out of
the analyzer filter, and I2is the light
intensity out of the last filter.
Ianalyzer I1 cos2
I2Ianalyzer cos2(90°)
I2I1cos2() cos2(90°)
Polarizing
axes
Polarized
light
Filter 1
Analyzer
Filter 2 90°
1493 m/s
17,000 Hz
v
f
(7.600103kg)(125 m/s)(tan 30.0°)
3.200103m/s
mpvp1(tan 30.0°)
vg
mgvg
mpvp1
356 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued

Physics: Principles and Problems Solutions Manual 357
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
17 Reflection and Mirrors
CHAPTER
Practice Problems
17.1 Reflection from Plane
Mirrors
pages 457–463
page 460
1. Explain why the reflection of light off
ground glass changes from diffuse to
specular if you spill water on it.
Water fills in the rough areas and
makes the surface smoother.
2. If the angle of incidence of a ray of light is
42°, what is each of the following?
a. the angle of reflection
r i 42°
b. the angle the incident ray makes with
the mirror
i, mirror 90° i 90° 42° 48°
c. the angle between the incident ray and
the reflected ray
i r 2i 84°
3. If a light ray reflects off a plane mirror at an
angle of 35° to the normal, what was the
angle of incidence of the ray?
ir35°
4. Light from a laser strikes a plane mirror at
an angle of 38° to the normal. If the laser
is moved so that the angle of incidence
increases by 13°, what is the new angle of
reflection?
ii, initial 13°
38° 13° 51°
ri51°
5. Two plane mirrors are positioned at right
angles to one another. A ray of light strikes
one mirror at an angle of 30° to the
normal. It then reflects toward the second
mirror. What is the angle of reflection of
the light ray off the second mirror?
r1 i1 30°
i2 90° r1
90° 30° 60°
Section Review
17.1 Reflection from Plane
Mirrors
pages 457–463
page 463
6. Reflection A light ray strikes a flat, smooth,
reflecting surface at an angle of 80° to the
normal. What is the angle that the reflected
ray makes with the surface of the mirror?
ri
80°
r, mirror 90° r
90° 80°
10°
7. Law of Reflection Explain how the law of
reflection applies to diffuse reflection.
The law of reflection applies to individ-
ual rays of light. Rough surfaces make
the light rays reflect in many different
directions.
8. Reflecting Surfaces Categorize each of the
following as a specular or a diffuse reflect-
ing surface: paper, polished metal, window
glass, rough metal, plastic milk jug, smooth
water surface, and ground glass.
Specular: window glass, smooth water,
polished metal. Diffuse: paper, rough
metal, ground glass, plastic milk jug.
9. Image Properties A 50-cm-tall dog stands
3 m from a plane mirror and looks at its
image. What is the image position, height,
and type?
di do
3 m
hi ho
50 cm
The image is virtual.
10. Image Diagram A car is following another
car down a straight road. The first car has a
rear window tilted 45°. Draw a ray diagram
showing the position of the Sun that would
cause sunlight to reflect into the eyes of the
driver of the second car.
The Sun’s position directly overhead
would likely reflect light into the driver’s
eyes, according to the law of reflection.
11. Critical Thinking Explain how diffuse
reflection of light off an object enables you
to see an object from any angle.
The incoming light reflects off the sur-
face of the object in all directions. This
enables you to view the object from any
location.
Practice Problems
17.2 Curved Mirrors
pages 464–473
page 469
12. Use a ray diagram, drawn to scale, to solve
Example Problem 2.
13. An object is 36.0 cm in front of a concave
mirror with a 16.0-cm focal length.
Determine the image position.
1
f
d
1
o
d
1
i
di
do
do
f
f
28.8 cm
14. A 3.0-cm-tall object is 20.0 cm from a
16.0-cm-radius concave mirror. Determine
the image position and image height.
1
f
d
1
o
d
1
i
di
do
do
f
f
13.3 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
2.0 cm
15. A concave mirror has a 7.0-cm focal length.
A 2.4-cm-tall object is 16.0 cm from the
mirror. Determine the image height.
1
f
d
1
o
d
1
i
di
do
do
f
f
12.4 cm
m
h
h
o
i
d
d
o
i
hi
1.9 cm
(12.4 cm)(2.4 cm)
16.0 cm
diho
do
(16.0 cm)(7.0 cm)
16.0 cm 7.0 cm
(13.3 cm)(3.0 cm)
20.0 cm
(20.0 cm)
16.0
2cm
20.0 cm
16.0
2cm
(36.0 cm)(16.0 cm)
36.0 cm 16.0 cm
FC
O1
I1
Horizontal scale:
1 block 1.0 cm
Vertical scale:
3 blocks 1.0 cm
Ray 1
Ray 2
45°
45°
45°
The Sun
Driver of
second car
Rear window
of first car
Road grade
358 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued

Physics: Principles and Problems Solutions Manual 359
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
16. An object is near a concave mirror of
10.0-cm focal length. The image is 3.0 cm
tall, inverted, and 16.0 cm from the mirror.
What are the object position and object
height?
1
f
d
1
o
d
1
i
do
di
d
if
f
26.7 cm
m
h
h
o
i
d
d
o
i
ho
d
d
o
i
hi
5.0 cm
page 472
17. An object is located 20.0 cm in front of a
convex mirror with a 15.0-cm focal
length. Find the image position using both
a scale diagram and the mirror equation.
d
1
o
d
1
i
1
f
so di
do
do
f
f
8.57 cm
18. A convex mirror has a focal length of
13.0 cm. A lightbulb with a diameter of
6.0 cm is placed 60.0 cm from the mirror.
What is the lightbulb’s image position and
diameter?
d
1
o
d
1
i
1
f
di
do
do
f
f
10.7 cm
m
h
h
o
i
d
d
o
i
m
(
60
1
.
0
0
.7
cm
cm)
0.178
hi mho (0.178)(6.0 cm)
1.1 cm
19. A convex mirror is needed to produce an
image that is three-fourths the size of an
object and located 24 cm behind the mir-
ror. What focal length should be specified?
1
f
d
1
i
d
1
o
f and m
d
d
o
i
so do
m
di
di 24 cm and m 0.75, so
do
(
0
2
.7
4
5
cm)
32 cm
f
96 cm
20. A 7.6-cm-diameter ball is located 22.0 cm
from a convex mirror with a radius of cur-
vature of 60.0 cm. What are the ball’s image
position and diameter?
1
f
d
1
o
d
1
i
di
do
do
f
f
12.7 cm
(22.0 cm)(30.0 cm)
22.0 cm (30.0 cm)
(32 cm)(24 cm)
32 cm (24 cm)
dodi
dodi
(60.0 cm)(13.0 cm)
60.0 cm (13.0 cm)
(20.0 cm)(15.0 cm)
20.0 cm (15.0 cm)
Ray 1
Ray 2 F
I1
di 8.6 cm
O1
Horizontal scale:
1 block 1.0 cm
(26.7 cm)(3.0 cm)
16.0 cm
(16.0 cm)(10.0 cm)
16.0 cm 10.0 cm
Chapter 17 continued

m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
4.4 cm
21. A 1.8-m-tall girl stands 2.4 m from a store’s
security mirror. Her image appears to be
0.36 m tall. What is the focal length of the
mirror?
m
h
h
o
i
d
d
o
i
di
d
h
o
o
hi
0.48 m
1
f
d
1
o
d
1
i
f
di
d
ido
do
0.60 m
Section Review
17.2 Curved Mirrors
pages 464–473
page 473
22. Image Properties If you know the focal
length of a concave mirror, where should
you place an object so that its image is
upright and larger compared to the object?
Will this produce a real or virtual image?
You should place the object between
the mirror and the focal point. The
image will be virtual.
23. Magnification An object is placed 20.0 cm
in front of a concave mirror with a focal
length of 9.0 cm. What is the magnification
of the image?
1
f
d
1
o
d
1
i
di
do
do
f
f
16.4 cm
m
d
d
o
i
21
06
.0
.4cc
m
m
0.82
24. Object Position The placement of an
object in front of a concave mirror with a
focal length of 12.0 cm forms a real image
that is 22.3 cm from the mirror. What is the
object position?
1
f
d
1
o
d
1
i
do
di
d
if
f
26.0 cm
25. Image Position and Height A 3.0-cm-tall
object is placed 22.0 cm in front of a
concave mirror having a focal length of
12.0 cm. Find the image position and
height by drawing a ray diagram to scale.
Verify your answer using the mirror and
magnification equations.
1
f
d
1
o
d
1
i
di
do
do
f
f
I1
O1
F
C
hi 3.6 cm
di 26.4 cm
Ray 1
Ray 2
Horizontal scale:
1 block 1.0 cm
Vertical scale:
1 block 1.0 cm
(22.3 cm)(12.0 cm)
22.3 cm 12.0 cm
(20.0 cm)(9.0 cm)
20.0 cm 9.0 cm
(0.48 m)(2.4 m)
0.48 m 2.4 m
(2.4 m)(0.36 m)
1.8 m
(12.7 cm)(7.6 cm)
22.0 cm
360 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued

Physics: Principles and Problems Solutions Manual 361
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
26.4 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
3.6 cm
26. Ray Diagram A 4.0-cm-tall object is
located 14.0 cm from a convex mirror with
a focal length of 12.0 cm. Draw a scale
ray diagram showing the image position
and height. Verify your answer using the
mirror and magnification equations.
1
f
d
1
o
di
do
do
f
f
6.46 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
1.8 cm
27. Radius of Curvature A 6.0-cm-tall object
is placed 16.4 cm from a convex mirror. If
the image of the object is 2.8 cm tall, what
is the radius of curvature of the mirror?
m
h
h
o
i
d
d
o
i
di
d
h
o
o
hi
7.7 cm
1
f
d
1
o
d
1
i
f
do
do
di
di
14.5 cm
r2f
(2)(14.5 cm)
29 cm
28. Focal Length A convex mirror is used to
produce an image that is two-thirds the
size of an object and located 12 cm behind
the mirror. What is the focal length of the
mirror?
m
h
h
o
i
d
d
o
i
do
m
di
18 cm
1
f
d
1
o
d
1
i
f
do
do
di
di
36 cm
29. Critical Thinking Would spherical aberra-
tion be less for a mirror whose height,
compared to its radius of curvature, is
small or large? Explain.
It would be less for a mirror whose
height is relatively small compared to
(12 cm)(18 cm)
12 cm 18 cm
(12 cm)
2
3
(7.7 cm)(16.4 cm)
7.7 cm 16.4 cm
(16.4 cm)(2.8 cm)
6.0 cm
(6.46 cm)(4.0 cm)
14.0 cm
(14.0 cm)(12.0 cm)
14.0 cm (12.0 cm)
1
di
I1
F
O1
Horizontal scale:
1 block 1.0 cm
Vertical scale:
3 blocks 2.0 cm
hi 1.8 cm
di 6.5 cm
Ray 1
Ray 2
(26.4 cm)(3.0 cm)
22.0 cm
(22.0 cm)(12.0 cm)
22.0 cm 12.0 cm
Chapter 17 continued
its radius of curvature; diverging light
rays from an object that strike the mir-
ror are more paraxial so they converge
more closely to create an image that is
not blurred.
Chapter Assessment
Concept Mapping
page 478
30. Complete the following concept map using
the following terms: convex, upright, inverted,
real, virtual.
Mastering Concepts
page 478
31. How does specular reflection differ from
diffuse reflection? (17.1)
When parallel light is reflected from a
smooth surface, the rays are reflected
parallel to each other.The result is an
image of the origin of the rays. When
light is reflected from a rough surface, it
is reflected in many different directions.
The rays are diffused or scattered. No
image of the source results.
32. What is meant by the phrase “normal to the
surface”? (17.1)
any line that is perpendicular to the
surface at any point
33. Where is the image produced by a plane
mirror located? (17.1)
The image is on a line that is
perpendicular to the mirror and the
same distance behind the mirror as the
object is in front of the mirror.
34. Describe the properties of a plane mirror.
(17.1)
A plane mirror is a flat, smooth
surface from which light is reflected by
specular reflection. The images created
by plane mirrors are virtual, upright,
and as far behind the mirror as the
object is in front of it.
35. A student believes that very sensitive
photographic film can detect a virtual
image. The student puts photographic film
at the location of a virtual image. Does this
attempt succeed? Explain. (17.1)
No, the rays do not converge at a virtual
image. No image forms and the student
would not get a picture. Some virtual
images are behind the mirror.
36. How can you prove to someone that an
image is a real image? (17.1)
Place a sheet of plain paper or photo-
graphic film at the image location and
you should be able to find the image.
37. An object produces a virtual image in a
concave mirror. Where is the object located?
(17.2)
Object must be located between Fand
the mirror.
38. What is the defect that all concave spherical
mirrors have and what causes it? (17.2)
Rays parallel to the axis that strike the
edges of a concave spherical mirror are
not reflected through the focal point.
This effect is called spherical aberration.
39. What is the equation relating the focal point,
object position, and image position? (17.2)
1
f
d
1
i
d
1
o
40. What is the relationship between the
center of curvature and the focal length
of a concave mirror? (17.2)
C 2f
362 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued
plane concave
Mirrors
convex
virtual real virtual virtual
upright inverted upright upright

Physics: Principles and Problems Solutions Manual 363
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
41. If you know the image position and object
position relative to a curved mirror, how can
you determine the mirror’s magnification?
(17.2)
The magnification is equal to the
negative of the image distance divided
by the object distance.
42. Why are convex mirrors used as rearview
mirrors? (17.2)
Convex mirrors are used as rearview
mirrors because they allow for a wide
range of view, allowing the driver to see
a much larger area than is afforded by
ordinary mirrors.
43. Why is it impossible for a convex mirror to
form a real image? (17.2)
The light rays always diverge.
Applying Concepts
pages 478–479
44. Wet Road A dry road is more of a
diffuse reflector than a wet road. Based
on Figure 17-16, explain why a wet
road appears blacker to a driver than
a dry road does.
■Figure 17-16
Less light is reflected back to the car
from a wet road.
45. Book Pages Why is it desirable that the
pages of a book be rough rather than
smooth and glossy?
The smoother and glossier the pages
are, the lesser the diffuse reflection of
light and the greater the glare from
the pages.
46. Locate and describe the physical properties
of the image produced by a concave mirror
when the object is located at the center of
curvature.
The image will be at C, the center of
curvature, inverted, real, and the same
size as the object.
47. An object is located beyond the center of
curvature of a spherical concave mirror.
Locate and describe the physical properties
of the image.
The image will be between Cand F, and
will be inverted, real, and smaller than
the object.
48. Telescope You have to order a large
concave mirror for a telescope that
produces high-quality images. Should you
order a spherical mirror or a parabolic
mirror? Explain.
You should order a parabolic mirror to
eliminate spherical aberrations.
49. Describe the properties of the image seen in
the single convex mirror in Figure 17-17.
■Figure 17-17
The image in a single convex mirror is
always virtual, erect, smaller than the
object, and located closer to the mirror
than the object.
Dry asphalt
Wet asphalt
Chapter 17 continued

50. List all the possible arrangements in which
you could use a spherical mirror, either
concave or convex, to form a real image.
You can use only a concave mirror with
the object beyond the focal point. A con-
vex mirror will not form a real image.
51. List all possible arrangements in which you
could use a spherical mirror, either concave
or convex, to form an image that is smaller
compared to the object.
You may use a concave mirror with the
object beyond the center of curvature
or a convex mirror with the object
anywhere.
52. Rearview Mirrors The outside rearview
mirrors of cars often carry the warning
“Objects in the mirror are closer than they
appear.” What kind of mirrors are these and
what advantage do they have?
Convex mirror; it provides a wider field
of view.
Mastering Problems
17.1 Reflection from Plane Mirrors
page 479
Level 1
53. A ray of light strikes a mirror at an angle of
38° to the normal. What is the angle that
the reflected angle makes with the normal?
r i
38°
54. A ray of light strikes a mirror at an angle of
53° to the normal.
a. What is the angle of reflection?
r i
53°
b. What is the angle between the incident
ray and the reflected ray?
i r
53° 53°
106°
55. A ray of light incident upon a mirror makes
an angle of 36° with the mirror. What is the
angle between the incident ray and the
reflected ray?
i 90° 36°
54°
r i
54°
i r
54° 54°
108°
Level 2
56. Picture in a Mirror Penny wishes to take a
picture of her image in a plane mirror, as
shown in Figure 17-18. If the camera is
1.2 m in front of the mirror, at what dis-
tance should the camera lens be focused?
■Figure 17-18
The image is 1.2 m behind the mirror, so
the camera lens should be set to 2.4 m.
57. Two adjacent plane mirrors form a right
angle, as shown in Figure 17-19. A light ray
is incident upon one of the mirrors at an
angle of 30° to the normal.
364 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued
Physics: Principles and Problems Solutions Manual 365
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
■Figure 17-19
a. What is the angle at which the light ray
is reflected from the other mirror?
Reflection from the first mirror:
r1 i1 30°
Reflection from the second mirror:
i2 90° r1
90° 30°
60°
r2 i2
60°
b. A retroreflector is a device that reflects
incoming light rays back in a direction
opposite to that of the incident rays.
Draw a diagram showing the angle of
incidence on the first mirror for which
the mirror system acts as a retroreflector.
58. Draw a ray diagram of a plane mirror to
show that if you want to see yourself from
your feet to the top of your head, the mirror
must be at least half your height.
The ray from the top of the head hits
the mirror halfway between the eyes
and the top of the head. The ray from
the feet hits the mirror halfway between
the eyes and the feet.The distance
between the point the two rays hit the
mirror is half the total height.
Level 3
59. Two plane mirrors are connected at their
sides so that they form a 45° angle between
them. A light ray strikes one mirror at an
angle of 30° to the normal and then reflects
off the second mirror. Calculate the angle of
reflection of the light ray off the second
mirror.
Reflection from the first mirror is
r, 1 i, 1 30°. The angle the ray
forms with the mirror is thus 90° 30°
60°. Because the two mirrors form a 45°
angle, the angle the ray reflecting off
the first mirror forms with the second
mirror is 180° 60° 45° 75°. The
angle the ray forms with the second
mirror is thus i, 2 90° 75° 15°.
The angle of reflection from the second
mirror is r, 2 i, 2 15°.
60. A ray of light strikes a mirror at an angle of
60° to the normal. The mirror is then rotated
18° clockwise, as shown in Figure 17-20.
What is the angle that the reflected ray
makes with the mirror?
■Figure 17-20
ii, old 18°
60° 18°
42°
60°
18°
Normal
Incident light
Mirror
ImageMirror
Eye
level
Feet
45°
30°
Chapter 17 continued
ri
42°
r, mirror 90° r
90° 42°
48°
17.2 Curved Mirrors
page 480
Level 1
61. A concave mirror has a focal length of
10.0 cm. What is its radius of curvature?
r 2f 2(10.0 cm) 20.0 cm
62. An object located 18 cm from a convex
mirror produces a virtual image 9 cm from
the mirror. What is the magnification of the
image?
m
d
d
o
i
(
1
8
9
c
c
m
m)
0.5
63. Fun House A boy is standing near a
convex mirror in a fun house at a fair. He
notices that his image appears to be
0.60 m tall. If the magnification of the
mirror is
1
3
, what is the boy’s height?
m
h
h
o
i
ho
m
hi
1.8 m
64. Describe the image produced by the object
in Figure 17-21 as real or virtual, inverted
or upright, and smaller or larger than the
object.
■Figure 17-21
real; inverted; larger
Level 2
65. Star Image Light from a star is collected by
a concave mirror. How far from the mirror
is the image of the star if the radius of
curvature is 150 cm?
Stars are far enough away that the
light coming into the mirror can be
considered to be parallel and parallel
light will converge at the focal point.
Since r 2f,
f
2
r
150
2cm
75 cm
66. Find the image position and height for the
object shown in Figure 17-22.
■Figure 17-22
1
f
d
1
o
d
1
i
di
do
do
f
f
(31 cm)(16 cm)
31 cm 16 cm
F
16 cm
3.8 cm
31 cm
CF
0.60 m
1
3
366 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued

Physics: Principles and Problems Solutions Manual 367
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
33 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
4.1 cm
67. Rearview Mirror How far does the image
of a car appear behind a convex mirror,
with a focal length of 6.0 m, when the car
is 10.0 m from the mirror?
1
f
d
1
o
d
1
i
di
do
do
f
f
3.8 m
68. An object is 30.0 cm from a concave mirror
of 15.0 cm focal length. The object is
1.8 cm tall. Use the mirror equation to
find the image position. What is the image
height?
d
1
o
d
1
i
1
f
di
do
do
f
f
30.0 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
1.8 cm
69. Dental Mirror A dentist uses a small mir-
ror with a radius of 40 mm to locate a
cavity in a patient’s tooth. If the mirror is
concave and is held 16 mm from the tooth,
what is the magnification of the image?
f
2
r
(40
2
mm)
20 mm
d
1
o
d
1
i
1
f
di
do
do
f
f
80 mm
m
d
d
o
i
(
16
80
m
m
m
m)
5
70. A 3.0-cm-tall object is 22.4 cm from a
concave mirror. If the mirror has a radius of
curvature of 34.0 cm, what are the image
position and height?
f
2
r
34.0
2cm
17.0 cm
1
f
d
1
o
d
1
i
di
do
do
f
f
70.5 cm
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
9.4 cm
Level 3
71. Jeweler’s Mirror A jeweler inspects a
watch with a diameter of 3.0 cm by placing
it 8.0 cm in front of a concave mirror of
12.0-cm focal length.
a. Where will the image of the watch
appear?
d
1
o
d
1
i
1
f
(70.5 cm)(3.0 cm)
22.4 cm
(22.4 cm)(17.0 cm)
22.4 cm 17.0 cm
(16 mm)(20 mm)
16 mm 20 mm
(30.0 cm)(1.8 cm)
(30.0 cm)
(30.0 cm)(15.0 cm)
30.0 cm 15.0 cm
(10.0 m)(6.0 m)
10.0 m (6.0 m)
(33 cm)(3.8 cm)
31 cm
Chapter 17 continued
di
do
do
f
f
24 cm
b. What will be the diameter of the image?
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
9.0 cm
72. Sunlight falls on a concave mirror and
forms an image that is 3.0 cm from the
mirror. An object that is 24 mm tall is
placed 12.0 cm from the mirror.
a. Sketch the ray diagram to show the
location of the image.
b. Use the mirror equation to calculate the
image position.
d
1
o
d
1
i
1
f
di
4.0 cm
c. How tall is the image?
m
d
d
o
i
12
4..0
0c
cm
m
0.33
hi mho (0.33)(24 mm)
8.0 mm
73. Shiny spheres that are placed on pedestals
on a lawn are convex mirrors. One such
sphere has a diameter of 40.0 cm.
A 12-cm-tall robin sits in a tree that is
1.5 m from the sphere. Where is the image
of the robin and how tall is the image?
r 20.0 cm, f 10.0 cm
d
1
o
d
1
i
1
f
di
do
fd
o
f
9.4 cm
m
d
d
o
i
(
1
5
9
0
.4
cm
cm)
0.063
hi mho (0.063)(12 cm) 0.75 cm
Mixed Review
pages 480–481
Level 1
74. A light ray strikes a plane mirror at an angle
of 28° to the normal. If the light source is
moved so that the angle of incidence
increases by 34°, what is the new angle of
reflection?
ii, initial 34°
28°34°
62°
ri
62°
75. Copy Figure 17-23 on a sheet of paper.
Draw rays on the diagram to determine the
height and location of the image.
■Figure 17-23
F
8.0 cm 4.0 cm
3.0 cm
(10.0 cm)(150 cm)
150 cm (10.0 cm)
(3.0 cm)(12.0 cm)
12.0 cm 3.0 cm
fdo
do f
I1
O1
CF
Ray 1
Ray 2
Horizontal scale:
1 block 1.0 cm
Vertical scale:
1 block 4 mm
(24 cm)(3.0 cm)
8.0 cm
(8.0 cm)(12.0 cm)
8.0 cm 12.0 cm
368 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued
Physics: Principles and Problems Solutions Manual 369
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The image height is 1.0 cm, and its
location is 2.7 cm from the mirror.
Level 2
76. An object is located 4.4 cm in front of a
concave mirror with a 24.0-cm radius.
Locate the image using the mirror equation.
f
2
r
24.0
2cm
12.0 cm
1
f
d
1
o
d
1
i
di
do
do
f
f
6.9 cm
77. A concave mirror has a radius of curvature
of 26.0 cm. An object that is 2.4 cm tall is
placed 30.0 cm from the mirror.
a. Where is the image position?
f
2
r
26.0
2cm
13.0 cm
1
f
d
1
o
d
1
i
di
do
do
f
f
22.9 cm
b. What is the image height?
m
h
h
o
i
hi
d
d
i
o
ho
1.8 cm
78. What is the radius of curvature of a concave
mirror that magnifies an object by a factor
of 3.2 when the object is placed 20.0 cm
from the mirror?
m
h
h
o
i
dimdo
(3.2)(20.0 cm)
64 cm
1
f
d
1
o
d
1
i
f
do
do
di
di
29 cm
r2f
(2)(29 cm)
58 cm
79. A convex mirror is needed to produce an
image one-half the size of an object and
located 36 cm behind the mirror. What
focal length should the mirror have?
m
h
h
o
i
d
d
o
i
do
d
h
i
i
ho
72 cm
1
f
d
1
o
d
1
i
(36 cm)ho
h
2
o
(20.0 cm)(64 cm)
20.0 cm (64 cm)
(22.9 cm)(2.4 cm)
30.0 cm
(30.0 cm)(13.0 cm)
30.0 cm 13.0 cm
(4.4 cm)(12.0 cm)
4.4 cm 12.0 cm
Horizontal scale:
1 block 1.0 cm
Vertical scale:
2 blocks 1.0 cm
F
I1hi 1.0 cm
di 2.7 cm
O1
Chapter 17 continued
f
do
do
di
di
72 cm
80. Surveillance Mirror A convenience store
uses a surveillance mirror to monitor the
store’s aisles. Each mirror has a radius of
curvature of 3.8 m.
a. What is the image position of a customer
who stands 6.5 m in front of the mirror?
A mirror that is used for surveillance
is a convex mirror. So the focal
length is the negative of half the
radius of curvature.
f
2r
3.
2
8m
1.9 m
1
f
d
1
o
d
1
i
di
do
do
f
f
1.5 m
b. What is the image height of a customer
who is 1.7 m tall?
m
h
h
o
i
d
d
o
i
hi
d
d
i
o
ho
0.38 m
Level 3
81. Inspection Mirror A production-line
inspector wants a mirror that produces an
image that is upright with a magnification
of 7.5 when it is located 14.0 mm from a
machine part.
a. What kind of mirror would do this job?
An enlarged, upright image results
only from a concave mirror, with the
object inside the focal length.
b. What is its radius of curvature?
m
d
d
o
i
di mdo (7.5)(14.0 mm)
105 mm
d
1
o
d
1
i
1
f
f
di
d
od
d
i
o
16 mm
r 2f (2)(16mm)
32 mm
82. The object in Figure 17-24 moves from
position 1 to position 2. Copy the diagram
onto a sheet of paper. Draw rays showing
how the image changes.
■Figure 17-24
83. A ball is positioned 22 cm in front of a spheri-
cal mirror and forms a virtual image. If the
spherical mirror is replaced with a plane mir-
ror, the image appears 12 cm closer to the mir-
ror. What kind of spherical mirror was used?
Horizontal scale:
1 block 10 cm
F
I2
I1
O1O2
Ray 1 Ray 1
12
C
Ray 2
Ray 2
FC
1
2
2.5 m
2.0 m
1.5 m
1.0 m
(14.0 mm)(105 mm)
14.0 mm (105 mm)
(1.5 m)(1.7 m)
6.5 m
(6.5 m)(1.9 m)
6.5 m (1.9 m)
(72 cm)(36 cm)
72 cm (36 cm)
370 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued
Physics: Principles and Problems Solutions Manual 371
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The object position for both mirrors is
22 cm. So, the image position for the
plane mirror is 22 cm.
Because the spherical mirror forms a
virtual image, the image is located
behind the mirror. Thus, the image posi-
tion for the spherical mirror is negative.
didi, plane 12 cm
22 cm 12 cm
34 cm
1
f
d
1
o
d
1
i
f
do
do
di
di
62 cm
The focal length is positive, so the
spherical mirror is a concave mirror.
84. A 1.6-m-tall girl stands 3.2 m from a convex
mirror. What is the focal length of the mirror
if her image appears to be 0.28 m tall?
m
h
h
o
i
d
d
o
i
di
h
h
i
o
do
0.56 m
1
f
d
1
o
d
1
i
f
do
do
di
di
0.68 m
85. Magic Trick A magician uses a concave
mirror with a focal length of 8.0 m to make a
3.0-m-tall hidden object, located 18.0 m from
the mirror, appear as a real image that is seen
by his audience. Draw a scale ray diagram to
find the height and location of the image.
The image is 2.4 m tall, and it is 14 m
from the mirror.
86. A 4.0-cm-tall object is placed 12.0 cm from a
convex mirror. If the image of the object is
2.0 cm tall, and the image is located at
6.0 cm, what is the focal length of the mir-
ror? Draw a ray diagram to answer the ques-
tion. Use the mirror equation and the mag-
nification equation to verify your answer.
1
f
d
1
o
d
1
i
f
do
do
di
di
12 cm
Thinking Critically
pages 481–482
87. Apply Concepts The ball in Figure 17-25
slowly rolls toward the concave mirror on the
right. Describe how the size of the ball’s image
changes as it rolls along.
■Figure 17-25
FC
(12.0 cm)(6.0 cm)
12.0 cm (6.0 cm)
Horizontal scale:
1 block 1.0 cm
Vertical scale:
3 blocks 2.0 cm
F
I1
f 12 cm
O1Ray 1
Ray 2
I1
O1
CF
Ray 1
Ray 2 Horizontal scale:
1 block 1.0 m
Vertical scale:
2 blocks 1.0 m
hi 2.4 m
di 14 m
(3.2 m)(0.56 m)
3.2 m (0.56 m)
(0.28 m)(3.2 m)
1.6 m
(22 cm)(34 cm)
22 cm (34 cm)
Chapter 17 continued
Beyond C, the image is smaller than the
ball. As the ball rolls toward the mirror,
the image size increases. The image is
the same size as the ball when the ball
is at C. The image size continues to
increase until there is no image when
the ball is at F. Past F, the size of the
image decreases until it equals the
ball’s size when the ball touches the
mirror.
88. Analyze and Conclude The object in
Figure 17-26 is located 22 cm from a
concave mirror. What is the focal length
of the mirror?
■Figure 17-26
f
2
r
d
2
o
222
cm
11 cm
89. Use Equations Show that as the radius of
curvature of a concave mirror increases to
infinity, the mirror equation reduces to the
relationship between the object position
and the image position for a plane mirror.
As f→,1/f→0. The mirror equation
then becomes 1/do 1/di,or do di.
90. Analyze and Conclude An object is located
6.0 cm from a plane mirror. If the plane mir-
ror is replaced with a concave mirror, the
resulting image is 8.0 cm farther behind the
mirror. Assuming that the object is located
between the focal point and the concave
mirror, what is the focal length of the con-
cave mirror?
di, initial do, initial
6.0 cm
didi, initial (8.0 cm)
6.0 cm (8.0 cm)
14.0 cm
1
f
d
1
o
d
1
i
f
do
do
di
di
f
f1.0101cm
91. Analyze and Conclude The layout of the
two-mirror system shown in Figure 17-11 is
that of a Gregorian telescope. For this
question, the larger concave mirror has a
radius of curvature of 1.0 m, and the
smaller mirror is located 0.75 m away. Why
is the secondary mirror concave?
The smaller mirror is concave to produce
a real image at the eyepiece that is
upright.The light rays are inverted by the
first concave mirror and then inverted
again by the secondary concave mirror.
92. Analyze and Conclude An optical arrange-
ment used in some telescopes is the
Cassegrain focus, shown in Figure 17-27.
This telescope uses a convex secondary
mirror that is positioned between the
primary mirror and the focal point of
the primary mirror.
■Figure 17-27
a. A single convex mirror produces only
virtual images. Explain how the convex
Convex
secondary mirror
Concave
primary mirror
Eyepiece
Telescope tube
F
(6.0 cm)(14.0 cm)
6.0 cm (14.0 cm)
22 cm
372 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued

Physics: Principles and Problems Solutions Manual 373
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
mirror in this telescope functions within
the system of mirrors to produce real
images.
The convex mirror is placed to inter-
cept the rays from a concave mirror
before they converge. The convex
mirror places the point of conver-
gence in the opposite direction back
toward the concave mirror, and
lengthens the total distance the light
travels before converging. This
effectively increases the focal length
compared to using the concave mir-
ror by itself, thus increasing the
total magnification.
b. Are the images produced by the
Cassegrain focus upright or inverted?
How does this relate to the number of
times that the light crosses?
Inverted; each time the light rays
cross the image inverts.
Writing in Physics
page 482
93. Research a method used for grinding, polish-
ing, and testing mirrors used in reflecting
telescopes. You may report either on meth-
ods used by amateur astronomers who make
their own telescope optics, or on a method
used by a project at a national laboratory.
Prepare a one-page report describing the
method, and present it to the class.
Answers will vary depending on the
mirrors and methods chosen by the stu-
dents. Amateur methods usually involve
rubbing two “blanks”against each other
with varying grits between them.
Methods used at national labs vary.
94. Mirrors reflect light because of their metal-
lic coating. Research and write a summary
of one of the following:
a. the different types of coatings used and
the advantages and disadvantages of each
Answers will vary. Student answers
should include information about
shininess as well as tarnish
resistance.
b. the precision optical polishing of alu-
minum to such a degree of smoothness
that no glass is needed in the process of
making a mirror
Answers will vary. Student answers
might include information about
deformation of a mirror from its own
weight as size increases and how a
mirror made of aluminum could
impact this problem.
Cumulative Review
page 482
95. A child runs down the school hallway and
then slides on the newly waxed floor. He
was running at 4.7 m/s before he started
sliding and he slid 6.2 m before stopping.
What was the coefficient of friction of the
waxed floor? (Chapter 11)
The work done by the waxed floor
equals the child’s initial kinetic energy.
KE
1
2
mv2 W Fd kmgd
The mass of the child cancels out, giving
k
2
v
g
2
d
0.18
96. A 1.0 g piece of copper falls from a height of
1.0104m from an airplane to the ground.
Because of air resistance it reaches the ground
moving at a velocity of 70.0 m/s. Assuming
that half of the energy lost by the piece was dis-
tributed as thermal energy to the copper, how
much did it heat during the fall? (Chapter 12)
Potential energy of the piece
E mgh
(0.0010 kg)(9.80 m/s2)(1.0104m)
9.8 J
Final energy
Ef
1
2
mv2
1
2
(0.0010 kg)(70.0 m/s)2
2.4 J
(4.7 m/s)2
(2)(9.80 m/s2)(6.2 m)
Chapter 17 continued

Heat added to the piece
Q
1
2
(E Ef)
1
2
(9.8 J 2.4 J)
3.7 J
T
m
Q
c
9.5°C
97. It is possible to lift a person who is sitting on a
pillow made from a large sealed plastic garbage
bag by blowing air into the bag through a soda
straw. Suppose that the cross-sectional area of
the person sitting on the bag is 0.25 m2and
the person’s weight is 600 N. The soda straw
has a cross-sectional area of 2105m2. With
what pressure must you blow into the straw to
lift the person that is sitting on the sealed
garbage bag? (Chapter 13)
Apply Pascal’s principle.
F2F1
A
A
1
2
(600 N)
2
01
.2
0
5
m
5m
2
2
0.048 N
P
A
F
2
2
2.4 kPa
or 2 kPa to one significant digit
not a very large pressure at all
98. What would be the period of a 2.0-m-long
pendulum on the Moon’s surface? The
Moon’s mass is 7.341022 kg, and its
radius is 1.74106m. What is the period of
this pendulum on Earth? (Chapter 14)
gm
1.62 m/s2
TMoon 2
g
l
2
1.6
22
.0m
m
/s2
7.0 s
TEarth 2
g
l
2
9.8
20
.0m
m
/s2
2.8 s
99. Organ pipes An organ builder must design
a pipe organ that will fit into a small space.
(Chapter 15)
a. Should he design the instrument to have
open pipes or closed pipes? Explain.
The resonant frequency of an open
pipe is twice that of a closed pipe
of the same length. Therefore, the
pipes of a closed-pipe organ need
be only half as long as open pipes
to produce the same range of
fundamental frequencies.
b. Will an organ constructed with open
pipes sound the same as one con-
structed with closed pipes? Explain.
No. While the two organs will have
the same fundamental tones,
closed pipes produce only the odd
harmonics, so they will have differ-
ent timbres than open pipes.
100. Filters are added to flashlights so that one
shines red light and the other shines green
light. The beams are crossed. Explain in
terms of waves why the light from both
flashlights is yellow where the beams
cross, but revert back to their original
colors beyond the intersection point.
(Chapter 16)
Waves can interfere, add, and then
pass through unaffected. Chapter 14
showed the amplitude of waves
adding. In this case, the waves retain
their color information as they cross
through each other.
Challenge Problem
page 470
An object of height hois located at dorelative to
a concave mirror with focal length f.
1. Draw and label a ray diagram showing the
focal length and location of the object if the
image is located twice as far from the
mirror as the object. Prove your answer
mathematically. Calculate the focal length
as a function of object position for this
placement.
(6.671011
Nm2/kg2)(7.341022 kg)
Gmm
d2m
0.048 N
2105m2
3.7 J
(0.0010 kg)(385 J/kg°C)
374 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 17 continued

Physics: Principles and Problems Solutions Manual 375
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1
f
d
1
o
d
1
i
f
do
do
di
di
d
d
o
o
(2d
2o
d
)
o
2. Draw and label a ray diagram showing the
location of the object if the image is located
twice as far from the mirror as the focal
point. Prove your answer mathematically.
Calculate the image height as a function of
the object height for this placement.
1
f
d
1
o
d
1
i
do
di
fd
if
2f
m
h
h
o
i
d
d
o
i
hi
d
di
o
ho
ho
3. Where should the object be located so that
no image is formed?
The object should be placed at the focal
point.
(2f)ho
2f
f(2f)
2ff
I1
C
O1Ray 1
di 2f
hi hO
F
Ray 2
2do
3
C
O1Ray 1
Ray 2
di 2dO
f
2dO
3
F
Chapter 17 continued


Physics: Principles and Problems Solutions Manual 377
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
18 Refraction and Lenses
CHAPTER
Practice Problems
18.1 Refraction of Light
pages 485–492
page 487
1. A laser beam in air is incident upon ethanol
at an angle of incidence of 37.0°. What is
the angle of refraction?
n1 sin 1 n2 sin 2
2 sin1
sin1
26.3°
2. Light in air is incident upon a piece of
crown glass at an angle of incidence of
45.0°. What is the angle of refraction?
n1 sin 1 n2 sin 2
2 sin1
sin1
27.7°
3. Light passes from air into water at 30.0° to
the normal. Find the angle of refraction.
n1 sin 1 n2 sin 2
2 sin1
sin1
22.1°
4. Light is incident upon a diamond facet at
45.0°. What is the angle of refraction?
n1 sin 1 n2 sin 2
2 sin1
sin1
17.0°
5. A block of unknown material is submerged
in water. Light in the water is incident on
the block at an angle of incidence of 31°.
The angle of refraction of the light in the
block is 27°. What is the index of refraction
of the material of the block?
n1 sin 1 n2 sin 2
n2
1.5
Section Review
18.1 Refraction of Light
pages 485–492
page 492
6. Index of Refraction You notice that when
a light ray enters a certain liquid from
water, it is bent toward the normal, but
when it enters the same liquid from crown
glass, it is bent away from the normal. What
can you conclude about the liquid’s index
of refraction?
nwater nliquid ncrown glass,therefore,
nliquid must be between 1.33 and 1.52.
7. Index of Refraction A ray of light has an
angle of incidence of 30.0° on a block
of unknown material and an angle of
refraction of 20.0°. What is the index of
refraction of the material?
n1 sin 1n2 sin 2
n2
1.46
(1.00)(sin 30.0°)
sin 20.0°
n1 sin 1
sin 2
(1.33)(sin 31°)
sin 27°
n1 sin 1
sin 2
(1.00)(sin 45.0°)
2.42
n1 sin 1
n2
(1.00)(sin 30.0°)
1.33
n1 sin 1
n2
(1.00)(sin 45.0°)
1.52
n1 sin 1
n2
(1.00)(sin 37.0°)
1.36
n1 sin 1
n2

8. Speed of Light Could an index of
refraction ever be less than 1? What would
this imply about the speed of light in that
medium?
No, it would mean the speed of light in
the medium is faster than it is in a
vacuum.
9. Speed of Light What is the speed of light
in chloroform (n1.51)?
n
vchloroform
1.99108m/s
10. Total Internal Reflection If you were to
use quartz and crown glass to make an
optical fiber, which would you use for the
cladding layer? Why?
crown glass because it has a lower
index of refraction and would produce
total internal reflection
11. Angle of Refraction A beam of light
passes from water into polyethylene with
n1.50. If i 57.5°, what is the angle of
refraction in the polyethylene?
n1 sin 1n2 sin 2
2sin1
sin1
48.4°
12. Critical Angle Is there a critical angle for
light traveling from glass to water? From
water to glass?
Yes, because nglass nwater.No.
13. Dispersion Why can you see the image of
the Sun just above the horizon when the
Sun itself has already set?
because of bending of light rays in the
atmosphere; refraction
14. Critical Thinking In what direction can
you see a rainbow on a rainy late after-
noon? Explain.
In the east, because the Sun sets in the
west and sunlight must shine from
behind you in order for you to see a
rainbow.
Practice Problems
18.2 Convex and Concave
Lenses
pages 493–499
page 496
15. A 2.25-cm-tall object is 8.5 cm to the left of
a convex lens of 5.5-cm focal length. Find
the image position and height.
di
15.6 cm, or 16 cm
m
hi
4.1 cm
16. An object near a convex lens produces a
1.8-cm-tall real image that is 10.4 cm from
the lens and inverted. If the focal length
of the lens is 6.8 cm, what are the object
position and height?
do
2.0101cm
(10.4 cm)(6.8 cm)
10.4 cm 6.8 cm
dif
di f
1
di
1
do
1
f
(15.6 cm)(2.25 cm)
8.5 cm
diho
do
di
do
hi
ho
(8.5 cm)(5.5 cm)
8.5 cm 5.5 cm
dof
do f
1
di
1
do
1
f
(1.33)(sin 57.5°)
1.50
n1 sin 1
n2
3.00108m/s
1.51
c
nchloroform
c
v
378 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 379
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
m
ho
3.4 cm
17. An object is placed to the left of a convex
lens with a 25-mm focal length so that its
image is the same size as the object. What
are the image and object positions?
with dodibecause
mand m1
Therefore,
di2f
2(25 mm)
5.0101mm
dodi5.0101mm
18. Use a scale ray diagram to find the image
position of an object that is 30 cm to the
left of a convex lens with a 10-cm focal
length.
di15 cm
19. Calculate the image position and height of
a 2.0-cm-tall object located 25 cm from a
convex lens with a focal length of 5.0 cm.
What is the orientation of the image?
di
6.2 cm
m
hi
0.50 cm (inverted image)
page 497
20. A newspaper is held 6.0 cm from a convex
lens of 20.0-cm focal length. Find the image
position of the newsprint image.
So di
8.6 cm
21. A magnifying glass has a focal length of
12.0 cm. A coin, 2.0 cm in diameter, is
placed 3.4 cm from the lens. Locate the
image of the coin. What is the diameter of
the image?
di
4.7 cm
hi
2.8 cm
(2.0 cm)(4.7 cm)
3.4 cm
hodi
do
(3.4 cm)(12.0 cm)
3.4 cm 12.0 cm
dof
dof
1
do
1
di
1
f
(6.0 cm)(20.0 cm)
6.0 cm 20.0 cm
dof
dof
1
do
1
di
1
f
(6.2 cm)(2.0 cm)
25 cm
diho
do
di
do
hi
ho
(25 cm)(5.0 cm)
25 cm 5.0 cm
dof
do f
1
di
1
do
1
f
FF
Horizontal scale:
1 block 1 cm
di 15 cm
Ray 1
Ray 2
I1
O1
2
di
1
f
di
do
1
do
1
di
1
f
(19.6 cm)(1.8 cm)
10.4 cm
dohi
di
di
do
hi
ho
Chapter 18 continued
22. A convex lens with a focal length of
22.0 cm is used to view a 15.0-cm-long
pencil located 10.0 cm away. Find the
height and orientation of the image.
di
18.3 cm
m
hi
27.5 cm (upright image)
23. A stamp collector wants to magnify a stamp
by 4.0 when the stamp is 3.5 cm from the
lens. What focal length is needed for the
lens?
m
dimdo(4.0)(3.5 cm)
14 cm
f
4.7 cm
24. A magnifier with a focal length of 30 cm
is used to view a 1-cm-tall object. Use ray
tracing to determine the location and
size of the image when the magnifier is
positioned 10 cm from the object.
The location should be about 15 cm on
the same side of the lens (15 cm) and
the image should be upright and about
1.5 cm tall.
Section Review
18.2 Convex and Concave
Lenses
pages 493–499
page 499
25. Magnification Magnifying glasses normal-
ly are used to produce images that are larger
than the related objects, but they also can
produce images that are smaller than the
related objects. Explain.
If the object is located farther than
twice the focal length from the lens, the
size of the image is smaller than the
size of the object.
26. Image Position and Height A 3.0-cm-tall
object is located 2.0 cm from a convex lens
having a focal length of 6.0 cm. Draw a ray
diagram to determine the location and size
of the image. Use the thin lens equation
and the magnification equation to verify
your answer.
di
3.0 cm
mdi
do
hi
ho
(2.0 cm)(6.0 cm)
2.0 cm 6.0 cm
dof
do f
1
di
1
do
1
f
I1
O1
Horizontal scale:
2 blocks 1.0 cm
Vertical scale:
1 block 1.0 cm
hi 4.5 cm
di 3.0 cm
FF
FF
O1
I1
hi 1.5 cm
di 15 cm
Horizontal scale:
1 block 2 cm
Vertical scale:
3 blocks 1 cm
(3.5 cm)(14 cm)
3.5 cm (14 cm)
dodi
do di
1
do
1
di
1
f
di
do
(18.3 cm)(15.0 cm)
10.0 cm
diho
do
di
do
hi
ho
(10.0 cm)(22.0 cm)
10.0 cm 22.0 cm
dof
do f
1
di
1
do
1
f
380 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 381
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
hi
4.5 cm
27. Types of Lenses The cross sections of four
different thin lenses are shown in Figure
18-16.
■Figure 18-16
a. Which of these lenses, if any, are
convex, or converging, lenses?
Lenses a and c are converging.
b. Which of these lenses, if any, are
concave, or diverging, lenses?
Lenses b and d are diverging.
28. Chromatic Aberration All simple lenses
have chromatic aberration. Explain, then,
why you do not see this effect when you
look through a microscope.
All precision optical instruments use
a combination of lenses, called an
achromatic lens, to minimize chromatic
aberration.
29. Chromatic Aberration You shine white
light through a convex lens onto a screen
and adjust the distance of the screen from
the lens to focus the red light. Which direc-
tion should you move the screen to focus
the blue light?
closer to the lens
30. Critical Thinking An air lens constructed
of two watch glasses is placed in a tank of
water. Copy Figure 18-17 and draw the
effect of this lens on parallel light rays
incident on the lens.
■Figure 18-17
The light rays will diverge.
Section Review
18.3 Applications of Lenses
pages 500–503
page 503
31. Refraction Explain why the cornea is the
primary focusing element in the eye.
The difference in index of refraction
between the air and the cornea is
greater than any other difference that
light rays encounter when traveling
toward the retina.
32. Lens Types Which type of lens, convex or
concave, should a nearsighted person use?
Which type should a farsighted person use?
A nearsighted person should use a con-
cave lens. A farsighted person should
use a convex lens.
Water
Water
Light rays n 1.3 n 1.0 n 1.3
Water
Water
Air
Light rays
(3.0 cm)(3.0 cm)
2.0 cm
diho
do
Chapter 18 continued

33. Focal Length Suppose your camera is
focused on a person who is 2 m away. You
now want to focus it on a tree that is farther
away. Should you move the lens closer to
the film or farther away?
Closer; real images are always farther
from the lens than the focal point. The
farther away the object is, the closer the
image is to the focal point.
34. Image Why is the image that you observe
in a refracting telescope inverted?
After the light rays pass through the
objective lens, they cross, forming an
image that is inverted. The eyepiece
maintains this orientation when it uses
this image as its object.
35. Prisms What are three benefits of having
prisms in binoculars?
The prisms extend the light’s path length
to make the binoculars more compact,
invert light rays so that the viewer sees
an upright image, and increase separa-
tion between objective lenses to improve
the three-dimensional view.
36. Critical Thinking When you use the
highest magnification on a microscope,
the image is much darker than it is at lower
magnifications. What are some possible
reasons for the darker image? What could
you do to obtain a brighter image?
You are using the light that strikes only
a small area of the object. A brighter
lamp could be used.
Chapter Assessment
Concept Mapping
page 508
37. Complete the following concept map using
the following terms: inverted, larger, smaller,
virtual.
Mastering Concepts
page 508
38. How does the angle of incidence compare
with the angle of refraction when a light ray
passes from air into glass at a nonzero
angle? (18.1)
The angle of incidence is larger than
the angle of refraction, because air has
a smaller index of refraction.
39. How does the angle of incidence compare
with the angle of refraction when a light ray
leaves glass and enters air at a nonzero
angle? (18.1)
The angle of incidence is smaller than
the angle of refraction, because glass
has a larger index of refraction.
40. Regarding refraction, what is the critical
angle? (18.1)
The term critical angle refers to the inci-
dent angle that causes the refracted ray
to lie right along the boundary of the
substance when a ray is passing from a
region of higher index of refraction to a
region of lower index of refraction. If the
incident angle exceeds the critical
angle, total internal reflection will occur.
Lenses
upright
virtual
convex concave
upright
virtual
inverted
real
larger
unchanged
size
smaller larger smaller
382 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 383
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
41. Although the light coming from the Sun is
refracted while passing through Earth’s
atmosphere, the light is not separated into
its spectrum. What does this indicate
about the speeds of different colors of light
traveling through air? (18.1)
The speeds of the different colors of
light traveling through air are the same.
42. Explain why the Moon looks red during a
lunar eclipse. (18.1)
During a lunar eclipse, Earth blocks the
Sun’s rays from the Moon. However,
sunlight refracting off Earth’s atmos-
phere is directed inward toward the
Moon. Because blue wavelengths of
light are dispersed more, red wave-
lengths of light reflect off the Moon
toward Earth.
43. How do the shapes of convex and concave
lenses differ? (18.2)
Convex lenses are thicker at the center
than at the edges. Concave lenses are
thinner in the middle than at the edges.
44. Locate and describe the physical properties
of the image produced by a convex lens
when an object is placed some distance
beyond 2F. (18.2)
It is a real image that is located
between F and 2F, and that is inverted
and smaller compared to the object.
45. What factor, other than the curvature of the
surfaces of a lens, determines the location
of the focal point of the lens? (18.2)
The index of refraction of the material
from which the lens is made also deter-
mines the focus.
46. To project an image from a movie projector
onto a screen, the film is placed between
F and 2F of a converging lens. This arrange-
ment produces an image that is inverted.
Why does the filmed scene appear to be
upright when the film is viewed? (18.2)
Another lens is included in the optics
system of the projector to invert the
image again. As a result, the image is
upright compared to the original object.
47. Describe why precision optical instruments
use achromatic lenses. (18.2)
All lenses have chromatic aberration,
which means different wavelengths of
light are bent at slightly different angles
near their edges. An achromatic lens is
a combination of two or more lenses
with different indices of refraction that
reduce this effect.
48. Describe how the eye focuses light. (18.3)
Light entering the eye is primarily
focused by the cornea. Fine focusing
occurs when muscles change the shape
of the lens, allowing the eye to focus on
either near or far objects.
49. What is the condition in which the focal
length of the eye is too short to focus light
on the retina? (18.3)
nearsightedness
50. What type of image is produced by the
objective lens in a refracting telescope?
(18.3)
real image, inverted
51. The prisms in binoculars increase the dis-
tance between the objective lenses. Why is
this useful? (18.3)
It improves the three-dimensional view.
52. What is the purpose of a camera’s reflex
mirror? (18.3)
The reflex mirror diverts the image onto
a prism so that it can be viewed before
taking a photograph. When the shutter
release button is pressed, the reflex
mirror moves out of the way so that the
lens focuses the image onto the film or
other photodetector.
Chapter 18 continued
Applying Concepts
pages 508—509
53. Which substance, A or B, in Figure 18-24
has a larger index of refraction? Explain.
■Figure 18-24
The angle in substance A is smaller, so
it has the larger index of refraction.
54. A light ray strikes the boundary between
two transparent media. What is the angle of
incidence for which there is no refraction?
An angle of incidence of 0°allows the
light to go through unchanged. Or if the
angle of incidence is greater than the
critical angle there is total internal
reflection.
55. How does the speed of light change as the
index of refraction increases?
As the index of refraction of a material
increases, the speed of light in that
material decreases.
56. How does the size of the critical angle
change as the index of refraction increases?
The critical angle decreases as the
index of refraction increases.
57. Which pair of media, air and water or air
and glass, has the smaller critical angle?
csin1
c, water/air sin1
48.8°
c, glass/air sin1
41.1°
Air and glass have the smaller critical
angle of 41.1°. The critical angle for air
and water is 48.8°.
58. Cracked Windshield If you crack the
windshield of your car, you will see a silvery
line along the crack. The glass has separated
at the crack, and there is air in the crack.
The silvery line indicates that light is reflect-
ing off the crack. Draw a ray diagram to
explain why this occurs. What phenomenon
does this illustrate?
This illustrates light reflected at angles
larger than the critical angle, or total
internal reflection.
59. Legendary Mirage According to legend,
Eric the Red sailed from Iceland and discov-
ered Greenland after he had seen the island
in a mirage. Describe how the mirage might
have occurred.
Even though Greenland is below the
horizon, it is visible as a mirage due to
the refraction of light.
Crack
n 1.0
From outside
To the driver’s eyes
nglass nglass
1 c1 c
1.00
1.52
1.00
1.33
n2
n1
AB
384 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued
Physics: Principles and Problems Solutions Manual 385
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
60. A prism bends violet light more than it
bends red light. Explain.
Violet light travels slower in a prism
than red light does.
61. Rainbows Why would you never see a rain-
bow in the southern sky if you were in the
northern hemisphere? In which direction
should you look to see rainbows if you are
in the southern hemisphere?
You can see a rainbow only when the
Sun’s rays come from behind you at an
angle not greater than 42°with the hori-
zon. When you are facing south in the
northern hemisphere, the Sun is never
behind you at an angle of 42°or less.
62. Suppose that Figure 18-14 is redrawn with
a lens of the same focal length but a larger
diameter. Explain why the location of the
image does not change. Would the image
be affected in any way?
The location of the image depends on
the focal length of the lens and the dis-
tance of the object from the lens.
Therefore, the location of the image
doesn’t change.
63. A swimmer uses a magnifying glass to
observe a small object on the bottom of a
swimming pool. She discovers that the mag-
nifying glass does not magnify the object
very well. Explain why the magnifying glass
is not functioning as it would in air.
The magnification is much less in water
than in air. The difference in the indices
of refraction for water and glass is
much less than the difference for air
and glass.
64. Why is there chromatic aberration for light
that goes through a lens but not for light
that reflects from a mirror?
Chromatic aberration for lenses is due to
the dispersion of light (different wave-
lengths of light have different speeds in
the lens and refract with slightly differ-
ent angles). Mirrors reflect, and reflec-
tion is independent of wavelength.
65. When subjected to bright sunlight, the pupils
of your eyes are smaller than when they are
subjected to dimmer light. Explain why your
eyes can focus better in bright light.
Eyes can focus better in bright light
because rays that are refracted into
larger angles are cut off by the iris.
Therefore, all rays converge at a
narrow angle, so there is less spherical
aberration.
66. Binoculars The objective lenses in binocu-
lars form real images that are upright
compared to their objects. Where are the
images located relative to the eyepiece
lenses?
Each side of the binoculars is like a
refracting telescope. Therefore, the
objective lens image must be between
the eyepiece lens and its focal point to
magnify the image.
Mastering Problems
18.1 Refraction of Light
pages 509—510
Level 1
67. A ray of light travels from air into a liquid,
as shown in Figure 18-25. The ray is inci-
dent upon the liquid at an angle of 30.0°.
The angle of refraction is 22.0°.
Mirage
Greenland Iceland
W
a
r
m
a
i
r
C
o
l
d
,
d
e
n
s
e
a
i
r
Chapter 18 continued
■Figure 18-25
a. Using Snell’s law, calculate the index of
refraction of the liquid.
n1 sin 1n2 sin 2
n2
1.33
b. Compare the calculated index of refrac-
tion to those in Table 18-1. What might
the liquid be?
water
68. Light travels from flint glass into ethanol.
The angle of refraction in the ethanol is
25.0°. What is the angle of incidence in the
glass?
n1 sin 1n2 sin 2
1sin1
sin1
20.8°
69. A beam of light strikes the flat, glass side of
a water-filled aquarium at an angle of 40.0°
to the normal. For glass, n 1.50.
a. At what angle does the beam enter the
glass?
nAsin Angsin g
gsin1
sin1
25.4°
b. At what angle does the beam enter the
water?
ngsin gnwsin w
wsin1
sin1
28.9°
70. Refer to Table 18-1. Use the index of refrac-
tion of diamond to calculate the speed of
light in diamond.
n
vdiamond
1.24108m/s
71. Refer to Table 18-1. Find the critical angle
for a diamond in air.
c, diamond/air sin1
sin1
24.4°
Level 2
72. Aquarium Tank A thick sheet of plastic,
n 1.500, is used as the side of an aquari-
um tank. Light reflected from a fish in the
water has an angle of incidence of 35.0°.
At what angle does the light enter the air?
n1 sin 1 n2 sin 2
nwater sin water nplastic sin plastic
plastic sin1
sin1
30.57°
nplastic sin plastic nair sin air
(1.33)(sin 35.0°)
1.500
nwater sin water
nplastic
1.00
2.42
n2
n1
3.00108m/s
2.42
c
ndiamond
c
v
(1.50)(sin 25.4°)
1.33
ngsin g
nw
(1.00)(sin 40.0°)
1.50
nA sin A
ng
(1.36)(sin 25.0°)
1.62
n2 sin 2
n1
(1.00)(sin 30.0°)
sin 22.0°
n1 sin 1
sin 2
30°
22°
Air
Liquid
386 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 387
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
air sin1
sin1
49.7°
73. Swimming-Pool Lights A light source is
located 2.0 m below the surface of a swim-
ming pool and 1.5 m from one edge of the
pool, as shown in Figure 18-26. The pool
is filled to the top with water.
■Figure 18-26
a. At what angle does the light reaching
the edge of the pool leave the water?
itan1
37°
Then find the angle in air.
nAsin Anwsin w
Asin1
sin1
53°
b. Does this cause the light viewed from
this angle to appear deeper or shallower
than it actually is?
tan 53°
side adjacent
1.1 m, shallower
74. A diamond’s index of refraction for red
light, 656 nm, is 2.410, while that for blue
light, 434 nm, is 2.450. Suppose that white
light is incident on the diamond at 30.0°.
Find the angles of refraction for red and
blue light.
nAsin Andsin d
dsin1
For red light
dsin1
12.0°
For blue light
dsin1
11.8°
75. The index of refraction of crown glass is 1.53
for violet light, and it is 1.51 for red light.
a. What is the speed of violet light in
crown glass?
v
1.96108m/s
b. What is the speed of red light in crown
glass?
v
1.99108m/s
76. The critical angle for a special glass in air is
41.0°. What is the critical angle if the glass
is immersed in water?
sin c, air
ng 1.524
sin c, water
c, water sin1
sin1
60.8°
1.33
1.524
nw
ng
nw
ng
1.00
sin 41.0°
nA
sin c, air
nA
ng
3.00108m/s
1.51
c
n
3.00108m/s
1.53
c
n
(1.00)(sin 30.0°)
2.450
(1.00)(sin 30.0°)
2.410
nAsin A
nd
1.5 m
tan 53°
side opposite
tan 53°
side opposite
side adjacent
(1.33)(sin 37°)
1.00
nwsin w
nA
1.5 m
2.0 m
1.5 m
2 m
(1.500)(sin 30.57°)
1.00
nplastic sin plastic
nair
Chapter 18 continued
Level 3
77. A ray of light in a tank of water has an
angle of incidence of 55.0°. What is the
angle of refraction in air?
n1 sin 1 n2 sin 2
2 sin1
sin1
sin1(1.09)
The value sin 21.09 is not defined.
Therefore, total internal reflection
occurs.
78. The ray of light shown in Figure 18-27 is
incident upon a 60°-60°-60° glass prism,
n 1.5.
■Figure 18-27
a. Using Snell’s law of refraction,
determine the angle, 2, to the nearest
degree.
nair sin 1nglass sin 2
2sin1
sin1
28°
b. Using elementary geometry, determine
the value of 1.
P90°28°62°
Q180°62°60°58°
190°58°32°
c. Determine 2.
nair sin 2nglass sin 1
2sin1
sin1
53°
79. The speed of light in a clear plastic is
1.90108m/s. A ray of light strikes the
plastic at an angle of 22.0°. At what angle is
the ray refracted?
nair sin air npsin pand np,so
nair sin air sin p
sin p
p sin1
sin1
13.7°
80. A light ray enters a block of crown glass,
as illustrated in Figure 18-28. Use a ray
diagram to trace the path of the ray until it
leaves the glass.
■Figure 18-28
nA sin Angsin g
gsin1
sin1
28°
Find the critical angle for crown glass.
sin c nA
ng
(1.00)(sin 45°)
1.52
nA sin A
ng
45°
(1.90108m/s)(1.00)(sin 22.0°)
3.00108m/s
vpnair sin air
c
vpnair sin air
c
c
vp
c
vp
(1.5)(sin 32°)
1.00
nglass sin 1
nair
1.00 sin 45°
1.5
nair sin 1
nglass
nglass 1.5
2
60°
60°60°
Air
PQ
R
Air
1 45°
21
Glass
(1.33)(sin 55.0°)
1.00
n1 sin 1
n2
388 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued
Physics: Principles and Problems Solutions Manual 389
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c sin1
sin1
41.1°
When the light ray in the glass strikes
the surface at a 62°angle, total internal
reflection occurs.
18.2 Convex and Concave Lenses
page 510
Level 1
81. The focal length of a convex lens is 17 cm.
A candle is placed 34 cm in front of the
lens. Make a ray diagram to locate the
image.
di34 cm
82. A converging lens has a focal length of
25.5 cm. If it is placed 72.5 cm from an
object, at what distance from the lens will
the image be?
di
39.3 cm
The image is 39.3 cm from the lens.
83. If an object is 10.0 cm from a converging
lens that has a focal length of 5.00 cm, how
far from the lens will the image be?
di
10.0 cm
Level 2
84. A convex lens is needed to produce an
image that is 0.75 times the size of the
object and located 24 cm from the lens on
the other side. What focal length should be
specified?
m
do
32 cm
f
14 cm
85. An object is located 14.0 cm from a convex
lens that has a focal length of 6.0 cm. The
object is 2.4 cm high.
a. Draw a ray diagram to determine the loca-
tion, size, and orientation of the image.
Horizontal scale:
1 block 1.0 cm
Vertical scale:
1 block 0.4 cm
hi 1.8 cm
di 10.5 cm
Ray 2
Ray 1
F
F
I1
O1
(32 cm)(24 cm)
32 cm 24 cm
dodi
dodi
1
di
1
do
1
f
(24 cm)
0.75
di
m
di
do
hi
ho
(10.0 cm)(5.00 cm)
10.0 cm 5.00 cm
dof
dof
1
di
1
do
1
f
(72.5 cm)(25.5 cm)
72.5 cm 25.5 cm
dof
dof
1
di
1
do
1
f
Horizontal scale:
1 block 2 cm
di 34 cm
Ray 2
Ray 1
F
F
I1
O1
45°45°
28°28°62°62°
1.00
1.52
nA
ng
Chapter 18 continued

b. Solve the problem mathematically.
di
10.5 cm
m
hi
1.8 cm, so the image is
inverted
86. A 3.0-cm-tall object is placed 22 cm in front
of a converging lens. A real image is formed
11 cm from the lens. What is the size of the
image?
m
hi
1.5 cm
The image is 1.5 cm tall.
Level 3
87. A 3.0-cm-tall object is placed 15.0 cm in
front of a converging lens. A real image is
formed 10.0 cm from the lens.
a. What is the focal length of the lens?
f
6.00 cm
b. If the original lens is replaced with a lens
having twice the focal length, what are
the image position, size, and orientation?
fnew 2f
2(6.00 cm)
12.0 cm
di, new
60.0 cm
m
hi, new
12 cm
The image is inverted compared to
the object.
88. A diverging lens has a focal length of
15.0 cm. An object placed near it forms a
2.0-cm-high image at a distance of 5.0 cm
from the lens.
a. What are the object position and object
height?
do
7.5 cm
m
ho
3.0 cm
(7.5 cm)(2.0 cm)
5.0 cm
dohi
di
di
do
hi
ho
(5.0 cm)(15.0 cm)
5.0 cm (15.0 cm)
dif
dif
1
di
1
do
1
f
(60.0 cm)(3.0 cm)
15 cm
di, newho
do
di
do
hi
ho
(15.0 cm)(12.0 cm)
15.0 cm 12.0 cm
dofnew
dofnew
1
di
1
do
1
f
(15.0 cm)(10.0 cm)
15.0 cm 10.0 cm
dodi
dodi
1
di
1
do
1
f
(11 cm)(3.0 cm)
22 cm
diho
do
di
do
hi
ho
(10.5 cm)(2.4 cm)
14.0 cm
diho
do
di
do
hi
ho
(14.0 cm)(6.0 cm)
14.0 cm 6.0 cm
dof
dof
1
di
1
do
1
f
390 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 391
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. The diverging lens is now replaced by a
converging lens with the same focal
length. What are the image position,
height, and orientation? Is it a virtual
image or a real image?
fnew f
(15.0 cm)
15.0 cm
di, new
15 cm
m
hi, new
6.0 cm
This is a virtual image that is upright
compared to the object.
18.3 Applications of Lenses
pages 510–511
Level 1
89. Camera Lenses Camera lenses are
described in terms of their focal length.
A 50.0-mm lens has a focal length of
50.0 mm.
a. A camera with a 50.0-mm lens is
focused on an object 3.0 m away. What
is the image position?
So di
51 mm
b. A 1000.0-mm lens is focused on an
object 125 m away. What is the image
position?
So di
1.01 m 1.01103mm
90. Eyeglasses To clearly read a book 25 cm
away, a farsighted girl needs the image to be
45 cm from her eyes. What focal length is
needed for the lenses in her eyeglasses?
So f
56 cm
Level 2
91. Copy Machine The convex lens of a copy
machine has a focal length of 25.0 cm. A
letter to be copied is placed 40.0 cm from
the lens.
a. How far from the lens is the copy
paper?
di
66.7 cm
b. How much larger will the copy be?
hi
1.67ho
The copy is enlarged and inverted.
(66.7 cm)(ho)
40.0 cm
diho
do
di
do
hi
ho
(40.0 cm)(25.0 cm)
40.0 cm 25.0 cm
dof
dof
1
do
1
di
1
f
(25 cm)(45 cm)
25 cm (45 cm)
dodi
dodi
1
do
1
di
1
f
(125 m)(1.0000 m)
125 m 1.00 m
dof
dof
1
do
1
di
1
f
(3.0103mm)(50.0 mm)
3.0103mm 50.0 mm
dof
dof
1
do
1
di
1
f
(15 cm)(3.0 cm)
7.5 cm
di, newho
do
di
do
hi
ho
(7.5 cm)(15 cm)
7.5 cm 15 cm
dofnew
dofnew
1
di, new
1
do
1
fnew
Chapter 18 continued

92. Camera A camera lens with a focal length
of 35 mm is used to photograph a distant
object. How far from the lens is the real
image of the object? Explain.
35 mm; for a distant object, docan be
considered at , thus 1/dois zero.
According to the thin lens equation,
dif.
Level 3
93. Microscope A slide of an onion cell is
placed 12 mm from the objective lens of
a microscope. The focal length of the
objective lens is 10.0 mm.
a. How far from the lens is the image
formed?
So di
6.0101mm
b. What is the magnification of this image?
mo 5.0
c. The real image formed is located
10.0 mm beneath the eyepiece lens.
If the focal length of the eyepiece is
20.0 mm, where does the final image
appear?
di
20.0 mm, or 20.0 mm beneath
the eyepiece
d. What is the final magnification of this
compound system?
me 2.00
mtotal mome(5.0)(2.00)
1.0101
94. Telescope The optical system of a toy
refracting telescope consists of a converging
objective lens with a focal length of
20.0 cm, located 25.0 cm from a converging
eyepiece lens with a focal length of
4.05 cm. The telescope is used to view a
10.0-cm-high object, located 425 cm from
the objective lens.
a. What are the image position, height,
and orientation as formed by the objec-
tive lens? Is this a real or virtual image?
di
21.0 cm
m
hi
0.494 cm
This is a real image that is inverted
compared to the object.
b. The objective lens image becomes the
object for the eyepiece lens. What are
the image position, height, and orienta-
tion that a person sees when looking
into the telescope? Is this a real or
virtual image?
do, new 25.0 cm di
25.0 cm 21.0 cm
4.0 cm
di, new
3.2102cm
(4.0 cm)(4.05 cm)
4.0 cm 4.05 cm
do, newfnew
do, new fnew
1
di, new
1
do, new
1
fnew
(21.0 cm)(10.0 cm)
425 cm
diho
do
di
do
hi
ho
(425 cm)(20.0 cm)
425 cm 20.0 cm
dof
dof
1
di
1
do
1
f
(20.0 mm)
10.0 mm
di
do
(10.0 mm)(20.0 mm)
10.0 mm 20.0 mm
dof
dof
1
do
1
di
1
f
6.0101mm
12 mm
di
do
(12 mm)(10.0 mm)
12 mm 10.0 mm
dof
dof
1
do
1
di
1
f
392 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 393
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
ho, new hi
0.494 cm
m
hi, new
4.0101cm
This is a virtual image that is invert-
ed compared to the object.
c. What is the magnification of the
telescope?
m
4.0
Mixed Review
pages 511—512
Level 1
95. A block of glass has a critical angle of 45.0°.
What is its index of refraction?
sin c
n1 ,n21.00 for air
n1
1.41
96. Find the speed of light in antimony trioxide
if it has an index of refraction of 2.35.
n
v
1.28108m/s
97. A 3.0-cm-tall object is placed 20 cm in front
of a converging lens. A real image is formed
10 cm from the lens. What is the focal
length of the lens?
f
7cm
Level 2
98. Derive nsin 1/sin 2from the general
form of Snell’s law of refraction,
n1sin 1 n2sin 2. State any assumptions
and restrictions.
The angle of incidence must be in air. If
we let substance 1 be air, then n1
1.000. Let n2n. Therefore,
n1sin 1n2sin 2
sin 1nsin 2
n
99. Astronomy How many more minutes
would it take light from the Sun to reach
Earth if the space between them were filled
with water rather than a vacuum? The Sun
is 1.5108km from Earth.
Time through vacuum
t
5.0102s
Speed through water
v
2.26108m/s
Time through water
t
660 s
t660 s 500 s 160 s
(160 s)(1 min/60 s) 2.7 min
(1.5108km)(1000 m/1 km)
2.26108m/s
d
v
3.00108m/s
1.33
c
n
(1.5108km)(1000 m/1 km)
3.00108m/s
d
c
sin 1
sin 2
(20 cm)(10 cm)
20 cm 10 cm
dodi
dodi
1
di
1
do
1
f
3.00108m/s
2.35
c
n
c
v
1.00
sin 45.0°
n2
sin c
n2
n1
4.0101cm
10.0 cm
hi, new
ho
(3.2102cm)(0.494 cm)
4.0 cm
di, newho, new
do, new
di
do
hi
ho
Chapter 18 continued
100. What is the focal length of the lenses in
your eyes when you read a book that is
35.0 cm from them? The distance from
each lens to the retina is 0.19 mm.
f
0.19 mm
Level 3
101. Apparent Depth Sunlight reflects diffu-
sively off the bottom of an aquarium.
Figure 18-29 shows two of the many light
rays that would reflect diffusively from a
point off the bottom of the tank and travel
to the surface. The light rays refract into the
air as shown. The red dashed line extending
back from the refracted light ray is a sight
line that intersects with the vertical ray at
the location where an observer would see
the image of the bottom of the tank.
■Figure 18-29
a. Compute the direction that the
refracted ray will travel above the
surface of the water.
n1sin 1n2sin 2
2sin1
sin1
6.7°
b. At what depth does the bottom of the
tank appear to be if you look into the
water? Divide this apparent depth into
the true depth and compare it to the
index of refraction.
Using right triangle geometry, (actu-
al depth)(tan 1) (apparent
depth)(tan 2)
apparent depth (12 cm)
8.9 cm
The refracted rays appear to inter-
sect 8.9 cm below the surface; this
is the apparent depth.
0.74
Also, 0.75
Therefore,
102. It is impossible to see through adjacent sides
of a square block of glass with an index of
refraction of 1.5. The side adjacent to the
side that an observer is looking through acts
as a mirror. Figure 18-30 shows the limiting
case for the adjacent side to not act like a
mirror. Use your knowledge of geometry and
critical angles to show that this ray configu-
ration is not achievable when nglass 1.5.
■Figure 18-30
The light ray enters the glass at an
angle 1and is refracted to an angle 2.
Air
Air
nglass 1.5
2
2 90°
1
1 90°
nair
nwater
apparent depth
true depth
1.0
1.33
nair
nwater
8.9 cm
12 cm
apparent depth
true depth
tan 5.0°
tan 6.7°
(1.33)(sin 5.0°)
1.0
n1sin 1
n2
5.0°
2
12 cm
(350 mm)(0.19 mm)
350 mm 0.19 mm
dodi
dodi
1
di
1
do
1
f
394 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 395
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
2sin1
sin1
42°
Therefore, 148°.
But the critical angle for glass is
csin1
sin1
42°
Because 1c, the light reflects
back into the glass and one cannot
see out of an adjacent side.
103. Bank Teller Window A 25-mm-thick sheet
of plastic, n 1.5, is used in a bank teller’s
window. A ray of light strikes the sheet at
an angle of 45°. The ray leaves the sheet at
45°, but at a different location. Use a ray
diagram to find the distance between the
ray that leaves and the one that would have
left if the plastic were not there.
8 mm
Thinking Critically
page 512
104. Recognize Spatial Relationships White
light traveling through air (n1.0003)
enters a slab of glass, incident at exactly
45°. For dense flint glass, n1.7708 for
blue light (435.8 nm) and n1.7273
for red light (643.8 nm). What is the
angular dispersion of the red and blue
light?
Find the angles of refraction for red
and blue light, and find the difference
in those angles in degrees.
Use Snell’s law, n1sin 1n2sin 2.
Thus, 2sin1
For red light
2sin1
24.173°
For blue light
2sin1
23.543°
Difference
24.173°23.543°0.630°
105. Compare and Contrast Find the critical
angle for ice (n 1.31). In a very cold
world, would fiber-optic cables made of
ice or those made of glass do a better job
of keeping light inside the cable? Explain.
sin c
csin1
sin1
49.8°
In comparison, the critical angle for
glass, n1.54, is 40.5°.The larger crit-
ical angle means that fewer rays would
be totally internally reflected in an ice
core than in a glass core. Thus, they
would not be able to transmit as much
light. Fiber optic cables made of glass
would work better.
1.00
1.31
nair
nice
nair
nice
(1.0003)(sin 45.000°)
1.7708
(1.0003)(sin 45.000°)
1.7273
n1sin 1
n2
25 mm
8 mm
28°
45°
45°
1.00
1.5
nA
ng
(1.00)(sin 90°)
1.5
nAsin A
ng
Chapter 18 continued

106. Recognize Cause and Effect Your lab
partner used a convex lens to produce an
image with di 25 cm and hi 4.0 cm.
You are examining a concave lens with a
focal length of 15 cm. You place the
concave lens between the convex lens and
the original image, 10 cm from the image.
To your surprise, you see a real image on
the wall that is larger than the object. You
are told that the image from the convex
lens is now the object for the concave lens,
and because it is on the opposite side of
the concave lens, it is a virtual object. Use
these hints to find the new image position
and image height and to predict whether
the concave lens changed the orientation
of the original image.
The new do10 cm. Thus,
di
30 cm
m 3
himho(3)(4.0 cm) 10 cm
The image orientation is not changed.
107. Define Operationally Name and describe
the effect that causes the rainbow-colored
fringe commonly seen at the edges of a
spot of white light from a slide or
overhead projector.
The light that passes through a lens
near the edges of the lens is slightly
dispersed, since the edges of a lens
resemble a prism and refract different
wavelengths of light at slightly different
angles. The result is that white light is
dispersed into its spectrum.The effect
is called chromatic aberration.
108. Think Critically A lens is used to project
the image of an object onto a screen.
Suppose that you cover the right half of
the lens. What will happen to the image?
It will get dimmer, because fewer light
rays will converge, but you will see a
complete image.
Writing in Physics
page 512
109. The process of accommodation, whereby
muscles surrounding the lens in the eye
contract or relax to enable the eye to
focus on close or distant objects, varies for
different species. Investigate this effect
for different animals. Prepare a report
for the class showing how this fine focus-
ing is accomplished for different eye
mechanisms.
Answers will vary depending on the
animals selected by the students.
110. Investigate the lens system used in an optical
instrument such as an overhead projector or
a particular camera or telescope. Prepare a
graphics display for the class explaining how
the instrument forms images.
Answers will vary. Students may find
that it is necessary to simplify their
chosen system for explanation
purposes.
Cumulative Review
page 512
111. If you drop a 2.0 kg bag of lead shot from
a height of 1.5 m, you could assume
that half of the potential energy will be
converted into thermal energy in the lead.
The other half would go to thermal energy
in the floor. How many times would you
have to drop the bag to heat it by 10°C?
(Chapter 12)
PE mgh
(2.0 kg)(9.80 m/s2)(1.5 m)
29.4 J
To heat the bag
QmCT
(2.0 kg)(130 J/kg°C)(10°C)
2600 J
N
180 times
2600 J
1
2
(29.4 J)
Q
1
2
PE
30 cm
10 cm
di
do
(15 cm)(10 cm)
10 cm (15 cm)
fdo
dof
396 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued
Physics: Principles and Problems Solutions Manual 397
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
112. A blacksmith puts an iron hoop or tire on
the outer rim of a wooden carriage wheel
by heating the hoop so that it expands to a
diameter greater than the wooden wheel.
When the hoop cools, it contracts to hold
the rim in place. If a blacksmith has a
wooden wheel with a 1.0000-m diameter
and wants to put a rim with a 0.9950-m
diameter on the wheel, what is the
minimum temperature change the iron
must experience? (iron 12106/°C)
(Chapter 13)
Liron LTwhere Lis the diameter
of the iron hoop. We want Lgreater
than 0.0050 m.
Therefore,
T
420°C
Actually he would heat it much hotter to
give room to fit over the wheel easily.
113. A car sounds its horn as it approaches a
pedestrian in a crosswalk. What does the
pedestrian hear as the car brakes to allow
him to cross the street? (Chapter 15)
The pitch of the horn heard by the
pedestrian will decrease as the car
slows down.
114. Suppose that you could stand on the
surface of the Sun and weigh yourself.
Also suppose that you could measure the
illuminance on your hand from the Sun’s
visible spectrum produced at that position.
Next, imagine yourself traveling to a
position 1000 times farther away from the
center of the Sun as you were when
standing on its surface. (Chapter 16)
a. How would the force of gravity on you
from the Sun at the new position com-
pare to what it was at the surface?
It is 1106
the value it was originally.
b. How would the illuminance on your
hand from the Sun at the new position
compare to what it was when you were
standing on its surface? (For simplicity,
assume that the Sun is a point source
at both positions.)
It is 1106
the value it was originally.
c. Compare the effect of distance upon
the gravitational force and illuminance.
They both follow the inverse square
law of distance.
115. Beautician’s Mirror The nose of a
customer who is trying some face powder
is 3.00-cm high and is located 6.00 cm in
front of a concave mirror having a 14.0-cm
focal length. Find the image position and
height of the customer’s nose by means of
the following. (Chapter 17)
a. a ray diagram drawn to scale
b. the mirror and magnification equations
di
10.5 cm
m
hi
5.25 cm
(10.5 cm)(3.00 cm)
6.00 cm
diho
do
di
do
hi
ho
(6.00 cm)(14.0 cm)
6.00 cm 14.0 cm
dof
do f
1
di
1
do
1
f
Horizontal scale:
1 block 1.0 cm
Vertical scale:
1 block 1.0 cm
hi 5.25 cm
di 10.5 cm
I1
O1
1
1,000,000
1
10002
1
1,000,000
1
(1000)2
0.0050
(12106/°C)(0.9950 m)
L
ironL
Chapter 18 continued
Challenge Problem
page 501
As light enters the eye, it first encounters the
air/cornea interface. Consider a ray of light that
strikes the interface between the air and a per-
son’s cornea at an angle of 30.0° to the normal.
The index of refraction of the cornea is approxi-
mately 1.4.
1. Use Snell’s law to calculate the angle of
refraction.
n1 sin 1 n2 sin 2
2 sin1
sin1
21°
2. What would the angle of refraction be if the
person was swimming underwater?
n1 sin 1 n2 sin 2
2 sin1
sin1
28°
3. Is the refraction greater in air or in water?
Does this mean that objects under water
seem closer or more distant than they
would in air?
Refraction is greater in air because the
angle to the normal is smaller. Objects
seem closer in water.
4. If you want the angle of refraction for the
light ray in water to be the same as it is
for air, what should the new angle of inci-
dence be?
n1 sin 1 n2 sin 2
1 sin1
sin1
22°
Air
2
Cornea
30.0°
(1.4)(sin 21°)
1.33
n2 sin 2
n1
(1.33)(sin 30.0°)
1.4
n1 sin 1
n2
(1.0)(sin 30.0°)
1.4
n1 sin 1
n2
398 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 18 continued

Physics: Principles and Problems Solutions Manual 399
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
19 Interference and
Diffraction
CHAPTER
Practice Problems
19.1 Interference
pages 515–523
page 519
1. Violet light falls on two slits separated by
1.90105m. A first-order bright band
appears 13.2 mm from the central bright
band on a screen 0.600 m from the slits.
What is ?
x
L
d
418 nm
2. Yellow-orange light from a sodium lamp of
wavelength 596 nm is aimed at two slits
that are separated by 1.90105m. What
is the distance from the central band to
the first-order yellow band if the screen is
0.600 m from the slits?
x
d
L
1.88102m 18.8 mm
3. In a double-slit experiment, physics stu-
dents use a laser with 632.8 nm. A
student places the screen 1.000 m from the
slits and finds the first-order bright band
65.5 mm from the central line. What is the
slit separation?
x
L
d
d
x
L
9.66106m 9.66 m
4. Yellow-orange light with a wavelength of
596 nm passes through two slits that are
separated by 2.25105m and makes an
interference pattern on a screen. If the dis-
tance from the central line to the first-order
yellow band is 2.00102m, how far is the
screen from the slits?
x
L
d
L
x
d
0.755 m
page 522
5. In the situation in Example Problem 2,
what would be the thinnest film that would
create a reflected red (635 nm) band?
2tm
1
2
n
oil
For the thinnest film, m0.
t
1
4
(6
43
)(
5
1.
n
4
m
5)
109 nm
6. A glass lens has a nonreflective coating
placed on it. If a film of magnesium
fluoride, n1.38, is placed on the glass,
n1.52, how thick should the layer be to
keep yellow-green light from being reflected?
Because nfilm nair, there is a phase
inversion on the first reflection.
Because nglass nfilm, there is a phase
inversion on the second reflection.
For destructive interference to keep
yellow-green from being reflected:
2tm
1
2
nfilm
noil
(2.00102m)(2.25105m)
596109m
(632.8109m)(1.000 m)
65.5103m
(13.2103m)(1.90105m)
0.600 m
(13.2103m)(1.90105m)
0.600 m

For the thinnest film, m0.
t
1
4
(5
45
)(
5
1.
n
3
m
8)
101 nm
7. A silicon solar cell has a nonreflective
coating placed on it. If a film of sodium
monoxide, n1.45, is placed on the sili-
con, n3.5, how thick should the layer be
to keep yellow-green light (555 nm)
from being reflected?
Because nfilm nair, there is a phase
inversion on the first reflection.
Because nsilicon nfilm, there is a phase
inversion on the second reflection.
For destructive interference to keep
yellow-green from being reflected:
2tm
1
2
For the thinnest film, m0.
t
1
4
(5
45
)(
5
1.
n
4
m
5)
95.7 nm
8. You can observe thin-film interference by
dipping a bubble wand into some bubble
solution and holding the wand in the air.
What is the thickness of the thinnest soap
film at which you would see a black stripe
if the light illuminating the film has a
wavelength of 521 nm? Use n1.33.
Because nfilm nair, there is a phase
change on the first reflection. Because
nair nfilm, there is no phase change on
the second reflection.
For destructive interference to get a
black stripe
2t
n
m
fil
m
For the thinnest film, m1.
t
2n
film
196 nm
9. What is the thinnest soap film (n1.33)
for which light of wavelength 521 nm will
constructively interfere with itself?
For constructive interference
2tm
1
2
For the thinnest film, m0.
t
1
4
(5
42
)(
1
1.
n
3
m
3)
97.9 nm
Section Review
19.1 Interference
pages 515–523
page 523
10. Film Thickness Lucien is blowing bubbles
and holds the bubble wand up so that a soap
film is suspended vertically in the air. What is
the second thinnest width of the soap film at
which he could expect to see a bright stripe if
the light illuminating the film has a wave-
length of 575 nm? Assume the soap solution
has an index of refraction of 1.33.
There is one phase inversion, so
constructive interference will be when
2tm
1
2
For the second thinnest thickness, m1.
t
3
4
324 nm
(3)(575 nm)
(4)(1.33)
nfilm
nfilm
nfilm
nfilm
521 nm
(2)(1.33)
nfilm
nfilm
nfilm
400 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 401
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
11. Bright and Dark Patterns Two very nar-
row slits are cut close to each other in a large
piece of cardboard. They are illuminated by
monochromatic red light. A sheet of white
paper is placed far from the slits, and a pat-
tern of bright and dark bands is seen on the
paper. Describe how a wave behaves when it
encounters a slit, and explain why some
regions are bright while others are dark.
When a wave encounters a slit, the
wave bends. Light is diffracted by the
slits. Light from one slit interferes with
light from the other. If interference is
constructive, there is a bright band; if
destructive, the region is dark.
12. Interference Patterns Sketch the pattern
described in problem 11.
13. Interference Patterns Sketch what hap-
pens to the pattern in problem 11 when the
red light is replaced by blue light.
The light bands become more closely
spaced.
14. Film Thickness A plastic reflecting film
(n1.83) is placed on an auto glass
window (n1.52).
a. What is the thinnest film that will
reflect yellow-green light?
Because nfilm nair, there is a phase
change on the first reflection.
Because nglass nfilm, there is not
a phase change on the second
reflection. For constructive interfer-
ence to reflect yellow-green light:
2tm
1
2
For the thinnest film, m0.
t
1
4
75.8 nm
b. Unfortunately, a film this thin cannot
be manufactured. What is the next-
thinnest film that will produce the
same effect?
For the next thinnest film, m1.
t
3
4
227 nm
15. Critical Thinking The equation for wave-
length from a double-slit experiment uses
the simplification that is small so that
sin tan . Up to what angle is this a
good approximation when your data has
two significant figures? Would the maxi-
mum angle for a valid approximation
increase or decrease as you increase the
precision of your angle measurement?
sin tan to two significant digits up
to 9.9°. An increase in the precision of the
measurement reduces this angle to 2.99°.
Practice Problems
19.2 Diffraction
pages 524–531
page 526
16. Monochromatic green light of wavelength
546 nm falls on a single slit with a width
of 0.095 mm. The slit is located 75 cm from
a screen. How wide will the central bright
band be?
(3)(555 nm)
(4)(1.83)
color
nfilm
555 nm
(4)(1.83)
color
nfilm
nfilm
Chapter 19 continued
Black
Red
Black
Red
Black
Red
Black
Repeats
and fades
Repeats
and fades
Blue
Black
Blue
Black
Blue
Black
Blue
Black
Blue
Black
Red
Black
Red
Black
Red
Black
Repeats
and fades
Repeats
and fades

xmin
w
L
4.3 mm
17. Yellow light with a wavelength of 589 nm
passes through a slit of width 0.110 mm and
makes a pattern on a screen. If the width of
the central bright band is 2.60102m,
how far is it from the slits to the screen?
2x1
2w
L
L
2.43 m
18. Light from a He-Ne laser (632.8 nm)
falls on a slit of unknown width. A pattern
is formed on a screen 1.15 m away, on
which the central bright band is 15 mm
wide. How wide is the slit?
2x1
2w
L
w
2
2
xL
1
9.7105 m
97 m
19. Yellow light falls on a single slit 0.0295 mm
wide. On a screen that is 60.0 cm away, the
central bright band is 24.0 mm wide. What
is the wavelength of the light?
2x1
2w
L
(2x
21
L
)w
5.90102nm
20. White light falls on a single slit that is
0.050 mm wide. A screen is placed 1.00 m
away. A student first puts a blue-violet filter
(441 nm) over the slit, then a red filter
(622 nm). The student measures the
width of the central bright band.
a. Which filter produced the wider band?
Red, because central peak width is
proportional to wavelength.
b. Calculate the width of the central bright
band for each of the two filters.
2x1
2w
L
For blue,
2x1
18 mm
For red,
2x1
25 mm
page 529
21. White light shines through a grating onto a
screen. Describe the pattern that is produced.
A full spectrum of color is seen.
Because of the variety of wavelengths,
dark fringes of one wavelength would
be filled by bright fringes of another
color.
22. If blue light of wavelength 434 nm shines
on a diffraction grating and the spacing
of the resulting lines on a screen that is
1.05 m away is 0.55 m, what is the spacing
between the slits in the grating?
dsin
d
sin
where tan1
L
x
9.410–7 m
434109
sin tan1
0
1.
.5
05
5m
m
sin tan1
L
x
2(6.22107m)(1.00 m)
5.0105m
2(4.41107m)(1.00 m)
5.0105m
(24.0103m)(0.0295103m)
(2)(60.0102m)
(2)(632.8109m)(1.15 m)
15103m
(2.60102 m)(0.110103 m)
(2)(589109 m)
(2x1)w
2
(5.46107m)(0.75 m)
9.5105m
xminw
L
402 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 403
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
23. A diffraction grating with slits separated by
8.60107m is illuminated by violet light
with a wavelength of 421 nm. If the screen is
80.0 cm from the grating, what is the sepa-
ration of the lines in the diffraction pattern?
dsin
sin
d
tan
L
x
xLtan
Ltan sin1
d
(0.800 m)tan sin1
0.449 m
24. Blue light shines on the DVD in Example
Problem 3. If the dots produced on a
wall that is 0.65 m away are separated
by 58.0 cm, what is the wavelength of
the light?
dsin dsin tan1
L
x
(7.41107 m)sin tan1
490 nm
25. Light of wavelength 632 nm passes through
a diffraction grating and creates a pattern
on a screen that is 0.55 m away. If the first
bright band is 5.6 cm from the central
bright band, how many slits per centimeter
does the grating have?
dsin
There is one slit per distance d, so
d
1
gives slits per centimeter.
d
sin
6.210–6 m 6.210–4 cm
6.2
1
1s
0l
–
i4
tcm
1.6103slits/cm
Section Review
19.2 Diffraction
pages 524–531
page 531
26. Distance Between First-Order Dark
Bands Monochromatic green light of wave-
length 546 nm falls on a single slit of width
0.080 mm. The slit is located 68.0 cm from
a screen. What is the separation of the first
dark bands on each side of the central
bright band?
2xmin
2w
L
9.3 mm
27. Diffraction Patterns Many narrow slits are
close to each other and equally spaced in a
large piece of cardboard. They are illumi-
nated by monochromatic red light. A sheet
of white paper is placed far from the slits,
and a pattern of bright and dark bands is
visible on the paper. Sketch the pattern that
would be seen on the screen.
Band spacing is exactly the same as in
the pattern produced by the two slits,
but now light bands are much thinner
and separated by wider dark bands.
28. Line Spacing You shine a red laser light
through one diffraction grating and form a
pattern of red dots on a screen. Then you
substitute a second diffraction grating for
the first one, forming a different pattern.
The dots produced by the first grating are
spread out more than those produced by
the second. Which grating has more lines
(2)(546109m)(68.0102m)
0.080103m
632109m
sin tan1
0
0
.0
.5
5
5
6m
m
sin tan1
L
x
0.58 m
0.65 m
421109m
8.60107m
Chapter 19 continued
Pattern
repeats
Pattern
repeats
Bright red lines
per millimeter?
x
L
d
, so the greater the dot spacings,
x, the narrower the slit spacing, d, and
thus more lines per millimeter.
29. Rayleigh Criterion The brightest star in the
winter sky in the northern hemisphere is
Sirius. In reality, Sirius is a system of two
stars that orbit each other. If the Hubble Space
Telescope (diameter 2.4 m) is pointed at the
Sirius system, which is 8.44 light-years from
Earth, what is the minimum separation there
would need to be between the stars in order
for the telescope to be able to resolve them?
Assume that the average light coming from
the stars has a wavelength of 550 nm.
xobj
2.21010 m
30. Critical Thinking You are shown a
spectrometer, but do not know whether
it produces its spectrum with a prism or
a grating. By looking at a white-light
spectrum, how could you tell?
Determine if the violet or the red end of
the spectrum makes the largest angle
with the direction of the beam of inci-
dent white light. A prism bends the vio-
let end of the spectrum the most,
whereas a grating diffracts red wave-
lengths the most.
Chapter Assessment
Concept Mapping
page 536
31. Monochromatic light of wavelength
illuminates two slits in a Young’s double-slit
experiment setup that are separated by a
distance, d. A pattern is projected onto a
screen a distance, L, away from the slits.
Complete the following concept map using
, L, and dto indicate how you could vary
them to produce the indicated change in the
spacing between adjacent bright bands, x.
Mastering Concepts
page 536
32. Why is it important that monochromatic light
was used to make the interference pattern in
Young’s interference experiment? (19.1)
When monochromatic light is used, you
get a sharp interference pattern; if you
use white light, you get sets of colored
bands.
33. Explain why the position of the central
bright band of a double-slit interference
pattern cannot be used to determine the
wavelength of the light waves. (19.1)
All wavelengths produce the line in the
same place.
34. Describe how you could use light of a
known wave-length to find the distance
between two slits. (19.1)
Let the light fall on the double slit, and
let the interference pattern fall on a
sheet of paper. Measure the spacings
between the bright bands, x, and use
the equation d
x
L
.
35. Describe in your own words what happens in
thin-film interference when a dark band is
produced by light shining on a soap film sus-
pended in air. Make sure you include in your
explanation how the wavelength of the light
and thickness of the film are related. (19.1)
1.22(330109 m)(7.991016 m)
2.4 m
1.22Lobj
D
404 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued
to increase x,
decrease increaseincrease
to decrease x,
decrease
x
L
d
Ld d L

Physics: Principles and Problems Solutions Manual 405
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
When the light strikes the front of the
film, some reflects off this surface and
some passes through the film and
reflects off the back surface of the film.
When light reflects off a medium with a
higher index of refraction, it undergoes
a phase shift of one-half wavelength;
this happens to the light that initially
reflects. In order for a dark band to be
produced, the two light rays must be
one-half wavelength out of phase. If the
thickness of the film is such that the ray
reflecting off the back surface goes
through a whole number of cycles while
passing through the film, the light rays
arriving at your eye will be out of phase
and destructively interfere. Remember
that the wavelength is altered by the
index of refraction of the film, so that
the thickness of the film must equal a
multiple of half a wavelength of the
light, divided by the film’s index of
refraction.
36. White light shines through a diffraction
grating. Are the resulting red lines spaced
more closely or farther apart than the
resulting violet lines? Why? (19.2)
The spacing is directly proportional to
the wavelength, and because red light
has a longer wavelength than violet, the
red lines will be spaced farther apart
than the violet lines.
37. Why do diffraction gratings have large
numbers of slits? Why are these slits so
close together? (19.2)
The large number of grooves in diffrac-
tion gratings increases the intensity of
the diffraction patterns. The grooves are
close together, producing sharper
images of light.
38. Why would a telescope with a small diam-
eter not be able to resolve the images of
two closely spaced stars? (19.2)
Small apertures have large diffraction
patterns that limit resolution.
39. For a given diffraction grating, which color
of visible light produces a bright line closest
to the central bright band? (19.2)
violet light, the color with the smallest
wavelength
Applying Concepts
page 536
40. For each of the following examples, indicate
whether the color is produced by thin-film
interference, refraction, or the presence of
pigments.
a. soap bubbles
interference
b. rose petals
pigments
c. oil films
interference
d. a rainbow
refraction
41. How can you tell whether a pattern is pro-
duced by a single slit or a double slit?
A double-slit interference pattern con-
sists of equally spaced lines of almost
equal brightness. A single-slit diffrac-
tion pattern has a bright, broad central
band and dimmer side bands.
42. Describe the changes in a single-slit
diffraction pattern as the width of the slit
is decreased.
The bands get wider and dimmer.
43. Science Fair At a science fair, one exhibi-
tion is a very large soap film that has a fairly
consistent width. It is illuminated by a light
with a wavelength of 432 nm, and nearly the
entire surface appears to be a lovely shade of
purple. What would you see in the following
situations?
a. the film thickness was doubled
complete destructive interference
b. the film thickness was increased by half
a wavelength of the illuminating light
complete constructive interference
Chapter 19 continued

c. the film thickness was decreased by one
quarter of a wavelength of the
illuminating light
complete destructive interference
44. What are the differences in the characteris-
tics of the diffraction patterns formed by
diffraction gratings containing 104lines/cm
and 105lines/cm?
The lines in the diffraction pattern are
narrower for the 105lines/cm grating.
45. Laser Pointer Challenge You have two
laser pointers, a red one and a green one.
Your friends Mark and Carlos disagree about
which has the longer wavelength. Mark
insists that red light has a longer wavelength,
while Carlos is sure that green has the longer
wavelength. You have a diffraction grating
handy. Describe what demonstration you
would do with this equipment and how you
would explain the results to Carlos and Mark
to settle their disagreement.
Shine each laser pointer through the grat-
ing onto a nearby wall.The color with the
longer wavelength will produce dots with
a greater spacing on the wall because the
spacing is directly proportional to the
wavelength. (Mark is correct; red light has
a longer wavelength than green light.)
46. Optical Microscope Why is blue light used
for illumination in an optical microscope?
Less diffraction results from the short
wavelength of blue light.
Mastering Problems
19.1 Interference
pages 536—537
Level 1
47. Light falls on a pair of slits 19.0 m apart
and 80.0 cm from a screen, as shown in
Figure 19-17. The first-order bright band is
1.90 cm from the central bright band. What
is the wavelength of the light?
■Figure 19-17 (Not to scale)
x
L
d
451 nm
48. Oil Slick After a short spring shower, Tom
and Ann take their dog for a walk and
notice a thin film of oil (n1.45) on a
puddle of water, producing different colors.
What is the minimum thickness of a place
where the oil creates constructive interfer-
ence for light with a wavelength of 545 nm?
There is one phase inversion, so
constructive interference will be when
2tm
1
2
For the minimum thickness, m0.
t
1
4
94.0 nm
Level 2
49. Light of wavelength 542 nm falls on a
double slit. First-order bright bands appear
4.00 cm from the central bright band. The
screen is 1.20 m from the slits. How far
apart are the slits?
x
L
d
d
x
L
16.3 m
50. Insulation Film Winter is approaching and
Alejandro is helping to cover the windows
(5.42107m)(1.20 m)
4.00102m
545 nm
(4)(1.45)
nfilm
nfilm
(19.0106m)(1.90102m)
80.0102m
ScreenDouble slit
80.0 cm
19.0 m
406 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 407
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
in his home with thin sheets of clear plastic
(n1.81) to keep the drafts out. After the
plastic is taped up around the windows such
that there is air between the plastic and the
glass panes, the plastic is heated with a hair
dryer to shrink-wrap the window. The thick-
ness of the plastic is altered during this
process. Alejandro notices a place on the
plastic where there is a blue stripe of color.
He realizes that this is created by thin-film
interference. What are three possible thick-
nesses of the portion of the plastic where
the blue stripe is produced if the wavelength
of the light is 4.40102nm?
There is one phase inversion, so
constructive interference will be when
2tm
1
2
Three possible thicknesses occur at
m0, 1, and 2.
t
1
4
for m0
60.8 nm
t
3
4
for m1
182 nm
t for m2
304 nm
Level 3
51. Samir shines a red laser pointer through
three different double-slit setups. In setup A,
the slits are separated by 0.150 mm and the
screen is 0.60 m away from the slits. In
setup B, the slits are separated by 0.175 mm
and the screen is 0.80 m away. Setup C has
the slits separated by 0.150 mm and the
screen a distance of 0.80 m away. Rank the
three setups according to the separation
between the central bright band and the
first-order bright band, from least to most
separation. Specifically indicate any ties.
x
L
d
x
d
L
Because is the same for each setup,
calculate
x
to compare the setups.
x
L
d
Setup A:
4.0103
Setup B:
4.6103
Setup C:
5.3103
xCxBxA
19.2 Diffraction
page 537
Level 1
52. Monochromatic light passes through a sin-
gle slit with a width of 0.010 cm and falls
on a screen 100 cm away, as shown in
Figure 19-18. If the width of the central
band is 1.20 cm, what is the wavelength of
the light?
■Figure 19-18 (Not to scale)
2x1
2w
L
x
L
w
ScreenSingle slit
100 cm
0.010 cm
0.80 m
1.50104m
0.80 m
1.75104m
0.60 m
1.50104m
(5)(4.40102nm)
(4)(1.81)
nfilm
5
4
(3)(4.40102nm)
(4)(1.81)
nfilm
4.40102nm
(4)(1.81)
nfilm
nfilm
Chapter 19 continued

600 nm
53. A good diffraction grating has 2.5103lines
per cm. What is the distance between two
lines in the grating?
d
4.0104cm
Level 2
54. Light with a wavelength of 4.5105cm
passes through a single slit and falls on a
screen 100 cm away. If the slit is 0.015 cm
wide, what is the distance from the center
of the pattern to the first dark band?
2x1
2w
L
2x1is the width of the bright band, so
to get the distance from the center to
the first dark band, divide by 2.
x1
w
L
0.3 cm
55. Hubble Space Telescope Suppose the Hubble
Space Telescope, 2.4 m in diameter, is in orbit
1.0105m above Earth and is turned to
view Earth, as shown in Figure 19-19. If
you ignore the effect of the atmosphere,
how large an object can the telescope
resolve? Use 5.1107m.
■Figure 19-19
1.2
D
2
xobj
2.6102m
2.6 cm
Level 3
56. Monochromatic light with a wavelength of
425 nm passes through a single slit and
falls on a screen 75 cm away. If the central
bright band is 0.60 cm wide, what is the
width of the slit?
2x1
2w
L
w
xL
1
x1
1
2
(2x1)0.30 cm
1.1102cm
57. Kaleidoscope Jennifer is playing with a
kaleidoscope from which the mirrors have
been removed. The eyehole at the end is
7.0 mm in diameter. If she can just distin-
guish two bluish-purple specks on the other
end of the kaleidoscope separated by 40 m,
what is the length of the kaleidoscope?
Use 650 nm and assume that the
resolution is diffraction limited through
the eyehole.
xobj
Lobj
0.4 m
(40106m)(7.0103m)
(1.22)(650109m)
xobjD
1.22
1.22Lobj
D
(4.25105cm)(75 cm)
0.30 cm
2L
2x1
(1.22)(5.1107m)(1.0105m)
2.4 m
1.22Lobj
D
xobj
Lobj
(4.5105cm)(100 m)
0.015 cm
1
2.5103lines/cm
(0.60 cm)(0.010 cm)
100 cm
408 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 409
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
58. Spectroscope A spectroscope uses a grat-
ing with 12,000 lines/cm. Find the angles at
which red light, 632 nm, and blue light,
421 nm, have first-order bright lines.
d8.33105cm
dsin
sin
d
For red light,
sin1
49.3°
For blue light,
sin1
30.3°
Mixed Review
page 538
Level 1
59. Record Marie uses an old 33
1
3
rpm record
as a diffraction grating. She shines a laser,
632.8 nm, on the record, as shown in
Figure 19-20. On a screen 4.0 m from the
record, a series of red dots 21 mm apart are
visible.
■Figure 19-20 (Not to scale)
a. How many ridges are there in a cen-
timeter along the radius of the record?
dsin
d
sin
1.2104m 1.2102cm
83 ridges/cm
b. Marie checks her results by noting that
the ridges represent a song that lasts
4.01 minutes and takes up 16 mm on
the record. How many ridges should
there be in a centimeter?
Number of ridges is
(4.01 min)(33.3 rev/min) 134 ridges
13
1
4
.6
ri
c
d
m
ges
84 ridges/cm
Level 2
60. An anti-reflective coating, n1.2, is
applied to a lens. If the thickness of the
coating is 125 nm, what is (are) the
color(s) of light for which complete
destructive interference will occur? Hint:
Assume the lens is made out of glass.
Because nfilm nair, there is a phase
inversion on the first reflection.
Because nlens 1.52 nfilm, there is a
phase inversion on the second reflection.
For destructive interference:
2dm
1
2
m1(3.0102nm)
For m0
1
2
1(3.0102nm)
6.0102nm
The light is reddish-orange. For other
values of m, the wavelength is shorter
than that of light.
1
2
(2)(125 nm)(1.2)
m
1
2
2dnfilm
m
1
2
nfilm
1
1.2102cm
1
d
632.8109m
sin tan1
214
.0
10
m
3m
sin tan1
L
x
21 mm
21 mm
Screen 4.0 m
Laser
Record
4.21105cm
8.33105cm
6.32105cm
8.33105cm
1
12,000 lines/cm
Chapter 19 continued

Level 3
61. Camera When a camera with a 50-mm
lens is set at f/8, its aperture has an opening
6.25 mm in diameter.
a. For light with 550 nm, what is
the resolution of the lens? The film is
50.0 mm from the lens.
xobj
5.4103mm
b. The owner of a camera needs to decide
which film to buy for it. The expensive
one, called fine-grained film, has
200 grains/mm. The less costly, coarse-
grained film has only 50 grains/mm. If
the owner wants a grain to be no smaller
than the width of the central bright spot
calculated in part a, which film should
he purchase?
Central bright band width
2x10.7103mm
The 200 grains/mm film has
2001
mm
between grains 5103mm, so
this film will work.
The 50 grains/mm has
50 1
mm
between grains 20103mm, so
this film won’t work.
Thinking Critically
page 538
62. Apply Concepts Yellow light falls on a dif-
fraction grating. On a screen behind the
grating, you see three spots: one at zero
degrees, where there is no diffraction, and
one each at 30° and 30°. You now add
a blue light of equal intensity that is in the
same direction as the yellow light. What
pattern of spots will you now see on the
screen?
A green spot at 0°, yellow spots at 30°
and 30°, and two blue spots slightly
closer in.
63. Apply Concepts Blue light of wavelength
passes through a single slit of width w. A
diffraction pattern appears on a screen. If
you now replace the blue light with a green
light of wavelength 1.5, to what width
should you change the slit to get the original
pattern back?
The angle of diffraction depends on the
ratio of slit width to wavelength.Thus,
you would increase the width to 1.5w.
64. Analyze and Conclude At night, the pupil
of a human eye has an aperture diameter
of 8.0 mm. The diameter is smaller in
daylight. An automobile’s headlights are
separated by 1.8 m.
a. Based upon Rayleigh’s criterion, how far
away can the human eye distinguish the
two headlights at night? Hint: Assume a
wavelength of 525 nm.
xobj
Lobj
1
x
.
o
2
b
2
jD
2.2104m 22 km
b. Can you actually see a car’s headlights
at the distance calculated in part a?
Does diffraction limit your eyes’ sensing
ability? Hypothesize as to what might
be the limiting factors.
No; a few hundred meters, not sever-
al kilometers, is the limit. Diffraction
doesn’t limit the sensing ability of
your eyes. More probable factors are
the refractive effects of the atmos-
phere, like those that cause stars to
twinkle, or the limitations of the reti-
na and the optic area of the brain to
separate two dim sources.
Writing in Physics
page 538
65. Research and describe Thomas Young’s con-
tributions to physics. Evaluate the impact of
his research on the scientific thought about
the nature of light.
(8.0103m)(1.80 m)
(1.22)(5.25107m)
1.22Lobj
D
(1.22)(5.5104mm)(50.0 mm)
6.25 mm
1.22Lobj
D
410 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 411
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Student answers will vary. Answers
should include Young’s two-slit experi-
ment that allowed him to precisely
measure the wavelength of light.
66. Research and interpret the role of diffrac-
tion in medicine and astronomy. Describe
at least two applications in each field.
Student answers will vary. Answers
could include diffraction in telescopes
and microscopes, as well as
spectroscopy.
Cumulative Review
page 538
67. How much work must be done to push a
0.5-m3block of wood to the bottom of a
4-m-deep swimming pool? The density of
wood is 500 kg/m3. (Chapter 13)
The block would float, but to submerge it
would require an extra force downward.
WFd
FFbuoyancy Fg
Fg Vg
(500 kg/m3)(0.5 m3)(9.80 m/s2)
2450 N
Fbuoyancy Vg
(1000 kg/m3)(0.5 m3)
(9.80 m/s2)
4900 N
Work (4900 N 2450 N)(4 m)
10 kJ
68. What are the wavelengths of microwaves in
an oven if their frequency is 2.4 GHz?
(Chapter 14)
c f
c
f
0.12 m
69. Sound wave crests that are emitted by an
airplane are 1.00 m apart in front of the
plane, and 2.00 m apart behind the plane.
(Chapter 15)
a. What is the wavelength of the sound in
still air?
1.50 m
b. If the speed of sound is 330 m/s, what
is the frequency of the source?
vf
f
v
3
1
3
.5
00
m
m
/s
220 Hz
c. What is the speed of the airplane?
The plane moves forward 0.50 m
for every 1.50 m that the sound wave
travels, so the plane’s speed is one-
third the speed of sound, or 110 m/s.
70. A concave mirror has a 48.0-cm radius. A
2.0-cm-tall object is placed 12.0 cm from
the mirror. Calculate the image position
and image height. (Chapter 17)
f
2
r
48.0
2cm
24.0 cm
1
f
d
1
o
d
1
i
di
24.0 cm
m
h
h
o
i
d
d
o
i
hi
d
di
o
ho
4.0 cm
71. The focal length of a convex lens is 21.0 cm.
A 2.00-cm-tall candle is located 7.50 cm
from the lens. Use the thin-lens equation
to calculate the image position and image
height. (Chapter 18)
1
f
d
1
o
d
1
i
(24.0 cm)(2.0 cm)
12.0 cm
(12.0 cm)(24.0 cm)
12.0 cm 24.0 cm
dof
do f
3.00108 m/s
2.4109 Hz
Chapter 19 continued

di
11.7 cm
m
h
h
o
i
hi
3.11 cm
Challenge Problem
page 526
You have several unknown substances and wish
to use a single-slit diffraction apparatus to deter-
mine what each one is. You decide to place a
sample of an unknown substance in the region
between the slit and the screen and use the data
that you obtain to determine the identity of each
substance by calculating its index of refraction.
1. Come up with a general formula for the
index of refraction of an unknown sub-
stance in terms of the wavelength of the
light, vacuum, the width of the slit, w, the
distance from the slit to the screen, L, and
the distance between the central bright
band and the first dark band, x1.
Use (1) ,(2) vsubstance f,
and (3) nsubstance .
Combine (2) and (3).
nsubstance (4),
because the frequency remains constant
as the light crosses a boundary.
Rewrite (1) in terms of a substance in
the space between the slits and the
screen.
substance (5)
Combine (4) and (5) and solve for x.
nsubstance
xmin
2. If the source you used had a wavelength of
634 nm, the slit width was 0.10 mm, the
distance from the slit to the screen was
1.15 m, and you immersed the apparatus
in water (nsubstance 1.33), then what
would you expect the width of the center
band to be?
x
5.510–3m
(634109m)(1.15 m)
(1.33)(0.10103m)
vacuumL
nsubstanced
vacuumL
nsubstancew
vacuum
xm
L
inw
xminw
L
vacuum
substance
vacuumf
substancef
c
v
xminw
L
Incoming light
Unknown
substance
L
x1
(11.7 cm)(2.00 cm)
7.50 cm
diho
do
di
do
(7.50 cm)(21.0 cm)
7.50 cm 21.0 cm
dof
dof
412 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued

Physics: Principles and Problems Solutions Manual 413
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
20 Static Electricity
CHAPTER
Section Review
20.1 Electric Charge
pages 541–545
page 545
1. Charged Objects After a comb is rubbed
on a wool sweater, it is able to pick up
small pieces of paper. Why does the comb
lose that ability after a few minutes?
The comb loses its charge to its sur-
roundings and becomes neutral once
again.
2. Types of Charge In the experiments
described earlier in this section, how could
you find out which strip of tape, B or T, is
positively charged?
Bring a positively charged glass rod
near the two strips of tape. The one that
is repelled by the rod is positive.
3. Types of Charge A pith ball is a small
sphere made of a light material, such as plas-
tic foam, often coated with a layer of graphite
or aluminum paint. How could you deter-
mine whether a pith ball that is suspended
from an insulating thread is neutral, is
charged positively, or is charged negatively?
Bring an object of known charge, such
as a negatively charged hard rubber
rod, near the pith ball. If the pith ball is
repelled, it has the same charge as the
rod. If it is attracted, it may have the
opposite charge or be neutral. To find
out which, bring a positively charged
glass rod near the pith ball. If they
repel, the pith ball is positive; if they
attract, the pith ball must be neutral.
4. Charge Separation A rubber rod can be
charged negatively when it is rubbed with
wool. What happens to the charge of the
wool? Why?
The wool becomes positively charged
because it gives up electrons to the
rubber rod.
5. Conservation of Charge An apple con-
tains trillions of charged particles. Why
don’t two apples repel each other when
they are brought together?
Each apple contains equal numbers of
positive and negative charges, so they
appear neutral to each other.
6. Charging a Conductor Suppose you hang
a long metal rod from silk threads so that
the rod is isolated. You then touch a
charged glass rod to one end of the metal
rod. Describe the charges on the metal rod.
The glass rod attracts electrons off
the metal rod, so the metal becomes
positively charged. The charge is dis-
tributed uniformly along the rod.
7. Charging by Friction You can charge a
rubber rod negatively by rubbing it with
wool. What happens when you rub a cop-
per rod with wool?
Because the copper is a conductor, it
remains neutral as long as it is in con-
tact with your hand.
8. Critical Thinking It once was proposed
that electric charge is a type of fluid that
flows from objects with an excess of the
fluid to objects with a deficit. Why is the
current two-charge model better than the
single-fluid model?
The two-charge model can better
explain the phenomena of attraction
and repulsion. It also explains how
objects can become charged when they
are rubbed together. The single-fluid
model indicated that the charge should
be equalized on objects that are in con-
tact with each other.

Practice Problems
20.2 Electric Force
pages 546–553
page 552
9. A negative charge of 2.0104C and a positive charge of 8.0104C are
separated by 0.30 m. What is the force between the two charges?
F
1.6104N
10. A negative charge of 6.0106C exerts an attractive force of 65 N on a second
charge that is 0.050 m away. What is the magnitude of the second charge?
F
qB
3.0106C
11. The charge on B in Example Problem 1 is replaced by a charge of 3.00 C.
Diagram the new situation and find the net force on A.
Magnitudes of all forces remain the same. The direction changes to 42°
above the xaxis, or 138°.
12. Sphere A is located at the origin and has a charge of 2.0106C. Sphere B
is located at 0.60 m on the x-axis and has a charge of 3.6106C.
Sphere C is located at 0.80 m on the x-axis and has a charge of 4.0106C.
Determine the net force on sphere A.
FB on A K(9.0109Nm2/C2)0.18 N
direction: toward the right
FC on A K(9.0109Nm2/C2)0.1125 N
direction: toward the left
Fnet FB on A FC on A (0.18 N) (0.1125 N) 0.068 N toward the right
13. Determine the net force on sphere B in the previous problem.
FAon B K
FC on B K
Fnet FC on B FAon B
KKqAqB
dAB2
qBqC
dBC2
qAqB
dAB2
qAqB
dAB2
(2.0106C)(4.0106C)
(0.80 m)2
qAqC
dAC2
(2.0106C)(3.6106C)
(0.60 m)2
qAqB
dAB2
(65 N)(0.050 m)2
(9.0109Nm2/C2)(6.0106C)
FdAB2
KqA
KqAqB
dAB2
(9.0109Nm2/C2)(2.0104C)(8.0104C)
(0.30 m)2
KqAqB
dAB2
414 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 415
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(9.0109Nm2/C2)
(9.0109Nm2/C2)
3.1 N toward the right
Section Review
20.2 Electric Force
pages 546–553
page 553
14. Force and Charge How are electric force
and charge related? Describe the force when
the charges are like charges and the force
when the charges are opposite charges.
Electric force is directly related to each
charge. It is repulsive between like
charges and attractive between oppo-
site charges.
15. Force and Distance How are electric force
and distance related? How would the force
change if the distance between two charges
were tripled?
Electric force is inversely related to
the square of the distance between
charges. If the distance is tripled, the
force will be one-ninth as great.
16. Electroscopes When an electroscope is
charged, the leaves rise to a certain angle
and remain at that angle. Why do they not
rise farther?
As the leaves move farther apart, the
electric force between them decreases
until it is balanced by the gravitational
force pulling down on the leaves.
17. Charging an Electroscope Explain how to
charge an electroscope positively using
a. a positive rod.
Touch the positive rod to the electro-
scope. Negative charges will move
to the rod, leaving the electroscope
positively charged.
b. a negative rod.
Bring the negative rod near, but not
touching the electroscope. Touch
(ground) the electroscope with your
finger, allowing electrons to be
repelled off of the electroscope into
your finger. Remove your finger and
then remove the rod.
18. Attraction of Neutral Objects What two
properties explain why a neutral object is
attracted to both positively and negatively
charged objects?
Charge separation, caused by the
attraction of opposite charges and the
repulsion of like charges, moves the
opposite charges in the neutral body
closer to the charged object and the
like charges farther away. The inverse
relation between force and distance
means that the nearer, opposite
charges will attract more than the more
distant, like charges will repel. The
overall effect is attraction.
19. Charging by Induction In an electroscope
being charged by induction, what happens
when the charging rod is moved away before
the ground is removed from the knob?
Charge that had been pushed into the
ground by the rod would return to the
electroscope from the ground, leaving
the electroscope neutral.
20. Electric Forces Two charged spheres are held
a distance, r, apart. One sphere has a charge of
3C, and the other sphere has a charge of
9C. Compare the force of the 3C
sphere on the 9C sphere with the force of
the 9C sphere on the 3C sphere.
The forces are equal in magnitude and
opposite in direction.
21. Critical Thinking Suppose that you are
testing Coulomb’s law using a small, posi-
tively charged plastic sphere and a large,
positively charged metal sphere. According
to Coulomb’s law, the force depends on
1/r2, where ris the distance between the
centers of the spheres. As the spheres get
(2.0106C)(3.6106C)
(0.60 m)2
(3.6106C)(4.0106C)
(0.20 m)2
Chapter 20 continued

close together, the force is smaller than
expected from Coulomb’s law. Explain.
Some charges on the metal sphere will
be repelled to the opposite side from
the plastic sphere, making the effective
distance between the charges greater
than the distance between the spheres’
centers.
Chapter Assessment
Concept Mapping
page 558
22. Complete the concept map below using the
following terms: conduction, distance, elemen-
tary charge.
Mastering Concepts
page 558
23. If you comb your hair on a dry day, the
comb can become positively charged. Can
your hair remain neutral? Explain. (20.1)
No. By conservation of charge, your
hair must become negatively charged.
24. List some insulators and conductors. (20.1)
Student answers will vary but may
include dry air, wood, plastic, glass,
cloth, and deionized water as insula-
tors; and metals, tap water, and your
body as conductors.
25. What property makes metal a good conduc-
tor and rubber a good insulator? (20.1)
Metals contain free electrons; rubber
has bound electrons.
26. Laundry Why do socks taken from a clothes
dryer sometimes cling to other clothes? (20.2)
They have been charged by contact as
they rub against other clothes, and
thus, are attracted to clothing that is
neutral or has an opposite charge.
27. Compact Discs If you wipe a compact disc
with a clean cloth, why does the CD then
attract dust? (20.2)
Rubbing the CD charges it. Neutral
particles, such as dust, are attracted to
a charged object.
28. Coins The combined charge of all electrons
in a nickel is hundreds of thousands of
coulombs. Does this imply anything about
the net charge on the coin? Explain. (20.2)
No. Net charge is the difference between
positive and negative charges. The coin
still can have a net charge of zero.
29. How does the distance between two
charges impact the force between them?
If the distance is decreased while the
charges remain the same, what happens
to the force? (20.2)
Electric force is inversely proportional
to the distance squared. As distance
decreases and charges remain the
same, the force increases as the square
of the distance.
30. Explain how to charge a conductor nega-
tively if you have only a positively charged
rod. (20.2)
Bring the conductor close to, but not
touching, the rod. Ground the conductor
in the presence of the charged rod; then,
remove the ground before removing the
charged rod. The conductor will have a
net negative charge.
Applying Concepts
page 558
31. How does the charge of an electron differ
from the charge of a proton? How are they
similar?
416 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued
Electric
Force
charging
conduction induction
Coulomb’s
law
charge
elementary
charge
distance
coulomb

Physics: Principles and Problems Solutions Manual 417
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The charge of the proton is exactly the
same size as the electron, but has the
opposite sign.
32. Using a charged rod and an electroscope,
how can you find whether or not an object
is a conductor?
Use a known insulator to hold one end
of the object against the electroscope.
Touch the other end with the charged
rod. If the electroscope indicates a
charge, the object is a conductor.
33. A charged rod is brought near a pile of tiny
plastic spheres. Some of the spheres are
attracted to the rod, but as soon as they
touch the rod, they are flung off in different
directions. Explain.
The natural spheres are initially attract-
ed to the charged rod, but they acquire
the same charge as the rod when they
touch it. As a result, they are repelled
from the rod.
34. Lightning Lightning usually occurs when a
negative charge in a cloud is transported to
Earth. If Earth is neutral, what provides the
attractive force that pulls the electrons
toward Earth?
The charge in the cloud repels elec-
trons on Earth, causing a charge sepa-
ration by induction. The side of Earth
closest to the cloud is positive, result-
ing in an attractive force.
35. Explain what happens to the leaves of a
positively charged electroscope when rods
with the following charges are brought
close to, but not touching, the electroscope.
a. positive
The leaves will move farther apart.
b. negative
The leaves will drop slightly.
36. As shown in Figure 20-13, Coulomb’s law
and Newton’s law of universal gravitation
appear to be similar. In what ways are the
electric and gravitational forces similar?
How are they different?
■Figure 20-13 (Not to scale)
Similar: inverse-square dependence on
distance, force proportional to product
of two masses or two charges; differ-
ent: only one sign of mass, so gravita-
tional force is always attractive; two
signs of charge, so electric force can
be either attractive or repulsive.
37. The constant, K, in Coulomb’s equation is
much larger than the constant, G, in the
universal gravitation equation. Of what sig-
nificance is this?
The electric force is much larger than
the gravitational force.
38. The text describes Coulomb’s method for
charging two spheres, A and B, so that the
charge on B was exactly half the charge on
A. Suggest a way that Coulomb could have
placed a charge on sphere B that was exactly
one-third the charge on sphere A.
After changing spheres A and B equally,
sphere B is touched to two other
equally sized balls that are touching
each other. The charge on B will be
divided equally among all three balls,
leaving one-third the total charge on it.
39. Coulomb measured the deflection of sphere
A when spheres A and B had equal charges
and were a distance, r, apart. He then made
the charge on B one-third the charge on A.
How far apart would the two spheres then
have had to be for A to have had the same
deflection that it had before?
To have the same force with one-third
the charge, the distance would have
to be decreased such that d21/3, or
0.58 times as far apart.
r
qAqB
Coulomb’s Law
FK
qAqB
r2
mB
mA
r
Law of
Universal Gravitation
FG
mAmB
r2
Chapter 20 continued

40. Two charged bodies exert a force of 0.145 N on each other. If they are moved
so that they are one-fourth as far apart, what force is exerted?
F
d
12
and F , so F16 times the original force.
41. Electric forces between charges are enormous in comparison to gravitational
forces. Yet, we normally do not sense electric forces between us and our
surroundings, while we do sense gravitational interactions with Earth. Explain.
Gravitational forces only can be attractive. Electric forces can be either
attractive or repulsive, and we can sense only their vector sums, which
are generally small. The gravitational attraction to Earth is larger and
more noticeable because of Earth’s large mass.
Mastering Problems
20.2 Electric Force
page 559
Level 1
42. Two charges, qAand qB, are separated by a distance, r, and exert a force, F, on
each other. Analyze Coulomb’s law and identify what new force would exist
under the following conditions.
a. qAis doubled
2qA, then new force 2F
b. qAand qBare cut in half
qAand qB, then new force
1
2
1
2
FF
c. ris tripled
3d, then new force F
d. ris cut in half
d, then new force F4F
e. qAis tripled and ris doubled
3qAand 2d, then new force F
43. Lightning A strong lightning bolt transfers about 25 C to Earth. How many
electrons are transferred?
(25 C)
1.61020 electrons
44. Atoms Two electrons in an atom are separated by 1.51010 m, the typical size
of an atom. What is the electric force between them?
F
Kq
d
A
2
qB
1.0108N, away from each other
(9.0109Nm2/C2)(1.601019 C)(1.601019 C)
(1.51010 m)2
1electron
1.601019 C
3
4
(3)F
(2)2
3
4
F
1
2
2
1
2
1
9
F
(3)2
1
4
1
2
1
2
1
1
4
2
418 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued
Physics: Principles and Problems Solutions Manual 419
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
45. A positive and a negative charge, each of magnitude 2.5105C, are separated
by a distance of 15 cm. Find the force on each of the particles.
F
2.5102N, toward the other charge
46. A force of 2.4102N exists between a positive charge of 8.0105C and a
positive charge of 3.0105C. What distance separates the charges?
F
d
0.30 m
47. Two identical positive charges exert a repulsive force of 6.4109N when
separated by a distance of 3.81010 m. Calculate the charge of each.
F
Kq
d
A
2
qB
K
d
q
2
2
q
3.21019 C
Level 2
48. A positive charge of 3.0 C is pulled on by two
negative charges. As shown in Figure 20-14, one
negative charge, 2.0 C, is 0.050 m to the west,
and the other, 4.0 C, is 0.030 m to the east.
What total force is exerted on the positive charge?
F1
22 N west
F2
120 N east
Fnet F2F1(1.2102N) (2.2101N)
98 N, east
49. Figure 20-15 shows two positively charged
spheres, one with three times the charge of the
other. The spheres are 16 cm apart, and the force
between them is 0.28 N. What are the charges
on the two spheres?
FK
q
d
Aq
2B
KqA3qA
d2
■Figure 20-15
q
16 cm
3q
(9.0109Nm2/C2)(3.0106C)(4.0106C)
(0.030 m)2
(9.0109Nm2/C2)(3.0106C)(2.0106C)
(0.050 m)2■Figure 20-14
2.0 C3.0 C
4.0 C
0.050 m 0.030 m
(6.4109N)(3.81010 m)2
9.0109Nm2/C2
Fd2
K
(9.0109Nm2/C2)(8.0105C)(3.0105C)
2.4102N
KqAqB
F
KqAqB
d2
(9.0109Nm2/C2)(2.5105C)(2.5105C)
(1.5101m)2
KqAqB
d2
Chapter 20 continued

qA
5.2107C
qB 3qA1.5106C
50. Charge in a Coin How many coulombs of charge are on the electrons in a nickel?
Use the following method to find the answer.
a. Find the number of atoms in a nickel. A nickel has a mass of about 5 g.
A nickel is 75 percent Cu and 25 percent Ni, so each mole of the coin’s
atoms will have a mass of about 62 g.
Acoin is 0.08 mole.
Thus, it has (0.08)(6.021023) 51022 atoms
b. Find the number of electrons in the coin. On average, each atom has
28.75 electrons.
(51022 atoms)(28.75 electrons/atom) 11024 electrons
c. Find the coulombs on the electrons.
(1.61019 coulombs/electron)(11024 electrons) 2105coulombs
51. Three particles are placed in a line. The left particle has a charge of 55 C, the
middle one has a charge of 45 C, and the right one has a charge of 78 C.
The middle particle is 72 cm from each of the others, as shown in Figure 20-16.
■Figure 20-16
a. Find the net force on the middle particle.
Let left be the negative direction
Fnet Fl(Fr)
Kq
d
m
2
ql
18 N, right
b. Find the net force on the right particle.
Fnet Fl (Fm)
K
(2
q
d
lq
)2
r
42 N, left
(9.0109Nm2/C2)(45106C)(78106C)
(0.72 m)2
(9.0109Nm2/C2)(55106C)(78106C)
(2(0.72 m))2
Kqmqr
d2
(9.0109Nm2/C2)(45106C)(78106C)
(0.72 m)2
(9.0109Nm2/C2)(45106C)(55106C)
(0.72 m)2
Kqmqr
d2
55 C45 C78 C
72 cm 72 cm
5 g
62 g
(0.28 N)(0.16 m)2
3(9.0109Nm2/C2)
Fd2
3K
420 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 421
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Mixed Review
page 559
Level 1
52. A small metal sphere with charge 1.2105C is touched to an identical neutral
sphere and then placed 0.15 m from the second sphere. What is the electric force
between the two spheres?
The two spheres share the charge equally, so
FK(9.0109Nm2C2)14 N
53. Atoms What is the electric force between an electron and a proton placed
5.31011 m apart, the approximate radius of a hydrogen atom?
FK(9.0109Nm2C2)8.2108N
54. A small sphere of charge 2.4 C experiences a force of 0.36 N when a second sphere
of unknown charge is placed 5.5 cm from it. What is the charge of the second sphere?
FK
qB 5.0108C
55. Two identically charged spheres placed 12 cm apart have an electric force of
0.28 N between them. What is the charge of each sphere?
FK, where qAqB
q
6.7107C
56. In an experiment using Coulomb’s apparatus, a sphere with a charge of
3.6108C is 1.4 cm from a second sphere of unknown charge. The force
between the spheres is 2.7102N. What is the charge of the second sphere?
FK
qB
1.6108C
57. The force between a proton and an electron is 3.51010 N. What is the distance
between these two particles?
FK
d K
q
F
Aq
2B
(9.0
109N
m2/C
2)
8.11010 m
(1.601019 C)(1.61019 C)
3.51010 N
qAqB
d2
(2.7102N)(1.4102m)2
(9.0109Nm2C2)(3.6108C)
Fd2
KqA
qAqB
d2
(0.28 N)(1.2101m)2
(9.0109Nm2C2)
Fd2
K
qAqB
d2
(0.36 N)(5.5102m)2
(9.0109Nm2C2)(2.4106C)
Fd2
KqA
qAqB
d2
(1.601019 C)(1.601019 C)
(5.31011 m)2
qAqB
d2
(6.0106C)(6.0106C)
(0.15 m)2
qAqB
d2
Chapter 20 continued

Thinking Critically
page 560
58. Apply Concepts Calculate the ratio of the electric force to the gravitational force
between the electron and the proton in a hydrogen atom.
F
F
g
e
G
K
m
qe
e
q
m
p
p
2.31039
59. Analyze and Conclude Sphere A, with a charge of 64 C, is positioned at the
origin. A second sphere, B, with a charge of 16 C, is placed at 11.00 m on
the x-axis.
a. Where must a third sphere, C, of charge 12 C be placed so there is no net
force on it?
The attractive and repulsive forces must cancel, so
FAC KKFBC, so
d
q
A
A
C2
d
q
B
B
C2
, and 16dAC264dBC2, or
dAC24dBC2, so dAC 2dBC
The third sphere must be placed at 2.00 m on the x-axis so it is twice
as far from the first sphere as from the second sphere.
b. If the third sphere had a charge of 6 C, where should it be placed?
The third charge, qc, cancels from the equation, so it doesn’t matter
what its magnitude or sign is.
c. If the third sphere had a charge of 12 C, where should it be placed?
As in part b, the magnitude and sign of the third charge, qc, do not matter.
60. Three charged spheres are located at the positions shown in Figure 20-17. Find
the total force on sphere B.
■Figure 20-17
F1FAon B
(9.0109Nm2/C2)(4.5106C)(8.2106C)
(0.040 m)2
KqAqB
d2
A
B
C
6.0 C
4.5 C8.2 C
3.0 cm
4.0 cm x
y
qBqC
dBC2
qAqC
dAC2
(9.0109Nm2/C2)(1.601019 C)2
(6.671011 Nm2/kg2)(9.111031 kg)(1.671027 kg)
K
q
d
eq
2p
G
m
d
em
2p
422 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 423
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
208 N 208 N, to left
The distance between the other two charges is
(0.040
m)2
(0.03
0 m)2
0.050 m
1tan1
0
0.
.0
03
40
0m
m
37° below the negative x-axis, or 217° from the positive x-axis.
F2FC on B
177 N 177 N at 217° from the positive x-axis (37° 180°)
The components of F2are:
F2xF2cos (177 N)(cos 217°) 142 N 142 N to the left
F2yF2sin (177 N)(sin 217°) 106 N 106 N down
The components of the net (resultant) force are:
Fnet, x208 N 142 N 350 N 350 N, to left
Fnet, y106 N, down
Fnet (350 N
)2(1
06 N)2
366 N 3.7102N
2tan1
17° below the negative x-axis
Fnet 3.7102N at 197° from the positive x-axis
61. The two pith balls in Figure 20-18 each have a mass of 1.0 g and an equal
charge. One pith ball is suspended by an insulating thread. The other is brought
to 3.0 cm from the suspended ball. The suspended ball is now hanging with the
thread forming an angle of 30.0° with the vertical. The ball is in equilibrium
with FE, Fg, and FT. Calculate each of the following.
■Figure 20-18
a. Fg on the suspended ball
Fgmg (1.0103kg)(9.80 m/s2) 9.8103N
b. FE
tan 30.0°
F
F
E
g
3.0 cm
30.0°
FE
106 N
350 N
(9.0109Nm2/C)(8.2106C)(6.0106C)
(0.050 m)2
KqCqB
d2
Chapter 20 continued

FEmg tan 30.0°
(1.0103kg)(9.80 m/s2)(tan 30.0°)
5.7103N
c. the charge on the balls
F
Kq
d
A
2
qB
F
q
2.4108C
62. Two charges, qAand qB, are at rest near a positive test charge, qT, of 7.2 C. The
first charge, qA, is a positive charge of 3.6 C located 2.5 cm away from qTat 35°;
qBis a negative charge of 6.6 C located 6.8 cm away at 125°.
a. Determine the magnitude of each of the forces acting on qT.
FA
Kq
d
T
2
qA
3.7102N, away (toward qT)
FB
Kq
d
T
2
qA
92 N, toward (away from qT)
b. Sketch a force diagram.
c. Graphically determine the resultant force acting on qT.
FB 92 N
FA 3.7102 N
F 3.8102 N
21°
35°
125°
92 N
3.7102 N
FA
FB
qB
qT
qA
35°
(9.0109Nm2/C2)(7.2106C)(6.6106C)
(0.068 m)2
(9.0109Nm2/C2)(7.2106C)(3.6106C)
(0.025 m)2
(5.7103N)(3.0102m2)
(9.0109Nm2/C2)
Fd2
K
Kq2
d2
424 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 425
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Writing in Physics
page 560
63. History of Science Research several
devices that were used in the seventeenth
and eighteenth centuries to study static
electricity. Examples that you might
consider include the Leyden jar and the
Wimshurst machine. Discuss how they
were constructed and how they worked.
Student answers will vary, but should
include information such as the follow-
ing. The Leyden jar, invented in the
mid-1740s, was the earliest capacitor. It
was used throughout the eighteenth and
nineteenth centuries to store charges for
electricity-related experiments and
demonstrations. The Wimshurst machine
was a device used in the nineteenth and
early twentieth centuries to produce and
discharge static charges. Wimshurst
machines, which were replaced by the
Van de Graaff generator in the twentieth
century, used Leyden jars to store the
charges prior to discharge.
64. In Chapter 13, you learned that forces exist
between water molecules that cause water to
be denser as a liquid between 0°C and 4°C
than as a solid at 0°C. These forces are elec-
trostatic in nature. Research electrostatic inter-
molecular forces, such as van der Waals forces
and dipole-dipole forces, and describe their
effects on matter.
Answers will vary, but students should
describe the interactions between
positive and negative charges at the
molecular level. Students should
note that the strength of these forces
accounts for differences in melting
and boiling points and for the unusual
behavior of water between 0°C and 4°C.
Cumulative Review
page 560
65. Explain how a pendulum can be used to
determine the acceleration of gravity.
(Chapter 14)
Measure the length and period of the
pendulum, and use the equation for the
period of a pendulum to solve for g.
66. A submarine that is moving 12.0 m/s sends
a sonar ping of frequency 1.50103 Hz
toward a seamount that is directly in front of
the submarine. It receives the echo 1.800 s
later. (Chapter 15)
a. How far is the submarine from the
seamount?
dvt (1533 m/s)(0.900 s) 1380 m
b. What is the frequency of the sonar wave
that strikes the seamount?
fdfs
(1.50103Hz)
1510 Hz
c. What is the frequency of the echo
received by the submarine?
fdfs
(1510 Hz)
1520 Hz
67. Security Mirror A security mirror is used
to produce an image that is three-fourths
the size of an object and is located 12.0 cm
behind the mirror. What is the focal length
of the mirror? (Chapter 17)
m
d
d
o
i
do
m
di
16.0 cm
1
f
d
1
o
d
1
i
f
do
do
didi
(12.0 cm)
3
4
1533 m/s (12.0 m/s)
1533 m/s 0.0 m/s
vvd
vvs
1533 m/s 0.0 m/s
1533 m/s 12.0 m/s
vvd
vvs
Chapter 20 continued

48.0 cm
68. A 2.00-cm-tall object is located 20.0 cm
away from a diverging lens with a focal
length of 24.0 cm. What are the image posi-
tion, height, and orientation? Is this a
real or a virtual image? (Chapter 18)
1
f
d
1
o
d
1
i
di
do
do
f
f
10.9 cm
m
h
h
o
i
d
d
o
i
hi
d
di
o
ho
1.09 cm
This is a virtual image that is upright in
orientation, relative to the object.
69. Spectrometer A spectrometer contains a
grating of 11,500 slits/cm. Find the angle
at which light of wavelength 527 nm has
a first-order bright band. (Chapter 19)
The number of centimeters per slit is
the slit separation distance, d.
11,500 slits/cm
d8.70105cm
dsin
sin1
d
sin1
0.00347°
Challenge Problem
page 552
As shown in the figure below, two spheres of
equal mass, m, and equal positive charge, q,
are a distance, r, apart.
■Figure 20-11
1. Derive an expression for the charge, q, that
must be on each sphere so that the spheres
are in equilibrium; that is, so that the
attractive and repulsive forces between
them are balanced.
The attractive force is gravitation, and
the repulsive force is electrostatic, so
their expressions may be set equal.
FgG
m
d
Am
2B
K
q
d
Aq
2B
Fe
The masses and charges are equal,
and the distance cancels, so
Gm2Kq2, and
qm
G
K
m
(8.611011 C/kg)m
2. If the distance between the spheres is dou-
bled, how will that affect the expression for
the value of qthat you determined in the
previous problem? Explain.
The distance does not affect the value
of qbecause both forces are inversely
related to the square of the distance,
and the distance cancels out of the
expression.
3. If the mass of each sphere is 1.50 kg, deter-
mine the charge on each sphere needed to
maintain the equilibrium.
q(8.611011 C/kg)(1.50 kg)
1.291010 C
(6.671011 Nm2/kg2)
(9.0109Nm2/C2)
r
mass m
charge q
mass m
charge q
527109m
8.70103m
1 slit
d
(10.9 cm)(2.00 cm)
20.0 cm
(20.0 cm)(24.0 cm)
20.0 cm (24.0 cm)
(16.0 cm)(12.0 cm)
16.0 cm (12.0 cm)
426 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 427
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
21 Electric Fields
CHAPTER
Practice Problems
21.1 Creating and Measuring
Electric Fields
pages 563–568
page 565
1. A positive test charge of 5.0106C is in an
electric field that exerts a force of 2.0104N
on it. What is the magnitude of the electric
field at the location of the test charge?
E
q
F
4.0101N/C
2. A negative charge of 2.0108C experi-
ences a force of 0.060 N to the right in an
electric field. What are the field’s magnitude
and direction at that location?
E
F
q
3.0106N/C
directed to the left
3. A positive charge of 3.0107C is located
in a field of 27 N/C directed toward the
south. What is the force acting on the charge?
E
F
q
FEq (27 N/C)(3.0107C)
8.1106N
4. A pith ball weighing 2.1103N is placed
in a downward electric field of 6.5104N/C.
What charge (magnitude and sign) must be
placed on the pith ball so that the electric
force acting on it will suspend it against the
force of gravity?
The electric force and the gravitational
force algebraically sum to zero because
the ball is suspended, i.e. not in motion:
FgFe0, so FeFg
E
F
q
e
q
F
E
e
3.2108C
The electric force is upward (opposite
the field), so the charge is negative.
5. You are probing the electric field of a charge
of unknown magnitude and sign. You first
map the field with a 1.0106-C test
charge, then repeat your work with a
2.0106-C test charge.
a. Would you measure the same forces at
the same place with the two test
charges? Explain.
No. The force on the 2.0-C charge
would be twice that on the 1.0-C
charge.
b. Would you find the same field
strengths? Explain.
Yes. You would divide the force by
the strength of the test charge, so
the results would be the same.
page 566
6. What is the magnitude of the electric field
strength at a position that is 1.2 m from a
point charge of 4.2106C?
E
q
F
K
(9109Nm2/C2)
2.6104N/C
7. What is the magnitude of the electric field
strength at a distance twice as far from the
point charge in problem 6?
Because the field strength varies as the
square of the distance from the point
charge, the new field strength will be
one-fourth of the old field strength, or
6.5103N/C.
8. What is the electric field at a position that
is 1.6 m east of a point charge of
7.2106C?
(4.2106C)
(1.2 m)2
q
d2
2.1103N
6.5104N/C
Fg
E
0.060 N
2.0108C
2.0104N
5.0106C

E
q
F
K
(9.0109Nm2/C2)
2.5104N/C
The direction of the field is east (away
from the positive point charge).
9. The electric field that is 0.25 m from a
small sphere is 450 N/C toward the sphere.
What is the charge on the sphere?
E
q
F
K
q
3.1109C
The charge is negative, because the
field is directed toward it.
10. How far from a point charge of 2.4106C
must a test charge be placed to measure a
field of 360 N/C?
E
q
F
K
d
K
E
q
7.7 m
Section Review
21.1 Creating and Measuring
Electric Fields
pages 563–568
page 568
11. Measuring Electric Fields Suppose you are
asked to measure the electric field in space.
How do you detect the field at a point? How
do you determine the magnitude of the
field? How do you choose the magnitude of
the test charge? What do you do next?
To detect a field at a point, place a test
charge at that point and determine if
there is a force on it.
To determine the magnitude of the field,
divide the magnitude of the force on the
test charge by the magnitude of the test
charge.
The magnitude of the test charge must
be chosen so that it is very small com-
pared to the magnitudes of the charges
producing the field.
The next thing you should do is mea-
sure the direction of the force on the
test charge. The direction of the field is
the same as the direction of the force if
the test charge is positive; otherwise, it
is in the opposite direction.
12. Field Strength and Direction A positive
test charge of magnitude 2.40108C
experiences a force of 1.50103N toward
the east. What is the electric field at the
position of the test charge?
E
F
q
6.25104N/C east
13. Field Lines In Figure 21-4, can you tell
which charges are positive and which are
negative? What would you add to complete
the field lines?
No. The field lines must have arrow-
heads indicating their directions, from
positive to negative charges.
14. Field Versus Force How does the electric
field, E, at the test charge differ from the
force, F, on it?
The field is a property of that region of
space, and does not depend on the test
charge used to measure it. The force
depends on the magnitude and sign of
the test charge.
15. Critical Thinking Suppose the top charge
in Figure 21-2c is a test charge measuring
the field resulting from the two negative
charges. Is it small enough to produce an
accurate measure? Explain.
1.50103N east
2.40108C
(9.0109Nm2/C2)(2.4106C)
360 N/C
q
d2
(450 N/C)(0.25 m)2
(9.0109Nm2/C2)
Ed2
K
q
d2
(7.2106C)
(1.6 m)2
q
d2
428 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 429
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
No. This charge is large enough to
distort the field produced by the other
charges with its own field. Compare
with Figure 21-4b.
Practice Problems
21.2 Applications of
Electric Fields
pages 569–579
page 571
16. The electric field intensity between two
large, charged, parallel metal plates is
6000 N/C. The plates are 0.05 m apart.
What is the electric potential difference
between them?
VEd (6000 N/C)(0.05 m)
300 J/C 3102V
17. A voltmeter reads 400 V across two charged,
parallel plates that are 0.020 m apart. What
is the electric field between them?
VEd
E
d
V
2104N/C
18. What electric potential difference is applied
to two metal plates that are 0.200 m apart
if the electric field between them is
2.50103N/C?
VEd (2.50103N/C)(0.200 m)
5.00102V
19. When a potential difference of 125 V is
applied to two parallel plates, the field
between them is 4.25103N/C. How far
apart are the plates?
VEd
d
E
V
2.94102m
20. A potential difference of 275 V is applied to
two parallel plates that are 0.35 cm apart.
What is the electric field between the plates?
E
d
V
7.9104N/C
page 572
21. What work is done when 3.0 C is moved
through an electric potential difference
of 1.5 V?
WqV(3.0 C)(1.5 V) 4.5 J
22. A 12-V car battery can store 1.44106C
when it is fully charged. How much work
can be done by this battery before it needs
recharging?
WqV(1.44106C)(12 V)
1.7107J
23. An electron in a television picture tube
passes through a potential difference of
18,000 V. How much work is done on the
electron as it passes through that potential
difference?
WqV(1.601019 C)(1.8104V)
2.91015 J
24. If the potential difference in problem 18 is
between two parallel plates that are 2.4 cm
apart, what is the magnitude of the electric
field between them?
E
d
V
5.0
0.
0
0
24
10
m
2V
2.1104N/C
25. The electric field in a particle-accelerator
machine is 4.5105N/C. How much work
is done to move a proton 25 cm through
that field?
WqVqEd
(1.601019 C)(4.5105N/C)(0.25 m)
1.81014 J
page 574
26. A drop is falling in a Millikan oil-drop appa-
ratus with no electric field. What forces are
acting on the oil drop, regardless of its accel-
eration? If the drop is falling at a constant
velocity, describe the forces acting on it.
Gravitational force (weight) downward,
friction force of air upward. The two
forces are equal in magnitude if the
drop falls at constant velocity.
275 V
3.5103m
125 V
4.25103N/C
400 V
0.020 m
Chapter 21 continued

27. An oil drop weighs 1.91015 N. It is sus-
pended in an electric field of 6.0103N/C.
What is the charge on the drop? How many
excess electrons does it carry?
Fg Eq
q
3.21019 C
# electrons
q
q
e
2
28. An oil drop carries one excess electron and
weighs 6.41015 N. What electric field
strength is required to suspend the drop so
it is motionless?
E
F
q
4.0104N/C
29. A positively charged oil drop weighing
1.21014 N is suspended between parallel
plates separated by 0.64 cm. The potential
difference between the plates is 240 V. What
is the charge on the drop? How many elec-
trons is the drop missing?
E
d
V
3.8104N/C
E
F
q
q
E
F
3.21019 C
# electrons
q
q
e
2
page 578
30. A 27-F capacitor has an electric potential
difference of 45 V across it. What is the
charge on the capacitor?
qCV(27106F)(45 V)
1.2103C
31. Both a 3.3-F and a 6.8-F capacitor are
connected across a 24-V electric potential
difference. Which capacitor has a greater
charge? What is it?
qCV, so the larger capacitor has a
greater charge.
q(6.8106F)(24 V) 1.6104C
32. The same two capacitors as in problem 31
are each charged to 3.5104C. Which has
the larger electric potential difference across
it? What is it?
V
C
q
, so the smaller capacitor has
the larger potential difference.
V1.1102V
33. A 2.2-F capacitor first is charged so that
the electric potential difference is 6.0 V.
How much additional charge is needed to
increase the electric potential difference to
15.0 V?
qCV
qC(V2V1)
(2.2106F)(15.0 V 6.0 V)
2.0105C
34. When a charge of 2.5105C is added to a
capacitor, the potential difference increases
from 12.0 V to 14.5 V. What is the capaci-
tance of the capacitor?
C
V2
q
V1
14
2
.5
.5V
1
0
12
5
.C
0V
1.0105F
Section Review
21.2 Applications of
Electric Fields
pages 569–579
page 579
35. Potential Difference What is the differ-
ence between electric potential energy and
electric potential difference?
Electric potential energy changes when
work is done to move a charge in an
electric field. It depends on the amount
of charge involved. Electric potential
difference is the work done per unit
charge to move a charge in an electric
field. It is independent of the amount of
charge that is moved.
3.5104C
3.5106F
3.41019 C
1.601019 C
1.21014 N
3.8104N/C
240 V
6.4103m
6.41015 N
1.601019 C
3.21019 C
1.601019 C
1.91015 N
6.0103N/C
Fg
E
430 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued
Physics: Principles and Problems Solutions Manual 431
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
36. Electric Field and Potential Difference
Show that a volt per meter is the same as a
newton per coulomb.
V/m J/Cm Nm/Cm N/C
37. Millikan Experiment When the charge on
an oil drop suspended in a Millikan appara-
tus is changed, the drop begins to fall. How
should the potential difference on the
plates be changed to bring the drop back
into balance?
The potential difference should be
increased.
38. Charge and Potential Difference In
problem 37, if changing the potential dif-
ference has no effect on the falling drop,
what does this tell you about the new
charge on the drop?
The drop is electrically neutral (no
electron excess or deficiency).
39. Capacitance How much charge is stored
on a 0.47-F capacitor when a potential
difference of 12 V is applied to it?
qCV(4.7107F)(12 V)
5.6106C
40. Charge Sharing If a large, positively
charged, conducting sphere is touched by a
small, negatively charged, conducting sphere,
what can be said about the following?
a. the potentials of the two spheres
The spheres will have equal
potentials.
b. the charges on the two spheres
The large sphere will have more
charge than the small sphere, but
they will be the same sign.The sign
of the charge will depend on which
sphere began with more charge.
41. Critical Thinking Referring back to
Figure 21-3a, explain how charge continues
to build up on the metal dome of a Van de
Graaff generator. In particular, why isn’t
charge repelled back onto the belt at point B?
The charges on the metal dome pro-
duce no field inside the dome. The
charges from the belt are transferred
immediately to the outside of the dome,
where they have no effect on new
charges arriving at point B.
Chapter Assessment
Concept Mapping
page 584
42. Complete the concept map below using the
following terms: capacitance, field strength,
J/C, work.
Mastering Concepts
page 584
43. What are the two properties that a test
charge must have? (21.1)
The test charge must be small in mag-
nitude relative to the magnitudes of the
charges producing the field and be
positive.
44. How is the direction of an electric field
defined? (21.1)
The direction of an electric field is the
direction of the force on a positive
charge placed in the field. This would
be away from a positive object and
toward a negative object.
Chapter 21 continued
force
field
strength
test charge
Electric Field
work
N/C
C/V
capacitance
J/C
potential
difference
45. What are electric field lines? (21.1)
lines of force
46. How is the strength of an electric field indi-
cated with electric field lines? (21.1)
The closer together the electric field
lines are, the stronger the electric field.
47. Draw some of the electric field lines
between each of the following. (21.1)
a. two like charges of equal magnitude
b. two unlike charges of equal magnitude
c. a positive charge and a negative charge
having twice the magnitude of the posi-
tive charge
d. two oppositely charged parallel plates
48. In Figure 21-15, where do the electric field
lines leave the positive charge end? (21.1)
■ Figure 21-15
They end on distant negative charges
somewhere beyond the edges of the
diagram.
49. What SI unit is used to measure electric
potential energy? What SI unit is used to
measure electric potential difference? (21.2)
electric potential energy: joule; electric
potential: volt
50. Define volt in terms of the change in poten-
tial energy of a charge moving in an electric
field. (21.2)
A volt is the change in electric potential
energy, PE, resulting from moving
a unit test charge, q, a distance, d,of
1 m in an electric field, E, of 1 N/C.
VPE/qEd
51. Why does a charged object lose its charge
when it is touched to the ground? (21.2)
The charge is shared with the surface of
Earth, which is an extremely large object.
52. A charged rubber rod that is placed on a
table maintains its charge for some time.
Why is the charged rod not discharged
immediately? (21.2)
The table is an insulator, or at least a
very poor conductor.
53. A metal box is charged. Compare the con-
centration of charge at the corners of the
box to the charge concentration on the
sides of the box. (21.2)
The concentration of charge is greater
at the corners.
Chapter 21 continued
432 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 433
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
54. Computers
Delicate parts
in electronic
equipment,
such as those
pictured in
Figure 21-16,
are contained
within a metal
box inside a
plastic case.
Why? (21.2)
The metal box shields the parts from
external electric fields, which do not
exist inside a hollow conductor.
Applying Concepts
pages 584–585
55. What happens to the strength of an electric
field when the charge on the test charge is
halved?
Nothing. Because the force on the test
charge also would be halved, the ratio
F/qand the electric field would remain
the same.
56. Does it require more energy or less energy
to move a constant positive charge through
an increasing electric field?
Energy is proportional to the force, and
the force is proportional to the electric
field. Therefore, it requires more energy.
57. What will happen to the electric potential
energy of a charged particle in an electric
field when the particle is released and free
to move?
The electric potential energy of the
particle will be converted into kinetic
energy of the particle.
58. Figure 21-17 shows three spheres with
charges of equal magnitude, with their
signs as shown. Spheres yand zare held
in place, but sphere xis free to move.
Initially, sphere xis equidistant from
spheres yand z. Choose the path that
sphere xwill begin to follow. Assume that
no other forces are acting on the spheres.
Sphere xwill follow path C. It will
experience forces shown by D and B.
The vector sum is C.
59. What is the unit of electric potential differ-
ence in terms of m, kg, s, and C?
VJ/C Nm/C (kgm/s2)(m/C)
kgm2/s2C
60. What do the electric field lines look like
when the electric field has the same
strength at all points in a region?
They are parallel, equally spaced lines.
61. Millikan Oil-Drop Experiment When
doing a Millikan oil-drop experiment, it is
best to work with drops that have small
charges. Therefore, when the electric field is
turned on, should you try to find drops that
are moving rapidly or slowly? Explain.
Slowly. The larger the charge, the
stronger the force, and thus, the larger
the (terminal) velocity.
62. Two oil drops are held motionless in a
Millikan oil-drop experiment.
a. Can you be sure that the charges are the
same?
No. Their masses could be different.
b. The ratios of which two properties of
the oil drops have to be equal?
charge to mass ratio, q/m(or m/q)
63. José and Sue are standing on an insulating
platform and holding hands when they are
given a charge, as in Figure 21-18. José is
larger than Sue. Who has the larger amount
of charge, or do they both have the same
amount?
zy
x
ED
B
C
A
■ Figure 21-17
■ Figure 21-16
Chapter 21 continued

José has a larger surface area, so he
will have a larger amount of charge.
64. Which has a larger capacitance, an alu-
minum sphere with a 1-cm diameter or one
with a 10-cm diameter?
The 10-cm diameter sphere has a larger
capacitance because the charges can
be farther apart, reducing potential rise
as it is charged.
65. How can you store different amounts of
charge in a capacitor?
Change the voltage across the capacitor.
Mastering Problems
21.1 Creating and Measuring Electric Fields
pages 585–586
The charge of an electron is 1.601019 C.
Level 1
66. What charge exists on a test charge that
experiences a force of 1.4108N at a
point where the electric field intensity is
5.0104N/C?
E
F
q
q
E
F
2.8105C
67. A positive charge of
1.0105C, shown
in Figure 21-19,
experiences a force
of 0.30 N when it is
located at a certain
point. What is the
electric field intensity
at that point?
E
F
q
3.0104N/C
in the same direction as the force
68. A test charge experiences a force of 0.30 N
on it when it is placed in an electric field
intensity of 4.5105N/C. What is the mag-
nitude of the charge?
E
F
q
q
E
F
6.7107C
69. The electric field in the atmosphere is about
150 N/C downward.
a. What is the direction of the force on a
negatively charged particle?
upward
b. Find the electric force on an electron
with charge 1.61019 C.
E
F
q
FqE (1.61019 C)(150 N/C)
2.41017 N
F2.41017 N directed upward
c. Compare the force in part bwith the
force of gravity on the same electron
(mass 9.11031 kg).
Fmg (9.11031 kg)(9.80 m/s2)
8.91030 N
F8.91030 N (downward), more
than one trillion times smaller
70. Carefully sketch each of the following.
a. the electric field produced by a 1.0-C
charge
1.0 C
0.30 N
4.5105N/C
0.30 N
1.0105C
1.0105 C
0.30 N
■ Figure 21-19
1.4108N
5.0104N/C
■ Figure 21-18
434 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued
Physics: Principles and Problems Solutions Manual 435
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. the electric field resulting from a 2.0-C
charge (Make the number of field lines
proportional to the change in charge.)
71. A positive test charge of 6.0106C is
placed in an electric field of 50.0-N/C
intensity, as in Figure 21-20. What is the
strength of the force exerted on the test
charge?
■ Figure 21-20
E
F
q
FqE (6.0106C)(50.0 N/C)
3.0104N
Level 2
72. Charges X, Y, and Z all are equidistant from
each other. X has a 1.0-C charge, Y has a
2.0-C charge, and Z has a small negative
charge.
a. Draw an arrow representing the force on
charge Z.
b. Charge Z now has a small positive
charge on it. Draw an arrow represent-
ing the force on it.
73. In a television picture tube, electrons are
accelerated by an electric field having a
value of 1.00105 NC.
a. Find the force on an electron.
E
F
q
FEq
(1.601019 C)(1.00105N/C)
1.601014 N
b. If the field is constant, find the
acceleration of the electron
(mass 9.111031 kg).
Fma
a
m
F
1.761016 m/s2
74. What is the electric field strength 20.0 cm
from a point charge of 8.0107C?
E, and F
so E
1.8105N/C
(9.0109Nm2/C2)(8.0107C)
(0.200 m)2
Kq
d2
Kqq
d2
F
q
1.601014 N
9.111031 kg
Z
Fx
F
Fy
Z
Y
Fx
F
Fy
X
q 6.0106 C
E 50.0 N/C
2.0 C
Chapter 21 continued

75. The nucleus of a lead atom has a charge of
82 protons.
a. What are the direction and magnitude
of the electric field at 1.01010 m
from the nucleus?
Q(82 protons)
(1.601019 C/proton)
1.311017 C
E
F
q
q
1
1.21013 N/C, outward
b. What are the direction and magnitude
of the force exerted on an electron
located at this distance?
FEq
(1.21013 N/C)(1.601019 C)
1.9106N, toward the nucleus
21.2 Applications of Electric Fields
pages 586–587
Level 1
76. If 120 J of work is performed to move 2.4 C
of charge from the positive plate to the nega-
tive plate shown in Figure 21-21, what
potential difference exists between the plates?
■ Figure 21-21
V
W
q
1
22
.4
0C
J
5.0101V
77. How much work is done to transfer 0.15 C
of charge through an electric potential dif-
ference of 9.0 V?
V
W
q
WqV(0.15 C)(9.0 V) 1.4 J
78. An electron is moved through an electric
potential difference of 450 V. How much
work is done on the electron?
V
W
q
WqV
(1.601019 C)(450 V)
7.21017 J
79. A 12-V battery does 1200 J of work
transferring charge. How much charge
is transferred?
V
W
q
q
W
V
11
22
00
VJ
1.0102C
80. The electric field intensity between two
charged plates is 1.5103N/C. The plates
are 0.060 m apart. What is the electric
potential difference, in volts, between the
plates?
VEd
(1.5103N/C)(0.060 m)
9.0101V
81. A voltmeter indicates that the electric
potential difference between two plates is
70.0 V. The plates are 0.020 m apart. What
electric field intensity exists between them?
VEd
E
d
V
0
7
.0
02
.0
0V
m
3500 V/m
3500 N/C
82. A capacitor that is connected to a 45.0-V
source contains 90.0 C of charge. What is
the capacitor’s capacitance?
C
q
V
90.0
4
5.
1
0
0
V
6C
2.00 µF
83. What electric potential difference exists
across a 5.4-F capacitor that has a charge
of 8.1104C?
C
q
V
V
1.5102V
8.1104C
5.4106F
q
C
2.4 C
(9.0109Nm2/C2)(1.311017 C)
(1.01010 m)2
KQ
d2
KqQ
d2
436 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 437
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
84. The oil drop shown in Figure 21-22 is neg-
atively charged and weighs 4.51015 N.
The drop is suspended in an electric field
intensity of 5.6103N/C.
■ Figure 21-22
a. What is the charge on the drop?
E
F
q
q
E
F
8.01019 C
b. How many excess electrons does it carry?
(8.01019 C)
5 electrons
85. What is the charge on a 15.0-pF capacitor
when it is connected across a 45.0-V source?
C
q
V
qCV(15.01012 F)(45.0 V)
6.751010 C
Level 2
86. A force of 0.065 N is required to move a
charge of 37 C a distance of 25 cm in a
uniform electric field, as in Figure 21-23.
What is the size of the electric potential
difference between the two points?
■ Figure 21-23
WFd
and V
W
q
F
q
d
4.4102V
87. Photoflash The energy stored in a capaci-
tor with capacitance C, and an electric
potential difference, V, is represented by
W
1
2
CV2. One application of this is in
the electronic photoflash of a strobe light,
like the one in Figure 21-24. In such a unit,
a capacitor of 10.0 F is charged to
3.0102V. Find the energy stored.
■ Figure 21-24
W
1
2
CV2
1
2
(10.0106F)(3.0102V)2
0.45 J
88. Suppose it took 25 s to charge the capacitor
in problem 87.
a. Find the average power required to
charge the capacitor in this time.
P
W
t
02
.4
55sJ
1.8102W
b. When this capacitor is discharged
through the strobe lamp, it transfers all
its energy in 1.0104s. Find the
power delivered to the lamp.
P
W
t
4.5103W
c. How is such a large amount of power
possible?
Power is inversely proportional to
the time. The shorter the time for a
given amount of energy to be
expended, the greater the power.
0.45 J
1.0104s
(0.065 N)(0.25 m)
37106C
25 cm
0.053 N
37 C
1 electron
1.601019 C
4.51015 N
5.6103N/C
8.51015 N
Chapter 21 continued

89. Lasers Lasers are used to try to produce
controlled fusion reactions. These lasers
require brief pulses of energy that are stored
in large rooms filled with capacitors. One
such room has a capacitance of 61103F
charged to a potential difference of 10.0 kV.
a. Given that W
1
2
CV2, find the energy
stored in the capacitors.
W
1
2
CV2
1
2
(61103F)(1.00104V)2
3.1106J
b. The capacitors are discharged in 10 ns
(1.0108s). What power is produced?
P
W
t
3.11014 W
c. If the capacitors are charged by a gener-
ator with a power capacity of 1.0 kW,
how many seconds will be required to
charge the capacitors?
t
W
P
3.1103s
Mixed Review
page 587
Level 1
90. How much work does it take to move
0.25 C between two parallel plates that
are 0.40 cm apart if the field between the
plates is 6400 N/C?
WqVqEd
(2.5107C)(6400 N/C)(4.0103m)
6.4106J
91. How much charge is stored on a 0.22-F
parallel plate capacitor if the plates are
1.2 cm apart and the electric field between
them is 2400 N/C?
qCVCEd
(2.2107F)(2400 N/C)(1.2102m)
6.3 C
92. Two identical small spheres, 25 cm apart,
carry equal but opposite charges of 0.060 C,
as in Figure 21-25. If the potential difference
between them is 300 V, what is the capaci-
tance of the system?
■ Figure 21-25
C
q
V
6.0
30
1
0
0
V
8C
21010 F
93. The plates of a 0.047 F capacitor are
0.25 cm apart and are charged to a poten-
tial difference of 120 V. How much charge
is stored on the capacitor?
C
q
V
qCV
(4.7108F)(120 V)
5.6106C 5.6 C
94. What is the strength of the electric field
between the plates of the capacitor in
Problem 93 above?
VEd
E
d
V
4.8104V/m
95. An electron is placed between the plates of
the capacitor in Problem 93 above, as in
Figure 21-26. What force is exerted on that
electron?
■ Figure 21-26
0.25 cm
C 0.047 F
V 120 V
120 V
2.5103m
25 cm
0.060 C0.060 C
V 300 V
3.1106J
1.0103W
3.1106J
1.0108s
438 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued
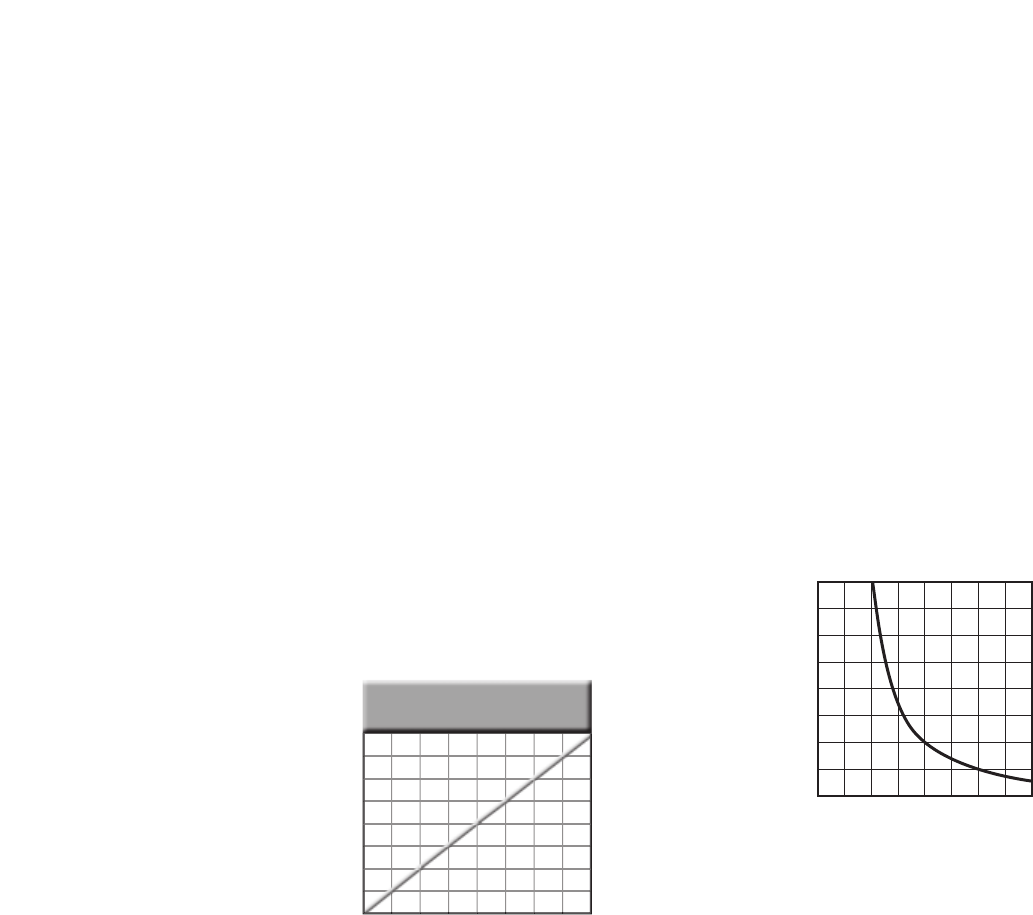
Physics: Principles and Problems Solutions Manual 439
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
E
F
q
FEq
(4.8104V/m)(1.61019 C)
7.71015 N
96. How much work would it take to move an
additional 0.010 C between the plates at
120 V in Problem 93?
V
W
q
WqV
(1.0108C)(120 V) 1.2106J
Level 2
97. The graph in Figure 21-27 represents the
charge stored in a capacitor as the charging
potential increases. What does the slope of
the line represent?
■Figure 21-27
capacitance of the capacitor
98. What is the capacitance of the capacitor
represented by Figure 21-27?
Cslope 0.50 F
99. What does the area under the graph line in
Figure 21-27 represent?
work done to charge the capacitor
100. How much work is required to charge the
capacitor in problem 98 to a potential dif-
ference of 25 V?
Warea
1
2
bh
1
2
(25 V)(12.5 C)
160 J
101. The work found in Problem 100 above is
not equal to qV. Why not?
The potential difference is not con-
stant as the capacitor is charged.
Therefore, the area under the graph
must be used to find work, not just
simple multiplication.
102. Graph the electric field strength near a
positive point charge as a function of
distance from it.
103. Where is the field of a point charge equal
to zero?
Nowhere, or at an infinite distance
from the point charge.
104. What is the electric field strength at a dis-
tance of zero meters from a point charge?
Is there such a thing as a true point charge?
Infinite. No.
Thinking Critically
pages 587–588
105. Apply Concepts Although a lightning rod
is designed to carry charge safely to the
ground, its primary purpose is to prevent
lightning from striking in the first place.
How does it do that?
The sharp point on the end of the rod
leaks charge into the atmosphere
before it has the chance to build up
enough potential difference to cause a
lightning strike.
E
d
q (C)
V (V)
5
0
10
15
10 20 30
Charge Stored
on Capacitor
Chapter 21 continued

106. Analyze and Conclude In an early set of experiments in 1911, Millikan
observed that the following measured charges could appear on a single oil drop.
What value of elementary charge can be deduced from these data?
a. 6.5631019 Cf. 18.081019 C
b. 8.2041019 Cg. 19.711019 C
c. 11 . 5 0 1019 Ch. 22.891019 C
d. 13.131019 Ci. 26.131019 C
e. 16.481019 C
1.631019 C. Subtracting adjacent values, ba,cb,dc,etc.
yields 1.6411019 C, 3.301019 C, 1.631019 C, 3.351019 C,
1.601019 C, 1.631019 C, 3.181019 C, 3.241019 C.
There are two numbers, approximately 1.6311019 C and 3.21019 C,
that are common. Averaging each similar group produces one charge of
1.631019 C and one charge of 3.271019 C (which is two times
1.6411019 C).
Dividing 1.631019 C into each piece of data yields nearly whole-num-
ber quotients, indicating it is the value of an elementary charge.
107. Analyze and Conclude Two small spheres,
A and B, lie on the x-axis, as in Figure 21-28.
Sphere A has a charge of 3.00106C.
Sphere B is 0.800 m to the right of sphere A
and has a charge of 5.00106C. Find the
magnitude and direction of the electric field
strength at a point above the x-axis that would
form the apex of an equilateral triangle with
spheres A and B.
Draw the spheres and vectors representing
the fields due to each charge at the given point.
Now do the math:
EA 4.22104N/C
EB 7.03104N/C
EAxEAcos 60.0°(4.22104N/C)(cos 60.0°) 2.11104N/C
EAyEAsin 60.0°(4.22104N/C)(sin 60.0°) 3.65104N/C
(9.0109Nm2/C2)(5.00106C)
(0.800 m)2
KqB
d2
FB
q
(9.0109Nm2/C2)(3.00106C)
(0.800 m)2
KqA
d2
FA
q
A0.800 m B
EB
ER
EA
440 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued
■ Figure 21-28
0.800 m
3.00106 C5.00106 C
AB
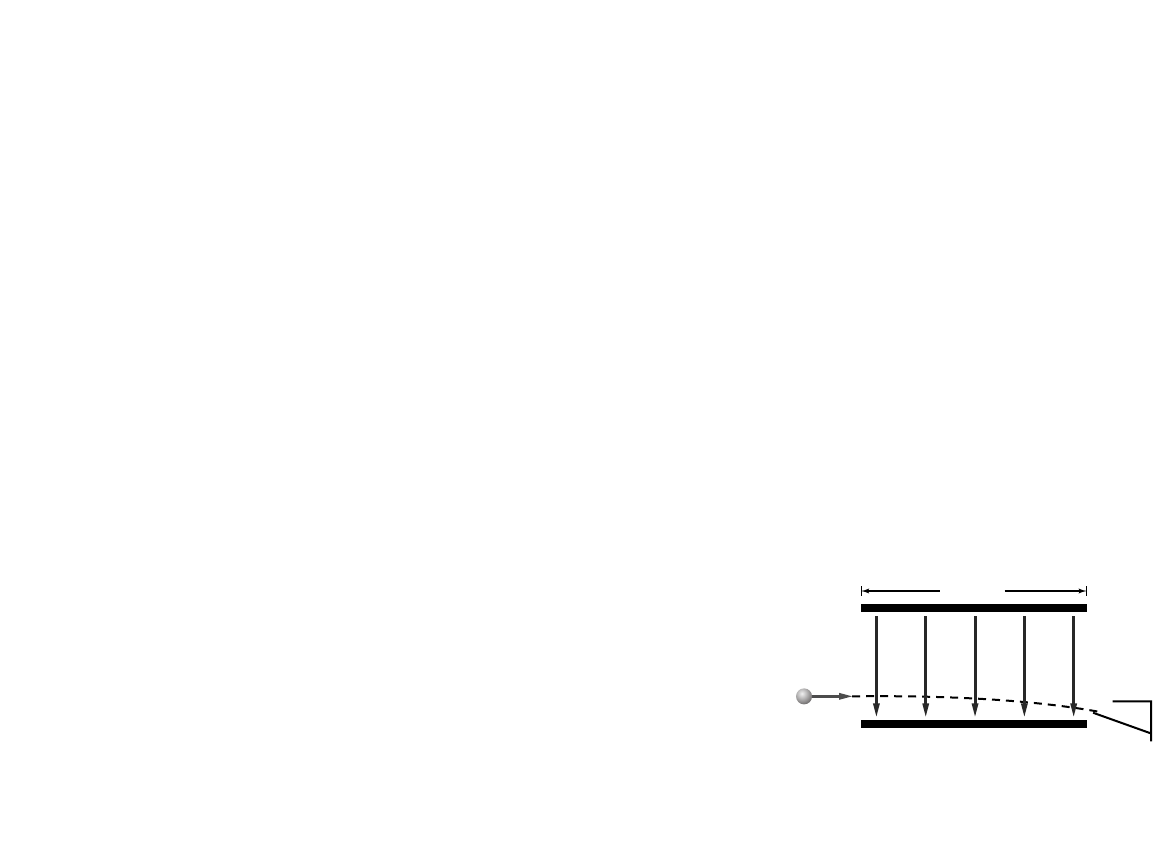
Physics: Principles and Problems Solutions Manual 441
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
EBxEBcos (60.0°)(7.03104N/C)(cos 60.0°) 3.52104N/C
EByEBsin (60.0°)(7.03104N/C)(sin 60.0°) 6.09104N/C
ExEAxEBx(2.11104N/C) (3.52104N/C) 5.63104N/C
EyEAyEBy(3.65104N/C) (6.09104N/C) 2.44104N/C
EREx2
Ey2
6.14104N/C
tan
tan1
tan1
23.4°
108. Analyze and Conclude In an ink-jet printer, drops of
ink are given a certain amount of charge before they
move between two large, parallel plates. The purpose
of the plates is to deflect the charges so that they are
stopped by a gutter and do not reach the paper. This
is shown in Figure 21-29. The plates are 1.5-cm long
and have an electric field of E1.2106N/C between
them. Drops with a mass m0.10 ng, and a charge
q1.01016 C, are moving horizontally at a speed,
v15 m/s, parallel to the plates. What is the vertical
displacement of the drops when they leave the plates?
To answer this question, complete the following steps.
a. What is the vertical force on the drops?
FEq
(1.01016 C)(1.2106N/C)
1.21010 N
b. What is their vertical acceleration?
a
m
F
1.2103m/s2
c. How long are they between the plates?
t
L
v
1.51
51m
0
/s
2m
1.0103s
d. How far are they displaced?
y
1
2
at2
1
2
(1.2103m/s2)(1.0103s)2
6.0104m 0.60 mm
1.21010 N
1.01013 kg
2.44104N/C
5.63104N/C
Ey
Ex
Ey
Ex
Chapter 21 continued
E 1.2106 N/C
1.5 cm
Gutter
q
mv
■ Figure 21-29

109. Apply Concepts Suppose the Moon had a net negative charge equal to q, and
Earth had a net positive charge equal to 10q. What value of q would yield the
same magnitude of force that you now attribute to gravity?
Equate the expressions for gravitational force and Coulombic force
between Earth and the Moon:
F
where qis the net negative charge of the Moon and qE, the net positive
charge of Earth, is 10q.
Solve symbolically before substituting numbers.
q
1.81013C
Writing in Physics
page 588
110. Choose the name of an electric unit, such as coulomb, volt, or farad, and
research the life and work of the scientist for whom it was named. Write a brief
essay on this person and include a discussion of the work that justified the
honor of having a unit named for him.
Student answers will vary. Some examples of scientists they could
choose are Volta, Coulomb, Ohm, and Ampère.
Cumulative Review
page 588
111. Michelson measured the speed of light by sending a beam of light to a mirror
on a mountain 35 km away. (Chapter 16)
a. How long does it take light to travel the distance to the mountain and back?
(35 km/trip)(2 trips)(1000 m/1 km)/ 3.00108m/s 2.3104s
b. Assume that Michelson used a rotating octagon with a mirror on each face
of the octagon. Also assume that the light reflects from one mirror, travels to
the other mountain, reflects off of a fixed mirror on that mountain, and
returns to the rotating mirrors. If the rotating mirror has advanced so that
when the light returns, it reflects off of the next mirror in the rotation, how
fast is the mirror rotating?
(8 mirrors/rev) 1.8103s/rev T
f 5.6102rev/s
Note that if students carry extra digits from part a to prevent round-
ing errors, they will get an answer of 5.4102rev/s.
1
1.8103s/rev
1
T
2.3104s
1 mirror
(6.671011 Nm2/kg2)(6.001024 kg)(7.311022 kg)
(10)(9.0109Nm2/C2)
GmEmM
10K
10Kq2
d2
KqEqM
d2
GmEmM
d2
442 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 443
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. If each mirror has a mass of 1.0101g
and rotates in a circle with an average
radius of 1.0101cm, what is the
approximate centripetal force needed
to hold the mirror while is it rotating?
Fc42mf2r
42(0.010 kg)(5.6102rev/s)2
(0.10 m)
1.2104N
Note that the answer should be
1.2104N regardless of whether
the students use 5.4102rev/s or
5.6104rev/s for f.
112. Mountain Scene You can see an image of
a distant mountain in a smooth lake just
as you can see a mountain biker next to
the lake because light from each strikes the
surface of the lake at about the same angle
of incidence and is reflected to your eyes.
If the lake is about 100 m in diameter, the
reflection of the top of the mountain is
about in the middle of the lake, the moun-
tain is about 50 km away from the lake,
and you are about 2 m tall, then approxi-
mately how high above the lake does the
top of the mountain reach? (Chapter 17)
Since the angle of incidence of the
light from the top of the mountain is
equal to its angle of reflection from the
lake, you and the reflection of the top
of the mountain form a triangle that is
similar to a triangle formed by the
mountain and the top of its reflection
in the lake. Your height makes up one
side, hyou 2 m and the top of the
mountain is halfway across the lake,
dyou 50 m. The mountain is a dis-
tance dmountain 50,000 m from its
reflection. Find hmountain by equating
the ratios of the sides of the two
similar triangles.
hmountain
(2 m)(
5
5
0
0,
m
000 m)
2000 m
113. A converging lens has a focal length of
38.0 cm. If it is placed 60.0 cm from an
object, at what distance from the lens will
the image be? (Chapter 18)
1
f
d
1
o
di
104 cm
The image is 104 cm from the lens.
114. A force, F, is measured between two
charges, Qand q, separated by a distance,
r. What would the new force be for each of
the following? (Chapter 20)
a. ris tripled
F/9
b. Qis tripled
3F
c. both rand Qare tripled
F/3
d. both rand Qare doubled
F/2
e. all three, r, Q, and q, are tripled
F
(60.0 cm)(38.0 cm)
60.0 cm 38.0 cm
dof
dof
1
di
hyoudmountain
dyou
hmountain
dmountain
hyou
dyou
Chapter 21 continued

Challenge Problem
page 579
The plates of a capacitor attract each other because they
carry opposite charges. A capacitor consisting of two parallel
plates that are separated by a distance, d, has capacitance, C.
1. Derive an expression for the force between the two
plates when the capacitor has charge, q.
Combine the following equations:
FEq,E, and V
FEq
qq
2. What charge must be stored on a 22-F capacitor to have a force of 2.0 N
between the plates if they are separated by 1.5 mm?
F
so qFCd
(2.0 N
)(2.2
105 F
)(1.5
103
m)
2.6104C
q2
Cd
q2
Cd
C
q
d
V
d
q
C
V
d
d
444 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 445
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
22 Current Electricity
CHAPTER
Practice Problems
22.1 Current and Circuits
pages 591–600
page 594
1. The current through a lightbulb connected
across the terminals of a 125-V outlet is
0.50 A. At what rate does the bulb convert
electric energy to light? (Assume 100 percent
efficiency.)
PIV (0.50 A)(125 V) 63 J/s 63 W
2. A car battery causes a current of 2.0 A
through a lamp and produces 12 V across
it. What is the power used by the lamp?
PIV (2.0 A)(12 V) 24 W
3. What is the current through a 75-W light-
bulb that is connected to a 125-V outlet?
PIV
I 0.60 A
4. The current through the starter motor of a
car is 210 A. If the battery maintains 12 V
across the motor, how much electric energy
is delivered to the starter in 10.0 s?
PIV and EPt
Thus, EIVt (210 A)(12 V)(10.0 s)
2.5104J
5. A flashlight bulb is rated at 0.90 W. If the
lightbulb drops 3.0 V, how much current
goes through it?
PIV
I 0.30 A
page 598
For all problems, assume that the battery voltage and
lamp resistances are constant, no matter what current
is present.
6. An automobile panel lamp with a resistance
of 33 is placed across a 12-V battery.
What is the current through the circuit?
I 0.36 A
7. A motor with an operating resistance of 32
is connected to a voltage source. The current
in the circuit is 3.8 A. What is the voltage of
the source?
VIR (3.8 A)(32 ) 1.2102V
8. A sensor uses 2.0104A of current when
it is operated by a 3.0-V battery. What is the
resistance of the sensor circuit?
R 1.5104
9. A lamp draws a current of 0.50 A when it is
connected to a 120-V source.
a. What is the resistance of the lamp?
R 2.4102
b. What is the power consumption of the
lamp?
PIV (0.50 A)(120 V) 6.0101W
10. A 75-W lamp is connected to 125 V.
a. What is the current through the lamp?
I 0.60 A
b. What is the resistance of the lamp?
R 2.1102
125 V
0.60 A
V
I
75 W
125 V
P
V
120 V
0.50 A
V
I
3.0 V
2.0104A
V
I
12 V
33
V
R
0.90 W
3.0 V
P
V
75 W
125 V
P
V
11. A resistor is added to the lamp in the previ-
ous problem to reduce the current to half of
its original value.
a. What is the potential difference across
the lamp?
The new value of the current is
0.30 A
VIR (0.30 A)(2.1102)
6.3101V
b. How much resistance was added to the
circuit?
The total resistance of the circuit
is now
Rtotal 4.2102
Therefore,
Rres Rtotal RIamp
4.21022.1102
2.1102
c. How much power is now dissipated in
the lamp?
PIV (0.30 A)(6.3101V) 19 W
page 600
12. Draw a circuit diagram to include a 60.0-V
battery, an ammeter, and a resistance of
12.5 in series. Indicate the ammeter read-
ing and the direction of the current.
I 4.80 A
13. Draw a series-circuit diagram showing a
4.5-V battery, a resistor, and an ammeter
that reads 85 mA. Determine the resistance
and label the resistor. Choose a direction
for the conventional current and indicate
the positive terminal of the battery.
R 53
14. Add a voltmeter to measure the potential
difference across the resistors in problems 12
and 13 and repeat the problems.
Both circuits will take the following form.
Because the ammeter resistance is
assumed zero, the voltmeter readings
will be 60.0 V for Practice Problem 12 and
4.5 V for Practice Problem 13.
15. Draw a circuit using a battery, a lamp, a
potentiometer to adjust the lamp’s bright-
ness, and an on-off switch.
16. Repeat the previous problem, adding an
ammeter and a voltmeter across the lamp.
V
A
Battery
Lamp
Switch Potentiometer
A
V
I
4.5 V
0.085 A
V
I
4.5 V
A
53
I
85 mA
60.0 V
12.5
V
R
60.0 V
A
12.5
I
4.80 A
125 V
0.30 A
V
I
0.60 A
2
446 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 447
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
22.1 Current and Circuits
pages 591–600
page 600
17. Schematic Draw a schematic diagram of a
circuit that contains a battery and a light-
bulb. Make sure the lightbulb will light in
this circuit.
18. Resistance Joe states that because RV/I,
if he increases the voltage, the resistance
will increase. Is Joe correct? Explain.
No, resistance depends on the device.
When Vincreases, so will I.
19. Resistance You want to measure the resis-
tance of a long piece of wire. Show how you
would construct a circuit with a battery, a
voltmeter, an ammeter, and the wire to be
tested to make the measurement. Specify
what you would measure and how you
would compute the resistance.
Measure the current through the wire
and the potential difference across it.
Divide the potential difference by the
current to obtain the wire resistance.
20. Power A circuit has 12 of resistance and
is connected to a 12-V battery. Determine
the change in power if the resistance
decreases to 9.0 .
P1V2/R1(12 V)2/12 12 W
P2V2/R2(12 V)2/9.0 16 W
PP2P116 W 12 W 4.0 W
4.0 W increase
21. Energy A circuit converts 2.2103J of
energy when it is operated for 3.0 min.
Determine the amount of energy it will
convert when it is operated for 1 h.
E
(60.0 min)
4.4104J
22. Critical Thinking We say that power is
“dissipated” in a resistor. To dissipate is to
use, to waste, or to squander. What is “used”
when charge flows through a resistor?
The potential energy of the charges
decreases as they flow through the resis-
tor.This decrease in potential energy is
used to produce heat in the resistor.
Practice Problems
22.2 Using Electric Energy
pages 601–605
page 603
23. A 15-electric heater operates on a 120-V
outlet.
a. What is the current through the heater?
I 8.0 A
b. How much energy is used by the heater
in 30.0 s?
EI2Rt (8.0 A)2(15 )(30.0 s)
2.9104J
c. How much thermal energy is liberated
in this time?
2.9104J, because all electric energy
is converted to thermal energy.
24. A 39-resistor is connected across a 45-V
battery.
a. What is the current in the circuit?
I 1.2 A
45 V
39
V
R
120 V
15
V
R
2.2103J
3.0 min
A
V
Chapter 22 continued

b. How much energy is used by the resistor
in 5.0 min?
Et
(5.0 min)(60 s/min)
1.6104J
25. A 100.0-W lightbulb is 22 percent efficient.
This means that 22 percent of the electric
energy is converted to light energy.
a. How many joules does the lightbulb
convert into light each minute it is in
operation?
EPt
(0.22)(100.0 J/s)(1.0 min)
(60 s/min)
1.3103J
b. How many joules of thermal energy does
the lightbulb produce each minute?
EPt
(0.78)(100.0 J/s)(1.0 min)
(60.0 s/min)
4.7103J
26. The resistance of an electric stove element at
operating temperature is 11 .
a. If 220 V are applied across it, what is
the current through the stove element?
I 2.0101A
b. How much energy does the element
convert to thermal energy in 30.0 s?
EI2Rt (2.0101A)2(11 )(30.0
s)
1.3105J
c. The element is used to heat a kettle con-
taining 1.20 kg of water. Assume that
65 percent of the heat is absorbed by
the water. What is the water’s increase
in temperature during the 30.0 s?
QmCTwith Q0.65E
T
17°C
27. A 120-V water heater takes 2.2 h to heat a
given volume of water to a certain tempera-
ture. How long would a 240-V unit operating
with the same current take to accomplish
the same task?
EIVt I(2V)
For a given amount of energy, doubling
the voltage will divide the time by 2.
t1.1 h
page 605
28. An electric space heater draws 15.0 A from a
120-V source. It is operated, on the average,
for 5.0 h each day.
a. How much power does the heater use?
PIV (15.0 A)(120 V)
1800 W 1.8 kW
b. How much energy in kWh does it con-
sume in 30 days?
EPt (1.8 kW)(5.0 h/day)(30 days)
270 kWh
c. At $0.12 per kWh, how much does it
cost to operate the heater for 30 days?
Cost ($0.12/kWh)(270 kWh)
$32.40
29. A digital clock has a resistance of 12,000
and is plugged into a 115-V outlet.
a. How much current does it draw?
I 9.6103A
b. How much power does it use?
PVI (115 V)(9.6103A) 1.1 W
c. If the owner of the clock pays $0.12 per
kWh, how much does it cost to operate
the clock for 30 days?
Cost (1.1103kWh)($0.12/kWh)
(30 days)(24 h/day)
$0.10
30. An automotive battery can deliver 55 A at
12 V for 1.0 h and requires 1.3 times as
much energy for recharge due to its less-
than-perfect efficiency. How long will it
115 V
12,000
V
R
2.2 h
2
t
2
(0.65)(1.3105 J)
(1.20 kg)(4180 J/kg°C)
0.65E
mC
220 V
11
V
R
(45 V)2
(39 )
V2
R
448 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 449
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
take to charge the battery using a current of
7.5 A? Assume that the charging voltage is
the same as the discharging voltage.
Echarge (1.3)IVt
(1.3)(55 A)(12 V)(1.0 h)
858 Wh
t 9.5 h
31. Rework the previous problem by assuming
that the battery requires the application of
14 V when it is recharging.
Echarge (1.3)IVt
(1.3)(55 A)(12 V)(1.0 h)
858 Wh
t 8.2 h
Section Review
22.2 Using Electric Energy
pages 601–605
page 605
32. Energy A car engine drives a generator,
which produces and stores electric charge in
the car’s battery. The headlamps use the elec-
tric charge stored in the car battery. List the
forms of energy in these three operations.
Mechanical energy from the engine con-
verted to electric energy in the genera-
tor; electric energy stored as chemical
energy in the battery; chemical energy
converted to electric energy in the bat-
tery and distributed to the headlamps;
electric energy converted to light and
thermal energy in headlamps.
33. Resistance A hair dryer operating from
120 V has two settings, hot and warm. In
which setting is the resistance likely to be
smaller? Why?
Hot draws more power, PIV, so the
fixed voltage current is larger. Because
IV/Rthe resistance is smaller.
34. Power Determine the power change in a
circuit if the applied voltage is decreased by
one-half.
P
P1
2
0.25
35. Efficiency Evaluate the impact of research
to improve power transmission lines on
society and the environment.
Research to improve power transmis-
sion lines would benefit society in cost
of electricity. Also, if less power was
lost during transmission, less coal and
other power-producing resources would
have to be used, which would improve
the quality of our environment.
36. Voltage Why would an electric range and
an electric hot-water heater be connected to
a 240-V circuit rather than a 120-V circuit?
For the same power, at twice the volt-
age, the current would be halved.The
I2Rloss in the circuit wiring would be
dramatically reduced because it is pro-
portional to the square of the current.
37. Critical Thinking When demand for elec-
tric power is high, power companies some-
times reduce the voltage, thereby producing
a “brown-out.” What is being saved?
Power, not energy; most devices will
have to run longer.
Chapter Assessment
Concept Mapping
page 610
38. Complete the concept map using the fol-
lowing terms: watt, current, resistance.
(0.5V1)2/R
V12
V22/R
V12/R
858 Wh
(7.5 A)(14 V)
E
IV
858 Wh
(7.5 A)(12 V)
E
IV
Chapter 22 continued
Electricity
rate of
conversion
rate of
flow
current
ampere watt
power
opposition
to flow
resistance
ohm

Mastering Concepts
page 610
39. Define the unit of electric current in terms
of fundamental MKS units. (22.1)
1 A 1 C/1 s
40. How should a voltmeter be connected in
Figure 22-12 to measure the motor’s
voltage? (22.1)
■Figure 22-12
The positive voltmeter lead connects
to the left-hand motor lead, and the
negative voltmeter lead connects to
the right-hand motor lead.
41. How should an ammeter be connected in
Figure 22-12 to measure the motor’s cur-
rent? (22.1)
Break the circuit between the battery
and the motor. Then connect the posi-
tive ammeter lead to the positive side of
the break (the side connected to the
positive battery terminal) and the nega-
tive ammeter lead to the negative side
nearest the motor.
42. What is the direction of the conventional
motor current in Figure 22-12? (22.1)
from left to right through the motor
43. Refer to Figure 22-12 to answer the follow-
ing questions. (22.1)
a. Which device converts electric energy to
mechanical energy?
4
b. Which device converts chemical energy
to electric energy?
1
c. Which device turns the circuit on and off?
2
d. Which device provides a way to adjust
speed?
3
44. Describe the energy conversions that occur
in each of the following devices. (22.1)
a. an incandescent lightbulb
electric energy to heat and light
b. a clothes dryer
electric energy to heat and kinetic
energy
c. a digital clock radio
electric energy to light and sound
45. Which wire conducts electricity with
the least resistance: one with a large
cross-sectional diameter or one with a
small cross-sectional diameter? (22.1)
A larger-diameter wire has a smaller
resistance because there are more
electrons to carry the charge.
46. A simple circuit consists of a resistor, a
battery, and connecting wires. (22.1)
a. Draw a circuit schematic of this simple
circuit.
b. How must an ammeter be connected in
a circuit for the current to be correctly
read?
The ammeter must be connected in
series.
II
4
1
2
3
450 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 451
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. How must a voltmeter be connected to
a resistor for the potential difference
across it to be read?
The voltmeter must be connected in
parallel.
47. Why do lightbulbs burn out more frequently
just as they are switched on rather than
while they are operating? (22.2)
The low resistance of the cold filament
allows a high current initially and a
greater change in temperature, subject-
ing the filament to greater stress.
48. If a battery is short-circuited by a heavy cop-
per wire being connected from one terminal
to the other, the temperature of the copper
wire rises. Why does this happen? (22.2)
The short circuit produces a high cur-
rent, which causes more electrons to
collide with the atoms of the wire. This
raises the atoms’kinetic energies and
the temperature of the wire.
49. What electric quantities must be kept small
to transmit electric energy economically
over long distances? (22.2)
the resistance of the wire and the
current in the wire
50. Define the unit of power in terms of funda-
mental MKS units. (22.2)
W
C
s
C
J
Applying Concepts
pages 610–611
51. Batteries When a battery is connected to a
complete circuit, charges flow in the circuit
almost instantaneously. Explain.
A potential difference is felt over the
entire circuit as soon as the battery is
connected to the circuit.The potential
difference causes the charges to begin
to flow. Note:The charges flow slowly
compared to the change in potential
difference.
52. Explain why a cow experiences a mild shock
when it touches an electric fence.
By touching the fence and the ground,
the cow encounters a difference in
potential and conducts current, thus
receiving a shock.
53. Power Lines Why can birds perch on high-
voltage lines without being injured?
No potential difference exists along the
wires, so there is no current through
the birds’bodies.
54. Describe two ways to increase the current in
a circuit.
Either increase the voltage or decrease
the resistance.
55. Lightbulbs Two lightbulbs work on a
120-V circuit. One is 50 W and the other is
100 W. Which bulb has a higher resistance?
Explain.
50-W bulb
P , so R
Therefore, the lower Pis caused by a
higher R.
56. If the voltage across a circuit is kept con-
stant and the resistance is doubled, what
effect does this have on the circuit’s current?
If the resistance is doubled, the current
is halved.
V2
P
V2
R
kgm2
s3
kg
m
s2
2
s
J
s
II
V
A
II
V
A
Chapter 22 continued
57. What is the effect on the current in a circuit
if both the voltage and the resistance are
doubled? Explain.
No effect. VIR, so IV/R, and if the
voltage and the resistance both are
doubled, the current will not change.
58. Ohm’s Law Sue finds a device that looks
like a resistor. When she connects it to a
1.5-V battery, she measures only 45106A,
but when she uses a 3.0-V battery, she mea-
sures 25103A. Does the device obey
Ohm’s law?
No. VIR, so RV/I. At 1.5 V,
R3.3104
At 3.0 V, R120
A device that obeys Ohm’s law has a
resistance that is independent of the
applied voltage.
59. If the ammeter in Figure 22-4a on page 596
were moved to the bottom of the diagram,
would the ammeter have the same reading?
Explain.
Yes, because the current is the same
everywhere in this circuit.
60. Two wires can be placed across the termi-
nals of a 6.0-V battery. One has a high resis-
tance, and the other has a low resistance.
Which wire will produce thermal energy at
a faster rate? Why?
the wire with the smaller resistance
P
Smaller Rproduces larger power P
dissipated in the wire, which produces
thermal energy at a faster rate.
Mastering Problems
22.1 Current and Circuits
pages 611–612
Level 1
61. A motor is connected to a 12-V battery, as
shown in Figure 22-13.
■Figure 22-13
a. How much power is delivered to the
motor?
PVI (12 V)(1.5 A) 18 W
b. How much energy is converted if the
motor runs for 15 min?
EPt (18 W)(15 min)(60 s/min)
1.6104J
62. Refer to Figure 22-14 to answer the follow-
ing questions.
■Figure 22-14
a. What should the ammeter reading be?
IV/R1.5 A
b. What should the voltmeter reading be?
27 V
c. How much power is delivered to the
resistor?
PVI (27 V)(1.5 A) 41 W
d. How much energy is delivered to the
resistor per hour?
EPt (41 W)(3600 s) 1.5105J
27 V
18
27 V
A
18
I
V
12 V
1.5 A
Motor
V2
R
3.0 V
25103 A
1.5 V
45106
452 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 453
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
63. Refer to Figure 22-15 to answer the follow-
ing questions.
■Figure 22-15
a. What should the ammeter reading be?
IV/R3.0 A
b. What should the voltmeter reading be?
27 V
c. How much power is delivered to the
resistor?
PVI (27 V)(3.0 A) 81 W
d. How much energy is delivered to the
resistor per hour?
EPt (81 W)(3600 s) 2.9105J
64. Refer to Figure 22-16 to answer the follow-
ing questions.
■Figure 22-16
a. What should the ammeter reading be?
IV/R0.50 A
b. What should the voltmeter reading be?
9.0 V
c. How much power is delivered to the
resistor?
PVI (9.0 V)(0.50 A) 4.5 W
d. How much energy is delivered to the
resistor per hour?
EPt (4.5 W)(3600 s) 1.6104J
65. Toasters The current through a toaster that
is connected to a 120-V source is 8.0 A.
What power is dissipated by the toaster?
PIV (8.0 A)(120 V) 9.6102W
66. Lightbulbs A current of 1.2 A is measured
through a lightbulb when it is connected
across a 120-V source. What power is dissi-
pated by the bulb?
PIV (1.2 A)(120 V) 1.4102W
67. A lamp draws 0.50 A from a 120-V generator.
a. How much power is delivered?
PIV (0.50 A)(120 V) 6.0101W
b. How much energy is converted in
5.0 min?
The definition of power is P
E
t
,so
EPt
(6.0101W)
18,000 J 1.8104J
68. A 12-V automobile battery is connected to
an electric starter motor. The current
through the motor is 210 A.
a. How many joules of energy does the
battery deliver to the motor each second?
PIV (210 A)(12 V) 2500 J/s
or 2.5103J/s
b. What power, in watts, does the motor
use?
P2.5103W
69. Dryers A 4200-W clothes dryer is connect-
ed to a 220-V circuit. How much current
does the dryer draw?
PIV
I
P
V
42
22
00
0V
W
19 A
60 s
min
5.0 min
1
9.0 V
18
I
V
9.0 V
A
18
27 V
9.0
27 V
A
9.0
I
V
Chapter 22 continued
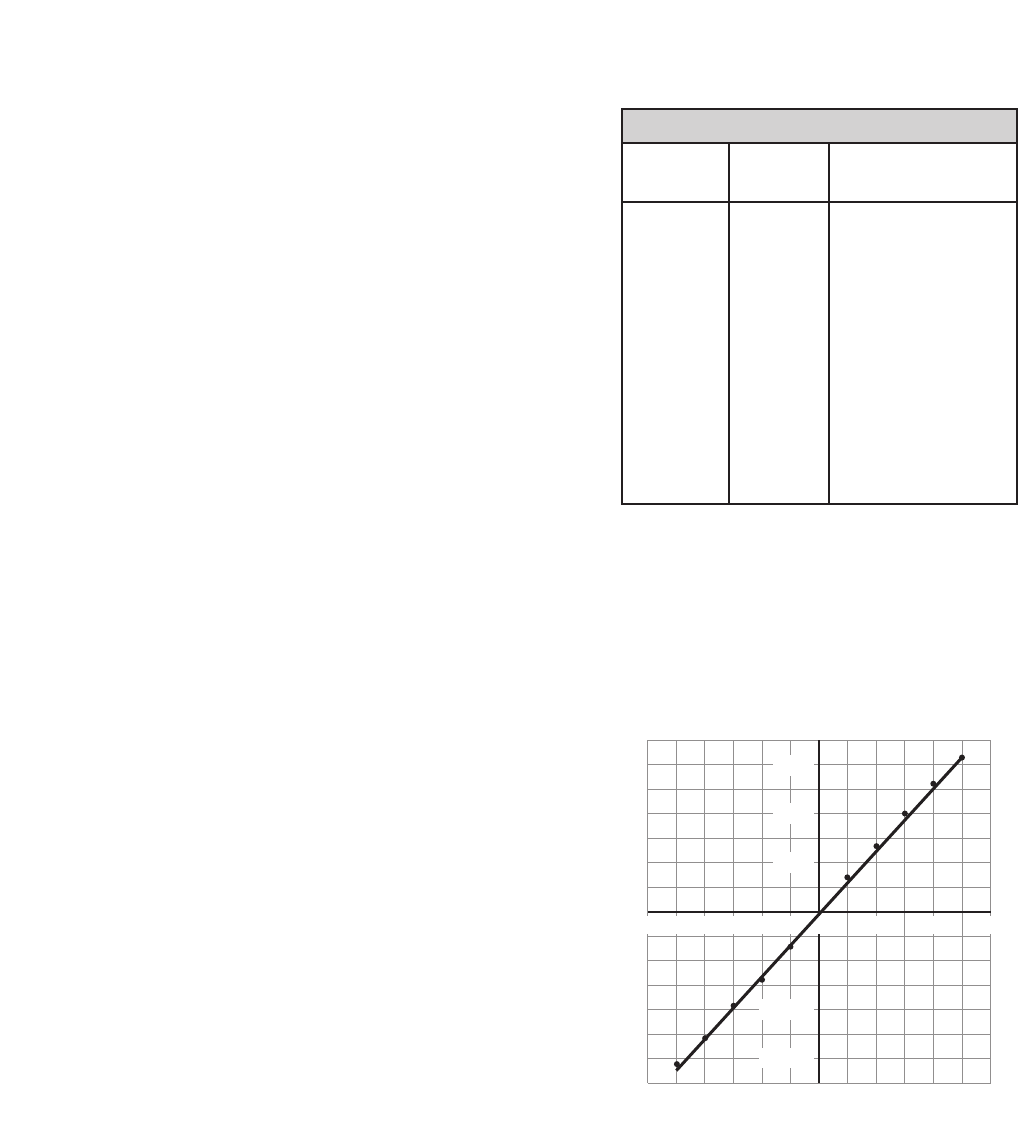
70. Flashlights A flashlight bulb is connected
across a 3.0-V potential difference. The cur-
rent through the bulb is 1.5 A.
a. What is the power rating of the bulb?
PIV (1.5 A)(3.0 V) 4.5 W
b. How much electric energy does the bulb
convert in 11 min?
The definition of power is P
E
t
,so
EPt
(4.5 W)(11 min)
6
m
0in
s
3.0103J
71. Batteries A resistor of 60.0 has a current
of 0.40 A through it when it is connected to
the terminals of a battery. What is the volt-
age of the battery?
VIR (0.40 A)(60.0 ) 24 V
72. What voltage is applied to a 4.0-resistor if
the current is 1.5 A?
VIR (1.5 A)(4.0 ) 6.0 V
73. What voltage is placed across a motor with
a 15-operating resistance if there is 8.0 A
of current?
VIR (8.0 A)(15 ) 1.2102V
74. A voltage of 75 V is placed across a 15-
resistor. What is the current through the
resistor?
VIR
I
1
75
5
V
5.0 A
Level 2
75. Some students connected a length of
nichrome wire to a variable power supply
to produce between 0.00 V and 10.00 V
across the wire. They then measured the
current through the wire for several volt-
ages. The students recorded the data for the
voltages used and the currents measured, as
shown in Table 22-2.
a. For each measurement, calculate the
resistance.
R143 ,R148 ,R150 ,
R154 ,R159 ,R143 ,
R143 ,R154 ,R157 ,
R161
b. Graph Iversus V.
c. Does the nichrome wire obey Ohm’s
law? If not, for all the voltages, specify the
voltage range for which Ohm’s law holds.
Ohm’s law is obeyed when the
resistance of a device is constant
and independent of the potential
difference. The resistance of the
nichrome wire increases somewhat
as the magnitude of the voltage
increases, so the wire does not
quite obey Ohm’s law.
0.0012.008.00 4.00 4.00 8.00 12.00
0.06
0.04
0.02
0.06
0.04
I (amps)
V (volts)
Table 22-2
Voltage, VCurrent, IResistance, RV/I
(volts) (amps) (amps)
2.00 0.0140 ______________
4.00 0.0270 ______________
6.00 0.0400 ______________
8.00 0.0520 ______________
10.00 0.0630 ______________
2.00 0.0140 ______________
4.00 0.0280 ______________
6.00 0.0390 ______________
8.00 0.0510 ______________
10.00 0.0620 ______________
V
R
454 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 455
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
76. Draw a series circuit diagram to include a
16-resistor, a battery, and an ammeter
that reads 1.75 A. Indicate the positive ter-
minal and the voltage of the battery, the
positive terminal of the ammeter, and the
direction of conventional current.
VIR (1.75 A)(16 ) 28 V
77. A lamp draws a 66-mA current when con-
nected to a 6.0-V battery. When a 9.0-V
battery is used, the lamp draws 75 mA.
a. Does the lamp obey Ohm’s law?
No. The voltage is increased by a
factor of
9
6.
.0
0
1.5, but the current
is increased by a factor of
7
65
6
1.1
b. How much power does the lamp dissi-
pate when it is connected to the 6.0-V
battery?
PIV (66103A)(6.0 V) 0.40 W
c. How much power does it dissipate at
9.0 V?
PIV (75103A)(9.0 V) 0.68 W
78. Lightbulbs How much energy does a 60.0-W
lightbulb use in half an hour? If the light-
bulb converts 12 percent of electric energy to
light energy, how much thermal energy does
it generate during the half hour?
P
E
t
EPt (60.0 W)(1800 s)
1.08105J
If the bulb is 12 percent efficient,
88 percent of the energy is lost to heat, so
Q(0.88)(1.08105J) 9.5104J
79. The current through a lamp connected
across 120 V is 0.40 A when the lamp is on.
a. What is the lamp’s resistance when it
is on?
VIR
R
V
I
3.0102
b. When the lamp is cold, its resistance is
1
5
as great as it is when the lamp is hot.
What is the lamp’s cold resistance?
1
5
(3.0102) 6.0101
c. What is the current through the lamp as
it is turned on if it is connected to a
potential difference of 120 V?
VIR
I 2.0 A
Level 3
80. The graph in Figure 22-17 shows the cur-
rent through a device called a silicon diode.
■Figure 22-17
a. A potential difference of 0.70 V is
placed across the diode. What is the
resistance of the diode?
From the graph, I22 m/A, and
VIR, so
R
V
I
32
b. What is the diode’s resistance when a
0.60-V potential difference is used?
R
V
I
1.2102
c. Does the diode obey Ohm’s law?
No. Resistance depends on voltage.
0.60 V
5.2103A
0.70 V
2.2102A
0.01
0.02
00.2 0.4 0.6 0.8
Voltage (V)
Current (A)
Current in a Diode
120 V
6.0101
V
R
120 V
0.40 A
V 28 V
A
16
I 1.75 A
I
Chapter 22 continued

81. Draw a schematic diagram to show a circuit
including a 90-V battery, an ammeter, and a
resistance of 45 connected in series. What
is the ammeter reading? Draw arrows show-
ing the direction of conventional current.
VIR
I
R
V
2 A
22.2 Using Electric Energy
pages 612–613
Level 1
82. Batteries A 9.0-V battery costs $3.00 and
will deliver 0.0250 A for 26.0 h before it
must be replaced. Calculate the cost per kWh.
EIVt (0.0250 A)(9.0 V)(26.0 h)
5.9 Wh 5.9103kWh
Rate
co
E
st
$510/kWh
83. What is the maximum current allowed in a
5.0-W, 220-resistor?
PI2R
I
R
P
0.15 A
84. A 110-V electric iron draws 3.0 A of current.
How much thermal energy is developed in
an hour?
QEVIt (110 V)(3.0 A)(1.0 h)(3600 s/h)
1.2106J
Level 2
85. For the circuit shown in Figure 22-18, the
maximum safe power is 5.0101W. Use the
figure to find the following:
■Figure 22-18
a. the maximum safe current
PI2R
I
1 A
b. the maximum safe voltage
PV2/R
VPR
(5.0
101W
)(40.0
)
45 V
86. Utilities Figure 22-19 represents an elec-
tric furnace. Calculate the monthly (30-day)
heating bill if electricity costs $0.10 per
kWh and the thermostat is on one-fourth of
the time.
■Figure 22-19
E
V
R
2
(t)
(2
4
4
.
0
8
.
0
0
V)2
(30 d)(24 h/d)(0.25)
2160 kWh
Cost (2160 kWh)($0.100/kWh) $216
87. Appliances A window air conditioner is esti-
mated to have a cost of operation of $50 per
30 days. This is based on the assumption that
the air conditioner will run half of the time
240.0 V 4.80
Thermostat
5.0101W
40.0
P
R
V40.0
I
5.0 W
220
$3.00
5.9103kWh
90 V
45
I
90 V
A
45
2 A
456 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued

Physics: Principles and Problems Solutions Manual 457
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
and that electricity costs $0.090 per kWh.
Determine how much current the air condi-
tioner will take from a 120-V outlet.
Cost (E)(rate)
E
C
ra
o
ts
et
$0.0$
95
00
/kWh
556 kWh
EIVt
I
V
Et
12.9 A
88. Radios A transistor radio operates by
means of a 9.0-V battery that supplies it
with a 50.0-mA current.
a. If the cost of the battery is $2.49 and it
lasts for 300.0 h, what is the cost per
kWh to operate the radio in this manner?
PIV (0.050 A)(9.0 V) 0.45 W
4.5104kW
Cost
$18.00/kWh
b. The same radio, by means of a converter,
is plugged into a household circuit by a
homeowner who pays $0.12 per kWh.
What does it now cost to operate the
radio for 300.0 h?
Cost ($0.12/kWh)
(4.5104 kW)(300 h)
$0.02
Mixed Review
page 613
Level 1
89. If a person has $5, how long could he or
she play a 200 W stereo if electricity costs
$0.15 per kWh?
E Pt
C
Ro
at
s
e
t
t
200 h
90. A current of 1.2 A is measured through a
50.0-resistor for 5.0 min. How much heat
is generated by the resistor?
QEI2Rt
(1.2 A)2(50.0 )(5.0 min)
6
m
0in
s
2.2104J
91. A 6.0-resistor is connected to a 15-V
battery.
a. What is the current in the circuit?
VIR
I
R
V
6
1
.5
0V
2.5 A
b. How much thermal energy is produced
in 10.0 min?
QEI2Rt
(2.5 A)2(6.0 )(10.0 min)
6
m
0in
s
2.3104J
Level 2
92. Lightbulbs An incandescent lightbulb with
a resistance of 10.0 when it is not lit and
a resistance of 40.0 when it is lit has
120 V placed across it.
a. What is the current draw when the bulb
is lit?
I
R
V
4
1
0
2
.0
0V
3.0 A
b. What is the current draw at the instant
the bulb is turned on?
I
R
V
1
1
0
2
.0
0V
12 A
c. When does the lightbulb use the most
power?
the instant it is turned on
93. A 12-V electric motor’s speed is controlled
by a potentiometer. At the motor’s slowest
setting, it uses 0.02 A. At its highest setting,
the motor uses 1.2 A. What is the range of
the potentiometer?
The slowest speed’s resistance is
RV/I12 V/0.02 A 600 . The
fastest speed’s resistance is
RV/I12 V/1.2 A 1.0101.
The range is 1.0101to 600 .
$5
($0.15/kWh)(200 W)
1
1
00
k
0
W
W
Cost
(Rate)(P)
$2.49
(4.5104kW)(300.0 h)
(556 kWh)(1000 W/kW)
(120 V)(30 d)(24 h/d)(0.5)
Chapter 22 continued

Level 3
94. An electric motor operates a pump that irri-
gates a farmer’s crop by pumping 1.0104L
of water a vertical distance of 8.0 m into a
field each hour. The motor has an operating
resistance of 22.0 and is connected across
a 110-V source.
a. What current does the motor draw?
VIR
I 5.0 A
b. How efficient is the motor?
EWmgd
(1104kg)(9.80 m/s2)(8.0 m)
8105J
EmIVt (5.0 A)(110 V)(3600 s)
2.0106J
Efficiency 100
100
40%
95. A heating coil has a resistance of 4.0 and
operates on 120 V.
a. What is the current in the coil while it is
operating?
VIR
I
R
V
3.0101A
b. What energy is supplied to the coil in
5.0 min?
EI2Rt
(3.0101A)2(4.0 )(5.0 min)
6
m
0in
s
1.1106J
c. If the coil is immersed in an insulated
container holding 20.0 kg of water,
what will be the increase in the temper-
ature of the water? Assume 100 percent
of the heat is absorbed by the water.
QmCT
T
m
Q
C
13°C
d. At $0.08 per kWh, how much does it
cost to operate the heating coil 30 min
per day for 30 days?
Cost
(30 days)
$4.40
96. Appliances An electric heater is rated at
500 W.
a. How much energy is delivered to the
heater in half an hour?
EPt (5102W)(1800 s)
9105J
b. The heater is being used to heat a room
containing 50 kg of air. If the specific
heat of air is 1.10 kJ/kg°C, and 50 per-
cent of the thermal energy heats the air
in the room, what is the change in air
temperature in half an hour?
QmCT
T
m
Q
C
8°C
c. At $0.08 per kWh, how much does it
cost to run the heater 6.0 h per day for
30 days?
Cost
(30 days)
$7
Thinking Critically
page 614
97. Formulate Models How much energy is
stored in a capacitor? The energy needed to
increase the potential difference of a charge, q,
$0.08
kWh
1kWH
3.6106J
3600 s
h
6.0 h
day
500 J
s
(0.5)(9105J)
(50.0 kg)(1100 J/kgC°)
$0.08
kWh
1kWh
3.6106J
30 min
day
1.1106J
5min
1.1106J
(20.0 kg)(4180 J/kgC°)
120 V
4.0
8105J
2.0106J
Ew
Em
110 V
22.0
V
R
458 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued
Physics: Principles and Problems Solutions Manual 459
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
is represented by EqV. But in a capacitor,
Vq/C. Thus, as charge is added, the poten-
tial difference increases. As more charge is
added, however, it takes more energy to add
the additional charge. Consider a 1.0-F
“supercap” used as an energy storage device
in a personal computer. Plot a graph of Vas
the capacitor is charged by adding 5.0 C to it.
What is the voltage across the capacitor? The
area under the curve is the energy stored in
the capacitor. Find the energy in joules. Is it
equal to the total charge times the final
potential difference? Explain.
Voltage V
C
q
5.0 V
Energy Earea under curve
(5.0 V)(5.0 C)
13 J
No. Graphically, total change times final
potential difference is exactly twice the
area under the curve. Physically, it
means that each coulomb would require
the same maximum amount of energy
to place it on the capacitor. Actually, the
amount of energy needed to add each
charge increases as charge accumu-
lates on the capacitor.
98. Apply Concepts A microwave oven oper-
ates at 120 V and requires 12 A of current.
Its electric efficiency (converting AC to
microwave radiation) is 75 percent, and its
conversion efficiency from microwave radia-
tion to heating water is also 75 percent.
a. Draw a block power diagram similar
to the energy diagram shown in
Figure 22-2b on page 593. Label the
function of each block according to
total joules per second.
b. Derive an equation for the rate of tem-
perature increase (T/s) from the infor-
mation presented in Chapter 12. Solve
for the rate of temperature rise given the
rate of energy input, the mass, and the
specific heat of a substance.
T
t
m
1
C
Q
t
c. Use your equation to solve for the rate
of temperature rise in degrees Celsius
per second when using this oven to heat
250 g of water above room temperature.
T
t
m
1
C
Q
t
0.78°C/s
d. Review your calculations carefully for
the units used and discuss why your
answer is in the correct form.
The kg unit cancels and the J unit
cancels, leaving °C/s.
e. Discuss, in general terms, different ways
in which you could increase the efficiency
of microwave heating.
The efficiency of conversion from
electric energy to microwave energy is
75 percent. It might be possible to find
a way to convert electric energy to
radiation using a different approach
that would be more efficient.The effi-
ciency of conversion from microwave
radiation to thermal energy in water is
75 percent. It might be possible to use
a different frequency of electromag-
netic radiation to improve this rating.
Or, it might be possible to find a new
810 J/s
(0.25 kg)(4180 J/kg°C)
1
2
5.0 C
1.0 F
1.0 2.0
0.0
1.0
2.0
3.0 4.0
Charge (C)
Potential difference (V)
5.0
3.0
4.0
5.0
Chapter 22 continued
Input
1440 J/s
Microwave
converter
1440 J/s
Heat
converter
1080 J/s
Wasted
360 J/s
Wasted
270 J/s
Useful
output
810 J/s
→→→
→
→

geometry of radiating objects to be
heated to improve the efficiency.
f. Discuss, in efficiency terms, why
microwave ovens are not useful for heat-
ing everything.
The conversion efficiency from
microwave energy to thermal energy
is good for water. It’s not as good
for other materials.The containers
and dishes designed for use with
microwave ovens convert little of the
energy.
g. Discuss, in general terms, why it is not
a good idea to run microwave ovens
when they are empty.
The empty oven means that the
microwave energy has to be dissi-
pated in the oven.This can lead to
overheating of the oven compo-
nents and to their failure.
99. Analyze and Conclude A salesclerk in an
appliance store states that microwave
ovens are the most electrically efficient
means of heating objects.
a. Formulate an argument to refute the
clerk’s claim. Hint: Think about heating
a specific object.
In the case of heating a cup of
water, an immersion heater uses
only resistance for energy conver-
sion and is nearly 100 percent effi-
cient. A microwave oven uses two
energy conversions (electricity to
microwave radiation to heat) and is
typically around 50 percent efficient.
b. Formulate an argument to support the
clerk’s claim. Hint: Think about heating
a specific object.
In the case of heating a potato, a
microwave oven heats mostly the
potato and is more efficient than an
electric oven or skillet, which also
heats the air, cabinets, racks, etc.
c. Formulate a diplomatic reply to the
clerk.
“It can be true, but it depends on
the specific application.”
100. Apply Concepts The sizes of 10-resis-
tors range from a pinhead to a soup can.
Explain.
The physical size of a resistor is deter-
mined by its power rating. Resistors
rated at 100 W are much larger than
those rated at 1 W.
101. Make and Use Graphs The diode graph
shown in Figure 22-17 on page 612 is
more useful than a similar graph for a
resistor that obeys Ohm’s law. Explain.
The volt–ampere graph for a resistor
obeying Ohm’s law is a straight line
and is seldom necessary.
102. Make and Use Graphs Based on what
you have learned in this chapter, identify
and prepare two parabolic graphs.
voltage–power and current–power
P V2
R
Amperes through a 10- resistor
Watts dissipated
120
10
20
30
40
P I2R
5
Voltage across a 10- resistor
Watts dissipated
10 15 200
10
20
30
40
460 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued

Physics: Principles and Problems Solutions Manual 461
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Writing in Physics
page 614
103. There are three kinds of equations encoun-
tered in science: (1) definitions, (2) laws,
and (3) derivations. Examples of these are:
(1) an ampere is equal to one coulomb
per second, (2) force is equal to mass
times acceleration, (3) power is equal to
voltage squared divided by resistance.
Write a one-page explanation of where
“resistance is equal to voltage divided by
current” fits. Before you begin to write,
first research the three categories given
above.
The student’s answer should include
the idea (1) that, for devices obeying
Ohm’s law, the voltage drop is propor-
tional to current through the device
and (2) that the formula RV/I,the
definition of resistance, is a derivation
from Ohm’s law.
104. In Chapter 13, you learned that matter
expands when it is heated. Research the
relationship between thermal expansion
and high-voltage transmission lines.
Answers will vary, but students should
determine that transmission lines can
become hot enough to expand and sag
when they have high currents. Sagging
lines can be dangerous if they touch
objects beneath them, such as trees or
other power lines.
Cumulative Review
page 614
105. A person burns energy at the rate of about
8.4106J per day. How much does she
increase the entropy of the universe in
that day? How does this compare to the
entropy increase caused by melting 20 kg
of ice? (Chapter 12)
SQ/Twhere Tis the body
temperature of 310 K.
S(8.4106J)/(310 K)
2.7104J/K
For melting ice
S(20 kg)(3.34105J/kg)/(273 K)
2.4104J/K
106. When you go up the elevator of a tall
building, your ears might pop because of
the rapid change in pressure. What is the
pressure change caused by riding in an ele-
vator up a 30-story building (150 m)? The
density of air is about 1.3 kg/m3at sea
level. (Chapter 13)
Pgh
(1.3 kg/m3)(9.80 m/s2)(150 m)
1.9 kPa or about 2/100 of
the total air pressure
107. What is the wavelength in air of a 17-kHz
sound wave, which is at the upper end of
the frequency range of human hearing?
(Chapter 15)
v f
0.020 m 2.0 cm
108. Light of wavelength 478 nm falls on a
double slit. First-order bright bands appear
3.00 mm from the central bright band.
The screen is 0.91 m from the slits. How
far apart are the slits? (Chapter 19)
x
L
d
d
x
L
1.4104m
109. A charge of 3.0106C is 2.0 m from a
second charge of 6.0105C. What is
the magnitude of the force between them?
(Chapter 20)
FK
(9.0109Nm2/C2)
0.41 N
(3.0106C)(6.0105C)
(2.0 m)2
qAqB
d2
(478109m)(0.91 m)
(3.00103m)
343 m/s
17,000 Hz
v
f
Chapter 22 continued

Challenge Problem
page 604
Use the figure to the right to help you answer the
questions below.
1. Initially, the capacitor is uncharged. Switch 1
is closed, and Switch 2 remains open.
What is the voltage across the capacitor?
15 V
2. Switch 1 is now opened, and Switch 2
remains open. What is the voltage across
the capacitor? Why?
It remains 15 V because there is no
path for the charge to be removed.
3. Next, Switch 2 is closed, while Switch 1
remains open. What is the voltage across the
capacitor and the current through the resis-
tor immediately after Switch 2 is closed?
15 V and 13 mA
4. As time goes on, what happens to the volt-
age across the capacitor and the current
through the resistor?
The capacitor voltage remains at 15 V
because there is no path to discharge
the capacitor; the current remains at
13 mA because the battery voltage is
constant at 15 V. However, if the bat-
tery and capacitor were real compo-
nents instead of ideal circuit compo-
nents, the capacitor voltage eventually
would become zero due to leakage,
and the current eventually would
become zero due to battery depletion.
1200
Switch 2
Switch 1
15 V
1.5 F
462 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued

Physics: Principles and Problems Solutions Manual 463
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
23 Series and Parallel Circuits
CHAPTER
Practice Problems
23.1 Simple Circuits
pages 617–626
page 619
1. Three 20-resistors are connected in series
across a 120-V generator. What is the equiv-
alent resistance of the circuit? What is the
current in the circuit?
RR1R2 R3
20 20 20
60
I 2 A
2. A 10-, 15-, and 5-resistor are connect-
ed in a series circuit with a 90-V battery.
What is the equivalent resistance of the cir-
cuit? What is the current in the circuit?
RR1R2 R3
10 15 5 30
I 3 A
3. A 9-V battery is in a circuit with three resis-
tors connected in series.
a. If the resistance of one of the resistors
increases, how will the equivalent resis-
tance change?
It will increase.
b. What will happen to the current?
I , so it will decrease.
c. Will there be any change in the battery
voltage?
No. It does not depend on the
resistance.
4. A string of holiday lights has ten bulbs with
equal resistances connected in series. When
the string of lights is connected to a 120-V
outlet, the current through the bulbs is
0.06 A.
a. What is the equivalent resistance of the
circuit?
R 2103
b. What is the resistance of each bulb?
Rbulb 2102
5. Calculate the voltage drops across the three
resistors in problem 2, and verify that their
sum equals the voltage of the battery.
V1 IR1 (3 A)(10 ) 30 V
V2 IR2 (3 A)(15 ) 45 V
V3 IR3 (3 A)(5 ) 15 V
V1 V2 V3 30 V 45 V 15 V
90 V
voltage of battery
page 622
6. The circuit shown in Example Problem 1 is
producing these symptoms: the ammeter
reads 0 A, VAreads 0 V, and VBreads 45 V.
What has happened?
RBhas failed. It has infinite resistance,
and the battery voltage appears across
it.
7. Suppose the circuit shown in Example
Problem 1 has these values: RA255 ,
RB292 , and VA17.0 V. No other
information is available.
a. What is the current in the circuit?
I 66.7 mA
b. What is the battery voltage?
First, find the total resistance, then
solve for voltage.
RRARB
255 292
547
VIR (66.7 mA)(547 ) 36.5 V
17.0 V
255.0
V
R
2103
10
R
10
120 V
0.06 A
V
I
V
R
90 V
30
V
R
120 V
60
V
R

c. What are the total power dissipation
and the individual power dissipations?
PIV (66.7 mA)(36.5 V) 2.43 W
PAI2RA
(66.7 mA)2(255 )
1.13 W
PBI2RB
(66.7 mA)2(292 )
1.30 W
d. Does the sum of the individual power
dissipations in the circuit equal the total
power dissipation in the circuit? Explain.
Yes. The law of conservation of ener-
gy states that energy cannot be cre-
ated or destroyed; therefore, the rate
at which energy is converted, or
power dissipated, will equal the sum
of all parts.
8. Holiday lights often are connected in series
and use special lamps that short out when
the voltage across a lamp increases to the
line voltage. Explain why. Also explain why
these light sets might blow their fuses after
many bulbs have failed.
If not for the shorting mechanism, the
entire set would go out when one lamp
burns out. After several lamps fail and
then short, the total resistance of the
remaining working lamps results in an
increased current that is sufficient to
blow the fuse.
9. The circuit in Example Problem 1 has
unequal resistors. Explain why the resistor
with the lower resistance will operate at a
lower temperature.
The resistor with the lower resistance
will dissipate less power, and thus will
be cooler.
10. A series circuit is made up of a 12.0-V bat-
tery and three resistors. The voltage across
one resistor is 1.21 V, and the voltage across
another resistor is 3.33 V. What is the volt-
age across the third resistor?
Vsource VAVBVC
VCVsource (VAVB)
12.0 V (1.21 V 3.33 V) 7.46 V
page 623
11. A 22-resistor and a 33-resistor are con-
nected in series and placed across a 120-V
potential difference.
a. What is the equivalent resistance of the
circuit?
RR1R222 33 55
b. What is the current in the circuit?
I 2.2 A
c. What is the voltage drop across each
resistor?
V1 IR1
R1
(22 )
48 V
V2 IR2
(33 ) 72 V
d. What is the voltage drop across the two
resistors together?
V48 V 72 V 1.20102V
12. Three resistors of 3.3 k, 4.7 k, and 3.9
kare connected in series across a 12-V
battery.
a. What is the equivalent resistance?
R3.3 k4.7 k3.9 k
1.2101k
b. What is the current through the resistors?
I
1.0 mA 1.0103A
c. What is the voltage drop across each
resistor?
VIR
V1(3.3 k)(1.0103A) 3.3 V
V2(4.7 k)(1.0103A) 4.7 V
12 V
12104
V
R
120 V
55
120 V
55
V
R
120 V
55
V
R
464 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued

Physics: Principles and Problems Solutions Manual 465
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
V3(3.9 k)(1.0103A) 3.9 V
so V3.3 V, 4.7 V, and 3.9 V
d. Find the total voltage drop across the
three resistors.
V3.3 V 4.7 V 3.9 V 11.9 V
13. A student makes a voltage divider from a
45-V battery, a 475-kresistor, and a 235-k
resistor. The output is measured across the
smaller resistor. What is the voltage?
VB 15 V
14. Select a resistor to be used as part of a volt-
age divider along with a 1.2-kresistor. The
drop across the 1.2-kresistor is to be 2.2 V
when the supply is 12 V.
VB
RARB
1.2 k
5.3 k
page 626
15. Three 15.0-resistors are connected in par-
allel and placed across a 30.0-V battery.
a. What is the equivalent resistance of the
parallel circuit?
R5.00
b. What is the current through the entire
circuit?
I 6.00 A
c. What is the current through each branch
of the circuit?
I 2.00 A
16. A 120.0-resistor, a 60.0-resistor, and a
40.0-resistor are connected in parallel
and placed across a 12.0-V battery.
a. What is the equivalent resistance of the
parallel circuit?
R20.0
b. What is the current through the entire
circuit?
I 0.600 A
c. What is the current through each branch
of the circuit?
I1 0.100 A
I2 0.200 A
I3 0.300 A
17. Suppose that one of the 15.0-resistors in
problem 15 is replaced by a 10.0-resistor.
a. Does the equivalent resistance change?
If so, how?
Yes, it gets smaller.
b. Does the amount of current through the
entire circuit change? If so, in what way?
Yes, it gets larger.
c. Does the amount of current through the
other 15.0-resistors change? If so,
how?
No, it remains the same. Currents
are independent.
18. A 150-branch in a circuit must be reduced
to 93 . A resistor will be added to this
branch of the circuit to make this change.
What value of resistance should be used and
how must the resistor be connected?
A parallel resistor will be required to
reduce the resistance.
1
RB
1
RA
1
R
12.0 V
40.0
V
R3
12.0 V
60.0
V
R2
12.0 V
120.0
V
R1
12.0 V
20.0
V
R
1
40.0
1
60.0
1
120.0
1
R3
1
R2
1
R1
1
R
30.0 V
15.0
V
R1
30.0 V
5.00
V
R
3
15.0
1
15.0
1
15.0
1
15.0
1
R3
1
R2
1
R1
1
R
(12.0 V)(1.2 k)
2.2 V
VRB
VB
VRB
RARB
(45 V)(235 k)
475 k 235 k
VRB
RARB
Chapter 23 continued

RA2.4102
2.4102in parallel with the 150-
resistance
19. A 12-, 2-W resistor is connected in paral-
lel with a 6.0-, 4-W resistor. Which will
become hotter if the voltage across them
keeps increasing?
Neither. They both reach maximum dis-
sipation at the same voltage.
P
VPR
The voltage is equal across parallel
resistors, so:
VP1R1
P2R2
(2 W)(
12 )
(4 W)(
6.0
)
5 V maximum
Section Review
23.1 Simple Circuits
pages 617–626
page 626
20. Circuit Types Compare and contrast the
voltages and the currents in series and par-
allel circuits.
The student’s answer should include
the following ideas:
(1) In a series circuit, the current in
each of the devices is the same, and the
sum of the device voltage drops equals
the source voltage.
(2) In a parallel circuit, the voltage drop
across each device is the same and the
sum of the currents through each loop
equals the source current.
21. Total Current A parallel circuit has four
branch currents: 120 mA, 250 mA, 380 mA,
and 2.1 A. How much current is supplied
by the source?
ITI1I2I3I4
120 mA 250 mA 380 mA 2.1
A
0.12 A 0.25 A 0.38 A 2.1 A
2.9 A
22. Total Current A series circuit has four
resistors. The current through one resistor is
810 mA. How much current is supplied by
the source?
810 mA. Current is the same every-
where in a series circuit.
23. Circuits A switch is connected in series
with a 75-W bulb to a source of 120 V.
a. What is the potential difference across
the switch when it is closed (turned on)?
0 V; VIR with R0
b. What is the potential difference across
the switch if another 75-W bulb is
added in series?
0 V; VIR with R0
24. Critical Thinking The circuit in Figure 23-8
has four identical resistors. Suppose that a
wire is added to connect points A and B.
Answer the following questions, and
explain your reasoning.
■Figure 23-8
a. What is the current through the wire?
0 A; the potentials of points A and B
are the same.
b. What happens to the current through
each resistor?
nothing
c. What happens to the current drawn
from the battery?
nothing
R
R
AB
R
R
V2
R
1
150
1
93
1
RB
1
R
1
RA
466 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Physics: Principles and Problems Solutions Manual 467
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
d. What happens to the potential differ-
ence across each resistor?
nothing
Practice Problems
23.2 Applications of Circuits
pages 627–631
page 630
25. A series-parallel circuit has three resistors:
one dissipates 2.0 W, the second 3.0 W, and
the third 1.5 W. How much current does
the circuit require from a 12-V battery?
By conservation of energy (and power):
PTP1P2P3
2.0 W 3.0 W 1.5 W
6.5 W
PTIV
I 0.54 A
26. There are 11 lights in series, and they are in
series with two lights in parallel. If the 13
lights are identical, which of them will burn
brightest?
The 11 lights in series will burn
brighter. The parallel lights each will
conduct half of the current of the series
lights and they will burn at one-fourth
the intensity of the series lights since
PI2R.
27. What will happen to the circuit in problem
26 if one of the parallel lights burns out?
Then, all of the working lights are in
series. The 12 working lights will burn
with equal intensity.
28. What will happen to the circuit in problem
26 if one of the parallel lights shorts out?
Then, the shorted light will reduce the
voltage across itself and its parallel
companion to 0. The 11 series lights will
burn with equal, but increased, intensity
and the two parallel lights will go out.
Section Review
23.2 Applications of Circuits
pages 627–631
page 631
Refer to Figure 23-13 for questions 29–33, and 35.
The bulbs in the circuit are identical.
■Figure 23-13
29. Brightness How do the bulb brightnesses
compare?
Bulbs 2 and 3 are equal in brightness
but dimmer than bulb 1.
30. Current If I3measures 1.7 A and I1mea-
sures 1.1 A, how much current is flowing in
bulb 2?
I3I1I2
I2I3I11.7 A 1.1 A 0.6 A
31. Circuits in Series The wire at point C is
broken and a small resistor is inserted in
series with bulbs 2 and 3. What happens to
the brightnesses of the two bulbs? Explain.
Both dim equally. The current in each is
reduced by the same amount.
32. Battery Voltage A voltmeter connected
across bulb 2 measures 3.8 V, and a volt-
meter connected across bulb 3 measures
4.2 V. What is the battery voltage?
These bulbs are in series, so:
VTV1V23.8 V 4.2 V 8.0 V
I3I1I2
V
A
AA
A
B
C
12
3
6.5 W
12 V
PT
V
Chapter 23 continued

33. Circuits Using the information from prob-
lem 32, determine if bulbs 2 and 3 are
identical.
No. Identical bulbs in series would have
identical voltage drops since their cur-
rents are the same.
34. Circuit Protection Describe three com-
mon safety devices associated with house-
hold wiring.
fuses, circuit breakers, ground-fault
circuit interrupters
35. Critical Thinking Is there a way to make
the three bulbs in Figure 23-13 burn with
equal intensity without using any additional
resistors? Explain.
Yes. Because intensity is proportional
to power, it would be necessary to use
a bulb at location 1 that has four times
the operating resistance of each of
those at locations 2 and 3.
V2/4R(V/2)2/R
Chapter Assessment
Concept Mapping
page 636
36. Complete the concept map using the fol-
lowing terms: series circuit, R R1R2
R3, constant current, parallel circuit, constant
potential.
Mastering Concepts
page 636
37. Why is it frustrating when one bulb burns
out on a string of holiday tree lights con-
nected in series? (23.1)
When one bulb burns out, the circuit is
open and all the bulbs go out.
38. Why does the equivalent resistance decrease
as more resistors are added to a parallel
circuit? (23.1)
Each new resistor provides an addition-
al path for the current.
39. Several resistors with different values are
connected in parallel. How do the values of
the individual resistors compare with the
equivalent resistance? (23.1)
The equivalent resistance will be less
than that of any of the resistors.
40. Why is household wiring constructed in
parallel instead of in series? (23.1)
Appliances in parallel can be run inde-
pendently of one another.
41. Why is there a difference in equivalent
resistance between three 60-resistors con-
nected in series and three 60-resistors
connected in parallel? (23.1)
In a series circuit, the current is
opposed by each resistance in turn. The
total resistance is the sum of the resis-
tors. In a parallel circuit, each resis-
tance provides an additional path for
current. The result is a decrease in total
resistance.
42. Compare the amount of current entering a
junction in a parallel circuit with that leav-
ing the junction. (A junction is a point
where three or more conductors are
joined.) (23.1)
The amount of current entering a junc-
tion is equal to the amount of current
leaving.
468 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Type of circuit parallel circuitseries circuit
constant
potential
constant
current
R
1
R
1
1
R
1
2
. . .
RR1R2R3 ...
Resistors in
circuits
Principle
Resistance

Physics: Principles and Problems Solutions Manual 469
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
43. Explain how a fuse functions to protect an
electric circuit. (23.2)
The purpose of a fuse is to prevent con-
ductors from being overloaded with cur-
rent, causing fires due to overheating. A
fuse is simply a short length of wire that
will melt from the heating effect if the
current exceeds a certain maximum.
44. What is a short circuit? Why is a short cir-
cuit dangerous? (23.2)
A short circuit is a circuit that has
extremely low resistance. A short cir-
cuit is dangerous because any potential
difference will produce a large current.
The heating effect of the current can
cause a fire.
45. Why is an ammeter designed to have a very
low resistance? (23.2)
An ammeter must have low resistance
because it is placed in series in the cir-
cuit. If its resistance were high, it would
significantly change the total resistance
of the circuit and thus serve to reduce
the current in the circuit, thereby chang-
ing the current it is meant to measure.
46. Why is a voltmeter designed to have a very
high resistance? (23.2)
A voltmeter is placed in parallel with the
portion of the circuit whose difference
in potential is to be measured. A volt-
meter must have very high resistance
for the same reason that an ammeter
has low resistance. If the voltmeter had
low resistance, it would lower the resis-
tance of the portion of the circuit it is
across and increase the current in the
circuit.This would produce a higher
voltage drop across the part of the cir-
cuit where the voltmeter is located,
changing the voltage it is measuring.
47. How does the way in which an ammeter is
connected in a circuit differ from the way in
which a voltmeter is connected? (23.2)
An ammeter is connected in series; a
voltmeter is connected in parallel.
Applying Concepts
page 636
48. What happens to the current in the other
two lamps if one lamp in a three-lamp
series circuit burns out?
If one of the lamp filaments burns out,
the current will cease and all the lamps
will go out.
49. Suppose the resistor, RA, in the voltage
divider in Figure 23-4 is made to be a vari-
able resistor. What happens to the voltage
output, VB, of the voltage divider if the
resistance of the variable resistor is
increased?
VBVRB/(RARB). As RAincreases,
VBwill decrease.
50. Circuit A contains three 60-resistors in
series. Circuit B contains three 60-resis-
tors in parallel. How does the current in the
second 60-resistor of each circuit change
if a switch cuts off the current to the first
60-resistor?
Circuit A:There will be no current in the
resistor.
Circuit B:The current in the resistor will
remain the same
51. What happens to the current in the other
two lamps if one lamp in a three-lamp par-
allel circuit burns out?
If one of the filaments burns out, the
resistance and the potential difference
across the other lamps will not change;
therefore, their currents will remain the
same.
52. An engineer needs a 10-resistor and a
15-resistor, but there are only 30-resis-
tors in stock. Must new resistors be pur-
chased? Explain.
No, the 30-resistors can be used in
parallel. Three 30-resistors in parallel
will give a 10-resistance. Two 30-
resistors in parallel will give a 15-
resistance.
Chapter 23 continued

53. If you have a 6-V battery and many 1.5-V
bulbs, how could you connect them so that
they light but do not have more than 1.5 V
across each bulb?
Connect four of the bulbs in series.
The voltage drop across each will be
(6.0 V)/4 1.5 V.
54. Two lamps have different resistances, one
larger than the other.
a. If the lamps are connected in parallel,
which is brighter (dissipates more
power)?
The lamp with the lower resistance:
PIV and IV/R, so PV2/R.
Because the voltage drop is the
same across both lamps, the smaller
Rmeans larger P, and thus will be
brighter.
b. When the lamps are connected in series,
which lamp is brighter?
The lamp with the higher resistance;
PIV and VIR, so PI2R.
Because the current is the same in
both lamps, the larger Rmeans larg-
er P, and thus will be brighter.
55. For each of the following, write the form of
circuit that applies: series or parallel.
a. The current is the same everywhere
throughout the entire circuit.
series
b. The total resistance is equal to the sum
of the individual resistances.
series
c. The voltage drop across each resistor in
the circuit is the same.
parallel
d. The voltage drop in the circuit is pro-
portional to the resistance.
series
e. Adding a resistor to the circuit decreases
the total resistance.
parallel
f. Adding a resistor to the circuit increases
the total resistance.
series
g. If the current through one resistor in the
circuit goes to zero, there is no current
in the entire circuit.
series
h. If the current through one resistor in the
circuit goes to zero, the current through
all other resistors remains the same.
parallel
i. This form is suitable for house wiring.
parallel
56. Household Fuses Why is it dangerous to
replace the 15-A fuse used to protect a
household circuit with a fuse that is rated at
30 A?
The 30-A fuse allows more current to
flow through the circuit, generating
more heat in the wires, which can be
dangerous.
Mastering Problems
23.1 Simple Circuits
pages 637–638
Level 1
57. Ammeter 1 in Figure 23-14 reads 0.20 A.
■Figure 23-14
a. What should ammeter 2 indicate?
0.20 A, because current is constant
in a series circuit.
b. What should ammeter 3 indicate?
0.20 A, because current is constant
in a series circuit.
V
22
15
A1
A2
A3
470 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Physics: Principles and Problems Solutions Manual 471
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
58. Calculate the equivalent resistance of these
series-connected resistors: 680 , 1.1 k,
and 10 k.
R680 1100 10,000
12 k
59. Calculate the equivalent resistance of these
parallel-connected resistors: 680 , 1.1 k,
and 10.2 k.
R
0.40 k
60. A series circuit has two voltage drops: 5.50 V
and 6.90 V. What is the supply voltage?
V5.50 V 6.90 V 12.4 V
61. A parallel circuit has two branch currents:
3.45 A and 1.00 A. What is the current in
the energy source?
I3.45 A 1.00 A 4.45 A
Level 2
62. Ammeter 1 in Figure 23-14 reads 0.20 A.
a. What is the total resistance of the circuit?
RR1R215 22 37
b. What is the battery voltage?
VIR (0.20 A)(37 ) 7.4 V
c. How much power is delivered to the
22-resistor?
P I2R(0.20 A)2(22 ) 0.88 W
d. How much power is supplied by the
battery?
PIV (0.20 A)(7.4 V) 1.5 W
63. Ammeter 2 in Figure 23-14 reads 0.50 A.
a. Find the voltage across the 22-resistor.
VIR (0.50 A)(22 ) 11 V
b. Find the voltage across the 15-resistor.
VIR (0.50 A)(15 ) 7.5 V
c. What is the battery voltage?
VV1V2(11 V) (7.5 V) 19 V
64. A 22-lamp and a 4.5-lamp are connect-
ed in series and placed across a potential dif-
ference of 45 V as shown in Figure 23-15.
■Figure 23-15
a. What is the equivalent resistance of the
circuit?
22 4.5 26
b. What is the current in the circuit?
I 1.7 A
c. What is the voltage drop across each
lamp?
VIR (1.7 A)(22 ) 37 V
VIR (1.7 A)(4.5 ) 7.7 V
d. What is the power dissipated in each
lamp?
PIV (1.7 A)(37 V) 63 W
PIV (1.7 A)(7.7 V) 13 W
65. Refer to Figure 23-16 to answer the follow-
ing questions.
■Figure 23-16
a. What should the ammeter read?
RR1R235 15
IV/R
(10.0 V)/(35 15 )
0.20 A
b. What should voltmeter 1 read?
VIR (0.20 A)(35 ) 7.0 V
A
35
15
10.0 V
V1
V2
45 V
27
V
R
22
4.5
45 V
1
0.68
1k
1.11k
10.2
1k
1
R3
1
R2
1
R1
1
R
Chapter 23 continued
c. What should voltmeter 2 read?
VIR (0.20 A)(15 ) 3.0 V
d. How much energy is supplied by the
battery per minute?
EPt
VIt
(10.0 V)(0.20 A)(1 min)(60 s/min)
120 J
66. For Figure 23-17, the voltmeter reads 70.0 V.
■Figure 23-17
a. Which resistor is the hottest?
50 . Since PI2Rand Iis con-
stant in a series circuit, the largest
value of resistance will produce the
most power.
b. Which resistor is the coolest?
15 . Since PI2Rand Iis con-
stant in a series circuit, the smallest
value of resistance will produce the
least power.
c. What will the ammeter read?
Use Ohm’s law: IV/R
(70.0 V)/(35 )
2.0 A
d. What is the power supplied by the
battery?
First, find the total resistance:
RR1R2R3
35 15 50
0.1 k
PI2R
(2.0 A)2(0.1 k)(1000 /k)
4102W
67. For Figure 23-18, the battery develops 110 V.
■Figure 23-18
a. Which resistor is the hottest?
10.0 . Since PV2/Rand Vis
constant in a parallel circuit, the
smallest resistor will dissipate the
most power.
b. Which resistor is the coolest?
50.0 . Since PV2/Rand Vis
constant in a parallel circuit, the
largest resistor will dissipate the
least power.
c. What will ammeter 1 read?
R
5.88
I 19A
d. What will ammeter 2 read?
I 5.5 A
e. What will ammeter 3 read?
I 2.2 A
f. What will ammeter 4 read?
I 11 A
68. For Figure 23-18, ammeter 3 reads 0.40 A.
a. What is the battery voltage?
VIR (0.40 A)(50.0 ) 2.0101V
1.1102V
10.0
V
R
1.1102V
50.0
V
R
1.1102V
20.0
V
R
1.1102V
5.88
V
R
1
20.1
0
50.1
0
10.1
0
1
R
1
1
R
1
2
R
1
3
1
R3
1
R2
1
R1
1
R
V
50.0 20.0 10.0
A4
A3
A2
A1
A
35
50
15
V
V
472 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued

Physics: Principles and Problems Solutions Manual 473
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What will ammeter 1 read?
Find the equivalent resistance:
R
5.88
I 3.4 A
c. What will ammeter 2 read?
I 1.0 A
d. What will ammeter 4 read?
I 2.0 A
69. What is the direction of the conventional cur-
rent in the 50.0-resistor in Figure 23-18?
down
70. The load across a battery consists of two
resistors, with values of 15 and 47 ,
connected in series.
a. What is the total resistance of the load?
RR1R215 47
62
b. What is the voltage of the battery if the
current in the circuit is 97 mA?
VIR (97 mA)(62 ) 6.0 V
71. Holiday Lights A string of 18 identical
holiday tree lights is connected in series to a
120-V source. The string dissipates 64 W.
a. What is the equivalent resistance of the
light string?
P
Req 2.3102
b. What is the resistance of a single light?
Ris the sum of the resistances of
18 lamps, so each resistance is
13
c. What power is dissipated by each light?
3.6 W
72. One of the lights in problem 71 burns out.
The light shorts out the bulb filament when
it burns out. This drops the resistance of the
lamp to zero.
a. What is the resistance of the light string
now?
There are now 17 lamps in series
instead of 18 lamps. The resistance
is
(2.3102) 2.2102
b. Find the power dissipated by the string.
P 65 W
c. Did the power increase or decrease
when the bulb burned out?
It increased.
73. A 16.0-and a 20.0-resistor are connect-
ed in parallel. A difference in potential of
40.0 V is applied to the combination.
a. Compute the equivalent resistance of
the parallel circuit.
R
8.89
b. What is the total current in the circuit?
I 4.50 A
c. What is the current in the 16.0-
resistor?
I1 2.50 A
40.0 V
16.0
V
R1
40.0 V
8.89
V
R
1
16.1
0
20.1
0
1
R
1
1
R
1
2
1
R2
1
R1
1
R
(120 V)2
2.2102
V2
R
17
18
64 W
18
2.3102
18
(120 V)2
64 W
V2
P
V2
Req
2.0101V
10.0
V
R
2.0101V
20.0
V
R
2.0101V
5.88
V
R
1
0.17
1
20.1
0
50.1
0
10.1
0
1
R
1
1
R
1
2
R
1
3
1
R3
1
R2
1
R1
1
R
Chapter 23 continued
74. Amy needs 5.0 V for an integrated-circuit
experiment. She uses a 6.0-V battery and
two resistors to make a voltage divider. One
resistor is 330 . She decides to make the
other resistor smaller. What value should it
have?
V2
R1R2
330 66
75. Pete is designing a voltage divider using a
12-V battery and a 82-resistor as RB.
What resistor should be used as RAif the
output voltage across RBis to be 4.0 V?
VB
RARB
RARB
82
1.6102
Level 3
76. Television A typical television dissipates
275 W when it is plugged into a 120-V
outlet.
a. Find the resistance of the television.
PIV and I, so P,or
R 52
b. The television and 2.5-wires connect-
ing the outlet to the fuse form a series cir-
cuit that works like a voltage divider. Find
the voltage drop across the television.
VA
110 V
c. A 12-hair dryer is plugged into the
same outlet. Find the equivalent resis-
tance of the two appliances.
R
9.8
d. Find the voltage drop across the televi-
sion and the hair dryer.
V1 96 V
23.2 Applications of Circuits
pages 638–639
Level 1
77. Refer to Figure 23-19 and assume that all
the resistors are 30.0 . Find the equivalent
resistance.
■Figure 23-19
The parallel combination of the two
30.0-resistors has an equivalent
resistance of 15.0 .
So R30.0 15.0 45.0
78. Refer to Figure 23-19 and assume that each
resistor dissipates 120 mW. Find the total
dissipation.
P3(120 mW) 360 mW
79. Refer to Figure 23-19 and assume that
IA13 mA and IB1.7 mA. Find IC.
ICIAIB
13 mA 1.7 mA
11 mA
IB
IA
IC
(120 V)(9.8 )
9.8 2.5
VRA
RARB
1
52
1
12
1
1
R
1
A
R
1
B
1
RB
1
RA
1
R
(120 V)(52 )
52 2.5
VRA
RARB
(120 V)2
275 W
V2
P
V2
R
V
R
(12 V)(82 )
4.0 V
VRB
VB
VRB
VB
VRB
RARB
(6.0 V)(330 )
5.0 V
VR2
V2
VR2
R1R2
474 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Physics: Principles and Problems Solutions Manual 475
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
80. Refer to Figure 23-19 and assume that
IB13 mA and IC1.7 mA. Find IA.
IAIBIC
13 mA 1.7 mA
15 mA
Level 2
81. Refer to Figure 23-20 to answer the follow-
ing questions.
■Figure 23-20
a. Determine the total resistance.
The 30.0-and 20.0-resistors are
in series.
R130.0 20.0 50.0
The 10.0-and 40.0-resistors are
in series.
R210.0 40.0 50.0
R1and R2are in parallel.
R
25.0 and is in series with the
25.0-resistor
RTotal 25.0 25.0 50.0
b. Determine the current through the 25-
resistor.
use Ohm’s law and RTotal
I0.50 A
c. Which resistor is the hottest? Coolest?
PI2R(0.50 A)2(25.0 ) 6.25 W
Half the total current is in each
parallel branch because the sum of
the resistances in each branch are
equal.
PI2R(0.25 A)2(30.0 ) 1.9 W
PI2R(0.25 A)2(20.0 ) 1.2 W
PI2R(0.25 A)2(10.0 ) 0.62 W
PI2R(0.25 A)2(40.0 ) 2.5 W
The 25.0-resistor is the hottest.
The 10.0-resistor is the coolest.
82. A circuit contains six 60-W lamps with a
resistance of 240-each and a 10.0-
heater connected in parallel. The voltage
across the circuit is 120 V. Find the current
in the circuit for the following situations.
a. Four lamps are turned on.
R0.060 k
I 2.0 A
b. All of the lamps are turned on.
R0.040 k
I 3.0 A
c. Six lamps and the heater are operating.
R8.0
I 15 A
120 V
8.0
V
R
4.0101
5
5
4.0101
1
10.0
1
0.040 k
1
R
120 V
0.040 k
V
R
240
6
6
240
1
R
120 V
0.060 k
V
R
240
4
4
240
1
240
1
240
1
240
1
240
1
R4
1
R3
1
R2
1
R1
1
R
25 V
50.0
V
RTotal
1
50.1
0
50.1
0
1
R
1
1
R
1
2
1
R2
1
R1
1
R
25 V
25.0 30.0 10.0
40.0
20.0
Chapter 23 continued
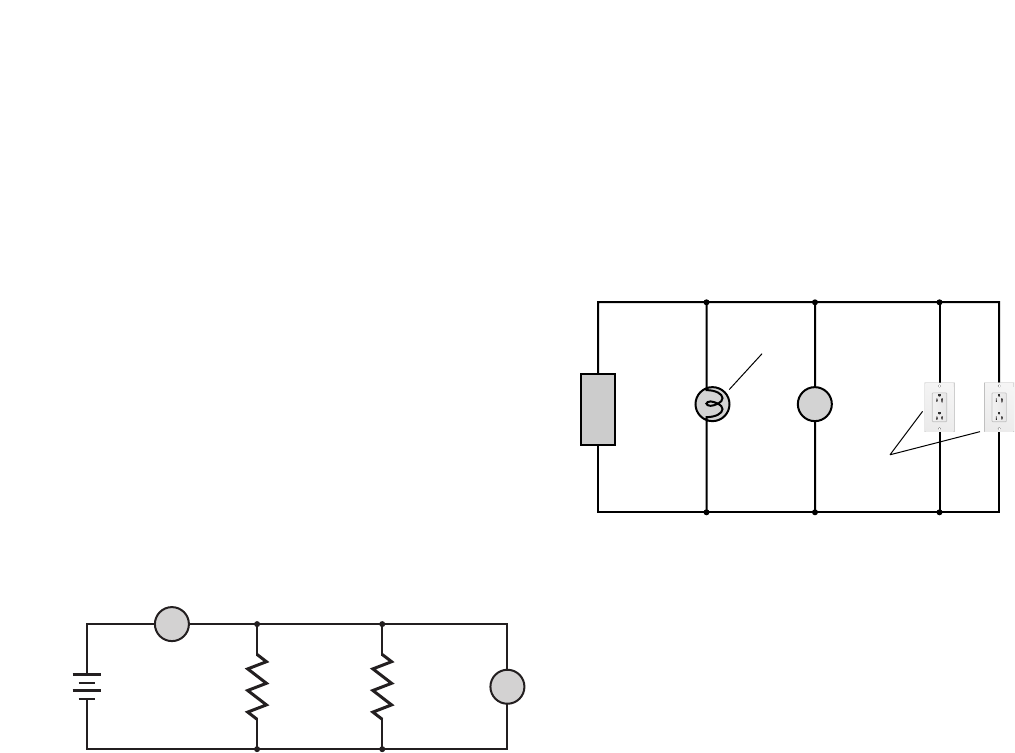
83. If the circuit in problem 82 has a 12-A fuse,
will the fuse melt if all the lamps and the
heater are on?
Yes. The 15-A current will melt the 12-A
fuse.
84. During a laboratory exercise, you are sup-
plied with a battery of potential difference
V, two heating elements of low resistance
that can be placed in water, an ammeter of
very small resistance, a voltmeter of extreme-
ly high resistance, wires of negligible resis-
tance, a beaker that is well insulated and has
negligible heat capacity, and 0.10 kg of water
at 25°C. By means of a diagram and stan-
dard symbols, show how these components
should be connected to heat the water as
rapidly as possible.
85. If the voltmeter used in problem 84 holds
steady at 45 V and the ammeter reading
holds steady at 5.0 A, estimate the time in
seconds required to completely vaporize the
water in the beaker. Use 4.2 kJ/kg°C as the
specific heat of water and 2.3106J/kg as
the heat of vaporization of water.
QmCT
(0.10 kg)(4.2 kJ/kg°C)(75°C)
32 kJ (energy needed to raise
temperature of water to 100°C)
QmHv(0.10 kg)(2.3106J/kg)
2.3102kJ (energy needed to
vaporize the water)
Qtotal 32 kJ 2.3102kJ
2.6102kJ (total energy need-
ed) Energy is provided at the
rate of
PIV (5.0 A)(45 V) 0.23 kJ/s.
The time required is
t1.1103s
86. Home Circuit A typical home circuit is
shown in Figure 23-21. The wires to the
kitchen lamp each have a resistance of
0.25 . The lamp has a resistance of
0.24 k. Although the circuit is parallel,
the lead lines are in series with each of
the components of the circuit.
■Figure 23-21
a. Compute the equivalent resistance of
the circuit consisting of just the lamp
and the lead lines to and from the
lamp.
R0.25 0.25 0.24 k
0.24 k
b. Find the current to the lamp.
I 0.50 A
c. Find the power dissipated in the lamp.
PIV (0.50 A)(120 V) 6.0101W
Mixed Review
page 639
Level 1
87. A series circuit has two voltage drops: 3.50
V and 4.90 V. What is the supply voltage?
V3.50 V 4.90 V 8.40 V
88. A parallel circuit has two branch currents:
1.45 A and 1.00 A. What is the current in
the energy source?
I1.45 A 1.00 A 2.45 A
89. A series-parallel circuit has three resistors,
dissipating 5.50 W, 6.90 W, and 1.05 W,
respectively. What is the supply power?
P5.50 W 6.90 W 1.05 W 13.45 W
120 V
0.24 k
V
R
0.25
0.25
Switch
box
120 V
Power
saw
Wall outlets
Kitchen
light 240
2.6102kJ
0.23 kJ/s
476 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
V
A
V
Heating
element
#1
Heating
element
#2

Physics: Principles and Problems Solutions Manual 477
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 2
90. Determine the maximum safe power in
each of three 150-, 5-W resistors
connected in series.
All will dissipate the same power.
P(3)(5 W) 15 W
91. Determine the maximum safe power in
each of three 92-, 5-W resistors connected
in parallel.
Each resistor will develop the same
power.
P(3)(5 W) 15 W
92. A voltage divider consists of two 47-k
resistors connected across a 12-V battery.
Determine the measured output for the
following.
a. an ideal voltmeter
VB
6.0 V
b. a voltmeter with a resistance of 85 k
The voltmeter resistance acts in
parallel:
RB3.0101k
VB
4.7 V
c. a voltmeter with a resistance of 10106
The voltmeter resistance acts in
parallel:
RB47 k
VB
6.0 V
The meter approaches the ideal
voltmeter.
Level 3
93. Determine the maximum safe voltage that
can be applied across the three series resistors
in Figure 23-22 if all three are rated at 5.0 W.
■Figure 23-22
Current is constant in a series circuit,
so the largest resistor will develop the
most power.
PI2R
I
0.151 A
The total resistance is now needed.
RTotal 92 150 220
462
Use Ohm’s law to find the voltage.
VIR
(0.151 A)(462 )
7.0101V
94. Determine the maximum safe total power
for the circuit in problem 93.
PV2/R11 W
(7.0101V)2
462
5.0 W
220
P
R
220 150 92
(12 V)(47 k)
47 k 47 k
VRB
RARB
1
2.1105
1
10106
1
47103
1
R2
1
R1
1
RB
(12 V)(3.0101k)
47 k 3.0101k
VRB
RARB
1
3.3105
1
85 k
1
47 k
1
R2
1
R1
1
RB
(12 V)(47 k)
47 k 47 k
VRB
RARB
Chapter 23 continued
95. Determine the maximum safe voltage that
can be applied across three parallel resistors
of 92 , 150 , and 220 , as shown in
Figure 23-23, if all three are rated at 5.0 W.
■Figure 23-23
The 92-resistor will develop the most
power because it will conduct the most
current.
P
VPR
(5.0 W
)(92
)
21 V
Thinking Critically
pages 639–640
96. Apply Mathematics Derive equations for
the resistance of two equal-value resistors in
parallel, three equal-value resistors in
parallel, and Nequal-value resistors in
parallel.
Req2
Req3
ReqN
97. Apply Concepts Three-way lamps, of the
type in Figure 23-24, having a rating of
50 W, 100 W, and 150 W, are common.
Draw four partial schematic diagrams that
show the lamp filaments and the switch
positions for each brightness level, as well as
the off position. (You do not need to show
the energy source.) Label each diagram.
■Figure 23-24
98. Apply Concepts Design a circuit that will
light one dozen 12-V bulbs, all to the cor-
rect (same) intensity, from a 48-V battery.
a. Design A requires that should one bulb
burn out, all other bulbs continue to
produce light.
48 V
R
N
R
3
3
R
1
R
1
R
1
R
1
Req3
R
2
2
R
1
R
1
R
1
Req2
V2
R
92
150
220
478 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Lower R
Higher R
150 W 50 W
100 W
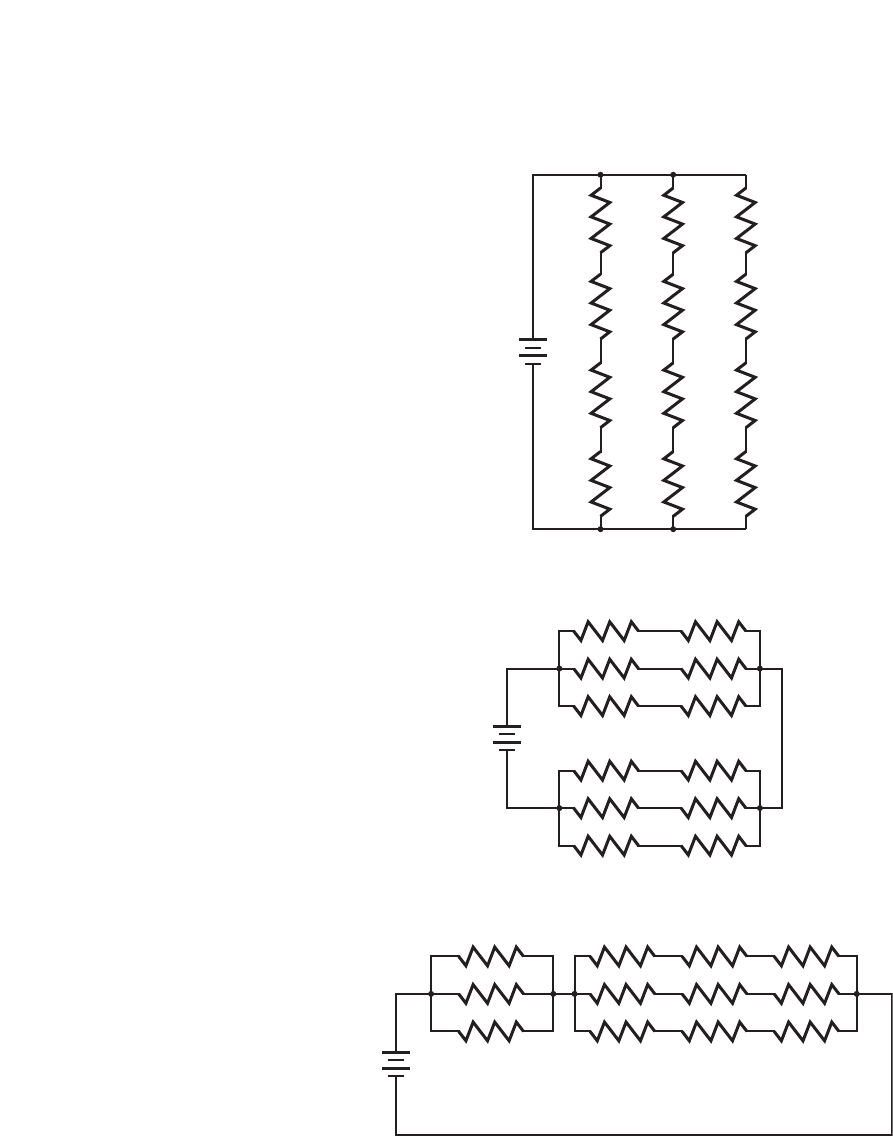
Physics: Principles and Problems Solutions Manual 479
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. Design B requires that should one bulb burn out, those bulbs that continue
working must produce the correct intensity.
c. Design C requires that should one bulb burn out, one other bulb also
will go out.
d. Design D requires that should one bulb burn out, either two others will go
out or no others will go out.
99. Apply Concepts A battery consists of an ideal source of potential difference in
series with a small resistance. The electric energy of the battery is produced by
chemical reactions that occur in the battery. However, these reactions also result in
a small resistance that, unfortunately, cannot be completely eliminated. A flash-
light contains two batteries in series, as shown in Figure 23-25. Each has a poten-
tial difference of 1.50 V and an internal resistance of 0.200 . The bulb has a
resistance of 22.0 .
48 V
48 V
48 V
Chapter 23 continued
■Figure 23-25
a. What is the current through the bulb?
The circuit has two 1.50-V batteries in
series with three resistors: 0.200 ,
0.200 , and 22.0 .The equivalent
resistance is 22.4 .The current is
I
0.134 A
b. How much power does the bulb
dissipate?
The power dissipated is
PI2R
(0.134 A)2(22.0 )
0.395 W
c. How much greater would the power be if
the batteries had no internal resistance?
PIV 0.409 W
P0.409 W 0.395 W 0.014 W
Power would be 0.014 W greater.
100. Apply Concepts An ohmmeter is made
by connecting a 6.0-V battery in series with
an adjustable resistor and an ideal amme-
ter. The ammeter deflects full-scale with a
current of 1.0 mA. The two leads are
touched together and the resistance is
adjusted so that 1.0 mA flows.
a. What is the resistance of the adjustable
resistor?
VIR
R 6.0 k
b. The leads are now connected to an
unknown resistance. What resistance
would produce a current of half-scale,
0.50 mA? Quarter-scale, 0.25 mA?
Three-quarters-scale, 0.75 mA?
R 12 k
and RTR1Re,so
ReRTR1
12 k6.0 k
6.0 k
R 24 k
and ReRTR1
24 k6.0 k
18 k
R 8.0 k
and ReRTR1
8.0 k6.0 k
2.0 k
c. Is the ohmmeter scale linear? Explain.
No. Zero ohms is at full-scale, 6 k
is at midscale, and infinite (or
open-circuit) is at zero-scale.
Writing in Physics
page 640
101. Research Gustav Kirchhoff and his laws.
Write a one-page summary of how they
apply to the three types of circuits
presented in this chapter.
Key ideas are:
(1) Kirchhoff’s Voltage Law (KVL) is
conservation of energy applied to
electric circuits.
(2) Kirchhoff’s Current Law (KCL) is
conservation of charge applied to
electric circuits.
(3) KVL states that the algebraic sum
of voltage drops around a closed
loop is zero. In a series circuit there
is one closed loop, and the sum of
voltage drops in the resistances
equals the source voltage. In a
6.0 V
0.75103 A
V
I
6.0 V
0.25103 A
V
I
6.0 V
0.50103 A
V
I
6.0 V
1.0103 A
V
I
(3.00 V)2
22.0
V2
R
2(1.50) V
(2(0.200 ) 22.0 )
V
R
Battery Battery
0.200 1.50 V 0.200 1.50 V
22.0
480 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued

Physics: Principles and Problems Solutions Manual 481
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
parallel circuit, there is a closed
loop for each branch, and KVL
implies that the voltage drop in
each branch is the same.
(4) KCL states that the algebraic sum
of currents at a node is zero. In a
series circuit, at every point the
current in equals current out; there-
fore, the current is the same every-
where. In a parallel circuit, there is
a common node at each end of the
branches. KCL implies that the sum
of the branch currents equals the
source current.
Cumulative Review
page 640
102. Airplane An airplane flying through still
air produces sound waves. The wave fronts
in front of the plane are spaced 0.50 m
apart and those behind the plane are
spaced 1.50 m apart. The speed of sound
is 340 m/s. (Chapter 15)
a. What would be the wavelength of the
sound waves if the airplane were not
moving?
1.00 m
b. What is the frequency of the sound
waves produced by the airplane?
fv/(340 m/s)/(1.00 m) 340 Hz
c. What is the speed of the airplane?
The airplane moves forward 0.50 m
for every 1.00 m that the sound
waves move, so its speed is one-
half the speed of sound, 170 m/s.
d. What is the frequency detected by an
observer located directly in front of the
airplane?
fv/
(340 m/s)/(0.50 m)
680 Hz, or
fdfs
(340 Hz)
680 Hz
e. What is the frequency detected by an
observer located directly behind the
airplane?
fv/
(340 m/s)/(1.50 m)
230 Hz, or
fdfs
(340 Hz)
230 Hz
103. An object is located 12.6 cm from a con-
vex mirror with a focal length of
18.0 cm. What is the location of the
object’s image? (Chapter 17)
di
7.41 cm
104. The speed of light in a special piece of
glass is 1.75108m/s. What is its index
of refraction? (Chapter 18)
n
1.71
105. Monocle An antireflective coating with an
index of refraction of 1.4 is applied
to a monocle with an index of refraction
of 1.52. If the thickness of the coating is
75 nm, what is/are the wavelength(s) of
light for which complete destructive
interference will occur? (Chapter 19)
Because nfilm nair, there is a phase
inversion on the first reflection.
Because nmonocle nfilm, there is a
phase inversion on the second
reflection.
For destructive interference:
2t m
nfilm
1
2
3.00108m/s
1.75108m/s
c
v
(12.6 cm)(18.0 cm)
12.6 cm (18.0 cm)
dof
dof
1
di
1
do
1
f
340 m/s 0
340 m/s (170 m/s)
vvd
v vs
340 m/s 0
340 m/s 170 m/s
vvd
v vs
Chapter 23 continued

m 1(2.1102 nm)
For m0
1(2.1102 nm)
4.2102nm
For m1
1(2.1102 nm)
2.8102nm
This is an ultraviolet wavelength, so it is not light. All other values of m
give wavelengths that are shorter than the light. So 4.2102nm is
the only wavelength of light for which destructive interference occurs.
106. Two charges of 2.0105C and 8.0106C experience a force between them
of 9.0 N. How far apart are the two charges? (Chapter 20)
FK, so d
Kq
F
Aq
B
0.40 m
107. A field strength, E, is measured a distance, d, from a point charge, Q. What
would happen to the magnitude of Ein the following situations? (Chapter 21)
E
a. dis tripled
b. Qis tripled
3E
c. both dand Qare tripled
d. the test charge qis tripled
E; by definition, field strength is force per unit test charge.
e. all three, d, Q, and q, are tripled
E
3
E
3
E
9
KQ
d2
(9.0109Nm2/C2)(2.0105C)(8.0106C)
9.0 N
qAqB
d2
3
2
1
2
1
2
(2)(75 nm)(1.4)
m
1
2
2tnfilm
m
1
2
482 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Physics: Principles and Problems Solutions Manual 483
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
108. The current flow in a 12-V circuit drops
from 0.55 A to 0.44 A. Calculate the
change in resistance. (Chapter 22)
R1V/I 12 V/0.55 A 21.8
R2V/I 12 V/0.44 A 27.3
RR2R1
5.5
Challenge Problem
page 628
When the galvanometer, a device used to mea-
sure very small currents or voltages, in this circuit
measures zero, the circuit is said to be balanced.
1. Your lab partner states that the only way to
balance this circuit is to make all the resis-
tors equal. Will this balance the circuit? Is
there more than one way to balance this cir-
cuit? Explain.
Yes; yes.You also can balance the cir-
cuit by adjusting the resistance values
so that R7/R3R4/R5remains equal.
2. Derive a general equation for a balanced
circuit using the given labels. Hint: Treat the
circuit as a voltage divider.
One definition of balance is that VAB
0. If this is so, then VR3 VR5. These
voltage drops can be defined using
Ohm’s law:
VR3 I1R3and VR5 I2R5
also, I1
and I2
substitute VR3
and VR5
VR3 VR5. Removing R3from the left
numerator and R5from the right
numerator gives the following:
3. Which of the resistors can be replaced with
a variable resistor and then used to balance
the circuit?
any resistor but R1
4. Which of the resistors can be replaced with
a variable resistor and then used as a sensi-
tivity control? Why would this be necessary?
How would it be used in practice?
R1. A galvanometer is a sensitive instru-
ment and can be damaged by too much
current flow. If R1is adjustable, it is set
for a high value before the circuit is
energized. This limits the current flow
through the galvanometer if the circuit
happens to be way out of balance. As
the balancing resistor is adjusted and
as the meter reading approaches zero,
the sensitivity then is increased by
decreasing R1.
R5
R4
R3
R2
1
R
R4
5
1
1
R
R2
3
1
V(I1I2)R1
R
R4
5
1
V(I1I2)R1
R
R2
3
1
R5V(I1I2)R1R5
R4R5
R3V(I1I2)R1R3
R2R3
V(I1I2)R1
R4R5
V(I1I2)R1
R2R3
12 V
0.55 A
12 V
0.44 A
Chapter 23 continued
R4
R5
A
VB
R2
R1
R3


Physics: Principles and Problems Solutions Manual 485
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
24 Magnetic Fields
CHAPTER
Practice Problems
24.1 Magnets: Permanent and
Temporary
pages 643–651
page 647
1. If you hold a bar magnet in each hand and
bring your hands close together, will the
force be attractive or repulsive if the mag-
nets are held in the following ways?
a. the two north poles are brought close
together
repulsive
b. a north pole and a south pole are
brought together
attractive
2. Figure 24-7 shows five disk magnets float-
ing above each other. The north pole of the
top-most disk faces up. Which poles are on
the top side of each of the other magnets?
■Figure 24-7
south, north, south, north
3. A magnet attracts a nail, which, in turn, attracts
many small tacks, as shown in Figure 24-3 on
page 645. If the north pole of the permanent
magnet is the left end, as shown, which end
of the nail is the south pole?
the bottom (the point)
4. Why do magnetic compasses sometimes
give false readings?
because Earth’s magnetic field is dis-
torted by objects made of iron, nickel, or
cobalt in the vicinity of the compass, and
by ore deposits of these same metals
page 650
5. A long, straight, current-carrying wire runs
from north to south.
a. A compass needle placed above the wire
points with its north pole toward the
east. In what direction is the current
flowing?
from south to north
b. If a compass is put underneath the wire,
in which direction will the compass
needle point?
west
6. How does the strength of a magnetic field,
1 cm from a current-carrying wire, compare
with each of the following?
a. the strength of the field that is 2 cm
from the wire
Because magnetic field strength
varies inversely with the distance
from the wire, the magnetic field at
1 cm will be twice as strong as the
magnetic field at 2 cm.
b. the strength of the field that is 3 cm
from the wire
Because magnetic field strength
varies inversely with the distance
from the wire, the magnetic field at
1 cm will be three times as strong as
the magnetic field at 3 cm.

7. A student makes a magnet by winding wire
around a nail and connecting it to a battery,
as shown in Figure 24-13. Which end of
the nail, the pointed end or the head, will
be the north pole?
■Figure 24-13
the pointed end
8. You have a spool of wire, a glass rod, an
iron rod, and an aluminum rod. Which rod
should you use to make an electromagnet
to pick up steel objects? Explain.
Use the iron rod. Iron would be attracted
to a permanent magnet and take on prop-
erties of a magnet, whereas aluminum or
glass would not.This effect would sup-
port the magnetic field in the wire coil and
thus make the strongest electromagnet.
9. The electromagnet in problem 8 works well,
but you decide that you would like to make its
strength adjustable by using a potentiometer
as a variable resistor. Is this possible? Explain.
Yes. Connect the potentiometer in
series with the power supply and the
coil. Adjusting the potentiometer for
more resistance will decrease the cur-
rent flow and the strength of the field.
Section Review
24.1 Magnets: Permanent and
Temporary
pages 643–651
page 651
10. Magnetic Fields Is a magnetic field real, or
is it just a means of scientific modeling?
Field lines are not real. The field is real.
11. Magnetic Forces Identify some magnetic
forces around you. How could you demon-
strate the effects of those forces?
Student answers may vary. Answers
could include magnets on a refrigerator
and Earth’s magnetic field. The effects
of these forces can be demonstrated by
bringing another magnet, or a material
that can be magnetized, nearby.
12. Magnetic Fields A current-carrying wire is
passed through a card on which iron filings
are sprinkled. The filings show the magnetic
field around the wire. A second wire is close
to and parallel to the first wire. There is an
identical current in the second wire. If the
two currents are in the same direction, how
will the first magnetic field be affected?
How will it be affected if the two currents
are in opposite directions?
It would be approximately twice as
large; it would be approximately zero.
13. Direction of a Magnetic Field Describe
the right-hand rule used to determine the
direction of a magnetic field around a
straight, current-carrying wire.
If you grasp the wire with your right hand,
with your thumb pointing in the direction
of the conventional current, your fingers
curl in the direction of the field.
14. Electromagnets A glass sheet is placed
over an active electromagnet, and iron fil-
ings sprinkled on the sheet create a pattern
on it. If this experiment is repeated with the
polarity of the power supply reversed, what
observable differences will result? Explain.
None. The filings would show the same
field pattern but a compass would show
the magnetic polarity reversal.
15. Critical Thinking Imagine a toy contain-
ing two parallel, horizontal metal rods, one
above the other. The top rod is free to move
up and down.
a. The top rod floats above the lower one. If
the top rod’s direction is reversed, however,
it falls down onto the lower rod. Explain
why the rods could behave in this way.
The metal rods could be magnets
with their axes parallel. If the top
486 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued

Physics: Principles and Problems Solutions Manual 487
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
magnet is positioned so that its
north and south poles are above the
north and south poles of the bottom
magnet, it will be repelled and float
above. If the top magnet is turned
end for end, it will be attracted to the
bottom magnet.
b. Assume that the top rod was lost and
replaced with another one. In this case,
the top rod falls on top of the bottom
rod no matter what its orientation is.
What type of replacement rod must
have been used?
If an ordinary iron bar is used on
top, it will be attracted to the bottom
magnet in any orientation.
Practice Problems
24.2 Forces Caused by
Magnetic Fields
pages 652–659
page 654
16. What is the name of the rule used to predict
the direction of force on a current-carrying
wire at right angles to a magnetic field?
Identify what must be known to use this rule.
Third right-hand rule. The direction of
the current and the direction of the field
must be known.
17. A wire that is 0.50 m long and carrying a
current of 8.0 A is at right angles to a 0.40-T
magnetic field. How strong is the force that
acts on the wire?
FBIL (0.40 N/Am)(8.0 A)(0.50 m)
1.6 N
18. A wire that is 75 cm long, carrying a current
of 6.0 A, is at right angles to a uniform
magnetic field. The magnitude of the force
acting on the wire is 0.60 N. What is the
strength of the magnetic field?
FBIL
B
IF
L
(6.0 0
A
.)
6
(0
0.N
75 m)
0.13 T
19. A 40.0-cm-long copper wire carries a cur-
rent of 6.0 A and weighs 0.35 N. A certain
magnetic field is strong enough to balance
the force of gravity on the wire. What is the
strength of the magnetic field?
FBIL, where Fweight of the wire
B
(6.0 A
0)
.(
3
0
5
.4
N
00 m)
0.15 T
20. How much current will be required to pro-
duce a force of 0.38 N on a 10.0 cm length
of wire at right angles to a 0.49-T field?
FBIL
I
B
F
L
7.8 A
page 658
21. In what direction does the thumb point when
using the third right-hand rule for an electron
moving at right angles to a magnetic field?
opposite to the direction of the electron
motion
22. An electron passes through a magnetic field
at right angles to the field at a velocity of
4.0106m/s. The strength of the magnetic
field is 0.50 T. What is the magnitude of the
force acting on the electron?
FBqv
(0.50 T)(1.601019 C)(4.0106m/s)
3.21013 N
23. A stream of doubly ionized particles (miss-
ing two electrons, and thus, carrying a net
charge of two elementary charges) moves at
a velocity of 3.0104m/s perpendicular to
a magnetic field of 9.0102T. What is the
magnitude of the force acting on each ion?
FBqv
(9.0102T)(2)(1.601019 C)
(3.0104m/s)
8.61016 N
24. Triply ionized particles in a beam carry a
net positive charge of three elementary
charge units. The beam enters a magnetic
field of 4.0102T. The particles have a
speed of 9.0106m/s. What is the magni-
tude of the force acting on each particle?
0.38 N
(0.49 T)(0.100 m)
F
IL
Chapter 24 continued

FBqv
(4.0102T)(3)(1.601019 C)
(9.0106m/s)
1.71013 N
25. Doubly ionized helium atoms (alpha parti-
cles) are traveling at right angles to a mag-
netic field at a speed of 4.0104m/s. The
field strength is 5.0102T. What force
acts on each particle?
FBqv
(5.0102T)(2)(1.601019 C)
(4.0104m/s)
6.41016 N
Section Review
24.2 Forces Caused by
Magnetic Fields
pages 652–659
page 659
26. Magnetic Forces Imagine that a current-
carrying wire is perpendicular to Earth’s
magnetic field and runs east-west. If the cur-
rent is east, in which direction is the force
on the wire?
up, away from the surface of Earth
27. Deflection A beam of electrons in a
cathode-ray tube approaches the deflecting
magnets. The north pole is at the top of the
tube; the south pole is on the bottom. If you
are looking at the tube from the direction of
the phosphor screen, in which direction are
the electrons deflected?
to the left side of the screen
28. Galvanometers Compare the diagram of a
galvanometer in Figure 24-18 on page 655
with the electric motor in Figure 24-20 on
page 656. How is the galvanometer similar
to an electric motor? How are they different?
Both the galvanometer and the electric
motor use a loop of wire positioned
between the poles of a permanent mag-
net. When a current passes through the
loop, the magnetic field of the perma-
nent magnet exerts a force on the loop.
The loop in a galvanometer cannot
rotate more than 180°.The loop in an
electric motor rotates through many
360° turns. The motor’s split-ring com-
mutator allows the current in the loop to
reverse as the loop becomes vertical in
the magnetic field, enabling the loop to
spin in the magnetic field.The gal-
vanometer measures unknown currents;
the electric motor has many uses.
29. Motors When the plane of the coil in a
motor is perpendicular to the magnetic
field, the forces do not exert a torque on the
coil. Does this mean that the coil does not
rotate? Explain.
Not necessarily; if the coil is already in
rotation, then rotational inertia will carry
it past the point of zero torque. It is the
coil’s acceleration that is zero, not the
velocity.
30. Resistance A galvanometer requires 180 A
for full-scale deflection. What is the total
resistance of the meter and the multiplier
resistor for a 5.0-V full-scale deflection?
R 28 k
31. Critical Thinking How do you know that
the forces on parallel current-carrying wires
are a result of magnetic attraction between
wires, and not a result of electrostatics?
Hint: Consider what the charges are like when
the force is attractive. Then consider what the
forces are when three wires carry currents in the
same direction.
If the currents are in the same direction,
the force is attractive. If it were due to
electrostatic forces, the like charges
would make the force repulsive. Three
wires would all attract each other, which
could never happen if the forces were
due to electrostatic charges.
50 V
180 A
V
I
488 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued
Chapter Assessment
Concept Mapping
page 664
32. Complete the following concept map using
the following: right-hand rule, F qvB, and
FILB.
Mastering Concepts
page 664
33. State the rule for magnetic attraction and
repulsion. (24.1)
Like poles repel one another; opposite
poles attract.
34. Describe how a temporary magnet differs
from a permanent magnet. (24.1)
A temporary magnet is like a magnet
only while under the influence of
another magnet. A permanent magnet
needs no outside influence.
35. Name the three most important common
magnetic elements. (24.1)
iron, cobalt, and nickel
36. Draw a small bar magnet and show the
magnetic field lines as they appear around
the magnet. Use arrows to show the direc-
tion of the field lines. (24.1)
37. Draw the magnetic field between two like
magnetic poles and then between two
unlike magnetic poles. Show the directions
of the fields. (24.1)
38. If you broke a magnet in two, would you
have isolated north and south poles?
Explain. (24.1)
No, new poles would form on each of
the broken ends.
39. Describe how to use the first right-hand rule
to determine the direction of a magnetic field
around a straight current-carrying wire. (24.1)
Grasp the wire with the right hand,
keeping thumb pointing in the direction
of the conventional current through the
wire. Fingers will encircle the wire and
point in the direction of the field.
40. If a current-carrying wire is bent into a
loop, why is the magnetic field inside the
loop stronger than the magnetic field out-
side? (24.1)
The magnetic field lines are concentrat-
ed inside the loop.
41. Describe how to use the second right-hand
rule to determine the polarity of an electro-
magnet. (24.1)
NN
NS
NS
Chapter 24 continued
exerted on a
has a
has a has a
given by given by given by
current-carrying
wire moving charge
direction
Force
resulting from
a magnetic field
magnitude magnitude
Physics: Principles and Problems Solutions Manual 489
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
FILB right-hand
rule FqvB

Grasp the coil with the right hand, keep-
ing the fingers encircling the coil in the
direction of the conventional current
flow through the loops.The thumb of
the right hand will point toward the
north pole of the electromagnet.
42. Each electron in a piece of iron is like a tiny
magnet. The iron, however, may not be a
magnet. Explain. (24.1)
The electrons are not all oriented and
moving in the same direction; their
magnetic fields have random directions.
43. Why will dropping or heating a magnet
weaken it? (24.1)
The domains are jostled out of alignment.
44. Describe how to use the third right-hand
rule to determine the direction of force on a
current-carrying wire placed in a magnetic
field. (24.2)
Point the fingers of your right hand in
the direction of the magnetic field. Point
your thumb in the direction of the con-
ventional current in the wire. The palm
of your hand then faces in the direction
of the force on the wire.
45. A strong current suddenly is switched on in a
wire. No force acts on the wire, however. Can
you conclude that there is no magnetic field
at the location of the wire? Explain. (24.2)
No, if a field is parallel to the wire, no
force would result.
46. What kind of meter is created when a shunt
is added to a galvanometer? (24.2)
an ammeter
Applying Concepts
pages 664–665
47. A small bar magnet is hidden in a fixed
position inside a tennis ball. Describe an
experiment that you could do to find the
location of the north pole and the south
pole of the magnet.
Use a compass.The north pole of the
compass needle is attracted to the south
pole of the magnet and vice versa.
48. A piece of metal is attracted to one pole of a
large magnet. Describe how you could tell
whether the metal is a temporary magnet or
a permanent magnet.
Move it to the other pole. If the same
end is attracted, it is a temporary
magnet; if the same end is repelled and
the other end is attracted, it is a perma-
nent magnet.
49. Is the magnetic force that Earth exerts on a
compass needle less than, equal to, or
greater than the force that the compass
needle exerts on Earth? Explain.
The forces are equal according to
Newton’s third law.
50. Compass Suppose you are lost in the
woods but have a compass with you.
Unfortunately, the red paint marking the
north pole of the compass needle has worn
off. You have a flashlight with a battery and
a length of wire. How could you identify
the north pole of the compass?
Connect the wire to the battery so that the
current is away from you in one section.
Hold the compass directly above and
close to that section of the wire. By the
right-hand rule, the end of the compass
needle that points right is the north pole.
51. A magnet can attract a piece of iron that is
not a permanent magnet. A charged rubber
rod can attract an uncharged insulator.
Describe the different microscopic processes
producing these similar phenomena.
The magnet causes the domains in the
iron to point in the same direction.The
charged rod separates the positive and
negative charges in the insulator.
52. A current-carrying wire runs across a labora-
tory bench. Describe at least two ways in
which you could find the direction of the
current.
490 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued
Physics: Principles and Problems Solutions Manual 491
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Use a compass to find the direction of
the magnetic field. Bring up a strong
magnet and find the direction of the force
on the wire, then use the right-hand rule.
53. In which direction, in relation to a magnetic
field, would you run a current-carrying wire
so that the force on it, resulting from the
field, is minimized, or even made to be zero?
Run the wire parallel to the magnetic field.
54. Two wires carry equal currents and run par-
allel to each other.
a. If the two currents are in opposite direc-
tions, where will the magnetic field
from the two wires be larger than the
field from either wire alone?
The magnetic field will be larger any-
where between the two wires.
b. Where will the magnetic field from both
be exactly twice as large as from one wire?
The magnetic field will be twice as
large along a line directly between
the wires that is equal in distance
from each wire.
c. If the two currents are in the same direc-
tion, where will the magnetic field be
exactly zero?
The magnetic field will be zero along
a line directly between the wires that
is equal in distance from each wire.
55. How is the range of a voltmeter changed
when the resistor’s resistance is increased?
The range of the voltmeter increases.
56. A magnetic field can exert a force on a
charged particle. Can the field change the
particle’s kinetic energy? Explain.
No, the force is always perpendicular
to the velocity. No work is done. The
energy is not changed.
57. A beam of protons is moving from the
back to the front of a room. It is deflected
upward by a magnetic field. What is the
direction of the field causing the deflection?
Facing the front of the room, the
velocity is forward, the force is upward,
and therefore, using the third right-hand
rule, B is to the left.
58. Earth’s magnetic field lines are shown in
Figure 24-23. At what location, poles or
equator, is the magnetic field strength
greatest? Explain.
■Figure 24-23
Earth’s magnetic field strength is
greatest at the poles. The field lines are
closer together at the poles.
Mastering Problems
24.1 Magnets: Permanent and Temporary
pages 665–666
Level 1
59. As the magnet below in Figure 24-24
moves toward the suspended magnet, what
will the magnet suspended by the string do?
■Figure 24-24
Move to the left or begin to turn. Like
poles repel.
60. As the magnet in Figure 24-25 moves
toward the suspended magnet, what will the
magnet that is suspended by the string do?
NN SS
Magnetic pole
Magnetic pole
North pole
South pole
N
S
Chapter 24 continued
■Figure 24-25
Move to the right. Unlike poles attract.
61. Refer to Figure 24-26 to answer the follow-
ing questions.
■Figure 24-26
a. Where are the poles?
4 and 2, by definition
b. Where is the north pole?
2, by definition and field direction
c. Where is the south pole?
4, by definition and field direction
62. Figure 24-27 shows the response of a compass
in two different positions near a magnet.
Where is the south pole of the magnet located?
■Figure 24-27
At the right end, unlike poles attract.
63. A wire that is 1.50 m long and carrying a
current of 10.0 A is at right angles to a uni-
form magnetic field. The force acting on the
wire is 0.60 N. What is the strength of the
magnetic field?
FILB
B
IF
L
(10.00
A
.6
)(
0
1N
.50 m)
0.040 N/Am
0.040 T
64. A conventional current flows through a
wire, as shown in Figure 24-28. Copy the
wire segment and sketch the magnetic field
that the current generates.
■Figure 24-28
65. The current is coming straight out of the
page in Figure 24-29. Copy the figure and
sketch the magnetic field that the current
generates.
■Figure 24-29
66. Figure 24-30 shows the end view of an elec-
tromagnet with current flowing through it.
■Figure 24-30
I
I
I
1
3
42
NS
NS
492 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued
Physics: Principles and Problems Solutions Manual 493
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. What is the direction of the magnetic
field inside the loops?
down into the page
b. What is the direction of the magnetic
field outside the loops?
up (out of the page)
Level 2
67. Ceramic Magnets The repulsive force
between two ceramic magnets was measured
and found to depend on distance, as given in
Table 24-1.
a. Plot the force as a function of distance.
b. Does this force follow an inverse square
law?
No.
24.2 Forces Caused by Magnetic Fields
pages 666–667
Level 1
68. The arrangement shown in Figure 24-31 is
used to convert a galvanometer to what
type of device?
■Figure 24-31
Ammeter, much of the current flows
through the resistor and allows the
measurement of higher currents.
69. What is the resistor shown in Figure 24-31
called?
Shunt; by definition shunt is another
word for parallel.
70. The arrangement shown in Figure 24-32 is
used to convert a galvanometer to what
type of device?
■Figure 24-32
Voltmeter; the added resistance
decreases the current for any given
voltage.
71. What is the resistor shown in Figure 24-32
called?
Multiplier; by definition since it multi-
plies the voltage range of the meter
72. A current-carrying wire is placed between the
poles of a magnet, as shown in Figure 24-33.
What is the direction of the force on the wire?
G
G
2.62.21.0 1.4 1.8 3.0
0.0
1.0
2.0
3.0
4.0
F (N)
d (cm)
Table 24-1
Separation, d(cm) Force, F(N)
1.0 3.93
1.2 0.40
1.4 0.13
1.6 0.057
1.8 0.030
2.0 0.018
2.2 0.011
2.4 0.0076
2.6 0.0053
2.8 0.0038
3.0 0.0028
Chapter 24 continued

■Figure 24-33
73. A wire that is 0.50 m long and carrying a
current of 8.0 A is at right angles to a uni-
form magnetic field. The force on the wire
is 0.40 N. What is the strength of the mag-
netic field?
FILB
B
IF
L
0.10 T
74. The current through a wire that is 0.80 m
long is 5.0 A. The wire is perpendicular to a
0.60-T magnetic field. What is the magni-
tude of the force on the wire?
FILB (5.0 A)(0.80 m)(0.60 N/Am)
2.4 N
75. A wire that is 25 cm long is at right angles
to a 0.30-T uniform magnetic field. The cur-
rent through the wire is 6.0 A. What is the
magnitude of the force on the wire?
FILB (6.0 A)(0.25 m)(0.30 N/Am)
0.45 N
76. A wire that is 35 cm long is parallel to a
0.53-T uniform magnetic field. The current
through the wire is 4.5 A. What force acts
on the wire?
If the wire is parallel to the field, no
cutting is taking place, so no force is
produced.
77. A wire that is 625 m long is perpendicular
to a 0.40-T magnetic field. A 1.8-N force acts
on the wire. What current is in the wire?
FILB
I
B
F
L
(0.401
T
.8
)(6
N
25 m)
0.0072 A
7.2 mA
78. The force on a 0.80-m wire that is perpen-
dicular to Earth’s magnetic field is 0.12 N.
What is the current in the wire? Use
5.0105T for Earth’s magnetic field.
FILB
I
B
F
L
3.0103A
3.0 kA
79. The force acting on a wire that is at right
angles to a 0.80-T magnetic field is 3.6 N.
The current in the wire is 7.5 A. How long
is the wire?
FILB
L
B
FI
0.60 m
Level 2
80. A power line carries a 225-A current from
east to west, parallel to the surface of Earth.
a. What is the magnitude of the force
resulting from Earth’s magnetic field
acting on each meter of the wire? Use
BEarth 5.0105T.
FILB
F
L
IB (225 A)(5.0105T)
0.011 N/m
b. What is the direction of the force?
The force would be downward.
c. In your judgment, would this force be
important in designing towers to hold
this power line? Explain.
No; the force is much smaller than
the weight of the wires.
3.6 N
(0.80 T)(7.5 A)
0.12 N
(5.0105T)(0.80 m)
0.40 N
(8.0 A)(0.50 m)
I
N
S
N
S
F
I
N
S
N
S
494 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued

Physics: Principles and Problems Solutions Manual 495
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
81. Galvanometer A galvanometer deflects
full-scale for a 50.0-A current.
a. What must be the total resistance of the
series resistor and the galvanometer to
make a voltmeter with 10.0-V full-scale
deflection?
VIR
R
V
I
2.00105
2.00102k
b. If the galvanometer has a resistance of
1.0 k, what should be the resistance of
the series (multiplier) resistor?
Total resistance 2.00102k,so
the series resistor is 2.00102k
1.0 k199 k.
82. The galvanometer in problem 81 is used to
make an ammeter that deflects full-scale for
10 mA.
a. What is the potential difference across the
galvanometer (1.0 kresistance) when a
current of 50 A passes through it?
VIR (50106A)(1.0103)
0.05 V
b. What is the equivalent resistance of par-
allel resistors having the potential differ-
ence calculated in a circuit with a total
current of 10 mA?
VIR
R
V
I
5
c. What resistor should be placed parallel
with the galvanometer to make the
resistance calculated in part b?
so
51
1.0
1
103
so R15
83. A beam of electrons moves at right angles to
a magnetic field of 6.0102T. The electrons
have a velocity of 2.5106m/s. What is the
magnitude of the force on each electron?
FBqv
(6.0102T)(1.61019 C)
(2.5106m/s)
2.41014 N
84. Subatomic Particle A muon (a particle
with the same charge as an electron) is
traveling at 4.21107m/s at right angles
to a magnetic field. The muon experiences
a force of 5.001012 N.
a. How strong is the magnetic field?
FqvB
B
q
F
v
0.742 T
b. What acceleration does the muon expe-
rience if its mass is 1.881028 kg?
Fma
a
2.661016 m/s2
85. A singly ionized particle experiences a force
of 4.11013 N when it travels at right
angles through a 0.61-T magnetic field.
What is the velocity of the particle?
FqvB
v
4.2106m/s
86. A room contains a strong, uniform magnetic
field. A loop of fine wire in the room has
current flowing through it. Assume that you
rotate the loop until there is no tendency for
it to rotate as a result of the field. What is the
direction of the magnetic field relative to the
plane of the coil?
The magnetic field is perpendicular to
the plane of the coil. The right-hand rule
would be used to find the direction of
the field produced by the coil. The field
in the room is in the same direction.
4.11013 N
(0.61 T)(1.601019 C)
F
Bq
5.001012 N
1.881028 kg
F
m
5.001012 N
(1.601019 C)(4.21107m/s)
1
R2
1
R
1
R1
1
R2
1
R1
1
R
5102V
0.01 A
10.0 V
50.0106A
Chapter 24 continued

87. A force of 5.781016 N acts on an
unknown particle traveling at a 90° angle
through a magnetic field. If the velocity of
the particle is 5.65104m/s and the field is
3.20102T, how many elementary
charges does the particle carry?
FqvB
q
3.201019 C
N(3.201019 C)
2 charges
Mixed Review
pages 667–668
Level 2
88. A copper wire of insignificant resistance
is placed in the center of an air gap
between two magnetic poles, as shown
in Figure 24-34. The field is confined
to the gap and has a strength of 1.9 T.
■Figure 24-34
a. Determine the force on the wire (direc-
tion and magnitude) when the switch is
open.
0 N. With no current, there is no mag-
netic field produced by the wire and
copper is not a magnetic material.
b. Determine the force on the wire (direc-
tion and magnitude) when the switch is
closed.
Up, 0.62 N.The direction of the force
is given by the third right-hand rule.
I
FILB
0.62 N
c. Determine the force on the wire (direc-
tion and magnitude) when the switch is
closed and the battery is reversed.
Down, 0.62 N. The direction of the
force is given by the third right-hand
rule and the magnitude of the force
is the same as in part b.
d. Determine the force on the wire (direc-
tion and magnitude) when the switch is
closed and the wire is replaced with a dif-
ferent piece having a resistance of 5.5 .
Up, 0.31 N.The direction of the force
is given by the third right-hand rule.
I
FILB
0.31 N
89. Two galvanometers are available. One has
50.0-A full-scale sensitivity and the other
has 500.0-A full-scale sensitivity. Both
have the same coil resistance of 855 . Your
challenge is to convert them to measure a
current of 100.0 mA, full-scale.
a. Determine the shunt resistor for the
50.0-A meter.
Find the voltage across the meter
coil at full scale.
VIR (50.0 A)(855 ) 0.0428 V
Calculate the shunt resistor.
R
0.428
b. Determine the shunt resistor for the
500.0-A meter.
Find the voltage across the meter
coil at full scale.
VIR (500.0 A)(855 ) 0.428 V
0.0428 V
100.0 mA 50.0 A
V
I
(24 V)(0.075 m)(1.9 T)
5.5 5.5
VLB
R
V
R
(24 V)(0.075 m)(1.9 T)
5.5
VLB
R
V
R
7.5 cm 5.5 Ω
24 V
N
S
1 charge
1.601019 C
5.781016 N
(3.20102T)(5.65104m/s)
F
Bv
496 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued

Physics: Principles and Problems Solutions Manual 497
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Calculate the shunt resistor.
R
4.30
c. Determine which of the two is better for
actual use. Explain.
The 50.0-A meter is better. Its
much lower shunt resistance will do
less to alter the total resistance of
the circuit being measured. An ideal
ammeter has a resistance of 0 .
90. Subatomic Particle A beta particle (high-
speed electron) is traveling at right angles to
a 0.60-T magnetic field. It has a speed of
2.5107m/s. What size force acts on the
particle?
FBqv
(0.60 T)(1.61019 C)(2.5107m/s)
2.41012 N
91. The mass of an electron is 9.111031 kg.
What is the magnitude of the acceleration of
the beta particle described in problem 90?
Fma
a
2.61018 m/s2
92. A magnetic field of 16 T acts in a direction
due west. An electron is traveling due south
at 8.1105m/s. What are the magnitude
and the direction of the force acting on the
electron?
FBqv
(16 T)(1.61019 C)(8.1105m/s)
2.11012 N, upward (right-hand
rule—remembering that electron flow is
opposite to current flow)
93. Loudspeaker The magnetic field in a loud-
speaker is 0.15 T. The wire consists of 250
turns wound on a 2.5-cm-diameter cylindri-
cal form. The resistance of the wire is 8.0 .
Find the force exerted on the wire when
15 V is placed across the wire.
I
L(# of turns)(circumference) nd
FBIL
F
BVR
nd
5.5 N
94. A wire carrying 15 A of current has a length
of 25 cm in a magnetic field of 0.85 T. The
force on a current-carrying wire in a uni-
form magnetic field can be found using the
equation FILB sin . Find the force on
the wire when it makes the following angles
with the magnetic field lines of
a. 90°
FILB sin
(15 A)(0.25 m)(0.85 T)(sin 90°)
3.2 N
b. 45°
FILB sin
(15 A)(0.25 m)(0.85 T)(sin 45°)
2.3 N
c. 0°
sin 0°0
so F0 N
95. An electron is accelerated from rest through
a potential difference of 20,000 V, which
exists between plates P1and P2, shown in
Figure 24-35. The electron then passes
through a small opening into a magnetic
field of uniform field strength, B. As indi-
cated, the magnetic field is directed into
the page.
■Figure 24-35
a. State the direction of the electric field
between the plates as either P1to P2or
P2to P1.
from P2to P1
XXXXXXX
XXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
P1P2
Electron
XX
(0.15 T)(15 V)(250)()(0.025 m)
8.0
V
R
2.41012 N
9.111031 kg
F
m
0.428 V
100.0 mA 500.0 A
V
I
Chapter 24 continued

b. In terms of the information given, cal-
culate the electron’s speed at plate P2.
KE qV(1.61019 C)
(20,000 J/C)
3.21015 J
KE mv2
v
8107m/s
c. Describe the motion of the electron
through the magnetic field.
clockwise
Thinking Critically
page 668
96. Apply Concepts A current is sent through
a vertical spring, as shown in Figure 24-36.
The end of the spring is in a cup filled with
mercury. What will happen? Why?
■Figure 24-36
When the current passes through the
coil, the magnetic field increases and
forces cause the spring to compress.
The wire comes out of the mercury,
the circuit opens, the magnetic field
decreases, and the spring drops down.
The spring will oscillate up and down.
97. Apply Concepts The magnetic field pro-
duced by a long, current-carrying wire is
represented by B(2107Tm/A)(I/d),
where Bis the field strength in teslas, Iis
the current in amps, and dis the distance
from the wire in meters. Use this equation
to estimate some magnetic fields that you
encounter in everyday life.
a. The wiring in your home seldom carries
more than 10 A. How does the magnetic
field that is 0.5 m from such a wire
compare to Earth’s magnetic field?
I10 A, d0.5 m, so
B
4106T
Earth’s field is 5105T, so Earth’s
field is about 12 times stronger than
that of the wire.
b. High-voltage power transmission lines
often carry 200 A at voltages as high as
765 kV. Estimate the magnetic field on
the ground under such a line, assuming
that it is about 20 m high. How does
this field compare with a magnetic field
in your home?
I200 A, d20 m, so
B
2106T
This is half as strong as the field in
part a.
c. Some consumer groups have recommend-
ed that pregnant women not use electric
blankets in case the magnetic fields cause
health problems. Estimate the distance
that a fetus might be from such a wire,
clearly stating your assumptions. If such a
blanket carries 1 A, find the magnetic field
at the location of the fetus. Compare this
with Earth’s magnetic field.
Assume only one wire runs over
“the fetus, and use the center of the
fetus (where the vital organs are) as
a reference point. At an early stage,
the fetus might be 5 cm from the
blanket. At later stages, the center
of the fetus may be 10 cm away.
I1 A, d0.05 m, so
B
(2107
dTm/A)I
(2107Tm/A)(1 A)
0.05 m
(2107Tm/A)(200 A)
20 m
(2107Tm/A)I
d
(2107Tm/A)(10 A)
0.5 m
(2107Tm/A)I
d
Mercury
Spring
(2)(3.21015 J)
9.111031 kg
2KE
m
1
2
498 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued

4106T
Earth’s magnetic field of 5105T is
about 12 times stronger.
98. Add Vectors In almost all cases described
in problem 97, a second wire carries the
same current in the opposite direction. Find
the net magnetic field that is a distance of
0.10 m from each wire carrying 10 A. The
wires are 0.01 m apart. Make a scale draw-
ing of the situation. Calculate the magni-
tude of the field from each wire and use a
right-hand rule to draw vectors showing the
directions of the fields. Finally, find the vec-
tor sum of the two fields. State its magni-
tude and direction.
From each wire I10 A, d0.10 m, so
B2105T
From the diagram, only the components
parallel to the line from the center of
the wires contribute to the net field
strength. The component from each
wire is B1Bsin , where sin
0
0
.0
.1
0
0
5m
m
0.05, so B1(2105T)
(0.05) 1106T. But, each wire con-
tributes the same amount, so the total
field is 2106T, about 1/25 Earth’s field.
Writing In Physics
page 668
99. Research superconducting magnets and write
a one-page summary of proposed future uses
for such magnets. Be sure to describe any
hurdles that stand in the way of the practical
application of these magnets.
Student answers may vary. Super-
conducting magnets currently are used
in magnetic resonance imaging (MRI), a
medical technology. They are being test-
ed for use in magnetically levitated high-
speed trains, and it is hoped that super-
conducting magnets will help to make
nuclear fusion energy practical. A draw-
back of superconducting magnets is that
they require extremely low temperatures
(near absolute zero). Scientists are try-
ing to develop materials that are super-
conductive at higher temperatures.
Cumulative Review
page 668
100. How much work is required to move a
charge of 6.40103C through a poten-
tial difference of 2500 V? (Chapter 21)
WqV (6.40103C)(2500 V) 16 J
101. The current flow in a 120-V circuit increas-
es from 1.3 A to 2.3 A. Calculate the
change in power. (Chapter 22)
PIV
P1I1V,P2I2V
PP2P1I2VI1V
V(I2I1)
(120 V)(2.3 A 1.3 A)
120 W
102. Determine the total resistance of three,
55-resistors connected in parallel and
then series-connected to two 55-resistors
connected in series. (Chapter 23)
55
1
55
1
55
1
Rparallel 18
Requiv Rparallel RR
18 55 55
128
3
55
1
R
1
R
1
R
1
Rparallel
(2107Tm/A)(10 A)
0.10 m
0.10 m
0.10 m Wire A
Iout
Iin
Wire B
0.005 m
B
A
B
B
B1
B1
0.005 m
Chapter 24 continued
Physics: Principles and Problems Solutions Manual 499
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Challenge Problem
page 656
The figure shows two identical motors with a
common shaft. For simplicity, the commutators
are not shown. Each armature coil consists of
48 turns of wire with rectangular dimensions of
17 cm wide by 35 cm deep. The armature
resistance is 12 . The red wire travels to the left
(along half the width) and then back to the rear
of the motor (along the depth). The magnetic
field is 0.21 T. The diameter of the pulley is
7.2 cm. A rope fixed to the pulley and the floor
prevents the motor shaft from turning.
1. Given FILB, derive an equation for the
torque on the armature for the position
shown.
Torque is defined as the product of the
force and the lever arm. In the case of
the motor armature position shown, the
lever arm is equal to half of the width of
the armature coil (the shaft is the center
of rotation and is at the midpoint of the
coil width). The length of the wire acted
upon by the field is equal to the depth
of the coil. This length is effectively
increased by n, the number of turns in
the coil. Finally, the torque is doubled
because as one side is pushed up by
the magnetic field, the other side is
pushed down according to the third
right-hand rule.
2nBI(depth)(width/2)
Simplifying and replacing (depth)(width)
with area, A, gives:
nBIA
The torque produced by the motor
armature, in the position shown, is
equal to the number of turns times the
field strength times the armature cur-
rent times the area of the armature coil.
2. With S1closed and S2open, determine the
torque on the shaft and the force on the
spring scale.
nBIA
(48)(0.21 T)
1
1
2
2
0
V
(0.35 m)(0.17 m)
6.0 Nm
Because the shaft cannot turn, the sys-
tem is in equilibrium and the force on
the spring scale is found by consider-
ing half the pulley diameter:
Fspring scale
0
6.
.0
03
N
6m
m
170 N
3. With both switches closed, determine the
torque on the shaft and the force on the
spring scale.
Both motors produce counterclockwise
torque:
1(48)(0.21 T)
1
1
2
2
0
V
(0.35 m)(0.17 m)
6.0 Nm
2(48)(0.21 T)
1
32
5
V
(0.35 m)(0.17 m)
1.7 Nm
net 7.7 Nm counterclockwise
Fspring scale
0
7.
.0
73
N
6m
m
210 N
4. What happens to torque if the armature is
in a different position?
The torque is reduced when there is
any rotation from the position shown
because the lever arm is reduced. With
90°rotation, the force on the armature
will be up and down (canceling) with
the effective lever arm equal to zero.
With the shown position as 0°:
nBIA cos
S1
120 V
S2
35 V
Shaft
Pulley
Spring
scale
N
S
N
S
500 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 24 continued

Physics: Principles and Problems Solutions Manual 501
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
25 Electromagnetic Induction
CHAPTER
Practice Problems
25.1 Electric Current from
Changing Magnetic Fields
pages 671–678
page 675
1. A straight wire, 0.5 m long, is moved
straight up at a speed of 20 m/s through
a 0.4-T magnetic field pointed in the
horizontal direction.
a. What EMF is induced in the wire?
EMF BLv
(0.4 T)(0.5 m)(20 m/s)
4 V
b. The wire is part of a circuit of total
resistance of 6.0 . What is the current
in the circuit?
I
EM
RF
64
.0V
0.7 A
2. A straight wire, 25 m long, is mounted on
an airplane flying at 125 m/s. The wire
moves in a perpendicular direction through
Earth’s magnetic field (B5.0105T).
What EMF is induced in the wire?
EMF BLv
(5.0105T)(25 m)(125 m/s)
0.16 V
3. A straight wire, 30.0 m long, moves at
2.0 m/s in a perpendicular direction
through a 1.0-T magnetic field.
a. What EMF is induced in the wire?
EMF BLv
(1.0 T)(30.0 m)(2.0 m/s)
6.0101V
b. The total resistance of the circuit of
which the wire is a part is 15.0 . What
is the current?
I
EM
RF
4.0 A
4. A permanent horseshoe magnet is mounted
so that the magnetic field lines are vertical. If
a student passes a straight wire between the
poles and pulls it toward herself, the current
flow through the wire is from right to left.
Which is the north pole of the magnet?
Using the right-hand rule, the north
pole is at the bottom.
page 678
5. A generator develops a maximum voltage
of 170 V.
a. What is the effective voltage?
Veff (0.707)Vmax (0.707)(170 V)
1.2102V
b. A 60-W lightbulb is placed across
the generator with an Imax of 0.70 A.
What is the effective current through
the bulb?
Ieff (0.707)Imax (0.707)(0.70 A)
0.49 A
c. What is the resistance of the lightbulb
when it is working?
R
V
Ie
e
f
f
f
f
V
Im
m
a
a
x
x
0
1.7
70
0V
A
2.4102
6. The RMS voltage of an AC household outlet
is 117 V. What is the maximum voltage
across a lamp connected to the outlet? If
the RMS current through the lamp is 5.5 A,
what is the maximum current in the lamp?
Vmax
0
V
.7
e
0
ff7
165 V
Imax
0.
I
7
ef
0
f7
7.8 A
7. An AC generator delivers a peak voltage of
425 V.
5.5 A
0.707
117 V
0.707
V
ma
2
x
I
ma
2
x
6.0101V
1.50

a. What is the Veff in a circuit placed
across the generator?
Veff 3.01102V
b. The resistance is 5.0102. What is the
effective current?
Ieff 0.60 A
8. If the average power dissipated by an electric
light is 75 W, what is the peak power?
P
1
2
Pmax
Pmax (2)P (2)(75 W) 1.5102W
Section Review
25.1 Electric Current from
Changing Magnetic Fields
pages 671–678
page 678
9. Generator Could you make a generator by
mounting permanent magnets on a rotating
shaft and keeping the coil stationary?
Explain.
Yes, only relative motion between the
coil and the magnetic field is important.
10. Bike Generator A bike generator lights the
headlamp. What is the source of the energy
for the bulb when the rider travels along a
flat road?
the stored chemical energy of the bike
rider
11. Microphone Consider the microphone
shown in Figure 25-3. When the diaphragm
is pushed in, what is the direction of the
current in the coil?
clockwise from the left
12. Frequency What changes to the generator
are required to increase the frequency?
increase the number of magnetic pole
pairs
13. Output Voltage Explain why the output
voltage of an electric generator increases
when the magnetic field is made stronger.
What else is affected by strengthening the
magnetic field?
The magnitude of the induced voltage is
directly related to the strength of the
magnetic field. A greater voltage is
induced in the conductor(s) if the field
strength is increased. The current and
the power in the generator circuit also
were affected.
14. Generator Explain the fundamental
operating principle of an electric generator.
Michael Faraday discovered that a volt-
age is induced in a length of electric wire
moving in a magnetic field.The induced
voltage may be increased by using a
stronger magnetic field, increasing the
velocity of the conductor, or increasing
the effective length of the conductor.
15. Critical Thinking A student asks, “Why
does AC dissipate any power? The energy
going into the lamp when the current is
positive is removed when the current is
negative. The net is zero.” Explain why this
reasoning is wrong.
Power is the rate at which energy is
transferred. Power is the product of
Iand V. When Iis positive, so is Vand
therefore, Pis positive. When Iis nega-
tive, so is V; thus, Pis positive again.
Energy is always transferred in the lamp.
Practice Problems
25.2 Changing Magnetic
Fields Induce EMF
pages 679–685
page 684
For the following problems, effective currents and
voltages are indicated.
16. A step-down transformer has 7500 turns
on its primary coil and 125 turns on its
secondary coil. The voltage across the pri-
mary circuit is 7.2 kV. What voltage is being
applied across the secondary circuit? If the
current in the secondary circuit is 36 A,
3.01102V
5.0102
Veff
R
425 V
2
Vmax
2
502 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 503
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
what is the current in the primary circuit?
V
V
p
s
N
N
p
s
Vs
V
N
pN
p
s
1.2102V
VpIp VsIs
Ip
V
V
s
p
Is
0.60 A
17. A step-up transformer has 300 turns on
its primary coil and 90,000 turns on its
secondary coil. The EMF of the generator
to which the primary circuit is attached is
60.0 V. What is the EMF in the secondary
circuit? The current in the secondary circuit is
0.50 A. What current is in the primary circuit?
Vs
V
N
pN
p
s
(60.0 V
3
)
0
(9
0
0,000)
1.80104V
Ip
V
V
s
p
Is
1.5102A
Section Review
25.2 Changing Magnetic
Fields Induce EMF
pages 679–685
page 685
18. Coiled Wire and Magnets You hang a coil
of wire with its ends joined so that it can
swing easily. If you now plunge a magnet
into the coil, the coil will swing. Which way
will it swing relative to the magnet and
why?
Away from the magnet. The changing
magnetic field induces a current in the
coil, producing a magnetic field.This
field opposes the field of the magnet,
and thus, the force between coil and
magnet is repulsive.
19. Motors If you unplugged a running vacu-
um cleaner from a wall outlet, you would
be much more likely to see a spark than
you would be if you unplugged a lighted
lamp from the wall. Why?
The inductance of the motor creates a
back-EMF that causes the spark.The
bulb has very low self-inductance, so
there is no back-EMF.
20. Transformers and Current Explain why a
transformer may only be operated on alter-
nating current.
In order to magnetically link the
primary and secondary coils, a varying
current must flow in the primary coil.
This changing current sets up a mag-
netic field that builds, expanding out-
wards, and collapses as the current
flow direction changes.
21. Transformers Frequently, transformer coils
that have only a few turns are made of very
thick (low-resistance) wire, while those with
many turns are made of thin wire. Why?
More current flows through the coil with
fewer turns, so the resistance must be
kept low to prevent voltage drops and
I2Rpower loss and heating.
22. Step-Up Transformers Refer to the step-up
transformer shown in Figure 25-13. Explain
what will happen to the primary current if
the secondary coil is short-circuited.
According to the transformer equations,
the ratio of primary to secondary cur-
rent is equal to the ratio of turns and
doesn’t change. Thus, if the secondary
current increases, so does the primary.
23. Critical Thinking Would permanent mag-
nets make good transformer cores? Explain.
No, the induced voltage depends on
a changing magnetic field through
the core. Permanent magnets are
“permanent” because they are made of
materials that resist such changes in
magnetic fields.
(1.80104V)(0.50 A)
60.0 V
(1.2102V)(36 A)
7.2103V
(7.2103V)(125)
7500
Chapter 25 continued
Chapter Assessment
Concept Mapping
page 690
24. Complete the following concept map using
the following terms: generator, back-EMF,
Lenz’s law.
Mastering Concepts
page 690
25. What is the armature of an electric
generator? (25.1)
The armature of an electric generator
consists of a number of wire loops
wound around an iron core and placed
in a strong magnetic field. As it rotates
in the magnetic field, the loops cut
through magnetic field lines and an
electric current is induced.
26. Why is iron used in an armature? (25.1)
Iron is used in an armature to increase
the strength of the magnetic field.
For problems 27–29, refer to Figure 25-16.
27. A single conductor moves through a mag-
netic field and generates a voltage. In what
direction should the wire be moved, relative
to the magnetic field to generate the mini-
mum voltage? (25.1)
The minimum amount of voltage (0 V), is
generated when the conductor is moving
parallel to the magnetic lines of force.
28. What is the polarity of the voltage induced
in the wire when it passes the south pole of
the magnetic field? (25.1)
A conductor moving by a south mag-
netic pole will have a positive induced
voltage.
29. What is the effect of increasing the net con-
ductor length in an electric generator? (25.1)
Increasing the conductor length results
in a net increase in induced voltage.
■ Figure 25-16
30. How were Oersted’s and Faraday’s results
similar? How were they different? (25.1)
They are similar in that they each show a
relationship between electricity and mag-
netism.They are different in that a steady
electric current produces a magnetic
field, but a change in magnetic field is
needed to produce an electric current.
31. You have a coil of wire and a bar magnet.
Describe how you could use them to gener-
ate an electric current. (25.1)
Either move the magnet into or out of
the coil, or move the coil up and down
over the end of the magnet.
32. What does EMF stand for? Why is the name
inaccurate? (25.1)
Electromotive force; it is not a force but
an electric potential (energy per unit of
charge).
33. What is the difference between a generator
and a motor? (25.1)
Bout of page
Wire
Lenz’s law
generator motor
EMF back-EMF
Michael
Faraday
504 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 505
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
In a generator, mechanical energy turns
an armature in a magnetic field.The
induced voltage produces current, thus
producing electric energy. In a motor,
voltage is placed across an armature coil
in a magnetic field.The voltage produces
current in the coil and the armature
turns, producing mechanical energy.
34. List the major parts of an AC generator. (25.1)
An AC generator consists of a perma-
nent magnet, an armature, a set of
brushes, and a slip ring.
35. Why is the effective value of an AC current
less than its maximum value? (25.1)
In an alternating-current generator, as
the armature turns, the generated
power varies between some maximum
value and zero. The average power is
equal to one-half the maximum power.
The effective current is the constant
value of current that would cause the
average power to be dissipated in the
load, R.
Pavg
1
2
Pmax
1
2
Imax2RIeff2R
Ieff
I
ma
2
x
Imax
36. Hydroelectricity Water trapped behind a
dam turns turbines that rotate generators.
List all the forms of energy that take part in
the cycle that includes the stored water and
the electricity produced. (25.1)
There is potential energy in the stored
water, kinetic energy in the falling water
and turning turbine, and electric energy
in the generator. In addition, there are
frictional losses in the turbine and gen-
erator resulting in thermal energy.
37. State Lenz’s law. (25.2)
An induced current always acts in such a
direction that its magnetic field opposes
the change by which the current is
induced.
38. What causes back-EMF in an electric motor?
(25.2)
This is Lenz’s law. Once the motor starts
turning, it behaves as a generator and
will generate current in opposition to the
current being put into the motor.
39. Why is there no spark when you close a
switch and put current through an inductor,
but there is a spark when you open the
switch? (25.2)
The spark is from the back-EMF that
tries to keep the current flowing.The
back-EMF is large because the current
has dropped quickly to zero. When clos-
ing the switch, the current increase isn’t
so fast because of the resistance in the
wires.
40. Why is the self-inductance of a coil a major
factor when the coil is in an AC circuit but a
minor factor when the coil is in a DC circuit?
(25.2)
An alternating current is always chang-
ing in the magnitude and direction.
Therefore, self-induction is a constant
factor. A direct current eventually
becomes steady, and thus, after a short
time, there is no changing magnetic field.
41. Explain why the word change appears so
often in this chapter. (25.2)
As Faraday discovered, only a changing
magnetic field induces EMF.
42. Upon what does the ratio of the EMF in the
primary circuit of a transformer to the EMF
in the secondary circuit of the transformer
depend? (25.2)
The ratio of number of turns of wire in
the primary coil to the number of turns
of wire in the secondary coil determines
the EMF ratio.
Applying Concepts
pages 690–692
43. Use unit substitution to show that the units
of BLv are volts.
The unit of BLv is (T)(m)(m/s).
T N/Am and A C/s.
So, BLv (Ns/Cm)(m)(m/s) Nm/C
Chapter 25 continued
Because J Nm and V J/C, the unit of
BLv is V (volts).
44. When a wire is moved through a magnetic
field, does the resistance of the closed
circuit affect current only, EMF only, both,
or neither?
current only
45. Biking As Logan slows his bike, what
happens to the EMF produced by his bike’s
generator? Use the term armature in your
explanation.
As Logan slows his bike, the rotation of
the armature in the magnetic field of the
generator slows, and the EMF is reduced.
46. The direction of AC voltage changes
120 times each second. Does this mean that
a device connected to an AC voltage alter-
nately delivers and accepts energy?
No; the signs of the current and voltage
reverse at the same time, and, therefore,
the product of the current and the volt-
age is always positive.
47. A wire is moved horizontally between the
poles of a magnet, as shown in Figure 25-17.
What is the direction of the induced current?
■ Figure 25-17
No current is induced because the
direction of the velocity is parallel to
the magnetic field.
48. You make an electromagnet by winding
wire around a large nail, as shown in
Figure 25-18. If you connect the magnet to
a battery, is the current larger just after you
make the connection or several tenths of a
second after the connection is made? Or, is
it always the same? Explain.
■ Figure 25-18
It is larger several tenths of a second
after the connection is made. The back-
EMF opposes current just after the con-
nection is made.
49. A segment of a wire loop is moving
downward through the poles of a magnet,
as shown in Figure 25-19. What is the
direction of the induced current?
■ Figure 25-19
The current direction is out-of-page to
the left along the path of the wire.
50. A transformer is connected to a battery
through a switch. The secondary circuit con-
tains a lightbulb, as shown in Figure 25-20.
Will the lamp be lighted as long as the switch
is closed, only at the moment the switch is
closed, or only at the moment the switch
is opened? Explain.
■ Figure 25-20
The bulb will light because there is a
current in the secondary circuit.This
will happen whenever the primary cur-
rent changes, so the bulb will glow
either when the switch is closed or
when it is opened.
Primary Secondary
v
N
S
N
S
N
S
N
S
506 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 507
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
51. Earth’s Magnetic Field The direction of
Earth’s magnetic field in the northern hemi-
sphere is downward and to the north as
shown in Figure 25-21. If an east-west wire
moves from north to south, in which direc-
tion is the current?
■ Figure 25-21
The current is from west to east.
52. You move a length of copper wire down
through a magnetic field, B, as shown in
Figure 25-19.
a. Will the induced current move to the
right or left in the wire segment in the
diagram?
The right-hand rule will show the
current moving left.
b. As soon as the wire is moved in the
field, a current appears in it. Thus, the
wire segment is a current-carrying wire
located in a magnetic field. A force must
act on the wire. What will be the direc-
tion of the force acting on the wire as a
result of the induced current?
The force will act in an upward
direction.
53. A physics instructor drops a magnet
through a copper pipe, as illustrated in
Figure 25-22. The magnet falls very slowly,
and the students in the class conclude that
there must be some force opposing gravity.
■ Figure 25-22
a. What is the direction of the current
induced in the pipe by the falling magnet
if the south pole is toward the bottom?
Induced EMF is perpendicular to both
the field and velocity, so the current
must be circumferential. Field lines
move in toward the south pole and
out from the north pole. By the right-
hand rule, current is clockwise near
the south pole and counterclockwise
near the north pole.
b. The induced current produces a magnetic
field. What is the direction of the field?
Near the south pole, the field inside
the pipe is down; near the north pole,
it is up.
c. How does this field reduce the
acceleration of the falling magnet?
Induced field exerts an upward force
on both poles.
54. Generators Why is a generator more diffi-
cult to rotate when it is connected to a cir-
cuit and supplying current than it is when it
is standing alone?
When the armature of a generator is
rotated, a force that opposes the direc-
tion of rotation is produced as a result
of induced current (Lenz’s law). When
standing alone, however, no current is
generated and consequently no oppos-
ing force is produced.
55. Explain why the initial start-up current is so
high in an electric motor. Also explain how
Lenz’s law applies at the instant t0.
If the armature (conductors) are not
rotating, no lines of force are being cut,
and no voltage is induced. Therefore,
the back-EMF is zero. Since there is no
current in the armature, no magnetic
field is formed around the stationary
conductor. It should be noted that this
explanation only holds true at the
instant of startup, at time just greater
than 0. The instant the armature begins
to rotate, it will be cutting the lines of
force and will have an induced voltage.
This voltage, the back-EMF, will have a
N
S
North magnetic pole
South magnetic pole
North pole
South pole
N
S
Chapter 25 continued

polarity such that it produces a magnetic
field opposing the field that created it.
This reduces the current in the motor.
Therefore, the motion of the motor
increases its apparent resistance.
56. Using Figure 25-10 in conjunction with
Lenz’s law, explain why all practical trans-
former cores incorporate a laminated core.
A laminated core is constructed from
thin sheets of steel, separated by a very
thin coating of varnish (insulation).
Eddy currents are greatly reduced
because of this insulation. Current in
the core is caused by the changing
magnetic flux within the core. The eddy
currents exist due to the induced volt-
age within the magnetic core.
57. A practical transformer is constructed with a
laminated core that is not a superconductor.
Because the eddy currents cannot be com-
pletely eliminated, there is always a small
core loss. This results, in part, in a net loss
of power within the transformer. What fun-
damental law makes it impossible to bring
this loss to zero?
Lenz’s law
58. Explain the process of mutual induction
within a transformer.
An AC current applied to the primary coil
of a transformer, results in a changing
current flow through the coil winding.
This current, in turn, generates a magnet-
ic flux, alternately building and collapsing
as the direction of current changes.This
strong magnetic field radiates outward in
all directions from the primary coil.When
the magnetic field reaches the stationary
secondary coil on the other side of the
core, a voltage is induced within that coil.
The voltage or EMF induced depends
upon the rate at which the magnetic field
alternates (supply frequency), number of
turns on the coil, and the strength of the
magnetic flux. Since the magnetic flux
is responsible for inducing a voltage in
the secondary coil, we say that it is
magnetically linked.
59. Shawn drops a magnet, north pole down,
through a vertical copper pipe.
a. What is the direction of the induced
current in the copper pipe as the bot-
tom of the magnet passes?
clockwise around the pipe, as
viewed from above
b. The induced current produces a magnet-
ic field. What is the direction of the
induced magnetic field?
down the pipe, at the location of the
south pole of the magnet (or oppo-
site the magnet’s field)
Mastering Problems
25.1 Electric Current from Changing
Magnetic Fields
pages 692–693
Level 1
60. A wire, 20.0-m long, moves at 4.0 m/s per-
pendicularly through a magnetic field. An
EMF of 40 V is induced in the wire. What is
the strength of the magnetic field?
EMF BLv
B
E
L
M
vF
0.5 T
61. Airplanes An airplane traveling at
9.50102km/h passes over a region where
Earth’s magnetic field is 4.5105T and
is nearly vertical. What voltage is induced
between the plane’s wing tips, which are
75 m apart?
EMF BLv
(4.5105T)(75 m)
(9.50102km/h)(1000 m/km)
(1 h/3600 s)
0.89 V
62. A straight wire, 0.75-m long, moves upward
through a horizontal 0.30-T magnetic field,
as shown in Figure 25-23, at a speed of
16 m/s.
a. What EMF is induced in the wire?
EMF BLv
40 V
(20.0 m)(4.0 m/s)
508 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 509
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(0.30 T)(0.75 m)(16 m/s)
3.6 V
b. The wire is part of a circuit with a total
resistance of 11 Ω. What is the current?
EMF IR
I
EM
RF
0.33 A
■Figure 25-23
63. At what speed would a 0.20-m length of
wire have to move across a 2.5-T magnetic
field to induce an EMF of 10 V?
EMF BLv
v
E
B
M
L
F
(2.5 T
1
)0
(0
V
.20 m)
20 m/s
64. An AC generator develops a maximum EMF
of 565 V. What effective EMF does the
generator deliver to an external circuit?
Veff
V
ma
2
x
4.00102V
65. An AC generator develops a maximum
voltage of 150 V. It delivers a maximum
current of 30.0 A to an external circuit.
a. What is the effective voltage of the
generator?
Veff (0.707)Vmax (0.707)(150 V)
110 V
b. What effective current does the generator
deliver to the external circuit?
Ieff (0.707)Imax (0.707)(30.0 V)
21.2 A
c. What is the effective power dissipated in
the circuit?
Peff IeffVeff
I
ma
2
x
V
ma
2
x
1
2
ImaxVmax
1
2
(150 V)(30.0 A)
2.3 kW
66. Electric Stove An electric stove is connected
to an AC source with an effective voltage of
240 V.
a. Find the maximum voltage across one of
the stove’s elements when it is operating.
Veff (0.707)Vmax
Vmax
0
V
.7
e
0
ff7
2
04
.7
0
0V
7
340 V
b. The resistance of the operating element
is 11 . What is the effective current?
Veff IeffR
Ieff 22 A
67. You wish to generate an EMF of 4.5 V by
moving a wire at 4.0 m/s through a 0.050-T
magnetic field. How long must the wire be,
and what should be the angle between the
field and direction of motion to use the
shortest wire?
EMF BLv
L
23 m
This is the shortest length of wire assum-
ing that the wire and the direction of
motion are each perpendicular to the field.
Level 2
68. A 40.0-cm wire is moved perpendicularly
through a magnetic field of 0.32 T with a
velocity of 1.3 m/s. If this wire is connected
into a circuit of 10.0-resistance, what is
the current?
EMF BLv
(0.32 T)(0.400 m)(1.3 m/s)
0.17 V
I
EM
RF
1
00
.1
.0
7
V
17 mA
69. You connect both ends of a copper wire with
a total resistance of 0.10 to the terminals of
a galvanometer. The galvanometer has a resis-
tance of 875 . You then move a 10.0-cm
segment of the wire upward at 1.0 m/s
through a 2.0102-T magnetic field. What
current will the galvanometer indicate?
4.5 V
(0.050 T)(4.0 m/s)
EMF
Bv
240 V
11
Veff
R
565 V
2
N
S
N
S
v
3.6 V
11
Chapter 25 continued
EMF BLv
(2.0102T)(0.100 m)(1.0 m/s)
2.0103V
I
R
V
2.08
7
1
5
0
3V
2.3106A
2.3 A
70. The direction of a 0.045-T magnetic field is
60.0º above the horizontal. A wire, 2.5-m
long, moves horizontally at 2.4 m/s.
a. What is the vertical component of the
magnetic field?
The vertical component of magnetic
field is
Bsin 60.0° (0.045 T)(sin 60.0°)
0.039 T
b. What EMF is induced in the wire?
EMF BLv
(0.039 T)(2.5 m)(2.4 m/s)
0.23 V
71. Dams A generator at a dam can supply
375 MW (375106W) of electrical power.
Assume that the turbine and generator are
85 percent efficient.
a. Find the rate at which falling water
must supply energy to the turbine.
eff
P
P
o
in
ut
100
Pin Pout
1
e
0
f0
f
375 MW
1
8
0
5
0
440 MW input
b. The energy of the water comes from a
change in potential energy, PE mgh.
What is the change in PE needed each
second?
440 MW 440 MJ/s
4.4108J each second
c. If the water falls 22 m, what is the mass
of the water that must pass through the
turbine each second to supply this
power?
PE mgh
m
P
gE
h
2.0106kg
72. A conductor rotating in a magnetic field has
a length of 20 cm. If the magnetic-flux den-
sity is 4.0 T, determine the induced voltage
when the conductor is moving perpendicu-
lar to the line of force. Assume that the
conductor travels at a constant velocity of
1 m/s.
When the conductor is moving perpen-
dicular to the line of force
Eind BLv
(4.0 T)(0.20 m)(1 m/s)
0.8 V
73. Refer to Example Problem 1 and
Figure 25-24 to determine the following.
■ Figure 25-24
a. induced voltage in the conductor
EMFind BLv
(7.0102T)(0.50 m)
(3.6 m/s)
0.13 V
b. current (I)
I
EM
R
Find
0.13 A
c. direction of flux rotation around the
conductor
Flux rotates clockwise around the
conductor when viewed from above.
d. polarity of point A relative to point B
Point A is negative relative to point B.
0.13 V
1.0
B 7.0102 T
A
EMF
A
v 3.6 m/s
R 1.0
L 0.50 m
Bout of page
4.4108J
(9.80 m/s2)(22 m)
510 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 511
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
25.2 Changing Magnetic Fields Induce EMF
page 693
Level 1
74. The primary coil of a transformer has
150 turns. It is connected to a 120-V source.
Calculate the number of turns on the
secondary coil needed to supply the follow-
ing voltages.
a. 625 V
V
V
p
s
N
N
p
s
Ns
V
V
p
s
Np
6
12
25
0V
V
(150)
781 turns, which rounds to 780
b. 35 V
Ns
V
V
p
s
Np
1
3
2
5
0V
V
(150)
44 turns
c. 6.0 V
Ns
V
V
p
s
Np
1
62
.0
0V
V
(150)
7.5 turns
75. A step-up transformer has 80 turns on its
primary coil and 1200 turns on its sec-
ondary coil. The primary circuit is supplied
with an alternating current at 120 V.
a. What voltage is being applied across the
secondary circuit?
V
V
p
s
N
N
p
s
Vs
V
N
pN
p
s
(120 V
8
)
0
(1200)
1.8 kV
b. The current in the secondary circuit is
2.0 A. What current is in the primary
circuit?
VpIp VsIs
Ip
V
V
s
p
Is
3.0101A
c. What are the power input and output of
the transformer?
VpIp (120 V)(30.0 A) 3.6 kW
VsIs (1800 V)(2.0 A) 3.6 kW
76. Laptop Computers The power supply in a
laptop computer requires an effective volt-
age of 9.0 V from a 120-V line.
a. If the primary coil has 475 turns, how
many does the secondary coil have?
V
V
p
s
N
N
p
s
Ns
V
V
sN
p
p
(9.0
12
V
0
)(
V
475)
36 turns
b. A 125-mA current is in the computer.
What current is in the primary circuit?
VpIp VsIs
Ip
V
V
s
p
Is
9.4 mA
Level 2
77. Hair Dryers A hair dryer manufactured for
use in the United States uses 10 A at 120 V.
It is used with a transformer in England,
where the line voltage is 240 V.
a. What should be the ratio of the turns of
the transformer?
V
V
p
s
N
N
p
s
2
14
20
0V
V
2
1.
.0
0
or 2 to 1
b. What current will the hair dryer now
draw?
VpIp VsIs
Ip
V
V
s
p
Is
(120
24
V
0
)(1
V
0A)
5 A
78. A 150-W transformer has an input voltage
of 9.0 V and an output current of 5.0 A.
a. Is this a step-up or step-down
transformer?
Pout VsIs
Vs
P
I
o
s
ut
1
5
5
.0
0A
W
3.0101V
step-up transformer
(9.0 V)(125 mA)
7200 V
(1.8103V)(2.0 A)
120 V
Chapter 25 continued

b. What is the ratio of Voutput to Vinput?
P VsIs
Vs
I
P
s
1
5
5
.0
0A
W
3.0101V
V
V
o
in
u
p
tp
u
u
t
t
3.0
9
.0
10
V
1V
1.0
3
.0
101
or 10 to 3
79. Scott connects a transformer to a 24-V
source and measures 8.0 V at the secondary
circuit. If the primary and secondary circuits
were reversed, what would the new output
voltage be?
The turns ratio is
N
N
p
s
V
V
p
s
8
2.4
0V
V
1
3.
.0
0
Reversed, it would be
3
1.
.0
0
.
Thus, the voltage would now be found by
N
N
p
s
V
V
p
s
Vs
N
N
p
s
Vp (3.0)(24 V) 72 V
Mixed Review
pages 693–694
Level 1
80. A step-up transformer’s primary coil has
500 turns. Its secondary coil has 15,000
turns. The primary circuit is connected to
an AC generator having an EMF of 120 V.
a. Calculate the EMF of the secondary circuit.
V
V
p
s
N
N
p
s
Vs
V
N
pN
p
s
(120 V
5
)
0
(1
0
5,000)
3.6103V
b. Find the current in the primary circuit if
the current in the secondary circuit is 3.0 A.
VpIp VsIs
Ip
V
V
s
p
Is
(3600
12
V
0
)(
V
3.0 A)
9.0101A
c. What power is drawn by the primary
circuit? What power is supplied by the
secondary circuit?
VpIp (120 V)(9.0101A)
1.1104W
VsIs (3600 V)(3.0 A) 1.1104W
81. With what speed must a 0.20-m-long wire
cut across a magnetic field for which Bis
2.5 T if it is to have an EMF of 10 V induced
in it?
EMF BLv
v
E
B
M
L
F
(2.5 T
1
)0
(0
V
.20 m)
20 m/s
82. At what speed must a wire conductor 50-cm
long be moved at right angles to a magnetic
field of induction 0.20 T to induce an EMF
of 1.0 V in it?
EMF BLv
v
E
B
M
L
F
1101m/s
83. A house lighting circuit is rated at 120-V
effective voltage. What is the peak voltage
that can be expected in this circuit?
Veff (0.707)Vmax
Vmax
0
V
.7
e
0
ff7
1
02
.7
0
0V
7
170 V
84. Toaster A toaster draws 2.5 A of alternating
current. What is the peak current through
this toaster?
Ieff (0.707)Imax
Imax
0.
I
7
ef
0
f7
3.5 A
85. The insulation of a capacitor will break down
if the instantaneous voltage exceeds 575 V.
What is the largest effective alternating volt-
age that may be applied to the capacitor?
Veff
V
ma
2
x
575
2
407 V
86. Circuit Breaker A magnetic circuit breaker
will open its circuit if the instantaneous
current reaches 21.25 A. What is the largest
effective current the circuit will carry?
2.5 A
0.707
1.0 V
(0.20 T)(0.5 m)
512 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 513
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Ieff
I
ma
2
x
21
.25
2
A
15.03 A
87. The electricity received at an electrical
substation has a potential difference of
240,000 V. What should the ratio of the
turns of the step-down transformer be to
have an output of 440 V?
N
N
p
s
V
V
p
s
244
04
,0
00
V
0V
51
45
primary : secondary 545 : 1
88. An alternating-current electric generator
supplies a 45-kW industrial electric heater.
If the system voltage is 660 Vrms, what is
the peak current supplied?
Irms
4
65
60
kW
V
68 A
Therefore, Ipeak 96 A
89. A certain step-down transformer has 100 turns
on the primary coil and 10 turns on the sec-
ondary coil. If a 2.0-kW resistive load is con-
nected to the transformer, what is the effective
primary current that flows? Assume that the
secondary voltage is 60.0 Vpk.
Vs, eff
Vs
,p
2
eak
60
.0
2
V
42.4 V
Is, eff
Vs
P
,eff
47 A
Ip, eff
N
N
p
s
Is, eff
1
1
0
0
0
47 A4.7 A
90. A transformer rated at 100 kVA has an
efficiency of 98 percent.
a. If the connected load consumes 98 kW
of power, what is the input power to the
transformer?
Pout 98 kW
Pin
90
8.9
k8
W
1.0102kW
b. What is the maximum primary current
with the transformer consuming its
rated reactive power? Assume that
VP600 V.
I
10
60
00
kV
VA
200 A
Level 2
91. A wire, 0.40-m long, cuts perpendicularly
across a magnetic field for which Bis 2.0 T
at a velocity of 8.0 m/s.
a. What EMF is induced in the wire?
EMF BLv
(2.0 T)(0.40 m)(8.0 m/s)
6.4 V
b. If the wire is in a circuit with a resis-
tance of 6.4 Ω, what is the size of the
current in the wire?
EMF IR
I
EM
RF
6
6.
.4
4
V
1.0 A
92. A coil of wire, which has a total length of
7.50 m, is moved perpendicularly to Earth’s
magnetic field at 5.50 m/s. What is the size
of the current in the wire if the total resis-
tance of the wire is 5.0102m? Assume
Earth’s magnetic field is 5105T.
EMF BLv and V IR, but EMF V,
so IR BLv, and
I
BR
Lv
4.1102A 41 mA
93. The peak value of the alternating voltage
applied to a 144-resistor is 1.00102V.
What power must the resistor be able to
handle?
P IV and V IR, so I
R
V
therefore,
Pmax
R
V
V
V
R
2
69.4 W
The average power is Pmax/2 so the
resistor must dissipate 34.7 W.
94. Television The CRT in a television uses a
step-up transformer to change 120 V to
48,000 V. The secondary side of the trans-
former has 20,000 turns and an output of
1.0 mA.
a. How many turns does the primary side
have?
(1.00102V)2
144
(5.0105T)(7.50 m)(5.50 m/s)
5.0102m
2.0103W
42.4 V
68 A
0.707
Chapter 25 continued

V
V
p
s
N
N
p
s
Np
N
V
sV
s
p
50 turns
b. What is the input current?
VpIp VsIs
Ip
V
V
s
p
Is
0.40 A
Thinking Critically
page 694
95. Apply Concepts Suppose that an “anti-
Lenz’s law” existed that meant a force was
exerted to increase the change in a magnetic
field. Thus, when more energy was demand-
ed, the force needed to turn the generator
would be reduced. What conservation law
would be violated by this new “law”? Explain.
It would violate the law of conversation
of energy. More energy would come out
than went in. A generator would create
energy, not just change it from one form
to another.
96. Analyze Real transformers are not
100 percent efficient. Write an expression for
transformer efficiency in percent using
power. A step-down transformer that has an
efficiency of 92.5 percent is used to obtain
28.0 V from a 125-V household voltage. The
current in the secondary circuit is 25.0 A.
What is the current in the primary circuit?
Efficiency
e
P
P
p
s
100
Secondary power:
Ps VsIs (28.0 V)(25.0 A)
7.00102W
Primary power:
Pp 757 W
Primary current:
Ip
P
V
p
p
7
15
27
5W
V
6.05 A
97. Analyze and Conclude A transformer that
supplies eight homes has an efficiency of 95
percent. All eight homes have operating
electric ovens that each draw 35 A from
240-V lines. How much power is supplied
to the ovens in the eight homes? How
much power is dissipated as heat in the
transformer?
Secondary power:
Ps(# of homes)VsIs
(8)(240 V)(35 A) 67 kW
67 kW is supplied to the ovens in the
eight homes.
Primary power:
Pp 71 kW
The difference between these two is the
power dissipated as heat, 4 kW.
Writing in Physics
page 694
98. Common tools, such as an electric drill, are
typically constructed using a universal
motor. Using your local library, and other
sources, explain how this type of motor
may operate on either AC or DC current.
A series DC Motor uses both an arma-
ture and series coil. When operated
on alternating current, the polarity on
both fields changes simultaneously.
Therefore, the polarity of the magnetic
field remains unchanged, and hence the
direction of rotation is constant.
Cumulative Review
page 694
99. Light is emitted by a distant star at a
frequency of 4.561014 Hz. If the star is
moving toward Earth at a speed of 2750
km/s, what frequency light will be detected
by observers on Earth? (Chapter 16)
fobs f1
v
c
(100)(67 W)
95
(100)Ps
e
(100)(7.00102 W)
92.5
(100)Ps
e
(48,000 V)(1.0103A)
120 V
(20,000)(120 V)
48 000 V
514 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued
Physics: Principles and Problems Solutions Manual 515
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Because they are moving toward each
other
fobs f1
v
c
(4.561014 Hz)1
4.60104Hz
100. A distant galaxy emits light at a frequency
of 7.291014 Hz. Observers on Earth
receive the light at a frequency of
6.141014 Hz. How fast is the galaxy mov-
ing, and in what direction? (Chapter 16)
The galaxy is moving away from Earth
because the observed frequency is
lower than the emitted frequency.To
find the speed:
fobs f1
v
c
Because the observed light has a
lower frequency, the galaxy must be
moving away from Earth. So, use the
negative form of the equation above
fobs f1
v
c
fo
f
bs
1
v
c
v
c
1
fo
f
bs
vc1
fo
f
bs
(3.00108 m/s)1
4.73107 m/s
101. How much charge is on a 22-F capacitor
with 48 V applied to it? (Chapter 21)
C
qCV
(22106F)(48 V)
1.1103C
102. Find the voltage across a 22-, 5.0-W
resistor operating at half of its rating.
(Chapter 22)
PV2/R
VPR
5.0
2W
(22
)
7.4 V
103. Determine the total resistance of three,
85-resistors connected in parallel and
then series-connected to two 85-resistors
connected in parallel, as shown in
Figure 25-25. (Chapter 23)
■ Figure 25-25
85
1
85
1
85
1
R3 in parallel 28.3
85
1
85
1
R2 in parallel 42.5
RR3 in parallel R2 in parallel
28.3 42.5
71
104. An electron with a velocity of 2.1106m/s
is at right angles to a 0.81-T magnetic field.
What is the force on the electron produced
by the magnetic field? What is the elec-
tron’s acceleration? The mass of an elec-
tron is 9.111031 kg. (Chapter 24)
FBqv
(0.81 T)(1.601019 C)(2.1106m/s)
2.71013 N
Fma
a
3.01017 m/s2
2.71013 N
9.111031 kg
F
m
1
R2 in parallel
1
R3 in parallel
85
85
85 85 85
q
V
6.141014 Hz
7.291014 Hz
2.75106m/s
3.00108m/s
Chapter 25 continued

Challenge Problem
page 685
A distribution transformer (T1) has its primary coil
connected to a 3.0-kV AC source. The secondary coil
is connected to the primary coil of a second trans-
former (T2) by copper conductors. Finally, the sec-
ondary coil of transformer T2connects to a load
that uses 10.0 kW of power. Transformer T1has a
turn ratio of 5:1, and T2has a load voltage of 120 V.
The transformer efficiencies are 100.0 percent and
97.0 percent, respectively.
1. Calculate the load current.
IL 83 A
2. How much power is being dissipated by
transformer T2?
P2 10.3 kW
P2is power input to transformer T2.Of
the 10.3 kW, 0.3 kW is dissipated by T2;
the other 10.0 kW is dissipated in the
load.
3. What is the secondary current of trans-
former T1?
Vs1
1
5
(3.0103V)
6.0102V
Is1 17 A
4. How much current is the AC source supply-
ing to T1?
Ip1
1
5
Is1
1
5
(17 A) 3.4 A
10.3103W
6.0102V
P2
Vs1
10.0 kW
0.970
PL
0.970
10.0 kW
120 V
PL
VL
516 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 25 continued

Physics: Principles and Problems Solutions Manual 517
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
26 Electromagnetism
CHAPTER
Practice Problems
26.1 Interactions of Electric and
Magnetic Fields and Matter
pages 697–704
page 700
Assume that all charged particles move perpendicular to a uniform magnetic field.
1. A proton moves at a speed of 7.5103m/s as it passes through a magnetic field of
0.60 T. Find the radius of the circular path. Note that the charge carried by the
proton is equal to that of the electron, but is positive.
Bqv
r
m
Bq
v
1.3104m
2. Electrons move through a magnetic field of 6.0102T balanced by an electric
field of 3.0103N/C. What is the speed of the electrons?
Bqv Eq
v
B
E
3
6
..
0
0
1
1
0
0
3
N
2/T
C
5.0104m/s
3. Calculate the radius of the circular path that the electrons in problem 2 follow in
the absence of the electric field.
Bqv
mr
v2
r
m
Bq
v
4.7106m
4. Protons passing without deflection through a magnetic field of 0.60 T are
balanced by an electric field of 4.5103N/C. What is the speed of the moving
protons?
Bqv Eq
v
B
E
4.5
0.1
60
0
3
T
N/C
7.5103m/s
(9.111031 kg)(5.0104m/s)
(6.0102T)(1.601019 C)
(1.671027 kg)(7.5103m/s)
(0.60 T)(1.601019 C)
mv2
r

page 703
5. A beam of singly ionized (1) oxygen atoms is sent through a mass spectrometer.
The values are B7.2102T, q1.601019 C, r0.085 m, and V110 V.
Find the mass of an oxygen atom.
m
B2
2r
V
2q
2.71026 kg
6. A mass spectrometer analyzes and gives data for a beam of doubly ionized (2)
argon atoms. The values are q2(1.601019 C), B5.0102T, r0.106 m,
and V66.0 V. Find the mass of an argon atom.
m
B2
2r
V
2q
6.81026 kg
7. A stream of singly ionized (1) lithium atoms is not deflected as it passes
through a magnetic field of 1.5103T that is perpendicular to an electric field
of 6.0102N/C. What is the speed of the lithium atoms as they pass through the
two fields?
Bqv Eq
v
B
E
4.0105m/s
8. In Example Problem 2, the mass of a neon isotope is determined. Another neon
isotope is found to have a mass of 22 proton masses. How far apart on the
photographic film would these two isotopes land?
Use the charge-to-mass ratio to find the ratio of the radii of the two
isotopes.
m
q
Thus, r
B
1
2V
qm
and,
r
r
2
2
2
0
m
m
2
2
2
0
The radius of the isotope with a mass of 22 proton masses, then, is
r22 r20
m
m
2
2
2
0
r20
2
22
0
r20
2
22
0
(0.053 m)
0.056 m
The difference in the radii is r22 r20 0.056 m 0.053 m 0.003 m
3 mm
22mp
20mp
B
1
2V
q
m2
2
B
1
2V
q
m2
0
2V
B2r2
6.0102N/C
1.5103T
(5.0102T)2(0.106 m)2(2)(1.601019 C)
(2)(66.0 V)
(7.2102T)2(0.085 m)2(1.601019 C)
(2)(110 V)
518 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued

Physics: Principles and Problems Solutions Manual 519
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Section Review
26.1 Interactions of Electric and
Magnetic Fields and Matter
pages 697–704
page 704
9. Cathode-Ray Tube Describe how a cathode-ray tube forms an electron beam.
Electrons are emitted by the cathode, accelerated by a potential difference,
and passed through slits to form a beam.
10. Magnetic Field The radius of the circular path of an ion in a mass spectrometer is
given by r(1/B)2Vm/q
. Use this equation to explain how a mass spectrometer
is able to separate ions of different masses.
Assuming all of the ions have the same charge, the only variable that is
not constant in the equation is the ion mass, m. As mincreases, the
radius of the ion’s path also increases. This results in separate paths for
each unique mass.
11. Magnetic Field A modern mass spectrometer can analyze molecules having
masses of hundreds of proton masses. If the singly charged ions of these mole-
cules are produced using the same accelerating voltage, how would the mass
spectrometer’s magnetic field have to be changed for the ions to hit the film?
Since r(1/B)2Vmq
, as mincreases, so too must B.If mis raised by
a factor of about 10, Bwould have to increase by a factor of about 3
because to keep rconstant, Bmust increase asm
.
12. Path Radius A proton moves at a speed of 4.2104m/s as it passes through a
magnetic field of 1.20 T. Find the radius of the circular path.
m
q
B
vr
r
v
qm
B
3.7104m
13. Mass A beam of doubly ionized (2) oxygen atoms is accelerated by a
potential difference of 232 V. The oxygen then enters a magnetic field of 75 mT
and follows a curved path with a radius of 8.3 cm. What is the mass of the
oxygen atom?
m
q
m
2.71026 kg
(2)(1.601019 C)(75103T)2(8.3102m)2
(2)(232 V)
qB2r2
2V
2V
B2r2
(4.2104m/s)(1.671027 kg)
(1.601019 C)(1.20 T)
Chapter 26 continued

14. Critical Thinking Regardless of the energy
of the electrons used to produce ions,
J. J. Thomson never could remove more
than one electron from a hydrogen atom.
What could he have concluded about the
positive charge of a hydrogen atom?
It must be only a single elementary
charge.
Practice Problems
26.2 Electric and Magnetic
Fields in Space
pages 705–713
page 706
15. What is the speed in air of an electromagnetic
wave having a frequency of 3.21019 Hz?
All electromagnetic waves travel through
air or a vacuum at c, 3.00108m/s.
16. What is the wavelength of green light
having a frequency of 5.701014 Hz?
c
f
5.26107m
17. An electromagnetic wave has a frequency
of 8.21014 Hz. What is the wavelength
of the wave?
c
f
3.7107m
18. What is the frequency of an electromagnetic
wave having a wavelength of 2.2102m?
c
f
f
c
1.41010 Hz
page 707
19. What is the speed of an electromagnetic
wave traveling through the air? Use
c299,792,458 m/s in your calculation.
v
2.99712108m/s
20. For light traveling through water, the
dielectric constant is 1.77. What is the
speed of light traveling through water?
v
2.25108m/s
21. The speed of light traveling through a
material is 2.43108m/s. What is the
dielectric constant of the material?
v
K
c
v
2
3
2.
.0
40
3
1
10
0
8
8m
m/
/s
s
21.52
Section Review
26.2 Electric and Magnetic
Fields in Space
pages 705–713
page 713
22. Wave Propagation Explain how electro-
magnetic waves are able to propagate
through space.
The changing electric field induces a
changing magnetic field, and the chang-
ing magnetic field induces a changing
electric field. The waves propagate as
these two fields regenerate each other.
23. Electromagnetic Waves What are some of
the primary characteristics of electromagnetic
waves? Do electromagnetic waves behave
differently from the way that other waves,
such as sound waves, behave? Explain.
Electromagnetic waves can be described
by frequency and wavelength.They
behave similarly to other waves in that
they reflect, refract, diffract, interfere, and
can be Doppler shifted.The difference
between the electromagnetic waves and
other waves, such as sound waves, is
that electromagnetic waves can travel
through a vacuum and can be polarized.
c
K
3.00108m/s
1.77
c
K
299,792,458 m/s
1.000
54
c
K
3.00108m/s
2.2102m
3.00108m/s
8.21014 Hz
3.00108m/s
5.701014 Hz
520 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued
magnetic
field
electric field
E B c
travel at the
speed of light
Electromagnetic
waves
Physics: Principles and Problems Solutions Manual 521
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
24. Frequency An electromagnetic wave is
found to have a wavelength of 1.5105m.
What is the frequency of the wave?
c
f
f
c
2.01013 Hz
25. TV Signals Television antennas normally
have metal rod elements that are oriented
horizontally. From this information, what
can you deduce about the directions of the
electric fields in television signals?
They also must be horizontal.
26. Parabolic Receivers Why is it important
for a parabolic dish’s receiving antenna to
be properly aligned with the transmitter?
Parabolic dish antennas are only able
to receive signals within a very narrow
range of angles. It is, therefore, neces-
sary to carefully align the dish receiver
with the transmitting antennas to maxi-
mize the received signal strength.
27. Antenna Design Television channels 2
through 6 have frequencies just below the
FM radio band, while channels 7 through
13 have much higher frequencies. Which
signals would require a longer antenna:
those of channel 7 or those of channel 6?
Provide a reason for your answer.
The signals of channel 6 would require a
longer antenna. Lower-frequency waves
would have longer wavelengths.
28. Dielectric Constant The speed of light
traveling through an unknown material is
1.98108m/s. Given that the speed of light
in a vacuum is 3.00108m/s, what is the
dielectric constant of the unknown material?
v
K
c
v
2
3
1.
.0
90
8
1
10
0
8
8m
m/
/s
s
22.30
29. Critical Thinking Most of the UV radiation
from the Sun is blocked by the ozone layer
in Earth’s atmosphere. In recent years,
scientists have discovered that the ozone layer
over both Antarctica and the Arctic Ocean is
thinning. Use what you have learned about
electromagnetic waves and energy to explain
why some scientists are very concerned about
the thinning ozone layer.
If the entire ozone layer is thinning, the
amount of UV radiation from the Sun
that is blocked by the ozone layer will
decrease, allowing more UV rays to
reach the surface of Earth. The wave-
lengths of UV waves are short enough,
and their energies are high enough, to
damage skin molecules. Thus, the
resulting increase in UV rays to which
humans would be exposed could
increase the prevalence of skin cancer.
Chapter Assessment
Concept Mapping
page 718
30. Complete the following concept map
using the following term and symbols:
E, c, magnetic field.
Mastering Concepts
page 718
31. What are the mass and charge of an
electron? (26.1)
The mass of an electron is
9.111031 kg.
Its charge is 1.601019 C.
32. What are isotopes? (26.1)
Isotopes are atoms of the same element
that have different masses.
c
K
3.00108m/s
1.5105m
Chapter 26 continued
33. The direction of an induced magnetic field
is always at what angle to the changing
electric field? (26.2)
An induced magnetic field is always at
right angles to the changing electric field.
34. Why must an AC generator be used to
propagate electromagnetic waves? If a DC
generator were used, when would it create
electromagnetic waves? (26.2)
An AC generator supplies the changing
electric field, which in turn generates a
changing magnetic field. A DC genera-
tor would only generate a changing
electric field when turned on or off.
35. A vertical antenna wire transmits radio
waves. Sketch the antenna and the electric
and magnetic fields that it creates. (26.2)
36. What happens to a quartz crystal when a
voltage is applied across it? (26.2)
Quartz crystals bend or deform when
voltage is placed across them.The
quartz crystal then will vibrate at a set
frequency.
37. How does an antenna’s receiving circuit
select electromagnetic radio waves of a
certain frequency and reject all others? (26.2)
By adjusting the capacitance of the
antenna circuit, the oscillation frequency
of the circuit equals the frequency of the
desired radio waves. Resonance occurs,
causing the electrons in the circuit to
oscillate at that frequency.
Applying Concepts
page 718
38. The electrons in a Thomson tube travel from
left to right, as shown in Figure 26-14.
Which deflection plate should be charged
positively to bend the electron beam upward?
■Figure 26-14
The top plate should be charged
positively.
39. The Thomson tube in question 38 uses a
magnetic field to deflect the electron
beam. What would the direction of the
magnetic field need to be to bend the
beam downward?
The magnetic field would be directed
into the plane of the paper.
40. Show that the units of E/B are the same as
the units for velocity.
B
E
AC
m
Because 1 A is 1 C/s, this becomes
B
E
C
s
m
C
m
s
41. The vacuum chamber of a mass spectrome-
ter is shown in Figure 26-15. If a sample of
ionized neon is being tested in the mass
spectrometer, in what direction must the
magnetic field be directed to bend the ions
into a clockwise semicircle?
N
C
AN
m
Upper charged
plate
Lower charged
plate
V
522 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued
Physics: Principles and Problems Solutions Manual 523
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
■Figure 26-15
The magnetic field is found by the
right-hand rule and would be directed
out from and perpendicular to the plane
of the paper.
42. If the sign of the charge on the particles in
question 41 is changed from positive to
negative, do the directions of either or both
of the fields have to be changed to keep the
particles undeflected? Explain.
You can either change both fields or
neither field, but you cannot change
only one field.
43. For each of the following properties,
identify whether radio waves, light waves,
or X rays have the largest value.
a. wavelength
Radio waves have the longest
wavelengths.
b. frequency
X rays have the highest frequencies.
c. velocity
All travel at the same velocity, which
is the speed of light.
44. TV Waves The frequency of television
waves broadcast on channel 2 is about
58 MHz. The waves broadcast on channel 7
are about 180 MHz. Which channel
requires a longer antenna?
Channel 2 waves have a lower frequency
and a longer wavelength, so channel 2
requires a longer antenna. The length of
an antenna is directly proportional to
wavelength.
45. Suppose the eyes of an alien being are
sensitive to microwaves. Would you expect
such a being to have larger or smaller eyes
than yours? Why?
The eyes would be much larger, because
the wavelength of microwave radiation is
much larger than that of visible light.
Mastering Problems
26.1 Interactions of Electric and
Magnetic Fields and Matter
page 719
Level 1
46. Electrons moving at 3.6104m/s pass
through an electric field with an intensity
of 5.8103N/C. How large a magnetic field
must the electrons also experience for their
path to be undeflected?
v
B
E
B
E
v
3
5.
.6
8
1
10
04
3
m
N//
C
s
0.16 T
47. A proton moves across a 0.36-T magnetic
field, as shown in Figure 26-16. If the
proton moves in a circular path with a radius
of 0.20 m, what is the speed of the proton?
■Figure 26-16
m
q
2
B
v
r
v
B
m
rq
6.9106m/s
(0.36 T)(0.20 m)(1.601019 C)
1.671027 kg
B
r
Path of charged particle
XX
XX
XX
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
XX
Vacuum chamber
Deflected
paths
Dual slits
Ion beam
Film plate
Chapter 26 continued

48. A proton enters a 6.0102-T magnetic field with a speed of 5.4104m/s.
What is the radius of the circular path it follows?
r
m
Bq
v
9.4103m
49. An electron is accelerated by a 4.5-kV potential difference. How strong a magnetic
field must be experienced by the electron if its path is a circle of radius 5.0 cm?
B
1
r
2V
qm
0.05
1
0m
4.5103T
50. A mass spectrometer yields the following data for a beam of doubly ionized
(2) sodium atoms: B8.0102T, q2(1.601019 C), r0.077 m,
and V156 V. Calculate the mass of a sodium atom.
m
q
m 3.91026 kg
Level 2
51. An alpha particle has a mass of approximately 6.61027 kg and has a charge
of 2. Such a particle is observed to move through a 2.0-T magnetic field along a
path of radius 0.15 m.
a. What speed does the particle have?
m
q
B
vr
v
B
m
qr
1.5107m/s
b. What is its kinetic energy?
KE
1
2
mv2
1
2
m
B
m
qr
2
q2
2
B
m
2r2
7.01013 J
c. What potential difference would be required to give it this kinetic energy?
KE qV
V 2.2106V
52. A mass spectrometer analyzes carbon-containing molecules with a mass of
175103proton masses. What percent differentiation is needed to produce a
sample of molecules in which only carbon isotopes of mass 12, and none of
mass 13, are present?
7.01013 J
(2)(1.601019 C)
KE
q
(2)(1.601019 C)(2.0 T)2(0.15 m)2
(2)(6.61027 kg)
(2.0 T)(2)(1.601019 C)(0.15 m)
6.61027 kg
(2)(1.601019 C)(8.0102T)2(0.077 m)2
(2)(156 V)
qB2r2
2V
2V
B2r2
(2)(4.5103V)(9.111031 kg)
1.601019 C
(1.671027 kg)(5.4104m/s)
(6.0102T)(1.601019 C)
524 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued
Physics: Principles and Problems Solutions Manual 525
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The difference between carbon-12
and carbon-13 is one proton mass.
To distinguish between these, a percent
differentiation of one proton mass out
of 175103is needed, or
1751
,000
100
17
1
50
percent.
53. Silicon Isotopes In a mass spectrometer,
ionized silicon atoms have curvatures, as
shown in Figure 26-17. If the smaller
radius corresponds to a mass of 28 proton
masses, what is the mass of the other sili-
con isotope?
■Figure 26-17
m
q
so mis proportional to r2
m
m
2
1
r
r
2
1
2
2
m2m1
r
r
2
1
2
(28 mp)
1
17
6.
.9
27
3c
cm
m
234mp
m234mp(34)(1.671027 kg)
5.71026 kg
26.2 Electric and Magnetic Fields in Space
page 719
Level 1
54. Radio Waves The radio waves reflected by a
parabolic dish are 2.0 cm long. How long
should the antenna be that detects the waves?
The antenna is
2
, or 1.0 cm long.
55. TV A television signal is transmitted on a
carrier frequency of 66 MHz. If the wires on
a receiving antenna are placed
1
4
apart,
determine the physical distance between the
receiving antenna wires.
1
4
1
4
c
f
(3
4.
)0
(6
06
11
00
8
6
m
H
/z
s)
1.1 m
56. Bar-Code Scanner A bar-code scanner
uses a laser light source with a wavelength
of about 650 nm. Determine the frequency
of the laser light source.
f
c
4.61014 Hz
57. What is the optimum length of a receiving
antenna that is to receive a 101.3-MHz radio
signal?
Optimum antenna length is
1
2
1
2
c
f
1.48 m
Level 2
58. An EM wave with a frequency of 100-MHz
is transmitted through a coaxial cable hav-
ing a dielectric constant of 2.30. What is the
velocity of the wave’s propagation?
v 1.98108m/s
3.00108m/s
2.30
c
K
3.00108m/s
(2)(101.3106Hz)
3.00108m/s
650109m
2V
B2r2
Film plate
Silicon ion beam
r1 16.23 cm
r2 17.97 cm
r1
r2
Vacuum chamber
Film plate
Dual slits
Chapter 26 continued

59. Cell Phone A certain cellular telephone
transmitter operates on a carrier frequency
of 8.00108Hz. What is the optimal length
of a cell phone antenna designed to receive
this signal? Note that single-ended antennas,
such as those used by cell phones, generate
peak EMF when their length is one-fourth
the wavelength of the wave.
For a single-ended antenna, optimum
antenna length is
1
4
1
4
c
f
0.0938 m
Mixed Review
page 720
Level 1
60. The mass of a doubly ionized (2) oxygen
atom is found to be 2.71026 kg. If the
mass of an atomic mass unit (amu) is equal
to 1.671027 kg, how many atomic mass
units are in the oxygen atom?
(2.71026 kg)
16 amu
61. Radio An FM radio station broadcasts
on a frequency of 94.5 MHz. What is the
antenna length that would give the best
reception for this station?
Optimum antenna length is
1
2
1
2
c
f
1.59 m
Level 2
62. At what frequency does a cell phone with
an 8.3-cm-long antenna send and receive
signals? Recall from question 59 that single-
ended antennas, such as those used by cell
phones, generate peak EMF when their
length is one-fourth the wavelength of the
wave they are broadcasting or receiving.
The antenna length is
0.083 m
1
4
1
4
c
f
The frequency, then, is
f
(4)(0.0
c83 m)
9.0108Hz
63. An unknown particle is accelerated by a
potential difference of 1.50102V. The
particle then enters a magnetic field of
50.0 mT, and follows a curved path with a
radius of 9.80 cm. What is the ratio of q/m?
m
q
B
2
2
V
r2
1.25107C/kg
Thinking Critically
page 720
64. Apply Concepts Many police departments
use radar guns to catch speeding drivers. A
radar gun is a device that uses a high-fre-
quency electromagnetic signal to measure
the speed of a moving object. The frequency
of the radar gun’s transmitted signal is
known. This transmitted signal reflects off
of the moving object and returns to the
receiver on the radar gun. Because the
object is moving relative to the radar gun,
the frequency of the returned signal is dif-
ferent from that of the originally transmit-
ted signal. This phenomenon is known as
the Doppler shift. When the object is mov-
ing toward the radar gun, the frequency of
the returned signal is greater than the fre-
quency of the original signal. If the initial
transmitted signal has a frequency of
10.525 GHz and the returned signal shows
a Doppler shift of 1850 Hz, what is the
speed of the moving object? Use the follow-
ing equation:
vtarget
2f
c
t
f
r
D
an
o
s
p
m
p
i
l
t
e
t
r
ed
Where,
vtarget velocity of target (m/s)
cspeed of light (m/s)
(2)(1.50102V)
(50.0103T)2(9.80102m)2
3.00108m/s
(4)(0.083 m)
3.00108m/s
(2)(94.5106Hz)
1amu
1.671027 kg
3.00108m/s
(4)(8.00108Hz)
526 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued

Physics: Principles and Problems Solutions Manual 527
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
fDoppler Doppler shift frequency (Hz)
ftransmitted frequency of transmitted wave (Hz)
vtarget 26.4 m/s
65. Apply Concepts H. G. Wells wrote a science-fiction novel called The Invisible Man,
in which a man drinks a potion and becomes invisible, although he retains all of
his other faculties. Explain why an invisible person would not be able to see.
To see, you must detect the light, which means the light will be absorbed or
scattered. Essentially, an invisible person would be completely
transparent so light would just pass through the eye without ever being
absorbed or scattered.
66. Design an Experiment You are designing a mass spectrometer using the
principles discussed in this chapter, but with an electronic detector replacing
the photographic film. You want to distinguish singly ionized (1) molecules of
175 proton masses from those with 176 proton masses, but the spacing between
adjacent cells in your detector is 0.10 mm. The molecules must have been accel-
erated by a potential difference of at least 500.0 V to be detected. What are some
of the values of V, B, and r that your apparatus should have?
The charge-to-mass ratio for isotopes in a mass spectrometer is
m
q
so the radius of the isotope’s path is r
B
1
2V
qm
.
The difference in the radii for the two isotopes is
0.10103mr176 r175
B
1
2
q
V
m176
m175
B
1
2
q
V
176m
p
175m
p
B
1
2V
q
mp
176
175
The magnetic field, then, is
B
2V
q
mp
1.2 T
The radius for the isotope with a mass equal to 176 proton masses
is r76
B
1
2V(17
q
6mp)
1.2
1T
3.6102m
When designing the spectrometer, you can choose any value of Vand
B, provided Vis at least 500.0 V. However, since q/mis constant, Vwill
be proportional to B2r2.
(2)(5.00 V)(176)(1.671027 kg)
1.601019 C
(2)(500.0 V)(1.671027kg)
1.601019 C
176
175
0.10103m
176
175
0.10103m
2V
B2r2
(3.00108m/s)(1850 Hz)
(2)(10.525109Hz)
cfDoppler
2ftransmitted
Chapter 26 continued

Writing in Physics
page 720
67. Compose a 1–2 page report in which you
outline the operation of a typical television,
DVD, or VCR infrared remote-control unit.
Explain why the simultaneous use of multi-
ple remote-control units typically does not
cause the units to interfere with each other.
Your report should include block diagrams
and sketches.
Remote controls use a broad range of
IR frequencies that are pulse-code mod-
ulated. Each button on the remote pro-
duces a unique sequence of short and
long pulses. Because of the wide range
of frequencies used by different manu-
facturers and the unique pulse codes
used, it is very unlikely that different
remote controls will interfere with each
other.
Cumulative Review
page 720
68. A He–Ne laser (633 nm) is used to illu-
minate a slit of unknown width, forming a
pattern on a screen that is located 0.95 m
behind the slit. If the first dark band is 8.5
mm from the center of the central bright
band, how wide is the slit? (Chapter 19)
x1
L
w
w
xL
1
7.1105m
69. The force between two identical metal
spheres with the charges shown in
Figure 26-18 is F. If the spheres are
touched together and returned to their
original positions, what is the new force
between them? (Chapter 20)
■Figure 26-18
The spheres share charges equally
when they are touched together, so they
each carry –1qof charge. The force
varies with the product of the charges,
so the new force is to the old force as
1q1qis to 4q2q, or 1:8.Therefore,
the new force is F/8.The direction of the
new force will be repulsive, rather than
attractive.
70. What is the electric field strength between
two parallel plates spaced 1.2 cm apart if a
potential difference of 45 V is applied to
them? (Chapter 21)
E
d
V
0.4
05
12
Vm
3.8103V/m or N/C
71. Calculate the daily cost of operating an air
compressor that runs one-fourth of the time
and draws 12.0 A from a 245-V circuit if the
cost is $0.0950 per kWh. (Chapter 22)
cost (E)(rate)
(IVt)(rate)
(120 A)(245 V)(6 h)
$0
k
.W
09
h
50
$1.68
72. A 440-cm length of wire carrying 7.7 A is
at right angles to a magnetic field. The force
on the wire is 0.55 N. What is the strength
of the field? (Chapter 24)
FBIL
B
IF
L
(7.70
A
.5
)(
5
4N
.4 m)
0.016 T
73. A north-south wire is moved toward the
east through a magnetic field that is point-
ing down, into Earth. What is the direction
of the induced current? (Chapter 25)
north
1 kW
1000 W
4q2q
(633109m)(0.95 m)
8.5103m
528 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued

Physics: Principles and Problems Solutions Manual 529
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Challenge Problems
page 709
Visible light makes up only a very small portion of
the entire electromagnetic spectrum. The wavelengths
for some of the colors of visible light are shown in
Table 26-1.
1. Which color of light has the longest wave-
length?
red
2. Which color travels the fastest in a vacuum?
They all travel at the same speed, c.
3. Waves with longer wavelengths diffract
around objects in their path more than
waves with shorter wavelengths. Which
color will diffract the most? The least?
Red light will diffract the most. Violet
light will diffract the least.
4. Calculate the frequency range for each color
of light given in Table 26-1.
The frequency is f
c
.
For 390 nm,
f
3
3
..
0
9
0
0
1
1
0
0
8
7
m
m
/s
7.691014 Hz
For 455 nm,
f
3
4.
.0
50
5
1
10
0
8
m
7m
/s
6.591014 Hz
For 492 nm,
f
3
4.
.0
90
2
1
10
0
8
m
7m
/s
6.101014 Hz
For 577 nm,
f
3
5.
.0
70
7
1
10
0
8
m
7m
/s
5.201014 Hz
For 597 nm,
f
3
5.
.0
90
7
1
10
0
8
m
7m
/s
5.031014 Hz
For 622 nm,
f
3
6.
.0
20
2
1
10
0
8
m
7m
/s
4.821014 Hz
For 700 nm,
f
3.
7
0
.0
0
0
10
1
8
0
m
7
/s
m4.291014 Hz
(41014 Hz to one significant digit)
Thus, the ranges are
Violet: 6.591014 Hz to 7.691014 Hz
Blue: 6.101014 Hz to 6.591014 Hz
Green: 5.201014 Hz to 6.101014 Hz
Yellow: 5.031014 Hz to 5.201014 Hz
Orange: 4.821014 Hz to 5.031014 Hz
Red: 4.291014 Hz to 4.821014 Hz
Table 26-1
Wavelengths of Visible Light
Color Wavelength (nm)
Violet–Indigo 390 to 455
Blue 455 to 492
Green 492 to 577
Yellow 577 to 597
Orange 597 to 622
Red 622 to 700
Chapter 26 continued


Physics: Principles and Problems Solutions Manual 531
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
27 Quantum Theory
CHAPTER
Practice Problems
27.1 A Particle Model
of Waves
pages 723–734
page 730
1. An electron has an energy of 2.3 eV. What is
the energy of the electron in joules?
(2.3 eV)
1.60
11
e
0
V
19 J
3.71019 J
2. What is the energy in eV of an electron with
a velocity of 6.2106m/s?
KE mv2
(9.111031 kg)(6.2106m/s)2
(1.751017 J)
1.1102eV
3. What is the velocity of the electron in
problem 1?
m9.111031 kg, KE mv2
v
2m
KE
9.0105m/s
4. The stopping potential for a photoelectric
cell is 5.7 V. Calculate the maximum kinetic
energy of the emitted photoelectrons in eV.
KE qV0
(1.601019 C)(5.7 J/C)
5.7 eV
5. The stopping potential required to prevent
current through a photocell is 3.2 V.
Calculate the maximum kinetic energy in
joules of the photoelectrons as they are
emitted.
KE qV0
(1.601019 C)(3.2 J/C)
5.11019 J
page 732
6. The threshold wavelength of zinc is 310 nm.
Find the threshold frequency, in Hz, and
the work function, in eV, of zinc.
f0
c
0
9.71014 Hz
Whf0
(6.631034 J/Hz)
(9.71014 Hz)
4.0 eV
7. The work function for cesium is 1.96 eV.
What is the kinetic energy, in eV, of photo-
electrons ejected when 425-nm violet light
falls on the cesium?
KEmax
1240
eVnm
hf0
124
42
05
en
Vm
nm
1.96 eV
0.960 eV
8. When a metal is illuminated with 193-nm
ultraviolet radiation, electrons with energies
of 3.5 eV are emitted. What is the work
function of the metal?
KE hfhf0
hf0hfKE
h
c
KE
1240
eVnm
KE
121
49
03
en
Vm
nm
3.5 eV
2.9 eV
1eV
1.601019 J
3.00108m/s
310109m
1eV
1.601019 J
(2)(3.71019 J)
9.111031 kg
1
2
1eV
1.601019 J
1
2
1
2

9. A metal has a work function of 4.50 eV.
What is the longest-wavelength radiation
that will cause it to emit photoelectrons?
hf04.50 eV, so
h
c
0
4.50 eV
Thus, 0276 nm
Section Review
27.1 A Particle Model
of Waves
pages 723–734
page 734
10. Photoelectric Effect Why is high-intensity,
low-frequency light unable to eject electrons
from a metal, whereas low-intensity, high-
frequency light can? Explain.
Light, a form of electromagnetic radia-
tion, is quantized and massless, yet it
does have kinetic energy. Each incident
photon interacts with a single electron. If
the incident photon does not have suffi-
cient energy, it cannot eject an electron.
Because energy is directly related to fre-
quency, low frequency light does not
have sufficient energy to eject an elec-
tron, whereas high frequency light does.
11. Frequency and Energy of Hot-Body
Radiation As the temperature of a body is
increased, how does the frequency of peak
intensity change? How does the total
amount of radiated energy change?
Both frequency of peak intensity and
total energy radiated increase. The peak
frequency increases as T, whereas the
total energy increases as T4.
12. Photoelectric and Compton Effects An
experimenter sends an X ray into a target.
An electron, but no other radiation,
emerges from the target. Explain whether
this event is a result of the photoelectric
effect or the Compton effect.
It is a result of the photoelectric effect,
which is the capture of a photon by an
electron in matter and the transfer of
the photon’s energy to the electron.
13. Photoelectric and Compton Effects
Distinguish the photoelectric effect from
the Compton effect.
The Compton effect is the scattering of
a photon by matter, resulting in a pho-
ton of lower energy and momentum.The
photoelectric effect is the emission of
electrons from a metal sample when radi-
ation of sufficient energy is incident on it.
14. Photoelectric Effect Green light
(532 nm) strikes an unknown metal,
causing electrons to be ejected. The ejected
electrons can be stopped by a potential of
1.44 V. What is the work function, in eV, of
the metal?
Egreen light
h
c
125
43
02
en
Vm
nm
2.33 eV
KEejected electron qV
(1.601019 C)
(1.44 J/C)
1.44 eV
WEgreen light KEejected electron
2.33 eV 1.44 eV
0.89 eV
15. Energy of a Photon What is the energy, in
eV, of the photons produced by a laser
pointer having a 650-nm wavelength?
E
h
c
126
45
00
en
Vm
nm
1.9 eV
16. Photoelectric Effect An X ray is absorbed in
a bone and releases an electron. If the X ray
has a wavelength of approximately 0.02 nm,
estimate the energy, in eV, of the electron.
E
h
c
12
0
4
.0
02
eV
n
m
nm
6104eV
17. Compton Effect An X ray strikes a bone,
collides with an electron, and is scattered.
How does the wavelength of the scattered
X ray compare to the wavelength of the
incoming X ray?
1eV
1.601019 J
1240 eVnm
4.50 eV
532 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued

Physics: Principles and Problems Solutions Manual 533
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The scattered X ray has a longer wave-
length than the incoming X ray.
18. Critical Thinking Imagine that the colli-
sion of two billiard balls models the inter-
action of a photon and an electron during
the Compton effect. Suppose the electron is
replaced by a much more massive proton.
Would this proton gain as much energy
from the collision as the electron does?
Would the photon lose as much energy as it
does when it collides with the electron?
The answer to both questions is no. A
tennis ball can transfer more kinetic
energy to a softball than it can to a
bowling ball.
Practice Problems
27.2 Matter Waves
pages 735–737
page 736
19. A 7.0-kg bowling ball rolls with a velocity
of 8.5 m/s.
a. What is the de Broglie wavelength of the
bowling ball?
(6
7..6
03k
g
1
)(
0
8
.5
34
m
J/
s
s)
1.11035 m
b. Why does the bowling ball exhibit no
observable wave behavior?
The wavelength is too small to show
observable effects.
20. What is the de Broglie wavelength and
speed of an electron accelerated by a poten-
tial difference of 250 V?
1
2
mv2qV,so
v
2m
qV
9.4106m/s
m
hv
7.71011 m
21. What voltage is needed to accelerate an
electron so it has a 0.125-nm wavelength?
h
p
, so p
h
KE
1
2
mv2
(1.5441017 J)
96.5 eV, so it would have to be
accelerated through 96.5 V.
22. The electron in Example Problem 3 has a
de Broglie wavelength of 0.14 nm. What
is the kinetic energy, in eV, of a proton
(m1.671027 kg) with the same
wavelength?
The de Broglie wavelength is
m
hv
so the velocity is v
m
h
The kinetic energy, then, is
KE
1
2
mv2
1
2
m
m
h
2
4.2102eV
Section Review
27.2 Matter Waves
pages 735–737
page 737
23. Wavelike Properties Describe the experi-
ment that confirmed that particles have
wavelike properties.
When a beam of electrons was aimed at a
crystal, the crystal acted like a diffraction
grating, causing the electrons to form a
diffraction pattern.The diffraction of the
electrons (particles) is similar to the dif-
fraction of light (waves) through a grating.
1eV
1.601019 J
(6.631034 Js)2
(2)(1.671027 kg)(0.14109m)2
h2
2m2
1eV
1.601019 J
6
0
..
6
1
3
2
5
10
1
0
3
4
9J
m
s
(2)(9.111031 kg)
h
2
2m
p2
2m
6.631034 Js
(9.111031 kg)(9.4106m/s)
(2)(1.601019 C)(250 J/C)
9.111031 kg
h
mv
Chapter 27 continued
24. Wave Nature Explain why the wave nature
of matter is not obvious.
The wavelengths of most objects are
much too small to be detected.
25. De Broglie Wavelength What is the
de Broglie wavelength of an electron
accelerated through a potential difference
of 125 V?
v
2
m
qV
6.63106m/s
pmv (9.111031 kg)(6.63106m/s)
6.041024 kgm/s
1.101010 m
0.110 nm
26. Wavelengths of Matter and Radiation
When an electron collides with a massive
particle, the electron’s velocity and wave-
length decrease. How is it possible to
increase the wavelength of a photon?
If the photon undergoes Compton scat-
tering with a fixed target, the wave-
length of the photon will increase. Note,
however, that the photon’s speed is not
changed. The photon still travels at c.
27. Heisenberg Uncertainty Principle When
light or a beam of atoms passes through a dou-
ble slit, an interference pattern forms. Both
results occur even when atoms or photons pass
through the slits one at a time. How does the
Heisenberg uncertainty principle explain this?
The Heisenberg uncertainty principle
states that you cannot simultaneously
know the precise position and momen-
tum of a particle. Thus, if you know the
precise position of a photon or an
atom as it passes through the slit, you
cannot know its precise momentum.
Because of the unknown momentum,
you cannot be sure which of the slits
the beam passed through, resulting in
the distribution of photons or atoms
seen in the interference pattern.
28. Critical Thinking Physicists recently made
a diffraction grating of standing waves of
light. Atoms passing through the grating
produce an interference pattern. If the
spacing of the slits in the grating were
1
2
(about 250 nm), what was the approximate
de Broglie wavelength of the atoms?
For diffraction gratings, dsin ,
where dis the spacing of the slits, and
is the angular separation between
consecutive peaks. The de Broglie
wavelength, then, is (250 nm) sin .
If we assume sin is around 0.1, then
the de Broglie wavelength is a few tens
of nanometers.
Chapter Assessment
Concept Mapping
page 742
29. Complete the following concept map using
these terms: dual nature, mass, wave proper-
ties, momentum, diffraction.
Mastering Concepts
page 742
30. Incandescent Light An incandescent light-
bulb is controlled by a dimmer. What happens
to the color of the light given off by the bulb as
the dimmer control is turned down? (27.1)
The light becomes redder.
6.631034 Js
6.041024 kgm/s
h
p
2(1.601019 C)(125 V)
9.111031 kg
534 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued
dual nature
interference diffraction mass momentum
particle
properties
wave properties

Physics: Principles and Problems Solutions Manual 535
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
31. Explain the concept of quantized energy.
(27.1)
Quantized energy means that energy
can exist only in multiples of some min-
imum value.
32. What is quantized in Max Planck’s interpre-
tation of the radiation of incandescent
bodies? (27.1)
The vibrational energy of the incandes-
cent atoms is quantized.
33. What is a quantum of light called? (27.1)
a photon
34. Light above the threshold frequency shines
on the metal cathode in a photocell. How
does Einstein’s photoelectric effect theory
explain the fact that as the light intensity
increases, the current of photoelectrons
increases? (27.1)
Each photon ejects a photoelectron.
Light with greater intensity contains
more photons per second; thus, it
causes the ejection of more photo-
electrons per second.
35. Explain how Einstein’s theory accounts for
the fact that light below the threshold fre-
quency of a metal produces no photoelec-
trons, regardless of the intensity of the
light. (27.1)
Photons below the threshold frequency
do not have sufficient energy to eject
an electron. If the intensity of the light
increases, the number of photons
increases but their energy does not;
the photons are still unable to eject an
electron.
36. Photographic Film Because certain types
of black-and-white film are not sensitive
to red light, they can be developed in a
darkroom that is illuminated by red light.
Explain this on the basis of the photon
theory of light. (27.1)
Red photons do not have enough energy
to cause the chemical reaction that
exposes film.
37. How does the Compton effect demonstrate
that photons have momentum as well as
energy? (27.1)
Elastic collisions transfer both momen-
tum and energy. Only if photons have
momentum can the equations be
satisfied.
38. The momentum, p, of a particle of matter is
given by pmv. Can you calculate the
momentum of a photon using the same
equation? Explain. (27.2)
No, using the equation yields a photon
momentum of zero because photons
are massless. This result is incorrect
because massless photons have non-
zero momenta.
39. Explain how each of the following electron
properties could be measured. (27.2)
a. charge
Balance the force of gravity against
the force of an electric field on the
charge.
b. mass
Balance the force of an electric field
against that of a magnetic field to
find m/q, then use the measured
value of q.
c. wavelength
Scatter electrons off a crystal and
measure the angles of diffraction.
40. Explain how each of the following photon
properties could be measured. (27.2)
a. energy
Measure the KE of the electrons
ejected from a metal for at least two
different wavelengths, or measure the
KE of the electrons ejected from a
known metal at only one wavelength.
b. momentum
Measure the change in wavelength
of X rays scattered by matter.
c. wavelength
Measure the angle of diffraction
when light passes through two slits
Chapter 27 continued

or a diffraction grating, measure the
width of a single-slit diffraction pat-
tern, or measure the angle the light is
bent when it passes through a prism.
Applying Concepts
page 742
41. Use the emission spectrum of an incandes-
cent body at three different temperatures
shown in Figure 27-1 on page 724 to
answer the following questions.
a. At what frequency does the peak emis-
sion intensity occur for each of the three
temperatures?
4000 K: ~2.51014 Hz, 5800 K:
~3.51014 Hz, 8000 K: ~4.61014 Hz
b. What can you conclude about the rela-
tionship between the frequency of peak
radiation emission intensity and tem-
perature for an incandescent body?
The frequency of the peak intensity
increases with increasing
temperature.
c. By what factor does the intensity of the
red light given off change as the body’s
temperature increases from 4000 K to
8000 K?
The intensity in the red portion of
the spectrum increases from approx-
imately 0.5 to 9.2, an increase by a
factor of slightly greater than 18.
42. Two iron bars are held in a fire. One glows
dark red, while the other glows bright
orange.
a. Which bar is hotter?
the rod glowing bright orange
b. Which bar is radiating more energy?
the rod glowing bright orange
43. Will high-frequency light eject a greater
number of electrons from a photosensitive
surface than low-frequency light, assuming
that both frequencies are above the thresh-
old frequency?
Not necessarily; the number of ejected
electrons is proportional to the number
of incident photons or the brightness of
the light, not the frequency of the light.
44. Potassium emits photoelectrons when
struck by blue light, whereas tungsten emits
photoelectrons when struck by ultraviolet
radiation.
a. Which metal has a higher threshold
frequency?
Blue light has a lower frequency and
energy than UV light.Thus, tungsten
has the higher threshold frequency.
b. Which metal has a larger work function?
tungsten
45. Compare the de Broglie wavelength of the
baseball shown in Figure 27-11 with the
diameter of the baseball.
■Figure 27-11
The diameter of the baseball is about
0.10 m, whereas the de Broglie wave-
length is 10–34 m; the baseball is about
1033 times larger than the wavelength.
Mastering Problems
27.1 A Particle Model of Waves
page 742–743
Level 1
46. According to Planck’s theory, how does the
frequency of vibration of an atom change if
it gives off 5.441019 J while changing its
value of nby 1?
Enhf , so
f
n
E
h
8.211014 Hz
47. What potential difference is needed to stop
electrons with a maximum kinetic energy of
4.81019 J?
5.441019 J
(1)(6.631034 Js)
0.10 m 21 m/s
536 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued
Physics: Principles and Problems Solutions Manual 537
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
KE qV0, so
V0
KE
q
3.0 V
48. What is the momentum of a photon of violet
light that has a wavelength of 4.0102nm?
p
h
1.71027 kgm/s
Level 2
49. The stopping potential of a certain metal is
shown in Figure 27-12. What is the maxi-
mum kinetic energy of the photoelectrons
in the following units?
■Figure 27-12
a. electron volts
KE qV0
(1 elementary charge)(5.0 V)
5.0 eV
b. joules
5.0
1eV
1.60
11
e
0
V
19 J
8.01019 J
50. The threshold frequency of a certain metal
is 3.001014 Hz. What is the maximum
kinetic energy of an ejected photoelectron if
the metal is illuminated by light with a
wavelength of 6.50102nm?
KE hfhf0
h
c
f0
(6.631034 Js)
3.001014 Hz
1.071019 J
51. The threshold frequency of sodium is
4.41014 Hz. How much work must be
done to free an electron from the surface
of sodium?
Work hf0
(6.631034 J/Hz)(4.41014 Hz)
2.91019 J
52. If light with a frequency of 1.001015 Hz
falls on the sodium in the previous prob-
lem, what is the maximum kinetic energy of
the photoelectrons?
KE hfhf0
h(ff0)
(6.631034 J/Hz)
(1.001015 Hz 4.41014 Hz)
3.71019 J
Level 3
53. Light Meter A photographer’s light meter
uses a photocell to measure the light falling
on the subject to be photographed. What
should be the work function of the cathode
if the photocell is to be sensitive to red light
(680 nm) as well as to the other colors
of light?
W
1240
e
0
Vnm
126
48
00
en
Vm
nm
1.8 eV
54. Solar Energy A home uses about 41011 J
of energy each year. In many parts of the
United States, there are about 3000 h of
sunlight each year.
a. How much energy from the Sun falls on
one square meter each year?
Earth receives about 1000 J/m2each
second, so
E(1000 J/m2s)
11010 J/m2per year
b. If this solar energy can be converted
to useful energy with an efficiency of
20 percent, how large an area of
converters would produce the energy
needed by the home?
3000 h
y
3600 s
h
3.00108m/s
6.50107m
Cathode Anode
5.0 V
6.631034 Js
4.0107m
4.81019 C
(1.601019 C)
Chapter 27 continued

Area
2102m2
27.2 Matter Waves
page 743
Level 1
55. What is the de Broglie wavelength of an
electron moving at 3.0106m/s?
2.41010 m
0.24 nm
56. What velocity would an electron need to
have a de Broglie wavelength of
3.01010 m?
m
hv
v
m
h
2.4106m/s
Level 2
57. A cathode-ray tube accelerates an electron
from rest across a potential difference of
5.0103V.
a. What is the velocity of the electron?
1
2
mv2qV
v
v
4.2107m/s
b. What is the wavelength associated with
the electron?
1.71011 m 0.017 nm
58. A neutron is held in a trap with a kinetic
energy of only 0.025 eV.
a. What is the velocity of the neutron?
KE (0.025 eV)
4.01021 J
mv2
v
2m
KE
2.2103m/s
b. Find the de Broglie wavelength of the
neutron.
1.81010 m
59. The kinetic energy of a hydrogen atom’s
electron is 13.65 eV.
a. Find the velocity of the electron.
KE mv2
v
2m
KE
2.19106m/s
b. Calculate the electron’s de Broglie
wavelength.
0.332 nm
c. Given that a hydrogen atom’s radius is
0.519 nm, calculate the circumference of
a hydrogen atom and compare it with
the de Broglie wavelength for the atom’s
electron.
C2r
6.631034 kgm/s
(9.111031 kg)(2.19106m/s)
h
mv
(2)(13.65 eV)(1.601019 JeV)
9.111031 kg
1
2
6.631034 Js
(1.671027 kg)(2.2103m/s)
h
mv
(2)(4.01021 J)
1.671027 kg
1
2
1.601019 J
eV
6.631034 J/Hz
(9.111031 kg)(4.2107m/s)
h
mv
(1.601019 C)(5.0103V)
1
2
(9.111031 kg)
qV
1
2
m
6.631034 J/Hz
(9.111031 kg)(3.01010 m)
6.631034 Js
(9.111031 kg)(3.0106m/s)
h
mv
41011 J
(0.2)(11010 J/m2)
538 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued

Physics: Principles and Problems Solutions Manual 539
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(2)(0.519 nm) 3.26 nm
The circumference is approximately equal to ten complete wavelengths.
Level 3
60. An electron has a de Broglie wavelength of 0.18 nm.
a. How large a potential difference did it experience if it started from rest?
The de Broglie wavelength is ,
which gives a velocity of v.
The kinetic energy, then, is
KE mv 2
m
m
h
2
In terms of voltage, the kinetic energy is KE qV.
Combining these and solving for voltage,
V
47 V
b. If a proton has a de Broglie wavelength of 0.18 nm, how large is the potential
difference that it experienced if it started from rest?
Using the same derivation as before, the voltage is
V
0.025 V
Mixed Review
page 743–744
Level 1
61. What is the maximum kinetic energy of photoelectrons ejected from a metal that
has a stopping potential of 3.8 V?
KE qV0(1 elementary charge)(3.8 V) 3.8 eV
62. The threshold frequency of a certain metal is 8.01014 Hz. What is the work
function of the metal?
Whf0
(6.631034 J/Hz)(8.01014 Hz)
5.31019 J
(6.631034 Js)2
(2)(1.671027 kg)(1.601019 C)(0.18109m)2
h2
2mq2
(6.631034 Js)2
(2)(9.111031 kg)(1.601019 C)(0.18109
h2
2mq2
h2
2m2
1
2
1
2
h
m
h
mv
Chapter 27 continued

63. If light with a frequency of 1.61015 Hz
falls on the metal in the previous problem,
what is the maximum kinetic energy of the
photoelectrons?
KE hfhf0
(6.631034 J/Hz)(1.61015 Hz)
5.31019 J
5.31019 J
64. Find the de Broglie wavelength of a
deuteron (nucleus of 2H isotope) of mass
3.31027 kg that moves with a speed of
2.5104m/s.
8.01012 m
Level 2
65. The work function of iron is 4.7 eV.
a. What is the threshold wavelength of
iron?
W
h
c
0
1240
e
0
Vnm
0
1240W
eVnm
124
4
0
.7
ee
V
V
nm
2.6102nm
b. Iron is exposed to radiation of wave-
length 150 nm. What is the maximum
kinetic energy of the ejected electrons
in eV?
KE
h
c
h
c
0
121
45
00
en
Vm
nm
4.7 eV
3.6 eV
66. Barium has a work function of 2.48 eV.
What is the longest wavelength of light
that will cause electrons to be emitted
from barium?
Work function 2.48 eV hf0
h
c
0
,so
0
5.01107m
501 nm
67. An electron has a de Broglie wavelength of
400.0 nm, the shortest wavelength of visible
light.
a. Find the velocity of the electron.
m
hv
v
m
h
1.82103m/s
b. Calculate the energy of the electron in eV.
KE
1
2
mv2
1
2
(9.111031 kg)(1.82103m/s)2
9.43106eV
68. Electron Microscope An electron micro-
scope is useful because the de Broglie wave-
lengths of electrons can be made smaller than
the wavelength of visible light. What energy
in eV has to be given to an electron for it to
have a de Broglie wavelength of 20.0 nm?
The de Broglie wavelength is
m
hv
,
which gives a velocity of v
m
h
.
The kinetic energy, then, is
KE
1
2
mv2
1
2
m
m
h
2
3.77103eV
1eV
1.601019 J
(6.631034 Js)2
(2)(9.111031 kg)(20.0109m)2
h2
2m2
eV
1.601019 J
6.631034 J/Hz
(9.111031 kg)(400.0109m)
(6.631034 Js)(3.00108m/s)
(2.48 eV)
1.60
1
1
e
0
V
19 J
hc
2.48 eV
6.631034 Js
(3.31027 kg)(2.5104m/s)
h
mv
540 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued
Physics: Principles and Problems Solutions Manual 541
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Level 3
69. Incident radiation falls on tin, as shown in
Figure 27-13. The threshold frequency of
tin is 1.21015 Hz.
■Figure 27-13
a. What is the threshold wavelength of tin?
cf
c
f
2.5107m
b. What is the work function of tin?
Whf0
(6.631034 J/Hz)(1.21015 Hz)
8.01019 J
c. The incident electromagnetic radiation
has a wavelength of 167 nm. What
is the kinetic energy of the ejected
electrons in eV?
KEmax
h
c
hf0
8.01019 J
3.91019 J
(3.91019 J)
2.4 eV
Thinking Critically
page 744
70. Apply Concepts A helium-neon laser emits
photons with a wavelength of 632.8 nm.
a. Find the energy, in joules, of each
photon emitted by the laser.
Each photon has energy
E
h
c
3.141019 J
b. A typical small laser has a power of
0.5 mW (equivalent to 5104J/s).
How many photons are emitted each
second by the laser?
n
P
E
21015 photons/s
71. Apply Concepts Just barely visible light
with an intensity of 1.51011 W/m2
enters a person’s eye, as shown in
Figure 27-14.
■Figure 27-14
a. If this light shines into the person’s eye
and passes through the person’s pupil,
what is the power, in watts, that enters
the person’s eye?
Power (intensity)(area)
(intensity)(r2)
(1.51011 W/m2)
((3.5103m)2)
5.81016 W
Cornea
550 nm Lens
Pupil
(diameter 7.0 mm)
5104J/s
3.141019 J/photon
(6.631034 Js)(3.00108m/s)
632.8109m
1eV
1.601019 J
(6.631034 J/Hz)(3.00108m/s)
167109m
3.00108m/s
1.21015 Hz
Cathode Anode
167 nm
Chapter 27 continued

b. Use the given wavelength of the inci-
dent light and information provided in
Figure 27-14 to calculate the number of
photons per second entering the eye.
Energy per photon
E
3.621019 J
n
1600 photons/s
72. Make and Use Graphs A student completed
a photoelectric-effect experiment and recorded
the stopping potential as a function of wave-
length, as shown in Table 27-1. The photo-
cell had a sodium cathode. Plot the data
(stopping potential versus frequency) and use
your calculator to draw the best-fit straight
line (regression line). From the slope and
intercept of the line, find the work function,
the threshold wavelength, and the value of
h/q from this experiment. Compare the value
of h/q to the accepted value.
Convert wavelength to frequency and
plot. Determine the best straight line
through the data.
Slope 4.181015 V/Hz
4.181015 J/HzC
The accepted value is
4.141015 J/HzC
From the graph, the threshold frequency
is f04.991014 Hz, which gives a
threshold wavelength of 0
f
c
0
601 nm and a work
function of
Whf0
(6.631034 J/Hz)(4.991014 Hz)
3.311019 J
Writing in Physics
page 744
73. Research the most massive particle for
which interference effects have been seen.
Describe the experiment and how the inter-
ference was created.
As of 2003, the largest is a buckyball, a
C60 molecule. Nano-formed metallic
grids were used as a diffraction grating.
Cumulative Review
page 744
74. The spring in a pogo stick is compressed
15 cm when a child who weighs 400.0 N
stands on it. What is the spring constant of
the spring? (Chapter 14)
F kx
k
F
x
0
4
.0
10
5N
m
3103N/m
75. A marching band sounds flat as it plays on
a very cold day. Why? (Chapter 15)
Answer:The pitch of a wind instrument
depends on the speed of sound in the
air within it. The colder the air, the lower
the speed of sound and the flatter the
pitch of the sound produced.
76. A charge of 8.0107C experiences a force
of 9.0 N when placed 0.02 m from a second
charge. What is the magnitude of the sec-
ond charge? (Chapter 20)
F K
qB
K
Fd
qA
2
qAqB
d2
3.00108m/s
4.991014 Hz
(6.631034 J/Hz)
(1.601019 C)
h
e
5.81016 J/s
3.621019 J/photon
P
E
(6.631034 Js)(3.00108m/s)
550109m
hc
542 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 27 continued
Table 27-1
Stopping Potential v. Wavelength
(nm) V0(eV)
200 4.20
300 2.06
400 1.05
500 0.41
600 0.03

Physics: Principles and Problems Solutions Manual 543
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5107 C
77. A homeowner buys a dozen identical 120-V
light sets. Each light set has 24 bulbs connect-
ed in series, and the resistance of each bulb is
6.0 . Calculate the total load in amperes if
the homeowner operates all the sets from a
single exterior outlet. (Chapter 23)
Itotal 12Iset
(12)
(12)
1.0101 A
78. The force on a 1.2-m wire is 1.1103N.
The wire is perpendicular to Earth’s magnetic
field. How much current is in the wire?
(Chapter 24)
FBIL
I
B
F
L
2101 A
Challenge Problem
page 731
Suppose a nickel with a mass of 5.0 g vibrates up
and down while it is connected to a spring. The
maximum velocity of the nickel during the oscil-
lations is 1.0 cm/s. Assume that the vibrating
nickel models the quantum vibrations of the
electrons within an atom, where the energy of
the vibrations is given by the equation Enhf.
1. Find the maximum kinetic energy of the
vibrating object.
KE mv2
(5.0103kg)(1.0102m/s)2
2.5107J
2. The vibrating object emits energy in
the form of light with a frequency of
5.01014 Hz. If the energy is emitted in
a single step, find the energy lost by the
object.
Ehf
(6.631034 J/Hz)(5.01014 Hz)
3.31019 J
3. Determine the number of equally sized
energy-step reductions that the object
would have to make in order to lose all
of its energy.
7.61011 steps
2.5107J
3.31019 J/step
1
2
1
2
Mass 5.0 g
Maximum velocity 1.0 cm/s
1.1103N
(5105T)(1.2 m)
120 V
(24)(6.0 )
V
24R
(9.0 N)(0.02 m)2
(9.0109Nm2C2)(8.0107C)
Chapter 27 continued


Physics: Principles and Problems Solutions Manual 545
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
28 The Atom
CHAPTER
Practice Problems
28.1 The Bohr Model of
the Atom
pages 747–759
page 757
1. Calculate the energies of the second, third,
and fourth energy levels in the hydrogen
atom.
En
E23.40 eV
E31.51 eV
E40.850 eV
2. Calculate the energy difference between E3
and E2in the hydrogen atom.
EE3E2(13.6 eV)
(13.6 eV)
1
9
1
4
1.89 eV
3. Calculate the energy difference between E4
and E2in the hydrogen atom.
EE4E2(13.6 eV)
(13.6 eV)
1
1
6
1
4
2.55 eV
4. The text shows the solution of the equation
rn
4
h
2
2
K
n
m
2
q2
for n1, the innermost
orbital radius of the hydrogen atom. Note
that with the exception of n2, all factors in
the equation are constants. The value of
r1is 5.31011 m, or 0.053 nm. Use this
information to calculate the radii of the
second, third, and fourth allowable energy
levels in the hydrogen atom.
rnn2k, where k5.31011 m
(We are using kfor the combination of
all the constants in the equation.)
r2(2)2(5.31011 m)
2.11010 m or 0.21 nm
r3(3)2(5.31011 m)
4.81010 m or 0.48 nm
r4(4)2(5.31011 m)
8.51010 m or 0.85 nm
5. The diameter of the hydrogen nucleus is
2.51015 m, and the distance between
the nucleus and the first electron is about
51011 m. If you use a ball with a diame-
ter of 7.5 cm to represent the nucleus, how
far away will the electron be?
0.07
x
5m
x2103m2 km, about 1 mile!
page 758
6. Find the wavelength of the light emitted in
Practice Problems 2 and 3. Which lines in
Figure 28-7 correspond to each transition?
3 to 2
hc
E
6.58107m658 nm
4 to 2
hc
E
4.88107m 488 nm
7. For a particular transition, the energy of a
mercury atom drops from 8.82 eV to 6.67 eV.
a. What is the energy of the photon emit-
ted by the mercury atom?
E8.82 eV 6.67 eV 2.15 eV
(6.631034 Js)(3.00108m/s)
(2.55 eV)(1.601019 J/eV)
(6.631034 Js)(3.00108m/s)
(1.89 eV)(1.601019 J/eV)
51011 m
2.51015 m
1
22
1
42
1
22
1
32
13.6 eV
(4)2
13.6 eV
(3)2
13.6 eV
(2)2
13.6 eV
n2

b. What is the wavelength of the photon
emitted by the mercury atom?
hc
E
5.78107m578 nm
8. The ground state of a helium ion is
54.4 eV. A transition to the ground state
emits a 304-nm photon. What was the
energy of the excited state?
hc
E
, so
E
h
c
123
40
04
en
Vm
nm
4.08 eV
Therefore Eexcited Eground E
54.4 eV 4.08 eV
50.3 eV
Section Review
28.1 The Bohr Model of
the Atom
pages 747–759
page 759
9. Rutherford’s Nuclear Model Summarize
the structure of the atom according to
Rutherford’s nuclear model.
In Rutherford’s nuclear model, all of an
atom’s positive charge and virtually all
of its mass are concentrated in a tiny,
centrally located nucleus around which
negatively charged electrons orbit.
10. Spectra How do the emission spectra of
incandescent solids and atomic gases differ?
In what ways are they similar?
Incandescent solids produce spectra
consisting of a continuous band of
colors, whereas gases produce spectra
made up of a set of discrete lines. All
spectra are created by energy-level
transitions in atoms.
11. Bohr Model Explain how energy is con-
served when an atom absorbs a photon of
light.
The initial sum of the energy of the
electron in the atom plus the energy
of the incident photon equals the final
energy of the electron in the atom.
12. Orbit Radius A helium ion behaves like a
hydrogen atom. The radius of the ion’s low-
est energy level is 0.0265 nm. According to
Bohr’s model, what is the radius of the sec-
ond energy level?
The radius depends on n2, so the
second level would have a radius
four times the first, or 0.106 nm.
13. Absorption Spectrum Explain how the
absorption spectrum of a gas can be deter-
mined. Describe the reasons for the spec-
trum’s appearance.
To obtain an absorption spectrum,
white light is passed through a sample
of gas and then a spectroscope.
Because the gas absorbs specific wave-
lengths, the normally continuous spec-
trum of white light contains dark lines.
14. Bohr Model Hydrogen has been detected
transitioning from the 101st to the 100th
energy levels. What is the radiation’s wave-
length? Where in the electromagnetic spec-
trum is this emission?
EE101 E100
(13.6 eV)
2.68105eV,
hc
E
46.3106nm 4.63 cm, the wave-
lengths indicates the radiation is a
microwave
1240 eVnm
2.68105eV
1
1002
1
1012
(6.631034 Js)(3.00108m/s)
(2.15 eV)(1.601019 J/eV)
546 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued

Physics: Principles and Problems Solutions Manual 547
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
15. Critical Thinking The nucleus of the
hydrogen atom has a radius of about
1.51015 m. If you were to build a model
of the hydrogen atom using a softball (r
5 cm) to represent the nucleus, where
would you locate an electron in the n 1
Bohr orbit? Would it be in your classroom?
The scale is 5 cm 1.51015 m, or
1 cm 3.01016 m. The Bohr radius
is 5.31011 m. In our model this would
be (5.31011/3.01016) 1 cm
1.8105cm, or 1.8 km.That would be
far larger than most schools.
Section Review
28.2 The Quantum Model of
the Atom
pages 760–765
page 765
16. Lasers Which of the lasers in Table 28-1
emits the reddest light (visible light with the
longest wavelength)? Which of the lasers
emit blue light? Which of the lasers emit
beams that are not visible to the human eye?
gallium aluminum arsenide laser in red;
argon ion and indium gallium nitride in
blue. Krypton-fluoride excimer, nitro-
gen, gallium arsenide, neodymium,
and carbon dioxide are not visible to
the human eye.
17. Pumping Atoms Explain whether green
light could be used to pump a red laser.
Why could red light not be used to pump
a green laser?
Yes. Red photons have less energy than
green ones. Red photons do not have
enough energy to put the atoms in
energy levels high enough to enable
them to emit green photons.
18. Bohr Model Limitations Although it was
able to accurately predict the behavior of
hydrogen, in what ways did Bohr’s atomic
model have serious shortcomings?
The Bohr model could not predict the
behavior of any other atom besides
hydrogen. The model also could not
explain why the laws of electromagnet-
ism do not apply within the atom.
19. Quantum Model Explain why the Bohr
model of the atom conflicts with the
Heisenberg uncertainty principle, whereas
the quantum model does not.
The uncertainty principle doesn’t allow
a particle to have a precisely known
position, such as a Bohr orbit.The
quantum model predicts only the proba-
bility that the radius of the electron
orbit will have any given value.
20. Lasers Explain how a laser makes use of
stimulated emission to produce coherent
light.
When a photon strikes an atom in the
excited state, it stimulates the excited
atom to emit a photon of the same ener-
gy and in step with the incident photon.
The incident photon remains unchanged
and these two photons in turn strike
other excited atoms, producing more
and more in-step, coherent light.
21. Laser Light What are the four characteris-
tics of laser light that make it useful?
concentrated, high power; directional;
single wavelength; coherent light
22. Critical Thinking Suppose that an elec-
tron cloud were to get so small that the
atom was almost the size of the nucleus.
Use the Heisenberg uncertainty principle to
explain why this would take a tremendous
amount of energy.
The smaller the electron cloud, the more
precisely we know the position of the
electrons. If a particle’s position is well
known, its momentum must be uncer-
tain. The uncertainty of the momentum
can be large only if momentum itself is
large. Therefore, the kinetic energy of
the electron also must be large, and it
takes lots of energy to do this.
Chapter 28 continued
Chapter Assessment
Concept Mapping
page 770
23. Complete the following concept map using
these terms: energy levels, fixed electron radii,
Bohr model, photon emission and absorption,
energy-level difference.
Mastering Concepts
page 770
24. Describe how Rutherford determined that
the positive charge in an atom is concen-
trated in a tiny region, rather than spread
throughout the atom. (28.1)
He directed a beam of charged parti-
cles at a thin metal sheet and measured
the number of particles deflected at var-
ious angles. The small but significant
number depleted at wide angles indi-
cates a concentrated nucleus.
25. How does the Bohr model explain why the
absorption spectrum of hydrogen contains
exactly the same frequencies as its emission
spectrum? (28.1)
Bohr said the energy of an emitted
photon or an absorbed photon is equal
to the change in energy of the atom,
which can have only specific values.
26. Review the planetary model of the atom.
What are some of the problems with a
planetary model of the atom? (28.1)
As the electrons undergo centripetal
acceleration, they would lose energy
and spiral into the nucleus. In addition,
all atoms should radiate at all wave-
lengths, not discrete wavelengths.
27. Analyze and critique the Bohr model of the
atom. What three assumptions did Bohr
make in developing his model? (28.1)
stationary states (quantized energy
levels), atom emits or absorbs radiation
only when it changes states, angular
momentum is quantized
28. Gas-Discharge Tubes Explain how line
spectra from gas-discharge tubes are pro-
duced. (28.1)
Energy is supplied to the gas, which
causes the electrons to excite and move
to higher energy levels.The electrons
then give off the difference in energy
between energy levels as they drop
back down to a less excited state.The
energy differences between levels corre-
sponds to spectral lines.
29. How does the Bohr model account for the
spectra emitted by atoms? (28.1)
Photon wavelengths are determined by
the difference in energies of allowed
levels as electrons jump inward to
stationary states.
30. Explain why line spectra produced by
hydrogen gas-discharge tubes are different
from those produced by helium gas-dis-
charge tubes. (28.1)
Each element has a different configura-
tion of electrons and energy levels.
31. Lasers A laboratory laser has a power of
only 0.8 mW (8104W). Why does it
seem more powerful than the light of a
100-W lamp? (28.2)
Light is concentrated into a narrow
beam, rather than being spread over a
wide area.
548 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued
has
that
include
with energy
equal to
fixed electron
radii
photon emission
and absorption
energy-level
difference
Bohr model
results
energy level
Physics: Principles and Problems Solutions Manual 549
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
32. A device similar to a laser that emits
microwave radiation is called a maser. What
words likely make up this acronym? (28.2)
Microwave Amplification by Stimulated
Emission of Radiation
33. What properties of laser light led to its use
in light shows? (28.2)
Lasers are directional and single, pure
colors.
Applying Concepts
page 770
34. As the complexity of energy levels changes
from atom to atom, what do you think
happens to the spectra that they produce?
Generally, the spectra become more
complex.
35. Northern Lights The northern lights are
caused by high-energy particles from the
Sun striking atoms high in Earth’s atmos-
phere. If you looked at these lights through
a spectrometer, would you see a continuous
or line spectrum? Explain.
Line spectrum; the light comes from
gas made of specific elements.
36. If white light were emitted from Earth’s sur-
face and observed by someone in space,
would its spectrum appear to be continu-
ous? Explain.
No, as white light passed through
Earth’s atmosphere, certain energies
would be absorbed by the gases com-
posing the atmosphere. Its spectrum,
therefore, would have black lines on it.
37. Is money a good example of quantization?
Is water? Explain.
Yes. Money comes in only certain dis-
crete values. No, water seems to come
in any possible quantity.
38. Refer to Figure 28-21. A photon with ener-
gy of 6.2 eV enters a mercury atom in the
ground state. Will it be absorbed by the
atom? Explain.
■ Figure 28-21
No, it takes 5.43 eV to raise the electron
to the E4level and 6.67 eV to E5. The
atom can absorb only photons that
have exactly the right energy.
39. A certain atom has four energy levels, with
E4being the highest and E1being the lowest.
If the atom can make transitions between
any two levels, how many spectral lines can
the atom emit? Which transition produces
the photon with the highest energy?
Six lines are possible. E4→E1has the
largest photon energy.
40. A photon is emitted when an electron in an
excited hydrogen atom drops through ener-
gy levels. What is the maximum energy that
the photon can have? If this same amount
of energy were given to the atom in the
ground state, what would happen?
The maximum energy is 13.6 eV. This
is also the ionization energy for hydro-
gen. The electron would have enough
energy to leave the nucleus.
41. Compare the quantum mechanical theory
of the atom with the Bohr model.
The Bohr model has fixed orbital radii.
The present model gives a probability
of finding an electron at a location.The
Bohr model allows for calculation of
only hydrogen atoms. The present
model can be used for all elements.
Ionization (0.00)
E9 (1.56)
E8 (1.57)
E7 (2.48)
E1 (10.38)
E6 (2.68)
E5 (3.71)
E4 (4.95)
E3 (5.52)
E2 (5.74)
10.38
8.82
8.81
7.90
7.70
6.67
5.43
4.86
0.00
4.64
Energy level (eV)
Energy above ground state (eV)
Energy Level Diagram for a Mercury Atom
Chapter 28 continued

42. Given a red, green, and blue laser, which
produces photons with the highest energy?
Blue light has a higher frequency and
therefore, higher energy.
Mastering Problems
28.1 The Bohr Model of the Atom
page 771
Level 1
43. A calcium atom drops from 5.16 eV above
the ground state to 2.93 eV above the
ground state. What is the wavelength of the
photon emitted?
Ehf
h
c
hc
E
556 nm
44. A calcium atom in an excited state, E2, has
an energy level 2.93 eV above the ground
state. A photon of energy 1.20 eV strikes the
calcium atom and is absorbed by it. To
what energy level is the calcium atom
raised? Refer to Figure 28-22.
■ Figure 28-22
2.93 eV 1.20 eV 4.13 eV E3
45. A calcium atom is in an excited state at the
E6energy level. How much energy is
released when the atom drops down to the
E2energy level? Refer to Figure 28-22.
E6E25.16 eV 2.93 eV 2.23 eV
46. A photon of orange light with a wavelength
of 6.00102nm enters a calcium atom in
the E6excited state and ionizes the atom.
What kinetic energy will the electron have
as it is ejected from the atom?
E
h
c
3.314 J 3.314 J
2.07 eV
Energy needed to ionize 6.08 eV
E65.16 eV
0.92 eV
Photon energy ionization energy
kinetic energy
2.07 eV 0.92 eV 1.15 eV
Level 2
47. Calculate the energy associated with the E7
and the E2energy levels of the hydrogen
atom.
E713.6 eV
13.6 eV
0.278 eV
E213.6 eV
13.6 eV
3.40 eV
48. Calculate the difference in energy levels in
the previous problem.
E713.6 eV
13.6 eV
0.278 eV
1
72
1
n2
1
22
1
n2
1
72
1
n2
1eV
1.601019 J
(6.631034 J/Hz)(3.00108m/s)
6.00107m
E10
E9
E8
E7
E6
E5
E4
E3
E2
E1
6.08 (Ionization)
5.58
5.49
5.32
0
Energy above ground state (eV)
1
2
3
4
5
6
5.18
5.16
4.62
4.55
4.13
2.93
Energy Level Diagram for a Calcium Atom
1240 eVnm
5.16 eV 2.93 eV
550 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued

Physics: Principles and Problems Solutions Manual 551
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
E213.6 eV
13.6 eV
3.40 eV
E7E20.278 eV (3.40 eV)
3.12 eV
Refer to Figure 28-21 for Problems 49 and 50.
49. A mercury atom is in an excited state at the
E6energy level.
a. How much energy would be needed to
ionize the atom?
E67.70 eV
10.38 eV 7.70 eV 2.68 eV
b. How much energy would be released
if the atom dropped down to the
E2energy level instead?
E24.64 eV
7.70 eV 4.64 eV 3.06 eV
50. A mercury atom in an excited state has an
energy of 4.95 eV. It absorbs a photon
that raises it to the next-higher energy level.
What is the energy and the frequency of the
photon?
E5E43.71 eV (4.95 eV)
1.24 eV
Ehf
f
E
h
2.991014 Hz
51. What energies are associated with a hydro-
gen atom’s energy levels of E2, E3, E4, E5,
and E6?
E23.40 eV
E31.51 eV
E40.850 eV
E50.544 eV
E60.378 eV
52. Using the values calculated in problem 51,
calculate the following energy differences.
a. E6E5
(0.378 eV) (0.544 eV) 0.166 eV
b. E6E3
(0.378 eV) (1.51 eV) 1.13 eV
c. E4E2
(0.850 eV) (3.40 eV) 2.55 eV
d. E5E2
(0.544 eV) (3.40 eV) 2.86 eV
e. E5E3
(0.544 eV) (1.51 eV) 0.97 eV
53. Use the values from problem 52 to deter-
mine the frequencies of the photons emit-
ted when an electron in a hydrogen atom
makes the energy level changes listed.
a. Ehf, so f
E
h
hfE6E50.166 eV
f
4.011013 Hz
b. hfE6E31.13 eV
f
2.731014 Hz
c. hfE4E22.55 eV
f
6.151014 Hz
d. hfE6E32.86 eV
f
6.901014 Hz
e. hfE6E30.97 eV
f
2.31014 Hz
54. Determine the wavelengths of the photons
having the frequencies that you calculated
in problem 53.
(0.97 eV)(1.601019 J/eV)
6.631034 J/Hz
(2.86 eV)(1.601019 J/eV)
6.631034 J/Hz
(2.55 eV)(1.601019 J/eV)
6.631034 J/Hz
(1.13 eV)(1.601019 J/eV)
6.631034 J/Hz
(0.166 eV)(1.601019 J/eV)
6.631034 J/Hz
13.6 eV
(6)2
13.6 eV
(5)2
13.6 eV
(4)2
13.6 eV
(3)2
13.6 eV
(2)2
13.6 eV
n2
1.24 eV
1.60
e
1
V
019 J
6.631034 Js
1
22
1
n2
Chapter 28 continued

a. cf
c
f
7.48106m7480 nm
b.
c
f
1.10106m1.10103nm
c.
c
f
4.88107m488 nm
d.
c
f
4.35106m435 nm
e.
c
f
1.3106m1.3103nm
Level 3
55. A hydrogen atom emits a photon with a wavelength of 94.3 nm when its falls to
the ground state. From what energy level did the electron fall?
cf
c
3.181015 Hz
EnE1(6.6261034 J/Hz)
(3.181015 Hz)
2.111018 J
E2.111018 J
EnE1E
2.171018 J(2.111018 J)
61020 J
61020 J
n236
n6
56. For a hydrogen atom in the n3 Bohr orbital, find the following.
a. the radius of the orbital
r
4.771010 m
(6.631034 Js)2(3)2
42(9.00109Nm2/C2)(9.111031 kg)(1.601019 C)2
h2n2
42Kmq2
2.171018 J
n2
3.00108m/s
9.43108m
3.00108m/s
2.31014 Hz
3.00108m/s
6.901014 Hz
3.00108m/s
6.151014 Hz
3.00108m/s
2.731014 Hz
3.00108m/s
4.011013 Hz
552 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued

Physics: Principles and Problems Solutions Manual 553
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. the electric force acting between the
proton and the electron
F
1.01109N
c. the centripetal acceleration of the
electron
Fma
a
m
F
1.111021 m/s2
d. the orbital speed of the electron
(Compare this speed with the speed
of light.)
a
var
(1.11
1021 m
/s2)(4.
7710
10 m
)
7.28105m/s, or 0.24% of c
28.2 The Quantum Model of the Atom
page 771
Level 1
57. CD Players Gallium arsenide lasers are
commonly used in CD players. If such a
laser emits at 840 nm, what is the difference
in eV between the two lasing energy levels?
cf
f
c
3
8
.4
00
0
1
10
0
8
9
m
m
/s
3.571014 Hz
Ehf
1.5 eV
58. A GaInNi laser lases between energy levels
that are separated by 2.90 eV.
a. What wavelength of light does it emit?
E
h
c
hc
E
122
4.
0
90
eV
e
V
nm
428 nm
b. In what part of the spectrum is this light?
blue
Level 2
59. A carbon-dioxide laser emits very high-
power infrared radiation. What is the energy
difference in eV between the two lasing
energy levels? Consult Table 28-1.
cf
f
c
2.831013 Hz
Ehf
0.117 eV
60. The power in a laser beam is equal to the
energy of each photon times the number of
photons per second that are emitted.
a. If you want a laser at 840 nm to have
the same power as one at 427 nm, how
many times more photons per second
are needed?
Since Ehf
h
c
, the ratio of energy
in each photon is
4
82
47
0
0.508.
Therefore, the ratio of number of
photons per second is
0.5
108
1.97
b. Find the number of photons per second
in a 5.0-mW 840-nm laser.
P(photons/s)(E/photon) nE so
nP/E.
Calculate the energy of the photon
in joules.
E
h
c
2.41019 J;
So, n
2.11016 photons/s
5.0103J/s
2.41019 J/photon
(1240 eVnm)(1.601019 J/eV)
840 nm
(6.631034 J/Hz)(2.831013 Hz)
1.601019 J/eV
3.00108m/s
10,600109m
(6.631034 J/Hz)(3.571014 Hz)
1.601019 J/eV
v2
r
1.01109N
9.111031 kg
(9.00109Nm2/C2)(1.601019 C)2
(4.771010 m)2
Kq2
r2
Chapter 28 continued

Level 3
61. HeNe Lasers The HeNe lasers used in many classrooms can be made to lase at
three wavelengths: 632.8 nm, 543.4 nm, and 1152.3 nm.
a. Find the difference in energy between the two states involved in the genera-
tion of each wavelength.
E
h
c
, so E;
substituting the three values of gives 1.96 eV, 2.28 eV, and 1.08 eV
b. Identify the color of each wavelength.
red, green, and infrared, respectively
Mixed Review
page 772
Level 1
62. A photon with an energy of 14.0 eV enters a hydrogen atom in the ground state
and ionizes it. With what kinetic energy will the electron be ejected from the
atom?
It takes 13.6 eV to ionize the atom, so 14.0 eV 13.6 eV 0.4 eV kinetic
energy.
63. Calculate the radius of the orbital associated with the energy levels E5and E6of
the hydrogen atom.
r5
1.33109m
r6
1.91109m
Level 2
64. A hydrogen atom is in the n2 level.
a. If a photon with a wavelength of 332 nm strikes the atom, show that the
atom will be ionized.
E23.40 eV, so 3.40 eV needed to ionize from
this level.
Ehf
h
c
5.991019 J
3.74 eV
Yes, the atom is ionized.
(6.631034 J/Hz)(3.00108m/s)
332109m
13.6 eV
(2)2
13.6 eV
n2
(6.631034 Js)2(6)2
42(9.00109Nm2/C2)(9.111031 kg)(1.601019 C)2
(6.631034 Js)2(5)2
42(9.00109Nm2/C2)(9.111031 kg)(1.601019 C)2
h2n2
42Kmq2
1240 eVnm
554 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued

Physics: Principles and Problems Solutions Manual 555
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. When the atom is ionized, assume that
the electron receives the excess energy
from the ionization. What will be the
kinetic energy of the electron in joules?
3.74 eV 3.40 eV 0.340 eV
5.41020 J
Level 3
65. A beam of electrons is directed onto a sam-
ple of atomic hydrogen gas. What minimum
energy of the electrons is needed for the
hydrogen atoms to emit the red light pro-
duced when the atom goes from the n3
to the n2 state?
There must be enough energy to transi-
tion a stable hydrogen atom to the
n3 state.
EE3E1
(13.6 eV)
(13.6 eV)
98
12.1 eV
66. The most precise spectroscopy experiments
use “two-photon” techniques. Two photons
with identical wavelengths are directed at
the target atoms from opposite directions.
Each photon has half the energy needed to
excite the atoms from the ground state to
the desired energy level. What laser wave-
length would be needed to make a precise
study of the energy difference between n1
and n2 in hydrogen?
EE2E1
(13.6 eV)
(13.6 eV)
3
4
10.2 eV
For each laser,
243 nm
Thinking Critically
page 772
67. Apply Concepts The result of projecting the
spectrum of a high-pressure mercury vapor
lamp onto a wall in a dark room is shown in
Figure 28-23. What are the differences in
energy levels for each of the three visible
lines?
■ Figure 28-23
436 nm (2.84 eV) from E6to E3since
124
43
06
en
Vm
nm
284 eV; see Fig 28-21 to
find energy levels.
546 nm (2.27 eV) from E6to E4
579 nm (2.14 eV) from E8to E5
68. Interpret Scientific Illustrations After the
emission of the visible photons described in
problem 67, the mercury atom continues to
emit photons until it reaches the ground
state. From an inspection of Figure 28-21,
determine whether or not any of these pho-
tons would be visible. Explain.
No. The three highest energy lines leave
the atom in states at least 4.64 eV above
the ground state. A photon with this
energy has a wavelength of 267 nm in
the ultraviolet.The change from E4to E2
involves an energy change of only 0.79
eV, resulting in light with a wavelength
of 1570 nm in the infrared.
69. Anaylze and Conclude A positronium atom
consists of an electron and its antimatter rela-
tive, the positron, bound together. Although the
lifetime of this “atom” is very short—on the
average it lives one-seventh of a microsecond—
its energy levels can be measured. The Bohr
model can be used to calculate energies with
the mass of the electron replaced by one-half its
mass. Describe how the radii of the orbits and
the energy of each level would be affected.
436 nm 546 nm 579 nm
1240 eVnm
10.2
2eV
hc
2
E
1
12
1
22
1
12
1
32
Chapter 28 continued

What would be the wavelength of the E2to E1
transition?
The radii would be twice as large
because mappears in the denominator
of the equation. The energies would be
half as large because mappears in the
numerator.Therefore, the wavelengths
would be twice as large. Thus, the light
emitted from E2to E1would be
(2)(121 nm) 242 nm.
Writing in Physics
page 772
70. Do research on the history of models of the
atom. Briefly describe each model and iden-
tify its strengths and weaknesses.
Students should describe the “raisin
pudding”model, a classical planetary
model, the Bohr model, and the quantum
model.The first explains how atoms can
have electrons and mass, but fails to
describe the results of Rutherford’s
experiments.The planetary explains
electrons and Rutherford’s results, but is
unstable and would collapse in about 1
ns. Bohr’s explains known spectra and
fits Rutherford’s nuclear model, but has
unexplained assumptions and fails the
uncertainty principle, as well as being
unable to describe atoms with more
than one electron.The quantum model
can explain all known facts, but is hard
to visualize and requires computers to
solve the equations.
71. Green laser pointers emit light with a wave-
length of 532 nm. Do research on the type
of laser used in this type of pointer and
describe its operation. Indicate whether
the laser is pulsed or continuous.
It uses a pulsed Nd laser at 1064 nm.
The IR is put into a “frequency doubling”
crystal. Light with half that wavelength,
or 532 nm, results.
Cumulative Review
page 772
72. The force on a test charge of 3.00107C
is 0.027 N. What is the electric field strength
at the position of the test charge?
(Chapter 21)
E
q
F
9.0104N/C
73. A technician needs a 4-resistor but only has
1-resistors of that value. Is there a way to
combine what she has? Explain. (Chapter 23)
Yes. Put four 1resistors in series.
RTR1R2R3R4
74. A 1.0-m–long wire is moved at right angles
to Earth’s magnetic field where the magnetic
induction is 5.0105T at a speed of
4.0 m/s. What is the EMF induced in the
wire? (Chapter 25)
EMF BLv
(5.0105T)(1.0 m)(4.0 m/s)
2.0104V0.20 mV
75. The electrons in a beam move at
2.8108m/s in an electric field of
1.4104N/C. What value must the magnetic
field have if the electrons pass through the
crossed fields undeflected? (Chapter 26)
v
B
E
B
E
v
2
1
.
.
8
4
1
1
0
08
4
m
N/
/
C
s
5.0105T5.0101T
76. Consider the modifications that J. J.
Thomson would need to make to his cath-
ode-ray tube so that it could accelerate pro-
tons (rather than electrons), then answer
the following questions. (Chapter 26)
a. To select particles of the same velocity,
would the ratio E/B have to be changed?
Explain.
No; V
B
E
, so ratio is same for a
given V.
b. For the deflection caused by the mag-
netic field alone to remain the same,
would the B field have to be made
smaller or larger? Explain.
For magnetic field only, Bqv mv2
r
0.027 N
3.00107C
556 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 28 continued

Physics: Principles and Problems Solutions Manual 557
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
and r
m
qB
v
for a bigger mass, B
must be bigger to keep v constant.
77. The stopping potential needed to return all
the electrons ejected from a metal is 7.3 V.
What is the maximum kinetic energy of the
electrons in joules? (Chapter 27)
KE (7.3 eV)
1.60
11
e
0
V
19 J
1.21018 J
Challenge Problem
page 759
Although the Bohr atomic model accurately
explained the behavior of a hydrogen atom, it
was unable to explain the behavior of any other
atom. Verify the limitations of the Bohr model by
analyzing an electron transition in a neon atom.
Unlike a hydrogen atom, a neon atom has ten
electrons. One of these electrons makes a transi-
tion between the n5 and the n3 energy
states, emitting a photon in the process.
1. Assuming that the neon atom’s electron can
be treated as an electron in a hydrogen
atom, what photon energy does the Bohr
model predict?
EEiEf(13.6 eV)
0.967 eV
2. Assuming that the neon atom’s electron can
be treated as an electron in a hydrogen
atom, what photon wavelength does the
Bohr model predict?
hc
E
12
0
4
.9
06
e
7
V
e
n
Vm
1280 nm
3. The actual wavelength of the photon emit-
ted during the transition is 632.8 nm. What
is the percent error of the Bohr model’s pre-
diction of photon wavelength?
Percent error
100
100 103%
The calculated wavelength is roughly
twice as large as the actual wavelength.
632.8 nm 1280 nm
6328 nm
Accepted value Predicted value
Accepted value
1
32
1
52
Chapter 28 continued


Physics: Principles and Problems Solutions Manual 559
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
29 Solid-State Electronics
CHAPTER
Practice Problems
29.1 Conduction in Solids
pages 775–783
page 778
1. Zinc, with a density of 7.13 g/cm3and an atomic mass of 65.37 g/mol, has
two free electrons per atom. How many free electrons are there in each cubic
centimeter of zinc?
free e/cm3
1.311023 free e/cm3
2. Silver has 1 free electron per atom. Use Appendix D and determine the number
of free electrons in 1 cm3of silver.
free e/cm3
5.851022 free e/cm3
3. Gold has 1 free electron per atom. Use Appendix D and determine the number
of free electrons in 1 cm3of gold.
free e/cm3
5.901022 free e/cm3
4. Aluminum has 3 free electrons per atom. Use Appendix D and determine the
number of free electrons in 1 cm3of aluminum.
free e/cm3
1.811023 free e/cm3
5. The tip of the Washington Monument was made of 2835 g of aluminum because
it was a rare and costly metal in the 1800s. Use problem 4 and determine the
number of free electrons in the tip of the Washington Monument.
free e(1.811023 free e/cm3)
1.901026 free ein the tip
page 780
6. In pure germanium, which has a density of 5.23 g/cm3and an atomic mass of
72.6 g/mol, there are 2.251013 free electrons/cm3at room temperature. How
many free electrons are there per atom?
2835 g
2.70 g/cm3
2.70 g
cm3
1 mol
26.982 g
6.021023 atoms
mol
3 e
atom
19.32 g
cm3
1 mol
196.97 g
6.021023 atoms
mol
1 free e
atom
10.49 g
cm3
1 mol
107.87 g
6.021023 atoms
mol
1 free e
atom
7.13 g
cm3
1 mol
65.37 g
6.021023 atoms
mol
2 free e
atom

free e/atom
5.191010 free e/atom
7. At 200.0 K, silicon has 1.89105free electrons/cm3. How many free electrons are
there per atom at this temperature? What does this temperature represent on the
Celsius scale?
free e/atom
3.781018 free e/atom
TKTC273°
TCTK273°
200.0° 273°
73°C
8. At 100.0 K, silicon has 9.231010 free electrons/cm3. How many free electrons
are there per atom at this temperature? What does this temperature represent on
the Celsius scale?
free e/atom
1.851032 free e/atom
TKTC273°
TCTK273°
100.0° 273°
173°C
9. At 200.0 K, germanium has 1.161010 free electrons/cm3. How many free
electrons are there per atom at this temperature?
free e/atom
2.671013 free e/atom
10. At 100.0 K, germanium has 3.47 free electrons/cm3. How many free electrons are
there per atom at this temperature?
free e/atom
8.001023 free e/atom
page 783
11. If you wanted to have 1104as many electrons from arsenic doping as thermally
free electrons in silicon at room temperature, how many arsenic atoms should
there be per silicon atom?
From Example Problem 3 you know that there are 4.991022
Si atoms/cm3,1.451010 free e/cm3in Si, and 1 free e/As atom.
3.47 free e
cm3
cm3
5.23 g
72.6 g
1 mol
1 mol
6.021023 atoms
1.161010 free e
cm3
cm3
5.23 g
72.6 g
1 mol
1 mol
6.021023 atoms
9.231010 free e
cm3
cm3
2.33 g
28.09 g
1 mol
1 mol
6.021023 atoms
1.89105 free e
cm3
cm3
2.33 g
28.09 g
1 mol
1 mol
6.021023 atoms
2.251013 free e
cm3
cm3
5.23 g
72.6 g
1 mol
1 mol
6.021023 atoms
560 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 561
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
efrom As (1104)(free efrom Si)
However, the ratio of atoms is needed, not electrons.
As atoms
free efrom Si (Si atoms)
Substituting into the expression for As atoms yields
As atoms
2.91109
12. If you wanted to have 5103as many electrons from arsenic doping as thermally
free electrons in the germanium semiconductor described in problem 6, how many
arsenic atoms should there be per germanium atom?
Using the solution in problem 11 as a go by
From problem 6, free e/cm3Ge 2.25103
From Example Problem 3, free e/atom As 1
Ge atoms/cm3
4.341022 atoms/cm3
2.59106
13. Germanium at 400.0 K, has 1.131015 thermally liberated carriers/cm3. If it is
doped with 1 As atom per 1 million Ge atoms, what is the ratio of doped carriers
to thermal carriers?
Use the solution to problem 12 as a starting point.
(free e/atom As)
(1)
38.4
4.341022
1.131015
1
1106
Ge atoms/cm3
free e/cm3Ge
As atoms
Ge atoms
doped e
Ge e
do
G
p
e
ed
e
e
fr
G
e
e
e
a
e
to
m
/c
s
m
/c
3
m
G
3
e
free e/atom As
As atoms
Ge atoms
(5103)
2
4.
.2
35
4
1
10
0
1
2
3
2
1
As atoms
Ge atoms
5.23 g
cm3
1 mol
72.6 g
6.021023 atoms
1 mol
(5103)
fG
re
e
ea
e
t
om
/cm
s/c
3
m
G3
e
free e/atom As
As atoms
Ge atoms
(1104)
1
4.
.4
95
9
1
10
0
1
2
0
2
1
(1104)
fS
re
ie
at
e
o
m
/c
s
m
/c
3
m
S
3i
free e/atom As
As atoms
Si atoms
(1104)(Si atoms)
fS
re
ie
at
e
o
m
/c
s
m
/c
3
m
S
3i
free e/atom As
free e/cm3Si
Si atoms/cm3
(1104)(free efrom Si)
free e/atom As
efrom As
free e/atom As
Chapter 29 continued

14. Silicon at 400.0 K, has 4.541012 thermally liberated carriers/cm3. If it is doped
with 1 As atom per 1 million Si, what is the ratio of doped carriers to thermal
carriers?
Using the solution problem 13 as a go by
(free e/atom As)
(1)
1.10104
15. Based on problem 14, draw a conclusion about the behavior of germanium
devices as compared to silicon devices at temperatures in excess of the boiling
point of water.
Germanium devices do not work well at such temperatures because the
ratio of doped carriers to thermal carriers is small enough that temperature
has too much influence on conductivity. Silicon is much better.
Section Review
29.1 Conduction in Solids
pages 775–783
page 783
16. Carrier Mobility In which type of material, a conductor, a semiconductor, or an
insulator, are electrons most likely to remain with the same atom?
insulator
17. Semiconductors If the temperature increases, the number of free electrons in an
intrinsic semiconductor increases. For example, raising the temperature by 8°C
doubles the number of free electrons in silicon. Is it more likely that an intrinsic
semiconductor or a doped semiconductor will have a conductivity that depends
on temperature? Explain.
An intrinsic one because all its conduction is from thermally freed elec-
trons, whereas the doped semiconductor depends on the charges from
the dopants, which depend little on temperature.
18. Insulator or Conductor? Silicon dioxide is widely used in the manufacture of
solid-state devices. Its energy-band diagram shows a gap of 9 eV between the
valence band and the conduction band. Is it more useful as an insulator or a
conductor?
insulator
19. Conductor or Insulator? Magnesium oxide has a forbidden gap of 8 eV. Is this
material a conductor, an insulator, or a semiconductor?
insulator
4.991022
4.541012
1
1106
Si atoms/cm3
free e/cm3Si
As atoms
Si atoms
doped e
Si e
562 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 563
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
20. Intrinsic and Extrinsic Semiconductors
You are designing an integrated circuit
using a single crystal of silicon. You want to
have a region with relatively good insulat-
ing properties. Should you dope this region
or leave it as an intrinsic semiconductor?
Leave it.
21. Critical Thinking Silicon produces a dou-
bling of thermally liberated carriers for
every 8°C increase in temperature, and ger-
manium produces a doubling of thermally
liberated carriers for every 13°C increase. It
would seem that germanium would be
superior for high-temperature applications,
but the opposite is true. Explain.
Even though rate of change for thermal
carrier production is greater for silicon,
at any given temperature silicon shows
far fewer thermally liberated carriers.
Practice Problems
29.2 Electronic Devices
pages 784–789
page 786
22. What battery voltage would be needed to
produce a current of 2.5 mA in the diode in
Example Problem 4?
1.7 V
Using Fig. 29-10, the diode has
Vd0.50 V at 2.5 mA
Vb IR Vd
(0.0025 A)(470 ) 0.50 V
1.7 V
23. What battery voltage would be needed to
produce a current of 2.5 mA if another
identical diode were added in series with
the diode in Example Problem 4?
VbIR VdVd
(0.0025 A)(470 ) 0.50 V 0.50 V
2.2 V
24. Describe how the diodes in the previous
problem should be connected.
The anode of one connects to the cath-
ode of the other and then the uncon-
nected anode must be connected to the
positive side of the circuit.
25. Describe what would happen in problem
23 if the diodes were connected in series
but with improper polarity.
It would be impossible to obtain 2.5 mA
of current with any reasonable power
supply voltage because one of the
diodes would be reverse-biased.
26. A germanium diode has a voltage drop of
0.40 V when 12 mA passes through it. If a
470-resistor is used in series, what battery
voltage is needed?
6.0 V
VbIR Vd
(0.012 A)(470 ) 0.40 V
6.0 V
Section Review
29.2 Electronic Devices
pages 784–789
page 789
27. Transistor Circuit The emitter current in a
transistor circuit is always equal to the sum
of the base current and the collector cur-
rent: IEIBIC. If the current gain from
the base to the collector is 95, what is the
ratio of emitter current to base current?
Gain 95
IEIBIC
Divide both sides by IB.
1 1 95 96
96 to 1
IC
IB
IE
IB
IC
IB
Chapter 29 continued
28. Diode Voltage Drop If the diode charac-
terized in Figure 29-10 is forward-biased by
a battery and a series resistor so that there is
more than 10 mA of current, the voltage
drop is always about 0.70 V. Assume that
the battery voltage is increased by 1 V.
a. By how much does the voltage across
the diode or the voltage across the resis-
tor increase?
Because the voltage across the
diode is always 0.70 V, the voltage
across the resistor increases by 1 V.
b. By how much does the current through
the resistor increase?
The current increases by I .
29. Diode Resistance Compare the resistance
of a pn-junction diode when it is forward-
biased and when it is reverse-biased.
It conducts much better when forward-
biased, so its resistance is much small-
er when forward-biased than when
reverse-biased.
30. Diode Polarity In a light-emitting diode,
which terminal should be connected to the
p-end to make the diode light?
The LED must be forward-biased, so the
positive terminal must be connected to
the p-end.
31. Current Gain The base current in a transis-
tor circuit measures 55 A and the collector
current measures 6.6 mA. What is the cur-
rent gain from base to collector?
Gain 120
32. Critical Thinking Could you replace an
npn-transistor with two separate diodes con-
nected by their p-terminals? Explain.
No, the p-region of an npn-transistor
must be thin enough to allow electrons
to pass through the base to the collector.
Chapter Assessment
Concept Mapping
page 794
33. Complete the concept map using the fol-
lowing terms: transistor, silicon diode, emits
light, conducts both ways.
Mastering Concepts
page 794
34. How do the energy levels in a crystal of an
element differ from the energy levels in a
single atom of that element? (29.1)
The energy levels of a single atom have
discrete and unique values.The energy
levels in a crystal have a small range
around the values found in a single
atom.
35. Why does heating a semiconductor increase
its conductivity? (29.1)
A higher temperature gives electrons
additional energy, permitting more elec-
trons to reach the conductive band.
36. What is the main current carrier in a p-type
semiconductor? (29.1)
positively-charged holes
37. An ohmmeter is an instrument that places a
potential difference across a device to be
tested, measures the current, and displays
the resistance of the device. If you connect
an ohmmeter across a diode, will the cur-
rent you measure depend on which end of
the diode was connected to the positive ter-
minal of the ohmmeter? Explain. (29.2)
Yes, one way you forward-bias the
diode; the other way you reverse-bias it.
6.6 mA
0.055 mA
IC
IB
1 V
R
564 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued
LED
silicon
diode
copper
wire transistor
emits
light
conducts
one way
conducts
both ways amplifies
Circuit
Components
Physics: Principles and Problems Solutions Manual 565
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
38. What is the significance of the arrowhead at
the emitter in a transistor circuit symbol?
(29.2)
The arrowhead shows the direction of
the conventional current.
39. Describe the structure of a forward-biased
diode, and explain how it works. (29.2)
A forward-biased diode has a p-type
and an n-type semiconductor layer,
connected to wires on either end
through metal caps.The p-type layer is
connected to the positive terminal of
the battery. New holes are created in the
p-type layer and those holes move
toward the boundary between the two
semiconductors. New electrons are
added to the n-type layer, and those
electrons move toward the boundary
between the two semiconductors. As
the holes and electrons combine, the
circuit is completed and there is cur-
rent. The current direction is from the p-
type semiconductor to the n-type.
Applying Concepts
pages 794–795
40. For the energy-band diagrams shown in
Figure 29-16, which one represents a mate-
rial with an extremely high resistance?
abc
■Figure 29-16
41. For the energy-band diagrams shown in
Figure 29-16, which have half-full conduc-
tion bands?
a
42. For the energy-band diagrams shown
in Figure 29-16, which ones represent
semiconductors?
b
43. The resistance of graphite decreases as tem-
perature rises. Does graphite conduct elec-
tricity more like copper or more like silicon
does?
more like Si
44. Which of the following materials would
make a better insulator: one with a forbidden
gap 8-eV wide, one with a forbidden gap
3-eV wide, or one with no forbidden gap?
one with an 8-eV gap
45. Consider atoms of the three materials in
problem 44. From which material would it
be most difficult to remove an electron?
one with an 8-eV gap
46. State whether the bulb in each of the circuits
of Figure 29-17 (a, b, and c) is lighted.
abc
■Figure 29-17
circuit a: no, circuit b: no, circuit c: yes
47. In the circuit shown in Figure 29-18, state
whether lamp L1, lamp L2, both, or neither
is lighted.
■Figure 29-18
L1is on, L2is off.
48. Use the periodic table to determine which
of the following elements could be added
to germanium to make a p-type semicon-
ductor: B, C, N, P, Si, Al, Ge, Ga, As, In, Sn,
or Sb.
B, Al, Ga, In
L1L2
Chapter 29 continued
49. Does an ohmmeter show a higher resistance
when a pn-junction diode is forward-biased
or reverse-biased?
The diode will have a lower resistance
when it is forward-biased.
50. If the ohmmeter in problem 49 shows the
lower resistance, is the ohmmeter lead on
the arrow side of the diode at a higher or
lower potential than the lead connected to
the other side?
higher potential, more positive
51. If you dope pure germanium with gallium
alone, do you produce a resistor, a diode, or
a transistor?
You make a resistor because there is no
junction.
52. Draw the time-versus-amplitude waveform
for point A in Figure 29-19a assuming
an input AC waveform as shown in
Figure 29-19b.
a
b
■Figure 29-19
Point A is negative with respect to
ground and the graph shows that the
alternating polarity of the input waveform
has been rectified to a negative polarity.
Mastering Problems
29.1 Conduction in Solids
page 795
Level 1
53. How many free electrons exist in a cubic cen-
timeter of sodium? Its density is 0.971 g/cm3,
its atomic mass is 22.99 g/mol, and there is
1 free electron per atom.
free e/cm3
2.541022 free e/cm3
Level 2
54. At a temperature of 0°C, thermal energy
frees 1.55109e/cm3in pure silicon. The
density of silicon is 2.33 g/cm3, and the
atomic mass of silicon is 28.09 g/mol. What
is the fraction of atoms that have free
electrons?
1.55109e/cm3
3.221013 atom/e
29.2 Electronic Devices
page 795
Level 1
55. LED The potential drop across a glowing
LED is about 1.2 V. In Figure 29-20, the
potential drop across the resistor is the dif-
ference between the battery voltage and the
LED’s potential drop. What is the current
through each of the following?
■Figure 29-20
a. the LED
VbIR Vd
1.2 V
Battery
V 6.0 V
R 240
LED
mol
28.09 g
2.33 g
cm3
6.021023 atoms
mol
mol
22.99 g
0.971 g
cm3
6.021023 atoms
mol
1 e
atom
Time
Output Voltage
Voltage
A
Time
AC voltage
566 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 567
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
I
2.0101mA
b. the resistor
2.0101mA
56. Jon wants to raise the current through the
LED in problem 55 up to 3.0101mA so
that it glows brighter. Assume that the
potential drop across the LED is still 1.2 V.
What resistor should be used?
R 160
Level 2
57. Diode A silicon diode with I/V characteris-
tics, as shown in Figure 29-10, is connected
to a battery through a 270-resistor. The
battery forward-biases the diode, and the
diode current is 15 mA. What is the battery
voltage?
Vb IR Vd
Vd0.70 V (from figure)
Vb(15 mA)(270 ) 0.70 V
4.8 V
Level 3
58. Assume that the switch shown in
Figure 29-21 is off.
■Figure 29-21
a. Determine the base current.
by inspection, the base circuit is off,
so it is zero
b. Determine the collector current.
by definition: when the base current
is zero, so is the collector current
c. Determine the voltmeter reading.
15 V
With no current flow, the drop
across the collector resistor is zero
and there is a 15-V drop across the
transistor.
59. Assume that the switch shown in Figure 29-
21 is on, and that there is a 0.70-V drop
across the base-emitter junction and a cur-
rent gain from base to collector of 220.
a. Determine the base current.
I
2.3105A
b. Determine the collector current.
220
IC220IB
(220)(2.3105A)
5.1103A
c. Determine the voltmeter reading.
Find the drop across the 1500
resistor:
Vresistor IR
(5.1103A)(1500 )
7.7 V
The meter is connected across the
transistor,
Vbattery Vresistor Vtransistor
Vmeter Vtransistor
Vbattery Vresistor
15 V 7.7 V
7.3 V
IC
IB
3.5 V 0.70 V
120,000
V
R
120,000
1500
15 V
3.5 V
A
A
V
6.0 V 1.2 V
3.0101mA
VbVd
I
6.0 V 1.2 V
240
VbVd
R
Chapter 29 continued
Mixed Review
pages 795–796
Level 1
60. The forbidden gap in silicon is 1.1 eV.
Electromagnetic waves striking the silicon
cause electrons to move from the valence
band to the conduction band. What is the
longest wavelength of radiation that could
excite an electron in this way? Recall that
E1240 eVnm/.
1100 nm in the near infrared
Level 2
61. Si Diode A particular silicon diode at 0°C
shows a current of 1.0 nA when it is reverse-
biased. What current can be expected if the
temperature increases to 104°C? Assume
that the reverse-bias voltage remains con-
stant. (The thermal carrier production of sil-
icon doubles for every 8°C increase in
temperature.)
Number of 8°C increases
13
The current will double 13 times
Current at 104°C (1 nA)(213) 8.2 A
62. Ge Diode A particular germanium diode at
0°C shows a current of 1.5 A when it is
reverse-biased. What current can be expected
if the temperature increases to 104°C?
Assume that the reverse-biasing voltage
remains constant. (The thermal charge-
carrier production of germanium doubles
for every 13°C increase in temperature.)
Number of 13°C increases 8
The current will double 8 times.
Current at 104°C (1.5 A)(28) 380 A
Level 3
63. LED A light-emitting diode (LED) produces
green light with a wavelength of 550 nm
when an electron moves from the conduction
band to the valence band. Find the width of
the forbidden gap in eV in this diode.
E2.25 eV
64. Refer to Figure 29-22.
■Figure 29-22
a. Determine the voltmeter reading.
0.70 V
by inspection and the approximation
that a silicon diode will drop 0.70 V
when it is forward biased
b. Determine the reading of A1.
0 A
by inspection; 0.70 V is not enough
to turn on two diodes in series.
c. Determine the reading of A2.
I 42 mA
Thinking Critically
page 796
65. Apply Concepts A certain motor, in
Figure 29-23, runs in one direction with a
given polarity applied and reverses direction
with the opposite polarity.
■Figure 29-23
M M
M
10.0 V 0.70 V
220
V
R
V
A1A2
220
10.0 V
All diodes
are silicon.
1240 eVnm
550 nm
104°C
13°C
104°C
8°C
1240 eVnm
1.1 eV
568 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued
ab
c

Physics: Principles and Problems Solutions Manual 569
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. Which circuit (a, b, or c) will allow the
motor to run in only one direction?
a
b. Which circuit will cause a fuse to blow
if the incorrect polarity is applied?
b
c. Which circuit produces the correct direc-
tion of rotation regardless of the
applied polarity?
c
d. Discuss the advantages and disadvan-
tages of all three circuits.
The circuit at a has the advantage of
simplicity. It has the disadvantage of
dropping 0.70 V, which can be
important in low-voltage circuits.
The circuit at b has the advantage of
not wasting 0.70 V. It has the disad-
vantage of having to replace fuses.
The circuit at c has the advantage of
always working, regardless of polari-
ty. It has the disadvantage of wast-
ing 1.4 V.
66. Apply Concepts The I/V characteristics of
two LEDs that glow with different colors are
shown in Figure 29-24. Each is to be con-
nected through a resistor to a 9.0-V battery.
If each is to be run at a current of 0.040 A,
what resistors should be chosen for each?
■Figure 29-24
Vb IR VD
R
R1 180
R2 160
67. Apply Concepts Suppose that the two
LEDs in problem 66 are now connected in
series. If the same battery is to be used and
a current of 0.035 A is desired, what resistor
should be used?
R
140
Writing in Physics
page 796
68. Research the Pauli exclusion principle and
the life of Wolfgang Pauli. Highlight his
outstanding contributions to science.
Describe the application of the exclusion
principle to the band theory of conduction,
especially in semiconductors.
Student answers will vary. Students
could discuss his contributions to
quantum mechanics, the Pauli matrices,
his suggestion of a neutral, massless
particle in beta decay (the neutrino),
and his proof of the spin-statistics
theorem.
69. Write a one-page paper discussing the Fermi
energy level as it applies to energy-band
diagrams for semiconductors. Include at
least one drawing.
Student answers will vary, but should
indicate that the Fermi energy is the
energy of the highest occupied state at
absolute zero. It applies when there are
many electrons in a system, and thus,
the electrons are forced into higher
energy levels due to the Pauli exclusion
principle.
9.0 V (1.75 V 2.5 V)
0.035 A
Vb (VD1 VD2)
I
9.0 V 2.5 V
0.040 A
9.0 V 1.75 V
0.040 A
Vb VD
I
0.5 2.51.512
0.02
0.04
Current (A)
Voltage (V)
0
LED Current v. Voltage
Chapter 29 continued
Cumulative Review
page 796
70. An alpha particle, a doubly ionized (2) helium atom, has a mass of
6.71027 kg and is accelerated by a voltage of 1.0 kV. If a uniform magnetic
field of 6.5102T is maintained on the alpha particle, what will be the
particle’s radius of curvature? (Chapter 26)
r
0.010 m
71. What is the potential difference needed to stop photoelectrons that have a
maximum kinetic energy of 8.01019 J? (Chapter 27)
KE 8.01019 J
5.0 eV, so 5.0 V
72. Calculate the radius of the orbital associated with the energy level E4of the
hydrogen atom. (Chapter 28)
r
8.491010 m 0.849 nm
Challenge Problem
page 786
Approximations often are used in diode
circuits because diode resistance is not con-
stant. For diode circuits, the first approxima-
tion ignores the forward voltage drop across
the diode. The second approximation takes
into account a typical value for the diode volt-
age drop. A third approximation uses addi-
tional information about the diode, often in
the form of a graph, as shown in the illustra-
tion to the right. The curve is the characteristic
current-volatage curve for the diode. The
straight line shows current-voltage conditions
for all possible diode voltage drops for a 180-
resistor, a 1.8-V battery, and a diode, from a
zero diode voltage drop and 10.0 mA at one
end, to a 1.8-V drop, 0.0 mA at the other end.
Use the diode circuit in Example Problem 4
with Vb1.8 V, but with R180 :
1.81.41.00.60.2
14.0
12.0
10.0
8.0
6.0
4.0
2.0
Current (mA)
Voltage (V)
0.0
Graphic solution
Diode Current v. Voltage
(6.6271034 Js)2(4)2
42(8.99109 Nm2/C2)(9.111031 kg)(1.601019 C)2
h2n2
42 Kmq2
1 eV
1.601019 J
(2)(1.0103V)(6.71027 kg)
(2)(1.601019 C)
1
(6.5102T)
2Vm
q
1
B
570 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 571
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
1. Determine the diode current using the first
approximation.
I 1.0101mA
2. Determine the diode current using the sec-
ond approximation and assuming a 0.70-V
diode drop.
I 6.1 mA
3. Determine the diode current using the third
approximation by using the accompanying
diode graph.
The straight line represents all the pos-
sible conditions for a 180-resistor
and a 1.8-V battery (from a diode volt-
age drop of 0.0 V at 10.0 mA on one end
to a 1.8-V drop at 0.0 mA on the other
end). The solution is the intersection of
both lines and occurs at I6.3 mA.
4. Estimate the error for all three approxima-
tions, ignoring the battery and resistor.
Discuss the impact of greater battery volt-
ages on the errors.
For the first approximation, the error is
(10.0 mA 6.1 mA)/6.1 mA, or 64 percent
(when the actual diode drop is 0.70 V).
This error decreases for greater battery
voltages. For the second approximation,
the error source is any deviation from
0.70 V as the actual diode drop. It cannot
be exactly determined, but it’s much less
than 64 percent.This error also decreases
with higher battery voltages. For the third
approximation, the error is due to graph-
ic resolution and is not affected by the
battery voltage.
1.8 V 0.70 V
180
V
R
1.8 V
180
V
R
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 573
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
30 Nuclear Physics
CHAPTER
Practice Problems
30.1 The Nucleus
pages 799–805
page 801
1. Three isotopes of uranium have mass numbers of 234, 235, and 238. The atomic
number of uranium is 92. How many neutrons are in the nuclei of each of these
isotopes?
AZneutrons
234 92 142 neutrons
235 92 143 neutrons
238 92 146 neutrons
2. An isotope of oxygen has a mass number of 15. How many neutrons are in the
nucleus of this isotope?
AZ15 8 7 neutrons
3. How many neutrons are in the mercury isotope 200
80Hg?
AZ200 80 120 neutrons
4. Write the symbols for the three isotopes of hydrogen that have zero, one, and
two neutrons in the nucleus.
1
1H, 2
1H, 3
1H
page 805
Use these values to solve the following problems: mass of hydrogen 1.007825 u,
mass of neutron 1.008665 u, 1 u 931.49 MeV.
5. The carbon isotope 12
6C has a mass of 12.0000 u.
a. Calculate its mass defect.
Mass defect (isotope mass) (mass of protons and electrons)
(mass of neutrons)
12.000000 u (6)(1.007825 u) (6)(1.008665 u)
0.098940 u
b. Calculate its binding energy in MeV.
Binding energy (mass defect)(binding energy of 1 u)
(0.098940 u)(931.49 MeV/u)
92.161 MeV

6. The isotope of hydrogen that contains one proton and one neutron is called
deuterium. The mass of the atom is 2.014102 u.
a. What is its mass defect?
Mass defect (isotope mass) (mass of proton and electron)
(mass of neutron)
2.014102 u 1.007825 u 1.008665 u
0.002388 u
b. What is the binding energy of deuterium in MeV?
Binding energy (mass defect)(binding energy of 1 u)
(0.002388 u)(931.49 MeV/u)
2.2244 MeV
7. A nitrogen isotope, 15
7N, has seven protons and eight neutrons. It has a mass of
15.010109 u.
a. Calculate the mass defect of this nucleus.
Mass defect (isotope mass) (mass of protons and electrons)
(mass of neutrons)
15.010109 u (7)(1.007825 u) (8)(1.008665 u)
0.113986 u
b. Calculate the binding energy of the nucleus.
Binding energy (mass defect)(binding energy of 1 u)
(0.113986 u)(931.49 MeV/u)
106.18 MeV
8. An oxygen isotope, 16
8O, has a nuclear mass of 15.994915 u.
a. What is the mass defect of this isotope?
Mass defect (isotope mass) (mass of protons and electrons)
(mass of neutrons)
15.994915 u (8)(1.007825 u) (8)(1.008665 u)
0.137005 u
b. What is the binding energy of its nucleus?
Binding energy (mass defect)(binding energy of 1 u)
(0.137005 u)(931.49 MeV/u)
127.62 MeV
Section Review
30.1 The Nucleus
pages 799–805
page 805
9. Nuclei Consider these two pairs of nuclei: 12
6C and 13
6C and 11
5B and 11
6C.
In which way are the two alike? In which way are they different?
574 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 575
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The first pair has the same number of protons, but a different number of
nucleons. The second pair has the same number of nucleons, but a differ-
ent number of protons.
10. Binding Energy When tritium, 3
1H, decays, it emits a beta particle and becomes
3
2He. Which nucleus would you expect to have a more negative binding energy?
The tritium nucleus, because tritium emits a particle with mass and kinet-
ic energy in its decay.
11. Strong Nuclear Force The range of the strong nuclear force is so short that only
nucleons that are adjacent to each other are affected by the force. Use this fact to
explain why, in large nuclei, the repulsive electromagnetic force can overcome the
strong attractive force and make the nucleus unstable.
The electric force is long range, so that all protons repel each other, even
in large nuclei.The strong force is short range, so that only neighboring
protons attract.The repulsive force grows, with increasing nuclear size,
faster than the strong force.
12. Mass Defect Which of the two nuclei in problem 10 has the larger mass defect?
the tritium nucleus
13. Mass Defect and Binding Energy The radioactive carbon isotope 14
6C has a
mass of 14.003074 u.
a. What is the mass defect of this isotope?
Mass defect (isotope mass) (mass of protons and electrons)
(mass of neutrons)
14.003074 u (6)(1.007825 u) (8)(1.008665 u)
0.113169 u
b. What is the binding energy of its nucleus?
Binding energy (mass defect)(binding energy of 1 u)
(0.113196 u)(931.49 MeV/u)
105.44 MeV
14. Critical Thinking In old stars, not only are helium and carbon produced by
joining more tightly bound nuclei, but so are oxygen (Z8) and silicon (Z
14). What is the atomic number of the heaviest nucleus that could be formed in
this way? Explain.
26, iron, because its binding energy is largest.
Practice Problems
30.2 Nuclear Decay and Reactions
pages 806–814
page 808
15. Write the nuclear equation for the transmutation of a radioactive uranium
isotope, 234
92U, into a thorium isotope, 230
90Th, by the emission of an particle.
234
92U →230
90Th 4
2He
Chapter 30 continued

16. Write the nuclear equation for the transmu-
tation of a radioactive thorium isotope,
230
90Th, into a radioactive radium isotope,
226
88Ra, by the emission of an particle.
230
90Th → 226
88Ra 4
2He
17. Write the nuclear equation for the transmu-
tation of a radioactive radium isotope,
226
88Ra, into a radon isotope, 222
86Rn, by decay.
226
88Ra → 222
86Rn 4
2He
18. A radioactive lead isotope, 214
82Pb, can
change to a radioactive bismuth isotope,
214
83Bi, by the emission of a particle and an
antineutrino. Write the nuclear equation.
214
82Pb → 214
83Bi 1
0e 0
0
19. A radioactive carbon isotope, 14
6C, under-
goes decay to become the nitrogen
isotope 14
7N. Write the nuclear equation.
14
6C → 14
7N 1
0e 0
0
page 809
20. Use the periodic table on page 916 to com-
plete the following.
a. 14
6C→?1
0e0
0
14
6C → Z
AX 1
0e 0
0
where Z6 (1) 0 7
A14 0 0 14
For Z7, the element must be
nitrogen.Thus, the isotope is 14
7N.
b. 55
24Cr →?1
0e0
0
55
24Cr → ? 1
0e 0
0
55
24Cr → Z
AX 1
0e 0
0
where Z24 (1) 0 25
A55 0 0 55
For Z25, the element must be
manganese. Thus, the isotope is
55
25Mn.
21. Write the nuclear equation for the transmu-
tation of a seaborgium isotope, 263
106Sg, into
a rutherfordium isotope, 259
104Rf, by the emis-
sion of an alpha particle.
263
106Sg →259
104Rf 4
2He
22. A proton collides with the nitrogen isotope
15
7N, forming a new isotope and an alpha
particle. What is the isotope? Write the
nuclear equation.
15
7N 1
1H →Z
AX 4
2He
where Z7 1 2 6
A15 1 4 12
For Z6, the element must be carbon.
Thus, the equation is
15
7N 1
1H →12
6C 4
2He.
23. Write the nuclear equations for the beta
decay of the following isotopes.
a. 210
80Pb
210
80Pb →Z
AX 1
0e 00
0
where Z80 (1) 0 81
A210 0 0 210.
For Z81, the element must be
thallium. Thus, the equation is
210
80Pb →210
81Tl 1
0e 00
0
.
b. 210
83Bi
210
83Bi →Z
AX 1
0e 0
0
where Z83 (1) 0 84
A210 0 0 210
For Z84, the element must be
polonium. Thus, the equation is
210
83Bi →210
84Po 1
0e 00
0
.
c. 234
90Th
234
90Th →Z
AX 1
0e 0
0
where Z90 (1) 0 91
A234 0 0 234
For Z91, the element must be
protactinium.Thus, the equation is
234
90Th →234
91Pa 1
0e 0
0
.
576 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 577
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
d. 239
93Np
239
93Np →Z
AX 1
0e 0
0
where Z93 (1) 0 94
A239 0 0 239
For Z94, the element must be
plutonium. Thus, the equation is
239
93Np →239
94Pu 1
0e 00
0
.
page 810
Refer to Figure 30-4 and Table 30-2 to solve the
following problems.
24. A sample of 1.0 g of tritium, 3
1H, is pro-
duced. What will be the mass of the tritium
remaining after 24.6 years?
24.6 years (2)(12.3 years), which is
2 half-lives.
remaining original
1
2
t
(1.0 g)
1
2
2
0.25 g
25. The isotope 238
93Np has a half-life of
2.0 days. If 4.0 g of neptunium is produced
on Monday, what will be the mass of
neptunium remaining on Tuesday of the
next week?
8.0 days (4)(2.0 days), which is
4 half-lives remaining
(original)
1
2
t
(4.0 g)
1
2
4
0.25 g
26. A sample of polonium-210 is purchased for
a physics class on September 1. Its activity is
2106Bq. The sample is used in an experi-
ment on June 1. What activity can be
expected?
The half-life of 210
84Po is 138 days.
There are 273 days or about 2 half-lives
between September 1 and June 1.
So the activity
2106
dec
s
ays
1
2
2
5105Bq
27. Tritium, 3
1H, once was used in some watches
to produce a fluorescent glow so that the
watches could be read in the dark. If the
brightness of the glow is proportional to
the activity of the tritium, what would be
the brightness of such a watch, in compari-
son to its original brightness, when the
watch is six years old?
Six years is about half of tritium’s
half-life of 12.3 years.Thus, the
brightness is
1
2
, or about
1
7
0
of the
original brightness.
Section Review
30.2 Nuclear Decay and
Reactions
pages 806–814
page 814
28. Beta Decay How can an electron be
expelled from a nucleus in beta decay if the
nucleus has no electrons?
In the nucleus a neutron changes into a
proton and emits an electron and an
antineutrino.
29. Nuclear Reactions The polonium isotope
210
84Po undergoes alpha decay. Write the
equation for the reaction.
210
84Po →Z
AX 4
2He
where Z 84 2 82
A 210 4 206
For Z 82, the element must be lead.
Thus, the equation is
210
84Po →206
82Pb 4
2He.
30. Half-Life Use Figure 30-4 and Table 30-2 to
estimate in how many days a sample of 131
53I
would have three-eighths its original activity.
From the graph, 3/8 are left at about
1.4 half lives. From the table, the half-
life is 8.07 days, so it would take about
11 days.
1
2
Chapter 30 continued

31. Nuclear Reactor Lead often is used as a radiation shield. Why is it not a good
choice for a moderator in a nuclear reactor?
Lead is used as a radiation shield because it absorbs radiation, including
neutrons. A moderator should only slow the neutrons so they can be
absorbed by the fissile material.
32. Fusion One fusion reaction involves two deuterium nuclei, 2
1H. A deuterium
molecule contains two deuterium atoms. Why doesn’t this molecule undergo fusion?
The nuclei in the molecule must be moving very fast to undergo fusion.
33. Energy Calculate the energy released in the first fusion reaction in the Sun,
1
1H1
1H→2
1H1
0e0
0.
The energy released is
E ((initial mass) (final mass))(931.49 MeV/u)
(2(mass of protium) (mass of deuterium) (mass of positron))
(931.49 MeV/u)
2(1.007825 u) 2.014102 u (9.111031kg)
(931.49 MeV/u)
0.931 MeV
34. Critical Thinking Alpha emitters are used in smoke detectors. An emitter is
mounted on one plate of a capacitor, and the particles strike the other plate.
As a result, there is a potential difference across the plates. Explain and predict
which plate has the more positive potential.
The plate being stuck by the particles has the more positive potential
because the positively charged particles move positive charge from the
emitter plate to the struck plate.
Practice Problems
30.3 The Building Blocks of Matter
pages 815–823
page 821
35. The mass of a proton is 1.671027 kg.
a. Find the energy equivalent of the proton’s mass in joules.
Emc2
(1.671027 kg)(3.00108m/s)2
1.501010 J
b. Convert this value to eV.
E
9.36108eV
1.501010 J
1.602171019 J/eV
1u
1.66051027 kg
578 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 579
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. Find the smallest total -ray energy that could result in a proton-antiproton pair.
The minimum energy is
(2)(9.36108eV) 1.87109eV
36. A positron and an electron can annihilate and form three gammas. Two gammas
are detected. One has an energy of 225 keV, the other 357 keV. What is the
energy of the third gamma?
As shown in this section, the energy equivalent of the positron and elec-
tron is 1.02 MeV. Thus, the energy of the third gamma is
1.02 MeV 0.225 MeV 0.357 MeV 0.438 MeV.
37. The mass of a neutron is 1.008665 u.
a. Find the energy equivalent of the neutron’s mass in MeV.
E(neutron mass in u)(931.49 MeV/u)
(1.008665 u)(931.49 MeV/u)
939.56 MeV
b. Find the smallest total -ray energy that could result in the production of a
neutron-antineutron pair.
The smallest possible -ray energy would be twice the neutron energy.
Etotal 2En(2)(939.56 MeV)
1879.1 MeV
38. The mass of a muon is 0.1135 u. It decays into an electron and two neutrinos.
What is the energy released in this decay?
Energy released (mass of muon mass of electron)(931.49 MeV/u)
0.1135 u (9.1091031 kg)
(931.49 MeV/u)
105.2 MeV
Section Review
30.3 The Building Blocks of Matter
pages 815–823
page 823
39. Nucleus Bombardment Why would a proton require more energy than a neu-
tron when used to bombard a nucleus?
The proton and nucleus both have positive charge, so they repel each
other.Therefore, the proton must have enough kinetic energy to overcome
the potential energy caused by the repulsion.The uncharged neutron does
not experience this repulsive force.
40. Particle Accelerator Protons in the Fermi Laboratory accelerator, Figure 30-11,
move counterclockwise. In what direction is the magnetic field of the bending
magnets?
down, into Earth
1u
1.66051027 kg
Chapter 30 continued
41. Pair Production Figure 30-18 shows the
production of two electron/positron pairs.
Why does the bottom set of tracks curve less
than the top pair of tracks?
The electron/positron pair at the bottom
has more kinetic energy, and therefore,
a greater velocity.
42. The Standard Model Research the limita-
tions of the Standard Model and possible
replacements.
Answers include:The Standard Model
has several parameters that can be
obtained only from experiment. The
Higgs particle that would set the energy
scale has not been found. It is not really
a theory that explains, and so is not
complete. Supersymmetry and string
theory are two possible replacements.
43. Critical Thinking Consider the following
equations.
u→dWand W→e
How could they be used to explain the
radioactive decay of a nucleon that results
in the emission of a positron and a neutri-
no? Write the equation involving nucleons
rather than quarks.
A nucleon containing a u quark could
decay by this process to a nucleon with
one less u and one more d quark. A
proton is uud and a neutron is uud, so
the following equation would work:
1
1p→1
0n0
1e0
0
Chapter Assessment
Concept Mapping
page 828
44. Organize the following terms into the
concept map: Standard Model, quarks,
gamma rays, force carriers, protons, neutrons,
leptons, W bosons, neutrinos, electrons, gluons.
Mastering Concepts
page 828
45. What force inside a nucleus acts to push the
nucleus apart? What force inside the nucle-
us acts to hold the nucleus together? (30.1)
The repulsive electric force between the
positive protons acts to push the nucle-
us apart. The strong nuclear force acts
to hold the nucleus together.
46. Define the mass defect of a nucleus. To
what is it related? (30.1)
The mass defect is the difference
between the sum of the masses of the
individual particles of the nucleus and
the mass of the nucleus. It is related to
binding energy through Emc2.
47. Which are generally more unstable, small or
large nuclei? (30.1)
Large nuclei are generally more
unstable. The greater number of
protons makes the repulsive electric
force overcome the attractive strong
force.
580 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued
Standard
Model
leptons
quarks force
carriers
gamma
rays gluons
W bosons
neutrinos
electrons
neutrons
protons
Includes
Which
compose Examples Examples

Physics: Principles and Problems Solutions Manual 581
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
48. Which isotope has the greater number of pro-
tons, uranium-235 or uranium-238? (30.1)
They both have the same number of pro-
tons, but different numbers of neutrons.
49. Define the term transmutation as used in
nuclear physics and give an example. (30.2)
Transmutation is the change of one ele-
ment into another by means of a
nuclear reaction caused by radioactive
decay or nuclear bombardment. For
example, uranium-238 decays into thori-
um-234 and an particle.
50. Radiation What are the common names
for an particle, particle, and radiation?
(30.2)
An a particle is a helium nucleus, a
particle is an electron, and radiation
is a high-energy photon.
51. What two quantities must always be con-
served in any nuclear equation? (30.2)
the atomic number, to conserve charge;
the mass number, to conserve the num-
ber of nucleons
52. Nuclear Power What sequence of events
must occur for a chain reaction to take place?
(30.2)
Many neutrons must be released by a fis-
sioned nucleus and absorbed by neigh-
boring nuclei, causing them to undergo
fission.
53. Nuclear Power What role does a modera-
tor play in a fission reactor? (30.2)
The moderator slows the fast neutrons,
increasing their probability of being
absorbed.
54. Fission and fusion are opposite processes.
How can each release energy? (30.2)
When a large atom, such as uranium,
undergoes fission, the mass of the
products is less than that of the original
nucleus. An amount of energy equiva-
lent to the difference in mass is
released. However, when small nuclei
fuse into a larger nucleus, the mass of
the more tightly bound, large nucleus is
less, and the extra mass appears as
energy.
55. High-Energy Physics Why would a linear
accelerator not work with a neutron? (30.3)
It accelerates particles using electric
force, and the neutron has no charge.
56. Forces In which of the four interactions
(strong, weak, electromagnetic, and gravita-
tional) do the following particles take part?
(30.3)
a. electron
electromagnetic, weak, gravitational
b. proton
strong, electromagnetic, gravitational
c. neutrino
weak
57. What happens to the atomic number and
mass number of a nucleus that emits a
positron? (30.3)
The atomic number decreases by 1, and
there is no change in the mass number.
Z → Z 1; A → A
58. Antimatter What would happen if a mete-
orite made of antiprotons, antineutrons,
and positrons landed on Earth? (30.3)
It would annihilate with an equivalent
amount of matter, producing an
extremely large amount of energy.
Applying Concepts
page 828
59. Fission A Web site claims that scientists
have been able to cause iron nuclei to
undergo fission. Is the claim likely to be
true? Explain.
It is not true. Iron is the most tightly
bound element, and thus the most sta-
ble nucleus. It cannot decay by either
fission or fusion.
Chapter 30 continued

60. Use the graph of binding energy per nucleon in Figure 30-2 to determine
whether the reaction 2
1H1
1H→3
2He is energetically possible.
The initial binding energy is less than the final binding energy and, there-
fore, the reaction is energetically possible.
61. Isotopes Explain the difference between naturally and artificially produced
radioactive isotopes.
A natural radioactive material is one that is found to exist normally in ores
and that experiences radioactive decay. Artificially, radioactive material
experiences radioactive decay only after being subjected to bombardment
by particles.
62. Nuclear Reactor In a nuclear reactor, water that passes through the core of the
reactor flows through one loop, while the water that produces steam for the turbines
flows through a second loop. Why are there two loops?
The water that passes through the core is at high pressure, so it doesn’t
boil. A second loop carries water at lower pressure, producing steam.
63. The fission of a uranium nucleus and the fusion of four hydrogen nuclei to pro-
duce a helium nucleus both produce energy.
a. Which produces more energy?
As shown in Section 30-2, the energy produced by the fission of one
uranium nucleus is 200 MeV. The energy produced by the fusion of
four hydrogen nuclei is 24 MeV.
b. Does the fission of a kilogram of uranium nuclei or the fusion of a kilogram
of hydrogen produce more energy?
The mass number of fissionable uranium is 238.The mass number
of hydrogen is 1. For an equal mass of the elements, you would have
238 times more hydrogen nuclei than uranium nuclei. The fission of
each uranium nucleus would produce 200 MeV of energy. The fusion of
238 nuclei of hydrogen to produce helium nuclei would produce
23
48
(25 MeV), or about 1500 MeV of energy.
c. Why are your answers to parts aand bdifferent?
Although the fission of one uranium nucleus produces more energy
than the fusion of four hydrogen nuclei to produce helium, there are
more than 200 times as many hydrogen nuclei in 1kg as there are ura-
nium nuclei.
Mastering Problems
30.1 The Nucleus
pages 828–829
Level 1
64. What particles, and how many of each, make up an atom of 109
47Ag?
47 electrons, 47 protons, 62 neutrons
582 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 583
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
65. What is the isotopic symbol (the one used in nuclear equations) of a zinc atom
composed of 30 protons and 34 neutrons?
64
30Zn
66. The sulfur isotope 32
16S has a nuclear mass of 31.97207 u.
a. What is the mass defect of this isotope?
mass defect (isotope mass) (mass of protons and electrons)
(mass of neutrons)
31.97207 u (16)(1.007825 u) (16)(1.008665 u)
0.29177 u
b. What is the binding energy of its nucleus?
Binding energy (mass defect)(binding energy of 1 u)
(0.29177 u)(931.5 MeV/u)
271.78 MeV
c. What is the binding energy per nucleon?
Binding energy per nucleon is
3
2
2n
71
u.
c
8
le
M
oe
n
V
s
8.494 MeV/nucleon
Level 2
67. A nitrogen isotope, 12
7N, has a nuclear mass of 12.0188 u.
a. What is the binding energy per nucleon?
Binding energy (mass of defect)(binding energy for 1 u)
((isotope mass) (mass of protons and electrons)
(mass of neutrons))(binding energy for 1 u)
((12.0188 u) (7)(1.007825 u) (5)(1.008665 u))
(931.49 MeV/u)
73.867 MeV
The binding energy per nucleon is
12
73
n
.8
u6
c7
leM
on
es
V
6.1556 MeV/nucleon
b. Does it require more energy to separate a nucleon from a 14
7N nucleus or
from a 12
7N nucleus? 14
7N has a mass of 14.00307 u.
For 14
7N, the binding energy is
Binding energy (mass defect)(binding energy for 1 u)
((isotope mass) (mass of protons and electrons)
(mass of neutrons))(binding energy for 1 u)
((14.00307 u (7)(1.007825 u)
(7)(1.008665 u))(931.49 MeV/u)
104.66 MeV
The binding energy per nucleon is
14
10
n
4
u
.6
c6
leM
on
es
V
7.4757 MeV/nucleon
Thus, removing a nucleon from 14
7N requires more energy.
Chapter 30 continued

68. The two positively charged protons in a helium nucleus are separated by about
2.01015 m. Use Coulomb’s law to find the electric force of repulsion between
the two protons. The result will give you an indication of the strength of the
strong nuclear force.
FK
(9.0109Nm2/C2)58 N
69. The binding energy for 4
2He is 28.3 MeV. Calculate the mass of a helium iso-
tope in atomic mass units.
mass of the isotope (mass defect) (mass of protons and electrons)
(mass of neutrons)
(mass of protons and electrons)
(mass of neutrons)
93
1
2
.4
89
.3M
M
e
e
V
V
/u
(2)(1.007825 u) (2)(1.008665 u)
4.00 u
30.2 Nuclear Decay and Reactions
page 829
Level 1
70. Write the complete nuclear equation for the alpha decay of 222
86Rn.
222
86Rn → Z
AX4
2He
where A222-4 218
Z86-2 84
For Z84, the element must be polonium. Thus, the equation is
222
86Rn → 218
84Po 4
2He
71. Write the complete nuclear equation for the beta decay of 89
36Kr.
89
36Kr Z
AX1
0e0
0
where Z36 (1) 0 37
A89 0 0 89
For Z37, the element must be rubidium. Thus, the equation is
89
36Kr 89
37Rb 1 1
0e0
0
72. Complete each nuclear reaction.
a. 225
89Ac →4
2He _____
225
89Ac → 4
2He 221
87Fr
b. 227
88Ra →1
0e _____ _____
227
88Ra → 1
0e227
89Ac 0
0
binding energy
binding energy of 1 u
(1.601019 C)(1.601019 C)
2.01015 m
qAqB
d2
584 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 585
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. 65
29Cu 1
0n→_____ →1
1p _____
65
29Cu 1
0n → 66
29Cu → 1
1p65
28Ni
d. 235
92U 1
0n→96
40Zr 3(1
0n) _____
235
92U1
0n → 96
40Zr 31
0n136
52Te
73. An isotope has a half-life of 3.0 days. What
percent of the original material will be left after
a. 6.0 days?
6
3.
.0
0d
d
2.0 half-lives
percent remaining
1
2
t 100
1
2
2.0 100
25%
b. 9.0 days?
9
3.
.0
0d
d
3.0 half-lives
percent remaining
1
2
t 100
1
2
3.0 100
13%
c. 12 days?
4 half-lives
percent remaining
1
2
t100
1
2
4.0 100
6.3%
74. In an accident in a research laboratory, a
radioactive isotope with a half-life of three
days is spilled. As a result, the radiation is
eight times the maximum permissible
amount. How long must workers wait
before they can enter the room?
For the activity to fall to
1
8
its present
amount, you must wait three half-lives,
or 9 days.
75. When a boron isotope, 11
5B, is bombarded
with protons, it absorbs a proton and emits
a neutron.
a. What element is formed?
carbon
b. Write the nuclear equation for this
reaction.
11
5B1
1p →A
6C1
0n
where A11 1 1 11
Thus, the equation is
11
5B1
1p → 11
6C1
0n
c. The isotope formed is radioactive and
decays by emitting a positron. Write
the complete nuclear equation for this
reaction.
11
6C → A
ZX1
0e0
0
where Z6 1 0 5
A11 0 0 11
For Z5, the element must be
boron.Thus, the equation is
11
6C→11
5B1
0e0
0
76. The first atomic bomb released an energy
equivalent of 2.0101kilotons of TNT. One
kiloton of TNT is equivalent to 5.01012 J.
Uranium-235 releases 3.211011 J/atom.
What was the mass of the uranium-235 that
underwent fission to produce the energy of
the bomb?
E(2.0101kton)(5.01012 J/kton)
1.2 kg
77. During a fusion reaction, two deuterons,
2
1H, combine to form a helium isotope,
3
2He. What other particle is produced?
2
1H2
1H → 3
2He A
ZX
where Z1 1 2 0
A2 2 3 1
Thus, the particle must be 1
0n, a neutron.
0.235 kg
mol
1mol
6.021023 atom
1 atom
3.211011 J
12 d
3.0 d
Chapter 30 continued

Level 2
78. 209
84Po has a half-life of 103 years. How long
would it take for a 100-g sample to decay so
that only 3.1 g of Po-209 was left?
remaining original
1
2
t
Let Rremaining mass and Iorigi-
nal mass
RI
1
2
t
2
It
2t
R
I
log(2t)log
R
I
tlog 2 log
R
I
t
5 half-lives
Therefore, the sample would take about
500 years to decay.
30.3 The Building Blocks of Matter
page 829
Level 1
79. What would be the charge of a particle
composed of three up quarks?
Each u quark has a charge of
2
3
.
uuu 3
2
3
2 elementary charges
80. The charge of an antiquark is opposite that
of a quark. A pion is composed of an up
quark and an anti-down quark, ud
. What
would be the charge of this pion?
u d
2
3
1
3
1 elementary
charge
81. Pions are composed of a quark and an anti-
quark. Find the charge of a pion made up
of the following.
a. uu
d u
2
3
2
3
0 charge
b. du
d u
1
3
2
3
1 charge
c. dd
u d
1
3
1
3
0 charge
82. Baryons are particles that are made of three
quarks. Find the charge on each of the fol-
lowing baryons.
a. neutron: ddu
d d u 2
1
3
2
3
0
b. antiproton: u
u
d
u
u
d
2
3
2
3
1
3
1
Level 2
83. The synchrotron at the Fermi Laboratory
has a diameter of 2.0 km. Protons circling
in it move at approximately the speed of
light in a vacuum.
a. How long does it take a proton to com-
plete one revolution?
v
d
t
where dis the circumference of the
synchrotron,
so t
d
v
2.1105s
b. The protons enter the ring at an energy
of 8.0 GeV. They gain 2.5 MeV each
revolution. How many revolutions must
they travel before they reach 400.0 GeV
of energy?
1.6105rev
c. How long does it take the protons to be
accelerated to 400.0 GeV?
t(1.6105rev)(2.1105s/rev)
3.4 s
d. How far do the protons travel during
this acceleration?
dvt (3.00108m/s)(3.4 s)
1.0109m, or about 1 million km
400.0109eV 8.00109eV
2.5106eV/rev
(2.0103m)
3.0108m/s
log
1
30
.1
0g
g
log 2
log
R
I
log 2
586 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 587
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
84. Figure 30-21 shows tracks in a bubble
chamber. What are some reasons one track
might curve more than another?
■Figure 30-21
The paths of faster-moving particles
would curve less.
Mixed Review
page 830
Level 1
85. Each of the following nuclei can absorb an
particle. Assume that no secondary parti-
cles are emitted by the nucleus. Complete
each equation.
a. 14
7N4
2He →_____
14
7N4
2He → Z
AX
where Z7 2 9
A14 4 18
For Z9, the element must be
fluorine. Thus, the equation is
14
7N 4
2He → 18
9F
b. 27
13Al 4
2He →_____
27
13Al 4
2He → A
ZX
where Z13 2 15
A27 4 31
For Z15, the element must be
phosphorus. Thus, the equation is
27
13Al 4
2He → 31
15P
86. 211
86Rn has a half-life of 15 h. What fraction
of a sample would be left after 60 h?
6
10
5h
h
4 half-lives, so
1
2
4
1
1
6
is left.
Level 2
87. One of the simplest fusion reactions
involves the production of deuterium,
2
1H(2.014102 u), from a neutron and a pro-
ton. Write the complete fusion reaction and
find the amount of energy released.
The equation for the reaction is
1
0n1
0p →2
1H
The energy released is
E ((initial mass) (final mass))
(931.49 MeV/u)
((mass of neutron)
(mass of proton) (mass of
deuterium))(931.49 MeV/u)
((1.008665 u) (1.007276 u)
(2.014102 u))(931.49 MeV/u)
1.7130 MeV
88. A 232
92U nucleus, mass 232.0372 u, decays
to 228
90Th, mass 228.0287 u, by emitting
an particle, mass 4.0026 u, with a
kinetic energy of 5.3 MeV. What must be
the kinetic energy of the recoiling thorium
nucleus?
The total kinetic energy of the decay
products is
KEtotal KEthorium KE
Thus,
KEthorium KEtotal KE
(mass defect)
(931.49 MeV/u)KE
((mass of 232
92U)
(mass of 228
90Th)
(mass of 4
2He))
(931.49 MeV/u) KE
((232.0372 u) (228.0287 u)
(4.0026 u))
(931.49 MeV/u) 5.3 MeV
0.2 MeV
Chapter 30 continued
Thinking Critically
page 830
89. Infer Gamma rays carry momentum. The
momentum of a gamma ray of energy Eis
equal to E/c, where cis the speed of light.
When an electron-positron pair decays into
two gamma rays, both momentum and
energy must be conserved. The sum of the
energies of the gamma rays is 1.02 MeV. If
the positron and electron are initially at rest,
what must be the magnitude and direction
of the momentum of the two gamma rays?
Because the initial momentum is zero,
this must be the final momentum.Thus,
the two gamma rays must have equal
and opposite momentum. The magni-
tude of the momenta is
p
1
2
C
E
2.721022 kgm/s
They move in opposite directions.
90. Infer An electron-positron pair, initially at
rest, also can decay into three gamma rays.
If all three gamma rays have equal energies,
what must be their relative directions? Make
a sketch.
The question becomes the following:
how can three particles, each with the
same momentum, have zero total
momentum? The three gamma rays
leave with angles of 120° between them
on a plane.
91. Estimate One fusion reaction in the Sun
releases about 25 MeV of energy. Estimate
the number of such reactions that occur
each second from the luminosity of the
Sun, which is the rate at which it releases
energy, 41026 W.
1 eV 1.60221019 J, so
25 MeV (25106eV/reaction)
(1.60221019 J/eV)
4.01012 J/reaction
The total power is 41026 J/s, so the
number of reactions occurring each
second is
1038 reactions/s
92. Interpret Data An isotope undergoing
radioactive decay is monitored by a radia-
tion detector. The number of counts in each
five-minute interval is recorded. The results
are shown in Table 30-3. The sample is
then removed and the radiation detector
records 20 counts resulting from cosmic
rays in 5 min. Find the half-life of the
isotope. Note that you should first subtract
the 20-count background reading from each
result. Then plot the counts as a function
of time. From your graph, determine the
half-life.
about 4 min
Writing in Physics
page 830
93. Research the present understanding of dark
matter in the universe. Why is it needed by
cosmologists? Of what might it be made?
About 25 percent of the universe is dark
matter. It is needed to explain galactic
rotation and the expansion of the uni-
verse. According to one theory, dark
matter is not made of ordinary matter
that is covered by the Standard Model.
It may interact with ordinary matter only
through gravity and weak nuclear
forces.
Table 30-3
Radioactive Decay
Measurements
Time (min) Counts
(per 5 min)
0987
5375
10 150
15 70
20 40
25 25
30 18
41026 J/s
4.01012 J/reaction
(1.02106eV)(1.601019 J/eV)
(2)(3.00108m/s)
588 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 589
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
94. Research the hunt for the top quark. Why
did physicists hypothesize its existence?
Theorists had predicted the existence
of different flavors of quarks.They real-
ized quarks occur in pairs. The up and
down quark pair and the charmed and
strange pair had been found by experi-
ments. When the bottom quark was
found in 1977, they felt it must have a
partner. The short lifetime and high
mass of the top quark made it difficult
to find. It finally was found at a Fermilab
experiment in 1995.
Cumulative Review
page 830
95. An electron with a velocity of 1.7106m/s
is at right angles to a 0.91-T magnetic field.
What is the force on the electron produced
by the magnetic field? (Chapter 24)
FBqv
(0.91 T)(1.601019 C)
(1.7106m/s)
2.51013 N
96. An EMF of 2.0 mV is induced in a wire that
is 0.10 m long when it is moving perpen-
dicularly across a uniform magnetic field at
a velocity of 4.0 m/s. What is the magnetic
induction of the field? (Chapter 25)
EMF BLv
B
E
L
M
vF
5.0103T 5.0 mT
97. An electron has a de Broglie wavelength of
400.0 nm, the shortest wavelength of visible
light. (Chapter 27)
a. Find the velocity of the electron.
m
hv
v
m
h
1.82103m/s
b. Calculate the energy of the electron in eV.
KE
1
2
mv2
1
2
(9.111031 kg)(1.82103 m/s)2
9.43106eV
98. A photon with an energy of 14.0 eV enters a
hydrogen atom in the ground state and ion-
izes it. With what kinetic energy will the
electron be ejected from the atom?
(Chapter 28)
KE (photon energy) (energy of
electron in the ground state)
14.0 eV (13.6 eV)
0.4 eV
99. A silicon diode (V0.70 V) that is con-
ducting 137 mA is in series with a resistor
and a 6.67-V power source. (Chapter 29)
a. What is the voltage drop across the
resistor?
VRVsource Vdiode
6.67 V 0.70 V
5.97 V
b. What is the value of the resistor?
R
V
I
1
5
3
.7
97
m
V
A
43.6
1 eV
1.601019 J
6.631034 J/Hz
(9.111031 kg)(400.0109m)
2.0103V
(0.10 m)(4.0 m/s)
Chapter 30 continued

Challenge Problem
page 821
238
92U decays by emission and two successive emissions back into uranium again.
1. Show the three nuclear decay equations.
For the emission, 238
92U → Z
AX4
2He
where Z92 – 2 90
A238 4 234
For Z90, the element must be thorium. Thus, the equation is
238
92U → 234
90Th 4
2He
For the first emission, 234
90Th → Z
AX 1
0e0
0
where Z90 (1) 0 91
A234 0 0 234
For Z91, the element must be protactinium.Thus, the equation is
234
90Th → 234
91Pa 1
0e0
0
For the second emission, 234
91Pa → Z
AX 1
0e0
0
where Z91 (1) 0 92
A234 0 0 234
For Z92, the element must be uranium. Thus, the equation is
234
91Pa → 234
92U 1
0e0
0
2. Predict the atomic mass number of the uranium formed.
A234
590 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Appendix B
Additional Problems
Chapter 1 . . . . . . . . . . . . . . . . . . . . . . . . 593
Chapter 2 . . . . . . . . . . . . . . . . . . . . . . . . 595
Chapter 3 . . . . . . . . . . . . . . . . . . . . . . . . 598
Chapter 4 . . . . . . . . . . . . . . . . . . . . . . . . 602
Chapter 5 . . . . . . . . . . . . . . . . . . . . . . . . 607
Chapter 6 . . . . . . . . . . . . . . . . . . . . . . . . 612
Chapter 7 . . . . . . . . . . . . . . . . . . . . . . . . 616
Chapter 8 . . . . . . . . . . . . . . . . . . . . . . . . 618
Chapter 9 . . . . . . . . . . . . . . . . . . . . . . . . 622
Chapter 10 . . . . . . . . . . . . . . . . . . . . . . . 626
Chapter 11 . . . . . . . . . . . . . . . . . . . . . . . 628
Chapter 12 . . . . . . . . . . . . . . . . . . . . . . . 631
Chapter 13 . . . . . . . . . . . . . . . . . . . . . . . 635
Chapter 14 . . . . . . . . . . . . . . . . . . . . . . . 638
Chapter 15 . . . . . . . . . . . . . . . . . . . . . . . 640
Chapter 16 . . . . . . . . . . . . . . . . . . . . . . . 641
Chapter 17 . . . . . . . . . . . . . . . . . . . . . . . 642
Chapter 18 . . . . . . . . . . . . . . . . . . . . . . . 644
Chapter 19 . . . . . . . . . . . . . . . . . . . . . . . 646
Chapter 20 . . . . . . . . . . . . . . . . . . . . . . . 649
Chapter 21 . . . . . . . . . . . . . . . . . . . . . . . 651
Chapter 22 . . . . . . . . . . . . . . . . . . . . . . . 655
Chapter 23 . . . . . . . . . . . . . . . . . . . . . . . 658
Chapter 24 . . . . . . . . . . . . . . . . . . . . . . . 662
Chapter 25 . . . . . . . . . . . . . . . . . . . . . . . 664
Chapter 26 . . . . . . . . . . . . . . . . . . . . . . . 665
Chapter 27 . . . . . . . . . . . . . . . . . . . . . . . 669
Chapter 28 . . . . . . . . . . . . . . . . . . . . . . . 672
Chapter 29 . . . . . . . . . . . . . . . . . . . . . . . 674
Chapter 30 . . . . . . . . . . . . . . . . . . . . . . . 677
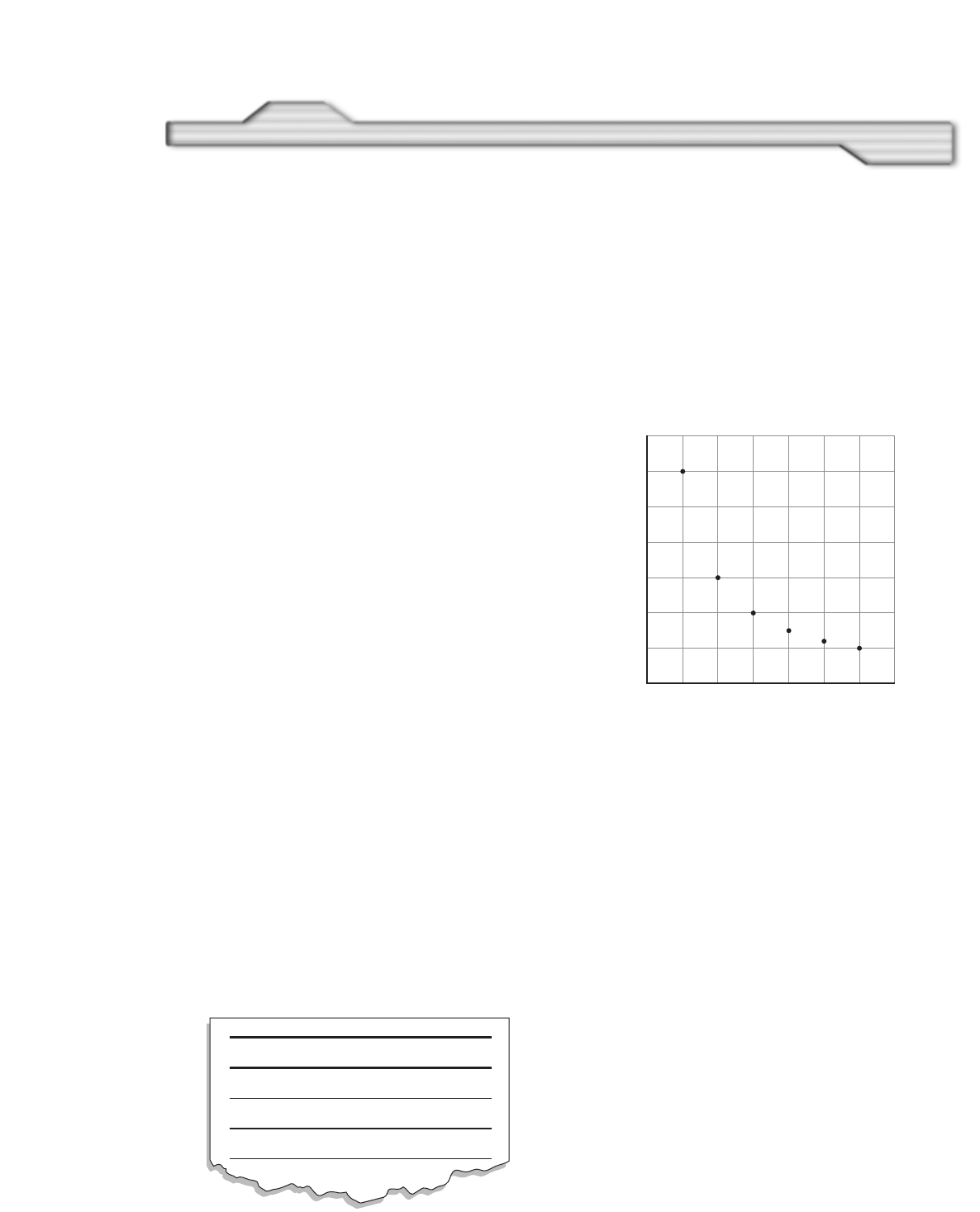
Physics: Principles and Problems Solutions Manual 593
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Appendix B
Chapter 1
page 858
1. The density, , of an object is given by the
ratio of the object’s mass, m, and volume, V,
according to the equation m/V. What is
the density of a cube that is 1.2 cm on each
side and has a mass of 25.6 g?
15 g/cm3
2. An object that is moving in a straight line
with speed vcovers a distance, dvt, in
time t. Rewrite the equation to find tin
terms of dand v. How long does it take
a plane that is traveling at 350 km/h to
travel 1750 km?
t 5.0 h
3. Convert 523 kg to milligrams.
523 kg (523 kg)
10
1
0
k
0
g
g
100
1
0
g
mg
5.23108mg
4. The liquid measure milliliter, mL, is the
same as 1 cm3. How many milliliters of
liquid can be held in a 2.5-m3container?
2.5 m3 (2.5 m3)
3
2.5106mL
5. Part of the label from a vitamin container
is shown below. The abbreviation “mcg”
stands for micrograms. Convert the values
to milligrams.
folic acid:
(400 mcg)(0.001 mg/mcg) 0.4 mg
vitamin B12:
(6 mcg)(0.001 mg/mcg) 0.006 mg
biotin:
(30 mcg)(0.001 mg/mcg) 0.03 mg
6. What type of relationship is shown in the
scatter plot? Write an equation to model
the data.
inverse relationship; y
7. How many significant digits are there in
each of the following measurements?
a. 100 m
1
b. 0.0023 m/s
2
c. 100.1 m
4
d. 2.0023
5
1.2
x
123456
0
0.2
0.4
0.6
0.8
1.0
1.2
Each Tablet Contains %DV
Folic Acid 400 mcg 100%
Vitamin B12 6 mcg 100%
Biotin 30 mcg 10%
1 mL
1 cm3
100 cm
1 m
1750 km
350 km/h
d
v
25.6 g
(1.2 cm)3
m
V
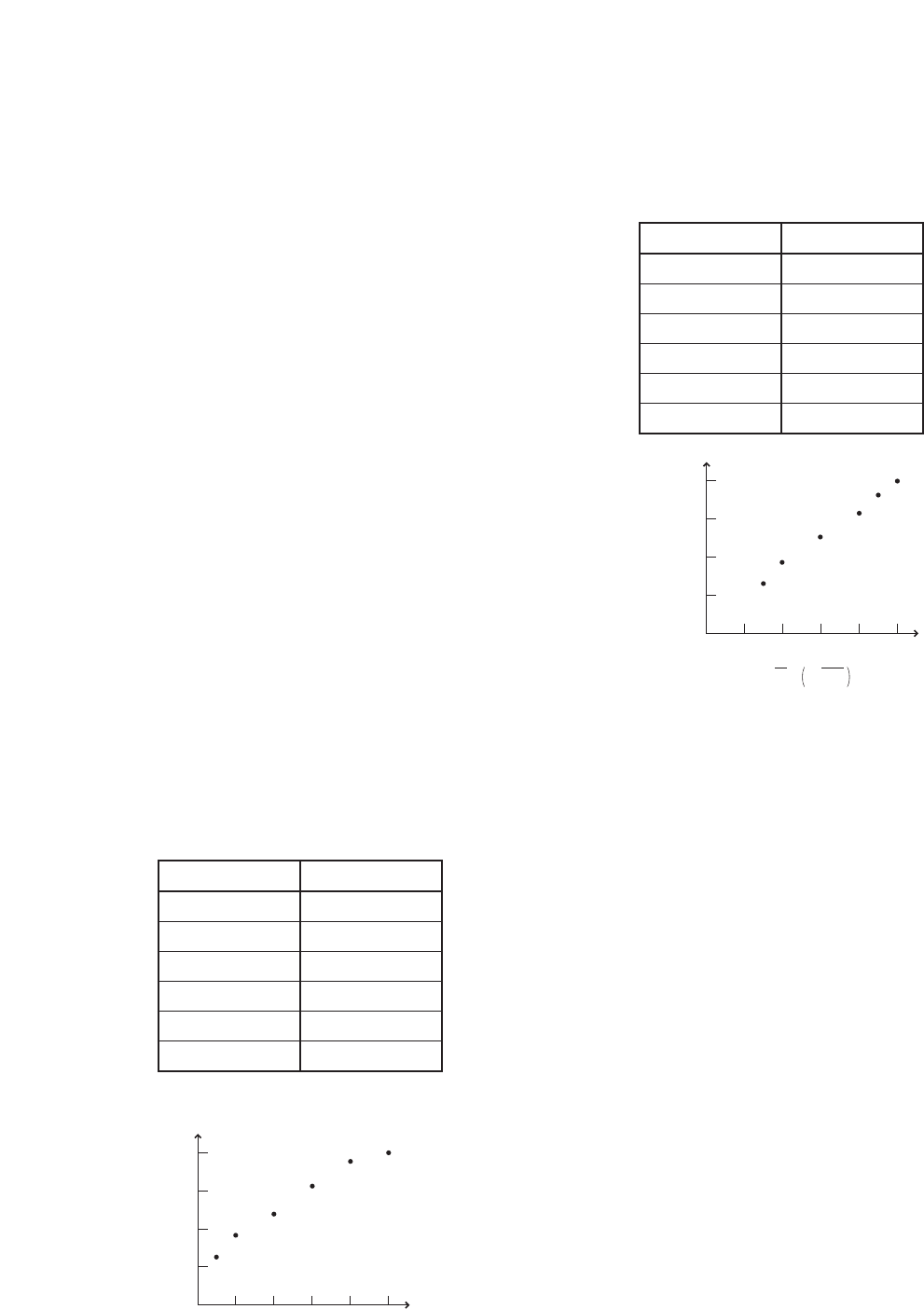
8. The buoyant (upward) force exerted by water
on a submerged object is given by the formula
FVg, where is the density of water
(1.0103kg/m3), Vis the volume of the
object in m3, and gis the acceleration due to
gravity (9.80 m/s2). The force is in newtons.
Rewrite the equation to find Vin terms of F.
Use this to find the volume of a submerged
barrel if the buoyant force on it is 9200 N.
V
F
g
0.94 m3
9. What is 2.3 kg 0.23 g?
2.3 kg 0.23 g 2.3103g 0.23 g
2.3103g 2.3 kg
10. Solve the following problems.
a. 15.5 cm 12.1 cm
188 cm2
b.
4.6 s
11. An experiment was performed to determine
the period of a pendulum as a function of
the length of its string. The data in the table
below were measured.
a. Plot period, T, versus length, l.
b. Are the data linear?
no
c. Plot the period versus the square root of
the length.
d. What is the relationship between the
period and the square root of the length?
The graph is linear, so the period is
proportional to the square root of
the length of the string.
12. Based on the previous problem, what should
be the period of a pendulum whose length
is 0.7 m?
around 1.7 s
1.0
Period (s)
2.0
0.0 0.4 0.80.2 0.6 1.0
l m
I
T
0.3 0.6
0.4 0.9
0.6 1.3
0.8 1.6
0.9 1.8
1.0 2.0
1.0
Period (s)
2.0
0.0
Length (m)
0.4 0.80.2 0.6 1.0
Length (m) Period (s)
0.1 0.6
0.2 0.9
0.4 1.3
0.6 1.6
0.8 1.8
1.0 2.0
14.678 m
3.2 m/s
9200 N
(1.0103kg/m3)(9.80 m/s2)
594 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 1 continued
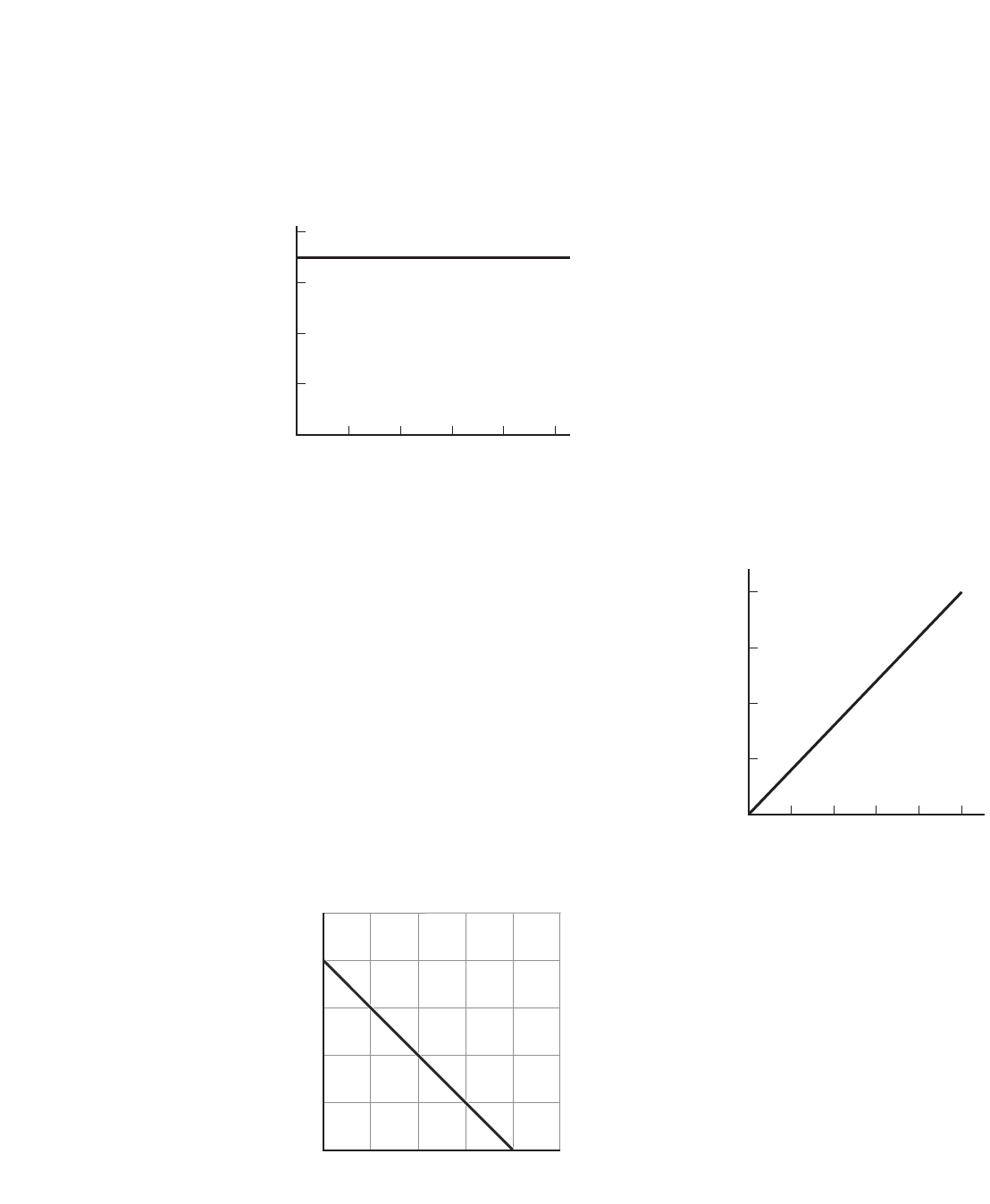
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2
pages 859–860
1. A position-time graph for a bicycle is shown
in the figure below.
a. What is the position of the bicycle at
1.00 min?
35.0 m
b. What is the position of the bicycle at
3.50 min?
35.0 m
c. What is the displacement of the
bicycle between the times 1.00 min
and 5.00 min?
0.00 m
d. Describe the motion of the bicycle.
The bicycle is not moving.
2. The position of an automobile is plotted as a
function of time in the accompanying figure.
a. What is the position of the car at
0.00 s?
40.0 m
b. What is the position of the automobile
after 2.00 s has elapsed?
20.0 m
c. How far did the automobile travel
between the times 1.00 s and 3.00 s?
distance traveled 30.0 m 10.0 m
20.0 m
3. A jogger runs at a constant rate of 10.0 m
every 2.0 s. The jogger starts at the origin, and
runs in the positive direction for 3600.0 s.
The figure below is a position-time graph
showing the position of the jogger from
time t0.0 s to time t20.0 s. Where is
the runner at time t5.0 s? t15.0 s?
At t 5.0 s the jogger is at 25.0 m.
At t 15.0 s the jogger is at 75.0 m.
4.0
0.0
8.0 12.0
Time (s)
16.0 20.0
25.0
50.0
75.0
100.0
Position (m)
0.0
10.0
20.0
30.0
40.0
Position (m)
1.00 2.00 3.00
Time (s)
4.00 5.00
50.0
1.000.00 2.00 3.00
Time (min)
4.00 5.00
10.0
20.0
30.0
4
0
.
0
Position (m)
Physics: Principles and Problems Solutions Manual 595
4. Two trains simultaneously leave the same
train station at noon. One train travels
north and the other travels south. The
position-time graph for both trains is
shown in the accompanying figure.
a. What is the position of the train
traveling north at 6.0 h?
600.0 km
b. What is the position of the train
traveling south at 6.0 h?
300.0 km
c. What is the distance between the trains
at 6.0 h? What is the distance at 10.0 h?
900.0 km, 1500.0 km
d. At what time are the trains 600.0 km
apart?
4.0 h
e. Which train is moving more quickly?
northbound train
5. Two cars head out in the same direction.
Car A starts 1.0 min before car B. The
position-time graphs for both cars are
shown in the accompanying figure.
a. How far apart are the two cars when
car B starts out at t1.0 min?
0.75 km
b. At what time do the cars meet?
2.0 min
c. How far apart are the cars at time
t3.0 min?
0.75 km
6. The position-time graph for two joggers, A
and B, is shown in the accompanying figure.
a. How far apart are the two runners at
10.0 min?
1.50 km
b. At what time are they 1.00 km apart?
20.0 min
c. How far apart are they at 50.0 min?
0.50 km
d. At what time do they meet?
40.0 min
10.00.00 20.0 30.0
Time (min)
40.0 50.0
0.50
1.00
1.50
Jogger B
Jogger A
2.00
Position (km)
1.00.0 2.0 3.0
Time (min)
4.0 5.0
0.5
1.0
1.5
Car A
Car B
2.0
Position (km)
0.0
1000.0
1000.0
Position (km)
4.0 6.0 Time (h)
North
South
8.0 10.0
596 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 2 continued
Physics: Principles and Problems Solutions Manual 597
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
e. What distance does jogger B cover
between 30.0 min and 50.0 min?
0.00 km
f. What distance does jogger A cover
between 30.0 min and 50.0 min?
1.00 km
7. A child’s toy train moves at a constant
speed of 2.0 cm/s.
a. Draw the position-time graph showing
the position of the toy for 1.0 min.
b. What is the slope of the line representing
the motion of the toy?
slope
2.0 cm/s, the same as the
train’s speed
8. The position of an airplane as a function
of time is shown in the figure below.
a. What is the average velocity of the
airplane?
velocity slope of line
2.0102km/h
b. What is the average speed of the
airplane?
speed absolute value of the velocity
2.0102km/h
9. The position-time graph for a hot-air
balloon that is in flight is shown in
the accompanying figure.
a. What is the average velocity of the
balloon?
velocity slope
8.0 km/h
b. What is the average speed of the
balloon?
speed absolute value of slope
8.0 km/h
0.00 km (40.0 km)
5.0 h 0.0 h
1.00.0 2.0 3.0
Time (h)
4.0 5.0
40.0
30.0
20.0
10.0
Position (km)
800.0 km 0.0 km
5.0 h 1.0 h
1.0 2.0 3.0
Time (h)
4.0 5.0
800.0
600.0
400.0
200.0
0.0
Position (km)
120 cm
60 s
rise
run
Position (cm)
90
60
30
010 20
Time (s)
30 40
120
50 60
Chapter 2 continued

Chapter 3
pages 861–862
1. Jason and his sister, Tara, are riding bicycles.
Jason tries to catch up to Tara, who has a
10.0-s head start.
a. What is Jason’s acceleration?
aJ
0.40 m/s2
b. What is Tara’s acceleration?
aT
0.20 m/s2
c. At what time do they have the same
velocity?
20.0 s
2. A dragster starts from rest and accelerates
for 4.0 s at a rate of 5.0 m/s2. It then travels
at a constant speed for 2.5 s. A parachute
opens, stopping the vehicle at a constant
rate in 2.0 s. Plot the v-t graph representing
the entire motion of the dragster.
3. A car traveling at 21 m/s misses the turnoff on
the road and collides into the safety guard rail.
The car comes to a complete stop in 0.55 s.
a. What is the average acceleration of
the car?
a
v
t
f
f
v
ti
i
38 m/s2
b. If the safety rail consisted of a section of
rigid rail, the car would stop in 0.15 s.
What would be the acceleration in this
case?
a
v
t
f
f
v
ti
i
1.4102m/s2
4. On the way to school, Jamal realizes that
he left his physics homework at home. His
car was initially heading north at 24.0 m/s.
It takes him 35.5 s to turn his car around
and head south at 15.0 m/s. If north is
designated to be the positive direction,
what is the average acceleration of the car
during this 35.5-s interval?
a
v
t
f
f
v
ti
i
1.10 m/s2
5. A cheetah can reach a top speed of 27.8 m/s
in 5.2 s. What is the cheetah’s average
acceleration?
a
v
t
f
f
v
ti
i
5.3 m/s2
6. After being launched, a rocket attains a speed
of 122 m/s before the fuel in the motor is
completely used. If you assume that the accel-
eration of the rocket is constant at 32.2 m/s2,
how much time does it take for the fuel to be
completely consumed?
a
v
t
t 3.79 s
122 m/s 0.00 m/s
32.2 m/s2
v
a
27.8 m/s 0.0 m/s
5.2 s
15.0 m/s 24.0 m/s
35.5 s
0.00 m/s 21 m/s
0.15 s
0.00 m/s 21 m/s
0.55 s
Velocity (m/s)
15.0
10.0
5.0
0.0 2.0 4.0
Time (s)
6.0 8.0
20.0
10.0
8.0 m/s 0.0 m/s
40.0 s 0.0 s
8.0 m/s 0.0 m/s
30.0 s 10.0 s
10.00.0 20.0 30.0
Time (s)
40.0
2.0
4.0
6.0
Jason
Tara
8.0
Velocity (m/s)
598 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Physics: Principles and Problems Solutions Manual 599
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. An object in free fall has an acceleration of
9.80 m/s2assuming that there is no air resis-
tance. What is the speed of an object dropped
from the top of a tall cliff 3.50 s after it has
been released, if you assume the effect of air
resistance against the object is negligible?
a
v
t
v a
t gt (9.80 m/s2)(3.50 s)
34.3 m/s
8. A train moving with a velocity of 51 m/s east
undergoes an acceleration of 2.3 m/s2as it
approaches a town. What is the velocity of the
train 5.2 s after it has begun to decelerate?
a
v
t
vfa
t vi
(2.3 m/s2)(5.2 s) 51 m/s
39 m/s
9. The v-t graph of a runner is shown in the
accompanying figure.
The displacement is the area under the
graph.
a. What is the displacement of the runner
between t0.00 s and t20.0 s?
d
(8.0 m/s)(20.0 s)
8.0101m
b. What is the displacement of the runner
between t 20.0 s and t 50.0 s?
d (8.0 m/s)(50.0 s 20.0 s)
240 m
c. What is the displacement of the runner
between t 50.0 s and t 60.0 s?
d
(8.0 m/s)(60.0 s 50.0 s)
4.0101m
10. Draw the v-t graph of an automobile that
accelerates uniformly from rest at t0.00 s
and covers a distance of 180.0 m in 12.0 s.
Since the car accelerates uniformly, the
v-t graph is a straight line. Starting from
the origin, the area is triangular.
Thus, d vmaxt
vmax
2
t
d
(2)(
1
1
2
8
.0
0.0
sm)
30.0 m/s
11. The v-t graph of a car is shown in the accom-
panying figure. What is the displacement of
the car from t0.00 s to t15.0 s?
displacement area under v-tgraph
The total displacement is the sum of
the displacements from 0.00 s to 4.00 s,
4.00 s to 6.00 s, 6.00 s to 8.00 s, 8.00 s to
10.0 s, and 10.0 s to 15.0 s:
4.00 8.00 12.00 16.00
15.0
0.00
30.0
Time (s)
15.0
30.0
Velocity (m/s)
Velocity (m/s)
15.0
0.0 2.0 4.0
Time (s)
6.0 8.0
30.0
10.0 12.0
1
2
1
2
1
2
10.0
0.00 20.0 30.0
Time (s)
40.0 50.0 60.0
2.0
4.0
6.0
8.0
Velocity (m/s)
vfvi
t
Chapter 3 continued

dtotal d1 d2 d3 d4 d5
(30.0 m/s)(4.00 s)
(30.0 m/s)(2.00 s)
(30.0 m/s)(2.00 s)
(30.0 m/s)(2.00 s)
(30.0 m/s)(5.00 s)
30.0 m
12. Suppose a car rolls down a 52.0-m-long
inclined parking lot and is stopped by a
fence. If it took the car 11.25 s to roll down
the hill, what was the acceleration of the
car before striking the fence?
df di vitf atf2
vi 0.00 m/s since the car starts
from rest
a 0.823 m/s2
13. A sky diver in free fall reaches a speed of
65.2 m/s when she opens her parachute.
The parachute quickly slows her down to
7.30 m/s at a constant rate of 29.4 m/s2.
During this period of acceleration, how far
does she fall?
vf2 vi2 2a(dfdi)
dfdi
71.4 m
She has fallen 71.4 m during the accel-
eration period.
14. A child rolls a ball up a hill at 3.24 m/s.
If the ball experiences an acceleration of
2.32 m/s2, how long will it take for the ball
to have a velocity of 1.23 m/s down the hill?
Let the positive direction be up the hill.
vf vi atf
tf
vf
a
vi
1.93 s
15. A cheetah can accelerate from rest to a speed
of 27.8 m/s in 5.20 s. The cheetah can main-
tain this speed for 9.70 s before it quickly
runs out of energy and stops. What distance
does the cheetah cover during this 14.9-s run?
During the acceleration period:
vf vi atf
a
vf
tf
vi
5.35 m/s2
With this acceleration the distance
during acceleration can be determined.
vf2 vi2 2a(dfdi)
dfdi
vf2
2
a
vi2
72.3 m
During the constant speed period,
a 0.00 m/s2.
d vt (27.8 m/s)(9.70 s)
2.70102m
The total distance is then the sum of
the two.
distance 2.70102m 72.3 m
342 m
16. A cab driver in a hurry is sitting at a red light.
When the light turns green she rapidly accel-
erates for 3.50 s at 6.80 m/s2. The next light
is still red. She then slams on the brakes,
accelerating at a rate of 9.60 m/s2before
coming to rest at the stop light. What was her
total distance for this trip?
During the first part of the trip,
df di vitf atf2
dfdi atf2
(6.80 m/s2)(3.50 s)2
41.6 m
1
2
1
2
1
2
(27.8 m/s)2(0.00 m/s)2
(2)(5.35 m/s2)
27.8 m/s 0.00 m/s
5.20 s
1.23 m/s 3.24 m/s
2.32 m/s2
(7.30 m/s)2(65.2 m/s)2
(2)(29.4 m/s2)
vf2vi2
2a
(2)(52.0 m)
(11.25 s)2
2(dfdi)
tf2
1
2
1
2
1
2
1
2
600 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 3 continued

Physics: Principles and Problems Solutions Manual 601
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
For the second part, first determine
the speed of the cab at the end of the
first acceleration period.
vf vi atf
(0.00 m/s) (6.80 m/s2)(3.50 s)
23.8 m/s
During the second acceleration period,
vf2 vi2 2a(dfdi)
dfdi
29.5 m
The total distance traveled is then the
sum of the two.
distance 41.6 m 29.5 m 71.1 m
17. A cyclist rides at a constant speed of 12.0 m/s
for 1.20 min and then coasts to a stop with
uniform acceleration 21.2 s later. If the total
distance traveled is 1321 m, then what is the
acceleration while the bike coasts to a stop?
During the first part of the motion,
the rider moves at constant speed,
or a 0.00 m/s2.
The distance covered is then
d vt (12.0 m/s)(72 s) 864 m.
The distance covered during the coast-
ing period is then 1321 864 457 m.
vf2 vi2 2a(dfdi)
a
0.158 m/s2
18. A hiker tosses a rock into a canyon. He
hears it strike water 4.78 s later. How far
down is the surface of the water?
Assume that downward is the positive
direction.
df di vitf atf2
0.00 m (0.00 m/s)(4.78 s)
(9.80 m/s2)(4.78 s)2
112 m
19. A rock is thrown upward with a speed of
26 m/s. How long after it is thrown will the
rock have a velocity of 48 m/s toward the
ground?
Take upward as the positive direction.
vf vi atfwhere a g
tf 7.6 s
20. The high-dive board at most pools is
3.00 m above the water. A diving instructor
dives off the board and strikes the water
1.18 s later.
a. What was the initial velocity of the
diver?
df di vitf atf2where a g
vi
3.24 m/s
b. How high above the board did the
diver rise?
At the highest point, the speed is
0.00 m/s.
vf2 vi2 2a(dfdi) where a g
dfdi
vf
2
2
(
g
v
)i2
0.536 m
(0.00 m/s)2(3.24 m/s)2
(2)(9.80 m/s2)
(3.00 m)
1
2
(9.80 m/s2)(1.18 s)2
1.18 s
(dfdi)
1
2
(g)tf2
tf
1
2
48 m/s 26 m/s
9.80 m/s2
vfvi
g
1
2
1
2
(0.00 m/s)2(12.0 m/s)2
(2)(457 m)
vf2vi2
2(dfdi)
(0.00 m/s) (23.8 m/s)2
(2)(9.60 m/s2)
vf2vi2
2a
Chapter 3 continued
Chapter 4
pages 862–864
1. Draw a free-body diagram for the space
shuttle just after it leaves the ground.
Identify the forces acting on the shuttle.
Make sure that you do not neglect air resis-
tance. Also be sure that you indicate the
direction of the acceleration, as well
as the net force.
The net force and acceleration are both
upward.
2. Draw a free-body diagram for a goldfish
that is motionless in the middle of a fish-
bowl. Identify the forces acting on the
fish. Indicate the direction of the net force
on the fish and the direction of the acceler-
ation of the fish.
The net force and the acceleration are
both zero.
3. Draw a free-body diagram for a submerged
beach ball as it rises toward the surface just
after being released. Identify the forces acting
on the beach ball and indicate the direction
of the net force and the acceleration.
The net force and acceleration vectors
are upward.
4. Muturi is rearranging some furniture. He
pushes the dresser with a force of 143 N,
and there is opposing frictional force of
112 N. What is the net force?
Fnet 143 N 112 N 31 N
5. One of the floats in a Thanksgiving Day
parade requires four people pulling on
ropes to maintain a constant speed of
3.0 km/h for the float. Two people pull
with a force of 210 N each, and the other
two pull with a force of 140 N each.
a. Draw a free-body diagram.
140 N (2)
Ff
210 N (2)
Fbuoyant
Fnet a
Fwater
resistance
Fg
Fbuoyant
Fg
Fthrust
Fg
Fair resistance
602 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 603
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What is the force of friction between the
float and the ground?
Fnet 210 N 210 N 140 N
140 N Ff
0 since speed is constant
Ff 7.0102N
6. Five people are playing tug-of-war. Anders
and Alyson pull to the right with 45 N and
35 N, respectively. Calid and Marisol pull to
the left with 53 N and 38 N, respectively.
With what force and in what direction does
Benito pull if the game is tied?
Assign the coordinate system so that
positive forces are to the right. Since
the rope is not accelerating:
Fnet FAnders FAlyson FCalid
FMarisol FBenito
0 N 45 N 35 N 53 N 38 N
FBenito
0 N 11 N FBenito
FBenito 11 N
Benito pulls to the right.
7. Two dogs fight over a bone. The larger of
the two pulls on the bone to the right with
a force of 42 N. The smaller one pulls to
the left with a force of 35 N.
a. Draw the free-body diagram for the bone.
b. What is the net force acting on the bone?
Fnet 42 N 35 N 7 N to the right
c. If the bone has a mass of 2.5 kg, what is
its acceleration?
Fnet ma
a 3 m/s2
8. A large model rocket engine can produce
a thrust of 12.0 N upon ignition. This
engine is part of a rocket with a total mass
of 0.288 kg when launched.
a. Draw a free-body
diagram of the rocket
just after launch.
b. What is the net force that is acting on
the model rocket just after it leaves the
ground?
Fnet Fthrust Fg
12.0 N (0.288 kg)(9.80 m/s2)
9.2 N upward
c. What is the initial acceleration of the
rocket?
Fnet ma
a
31.8 m/s2
9. Erika is on an elevator and presses the
button to go down. When the elevator
first starts moving, it has an acceleration of
2.5 m/s2downward. Erika and the elevator
have a combined mass of 1250 kg.
1.20 N (0.288 kg)(9.80 m/s2)
0.288 kg
Fnet
m
Fthrust
Fg
7 N
2.5 kg
Fnet
m
35 N 42 N
Do
g
1 Do
g
2
Chapter 4 continued

a. Draw a free-body diagram for the
elevator.
b. What is the tension in the cable that
provides the upward force on the
elevator car?
Fnet FT Fg ma
FT ma Fg
(1250 kg)(2.5 m/s2)
(1250 kg)(9.80 m/s2)
9100 N upward
10. Ngan has a weight of 314.5 N on Mars and
a weight of 833.0 N on Earth.
a. What is Ngan’s mass on Mars?
Fg, Earth mgEarth
m 85.0 kg
b. What is the acceleration due to gravity
on Mars, gMars?
Fg, Mars mgMars
gMars
3.70 m/s2
11. Alex is on the wrestling team and has a mass
of 85.3 kg. Being a whiz at physics, he real-
izes that he is over the 830.0-N cutoff for his
weight class. If he can convince the trainers
to measure his weight in the elevator, what
must be the acceleration of the elevator so
that he just makes his weight class?
Fnet Fg, apparent Fg ma
a
0.0696 m/s2
a 0.0696 m/s2down
12. During a space launch, an astronaut typically
undergoes an acceleration of 3 gs, which
means he experiences an acceleration that
is three times that of gravity alone. What
would be the apparent weight of a 205-kg
astronaut that experiences a 3-gliftoff?
Let up be the negative direction.
Fnet Fg, apparent Fg ma
Fg, apparent Fg ma
(205 kg)(9.80 m/s2)
(205 kg)(3)(9.80 m/s2)
8040 N
13. Alfonso and Sarah like to go sky diving
together. Alfonso has a mass of 88 kg, and
Sarah has a mass of 66 kg. While in free fall
together, Alfonso pushes Sarah horizontally
with a force of 12.3 N.
a. What is Alfonso’s horizontal acceleration?
Fon Sarah mSarahaSarah
aSarah
0.19 m/s2
b. What is Sarah’s horizontal acceleration?
Fon Alphonso Fon Sarah
mAlphonsoaAlphonso
aAlphonso
0.14 m/s2
14. A 7.25-g bullet is fired from a gun. The
muzzle velocity of the bullet is 223 m/s.
Assume that the bullet accelerates at a
constant rate along the barrel of the gun
before it emerges with constant speed.
The barrel of the gun is 0.203 m long.
What average force does the bullet exert
on the gun?
by Newton’s third law
Fon bullet Fon gun
12.3 N
88 kg
Fon Alphonso
mAlphonso
12.3 N
66 kg
Fon Sarah
mSarah
830.0 kg (85.3 kg)(9.80 m/s2)
85.3 kg
Fg, apparent Fg
m
314.5 N
85.0 kg
Fg, Mars
m
833.0 N
9.80 m/s2
Fg, Earth
gEarth
FT
Fg
604 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued
Physics: Principles and Problems Solutions Manual 605
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Fon bullet mbulletabullet
vf2 vi2 2abullet(df di)
abullet 1.22105m/s2
Fon bullet mbulletabullet
(0.00725 kg)(1.22105m/s2)
888 N
so, 888 N on the gun
15. A 15.2-kg police battering ram exerts an
average force of 125 N on a 10.0-kg door.
a. What is the average acceleration of the
door?
By Newton’s third law,
Fdoor Fram
Fdoor mdooradoor
adoor
1
1
0
2
.0
5k
N
g
12.5 m/s2
b. What is the average acceleration of the
battering ram?
Fram mramaram
aram 8.22 m/s2
16. As a demonstration, a physics teacher
attaches a 7.5-kg object to the ceiling by a
nearly massless string. This object then sup-
ports a 2.5-kg object below it by another
piece of string. Finally, another piece of
string hangs off the bottom of the lower
object to be pulled with ever increasing force
until the string breaks somewhere. The string
will break when the tension reaches 156 N.
a. Which length of string will break first?
A free-body diagram can be drawn
for the 2.5-kg mass, m1, and the two
masses taken together, m1 m2. Let
FT1 be the tension in the top string,
and FT2 the tension in the middle
string, and FT3 the tension applied
by the physics teacher.
FT2 FT3 Fg 0
FT2 (2.5 kg)(9.80 m/s2) FT3
24.5 N FT3
FT1 FT3 Fg 0
FT1 (10.0 kg)(9.80 m/s2) FT3
98.0 N FT3
Regardless of the applied force
FT1 FT2 FT3. Therefore, the upper
string will break first.
b. What is the maximum downward force
the physics teacher can apply before the
string breaks?
FT2
Fg
FT1
Fg
FT3
FT3
2.5 kg m110.0 kg m1 m2
2.5 kg
7.5 kg
125 N
15.2 kg
Fram
mram
Fdoor
mdoor
(223 m/s)2
(2)(0.203 m)
Chapter 4 continued

The string breaks when FT1 156 N.
FT1 98.0 N FT3
FT3 FT1 98.0 N 156 N 98.0 N
58 N
17. A 10.0-kg object is held up by a string
that will break when the tension exceeds
1.00102N. At what upward acceleration
will the string break?
Fnet FT Fg ma
a
0.200 m/s2
18. A large sculpture is lowered into place by a
crane. The sculpture has a mass of 2225 kg.
When the sculpture makes contact with the
ground, the crane slowly releases the ten-
sion in the cable as workers make final
adjustments to the sculpture’s position on
the ground.
a. Draw a free-body diagram of the sculp-
ture when it is in contact with the
ground, and there is still tension in
the cable while the workers make the
final adjustments.
b. What is the normal force on the sculp-
ture when the tension in the cable is
19,250 N?
What is the normal force on the
sculpture when the tension in the
cable is 19,250 N?
Fnet FT FN Fg 0
FN Fg FT
(2225 kg)(9.80 m/s2)
19,250 N
2560 N
2560 N upward
FT
Fg
FN
1.00102N(10.0 kg)(9.80 m/s2)
10.0 kg
FTFg
m
606 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 4 continued

Physics: Principles and Problems Solutions Manual 607
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5
pages 865–867
1. A soccer ball is kicked from a 22-m-tall platform. It lands 15 m from the base of
the platform. What is the net displacement of the ball?
Since the two distances are perpendicular, use the Pythagorean theorem.
R2 A2 B2
R A2
B2
(22 m
)2(1
5 m)2
27 m
2. If the net displacement is 32 m for the same situation, as described in problem 1,
how far from the platform base must the ball land?
R2 A2 B2
B R2
A2
(32 m
)2(2
2 m)2
23 m
3. For any single force vector, there is only one angle for which its x- and
y-components are equal in size.
a. What is that angle?
Rsin Rcos
c
so
in
s
tan1
tan1(1) 45°
b. How many times bigger is a vector at this particular angle than either of its
components?
Rs
R
in
sin
1
1.4 times bigger
4. A cue ball on a billiards table travels at 1.0 m/s for 2.0 s.
After striking another ball, it travels at 0.80 m/s for 2.5 s at
an angle of 60.0° from its original path.
a. How far does the cue ball travel before and after it strikes
the other ball?
In first leg it goes
xbefore vbeforetbefore
(1.0 m/s)(2.0 s)
2.0 m
and in second leg
xafter vaftertafter
(0.80 m/s)(2.5 s)
2.0 m
120.0°
1
sin 45°
R
R
R
R
b. What is the net displacement of the cue ball for the entire 4.5-s time interval?
Note that the angle between the two legs is 120.0°, not 60.0°.
Using the law of cosines
R2 x2 y2 2xy(cos )
R x2 y
2 2x
y(cos
)
(2.0 m
)2(2
.0 m)2
(2)
(2.0 m
)(2.0 m
)(cos
120.0
°)
3.5 m
5. The table below represents a set of force vectors. These vectors
begin at the origin of a coordinate system, and end at the
coordinates given in the table.
a. What is the magnitude of the resultant of
the sum of these three vectors?
Rx AxBxCx
0.0 N 5.0 N 0.0 N 5.0 N
Ry AyByCy
6.0 N 0.0 N (10.0 N) 4.0 N
R Rx2
Ry2
(5.0 N
)2(
4.0 N)
2
6.4 N
b. What is the size of the angle, , that the resultant makes with the horizontal?
tan1
R
Ry
x
tan1
54
.0
.0N
N
39°
c. Into which quadrant does the resultant point?
Because the x-component is positive and the y-component is negative,
the resultant points into quadrant 4.
6. A 9.0-kg crate sits on a level, rough floor. A 61-N force is needed just to start it
moving. What is the size of the coefficient of maximum static friction?
if there is no motion, Fapplied Ff sFN;
therefore,
s
Fap
F
p
N
lied
Fa
m
pp
g
lied
0.69
61 N
(9.0 kg)(9.80 m/s2)
Vector # x-value (N) y-value (N)
A0.0 6.0
B5.0 0.0
C0.0 10.0
608 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued
y
x
A
C
B
R
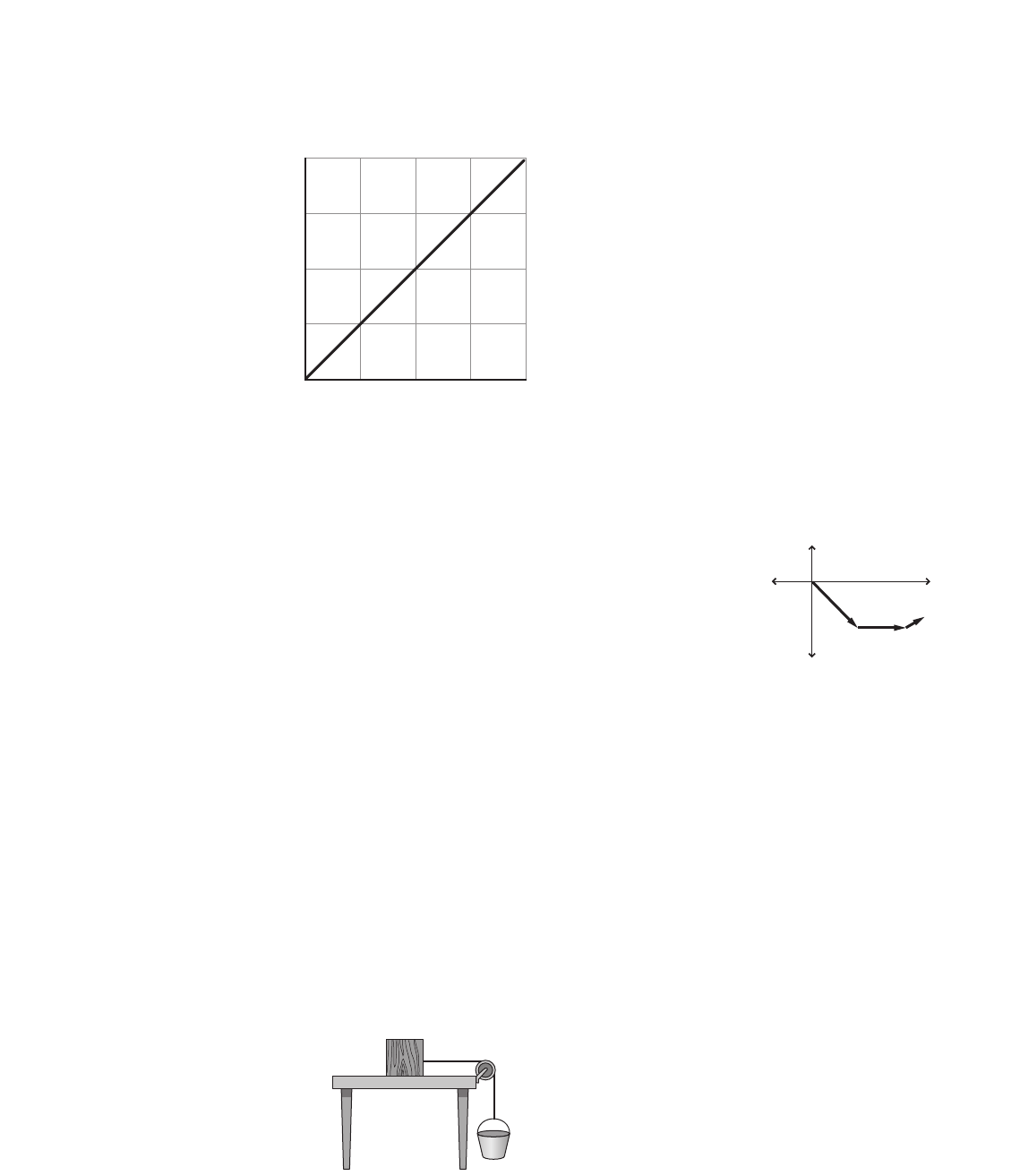
Physics: Principles and Problems Solutions Manual 609
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. Given the graph below, answer the following
questions.
a. What is the value of kfor this system?
kis the slope of the line.
4
8N
N
0
0N
N
0.5
b. If the frictional force is 1.5 N, what is FN?
From the graph, FN 3 N
c. Does tripling FNtriple Fapplied?
Yes, they are directly proportional.
d. Do Fapplied and FNact in the same
direction? Explain why or why not.
No, the friction force acts horizontally
and opposite to applied force, while
the normal force acts perpendicular
to the fixed surface.
8. A wooden block sits on a level lab table. A
string draped over a pulley connects to a
bucket that can be filled with lead pellets.
Maggie wants to measure how much applied
mass (pellets bucket) is needed to move
the block along the table at a constant speed.
a. If the applied mass of the bucket and
the lead pellets is 0.255 kg, and the
block has a weight of 12 N, what is
the value of k?
If vis constant, Fapplied Ff kFN
k
Fap
F
p
N
lied
0.21
b. If some extra pellets are added, describe
the behavior of the block.
Since Fapplied now exceeds Ff,
Fnet 0, the block will accelerate
over time.
9. A boat travels 75 km southeast, then 56 km
due east, then 25 km 30.0° north of east.
a. Sketch the vector set on a N-E-S-W grid.
b. Find its net E-W component of displace-
ment and net N-S component of
displacement.
REW AEW BEW CEW
(75 km)(cos (45°))
(56 km)(cos 0.0°)
(25 km)(cos 30.0°)
1.3102 km
RNS ANS BNS CNS
(75 km)(sin (45°))
(56 km)(sin 0.0°)
(25 km)(sin 30.0°)
41 km
c. Find its net displacement.
R REW2
RNS
2
(1.3
102km
)2(
41 km
)2
136 km
S
N
WE
(0.255 kg)(9.80 m/s2)
12 N
mbucket leadg
FN
2468
0
1
2
3
Ff (N)
FN (N)
4
Chapter 5 continued

d. Find its net angle relative to an E-W axis.
tan 1
tan 1
1.3
41
10k
2m
km
18°
18° south of east
10. A 1.25-kg box is being pulled across a level
surface where kis 0.80. If the string is sud-
denly cut, causing the applied force to
immediately go to 0.0 N, what is the rate of
acceleration of the block?
Let the direction of the applied force be
positive.
The net force on the box is due to
friction and is in the negative direction.
Fnet ma Ff kFN kmg
a kg (0.80)(9.80 m/s2)
7.8 m/s2in the negative direction
11. If the velocity of the box in problem 10 was
5.0 m/s at time zero, what will be its speed
after 0.50 s? How far will it travel in that
time interval?
vf vi at
vf 5.0 m/s (7.8 m/s2)(0.50 s)
1.1 m/s
d
1.5 m
12. A 0.17-kg hockey puck leaves the stick on a
slap shot traveling 21 m/s. If no other forces
act on the puck, friction eventually will
bring it to rest 62 m away.
a. Based on these data, determine the
value of kfor this hockey puck on ice.
Let the direction of motion be posi-
tive. Thus, the force of friction is in
the negative direction.
Ff kFN (Remember: friction is in
the negative direction.)
Ff Fnet ma (No negative sign
here because the value of ashould
incorporate that.)
Thus,
kFN ma
kmg ma
k
vf2 vi2 2ad, so a
vf2
2
d
vi2
k
0.36
b. Will the answer change if a puck of
different mass, but same material and
shape is used? Explain why or why not.
No, the result is independent of
mass. Note how it cancels in above
solution.
13. A 105-N suitcase sits on a rubber ramp at
an airport carousel at a 25° angle. The
weight vector can be broken into two
perpendicular components.
a. What is the magnitude of the compo-
nent parallel to the ramp surface?
Fx Fw sin (105 N)(sin 25°)
44 N
b. What is the magnitude of the compo-
nent at a right angle to the ramp
surface?
Fy Fw cos (105 N)(cos 25°)
95 N
FxFy
105 N
Fg
((0.0 m/s)2(21 m/s)2)
(2)(62 m)(9.80 m/s2)
(vf2vi2)
2dg
vf2
2
d
vi2
g
a
g
(1.1 m/s)2(5.0 m/s)2
(2)(7.8 m/s2)
vf2vi2
2a
RNS
REW
610 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 5 continued

Physics: Principles and Problems Solutions Manual 611
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
c. Which of those components is the
normal force?
Fy
14. In problem 13, which force offsets the
kinetic friction force? If Fxexceeds Ff, will
the suitcase accelerate down the ramp?
The component parallel to ramp, Fx,
offsets the friction force. Since Fnet
along ramp no longer equals zero,
the suitcase will accelerate.
15. Dalila decides to determine the coefficient
of maximum static friction for wood against
wood by conducting an experiment. First
she places a block of wood on a small
plank; next, she slowly lifts one end of the
plank upward. She notes the angle at which
the block just begins to slide, and claims
that s tan . She is correct. Show why.
If there is no motion, Fnet along the
ramp 0 and
Fx Fwsin Ff sFN sFw cos
Thus, s
F
F
w
wc
s
o
in
s
tan
This works, regardless of the weight of
the block.
16. Jonathan, with a mass of 81 kg, starts at rest
from the top of a water slide angled at 42°
from the ground. He exits at the bottom
3.0 s later going 15 m/s. What is k?
vf vi at where vi 0
a
v
tf
Fnet ma Fg Ff Fg kFn
mg sin kmg cos
k
mg
m
s
g
in
c
os
ma
0.21
17. A 64-N box is pulled by a rope at a constant
speed across a rough horizontal surface.
If the coefficient of kinetic friction is 0.81,
what is the magnitude of the applied force
if that force is directed parallel to the floor?
Fapplied Ffsince Fnet 0
Ff kFN (0.81)(64 N) 52 N
18. Suppose that in problem 17 the applied
force is directed by the rope at an angle, ,
to the floor.
a. The normal force is no longer simply Fg.
Show how to compute net vertical force.
Fnet, y Fg (Fapplied sin )
b. The frictional force still opposes the
horizontal motion of the box. Show
how to compute net horizontal force.
Fnet, x Fapplied cos (Ff)
Fapplied cos kFN
Fapplied cos kFnet, y
(9.80 m/s2)(sin 42°)
13
5.0
ms
/s
(9.80 m/s2)(cos 42°)
gsin
v
tf
gcos
gsin a
gcos
Chapter 5 continued
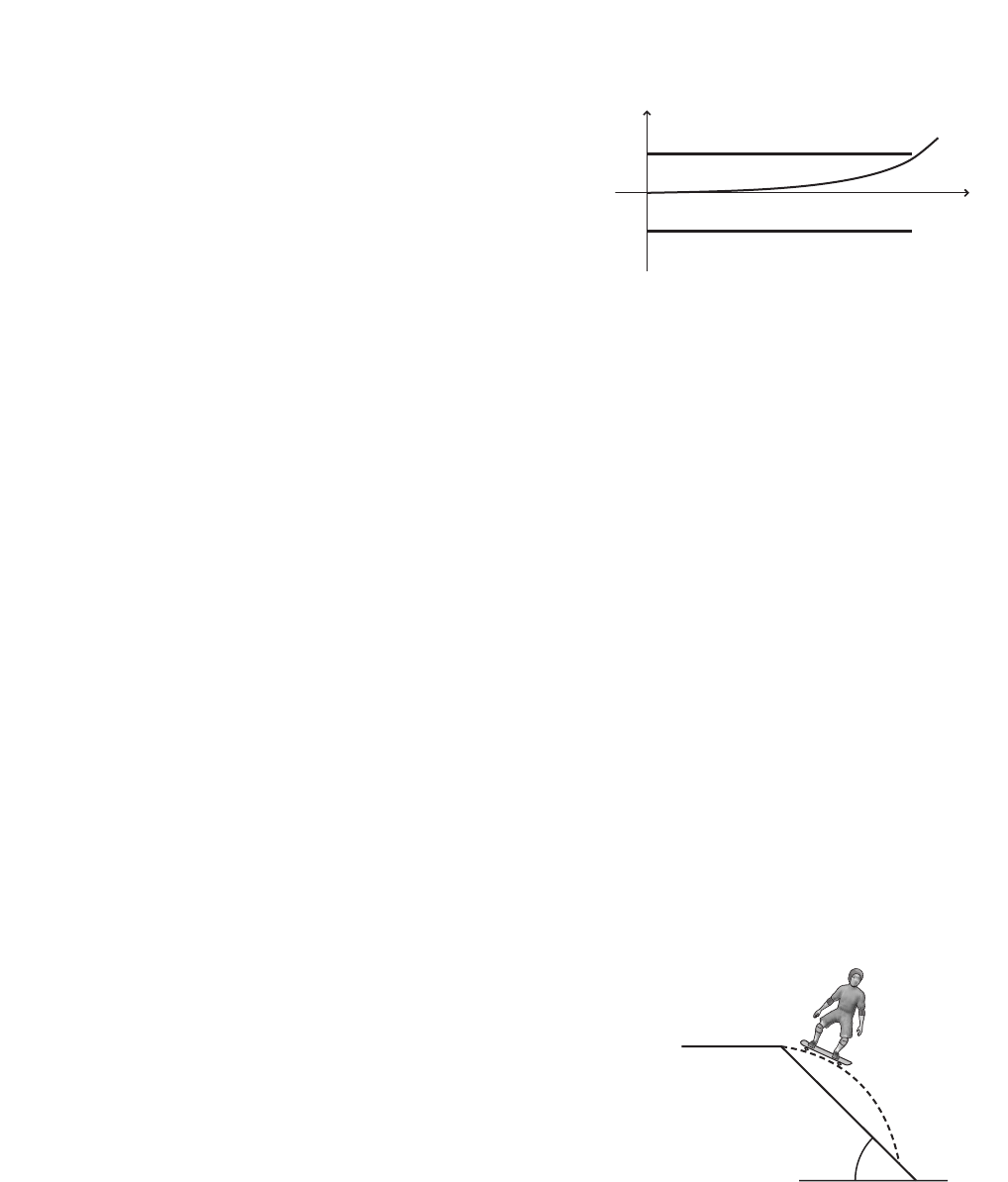
Chapter 6
pages 867–868
1. A football player kicks a field goal from a dis-
tance of 45 m from the goalpost. The football
is launched at a 35° angle above the horizon-
tal. What initial velocity is required so that the
football just clears the goalpost crossbar that
is 3.1 m above the ground? Ignore air resis-
tance and the dimensions of the football.
The origin of the coordinate system is
at the point of the kick.
vxivi cos
vyivi sin
Let tbe the time when the football
crosses the vertical plane of the
uprights. Then:
x vxit
so t
v
x
xi
y vyit
vyi
v
x
xi
(visin )
(tan )(x)
vi
23 m/s
2. In a certain cathode-ray tube, a beam of
electrons, moving at a constant velocity,
enters a region of constant electric force
midway between two parallel plates that are
10.0 cm long and 1.0 cm apart. In this
region, the electrons experience an accelera-
tion, a, toward the upper plate. If the elec-
trons enter this region at a velocity of
3.0106m/s, what is the acceleration that
needs to be applied so that the electrons
just miss the upper deflection plate?
Locate the origin of the coordinate sys-
tem midway between the plates at the
left edge. Thereby yi 0 and vyi 0.
The position of an electron in the region
of the plates is given by:
x vxit,y
Eliminating tgives the trajectory:
y
v
x
xi
2 x2
We require the trajectory to pass through
the point just beyond the deflection plate:
y x2
Then,
a
9.01012 m/s2
3. A skateboard track has a horizontal segment
followed by a ramp that declines at a 45°
angle, as shown.
a. How long would the ramp need to be to
provide a landing for a skateboarder who
launches from the horizontal segment at
a velocity of 5.0 m/s?
The skateboarder’s trajectory is
given by:
y x2,for 0x xL
g
2vxi2
45°
(2)(3.0106m/s)2
0.01
2
0m
(0.100 m)2
2vxi2y
x2
a
2vxi2
a
2vxi2
a
2
at2
2
y
x
d
d
Electron beam
Deflector plates
(9.80 m/s2)(45 m)2
(2)(cos 35°)2((tan 35°)(45 m) 3.1 m)
gx2
2(cos )2((tan )(x) y)
gx2
2vi2(cos )2
x2
(vicos )2
g
2
x
vicos
g
v
x
xi
2
2
gt2
2
612 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 613
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The ramp can be represented by the
equation:
y x
By eliminating y, we can find the val-
ues of xthat satisfy both equations.
x2 x x 1x 0
x 0, x
2v
g
xi2
xL
The second solution represents the
point where the skateboarder returns
to the ramp.
xL 5.1 m
yL xL 5.1 m
xL Lramp cos
Lramp 7.2 m
The negative sign is because of the
coordinate system assigned.The
length of the ramp is a positive
value: 7.2 m.
b. If the initial velocity is doubled, what
happens to the required length of the
ramp?
Note that the required ramp length is
proportional to the square of the ini-
tial velocity. Therefore, the required
ramp length is quadrupled to 28.8 m.
4. In an attempt to make a 3-point shot from
a distance of 6.00 m, a basketball player
lofts the ball at an angle of 68° above the
horizontal. The ball has an initial velocity
of 10.0 m/s and an initial distance from the
floor of 1.50 m.
a. What is the maximum height reached
by the ball?
The vertical component of the veloc-
ity over time is:
vy vyi gt
The maximum height occurs at time
t1when the vertical velocity is zero.
t
v
g
yi
If the coordinate system is chosen
so that the origin is on the floor at
the point the ball is thrown, then the
height of the ball over time is:
y yi vyit
At time t, the maximum height is
ymax yi vyi
2
yi
yi yi
1.50 m
5.9 m
b. If the basket rim height is 3.05 m, how
far above the rim is the ball?
The horizontal position of the ball
over time is:
x vxit (vicos )(t)
so t
The height of the ball then is:
yrim yi vyit
yi visin
2
yi tan x
1.50 m (tan 68°)(6.00 m)
3.78 m
height above rim 3.78 m 3.05 m
0.73 m
The ball is 0.73 m above the rim.
5. How far does a baseball that is thrown hori-
zontally at 42.5 m/s drop over a horizontal
distance of 18.4 m?
(9.80 m/s2)(6.00 m)2
(2)(10.0 m/s)2(cos 68°)2
gx2
vi2(cos )2
x
vicos
g
2
x
vicos
gt2
2
x
vicos
(10.0 m/s)2(sin 68°)2
(2)(9.80 m/s2)
vi2(sin )2
2g
vyi2
2g
gvyi2
2g2
vyi2
g
vyi
g
g
2
vyi
g
gt2
2
5.1 m
cos 45°
xL
cos
(2)(5.0 m/s)2
9.80 m/s2
g
2vxi2
g
2vxi2
Chapter 6 continued

The time needed by the baseball to travel
18.4 m is
x vxt, so t
In this time interval the ball drops
y
2
2
0.918 m
6. A projectile is launched from zero height
with an initial angle, , above the horizon-
tal and with an initial velocity, vi.
a. Show that the range of the projectile—
the distance from the launch point at
which the height is again zero—is
given by:
R
v
g
i2
sin 2
Locate the origin of the coordinate
system at the point of launch.The
projectile coordinates over time are
given by:
x vxit,y vyit gt2
Eliminating tgives the trajectory
path.
y x x2
x x
Setting y 0 gives the two roots of
this equation.
x 0, x 0
The second is the solution of interest.
Solve for xand rename it as R.
R
Substitute:
vxi vicos ,vyi visin ,
R
and use the trigonometric identity
2 sin cos sin 2 to get
R sin 2
b. What launch angle, , results in the
largest range?
sine has a maximum value at 90° so,
2 90°
45°
Ris maximum when 45°
7. If a ring were constructed as part of a space
station, how fast must a 50.0-m-radius ring
rotate to simulate Earth’s gravity?
For objects in uniform circular motion,
the centripetal acceleration is ac .
To simulate Earth’s gravity, set the
centripetal acceleration to g.
ac g
v2 gr
v gr
(9.80
m/s2)
(50.0
m)
22.1 m/s
The required period Tis
T 14.2 s
8. A turntable for vinyl records works by con-
straining the needle to track inside a groove
in a very close approximation of uniform
circular motion. If the turntable rotational
speed is 33
1
3
rpm, what is the needle’s
centripetal acceleration when it is 14.6 cm
from the center?
(33 rev/min) 0.55 rev/s
T 1.80 s
ac 3.20 m/s2
42(0.146 m)
1.80 s
42r
T2
1
0.556 rev/s
1
3
(2)(50.0 m)
22.1 m/s
2r
v
v2
r
v2
r
vi2
g
(vi2)(2)(sin )(cos )
g
(2)(vicos )(visin )
g
2vxivyi
g
g
2vxi2
vyi
vxi
g
2vxi2
vyi
vxi
g
2vxi2
vyi
vxi
1
2
18.4 m
42.5 m/s
9.80 m/s2
2
x
vx
g
2
gt2
2
x
vx
614 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued
Physics: Principles and Problems Solutions Manual 615
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
9. A park ride is designed so that the rider is
on the edge of a revolving platform, 3.5 m
from the platform’s center. This platform is
mounted 8.0 m from the center of a larger
revolving platform. The smaller platform
makes one revolution in 6.0 s and com-
pletes 2.0 rev for each revolution of the
larger platform. All rotations are counter-
clockwise. At the instant shown, what are
the magnitude and the direction of the
rider’s velocity with respect to the ground?
Let the velocity of the rider Rwith
respect to point Pbe vRP. The period of
platform Pis 6.0 s, so the magnitude
and direction of vRP is
vRP
3.7 m/s, north
The period of platform Qis (2.0)(6.0 s)
12 s, so the magnitude and direction
of vPQ is
vPQ
4.2 m/s, east
The velocity of the rider with respect to
the ground is
vRQ vRP vPQ
vRQ vRP2
vPQ2
vRQ(3.7 m
/s)2
(4.2 m
/s)2
5.6 m/s
The direction is:
tan1
tan1
41° north of east
10. Two objects are placed on a flat turntable
at 10.0 cm and 20.0 cm from the center,
respectively. The coefficient of static friction
with the turntable is 0.50. The turntable’s
rotational speed is gradually increased.
a. Which of the two objects will begin to
slide first? Why?
The outer object slides first.The
centripetal acceleration ac is
proportional to the radius, r. The
centripetal acceleration is provided
by the frictional force up to the limit
specified by the coefficient of static
friction. Therefore, at any given rota-
tional speed, the frictional force is
greater for the object at the larger
radius, and the force on that object
reaches the limit first.
b. At what rotational speed does the inner
object begin to slide?
Let vbe the velocity in m/s. Then,
v , and ac .
At the maximum angular velocity,
the frictional force Ff sFN
smg must be equal to mac.
smg
v sgr
(0.50)
(9.80
m/s2)
(0.10
m)
0.70 m/s
11. An airplane’s airspeed is 2.0102km/h
due east. Because of a wind blowing to
the north, it is approaching its destination
15° north of east.
a. What is the wind speed?
tan vwind
vair
mv2
r
v2
r
2r
T
42r
T2
3.7 m/s
4.2 m/s
vRP
vPQ
(2)(8.0 m)
12 s
2r
T
(2)(3.5 m)
6.0 s
2r
T
3.5 m
8.0 m
Q
P
R
vRP
vPQ
Chapter 6 continued

vwind vair tan
(2.0102 km/h)(tan 15°)
54 km/h
b. How fast is the airplane approaching its
destination?
cos
vground
2.1102 km/h
12. A river is flowing 4.0 m/s to the east. A
boater on the south shore plans to reach a
dock on the north shore 30.0° downriver by
heading directly across the river.
a. What should be the boat’s speed relative
to the water?
Let vb/w be the boat’s speed relative
to the water. Then,
tan
vb/w
6.9 m/s
b. What is the boat’s speed relative to the
dock?
vb/d vw2
vb/w2
(4.0 m
/s)2
(6.9 m
/s)2
8.0 m/s
Chapter 7
pages 868–869
1. A year is defined as the time it takes for a
planet to travel one full revolution around
the Sun. One Earth year is 365 days. Using
the data in Table 7-1, calculate the number
of Earth days in one Neptune year. If
Neptune takes about 16 h to complete one
of its days, how many Neptunian days long
is Neptune’s year?
2
3
TN
TE
r
2
E
r
3
N
3
6.00104Earth days
For every 16 Earth days, there will be
24 Neptunian days,
(6.00104Earth days)
9.00104Neptunian days
2. Suppose a new planet was discovered to
orbit the Sun with a period 5 times that
of Pluto. Using the data in Table 7-1, calcu-
late the average distance from the Sun
for this new planet.
2
3
Let TP period for Pluto
TA period for new planet 5TP
rA
3
TA
T
2
P
r
2
P
3
3
1.721013 m
3. If a meteorite hit the Earth and moved it
2.411010 m closer to Venus, how many
days would there be in an Earth year? Use
the data in Table 7-1.
(5TP)2(5.871012 m)3
TP2
rA
rP
TA
TP
24 Neptunian days
16 Earth days
(365 days)2(4.501012 m)3
(1.501011 m)3
rN
rE
TN
TE
4.0 m/s
tan 30.0°
vw
tan
vw
vb/w
30.0°
2.0102km/h
cos 15°
vair
cos
vair
vground
616 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 6 continued

Physics: Principles and Problems Solutions Manual 617
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
New average distance from the Sun
2
3
TA
TB
r
2
B
r
3
A
3
281 days
4. The Moon is a satellite of the Earth. The Moon travels one full revolution around
the Earth in 27.3 days. Given that the mass of the Earth is 5.971024 kg, what is
the average distance from the Earth to the Moon?
Look at units first:The period is given to us in days, which must be
converted to seconds due to the units of G.
(27.3 days)
2.36106 s
T 2
r
3
3
3.83108m
5. A satellite travels 7.18107m from the center of one of the planets in our solar
system at a speed of 4.20104m/s. Using the data in Table 7-1, identify the planet.
v
M 1.901027 kg, Jupiter
6. Earth’s atmosphere is divided into four layers: the troposphere (0–10 km), the
stratosphere (10–50 km), the mesosphere (50–80 km), and the thermosphere
(80–500 km). What is the minimum velocity an object must have to enter the
thermosphere?
r h rE 8.0104m 6.38106m
v
7.8103m/s
(6.671011 Nm2/kg2)(5.971024 kg)
8.0104m 6.38106m
GME
r
(4.20104m/s)2(7.18107m)
6.671011 Nm2/kg2
v2r
G
GM
r
(2.36106s)2(6.671011 Nm2/kg2)(5.971024 kg)
42
T2GME
42
r3
GME
60 s
1 min
60 min
1 h
24 h
1 day
(365 days)2(1.501011 m 2.411010 m)3
(1.501011 m)3
rA
rB
TA
TB
Chapter 7 continued

Chapter 8
pages 869–870
1. The rotational velocity of a merry-go-
round is increased at a constant rate from
1.5 rad/s to 3.5 rad/s in a time of 9.5 s.
What is the rotational acceleration of
the merry-go-round?
0.21 rad/s2
2. A record player’s needle is 6.5 cm from the
center of a 45-rpm record. What is the
velocity of the needle?
First convert rpm to rad/s.
4.71 rad/s
v r (6.5 cm)
(4.71 rad/s)
0.31 m/s
3. Suppose a baseball rolls 3.2 m across the
floor. If the ball’s angular displacement is
82 rad, what is the circumference of the ball?
d r
r 0.039 m
c 2r 2(0.039 m) 0.25 m
4. A painter uses a 25.8-cm long screwdriver to
pry the lid off of a can of paint. If a force of
85 N is applied to move the screwdriver 60.0°
from the perpendicular, calculate the torque.
Fr sin (85 N)(0.258 m)(sin 60.0°)
19 Nm
5. A force of 25 N is applied vertically at the
end of a wrench handle that is 45 cm long
to tighten a bolt in the clockwise direction.
What torque is needed by the bolt to keep
the wrench from turning?
In order to keep the wrench from turn-
ing, the torque on the bolt must be equal
in magnitude but opposite in direction of
the torque applied by the wrench.
Fr sin (25 N)(0.45 m)(sin 90.0°)
11 Nm counterclockwise
6. A 92-kg man uses a 3.05-m board to attempt
to move a boulder, as shown in the diagram
below. He pulls the end of the board with a
force equal to his weight and is able to move
it to 45° from the perpendicular. Calculate
the torque applied.
Fr sin
mgr sin
(92 kg)(9.80 m/s2)(3.05 m)(sin 45°)
1.9103Nm
7. If a 25-kg child tries to apply the same torque
as in the previous question using only his or
her weight for the applied force, what would
the length of the lever arm need to be?
L rsin
7.8 m
8. Logan, whose mass is 18 kg, sits 1.20 m
from the center of a seesaw. If Shiro must
sit 0.80 m from the center to balance
Logan, what is Shiro’s mass?
FLrL FSrS
mLgrL mSgrS
mS
27 kg
9. Two forces—55-N clockwise and 35-N
counterclockwise—are applied to a merry-
go-round with a diameter of 4.5 m. What is
the net torque?
(18 kg)(1.20 m)
0.80 m
mLrL
rS
1.9103Nm
(25 kg)(9.80 m/s2)
mg
F
45°
3.2 m
82 rad
d
1 m
100 cm
1 min
60 s
2rad
1 rev
45 rev
1 min
(3.5 rad/s) (1.5 rad/s)
9.5 s
t
618 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Physics: Principles and Problems Solutions Manual 619
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
The net torque is the sum of the
individual torques.
net ccw cw
Fccwrsin Fcwrsin
(Fccw Fcw)rsin
(35 N 55 N)
(sin 90.0°)
45 Nm
45 Nm clockwise
10. A student sits on a stool holding a 5.0-kg
dumbbell in each hand. He extends his arms
such that each dumbbell is 0.60 m from the
axis of rotation. The student’s moment of
inertia is 5.0 kgm2. What is the moment of
inertia of the student and the dumbbells?
Isingle dumbbell mr2 (5.0 kg)(0.60 m)2
1.8 kgm2
Itotal 2Isingle dumbbell Istudent
(2)(1.8 kgm2) 5.0 kgm2
8.6 kgm2
11. A basketball player spins a basketball with a
radius of 15 cm on his finger. The mass of
the ball is 0.75 kg. What is the moment of
inertia about the basketball?
I mr2
(0.75 kg)(0.15 m)2
6.8103kgm2
12. A merry-go-round in the park has a radius
of 2.6 m and a moment of inertia of
1773 kgm2. What is the mass of the
merry-go-round?
I mr2
m
5.2102kg
13. The merry-go-round described in the previ-
ous problem is pushed with a constant force
of 53 N. What is the angular acceleration?
7.8102rad/s2
14. What is the angular velocity of the merry-
go-round described in problems 12 and 13
after 85 s, if it started from rest?
i 0 since it started from rest
f t
(7.8102rad/s2)(85 s)
6.6 rad/s
15. An ice-skater with a moment of inertia of
1.1 kgm2begins to spin with her arms
extended. After 25 s, she has an angular
velocity of 15 rev/s. What is the net torque
acting on the skater?
net I
4.1 Nm
2rad
rev
(1.1 kgm2)(15 rev/s 0 rev/s)
255
I(fi)
t
fi
t
t
(53 N)(2.6 m)(sin 90.0°)
1773 kgm2
Fr sin
1
net
I
(2)(1773 kgm2)
(2.6 m)2
2I
r2
1
2
2
5
2
5
4.5 m
2
35 N
55 N
4.5 m
Chapter 8 continued

16. A board that is 1.5 m long is supported in two places. If the force exerted by the
first support is 25 N and the forced exerted by the second is 62 N, what is the
mass of the board?
Fnet F1 F2 (Fg)
Since the system is in equilibrium,
Fnet 0.
0 F1 F2Fg
Fg F1 F2
mg F1 F2
m
8.9 kg
17. A child begins to build a house of cards by laying an 8.5-cm-long playing card
with a mass of 0.75 g across two other playing cards: support card A and support
card B. If support card A is 2.0 cm from the end and exerts a force of 1.5103N,
how far from the end is support card B located? Let the axis of rotation be at the
point support card A comes in contact with the top card.
Fnet FA FB (Fg)
Since the system is in equilibrium,
Fnet 0.
0FA FBFg
FB FgFA
mg FA
Since the axis of rotation is about support card A, A 0.
so net B g
The system is in equilibrium, so net 0.
0 B g
B g
B rBFBand g rgFg
rBFB rgFg
rB
2.8102m
28 cm
1
2
(0.085 m) 0.020 m(7.5104kg)(9.80 m/s2)
(7.5104kg)(9.80 m/s2)1.5103N
rgmg
mg FA
rgFg
FB
25 N 62 N
9.80 m/s2
F1F2
g
620 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 8 continued

Physics: Principles and Problems Solutions Manual 621
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
18. If support card A in the previous problem was moved so that it now is 2.5 cm
from the end, how far from the other end does support card B need to be to
reestablish equilibrium?
rB
2.2102m
22 cm
1
2
(0.085 m) 0.025 m(7.5104kg)(9.80 m/s2)
(7.5104kg)(9.80 m/s2)1.5103N
rgmg
mg FA
Chapter 8 continued

Chapter 9
pages 870–871
1. A ball with an initial momentum of 6.00 kgm/s bounces off a wall and travels in
the opposite direction with a momentum of 4.00 kgm/s. What is the magnitude
of the impulse acting on the ball?
Choose the direction away from the wall to be positive.
pf 4.00 kgm/s
pi 6.00 kgm/s
Impulse pfpi (4.00 kgm/s) (6.00 kgm/s)
10.0 kgm/s
2. If the ball in the previous problem interacts with the wall for a time interval of
0.22 s, what is the average force exerted on the wall?
Impulse Ft
F 45 N
3. A 42.0-kg skateboarder traveling at 1.50 m/s hits a wall and bounces off of it.
If the magnitude of the impulse is 150.0 kg·m/s, calculate the final velocity of the
skateboarder.
Choose the direction away from the wall to be positive.
Impulse pfpi mvf(mvi)
m(vf vi)
vf vi
1.50 m/s
2.07 m/s
4. A 50.0-g toy car traveling with a velocity of 3.00 m/s due north collides head-on
with an 180.0-g fire truck traveling with a velocity of 0.50 m/s due south. The
toys stick together after the collision. What are the magnitude and direction of
their velocity after the collision?
Choose north to be positive.
pi pf
pci pti pf
mcvci mtvti (mc mt)vf
vf
0.26 m/s, due north
(50.0 g)(3.00 m/s) (180.0 g)(0.50 m/s)
50.0 g 180.0 g
mcvci mtvti
mcmt
150.0 kgm/s
42.0 kg
Impulse
m
10.0 kgm/s
0.22 s
Impulse
t
622 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 623
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5. A 0.040-kg bullet is fired into a 3.50-kg
block of wood, which was initially at rest.
The bullet remains embedded within the
block of wood after the collision. The
bullet and the block of wood move at a
velocity of 7.40 m/s. What was the original
velocity of the bullet?
pi pf
pbi pwi pf
mbvbi mwvwi (mb mw)vf
where vwi 0. Thus,
vbi
6.5102m/s
6. Ball A, with a mass of 0.20 kg, strikes ball B,
with a mass of 0.30 kg. The initial velocity
of ball A is 0.95 m/s. Ball B is initially at
rest. What are the final speed and direction
of ball A and B after the collision if they
stick together?
pi pf
mAvAi (mA mB)vf
vf
0.38 m/s in the same direction as
ball A’s initial velocity
7. An ice-skater with a mass of 75.0 kg pushes
off against a second skater with a mass of
42.0 kg. Both skaters are initially at rest.
After the push, the larger skater moves off
with a speed of 0.75 m/s eastward. What
is the velocity (magnitude and direction) of
the smaller skater after the push?
pi pf
m1vf1 m2vf2
vf2
1.3 m/s
The second skater moves west with a
velocity of 1.3 m/s.
8. Suppose a 55.0-kg ice-skater, who was
initially at rest, fires a 2.50-kg gun. The
0.045-kg bullet leaves the gun at a velocity
of 565.0 m/s. What is the velocity of the
ice-skater after she fires the gun?
pi pf
0 pfs pfb
(ms mg)vfs mbvfb
because the final mass of the skater
includes the mass of the gun held by
the skater. Then,
vfs
0.44 m/s
9. A 1200-kg cannon is placed at rest on
an ice rink. A 95.0-kg cannonball is shot
from the cannon. If the cannon recoils at
a speed of 6.80 m/s, what is the speed of
the cannonball?
pi pf
Since the cannon and cannonball are at
rest before the blast, pi 0.00 kgm/s.
So pfc pfb
mcvfc mbvfb
vfb
86 m/s
10. An 82-kg receiver, moving 0.75 m/s north,
is tackled by a 110.0-kg defensive lineman
moving 0.15 m/s east. The football players
hit the ground together. Calculate their final
velocity (magnitude and direction).
pri mrvri, y (82 kg)(0.75 m/s)
62 kgm/s north
pdi mdvdi, x (110.0 kg)(0.15 m/s)
16 kgm/s, east
(1200 kg)(6.80 m/s)
95.0 kg
mcvfc
mb
(0.045 kg)(565.0 m/s)
55.0 kg 2.50 kg
mbvfb
msmg
(75.0 kg)(0.75 m/s)
42.0 kg
m1vf1
m2
(0.20 kg)(0.95 m/s)
0.20 kg 0.30 kg
mAvAi
mAmB
(0.040 kg 3.50 kg)(7.40 m/s)
0.040 kg
Chapter 9 continued
Law of conservation of momentum states
pi pf
pf, x pi, x 16 kgm/s
pf, y pi, y 62 kgm/s
pf (pf, x2 pf, y2)
1
2
((16 kgm/s)2 (62 kgm/s)2)
1
2
64 kgm/s
vf
0.33 m/s
tan1
tan1
tan1
75°
11. A 985-kg car traveling south at
29.0 m/s hits a truck traveling
18.0 m/s west, as shown in the figure
below. After the collision, the vehicles
stick together and travel with a final
momentum of 4.0104kgm/s at
an angle of 45°. What is the mass
of the truck?
pf2 pfx2 pfy2
pf2 pix2 piy2
pf2 mc2vci2 mt2vti2
mt
1
2
1
2
1.6103kg
(4.0104kgm/s) (985 kg)2(29.0 m/s)2
(18.0 m/s)2
pf2 mc2vci2
vti2
29.0 m/s
18.0 m/s
p 4.0104 kgm/s
45°
(82 kg)(0.75 m/s)
(110.0 kg)(0.15 m/s)
mrvri, y
mdvdi, x
pf,y
pf,x
64 kgm/s
82 kg 110.0 kg
pf
mrmd
624 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 9 continued

Physics: Principles and Problems Solutions Manual 625
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
12. A 77.0-kg woman is walking 0.10 m/s east in the gym. A man throws a 15.0-kg
ball south and accidentally hits the woman. The woman and the ball move
together with a velocity of 0.085 m/s. Calculate the direction the woman and
the ball move.
cos1
cos1
cos1
cos1
1.0101degrees south of east
(77.0 kg)(0.10 m/s)
(77.0 kg 15.0 kg)(0.085 m/s)
mwviw
(mwmb)vf
pix
pf
pfx
pf
Chapter 9 continued

Chapter 10
page 871
1. A toy truck is pushed across a table 0.80 m
north, and pulled back across the table
0.80 m south. If a constant horizontal force
of 15 N was applied in both directions,
what is the net work?
Choose north to be the positive direction.
Wnet Wnorth Wsouth
(Fd) (Fd )
(15 N)(0.80 m) (15 N)(0.80 m)
0.0 J
2. A 15-kg child experiences an acceleration of
0.25 m/s2as she is pulled 1.7 m horizontally
across the floor by her sister. Calculate the
change in the child’s kinetic energy.
KE W Fd mad
(15 kg)(0.25 m/s2)(1.7 m)
6.4 J
3. A man pushes a couch a distance of 0.75 m.
If 113 J of work is done, what is the magni-
tude of the horizontal force applied?
W Fd
F 1.5102N
4. Two blocks are tied together by a horizontal
string and pulled a distance of 2.7 m across
an air hockey table with a constant force of
35 N. The force is directed at an upward
angle of 35° from the 9.0-kg block, as
shown in the figure. What is the change in
kinetic energy in the two-block system?
W KE Fd cos
(35 N)(2.7 m)(cos 35°)
77 J
5. If the two-block system described in the
previous problem was initially at rest, what
is the final velocity?
KE mv2
m(vfvi)2
vi 0 since blocks were initially at rest.
So KE mvf2
vf
3.2 m/s
6. A toy car with a mass of 0.75 kg is pulled
3.2 m across the floor with a constant force
of 110 N. If 67 J of work is done, what is the
upward angle of the force?
W Fd cos
cos1
cos1
79°
7. If a 75-W lightbulb is left on for 2.0 h, how
much work is done?
(2.0 h)
7.2103s
P
W Pt (75 W)(7.2103s)
5.4105J
8. A 6.50-horsepower (hp) self-propelled
lawn mower is able to go from 0.00 m/s
to 0.56 m/s in 0.050 s. If the mass of the
lawn mower is 48.0 kg, what distance
does the lawn mower travel in this time?
(Use 1 hp 746 W.)
(6.50 hp)
4.85103W
a v
t
746 W
1 hp
W
t
3600 s
1.0 h
67 J
(110 N)(3.2 m)
W
Fd
(2)(77 J)
15 kg
2KE
m
1
2
1
2
1
2
35°
35 N
6.0 kg 9.0 kg
113 J
0.75 m
W
d
626 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 627
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
P
d
0.45 m
9. A winch that’s powered by a 156-W motor
lifts a crate 9.8 m in 11 s. What is the mass
of the crate?
vavg 0.89 m/s
If the crate is initially at rest:
vavg
vf 2vavg (2)(0.89 m/s) 1.8 m/s
P
m
1.1103kg
10. A man exerts a force of 310 N on a lever to
raise a crate with a mass of 910 kg. If the
efficiency of the lever is 78 percent, what
is the lever’s IMA?
(100)
(100)
(100)
78
37
11. A worker uses a pulley to lift a 45-kg object.
If the mechanical advantage of the pulley is
5.2, what is the effort force exerted by the
worker?
MA
Fe
85 N
12. When the chain on a bicycle is pulled
0.95 cm, the rear wheel rim moves a
distance of 14 cm. If the gear has a radius
of 3.5 cm, what is the radius of the rear
wheel?
IMA
rr
52 cm
(3.50 cm)(14.0 cm)
0.95 cm
redr
de
re
rr
de
dr
(45 kg)(9.80 m/s2)
5.2
mg
MA
Fr
MA
Fr
Fe
(910 kg)(9.80 m/s2)
310 N
m
Fe
g
e
F
F
e
r
e
(2)(156 W)(11 s)
(1.8 m/s)2
2Pt
(vfvi)2
2Pt
v2
mv2
2t
KE
t
W
t
vf
2
vivf
2
9.8 m
11 s
d
t
(4.85103W)(0.050 s)2
(48.0 kg)(0.36 m/s 0.00 m/s)
Pt2
m(vfvi)
m(vfvi)d
t2
m
tv
d
t
mad
t
Fd
t
W
t
Chapter 10 continued
Chapter 11
page 872
1. A crate with a mass of 210 kg is horizontally
accelerated by a force of 95 N. The force
is directed at an upward angle so that the
vertical part of the force is 47.5 N and
the horizontal part of the force is 82.3 N
(see the diagram below). If the crate is
pulled 5.5 m across the floor, what is the
change in kinetic energy of the crate?
WKE Fd
(82.3 N)(5.5 m)
4.5102J
2. Assuming that the crate described in prob-
lem 1 was initially at rest, what is the final
velocity of the crate?
KE KEfKEi
KEf
1
2
mvf2
KEi
1
2
mvi2
Since the crate was initially at rest,
KEi0.
So, KE KEf
1
2
mvf2
vf
2
m
KE
2.1 m/s
3. If the crate described in problem 1
experienced a frictional force of 15 N,
what is the final kinetic energy of the crate?
Let the direction of the motion of the
crate be positive.
WKE Fd
FFHFf82.3 N (15 N)
67 N
KE WFd (67 N)(5.5 m)
3.7102J
Since the crate was initially at rest,
KE KEf
KEf3.7102J
4. A 150-kg roller-coaster car climbs to the
top of a 91-m-high hill. How much work
is done against gravity as the car is lifted
to the top of the hill?
WFd
Fmg
Wmgd
(150 kg)(9.80 m/s2)(91 m)
1.3105J
5. A pendulum bob with a mass of 0.50 kg
swings to a maximum height of 1.0 m. What
is the kinetic energy when the pendulum
bob is at a height of 0.40 m?
Etot KE PE
Since energy is conserved, the total
energy is constant.
When the pendulum bob is at the top of
the swing, Etot PE at the top of the
swing.
PE mgh (0.50 kg)(9.80 m/s2)(1.0 m)
4.9 J
When the pendulum bob is at 0.40 m,
PE mgh (0.50 kg)(9.80 m/s2)(0.40 m)
2.0 J
KE Etot PE 4.9 J 2.0 J
2.9 J
6. A sled and its rider, with a total mass of
95 kg, are perched on top of a 25-m-tall
hill. A second hill is 12 m tall (see the dia-
gram below). The rider is given an initial
push providing 3674 J of kinetic energy.
Neglecting friction, what is the velocity at the
top of the top of the 12-m-tall hill?
(2)(4.5102J)
210 kg
210 kg
47.5 N
82.3 N
95 N
Smooth floor
628 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 629
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
EKE PE
At the top of the 25-m-high hill:
KE 3674 J
PE mgh (95 kg)(9.80 m/s2)(25 m)
2.3104J
EKE PE 3674 J 2.3104J
2.7104J
At the top of the 12-m-high hill:
PE mgh (95 kg)(9.80 m/s2)(12 m)
1.1104J
KE EPE 2.7104J1.1104J
1.6104J
v
2m
KE
(2)(1
9
.
6
5
k
1
g
0
4J)
18 m/s
7. A 35-kg child is riding on a swing that rises
to a maximum height of 0.80 m. Neglecting
friction, what is the child’s gravitational
potential energy at the top of the swing?
What is the child’s kinetic energy at the top
of the swing?
PE mgh (35 kg)(9.80 m/s2)(0.80 m)
2.7102J
When the swing is at its maximum
height, the velocity is zero.
KE
1
2
mv20 J
8. A sled and its rider are perched at the top of
a hill that is 35 m tall. If the gravitational
potential energy is 3.0104J, what is the
weight of the sled and rider?
PE mgh
Fgmg
PE Fgh
Fg
P
h
E
3.0
3
51
m
04J
8.6102N
9. The big hill on a roller-coaster ride is 91 m
tall. If the mass of the roller-coaster car and
its two riders is 314 kg and the maximum
velocity reached by this roller-coaster ride
is 28 m/s, how much energy was lost to
friction?
At the top of the 91-m-high hill:
EPE mgh
(314 kg)(9.80 m/s2)(91 m)
2.8105J
At the bottom of the hill:
EKE
1
2
mv2
v
2m
KE
42 m/s if no energy is lost to friction
The actual KE at the bottom of the hill:
KE
1
2
mv2
1
2
(314 kg)(28 m/s)2
1.2105J
EKE Ef
EfEKE 2.8105J1.2105J
1.6105J
10. A dartboard with a mass of 2.20 kg is
suspended from the ceiling such that it is
initially at rest. A 0.030-kg dart is thrown
at the dartboard with a velocity of 1.3 m/s.
After the dart hits the dartboard, the dart
and the board initially move with a velocity
of 0.025 m/s. How much kinetic energy is
lost in the system?
KEi
1
2
mdvd2
1
2
(0.030 kg)(1.3 m/s)2
2.5102J
KEf
1
2
(mdmb)vf2
1
2
(0.030 kg 2.20 kg)(0.025 m/s)2
6.97104J
(2)(2.8105J)
314 kg
25 m
12 m
Chapter 11 continued
Elost KEiKEf
(2.5102J) (6.97104J)
2.4102J
11. In a physics laboratory, students crash carts
together on a frictionless track. According
to the following data, was kinetic energy
conserved?
KEiA
1
2
mAviA2
1
2
(0.25 kg)(0.18 m/s)2
4.0103J
KEiB
1
2
mBviB2
1
2
(0.36 kg)(0.20 m/s)2
7.2103J
KEfA
1
2
mAvfA2
1
2
(0.25 kg)(0.21 m/s)2
5.5103J
KEfB
1
2
mBvfB2
1
2
(0.36 kg)(0.11 m/s)2
2.2103J
If KE is conserved:
KEiKEf
KEiKEiA KEiB
4.0103J7.2103J
11.2103J
KEfKEfA KEfB
5.5103J2.2103J
7.7103J
KE is not conserved.
12. A 0.150-kg ball that is thrown at a velocity of
30.0 m/s hits a wall and bounces back in the
opposite direction with a speed of 25.0 m/s.
How much work was done by the ball?
Conservation of energy:
Wball KE 0
Wball KE KEf KEi
KEi
1
2
mvi2
1
2
(0.150 kg)(30.0 m/s)2
67.5 J
KEf
1
2
mvf2
1
2
(0.150 kg)(25.0 m/s)2
46.9 J
Wball KEf KEi
46.9 J 67.5 J
20.6 J
Mass (kg) vi(m/s) vf(m/s)
Cart A 0.25 0.18 0.21
Cart B 0.36 0.20 0.11
630 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 11 continued
Physics: Principles and Problems Solutions Manual 631
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12
pages 872–874
1. Convert the following Celsius temperatures
to Kelvin temperatures.
a. 196°C
TKTC273 196 273 77 K
b. 32°C
TKTC273 32 273 305 K
c. 212°C
TKTC273 212 273 485 K
d. 273°C
TKTC273 273 273 0 K
e. 273°C
TKTC273 273 273 546 K
f. 27°C
TKTC273 27 273 300 K
2. Find the Celsius and the Kelvin tempera-
tures for the following objects.
a. average body temperature
98.6°F is about 37°C, 310 K
b. hot coffee
about 70°C, 343 K
c. iced tea
about 0°C, 273 K
d. boiling water
100°C, 373 K
3. Convert the following Kelvin temperatures
to Celsius temperatures.
a. 4 K
TCTK273 4 273 269°C
b. 25 K
TCTK 273 25 273 248°C
c. 272 K
TCTK 273 272 273 1°C
d. 373 K
TCTK 273 373 273 100°C
e. 298 K
TCTK 273 298 273 25°C
f. 316 K
TCTK 273 316 273 43°C
4. A 9.8-g lead bullet with a muzzle velocity
of 3.90102m/s is stopped by a wooden
block. What is the change in temperature of
the bullet if one-fourth of its original kinetic
energy goes into heating the bullet?
KE
1
2
mv2
and
1
4
KE QmCT
1
4
1
2
mv2mCT
T
1.5102 K
5. What is the change in temperature of 2.2 kg of
the following substances if 8.5103J of ther-
mal energy is added to each of the substances?
a. ice
T
m
Q
C
1.9 K
b. water
T
m
Q
C
0.92 K
8.5103J
(2.2 kg)(4180 J/kgK)
8.5103J
(2.2 kg)(2060 J/kgK)
1
8
(3.90102m/s)2
130 J/kgK
1
8
v2
C
v 3.90102 m/s
Bullet
m 9.8 g
Wooden
block

c. steam
T
m
Q
C
1.9 K
d. aluminum
T
m
Q
C
4.3 K
e. silver
T
m
Q
C
16 K
f. copper
T
m
Q
C
1.0101K
6. A 2350-kg granite tombstone absorbs 2.8107J of energy from the Sun to
change its temperature from 5.0°C at night to 20.0°C during an autumn day.
Determine the specific heat of granite from this information.
QmCT
C
m
Q
T
7.9102J/kgK
7. A 2.00103-g sample of water at 100.0°C is mixed with a 4.00103-g sample of
water at 0.0°C in a calorimeter. What is the equilibrium temperature of the mixture?
mACA(Tf TAi)mBCB(TfTBi)0
Since CACBin this case, the specific heat cancels out.
Tf 33°C
(2.00 kg)(100.0°C) (4.00 kg)(0.0°C)
2.00 kg 4.00 kg
mATAi mBTBi
mAmB
2.8107J
(2350 kg)(20.0°C 5.0°C)
8.5103J
(2.2 kg)(300 J/kgK)
8.5103J
(2.2 kg)(235 J/kgK)
8.5103J
(2.2 kg)(897 J/kgK)
8.5103J
(2.2 kg)(2020 J/kgK)
632 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued
Physics: Principles and Problems Solutions Manual 633
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
8. A 220-g iron horseshoe is heated to 825°C and
then plunged into a bucket filled with 20.0 kg
of water at 25.0°C. Assuming that no energy is
transferred to the surroundings, what is the
final temperature of the water at equilibrium?
mACA(TfTAi)mBCB(TfTBi)0
Tf
26°C
9. A cook adds 1.20 kg of soup bones to
12.5 kg of hot broth for flavoring. The
temperatures of the bones and the broth
are 20.0°C and 90.0°C, respectively.
Assume that the specific heat of the broth
is the same as that of water. Also assume that
no heat is lost to the environment. If the
equilibrium temperature is 87.2°C, what is
the specific heat of the bones?
mACA(TfTAi)mBCB(TfTBi)0
CA
1.81103J/kgK
10. A 150.0-g copper cylinder at 425°C is placed on a large block of ice at 0.00°C.
Assume that no energy is transferred to the surroundings. What is the mass of the
ice that will melt?
The energy for melting the ice comes from the cooling of the copper.
QmCT
This quantity of energy is available to melt the ice, so
QmiceHf
mice
H
Q
f
mC
H
f
T
0.0735 kg of ice
(0.1500 kg)(385 J/kg°C)(425°C 0.00°C)
3.34105J/kg
(12.5 kg)(4180 J/kgK)(87.2°C 90.0°C)
(1.20 kg)(87.2°C 20.0°C)
mBCB(TfTBi)
mA(TfTAi)
t 20.0C
Bones
Broth
T 90.0C
m 1.20 kg
(0.22 kg)(450 J/kgK)(825°C) (20.0 kg)(4180 J/kgK)(25.0°C)
(0.22 kg)(450 J/kgK) (20.0 kg)(4180 J/kg°K)
mACATAi mBCBTBi
mACAmBCB
Water
T 25.0°C
Horseshoe
T 825°C
m 20.0 kg
Chapter 12 continued

11. How much energy is needed to melt one troy
ounce, 31.1 g, of gold at its melting point?
QmHf
(0.0311 kg)(6.30104J/kg)
1.96103J
12. Trying to make an interesting pattern,
an artist slowly pours 1.00 cm3of liquid
gold onto a large block of ice at 0.00°C.
While being poured, the liquid gold is at its
melting point of 1064°C. The density of
gold is 19.3 g/cm3, and its specific heat is
128 J/kgK. What mass of ice will melt after
all the gold cools to 0.00°C?
The energy to melt the ice comes from
the energy released when the gold solid-
ifies and then released as the gold cools
from its melting temperature to 0.00°C.
Qtot Qsolidification Qcooling
Qsolidification mHf
(0.0193 kg/cm3)(1.00 cm3)
(6.30104J/kg)
1216 J
Qcooling mCT
(0.0193 kg/cm3)(1.00 cm3)
(128 J/kg°C)
(1064°C 0.00 °C)
2628 J
Qtot 1216 J 2628 J 3844 J
Qice mHf
m
1.15102kg
13. A cylinder containing 1.00 g of water at the
boiling point is heated until all the water
turns into steam. The expanding steam
pushes a piston 0.365 m. There is a 215-N
frictional force acting against the piston.
What is the change in the thermal energy
of the water?
UQW
QmHv
(1.00103kg)(2.26106J/kg)
2.26103J
WFd (215 N)(0.365 m) 78.5 J
UQW
2.26103J – 78.5 J
2.18103 J
14. What is the change in temperature of water
after falling over a 50.0-m-tall waterfall?
Assume that the water is at rest just before
falling off and just after it reaches the
bottom of the falls.
UQ– W
U0 and WKE PE mgh
QmCT
Thus, mCTmgh
T
g
C
h
0.117 K
15. Two 6.35-kg lead bricks are rubbed against
each other until their temperature rises by
1.50 K. How much work was done on the
bricks?
UQW and U0
WQmCT
(12.70 kg)(130 J/kg)(1.50 K)
2500 J
(9.80 m/s2)(50.0 m)
4180 J/kgK
3844 J
3.34105J/kg
Qice
Hf
634 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 12 continued

Physics: Principles and Problems Solutions Manual 635
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13
pages 874–875
1. Use Table 13.1 to estimate the pressure
in atmospheres (atm) on a climber stand-
ing atop Mt. Everest. Is this more or less
than half standard atmospheric pressure
(1.0 atm)?
(3104Pa)
0.3 atm
This is less than half of standard
atmospheric pressure.
2. A woman wearing high heels briefly supports
all her weight on the heels. If her mass is
45 kg and each heel has an area of 1.2 cm2,
what pressure does she exert on the floor?
P
A
F
m
A
g
10
1
0m
cm
2
1.8103kPa
3. A typical brick has dimensions of
20.0 cm 10.0 cm 5.0 cm and weighs
20.0 N. How does the pressure exerted
by a typical brick when it is resting on
its smallest side compare to the pressure
exerted when it is resting on its largest side?
psmall
As
F
mall
10
1
0m
cm
2
4.0103Pa
plarge
Ala
F
rge
10
1
0m
cm
2
1.00103Pa
The pressure is four times as large
when the brick rests on its smallest
side.
4. As shown in the figure below, a bubble of
gas with a volume of 1.20 cm3is released
under water. As it rises to the surface, the
temperature of the bubble increases from
27°C to 54°C, and the pressure is cut to
one-third of its initial value. What is the
volume of the bubble at the surface?
T127 273 300 K
T254 273 327 K
V2
3.9 cm3
5. A sample of ethane gas (molar mass
30.1 g/mol) occupies 1.2102m3at 46°C
and 2.4105Pa. How many moles of ethane
are present in the sample? What is the mass
of the sample?
n
1.1 mol of ethane
mMn
(30.1 g/mol)(1.1 mol)
33 g
(2.4105Pa)(1.2102m3)
(8.31 Pam3/molK)(319 K)
PV
RT
P1(1.20 cm3)(327 K)
(300 K)
1
3
P1
P1V1T2
T1P2
P2V2
T2
P1V1
T1
20.0 N
(20.0 cm)(10.0 cm)
20.0 N
(10.0 cm)(5.0 cm)
(45 kg)(9.80 m/s2)
(2)(1.2 cm2)
1.0 atm
1.0105Pa
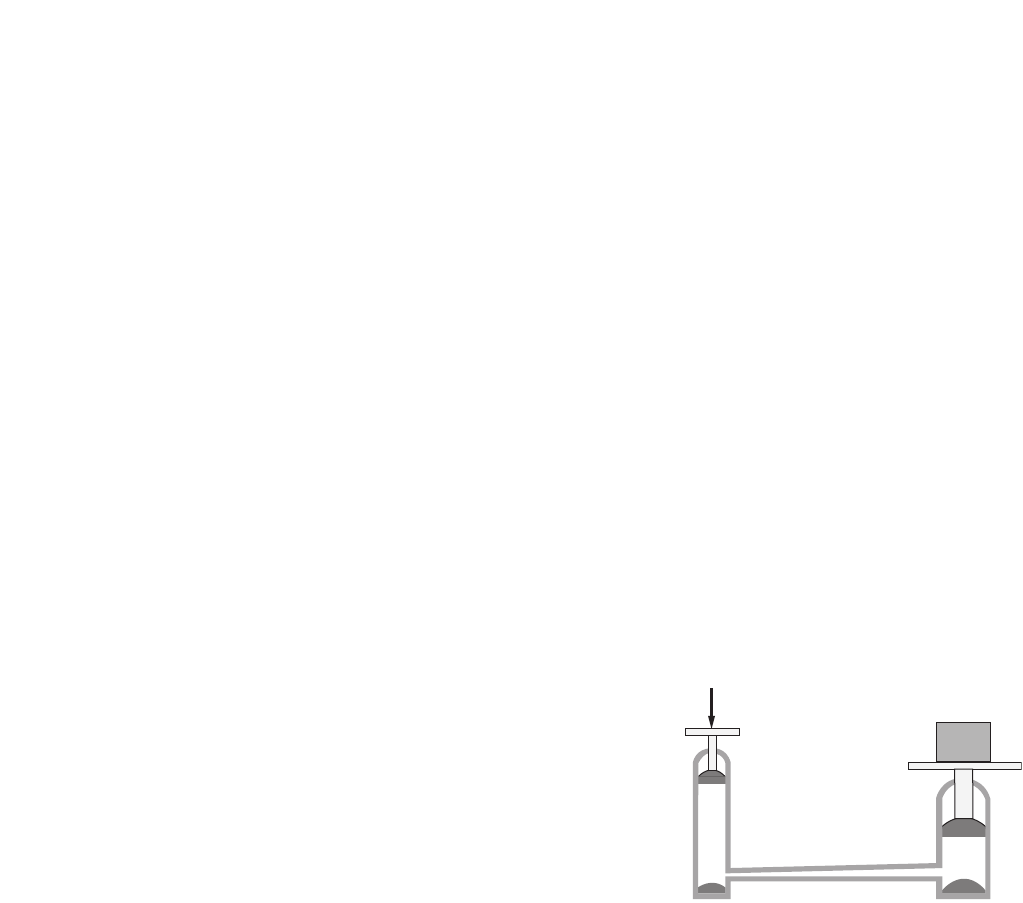
6. The constant Requals 8.31 Pam3/molK as it is presented in the ideal gas law in
this chapter. One mole of an ideal gas occupies 22.4 L at standard temperature
and pressure, STP, which is defined as 0.00°C and 1.00 atm. Given this
information, deduce the value of R in Latm/molK.
R
P
nV
T
0.0821 Latm/molK
7. Suppose that two linked pistons are both cylindrical in shape. Show that the
ratio of forces generated is directly proportional to the square of the radii of the
two cross-sectional circular areas.
, a direct proportion
8. The cross-sectional areas of the pistons
in the system shown below have a ratio
of 25 to 1. If the maximum force that can
be applied to the small piston is 12 N,
what is the maximum weight that can be
lifted?
F1
3.0102N
9. A car of mass 1.35103kg sits on a large piston that has a surface area of 1.23 m2.
The large piston is linked to a small piston of area 144 cm2. What is the weight of
the car? What force must a mechanic exert on the small piston to raise the car?
Fgmg (1.35103kg)(9.80 m/s2)
1.32104N
F2
155 N
(1.35103kg)(9.80 m/s2)(1.44102m2)
1.23 m2
mgA2
A1
F1A2
A1
(12 N)(25)
1
F2A1
A2
F
r12
r22
F1
F2
F2
r22
F1
r12
F2
A2
F1
A1
(1.00 atm)(22.4 L)
(1 mol)(273 K)
636 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 637
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
10. At what depth in freshwater does the water
exert a pressure of 1.00 atm (1 atm
1.013105Pa) on a scuba diver?
Pgh
h
P
g
10.3 m
11. An iceberg floats in seawater, partly under
water and partly exposed. Show that the
value of Vsubmerged/Vtotal equals ice/seawater.
What percentage of the iceberg is exposed?
Use 1.03103kg/m3for the density of sea-
water, and 0.92103kg/m3for the density
of ice.
Because the ice floats,
Fbuoyant Fg
seawaterVsubmergedgiceVtotalg
This is a general result for floating
solids.
0.89
So, 89 percent is submerged and
11 percent is exposed.
12. A concrete block (36106°C1) of
volume 0.035 m3at 30.0°C is cooled to
10.0°C. What is the change in volume?
VVT
(36106°C1)(0.035 m3)
(10.0°C 30.0°C)
5.0105m3
13. A glass mirror used in a mountaintop
telescope is subject to temperatures ranging
from 15°C to 45°C. At the lowest temper-
ature, it has a diameter of 5.1 m. If the
coefficient of linear expansion for this glass
is 3.0106°C1, what is the maximum
change in diameter the mirror undergoes
due to thermal expansion?
LLT
(3.0106°C1)(5.1 m)
(45°C (15°C))
9.2104m
14. As shown in the figure below, a bimetallic
strip is made from a piece of copper
(16106°C1) and a piece of steel
(8106°C1). The two pieces are
equal in length at room temperature.
a. As the strip is heated from room tem-
perature, what is the ratio of the change
in the length of the copper to that of
the steel?
2
1
b. How will the strip bend when it is heated
above room temperature? When it is
cooled below room temperature?
When heated, it bends with copper
on the outside of the arc. When it is
cooled, the copper will be on the
inside of the bend.
16106°C1
8106°C1
copper
steel
copperL1T
steelL1T
Lcopper
Lsteel
Wooden
handle
Copper
Steel
0.92103kg/m3
1.03103kg/m3
ice
seawater
ice
seawater
Vsubmerged
Vtotal
1.013105N/m2
(1.00103kg/m3)(9.80 m/s2)
Chapter 13 continued

15. A fishing line’s lead sinker has a volume
of 1.40105m3. The density of lead is
1.2104kg/m3. What is the apparent
weight of the sinker when immersed in
freshwater? Seawater is slightly denser than
freshwater. Is the sinker’s apparent weight
bigger or smaller in seawater? Explain.
Fapparent FgFbuoyant
leadgV watergV
gV(lead water)
(9.80 m/s2)(1.40105m3)
(1.2104kg/m3
1.00103kg/m3)
1.5 N
The buoyant force is slightly bigger in
seawater, due to its greater density.
Thus, the apparent weight is slightly
smaller than in freshwater.
Chapter 14
pages 875–876
1. What is the mass of the watermelon shown
below, if the spring constant is 128 N/m?
Fkx mg
m
k
g
x
6.3 kg
2. How many centimeters will a spring stretch
when a 2.6-kg block is hung vertically from
a spring with a spring constant of 89 N/m?
Fkx mg
x
m
k
g
0.29 m or 29 cm
3. How much elastic potential energy does
a spring with a constant of 54 N/m have
when it is stretched 18 cm?
PEsp
1
2
kx2
1
2
(54 N/m)(0.18 m)2
0.87 J
4. What is the period of
the pendulum of the
clock below?
T 2
g
l
2
1.6 s
0.62 m
9.80 m/s2
62 cm
0.52 kg
XII
VI
VII V
XI I
VIII IV
XII
IIIIX
(2.6 kg)(9.80 m/s2)
89 N/m
(128 N/m)(0.48 m)
9.80 m/s2
0.48 m
638 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 13 continued

Physics: Principles and Problems Solutions Manual 639
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5. A clock pendulum has a period of 0.95 s.
How much longer will it have to be to have
a period of 1.0 s?
T2
g
l
l
l2l1(T22T12)
((1.0 s)2(0.95 s)2)
0.024 m 2.4 cm
The pendulum will have to be 2.4 cm
longer.
6. What is the length of a pendulum with a
period of 89.4 ms?
T2
g
l
l
1.98103m1.98 mm
7. Al is chopping wood across a clearing from
Su. Su sees the axe come down and hears
the sound of the impact 1.5 s later. How
wide is the clearing?
dvt
(343 m/s)(1.5 s) 5.1102m
8. When an orchestra is tuning up, the first
violinist plays a note at 256 Hz.
a. What is the wavelength of that sound
wave if the speed of sound in the con-
cert hall is 340 m/s?
v
f
1.3 m
b. What is the period of the wave?
T
1
f
256
1Hz
0.00391 s or 3.91 ms
9. Geo is standing on a breakwater and he
notices that one wave goes by every 4.2 s.
The distance between crests is 12.3 m.
a. What is the frequency of the wave?
f
4.2
1s
0.24 Hz
b. What is the speed of the wave?
vf
(12.3 m)
4.2
1s
2.9 m/s
1
T
1
T
340 m/s
256 Hz
(9.80 m/s2)(89.4103s)2
42
gT 2
42
9.80 m/s2
42
g
42
gT2
42
Chapter 14 continued
Chapter 15
page 876
1. Sound waves are being used to determine
the depth of a freshwater lake, as shown in
the figure below. If the water is 25°C and
it takes 1.2 s for the echo to return to the
sensor, how deep is the lake?
depth vt (1493 m/s)
9.0102m
2. Find the wavelength of an 8300-Hz wave in
copper.
v
f
3
8
5
3
6
0
0
0m
H/
z
s
0.43 m
3. Janet is standing 58.2 m from Ninovan.
If Ninovan shouts, how long will it take
Janet to hear her? Use 343 m/s for the
speed of sound.
t
d
v
0.170 s
4. The engine on a motorcycle hums at 85 Hz.
If the motorcycle travels toward a resting
observer at a velocity of 29.6 m/s, what fre-
quency does the observer hear? Use 343 m/s
for the speed of sound.
fdfs
v
v
v
vd
s
and vd0, so
fdfs
(85 Hz)
93 Hz
5. If the speed of a wave on a 78-cm-long
guitar string is known to be 370 m/s, what
is the fundamental frequency?
12L(2)(0.78 m) 1.56 m
f1
2
v
L
3
1
7
.5
06
m
m
/s
240 Hz
6. Boat A is traveling at 4.6 m/s. Boat B is
moving away from boat A at 9.2 m/s, as
shown in the figure below. The captain of
boat B blows an air horn with a frequency
of 550 Hz. What frequency does boat A
hear? Use 343 m/s for the speed of sound.
fdfs
v
v
v
vd
s
(550 Hz)
5.3102Hz
7. A submarine is traveling toward a stationary
detector. If the submarine emits a 260-Hz
sound that is received by the detector as a
262-Hz sound, how fast is the submarine
traveling? Use 1533 m/s for the speed of
sound in seawater.
fdfs
v
v
v
vd
s
and vd0, so
vvs
f
f
s
d
v
vsv1
f
f
d
s
(1533 m/s)1
2
26
60
2H
Hz
z
12 m/s
343 m/s 4.6 m/s
343 m/s (9.2 m/s)
vdvs
Boat A Boat B
1
1
2
39
4.3
6m
m//s
s
1
1
v
v
s
58.2 m
343 m/s
1.2 s
2
Sound
source
Detector
640 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Physics: Principles and Problems Solutions Manual 641
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
8. The end of a pipe is inserted into water.
A tuning fork is held over the pipe. If the
pipe resonates at lengths of 15 cm and
35 cm, what is the frequency of the tuning
fork? Use 343 m/s for the speed of sound.
closed pipe:
2(LB LA)
(2)(0.35 m 0.15 m) 0.40 m
f
v
3
0
4
.4
30
m
m
/s
8.6102Hz
9. A 350-Hz tuning fork is held over the end of
a pipe that is inserted into water. What is the
spacing between the resonance lengths of
the pipe if the speed of sound is 348 m/s?
v
f
and
LBLA
2
for a closed pipe, so
LBLA
2
v
f
Chapter 16
pages 876–877
1. What is the distance, r, between the light-
bulb and the table in the figure below?
E
r
0.98 m
2. What is the luminous flux of a flashlight
that provides an illuminance of 145 lx to
the surface of water when held 0.50 m
above the water?
E
P4r2E4(0.50 m)2(145 lx)
4.6102lm
3. An overhead light fixture holds three light-
bulbs. Each lightbulb has a luminous flux of
1892 lm. The light fixture is 1.8 m above the
floor. What is the illuminance on the floor?
E 1.4102lx
4. What is the wavelength in air of light that
has a frequency of 4.61014 Hz?
c
f
6.5107m650 nm
3.00108m/s
4.61014 Hz
(3)(1892 lm)
4(1.8 m)2
P
4r2
P
4r2
2152 lm
4(180 lx)
P
4E
P
4r2
P 2152 lm
E 180 lx
r
348 m/s
(2)(350 Hz) 0.50 m
Chapter 15 continued

5. A helium atom is in a galaxy traveling at
a speed of 4.89106m/s away from the
Earth. An astronomer on Earth observes
a frequency from the helium atom of
6.521014 Hz. What frequency of light
is emitted from the helium atom?
fobs f1
v
c
They are moving away from each other
so use the plus form.
ffobs1
v
c
(6.521014 Hz)1
6.631014 Hz
6. An astronomer observes that a molecule
in a galaxy traveling toward Earth emits
light with a wavelength of 514 nm. The
astronomer identifies the molecule as one
that actually emits light with a wavelength
of 525 nm. At what velocity is the galaxy
moving?
obs
5.14107m5.25107m
v
c
vc
(3.00108m/s)
6.29106m/s
Chapter 17
page 877
1. A light ray is reflected off a plane mirror at
an angle of 25° from the normal. A light
ray from another source is reflected 54°
from the normal. What is the difference in
the angles of incidence for the two light
sources?
Difference 54° 25°
29°
2. A light ray is reflected off a plane mirror, as
shown. What is the angle of reflection?
i90° angle to mirror
90° 13° 77°
ri
77°
3. The angle between an incident and a reflected
ray is 70.0°. What is the angle of reflection?
ri
70
2
.0°
35.0°
4. An image is produced by a concave mirror,
as shown. What is the object’s position?
f
2
r
152
cm
7.5 cm
C
15 cm
25 cm
Image
13°
5.14107m5.25107m
5.25107m
4.89106m/s
3.00108m/s
642 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 16 continued

Physics: Principles and Problems Solutions Manual 643
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
do
1.0101cm
5. What is the magnification of the object in
problem 4?
m
2.3
6. If the object in problem 4 is 3.5 cm tall,
how tall is the image?
m
himho
(2.3)(3.5 cm)
8.2 cm
The image is 8.2 cm tall. The negative
sign means it is inverted.
7. A 6.2-m-tall object is 2.3 m from a convex
mirror with a 0.8-m focal length. What
is the magnification?
di
0.6 m
m
0.3
8. How tall is the image in problem 7?
m
himho
(0.3)(6.2 m)
2 m
9. A ball is 6.5 m from a convex mirror with a
magnification of 0.75. If the image is 0.25 m
in diameter, what is the diameter of the
actual ball?
m
The variable hcan be used for any
dimension in plane and spherical
mirrors. In this problem, hodiameter
of the ball.
ho
m
hi
0.
0
2
.5
75
m
0.33 m
hi
ho
hi
ho
(0.6 m)
2.3 m
di
do
(0.8 m)(2.3 m)
2.3 m (0.8 m)
fdo
dof
hi
ho
25 cm
11 cm
di
do
(7.5 cm)(25 cm)
25 cm 7.5 cm
fdi
dif
Chapter 17 continued
Chapter 18
pages 877–878
1. A piece of flint glass
is lying on top of a con-
tainer of water (see figure
below). When a red beam
of light in air is incident
upon the flint glass at an
angle of 28°, what is the
angle of refraction in the
flint glass?
n1sin 1n2sin 2
2sin1
sin1
17°
2. When the angle of refraction in the flint
glass of problem 1 is 22°, what is the angle
of refraction in the water?
n1sin 1n2sin 2
2sin1
sin1
27°
3. When the beam of light in problem 1 enters
the flint glass from the water, what is the
maximum angle of incidence in the water
such that light will transmit into the air above
the flint glass? Hint: Use an angle of refraction
of the light beam in air that is almost 90°.
This will occur when the angle of
refraction of the light beam in the air is
almost 90°. Use 289.9°.
n1sin 1n2sin 2
At the flint glass and air boundary:
1sin1
sin1
38.1°
At the water and flint glass boundary:
1sin1
sin1
48.7°
4. An object that is 24 cm from a convex
lens produces a real image that is 13 cm
from the lens. What is the focal length of
the lens?
f
8.4 cm
5. A 5.0-cm-tall object is placed 16 cm from a
convex lens with a focal length of 8.4 cm.
What are the image height and orientation?
di
17.7 cm
m
hi
5.5 cm
The image is inverted relative to the
object.
6. An object is 185 cm from a convex lens
with a focal length of 25 cm. When an
inverted image is 12 cm tall, how tall is
the associated object?
di
29 cm
m
ho
77 cm
The object is 77 cm tall.
(185 cm)(12 cm)
29 cm
dohi
di
di
do
hi
ho
(25 cm)(185 cm)
185 cm 25 cm
fdo
dof
(17.7 cm)(5.0 cm)
16 cm
diho
do
di
do
hi
ho
(8.4 cm)(16 cm)
16 cm 8.4 cm
fdo
dof
(13 cm)(24 cm)
13 cm 24 cm
dido
dido
(1.62)(sin 38.1°)
1.33
n2sin 2
n1
(1.0003)(sin 89.9°)
1.62
n2sin 2
n1
(1.62)(sin 22°)
1.33
n1sin 1
n2
(1.0003)(sin 28°)
1.62
n1sin 1
n2
Air
Flint glass
Water
644 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
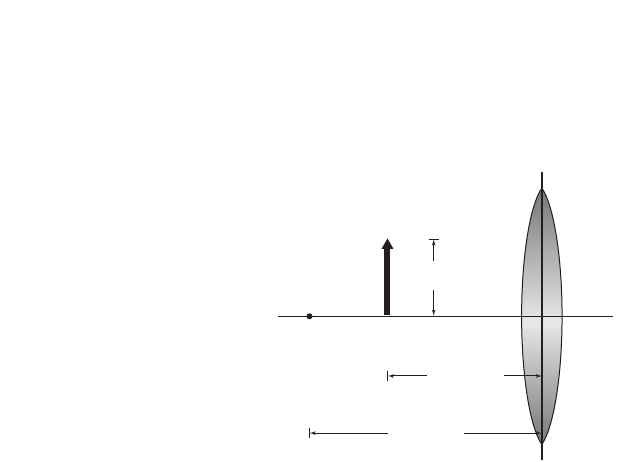
Physics: Principles and Problems Solutions Manual 645
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. What are the image height and orientation
produced by the setup in the following figure?
di
3.0101cm
m
hi
15 cm
The image is upright relative to the
object.
8. A convex lens can be used as a magnifying
glass. When an object that is 15.0 cm from
the lens has an image that is exactly 55 times
the size of the object, what is the focal length
of the lens?
m
dimdo(55)(15.0 cm)
825 cm
f
15.3 cm
9. A concave lens with a focal length of
220 cm produces a virtual image that
is 36 cm tall. When the object is placed
128 cm from the lens, what is the
magnification?
di
81 cm
m 0.63
(81 cm)
128 cm
di
do
(220 cm)(128 cm)
128 cm (220 cm)
fdo
dof
(825 cm)(15.0 cm)
(825 cm) (15.0 cm)
dido
dido
di
do
(3.0101cm)
10.0 cm
diho
do
di
do
hi
ho
(15.0 cm)(10.0 cm)
10.0 cm 15.0 cm
fdo
dof
F
5.0 cm
Object
10.0 cm
15.0 cm
Chapter 18 continued
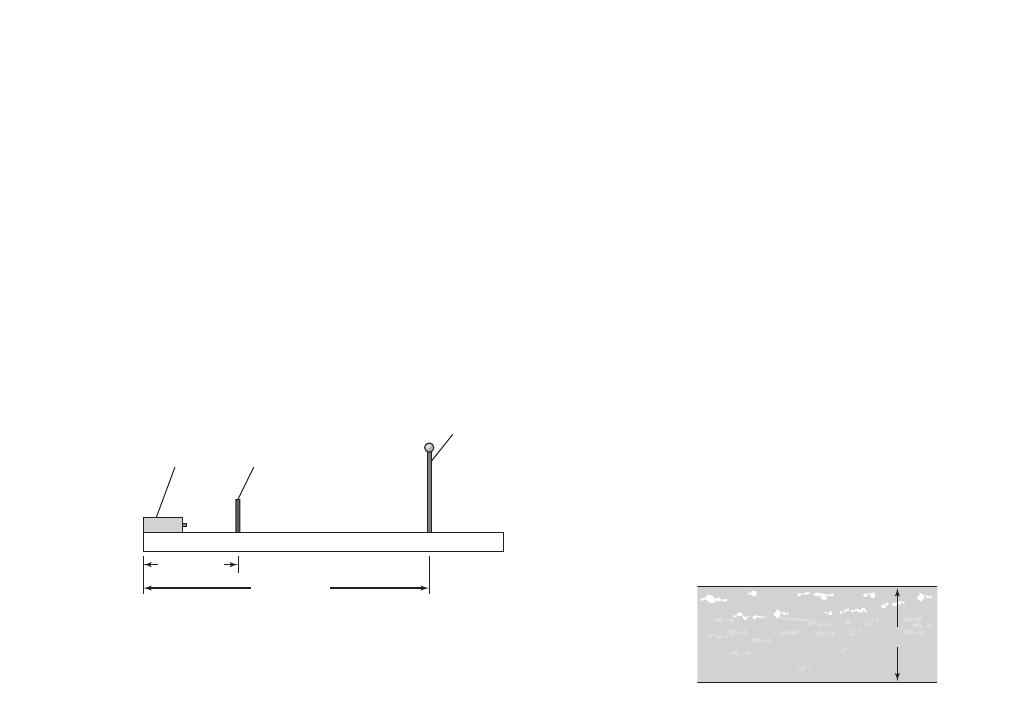
Chapter 19
pages 878–879
1. A physics student performs a double-slit
diffraction experiment on an optical bench,
as shown in the figure below. The light
from a helium-neon laser has a wavelength
of 632.8 nm. The laser light passes through
two slits separated by 0.020 mm. What is
the distance between the centers of the
central band and the first-order band?
L150.0 cm 50.0 cm
100.0 cm
x
L
d
x
d
L
3.2102m3.2 cm
2. A laser of unknown wavelength replaces
the helium-neon laser in the experiment
described in problem 1. To obtain the best
diffraction pattern, the screen had to be
moved to 104.0 cm. The distance between
the centers of the central band and the first-
order band is 1.42 cm. What wavelength of
light is produced by the laser?
L104.0 cm 50.0 cm
54.0 cm
x
L
d
5.3107m530 nm
3. Light with a wavelength of 454.5 nm passes
through two slits that are 95.2 cm from a
screen. The distance between the centers
of the central band and the first-order band
is 15.2 mm. What is the slit separation?
x
L
d
d
x
L
2.85105m
4. What color of light would be reflected from
the soapy water film shown in the figure
below?
2dm
1
2
n
sw
For m0, 2d
1
2
n
sw
.
4dnsw
(4)(76.1 nm)(1.33)
405 nm
The light is violet in color.
5. A 95.7-nm film of an unknown substance is
able to prevent 555-nm light from being
reflected when surrounded by air. What is
the index of refraction of the substance?
2dm
1
2
ns
ub
For m0, 2d
1
2
ns
ub
.
nsub
4
d
(4)5
(9
55
5.7
nm
nm)
1.45
76.1 nm
Soapy water
Air
Air
nSW 1.33
(4.545107m)(0.952 m)
0.0152 m
(1.42102m)(2.0105m)
0.540 m
(6.328107m)(1.000 m)
2.0105m
Laser Diffraction
grating
Screen
150.0 cm
50.0 cm
646 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 647
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
6. An oil film (n1.45) on the surface of a
puddle of water on the street is 118 nm
thick. What frequency of light would be
reflected?
2dm
1
2
n
oil
For m0, 2d
1
2
n
oil
.
4dnoil
(4)(118 nm)(1.45)
685 nm
c
f
f
c
4.381014 Hz
7. Violet light (415 nm) falls on a slit that
is 0.040 mm wide. The distance between
the centers of the central bright band and
the third-order dark band is 18.7 cm. What
is the distance from the slit to the screen?
xm
L
6.0 m
8. Red light (685 nm) falls on a slit that is
0.025 mm wide. The distance between the
centers of the central bright band and the
second-order dark band is 6.3 cm. What is
the width of the central band?
xm
L
1.1 m
2x1
0.063 m
9. The width of the central bright band of a
diffraction pattern is 2.9 cm. Laser light
of unknown wavelength passes through a
single slit that is 0.042 mm wide and onto
a screen that is 1.5 m from the slit. What
is the wavelength of the light?
2x1
4.1107m
10. A diffraction grating has 13,400 lines per
inch. What is the slit separation distance?
(Use 1 in 2.54 cm)
d
1.90106m/line
11. Light from a helium-neon laser (
632.8 nm) passes through the diffraction
grating described in problem 10. What is
the angle between the central bright line
and the first-order bright line?
dsin
sin1
sin1
19.5°
6.328107m
1.90106m
d
1 m
100 cm
2.54 cm
1 in
1 in
13,400 lines
(0.029 m)(4.2105m)
(2)(1.5 m)
2x1w
2L
2L
w
(2)(6.85107m)(1.1 m)
2.5105m
2L
w
(0.063 m)(2.5105m)
(2)(6.85107m)
xmw
m
mL
w
(0.187 m)(4.0105m)
(3)(4.15107m)
xmw
m
mL
w
3.00108m/s
6.85107m
Chapter 19 continued

12. A diffraction grating with slits separated by 3.40106m is illuminated by light
with a wavelength of 589 nm. The separation between lines in the diffraction
pattern is 0.25 m. What is the distance between the diffraction grating and the
screen?
dsin
sin1
sin1
9.98°
tan
L
x
L
tax
n
ta
0
n
.29
5.9
m
8°
1.4 m
5.89107m
3.40106m
d
648 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 19 continued
Physics: Principles and Problems Solutions Manual 649
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20
page 879
1. The magnitude of a charge, q, is to be deter-
mined by transferring the charge equally to
two pith balls. Each of the pith balls has a mass
of m, and is suspended by an insulating thread
of length l. When the charge is transferred, the
pith balls separate to form an equilibrium in
which each thread forms an angle, , with the
vertical.
a. Draw a force diagram showing the forces
that are acting on the rightmost pith ball.
where:
FTthread tension
FEelectrostatic force
Fggravitational force
b. Derive an expression for qas a function of , m, and l.
Since the system is in equilibrium, the net horizontal and vertical
forces must be zero.
FTsin FE0
FTcos Fg0
Rearrange and substitute FEand Fg.
FTsin FEKKK
FTcos Fgmg
Divide the first equation by the second to eliminate FT.
c
so
in
s
tan Kq2
16mgd2
q2
16d2
q
2
2
4d2
qAqB
(2d)2
FT
FE
Fg
dd
l

From the diagram, dlsin . Substitute for dand solve for q.
q2
q4lsin
mg
K
ta
n
c. Use your derived expression to determine the value of qwhen 5.00°,
m2.00 g, and l10.0 cm.
q(4)(10.0102m)(sin 5.0°)
1.52108C
2. As shown in the figure below, four charges, each with charge q, are distributed sym-
metrically around the origin, O(0, 0), at A(1.000, 0), B(0, 1.000), C(1.000, 0),
and D(0, 1.000). Find the force on a fifth charge, qT, located at T(5.000, 0).
Because of symmetry, the force components on charge Tin the direction
of the y-axis cancel, and only the x-direction forces need to be computed.
FT, xFAT, xFBT, xFCT, xFDT, x
KqqT
KqqT
1
1
6
(2)
3
1
6
1252
0.1657KqqTN
3. Consider that the four charges in the previous problem are now combined into a
single charge, 4q, located at the origin. What is the force on charge qT?
KKqqT
2
4
5
0.1600KqqTN
A charge uniformly spread over a spherical surface may be treated as if
all of the charge is concentrated at the sphere’s center. The previous
problem is a two-dimensional approximation of this condition.
(4q)(qT)
52
5
125
2
cos D
DT 2
1
CT 2
cos B
BT 2
1
AT 2
y (m)
x (m)
0
D
CT
B
A
(2.00103kg)(9.80 m/s2)(tan 5.0°)
(9.0109 Nm2/C2)
16mgl2sin2tan
K
650 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 20 continued

Physics: Principles and Problems Solutions Manual 651
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21
pages 879–880
1. What are the magnitude and the sign of a
point charge that experiences a force of
0.48 N east when placed in an electric
field of 1.6105N/C west?
q
E
F
3.0106C
Because the force exerted on the charge
is opposite the direction of the electric
field, the charge must be negative.
2. A test charge of 1.0106C, located at
the point T(0, 1) m, experiences a force of
0.19 N directed toward the origin, along the
y-axis, due to two identical point charges
located at A(1, 0) m and B(1, 0) m.
a. What is the sign of the charges at A
and B?
The charges at Aand Bmust be
positive to cause an attractive force
on the test charge.
b. What are the magnitude and direction
of the electric field at T?
E
F
q
E1.9105N/C
The direction is opposite the force
because it is a negative charge. So,
E1.9105N/C, away from the
origin.
3. A test charge of 0.5107C is placed in
an electric field of 6.2104N/C, directed
15° north of east. What is the force experi-
enced by the charge?
FqE
(0.5107C)(6.2104N/C)
3.1103N
The direction is opposite that of
the electric field because the charge
is negative. So, E3.1103N,
15° south of west
4. By what percent must the distance from a
point charge increase in order to have a
reduction in the electric field strength by
40 percent?
The electric field strength of a point
charge,
EK,
is inversely proportional to the square
of the distance from the charge.
E
E1
2
r22
E
E1
2
r12
r2
E
E1
2
r1
In this case, E2(1 0.40)E10.60E1
Then, r2
0.1
60
r11.2r1
The distance must increase by
30 percent.
5. A particle of mass m2.0106kg is
in a circular orbit about a point charge.
The charge, q,is 3.0105C and is at a
distance of r20.0 cm.
a. What is the electric field strength at
all points on the orbit around the
point charge?
FE
q
20.0 cm
r22
r12
q
r2
0.19 N
1.0106C
y
T(0, 1)qT
qAqB
A(1, 0) B(1, 0)
x
0.48 N
1.6105N/C

Since the orbit is circular, the
distance of the particle from the
point charge is constant. From
Example Problem 2, the electric
field strength depends only on the
distance and the charge, and is
given by
EK
(9.0109Nm2/C2)
3
(.
0
0
.
20
1
0
0
m
5
)2
C
6.8106N/C, radially outward at
all points on the orbit
b. Considering only electrostatic forces,
what charge, q, on the particle is
required to sustain an orbital period
of 3.0103s?
The electrostatic force FEmust be
toward the point charge to account
for the centripetal acceleration of
the particle in orbit. Therefore, the
particle charge must be negative.
The force required to keep the
particle in orbit is (see Chapter 6,
Motion in Two Dimensions):
FEmacm
4T
2
2r
, radially inward.
The charge on the particle must then
be
q
F
E
E
2.6107C
6. Two charges of equal magnitude and
opposite sign are placed 0.50 m apart. The
electric field strength midway between them
is 4.8104N/C toward the negative charge.
What is the magnitude of each charge?
The electric field strength is the sum
of two components, one due to each
charge, both pointing toward the
negative charge. At the midpoint,
the magnitudes of the component
field strengths are equal.
EEqEq
Solve for qin terms of E.
q
1.7107C
7. A pith ball weighing 3.0102N carries a
charge of 1.0106C. The pith ball is
placed between two large, parallel, metal
plates, that are separated by 0.050 m. What
is the potential difference, V, that must be
applied in order to suspend the pith ball
between the plates?
VEd
F
q
Ed
1.5103V
8. The electric field strength, defined as a force
per unit charge, has the units newtons per
coulomb, N/C. The formula for electric
potential difference, VEd, however,
suggests that Ealso can be expressed as
volts per meter, V/m.
a. By analysis of the units, show that these
two expressions for the units of electric
field strength are equivalent.
m
V
J
m
/C
(N
m
m)/C
N
C
b. Suggest a reason why V/m is often a
more useful way to express electric
field strength.
In practice, electric potential differ-
ences and distances are much easier
to measure than forces on charges.
(3.0102N)(0.050 m)
1.0106C
(4.8104N/C)(0.50 m)2
(8)(9.0109Nm2/C2)
Er2
8K
8Kq
r2
2Kq
2
r
2
qqE
r
2
r
2
42(0.200 m)(2.0106kg)
(6.8106N/C)(3.0103s)2
42rm
ET2
q
r2
652 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 653
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
9. Suppose you have two parallel, metal plates
that have an electric field between them of
strength 3.0104N/C, and are 0.050 m
apart. Consider a point, P, located 0.030 m
from plate A,the negatively charged plate,
when answering the following questions.
a. What is the electric potential at P
relative to plate A?
VPA (3.0104V/m)(0.030 m)
9.0102V
b. What is the electric potential at P relative
to plate B,the positively charged plate?
VPB (3.0104V/m)(0.020 m)
6.0102V
10. A certain 1.5-V size-AA battery has a storage
capacity of 2500 C. How much work can
this battery perform?
WqV(2.5103C)(1.5 V)
3.8103J
11. In a vacuum tube, electrons accelerate from
the cathode element to the plate element,
which is maintained at a positive potential
with respect to the cathode. If the plate volt-
age is 240 V, how much kinetic energy
has an electron acquired when it reaches
the plate?
The kinetic energy gained by an electron
is the same as the potential energy lost
by the electron as it moves through the
potential difference of 240 V.
KE WeV
(1.601019 C)(240 V)
3.81017 J
12. An oil drop with five excess electrons is sus-
pended in an electric field of 2.0103N/C.
What is the mass of the oil drop?
Fgmg FEqE neE
m
ne
gE
1.61016 kg
13. An oil drop weighing 7.51015 N carries
three excess electrons.
a. What potential difference is required
to suspend the drop between parallel
plates separated by 2.3 cm?
FgFEqE neE ne
V
F
n
g
e
d
3.6102V
b. If the oil drop picks up another electron,
by how much must the potential differ-
ence between the plates be reduced to
maintain the oil drop in suspension?
V
So the potential difference is
inversely proportional to the
number of excess electrons.
V
V2
1
n
n1
2
V2
n
n1
2
V1
3
4
(3.6102V) 2.7102V
Reduction of 90 V
14. A charge of 2.00106C is moved against
a constant electric field. If 4.50104J of
work is done on the charge, what is the
potential difference between the initial
and the final locations of the charge?
V
W
q
q
225 V
15. Capacitors C1 220 F and C2470 F are
connected across a 48.0-V electric potential
difference.
a. What are the charges, q1and q2, on each
of the capacitors?
C
q
V
4.50104J
2.00106C
Fgd
ne
(7.51015 N)(2.3102m)
(3)(1.601019 C)
V
d
(5)(1.601019 C)(2.0103N/C)
9.80 m/s2
Fg
g
Chapter 21 continued
q1C1V(220106F)(48.0 V)
1.1102C
q2C2V(470106F)(48.0 V)
2.3102C
b. What is the total charge, qT, on both
capacitors?
qTq1q2
C1VC2V
(C1C2)V
(220106F470106F)
(48.0 V)
3.3102C
c. Repeat steps aand bfor a new potential
difference, v96.0 V.
q1C1V(220106F)(96.0 V)
2.1102C
q2C2V(470106F)(96.0 V)
4.5102C
qTq1 q2
(C1C2)V
(220106F470106F)
(96.0 V)
6.6102C
d. Now consider the two capacitors as a
system. What would be a single equiva-
lent capacitor, Ceq, that could replace C1
and C2, and be capable of yielding the
same results?
Let Ceq C1C2690 F
Then,
qTCeqV
(690106F)(48.0 V)
3.3102C
and
qTCeqV
(690106F)(96.0 V)
6.6102C
yielding similar results as previously.
e. Based on your responses to the above,
make a conjecture concerning the
equivalent capacitance of a system of
capacitors—all of which are connected
across the same potential difference.
The equivalent capacitance is
the sum of all of the individual
capacitances.
16. A new 90.0-V battery with a storage capacity
of 2.5104C charges a 6800-F capacitor
with the switch in position A. Then the
switch is thrown to position B to discharge
the capacitor.
a. How many times can this cycle be
repeated before the battery is
completely discharged?
When the capacitor is completely
charged, it contains
qcCV(6800106F)(90.0 V)
0.61 C
The number of cycles Nis
N
02
.6
.5
1
C
1
/c
0y
4
c
C
le
4.1104cycles
b. If the capacitor discharge occurs in
120 ms, what is the average power
dissipated in the discharge circuit
during one cycle?
The energy stored in the fully
charged capacitor equals the work
performed to store the charge.
WqcV
The average power dissipated
equals the total energy dissipated
divided by the time required.
P
E
t
W
t
qcV
t
90.0 V
Discharge
circuit
BA
654 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 21 continued

Physics: Principles and Problems Solutions Manual 655
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
(0.61
0
C
.1
)
2
(9
s
0.0 V)
4.6102W
17. A 0.68-F capacitor carries a charge on one
plate of 1.36105C. What is the potential
difference across the leads of this capacitor?
C
q
V
V
C
q
2.0101V
Chapter 22
pages 881–882
1. A decorative lightbulb rated at 7.50 W
draws 60.0 mA when lit. What is the
voltage drop across the bulb?
PVI
V
P
I
(60
(
.0
7
.5
1
0
0
W
3
)
A)
125 V
2. A 1.2-V nickel-cadmium battery has a
rated storage capacity of 4.0103mAh
(milliamp-hours).
a. What is the battery charge capacity in
coulombs? Hint: 1 C 1 As.
q(4.0103mAh)
100
1
0A
mA
1.4104As1.4104C
b. How long can this battery supply a
current of 125 mA?
qIt
t32 h
3. A heating element of an electric furnace
consumes 5.0103W when connected
across a 240-V source. What current flows
through the element?
PVI
I
5.0
2
41
00
V
3W
21 A
4. The cold filament resistance of a lightbulb
is 20.0 . The bulb consumes 75 W when it
is operating from a 120-V source. By what
factor does the start-up current in the bulb
exceed the operating current?
Istart
R
V
Ioperate
P
V
Io
I
p
s
e
ta
ra
rt
te
R
VP
2
(20.
(
0
12
0
)(
V
7
)
5
2
W)
9.6
The start-up current is 9.6 times larger
than the operating current.
R
V
P
V
P
V
4.0103mAh
125 mA
3600 s
1 h
1.36105C
0.68106F
Chapter 21 continued
5. In the circuit shown below, a potentiometer
is used to vary the current to the lamp. If
the only resistance is due to the lamp, what
is the current in the circuit?
I
Rla
V
mp
21
02
.0V
0.60 A
6. An electric toaster consumes 1875 W in
operation. If it is plugged into a 125-V
source, what is its resistance?
P
V
R
2
R
V
P
2
(
1
1
8
2
7
5
5
V
W
)2
8.33
7. Draw a circuit diagram to include a 90.0-V
battery, a 220-resistor, and a 680-
resistor in series. Show the direction of
conventional current.
8. Modify the diagram of the previous problem
to include an ammeter and a voltmeter to
measure the voltage drop across the 680-
resistor.
9. If the total resistance in the circuit
in problem 8 is 9.0102, what would
the ammeter and the voltmeter indicate?
Ammeter reading is
I
R
V
9.0
9
0.
1
0
0V
2
0.10 A
Voltmeter reading is
VIR
(0.10 A)(680 )68 V
10. An electric motor with a load delivers
5.2 hp to its shaft (1 hp 746 W). Under
these conditions, it operates at 82.8 percent
efficiency. (Efficiency is defined as the ratio
of power output to power input.)
a. How much current does the motor draw
from a 240-V source?
Efficiency
P
P
o
in
u
p
tp
u
u
t
t
0.828
I
Pin
V
put
240 V
2.0101A
(5.2 hp)(746 W/hp)
0.828
Ef
P
fio
c
u
it
e
p
n
uc
ty
V
90.0 V
220
680
I
I
A
V
90.0 V
220
680
I
I
I
Rlamp 20.0
12 V
656 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 22 continued

Physics: Principles and Problems Solutions Manual 657
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. What happens to the remaining
17.2 percent of the input power?
It is primarily dissipated as I2R
losses in the motor windings.
Ultimately, this energy is converted
to thermal energy and must be
removed from the motor by fans
or other means.
11. An industrial heating process uses a current
of 380 A supplied at 440-V potential.
a. What is the effective resistance of the
heating element?
R
V
I
3
48
40
0A
V
1.2
b. How much energy is used by this
process during an 8-h shift?
EPt VIt
(440 V)(380 A)(8 h)
36
1
00
hs
5109J
12. An 8.0-electric heater operates from
a 120-V source.
a. How much current does the heater
require?
I
R
V
1
82
.0
0
V
15 A
b. How much time does the heater need to
generate 2.0104J of thermal energy?
EPt VIt
t
V
EI
(1
2
2
.
0
0
V
1
)(
0
1
4
5
J
A)
11 s
13. A manufacturer of lightbulbs advertises that
its 55-W bulb, which produces 800.0 lm of
light output, provides almost the same light
as a 60.0-W bulb with an energy savings.
The 60.0-W bulb produces 840.0 lm.
a. Which bulb most efficiently converts
electric energy to light?
The 55-W bulb produces
80
5
0
5
.0
W
lm
,
or 14.5 lm/W. The 60.0-W bulb
produces
8
6
4
0
0
..
0
0W
lm
, or 14.0 lm/W.
The 55-W bulb is more efficient.
b. Assume a bulb has a lifetime of
1.0103h and an electric energy cost
of $0.12/kWh. How much less does
the 55-W bulb cost to operate over
its lifetime?
The 60.0-W bulb costs
(0.0600 kW)(1.0103h)($0.12/kWh)
$7.20
The 55-W bulb costs
(0.055 kW)(1.0103h)($0.12/kWh)
$6.60
The difference in cost is
$7.20 $6.60 $0.60
c. Is most of the cost savings due to
higher bulb efficiency, or due to the
consumer’s willingness to accept lower
light output?
Most of the savings is due to a
willingness to accept lower light
output. If the 60.0-W bulb could
be made to output 800.0 Im, its
cost would be
8
80
40
0.
.0
0
($7.20) $6.86,resulting in a
savings of $0.26 for the 55-W bulb.
So of the $0.60 savings over the bulb
lifetime, only $0.26, or 43 percent, is
due to higher efficiency.
14. By what factor would the I2Rloss in trans-
mission wires be reduced if the transmission
voltage were boosted from 220 V to 22 kV?
Assume that the rate of energy delivered is
unchanged.
The power required is the same. The
current, however, would be reduced by
the same factor that the voltage was
boosted, 102. The I2Rloss would be
reduced by a factor of 104because the
current is squared.
15. The electric-utility invoice for a household
shows a usage of 1245 kWh during a
certain 30-day period. What is the average
power consumption during this period?
P
E
t
1.245
3
01d
06Wh
2
1
4d
h
2103W
Chapter 22 continued
Chapter 23
pages 882–884
1. A series circuit contains a 47-resistor, an
82-resistor, and a 90.0-V battery. What
resistance, R3, must be added in series to
reduce the current to 350 mA?
I
Vso
R
urce
R
VsoI
urce
0
9
.3
05
.0
0V
A
257
For a series circuit, RR1R2R3
R3RR1R2
257 47 82
128
2. What is the minimum number of 100.0-
resistors that must be connected in series
together with a 12.0-battery to ensure
that the current does not exceed 10.0 mA?
I
Vso
R
urce
, where I0.0100 A
Let nequal the number of 100.0-
resistors.Thus, for this series circuit,
R100.0n
0.0100 A
12R
.0 V
0.0100 A
1
10
20
.0
.0
V
n
n
(0.010
1
0
2
).(
0
100.0)
12.0
There must be at least 12 resistors.
3. A 120.0-generator is connected in series
with a 100.0-resistor, a 400.0-resistor,
and a 700.0-resistor.
a. How much current is flowing in the
circuit?
I
Vso
R
urce
0.1000 A
b. What is the voltage drop in the 400-
resistor?
V400 IR400
(0.1000 A)(400.0 )
40.00 V
4. Show that the total power dissipated in
a circuit of series-connected resistors is
PI2R, where Ris the equivalent resistance.
The total dissipated power is equal to
the sum of the power dissipations in
each of the resistors.
PP1P2…
I2R1I2R2…
I2(R1R2…)
I2R
5. In an experiment, three identical lightbulbs
are connected in series across a 120.0-V
source, as shown. When the switch is closed,
all of the bulbs are illuminated. However,
when the experiment is repeated the next
day, bulbs A and B are illuminated brighter
than normal, and bulb C is dark. A volt-
meter is used to measure the voltages in the
circuit as shown. The voltmeter readings are:
V1120.0 V
V260.0 V
V30.0 V
a. What has happened in this circuit?
Bulb C has developed a short circuit
in its base and thus, no current flows
through its filament and it remains
dark.The short acts as a zero resis-
tance and allows the circuit current
V3
V2
V1
(Bulb A)
RA
(Bulb B)
RB
(Bulb C)
RC
120.0 V
120.0 V
100.0 400.0 700.0
658 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 659
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
to flow.The measurements confirm
that the available voltage is dropped
across the remaining two bulbs.
b. Explain why bulbs A and B are brighter
than normal.
The voltage drop across each bulb
increased from
120
3
.0 V
40.00 V,
to
120
2
.0 V
60.00 V. The power
dissipated in each bulb, P,
has increased because of the
increased V.
c. Is there more or less current flowing
now in the circuit?
More current flows through the
circuit. The equivalent resistance of
two bulbs and a short circuit is
lower than that of three bulbs. This
lower equivalent resistance results
in an increased current.
6. A string of holiday lights has 25 identical
bulbs connected in series. Each bulb dissi-
pates 1.00 W when the string is connected
to a 125-V outlet.
a. How much power must be supplied by
the 125-V source?
P(25 bulbs)(1.00 W/bulb)
25.0 W
b. What is the equivalent resistance of
this circuit?
P
R
(
2
1
5
2
.
5
0
V
W
)2
625
c. What is the resistance of each bulb?
Because the bulbs are in series,
Rbulb
2
R
5
62
2
5
5
25.0
d. What is the voltage drop across each
bulb?
Because the bulbs are in series,
Vbulb
2
V
5
12
2
5
5V
5.00 V
7. Two resistors are connected in series across
a 12.0-V battery. The voltage drop across
one of the resistors is 5.5 V.
a. What is the voltage drop across the
other resistor?
12.0 V 5.5 V 6.5 V
b. If the current in the circuit is 5.0 mA,
what are the two resistor values?
R
V
I
R1
0.0
50
.5
50
VA
1100
R2
0.0
60
.5
50
VA
1300
8. In problem 7, the specifications for the
resistors state that their resistance may vary
from the listed nominal value. If the possi-
ble ranges of actual resistance values are
as follows, 1050 R1 1160 , and
1240 R21370 , what is the possi-
ble minimum and maximum value of the
nominal 5.5-V voltage drop?
Construct a table to determine the volt-
age drops resulting from the extreme
values of the resistors. The voltage drop
is calculated using the equation
R
1
1
2
R
R
1
2
.
The voltage drop will range from 5.2 V
to 5.8 V.
Resistor R1Resistor R2Voltage Drop
kk(V)
1.05 1.24 5.5
1.05 1.37 5.2
1.16 1.24 5.8
1.16 1.37 5.5
V2
P
V2
R
V2
R
Chapter 23 continued

9. A voltage-divider circuit is constructed with
a potentiometer, as shown below. There are
two fixed resistances of 113 kand 294 k.
The resistance of the potentiometer can
range from 0.0 to 100.0 k.
a. What is Vout when the potentiometer
is at its minimum setting of 0.0 ?
Vout Vmin
(100.0 V)
58.0 V
b. What is Vout when the potentiometer
is at its maximum setting of 100.0 k?
Vout Vmax
(100.0 V)
77.7 V
c. What potentiometer setting is required
to adjust Vout to exactly 65.0 ?
The setting is the same as the ratio
of the range from Vmin to 65.0 V to
the total available range.
(6
V
5
m
.0
ax
V
)
V
V
m
m
in
in
6
75
7.
.0
7V
V
5
58
8.
.0
0V
V
35.5%
10. Two lightbulbs, one rated at 25.0 W and
one rated at 75.0 W, are connected in
parallel across a 125-V source.
a. Which bulb is the brightest?
The 75.0-W bulb dissipates the
most power and therefore burns
the brightest.
b. What is the operating resistance of each
of the bulbs?
Since the bulbs are connected
in parallel, the same voltage is
connected across each of them.
P
R
R75
(
7
1
5
2
.
5
0
V
W
)2
208
R25
(
2
1
5
2
.
5
0
V
W
)2
625
c. The bulbs are rewired in series. What is
the dissipated power in each bulb?
Which bulb is the brightest?
The current in the circuit is now:
I
Vso
R
urce
R25
VR75
8
13
23
5
V
0.150 A
The power dissipated in each bulb is:
P75 I2R75 (0.150 A)2(208 )
4.68 W
P25 I2R25 (0.150 A)2(625 )
14.1 W
The 25-W bulb is the brightest.
11. A 10.0-V battery has an internal resistance
of 0.10 . The internal resistance can be
modeled as a series resistor, as shown.
RL
RI 0.10
10.0 V
Battery Load
V
V2
P
V2
R
294 k100.0 k
294 k100.0 k113 k
294 k
294 k100.0 k113 k
294 k
100.0 k
Vout
113 k
100.0 V
660 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
Physics: Principles and Problems Solutions Manual 661
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
a. Derive an expression for the battery
terminal voltage, V, as a function of
the current, I.
voltage rise sum of voltage drops
10.0 IRIV
V10.0 IRI
10.0 – 0.10I
b. Create a graph of voltage versus current
for a current range of 0.0 to 1.0 A.
c. What value of load resistor RLneeds to
be placed across the battery terminals to
give a current of 1.0 A?
I
R
V
I
s
our
R
ce
L
RL
VsoI
urce
RI
1
1
0
.0
.0A
V
0.10
9.9
d. How does the V-I function differ from
that of an ideal voltage source?
An ideal voltage source provides
the specified potential difference
regardless of the amount of current
drawn from it.
12. Show that the total power dissipated in a
circuit of parallel-connected resistors is:
P
V
R
2
, where Ris the equivalent resistance.
The total dissipated power is equal to
the sum of the power dissipations in
each of the resistors.
PP1P2…
P…
V2…
13. A holiday light string of ten bulbs is
equipped with shunts that short out the
bulbs when the voltage drop increases to
line voltage, which happens when a bulb
burns out. Each bulb has a resistance
of 200.0 . The string is connected to a
household circuit at 120.0 V. If the string
is protected by a 250.0-mA fuse, how many
bulbs can fail without blowing the fuse?
The string will operate as long as the
current is less than 250.0 mA.
I
R
V
0.250 A
nR
V
bulb
0.250 A
(n)
1
(2
20
00
.0
.0
V
)
n
n2.4
The string will operate with at least
three good bulbs, or no more than
seven failed bulbs.
14. A 60.0-W lightbulb and a 75.0-W lightbulb
are connected in series with a 120-V source.
a. What is the equivalent resistance of
the circuit?
P
R
60.0
(
W
120
V
7
)
5
2
.0 W
1.1102
b. Suppose an 1875-W hair dryer is now
plugged into the parallel circuit with the
lightbulbs. What is the new equivalent
resistance of the circuit?
R
7.2
(120 V)2
60.0 W 75.0 W 1875 W
V2
P
V2
P
V2
R
120.0 V
(0.250 A)(200.0 )
V2
R
1
R2
1
R1
V2
R2
V2
R1
Vsource
R
Voltage (V)
Current (Amps)
10.0
9.9
0
00.5 1.0
(1.0 A, 9.9 V)
Chapter 23 continued
15. What is the equivalent resistance of the
following resistor network?
R129.4 k
R23 6.34 k7.87 k
14.21 k
R45 25.5 k47.5 k
73.0 k
R
1
p
R
1
23
R
1
45
14.21
1k
73.0
1k
Rp 11.9 k
R R1Rp 29.4 k11.9 k
41.3 k
Chapter 24
pages 884–885
1. The magnetic field of Earth resembles
the field of a bar magnet. The north pole of
a compass needle, used for navigation, gen-
erally points toward the geographic north
pole. Which magnetic pole of the Earth is
the compass needle pointing toward?
the south magnetic pole of Earth
2. A magnet is used to collect some spilled
paper clips. What is the magnetic pole at
the end of the paper clip that is indicated
in the figure?
north
3. Jingdan turned a screwdriver into a magnet
by rubbing it with a strong bar magnet to
pick up a screw that has fallen into an
inaccessible spot. How could he demagnetize
his screwdriver after picking up the screw?
He could drop it, heat it, hit it with a
hammer, or somehow otherwise jiggle
the magnetic domains into randomness.
4. A long, straight, current-carrying wire carries
a current from west to east. A compass is
held above the wire.
a. Which direction does the north pole of
the compass point?
south
b. When the compass is moved underneath
the wire, in which direction does the
north pole point?
north
N
S
25.5 k29.4 k
6.34 k
7.87 k
47.5 k
662 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 23 continued
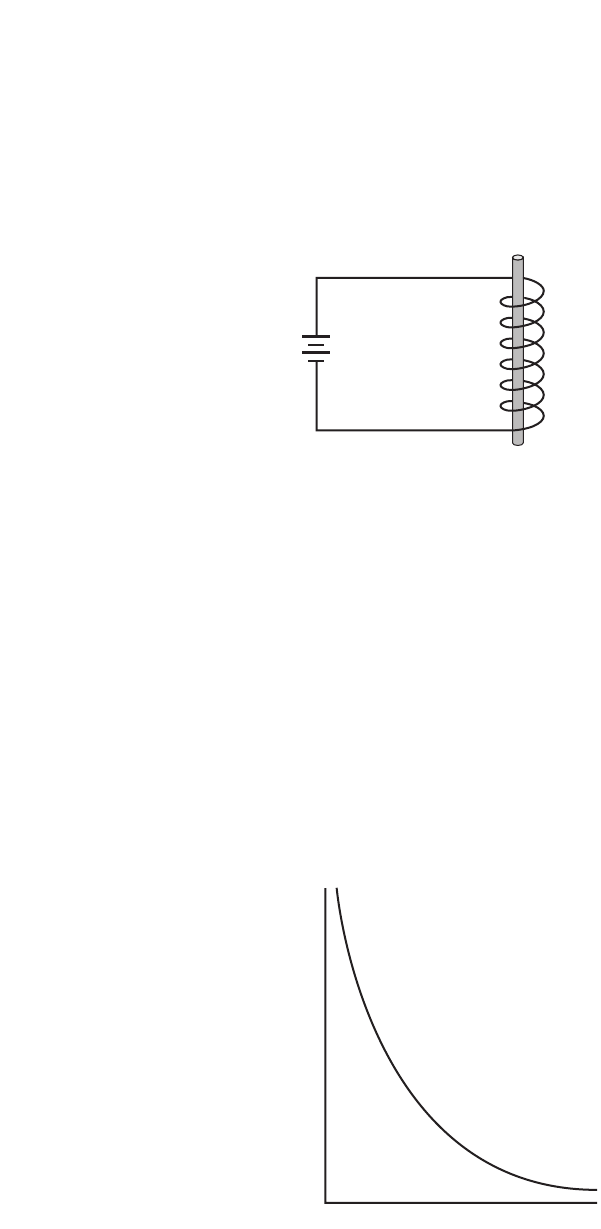
Physics: Principles and Problems Solutions Manual 663
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5. Consider the sketch of the electromagnet in
the figure below. Which components could
you change to increase or decrease the
strength of the electromagnet? Explain your
answer.
To increase the strength of the magnet,
the voltage of the power source could
be increased, the number of the wraps
could be increased, or ferromagnetic
cores could be added.
To decrease the strength of the magnet,
the voltage of the power source could
be decreased, fewer wraps could be
used, or hollow or nonmagnetic cores
could be used.
6. Sketch a graph showing the relationship
between the magnetic field around a
straight, current-carrying wire, and the
distance from the wire.
This is a graph of y1/x.The units/num-
bers do not matter. The y-axis should be
labeled magnetic field strength and the
x-axis distance from wire.
7. How long is a wire in a 0.86-T field that
carries a current of 1.4 A and experiences
a force of 13 N?
FILB
L
IF
B
(1.4 A
1)
3
(0
N
.86 T)
11 m
8. A 6.0-T magnetic field barely prevents a
0.32-m length of copper wire with a current
of 1.8 A from dropping to the ground.
What is the mass of the wire?
FILB mg
m
IL
g
B
0.35 kg
9. How much current will be needed to
produce a force of 1.1 N on a 21-cm-long
piece of wire at right angles to a 0.56-T field?
I
L
F
B
(0.21 1
m
.1
)(0
N
.56 T)
9.4 A
10. Alpha particles (particles containing two
protons, two neutrons, but no electrons)
are traveling at right angles to a 47-T field
with a speed of 36 cm/s. What is the force
on each particle?
FqvB
(3.201019 C)(0.36 m/s)(4.7105T)
5.41024 N
11. A force of 7.11012 N is exerted on some
Al3ions (an atom missing three electrons)
that are traveling at 430 km/s perpendicular
to a magnetic field. What is the magnetic
field?
B
q
F
v
34 T
12. Electrons traveling at right angles to a
magnetic field experience a force of
8.31013 N when they are in a magnetic
field of 6.2101T. How fast are the
electrons moving?
v
q
F
B
8.4106m/s
8.31013 N
(1.601019 C)(6.2101T)
7.11012 N
(4.801019 C)(4.3105m/s)
(1.8 A)(0.32 m)(6.0 T)
9.80 m/s2
Magnetic field strength
Distance from wire
Chapter 24 continued

Chapter 25
page 885
1. A 72-cm wire is moved at an angle of 72°
through a magnetic field of 1.7102T
and experiences an EMF of 1.2 mV. How
fast is the wire moving?
v
LB
EM
siF
n
0.10 m/s
2. A 14.2-m wire moves 3.12 m/s perpendicular
to a 4.21-T field.
a. What EMF is induced in the wire?
EMF BLv sin
(4.21 T)(14.2 m)(3.12 m/s)
(sin 90.0°)
187 V
b. Assume that the resistance in the wire is
0.89 . What is the amount of current
in the wire?
I
R
V
0
1
.8
87
9V
2.1102A
3. A 3.1-m length of straight wire has a
resistance of 3.1 . The wire moves at
26 cm/s at an angle of 29° through a
magnetic field of 4.1 T. What is the
induced current in the wire?
EMF BLv sin
(4.1 T)(3.1 m)(0.26 m/s2)(sin 29°)
1.6 V
I
EM
RF
3
1.
.1
6
V
0.52 A
4. A generator delivers an effective current
of 75.2 A to a wire that has a resistance
of 0.86 .
a. What is the effective voltage?
Veff IeffR(75.2)(0.86) 65 V
b. What is the peak voltage of the generator?
Vmax 92 V
5. What is the RMS voltage of a household
outlet if the peak voltage is 125 V?
Veff 2
Vmax (2
)(165 V) 117 V
6. An outlet has a peak voltage of 170 V.
a. What is the effective voltage?
Veff 2
Vmax
(2
)(170 V) 120 V
b. What effective current is delivered to an
11 - toaster?
I
R
V
1
1
2
1
0
V
11 A
7. A step-up transformer has a primary coil
consisting of 152 turns and a secondary coil
with 3040 turns. The primary coil receives a
peak voltage of 98 V.
a. What is the effective voltage in the
primary coil?
Veff 2
Vmax (2
)(98 V) 69 V
b. What is the effective voltage in the
secondary coil?
V2
n
n2
1
V1
3
1
0
5
4
2
0
(69 V) 1.4 kV
8. A step-down transformer has 9000 turns
on the primary coil and 150 turns on the
secondary coil. The EMF in the primary
coil is 16 V. What is the voltage being
applied to the secondary coil?
V1
n
n1
2
V2
9
1
0
5
0
0
0
(16 V) 0.27 V
9. A transformer has 124 turns on the
primary coil and 18,600 turns on the
secondary coil.
a. Is this a step-down or a step-up
transformer?
step-up
Veff
2
1.2103V
(0.72 m)(1.7102T)(sin 72°)
664 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 665
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
b. If the effective voltage in the secondary
coil is 3.2 kV, what is the peak voltage
being delivered to the primary coil?
V1, eff
n
n1
2
V2, eff
18
1,2
64
00
(3.2 kV) 21 V
V1, max 2
V1, eff (2
)(21 V)
3.0101
Chapter 26
pages 885–886
1. A stream of singly ionized (1) fluorine
atoms passes undeflected through a mag-
netic field of 2.5103T that is balanced
by an electric field of 3.5103V/m. The
mass of the fluorine atoms is 19 times that
of a proton.
a. What is the speed of the fluorine ions?
The electric force and magnetic
forces balance each other.
Bqv Eq
v
B
E
1.4106m/s
b. If the electric field is switched off, what is
the radius of the circular path followed
by the ions?
The magnetic force acts as a cen-
tripetal force.
Bqv
r
m
Bq
v
110 m
2. An electron moves perpendicular to Earth’s
magnetic field with a speed of 1.78106m/s.
If the strength of Earth’s magnetic field is
about 5.00105T, what is the radius of the
electron’s circular path?
Bqv
r
m
Bq
v
0.203 m
(9.111031 kg)(1.78106m/s)
(5.00105T)(1.601019 C)
mv2
r
(19)(1.671027 kg)(1.4106m/s)
(1.601019 C)(2.5103T)
mv2
r
3.5103V/m
2.5103T
Chapter 25 continued

3. A proton with a velocity of 3.98104m/s perpendicular to the direction of a
magnetic field follows a circular path with a diameter of 4.12 cm. If the mass of
a proton is 1.671027 kg, what is the strength of the magnetic field?
Bqv
B
m
rq
v
2.02102 T
4. A beam of doubly ionized (2) calcium atoms is analyzed by a mass spectrome-
ter. If B4.5103T, r0.125 m, and the mass of the calcium ions is
6.681026 kg, what is the voltage of the mass spectrometer?
V
0.76 V
5. The speed of light in crown glass is 1.97108m/s. What is the dielectric
constant of crown glass?
v
K
2
2
2.32
6. The dielectric constant of diamond is 6.00. What is the speed of light in dia-
mond?
v
1.22108m/s
3.00108m/s
6.00
c
K
3.00108m/s
1.97108m/s
c
v
c
K
(3.201019 C)(4.5103T)2(0.125 m)2
(2)(6.681026 kg)
qB2r2
2m
2V
B2r2
q
mcalcium
(1.671027 kg)(3.98104m/s)
(2.06102m)(1.601019 C)
mv2
r
666 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued
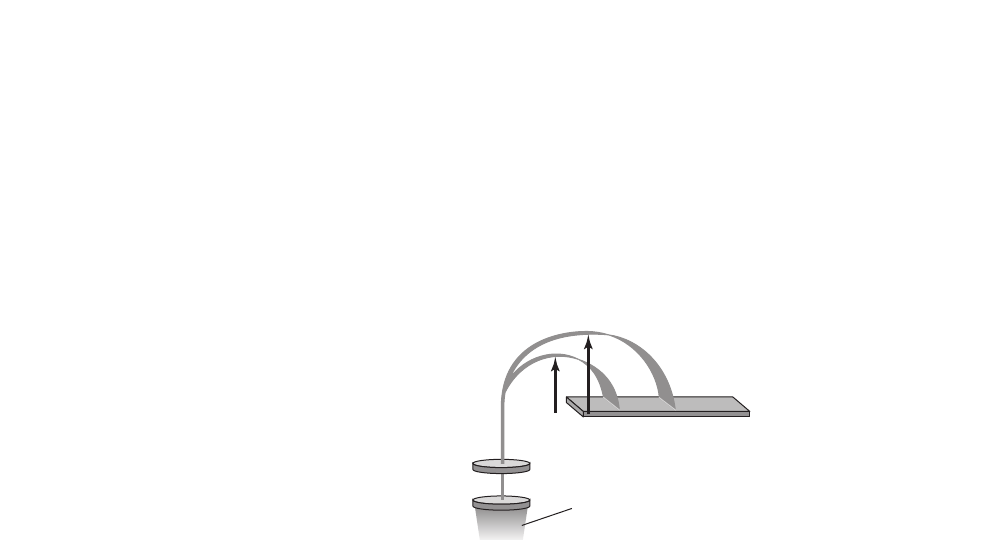
Physics: Principles and Problems Solutions Manual 667
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. By curving different isotopes through paths with different radii, a mass spectrom-
eter can be used to purify a sample of mixed uranium-235 and uranium-238 iso-
topes. Assume that B 5.00103T, V 55.0 V, and that each uranium isotope
has a 5ionization state. Uranium-235 has a mass that is 235 times that of a pro-
ton, while uranium-238 has a mass that is 238 times that of a proton. By what dis-
tance will the two isotopes be separated by the mass spectrometer?
m
q
rU-235
1.47 m
rU-238
1.48 m
Separation rU-238 rU-235
1.48 m 1.47 m
0.01 m
8. A mass spectrometer often is used in carbon dating to determine the ratio of C-14
isotopes to C-12 isotopes in a biological sample. This ratio then is used to estimate
how long ago the once-living organism died. Because a mass spectrometer is sensi-
tive to the charge-to-mass ratio, it is possible for a contaminant particle to alter the
value measured for the C-14/C-12 ratio, and thus, yield erroneous results. When ion-
ized, C-14 forms an ion with a 4 charge, and the mass of C-14 is 14 times that of a
proton. Consider a contaminant lithium particle. If the most common lithium iso-
tope has a mass that is seven times that of a proton, what must be the charge of the
lithium ion needed to contaminate a carbon-14 experiment?
m
qC
C
m
qL
L
i
i
qLi qC
m
m
L
C
i
2V
B2r2
(2)(55.0 V)(238)(1.671027 kg)
(5)(1.601019 kg)(5.00103T)2
2Vm
qB2
(2)(55.0 V)(235)(1.671027 kg)
(5)(1.601019 kg)(5.00103T)2
2Vm
qB2
2V
B2r2
Uranium ion beam
R2 Uranium-238
R1 Uranium-235
R2
R1
Chapter 26 continued

(4)
1
7
4
m
m
p
p
2
9. What is the wavelength of a radio wave with
a frequency of 90.7 MHz?
c
f
3.31m
10. What is the frequency of a microwave with
a wavelength of 3.27 mm?
c
f
f
c
9.171010 Hz
11. What is the frequency of an X ray with a
wavelength of 1.001010 m?
c
f
f
c
3.001018 Hz
12. In recent years, physicists have slowed the
speed of light passing through a material to
about 1.20 mm/s. What is the dielectric
constant of this material?
v
K
2
2
6.251022
3.00108m/s
1.20103m/s
c
v
c
K
3.00108m/s
1.001010 m
3.00108m/s
3.27103m
3.00108m/s
90.7106Hz
668 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 26 continued

Chapter 27
pages 886–887
1. If the maximum kinetic energy of emitted photoelectrons is 1.41018 J, what
is the stopping potential of a certain photocell?
KE qV0
V0
8.8 V
2. The stopping potential of a photocell is 2.3 V. What is the initial velocity of an
emitted photoelectron that is brought to a stop by the photocell?
KE qV0
1
2
mv2
v
9.0105m/s
3. If a photoelectron traveling at 8.7105m/s is stopped by a photocell, what is
the photocell’s stopping potential?
KE qV0
1
2
mv2
V0
2.2 V
4. Light with a frequency of 7.51014 Hz is able to eject electrons from the metal
surface of a photocell that has a threshold frequency of 5.21014 Hz. What
stopping potential is needed to stop the emitted photoelectrons?
KE hfhf0 h(ff0) and KE qV0
Thus,
V0
q
KE
0.95 V
(6.6261034 J/Hz)(7.51014 Hz 5.21014 Hz)
1.601019 C
h(ff0)
q
(9.111031 kg)(8.7105m/s)2
(2)(1.601019 C)
mv2
2q
(2)(1.601019 C)(2.3 V)
9.111031 kg
2qV0
m
1.41018 J
1.601019 C
KE
q
Physics: Principles and Problems Solutions Manual 669
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

5. A metal has a work function of 4.80 eV. Will ultraviolet radiation with a wave-
length of 385 nm be able to eject a photoelectron from the metal?
First calculate the energy of the photon.
E
3.22 eV
To eject a photoelectron from the metal, the energy of the incident radiation
must be greater than the work function of the metal. Because the energy of
the incident radiation, 3.22 eV, is less than the work function, 4.80 eV, a
photoelectron will not be ejected.
6. When a metal is illuminated with radiation
with a wavelength of 152 nm, photoelectrons
are ejected with a velocity of 7.9105m/s.
What is the work function, in eV, of the metal?
First calculate the energy of the photon
in joules.
E
h
c
1.311018 J
Next, calculate the kinetic energy.
KE
1
2
mv2
1
2
(9.111031 kg)(7.9105m/s)2
2.81019 J
KE EW
W EKE
1.311018 J 2.81019 J
1.01018 J
(1.01018 J)
6.2 eV
1 eV
1.601019 J
(6.6261034 J/Hz)(2.998108m/s)
1.52107m
Cathode
Incident
radiation
v 7.9105 m/s
152 nm
Anode
1240 eVnm
385 nm
1240 eVnm
Chapter 27 continued
670 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 671
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
7. The de Broglie wavelength for an electron traveling at 9.6105m/s is 7.61010 m.
What is the mass of the electron?
m
hv
m
h
v
9.11031 kg
8. What is the de Broglie wavelength of a 68-kg man moving with a kinetic energy
of 8.5 J?
KE
1
2
mv2
v
The de Broglie wavelength is then,
m
hv
h(2mKE)
(6.6261034 J/Hz)((2)(68 kg)(8.5 J))
1.91035 m
9. An electron has a de Broglie wavelength of 5.21010 m. What potential
difference is responsible for this wavelength?
m
hv
v
h
m
and
KE –qV0
1
2
mv2
V0
2
m
q
v2
5.6 V
(6.6261034 J/Hz)2
(2)(1.601019 C)(5.21010 m)2(9.111031 kg)
h2
2q2m
mh2
2q2m2
1
2
1
2
m
2KE
h
m
2KE
m
6.6261034 J/Hz
(7.61010 m)(9.6105m/s)
Chapter 27 continued

Chapter 28
page 887
1. An electron in a hydrogen atom makes a transition from E3to E1. How much
energy does the atom lose?
En 13.6 eV
E E1E3
12.1 eV
2. An electron in the hydrogen atom loses 3.02 eV as it falls to energy level E2.
From which energy level did the atom fall?
E EfEi
3.02 eV 13.6
3.02 eV 3.40 eV
nx 6
3. Which energy level in a hydrogen atom has a radius of 7.63109m?
r
n
12
Alternatively, r r0m2where r0is the Bohr radius in hydrogen, 530 mm.
Thus, m
144
12
4. When an electron falls from E4to E1, what is the frequency of the emitted photon?
E E1E4
(2.171018 J)
(2.171018 J)
2.041018J
E hf
f
E
h
3.081015 Hz
2.041018 J
6.6261034 Js
1
42
1
12
7.63109m
5.301011 m
r
r0
42(9.0109Nm2/C2)(9.111031 kg)(1.601019 C)2(7.63109m)
(6.6261034 Js)2
42Kmq2r
h2
h2n2
42Kmq2
13.6 eV
nx2
1
nx2
1
ny2
13.6
32
13.6
12
1
n2
672 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 673
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
5. If an electron moves from E3to E5, what is the wavelength of the photon
absorbed by the atom?
E E5E3
(2.171018 J)
(2.171018 J)
1.541019 J
E hf
h
d
c
d
hc
E
1.29106m
6. If a hydrogen atom in its ground state absorbs a photon with a wavelength of
93 nm, it jumps to an excited state. What is the value of the energy in that
excited state?
E hf
h
c
2.141018 J
(2.141018 J)
13.3 eV absorbed
Ef Ei E
13.6 eV 13.3 eV
0.27 eV
1 eV
1.601019 J
(6.6261034 Js)(3.00108m/s)
9.3108m
(6.6261034 Js)(3.00108m/s)
1.541019 J
1
32
1
52
Chapter 28 continued

Chapter 29
pages 887–888
1. Indium has 3 free electrons per atom. Use Appendix D and determine the num-
ber of free electrons in 1.0 kg of indium.
(free e/atom)(NA)
M
1
Substitute: free e/atom 3 free e/1 atom,
NA 6.021023 atoms/mol, M 114.82 g/mol
1.571025 free e/kg for indium
2. Cadmium has 2 free electrons per atom. Use Appendix D and determine the
number of free electrons in 1.0 dm3of Cd.
(free e/atom)(NA)
M
1
()
Substitute: free e/atom 2 free e/1 atom,
NA 6.021023 atoms/mol, M 112.41 g/mol,
8.65 g/cm3
9.261025 free e/dm3in cadmium
3. Copper has 1 free electron per atom. What length of 1.00-mm diameter copper
wire contains 7.811024 free electrons? Use Appendix D for physical constants.
Lwire
(number of free e)
(M)
Substitute: NA 6.021023 atoms/mol,
M 63.546 g/mol, 8.92 g/cm3,
number of free e 7.811024 free e,
rwire 1.00 mm/2 0.50 mm 0.050 cm
Lwire
(7.811024 free e)
1.18104cm 118 m
1 cm3
8.92 g
63.546 g
1 mol
1 mol
6.0221023 atoms
1 atom
1 free e
1
0.102
0cm
2
1
1
NA
atoms
free e
1
r2
1000 cm3
1 dm3
8.65 g
1 cm3
1 mol
112.41 g
6.021023 atoms
1 mol
2 free e
1 atom
free e
dm3
1000 cm3
1 dm3
free e
dm3
1000 g
1 kg
1 mol
114.82 g
6.021023 atoms
1 mol
3 free e
1 atom
free e
kg
1000 g
1 kg
free e
kg
674 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.

Physics: Principles and Problems Solutions Manual 675
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
4. At 400.0 K, germanium has 1.131015 free electrons/cm3. How many free
electrons per Ge atom are there at this temperature?
N
1
A
(M)
1
(free ecm3for Ge)
Substitute: NA 6.021023 atoms/mol,
M 72.63 g/mol, 5.23 g/cm3,
free e/cm3for Ge 1.131015 free e/cm3
free e/atom of Ge at 400.0 K 2.61108
5. At 400.0 K, silicon has 4.541012 free electrons/cm3. How many free electrons
per Si atom are there at this temperature?
N
1
A
(M)
1
(4.541012 free e/cm3for Si)
Substitute: NA 6.021023 atoms/mol, M 28.09 g/mol, 2.33 g/cm3,
free e/cm3for Si 4.541012 free e/cm3at 400.0 K
free e/atom of Si at 400.0 K 9.091011
6. At 200.0 K, silicon has 3.791018 free electrons per atom. How many free
electrons/cm3are there in silicon at this temperature?
(NA)
M
1
()
Substitute: free e/atom 3.791018 free e/1 atom,
NA 6.021023 atoms/mol, M 28.09 g/mol, 2.33 g/cm3
1.89105free e/cm3in silicon at 200 K
7. Silicon has 1.451010 free electrons/cm3at room temperature. If you wanted to
have 3106as many electrons from arsenic doping as thermal free electrons
from silicon at room temperature, how many arsenic atoms should there be for
each silicon atom? Each arsenic atom provides 1 free electron. Use Appendix D
for physical constants.
(M)
Substitute: M 28.09 g/mol, NA 6.021023 atoms/mol, 2.33 g/cm3,
1 As atom 1 As e,3106As e/thermal e,
number of thermal e/cm3 1.451010 e/cm3
1
1
NA
number of thermal e
cm3
number of As e
thermal e
number As atoms
As e
As atoms
Si atoms
2.33 g
1 cm3
1 mol
28.09 g
6.021023 atoms
1 mol
3.791018 e
1 atom
free e
cm3
free e
atom
free e
cm3
4.541012 free e
cm3
1 cm3
2.33 g
28.09 g
1mol
1 mol
6.021023 atoms
free e
atom
free e
atom
1.131015 free e
cm3
1 cm3
5.23 g
72.63 g
1 mol
1 mol
6.021023 atoms
free e
atom
free e
atom
Chapter 29 continued

28
m
.0
o
9
l
g
8.71107
8. At 200.0 K, germanium has 1.161010 thermally liberated charge carriers/cm3. If it
is doped with 1 As atom to 525,000 Ge atoms, what is the ratio of doped carriers
to thermal carriers at this temperature? See Appendix D for physical constants.
(NA)
()
Substitute: M 72.6 g/mol,
NA 6.021023 atoms/mol, 5.23 g/cm3
thermal carriers 1.161010 thermal carriers/cm3
7.12106
9. At 200.0 K, silicon has 1.89105thermally liberated charge carriers/cm3. If it is
doped with 1 As atom to 3.75 million Si atoms, what is the ratio of doped carri-
ers to thermal carriers at this temperature? See Appendix D for physical constants.
(NA)
()
Substitute: M 28.09 g/mol,
NA 6.021023 atoms/mol, 2.33 g/cm3
thermal carriers 1.89105thermal carriers/cm3
7.051010
10. The diode shown below has a voltage drop, Vd,
of 0.45 V when I11 mA. If a 680-resistor, R,
is connected in series, what power supply voltage,
Vbis needed?
Vb IR Vd (0.011 A)(680 ) 0.45 V
7.9 V
I
R
Diode
Vd
Vb
cm3
1.89105thermal carriers
2.33 g
cm3
mol
28.09 g
6.021023 atoms
mol
1 doped carrier
3.75106atoms
doped carriers
thermal carriers
1
thermal carriers
1
M
doped carriers
3.75106atoms
doped carriers
thermal carriers
cm3
1.161010 thermal carriers
5.23 g
cm3
mol
72.6 g
6.021023 atoms
mol
1 doped carrier
5.25105atoms
doped carriers
thermal carriers
1
thermal carriers
1
M
doped carriers
5.25105atoms
doped carriers
thermal carriers
cm3
2.33 g
mol
6.021023 Si atoms
1.451010 thermal e
cm3
3106As e
thermal e
1 As atoms
1 As e
As atoms
Si atoms
676 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 29 continued

Physics: Principles and Problems Solutions Manual 677
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
11. A diode in a circuit similar to the one in
Figure 29-26 has a voltage drop, Vd, of
0.95 V when I18 mA. If a 390-resistor,
R, is connected in series, what power supply
voltage, Vbis needed?
Vb IR Vd
(0.018 A)(390 ) 0.95 V
8.0 V
12. What power supply voltage would be needed
to produce a current of 27 mA in the circuit
in problem 10? Assume the diode voltage is
uncharged.
Vb IR Vd
(0.027 A)(680 ) 0.45 V
19 V
Chapter 30
pages 888–889
1. Carbon-14, or 14C, is an isotope of the
common 12
6C, and is used in dating ancient
artifacts. What is the composition of its
nucleus?
six protons (equal to Z) and eight
neutrons (equal to AZ)
2. An isotope of iodine (Z53) is used to
treat thyroid conditions. Its mass number is
131. How many neutrons are in its nucleus?
131 53 78 neutrons
3. The only nonradioactive isotope of fluorine
has nine protons and ten neutrons.
a. What is its mass number?
mass number (A) 19
b. The atomic mass unit, u, is equal to
1.661027 kg. What is fluorine-19’s
approximate mass in kilograms?
(19 nucleons)(1.661027 kg/nucleon)
3.1510–26 kg
c. Write the full symbol of this atom.
19
9F
4. The magnesium isotope 25
12Mg has a mass of
24.985840 u.
a. Calculate its mass defect.
mass defect (isotope mass)
(mass of protons and electrons)
(mass of neutrons)
24.985840 u (12)(1.007825 u)
(13)(1.008665 u)
0.220705 u
b. Calculate its binding energy in MeV.
binding energy (mass defect)
(binding energy of 1 u)
(0.220705 u)(931.49 MeV/u)
205.58 MeV
Chapter 29 continued
5. The isotope 10
5B has a mass of 10.012939 u.
a. Calculate the mass defect.
mass defect (isotope mass)
(mass of protons and electrons)
(mass of neutrons)
10.012939 u (5)(1.007825 u)
(5)(1.008665 u)
0.069511 u
b. Calculate its binding energy in MeV.
binding energy (mass defect)
(binding energy of 1 u)
(0.069511 u)(931.49 MeV/u)
64.749 MeV
c. Calculate its binding energy per nucleon.
binding energy per nucleon is
6.4749 MeV/nucleon
6. The most stable isotope of all is 56
26Fe.
Its binding energy per nucleon is
8.75 MeV/nucleon.
a. What is the binding energy of this
isotope?
(56 nucleons)(–8.75 MeV/nucleon)
–4.90102MeV
b. What is the mass defect of this isotope?
mass defect
0.526 u
7. The isotope 239
94Pu can be transmuted to an
isotope of uranium, 235
92U.
a. Write the nuclear equation for this
transmutation.
94
239Pu →235
92UA
ZX
where Z 94 92 2
A 239 235 4
For Z 2, the element must be
helium. Thus the equation is
239
94Pu →235
92U 4
2He
b. Identify the particle that is ejected.
an particle
8. The radioisotope 222
84Po undergoes alpha
decay to form an isotope of lead (lead has
atomic number 82). Determine what the
mass number of that isotope must be by
writing a nuclear equation.
222
84Po →A
ZPb 4
2He
where Z 84 2 82
A 222 4 218
Thus the equation is 222
84Po →218
82Pb 4
2He
The mass number is 218.
9. The graph below shows a sequence of alpha
and beta decays, labeled 1, 2, 3, and 4.
Consult Table 30-1 as needed.
a. Which represent alpha decays, and
which represent beta decays?
alpha decays: 1 and 4, in which
mass number decreases by 4 and
atomic number by 2; beta decays: 2
and 3, in which atomic number
increases by 1 and mass number
stays the same
b. What is the overall change in mass in the
sequence? In the number of neutrons?
Overall change in mass is 218 u
210 u 8 u lower. Overall change in
Zis 84 – 82 2 lower. Thus, overall
change in the number of neutrons is
6 lower (8 nucleons less, 2 protons
less, so 6 neutrons less).
80 82
Atomic number
84 Z
210
212
214
216
218
1
2
3
4
A
Mass number
4.90102MeV
931.49 MeV/u
binding energy
binding energy of 1 u
64.744 MeV
10 nucleons
678 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued

Physics: Principles and Problems Solutions Manual 679
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
10. Use Appendix D to complete the two
nuclear equations. Include correct
subscripts and superscripts for each
of the particles.
a. 32
15P→?antineutrino
32
15P →A
ZX 1
0e 0
0
where Z 15 (1) 0 16
A 32 0 0 32
For Z 16, the element must be
sulfur. Thus, the equation is
32
15P →32
16S 1
0e 0
0
b. 235
92U→?
235
92U →A
ZX 4
2He
where Z 92 2 90
A 235 4 231
For Z 90, the element must be
thorium. Thus, the equation is
235
92U → 231
90Th 4
2He
11. Write the complete nuclear equation for the
beta decay of 34
16S.
34
16S → A
ZX 1
0e 0
0
where Z 16 (1) 0 17
A 34 0 0 34
For Z 17, the element must be
chlorine. Thus, the equation is
34
16S → 34
17Cl 1
0e 0
0
12. A positron is identical to a beta particle,
except that its charge is 1 instead of 1.
37
19K undergoes spontaneous positron
decay to form an isotope of argon. Identify
the isotope of argon by writing a nuclear
equation.
37
19K → A
ZAr 1
0e 0
0
where Z 19 1 0 18
A 37 0 0 37
Thus the equation is
37
19K → 37
18Ar 1
0e 0
0
The isotope is argon 37.
13. Iodine-131 has a half-life of 8.0 days. If
there are 60.0 mg of this isotope at time
zero, how much remains 24 days later?
3.0 half-lives
remaining original
t
(60.0 mg)
3.0
7.5 mg
14. Refer to Table 30-2. Given a sample of
cobalt-60,
a. how long a time is needed for it to go
through four half-lives?
(4)(30 years) 120 years
b. what fraction remains at the end of that
time?
remaining original
t
original
4
original
15. The graph shows the activity of a certain
radioisotope over time. Deduce its half-life
from this data.
Every 3.0 h the activity is half of the pre-
vious activity, so the half-life is 3.0 h.
3
069
Time (h)
Activity105 (Bq)
12
12
24
36
48
1
16
1
2
1
2
1
2
1
2
24 days
8.0 days/half-life
Chapter 30 continued
16. The mass of a proton and of an antiproton
is 1.00728 u. Recall that the conversion of
exactly 1 u into energy yields 931.5 MeV.
a. Calculate the mass used up when a
proton and an antiproton annihilate
one another.
(2)(1.00728 u) 2.01456 u
b. Calculate the energy released here.
(2.01456 u)(931.5 MeV/u) 1876.5 MeV
17. One source of a star’s energy is the fusion of
two deuterons to form an alpha particle
plus a gamma ray.
a. Write the nuclear equation for this
fusion.
2
1H 2
1H →4
2He 0
0
b. Calculate the mass “lost” in this process.
mass before mass after
2(2.0136 u) 4.0026 u
0.0246 u
c. Calculate the energy released in MeV.
(0.0246 u)(931.49 MeV/u) 22.9 MeV
18. When 1 mol (235 g) of uranium-235
undergoes fission, about 2.01010 kJ of
energy are released. When 4.0 g of hydro-
gen undergoes fusion, about 2.0109kJ are
released.
a. For each, calculate the energy yield per
gram of fuel.
5.0108
kJ/g for fusion of hydrogen;
8.5107
kJ/g for fission of uranium
b. Which process produces more energy
per gram of fuel?
Fusion releases about six times as
much energy per gram of fuel as
fission.
2.01010 kJ
235 g
2.0109kJ
4.0 g
Particle Mass in u
2
1H2.0136
4
2He 4.0026
0
00.0000
680 Solutions Manual Physics: Principles and Problems
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
Chapter 30 continued