Solutions Manual

User Manual: Pdf

Open the PDF directly: View PDF .
Page Count: 223 [warning: Documents this large are best viewed by clicking the View PDF Link!]

An Introduction to Mathematical

Cryptography

Solution Manual

Jeﬀrey Hoﬀstein, Jill Pipher, Joseph H. Silverman

°2008 by J. Hoﬀstein, J. Pipher, J.H. Silverman

July 31, 2008

Chapter 1

An Introduction to

Cryptography

Exercises for Chapter 1

Section. Simple substitution ciphers

1.1. Build a cipher wheel as illustrated in Figure 1.1, but with an inner wheel

that rotates, and use it to complete the following tasks. (For your convenience,

there is a cipher wheel that you can print and cut out at www.math.brown.

edu/~jhs/MathCrypto/CipherWheel.pdf.)

(a) Encrypt the following plaintext using a rotation of 11 clockwise.

“A page of history is worth a volume of logic.”

(b) Decrypt the following message, which was encrypted with a rotation of 7

clockwise.

AOLYLHYLUVZLJYLAZILAALYAOHUAOLZLJYLALZAOHALCLYFIVKFNBLZZLZ

wise for the ﬁrst letter, then 2 clockwise for the second letter, etc.

XJHRFTNZHMZGAHIUETXZJNBWNUTRHEPOMDNBJMAUGORFAOIZOCC

Solution to Exercise 1.1.

(a) apageofhistoryisworthavolumeoflogic

LALRPZQSTDEZCJTDHZCESLGZWFXPZQWZRTN

This quote is in a court decision of Oliver Wendell Holmes, Jr. (1921).

(b) therearenosecretsbetterthanthesecretsthateverybodyguesses

AOLYLHYLUVZLJYLAZILAALYAOHUAOLZLJYLAZAOHALCLYFIVKFNBLZZLZ

There are no secrets better than the secrets that everybody

guesses.

This quote is due to George Bernard Shaw, Mrs. Warren’s Profession (1893)

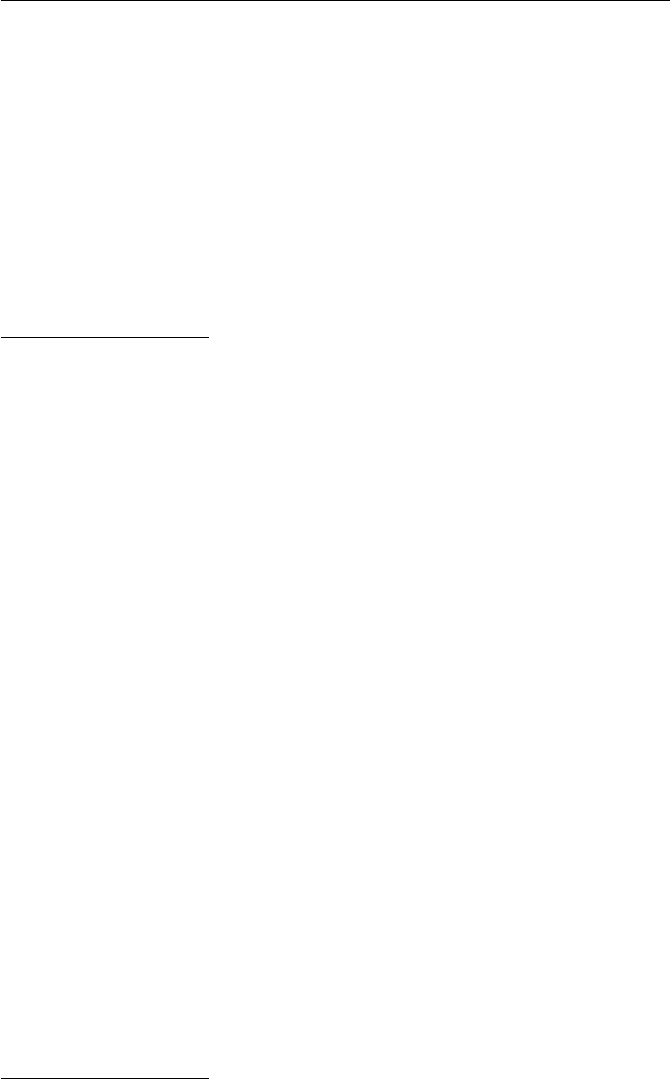
2 Exercises for Chapter 1

XJHRFTNZHMZGAHIUETXZJNBWNUTRHEPOMDNBJMAUGORFAOIZOCC

When angry, count ten before you speak; if very angry, an hundred.

This quote is due to Thomas Jeﬀerson, A Decalogue of Canons. . . (1825).

1.2. Decrypt each of the following Caesar encryptions by trying the various

possible shifts until you obtain readable text.

(a) LWKLQNWKDWLVKDOOQHYHUVHHDELOOERDUGORYHOBDVDWUHH

(b) UXENRBWXCUXENFQRLQJUCNABFQNWRCJUCNAJCRXWORWMB

Solution to Exercise 1.2.

(a) ithinkthatishallneverseeabillboardlovelyasatree

LWKLQNWKDWLVKDOOQHYHUVHHDELOOERDUGORYHOBDVDWUHH

I think that I shall never see, a billboard lovely as a tree.

This quote is due to Ogden Nash, Many Long Years Ago (1945), Song of the

Open Road.

(b) loveisnotlovewhichalterswhenitalterationfinds

UXENRBWXCUXENFQRLQJUCNABFQNWRCJUCNAJCRXWORWMB

Love is not love which alters when it alteration ﬁnds.

This quote is due to William Shakespeare, Sonnet 116.

BGUTBMBGZTFHNLXMKTIPBMAVAXXLXTEPTRLEXTOXKHHFYHKMAXFHNLX

In baiting a mousetrap with cheese, always leave room for the

mouse.

This quote is due to H.H. Munro (Saki), The Square Egg (1924).

1.3. For this exercise, use the simple substitution table given in Table 1.11.

(a) Encrypt the plaintext message

The gold is hidden in the garden.

(b) Make a decryption table, that is, make a table in which the ciphertext

alphabet is in order from Ato Zand the plaintext alphabet is mixed up.

IBXLX JVXIZ SLLDE VAQLL DEVAU QLB

Solution to Exercise 1.3.

(a)

Exercises for Chapter 1 3

abcdefghijklmnopqrstuvwxyz

SCJAXUFBQKTPRWEZHVLIGYDNMO

Table 1.1: Simple substitution encryption table for exercise 1.3

thegoldishiddeninthegarden

IBXFEPAQLBQAAXWQWIBXFSVAXW

Breaking it into ﬁve letter blocks gives the ciphertext

IBXFE PAQLB QAAXW QWIBX FSVAX W

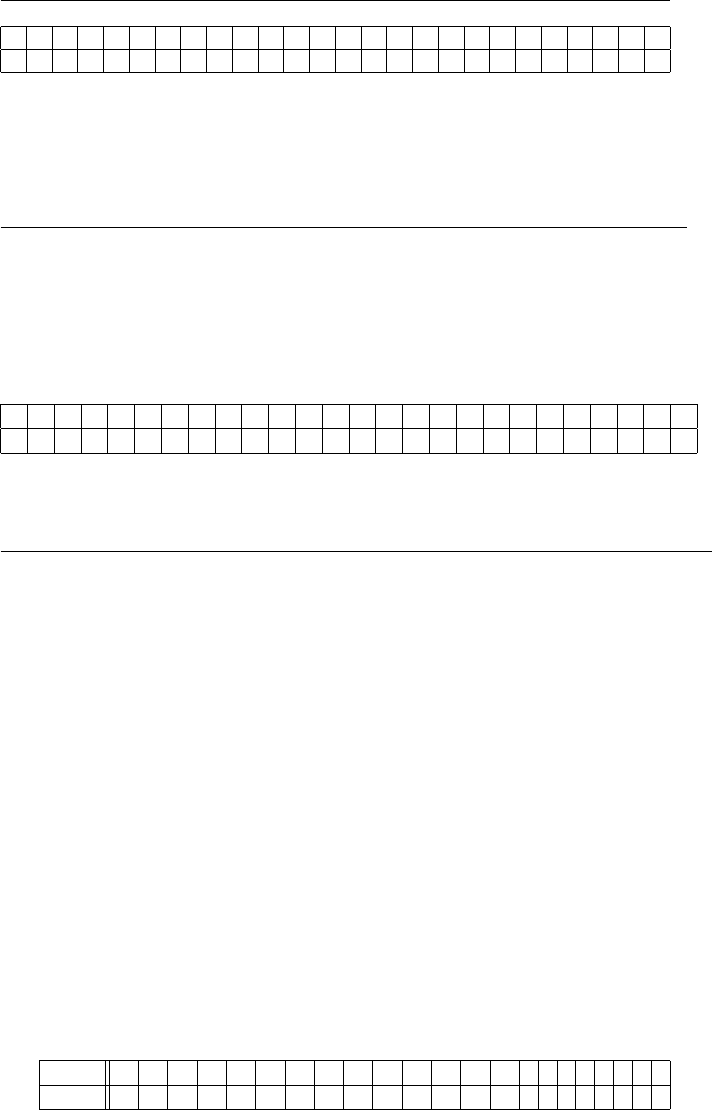
(b)

dhbwoguqtcjsyxzlimakfrnevp

ABCDEFGHIJKLMNOPQRSTUVWXYZ

(c)

thesecretpasswordisswordfish

IBXLXJVXIZSLLDEVAQLLDEVAUQLB

Putting in word breaks gives the plaintext

The secret password is swordfish.

1.4. Each of the following messages has been encrypted using a simple sub-

stitution cipher. Decrypt them. For your convenience, we have given you a

frequency table and a list of the most common bigrams that appear in the

ciphertext. (If you do not want to recopy the ciphertexts by hand, they can

be downloaded or printed from the web site listed in the preface.)

(a) “A Piratical Treasure”

JNRZR BNIGI BJRGZ IZLQR OTDNJ GRIHT USDKR ZZWLG OIBTM NRGJN

IJTZJ LZISJ NRSBL QVRSI ORIQT QDEKJ JNRQW GLOFN IJTZX QLFQL

WBIMJ ITQXT HHTBL KUHQL JZKMM LZRNT OBIMI EURLW BLQZJ GKBJT

QDIQS LWJNR OLGRI EZJGK ZRBGS MJLDG IMNZT OIHRK MOSOT QHIJL

QBRJN IJJNT ZFIZL WIZTO MURZM RBTRZ ZKBNN LFRVR GIZFL KUHIM

MRIGJ LJNRB GKHRT QJRUU RBJLW JNRZI TULGI EZLUK JRUST QZLUK

EURFT JNLKJ JNRXR S

The ciphertext contains 316 letters. Here is a frequency table:

R J I L Z T N Q B G K U M O S H W F E D X V

Freq 33 30 27 25 24 20 19 16 15 15 13 12 12 10 9 8 7 6 5 5 3 2

4 Exercises for Chapter 1

The most frequent bigrams are: JN (11 times), NR (8 times), TQ (6 times),

and LW,RB,RZ, and JL (5 times each).

(b) “A Botanical Code”

KZRNK GJKIP ZBOOB XLCRG BXFAU GJBNG RIXRU XAFGJ BXRME MNKNG

BURIX KJRXR SBUER ISATB UIBNN RTBUM NBIGK EBIGR OCUBR GLUBN

JBGRL SJGLN GJBOR ISLRS BAFFO AZBUN RFAUS AGGBI NGLXM IAZRX

RMNVL GEANG CJRUE KISRM BOOAZ GLOKW FAUKI NGRIC BEBRI NJAWB

OBNNO ATBZJ KOBRC JKIRR NGBUE BRINK XKBAF QBROA LNMRG MALUF

BBG

The ciphertext contains 253 letters. Here is a frequency table:

B R G N A I U K O J L X M F S E Z C T W P V Q

Freq 32 28 22 20 16 16 14 13 12 11 10 10 8 8 7 7 6 5 3 2 1 1 1

The most frequent bigrams are: NG and RI (7 times each), BU (6 times),

and BR (5 times).

occurrences of the word “the” from the plaintext.

“A Brilliant Detective”

GSZES GNUBE SZGUG SNKGX CSUUE QNZOQ EOVJN VXKNG XGAHS AWSZZ

BOVUE SIXCQ NQESX NGEUG AHZQA QHNSP CIPQA OIDLV JXGAK CGJCG

SASUB FVQAV CIAWN VWOVP SNSXV JGPCV NODIX GJQAE VOOXC SXXCG

OGOVA XGNVU BAVKX QZVQD LVJXQ EXCQO VKCQG AMVAX VWXCG OOBOX

VZCSO SPPSN VAXUB DVVAX QJQAJ VSUXC SXXCV OVJCS NSJXV NOJQA

MVBSZ VOOSH VSAWX QHGMV GWVSX CSXXC VBSNV ZVNVN SAWQZ ORVXJ

CVOQE JCGUW NVA

The ciphertext contains 313 letters. Here is a frequency table:

V S X G A O Q C N J U Z E W B P I H K D M L R F

Freq 39 29 29 22 21 21 20 20 19 13 11 11 10 8 8 6 5 5 5 4 3 2 1 1

The most frequent bigrams are: XC (10 times), NV (7 times), and CS,OV,

QA, and SX (6 times each).

Solution to Exercise 1.4.

(a) The message was encrypted using the table:

abcdefghijklmnopqrstuvwxyz

IEBHRWDNTPXUOQLMAGZJKVFCSY

The plaintext reads:

“These characters, as one might readily guess, form a cipher—that is to

say, they convey a meaning; but then, from what is known of Captain Kidd,

I could not suppose him capable of constructing any of the more abstruse

cryptographs. I made up my mind, at once, that this was of a simple species—

such, however, as would appear, to the crude intellect of the sailor, absolutely

insoluble without the key.” (The Gold-Bug, 1843, Edgar Allan Poe)

(b) The message was encrypted using the table:

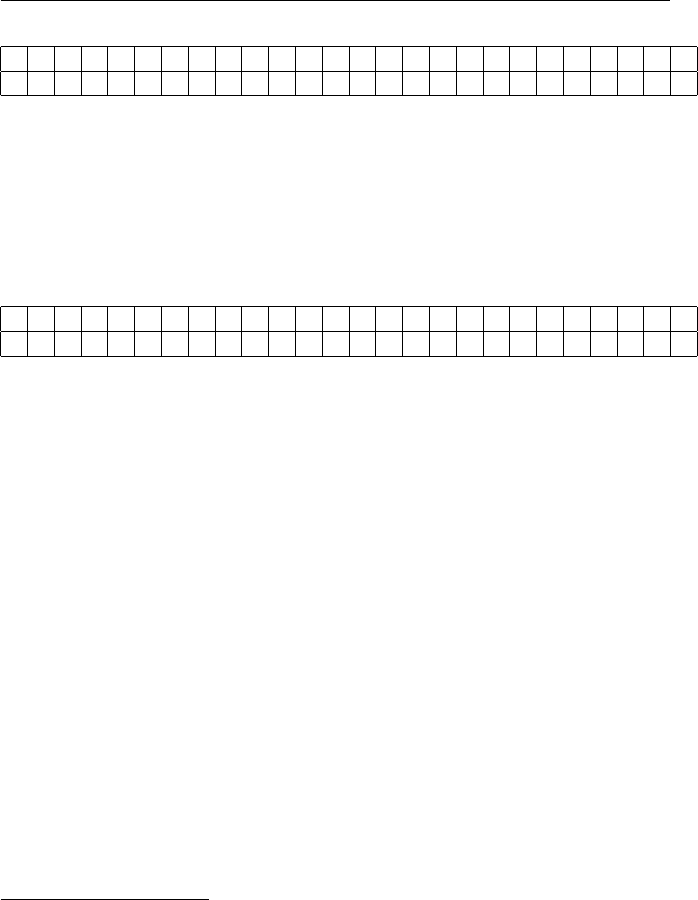
Exercises for Chapter 1 5

abcdefghijklmnopqrstuvwxyz

RVCXBFSJKQPOEIAWDUNGLTZYMH

The plaintext reads:

“I was, I think, well educated for the standard of the day. My sister and

I had a German governess. A very sentimental creature. She taught us the

language of ﬂowers—a forgotten study nowadays, but most charming. A yellow

tulip, for instance, means Hopeless Love, while a China Aster means I die of

Jealousy at your feet.” (The Four Suspects, 1933, Agatha Christie)

abcdefghijklmnopqrstuvwxyz

SDJWVEHCGLRUZAQPTNOXIMKYBF

The plaintext reads (all occurrences of the word “the” were omitted from the

text before encryption):

I am fairly familiar with all forms of secret writing, and am myself (the)

author of a triﬂing monograph upon (the) subject, in which I analyze one

hundred separate ciphers, but I confess that this is entirely new to me. (The)

object of those who invented this system has apparently been to conceal that

these characters convey a message, and to give (the) idea that they are (the)

mere random sketches of children. (The Adventure of the Dancing Men, 1903,

Sir Arthur Conan Doyle)

1.5. Suppose that you have an alphabet of 26 letters.

(a) How many possible simple substitution ciphers are there?

(b) A letter in the alphabet is said to be ﬁxed if the encryption of the letter

is the letter itself. How many simple substitution ciphers are there that

leave:

(i) no letters ﬁxed?

(ii) at least one letter ﬁxed?

(iii) exactly one letter ﬁxed?

(iv) at least two letters ﬁxed?

(Part (b) is quite challenging! You might try doing the problem ﬁrst with an

alphabet of four or ﬁve letters to get an idea of what is going on.)

Solution to Exercise 1.5.

(a) We can assign Ato any of 26 letters, then Bto any of the remaining 25

letters, etc. So there are 26! = 403291461126605635584000000 diﬀerent simple

substitution ciphers.

(b) Let S(n, k) denote the number of permutations of nelements that ﬁx at

least kelements. You might guess that since there are ¡n

k¢ways to choose k

elements to ﬁx and (n−k)! permutations of the remaining n−kelements,

S(n, k) = µn

k¶(n−k)! ←− Incorrect Formula.(1.1)

6 Exercises for Chapter 1

But this overcounts because any permutation ﬁxing more than n−kele-

ments will be counted multiple times. We can, however, get a useful formula

out of this mistake by modifying it somewhat. If we let R(n, k) denote the

number of permutations of nelements that ﬁx exactly kelements, and !(n−k)

(the subfactorial of (n−k)) denote the number of permutations of n−kele-

ments that ﬁx no elements (such permutations are called derangements), then

the following equation holds:

R(n, k) = µn

k¶!(n−k).(1.2)

How can we compute !n? One way would be to consider cycle decompo-

sitions of permutations of n elements, since any derangement of nelements

decomposes into a disjoint union of cycles, with the size of the cycles summing

to n. This, however, is only feasible for relatively small n. It would also be

possible to formulate a recurrence relation, but a method following that tack

would take several steps. We’ll instead use the following fact:

!n=n!−#{permutations that ﬁx at least 1 element}.(1.3)

Now if we notice that

#{permutations that ﬁx at least 1 element}=

#{permutations that ﬁx element 1}

∪{permutations that ﬁx element 2}

∪··· ∪ {permutations that ﬁx element n}(1.4)

and use an analogue of the following formula in probability (often called the

inclusion–exclusion principle):

P(E1∪E2∪ ··· ∪ En) =

i=1

P(Ei) + X

i1<i2

P(Ei1∩Ei2) + . . .

+(−1)r+1 X

i1<i2<···<ir

P(Ei1∩Ei2∩Eir) + . . .

+(−1)n+1P(E1∩E2∩ ··· ∩ En) (1.5)

we see that

!n=

i=1

#{permutations that ﬁx element i}

−

i1<i2

#{permutations that ﬁx elements i1and i2}+. . .

+(−1)r+1 X

i1<i2<···<ir

#{permutations that ﬁx elements i1,i2, . . . ir}+. . .

+(−1)n+1#{permutations that ﬁx everything}.(1.6)

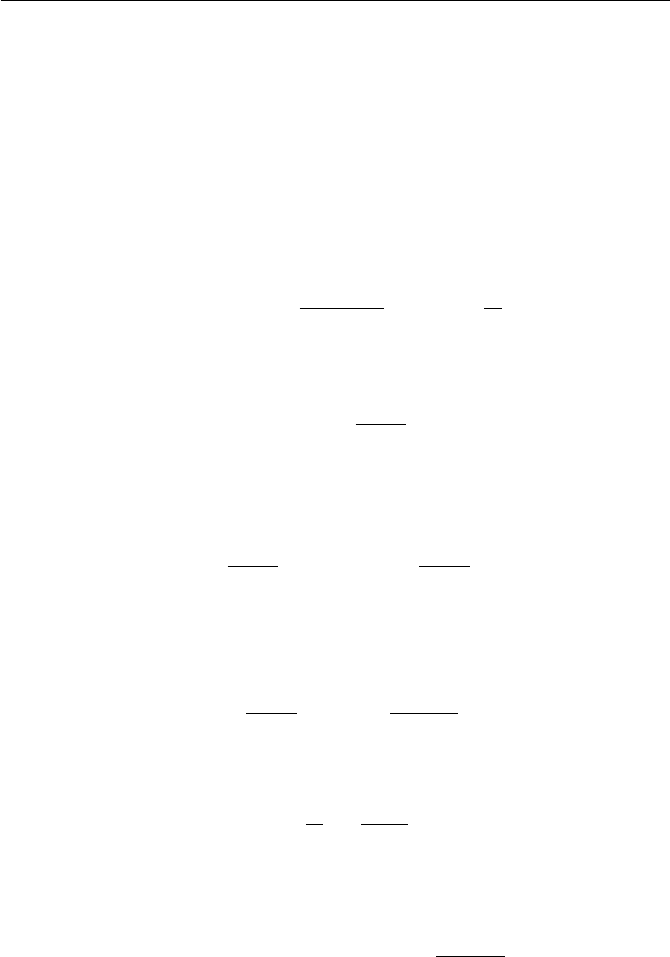
Exercises for Chapter 1 7

Given kelements, the number of permutations ﬁxing them is (n−k)!

regardless of which kelements you ﬁx, and there are ¡n

k¢ways to choose k

elements to ﬁx. So the above equation becomes

!n=µn

1¶(n−1)! −µn

2¶(n−2)! + . . .

+(−1)k+1µn

k¶(n−k)! + ··· + (−1)n+1(n−n)!.(1.7)

Now noticing that

µn

k¶(n−k)! = n!

(n−k)!k!(n−k)! = n!

k!,(1.8)

the formula (??) becomes

!n=n!

k=0

(−1)k

k!.(1.9)

This sum is somewhat cumbersome to compute when nis large, but notice

that it resembles the series for e−1. Thus

k=0

(−1)k

k!=e−1−∞

k=n+1

(−1)k

k!.

Since the series is alternating and the terms are decreasing in magnitude, each

term is larger than the sum of the remaining terms (alternating series test).

¯¯¯

k=0

(−1)k

k!−e−1¯¯¯<1

(n+ 1)!.

Multiplying by n! and using (??) yields

¯¯¯!n−n!

e¯¯¯<1

n+ 1.

Hence !nis the closest integer to n!/e.

Now that we’re able to compute !n, we can compute

R(n, k) = µn

k¶!(n−k) = µn

k¶¹(n−k)!

e¼,

and then we can compute S(n, k) using

S(n, k) =

j=k

R(n, j) = n!−

k−1

j=0

R(n, j).(1.10)

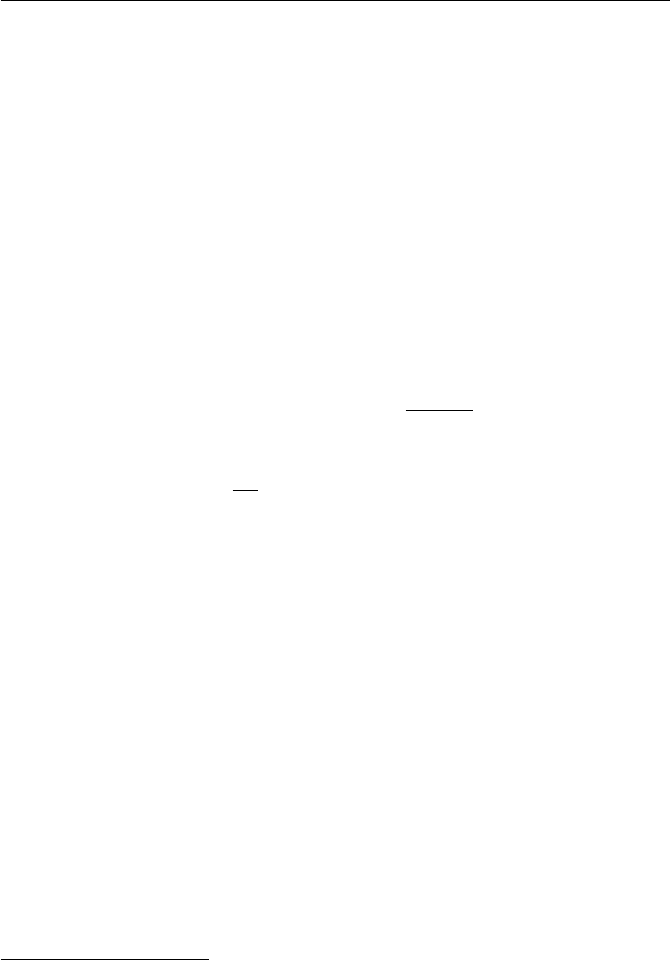
8 Exercises for Chapter 1

(b-i) No letters ﬁxed is R(n, 0) =!nis the nth derangement number. For n=

26 we get

R(26,0) =!26 = b26!/ee=b148362637348470135821287824.964e

= 148362637348470135821287825.

(b-ii) At least one letter ﬁxed is n! minus no letters ﬁxed, so

S(n, 1) = n!−R(n, 0) = n!−!n=n!− bn!/ee.

Hence

S(26,1) = 26! − b26!/ee= 254928823778135499762712175.

(b-iii) Exactly 1 letter ﬁxed is

R(n, 1) = n·!(n−1) = n¹(n−1)!

e¼,

R(26,1) = 26 ¹25!

e¼= 148362637348470135821287824.

(b-iv) At least two letters ﬁxed is n! minus zero or one letters ﬁxed, so

S(n, 1) = n!−R(n, 0) −R(1,0) = n!−!n−n·!(n−1)

=n!− bn!/ee − nb(n−1)!/ee.

Hence

S(26,1) = 26! − b26!/ee − 26 · b25!/ee= 106566186429665363941424351.

Section. Divisibility and greatest common divisors

1.6. Let a, b, c ∈Z. Use the deﬁnition of divisibility to directly prove the

following properties of divisibility. (This is Proposition 1.4.)

(a) If a|band b|c, then a|c.

(b) If a|band b|a, then a=±b.

Solution to Exercise 1.6.

(a) By deﬁnition we have b=aA and c=bB for some integers Aand B.

Multiplying gives bc =aAbB, and dividing by byields c=aAB. (Note that b

is nonzero, since zero is not allowed to divide anything.) Hence cis an integer

multiple of a, so a|c.

(b) By deﬁnition we have b=aA and a=bB for some integers Aand B.

Multiplying gives ab =aAbB, and dividing by ab yields 1 = AB. (Note that a

Exercises for Chapter 1 9

and bare nonzero, since zero is not allowed to divide anything.) But the only

way for two integers to have product 1 is for A=B=±1.

b±c=au ±av =a(u±v),

so both b+cand b−care integer multiples of a. Hence both are divisible

by a.

1.7. Use a calculator and the method described in Remark 1.9 to compute

the following quotients and remainders.

(a) 34787 divided by 353.

(b) 238792 divided by 7843.

(d) 1498387487 divided by 76348.

Solution to Exercise 1.7.

(a) a= 34787, b= 353, a/b = 98.54674221, q= 98, r=a−b·q= 193.

(b) a= 238792, b= 7843, a/b = 30.44651281, q= 30, r=a−b·q= 3502.

a−b·q= 60788.

(d) a= 1498387487, b= 76348, a/b = 19625.75950909, q= 19625, r=

a−b·q= 57987.

1.8. Use a calculator and the method described in Remark 1.9 to compute

the following remainders, without bothering to compute the associated quo-

tients.

(a) The remainder of 78745 divided by 127.

(b) The remainder of 2837647 divided by 4387.

(d) The remainder of 4536782793 divided by 9784537.

Solution to Exercise 1.8.

(a) a= 78745, b= 127, a/b = 620.03937008.

r≈127 ·0.03937008 ≈4.99999889,so r= 5.

(b) a= 2837647, b= 4387, a/b = 646.83086392.

r≈4387 ·0.83086392 ≈3644.99997317,so r= 3645.

r≈18754 ·0.91889730 ≈17232.99996420,so r= 17233.

(d) a= 4536782793, b= 9784537, a/b = 463.66862254.

r≈9784537 ·0.66862254 ≈6542161.98166398,so r= 6542162.

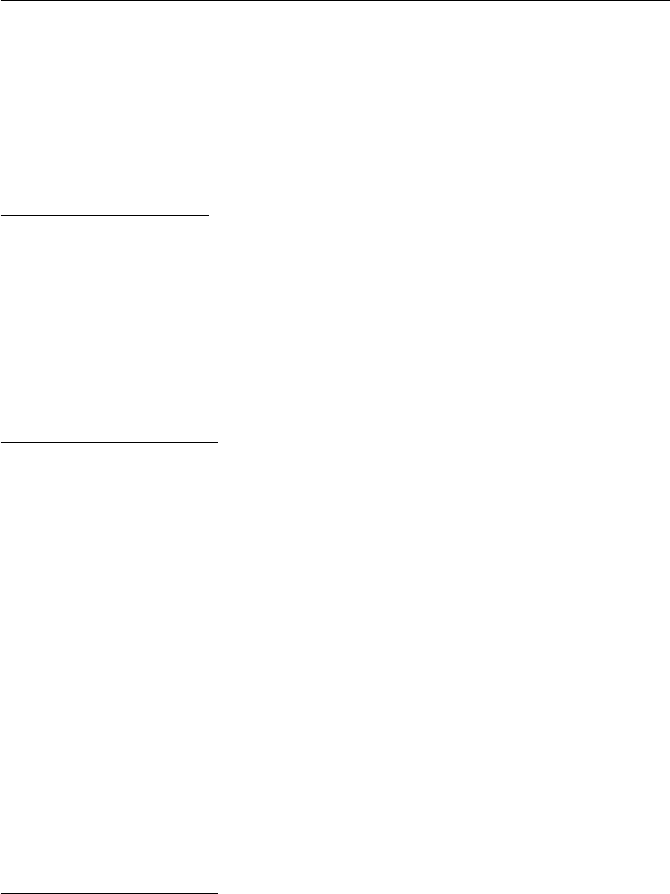
10 Exercises for Chapter 1

1.9. Use the Euclidean algorithm to compute the following greatest common

divisors.

(a) gcd(291,252).

(b) gcd(16261,85652).

(d) gcd(16534528044,8332745927).

Solution to Exercise 1.9.

(a) gcd(291,252) = 3.

(b) gcd(16261,85652) = 161.

(d) gcd(16534528044,8332745927) = 43.

1.10. For each of the gcd(a, b) values in Exercise 1.9, use the extended

Euclidean algorithm (Theorem 1.11) to ﬁnd integers uand vsuch that

au +bv = gcd(a, b).

Solution to Exercise 1.10.

(a) 291 ·13 −252 ·15 = 3

(b) 16261 ·85573 −85652 ·16246 = 161

(d) 16534528044 ·81440996 −8332745927 ·161602003 = 43

1.11. Let aand bbe positive integers.

(a) Suppose that there are integers uand vsatisfying au +bv = 1. Prove that

gcd(a, b) = 1.

(b) Suppose that there are integers uand vsatisfying au +bv = 6. Is it nec-

essarily true that gcd(a, b) = 6? If not, give a speciﬁc counterexample,

and describe in general all of the possible values of gcd(a, b)?

tion au +bv = 1. Prove that adivides v2−v1and that bdivides u2−u1.

(d) More generally, let g= gcd(a, b) and let (u0, v0) be a solution in integers

to au +bv =g. Prove that every other solution has the form u=u0+

kb/g and v=v0−ka/g for some integer k. (This is the second part of

Theorem 1.11.)

Solution to Exercise 1.11.

(a) Let g= gcd(a, b). Then a=gA and b=gB for some integers Aand

B. Substituting into the given equation au +bv = 1 yields

1 = au +bv =gAu +gBv =g(Au +Bv).

Thus gdivides 1, so we must have g= 1.

then we can solve aU +bV = 1, and multiplying this equation by 6 gives

a(6U)+b(6V) = 6. For a speciﬁc counterexample, take a= 3 and b= 2. Then

Exercises for Chapter 1 11

a·6 + b·(−6) = 6,

but gcd(a, b) = 1.

In general, if au +bv =chas a solution, then cdivides gcd(a, b). To see

this, let g= gcd(a, b) and divide cby gwith remainder, say

c=gq +rwith 0 ≤r < g.

We know that we can ﬁnd a solution to g=ax +by, so we get

au +bv =c=gq +r= (ax +by)q+r.

Rearranging this yields

a(u−xq) + b(v−yq) = r.

In other words, we have a solution to aX +bY =rwith 0 ≤r < g. The

left-hand side is divisible by g. (Remember that g= gcd(a, b), so gdivides

both aand b.) Hence g|r. But the only rsatisfying 0 ≤r < g and g|ris

r= 0. Therefore c=gq, which completes the proof that gcd(a, b) divides c.

(d) We are given that

au +bv =gand au0+bv0=g.

Subtracting and rearranging yields

a(u−u0) = −b(v−v0).

Dividing both sides by ggives

g(u−u0) = −b

g(v−v0).

We observe that gcd(a/g, b/g) = 1. (To see this, we note that (a/g)u0+

(b/g)v0= 1, so (a) tells us that gcd(a/g, b/g) = 1.) Thus a/g divides (b/g)(v−

v0) and is relatively prime to (b/g), so it must divide v−v0. Hence

v−v0=a

gxfor some integer x.

The same reasoning tells us that

u−u0=b

gyfor some integer y.

Hence

u=u0+b

gyand v=v0+a

gx.

Substituting into the equation a

g(u−u0) = −b

g(v−v0) from above yields

12 Exercises for Chapter 1

gy=−b

gx,

so y=−x. If we use the letter kinstead of the letter y, we have shown that

u=u0+b

gkand v=v0−a

gk,

which is exactly what we were trying to prove.

1.12. The method for solving au +bv = gcd(a, b) described in Section 1.2 is

somewhat ineﬃcient. This exercise describes a method to compute uand v

that is well suited for computer implementation. In particular, it uses very

little storage.

(a) Show that the following algorithm computes the greatest common divi-

sor gof the positive integers aand b, together with a solution (u, v) in

integers to the equation au +bv = gcd(a, b).

1. Set u= 1,g=a,x= 0, and y=b

2. If y= 0, set v= (g−au)/b and return the values (g, u, v)

3. Divide gby ywith remainder, g=qy +t, with 0≤t < y

4. Set s=u−qx

5. Set u=xand g=y

6. Set x=sand y=t

7. Go To Step (2)

(b) Implement the above algorithm on a computer using the computer lan-

guage of your choice.

equation au +bv =gfor the following pairs (a, b).

(i) (527,1258)

(ii) (228,1056)

(iii) (163961,167181)

(iv) (3892394,239847)

(d) What happens to your program if b= 0? Fix the program so that it deals

with this case correctly.

(e) It is often useful to have a solution with u > 0. Modify your program so

that it returns a solution with u > 0 and uas small as possible. [Hint.

If (u, v) is a solution, then so is (u+b/g, v −a/g).] Redo (c) using your

modiﬁed program.

Solution to Exercise 1.12.

(a) A solution for this exercise is not currently available.

(b) A solution for this exercise will not be provided.

(ii) 228 ·51 −1056 ·11 = 12

(iii) 163961 ·4517 −167181 ·4430 = 7

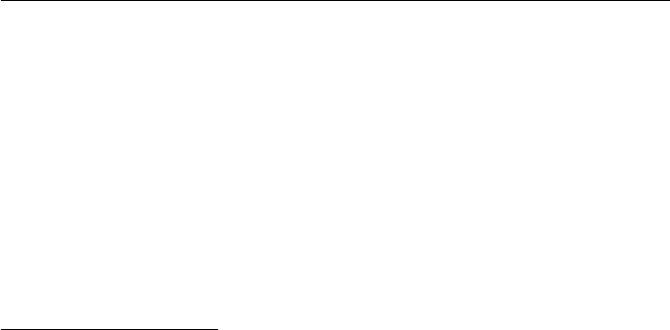
Exercises for Chapter 1 13

(iv) 3892394 ·59789 −239847 ·970295 = 1

(d) If b= 0, then there is a “division by zero” error in step 2. So the program

should check if b= 0, if in that case it should return (a, 1,0).

1.13. Let a1, a2, . . . , akbe integers with gcd(a1, a2, . . . , ak) = 1, i.e., the

largest positive integer dividing all of a1, . . . , akis 1. Prove that the equa-

tion

a1u1+a2u2+··· +akuk= 1

has a solution in integers u1, u2, . . . , uk. (Hint. Repeatedly apply the extended

Euclidean algorithm, Theorem 1.11. You may ﬁnd it easier to prove a more

general statement in which gcd(a1, . . . , ak) is allowed to be larger than 1.)

Solution to Exercise 1.13.

We prove more generally that for any integers a1, . . . , ak(not all zero),

there is a solution to

a1u1+a2u2+··· +akuk= gcd(a1, . . . , ak).

We give the proof using induction on k. If k= 1 there is nothing to prove,

since a1·1 = gcd(a1). For k= 2, this is already proven in the extended

Euclidean algorithm. So assume now that we know the result for fewer than k

integers, where k≥3, and we want to prove it for kintegers. By the induction

hypothesis, we can ﬁnd a solution to

a1u1+a2u2+··· +ak−1uk−1= gcd(a1, . . . , ak−1).

To ease notation, we let b= gcd(a1, . . . , ak−1). We apply the extended Eu-

clidean algorithm to the two numbers band ak, which gives us a solution

bv +akw= gcd(b, ak).

Multiplying the earlier equation by vand subtituting this equation gives

a1u1v+a2u2v+··· +ak−1uk−1v= gcd(a1, . . . , ak−1)v

=bv by deﬁnition of b,

=−akw+ gcd(b, ak).

Hence

a1u1v+a2u2v+··· +ak−1uk−1v+akw= gcd(b, ak).

This completes the proof, since from the deﬁnition of gcd as the largest integer

dividing all of the listed integers, it’s clear that

gcd(b, ak) = gcd¡gcd(a1, . . . , ak−1), ak¢= gcd(a1, . . . , ak−1, ak).

Section. Modular arithmetic

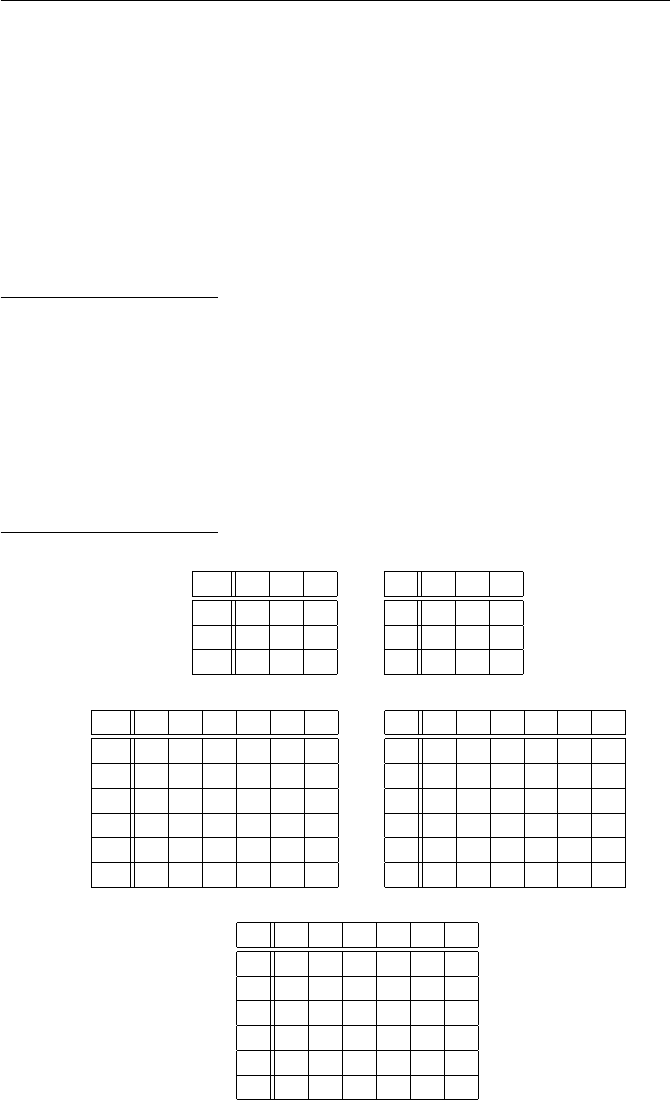
14 Exercises for Chapter 1

1.14. Let m≥1 be an integer and suppose that

a1≡a2(mod m) and b1≡b2(mod m).

Prove that

a1±b1≡a2±b2(mod m) and a1·b1≡a2·b2(mod m).

(This is Proposition 1.13(a).)

Solution to Exercise 1.14.

1.15. Write out the following tables for Z/mZand (Z/mZ)∗, as we did in

Figures 1.4 and 1.5.

(a) Make addition and multiplication tables for Z/3Z.

(b) Make addition and multiplication tables for Z/6Z.

(d) Make a multiplication table for the unit group (Z/16Z)∗.

Solution to Exercise 1.15.

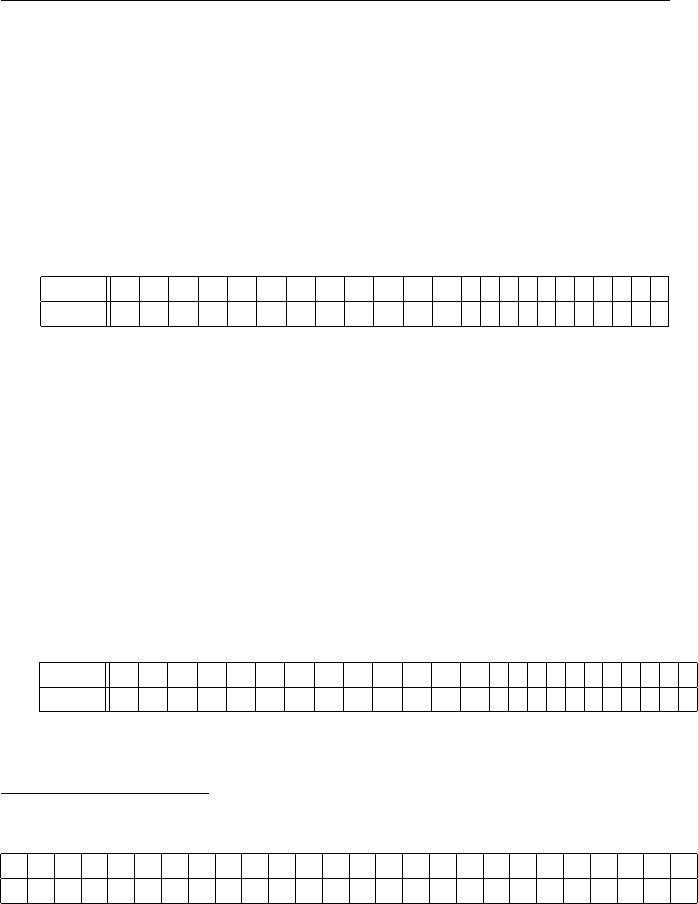
(a)

+ 0 1 2

0 0 1 2

1 1 2 0

2 2 0 1

·012

0 0 0 0

1 0 1 2

2 0 2 1

(b)

+ 012345

0 012345

1 123450

2 234501

3 345012

4 450123

5 501234

·012345

0 000000

1 012345

2 024024

3 030303

4 042042

5 054321

(c)

·124578

1 124578

2 248157

4 487215

5 512784

7 751842

8 875421

Exercises for Chapter 1 15

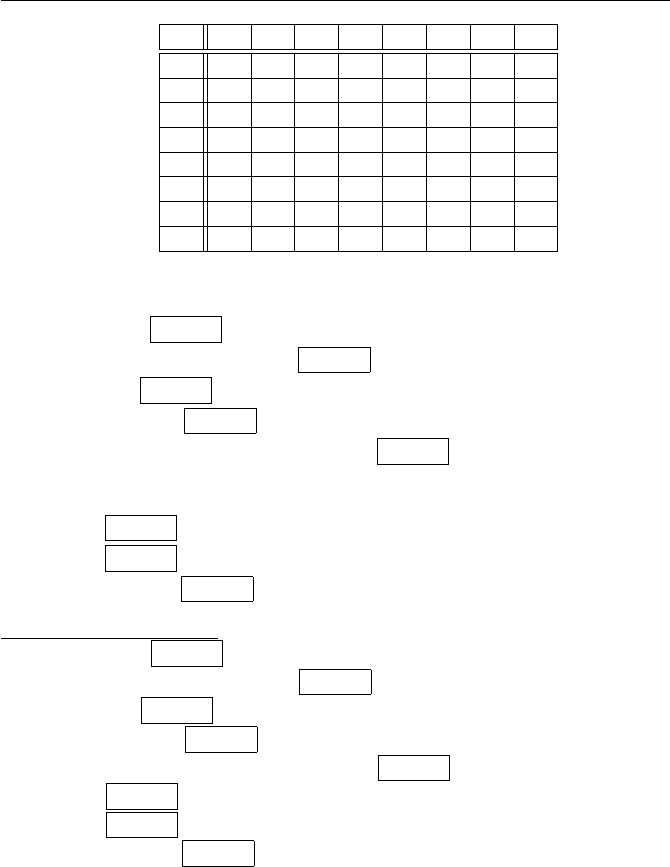
(d)

·1 3 5 7 9 11 13 15

1 1 3 5 7 9 11 13 15

3 3 9 15 5 11 1 7 13

5 5 15 9 3 13 7 1 11

7 7 5 3 1 15 13 11 9

9 9 11 13 15 1 3 5 7

11 11 1 7 13 3 9 15 5

13 13 7 1 11 5 15 9 3

15 15 13 11 9 7 5 3 1

1.16. Do the following modular computations. In each case, ﬁll in the box

with an integer between 0 and m−1, where mis the modulus.

(a) 347 + 513 ≡(mod 763).

(b) 3274 + 1238 + 7231 + 6437 ≡(mod 9254).

(d) 357 ·862 ·193 ≡(mod 943).

(e) 5327 ·6135 ·7139 ·2187 ·5219 ·1873 ≡(mod 8157).

(Hint. After each multiplication, reduce modulo 8157 before doing the

next multiplication.)

(f) 1372≡(mod 327).

(g) 3736≡(mod 581).

(h) 233·195·114≡(mod 97).

Solution to Exercise 1.16.

(a) 347 + 513 ≡97 (mod 763).

(b) 3274 + 1238 + 7231 + 6437 ≡8926 (mod 9254).

(d) 357 ·862 ·193 ≡636 (mod 943).

(e) 5327 ·6135 ·7139 ·2187 ·5219 ·1873 ≡603 (mod 8157).

(f) 1372≡130 (mod 327).

(g) 3736≡463 (mod 581).

(h) 233·195·114≡93 (mod 97).

1.17. Find all values of xbetween 0 and m−1 that are solutions of the

following congruences. (Hint. If you can’t ﬁgure out a clever way to ﬁnd the

solution(s), you can just substitute each value x= 1, x= 2,. . . , x=m−1

and see which ones work.)

(a) x+ 17 ≡23 (mod 37).

(b) x+ 42 ≡19 (mod 51).

(d) x2≡2 (mod 13).

(e) x2≡1 (mod 8).

16 Exercises for Chapter 1

(f) x3−x2+ 2x−2≡0 (mod 11).

(g) x≡1 (mod 5) and also x≡2 (mod 7). (Find all solutions modulo 35,

that is, ﬁnd the solutions satisfying 0 ≤x≤34.)

Solution to Exercise 1.17.

(a) x≡23 −17 ≡6 (mod 37).

(b) x≡19 −42 ≡ −23 ≡28 (mod 51).

etc. The full list is {0,1,4,9,5,3,3,5,9,4,1}. Thus 52≡2 (mod 11) and

62≡2 (mod 11), so there are two solutions, x= 5 and x= 6 .

(d) The squares modulo 13 are {0,1,4,9,3,12,10,10,12,3,9,4,1}. Thus x2≡

2 (mod 13) has no solutions .

(e) The solutions to x2≡1 (mod 8) are x= 1, x= 3, x= 5 and x= 7 .

(f) Plugging x= 0,1,2, . . . , 10 into x3−x2+ 2x−2 and reducing modulo 11,

we ﬁnd the three solutions x= 1, x= 3, and x= 8 .

(g) One method is to try all values x= 0,1,2, . . . , 34. A faster method is

to list the solutions to x≡1 (mod 5), namely 1,6,11,16,21,26,31, . . . and

reduce them modulo 7 to see which ones are congruent to 2 modulo 7. Thus

working modulo 7,

1≡1,6≡6,11 ≡4,16 ≡2,21 ≡0,26 ≡5,31 ≡3.

Thus the solution is x= 16 .

1.18. Suppose that ga≡1 (mod m) and that gb≡1 (mod m). Prove that

ggcd(a,b)≡1 (mod m).

Solution to Exercise 1.18.

The extended Euclidean algorithm says that there are integers uand v

satisfying au +bv = gcd(a, b). Then

ggcd(a,b)≡gau+bv ≡(ga)u·(gb)v≡1u·1v≡1 (mod p).

1.19. Prove that if a1and a2are units modulo m, then a1a2is a unit modulo

Solution to Exercise 1.19.

By deﬁnition of unit, there are numbers b1and b2so that

a1b1≡1 (mod m) and a2b2≡1 (mod m).

Then

(a1a2)(b1b2)≡(a1b1)(a2b2)≡1·1≡1 (mod m),

so a1a2is a unit. Its inverse is b1b2.

Exercises for Chapter 1 17

1.20. Prove that mis prime if and only if φ(m) = m−1, where φis Euler’s

phi function.

Solution to Exercise 1.20.

Suppose ﬁrst that mis prime. Let kbe any number between 1 and m−1

and let d= gcd(k, m). Then d|m, so the fact that mis prime tells us that

either d= 1 or d=m. But also d|kand 1 ≤k < m, so we have d <

m. Hence d= 1. This proves that every number kbetween 1 and m−1

satisﬁes gcd(k, m) = 1. Hence

φ(m) = #©1≤k < m : gcd(k, m) = 1ª= #{1,2,3, . . . , m −1}=m−1.

Next suppose that φ(m) = m−1. This means that every number kbe-

tween 1 and m−1 satisﬁes gcd(k, m) = 1. Suppose that ddivides mand

that d6=m. Then 1 ≤d≤m−1, so gcd(d, m) = 1. But the fact that d

divides mimplies that gcd(d, m) = d. Hence d= 1. This proves that the only

divisors of mare 1 and m, so mis prime.

1.21. Let m∈Z.

(a) Suppose that mis odd. What integer between 1 and m−1 equals 2−1mod m?

(b) More generally, suppose that m≡1 (mod b). What integer between 1

and m−1 is equal to b−1mod m?

Solution to Exercise 1.21.

(a) The fact that mis odd means that m+1

2is an integer, and clearly

2·m+ 1

2=m+ 1 ≡1 (mod m).

(b) The assumption that m≡1 (mod b) means that m−1

bis an integer, so

we have

b·m−1

b=m−1≡ −1 (mod m).

This is almost what we want, so multiply by −1 to get

b·1−m

b= 1 −m≡1 (mod m).

Unfortunately, 1−m

bis negative, but we can add on multiples of mwithout

changing its value modulo m. Thus 1−m

b+m=1+(b−1)m

bis an integer and

b·1+(b−1)m

b= 1 + (b−1)m≡1 (mod m).

Hence b−1mod mis equal to 1+(b−1)m

1.22. Let mbe an odd integer and let abe any integer. Prove that 2m+a2

can never be a perfect square. (Hint. If a number is a perfect square, what

are its possible values modulo 4?)

18 Exercises for Chapter 1

Solution to Exercise 1.22.

Any number squared is either 0 or 1 modulo 4. But

2m+a2≡2 + a2≡(2 + 0 ≡2 if ais even,

2 + 1 ≡3 if ais odd.

Thus 2m+a2is either 2 or 3 modulo 4, so it can never be a perfect square.

1.23. (a) Find a single value xthat simultaneously solves the two congruences

x≡3 (mod 7) and x≡4 (mod 9).

(Hint. Note that every solution of the ﬁrst congruence looks like x= 3+7y

for some y. Substitute this into the second congruence and solve for y;

then use that to get x.)

(b) Find a single value xthat simultaneously solves the two congruences

x≡13 (mod 71) and x≡41 (mod 97).

x≡4 (mod 7), x ≡5 (mod 8),and x≡11 (mod 15).

(d) Prove that if gcd(m, n) = 1, then the pair of congruences

x≡a(mod m) and x≡b(mod n)

has a solution for any choice of aand b. Also give an example to show

that the condition gcd(m, n) = 1 is necessary.

Solution to Exercise 1.23.

(a) x= 31 (b) x= 5764 (c) x= 221

(d) The solutions to the ﬁrst congruence look like x=a+my for any

integer y. Substituting into the second congruence yields

a+my ≡b(mod n),

so we want to ﬁnd a value of zsuch that

a+my −b=nz.

In other words, we need integers yand zsatisfying

my −nz =b−a.

We are given that gcd(m, n) = 1, so we can ﬁnd integers uand vsatisfying

mu +nv = 1. Multiplying this by b−agives

mu(b−a) + nv(b−a) = b−a,

Exercises for Chapter 1 19

so we can take y=u(b−a) and z=v(b−a). Then we have x=a+my =

a+mu(b−a).

To summarize, we ﬁrst solve mu +nv = 1 and then we take

x=a+mu(b−a) = a+ (1 −nv)(b−a) = b+nv(b−a).

The two expressions for xshow that x≡a(mod m) and x≡v(mod n).

This exercise is a special case of the Chinese remainder theorem, which is

covered in Chapter 2.

1.24. Let N,g, and Abe positive integers (note that Nneed not be

prime). Prove that the following algorithm, which is a low-storage variant

of the square-and-multiply algorithm described in Section 1.3.2, returns the

value gA(mod N). (In Step 4 we use the notation bxcto denote the greatest

integer function, i.e., round xdown to the nearest integer.)

Input. Positive integers N,g, and A.

1. Set a=gand b= 1.

2. Loop while A > 0.

3. If A≡1 (mod 2), set b=b·a(mod N).

4. Set a=a2(mod N) and A=bA/2c.

5. If A > 0, continue with loop at Step 2.

6. Return the number b, which equals gA(mod N).

Solution to Exercise 1.24.

*** ﬁll in solution

1.25. Use the square-and-multiply algorithm described in Section 1.3.2, or the

more eﬃcient version in Exercise 1.24, to compute the following powers.

(a) 17183 (mod 256).

(b) 2477 (mod 1000).

Solution to Exercise 1.25.

(a) 183 = 1 + 2 + 22+ 24+ 25+ 27,17183 (mod 256) = 113 .

(b) 477 = 1 + 22+ 23+ 24+ 26+ 27+ 28,2477 (mod 1000) = 272

Section. Prime numbers, unique factorization, and ﬁnite ﬁelds

1.26. Let {p1, p2, . . . , pr}be a set of prime numbers, and let

N=p1p2···pr+ 1.

20 Exercises for Chapter 1

Prove that Nis divisible by some prime not in the original set. Use this fact

to deduce that there must be inﬁnitely many prime numbers. (This proof of

the inﬁnitude of primes appears in Euclid’s Elements. Prime numbers have

been studied for thousands of years.)

Solution to Exercise 1.26.

Let qbe any prime that divides N. (Since N≥2, we know that it must

be divisible by some prime.) Suppose that qwere equal to some pi. Then we

would have

1 = N−p1p2···pr≡0 (mod q),

since qwould divide both of the terms Nand p1···pr. But then q|1, which

is impossible. Therefore qis not equal to any of the pi’s.

Next suppose that there were only ﬁnitely many primes. That means we

can list them, say p1, p2, . . . , pr. But from the ﬁrst part of the exercise, we can

create a new prime that’s not in our list. This contradicts the assumption that

there are ﬁnitely many primes, and hence proves that there must be inﬁnitely

many primes.

1.27. Without using the fact that every integer has a unique factorization

into primes, prove that if gcd(a, b) = 1 and if a|bc, then a|c. (Hint. Use the

fact that it is possible to ﬁnd a solution to au +bv = 1.)

Solution to Exercise 1.27.

From the extended Euclidean algorithm, we can solve au+bv = 1. Multiply

by cto get acu +bcv =c. We are given that a|bc, so there is an integer d

satisfying bc =ad. Substituting this gives acu +adv =c. Thus a(cu +dv) = c,

which shows that a|c.

1.28. Compute the following ordpvalues:

(a) ord2(2816).

(b) ord7(2222574487).

Solution to Exercise 1.28.

(a) ord2(2816) = 8.

(b) ord7(2222574487) = 5.

ord11(a) = 0.

1.29. Let pbe a prime number. Prove that ordphas the following proper-

ties.

(a) ordp(ab) = ordp(a) + ordp(b). (Thus ordpresembles the logarithm func-

tion, since it converts multiplication into addition!)

(b) ordp(a+b)≥min©ordp(a),ordp(b)ª.

A function satisfying properties (a) and (b) is called a valuation.

Exercises for Chapter 1 21

Solution to Exercise 1.29.

(a) By deﬁnition of ordp, we have

a=pordp(a)Aand b=pordp(b)Bwith p-Aand p-B.

Then

ab =pordp(a)A·pordp(b)B=pordp(a)+ordp(b)AB with p-AB,

so by deﬁnition,

ordp(ab) = ordp(a) + ordp(b).

(b) We continue with the notation from (a) and, without loss of generality,

we switch aand bif necessary so that ordp(a)≥ordp(b). Then

a+b=pordp(a)A+pordp(b)B=pordp(b)³pordp(a)−ordp(b)A+B´.

Thus pordp(b)|a+b, so by deﬁnition of ordpwe have

ordp(a+b)≥ordp(b).

(Note that we’ve set things up so that ordp(b) = min{ordp(a),ordp(b)}, so

this is the result that we want.)

given that ordp(a)>ordp(b). We also know that p-B, so it follows that

p-³pordp(a)−ordp(b)A+B´,

since the exponent of pon the ﬁrst term is positive. Hence pordp(b)is the

largest power of pdividing a+b, which proves that

ordp(a+b) = ordp(b).

Section. Powers and primitive roots in ﬁnite ﬁelds

1.30. For each of the following primes pand numbers a, compute a−1mod p

in two ways: (i) Use the extended Euclidean algorithm. (ii) Use the fast power

algorithm and Fermat’s little theorem. (See Example 1.28.)

(a) p= 47 and a= 11.

(b) p= 587 and a= 345.

Solution to Exercise 1.30.

(a) (i) We use the extended Euclidean algorithm to solve

11u+ 47v= 1.

22 Exercises for Chapter 1

The solution is (u, v) = (−17,4), so 11−1≡ −17 ≡30 (mod 47). (ii) Fermat’s

little theorem gives

11−1≡1145 ≡30 (mod 47).

(b) (i) We use the extended Euclidean algorithm to solve

345u+ 587v= 1.

The solution is (u, v) = (114,−67), so 345−1≡114 (mod 587). (ii) Fermat’s

little theorem gives

345−1≡345585 ≡114 (mod 587).

78467u+ 104801v= 1.

The solution is (u, v) = (1763,−1320), so 78467−1≡1763 (mod 104801). (ii)

Fermat’s little theorem gives

78467−1≡78467104799 ≡1763 (mod 104801).

1.31. Let pbe a prime and let qbe a prime that divides p−1.

(a) Let a∈F∗

pand let b=a(p−1)/q. Prove that either b= 1 or else bhas

order q. (Recall that the order of bis the smallest k≥1 such that bk= 1

in F∗

p.Hint. Use Proposition 1.30.)

(b) Suppose that we want to ﬁnd an element of F∗

pof order q. Using (a), we

can randomly choose a value of a∈F∗

pand check whether b=a(p−1)/q

satisﬁes b6= 1. How likely are we to succeed? In other words, compute

the value of the ratio

#{a∈F∗

p:a(p−1)/q 6= 1}

#F∗

(Hint. Use Theorem 1.31.)

Solution to Exercise 1.31.

(a) Let kbe the order of b, i.e., the smallest exponent such that bk= 1. We

know that bq=ap−1= 1 from Fermat’s little theorem. Then Proposition 1.30

tells us that kdivides q, and since qis prime, it follows that either k=q

or k= 1. Thus either bhas order q, or else it has order 1, in which case b=

b1= 1.

(b) Let g∈F∗

pbe a primitive root. Then every a∈F∗

phas the form gifor

some 0 ≤i < p −1. We’ll count the number of awith a(p−1)/q = 1. Thus

Exercises for Chapter 1 23

#{a∈F∗

p:a(p−1)/q = 1}= #{0≤i < p −1 : (gi)(p−1)/q = 1}

= #{0≤i < p −1 : gi(p−1)/q = 1}.

Since ghas order p−1, we have gk= 1 if and only if p−1|k. Hence

gi(p−1)/q = 1 ⇐⇒ p−1|i(p−1)/q ⇐⇒ q|i.

Hence

#{a∈F∗

p:a(p−1)/q = 1}= #{0≤i < p −1 : q|i}=p−1

It follows that

#{a∈F∗

p:a(p−1)/q 6= 1}=p−1−#{a∈F∗

p:a(p−1)/q = 1}

=p−1−p−1

q= (p−1) µ1−1

q¶.

Hence #{a∈F∗

p:a(p−1)/q 6= 1}

#F∗

= 1 −1

so if qis large, we have a very good chance of succeeding on our ﬁrst try.

1.32. Recall that gis called a primitive root modulo pif the powers of ggive

all nonzero elements of Fp.

(a) For which of the following primes is 2 a primitive root modulo p?

(i) p= 7 (ii) p= 13 (iii) p= 19 (iv) p= 23

(b) For which of the following primes is 3 a primitive root modulo p?

(i) p= 5 (ii) p= 7 (iii) p= 11 (iv) p= 17

(i) p= 23 (ii) p= 29 (iii) p= 41 (iv) p= 43

(d) Find all primitive roots modulo 11. Verify that there are exactly φ(10) of

them, as asserted in Remark 1.33.

(e) Write a computer program to check for primitive roots and use it to ﬁnd

all primitive roots modulo 229. Verify that there are exactly φ(229) of

them.

(f) Use your program from (e) to ﬁnd all primes less than 100 for which 2 is

a primitive root.

(g) Repeat the previous exercise to ﬁnd all primes less than 100 for which 3

is a primitive root. Ditto to ﬁnd the primes for which 4 is a primitive

root.

Solution to Exercise 1.32.

(a) (i) No. (ii) Yes. (iii) Yes. (iv) No.

(b) (i) Yes. (ii) Yes. (iii) No. (iv) Yes.

24 Exercises for Chapter 1

(i) p= 23, g= 5. (ii) p= 29, g= 2. (iii) p= 41, g= 6. (iv) p= 43, g= 3.

(d) The primitive roots modulo 11 are {2,6,7,8}. There are φ(10) = 4 of

them.

(e) The primitive roots modulo 229 are

{6,7,10,23,24,28,29,31,35,38,39,40,41,47,50,59,63,65,66,

67,69,72,73,74,77,79,87,90,92,96,98,102,105,110,112,113,

116,117,119,124,127,131,133,137,139,142,150,152,155,156,157,

160,162,163,164,166,170,179,182,188,189,190,191,194,198,200,

201,205,206,219,222,223}.

There are exactly φ(228) = 72 of them.

(f) 2 is a primitive root modulo pfor p∈ {3,5,11,1319,29,37,53,59,61,67,83}

and for no other primes less than 100. It is conjectured that 2 is a primitive

root for inﬁnitely many primes (Artin’s conjecture).

(g) 3 is a primitive root modulo pfor p∈ {5,7,17,19,29,31,43,53,79,89}

and for no other primes less than 100. On the other hand, there are no primes

for which 4 is a primitive root. This is because 4 = 22is a square, so the

powers of 4 can hit at most half of the possible nonzero values modulo p.

1.33. Let pbe a prime such that q=1

2(p−1) is also prime. Suppose that g

is an integer satisfying

g6≡ ±1 (mod p) and gq6≡ 1 (mod p).

Prove that gis a primitive root modulo p.

Solution to Exercise 1.33.

Let nbe the order of g, i.e., the smallest power of gthat is congruent to 1.

Then ndivides p−1 from Proposition 1.30. Since p−1 = 2qwith qprime,

this means that

n= 1 orn= 2 orn=qorn= 2q.

We are given that g6≡ ±1 (mod p), so n6= 1 and n6= 2, and we are also given

that gq6≡ ±1 (mod p), so n6=q.The only value left is n= 2q. This proves

that n=p−1, so gis a primitive root modulo p.

1.34. This exercise begins the study of squares and square roots modulo p.

(a) Let pbe an odd prime number and let bbe an integer with p-b. Prove

that either bhas two square roots modulo por else bhas no square roots

modulo p. In other words, prove that the congruence

X2≡b(mod p)

has either two solutions or no solutions in Z/pZ. (What happens for p=

2? What happens if p|b?)

Exercises for Chapter 1 25

(b) For each of the following values of pand b, ﬁnd all of the square roots

of bmodulo p.

(i) (p, b) = (7,2) (ii) (p, b) = (11,5)

(iii) (p, b) = (11,7) (iv) (p, b) = (37,3)

tradict the assertion in (a)?

(d) Let pbe an odd prime and let gbe a primitive root modulo p. Then

any number ais equal to some power of gmodulo p, say a≡gk(mod p).

Prove that ahas a square root modulo pif and only if kis even.

Solution to Exercise 1.34.

(a) If X=a1and X=a2are square roots of bmodulo p, then pdivides

1−band pdivides a2

2−b, so pdivides their diﬀerence

(a2

1−b)−(a2

2−b) = a2

1−a2

2= (a1−a2)(a1+a2).

It follows that pdivides either a1−a2or a1+a2. If the former, then a1≡a2

(mod p), and if the latter, then a1≡ −a2(mod p). Thus there are at most

two possibilities.

Further, if there is one solution aand if p≥3, then p−ais a second

solution diﬀerent from a, so if there are any solutions, then there are exactly

two solutions. On the other hand, if p= 2, then X2≡b(mod p) always has

exactly one solution, namely X=b.

(b) (i) 3 and 4.

(ii) 4 and 7.

(iii) None.

(iv) 15 and 22.

square roots modulo 35. This does not contradict (a), since the modulus 35

is not prime.

(d) Suppose ﬁrst that kis even, say k= 2j. Then

a≡gk≡g2j≡(gj)2(mod p),

so ais a square modulo p.

Next suppose ais a square, say a≡b2(mod p). Since gis a primitive root,

we can write b≡gi(mod p) for some exponent i. Then

gk≡a≡b2≡(gi)2≡g2i(mod p).

Thus gk−2i≡1 (mod p), and the fact that gis a primitive root implies

that p−1 divides k−2i. But p−1 is even, hence 2 divides k−2i, so 2

divides k.

1.35. Let p≥3 be a prime and suppose that the congruence

X2≡b(mod p)

has a solution.

26 Exercises for Chapter 1

(a) Prove that for every exponent e≥1 the congruence

X2≡b(mod pe) (1.11)

has a solution. (Hint. Use induction on e. Build a solution modulo pe+1

by suitably modifying a solution modulo pe.)

(b) Let X=αbe a solution to X2≡b(mod p). Prove that in (a), we can ﬁnd

a solution X=βto X2≡b(mod pe) that also satisﬁes β≡α(mod p).

(d) Use Exercise 1.34 to deduce that the congruence (1.14) has either two

solutions or no solutions modulo pe.

Solution to Exercise 1.35.

We do (a), (b), and (c) simultaneously. We are given that X=αis a

solution to X2≡b(mod p). We are going to prove by induction that for

every e≥1 there is a unique value βmod pesatisfying both

β2≡b(mod pe) and β≡α(mod p).

The case e= 1 is given to us, we must take β=α. Now suppose that we

have a value of βthat works for e, and we ask for all solutions that work for

e+ 1. Note that if γis a solution for e+ 1, then γmod peis a solution for e.

So by the uniqueness part of the induction hypothesis, we would need to have

γ≡β(mod pe). In other words, if there are any solutions γfor e+ 1, then γ

is forced to have the form

γ=β+ypefor some integer y.

What we want to do is show that there is a unique value of ymodulo pthat

makes γinto a solution of X2≡b(mod pe+1).

We also want to use the fact that βis a solution to X2≡b(mod pe). This

means that

β2=b+peBfor some integer B.

Now we substitute γ=β+ypeinto the congruence X2≡b(mod pe+1) and

try to solve for y. Thus

(β+ype)2≡b(mod pe+1)

β2+ 2ype+y2p2e≡b(mod pe+1)

β2+ 2ype≡b(mod pe+1) since 2e≥e+ 1,

b+peB+ 2ype≡b(mod pe+1) since β2=b+peB,

pe(B+ 2y)≡0 (mod pe+1).

Thus we need to solve

B+ 2y≡0 (mod p).

Exercises for Chapter 1 27

This has a unique solution for y. (Note that pis assumed to be an odd prime.

If p= 2, the argument does not work.) We can even solve explicitly,

y≡p−1

2B(mod p).

This completes the proof that for every e≥1 there exists a unique value of β

(mod pe) satisfying

β2≡b(mod pe) and β≡α(mod p),

which gives all of the statements in (a), (b), and (b).

(d) From the earlier exercise we know that X2≡b(mod p) has either 0

or 2 solutions. If it has no solutions, there there certainly aren’t any solutions

to X2≡b(mod pe) for e≥2, since any such solution could always be

reduced modulo p. On the other hand, if X2≡b(mod p) has two solutions,

then (a), (b), and (c) together imply that there are also two solutions to

X2≡b(mod pe) for each e≥1, since the solutions to X2≡b(mod p) are

matched up one-to-one with the solutions to X2≡b(mod pe).

This exercise is a very special case of Hensel’s lemma.

1.36. Compute the value of

2(p−1)/2(mod p)

for every prime 3 ≤p < 20. Make a conjecture as to the possible values of

2(p−1)/2(mod p) when pis prime and prove that your conjecture is correct.

Solution to Exercise 1.36.

p= 3 21= 2 ≡2

p= 5 22= 4 ≡4

p= 7 23= 8 ≡1

p= 11 25= 32 ≡10

p= 13 26= 64 ≡12

p= 17 28= 256 ≡1

p= 19 29= 512 ≡18

Conjecture: 2(p−1)/2is congruent to either 1 or p−1 modulo p.

Proof : Let a= 2(p−1)/2. Then a2≡2p−1≡1 (mod p) by Fermat’s little

theorem. Therefore a≡ ±1 (mod p). To see this last fact, note that p|(a2−1),

so p|(a−1)(a+ 1), so since pis prime, it divides one of a−1 or a+ 1, which

is just another way of saying that a≡ ±1 (mod p).

Section. Cryptography by hand

28 Exercises for Chapter 1

1.37. Write a 2 to 5 page paper on one of the following topics, including both

cryptographic information and placing events in their historical context:

(a) Cryptography in the Arab world to the 15th century.

(b) European cryptography in the 15th and early 16th centuries.

(d) Cryptography and cryptanalysis in the 19th century.

(e) Cryptography and cryptanalysis during World War I.

(f) Cryptography and cryptanalysis during World War II.

(Most of these topics are too broad for a short term paper, so you should

choose a particular aspect on which to concentrate.)

Solution to Exercise 1.37.

A solution for this exercise will not be provided.

1.38. Ahomophonic cipher is a substitution cipher in which there may be

more than one ciphertext symbol for each plaintext letter. Here is an example

of a homophonic cipher, where the more common letters have several possible

replacements.

a b c d e f g h i j k l m n o p q r s t u v w x y z

! 4 # $ 1 % & * ( ) 3 2 = + [ 9 ] { } : ; 7<>5?

♥ ◦ ℵ6%♦ ∧ & ∆∇8♣Ω∨ ⊗ ♠ 

Θ∞ ⇑ • ¯ ⊕ ⇐

. ⇓ ⇒ -

Decrypt the following message.

( % ∆♠ ⇒ # 4 ∞:♦6% ¯ [ℵ8%2[7⇓ ♣ & ♥ 5¯ ∇

Solution to Exercise 1.38.

( % ∆♠ ⇒ # 4 ∞:♦6% ¯ [ℵ8

I f m u s i c b e t h e f o o d o

% 2 [ 7 ⇓ ♣ & ♥ 5¯ ∇

f l o v e p l a y o n

From Shakespeare’s Twelfth Night:If music be the food of love, play

on...

1.39. Atransposition cipher is a cipher in which the letters of the plaintext

remain the same, but their order is rearranged. Here is a simple example in

which the message is encrypted in blocks of 25 letters at a time.1Take the

given 25 letters and arrange them in a 5-by-5 block by writing the message

horizontally on the lines. For example, the ﬁrst 25 letters of the message

Now is the time for all good men to come to the aid...

is written as

1If the number of letters in the message is not an even multiple of 25, then extra random

letters are appended to the end of the message.

Exercises for Chapter 1 29

NOWIS

THETI

MEFOR

ALLGO

ODMEN

Now the cipehrtext is formed by reading the letters down the columns, which

gives the ciphertext

NTMAO OHELD WEFLM ITOGE SIRON.

(a) Use this transposition cipher to encrypt the ﬁrst 25 letters of the message

Four score and seven years ago our fathers...

(b) The following message was encrypted using this transposition cipher. De-

crypt it.

WNOOA HTUFN EHRHE NESUV ICEME

into a rectangle instead of a square, and we can use various patterns to

place the letters into the rectangle and to read them back out. Try to

decrypt the following ciphertext, in which the letters were placed hor-

izontally into a rectangle of some size and then read oﬀ vertically by

columns. WHNCE STRHT TEOOH ALBAT DETET SADHE

LEELL QSFMU EEEAT VNLRI ATUDR HTEEA

(For convenience, we’ve written the ciphertext in 5 letter blocks, but that

doesn’t necessarily mean that the rectangle has a side of length 5.)

Solution to Exercise 1.39.

(a) Ciphertext: FCNER OODNS URSYA REEEG SAVAO

F O U R S

C O R E A

N D S E V

E N Y E A

R S A G O

(b) Plaintext: When in the course of human events it becomes necessary...

Hopefully everyone recognizes the ﬁrst few words of the American Decla-

ration of Independence.

W H E N I

N T H E C

O U R S E

O F H U M

A N E V E

30 Exercises for Chapter 1

are created equal, that they are endowed by their Creator...

Another excerpt from the Declaration of Independence. It was encrypted

using a 15-by-4 rectangle.

W E H O L D T H E S E T R U T

H S T O B E S E L F E V I D E

N T T H A T A L L M E N A R E

C R E A T E D E Q U A L T H A

Section. Symmetric ciphers and asymmetric ciphers

1.40. Encode the following phrase (including capitalization, spacing and

punctuation) into a string of bits using the ASCII encoding scheme given

in Table 1.10.

Bad day, Dad.

Solution to Exercise 1.40.

Bad day,

66 97 100 32 100 97 121 44

01000010 01100001 01100100 00100000 01100100 01100001 01111001 00101100

D a d .

32 68 97 100 46

00100000 01000100 01100001 01100100 00101110

Thus the phrase “Bad day, Dad.” becomes the ASCII list of bits

0100001001100001011001000010000001100100011000010111

1001001011000010000001000100011000010110010000101110

1.41. Consider the aﬃne cipher with key k= (k1, k2) whose encryption and

decryption functions are given by (1.11) on page 43.

(a) Let p= 541 and let the key be k= (34,71). Encrypt the message m=

204. Decrypt the ciphertext c= 431.

(b) Assuming that pis public knowledge, explain why the aﬃne cipher is

vulnerable to a chosen plaintext attack. (See Property 4 on page 38.)

How many plaintext/ciphertext pairs are likely to be needed in order to

recover the private key?

value of pis public knowledge, and Eve intercepts the ciphertexts c1=

324 and c2= 381 and also manages to ﬁnd out that the corresponding

plaintexts are m1= 387 and m2= 491. Determine the private key and

then use it to encrypt the message m3= 173.

(d) Suppose now that pis not public knowledge. Is the aﬃne cipher still

vulnerable to a chosen plaintext attack? If so, how many plaintext/cipher-

text pairs are likely to be needed in order to recover the private key?

Exercises for Chapter 1 31

Solution to Exercise 1.41.

(a) The encryption of m= 204 is c≡34·204+71 ≡7007 ≡515 (mod 541).

The inverse of k1is 34−1≡366 (mod 541). The decryption of c= 431 is

m≡366(431 −71) ≡297 (mod 541).

(b) Given two plaintext/ciphertext pairs, one can solve the two linear con-

gruences

c1≡k1·m1+k2(mod p) and c2≡k1·m2+k2(mod p)

for the two unknowns k1and k2.

324 ≡k1·387 + k2(mod 601) and 381 ≡k1·491 + k2(mod 601)

She subtracts the ﬁrst equation from the second to get

57 ≡k1·104 (mod 601).

She computes 104−1≡549 (mod 601), and hence

k1≡57 ·104−1≡41 (mod 601).

Then she uses either of the above congruences to recover k2,

k2≡324 −k1·387 ≡83 (mod 601).

Eve now knows Alice and Bob’s private key, so she can encrypt a message,

c3≡k1·m3+k2≡41 ·173 + 83 ≡565 (mod 601).

(d) Yes. Suppose that we have three plaintext/ciphertext pairs,

(m1, c1),(m2, c2),(m3, c3).

This gives us a system of three congruences

c1≡k1m1+k2(mod p)

c2≡k1m2+k2(mod p)

c3≡k1m3+k2(mod p)

We can write this in suggestive matrix and vector notation at





c1m11

c2m21

c3m31

¡1−k1−k2¢≡¡0 0 0¢(mod p).

Using linear algebra modulo p, this implies that the determinant of the matrix

satisﬁes

32 Exercises for Chapter 1

det 



c1m11

c2m21

c3m31

≡0 (mod p).

Thus three plaintext/ciphertext pairs allows Eve to compute a number,

namely

D= det 



c1m11

c2m21

c3m31



that is divisible by the secret prime p. If Eve can factor D, then at worst she

has a few possible values of pto check. So three pairs may be enough to break

the cipher.

More generally, if Eve has ndiﬀerent pairs, she can compute determinant

values D1, . . . , Dn−2by using diﬀerent pairs in the last row of the matrix

(keeping the ﬁrst two rows the same). This gives her a bunch of numbers that

are divisible by p, and within a short time she will almost certain ﬁnd that

gcd(D1, . . . , Dn−2) is equal to p.

1.42. Consider the Hill cipher deﬁned by (1.11),

ek(m)≡k1·m+k2(mod p) and dk(c)≡k−1

1·(c−k2) (mod p),

where m,c, and k2are column vectors of dimension n, and k1is an n-by-n

matrix.

(a) We use the vector Hill cipher with p= 7 and the key k1= ( 1 3

2 2 )

and k2= ( 5

4).

(i) Encrypt the message m= ( 2

1).

(ii) What is the matrix k−1

1used for decryption?

(iii) Decrypt the message c= ( 3

5).

(b) Explain why the Hill cipher is vulnerable to a chosen plaintext attack.

pher with the prime p= 11. Find the keys k1and k2.

m1= ( 5

4), c1= ( 1

8), m2= ( 8

10 ), c2= ( 8

5), m3= ( 7

1), c3= ( 8

7).

(d) Explain how any simple substitution cipher that involves a permutation

of the alphabet can be thought of as a special case of a Hill cipher.

Solution to Exercise 1.42.

(a-i) ek(m) = 5 3 .

(a −ii)k−1

1=3 6

4 5 .

(a −iii)dk(c) = 0 4 .

(b) Each known plaintext/ciphertext pair gives a congruence of the form

c≡k1·m+k2(mod p). Writing this out gives nlinear equations for the n2+n

unknown entries of k1and k2. Hence n+1 plaintext/ciphertext pairs probably

gives enough equations to solve for the keys k1and k2.

Exercises for Chapter 1 33

z w ) and k2= ( u

v). Then the congruence c1=k1m1+

k2(mod 11) becomes the matrix equation

µ1

8¶=µx y

z w¶µ5

4¶+µu

v¶=µ5x+ 4y+u

5z+ 4w+v¶(mod 11).

So this gives the two congruences

5x+ 4y+u≡1 (mod 11) and 5z+ 4w+v≡8 (mod 11).

Similarly, the congruence c2=k1m2+k2(mod 11) gives

8x+ 10y+u≡8 (mod 11) and 8z+ 10w+v≡5 (mod 11).

and c3=k1m3+k2(mod 11) gives

7x+y+u≡8 (mod 11) and 7z+w+v≡7 (mod 11).

This gives us 6 equations for the 6 unknowns x, y, z, w, u, v. Further, three of

the equations only involve x, y, u and the other three only involve z, w, v, so

it’s really two sets of 3-by-3 equations to solve:

5x+ 4y+u= 1 5z+ 4w+v= 8

8x+ 10y+u= 8 8z+ 10w+v= 5

7x+y+u= 8 7z+w+v= 7.

(All equations are modulo 11.) These are easily solved using basic linear al-

gebra methods, and we ﬁnd that

(x, y, u) = (3,7,2) and (z, w, v) = (4,3,9).

Hence

k1=µ3 7

4 3¶and k2=µ2

9¶.

(d) We work with vectors of dimension 26. Let e1, . . . , e26 be the usual basis

vectors for R26, i.e., eihas a 1 in the ith place and 0’s elsewhere. For the

plaintext, we use e1to represent (a), we use e2to represent (b), and so

on. We view the the simple substitution cipher as a function that takes each

plaintext letter and assigns it to a ciphertext letter. Equivalently, it takes

each eiand assigns it to some eπ(i), where πis a one-to-one function

π:{1,2,...,26} −→ {1,2, . . . , 26}.

In the Hill cipher, we now take k1to be the matrix whose ijth entry is 1 if

e(i) = j, and otherwise it is 0. We also take k2= 0. Then k1·ei=eπ(i), so

the encryption of the plaintext eiis equal to eπ(i), as desired.

34 Exercises for Chapter 1

1.43. Let Nbe a large integer and let K=M=C=Z/NZ. For each of the

functions

e:K × M −→ C

listed in (a), (b), and (c), answer the following questions:

•Is ean encryption function?

•If eis an encryption function, what is its associated decryption function d?

•If eis not an encryption function, can you make it into an encryption

function by using some smaller, yet reasonably large, set of keys?

(a) ek(m)≡k−m(mod N).

(b) ek(m)≡k·m(mod N).

Solution to Exercise 1.43.

(a) Yes, eis an encryption function. The decryption function dk(c) = k−c

is the same as e!

(b) No, eis not an encryption function, it is not one-to-one. However, if we

restrict the keys to K= (Z/NZ)∗(i.e., gcd(k, N ) = 1), then eis an encryption

function, with decryption function dk(c)≡k−1c(mod N).

set of keys will make it one-to-one. However, one might deﬁne a decryption

“function” by dk(c)≡√c−k(mod N). Assuming that one knows how to

compute square roots modulo N, this gives two possibly decryptions, since

it’s really ±√c. In practice, one might be able to use some property of valid

messages to ﬁgure out which one is correct.

1.44. (a) Convert the 12 bit binary number 110101100101 into a decimal

integer between 0 and 212 −1.

(b) Convert the decimal integer m= 37853 into a binary number.

(d) Use exclusive or (XOR) to “add” the bit strings 11001010 ⊕10011010.

(e) Convert the decimal numbers 8734 and 5177 into binary numbers, com-

bine them using XOR, and convert the result back into a decimal number.

Solution to Exercise 1.44.

(a) 211 + 210 + 28+ 26+ 25+ 22+ 20= 3429

(b) 37853 = 215 + 212 + 29+ 28+ 27+ 26+ 24+ 23+ 22+ 20, so the binary

form of 37853 is 1001001111011101 .

of 9487428 is 100100001100010001000100 .

(d) 11001010 ⊕10011010 = 01010000 .

(e)

Exercises for Chapter 1 35

8734 = ‘10001000011110’,

5177 = ‘01010000111001’,

8734 ⊕5177 = 10001000011110 ⊕01010000111001 = 11011000100111,

‘11011000100111’ = 13863 .

1.45. Alice and Bob choose a key space Kcontaining 256 keys. Eve builds a

special-purpose computer that can check 10,000,000,000 keys per second.

(a) How many days does it take Eve to check half of the keys in K?

(b) Alice and Bob replace their key space with a larger set containing 2Bdif-

ferent keys. How large should Alice and Bob choose Bin order to force

Eve’s computer to spend 100 years checking half the keys? (Use the ap-

proximation that there are 365.25 days in a year.)

For many years the United States government recommended a symmetric

cipher called DES that used 56 bit keys. During the 1990s, people built special

purpose computers demonstrating that 56 bits provided insuﬃcient security.

A new symmetric cipher called AES, with 128 bit keys, was developed to

replace DES. See Section 8.10 for further information about DES and AES.

Solution to Exercise 1.45.

(a)

(256 keys) ·µ1 second

10,000,000,000 keys¶·µ1 minute

60 seconds¶

·µ1 hour

60 minutes¶·µ1 day

24 hours¶≈83.4 days.

It thus takes about 83.4 days to check all the keys, so about 41.7 days to

check half the keys.

(b)

µ10,000,000,000 keys

1 second ¶·µ60 seconds

1 minute ¶·µ60 minutes

1 hour ¶

·µ24 hours

1 day ¶·µ365.25 days

1 year ¶·(100 years)

= 31557600000000000000 keys ≈264.775 keys.

Thus it takes Eve’s computer 100 years to check 264.775 keys. The problem says

that this should be half the keys, so Alice and Bob should have at least 265.775

diﬀerent keys. In practice, it is easiest to choose an integral power of 2, so Alice

and Bob’s key space should contain (at least) 266 keys.

Comparing (a) and (b), notice that by increasing the keylength from 56 bits

to 66 bits, Alice and Bob’s security goes from 42 days to 100 years. Thus even a

36 Exercises for Chapter 1

small increase in the keylength results in an enormous increase in the breaking

time by exhaustive search. This reﬂects the fact that exponential functions

grow extremely rapidly.

1.46. Explain why the cipher

ek(m) = k⊕mand dk(c) = k⊕c

deﬁned by XOR of bit strings is not secure against a chosen plaintext attack.

Demonstrate your attack by ﬁnding the private key used to encrypt the 16-bit

ciphertext c= 1001010001010111 if you know that the corresponding plaintext

is m= 0010010000101100.

Solution to Exercise 1.46.

If you know mand c, since they are related by c=k⊕m, it follows that

c⊕m=k⊕m⊕m=k. For the example,

k=c⊕m= 1001010001010111 ⊕0010010000101100 = 1011000001111011 .

1.47. Alice and Bob create a symmetric cipher as follows. Their private key k

is a large integer and their messages (plaintexts) are d-digit integers

M={m∈Z: 0 ≤m < 10d}.

To encrypt a message, Alice computes √kto ddecimal places, throws away

the part to the left of the decimal point, and keeps the remaining ddigits.

Let αbe this d-digit number. (For example, if k= 23 and d= 6, then

√87 = 9.32737905 . . . and α= 327379.)

Alice encrypts a message mas

c≡m+α(mod 10d).

Since Bob knows k, he can also ﬁnd α, and then he decrypts cby comput-

ing m≡c−α(mod 10d).

(a) Alice and Bob choose the secret key k= 11 and use it to encrypt 6-digit

integers (i.e., d= 6). Bob wants to send Alice the message m= 328973.

What is the ciphertext that he sends?

(b) Alice and Bob use the secret key k= 23 and use it to encrypt 8-digit

integers. Alice receives the ciphertext c= 78183903. What is the plain-

text m?

the formula

α=j10d³√k− b√kc´k,

where btcdenotes the greatest integer that is less than or equal to t.

Exercises for Chapter 1 37

(d) (Challenge Problem) If Eve steals a plaintext/ciphertext pair (m, c), then

it is clear that she can recover the number α, since α≡c−m(mod 10d).

If 10dis large compared to k, can she also recover the number k? This

might be useful, for example, if Alice and Bob use some of the other digits

of √kto encrypt subsequent messages.

Solution to Exercise 1.47.

(a) √11 = 3.3166247903 ..., so α= 316624 and the ciphertext is c=

328973 + 316624 = 645597 .

(b) √23 = 4.7958315233127195 . . . , so α= 79583152 and the plaintext is

c= 78183903 −79583152 = −1399249 ≡98600751 (mod 108).

right of the decimal point. The remaining part of the formula simply shifts

the digits dplaces to the left and then discards everything after the decimal

point.

(d) The answer is yes, Eve should be able to recover k, but probably not

using the tools that we’ve developed so far. Let β=α/10d. Then

√k=L+βfor some L∈Z.

There are two unknowns here, kand L, and all that Eve knows is that they

are both integers. Squaring both sides gives

k=L2+ 2Lβ +β2.

Thus there are integers Aand Bsatisfying

β2+Aβ +B= 0,

namely A= 2Land B=L2−k. Of course, Eve doesn’t know Aor B, either.

However, there are algorithms based on lattice reduction that are very good at

ﬁnding the smallest (quadratic) polynomial with integer coeﬃcients satisﬁed

by a given decimal number. Using these algorithms, Eve should be able to

ﬁnd Aand B, from which it is easy to recover kas k=1

4A2−B.

1.48. Bob and Alice use a cryptosystem in which their private key is a (large)

prime kand their plaintexts and ciphertexts are integers. Bob encrypts a

message mby computing the product c=km. Eve intercepts the following

two ciphertexts:

c1= 12849217045006222, c2= 6485880443666222.

Use the gcd method described in Section 1.7.4 to ﬁnd Bob and Alice’s private

key.

Solution to Exercise 1.48.

We compute

gcd(c1, c2) = 174385766.

This factors as 174385766 = 2 ·87192883 and 87192883 is prime, so it is Bob

and Alice’s key.

Chapter 2

Discrete Logarithms and

Diﬃe–Hellman

Exercises for Chapter 2

Section. Diﬃe–Hellman and RSA

2.1. Write a one page essay giving arguments, both pro and con, for the

following assertion:

If the government is able to convince a court that there is a valid

reason for their request, then they should have access to an in-

dividual’s private keys (even without the individual’s knowledge),

in the same way that the government is allowed to conduct court

authorized secret wiretaps in cases of suspected criminal activity

or threats to national security.

Based on your arguments, would you support or oppose the government be-

ing given this power? How about without court oversight? The idea that all

private keys should be stored at a secure central location and be accessible to

government agencies (with or without suitably stringent legal conditions) is

called key escrow.

Solution to Exercise 2.1.

A solution for this exercise will not be provided.

2.2. Research and write a one to two page essay on the classiﬁcation of cryp-

tographic algorithms as munitions under ITAR (International Traﬃc in Arms

Regulations). How does that act deﬁne “export”? What are the potential

ﬁnes and jail terms for those convicted of violating the Arms Export Control

Act? Would teaching non-classiﬁed cryptographic algorithms to a college class

that includes non-US citizens be considered a form of export? How has US

government policy changed from the early 1990s to the present?

40 Exercises for Chapter 2

Solution to Exercise 2.2.

Some historical material:

Press Release

Law Professor Sues Federal Government Over Computer Privacy Issues

Federal Civil Rights Action Seeks Injunction Against State Department

And National Security Agency

Cleveland Scholar Attacks Prohibition On Discussing Cryptographic Soft-

ware With Foreign Students And Colleagues

For Immediate Release

Cleveland, Wednesday, August 7, 1996

A Case Western Reserve University law professor ﬁled suit today in federal

court, challenging government regulations which restrict his ability to teach

a course in computer law. Peter Junger, a twenty-ﬁve year veteran of the

law school faculty, will ﬁle a federal civil rights action this afternoon in the

United States District Court in Cleveland. The suit names the Department

of State and the secretive National Security Agency, which administer federal

regulations limiting Professor Junger’s ability to teach.

The case involves the International Traﬃc in Arms Regulations, or ITAR,

federal regulations which restrict the export of military technology. Under the

ITAR, cryptographic computer software, which encodes text to preserve the

privacy of messages on the Internet, is considered a “munition” and subject to

strict export control. The regulations raise signiﬁcant First Amendment ques-

tions by deﬁning “export” to include discussing technical information about

non-classiﬁed software with foreign nationals, such as students registered for

Professor Junger’s course.

In recent months, the State Department has sent a series of letters threat-

ening possible criminal action to a Florida man who posted a simple crypto-

graphic algorithm to the ”sci.crypt” Usenet Newsgroup, an Internet site pop-

ular with cryptography enthusiasts. These and similar incidents have caused

Professor Junger to limit his discussions of cryptographic material with foreign

colleagues, for fear of violating the ITAR. Penalties for unlicensed disclosure

of cryptographic information are severe: federal law provides ten year prison

terms and One Million Dollar ﬁnes for those convicted of violating the Arms

Export Control Act, the legislation under which the ITAR was promulgated.

————————————

Statement by Ambassador David Aaron

US Envoy for Cryptography

RSA Data Security Conference, January 28, 1997

International Views of Key Recovery

These concerns are being heard in Washington. The Administration has

taken the following steps - many based on the direct recommendations of

industry representatives:

First, at the end of last year, jurisdiction for licenses of encryption exports

was transferred from the Department of State to the Department of Com-

merce. Commercial encryption is no longer treated as a munition and thereby

Exercises for Chapter 2 41

subject to various foreign policy embargoes. We hope this will both speed up

and simplify the tasks of obtaining licenses.

Second, and very important, the Administration will license the export of

encryption products, of any algorithm and any key length, if they incorporate

key recovery.

Third, the Administration will also permit the export, over the next two

years, of 56-bit DES and equivalent encryption products without key recovery

provided exporters make commitments to develop key recovery products. I

am pleased to report that already at least 4 vendors have formally ﬁled key

recovery commitments and several more companies are in the initial stages of

dialogue with the Department of Commerce.

And last, a point which is often lost in the debate, domestic use of key

recovery will be voluntary as announced by the Vice President last October.

All Americans will remain free to use any encryption system in the United

States.

———————————

In 1992, the Software Publishers Association and the State Department

reached an agreement which allows the export of programs containing RSA

Data Security’s RC2 and RC4 algorithms, but only when the key size is set

to 40 bits or less. 40 bits is not very secure, and application of a distributed

attack using standard workstations in a good-size lab can break these in at

most a few days. This theory was demonstrated quite visibly in mid-1995

when two independent groups broke 40-bit keys used in the export version of

the Netscape browser.

Section. The discrete logarithm problem

2.3. Let gbe a primitive root for Fp.

(a) Suppose that x=aand x=bare both integer solutions to the congruence

gx≡h(mod p). Prove that a≡b(mod p−1). Explain why this implies

that the map (2.1) on page 63 is well-deﬁned.

(b) Prove that logg(h1h2) = logg(h1) + logg(h2) for all h1, h2∈F∗

pand n∈Z.

Solution to Exercise 2.3.

(a) We are given that ga≡gb(mod p), since they are both congruent

to h. Hence ga−b≡1 (mod p). But gis a primitive root, so its order is p−1,

which implies that p−1 divides a−b. Hence a≡b(mod p−1). This means

the logg(h) is well-deﬁned up to adding or subtracting multiples of p−1, so

the map (2.1) on page 63 is well-deﬁned.

(b) We have

glogg(h1)+logg(h2)=glogg(h1)·glogg(h2)

≡h1·h2(mod p)

≡glogg(h1h2)(mod p).

42 Exercises for Chapter 2

Hence logg(h1) + logg(h2) = logg(h1h2), or more precisely, the are congruent

modulo p−1.

gnlogg(h)=³glogg(h)´n≡hn≡glogg(hn)(mod p).

Hence nlogg(h) = logg(hn).

2.4. Compute the following discrete logarithms.

(a) log2(13) for the prime 23, i.e., p= 23, g= 2, and you must solve the

congruence 2x≡13 (mod 23).

(b) log10(22) for the prime p= 47.

Table 2.1 on page 64.)

Solution to Exercise 2.4.

(a) log2(13) = 7 in F23, since 213 = 128 ≡13 (mod 23).

(b) log10(22) = 11 in F47.

in F941.

2.5. Let pbe an odd prime and let gbe a primitive root modulo p. Prove

that ahas a square root modulo pif and only if its discrete logarithm logg(a)

modulo pis even.

Solution to Exercise 2.5.

This solution is taken from the proof of Proposition 3.60.

Let m= logg(a), so a=gm. If m= 2kis even, then gm=g2k= (gk)2is

a square.

On the other hand, let mbe odd, say m= 2k+ 1, and suppose that gm

is a square modulo p, say gm≡c2(mod p). Fermat’s little theorem (Theo-

rem 1.25) tells us that

cp−1≡1 (mod p).

However, cp−1(mod p) is also equal to

cp−1≡(c2)p−1

2≡(gm)p−1

2≡(g2k+1)p−1

2≡gk(p−1) ·gp−1

2(mod p).

Another application of Fermat’s little theorem tells us that

gk(p−1) ≡(gp−1)k≡1k≡1 (mod p),

so we ﬁnd that

gp−1

2≡1 (mod p).

This contradicts the fact that gis a primitive root, which proves that every

odd power of gis not a square modulo p.

Section. Diﬃe–Hellman key exchange

Exercises for Chapter 2 43

2.6. Alice and Bob agree to use the prime p= 1373 and the base g= 2 for

a Diﬃe–Hellman key exchange. Alice sends Bob the value A= 974. Bob asks

your assistance, so you tell him to use the secret exponent b= 871. What

value Bshould Bob send to Alice, and what is their secret shared value? Can

you ﬁgure out Alice’s secret exponent?

Solution to Exercise 2.6.

Bob sends B=gb= 2871 ≡805 (mod 1373) to Alice. Their shared value

is Ab= 974871 ≡397 (mod 1373). There is no really easy way to determine

Alice’s secret exponent, but with a computer or even a progammable calcu-

lator, it does not take long to compute all of the powers of 2 modulo 1373.

(Using the babystep–giantstep method is even faster, you only need to make

two lists of length approximately √1373 = 37.04 . . . . If you do this, you will

ﬁnd that 2587 ≡974 (mod 1373), so Alice’s secret exponent is 587.

2.7. Let pbe a prime and let gbe an integer. The Diﬃe–Hellman Decision

Problem is as follows. Supoose that you are given three numbers A,B, and C,

and suppose that Aand Bare equal to

A≡ga(mod p) and B≡gb(mod p),

but that you do not necessarily know the values of the exponents aand b.

Determine whether Cis equal to gab (mod p). Notice that this is diﬀerent

from the Diﬃe–Hellman problem described on page 67. The Diﬃe–Hellman

problem asks you to actually compute the value of gab.

(a) Prove that an algorithm that solves the Diﬃe–Hellman problem can be

used to solve the Diﬃe–Hellman decision problem.

(b) Do you think that the Diﬃe–Hellman decision problem is hard or easy?

Why?

See Exercise 5.35 for a related example in which the decision problem is easy,

but it is believed that the associated computational problem is hard.

Solution to Exercise 2.7.

(a) This is obvious. If you can compute gab from g,ga, and gb, then you

can simply compare the value of gab with the value of Cand check if they are

equal.

(b) No one currently knows how to solve the Diﬃe–Hellman decision problem

without solving the Diﬃe–Hellman computational problem.

Section. The ElGamal public key cryptosystem

2.8. Alice and Bob agree to use the prime p= 1373 and the base g= 2 for

communications using the ElGamal public key cryptosystem.

(a) Alice chooses a= 947 as her private key. What is the value of her public

key A?

(b) Bob chooses b= 716 as his private key, so his public key is

B≡2716 ≡469 (mod 1373).

44 Exercises for Chapter 2

Alice encrypts the message m= 583 using the ephemeral key k= 877.

What is the ciphertext (c1, c2) that Alice sends to Bob?

key A≡2299 ≡34 (mod 1373). Bob encrypts a message using Alice’s

public key and sends her the ciphertext (c1, c2) = (661,1325). Decrypt

the message.

(d) Now Bob chooses a new private key and publishes the associated public

key B= 893. Alice encrypts a message using this public key and sends the

ciphertext (c1, c2) = (693,793) to Bob. Eve intercepts the transmission.

Help Eve by solving the discrete logarithm problem 2b≡893 (mod 1373)

and using the value of bto decrypt the message.

Solution to Exercise 2.8.

(a) A≡2947 ≡177 (mod 1373), so Alice’s public key is A= 177 .

(b) c1≡2877 ≡719 (mod 1373) and c2≡583 ·469877 ≡623 (mod 1373).

Alice sends the ciphertext (c1, c2) = (719,623) to Bob.

1)−1·c2≡(661299)−1·1325 ≡645−1·1325 ≡794 ·1325 ≡332

(mod 1373). Thus the plaintext is m=332 . It turns out that the ephemeral

key is k= 566, but Alice does not know this value.

(d) The solution to 2b≡893 (mod 1373) is b= 219 , which is Bob’s private

key. It is now easy to decrypt,

(ca

1)−1·c2≡(693219)−1·793 ≡431−1·793 ≡532 ·793 ≡365 (mod 1373).

Thus Alice’s message to Bob is m= 365 . (The ephemeral key was k= 932.)

2.9. Suppose that an oracle oﬀers to solve the Diﬃe–Hellman problem for

you. (See page 67 for a description of the Diﬃe–Hellman problem.) Explain

how you can use the oracle to decrypt messages that have been encrypted

using the ElGamal public key cryptosystem.

Solution to Exercise 2.9.

In the ElGamal PKC, you know Alice’s public key A≡ga(mod p) and

you know the ciphertext consisting of the two quantities c1≡gk(mod p) and

c2≡m·Ak(mod p), where kis Bob’s secret ephemeral key. You thus know

the values of gaand gk, so the Diﬃe–Hellman problem oracle will take those

values and tell you the value of gak (mod p). But gak ≡Ak(mod p), so you

can recover Bob’s plaintext message by computing (gak)−1·c2≡m(mod p).

2.10. The exercise describes a public key cryptosystem that requires Bob and

Alice to exchange several messages. We illustrate the system with an example.

Bob and Alice ﬁx a publicly known prime p= 32611, and all of the other

numbers used are private. Alice takes her message m= 11111, chooses a ran-

dom exponent a= 3589, and sends the number u=ma(mod p) = 15950 to

Bob. Bob chooses a random exponent b= 4037 and sends v=ub(mod p) = 15422

back to Alice. Alice then computes w=v15619 ≡27257 (mod 32611) and

Exercises for Chapter 2 45

sends w= 27257 to Bob. Finally, Bob computes w31883 (mod 32611) and

recovers the value 11111 of Alice’s message.

(a) Explain why this algorithm works. In particular, Alice uses the numbers

a= 3589 and 15619 as exponents. How are they related? Similarly, how

are Bob’s exponents b= 4037 and 31883 related?

(b) Formulate a general version of this cryptosystem, i.e., using variables, and

show that it works in general.

many times must Alice and Bob exchange data?)

(d) Are there any advantages of this cryptosystem over ElGamal? In partic-

ular, can Eve break it if she can solve the discrete logarithm problem?

Can Eve break it if she can solve the Diﬃe–Hellman problem?

Solution to Exercise 2.10.

(a) Alice’s and Bob’s exponents satisfy

3589 ·15619 ≡1 (mod 32610) and 4037 ·31883 ≡1 (mod 32610)

The reason why the algorithm works is discussed in the answer to (b).

(b) In the general formulation, a public prime pis ﬁxed. Alice choose a plain-

text mmod pand a random exponent asatisfying gcd(a, p −1) = 1. She send

u≡ma(mod p)

to Bob. Bob chooses a random exponent bsatisfying gcd(b, p −1) = 1, com-

putes

v≡ub(mod p),

and send vto Alice. Alice now computes the inverse of amodulo p−1, i.e.,

she solves ax ≡1 (mod p−1) for x. Let a0=a−1mod p−1. Alice computes

w≡va0(mod p)

and sends it to Bob. Finally, Bob computes the inverse b0=b−1(mod p−1)

and then wb0mod pis equal to m.

To see that this last assertion is true, we compute

wb0≡va0b0≡uba0b0≡maba0b0(mod p).

We know that

aa0≡1 (mod 1) (mod p−1) and bb0≡1 (mod 1) (mod p−1),

so the exponent aba0b0is congruent to 1 modulo p−1. Then Fermat’s little

theorem tells us that maba0b0≡m(mod p).

tosystem requires Alice to send Bob two messages and for Bob to send a

46 Exercises for Chapter 2

message back to Alice. So this new system is much more interactive and re-

quires a lot more communication than does ElGamal.

(d) The advantage of this new system is that Alice and Bob reveal somewhat

less information than in ElGamal. Of course, if Eve can solve the DLP, then

since she knows u,vand w, she can solve

w≡vx(mod p)

to recover x=a0, and then she can recover m, because

ua0≡maa0≡m(mod p).

However, there does not appear to be an easy way for Eve to break the

system if she knows how to solve the Diﬃe–Hellman Problem. Thus this new

cryptosystem is potentially more secure than ElGamal, if it turns out that

the DHP is easier to solve than the DLP.

Section. An overview of the theory of groups

2.11. The group S3consists of the following six distinct elements

e, σ, σ2, τ, στ, σ2τ,

where eis the identity element and multiplication is performed using the rules

σ3=e, τ2= 1, τσ =σ2τ.

Compute the following values in the group S3:

(a) τσ2(b) τ(στ ) (c) (στ)(στ ) (d) (στ)(σ2τ).

Is S3a commutative group?

Solution to Exercise 2.11.

(a) τσ2= (τσ)σ= (σ2τ)σ=σ2(τσ) = σ2(σ2τ) = σ4τ= (σ3)στ =στ.

(b) τ(στ) = (τσ)τ= (σ2τ)τ=σ2τ2=σ2.

(d) (στ)(σ2τ) = σ(τσ)στ =σ(σ2τ)στ =σ3(τσ)τ=e(σ2τ)τ=σ2τ2=σ2.

No, S3is not a commutative group. For example τσ =σ2τ, which is diﬀerent

from στ.

2.12. Let Gbe a group, let d≥1 be an integer, and deﬁne a subset of Gby

G[d] = {g∈G:gd=e}.

(a) Prove that if gis in G[d], then g−1is in G[d].

(b) Suppose that Gis commutative. Prove that if g1and g2are in G[d], then

their product g1 g2is in G[d].

(d) Show by an example that if Gis not a commutative group, then G[d]

need not be a group. (Hint. Use Exercise 2.11.)

Exercises for Chapter 2 47

Solution to Exercise 2.12.

(a) For any element hof Gand any positive integer n, we have

(h−1)n hn= (h−1 h−1···  h−1)(hh···  h) = e,

since there are ncopies of h−1to cancel the ncopies of h. Thus (h−1)nis the

inverse of hn, which we can write succintly as (h−1)n= (hn)−1. We apply this

with h=gand n=dand use the assumption that gd=eto conclude that

(g−1)d= (gd)−1=e−1=e.

Hence g−1is in G[d].

(b) We are given that gd

1=eand gd

2=e. We use the commutativity to

compute

(g1g2)d=g1g2g1g2···g1g2=gd

1gd

2=ee =e.

Therefore g1g2∈G[d].

and their inverses are in G[d]. Also clearly eis in G[d]. This gives the ﬁrst

two axioms, and the third (associativity) is automatic, since it’s true for all

elements in G.

(d) Using the group S3in Exercise 2.11, we have τ2=eand (στ )2=e. (The

ﬁrst is true from the description of the group, and the second is true form

part (c) of the exercise.) However, (στ)τ=στ 2=σdoes not satisfy σ2=e.

To see why, note that σ3=e, so if also σ2=e, then we would have e=σ3=

(σ2)σ=eσ =σ, which is not true.

An alternative solution is to use the group of 2-by-2 matrices with integer

coeﬃcients. The matrix A= ( 0 1

1 0 ) satisﬁes A2=Iand the matrix B=¡1−1

0−1¢

satisﬁes B2=I, but AB =¡1−1

0−1¢actually has order 3, i.e., (AB)3=I.

2.13. Let Gand Hbe groups. A function φ:G→His called a (group)

homomorphism if it satisﬁes

φ(g1 g2) = φ(g1) φ(g2) for all g1, g2∈G.

(Note that the product g1 g2uses the group law in the group G, while the

product φ(g1) φ(g2) uses the group law in the group H.)

(a) Let eGbe the identity element of G, let eHbe the identity element of H,

and let g∈G. Prove that

φ(eG) = eHand φ(g−1) = φ(g)−1.

(b) Let Gbe a commutative group. Prove that the map φ:G→Gdeﬁned

by φ(g) = g2is a homomorphism. Give an example of a noncommutative

group for which this map is not a homomorphism.

Solution to Exercise 2.13.

A solution for this exercise is not currently available.

48 Exercises for Chapter 2

2.14. Prove that each of the following maps is a group homomorphism.

(a) The map φ:Z→Z/NZthat sends a∈Zto amod Nin Z/NZ.

(b) The map φ:R∗→GL2(R) deﬁned by φ(a) = ¡a0

0a−1¢.

p→Z/(p−1)Z, where gis a primitive

root modulo p.

Solution to Exercise 2.14.

A solution for this exercise is not currently available.

2.15. (a) Prove that GL2(Fp) is a group.

(b) Show that GL2(Fp) is a noncommutative group for every prime p.

multiplication table.

(d) How many elements are there in the group GL2(Fp)?

(e) How many elements are there in the group GLn(Fp)?

Solution to Exercise 2.15.

(a) The identity element is the usual matrix ( 1 0

0 1 ). The deﬁnition of GL2(Fp)

ensures that every element has an inverse. Finally, the associative law is true

because it’s true in general for matrix multiplication. (But feel free to write

it out explicitly for the product of three 2-by-2 matrices.)

(b) Here’s an example of noncommuting matrices:

µ1 1

0 1¶µ1 0

1 1¶=µ2 1

1 1¶and µ1 0

1 1¶µ1 1

0 1¶=µ1 1

1 2¶.

(If p= 2, then 2 = 0, but they are still diﬀerent matrices.)

e=µ1 0

0 1¶α=µ1 1

1 0¶β=µ0 1

1 1¶

γ=µ0 1

1 0¶δ=µ1 1

0 1¶=µ1 0

1 1¶

They satisfy many relations, for example β=α2and =α2γ. In fact, we can

get all 6 elements as

e, α, α2, γ, αγ, α2γ,

and the group operation is determined by the rules

α3=e, γ2=e, γα =α2γ.

Comparing with Exercise 2.11 we see that GL2(F2) is the same as the group S3

described in that exercise, we’ve just named the generating elements αand γ

instead of σand τ.

(d) Let αbe a matrix in GL2(Fp). The ﬁrst row can be any vector except for

the 0 vector, so there are p2−1 possibilities for the ﬁrst row. The second row

Exercises for Chapter 2 49

can be any vector that is not a scalar multiple of the ﬁrst row. There are p

possible scalar multiples of the ﬁrst row, so there are p2−ppossibilities for

the second row. Hence

# GL2(Fp)=(p1−1)(p2−p) = (p−1)2p(p+ 1).

(e) Using the same reasoning as in (d), there are pn−1 allowable ﬁrst rows,

then pn−pallowable second rows, then pn−p2allowable third rows (since

we have to disallow all linear combinations of the ﬁrst two rows), etc. Hence

# GLn(Fp) =

n−1

i=0

(pn−pi).

Section. How hard is the discrete logarithm problem?

2.16. Verify the following assertions from Example 2.17.

(a) x2+√x=O¡x2¢. (d) (ln k)375 =O¡k0.001¢.

(b) 5 + 6x2−37x5=O¡x5¢. (e) k22k=O¡e2k¢.

Solution to Exercise 2.16.

A solution for this exercise is not currently available.

Section. A Collision Algorithm for the DLP

2.17. Use Shanks’s babystep–giantstep method to solve the following discrete

logarithm problems. (For (b) and (c), you may want to write a computer

program implementing Shanks’s algorithm.)

(a) 11x= 21 in F71.

(b) 156x= 116 in F593.

Solution to Exercise 2.17.

(a) The number 11 has order 70 in F71. Set N=d√70 e= 9 and H=

h−N= 11−9= 7. From Table ?? we see that

111= 21 ·74= 11 in F71.

Hence

21 = 111·7−4= 111·(119)4= 1137 in F71,

so the solution is x=37 .

(b) The number 156 has order 148 in F593. Set N=d√148 e= 13 and

H=h−N= 156−13 = 297. From Table ?? we see that

1567= 116 ·2974= 452 in F593.

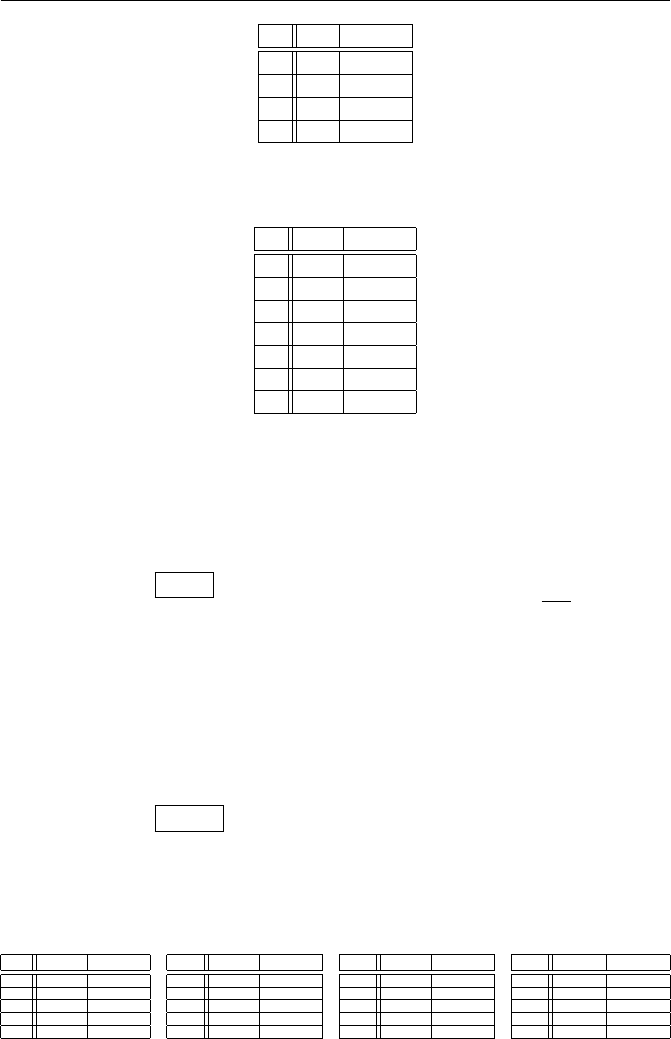
50 Exercises for Chapter 2

k hka·Hk

1 11 5

2 50 35

3 53 32

4 15 11

Table 2.1: Solve 11x≡21 (mod 71) with babystep–giantstep

k hka·Hk

1 156 58

2 23 29

3 30 311

4 529 452

5 97 226

6 307 113

7 452 353

Table 2.2: Solve 156x≡116 (mod 593) via babystep–giantstep

Hence

116 = 1567·297−4= 1567·(15613)4= 15659 in F593,

so the solution is x=59 .

H=h−N= 650−23 = 1925. Table ?? lists the values of hkand a·Hkfor

k= 1,2, . . .. From the table we see that

65020 = 2213 ·192513 = 3011 in F3571.

Using the fact that 1925 = 650−23, we compute

2213 = 65020 ·1925−13 = 65020 ·(65023)13 = 650319 in F3571,

so the solution is x=319 .

Section. The Chinese remainder theorem

2.18. Solve each of the following simultaneous systems of congruences (or

explain why no solution exists).

k hka·Hk

1 650 3393

2 1122 166

3 816 1731

4 1892 432

5 1376 3128

k hka·Hk

6 1650 694

7 1200 396

8 1522 1677

9 133 41

10 746 363

k hka·Hk

11 2815 2430

12 1398 3311

13 1666 3011

14 887 442

15 1619 952

k hka·Hk

16 2476 677

17 2450 3381

18 3405 2063

19 2801 323

20 3011 421

Table 2.3: Solve 650x≡2213 (mod 3571) using babystep–giantstep

Exercises for Chapter 2 51

(a) x≡3 (mod 7) and x≡4 (mod 9).

(b) x≡137 (mod 423) and x≡87 (mod 191).

(d) x≡5 (mod 9), x ≡6 (mod 10),and x≡7 (mod 11).

(e) x≡37 (mod 43), x ≡22 (mod 49),and x≡18 (mod 71).

Solution to Exercise 2.18.

(a) x≡31 (mod 63).

(b) x≡27209 (mod 80793).

ent to one another modulo 41.

(d) x≡986 (mod 990).

(e) x≡11733 (mod 149597).

2.19. Solve the 1700-year-old Chinese remainder problem from the Sun Tzu

Suan Ching stated on page 82.

Solution to Exercise 2.19.

In the modern notation, the solution in the Sun Tzu Suan Ching uses the

fact that:

70 ≡1 (mod 3) ≡0 (mod 5) ≡0 (mod 7),

21 ≡0 (mod 3) ≡1 (mod 5) ≡0 (mod 7),

15 ≡0 (mod 3) ≡0 (mod 5) ≡1 (mod 7).

Hence (2 ∗70) + (3 ∗21) + (2 ∗15) = 233 satisﬁes the desired congruences.

Since any multiple of 105 is divisible by 3, 5 and 7, we can subtract 2 ∗105

from 233 to get 23 as the smallest positive solution.

Problem 26 is the only problem in the Sun Tzu Suan Ching that illus-

trates the Chinese remainder theorem. Thus it is not known if the author had

developed a general method to solve such problems.

2.20. Let a, b, m, n be integers with gcd(m, n) = 1. Let

c≡(b−a)·m−1(mod n).

Prove that x=a+cn is a solution to

x≡a(mod m) and x≡b(mod n),(2.1)

and that every solution to (2.24) has the form x=a+cn+ymn for some y∈Z.

Solution to Exercise 2.20.

A solution for this exercise is not currently available.

2.21. Let x=cand x=c0be two solutions of the system of simultaneous

congruences (2.7) in the Chinese remainder theorem (Theorem 2.25). Prove

that

c≡c0(mod m1m2···mk).

52 Exercises for Chapter 2

Solution to Exercise 2.21.

A solution for this exercise is not currently available.

2.22. For those who have studied ring theory, this exercise sketches a short, al-

beit nonconstructive, proof of the Chinese remainder theorem. Let m1, . . . , mk

be integers and let m=m1m2···mkbe their product.

(a) Prove that the map

mZ−−−−→ Z

m1Z×Z

m2Z×Z

mkZ

amod m−−−−→ (amod m1, a mod m2, . . . , a mod mk)

(2.2)

is a well-deﬁned homomorphism of rings. (Hint. First deﬁne a homomor-

phism from Zto the right-hand side of (2.25), and then show that mZis

in the kernel.)

(b) Assume that m1, . . . , mkare pairwise relatively prime. Prove that the

map given by (2.25) is one-to-one. (Hint. What is the kernel?)

wise relatively prime, prove that the map (2.25) is onto. (Hint. Use (b)

and count the size of both sides.)

(d) Explain why the Chinese remainder theorem (Theorem 2.25) is equivalent

to the assertion that (b) and (c) are true.

Solution to Exercise 2.22.

A solution for this exercise is not currently available.

2.23. Use the method described in Section 2.8.1 to ﬁnd square roots modulo

the following composite moduli.

(a) Find a square root of 340 modulo 437. (Note that 437 = 19 ·23.)

(b) Find a square root of 253 modulo 3143.

4189 = 59 ·71. Note that your four square roots should be distinct mod-

ulo 4189.)

(d) Find eight square roots of 813 modulo 868.

Solution to Exercise 2.23.

(a) The square roots of 340 modulo 437 are 146, 215, 222, and 291.

(b) The square roots of 253 modulo 3143 are 489, 1387, 1756, 2654. (Note

3143 = 7 ·449 and 449 is prime.)

(d) We factor 868 = 4 ·7·31. The eight square roots of 813 modulo 868 are

41, 83, 351, 393, 475, 517, 785, and 827.

2.24. Let pbe an odd prime and let bbe a square root of amodulo p. This

exercise investigates the square root of amodulo powers of p.

(a) Prove that for some choice of k, the number b+kp is a square root of a

modulo p2, i.e., (b+kp)2≡a(mod p2).

Exercises for Chapter 2 53

(b) The number b= 537 is a square root of a= 476 modulo the prime

p= 1291. Use the idea in (a) to compute a square root of 476 modulo p2.

of j, the number b+jpnis a square root of amodulo pn+1.

(d) Explain why (c) implies the following statement: If pis an odd prime and

if ahas a square root modulo p, then ahas a square root modulo pnfor

every power of p. Is this true if p= 2?

(e) Use the method in (c) to compute the square root of 3 modulo 133, given

that 92≡3 (mod 13).

Solution to Exercise 2.24.

(a),(c),(d) A solution for this exercise is not currently available.

(b) (b+k·p)2≡a(mod p2) gives 1074k+ 223 ≡0 (mod p), and hence

k≡239 (mod p). This gives 309086 as the square root of amodulo p2.

(e) 9863 is the square root of 3 modulo 133.

2.25. Suppose n=pq with pand qboth primes.

(a) Suppose that gcd(a, pq) = 1. Prove that if the equation x2≡a(mod n)

has any solutions, then it has four solutions.

(b) Suppose you had a machine that could ﬁnd all four solutions for some

given a. How could you use this machine to factor n?

Solution to Exercise 2.25.

A solution for this exercise is not currently available.

Section. The Pohlig–Hellman algorithm

2.26. Let Fpbe a ﬁnite ﬁeld and let N|p−1. Prove that F∗

phas an element

of order N. This is true in particular for any prime power that divides p−1.

(Hint. Use the fact that F∗

phas a primitive root.)

Solution to Exercise 2.26.

Let gbe a primitive root. Then ghas order p−1, so h=g(p−1)/N has

order N.

2.27. Write out your own proof that the Pohlig–Hellman algorithm works in

the particular case that p−1 = q1·q2is a product of two distinct primes.

This provides a good opportunity for you to understand how the proof works

and to get a feel for how it was discovered.

Solution to Exercise 2.27.

A solution for this exercise will not be provided.

2.28. Use the Pohlig–Hellman algorithm (Theorem 2.32) to solve the discrete

logarithm problem

gx=ain Fp

in each of the following cases.

(a) p= 433, g= 7, a= 166.

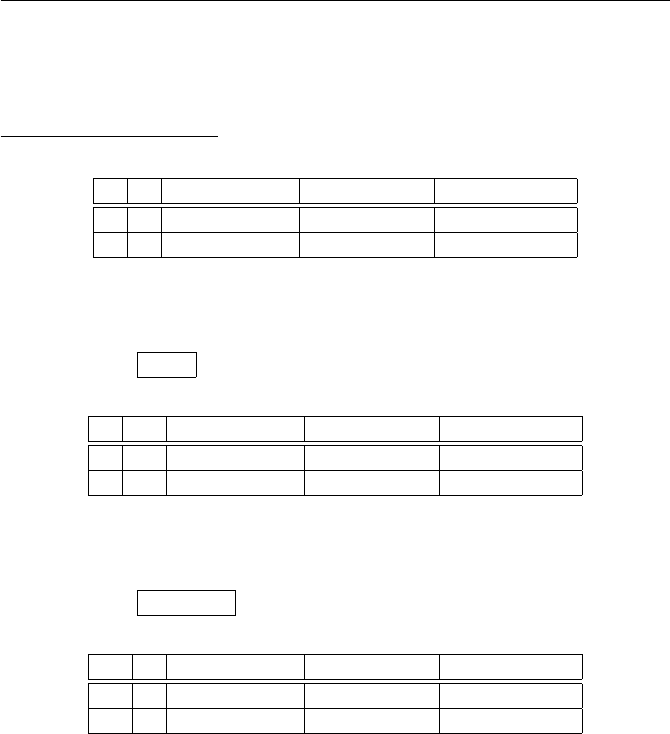
54 Exercises for Chapter 2

(b) p= 746497, g= 10, a= 243278.

(d) p= 1291799, g= 17, a= 192988. (Hint.p−1 has a factor of 709.)

Solution to Exercise 2.28.

(a) Step 1 is to solve

q e h =g(p−1)/qeb=a(p−1)/qeywith hy=b

2 4 265 250 15

3 3 374 335 20

Step 2 is to solve

x≡15 (mod 24), x ≡20 (mod 33).

The solution is x=47 .

(b) Step 1 is to solve

q e h =g(p−1)/qeb=a(p−1)/qeywith hy=b

2 10 4168 38277 523

3 6 674719 322735 681

Step 2 is to solve

x≡523 (mod 210), x ≡681 (mod 36).

The solution is x=223755 .

q e h =g(p−1)/qeb=a(p−1)/qeywith hy=b

2 1 41022298 1 0

29 5 4 11844727 13192165

In order to solve the discrete logarithm problem modulo 295, it is best to solve

it step by step. Note that 4294= 18794375 is an element of order 29 in F∗

p. To

avoid notational confusion, we use the letter ufor the exponents.

First solve 18794375u0=¡11844727¢294

= 987085. The solution is u0= 7.

The value of uso far is u= 7.

Solve 18794375u1=¡11844727·4−7¢293

= 8303208. The solution is u1= 8.

The value of uso far is u= 239 = 7 + 8 ·29.

Solve 18794375u2=¡11844727 ·4−239¢292

= 30789520. The solution is

u2= 26. The value of uso far is u= 22105 = 7 + 8 ·29 + 26 ·292.

Solve 18794375u3=¡11844727 ·4−22105¢291

= 585477. The solution is

u3= 18. The value of uso far is u= 461107 = 7 + 8 ·29 + 26 ·292+ 18 ·293.

Solve 18794375u4=¡11844727 ·4−461107¢290

= 585477. The solution is

u4= 18. The ﬁnal value of uis u= 13192165 = 7 + 8 ·29 + 26 ·292+ 18 ·293+

18 ·294, which is the number you see in the last column of the table.

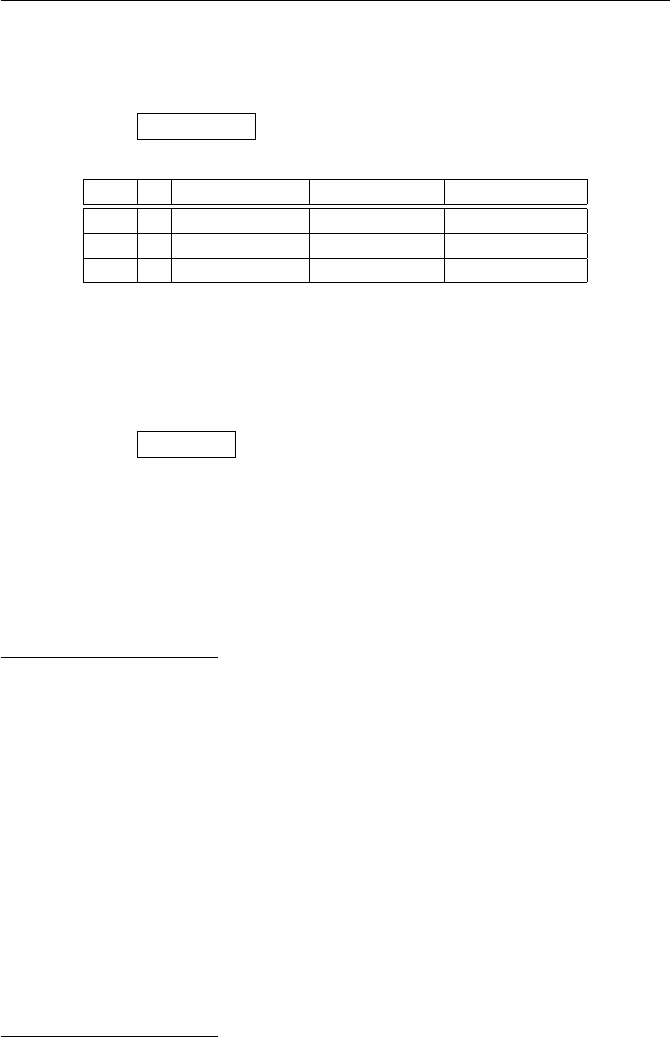
Exercises for Chapter 2 55

Step 2 is to solve

x≡0 (mod 2), x ≡13192165 (mod 295).

The solution is x=33703314 .

(d) Step 1 is to solve

q e h =g(p−1)/qeb=a(p−1)/qeywith hy=b

2 1 1291798 1 0

709 1 679773 566657 322

911 1 329472 898549 534

There is no magical way to solve the DLP’s modulo 709 or 911, although

they are easily solved by an exhaustive search on a computer, and a collision

algorithm is even faster. Step 2 is to solve

x≡0 (mod 2), x ≡322 (mod 709), x ≡534 (mod 911).

The solution is x=984414 .

Section. Rings, quotient rings, polynomial rings, and ﬁnite ﬁelds

2.29. Let Rbe a ring with the property that the only way that a product a·b

can be 0 is if a= 0 or b= 0. (In the terminology of Example 2.56, the ring R

has no zero divisors.) Suppose further that Rhas only ﬁnitely many elements.

Prove that Ris a ﬁeld. (Hint. Let a∈Rwith a6= 0. What can you say about

the map R→Rdeﬁned by b7→ a·b?)

Solution to Exercise 2.29.

A solution for this exercise is not currently available.

2.30. Let Rbe a ring. Prove the following properties of Rdirectly from the

ring axioms described in Section 2.10.1.

(a) Prove that the additive identity element 0 ∈Ris unique, i.e., prove that

there is only one element in Rsatisfying 0+a=a+0 = 0 for every a∈R.

(b) Prove that the multiplicative identity element 1 ∈Ris unique.

(d) Prove that 0  a =a  0 = 0 for all a∈R.

(e) We denote the additive inverse of aby −a. Prove that −(−a) = a.

(f) Let −1 be the additive inverse of the multiplicative identity element 1 ∈

R. Prove that (−1) (−1) = 1.

(g) Prove that b|0 for every nonzero b∈R.

(h) Prove that an element of Rhas at most one multiplicative inverse.

Solution to Exercise 2.30.

(a) If 0 and 00are both additive identities, then

00= 00+ 0 = 0.

56 Exercises for Chapter 2

(b) If 1 and 10are both multiplicative identities, then

10= 101 = 1.

b=b+ 0 = b+ (c+b0) = (b+c) + b0= 0 + b0=b0.

(d)

0 a = (0 + 0)  a = (0  a) + (0  a).

Subtracting 0  a from both sides give 0  a = 0. (Note “subtraction” really

means to add the additive inverse.)

(e) Let b=−(−a). Then by deﬁnition, b+ (−a) = 0. But we also know by

deﬁnition that a+ (−a) = 0. Since additive inverses are unique from (c), it

follows that b=a.

(f) To ease notation, we let i= 1 and u=−1. Then

0 = 0  u = (i+u) u = (iu)+(uu) = u+ (uu).

Thus uu is the additive inverse of u. Using (e) gives (−1)(−1) = −(−1) = 1.

(g) We have b  0 = 0 from (d), so b|0 by deﬁnition of divisibility.

(h) Let a∈Rand suppose that ab = 1 and ac = 1, so band care both

multiplicative inverses of a. Then

b=b·1 = b·(a·c) = (a·b)·c= 1 ·c=c.

Thus b=c, so ahas at most one multiplicative inverse.

2.31. Prove Proposition 2.42.

Solution to Exercise 2.31.

A solution for this exercise is not currently available.

2.32. Prove Proposition 2.44. (Hint. First use Exercise 2.31 to prove that the

congruence classes a+band abdepend only on the congruence classes of a

and b.)

Solution to Exercise 2.32.

A solution for this exercise is not currently available.

2.33. Let Fbe a ﬁeld and let aand bbe nonzero polynomials in F[x].

(a) Prove that deg(a·b) = deg(a) + deg(b).

(b) Prove that ahas a multiplicative inverse in F[x] if and only if ais in F,

i.e., if and only if ais a constant polynomial.

irreducible polynomials. (Hint. Use (a), (b), and induction on the degree

of the polynomial.)

Exercises for Chapter 2 57

(d) Let Rbe the ring Z/6Z. Give an example to show that (a) is false for

some polynomials aand bin R[x].

Solution to Exercise 2.33.

(a) A solution for this exercise is not currently available.

(b) If a·b= 1, then taking degrees and using (a) gives

0 = deg(1) = deg(a·b) = deg(a) + deg(b).

The degree of a nonzero polynomial is a nonnegative integer, so we conclude

that deg(a) = deg(b) = 0. Hence aand bare constant polynomials.

that every polynomial of degree smaller than ncan be factored into a product

of irreducible polynomials, and let a∈F[x] have degree n. If ais itself irre-

ducible, we’re done. Otherwise it factors as a=b·c, where neither bnor c

is a unit. It follows from (b) that band cboth have degree at least 1, so

using (a) we ﬁnd that band chave degrees that are strictly smaller than the

degree of a. Hence by induction, both band ccan be factored as a product

of irreducible polynomials. But then their product, which equals a, is also a

product of irreducible polynomials.

(d) Let a= 2x+ 1 and bfb = 3x+ 1, then a·b= 6x2+ 5x+ 1 = 5x+ 1,

since 6 = 0 in Z/6Z. Hence

deg(a) = deg(b) = deg(a·b) = 1,

so the degree formula in (a) is false.

2.34. Let aand bbe the polynomials

a=x5+ 3x4−5x3−3x2+ 2x+ 2,

b=x5+x4−2x3+ 4x2+x+ 5.

Use the Euclidean algorithm to compute gcd(a,b) in each of the following

rings.

(a) F2[x] (b) F3[x] (c) F5[x] (d) F7[x].

Solution to Exercise 2.34.

(a) gcdF2[x](a,b) = x3+x2+x+ 1.

(b) gcdF3[x](a,b) = x2+x+ 2.

(d) gcdF7[x](a,b) = 1.

(Note for instructor: The resultant of aand bis −23·32·5·59 ·107, so

gcd(a,b) = 1 in Fp[x] unless p∈ {2,3,5,59,107}.)

2.35. Continuing with the same polynomials aand bas in Exercise 2.34,

for each of the polynomial rings (a), (b), (c), and (d) in Exercise 2.34, ﬁnd

polynomials uand vsatisfying

a·u+b·v= gcd(a,b).

58 Exercises for Chapter 2

Solution to Exercise 2.35.

(a) u= 1 and v= 1.

(b) u=x+ 1 and v= 2x.

(d) u= 3x4+ 3x3+x2+ 5x+ 4 and v= 4x4+ 5x3+x2+ 2x.

2.36. Prove that the polynomial x3+x+ 1 is irreducible in F2[x]. (Hint.

Think about what a factorization would have to look like.)

Solution to Exercise 2.36.

If x3+x+ 1 factors, then it can be written as the product of a linear

polynomial and a quadratic polynomial. Since the only possible coeﬃcients

are 0 and 1, this means we would have

x3+x+ 1 = (x+a)(x2+bx +c) in F2[x].

Putting x= 0 yields 1 = ac, so we must have a=c= 1. (Remember that a

and care in F2, so they are either 0 or 1.) Now we have

x3+x+ 1 = (x+ 1)(x2+bx + 1),

and putting x= 1 yields 1 = 2 ·(2 + b) = 0. This contradiction shows

that x3+x+ 1 does not factor in F2[x].

2.37. The multiplication table for the ﬁeld F2[x]/(x3+x+ 1) is given in

Table 2.5, but we have omitted fourteen entries. Fill in the missing entries.

(This is the ﬁeld described in Example 2.58. You can download and print

a copy of Table 2.5 at www.math.brown.edu/~jhs/MathCrypto/Table2.5.

pdf.)

Solution to Exercise 2.37.

Note that it’s not necessary to compute both a·band b·a. Half missing

entries in the table are

1·x2=x2

x·(x2+x) = x2+x+ 1

x2·x=x+ 1

(x+ 1) ·1 = x+ 1

(x2+ 1) ·(x+ 1) = x2

(x2+x)·(x2+x+ 1) = x2

(x2+x+ 1) ·(x2+ 1) = x2+x.

The other half are the same products in the opposite order.

Exercises for Chapter 2 59

0 1 x x21 + x1 + x2x+x21 + x+x2

0 0 0 0 0 0 0 0 0

1 0 1 x1 + x2x+x21 + x+x2

x0x x2x+x21 1 + x2

x20x+x21 + x+x2x1 + x21

1 + x0x+x21 + x+x21 + x21x

1 + x20 1 + x21x1 + x+x21 + x

x+x20x+x21 + x21 1 + x x

1 + x+x20 1 + x+x21 + x21x1 + x

Table 2.4: Multiplication table for the ﬁeld F2[x]/(x3+x+ 1)

2.38. The ﬁeld F7[x]/(x2+ 1) is a ﬁeld with 49 elements, which for the mo-

ment we denote by F49. (See Example 2.59 for a convenient way to work

with F49.)

(a) Is 2 + 5xa primitive root in F49?

(b) Is 2 + xa primitive root in F49?

(Hint. Lagrange’s theorem says that the order of u∈F49 must divide 48. So

if uk6= 1 for all proper divisors kof 48, then uis a primitive root.)

Solution to Exercise 2.38.

(a) No, (2 + x)8= 1.

(b) Yes. It suﬃces to check that (2 + x)16 = 4 and (2+x)24 = 6 are not equal

to 1.

2.39. Let pbe a prime number and let e≥2. The quotient ring Z/peZand

the ﬁnite ﬁeld Fpeare both rings and both have the same number of elements.

Describe some ways in which they are intrinsically diﬀerent.

Solution to Exercise 2.39.

Every nonzero element in the ﬁeld Fpehas a multiplicative inverse,

while Z/(pe) has lots of elements that do not have inverses, for example all el-

ements of the form kp with 1 ≤k < pe−1. In the ﬁeld Fpe, if a product ab = 0,

then either a= 0 or b= 0. (To see this, note that if a6= 0, then a−1exists, so

multiplying ab = 0 by a−1shows that b= 0.) On the other hand, Z/(pe) does

not have this property. For example, p·pe−1= 0, but neither pnor pe−1is 0

in Z/(pe). A subtler property is that every element αof Fpesatisﬁes αpe=α,

but this is not true in Z/(pe). For example, if we take α=p, the αpe= 0.

2.40. Let Fbe a ﬁnite ﬁeld.

(a) Prove that there is an integer m≥1 such that if we add 1 to itself m

times,

1+1+··· + 1

| {z }

mones

60 Exercises for Chapter 2

then we get 0. Note that here 1 and 0 are the multiplicative and additive

identity elements of the ﬁeld F. If the notation is confusing, you can let u

and zbe the multiplicative and additive identity elements of F, and then

you need to prove that u+u+···+u=z. (Hint. Since Fis ﬁnite, the

numbers 1, 1 + 1, 1 + 1 + 1,. . . cannot all be diﬀerent.)

(b) Let mbe the smallest positive integer with the property described in (a).

Prove that mis prime. (Hint. If mfactors, show that there are nonzero

elements in Fwhose product is zero, so Fcannot be a ﬁeld.) This prime

is called the characteristic of the ﬁeld F.

space over the ﬁeld Fpof pelements.

(d) Use (c) to deduce that Fhas pdelements for some d≥1.

Solution to Exercise 2.40.

(a) The fact that Fis ﬁnite means that when we look at

1,1 + 1,1 + 1 + 1,1+1+1+1, . . .

eventually we get a repeated value. Subtracting the smaller number of terms

from the larger, it follows that some sum of 1’s is equal to 0 in F.

(b) Suppose that mfactors as m=qr. Then we have

1+1+··· + 1

| {z }

qones ·1 + 1 + ··· + 1

| {z }

rones

= 1 + 1 + ··· + 1

| {z }

mones

= 0.

Since Fis a ﬁeld, the only way for a product to be 0 is for one of the factors

to be 0, so we have either

1+1+··· + 1

| {z }

qones

= 0 or 1 + 1 + ··· + 1

| {z }

rones

= 0 in F.

But we deﬁned mto be the smallest number of 1’s that sums to 0, so either q≥

mor r≥m. Since we also have m=qr, it follows that either q=m(and

r= 1) or r=m(and q= 1). This proves that mis prime.

1 + 1 to 1 + 1, etc. The axioms for a ﬁeld show that this makes Finto a

vector space using Fpas scalars. By standard linear algebra, Fhas a basis as

a vector space over Fp, and the basis is ﬁnite since Fitself is ﬁnite. Hence F

is a ﬁnite-dimensional vector space over Fp.

(d) Let v1,...,vdbe a basis for Fas a vector space over Fp. Then every

element of Fcan be written uniquely as

a1v1+a2v2+··· +advdwith a1, . . . , ad∈Fp.

There are pchoices of a1, and pchoices of a2, and pchoices of a3, etc. So

there are pddistinct elements in F.

Chapter 3

Integer Factorization and

RSA

Exercises for Chapter 3

Section. Euler’s theorem and roots modulo pq

3.1. Solve the following congruences.

(a) x19 ≡36 (mod 97).

(b) x137 ≡428 (mod 541).

(d) x751 ≡677 (mod 8023).

(e) x38993 ≡328047 (mod 401227). (Hint. 401227 = 607 ·661.)

Solution to Exercise 3.1.

(a) 97 is prime. The congruence 19d≡1 (mod 96) has solution d≡91

(mod 96). Then x≡3691 ≡36 (mod 97).

(b) 541 is prime. The congruence 137d≡1 (mod 540) has solution d≡473

(mod 540). Then x≡428473 ≡213 (mod 541).

has solution d≡577 (mod 1080). Then x≡614577 ≡158 (mod 1159).

More eﬃciently, g= gcd(18,60) = 6 and (18)(60)/6 = 180. The congruence

73d≡1 (mod 180) has solution d≡37 (mod 180). Then x≡61437 ≡158

(mod 1159).

(d) 8023 = 71 ·113 and 71 ·112 = 7840. The congruence 751d≡1

(mod 7840) has solution d≡7151 (mod 7840). Then x≡6777151 ≡1355

(mod 8023). More eﬃciently, g= gcd(70,112) = 14 and (70)(112)/14 = 560.

The congruence 751d≡1 (mod 560) has solution d≡431 (mod 560). Then

x≡677431 ≡1355 (mod 8023).

(e) 401227 = 607 ·661 and 608 ·660 = 399960. The congruence 38993d≡

1 (mod 399960) has the solution d≡265457 (mod 399960). Then x≡

62 Exercises for Chapter 3

328047265457 ≡36219 (mod 401227). More eﬃciently, g= gcd(606,660) = 6

and (606)(660)/6 = 66660. The congruence 38993d≡1 (mod 66660) has

the solution d≡65477 (mod 66660). Then x≡32804765477 ≡36219

(mod 401227).

3.2. Let pand qbe distinct primes and let eand dbe integers satisfying

de ≡1 (mod (p−1)(q−1)).

Suppose further that cis an integer with gcd(c, pq)>1. Prove that

x≡cd(mod pq) is a solution to the congruence xe≡c(mod pq),

thereby completing the proof of Proposition 3.4.

Solution to Exercise 3.2.

If pq |c, then the solution is x= 0. So the interesting case is when cis

divisible by exactly one of pand q, say p|cand q-c. Then x≡cd≡0 (mod p)

is a solution to xe≡c≡0 (mod p), so we only need to check that it is true

modulo q. We compute

(cd)e≡c1+k(p−1)(q−1) ≡c·(cq−1)k(p−1) ≡c(mod q),

since cq−1≡1 (mod q) from Fermat’s little theorem.

3.3. Recall from Section 1.3 that Euler’s phi function φ(N) is the function

deﬁned by

φ(N) = #{0≤k < N : gcd(k, N) = 1}.

In other words, φ(N) is the number of integers between 0 and N−1 that are

relatively prime to N, or equivalently, the number of elements in Z/N Zthat

have inverses modulo N.

(a) Compute the values of φ(6), φ(9), φ(15), and φ(17).

(b) If pis prime, what is the value of φ(p)?

aφ(N)≡1 (mod N) for all integers asatisfying gcd(a, N) = 1.

(Hint. Mimic the proof of Fermat’s little theorem (Theorem 1.25), but

instead of looking at all of the multiples of aas was done in (1.8), just

take the multiples ka of afor values of ksatisfying gcd(k, N) = 1.)

Solution to Exercise 3.3.

A solution for this exercise is not currently available.

3.4. Euler’s phi function has many beautiful properties.

(a) If pand qare distinct primes, how is φ(pq) related to φ(p) and φ(q)?

Exercises for Chapter 3 63

(b) If pis prime, what is the value of φ(p2)? How about φ(pj)? Prove that

your formula for φ(pj) is correct. (Hint. Among the numbers between 0

and pj−1, remove the ones that have a factor of p. The ones that are

left are relatively prime to p.)

cation formula

φ(MN) = φ(M)φ(N).

(d) Let p1, p2, . . . , prbe the distinct primes that divide N. Use your results

from (b) and (c) to prove the following formula:

φ(N) = N

i=1 µ1−1

pi¶.

(e) Use the formula in (d) to compute the following values of φ(N).

(i) φ(1728). (ii) φ(1575). (iii) φ(889056) (Hint. 889056 = 25·34·73).

Solution to Exercise 3.4.

(a)–(d) A solution for this exercise is not currently available.

(e) (i) φ(1728) = 576, (ii) φ(1575) = 720, (iii) φ(889056) = 254016.

3.5. Let N,c, and ebe positive integers satisfying the conditions gcd(N, c) = 1

and gcd¡e, φ(N)¢= 1.

(a) Explain how to solve the congruence

xe≡c(mod N),

assuming that you know the value of φ(N). (Hint. Use the formula in

Exercise 3.3(c).)

(b) Solve the following congruences. (The formula in Exercise 3.4(d) may be

helpful for computing the value of φ(N).)

(i) x577 ≡60 (mod 1463).

(ii) x959 ≡1583 (mod 1625).

(iii) x133957 ≡224689 (mod 2134440).

Solution to Exercise 3.5.

(a) A solution for this exercise is not currently available.

(b) (i) N= 7 ·11 ·19, so

φ(1463) = 1463 µ1−1

7¶µ1−1

11¶µ1−1

19¶= 1080.

We compute d≡577−1≡73 (mod 1080), so

x≡6073 ≡1390 (mod 1463).

64 Exercises for Chapter 3

Check: 1390577 ≡60 (mod 1463). X

(ii) N= 53·13, so

φ(1625) = 1625 µ1−1

5¶µ1−1

13¶= 1200.

We compute d≡959−1≡239 (mod 1200), so

x≡1583239 ≡147 (mod 1625).

Check: 147959 ≡1583 (mod 1625). X

(iii) N= 23·32·5·72·112, so

φ(2134440) = 2134440 µ1−1

2¶µ1−1

3¶µ1−1

5¶µ1−1

7¶µ1−1

11¶

= 443520.

We compute d≡133957−1≡326413 (mod 443520), so

x≡224689326413 ≡1892929 (mod 2134440).

Check: 1892929133957 ≡224689 (mod 2134440). X

Section. The RSA public key cryptosystem

3.6. Alice publishes her RSA public key: modulus N= 2038667 and exponent

e= 103.

(a) Bob wants to send Alice the message m= 892383. What ciphertext does

Bob send to Alice?

(b) Alice knows that her modulus factors into a product of two primes, one

of which is p= 1301. Find a decryption exponent dfor Alice.

Solution to Exercise 3.6.

(a) Bob sends c=me= 892383103 ≡45293 (mod 2038667).

(b) The modulus is N= 2038667 = 1301 ·1567, so φ(N) = 1300 ·1568 =

2035800. A decryption exponent is given by a solution to

103d≡1 (mod 2035800).

The solution is d≡810367 (mod 2035800).

m103 ≡317730 (mod 2038667).

Raising both sides to the dth power, where d= 810367 is her decryption

exponent, yields

m≡317730810367 ≡514407 (mod 2038667).

Exercises for Chapter 3 65

3.7. Bob’s RSA public key has modulus N= 12191 and exponent e= 37.

Alice sends Bob the ciphertext c= 587. Unfortunately, Bob has chosen too

small a modulus. Help Eve by factoring Nand decrypting Alice’s message.

(Hint.Nhas a factor smaller than 100.)

Solution to Exercise 3.7.

The modulus factors as N= 12191 = 73 ·167, so φ(N) = 72 ·168 = 11952.

The congruence

37d≡1 (mod 11952)

has solution d≡11629 (mod 11952). Then

m≡58711629 ≡4894 (mod 12191)

is a solution to m37 ≡587 (mod 12191).

It is possible to be a bit more eﬃcient, using the fact that g= gcd(72,166) =

2 and (72)(166)/2 = 5976. Thus a solution to the congruence

37d≡1 (mod 5976)

is a decryption exponent, giving the smaller decryption exponent d≡5653

(mod 5976). Of course, this gives the same plaintext

m≡5875653 ≡4894 (mod 12191).

3.8. For each of the given values of N=pq and (p−1)(q−1), use the method

described in Remark 3.10 to determine pand q.

(a) N=pq = 352717 and (p−1)(q−1) = 351520.

(b) N=pq = 77083921 and (p−1)(q−1) = 77066212.

(d) N=pq = 172205490419 and (p−1)(q−1) = 172204660344.

Solution to Exercise 3.8.

(a) Suppose that N=pq = 352717 and (p−1)(q−1) = 351520. Then

p+q=N+ 1 −(p−1)(q−1) = 1198, so

X2−(p+q)X+N=X2−1198X+ 352717 = (X−677)(X−521).

Hence N= 352717 = 677 ·521.

(b) Suppose that N=pq = 77083921 and (p−1)(q−1) = 77066212. Then

p+q=N+ 1 −(p−1)(q−1) = 17710, so

X2−(p+q)X+N=X2−17710X+ 77083921 = (X−10007)(X−7703).

Hence N= 77083921 = 10007 ·7703.

p+q=N+ 1 −(p−1)(q−1) = 23550, so

66 Exercises for Chapter 3

X2−(p+q)X+N=X2−23550X+ 109404161 = (X−6367)(X−17183).

Hence N= 109404161 = 6367 ·17183.

(d) Suppose that N=pq = 172205490419 and (p−1)(q−1) = 172204660344.

Then p+q=N+ 1 −(p−1)(q−1) = 830076, so

X2−(p+q)X+N=X2−830076X+172205490419 = (X−407893)(X−422183).

Hence N= 172205490419 = 407893 ·422183.

3.9. Adecryption exponent for an RSA public key (N, e) is an integer dwith

the property that ade ≡a(mod N) for all integers athat are relatively prime

to N.

(a) Suppose that Eve has a magic box that creates decryption exponents

for (N, e) for a ﬁxed modulus Nand for a large number of diﬀerent

encryption exponents e. Explain how Eve can use her magic box to try

to factor N.

(b) Let N= 38749709. Eve’s magic box tells her that the encryption ex-

ponent e= 10988423 has decryption exponent d= 16784693 and

that the encryption exponent e= 25910155 has decryption exponent

d= 11514115. Use this information to factor N.

tion/decryption pairs for N:

(70583995,4911157),(173111957,7346999),(180311381,29597249).

Use this information to factor N.

(d) Let N= 1291233941. Eve’s magic box tells her the following three en-

cryption/decryption pairs for N:

(1103927639,76923209),(1022313977,106791263),(387632407,7764043).

Use this information to factor N.

Solution to Exercise 3.9.

Let e1, e2, . . . , enbe a bunch of random encryption exponents, and suppose

that Eve uses her magic box to create decryption exponents d1, d2, . . . , dn.

The numbers Kwith the property that aK≡a(mod N) for all asatisfying

gcd(a, N) = 1 are numbers satisfying

K≡1µmod (p−1)(q−1)

gcd(p−1, q −1)¶.

Thus diei−1 is a multiple of (p−1)(q−1)/gcd(p−1, q −1) for all 1 ≤i≤n.

Assuming that the ei’s are reasonably random, Eve will ﬁnd that

T= gcd(d1e1−1, d2e2−1, d3e3−1, . . . , dnen−1) (3.1)

Exercises for Chapter 3 67

is equal to a small multiple of

(p−1)(q−1)

gcd(p−1, q −1).

Next Eve uses the fact that gcd(p−1, q −1) is even and tends to be fairly

small. So she ﬁrst assumes that T= (p−1)(q−1)/2 and uses this to compute

R=N+ 1 −(p−1)(q−1) = N+ 1 −2T. If she is right about the value of T,

then Rwill equal p+q, and she can recover pand qby factoring x2−T x+N. If

this doesn’t work, she repeats the process with R=N+1−3T,R=N+1−4T,

etc. Continuing in this fashion, she should recover pand qfairly quickly.

Eve can save a bit of time in ﬁnding the right multiple of T. The idea is

that N+ 1 −kT should equal p+q, and in practice pand qwill have more or

less the same order of magnitude. So Eve wants N+ 1 −kT ≈2√N, which

means that she should take k≈(N+ 1 −2√N)/T .

(b)

gcd(16784693 ·10988423 −1,11514115 ·25910155 −1)

= gcd(184437306609138,298332504337824)

= 19368558

First Eve tries N+ 1 −1·gcd = 19381152, but x2−19381152x+ 38749709

is irreducible. Next she tries N+ 1 −2·gcd = 12594, and this time she ﬁnds

that x2−12594x+ 38749709 = (x−7247)(x−5347). Hence N= 38749709 =

7247 ·5347.

(c)

gcd(4911157 ·70583995 −1,7346999 ·173111957 −1,

29597249 ·180311381 −1)

= gcd(346649081132214,1271853374967042,5336720840990868)

= 37498566

Eve computes (√225022969 −1)2/37498566 ≈6.00004193, which suggests

that she should try N+ 1 −6·gcd = 31574. This given

x2−31574x+ 225022969 = (x−20707)(x−10867).

Hence N= 225022969 = 20707 ·10867.

(d)

gcd(76923209 ·1103927639 −1,106791263 ·1022313977 −1,

7764043 ·387632407 −1)

= gcd(84917656495673550,109174200786382950,3009594676141500)

= 129112350

68 Exercises for Chapter 3

Eve computes (√1291233941 −1)2/129112350 ≈10.0002987, which suggests

that she should use N+ 1 −10 ·gcd = 110442. This yields

x2−110442x+ 1291233941 = (x−97151)(x−13291).

Hence N= 1291233941 = 97151 ·13291.

3.10. Here is an example of a public key system that was proposed at a

cryptography conference. It is supposed to be faster and more eﬃcient than

RSA.

Alice chooses two large primes pand qand she publishes N=pq. It is as-

sumed that Nis hard to factor. Alice also chooses three random numbers g,r1,

and r2modulo Nand computes

g1≡gr1(p−1) (mod N) and g2≡gr2(q−1) (mod N).

Her public key is the triple (N, g1, g2) and her private key is the pair of

primes (p, q).

Now Bob wants to send the message mto Alice, where mis a number

modulo N. He chooses two random integers s1and s2modulo Nand computes

c1=≡mgs1

1(mod N) and c2≡mgs2

2(mod N).

Bob sends the ciphertext (c1, c2) to Alice.

Decryption is extremely fast and easy. Alice use the Chinese remainder

theorem to solve the pair of congruences

x≡c1(mod p) and x≡c2(mod q).

(a) Prove that Alice’s solution xis equal to Bob’s plaintext m.

(b) Explain why this cryptosystem is not secure.

Solution to Exercise 3.10.

(a) Notice that

c1≡mgs1

1≡mgs1r1(p−1) ≡m(mod p)

by Fermat’s little theorem, and similarly c2≡m(mod q). Hence Alice’s

solutions satisﬁes x≡m(mod pq).

(b) As in (a), we observe that g1≡1 (mod p) from Fermat’s little theorem.

On the other hand, most likely g16≡ 1 (mod q). So Eve can recover pfrom

the trivial gcd computation

gcd(g1−1, N) = p.

(If, by some rare coincidence, g1≡1 (mod q), then c1≡m(mod N), so

although Eve cannot factor N, she can read Bob’s message.)

Section. Implementation and security issues

Exercises for Chapter 3 69

3.11. Formulate a man-in-the-middle attack, similar to the attack described

in Example 3.12 on page 122, for the following public key cryptosystems.

(a) The ElGamal public key cryptosystem (Table 2.3 on page 70).

(b) The RSA public key cryptosystem (Table 3.1 on page 119).

Solution to Exercise 3.11.

A solution for this exercise is not currently available.

3.12. Alice decides to use RSA with the public key N= 1889570071. In

order to guard against transmission errors, Alice has Bob encrypt his message

twice, once using the encryption exponent e1= 1021763679 and once using

the encryption exponent e2= 519424709. Eve intercepts the two encrypted

messages

c1= 1244183534 and c2= 732959706.

Assuming that Eve also knows Nand the two encryption exponents e1and e2,

use the method described in Example 3.14 to help Eve recover Bob’s plaintext

without ﬁnding a factorization of N.

Solution to Exercise 3.12.

With notation as in Example 3.14, we ﬁnd that

u·c1+v·c2= 1

with

u= 252426389 and v=−496549570.

Then the plaintext is

m≡cu

1·cv

2≡1054592380 (mod N).

Section. Primality testing

3.13. We stated that the number 561 is a Carmichael number, but we never

checked that a561 ≡a(mod 561) for every value of a.

(a) The number 561 factors as 3 ·11 ·17. First use Fermat’s little theorem to

prove that

a561 ≡a(mod 3), a561 ≡a(mod 11),and a561 ≡a(mod 17)

for every value of a. Then explain why these three congruences imply that

a561 ≡a(mod 561) for every value of a.

(b) Mimic the idea used in (a) to prove that each of the following numbers is

a Carmichael number. (To assist you, we have factored each number into

primes.)

(i) 1729 = 7 ·13 ·19

(ii) 10585 = 5 ·29 ·73

70 Exercises for Chapter 3

(iii) 75361 = 11 ·13 ·17 ·31

(iv) 1024651 = 19 ·199 ·271

(d) Prove that a Carmichael number must be a product of distinct primes.

(e) Look up Korselt’s criterion in a book or online, write a brief description of

how it works, and use it to show that 29341 = 13·37·61 and 172947529 =

307 ·613 ·919 are Carmichael numbers.

Solution to Exercise 3.13.

A solution for this exercise is not currently available.

Here is a list of all Carmichael up to 100000, plus a few others.

•561 = 3 ·11 ·17

•1105 = 5 ·13 ·17

•1729 = 7 ·13 ·19

•2465 = 5 ·17 ·29

•2821 = 7 ·13 ·31

•6601 = 7 ·23 ·41

•8911 = 7 ·19 ·67

•10585 = 5 ·29 ·73

•15841 = 7 ·31 ·73

•29341 = 13 ·37 ·61

•41041 = 7 ·11 ·13 ·41

•46657 = 13 ·37 ·97

•52633 = 7 ·73 ·103

•62745 = 3 ·5·47 ·89

•63973 = 7 ·13 ·19 ·37

•75361 = 11 ·13 ·17 ·31

•294409 = 37 ·73 ·109

•56052361 = 211 ·421 ·631

•118901521 = 271 ·541 ·811

•172947529 = 307 ·613 ·919

Exercises for Chapter 3 71

•1024651 = 19 ·199 ·271

3.14. Use the Miller–Rabin test on each of the following numbers. In each

case, either provide a Miller–Rabin witness for the compositeness of n, or

conclude that nis probably prime by providing 10 numbers that are not

Miller–Rabin witnesses for n.

(a) n= 1105. (Yes, 5 divides n, but this is just a warm-up exercise!)

(b) n= 294409 (c) n= 294409

(d) n= 118901509 (e) n= 118901521

(f) n= 118901527 (g) n= 118915387

Solution to Exercise 3.14.

(a) n−1 = 1104 = 24·69.

269 ≡ −138 (mod 1105)

22·69 ≡259 (mod 1105)

24·69 ≡ −324 (mod 1105)

28·69 ≡1 (mod 1105)

Thus 1105 is composite. It factors as n= 5 ·13 ·17.

(b) n−1 = 294408 = 23·36801.

236801 ≡512 (mod 294409)

22·36801 ≡ −32265 (mod 294409)

24·36801 ≡1 (mod 294409)

Thus 294409 is composite. It factors as n= 37 ·73 ·109.

2147219 ≡1 (mod 294439)

3147219 ≡ −1 (mod 294439)

5147219 ≡1 (mod 294439)

Thus 2, 3, 5 are not Miller–Rabin witnesses for 294439. It turns out that

294439 is prime.

(d) n−1 = 118901508 = 22·29725377.

72 Exercises for Chapter 3

229725377 ≡7906806 (mod 118901509)

22·29725377 ≡ −1 (mod 118901509)

329725377 ≡ −1 (mod 118901509)

32·29725377 ≡1 (mod 118901509)

529725377 ≡ −1 (mod 118901509)

52·29725377 ≡1 (mod 118901509)

729725377 ≡7906806 (mod 118901509)

72·29725377 ≡ −1 (mod 118901509)

1129725377 ≡ −1 (mod 118901509)

112·29725377 ≡1 (mod 118901509)

Thus 2, 3, 5, 7, and 11 are not Miller–Rabin witnesses for 118901509. It turns

out that 118901509 is prime.

(e) n−1 = 118901520 = 24·7431345

27431345 ≡45274074 (mod 118901521)

22·7431345 ≡1758249 (mod 118901521)

24·7431345 ≡1 (mod 118901521)

28·7431345 ≡1 (mod 118901521)

Thus 118901521 is composite. It factors as 118901521 = 271 ·541 ·811.

(f) n−1 = 118901526 = 21·59450763.

259450763 ≡1 (mod 118901527)

359450763 ≡ −1 (mod 118901527)

559450763 ≡ −1 (mod 118901527)

759450763 ≡1 (mod 118901527)

1159450763 ≡1 (mod 118901527)

Thus 2, 3, 5, 7, and 11 are not Miller–Rabin witnesses for 118901527. It turns

out that 118901527 is prime.

(g) n−1 = 118915386 = 21·59457693.

259457693 ≡ −5081012 (mod 118915387)

Thus 118915387 is composite. It factors as n= 6571 ·18097.

3.15. Looking back at Exercise 3.9, let’s suppose that for a given N, the magic

box can produce only one decryption exponent. Equivalently, suppose that an

RSA key pair has been compromised and that the private decryption exponent

corresponding to the public encryption exponent has been discovered. Show

how the basic idea in the Miller–Rabin primality test can be applied to use

this information to factor N.

Exercises for Chapter 3 73

Solution to Exercise 3.15.

We are given an encryption/decryption pair (e, d), which means that

ade ≡a(mod N) for all 1 ≤a < N.

So for most values of awe have ade−1≡1 (mod N). (This is true un-

less gcd(a, N)>1, in which case gcd(a, N ) is a nontrivial factor of N.) Using

the idea of the Miller–Rabin test, we factor

de = 2krwith rodd.

Then for random choices of a, we look at

ar, a2r, a4r, . . . , a2krmod N.

We know that the last entry in the list is 1.

Now suppose that Nfactors as pq, where we do not know pand q. We

choose a value for a. The Miller–Rabin test applied to ptells us that either

ar≡1 (mod p),or else a2ir≡ −1 (mod p) for some 0 ≤i < k.

(If the latter is true, we take ito be the smallest such value.) Note that we

do not know the value of i, because we do not know the value of p, but that’s

okay. Next we do the same thing with q. Thus the Miller–Rabin test tells us

that either

ar≡1 (mod q),or else a2jr≡ −1 (mod p) for some 0 ≤j < k,

where again we choose the smallest such j.

We now consider several cases. If ar≡1 (mod p) and αr6≡ 1 (mod q),

then we recover pby computing

gcd(N, ar−1) = p.

Similarly, if ar6≡ 1 (mod p) and αr≡1 (mod q), then gcd(N, ar−1) = q, so

again we win. On the other hand, if ar≡1 (mod N), then we get no useful

information, so we need to go try a diﬀerent value for a.

In the remaining cases we have ar6≡ 1 (mod p) and αr6≡ 1 (mod q).

Suppose that iand jare diﬀerent, say i < j. Then

a2ir≡ −1 (mod p) and a2ir6≡ −1 (mod q),

So computing gcd(N, a2ir+1) = precovers p. A similar method works if j < i.

And ﬁnally, if i=j, then we get no useful information and need to try a

diﬀerent value for a.

We can summarize the above solution as the following algorithm:

1. Choose a random value 1 < a < N .

74 Exercises for Chapter 3

2. Compute gcd(a, N). If it is not equal to 1, then it is a nontrivial factor

of N.

3. Let (e, d) be the encryption/decryption pair. Factor de −1 = 2krwith r

odd.

4. Compute gcd(N, ar−1). If it is a nontrivial factor of N, you’re are done.

5. For each 0 ≤i < k, compute gcd(N, a2ir+ 1). If it is a nontrivial factor

of N, you’re done.

6. If you haven’t found a factor of N, go back to Step 1 and choose a new

value of a.

3.16. The function π(X) counts the number of primes between 2 and X.

(a) Compute the values of π(20), π(30), and π(100).

(b) Write a program to compute π(X) and use it to compute π(X) and

the ratio π(X)/(X/ ln(X)) for X= 100, X= 1000, X= 10000, and

X= 100000. Does your list of ratios make the prime number theorem

plausible?

Solution to Exercise 3.16.

X π(X)π(X)/(X/ ln(X)

10 4 0.921

20 8 1.198

30 10 1.134

100 25 1.151

1000 168 1.161

10000 1229 1.132

100000 9592 1.104

1000000 78498 1.084

3.17. Let

π1(X) = (# of primes pbetween 2 and Xsatisfying p≡1 (mod 4)),

π3(X) = (# of primes pbetween 2 and Xsatisfying p≡3 (mod 4)).

Thus every prime other than 2 gets counted by either π1(X) or by π3(X).

(a) Compute the values of π1(X) and π3(X) for each of the following values

of X. (i) X= 10. (ii) X= 25. (iii) X= 100.

(b) Write a program to compute π1(X) and π3(X) and use it to compute their

values and the ratio π3(X)/π1(X) for X= 100, X= 1000, X= 10000,

and X= 100000.

of π1(X) and π3(X). Which one do you think is larger? What do you

think is the limit of the ratio π3(X)/π1(X) as X→ ∞?

Solution to Exercise 3.17.

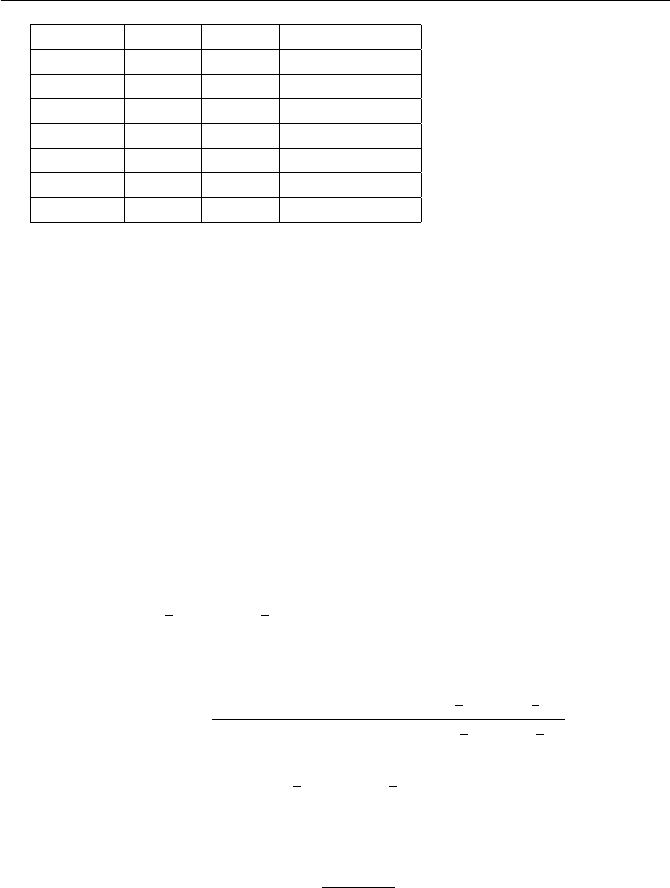
Exercises for Chapter 3 75

X π1(X)π3(X)π3(X)/π1(X)

10 1 2 2.0000

25 3 5 1.6667

100 11 13 1.1818

1000 80 87 1.0875

10000 609 619 1.0164

100000 4783 4808 1.0052

1000000 39175 39322 1.0038

actually false, but the ﬁrst Xfor which the inequality is reversed is ex-

tremely large. In any case, the ratio satisﬁes limX→∞ π3(X)/π1(X) = 1.

This is a special case of Dirichlet’s theorem on primes in arithmetic pro-

gressions, which says the following. Let gcd(a, N) = 1 and let πa,N (X) be

the number of primes pbetween 2 and Xsatisfying p≡a(mod N). Then

limX→∞ πa,N (X)/π(X) = 1/φ(N).

3.18. We noted in Section 3.4 that it really makes no sense to say that the

number nhas probability 1/ln(n) of being prime. Any particular number that

you choose either will be prime or will not be prime; there are no numbers

that are 35% prime and 65% composite! In this exercise you will prove a

result that gives a more sensible meaning to the statement that a number has

a certain probability of being prime. You may use the prime number theorem

(Theorem 3.20) for this problem.

(a) Fix a (large) number Nand suppose that Bob chooses a random number n

in the interval 1

2N≤n≤3

2N. If he repeats this process many times, prove

that approximately 1/ln(N) of his numbers will be prime. More precisely,

deﬁne

P(N) = number of primes between 1

2Nand 3

number of integers between 1

2Nand 3

="Probability that an integer nin the

interval 1

2N≤n≤3

2Nis a prime num-

ber #,

and prove that

lim

N→∞

P(N)

1/ln(N)= 1.

This shows that if Nis large, then P(N) is approximately 1/ln(N).

(b) More generally, ﬁx two numbers c1and c2satisfying c1< c2. Bob chooses

random numbers nin the interval c1N≤n≤c2N. Keeping c1and c2

ﬁxed, let

P(c1, c2;N) = "Probability that an integer nin the in-

terval c1N≤n≤c2Nis a prime num-

ber #.

76 Exercises for Chapter 3

In the following formula, ﬁll in the box with a simple function of Nso

that the statement is true:

lim

N→∞

P(c1, c2;N)= 1.

Solution to Exercise 3.18.

We will just write P(N), instead of P(c1, c2;N).

P(N) = # of primes between c1Nand c2N

=π(c2N)−π(c2N)

=c2

ln(c2N)−c1

ln(c1N)+oµ1

ln(N)¶from the prime number theorem

=(c2−c1) ln(N) + O(1)

ln(c1N) ln(c2N)+oµ1

ln(N)¶

=c2−c1

ln(N)+oµ1

ln(N)¶

Hence P(N) divided by (c2−c1)/ln(N) goes to 1 as N→ ∞, or equivalently,

lim

N→∞

P(N)

ln(N)=c2−c1.

For part (a), we have c1=1

2and c2=3

2, so the limit is 1.

3.19. Continuing with the previous exercise, explain how to make mathemat-

ical sense of the following statements.

(a) A randomly chosen odd number Nhas probability 2/ln(N) of being

prime. (What is the probability that a randomly chosen even number is

prime?)

(b) A randomly chosen number Nsatisfying N≡1 (mod 3) has probability

3/(2 ln(N)) of being prime.

3/ln(N) of being prime.

(d) Let m=p1p2···prbe a product of distinct primes and let kbe a number

satisfying gcd(k, m) = 1. What number should go into the box to make

statement (3.35) correct? Why?

A randomly chosen number Nsatisfying

N≡k(mod m) has probabil-

ity /ln(N) of being prime.

(3.2)

(e) Same question, but for arbitrary m, not just for mthat are products of

distinct primes.

Exercises for Chapter 3 77

Solution to Exercise 3.19.

(a,b,c) A solution for this exercise is not currently available.

(d) If m=p1···pr, then the probability that N≡k(mod m) is prime is

approximately r

i=1 µpi

pi−1¶·1

ln(N).

(e) More generally, for arbitrary mand ksatisfying gcd(m, k) = 1, the prob-

ability that N≡k(mod m) is prime is approximately

p|mµp

p−1¶·1

ln(N).

This is often written as

p|mµ1−1

p¶−1

·1

ln(N),

which is also equal to N/(φ(N) ln(N)), where φ(N) is Euler’s phi function.

3.20. The logarithmic integral function Li(X) is deﬁned to be

Li(X) = ZX

ln t.

(a) Prove that

Li(X) = X

ln X+ZX

(ln t)2+O(1).

(Hint. Integration by parts.)

(b) Compute the limit

lim

X→∞

Li(X)

X/ ln X.

(Hint. Break the integral in (a) into two pieces, 2 ≤t≤√Xand √X≤

t≤X, and estimate each piece separately.)

theorem (Theorem 3.20).

Solution to Exercise 3.20.

A solution for this exercise is not currently available.

Section. Pollard’s p−1factorization algorithm

3.21. Use Pollard’s p−1 method to factor each of the following numbers.

(a) n= 1739 (b) n= 220459 (c) n= 48356747

78 Exercises for Chapter 3

Be sure to show your work and to indicate which prime factor pof nhas the

property that p−1 is a product of small primes.

Solution to Exercise 3.21.

(a)

23! −1≡63 (mod 1739) gcd(23! −1,1739) = 1

24! −1≡1082 (mod 1739) gcd(24! −1,1739) = 1

25! −1≡1394 (mod 1739) gcd(25! −1,1739) = 1

26! −1≡1443 (mod 1739) gcd(26! −1,1739) = 37

This give 1739 = 37 ·47. Note that p−1 = 36 = 22·32and q−1 = 46 = 2 ·23.

(b)

23! −1≡63 (mod 220459) gcd(23! −1,220459) = 1

24! −1≡22331 (mod 220459) gcd(24! −1,220459) = 1

25! −1≡85053 (mod 220459) gcd(25! −1,220459) = 1

26! −1≡4045 (mod 220459) gcd(26! −1,220459) = 1

27! −1≡43102 (mod 220459) gcd(27! −1,220459) = 1

28! −1≡179600 (mod 220459) gcd(28! −1,220459) = 449

This gives 220459 = 449 ·491. Note that p−1 = 448 = 26·7 and q−1 =

490 = 2 ·5·72.

(c)

215! −1≡46983890 (mod 48356747) gcd(215! −1,48356747) = 1

216! −1≡8398520 (mod 48356747) gcd(216! −1,48356747) = 1

217! −1≡9367159 (mod 48356747) gcd(217! −1,48356747) = 1

218! −1≡17907955 (mod 48356747) gcd(218! −1,48356747) = 1

219! −1≡13944672 (mod 48356747) gcd(219! −1,48356747) = 6917

This gives 48356747 = 6917 ·6991. Note that p−1 = 6916 = 22·7·13 ·19 and

q−1 = 6990 = 2 ·3·5·233.

3.22. A prime of the form 2n−1 is called a Mersenne prime.

(a) Factor each of the numbers 2n−1 for n= 2,3, . . . , 10. Which ones are

Mersenne primes?

(b) Find the ﬁrst seven Mersenne primes. (You may need a computer.)

(d) If 3 |nand n > 3, prove that 2n−1 is not prime.

(e) More generally, prove that if nis a composite number, then 2n−1 is not

prime. Thus all Mersenne primes have the form 2p−1 with pa prime

number.

Exercises for Chapter 3 79

(f) What is the largest known Mersenne prime? Are there any larger primes

known? (You can ﬁnd out at the “Great Internet Mersenne Prime Search”

web site www.mersenne.org/prime.htm.)

(g) Write a one page essay on Mersenne primes, starting with the discoveries

of Father Mersenne and ending with GIMPS.

Solution to Exercise 3.22.

The factorization of 2n−1 for 2 ≤n≤20 is

22−1=3=3

23−1=7=7

24−1 = 15 = 3 ·5

25−1 = 31 = 31

26−1 = 63 = 32·7

27−1 = 127 = 127

28−1 = 255 = 3 ·5·17

29−1 = 511 = 7 ·73

210 −1 = 1023 = 3 ·11 ·31

211 −1 = 2047 = 23 ·89

212 −1 = 4095 = 32·5·7·13

213 −1 = 8191 = 8191

214 −1 = 16383 = 3 ·43 ·127

215 −1 = 32767 = 7 ·31 ·151

216 −1 = 65535 = 3 ·5·17 ·257

217 −1 = 131071 = 131071

218 −1 = 262143 = 33·7·19 ·73

219 −1 = 524287 = 524287

220 −1 = 1048575 = 3 ·52·11 ·31 ·41

Thus the ﬁrst few Mersenne primes are

22−1=3,23−1 = 7,25−1 = 31,27−1 = 127,

213 −1 = 8191,217 −1 = 131071,219 −1 = 524287.

Notice that 2p−1 is prime for all primes p < 20 except for p= 11. However,

this is somewhat misleading. For the primes 20 < p < 40, only 231 −1 yields

a Mersenne prime.

223 −1 = 8388607 = 47 ·178481

229 −1 = 536870911 = 233 ·1103 ·2089

231 −1 = 2147483647 = 2147483647

237 −1 = 137438953471 = 223 ·616318177

241 −1 = 2199023255551 = 13367 ·164511353

243 −1 = 8796093022207 = 431 ·9719 ·2099863

247 −1 = 140737488355327 = 2351 ·4513 ·13264529

2n−1 is composite unless 2m−1 = 1, i.e. unless m= 1 and n= 2.

80 Exercises for Chapter 3

(d) Similarly, 23m−1 = (2m−1)(22m+ 2m+ 1), so it is composite unless

m= 1.

(e) More generally,

2km −1 = (2m−1)(2(k−1)m+ 2(k−2)m+··· + 22m+ 2m+ 1),

so 2km −1 is composite unless m= 1 or k= 1. Notice that what we are really

doing is using the standard identity

xk−1 = (x−1)(x(k−1) +x(k−2) +··· +x2+x+ 1)

with x= 2m.

(f) As of January 2008, the largest known Mersenne prime is 232582657 −1,

which was discovered in September 2006 as part of the GIMPS project.

Exercises for Chapter 3 81

Section. Factorization via diﬀerence of squares

3.23. For each of the following numbers N, compute the values of

N+ 12, N + 22, N + 32, N + 42, . . .

as we did in Example 3.33 until you ﬁnd a value N+b2that is a perfect

square a2. Then use the values of aand bto factor N.

(a) N= 53357 (b) N= 34571 (c) N= 25777 (d) N= 64213

Solution to Exercise 3.23.

(a)

53357 + 12= 53358 not a square,

53357 + 22= 53361 = 2312** square **.

Thus

53357 = 2312−22= (231 + 2)(231 −2) = 233 ·229.

(b)

34571 + 12= 34572 not a square,

34571 + 22= 34575 not a square,

34571 + 32= 34580 not a square,

34571 + 42= 34587 not a square,

34571 + 52= 34596 = 1862** square **.

Thus

34571 = 1862−52= (186 + 5)(186 −5) = 191 ·181.

(c)

25777 + 12= 25778 not a square

25777 + 22= 25781 not a square

25777 + 32= 25786 not a square

25777 + 42= 25793 not a square

25777 + 52= 25802 not a square

25777 + 62= 25813 not a square

25777 + 72= 25826 not a square

25777 + 82= 25841 not a square

25777 + 92= 25858 not a square

25777 + 102= 25877 not a square

25777 + 112= 25898 not a square

25777 + 122= 25921 = 1612** square **

82 Exercises for Chapter 3

Thus

25777 = 1612−122= (161 + 12)(161 −12) = 173 ·149.

(d) Most people will give up before ﬁnishing this one unless they write a

computer program! It is included to make people aware that this method

doesn’t always work.

64213 + 12= 64214 not a square

64213 + 22= 64217 not a square

64213 + 32= 64222 not a square

64213 + 42= 64229 not a square

64213 + 1212= 78854 not a square

64213 + 1222= 79097 not a square

64213 + 1232= 79342 not a square

64213 + 1242= 79589 not a square

64213 + 1252= 79838 not a square

64213 + 1262= 80089 = 2832** square **

Thus

64213 = 2832−1262= (283 + 126)(283 −126) = 409 ·157.

3.24. For each of the listed values of N,k, and binit, factor Nby making

a list of values of k·N+b2, starting at b=binit and incrementing buntil

k·N+b2is a perfect square. Then take greatest common divisors as we did

in Example 3.34.

(a) N= 143041 k= 247 binit = 1

(b) N= 1226987 k= 3 binit = 36

Solution to Exercise 3.24.

(a)

247 ·143041 + 12= 35331128 not a square

247 ·143041 + 22= 35331131 not a square

247 ·143041 + 32= 35331136 = 59442** square **

Thus

247 ·143041 = 59442−32= (5944 + 3)(5944 −3) = 5947 ·5941.

Exercises for Chapter 3 83

gcd(143041,5947) = 313,gcd(143041,5941) = 457

(b)

3·1226987 + 362= 3682257 not a square

3·1226987 + 372= 3682330 not a square

3·1226987 + 382= 3682405 not a square

3·1226987 + 392= 3682482 not a square

3·1226987 + 402= 3682561 = 19192** square **

Thus

3·1226987 = 19192−402= (1919 + 40)(1919 −40) = 1959 ·1879.

gcd(1226987,1959) = 653,gcd(1226987,1879) = 1879

(c)

21 ·2510839 + 902= 52735719 not a square

21 ·2510839 + 912= 52735900 not a square

21 ·2510839 + 922= 52736083 not a square

21 ·2510839 + 932= 52736268 not a square

21 ·2510839 + 942= 52736455 not a square

21 ·2510839 + 952= 52736644 = 72622** square **

Thus

21 ·2510839 = 72622−952= (7262 + 95)(7262 −95) = 7357 ·7167.

gcd(2510839,7357) = 1051,gcd(2510839,7167) = 2389

3.25. For each part, use the data provided to ﬁnd values of aand bsatisfying

a2≡b2(mod N), and then compute gcd(N, a −b) in order to ﬁnd a nontrivial

factor of N, as we did in Examples 3.36 and 3.37.

(a) N= 61063

18822≡270 (mod 61063) and 270 = 2 ·33·5

18982≡60750 (mod 61063) and 60750 = 2 ·35·53

(b) N= 52907

3992≡480 (mod 52907) and 480 = 25·3·5

7632≡192 (mod 52907) and 192 = 26·3

7732≡15552 (mod 52907) and 15552 = 26·35

9762≡250 (mod 52907) and 250 = 2 ·53

84 Exercises for Chapter 3

11892≡27000 (mod 198103) and 27000 = 23·33·53

16052≡686 (mod 198103) and 686 = 2 ·73

23782≡108000 (mod 198103) and 108000 = 25·33·53

28152≡105 (mod 198103) and 105 = 3 ·5·7

(d) N= 2525891

15912≡5390 (mod 2525891) and 5390 = 2 ·5·72·11

31822≡21560 (mod 2525891) and 21560 = 23·5·72·11

47732≡48510 (mod 2525891) and 48510 = 2 ·32·5·72·11

52752≡40824 (mod 2525891) and 40824 = 23·36·7

54012≡1386000 (mod 2525891) and 1386000 = 24·32·53·7·11

Solution to Exercise 3.25.

(a)

18822·18982≡(2 ·33·5)(2 ·35·53) (mod 61063)

= (2 ·34·52)2

= 40502

gcd(61063,1882 ·1898 −4050) = 227 Eureka!

(b) The most natural combination to try ﬁrst is

7632·7732≡(26·3)(26·35) (mod 52907)

= (26·33)2

= 17282

gcd(52907,763 ·773 −1728) = 277 Eureka!

So this works. However, if instead we use

3992·7632·9762≡(25·3·5)(26·3)(2 ·53) (mod 52907)

= (26·3·52)2

= 48002,

then we do not win, since

gcd(52907,399 ·763 ·976 −4800) = 52907 No help

Exercises for Chapter 3 85

11892·23782≡(23·33·53)(25·33·53) (mod 198103)

= (24·33·53)2

= 540002

gcd(198103,1189 ·2378 −54000) = 198103 No help

This didn’t work, so next we try

11892·16052·28152≡(23·33·53)(2 ·73)(3 ·5·7) (mod 198103)

= (22·32·52·72)2

= 441002

gcd(198103,1189 ·1605 ·2815 −44100) = 499 Eureka!

(d) First we try

15912·31822≡(2 ·5·72·11)(23·5·72·11) (mod 2525891)

= (22·5·72·11)2

= 107802

gcd(2525891,1591 ·3182 −10780) = 2525891 No help

Next we try

15912·47732≡(2 ·5·72·11)(2 ·32·5·72·11) (mod 2525891)

= (2 ·3·5·72·11)2

= 161702

gcd(2525891,1591 ·4773 −16170) = 2525891 No help

Finally we win when we try

15912·52752·54012

≡(2 ·5·72·11)(23·36·7)(24·32·53·7·11) (mod 2525891)

= (24·34·52·72·11)2

= 174636002

gcd(2525891,1591 ·5275 ·5401 −17463600) = 1637 Eureka!

Section. Smooth numbers, sieves, and building relations for factorization

3.26. Compute the following values of ψ(X, B), the number of B-smooth

numbers between 2 and X(see page 146).

(a) ψ(25,3) (b) ψ(35,5) (c) ψ(50,7) (d) ψ(100,5)

(e) ψ(100,7)

86 Exercises for Chapter 3

Solution to Exercise 3.26.

(a) ψ(25,3) = 10

(b) ψ(35,5) = 18

(d) ψ(100,5) = 33

(e) ψ(100,7) = 45

3.27. An integer Mis called B-power-smooth if every prime power pedi-

viding Msatisﬁes pe≤B. For example, 180 = 22·32·5 is 10-power-smooth,

since the largest prime power dividing 180 is 9, which is smaller than 10.

(a) Suppose that Mis B-power-smooth. Prove that Mis also B-smooth.

(b) Suppose that Mis B-smooth. Is it always true that Mis also B-power-

smooth? Either prove that it is true or give an example for which it is

not true.

sorted from smallest to largest. Which of these numbers are 10-power-

smooth? Which of them are 10-smooth?

{84,141,171,208,224,318,325,366,378,390,420,440,

504,530,707,726,758,765,792,817}

(d) Prove that Mis B-power-smooth if and only if Mdivides the least com-

mon multiple of [1,2, . . . , B]. (The least common multiple of a list of

numbers k1, . . . , kris the smallest number Kthat is divisible by every

number in the list.)

Solution to Exercise 3.27.

(a,b,d) A solution for this exercise is not currently available.

10-power-smooth. They are also 10-smooth, of course, as are the additional

numbers 224 = 25·7 and 378 = 2 ·33·7.

3.28. Let L(N) = e√(ln N)(ln ln N)as usual. Suppose that a computer does

one billion operations per second.

(a) How many seconds does it take to perform L(2100) operations?

(b) How many hours does it take to perform L(2250) operations?

(d) How many years does it take to perform L(2500) operations?

(e) How many years does it take to perform L(2750) operations?

(f) How many years does it take to perform L(21000) operations?

(g) How many years does it take to perform L(22000) operations?

(For simplicity, you may assume that there are 365.25 days in a year.)

Solution to Exercise 3.28.

(a) N= 2100 :L(N) = 224.73 steps takes 0.03 seconds.

(b) N= 2250 :L(N) = 243.12 steps takes 2.65 hours.

Exercises for Chapter 3 87

(d) N= 2500 :L(N) = 264.95 steps takes 1129.30 years.

(e) N= 2750 :L(N) = 282.26 steps takes 108.26 years.

(f) N= 21000 :L(N) = 297.14 steps takes 1012.74 years.

(g) N= 22000 :L(N) = 2144.48 steps takes 1026.99 years.

3.29. Prove that the function L(X) = e√(ln X)(ln ln X)is subexponential. That

is, prove the following two statements.

(a) For every positive constant α, no matter how large, L(X) = Ω¡(ln X)α¢.

(b) For every positive constant β, no matter how small, L(X) = O¡Xβ).

Solution to Exercise 3.29.

A solution for this exercise is not currently available.

3.30. For any ﬁxed positive constants aand b, deﬁne the function

Fa,b(X) = e(ln X)1/a (ln ln X)1/b .

Prove the following properties of Fa,b(X).

(a) If a > 1, prove that Fa,b(X) is subexponential.

(b) If a= 1, prove that Fa,b(X) is exponential.

Solution to Exercise 3.30.

A solution for this exercise is not currently available.

3.31. This exercise asks you to verify an assertion in the proof of Corol-

lary 3.44. Let L(X) be the usual function L(X) = e√(ln X)(ln ln X).

(a) Prove that there is a value of  > 0 such that

(ln X)²<ln L(X)<(ln X)1−²for all X > 10.

(b) Let c > 0, let Y=L(X)c, and let u= (ln X)/(ln Y). Prove that

u−u=L(X)−1

2c(1+o(1)).

Solution to Exercise 3.31.

(a) is clear, any  < 1

2will work.

(b) We ﬁrst compute

u=ln X

ln L(X)c=ln X

cp(ln X)(ln ln X)=1

crln X

ln ln X.

Then

88 Exercises for Chapter 3

uln u=1

crln X

ln ln Xln Ã1

crln X

ln ln X!

crln X

ln ln X·1

2ln ln X−1

2ln ln ln X−ln c¸

2c√ln Xln ln X¡1 + o(1)¢

2c¡ln L(X)¢¡1 + o(1)¢.

Hence

uu=L(X)1

2c(1+o(1)).

3.32. Proposition 3.47 assumes that we choose random numbers amodulo N,

compute a2(mod N), and check whether the result is B-smooth. We can

achieve better results if we take values for aof the form

a=¥√N¦+kfor 1 ≤k≤K.

(For simplicity, you may treat Kas a ﬁxed integer, independent of N. More

rigorously, it is necessary to take Kequal to a power of L(N), which has a

small eﬀect on the ﬁnal answer.)

(a) Prove that a2−N≤2K√N+K2, so in particular, a2(mod N) is smaller

than a multiple of √N.

(b) Prove that L(√N)≈L(N)1/√2by showing that

lim

N→∞

log L(√N)

log L(N)1/√2= 1.

More generally, prove that in the same sense, L(N1/r )≈L(N)1/√rfor

any ﬁxed r > 0.

B=L(N)cand ﬁnd the optimal value of c. Approximately how many

relations are needed to factor N?

Solution to Exercise 3.32.

(a) We have a=√N++kfor some 0 ≤ < 1. Hence a2−N=

2(+k)√N+ (+k)2≤2K√N+K2.

(b) A rough computation shows that

L(√N) = e√(ln √N)(ln ln √N)

=e√(1

2ln N)(ln 1

2ln N)

≈e√(1

2ln N)(ln ln N)=L(N)1/√2.

Exercises for Chapter 3 89

More precisely, we ﬁrst simplify

log L(N1/r)

log L(N)1/√r=√ln N1/r ln ln N1/r

(1/√r)√ln Nln ln N

=s(1/r)(ln N)(ln(1/r) + ln ln N)

(1/r)(ln N)(ln ln N)

=r−ln r

ln ln N+ 1.

It is clear that if ris ﬁxed, then this last expression goes to 1 as N→ ∞.

number that is approximately √Nis B-smooth is ψ(√N, B)/√N, and we

need approximately π(B) relations, so we need to check approximately

π(B)

ψ(√N, B)/√Nnumbers. (3.3)

We set B=L(√N)c, substitute into ??, and use Theorem ?? and the prime

number theorem (Theorem 3.20) to get (we ignore various lower-order log

terms)

π(L(√N)c)

ψ(√N, L(√N)c)/√N≈L(√N)c

L(√N)−1/2c≈L(N)1

√2(c+1

2c).

The exponent is minimized when c=1

√2, so we should take B=L(√N)1/√2≈

L(N)1/2and we need to check approximately L(N) numbers in order to fac-

tor N. Of course, our assumptions mean that this is an underestimate, but

this exercise suggests that without some signiﬁcant new idea, the running time

of this method will be at least O(L(N)).

3.33. Illustrate the quadratic sieve, as was done in Figure 3.3 (page 157), by

sieving prime powers up to Bon the values of F(T) = T2−Nin the indicated

range.

(a) Sieve N= 493 using prime powers up to B= 11 on values from F(23)

to F(38). Use the relation(s) that you ﬁnd to factor N.

(b) Extend the computations in (a) by using prime powers up to B= 16 and

sieving values from F(23) to F(50). What additional value(s) are sieved

down to 1 and what additional relation(s) do they yield?

Solution to Exercise 3.33.

(a) We sieve the following values, as illustrated in Table ??:

•The congruence t2≡493 ≡1 (mod 2) has solution t≡1 (mod 2), so we

sieve 2 from F(23), F(25), F(27),. . . .

90 Exercises for Chapter 3

•The congruence t2≡493 ≡1 (mod 3) has solutions t≡1 (mod 3) and

t≡2 (mod 3), so ﬁrst we sieve 3 from F(23), F(26), F(29),. . . , and

then we sieve 3 from F(25), F(28), F(31),. . . .

•The congruence t2≡493 ≡1 (mod 4) has solution t≡1 (mod 2), so we

sieve another 2 from F(23), F(25), F(27),. . . .

•The congruence t2≡493 ≡3 (mod 5) has no solutions.

•The congruence t2≡493 ≡3 (mod 7) has no solutions.

•The congruence t2≡493 ≡5 (mod 8) has no solutions.

•The congruence t2≡493 ≡7 (mod 9) has solutions t≡4 (mod 9) and

t≡5 (mod 9), so ﬁrst we sieve another 3 from F(31) and then we sieve

another 3 from F(23) and F(32).

•The congruence t2≡493 ≡9 (mod 11) has solutions t≡3 (mod 11)

and t≡8 (mod 11), so ﬁrst we sieve 11 from F(25) and F(36) and then

we sieve 11 from F(30).

The two values F(23) and F(25) have been sieved down to 1, yielding the

congruences

F(23) ≡36 ≡22·32(mod 493) and F(25) ≡132 ≡22·3·11 (mod 493).

Since F(23) is itself congruent to a square, we can compute

gcd(23 −2·3,493) = 17,

which gives the factorization 493 = 17 ·29.

(b) The ﬁrst step is to make Table ?? wider, i.e. sieve the values from F(23)

to F(50) using prime powers up to B= 11. The next step is to sieve out the

additional prime powers up to B= 16.

The congruence t2≡493 ≡12 (mod 13) has solutions t≡5 (mod 13)

and t≡8 (mod 13), so ﬁrst we sieve 13 from F(31) and F(44), and then we

sieve 13 from F(34) and F(47). The only other prime power up to B= 16

is 16, and the congruence t2≡493 ≡13 (mod 16) has no solutions (as indeed

it cannot, since we already noted that t2≡493 (mod 8) has no solutions).

We do not give the entire sieve table, but merely observe that two more

values have been sieved down to 1, namely

F(31) = 468 ≡22·32·13 (mod 493) and F(47) = 1716 ≡22·3·11·13 (mod 493).

Combining these with the earlier fully sieved values gives the relation

(25·31·47)2≡(22·3·11)·(22·32·13)·(22·3·11·13) ≡(23·32·11·13)3(mod 493).

Unfortunately,

gcd(25 ·31 ·47 −23·32·11 ·13,493) = gcd(26129,493) = 493,

so this relation does not give a factorization of 493.

Exercises for Chapter 3 91

23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

36 83 132 183 236 291 348 407 468 531 596 663 732 803 876 951

↓2↓2↓2↓2↓2↓2↓2↓2

18 83 66 183 118 291 174 407 234 531 298 663 366 803 438 951

↓3↓3↓3↓3↓3↓3

6 83 66 61 118 291 58 407 234 177 298 663 122 803 438 317

↓3↓3↓3↓3↓3

6 83 22 61 118 97 58 407 78 177 298 221 122 803 146 317

↓2↓2↓2↓2↓2↓2↓2↓2

3 83 11 61 59 97 29 407 39 177 149 221 61 803 73 317

↓3

3 83 11 61 59 97 29 407 13 177 149 221 61 803 73 317

↓3↓3

1 83 11 61 59 97 29 407 13 59 149 221 61 803 73 317

↓11 ↓11

1 83 1 61 59 97 29 407 13 59 149 221 61 73 73 317

↓11

1 83 1 61 59 97 29 37 13 59 149 221 61 73 73 317

Table 3.1: Sieving N= 493

3.34. Let Z[β] be the ring described in Example 3.54, i.e., βis a root of f(x) =

1+3x−2x3+x4. For each of the following pairs of elements u, v ∈Z[β],

compute the sum u+vand the product uv. Your answers should involve only

powers of βup to β3.

(a) u=−5−2β+ 9β2−9β3and v= 2 + 9β−7β2+ 7β3.

(b) u= 9 + 9β+ 6β2−5β3and v=−4−6β−2β2−5β3.

Solution to Exercise 3.34.

(a) u+v=−3+7β+ 2β2−2β3and uv = 148 + 425β+ 98β2−85β3.

(b) u+ 4 = 5 + 3β+ 4β2−10β3and uv =−69 −219β−211β2−88β3.

Section. The index calculus and discrete logarithms

3.35. This exercise asks you to use the index calculus to solve a discrete

logarithm problem. Let p= 19079 and g= 17.

(a) Verify that gi(mod p) is 5-smooth for each of the values i= 3030,

i= 6892, and i= 18312.

(b) Use your computations in (a) and linear algebra to compute the discrete

logarithms logg(2), logg(3), and logg(5). (Note that 19078 = 2 ·9539 and

that 9539 is prime.)

92 Exercises for Chapter 3

(d) Use the values from (b) and the computation in (c) to solve the discrete

logarithm problem

17x≡19 (mod 19079).

Solution to Exercise 3.35.

(a) We have

g3030 ≡22·36·5, g6892 ≡211 ·32, g18312 ≡24·3·53.

(b) We get the linear equations

3030 = 2x2+ 6x3+x5

6892 = 11x2+ 2x3

18312 = 4x2+x3+ 2x5

Solving modulo 2 and modulo 9539 gives

(x2, x3, x5)≡(0,0,0) (mod 2),

(x2, x3, x5)≡(8195,1299,7463) (mod 9539).

Hence

(x2, x3, x5)≡(17734,10838,17002) (mod 19079).

h·g−12224 ≡213 (mod 19079).

(d) Hence

logg(h) = 12224 + 13 ·logg(2) = 242766 ≡13830 (mod p−1).

We check that 1713830 ≡19 (mod 19079). X

Section. Quadratic residues and quadratic reciprocity

3.36. Let pbe an odd prime and let abe an integer with p-a.

(a) Prove that a(p−1)/2is congruent to either 1 or −1 modulo p.

(b) Prove that a(p−1)/2is congruent to 1 modulo pif and only if ais a

quadratic residue modulo p. (Hint. Let gbe a primitive root for pand

use the fact, proven during the course of proving Proposition 3.60, that gm

is a quadratic residue if and only if mis even.)

p¢(mod p). (This holds even if p|a.)

(d) Use (c) to prove Theorem 3.61(a), that is, prove that

µ−1

p¶=(1 if p≡1 (mod 4),

−1 if p≡3 (mod 4).

Solution to Exercise 3.36.

A solution for this exercise is not currently available.

Exercises for Chapter 3 93

3.37. Prove that the three parts of the quadratic reciprocity theorem (Theo-

rem 3.61) are equivalent to the following three concise formulas, where pand q

are odd primes:

(a) µ−1

p¶= (−1)p−1

2(b) µ2

p¶= (−1)p2−1

8(c) µp

q¶µq

p¶= (−1)p−1

2·q−1

Solution to Exercise 3.37.

A solution for this exercise is not currently available.

3.38. Let pbe a prime satisfying p≡3 (mod 4).

(a) Let abe a quadratic residue modulo p. Prove that the number

b≡ap+1

4(mod p)

has the property that b2≡a(mod p). (Hint. Write p+1

2as 1 + p−1

2and

use Exercise 3.36.) This gives an easy way to take square roots modulo p

for primes that are congruent to 3 modulo p.

(b) Use (a) to compute the following square roots modulo p. Be sure to check

your answers.

(i) Solve b2≡116 (mod 587).

(ii) Solve b2≡3217 (mod 8627).

(iii) Solve b2≡9109 (mod 10663).

Solution to Exercise 3.38.

This was proven in Chapter 2, see Proposition 2.27, but it is included here

as an exercise because of its importance, and because the use of the Legendre

symbol makes for a short proof.

(a)

b2≡ap+1

2≡a1+ p−1

2≡a·µa

p¶≡a(mod p).

We are using ap−1

2≡¡a

p¢from the previous exercise and the assumption that a

is a quadratic residue, which tells us that ¡a

p¢= 1.

(b) (i) 116(587+1)/4= 116147 ≡65 (mod 587). Check: 652≡116 (mod 587).

(ii) 3217(8627+1)/4≡18652157 ≡2980 (mod 8627). Check: 29802≡3217

(mod 8627).

(iii) 9109(10663+1)/4≡91092666 ≡3502 (mod 10663). Check: 35022≡1554

(mod 10663). Oops, what’s going on? The problem is that ¡9109

10663¢=−1, so

9109 is not a quadratic residue modulo 10663. In fact, the previous exercise

tells us that b2≡¡a

p¢a(mod p), and indeed in this case we have 35022≡ −9109

(mod 10663).

3.39. Recall that for any a∈F∗

p, the discrete logarithm of a(with respect to

a primitive root g) is a number logg(a) satisfying

94 Exercises for Chapter 3

glogg(a)≡a(mod p).

Prove that µa

p¶= (−1)logg(a)for all a∈F∗

Thus quadratic reciprocity gives a fast method to compute the parity of logg(a).

Solution to Exercise 3.39.

To ease notation,let k= logg(a). Then

µa

p¶≡a(p−1)/2(mod p) from earlier exercise,

≡gk(p−1)/2(mod p) from deﬁnition of discrete log,

≡(−1)k(mod p) since g(p−1)/2≡1 (mod p).

3.40. Let p≥5 be a prime. We say that ais a cubic residue modulo pif p-a

and there is an integer csatisfying a≡c3(mod p).

(a) Let aand bbe cubic residues modulo p. Prove that ab is a cubic residue

modulo p.

(b) Give an example to show that (unlike the case with quadratic residues)

it is possible for none of a,b, and ab to be a cubic residue modulo p.

modulo pif and only if 3 |logg(a), where logg(a) is the discrete logarithm

of a.

Solution to Exercise 3.40.

It is easiest to prove (c) ﬁrst, but we give a direct proof of (a). The as-

sumption is that there are numbers cand dsatisfying

a≡c3mod pand b≡d3(mod p).

Then ab = (cd)3(mod p), so ab is also a cubic residue modulo p.

(b,c) A solution for this exercise is not currently available.

Section. Probabilistic encryption and the Goldwasser–Micali cryptosystem

3.41. Perform the following encryptions and decryptions using the Goldwas-

ser–Micali public key cryptosystem (Table 3.9).

(a) Bob’s public key is the pair N= 1842338473 and a= 1532411781. Alice

encrypts three bits and sends Bob the ciphertext blocks

1794677960,525734818,and 420526487.

Decrypt Alice’s message using the factorization

N=pq = 32411 ·56843.

Exercises for Chapter 3 95

(b) Bob’s public key is N= 3149 and a= 2013. Alice encrypts three bits

and sends Bob the ciphertext blocks 2322, 719, and 202. Unfortunately,

Bob used primes that are much too small. Factor Nand decrypt Alice’s

message.

three bits 1, 1, 0 using, respectively, the three random values

r= 705130839, r = 631364468, r = 67651321.

Solution to Exercise 3.41.

(a) Decrypt c= 1794677960 by computing ¡1794677960

32411 ¢=−1, which gives

the plaintext bit m= 1. Decrypt c= 525734818 by computing ¡525734818

32411 ¢= 1,

which gives the plaintext bit m= 0. Decrypt c= 420526487 by computing

¡420526487

32411 ¢=−1, which gives the plaintext bit m= 1. Alice’s plaintext is

(1,0,1).

(b) The factorization of mis m= 3149 = 47 ·57. Decrypt c= 2322 by

computing ¡2322

47 ¢=−1, which gives the plaintext bit m= 1. Decrypt c= 719

by computing ¡719

47 ¢= 1, which gives the plaintext bit m= 0. Decrypt c= 202

by computing ¡202

47 ¢= 1, which gives the plaintext bit m= 0. Thus Alice’s

plaintext is (1,0,0).

781044643 = 22109 ·35327. Encrypt m= 1 using r= 705130839. Compute

c≡ar2≡568980706 ·7051308392≡517254876 (mod 781044643). Encrypt

m= 1 using r= 631364468. Compute c≡ar2≡568980706 ·6313644682≡

4308279 (mod 781044643). Encrypt m= 0 using r= 67651321. Compute c≡

r2≡676513212≡660699010 (mod 781044643). The ciphertext for (1,1,0) is

(517254876,4308279,660699010).

3.42. Suppose that the plaintext space Mof a certain cryptosystem is the

set of bit strings of length 2b. Let ekand dkbe the encryption and decryption

functions associated with a key k∈ K. This exercise describes one method

of turning the original cryptosystem into a probabilistic cryptosystem. Most

practical cryptosystems that are currently in use rely on more complicated

variants of this idea in order to thwart certain types of attacks. (See Section 8.6

for further details.)

Alice sends Bob an encrypted message by performing the following steps:

1. Alice chooses a b-bit message m0to be encrypted.

2. Alice chooses a string rconsisting of brandom bits.

3. Alice sets m=rk(r⊕m0), where kdenotes concatenation1and ⊕denotes

exclusive or (see Section 1.7.4). Notice that mhas length 2bbits.

4. Alice computes c=ek(m) and sends the ciphtertext cto Bob.

1The concatenation of two bit strings is formed by placing the ﬁrst string before the

second string. For example, 1101 k1001 is the bit string 11011001.

96 Exercises for Chapter 3

(a) Explain how Bob decrypts Alice’s message and recovers the plaintext m0.

We assume, of course, that Bob knows the decryption function dk.

(b) If the plaintexts and the ciphertexts of the original cryptosystem have the

same length, what is the message expansion ratio of the new probabilistic

cryptosystem?

ratio of µ, what is the message expansion ratio of the new probabilistic

cryptosystem?

Solution to Exercise 3.42.

(a) Bob decrypts cto recover m=dk(c). He splits mup into two pieces

m=rks, where rconsists of the ﬁrst bbits of mand sconsists of the

last bbits of m. Then he recovers Alice’s plaintext m0by computing r⊕s.

(b) The new probabilistic cryptosystem has plaintext length bbits and ci-

phertext length 2bbits, so its message expansion ratio is 2.

has message expansion µ, so its ciphertexts have length 2bµ bits. The new

probabilistic cryptosystem has plaintext length bbits, so its message expansion

ratio is 2bµ/b = 2µ.

Chapter 4

Combinatorics, Probability,

and Information Theory

Exercises for Chapter 4

Section. Basic principles of counting

4.1. The Rhind papyrus is an ancient Egyptian mathematical manuscript

that is more than 3500 years old. Problem 79 of the Rhind papyrus poses a

problem that can be paraphrased as follows: there are seven houses; in each

house lives seven cats; each cat kills seven mice; each mouse has eaten seven

spelt seeds1; each spelt seed would have produced seven hekat2of spelt. What

is the sum of all of the named items? Solve this 3500 year old problem.

Solution to Exercise 4.1.

|{z}

houses

+ 72

|{z}

cats

+ 73

|{z}

mice

+ 74

|{z}

spelt

+ 75

|{z}

hekat

= 19607.

As stated in the Rhind papyrus, the problem and solution looks more or

less as follows:

houses 7

1 2,801 cats 49

2 5,602 mice 343

4 11,204 spelt 2,301

hekat 16,807

Total 19,607 Total 19,607

1Spelt is an ancient type of wheat.

2Ahekat is 1

30 of a cubic cubit, which is approximately 4.8 liters.

98 Exercises for Chapter 4

Notice that the author has made a mistake in the value of 74= 2401, but

that his ﬁnal answer is correct. The last column in the Rhind papyrus is

the same as our solution, adding up powers of 7. In the ﬁrst column the

author gives an alternative computational method based on the fact that

2801 = 1 + 7 + 72+ 73+ 74. Thus he computes

7 + 72+ 73+ 74+ 75= 7 ·(1 + 7 + 72+ 73+ 74)

= (1 + 2 + 4) ·(1 + 7 + 72+ 73+ 74)

= 2801 + 2 ·2801 + 4 ·2801.

This double-and-add method is very reminiscent of many modern algorithms.

4.2. (a) How many n-tuples (x1, x2, . . . , xn) are there if the coordinates are

required to be integers satisfying 0 ≤xi< q?

(b) Same question as (a), except now there are separate bounds 0 ≤xi< qi

for each coordinate.

integers satisfying 0 ≤xi,j < q?

(d) Same question as (a), except now the order of the coordinates does not

matter. So for example, (0,0,1,3) and (1,0,3,0) are considered the same.

(This one is rather tricky.)

(e) Twelve students are each taking four classes, for each class they need two

loose-leaf notebooks, for each notebook they need 100 sheets of paper, and

each sheet of paper has 32 lines on it. Altogether, how many students,

classes, notebooks, sheets, and lines are there? (Bonus. Make this or a

similar problem of your own devising into a rhyme like the St. Ives riddle.)

Solution to Exercise 4.2.

(a) There are qchoices for each coordinate, so a total of qnpossible n-

tuples.

(b) Now there are q1choices for x1, and q2choices for x2, and so on. Hence

the total number of possibilities is the product q1q2···qn.

So there are qn2possible matrices.

(d) The idea is to count the quantity of each number that appears. Say there

are k0zeros, k1ones, etc. Then k0+k1+···+kq−1=n, so we need to count

the number of ways to split ninto a sum of qnonnegative pieces. The answer

to this is ¡q+n−1

q−1¢, which is also equal to ¡q+n−1

n¢.

(e) The total number of students, classes, notebooks, sheets, and lines is

307200 = 12

|{z}

students ·4

|{z}

classes ·2

|{z}

notebooks ·100

|{z}

sheets ·32

|{z}

lines

4.3. (a) List all of the permutations of the set {A, B, C}.

(b) List all of the permutations of the set {1,2,3,4}.

Exercises for Chapter 4 99

(d) Seven students are to be assigned to seven dormitory rooms, each student

receiving his or her own room. In how many ways can this be done?

(e) How many diﬀerent words can be formed with the four symbols A, A, B, C?

Solution to Exercise 4.3.

(a)

(A, B, C),(A, C, B),(B, A, C),(B, C, A),(C, A, B),(C, B, A).

(b) There are 24 permutations of {1,2,3,4}. They are

(1,2,3,4) (1,2,4,3) (1,3,2,4) (1,3,4,2) (1,4,2,3) (1,4,3,2)

(2,1,3,4) (2,1,4,3) (2,3,1,4) (2,3,4,1) (2,4,1,3) (2,4,3,1)

(3,1,2,4) (3,1,4,2) (3,2,1,4) (3,2,4,1) (3,4,1,2) (3,4,2,1)

(4,1,2,3) (4,1,3,2) (4,2,1,3) (4,2,3,1) (4,3,1,2) (4,3,2,1)

{1,2,...,20}.

(d) If the rooms are labeled 1,2, . . . , 7, then each permutation of the students

gives a way of assigning rooms, by putting the ﬁrst listed student in room #1,

the second listed student in room #2, etc. So there are 7! = 5040 ways to

assign rooms.

(e) There are 4 choices for placement of B, then 3 choices for placement of C,

after which the two A’s go in the remaining places, so there are 12 words.

4.4. (a) List the 24 possible permutations of the letters A1, A2, B1, B2. If A1is

indistinguishable from A2, and B1is indistinguishable from B2, show how

the permutations become grouped into 6 distinct letter arrangements,

each containing 4 of the original 24 permutations.

(b) Using the seven symbols A, A, A, A, B, B, B, how many diﬀerent seven

letter words can be formed?

(d) Using the seven symbols A, A, A, A, B, B, B, how many diﬀerent ﬁve letter

words can be formed?

Solution to Exercise 4.4.

(a) Here are the 24 permutations.

(A1, A2, B1, B2) (A1, A2, B2, B1) (A2, A1, B1, B2) (A2, A1, B2, B1)

(A1, B1, A2, B2) (A1, B2, A2, B1) (A2, B1, A1, B2) (A2, B2, A1, B1)

(A1, B1, B2, A2) (A1, B2, B1, A2) (A2, B1, B2, A1) (A2, B2, B1, A1)

(B1, B2, A2, A1) (B1, B2, A1, A2) (B2, B1, A1, A2) (B2, B1, A2, A1)

(B1, A1, A2, B2) (B1, A2, A1, B2) (B2, A1, A2, B1) (B2, A2, A1, B1)

(B1, A1, B2, A2) (B1, A2, B2, A1) (B2, A1, B1, A2) (B2, A2, B1, A1)

If A1=A2and B1=B2, then the four entries in each row become the

same.

100 Exercises for Chapter 4

(b) We need to pick 4 of the 7 spots for the A’s, then the B’s go into the

remaining 3 spots. Hence there are ¡7

4¢= 35 such words.

the remaining 5 spots for the B’s, then the C’s go into the remaining 2 spots.

Hence there are ¡9

4¢¡5

3¢= 126 ·10 = 1260 such words.

(d) We can form ﬁve letter words using anywhere from two to four A’s. So

we need to count the number of ﬁve letter words using each of

{A, A, A, A, B},{A, A, A, B, B},and {A, A, B, B, B}.

So there are

µ5

4¶+µ5

3¶+µ5

2¶= 25 diﬀerent ﬁve letter words.

4.5. (a) There are 100 students eligible for an award, and the winner gets

to choose from among 5 diﬀerent possible prizes. How many possible

outcomes are there?

(b) Same as in (a), but this time there is a ﬁrst place winner, a second place

winner, and a third place winner, each of whom gets to select a prize.

However, there is only one of each prize. How many possible outcomes

are there?

each of the three winners may choose any of the prizes. Now how many

possible outcomes are there? Is this larger or smaller than your answer

from (b)?

(d) Same as in (c), except that rather than specifying a ﬁrst, second, and

third place winner, we just choose three winning students without dif-

ferentiating between them. Now how many possible outcomes are there?

Compare the size of your answers to (b), (c), and (d).

Solution to Exercise 4.5.

(a) There are 100 ·5 = 500 outcomes.

(b) This can be split into ﬁrst choosing the three winners (in order), which

can be done in 100 ·99 ·98 ways, and then choosing the three prizes (in order),

which can be done in 5 ·4·3 ways. Then using the basic counting principle,

the total number of outcomes is

100 ·99 ·98 ·5·4·3 = 58212000 ≈107.77.

(b) This time there are 5 ·5·5 ways to choose the prizes, so the total number

of outcomes is

100 ·99 ·98 ·5·5·5 = 121275000 ≈108.08.

3¢=

100·99·98

3! ways to choose the students. Hence the total number of outcomes is

Exercises for Chapter 4 101

100 ·99 ·98

3! ·5·5·5 = 20212500 ≈107.31.

4.6. Use the binomial theorem (Theorem 4.10) to compute each of the fol-

lowing quantities.

(a) (5z+ 2)3(b) (2a−3b)4(c) (x−2)5

Solution to Exercise 4.6.

(a) (5z+ 2)3= 125z3+ 225z2+ 135z+ 27.

(b) (2a−3b)4= 16a4−96a3b+ 216a2b2−216ab3+ 81b4.

4.7. The binomial coeﬃcients satisfy many interesting identities. Give three

proofs of the identity

µn

j¶=µn−1

j−1¶+µn−1

j¶.

(a) For Proof #1, use the deﬁnition of ¡n

j¢as n!

(n−j)!j!.

(b) For Proof #2, use the binomial theorem (Theorem 4.10) and compare the

coeﬃcients of xjyn−jon the two sides of the identity

(x+y)n= (x+y)(x+y)n−1.

objects can be decomposed into either choosing j−1 objects from n−1

objects or choosing jobjects from n−1 objects.

Solution to Exercise 4.7.

Proof #1:

µn−1

j−1¶+µn−1

j¶=(n−1)!

(n−j)!(j−1)! +(n−1)!

(n−1−j)!j!

=(n−1)!

(n−1−j)!(j−1)! ·1

n−j+1

j¸

=(n−1)!

(n−1−j)!(j−1)! ·n

(n−j)j

=n!

(n−j)!j!

=µn

j¶.

Proof #2: Expand both sides of (x+y)n= (x+y)(x+y)n−1using the

binomial theorem:

102 Exercises for Chapter 4

j=0 µn

j¶xjyn−j= (x+y)

n−1

j=0 µn−1

j¶xjyn−1−j

n−1

j=0 µn−1

j¶xj+1yn−1−j+

n−1

j=0 µn−1

j¶xjyn−j

j=1 µn−1

j−1¶xjyn−j+

n−1

j=0 µn−1

j¶xjyn−j

=xn+

n−1

j=1 ·µn−1

j−1¶+µn−1

j¶xjyn−j¸+yn.

Comparing the coeﬃcients of xjyn−jon the two sides gives the desired iden-

tity.

Another way to illustrate the same proof is to write the expansion of (x+

y)nfor n= 0,1,2,3, . . . in the form of a triangle called Pascal’s triangle.

Proof #3: Let the nobjects be A1,··· , An. Treat the last one as special, so

label them as A1, . . . , An−1, B. In choosing jof these nobjects, there are two

possibilities, namely either Bis chosen or it is not chosen. The number of ways

to choose jobjects without Bis ¡n−1

j¢, since we are choosing jobjects from

among the n−1A’s. The number of ways to choose jobjects including B

is ¡n−1

j−1¢, since having already selected B, we are need to choose j−1 objects

from among the n−1A’s.

4.8. Let pbe a prime number. This exercise sketches another proof of Fermat’s

little theorem (Theorem 1.25).

(a) If 1 ≤j≤p−1, prove that the binomial coeﬃcient ¡p

j¢is divisible by p.

(b) Use (a) and the binomial theorem (Theorem 4.10) to prove that

(a+b)p≡ap+bp(mod p) for all a, b ∈Z.

all a≥0.

(d) Use (c) to deduce that ap−1≡1 (mod p) for all awith gcd(p, a) = 1.

Solution to Exercise 4.8.

(a) µp

j¶=p(p−1)(p−2) ···(p−j+ 1)

j!.

The denominator has no factors of p, so the pin the numerator does not

cancel.

(b)

(a+b)p=

j=0 µp

j¶ajbp−j≡ap+bp(mod p),

Exercises for Chapter 4 103

since (a) tells us that the middle terms in the sum are all divisible by p.

value a= 0. Then using (b) we have

(a+ 1)p≡ap+ 1 ≡a+ 1 (mod p).

Hence the result is also true for a+ 1. By induction, it is true for all a≥0.

(d) If p-a, then we can multiply both sides of ap≡a(mod p) by a−1mod p.

4.9. We know that there are n! diﬀerent permutations of the set {1,2, . . . , n}.

(a) How many of these permutations leave no number ﬁxed?

(b) How many of these permutations leave at least one number ﬁxed?

(d) How many of these permutations leave at least two numbers ﬁxed?

For each part of this problem, give a formula or algorithm that can be used to

compute the answer for an arbitrary value of n, and then compute the value

for n= 10 and n= 26. (This exercise generalizes Exercise 1.5.)

Solution to Exercise 4.9.

Let S(n, k) denote the number of permutations of nelements that ﬁx at

least kelements, let R(n, k) denote the number of permutations of nele-

ments that ﬁx exactly kelements, and let !n(the subfactorial of n) denote

the number of permutations of nelements that ﬁx no elements (such permu-

tations are called derangements). Notice that !n=R(n, 0). See the solution

to Exercise exercise:derangement for the derivation of the following formulas:

!n=n!

k=0

(−1)k

k!=bn!/ee,

R(n, k) = µn

k¶!(n−k) = µn

k¶¹(n−k)!

e¼,

S(n, k) =

j=k

R(n, j) = n!−

k−1

j=0

R(n, j).

(a) No letters ﬁxed is R(n, 0) =!n. This is called the nth derangement number.

For n= 10 we get

R(10,0) =!10 = b10!/ee=b1334960.916e= 1334961.

For n= 26 we get

R(26,0) =!26 = b26!/ee=b148362637348470135821287824.964e

= 148362637348470135821287825.

(b) At least one letter ﬁxed is n! minus no letters ﬁxed, so

104 Exercises for Chapter 4

S(n, 1) = n!−R(n, 0) = n!−!n=n!− bn!/ee.

Hence

S(10,1) = 10! − b10!/ee= 2293839,

S(26,1) = 26! − b26!/ee= 254928823778135499762712175.

R(n, 1) = n·!(n−1) = n¹(n−1)!

e¼,

R(10,1) = 10 ¹9!

e¼= 1334960,

R(26,1) = 26 ¹25!

e¼= 148362637348470135821287824.

(d) At least two letters ﬁxed is n! minus zero or one letters ﬁxed, so

S(n, 1) = n!−R(n, 0) −R(1,0) = n!−!n−n·!(n−1)

=n!− bn!/ee − nb(n−1)!/ee.

Hence

S(10,1) = 10! − b10!/ee − 10 · b9!/ee= 958879,

S(26,1) = 26! − b26!/ee − 26 · b25!/ee= 106566186429665363941424351.

Section. The Vigen`ere cipher

4.10. Encrypt each of the following Vigen`ere plaintexts using the given key-

word and the Vigen`ere tableau (Table 4.1).

(a) Keyword: hamlet

Plaintext: To be, or not to be, that is the question.

(b) Keyword: fortune

Plaintext: The treasure is buried under the big W.

Solution to Exercise 4.10.

(a) Vigen`ere Keyword: hamlet

tobeornottobethatisthequestion

hamlethamlethamlethamlethamlet

aonpskuofesulttlxbzttpunlsftsg

(b) Vigen`ere Keyword: fortune

thetreasureisburiedunderthebigw

fortunefortunefortunefortunefor

yvvmlrexiixcffzfzxxhrisimbrfnun

Exercises for Chapter 4 105

4.11. Decrypt each of the following Vigen`ere ciphertexts using the given key-

word and the Vigen`ere tableau (Table 4.1).

(a) Keyword: condiment

Ciphertext: rsghz bmcxt dvfsq hnigq xrnbm

pdnsq smbtr ku

(b) Keyword: rabbithole

Ciphertext: khfeq ymsci etcsi gjvpw ffbsq

moapx zcsfx epsox yenpk daicx

cebsm ttptx zooeq laflg kipoc

zswqm taujw ghboh vrjtq hu

Solution to Exercise 4.11.

(a) Vigen`ere Keyword: condiment

Ciphertext: rsghz bmcxt dvfsq hnigq xrnbm

Keyword: condi mentc ondim entco ndime

Plaintext: peter piper picke dapec kofpi

Ciphertext: pdnsq smbtr ku

Keyword: ntcon dimen tc

Plaintext: ckled peppe rs

Plaintext. Peter Piper picked a peck of pickled peppers!

(b) Vigen`ere Keyword: rabbithole

Ciphertext: khfeq ymsci etcsi gjvpw ffbsq

Keyword: rabbi thole rabbi thole rabbi

Plaintext: thedi ffere ntbra nches ofari

Ciphertext: moapx zcsfx epsox yenpk daicx

Keyword: thole rabbi thole rabbi thole

Plaintext: thmet icrep liedt hemoc kturt

Ciphertext: cebsm ttptx zooeq laflg kipoc

Keyword: rabbi thole rabbi thole rabbi

Plaintext: leare ambit iondi strac tionu

Ciphertext: zswqm taujw ghboh vrjtq hu

Keyword: thole rabbi thole rabbi th

Plaintext: glifi catio nandd erisi on

Plaintext. The diﬀerent branches of arithmetic, replied the Mock Turtle, are

ambition, distraction, ugliﬁcation, and derision. (From Lewis Carroll’s Alice

in Wonderland.)

4.12. Explain how a cipher wheel with rotating inner wheel (see Figure 1.1

on page 3) can be used in place of a Vige`nere tableau (Table 4.1) to perform

Vigen`ere encryption and decryption. Illustrate by describing the sequence of

rotations used to perform a Vigen`ere encryption with the keyword mouse.

106 Exercises for Chapter 4

Solution to Exercise 4.12.

A solution for this exercise is not currently available.

4.13. Let

s= “I am the very model of a modern major general.”

t= “I have information vegetable, animal, and mineral.”

(a) Make frequency tables for sand t.

(b) Compute IndCo(s) and IndCo(t).

Solution to Exercise 4.13.

(a)

ABCDEFGHIJKLMNOPQRSTUVWXYZ

Freq s40026111110242400401010010

Freq t81014111500335200202020000

(b) IC(s) = 0.0424 and IC(t) = 0.0544.

4.14. The following strings are blocks from a Vigen`ere encryption. It turns

out that the keyword contains a repeated letter, so two of these blocks were

encrypted with the same shift. Compute MutIndCo(si,sj) for 1 ≤i < j ≤3

and use these values to deduce which two strings were encrypted using the

same shift.

s1=iwseesetftuonhdptbunnybioeatneghictdnsevi

s2=qibfhroeqeickxmirbqlflgkrqkejbejpepldfjbk

s3=iesnnciiheptevaireittuevmhooottrtaaflnatg

Solution to Exercise 4.14.

(a)

abcdefghijklmnopqrstuvwxyz

Freq s112126112400005210035211010

Freq s204115311334310124300000100

Freq s340105112500113310217120000

MutIndCo(s1,s2) = 0.0375,

MutIndCo(s1,s3) = 0.0744,

MutIndCo(s2,s3) = 0.0369.

Thus s1and s3were probably encrypted using the same shift, so the ﬁrst and

third letters of the keyword are probably the same.

4.15. (a) One of the following two strings was encrypted using a simple sub-

stitution cipher, while the other is a random string of letters. Compute

the index of coincidence of each string and use the results to guess which

is which.

Exercises for Chapter 4 107

s1=RCZBWBFHSLPSCPILHBGZJTGBIBJGLYIJIBFHCQQFZBYFP,

s2=KHQWGIZMGKPOYRKHUITDUXLXCWZOTWPAHFOHMGFEVUEJJ.

(b) One of the following two strings was encrypted using a simple substitution

cipher, while the other is a random permutation of the same set of letters.

s1=NTDCFVDHCTHKGUNGKEPGXKEWNECKEGWEWETWKUEVHDKK

CDGCWXKDEEAMNHGNDIWUVWSSCTUNIGDSWKE

s2=IGWSKGEHEXNGECKVWNKVWNKSUTEHTWHEKDNCDXWSIEKD

AECKFGNDCPUCKDNCUVWEMGEKWGEUTDGTWHD

Thus their Indices of Coincidence are identical. Develop a method to

compute a bigram index of coincidence, i.e., the frequency of pairs of

letters, and use it to determine which string is most likely the encrypted

text.

(Bonus: Decrypt the encrypted texts in (a) and (b), but be forewarned that

the plaintexts are in Latin.)

Solution to Exercise 4.15.

(a) The Indices of Coincidence of the two strings are IndCo(s1) = 0.0576

and IndCo(s2) = 0.0303, so most likely s1is the encrypted text and s2is

the random string. The plaintext for s1is “Facilius per partes in cognitionem

totius adducimur,” which translated into English says “We are more easily led

part by part to an understanding of the whole.” The phrase is due to Seneca.

(b) The Indices of Coincidence are identical, IndCo(s1) = IndCo(s2) =

0.0672. In general, let A={a1, a2, . . . , ak}be a set of distinct objects (letters,

bigrams, turtles, etc.) and let B= (b1, b2, . . . , bn) be a list of elements from A,

where the bido not need to be distinct. For each 1 ≤i≤k, let Fidenote

the number of b’s that are equal to ai, i.e., Fiis the frequency with which ai

appears in the list B. Then the index of coincidence of the set Bis

IndCo(B) = 1

n(n−1)

i=1

Fi(Fi−1).

So now we can apply the theory of Index of Coincidence to the set of

bigrams that appear in a string. And we would expect that the index should

be higher for the string that is the encrypted message and lower for the string

with the same letters, but randomly rearranged. We ﬁnd that

IndCo(Bigrams in s1) = 0.004,

IndCo(Bigrams in s2) = 0.010.

Thus it seems likely that the second string s2is the encrypted plaintext.

This is the case, and the plaintext for s2is “Frustra laborant quotquot se

calculationibus fatigant pro inventione quadraturae circuli,” which translated

into English says “Futile is the labor of those who fatigue themselves with

calculations to square the circle.” The phrase is due to Michael Stifel (1544).

108 Exercises for Chapter 4

nhqrk vvvfe fwgjo mzjgc kocgk lejrj wossy wgvkk hnesg kwebi

bkkcj vqazx wnvll zetjc zwgqz zwhah kwdxj fgnyw gdfgh bitig

mrkwn nsuhy iecru ljjvs qlvvw zzxyv woenx ujgyr kqbfj lvjzx

dxjfg nywus rwoar xhvvx ssmja vkrwt uhktm malcz ygrsz xwnvl

lzavs hyigh rvwpn ljazl nispv jahym ntewj jvrzg qvzcr estul

fkwis tfylk ysnir rddpb svsux zjgqk xouhs zzrjj kyiwc zckov

qyhdv rhhny wqhyi rjdqm iwutf nkzgd vvibg oenwb kolca mskle

cuwwz rgusl zgfhy etfre ijjvy ghfau wvwtn xlljv vywyj apgzw

trggr dxfgs ceyts tiiih vjjvt tcxfj hciiv voaro lrxij vjnok

mvrgw kmirt twfer oimsb qgrgc

Table 4.1: A Vigen`ere ciphertext for Exercise 4.16

4.16. Table 4.13 is a Vigen`ere ciphertext in which we have marked some of

the repeated trigrams for you. How long do you think the keyword is? Why?

Bonus: Complete the cryptanalysis and recover the plaintext.

Solution to Exercise 4.16.

Trigram Appears at places Diﬀerences

hyi 109, 206 and 313 97 = 97

107 = 107

204 = 22·3·17

jjv 117, 235, 372, and 422 118 = 2 ·59

137 = 137

255 = 3 ·5·17

305 = 5 ·61

187 = 11 ·17

50 = 2 ·52

nyw 88, 156, and 309 68 = 22·17

221 = 13 ·17

153 = 32·17

The keyword has length 17 . The keyword used for encryption was

fourscoreandseven .

The plaintext is

It was the best of times, it was the worst of times, it was the age of

wisdom, it was the age of foolishness, it was the epoch of belief, it

was the epoch of incredulity, it was the season of Light, it was the

season of Darkness, it was the spring of hope, it was the winter of

despair, we had everything before us, we had nothing before us,

we were all going direct to Heaven, we were all going direct the

other way—in short, the period was so far like the present period,

Exercises for Chapter 4 109

togmg gbymk kcqiv dmlxk kbyif vcuek cuuis vvxqs pwwej koqgg

phumt whlsf yovww knhhm rcqfq vvhkw psued ugrsf ctwij khvfa

thkef fwptj ggviv cgdra pgwvm osqxg hkdvt whuev kcwyj psgsn

gfwsl jsfse ooqhw tofsh aciin gfbif gabgj adwsy topml ecqzw

asgvs fwrqs fsfvq rhdrs nmvmk cbhrv kblxk gzi

Table 4.2: A Vigen`ere ciphertext for Exercise 4.17

Blocks Shift Amount

i j 0123456789101112

1 2 .044 .047 .021 .054 .046 .038 .022 .034 .057 .035 .040 .023 .038

1 3 .038 .031 .027 .037 .045 .036 .034 .032 .039 .039 .047 .038 .050

1 4 .025 .039 .053 .043 .023 .035 .032 .043 .029 .040 .041 .050 .027

1 5 .050 .050 .025 .031 .038 .045 .037 .028 .032 .038 .063 .033 .034

2 3 .035 .037 .039 .031 .031 .035 .047 .048 .034 .031 .031 .067 .053

2 4 .040 .033 .046 .031 .033 .023 .052 .027 .031 .039 .078 .034 .029

2 5 .042 .040 .042 .029 .033 .035 .035 .038 .037 .057 .039 .038 .040

3 4 .032 .033 .035 .049 .053 .027 .030 .022 .047 .036 .040 .036 .052

3 5 .043 .043 .040 .034 .033 .034 .043 .035 .026 .030 .050 .068 .044

4 5 .045 .033 .044 .046 .021 .032 .030 .038 .047 .040 .025 .037 .068

Blocks Shift Amount

i j 13 14 15 16 17 18 19 20 21 22 23 24 25

1 2 .040 .063 .033 .025 .032 .055 .038 .030 .032 .045 .035 .030 .044

1 3 .026 .046 .042 .053 .027 .024 .040 .047 .048 .018 .037 .034 .066

1 4 .042 .050 .042 .031 .024 .052 .027 .051 .020 .037 .042 .069 .031

1 5 .030 .048 .039 .030 .034 .038 .042 .035 .036 .043 .055 .030 .035

2 3 .039 .015 .030 .045 .049 .037 .023 .036 .030 .049 .039 .050 .037

2 4 .027 .048 .050 .037 .032 .021 .035 .043 .047 .041 .047 .042 .035

2 5 .033 .035 .039 .033 .037 .047 .037 .028 .034 .066 .054 .032 .022

3 4 .040 .048 .041 .044 .033 .028 .039 .027 .036 .017 .038 .051 .065

3 5 .039 .029 .045 .040 .033 .028 .031 .037 .038 .036 .033 .051 .036

4 5 .049 .033 .029 .043 .028 .033 .020 .040 .040 .041 .039 .039 .059

Table 4.3: Mutual indices of coincidence for Exercise 4.17

that some of its noisiest authorities insisted on its being received,

for good or for evil, in the superlative degree of comparison only.

These are the opening lines of A Tale of Two Cities by Charles Dickens.

4.17. We applied a Kasiski test to the Vigen`ere ciphertext listed in Table 4.14

and found that the key length is probably 5. We then performed a mutual

index of coincidence test to each shift of each pair of blocks and listed the

results for you in Table 4.15. (This is the same type of table as Table 4.5 in

the text, except that we haven’t underlined the large values.) Use Table 4.15

to guess the relative rotations of the blocks, as we did in Table 4.6. This

will give you a rotated version of the keyword. Try rotating it, as we did in

Table 4.7, to ﬁnd the correct keyword and decrypt the text.

Solution to Exercise 4.17.

The table of likely shift relations gives

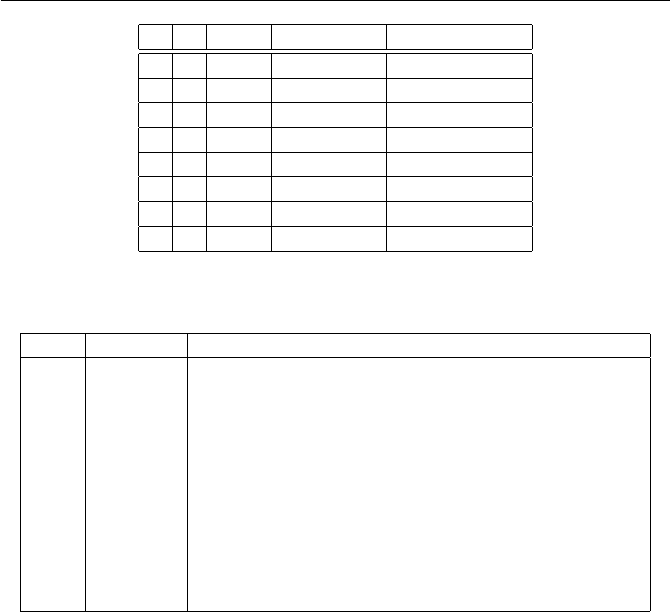
110 Exercises for Chapter 4

i j Shift MutIndCo Shift Relation

2 3 11 0.067 β2−β3= 11

2 4 10 0.078 β2−β4= 10

3 5 11 0.068 β3−β5= 11

4 5 12 0.068 β4−β5= 12

1 3 25 0.066 β1−β3= 25

1 4 24 0.069 β1−β4= 24

2 5 22 0.066 β2−β5= 22

3 4 25 0.065 β3−β4= 25

Table 4.4: Large indices of coincidence and shift relations

Shift Keyword Decrypted Text

0 AMBCQ tcfkqgpxkukqpgfdakvukpxgpvqtcucitgcvjwocpk

1 BNCDR sbejpfowjtjpofeczjutjowfoupsbtbhsfbuivnboj

2 CODES radioenvisionedbyitsinventorasagreathumani

3 DPEFT qzchndmuhrhnmdcaxhsrhmudmsnqzrzfqdzsgtlzmh

4 EQFGU pybgmcltgqgmlcbzwgrqgltclrmpyqyepcyrfskylg

5 FRGHV oxaflbksfpflkbayvfqpfksbkqloxpxdobxqerjxkf

6 GSHIW nwzekajreoekjazxuepoejrajpknwowcnawpdqiwje

7 HTIJX mvydjziqdndjizywtdondiqziojmvnvbmzvocphvid

8 IUJKY luxciyhpcmcihyxvscnmchpyhnilumualyunboguhc

Table 4.5: Decryption using shifts of the keyword AJCHWJZ

β2=β1+ 12, β3=β1+ 1, β4=β1+ 2, β5=β1+ 16.

Hence the keyword is a rotation of AMBCQ. The table lists the rotations of

this word with the corresponding decryptions. We see immediately that the

keyword is CODES. The full plaintext reads as follows:

Radio, envisioned by its inventor as a great humanitarian contri-

bution, was seized upon by the generals soon after its birth and

impressed as an instrument of war. But radio turned over to the

commander a copy of every enemy cryptogram it conveyed. Radio

made cryptanalysis an end in itself.

The Code-Breakers, Chapter 10, 1967, David Kahn

4.18. Table 4.16 gives a Vigen`ere ciphertext for you to analyze from scratch.

It is probably easiest to do so by writing a computer program, but you are

welcome to try to decrypt it with just paper and pencil.

(a) Make a list of matching trigrams as we did in Table 4.3. Use the Kasiski

test on matching trigrams to ﬁnd the likely key length.

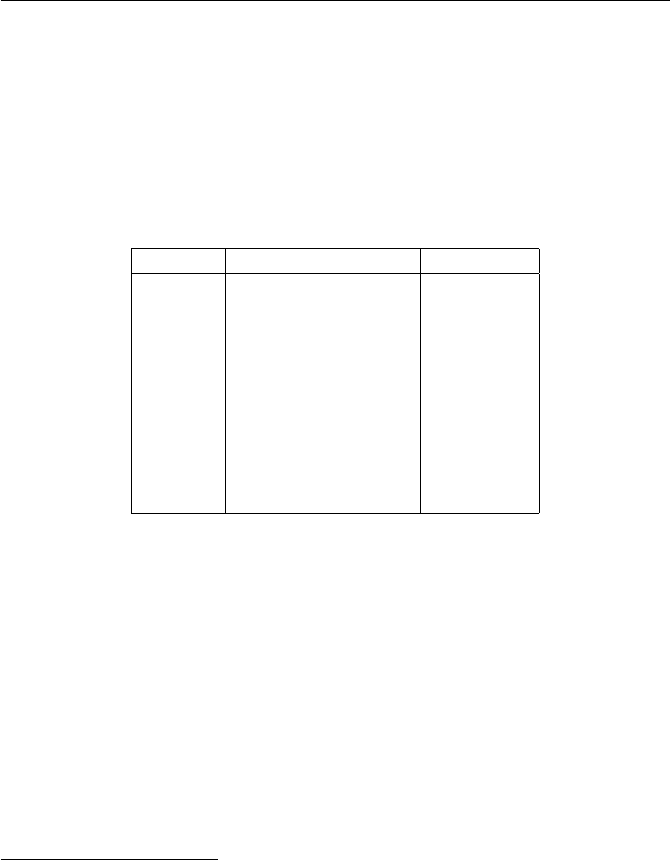
Exercises for Chapter 4 111

mgodt beida psgls akowu hxukc iawlr csoyh prtrt udrqh cengx

uuqtu habxw dgkie ktsnp sekld zlvnh wefss glzrn peaoy lbyig

uaafv eqgjo ewabz saawl rzjpv feyky gylwu btlyd kroec bpfvt

psgki puxfb uxfuq cvymy okagl sactt uwlrx psgiy ytpsf rjfuw

igxhr oyazd rakce dxeyr pdobr buehr uwcue ekfic zehrq ijezr

xsyor tcylf egcy

Table 4.6: A Vigen`ere ciphertext for Exercise 4.18

Trigram Appears at places Diﬀerence

awl 27 and 118 91

ehr 228 and 242 14

gki 62 and 153 91

gls 13 and 174 161

lsa 14 and 175 161

psg 11 and 151 and 186 140 and 35

sgl 12 and 85 73

tps 150 and 192 42

uxf 157 and 161 4

wlr 28 and 119 and 182 91 and 63

Table 4.7: Repeated trigrams in the ciphertext

(b) Make a table of indices of coincidence for various key lengths, as we did

in Table 4.4. Use your results to guess the probable key length.

indices of coincidence between rotated blocks, as we did in Table 4.5. Pick

the largest indices from your table and use them to guess the relative

rotations of the blocks, as we did in Table 4.6.

(d) Use your results from (c) to guess a rotated version of the keyword, and

then try the diﬀerent rotations as we did in Table 4.7 to ﬁnd the correct

keyword and decrypt the text.

Solution to Exercise 4.18.

A list of repeated trigrams for the Kasiski test is given in the Table. The

list of diﬀerences (sorted) is

{4,14,35,42,63,73,91,91,91,140,154,161,161,175}.

Thus a good guess for the period is 7.

Solving the relations in the table gives

β2=β1+ 9, β3=β1+ 2, β4=β1+ 7, β5=β1+ 22, β6=β1+ 9.

(There is actually one erroneous relation, namely β2−β5= 24, but our solution

satisﬁes the other 10 relations, which makes it likely that it is correct.) In order

112 Exercises for Chapter 4

Block Average Individual Indices

Size Index of Coincidence

4 0.043 0.038, 0.043, 0.042, 0.046

5 0.044 0.048, 0.052, 0.046, 0.030, 0.041

6 0.042 0.036, 0.050, 0.042, 0.051, 0.038, 0.035

7 0.060 0.058, 0.060, 0.081, 0.054, 0.059, 0.065, 0.047

8 0.046 0.042, 0.051, 0.030, 0.053, 0.040, 0.051, 0.057, 0.040

9 0.041 0.041, 0.053, 0.042, 0.037, 0.052, 0.030, 0.054, 0.030, 0.030

Table 4.8: Index of coincidence for various block sizes

Blocks Shift Amount

i j 0123456789101112

1 2 .037 .035 .043 .037 .045 .035 .053 .046 .035 .034 .046 .030 .024

1 3 .020 .046 .035 .041 .046 .030 .033 .039 .037 .033 .040 .048 .036

1 4 .038 .031 .045 .035 .039 .030 .046 .043 .050 .041 .026 .035 .039

1 5 .053 .037 .027 .034 .065 .048 .038 .036 .048 .028 .022 .036 .044

1 6 .024 .027 .048 .044 .039 .043 .043 .040 .024 .036 .053 .043 .039

1 7 .048 .055 .038 .036 .033 .031 .037 .047 .041 .023 .035 .041 .049

2 3 .040 .035 .026 .046 .039 .027 .051 .071 .022 .026 .062 .033 .039

2 4 .038 .045 .070 .029 .034 .044 .035 .037 .042 .038 .030 .042 .037

2 5 .041 .038 .051 .032 .021 .028 .043 .025 .031 .049 .039 .031 .044

2 6 .067 .034 .028 .050 .048 .027 .036 .045 .028 .023 .034 .056 .031

2 7 .030 .030 .047 .031 .035 .035 .056 .031 .034 .051 .048 .031 .033

3 4 .033 .048 .035 .033 .044 .046 .040 .023 .044 .028 .048 .037 .037

3 5 .034 .040 .054 .042 .026 .026 .056 .042 .036 .032 .046 .031 .035

3 6 .050 .042 .022 .029 .047 .038 .036 .033 .041 .041 .030 .030 .038

3 7 .033 .025 .032 .059 .038 .039 .028 .037 .033 .053 .039 .026 .039

4 5 .053 .040 .036 .021 .042 .032 .031 .038 .035 .033 .038 .058 .045

4 6 .020 .037 .041 .040 .043 .041 .031 .015 .030 .049 .043 .035 .030

4 7 .040 .038 .030 .028 .052 .032 .041 .041 .058 .029 .030 .036 .045

5 6 .022 .045 .050 .031 .034 .053 .047 .023 .037 .044 .030 .024 .044

5 7 .039 .034 .028 .038 .044 .020 .039 .050 .057 .028 .035 .050 .038

6 7 .032 .029 .052 .049 .028 .037 .035 .031 .031 .058 .055 .024 .033

Blocks Shift Amount

i j 13 14 15 16 17 18 19 20 21 22 23 24 25

1 2 .047 .047 .021 .030 .070 .043 .030 .046 .038 .028 .030 .039 .029

1 3 .033 .051 .030 .047 .044 .032 .026 .055 .031 .016 .046 .080 .024

1 4 .035 .037 .058 .039 .021 .036 .062 .042 .036 .042 .024 .033 .039

1 5 .031 .028 .054 .052 .036 .040 .049 .041 .022 .032 .039 .030 .030

1 6 .046 .038 .014 .033 .066 .039 .024 .043 .036 .021 .036 .055 .041

1 7 .040 .040 .048 .038 .026 .023 .053 .041 .033 .031 .053 .030 .029

2 3 .035 .038 .029 .042 .037 .044 .023 .044 .035 .040 .049 .033 .033

2 4 .050 .029 .045 .035 .039 .033 .026 .033 .033 .039 .028 .054 .036

2 5 .064 .041 .032 .033 .044 .025 .020 .038 .037 .037 .037 .072 .048

2 6 .025 .038 .034 .036 .028 .043 .047 .038 .038 .048 .048 .026 .043

2 7 .043 .034 .033 .036 .041 .023 .048 .044 .056 .031 .042 .038 .039

3 4 .027 .034 .033 .042 .048 .055 .022 .021 .073 .039 .033 .042 .035

3 5 .028 .050 .033 .035 .054 .054 .036 .033 .040 .043 .031 .024 .041

3 6 .047 .049 .042 .050 .026 .018 .065 .048 .027 .050 .041 .024 .035

3 7 .043 .046 .035 .041 .041 .042 .027 .029 .039 .047 .036 .033 .059

4 5 .036 .032 .044 .038 .037 .033 .040 .029 .029 .053 .048 .046 .034

4 6 .038 .035 .036 .041 .047 .048 .034 .038 .046 .041 .038 .063 .043

4 7 .044 .037 .037 .021 .041 .038 .053 .037 .043 .032 .041 .033 .042

5 6 .065 .031 .021 .039 .042 .028 .028 .058 .035 .024 .043 .057 .042

5 7 .034 .033 .050 .028 .028 .035 .045 .030 .042 .053 .056 .029 .037

6 7 .036 .042 .032 .048 .050 .025 .032 .037 .056 .035 .030 .045 .038

Table 4.9: Mutual indices of coincidence for shifted blocks

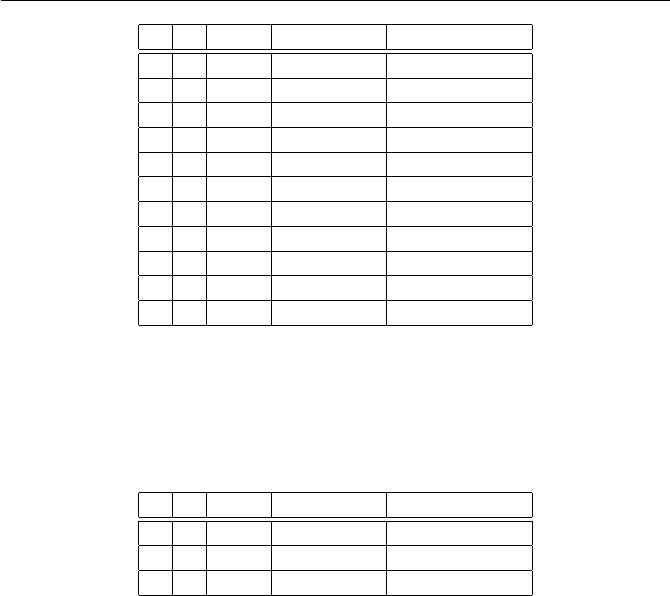
Exercises for Chapter 4 113

i j Shift MutIndCo Shift Relation

1 5 4 0.065 β1−β5= 4

2 3 7 0.071 β2−β3= 7

2 4 2 0.070 β2−β4= 2

2 6 0 0.067 β2−β6= 0

1 2 17 0.070 β1−β2= 17

1 3 24 0.080 β1−β3= 24

1 6 17 0.066 β1−β6= 17

2 5 24 0.072 β2−β5= 24

3 4 21 0.073 β3−β4= 21

3 6 19 0.065 β3−β6= 19

5 6 13 0.065 β5−β6= 13

Table 4.10: Large indices of coincidence and shift relations

to ﬁnd β7, we look at the mutual indices that involve Block 7 and are greater

than 0.058. There are three of them:

i j Shift MutIndCo Shift Relation

3 7 3 0.059 β3−β7= 3

3 7 25 0.059 β3−β7= 25

4 7 8 0.058 β4−β7= 8

Only one of the ﬁrst two can be correct, but the third yields β7=β1+ 25.

This agrees with β7=β3−3 = 25, so is probably correct. Thus the amounts

that Blocks 2 through 7 are rotated exceed the amount that Block 1 is rotated

by 9, 2, 7, 22, 9, and 25, respectively. For example, if the ﬁrst letter of the

keyword is A, then the full keyword is AJCHWJZ. The shifts of this keyword

and decryptions are listed in the table.

We ﬁnd that the keyword is ENGLAND, and the full plaintext reads as fol-

lows:

It is to be questioned whether in the whole length and breadth

of the world there is a more admirable spot for a man in love to

pass a day or two than the typical English village. It combines the

comforts of civilization with the restfulness of solitude in a manner

equalled by no other spot except the New York Public Library.

A Damsel in Distress, 1919, P.G. Wodehouse

4.19. The autokey cipher is similar to the Vigen`ere cipher, except that rather

than repeating the key, it simply uses the key to encrypt the ﬁrst few letters

and then uses the plaintext itself (shifted over) to continue the encryption. For

example, in order to encrypt the message “The autokey cipher is cool”

using the keyword random, we proceed as follows:

114 Exercises for Chapter 4

Shift Keyword Decrypted Text

0 AJCHWJZ mxmwxsfiuyiwxmsrihalixlivmrxlialspipirkxle

1 BKDIXKA lwlvwrehtxhvwlrqhgzkhwkhulqwkhzkrohohqjwkd

2 CLEJYLB kvkuvqdgswguvkqpgfyjgvjgtkpvjgyjqngngpivjc

3 DMFKZMC jujtupcfrvftujpofexifuifsjouifxipmfmfohuib

4 ENGLAND itistobequestionedwhetherinthewholelengtha

5 FOHMBOE hshrsnadptdrshnmdcvgdsgdqhmsgdvgnkdkdmfsgz

6 GPINCPF grgqrmzcoscqrgmlcbufcrfcpglrfcufmjcjclerfy

7 HQJODQG fqfpqlybnrbpqflkbatebqebofkqebtelibibkdqex

8 IRKPERH epeopkxamqaopekjazsdapdanejpdasdkhahajcpdw

9 JSLQFSI dodnojwzlpznodjizyrczoczmdioczrcjgzgzibocv

Table 4.11: Decryption using shifts of the keyword AJCHWJZ

Plaintext theautokeycipheriscool

Key randomtheautokeycipher

Ciphertext khrdifhriywbdripkarvsc

The autokey cipher has the advantage that diﬀerent messages are encrypted

using diﬀerent keys (except for the ﬁrst few letters). Further, since the key does

not repeat, there is no key length, so the autokey is not directly susceptible

to a Kasiski or index of coincidence analysis. A disadvantage of the autokey

is that a single mistake in encryption renders the remainder of the message

unintelligible. According to [58], Vigen`ere invented the autokey cipher in 1586,

but his invention was ignored and forgotten before being reinvented in the

1800s.

(a) Encrypt the following message using the autokey cipher:

Keyword: LEAR

Plaintext: Come not between the dragon and his wrath.

(b) Decrypt the following message using the autokey cipher:

Keyword: CORDELIA

Ciphertext: pckkm yowvz ejwzk knyzv vurux cstri tgac

nying plaintext:

Plaintext ifmusicbethefoodofloveplayon

Ciphertext azdzwqvjjfbwnqphhmptjsszfjci

Help Eve to ﬁgure out the keyword that was used for encryption. Describe

your method in suﬃcient generality to show that the autokey cipher is

susceptible to chosen plaintext attacks.

(d) Bonus Problem: Try to formulate a statistical or algebraic attack on the

autokey cipher, assuming that you are given a large amount of ciphertext

to analyze.

Exercises for Chapter 4 115

Solution to Exercise 4.19.

(a)

comenotbetweenthedragonandhiswrath

learcomenotbetweenthedragonandhisw

nsmvpcffrhpfigpliqkhkreatruifzyild

The ciphertext is nsmvp cffrh pfigp liqkh kreat ruifz yild.

(b)

pckkmyowvzejwzkknyzvvuruxcstritgac

cordelianothingwillcomeofnothingsp

nothingwillcomeofnothingspeakagain

The plaintext is Nothing will come of nothing. Speak again. These are

King Lear’s tragically inaccurate words to his youngest daughter Cordelia.

and the full encryption is

ifmusicbethefoodofloveplayon

surfeitifmusicbethefoodoflov

azdzwqvjjfbwnqphhmptjsszfjci

116 Exercises for Chapter 4

Section. Probability theory

4.20. Use the deﬁnition (4.15) of the probability of an event to prove the

following basic facts about probability theory.

(a) Let Eand Fbe disjoint events. Then

Pr(E∪F) = Pr(E) + Pr(F).

(b) Let Eand Fbe events that need not be disjoint. Then

Pr(E∪F) = Pr(E) + Pr(F)−Pr(E∩F).

(d) Let E1, E2, E3be events. Prove that

Pr(E1∪E2∪E3) = Pr(E1) + Pr(E2) + Pr(E3)−Pr(E1∩E2)

−Pr(E1∩E3)−Pr(E2∩E3) + Pr(E1∩E2∩E3).

The formulas in (b) and (d) and their generalization to nevents are known

as the inclusion–exclusion principle.

Solution to Exercise 4.20.

A solution for this exercise is not currently available.

4.21. We continue with the coin tossing scenario from Example 4.23, so our

experiment consists in tossing a fair coin ten times. Compute the probabilities

of the following events.

(a) The ﬁrst and last tosses are both heads.

(b) Either the ﬁrst toss or the last toss (or both) are heads.

(d) There are exactly kheads and 10 −ktails. Compute the probability for

each value of kbetween 0 and 10. (Hint. To save time, note that the

probability of exactly kheads is the same as the probability of exactly k

tails.)

(e) There is an even number of heads.

(f) There is an odd number of heads.

Solution to Exercise 4.21.

We label the events in the parts of this problem as E(a),E(b),E(c,k), etc.

(a) Pr(E(a)) = 1

(b) Pr(E(b)) = 1 −Pr(Ec

(b)) = 1 −1

4=3

(d)

Pr(E(d,0)) = µ10

0¶·1

210 =1

1024 =1

1024 ≈0.0010

Exercises for Chapter 4 117

Pr(E(d,1)) = µ10

1¶·1

210 =10

1024 =5

512 ≈0.0098

Pr(E(d,2)) = µ10

2¶·1

210 =45

1024 =45

1024 ≈0.0439

Pr(E(d,3)) = µ10

3¶·1

210 =120

1024 =15

128 ≈0.1172

Pr(E(d,4)) = µ10

4¶·1

210 =210

1024 =105

512 ≈0.2051

Pr(E(d,5)) = µ10

5¶·1

210 =252

1024 =63

256 ≈0.2461

Pr(E(d,6)) = µ10

6¶·1

210 =210

1024 =105

512 ≈0.2051

Pr(E(d,7)) = µ10

7¶·1

210 =120

1024 =15

128 ≈0.1172

Pr(E(d,8)) = µ10

8¶·1

210 =45

1024 =45

1024 ≈0.0439

Pr(E(d,9)) = µ10

9¶·1

210 =10

1024 =5

512 ≈0.0098

Pr(E(d,10)) = µ10

10¶·1

210 =1

1024 =1

1024 ≈0.0010

(e)

Pr(E(e)) = Pr(Even number of heads) = X

keven

Pr(E(c,k)) = 1

(f) Pr(E(f)) = Pr(E(d)) = 1

4.22. Alice oﬀers to make the following bet with you. She will toss a fair

coin 14 times. If exactly 7 heads come up, she will give you $4; otherwise you

must give her $1. Would you take this bet? If so, and if you repeated the bet

10000 times, how much money would you expect to win or lose?

Solution to Exercise 4.22.

The probability of winning the bet is

µ14

7¶·1

214=3432

16384 =429

2048 ≈0.2095.

Thus your probability of winning the bet is slightly larger than 1

5, so it is

worthwhile making the bet. (Note that if the probability of winning were

exactly 1

5, then in ﬁve trials you would expect to win once for plus $4 and

lose four times for minus $4, so you would end up even.) In 10000 trials, you

118 Exercises for Chapter 4

would expect to win the bet approximately 2095 times, for a gain of $8380,

and to lose the bet approximately 7905 times, for a loss of $7905. Hence your

average net gain for 10000 trials is $475.

4.23. Let Eand Fbe events.

(a) Prove that Pr(E|E) = 1. Explain in words why this is reasonable.

(b) If Eand Fare disjoint, prove that Pr(F|E) = 0. Explain in words why

this is reasonable.

that F1, . . . , Fnare pairwise disjoint. Prove then that

Prµn

[

i=1

Fi¶=

i=1

Pr(Fi).

(d) Let F1, . . . , Fnbe pairwise disjoint as in (c), and assume further that

F1∪ ··· ∪ Fn= Ω,

where recall that Ω is the entire sample space. Prove the following general

version of the decomposition formula (4.20) in Proposition 4.24(a):

Pr(E) =

i=1

Pr(E|Fi) Pr(Fi).

(e) Prove a general version of Bayes’s formula:

Pr(Fi|E) = Pr(E|Fi) Pr(Fi)

Pr(E|F1) Pr(F1) + Pr(E|F2) Pr(F2) + ··· + Pr(E|Fn) Pr(Fn).

Solution to Exercise 4.23.

(a) Pr(E|E) = Pr(E∩E)

Pr(E)=Pr(E)

Pr(E)= 1. It is clear that if we know

that Eoccurs, then the probability that Eoccurs is 1.

(b) Pr(F|E) = Pr(F∩E)

Pr(E)=Pr(∅)

Pr(E)= 0. If Eoccurs and Fis disjoint

from E, then none of the individual events in Fcan possibly occur, so the

probability of Fis clearly 0.

induction on n, since we already know the formula for n= 2.

(d) The assumptions of F1, . . . , Fnimply that

[

i=1

(E∩Fi) and (E∩Fi)∩(E∩Ej) = ∅for i6=j.

Hence

Exercises for Chapter 4 119

Pr(E) = Prµn

[

i=1

(E∩Fi)¶

i=1

Pr(E∩Fi) since the E∩Fiare disjoint from one another,

i=1

Pr(E|Fi) Pr(Fi).

4.24. There are two urns containing pens and pencils. Urn #1 contains three

pens and seven pencils and Urn #2 contains eight pens and four pencils.

(a) An urn is chosen at random and an object is drawn. What is the proba-

bility that it is a pencil?

(b) An urn is chosen at random and an object is drawn. If the object drawn

is a pencil, what is the probability that it came from Urn #1?

what is the probability that both are pencils?

Solution to Exercise 4.24.

Deﬁne events

E={Urn #1 is selected},

F={A pencil is selected}.

(a) We compute

Pr(F) = Pr(F|E) Pr(E) + Pr(F|Ec) Pr(Ec)

10 ·1

2+4

12 ·1

=31

60 ≈0.517.

(b) We compute

Pr(E|F) = Pr(F|E) Pr(E)

Pr(F)Baye’s law,

=(7/10) ·(1/2)

31/60 using (a) to get Pr(F),

=21

31 ≈0.677.

E={Urn #1 is selected},

F={First item selected is a pencil},

G={Second item selected is a pencil}.

120 Exercises for Chapter 4

Then

Pr(Fand G) = Pr(F) Pr(G|F).

We already know Pr(F) = 31/60 from (a). To compute Pr(G|F), we do a

calculation similar to the calculation in (a). Thus

Pr(G|F) = Pr(G|F&E) Pr(F&E) + Pr(G|F&Ec) Pr(F&Ec)

= Pr(G|F&E) Pr(F|E) Pr(E) + Pr(G|F&Ec) Pr(F|Ec) Pr(Ec)

9·7

10 ·1

2+3

11 ·4

12 ·1

=46

165 ≈0.279.

4.25. An urn contains 20 silver coins and 10 gold coins. You are the sixth

person in line to randomly draw and keep a coin from the urn.

(a) What is the probability that you draw a gold coin?

(b) If you draw a gold coin, what is the probability that the ﬁve people ahead

of you all drew silver coins?

Solution to Exercise 4.25.

(a) It doesn’t matter if you are the sixth to draw a coin, or the ﬁrst, or

the last, your chance of getting a gold coin is 10/30, since there are 10 gold

coins and 30 coins altogether. (If you had some information about the color

of the coins drawn by the people ahead of you, that would change the answer,

but the problem does not give you any such information.)

(b) This part is more diﬃcult. We deﬁne events:

E={You draw a gold coin},

F={Previous 5 people drew silver coins}.

We want to compute Pr(F|E) and we will use Baye’s law in the form

Pr(F|E) = Pr(E|F) Pr(F)

Pr(E).

As already explained, Pr(E) = 1/3. Similarly, it is easy to compute Pr(E|F).

The assumption that Fis true means that when you draw your coin, the urn

now contains 15 silver coins and 10 gold coins, so your probability of drawing

a gold coin is Pr(E|F) = 10/25 = 2/5.

Finally, to compute Pr(F), deﬁne events F1, . . . , F5by

Fi={Person #idraws a silver coin}.

Then

Exercises for Chapter 4 121

Pr(F) = Pr(F1&F2&F3&F4&F5)

= Pr(F1)·Pr(F2|F1)·Pr(F3|F1&F2)·Pr(F4|F1&F2&F3)

·Pr(F5|F1&F2&F3&F4)

=20

30 ·19

29 ·18

28 ·17

27 ·16

=2584

23751 ≈0.109.

We now have the values needed to solve the problem:

Pr(F|E) = Pr(E|F) Pr(F)

Pr(E)=(2/5) ·(2584/23751)

1/3=5168

39585 ≈0.131.

Thus with no other knowledge, there is approximately an 11% chance

that the ﬁrst ﬁve coins chosen are silver, but if we know that the sixth coin

chosen is gold, then the probability that the ﬁrst ﬁve were silver increases to

approximately 13%.

4.26. (The Monty Hall Problem) Monty Hall gives Dan, a contestant, the

choice of three boxes. One box contains a valuable prize and the other two

contain nothing. Dan chooses a box, but does not yet open it. Monty Hall

then opens one of the other boxes, shows that it is empty, and oﬀers Dan the

option of keeping his original box or of switching it for the remaining box.

The Monty Hall problem is to ﬁgure out Dan’s best strategy: “To hold or to

switch?”

The answer may depend on the strategy that Monty Hall employs in decid-

ing which box to open when he has a choice, i.e., when Dan initially chooses

the prize box and the other two boxes are empty. This problem considers

various strategies. (We assume in all cases that Dan is aware of Monty Hall’s

chosen strategy.)

(a) Suppose that when Monty Hall has a choice, he randomly opens one of the

two empty boxes. Should Dan hold or switch, and what is his probability

of winning?

(b) Suppose that Monty Hall has mentally labeled the boxes 0, 1, and 2, and

that if Dan chooses Box nand if the other two boxes are empty, then

Monty Hall opens Box n+ 1. (If n= 2, then he opens Box 0.) Should

Dan hold or switch, and what is his probability of winning?

but now suppose that Monty Hall always opens the lowest-numbered

empty box. What is Dan’s best strategy and what is his probability of

winning? (You may assume that the prize is placed in each box with equal

probability.)

(d) Same questions as in (b) and (c), except that Dan also knows how the

boxes are labeled.

(e) With the same assumptions as in (c), suppose that Dan employs his best

strategy and that Monty Hall knows that Dan is employing this strategy.

122 Exercises for Chapter 4

Can Monty Hall hurt Dan’s chances of winning by placing the prize in

one box more often than the others? But if he does so and if Dan knows,

can Dan do better by changing his strategy?

(f) Suppose that we return to the scenario in (a), but we give Monty Hall

another option, namely he can force Dan to keep the box that Dan initially

chose. Now what is Dan’s best strategy to win the prize and what is Monty

Hall’s best strategy to stop Dan?

Solution to Exercise 4.26.

A solution for this exercise is not currently available.

4.27. Let Sbe a set, let Abe a property of interest, and suppose that for m∈

S, we have Pr(mhas property A) = δ. Suppose further that a Monte Carlo

algorithm applied to mand a random number rsatisfy:

(1) If the algorithm returns Yes, then mdeﬁnitely has property A.

(2) If mhas property A, then the probability that the algorithm returns

Yes is at least p.

Notice that we can restate (1) and (2) as conditional probabilities:

(1) Pr(mhas property A|algorithm returns Yes) = 1,

(2) Pr(algorithm returns Yes |mhas property A)≥p.

Suppose that we run the algorithm Ntimes on the number m, and suppose

that the algorithm returns No every single time. Derive a lower bound, in

terms of δ,p, and N, for the probability that mdoes not have property A.

(This generalizes the version of the Monte Carlo method that we studied in

Section 4.3.3 with δ= 0.01 and p=1

2. Be careful to distinguish pfrom 1 −p

in your calculations.)

Solution to Exercise 4.27.

Let

E={an element m∈ S does not have property A}.

F={the algorithm returns No Ntimes in a row}.

We want a lower bound for the conditional probability Pr(E|F), that is,

the probability that mdoes not have property Adespite the fact that the

algorithm returned No Ntimes. We compute this probability using Bayes’s

formula

Pr(E|F) = Pr(F|E) Pr(E)

Pr(F|E) Pr(E) + Pr(F|Ec) Pr(Ec).

We are given that the probability of have property Ais δ, so

Pr(E) = Pr(not A)=1−δand Pr(Ec) = Pr(A) = δ.

Exercises for Chapter 4 123

Next consider Pr(F|E). If mdoes not have property A, which is our assump-

tion on this conditional probability, then the algorithm always returns No,

since Property (1) tells us that a Yes output forces mto have property A.

Thus

Pr(No |not A) = Pr(A|Yes) = 1,

from which it follows that Pr(F|E) = Pr(No |not A)N= 1.

Finally, we must compute the value of Pr(F|Ec). Since the algorithm is

run Nindependent times, we have

Pr(F|Ec) = Pr(Output is No |mhas property A)N

=¡1−Pr(Output is Yes |mhas property A)¢N

≤(1 −p)Nfrom Property (2) of the Monte Carlo method.

Substituting these values into Bayes’s formula, we ﬁnd that if the algorithm

returns No Ntimes in a row, then the probability that the integer mdoes not

have property Ais

Pr(E|F)≥1·(1 −δ)

1·(1 −δ) + (1 −p)N·δ=1−δ

1−δ+ (1 −p)N·δ.

If δand pare not too small and Nis large, this can be approximated by

Pr(E|F)≥1−(1 −p)N·δ

1−δ+ (1 −p)N·δ≈1−(1 −p)N·δ

1−δ= 1 −(1 −p)N

δ−1−1.

4.28. We continue with the setup described in Exercise 4.27.

(a) Suppose that δ=9

10 and p=3

4. If we run the algorithm 25 times on the

input mand always get back No, what is the probability that mdoes not

have property A?

(b) Same question as (a), but this time we run the algorithm 100 times.

100 and p=1

2. How many times should we run the

algorithm on mto be 99% conﬁdent that mdoes not have property A,

assuming that every output is No?

(d) Same question as (c), except now we want to be 99.9999% conﬁdent.

Solution to Exercise 4.28.

A solution for this exercise is not currently available.

4.29. If an integer nis composite, then the Miller–Rabin test has at least

a 75% chance of succeeding in proving that nis composite, while it never

misidentiﬁes a prime as being composite. (See Table 3.2 in Section 3.4 for a

description of the Miller–Rabin test.) Suppose that we run the Miller–Rabin

test Ntimes on the integer nand that it fails to prove that nis composite.

Show that the probability that nis prime satisﬁes (approximately)

124 Exercises for Chapter 4

Pr(nis prime |the Miller–Rabin test fails Ntimes) ≥1−ln(n)

4N.

(Hint. Use Exercise 4.27 with appropriate choices of A,S,δ, and p. You may

also use the estimate from Section 3.4.1 that the probability that nis prime

is approximately 1/ln(n).)

Solution to Exercise 4.29.

In Exercise 4.27 we let Abe the property of being composite and we

let p=3

4, since we know that if nis composite, then the Miller–Rabin test

returns Yes at least 75% of the time. Further, we have δ≈1−1/ln(n), since δ

is the probability that nis composite, which is 1 minus the probability that

it is prime. The solution to that exercise says that (approximately)

Pr(nis prime |the Miller–Rabin test fails Ntimes)

≥1−(1 −p)N

δ−1−1

≈1−ln(n)−1

≈1−ln(n)

4N.

4.30. Let fX(k) be the binomial density function (4.23). Prove directly, using

the binomial theorem, that Pn

k=0 fX(k) = 1.

Solution to Exercise 4.30.

Let q= 1 −p, so p+q= 1. Then we use the binomial theorem to compute

k=0

fX(k) =

k=0 µn

k¶pk(1 −p)n−k=

k=0 µn

k¶pkqn−k= (p+q)n= 1n= 1.

4.31. In Example 4.37 we used a diﬀerentiation trick to compute the value

of the inﬁnite series P∞

n=1 np(1 −p)n−1. This exercise further develops this

useful technique. The starting point is the formula for the geometric series

∞

n=0

xn=1

1−xfor |x|<1. (4.1)

(a) Prove that ∞

n=1

nxn−1=1

(1 −x)2(4.2)

by diﬀerentiating both sides of (4.57) with respect to x. For which xdoes

the left-hand side of (4.58) converge? (Hint. Use the ratio test.)

Exercises for Chapter 4 125

(b) Diﬀerentiate again to prove that

∞

n=2

n(n−1)xn−2=2

(1 −x)3.(4.3)

∞

n=0 µn+k

k¶xn=1

(1 −x)k+1 .(4.4)

(Hint. Use induction on k.)

(d) Prove that ∞

n=0

n2xn=x+x2

(1 −x)3.(4.5)

(Hint. Multiply (4.58) by xand (4.59) by x2and then add them together.)

(e) Find a formula for ∞

n=0

n3xn.(4.6)

(f) Prove that for every value of kthere is a polynomial Fk(x) such that

∞

n=0

nkxn=Fk(x)

(1 −x)k+1 .(4.7)

(Hint. Use induction on k.) Compute the polynomials F0(x), F1(x),

and F2(x).

(g) Prove that the polynomial Fk(x) in (f) has degree k.

Solution to Exercise 4.31.

(a) Term-by-term diﬀerentiation gives the formula. We compute

ρ= lim

n→∞ |(n+ 1)xn+1|

|nxn|= lim

n→∞

n+ 1

n|x|=|x|.

The ratio test tells us that the series converges for |x|<1 and diverges

for |x|>1. And the series clearly also diverges for |x|= 1.

(b) Term-by-term diﬀerentiation of (a) gives the formula.

∞

n=0

n(n−1)(n−2) ···(n−k+ 1)xn−k=1·2·3···k

(1 −x)k+1 .

(If one wants to be formal, one can prove this formula by induction on k.) Now

divide both sides by k! and use the deﬁnition of the combinatorial symbol to

get

126 Exercises for Chapter 4

∞

n=kµn

k¶xn−k=1

(1 −x)k+1 .

(Notice that we only need to start the summation with n=k, since terms

with n= 0,1, . . . , k−1 give 0.) Finally, in the summation on the left, replace n

by n+k, so now the sum starts at n= 0. This gives

∞

n=0 µn+k

k¶xn=1

(1 −x)k+1 .

(d) Following the hint, we ﬁrst compute

x∞

n=1

nxn−1+x2∞

n=2

n(n−1)xn−2=∞

n=0¡n+n(n−1)¢xn=∞

n=0

n2xn.

Then, according to our results in (a) and (b), this is also equal to

(1 −x)2+2x2

(1 −x)3=x+x2

(1 −x)3.

(e) One way to do this is to diﬀerentiate (b) and then combine various quan-

tities to get the desired result. An easier method is to diﬀerentiate both sides

of (d). Thus

dxµ∞

n=0

n2xn¶=d

dx µx+x2

(1 −x)3¶

∞

n=0

n3xn−1=1 + 4x+x2

(1 −x)4.

Multiplying both sides by xgives the desired result,

∞

n=0

n3xn=x+ 4x2+x3

(1 −x)4.

(f,g)From the geometric series we have F0(x) = 1, and (a) and (d) give F1(x) =

xand F2(x) = x+x2. Now assume that

∞

n=0

nkxn=Fk(x)

(1 −x)k+1

is true for k, where Fk(x) is a polynomial of degree k. Diﬀerentiating both

sides and using the diﬀerentiation rule for quotients yields

∞

n=0

nk+1xn−1=(1 −x)k+1F0

k(x)−(k+ 1)(1 −x)k(−1)Fk(x)

(1 −x)2k+2

=(1 −x)F0

k(x)+(k+ 1)Fk(x)

(1 −x)k+2

Exercises for Chapter 4 127

Multiplying both sides by xgives

∞

n=0

nk+1xn=(x−x2)F0

k(x)+(k+ 1)xFk(x)

(1 −x)k+2 ,

so the desired formula is true with

Fk+1(x) = (x−x2)F0

k(x) + (k+ 1)xFk(x).

Since the degree of F0

k(x) is one smaller than the degree of Fk(x), we also see

that

deg Fk+1(x) = 1 + deg Fk(x).

Since deg F0(x) = 0, we conclude that deg Fk(x) = k.

4.32. In each case, compute the expectation of the random variable X.

(a) The values of Xare uniformly distributed on the set {0,1,2, . . . , N −1}.

(See Example 4.28.)

(b) The values of Xare uniformly distributed on the set {1,2, . . . , N }.

(d) Xis a random variable with a binomial density function (see (4.23) on

page 221).

Solution to Exercise 4.32.

(a)

E(X) = 0 ·1

N+ 1 ·1

N+ 2 ·1

N+··· + (N−1) ·1

=0 + 1 + 2 + ···+ (N−1)

2(N−1)N

=N−1

(b)

E(X) = 1 ·1

N+ 2 ·1

N+ 3 ·1

N+··· +N·1

=1 + 2 + 3 + ···+N

2N(N+ 1)

=N+ 1

(c)

128 Exercises for Chapter 4

E(X) = 1+3+7+11+19+23

6=64

6=32

(d)

E(X) =

k=0

k·fX(k)

k=0

kµn

k¶pk(1 −p)n−k

= (1 −p)n

k=0

kµn

k¶µ p

1−p¶k

If we let x=p/(1 −p), then we need to compute the value of the sum

k=0

kµn

k¶xk.

To do this, we start with the binomial theorem

k=0 µn

k¶xk= (x+ 1)n

and diﬀerentiate both sides with respect to xto get

k=0

kµn

k¶xk−1=n(x+ 1)n−1.

Now multiply both sides by xto get

k=0

kµn

k¶xk=nx(x+ 1)n−1.

This gives the value

E(X) = (1−p)n·n·p

1−p·µp

1−p+ 1¶n−1

= (1−p)n·n·p

1−p·µ1

1−p¶n−1

=np.

This makes sense, since if we perform the experiment ntimes and have a

probability pof succeeding each time, we would expect to succeed, on average,

a total of np times.

4.33. Let Xbe a random variable on the probability space Ω. It might seem

more natural to deﬁne the expected value of Xby the formula

ω∈Ω

X(ω)·Pr(ω).(4.8)

Prove that the formula (4.64) gives the same value as equation (4.27) on

page 225, which we used in the text to deﬁne E(X).

Exercises for Chapter 4 129

Solution to Exercise 4.33.

We compute (the key step comes in the middle where we reverse the order

of summation):

E(X) =

i=1

xi·fX(xi)

i=1

xi·Pr(X=xi)

i=1

xiPr©ω∈Ω : X(ω) = xiª

i=1

xiXω∈Ω

X(ω)=xiPr(ω)

ω∈Ω

Pr(ω)X

1≤i≤n

xi=X(ω)

ω∈Ω

Pr(ω)·X(ω),

where for the ﬁnal equality we use that fact that x1, . . . , xnare distinct, so

each X(ω) is equal to exactly one of the xivalues.

Section. Collision algorithms and the birthday paradox

4.34. (a) In a group of 23 strangers, what is the probability that at least two

of them have the same birthday? How about if there are 40 strangers?

In a group of 200 strangers, what is the probability that one of them

has the same birthday as your birthday? (Hint. See the discussion in

Section 4.4.1.)

(b) Suppose that there are Ndays in a year (where Ncould be any num-

ber) and that there are npeople. Develop a general formula, analogous

to (4.28), for the probability that at least two of them have the same

birthday. (Hint. Do a calculation similar to the proof of (4.28) in the col-

lision theorem (Theorem 4.38), but note that the formula is a bit diﬀerent

because the birthdays are being selected from a single list of Ndays.)

Pr(at least one match) ≥1−e−(some function of nand N)

for the probability in (b), analogous to the estimate (4.29).

Solution to Exercise 4.34.

We start by doing (b).

130 Exercises for Chapter 4

Pr µat least one match

in nattempts ¶= 1 −Pr µall nbirthdays

are diﬀerent ¶

= 1 −

i=1

Pr 



ith birthday is diﬀerent

from all of the

previous i−1 birthdays



= 1 −

i=1

N−(i−1)

= 1 −

n−1

i=1 µ1−i

N¶.

Then the answer to the ﬁrst part of (a) is obtained by setting N= 365

and n= 23, which gives

(a) Pr(match) = 1 −

i=1 µ1−i

365¶≈50.73%.

Similarly, N= 365 and n= 40 gives the answer to the second part of (a),

(b) Pr(match) = 1 −

i=1 µ1−i

365¶≈89.12%.

The ﬁnal part of (a) is

Pr(someone has your birthday) = 1 −Pr(no one has your birthday)

= 1 −Pr(one person does not have your birthday)200

= 1 −µ364

365¶200

≈42.23%.

For (c) we use the lower bound e−x≥1−xwith x=i/N to compute

Pr µat least one match

in nattempts ¶= 1 −

n−1

i=1 µ1−i

N¶

≥1−

n−1

i=1

e−i/N

= 1 −e−(1+2+···+(n−1))/N

= 1 −e−(n−1)n/2N

≈1−e−n2/2N.

Notice that we have used the well known formula

Exercises for Chapter 4 131

1 + 2 + ·+ (n−1) = n(n−1)

4.35. A deck of cards is shuﬄed and the top eight cards are turned over.

(a) What is the probability that the king of hearts is visible?

(b) A second deck is shuﬄed and its top eight cards are turned over. What

is the probability that a visible card from the ﬁrst deck matches a visible

card from the second deck? (Note that this is slightly diﬀerent from Ex-

ample 4.39 because the cards in the second deck are not being replaced.)

Solution to Exercise 4.35.

A solution for this exercise is not currently available.

4.36. (a) Prove that

e−x≥1−xfor all values of x.

(Hint. Look at the graphs of e−xand 1 −x, or use calculus to compute

the minimum of the function f(x) = e−x−(1 −x).)

(b) Prove that for all a > 1, the inequality

e−ax ≤(1 −x)a+1

2ax2is valid for all 0 ≤x≤1.

(This is a challenging problem.)

in the collision theorem (Theorem 4.38). Use (b) to prove that

Pr(at least one red) ≤1−e−mn/N +mn2

2N2.

Thus if Nis large and mand nare not much larger than √N, then the

estimate

Pr(at least one red) ≈1−e−mn/N

is quite accurate. (Hint. Use (b) with a=mand x=n/N.)

Solution to Exercise 4.36.

(a) Let f(x) = e−x−1+x. Then f(0) = f0(0) = 0. Then generalized mean

value theorem says that

f(x) = f(0) + f0(0)x+1

2f00(z)x2for some 0 ≤z≤x,

so we ﬁnd that f(x) = 1

2e−zx2≥0. This is the desired inequality.

(b) Let

f(x) = (1 −x)a+1

2ax2−e−ax.

132 Exercises for Chapter 4

Since f(0) = 0, it suﬃces to prove that

f0(x) = −a(1 −x)a−1+ax +ae−ax

is positive for 0 < x < 1. We can divide by a, and for notational convenience,

we let a=b+ 1. So we need to prove that

g(x) = −(1 −x)b+x+e−(b+1)x

is positive for 0 <x<1 and b > 0.

From (a) we know that e−x>1−x, so raising both sides to the bth power

and multiplying by −1 gives

−(1 −x)b>−e−bx.

Substituting this into g(x), we ﬁnd that

g(x)>−e−bx +x+e−(b+1)x=x−e−bx(1 −e−x).

It is clear that this last expression is increasing as bincreases. (To be more

formal, its derivative with respect to bis be−bx(1 −e−x), which is strictly

positive for 0 < x < 1.) Hence the expression is minimized when b= 0, so we

get

g(x)> x −(1 −e−x) = e−x−(1 −x).

Using (a) again gives g(x)>0.

Remark: It appears to be true numerically that f(x)≥0 provided that a >

0.8526055 . . . , where c= 0.8526055 ... is the unique real solution to cec= 2.

Pr µat least

one red ¶= 1 −³1−n

N´mfrom the Collision Theorem

≤1−µe−mn/N −mn2

2N2¶use (b) with a=mand x=n

4.37. Solve the discrete logarithm problem 10x= 106 in the ﬁnite ﬁeld F811

by ﬁnding a collision among the random powers 10iand 106 ·10ithat are

listed in Table 4.17.

Solution to Exercise 4.37.

From Table 4.17 we see that

10234 = 106 ·10399 = 304 in F811.

Hence

10234 ·10−399 = 10−165 = 10645 = 106 in F811.

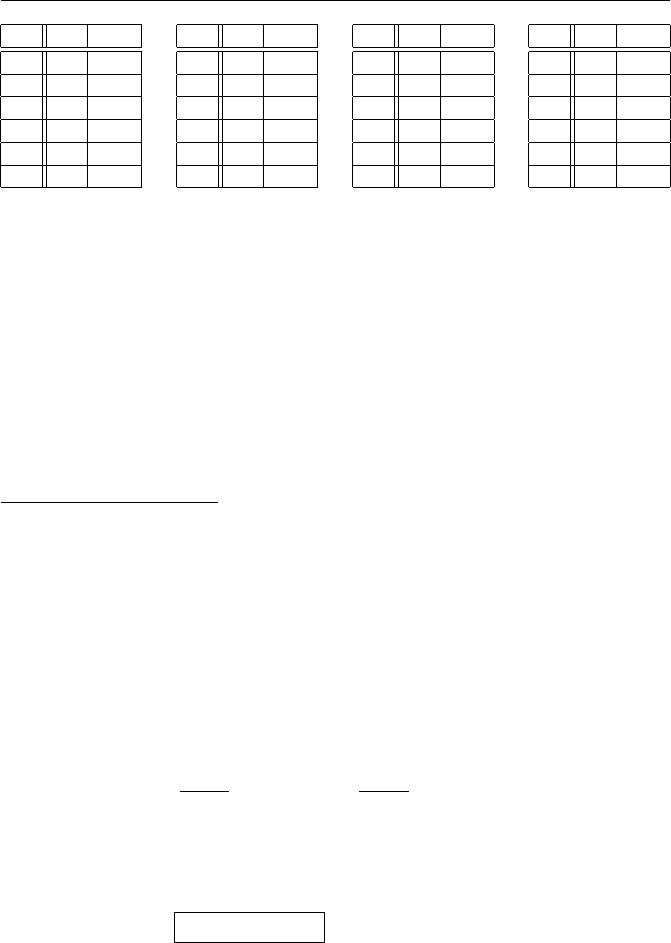
Exercises for Chapter 4 133

i hia·hi

116 96 444

497 326 494

225 757 764

233 517 465

677 787 700

622 523 290

i hia·hi

519 291 28

286 239 193

298 358 642

500 789 101

272 24 111

307 748 621

i hia·hi

791 496 672

385 437 95

178 527 714

471 117 237

42 448 450

258 413 795

i hia·hi

406 801 562

745 194 289

234 304 595

556 252 760

326 649 670

399 263 304

Table 4.12: Data for Exercise 4.37, h= 10, a= 106, p= 811

Section. Pollard’s ρmethod

4.38. Table 4.18 gives some of the computations for the solution of the discrete

logarithm problem

11t= 41387 in F81799 (4.9)

using Pollard’s ρmethod. (It is similar to Table 4.11 in Example 4.51.) Use

the data in Table 4.18 to solve (4.65).

Solution to Exercise 4.38.

x308 =x154 = 15386 in F81799.

α154 = 81756, β154 = 9527, γ154 = 67782, δ154 = 28637.

1181756 ·413879527 = 1167782 ·4138728637 in F81799.

1113974 = 4138719110 in F81799.

gcd(19110,81798) = 6.

81340 ·19110 ≡6 (mod 81798).

1113974·81340 = 111136645160 = 1161950 = 413876in F81799.

61950

6= 10325,81798

6= 13633.

log11(41387) ∈ {10325 + 13633 ·k: 0 ≤k < 6}

={10325,23958,37591,51224,64857,78490}.

1110325 = 73192,1123958 = 40412,1137591 = 49019,1151224 = 8607,

1164857 = 41387 ,1178490 = 32780.

4.39. Table 4.19 gives some of the computations for the solution of the discrete

logarithm problem

7t= 3018 in F7963 (4.10)

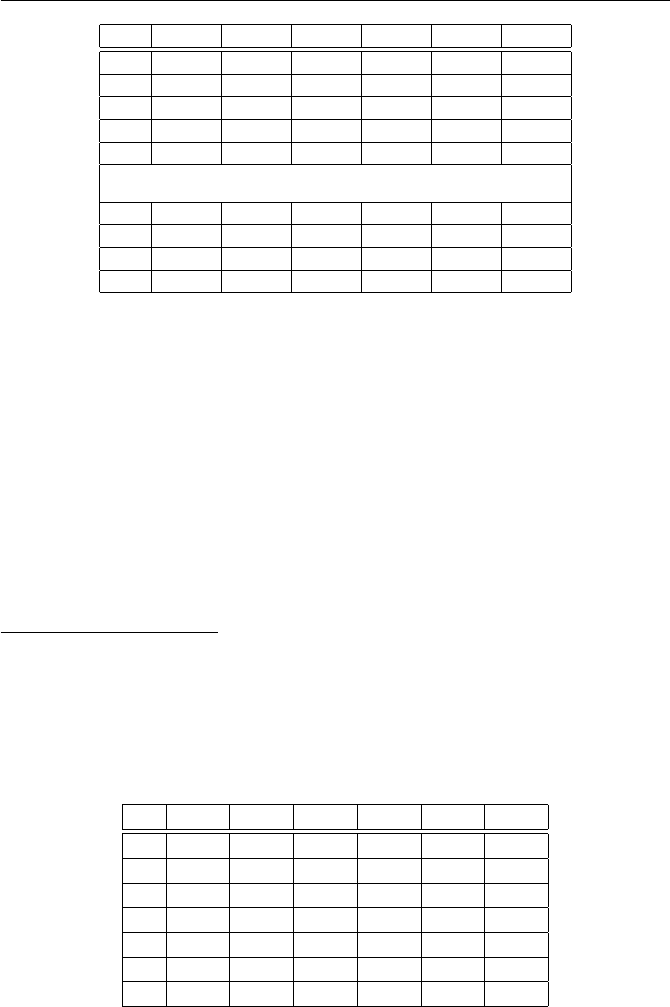
134 Exercises for Chapter 4

i xiyiαiβiγiδi

0 1 1 0 0 0 0

1 11 121 1 0 2 0

2 121 14641 2 0 4 0

3 1331 42876 3 0 12 2

4 14641 7150 4 0 25 4

151 4862 33573 40876 45662 29798 73363

152 23112 53431 81754 9527 37394 48058

153 8835 23112 81755 9527 67780 28637

154 15386 15386 81756 9527 67782 28637

Table 4.13: Computations to solve 11t= 41387 in F81799 for Exercise 4.38

using Pollard’s ρmethod. (It is similar to Table 4.11 in Example 4.51.) Extend

Table 4.19 until you ﬁnd a collision (we promise that it won’t take too long)

and then solve (4.66).

Solution to Exercise 4.39.

Extending the table:

i xiyiαiβiγiδi

87 1329 1494 6736 7647 3148 3904

88 1340 1539 6737 7647 3150 3904

89 1417 4767 6738 7647 6302 7808

90 1956 1329 6739 7647 4642 7655

91 5729 1417 6740 7647 4644 7655

92 2449 5729 6740 7648 4646 7655

93 1217 1217 6741 7648 4647 7656

Exercises for Chapter 4 135

x186 =x93 = 1217 in F7963.

α93 = 6741, β93 = 7648, γ93 = 4647, δ93 = 7656.

76741 ·30187648 = 74647 ·30187656 in F7963.

72094 = 30188in F7963.

gcd(8,7962) = 2.

6967 ·8≡2 (mod 7962).

72094·6967 = 714588898 = 72514 = 30182in F7963.

2514

2= 1257,7962

2= 3981.

log7(3018) ∈ {1257 + 3981 ·k: 0 ≤k < 2}={1257,5238}.

71257 = 4945,75238 = 3018.

i xiyiαiβiγiδi

0110000

1 7 49 1 0 2 0

2 49 2401 2 0 4 0

3 343 6167 3 0 6 0

4 2401 1399 4 0 7 1

87 1329 1494 6736 7647 3148 3904

88 1340 1539 6737 7647 3150 3904

89 1417 4767 6738 7647 6302 7808

90 1956 1329 6739 7647 4642 7655

Table 4.14: Computations to solve 7t= 3018 in F7963 for Exercise 4.39

4.40. Write a computer program implementing Pollard’s ρmethod for solving

the discrete logarithm problem and use it to solve each of the following:

(a) 2t= 2495 in F5011.

(b) 17t= 14226 in F17959.

Solution to Exercise 4.40.

(a) 23351 = 2495 .

(b) 1714557 = 14226 .

136 Exercises for Chapter 4

4.41. Evaluate the integral I=R∞

0t2e−t2/2dt appearing in the proof of

Theorem 4.47. (Hint. Write I2as an iterated integral,

I2=Z∞

0Z∞

x2e−x2/2·y2e−y2/2dx dy,

and switch to polar coordinates.)

Solution to Exercise 4.41.

Following the hint, we have

I2=Z∞

0Z∞

x2e−x2/2y2e−y2/2dx dy

=Z∞

0Z∞

x2y2e−(x2+y2)/2dx dy

=Z∞

0Zπ/2

(rsin θ)2(rcos θ)2e−r2/2r dr dθ

=ÃZπ/2

sin2θcos2θ dθ!µZ∞

r5e−r2/2dr¶.

Each of these integrals is now a moderately hard freshman calculus exercise.

For the ﬁrst one we can use

sin2θcos2θ= (sin θcos θ)2=µ1

2sin(2θ)¶2

4·1−cos(4θ)

Then

Zπ/2

sin2θcos2θ dθ =Zπ/2

1−cos(4θ)

8dθ =θ

8−sin(4θ)

32 ¯¯¯¯

π/2

=π

16.

For the second integral we substitute r2=zand then integrate by parts twice.

Thus

Z∞

r5e−r2/2dr =Z∞

z2e−z/21

2dz

=−z2e−z/2¯¯¯∞

0+ 2 Z∞

ze−z/2dz

= 2 Z∞

ze−z/2dz

=−4ze−z/2¯¯¯∞

0+ 4 Z∞

e−z/2dz

= 4 Z∞

e−z/2dz

=−8e−z/2¯¯¯∞

0= 8.

Hence I2=π/16 ·8 = π/2, so I=pπ/2.

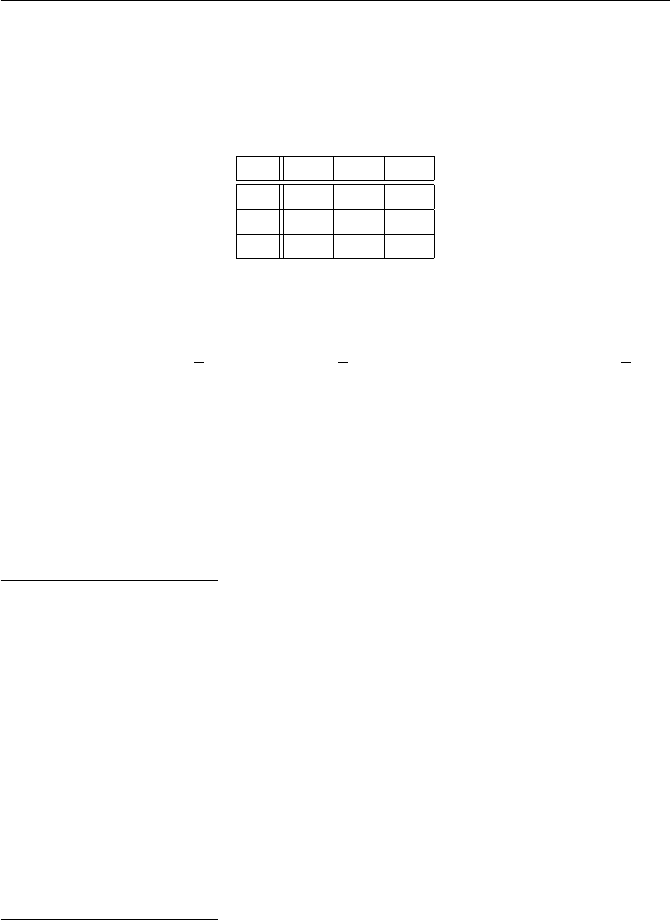
Exercises for Chapter 4 137

Section. Information theory

4.42. Consider the cipher that has three keys, three plaintexts, and four

ciphertexts that are combined using the following encryption table (which is

similar to Table 4.12 used in Example 4.53 on page 246).

m1m2m3

k1c2c4c1

k2c1c3c2

k3c3c1c2

Suppose further that the plaintexts and keys are used with the following

probabilities:

f(m1) = f(m2) = 2

5, f(m3) = 1

5, f(k1) = f(k2) = f(k3) = 1

(a) Compute f(c1), f(c2), f(c3), and f(c4).

(b) Compute f(c1|m1), f(c1|m2), and f(c1|m3). Does this cryptosystem

have perfect secrecy?

(d) Compute f(k1|c3) and f(k2|c3).

Solution to Exercise 4.42.

A solution for this exercise is not currently available.

4.43. Suppose that a shift cipher is employed such that each key, i.e., each

shift amount from 0 to 25, is used with equal probability and such that a new

key is chosen to encrypt each successive letter. Show that this cryptosystem

has perfect secrecy by ﬁlling in the details of the following steps.

(a) Show that Pk∈K fM(dk(c)) = 1 for every ciphertext c∈ C.

(b) Compute the ciphertext density function fCusing the formula

fC(c) = X

k∈K

fK(k)fM(dk(c)).

Solution to Exercise 4.43.

A solution for this exercise is not currently available.

4.44. Suppose that a cryptosystem has the same number of plaintexts as it

does ciphertexts (#M= #C). Prove that for any given key k∈ K and any

given ciphertext c∈ C, there is a unique plaintext m∈ M that encrypts to c

using the key k. (We used this fact during the proof of Theorem 4.55. Notice

that the proof does not require the cryptosystem to have perfect secrecy; all

that is needed is that #M= #C.)

138 Exercises for Chapter 4

Solution to Exercise 4.44.

Fix k∈ K. The encryption map ek:M → C is injective by deﬁnition

of a cryptosystem, so our assumption that #M= #Cimplies that ekis also

surjective, and hence is a bijective map from Mto C. This is equivalent to the

assertion that for every c∈ C, there is a unique m∈ M satisfying ek(m) = c,

which is the desired result.

4.45. Let Sm,c =©k∈ K :ek(m) = cªbe the set used during the proof of

Theorem 4.55. Prove that if c6=c0, then Sm,c ∩Sm,c0=∅. (Prove this for any

cryptosystem; it is not necessary to assume perfect secrecy.)

Solution to Exercise 4.45.

Suppose that k∈ Sm,c∩Sm,c0. Then c=ek(m) = c0. Hence Sm,c∩Sm,c06=∅

implies that c=c0.

4.46. Suppose that a cryptosystem satisﬁes #K= #M= #Cand that it

has perfect secrecy. Prove that every ciphertext is used with equal probability

and that every plaintext is used with equal probability. (Hint. We proved one

of these during the course of proving Theorem 4.55. The proof of the other is

similar.)

Solution to Exercise 4.46.

A solution for this exercise is not currently available.

4.47. Prove the “only if” part of Theorem 4.55, i.e., prove that if a cryp-

tosystem with an equal number of keys, plaintexts, and ciphertexts satisﬁes

conditions (a) and (b) of Theorem 4.55, then it has perfect secrecy.

Solution to Exercise 4.47.

A solution for this exercise is not currently available.

4.48. Let Xbe an experiment (random variable) with outcomes x1, . . . , xn

occurring with probabilities p1, . . . , pn, and similarly let Ybe an experiment

with outcomes y1, . . . , ymoccurring with probabilities q1, . . . , qm. Consider the

experiment Zconsisting of ﬁrst performing Xand then performing Y. Thus

the outcomes of Zare the mn pairs (xi, yj) occurring with probabilities piqj.

Use the formula for entropy (4.51) to prove that

H(Z) = H(X) + H(Y).

Thus entropy is additive on independent compound events, which is a special

case of Property H3on page 250.

Solution to Exercise 4.48.

Using the formula for entropy, we compute

Exercises for Chapter 4 139

H(Z) = −

i=1

j=1

piqjlog(piqj)

=−

i=1

j=1

piqj(log pi+ log qj)

=−

i=1

pilog pi

j=1

qj−

i=1

j=1

qjlog qj

=H(X)·1 + 1 ·H(Y).

4.49. Let F(t) be a twice diﬀerentiable function with the property that F00(t)<0

for all xin its domain. Prove that Fis concave in the sense of (4.52). Conclude

in particular that the function F(t) = log tis concave for all t > 0.

Solution to Exercise 4.49.

A solution for this exercise is not currently available.

4.50. Use induction to prove Jensen’s inequality (Theorem 4.59).

Solution to Exercise 4.50.

The case n= 2 is true by deﬁnition of concavity. Assume now that it is

true for n. The idea is to combine two of the terms in the sum α1t1+··· +

αntn+αn+1tn+1 into one term, say the last two. In other words, we want to

write

αntn+αn+1tn+1 as βnyn,

but we need to make sure that α1+α2+···+αn−1+βn= 1. So we need to

take βn=αn+αn+1, which means that we need to take

yn=αntn+αn+1tn+1

αn+αn+1

With this choice of βnand yn, we have α1+··· +αn−1+βn= 1, so we can

apply the induction hypothesis to conclude that

f(α1t1+···+αn−1tn−1+βnyn)≤α1f(t1) + ··· +αn−1f(tn−1) + βnf(yn).

We are also going to apply the induction hypothesis to f(yn). We can write yn

yn=αn

αn+αn+1

tn+αn+1

αn+αn+1

tn+1 =γtn+δtn+1,

where notice that γand δsatisfy γ+δ= 1. Hence the induction hypothesis

tells us that

f(yn) = f(γtn+δtn+1)≤γf (tn) + δf (tn+1).

140 Exercises for Chapter 4

Now multiplying both sides by βnand substituting in the values γ,δ, and βn

yields

βnf(yn)≤βnγf(tn) + βnδf(tn+1) = αnf(tn) + αn+1f(tn+1).

Finally, substituting this in above gives the desired inequality

f(α1t1+···+αntn+αn+1tn+1)≤α1f(t1) + ··· +αnf(tn) + αn+1f(tn+1).

The induction proof that there is equality if and only if all of the ti’s are equal

is similar.

4.51. Let Xand Ybe independent random variables.

(a) Prove that the equivocation H(X|Y) is equal to the entropy H(X).

(b) If H(X|Y) = H(X), is it necessarily true that Xand Yare independent?

Solution to Exercise 4.51.

Independence means that f(x|y) = f(x), so

H(X|Y) = −X

x,y

f(y)f(x|y) log f(x|y)

=−X

x,y

f(y)f(x) log f(x)

=−X

f(y)X

f(x) log f(x)

= 1 ·H(X).

For the converse, notice that

H(X) = −X

f(x) log f(x)

=−X

x³X

f(x, y)´log f(x)

=−X

x,y

f(y)f(x|y) log f(x),

H(X)−H(X|Y) = −X

x,y

f(y)f(x|y) log f(x)

f(x|y)

=−X

x,y

f(x, y) log f(x)f(y)

f(x, y).

It is likely that one could come up with dependent random variables Xand Y

making this quantity vanish.

Exercises for Chapter 4 141

4.52. Suppose a cryptosystem has two keys, K={k1, k2}, each of which

is equally likely to be used, and suppose that it has three plaintexts M=

{m1, m2, m3}that occur with probabilities f(m1) = 1

2,f(m2) = 1

4, and

f(m3) = 1

(a) Create an encryption function for this cipher, similar to Example 4.53,

such that there are three ciphertexts C={c1, c2, c3}and such that the

ciphertext c1occurs with probability 1

2. (There is more than one correct

answer to this problem.)

(b) Compute the entropies H(K), H(M), and H(C) of your encryption

scheme in (a).

(d) Use your answer in (c) to explain why each ciphertext leaks information.

Solution to Exercise 4.52.

A solution for this exercise is not currently available.

4.53. Suppose that the key equivocation of a certain cryptosystem vanishes,

i.e., suppose that H(K|C) = 0. Prove that even a single observed ciphertext

uniquely determines which key was used.

Solution to Exercise 4.53.

A solution for this exercise is not currently available.

4.54. Write a computer program that reads a text ﬁle and performs the

following tasks:

[1] Convert all alphabetic characters to lowercase and convert all strings of

consecutive nonalphabetic characters to a single space. (The reason for

leaving in a space is that when you count bigrams and trigrams, you will

want to know where words begin and end.)

[2] Count the frequency of each letter a-to-z, print a frequency table, and use

your frequency table to estimate the entropy of a single letter in English,

as we did in Section 4.6.3 using Table 1.3.

[3] Count the frequency of each bigram aa,ab,. . . ,zz, being careful to in-

clude only bigrams that appear within words. (As an alternative, also

allow bigrams that either start or end with a space, in which case

there are 272−1 = 728 possible bigrams.) Print a frequency table of

the 25 most common bigrams and their probabilities, and use your full

frequency table to estimate the entropy of bigrams in English. In the

notation of Section 4.6.3, this is the quantity H(L2). Compare 1

2H(L2)

with the value of H(L) from step [1].

[4] Repeat [3], but this time with trigrams. Compare 1

3H(L3) with the values

of H(L) and 1

2H(L2) from [2] and [3]. (Note that for this part, you will

need a large quantity of text in order to get some reasonable frequencies.)

Try running your program on some long blocks of text. For example, the

following noncopyrighted material is available in the form of ordinary text ﬁles

from Project Gutenberg at http://www.gutenberg.net/. To what extent

142 Exercises for Chapter 4

are the letter frequencies similar and to what extent do they diﬀer in these

diﬀerent texts?

(a) Alice’s Adventures in Wonderland by Lewis Carroll,

http://www.gutenberg.net/etext/11

(b) Relativity: the Special and General Theory by Albert Einstein,

http://www.gutenberg.net/etext/5001

http://www.gutenberg.net/etext/1609

(d) 20000 Lieues Sous Les Mers (20000 Leagues Under the Sea) by Jules

Verne, http://www.gutenberg.net/etext/5097. Note that this one is a

little trickier, since ﬁrst you will need to convert all of the letters to their

unaccented forms.

Chapter 5

Elliptic Curves and

Cryptography

Exercises for Chapter 5

Section. Elliptic curves

5.1. Let Ebe the elliptic curve E:Y2=X3−2X+ 4 and let P= (0,2) and

Q= (3,−5). (You should check that Pand Qare on the curve E.)

(a) Compute P⊕Q.

(b) Compute P⊕Pand Q⊕Q.

Solution to Exercise 5.1.

(a) P⊕Q= (22/9,100/27).

(b) P⊕P=Q⊕Q= (1/4,−15/8).

5.2. Check that the points P= (−1,4) and Q= (2,5) are points on the

elliptic curve E:Y2=X3+ 17.

(a) Compute the points P⊕Qand PªQ.

(b) Compute the points 2Pand 2Q.

(Bonus. How many points with integer coordinates can you ﬁnd on E?)

Solution to Exercise 5.2.

(a) P+Q=¡−8

9,−109

27 ¢and P−Q= (8,23).

(b) 2P=¡137

64 ,−2651

512 ¢and 2Q=¡−64

25 ,59

125 ¢

Bonus. This curve has 16 points with integer coordinates, including one

that is quite large. This is somewhat surpising number. The points are

(−2,±3), (−1,±4), (2,±5), (4,±9), (8,±23), (43,±282), (52,±375), (5234,±378661).

There are no others, but that’s not so easy to prove.

143

144 Exercises for Chapter 5

5.3. Suppose that the cubic polynomial X3+AX +Bfactors as

X3+AX +B= (X−e1)(X−e2)(X−e2).

Prove that 4A3+ 27B2= 0 if and only if two (or more) of e1,e2, and e3are

the same. (Hint. Multiply out the right-hand side and compare coeﬃcients to

relate Aand Bto e1,e2, and e3.)

Solution to Exercise 5.3.

We have

X3+AX +B=X3−(e1+e2+e3)X2+ (e1e2+e1e3+e2e3)X−e1e2e3,

and comparing the coeﬃcients gives three relations

e1+e2+e3= 0,

e1e2+e1e3+e2e3=A,

e1e2e3=B.

Suppose ﬁrst that two of the eiare the same, say e2=e3. Then we get

e1+ 2e2= 0,2e1e2+e2

2=A, e1e2

2=B.

So e1=−2e2, and substituting this into the second and third equations gives

−3e2

2=Aand −2e3

2=B.

Hence

4A3+ 27B2= 4(−3e2

2)3+ 27(−2e3

2)2= 0.

Conversely, suppose that 4A3+ 27B2= 0. Substituting the expressions

for Aand Bfrom above and multiplying it out gives the rather complicated

expression

4A3+ 27B2= (4e3

2+ 12e3e2

2+ 12e2

3e2+ 4e3

3)e3

1+ (12e3e3

2+ 51e2

3e2

2+ 12e3

3e2)e2

+ (12e2

3e3

2+ 12e3

3e2

2)e1

+ 4e3

3e3

Next we substitute e1=−e2−e3to get

4A3+ 27B2=−4e6

2−12e3e5

2+ 3e2

3e4

2+ 26e3

3e3

2+ 3e4

3e2

2−12e5

3e2−4e6

We’d like to know that this last expression vanishes if any two of the eiare

the same. It is not hard to check that it is a multiple of e2−e3, and indeed a

multiple of (e2−e3)2. But we’d also like it to vanish when e3=e1, which is

the same as when e3=−e2−e3. So we check and ﬁnd that the expression is

divisible by e2+ 2e3, and in fact it is divisible by (e2+ 2e3)2. Similarly, it is

divisible by (e3+ 2e2)2. So we ﬁnd that

Exercises for Chapter 5 145

4A3+ 27B2=−(e2−e3)2(e2+ 2e3)2(e3+ 2e2)2.

Hence using the fact that e1+e2+e3= 0, we ﬁnd that

4A3+ 27B2if and only if (e2−e3)2(e1−e3)2(e1−e2)2= 0,

5.4. Sketch each of the following curves, as was done in Figure 5.1 on

page 280.

(a) E:Y2=X3−7X+ 3.

(b) E:Y2=X3−7X+ 9.

(d) E:Y2=X3−3X+ 2.

(e) E:Y2=X3.

Notice that the curves in (d) and (e) have ∆E= 0, so they are not elliptic

curves. How do their pictures diﬀer from the pictures in (a), (b), and (c)?

Each of the curves (d) and (e) has one point that is somewhat unusual. These

unusual points are called singular points.

Section. Elliptic curves over ﬁnite ﬁelds

5.5. For each of the following elliptic curves Eand ﬁnite ﬁelds Fp, make a

list of the set of points E(Fp).

(a) E:Y2=X3+ 3X+ 2 over F7.

(b) E:Y2=X3+ 2X+ 7 over F11.

(d) E:Y2=X3+ 9X+ 5 over F11.

(e) E:Y2=X3+ 9X+ 5 over F13.

Solution to Exercise 5.5.

(a) #E(F7) = 9

E(F7) = {O,(0,3),(0,4),(2,3),(2,4),(4,1),(4,6),(5,3),(5,4)}

(b) #E(F11) = 7

E(F11) = {O,(6,2),(6,9),(7,1),(7,10),(10,2),(10,9)}

E(F11) = {O,(0,4),(0,7),(3,0),(6,5),(6,6),(9,0),(10,0)}

(d) #E(F11) = 14

E(F11) = {O,(0,4),(0,7),(1,2),(1,9),(2,3),(2,8),(3,2),(3,9),(6,0),

(7,2),(7,9),(9,1),(9,10)}

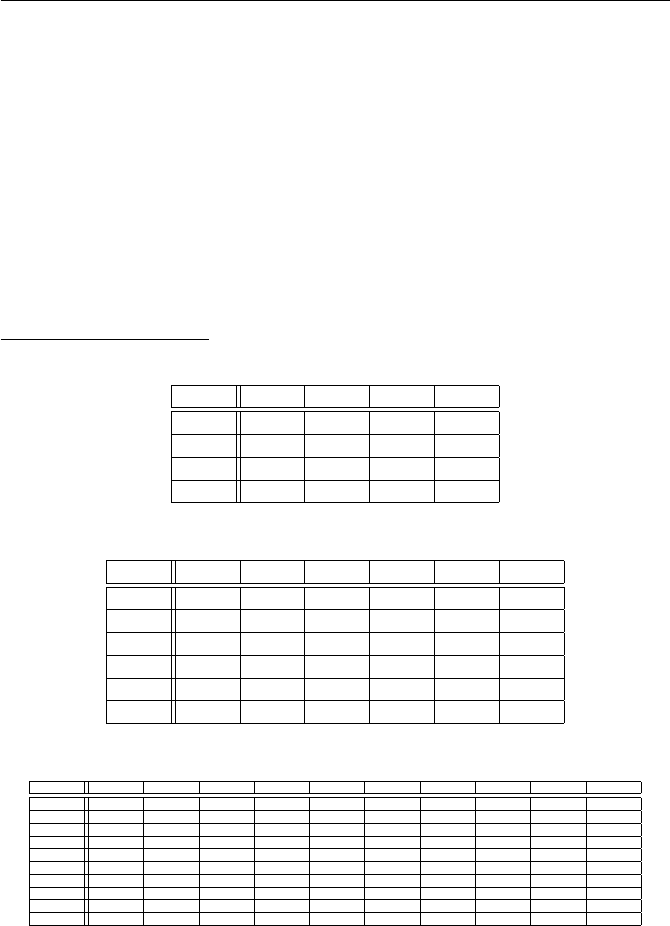
146 Exercises for Chapter 5

(e) #E(F13) = 9

E(F13) = {O,(4,1),(4,12),(8,2),(8,11),(9,3),(9,10),(10,4),(10,9)}

5.6. Make an addition table for Eover Fp, as we did in Table 5.1.

(a) E:Y2=X3+X+ 2 over F5.

(b) E:Y2=X3+ 2X+ 3 over F7.

You may want to write a computer program for (c), since E(F11) has a lot

of points!

Solution to Exercise 5.6.

(a) E(F5) = {O,(1,2),(1,3),(4,0)}.

O(1,2) (1,3) (4,0)

O O (1,2) (1,3) (4,0)

(1,2) (1,2) (4,0) O(1,3)

(1,3) (1,3) O(4,0) (1,2)

(4,0) (4,0) (1,3) (1,2) O

(b) E(F7) = {O,(2,1),(2,6),(3,1),(3,6),(6,0)}.

O(2,1) (2,6) (3,1) (3,6) (6,0)

O O (2,1) (2,6) (3,1) (3,6) (6,0)

(2,1) (2,1) (3,6) O(2,6) (6,0) (3,1)

(2,6) (2,6) O(3,1) (6,0) (2,1) (3,6)

(3,1) (3,1) (2,6) (6,0) (3,6) O(2,1)

(3,6) (3,6) (6,0) (2,1) O(3,1) (2,6)

(6,0) (6,0) (3,1) (3,6) (2,1) (2,6) O

O(0,4) (0,7) (3,4) (3,7) (4,0) (8,4) (8,7) (9,2) (9,9)

O O (0,4) (0,7) (3,4) (3,7) (4,0) (8,4) (8,7) (9,2) (9,9)

(0,4) (0,4) (9,2) O(8,7) (9,9) (8,4) (3,7) (4,0) (3,4) (0,7)

(0,7) (0,7) O(9,9) (9,2) (8,4) (8,7) (4,0) (3,4) (0,4) (3,7)

(3,4) (3,4) (8,7) (9,2) (8,4) O(9,9) (0,7) (3,7) (4,0) (0,4)

(3,7) (3,7) (9,9) (8,4) O(8,7) (9,2) (3,4) (0,4) (0,7) (4,0)

(4,0) (4,0) (8,4) (8,7) (9,9) (9,2) O(0,4) (0,7) (3,7) (3,4)

(8,4) (8,4) (3,7) (4,0) (0,7) (3,4) (0,4) (9,2) O(9,9) (8,7)

(8,7) (8,7) (4,0) (3,4) (3,7) (0,4) (0,7) O(9,9) (8,4) (9,2)

(9,2) (9,2) (3,4) (0,4) (4,0) (0,7) (3,7) (9,9) (8,4) (8,7) O

(9,9) (9,9) (0,7) (3,7) (0,4) (4,0) (3,4) (8,7) (9,2) O(8,4)

5.7. Let Ebe the elliptic curve

E:y2=x3+x+ 1.

Compute the number of points in the group E(Fp) for each of the following

primes:

(a) p= 3. (b) p= 5. (c) p= 7. (d) p= 11.

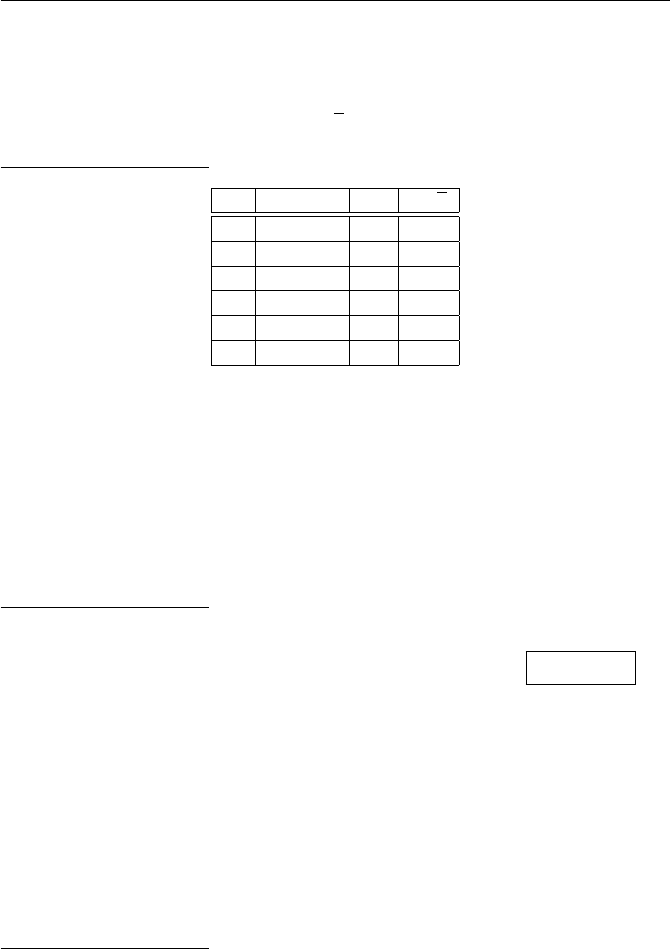
Exercises for Chapter 5 147

In each case, also compute the trace of Frobenius

tp=p+ 1 −#E(Fp)

and verify that |tp|is smaller than 2√p.

Solution to Exercise 5.7.

p#E(Fp)tp2√p

3 4 0 3.46

5 9 −3 4.47

7 5 3 5.29

11 14 −2 6.63

13 18 −4 7.21

17 18 0 8.25

Section. The elliptic curve discrete logarithm problem

5.8. Let Ebe the elliptic curve

E:y2=x3+x+ 1

and let P= (4,2) and Q= (0,1) be points on Emodulo 5. Solve the elliptic

curve discrete logarithm problem for Pand Q, that is, ﬁnd a positive integer n

such that Q=nP .

Solution to Exercise 5.8.

We compute the multiples of P:

P= (4,2),2P= (3,4),3P= (2,4),4P= (0,4),5P= (0,1)

6P= (2,1),7P= (3,1),8P= (4,3),9P=O.

Thus logP(Q) = 5 in E(F5). It turns out that E(F5) contains 9 points, and

the multiples of Pgive all of them.

5.9. Let Ebe an elliptic curve over Fpand let Pand Qbe points in E(Fp).

Assume that Qis a multiple of Pand let n0>0 be the smallest solution

to Q=nP . Also let s > 0 be the smallest solution to sP =O. Prove that

every solution to Q=nP looks like n0+is for some i∈Z. (Hint. Write nas

n=is +rfor some 0 ≤r < s and determine the value of r.)

Solution to Exercise 5.9.

Following the hint, we write nas n=is +rfor some 0 ≤r < s. Then

Q=nP = (is +r)P=i(sP ) + rP =iO+rP =rP,

since by deﬁnition sP =O. But n0Pis the smallest multiple of Pthat is

equal to Q, so we must have r≥n0. If r=n0, we’re done, so suppose instead

that r > n0.

148 Exercises for Chapter 5

Then

O=Q−Q=rP −n0P= (r−n0)P,

and we know that sP is the smallest (nonzero) multiple of Pthat is equal

to O, so r−n0≥s. But this contradicts r < s. Hence r=n0, which proves

that n=is +n0.

5.10. Use the double-and-add algorithm (Table 5.3) to compute nP in E(Fp)

for each of the following curves and points, as we did in Figure 5.4.

(a) E:Y2=X3+ 23X+ 13, p = 83, P = (24,14), n = 19;

(b) E:Y2=X3+ 143X+ 367, p = 613, P = (195,9), n = 23;

(d) E:Y2=X3+ 1541X+ 1335, p = 3221, P = (2898,439), n = 3211.

Solution to Exercise 5.10.

(a) Solution: 19 ∗(24,14) = (24,69).

Step i n Q = 2iP R

0 19 (24,14) O

1 9 (30,8) (24,14)

2 4 (24,69) (30,75)

3 2 (30,75) (30,75)

4 1 (24,14) (30,75)

5 0 (30,8) (24,69)

Compute 19 ·(24,14) on Y2=X3+ 23X+ 13 modulo 83.

(b) Solution: 23 ∗(195,9) = (485,573).

Step i n Q = 2iP R

0 23 (195,9) O

1 11 (407,428) (195,9)

2 5 (121,332) (182,355)

3 2 (408,110) (194,565)

4 1 (481,300) (194,565)

5 0 (401,150) (485,573)

Compute 23 ·(195,9) on Y2=X3+ 143X+ 367 modulo 613

Step i n Q = 2iP R

0 11 (1756,348) O

1 5 (1526,1612) (1756,348)

2 2 (1657,1579) (1362,998)

3 1 (1849,225) (1362,998)

4 0 (586,959) (1068,1540)

Compute 11 ·(1756,348) on Y2=X3+ 1828X+ 1675 modulo 1999

Exercises for Chapter 5 149

(d) Solution: 3211 ∗(2898,439) = (243,1875).

Step i n Q = 2iP R

0 3211 (2898,439) O

1 1605 (2964,2977) (2898,439)

2 802 (1372,2349) (781,2494)

3 401 (2956,1288) (781,2494)

4 200 (1045,1606) (341,1727)

5 100 (770,285) (341,1727)

6 50 (2589,1698) (341,1727)

7 25 (2057,2396) (341,1727)

8 12 (1017,828) (2117,1162)

9 6 (1988,1949) (2117,1162)

10 3 (1397,1477) (2117,1162)

11 1 (420,1274) (2362,757)

12 0 (2583,2597) (243,1875)

Compute 3211 ·(2898,439) on Y2=X3+ 1541X+ 1335 modulo 3221

5.11. Convert the proof of Proposition 5.18 into an algorithm and use it to

write each of the following numbers nas a sum of positive and negative powers

of 2 with at most 1

2blog nc+1 nonzero terms. Compare the number of nonzero

terms in the binary expansion of nwith the number of nonzero terms in the

ternary expansion of n.

(a) 349. (b) 9337. (c) 38728. (d) 8379483273489.

Solution to Exercise 5.11.

(a) Binary expansion has 6 terms. Ternary expansion has 5 terms.

349 = +21+ 23+ 24+ 25+ 27+ 29

= +21−23−26−28+ 210

(b) Binary expansion has 7 terms. Ternary expansion has 5 terms.

9337 = +21+ 24+ 25+ 26+ 27+ 211 + 214

= +21−24+ 28+ 211 + 214

38728 = +24+ 27+ 29+ 210 + 211 + 213 + 216

= +24+ 27−29−212 + 214 + 216

(d) Binary expansion has 21 terms. Ternary expansion has 10 terms.

8379483273489 = +21+ 25+ 29+ 212 + 213 + 214 + 216 + 217 + 218 + 219

+ 220 + 221 + 233 + 234 + 235 + 236 + 237 + 240 + 241

+ 242 + 243

= +21+ 25+ 29−212 −215 + 222 −233 + 238 −240 + 244

150 Exercises for Chapter 5

5.12. In Section 4.5 we gave an abstract description of Pollard’s ρmethod,

and in Section 4.5.2 we gave an explicit version to solve the discrete logarithm

problem in Fp. Adapt this material to create a Pollard ρalgorithm to solve

the ECDLP.

Solution to Exercise 5.12.

We want to ﬁnd nso that Q=nP , where P, Q ∈E(Fp) are given. We

also assume that we know an integer Nsuch that NP =Oand NQ =O.

For example, we can take N= #E(Fp). To apply Pollard’s method, we need

a function f:E(Fp)→E(Fp) that mixes up the points reasonably well.

Following the ideas from Section 4.5.2, we deﬁne

f:E(Fp)−→ E(Fp), f(T) = 









P+Tif 0 ≤xT< p/3,

2Tif p/3≤xT<2p/3,

Q+Tif 2p/3≤xT< p.

Then after isteps, we have

fi(O) = αiP+βiQand f2i(O) = γiP+δiQ

for certain integer values of αi, βi, γi, δi. We can keep track of the val-

ues of αi, βi, γi, δijust as we did in Section 4.5.2. Note that the values

of αi, βi, γi, δishould be computed modulo N, which prevents them from

getting too big.

After O(√N) steps, we expect to ﬁnd a match

fi(O) = f2i(O).

This means that

(αi−γi)P= (δi−βi)Qin E(Fp).

If gcd(δi−βi, N) = 1, we can multiply both sides by

(δi−βi)−1mod N

to express Qas a multiple of P. More generally, we can use the same sort of

calculation described in Section 4.5.2 to ﬁnd gcd(δi−βi, N) possible values

of n, and then we can test each of them to see if nP is equal to Q. (In

practice, Nwill be prime, or at worst a small multiple of a large prime, so

there will be few cases to check.)

Section. Elliptic curve cryptography

5.13. Alice and Bob agree to use elliptic Diﬃe–Hellman key exchange with

the prime, elliptic curve, and point

p= 2671, E :Y2=X3+ 171X+ 853, P = (1980,431) ∈E(F2671).

Exercises for Chapter 5 151

(a) Alice sends Bob the point QA= (2110,543). Bob decides to use the secret

multiplier nB= 1943. What point should Bob send to Alice?

(b) What is their secret shared value?

you know how to program, use a computer to ﬁnd nA.

(d) Alice and Bob decide to exchange a new piece of secret information using

the same prime, curve, and point. This time Alice sends Bob only the

x-coordinate xA= 2 of her point QA. Bob decides to use the secret

multiplier nB= 875. What single number modulo pshould Bob send to

Alice, and what is their secret shared value?

Solution to Exercise 5.13.

(a) Bob sends B=gb= 2871 ≡805 (mod 1373) to Alice. Their shared

value (a) Bob sends the point QB= 1943P= (1432,667) ∈E(F2671) to

Alice.

(b) Their secret shared value is the x-coordinate x=2424 of the point

nBQA= 1943(2110,543) = (2424,911) ∈E(F2671).

not too hard on a computer. Alice’s secret value was nA= 2045, but it turns

out that the point Phas order 1319, so in the smallest value that works is

nA= 726 , since 726P= (2110,543) = QA∈E(F2671).

(d) Bob computes QB= 875P= (161,2040) ∈E(F2671), but he sends Al-

ice only the x-coordinate xB= 161 . In order to ﬁnd the shared value, Bob

computes

A=x3

A+ 171xA+ 853 = 23+ 171 ·2 + 853 = 1203,

yA= 1203(2671+1)/4= 1203668 ≡2575 (mod 2671),

nB(xA, yA) = 875(2,2575) = (1708,1419) ∈E(F2671).

The shared value is the x-coordinate x= 1708 .

5.14. Exercise 2.10 on page 107 describes a multistep public key cryptosystem

based on the discrete logarithm problem for Fp. Describe a version of this cryp-

tosystem that uses the elliptic curve discrete logarithm problem. (You may

assume that Alice and Bob know the order of the point Pin the group E(Fp),

i.e., they know the smallest integer N≥1 with the property that NP =O.)

Solution to Exercise 5.14.

A solution for this exercise is not currently available.

5.15. A shortcoming of using an elliptic curve E(Fp) for cryptography is the

fact that it takes two coordinates to specify a point in E(Fp). However, as

discussed brieﬂy at the end of Section 5.4.2, the second coordinate actually

conveys very little additional information.

152 Exercises for Chapter 5

(a) Suppose that Bob wants to send Alice the value of a point R∈E(Fp). Ex-

plain why it suﬃces for Bob to send Alice the x-coordinate of R= (xR, yR)

together with the single bit

βR=(0 if 0 ≤yR<1

2p,

1 if 1

2p < yR< p.

(You may assume that Alice is able to eﬃciently compute square roots

modulo p. This is certainly true, for example, if p≡3 (mod 4); see Propo-

sition 2.27.)

(b) Alice and Bob decide to use the prime p= 1123 and the elliptic curve

E:Y2=X3+ 54X+ 87.

Bob sends Alice the x-coordinate x= 278 and the bit β= 0. What point

is Bob trying to convey to Alice? What about if instead Bob had sent

β= 1?

Solution to Exercise 5.15.

(a) Alice computes x3

R+AxR+B. This quantity has two square roots,

say band p−b. One of bor p−bis between 0 and 1

2p, the other is between 1

and p. So the value of βRtells Alice exactly which square root to take for yR.

(b) First compute u= 2783+ 54 ·278 + 87 ≡216 (mod 1123). Then compute

u(1123+1)/4≡487 (mod 1123). So the two possible points are (278,487) and

(278,636), since 636 = 1123 −487. From the way that βis chosen, we have

β= 0 =⇒R= (278,487) and β= 1 =⇒R= (278,636)

5.16. The Menezes–Vanstone variant of the elliptic ElGamal public key cryp-

tosystem improves message expansion while avoiding the diﬃculty of directly

attaching plaintexts to points in E(Fp). The MV-ElGamal cryptosystem is

described in Table 5.12 on page 343.

(a) The last line of Table 5.12 claims that m0

1=m1and m0

2=m2. Prove

that this is true, so the decryption process does work.

(b) What is the message expansion of MV-ElGamal?

p= 1201, E :Y2=X3+ 19X+ 17, P = (278,285) ∈E(Fp),

for MV-ElGamal. Alice’s secret value is nA= 595. What is her public key?

Bob sends Alice the encrypted message ((1147,640),279,1189). What is

the plaintext?

Solution to Exercise 5.16.

Exercises for Chapter 5 153

(a) Suppose that Bob has encrypted the plaintext (m1, m2) using the ran-

dom number kas described in Table 5.12 and that he sends Alice his cipher-

text (R, c1, c2). Alice’s ﬁrst step is to compute T=nAR. However, using the

deﬁnition of R,Sand QA, we see that Alice is actually computing

T=nAR=nA(kP ) = k(nAP) = kQA=S.

Thus xS=xTand yS=yT, so Alice’s second step yields

1≡x−1

Tc1≡x−1

S(xSm1)≡m1(mod p),

2≡y−1

Tc2≡y−1

S(ySm2)≡m2(mod p).

This shows that Alice recovers Bob’s plaintext. Notice how she uses her secret

multiplier nAduring the decryption process.

(b) The plaintext (m1, m2) consists of two numbers modulo p. The cipher-

text (R, c1, c2) consists of four numbers modulo p, since Rhas two coordinates.

So the message expansion ratio is 2-to-1 . This can be improved if Bob sends

only the x-coordinate of R, plus one extra bit to enable Alice to determine the

correct y-coordinate. In that case, the cipher text is three numbers modulo p

(plus one bit), so the message expansion ratio is approximately 3-to-2 .

decrypt, Alice computes T=nA(1147,640) = 595(1147,640) = (942,476).

She then computes x−1

Tc1= 941−1·279 ≡509 (mod 1201) and y−1

Tc2=

476−1·1189 ≡767 (mod 1201). So the plaintext is (509,767) .

5.17. This exercise continues the discussion of the MV-ElGamal cryptosystem

described in Table 5.12 on page 343.

(a) Eve knows the elliptic curve Eand the ciphertext values c1and c2. Show

how Eve can use this knowledge to write down a polynomial equation

(modulo p) that relates the two pieces m1and m2of the plaintext. In

particular, if Eve can ﬁgure out one piece of the plaintext, then she can

recover the other piece by ﬁnding the roots of a certain polynomial mod-

ulo p.

(b) Alice and Bob exchange a message using MV-ElGamal with the prime,

elliptic curve, and point in Exercise 5.16(c). Eve intercepts the ciphertext

((269,339),814,1050) and, through other sources, she discovers that the

ﬁrst part of the plaintext is m1= 1050. Use your algorithm in (a) to

recover the second part of the plaintext.

Solution to Exercise 5.17.

(a) Eve knows the equation of the elliptic curve,

E:Y2=X3+AX +B.

The coordinates of the point S∈E(Fp) satisfy

154 Exercises for Chapter 5

xS≡m−1

1c1(mod p),

yS≡m−1

2c2(mod p),

and the point (xS, yS) satisﬁes the equation for E, so Eve knows that

(m−1

2c2)2≡(m−1

1c1)3+A(m−1

1c1) + B(mod p).

Eve clears denominators by multiplying by m3

1m2

2, so

2m3

1≡c3

1m2

2+Ac1m2

1m2

2+Bm3

1m2

2(mod p).

Thus (m1, m2) is a solution to the congruence

2u3≡c3

1v2+Ac1u2v2+Bu3v2(mod p),

so in particular, if Eve knows either m1or m2, then she can ﬁnd the other

one by substituting in the known value and ﬁnding the roots modulo pof the

resulting polynomial.

(b) m2= 179. A solution for this exercise is not currently available.

Section. Lenstra’s elliptic curve factorization algorithm

5.18. Use the elliptic curve factorization algorithm to factor each of the num-

bers Nusing the given elliptic curve Eand point P.

(a) N= 589, E :Y2=X3+ 4X+ 9, P = (2,5).

(b) N= 26167, E :Y2=X3+ 4X+ 128, P = (2,12).

(d) N= 28102844557, E :Y2=X3+ 18X−453, P = (7,4).

Solution to Exercise 5.18.

(a)

n n!·Pmod 589

1P= (2,5)

2 2! ·P= (564,156)

3 3! ·P= (33,460)

4 4! ·P= (489,327)

Factorial multiples of Pon Y2=X3+ 4X+ 9 modulo 589

Computation of 5! ·Pgives 589 = 19 ·31.

(b)

n n!·Pmod 26167

1P= (2,12)

2 2! ·P= (23256,1930)

3 3! ·P= (21778,1960)

4 4! ·P= (22648,14363)

5 5! ·P= (5589,11497)

6 6! ·P= (7881,16198)

Exercises for Chapter 5 155

Public Parameter Creation

A trusted party chooses and publishes a (large) prime p,

an elliptic curve Eover Fp, and a point Pin E(Fp).

Alice Bob

Key Creation

Chooses a secret multiplier nA.

Computes QA=nAP.

Publishes the public key QA.

Encryption

Chooses plaintext values m1and m2

modulo p.

Chooses a random number k.

Computes R=kP .

Computes S=kQAand writes it

as S= (xS, yS).

Sets c1≡xSm1(mod p) and

c2≡ySm2(mod p).

Sends ciphtertext (R, c1, c2) to Alice.

Decryption

Computes T=nARand writes

it as T= (xT, yT).

Sets m0

1≡x−1

Tc1(mod p) and

2≡y−1

Tc2(mod p).

Then m0

1=m1and m0

2=m2.

Table 5.1: Menezes–Vanstone variant of ElGamal (Exercises 5.16, 5.17)

Factorial multiples of Pon Y2=X3+ 4X+ 128 modulo 26167.

Computation of 7! ·Pgives 26167 = 191 ·137.

(c)

n n!·Pmod 1386493

1P= (1,1)

2 2! ·P= (7,1386474)

3 3! ·P= (1059434,60521)

4 4! ·P= (81470,109540)

5 5! ·P= (870956,933849)

6 6! ·P= (703345,474777)

7 7! ·P= (335675,1342927)

8 8! ·P= (1075584,337295)

9 9! ·P= (149824,1003869)

10 10! ·P= (92756,1156933)

156 Exercises for Chapter 5

Factorial multiples of Pon Y2=X3+ 3X−3 modulo 1386493

Computation of 11! ·Pgives 1386493 = 1069 ·1297.

(d)

n n!·Pmod 28102844557

1P= (7,4)

2 2! ·P= (1317321250,11471660625)

3 3! ·P= (15776264786,10303407105)

4 4! ·P= (27966589703,26991329662)

5 5! ·P= (11450520276,14900134804)

24 24! ·P= (25959867777,9003083411)

25 25! ·P= (10400016599,11715538594)

26 26! ·P= (22632202481,6608272585)

27 27! ·P= (25446531195,2223850203)

28 28! ·P= (12412875644,7213676617)

Factorial multiples of Pon Y2=X3+ 18X+ 28102844104 modulo

28102844557.

Computation of 29! ·Pgives 28102844557 = 117763 ·238639.

Section. Elliptic curves over F2and over F2k

5.19. Let Ebe an elliptic curve given by a generalized Weierstrass equation

E:Y2+a1XY +a3Y=X3+a2X2+a4X+a6.

Let P1= (x1, y1) and P2= (x2, y2) be points on E. Prove that the following

algorithm computes their sum P3=P1+P2.

First, if x1=x2and y1+y2+a1x2+a3= 0, then P1+P2=O.

Otherwise deﬁne quantities λand νas follows:

[If x16=x2]λ=y2−y1

x2−x1

, ν =y1x2−y2x1

x2−x1

[If x1=x2]λ=3x2

1+ 2a2x1+a4−a1y1

2y1+a1x1+a3

, ν =−x3

1+a4x1+ 2a6−a3y1

2y1+a1x1+a3

Then

P3=P1+P2= (λ2+a1λ−a2−x1−x2,−(λ+a1)x3−ν−a3).

Solution to Exercise 5.19.

This is proven in any basic text on elliptic curves. See for example Group

Law Algorithm 2.3 in [123, §2.2].

5.20. Let F8=F2[T]/(T3+T+ 1) be as in Example 5.28, and let Ebe the

elliptic curve

E:Y2+XY +Y=X3+T X + (T+ 1).

Exercises for Chapter 5 157

(a) Calculate the discriminant of E.

(b) Verify that the points

P= (1 + T+T2,1 + T), Q = (T2, T ), R = (1 + T+T2,1 + T2),

are in E(F8) and compute the values of P+Qand 2R.

(d) Find a point P∈E(F8) such that every point in E(F8) is a multiple of P.

Solution to Exercise 5.20.

(a) ∆ = 1 + T2.

(b) P+Q= (1 + T+T2,1 + T2) and 2R= (T2, T ).

(c,d) The point P= (1 + T+T2,1 + T2) satisﬁes

P= (1 + T+T2,1 + T2)

2P= (T2, T )

3P= (1,0)

4P= (T2,1 + T+T2)

5P= (1 + T+T2,1 + T)

6P=O,

and this is the complete set of points in E(F8). (One can check this directly, or

note that if there were more points, since the order of an element divides the

order of a group, it would follow that #E(F8) is at least 12, which contradicts

the Hasse bound of 8 + 1 + 2√8≈11.83.) The multiples of the point 5Palso

give all of #E(F8).

5.21. Let τ(α) = αpbe the Frobenius map on Fpk.

(a) Prove that

τ(α+β) = τ(α)+τ(β) and τ(α·β) = τ(α)·τ(β) for all α, β ∈Fpk.

(Hint. For the addition formula, use the binomial theorem (Theorem 4.10).)

(b) Prove that τ(α) = αfor all α∈Fp.

Frobenius map from E(Fpk) to itself. Prove that

τ(P+Q) = τ(P) + τ(Q) for all P∈E(Fpk).

5.22. Let E0be the Koblitz curve Y2+XY =X3+ 1 over the ﬁeld F2, and

for every k≥1, let

tk= 2k+ 1 −#E(F2k).

(a) Prove that t1=−1 and t2=−3.

158 Exercises for Chapter 5

(b) Prove that tksatisﬁes the recursion

tk=t1tk−1−ptk−2for all t≥3.

(You may use the formula (5.12) that we stated, but did not prove, on

page 313.)

(d) Program a computer to calculate the recursion and use it to compute the

values of #E(F211 ), #E(F231 ), and #E(F2101 ).

Solution to Exercise 5.22.

(a) A solution for this exercise is not currently available.

(b) A solution for this exercise is not currently available.

(d) #E(F211 ) = 2116.

#E(F231 ) = 2147574356.

#E(F2101 ) = 2535301200456455833701195805484.

5.23. Let τsatisfy τ2=−2−τ. Prove that the following algorithm gives

coeﬃcients vi∈ {−1,0,1}such that the positive integer nis equal to

n=v0+v1τ+v2τ2+···+v`τ`.(5.1)

Further prove that at most one-third of the viare nonzero and that ≤log(n).

[1] Set n0=nand n1= 0 and i= 0

[2] Loop while n06= 0 or n16= 0

[3] If n0is odd

[4] Set vi= 2 −¡(n0−2n1) mod 4¢

[5] Set n0=n0−vi

[6] Else

[7] Set vi= 0

[8] End If

[9] Set i=i+ 1

[10] Set (n0, n1) = ¡n1−1

2n0,−1

2n0¢

[11] End Loop

Solution to Exercise 5.23.

A solution for this exercise is not currently available.

5.24. Implement the algorithm in Exercise 5.23 and use it to compute the τ-

expansion (5.19) of the following integers. What is the highest power of τthat

appears and how many nonzero terms are there?

(a) n= 931 (b) n= 32755 (c) n= 82793729188

Solution to Exercise 5.24.

(a)

Exercises for Chapter 5 159

931 = −1 + τ2+τ10 +τ14 −τ17 −τ19 −τ21.

The highest power of τis τ21 and the τ-expansion has 7 nonzero terms.

(b)

32755 = −1 + τ2+τ4+τ6+τ8+τ15 −τ17 +τ19 −τ22 +τ28 −τ31.

The highest power of τis τ31 and the τ-expansion has 11 nonzero terms.

(c)

82793729188 = τ2+τ8−τ10 −τ12 +τ15 +τ18

+τ20 −τ24 −τ27 +τ30 −τ34 +τ36 −τ40

+τ44 +τ46 −τ48 +τ50 −τ52 +τ55 +τ58

+τ61 +τ68 −τ71 −τ73.

The highest power of τis τ73 and the τ-expansion has 24 nonzero terms.

Section. Bilinear pairings on elliptic curves

5.25. Let R(x) and S(x) be rational functions. Prove that the divisor of a

product is the sum of the divisors, i.e.,

div¡R(x)S(x)¢= div¡R(x)¢+ div¡S(x)¢.

5.26. Prove that the Weil pairing satisﬁes

em(P, Q) = em(Q, P )−1for all P, Q, ∈E[m].

(Hint. Use the fact that em(P+Q, P +Q) = 1 and expand using bilinearity.)

5.27. This exercise asks you to verify that the Weil pairing emis well-

deﬁned.

(a) Prove that the value of em(P, Q) is independent of the choice of rational

functions fPand fQ.

(b) Prove that the value of em(P, Q) is independent of the auxiliary point S.

(Hint. Fix the points Pand Qand consider the quantity

F(S) = fP(Q+S)

fP(S)ÁfQ(P−S)

fQ(−S)

as a function of S. Compute the divisor of Fand use the fact that every

nonconstant function on Ehas at least one zero.)

You might also try to prove that the Weil pairing is bilinear, but do not be

discouraged if you do not succeed, since the standard proofs use more tools

than we have developed in the text.

5.28. Choose a basis {P1, P2}for E[m] and write each P∈E[m] as a linear

combination P=aPP1+bPP2. (See Remark 5.39.) Use the basic properties

of the Weil pairing described in Theorem 5.38 to prove that

em(P, Q) = em(P1, P2)det³aPaQ

bPbQ´=em(P1, P2)aPbQ−aQbP.

160 Exercises for Chapter 5

5.29. Complete the proof of Proposition 5.51 by proving that φ(2P) = 2φ(P).

5.30. For each of the following elliptic curves E, ﬁnite ﬁelds Fp, points P

and Qof order m, and auxiliary points S, use Miller’s algorithm to compute

the Weil pairing em(P, Q). (See Example 5.43.)

E p P Q m S

(a) y2=x3+ 23 1051 (109 203) (240 203) 5 (1,554)

(b) y2=x3−35x−9 883 (5, 66) (103, 602) 7 (1,197)

(d) y2=x3+ 37x1009 (417, 952) (561, 153) 7 (0,0)

Notice that (c) and (d) use the same elliptic curve. Letting P0and Q0denote

the points in (d), verify that

P0= 2P, Q0= 3Q, and e7(P0, Q0) = e7(P, Q)6.

Solution to Exercise 5.30.

(a) We have #E(F1051 = 1075 = 52·43. The point Shas order 215. Miller’s

algorithm gives

fP(Q+S)

fP(S)=109

306 = 203 and fQ(P−S)

fQ(−S)=552

406 = 312.

Taking the ratio of these two values yields

e5(P, Q) = 203

312 = 671 ∈F1051.

(b) We have #E(F883) = 882 = 2 ·32·72The point Shas order 126. Miller’s

algorithm gives

fP(Q+S)

fP(S)=387

413 = 730 and fQ(P−S)

fQ(−S)=454

161 = 469.

Taking the ratio of these two values yields

e7(P, Q) = 730

469 = 749 ∈F883.

algorithm gives

fP(Q+S)

fP(S)=92

478 = 739 and fQ(P−S)

fQ(−S)=800

810 = 574.

Taking the ratio of these two values yields

Exercises for Chapter 5 161

e7(P, Q) = 739

574 = 105 ∈F1009.

(d) Miller’s algorithm gives

fP(Q+S)

fP(S)=86

531 = 384 and fQ(P−S)

fQ(−S)=919

759 = 969.

Taking the ratio of these two values yields

e7(P, Q) = 384

969 = 394 ∈F1009.

Finally, we check that

e7(P, Q)6= 1056= 394 = e7(P0, Q0),

which is in accordance with P0= 2Pand Q0= 3Q.

5.31. Let Eover Fqand be as described in Theorem 5.44. Prove that the

modiﬁed Tate pairing is symmetric, in the sense that

ˆτ(P, Q) = ˆτ(Q, P ) for all P, Q ∈E(Fq)[].

Solution to Exercise 5.31.

By assumption we have E(Fq)[] = Z/Z, a cyclic group. Let Tbe a

generator. Then any P, Q ∈E(Fq)[] can be written as P=uT and Q=vT

for some u, v ∈Z/Z. But then the linearity of that Tate pairing gives

ˆτ(P, Q) = ˆτ(uT, vT ) = ˆτ(T, T )uv,

ˆτ(Q, P ) = ˆτ(vT, uT ) = ˆτ(T, T )vu,

which are clearly the same value.

5.32. Let Ebe an elliptic curve over Fqand let P, Q ∈E(Fq)[]. Prove that

the Weil pairing and the Tate pairing are related by the formula

e`(P, Q) = τ(P, Q)

τ(Q, P ),

provided that the Tate pairings on the right-hand side are computed properly.

Thus the Weil pairing requires approximately twice as much work to compute

as does the Tate pairing.

Section. The Weil pairing over ﬁelds of prime power order

5.33. Prove Proposition 5.51(b) in the case P1=P2.

5.34. Let Ebe an elliptic curve over Fpand let be a prime. Suppose

that E(Fp) contains a point of order and that  > √p+ 1. Prove that

E(Fp)[]∼

=Z/Z.

162 Exercises for Chapter 5

Solution to Exercise 5.34.

Hasse’s theorem says that

#E(Fp)≤p+1+2√p= (√p+ 1)2.

The assumption on then tells us that #E(Fp)< 2. But if E(Fp)[] is larger

than Z/Z, then it is equal to Z/Z×Z/Z, so we would have 2elements,

contradicting #E(Fp)< 2.

5.35. Let Ebe an elliptic curve over a ﬁnite ﬁeld Fqand let be a prime.

Suppose that we are given four points P, aP, bP, cP ∈E(Fq)[]. The (elliptic)

decision Diﬃe–Hellman problem is to determine whether cP is equal to abP .

Of course, if we could solve the Diﬃe–Hellman problem itself, then we could

compute abP and compare it with cP , but the Diﬃe–Hellman problem is often

diﬃcult to solve.

Suppose that there exists a distortion map φfor E[]. Show how to use

the modiﬁed Weil pairing to solve the elliptic decision Diﬃe–Hellman problem

without actually having to compute abP .

Solution to Exercise 5.35.

Compute

ˆe`(aP, bP ) = ˆe`(P, P )ab and ˆe`(P, cP ) = ˆe`(P, P )c.

If they agree, then cP =abP , otherwise cP 6=abP .

5.36. Let Ebe the elliptic curve E:y2=x3+xand let φ(x, y) = (−x, αy)

be the map described in Proposition 5.51. Prove that φ(φ(P)) = −Pfor

all P∈E. (Intuitively, φbehaves like multiplication by √−1 when it is

applied to points of E.)

Solution to Exercise 5.36.

Let P= (x, y). We compute

φ(φ(P)) = φ(−x, αy) = ¡−(−x), α ·αy¢= (x, α2y) = (x, −y) = −P.

5.37. Let p≡3 (mod 4), let E:y2=x3+x, let P∈E(Fp)[], and

let φ(x, y)=(−x, αy) be the -distortion map for Pdescribed in Proposi-

tion 5.52. Suppose further that ≡3 (mod 4). Prove that φis an -distortion

map for every point in E[]. In other words, if Q∈Eis any point of order ,

prove that e`(Q, φ(Q)) is a primitive th root of unity.

Solution to Exercise 5.37.

We can write Q=aP +bφ(P), since {P, φ(P)}is a basis for E[]. We have

φ(Q) = φ(aP +bφ(P)) = aφ(P) + bφ(φ(P)).

Exercises for Chapter 5 163

Note that

φ(φ(P)) = φ(φ(x, y)) = φ(−x, αy) = (x, α2y) = (x, −y) = −P.

(This was a previous exercise.) So φ(Q) = −bP +aφ(P). Hence

e`(Q, φ(Q)) = e`(aP +bφ(P),−bP +aφ(P))

=e`(P, P )−abe`(P, φ(P))a2e`(φ(P), P )−b2e`(φ(P), φ(P))ab

=e`(P, φ(P))a2+b2.

We know that e`(P, φ(P)) is a primitive th-root of unity, so either e`(Q, φ(Q))

is a primitive th-root of unity, or else a2+b2is a multiple of . (Note that

we can assume that take 0 ≤a, b <  and that aand bare not both 0.) But

if divides a2+b2, then we get

1 = µa2

¶=µ−b2

¶=µ−1

¶µb2

¶=µ−1

¶,

so −1 is a square modulo . From an easy piece of quadratic reciprocity, this

implies that ≡1 (mod 4), contradicting our assumption that ≡3 (mod 4).

5.38. Let Ebe the elliptic curve

E:y2=x3+ 1

over a ﬁeld K, and suppose that Kcontains an element β6= 1 satisfying β3=

1. (We say that βis a primitive cube root of unity.) Deﬁne a map φby

φ(x, y)=(βx, y) and φ(O) = O.

(a) Let P∈E(K). Prove that φ(P)∈E(K).

(b) Prove that φrespects the addition law on E, i.e., φ(P1+P2) = φ(P1) +

φ(P2) for all P1, P2∈E(K).

5.39. Let E:y2=x3+ 1 be the elliptic curve in Exercise 5.38.

(a) Let p≥3 be a prime with p≡2 (mod 3). Prove that Fpdoes not contain

a primitive cube root of unity, but that Fp2does contain a primitive cube

root of unity.

(b) Let β∈Fp2be a primitive cube root of unity and deﬁne a map φ(x, y) =

(βx, y) as in Exercise 5.38. Suppose that E(Fp) contains a point Pof

prime order ≥5. Prove that φis an -distortion map for P.

Solution to Exercise 5.39.

(b) This is the same as the proof of Proposition 5.52. The multiples of P

are in E(Fp), but φ(P) is not unless its x-coordinate is 0. Then on checks

that points on Eof the form (0, y) are points of order 3. Hence φ(P) is

not a multiple of P, and then Proposition 5.49 tells us that e`(P, φ(P)) is a

primitive th-root of unity.

164 Exercises for Chapter 5

5.40. Let Ebe the elliptic curve E:y2=x3+xover the ﬁeld F691. The

point P= (301,14) ∈#E(F691) has order 173. Use the distortion map on E

from Exercises 5.38 and 5.39 to compute ˆe173(P, P ) (cf. Example 5.54). Verify

that the value is a primitive 173rd root of unity.

Solution to Exercise 5.40.

We have φ(P) = (−301,14i) = (390,14i). We randomly choose a point

S= (499 + 325i, 41 + 140i)∈E(F6912)

and use Miller’s algorithm to compute

fP(φ(P) + S)

fP(S)=452 + 325i

236 + 219i= 432 + 271i,

fφ(P)(P−S)

fφ(P)(−S)=48 + 608i

115 + 533i= 259 + 271i.

Then

ˆe(P, P ) = e173(P, φ(P)) = 432 + 271i

259 + 271i= 242 + 92i∈F6912.

We check that (242 + 92i)173 = 1.

5.41. Continuing with the curve E, prime p= 691, and point P= (301,14)

from Exercise 5.40, let

Q= (143,27) ∈E(F691).

Use the MOV method to solve the ECDLP for Pand Q, i.e., compute ˆe173(P, Q)

and express it as the nth power of ˆe173(P, P ). Check your answer by verifying

that nP is equal to Q.

Solution to Exercise 5.41.

The distortion map gives φ(Q) = (548,278i), and we use the randomly

chosen point S= (379 + 605i, 205 + 534i)∈E(F6912) to compute

ˆe173(P, Q) = e173(P, φ(Q)) =

139+432i

506+550i

239+375i

142+299i

= 500 + 603i∈F6912.

From the previous exercise we have ˆe173(P, P ) = 242+92i, so we need to solve

the DLP

(242 + 92i)n= 500 + 603iin F6912.

The solution to this DLP is n= 122, and we can check that Q=P, so n= 122

is also a solution to the ECDLP.

Section. Applications of the Weil pairing

Exercises for Chapter 5 165

5.42. Alice, Bob, and Carl use tripartite Diﬃe–Hellman with the curve

E:y2=x3+xover the ﬁeld F1723.

They use the point

P= (668,995) of order 431.

(a) Alice chooses the secret value nA= 278. What is Alice’s public point QA?

(b) Bob’s public point is QB= (1275,1550) and Carl’s public point is QC=

(897,1323). What is the value of ˆe431(QB, QC)?

(d) Bob’s secret value is nB= 224. Verify that ˆe431(QA, QC)nBis the same

as the value that you got in (c).

(e) Figure out Carl’s secret value nC. (Since Phas order 431, you can do

this on a computer by trying all possible values.)

Solution to Exercise 5.42.

(a) Alice’s public point is QA=nAP= (726,1127).

(b) ˆe431(QB, QC) = 1444 + 1288i.

(d) ˆe431(QA, QC)224 = (1264 + 1083i)224 = 68 + 428i.

(e) Carl’s secret value is nC= 145. We check that he gets the same shared

value, ˆe431(QA, QB)145 = (977 + 1163i)145 = 68 + 428i.

5.43. Show that Eve can break tripartite Diﬃe–Hellman key exchange as

described in Table 5.10.1 if she knows how to solve the Diﬃe–Hellman problem

(page 67) for the ﬁeld Fq.

Solution to Exercise 5.43.

Eve can compute

ˆe`(P, P ) and ˆe`(QA, P ) = ˆe`(nAP, P ) = ˆe`(P, P )nA.

But she can also compute

ˆe`(QB, QC) = ˆe`(P, P )nBnC.

Thus Eve knows the quantities

gnAand gnBnC

for a certain primitive th root of unity gin F∗

q. If she can solve the Diﬃe–

Hellman problem in F∗

q, then she can use these known values to compute Alice,

Bob, and Carl’s shared value gnAnBnC.

Chapter 6

Lattices and Cryptography

Exercises for Chapter 6

Section. A congruential public key cryptosystem

6.1. Alice uses the congruential cryptosystem with q= 918293817 and private

key (f, g) = (19928,18643).

(a) What is Alice’s public key h?

(b) Alice receives the ciphertext e= 619168806 from Bob. What is the plain-

text?

using the ephemeral key r= 19564. What is the ciphertext that Bob sends

to Alice?

Solution to Exercise 6.1.

(a) h= 767748560.

(b) First compute

a≡fe ≡600240756 (mod q)

Then

m=f−1a= 9764 ·600240756 ≡11818 (mod g).

(The ephemeral key was 19564.)

(c)

e≡rh +m≡619167208 (mod q).

Section. Subset-sum problems and knapsack cryptosystems

6.2. Use the algorithm described in Proposition 6.5 to solve each of the fol-

lowing subset-sum problems. If the “solution” that you get is not correct,

explain what went wrong.

(a) M= (3,7,19,43,89,195), S= 260.

167

168 Exercises for Chapter 6

(b) M= (5,11,25,61,125,261), S= 408.

(d) M= (4,12,15,36,75,162), S= 214.

Solution to Exercise 6.2.

(a) Output from algorithm is x= (1,0,1,1,0,1). Sum is correct.

(b) Output from algorithm is x= (1,1,0,0,1,1). Sum is 402 instead of 408.

Incorrect. Superincreasing, but this Shas no solution.

(d) Output from algorithm is x= (0,0,1,1,0,1). Sum is 213 instead of 214.

Incorrect. Mis not superincreasing, this problem has a solution (1,1,0,1,0,1),

but it is not found by the algorithm.

6.3. Alice’s public key for a knapsack cryptosystem is

M= (5186,2779,5955,2307,6599,6771,6296,7306,4115,7039).

Eve intercepts the encrypted message S= 26560. She also breaks into Alice’s

computer and steals Alice’s secret multiplier A= 4392 and secret modulus

B= 8387. Use this information to ﬁnd Alice’s superincreasing private se-

quence rand then decrypt the message.

Solution to Exercise 6.3.

A solution for this exercise is not currently available.

6.4. Proposition 6.3 gives an algorithm that solves an n-dimensional knap-

sack problem in O(2n/2) steps, but it requires O(2n/2) storage. Devise an

algorithm, similar to Pollard’s ρalgorithm (Section 4.5), that takes O(2n/2)

steps, but requires only O(1) storage.

Solution to Exercise 6.4.

A solution for this exercise is not currently available.

Section. A brief review of vector spaces

6.5. (a) Let

B={(1,3,2),(2,−1,3),(1,0,2)},B0={(−1,0,2),(3,1,−1),(1,0,1)}.

Each of the sets Band B0is a basis for R3. Find the change of basis

matrix that transforms B0into B.

(b) Let v= (2,3,1) and w= (−1,4,−2). Compute the lengths kvkand kwk

and the dot product v·w. Compute the angle between vand w.

Solution to Exercise 6.5.

(a) Let

B=



1 3 2

2−1 3

1 0 2

and C=

−1 0 2

3 1 −1

101



Exercises for Chapter 6 169

Then

C−1=



−1

302

31−5

301



and A=BC−1=



33−11

−1−1 4

304





(b) kvk=√14 ≈3.7417. kwk=√21 ≈4.5826. v·w= 8.

cos(θ) = 8/√14 ·√21 ≈0.4666, so

θ≈cos−1(0.4666) ≈1.0854 radians ≈62.188 degrees.

6.6. Use the Gram–Schmidt algorithm (Theorem 6.13) to ﬁnd an orthogonal

basis from the given basis.

(a) v1= (1,3,2),v2= (4,1,−2),v3= (−2,1,3).

(b) v1= (4,1,3,−1),v2= (2,1,−3,4),v3= (1,0,−2,7).

Solution to Exercise 6.6.

(a)

v∗

1= (1,3,2),v∗

2= (53/14,5/14,−17/7),v∗

3= (56/285,−14/57,77/285).

(b)

v∗

1= (4,1,3,−1),v∗

2= (70/27,31/27,−23/9,104/27),

v∗

3= (−287/397,−405/397,799/397,844/397).

Section. Lattices: Basic deﬁnitions and properties

6.7. Let Lbe the lattice generated by {(1,3,−2),(2,1,0),(−1,2,5)}. Draw a

picture of a fundamental domain for Land ﬁnd its volume.

Solution to Exercise 6.7.

The volume is ¯¯¯¯¯¯

det 



1 3 −2

2 1 0

−1 2 5 

¯¯¯¯¯¯

= 35.

6.8. Let L⊂Rmbe an additive subgroup with the property that there is a

positive constant  > 0 such that

Prove that Lis discrete, and hence is a lattice. (In other words, show that in

the deﬁntion of discrete subgroup, it suﬃces to check that (6.8) is true for the

single vector v=0.)

170 Exercises for Chapter 6

Solution to Exercise 6.8.

A solution for this exercise is not currently available.

6.9. Prove that a subset of Rmis a lattice if and only if it is a discrete additive

subgroup.

Solution to Exercise 6.9.

A solution for this exercise is not currently available.

6.10. This exercise describes a result that you may have seen in your linear

algebra course.

Let Abe an n-by-nmatrix with entries aij , and for each pair of indices i

and j, let Aij denote the (n−1)-by-(n−1) matrix obtained by deleting the ith

row of Aand the jth column of A. Deﬁne a new matrix Bwhose ijth entry bij

is given by the formula

bij = (−1)i+jdet(Aji).

(Note that bij is the determinant of the submatrix Aji, i.e., the indices are

reversed.) The matrix Bis called the adjoint of A.

(a) Prove that

AB =BA = det(A)In,

where Inis the n-by-nidentity matrix.

(b) Deduce that if det(A)6= 0, then

A−1=1

det(A)B.

entries if and only if det(A) = ±1.

(d) For those who know ring theory from Section 2.10 or from some other

source, suppose that Ahas entries in a ring R. Prove that A−1exists and

has entries in Rif and only if det(A) is a unit in R.

Solution to Exercise 6.10.

A solution for this exercise is not currently available.

6.11. Recall from Remark 6.16 that the general linear group GLn(Z) is the

group of n-by-nmatrices with integer coeﬃcients and determinant ±1. Let A

and Bbe matrices in GLn(Z).

(a) Prove that AB ∈GLn(Z).

(b) Prove that A−1∈GLn(Z).

(d) Prove that GLn(Z) is a group. (Hint. You have already done most of the

work in proving (a), (b), and (c). For the associative law, either prove it

directly or use the fact that you know that it is true for matrices with

real coeﬃcients.)

Exercises for Chapter 6 171

(e) Is GLn(Z) a commutative group?

Solution to Exercise 6.11.

(a) By assumption, A−1and B−1have integer entries. Hence (AB)−1=

B−1A−1also has integer entries, so AB ∈GLn(Z).

(b) (A−1)−1is equal to A, so it has integer entries. Hence A−1∈GLn(Z).

also has integer entries, so I∈GLn(Z).

(d) As the hint says, (a), (b) and (c) show that the product and inverse of

matrices in GLn(Z) are again in GLn(Z) and the identity matrix is in GLn(Z),

so really just need to check the associative law (AB)C=A(BC). But you

proved the associative law for matrix multiplication in linear algebra when

the entries are real numbers (or maybe even more generally), so it is certainly

true when the entries are integers.

(e) No, GLn(Z) is not commutative for n≥2. For example, ( 1 0

1 1 ) and ( 1 1

0 1 )

do not commute, and similar examples exist for any n≥2. Of course, for n=

1, GL1(Z) = {±1}is commutative.

6.12. Which of the following matrices are in GLn(Z)? Find the inverses of

those matrices that are in GLn(Z).

(a) A1=µ3 1

2 2¶(b) A2=µ3−2

2−1¶



3 2 2

2 1 2

−1 3 1

(d) A4=

−3−1 2

1−3−1

3 0 −2



Solution to Exercise 6.12.

(a) No, since det = 4.

(b) Yes, since det = 1. A−1

2=µ−1 2

−2 3¶.

(d) Yes, since det = 1. A−2

4=



6−2 7

−1 0 −1

9−3 10 

.

6.13. Let Lbe the lattice given by the basis

Which of the following sets of vectors are also bases for L? For those that are,

express the new basis in terms of the basis B, i.e., ﬁnd the change of basis

matrix.

(a) B1={(5,13,−13),(0,−4,2),(−7,−13,18)}.

(b) B2={(4,−2,3),(6,6,−6),(−2,−4,7)}.

172 Exercises for Chapter 6

Solution to Exercise 6.13.

(a) Yes. The change of basis matrix is





5 13 −13

0−4 2

−7−13 18 

.=



0−3 2

1 1 −1

−2 3 −1





3 1 −2

1−3 5

4 2 1 



The inverse matrix is





0−3 2

1 1 −1

−2 3 −1



−1

=



231

342

563



which shows that Band B1generate the same lattice.

(b) No, since det(B) = −48 and det(B2) = 96.

6.14. Let L⊂Rmbe a lattice of dimension nand let v1, . . . , vnbe a basis

for L. (Note that we are allowing nto be smaller than m.) The Gram matrix

of v1, . . . , vnis the matrix

Gram(v1, . . . , vn) = ¡vi·vj¢1≤i,j≤n.

(a) Let F(v1,...,vn) be the matrix (6.11) described in Proposition (6.20),

except that now F(v1, . . . , vn) is an n-by-mmatrix, so it need not be

square. Prove that

Gram(v1, . . . , vn) = F(v1, . . . , vn)F(v1, . . . , vn)t,

where F(v1, . . . , vn)tis the transpose matrix, i.e., the matrix with rows

and columns interchanged.

(b) If m=n, prove that

det¡Gram(v1, . . . , vn)¢= det(L)2.(6.1)

of a fundamental domain for L, so we can use (6.61) to compute det(L).

(d) Let L⊂R4be the 3-dimensional lattice with basis

v1= (1,0,1,−1),v2= (1,2,0,4),v3= (1,−1,2,1).

Compute the Gram matrix of this basis and use it to compute det(L).

(e) Let v∗

1, . . . , v∗

nbe the Gram–Schmidt orthogonalized vectors (Theo-

rem 6.13) associated to v1, . . . , vn. Prove that

Gram(v1, . . . , vn) = kv∗

1k2kv∗

2k2···kv∗

nk2.

Exercises for Chapter 6 173

Solution to Exercise 6.14.

(a–c) A solution for this exercise is not currently available.

(d)

Gram(v1, . . . , vn) = 



101−1

1204

1−1 2 1 







111

0 2 −1

102

−1 4 1





=



3−3 2

−3 21 3

2 3 7



Then

det(L) = pdet Gram(v1, . . . , vn) = √231.

Section. The shortest and closest vector problems

6.15. Let Lbe a lattice and let Fbe a fundamental domain for L. This

exercise sketches a proof that

lim

R→∞

#¡BR(0)∩L¢

Vol¡BR(0)¢=1

Vol(F).(6.2)

(a) Consider the translations of Fthat are entirely contained within BR(0),

and also those that have nontrivial intersection with BR(0). Prove the

inclusion of sets

[

v∈L

F+v⊂BR(0)

(F+v)⊂BR(0)⊂[

v∈L

(F+v)∩BR(0)6=∅

(F+v).

(b) Take volumes in (a) and prove that

(Hint. Proposition 6.18 says that the diﬀerent translates of Fare disjoint.)

being entirely contained within BR(0) is comparatively small compared

to the number of translates Fvthat are entirely contained within BR(0).

(This is the hardest part of the proof.)

(d) Use (b) and (c) to prove that

Vol¡BR(0)¢= #¡BR(0)∩L¢·Vol(F) + (smaller term).

Divide by Vol¡BR(0)¢and let R→ ∞ to complete the proof of (6.62).

Solution to Exercise 6.15.

A solution for this exercise is not currently available.

174 Exercises for Chapter 6

6.16. A lattice Lof dimension n= 251 has determinant det(L)≈22251.58.

With no further information, approximately how large would you expect the

shortest nonzero vector to be?

Solution to Exercise 6.16.

The Gaussian heuristic (6.21) predicts that the shortest nonzero vector in

Lhas length approximately

σ(L) = rn

2πe (det L)1/n ≈1922.96.

Section. Babai’s algorithm and solving CVP with a “good” basis

6.17. Let L⊂R2be the lattice given by the basis v1= (213,−437) and

v2= (312,105), and let w= (43127,11349).

(a) Use Babai’s algorithm to ﬁnd a vector v∈Lthat is close to w. Compute

the distance kv−wk.

(b) What is the value of the Hadamard ratio det(L)/kv1kkv2k? Is the ba-

sis {v1,v2}a “good” basis?

1= (2937,−1555) and v0

2= (11223,−5888) are

also a basis for Lby expressing them as linear combinations of v1and v2

and checking that the change-of-basis matrix has integer coeﬃcients and

determinant ±1.

(d) Use Babai’s algorithm with the basis {v0

1,v0

2}to ﬁnd a vector v0∈L.

Compute the distance kv0−wkand compare it to your answer from (a).

(e) Compute the Hadamard ratio using v0

1and v0

2. Is {v0

1,v0

2}a good basis?

Solution to Exercise 6.17.

(a) (t1, t2) = (6.22,133.98), so v= 6v1+ 134v2= (43086,11448). Then

kv−wk= 107.15.

(b) det(L)/kv1kkv2k= 158709/(486.15)(329.19) = 0.9917. The ratio is close

to 1, so {v0

1,v0

2}a good basis.

1= 5v1+ 6v2and v0

2= 19v1+ 23v2. We have det ( 5 6

19 23 ) = 1.

(d) (t1, t2)=(−2402.52,632.57), so v0=−2403v0

1+ 633v0

2= (46548,9561).

Then kv−wk= 3860.08.

(e) det(L)/kv0

1kkv0

2k= 158709/(3323.25)(12673.76) = 0.00377. The ratio is

very small, so {v0

1,v0

2}a bad basis.

Section. The GGH public key cryptosystem

6.18. Alice uses the GGH cryptosystem with private basis

v1= (4,13),v2= (−57,−45),

and public basis

w1= (25453,9091),w2= (−16096,−5749).

Exercises for Chapter 6 175

(a) Compute the determinant of Alice’s lattice and the Hadamard ratio of

the private and public bases.

(b) Bob sends Alice the encrypted message e= (155340,55483). Use Alice’s

private basis to decrypt the message and recover the plaintext. Also de-

termine Bob’s random perturbation r.

basis {w1,w2}. Is the output equal to the plaintext?

Solution to Exercise 6.18.

(a) det(L) = 561, The Hadamard ratio of the private key is 0.75362. and

the Hadamard ratio of the public key is 0.0011.

(b)

e≈ −6823.12v1−3204.08v2.

v=−6823v1−3204v2

= (155336,55481)

= 8w1+ 3w2.

So the plaintext is m= (8,3). Also r=w−v= (4,2).

(c)

e≈ −8.39w1−22.92w2.

This yields the incorrect plaintext (−8,−23).

6.19. Alice uses the GGH cryptosystem with private basis

v1= (58,53,−68),v2= (−110,−112,35),v3= (−10,−119,123)

and public basis

w1= (324850,−1625176,2734951),

w2= (165782,−829409,1395775),

w3= (485054,−2426708,4083804).

(a) Compute the determinant of Alice’s lattice and the Hadamard ratio of

the private and public bases.

(b) Bob sends Alice the encrypted message e= (8930810,−44681748,75192665).

Use Alice’s private basis to decrypt the message and recover the plaintext.

Also determine Bob’s random perturbation r.

basis {w1,w2,w3}. Is the output equal to the plaintext?

Solution to Exercise 6.19.

(a) det(L) = −672858, The Hadamard ratio of the private key is 0.61697

and the Hadamard ratio of the public key is 0.00003.

(b)

176 Exercises for Chapter 6

e≈ −334865.23v1−304373.02v2+ 512803.95v3.

v=−334865v1−304373v2+ 512804v3

= (8930820,−44681745,75192657)

=−50w1−91w2+ 83w3.

So the plaintext is m= (−50,−91,83). Also r=w−v= (−10,−3,8).

(c)

e≈51.59w1+ 416.67w2−158.55w3.

This yields the incorrect plaintext (52,417,−159).

6.20. Bob uses the GGH cryptosystem to send some messages to Alice.

(a) Suppose that Bob sends the same message mtwice, using diﬀerent ran-

dom perturbations rand r0. Explain what sort of information Eve can

deduce from the ciphertexts e=mW+rand e0=mW+r0.

(b) For example, suppose that n= 5 and that random permutations are

chosen with coordinates in the set {−2,−1,0,1,2}. This means that there

are 55= 3125 possibilities for r. Suppose further that Eve intercepts two

ciphertexts

e= (−9,−29,−48,18,48) and e0= (−6,−26,−51,20,47)

having the same plaintext. With this information, how many possibilities

are there for r?

diﬀerent messages. Explain what sort of information Eve can deduce from

the ciphertexts e=mW+rand e0=m0W+r.

Solution to Exercise 6.20.

(a) Eve can compute e0−e=r0−rand use this information to narrow

down the possibilities for rand r0.

(b) Eve computes

e−e0=r−r0= (−3,−3,3,−2,1).

Thus

r1=r0

1−3, r2=r0

2−3, r3=r0

3+ 3, r4=r0

4−2, r5=r0

5+ 1.

Further, Eve knows that all of the riand all of the r0

iare between −2 and 2.

Thus each equation puts some restrictions on the coordinates of r. For example

r1=r0

1−3≤2−3 = −1,so r1∈ {−2,−1},

and similarly

Exercises for Chapter 6 177

r2=r0

2−3≤ −2 + 3 = 1,so r2∈ {−2,−1},

r3=r0

3+ 3 ≥ −2 + 3 = 1,so r3∈ {1,2},

r4=r0

4−2≤2−2 = 0,so r4∈ {−2,−1,0},

r5=r0

5+ 1 ≥ −2 + 1 = −1,so r1∈ {−1,0,1,2}.

Hence the number of possibilities for rhas been reduced to 2 ·2·2·3·3 = 72,

which is far less than 3125.

that mand m0are small again allows Eve to narrow down the possibilities.

Section. Convolution polynomial rings

6.21. Compute (by hand!) the polynomial convolution product c=ab

using the given value of N.

(a) N= 3,a(x) = −1+4x+ 5x2,b(x) = −1−3x−2x2;

(b) N= 5,a(x) = 2 −x+ 3x3−3x4,b(x) = 1 −3x2−3x3−x4;

(d) N= 10,a(x) = x+x2+x3+x4+x6+x7+x9,

b(x) = x2+x3+x6+x8.

Solution to Exercise 6.21.

(a) c=ab=−22 −11x−15x2.

(b) c=ab=−6−x+ 3x3−2x4.

(d) c=ab= 3 + 2x+ 3x2+ 2x3+ 3x4+ 4x5+ 2x6+ 3x7+ 2x8+ 4x9.

6.22. Compute the polynomial convolution product c=abmodulo qusing

the given values of qand N.

(a) N= 3, q = 7,a(x) = 1 + x, b(x) = −5+4x+ 2x2;

(b) N= 5, q = 4,a(x) = 2 + 2x−2x2+x3−2x4,

b(x) = −1+3x−3x2−3x3−3x4;

(d) N= 10, q = 2,a(x) = x2+x5+x7+x8+x9,

b(x) = 1 + x+x3+x4+x5+x7+x8+x9.

Solution to Exercise 6.22.

(a) c≡ab≡4+6x+ 6x2(mod 7).

(b) c≡ab≡1 + x+x2+ 3x3+ 3x4(mod 4).

(d) c≡ab≡x+x2+x4+x6(mod 2).

6.23. Let a(x)∈(Z/qZ)[x], where qis a prime.

178 Exercises for Chapter 6

(a) Prove that

a(1) ≡0 (mod q) if and only if (x−1) |a(x) in (Z/qZ)[x].

(b) Suppose that a(1) ≡0 (mod q). Prove that a(x) is not invertible in Rq.

Solution to Exercise 6.23.

(a) Working in (Z/qZ)[x], we use division with remainder to divide a(x)

by x−1. The result is

a(x) = (x−1)b(x) + r(x) with deg r<deg(x−1) = 1.

Thus either r(x) = 0 or deg r(x) = 0, so in any case, r(x) is a constant. Thus

a(x) = (x−1)b(x) + cfor some c∈Z/qZ.

We can determine cby substituting x= 1, which gives c=a(1). Thus

a(x) = (x−1)b(x) + a(1).

Now (a) is obvious, since this equation shows that a(x) is a multiple of x−1

if and only if a(1) = 0.

(b) Suppose that a(x) is invertible in Rq, say a(x)b(x) = 1 in Rq. We have

a well-deﬁned map Rq→Z/qZdeﬁned by evaluating a polynomial at x= 1.

This map is well-deﬁned because the extra relation xN= 1 is true when we

set x= 1. Further, the map respects addition and multiplication. Hence the

relation a(x)b(x) = 1 in Rqleads to the relation a(1)b(1) = 1 in Z/qZ. In

particular, we certainly can’t have a(1) = 0. This proves

a(x) invertible =⇒a(1) 6= 0,

which is equivalent to the statement

a(1) = 0 =⇒a(x) is not invertible.

6.24. Let N= 5 and q= 3 and consider the two polynomials

a(x) = 1 + x2+x3∈R3and b(x) = 1 + x2−x3∈R3.

One of these polynomials has an inverse in R3and the other does not. Com-

pute the inverse that exists, and explain why the other doesn’t exist.

Solution to Exercise 6.24.

a(x) does not have an inverse, because a(1) ≡0 (mod 3). The previous

exercise then implies that a(x) does not have an inverse. Alternatively, using

the Euclidean algorithm, one ﬁnds that

Exercises for Chapter 6 179

gcd¡a(x), x5−1¢= 1 −xin (Z/3Z)[x],

so a(x) does not have an inverse from Proposition 6.45.

Similarly, gcd(b(x), x5−1) = 1 in (Z/3Z)[x], and using the extended

Euclidean algorithm, we ﬁnd that

b(x)−1= 1 −x−x2−x3in (Z/3Z)[x].

6.25. For each of the following values of N,q, and a(x), either ﬁnd a(x)−1

in Rqor show that the inverse does not exist.

(a) N= 5, q= 11, and a(x) = x4+ 8x+ 3;

(b) N= 5, q= 13, and a(x) = x3+ 2x−3.

Solution to Exercise 6.25.

(a) a(x)−1= 7x4+ 8x3+ 3x2+ 2x+ 3 in F11[x].

(b) gcd(a(x), x5−1) = x+ 12 in F13[x], so no inverse.

6.26. This exercise illustrates how to ﬁnd inverses in

Rm=(Z/mZ)[x]

(xN−1)

when mis a prime power pe.

(a) Let f(x)∈Z[x]/(XN−1) be a polynomial, and suppose that we have

already found a polynomial F(x) such that

f(x) F (x)≡1 (mod pi)

for some i≥1. Prove that the polynomial

G(x) = F(x)¡2−f(x) F (x)¢

satisﬁes

f(x) G(x)≡1 (mod p2i).

(b) Suppose that we know an inverse of f(x) modulo p. Using (a) repeatedly,

how many convolution multiplications does it take to compute the inverse

of f(x) modulo pe?

where to ease your task, we have given you the inverse modulo p.

180 Exercises for Chapter 6

(i) N= 5, m = 24, f(x) = 7 + 3x+x2,

f(x)−1≡1 + x2+x3(mod 2).

(ii) N= 5, m = 27, f(x) = 22 + 11x+ 5x2+ 7x3,

f(x)−1≡1 + x2+x3(mod 2).

(iii) N= 7, m = 55, f(x) = 112 + 34x+ 239x2+ 234x3+ 105x4

+ 180x5+ 137x6,

f(x)−1≡1+3x2+ 2x4(mod 5).

Solution to Exercise 6.26.

(a) We have

fG −1 = f(F(2 −f F )) −1

= 2fF −(f F )2−1

=−(fF −1)2.

We are assuming that f F ≡1 (mod pi), say fF = 1 + piH. Then

fG −1 = −(f F −1)2=p2iH,

so fG ≡1 (mod p2i).

(b) Each iteration of (a) takes two convolution multiplications, and each dou-

bles the exponent of p. So after kiterations, we’ve done 2kconvolution multi-

plications and we have an inverse of fmodulo p2k. So we need 2k≥e, which

means that k=dlog2ee(or one less, if eis a power of 2). Then the number

of convolution multiplications is 2dlog2ee.

(ii) f(x)−1mod 27= 101 + 12X+X2+ 17X3+ 34X4.

(iii) f(x)−1mod 55= 840 + 711X+ 710X2+ 268X3+ 1710X4+ 1142X5+

2430X6.

Section. The NTRU public key cryptosystem

6.27. Alice and Bob agree to communicate using the NTRU cryptosystem

with

(N, p, q) = (7,2,37).

Alice’s private key is

f(x) = x+x3+x6and F2(x) = 1 + x+x4+x5+x6.

(You can check that fF2≡1 (mod 2).) Alice receives the ciphertext

e(x) = 1 + 3x+ 3x2+ 4x3+ 4x4+x5+ 35x6

from Bob. Decipher the message and ﬁnd the plaintext.

Exercises for Chapter 6 181

Solution to Exercise 6.27.

Alice ﬁrst computes

a≡fe≡5+5x+ 5x2+ 8x3+ 8x4+ 5x5+ 6x6(mod 37).

Then she computes

F2a= 29 + 31x+ 31x2+ 32x3+ 32x4+ 29x5+ 26x6

≡1 + x+x2+x5(mod 2).

The plaintext is m= 1 + x+x2+x4+x6.

6.28. Alice and Bob decide to communicate using the NTRU cryptosystem

with parameters (N, p, q) = (7,2,29). Alice’s public key is

h(x) = 23 + 23x+ 23x2+ 24x3+ 23x4+ 24x5+ 23x6.

Bob sends Alice the plaintext message m(x) = 1 + x5using the ephemeral

key r(x) = 1 + x+x3+x6.

(a) What ciphertext does Bob send to Alice?

(b) Alice’s secret key is f(x) = 1 + x+x2+x4+x5and F2(x) = 1 + x5+x6.

Check your answer in (a) by using fand F2to decrypt the message.

Solution to Exercise 6.28.

(a) c≡2rh+m≡11+12x+12x2+12x3+14x4+13x5+14x6(mod 29).

(b) First compute

b≡fc≡4+5x+ 4x2+ 5x3+ 5x4+ 4x5+ 7x6(mod 37).

Then compute

Fb= 13 + 14x+ 14x2+ 14x3+ 16x4+ 15x5+ 16x6

≡1 + x5(mod 2).

This agrees with the plaintext.

6.29. What is the message expansion of NTRU in terms of N,p, and q?

Solution to Exercise 6.29.

The plaintext is Nnumbers modulo p, so consists of Nlog2(p) bits. The

ciphertext is Nnumbers modulo q, so consists of Nlog2(q) bits. Hence the

message expansion of NTRU is log2(q)/log2(p).

6.30. The guidelines for choosing NTRU public parameters (N, p, q, d) require

that gcd(p, q) = 1. Prove that if p|q, then it is very easy for Eve to decrypt

the message without knowing the private key. (Hint. First do the case that

p=q.)

182 Exercises for Chapter 6

Solution to Exercise 6.30.

We always have

e(x)≡pr(x)h(x) + m(x)≡m(x) (mod q).

If p=q, then this reduces to e(x) = m(x), so the ciphertext is equal to

the plaintext. In general, if p|q, then reducing e(x) modulo pgives the

plaintext m(x).

6.31. Alice uses the NTRU cryptosystem with p= 3 to send messages to

Bob.

(a) Suppose that Alice uses the same ephemeral key r(x) to encrypt two dif-

ferent plaintexts m1(x) and m2(x). Explain how Eve can use the two

ciphertexts e1(x) and e2(x) to determine approximately 2

9of the coeﬃ-

cients of m1(x). (See Exercise 6.34 for a way to exploit this information.)

(b) For example, suppose that N= 8, so there are 38possibilities for m1(x).

Suppsoe that Eve intercepts two ciphertexts

e1(x) = 32 + 21x−9x2−20x3−29x4−29x5−19x6+ 38x7,

e2(x) = 33 + 21x−7x2−19x3−31x4−27x5−19x6+ 38x7,

that were encrypted using the same ephemeral key r(x). How many coef-

ﬁcients of m1(x) can she determine exactly? How many possibilities are

there for m1(x)?

and r2(x) to encrypt the same plaintext m(x). (Hint. Do it ﬁrst assum-

ing that h(x) has an inverse in Rq. The problem is harder without this

assumption.)

Solution to Exercise 6.31.

(a) Eve computes

e1(x)−e2(x)≡¡r(x)h(x) + m1(x)¢−¡r(x)h(x) + m2(x)¢(mod q)

≡m1(x)−m2(x) (mod q).

The coeﬃcients of m1(x)−m2(x) are in the set {−2,−1,0,1,2}, so since q > 5,

Eve recovers m1(x)−m2(x) exactly. Any coeﬃcient that is nonzero limits the

possibilities for that coeﬃcient of m1(x). (This is the same as the analogous

GGH exercise.)

More precisely, Eve can recover the ith coeﬃcient of m1(x) if the ith coef-

ﬁcient of both m1(x) and m2(x) are both +1 or both −1. Assuming that the

coeﬃcients are random, the probability of this happening is 2 ·1

3·1

3=2

9. So

Eve recovers approximately 2

9of the coeﬃcients of m1(x).

(b) Eve ﬁnds that

m1(x)−m2(x) = e1(x)−e2(x) = −1−2x2−x3+ 2x4−2x5

Exercises for Chapter 6 183

The coeﬃcients of x2,x4and x5for m1are determined, they are −x2+x4−x5.

So Eve knows three of the coeﬃcients of m1.

More generally, m1(x) looks like

A+Bx −x2+Cx3+x4−x5+Dx6+Ex7.

Further, Eve knows that A∈ {0,1}and C∈ {0,1}. So there are 2 ·3·2·3·3 =

108 possibilities for m1(x), which is much smaller than 38= 6561.

h(x)−1¡e1(x)−e2(x)¢=h(x)−1¡pr1(x)h(x)−pr2(x)h(x)¢(mod q)

=r1(x)−r2(x) (mod q).

Then the analysis is the same as in (a), since r1and r2have ternary coeﬃ-

cients.

In general, however, h(x) is not invertible, since g(x) is not invertible,

since g(1) = 0. One way around this problem is to develop a theory of “almost

inverses” based on the fact that the ring Z[x]/(xN−1) is isomorphic to Z×

Z[x]/¡Φ(x)¢, where Φ(x) = xN−1+xN−2+···+x+ 1. The image of g(x) in

the product ring is (0, g(x)), so one inverts the second factor.

Section. NTRU as a lattice cryptosystem

6.32. This exercise explains how to formulate NTRU message recovery as a

closest vector problem. Let h(x) be an NTRU public key and let

e(x)≡pr(x)h(x) + m(x) (mod q)

be a message encrypted using h(x).

(a) Prove that the vector (pr,e−m) is in LNTRU

(b) Prove that the lattice vector in (a) is almost certainly the closest lattice

vector to the known vector (0,e). Hence solving CVP reveals the plain-

text m. (For simplicity, you may assume that d≈N/3 and q≈2N, as

we did in Proposition 6.61.)

the determinant, by using instead a modiﬁed NTRU lattice of the form

µ1ph

0q¶.

Solution to Exercise 6.32.

(a) By the deﬁnition of e, we can ﬁnd a polynomial v(x) satisfying

e=prh+m+qv(x).

Thus

184 Exercises for Chapter 6

(pr,v)MNTRU

h= (pr,v)µ1h

0q¶

= (pr, prh+qv)

= (pr,e−m).

This shows that (pr,e−m) is in the NTRU lattice LNTRU

hspanned by the

rows of MNTRU

h. Also notice that

(pr,e−m) =

Eve knows this vector

z}|{

(0,e) +

a short vector

z }| {

(pr,−m).

(b) We have

°(pr,e−m)−(0,e)°

°=°

°(pr,−m)°

=pp2·2d+ 2d

≈p(p2+ 1)2N/3.

Since pis small, typically 2 or 3, this is between 1.83√Nand 2.58√N. But as

in the Proposition, the Gaussian heuristic predicts that a random CVP has a

solution of size approximately σ(LNTRU

h)≈0.484N.

ANTRU

h=µ1ph

0q¶.

Then with notation as in (a), we have

(r,v)ANTRU

h= (r,v)µ1ph

0q¶

= (pr, prh+qv)

= (pr,e−m).

This shows that (r,e−m) is in the lattice spanned by the rows of ANTRU

And det(ANTRU

h) = qN, which is the same as det(MNTRU

h).

Now reworking (b), we see that

°(r,e−m)−(0,e)°

°=°

°(r,−m)°

=√4d≈p4N/3≈1.15√N .

So the distance to the closest vector using this new lattice is less than when

using the old lattice.

6.33. The guidelines for choosing NTRU public parameters (N, p, q, d) include

the assumption that Nis prime. To see why, suppose (say) that Nis even.

Explain how Eve can recover the private key by solving a lattice problem in

dimension N, rather than in dimension 2N.Hint. Use the natural map

Z[x]/(xN−1) →Z[x]/(xN/2−1).

Exercises for Chapter 6 185

Solution to Exercise 6.33.

This method of breaking NTRU when Nis composite is due to Craig

Gentry, Key recovery and message attacks on NTRU-composite, Advances in

cryptology—EUROCRYPT 2001 (Innsbruck), Lecture Notes in Comput. Sci.

2045, 182–194, Springer, Berlin, 2001.

6.34. Suppose that Bob and Alice are using NTRU to exchange messages

and that Eve intercepts a ciphertext e(x) for which she already knows part of

the plaintext m(x). (This is not a ludicrous assumption; see Exercise 6.31, for

example.) More precisely, suppose that Eve knows tof the coeﬃcients of m(x).

Explain how to set up a CVP to ﬁnd m(x) using a lattice of dimension 2N−2t.

Solution to Exercise 6.34.

A solution for this exercise is not currently available.

Section. Lattice reduction algorithms

6.35. Let b1and b2be vectors, and set

t=b1·b2/kb1k2and b∗

2=b2−tb1.

Prove that b∗

2·b1= 0 and that b∗

2is the projection of b2onto the orthogonal

complement of b1.

Solution to Exercise 6.35.

A solution for this exercise is not currently available.

6.36. Let aand bbe nonzero vectors in Rn.

(a) What value of t∈Rminimizes the distance ka−tbk? (Hint. It’s easier

to minimize the value of ka−tbk2.)

(b) What is the minimum distance in (a)?

orthogonal complement of b.

(d) If the angle between aand bis θ, use your answer in (b) to show that

the minimum distance is kaksin θ. Draw a picture illustrating this result.

Solution to Exercise 6.36.

(a) We have

F(t) = ka−tbk2

= (a−tb)·(a−tb)

=kak2−2ta·b+t2kbk2.

One can then use calculus (i.e., set F0(t) = 0) or complete the square to

minimize the value of the quadratic polynomial. The minimizing value of tis

t=a·b

kbk2.

(b) Substituting this value of tand simplifying gives the minimum distance

186 Exercises for Chapter 6

skak2kbk2−(a·b)2

kbk2.

(d) Substitute a·b=kakkbkcos θinto (b) and use

kak2kbk2−(a·b)2=kak2kbk2−¡kakkbkcos θ¢2

=kak2kbk2(1 −cos2θ)

=kak2kbk2sin2θ.

6.37. Apply Gauss’s lattice reduction algorithm (Proposition 6.63) to solve

SVP for the following two dimensional lattices having the indicated basis vec-

tors. How many steps does the algorithm take?

(a) v1= (120670,110521) and v2= (323572,296358).

(b) v1= (174748650,45604569) and v2= (35462559,9254748).

Solution to Exercise 6.37.

(a)

Step v1v2m

1 (120670,110521) (323572,296358) 3

2 (−38438,−35205) (120670,110521) −3

3 (5356,4906) (−38438,−35205) −7

4 (−946,−863) (5356,4906) −6

5 (−320,−272) (−946,−863) 3

6 (14,−47) (−320,−272) 3

7 (14,−47) (−362,−131) 0

The solution to SVP is v= (14,−47).

(b)

Step v1v2m

1 (35462559,9254748) (174748650,45604569) 5

2 (−2564145,−669171) (35462559,9254748) −14

3 (−435471,−113646) (−2564145,−669171) 6

4 (48681,12705) (−435471,−113646) −9

5 (2658,699) (48681,12705) 18

6 (837,123) (2658,699) 3

7 (147,330) (837,123) 1

8 (147,330) (690,−207) 0

The solution to SVP is v= (147,330).

(c)

Exercises for Chapter 6 187

Step v1v2m

1 (725734520,613807887) (3433061338,2903596381) 5

2 (−195611262,−165443054) (725734520,613807887) −4

3 (−56710528,−47964329) (−195611262,−165443054) 3

4 (−25479678,−21550067) (−56710528,−47964329) 2

5 (−5751172,−4864195) (−25479678,−21550067) 4

6 (−2474990,−2093287) (−5751172,−4864195) 2

7 (−801192,−677621) (−2474990,−2093287) 3

8 (−71414,−60424) (−801192,−677621) 11

9 (−15638,−12957) (−71414,−60424) 5

10 (6776,4361) (−15638,−12957) −3

11 (4690,126) (6776,4361) 1

12 (4690,126) (2086,4235) 0

The solution to SVP is v= (4690,126).

6.38. Let Vbe a vector space, let W⊂Vbe a vector subspace of V, and

let W⊥be the orthogonal complement of Win V.

(a) Prove that W⊥is also a vector subspace of V.

(b) Prove that every vector v∈Vcan be written as a sum v=w+w0for

unique vectors w∈Wand w0∈W⊥. (One says that Vis the direct sum

of the subspaces Wand W⊥.)

kvk2=a2kwk2+b2kw0k2.

Solution to Exercise 6.38.

A solution for this exercise is not currently available.

6.39. Let Lbe a lattice with basis vectors v1= (161,120) and v2=

(104,77).

(a) Is (0,1) in the lattice?

(b) Find an LLL reduced basis.

2,11¢.

Solution to Exercise 6.39.

A solution for this exercise is not currently available.

6.40. Use the LLL algorithm to reduce the lattice with basis

v1= (20,16,3),v2= (15,0,10),v3= (0,18,9).

You should do this exercise by hand, writing out each step.

Solution to Exercise 6.40.

Compute

µ2,1=300 + 30

400 + (14)2+ 64 =330

665 <1

188 Exercises for Chapter 6

Checking the Lov´asz condition for v2amounts to checking that kv2k2≥

4kv1k2and kv2k2= 225 + 100 = 325,kv1k2= 665, so swap. Now v1=

(15,0,10) and v2= (20,16,3). Recompute µ2,1=356

325 and subtract one mul-

tiple of v1from v2. New v2= (5,16,−7). Note that the (new) µ2,1is now

(75 −70)/325 = −5/325.

Move on to v3computing

µ3,1=−75 + 160

325 =85

325 <1

µ3,2=225

330 >1

Subtract one multiple of v2from v3obtaining the new v3= (−5,2,16).

On to the Lov´asz condition, computing

kv∗

3+µ3,2v∗

2k2=kv3−µ3,1v1k2=k(−5,2,16)−85

325(15,0,10)k2=k1

13(−14,26,174)k2.

Next compute

kv∗

2k2=k1

13(62,208,3)k2

and we ﬁnd the condition (2) is not satisﬁed, so we swap. At this point,

v1= (15,0,10),v2= (−5,2,16),v3= (5,16,−7).

Checking condition (2) for (the new) v2:kv2k2= 285, which is larger than

3/4 times kv1k2= 325. (If, instead of 3/4, we had chosen a constant closer

to 1, like .99, then we would perform the swap step again. This makes sense

since the length of v2is smaller than the length of v1.) Now check the value

µ3,2=−105

285

and the Lov´asz condition for v3, which is satisﬁed. So we now have an LLL

reduced basis.

6.41. Let Lbe the lattice generated by the rows of the matrix







20 51 35 59 73 73

14 48 33 61 47 83

95 41 48 84 30 45

0 42 74 79 20 21

6 41 49 11 70 67

23 36 6 1 46 4







Implement the LLL algorithm (Figure 6.7) on a computer and use your pro-

gram to answer the following questions.

(a) Compute det(L) and H(M). What is the shortest basis vector?

Exercises for Chapter 6 189

(b) Apply LLL to M. How many swaps (Step [11]) are required? What is the

value of H(MLLL)? What is the shortest basis vector in the LLL reduced

basis? How does it compare with the Gaussian expected shortest length?

How many swaps are required? What is the value of H(MLLL) and what

is the shortest basis vector?

(d) Apply LLL to the original matrix M, but in the Lov´asz condition

(Step [8]), use 0.99 instead of 3

4. How many swaps are required? What is

the value of H(MLLL) and what is the shortest basis vector?

Solution to Exercise 6.41.

(a) det(L) = 21242880806, H(M) = 0.45726, smallest basis vector is

kv6k= 63.198,

(b) The output is







−6−3−2 2 −26 10

11 30 2 5 −6 24

−14 −10 14 −48 −3−6

−3 24 43 23 −33 −38

64 −44 −16 −46 −13 4

−28 −25 41 5 30 39







There are 11 swap steps. We have H(MLLL)=0.91981 and the shortest

vector is kv1k= 28.792. Gaussian expected shortest is σ(L) = 40.0239. This

suggests that v1is probably the shortest vector in L.







6 3 2 −2 26 −10

11 30 2 5 −6 24

14 10 −14 48 3 6

−28 −25 41 5 30 39

−3 24 43 23 −33 −38

47 −35 54 30 −13 11







There are 8 swap steps. We have H(MLLL) = 0.94427 and the shortest vector

is kv1k= 28.792.

(d) With Lov´asz condition 0.99,







−6−3−2 2 −26 10

11 30 2 5 −6 24

−14 −10 14 −48 −3−6

−3 24 43 23 −33 −38

−28 −25 41 5 30 39

47 −35 54 30 −13 11







There are 12 swap steps. We have H(MLLL)=0.944270 and the shortest

vector is kv1k= 28.792. This is the same basis as in (c), in a diﬀerent order.

190 Exercises for Chapter 6

6.42. A more eﬃcient way to implement the LLL algorithm is described in

Figure 6.8, with Reduce and Swap subroutines given in Figure 6.9. (This

implementation of LLL follows [26, Algorithm 2.6.3]. We thank Henri Cohen

for his permission to include it here.)

(a) Prove that the algorithm described in Figures 6.8 and 6.9 returns an LLL

reduced basis.

(b) For any given Nand q, let LN,q be the N-dimensional lattice with ba-

sis v1, . . . , vNdescribed by the formulas

vi= (ri1, ri2, . . . , riN ), rij ≡(i+N)j(mod q),0≤rij < q.

Implement the LLL algorithm and use it to LLL reduce LN,q for each of

the following values of Nand q:

(i) (N, q) = (10,541) (ii) (N, q) = (20,863)

(iii) (N, q) = (30,1223) (iv) (N, q) = (40,3571)

In each case, compare the Hadamard ratio of the original basis to the

Hadamard ratio of the LLL reduced basis, and compare the length of the

shortest vector found by LLL to the Gaussian expected shortest length.

Solution to Exercise 6.42.

(b) We write Lfor the original basis and L0for the LLL reduced basis,

and we write vfor the shortest vector in the original basis and v0for the

shortest vector in the LLL reduced basis. Here are the shortest vectors in the

LLL reduced basis (N.B. the shortest vector was not always the ﬁrst vector):

(i) v0= (−98,166,−131,−18,100,28,81,50,−39,−39).

(ii) v0= (−122,−33,−59,166,9,−394,−46,227,−148,−86,−46,108,−214,

173,−107,171,34,−86,−153,−117).

(iii) v0= (98,−148,−263,−370,76,53,258,−128,221,−435,−119,−59,142,

−336,311,290,89,−538,16,437,108,361,322,−374,56,−117,

−208,−131,645,42).

(iv) v0= (192,−1426,552,−292,52,482,1046,−1344,−414,−226,−1413,

−1466,−447,653,−484,−553,−284,232,1975,1944,27,1203,

−1363,707,91,−549,−831,974,768,1074,57,−966,1997,

2099,828,−1295,−972,−842,185,−2271).

The lengths, Hadamard ratios, and Gaussian expected shortest lengths are

given in the following table:

kvk kv0k H(L)H(L0)σ(L)

(i) 632.369 278.446 0.309773 0.853005 241.775

(ii) 1846.49 679.056 0.253273 0.694868 659.505

(iii) 3133.91 1505.95 0.304603 0.579003 1613.89

(iv) 10711.4 6706.75 0.281214 0.470440 5775.49

Exercises for Chapter 6 191

[1] Input a basis {v1, . . . , vn}for a lattice L

[2] Set k= 2,kmax = 1,v∗

1=v1, and B1=kv1k2

[3] If k≤kmax go to Step [9]

[4] Set kmax =kand v∗

k=vk

[5] Loop j= 1,2, . . . , k −1

[6] Set µk,j =vk·v∗

j/Bjand v∗

k=v∗

k−µk,j v∗

[7] End jLoop

[8] Set Bk=kv∗

kk2

[9] Execute Subroutine RED(k, k −1)

[10] If Bk<³3

4−µ2

k,k−1´Bk−1

[11] Execute Subroutine SWAP(k)

[12] Set k= max(2, k −1) and go to Step [9]

[13] Else

[14] Loop =k−2, k −3,...,2,1

[15] Execute Subroutine RED(k, )

[16] End Loop

[17] Set k=k+ 1

[18] End If

[19] If k≤ngo to Step [3]

[20] Return LLL reduced basis {v1,...,vn}

Figure 6.1: The LLL algorithm—Main routine

6.43. Let 1

4< α < 1 and suppose that we replace the Lov´asz condition with

the condition

kv∗

ik2≥¡α−µ2

i,i−1¢kv∗

i−1k2for all 1 < i ≤n.

(a) Prove a more version of Theorem 6.66. What quantity, depending on α,

replaces the 2 that appears in the estimates (6.53), (6.54), and (6.55)?

(b) Prove a version of Theorem 6.68. In particular, how does the upper bound

for the number of swap steps depend on α? What happens as α→1?

Solution to Exercise 6.43.

A solution for this exercise is not currently available.

6.44. Let v1, . . . , vnbe an LLL reduced basis for a lattice L.

(a) Prove that there are constants C1>1> C2>0 such that for

all y1, . . . , yn∈Rwe have

i=1

ikvik2≥°

i=1

yivi°

≥Cn

i=1

ikvik2.(6.3)

(This is a hard exercise.) We observe that the inequality (6.63) is another

way of saying that the basis v1,...,vnis quasi-orthogonal, since if it

192 Exercises for Chapter 6

—— Subroutine RED(k, )——

[1] If |µk,`| ≤ 1

2, return to Main Routine

[2] Set m=bµk,`e

[3] Set vk=vk−mv`and µk,` =µk,` −m

[4] Loop i= 1,2, . . . ,  −1

[5] Set µk,i =µk,i −mµ`,i

[6] End iLoop

[7] Return to Main Routine

—— Subroutine SWAP(k)——

[1] Exchange vk−1and vk

[2] Loop j= 1,2, . . . , k −2

[3] Exchange µk−1,j and µk,j

[4] End jLoop

[5] Set µ=µk,k−1and B=Bk−µ2Bk−1

[6] Set µk,k−1=µBk−1/B and Bk=Bk−1Bk/B and Bk−1=B

[7] Loop i=k+ 1, k + 2, . . . , kmax

[8] Set m=µi,k and µi,k =µi,k−1−µm and µi,k−1=m+µk,k−1µi,k

[9] End iLoop

[10] Return to Main Routine

Figure 6.2: The LLL algorithm—RED and SWAP subroutines

were truly orthogonal, then we would have an equality kPyivik2=

Py2

ikvik2.

(b) Prove that there is a constant Csuch that for any target vector w∈Rn,

Babai’s algorithm (Theorem 6.34) ﬁnds a lattice vector v∈Lsatisfying

kw−vk ≤ Cnmin

u∈Lkw−uk.

Thus Babai’s algorithm applied with an LLL reduced basis solves ap-

prCVP to within a factor of Cn. This is Theorem 6.73.

Solution to Exercise 6.44.

(a) This is a hard exercise. We follow the proof given in [?,§5.7].

Fix a basis v1,...,vn, let v∗

1, . . . , v∗

nbe the associated Gram–Schmidt

orthogonalized basis, and let

ei=v∗

i/kv∗

ik,1≤i≤n,

be the associated orthonormal basis. Let µi,j be as usual (settting µi,i = 1

and µi,j = 0 for i > j), so the change of basis matrix M= (µi,j ) satisﬁes

V=V∗M.

Exercises for Chapter 6 193

(The rows of Vare v1, . . . , vnand the rows of V∗are v∗

1, . . . , v∗

n.)

In general, for any linear transformation A, we write A= (ai,j ) as a matrix

relative to the orthonormal basis e∗

1, . . . , e∗

nand deﬁne

kAk= sup

06=v∈RnkvAk

kvkand kAke= sup

i,j |ai,j |.

We observe that if v=Pxie∗

i, then kvk2=Px2

iand we have

kvAk2=°

i=1

j=1

ai,j ej°

j=1µn

i=1

xiai,j ¶2

≤

j=1 kvk2ka·,j k2(Cauchy–Schwartz),

≤

j=1 kvk2nkA|2

=n2kAk2

ekvk2.

Taking square roots, dividing by kvk, and taking the sup over nonzero vyields

kAk ≤ nkAke.

To ease notation, we let

ci=kv∗

ik,so v∗

i=ciei.

Now we compute

eiM=c−1

iv∗

iM=c−1

ivi=c−1

iµv∗

i−1

j=1

µi,j v∗

j¶=c−1

iµciei+

i−1

j=1

µi,j cjej¶

=ei+

i−1

j=1

µi,j c−1

icjej.

So relative to the ebasis, the linear transformation Mhas a matrix that is

lower triangular with 1’s on the diagonal and with ijth entry satisfying

|µi,j c−1

icj| ≤ 1

2·kv∗

kv∗

ik≤2(i−j)/2−1,(6.4)

where for the last inequality we use (6.57) (N.B. This is where we use the

fact that the basis is reduced, since the size condition gives |µi,j | ≤ 1

2and the

Lov´asz condition implies the estimate (6.57).) Therefore,

194 Exercises for Chapter 6

kMke≤max

1≤j≤i≤n2(i−j)/2−1= 2(n−3)/2.

(If n≤2, we need to replace this upper bound by 1.)

This allows us to get an upper bound

i=1

yivi°

=kyVk2=kyV∗Mk≤kyV∗kkMk ≤ kyV∗k · nkMke

≤ kyV∗kn2(n−3)/2=n2(n−3)/2

i=1

ikv∗

ik2.(6.5)

To obtain a lower bound, we observe that

i=1

ikv∗

ik2=kyV∗k2=°

°yV M−1°

°2

≤ kyVk°

°M−1°

°2=°

°M−1°

°2°

i=1

yivi°

.(6.6)

So we need an upper bound for °

°M−1°

°.

Note that

M=I−N,

where Nis lower triangular with 0’s on the diagonal, so Nis nilpotent, and

indeed it satisﬁes Nn= 0. Hence

M−1=I+N+N2+··· +Nn−1.

The following lemma provides the necessary estimate. We refer the reader

to [?, Lemma 7.10] for the proof.

Lemma 6.1. Let B= (bi,j )be the matrix of a linear transformation relative

to an orthonormal basis {ei}. Suppose that there are positive constants βand γ

so that

bi,j = 0 for i≤jand |bi,j | ≤ γδj−ifor i > j.

Then °

°B+B2+B3+···+Bn−1°

°e≤γ(γ+ 1)n−2δn−1.

Note that (??) tells us that the coeﬃcients of Nsatisfy

|coef. of N| ≤ 2(i−j)/2−1=1

2·µ1

√2¶j−i

So we can apply the lemma to Nwith γ= 1/2 and δ= 1/√2, which gives

°N+N2+···+Nn−1°

°e≤1

2·µ3

2¶n−2

·µ1

√2¶n−1

3µ9

8¶(n−1)/2

Exercises for Chapter 6 195

Hence

°M−1°

°≤n°

°M−1°

°e≤n¡1 + °

°N+N2+···+Nn−1°

°e¢

≤n+n

3µ9

8¶(n−1)/2

≤nµ9

8¶(n−1)/2

(The last inequality is valid for n≥8. For smaller n, one can put in a small

correction factor.)

Substituting into (??) gives

i=1

ikv∗

ik2≤n2µ9

8¶n−1°

i=1

yivi°

.(6.7)

We now apply (6.54) from Theorem 6.66, which says that kv∗

ik2≥2−(i−1)kvik2.

This yields

i=1

yivi°

≥n−2µ8

9¶n−1n

i=1

i·2−(i−1)kvik2≥n−2µ4

9¶n−1n

i=1

ikvik2.

(b) Let a=Paivi∈Lbe any lattice vector, for example, it could be the

lattice vector that is closest to w. Write

w=Xβiviwith βi∈R,

and let

b=Xbiviwith bi=bβie

be the vector returned by Babai’s algorithm. Also write

βi=bi+δiwith |δi| ≤ 1

Then

kw−ak2=°

°X(βi−ai)vi°

≥Cn

2X(βi−ai)2kvik2from (6.63),

=Cn

2X(bi−ai+δi)2kvik2.

If ai6=bi, then |bi−ai| ≥ 1, so

(bi−ai+δi)2≥1

4(bi−ai)2,

and clearly this is also valid if ai=bi. Hence using the other inequality

in (6.63),

196 Exercises for Chapter 6

Input a basis v1, . . . , vnof a lattice L.

Input a target vector t.

Compute Gram–Schmidt orthogonalized vectors v∗

1, . . . , v∗

n(Theorem 6.13).

Set w=t.

Loop i=n, n −1, . . . , 2,1

Set w=w−¥w·v∗

i/kv∗

ik2¨vi.

End iLoop

Return the lattice vector t−w.

Figure 6.3: Babai’s closest plane algorithm

kw−ak2≥Cn

2X1

4(bi−ai)2kvik2

≥1

4Cn

2C−n

1°

°X(bi−ai)vi°

4Cn

2C−n

1kb−ak2.

Using the triangle inequality, we ﬁnd that

kw−ak ≥ 1

2(C2/C1)n/2kb−ak ≥ 1

2(C2/C1)n/2¡kb−wk−kw−ak¢,

and now a little bit of algebra yields

kw−bk ≤ Ã2µC1

C2¶n/2

+ 1!kw−ak.

This shows that the Babai vector bis the closest vector to wup to a factor

of 2(C1/C2)n/2+ 1.

6.45. Babai’s Closest Plane Algorithm, which is described in Figure 6.10, is

an alternative rounding method that uses a given basis to solve apprCVP. As

usual, the more orthogonal the basis, the better the solution, so generally

people ﬁrst use LLL to create a quasi-orthogonal basis and then apply one of

Babai’s methods. In both theory and practice, Babai’s closest plane algorithm

seems to yield better results than Babai’s closest vertex algorithm.

Implement both of Babai’s algorithms (Theorem 6.34 and Figure 6.10)

and use them to solve apprCVP for each of the following lattices and target

vectors. Which one gives the better result?

(a) Lis the lattice generated by the rows of the matrix

Exercises for Chapter 6 197

ML=







−5 16 25 25 13 8

26 −3−11 14 5 −26

15 −28 16 −7−21 −4

32 −3 7 −30 −6 26

15 −32 −17 32 −3 11

5 24 0 −13 −46 15







and the target vector is t= (−178,117,−407,419,−4,252). (Notice that

the matrix MLis LLL reduced.)

(b) Lis the lattice generated by the rows of the matrix

ML=







−33 −15 22 −34 −32 41

10 9 45 10 −6−3

−32 −17 43 37 29 −30

26 13 −35 −41 42 −15

−50 32 18 35 48 45

2−5−2−38 38 41







and the target vector is t= (−126,−377,−196,455,−200,−234). (Notice

that the matrix MLis not LLL reduced.)

methods to solve apprCVP. Do you get better solutions?

Solution to Exercise 6.45.

(a) The Closest Plane Algorithm gives the vector

w= (−185,105,−414,419,−8,277) = (−1,−4,−13,−3,12,5)ML∈L.

It satisﬁes kt−wk= 29.7153. The Closest Vertex Algorithm gives the vector

w= (−159,102,−425,433,−3,251) = (−1,−3,−13,−3,12,5)ML∈L.

It satisﬁes kt−wk= 33.2866. So the Closest Plane Algorithm gives a slightly

better result than the Closest Vertex Algorithm.

(b) The Closest Plane Algorithm gives the vector

w= (−166,−394,−203,460,−196,−204) = (−6,−13,4,−12,−4,3)ML∈L.

It satisﬁes kt−wk= 53.6563. The Closest Vertex Algorithm gives the vector

w= (−156,−385,−158,470,−202,−207) = (−6,−12,4,−12,−4,3)ML∈L.

It satisﬁes kt−wk= 58.0172. So the Closest Plane Algorithm gives a slightly

better result than the Closest Vertex Algorithm.







10 9 45 10 −6−3

9−3 11 37 28 15

−24 −18 33 3 −4 56

2−5−2−38 38 41

−41 −14 32 0 1 −45

−35 53 −26 −5 24 −26







198 Exercises for Chapter 6

The Closest Plane Algorithm gives the vector

w= (−132,−367,−191,467,−198,−263) = (−12,6,1,−9,4,−4)ML∈L.

It satisﬁes kt−wk= 33.9116. The Closest Vertex Algorithm gives the exact

same result. So starting with an LLL reduced basis yields a signiﬁcantly better

solution to apprCVP.

Section. Applications of LLL to cryptanalysis

6.46. You have been spying on George for some time and overhear him re-

ceiving a ciphertext e= 83493429501 that has been encrypted using the con-

gruential cryptosystem described in Section 6.1. You also know that George’s

public key is h= 24201896593 and the public modulus is q= 148059109201.

Use Gaussian lattice reduction to recover George’s private key (f, g) and the

message m.

Solution to Exercise 6.46.

Gaussian lattice reduction on the lattice generated by

(1,24201896593) and (0,148059109201)

gives the short basis

(233444,255333) and (330721,−272507),

so the private key is

f= 233444 and g= 255333.

We check that

f−1g≡133037176740 ·255333 ≡24201896593 ≡h(mod q).

In order to decrypt the message, we ﬁrst compute

a≡fe ≡94843884201 (mod q).

Then we do a computation modulo gto recover the plaintext m,

m=f−1a= 94649 ·94843884201 ≡186000 (mod g).

6.47. Let

M= (81946,80956,58407,51650,38136,17032,39658,67468,49203,9546)

and let S= 168296. Use the LLL algorithm to solve the subset-sum problem

for Mand S, i.e., ﬁnd a subset of the elements of Mwhose sum is S.

Exercises for Chapter 6 199

Solution to Exercise 6.47.

We apply LLL to the matrix







2 0 0 0 0 0 0 0 0 0 81946

0 2 0 0 0 0 0 0 0 0 80956

0 0 2 0 0 0 0 0 0 0 58407

0 0 0 2 0 0 0 0 0 0 51650

0 0 0 0 2 0 0 0 0 0 38136

0 0 0 0 0 2 0 0 0 0 17032

0 0 0 0 0 0 2 0 0 0 39658

0 0 0 0 0 0 0 2 0 0 67468

0 0 0 0 0 0 0 0 2 0 49203

0 0 0 0 0 0 0 0 0 2 9546

1 1 1 1 1 1 1 1 1 1 168296







It takes LLL 102 swaps to ﬁnd the reduced matrix







1−1 1 1 −1 1 −1 1 1 −1 0

1−1 1 1 −1 1 1 1 −1 1 1

3 1 1 3 1 1 1 −3 1 −1 0

3 1 1 −1 3 1 −31112

−2 0 2 −24022202

−2−2 4 −4−20200−2−2

−1−3−1 1 1 −3−3−1 1 1 3

−2 2 0 4 −2−4−2 0 0 2 −2

−2 4 4 0 −2 2 0 −2 2 0 1

−4−2 0 2 4 0 0 2 −4−2 0

2 4 2 0 −2−2−2 2 −4−4−1







The top row gives the solution

(0,−1,0,0,−1,0,−1,0,0,−1,1),

i.e., we have

80956 + 38136 + 39658 + 9546 = 168296.

This problem was created using the superincreasing sequence

r= (73,160,323,657,1325,2660,5348,10698,21396,42807)

and the multiplier and modulus A= 79809 and B= 85733.

6.48. Alice and Bob communicate using the GGH cryptosystem. Alice’s pub-

lic key is the lattice generated by the rows of the matrix







10305608 −597165 45361210 39600006 12036060

−71672908 4156981 −315467761 −275401230 −83709146

−46304904 2685749 −203811282 −177925680 −54081387

−68449642 3969419 −301282167 −263017213 −79944525

−46169690 2677840 −203215644 −177405867 −53923216







200 Exercises for Chapter 6

Bob sends her the encrypted message

e= (388120266,−22516188,1708295783,1491331246,453299858).

Use LLL to ﬁnd a reduced basis for Alice’s lattice, and then use Babai’s

algorithm to decrypt Bob’s message.

Solution to Exercise 6.48.

LLL takes 52 swaps to produce the following matrix whose Hadamard

ratio is H= 0.963, so it is quite orthogonal:







72 −116 172 −290 −51

180 −218 −53 298 161

−158 −301 −230 −185 −25

114 172 −148 −311 297

462 164 −258 91 −491







Babai’s closest vertex method gives the lattice vector

(388120256,−22516180,1708295793,1491331242,453299848)

that is close to the target vector e. If we let v1, . . . , v5be the LLL-reduced

basis vectors and w1, . . . , w5be the original basis vectors, then

(388120256,−22516180,1708295793,1491331242,453299848)

= 1622959v1+ 2403687v2−4093270v3−1942134v4−1269978v5

=−3w1−9w2+ 0w3+ 6w4−4w5.

So Bob’s plaintext is the vector (−3,−9,0,6,−4).

6.49. Alice and Bob communicate using the NTRU cryptosystem with public

parameters (N, p, q, d) = (11,3,97,3). Alice’s public key is

h= 39 + 9x+ 33x2+ 52x3+ 58x4+ 11x5+ 38x6+ 6x7+x8+ 48x9+ 41x10.

Apply the LLL algorithm to the associated NTRU lattice to ﬁnd an NTRU

private key (f,g) for h. Check your answer by verifying that g≡fh(mod q).

Use the private key to decrypt the ciphertext

e= 52 + 50x+ 50x2+ 61x3+ 61x4+ 7x5+ 53x6+ 46x7+ 24x8+ 17x9+ 50x10.

Solution to Exercise 6.49.

We apply LLL to the 22 dimensional NTRU lattice LNTRU

hassociated to h.

It requires 322 swaps and returns the LLL reduced the matrix

Exercises for Chapter 6 201







−1−1−1 0 0 −1 0 1 0 1 1 1 1 −1 0 0 −1−1 0 1 0 −1

1−1−1−1 0 0 −1 0 1 0 1 −1 1 1 −1 0 0 −1−1 0 1 0

0 1 0 0 0 1 0 1 −1 0 −2 0 −1 0 0 −1 1 1 0 −1 1 0

0 1 0 0 0 0 −2 1 −1 1 1 0 1 0 1 0 0 0 0 −1 1 −1

0 1 1 −1−1−1 0 0 −1 0 1 1 0 −1 1 1 −1 0 0 −1−1 0

0 0 2 1 0 −10011−1 1 0 1 0 0 0 1 1 0 −1 0

−1 0 0 0 −1 0 −1 1 0 2 0 1 0 0 1 −1−1 0 1 −1 0 0

1−1 1 1 0 1 0 0 0 0 −2 0 −1 1 −1 0 1 0 1 0 0 0

−1 0 2 1 0 1 −1 1 0 0 −1 0 0 0 0 0 0 1 2 −1 0 0

0 0 0 0 −1 0 0 −1−1 0 −2 0 −2 0 0 −1 0 0 0 −1−1 0

1 1 1 −11100−2 0 0 0 −1 0 1 1 0 1 0 −1 1 0

−4 8 0 2 −7 0 1 −8 13 −4−2 4 −9−1 0 7 −7−6 1 2 18 −10

9 2 3 −7−1 0 −9 12 −4−4−3−10 0 0 7 −6−5 1 1 17 −11 4

−6−2−5 3 13 2 0 1 5 −11 −1 16 −3 9 5 3 2 −8−5−14 −4−2

−3 7 2 0 8 −12 3 3 4 −8−1 0 −7 7 6 −1−2−17 12 −5 9 1

−9 7 7 −8−14 2 −10 −8−2 1 −1 4 −3 1 −6 2 0 3 −1 21 12 −1

7 1 0 9 −12 4 4 3 −9−2−3−7 6 5 −1−1−17 11 −4 10 0 0

−2−3 9 2 3 −6−1 0 −8 13 −4−11 4 −8 0 0 8 −6−5 1 2 18

13 3 −4 1 3 4 −12 −2 9 −14 −2 14 −2−7 2 −10 −12 3 3 8 4 −4

−1−5 11 1 6 2 5 −3−13 −2 0 5 14 4 2 −16 3 −9−5−3−2 8

−6 11 0 6 2 5 −3−11 −3 1 −2 15 4 1 −16 2 −9−5−3−2 9 4

−3−3−3 9 2 1 −8−1 0 −7 13 18 −10 5 −9 0 0 7 −7−5 1 0







The top row is

(−1,−1,−1,0,0,−1,0,1,0,1,1,1,1,−1,0,0,−1,−1,0,1,0,−1),

which gives the private key polynomials

f(x) = −1−x−x2−x5+x7+x9+x10

g(x) = 1 + x−x2−x5−x6+x8−x10.

To decipher the message, we compute

a≡fe≡ −11−13x−1x2+3x3−4x4+2x5+16x6+4x7+4x9−2x10 (mod q).

Then we use

f−1≡ −1 + x−x3+x4−x6+x7−x8−x9+x10 (mod 3)

to compute the plaintext

m≡af−11−x−x2−x3−x4+x7+x10 (mod 3).

In vector form, m= (1,−1,−1,−1,−1,0,0,1,0,0,1).

6.50. (a) Suppose that kis a 10 digit integer, and suppose that when √kis

computed, the ﬁrst 15 digits after the decimal place are 418400286617716.

Find the number k. (Hint. Reformulate it as a lattice problem.)

(b) More generally, suppose that you know the ﬁrst d-digits after the decimal

place of √K. Explain how to set up a lattice problem to ﬁnd K.

See Exercise 1.47 for a cryptosystem associated to this problem.

Solution to Exercise 6.50.

We do (b) ﬁrst, then illustrate the general idea by doing (a). Let αbe the d-

digit number consisting of the ﬁrst ddigits after the decimal place of √K. If

we let β=α/10d, then we can write

√K≈J+βfor some J∈Z.

202 Exercises for Chapter 6

There are two unknowns here, Kand J, and all that we know is that they

are both integers. Squaring both sides gives

K≈J2+ 2Jβ +β2.

Thus there are integers Aand Bsatisfying

β2+Aβ +B≈0,

namely A= 2Jand B=J2−K. Of course, we don’t know Aor B, so we now

describe a lattice reduction problem that ﬁnds a (quadratic) polynomial with

small integer coeﬃcients that has a given decimal number as an (approximate)

root. Once we ﬁnd Aand B, it is easy to recover Kas K=1

4A2−B.

Let Lbe the lattice generated by the rows of the matrix

M=



100 c

010 cβ

0 0 t cβ2

,

where we will choose tand clater. Notice that

¡B A 1¢



100 c

010 cβ

0 0 t cβ2

=¡B A t c(B+Aβ +β2)¢.

So if B+Aβ +β2is small, then we have found a small vector in the lattice. In

other words, if we ﬁnd a small vector in the lattice having the form (B, A, ∗),

then we have probably found the values of Aand Bthat we want. (We choose t

reasonably large to force the relation to look like (B, A, 1), instead of (B, A, C)

for some larger C.)

(b) A solution for this exercise is not currently available.

Chapter 7

Digital Signatures

Exercises for Chapter 7

Section. RSA digital signatures

7.1. Samantha uses the RSA signature scheme with primes p= 541 and

q= 1223 and public veriﬁcation exponent v= 159853.

(a) What is Samantha’s public modulus? What is her private signing key?

(b) Samantha signs the digital document D= 630579. What is the signature?

Solution to Exercise 7.1.

(a) Samantha’s public modulus is N=p·q= 541 ·1223 = 661643. Saman-

tha knows that (p−1)(q−1) = 540 ·1222 = 659880, so she can solve

vs ≡1 (mod (p−1)(q−1)),159853 ·s≡1 (mod 659880),

for the private signing key s= 561517.

(b) Samantha takes the document D= 630579 and computes

S=Ds(mod N),630579561517 ≡206484 (mod 661643).

So the signature is S= 206484.

She can check that this is correct by computing

C≡Sv(mod N), C ≡206484159853 ≡630579 (mod 661643)

and noting that this value agrees with D= 630579.

7.2. Samantha uses the RSA signature scheme with public modulus N=

1562501 and public veriﬁcation exponent v= 87953. Adam claims that

Samantha has signed each of the documents

D= 119812, D0= 161153, D00 = 586036,

203

204 Exercises for Chapter 7

and that the associated signatures are

S= 876453, S0= 870099, S00 = 602754.

Which of these are valid signatures?

Solution to Exercise 7.2.

Victor uses Samantha’s public key (N, v) = (1562501,87953) to compute:

C≡Sv(mod N), C ≡87645387953 ≡772481 (mod 1562501),

C0≡S0v(mod N), C0≡87009987953 ≡161153 (mod 1562501),

C00 ≡S00v(mod N), C00 ≡60275487953 ≡586036 (mod 1562501).

Comparing the values of C, C0, C00 with the document values D, D0, D00, we see

that S0and S00 are valid signatures, but Sis not. We remark that Samantha’s

private factorization is

N=p·q= 1301 ·1201 = 1562501

and her signing key is s= 261617.

7.3. Samantha uses the RSA signature scheme with public modulus and pub-

lic veriﬁcation exponent

N= 27212325191 and v= 22824469379.

Use whatever method you want to factor N, and then forge Samantha’s sig-

nature on the document D= 12910258780.

Solution to Exercise 7.3.

The factorization of Samantha’s public modulus is

N=p·q= 128311 ·212081 = 27212325191.

Then (p−1)(q−1) = 128310 ·212080 = 27211984800, so we can solve

vs ≡1 (mod (p−1)(q−1)),22824469379 ·s≡1 (mod 27211984800)

for Samantha’s private signing exponent s= 18408628619. We can then sign

the document D= 12910258780 by computing

S≡Ds(mod N),

1291025878018408628619 ≡22054770669 (mod 27212325191).

To check that this signature is correct, we compute

C≡Sv(mod N),

C≡2205477066922824469379 ≡12910258780 (mod 27212325191)

and note that it agrees with D= 12910258780.

Exercises for Chapter 7 205

Section. Discrete logarithm digital signatures

7.4. Samantha uses the ElGamal signature scheme with prime p= 6961 and

primitive root g= 437.

(a) Samantha’s private signing key is s= 6104. What is her public veriﬁcation

key?

(b) Samantha signs the digital document D= 5584 using the ephemeral key

e= 4451. What is the signature?

Solution to Exercise 7.4.

(a)

v≡4376104 ≡2065 (mod 6961).

(b)

S1≡4374451 ≡3534 (mod 6961),

S2≡(5584 −6104 ·3534)4451−1≡5888 (mod 6960).

So the signature on Dis (3534,5888).

7.5. Samantha uses the ElGamal signature scheme with prime p= 6961 and

primitive root g= 437. Her public veriﬁcation key is v= 4250. Adam claims

that Samantha has signed each of the documents

D= 1521, D0= 1837, D00 = 1614,

and that the associated signatures are

(S1, S2) = (4129,5575),(S0

1, S0

2) = (3145,1871),(S00

1, S00

2) = (2709,2994).

Which of these are valid signatures?

Solution to Exercise 7.5.

(a)

vS1·SS2

1≡(42504129)·41295575 ≡231 (mod 6961).

gD≡4371521 ≡231 (mod 6961).

So the signature is valid. (The ephemeral key was e= 5627.)

(b)

vS1·SS2

1≡(42503145)·31451871 ≡6208 (mod 6961).

gD≡4371837 ≡2081 (mod 6961).

So the signature is not valid.

(c)

vS1·SS2

1≡(42502709)·27092994 ≡2243 (mod 6961).

gD≡4371614 ≡2243 (mod 6961).

So the signature is valid. (The ephemeral key was e= 3997.)

(Samantha’s private signing key is s= 4804.)

206 Exercises for Chapter 7

7.6. Let pbe a prime and let iand jbe integers with gcd(j, p −1) = 1. Set

S1≡givj(mod p), S2≡ −S1j−1(mod p−1), D ≡ −S1ij−1(mod p−1).

Prove that (S1, S2) is a valid ElGamal signature on the document Dfor the

veriﬁcation key v. Thus Eve can produce signatures on random documents.

Solution to Exercise 7.6.

We compute

vS1SS2

1≡vS1(givj)−S1j−1(mod p)

≡vS1g−ij−1S1v−S1(mod p)

≡gD(mod p).

7.7. Suppose that Samantha is using the ElGamal signature scheme and that

she is careless and uses the same ephemeral key eto sign two documents D

and D0.

(a) Explain how Eve can tell at a glance whether Samantha has made this

mistake.

(b) If the signature on Dis (S1, S2) and the signature on D0is (S0

1, S0

2),

explain how Eve can recover s, Samantha’s private signing key.

tha’s signing key s, where Samantha is using the prime p= 348149,

base g= 113459, and veriﬁcation key v= 185149.

D= 153405, S1= 208913, S2= 209176,

D0= 127561, S0

1= 208913, S0

2= 217800.

Solution to Exercise 7.7.

(a) Since S1≡geand S0

1=ge0, Eve can check if the two signatures used

the same ephemeral key by checking if S1=S0

(b) Using discrete logarithms to the base g, the veriﬁcation conditions are

S1log(v) + S2log(S1)≡D(mod p−1),

1log(v) + S0

2log(S0

1)≡D0(mod p−1).

Since S1=S0

1from (a), this becomes

S1s+S2log(S1)≡D(mod p−1),

S1s+S0

2log(S1)≡D0(mod p−1),

where s= log(v) is Samantha’s secret signing key. Taking S0

2times the ﬁrst

congruence and subtracting S2times the second congruence, we obtain

S1(S0

2−S2)s≡S0

2D−S2D0(mod p−1).

Exercises for Chapter 7 207

For notational convenience we write this congruence as

As ≡B(mod p−1),

where we know the values of Aand B. If gcd(A, p −1) = 1, we can solve

uniquely for s. In general, if gcd(A, p −1) >1 (it’s unlikely to be too large),

then there are gcd(A, p −1) solutions for s, and after computing them, we can

decide which one is correct by checking which one yields gs≡v(mod p).

A≡S1(S0

2−S2)≡347960 (mod p−1),

B≡S0

2D−S2D0≡252868 (mod p−1).

We need to solve As ≡B(mod p−1), so we need to solve

347960s≡252868 (mod 348148).

This congruence has several solutions. More precisely, since gcd(347960,348148) =

4 and 4 |252868, we divide through by 4 to get

86990s≡63217 (mod 87037).

Then gcd(86990,87037) = 1, so we can solve this congruence. The solution is

s≡72729 (mod 87037).

Adding on multiples of (p−1)/4 = 87037 yields the four solutions

s≡72729,159766,246803,333840 (mod 348148)

to the original congruence. We can pick out which solution is correct from the

relation gs≡v(mod p), i.e., the correct value of sshould satisfy

113459s≡185149 (mod 348149).

We compute

11345972729 ≡185149 (mod 348149),

113459159766 ≡137653 (mod 348149),

113459246803 ≡163000 (mod 348149),

113459333840 ≡210496 (mod 348149).

Hence Samantha’s secret signing key is

s= 72729.

208 Exercises for Chapter 7

7.8. Samantha uses DSA with public parameters (p, q, g) = (22531,751,4488).

She chooses the secret signing key s= 674.

(a) What is Samantha’s public veriﬁcation key?

(b) Samantha signs the document D= 244 using the ephemeral key e= 574.

What is the signature?

Solution to Exercise 7.8.

(a) Samantha’s public veriﬁcation key is

v≡4488674 ≡4940 (mod 22531).

(b) The signature is

S1= (4488574 mod 22531) mod 751 = 444,

S2≡(244 + 674 ·444)574−1≡56 (mod 751).

7.9. Samantha uses DSA with public parameters (p, q, g) = (22531,751,4488).

Her public veriﬁcation key is v= 22476.

(a) Is (S1, S2) = (183,260) a valid signature on the document D= 329?

(b) Is (S1, S2) = (211,97) a valid signature on the document D= 432?

Solution to Exercise 7.9.

(a) Victor computes

V1≡329 ·260−1≡293 (mod 751) and V2≡183 ·260−1≡252 (mod 751).

He then computes

gV1vV2≡4488293 ·22476252 ≡6191 (mod 22531)

and veriﬁes that 6191 mod 751 = 183 is equal to S1. So the signature is valid.

(Samantha’s secret signing key happens to be s= 38.)

(b) Victor computes

V1≡432 ·97−1≡709 (mod 751) and V2≡211 ·97−1≡428 (mod 751).

He then computes

gV1vV2≡4488709 ·22476428 ≡3979 (mod 22531).

Then he observes that

(gV1vV2mod p) mod q= 3979 mod 751 = 224

is not equal to S1= 211. So the signature is not valid.

Exercises for Chapter 7 209

7.10. Samantha’s DSA public parameters are (p, q, g) = (103687,1571,21947),

and her public veriﬁcation key is v= 31377. Use whatever method you prefer

(brute-force, collision, index calculus, . . . ) to solve the DLP and ﬁnd Saman-

tha’s private signing key. Use her key to sign the document D= 510 using

the ephemeral key e= 1105.

Solution to Exercise 7.10.

Solving 31377 ≡21947s(mod 103687) gives s= 602. Then the signature

on D= 510 using the ephemeral key e= 1105 is

S1= (219471105 mod 103687) mod 1571 = 439

S2≡(510 + 602 ·439)1105−1≡1259 (mod 1571).

7.11. The Elliptic Curve Digital Signature Algorithm (ECDSA) is described

in Table 7.7. Prove that ECDSA works, i.e., prove that the veriﬁcation step

succeeds in verifying a valid signature.

Solution to Exercise 7.11.

We compute

v1G+v2V=ds−1

2G+s1s−1

2(sG)

= (d+ss1)s−1

= (es2)s−1

=eG ∈E(Fp).

Hence

x(v1G+v2V) mod q=x(eG) mod q=s1.

7.12. This exercise asks you to compute some numerical instances of the

elliptic curve digital signature algorithm described in Table 7.7 for the public

parameters

E:y2=x3+231x+473, p = 17389, q = 1321, G = (11259,11278) ∈E(Fp).

You should begin by verifying that Gis a point of order qin E(Fp).

(a) Samantha’s private signing key is s= 542. What is her public veriﬁcation

key? What is her digital signature on the document d= 644 using the

ephemeral key e= 847?

(b) Tabitha’s public veriﬁcation key is V= (11017,14637). Is (s1, s2) =

(907,296) a valid signature on the document d= 993?

that you want to ﬁnd Umberto’s private signing key, and then use the

private key to forge his signature on the document d= 516 using the

ephemeral key e= 365.

210 Exercises for Chapter 7

Public Parameter Creation

A trusted party chooses a ﬁnite ﬁeld Fp, an elliptic curve E/Fp,

and a point G∈E(Fp) of large prime order q.

Samantha Victor

Key Creation

Choose secret signing key

1<s<q−1.

Compute V=sG ∈E(Fp).

Publish the veriﬁcation key V.

Signing

Choose document dmod q.

Choose ephemeral key emod q.

Compute eG ∈E(Fp) and then,

s1=x(eG) mod qand

s2≡(d+ss1)e−1(mod q).

Publish the signature (s1, s2).

Veriﬁcation

Compute v1≡ds−1

2(mod q) and

v2≡s1s−1

2(mod q).

Compute v1G+v2V∈E(Fp) and ver-

ify that

x(v1G+v2V) mod q=s1.

Table 7.1: The elliptic curve digital signature algorithm (ECDSA)

Solution to Exercise 7.12.

(a) Samantha’s public veriﬁcation key is

V= 542(11259,11278) = (8689,1726) ∈E(Fp).

Her signature on d= 644 using e= 847 is obtained by ﬁrst computing eG =

(8417,8276) ∈E(Fp) and then

s1=x(eG) mod q= 491 and s2≡(d+ss1)e−1≡290 (mod q).

(b) Victor computes

v1≡ds−1

2≡106 (mod q) and v2≡s1s−1

2≡311 (mod q).

Then v1G+v2V= (8833,4526) ∈E(Fp), and

x(v1G+v2V) mod q= 8833 mod 1321 = 907

is equal to s1, so the signature is valid.

since

Exercises for Chapter 7 211

1294G= 1294(11259,11278) = (14594,308) ∈E(Fp).

We can then forge a signature on the document d= 516 using the ephemeral

key e= 365 by ﬁrst computing eG = (3923,12121) ∈E(Fp) and then

s1=x(eG) mod q= 1281 and s2≡(d+ss1)e−1≡236 (mod q).

To check that the signature is valid, we compute v1G+v2V= (3923,12121) ∈

E(Fp), and

x(v1G+v2V) mod q= 3923 mod 1321 = 1281,

which is equal to s1.

Section. Lattice-based digital signatures

7.13. Samantha uses the GGH digital signature scheme with private and

public bases

v1= (−20,−8,1),w1= (−248100,220074,332172),

v2= (14,11,23),w2= (−112192,99518,150209),

v3= (−18,1,−12),w3= (−216150,191737,289401).

What is her signature on the document

d= (834928,123894,7812738)?

Solution to Exercise 7.13.

Samantha uses Babai’s algorithm with the good basis to ﬁnd the vector

s= 283411v1+ 233700v2−179519v3= (834922,123893,7812739)

that is close to d,

ks−dk ≈ 6.16.

She then expresses the signature in terms of bad basis,

s= 785152901w1−1383699316w2−183004589w3

and publishes the signature (785152901,−1383699316,−183004589).

7.14. Samantha uses the GGH digital signature scheme with public basis

w1= (3712318934,−14591032252,11433651072),

w2= (−1586446650,6235427140,−4886131219),

w3= (305711854,−1201580900,941568527).

She publishes the signature

(6987814629,14496863295,−9625064603)

on the document

d= (5269775,7294466,1875937).

If the maximum allowed distance from the signature to the document is 60,

verify that Samantha’s signature is valid.

212 Exercises for Chapter 7

Solution to Exercise 7.14.

We ﬁrst compute

s= 6987814629w1+ 14496863295w2−9625064603w3

= (5269774,7294492,1875902) ∈L.

Then we compute the distance

ks−dk ≈ 43.61

and verify that it is smaller than the cutoﬀ value of 60, so the signature is

valid.

7.15. Samantha uses the GGH digital signature scheme with public basis

w1= (−1612927239,1853012542,1451467045),

w2= (−2137446623,2455606985,1923480029),

w3= (2762180674,−3173333120,−2485675809).

Use LLL or some other lattice reduction algorithm to ﬁnd a good basis for

Samantha’s lattice, and then use the good basis to help Eve forge a signature

on the document

d= (87398273893,763829184,118237397273).

What is the distance from your forged signature lattice vector to the target

vector? (You should be able to get a distance smaller than 100.)

Solution to Exercise 7.15.

Eve’s implementation of LLL gives the basis

v1= (−9,−147,−136),v2= (73,169,−41),v3= (109,−132,−110).

Using this LLL reduced basis, she computes

s=−1542740188v1−532211991v2+ 1030872363v3

= (87398273916,763829241,118237397269) ∈L.

It satisﬁes

ks−dk ≈ 61.60,

so is quite a good solution. To ﬁnd the signature, Eve expresses sin terms of

the original bad basis,

s= 203927306009123w1+ 225365519245447w2+ 293473443761381w3.

The signature is

(203927306009123,225365519245447,293473443761381).

Exercises for Chapter 7 213

Section. NTRU digital signatures

7.16. Samantha uses an NTRU digital signature with (N, q, d) = (11,23,3).

(a) Samantha’s private key is

f= (1,−1,1,0,1,0,−1,1,0,−1,0),

g= (0,−1,0,1,1,0,0,1,−1,1,−1),

F= (0,−1,−1,1,−3,−1,0,−3,−3,−2,2),

G= (−3,−1,2,4,3,−4,−1,3,5,5,−1).

She uses her private key to sign the digital document D= (D1,D2) given

D1= (0,8,−6,−6,−5,−1,9,−2,−6,−4,−6),

D2= (9,9,−10,2,−3,2,6,6,5,0,8).

Compute the signature s.

(b) Samantha’s public veriﬁcation key is

h= (5,8,−5,−11,8,8,8,5,3,−10,5).

Compute the other part of the signature t≡hs(mod q) and ﬁnd the

distance between the lattice vector (s,t) and the target vector D.

tors (1,h) and (0,q). What signature (s0,t0) does she get and how far is

it from the target vector D?

Solution to Exercise 7.16.

(a) Samantha ﬁrst computes

v1=¥¡−164

23 ,−64

23 ,32

23 ,143

23 ,146

23 ,1

23 ,−178

23 ,−1,120

23 ,108

23 ,25

23 ¢¨

= (−7,−3,1,6,6,0,−8,−1,5,5,1),

v2=¥¡27

23 ,13

23 ,0,35

23 ,−27

23 ,4

23 ,2

23 ,16

23 ,11

23 ,−24

23 ,−4

23 ¢¨

= (1,1,0,2,−1,0,0,1,0,−1,0),

and then

s= (−2,8,−4,−7,−5,−2,9,−4,−9,−4,−8).

(b)

t≡hs≡(11,9,−9,2,−4,5,4,8,4,0,11) (mod 23).

Then

k(s,t)−Dk= 7.74597.

214 Exercises for Chapter 7

s0= (0,8,−6,−6,−5,−1,9,−2,−6,−4,−6),

t0= (5,17,−3,9,3,2,14,13,2,10,1).

It satisﬁes

k(s0,t0)−Dk= 22.0227.

7.17. Samantha uses an NTRU digital signature with (N, q, d) = (11,23,3).

(a) She creates a private key using the ternary vectors

f= (1,1,1,1,0,−1,−1,0,0,0,−1),

g= (−1,0,1,1,−1,0,0,1,−1,0,1).

Use the algorithm described in Table 7.6 to ﬁnd short vectors Fand G

satisfying fG−gF=q.

(b) Samantha uses the private signing key (f,g,F,G) to sign the digital

document D= (D1,D2) given by

D1= (5,5,−5,−10,3,−7,−3,2,0,−5,−11),

D2= (8,9,−10,−7,6,−3,1,4,4,4,−7).

What the signature s?

(d) Compute t≡hs(mod q) and determine the distance from the lattice

vector (s,t) to the target vector D.

Solution to Exercise 7.17.

(a) First she computes

f1= (1363,−944,786,358,482,80,−133,368,955,126,476),

f2= (−2554,419,1205,1563,682,343,368,955,126,476,0),

g1= (−63,121,−173,−232,208,−251,96,172,620,799,574),

g2= (−1808,−121,110,290,−197,−275,53,−46,−799,−574,0).

The resultants are Rf= 3917 and Rg= 1871, and then Sf=−866 and

Sg= 1813 satisﬁes SfRf+SgRg= 1. Then we ﬁnd that

A= (2627037,−5045579,7213927,9674168,−8673392,10466449,

−4003104,−7172228,−25853380,−33317501,−23935226),

B= (−27148234,18802592,−15655548,−7130644,−9600476,−1593440,

2649094,−7329824,−19021690,−2509668,−9480968).

Next we use

Exercises for Chapter 7 215

f−1= (0.35,−0.24,0.20,0.09,0.12,0.02,−0.03,0.09,0.24,0.03,0.12),

g−1= (−0.03,0.06,−0.09,−0.12,0.11,−0.13,0.05,0.09,0.33,0.43,0.31),

to compute

C= (−2522997,−13372262,753797,−4259685,−6431876,−1572245,

−16151212,−8516655,−12881295,−9762142,−3302247).

Using this yields

F= (−1,−1,1,2,0,2,0,0,−3,−5,−5),

G= (4,−4,3,2,1,0,0,2,3,0,2).

These are reasonably short, kFk= 8.36660 and kGk= 7.93725.

(b)

v1=¥¡−2

23 ,−117

23 ,−116

23 ,−37

23 ,51

23 ,−40

23 ,7

23 ,1,−22

23 ,−2

23 ¢¨

= (0,−5,−5,−2,2,−2,0,0,1,−1,0)

v2=¥¡−4

23 ,55

23 ,1

23 ,−53

23 ,21

23 ,5

23 ,−21

23 ,−15

23 ,37

23 ,31

23 ,−22

23 ¢¨

= (0,2,0,−2,1,0,−1,−1,2,1,−1)

Then

s= (7,3,−4,−10,4,−6,−3,1,1,−5,−10).

f−1mod 23 = (−9,−10,−6,−8,−10,−5,4,0,5,−5,−1),

h= (−3,−2,2,−1,3,−5,11,−10,−2,−6,−9).

(d)

t= (9,6,−9,−7,4,−4,0,4,5,−2,−5).

k(s,t)−Dk= 8.48528.

7.18. Let a∈RNbe a ﬁxed vector.

(a) Suppose that bis an N-dimensional vector whose coeﬃcients are chosen

randomly from the set {−1,0,1}. Prove that the expected values of kbk2

and kabk2are given by

E¡kbk2¢=2

3Nand E¡kabk2¢=kak2E¡kbk2¢.

(b) More generally, suppose that the coeﬃcients of bare chosen at random

from the set of integers {−T, −T+1, . . . , T −1, T }. Compute the expected

values of kbk2and kabk2as in (a).

216 Exercises for Chapter 7

uniformly and independently in the interval from −Rto R. Prove that

E¡kbk2¢=R2N

3and E¡kabk2¢=kak2E¡kbk2¢.

(Hint. The most direct way to do (c) is to use continuous probability

theory. As an alternative, let the coeﬃcients of bbe chosen uniformly and

independently from the set {jR/T :−T≤j≤T}, redo the computation

from (b), and then let T→ ∞.)

Solution to Exercise 7.18.

Let c=ab. Then

kck2=X

kmod N

kmod NµX

i+j≡k(mod N)

aibj¶2

kmod NX

i+j≡k(mod N)

aibjX

u+v≡k(mod N)

aubv

i+j≡u+v(mod N)

aiaubjbv.

Note that this last sum is over all 4-tuples (i, j, u, v) mod Nsatisfying i+j≡

u+v(mod N). We suppose now that the coeﬃcients of bare independent

random variables whose average value is 0, i.e., we assume that E(bi) = 0.

This is a valid assumption in (a), (b), and (c). Since the coeﬃcients of aare

ﬁxed, we can compute

E¡kabk2¢=X

i+j≡u+v(mod N)

E(aiaubjbv)

i+j≡u+v(mod N)

aiauE(bjbv)

i+j≡u+v(mod N)

j6=v

aiauE(bj)E(bv) + X

imod NX

jmod N

iE(b2

imod N

jmod N

E(b2

=kak2E(b2

0+··· +b2

N−1)

=kak2E¡kbk2¢.

Hence in all cases we have

E¡kabk2¢=kak2E¡kbk2¢.

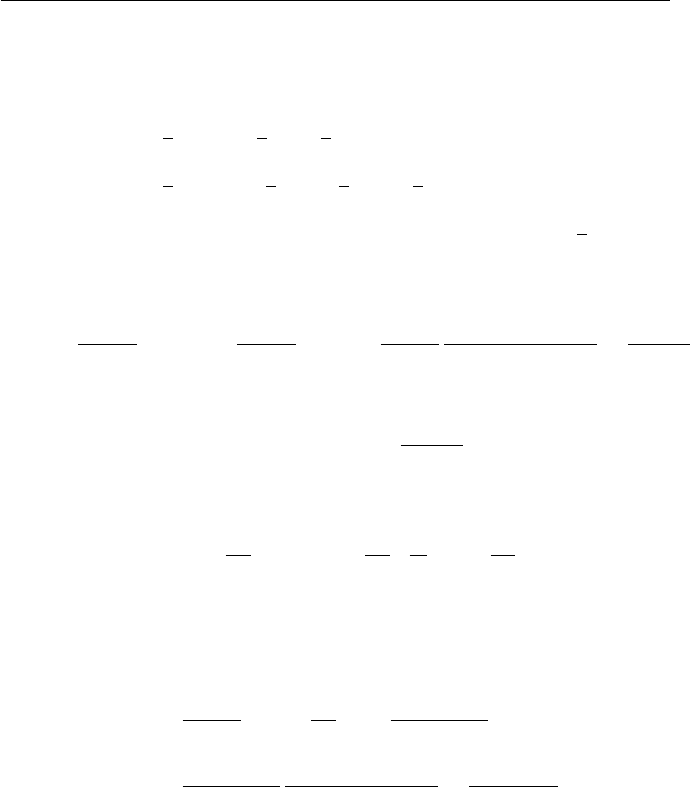
Exercises for Chapter 7 217

It remains to compute E¡kbk2¢under the various scenarios.

(a) The coeﬃcients of bare independent random variables taking values

in {−1,0,1}with equal probabilities, so

E(bi) = 1

3·(−1) + 1

3·0 + 1

3·1 = 0,

E(b2

i) = 1

3·(−1)2+1

3·02+1

3·12=2

E¡kbk2¢=E(b2

0+··· +b2

N−1) = E(b2

0) + ··· +E(b2

N−1) = 2

3N.

(b) Similar to (a), but now the values are integers between −Tand T. So

E(b2

i) = 1

2T+ 1

j=−T

j2=2

2T+ 1

j=1

j2=2

2T+ 1

T(T+ 1)(2T+ 1)

6=T2+T

Hence

E¡kbk2¢=

N−1

i=0

E(b2

j) = T2+T

3N.

E(b2

i) = 1

2RZR

−R

b2db =1

2R·b3

3¯¯R

−R=R2

Hence E¡kbk2¢=R2N/3.

The alternative computation using the hint gives, for any particular value

of T,

E(b2

i) = 1

2T+ 1

j=−TµjR

T¶2

=2R2

(2T+ 1)T2

j=1

=2R2

(2T+ 1)T2

T(T+ 1)(2T+ 1)

6=R2(T+ 1)

3T.

Letting T→ ∞ yields E(b2

i) = R2/3, and then

E¡kbk2¢=NR2/3.

7.19. Let (f,g,F,G) be an NTRU digital signature private key and let

h≡f−1g(mod q)

be the associated public key. Suppose that (s,t) is the signature on the doc-

ument D= (D1,D2), so in particular, the vector (s,t) is in the NTRU lat-

tice LNTRU

218 Exercises for Chapter 7

(a) Prove that for every vector w∈ZN, the vector

(s+wf,t+wg)

is in the NTRU lattice LNTRU

(b) Let f−1be the inverse of fin the ring R[x]/(xN−1) (cf. Table 7.6). Prove

that the vector

s0=s+b−f−1D1ef

is a signature on a document of the form D0= (0,D2+D3) for some D3

that depends on D1.

able to sign documents of the form (D1,D2). Hence in the NTRU digital

signature scheme (Table 7.5), we might as well assume that the document

being signed is of the form (0,D2). This has several beneﬁts, including

speeding the computation of v1and v2.

Solution to Exercise 7.19.

(a) The NTRU lattice is characterized as the set of vectors

LNTRU

We are given that (s,t)∈LNTRU

h, so

(s+wf)h≡sh+wfh≡t+wg(mod q),

where we have used the fact that h≡f−1g(mod q).

(b) For notational convenience, we let w=b−f−1D1e. Then

wf=−D1+²f,

where the coeﬃcients of ²are between −1

2and 1

2. Hence

s0=s+wf=s−D1+²f.

We know that ks−D1kis small, so we ﬁnd that

ks0k ≤ ks−D1k+k²fk ≈ ks−D1k+k²kkfk

is also small.

Next we compute

t0≡s0h≡sh+wfh≡t+wg(mod q).

Since tis close to D2, we ﬁnd that t0is close to D2+D3, where

D3=wg=b−f−1D1eg.

that she wants to sign (D1,D2). She starts by ﬁnding a signature s0to the

document

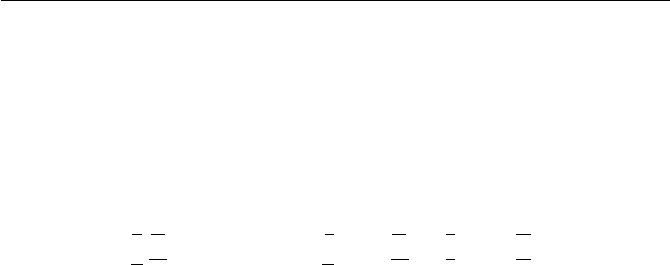
Exercises for Chapter 7 219

¡0,D2+b−f−1D1eg¢.

Then from the calculations in (b), she sees that

s=s0− b−f−1D1eg

is a signature on (D1,D2).

7.20. Verify the identity

µf F

g G¶µf g

F G¶=µff+FF g f+GF

fg+FG g f+GF¶,

where bar indicates reversal of a vector as in Remark 7.13. Prove that the

corresponding 2N-by-2Nmatrix is the Gram matrix associated to the 2N-by-

2Nmatrix ¡f g

F G ¢. (See Exercise 6.14 for the deﬁnition of the Gram matrix.)

Chapter 8

Additional Topics in

Cryptography

221

http://www.springer.com/978-0-387-77993-5

Solutions Manual

Navigation menu

Versions of this User Manual:

Views

Navigation