TMVA Users Guide TMVAUsers
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 158 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introduction
- TMVA Quick Start
- Using TMVA
- The TMVA Factory
- Specifying training and test data
- Negative event weights
- Defining input variables, spectators and targets
- Preparing the training and test data
- Booking MVA methods
- Help option for MVA booking
- Training the MVA methods
- Testing the MVA methods
- Evaluating the MVA methods
- Classification performance evaluation
- Regression performance evaluation
- Overtraining
- Other representations of MVA outputs for classification: probabilities and probability integral transformation (Rarity)
- ROOT macros to plot training, testing and evaluation results
- The TMVA Reader
- An alternative to the Reader: standalone C++ response classes
- The TMVA Factory
- Data Preprocessing
- Probability Density Functions – the PDF Class
- Optimisation and Fitting
- Boosting and Bagging
- The TMVA Methods
- Rectangular cut optimisation
- Projective likelihood estimator (PDE approach)
- Multidimensional likelihood estimator (PDE range-search approach)
- Likelihood estimator using self-adapting phase-space binning (PDE-Foam)
- k-Nearest Neighbour (k-NN) Classifier
- H-Matrix discriminant
- Fisher discriminants (linear discriminant analysis)
- Linear discriminant analysis (LD)
- Function discriminant analysis (FDA)
- Artificial Neural Networks (nonlinear discriminant analysis)
- Deep Neural Networks
- Support Vector Machine (SVM)
- Boosted Decision and Regression Trees
- Predictive learning via rule ensembles (RuleFit)
- The PyMVA Methods
- Combining MVA Methods
- Which MVA method should I use for my problem?
- TMVA implementation status summary for classification and regression
- Conclusions and Plans
- Acknowledgements
- More Classifier Booking Examples
- Bibliography
- Index
arXiv:physics/0703039 [Data Analysis, Statistics and Probability]
CERN-OPEN-2007-007
TMVA version 4.2.0
March 3, 2017
http:// tmva.sourceforge.net
TMVA 4
Toolkit for Multivariate Data Analysis with ROOT
Users Guide
A. Hoecker, P. Speckmayer, J. Stelzer, J. Therhaag, E. von Toerne, H. Voss
Contributed to TMVA have:
M. Backes, T. Carli, O. Cohen, A. Christov, D. Dannheim, K. Danielowski,
S. Henrot-Versill ´
e, M. Jachowski, K. Kraszewski, A. Krasznahorkay Jr.,
M. Kruk, Y. Mahalalel, R. Ospanov, X. Prudent, A. Robert, C. Rosemann,
D. Schouten, F. Tegenfeldt, A. Voigt, K. Voss, M. Wolter, A. Zemla, J. Zhong, A. Moudgil

Abstract — In high-energy physics, with the search for ever smaller signals in ever larger data sets, it has
become essential to extract a maximum of the available information from the data. Multivariate classification
methods based on machine learning techniques have become a fundamental ingredient to most analyses.
Also the multivariate classifiers themselves have significantly evolved in recent years. Statisticians have
found new ways to tune and to combine classifiers to further gain in performance. Integrated into the anal-
ysis framework ROOT, TMVA is a toolkit which hosts a large variety of multivariate classification algorithms.
Training, testing, performance evaluation and application of all available classifiers is carried out simulta-
neously via user-friendly interfaces. With version 4, TMVA has been extended to multivariate regression
of a real-valued target vector. Regression is invoked through the same user interfaces as classification.
TMVA 4 also features more flexible data handling allowing one to arbitrarily form combined MVA methods.
A generalised boosting method is the first realisation benefiting from the new framework.
TMVA 4.2.0 – Toolkit for Multivariate Data Analysis with ROOT
Copyright c
2005-2009, Regents of CERN (Switzerland), DESY (Germany), MPI-Kernphysik Heidelberg
(Germany), University of Bonn (Germany), and University of Victoria (Canada).
BSD license: http://tmva.sourceforge.net/LICENSE.
Authors:
Andreas Hoecker (CERN, Switzerland) handreas.hoecker@cern.chi,
Peter Speckmayer (CERN, Switzerland) hpeter.speckmayer@cern.chi,
J¨
org Stelzer (CERN, Switzerland) hjoerg.stelzer@cern.chi,
Jan Therhaag (Universit ¨
at Bonn, Germany) htherhaag@physik.uni-bonn.dei,
Eckhard von Toerne (Universit¨
at Bonn, Germany) hevt@physik.uni-bonn.dei,
Helge Voss (MPI f¨
ur Kernphysik Heidelberg, Germany) hhelge.voss@cern.chi,
Moritz Backes,Tancredi Carli,Or Cohen,Asen Christov,Krzysztof Danielowski,Dominik Dannheim,Sophie
Henrot-Versill´
e,Matthew Jachowski,Kamil Kraszewski,Attila Krasznahorkay Jr.,Maciej Kruk,Yair
Mahalale,Rustem Ospanov,Xavier Prudent,Doug Schouten,Fredrik Tegenfeldt,Arnaud Robert,Christoph
Rosemann,Alexander Voigt,Kai Voss,Marcin Wolter,Andrzej Zemla,Jiahang Zhong,Abhinav Moudgil and
valuable contributions from many users, please see acknowledgements.

CONTENTS i
Contents
1 Introduction 1
Copyrights and credits ............... 3
2 TMVA Quick Start 4
2.1 How to download and build TMVA ...... 4
2.2 Version compatibility ............. 5
2.3 Avoiding conflicts between external TMVA
and ROOT’s internal one ........... 5
2.4 The TMVA namespace ............ 5
2.5 Example jobs ................. 5
2.6 Running the example ............. 6
2.7 Displaying the results ............. 7
2.8 Getting help .................. 9
3 Using TMVA 11
3.1 The TMVA Factory .............. 13
3.1.1 Specifying training and test data . . . 13
3.1.2 Negative event weights ........ 18
3.1.3 Defining input variables, spectators
and targets .............. 18
3.1.4 Preparing the training and test data .20
3.1.5 Booking MVA methods ........ 23
3.1.6 Help option for MVA booking . . . . 23
3.1.7 Training the MVA methods ...... 23
3.1.8 Testing the MVA methods ...... 24
3.1.9 Evaluating the MVA methods ..... 24
3.1.10 Classification performance evaluation 25
3.1.11 Regression performance evaluation .26
3.1.12 Overtraining .............. 28
3.1.13 Other representations of MVA outputs
for classification: probabilities and prob-
ability integral transformation (Rarity)29
3.2 ROOT macros to plot training, testing and
evaluation results ............... 30
3.3 The TMVA Reader .............. 31
3.3.1 Specifying input variables ...... 33
3.3.2 Booking MVA methods ........ 33
3.3.3 Requesting the MVA response . . . . 34
3.4 An alternative to the Reader: standalone C++
response classes ............... 36
4 Data Preprocessing 38
4.1 Transforming input variables ......... 38
4.1.1 Variable normalisation ........ 39
4.1.2 Variable decorrelation ........ 40
4.1.3 Principal component decomposition .40
4.1.4 Uniform and Gaussian transformation
of variables (“Uniformisation” and “Gaus-
sianisation”) .............. 41
4.1.5 Booking and chaining transformations
for some or all input variables . . . . 42
4.2 Variable selection based on variance . . . . 43
4.3 Binary search trees .............. 44
5 Probability Density Functions – the PDF Class 44
5.1 Nonparametric PDF fitting using spline func-
tions ...................... 45
5.2 Nonparametric PDF parameterisation using
kernel density estimators .......... 47
6 Optimisation and Fitting 49
6.1 Monte Carlo sampling ............ 49
6.2 Minuit minimisation .............. 50
6.3 Genetic Algorithm ............... 50
6.4 Simulated Annealing ............. 53
6.5 Combined fitters ................ 54
7 Boosting and Bagging 55
7.1 Adaptive Boost (AdaBoost) .......... 56
7.2 Gradient Boost ................ 57
7.3 Bagging .................... 58
8 The TMVA Methods 60
8.1 Rectangular cut optimisation ......... 60
8.1.1 Booking options ............ 62
8.1.2 Description and implementation . . . 63
8.1.3 Variable ranking ............ 64
8.1.4 Performance .............. 64
8.2 Projective likelihood estimator (PDE approach) 65
8.2.1 Booking options ............ 65
8.2.2 Description and implementation . . . 65
8.2.3 Variable ranking ............ 66
8.2.4 Performance .............. 67
8.3 Multidimensional likelihood estimator (PDE
range-search approach) ........... 67
8.3.1 Booking options ............ 68
8.3.2 Description and implementation . . . 68
8.3.3 Variable ranking ............ 71
8.3.4 Performance .............. 72

ii Contents
8.4 Likelihood estimator using self-adapting phase-
space binning (PDE-Foam) .......... 72
8.4.1 Booking options ............ 72
8.4.2 Description and implementation of the
foam algorithm ............ 73
8.4.3 Classification ............. 78
8.4.4 Regression .............. 80
8.4.5 Visualisation of the foam via projec-
tions to 2 dimensions ......... 82
8.4.6 Variable ranking ............ 83
8.4.7 Performance .............. 83
8.5 k-Nearest Neighbour (k-NN) Classifier . . . 83
8.5.1 Booking options ............ 83
8.5.2 Description and implementation . . . 84
8.5.3 Ranking ................ 86
8.5.4 Performance .............. 86
8.6 H-Matrix discriminant ............. 87
8.6.1 Booking options ............ 87
8.6.2 Description and implementation . . . 87
8.6.3 Variable ranking ............ 88
8.6.4 Performance .............. 88
8.7 Fisher discriminants (linear discriminant anal-
ysis) ...................... 88
8.7.1 Booking options ............ 88
8.7.2 Description and implementation . . . 89
8.7.3 Variable ranking ............ 90
8.7.4 Performance .............. 90
8.8 Linear discriminant analysis (LD) ...... 90
8.8.1 Booking options ............ 90
8.8.2 Description and implementation . . . 91
8.8.3 Variable ranking ............ 92
8.8.4 Regression with LD .......... 92
8.8.5 Performance .............. 92
8.9 Function discriminant analysis (FDA) . . . . 92
8.9.1 Booking options ............ 93
8.9.2 Description and implementation . . . 94
8.9.3 Variable ranking ............ 94
8.9.4 Performance .............. 94
8.10 Artificial Neural Networks (nonlinear discrim-
inant analysis) ................. 95
8.10.1 Description and implementation . . . 99
8.10.2 Network architecture ......... 101
8.10.3 Training of the neural network . . . . 101
8.10.4 Variable ranking ............ 104
8.10.5 Bayesian extension of the MLP . . . 104
8.10.6 Performance .............. 104
8.11 Deep Neural Networks ............ 105
8.11.1 Building the CPU and GPU Backends 105
8.11.2 Training of Deep Neural Networks . . 105
8.11.3 Test and Evaluation Set ....... 106
8.11.4 Booking of the DNN Method ..... 106
8.11.5 Network Layout ............ 107
8.11.6 Training Strategy ........... 108
8.12 Support Vector Machine (SVM) ....... 110
8.12.1 Booking options ............ 110
8.12.2 Description and implementation . . . 110
8.12.3 Variable ranking ............ 114
8.12.4 Performance .............. 114
8.13 Boosted Decision and Regression Trees . . 114
8.13.1 Booking options ............ 115
8.13.2 Description and implementation . . . 119
8.13.3 Boosting, Bagging and Randomising 119
8.13.4 Variable ranking ............ 121
8.13.5 Performance .............. 121
8.14 Predictive learning via rule ensembles (Rule-
Fit) ....................... 122
8.14.1 Booking options ............ 123
8.14.2 Description and implementation . . . 123
8.14.3 Variable ranking ............ 126
8.14.4 Friedman’s module .......... 127
8.14.5 Performance .............. 128
9 The PyMVA Methods 129
9.1 Keras ..................... 129
9.1.1 Training and Testing Data ...... 129
9.1.2 Booking Options ........... 129
9.1.3 Model Definition ............ 130
9.1.4 Variable Ranking ........... 131
10 Combining MVA Methods 131
10.1 Boosted classifiers .............. 132
10.1.1 Booking options ............ 132
10.1.2 Boostable classifiers ......... 134
10.1.3 Monitoring tools ............ 134
10.1.4 Variable ranking ............ 135
10.2 Category Classifier .............. 135

CONTENTS iii
10.2.1 Booking options ............ 136
10.2.2 Description and implementation . . . 137
10.2.3 Variable ranking ............ 138
10.2.4 Performance .............. 138
11 Which MVA method should I use for my prob-
lem? 138
12 TMVA implementation status summary for clas-
sification and regression 141
13 Conclusions and Plans 144
Acknowledgements 146
A More Classifier Booking Examples 148
Bibliography 151
Index 153

1
1 Introduction
The Toolkit for Multivariate Analysis (TMVA) provides a ROOT-integrated [1] environment for
the processing, parallel evaluation and application of multivariate classification and – since TMVA
version 4 – multivariate regression techniques.1All multivariate techniques in TMVA belong to
the family of “supervised learnning” algorithms. They make use of training events, for which
the desired output is known, to determine the mapping function that either discribes a decision
boundary (classification) or an approximation of the underlying functional behaviour defining the
target value (regression). The mapping function can contain various degrees of approximations and
may be a single global function, or a set of local models. TMVA is specifically designed for the
needs of high-energy physics (HEP) applications, but should not be restricted to these. The package
includes:
•Rectangular cut optimisation (binary splits, Sec. 8.1).
•Projective likelihood estimation (Sec. 8.2).
•Multi-dimensional likelihood estimation (PDE range-search – Sec. 8.3, PDE-Foam – Sec. 8.4,
and k-NN – Sec. 8.5).
•Linear and nonlinear discriminant analysis (H-Matrix – Sec. 8.6, Fisher – Sec. 8.7, LD –
Sec. 8.8, FDA – Sec. 8.9).
•Artificial neural networks (three different multilayer perceptron implementations – Sec. 8.10).
•Support vector machine (Sec. 8.12).
•Boosted/bagged decision trees (Sec. 8.13).
•Predictive learning via rule ensembles (RuleFit, Sec. 8.14).
•A generic boost classifier allowing one to boost any of the above classifiers (Sec. 10).
•A generic category classifier allowing one to split the training data into disjoint categories
with independent MVAs.
The software package consists of abstract, object-oriented implementations in C++/ROOT for
each of these multivariate analysis (MVA) techniques, as well as auxiliary tools such as parameter
fitting and transformations. It provides training, testing and performance evaluation algorithms
1A classification problem corresponds in more general terms to a discretised regression problem. A regression is the
process that estimates the parameter values of a function, which predicts the value of a response variable (or vector)
in terms of the values of other variables (the input variables). A typical regression problem in High-Energy Physics
is for example the estimation of the energy of a (hadronic) calorimeter cluster from the cluster’s electromagnetic
cell energies. The user provides a single dataset that contains the input variables and one or more target variables.
The interface to defining the input and target variables, the booking of the multivariate methods, their training and
testing is very similar to the syntax in classification problems. Communication between the user and TMVA proceeds
conveniently via the Factory and Reader classes. Due to their similarity, classification and regression are introduced
together in this Users Guide. Where necessary, differences are pointed out.

2 1 Introduction
and visualisation scripts. Detailed descriptions of all the TMVA methods and their options for
classification and (where available) regression tasks are given in Sec. 8. Their training and testing
is performed with the use of user-supplied data sets in form of ROOT trees or text files, where
each event can have an individual weight. The true sample composition (for event classification)
or target value (for regression) in these data sets must be supplied for each event. Preselection
requirements and transformations can be applied to input data. TMVA supports the use of variable
combinations and formulas with a functionality similar to the one available for the Draw command
of a ROOT tree.
TMVA works in transparent factory mode to provide an objective performance comparison between
the MVA methods: all methods see the same training and test data, and are evaluated following
the same prescriptions within the same execution job. A Factory class organises the interaction
between the user and the TMVA analysis steps. It performs preanalysis and preprocessing of
the training data to assess basic properties of the discriminating variables used as inputs to the
classifiers. The linear correlation coefficients of the input variables are calculated and displayed.
For regression, also nonlinear correlation measures are given, such as the correlation ratio and mutual
information between input variables and output target. A preliminary ranking is derived, which is
later superseded by algorithm-specific variable rankings. For classification problems, the variables
can be linearly transformed (individually for each MVA method) into a non-correlated variable
space, projected upon their principle components, or transformed into a normalised Gaussian shape.
Transformations can also be arbitrarily concatenated.
To compare the signal-efficiency and background-rejection performance of the classifiers, or the
average variance between regression target and estimation, the analysis job prints – among other
criteria – tabulated results for some benchmark values (see Sec. 3.1.9). Moreover, a variety of
graphical evaluation information acquired during the training, testing and evaluation phases is
stored in a ROOT output file. These results can be displayed using macros, which are conveniently
executed via graphical user interfaces (each one for classification and regression) that come with
the TMVA distribution (see Sec. 3.2).
The TMVA training job runs alternatively as a ROOT script, as a standalone executable, or as
a python script via the PyROOT interface. Each MVA method trained in one of these applica-
tions writes its configuration and training results in a result (“weight”) file, which in the default
configuration has human readable XML format.
A light-weight Reader class is provided, which reads and interprets the weight files (interfaced by
the corresponding method), and which can be included in any C++ executable, ROOT macro, or
python analysis job (see Sec. 3.3).
For standalone use of the trained MVA method, TMVA also generates lightweight C++ response
classes (not available for all methods), which contain the encoded information from the weight files
so that these are not required anymore. These classes do not depend on TMVA or ROOT, neither
on any other external library (see Sec. 3.4).
We have put emphasis on the clarity and functionality of the Factory and Reader interfaces to the
user applications, which will hardly exceed a few lines of code. All MVA methods run with reasonable
default configurations and should have satisfying performance for average applications. We stress

3
however that, to solve a concrete problem, all methods require at least some specific tuning to deploy
their maximum classification or regression capabilities. Individual optimisation and customisation
of the classifiers is achieved via configuration strings when booking a method.
This manual introduces the TMVA Factory and Reader interfaces, and describes design and imple-
mentation of the MVA methods. It is not the aim here to provide a general introduction to MVA
techniques. Other excellent reviews exist on this subject (see, e.g., Refs. [2–4]). The document
begins with a quick TMVA start reference in Sec. 2, and provides a more complete introduction
to the TMVA design and its functionality for both, classification and regression analyses in Sec. 3.
Data preprocessing such as the transformation of input variables and event sorting are discussed in
Sec. 4. In Sec. 5, we describe the techniques used to estimate probability density functions from the
training data. Section 6introduces optimisation and fitting tools commonly used by the methods.
All the TMVA methods including their configurations and tuning options are described in Secs. 8.1–
8.14. Guidance on which MVA method to use for varying problems and input conditions is given
in Sec. 11. An overall summary of the implementation status of all TMVA methods is provided in
Sec. 12.
Copyrights and credits
TMVA is an open source product. Redistribution and use of TMVA in source and binary forms, with or with-
out modification, are permitted according to the terms listed in the BSD license.2Several similar combined
multivariate analysis (“machine learning”) packages exist with rising importance in most fields of science
and industry. In the HEP community the package StatPatternRecognition [5,6] is in use (for classification
problems only). The idea of parallel training and evaluation of MVA-based classification in HEP has been
pioneered by the Cornelius package, developed by the Tagging Group of the BABAR Collaboration [7]. See
further credits and acknowledgments on page 146.
2For the BSD l icense, see http://tmva.sourceforge.net/LICENSE.
4 2 TMVA Quick Start
2 TMVA Quick Start
To run TMVA it is not necessary to know much about its concepts or to understand the detailed
functionality of the multivariate methods. Better, just begin with the quick start tutorial given
below.
Classification and regression analyses in TMVA have similar training, testing and evaluation phases,
and will be treated in parallel in the following.
2.1 How to download and build TMVA
TMVA is built upon ROOT (http://root.cern.ch/), so that for TMVA to run ROOT must be installed.
Since ROOT version 5.11/06, TMVA comes as integral part of ROOT and can be used from the
ROOT prompt without further preparation. For older ROOT versions or if the latest TMVA
features are desired, the TMVA source code can either be downloaded as a gzipped tarfile from
Sourceforge.net .Since we do not provide prebuilt libraries for any platform, the library must be
built by the user (easy – see below). While the source code is known to compile with VisualC++ on
Windows (which is a requirement for ROOT), we do not provide project support for this platform
yet. For Unix and most Linux flavours custom Makefiles are provided with the TMVA distribution,
so that the library can be built by typing:
~> cd tmva
~/tmva> make
~/tmva> cd test
~/tmva/test> source setup.sh # for c-shell family: source setup.csh
Code Example 1: Building the TMVA library under Linux/Unix using the provided Makefile. The setup.
[c]sh script must be executed to ensure the correct setting of symbolic links and library paths required by
TMVA.
After compilation, the library tmva/lib/libTMVA.1.so should be present.
If you run TMVA in a working directory other than ∼/tmva/test, then you simply need to copy
the setup.[c]sh file into your work directory and “source” it while giving it as an argument the
TMVA installation directory:
2.2 Version compatibility 5
~> cd MyWorkDir
~/MyWorkDir> cp ~/tmva/test/setup.[c]sh .
~/MyWorkDir> source setup.[c]sh <Your TMVA installation path>
Code Example 2: Using the built TMVA library under Linux/Unix from an arbritrary work directory.
The setup.[c]shhpathToYourTMVAInstallationiscript must be executed to ensure the correct setting of
symbolic links and library paths required by TMVA.
2.2 Version compatibility
TMVA can be run with any ROOT version equal or above v5.08. The few occurring conflicts due to
ROOT source code evolution after v5.08 are intercepted in TMVA via C++ preprocessor conditions.
2.3 Avoiding conflicts between external TMVA and ROOT’s internal one
A ROOT installation typcially comes a TMVA version already. To use a more recent version of
TMVA than the one present in the local ROOT installation, one needs to download the desired
TMVA release as described above, compile it against the local ROOT version and make sure the
newly built library tmva/lib/libTMVA.1.so is used instead of ROOT’s internal one. While execut-
ing the setup.[c]sh script is usually sufficient to ensure the latter, on MAC OSX systems it may
be neccessary to load the library exlicitly when running TMVA in CINT: gSystem->Load("tmva/
lib/libTMVA.1"). This can be done directly in the macro or in a file that is automatically loaded
at the start of CINT (for an example, see the files .rootrc and TMVAlogon.C in the tmva/test/
directory). When running TMVA in an executable, the corresponding shared library needs to be
linked. Once this is done, ROOT’s own libTMVA.so library will not be invoked anymore.
2.4 The TMVA namespace
All TMVA classes are embedded in the namespace TMVA. For interactive access, or use in macros
the classes must thus be preceded by TMVA::, or one may use the command using namespace TMVA
instead.
2.5 Example jobs
TMVA comes with example jobs for the training phase (this phase actually includes training,
testing and evaluation) using the TMVA Factory, as well as the application of the training re-
sults in a classification or regression analysis using the TMVA Reader. The training examples are
TMVAClassification,TMVAMulticlass.C and TMVARegression, and the application examples are
TMVAClassificationApplication,TMVAMulticlassApplication.C and TMVARegressionApplication.

6 2 TMVA Quick Start
The above macros (extension .C) are located in the directory tmva/test/.
All examples are also provided in form of C++ executables (replace .C by .cxx). To build the exe-
cutables, go to tmva/test/, type make and then simply execute them by typing ./TMVAClassification,
./TMVAMulticlass or ./TMVARegression (and similarly for the applications). To illustrate how
TMVA can be used in a python script via PyROOT we also provide the script TMVAClassification.
py located in TMVA/python/, which has the same functionality as the macro TMVAClassification.C
(the other macros are not provided as python scripts).
2.6 Running the example
The most straightforward way to get started with TMVA is to simply run the TMVAClassification.
Cor TMVARegression.C example macros. Both use academic toy datasets for training and testing,
which, for classification, consists of four linearly correlated, Gaussian distributed discriminating
input variables, with different sample means for signal and background, and, for regression, has
two input variables with fuzzy parabolic dependence on the target (fvalue), and no correlations
among themselves. All classifiers are trained, tested and evaluated using the toy datasets in the
same way the user is expected to proceed for his or her own data. It is a valuable exercise to look at
the example file in more detail. Most of the command lines therein should be self explaining, and
one will easily find how they need to be customized to apply TMVA to a real use case. A detailed
description is given in Sec. 3.
The macros automatically fetch the data file from the web using the corresponding TFile construc-
tor, e.g., TFile::Open("http://root.cern.ch/files/tmva class example.root") (tmva reg
example.root for regression). The example ROOT macros can be run directly in the tmva/test/
directory, or in any designated test directory workdir, after adding the macro directory to ROOT’s
macro search path:
~/workdir> echo "Unix.*.Root.MacroPath: $ROOTSYS/tmva/test" >> .rootrc
~/workdir> root -l $ROOTSYS/tmva/test/TMVAClassification.C
Code Example 3: Running the example TMVAClassification.C.
It is also possible to explicitly select the MVA methods to be processed:
~/workdir> root -l $ROOTSYS/tmva/test/TMVAClassification.C\(\"Fisher\"\)
Code Example 4: Running the example TMVAClassification.C and processing only the Fisher classifier.
Note that the backslashes are mandatory. Multiple classifiers are separated by commas. The others macros
can be called accordingly.
where the names of the MVA methods are predifined in the macro.

2.7 Displaying the results 7
The training job provides formatted output logging containing analysis information such as: lin-
ear correlation matrices for the input variables, correlation ratios and mutual information (see
below) between input variables and regression targets, variable ranking, summaries of the MVA
configurations, goodness-of-fit evaluation for PDFs (if requested), signal and background (or regres-
sion target) correlations between the various MVA methods, decision overlaps, signal efficiencies at
benchmark background rejection rates (classification) or deviations from target (regression), as well
as other performance estimators. Comparison between the results for training and independent test
samples provides overtraining validation.
2.7 Displaying the results
Besides so-called “weight” files containing the method-specific training results, TMVA also provides
a variety of control and performance plots that can be displayed via a set of ROOT macros available
in $ROOTSYS/tmva/test/. The macros are summarized in Tables 2and 4on page 32. At the end
of the example jobs a graphical user interface (GUI) is displayed, which conveniently allows to run
these macros (see Fig. 1).
Examples for plots produced by these macros are given in Figs. 3–5for a classification problem.
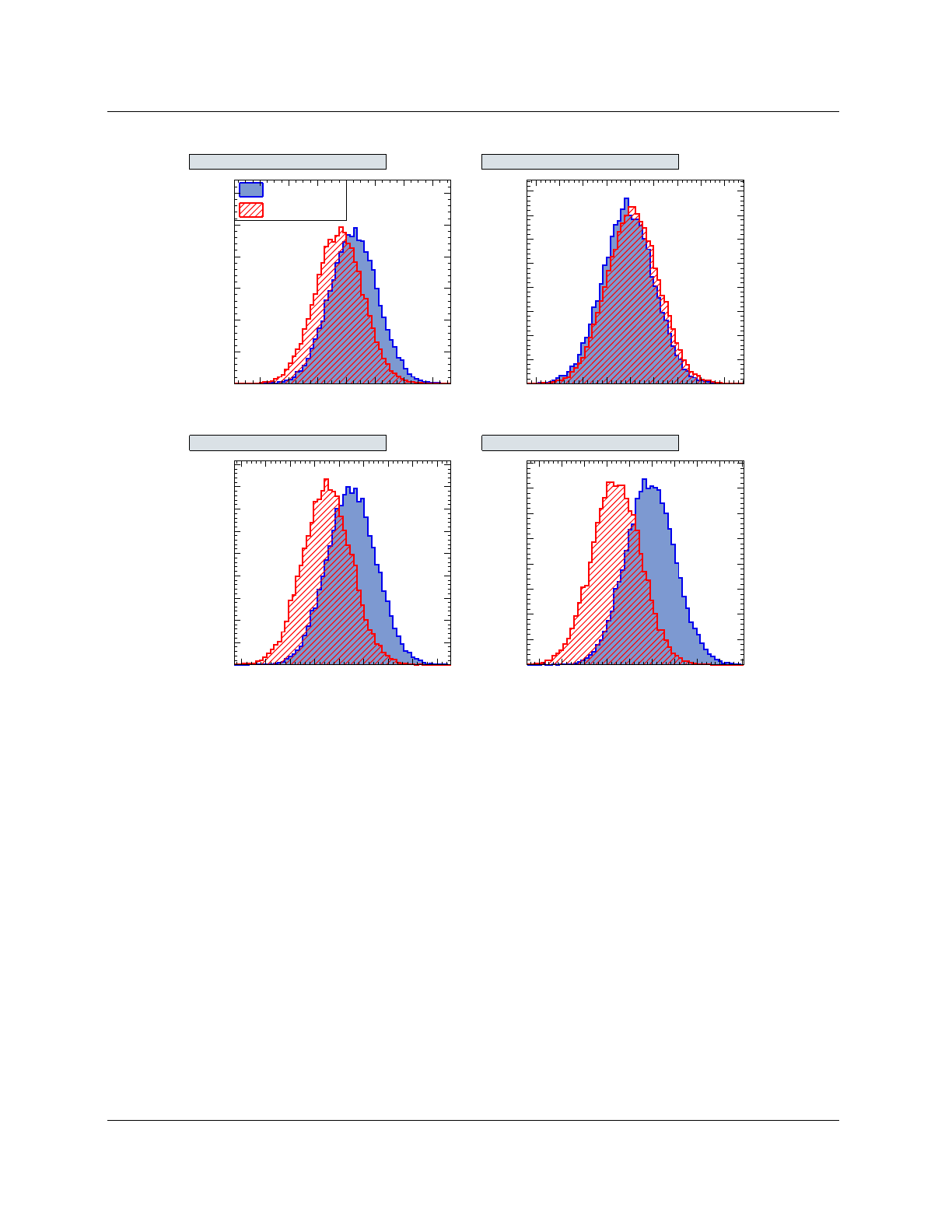
The distributions of the input variables for signal and background according to our example job
are shown in Fig. 2. It is useful to quantify the correlations between the input variables. These
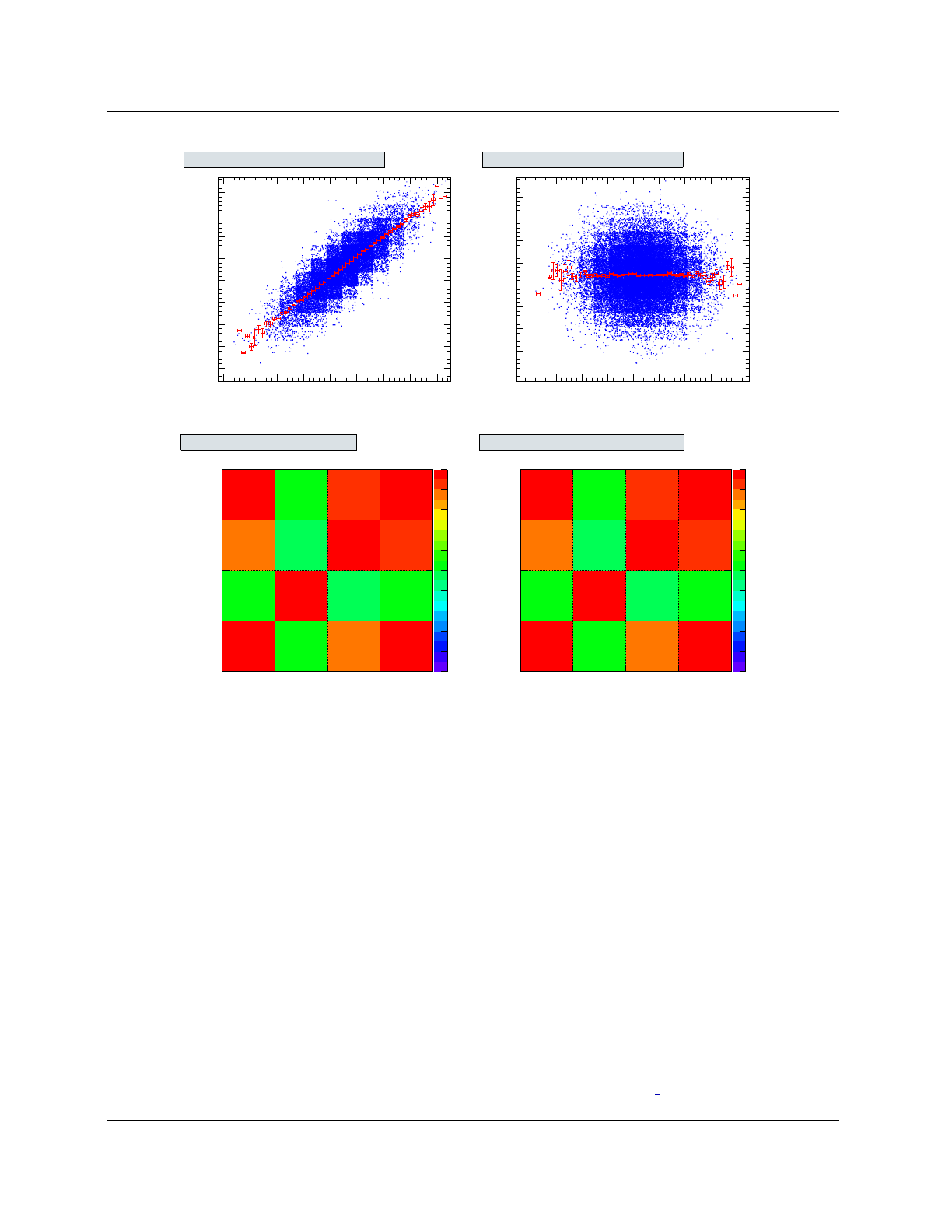
are drawn in form of a scatter plot with the superimposed profile for two of the input variables in
Fig. 3(upper left). As will be discussed in Sec. 4, TMVA allows to perform a linear decorrelation
transformation of the input variables prior to the MVA training (for classification only). The result
of such decorrelation is shown at the upper right hand plot of Fig. 3. The lower plots display the
linear correlation coefficients between all input variables, for the signal and background training
samples of the classification example.
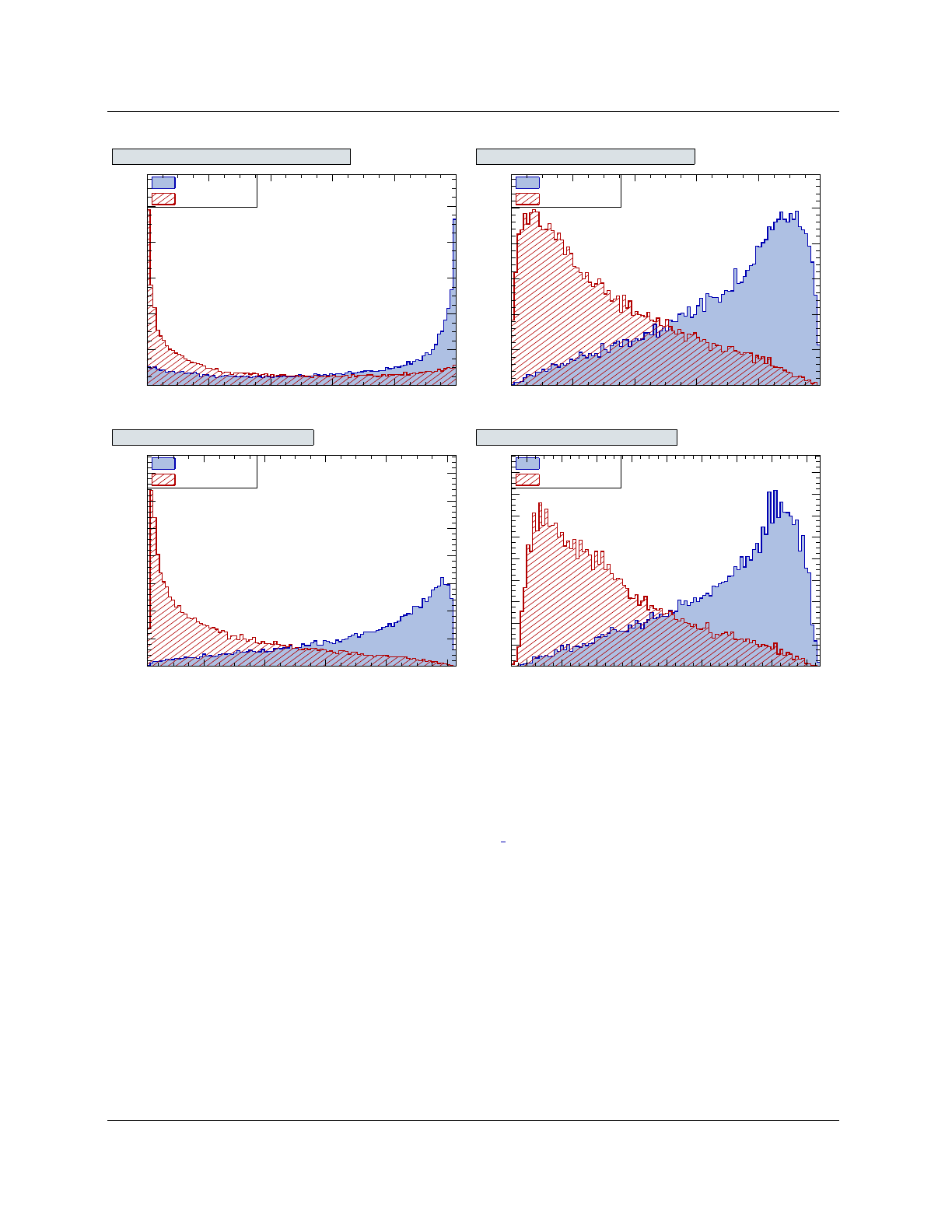
Figure 4shows several classifier output distributions for signal and background events based on
the test sample. By TMVA convention, signal (background) events accumulate at large (small)
classifier output values. Hence, cutting on the output and retaining the events with ylarger than
the cut requirement selects signal samples with efficiencies and purities that respectively decrease
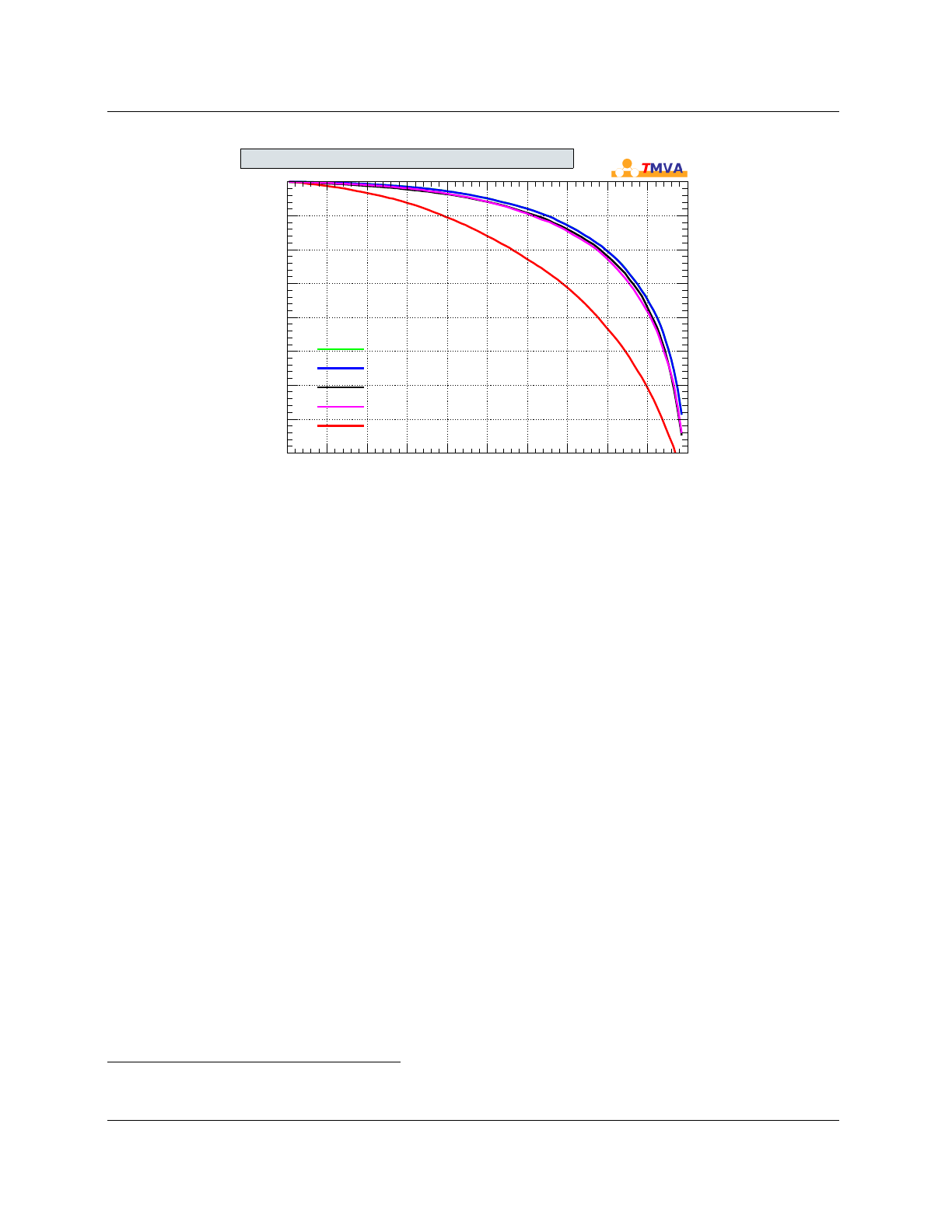
and increase with the cut value. The resulting relations between background rejection versus signal
efficiency are shown in Fig. 5for all classifiers that were used in the example macro. This plot
belongs to the class of Receiver Operating Characteristic (ROC) diagrams, which in its standard
form shows the true positive rate versus the false positive rate for the different possible cutpoints
of a hypothesis test.
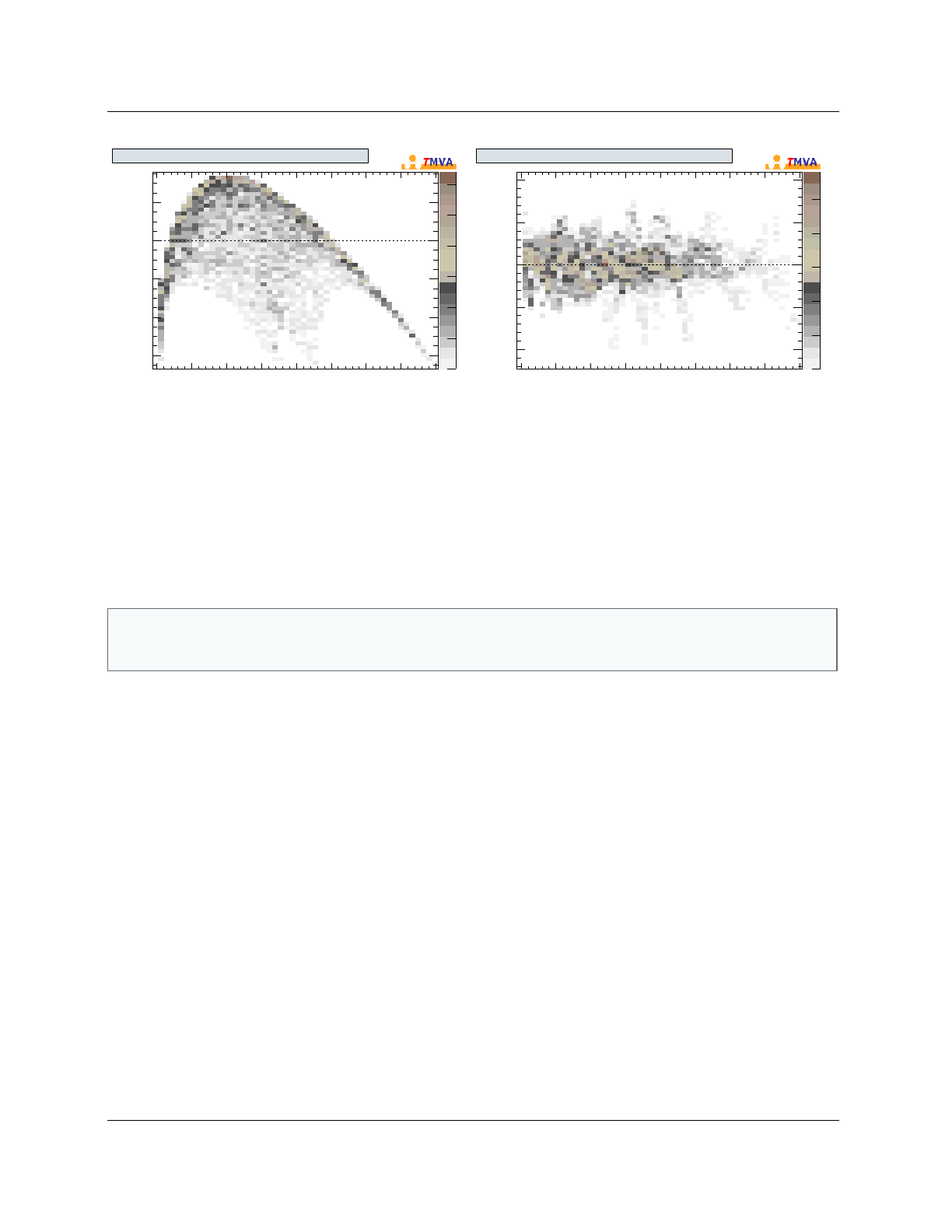
As an example for multivariate regression, Fig. 6displays the deviation between the regression
output and target values for linear and nonlinear regression algorithms.
More macros are available to validate training and response of specific MVA methods. For example,
the macro likelihoodrefs.C compares the probability density functions used by the likelihood
classifier to the normalised variable distributions of the training sample. It is also possible to
visualize the MLP neural network architecture and to draw decision trees (see Table 4).

8 2 TMVA Quick Start
Figure 1: Graphical user interfaces (GUI) to execute macros displaying training, test and evaluation results
(cf. Tables 2and 4on page 32) for classification (left) and regression problems (right). The multiclass classi-
fication GUI is similar to the classification GUI, where some functionality is not available. The classification
GUI can be launched manually by executing the script $ROOTSYS/tmva/test/TMVAGui.C in a ROOT ses-
sion. To launch the multiclass or regression GUIs use the macros TMVARegGui.C or TMVAMultiClassGui.C,
respectively.
Classification (left). The buttons behave as follows: (1a) plots the signal and background distributions of input vari-
ables (training sample), (1b–d) the same after applying the corresponding preprocessing transformation of the input
variables, (2a–f) scatter plots with superimposed profiles for all pairs of input variables for signal and background and
the applied transformations (training sample), (3) correlation coefficients between the input variables for signal and
background (training sample), (4a/b) signal and background distributions for the trained classifiers (test sample/test
and training samples superimposed to probe overtraining), (4c,d) the corresponding probability and Rarity distri-
butions of the classifiers (where requested, cf. see Sec. 3.1.13), (5a) signal and background efficiencies and purities
versus the cut on the classifier output for the expected numbers of signal and background events (before applying
the cut) given by the user (an input dialog box pops up, where the numbers are inserted), (5b) background rejection
versus signal efficiency obtained when cutting on the classifier outputs (ROC curve, from the test sample), (6) plot
of so-called Parallel Coordinates visualising the correlations among the input variables, and among the classifier and
the input variables, (7–13) show classifier specific diagnostic plots, and (14) quits the GUI. Titles greyed out indicate
actions that are not available because the corresponding classifier has not been trained or because the transformation
was not requested.
Regression (right). The buttons behave as follows: (1–3) same as for classification GUI, (4a–d) show the linear devia-
tions between regression targets and estimates versus the targets or input variables for the test and training samples,
respectively, (5) compares the average deviations between target and MVA output for the trained methods, and (6–8)
are as for the classification GUI.
2.8 Getting help 9
var1+var2
-6 -4 -2 0 2 4 6
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3 Signal
Background
var1+var2
-6 -4 -2 0 2 4 6
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
Input variables (training sample): var1+var2
var1-var2
-4 -3 -2 -1 0 1 2 3 4
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
var1-var2
-4 -3 -2 -1 0 1 2 3 4
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
Input variables (training sample): var1-var2
var3
-4 -3 -2 -1 0 1 2 3 4
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
var3
-4 -3 -2 -1 0 1 2 3 4
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
Input variables (training sample): var3
var4
-4 -3 -2 -1 0 1 2 3 4 5
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
var4
-4 -3 -2 -1 0 1 2 3 4 5
Normalised
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
Input variables (training sample): var4
Figure 2: Example plots for input variable distributions. The histogram limits are chosen to zoom into
the bulk of the distributions, which may lead to truncated tails. The vertical text on the right-hand side
of the plots indicates the under- and overflows. The limits in terms of multiples of the distribution’s RMS
can be adjusted in the user script by modifying the variable (TMVA::gConfig().GetVariablePlotting())
.fTimesRMS (cf. Code Example 20).
2.8 Getting help
Several help sources exist for TMVA (all web address given below are also linked from the TMVA
home page http://tmva.sourceforge.net).
•Information on how to download and install TMVA, and the TMVA Quick-start commands
are also available on the web at: http://tmva.sourceforge.net/howto.shtml.
•TMVA tutorial: https://twiki.cern.ch/twiki/bin/view/TMVA.
•An up-to-date reference of all configuration options for the TMVA Factory, the fitters, and all
the MVA methods: http://tmva.sourceforge.net/optionRef.html.
10 2 TMVA Quick Start
var3
-4 -3 -2 -1 0 1 2 3 4
var4
-4
-3
-2
-1
0
1
2
3
4
var3
-4 -3 -2 -1 0 1 2 3 4
var4
-4
-3
-2
-1
0
1
2
3
4
var4 versus var3 (signal)_NoTransform
var3
-4 -3 -2 -1 0 1 2 3 4
var4
-4
-3
-2
-1
0
1
2
3
4
var3
-4 -3 -2 -1 0 1 2 3 4
var4
-4
-3
-2
-1
0
1
2
3
4
var4 versus var3 (signal)_DecorrTransform
-100
-80
-60
-40
-20
0
20
40
60
80
100
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
Correlation Matrix (signal)
100 0 77 92
0 100 -8 9
77 -8 100 85
92 9 85 100
linear correlation coefficients in %
-100
-80
-60
-40
-20
0
20
40
60
80
100
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
var1+var2
var1-var2
var3
var4
Correlation Matrix (background)
100 0 77 92
0 100 -9 8
77 -9 100 85
92 8 85 100
linear correlation coefficients in %
Figure 3: Correlation between input variables. Upper left: correlations between var3 and var4 for the signal
training sample. Upper right: the same after applying a linear decorrelation transformation (see Sec. 4.1.2).
Lower plots: linear correlation coefficients for the signal and background training samples.
•On request, the TMVA methods provide a help message with a brief description of the method,
and hints for improving the performance by tuning the available configuration options. The
message is printed when the option ”H” is added to the configuration string while booking
the method (switch off by setting ”!H”). The very same help messages are also obtained by
clicking the “info” button on the top of the reference tables on the options reference web page:
http://tmva.sourceforge.net/optionRef.html.
•The web address of this Users Guide: http://tmva.sourceforge.net/docu/TMVAUsersGuide.pdf.
•The TMVA talk collection: http://tmva.sourceforge.net/talks.shtml.
•TMVA versions in ROOT releases: http://tmva.sourceforge.net/versionRef.html.
•Direct code views via ViewVC: http://tmva.svn.sourceforge.net/viewvc/tmva/trunk/TMVA.
•Class index of TMVA in ROOT: http://root.cern.ch/root/htmldoc/TMVA Index.html.
11
Likelihood
0 0.2 0.4 0.6 0.8 1
Normalized
0
2
4
6
8
10
Signal
Background
Likelihood
0 0.2 0.4 0.6 0.8 1
Normalized
0
2
4
6
8
10
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA output for classifier: Likelihood
PDERS
0 0.2 0.4 0.6 0.8 1
Normalized
0
0.5
1
1.5
2
2.5
Signal
Background
PDERS
0 0.2 0.4 0.6 0.8 1
Normalized
0
0.5
1
1.5
2
2.5
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA output for classifier: PDERS
MLP
0.2 0.4 0.6 0.8 1
Normalized
0
1
2
3
4
5
6
7Signal
Background
MLP
0.2 0.4 0.6 0.8 1
Normalized
0
1
2
3
4
5
6
7
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA output for classifier: MLP
BDT
-0.8 -0.6 -0.4 -0.2 -0 0.2 0.4 0.6 0.8
Normalized
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8 Signal
Background
BDT
-0.8 -0.6 -0.4 -0.2 -0 0.2 0.4 0.6 0.8
Normalized
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA output for classifier: BDT
Figure 4: Example plots for classifier output distributions for signal and background events from the academic
test sample. Shown are likelihood (upper left), PDE range search (upper right), Multilayer perceptron (MLP
– lower left) and boosted decision trees.
•Please send questions and/or report problems to the tmva-users mailing list:
http://sourceforge.net/mailarchive/forum.php?forum name=tmva-users (posting messages requires
prior subscription: https://lists.sourceforge.net/lists/listinfo/tmva-users).
3 Using TMVA
A typical TMVA classification or regression analysis consists of two independent phases: the training
phase, where the multivariate methods are trained, tested and evaluated, and an application phase,
where the chosen methods are applied to the concrete classification or regression problem they have
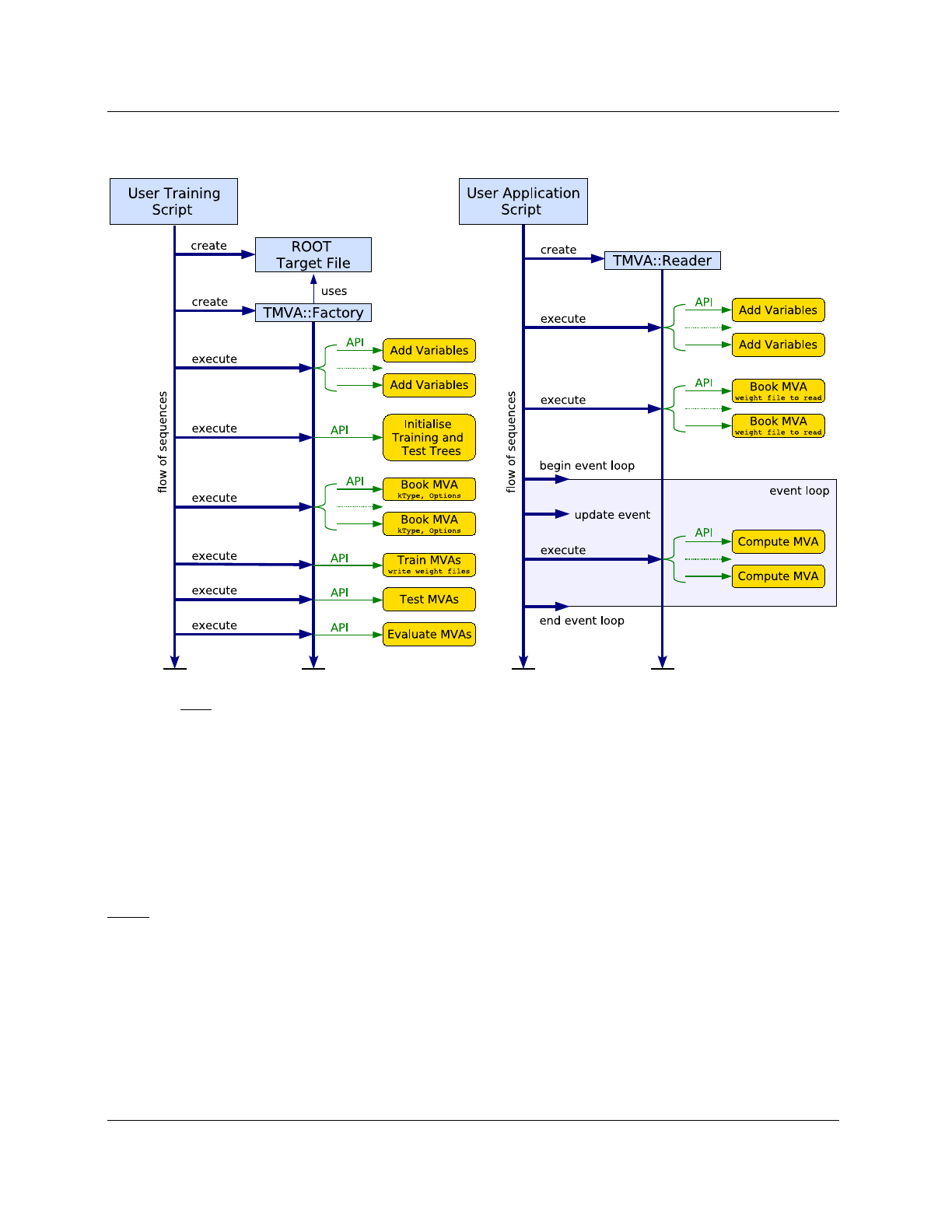
been trained for. An overview of the code flow for these two phases as implemented in the examples
TMVAClassification.C and TMVAClassificationApplication.C (for classification – see Sec. 2.5),
and TMVARegression.C and TMVARegressionApplication.C (for regression) are sketched in Fig. 7.
12 3 Using TMVA
Signal efficiency
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Background rejection
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Signal efficiency
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Background rejection
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
MVA Method:
Fisher
MLP
BDT
PDERS
Likelihood
Background rejection versus Signal efficiency
Figure 5: Example for the background rejection versus signal efficiency (“ROC curve”) obtained by cutting
on the classifier outputs for the events of the test sample.
Multiclass classification does not differ much from two class classification from a technical point of
view and differences will only be highlighted where neccessary.
In the training phase, the communication of the user with the data sets and the MVA methods
is performed via a Factory object, created at the beginning of the program. The TMVA Factory
provides member functions to specify the training and test data sets, to register the discriminating
input and – in case of regression – target variables, and to book the multivariate methods. Sub-
sequently the Factory calls for training, testing and the evaluation of the booked MVA methods.
Specific result (“weight”) files are created after the training phase by each booked MVA method.
The application of training results to a data set with unknown sample composition (classification) /
target value (regression) is governed by the Reader object. During initialisation, the user registers
the input variables3together with their local memory addresses, and books the MVA methods that
were found to be the most appropriate after evaluating the training results. As booking argument,
the name of the weight file is given. The weight file provides for each of the methods full and
consistent configuration according to the training setup and results. Within the event loop, the
input variables are updated for each event and the MVA response values are computed. Some
methods also provide the computation of errors.
For standalone use of the trained MVA methods, TMVA also generates lightweight C++ response
classes, which contain the encoded information from the weight files so that these are not required
anymore (cf. Sec. 3.4).
3This somewhat redundant operation is required to verify the correspondence between the Reader analysis and the
weight files used.
3.1 The TMVA Factory 13
fvalue
0 50 100 150 200 250 300 350 400
true
- fvalue
regression
fvalue
-60
-40
-20
0
20
0
5
10
15
20
25
30
Output deviation for method: LD (test sample)
fvalue
0 50 100 150 200 250 300 350 400
true
- fvalue
regression
fvalue
-10
-5
0
5
10
0
5
10
15
20
25
Output deviation for method: MLP (test sample)
Figure 6: Example plots for the deviation between regression output and target values for a Linear Dis-
criminant (LD – left) and MLP (right). The dependence of the input variables on the target being strongly
nonlinear, LD cannot appropriately solve the regression problem.
3.1 The TMVA Factory
The TMVA training phase begins by instantiating a Factory object with configuration options
listed in Option-Table 1.
TMVA::Factory* factory
= new TMVA::Factory( "<JobName>", outputFile, "<options>" );
Code Example 5: Instantiating a Factory class object. The first argument is the user-defined job name that
will reappear in the names of the weight files containing the training results. The second argument is the
pointer to a writable TFile output file created by the user, where control and performance histograms are
stored.
3.1.1 Specifying training and test data
The input data sets used for training and testing of the multivariate methods need to be handed
to the Factory. TMVA supports ROOT TTree and derived TChain objects as well as text files. If
ROOT trees are used for classification problems, the signal and background events can be located
in the same or in different trees. Data trees can be provided specifically for the purpose of either
training or testing or for both purposes. In the latter case the factory then splits the tree into one
part for training, the other for testing (see also section 3.1.4).
Overall weights can be specified for the signal and background training data (the treatment of
event-by-event weights is discussed below).
Specifying classification training and test data in ROOT tree format with signal and back-
ground events being located in different trees:
14 3 Using TMVA
Figure 7: Left: Flow (top to bottom) of a typical TMVA training application. The user script can be a
ROOT macro, C++ executable, python script or similar. The user creates a ROOT TFile, which is used by
the TMVA Factory to store output histograms and trees. After creation by the user, the Factory organises
the user’s interaction with the TMVA modules. It is the only TMVA object directly created and owned by
the user. First the discriminating variables that must be TFormula-compliant functions of branches in the
training trees are registered. For regression also the target variable must be specified. Then, selected MVA
methods are booked through a type identifier and a user-defined unique name, and configuration options are
specified via an option string. The TMVA analysis proceeds by consecutively calling the training, testing
and performance evaluation methods of the Factory. The training results for all booked methods are written
to custom weight files in XML format and the evaluation histograms are stored in the output file. They can
be analysed with specific macros that come with TMVA (cf. Tables 2and 4).
Right: Flow (top to bottom) of a typical TMVA analysis application. The MVA methods qualified by the
preceding training and evaluation step are now used to classify data of unknown signal and background com-
position or to predict a regression target. First, a Reader class object is created, which serves as interface
to the method’s response, just as was the Factory for the training and performance evaluation. The dis-
criminating variables and references to locally declared memory placeholders are registered with the Reader.
The variable names and types must be equal to those used for the training. The selected MVA methods are
booked with their weight files in the argument, which fully configures them. The user then runs the event
loop, where for each event the values of the input variables are copied to the reserved memory addresses, and
the MVA response values (and in some cases errors) are computed.

3.1 The TMVA Factory 15
Option Array Default Predefined Values Description
V–False –Verbose flag
Color –True –Flag for coloured screen output (de-
fault: True, if in batch mode: False)
Transformations – – List of transformations to test;
formatting example: Transforma-
tions=I;D;P;U;G,D, for identity,
decorrelation, PCA, Uniform and
Gaussianisation followed by decorre-
lation transformations
Silent –False –Batch mode: boolean silent flag in-
hibiting any output from TMVA after
the creation of the factory class object
(default: False)
DrawProgressBar –True –Draw progress bar to display training,
testing and evaluation schedule (de-
fault: True)
AnalysisType –Auto Classification,
Regression,
Multiclass, Auto
Set the analysis type (Classification,
Regression, Multiclass, Auto) (de-
fault: Auto)
Option Table 1: Configuration options reference for class: Factory. Coloured output is switched on by default,
except when running ROOT in batch mode (i.e., when the ’-b’ option of the CINT interpreter is invoked). The
list of transformations contains a default set of data preprocessing steps for test and visualisation purposes
only. The usage of preprocessing transformations in conjunction with MVA methods must be configured
when booking the methods.
// Get the signal and background trees from TFile source(s);
// multiple trees can be registered with the Factory
TTree* sigTree = (TTree*)sigSrc->Get( "<YourSignalTreeName>" );
TTree* bkgTreeA = (TTree*)bkgSrc->Get( "<YourBackgrTreeName_A>" );
TTree* bkgTreeB = (TTree*)bkgSrc->Get( "<YourBackgrTreeName_B>" );
TTree* bkgTreeC = (TTree*)bkgSrc->Get( "<YourBackgrTreeName_C>" );
// Set the event weights per tree (these weights are applied in
// addition to individual event weights that can be specified)
Double_t sigWeight = 1.0;
Double_t bkgWeightA = 1.0, bkgWeightB = 0.5, bkgWeightC = 2.0;
// Register the trees
factory->AddSignalTree ( sigTree, sigWeight );
factory->AddBackgroundTree( bkgTreeA, bkgWeightA );
factory->AddBackgroundTree( bkgTreeB, bkgWeightB );
factory->AddBackgroundTree( bkgTreeC, bkgWeightC );
Code Example 6: Registration of signal and background ROOT trees read from TFile sources. Overall signal
and background weights per tree can also be specified. The TTree object may be replaced by a TChain. The
trees will be later split by the factory into subsamples used for testing and training.

16 3 Using TMVA
Specifying classification training and test data in ROOT tree format with signal and back-
ground events being located in the same tree:
TTree* inputTree = (TTree*)source->Get( "<YourTreeName>" );
TCut signalCut = ...; // how to identify signal events
TCut backgrCut = ...; // how to identify background events
factory->SetInputTrees( inputTree, signalCut, backgrCut );
Code Example 7: Registration of a single ROOT tree containing the input data for signal and background,
read from a TFile source. The TTree object may be replaced by a TChain. The cuts identify the event
species.
Specifying classification data in ROOT tree format with signal and background training/test
events being located in separate trees:
#include "TMVA/Types.h"
// Get the signal and background training and test trees from TFile source(s);
TTree* sigTreeTrain = (TTree*)sigSrc->Get( "<YourSignalTrainTreeName>" );
TTree* bkgTreeTrain = (TTree*)bkgSrc->Get( "<YourBackgrTrainTreeName>" );
TTree* sigTreeTest = (TTree*)sigSrc->Get( "<YourSignalTestTreeName>" );
TTree* bkgTreeTest = (TTree*)bkgSrc->Get( "<YourBackgrTestTreeName>" );
// Set the event weights (these weights are applied in
// addition to individual event weights that can be specified)
Double_t sigWeight = 1.0;
Double_t bkgWeight = 1.0;
// Register the trees
factory->AddSignalTree ( sigTreeTrain, sigWeight, TMVA::Types::kTraining);
factory->AddBackgroundTree( bkgTreeTrain, bkgWeight, TMVA::Types::kTraining);
factory->AddSignalTree ( sigTreeTest, sigWeight, TMVA::Types::kTesting);
factory->AddBackgroundTree( bkgTreeTest, bkgWeight, TMVA::Types::kTesting);
Code Example 8: Registration of signal and background ROOT trees read from TFile sources. The first
two tree are specified to be used only for training the other two only for testing. Please note that the tree
type testing/training requires the inclusion of the header file TMVA/Types.h.
Specifying classification training and test data in text format:
3.1 The TMVA Factory 17
// Text file format (available types: ’F’ and ’I’)
// var1/F:var2/F:var3/F:var4/F
// 0.21293 -0.49200 -0.58425 -0.70591
// ...
TString sigFile = "signal.txt"; // text file for signal
TString bkgFile = "background.txt"; // text file for background
Double_t sigWeight = 1.0; // overall weight for all signal events
Double_t bkgWeight = 1.0; // overall weight for all background events
factory->SetInputTrees( sigFile, bkgFile, sigWeight, bkgWeight );
Code Example 9: Registration of signal and background text files used for training and testing. Names and
types of the input variables are given in the first line, followed by the values.

18 3 Using TMVA
Specifying regression training and test data in ROOT tree format:
factory->AddRegressionTree( regTree, weight );
Code Example 10: Registration of a ROOT tree containing the input and target variables. An overall weight
per tree can also be specified. The TTree object may be replaced by a TChain.
Rather than having only global weighting factors for individual input trees which allow to scale
them to the same “luminosity”, individual event weights can be applied as well. These weights
should be available event-by-event, i.e. as a column or a function of columns of the input data sets.
To specify the weights to be used for the training use the command:
factory->SetWeightExpression( "<YourWeightExpression>" );
or if you have different expressions (variables) used as weights in the signal and background trees:
factory->SetSignalWeightExpression( "<YourSignalWeightExpression>" );
factory->SetBackgroundWeightExpression( "<YourBackgroundWeightExpression>" );
Code Example 11: Specification of individual weights for the training events. The expression must be a
function of variables present in the input data set.
3.1.2 Negative event weights
In next-to-leading order Monte Carlo generators, events with (unphysical) negative weights may
occur in some phase space regions. Such events are often troublesome to deal with, and it depends
on the concrete implementation of the MVA method, whether or not they are treated properly.
Among those methods that correctly incorporate events with negative weights are likelihood and
multi-dimensional probability density estimators, but also decision trees. A summary of this feature
for all TMVA methods is given in Table 7. In cases where a method does not properly treat events
with negative weights, it is advisable to ignore such events for the training - but to include them in
the performance evaluation to not bias the results. This can be explicitly requested for each MVA
method via the boolean configuration option IgnoreNegWeightsInTraining (cf. Option Table 9on
page 61).
3.1.3 Defining input variables, spectators and targets
The variables in the input trees used to train the MVA methods are registered with the Factory using
the AddVariable method. It takes the variable name (string), which must have a correspondence in
the input ROOT tree or input text file, and optionally a number type (’F’ (default) and ’I’). The
type is used to inform the method whether a variable takes continuous floating point or discrete

3.1 The TMVA Factory 19
values.4Note that ’F’ indicates any floating point type, i.e., float and double. Correspondingly,
’I’ stands for integer, including int,short,char, and the corresponding unsigned types. Hence,
if a variable in the input tree is double, it should be declared ’F’ in the AddVariable call.
It is possible to specify variable expressions, just as for the TTree::Draw command (the expression
is interpreted as a TTreeFormula, including the use of arrays). Expressions may be abbreviated for
more concise screen output (and plotting) purposes by defining shorthand-notation labels via the
assignment operator :=.
In addition, two more arguments may be inserted into the AddVariable call, allowing the user to
specify titles and units for the input variables for displaying purposes.
The following code example revises all possible options to declare an input variable:
factory->AddVariable( "<YourDescreteVar>", ’I’ );
factory->AddVariable( "log(<YourFloatingVar>)", ’F’ );
factory->AddVariable( "SumLabel := <YourVar1>+<YourVar2>", ’F’ );
factory->AddVariable( "<YourVar3>", "Pretty Title", "Unit", ’F’ );
Code Example 12: Declaration of variables used to train the MVA methods. Each variable is specified by
its name in the training tree (or text file), and optionally a type (’F’ for floating point and ’I’ for integer,
’F’ is default if nothing is given). Note that ’F’ indicates any floating point type, i.e., float and double.
Correspondingly, ’I’ stands for integer, including int,short,char, and the corresponding unsigned types.
Hence, even if a variable in the input tree is double, it should be declared ’F’ here. Here, YourVar1 has
discrete values and is thus declared as an integer. Just as in the TTree::Draw command, it is also possible
to specify expressions of variables. The := operator defines labels (third row), used for shorthand notation in
screen outputs and plots. It is also possible to define titles and units for the variables (fourth row), which are
used for plotting. If labels and titles are defined, labels are used for abbreviated screen outputs, and titles
for plotting.
It is possible to define spectator variables, which are part of the input data set, but which are not
used in the MVA training, test nor during the evaluation. They are copied into the TestTree,
together with the used input variables and the MVA response values for each event, where the
spectator variables can be used for correlation tests or others. Spectator variables are declared as
follows:
factory->AddSpectator( "<YourSpectatorVariable>" );
factory->AddSpectator( "log(<YourSpectatorVariable>)" );
factory->AddSpectator( "<YourSpectatorVariable>", "Pretty Title", "Unit" );
Code Example 13: Various ways to declare a spectator variable, not participating in the MVA anlaysis, but
written into the final TestTree.
4For example for the projective likelihood method, a histogram out of discrete values would not (and should not)
be interpolated between bins.
20 3 Using TMVA
For a regression problem, the target variable is defined similarly, without however specifying a
number type:
factory->AddTarget( "<YourRegressionTarget1>" );
factory->AddTarget( "log(<YourRegressionTarget2>)" );
factory->AddTarget( "<YourRegressionTarget3>", "Pretty Title", "Unit" );
Code Example 14: Various ways to declare the target variables used to train a multivariate regression
method. If the MVA method supports multi-target (multidimensional) regression, more than one regression
target can be defined.
3.1.4 Preparing the training and test data
The input events that are handed to the Factory are internally copied and split into one training and
one test ROOT tree. This guarantees a statistically independent evaluation of the MVA algorithms
based on the test sample.5The numbers of events used in both samples are specified by the user.
They must not exceed the entries of the input data sets. In case the user has provided a ROOT
tree, the event copy can (and should) be accelerated by disabling all branches not used by the input
variables.
It is possible to apply selection requirements (cuts) upon the input events. These requirements can
depend on any variable present in the input data sets, i.e., they are not restricted to the variables
used by the methods. The full command is as follows:
TCut preselectionCut = "<YourSelectionString>";
factory->PrepareTrainingAndTestTree( preselectionCut, "<options>" );
Code Example 15: Preparation of the internal TMVA training and test trees. The sizes (number of events)
of these trees are specified in the configuration option string. For classification problems, they can be set
individually for signal and background. Note that the preselection cuts are applied before the training and
test samples are created, i.e., the tree sizes apply to numbers of selected events. It is also possible to choose
among different methods to select the events entering the training and test trees from the source trees. All
options are described in Option-Table 2. See also the text for further information.
For classification, the numbers of signal and background events used for training and testing are
specified in the configuration string by the variables nTrain Signal,nTrain Background,nTest
Signal and nTest Background (for example, "nTrain Signal=5000:nTrain Background=5000:
nTest Signal=4000:nTest Background=5000"). The default value (zero) signifies that all available
events are taken, e.g., if nTrain Signal=5000 and nTest Signal=0, and if the total signal sample
has 15000 events, then 5000 signal events are used for training and the remaining 10000 events are
5A fully unbiased training and evaluation requires at least three statistically independent data sets. See comments
in Footnote 9on page 29.

3.1 The TMVA Factory 21
used for testing. If nTrain Signal=0 and nTest Signal=0, the signal sample is split in half for
training and testing. The same rules apply to background. Since zero is default, not specifying
anything corresponds to splitting the samples in two halves.
For regression, only the sizes of the train and test samples are given, e.g., "nTrain Regression=0:
nTest Regression=0", so that one half of the input sample is used for training and the other half
for testing. If a tree is given to the factory as a training tree. The events of that tree can only be
used for training. The same is true for test trees.
The option SplitMode defines how the training and test samples are selected from the source trees.
With SplitMode=Random, events are selected randomly. With SplitMode=Alternate, events are
chosen in alternating turns for the training and test samples as they occur in the source trees
until the desired numbers of training and test events are selected. The training and test samples
should contain the same number of events for each event class. In the SplitMode=Block mode
the first nTrain Signal and nTrain Background (classification), or nTrain Regression events
(regression) of the input data set are selected for the training sample, and the next nTest Signal
and nTest Background or nTest Regression events comprise the test data. This is usually not
desired for data that contains varying conditions over the range of the data set. For the Random
selection mode, the seed of the random generator can be set. With SplitSeed=0 the generator
returns a different random number series every time. The default seed of 100 ensures that the same
training and test samples are used each time TMVA is run (as does any other seed apart from 0).
The option MixMode defines the order of how the training and test events of the different classes are
combined into a training sample. It also defines the order in which they appear in the test sample.
The available options for MixMode are the same as for SplitMode. By default, the same option
is chosen for the MixMode as given in SplitMode. Again, with MixMode=Random, the order of the
events in the samples is random. With MixMode=Alternate subsequent events are always of the
next class (e.g. 0, 1, 2, 3, 0, 1, 2, 3, ···). With MixMode=Block all events of one class are inserted
in a block into the training/test samples (e.g. 0, 0, ···, 0, 1, 1, ···, 1, 2, 2, ···, 2, ··· ).
In some cases event weights are given by Monte Carlo generators, and may turn out to be overall
very small or large numbers. To avoid artifacts due to this, TMVA can internally renormalise the
signal and background training(!) weights such that their respective sums of effective (weighted)
events is equal. This is the default renormalisation and it can be modified with the configuration
option NormMode (cf. Table 2). Possible settings are: None: no renormalisation is applied (the
weights are used as given), NumEvents : renormalisation of the training events such that the sum
of event weights of the Signal and Background events, respectively are equal to the number of
events Ns,Nb requested in the call Factory::PrepareTrainingAndTestTree("","nTrain Signal=
Ns,nTrain Background=Nb...",EqualNumEvents (default): the event weights are renormalised
such that both, the sum of all weighted signal training events equals the sum of all weights of
the background training events. Note: All this renormalisation only affects the training events as
the training of some classifiers is sensitive to the relative amount of signal and background in the
training data. On the other hand, the background or signal efficiency of the trained classifier as
determined from the test sample is independent of the relative abundance of signal and background
events.

22 3 Using TMVA
Option Array Default Predefined Values Description
SplitMode –Random Random,
Alternate,
Block
Method of picking training and testing
events (default: random)
MixMode –SameAsSplitModeSameAsSplitMode,
Random,
Alternate,
Block
Method of mixing events of dif-
fernt classes into one dataset (default:
SameAsSplitMode)
SplitSeed –100 –Seed for random event shuffling
NormMode –EqualNumEvents None, NumEvents,
EqualNumEvents
Overall renormalisation of event-by-
event weights used in the training (Nu-
mEvents: average weight of 1 per
event, independently for signal and
background; EqualNumEvents: aver-
age weight of 1 per event for signal,
and sum of weights for background
equal to sum of weights for signal)
nTrain Signal –0–Number of training events of class Sig-
nal (default: 0 = all)
nTest Signal –0–Number of test events of class Signal
(default: 0 = all)
nTrain Background –0–Number of training events of class
Background (default: 0 = all)
nTest Background –0–Number of test events of class Back-
ground (default: 0 = all)
V–False –Verbosity (default: true)
VerboseLevel –Info Debug, Verbose,
Info
VerboseLevel (Debug/Verbose/Info)
Option Table 2: Configuration options reference in call Factory::PrepareTrainingAndTestTree(..). For
regression, nTrain Signal and nTest Signal are replaced by nTrain Regression and nTest Regression,
respectively, and nTrain Background and nTest Background are removed. See also Code-Example 15 and
comments in the text.
3.1 The TMVA Factory 23
3.1.5 Booking MVA methods
All MVA methods are booked via the Factory by specifying the method’s type, plus a unique name
chosen by the user, and a set of specific configuration options encoded in a string qualifier.6If
the same method type is booked several times with different options (which is useful to compare
different sets of configurations for optimisation purposes), the specified names must be different to
distinguish the instances and their weight files. A booking example for the likelihood method is
given in Code Example 16 below. Detailed descriptions of the configuration options are given in
the corresponding tools and MVA sections of this Users Guide, and booking examples for most of
the methods are given in Appendix A. With the MVA booking the initialisation of the Factory is
complete and no MVA-specific actions are left to do. The Factory takes care of the subsequent
training, testing and evaluation of the MVA methods.
factory->BookMethod( TMVA::Types::kLikelihood, "LikelihoodD",
"!H:!V:!TransformOutput:PDFInterpol=Spline2:\
NSmoothSig[0]=20:NSmoothBkg[0]=20:NSmooth=5:\
NAvEvtPerBin=50:VarTransform=Decorrelate" );
Code Example 16: Example booking of the likelihood method. The first argument is a unique type enumer-
ator (the available types can be looked up in src/Types.h), the second is a user-defined name which must
be unique among all booked MVA methods, and the third is a configuration option string that is specific to
the method. For options that are not explicitly set in the string default values are used, which are printed to
standard output. The syntax of the options should be explicit from the above example. Individual options
are separated by a ’:’. Boolean variables can be set either explicitly as MyBoolVar=True/False, or just via
MyBoolVar/!MyBoolVar. All specific options are explained in the tools and MVA sections of this Users Guide.
There is no difference in the booking of methods for classification or regression applications. See Appendix A
on page 148 for a complete booking list of all MVA methods in TMVA.
3.1.6 Help option for MVA booking
Upon request via the configuration option ”H” (see code example above) the TMVA methods print
concise help messages. These include a brief description of the algorithm, a performance assessment,
and hints for setting the most important configuration options. The messages can also be evoked
by the command factory->PrintHelpMessage("<MethodName>").
3.1.7 Training the MVA methods
The training of the booked methods is invoked by the command:
6In the TMVA package all MVA methods are derived from the abstract interface IMethod and the base class
MethodBase.

24 3 Using TMVA
factory->TrainAllMethods();
Code Example 17: Executing the MVA training via the Factory.
The training results are stored in the weight files which are saved in the directory weights (which, if
not existing is created).7The weight files are named Jobname MethodName.weights.hextensioni,
where the job name has been specified at the instantiation of the Factory, and MethodName is the
unique method name specified in the booking command. Each method writes a custom weight file
in XML format (extension is xml), where the configuration options, controls and training results for
the method are stored.
3.1.8 Testing the MVA methods
The trained MVA methods are applied to the test data set and provide scalar outputs according
to which an event can be classified as either signal or background, or which estimate the regression
target.8The MVA outputs are stored in the test tree (TestTree) to which a column is added for
each booked method. The tree is eventually written to the output file and can be directly analysed
in a ROOT session. The testing of all booked methods is invoked by the command:
factory->TestAllMethods();
Code Example 18: Executing the validation (testing) of the MVA methods via the Factory.
3.1.9 Evaluating the MVA methods
The Factory and data set classes of TMVA perform a preliminary property assessment of the input
variables used by the MVA methods, such as computing correlation coefficients and ranking the
variables according to their separation (for classification), or according to their correlations with
the target variable(s) (for regression). The results are printed to standard output.
The performance evaluation in terms of signal efficiency, background rejection, faithful estimation
of a regression target, etc., of the trained and tested MVA methods is invoked by the command:
7The default weight file directory name can be modified from the user script through the global configuration
variable (TMVA::gConfig().GetIONames()).fWeightFileDir.
8In classification mode, TMVA discriminates signal from background in data sets with unknown composition of
these two samples. In frequent use cases the background (sometimes also the signal) consists of a variety of different
populations with characteristic properties, which could call for classifiers with more than two discrimination classes.
However, in practise it is usually possible to serialise background fighting by training individual classifiers for each
background source, and applying consecutive requirements to these. Since TMVA 4, the framework directly supports
multi-class classification. However, some MVA methods have not yet been prepared for it.

3.1 The TMVA Factory 25
factory->EvaluateAllMethods();
Code Example 19: Executing the performance evaluation via the Factory.
The performance measures differ between classification and regression problems. They are sum-
marised below.
3.1.10 Classification performance evaluation
After training and testing, the linear correlation coefficients among the classifier outputs are printed.
In addition, overlap matrices are derived (and printed) for signal and background that determine the
fractions of signal and background events that are equally classified by each pair of classifiers. This
is useful when two classifiers have similar performance, but a significant fraction of non-overlapping
events. In such a case a combination of the classifiers (e.g., in a Committee classifier) could improve
the performance (this can be extended to any combination of any number of classifiers).
The optimal method to be used for a specific analysis strongly depends on the problem at hand
and no general recommendations can be given. To ease the choice TMVA computes a number of
benchmark quantities that assess the performance of the methods on the independent test sample.
For classification these are
•The signal efficiency at three representative background efficiencies (the efficiency is
equal to 1 −rejection) obtained from a cut on the classifier output. Also given is the area of
the background rejection versus signal efficiency function (the larger the area the better the
performance).
•The separation hS2iof a classifier y, defined by the integral [7]
hS2i=1
2Z(ˆyS(y)−ˆyB(y))2
ˆyS(y) + ˆyB(y)dy , (1)
where ˆySand ˆyBare the signal and background PDFs of y, respectively (cf. Sec. 3.1.13). The
separation is zero for identical signal and background shapes, and it is one for shapes with no
overlap.
•The discrimination significance of a classifier, defined by the difference between the classifier
means for signal and background divided by the quadratic sum of their root-mean-squares.
The results of the evaluation are printed to standard output. Smooth background rejection/efficiency
versus signal efficiency curves are written to the output ROOT file, and can be plotted using custom
macros (see Sec. 3.2).

26 3 Using TMVA
3.1.11 Regression performance evaluation
Ranking for regression is based on the correlation strength between the input variables or MVA
method response and the regression target. Several correlation measures are implemented in TMVA
to capture and quantify nonlinear dependencies. Their results are printed to standard output.
•The Correlation between two random variables Xand Yis usually measured with the
correlation coefficient ρ, defined by
ρ(X, Y ) = cov(X, Y )
σXσY
.(2)
The correlation coefficient is symmetric in Xand Y, lies within the interval [−1,1], and
quantifies by definition a linear relationship. Thus ρ= 0 holds for independent variables, but
the converse is not true in general. In particular, higher order functional or non-functional
relationships may not, or only marginally, be reflected in the value of ρ(see Fig. 8).
•The correlation ratio is defined by
η2(Y|X) = σE(Y|X)
σY
,(3)
where
E(Y|X) = Zy P (y|x)dy , (4)
is the conditional expectation of Ygiven Xwith the associated conditional probability density
function P(Y|X). The correlation ratio η2is in general not symmetric and its value lies within
[0,1], according to how well the data points can be fitted with a linear or nonlinear regression
curve. Thus non-functional correlations cannot be accounted for by the correlation ratio. The
following relations can be derived for η2and the squared correlation coefficient ρ2[9]:
◦ρ2=η2= 1, if Xand Yare in a strict linear functional relationship.
◦ρ2≤η2= 1, if Xand Yare in a strict nonlinear functional relationship.
◦ρ2=η2<1, if there is no strict functional relationship but the regression of Xon Yis
exactly linear.
◦ρ2< η2<1, if there is no strict functional relationship but some nonlinear regression
curve is a better fit then the best linear fit.
Some characteristic examples and their corresponding values for η2are shown in Fig. 8. In
the special case, where all data points take the same value, ηis undefined.
•Mutual information allows to detect any predictable relationship between two random
variables, be it of functional or non-functional form. It is defined by [10]
I(X, Y ) = X
X,Y
P(X, Y ) ln P(X, Y )
P(X)P(Y),(5)
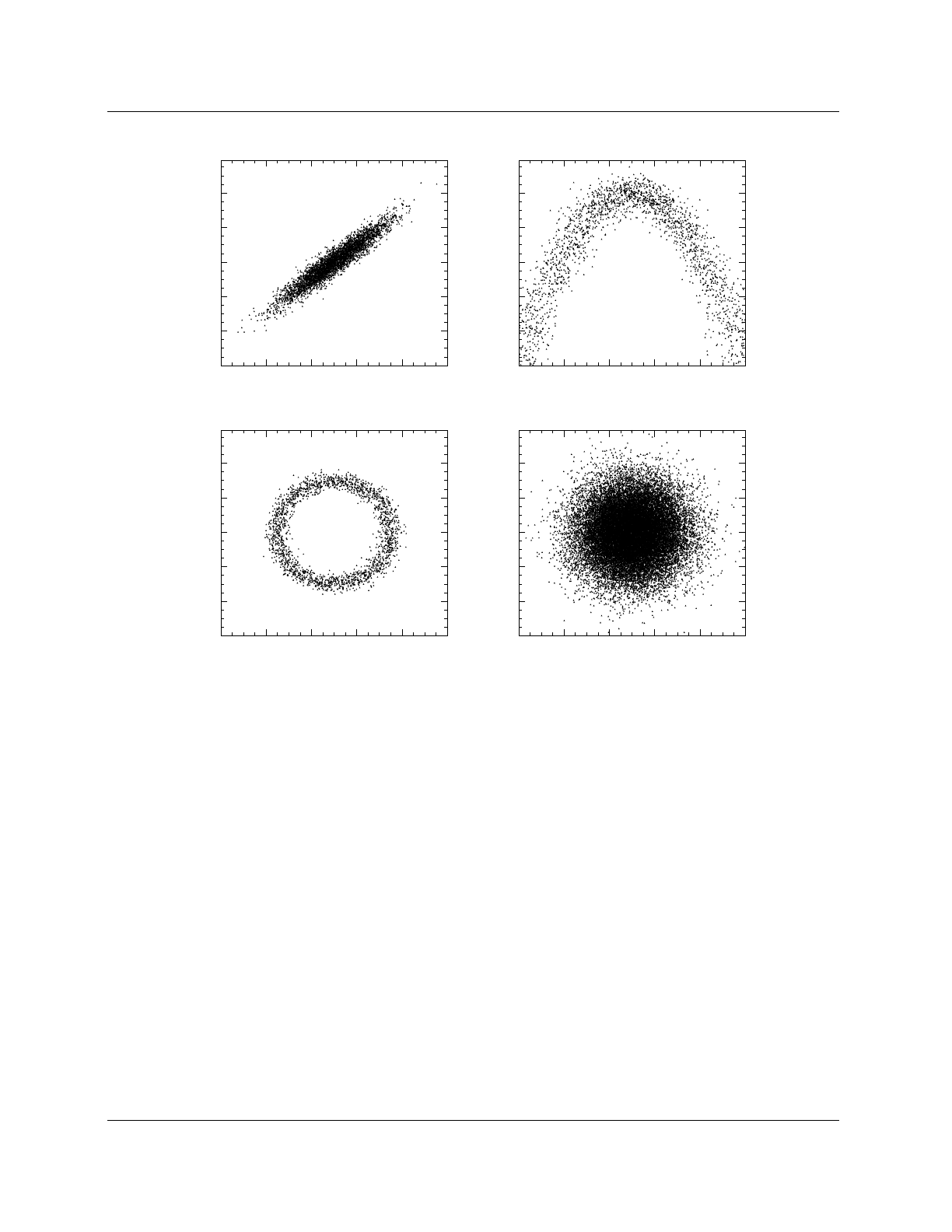
3.1 The TMVA Factory 27
X
0 0.2 0.4 0.6 0.8 1
Y
0
0.2
0.4
0.6
0.8
1
= 0.9498ρ = 0.9008
2
ηI = 1.243
X
0 0.2 0.4 0.6 0.8 1
Y
0
0.2
0.4
0.6
0.8
1
= 0.002ρ = 0.7664
2
ηI = 1.4756
X
0 0.2 0.4 0.6 0.8 1
Y
0
0.2
0.4
0.6
0.8
1
= 0.0029ρ = 0.0293
2
ηI = 1.0016
X
0 0.2 0.4 0.6 0.8 1
Y
0
0.2
0.4
0.6
0.8
1
= 0.0064ρ = 0.0026
2
ηI = 0.0661
Figure 8: Various types of correlations between two random variables and their corresponding values for
the correlation coefficient ρ, the correlation ratio η, and mutual information I. Linear relationship (upper
left), functional relationship (upper right), non-functional relationship (lower left), and independent variables
(lower right).
where P(X, Y ) is the joint probability density function of the random variables Xand Y,
and P(X), P(Y) are the corresponding marginal probabilities. Mutual information originates
from information theory and is closely related to entropy which is a measure of the uncertainty
associated with a random variable. It is defined by
H(X) = −X
X
P(X) ln P(X),(6)
where Xis the discrete random variable and P(X) the associated probability density function.

28 3 Using TMVA
ρPDF 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.9999
ρ0.006 0.092 0.191 0.291 0.391 0.492 0.592 0.694 0.795 0.898 1.0
η20.004 0.012 0.041 0.089 0.156 0.245 0.354 0.484 0.634 0.806 1.0
I0.093 0.099 0.112 0.139 0.171 0.222 0.295 0.398 0.56 0.861 3.071
Table 1: Comparison of the correlation coefficient ρ, correlation ratio η, and mutual information
Ifor two-dimensional Gaussian toy Monte-Carlo distributions with linear correlations as indicated
(20000 data points/100 ×100 bins .
The connection between the two quantities is given by the following transformation
I(X, Y ) = X
X,Y
P(X, Y ) ln P(X, Y )
P(X)P(Y)(7)
=X
X,Y
P(X, Y ) ln P(X|Y)
PX(X)(8)
=−X
X,Y
P(X, Y ) ln P(X) + X
X,Y
P(X, Y ) ln P(X|Y) (9)
=−X
X,Y
P(X) ln P(X)−(−X
X,Y
P(X, Y ) ln P(X|Y)) (10)
=H(X)−H(X|Y),(11)
where H(X|Y) is the conditional entropy of Xgiven Y. Thus mutual information is the
reduction of the uncertainty in variable Xdue to the knowledge of Y. Mutual information
is symmetric and takes positive absolute values. In the case of two completely independent
variables I(X, Y ) is zero.
For experimental measurements the joint and marginal probability density functions are a
priori unknown and must be approximated by choosing suitable binning procedures such as
kernel estimation techniques (see, e.g., [11]). Consequently, the values of I(X, Y ) for a given
data set will strongly depend on the statistical power of the sample and the chosen binning
parameters.
For the purpose of ranking variables from data sets of equal statistical power and identical
binning, however, we assume that the evaluation from a simple two-dimensional histogram
without further smoothing is sufficient.
A comparison of the correlation coefficient ρ, the correlation ratio η, and mutual information Ifor
linearly correlated two-dimensional Gaussian toy MC simulations is shown in Table 1.
3.1.12 Overtraining
Overtraining occurs when a machine learning problem has too few degrees of freedom, because too
many model parameters of an algorithm were adjusted to too few data points. The sensitivity to

3.1 The TMVA Factory 29
overtraining therefore depends on the MVA method. For example, a Fisher (or linear) discriminant
can hardly ever be overtrained, whereas, without the appropriate counter measures, boosted deci-
sion trees usually suffer from at least partial overtraining, owing to their large number of nodes.
Overtraining leads to a seeming increase in the classification or regression performance over the
objectively achievable one, if measured on the training sample, and to an effective performance
decrease when measured with an independent test sample. A convenient way to detect overtraining
and to measure its impact is therefore to compare the performance results between training and
test samples. Such a test is performed by TMVA with the results printed to standard output.
Various method-specific solutions to counteract overtraining exist. For example, binned likelihood
reference distributions are smoothed before interpolating their shapes, or unbinned kernel density
estimators smear each training event before computing the PDF; neural networks steadily monitor
the convergence of the error estimator between training and test samples9suspending the training
when the test sample has passed its minimum; the number of nodes in boosted decision trees can
be reduced by removing insignificant ones (“tree pruning”), etc.
3.1.13 Other representations of MVA outputs for classification: probabilities and probabil-
ity integral transformation (Rarity)
In addition to the MVA response value yof a classifier, which is typically used to place a cut for
the classification of an event as either signal or background, or which could be used in a subse-
quent likelihood fit, TMVA also provides the classifier’s signal and background PDFs, ˆyS(B). The
PDFs can be used to derive classification probabilities for individual events, or to compute any
kind of transformation of which the Probability integral transformation (Rarity) transformation is
implemented in TMVA.
•Classification probability: The techniques used to estimate the shapes of the PDFs are
those developed for the likelihood classifier (see Sec. 8.2.2 for details) and can be customised
individually for each method (the control options are given in Sec. 8). The probability for
event ito be of signal type is given by,
P
S(i) = f
S·ˆyS(i)
f
S·ˆyS(i) + (1 −f
S)·ˆyB(i),(12)
where f
S=N
S/(N
S+N
B) is the expected signal fraction, and N
S(B)is the expected number
of signal (background) events (default is f
S= 0.5).10
9Proper training and validation requires three statistically independent data sets: one for the parameter optimi-
sation, another one for the overtraining detection, and the last one for the performance validation. In TMVA, the
last two samples have been merged to increase statistics. The (usually insignificant) bias introduced by this on the
evaluation results does not affect the analysis as far as classification cut efficiencies or the regression resolution are
independently validated with data.
10The P
Sdistributions may exhibit a somewhat peculiar structure with frequent narrow peaks. They are generated
by regions of classifier output values in which ˆyS∝ˆyBfor which P
Sbecomes a constant.
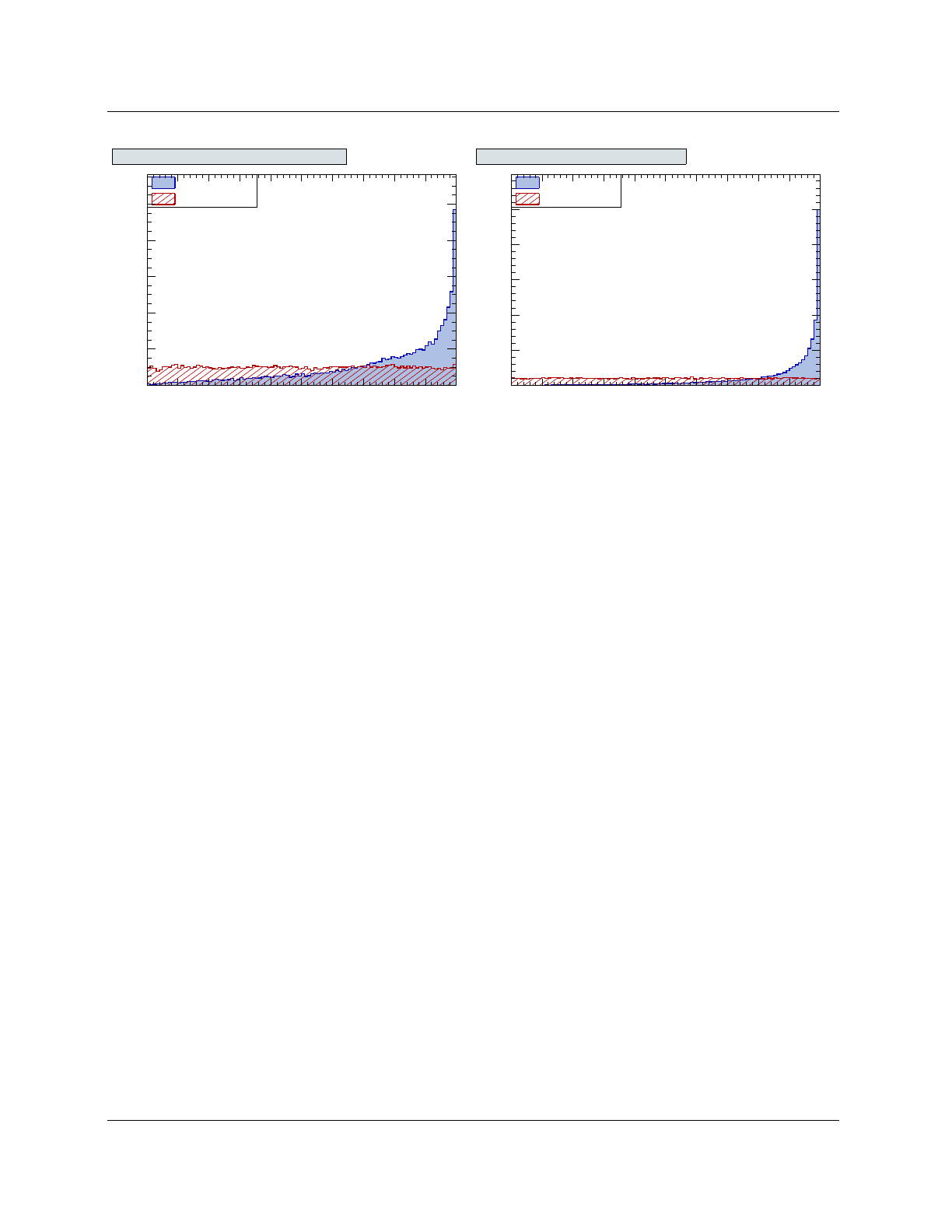
30 3 Using TMVA
Signal rarity
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Normalized
0
2
4
6
8
10
Signal
Background
Signal rarity
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Normalized
0
2
4
6
8
10
U/O-flow (S,B): (0.0, 0.0)% / (0.7, 0.0)%
TMVA Rarity for classifier: Likelihood
Signal rarity
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Normalized
0
5
10
15
20
25
Signal
Background
Signal rarity
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Normalized
0
5
10
15
20
25
U/O-flow (S,B): (0.0, 0.0)% / (3.0, 0.0)%
TMVA Rarity for classifier: Fisher
Figure 9: Example plots for classifier probability integral transformation distributions for signal and back-
ground events from the academic test sample. Shown are likelihood (left) and Fisher (right).
•Probability Integral Transformation: The Probability integral transformation R(y) of a
classifier yis given by the integral [8]
R(y) =
y
Z
−∞
ˆyB(y0)dy0,(13)
which is defined such that R(yB) for background events is uniformly distributed between 0 and
1, while signal events cluster towards 1. The signal distributions can thus be directly compared
among the various classifiers. The stronger the peak towards 1, the better is the discrimination.
Another useful aspect of the probability integral transformation is the possibility to directly
visualise deviations of a test background (which could be physics data) from the training
sample, by exhibition of non-uniformity.
The probability integral transformation distributions of the Likelihood and Fisher classifiers
for the example used in Sec. 2are plotted in Fig. 9. Since Fisher performs better (cf. Fig. 5on
page 12), its signal distribution is stronger peaked towards 1. By construction, the background
distributions are uniform within statistical fluctuations.
The probability and probability integral transformation distributions can be plotted with dedicated
macros, invoked through corresponding GUI buttons.
3.2 ROOT macros to plot training, testing and evaluation results
TMVA provides simple GUIs (TMVAGui.C and TMVARegGui.C, see Fig. 1), which interface ROOT
macros that visualise the various steps of the training analysis. The macros are respectively located
in TMVA/macros/ (Sourceforge.net distribution) and $ROOTSYS/tmva/test/ (ROOT distribution),
and can also be executed from the command line. They are described in Tables 2and 4. All plots

3.3 The TMVA Reader 31
drawn are saved as png files (or optionally as eps,gif files) in the macro subdirectory plots which,
if not existing, is created.
The binning and histogram boundaries for some of the histograms created during the training,
testing and evaluation phases are controlled via the global singleton class TMVA::Config. They can
be modified as follows:
// Modify settings for the variable plotting
(TMVA::gConfig().GetVariablePlotting()).fTimesRMS = 8.0;
(TMVA::gConfig().GetVariablePlotting()).fNbins1D = 60.0;
(TMVA::gConfig().GetVariablePlotting()).fNbins2D = 300.0;
// Modify the binning in the ROC curve (for classification only)
(TMVA::gConfig().GetVariablePlotting()).fNbinsXOfROCCurve = 100;
// For file name settings, modify the struct TMVA::Config::IONames
(TMVA::gConfig().GetIONames()).fWeightFileDir = "myWeightFileDir";
Code Example 20: Modifying global parameter settings for the plotting of the discriminating input variables.
The values given are the TMVA defaults. Consult the class files Config.h and Config.cxx for all available
global configuration variables and their default settings, respectively. Note that the additional parentheses
are mandatory when used in CINT.
3.3 The TMVA Reader
After training and evaluation, the most performing MVA methods are chosen and used to classify
events in data samples with unknown signal and background composition, or to predict values of a
regression target. An example of how this application phase is carried out is given in TMVA/macros/
TMVAClassificationApplication.C and TMVA/macros/TMVARegressionApplication.C (Source-
forge.net), or $ROOTSYS/tmva/test/TMVAClassificationApplication.C and $ROOTSYS/tmva/test/
TMVARegressionApplication.C (ROOT).
Analogously to the Factory, the communication between the user application and the MVA methods
is interfaced by the TMVA Reader, which is created by the user:
TMVA::Reader* reader = new TMVA::Reader( "<options>" );
Code Example 21: Instantiating a Reader class object. The only options are the booleans: Vfor verbose,
Color for coloured output, and Silent to suppress all output.

32 3 Using TMVA
Macro Description
variables.C Plots the signal and background MVA input variables (training sam-
ple). The second argument sets the directory, which determines the
preprocessing type (InputVariables Id for default identity transfor-
mation, cf. Sec. 4.1). The third argument is a title, and the fourth
argument is a flag whether or not the input variables served a regres-
sion analysis.
correlationscatter.C Plots superimposed scatters and profiles for all pairs of input vari-
ables used during the training phase (separate plots for signal and
background in case of classification). The arguments are as above.
correlations.C Plots the linear correlation matrices for the input variables in the
training sample (distinguishing signal and background for classifica-
tion).
mvas.C Plots the classifier response distributions of the test sample for signal
and background. The second argument (HistType=0,1,2,3) allows
to also plot the probability (1) and probability integral transforma-
tion (2) distributions of the classifiers, as well as a comparison of
the output distributions between test and training samples. Plot-
ting of probability and probability integral transformation requires
the CreateMVAPdfs option for the classifier to be set to true.
mvaeffs.C Signal and background efficiencies, obtained from cutting on the clas-
sifier outputs, versus the cut value. Also shown are the signal purity
and the signal efficiency times signal purity corresponding to the ex-
pected number of signal and background events before cutting (num-
bers given by user). The optimal cuts according to the best signifi-
cance are printed on standard output.
efficiencies.C Background rejection (second argument type=2, default), or back-
ground efficiency (type=1), versus signal efficiency for the classifiers
(test sample). The efficiencies are obtained by cutting on the classi-
fier outputs. This is traditionally the best plot to assess the overall
discrimination performance (ROC curve).
paracoor.C Draws diagrams of “Parallel coordinates” [33] for signal and back-
ground, used to visualise the correlations among the input variables,
but also between the MVA output and input variables (indicating the
importance of the variables).
Table 2: ROOT macros for the representation of the TMVA input variables and classification results. All
macros take as first argument the name of the ROOT file containing the histograms (default is TMVA.root).
They are conveniently called via the TMVAGui.C GUI (the first three macros are also called from the regression
GUI TMVARegGui.C). Macros for the representation of regression results are given in Table 3. Plotting macros
for MVA method specific information are listed in Table 4.

3.3 The TMVA Reader 33
Macro Description
deviations.C Plots the linear deviation between regression target value and MVA
response or input variables for test and training samples.
regression averagedevs.C Draws the average deviation between the MVA output and the regres-
sion target value for all trained methods.
Table 3: ROOT macros for the representation of the TMVA regression results. All macros take as first
argument the name of the ROOT file containing the histograms (default is TMVA.root). They are conveniently
called from the TMVARegGui.C GUI.
3.3.1 Specifying input variables
The user registers the names of the input variables with the Reader. They are required to be
the same (and in the same order) as the names used for training (this requirement is not actually
mandatory, but enforced to ensure the consistency between training and application). Together with
the name is given the address of a local variable, which carries the updated input values during the
event loop.
Int_t localDescreteVar;
Float_t localFloatingVar, locaSum, localVar3;
reader->AddVariable( "<YourDescreteVar>", &localDescreteVar );
reader->AddVariable( "log(<YourFloatingVar>)", &localFloatingVar );
reader->AddVariable( "SumLabel := <YourVar1>+<YourVar2>", &locaSum );
reader->AddVariable( "<YourVar3>", &localVar3 );
Code Example 22: Declaration of the variables and references used as input to the methods (cf. Code
Example 12). The order and naming of the variables must be consistent with the ones used for the training.
The local variables are updated during the event loop, and through the references their values are known to
the MVA methods. The variable type must be either float or int (double is not supported).
3.3.2 Booking MVA methods
The selected MVA methods are booked with the Reader using the weight files from the preceding
training job:

34 3 Using TMVA
Macro Description
likelihoodrefs.C Plots the reference PDFs of all input variables for the projective likeli-
hood method and compares it to original distributions obtained from
the training sample.
network.C Draws the TMVA-MLP architecture including weights after training
(does not work for the other ANNs).
annconvergencetest.C Plots the MLP error-function convergence versus the training epoch
for training and test events (does not work for the other ANNs).
BDT.C(i) Draws the ith decision tree of the trained forest (default is i=1). The
second argument is the weight file that contains the full architecture
of the forest (default is weights/TMVAClassification BDT.weights.
xml).
BDTControlPlots.C Plots distributions of boost weights throughout forest, boost weights
versus decision tree, error fraction, number of nodes before and after
pruning and the coefficient α.
mvarefs.C Plots the PDFs used to compute the probability response for a clas-
sifier, and compares it to the original distributions.
PlotFoams.C Draws the signal and background foams created by the method PDE-
Foam.
rulevis.C Plots the relative importance of rules and linear terms. The 1D plots
show the accumulated importance per input variable. The 2D scat-
ter plots show the same but correlated between the input variables.
These plots help to identify regions in the parameter space that are
important for the model.
Table 4: List of ROOT macros representing results for specific MVA methods. The macros require that
these methods have been included in the training. All macros take as first argument the name of the ROOT
file containing the histograms (default is TMVA.root).
reader->BookMVA( "<YourMethodName>", "<path/JobName_MethodName.weights.xml>" );
Code Example 23: Booking a multivariate method. The first argument is a user defined name to distinguish
between methods (it does not need to be the same name as for training, although this could be a useful choice).
The true type of the method and its full configuration are read from the weight file specified in the second
argument. The default structure of the weight file names is: path/hJobNamei hMethodNamei.weights.xml.
3.3.3 Requesting the MVA response
Within the event loop, the response value of a classifier, and – if available – its error, for a given
set of input variables computed by the user, are obtained with the commands:

3.3 The TMVA Reader 35
localDescreteVar = treeDescreteVar; // reference could be implicit
localFloatingVar = log(treeFloatingVar);
locaSum = treeVar1 + treeVar2;
localVar3 = treeVar3; // reference could be implicit
// Classifier response
Double_t mvaValue = reader->EvaluateMVA( "<YourMethodName>" );
// Error on classifier response - must be called after "EvaluateMVA"
// (not available for all methods, returns -1 in that case)
Double_t mvaErr = reader->GetMVAError();
Code Example 24: Updating the local variables for an event, and obtaining the corresponding classifier
output and error (if available – see text).
The output of a classifier may then be used for example to put a cut that increases the signal purity
of the sample (the achievable purities can be read off the evaluation results obtained during the
test phase), or it could enter a subsequent maximum-likelihood fit, or similar. The error reflects the
uncertainty, which may be statistical, in the output value as obtained from the training information.
For regression, multi-target response is already supported in TMVA, so that the retrieval command
reads:
// Regression response for one target
Double_t regValue = (reader->EvaluateRegression( "<YourMethodName>" ))[0];
Code Example 25: Obtaining the regression output (after updating the local variables for an event – see
above). For mult-target regression, the corresponding vector entries are filled.
The output of a regression method could be directly used for example as energy estimate for a
calorimeter cluster as a function of the cell energies.
The rectangular cut classifier is special since it returns a binary answer for a given set of input
variables and cuts. The user must specify the desired signal efficiency to define the working point
according to which the Reader will choose the cuts:
Bool_t passed = reader->EvaluateMVA( "Cuts", signalEfficiency );
Code Example 26: For the cut classifier, the second parameter gives the desired signal efficiency according
to which the cuts are chosen. The return value is 1 for passed and 0 for retained. See Footnote 20 on page 61
for information on how to determine the optimal working point for known signal and background abundance.

36 3 Using TMVA
Instead of the classifier response values, one may also retrieve the ratio (12) from the Reader, which,
if properly normalised to the expected signal fraction in the sample, corresponds to a probability.
The corresponding command reads:
Double_t pSig = reader->GetProba( "<YourClassifierName>", sigFrac );
Code Example 27: Requesting the event’s signal probability from a classifier. The signal fraction is the
parameter f
Sin Eq. (12).
Similarly, the probability integral transformation (Rarity) (13) of a classifier is retrieved by the
command
Double_t rarity = reader->GetRarity( "<YourClassifierName>" );
Code Example 28: Requesting the event’s probability integral transformation distribution from a classifier.
3.4 An alternative to the Reader: standalone C++ response classes
To simplify the portability of the trained MVA response to any application the TMVA methods
generate after the training lightweight standalone C++ response classes including in the source
code the content of the weight files.11 These classes do not depend on ROOT, neither on any other
non-standard library. The names of the classes are constructed out of Read+"MethodName", and
they inherit from the interface class IClassifierReader, which is written into the same C++ file.
These standalone classes are presently only available for classification.
An example application (ROOT script here, not representative for a C++ standalone application)
for a Fisher classifier is given in Code-Example 29. The example is also available in the macro
TMVA/macros/ClassApplication.C (Sourceforge.net). These classes are C++ representations of
the information stored in the weight files. Any change in the training parameters will generate a
new class, which must be updated in the corresponding application.12
For a given test event, the MVA response returned by the standalone class is identical to the one
returned by the Reader. Nevertheless, we emphasise that the recommended approach to apply the
training results is via the Reader.
11At present, the class making functionality has been implemented for all MVA methods with the exception of cut
optimisation, PDE-RS, PDE-Foam and k-NN. While for the former classifier the cuts can be easily implemented into
the user application, and do not require an extra class, the implementation of a response class for PDE-RS or k-NN
requires a copy of the entire analysis code, which we have not attempted so far. We also point out that the use of the
standalone C++ class for BDT is not practical due to the colossal size of the generated code.
12We are aware that requiring recompilation constitutes a significant shortcoming. we consider to upgrade these
classes to reading the XML weight files, which entails significant complications if the independence of any external
library shall be conserved.

3.4 An alternative to the Reader: standalone C++ response classes 37
// load the generated response class into macro and compile it (ROOT)
// or include it into any C++ executable
gROOT->LoadMacro( "TMVAClassification_Fisher.class.C++" ); // usage in ROOT
// define the names of the input variables (same as for training)
std::vector<std::string> inputVars;
inputVars.push_back( "<YourVar1>" );
inputVars.push_back( "log(<YourVar2>)" );
inputVars.push_back( "<YourVar3>+<YourVar4>" );
// create a class object for the Fisher response
IClassifierReader* fisherResponse = new ReadFisher( inputVars );
// the user’s event loop ...
std::vector<double> inputVec( 3 );
for (...) {
// compute the input variables for the event
inputVec[0] = treeVar1;
inputVec[1] = TMath::Log(treeVar2);
inputVec[2] = treeVar3 + treeVar4;
// get the Fisher response
double fiOut = fisherResponse->GetMvaValue( inputVec );
// ... use fiOut
}
Code Example 29: Using a standalone C++ class for the classifier response in an application (here of the
Fisher discriminant). See also the example code in TMVA/macros/ClassApplication.C (Sourceforge.net).

38 4 Data Preprocessing
4 Data Preprocessing
It is possible to preprocess the discriminating input variables or the training events prior to pre-
senting them to a multivariate method. Preprocessing can be useful to reduce correlations among
the variables, to transform their shapes into more appropriate forms, or to accelerate the response
time of a method (event sorting).
The preprocessing is completely transparent to the MVA methods. Any preprocessing performed
for the training is automatically performed in the application through the Reader class. All the
required information is stored in the weight files of the MVA method. The preprocessing methods
normalisation and principal component decomposition are available for input and target variables,
gaussianization, uniformization and decorrelation discussed below can only be used for input vari-
ables.
Apart from five variable transformation methods mentioned above, an unsupervised variable selec-
tion method Variance Threshold is also implemented in TMVA. It follows a completely different
processing pipeline. It is discussed in detail in section 4.2.
4.1 Transforming input variables
Currently five preprocessing transformations are implemented in TMVA:
•variable normalisation;
•decorrelation via the square-root of the covariance matrix ;
•decorrelation via a principal component decomposition;
•transformation of the variables into Uniform distributions (“Uniformization”).
•transformation of the variables into Gaussian distributions (“Gaussianisation”).
Normalisation and principal component decomposition can be applied to input and target vari-
ables, the other transformations can only be used for the input variables. The transformations be
performed for all input variables of for a selected subset of the input variables only. The latter is
especially useful in situations where only some variables are correlated or the correlations are very
different for different subsets.
All transformations can be performed separately for signal and background events because their
correlation patterns are usually different.13
Technically, any transformation of the input and target variables is performed “on the fly” when the
event is requested from the central DataSet class. The preprocessing is hence fully transparent to
13Different transformations for signal and background events are only useful for methods that explicitly distinguish
signal and background hypotheses. This is the case for the likelihood and PDE-RS classifiers. For all other methods
the user must choose which transformation to use.
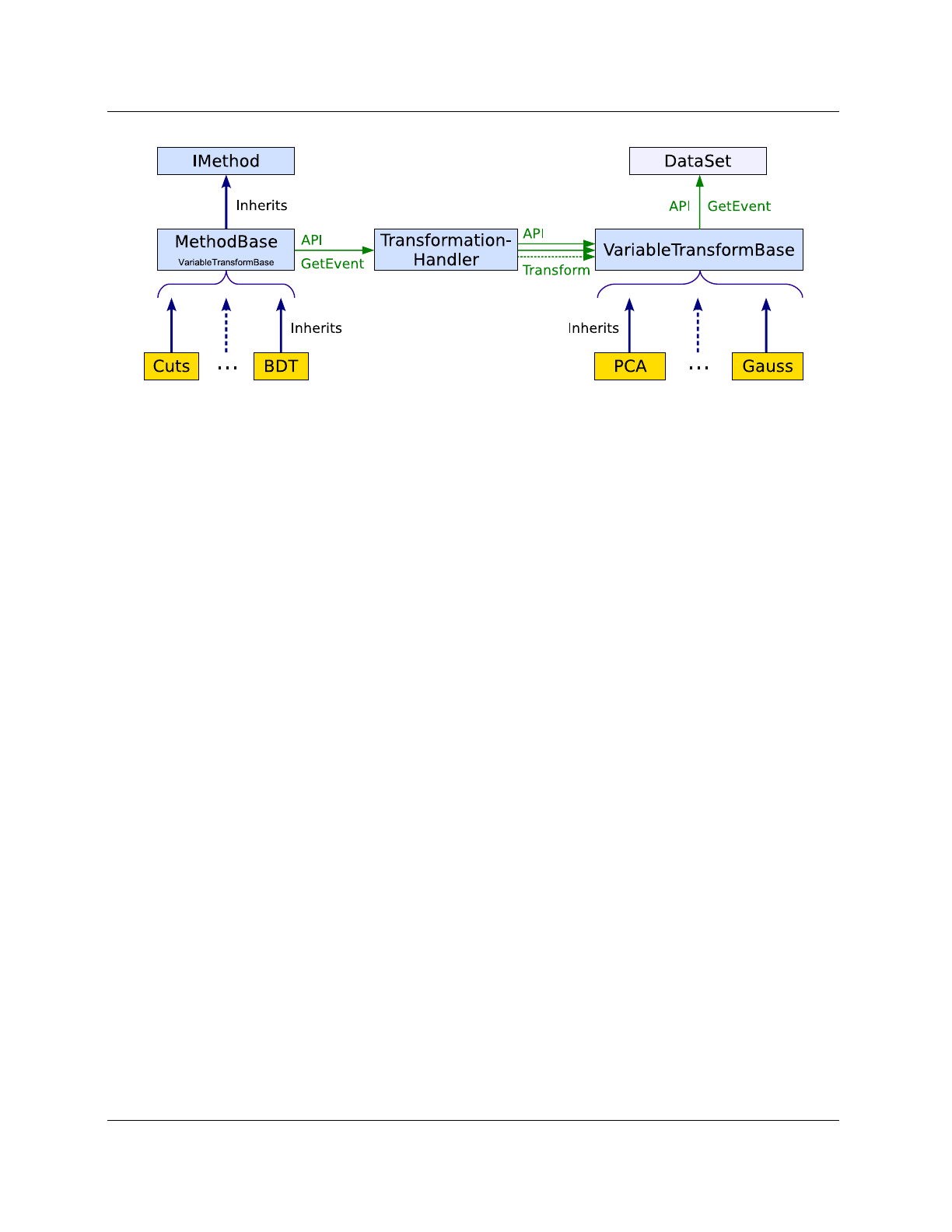
4.1 Transforming input variables 39
Figure 10: Schematic view of the variable transformation interface implemented in TMVA. Each concrete
MVA method derives from MethodBase (interfaced by IMethod), which holds a protected member object
of type TransformationHandler. In this object a list of objects derived from VariableTransformBase
which are the implementations of the particular variable transformations available in TMVA is stored. The
construction of the concrete variable transformation objects proceeds in MethodBase according to the trans-
formation methods requested in the option string. The events used by the MVA methods for training, testing
and final classification (or regression) analysis are read via an API of the TransformationHandler class,
which itself reads the events from the DataSet and applies subsequently all initialised transformations. The
DataSet fills the current values into the reserved event addresses (the event content may either stem from the
training or testing trees, or is set by the user application via the Reader for the final classification/regression
analysis). The TransformationHandler class ensures the proper transformation of all events seen by the
MVA methods.
the MVA methods. Any preprocessing performed for the training is automatically also performed
in the application through the Reader class. All the required information is stored in the weight
files of the MVA method. Each MVA method carries a variable transformation type together with a
pointer to the object of its transformation class which is owned by the DataSet. If no preprocessing
is requested, an identity transform is applied. The DataSet registers the requested transformations
and takes care not to recreate an identical transformation object (if requested) during the training
phase. Hence if two MVA methods wish to apply the same transformation, a single object is
shared between them. Each method writes its transformation into its weight file once the training
has converged. For testing and application of an MVA method, the transformation is read from
the weight file and a corresponding transformation object is created. Here each method owns its
transformation so that no sharing of potentially different transformation objects occurs (they may
have been obtained with different training data and/or under different conditions). A schematic
view of the variable transformation interface used in TMVA is drawn in Fig. 10.
4.1.1 Variable normalisation
Minimum and maximum values for the variables to be transformed are determined from the training
events and used to linearly scale these input variables to lie within [−1,1]. Such a transformation is
useful to allow direct comparisons between the MVA weights assigned to the variables, where large

40 4 Data Preprocessing
absolute weights may indicate strong separation power. Normalisation may also render minimisation
processes, such as the adjustment of neural network weights, more effective.
4.1.2 Variable decorrelation
A drawback of, for example, the projective likelihood classifier (see Sec. 8.2) is that it ignores
correlations among the discriminating input variables. Because in most realistic use cases this is
not an accurate conjecture it leads to performance loss. Also other classifiers, such as rectangular
cuts or decision trees, and even multidimensional likelihood approaches underperform in presence
of variable correlations.
Linear correlations, measured in the training sample, can be taken into account in a straightforward
manner through computing the square-root of the covariance matrix. The square-root of a matrix
Cis the matrix C0that multiplied with itself yields C:C= (C0)2. TMVA computes the square-root
matrix by means of diagonalising the (symmetric) covariance matrix
D=STCS ⇒C0=S√DST,(14)
where Dis a diagonal matrix, and where the matrix Sis symmetric. The linear decorrelation of
the selected variables is then obtained by multiplying the initial variable tuple xby the inverse of
the square-root matrix
x7→ (C0)−1x.(15)
The decorrelation is complete only for linearly correlated and Gaussian distributed variables. In sit-
uations where these requirements are not fulfilled only little additional information can be recovered
by the decorrelation procedure. For highly nonlinear problems the performance may even become
worse with linear decorrelation. Nonlinear methods without prior variable decorrelation should be
used in such cases.
4.1.3 Principal component decomposition
Principal component decomposition or principal component analysis (PCA) as presently applied in
TMVA is not very different from the above linear decorrelation. In common words, PCA is a linear
transformation that rotates a sample of data points such that the maximum variability is visible.
It thus identifies the most important gradients. In the PCA-transformed coordinate system, the
largest variance by any projection of the data comes to lie on the first coordinate (denoted the
first principal component), the second largest variance on the second coordinate, and so on. PCA
can thus be used to reduce the dimensionality of a problem (initially given by the number of input
variables) by removing dimensions with insignificant variance. This corresponds to keeping lower-
order principal components and ignoring higher-order ones. This latter step however goes beyond
straight variable transformation as performed in the preprocessing steps discussed here (it rather
represents itself a full classification method). Hence all principal components are retained here.
The tuples xPC
U(i) = (xPC
U,1(i), . . . , xPC
U,nvar (i)) of principal components of a tuple of input variables
x(i)=(x1(i), . . . , xnvar (i)), measured for the event ifor signal (U=S) and background (U=B),
4.1 Transforming input variables 41
are obtained by the transformation
xPC
U,k(i) =
nvar
X
`=1
(xU,`(i)−xU,`)v(k)
U,` ,∀k= 1, nvar .(16)
The tuples xUand v(k)
Uare the sample means and eigenvectors, respectively. They are computed by
the ROOT class TPrincipal. The matrix of eigenvectors VU= (v(1)
U,...,v(nvar)
U) obeys the relation
CU·VU=DU·VU,(17)
where Cis the covariance matrix of the sample U, and DUis the tuple of eigenvalues. As for
the preprocessing described in Sec. 4.1.2, the transformation (16) eliminates linear correlations for
Gaussian variables.
4.1.4 Uniform and Gaussian transformation of variables (“Uniformisation” and “Gaussian-
isation”)
The decorrelation methods described above require linearly correlated and Gaussian distributed
input variables. In real-life HEP applications this is however rarely the case. One may hence trans-
form the variables prior to their decorrelation such that their distributions become Gaussian. The
corresponding transformation function is conveniently separated into two steps: first, transform a
variable into a uniform distribution using its cumulative distribution function14 obtained from the
training data (this transformation is identical to the probability integral transformation (“Rarity”)
introduced in Sec. 3.1.13 on page 29); second, use the inverse error function to transform the uniform
distribution into a Gaussian shape with zero mean and unity width. As for the other transforma-
tions, one needs to choose which class of events (signal or background) is to be transformed and
hence, for the input variables (Gaussianisation is not available for target values), it is only possible
to transform signal or background into proper Gaussian distributions (except for classifiers testing
explicitly both hypotheses such as likelihood methods). Hence a discriminant input variable xwith
the probability density function ˆxis transformed as follows
x7→ √2·erf−1
2·
x
Z
−∞
ˆx(x0)dx0−1
.(18)
A subsequent decorrelation of the transformed variable tuple sees Gaussian distributions, but most
likely non-linear correlations as a consequence of the transformation (18). The distributions ob-
tained after the decorrelation may thus not be Gaussian anymore. It has been suggested that
iterating Gaussianisation and decorrelation more than once may improve the performance of likeli-
hood methods (see next section).
14The cumulative distribution function F(x) of the variable xis given by the integral F(x) =
x
R
−∞
ˆx(x0)dx0, where ˆx
is the probability density function of x.

42 4 Data Preprocessing
4.1.5 Booking and chaining transformations for some or all input variables
Variable transformations to be applied prior to the MVA training (and application) can be defined
independently for each MVA method with the booking option VarTransform=<type>, where <type>
denotes the desired transformation (or chain of transformations). The available transformation
types are normalisation, decorrelation, principal component analysis and Gaussianisation, which
are labelled by Norm,Deco,PCA,Uniform,Gauss, respectively, or, equivalently, by the short-hand
notations N,D,P,U,G.
Transformations can be chained allowing the consecutive application of all defined transformations
to the variables for each event. For example, the above Gaussianisation and decorrelation se-
quence would be programmed by VarTransform=G,D, or even VarTransform=G,D,G,D in case of
two iterations (instead of the comma “,”, a “+” can be equivalently used as chain operator, i.e.
VarTransform=G+D+G+D). The ordering of the transformations goes from left (first) to right (last).
factory->BookMethod( TMVA::Types::kLD, "LD_GD", "H:!V:VarTransform=G,D");
Code Example 30: Booking of a linear discriminant (LD) classifier with Gaussianisation and decorrelation
for all input variables.
By default, the transformations are computed with the use of all training events. It is possible to
specify the use of a specific class only (e.g., Signal,Background,Regression) by attaching <class
name> to the user option – where <class name> has to be replaced by the actual class name (e.g.,
Signal) – which defines the transformation (e.g., VarTransform=G Signal). A complex transfor-
mation option might hence look like VarTransform=D,G Signal,N. The attachment AllClasses
is equivalent to the default, where events from all classes are used.
factory->BookMethod( TMVA::Types::kLD, "LD_GDSignal", "H:!V:VarTransform= \
G_Signal,D_Signal");
Code Example 31: Booking of a linear discriminant (LD) classifier where the Gaussianisation and decorre-
lation transformations are computed from the signal events only.
By default, all input variables are transformed when booking a transformation. In many situations
however, it is desirable to apply a transformation only to a subset of all variables15. Such a selec-
tion can be achieved by specifying the variable names separated by commas in brackets after the
transformation name, i.e. VarTransform=N(var2,var1,myvar3). Alternatively the variables and
targets can be denoted by their position Vhindexi(for input variables) and Thindexi(for targets)
where the index is the position of the variable (target) according to the order in which the variables
where defined to the factory (e.g. VarTransform=N( V0 , V3 , T3 ). The numbering starts with
15As decorrelation for example is only reasonable if the variables have strong “linear” correlations, it might be wise
to apply the decorrelation only to those variables that have linear correlations

4.2 Variable selection based on variance 43
0 and the ordering of the variables within the parentheses has no impact. To address all variables
(targets) the keywords Vand Tcan be used. The result of a transformation is written back into
the same variables. For instance in the case of the principal component analysis transformation
the first (and most important) eigenvalue is written into the variable with the smallest index, the
second eigentvalue into the variable with the second lowest index and so forth. Input variables and
targets can only be transformed at the same time if each variable is transformed independently.
This is the case for the normalisation transformation.
Transformations of variable subsets can also be chained. For example, in VarTransform=N+P(
V0 ,var2, V4 )+P( T ) Background+G Signal, first all variables and targets are normalized with
respect to all events, then the variables with the indices 0 and 4 and the variable var2 are PCA
transformed, subsequently all targets are PCA transformed with respect to the background events
and finally all variables are gaussianised with respect to the signal events.
factory->BookMethod( TMVA::Types::kLD, "LD_DSubset", "H:!V:VarTransform= \
D(_V0_,var2)");
Code Example 32: Booking of a linear discriminant (LD) classifier where only the first variable and the
variable labeled var2 are subject to a decorrelation transformation.
4.2 Variable selection based on variance
In high energy physics and machine learning problems, we often encounter datasets which have
large number of input variables. However to extract maximum information from the data, we
need to select the relevant input variables for the multivariate classification and regression methods
implemented in TMVA. Variance Threshold is a simple unsupervised variable selection method
which automates this process. It computes weighted variance σ2
jfor each variable j= 1, . . . , nvar
and ignores the ones whose variance lie below a specific threshold. Weighted variance for each
variable is defined as follows:
σ2
j=PN
i=1 wi(xj(i)−µj)2
PN
i=1 wi
(19)
where Nis the total number of events in a dataset, x(i)=(x1(i), . . . , xnvar (i)) denotes each event i
and wiis the weight of each event. Weighted mean µjis defined as:
µj=PN
i=1 wixj(i)
PN
i=1 wi
(20)
Unlike above five variable transformation method, this Variance Threshold method is implemented
in DataLoader class. After loading dataset in the DataLoader object, we can apply this method. It
returns a new DataLoader with the selected variables which have variance strictly greater than the
threshold value passed by user. Default value of threshold is zero i.e. remove the variables which
have same value in all the events.
44 5 Probability Density Functions – the PDF Class
// Threshold value of variance = 2.95
TMVA::DataLoader* transformed_loader1 = loader->VarTransform("VT(2.95)");
// No threshold value passed in below example, hence default value = 0
TMVA::DataLoader* transformed_loader2 = loader->VarTransform("VT");
Code Example 33: VT stands for Variance Threshold. Parameter passed to VarTransform method is just a
single string. String strictly follows either of the above two formats for Variance Threshold otherwise method
would raise an error.
4.3 Binary search trees
When frequent iterations over the training sample need to be performed, it is helpful to sort the
sample before using it. Event sorting in binary trees is employed by the MVA methods rectangular
cut optimisation, PDE-RS and k-NN. While the former two classifiers rely on the simplest possible
binary tree implementation, k-NN uses on a better performing kd-tree (cf. Ref. [12]).
Efficiently searching for and counting events that lie inside a multidimensional volume spanned
by the discriminating input variables is accomplished with the use of a binary tree search algo-
rithm [13].16 It is realised in the class BinarySearchTree, which inherits from BinaryTree, and
which is also employed to grow decision trees (cf. Sec. 8.13). The amount of computing time needed
to sort Nevents into the tree is [14]∝PN
i=1 ln2(i) = ln2(N!) 'Nln2N. Finding the events within
the tree which lie in a given volume is done by comparing the bounds of the volume with the co-
ordinates of the events in the tree. Searching the tree once requires a CPU time that is ∝ln2N,
compared to ∝Nnvar without prior event sorting.
5 Probability Density Functions – the PDF Class
Several methods and functionalities in TMVA require the estimation of probability densities (PDE)
of one or more correlated variables. One may distinguish three conceptually different approaches to
PDEs: (i) parametric approximation, where the training data are fitted with a user-defined para-
metric function, (ii) nonparametric approximation, where the data are fitted piecewise using simple
standard functions, such as a polynomial or a Gaussian, and (iii) nearest-neighbour estimation,
where the average of the training data in the vicinity of a test event determines the PDF.
16The following is extracted from Ref. [14] for a two-dimensional range search example. Consider a random sequence
of signal events ei(x1, x2), i= 1,2, . . . , which are to be stored in a binary tree. The first event in the sequence becomes
by definition the topmost node of the tree. The second event e2(x1, x2) shall have a larger x1-coordinate than the
first event, therefore a new node is created for it and the node is attached to the first node as the right child (if the
x1-coordinate had been smaller, the node would have become the left child). Event e3shall have a larger x1-coordinate
than event e1, it therefore should be attached to the right branch below e1. Since e2is already placed at that position,
now the x2-coordinates of e2and e3are compared, and, since e3has a larger x2,e3becomes the right child of the
node with event e2. The tree is sequentially filled by taking every event and, while descending the tree, comparing
its x1and x2coordinates with the events already in place. Whether x1or x2are used for the comparison depends on
the level within the tree. On the first level, x1is used, on the second level x2, on the third again x1and so on.
5.1 Nonparametric PDF fitting using spline functions 45
All multidimensional PDEs used in TMVA are based on nearest-neighbour estimation with however
quite varying implementations. They are described in Secs. 8.3,8.4 and 8.5.
One-dimensional PDFs in TMVA are estimated by means of nonparametric approximation, because
parametric functions cannot be generalised to a-priori unknown problems. The training data can be
in form of binned histograms, or unbinned data points (or “quasi-unbinned” data, i.e., histograms
with very narrow bins). In the first case, the bin centres are interpolated with polynomial spline
curves, while in the latter case one attributes a kernel function to each event such that the PDF
is represented by the sum over all kernels. Beside a faithful representation of the training data, it
is important that statistical fluctuations are smoothed out as much as possible without destroying
significant information. In practise, where the true PDFs are unknown, a compromise determines
which information is regarded significant and which is not. Likelihood methods crucially depend on
a good-quality PDF representation. Since the PDFs are strongly problem dependent, the default
configuration settings in TMVA will almost never be optimal. The user is therefore advised to
scrutinise the agreement between training data and PDFs via the available plotting macros, and to
optimise the settings.
In TMVA, all PDFs are derived from the PDF class, which is instantiated via the command (usually
hidden in the MVA methods for normal TMVA usage):
PDF* pdf = new PDF( "<options>", "Suffix", defaultPDF );
pdf->BuildPDF( SourceHistogram );
double p = pdf->GetVal( x );
Code Example 34: Creating and using a PDF class object. The first argument is the configuration options
string. Individual options are separated by a ’:’. The second optional argument is the suffix appended to
the options used in the option string. The suffix is added to the option names given in the Option Table 3
in order to distinguish variables and types. The third (optional) object is a PDF from which default option
settings are read. The histogram specified in the second line is a TH1* object from which the PDF is built.
The third line shows how to retrieve the PDF value at a given test value ’x’.
Its configuration options are given in Option Table 3.
5.1 Nonparametric PDF fitting using spline functions
Polynomial splines of various orders are fitted to one-dimensional (1D) binned histograms according
to the following procedure.
1. The number of bins of the TH1 object representing the distribution of the input variable is
driven by the options NAvEvtPerBin or Nbins (cf. Option Table 3). Setting Nbins enforces a
fixed number of bins, while NAvEvtPerBin defines an average number of entries required per
bin. The upper and lower bounds of the histogram coincide with the limits found in the data
(or they are [−1,1] if the input variables are normalised).

46 5 Probability Density Functions – the PDF Class
Option Values Description
PDFInterpol KDE,
Spline0,
Spline1,
Spline2*,
Spline3,
Spline5
The method of interpolating the reference histograms:
either by using the unbinned kernel density estima-
tor (KDE), or by various degrees of spline functions
(note that currently the KDE characteristics cannot
be changed individually but apply to all variables that
select KDE)
NSmooth 0 Number of smoothing iterations for the input his-
tograms; if set, MinNSmooth and MaxNSmooth are ig-
nored
MinNSmooth -1 Minimum number of smoothing iteration for the input
histograms; for bins with least relative error (see text)
MaxNSmooth -1 Maximum number of smoothing iteration for the input
histograms; for bins with most relative error (see text)
Nbins 0 Number of bins used to build the reference histogram;
if set to value >0, NAvEvtPerBin is ignored
NAvEvtPerBin 50 Average number of events per bin in the reference his-
togram (see text)
KDEtype Gauss* KDE kernel type (currently only Gauss)
KDEiter Nonadaptive*,
Adaptive
Non-adaptive or adaptive number of iterations (see
text)
KDEFineFactor 1 Fine-tuning factor for the adaptive KDE
KDEborder None*, Renorm,
Mirror
Method for correcting histogram boundary/border ef-
fects
CheckHist False Sanity comparison of derived high-binned interpolated
PDF histogram versus the original PDF function
Option Table 3: Configuration options for class: PDF. Values given are defaults. If predefined categories
exist, the default category is marked by a ’?’. In case a suffix is defined for the PDF, it is added in the end
of the option name. For example for PDF with suffix MVAPdf the number of smoothing iterations is given by
the option NSmoothMVAPdf (see Option Table 11 on page 65 for a concrete use of the PDF options in a MVA
method).

5.2 Nonparametric PDF parameterisation using kernel density estimators 47
2. The histogram is smoothed adaptively between MinNSmooth and MaxNSmooth times, using
TH1::Smooth(.) – an implementation of the 353QH-twice algorithm [20]. The appropriate
number of smoothing iterations is derived with the aim to preserve statistically significant
structures, while smoothing out fluctuations. Bins with the largest (smallest) relative sta-
tistical error are maximally (minimally) smoothed. All other bins are smoothed between
MaxNSmooth and MinNSmooth times according to a linear function of their relative errors.
During the smoothing process a histogram with the suffix NSmooth is created for each vari-
able, where the number of smoothing iterations applied to each bin is stored.
3. The smoothed TH1 object is internally cloned and the requested polynomial splines are used to
interpolate adjacent bins. All spline classes are derived from ROOT’s TSpline class. Available
are: polynomials of degree 0 (the original smoothed histogram is kept), which is used for
discrete variables; degree 1 (linear), 2 (quadratic), 3 (cubic) and degree 5. Splines of degree
two or more render the PDF continuous and differentiable in all points excluding the interval
borders. In case of a likelihood analysis, this ensures the same property for the likelihood
ratio (36). Since cubic (and higher) splines equalise the first and second derivatives at the
spline transitions, the resulting curves, although mathematically smooth, can wiggle in quite
unexpected ways. Furthermore, there is no local control of the spline: moving one control
point (bin) causes the entire curve to change, not just the part near the control point. To
ensure a safe interpolation, quadratic splines are used by default.
4. To speed up the numerical access to the probability densities, the spline functions are stored
into a finely binned (104bins) histogram, where adjacent bins are interpolated by a linear
function. Only after this step, the PDF is normalised according to Eq. (38).
5.2 Nonparametric PDF parameterisation using kernel density estimators
Another type of nonparametric approximation of a 1D PDF are kernel density estimators (KDE).
As opposed to splines, KDEs are obtained from unbinned data. The idea of the approach is to
estimate the shape of a PDF by the sum over smeared training events. One then finds for a PDF
p(x) of a variable x[21]
p(x) = 1
N h
N
X
i=1
Kx−xi
h=1
N
N
X
i=1
Kh(x−xi),(21)
where Nis the number of training events, Kh(t) = K(t/h)/h is the kernel function, and his the
bandwidth of the kernel (also termed the smoothing parameter). Currently, only a Gaussian form of
Kis implemented in TMVA, where the exact form of the kernel function is of minor relevance for
the quality of the shape estimation. More important is the choice of the bandwidth.
The KDE smoothing can be applied in either non-adaptive (NA) or adaptive form (A), the choice
of which is controlled by the option KDEiter. In the non-adaptive case the bandwidth hNA is kept
constant for the entire training sample. As optimal bandwidth can be taken the one that minimises
the asymptotic mean integrated square error (AMISE). For the case of a Gaussian kernel function

48 5 Probability Density Functions – the PDF Class
this leads to [21]
hNA =4
3
1/5
σxN−1/5,(22)
where σxis the RMS of the variable x.
The so-called sample point adaptive method uses as input the result of the non-adaptive KDE, but
also takes into account the local event density. The adaptive bandwidth hAthen becomes a function
of p(x) [21]
hA(x) = hNA
pp(x).(23)
The adaptive approach improves the shape estimation in regions with low event density. However,
in regions with high event density it can give rise to “over-smoothing” of fine structures such as
narrow peaks. The degree of smoothing can be tuned by multiplying the bandwidth hA(x) with the
user-specified factor KDEFineFactor.
For practical reasons, the KDE implementation in TMVA differs somewhat from the procedure
described above. Instead of unbinned training data a finely-binned histogram is used as input, which
allows to significantly speed up the algorithm. The calculation of the optimal bandwidth hNA is
performed in the dedicated class KDEKernel. If the algorithm is run in the adaptive mode, the non-
adaptive step is also performed because its output feeds the computation of hA(x) for the adaptive
part. Subsequently, a smoothed high-binned histogram estimating the PDF shape is created by
looping over the bins of the input histogram and summing up the corresponding kernel functions,
using hNA (hA(x)) in case of the non-adaptive (adaptive) mode. This output histogram is returned
to the PDF class.
Both the non-adaptive and the adaptive methods can suffer from the so-called boundary problem
at the histogram boundaries. It occurs for instance if the original distribution is non-zero below
a physical boundary value and zero above. This property cannot be reproduced by the KDE
procedure. In general, the stronger the discontinuity the more acute is the boundary problem.
TMVA provides three options under the term KDEborder that allow to treat boundary problems.
•KDEborder=None
No boundary treatment is performed. The consequence is that close to the boundary the KDE
result will be inaccurate: below the boundary it will underestimate the PDF while it will not
drop to zero above. In TMVA the PDF resulting from KDE is a (finely-binned) histogram,
with bounds equal to the minimum and the maximum values of the input distribution. Hence,
the boundary value will be at the edge of the PDF (histogram), and a drop of the PDF due to
the proximity of the boundary can be observed (while the artificial enhancement beyond the
boundary will fall outside of the histogram). In other words, for training events that are close
to the boundary some fraction of the probability “flows” outside the histogram (probability
leakage). As a consequence, the integral of the kernel function inside the histogram borders is
smaller than one.
•KDEborder=Renorm
The probability leakage is compensated by renormalising the kernel function such that the
integral inside the histogram borders is equal to one.

49
Option Values Description
FitMethod MC, MINUIT, GA, SA Fitter method
Converger None*, MINUIT Converger which can be combined with MC or
GA (currently only used for FDA) to improve
finding local minima
Option Table 4: Configuration options for the choice of a fitter. The abbreviations stand for Monte Carlo
sampling, Minuit, Genetic Algorithm, Simulated Annealing. By setting a Converger (only Minuit is currently
available) combined use of Monte Carlo sampling and Minuit, and of Genetic Algorithm and Minuit is possible.
The FitMethod option can be used in any MVA method that requires fitting. The option Converger is
currently only implemented in FDA. The default fitter depends on the MVA method. The fitters and their
specific options are described below.
•KDEborder=Mirror
The original distribution is “mirrored” around the boundary. The same procedure is applied
to the mirrored events and each of them is smeared by a kernel function and its contribution
inside the histogram’s (PDF) boundaries is added to the PDF. The mirror copy compensates
the probability leakage completely.
6 Optimisation and Fitting
Several MVA methods (notably cut optimisation and FDA) require general purpose parameter
fitting to optimise the value of an estimator. For example, an estimator could be the sum of
the deviations of classifier outputs from 1 for signal events and 0 for background events, and the
parameters are adjusted so that this sum is as small as possible. Since the various fitting problems
call for dedicated solutions, TMVA has a fitter base class, used by the MVA methods, from which
all concrete fitters inherit. The consequence of this is that the user can choose whatever fitter is
deemed suitable and can configure it through the option string of the MVA method. At present,
four fitters are implemented and described below: Monte Carlo sampling, Minuit minimisation, a
Genetic Algorithm, Simulated Annealing. They are selected via the configuration option of the
corresponding MVA method for which the fitter is invoked (see Option Table 4). Combinations of
MC and GA with Minuit are available for the FDA method by setting the Converger option, as
described in Option Table 16.
6.1 Monte Carlo sampling
The simplest and most straightforward, albeit inefficient fitting method is to randomly sample the
fit parameters and to choose the set of parameters that optimises the estimator. The priors used
for the sampling are uniform or Gaussian within the parameter limits. The specific configuration
options for the MC sampling are given in Option Table 5.

50 6 Optimisation and Fitting
Option Array Default Predefined Values Description
SampleSize –100000 –Number of Monte Carlo events in toy
sample
Sigma –-1 –If >0: new points are generated ac-
cording to Gauss around best value
and with Sigma in units of interval
length
Seed –100 –Seed for the random generator (0 takes
random seeds)
Option Table 5: Configuration options reference for fitting method: Monte Carlo sampling (MC).
For fitting problems with few local minima out of which one is a global minimum the performance can
be enhanced by setting the parameter Sigma to a positive value. The newly generated parameters are
then not any more independent of the parameters of the previous samples. The random generator
will throw random values according to a Gaussian probability density with the mean given by the
currently known best value for that particular parameter and the width in units of the interval size
given by the option Sigma. Points which are created out of the parameter’s interval are mapped
back into the interval.
6.2 Minuit minimisation
Minuit is the standard multivariate minimisation package used in HEP [17]. Its purpose is to find
the minimum of a multi-parameter estimator function and to analyse the shape of the function
around the minimum (error analysis). The principal application of the TMVA fitters is simple
minimisation, while the shape of the minimum is irrelevant in most cases. The use of Minuit is
therefore not necessarily the most efficient solution, but because it is a very robust tool we have
included it here. Minuit searches the solution along the direction of the gradient until a minimum
or an boundary is reached (MIGRAD algorithm). It does not attempt to find the global minimum
but is satisfied with local minima. If during the error analysis with MINOS, the minimum smaller
values than the local minimum might be obtained. In particular, the use of MINOS may as a
side effect of an improved error analysis uncover a convergence in a local minimum, in which case
MIGRAD minimisation is invoked once again. If multiple local and/or global solutions exist, it
might be preferable to use any of the other fitters which are specifically designed for this type of
problem.
The configuration options for Minuit are given in Option Table 6.
6.3 Genetic Algorithm
A Genetic Algorithm is a technique to find approximate solutions to optimisation or search problems.
The problem is modelled by a group (population) of abstract representations (genomes) of possible

6.3 Genetic Algorithm 51
Option Array Default Predefined Values Description
ErrorLevel –1–TMinuit: error level: 0.5=logL fit,
1=chi-squared fit
PrintLevel –-1 –TMinuit: output level: -1=least, 0,
+1=all garbage
FitStrategy –2–TMinuit: fit strategy: 2=best
PrintWarnings –False –TMinuit: suppress warnings
UseImprove –True –TMinuit: use IMPROVE
UseMinos –True –TMinuit: use MINOS
SetBatch –False –TMinuit: use batch mode
MaxCalls –1000 –TMinuit: approximate maximum
number of function calls
Tolerance –0.1 –TMinuit: tolerance to the function
value at the minimum
Option Table 6: Configuration options reference for fitting method: Minuit. More information on the Minuit
parameters can be found here: http://root.cern.ch/root/html/TMinuit.html.
solutions (individuals). By applying means similar to processes found in biological evolution the
individuals of the population should evolve towards an optimal solution of the problem. Processes
which are usually modelled in evolutionary algorithms — of which Genetic Algorithms are a subtype
— are inheritance, mutation and “sexual recombination” (also termed crossover).
Apart from the abstract representation of the solution domain, a fitness function must be defined.
Its purpose is the evaluation of the goodness of an individual. The fitness function is problem
dependent. It either returns a value representing the individual’s goodness or it compares two
individuals and indicates which of them performs better.
The Genetic Algorithm proceeds as follows:
•Initialisation: A starting population is created. Its size depends on the problem to be solved.
Each individual belonging to the population is created by randomly setting the parameters of
the abstract representation (variables), thus producing a point in the solution domain of the
initial problem.
•Evaluation: Each individual is evaluated using the fitness function.
•Selection: Individuals are kept or discarded as a function of their fitness. Several selection
procedures are possible. The simplest one is to separate out the worst performing fraction
of the population. Another possibility is to decide on the individual’s survival by assigning
probabilities that depend on the individual’s performance compared to the others.
•Reproduction: The surviving individuals are copied, mutated and crossed-over until the initial
population size is reached again.

52 6 Optimisation and Fitting
Option Array Default Predefined Values Description
PopSize –300 –Population size for GA
Steps –40 –Number of steps for convergence
Cycles –3–Independent cycles of GA fitting
SC steps –10 –Spread control, steps
SC rate –5–Spread control, rate: factor is changed
depending on the rate
SC factor –0.95 –Spread control, factor
ConvCrit –0.001 –Convergence criteria
SaveBestGen –1–Saves the best n results from each gen-
eration. They are included in the last
cycle
SaveBestCycle –10 –Saves the best n results from each cy-
cle. They are included in the last cy-
cle. The value should be set to at least
1.0
Trim –False –Trim the population to PopSize after
assessing the fitness of each individual
Seed –100 –Set seed of random generator (0 gives
random seeds)
Option Table 7: Configuration options reference for fitting method: Genetic Algorithm (GA).
•Termination: The evaluation, selection and reproduction steps are repeated until a maximum
number of cycles is reached or an individual satisfies a maximum-fitness criterion. The best
individual is selected and taken as solution to the problem.
The TMVA Genetic Algorithm provides controls that are set through configuration options (cf.
Table 7). The parameter PopSize determines the number of individuals created at each generation
of the Genetic Algorithm. At the initialisation, all parameters of all individuals are chosen randomly.
The individuals are evaluated in terms of their fitness, and each individual giving an improvement
is immediately stored.
Individuals with a good fitness are selected to engender the next generation. The new individuals
are created by crossover and mutated afterwards. Mutation changes some values of some parameters
of some individuals randomly following a Gaussian distribution function. The width of the Gaussian
can be altered by the parameter SC\factor. The current width is multiplied by this factor when
within the last SC\steps generations more than SC\rate improvements have been obtained. If
there were SC\rate improvements the width remains unchanged. Were there, on the other hand,
less than SC\rate improvements, the width is divided by SC\factor. This allows to influence the
speed of searching through the solution domain.
The cycle of evaluating the fitness of the individuals of a generation and producing a new generation
is repeated until the improvement of the fitness within the last Steps has been less than ConvCrit.

6.4 Simulated Annealing 53
The minimisation is then considered to have converged. The whole cycle from initialisation over
fitness evaluation, selection, reproduction and determining the improvement is repeated Cycles
times, before the Genetic Algorithm has finished.
Guidelines for optimising the GA
PopSize is the most important value for enhancing the quality of the results. This value is by
default set to 300, but can be increased to 1000 or more only limited by the resources available.
The calculation time of the GA should increase with O(PopSize).
Steps is set by default to 40. This value can be increased moderately to about 60. Time consumption
increases non linearly but at least with O(Steps).
Cycles is set by default to 3. In this case, the GA is called three times independently from each
other. With SaveBestCycle and SaveBestGen it is possible to set the number of best results which
shall be stored each cycle of even each generation. These stored results are reused in the last cycle.
That way the last cycle is not independent from the others, but incorporates their best results. The
number of cycles can be increased moderately to about 10. The time consumption of GA rises with
about O(Cycles).
6.4 Simulated Annealing
Simulated Annealing also aims at solving a minimisation problem with several discrete or continuous,
local or global minima. The algorithm is inspired by the process of of annealing which occur in
condensed matter physics. When first heating and then slowly cooling down a metal (“annealing”)
its atoms move towards a state of lowest energy, while for sudden cooling the atoms tend to freeze
in intermediate states higher energy. For infinitesimal annealing activity the system will always
converge in its global energy minimum (see, e.g., Ref. [18]). This physical principle can be converted
into an algorithm to achieve slow, but correct convergence of an optimisation problem with multiple
solutions. Recovery out of local minima is achieved by assigning the probability [19]
p(∆E)∝exp −∆E
T,(24)
to a perturbation of the parameters leading to a shift ∆Ein the energy of the system. The
probability of such perturbations to occur decreases with the size of a positive energy coefficient of
the perturbation, and increases with the ambient temperature (T).
Guidelines for optimising SA
The TMVA implementation of Simulated Annealing includes various different adaptive adjustments
of the perturbation and temperature gradients. The adjustment procedure is chosen by setting
KernelTemp to one of the following values.

54 6 Optimisation and Fitting
•Increasing Adaptive Approach (IncAdaptive). The algorithm seeks local minima and ex-
plores their neighbourhood, while changing the ambient temperature depending on the number
of failures in the previous steps. The performance can be improved by increasing the number
of iteration steps (MaxCalls), or by adjusting the minimal temperature (MinTemp). Manual
adjustments of the speed of the temperature increase (TempScale and AdaptiveSpeed) for
individual data sets might also improve the performance.
•Decreasing Adaptive Approach (DecAdaptive). The algorithm calculates the initial temper-
ature (based on the effectiveness of large steps) and defines a multiplier to ensure that the
minimal temperature is reached in the requested number of iteration steps. The performance
can be improved by adjusting the minimal temperature (MinTemp) and by increasing number
of steps (MaxCalls).
•Other Kernels. Several other procedures to calculate the temperature change are also imple-
mented. Each of them starts with the maximum temperature (MaxTemp) and decreases while
changing the temperature according to :
Temperature(k)=
Sqrt :InitialTemp
√k+2 ·TempScale
Log :InitialTemp
ln(k+2) ·TempScale
Homo :InitialTemp
k+2 ·TempScale
Sin :sin(k/TempScale)+1
k+1 ·InitialTemp +ε
Geo :CurrentTemp ·TempScale
Their performances can be improved by adjusting the initial temperature InitialTemp
(= Temperature(k=0)), the number of iteration steps (MaxCalls), and the multiplier that scales
the temperature decrease (TempScale).
The configuration options for the Simulated Annealing fitter are given in Option Table 8.
6.5 Combined fitters
For MVA methods such as FDA, where parameters of a discrimination function are adjusted to
achieve optimal classification performance (cf. Sec. 8.9), the user can choose to combine Minuit
parameter fitting with Monte Carlo sampling or a Genetic Algorithm. While the strength of Minuit
is the speedy detection of a nearby local minimum, it might not find a better global minimum. If
several local minima exist Minuit will find different solutions depending on the start values for the
fit parameters. When combining Minuit with Monte Carlo sampling or a Genetic Algorithm, Minuit
uses starting values generated by these methods. The subsequent fits then converge in local minima.
Such a combination is usually more efficient than the uncontrolled sampling used in Monte Carlo
techniques. When combined with a Genetic Algorithm the user can benefit from the advantages of
both methods: the Genetic Algorithm to roughly locate the global minimum, and Minuit to find
an accurate solution for it (for an example see the FDA method).
55
Option Array Default Predefined Values Description
MaxCalls –100000 –Maximum number of minimisation
calls
InitialTemp –1e+06 –Initial temperature
MinTemp –1e-06 –Mimimum temperature
Eps –1e-10 –Epsilon
TempScale –1–Temperature scale
AdaptiveSpeed –1–Adaptive speed
TempAdaptiveStep –0.009875 –Step made in each generation temper-
ature adaptive
UseDefaultScale –False –Use default temperature scale for tem-
perature minimisation algorithm
UseDefaultTemp –False –Use default initial temperature
KernelTemp –IncAdaptive IncAdaptive,
DecAdaptive,
Sqrt, Log, Sin,
Homo, Geo
Temperature minimisation algorithm
Option Table 8: Configuration options reference for fitting method: Simulated Annealing (SA).
The configuration options for the combined fit methods are the inclusive sum of all the individual
fitter options. It is recommended to use Minuit in batch mode (option SetBatch) and without
MINOS (option !UseMinos) to prevent TMVA from flooding the output with Minuit messages
which cannot be turned off, and to speed up the individual fits. It is however important to note
that the combination of MIGRAD and MINOS together is less susceptible to getting caught in local
minima.
7 Boosting and Bagging
Boosting is a way of enhancing the classification and regression performance (and increasing the
stability with respect to statistical fluctuations in the training sample) of typically weak MVA
methods by sequentially applying an MVA algorithm to reweighted (boosted) versions of the training
data and then taking a weighted majority vote of the sequence of MVA algorithms thus produced.
It has been introduced to classification techniques in the early ’90s [25] and in many cases this
simple strategy results in dramatic performance increases.
Although one may argue that bagging (cf. Sec. 7.3) is not a genuine boosting algorithm, we include
it in the same context and typically when discussing boosting we also refer to bagging. The most
commonly boosted methods are decision trees. However, as described in Sec. 10.1 on page 132,
any MVA method may be boosted with TMVA. Hence, although the following discussion refers
to decision trees, it also applies to other methods. (Note however that “Gradient Boost” is only

56 7 Boosting and Bagging
available for decision trees).
7.1 Adaptive Boost (AdaBoost)
The most popular boosting algorithm is the so-called AdaBoost (adaptive boost) [26]. In a clas-
sification problem, events that were misclassified during the training of a decision tree are given a
higher event weight in the training of the following tree. Starting with the original event weights
when training the first decision tree, the subsequent tree is trained using a modified event sample
where the weights of previously misclassified events are multiplied by a common boost weight α.
The boost weight is derived from the misclassification rate, err, of the previous tree17,
α=1−err
err .(25)
The weights of the entire event sample are then renormalised such that the sum of weights remains
constant.
We define the result of an individual classifier as h(x), with (xbeing the tuple of input variables)
encoded for signal and background as h(x) = +1 and −1, respectively. The boosted event classifi-
cation yBoost(x) is then given by
yBoost(x) = 1
Ncollection ·
Ncollection
X
i
ln(αi)·hi(x),(26)
where the sum is over all classifiers in the collection. Small (large) values for yBoost(x) indicate a
background-like (signal-like) event. Equation (26) represents the standard boosting algorithm.
AdaBoost performs best on weak classifiers, meaning small indivdidual decision trees with a tree
depth of often as small 2 or 3, that have very little discrimination power by themselves. Given
such small trees, they are much less prone to overtraining compared to simple decision trees and
as an ensemble outperform them typically by far. The performance is often further enhanced by
forcing a “slow learing” and allowing a larger number of boost steps instead. The learning rate of
the AdaBoost algorithm is controled by a parameter βgiving as an exponent to the boost weight
α→αβ, which can be modified using the configuration option string of the MVA method to be
boosted (see Option Tables 25 and 27 on pages 116 and 116 for boosted decision trees, and Option
Table 30 for general classifier boosting 10.1).
For regression trees, the AdaBoost algorithm needs to be modified. TMVA uses here the so-called
AdaBoost.R2 algorithm [28]. The idea is similar to AdaBoost albeit with a redefined loss per event
to account for the deviation of the estimated target value from the true one. Moreover, as there
are no longer correctly and wrongly classified events, all events need to be reweighted depending on
17By construction, the error rate is err ≤0.5 as the same training events used to classify the output nodes of the
previous tree are used for the calculation of the error rate.

7.2 Gradient Boost 57
their individual loss, which – for event k– is given by
Linear :L(k) = |y(k)−ˆy(k)|
max
events k0(|y(k0)−ˆy(k0|),(27)
Square :L(k) = |y(k)−ˆy(k)|
max
events k0(|y(k0)−ˆy(k0|)2
,(28)
Exponential :L(k)=1−exp −|y(k)−ˆy(k)|
max
events k0(|y(k0)−ˆy(k0|).(29)
The average loss of the classifier y(i)over the whole training sample, hLi(i)=Pevents k0w(k0)L(i)(k0),
can be considered to be the analogon to the error fraction in classification. Given hLi, one computes
the quantity β(i)=hLi(i)/(1 − hLi(i)), which is used in the boosting of the events, and for the
combination of the regression methods belonging to the boosted collection. The boosting weight,
w(i+1)(k), for event kand boost step i+ 1 thus reads
w(i+1)(k) = w(i)(k)·β1−L(i)(k)
(i).(30)
The sum of the event weights is again renormalised to reproduce the original overall number of
events. The final regressor, yBoost, uses the weighted median, ˜y(i), where (i) is chosen so that it is
the minimal (i) that satisfies the inequality
X
t∈sorted collection
t≤i
ln 1
β(t)≥1
2
Ncollection
X
t
ln 1
β(t)
(31)
7.2 Gradient Boost
The idea of function estimation through boosting can be understood by considering a simple additive
expansion approach. The function F(x) under consideration is assumed to be a weighted sum of
parametrised base functions f(x;am), so-called “weak learners”. From a technical point of view any
TMVA classifier could act as a weak learner in this approach, but decision trees benefit most from
boosting and are currently the only classifier that implements GradientBoost (a generalisation may
be included in future releases). Thus each base function in this expansion corresponds to a decision
tree
F(x;P) =
M
X
m=0
βmf(x;am); P∈ {βm;am}M
0.(32)
The boosting procedure is now employed to adjust the parameters Psuch that the deviation between
the model response F(x) and the true value yobtained from the training sample is minimised. The
deviation is measured by the so-called loss-function L(F, y), a popular choice being squared error
loss L(F, y) = (F(x)−y)2. It can be shown that the loss function fully determines the boosting
procedure.
The most popular boosting method, AdaBoost, is based on exponential loss, L(F, y) = e−F(x)y,
which leads to the well known reweighting algorithm described in Sec. 7.1. Exponential loss has

58 7 Boosting and Bagging
the shortcoming that it lacks robustness in presence of outliers or mislabelled data points. The
performance of AdaBoost therefore is expected to degrade in noisy settings.
The GradientBoost algorithm attempts to cure this weakness by allowing for other, potentially more
robust, loss functions without giving up on the good out-of-the-box performance of AdaBoost. The
current TMVA implementation of GradientBoost uses the binomial log-likelihood loss
L(F, y) = ln 1 + e−2F(x)y,(33)
for classification. As the boosting algorithm corresponding to this loss function cannot be obtained
in a straightforward manner, one has to resort to a steepest-descent approach to do the minimisation.
This is done by calculating the current gradient of the loss function and then growing a regression
tree whose leaf values are adjusted to match the mean value of the gradient in each region defined by
the tree structure. Iterating this procedure yields the desired set of decision trees which minimises
the loss function. Note that GradientBoost can be adapted to any loss function as long as the
calculation of the gradient is feasible.
Just like AdaBoost, GradientBoost works best on weak classifiers, meaning small indivdidual de-
cision trees with a depth of often just 2 to 4. Given such small trees, they are much less prone
to overtraining compared to simple decision trees. Its robustness can be enhanced by reducing the
learning rate of the algorithm through the Shrinkage parameter (cf. Option Table 25 on page 116),
which controls the weight of the individual trees. A small shrinkage (0.1–0.3) demands more trees
to be grown but can significantly improve the accuracy of the prediction in difficult settings.
In certain settings GradientBoost may also benefit from the introduction of a bagging-like resampling
procedure using random subsamples of the training events for growing the trees. This is called
stochastic gradient boosting and can be enabled by selecting the UseBaggedGrad option. The sample
fraction used in each iteration can be controlled through the parameter BaggingSampleFraction,
where typically the best results are obtained for values between 0.5 and 0.8.
For regression tasks, GradientBoost employs the Huber loss function [47], which features the ro-
bustness of least-absolute-deviation loss for error distributions with broad tails, while maintaining
the high efficiency of least-squares loss for normally distributed errors. For moderately broad tails,
it should surpass both least-squares and least-absolute-deviation loss.
L(F, y) = (1
2(y−F(x))2|y−F| ≤ δ ,
δ(|y−F| − δ/2) |y−F|> δ . (34)
All GradientBoost options for classification described above can be also applied for regression tasks,
but tests have shown that stochastic gradient boosting may not perform very well for regression
problems.
7.3 Bagging
The term Bagging denotes a resampling technique where a classifier is repeatedly trained using
resampled training events such that the combined classifier represents an average of the individual

7.3 Bagging 59
classifiers. A priori, bagging does not aim at enhancing a weak classifier in the way adaptive or
gradient boosting does, and is thus not a “boosting” algorithm in a strict sense. Instead it effectively
smears over statistical representations of the training data and is hence suited to stabilise the
response of a classifier. In this context it is often accompanied also by a significant performance
increase compared to the individual classifier.
Resampling includes the possibility of replacement, which means that the same event is allowed
to be (randomly) picked several times from the parent sample. This is equivalent to regarding
the training sample as being a representation of the probability density distribution of the parent
sample: indeed, if one draws an event out of the parent sample, it is more likely to draw an event
from a region of phase-space that has a high probability density, as the original data sample will have
more events in that region. If a selected event is kept in the original sample (that is when the same
event can be selected several times), the parent sample remains unchanged so that the randomly
extracted samples will have the same parent distribution, albeit statistically fluctuated. Training
several classifiers with different resampled training data, and combining them into a collection,
results in an averaged classifier that, just as for boosting, is more stable with respect to statistical
fluctuations in the training sample.
Technically, resampling is implemented by applying random Poisson weights to each event of the
parent sample.

60 8 The TMVA Methods
8 The TMVA Methods
All TMVA classification and regression methods (in most cases, a method serves both analysis
goals) inherit from MethodBase, which implements basic functionality like the interpretation of
common configuration options, the interaction with the training and test data sets, I/O operations
and common performance evaluation calculus. The functionality each MVA method is required to
implement is defined in the abstract interface IMethod.18 Each MVA method provides a function
that creates a rank object (of type Ranking), which is an ordered list of the input variables prioritised
according to criteria specific to that method. Also provided are brief method-specific help notes
(option Help, switched off by default) with information on the adequate usage of the method and
performance optimisation in case of unsatisfying results.
If the option CreateMVAPdfs is set TMVA creates signal and background PDFs from the corre-
sponding MVA response distributions using the training sample (cf. Sec. 3.1.7). The binning and
smoothing properties of the underlying histograms can be customised via controls implemented in
the PDF class (cf. Sec. 5and Option Table 3on page 46). The options specific to MethodBase are
listed in Option Table 9. They can be accessed by all MVA methods.
The following sections describe the methods implemented in TMVA. For each method we proceed
according to the following scheme: (i) a brief introduction, (ii) the description of the booking options
required to configure the method, (iii) a description of the the method and TMVA implementation
specifications for classification and – where available – for regression, (iv) the properties of the
variable ranking, and (v) a few comments on performance, favourable (and disfavoured) use cases,
and comparisons with other methods.
8.1 Rectangular cut optimisation
The simplest and most common classifier for selecting signal events from a mixed sample of signal
and background events is the application of an ensemble of rectangular cuts on discriminating
variables. Unlike all other classifiers in TMVA, the cut classifier only returns a binary response
(signal or background).19 The optimisation of cuts performed by TMVA maximises the background
rejection at given signal efficiency, and scans over the full range of the latter quantity. Dedicated
analysis optimisation for which, e.g., the signal significance is maximised requires the expected
signal and background yields to be known before applying the cuts. This is not the case for a
18Two constructors are implemented for each method: one that creates the method for a first time for training
with a configuration (“option”) string among the arguments, and another that recreates a method from an existing
weight file. The use of the first constructor is demonstrated in the example macros TMVAClassification.C and
TMVARegression.C, while the second one is employed by the Reader in TMVAClassificationApplication.C and
TMVARegressionApplication.C. Other functions implemented by each methods are: Train (called for training),
Write/ReadWeightsToStream (I/O of specific training results), WriteMonitoringHistosToFile (additional specific
information for monitoring purposes) and CreateRanking (variable ranking).
19Note that cut optimisation is not a multivariate analyser method but a sequence of univariate ones, because no
combination of the variables is achieved. Neither does a cut on one variable depend on the value of another variable
(like it is the case for Decision Trees), nor can a, say, background-like value of one variable in a signal event be
counterweighed by signal-like values of the other variables (like it is the case for the likelihood method).
8.1 Rectangular cut optimisation 61
Option Array Default Predefined Values Description
V–False –Verbose output (short form of Ver-
bosityLevel below - overrides the latter
one)
VerbosityLevel –Default Default, Debug,
Verbose, Info,
Warning, Error,
Fatal
Verbosity level
VarTransform –None –List of variable transformations
performed before training, e.g.,
D Background,P Signal,G,N AllClasses
for: Decorrelation, PCA-
transformation, Gaussianisation,
Normalisation, each for the given
class of events (’AllClasses’ denotes
all events of all classes, if no class
indication is given, ’All’ is assumed)
H–False –Print method-specific help message
CreateMVAPdfs –False –Create PDFs for classifier outputs (sig-
nal and background)
IgnoreNegWeightsInTraining–False –Events with negative weights are ig-
nored in the training (but are included
for testing and performance evalua-
tion)
Option Table 9: Configuration options that are common for all classifiers (but which can be controlled
individually for each classifier). Values given are defaults. If predefined categories exist, the default category
is marked by a *. The lower options in the table control the PDF fitting of the classifiers (required, e.g., for
the Rarity calculation).
multi-purpose discrimination and hence not used by TMVA. However, the cut ensemble leading to
maximum significance corresponds to a particular working point on the efficiency curve, and can
hence be easily derived after the cut optimisation scan has converged.20
TMVA cut optimisation is performed with the use of multivariate parameter fitters interfaced by
the class FitterBase (cf. Sec. 6). Any fitter implementation can be used, where however because
of the peculiar, non-unique solution space only Monte Carlo sampling, Genetic Algorithm, and
20 Assuming a large enough number of events so that Gaussian statistics is applicable, the significance for a signal
is given by S=ε
SN
S/pε
SN
S+ε
B(ε
S)N
S, where ε
S(B)and N
S(B)are the signal and background efficiencies for a cut
ensemble and the event yields before applying the cuts, respectively. The background efficiency ε
Bis expressed as a
function of ε
Susing the TMVA evaluation curve obtained form the test data sample. The maximum significance is
then found at the root of the derivative
dS
dε
S
=N
S
2ε
B(ε
S)N
B+ε
SN
S−dε
B(ε
S)
dε
SN
B
2 (ε
SN
S+ε
B(ε
S)N
B)3/2= 0 ,(35)
which depends on the problem.

62 8 The TMVA Methods
Option Array Default Predefined Values Description
FitMethod –GA GA, SA, MC,
MCEvents,
MINUIT,
EventScan
Minimisation Method (GA, SA, and
MC are the primary methods to be
used; the others have been introduced
for testing purposes and are depreci-
ated)
EffMethod –EffSel EffSel, EffPDF Selection Method
CutRangeMin Yes -1 –Minimum of allowed cut range (set per
variable)
CutRangeMax Yes -1 –Maximum of allowed cut range (set per
variable)
VarProp Yes NotEnforced NotEnforced,
FMax, FMin,
FSmart
Categorisation of cuts
Option Table 10: Configuration options reference for MVA method: Cuts. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
Simulated Annealing show satisfying results. Attempts to use Minuit (SIMPLEX or MIGRAD)
have not shown satisfactory results, with frequently failing fits.
The training events are sorted in binary trees prior to the optimisation, which significantly reduces
the computing time required to determine the number of events passing a given cut ensemble (cf.
Sec. 4.3).
8.1.1 Booking options
The rectangular cut optimisation is booked through the Factory via the command:
factory->BookMethod( Types::kCuts, "Cuts", "<options>" );
Code Example 35: Booking of the cut optimisation classifier: the first argument is a predefined enumerator,
the second argument is a user-defined string identifier, and the third argument is the configuration options
string. Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The configuration options for the various cut optimisation techniques are given in Option Table 10.

8.1 Rectangular cut optimisation 63
8.1.2 Description and implementation
The cut optimisation analysis proceeds by first building binary search trees for signal and back-
ground. For each variable, statistical properties like mean, root-mean-squared (RMS), variable
ranges are computed to guide the search for optimal cuts. Cut optimisation requires an estimator
that quantifies the goodness of a given cut ensemble. Maximising this estimator minimises (max-
imises) the background efficiency, ε
B(background rejection, r
B= 1 −ε
B) for each signal efficiency
ε
S.
All optimisation methods (fitters) act on the assumption that one minimum and one maximum
requirement on each variable is sufficient to optimally discriminate signal from background (i.e.,
the signal is clustered). If this is not the case, the variables must be transformed prior to the cut
optimisation to make them compliant with this assumption.
For a given cut ensemble the signal and background efficiencies are derived by counting the training
events that pass the cuts and dividing the numbers found by the original sample sizes. The resulting
efficiencies are therefore rational numbers that may exhibit visible discontinuities when the number
of training events is small and an efficiency is either very small or very large. Another way to compute
efficiencies is to parameterise the probability density functions of all input variables and thus to
achieve continuous efficiencies for any cut value. Note however that this method expects the input
variables to be uncorrelated! Non-vanishing correlations would lead to incorrect efficiency estimates
and hence to underperforming cuts. The two methods are chosen with the option EffMethod set to
EffSel and EffPDF, respectively.
Monte Carlo sampling
Each generated cut sample (cf. Sec. 6.1) corresponds to a point in the (ε
S, r
B) plane. The ε
S
dimension is (finely) binned and a cut sample is retained if its r
Bvalue is larger than the value
already contained in that bin. This way a reasonably smooth efficiency curve can be obtained if the
number of input variables is not too large (the required number of MC samples grows with powers
of 2nvar).
Prior information on the variable distributions can be used to reduce the number of cuts that
need to be sampled. For example, if a discriminating variable follows Gaussian distributions for
signal and background, with equal width but a larger mean value for the background distribution,
there is no useful minimum requirement (other than −∞) so that a single maximum requirement
is sufficient for this variable. To instruct TMVA to remove obsolete requirements, the option
VarProp[i] must be used, where [i] indicates the counter of the variable (following the order in
which they have been registered with the Factory, beginning with 0) must be set to either FMax or
FMin. TMVA is capable of automatically detecting which of the requirements should be removed.
Use the option VarProp[i]=FSmart (where again [i] must be replaced by the appropriate variable
counter, beginning with 0). Note that in many realistic use cases the mean values between signal
and background of a variable are indeed distinct, but the background can have large tails. In such
a case, the removal of a requirement is inappropriate, and would lead to underperforming cuts.

64 8 The TMVA Methods
Genetic Algorithm
Genetic Algorithm (cf. Sec. 6.3) is a technique to find approximate solutions to optimisation or
search problems. Apart from the abstract representation of the solution domain, a fitness function
must be defined. In cut optimisation, the fitness of a rectangular cut is given by good background
rejection combined with high signal efficiency.
At the initialization step, all parameters of all individuals (cut ensembles) are chosen randomly.
The individuals are evaluated in terms of their background rejection and signal efficiency. Each cut
ensemble giving an improvement in the background rejection for a specific signal efficiency bin is
immediately stored. Each individual’s fitness is assessed, where the fitness is largely determined by
the difference of the best found background rejection for a particular bin of signal efficiency and the
value produced by the current individual. The same individual that has at one generation a very
good fitness will have only average fitness at the following generation. This forces the algorithm
to focus on the region where the potential of improvement is the highest. Individuals with a good
fitness are selected to produce the next generation. The new individuals are created by crossover
and mutated afterwards. Mutation changes some values of some parameters of some individuals
randomly following a Gaussian distribution function, etc. This process can be controlled with the
parameters listed in Option Table 7, page 52.
Simulated Annealing
Cut optimisation using Simulated Annealing works similarly as for the Genetic Algorithm and
achieves comparable performance. The same fitness function is used to estimator the goodness of a
given cut ensemble. Details on the algorithm and the configuration options can be found in Sec. 6.4
on page 53.
8.1.3 Variable ranking
The present implementation of Cuts does not provide a ranking of the input variables.
8.1.4 Performance
The Genetic Algorithm currently provides the best cut optimisation convergence. However, it is
found that with rising number of discriminating input variables the goodness of the solution found
(and hence the smoothness of the background-rejections versus signal efficiency plot) deteriorates
quickly. Rectangular cut optimisation should therefore be reduced to the variables that have the
largest discriminating power.
If variables with excellent signal from background separation exist, applying cuts can be quite
competitive with more involved classifiers. Cuts are known to underperform in presence of strong
nonlinear correlations and/or if several weakly discriminating variables are used. In the latter case,

8.2 Projective likelihood estimator (PDE approach) 65
Option Array Default Predefined Values Description
TransformOutput –False –Transform likelihood output by inverse
sigmoid function
Option Table 11: Configuration options reference for MVA method: Likelihood. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
a true multivariate combination of the information will be rewarding.
8.2 Projective likelihood estimator (PDE approach)
The method of maximum likelihood consists of building a model out of probability density functions
(PDF) that reproduces the input variables for signal and background. For a given event, the
likelihood for being of signal type is obtained by multiplying the signal probability densities of all
input variables, which are assumed to be independent, and normalising this by the sum of the
signal and background likelihoods. Because correlations among the variables are ignored, this PDE
approach is also called “naive Bayes estimator”, unlike the full multidimensional PDE approaches
such as PDE-range search, PDE-foam and k-nearest-neighbour discussed in the subsequent sections,
which approximate the true Bayes limit.
8.2.1 Booking options
The likelihood classifier is booked via the command:
factory->BookMethod( Types::kLikelihood, "Likelihood", "<options>" );
Code Example 36: Booking of the (projective) likelihood classifier: the first argument is the predefined
enumerator, the second argument is a user-defined string identifier, and the third argument is the configuration
options string. Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The likelihood configuration options are given in Option Table 11.
8.2.2 Description and implementation
The likelihood ratio yL(i) for event iis defined by
yL(i) = LS(i)
LS(i) + LB(i),(36)

66 8 The TMVA Methods
where
LS(B)(i) =
nvar
Y
k=1
pS(B),k(xk(i)) ,(37)
and where pS(B),k is the signal (background) PDF for the kth input variable xk. The PDFs are
normalised
+∞
Z
−∞
pS(B),k(xk)dxk= 1 ,∀k. (38)
It can be shown that in absence of model inaccuracies (such as correlations between input variables
not removed by the de-correlation procedure, or an inaccurate probability density model), the
ratio (36) provides optimal signal from background separation for the given set of input variables.
Since the parametric form of the PDFs is generally unknown, the PDF shapes are empirically
approximated from the training data by nonparametric functions, which can be chosen individually
for each variable and are either polynomial splines of various degrees fitted to histograms or unbinned
kernel density estimators (KDE), as discussed in Sec. (5).
A certain number of primary validations are performed during the PDF creation, the results of
which are printed to standard output. Among these are the computation of a χ2estimator between
all nonzero bins of the original histogram and its PDF, and a comparison of the number of outliers
(in sigmas) found in the original histogram with respect to the (smoothed) PDF shape, with the
statistically expected one. The fidelity of the PDF estimate can be also inspected visually by
executing the macro likelihoodrefs.C (cf. Table 4).
Transforming the likelihood output
If a data-mining problem offers a large number of input variables, or variables with excellent sepa-
ration power, the likelihood response yLis often strongly peaked at 0 (background) and 1 (signal).
Such a response is inconvenient for the use in subsequent analysis steps. TMVA therefore allows to
transform the likelihood output by an inverse sigmoid function that zooms into the peaks
yL(i)−→ y0
L(i) = −τ−1lny−1
L−1,(39)
where τ= 15 is used. Note that y0
L(i) is no longer contained within [0,1] (see Fig. 11). The
transformation (39) is enabled (disabled) with the booking option TransformOutput=True(False).
8.2.3 Variable ranking
The present likelihood implementation does not provide a ranking of the input variables.
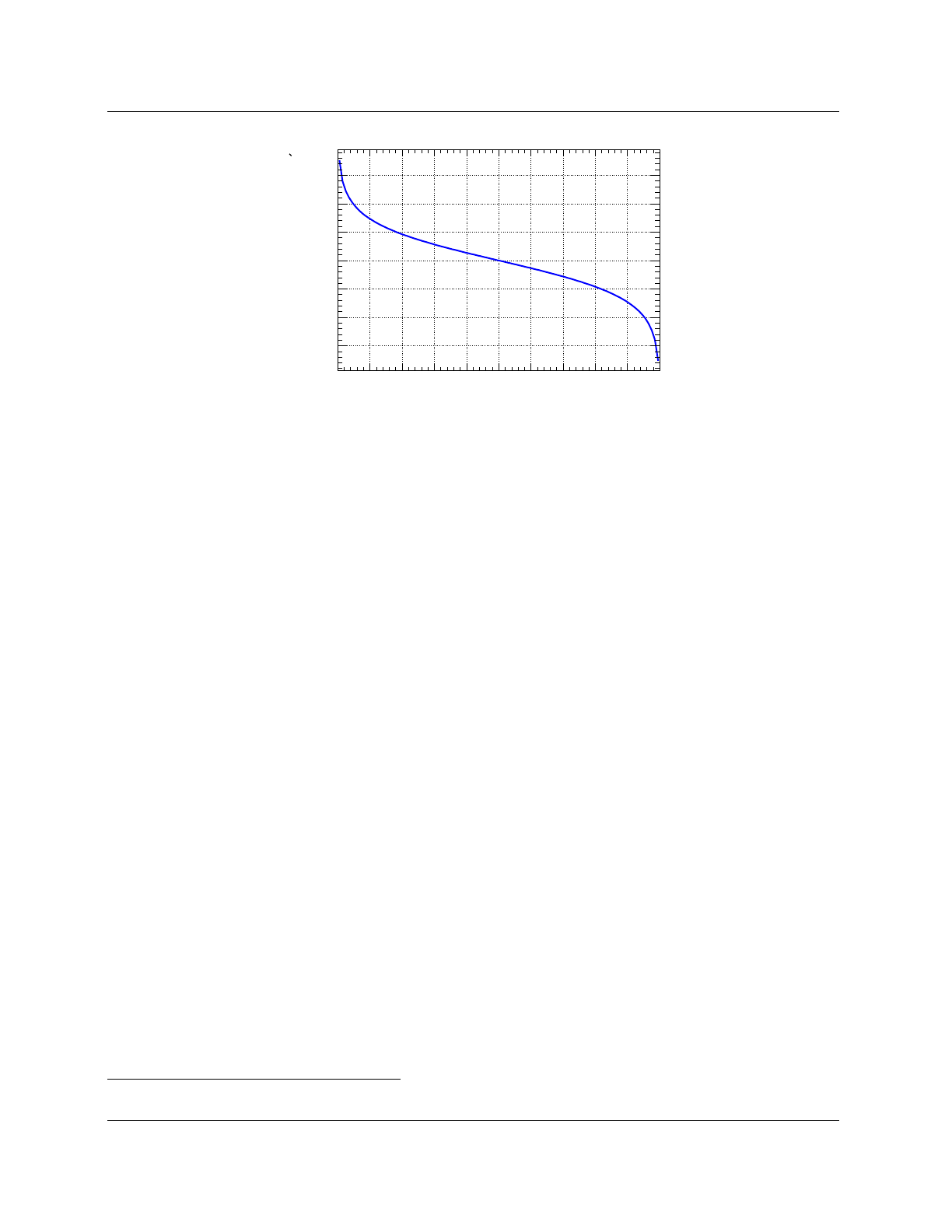
8.3 Multidimensional likelihood estimator (PDE range-search approach) 67
L
R
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
L
R
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Figure 11: Transformation (39) of the likelihood output.
8.2.4 Performance
Both the training and the application of the likelihood classifier are very fast operations that are
suitable for large data sets.
The performance of the classifier relies on the accuracy of the likelihood model. Because high
fidelity PDF estimates are mandatory, sufficient training statistics is required to populate the tails
of the distributions. The neglect of correlations between input variables in the model (37), often
leads to a diminution of the discrimination performance. While linear Gaussian correlations can
be rotated away (see Sec. 4.1), such an ideal situation is rarely given. Positive correlations lead to
peaks at both yL→0,1. Correlations can be reduced by categorising the data samples and building
an independent likelihood classifier for each event category. Such categories could be geometrical
regions in the detector, kinematic properties, etc. In spite of this, realistic applications with a large
number of input variables are often plagued by irreducible correlations, so that projective likelihood
approaches like the one discussed here are under-performing. This finding led to the development
of the many alternative classifiers that exist in statistical theory today.
8.3 Multidimensional likelihood estimator (PDE range-search approach)
This is a generalization of the projective likelihood classifier described in Sec. 8.2 to nvar dimensions,
where nvar is the number of input variables used. If the multidimensional PDF for signal and back-
ground (or regression data) were known, this classifier would exploit the full information contained
in the input variables, and would hence be optimal. In practice however, huge training samples are
necessary to sufficiently populate the multidimensional phase space.21 Kernel estimation methods
may be used to approximate the shape of the PDF for finite training statistics.
A simple probability density estimator denoted PDE range search, or PDE-RS, has been suggested
21Due to correlations between the input variables, only a sub-space of the full phase space may be populated.
68 8 The TMVA Methods
in Ref. [14]. The PDE for a given test event (discriminant) is obtained by counting the (normalised)
number of training events that occur in the ”vicinity” of the test event. The classification of the
test event may then be conducted on the basis of the majority of the nearest training events. The
nvar-dimensional volume that encloses the ”vicinity” is user-defined and can be adaptive. A search
method based on sorted binary trees is used to reduce the computing time for the range search. To
enhance the sensitivity within the volume, kernel functions are used to weight the reference events
according to their distance from the test event. PDE-RS is a variant of the k-nearest neighbour
classifier described in Sec. 8.5.
8.3.1 Booking options
The PDE-RS classifier is booked via the command:
factory->BookMethod( Types::kPDERS, "PDERS", "<options>" );
Code Example 37: Booking of PDE-RS: the first argument is a predefined enumerator, the second argument
is a user-defined string identifier, and the third argument is the configuration options string. Individual
options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The configuration options for the PDE-RS classifier are given in Option Table 12.
8.3.2 Description and implementation
Classification
To classify an event as being either of signal or of background type, a local estimate of the probability
density of it belonging to either class is computed. The method of PDE-RS provides such an estimate
by defining a volume (V) around the test event (i), and by counting the number of signal (nS(i, V ))
and background events (nB(i, V )) obtained from the training sample in that volume. The ratio
yPDE-RS(i, V ) = 1
1 + r(i, V ),(40)
is taken as the estimate, where r(i, V )=(nB(i, V )/NB)·(NS/nS(i, V )), and NS(B)is the total
number of signal (background) events in the training sample. The estimator yPDE-RS(i, V ) peaks at
1 (0) for signal (background) events. The counting method averages over the PDF within V, and
hence ignores the available shape information inside (and outside) that volume.
Binary tree search
Efficiently searching for and counting the events that lie inside the volume is accomplished with the
use of a nvar-variable binary tree search algorithm [13] (cf. Sec. 4.3).

8.3 Multidimensional likelihood estimator (PDE range-search approach) 69
Option Array Default Predefined Values Description
VolumeRangeMode –Adaptive Unscaled,
MinMax, RMS,
Adaptive, kNN
Method to determine volume size
KernelEstimator –Box Box, Sphere,
Teepee, Gauss,
Sinc3, Sinc5,
Sinc7, Sinc9,
Sinc11,
Lanczos2,
Lanczos3,
Lanczos5,
Lanczos8, Trim
Kernel estimation function
DeltaFrac –3–nEventsMin/Max for minmax and rms
volume range
NEventsMin –100 –nEventsMin for adaptive volume range
NEventsMax –200 –nEventsMax for adaptive volume
range
MaxVIterations –150 –MaxVIterations for adaptive volume
range
InitialScale –0.99 –InitialScale for adaptive volume range
GaussSigma –0.1 –Width (wrt volume size) of Gaussian
kernel estimator
NormTree –False –Normalize binary search tree
Option Table 12: Configuration options reference for MVA method: PDE-RS. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
Choosing a volume
The TMVA implementation of PDE-RS optionally provides four different volume definitions selected
via the configuration option VolumeRangeMode.
•Unscaled
The simplest volume definition consisting of a rigid box of size DeltaFrac, in units of the
variables. This method was the one originally used by the developers of PDE-RS [14].
•MinMax
The volume is defined in each dimension (i.e., input variable) with respect to the full range of
values found for that dimension in the training sample. The fraction of this volume used for
the range search is defined by the option DeltaFrac.
•RMS
The volume is defined in each dimension with respect to the RMS of that dimension (input

70 8 The TMVA Methods
variable), estimated from the training sample. The fraction of this volume used for the range
search is defined by the option DeltaFrac.
•Adaptive
A volume is defined in each dimension with respect to the RMS of that dimension, estimated
from the training sample. The overall scale of the volume is adjusted individually for each test
event such that the total number of events confined in the volume lies within a user-defined
range (options NEventsMin/Max). The adjustment is performed by the class RootFinder,
which is a C++ implementation of Brent’s algorithm (translated from the CERNLIB function
RZERO). The maximum initial volume (fraction of the RMS) and the maximum number
of iterations for the root finding is set by the options InitialScale and MaxVIterations,
respectively. The requirement to collect a certain number of events in the volume automatically
leads to small volume sizes in strongly populated phase space regions, and enlarged volumes
in areas where the population is scarce.
Although the adaptive volume adjustment is more flexible and should perform better, it significantly
increases the computing time of the PDE-RS discriminant. If found too slow, one can reduce the
number of necessary iterations by choosing a larger NEventsMin/Max interval.
Event weighting with kernel functions
One of the shortcomings of the original PDE-RS implementation is its sensitivity to the exact
location of the sampling volume boundaries: an infinitesimal change in the boundary placement
can include or exclude a training event, thus changing r(i, V ) by a finite amount.22 In addition, the
shape information within the volume is ignored.
Kernel functions mitigate these problems by weighting each event within the volume as a function
of its distance to the test event. The farer it is away, the smaller is its weight. The following kernel
functions are implemented in TMVA, and can be selected with the option KernelEstimator.
•Box
Corresponds to the original rectangular volume element without application of event weights.
•Sphere
A hyper-elliptic volume element is used without application of event weights. The hyper-
ellipsoid corresponds to a sphere of constant fraction in the MinMax or RMS metrics. The size
of the sphere can be chosen adaptive, just as for the rectangular volume.
•Teepee
The simplest linear interpolation that eliminates the discontinuity problem of the box. The
training events are given a weight that decreases linearly with their distance from the centre
of the volume (the position of the test event). In other words: these events are convolved with
the triangle or tent function, becoming a sort of teepee in multi-dimensions.
22Such an introduction of artefacts by having sharp boundaries in the sampled space is an example of Gibbs’s
phenomenon, and is commonly referred to as ringing or aliasing.
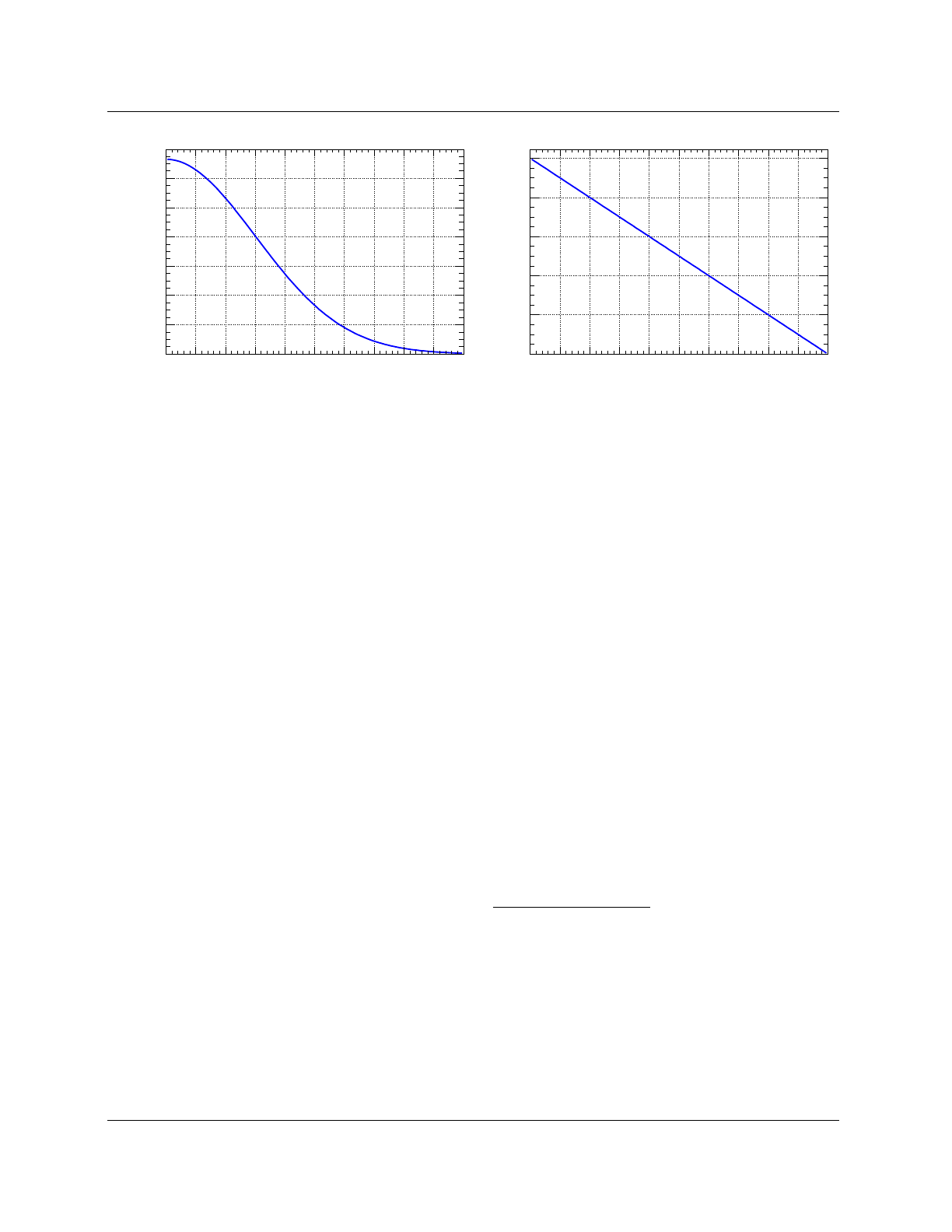
8.3 Multidimensional likelihood estimator (PDE range-search approach) 71
Radial distance from test discriminant
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Kernel weight
0
0.2
0.4
0.6
0.8
1
1.2
Radial distance from test discriminant
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Kernel weight
0
0.2
0.4
0.6
0.8
1
Figure 12: Kernel functions (left: Gaussian, right: Teepee) used to weight the events that are found inside
the reference volume of a test event.
•Trim
Modified Teepee given by the function (1 −ˆx3)3, where ˆxis the normalised distance between
test event and reference.
•Gauss
The simplest well behaved convolution kernel. The width of the Gaussian (fraction of the
volume size) can be set by the option GaussSigma.
Other kernels implemented for test purposes are “Sinc” and ”Lanczos” functions ∝sin x/x of
different (symmetric) orders. They exhibit strong peaks at zero and oscillating tails. The Gaussian
and Teepee kernel functions are shown in Fig. 12.
Regression
Regression with PDE-RS proceeds similar to classification. The difference lies in the replacement
of Eq. (40) by the average target value of all events belonging to the volume Vdefined by event i
(the test event)
yPDE-RS(i, V ) = ht(i, V )i=Pj∈Vwjtjf(dis(i, j))
Pj∈Vwjf(dis(i, j)) ,(41)
where the sum is over all training events in V,wjand tjare the weight and target value of event j
in V, dis(i, j) is a measure of the distance between events iand j, and f(. . . ) is a kernel function.
8.3.3 Variable ranking
The present implementation of PDE-RS does not provide a ranking of the input variables.
72 8 The TMVA Methods
8.3.4 Performance
As opposed to many of the more sophisticated data-mining approaches, which tend to present the
user with a ”black box”, PDE-RS is simple enough that the algorithm can be easily traced and
tuned by hand. PDE-RS can yield competitive performance if the number of input variables is
not too large and the statistics of the training sample is ample. In particular, it naturally deals
with complex nonlinear variable correlations, the reproduction of which may, for example, require
involved neural network architectures.
PDE-RS is a slowly responding classifier. Only the training, i.e., the fabrication of the binary tree is
fast, which is usually not the critical part. The necessity to store the entire binary tree in memory
to avoid accessing virtual memory limits the number of training events that can effectively be used
to model the multidimensional PDF. This is not the case for the other classifiers implemented in
TMVA (with some exception for Boosted Decision Trees).
8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam)
The PDE-Foam method [16] is an extension of PDE-RS, which divides the multi-dimensional phase
space in a finite number of hyper-rectangles (cells) of constant event density. This “foam” of
cells is filled with averaged probability density information sampled from the training data. For
a given number of cells, the binning algorithm adjusts the size and position of the cells inside the
multi-dimensional phase space based on a binary split algorithm that minimises the variance of the
event density in the cell. The binned event density information of the final foam is stored in cells,
organised in a binary tree, to allow a fast and memory-efficient storage and retrieval of the event
density information necessary for classification or regression. The implementation of PDE-Foam is
based on the Monte-Carlo integration package TFoam [15] included in ROOT.
In classification mode PDE-Foam forms bins of similar density of signal and background events or
the ratio of signal to background. In regression mode the algorithm determines cells with small
varying regression targets. In the following, we use the term density (ρ) for the event density in
case of classification or for the target variable density in case of regression.
8.4.1 Booking options
The PDE-Foam classifier is booked via the command:
factory->BookMethod( Types::kPDEFoam, "PDEFoam", "<options>" );
Code Example 38: Booking of PDE-Foam: the first argument is a predefined enumerator, the second argu-
ment is a user-defined string identifier, and the third argument is the configuration options string. Individual
options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.

8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam) 73
The configuration options for the PDE-Foam method are summarised in Option Table 13.
Table 5gives an overview of supported combinations of configuration options.
Classification Regression
Option Separated foams Single foam Mono target Multi target
SigBgSeparate True False – –
MultiTargetRegression – – False True
Kernel • • • •
TargetSelection ◦ ◦ ◦ •
TailCut • • • •
UseYesNoCell • • ◦ ◦
MaxDepth • • • •
Table 5: Availability of options for the two classification and two regression modes of PDE-Foam. Supported
options are marked by a ’•’, while disregarded ones are marked by a ’◦’.
8.4.2 Description and implementation of the foam algorithm
Foams for an arbitrary event sample are formed as follows.
1. Setup of binary search trees. A binary search tree is created and filled with the d-dimensional
event tuples form the training sample as for the PDE-RS method (cf. Sec. 8.3).
2. Initialisation phase. A foam is created, which at first consists of one d-dimensional hyper-
rectangle (base cell). The coordinate system of the foam is normalised such that the base cell
extends from 0 to 1 in each dimension. The coordinates of the events in the corresponding
training tree are linearly transformed into the coordinate system of the foam.
3. Growing phase. A binary splitting algorithm iteratively splits cells of the foam along axis-
parallel hyperplanes until the maximum number of active cells (set by nActiveCells) is
reached. The splitting algorithm minimises the relative variance of the density σρ/hρiacross
each cell (cf. Ref. [15]). For each cell nSampl random points uniformly distributed over the
cell volume are generated. For each of these points a small box centred around this point is
defined. The box has a size of VolFrac times the size of the base cell in each dimension. The
density is estimated as the number of events contained in this box divided by the volume of
the box.23 The densities obtained for all sampled points in the cell are projected onto the d
axes of the cell and the projected values are filled in histograms with nBin bins. The next
cell to be split and the corresponding division edge (bin) for the split are selected as the ones
that have the largest relative variance. The two new daughter cells are marked as ‘active’
cells and the old mother cell is marked as ‘inactive’. A detailed description of the splitting
algorithm can be found in Ref. [15]. The geometry of the final foam reflects the distribution of
the training samples: phase-space regions where the density is constant are combined in large
23In case of regression this is the average target value computed according to Eq. (41), page 71.

74 8 The TMVA Methods
Option Array Default Predefined Values Description
SigBgSeparate –False –Separate foams for signal and back-
ground
TailCut –0.001 –Fraction of outlier events that are ex-
cluded from the foam in each dimen-
sion
VolFrac –0.0666667 –Size of sampling box, used for den-
sity calculation during foam build-up
(maximum value: 1.0 is equivalent to
volume of entire foam)
nActiveCells –500 –Maximum number of active cells to be
created by the foam
nSampl –2000 –Number of generated MC events per
cell
nBin –5–Number of bins in edge histograms
Compress –True –Compress foam output file
MultiTargetRegression –False –Do regression with multiple targets
Nmin –100 –Number of events in cell required to
split cell
MaxDepth –0–Maximum depth of cell tree (0=unlim-
ited)
FillFoamWithOrigWeights–False –Fill foam with original or boost
weights
UseYesNoCell –False –Return -1 or 1 for bkg or signal like
events
DTLogic –None None, GiniIndex,
MisClassificationError,
CrossEntropy,
GiniIndexWithLaplace,
SdivSqrtSplusB
Use decision tree algorithm to split
cells
Kernel –None None, Gauss,
LinNeighbors
Kernel type used
TargetSelection –Mean Mean, Mpv Target selection method
Option Table 13: Configuration options reference for MVA method: PDE-Foam. The options in Option
Table 9on page 61 can also be configured.

8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam) 75
variable 1
-4 -2 0 2 4
variable 2
-3
-2
-1
0
1
2
3
0
50
100
150
200
250
300
350
400
450
(a) foam projection without kernel
variable 1
-4 -2 0 2 4
variable 2
-3
-2
-1
0
1
2
3
0
50
100
150
200
250
300
350
400
(b) foam projection with Gaussian kernel
Figure 13: Projections of a two-dimensional foam with 500 cells for a Gaussian distribution on a two-
dimensional histogram. The foam was created with 5000 events from the input tree. (a) shows the re-
constructed distribution without kernel weighting and (b) shows the distribution weighted with a Gaussian
kernel. The grey shades indicate the event density of the drawn cell. For more details about the projection
function see the description on page 82.
cells, while in regions with large density gradients many small cells are created. Figure 13(a)
displays a foam obtained from a two-dimensional Gaussian-distributed training sample.
4. Filling phase. Each active cell is filled with values that classify the event distribution within
this cell and which permit the calculation of the classification or regression discriminator.
5. Evaluation phase. The estimator for a given event is evaluated based on the information stored
in the foam cells. The corresponding foam cell, in which the event variables (d-dimensional
vector) of a given event is contained, is determined with a binary search algorithm.24
The initial trees which contain the training events and which are needed to evaluate the densities
for the foam build-up, are discarded after the training phase. The memory consumption for the
foam is 160 bytes per foam cell plus an overhead of 1.4 kbytes for the PDE-Foam object on a 64
bit architecture. Note that in the foam all cells created during the growing phase are stored within
a binary tree structure. Cells which have been split are marked as inactive and remain empty. To
reduce memory consumption, the cell geometry is not stored with the cell, but rather obtained
recursively from the information about the division edge of the corresponding mother cell. This
way only two short integer numbers per cell represent the information of the entire foam geometry:
the division coordinate and the bin number of the division edge.
PDE-Foam options
•TailCut –boundaries for foam geometry
24For an event that falls outside the foam boundaries, the cell with the smallest Cartesian distance to the event is
chosen.

76 8 The TMVA Methods
A parameter TailCut is used to define the geometry of the base cell(s) such that outliers of
the distributions in the training ensemble are not included in the volume of the base cell(s).
In a first step, the upper and lower limits for each input variable are determined from the
training sample. Upper and a lower bounds are then determined for each input variable,
such that on both sides a fraction TailCut of all events is excluded. The default value of
TailCut=0.001 ensures a sufficient suppression of outliers for most input distributions. For
cases where the input distributions have a fixed range or where they are discontinuous and/or
have peaks towards the edges, it can be appropriate to set TailCut to 0. Note that for event
classification it is guaranteed that the foam has an infinite coverage: events outside the foam
volume are assigned to the cell with the smallest Cartesian distance to the event.
•nActiveCells –maximum number of active foam cells
In most cases larger nActiveCells values result in more accurate foams, but also lead to
longer computation time during the foam formation, and require more storage memory. The
default value of 500 was found to be a good compromise for most practical applications if the
size of the training samples is of the order of 104events. Note that the total number of cells,
nCells, is given as nCells =nActiveCells ·2−1, since the binary-tree structure of the foam
requires all inactive cells to remain part of the foam (see Growing phase).
•VolFrac –size of the probe volume for the density sampling of the training data
The volume is defined as a d-dimensional box with edge length VolFrac times the extension
of the base cell in each dimension. The default of 1/15 results in a box with volume 1/15d
times the volume of the base cell. Smaller values of VolFrac increase the sampling speed,
but also make the algorithm more vulnerable to statistical fluctuations in the training sample
(overtraining). In cases with many observables (>5) and small training samples (<104),
VolFrac should be increased for better classification results.
•nSampl –number of samplings per cell and per cell-division step
The computation time for the foam formation scales linearly with the number of samplings.
The default of 2000 was found to give sufficiently accurate estimates of the density distributions
with an acceptable computation time.25
•nBin –number of bins for edge histograms
The number of bins for the edge histograms used to determine the variance of the sampled
density distributions within one cell are set with the parameter nBin. The performance in
typical applications was found to be rather insensitive to the number of bins. The default value
of 5 gives the foam algorithm sufficient flexibility to find the division points, while maintaining
sufficient statistical accuracy also in case of small event samples.
•Nmin –Minimal number of events for cell split
If Nmin is set to a value greater than zero, the foam will only consider cells with a number of
events greater than Nmin to be split. If no more cells are found during the growing phase for
which this condition is fulfilled, the foam will stop splitting cells, even if the target number of
cells is not yet reached. This option prevents the foam from adapting to statistical fluctuations
25Contrary to the original application where an analytical function is used, increasing the number of samplings does
not automatically lead to better accuracy. Since the density is defined by a limited event sample, it may occur that
always the same event is found for all sample points.

8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam) 77
in the training samples (overtraining). Note that event weights are not taken into account for
evaluating the number of events in the cell.
In particular for training samples with small event numbers of less than 104events this cut
improves the performance. The default value of (Nmin=100) was found to give good results in
most cases. It should be reduced in applications with very small training samples (less than
200 training events) and with many cells.
•Kernel –cell weighting with kernel functions:
A Gaussian Kernel smoothing is applied during the evaluation phase, if the option Kernel
is set to “Gauss”. In this case all cells contribute to the calculation of the discriminant for
a given event, weighted with their Gaussian distance to the event. The average cell value v
(event density in case of separated foams, and the ratio nS/(nS+nB) in case of a single foam)
for a given event x= (x1, . . . , xnvar ) is calculated by
v=Pall cells iG(D(i, x),0,VolFrac)·vi
Pall cells iG(D(i, x),0,VolFrac),(42)
where viis the output value in cell i,G(x, x0, σ) = exp(−(x−x0)2/2σ2), and D(i, x) is the
minimal Euclidean distance between xand any point yin cell i
D(i, x) = min
y∈cell i|x−y|.(43)
The Gaussian kernel avoids discontinuities of the discriminant values at the cell boundaries.
In most cases it results in an improved separation power between signal and background.
However, the time needed for classification increases due to the larger number of computations
performed. A comparison between foams with and without Gaussian kernel can be seen in
Fig. 13.
A linear interpolation with adjacent cells in each dimension is applied during the classification
phase, if the option Kernel is set to “LinNeighbors”. This results in faster classification than
the Gauss weighting of all cells in the foam.
•UseYesNoCell –Discrete classification output
If UseYesNoCell is set to False (default), the discriminant (48) is returned as classification
output. If UseYesNoCell is set to True,−1 is returned for events with discriminant <0.5
(background-like) and +1 is returned for events with ≥0.5 (signal-like).
•MaxDepth –Maximum cell tree depth
The cell tree depth can be limited by using this option. When MaxDepth is set to an integer
value greater than zero, the created cell tree will not be deeper than MaxDepth. By convention
the root node has depth 1, which implies that a foam with 2 active cells (3 cells in total) has
depth 2. If nActiveCells ≥2MaxDepth−1the resulting cell tree will be completely balanced.
When MaxDepth is set to 0, the cell tree depth is not limited.
•DTLogic –Cell split algorithm
In order to emulate a decision tree-like cell splitting algorithm, the option DTLogic was intro-
duced. When set to GiniIndex,MisClassificationError or CrossEntropy, the algorithm

78 8 The TMVA Methods
projects all events in a cell onto the cell edges and probes nBin-1 division points such that
the separation gain
gain(parent cell) −gain(daughter cell 1) −gain(daughter cell 2) (44)
is maximal (see Sec. 8.13.3). For a given separation type and a given cell the gain is defined
as
GiniIndex : gain(cell) = p(1 −p),(45)
MisClassificationError : gain(cell) = 1 −max(p, 1−p),(46)
CrossEntropy : gain(cell) = −plog p−(1 −p) log(1 −p),(47)
where p=nS/(nS+nB) in the considered cell. When DTLogic is set to None (default), the
PDE-Foam cell splitting algorithm (see Sec. 8.4.2) is used. This option is available only for
classification and is an alternative to the classification with two separate foams or one single
foam (see Sec. 8.4.3).
•FillFoamWithOrigWeights –Event weights for boosting
Since the PDE-Foam cells are filled with events after the splitting, it is in principle pos-
sible to use different event weights for the filling than for the foam build-up. The option
FillFoamWithOrigWeights was created to choose either the original or the full event weight
(including the boost weight) to be filled into the foam cells after the build-up. This option
is only relevant for boosting, because for non-boosted classifiers the boost weights are always
1. When setting FillFoamWithOrigWeights=T, one would only boost the foam geometry,
instead of the cell content. This would slow down the boosting process, because the boost
weights are ignored in the classification. In most cases studied FillFoamWithOrigWeights=T
leads to worse classification results than FillFoamWithOrigWeights=F for the same number
of boosts. However, when using stronger boosting by choosing AdaBoostBeta accordingly,
filling the original weights into the foam can improve the performance.
The PDE-Foam algorithm exhibits stable performance with respect to variations in most of the
parameter settings. However, optimisation of the parameters is required for small training samples
(<104events) in combination with many observables (>5). In such cases, VolFrac should be
increased until an acceptable performance is reached. Moreover, in cases where the classification
time is not critical, one of the Kernel methods should be applied to further improve the classi-
fication performance. For large training samples (>105) and if the training time is not critical,
nActiveCells should be increased to improve the classification performance.
8.4.3 Classification
To classify an event in a d-dimensional phase space as being either of signal or of background type,
a local estimator of the probability that this event belongs to either class can be obtained from the
foam’s hyper-rectangular cells. The foams are created and filled based on samples of signal and
background training events. For classification two possibilities are implemented. One foam can be
used to separate the S/B probability density or two separate foams are created, one for the signal
events and one for background events.
8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam) 79
1) Separate signal and background foams
If the option SigBgSeparate=True is set, the method PDE-Foam treats the signal- and background
distributions separately and performs the following steps to form the two foams and to calculate
the classifier discriminator for a given event:
1. Setup of training trees. Two binary search trees are created and filled with the d-dimensional
observable vectors of all signal and background training events, respectively.
2. Initialisation phase. Two independent foams for signal and background are created.
3. Growing phase. The growing is performed independently for the two foams. The density of
events is estimated as the number of events found in the corresponding tree that are contained
in the sampling box divided by the volume of the box (see VolFrac option). The geometries of
the final foams reflect the distribution of the training samples: phase-space regions where the
density of events is constant are combined in large cells, while in regions with large gradients
in density many small cells are created.
4. Filling phase. Both for the signal and background foam each active cell is filled with the
number of training events, nS(signal) or nB(background), contained in the corresponding
cell volume, taking into account the event weights wi:nS=Psig. cell wi,nB=Pbg. cell wi.
5. Evaluation phase. The estimator for a given event is evaluated based on the number of events
stored in the foam cells. The two corresponding foam cells that contain the event are found.
The number of events (nSand nB) is read from the cells. The estimator yPDE-Foam(i) is then
given by
yPDE-Foam(i) = nS/VS
nB
VB+nS
VS
,(48)
where VSand VBare the respective cell volumes. The statistical error of the estimator is
calculated as:
σyPDE-Foam (i) = snS√nB
(nS+nB)22
+nB√nS
(nS+nB)22
.(49)
Note that the so defined discriminant approximates the probability for an event from within
the cell to be of class signal, if the weights are normalised such that the total number of
weighted signal events is equal to the total number of weighted background events. This can
be enforced with the normalisation mode “EqualNumEvents” (cf. Sec. 3.1.4).
Steps 1-4 correspond to the training phase of the method. Step 5 is performed during the testing
phase. In contrast to the PDE-RS method the memory consumption and computation time for the
testing phase does not depend on the number of training events.
Two separate foams for signal and background allow the foam algorithm to adapt the foam geome-
tries to the individual shapes of the signal and background event distributions. It is therefore well
suited for cases where the shapes of the two distributions are very different.

80 8 The TMVA Methods
2) Single signal and background foam
If the option SigBgSeparate=False is set (default), the PDE-Foam method creates only one foam,
which holds directly the estimator instead of the number of signal and background events. The
differences with respect to separate signal and backgrounds foams are:
1. Setup of training trees. Fill only one binary search tree with both signal events and background
events. This is possible, since the binary search tree has the information whether a event is
of signal or background type.
2. Initialisation phase. Only one foam is created. The cells of this foam will contain the estimator
yPDE-Foam(i) (see eq. (48)).
3. Growing phase. The splitting algorithm in this case minimises the variance of the estimator
density σρ/hρiacross each cell. The estimator density ρis sampled as the number of weighted
signal events nSover the total number of weighted events nS+nBin a small box around the
sampling points:
ρ=nS
nS+nB
1
VolFrac (50)
In this case the geometries of the final foams reflect the distribution of the estimator density in
the training sample: phase-space regions where the signal to background ratio is constant are
combined in large cells, while in regions where the signal-to-background ratio changes rapidly
many small cells are created.
4. Filling phase. Each active cell is filled with the estimator given as the ratio of weighted signal
events to the total number of weighted events in the cell:
yPDE-Foam(i) = nS
nS+nB
.(51)
The statistical error of the estimator (49) also is stored in the cell.
5. Evaluation phase. The estimator for a given event is directly obtained as the discriminator
that is stored in the cell which contains the event.
For the same total number of foam cells, the performance of the two implementations was found to
be similar.
8.4.4 Regression
Two different methods are implemented for regression. In the first method, applicable for single
targets only (mono-target regression), the target value is stored in each cell of the foam. In the
second method, applicable to any number of targets (multi-target regression), the target values are
stored in higher foam dimensions.
In mono-target regression the density used to form the foam is given by the mean target density
in a given box. The procedure is as follows.

8.4 Likelihood estimator using self-adapting phase-space binning (PDE-Foam) 81
1. Setup of training trees. A binary search tree is filled with all training events.
2. Growing phase. One nvar-dimensional foam is formed: the density ρis given by the mean
target value htiwithin the sampling box, divided by the box volume (given by the VolFrac
option):
ρ=hti
VolFrac ≡PNbox
i=1 ti
Nbox ·VolFrac ,(52)
where the sum is over all Nbox events within the sampling box, and tiis the target value of
event i.
3. Filling phase. The cells are filled with their average target values, hti=PNbox
i=1 t(i)/Nbox.
4. Evaluation phase. Estimate the target value for a given test event: find the corresponding
foam cell in which the test event is situated and read the average target value htifrom the
cell.
For multi-target regression the target information is stored in additional foam dimensions. For a
training sample with nvar (ntar) input variables (regression targets), one would form a (nvar +ntar)-
dimensional foam. To compute a target estimate for event i, one needs the coordinates of the cell
centre C(i, k) in each foam dimension k. The procedure is as follows.
1. Setup of training trees. A binary search tree is filled with all training events.
2. Growing phase. A (nvar +ntar)-dimensional foam is formed: the event density ρis estimated
by the number of events Nbox within a predefined box of the dimension (nvar +ntar), divided
by the box volume, whereas the box volume is given by the VolFrac option
ρ=Nbox
VolFrac .(53)
3. Filling phase. Each foam cell is filled with the number of corresponding training events.
4. Evaluation phase. Estimate the target value for a given test event: find the Ncells foam cells
in which the coordinates (x1, . . . , xnvar ) of the event vector are situated. Depending on the
TargetSelection option, the target value tk(k= 1, . . . , ntar) is
(a) the coordinate of the cell centre in direction of the target dimension nvar +kof the cell
j(j= 1, . . . , Ncells), which has the maximum event density
tk=C(j, nvar +k),(54)
if TargetSelection=Mpv.
(b) the mean cell centre in direction of the target dimension nvar +kweighted by the event
densities dev(j) (j= 1, . . . , Ncells) of the cells
tk=PNcells
j=1 C(j, nvar +k)·dev(j)
PNcells
j=1 dev(j)(55)
if TargetSelection=Mean.

82 8 The TMVA Methods
Kernel functions for regression
The kernel weighting methods have been implemented also for regression, taking into account the
modified structure of the foam in case of multi-target regression.
8.4.5 Visualisation of the foam via projections to 2 dimensions
A projection function is used to visualise the foam in two dimensions. It is called via:
TH2D *proj = foam->Project2( dim1, dim2, cell_value, kernel, nbin );
Code Example 39: Call of the projection function. The first two arguments are the dimensions one wishes
to project on, the third specifies the quantity to plot (kValue,kValueError,kValueDensity,kMeanValue,
kRms,kRmsOvMean,kCellVolume), and the fourth argument chooses the kernel (default value is NULL which
means that no kernel is used). By the optional parameter nbin one can set the number of bins of the resulting
histogram (default value is 50).
For each bin in the histogram the algorithm finds all cells which match the bin coordinate and fills
the cell values, depending on cell value, into the bin. This implies that in the case of more than
two dimensions the cell values in the dimensions that are not visible are summed.
•cell value==kValue –projecting the cell value
When this option is given, the standard cell values are visualized. The concrete values depend
on the foam type.
In case of classification with separate signal and background foams or multi-target regression,
the cell value is the number of events found in the phase space region of the cell.
In the single foam approach (SigBgSeparate==False) the foam cells are filled with the dis-
criminator. The value v(i), filled in the histogram is equal to the discriminator y(i) stored in
cell i, multiplied by the cell volume, excluding the dimensions dim1 and dim2
v(i) = y(i)
d
Y
k=1
k6=dim1
k6=dim2
L(i, k),(56)
where L(i, k) is the length of the foam cell iin the direction kof a d-dimensional foam.
This means that the average discriminator weighted with the cell size of the non-visualised
dimensions is filled.
In case of a mono-target regression foam (MultiTargetRegression==False) the foam cells
are filled with the target, which is then directly filled into the histogram.
•cell value==kRms,cell value==kRmsOvMean –projection of cell variances
The variance (RMS) and the mean of the event distribution are saved in every foam cell,

8.5 k-Nearest Neighbour (k-NN) Classifier 83
independent of the foam type. If cell value==kRms, then the plotted value is the RMS of
the event distribution in the cell. If cell value==kRmsOvMean, then the RMS divided by the
mean of the event distribution in the cell is filled into the histogram.
•kernel –Using kernels for projecting
Instead of filling the cell values directly into the histogram, one can use a PDEFoam kernel
estimator to interpolate between cell values. In this case the cell value (set by the cell value
option) is passed to the kernel estimator, whose output is filled into the histogram. See page 77
for more details on kernels available for PDE-Foam.
8.4.6 Variable ranking
In PDE-Foam the input variables are ranked according to the number of cuts made in each PDE-
Foam dimension.26 The dimension (the input variable) for which the most cuts were done is ranked
highest.
8.4.7 Performance
Like PDE-RS (see Sec. 8.3), this method is a powerful classification tool for problems with highly
non-linearly correlated observables. Furthermore PDE-Foam is a fast responding classifier, because
of its limited number of cells, independent of the size of the training samples.
An exception is the multi-target regression with Gauss kernel because the time scales with the
number of cells squared. Also the training can be slow, depending on the number of training events
and number of cells one wishes to create.
8.5 k-Nearest Neighbour (k-NN) Classifier
Similar to PDE-RS (cf. Sec. 8.3), the k-nearest neighbour method compares an observed (test) event
to reference events from a training data set [2]. However, unlike PDE-RS, which in its original form
uses a fixed-sized multidimensional volume surrounding the test event, and in its augmented form
resizes the volume as a function of the local data density, the k-NN algorithm is intrinsically adaptive.
It searches for a fixed number of adjacent events, which then define a volume for the metric used.
The k-NN classifier has best performance when the boundary that separates signal and background
events has irregular features that cannot be easily approximated by parametric learning methods.
8.5.1 Booking options
The k-NN classifier is booked via the command:
26Variable ranking is available for PDE-Foam since TMVA version 4.1.1.
84 8 The TMVA Methods
Option Array Default Predefined Values Description
nkNN –20 –Number of k-nearest neighbors
BalanceDepth –6–Binary tree balance depth
ScaleFrac –0.8 –Fraction of events used to compute
variable width
SigmaFact –1–Scale factor for sigma in Gaussian ker-
nel
Kernel –Gaus –Use polynomial (=Poln) or Gaussian
(=Gaus) kernel
Trim –False –Use equal number of signal and back-
ground events
UseKernel –False –Use polynomial kernel weight
UseWeight –True –Use weight to count kNN events
UseLDA –False –Use local linear discriminant - experi-
mental feature
Option Table 14: Configuration options reference for MVA method: k-NN. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
factory->BookMethod( Types::kKNN, "kNN", "<options>" );
Code Example 40: Booking of the k-NN classifier: the first argument is a predefined enumerator, the second
argument is a user-defined string identifier, and the third argument is the configuration options string.
Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The configuration options for the k-NN classifier are listed in Option Table 14 (see also Sec. 6).
8.5.2 Description and implementation
The k-NN algorithm searches for kevents that are closest to the test event. Closeness is thereby
measured using a metric function. The simplest metric choice is the Euclidean distance
R= nvar
X
i=1 |xi−yi|2!1
2
.(57)
where nvar is the number of input variables used for the classification, xiare coordinates of an event
from a training sample and yiare variables of an observed test event. The kevents with the smallest
values of Rare the k-nearest neighbours. The value of kdetermines the size of the neighbourhood
for which a probability density function is evaluated. Large values of kdo not capture the local
behavior of the probability density function. On the other hand, small values of kcause statistical

8.5 k-Nearest Neighbour (k-NN) Classifier 85
0
x
0 0.5 1 1.5
1
x
0
0.5
1
1.5
0
x
0 0.5 1 1.5
2
x
0
0.5
1
1.5
1
x
0 0.5 1 1.5
2
x
0
0.5
1
1.5
Figure 14: Example for the k-nearest neighbour algorithm in a three-dimensional space (i.e., for three
discriminating input variables). The three plots are projections upon the two-dimensional coordinate planes.
The full (open) circles are the signal (background) events. The k-NN algorithm searches for 20 nearest points
in the nearest neighborhood (circle) of the query event, shown as a star. The nearest neighborhood counts 13
signal and 7 background points so that query event may be classified as a signal candidate.
fluctuations in the probability density estimate. A case study with real data suggests that values
of kbetween 10 and 100 are appropriate and result in similar classification performance when the
training sample contains hundreds of thousands of events (and nvar is of the order of a few variables).
The classification algorithm finds k-nearest training events around a query point
k=kS+kB,(58)
where kS(B)is number of the signal (background) events in the training sample. The relative
probability that the test event is of signal type is given by
PS=kS
kS+kB
=kS
k.(59)
The choice of the metric governs the performance of the nearest neighbour algorithm. When input
variables have different units a variable that has a wider distribution contributes with a greater
weight to the Euclidean metric. This feature is compensated by rescaling the variables using a scaling
fraction determined by the option ScaleFrac. Rescaling can be turned off by setting ScaleFrac to
0. The scaling factor applied to variable iis determined by the width wiof the xidistribution for
the combined sample of signal and background events: wiis the interval that contains the fraction
ScaleFrac of xitraining values. The input variables are then rescaled by 1/wi, leading to the
rescaled metric
Rrescaled = d
X
i=1
1
w2
i|xi−yi|2!1
2
.(60)
Figure 14 shows an example of event classification with the k-nearest neighbour algorithm.27
27The number of training events shown has been greatly reduced to illustrate the principle of the algorithm. In a
real application a typical k-NN training sample should be ample.

86 8 The TMVA Methods
The output of the k-nearest neighbour algorithm can be interpreted as a probability that an event
is of signal type, if the numbers (better: sum of event weights) of signal and background events in
the training sample are equal. This can be enforced via the Trim option. If set training events of
the overabundant type are randomly removed until parity is achieved.
Like (more or less) all TMVA classifiers, the k-nearest neighbour estimate suffers from statistical
fluctuations in the training data. The typically high variance of the k-NN response is mitigated by
adding a weight function that depends smoothly on the distance from a test event. The current
k-NN implementation uses a polynomial kernel
W(x) = ((1 − |x|3)3if |x|<1,
0 otherwise .(61)
If Rkis the distance between the test event and the kth neighbour, the events are weighted according
to the formula:
WS(B)=
kS(B)
X
i=1
WRi
Rk,(62)
where kS(B)is number of the signal (background) events in the neighbourhood. The weighted signal
probability for the test event is then given by
PS=WS
WS+WB
.(63)
The kernel use is switched on/off by the option UseKernel.
Regression
The k-NN algorithm in TMVA also implements a simple multi-dimensional (multi-target) regression
model. For a test event, the algorithm finds the k-nearest neighbours using the input variables, where
each training event contains a regression value. The predicted regression value for the test event is
the weighted average of the regression values of the k-nearest neighbours, cf. Eq. (41) on page 71.
8.5.3 Ranking
The present implementation of k-NN does not provide a ranking of the input variables.
8.5.4 Performance
The simplest implementation of the k-NN algorithm would store all training events in an array. The
classification would then be performed by looping over all stored events and finding the k-nearest
neighbours. As discussed in Sec. 4.3, such an implementation is impractical for large training
samples. The k-NN algorithm therefore uses a kd-tree structure [12] that significantly improves the
performance.
8.6 H-Matrix discriminant 87
The TMVA implementation of the k-NN method is reasonably fast to allow classification of large
data sets. In particular, it is faster than the adaptive PDE-RS method (cf. Sec. 8.3). Note that
the k-NN method is not appropriate for problems where the number of input variables exceeds
nvar &10. The neighbourood size Rdepends on nvar and the size of the training sample Nas
RN∝1
nvar
√N.(64)
A large training set allows the algorithm to probe small-scale features that distinguish signal and
background events.
8.6 H-Matrix discriminant
The origins of the H-Matrix approach dates back to works of Fisher and Mahalanobis in the context
of Gaussian classifiers [22,23]. It discriminates one class (signal) of a feature vector from another
(background). The correlated elements of the vector are assumed to be Gaussian distributed, and the
inverse of the covariance matrix is the H-Matrix. A multivariate χ2estimator is built that exploits
differences in the mean values of the vector elements between the two classes for the purpose of
discrimination.
The H-Matrix classifier as it is implemented in TMVA is equal or less performing than the Fisher
discriminant (see Sec. 8.7), and has been only included for completeness.
8.6.1 Booking options
The H-Matrix discriminant is booked via the command:
factory->BookMethod( Types::kHMatrix, "HMatrix", "<options>" );
Code Example 41: Booking of the H-Matrix classifier: the first argument is a predefined enumerator, the
second argument is a user-defined string identifier, and the third argument is the configuration options string.
Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
No specific options are defined for this method beyond those shared with all the other methods (cf.
Option Table 9on page 61).
8.6.2 Description and implementation
For an event i, each one χ2estimator (χ2
S(B)) is computed for signal (S) and background (B),
using estimates for the sample means (xS(B),k) and covariance matrices (CS(B)) obtained from the
88 8 The TMVA Methods
training data
χ2
U(i) =
nvar
X
k,`=1
(xk(i)−xU,k)C−1
U,k` (x`(i)−xU,`),(65)
where U=S, B. From this, the discriminant
yH(i) = χ2
B(i)−χ2
S(i)
χ2
B(i) + χ2
S(i),(66)
is computed to discriminate between the signal and background classes.
8.6.3 Variable ranking
The present implementation of the H-Matrix discriminant does not provide a ranking of the input
variables.
8.6.4 Performance
The TMVA implementation of the H-Matrix classifier has been shown to underperform in compar-
ison with the corresponding Fisher discriminant (cf. Sec. 8.7), when using similar assumptions and
complexity. It might therefore be considered to be depreciated.
8.7 Fisher discriminants (linear discriminant analysis)
In the method of Fisher discriminants [22] event selection is performed in a transformed variable
space with zero linear correlations, by distinguishing the mean values of the signal and background
distributions. The linear discriminant analysis determines an axis in the (correlated) hyperspace
of the input variables such that, when projecting the output classes (signal and background) upon
this axis, they are pushed as far as possible away from each other, while events of a same class are
confined in a close vicinity. The linearity property of this classifier is reflected in the metric with
which ”far apart” and ”close vicinity” are determined: the covariance matrix of the discriminating
variable space.
8.7.1 Booking options
The Fisher discriminant is booked via the command:
factory->BookMethod( Types::kFisher, "Fisher", "<options>" );
Code Example 42: Booking of the Fisher discriminant: the first argument is a predefined enumerator, the
second argument is a user-defined string identifier, and the third argument is the configuration options string.
Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.

8.7 Fisher discriminants (linear discriminant analysis) 89
Option Array Default Predefined Values Description
Method –Fisher Fisher,
Mahalanobis
Discrimination method
Option Table 15: Configuration options reference for MVA method: Fisher. Values given are defaults. If
predefined categories exist, the default category is marked by a ’star’. The options in Option Table re-
fopt:mva::methodbase on page pagerefopt:mva::methodbase can also be configured.
The configuration options for the Fisher discriminant are given in Option Table 15.
8.7.2 Description and implementation
The classification of the events in signal and background classes relies on the following characteris-
tics: the overall sample means xkfor each input variable k= 1, . . . , nvar, the class-specific sample
means xS(B),k, and total covariance matrix Cof the sample. The covariance matrix can be decom-
posed into the sum of a within- (W) and a between-class matrix (B). They respectively describe
the dispersion of events relative to the means of their own class (within-class matrix), and relative
to the overall sample means (between-class matrix)28.
The Fisher coefficients,Fk, are then given by
Fk=√N
SN
B
N
S+N
B
nvar
X
`=1
W−1
k` (xS,` −xB,`),(67)
where N
S(B)are the number of signal (background) events in the training sample. The Fisher
discriminant yFi(i) for event iis given by
yFi(i) = F0+
nvar
X
k=1
Fkxk(i).(68)
The offset F0centers the sample mean yFi of all N
S+N
Bevents at zero.
Instead of using the within-class matrix, the Mahalanobis variant determines the Fisher coefficients
28The within-class matrix is given by
Wk` =X
U=S,B
hxU,k −xU,kihxU,` −xU,`i=CS,k` +CB,k` ,
where CS(B)is the covariance matrix of the signal (background) sample. The between-class matrix is obtained by
Bk` =1
2X
U=S,B
(xU,k −xk) (xU,` −x`),
where xS(B),k is the average of variable xkfor the signal (background) sample, and xkdenotes the average for the
entire sample.

90 8 The TMVA Methods
as follows [23]
Fk=√N
SN
B
N
S+N
B
nvar
X
`=1
C−1
k` (xS,` −xB,`),(69)
where Ck` =Wk` +Bk`.
8.7.3 Variable ranking
The Fisher discriminant analysis aims at simultaneously maximising the between-class separation
while minimising the within-class dispersion. A useful measure of the discrimination power of a
variable is therefore given by the diagonal quantity Bkk/Ckk, which is used for the ranking of the
input variables.
8.7.4 Performance
In spite of the simplicity of the classifier, Fisher discriminants can be competitive with likelihood
and nonlinear discriminants in certain cases. In particular, Fisher discriminants are optimal for
Gaussian distributed variables with linear correlations (cf. the standard toy example that comes
with TMVA).
On the other hand, no discrimination at all is achieved when a variable has the same sample mean
for signal and background, even if the shapes of the distributions are very different. Thus, Fisher
discriminants often benefit from suitable transformations of the input variables. For example, if a
variable x∈[−1,1] has a a signal distributions of the form x2, and a uniform background distribu-
tions, their mean value is zero in both cases, leading to no separation. The simple transformation
x→ |x|renders this variable powerful for the use in a Fisher discriminant.
8.8 Linear discriminant analysis (LD)
The linear discriminant analysis provides data classification using a linear model, where linear refers
to the discriminant function y(x) being linear in the parameters β
y(x) = x>β+β0,(70)
where β0(denoted the bias) is adjusted so that y(x)≥0 for signal and y(x)<0 for background. It
can be shown that this is equivalent to the Fisher discriminant, which seeks to maximise the ratio
of between-class variance to within-class variance by projecting the data onto a linear subspace.
8.8.1 Booking options
The LD is booked via the command:

8.8 Linear discriminant analysis (LD) 91
factory->BookMethod( Types::kLD, "LD" );
Code Example 43: Booking of the linear discriminant: the first argument is a predefined enumerator, the
second argument is a user-defined string identifier. No method-specific options are available. See Sec. 3.1.5
for more information on the booking.
No specific options are defined for this method beyond those shared with all the other methods (cf.
Option Table 9on page 61).
8.8.2 Description and implementation
Assuming that there are m+1 parameters β0,··· , βmto be estimated using a training set comprised
of nevents, the defining equation for βis
Y=Xβ , (71)
where we have absorbed β0into the vector βand introduced the matrices
Y=
y1
y2
.
.
.
yn
and X=
1x11 ··· x1m
1x21 ··· x2m
.
.
..
.
.....
.
.
1xn1··· xnm
,(72)
where the constant column in Xrepresents the bias β0and Yis composed of the target values
with yi= 1 if the ith event belongs to the signal class and yi= 0 if the ith event belongs to the
background class. Applying the method of least squares, we now obtain the normal equations for
the classification problem, given by
XTXβ =XTY⇐⇒ β= (XTX)−1XTY . (73)
The transformation (XTX)−1XTis known as the Moore-Penrose pseudo inverse of Xand can be
regarded as a generalisation of the matrix inverse to non-square matrices. It requires that the matrix
Xhas full rank.
If weighted events are used, this is simply taken into account by introducing a diagonal weight
matrix Wand modifying the normal equations as follows:
β= (XTW X)−1XTW Y . (74)
Considering two events x1and x2on the decision boundary, we have y(x1) = y(x2) = 0 and hence
(x1−x2)Tβ= 0. Thus we see that the LD can be geometrically interpreted as determining the
decision boundary by finding an orthogonal vector β.

92 8 The TMVA Methods
8.8.3 Variable ranking
The present implementation of LD provides a ranking of the input variables based on the coefficients
of the variables in the linear combination that forms the decision boundary. The order of importance
of the discriminating variables is assumed to agree with the order of the absolute values of the
coefficients.
8.8.4 Regression with LD
It is straightforward to apply the LD algorithm to linear regression by replacing the binary targets
yi∈0,1 in the training data with the measured values of the function which is to be estimated. The
resulting function y(x) is then the best estimate for the data obtained by least-squares regression.
8.8.5 Performance
The LD is optimal for Gaussian distributed variables with linear correlations (cf. the standard toy
example that comes with TMVA) and can be competitive with likelihood and nonlinear discrimi-
nants in certain cases. No discrimination is achieved when a variable has the same sample mean
for signal and background, but the LD can often benefit from suitable transformations of the input
variables. For example, if a variable x∈[−1,1] has a signal distribution of the form x2and a
uniform background distribution, their mean value is zero in both cases, leading to no separation.
The simple transformation x→ |x|renders this variable powerful for the use with LD.
8.9 Function discriminant analysis (FDA)
The common goal of all TMVA discriminators is to determine an optimal separating function in
the multivariate space of all input variables. The Fisher discriminant solves this analytically for the
linear case, while artificial neural networks, support vector machines or boosted decision trees pro-
vide nonlinear approximations with – in principle – arbitrary precision if enough training statistics
is available and the chosen architecture is flexible enough.
The function discriminant analysis (FDA) provides an intermediate solution to the problem with
the aim to solve relatively simple or partially nonlinear problems. The user provides the desired
function with adjustable parameters via the configuration option string, and FDA fits the parameters
to it, requiring the function value to be as close as possible to the real value (to 1 for signal and
0 for background in classification). Its advantage over the more involved and automatic nonlinear
discriminators is the simplicity and transparency of the discrimination expression. A shortcoming
is that FDA will underperform for involved problems with complicated, phase space dependent
nonlinear correlations.

8.9 Function discriminant analysis (FDA) 93
Option Array Default Predefined Values Description
Formula –(0) –The discrimination formula
ParRanges –() –Parameter ranges
FitMethod –MINUIT MC, GA, SA,
MINUIT
Optimisation Method
Converger –None None, MINUIT FitMethod uses Converger to improve
result
Option Table 16: Configuration options reference for MVA method: FDA. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured. The input variables In the discriminator expression are denoted x0,x1, . . . (until
nvar −1), where the number follows the order in which the variables have been registered with the Factory;
coefficients to be determined by the fit must be denoted (0),(1), . . . (the number of coefficients is free)
in the formula; allowed is any functional expression that can be interpreted by a ROOT TFormula. See
Code Example 45 for an example expression. The limits for the fit parameters (coefficients) defined in the
formula expression are given with the syntax: ”(-1,3);(2,10);...”, where the first interval corresponds
to parameter (0). The converger allows to use (presently only) Minuit fitting in addition to Monte Carlo
sampling or a Genetic Algorithm. More details on this combination are given in Sec. 6.5. The various fitters
are configured using the options given in Tables 5,6,7and 8, for MC, Minuit, GA and SA, respectively.
8.9.1 Booking options
FDA is booked via the command:
factory->BookMethod( Types::kFDA, "FDA", "<options>" );
Code Example 44: Booking of the FDA classifier: the first argument is a predefined enumerator, the second
argument is a user-defined string identifier, and the third argument is the configuration options string.
Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The configuration options for the FDA classifier are listed in Option Table 16 (see also Sec. 6).
A typical option string could look as follows:

94 8 The TMVA Methods
"Formula=(0)+(1)*x0+(2)*x1+(3)*x2+(4)*x3:\
ParRanges=(-1,1);(-10,10);(-10,10);(-10,10);(-10,10):\
FitMethod=MINUIT:\
ErrorLevel=1:PrintLevel=-1:FitStrategy=2:UseImprove:UseMinos:SetBatch"
Code Example 45: FDA booking option example simulating a linear Fisher discriminant (cf. Sec. 8.7). The
top line gives the discriminator expression, where the xi denote the input variables and the (j) denote the
coefficients to be determined by the fit. Allowed are all standard functions and expressions, including the
functions belonging to the ROOT TMath library. The second line determines the limits for the fit parameters,
where the numbers of intervals given must correspond to the number of fit parameters defined. The third
line defines the fitter to be used (here Minuit), and the last line is the fitter configuration.
8.9.2 Description and implementation
The parsing of the discriminator function employs ROOT’s TFormula class, which requires that
the expression complies with its rules (which are the same as those that apply for the TTree::
Draw command). For simple formula with a single global fit solution, Minuit will be the most
efficient fitter. However, if the problem is complicated, highly nonlinear, and/or has a non-unique
solution space, more involved fitting algorithms may be required. In that case the Genetic Algorithm
combined or not with a Minuit converger should lead to the best results. After fit convergence, FDA
prints the fit results (parameters and estimator value) as well as the discriminator expression used
on standard output. The smaller the estimator value, the better the solution found. The normalised
estimator is given by
For classification: E=1
W
SPN
S
i=1 (F(xi)−1)2wi+1
W
BPN
B
i=1 F2(xi)wi,
For regression: E=1
WPN
i=1 (F(xi)−ti)2wi,
(75)
where for classification the first (second) sum is over the signal (background) training events, and
for regression it is over all training events, F(xi) is the discriminator function, xiis the tuple of the
nvar input variables for event i,wiis the event weight, tithe tuple of training regression targets,
W
S(B)is the sum of all signal (background) weights in the training sample, and Wthe sum over all
training weights.
8.9.3 Variable ranking
The present implementation of FDA does not provide a ranking of the input variables.
8.9.4 Performance
The FDA performance depends on the complexity and fidelity of the user-defined discriminator
function. As a general rule, it should be able to reproduce the discrimination power of any linear
8.10 Artificial Neural Networks (nonlinear discriminant analysis) 95
discriminant analysis. To reach into the nonlinear domain, it is useful to inspect the correlation
profiles of the input variables, and add quadratic and higher polynomial terms between variables as
necessary. Comparison with more involved nonlinear classifiers can be used as a guide.
8.10 Artificial Neural Networks (nonlinear discriminant analysis)
An Artificial Neural Network (ANN) is most generally speaking any simulated collection of inter-
connected neurons, with each neuron producing a certain response at a given set of input signals.
By applying an external signal to some (input) neurons the network is put into a defined state that
can be measured from the response of one or several (output) neurons. One can therefore view the
neural network as a mapping from a space of input variables x1, . . . , xnvar onto a one-dimensional
(e.g. in case of a signal-versus-background discrimination problem) or multi-dimensional space of
output variables y1, . . . , ymvar . The mapping is nonlinear if at least one neuron has a nonlinear
response to its input.
In TMVA four neural network implementations are available to the user. The first was adapted
from a FORTRAN code developed at the Universit´e Blaise Pascal in Clermont-Ferrand,29 the sec-
ond is the ANN implementation that comes with ROOT. The third is a newly developed neural
network (denoted MLP) that is faster and more flexible than the other two and is the recommended
neural network to use with TMVA. The fourth implementation is a highly optimized one which
provides functionality to perform the training on multi-core and GPU architectures (see 8.11). This
implementation has been developed specifically for the training of very complex neural networks
with several hidden layers, so called deep neural networks. All four neural networks are feed-forward
multilayer perceptrons.
The Clermont-Ferrand neural network
The Clermont-Ferrand neural network is booked via the command:
factory->BookMethod( Types::kCFMlpANN, "CF_ANN", "<options>" );
Code Example 46: Booking of the Clermont-Ferrand neural network: the first argument is a predefined
enumerator, the second argument is a user-defined string identifier, and the third argument is the options
string. Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The configuration options for the Clermont-Ferrand neural net are given in Option Table 17. Since
CFMlpANN is less powerful than the other neural networks in TMVA, it is only kept for backward
compatibility and we do not recommend to use it when starting a new analysis.
29The original Clermont-Ferrand neural network has been used for Higgs search analyses in ALEPH, and background
fighting in rare B-decay searches by the BABAR Collaboration. For the use in TMVA the FORTRAN code has been
converted to C++.

96 8 The TMVA Methods
Option Array Default Predefined Values Description
NCycles –3000 –Number of training cycles
HiddenLayers –N,N-1 –Specification of hidden layer architec-
ture
Option Table 17: Configuration options reference for MVA method: CFMlpANN. Values given are defaults.
If predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on
page 61 can also be configured. See Sec. 8.10.2 for a description of the network architecture configuration.
Option Array Default Predefined Values Description
NCycles –200 –Number of training cycles
HiddenLayers –N,N-1 –Specification of hidden layer architec-
ture (N stands for number of variables;
any integers may also be used)
ValidationFraction –0.5 –Fraction of events in training tree used
for cross validation
LearningMethod –Stochastic Stochastic,
Batch,
SteepestDescent,
RibierePolak,
FletcherReeves,
BFGS
Learning method
Option Table 18: Configuration options reference for MVA method: TMlpANN. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured. See Sec. 8.10.2 for a description of the network architecture configuration.
The ROOT neural network (class TMultiLayerPerceptron)
This neural network interfaces the ROOT class TMultiLayerPerceptron and is booked through
the Factory via the command line:
factory->BookMethod( Types::kTMlpANN, "TMlp_ANN", "<options>" );
Code Example 47: Booking of the ROOT neural network: the first argument is a predefined enumerator,
the second argument is a user-defined string identifier, and the third argument is the configuration options
string. See Sec. 3.1.5 for more information on the booking.
The configuration options for the ROOT neural net are given in Option Table 18.
8.10 Artificial Neural Networks (nonlinear discriminant analysis) 97
The MLP neural network
The MLP neural network is booked through the Factory via the command line:
factory->BookMethod( Types::kMLP, "MLP_ANN", "<options>" );
Code Example 48: Booking of the MLP neural network: the first argument is a predefined enumerator, the
second argument is a user-defined string identifier, and the third argument is the options string. See Sec. 3.1.5
for more information on the booking.
The configuration options for the MLP neural net are given in Option Tables 19 and 20. The option
UseRegulator is of special interest since it invokes the Bayesian extension of the MLP, which is
descibed in Section .
The TMVA implementation of MLP supports random and importance event sampling. With event
sampling enabled, only a fraction (set by the option Sampling) of the training events is used for the
training of the MLP. Values in the interval [0,1] are possible. If the option SamplingImportance
is set to 1, the events are selected randomly, while for a value below 1 the probability for the
same events to be sampled again depends on the training performance achieved for classification
or regression. If for a given set of events the training leads to a decrease of the error of the test
sample, the probability for the events of being selected again is multiplied with the factor given
in SamplingImportance and thus decreases. In the case of an increased error of the test sample,
the probability for the events to be selected again is divided by the factor SamplingImportance
and thus increases. The probability for an event to be selected is constrained to the interval [0,1].
For each set of events, the importance sampling described above is performed together with the
overtraining test.
Event sampling is performed until the fraction specified by the option SamplingEpoch of the total
number of epochs (NCycles) has been reached. Afterwards, all available training events are used for
the training. Event sampling can be turned on and off for training and testing events individually
with the options SamplingTraining and SamplingTesting.
The aim of random and importance sampling is foremost to speed-up the training for large training
samples. As a side effect, random or importance sampling may also increase the robustness of the
training algorithm with respect to convergence in a local minimum.
Since it is typically not known beforehand how many epochs are necessary to achieve a suf-
ficiently good training of the neural network, a convergence test can be activated by setting
ConvergenceTests to a value above 0. This value denotes the number of subsequent convergence
tests which have to fail (i.e. no improvement of the estimator larger than ConvergenceImprove)
to consider the training to be complete. Convergence tests are performed at the same time as
overtraining tests. The test frequency is given by the parameter TestRate.
It is recommended to set the option VarTransform=Norm, such that the input (and in case of
regression the output as well) is normalised to the interval [−1,1].

98 8 The TMVA Methods
Option Array Default Predefined Values Description
NCycles –500 –Number of training cycles
HiddenLayers –N,N-1 –Specification of hidden layer architec-
ture
NeuronType –sigmoid –Neuron activation function type
RandomSeed –1–Random seed for initial synapse
weights (0 means unique seed for each
run; default value ’1’)
EstimatorType –MSE MSE, CE, linear,
sigmoid, tanh,
radial
MSE (Mean Square Estimator) for
Gaussian Likelihood or CE(Cross-
Entropy) for Bernoulli Likelihood
NeuronInputType –sum sum, sqsum,
abssum
Neuron input function type
TrainingMethod –BP BP, GA, BFGS Train with Back-Propagation (BP),
BFGS Algorithm (BFGS), or Genetic
Algorithm (GA - slower and worse)
LearningRate –0.02 –ANN learning rate parameter
DecayRate –0.01 –Decay rate for learning parameter
TestRate –10 –Test for overtraining performed at
each #th epochs
EpochMonitoring –False –Provide epoch-wise monitoring plots
according to TestRate (caution:
causes big ROOT output file!)
Sampling –1–Only ’Sampling’ (randomly selected)
events are trained each epoch
SamplingEpoch –1–Sampling is used for the first ’Sam-
plingEpoch’ epochs, afterwards, all
events are taken for training
SamplingImportance –1–The sampling weights of events in
epochs which successful (worse estima-
tor than before) are multiplied with
SamplingImportance, else they are di-
vided.
SamplingTraining –True –The training sample is sampled
SamplingTesting –False –The testing sample is sampled
ResetStep –50 –How often BFGS should reset history
Tau –3–LineSearch size step
BPMode –sequential sequential,
batch
Back-propagation learning mode: se-
quential or batch
Option Table 19: Configuration options reference for MVA method: MLP. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on
page 61 can also be configured. See Sec. 8.10.2 for a description of the network architecture configuration.
Continuation in Table 20.

8.10 Artificial Neural Networks (nonlinear discriminant analysis) 99
Option Array Default Predefined Values Description
BatchSize –-1 –Batch size: number of events/batch,
only set if in Batch Mode, -1 for Batch-
Size=number of events
ConvergenceImprove –1e-30 –Minimum improvement which counts
as improvement (<0 means automatic
convergence check is turned off)
ConvergenceTests –-1 –Number of steps (without improve-
ment) required for convergence (<0
means automatic convergence check is
turned off)
UseRegulator –False –Use regulator to avoid over-training
UpdateLimit –10000 –Maximum times of regulator update
CalculateErrors –False –Calculates inverse Hessian matrix at
the end of the training to be able to
calculate the uncertainties of an MVA
value
WeightRange –1–Take the events for the estimator cal-
culations from small deviations from
the desired value to large deviations
only over the weight range
Option Table 20: Configuration options reference for MVA method: MLP. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured. See Sec. 8.10.2 for a description of the network architecture configuration. See also
Table 19.
8.10.1 Description and implementation
The behaviour of an artificial neural network is determined by the layout of the neurons, the weights
of the inter-neuron connections, and by the response of the neurons to the input, described by the
neuron response function ρ.
Multilayer Perceptron
While in principle a neural network with nneurons can have n2directional connections, the com-
plexity can be reduced by organising the neurons in layers and only allowing direct connections from
a given layer to the following layer (see Fig. 15). This kind of neural network is termed multi-layer
perceptron; all neural net implementations in TMVA are of this type. The first layer of a multilayer
perceptron is the input layer, the last one the output layer, and all others are hidden layers. For
a classification problem with nvar input variables the input layer consists of nvar neurons that hold
the input values, x1, . . . , xnvar , and one neuron in the output layer that holds the output variable,
the neural net estimator yANN.
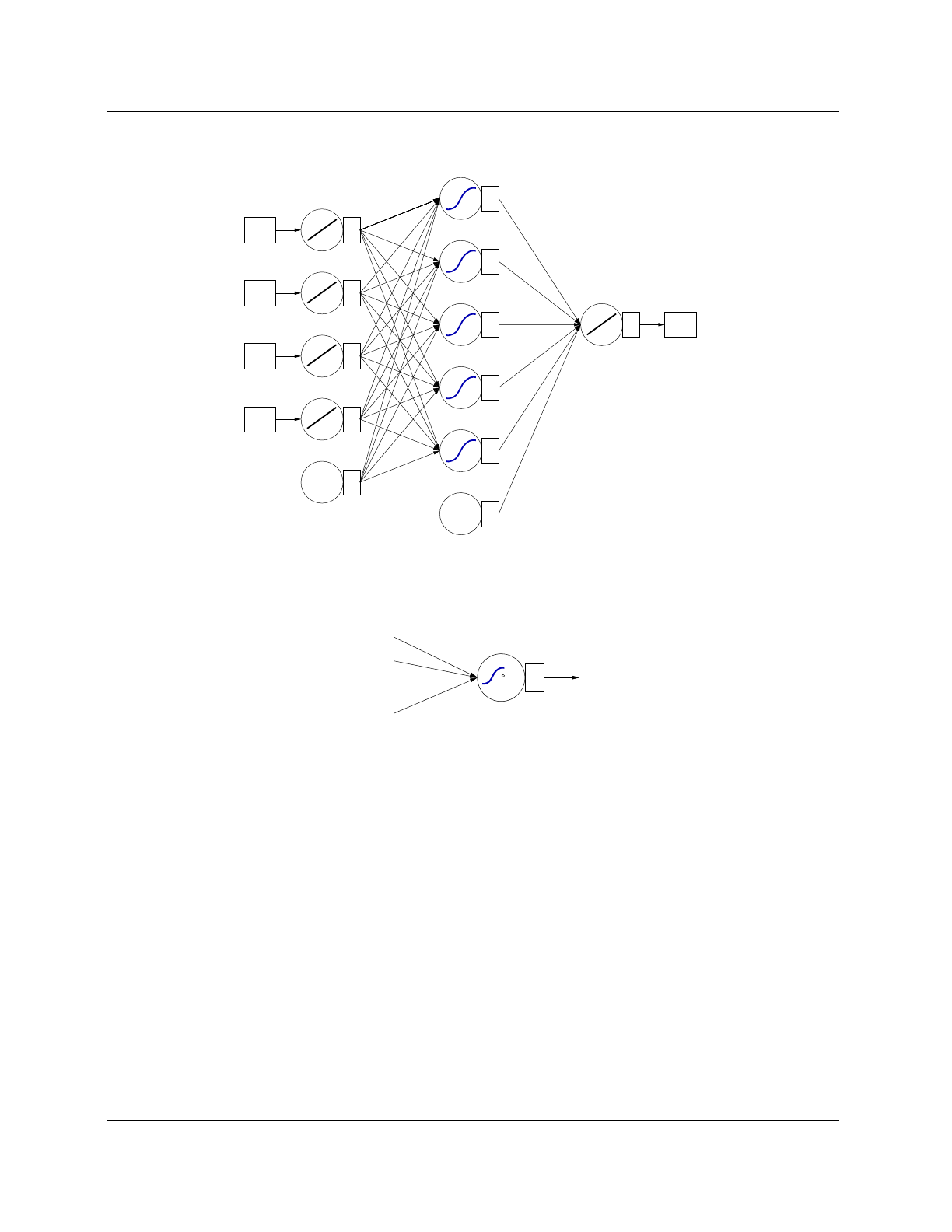
100 8 The TMVA Methods
1
x
2
x
3
x
11
w1
12
w1
y2
1
y2
2
y2
3
y2
4
y2
5
y1
3
y1
1
y1
2
y1
4
y3
1
11
w2
51
w2
01
w2
05
w1
45
w1
4
x
Input Layer Output Layer
Hidden Layer
Bias
Bias
y
ANN
1
1
Figure 15: Multilayer perceptron with one hidden layer.
yl
j
wl−1
1j
wl−1
2j
.
.
.
yl−1
2
yl−1
1
wl−1
nj
yl−1
n
Σ
Output
Input
ρ
Figure 16: Single neuron jin layer `with ninput connections. The incoming connections carry a weight of
w(l−1)
ij .
For a regression problem the network structure is similar, except that for multi-target regression
each of the targets is represented by one output neuron. A weight is associated to each directional
connection between the output of one neuron and the input of another neuron. When calculating
the input value to the response function of a neuron, the output values of all neurons connected to
the given neuron are multiplied with theses weights.
Neuron response function
The neuron response function ρmaps the neuron input i1, . . . , inonto the neuron output (Fig. 16).
Often it can be separated into a Rn7→ R synapse function κ, and a R 7→ R neuron activation

8.10 Artificial Neural Networks (nonlinear discriminant analysis) 101
function α, so that ρ=α◦κ. The functions κand αcan have the following forms:
κ: (y(`)
1, .., y(`)
n|w(`)
0j, .., w(`)
nj )→
w(`)
0j+
n
P
i=1
y(`)
iw(`)
ij Sum,
w(`)
0j+
n
P
i=1 y(`)
iw(`)
ij 2Sum of squares,
w(`)
0j+
n
P
i=1 |y(`)
iw(`)
ij |Sum of absolutes,
(76)
α:x→
xLinear,
1
1 + e−kx Sigmoid,
ex−e−x
ex+e−xTanh,
e−x2/2Radial.
(77)
8.10.2 Network architecture
The number of hidden layers in a network and the number of neurons in these layers are configurable
via the option HiddenLayers. For example the configuration "HiddenLayers=N-1,N+10,3" creates
a network with three hidden layers, the first hidden layer with nvar −1 neurons, the second with
nvar + 10 neurons, and the third with 3 neurons.
When building a network two rules should be kept in mind. The first is the theorem by Weierstrass,
which if applied to neural nets, ascertains that for a multilayer perceptron a single hidden layer is
sufficient to approximate a given continuous correlation function to any precision, provided that a
sufficiently large number of neurons is used in the hidden layer. If the available computing power
and the size of the training data sample suffice, one can increase the number of neurons in the
hidden layer until the optimal performance is reached.
It is likely that the same performance can be achieved with a network of more than one hidden
layer and a potentially much smaller total number of hidden neurons. This would lead to a shorter
training time and a more robust network.
8.10.3 Training of the neural network
Back-propagation (BP)
The most common algorithm for adjusting the weights that optimise the classification performance
of a neural network is the so-called back propagation. It belongs to the family of supervised learning
methods, where the desired output for every input event is known. Back propagation is used by all
neural networks in TMVA. The output of a network (here for simplicity assumed to have a single
hidden layer with a Tanh activation function, and a linear activation function in the output layer)

102 8 The TMVA Methods
is given by
yANN =
nh
X
j=1
y(2)
jw(2)
j1=
nh
X
j=1
tanh nvar
X
i=1
xiw(1)
ij !·w(2)
j1,(78)
where nvar and nhare the number of neurons in the input layer and in the hidden layer, respectively,
w(1)
ij is the weight between input-layer neuron iand hidden-layer neuron j, and w(2)
j1is the weight
between the hidden-layer neuron jand the output neuron. A simple sum was used in Eq. (78) for
the synapse function κ.
During the learning process the network is supplied with Ntraining events xa= (x1, . . . , xnvar )a,
a= 1, . . . , N. For each training event athe neural network output yANN,a is computed and compared
to the desired output ˆya∈ {1,0}(in classification 1 for signal events and 0 for background events).
An error function E, measuring the agreement of the network response with the desired one, is
defined by
E(x1,...,xN|w) =
N
X
a=1
Ea(xa|w) =
N
X
a=1
1
2(yANN,a −ˆya)2,(79)
where wdenotes the ensemble of adjustable weights in the network. The set of weights that
minimises the error function can be found using the method of steepest or gradient descent, provided
that the neuron response function is differentiable with respect to the input weights. Starting from
a random set of weights w(ρ)the weights are updated by moving a small distance in w-space into
the direction −∇wEwhere Edecreases most rapidly
w(ρ+1) =w(ρ)−η∇wE , (80)
where the positive number ηis the learning rate.
The weights connected with the output layer are updated by
∆w(2)
j1=−η
N
X
a=1
∂Ea
∂w(2)
j1
=−η
N
X
a=1
(yANN,a −ˆya)y(2)
j,a ,(81)
and the weights connected with the hidden layers are updated by
∆w(1)
ij =−η
N
X
a=1
∂Ea
∂w(1)
ij
=−η
N
X
a=1
(yANN,a −ˆya)y(2)
j,a (1 −y(2)
j,a )w(2)
j1xi,a ,(82)
where we have used tanh0x= tanh x(1 −tanh x). This method of training the network is denoted
bulk learning, since the sum of errors of all training events is used to update the weights. An
alternative choice is the so-called online learning, where the update of the weights occurs at each
event. The weight updates are obtained from Eqs. (81) and (82) by removing the event summations.
In this case it is important to use a well randomised training sample. Online learning is the learning
method implemented in TMVA.

8.10 Artificial Neural Networks (nonlinear discriminant analysis) 103
BFGS
The Broyden-Fletcher-Goldfarb-Shannon (BFGS) method [24] differs from back propagation by the
use of second derivatives of the error function to adapt the synapse weight by an algorithm which
is composed of four main steps.
1. Two vectors, Dand Yare calculated. The vector of weight changes Drepresents the evolution
between one iteration of the algorithm (k−1) to the next (k). Each synapse weight corresponds
to one element of the vector. The vector Yis the vector of gradient errors.
D(k)
i=w(k)
i−w(k−1)
i,(83)
Y(k)
i=g(k)
i−g(k−1)
i,(84)
where iis the synapse index, giis the i-th synapse gradient,30 wiis the weight of the i-th
synapse, and kdenotes the iteration counter.
2. Approximate the inverse of the Hessian matrix, H−1, at iteration kby
H−1(k)=D·DT·(1 + YT·H−1(k−1) ·Y)
YT·D−D·YT·H+H·Y·DT+H−1(k−1) ,(85)
where superscripts (k) are implicit for Dand Y.
3. Estimate the vector of weight changes by
D(k)=−H−1(k)·Y(k).(86)
4. Compute a new vector of weights by applying a line search algorithm. In the line search the
error function is locally approximated by a parabola. The algorithm evaluates the second
derivatives and determines the point where the minimum of the parabola is expected. The
total error is evaluated for this point. The algorithm then evaluates points along the line
defined by the direction of the gradient in weights space to find the absolute minimum. The
weights at the minimum are used for the next iteration. The learning rate can be set With
the option Tau. The learning parameter, which defines by how much the weights are changed
in one epoch along the line where the minimum is suspected, is multiplied with the learning
rate as long as the training error of the neural net with the changed weights is below the one
with unchanged weights. If the training error of the changed neural net were already larger
for the initial learning parameter, it is divided by the learning rate until the training error
becomes smaller. The iterative and approximate calculation of H−1(k)turns less accurate
with an increasing number of iterations. The matrix is therefore reset to the unit matrix
every ResetStep steps.
The advantage of the BFGS method compared to BG is the smaller number of iterations. However,
because the computing time for one iteration is proportional to the squared number of synapses,
large networks are particularly penalised.
30The synapse gradient is estimated in the same way as in the BP method (with initial gradient and weights set to
zero).

104 8 The TMVA Methods
8.10.4 Variable ranking
The MLP neural network implements a variable ranking that uses the sum of the weights-squared
of the connections between the variable’s neuron in the input layer and the first hidden layer. The
importance Iiof the input variable iis given by
Ii=x2
i
nh
X
j=1 w(1)
ij 2, i = 1, . . . , nvar ,(87)
where xiis the sample mean of input variable i.
8.10.5 Bayesian extension of the MLP
Achieiving a good test performance with MLP is a tradeoff between using a network architecture
that is flexible enough to allow for the modelling of complex functions and the avoidance of over-
training. Avoiding overtraining by limiting the flexibility of the network in the first place by keeping
the number of hidden units/layers small is a very rigid approach which will typically hurt the per-
formance of the neural network. The Bayesian extension of MLP offers a means to allow for more
complex network architectures while at the same time regularizing the model complexity adaptively
to avoid unwanted overfitting effects. The price to pay is an increase in computation time. The
extension is enabled with the option UseRegulator and should typically be used in difficult setting
where the problem calls for a network architecture with many hidden units and/or several layers.
Enabling the Bayesian extension of the MLP will add an additional term to the network error func-
tion E(w) (which is equivalent to minus the log-likelihood of the training data given the network
model): ˜
E(w) = E(w) + α|w|2(88)
The penalty term is proportional to the squared norm of the weight ensemble wof the network and
effectively penalizes large weights which results in a reduced model complexity. The metaparameter
αcontrols the amount of regularization applied and thus ultimatively controls the level of model
complexity the network can exhibit. This is called a Bayesian extension since it is equivalent to
introducing a Gaussian prior for the network weights, whose width is controlled by the parameter α.
Since choosing αmanually would only shift the problem of picking the correct network complexity to
picking the right α, TMVA automatically infers the best value of αfrom the training data by doing
a complexity analysis based on the so-called evidence approximation. The user can therefore choose
to train a large network which will then automatically be regularized to a degree that optimally fits
the data.
8.10.6 Performance
In the tests we have carried out so far, the MLP and ROOT networks performed equally well,
however with a clear speed advantage for the MLP. The Clermont-Ferrand neural net exhibited
worse classification performance in these tests, which is partly due to the slow convergence of its
training (at least 10k training cycles are required to achieve approximately competitive results).

8.11 Deep Neural Networks 105
8.11 Deep Neural Networks
Adeep neural network (DNN) is an artificial neural network (see Section 8.10) with several hidden
layers and a large number of neurons in each layer. Recent developments in machine learning have
shown that these networks are capable of learning complex, non-linear relations when trained on a
sufficiently large amount of training data. For an article describing the application of DNNs to a
classification problem in particle physics see the article by Baldi, Sadowski and Whiteson [48].
The purpose of this deep neural network implementation is to provide an optimized implementation
of feed-forward multilayer perceptrons that can be efficiently trained on modern multi-core and GPU
architectures. To this end the implementation provides several backends. The standard backend is
the fall-back implementation and will work on any platform where Root can be installed. The CPU
backend uses multithreading to perform the training in parallel on multi-core CPU architectures
and requires a multithreaded BLAS implementation and the Intel TBB library. The GPU backend
can be used to perform the training on CUDA-capable GPU architectures.
8.11.1 Building the CPU and GPU Backends
To be able to use the CPU backend an implementation of the BLAS library as well as the In-
tel TBB library must be available on the system and detected by CMake. Note that the BLAS
implementation must be multithreaded in order to exploit the multithreading capabilities of the
underlying hardware. Furthermore, the IMT CMake flag must be set to enable multithreading for
Intel architectures in Root.
For the GPU backend, a CUDA installation is required on the system and must be successfully
detected by CMake. This requires the user to set the CUDA CMake flag when installing Root.
If the user tries to use a backend that is not installed, the training of the DNN method will abort
with a fatal error.
8.11.2 Training of Deep Neural Networks
As common for deep neural networks, this implementation uses the stochastic batch gradient descend
method to train the network. This means that in each training step the weights Wk
i,j and bias terms
θk
iof a given layer kare updated using
Wk
i,j →Wk
i,j −α∂J(xb,yb)
∂W k
i,j
(89)
θk
i→θk
i−α∂J(xb,yb)
∂θk
i
(90)
Here J(xb,yb) is the value of the loss function corresponding to the randomly chosen input batch xb

106 8 The TMVA Methods
and expected output yb. If regularization is applied, the loss may as well contain contributions from
the weight terms Wk
i,j of each layer. This implementation also supports training with momentum.
In this case training updates take the form:
∆Wk
i,j →p∆Wk
i,j + (1.0−p)∂J(xb,yb)
∂W k
i,j
(91)
Wk
i,j →Wk
i,j −α∆Wk
i,j (92)
∆θk
i→p∆θk
i+ (1.0−p)∂J(xb,yb)
∂θk
i
(93)
θk
i→θk
i−α∆θk
i(94)
Note that for p= 0 the standard stochastic batch gradient descent method is obtained.
The training batch (xb,yb) is chosen randomly and without replacement from the set of training
samples. The number of training steps necessary to traverse the whole training set one time is
referred to as an epoch.
The training of the deep neural network is performed in one or multiple training phases. A training
phase ends when the test error did not decrease for a user-specified number of epochs.
8.11.3 Test and Evaluation Set
The user should note that this implementation uses the error on the TMVA test set to check for
convergence. Therefore the TMVA test error reported by TMVA may overestimate the performance
of the model. To properly evaluate the performance, the model should be evaluated on a completely
separate data set.
8.11.4 Booking of the DNN Method
The booking of the DNN method is similar to any other method in TMVA. The method specific
options are passed in the form of an option string hoptionsito the method.
factory->BookMethod(dataloader, TMVA::Types::kDNN, "DNN", <options>);
Code Example 49: Booking of a deep neural network: The first argument is a TMVA::DataLoader object,
which holds training and test data. The second argument is the predefined enumerator object that represents
the deep neural network implementation. The third argument is a string holding a user defined name for
the method. The fourth argument is the option string holding the options for the method. See Sec. 3.1.5 for
more information on the booking.

8.11 Deep Neural Networks 107
The Architecture parameter is used to specify the backend used for the training. The standard
backend will work with any Root installation, but is not optimized with respect to performance. The
standard backend also supports multithreading, which can be enabled for each training phase sepa-
rately (see 8.11.6). The multi-core CPU and GPU backends must be enabled during the installation
of Root.
The method used to initialize the weight matrices before beginning the training is specified using the
WeightInitialization argument. Possible values are XAVIER, which initializes the weights with
zero-mean Gaussian distributed random values, and XAVIERUNIFORM, which initializes the weights
with uniformly distributed values.
The complete set of options that can be set in the options string are summarized in Table 21.
Option Array Default Predefined Values Description
Architecture –STANDARD STANDARD, CPU,
GPU
Compute architecture backend to use
for the training of the network
ErrorStrategy –CROSSENTROPY CROSSENTROPY,
SUMOFSQUARES
Loss functions used for the training
Layout – – See Section
8.11.5
Layout of the network
TrainingStrategy – – See Section
8.11.6
Training Settings
WeightInitialization –XAVIER XAVIER,
XAVIERUNIFORM
Weight initialization method
Option Table 21: Configuration options reference for MVA method: DNN.
8.11.5 Network Layout
The structure of the deep neural network is specified by the Layout parameter of the option string.
This string specifies the activation function and the number of neurons of each layer of the network.
Different layers are separated by ’,’ characters while activation function and number of neurons are
separated by ’|’ characters. For example the layout string
Layout=TANH|128,TANH|128,TANH|128,LINEAR
defines a network with three hidden layers with 128 neurons and tanh activation functions. The
neurons of the output layer are inferred automatically from the number of classes (in the case of
classification) or the number of target variables (in the case of regression). The available activatio-
functions are given in Table 22.

108 8 The TMVA Methods
Name Activation Function
IDENTITY f(x) = x
RELU f(x) = (x, if x≥0
0,otherwise
TANH f(x) = tanh(x)
SIGMOID f(x) = 1
1+exp(−x)
SOFTSIGN f(x) = x
1+|x|
GAUSS f(x) = exp(−x2)
SYMMRELU f(x) = (x, if x≥0
−x, otherwise
Option Table 22: DNN Activation Functions
8.11.6 Training Strategy
The training of deep neural networks is performed in one or several consecutive training phases
that are specified using the TrainingStategy argument of the hoptionsistring passed to the
BookMethod call. A single phase is specified by the parameters described in Table 23. Different
training phases are separated by |characters. As an example, a valid training strategy string would
be the following:
TrainingStrategy = LearningRate=1e-1, BatchSize=256
| LearningRate=1e-2, BatchSize=256
| LearningRate=1e-3, BatchSize=256
This training strategy trains the network in three training phases each with a lower learning rate.
Dropout is a regularization technique that with a certain probability sets neuron activations to zero.
This probability can be set for all layers at once by giving a single floating point value or a value
for each hidden layer of the network separated by ’+’ signs. Probabilities should be given by a value
in the interval [0,1].

8.11 Deep Neural Networks 109
Option Array Default Predefined Values Description
BatchSize –30 –Batch size used for this training phase.
ConvergenceSteps –100 –Convergence criterion: Number of
training epochs without improvement
in test error to be performed before
ending the training phase
DropConfig –0.0 –Dropout fractions for each layer sepa-
rated by ’+’ signs or a single number
if the same for all layers.
LearningRate –10−5–Learning rate αto use for the current
training phase.
Momentum –0.0 –The momentum pto use for the train-
ing. See section 8.11.2.
Regularization –NONE NONE, L1 ,L2 Type of regularization
Multithreading –T T, F Whether to use multithreading with
the standard backend or not. Does not
affect CPU and GPU backend.
TestRepetitions –7–Interval for evaluation of the test set
error in epochs.
WeightDecay –0.0 –Scaling factor applied to the L1 or L2
norms of the weight matrices when us-
ing regularization.
Option Table 23: Configuration options reference for MVA method: DNN.

110 8 The TMVA Methods
8.12 Support Vector Machine (SVM)
In the early 1960s a linear support vector method has been developed for the construction of
separating hyperplanes for pattern recognition problems [39,40]. It took 30 years before the method
was generalised to nonlinear separating functions [41,42] and for estimating real-valued functions
(regression) [43]. At that moment it became a general purpose algorithm, performing classification
and regression tasks which can compete with neural networks and probability density estimators.
Typical applications of SVMs include text categorisation, character recognition, bio-informatics and
face detection.
The main idea of the SVM approach to classification problems is to build a hyperplane that sep-
arates signal and background vectors (events) using only a minimal subset of all training vectors
(support vectors). The position of the hyperplane is obtained by maximizing the margin (distance)
between it and the support vectors. The extension to nonlinear SVMs is performed by mapping
the input vectors onto a higher dimensional feature space in which signal and background events
can be separated by a linear procedure using an optimally separating hyperplane. The use of ker-
nel functions eliminates thereby the explicit transformation to the feature space and simplifies the
computation.
The implementation of the newly introduced regression is similar to the approach in classification.
It also maps input data into higher dimensional space using previously chosen support vectors.
Instead of separating events of two types, it determines the hyperplane with events of the same
value (which is equal to the mean from all training events). The final value is estimated based on
the distance to the hyperplane which is computed by the selected kernel function.
8.12.1 Booking options
The SVM classifier is booked via the command:
factory->BookMethod( TMVA::Types::kSVM, "SVM", "<options>" );
Code Example 50: Booking of the SVM classifier: the first argument is a unique type enumerator, the second
is a user-defined name which must be unique among all booked classifiers, and the third argument is the
configuration option string. Individual options are separated by a ’:’. For options that are not set in the
string default values are used. See Sec. 3.1.5 for more information on the booking.
The configuration options for the SVM classifier are given in Option Table 24.
8.12.2 Description and implementation
A detailed description of the SVM formalism can be found, for example, in Ref. [44]. Here only a
brief introduction of the TMVA implementation is given.

8.12 Support Vector Machine (SVM) 111
Option Array Default Predefined Values Description
Gamma –1–RBF kernel parameter: Gamma (size
of the Kernel)
C–1–Cost parameter
Tol –0.01 –Tolerance parameter
MaxIter –1000 –Maximum number of training loops
Option Table 24: Configuration options reference for MVA method: SVM. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
Linear SVM
Consider a simple two-class classifier with oriented hyperplanes. If the training data is linearly
separable, a vector-scalar pair ( ~w, b) can be found that satisfies the constraints
yi(~xi·~w +b)−1≥0,∀i,(95)
where ~xiare the input vectors, yithe desired outputs (yi=±1), and where the pair ( ~w, b) defines
a hyperplane. The decision function of the classifier is f(~xi) = sign(~xi·~w +b), which is +1 for all
points on one side of the hyperplane and −1 for the points on the other side.
Intuitively, the classifier with the largest margin will give better separation. The margin for this
linear classifier is just 2/|~w|. Hence to maximise the margin, one needs to minimise the cost function
W=|~w|2/w with the constraints from Eq. (95).
At this point it is beneficial to consider the significance of different input vectors ~xi. The training
events lying on the margins, which are called the support vectors (SV), are the events that contribute
to defining the decision boundary (see Fig. 17). Hence if the other events are removed from the
training sample and the classifier is retrained on the remaining events, the training will result in
the same decision boundary. To solve the constrained quadratic optimisation problem, we first
reformulate it in terms of a Lagrangian
L(~w, b, ~α) = 1
2|~w|2−X
i
αi(yi((~xi·~w) + b)−1) (96)
where αi≥0 and the condition from Eq. (95) must be fulfilled. The Lagrangian Lis minimised
with respect to ~w and band maximised with respect to ~α. The solution has an expansion in terms
of a subset of input vectors for which αi6= 0 (the support vectors):
~w =X
i
αiyi~xi,(97)
because ∂L/∂b = 0 and ∂L/∂ ~w = 0 hold at the extremum. The optimisation problem translates to
finding the vector ~α which maximises
L(~α) = X
i
αi−1
2X
ij
αiαjyiyj~xi·~xj.(98)
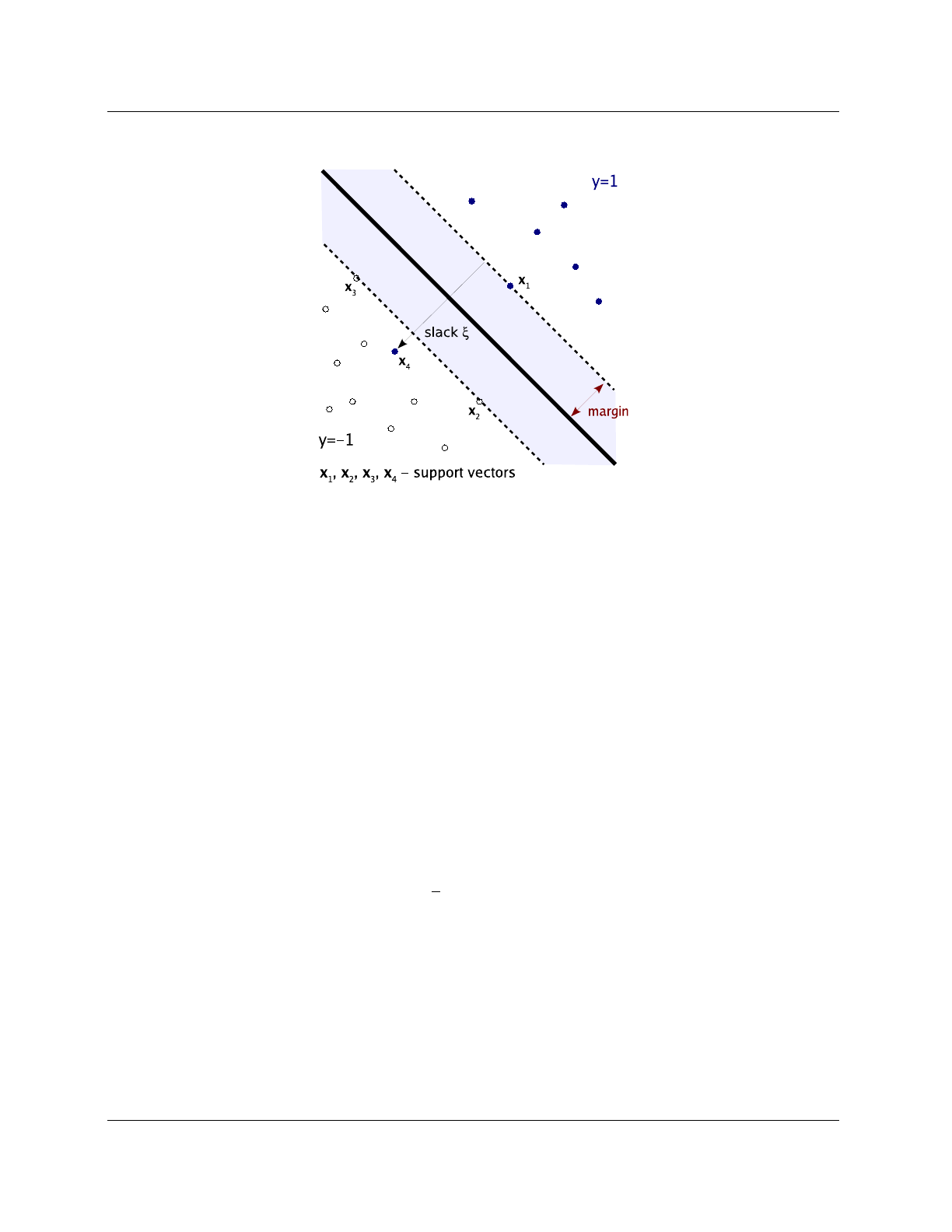
112 8 The TMVA Methods
Figure 17: Hyperplane classifier in two dimensions. The vectors (events) x1−4define the hyperplane and
margin, i.e., they are the support vectors.
Both the optimisation problem and the final decision function depend only on scalar products
between input vectors, which is a crucial property for the generalisation to the nonlinear case.
Nonseparable data
The above algorithm can be extended to non-separable data. The classification constraints in
Eq. (95) are modified by adding a “slack” variable ξito it (ξi= 0 if the vector is properly classified,
otherwise ξiis the distance to the decision hyperplane)
yi(~xi·~w +b)−1 + ξi≥0, ξi≥0,∀i.(99)
This admits a certain amount of misclassification. The training algorithm thus minimises the
modified cost function
W=1
2|~w|2+CX
i
ξi,(100)
describing a trade-off between margin and misclassification. The cost parameter Csets the scale by
how much misclassification increases the cost function (see Tab. 24).
Nonlinear SVM
The SVM formulation given above can be further extended to build a nonlinear SVM which can
classify nonlinearly separable data. Consider a function Φ : Rnvar → H, which maps the training

8.12 Support Vector Machine (SVM) 113
data from Rnvar , where nvar is the number of discriminating input variables, to some higher dimen-
sional space H. In the Hspace the signal and background events can be linearly separated so that
the linear SVM formulation can be applied. We have seen in Eq. (98) that event variables only
appear in the form of scalar products ~xi·~xj, which become Φ(~xi)·Φ(~xj) in the higher dimensional
feature space H. The latter scalar product can be approximated by a kernel function
K(~xi, ~xj)≈Φ(~xi)·Φ(~xj),(101)
which avoids the explicit computation of the mapping function Φ(~x). This is desirable because the
exact form of Φ(~x) is hard to derive from the training data. Most frequently used kernel functions
are K(~x, ~y) = (~x ·~y +θ)dPolynomial,
K(~x, ~y) = exp −|~x −~y|2/2σ2Gaussian,
K(~x, ~y) = tanh (κ(~x ·~y) + θ)Sigmoidal,
(102)
of which currently only the Gaussian Kernel is implemented in TMVA. It was shown in Ref. [43]
that a suitable function kernel must fulfill Mercer’s condition
ZK(~x, ~y)g(~x)g(~y)d~xd~y ≥0,(103)
for any function gsuch that Rg2(~x)d~x is finite. While Gaussian and polynomial kernels are known
to comply with Mercer’s condition, this is not strictly the case for sigmoidal kernels. To extend the
linear methodology to nonlinear problems one substitutes ~xi·~xjby K(~xi, ~xj) in Eq. (98). Due to
Mercer’s conditions on the kernel, the corresponding optimisation problem is a well defined convex
quadratic programming problem with a global minimum. This is an advantage of SVMs compared
to neural networks where local minima occur.
For regression problems, the same algorithm is used as for classification with the exception that
instead of dividing events based on their type (signal/background), it separates them based on the
value (larger/smaller than average). In the end, it does not return the sigmoid of the distance
between the event and the hyperplane, but the distance itself – increased by the average target
value.
Implementation
The TMVA implementation of the Support Vector Machine follows closely the description given
in the literature. It employs a sequential minimal optimisation (SMO) [45] to solve the quadratic
problem. Acceleration of the minimisation is achieved by dividing a set of vectors into smaller
subsets [46]. The number of training subsets is controlled by option NSubSets. The SMO method
drives the subset selection to the extreme by selecting subsets of two vectors (for details see Ref. [44]).
The pairs of vectors are chosen, using heuristic rules, to achieve the largest possible improvement
(minimisation) per step. Because the working set is of size two, it is straightforward to write down
the analytical solution. The minimisation procedure is repeated recursively until the minimum
is found. The SMO algorithm has proven to be significantly faster than other methods and has
become the most common minimisation method used in SVM implementations. The precision of

114 8 The TMVA Methods
the minimisation is controlled by the tolerance parameter Tol (see Tab. 24). The SVM training
time can be reduced by increasing the tolerance. Most classification problems should be solved with
less then 1000 training iterations. Interrupting the SVM algorithm using the option MaxIter may
thus be helpful when optimising the SVM training parameters. MaxIter can be released for the
final classifier training.
8.12.3 Variable ranking
The present implementation of the SVM classifier does not provide a ranking of the input variables.
8.12.4 Performance
The TMVA SVM algorithm comes currently only with the Gaussian kernel function. With sufficient
training statistics, the Gaussian kernel allows to approximate any separating function in the input
space. It is crucial for the performance of the SVM to appropriately tune the kernel parameters and
the cost parameter C. In case of a Gaussian, the kernel is tuned via option Gamma which is related
to the width σby Γ = 1/(2σ2). The optimal tuning of these parameters is specific to the problem
and must be done by the user.
The SVM training time scales with n2, where nis the number of vectors (events) in the training
data set. The user is therefore advised to restrict the sample size during the first rough scan of the
kernel parameters. Also increasing the minimisation tolerance helps to speed up the training.
SVM is a nonlinear general purpose classification and regression algorithm with a performance
similar to neural networks (Sec. 8.10) or to a multidimensional likelihood estimator (Sec. 8.3).
8.13 Boosted Decision and Regression Trees
Adecision (regression) tree is a binary tree structured classifier (regressor) similar to the one
sketched in Fig. 18. Repeated left/right (yes/no) decisions are taken on one single variable at
a time until a stop criterion is fulfilled. The phase space is split this way into many regions that are
eventually classified as signal or background, depending on the majority of training events that end
up in the final leaf node. In case of regression trees, each output node represents a specific value of
the target variable.31 The boosting (see Sec. 7) of a decision (regression) tree extends this concept
from one tree to several trees which form a forest. The trees are derived from the same training
ensemble by reweighting events, and are finally combined into a single classifier (regressor) which
is given by a (weighted) average of the individual decision (regression) trees. Boosting stabilizes
the response of the decision trees with respect to fluctuations in the training sample and is able to
considerably enhance the performance w.r.t. a single tree. In the following, we will use the term
decision tree for both, decision- and regression trees and we refer to regression trees only if both
types are treated differently.
31The target variable is the variable the regression “function” is trying to estimate.
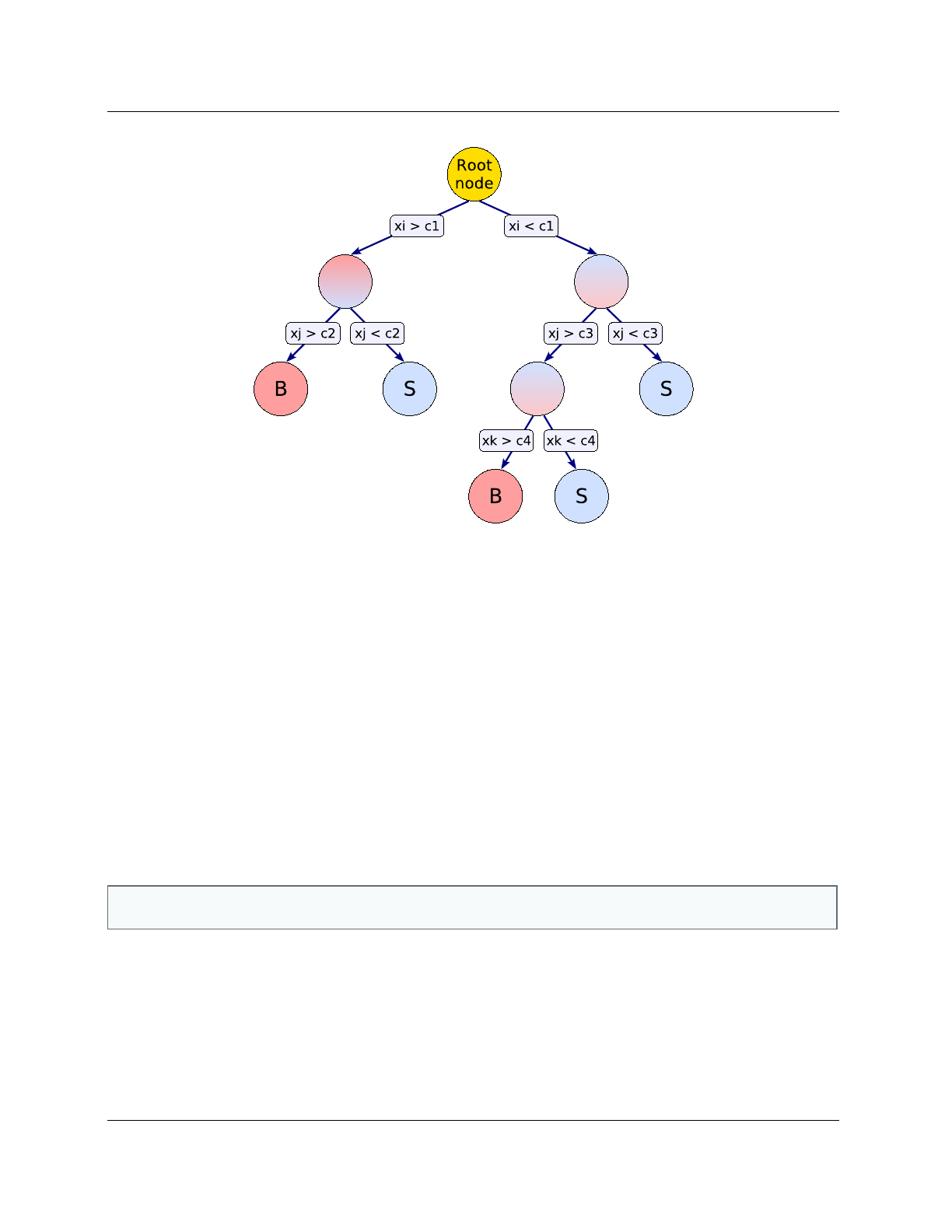
8.13 Boosted Decision and Regression Trees 115
Figure 18: Schematic view of a decision tree. Starting from the root node, a sequence of binary splits using
the discriminating variables xiis applied to the data. Each split uses the variable that at this node gives the
best separation between signal and background when being cut on. The same variable may thus be used at
several nodes, while others might not be used at all. The leaf nodes at the bottom end of the tree are labeled
“S” for signal and “B” for background depending on the majority of events that end up in the respective
nodes. For regression trees, the node splitting is performed on the variable that gives the maximum decrease
in the average squared error when attributing a constant value of the target variable as output of the node,
given by the average of the training events in the corresponding (leaf) node (see Sec. 8.13.3).
8.13.1 Booking options
The boosted decision (regression) treee (BDT) classifier is booked via the command:
factory->BookMethod( Types::kBDT, "BDT", "<options>" );
Code Example 51: Booking of the BDT classifier: the first argument is a predefined enumerator, the second
argument is a user-defined string identifier, and the third argument is the configuration options string.
Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
Several configuration options are available to customize the BDT classifier. They are summarized
in Option Tables 25 and 27 and described in more detail in Sec. 8.13.2.

116 8 The TMVA Methods
Option Array Default Predefined Values Description
NTrees –800 –Number of trees in the forest
MaxDepth –3–Max depth of the decision tree allowed
MinNodeSize –5% –Minimum percentage of training
events required in a leaf node (default:
Classification: 5%, Regression: 0.2%)
nCuts –20 –Number of grid points in variable
range used in finding optimal cut in
node splitting
BoostType –AdaBoost AdaBoost,
RealAdaBoost,
Bagging,
AdaBoostR2,
Grad
Boosting type for the trees in the for-
est (note: AdaCost is still experimen-
tal)
AdaBoostR2Loss –Quadratic Linear,
Quadratic,
Exponential
Type of Loss function in AdaBoostR2
UseBaggedGrad –False –Use only a random subsample of all
events for growing the trees in each it-
eration. (Only valid for GradBoost)
Shrinkage –1–Learning rate for GradBoost algo-
rithm
AdaBoostBeta –0.5 –Learning rate for AdaBoost algorithm
UseRandomisedTrees –False –Determine at each node splitting the
cut variable only as the best out of
a random subset of variables (like in
RandomForests)
UseNvars –2–Size of the subset of variables used
with RandomisedTree option
UsePoissonNvars –True –Interpret UseNvars not as fixed num-
ber but as mean of a Possion dis-
tribution in each split with Ran-
domisedTree option
BaggedSampleFraction –0.6 –Relative size of bagged event sample to
original size of the data sample (used
whenever bagging is used (i.e. Use-
BaggedGrad, Bagging,)
UseYesNoLeaf –True –Use Sig or Bkg categories, or the pu-
rity=S/(S+B) as classification of the
leaf node ->Real-AdaBoost
Option Table 25: Configuration options reference for MVA method: BDT. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured. The table is continued in Option Table 27.

8.13 Boosted Decision and Regression Trees 117
Option Array Default Predefined Values Description
NegWeightTreatment –InverseBoostNegWeightsInverseBoostNegWeights,
IgnoreNegWeightsInTraining,
PairNegWeightsGlobal,
Pray
How to treat events with negative
weights in the BDT training (partic-
ular the boosting) : IgnoreInTrain-
ing; Boost With inverse boostweight;
Pair events with negative and positive
weights in traning sample and *anni-
hilate* them (experimental!)
NodePurityLimit –0.5 –In boosting/pruning, nodes with pu-
rity >NodePurityLimit are signal;
background otherwise.
SeparationType –GiniIndex CrossEntropy,
GiniIndex,
GiniIndexWithLaplace,
MisClassificationError,
SDivSqrtSPlusB,
RegressionVariance
Separation criterion for node splitting
DoBoostMonitor –False –Create control plot with ROC integral
vs tree number
UseFisherCuts –False –Use multivariate splits using the
Fisher criterion
MinLinCorrForFisher –0.8 –The minimum linear correlation be-
tween two variables demanded for use
in Fisher criterion in node splitting
UseExclusiveVars –False –Variables already used in fisher crite-
rion are not anymore analysed individ-
ually for node splitting
DoPreselection –False –and and apply automatic pre-selection
for 100% efficient signal (bkg) cuts
prior to training
RenormByClass –False –Individually re-normalize each event
class to the original size after boost-
ing
SigToBkgFraction –1–Sig to Bkg ratio used in Training (sim-
ilar to NodePurityLimit, which cannot
be used in real adaboost
Option Table 26: Continuation of Option Table 25.

118 8 The TMVA Methods
Option Array Default Predefined Values Description
PruneMethod –NoPruning NoPruning,
ExpectedError,
CostComplexity
Note: for BDTs use small trees
(e.g.MaxDepth=3) and NoPruning:
Pruning: Method used for pruning
(removal) of statistically insignificant
branches
PruneStrength –0–Pruning strength
PruningValFraction –0.5 –Fraction of events to use for optimizing
automatic pruning.
nEventsMin –0–deprecated: Use MinNodeSize (in % of
training events) instead
GradBaggingFraction –0.6 –deprecated: Use *BaggedSampleFrac-
tion* instead: Defines the fraction of
events to be used in each iteration, e.g.
when UseBaggedGrad=kTRUE.
UseNTrainEvents –0–deprecated: Use *BaggedSampleFrac-
tion* instead: Number of randomly
picked training events used in ran-
domised (and bagged) trees
NNodesMax –0–deprecated: Use MaxDepth instead to
limit the tree size
Option Table 27: Some deprecated options for the BDT Method that are for the moment still kept for
compatibility.

8.13 Boosted Decision and Regression Trees 119
8.13.2 Description and implementation
Decision trees are well known classifiers that allow a straightforward interpretation as they can be
visualized by a simple two-dimensional tree structure. They are in this respect similar to rectangular
cuts. However, whereas a cut-based analysis is able to select only one hypercube as region of phase
space, the decision tree is able to split the phase space into a large number of hypercubes, each
of which is identified as either “signal-like” or “background-like”, or attributed a constant event
(target) value in case of a regression tree. For classification trees, the path down the tree to each
leaf node represents an individual cut sequence that selects signal or background depending on the
type of the leaf node.
A shortcoming of decision trees is their instability with respect to statistical fluctuations in the
training sample from which the tree structure is derived. For example, if two input variables exhibit
similar separation power, a fluctuation in the training sample may cause the tree growing algorithm
to decide to split on one variable, while the other variable could have been selected without that
fluctuation. In such a case the whole tree structure is altered below this node, possibly resulting
also in a substantially different classifier response.
This problem is overcome by constructing a forest of decision trees and classifying an event on a
majority vote of the classifications done by each tree in the forest. All trees in the forest are derived
from the same training sample, with the events being subsequently subjected to so-called boosting
(see 7), a procedure which modifies their weights in the sample. Boosting increases the statistical
stability of the classifier and is able to drastically improve the separation performance compared to
a single decision tree. However, the advantage of the straightforward interpretation of the decision
tree is lost. While one can of course still look at a limited number of trees trying to interpret the
training result, one will hardly be able to do so for hundreds of trees in a forest. Nevertheless,
the general structure of the selection can already be understood by looking at a limited number
of individual trees. In many cases, the boosting performs best if applied to trees (classifiers) that,
taken individually, have not much classification power. These so called “weak classifiers” are small
trees, limited in growth to a typical tree depth of as small as two, depending on the how much
interaction there is between the different input variables. By limiting the tree depth during the
tree building process (training), the tendency of overtraining for simple decision trees which are
typically grown to a large depth and then pruned, is almost completely eliminated.
8.13.3 Boosting, Bagging and Randomising
The different “boosting” algorithms (in the following we will call also baggand and randomised trees
“boosted”) available for decision trees in TMVA are currently:
•AdaBoost (Discreate AdaBoost, see Sec. 7.1), RealAdaBoost (see below and [27]) and Ad-
aBoostR2(see Sec. 31) for regression
•Gradient Boost (see Sec. 7.2)
•Bagging (see Sec. 7.3)

120 8 The TMVA Methods
•Randomised Trees, like the Random Forests of L. Breiman [30]. Each tree is grown in such a
way that at each split only a random subset of all variables is considered. Moreover, each tree
in the forest is grown using only a (resampled) subset of the original training events. The size
of the subset as well as the number of variables considered at each split can be set using the
options UseNTrainEvents and UseNVars.
A possible modification of Eq. (26) for the result of the combined classifier from the forest is to
use the training purity32 in the leaf node as respective signal or background weights rather than
relying on the binary decision. This is then called Real-AdaBoost can be chosen as one of the
boost algorithms. For other boosting algorithms rather than AdaBoost, the same averaging of the
individual trees can be chosen using the option UseYesNoLeaf=False .
Training (Building) a decision tree
The training, building or growing of a decision tree is the process that defines the splitting criteria
for each node. The training starts with the root node, where an initial splitting criterion for the
full training sample is determined. The split results in two subsets of training events that each go
through the same algorithm of determining the next splitting iteration. This procedure is repeated
until the whole tree is built. At each node, the split is determined by finding the variable and
corresponding cut value that provides the best separation between signal and background. The
node splitting stops once it has reached the minimum number of events which is specified in the
BDT configuration (option nEventsMin). The leaf nodes are classified as signal or background
according to the class the majority of events belongs to. If the option UseYesNoLeaf is set the
end-nodes are classified in the same way. If UseYesNoLeaf is set to false the end-nodes are classified
according to their purity.
A variety of separation criteria can be configured (option SeparationType see Option Table 27)
to assess the performance of a variable and a specific cut requirement. Because a cut that selects
predominantly background is as valuable as one that selects signal, the criteria are symmetric with
respect to the event classes. All separation criteria have a maximum where the samples are fully
mixed, i.e., at purity p= 0.5, and fall off to zero when the sample consists of one event class only.
Tests have revealed no significant performance disparity between the following separation criteria:
•Gini Index [default], defined by p·(1 −p);
•Cross entropy, defined by −p·ln(p)−(1 −p)·ln(1 −p);
•Misclassification error, defined by 1 −max(p, 1−p);
•Statistical significance, defined by S/√S+B;
•Average squared error, defined by 1/N ·PN(y−ˆy)2for regression trees where y is the regression
target of each event in the node and ˆyis its mean value over all events in the node (which
would be the estimate of y that is given by the node).
32The purity of a node is given by the ratio of signal events to all events in that node. Hence pure background
nodes have zero purity.

8.13 Boosted Decision and Regression Trees 121
Since the splitting criterion is always a cut on a single variable, the training procedure selects the
variable and cut value that optimises the increase in the separation index between the parent node
and the sum of the indices of the two daughter nodes, weighted by their relative fraction of events.
The cut values are optimised by scanning over the variable range with a granularity that is set
via the option nCuts. The default value of nCuts=20 proved to be a good compromise between
computing time and step size. Finer stepping values did not increase noticeably the performance
of the BDTs. However, a truly optimal cut, given the training sample, is determined by setting
nCuts=-1. This invokes an algorithm that tests all possible cuts on the training sample and finds
the best one. The latter is of course “slightly” slower than the coarse grid.
In principle, the splitting could continue until each leaf node contains only signal or only background
events, which could suggest that perfect discrimination is achievable. However, such a decision tree
would be strongly overtrained. To avoid overtraining a decision tree must be pruned.
Pruning a decision tree
Pruning is the process of cutting back a tree from the bottom up after it has been built to its maxi-
mum size. Its purpose is to remove statistically insignificant nodes and thus reduce the overtraining
of the tree. For simple decision trees It has been found to be beneficial to first grow the tree to its
maximum size and then cut back, rather than interrupting the node splitting at an earlier stage.
This is because apparently insignificant splits can nevertheless lead to good splits further down the
tree. For Boosted Decision trees however, as the boosting algorithms perform best on weak classi-
fiers, pruning is unnecessary as one should rather drastically limit the tree depth far stronger than
any pruning algorithm would do afterwards. Hence, while pruning algorithms are still implemented
in TMVA, they are obsolete as they should not be used.
8.13.4 Variable ranking
A ranking of the BDT input variables is derived by counting how often the variables are used to
split decision tree nodes, and by weighting each split occurrence by the separation gain-squared it
has achieved and by the number of events in the node [32]. This measure of the variable importance
can be used for a single decision tree as well as for a forest.
8.13.5 Performance
Only limited experience has been gained so far with boosted decision trees in HEP. In the literature
decision trees are sometimes referred to as the best “out of the box” classifiers. This is because little
tuning is required in order to obtain reasonably good results. This is due to the simplicity of the
method where each training step (node splitting) involves only a one-dimensional cut optimisation.
Decision trees are also insensitive to the inclusion of poorly discriminating input variables. While
for artificial neural networks it is typically more difficult to deal with such additional variables,
the decision tree training algorithm will basically ignore non-discriminating variables as for each

122 8 The TMVA Methods
node splitting only the best discriminating variable is used. However, the simplicity of decision
trees has the drawback that their theoretically best performance on a given problem is generally
inferior to other techniques like neural networks. This is seen for example using the academic
training samples included in the TMVA package. For this sample, which has equal RMS but
shifted mean values for signal and background and linear correlations between the variables only,
the Fisher discriminant provides theoretically optimal discrimination results. While the artificial
neural networks are able to reproduce this optimal selection performance the BDTs always fall
short in doing so. However, in other academic examples with more complex correlations or real
life examples, the BDTs often outperform the other techniques. This is because either there are
not enough training events available that would be needed by the other classifiers, or the optimal
configuration (i.e. how many hidden layers, which variables) of the neural network has not been
specified. We have only very limited experience at the time with the regression, hence cannot really
comment on the performance in this case.
8.14 Predictive learning via rule ensembles (RuleFit)
This classifier is a TMVA implementation of Friedman-Popescu’s RuleFit method described in [34].
Its idea is to use an ensemble of so-called rules to create a scoring function with good classification
power. Each rule riis defined by a sequence of cuts, such as
r1(x) = I(x2<100.0) ·I(x3>35.0) ,
r2(x) = I(0.45 < x4<1.00) ·I(x1>150.0) ,
r3(x) = I(x3<11.00) ,
where the xiare discriminating input variables, and I(. . . ) returns the truth of its argument. A
rule applied on a given event is non-zero only if all of its cuts are satisfied, in which case the rule
returns 1.
The easiest way to create an ensemble of rules is to extract it from a forest of decision trees (cf.
Sec. 8.13). Every node in a tree (except the root node) corresponds to a sequence of cuts required
to reach the node from the root node, and can be regarded as a rule. Hence for the tree illustrated
in Fig. 18 on page 115 a total of 8 rules can be formed. Linear combinations of the rules in the
ensemble are created with coefficients (rule weights) calculated using a regularised minimisation
procedure [35]. The resulting linear combination of all rules defines a score function (see below)
which provides the RuleFit response yRF(x).
In some cases a very large rule ensemble is required to obtain a competitive discrimination between
signal and background. A particularly difficult situation is when the true (but unknown) scoring
function is described by a linear combination of the input variables. In such cases, e.g., a Fisher
discriminant would perform well. To ease the rule optimisation task, a linear combination of the
input variables is added to the model. The minimisation procedure will then select the appropriate
coefficients for the rules and the linear terms. More details are given in Sec. 8.14.2 below.

8.14 Predictive learning via rule ensembles (RuleFit) 123
8.14.1 Booking options
The RuleFit classifier is booked via the command:
factory->BookMethod( Types::kRuleFit, "RuleFit", "<options>" );
Code Example 52: Booking of RuleFit: the first argument is a predefined enumerator, the second argument
is a user-defined string identifier, and the third argument is the configuration options string. Individual
options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The RuleFit configuration options are given in Option Table 28.
8.14.2 Description and implementation
As for all TMVA classifiers, the goal of the rule learning is to find a classification function yRF(x)
that optimally classifies an event according to the tuple of input observations (variables) x. The
classification function is written as
yRF(x) = a0+
MR
X
m=1
amfm(x),(104)
where the set {fm(x)}MRforms an ensemble of base learners with MRelements. A base learner
may be any discriminating function derived from the training data. In our case, they consist of
rules and linear terms as described in the introduction. The complete model then reads
yRF(x) = a0+
MR
X
m=1
amrm(x) +
nvar
X
i=1
bixi.(105)
To protect against outliers, the variables in the linear terms are modified to
x0
i= min(δ+
i,max(δ−
i)) ,(106)
where δ±
iare the lower and upper βquantiles33 of the variable xi. The value of βis set by the
option LinQuantile. If the variables are used “as is”, they may have an unequal a priori influence
relative to the rules. To counter this effect, the variables are normalised
x0
i→σr·x0
i/σi,(107)
where σrand σiare the estimated standard deviations of an ensemble of rules and the variable x0
i,
respectively.
33Quantiles are points taken at regular intervals from the PDF of a random variable. For example, the 0.5 quantile
corresponds to the median of the PDF.

124 8 The TMVA Methods
Option Array Default Predefined Values Description
GDTau –-1 –Gradient-directed (GD) path: default
fit cut-off
GDTauPrec –0.01 –GD path: precision of tau
GDStep –0.01 –GD path: step size
GDNSteps –10000 –GD path: number of steps
GDErrScale –1.1 –Stop scan when error >scale*errmin
LinQuantile –0.025 –Quantile of linear terms (removes out-
liers)
GDPathEveFrac –0.5 –Fraction of events used for the path
search
GDValidEveFrac –0.5 –Fraction of events used for the valida-
tion
fEventsMin –0.1 –Minimum fraction of events in a split-
table node
fEventsMax –0.9 –Maximum fraction of events in a split-
table node
nTrees –20 –Number of trees in forest.
ForestType –AdaBoost AdaBoost, Random Method to use for forest generation
(AdaBoost or RandomForest)
RuleMinDist –0.001 –Minimum distance between rules
MinImp –0.01 –Minimum rule importance accepted
Model –ModRuleLinear ModRule,
ModRuleLinear,
ModLinear
Model to be used
RuleFitModule –RFTMVA RFTMVA,
RFFriedman
Which RuleFit module to use
RFWorkDir –./rulefit –Friedman’s RuleFit module (RFF):
working dir
RFNrules –2000 –RFF: Mximum number of rules
RFNendnodes –4–RFF: Average number of end nodes
Option Table 28: Configuration options reference for MVA method: RuleFit. Values given are defaults. If
predefined categories exist, the default category is marked by a ’?’. The options in Option Table 9on page 61
can also be configured.
Rule generation
The rules are extracted from a forest of decision trees. There are several ways to generate a forest.
In the current RuleFit implementation, each tree is generated using a fraction of the training sample.
The fraction depends on which method is used for generating the forest. Currently two methods
are supported (selected by option ForestType); AdaBoost and Random Forest. The first method

8.14 Predictive learning via rule ensembles (RuleFit) 125
is described in Sec. 8.13.2. In that case, the whole training set is used for all trees. The diversity
is obtained through using different event weights for each tree. For a random forest, though, the
diversity is created by training each tree using random sub-samples. If this method is chosen, the
fraction is calculated from the training sample size N(signal and background) using the empirical
formula [36]
f= min(0.5,(100.0+6.0·√N)/N ).(108)
By default, AdaBoost is used for creation of the forest. In general it seems to perform better than
the random forest.
The topology of each tree is controlled by the parameters fEventsMin and fEventsMax. They define
a range of fractions which are used to calculate the minimum number of events required in a node
for further splitting. For each tree, a fraction is drawn from a uniform distribution within the given
range. The obtained fraction is then multiplied with the number of training events used for the tree,
giving the minimum number of events in a node to allow for splitting. In this way both large trees
(small fraction) giving complex rules and small trees (large fraction) for simple rules are created.
For a given forest of Nttrees, where each tree has n`leaf nodes, the maximum number of possible
rules is
MR,max =
Nt
X
i=1
2(n`,i −1) .(109)
To prune similar rules, a distance is defined between two topologically equal rules. Two rules are
topologically equal if their cut sequences follow the same variables only differing in their cut values.
The rule distance used in TMVA is then defined by
δ2
R=X
i
δ2
i,L +δ2
i,U
σ2
i
,(110)
where δi,L(U)is the difference in lower (upper) limit between the two cuts containing the variable xi,
i= 1, . . . , nvar. The difference is normalised to the RMS-squared σ2
iof the variable. Similar rules
with a distance smaller than RuleMinDist are removed from the rule ensemble. The parameter can
be tuned to improve speed and to suppress noise. In principle, this should be achieved in the fitting
procedure. However, pruning the rule ensemble using a distance cut will reduce the fitting time and
will probably also reduce the number of rules in the final model. Note that the cut should be used
with care since a too large cut value will deplete the rule ensemble and weaken its classification
performance.
Fitting
Once the rules are defined, the coefficients in Eq. (105) are fitted using the training data. For
details, the fitting method is described in [35]. A brief description is provided below to motivate
the corresponding RuleFit options.
Aloss function L(yRF(x)|ˆy), given by the “squared-error ramp” [35]
L(yRF|ˆy) = (ˆy−H(yRF))2,(111)

126 8 The TMVA Methods
where H(y) = max(−1,min(yRF,1)), quantifies the “cost” of misclassifying an event of given true
class ˆy. The risk Ris defined by the expectation value of Lwith respect to xand the true class.
Since the true distributions are generally not known, the average of Ntraining events is used as an
estimate
R=1
N
N
X
i=1
L(yRF(xi)|ˆyi).(112)
A line element in the parameter space of the rule weights (given by the vector aof all coefficients)
is then defined by
a(+δ) = a() + δ ·g(),(113)
where δ is a positive small increment and g() is the negative derivative of the estimated risk R,
evaluated at a(). The estimated risk-gradient is evaluated using a sub-sample (GDPathEveFrac) of
the training events.
Starting with all weights set to zero, the consecutive application of Eq. (113) creates a path in the a
space. At each step, the procedure selects only the gradients gkwith absolute values greater than a
certain fraction (τ) of the largest gradient. The fraction τis an a priori unknown quantity between
0 and 1. With τ= 0 all gradients will be used at each step, while only the strongest gradient
is selected for τ= 1. A measure of the “error” at each step is calculated by evaluating the risk
(Eq. 112) using the validation sub-sample (GDValidEveFrac). By construction, the risk will always
decrease at each step. However, for the validation sample the value will increase once the model
starts to be overtrained. Currently, the fitting is crudely stopped when the error measure is larger
than GDErrScale times the minimum error found. The number of steps is controlled by GDNSteps
and the step size (δ in Eq. 113) by GDStep.
If the selected τ(GDTau) is a negative number, the best value is estimated by means of a scan. In
such a case several paths are fitted in parallel, each with a different value of τ. The number of paths
created depend on the required precision on τgiven by GDTauPrec. By only selecting the paths
being “close enough” to the minimum at each step, the speed for the scan is kept down. The path
leading to the lowest estimated error is then selected. Once the best τis found, the fitting proceeds
until a minimum is found. A simple example with a few scan points is illustrated in Fig. 19.
8.14.3 Variable ranking
Since the input variables are normalised, the ranking of variables follows naturally from the co-
efficients of the model. To each rule m(m= 1, . . . , MR) can be assigned an importance defined
by
Im=|am|psm(1.0−sm),(114)
where smis the support of the rule with the following definition
sm=1
N
N
X
n=1
rm(xn).(115)
The support is thus the average response for a given rule on the data sample. A large support implies
that many events pass the cuts of the rule. Hence, such rules cannot have strong discriminating
8.14 Predictive learning via rule ensembles (RuleFit) 127
*
τ(1) τ(2)
τ(3)
a
a1
2
Best point
Figure 19: An example of a path scan in two dimensions. Each point represents an in Eq. (113) and each
step is given by δ. The direction along the path at each point is given by the vector g. For the first few
points, the paths τ(1,2,3) are created with different values of τ. After a given number of steps, the best path
is chosen and the search is continued. It stops when the best point is found. That is, when the estimated
error-rate is minimum.
power. On the other hand, rules with small support only accept few events. They may be important
for these few events they accept, but they are not in the overall picture. The definition (114) for
the rule importance suppresses rules with both large and small support.
For the linear terms, the definition of importance is
Ii=|bi| · σi,(116)
so that variables with small overall variation will be assigned a small importance.
A measure of the variable importance may then be defined by
Ji=Ii+X
m|xi∈rm
Im/qm,(117)
where the sum is over all rules containing the variable xi, and qmis the number of variables used
in the rule rm. This is introduced in order to share the importance equally between all variables in
rules with more than one variable.
8.14.4 Friedman’s module
By setting RuleFitModule to RFFriedman, the interface to Friedman’s RuleFit is selected. To use
this module, a separate setup is required. If the module is selected in a run prior to setting up the

128 8 The TMVA Methods
environment, TMVA will stop and give instructions on how to proceed. A command sequence to
setup Friedman’s RuleFit in a UNIX environment is:
~> mkdir rulefit
~> cd rulefit
~> wget http://www-stat.stanford.edu/~jhf/r-rulefit/linux/rf_go.exe
~> chmod +x rf_go.exe
Code Example 53: The first line creates a working directory for Friedman’s module. In the third line, the
binary executable is fetched from the official web-site. Finally, it is made sure that the module is executable.
As of this writing, binaries exists only for Linux and Windows. Check J. Friedman’s home page at
http://www-stat.stanford.edu/∼jhf for updated information. When running this module from TMVA,
make sure that the option RFWorkDir is set to the proper working directory (default is ./rulefit).
Also note that only the following options are used: Model,RFWorkDir,RFNrules,RFNendnodes,
GDNSteps,GDStep and GDErrScale. The options RFNrules and RFNendnodes correspond in the
package by Friedman-Popescu to the options max.rules and tree.size, respectively. For more
details, the reader is referred to Friedman’s RuleFit manual [36].
Technical note
The module rf go.exe communicates with the user by means of both ASCII and binary files.
This makes the input/output from the module machine dependant. TMVA reads the output from
rf go.exe and produces the normal machine independent weight (or class) file. This can then be
used in other applications and environments.
8.14.5 Performance
Rule ensemble based learning machines are not yet well known within the HEP community, although
they start to receive some attention [37]. Apart from RuleFit [34] other rule ensemble learners exists,
such as SLIPPER [38].
The TMVA implementation of RuleFit follows closely the original design described in Ref. [34].
Currently the performance is however slightly less robust than the one of the Friedman-Popescu
package. Also, the experience using the method is still scarce at the time of this writing.
To optimise the performance of RuleFit several strategies can be employed. The training consists of
two steps, rule generation and rule ensemble fitting. One approach is to modify the complexity of
the generated rule ensemble by changing either the number of trees in the forest, or the complexity
of each tree. In general, large tree ensembles with varying trees sizes perform better than short
non-complex ones. The drawback is of course that fitting becomes slow. However, if the fitting
performs well, it is likely that a large amount of rules will have small or zero coefficients. These can

129
be removed, thus simplifying the ensemble. The fitting performance can be improved by increasing
the number of steps along with using a smaller step size. Again, this will be at the cost of speed
performance although only at the training stage. The setting for the parameter τmay greatly affect
the result. Currently an automatic scan is performed by default. In general, it should find the
optimum τ. If in doubt , the user may set the value explicitly. In any case, the user is initially
advised to use the automatic scan option to derive the best path.
9 The PyMVA Methods
PyMVA is the interface for third-party MVA tools based on Python. It is created to make powerful
external libraries easily accessible with a direct integration into the TMVA workflow. All PyMVA
methods provide the same plug-and-play mechanisms than the TMVA methods described in section
8.
Because the base method of PyMVA is inherited from the TMVA base method, all options from
the Option Table 9apply for PyMVA methods as well.
9.1 Keras
Keras (www.keras.io) is a high-level wrapper for the machine learning frameworks Theano (www.
deeplearning.net/software/theano/) and TensorFlow (www.tensorflow.org), which are mainly used
to set up deep neural networks.
9.1.1 Training and Testing Data
Please note that data defined as testing data in the dataloader is used for validation of the model
after each epoch. Such as stated in section 8.11.3, a proper evaluation of the performance should
be done on a completely independent dataset.
9.1.2 Booking Options
The Keras method is booked mainly similar to other TMVA methods such as shown in Code
Example 54. The different part is the definition of the neural network model itself. These options
are not set in the options string of TMVA, but these are defined in Python and exported to a model
file, which is later on loaded by the method. The definition of such a model using the Keras API is
explained in detail in section 9.1.3. The settings in the method’s option string manage the training
process.
The full list of possible settings that can be used in the option string is presented in Table 29.

130 9 The PyMVA Methods
factory->BookMethod(dataloader, TMVA::Types::kPyKeras, "Keras", <options>);
Code Example 54: Booking of the PyKeras method
Option Array Default Predefined Values Description
FilenameModel – – – Filename of the neural network model
defined by Keras
FilenameTrainedModel –Placed in
weights
directory of
dataloader
–Filename of the model with trained
weights. By default, the file is placed
in the weights directory of the dat-
aloader, but you can define with this
option a custom path to the model file
with trained weights.
BatchSize –100 –Batch size used for a single gradient
step during training
NumEpochs –10 –Number of training epochs
Verbose –1–Verbosity during training
ContinueTraining –false –Continue training by loading weights
from FilenameTrainedModel at begin-
ning of training
SaveBestOnly –true –Store only weights with smallest vali-
dation loss
TriesEarlyStopping –-1 –Number of epochs with no improve-
ment in validation loss after which
training will be stopped. The default
or a negative number deactivates this
option.
LearningRateSchedule –’’ –Set new learning rate during training
at specific epochs, e.g., set new learn-
ing rate at epochs 50 and 70 with ’50,
0.01;70,0.005’. By default, there is
no schedule set.
Option Table 29: Configuration options reference for PyMVA method PyKeras.
9.1.3 Model Definition
The model of the neural network is defined in Python using the Keras API, stored to a file and then
loaded by the Keras method of PyMVA. This section gives an detailed example how this can be
done for a classification task. The final reference to build a Keras model is the Keras documentation
itself (www.keras.io). As well, ROOT ships with TMVA tutorials, which include examples for the
usage of the PyKeras method for binary classification, multiclass classification and regression.

131
Code Example 55 shows as an example a simple three-layer neural network, which can be applied
for any classification task. After running this script, the model file, e.g. model.h5 in this example,
has to be set as the option FilenameModel of the method.
from keras.models import Sequential
from keras.layers.core import Dense
# Define model architecture
model = Sequential()
model.add(Dense(64, init=’glorot_normal’, activation=’relu’,
input_dim=num_input_variables))
model.add(Dense(num_output_classes, init=’glorot_uniform’,
activation=’softmax’))
# Set loss function and optimizer algorithm
model.compile(loss=’categorical_crossentropy’, optimizer=’Adam’,
metrics=[’accuracy’,])
# Store model to file
model.save(’model.h5’)
Code Example 55: Definition of a classification model in Python using Keras. The placeholders num input
variables and num output classes have to be set accordingly to the specific task.
9.1.4 Variable Ranking
A variable ranking is not supported.
10 Combining MVA Methods
In challenging classification or regression problems with a high demand for optimisation, or when
treating feature spaces with strongly varying properties, it can be useful to combined MVA methods.
There is large room for creativity inherent in such combinations. For TMVA we distinguish three
classes of combinations:
1. Boosting MVA methods,
2. Categorising MVA methods,
3. Building committees of MVA methods.
While the first two combined methods are available since TMVA 4.1, the third one is still under
development. The MVA booster is a generalisation of the Boosted Decision Trees approach (see

132 10 Combining MVA Methods
Sec. 8.13) to any method in TMVA. Category methods allow the user to specify sub-regions of phase
space, which are assigned by requirements on input or spectator variables, and which define disjoint
sub-populations of the training sample, thus improving the modelling of the training data. Finally,
Committee methods allow one to input MVA methods into other MVA methods, a procedure that
can be arbitrarily chained.
All of these combined methods are of course MVA methods themselves, treated just like any other
method in TMVA for training, testing, evaluation and application. This also allows to categorise a
committee method, for example.
10.1 Boosted classifiers
Since generalised boosting is not yet available for regression in TMVA, we restrict the following
discussion to classification applications. A boosted classifier is a combination of a collection of
classifiers of the same type trained on the same sample but with different events weights.34 The
response of the final classifier is a weighted response of each individual classifier in the collection. The
boosted classifier is potentially more powerful and more stable with respect to statistical fluctuations
in the training sample. The latter is particularly the case for bagging as “boost” algorithm (cf.
Sec. 7.3, page 58).
The following sections do not apply to decision trees. We refer to Sec. 8.13 (page 114) for a
description of boosted decision trees. In the current version of TMVA only the AdaBoost and
Bagging algorithms are implemented for the boost of arbitrary classifiers. The boost algorithms are
described in detail in Sec. 7on page 55.
10.1.1 Booking options
To book a boosted classifier, one needs to add the booster options to the regular classifier’s option
string. The minimal option required is the number of boost iterations Boost Num, which must be
set to a value larger than zero. Once the Factory detects a Boost Numi0in the option string it
books a boosted classifier and passes all boost options (recognised by the prefix Boost ) to the
Boost method and the other options to the boosted classifier.
factory->BookMethod( TMVA::Types::kLikelihood, "BoostedLikelihood",
"Boost_Num=10:Boost_Type=Bagging:Spline=2:NSmooth=5:NAvEvtPerBin=50" );
Code Example 56: Booking of the boosted classifier: the first argument is the predefined enumerator, the
second argument is a user-defined string identifier, and the third argument is the configuration options string.
All options with the prefix Boost (in this example the first two options) are passed on to the boost method,
the other options are provided to the regular classifier (which in this case is Likelihood). Individual options
are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
34The Boost method is at the moment only applicable to classification problems.

10.1 Boosted classifiers 133
Option Array Default Predefined Values Description
Boost Num –100 –Number of times the classifier is
boosted
Boost MonitorMethod –True –Write monitoring histograms for each
boosted classifier
Boost DetailedMonitoring–False –Produce histograms for detailed boost-
wise monitoring
Boost Type –AdaBoost AdaBoost,
Bagging,
HighEdgeGauss,
HighEdgeCoPara
Boosting type for the classifiers
Boost BaggedSampleFraction–0.6 –Relative size of bagged event sample to
original size of the data sample (used
whenever bagging is used)
Boost MethodWeightType –ByError ByError,
Average, ByROC,
ByOverlap,
LastMethod
How to set the final weight of the
boosted classifiers
Boost RecalculateMVACut–True –Recalculate the classifier MVA Signal-
like cut at every boost iteration
Boost AdaBoostBeta –1–The ADA boost parameter that sets
the effect of every boost step on the
events’ weights
Boost Transform –step step, linear,
log, gauss
Type of transform applied to every
boosted method linear, log, step
Boost RandomSeed –0–Seed for random number generator
used for bagging
Option Table 30: Boosting configuration options. These options can be simply added to a simple classifier’s
option string or used to form the option string of an explicitly booked boosted classifier.
The boost configuration options are given in Option Table 30.
The options most relevant for the boost process are the number of boost iterations, Boost Num, and
the choice of the boost algorithm, Boost Type. In case of Boost Type=AdaBoost, the option Boost
Num describes the maximum number of boosts. The algorithm is iterated until an error rate of 0.5 is
reached or until Boost Num iterations occurred. If the algorithm terminates after to few iterations,
the number might be extended by decreasing the βvariable (option Boost AdaBoostBeta). Within
the AdaBoost algorithm a decision must be made how to classify an event, a task usually done by
the user. For some classifiers it is straightforward to set a cut on the MVA response to define signal-
like events. For the others, the MVA cut is chosen that the error rate is minimised. The option
Boost RecalculateMVACut determines whether this cut should be recomputed for every boosting
iteration. In case of Bagging as boosting algorithm the number of boosting iterations always reaches
Boost Num.
134 10 Combining MVA Methods
By default boosted classifiers are combined as a weighted average with weights computed from the
misclassification error (option Boost MethodWeightType=ByError). It is also possible to use the
arithmetic average instead (Boost MethodWeightType=Average).
10.1.2 Boostable classifiers
The boosting process was originally introduced for simple classifiers. The most commonly boosted
classifier is the decision tree (DT – cf. Sec. 8.13, page 114). Decision trees need to be boosted a few
hundred times to effectively stabilise the BDT response and achieve optimal performance.
Another simple classifier in the TMVA package is the Fisher discriminant (cf. Sec. 8.7, page 88 –
which is equivalent to the linear discriminant described in Sec. 8.8). Because the output of a Fisher
discriminant represents a linear combination of the input variables, a linear combination of different
Fisher discriminants is again a Fisher discriminant. Hence linear boosting cannot improve the per-
formance. It is nevertheless possible to effectively boost a linear discriminant by applying the linear
combination not on the discriminant’s output, but on the actual classification results provided.35
This corresponds to a “non-linear” transformation of the Fisher discriminant output according to a
step function. The Boost method in TMVA also features a fully non-linear transformation that is
directly applied to the classifier response value. Overall, the following transformations are available:
•linear: no transformation is applied to the MVA output,
•step: the output is −1 below the step and +1 above (default setting),
•log: logarithmic transformation of the output.
The macro Boost.C (residing in the macros (test) directory for the sourceforge (ROOT) version
of TMVA) provides examples for the use of these transformations to boost a Fisher discriminant.
We point out that the performance of a boosted classifier strongly depends on its characteristics as
well as on the nature of the input data. A careful adjustment of options is required if AdaBoost is
applied to an arbitrary classifier, since otherwise it might even lead to a worse performance than
for the unboosted method.
10.1.3 Monitoring tools
The current GUI provides figures to monitor the boosting process. Plotted are the boost weights, the
classifier weights in the boost ensemble, the classifier error rates, and the classifier error rates using
unboosted event weights. In addition, when the option Boost MonitorMethod=T is set, monitoring
histograms are created for each classifier in the boost ensemble. The histograms generated during
the boosting process provide useful insight into the behaviour of the boosted classifiers and help
35Note that in the TMVA standard example, which uses linearly correlated, Gaussian-distributed input variables
for signal and background, a single Fisher discriminant already provides the theoretically maximum separation power.
Hence on this example, no further gain can be expected by boosting, no matter what “tricks” are applied.

10.2 Category Classifier 135
to adjust to the optimal number of boost iterations. These histograms are saved in a separate
folder in the output file, within the folder of MethodBoost/<Title>/. Besides the specific classifier
monitoring histograms, this folder also contains the MVA response of the classifier for the training
and testing samples.
10.1.4 Variable ranking
The present boosted classifier implementation does not provide a ranking of the input variables.
10.2 Category Classifier
The Category method allows the user to separate the training data (and accordingly the application
data) into disjoint sub-populations exhibiting different properties. The separation into phase space
regions is done by applying requirements on the input and/or spectator variables (variables defined
as spectators are not used as direct inputs to MVA methods). It thus reaches beyond a simple sub-
classification of the original feature space. In each of these disjoint regions (each event must belong
to one and only one region), an independent training is performed using the most appropriate MVA
method, training options and set of training variables in that zone. The division into categories
in presence of distinct sub-populations reduces the correlations between the training variables, im-
proves the modelling, and hence increases the classification and regression performance.36 Another
common application is when variables are not available in some phase space regions. For example,
a sub-detector may only cover a fraction of the training data sample. By defining two categories the
variables provided by this detector could be excluded from the training in the phase space region
outside of its fiducial volume. Finally, an advantage of categorisation, often exploited in likelihood
fits, also lies in the gain of signal significance when the fraction of signal events in the event sample
differs between the categories.
We point out that the explicit use of the Category method is not mandatory. The categorisation
functionality can be achieved by hand by training independent MVAs in each of the disjoint regions.
Our experience however shows that often the corresponding bookkeeping is considered too cumber-
some and the required categorisation is not performed, thus leading to performance loss.37 The
Category method is straightforward to implement and should help in almost all analyses to bet-
ter describe the training sample. Performance comparison with the corresponding non-categorised
method should guide the user in his/her choice.
For the current release, the Category method is only implemented for classification. Extension to
regression is however straightforward and should follow soon.
36This is particularly the case for projective likelihood methods, even when including prior decorrelation of the
input data (cf. Sec. 8.2).
37In the above example with the reduced detector fiducial acceptance, it often occurs that non-physical values
(“−99”) are assigned to the variables for events where they are not available. Inserting such meaningless (apart from
indicating the category) values into an MVA penalises its performance.
136 10 Combining MVA Methods
10.2.1 Booking options
The Category method is booked via the command:
TMVA::IMethod* category = factory->BookMethod( TMVA::Types::kCategory,
"Category",
"<options>" );
Code Example 57: Booking of the Category method: the first argument is a predefined enumerator, the
second argument is a user-defined string identifier, and the third argument is the configuration options
string. Individual options are separated by a ’:’. See Sec. 3.1.5 for more information on the booking.
The categories and sub-classifiers are defined as follows:
TMVA::MethodCategory* mcategory = dynamic_cast<TMVA::MethodCategory*>(category);
mcategory->AddCategory( "<cut>",
"<variables>",
TMVA::Types::<enumerator>,
"<sub-classifier name>",
"<sub-classifier options>" );
Code Example 58: Adding a category to the Category method: the first argument is the cut that defines
the category, the second defines is the set of variables used to train this sub-classifier, the third argument is
the predefined enumerator of the sub-classifier, the fourth argument is a user-defined string identifier of the
sub-classifier, and the last argument sets the configuration options of the sub-classifier. Individual variables
and options are both separated by a ’:’. See Sec. 10.2.2 for further information on cuts and variables. The
dynamic cast is required to allow access to specific Category members.
There are no options implemented for the Category method itself, apart from those common to all
methods (cf. Option Table 9on page 61). The available options for the sub-classifiers are found in
the corresponding sections of this Users Guide.
The following example illustrates how sub-classifiers are added:

10.2 Category Classifier 137
mcategory->AddCategory( "abs(eta)<=1.3",
"var1:var2:var3:var4:",
TMVA::Types::kFisher,
"Category_Fisher",
"H:!V:Fisher" );
mcategory->AddCategory( "abs(eta)>1.3",
"var1:var2:var3:",
TMVA::Types::kFisher,
"Category_Fisher",
"H:!V:Fisher" );
Code Example 59: Adding a category with sub-classifier of type Fisher: the cut in the first argument
defines the region to which each of the sub-classifiers are applied, the second argument is the list of variables
which are to be considered for this region (in this example var4 is not available when abs(eta)>1.3), the
third argument contains the internal enumerator for a classifier of type Fisher (the MVA method may differ
between categories, the fourth argument is the user-defined identifier, and the fifth argument contains the
options string for the Fisher classifier. The variable eta must have been defined as an input or spectator
variable.
10.2.2 Description and implementation
The Category method is implemented in an entirely transparent way, conserving full flexibility for
the user on which input variables, MVA method and options to use in each category, and how the
category should be defined.
The categories are defined via cuts on the input and/or spectator variables. These cuts can be
arbitrary boolean expressions or may involve any number of variables. In case of particularly
intricate category definitions it may turn out advantageous for the user to pre-define and pre-fill
category variables, and use those as spectators in TMVA to set an event’s category. It is required
that the cuts are defined in such a way that they create disjoint event samples. TMVA will issue a
fatal error in case of an ambiguous category definition.
The variables used for the training of each of the sub-classifiers can be chosen from the variables
and spectators that have been defined in the TMVA script. The individual variables have to be
separated by a ’:’. The distinction between input variables and spectators is necessary to allow per-
formance comparisons between categorised and non-categorised methods within the same training
and evaluation job (spectator variables would not be used by non-categorised methods).
The advantage offered by the Category classifier is illustrated with the following academic example.
We consider four uncorrelated and Gaussian distributed input variables for training. The mean
values of the variables are shifted between signal and background, hence providing classification
information. In addition, all mean values (signal and background) depend on a spectator variable
eta: for abs(eta)>1.3 (abs(eta)<=1.3) they have a positive (negative) offset. Hence, the Gaus-
sians are broader and the variables receive an effective correlation when integrating over eta. The
distributions for signal and background of one out of the four variables is shown for both abs(eta)

138 11 Which MVA method should I use for my problem?
categories in Fig. 20. Figure 21 shows the ROC curves (cf. Sec. 2.7) of the categorised and non-
categorised Fisher and Projective Likelihood classifiers. Optimum performance is recovered by the
Category classifier.
10.2.3 Variable ranking
Due to the nature of the Category classifier it does not provide a general variable ranking. As far
as available, the sub-classifiers will provide ranking for each category.
10.2.4 Performance
The performance of the Category method depends entirely on the judicious choice of the categories,
properly separating events with different properties, and on the performance of the sub-methods
within these categories. Control by performance comparison with the corresponding non-categorised
methods allows to measure the performance gain, and to assess whether categorisation improves
the classification.
11 Which MVA method should I use for my problem?
There is obviously no generally valid answer to this question. To guide the user, we have attempted
a coarse assessment of various MVA properties in Table 6. Simplicity is a virtue, but only if it is
not at the expense of significant loss of discrimination power. A properly trained Neural Network
with the problem dependent optimal architecture or a Support Vector Machine with the appropriate
kernel size should theoretically give superior performance compared to a more robust “out of the
box” Boosted Decision Trees38, which in practice often outperforms the former.
To assess whether a linear discriminant analysis (LDA) could be sufficient for a classification (re-
gression) problem, the user is advised to analyse the correlations among the discriminating variables
(among the variables and regression target) by inspecting scatter and profile plots (it is not enough
to print the correlation coefficients, which by definition are linear only). Using an LDA greatly
reduces the number of parameters to be adjusted and hence allow smaller training samples. It
usually is robust with respect to generalisation to larger data samples. For moderately intricate
problems, the function discriminant analysis (FDA) with some added nonlinearity may be found
sufficient. It is always useful to cross-check its performance against several of the sophisticated
nonlinear methods to see how much can be gained over the use of the simple and very transparent
FDA.
For problems that require a high degree of optimisation and allow to use a large number of input
38Note, in an earlier version we noted the problem of overtraining in BDTs when using large trees and trying to
regulate them using pruning. This however is overcome completely when using tress with limited depth (say 2 to
4) and minimal leaf node size (some % of training sample size) instead of pruning, which in addition gives superior
performance.
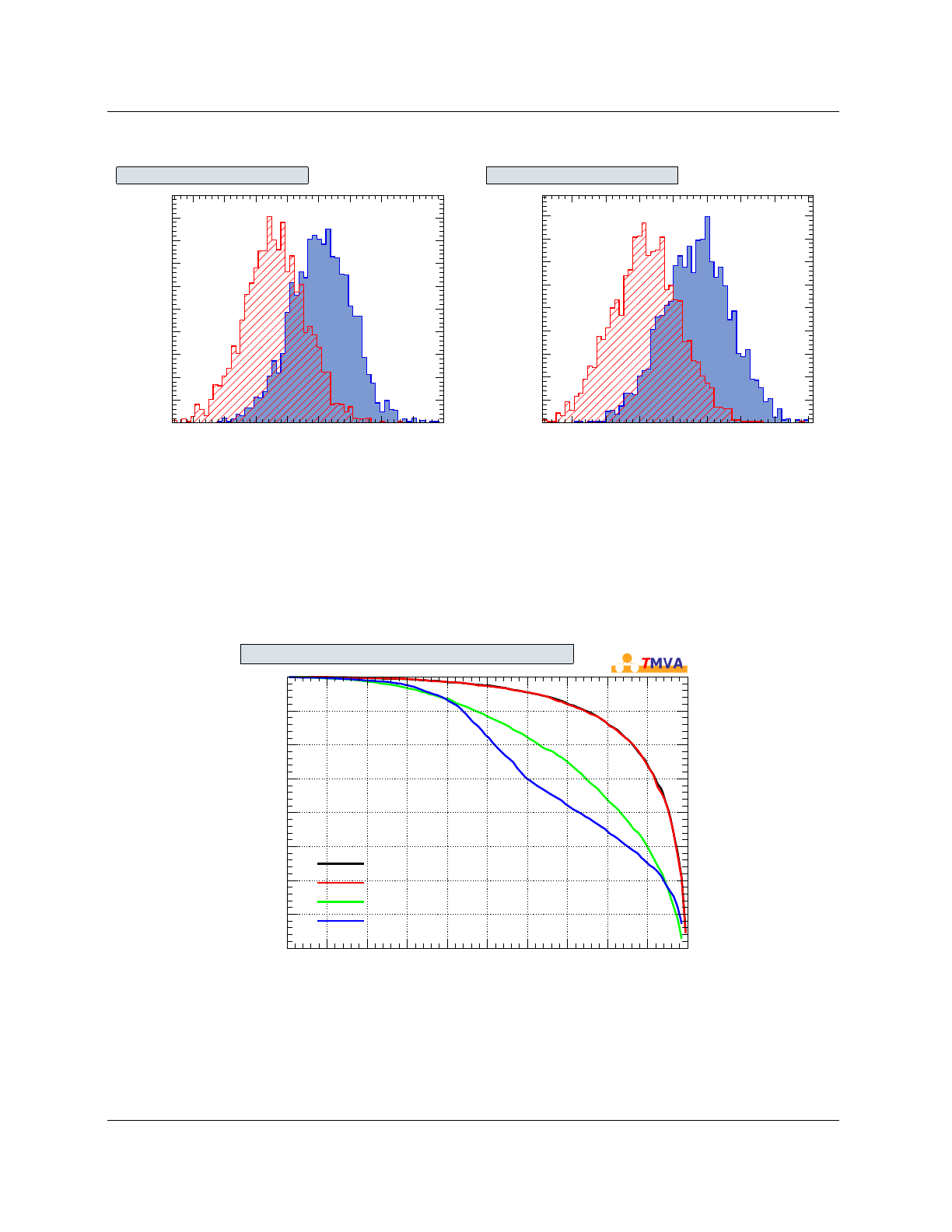
139
var4
-4 -3 -2 -1 0 1 2 3
0.144
/
(1/N) dN
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
TMVA Input Variables: var4
var4
-4 -3 -2 -1 0 1 2 3
0.144
/
(1/N) dN
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA Input Variables: var4
var4
-2 -1 0 1 2 3 4 5
0.134
/
(1/N) dN
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
TMVA Input Variables: var4
var4
-2 -1 0 1 2 3 4 5
0.134
/
(1/N) dN
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
U/O-flow (S,B): (0.0, 0.0)% / (0.0, 0.0)%
TMVA Input Variables: var4
Figure 20: Examples for the usage of categories. The variable var4 depends on abs(eta): for abs(eta)<=1.3
(left plot), the signal and background Gaussian distributions are both shifted to lower values, while for
abs(eta)>1.3 (right plot) shifts to larger values have been applied. Ignoring this dependence, broadens
the inclusive Gaussian distributions and generates variable correlations (here a coefficient of +0.4 between
var3 and var4) due to the existence of distinct subsamples. The Category classifier treats the two cases
independently, thus recovering optimal separation.
Signal efficiency
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Background rejection
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Signal efficiency
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Background rejection
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
MVA Method:
FisherCat
LikelihoodCat
Fisher
Likelihood
Background rejection versus Signal efficiency
Figure 21: ROC curves for categorised and non-categorised Fisher and Projective Likelihood classifiers applied
to an academic four-Gaussian example with eta-dependent mean values distinguishing two categories (cf.
Fig. 20 for the category-dependent signal and background distributions of one of the four input variables). The
categorised (“...Cat”) classifiers recover optimum performance (their red and black curves are superimposed).

140 11 Which MVA method should I use for my problem?
MVA METHOD
CRITERIA Cuts Likeli-
hood
PDE-
RS /
k-NN
PDE-
Foam
H-
Matrix
Fisher
/ LD
MLP BDT Rule-
Fit
SVM
Perfor-
No or linear
correlations
? ?? ? ? ? ?? ?? ? ?? ?
mance Nonlinear
correlations ◦ ◦ ?? ?? ◦ ◦ ?? ?? ?? ??
Training ◦?? ?? ?? ?? ?? ? ? ? ◦
Speed Response ?? ?? ◦? ?? ?? ?? ? ?? ?
Robust- Overtraining ?? ? ? ? ?? ?? ? ?39 ? ??
ness Weak variables ?? ? ◦ ◦ ?? ?? ? ?? ? ?
Curse of dimensionality ◦?? ◦ ◦ ?? ?? ? ? ?
Transparency ?? ?? ? ? ?? ?? ◦ ◦ ◦ ◦
Table 6: Assessment of MVA method properties. The symbols stand for the attributes “good” (??), “fair”
(?) and “bad” (◦). “Curse of dimensionality” refers to the “burden” of required increase in training statistics
and processing time when adding more input variables. See also comments in the text. The FDA method is
not listed here since its properties depend on the chosen function.
variables, complex nonlinear methods like neural networks, the support vector machine, boosted
decision trees and/or RuleFit are more appropriate.
Very involved multi-dimensional variable correlations with strong nonlinearities are usually best
mapped by the multidimensional probability density estimators such as PDE-RS, k-NN and PDE-
Foam, requiring however a reasonably low number of input variables.
For RuleFit classification we emphasise that the TMVA implementation differs from Friedman-
Popescu’s original code [34], with slightly better robustness and out-of-the-box performance for the
latter version. In particular, the behaviour of the original code with respect to nonlinear correlations
and the curse of dimensionality would have merited two stars.40 We also point out that the excellent
performance for by majority linearly correlated input variables is achieved somewhat artificially by
adding a Fisher-like term to the RuleFit classifier (this is the case for both implementations, cf.
Sec. 8.14 on page 122).
In Fig 5(page 12) we have shown the example of ROC-curves obtained from various linear and
non-linear classifiers on a simple toy Monte Carlo sample of linear correlated Gaussian distribution
functions. Here all classifiers capable of dealing with such type of correlations are equally performing.
Only the projective likelihood method, which ignores all correlations, performs significantly worse
(it recovers optimum performance after prior decorrelation of the variables). For such a problem, a
Fisher (aka linear) discriminant is optimal by construction, and the non-linear methods effectively
reduce in the training to linear discriminants achieving competitive, but somewhat less robust
40An interface to Friedman-Popescu’s original code can be requested from the TMVA authors. See Sec. 8.14.4.

141
performance.
For another academic toy Monte Carlo example however, which exhibits strongly non-linear correla-
tions in form of a “Schachbrett” (chess board with two-dimensional Gaussian-distributed signal and
background spots – see Fig. 22), the limitations of the linear classifiers, being unable to capture the
features of the data, become manifest. Non-linear classifiers, once appropriately optimised such as
choosing a sufficiently complex network architecture for the MLP, or the proper kernel functions in
the SVM, all non-linear methods reproduce or approximate the theoretical limit of this classification
problem (indicated by the thick red line in the ROCc curve in the lower plot of Fig. 22).
12 TMVA implementation status summary for classification and re-
gression
All TMVA methods are fully operational for user analysis, requiring training, testing, evaluating
and reading for the application to unknown data samples. Additional features are optional and –
despite our attempts to provide a fully transparent analysis – not yet uniformly available. A status
summary is given in Table 7and annotated below.
Although since TMVA 4 the framework supports multi-dimensional MVA outputs it has not yet been
implemented for classification. For regression, only a few methods are fully multi-target capable so
far (see Table 7).
Individual event-weight support is now commonly realised, only missing (and not foreseen to be
provided) for the less recommended neural network CFMlpANN. Support of negative event weights
occurring, e.g., in NLO MC requires more scrutiny as discussed in Sec. 3.1.2 on page 18.
Ranking of the input variables cannot be defined in a straightforward manner for all MVA methods.
Transparent and objective variable ranking through performance comparison of the MVA method
under successive elimination of one input variable at a time is under consideration (so far only
realised for the naive-Bayes likelihood classifier).
Standalone C++ response classes (not required when using the Reader application) are generated
by the majority of the classifiers, but not yet for regression analysis. The missing ones for PDE-RS,
PDE-Foam, k-NN, Cuts and CFMlpANN will only be considered on explicit request.
The availability of help messages, which assist the user with the performance tuning and which are
printed on standard output when using the booking option ’H’, is complete.
Finally, custom macros are provided for some MVA methods to analyse specific properties, such
as the fidelity of likelihood reference distributions or the neural network architecture, etc. More
macros can be added upon user request.
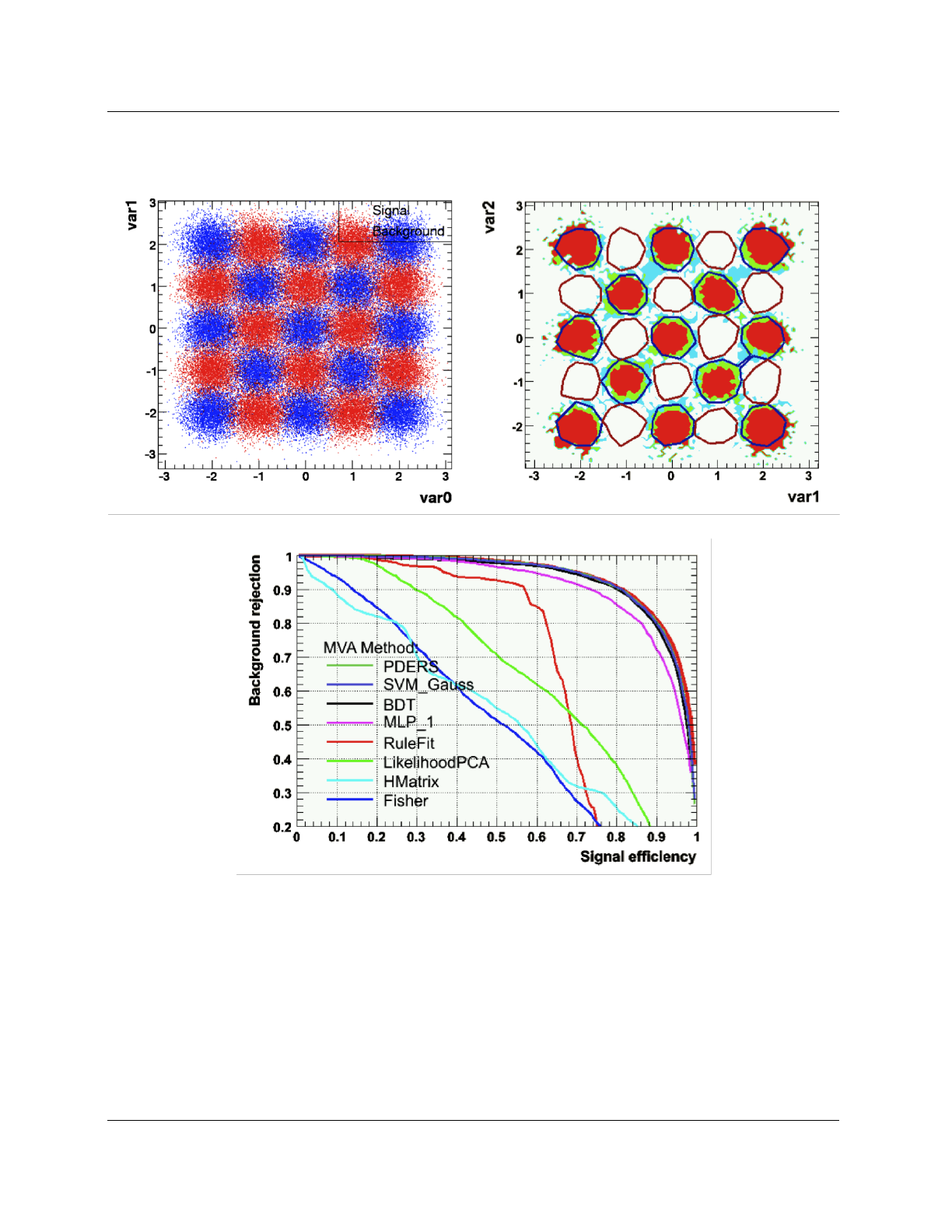
142 12 TMVA implementation status summary for classification and regression
Figure 22: The top left plot shows the two-dimensional Gaussian-distributed signal (blue) and background
(red) distributions for the “Schachbrett” toy Monte Carlo sample. In the top right plot is drawn as an
example the Support Vector Machine’s classification response in terms of the weights given to events in
the two dimensional plane. Dark red signifies large MVA output values, i.e. signal like event regions. The
bottom plot gives the ROC curves obtained with several TMVA classifiers for this example after training.
The theoretically best ROC curve is known and shown by the thick red outer line. While all the non-linear
classification methods (after carefully tuning their parameters) are able to approximate the theoretical limit,
the linear methods strongly underperform.
143
Classi- Regress- Multi-class/target Treats event weights: Variable Standalone Help Custom
MVA method fication ion classification regression positive negative ranking response class messages macros
Cut optimisation • ◦ ◦ ◦ • ◦ ◦ ◦ • ◦
Likelihood • ◦ ◦ ◦ • • • • • •
PDE-RS • • ◦ ◦ • • ◦ ◦ • ◦
PDE-Foam • • • • • • • ◦ • •
k-NN • • ◦ • • • ◦ ◦ • ◦
H-Matrix • ◦ ◦ ◦ • ◦ • • • ◦
Fisher • ◦ ◦ ◦ • ◦ • • • ◦
LD • • ◦ ◦ • ◦ • • • ◦
FDA • • ◦ ◦ • ◦ ◦ • • ◦
MLP • • ◦ • • ◦ • • • •
TMlpANN(?)• ◦ ◦ ◦ • ◦ ◦ • • ◦
CFMlpANN • ◦ ◦ ◦ ◦ ◦ ◦ ◦ ◦ ◦
SVM • ◦ ◦ ◦ • • ◦ • • ◦
BDT • • ◦ ◦ • • • • • •
RuleFit • ◦ ◦ ◦ • ◦ • • • •
(?)Not a generic TMVA method −interface to ROOT class TMultiLayerPerceptron.
Table 7: Status of the methods with respect to various TMVA features. See text for comments. Note that the column “Standalone response
class” only refers to classification. It is yet unavailable for regression.

144 13 Conclusions and Plans
13 Conclusions and Plans
TMVA is a toolkit that unifies highly customisable multivariate (MVA) classification and regression
algorithms in a single framework thus ensuring convenient use and an objective performance assess-
ment. It is designed for machine learning applications in high-energy physics, but not restricted to
these. Source code and library of TMVA-v.3.5.0 and higher versions are part of the standard ROOT
distribution kit (v5.14 and higher). The newest TMVA development version can be downloaded
from Sourceforge.net at http://tmva.sourceforge.net.
This Users Guide introduced the main steps of a TMVA analysis allowing a user to optimise and
perform her/his own multivariate classification or regression. Let us recall the main features of the
TMVA design and purpose:
•TMVA works in transparent factory mode to allow an unbiased performance assessment and
comparison: all MVA methods see the same training and test data, and are evaluated following
the same prescription.
•A complete TMVA analysis consists of two steps:
1. Training: the ensemble of available and optimally customised MVA methods are trained
and tested on independent signal and background data samples; the methods are evalu-
ated and the most appropriate (performing and concise) ones are selected.
2. Application: selected trained MVA methods are used for the classification of data sam-
ples with unknown signal and background composition, or for the estimate of unknown
target values (regression).
•A Factory class object created by the user organises the customisation and interaction with
the MVA methods for the training, testing and evaluation phases of the TMVA analysis. The
training results together with the configuration of the methods are written to result (“weight”)
files in XML format.
•Standardised outputs during the Factory running, and dedicated ROOT macros allow a refined
assessment of each method’s behaviour and performance for classification and regression.
•Once appropriate methods have been chosen by the user, they can be applied to data samples
with unknown classification or target values. Here, the interaction with the methods occurs
through a Reader class object created by the user. A method is booked by giving the path to
its weight file resulting from the training stage. Then, inside the user’s event loop, the MVA
response is returned by the Reader for each of the booked MVA method, as a function of the
event values of the discriminating variables used as input for the classifiers. Alternatively, for
classification, the user may request from the Reader the probability that a given event belongs
to the signal hypothesis and/or the event’s Rarity.
•In parallel to the XML files, TMVA generates standalone C++ classes after the training,
which can be used for classification problems (feature not available yet for regression). Such
classes are available for all classifiers except for cut optimisation, PDE-RS, PDE-Foam, k-NN
and the old CFMlpANN.

145
We give below a summary of the TMVA methods, outlining the current state of their implementa-
tion, their advantages and shortcomings.
•Rectangular Cut Optimisation
The current implementation is mature. It includes speed-optimised range searches using
binary trees, and three optimisation algorithms: Monte Carlo sampling, a Genetic Algorithm
and Simulated Annealing. In spite of these tools, optimising the cuts for a large number
of discriminating variables remains challenging. The user is advised to reduce the available
dimensions to the most significant variables (e.g., using a principal component analysis) prior
to optimising the cuts.
•Likelihood
Automatic non-parametric probability density function (PDF) estimation through histogram
smoothing and interpolation with various spline functions and quasi-unbinned kernel density
estimators is implemented. The PDF description can be individually tuned for each input
variable.
•PDE-RS
The multidimensional probability density estimator (PDE) approach is in an advanced devel-
opment stage featuring adaptive range search, several kernel estimation methods, and speed
optimised range search using event sorting in binary trees. It has also been extended to
regression.
•PDE-Foam
This new multidimensional PDE algorithm uses self-adapting phase-space binning and is a
fast realisation of PDE-RS in fixed volumes, which are determined and optimised during the
training phase. Much work went into the development of PDE-Foam. It has been thor-
oughly tested, and can be considered a mature method. PDE-Foam performs classification
and regression analyses.
•k-NN
The k-Nearest Neighbour classifier is also in a mature state, featuring both classification and
regression. The code has been well tested and shows satisfactory results. With scarce training
statistics it may slightly underperform in comparison with PDE-RS, whereas it is significantly
faster in the application to large data samples.
•Fisher and H-Matrix
Both are mature algorithms, featuring linear discrimination for classification only. Higher-
order correlations are taken care of by FDA (see below).
•Linear Discriminant (LD)
LD is equivalent to Fisher but providing both classification and linear regression.
•Function Discriminant Analysis (FDA)
FDA is a mature algorithm, which has not been extensively used yet. It extends the linear
discriminant to moderately non-linear correlations that are fit to the training data.

146 13 Conclusions and Plans
•Artificial Neural Networks
Significant work went into the implementation of fast feed-forward multilayer perceptron algo-
rithms into TMVA. Two external ANNs have been integrated as fully independent methods,
and another one has been newly developed for TMVA, with emphasis on flexibility and speed.
The performance of the latter ANN (MLP) has been cross checked against the Stuttgart
ANN (using as an example τidentification in ATLAS), and was found to achieve competitive
performance. The MLP ANN also performs multi-target regression.
•Support Vector Machine
SVM is a relatively new multivariate analysis algorithm with a strong statistical background.
It performs well for nonlinear discrimination and is insensitive to overtraining. Optimisation is
straightforward due to a low number of adjustable parameters (only two in the case of Gaussian
kernel). The response speed is slower than for a not-too-exhaustive neural network, but
comparable with other nonlinear methods. SVM is being extended to multivariate regression.
•Boosted Decision Trees
The BDT implementation has received constant attention over the years of its development.
The current version includes additional features like bagging or gradient boosting, and manual
or automatic pruning of statistically insignificant nodes. It is a highly performing MVA method
that also applies to regression problems.
•RuleFit
The current version has the possibility to run either the original program written by J. Fried-
man [34] or an independent TMVA implementation. The TMVA version has been improved
both in speed and performance and achieves almost equivalent results with respect to the
original one, requiring however somewhat more tuning.
The new framework introduced with TMVA 4 provides the flexibility to combine MVA methods in
a general fashion. Exploiting these capabilities for classification and regression however requires to
create so-called committee methods for each combination. So far, we provide a generalised Boost
method, allowing to boost any classifier by simply setting the variable Boost Num in the configuration
options to a positive number (plus possible adjustment of other configuration parameters). The
result is a potentially powerful committee method unifying the excellent properties of boosting with
MVA methods that already represent highly optimised algorithms.
Boosting is not the only combination the new framework allows us to establish. TMVA now also
supports the categorisation of classification according to the phase space, which allows a better
modelling and hence simplifies the mapping of the feature space. This particularly improves simple
methods, such las projective likelihood and linear discriminants.
Acknowledgements
The fast growth of TMVA would not have been possible without the contribution and feedback from many
developers (also co-authors of this Users Guide) and users to whom we are indebted. We thank in particular
the CERN Summer students Matt Jachowski (Stanford U.) for the implementation of TMVA’s MLP neural

147
network, and Yair Mahalalel (Tel Aviv U.) for a significant improvement of PDE-RS. The Support Vector
Machine has been contributed to TMVA by Andrzej Zemla and Marcin Wolter (IFJ PAN Krakow), and the
k-NN method has been written by Rustem Ospanov (Texas U.). We are grateful to Lucian Ancu, Doug
Applegate, Kregg Arms, Ren´e Brun and the ROOT team, Andrea Bulgarelli, Marc Escalier, Zhiyi Liu, Colin
Mclean, Elzbieta Richter-Was, Alfio Rizzo, Lydia Roos, Vincent Tisserand, Alexei Volk, Jiahang Zhong for
helpful feedback and bug reports. Thanks also to Lucian Ancu for improving the plotting macros.

148 A More Classifier Booking Examples
A More Classifier Booking Examples
The Code Examples 60 and 61 give a (non-exhaustive) collection of classifier bookings with appro-
priate default options. They correspond to the example training job TMVAClassification.C.
// Cut optimisation using Monte Carlo sampling
factory->BookMethod( TMVA::Types::kCuts, "Cuts",
"!H:!V:FitMethod=MC:EffSel:SampleSize=200000:VarProp=FSmart" );
// Cut optmisation using Genetic Algorithm
factory->BookMethod( TMVA::Types::kCuts, "CutsGA",
"H:!V:FitMethod=GA:CutRangeMin=-10:CutRangeMax=10:VarProp[1]=FMax:EffSel:\
Steps=30:Cycles=3:PopSize=400:SC_steps=10:SC_rate=5:SC_factor=0.95" );
// Cut optmisation using Simulated Annealing algorithm
factory->BookMethod( TMVA::Types::kCuts, "CutsSA",
"!H:!V:FitMethod=SA:EffSel:MaxCalls=150000:KernelTemp=IncAdaptive:\
InitialTemp=1e+6:MinTemp=1e-6:Eps=1e-10:UseDefaultScale" );
// Likelihood classification (naive Bayes) with Spline PDF parametrisation
factory->BookMethod( TMVA::Types::kLikelihood, "Likelihood",
"H:!V:TransformOutput:PDFInterpol=Spline2:NSmoothSig[0]=20:\
NSmoothBkg[0]=20:NSmoothBkg[1]=10:NSmooth=1:NAvEvtPerBin=50" );
// Likelihood with decorrelation of input variables
factory->BookMethod( TMVA::Types::kLikelihood, "LikelihoodD",
"!H:!V:!TransformOutput:PDFInterpol=Spline2:NSmoothSig[0]=20:\
NSmoothBkg[0]=20:NSmooth=5:NAvEvtPerBin=50:VarTransform=Decorrelate" );
// Likelihood with unbinned kernel estimator for PDF parametrisation
factory->BookMethod( TMVA::Types::kLikelihood, "LikelihoodKDE",
"!H:!V:!TransformOutput:PDFInterpol=KDE:KDEtype=Gauss:KDEiter=Adaptive:\
KDEFineFactor=0.3:KDEborder=None:NAvEvtPerBin=50" );
Code Example 60: Examples for booking MVA methods in TMVA for application to classification and –
where available – to regression problems. The first argument is a unique type enumerator (the avaliable types
can be looked up in src/Types.h), the second is a user-defined name (must be unique among all booked
classifiers), and the third a configuration option string that is specific to the classifier. For options that
are not set in the string default values are used. The syntax of the options should become clear from the
above examples. Individual options are separated by a ’:’. Boolean variables can be set either explicitly as
MyBoolVar=True/False, or just via MyBoolVar/!MyBoolVar. All concrete option variables are explained in
the tools and classifier sections of this Users Guide. The list is continued in Code Example 61.

149
// Probability density estimator range search method (multi-dimensional)
factory->BookMethod( TMVA::Types::kPDERS, "PDERS",
"!H:V:NormTree=T:VolumeRangeMode=Adaptive:KernelEstimator=Gauss:\
GaussSigma=0.3:NEventsMin=400:NEventsMax=600" );
// Multi-dimensional PDE using self-adapting phase-space binning
factory->BookMethod( TMVA::Types::kPDEFoam, "PDEFoam",
"H:V:SigBgSeparate=F:TailCut=0.001:VolFrac=0.0333:nActiveCells=500:\
nSampl=2000:nBin=5:CutNmin=T:Nmin=100:Kernel=None:Compress=T" );
// k-Nearest Neighbour method (similar to PDE-RS)
factory->BookMethod( TMVA::Types::kKNN, "KNN",
"H:nkNN=20:ScaleFrac=0.8:SigmaFact=1.0:Kernel=Gaus:UseKernel=F:\
UseWeight=T:!Trim" );
// H-matrix (chi-squared) method
factory->BookMethod( TMVA::Types::kHMatrix, "HMatrix", "!H:!V" );
// Fisher discriminant (also creating Rarity distribution of MVA output)
factory->BookMethod( TMVA::Types::kFisher, "Fisher",
"H:!V:Fisher:CreateMVAPdfs:PDFInterpolMVAPdf=Spline2:NbinsMVAPdf=60:\
NsmoothMVAPdf=10" );
// Fisher discriminant with Gauss-transformed input variables
factory->BookMethod( TMVA::Types::kFisher, "FisherG", "VarTransform=Gauss" );
// Fisher discriminant with principle-value-transformed input variables
factory->BookMethod( TMVA::Types::kFisher, "FisherG", "VarTransform=PCA" );
// Boosted Fisher discriminant
factory->BookMethod( TMVA::Types::kFisher, "BoostedFisher",
"Boost_Num=20:Boost_Transform=log:\
Boost_Type=AdaBoost:Boost_AdaBoostBeta=0.2");
// Linear discriminant (same as Fisher, but also performing regression)
factory->BookMethod( TMVA::Types::kLD, "LD", "H:!V:VarTransform=None" );
// Function discrimination analysis (FDA), fitting user-defined function
factory->BookMethod( TMVA::Types::kFDA, "FDA_MT",
"H:!V:Formula=(0)+(1)*x0+(2)*x1+(3)*x2+(4)*x3:\
ParRanges=(-1,1);(-10,10);(-10,10);(-10,10);(-10,10):FitMethod=MINUIT:\
ErrorLevel=1:PrintLevel=-1:FitStrategy=2:UseImprove:UseMinos:SetBatch" );
Code Example 61: Continuation from Code Example 60. Continued in Code Example 61.

150 A More Classifier Booking Examples
// Artificial Neural Network (Multilayer perceptron) - TMVA version
factory->BookMethod( TMVA::Types::kMLP, "MLP",
"H:!V:NeuronType=tanh:VarTransform=N:NCycles=600:HiddenLayers=N+5:\
TestRate=5" );
// NN with BFGS quadratic minimisation
factory->BookMethod( TMVA::Types::kMLP, "MLPBFGS",
"H:!V:NeuronType=tanh:VarTransform=N:NCycles=600:HiddenLayers=N+5:\
TestRate=5:TrainingMethod=BFGS" );
// NN (Multilayer perceptron) - ROOT version
factory->BookMethod( TMVA::Types::kTMlpANN, "TMlpANN",
"!H:!V:NCycles=200:HiddenLayers=N+1,N:LearningMethod=BFGS:
ValidationFraction=0.3" );
// NN (Multilayer perceptron) - ALEPH version (depreciated)
factory->BookMethod( TMVA::Types::kCFMlpANN, "CFMlpANN",
"!H:!V:NCycles=2000:HiddenLayers=N+1,N" );
// Support Vector Machine
factory->BookMethod( TMVA::Types::kSVM, "SVM", "Gamma=0.25:Tol=0.001" );
// Boosted Decision Trees with adaptive boosting
factory->BookMethod( TMVA::Types::kBDT, "BDT",
"!H:!V:NTrees=400:nEventsMin=400:MaxDepth=3:BoostType=AdaBoost:\
SeparationType=GiniIndex:nCuts=20:PruneMethod=NoPruning" );
// Boosted Decision Trees with gradient boosting
factory->BookMethod( TMVA::Types::kBDT, "BDTG",
"!H:!V:NTrees=1000:BoostType=Grad:Shrinkage=0.30:UseBaggedGrad:\
GradBaggingFraction=0.6:SeparationType=GiniIndex:nCuts=20:\
PruneMethod=CostComplexity:PruneStrength=50:NNodesMax=5" );
// Boosted Decision Trees with bagging
factory->BookMethod( TMVA::Types::kBDT, "BDTB",
"!H:!V:NTrees=400:BoostType=Bagging:SeparationType=GiniIndex:\
nCuts=20:PruneMethod=NoPruning" );
// Predictive learning via rule ensembles (RuleFit)
factory->BookMethod( TMVA::Types::kRuleFit, "RuleFit",
"H:!V:RuleFitModule=RFTMVA:Model=ModRuleLinear:MinImp=0.001:\
RuleMinDist=0.001:NTrees=20:fEventsMin=0.01:fEventsMax=0.5:\
GDTau=-1.0:GDTauPrec=0.01:GDStep=0.01:GDNSteps=10000:GDErrScale=1.02" );
Code Example 62: Continuation from Code Example 61.

REFERENCES 151
References
[1] R. Brun and F. Rademakers, “ROOT - An Object Oriented Data Analysis Framework”, Nucl.
Inst. Meth. in Phys. Res. A 389, 81 (1997).
[2] J. Friedman, T. Hastie and R. Tibshirani, “The Elements of Statistical Learning”, Springer
Series in Statistics, 2001.
[3] A. Webb, “Statistical Pattern Recognition”, 2nd Edition, J. Wiley & Sons Ltd, 2002.
[4] L.I. Kuncheva, “Combining Pattern Classifiers”, J. Wiley & Sons, 2004.
[5] I. Narsky, “StatPatternRecognition: A C++ Package for Statistical Analysis of High Energy
Physics Data”, physics/0507143 (2005).
[6] The following web pages give information on available statistical tools in HEP and other areas
of science: https://plone4.fnal.gov:4430/P0/phystat/,http://astrostatistics.psu.edu/statcodes/.
[7] The BABAR Physics Book, BABAR Collaboration (P.F. Harrison and H. Quinn (editors) et
al.), SLAC-R-0504 (1998); S. Versill´e, PhD Thesis at LPNHE, http://lpnhe-babar.in2p3.fr/theses/
these SophieVersille.ps.gz (1998).
[8] To our information, the Rarity has been originally defined by F. Le Diberder in an unpublished
Mark II internal note. In a single dimension, as defined in Eq. (13), it is equivalent to the
µ-transform developed in: M. Pivk, “Etude de la violation de CP dans la d´esint´egration B0→
h+h−(h=π, K)aupr`es du d´etecteur BABAR `a SLAC”, PhD thesis (in French), http://tel.
archives-ouvertes.fr/documents/archives0/00/00/29/91/index fr.html (2003).
[9] M. Kendall, A. Stuart, K.J. Ord, and S. Arnold, Kendall’s Advanced Theory of Statistics:
Volume 2A – Classical Inference and and the Linear Model (Kendall’s Library of Statistics), A
Hodder Arnold Publication, 6th edition, April 1999.
[10] T.M. Cover and J.A. Thomas, “Elements of information theory”, Wiley-Interscience, New
York, NY, USA, 1991.
[11] Y.-I. Moon, B. Rajagopalan, and U. Lall, Phys. Rev. E, 52 (no. 3), 2318 (1995).
[12] J.L. Bentley, “Multidimensional Binary Search Trees Used for Associate Searching”, Commu-
nications of the ACM, 18, 509 (1975); J.L. Bentley, “Multidimensional Divide-and-Conquer”,
Communications of the ACM, 23(4), 214 (1980); J.H. Friedman, J.L. Bentley and R.A. Finkel,
“An Algorithm for Finding Matches in Logarithmic Expected Time”, ACM Trans. on Mathe-
matical Software, 3(3), 209 (1977).
[13] R. Sedgewick, “Algorithms in C++”, Addison Wesley, Chapter 26, Boston, USA (1992).
[14] T. Carli and B. Koblitz, Nucl. Instrum. Meth. A 501, 576 (2003) [hep-ex/0211019].
[15] S. Jadach, Comput. Phys. Commun. 130, 244 (2000); S. Jadach, Comput. Phys. Commun. 152,
55 (2003).

152 References
[16] D. Dannheim et al., Nucl. Instr. and Meth. A 606, 717 (2009).
[17] F. James, “MINUIT, Function Minization and ERROR Analysis”, Version 94.1, CERN pro-
gram Library long writeup D506.
[18] P.J.M. Van Laarhoven and E.H.L. Aart, “Simulated Annealing: Theory and Application”,
D. Reidel Publishing, Dordrecht, Holland, 1987.
[19] N. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, A.M. Teller, and E. Teller, J. Chem. Phys.
21, 6, 1087 (1953).
[20] 353QH twice smoothing algorithm, presented by J. Friedman in Proc. of the 1974 CERN School
of Computing, Norway, Aug 11-24, 1974.
[21] D.W. Scott, “Multivariate Density Estimation, Theory, Practice, and Visualization”, Wiley-
Interscience, New York, 1992.
[22] R.A. Fisher, Annals Eugenics 7, 179 (1936).
[23] P.C. Mahalanobis, Proc. Nat. Inst. Sci. India, Part 2A, 49 (1936); P.C. Mahalanobis, “On the
generalized distance in statistics”, Proceedings of the National Institute of Science, Calcutta,
12, 49 (1936).
[24] C.G. Broyden, “The Convergence of a Class of Double-rank Minimization Algorithms”, J.
Inst. of Math. and App. 6, 76 (1970); R. Fletcher, “A New Approach to Variable Metric
Algorithms”, Computer J. 13, 317 (1970); D. Goldfarb, ”A Family of Variable Metric Updates
Derived by Variational Means”, Math. Comp. 24, 23 (1970); D.F. Shannon, “Conditioning of
Quasi-Newton Methods for Function Minimization”, Math. Comp. 24, 647 (1970).
[25] R.E. Schapire, “The strenght of weak learnability, (1990) Machine Learning 5 197-227; Y. Freud,
“Boosting a weak learning algorithm by majority (1995) Inform. and Comput. 121 256-285;
[26] Y. Freund and R.E. Schapire, J. of Computer and System Science 55, 119 (1997).
[27] Robert E. Schapire, Yoram Singer, Improved Boosting Algorithms Using Confidence-rated Pre-
dictions, Machine Learning , Vol.37, No. 3, (297-336) 1999.
[28] H. Drucker,Improving regressors using boosting techniques,In D. H. Fisher (Ed.), Proceedings
of the fourteenth international conference on machine learning (ICML 1997) (pp. 107115).
Nashville, TN, USA, July 812. Morgan Kaufmann, ISBN 1558604863.
[29] Wei Fan and Salvatore J. Stolfo, AdaCost: misclassification cost-sensitive boosting, Proceedings
of the 16th International conference on machine learning (ICML 1999).
[30] L. Breiman, Random Forests, Technical Report, University of California 2001.
[31] Y.R. Quinlan, “Simplifying Decision Trees”, Int. J. Man-Machine Studies, 28, 221 (1987).
[32] L. Breiman, J. Friedman, R. Olshen and C. Stone, “Classification and Regression Trees”,
Wadsworth (1984).

REFERENCES 153
[33] We use the ROOT class TParallelCoord by B. Dalla Piazza, 2007.
[34] J. Friedman and B.E. Popescu, “Predictive Learning via Rule Ensembles”, Technical Report,
Statistics Department, Stanford University, 2004.
[35] J. Friedman and B.E. Popescu, “Gradient Directed Regularization for Linear Regression and
Classification”, Technical Report, Statistics Department, Stanford University, 2003.
[36] RuleFit web site: http:/www-stat.stanford.edu/∼jhf/r-rulefit/RuleFit help.html.
[37] J. Conrad and F. Tegenfeldt, JHEP 0607, 040 (2006) [hep-ph/0605106].
[38] W. Cohen and Y. Singer, Proceedings of the Sixteenth National Conference on Artificial Intel-
ligence (AAAI-99), 335, AAAI Press, 1999.
[39] V. Vapnik and A. Lerner, “Pattern recognition using generalized portrait method”, Automation
and Remote Control, 24, 774 (1963).
[40] V. Vapnik and A. Chervonenkis, “A note on one class of perceptrons”, Automation and Remote
Control, 25 (1964).
[41] B.E. Boser, I.M. Guyon, and V.N. Vapnik, “A training algorithm for optimal margin classi-
fiers”, in D. Haussler, ed., Proceedings of the 5th Annual ACM Workshop on Computational
Leraning Theory, 144, ACM Press (1992).
[42] C. Cortes and V. Vapnik, “Support vector networks”, Machine Learning, 20, 273 (1995).
[43] V. Vapnik, “The Nature of Statistical Learning Theory”, Springer Verlag, New York, 1995.
[44] C.J.C. Burges, “A Tutorial on Support Vector Machines for Pattern Recognition”, Data Mining
and Knowledge Discovery, 2, 1 (1998).
[45] J. Platt, “Fast training of support vector machines using sequential minimal optimization”, in
B. Scholkopf, C. Burges and A. Smola, eds., Advances in Kernel Methods – Support Vector
Learning, ch. 12, pp. 185, MIT Press, 1999.
[46] S. Keerthi, S. Shevade, C. Bhattacharyya and K. Murthy, “Improvements to Platt’s SMO
algorithm for SVM classifier design”, Technical Report CD-99-14, Dept. of Mechanical and
Production Engineering, Natl. Univ. Singapore, Singapore, 1999.
[47] P. Huber, “Robust estimation of a location parameter”, Annals of Mathematical Statistics, 35,
73-101,1964
[48] P. Baldi, P. Sadowski, D. Whiteson, “Searching for Exotic Particles in High-Energy Physics
with Deep Learning”, Nature Communications 5, Article number: 4308 (2014)