BIOL340: Ecology Lab Manual Bookdown

User Manual: Pdf

Open the PDF directly: View PDF PDF.
Page Count: 111 [warning: Documents this large are best viewed by clicking the View PDF Link!]

BIOL340: Ecology Lab Manual
Daniel J. Hocking
2018-02-14
2
Contents
Course Information 7
LearningOutcomes............................................. 7
Grades: ................................................... 7
ExpectationofStudentWork ....................................... 8
GeneralLaboratoryInformation ..................................... 8
CourseTopicsandSchedule........................................ 9
Importantdatesandinformation ..................................... 9
Attendance ................................................. 10
ClassPolicies ................................................ 10
Condentiality and Mandatory Reporting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
AcademicHonesty ............................................. 11
PersonswithDisabilities.......................................... 11
1 Biology Field Safety Regulations 13
BasicSafetyRules ............................................. 13
Students’ Responsibility Statement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2 Introduction: From Observation to Experimentation 17
2.1 ActiveGroupObservation...................................... 17
2.2 Hypotheses .............................................. 17
2.3 Observations ............................................. 17
2.4 Observation: Starting the Process of Ecological Study . . . . . . . . . . . . . . . . . . . . . . 18
2.5 Homework............................................... 19
3 Data Organization in Spreadsheets 21
3.1 ProblemswithSpreadsheets..................................... 22
3.2 Activity ................................................ 23
4 Introduction to Scientic Thinking and Statistics in Ecology 25
4.1 IntroductiontoStatistics ...................................... 25
4.2 Describing Central Tendancy and Variation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
4.3 Explaining Variation: Measuring association with the Coecient of Determination . . . . . . 28
4.4 Explaining Variation by Association: Regression . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.5 Explaining Variation: Identifying random and nonrandom variation with probabilities . . . . 31
4.6 Explaining Variation: Associating dierences with group membership . . . . . . . . . . . . . 31
4.7 Activity ................................................ 33
4.8 Introduction to Scientic Programming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.9 AssignandRecallanObject..................................... 35
4.10 Calculate the Mean, SD, and Variance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.11ImportData ............................................. 36
4.12 Calculate Summary Statistics on the Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
4.13 Subset and Recalculate Summary Statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3
4CONTENTS
4.14SaveScript .............................................. 37
5 Sampling Populations 39
5.1 Introduction.............................................. 39
5.2 SamplingSchemes .......................................... 39
5.3 SequentialSampling ......................................... 41
5.4 TheEectsofDistributions..................................... 42
5.5 Mark Recapture (Capture Recapture) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
6 Life Tables and Population Demographics 45
6.1 Objectives............................................... 45
6.2 Introduction.............................................. 45
6.3 Materials ............................................... 45
6.4 Methods................................................ 45
7 Logistic Population Growth 53
7.1 Labactivities ............................................. 53
7.2 Objectives............................................... 53
7.3 Introduction.............................................. 53
7.4 Materials ............................................... 55
7.5 Methods................................................ 56
7.6 Questions ............................................... 56
8 Community Ecology: Diversity 59
8.1 Labactivities ............................................. 59
8.2 Objectives............................................... 59
8.3 Introduction.............................................. 59
8.4 FieldMethods ............................................ 62
8.5 QuestionsForHomework ...................................... 63
9 Ant Spatial Distributions 65
9.1 Materials ............................................... 65
9.2 LabActivities............................................. 65
9.3 Review................................................. 65
9.4 Homework............................................... 66
10 Population Growth 67
10.1Introduction.............................................. 67
10.2Objectives............................................... 70
10.3Materials ............................................... 70
10.4InitialSet-Up............................................. 70
10.5Assignment .............................................. 71
11 Competition and Allometry 73
11.1Labactivities ............................................. 73
11.2Objectives............................................... 73
11.3Introduction.............................................. 73
11.4Hypotheses .............................................. 74
11.5Materials ............................................... 74
11.6PlantingMethods........................................... 75
11.7MeasurementMethods........................................ 75
11.8AnalysisMethods........................................... 75
11.9ResultsandDiscussion........................................ 76
11.10LiteratureCited ........................................... 76
11.11Homework–LabReport....................................... 77
CONTENTS 5
11.12Grading key to the lab report on competition and mass-density scaling . . . . . . . . . . . . . 77
12 Turtle Ecology 79
12.1Objectives............................................... 79
12.2Labactivities ............................................. 79
12.3 Mark Recapture (Capture Recapture) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
12.4QuestionsforLabAssignment.................................... 80
13 Population Spatial Variation 81
13.1Labactivities ............................................. 81
13.2Objectives............................................... 81
13.3Introduction.............................................. 81
13.4Hypotheses .............................................. 81
13.5Materials ............................................... 81
13.6Methods................................................ 81
13.7LiteratureCited ........................................... 82
13.8Homework–LabReport....................................... 82
14 Forest Stand Dynamics 83
14.1Labactivities ............................................. 83
14.2Objectives............................................... 83
14.3Introduction.............................................. 83
14.4Materials ............................................... 84
14.5Methods................................................ 84
14.6LiteratureCited ........................................... 85
14.7Homework–LabReport....................................... 85
15 Phenology 87
15.1Activity ................................................ 87
16 Lab 2: Population Setup and Statistics 89
16.1 Population Density Dependence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
16.2 Review of Introductory Statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
16.3 Introduction to Scientic Programming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
16.4BasicStatisticswithR........................................ 89
17 Migration 91
17.1Labactivities ............................................. 91
17.2Objectives............................................... 92
17.3Introduction.............................................. 92
17.4Hypotheses .............................................. 92
17.5Materials ............................................... 92
17.6PlantingMethods........................................... 92
17.7MeasurementMethods........................................ 92
17.8AnalysisMethods........................................... 92
17.9ResultsandDiscussion........................................ 92
17.10LiteratureCited ........................................... 92
17.11Homework–LabReport....................................... 92
18 Population Growth 93
18.1InitialSet-Up............................................. 93
18.2Assignment .............................................. 95
19 Cemetery Demographics and Life Tables0 97
19.1SynopsisofToday’sLab........................................ 97
6CONTENTS
19.2Introduction.............................................. 97
19.3Methods................................................ 98
19.4GeneralInstructions ......................................... 99
19.5DataAnalysis............................................. 99
20 Lab 3: Introduction of Scientic Writing 103
Course Information 105
LearningOutcomes.............................................105
Grades: ...................................................105
ExpectationofStudentWork .......................................106
GeneralLaboratoryInformation .....................................107
CourseTopicsandSchedule........................................107
Importantdatesandinformation ..................................... 108
Attendance .................................................108
ClassPolicies ................................................108
Condentiality and Mandatory Reporting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
AcademicHonesty .............................................109
PersonswithDisabilities.......................................... 109
Course Information
Instructor
Dr. Daniel Hocking, Compton 309, djhocking@frostburg.edu, 301-687-4343
Meeting Times and Locations
Lecture: Tuesday/Thursday 8:00-8:50 am; Compton 327
Laboratory:
• Section 1: Tuesday 2:00-5:50 pm; Compton 321
• Section 2: Wednesday 8:00-11:50 am; Compton 321
Oce Hours: Compton 309; Monday 10:00-11:00 am, Tuesday & Thursday 9:00-10:30 am, Wednesday
3:00-4:00 pm, or by appointment
Description
Environmental relationships of plants and animals. Field laboratory experience. Measuring environmental
variables in terrestrial and aquatic ecosystems. Two hrs. lecture, one 4-hr. lab. Every semester.
Prerequisites
BIOL 150, 160 or 161; CHEM 202 (or CHEM 201 and permission of the instructor); MATH 109/209.
Learning Outcomes
The primary objective of the lab section is to provide you with experience collecting real, relevant ecological
data. Specically you will:
1. become familiar with ecological data collection for various taxa and in a variety of ecosystems.
2. be able to analyze data and interpret results.
3. practice and improve writtn and oral communication skills.
Grades:
7
8CONTENTS
Task Pct Grade
Lecture Exams 45% A >= 90%
Homework, quizzes, & In-class work 10% B = 80 – 89%
Final Exam, comprehensive 20% C = 70 – 79%
Lab Reports 25% D = 60 – 69%
F < 60%
Total points, percentages, and assignments may change to accommodate teaching and learning parameters.
Grades are still based on percentage of total points. Grades from individual assignments will be posted on
blackboard; however, the grade calculated by blackboard could be incorrect because of dier-
ences in weighting of assignments. It is your responsibility to calculate your current grade based on the
grading scheme described above.
Extra Credit
Extra credit may total up to 10% on your lowest exam grade (except the nal).
• Species of the week (1 pt per approved submission - see below)
• Diving vans for eld trips (1 pt for training/registration + 1 pt per trip driving)
Species of the Week
Over the course of the semester (no more than one submision per week), each student may upload to
blackboard a description of the ecology and life history of a species observed in the wild. This can be any
wild plant or animal but must be positively identied to species (non-native species and planted trees count
but not planted owers). The description and location of the sighting should be included. No animals should
be disturbed or handled for this assignment. Additional instructions on uploading will be provided in lab.
Once a species has been reported, another member of class may not receive credit for it. The description of
the ecology and life history must be a minimum of 1 page, single-spaced with 12 pt font and 1 inch margins.
Students will receive 1 pt for each approved submission up to a total maximum of 10.
Expectation of Student Work
Student work is dened as assignments, homework, and other academic activities to be completed outside
of instructional time, including reading, studying, writing, research etc. Students should expect to spend a
minimum of two hours per week completing this work for each credit hour enrolled (thus 6 hours of work
outside of class for a 3-credit course), although the time spent outside of class may increase based on the
topic and level of the course.
Late Policy: Assignments turned in after the due date will lose 10% per day for a maximum of 3 days, after
which they will not be accepted and will receive a zero. Assignments turned in at any point after the time
due (even 1 minute late) will lose a minimum of 10%. This excludes quizzes, in-class assignments, in-lab
activities, exams, and presentations, which can not be turned in late or made up without prior arrangement
with the instructor for extremely extenuating circumstances.
General Laboratory Information
Labs are an opportunity to gain hands-on experience with ecological techniques and gain a greater appreci-
ation of the scientic process. Lab assignments will help guide you through the development of ecological
CONTENTS 9
questions, formation of hypotheses, and design of ecological studies. Studies will be conducted in the eld or
via computer simulation. Students will learn and be expected to use appropriate statistical techniques along
with data visualizations (e.g. gures/plots/graphs) to summarize the data and test the hypotheses. Some
labs will require full reports (intro, methods, results, dicussion, literature cited) but most will just require
answering a series of questions to help guide inference and understanding of the results.
Please note that many of our labs will be conducted at local eld sites. These labs will be
conducted outside so you are expected to use common sense in deciding what to wear and
what to bring. You will get dirty and you will get wet during these labs. Be prepared to
spend 4 hours in areas without restrooms, if you have questions about outdoor restroom etiquette please
consult leave-no-trace (lnt) principles: http://www.lnt.org/training/educationaltraining.php, http://lnt.org/
training/OnlineCourse/ or ask the instructor if you have specic questions. You must notify the instructor
during the rst week of class if you are allergic to bees or have never been stung by a bee. Refer to the safety
1 section for additional information.
Course Topics and Schedule
The laboratory schedule is exible based on previous lab timing and weather. We will often go out in the
eld during inclement weather as long as it does not result in undue risk of injury. Thus, come to all labs
prepared to go out in the eld and get wet and dirty. More about the lab schedule will be provided during
your lab section. Below is a tentative laboratory schedule.
+——+———————————–+———————-+ | Week | Activity | Assignment Due | +:=====+:==================================+:=====================+
| 1 | No Lab | | +——+———————————–+———————-+ | 2 | Set up population and com-
petition | | | | experiments | | +——+———————————–+———————-+ | 3 | Questions,
Hypotheses | | +——+———————————–+———————-+ | 4 | Sampling | Qs & Hypotheses
from | | | | 3 scientic papers | +——+———————————–+———————-+ | 5 | Excel,
graphics, and statistics | Sampling lab | +——+———————————–+———————-+ | 6 |
Cemetery demographics | Excel & Stats | +——+———————————–+———————-+ | 7
| Food Webs | Cemetery lab | +——+———————————–+———————-+ | 8 | SPRING
BREAK - no classes | | +——+———————————–+———————-+ | 9 | Ant distribu-
tions | | +——+———————————–+———————-+ | 10 | Forest stand dynamics | Forest
stand reading | +——+———————————–+———————-+ | 11 | No Lab - Count Beetles
| Forest lab | +——+———————————–+———————-+ | 12 | Sampling invertebrates |
| +——+———————————–+———————-+ | 13 | Invertebrate diversity; Radishes | |
+——+———————————–+———————-+ | 14 | Turtle Mark-Recapture | Diversity lab |
+——+———————————–+———————-+ | 15 | Beetle populations | Raddish comp lab |
+——+———————————–+———————-+
Important dates and information
• February 2: Last day to add/drop courses
• February 16: Last day to le pass/fail option
• April 6: last day to withdraw with a “W”
• May 15: Last day of classes
•Friday May 18: Final Exam, 2:30 - 5:00 pm, Compton 327
• Email and Blackboard: access to your email and Blackboard is required for this class. Check your
email daily.
10 CONTENTS
Attendance
If you miss class, you miss whatever quizzes, exams, or activities that were administered and you will receive a
zero. Attendance is critical to success. Makeup exams are extremely rare, and will likely be a dierent format
from the original exam. However, you will be allowed to make up missed exams if you have a documented,
excused absence. Additionally, if the absence was planned, you must notify me before the absence.
Attendance is required for all laboratory sessions. You will receive a zero for any work associated with that
lab. Additionally, any assignments due in lab that day will be late. If you show up late to lab and miss the
van, it will be considered an absence. The van will not wait for anyone. For indoor labs, arriving more than
15 minutes late will count as an absence, but you will be able to participate for half credit in any activities
associated with the lab.
Documented excused absences are generally limited to the following examples: university sanctioned events
(eld trips, or events where the student is an athlete/performer), funerals (requires an obituary or other proof),
or illness/medical emergencies (requires a doctor’s note or other proof). For all of these, documentation must
be provided. If a student is participating in extracurricular activities or has an excused absence, I must be
notied within one week to arrange makeup assignments.
If you have an unexcused absence, you do not need to contact me. Common examples of unexcused absences
are “family emergencies”, “car trouble”, and “my ride is leaving early this week.” While you may deem these
as legitimate excuses, accepting them as excusable absences and allowing students to make up work will only
encourage widespread abuse. Makeups of any kind are not allowed for unexcused absences.
Class Policies
There will be no cell phones on the desk or in lab. There will be no use of laptops unless prior consent
is obtained for special circumstances. You may not eat food or use tobacco products including electronic
cigarettes in class or labs. Disruptive behavior (using phones, talking, etc.): I will kick you out if I think
you are being disruptive.
“The University will not tolerate disorderly or disruptive conduct which substantially threatens, harms, or
interferes with university personnel or orderly university processes and functions. A faculty member may
require a student to leave the classroom when his/her behavior disrupts the learning environment of the class.
A student found responsible for disruptive behavior in the classroom may be administratively withdrawn
from the course.”
Beacon Early Warning System: all students should have a network of people who will support them in
their educational journey. For that reason, the University uses a system known as Beacon, whereby your
instructors and coaches, if applicable, can post notices about your academic behavior. For instance, if you
are absent repeatedly from a class or are not completing assignments, your instructor may post a notice on
Beacon. That information may be shared with your other instructors and/or your athletic coach. I will be
monitoring notices posted on Beacon so that you and I may address any issues before they become obstacles
to your academic success.
Condentiality and Mandatory Reporting
Frostburg State University and its faculty are committed to maintaining a safe learning environment and
supporting survivors of violence. To meet this commitment and comply with federal and state law, FSU re-
quires all faculty and sta (other than the condential employees in CAPS and Brady Health) to report any
instances of gender-based harassment, sexual misconduct, relationship violence, or stalking against students.
This means if you share your or another FSU student’s experience with gender-based harassment, sexual mis-
conduct, relationship violence, or, stalking, I have a duty to report the information to the University’s Title
CONTENTS 11
IX Coordinator. The only exception to my reporting obligation is when such incidents are communicated
during class discussion, as part of an assignment for a class, or as part of a University-approved research
project.
Faculty and sta are also obligated to report allegations of child abuse and neglect to University Police and
to Child Protective Services. This obligation extends to disclosures of past abuse even if the victim is now an
adult and the abuser is deceased. My duty to report suspected child abuse and neglect extends to disclosures
that are made as part of classroom discussions and in writing assignments.
If you or someone you know has experienced an incident of harassment or violence, please go to www.
frostburg.edu/titleix to nd information on reporting options and the resources and services available for
support.
Academic Honesty
Denition of Academic Dishonesty from your student handbook: “Academic dishonesty is dened to include
any form of cheating and/or plagiarism. Cheating includes, but is not limited to, such acts as stealing or
altering testing instruments; falsifying the identity of persons for any academic purpose; oering, giving
or receiving unauthorized assistance on an examination, quiz or other written or oral material in a course;
or falsifying information on any type of academic record. Plagiarism is the presentation of written or oral
material in a manner which conceals the true source of documentary material; or the presentation of materials
which uses hypotheses, conclusions, evidence, data or the like, in a way that the student appears to have done
work which he/she did not, in fact, do. In cases involving academic dishonesty, a failing grade or a grade
of zero (0) for either an assignment and/or a course may be administered. Students who are expelled or
suspended for reasons of academic dishonesty are not admissible to other institutions within the University
System of Maryland. Suspension or expulsion for academic dishonesty is noted on a student’s academic
transcript.”
Any violation of academic honesty will result in a zero for that graded work, and a repeat
violation will result in failure of the course. Cheating will be reported and further disciplinary
action may be pursued by the University Judicial Board This includes plagiarism. I will check long
answers, essays, and lab reports with plagiarism-checking software. When in doubt, just cite the source.
There’s nothing wrong with building on somone else’s ideas, in fact it’s the way progress in made in science.
Just give that person credit.
Persons with Disabilities
Frostburg State University is committed to providing equal educational opportunities for students with
documented disabilities. Students who require disability serves or reasonable accommodations must identify
themselves as having a disability and provide current diagnostic documentation to Disability Support Services.
All information is condential. Please call 4483 or visit 150 Pullen Hall for more information.
12 CONTENTS
Chapter 1
Biology Field Safety Regulations
Basic Safety Rules
General Field Safety
1. Safety is paramount. A student who willfully endangers the safety and welfare of him/herself or another
will be required to leave the eld and return home at the student’s own expense.
2. Footwear: Closed-toe shoes and boots with a good sole are essential in avoiding accidents and falls. Be
prepared to walk o of trails and encounter slippery conditions. Watch before you step.
3. Clothing: Students are required to be prepared for outside conditions, including raingear, warm coats
and clothing, hats, and gloves.
4. Additional equipment: Insect repellant and hand sanitizer are benecial additions to any eld bag.
5. Field participants will take part in activities of the eld trip group or one of the eld trip subgroups
at all times. You are not allowed to leave the group at any point.
6. Fieldtrip leaders will make the nal decision on whether any proposed activity is appropriate or not,
and participants will abide by that decision.
7. When students return from a eldtrip, each person will be responsible for helping to clean the equipment
and return it to its proper spot in the storeroom.
8. All accidents must be reported to the instructor or supervisor.
Field Hazards
1. Bees and other stinging creatures may be encountered during eld experiences. If you are allergic to
bees, it is your responsibility to notify the instructor of the course during the rst week of the course.
If you have never been stung by a bee before, you must also notify the instructor of the course during
the rst week of the course. If you require the use of an epi-pen you must bring your own prescription
pen and self-administer the medicine in case of a bee sting.
2. Poisonous plants: eastern poison ivy and poison sumac are both native and naturally occurring in the
area and may cause adverse reactions. Please be aware that you may encounter poisonous plants.
3. Do not consume any part of any plant or fungi material during laboratory activities. Doing so, even
if you are aware of the species, is not safe.
4. Animals: venomous snakes and other hazardous animals are present in the eld. Please be aware of
your surroundings, stay together as a group, and do not handle animals of any kind.
13
14 CHAPTER 1. BIOLOGY FIELD SAFETY REGULATIONS
Alcohol and Drugs
1. All eldtrips and eld labs are tobacco-free, no dipping, chewing or smoking in vans or in the eld.
2. All eldtrips and eld labs are “dry” and drug-free. This means that students who go on eldtrips
agree not to consume alcoholic beverages of any kind or to use illegal substances for the duration of
the eldtrip, including during the evenings. A student or students violating this rule will be required
to leave the eld trip and return home at the student’s own expense.
3. Drinks containing any percentage of alcohol are considered alcoholic beverages.
Vehicle Use
1. All students who operate vans for eldtrip activities must be recognized by the college as qualied
drivers. Qualication to operate vans for college-sanctioned events does not, however, give any individ-
ual the right to drive a van. The eld trip leader will use his/her discretion in deciding which qualied
students will drive the vans.
2. The eld trip leader will hold all van keys during o hours, and students will not normally be permitted
to drive the vans if not accompanied by the eld trip leader.
3. When more than 1 van is used on a eldtrip vans are required to stay together while traveling to and
from destinations.
4. Students will not be permitted to sleep in the vans during the night, nor will students be allowed to
prepare food or eat meals in the vans.
In Case of Illness or Health Emergency
1. If a student is injured, becomes ill, faints or has a seizure, carefully move them to the ground or keep
them on the ground until emergency help arrives. The instructor must stay with the student while
someone else calls 911 and Campus Police (301-687-4222) for emergency assistance or gets help to do
so from a faculty member, lab manager or administrative assistant.
2. Keep the student prone and calm until help arrives. Do not give them anything to eat or drink.
3. Do not administer rst aid unless trained to do so or get the help of someone who is trained in First Aid.
4. Report the incident to the Chair of the Department and complete an incident report.
15
Students’ Responsibility Statement
I, the undersigned, have received a copy of the Field Safety Procedures. These safety procedures were
explained to my satisfaction. I have been notied by the instructor on proper eld attire and the hazards
of eld exercises I agree to follow these eld safety regulations as require by this course. I understand that
failure to follow these regulations can result in my dismissal from the eld and will have a negative impact
on my grade for this course.
Signature __________________________________
Print Name ________________________________
Date ______________________________________
Course and Section _______________________________
Safety Instructor _______________________________
In case of an accident, name, address and telephone numbers of who should be notied. (Optional)
__________________________________________
__________________________________________
__________________________________________
__________________________________________
16 CHAPTER 1. BIOLOGY FIELD SAFETY REGULATIONS
Chapter 2
Introduction: From Observation to
Experimentation
Research is to see what everybody else has seen, and to think what nobody else has thought. - Arthur
Schopenhauer
An important part of any science, and ecology in particular, is the creative process of turning observations
into hypotheses.
2.1 Active Group Observation
If weather is acceptable, go outside and make observations as a group and discuss the process of turning
these into ecological questions and testable hypotheses. If poor weather conditions, use photographs to
demonstrate observations and the process.
2.2 Hypotheses
Discuss strong vs weak hypotheses with examples.
2.3 Observations
Walk then sit quietly for 10-15 minutes. Write down ecological observations. If the weather isn’t suitable,
have students think about patterns of species abundances or distributions they’ve previously noticed and
develop questions from those.
Share some observations.
Turn at least 1 observation into a (strong) hypothesis.
17
18 CHAPTER 2. INTRODUCTION: FROM OBSERVATION TO EXPERIMENTATION
2.4 Observation: Starting the Process of Ecological Study
1.___________________________________________________________________________________
2.___________________________________________________________________________________
3.___________________________________________________________________________________
4.___________________________________________________________________________________
5.___________________________________________________________________________________
6.___________________________________________________________________________________
7.___________________________________________________________________________________
8.___________________________________________________________________________________
9.___________________________________________________________________________________
10.__________________________________________________________________________________
11.__________________________________________________________________________________
12.__________________________________________________________________________________
13.__________________________________________________________________________________
14.__________________________________________________________________________________
15.__________________________________________________________________________________
16.__________________________________________________________________________________
17.__________________________________________________________________________________
18.__________________________________________________________________________________
19.__________________________________________________________________________________
20.__________________________________________________________________________________
21.__________________________________________________________________________________
22.__________________________________________________________________________________
23.__________________________________________________________________________________
24.__________________________________________________________________________________
25.__________________________________________________________________________________
26.__________________________________________________________________________________
27.__________________________________________________________________________________
28.__________________________________________________________________________________
29.__________________________________________________________________________________
30.__________________________________________________________________________________
2.4.1 Hypothesis
Hypothesis 1.
Null:
2.5. HOMEWORK 19
Alternative:
Hypothesis 2.
Null:
Alternative:
Hypothesis 3.
Null:
Alternative:
2.4.2 Research Design
2.5 Homework
Read three scientic papers from the journal Ecology and write down the questions/objectives and hypotheses
tested in each paper. Include citations for the papers in the format used in the journal Ecology. This will
be due in class next week and should be typed and printed out. Regardless of “printer issues” it will be
considered late if not submitted at the start of class.
20 CHAPTER 2. INTRODUCTION: FROM OBSERVATION TO EXPERIMENTATION
Chapter 3
Data Organization in Spreadsheets
Christie Bahlai and Tracy Teal (eds): “Data Carpentry: Data Organization in Spreadsheets Ecology lesson.”
Version 2017.04.0, April 2017, http://www.datacarpentry.org/spreadsheet-ecology-lesson/
Authors:Christie Bahlai,Aleksandra Pawlik
Good data organization is the foundation of your research project. Most researchers have data or do data
entry in spreadsheets. Spreadsheet programs are very useful graphical interfaces for designing data tables
and handling very basic data quality control functions.
3.0.1 Spreadsheet outline
In this lesson, we’re going to talk about:
• Good data entry practices - formatting data tables in spreadsheets
• How to avoid common formatting mistakes
• Dates as data - beware!
• Basic quality control and data manipulation in spreadsheets
• Exporting data from spreadsheets
Overall good data practices
Spreadsheets are good for data entry. Therefore we have a lot of data in spreadsheets. Much of your time
as a researcher will be spent in this ‘data wrangling’ stage. It’s not the most fun, but it’s necessary. We’ll
teach you how to think about data organization and some practices for more eective data wrangling.
3.0.2 What this lesson will not teach you
• How to do statistics in a spreadsheet
• How to do plotting in a spreadsheet
• How to write code in spreadsheet programs
If you’re looking to do this, a good reference is Head First Excel, published by O’Reilly
3.0.3 Why aren’t we teaching data analysis in spreadsheets
• Data analysis in spreadsheets usually requires a lot of manual work. If you want to change a parameter
or run an analysis with a new dataset, you usually have to redo everything by hand. (We do know
that you can create macros, but see the next point.)
21
22 CHAPTER 3. DATA ORGANIZATION IN SPREADSHEETS
• It is also dicult to track or reproduce statistical or plotting analyses done in spreadsheet programs
when you want to go back to your work or someone asks for details of your analysis.
3.0.4 Spreadsheet programs
Many spreadsheet programs are available. Since most participants utilize Excel as their primary spreadsheet
program, this lesson will make use of Excel examples.
A free spreadsheet program that can also be used is LibreOce
Commands may dier a bit between programs, but the general idea is the same. Spreadsheets encompass a
lot of the things we need to be able to do as researchers. We can use them for:
• Data entry
• Organizing data
• Subsetting and sorting data
• Statistics
• Plotting
We do a lot of dierent operations in spreadsheets. What kind of operations do you do in spreadsheets?
Which ones do you think spreadsheets are good for?
3.1 Problems with Spreadsheets
Spreadsheets are good for data entry, but in reality we tend to use spreadsheet programs for much more
than data entry. We use them to create data tables for publications, to generate summary statistics, and
make gures.
Generating tables for publications in a spreadsheet is not optimal - often, when formatting a data table for
publication, we’re reporting key summary statistics in a way that is not really meant to be read as data,
and often involves special formatting (merging cells, creating borders, making it pretty). We advise you to
do this sort of operation within your document editing software.
The latter two applications, generating statistics and gures, should be used with caution: because of the
graphical, drag and drop nature of spreadsheet programs, it can be very dicult, if not impossible, to
replicate your steps (much less retrace anyone else’s), particularly if your stats or gures require you to do
more complex calculations. Furthermore, in doing calculations in a spreadsheet, it’s easy to accidentally
apply a slightly dierent formula to multiple adjacent cells. When using a command-line based statistics
program like R or SAS, it’s practically impossible to apply a calculation to one observation in your dataset
but not another unless you’re doing it on purpose.
3.1.1 Using Spreadsheets for Data Entry and Cleaning
However, there are circumstances where you might want to use a spreadsheet program to produce “quick and
dirty” calculations or gures, and some of these features can be used in data cleaning, prior to importation
into a statistical analysis program. We will show you how to use some features of spreadsheet programs to
check your data quality along the way and produce preliminary summary statistics.
In this lesson, we will assume that you are most likely using Excel as your primary spreadsheet program -
there are others (gnumeric, Calc from OpenOce), and their functionality is similar, but Excel seems to be
the program most used by biologists and ecologists.
In this lesson we’re going to talk about:
1. Formatting data tables in spreadsheets
3.2. ACTIVITY 23
2. Formatting problems
3. Dates as data
4. Quality control
5. Exporting data
3.2 Activity
Go through the lessons on the Data Carpentry Spreadsheet website: http://www.datacarpentry.org/
spreadsheet-ecology-lesson/ and reorganize the test data they provide. I will come around and answer
questions and then we will regroup to discuss the challenges, issues, and best practices when organizing
data in spreadsheets.
24 CHAPTER 3. DATA ORGANIZATION IN SPREADSHEETS
Chapter 4
Introduction to Scientic Thinking
and Statistics in Ecology
Adapted from:
Taylor, J. 2008. Appendix A: A Primary of Biometry. Ecology Laboratory Manual. University of New
Hampshire.
4.1 Introduction to Statistics
To do science is to describe and explain nature through observation. In ecology, most of these observations
are quantitative. They are either measurements (e.g. temperature, pH, mass) or counts (e.g. number of
individuals in a population). Unfortunately, quantitative phenomena are highly variable, as two observations
are rarely identical. We even use “variable” as a synonym for the ecological attirbutes we measure. Therefore,
in order to describe nature, we must nd ways to describe and expalin the variation we observe. Similarly,
we only sample nature so we need to use statistics to test hypotheses if we want our inferences to be relevant
to populations rather than just to the specic samples we took.
4.2 Describing Central Tendancy and Variation
The rst step in describing observations or samples is to summarize them by reducing many individual
observations to one or two statistics that describe the original observations without listing all of them. The
simplest descriptive statistics is the mean (sometimes call the average). The mean is dened as
¯
X=ΣXi
n
where ΣXiis the sum of all observations and nis the total number of observations.
The mean can reduce many observations into a single number for descriptive or comparative purposes.
However, the mean does not describe the amount of variation among observations. It is possible for two
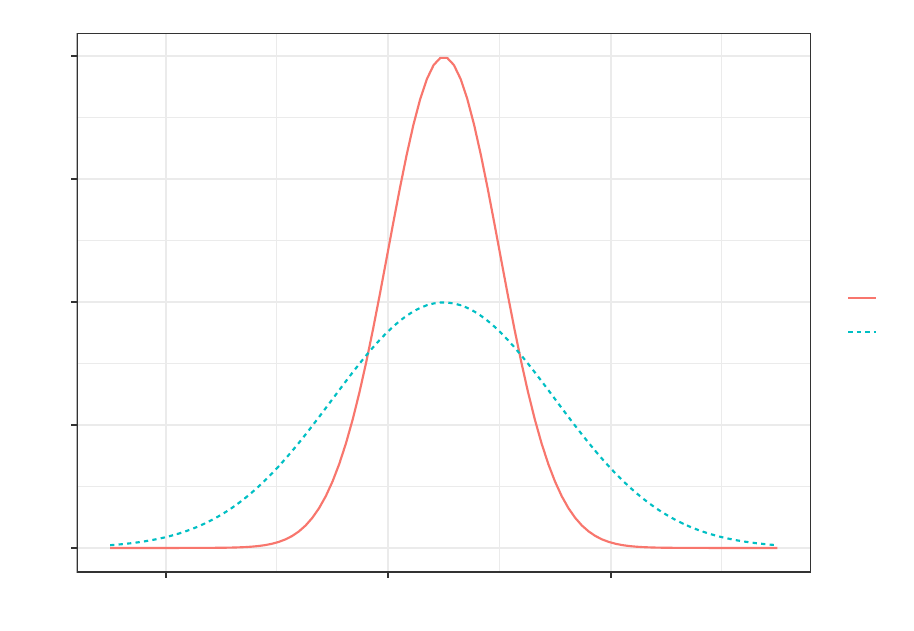
dierent groups of observations to have the same mean, but dierent amounts of variation. Consider Figure
4.1, which shows two normal curves with the same mean(5), but with dierent variances.
Note that in the sample with less variation (the taller, narrower one), most of the observationsare close to
the mean, while in the sample with more variation, there are more observations at greater distances from the
mean. This provideds a clue about ways to measure variation: Find a statistics that summarized distances
25
26 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
0.0
0.1
0.2
0.3
0.4
048
Abundance of organism
Frequency (proportion of samples)
dist
sd1
sd2
Normal Distribution
Figure 4.1: Two curves with equal means (5), but unequal variances. The higher, narrower curve has a
variance of 1, while the broader, atter curve has a variance of 2
4.2. DESCRIBING CENTRAL TENDANCY AND VARIATION 27
from the mean to all the observations. Distance from the mean is simply xi−¯
X, where xirepresents any
one observation and barX represents the mean of all the observations. Distance from the mean tells us how
deviant a single observation is. To summarize all thedistances into an estimate of variability, we calculate
the variance, which is the average squared distance from the mean. To calculate variance, subtract the
mean from each observation:
xi−¯
X
Square each deviation (This removes negative distances):
(xi−¯
X)2
Sum the squared deviations:
(xi−¯
X)2
Find the average of the squared deviations. When taking an average we typically divide by n, the number of
observations. In this case, however, we calculate the average by dividing by n−1instead of n. This corrects
for a bias caused by sampling only a few of all possible observations. If we observed all members, then it is
apprpriate to divide by n.
(xi−¯
X)2
n−1
The average of all the squared deviations is also known as the variance, and it is traditionally reresented by
σ2. The variance is a very important descriptor of ecological variation: The greater the variation among the
observations, the greater the variance. Knowing the amount of variation in ecological attributes can tell us
much about ecological patterns and processes.
Another descriptor of variation is the standard deviation, abbreviated as σor SD, which is the positive
square-root of the variance:
σ=√σ2
The standard deviation may be thought of as the average absolute deviation from the mean. It has the same
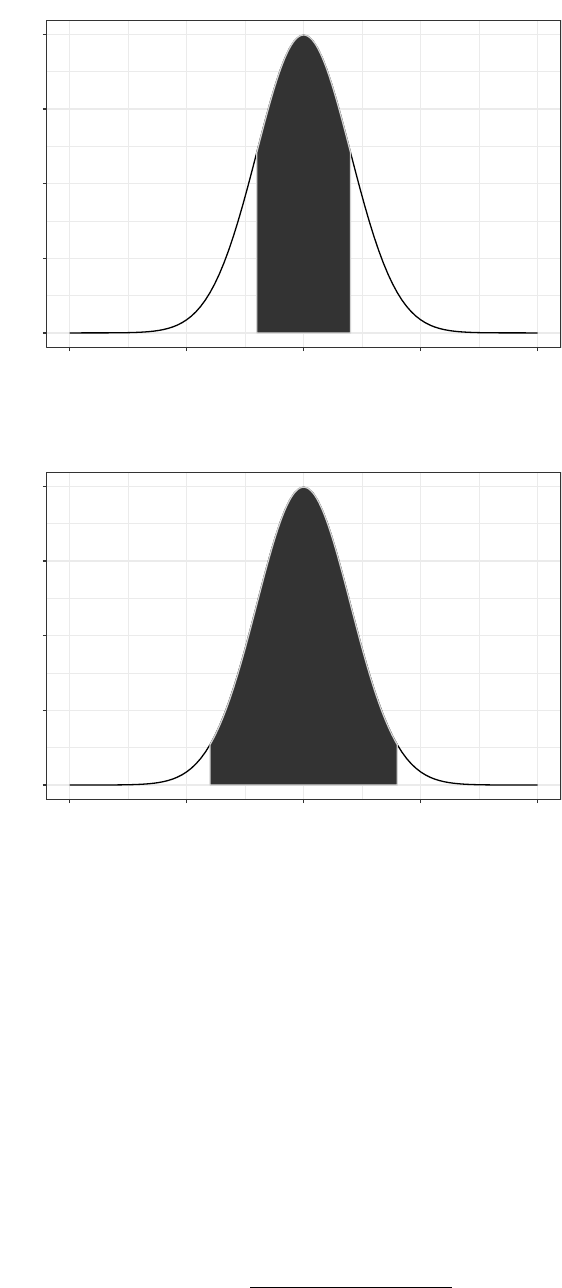
units as the original observations. If our data are normally distributed, such as in Figure 4.1, then about
68% of the observations will fall within 1 standard deviation on either side of the mean (Figure 4.2), and
about 95% of the observations will fall within 2 standard deviations of the mean (Figure 4.2).
28 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
\begin{gure}
0.0
0.1
0.2
0.3
0.4
0.0 2.5 5.0 7.5 10.0
Abundance of organism
Frequency (proportion of samples)
Normal Distribution
\caption{Normal curve
with colored area indicating occurance of +/-1 standard deviation. Approximately 68% of all observations
fall in this area.} \end{gure}
\begin{gure}
0.0
0.1
0.2
0.3
0.4
0.0 2.5 5.0 7.5 10.0
Abundance of organism
Frequency (proportion of samples)
Normal Distribution
\caption{Normal curve
with colored area indicating occurance of +/-2 standard deviation. Approximately 95% of all observations
fall in this area.} \end{gure}
4.3 Explaining Variation: Measuring association with the Coe-
cient of Determination
To explain things, we try to nd other things that are associated with them that change as they change
and remain constant when they stay constant. The search for pattern in nature is thus often a search for
associations. Although cause and eect can rarely be inferred from such associations, the do have predictive
use. If you variables are associated with each other, then knowledge of one tells us something about the
other.
A good descriptor of the association between two variables is the Coecient of Determination,R2. It is
the ratio of the variance shared with another variable to the total variance in the two variables.
R2=V ariance in Common
T otal V ariance
4.4. EXPLAINING VARIATION BY ASSOCIATION: REGRESSION 29
Thus, R2is the proportion of the variance in one variable explained by, or associated with, another variable.
As a proportion, it is a unitless number ranging from 0 to 1. High values, those approaching 1, indicate very
close association, because one variable explains a large proprotion of the variance in another variable. Low
values, those approaching 0, indicate little or no association. The equation for calculating the Coecient of
Determination is
R2=(xi−¯
X)(yi−¯
Y)
n−12
σ2
xσ2
y
where X and Y are the data for the two variables and σ2
xand σ2
yare the variances of the two variables. The
part within the parentheses is the covariance.
R2can also be used to determine which of several hyptheses best explains an association. The hypothesis
that generates the largest R2between two variables is the best explanation of their association. There are
other, better methods ecologists generally use for model comparison, but they are much more complicated
and R2will be useful for our purposes.
The Correlation Coecient,r, is another measure of association. It varies from 1 (perfect association
where the two variables increase or decrease together), to 0 (no association), to -1 (perfect inverse association,
where one variable increasesas the other decreases). It is caluclated as the square root of the Coecient of
Determination:
r=√R2
Computers easily calculate rand R2.
4.4 Explaining Variation by Association: Regression
R2gives us a measure of the relationship between two variables, tellingus how much variation in one variable
is explained by another variable. Sometimes, however, we would like to visualize the relationship. One way
to do this is to t a trend line that shows the change in one variable with change in another. The simplest
trend line is a straight line drawn through the data, such that it minimizes the distance from each observation
to the line. This is called linear regression.
Figure 4.2 shows a linear (straight-line) regression tted to measurements on some iris owers. It illustrates
the trend of increasing ower petal length with increasing petal with. The equation for a straight line is
Y=mX +b
and is often written as Y=b+mX since the order of addition doesn’t matter and brepresents the intercept
or overall mean before accounting for the eect of the the independent variable X. In this case, mis the
slope of the line (change in Yfor one unit change in X), which represents the eect of Xon the dependent
or response variable Y. The distance between each observed point and the best tted line are referred to as
the residuals and in a linear regression it must be assumed that they are normally distributed with a mean
of zero (equal amount over and under the line).
It is also possible to t other lines to data or manipulate equations so they t the linear regression equation.
Figure 4.3 shows the same data with a log-log linear regression.
This assumes an equation following
Y=bXm
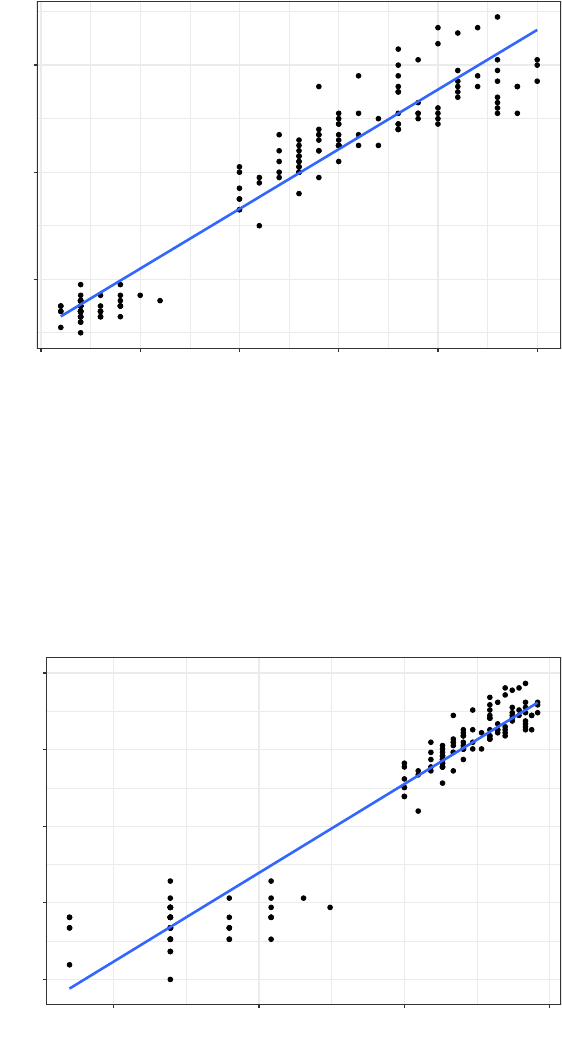
30 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
2
4
6
0.0 0.5 1.0 1.5 2.0 2.5
Petal width (cm)
Petal length (mm)
Figure 4.2: Example of a linear regression plot.
y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932y=1.3 +0.58 ⋅x, r2 = 0.932
0.0
0.5
1.0
1.5
2.0
−2 −1 0 1
Log of petal width (cm)
Log petal length (mm)
Figure 4.3: Example of a linear regression plot.
4.5. EXPLAINING VARIATION: IDENTIFYING RANDOM AND NONRANDOM VARIATION WITH PROBABILITIES31
and would require a nonlinear regression without transformation of the data. By taking the logarithm of
both sides of the equation is is transformed into
log(Y) = m∗log(X) + log(b)
Which of the two lines ts the data better? To answer this kind of question, one is interested in the R2value.
However, they both assume that the data meet the assumptions for the model which must be checked after
the analysis.
4.5 Explaining Variation: Identifying random and nonrandom
variation with probabilities
Odd things do happen, even if the probability of their occurrence is extremely small. For example, the
probability that two dierent states would pick the same fout-diit lottery number on the sam day seems
remote (it’s typically on the order of 1 in one hundred million on any given day), but it has happened.
Likewise, it is possible that a seemingly meaningful R2or other statistic of association was derived by
chance alone rather than from variables that were actually related. To guard against this possibility we can
determine the probability that the observed result did occur by chance. If this probability is low, then we
can be reasonably (but never absolutely) sure that there is a real association in our observations. A “low”
probability is often, but not always, dened as 0.05, or one chance in 20 that the result occurred by chance.
The probability of getting a certain result by chance is called its statistical signicance. Signicance is
calculated from the known behavior of random variables, and the particular method depends on the statistic
of interest. Computer programs are adept at calculating signicance in an apprpriate manner. Signicance
is often reported as “p =”, were pstands for probability. The probability values are often termed “p-values”.
Thus, when inferring an association in your data, always look at the p-value as well as the measure of
association or eect size of a variable. Only if the p-values is low (e.g., less than 0.05) can one have
condence that one has discovered a real relationship.
4.6 Explaining Variation: Associating dierences with group
membership
Sometimes one wishes to determine if certain attributes are associate with certain groups or determine
whether some characteristic diers among groups. For example, we might hypothesize that wormwood
plants growing in the open are taller than those growing in the shade. In this example, we want to determine
if “taller” is associated with “open” and if “shorter” is associated with “shade”. In order for this to be true,
the two populations must be truly dierent from each other. Suppose we collect data on sun grown plants
and shade grown plants and observe the results in Figure 4.4.
We observe a dierence btween the two samples, because they do not totally overlap and the means are
slightly dierent (the mean for the shade plants is 5 and the mean for the sun plants is 8). They both
have a standard deviation of 2. Can we conclude that our hypothesis (“taller” is associated with “sun” and
“shorter” is associated with “shade”) is true? The dierences between the two groups could be due to chance
or sampling erros. We didn’t measure every wormwood in the whole world, and we may have accidentally
take more taller plants from the “sun” group, when in fact the “sun” may have no aect on wormwood size.
Because out results do suggest a dierence in plant height between the two groups, we ask ourselves, “What
is the probability of obtaining our results when in fact the observed dierence between groups is jus due to
sampling error?”. If the probability of getting our results when there is no true dierence is low, then the
32 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
0.00
0.05
0.10
0.15
0.20
0 5 10 15
Height (cm)
Frequency (proportion of samples)
light
shade
sun
Figure 4.4: Two wormwood populations grown in sun and shade.
dierence is probably real. Low probabilities of dierences due to chance alone usually indicate meaningful
(signicant) dierences between groups.
There are many ways of determining the probability of obtaining our result when there is no true dierence.
The two simpliest and most common ways are t-tests and the Analysis of Variance (ANOVA). There
are many variations of each and choosing the appropriate form requires skill and experience. In pratice it’s
best to consult with a statistician when designing and analyzing your study. For this course, you will gain
experience determining the appropriate analysis, analyzing data, and drawing inference based on the analysis.
We will stick to basic forms of analysis that you can build from in future courses, projects, and jobs.
An ANOVA is used for testing for a dierence among multiple groups. A t-test is essentially a special case
of an ANOVA when there are only two groups. Since ANOVA can still be used in cases of two groups, we
will focus on ANOVA for this class.
4.7. ACTIVITY 33
4.7 Activity
Determine what type of test you would use to test each of your hypotheses developed previously? What
data would you need to test the hypotheses?
What is one additional question that you had that would require a regression to evaluate (not one used for
your hypotheses)?
What are general types of hypotheses that you can test with regression analysis?
34 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
What is the hypothesis you would test with an ANOVA?
When do you need to use an ANOVA instead of a t-test to answer the same type of question?
4.8. INTRODUCTION TO SCIENTIFIC PROGRAMMING 35
4.8 Introduction to Scientic Programming
Microsoft Excel is capable of doing some basic statistics including t-tests, ANOVA, and regression. However,
the user has little control over the analysis, the software is proprietary, and you cannot build on these basics
to analyze more complicated data or ask more interesting questions. MS Excel also varies considerably
among computer operating systems and versions. Therefore, we are going to be using software designed
for statistical analysis in this course, although you may use any appropriate means on your own homework
(e.g. hand calculations, MS Excel, Stata, JMP, SAS, SPSS, Minitab, R, etc.). The demonstrations and in-
struction in this course will be using the R Statistical Programming Language and associated integrated
development environment (IDE) RStudio. Both of these programs are free and open source and available on
all major computer operating systems. They also generally look and act the same across operating systems
and versions.
R has become the lingua franca of statistics and in the eld of ecology. Besides the utility in this course and
other science courses, having some familiarity with R and programming languages in general can open many
graduate school and profession opportunities.
4.9 Assign and Recall an Object
The most basic action in R is to assign a value to an object so you can use the object or recall it later.
a <- 5
b <- c(1,2,2,3)
print(a)
## [1] 5
b# you generally don't need the "print" command
##[1]1223
a * b
## [1] 5 10 10 15
4.10 Calculate the Mean, SD, and Variance
R also has a massive number of built-in functions, especially associated with data manipulation, printing,
and statistics. Therefore, it’s easy to calculate basic summary statistics such as the mean, median, mode,
SD, and Variance.
mean(b)
## [1] 2
median(b)
## [1] 2
sd(b)
## [1] 0.8164966
var(b)
## [1] 0.6666667
36 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
sd(b)^2
## [1] 0.6666667
sqrt(var(b))
## [1] 0.8164966
4.11 Import Data
When interested in real data, we have to import the data into R. You can code it which as the advantage of
being reproducible (like other methods in science).
salamander_data <- read.csv(file = "Data/salamanders.csv",header = TRUE,stringsAsFactors = FALSE)
RStudio also has the option under File -> Import Dataset to do this through the GUI.
4.12 Calculate Summary Statistics on the Data
One you have imported a dataset and assigned it to an object in R, you are ready to work with it. R has a
nice summary function for datasets. You can also view the data through the options in RStudio or through
R functions.
summary(salamander_data)
## Plot Species Date Count
## Length:72 Length:72 Length:72 Min. :0.0000
## Class :character Class :character Class :character 1st Qu.:0.0000
## Mode :character Mode :character Mode :character Median :0.0000
## Mean :0.4444
## 3rd Qu.:0.0000
## Max. :5.0000
## Cover_Objects
## Min. : 0.00
## 1st Qu.:10.00
## Median :15.50
## Mean :15.22
## 3rd Qu.:17.00
## Max. :35.00
head(salamander_data)
## Plot Species Date Count Cover_Objects
## 1 1--1 Allegheny Mountain Dusky Salamander 10/4/16 0 19
## 2 1--2 Allegheny Mountain Dusky Salamander 10/4/16 1 15
## 3 1--3 Allegheny Mountain Dusky Salamander 10/4/16 0 16
## 4 1--4 Allegheny Mountain Dusky Salamander 10/4/16 0 13
## 5 1--5 Allegheny Mountain Dusky Salamander 10/4/16 0 15
## 6 1--6 Allegheny Mountain Dusky Salamander 10/4/16 0 17
str(salamander_data)
## 'data.frame': 72 obs. of 5 variables:
## $ Plot : chr "1--1" "1--2" "1--3" "1--4" ...
4.13. SUBSET AND RECALCULATE SUMMARY STATISTICS 37
## $ Species : chr "Allegheny Mountain Dusky Salamander" "Allegheny Mountain Dusky Salamander" "Allegheny Mountain Dusky Salamander" "Allegheny Mountain Dusky Salamander" ...
## $ Date : chr "10/4/16" "10/4/16" "10/4/16" "10/4/16" ...
## $ Count : int 0 1 0 0 0 0 3 1 1 0 ...
## $ Cover_Objects: int 19 15 16 13 15 17 10 8 16 6 ...
4.13 Subset and Recalculate Summary Statistics
You can also subset the data and perform actions on the new object.
pcinereus <- salamander_data[which(salamander_data$Species == "Red-backed Salamander"), ]
summary(pcinereus)
## Plot Species Date Count
## Length:18 Length:18 Length:18 Min. :0.0000
## Class :character Class :character Class :character 1st Qu.:0.0000
## Mode :character Mode :character Mode :character Median :0.0000
## Mean :0.9444
## 3rd Qu.:2.0000
## Max. :5.0000
## Cover_Objects
## Min. : 0.00
## 1st Qu.:10.75
## Median :15.50
## Mean :15.22
## 3rd Qu.:17.00
## Max. :35.00
mean(pcinereus$Count)
## [1] 0.9444444
sd(pcinereus$Count)
## [1] 1.349171
4.14 Save Script
Once you have nished working on something, it’s important to save the script so you can rerun the analysis
later, share the code, or reuse code in other places. You do this through RStudio and the le ending is .R.
You can also output objects as CSV les or as RData les to work with later or work with outside of R.
38 CHAPTER 4. INTRODUCTION TO SCIENTIFIC THINKING AND STATISTICS IN ECOLOGY
Chapter 5
Sampling Populations
Adapted from Johnson, P. 2008. Sampling Populations. Ecology Laboratory Manual. University of New
Hampshire.
5.1 Introduction
Ecologists expend a considerable amount of eort estimating the characteristics of populations. Two pa-
rameters of particular interest are density and dispersion. The exercise below will demonstrate the basic
principals of population sampling. The steps in most sampling programs include:
1. Selecting the sampling universe. What are the limits of the area within which you want to estimate
these population parameters? The universe may be of any size or shape suitable to your goal.
2. Selecting an appropriate sampling unit, or quadrat. In practice this may be a leaf, a plant, a specic
volume of soil, etc. Whatever unit is appropriate to your population.
3. Selecting a sampling scheme.
5.2 Sampling Schemes
The most appropriate scheme from a statistical point of view is an unrestricted random sample, where
every quadrat in the sampling universe has an equal opportunity to be selected at each sampling event.
Frequently the sampling universe will include more than one type of habitat represented in varying amounts
within the universe. Since individuals may be unequally distributed among these habitats, a completely
random scheme might misrepresent the true population density. In this case, to ensure proportionate repre-
sentation of each habitat, we may use a stratied random sample. Each sector (or strata) is sampled at
an intensity relative to its proportionate representation, but samples are drawn at random within the sector.
Often it is possible to use systematic sampling, selecting quadrats at regular intervals throughout the
universe. One advantage is the inclusion of all of the sampling universe in equal proportions. In many
cases, this is the easiest scheme to design and implement and can give good results in spite of violating
the statistical assumption of random sampling. You must be sure, however, that your selection of sample
locations does not bias your results. This requires a good background knowledge of the population’s biology.
39
40 CHAPTER 5. SAMPLING POPULATIONS
Figure 5.1: Sampling Schemes
5.2.1 Sampling scheme methods
1. Measure approximately 200 grains of white rice (3.8 g)
2. Gently shake the grains of rice onto your sampling universe.
3. First try an unrestricted random sample using the supplied random number table. This will be your
row and column to sample.
4. Count 12 random quadrats and record your results for each quadrat. Be careful not to disturb the
grains of rice during the sampling process.
5. Next, without disturbing the rice, apply a stratied random sampling scheme and count three
quadrats randomly from each of the four sectors (A, B, C, D). Ignore the random numbers for a sector
once you’ve collected three samples from that sector.
6. Finally, use a systematic sampling scheme for 12 quadrats to estimate the parameters. Record the
results on your data sheet and perform the calculations.
Still do not disturb the rice!
Density: Mean number of individuals per quadrat (1 cm2).
x=Ni
n
Dispersion: The index of patichness (IP) is one of the commonly used indices of dispersion. First compute
the Mean Crowding (MC)
MC =Ni(Ni−1)
Ni
Next compute the IP by dividing MC by the mean density
5.3. SEQUENTIAL SAMPLING 41
IP =MC
x
• IP < 1 is Regular/Uniform
• IP = 1 is Random
• IP > 1 is Aggregate/Clumped
5.3 Sequential Sampling
A variation on this type of sampling is often used in quality control or pest control situations where our
interest is in classifying or approximating the population density or in situations when we do not have a
good idea how many samples are needed and are constrained in the number of samples we can take.
One basic form of sequential sampling uses the cumulative average density with the number of samples and
looks for a leveling o point. This is a type of rarefaction curve. To do this, randomly sample one quadrat
and plot the density on the y-axis. Repeat this but for sample two (x-axis), plot the mean density on the
y-axis (average density from sample 1 and sample 2). Continue this until the mean density has stabilized.
Use the graph paper to record this.
5.3.1 Sequential sampling questions
How many samples are required to reach a decision on the density (and hence population size)? How did
you decide?
Does this agree with the estimates from your previous sampling procedures?
Was this more ecient than your previous sampling procedures(i.e. did you get the correct estimate of
density/abundance in fewer than 12 samples)?
42 CHAPTER 5. SAMPLING POPULATIONS
5.4 The Eects of Distributions
Repeat steps 1-6 from the sampling schemes for
A. Uniformly distributed individuals (place ~2 grains of rice per quadrat) B. Clumped distributions of
individuals (put most of the rice into 5 clusters)
5.4.1 Distribution Questions
Does the best sampling scheme depend on the distribution of the individuals in the population?
How do you think matching of the clustering with your stratication would eect the estimates?
5.5. MARK RECAPTURE (CAPTURE RECAPTURE) 43
5.5 Mark Recapture (Capture Recapture)
For species that are dicult to capture or detect, mark-recapture can provide a much better estimate
of population size (abundance) or density. The simplest form of mark-recapture is the Lincoln-Peterson
estimator with a single marking (cohort marking) and single recapture eect. The estimator is calculated as
N=nM
R
where Nis the esimate of the total population size, nis the number of the sample size, Mis the number
of marked individuals released back into the population, and Ris the number of marked recaptures in the
sample.
5.5.1 Mark-Recapture Simulation Method
1. Measure approximately 100 grains of white rice and 100 grains of colored rice (1.9 g each)
2. Mix your marked rice thoroughly with the rest of your unmarked population
3. Take a sample from the population consisting of roughly 0.2 g (5% of population)
4. Record the number of marked and unmarked rice in the sample and calculate the total population size
using the Lincoln-Peterson Index.
5. Mix the rice back together and repeat with 0.4 g (10%) and 0.8 g (20%) samples.
5.5.2 Mark-Recapture Questions
Comment on the accuracy of your mark-recapture estimates. Does the size of the sample aect the accuracy
of the estimate?
44 CHAPTER 5. SAMPLING POPULATIONS
Chapter 6
Life Tables and Population
Demographics
Adapted from Johnson, P. 2008. Sampling Populations. Ecology Laboratory Manual. University of New
Hampshire.
6.1 Objectives
• Learn how life tables are constructed
• Learn to calculate population parameters from life tables
• Develop understanding of inference and limitations of life tables
6.2 Introduction
By sampling a population (Chapter 5), we can construct age class distributions for a population. This infor-
mation can be used to generate survivorship curves, construct life tables, which are age-specic summaries
of this important life history information.
6.3 Materials
• 100 grains of 5-colored rice (approximated by weighing 1.9 g)
• Sampling universe (1 x 1 cm grid paper)
• Tray to keep rice from going everywhere
• Data sheets
• Calculator (Computer with excel or other software may be used, but not on an exam)
6.4 Methods
Let’s pretend that our rice represents a population of an organism with ve distinct age classes that are readily
available. This could be an insect with an egg, 2 larvae stages, pupa stage, and adult stage. Similarly, it
could be a species of frog that lives a maximum of ve years. Alternatively, it could be a long-lived animal
(think turtle) or tree where we bin the ages into ve classes.
45
46 CHAPTER 6. LIFE TABLES AND POPULATION DEMOGRAPHICS
We can use the unrestricted random sampling scheme from the distribution lab (Chapter 5, to construct a
life table. This is a static approach to life table generation, which assumes our populations are increasing
or decreasing at a constant rate or are stable and have reached a stable age distribution. This is probably a
safe assumption for our rice population.
1. Sample your population and keep track of the various age classes. You can use the table below, relating
color to rice age class.
Age Class Color
0 White
1 Yellow
2 Green
3 Blue
4 Red
2. Fill in table 6.1 with your sampling results and use this data to compute the proportion of each age
class relative to the rst age class. To do this, calculate the total number of individuals of age class
in the population (mean density * total area), then divide that abundance by the total abundance of
Age Class 0 individuals. This will be the survivorship data (lx) needed for our life table.
lx=nx
n0
The life table parameters are dened in the table below. The data used to generate a life table is either
the number of individuals (nx) surviving from a chorot of individuals born at the same time (a cohort or
horizontal table) or the proportion of individuals (lx) surviving to each life stage as derived from the age
structure of a population (static life table or vertical table). In our case, we will use the proportionate
survivorship group data from our sampling.
x Age class Calculation
nxNumber of surviving in cohort Data or 1000 ∗lx
lxSurvivorship for xto x+ 1 Data or nx
n0
dxDeaths for xto x+ 1 $
qxMortality rate for xto x+ 1 dx
nx
LxAverage number alive during age interval x
to x+ 1
nx+nx+1
2
TxTotal years lived into the future by
individuals of age class xXmax
xLx
exLife expectancy for age class xTx
nx
Note that we have set the initial nxvalue to 1000. This is the traditional cohort, although you can use any
value and get the same results. For the expectation of further life, sum the Lxvalues from the target age
class (x) to the bottom of the life table.
ex=∞
xLx
nx
6.4. METHODS 47
Age Class 0
Age Class 1
Age Class 2
Age Class 3
Age Class 4
White
Yellow
Green
Blue
Red
x
count
x
count
x
count
x
count
x
count
1
1
1
1
1
2
2
2
2
2
3
3
3
3
3
4
4
4
4
4
5
5
5
5
5
6
6
6
6
6
7
7
7
7
7
8
8
8
8
8
9
9
9
9
9
10
10
10
10
10
11
11
11
11
11
12
12
12
12
12
13
13
13
13
13
14
14
14
14
14
15
15
15
15
15
16
16
16
16
16
17
17
17
17
17
18
18
18
18
18
19
19
19
19
19
20
20
20
20
20
Σ
Σ
Σ
Σ
Σ
Mean
Density
Mean
Density
Mean
Density
Mean
Density
Mean
Density
nx
nx
nx
nx
nx
Number Surviving to Age Class (nx)
Age Class 0
Age Class 1
Age Class 2
Age Class 3
Age Class 4
White
Yellow
Green
Blue
Red
Lab:
Survivorship (lx)
Age Class 0
Age Class 1
Age Class 2
Age Class 3
Age Class 4
White
Yellow
Green
Blue
Red
Team:
Lab:
Figure 6.1: Demographic sampling data sheet
48 CHAPTER 6. LIFE TABLES AND POPULATION DEMOGRAPHICS
Fill in life table 6.2 below using the data for our lab population data.
In order to use life table information to estimate population growth, we must add an additional column to
our life table, the age specic fertility or birth rate (bx). This is the average number of ospring produced
per female of age class x, so it is technically fertility, not fecundity, although you often hear it referred to as
the age specic fecundity rate.
Since the calculations that follow use products of x,lx, and bx, we have added appropriate columns to the
life table. Fill in life table 6.3 using the birth rate information provided.
We can now compute the average generation time, G, for our population. This is sometimes expressed as T
so be careful not to get it confused with Tx.
G=∞
0xlxbx
R0
where R0is the net reproductive rate calculated as
R0=
i=∞
i=0
lxbx
From this we can estimate the intrinsic growth rate of the population, ras
r=lnR0
G
where ln is the base of the natural logrithm, also written as loge. With this estimate, we can model population
growth for a rice grain population with a stable age class distribution using the exponential growth equation
Nt=N0ert
where Ntis the population abundance at time tand N0is the starting population size. Fill in the table
and graph (Figure 6.1) provided by computing population values at each of the time points on the x-axis,
beginning with a population of 50 females at time zero.
6.4. METHODS 49
Age$(x)$
lx#
nx#
dx#
qx#
Lx#
ex#
0"
1.00"
1000"
""
""
""
""
1"
""
""
""
""
""
""
2"
""
""
""
""
""
""
3"
""
""
""
""
""
""
4"
""
""
""
""
""
""
"
Figure 6.2: Life Table
50 CHAPTER 6. LIFE TABLES AND POPULATION DEMOGRAPHICS
!
!
Age$Class$(x)$
lx#
bx#
lxbx#
xlxbx#
0!
1!
0!
!
!
1!
!
1!
!
!
2!
!
4!
!
!
3!
!
2!
!
!
4!
!
0!
!
!
!
𝑅"= Σ𝑙𝑥𝑏𝑥!
!!
!
Figure 6.3: Life Table Calculations
6.4. METHODS 51
Days%(t)%
r#
rt#
ert#
N0ert#
10#
##
##
##
##
20#
##
##
##
##
30#
##
##
##
##
40#
##
##
##
##
50#
##
##
##
##
#
#
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
Population%
Size%
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
##
##
##
##
##
#
0%
10%
20%
30%
40%
50%
%
Time%
(days)%
#
#
Figure 6.4: Population project from a life table
52 CHAPTER 6. LIFE TABLES AND POPULATION DEMOGRAPHICS
Chapter 7
Logistic Population Growth
7.1 Lab activities
1. Count our beetles
2. Conduct logistic growth simulations
3. Answer population growth questions
4. Review for Exam 2
5. Brief lecture on science writing
6. Writing workshop optional
7.2 Objectives
• To demonstrate exponential and logistic population growth
• To understand how the growth rate and carrying capacity inuences the shapes of these population
growth curves
• Develop ability to relate equations and graphs to the concepts of population growth
7.3 Introduction
All organisms tend to show the capability of unlimited exponential growth. Consequently, mathematical
models have been developed to try to simulate this phenomenon. It is hoped that by creating models
that include enough realism one might be able to explain and even predict the changes that occur in real
populations. Realistically, no population grows in an exponential manner forever. Populations are limited
by food, space, light, waste build-up, and by populations of other organisms. Once a particular resource
becomes limiting, population growth will slow and eventually stop. Populations that are limited by the
environment typically exhibit logistic growth.
Mathematical models are created to describe and understand natural phenomena. Based on our knowledge
of the reproductive processes of organisms we understand that with unlimited resources a population of
organisms will grow exponentially. This happens when there is nothing hindering an individual’s ability to
access whatever resources it needs. Exponential growth is characterized by a j-shaped numerical response
curve (number of organisms vs. time). The number of organisms at any time (Nt) depends on time, intrinsic
growth rate (r), and the number of organisms at time zero (N0) (Figure 7.1). The slope of the exponential
growth curve (dN
dt ) is constantly increasing and is directly proportional to the number of organisms at any
time (dN
dt =rN). The proportionality constant is the intrinsic growth rate (r). The population size at any
53
54 CHAPTER 7. LOGISTIC POPULATION GROWTH
point in time can be calculated following Nt=N0ert. Remember that eis a constant equal to the base of
natural logarithms (2.71828).
0
500
1000
1500
0 10 20 30 40 50
Time (days)
Population size (N)
Figure 7.1: Exponential growth
It is important to realize that all populations have the potential to grow exponentially, but few ever do
in reality. This is because there are restrictions that limit an organism’s ability to survive. Some of these
restrictions are brought about by an limited supply of resources (food, light, space) and/or competition for
with other populations for these limited resources. As more organisms compete for the same resources, fewer
are able to reproduce and population growth slows. When the number of organisms in the population directly
inuences population growth, growth becomes density-dependent. In this situation, the population ex-
hibits logistic growth, and the numerical response curve has an s-shape (Figure 7.2). The maximum number
of individuals that can exist in a habitat with limiting resources is referred to as the carrying capacity (K).
The slope of the logistic growth curve (dN
dt ) increases quickly with time but gradually slows to zero (verify
this by examining (Figure 7.2)).
10
20
30
40
0 10 20 30 40 50
Time (days)
Population size (N)
Figure 7.2: Logistic growth where K = 40
7.4. MATERIALS 55
The equation for the slope of the logistic curveis similar to the equation for the slope of the exponential
curve except that it includes slowing factor that reduces population growth to zero as N approaches K. The
rate of population growth follows
dN
dt =rN1−N
K
When a population is very small (2-4 individuals) and far from its carrying capacity, it will grow exponentially.
Verify this by examining the value of the slowing factor (1−N
K) for a population whose K= 200. What is
the value of (dN
dt ) when N= 199?
The population size at a given point in time (Nt) can be calculated using
Nt=K
1 + K−N0
N0e−rt
Sometimes population growth is restricted not by resource limitation but by abiotic factors from outside of
the habitat. Storms, res, earthquakes, and meteor impacts can all limit the growth of a population. These
factors typically aect a specic proportion of the population (for example 30%) regardless of the population
density. Therefore, they are referred to as density-independent factors.
7.3.1 Logistic Growth Assumptions
The logistic growth model is certainly more realistic than the exponential growth model but it still requires
a variety of assumptions:
1. All individuals in the population have identical ecological properties, that is, they have equal probability
of producing young, death, and predation.
2. Changes in the population’s birth and death rate occur instantaneously, without lag, with changes in
population density.
3. All members of the population are equally aected by crowding. This is true only if the population is
dispersed uniformly.
4. There is a constant upper limit to population size (K is constant), implying that the environment is
constant and the population never increases over K.
5. The population has a stable age distribution
6. Birth and death rates are not aected by abiotic factors in the environment (density independent
events).
Despite these seemly restrictive assumptions, biologists can frequently appoximate populations reasonably
well using the logistic growth equation. This is especially true for populations in simple environments. Some
populations follow this pattern on average but with stochastic variation around the expected prediction. Ad-
ditionally, biologists can use this model but allowing rand Kto vary over time based on density independent
factors. These density-independent factors are generally environmental conditions such as temperature and
precipitation. In our next module, we will also see ways that competitors and predators can be added into
this type of model to increase realism.
7.4 Materials
• Beans
• Spoons
• Container
56 CHAPTER 7. LOGISTIC POPULATION GROWTH
7.5 Methods
1. In groups of 8-10, start with 20 beans in your habitat (plastic container).
2. Start with 1 person acting as a bean predator. Gather as many beans as you can in 15 seconds
3. Use the following table to determine your survival and reproduction
Num Beans Result
<4Die
4−6Survive
7−10 Survive + 1 ospring
>10 Survive + 2 ospring
4. Record the number of births and deaths and the new population size
5. Grow 15 new beans
6. New ospring join the population and repeat
7.6 Questions
1. Plot the data and draw a line through the points.
2. Does the line atten out? Why or why not? What is the value of K?
3. What were the limiting resources in our scenario?
7.6. QUESTIONS 57
4. If a bacterial colony starts with 100 individuals and its population size at sampling time 1000 (hrs)
was 20,000; what is r? What would the bacterial colonies population size be after 1 day (sampling
time 2400)?
5. Calculate the population size at year seven of a lion population with an initial population size of 20
and an instantaneous growth rate of 0.1 (rounded to the nearest whole number).
6. The endangered purple falcon, which is endemic to your state, had a population size of 100 individuals
in 2012. The population’s instantaneous growth rate over the past decade has been 0.05 assuming
a continuously growing population. Delisting of the falcon from the Endangered Species List can
occur when the population reaches 1000 individuals. Using the density-independent population growth
equation, when should the falcon be delisted?
7. For the population of purple falcon described above, assume there is actually some density dependence
and the carrying capacity is only 2000 individuals. What is the expected abundance of the population
in 2020, 2050, and 2100?
58 CHAPTER 7. LOGISTIC POPULATION GROWTH
8. A population of common red-bellied snipe is limited by the number of nesting sites in their habitat.
Thus, they grow according to the density- dependent logistic growth equation. Calculate the population
growth rate for snipe populations of 25 and 75 given that their instantaneous growth equals 0.1 and
their carrying capacity equals 100. Are the growth rates the same or dierent? Why?
Chapter 8
Community Ecology: Diversity
8.1 Lab activities
1. Collect invertebrates using D-net sweeps of water column and benthic zone (Potential: Leaf litter or
pine cone invertebrates with Berlese Funnels)
2. Preserve all invertebrates in 95% ethanol
3. Sort invertebrates into taxonomic units (Order or Family) and record number of each
4. Discuss expectations for lab assignment
8.2 Objectives
• Become familiar with invertebrate groups
• Gain experience with standard invertebrate sampling techniques
• Learn various measures to quantify biological diversity
• Practice organizing and visualizing biological data
• Gain experience with diversity calculations
8.3 Introduction
Lab adapted from Tiany Troxler’s PCB3043L lab manual at Florida International University
8.3.1 Ecological communities
Ecological communities are assemblages of populations of interacting species. People conceptually recognize
communities because they are perceptually obvious. Examples of ecological communities include forests,
prairies, wetlands, estuaries, lakes, deep ocean hydrothermal vents, and coral reefs. The essential feature of
communities is that they are assemblages of species that predictably co-occur.
The structure of ecological communities is measured with a number of dierent metrics. One method of
analyzing ecological communities is the construction of food webs, which address the functional relationships
among the species of a community. Species diversity and species richness are also important measures
of community structure. Species richness is a measure of the number of species per unit area. Species
diversity is a non-dimensional, numerical index generated for a given community, which takes into account
both richness and abundance of individual species. Because of the problems associated with mathematical
59
60 CHAPTER 8. COMMUNITY ECOLOGY: DIVERSITY
measures of species richness that arise in certain situations, many ecologists elect to use measures of species
diversity to describe ecological communities.
8.3.2 Sampling eort curves and diversity indices
Ecologists face two main problems when quantifying dierences in the abundances of species in communities.
First, the total number of species found correlates with the sample size because you are more likely to nd a
rare species as you increase your sampling frequency. This means that diversity cannot be compared between
communities that were sampled at dierent intensities. Second, the number of individuals representing a
species may not be a good indication of the functional importance of that species to the community. To some
degree, the functional roles that species play in a community vary in proportion to their overall abundance.
There are cases where this is not true, however. An excellent example of a species whose functional role is not
proportional to its overall abundance in a community is a keystone predator. A keystone predator species
may be represented by only a few individuals, but it plays a critical role in structuring the community in
which it lives. The Florida panther in the Everglades is a good example of such a keystone predator. Thus, it
is best to have some measure of the functional roles of species in a community in addition to simple measures
of the numbers of individuals that represent each species.
One part of the discovery process in assessing communities is identifying when we have exerted a
sucient sampling eort to determine species richness and diversity with some level of condence.
Construction of a species-area curve (Figure 8.1) is one approach to determining adequate sampling
eort. Species-area curves plot the area examined with repeated samplings (x-axis) versus the total
number of species found in those samplings (y-axis). Alternatively, a sampling eort curve (Figure
@ref(g:cumulative_species_sampling)) plots the cumulative number of individuals sampled (x-axis) or
the number of samples taken (as in this lab) against the total number of species represented by those
individuals (y-axis). Both curve types address the same question (i.e., whether species richness is increasing
or has leveled o in your sample) but may be appropriate for dierent situations. For example, data from
rapid ecological assessments of species richness with far-reaching conservation consequences frequently do
not include accurate measures of area covered but do include numbers of individuals sampled. In such a
scenario, a sampling eort curve would be more informative than a species-area curve.
The result for both curve types is a line that increases steeply at rst but eventually levels o at an asymptote.
The point at which the species-area and sampling eort curves level o is the point where additional sampling
is yielding no additional information about the number of species. In other words, the leveling o point or
asymptote represents the optimal sample size in terms of area or individuals, depending on the type of curve.
The total number of species in a community strongly determines how large the sample should be to reach
this optimum, though the number of rare species also plays a critical role.
## `geom_smooth()` using method = 'loess'
Once you have adequately sampled the species in a community, you can also calculate an index to quantify
the species diversity in that community. The two most common indices of species diversity are Simpson’s
index (D) and the Shannon-Wiener index (H). Higher values of D and H represent greater diversity.
Both indices are calculated from the proportions (pi) of individuals in the total sample (Ntotal) that are
represented by a given species (i), such that…
pi=ni
Ntotal
…for each species. Simpson’s index (D) is calculated as…
D=p2
i
but the most useful way to use Simpson’s Index is with relation the the reciprocal.
8.3. INTRODUCTION 61
12
15
18
21
123
Cumulative sampling area ( m2 )
Cumulative number of species (S)
Figure 8.1: Herbaceous plant species-area curve
5
10
15
20
10 20 30 40
Cumulative number of individuals sampled (N)
Cumulative number of species (S)
Figure 8.2: Herbaceous plant sampling curve. The line can be drawn by hand or tted using a smoothing
spline or loess t. However, S is always at least the number of species you caught. Alternatively, you can
just connect all the points with a line graph.
62 CHAPTER 8. COMMUNITY ECOLOGY: DIVERSITY
D′=1
p2
i
This sets the lowest value as 1, representing a coummunity with only one species. The higher the value, the
greater the species diversity. The maximal values is equal to the species richenss (S).
The Shannon-Wiener index (H) is calculated as…
H=−
S
i=1
piln(pi)
WHERE:
• H = symbol for the diversity in a sample of S species or kinds
• S = the number of species in the sample
•pi= relative abundance of ith species or kinds measures, = ni/N or (# individuals of each species) /
( total # individuals in the plot)
• N = total number of individuals of all species or kinds
•ni= number of individuals of ith species
• ln = log to base e
•Hmax = ln(S)= maximum possible diversity given the number of species in the plot
Reminder: S is the species richness (or the number of dierent species)
Evenness (J)is a component of biological diversity and is a measure of the relative abundances of dierent
species in a community. Note: your textbook uses EHfor evenness, rather than J, but this is much less
common in my experience. Evenness is calculated as:
J=H
Hmax
If all species have the same relative abundance in a community, J= 1. For example:
Figure 8.3: Example calculation of D, D’, H and J
8.4 Field Methods
Directions will be given by your laboratory instructor. Generally, a sample of habitat will be taken. The
invertebrates will be sorted and later identied to the lowest taxonomic unit possible. The number of each
8.5. QUESTIONS FOR HOMEWORK 63
species in each sample or unit area will be the primary unit of data to start.
Enter these data into a Google Doc for sharing: https://docs.google.com/spreadsheets/d/1dtevbDPMBdJCWaX44GH0TDTlAWXDMWnxZzoaN6ZmHys/
edit?usp=sharing
8.5 Questions For Homework
Use data from Blackboard and not directly from the google sheet where it was entered. I will
clean up and organize the data and post it to blackboard under course documents.
1. Generate a sampling eort curve to determine whether or not your lab samples approach a sucient
sample size to infer aquatic macroinvertebrate diversity. Either make one plot per habitat type (if
more than one habitat type listed) or use dierent symbols for each habitat on a single plot. Be sure
to label the axes and symbols. Use data from all dates and years provided.
2. How many species (or taxonomic groups) did we nd in total per habitat type (observed S)?
3. How many species (or taxonomic groups) do you estimate there are in each habitat based on your
species area or sampling eort curves?
4. Did we do enough sampling to accurately estimate the number of species (Order/Family groups in our
case)? How can you tell? If we did not do enough, how many do you think we would have to do?
5. Calculate D,D′H,Hmax, and Jusing the combined class data (from Tuesday and Wednesday lab
sections) for each habitat type. Show your work to receive credit. If done in excel, the table should be
formatted to be easily readable.
6. Which habitat has the highest species richness (S)?
7. Which habitat has the highest diversity?
64 CHAPTER 8. COMMUNITY ECOLOGY: DIVERSITY
Chapter 9
Ant Spatial Distributions
The Allegheny mound ant (Formica exsectoides) occurs throughout the Appalachian Mountains in the eastern
United States. They are conspicuous in the large mounds they build for which they get their name. These
mounds can be up to 1 m in height. They occur in old elds and other open habitats and maintain these
habitats by killing nearby plants with injections of formic acid.
9.1 Materials
• Tape Measures
• Pin Flags
• Permanent Markers
• Meter Sticks or small tape measures
• Datasheets
• Clipboards
• Pencils
9.2 Lab Activities
In this lab we will examine the distribution of Allegheny Mound Ants at Glendenning Park in Frostburg.
Most ants, including Allegheny Mound Ants, will bite and sting to defend homes, food, or territories. These
ants are not especially dangerous but do be careful to not excessively disturb the mounds. Watch around
your feet so as to not get attacked by angry ants.
1. 20 x 20 m grid with 2 m square quadrants. Rows A –K and columns 0-9. In each quadrant, measure
the height and diameter of each mount that falls primarily in that quadrant. 2-3 people do all columns
within each of ~2 rows.
2. Count the number of trees >2 cm in diameter within the quadrant.
3. Enter the data into a google sheet
9.3 Review
Below is a review from the sampling lab
Density: Mean number of individuals per quadrat (1 cm2).
65
66 CHAPTER 9. ANT SPATIAL DISTRIBUTIONS
x=Ni
n
Dispersion: The index of patichness (IP) is one of the commonly used indices of dispersion. First compute
the Mean Crowding (MC)
MC =Ni(Ni−1)
Ni
Next compute the IP by dividing MC by the mean density
IP =MC
x
• IP < 1 is Regular/Uniform
• IP = 1 is Random
• IP > 1 is Aggregate/Clumped
9.4 Homework
For next week, answer each of the following questions. Answers should be typed using 12 point font and 1
inch margins. Some questions may involve looking up information about the species on your own
1. Make a map of the distribution of ant mounds
2. Calculate the mean density, mean crowding, and index of patchiness of ant mounts. Are they uniformly
distributed, randomly distributed, or clumped?
3. Assume a 15 cm diameter mound supports approximately 500 ants, a 45 cm mound has about 2,000
ants, a 1 m mound has approximately 4,500 ants, and a 2 m diameter mound supports approximately
10,000 ants. Make a plot of mound diameter versus ant abundance. Use this information to determine
the mean number of ants per meter squared and per hectare.
4. Do another regression to assess the eect of mound size on tree density. Make the plot, report the
regression equation, and the variance explained (R2). hint: this will require a linear regression
5. What is the life cycle of Allegheny Mound Ants?
6. Do these ant colonies have 1 or more ants per mound?
7. Describe the timing and formation of mounds.
8. What do Allegheny Mound Ants eat?
9. What do people say Allegheny Mound Ants taste like?
Chapter 10
Population Growth
Lab adapted from:
Shanholtzer, S. and A.S. Lumsden. 2012. Proceedings of the Association for Biology Laboratory Education.
Vol. 33, 195–207, 2012
Johnson, P. 2008. University of New Hampshire Ecology Laboratory Manual: Red Flour Beetle Resource
Limited Growth.
10.1 Introduction
When populations of organisms are allowed to grow under constant conditions, the increase in numbers follows
a predict- able pattern. A type of graph called a population growth curve is used to describe these patterns
by showing the number of organisms on the y-axis (vertical) and the time (or number of generations on the
x-axis (horizontal). These curves are usually S-shaped like Figure 10.1 because the numbers of organisms
start low, increase ever faster for a while and then eventually reach an upper limit beyond which they do
not increase.
The shape of an S-shaped population growth curve is the result of two processes. When the population is
small relative to its resources, each individual organism is very successful at producing ospring, and the
population grows each generation. If each individual produces three ospring, the population will triple in
each generation. When this occurs, population growth is said to be geometric, that is, it increases by a certain
factor (by a factor of 3 in this example) in each generation. If population growth continued in this geometric
mode, the growth curve would resemble the upper gure boundary in Figure 10.2, and theoretically, would
eventually reach innity.
In real life however, this can never happen. As population size increases, a wide variety of negative inuences
will begin to act either on the reproducing individuals or their ospring that decreases their reproductive
success. Each adult will produce fewer ospring. Finally when individuals produce, on average, only a
single ospring, the population increase will stop. There are many factors that have a negative eect on
reproductive success, and they may act on either survival or reproduction. Ex- amples of such factors
include space, nest sites, food, disease, shelter, predation, accumulation of wastes, or migration. These
negative inuences on reproduction and survival gradually put the brakes on population growth until it
nally ceases and the population size reaches an upper limit (Figure 10.2).
The upper limit of population size is called the carrying capacity (K) for that population. The carrying
capacity is a characteristic determined by both the organism and the environment. Carrying capacity may
be determined by the same factors that slowed the rate of growth, such as availability of food, shelter,
nesting sites, or space, disease, etc. As these environmental conditions change, the carrying capacity of an
environment may also change.
67
68 CHAPTER 10. POPULATION GROWTH
Figure 10.1: Exponential and logistic population growth
Figure 10.2: Exponential and logistic population growth
10.1. INTRODUCTION 69
Figure 10.3: Life cycle of the red our beetle including the signicant cannibalistic interactions.
Another way of looking at populations and population growth is from the point of view of the processes
that result in changes of population size. There are four such processes: 1) birth, 2) death, 3) emigration
and 4) immigration. Births and immigration represent gains in the population, while deaths and emigration
represent losses. When:
Birth Rate + Immigration Rate = Death Rate + Emigration Rate
the population size will be stable, neither increasing nor decreasing. There are many factors that inuence
these four factors.
The nature of the factors that result in population growth and stabilization are central questions in ecology,
and have been the subject of a great deal of research. In real life, populations of species generally interact
not only with members of their population but with other species as well as their physical environment. This
makes understanding and predicting population growth in natural populations very complex and dicult
undertaking.
We are going to demonstrate the principles of population growth by studying it in a simplied system with
only one species and a non-renewing environment. To do this we will use our beetles. The our beetles
of the genus Tribolium are ideal subjects for this study. They are small, have short life cycles, require little
care because they spend their entire life cycle in dry our, can be easily counted at intervals, and can take
the kind of abuse that you can dish out (please don’t test this theory). The vial of our is their universe - it
both supports them and limits them.
The Red Flour Beetle (Tribolium castaneum) is an insect pest of our and other stored grain products. Like
many other insects, they go through a complete metamorphosis (Figure ??). During complete metamorphosis,
the immature stages do not resemble the adult stages (for example, caterpillars and butteries). Adult female
beetles can lay up to 400-500 eggs in stored grains. In 3-5 days the eggs hatch into the actively feeding stage
called the larva. A larva grows by periodically shedding (molting) its skin (exoskeleton) until it reaches the
size of the adult. It then molts into the pupa, which is the resting stage. This stage nally molts into the
adult (Figure 10.4). The adult then matures and within days is able to reproduce by mating and laying eggs.
The our beetle is a good insect for life cycle observations. All of its life stages are easy to rear and
retrieve, and the life cycle is short. The life expectancy is approximately 6 months. The Red Flour Beetle
is particularly ineresting because in addition to the intrinsic rate of increase, cannibalism at multiple levels
deterines the population growth rate. These are depicted in Figure 10.3 (following Cushing et al. 2003).
By careful observations you will be able to see a number of interesting phenomena for yourself. We will
70 CHAPTER 10. POPULATION GROWTH
Figure 10.4: Life stages of our beetles: A. Eggs, B-H. Larval instars, I. Pupa, J. Adult, from Lumsden et
al. 2010.
manipulate the amount of resource to try to determine the impact of resource limited growth on the Red Flour
Beetle population. We will also compare the eect of dierent type of food resources on their populations.
10.2 Objectives
• To understand and perform the elements of the scientic method by performing a population growth
experiment with our beetles
• To improve understanding of resouce limitation on population growth
• Practice developing and testing hypotheses regarding the eects of dierent environments on popula-
tions
10.3 Materials
• 4 glass vials (per group)
• Petri dish or tray
• Beetle growth medium (whole wheat our)
• Tape (to label vials)
• 8 beetles (per vial)
• Marking pen
• Funnels
• Sifters
• Data table
• Data graph
• Calculator
• Paint brushes
• Petri dish with agar medium
10.4 Initial Set-Up
1. In groups of three, you will be assigned one of two type of food and will do four levels of that resource,
requiring four vials.
2. Fill the vials with 2, 4, 8, or 16 g of food resource.
10.5. ASSIGNMENT 71
3. Mark each with a piece of tape with your group ID, date, lab section, and amount of the resource
written on it.
4. Add 8 beetles to each vial if your instructor has enough, otherwise add 4 individuals.
5. Stopper the vials with cotton or a porous plug.
6. Make your rst entry on your lab data sheet and in the laboratory computers.
7. The instructor will put the beetles in an incubator at a constant temperature and complete darkness.
8. Each week count the number of living adult beetles and number of dead adult beetles in the vial during
your lab period or during another arranged time, recording the data on your data sheet and in the
computer. Again, be careful not to leave our on the tabletop. Depending on time, you may count the
number of larvae and pupae in the vials.
In order to count the number of beetles, pour the contents of the vial into the sifter. Sift the our into the
tray. After counting the number of adult beetles, return the beetles and the medium to the vial using a
funnel (NOTE: Do not leave any our on the table top. This our may contain eggs)
10.5 Assignment
Near the end of the semester, we will do nal counts and organize and distribute all the data from both lab
sections. You will then answer a set of questions relating the experiment to ecological and scientic concepts.
A rough outline of the questions are listed below but will be provided in more detail in lab during the nal
beetle count day.
1. During the last week of observation, make a nal population count of the adult and larval beetles in
your vial. Enter the data into the class Google Doc.
2. Your instructor will organize a table of the compiled class data from the Google Doc and post it under
“Course Materials” on Blackboard. From these data, plot week (on the x axis) versus mean adult
population size (on the y axis) for each food type. Use the data on your graph to determine the
slope during each time interval (REMEMBER: slope is the change in y over the change in x, or rise
over run; i.e., slope =∆y
∆x). Record the slopes for each week in a table.
Between weeks 1 and 2
Between weeks 2 and 3
Between weeks 3 and 4
Between weeks 4 and 5
etc.
3. How do the slopes change? What does this tell you about the beetle population growth over the course
of the semester? Does food type matter? What would happen to the population growth if all the
slopes were the same?
4. Plot the abundance (y-axis) over time (x-axis) of adult beetles for each food amount. Do the same
thing for larvae. How does the amount of food aect the pattern of population growth? Do the patterns
look the same for larvae and adults?
5. If the beetle population reached a peak, why did it not stablize at that point? What could be done to
maintain a stable population level?
72 CHAPTER 10. POPULATION GROWTH
Chapter 11
Competition and Allometry
Lab adapted from the University of New Mexico Biology 310L, Principles of Ecology Lab Manual
11.1 Lab activities
1. Collect data on survival, size, and mass of plants
2. Plan data entry
3. Discuss our ndings
4. Discuss expectations for lab report
11.2 Objectives
You should get a feeling for how to think and work through a controlled experiment, with treatments,
controls, and replicates. You should understand the concept of competition in the sense of what happens
to individuals and in the sense of how it can contribute to the development of community structure. You
should also be getting comfortable with how to bring real data and models together to produce deep insights
into how nature works.
11.3 Introduction
The theory of natural selection assumes that living organisms compete for limited resources. Those indi-
viduals with phenotypes that allow them to more eciently gather those limited resources and turn them
into viable ospring are favored over time and are selected for. In the case of plants, competition between
neighbors for sunlight, water, and nutrients inuence patterns of growth and reproduction (Harper 1977).
In other words, nearby competitors of the same or other species reduce the amount of resources available
to an individual, which may then suer reductions in growth, reproduction, germination, and survival. In
addition, competition may aect how plants allocate resources to aboveground or belowground growth and
reproductive structures (such as owers) (Harper 1961).
Plants have developed mechanisms to deal with competition. Competition for light results from shading by
the leaves and stems of neighboring plants. To compensate for the reduced light availability caused by their
neighbors, plants may change leaf morphology to capture more of the available sunlight (recall performing
an ANOVA using MS Excel or the Anova function in R during the Statistics Lab (Chapter 4) to test for
dierences in petal length among species of iris). Competition for water and nutrients occurs belowground.
73
74 CHAPTER 11. COMPETITION AND ALLOMETRY
Plants have evolved root structures to access water in dierent parts of the soil column (such as on the surface
or deeper down), allowing some plants to grow a little closer together without experiencing quite as much
competition. And some plants, such as creosote bush (Larrea tridentata), may even excrete chemicals into
the soil that inhibit the growth of nearby plants (known as allelopathy), eectively reducing the competition
experienced by the allelopathic plant (Mahall and Callaway 1992).
Competition also contributes to the development of plant communities. Have you ever noticed that mature
forests tend to have widely spaced trees, whereas younger forests tend to have trees spaced more closely
together? When a forest begins to regrow after a disturbance, many seeds may germinate, and many small
young trees will begin to grow. As the trees get larger however, their demand for nutrients increases, causing
increased competition among the trees. Ultimately, many of the young trees die out, leaving a maturing
forest with more widely spaced trees. This decreasing density of stems as the stems get larger is called
self-thinning.
The negative relationship between the number of plants and the size of the plants follows a power law. We
can write:
M=kDθ
where Mis plant mass, Dis plant density, θis the exponent characterizing the relationship, and kis the
prefactor (intercept in a log-link regression).
Original estimates of θwere −3/2, tting a simple geometric model of plant growth (Yoda et al. 1963). The
geometric model is based on the idea that plants ll a three-dimensional space but cover ground in only
two dimensions (thus 3 over 2). Recent evaluations of the rule suggest a value of θ=−4/3, which can be
accounted for by a fractal model of plant allometry (Weller 1987, Niklas 1994, Enquist et al. 1998). An
allometric relation, again, is one where traits of various organisms can be linked to body mass via a power
law. In this case, the fractal branching of a plant’s roots and stems determines how much space is required
by a plant of a given body size, which in turn determines how many individuals can t in an area. Try to
imagine how a tree’s branches and roots fan out and begin to intermingle with the branches and roots of
neighboring trees. Branching structure determines how much space a plant needs. The exponent is −4/3
because the plant is operating in three dimensions plus time (four dimensions) to move resources through
the branching network, but they do it through space (thus 4 over 3).
In this exercise, we will perform a controlled greenhouse experiment with cultivated radish to measure
competition in plants and test the theory that plant mass scales with density to the −4/3power. We will
plant seeds at a variety of densities, watch them grow, and measure the relationship between size and density
at the end of the experiment. Because competition impacts survivorship, growth, and reproduction, we also
will examine the eects of density on survivorship and on the tendency to store energy in tubers (the radish
itself).
11.4 Hypotheses
1. There will be lower survivorship as densities increase,
2. The plants will grow larger at lower densities, creating a negative relationship between plant mass and
density,
3. The mass of the plants will scale to density to the -4/3 power,
4. The plants will be less likely to store energy in tubers at higher densities.
11.5 Materials
• 12-cm plastic pots (1 per student)
• Marker stakes or label tape
11.6. PLANTING METHODS 75
• plastic starter trays
• Sand and potting soil thoroughly mixed at a 1:1 ratio
• ~850 radish seeds
• Rulers
• Electronic balance
11.6 Planting Methods
1. Set up the pots in the trays. We will decide on replicates and treatments in class, but we often have
4-8 replicates of four density treatment (2, 5, 15, or 30 plants). Each student will be randomly assigned
an experimental treatment.
2. Optional: Tear (~15 cm by ~15 cm) squares of newspaper and crimp into the bottom of each pot.
3. Mix the potting soil.
4. Fill each pot with an equal amount of soil. The easiest way to do this is to ll the pots up to about
1.5 cm from the top of the pot, or to the point where the pot gets a little wider, if it does, or to a lip
in the pot, if there is one. Try not to let the soil quantity vary from pot to pot.
5. Label pots with your name, date, and experimental treatment and which lab section you are in.
6. Lay the correct number of seeds out for each pot. Add extra seeds to make sure that if not all seeds
germinate that we will still have the correct number of plants (we will decide as a class how many extra
to add). After germination, we will randomly prune the seedlings down to the correct treatment level.
7. Push the seeds no more than ¼ inch into the soil and cover with a small amount of soil.
8. Lightly spray the top of the soil with water and ll the tray up to about 1 inch deep with water.
9. If greenhouse technician is not available: Sign up to water the plants, and note your watering days on
your calendar. On every other day, we will rotate the ats so that they all get equal exposure to the
light during the course of the experiment.
10. We will thin the pots after about two weeks.
11.7 Measurement Methods
1. We will do all of the measurements on the day the competition lab is scheduled. Bring all of the plant
trays into the lab.
2. When we get started, always take care to note which treatment and replicate you have.
3. Count the number of surviving stems in each pot. You may have to decide what constitutes “surviving”
because some plants will be yellowing and not dead yet. Assume that the original number of plants in
a pot can be determined by the total number of living and dead shoots.
4. Measure the height of the plants from the soil surface to the extent of the tallest leaf. Grab the
tallest leaf of all of the plants and estimate the highest extent for the plants as a group, and take your
measurement there.
5. Dig up the plant and shake the soil loose from the roots if the soil is dry enough. If the soil does
not all easily come o, you will need to rise them in water then gently pat them dry before weighing.
Determine the mass of the plant by weighing it on the electronic balance. Cut o the radish itself and
weigh that. Now we have the whole plant mass, the aboveground mass, and the belowground mass.
6. If the plants have sent up inorescences (owering stalks), we will want to quantify the number, height,
and perhaps number of owers, too.
11.8 Analysis Methods
1. Enter measurements into a spreadsheet, pool among sections, and distributet to whole class (try Google
Form or Sheet).
76 CHAPTER 11. COMPETITION AND ALLOMETRY
2. Calculate the mean above-ground, below-ground, and total mass of the plants for each pot. Do this
for separately for plants that owered and for plants that owered. That is, for each pot, there are
going to be two sets of averages.
3. Take the log (base 10) of the masses and the density.
4. Plot all three types of log mass (whole plant, above ground, and below ground) against log density.
There should be two plots: one for plants that owered and one for plants that did not.
5. Add the linear regression trendlines and their equations to the graph along with the R2value (or report
in the gure description). Make sure that the legend and/or gure description clearly states which set
of data are plotted with each color or symbol.
6. Using the coecients from the regression equation above, produce the power laws that relate each type
of plant mass to density. You might consider putting all of the power laws in a table in the lab report.
7. Evaluate the scaling relation between owering and density: do the same type of plot as above. This
time however, plot the log(density) on the x-axis and the log(average # of owers) on the y-axis.
8. Fit a linear trendline and add R2and equation to the graph (or gure description). Make sure to use
only the set of data for plants that owered.
11.9 Results and Discussion
These questions are just to stimulate your thought for the discussion section of your lab report. They shouldn’t
be answered in a numbered section but rather in paragraph form weaved into the discussion.
1. Did the plants get smaller as density increased?
2. Can you list the resources for which the plants competed that would cause this pattern?
3. Were there any results, perhaps a particular treatment, that came out other than expected? Was there
a lot of within-treatment variation? What would cause the variation?
4. Did we nd the expected power law between size and density? What was the scaling exponent? Was
this close enough to -4/3 to believe that is really what we found? If not, why do you think it wasn’t?
5. Did the experiment give an adequate test of the theory?
11.10 Literature Cited
Enquist, B. J., J. H. Brown, and G. B. West. 1998. Allometric scaling of plant energetics and population
density. Nature 395:163-165.
Harper, J. L. 1961. Approaches to the study of plant competition. Pp 1-39 in Mechanisms in Biological
Competition (F.L. Milthorpe, ed.), Symposium No. 15, Society for Experimental Biology. Cambridge
University Press, Cambridge.
Harper, J. L. 1977. Population Biology of Plants. Academic Press, London. Mahall, B. E., and R. M.
Callaway. 1992. Root communication mechanisms and intracommunity distributions of two Mojave desert
shrubs. Ecology 73:2145-2151.
Niklas, K. J. 1994. Plant Allometry: The Scaling of Form and Process. University of Chicago Press, Chicago.
Weller, D. E. 1987. A reevaluation of the -3/2 power rule of plant self-thinning. Ecological Monographs
57:23-43.
Yoda, K., T. Kira, H. Ogawa, and K. Hozumi. 1963. Self-thinning in overcrowded pure stands under
cultivated and natural conditions. Journal of Biology Osaka City University. 14:107-129.
11.11. HOMEWORK – LAB REPORT 77
11.11 Homework – Lab Report
You will write up a lab report covering this chapter’s questions and analyses. The report is due on November
15 (Tuesday section) and 16 (Wednesday section). Write a short but complete report that tells what your
question was, how you answered it, and what the answer was.
What needs to be in the report:
1. Introduction
Introduce the topic of intraspecic competition and how it inuences access to resources and growth. In
your own words describe the theory relating plant size to density. Describe how your study relates to that
theory. What specic questions are you asking? Generally, how are you going to answer them? Specify
what needs to be shown to support or refute your hypothesis. Strategically, you want to pose a compelling
question that is answerable by the results, thereby creating a meaningful storyline for the reader to follow.
2. Methods
Describe what you did in just enough detail to allow someone else to repeat your study.
3. Results
Without any discussion our interpretation, describe what you found. You must include the gures discussed
in 2 and 3 of the analytical methods above. The graphs must be produced in a spreadsheet program. Each
graph must have clearly labeled x- and y-axes and a gure legend (below the gure) that orients the reader
to the result. In the text, describe the results in words. For example, you could say, “Survival of plants
declined with increasing density of plants (Figure 1),” or “Plants were taller in the low-density treatments
(Figure 2)”. Say what you found as simply and directly as possible. As an author, your task is to guide
the reader’s attention to the key information. Some specic style requirements are 1) use the past tense,
as you have already conducted the study, and 2) do not add additional tables of data or printouts of your
spreadsheet.
4. Discussion
What is/are the answer/s to your question? Is it what you expected? If not, why not? Were the methods
insucient? Were there enough data? How does this study relate to the major studies? Was there something
we did that limits what we can say from our results? Do you have alternative interpretations that are
consistent with your results?
5. Literature cited
Properly list the references cited in your text. The list should denitely include Enquist et al. (1998). It
should also include at least two other peer-reviewed journal articles that you have found. Format references
like the Literature Cited of this chapter.
11.12 Grading key to the lab report on competition and mass-
density scaling
Use this key to help you include the necessary components of the paper (30 points total).
11.12.1 Introduction (6 points)
• General opening to paper (1)
• Dened competition (1)
• Described theory of size-density scaling (i.e., the power law that relates them) (1)
• Stated hypothesis/question (1)
78 CHAPTER 11. COMPETITION AND ALLOMETRY
• Errors and readability (2)
11.12.2 Methods (8 points)
• Explained our experimental setup (2)
• Explained our eorts at reducing bias and confounding variables (1)
• Explained how we determined owering, density, and mass (1)
• Explained how we determined the power law in our study (2)
• Errors and readability (2)
11.12.3 Results (9 points)
• All three gures included with legends (3)
• Presented relationship between density and owering (1)
• Presented relationship between density and mass (2)
• Errors and readability (2)
11.12.4 Discussion (7 points)
• Discussed relationship between density and owering (1)
• Discussed relationship between density and mass (2)
• Two additional references (2)
• Critique of methods (1)
• Errors and readability (2)
Chapter 12
Turtle Ecology
Lab adapted from “Turtle Population Biology” by Greg Haenel at Elon University
12.1 Objectives
• Understand important demographic parameters to estimate
• Become familiar with various local pond turtle species
• Learn how to collect mark recapture data
• Learn how to mark turtles
• Learn how to measure and sex turtles
• Practice applying basic mark-recapture calculations
12.2 Lab activities
Goals of today: Catch turtles, see if they are marked, if not, mark them, and measure them. Take data and
photos.
You will need to dress appropriately for being outdoors. You may want to bring water, a hat, sunscreen,
long pants, and shoes that protect your feet. Flip ops and shorts will not be adequate for outdoor labs. If
you have any allergies to bee stings (or similar issues) please inform your instructor at the beginning of class.
Waders may be benecial but are not required.
This week we will focus on mark recapture techniques using pond turtles as a model system. You have read a
little background on some of the more common species found in ponds of the region. You will be taking part
in an ongoing mark-recapture study of the turtles in the C&O Canal National Historic Park. One of the key
questions in population biology is, “what are the current and future population sizes of a given organism?”
Current population sizes can be estimated using mark-recapture methods. To predict future population size
we need to also estimate survivorship, reproductive schedules (birth rates), death rates, immigration, and
emigration rates. Some of these parameters are beyond the scope our lab but we can estimate some as we
collect more data over more semesters. As you observe the pond ask yourself the following questions:
• What factors might impact survivorship of the turtles?
• Would survivorship of hatchling and adult turtles be similar?
• What may be impact growth rates of the turtles?
• What could be impacting birth rates?
• Is there a relationship between growth rates of turtle and fecundity (or birth rates)?
79
80 CHAPTER 12. TURTLE ECOLOGY
• These turtles lay eggs that they bury in the ground. What factors may be impacting the success of
female nesting?
12.3 Mark Recapture (Capture Recapture)
For species that are dicult to capture or detect, mark-recapture can provide a much better estimate
of population size (abundance) or density. The simplest form of mark-recapture is the Lincoln-Peterson
estimator with a single marking (cohort marking) and single recapture eect. The estimator is calculated as
N=nM
R
where Nis the esimate of the total population size, nis the number of animals captured in the sample
(number caught on day 2), Mis the number of marked individuals released back into the population (usually
number of animals caught on day 1), and Ris the number of marked recaptures in the sample (day 2).
12.4 Questions for Lab Assignment
1. What dierence is there between the claws on the front feet of male and female painted turtles?
2. What is the average size of female painted turtles?
3. What is typical food of a painted turtle? Are adult painted turtles are carnivorous, omnivorous, or
herbivorous? Dene each term.
4. How do you sex snapping turtles?
5. Use the class data from the rst two trapping days (posted on blackboard) to calculate the total
abundance of each species.
6. What are the assumptions of the Lincoln-Peterson population estimator? Look up and describe at
least one more robust mark-recapture population estimator and indicate why it might be better.
7. What are the sex ratios of each species?
8. Plot the size distribution (histogram) of each species using one of the measurements we took. Why did
you choose this measurement? Be sure to label your axes and any other symbols used
Prior to the start of this lab we will continue activities related to ongoing experiments:
Chapter 13
Population Spatial Variation
• Go over literature cited 10 sources and topics
• Count ies and pupa
• Thin plants to treatment density, water, 1/4 turn
13.1 Lab activities
1. Learn salamander and invertebrate identication
2. Plan data entry
3. Collect natural cover object eld data on replicate plots
4. Discuss expectations for lab report
13.2 Objectives
13.3 Introduction
13.4 Hypotheses
13.5 Materials
• Tape measures
• Pin ags
• Data sheets
• Clipboards
• Pen/Pencils
13.6 Methods
1. In groups of 3-4 students, establish a 4 x 25 m plot, ensuring that sides of the plot are parallel
(rectangular plot). Use ags for the corners of the plot.
2. Flip all natural cover objects (rocks and logs) that you can move, which have a contact patch with the
ground greater than 400 cm2.
81
82 CHAPTER 13. POPULATION SPATIAL VARIATION
3. Tally the number of each salamander spp., beetles, centipedes, and millipedes found the plot.
4. Record the number of cover objects ipped in each plot.
5. Back in the lab: Enter measurements into a spreadsheet, pool among sections, and distribute to whole
class.
13.7 Literature Cited
13.8 Homework – Lab Report
For next week, answer each of the following questions. Answers should be typed using 12 point font and 1
inch margins. Late homework will not be accepted.
1. Make a table with the mean and standard deviation for each taxa across all replicate plots.
2. Which species/taxa has the highest variability in counts? What species/taxa is most abundant?
3. Is there a signicant dierence in the counts among species? How do you know? Show your work/results
(hint: this will require an ANOVA).
4. Does the number of cover objects ipped in a plot inuence the number of salamanders found? (hint:
this will require a linear regression). Plot the number of objects ipped vs the count of salamanders
in each plot. Add the linear regression trendlines and their equations to the graph along with the R2
value (or report in the gure desription).
5. What might be a better measure of search eort and available habitat rather than the number of cover
objects ipped?
6. If this were a real observational eld study, what are some other variables that you would want to
record?
Chapter 14
Forest Stand Dynamics
14.1 Lab activities
1. Plan data entry
2. Collect data on forest stand characteristics
3. Discuss expectations for lab assignment
14.2 Objectives
• Become familiar with the stages of forest succession
• Gain experience with standard forest measurement techniques
• Be able to visually identify stands at dierent stages of succession
• Contextualize eld observations with reading on stand development patterns
• Gain additional pratice in hypothesis testing
14.3 Introduction
Ecosystems are constantly in ux. Some changes are subtle and short-term while other changes alter the
entire structure and function of an ecosystem. Even long-lived forests that may appear relatively stable
change over time. Community ecologists are interested in understanding and predicting the changes in
community structure including the dierent species present, relative abundance of dierent species, and the
interactions among these species. Ecosystem ecologists are interested in how these changes alter the processes
such as nitrogen and carbon cycling and exchange of materials into and out of the system. Fish and wildlife
biologists are often interested in how the changes in the major plant communities aects populations of sh
and wildlife through altered food resources and habitat structure. Finally, conservation biologists and land
managers are frequently concerned with the protection of rare species, habitats, or communities. Today we
will examine the process of change in forest communities. We will refer to the change in forests over time as
forest stand dynamics. Below are denitions of a few important terms we will use in this lab.
Astand is a spatially continuous group of trees having similar structures, growing under similar conditions,
and often started development following the same stand-replacing disturbance (Oliver and Larson 1996).
DBH is the diameter at breast height is the diameter of a tree at 1.35 m (4.5 ft) above ground. When on
a slope this is measured from the upslope side of the tree. If the tree splits into multiple trunks below this
height, each trunk is measured independently.
83
84 CHAPTER 14. FOREST STAND DYNAMICS
CWD stands for coarse woody debris and refers to dead fallen logs on the forest oor.
Species Richness refers to the number of species in a given area.
Common trees in the area (You should familiarize yourself with these before lab):
• Pin cherry
• Black cherry
• Witch hazel
• Red maple
• Sugar maple
• Red oak
• Chinkapin oak
• Pitch pine
• Tulip poplar
• Yellow birch
• Eastern hemlock
• Striped maple
• Black locus
• Sassafras
• Pignut hickory
• Shagbark hickory
• American chestnut (rare but at the site)
• Sumac (Rhus spp.)
14.4 Materials
• Tape measures
• Pin ags
• DBH tape
• Spherical densiometer
• Tree/CWD calipers
• Data sheets
• Clipboards
• Pen/Pencils
14.5 Methods
1. In groups of 3-4 students, establish a 5 x 5 m plot in the recent clearcut or a 10 x 10 m plot in the
other forest stands. Use ags for the corners of the plot.
2. Count the number of stems above 2 m tall in the plot by species.
3. Measure the DBH of the 5 largest trees in the plot.
4. In each coner, measure the canopy cover using the spherical densiometer.
5. Measure the diameter of any CWD in the plot at the midpoint of the log.
6. Back in the lab: Enter measurements into a Google spreadsheet, pool among sections, and distribute
to whole class.
14.6. LITERATURE CITED 85
14.6 Literature Cited
14.7 Homework – Lab Report
For next week, read Chapter 5 of Forest Stand Dynamics (Oliver and Larson 1996) posted under Readings
on blackboard. Answer each of the following questions. Answers should be typed using 12 point font and 1
inch margins. Late homework will not be accepted.
1. What are the stages of stand development?
2. Species composition during stand initiation is often largely determined by the type of disturbance that
initiated development. How might disturbance from a stand-replacing re change the early species
composition relative to logging (which we observed)? Don’t focus on specic species bur rather general
dierences in the types of species or source of species that would rst dominate.
3. Which strata did you observe in the second forest stand we visited and which stage of development do
you think this stand is in? Why?
4. Make a null and alternative hypothesis regarding the species richness in the dierence forst stands.
5. Test your hypothesis using the data. Did you reject or accept your null hypothesis? (hint: In which
stand did you observe the most species, be sure to compare per unit area if you didn’t use plots of the
same size? Was the dierence in species richness signicantly (statistically) dierent among stands?
Show your evidence).
86 CHAPTER 14. FOREST STAND DYNAMICS
Chapter 15
Phenology
Phenology is the study of cyclic and seasonal natural phenomena, especially in relation to climate and
plant and animal life. It has been referred to as “nature’s calendar”. The root phaner originates from the
Greek phaneros meaning visible, open, evident, or to show. This in turn relates to the Greek phainomenon,
that which is seen. This is where we get our English term “phenomenon” and phenology being short for
phenomenology. This basis in the root meaning “to show” is why phenology (birds show up in the spring,
owers appear and become evident) and phenotype (outward appearance or expression of the genotype).
-From E.C. Jaeger. 1955. A source-book of biological names and terms. Third Edition.
15.1 Activity
Recording phenology data over broad spatial extents and long time periods is generally more than a single
research can accomplish. As such, the USA National Phenology Network maintains data submitted by
researcher and volunteer citizen scientists. They hae accumulated more than 10 million phenologic records.
Your task today is to
1. go to their data portal https://www.usanpn.org/node/21094 and download phenology data for a place
and species of interest.
2. Filter, sort, and summarize the data in MS Excel as necessary (remember the magic of pivot tables)
3. Make a Line plot of one or two phenologic traits (e.g. egg laying, edging, owering, arrival, etc.) for
that species and a particular location or region.
4. Add a trendline to see if there is a change in the phenology over time.
5. Share with the class what species and location you picked, what the trend looked like, how variable
the trait was, and any other interesting information you found.
If you get interested in this and want to contribute to science, you can contribute data to their Nature’s
Notebook Project at https://www.usanpn.org/natures_notebook.
87
88 CHAPTER 15. PHENOLOGY
Chapter 16
Lab 2: Population Setup and
Statistics
16.1 Population Density Dependence
16.2 Review of Introductory Statistics
16.3 Introduction to Scientic Programming
16.4 Basic Statistics with R
We can use an Analysis of Variance (ANOVA) to test whether petal length diers among species of iris.
# Conduct and save the analysis
length_anova <- aov(formula = Petal.Length ~ Species, data = iris)
# View the summary results
summary(length_anova)
## Df Sum Sq Mean Sq F value Pr(>F)
## Species 2 437.1 218.55 1180 <2e-16 ***
## Residuals 147 27.2 0.19
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
89
90 CHAPTER 16. LAB 2: POPULATION SETUP AND STATISTICS
Chapter 17
Migration
Prior to the start of this lab we will continue activities related to ongoing experiments:
• Go over literature cited 10 sources and topics
• Count ies and pupa
• Thin plants to treatment density, water, 1/4 turn
17.1 Lab activities
1. Learn diurnal raptor identication
2. Sign out binoculars
3. Review binocular use
4. Collect data on migrating hawks
5. Return binoculars
6. Discuss lab homework
91
92 CHAPTER 17. MIGRATION
17.2 Objectives
17.3 Introduction
17.4 Hypotheses
17.5 Materials
17.6 Planting Methods
17.7 Measurement Methods
17.8 Analysis Methods
17.9 Results and Discussion
17.10 Literature Cited
17.11 Homework – Lab Report
Chapter 18
Population Growth
Lab adapted from Heaps et al. (2016)
18.1 Initial Set-Up
Step 1: Obtain Supplies
You will be working in groups of four. You will need two vials and two jars for each group, a culture of fruit
ies, FlyNap, and a wand. Prepare your culture medium in each container using 1 part dry akes, 1 part
water (20 ml of each; it should be the consistency of peanut butter), and a pinch of yeast (a few grains).
You will prepare the following four set-ups within your group:
• Large jar, warm conditions (25 C)
• Small vial, warm conditions (25 C)
• Large jar, cold conditions (20 C)
• Small vial, cold conditions (20 C)
Step 2: Anesthetize Fruit Flies
1. Dip absorbent end of the wand into the FlyNap.
2. Tap the culture vial of ies on the table top to knock the ies to the bottom of the vial and with one
nger push the plug very slightly to one side.
3. Remove wand from vial of FlyNap; quickly stick anesthetic end into culture vial just below plug. Be
careful not to touch the wand to the foam cap!
4. Immediately replace the cap on the FlyNap vial.
5. Tip vial on its side and wait approximately 1 minute with wand in place—just until all but one or two
ies are asleep (too long will kill them!). Do not touch the culture medium with the wand.
6. Remove wand and plug from culture vial and spill ies onto card for study.
7. Replace plug in culture vial; return wand to box.
Step 3: Determining the sex of your ies
You will need to obtain one male and one female fruit y. This means you will have to determine their
sex. You should have researched this at home. Discuss your ndings with your group members and your
instructor to be sure that you understand how to do this. After you have sexed them you will place one
male and one female into your jar.
Place the fruit ies in your jar but keep them on their side. Be sure that they do not fall into the medium
where they can drown. After you have your ies in the jar you will plug it with the provided foam and leave
93
94 CHAPTER 18. POPULATION GROWTH
it on its side (your instructor will place it upright once the ies wake up later in the day, or we will do it at
the end of the lab period).
Predictions:
Discuss with your group your four dierent set-ups (two dierent jar types and two dierent y types).
Consider and answer the following questions together:
18.2. ASSIGNMENT 95
1. How do you think jar type will aect your population size over the next ten weeks? Why?
2. How do you think temperature will aect your population size over the next ten weeks? Why?
3. Do you expect that container size will interact with temperature to aect your population size over
the next ten weeks? Why?
4. Make a prediction as to approximately how many ies you think you will get in each of the four set-ups.
Step 4: Your Assignment—Counting your fruit y population
Each week you will count the new ospring in your jars/vials. In order to do this you will need a little
background on the lifecycle of a fruit y. Your assignment is to go home and research Drosophila. Specically,
investigate information regarding their life expectancy, breeding cycles, life stages, etc. You will need to come
up with a feasible way to determine your population size each week. This research will also help you to more
accurately predict how many ies you think you will have in each set-up at the end of ten weeks.
18.2 Assignment
For your lab, you will be looking at how fruit ies grow in an ideal environment. At the beginning of the
semester, you placed two male and two female ies in a jar with food and closed the lid. These fruit ies
then reproduced over the course of the semester.
1. Based on your background research, draw below the life cycle of a fruit y including approximate
timing below.
2. If we start with four fruit ies in a jar with an abundance of food, what do you think the population
will be after reproducing for a week? a month? four months? Record the expected numbers based on
96 CHAPTER 18. POPULATION GROWTH
exponential growth (Nt=N0ert) assuming an intrinsic rate of growth of 0.18. What would you have
to do in order to keep the population growing indenitely?
3. Plot week (on the x axis) versus adult population size (on the y axis) for cold (20 C) and warm (25
C) vials. Just use the data from your group (unless you never had any reproduction, in which case
you data from a dierent group). Use the data on your graph to determine the slope during each time
interval (REMEMBER: slope is the change in y over the change in x, or rise over run; i.e., slope =∆y
∆x).
Record the slopes for each week in a table.
Between weeks 1 and 2
Between weeks 2 and 3
Between weeks 3 and 4
Between weeks 4 and 5
etc.
4. How do the slopes change? What does this tell you about the fruit y population growth over the
course of the semester? What would happen to the population growth if all the slopes were the same?
Are these curves better represented by an exponential or logistic growth curve? Why? If it looks
logistic, what is the carrying capacity?
5. Repeat question 3 but using pupa rather than adult ies and do it for all four experimental treatments
(temperature X small/large). How do they compare? Which ies did best (explain)? Which did worst
(explain)? Can you hypothesize factors that might have caused dierences between treatments?
6. If you were to repeat this experiment, what would you do dierently?
7. If you were to design a population growth experiment for this class, what treatments would you use
(i.e. what factors would you experimentally manipulate) and why?
Chapter 19
Cemetery Demographics and Life
Tables0
Note: This handout is modied from the following lab activities 1) “Cemetery Demography” by Nancy
Flood (U. Toronto) in the Ecological Society of America’s Experiments to Teach Ecology, edited by Dr. Jane
Beiswenger and 2) Human Population Ecology by Dr. Bruce W. Grant, Department of Biology, Widener
University, Chester, PA.
19.1 Synopsis of Today’s Lab.
Today we will travel to a local cemetery and record dates of birth and death etched on the headstones com-
memorating previous local residents. After lab, I will pool the class data and you will examine demographic
parameters such as survivorship and mortality of males and females during two time intervals: pre-1950 and
1950 to the present.
19.2 Introduction
Demography is the study of the internal composition of populations and the eects of that composition on
population growth. Patterns of survival vary a great deal from one species to another. Moreover, depending
upon the environment, there may be substantial variation in survivorship within a species. Age is an
important structuring component for many populations because fecundity and survivorship frequently vary
with age.
Humans are one species whose fecundity and survivorship is aected by age and the environment. This
includes occupation and the time period in which they live. One way that biologists attempt to discern
patterns in survivorship rates is to use a bookkeeping system called a life table. Life tables were developed
by the insurance industry because in essence, they are betting on how long you may live. Life tables permit
them to keep track of how long dierent segments of the population have lived. From this, they try to predict
how long the current population will survive. Ecologists have adopted this technique to help them study the
population patterns of plants and animals.
The basic data in a life table are the number of individuals in each age class. There are two dierent
approaches to constructing life tables; a cohort life table and a static life table. The most straightforward
of the two is the cohort life table. It starts with a group of individuals born at the same time and tracks
their mortality until the last one dies. Cohort data are dicult to obtain, so these data sets are not common.
The other way to construct a life table is to record the age at death of a large number of individuals. This
97
98 CHAPTER 19. CEMETERY DEMOGRAPHICS AND LIFE TABLES0
information can be used to calculate mortality and survival and thus create a static life table. The table is
called static because the method involves a snapshot of survival within a population during a short interval
of time. Your sampling will create a static life table over a long period of time.
Local cemeteries are an excellent place to study human demography. Etched in the gravestones are the
dates of birth and death of the person below, at least in most cases. From these data we can calculate
death rates and draw survivorship curves. A survivorship curve is simply a graphical representation of
the chance that an individual will survive from birth to any particular age. By comparing survivorship
curves for dierent periods of time we may look for historical trends in demography over the decades. Also,
dierent cemeteries may represent dierent socio-economic cross-sections of the population, and comparing
data among cemeteries may reveal dierent patterns of mortality.
Over the last few centuries, advances in health care and large-scale global political conict have left rather
opposing marks on the demographics of our population. In this lab, you will investigate how three major
time intervals in American history impact the survivorship of this local population. Pre-1900, the U.S.
experienced its own Industrial Revolution, the Civil War, a 2nd Industrial Revolution following the Civil
War, and a lot of changes in politics. The period between 1900 and 1950 includes periods of prosperity (the
roaring 20’s) WWI, the Great Depression and WWII. Following 1950, numerous vaccines and antibiotics
were widely used and, with the exception of the Korean, Vietnam, and Gulf Wars (not to mention a few
other incidents…), this has been an era of relative peace in North America (in the greater historic context).
What are your predictions about how the demographics of the local human population have changed during
these two time periods?
In order to study the demography of the entire human population that once lived in the area, we would
have to study all of the local cemeteries and assume that no one emigrated from the area and was buried
elsewhere. Neither is likely. We only have a few hours, and many deceased local residents were buried, or
otherwise, elsewhere. Thus for now, we will assume that the cemeteries we will visit are representative of all
humans in this area, although we should be aware of these sorts of biases in the data.
19.3 Methods
Location: Frostburg, MD.
Data Collection: The cemetery is typical of many of the local churches. Older headstones are close to the
main church, and more recent ones are farther away as the cemetery expanded. We will collect data from
headstones in a manner so that everyone can investigate both old and new headstones. You will work in
pairs, rst in the older portion, then in the newer one. One person from each pair will collect data on females
and one will collect data on males. Collect data from as many headstones as possible without overlapping
the progress of others. To help prevent overlap, each pair will start at the beginning of a row. When you
are done, you collectively will have gathered data on;
• Group 1: FEMALES WHO DIED BEFORE 1900 Group 2: MALES WHO DIED BEFORE 1900
• Group 3: FEMALES WHO DIED AFTER 1900 BUT BEFORE 1950 Group 4: MALES WHO DIED
AFTER 1900 BUT BEFORE 1950 Group 5: FEMALES WHO DIED AFTER 1950
• Group 6: MALES WHO DIED AFTER 1950
!!PLEASE CALCULATE THE AGE AT DEATH FOR ALL INDIVIDUALS!!
Back in the lab we will enter all the data into a google spreadsheet and I will check it over and post a nal
copy to blackboard for your use in answering the questions.
19.5. DATA ANALYSIS 99
19.4 General Instructions
Record what group you are collecting data for at the top of the Data Sheet #1. Record your names. Enter
the data from the headstones. There are spaces for the birth year, death year and age at death. The cells
of the data sheet are designed so that you can calculate one bit of data from the other two.
Some guidelines for collecting data. If you are unable to tell from the name or other evidence whether
an individual was male or female, omit him or her. If only initials are used rather than given names, the
individual was probably male. Occasionally infants or stillborn children were recorded as simply “baby”,
“infant” or some other designation from which sex cannot be determined. Tally these and put half in one sex
and half in the other of the 0 category.
Please exercise restraint when collecting these data. Do not run, shout, stomp on graves, etc. Be respectful
of the dead and those who mourn the dead. If there are burials or mourners we will stay a minimum of two
rows from them.
19.5 Data Analysis
To estimate demographic characteristics of the local population, we need to know the ages of people when
they died for each sex and time interval. To get this, simply examine your eld data sheets, and count the
number of people who died in each age interval, 0-0.9; 1-9; 10-19, etc.
The life table parameters are dened in the table below. The data used to generate a life table is either
the number of individuals (nx) surviving from a chorot of individuals born at the same time (a cohort or
horizontal table) or the proportion of individuals (lx) surviving to each life stage as derived from the age
structure of a population (static life table or vertical table). In our case, we will use the proportionate
survivorship group data from our sampling.
x Age class Calculation
nxNumber of surviving in cohort Data or 1000 ∗lx
lxSurvivorship for xto x+ 1 Data or nx
n0
dxDeaths for xto x+ 1 |nx+1 −nx|
qxMortality rate for xto x+ 1 dx
nx
LxAverage number alive during age interval x
to x+ 1
nx+nx+1
2
TxTotal years lived into the future by
individuals of age class xXmax
xLx
exLife expectancy for age class xTx
nx
Note that we have set the initial nxvalue to 1000. This is the traditional cohort, although you can use any
value and get the same results. For the expectation of further life, sum the Lxvalues from the target age
class (x) to the bottom of the life table.
ex=∞
xLx
nx
100 CHAPTER 19. CEMETERY DEMOGRAPHICS AND LIFE TABLES0
In order to use life table information to estimate population growth, we must add an additional column to
our life table, the age specic fertility or birth rate (bx). This is the average number of ospring produced
per female of age class x, so it is technically fertility, not fecundity, although you often hear it referred to as
the age specic fecundity rate.
Since the calculations that follow use products of x,lx, and bx, we have added appropriate columns to the
life table. Below is an example life table 6.3 including birth rate information.
We can now compute the average generation time, G, for our population. This is sometimes expressed as T
so be careful not to get it confused with Tx.
G=∞
0xlxbx
R0
where R0is the net reproductive rate calculated as
R0=
i=∞
i=0
lxbx
From this we can estimate the intrinsic growth rate of the population, ras
r=lnR0
G
where ln is the base of the natural logrithm, also written as loge. With this estimate, we can model population
growth for a rice grain population with a stable age class distribution using the exponential growth equation
Nt=N0ert
where Ntis the population abundance at time tand N0is the starting population size.
1. Create a life table (clearly labeled) for each of the four demographic groups, e.g. MALES or FEMALES
and BEFORE 1950 or AFTER 1950, that includes one column for each of the parameters listed in the
table above. Use the age groups (0-0.9, 1-9, 10-19, 20-29, up to 100-109).
2. Make two separate graphs, one with survivorship curves, plotting them on an arithmetic basis and
one plotting them on a logarithmic basis. Each graph should be large enough to clearly show the
survivorship dierences for each of the demographic groups. Which graph, arithmetic or log, permits
you to accurately compare trends among the four curves? WHY?
3. What are the trends for infant & child (ages 0-19) mortality rates for males and for females in each
time period? List and describe all factors that might account for any dierences you see.
4. What are the trends for mortality rates for reproductive age adults (age 20-39) for males and for
females in each time period? List and describe all factors that might account for any dierences?
Note: Many of the men who died during WWI and WWII were not returned to the United
States.
5. What are the trends for mortality rates for adults ages 80 and onward (upward) for males and for
females in each time period? List all and describe all factors that might account for any dierences
you see.
6. What shifts in the survivorship curves would you expect if environmental problems worsen and
pollution-related diseases increase? Explain why.
7. What shifts in the survivorship curves would you expect if cutbacks to social services such as prenatal
and infant care are enacted? Explain why.
19.5. DATA ANALYSIS 101
!
!
Age$Class$(x)$
lx#
bx#
lxbx#
xlxbx#
0!
1!
0!
!
!
1!
!
1!
!
!
2!
!
4!
!
!
3!
!
2!
!
!
4!
!
0!
!
!
!
𝑅"= Σ𝑙𝑥𝑏𝑥!
!!
!
Figure 19.1: Life Table Calculations
102 CHAPTER 19. CEMETERY DEMOGRAPHICS AND LIFE TABLES0
8. What was the initial life expectancy for a male born before 1950? After 1950?
9. Assume age specic birth rates (bx) of 0.25, 1.0, and 0.75 for females of age classes 10-19, 20-29, 30-39
respectively and zero for all other age classes. Calculate R0and Gfrom these in a fecundity table.
10. Calculate rfor females post-1950 and assuming an initial population size of 2,000 females, how many
are expected after 25 years (Nt=25)?
Chapter 20
Lab 3: Introduction of Scientic
Writing
103
104 CHAPTER 20. LAB 3: INTRODUCTION OF SCIENTIFIC WRITING
Course Information
Instructor
Dr. Daniel Hocking, Compton 309, djhocking@frostburg.edu, 301-687-4343
Meeting Times and Locations
Lecture: Tuesday/Thursday 8:00-8:50 am; Compton 327
Laboratory:
• Section 1: Tuesday 2:00-5:50 pm; Compton 321
• Section 2: Wednesday 2:00-5:50 pm; Compton 321
Oce Hours: Compton 309; Monday 11:00 - 12:00; Tuesday & Thursday 9:00 - 10:30 AM, Wednesday 9:00
- 10:00 AM; or by appointment
Description
Environmental relationships of plants and animals. Field laboratory experience. Measuring environmental
variables in terrestrial and aquatic ecosystems. Two hrs. lecture, one 4-hr. lab. Every semester.
Prerequisites
BIOL 150, 160 or 161; CHEM 202 (or CHEM 201 and permission of the instructor); MATH 109/209.
Learning Outcomes
The primary objective of the lab section is to provide you with experience collecting real, relevant ecological
data. Specically you will:
1. become familiar with ecological data collection for various taxa and in a variety of ecosystems.
2. be able to analyze data and interpret results.
3. practice and improve written and oral communication skills.
Grades:
105
106 CHAPTER 20. LAB 3: INTRODUCTION OF SCIENTIFIC WRITING
Task Pct Grade
Lecture Exams 45% A >= 90%
Homework, & In-class assignments 5% B = 80 – 89%
Final Exam, comprehensive 20% C = 70 – 79%
Lab Reports 10% D = 60 – 69%
Literature Review Paper 15% F < 60%
Literature Review Presentation 5%
Total points, percentages, and assignments may change to accommodate teaching and learning parameters.
Grades are still based on percentage of total points. Grades from individual assignments will be posted on
blackboard; however, the grade calculated by blackboard could be incorrect because of dier-
ences in weighting of assignments. It is your responsibility to calculate your current grade based on the
grading scheme described above.
Literature Review
The purpose of this exercise is two-fold. First, it is designed to illustrate the problems that a researcher in
ecology has when he/she must submit a grant proposal or manuscript for publication. In both of these cases
the author must demonstrate that he/she has found and considered many important references to previous
work on the subject. Additionally, this assignment will force you to read some of the primary literature to
see how actual research is done and presented before it is synthesized by textbooks. Specic instructions
will be provided in class.
Extra Credit
Extra credit may total up to 5% of your grade.
• Species of the week (1 pt per approved submission - see below)
• Diving vans for eld trips (1 pt for training/registration + 1 pt per trip driving)
Species of the Week
Over the course of the semester (no more than one submision per week), each student may upload to
blackboard a description of the ecology and life history of a species observed in the wild. This can be any
wild plant or animal but must be positively identied to species (non-native species and planted trees count
but not planted owers). The description and location of the sighting should be included. No animals should
be disturbed or handled for this assignment. Additional instructions on uploading will be provided in lab.
It is important to remember that Species of the Week is a competition! As such, once a species has been
reported, another member of class may not receive credit for it. The description of the ecology and life
history must be a minimum of 1 page, single-spaced with 12 pt font and 1 inch margins. Students will
receive 1 pt for each approved submission up to a total maximum of ve.
Expectation of Student Work
Student work is dened as assignments, homework, and other academic activities to be completed outside
of instructional time, including reading, studying, writing, research etc. Students should expect to spend a
minimum of two hours per week completing this work for each credit hour enrolled (thus 6 hours of work
outside of class for a 3-credit course), although the time spent outside of class may increase based on the
topic and level of the course.
107
Late Policy: Assignments turned in after the due date will lose 10% per day for a maximum of 3 days, after
which they will not be accepted and will receive a zero. Assignments turned in at any point after the time
due (even 1 minute late) will lose a minimum of 10%. This excludes quizzes, in-class assignments, in-lab
activities, exams, and presentations, which can not be turned in late or made up without prior arrangement
with the instructor for extremely extenuating circumstances.
General Laboratory Information
Labs are an opportunity to gain hands-on experience with ecological techniques and gain a greater appreci-
ation of the scientic process. Lab assignments will help guide you through the development of ecological
questions, formation of hypotheses, and design of ecological studies. Studies will be conducted in the eld or
via computer simulation. Students will learn and be expected to use appropriate statistical techniques along
with data visualizations (e.g. gures/plots/graphs) to summarize the data and test the hypotheses. Some
labs will require full reports (intro, methods, results, dicussion, literature cited) but most will just require
answering a series of questions to help guide inference and understanding of the results.
Please note that many of our labs will be conducted at local eld sites. These labs will be
conducted outside so you are expected to use common sense in deciding what to wear and
what to bring. You will get dirty and you will get wet during these labs. Be prepared to
spend 4 hours in areas without restrooms, if you have questions about outdoor restroom etiquette please
consult leave-no-trace (lnt) principles: http://www.lnt.org/training/educationaltraining.php, http://lnt.org/
training/OnlineCourse/ or ask the instructor if you have specic questions. You must notify the instructor
during the rst week of class if you are allergic to bees or have never been stung by a bee. Refer to the safety
1 section for additional information.
Course Topics and Schedule
The laboratory schedule is exible based on previous lab timing and weather. We will often go out in the
eld during inclement weather as long as it does not result in undue risk of injury. Thus, come to all labs
prepared to go out in the eld and get wet and dirty. More about the lab schedule will be provided during
your lab section. Below is a tentative laboratory schedule.
Week Activity Assignment Due
1 No Lab
2 Set up experiments, intro lit review
3 Questions, Hypotheses, and Data Management Literature review
4 Turtle Mark Recapture Turtle pre lab
5 Turtle Population 2 Lit review outline
6 Invertebrate Diversity Field Turtle Lab Qs
7 Invertebrate Diversity ID Lit review draft
8 Forest Succession and Diversity Diversity Lab Qs
9 Sampling Rice and Ant Mounts Peer review
10 Life Tables and Demography Forest Lab Qs
11 Writing Workshop Ant Sampling Qs
12 Finish Beetle and Radish Labs Final draft
13 THANKSGIVING BREAK NO LAB
14 Presentations Radish comp lab
15 Presentations Writing reection
108 CHAPTER 20. LAB 3: INTRODUCTION OF SCIENTIFIC WRITING
Important dates and information
• November 3: last day to withdraw with a “W”
• November 22 - 26: no classes (Thanksgiving Break)
• December 11: last day of classes
• Email and Blackboard: access to your email and Blackboard is required for this class. Check your
email daily.
Attendance
Attendance is required for all laboratory sessions. Each missed lab will result in a 5% reduction in
your overall grade and you will receive a zero for any work associated with that lab. Additionally, any
assignments due in lab that day will be late. If you show up late to lab and miss the van, it will be considered
an absence. The van will not wait for anyone. For indoor labs, arriving more than 15 minutes late will
count as an absence (5% reduction in grade), but you will be able to participate for credit in any activities
associated with the lab.
Documented excused absences are generally limited to the following examples: university sanctioned events
(eld trips, or events where the student is an athlete/performer), funerals (requires an obituary or other proof),
or illness/medical emergencies (requires a doctor’s note or other proof). For all of these, documentation must
be provided. If a student is participating in extracurricular activities or has an excused absence, I must be
notied within one week to arrange makeup assignments.
If you have an unexcused absence, you do not need to contact me. Common examples of unexcused absences
are “family emergencies”, “car trouble”, and “my ride is leaving early this week.” While you may deem these
as legitimate excuses, accepting them as excusable absences and allowing students to make up work will only
encourage widespread abuse. Makeups of any kind are not allowed for unexcused absences.
Class Policies
There will be no cell phones on the desk or in lab. There will be no use of laptops unless prior consent
is obtained for special circumstances. You may not eat food or use tobacco products including electronic
cigarettes in class or labs. Disruptive behavior (using phones, talking, etc.): I will kick you out if I think
you are being disruptive.
“The University will not tolerate disorderly or disruptive conduct which substantially threatens, harms, or
interferes with university personnel or orderly university processes and functions. A faculty member may
require a student to leave the classroom when his/her behavior disrupts the learning environment of the class.
A student found responsible for disruptive behavior in the classroom may be administratively withdrawn
from the course.”
Beacon Early Warning System: all students should have a network of people who will support them in
their educational journey. For that reason, the University uses a system known as Beacon, whereby your
instructors and coaches, if applicable, can post notices about your academic behavior. For instance, if you
are absent repeatedly from a class or are not completing assignments, your instructor may post a notice on
Beacon. That information may be shared with your other instructors and/or your athletic coach. I will be
monitoring notices posted on Beacon so that you and I may address any issues before they become obstacles
to your academic success.
109
Condentiality and Mandatory Reporting
Frostburg State University and its faculty are committed to maintaining a safe learning environment and
supporting survivors of violence. To meet this commitment and comply with federal and state law, FSU re-
quires all faculty and sta (other than the condential employees in CAPS and Brady Health) to report any
instances of gender-based harassment, sexual misconduct, relationship violence, or stalking against students.
This means if you share your or another FSU student’s experience with gender-based harassment, sexual mis-
conduct, relationship violence, or, stalking, I have a duty to report the information to the University’s Title
IX Coordinator. The only exception to my reporting obligation is when such incidents are communicated
during class discussion, as part of an assignment for a class, or as part of a University-approved research
project.
Faculty and sta are also obligated to report allegations of child abuse and neglect to University Police and
to Child Protective Services. This obligation extends to disclosures of past abuse even if the victim is now an
adult and the abuser is deceased. My duty to report suspected child abuse and neglect extends to disclosures
that are made as part of classroom discussions and in writing assignments.
If you or someone you know has experienced an incident of harassment or violence, please go to
www.frostburg.edu/titleix to nd information on reporting options and the resources and services available
for support.
Academic Honesty
Denition of Academic Dishonesty from your student handbook: “Academic dishonesty is dened to include
any form of cheating and/or plagiarism. Cheating includes, but is not limited to, such acts as stealing or
altering testing instruments; falsifying the identity of persons for any academic purpose; oering, giving
or receiving unauthorized assistance on an examination, quiz or other written or oral material in a course;
or falsifying information on any type of academic record. Plagiarism is the presentation of written or oral
material in a manner which conceals the true source of documentary material; or the presentation of materials
which uses hypotheses, conclusions, evidence, data or the like, in a way that the student appears to have done
work which he/she did not, in fact, do. In cases involving academic dishonesty, a failing grade or a grade
of zero (0) for either an assignment and/or a course may be administered. Students who are expelled or
suspended for reasons of academic dishonesty are not admissible to other institutions within the University
System of Maryland. Suspension or expulsion for academic dishonesty is noted on a student’s academic
transcript.”
Any violation of academic honesty will result in a zero for that graded work, and a repeat
violation will result in failure of the course. Cheating will be reported and further disciplinary
action may be pursued by the University Judicial Board This includes plagiarism. I will check long
answers, essays, and lab reports with plagiarism-checking software. When in doubt, just cite the source.
There’s nothing wrong with building on somone else’s ideas, in fact it’s the way progress in made in science.
Just give that person credit.
Persons with Disabilities
Frostburg State University is committed to providing equal educational opportunities for students with
documented disabilities. Students who require disability serves or reasonable accommodations must identify
themselves as having a disability and provide current diagnostic documentation to Disability Support Services.
All information is condential. Please call 4483 or visit 150 Pullen Hall for more information.
110 CHAPTER 20. LAB 3: INTRODUCTION OF SCIENTIFIC WRITING
Bibliography
111

Navigation menu