Exam Instructions
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 5

LABORATÓRIO - 2018
DCTA - ITA - IEC
Objetivo: Implementar algoritmo aproximativo para o Problema do Caixeiro Viajante.
Descrição
O Problema do Caixeiro Viajante (Travelling Salesman Problem) é um conhecido
problema de combinatória, que pode ser formulado da seguinte maneira: dadas n cidades e
as distâncias entre elas, qual é o menor ciclo possível que passe por todas? Este problema
tem grande importância na Teoria de Computação: é NP-Difícil, ou seja, não se conhece
nenhuma resolução de tempo polinomial em n.
No entanto, há um conhecido algoritmo aproximativo de tempo polinomial em n
para este problema, que encontra uma solução cujo valor é menor que o dobro da solução
ótima. Para que este algoritmo possa ser aplicado, algumas condições são necessárias:
a) O grafo referente às cidades deve ser completo, ou seja, sempre há um caminho
entre qualquer par de cidades.
b) As distâncias entre os vértices são euclideanas.
Vamos descrever este algoritmo através de um exemplo. Considere o mapa abaixo,
com n = 8, e o seu arquivo de entrada:
Seu programa deverá ler o arquivo de entrada e gerar o correspondente grafo com-
pleto. Repare que os vértices serão sempre representados por números de 1 a n. Lembre-se
também de que, a partir das coordenadas de cada par de vértices, será preciso calcular a
distância entre eles. Para evitar divergências no arredondamento, a distância deverá ser um
valor inteiro. Considerando os vértices i e j, a distância dij entre eles deverá ser calculada
do seguinte modo, onde a função nint(x) deve ser calculada como (int) (x + 0.5):
8
1 2 5
2 2 3
3 1 2
4 4 5
5 5 4
6 4 3
7 6 3
8 3 1
xd = x[i] - x[j];
yd = y[i] - y[j];
dij = nint( sqrt( xd*xd + yd*yd) );
Considere que o
valor n é sempre
maior ou igual a 1
\n no final
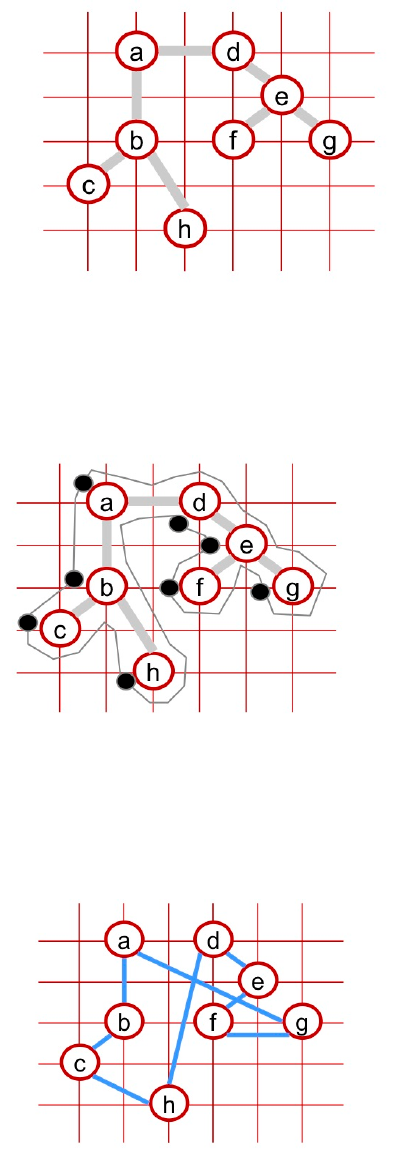
Em seguida, você deverá encontrar a árvore geradora de custo mínimo deste grafo,
apresentado no Capítulo 9 do nosso curso. No exemplo anterior, veja a árvore correspon-
dente, que chamaremos de T:
Uma possível solução para o Problema do Caixeiro Viajante pode ser obtida atra-
vés de um ciclo C' ao redor de T, onde cada aresta dessa árvore é percorrida duas vezes.
Veja na figura abaixo como seria C' calculado a partir da cidade a, (os pontos negros indi-
cam a primeira vez que cada vértice é visitado):
Repare que o ciclo C' pode ser encontrado a partir de um percurso pré-ordem em T.
Por outro lado, esta solução pode ser melhorada evitando-se arestas que incidam em vérti-
ces já visitados, ou seja, incluem-se apenas arestas para o próximo vértice ainda não visita-
do. Veja abaixo como ficaria o novo ciclo calculado, chamado de C, que pode ser construí-
do a partir de C' e dos pontos negros:
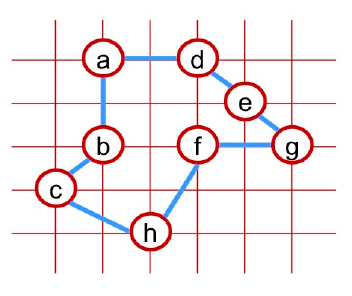
Este ciclo C é a nossa solução aproximada. Como foi dito, não há nenhuma garantia
de que seja ótima. Para este exemplo, o ciclo de custo mínimo C* está indicado na figura
abaixo:
T
C'
C
No entanto, é possível demonstrar uma importante propriedade da solução C. Lem-
brando:
• T: árvore de espalhamento de custo mínimo
• C': ciclo ao redor de T, com repetição de arestas
• C: ciclo baseado em C', sem repetição de arestas
• C*: ciclo de custo mínimo
Seja c(G) o custo associado a um grafo G. Se removermos uma aresta qualquer do
ciclo mínimo C*, obteremos uma árvore de espalhamento. Portanto, c(T) < c(C*).
Em C', cada aresta de T ocorre exatamente 2 vezes. Logo, c(C) ≤ c(C') = 2.c(T), ou
seja, c(C) < 2.c(C*). Em outras palavras, a solução C não é necessariamente ótima, mas
seu custo é sempre menor que o dobro da solução ótima.
C*

Entrada
Seu programa deverá ler do console um número inteiro positivo m, onde 1 ≤ m ≤
99. Em seguida, deverá ler automaticamente m arquivos de entrada, presentes no mesmo
diretório em que seu programa foi compilado, cujos nomes são ent01.txt, ent02.txt, ...,
entm.txt, considerando m com exatamente dois dígitos decimais.
Cada um desses m arquivos terá o seguinte formato:
a) Primeira linha: um número n de cidades.
b) Próximas n linhas: são formadas por 3 valores. O primeiro valor é um inteiro
positivo i, onde 1 ≤ i ≤ n, sem repetição, que é o índice de cada cidade. Na frente de i, há
dois valores reais, que correspondem às coordenadas x[i] e y[i].
Seu programa deverá representar cada uma dessas entradas através de um grafo não
orientado, utilizando listas ou matrizes de adjacências, como visto em sala de aula. Caso
deseje armazená-los como listas de adjacências, utilize, por exemplo, a seguinte estrutura
de dados (vertices é um vetor alocado dinamicamente):
Importante:
• Nos grafos não orientados, lembre-se de que cada aresta deve estar presente na
lista de adjacências de ambos os vértices incidentes.
• Cuidado para não "estourar" a memória ao longo da bateria de m testes. Para is-
so, utilize uma forma adequada de alocação, cada vez que for necessário criar
um novo grafo.
Saída
Seu programa deverá gerar um único arquivo saida.txt com exatamente m linhas,
onde na linha i, 1 ≤ i ≤ m, estará apenas um número inteiro positivo correspondente ao va-
lor da solução encontrada para a entrada enti.txt.
struct CelAdj {
int vert;
int distancia;
CelAdj *prox;
};
struct CelVert {
CelAdj *listaAdj;
};
struct grafo {
int nvert;
CelVert *vertices;
};

Importante
• Não é necessário verificar a consistência dos dados de entrada: você pode supor
que cada arquivo de entrada seguirá perfeitamente a estrutura indicada acima.
• O processo de correção consistirá na submissão automática do seu programa a essa
bateria de m testes. Por isso, a formatação de entrada e de saída deve ser obedecida
rigorosamente.
• Para que todos os alunos encontrem a mesma solução em cada teste, serão estabele-
cidas as seguintes regras:
o O vértice 1 será sempre a raiz da árvore T.
o T deverá ser encontrada através do algoritmo de Prim. Em cada passo deste
algoritmo, o novo vértice a ser incluído será o mais próximo de T, dentre
aqueles que ainda não pertencem a T. Em caso de empate, será escolhido o
que for adjacente ao vértice de menor índice em T. Em caso de novo empa-
te, será escolhido o vértice de menor índice.
o Na sequência de visitas em T que gera o circuito C', sempre será dada prio-
ridade ao vizinho mais próximo. Se houver vizinhos com a mesma distân-
cia, o desempate será através do menor índice.
• Seu programa deverá estar escrito necessariamente em linguagem C++ ou C, e será
compilado pelo CodeBlocks.
• Ele deverá estar em um único arquivo de código fonte, chamado TSP.cpp. Para en-
trada e saída, use a biblioteca stdio.h (e não conio.h).
• No programa principal, escreva int main (e não void main).
• Atenção com o prazo de entrega, indicado abaixo. Será descontado 1 ponto da nota
por dia de atraso.
• Sugestão: não deixe para fazer seu upload no último momento, pois sempre há o
risco de falta de energia elétrica, o que impossibilitaria o funcionamento do Tidia.
Entrega (através do TIDIA)
• Prazo impreterível: 20 de junho, quarta-feira, às 23h55.