FrailtyEM: An R Package For Estimating Semiparametric Shared Frailty S EM Manual
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 24

frailtyEM: An RPackage for Estimating
Semiparametric Shared Frailty Models
Theodor Adrian Balan
Leiden University Medical Center
Hein Putter
Leiden University Medical Center
Abstract
When analyzing correlated time to event data, shared frailty (random effect) models
are particularly attractive. However, the estimation of such models has proved challenging.
In semiparametric models, this is further complicated by the presence of the nonparamet-
ric baseline hazard. Although recent years have seen an increased availability of software
for fitting frailty models, most software packages focus either on a small number of distri-
butions of the random effect, or support only on a few data scenarios. frailtyEM is an R
package that provides maximum likelihood estimattion of semiparametric shared frailty
models using the Expectation-Maximization algorithm. The implementation is consistent
across several scenarios, including possibly left truncated clustered failures and recurrent
events in both calendar time and gap time formulation. A large number of frailty distri-
butions belonging to the Power Variance Function family are supported. Several methods
facilitate access to predicted survival and cumulative hazard curves, both for an individ-
ual and on a population level. An extensive number of summary measures and statistical
tests are also provided.
Keywords: shared frailty, EM algorithm, recurrent events, clustered failures, left truncation,
survival analysis, R.
1. Introduction
Time-to-event data is very common in medical applications. Often, these data are marked
by incomplete observations. For example, the phenomena of right censoring occurs when the
actual event time is not observed, but the only thing that is known is that the event has not
taken place by the end of follow-up. Sometimes, individuals enter the data set only if they
have not experienced the event before a certain time point. This is known as left truncation,
which, if not accounted for correctly, leads to bias. Regression models for such data have
been developed in the field of survival analysis. The most popular is the Cox proportional
hazards model (Cox 1972), which is semiparametric in nature: the effect of the covariates is
assumed to be time-constant and fully parametric, while the time-dependent probability of
observing an event arises from the nonparametric baseline hazard. Cox regression has been
the standard in survival analysis for a few reasons. First, it does not require any a priori
assumptions about the baseline hazard. Second, under the proportional hazards assumption,
maximum likelihood estimation can be carried out efficiently using Cox’s partial likelihood.
Nowadays, such models may be estimated with most statistical software, such as R(R Core
Team 2016)Stata (StataCorp 2017), SAS (SAS Institute Inc. 2003) or SPSS (IBM Corp 2016).
2frailtyEM: An R package for shared frailty models
When individuals belong to clusters, or may experience recurrent events, the observations are
correlated. In this case the Cox model is not appropriate for modeling individual risk. A
natural extension is represented by random effect “shared frailty” models. Originating from
the field of demographics (Vaupel, Manton, and Stallard 1979), these models traditionally
assume that the proportional hazards model holds conditional on the frailty, a random effect
that acts multiplicatively on the hazard. The variance of the frailty is usually indicative of the
degree of heterogeneity in the data. This makes the choice of the random effect distribution
relevant. However, the simplicity that made the Cox model so popular does not carry over to
such models.
Arguably the most popular way of fitting semiparametric shared frailty models is via the
penalized likelihood method (Therneau, Grambsch, and Pankratz 2003), available for the
gamma and log-normal frailty distributions. This is the standard in the survival package
(Therneau and Grambsch 2000;Therneau 2015a) in R, in the PHREG command in SAS and
the streg procedure in Stata. This method has the advantage that it is generally fast and the
Cox model is contained as a limiting case when the variance of the frailty is 0. However, this
algorithm can not be used for estimating other frailty distributions or left-truncated data,
and the provided standard errors are presented under the assumption that the estimated
parameters of the frailty distribution are fixed. Log-normal frailty models may also be esti-
mated in Rvia Laplace approximation in coxme (Therneau 2015b), h-likelihood in frailtyHL
(Do Ha, Noh, and Lee 2012) or Monte Carlo Expectation-Maximization phmm Donohue and
Xu (2013); Vaida and Xu (2000); Donohue, Overholser, Xu, and Florin (2011). Parametric
and spline based shared frailty models are implemented for the gamma and log-normal dis-
tributions in the frailtypack package (Rondeau, Mazroui, and Gonzalez 2012;Rondeau and
Gonzalez 2005).
In Hougaard (2000), the Power Variance Function (PVF) family was proposed for modeling
the frailty distribution. These include the gamma, positive stable (PS), inverse gaussian (IG)
and compound Poisson distributions with mass at 0. Each choice of the distribution for
the frailty implies a different marginal model, with some emphasizing early depence of the
observations (IG) and others the late dependence (gamma). Of particular interest is the PS
distribution; for all the others, the hazards are assumed to be proportional conditional on the
frailty, but not on the marginal level. For the PS frailty model, the hazards are assumed to
be proportional on both levels. Therefore, this is the only distribution where the potential
violation of the proportional hazards is not confounded with a frailty effect.
The software implementation of these distributions has so far been limited. At this time, two
Rpackages provide some capabilities: the frailtySurv package (Monaco, Gorfine, and Hsu
2017;Gorfine, Zucker, and Hsu 2006) implements the above mentioned distributions except
the PS via a pseudo full likelihood approach and the parfm package (Munda, Rotolo, Legrand
et al. 2012) estimates fully parametric gamma, IG, PS and log-normal frailty models.
In this paper we present frailtyEM (Balan and Putter 2017), an Rpackage which uses the
general Expectation-Maximization (EM) algorithm (Dempster, Laird, and Rubin 1977) for
fitting semiparametric shared frailty models. This implementation comes to complete the
landscape of packages that may be used for such models, with support for the whole PVF
family of distributions for the scenarios of clustered failures, clusted failures with left trun-
cation and recurrent events data in both calendar time and gap time formulations. Point
estimates for regression coefficients are provided with confidence intervals that take into ac-
count the estimation of the frailty distribution parameters, and plotting methods facilitate the
Theodor Adrian Balan, Hein Putter 3
visualization of both conditional and marginal survival or cumulative hazard curves with 95%
confidence bands, marginal covariate effects, and empirical Bayes estimates of the random
effects. A comparison with respect to functionality between frailtyEM and other Rpackages
is provided in Table 1.
The rest of this paper is structured as follows. In Section 2we present a brief overview the
semiparametric shared frailty model, and the implications of left truncation. In Section 3we
discuss the estimation method and its implementation. In Section 4we illustrate the usage
of the functions from the frailtyEM package on two classical data sets available in R.
2. Model
We consider the following framework: there are Iclusters and Jiindividuals in cluster i. The
outcome from each individual is represented by a realization of a counting process Nij . We
specify the intensity of Nij as
λij(t|Zi) = Yij (t)Ziexp(β>xij(t))λ0(t) (1)
where Yij(t) indicates whether Nij is under observation at time t,Ziis an unobserved random
effect common to all individuals from cluster i(the “shared frailty”), xij(t) a vector of possibly
time-dependent covariates, βa vector of unknown regression coefficients and λ0(t)≥0 an
unspecified baseline intensity function. We assume that event times are independent given
Zi=zi. We consider the general case where the Zifollows a distribution with positive
support from the infinitely divisible family, i.e., they are i.i.d. realizations of a random variable
described by the Laplace transform
LZ(c;α, γ)≡E[exp(−Zc)] = exp(−αψ(c;γ)) (2)
with α > 0 and γ > 0. This formulation includes several distributions, such as the gamma, PS,
IG an the general PVF case. These distributions have been extensively studied in Hougaard
(2000). Denote θ= (α, γ) as the parameter vector that describes the distribution. The
parametrizations used are described in Appendix A1.
2.1. Likelihood
The maximum likelihood problem is to maximize the marginal likelihood, based only on the
observed data. With the specification (1), the marginal likelihood is obtained as the product
over clusters of expected marginal contributions, i.e.,
L(θ, β, λ0(·)) = Y
i
Eθ
Y
jZ∞
0nYij(t)Ziexp(β>xij (t)λ0(t)odNij (t)
×exp
−X
jZ∞
0
Yij(t)Ziexp(β>xij (t))λ0(t)dt
To make the connection with how this is reflected in the data, we consider that (i, j, k) refers
to the k-th observation from the j-th individual in the i-th cluster. Thus, tijk is the event or

4frailtyEM: An R package for shared frailty models
frailtyEM survival coxme frailtySurv frailtyHL frailtypack parfm phmm
Distributions
Gamma yes yes no yes no yes yes no
Log-normal no yes yes yes yes yes yes yes
PS yes no no no no no yes no
IG yes no no yes no no yes no
Compound Poisson yes no no no no no no no
PVF yes no no yes no no no no
Data
Clustered failures yes yes yes yes yes yes yes yes
Recurrent events (AG) yes yes yes no no yes no no
Left truncation yes no no no no yes yes no
Correlated structure no no yes no no yes no yes
Estimation
Semiparametric yes yes yes yes yes no no yes
Posterior frailties yes yes no no no yes no no
Conditional Λ0, S0yes limited no yes no yes yes no
Marginal Λ0, S0yes no no no no no no no
Table 1: Comparsion of Rpackages for frailty models. Versions: frailtyEM 0.7.0, survival 2.40-1, coxme 2.2-5, frailtyHL 1.1, frailtypack
2.10.5, parfm 2.7.1, phmm 0.7-5.

Theodor Adrian Balan, Hein Putter 5
censoring time and δijk =dNij(tijk) is the event indicator for (i, j, k). We write the value of
the covariate vector for this observation as xijk. In the most basic case of clustered failures,
k≡1, while in the case of recurrent events j≡1. More observations for one individual
may also arise in the case of clustered failures when the covariates are time-dependent, and
the individual is artificially censored at the time when the value of the covariates changes.
Nevertheless, the (i, j, k) pair refers to a certain cluster, individual, and a period of time where
the covariate vector does not change.
The baseline cumulative hazard for observation (i, j, k) is denoted as Λ0,ijk. Also, let
˜
Λi=Pjk exp(β>xijk)Λ0,ijk. The marginal likelihood can be written as
L(θ, β, λ0(·)) = Y
i
Eθ
Y
j(Y
k
(Ziexp(β>xijk)λ0(tk))δijk )exp(−zi˜
Λi)
.
We consider the Breslow estimator for the baseline hazard, i.e., λ0(t)≡λ0tfor tan event
time, and 0 otherwise. By using (2), the marginal likelihood can be rewritten as
L(θ, β, λ0(·)) = Y
i
Y
j(Y
k
(exp(β>xijk)λ0(tk))δijk )(−1)niL(ni)
Z(˜
Λi)
,(3)
where L(k)
Zis the k-th derivative of the Laplace transform and niis the total number of events
in cluster i.
2.2. Ascertainment and left truncation
The problem of ascertainment with random effect time-to-event data is usually a difficult one.
Consider that the event of observing the cluster iin the data set is Ai. Thus, the distribution
of the random effect in cluster iis described by the Laplace transform of Zi|Ai, which follows
from Bayes’ rule as
LZi|Ai(c) = E[P(Ai|Zi) exp(−cZi)]
E[P(Ai|Zi)] .(4)
Expressing P(Ai|Z=z) depends on the type of the study at hand and on the way the data
were collected. In frailtyEM an option is included to deal with the classical scenario of left
truncation, i.e., where
P(Ai|Zi=zi) = P(Ti1> tL,i1, Ti2> tL,i2...TJi> tL,iJi|Zi=zi)
Assume that, given zi, the left truncation times tL,i are independent and the cluster size is
not informative. In this case,
P(Ai|Zi=zi) =
Ji
Y
j=1
exp −ziZtL,ij
0
exp(β>xij(t))λ0(t)dt.(5)
A difficulty here is that the values of the covariate vector and of the baseline intensity must
be known prior to the entry time in the study. To assign a value for xbefore the entry time
is speculative. Therefore, we only consider this case when xiis time constant.

6frailtyEM: An R package for shared frailty models
With the previous notation, denote the risk accumulated before each of the entry times of
cluster ias
˜
ΛL,i =X
j
exp(β>xij)Λ0L,ij
where Λ0L,ij =RtL,ij
0λ0(t)dt. Then, it follows from (2), (4) and (5) that the Laplace transform
can be written as
LZ|Ai(c;α, γ) = exp(−αψ(c+˜
ΛL,i;γ))
exp(−αψ(˜
ΛL,i;γ)) = exp(−α˜
ψ(c;˜
ΛL,i, γ)) (6)
where ˜
ψ(c; ΛL,i, γ) = ψ(c+ ΛL,i;γ)−ψ(ΛL,i;γ). Thus, the random effect stays in the same
infinitely divisible family of distributions under this ascertainment scheme.
Note that, in general, the ascertainment scheme does not have a simple description and
P(Ai|Zi=zi) may or may not be available in closed form. For example, in family studies,
the families may be selected only when a number of individuals live long enough (Rodr´ıguez-
Girondo, Deelen, Slagboom, and Houwing-Duistermaat 2016). In this case, (5) does not hold.
In the case of registry data on recurrent events, individuals (clusters) may be selected only if
they have at least one event during a certain time window (Balan, Jonker, Johannesma, and
Putter 2016b). These specific cases are not currently accommodated by frailtyEM.
2.3. Goodness of fit and measures of dependence
A reasonable question when fitting random effect models is whether there is evidence for
heterogeneity. To answer this a priori , the score test introduced in Commenges and Andersen
(1995) may be used. This test is referred in frailtyEM as the Commenges-Andersen test, and
is performed before the actual maximization of the likelihood, as it does not depend on the
frailty distribution and it does not require the actual estimation of the frailty model.
After fitting the model, the likelihood ratio test may be used to assess whether the model
with the frailty is a better fit than a model without frailty. In this case, the null model is
the model without frailty. With the parametrizations described in Appendix A1, this test lies
at the edge of the parameter space, and the test statistic under the null hypothesis follows
asymptotically a mixture of χ2(0) and χ2(1) distribution (Zhi, Grambsch, and Eberly 2005).
An explicit assumption of model (1) is that the censoring is non-informative on the frailty.
This assumption is usually difficult to test. In frailtyEM, a correlation score test is imple-
mented for the gamma distribution, following Balan, Boonk, Vermeer, and Putter (2016a).
This can also be used, for example, for testing whether a recurrent event event process and a
terminal event are associated.
Several measures of dependence are implemented in frailtyEM. The first is the variance of
the estimated frailty distribution Z, which is useful for the gamma and the PVF family. The
variance of log Zis also useful for the positive stable distribution for which the variance is
infinite. Other measures of association include Kendall’s τand the median concordance. A
thorough discussion and comparison of these measures can be found in Hougaard (2000).
3. Estimation and implementation
Theodor Adrian Balan, Hein Putter 7
frailtyEM implements a general full-likelihood estimation procedure for the gamma, positive
stable and PVF frailty models, based on a profile likelihood method and making use of the
expectation-maximization (EM) algorithm Dempster et al. (1977). For fixed parameters of
the frailty distribution θ, we define the profile maximum likelihood
b
L(θ) = max
β,λ0
L(β, λ0|θ).(7)
For each θ, denote ˆ
β(θ) and ˆ
λ0(θ) the value of the parameters that maximize L(β, λ0|θ). A
first observation is that, if ˆ
θmaximizes L(θ), then (ˆ
θ, ˆ
β(ˆ
θ),ˆ
λ0(ˆ
θ)) maximize L(θ, β, λ0). Thus,
we split the problem of maximizing the likelihood into two: obtaining ˆ
β(θ),ˆ
λ0(θ) for a fixed
θ(the “inner problem”) and maximizing L(θ) over θ(the “outer problem”).
The frailtyEM package is loaded in the usual way,
R> library("frailtyEM")
The main fitting function of the frailtyEM package is emfrail, with a syntax like:
R> emfrail(formula, data, distribution, control, ...)
The formula argument contains a Surv object on the left hand side and a +cluster()
statement on the right hand side which determines which observations share the same frailty.
The Surv object accepts both (start, status) for clustered failures and recurrent events in
gap time and (start, stop, status) for clustered failures with left truncation or recurrent
events in calendar time. The distribution argument determines the distribution of the
frailty. It may be generated by the emfrail_dist() function, with the structure:
R> str(emfrail_dist())
List of 4
$ dist : chr "gamma"
$ theta : num 2
$ pvfm : num -0.5
$ left_truncation: logi FALSE
- attr(*, "class")= chr "emfrail_dist"
where dist may be one of c("gamma", "stable", "pvf"). For "pvf", the mparameter
determines the precise distribution: for m=−1/2 for the IG, m∈(−1,0) for the so-called
Hougaard distribution and m > 0 a compound Poisson distribution with mass at 0. The
theta parameter determines the starting value of the optimization and left_truncation
determines whether the start column, if specified, refers to left truncation. If TRUE, then the
adjustment described in Section 2.2 is performed.
Finally, the control argument may be generated by the emfrail_control() function and
regulates parameters regarding to the estimation.
Once the user input is checked and processed, the Commenges-Andersen test for heterogene-
ity is performed and a few calculations regarding the risk sets at different time points are
calculated once and cached for use in the maximization.

8frailtyEM: An R package for shared frailty models
3.1. Outer problem
The “outer” problem refers to finding b
θwhich maximizes the profile likelihood (7). The
resulting b
θis the maximum likelihood estimator and the maximum likelihood is obtained
at b
L(b
θ). For the infinitely divisible distributions in frailtyEM,θis one dimensional. For
numerical stability, θis introduced on the log-scale in the general purpose maximizer nlm
from the stats package, together with a function that maximizes L(β, λ0|θ). The parameters
controling the optimization parameters of nlm may be passed on from the control argument.
3.2. The inner problem
For the inner problem of maximizing L(β, λ0|θ) the EM algorithm is used. This has been first
proposed for the gamma frailty model in Nielsen, Gill, Andersen, and Sørensen (1992) and
Klein (1992), and a generalization is discussed in Hougaard (2000).
Most ideas from Nielsen et al. (1992) are used here. The crucial observation is that the
E step involves calculating the empirical Bayes estimates of the frailties bzi=E[Zi|data].
This expectation is taken with respect to the “posterior” distribution of the random effect.
Afterwards, the M step is essentially a proportional hazards model with the log bzias offset
for each cluster.
The E step For the E step βand λ0are fixed, either at their initial values or at the values
from the previous M step. Let ni=Pj,k δijk be the number of events in cluster i. The
conditional distribution of Zigiven the data is described by the Laplace transform
L(c) =
EhZni
iexp(−Zi˜
Λi) exp(−Zic)i
EhZni
iexp(−Zi˜
Λi)i=L(ni)(c+˜
Λi)
L(ni)(˜
Λi).(8)
The E step reduces to calculating the expectation of this distribution, i.e. the derivative of
(8) in 0:
bzi=−L(ni+1)(˜
Λi)
L(ni)(˜
Λi).(9)
The marginal (log-)likelihood is also calculated at this point to keep track of convergence of
the EM algorithm. It can be seen that (3) involves the denominator of (8) in addition to a
straight forward expression of βand λ0.
The E step is generally the expensive operation of the EM algorithm. In a few scenarios (9)
may be expressed in a closed form: for the gamma and the inverse gaussian distributions. In
these scenarios, the E step is calculated with the fast_estep() routine. For all other cases,
the E step is calculated via a recursive algorithm with an internal routine which is described
in Appendix A2. For easing the computational burden, this is implemented in C++ and is
interfaced with Rvia the Rcpp library (Eddelbuettel and Fran¸cois 2011;Eddelbuettel 2013).
The M step With the same argument as made in Nielsen et al. (1992), the M step is
equivalent to a regular proportional hazards model with log bziadded as an offset for all the
cases in zi. This is done via the agreg.fit() function in the survival package, which estimates
of βvia Cox’s partial likelihood. Afterwards, λ0and the subsequent calculations of ˜
Λi(and,
eventually ˜
ΛL,i, in the case of left truncation) are calculated.
Theodor Adrian Balan, Hein Putter 9
The EM algorithm stops after the marginal log-likelihood has converged, i.e., when difference
in b
L(θ) is smaller than εbetween two consecutive iterations. The value of εcan be set with
the control argument of emfrail.
3.3. Standard errors and confidence intervals
Once the the outer maximization is finished and d
log θhas been obtained, the Hessian is
collected from nlm and, using the delta method as implemented in the msm (Jackson 2011)
package, the variance of b
θis obtained. The 95% confidence interval for b
θis calculated from a
symmetric confidence interval on the log scale, then exponentiated. The resulting asymmetric
confidence interval has been seen to provide good coverage (Balan et al. 2016b).
A more precise yet computationally intensive method for quantifying the uncertainty in d
log θ
or θis through likelihood-based confidence intervals. This requires finding the b
θvalues for
which the difference between the maximum likelihood and the specific profile maximum likeli-
hood values at θequals a critical value, calculated from the χ2(1) distribution, and is discussed
in Appendix A3. This is achieved with the root-finding routine uniroot() function in the
stats package. The major advantage of likelihood-based confidence intervals is that they are
invariant to any transformation of the parameter of interest.
The standard error of the estimates for βand λ0(·) are calculated with Louis’ formula (Louis
1982), for θfixed to the maximum likelihood estimate. The resulting information matrix leads
to an underestimate of the standard errors, because it does not account for the uncertainty
in estimating θ. These standard errors as provided by the statistical packages that use the
penalized likelihood approach, for example. In frailtyEM, adjusted standard errors are also
obtained by recalcuating the information matrix for βand λ0also at ˆ
θ±ε. This is described in
more detail in Appendix A3. 95% confidence intervals may be built based on the asymptotic
normality of these maximum likelihood estimators.
3.4. Output, summary and prediction
The return object type is emfrail, which is essentially a list that contains the results of the
“outer” maximization, the results of the “inner” maximization at this estimate, and a few other
fields which are used for different methods. The object type is documented in ?emfrail.
By itself, the print.emfrail() method prints the call, a summary of “outer” optimization,
the estimates of the covariates and the pvalue of the Commenges-Andersen test. A more
user-readable summary of an emfrail object is provided by the summary.emfrail() method.
This returns an object of the class emfrail_summary that contains general fit information,
covariate estimates and several distribution-specific measures of fit and dispersion described
in Section 2.3. Arguments to summary.emfrail() may be used to show confidence intervals
either likelihood based or delta method based, as described in Section 3.3.
A method for predicting cumulative hazard and survival curves, both conditional and marginal,
is implemented in predict.emfrail(). Confidence bands are based on the asymptotic nor-
mality of the estimated λ0, and available both for adjusted and un-adjusted for the uncertainty
of θ. The user can specify which quantities to obtain for a number of individuals, specified
either by a data frame of covariate values or a vector of linear predictor values at which to
calculate these curves. With the individual argument, predicted curves may be produced
for individuals with non-specific at-risk patterns (for example, if an individual is not at risk
10 frailtyEM: An R package for shared frailty models
during a certain time frame), or for individuals with time dependent covariates. The function
returns a data frame from which several plots can be easily created.
Two plot methods are provided based on both graphics package via plot.emfrail() and
the ggplot2 package, via autoplot.emfrail(), both with identical syntax. The type ar-
gument may be specified as type = "hist" for a histogram of the posterior estimates of
the frailties, type = "pred" for plotting marginal and conditional cumulative hazard or sur-
vival curves, and type = "hr" for plotting marginal and conditional estimated hazard ratios.
Furthermore, a scatter plot of the posterior estimates of the frailties may be obtained from
autoplot.emfrail with type = "frail", which also includes quantiles of the posterior dis-
tribution in the case of the gamma distribution.
An additional function is provided to calculate the marginal log-likelihood for a vector of
values of θ,emfrail_pll(), without actually performing the outer optimizaion. This may be
useful for visualizing the profile log-likelihood or when debugging (e.g., to see if the maximum
likelihood estimate of θlies on the boundary).
Other methods for emfrail objects include residuals.emfrail(), which may be used to
obtain martingale residuals, aggregated or individual. Using the notation of section 2, if type
= "cluster", then the vector of ˜
Λiare returned. If type = "individual", then for each
row in the data (i, j, k) a vector containing
bziexp(b
β>xijk)Λ0,ijk
is returned.
4. Illustration
The features of the package will now be illustrated with two well-known data sets available
in R.
4.1. CGD
The data are from a placebo controlled trial of gamma interferon in chronic granulotomous
disease (CGD) and is available in the survival package. It contains the time to recurrence of
serious infections observed, from randomizatio until end of study for each patient.
R> data("cgd")
For the purpose of illustration, we will use treat (treatment or placebo) and sex (female or
male) as covariates, althought a larger number of variables are recorded in the data set.
A basic gamma frailty model can be fitted like this:
R> gam <- emfrail(Surv(tstart, tstop, status) ~ sex + treat + cluster(id),
+ data = cgd)
R> summary(gam, lik_ci = TRUE)
Call:
emfrail(formula = Surv(tstart, tstop, status) ~ sex + treat +
Theodor Adrian Balan, Hein Putter 11
cluster(id), data = cgd)
Regression coefficients:
coef exp(coef) se(coef) adj. se z p
sexfemale -0.227 0.797 0.396 0.396 -0.575 0.57
treatrIFN-g -1.052 0.349 0.310 0.310 -3.389 0.00
Estimated distribution: gamma / left truncation: FALSE
Fit summary:
Commenges-Andersen test for heterogeneity: p-val 0.00172
no-frailty Log-likelihood: -331.997
Log-likelihood: -326.619
LRT: 1/2 * pchisq(10.8), p-val 0.00052
Frailty summary:
frailty variance = 0.821 / 95% CI: [0.231, 1.854]
Kendall's tau: 0.291 / 95% CI: [0.104, 0.481]
Median concordance: 0.289 / 95% CI: [0.101, 0.491]
E[log Z]: -0.464 / 95% CI: [-1.164, -0.12]
Var[log Z]: 1.241 / 95% CI: [0.26, 4.341]
theta = 1.218 (0.59) / 95% CI: [0.539, 4.326]
Confidence intervals based on the likelihood function
The first two parts of this output, about regression coefficients and fit summary, exist regard-
less of the frailty distributions. The last part, “frailty summary”, provides a useful output
according to the distribution. The calculations behind this part are described for each distri-
bution in Appendix A1. Since only log θis actually estimated in the “outer” step, the delta
method is employed to obtain standard errors for all derived quantities. The confidence in-
tervals may be obtained either likelihood-based or delta method-based, see Appendix A3 for
details. The delta method based confidence intervals are shown with the option lik_ci =
FALSE.
Both the Commenges-Andersen test for heterogeneity and the one-sided likelihood ratio test
deems the random effect highly significant. This is also suggested by the confidence interval
for the frailty variance, which is far from 0.
To illustrate the predicted cumulative hazard curves we take two individuals, one from the
treatment arm and one from the placebo arm, both males:
R> library("ggplot2")
R> p1 <- autoplot(gam, type = "pred",
+ newdata = data.frame(sex = "male", treat = "rIFN-g")) +
+ ggtitle("rIFN-g") + ylim(c(0, 2)) + theme_minimal()
R> p2 <- autoplot(gam, type = "pred",
+ newdata = data.frame(sex = "male", treat = "placebo")) +
+ ggtitle("placebo") + ylim(c(0, 2)) + theme_minimal()
The two plots are shown in Figure 1.
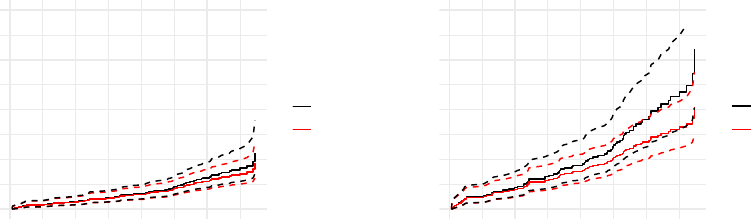
12 frailtyEM: An R package for shared frailty models
0.0
0.5
1.0
1.5
2.0
0 100 200 300
time
cumhaz
type
conditional
marginal
rIFN−g
0.0
0.5
1.0
1.5
2.0
0 100 200 300
time
cumhaz
type
conditional
marginal
placebo
Figure 1: Predicted conditional and marginal cumulative hazards for males, one from the
treatment arm and one from the placebo arm, as produced by autplot.emfrail() with type
= "pred".
The cumulative hazard in this case can be interpreted as the expected number of events at
a certain time. It can be seen that the frailty “drags down” the marginal hazard. This is
a well-known effect observed in frailty models, as described in Aalen, Borgan, and Gjessing
(2008, ch. 7).
If autoplot.emfrail() is called with type = "pred", this will also call predict.emfrail().
All prediction results could also be obtained directly:
R> dat_pred <- data.frame(sex = c("male", "male"),
+ treat = c("rIFN-g", "placebo"))
R> predict(gam, dat_pred)
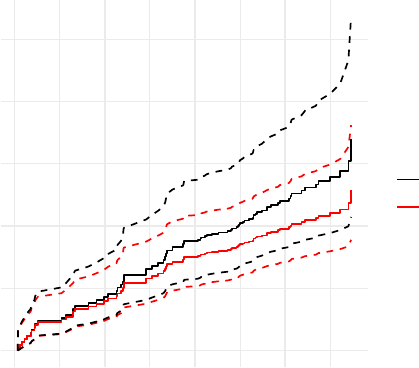
For a hypothetical individual that changes treatment from placebo to rIFN-g at time 200,
predictions may also be obtained:
R> dat_pred_b <- data.frame(sex = c("male", "male"),
+ treat = c("placebo", "rIFN-g"),
+ tstart = c(0, 200), tstop = c(200, Inf))
R> p <- autoplot(gam, type = "pred", newdata = dat_pred_b, individual = TRUE) +
+ ggtitle("change placebo to rIFN-g at time 200") + theme_minimal()
This plot is shown in Figure 2.
A positive stable frailty model can also be fitted by specifying the distribution argument.
R> stab <- emfrail(Surv(tstart, tstop, status) ~ sex + treat + cluster(id),
+ data = cgd,
+ distribution = emfrail_dist(dist = "stable"))
R> summary(stab)
Call:
emfrail(formula = Surv(tstart, tstop, status) ~ sex + treat +
Theodor Adrian Balan, Hein Putter 13
0.0
0.5
1.0
0 100 200 300
time
cumhaz
type
conditional
marginal
change placebo to rIFN−g at time 200
Figure 2: Predicted conditional and marginal cumulative hazards for a male that switches
treatment from placebo to rIFN-g at time 200 as produced by autoplot.emfrail() with
type = "pred"
cluster(id), data = cgd, distribution = emfrail_dist(dist = "stable"))
Regression coefficients:
coef exp(coef) se(coef) adj. se z p
sexfemale -0.137 0.872 0.407 0.407 -0.337 0.74
treatrIFN-g -1.085 0.338 0.332 0.336 -3.230 0.00
Estimated distribution: stable / left truncation: FALSE
Fit summary:
Commenges-Andersen test for heterogeneity: p-val 0.00172
no-frailty Log-likelihood: -331.997
Log-likelihood: -329.39
LRT: 1/2 * pchisq(5.21), p-val 0.0112
Frailty summary:
Kendall's tau: 0.104 / 95% CI: [0.011, 0.236]
Median concordance: 0.102 / 95% CI: [0.011, 0.233]
E[log Z]: 0.067 / 95% CI: [0.006, 0.179]
Var[log Z]: 0.406 / 95% CI: [0.037, 1.176]
Attenuation factor: 0.896 / 95% CI: [0.764, 0.989]
theta = 8.572 (5.41) / 95% CI: [3.232, 90.316]
Confidence intervals based on the likelihood function
The coefficient estimates are similar to those of the gamma frailty fit. The “Frailty summary”
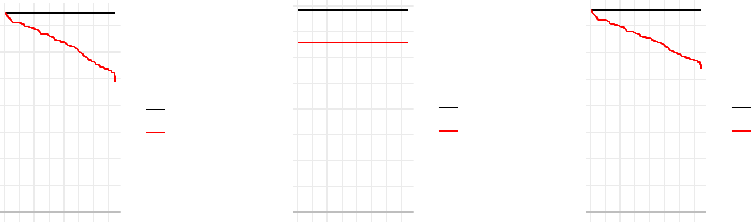
14 frailtyEM: An R package for shared frailty models
1.0
1.5
2.0
2.5
0 100 200 300
time
hazard ratio
type
conditional
marginal
gamma
1.0
1.5
2.0
2.5
3.0
0 100 200 300
time
hazard ratio
type
conditional
marginal
PS
1.0
1.5
2.0
2.5
0 100 200 300
time
hazard ratio
type
conditional
marginal
IG
Figure 3: Conditional and marginal hazard ratio between two males from the placebo
and rIFN-g treatment arms from the gamma, PS and IG frailty models as produced by
autoplot.emfrail() with type = "hr".
part is quite different though. For the positive stable distribution, the variance is not defined.
However, Kendall’s τis easily obtained, and in this case it is smaller than in the gamma
frailty model. Unlike the gamma or PVF distributions, the positive stable frailty predicts a
marginal model with proportional hazards where the marginal hazard ratios are an attenuated
version of the conditional hazard ratios shown in the output. The calculations are detailed in
Appendix A1.
The conditional and marginal hazard betw ratios from different distributions can also be
visualized easily. We also fitted an IG frailty model on the same data, and plots of the hazard
ratio between two males from different treatment arms created below are shown in Figure 3.
R> ig <- emfrail(Surv(tstart, tstop, status) ~ sex + treat + cluster(id),
+ data = cgd,
+ distribution = emfrail_dist(dist = "pvf"))
R> newdata <- data.frame(treat = c("placebo", "rIFN-g"),
+ sex = c("male", "male"))
R> pl1 <- autoplot(gam, type = "hr", newdata = newdata) +
+ ggtitle("gamma") + theme_minimal()
R> pl2 <- autoplot(stab, type = "hr", newdata = newdata) +
+ ggtitle("PS") + theme_minimal()
R> pl3 <- autoplot(ig, type = "hr", newdata = newdata) +
+ ggtitle("IG") + theme_minimal()
While all models shrink the hazard ratio towards 1, it can be seen that this effect is slightly
more pronounced for the gamma than for the IG, while the PS exhibits a constant “average”
shrinkage. This type of behaviour from the PS is seen as a strength of the model (Hougaard
2000).
4.2. Kidney
The kidney data set is also available in the survival package. The data, presented originally
in McGilchrist and Aisbett (1991), contains the time to infection for kidney patients using
Theodor Adrian Balan, Hein Putter 15
a portable dialysis equipment. The infection may occur at the insertion of the catheter
and at that point, the catheter must be removed, the infection cleared up, and the catheter
reinserted. Each of the 38 patients has exactly 2 observations, representing recurrence times
from insertion until the next infection. There are 3 covariates: sex, age and disease (a factor
with 4 levels). A data analysis based on frailty models is described in Therneau and Grambsch
(2000, ch. 9.5.2). The authors note that, when disease is included in the model, a gamma
frailty model offers no evidence of heterogeneity. However, when disease is removed from
the model, then there seems to be moderate evidence for heterogeneity. This is an example
where the frailty may be interpreted as a missing covariate.
R> data("kidney")
R> kidney$sex <- ifelse(kidney$sex == 1, "male", "female")
R> m_gam <- emfrail(Surv(time, status) ~ age + sex + cluster(id),
+ data = kidney)
R> s_gam <- summary(m_gam)
R> s_gam
Call:
emfrail(formula = Surv(time, status) ~ age + sex + cluster(id),
data = kidney)
Regression coefficients:
coef exp(coef) se(coef) adj. se z p
age 0.00544 1.00545 0.01158 0.01170 0.46481 0.64
sexmale 1.55284 4.72487 0.44518 0.49952 3.10868 0.00
Estimated distribution: gamma / left truncation: FALSE
Fit summary:
Commenges-Andersen test for heterogeneity: p-val 0.00238
no-frailty Log-likelihood: -184.657
Log-likelihood: -182.053
LRT: 1/2 * pchisq(5.21), p-val 0.0112
Frailty summary:
frailty variance = 0.397 / 95% CI: [0.046, 1.031]
Kendall's tau: 0.166 / 95% CI: [0.022, 0.34]
Median concordance: 0.162 / 95% CI: [0.022, 0.341]
E[log Z]: -0.212 / 95% CI: [-0.597, -0.023]
Var[log Z]: 0.486 / 95% CI: [0.047, 1.721]
theta = 2.517 (1.49) / 95% CI: [0.97, 21.802]
Confidence intervals based on the likelihood function
Therneau and Grambsch discuss these models and they conclude that an outlier case is at
the source of the frailty effect. With the frailtyEM package, the positive stable frailty model
may also be fitted. Unlike the gamma frailty model, the positive stable does not attempt to
“correct” non-proportional hazards.
16 frailtyEM: An R package for shared frailty models
R> m_stab <- emfrail(Surv(time, status) ~ age + sex + cluster(id),
+ data = kidney,
+ distribution = emfrail_dist(dist = "stable"))
R> s_stab <- summary(m_stab)
R> s_stab
Call:
emfrail(formula = Surv(time, status) ~ age + sex + cluster(id),
data = kidney, distribution = emfrail_dist(dist = "stable"))
Regression coefficients:
coef exp(coef) se(coef) z p
age 0.00218 1.00218 0.00922 0.23649 0.81
sexmale 0.82100 2.27278 0.29873 2.74831 0.01
Estimated distribution: stable / left truncation: FALSE
Fit summary:
Commenges-Andersen test for heterogeneity: p-val 0.00238
no-frailty Log-likelihood: -184.657
Log-likelihood: -184.657
LRT: 1/2 * pchisq(0), p-val>0.5
Frailty summary:
Kendall's tau: 0 / 95% CI: [0, 0.258]
Median concordance: 0 / 95% CI: [0, 0.255]
E[log Z]: 0 / 95% CI: [0, 0.201]
Var[log Z]: 0 / 95% CI: [0, 1.342]
Attenuation factor: 1 / 95% CI: [0.742, 1]
theta = 42445.25 (Inf) / 95% CI: [2.878, Inf]
Confidence intervals based on the likelihood function
The Commenges-Andersen test for heterogeneity shows the same evidence as before, as it
does not depend on the frailty distribution. However, the positive stable parameter lies at the
edge of the parameter space (θis between 0 and 1 for the PS distribution). Therefore, the
LRT is not significant. The major difference with the gamma frailty fit is that the regression
coefficient for sex is much smaller. To untangle this effect, one can check the (marginal)
proportional hazards assumption.
A test for proportionality, based on Schoenfeld residuals, is implemented in the survival
package. This reveals that sex has a significantly non-proportional effect on the marginal
hazards:
R> zph1 <- cox.zph(coxph(Surv(time, status) ~ age + sex + cluster(id),
+ data = kidney))
R> zph1
rho chisq p
age 0.0214 0.0231 8.79e-01
Theodor Adrian Balan, Hein Putter 17
sexmale -0.4390 29.2598 6.33e-08
GLOBAL NA 29.3325 4.27e-07
The same test may be performed with two other models, by including the estimated frailties
as offset. This would be a test for proportionality, conditional on the frailties.
R> off_z_gam <- log(s_gam$frail$z)[match(kidney$id, s_gam$frail$id)]
R> off_z_stab <- log(s_stab$frail$z)[match(kidney$id, s_stab$frail$id)]
R> zph_gam <- cox.zph(coxph(Surv(time, status) ~
+ age + sex + offset(off_z_gam) + cluster(id),
+ data = kidney))
R> zph_stab <- cox.zph(coxph(Surv(time, status) ~
+ age + sex + offset(off_z_stab) + cluster(id),
+ data = kidney))
R> zph_gam
rho chisq p
age -0.0145 0.00427 0.948
sexmale -0.2170 1.39043 0.238
GLOBAL NA 1.41146 0.494
R> zph_stab
rho chisq p
age 0.0214 0.0231 8.79e-01
sexmale -0.4390 29.2553 6.34e-08
GLOBAL NA 29.3279 4.28e-07
In this case, it can be seen that the gamma frailty corrects for proportionality while the PS
distribution does not, indicating that there might be that the gamma frailty might pick up
the marginal non-proportionality rather than heterogeneity.
5. Conclusion
In the current landscape for modeling random effects in survival analysis, frailtyEM is a
contribution that focuses on implementing classical methodology in an efficient way. We
have shown that the EM based approach has certain advantages in the context of frailty
models. First of all, it is semiparametric, which means that it is a direct extension of the Cox
proportional hazards model. In this way, classical results from semiparametric frailty models
(for example, based on the data sets in Section 4) can be replicated and further insight may
be obtained by fitting models with different frailty distributions. Until now, the Commenges-
Andersen test, positive stable and PVF family, have not all been implemented in a consistent
way in an Rpackage. Another advantage of the EM algorithm is that, by its nature, it is a
full maximum likelihood approach, and the estimators have well known desirable asymptotic
properties.
To our knowledge, no other statistical package provides similar capabilities for visualizing
conditional and marginal survival curves, or the marginal effect of covariates. Since this is

18 frailtyEM: An R package for shared frailty models
implemented across a large number of distributions, this might come to the aid of both applied
and theoretical research into shared frailty models. While the question of model selection with
different random effect distributions is still an open one, the functions included frailtyEM may
be useful for further research in this direction.
Evaluating goodness of fit for shared frailty models is still a complicated issue, particularly
in semiparametric models. However, tests based on martingale residuals, such as that of
Commenges and Rondeau (2000), should be now possible by extrating the necessary quantities
from an emfrail fit.
In this paper we have not exemplified the left truncation adjustment. In this respect, the
implementation from frailtyEM is very similar to that from the parfm package. However,
performing of a larger simulation study to assess the effects of left truncation in clustered fail-
ure data with semiparametric frailty models is now possible. The scenario of time dependent
covariates and left truncation is not supported at this time. This is because this would require
also specifying values of these covariates from time 0 to the left truncation time, which would
probably involve some speculation.
Technically, extending the package to other distributions is possible, as long as their Laplace
transform and the corresponding derivatives may be specified in closed form. An interesting
extension would be to choose discrete distributions from the infinitely divisible family for the
random effect, such as the Poisson distribution. The newest features will be implemented in
the development version of the package at https://github.com/tbalan/frailtyEM.
Appendix A1: Results for the Laplace transforms
We consider distributions from the infinitely divisible family (Ash 1972, ch 8.5) with the
Laplace transform
LY(c) = exp(−αψ(c;γ)).
We now consider how αand γcan be represented as a function of a positive parameter θ.
The gamma distribution For Ya gamma distributed random variable, ψ(c;γ) = log(γ+
c)−log(γ), the derivatives of which are
ψ(k)(c;γ) = (−1)k−1(k−1)!(γ+c)−k.
For identifiability, the restriction EY= 1 is imposed; this leads to α=γ. The distribution
is parametrized with θ > 0, θ=α=γ. The variance of Yis VARY=θ−1. Kendall’s τ
is then τ=1
1+2θand the median concordance is κ= 4 21+1/θ −1−θ−1. Furthermore,
Elog Y=ψ(θ)−log θand VAR log Y=ψ0(θ) where ψand ψ0are the digamma and trigamma
functions.
The positive stable distribution For Ya positive stable random variable, ψ(c;γ) = cγ
with γ∈(0,1), the derivatives of which are
ψ(k)(c;γ) = Γ(k−β)
Γ(1 −γ)(−1)k−1cγ−k.
Theodor Adrian Balan, Hein Putter 19
For identifiability, the restriction α= 1 is made; EYis undefined and VARY=∞. The
distribution is parametrized with θ > 0, γ=θ
θ+1 .
Kendall’s τis then τ= 1−θ
θ+1 and the median concordance is κ= 22−2θ
θ+1 −1. Furthermore,
Elog Y=−nθ
1+θo−1−1ψ(1) and VAR log Y=nθ
1+θo−2−1ψ0(1).
In the case of the PS distribution, the marginal hazard ratio is an attenuated version of the
conditional hazard ratio. If the conditional log-hazard ratio is β, the marginal hazard ratio
is equal to βθ
θ+1 .
The PVF distributions For Ya PVF distribution with fixed parameter m∈R,m > −1
and m6= 0,
ψ(c;γ) = (1 −γm(γ+c)−m).
This is the same parametrizaion as in Aalen et al. (2008). The derivatives of ψare
ψ(k)(c;γ) = (−γ)m(γ+c)−m−k(−1)k+1 Γ(m+k)
Γ(m).
The expectation of this distribution can be calculated as minus the first derivative of the
Laplace transform calculated in 0, i.e.,
EY=αψ0(0; γ)L(0; α, γ) = α
γm.
The second moment of the distribution can be calculated as the second derivative of the
Laplace transform at 0,
EY2=α2ψ02(0) −αψ00(0) = α2
γ2m2+α
γ2m(m+ 1).
For identifiability, we set EY= 1. The distribution is parametrized through a parameter
θ > 0 which is determined by γ= (m+ 1)θand α=m+1
mθ. This results in VARY=θ−1.
A slightly different parametrization is presented in Hougaard (2000), dependent on the pa-
rameter ηH. The correspondence is obtained by setting ηH= (m+ 1)θ.
The PVF family of distributions includes the gamma as a limiting case when m→0. When
γ→0 the positive stable distribution is obtained. When m=−1 the distribution is degen-
erate, and with m= 1 a non-central gamma distribution is obtained. Of special interest is
the case m=−0.5, when the inverse Gaussian distribution is obtained. With m > 0, the
distribution is compound Poisson with mass at 0. In this case, P(Y= 0) = exp(−m+1
mθ).
For m < 0, closed forms for Kendall’s τand median concordance are given in Hougaard (2000,
Section 7.5).
Left truncation
To determine the Laplace transform under left truncation, we determine ˜
ψfrom (6).
For the gamma distribution, we have
˜
ψ(c;γ, ΛL) = log(γ+ ΛL+c)−log(γ+ ΛL)

20 frailtyEM: An R package for shared frailty models
which implies that the frailty of the survivors is still gamma distributed, but with a change
in the parameter γ.
For the positive stable we have
˜
ψ(c;γ, ΛL)=(c+ ΛL)γ−Λγ
L,
which is not a positive stable distribution any more.
For the PVF distributions, we have
˜
ψ(c;γ, ΛL) = sign(m)γm(γ+ ΛL)−m−(γ+ ΛL)m(γ+ ΛL+c)−m,
which is not PVF any more.
Closed forms
The gamma distribution leads to a Laplace transform for which the derivatives can be calcu-
lated in closed form. It can be seen that
L(c;α, γ) = γα(γ+c)−α.
The k-th derivative of this expression is
L(k)(c;α, γ) = γα(γ+c)−γ−kΓ(α+k)
Γ(α).
This can be exploited also in the case of left truncation, since the gamma frailty is preserved,
as shown in the previous section.
The inverse gaussian distribution is obtained when the PVF parameter is m=−1
2. Under
the current parametrization, we have γ=θ/2 and α=θ. In this case, the Laplace transform
is
L(c;θ) = exp nθ1−p1+2c/θo.
The k-th derivative of this can be written as
L(k)(c;θ)=(−1)k2
θc+ 1−k/2Kk−1/2q2θc+θ
2
K1/2q2θc+θ
2
where Kis the modified Bessel function of the second kind.
The emfrail() uses the closed form formulas when possible, by default.
Appendix A2: A general E step
As shown in (8), the calculation of the E step for the general case involves taking derivatives
of Laplace transforms of the form
L(c) = exp(g(c))

Theodor Adrian Balan, Hein Putter 21
where for simplicity we denote g(c) = −αψ(c;γ). The expression for the k-th derivative of
L(c) can be obtained with a classical calculus result, di Bruno’s formula, i.e.,
L(n)(c) = X
m∈Mn
n!
m1!m2!...mn!
n
Y
j=1 g(j)(c)
j!!mj
L(c),(10)
where Mn={(m1, ..., mn)|Pn
j=1 j×mj=n}. For example, for n= 3,
M3={(3,0,0),(1,1,0),(0,0,1)}.
This corresponds to the “partitions of the integer” 3, i.e., all the integers that sum up to 3:
{(1,1,1),(1,2,0),(3,0,0)}.
We implemented a recursive algorithm in C++ which resides in the emfrail_estep.cpp
which loops through these partitions, calculates the corresponding derivatives of ψand the
coefficients.
Appendix A3: Standard errors
The outer maximization of b
L(θ) is carried out on the log-scale, as described in section 3, and
the numeric hessian is used to obtain VAR(b
θ). Afterwards, the delta method is employed
to derive standard errors for θand the other functionals of θdescribed in Appendix A1.
However, the standard error is not very meaningul for parameters with skewed distributions.
Confidence intervals are constructed in two ways.
The first type of confidence intervals provided by frailtyEM are based on the the asymptotic
normality of d
log θ, by constructing a 95% symmetric confidence interval on the log-scale, and
then translating it to the other functionals of θ.
The second type are likelihood-based confidence intervals. Under the null hypothesis, the
likelihood ratio test statistic follows a χ2(0) +χ2(1) distribution. The critical value associated
with this test statistic is approximately 1.92. Using the root-finding algorithm implemented in
the uniroot() function in the stats package, a confidence interval is obtained from the values
of θwith the property that b
L(θ)≥b
L(b
θ)−1.92. This confidence interval is then translated to
the functionals of θ.
The likelihood-based confidence intervals are the default in emfrail() because the coverage
is guaranteed to be the same for all transformations of θ.
Considering the vector of parameters η= (β, λ0(·)), the information matrix for (θ, η) can be
written as follows:
I=Iθ,θ Iθ,η
Iη,θ Iη,η.
The part corresponding to η,Iη,η is calculated using Louis’ formula, which has been com-
monly employed to obtain this quantity from EM algorithms Louis (1982). This is done
under the assumption of θfixed to the maximum likelihood estimate ˆ
θ. This leads to an
underestimate of the standard errors, as is noted also in Therneau and Grambsch (2000, sec.
9.5). The calculation of the variance-covariance matrix I−1in this case involves approximat-
ing Iη,θ and adjusting Iη,η, as described in Hougaard (2000, Appendix B.3) and Putter and
Van Houwelingen (2015).
22 frailtyEM: An R package for shared frailty models
Confidence intervals for the conditional cumulative hazard are obtained from the part of
the variance-covariance matrix corresponding to λ0(·), and confidence intervals for Λ0(t) =
Ps≤tλ0(t) are obtained with the usual formula. For confidence intervals, the delta method
is used to calculate a symmetric confidence interval for log Λ0(t) for all t, which is then
exponentiated.
References
Aalen O, Borgan O, Gjessing H (2008). Survival and Event History Analysis: A Process Point
of View. Springer-Verlag New York. doi:10.1007/978-0-387-68560-1.
Ash RP (1972). Real Analysis and Probability. Academic press.
Balan TA, Boonk SE, Vermeer MH, Putter H (2016a). “Score Test for Association Between
Recurrent Events and a Terminal Event.” Statistics in Medicine,35(18), 3037–3048. doi:
10.1002/sim.6913.
Balan TA, Jonker MA, Johannesma PC, Putter H (2016b). “Ascertainment Correction in
Frailty Models for Recurrent Events Data.” Statistics in Medicine,35(23), 4183–4201.
doi:10.1002/sim.6968.
Balan TA, Putter H (2017). frailtyEM: Fitting Frailty Models with the EM Algorithm. R
package version 0.5.4, URL https://CRAN.R-project.org/package=frailtyEM.
Commenges D, Andersen PK (1995). “Score Test of Homogeneity for Survival Data.” Lifetime
Data Analysis,1(2), 145–156. doi:10.1007/BF00985764.
Commenges D, Rondeau V (2000). “Standardized martingale residuals applied to grouped
left truncated observations of dementia cases.” Lifetime Data Analysis,6(3), 229–235.
Cox DR (1972). “Regression Models and Life-Tables.” Journal of the Royal Statistical Society
B,34(2), 187–220. ISSN 00359246. URL http://www.jstor.org/stable/2985181.
Dempster AP, Laird NM, Rubin DB (1977). “Maximum Likelihood from Incomplete Data via
the EM Algorithm.” Journal of the Royal Statistical Society B, pp. 1–38.
Do Ha I, Noh M, Lee Y (2012). “frailtyHL: A Package for Fitting Frailty Models with h-
likelihood.” R Journal,4(2), 28–36.
Donohue MC, Overholser R, Xu R, Florin V (2011). “Conditional Akaike Information under
Generalized Linear and Proportional Hazards Mixed Models.” Biometrika, (98, 3), 685–700.
doi:10.1093/biomet/asr023.
Donohue MC, Xu R (2013). phmm: Proportional Hazards Mixed-effects Models. R package
version 0.7-5.
Eddelbuettel D (2013). Seamless Rand C++ Integration with Rcpp. Springer-Verlag New
York. doi:10.1007/978-1-4614-6868-4. ISBN 978-1-4614-6867-7.
Theodor Adrian Balan, Hein Putter 23
Eddelbuettel D, Fran¸cois R (2011). “Rcpp: Seamless Rand C++ Integration.” Journal
of Statistical Software,40(8), 1–18. doi:10.18637/jss.v040.i08. URL http://www.
jstatsoft.org/v40/i08/.
Gorfine M, Zucker DM, Hsu L (2006). “Prospective Survival Analysis with a General Semi-
parametric Shared Frailty Model: A Pseudo Full Likelihood Approach.” Biometrika, pp.
735–741.
Hougaard P (2000). Analysis of Multivariate Survival Data. Springer-Verlag, New York.
doi:10.1007/978-1-4612-1304-8.
IBM Corp (2016). IBM SPSS Statistics for Windows, Version 24.0. IBM Corp, Armonk, NY.
URL https://www.ibm.com/analytics/us/en/technology/spss/.
Jackson CH (2011). “Multi-State Models for Panel Data: The msm Package for R.” Journal
of Statistical Software,38(8), 1–29. doi:10.18637/jss.v038.i08. URL http://www.
jstatsoft.org/v38/i08/.
Klein JP (1992). “Semiparametric Estimation of Random Effects using the Cox Model based
on the EM Algorithm.” Biometrics, pp. 795–806.
Louis TA (1982). “Finding the Observed Information Matrix When Using the EM Algorithm.”
Journal of the Royal Statistical Society B, pp. 226–233.
McGilchrist C, Aisbett C (1991). “Regression with Frailty in Survival Analysis.” Biometrics,
pp. 461–466. doi:10.2307/2532138.
Monaco JV, Gorfine M, Hsu L (2017). frailtySurv: General Semiparametric Shared
Frailty Model. R package version 1.3.2, URL https://CRAN.R-project.org/package=
frailtySurv.
Munda M, Rotolo F, Legrand C, et al. (2012). “parfm: Parametric Frailty Models in R.”
Journal of Statistical Software,51(1), 1–20. doi:10.18637/jss.v051.i11.
Nielsen GG, Gill RD, Andersen PK, Sørensen TI (1992). “A Counting Process Approach to
Maximum Likelihood Estimation in Frailty Models.” Scandinavian Journal of Statistics,
pp. 25–43.
Putter H, Van Houwelingen HC (2015). “Dynamic Frailty Models Based on Compound Birth–
Death Processes.” Biostatistics,16(3), 550–564. doi:10.1093/biostatistics/kxv002.
R Core Team (2016). R: A Language and Environment for Statistical Computing. R Founda-
tion for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Rodr´ıguez-Girondo M, Deelen J, Slagboom EP, Houwing-Duistermaat JJ (2016). “Survival
Analysis with Delayed Entry in Selected Families with Application to Human Longevity.”
Statistical Methods in Medical Research, p. 0962280216648356.
Rondeau V, Gonzalez JR (2005). “frailtypack: A computer program for the analysis of
correlated failure time data using penalized likelihood estimation.” Computer Methods and
Programs in Biomedicine,80(2), 154–164. doi:10.1016/j.cmpb.2005.06.010.
24 frailtyEM: An R package for shared frailty models
Rondeau V, Mazroui Y, Gonzalez JR (2012). “frailtypack: An RPackage for the Analysis
of Correlated Survival Data with Frailty Models Using Penalized Likelihood Estimation or
Parametrical Estimation.” Journal of Statistical Software,47(4), 1–28. doi:10.18637/
jss.v047.i04. URL http://www.jstatsoft.org/v47/i04/.
SAS Institute Inc (2003). SAS/STAT Software, Version 9.1. Cary, NC. URL http://www.
sas.com/.
StataCorp (2017). Stata Statistical Software: Release 15. StataCorp LLC, College Station,
TX. URL http://www.stata.com.
Therneau TM (2015a). A Package for Survival Analysis in S. Version 2.38, URL https:
//CRAN.R-project.org/package=survival.
Therneau TM (2015b). coxme: Mixed Effects Cox Models. R package version 2.2-5, URL
https://CRAN.R-project.org/package=coxme.
Therneau TM, Grambsch PM (2000). Modeling Survival Data: Extending the Cox
Model. Springer-Verlag, New York, New York. ISBN 0-387-98784-3. doi:10.1007/
978-1-4757-3294-8.
Therneau TM, Grambsch PM, Pankratz VS (2003). “Penalized Survival Models and Frailty.”
Journal of Computational and Graphical Statistics,12(1), 156–175. ISSN 10618600. doi:
10.2307/1391074. URL http://www.jstor.org/stable/1391074.
Vaida F, Xu R (2000). “Proportional Hazards Model with Random Effects.” Statistics in
Medicine, (19), 3309–3324.
Vaupel JW, Manton KG, Stallard E (1979). “The Impact of Heterogeneity in Individual Frailty
on the Dynamics of Mortality.” Demography,16(3), 439–454. doi:10.2307/2061224.
Zhi X, Grambsch PM, Eberly LE (2005). “Likelihood Ratio Test for the Variance Component
in a Semi-Parametric Shared Gamma Frailty Model.” Research Report 2005-5.
Affiliation:
Theodor Adrian Balan
Department of Medical Statistics and Bioinformatics
Leiden University Medical Center
2300 RC Leiden, The Netherlands
E-mail: t.a.balan@lumc.nl