Manual SPECFEM2D
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 56
- Contents
- 1 Introduction
- 2 Getting Started
- 3 Mesh Generation
- 4 Running the Solver xspecfem2D
- 4.1 How to run elastic wave simulations
- 4.2 How to run axisymmetric wave simulations
- 4.3 How to run anisotropic wave simulations
- 4.4 How to run poroelastic wave simulations
- 4.5 Coupled simulations
- 4.6 How to choose the time step
- 4.7 How to set plane waves as initial conditions
- 4.8 Note on the viscoelastic model used
- 4.9 Note on viscoelasticity in the 2D plane strain approximation
- 5 Adjoint Simulations
- 6 Doing tomography, i.e., updating the model based on the sensitivity kernels obtained
- 7 Oil and gas industry simulations
- 8 Information for developers of the code, and for people who want to learn how the technique works
- Notes & Acknowledgments
- Copyright
- Bibliography
- A Troubleshooting
- B License

User Manual
COMPUTATIONAL INFRASTRUCTURE FOR GEODYNAMICS (CIG)
Version 7.0
CNRS (FRANCE)
PRINCETON UNIVERSITY (USA)
SPECFEM 2D
SPECFEM2D
User Manual
© CNRS (France) and Princeton University (USA)
Version 7.0
December 12, 2017
1
Authors
The SPECFEM2D package was first developed by Dimitri Komatitsch and Jean-Pierre Vilotte at Institut de Physique
du Globe (IPGP) in Paris, France from 1995 to 1997 and then by Dimitri Komatitsch at Harvard University (USA),
Caltech (USA) and then CNRS and University of Pau (France) from 1998 to 2005. The story started on April 4,
1995, when Prof. Yvon Maday from CNRS and University of Paris, France, gave a lecture to Dimitri Komatitsch
and Jean-Pierre Vilotte at IPG about the nice properties of the Legendre spectral-element method with diagonal mass
matrix that he had used for other equations. We are deeply indebted and thankful to him for that. That followed a
visit by Dimitri Komatitsch to OGS (Istituto Nazionale di Oceanografia e di Geofisica Sperimentale) in Trieste, Italy,
in February 1995 to meet with Géza Seriani and Enrico Priolo, who introduced him to their 2D Chebyshev version
of the spectral-element method with a non-diagonal mass matrix. We are deeply indebted and thankful to them for that.
Since then it has been developed and maintained by a development team: in alphabetical order, Étienne Bachmann,
Alexis Bottero, Quentin Brissaud, Paul Cristini, Dimitri Komatitsch, Jesús Labarta, Nicolas Le Goff, Pieyre Le Loher,
Qinya Liu, Youshan Liu, Roland Martin, René Matzen, Christina Morency, Daniel Peter, Carl Tape, Jeroen Tromp,
Jean-Pierre Vilotte, Zhinan Xie.
The code is released open-source under the GNU version 3 license, see the license at the end of this manual.

2
Current and past main participants or main sponsors of the SPECFEM project
(in no particular order)
Contents
Contents 3
1 Introduction 5
1.1 Citation .................................................. 6
1.2 Support .................................................. 8
2 Getting Started 9
2.1 Visualizing the subroutine calling tree of the source code ........................ 10
2.2 Becoming a developer of the code, or making small modifications in the source code ......... 10
3 Mesh Generation 11
3.1 How to use SPECFEM2D ......................................... 11
3.2 How to use Gmsh to generate an external mesh ............................. 13
3.3 How to use Cubit/Trelis to generate an external mesh .......................... 14
3.3.1 Note about Cubit/Trelis built-in Python ............................. 15
3.4 Notes about absorbing PMLs ....................................... 15
3.5 Controlling the quality of an external mesh ............................... 16
3.6 Controlling how the mesh samples the wave field ............................ 18
4 Running the Solver xspecfem2D 19
4.1 How to run elastic wave simulations ................................... 23
4.2 How to run axisymmetric wave simulations ............................... 23
4.3 How to run anisotropic wave simulations ................................. 25
4.4 How to run poroelastic wave simulations ................................. 26
4.5 Coupled simulations ........................................... 27
4.6 How to choose the time step ....................................... 28
4.7 How to set plane waves as initial conditions ............................... 28
4.8 Note on the viscoelastic model used ................................... 29
4.9 Note on viscoelasticity in the 2D plane strain approximation ...................... 29
5 Adjoint Simulations 30
5.1 How to obtain finite sensitivity kernels .................................. 30
5.2 Remarks about adjoint runs and solving inverse problems ........................ 31
5.3 Caution .................................................. 31
6 Doing tomography, i.e., updating the model based on the sensitivity kernels obtained 32
7 Oil and gas industry simulations 33
8 Information for developers of the code, and for people who want to learn how the technique works 34
Notes & Acknowledgments 35
Copyright 36
3
Chapter 1
Introduction
SPECFEM2D allows users to perform 2D and 2.5D (i.e., axisymmetric) simulations of acoustic, elastic, viscoelastic,
and poroelastic seismic wave propagation as well as full waveform imaging (FWI) or adjoint tomography.
In fluids, SPECFEM2D uses the classical linearized Euler equation; thus if you have sharp local variations
of density in the fluid (highly heterogeneous fluids in terms of density) or if density becomes extremely small
in some regions of your model (e.g. for upper-atmosphere studies), before using the code please make sure the
linearized Euler equation is a valid approximation in the case you want to study. For more details on that see
e.g. Jensen et al. [2011].
The 2D spectral-element solver accommodates regular and unstructured meshes, generated for example by Cubit
(http://cubit.sandia.gov), Gmsh (http://geuz.org/gmsh) or GiD (http://www.gid.cimne.
upc.es). Even mesh creation packages that generate triangles, for instance Delaunay-Voronoi triangulation codes,
can be used because each triangle can then easily be decomposed into three quadrangles by linking the barycenter to
the center of each edge; while this approach does not generate quadrangles of optimal quality, it can ease mesh creation
in some situations and it has been shown that the spectral-element method can very accurately handle distorted mesh
elements.
With version 7.0, the 2D spectral-element solver accommodates Convolution PML absorbing layers and well as
higher-order time schemes (4th order Runge-Kutta and LDDRK4-6). Convolution or Auxiliary Differential Equation
Perfectly Matched absorbing Layers (C-PML or ADE-PML) are described in Martin et al. [2008b,c], Martin and Ko-
matitsch [2009], Martin et al. [2010], Komatitsch and Martin [2007].
The solver has adjoint capabilities and can calculate finite-frequency sensitivity kernels [Tromp et al.,2008,Peter
et al.,2011] for acoustic, (an)elastic, and poroelastic media. The package also considers 2D SH and P-SV wave propa-
gation. Finally, the solver can run both in serial and in parallel. See SPECFEM2D (http://www.geodynamics.
org/cig/software/packages/seismo/specfem2d) for the source code.
The SEM is a continuous Galerkin technique [Tromp et al.,2008,Peter et al.,2011], which can easily be made dis-
continuous [Bernardi et al.,1994,Chaljub,2000,Kopriva et al.,2002,Chaljub et al.,2003,Legay et al.,2005,Kopriva,
2006,Wilcox et al.,2010,Acosta Minolia and Kopriva,2011]; it is then close to a particular case of the discontinuous
Galerkin technique [Reed and Hill,1973,Lesaint and Raviart,1974,Arnold,1982,Johnson and Pitkäranta,1986,
Bourdel et al.,1991,Falk and Richter,1999,Hu et al.,1999,Cockburn et al.,2000,Giraldo et al.,2002,Rivière and
Wheeler,2003,Monk and Richter,2005,Grote et al.,2006,Ainsworth et al.,2006,Bernacki et al.,2006,Dumbser and
Käser,2006,De Basabe et al.,2008,de la Puente et al.,2009,Wilcox et al.,2010,De Basabe and Sen,2010,Étienne
et al.,2010], with optimized efficiency because of its tensorized basis functions [Wilcox et al.,2010,Acosta Minolia
and Kopriva,2011]. In particular, it can accurately handle very distorted mesh elements [Oliveira and Seriani,2011].
It has very good accuracy and convergence properties [Maday and Patera,1989,Seriani and Priolo,1994,Deville
et al.,2002,Cohen,2002,De Basabe and Sen,2007,Seriani and Oliveira,2008,Ainsworth and Wajid,2009,2010,
5
CHAPTER 1. INTRODUCTION 6
Melvin et al.,2012]. The spectral element approach admits spectral rates of convergence and allows exploiting hp-
convergence schemes. It is also very well suited to parallel implementation on very large supercomputers [Komatitsch
et al.,2003,Tsuboi et al.,2003,Komatitsch et al.,2008,Carrington et al.,2008,Komatitsch et al.,2010b] as well as
on clusters of GPU accelerating graphics cards [Komatitsch,2011,Michéa and Komatitsch,2010,Komatitsch et al.,
2009,2010a]. Tensor products inside each element can be optimized to reach very high efficiency [Deville et al.,2002],
and mesh point and element numbering can be optimized to reduce processor cache misses and improve cache reuse
[Komatitsch et al.,2008]. The SEM can also handle triangular (in 2D) or tetrahedral (in 3D) elements [Wingate and
Boyd,1996,Taylor and Wingate,2000,Komatitsch et al.,2001,Cohen,2002,Mercerat et al.,2006] as well as mixed
meshes, although with increased cost and reduced accuracy in these elements, as in the discontinuous Galerkin method.
Note that in many geological models in the context of seismic wave propagation studies (except for instance for
fault dynamic rupture studies, in which very high frequencies or supershear rupture need to be modeled near the fault,
see e.g. Benjemaa et al. [2007,2009], de la Puente et al. [2009], Tago et al. [2010]) a continuous formulation is
sufficient because material property contrasts are not drastic and thus conforming mesh doubling bricks can efficiently
handle mesh size variations [Komatitsch and Tromp,2002,Komatitsch et al.,2004,Lee et al.,2008,2009a,b].
For a detailed introduction to the SEM as applied to regional seismic wave propagation, please consult Peter et al.
[2011], Tromp et al. [2008], Komatitsch and Vilotte [1998], Komatitsch and Tromp [1999], Chaljub et al. [2007] and
in particular Lee et al. [2009b,a,2008], Godinho et al. [2009], van Wijk et al. [2004], Komatitsch et al. [2004]. A
detailed theoretical analysis of the dispersion and stability properties of the SEM is available in Cohen [2002], De
Basabe and Sen [2007], Seriani and Oliveira [2007], Seriani and Oliveira [2008] and Melvin et al. [2012].
The SEM was originally developed in computational fluid dynamics [Patera,1984,Maday and Patera,1989] and
has been successfully adapted to address problems in seismic wave propagation. Early seismic wave propagation ap-
plications of the SEM, utilizing Legendre basis functions and a perfectly diagonal mass matrix, include Cohen et al.
[1993], Komatitsch [1997], Faccioli et al. [1997], Casadei and Gabellini [1997], Komatitsch and Vilotte [1998] and
Komatitsch and Tromp [1999], whereas applications involving Chebyshev basis functions and a non-diagonal mass
matrix include Seriani and Priolo [1994], Priolo et al. [1994] and Seriani et al. [1995]. In the Legendre version that
we use in SPECFEM the mass matrix is purposely slightly inexact but diagonal (but can be made exact if needed, see
Teukolsky [2015]), while in the Chebyshev version it is exact but non diagonal.
All SPECFEM2D software is written in Fortran2003 with full portability in mind, and conforms strictly to the
Fortran2003 standard. It uses no obsolete or obsolescent features of Fortran. The package uses parallel programming
based upon the Message Passing Interface (MPI) [Gropp et al.,1994,Pacheco,1997].
This new release of the code includes support for GPU graphics card acceleration [Komatitsch,2011,Michéa and
Komatitsch,2010,Komatitsch et al.,2009,2010a].
The code uses the plane strain convention when the standard P-SV equation case is used, i.e., the off-plane strain
zz is zero by definition of the plane strain convention but the off-plane stress σzz is not equal to zero, one has
σzz =λ(xx+yy). This implies, as in any plain strain software package, that the P-SV source is a line source along the
direction perpendicular to the plane (see file discussion_of_2D_sources_and_approximations_from_Pilant_1979.pdf
for more details).
1.1 Citation
You can find all the references below in BIBT
EXformat in file doc/USER_MANUAL/bibliography.bib.
If you use this code for your own research, please cite at least one article written by the developers of the package,
for instance:
•Tromp et al. [2008],
•Peter et al. [2011],
CHAPTER 1. INTRODUCTION 7
•Vai et al. [1999],
•Lee et al. [2009a],
•Lee et al. [2008],
•Lee et al. [2009b],
•Komatitsch et al. [2010a],
•Komatitsch et al. [2009],
•Liu et al. [2004],
•Chaljub et al. [2007],
•Komatitsch and Vilotte [1998],
•Komatitsch and Tromp [1999],
•Komatitsch et al. [2004],
•Morency and Tromp [2008],
•Blanc et al. [2016],
• and/or other articles from http://komatitsch.free.fr/publications.html.
If you use the C-PML absorbing layer capabilities of the code, please cite at least one article written by the developers
of the package, for instance:
•Xie et al. [2014],
•Xie et al. [2016].
If you use the UNDO_ATTENUATION option of the code in order to produce full anelastic/viscoelastic sensitivity
kernels, please cite at least one article written by the developers of the package, for instance (and in particular):
•Komatitsch et al. [2016].
More generally, if you use the attenuation (anelastic/viscoelastic) capabilities of the code, please cite at least one article
written by the developers of the package, for instance:
•Komatitsch et al. [2016],
•Blanc et al. [2016].
If you use the kernel capabilities of the code, please cite at least one article written by the developers of the package,
for instance:
•Tromp et al. [2008],
•Peter et al. [2011],
•Liu and Tromp [2006],
•Morency et al. [2009].
If you use the SCOTCH / CUBIT non-structured capabilities, please cite:
•Martin et al. [2008a].
If you use axisymmetric geometries please also cite:
•Bottero et al. [2016]
The corresponding BibT
EX entries may be found in file doc/USER_MANUAL/bibliography.bib.
CHAPTER 1. INTRODUCTION 8
1.2 Support
This material is based upon work supported by the USA National Science Foundation under Grants No. EAR-0406751
and EAR-0711177, by the French CNRS, French Inria Sud-Ouest MAGIQUE-3D, French ANR NUMASIS under
Grant No. ANR-05-CIGC-002, and European FP6 Marie Curie International Reintegration Grant No. MIRG-CT-
2005-017461. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the
authors and do not necessarily reflect the views of the USA National Science Foundation, CNRS, Inria, ANR or the
European Marie Curie program.
Chapter 2
Getting Started
To download the SPECFEM2D software package, type this:
git clone --recursive --branch devel https://github.com/geodynamics/specfem2d.git
We recommend that you add ulimit -S -s unlimited to your .bash_profile file and/or limit
stacksize unlimited to your .cshrc file to suppress any potential limit to the size of the Unix stack.
Then, to configure the software for your system, run the configure shell script. This script will attempt to guess
the appropriate configuration values for your system. However, at a minimum, it is recommended that you explicitly
specify the appropriate command names for your Fortran compiler (another option is to define FC, CC and MPIF90 in
your .bash_profile or your .cshrc file):
./configure FC=gfortran CC=gcc
If you want to run in parallel, i.e., using more than one processor core, then you would type
./configure FC=gfortran CC=gcc MPIFC=mpif90 --with-mpi
You can replace the GNU compilers above (gfortran and gcc) with other compilers if you want to; for instance for
Intel ifort and icc use FC=ifort CC=icc instead.
Before running the configure script, you should probably edit file flags.guess to make sure that it contains
the best compiler options for your system. Known issues or things to check are:
Intel ifort compiler See if you need to add -assume byterecl for your machine. In the case of that
compiler, we have noticed that initial release versions sometimes have bugs or issues that can lead to
wrong results when running the code, thus we strongly recommend using a version for which at least one
service pack or update has been installed.
IBM compiler See if you need to add -qsave or -qnosave for your machine.
Mac OS You will probably need to install XCODE.
IBM Blue Gene machines Please refer to the manual of SPECFEM3D_Cartesian, which contains detailed in-
structions on how to run on Blue Gene.
The SPECFEM2D software package relies on the SCOTCH library to partition meshes. The SCOTCH library
[Pellegrini and Roman,1996] provides efficient static mapping, graph and mesh partitioning routines. SCOTCH is a
free software package developed by François Pellegrini et al. from LaBRI and Inria in Bordeaux, France, download-
able from the web page https://gforge.inria.fr/projects/scotch/. In case no SCOTCH libraries
can be found on the system, the configuration will bundle the version provided with the source code for compilation.
The path to an existing SCOTCH installation can to be set explicitly with the option --with-scotch-dir. Just as
an example:
./configure FC=ifort MPIFC=mpif90 --with-mpi --with-scotch-dir=/opt/scotch
9
CHAPTER 2. GETTING STARTED 10
If you use the Intel ifort compiler to compile the code, we recommend that you use the Intel icc C compiler to compile
Scotch, i.e., use:
./configure CC=icc FC=ifort MPIFC=mpif90
For further details about the installation of SCOTCH, go to subdirectory scotch_5.1.11/ and read INSTALL.txt.
You may want to download more recent versions of SCOTCH in the future from (http://www.labri.fr/
perso/pelegrin/scotch/scotch_en.html) . Support for the METIS graph partitioner has been discon-
tinued because SCOTCH is more recent and performs better.
When compiling the SCOTCH source code, if you get a message such as: "ld: cannot find -lz", the Zlib com-
pression development library is probably missing on your machine and you will need to install it or ask your system
administrator to do so. On Linux machines the package is often called "zlib1g-dev" or similar. (thus "sudo apt-get
install zlib1g-dev" would install it)
You may edit the Makefile for more specific modifications. Especially, there are several options available:
•-DUSE_MPI compiles with use of an MPI library.
•-DUSE_SCOTCH enables use of graph partitioner SCOTCH.
After these steps, go back to the main directory of SPECFEM2D/ and type
make
to create all executables which will be placed into the folder ./bin/.
By default, the solver runs in single precision. This is fine for most application, but if for some reason you want
to run the solver in double precision, run the configure script with option “--enable-double-precision”.
Keep in mind that this will of course double total memory size and will also make the solver around 20 to 30% slower
on many processors.
If your compiler has problems with the use mpi statements that are used in the code, use the script called
replace_use_mpi_with_include_mpif_dot_h.pl in the root directory to replace all of them with include
‘mpif.h’ automatically.
If you have problems configuring the code on a Cray machine, i.e. for instance if you get an error message
from the configure script, try exporting these two variables: MPI_INC=$CRAY_MPICH2_DIR/include and
FCLIBS=" ", and for more details if needed you can refer to the utils/Cray_compiler_information
directory.
2.1 Visualizing the subroutine calling tree of the source code
Packages such as doxywizard can be used to visualize the subroutine calling tree of the source code. Doxywizard
is a GUI front-end for configuring and running doxygen.
2.2 Becoming a developer of the code, or making small modifications in the
source code
If you want to develop new features in the code, and/or if you want to make small changes, improvements, or bug
fixes, you are very welcome to contribute. To do so, i.e. to access the development branch of the source code with
read/write access (in a safe way, no need to worry too much about breaking the package, there is a robot called
BuildBot that is in charge of checking and validating all new contributions and changes), please visit this Web page:
https://github.com/geodynamics/specfem2d/wiki/Using-Hub.
To visualize the call tree (calling tree) of the source code, you can see the Doxygen tool available in directory
doc/call_trees_of_the_source_code.
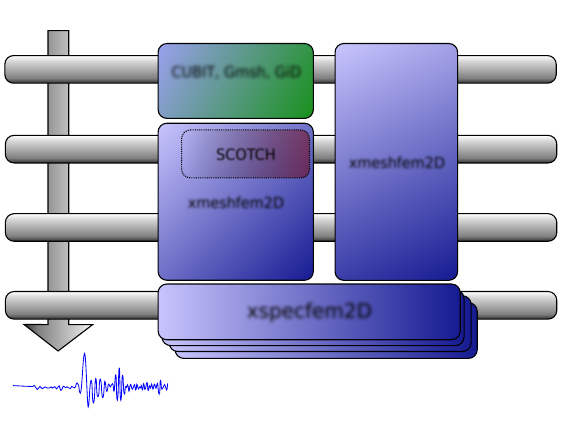
Chapter 3
Mesh Generation
3.1 How to use SPECFEM2D
Mesher
Partitioner
Databases
Solver
CUBIT, Gmsh, GiD
SCOTCH
xmeshfem2D
xmeshfem2D
xspecfem2D
Figure 3.1: Schematic workflow for a SPECFEM2D simulation. The executable xmeshfem2D creates the GLL mesh
points and assigns specific model parameters. The executable xspecfem2D solves the seismic wave propagation.
To run the mesher, please follow these steps:
• edit the input file DATA/Par_file, which describes the simulation. The default DATA/Par_file pro-
vided in the root directory of the code contains detailed comments and should be almost self-explanatory
(note that some of the older DATA/Par_file files provided in the EXAMPLES directory work fine but
some of the comments they contain may be obsolete or even wrong; thus refer to the default DATA/Par_file
instead for reliable explanations). If you need more details we do not have a detailed description of all the
parameters for the 2D version in this manual but you can find useful information in the manuals of the 3D ver-
sions, since many parameters and the general philosophy is similar. They are available at (https://github.
com/geodynamics/specfem3d/tree/master/doc/USER_MANUAL). To create acoustic (fluid) re-
gions, just set the S wave speed to zero and the code will see that these elements are fluid and switch to the right
equations there automatically, and automatically match them with the solid regions
• if you are using an external mesher (like GiD or CUBIT / Trelis), you should set read_external_mesh to
.true.:
11
CHAPTER 3. MESH GENERATION 12
mesh_file is the file describing the mesh : first line is the number of elements, then a list of 4 nodes (quadri-
laterals only) forming each elements on each line.
nodes_coords_file is the file containing the coordinates (xand z) of each node: number of nodes on the
first line, then coordinates x and z on each line.
materials_file is the number of the material for every element : an integer ranging from 1 to nbmodels
on each line.
free_surface_file is the file describing the edges forming the acoustic free surface: number of edges on
the first line, then on each line: number of the element, number of nodes forming the free surface (1 for
a point, 2 for an edge), the nodes forming the free surface for this element. If you do not want any free
surface, just put 0 on the first line; you then get a rigid surface instead.
axial_elements_file is the file describing the axial elements in the case of an axisymmetric simulation.
See Section 4.2.
absorbing_surface_file is the file describing the edges forming the absorbing boundaries: number of
edges on the first line, then on each line: number of the element, number of nodes forming the absorbing
edge (must always be equal to 2), the two nodes forming the absorbing edge for this element, and then the
type of absorbing edge: 1 for BOTTOM, 2 for RIGHT, 3 for TOP and 4 for LEFT. Only two nodes per
element can be listed, i.e., the second parameter of each line must always be equal to 2. If one of your
elements has more than one edge along a given absorbing contour (e.g., if that contour has a corner) then
list it twice, putting the first edge on the first line and the second edge on the second line. Do not list
the same element with the same absorbing edge twice or more, otherwise absorption will not be correct
because the edge integral will be improperly subtracted several times. If one of your elements has a single
point along the absorbing contour rather than a full edge, do NOT list it (it would have no weight in the
contour integral anyway because it would consist of a single point). If you use 9-node elements, list only
the first and last points of the edge and not the intermediate point located around the middle of the edge;
the right 9-node curvature will be restored automatically by the code.
tangential_detection_curve_file contains points describing the envelope, that are used for the
source_normal_to_surface and rec_normal_to_surface. Should be fine grained, and or-
dered clockwise. Number of points on the first line, then (x,z) coordinates on each line.
• if you have compiled with MPI, you must specify the number of processes.
Then type
./bin/xmeshfem2D
to create the mesh (which will be stored in directory OUTPUT_FILES/). xmeshfem2D is serial; it will output
several files called Database??????.bin, one for each process.
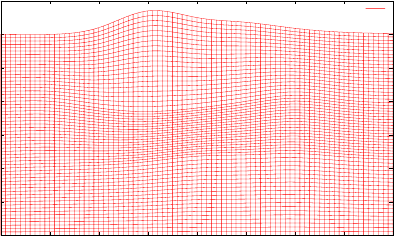
0
500
1000
1500
2000
2500
3000
3500
0 500 1000 1500 2000 2500 3000 3500 4000
'OUTPUT_FILES.default.M2_UPPA/gridfile.gnu'
Figure 3.2: Example of a grid file generated by xmeshfem2D and visualized with gnuplot (within gnuplot, type
‘plot "OUTPUT_FILES/gridfile.gnu" w l’).
Regarding mesh point numbering in the files created by the mesher, we use the classical convention of 4-node and
9-node finite elements:

CHAPTER 3. MESH GENERATION 13
4....7....3
. .
. eta .
.|.
8 9--xi 6
. .
. .
. .
1....5....2
the local coordinate system being ξand η(xi and eta). Note that this convention is used to describe the geometry
only. In the solver the wave field is then described based on high-order Lagrange interpolants at Gauss-Lobatto-
Legendre points, as is classical in spectral-element methods.
3.2 How to use Gmsh to generate an external mesh
Gmsh1is a 3D finite element grid generator which can be used for the generation of quadrangle and hexahedral
meshes. It is therefore a good candidate for generating meshes which can be processed by SPECFEM2D. Only two
modules of Gmsh are of interest for the SPECFEM2D users : the geometry and the mesh modules. An example is
given in directory EXAMPLES/Gmsh_example which illustrates the generation of an external mesh using these two
modules. The model that is considered consists of a homogeneous square containing two circles filled with a different
material.
The geometry is generated by loading file SqrCirc.geo into Gmsh. The end of the .geo file contains several
lines which are required in order to define the sides of the box and the media. This is done using the following
conventions :
Physical Line("Top") = {1}; line corresponding to the top of the box
Physical Line("Left") = {2}; line corresponding to the left side of the box
Physical Line("Bottom") = {3}; line corresponding to the bottom of the box
Physical Line("Right") = {4}; line corresponding to the right side of the box
Physical Surface("M1") = {10}; surrounding medium
Physical Surface("M2") = {11,12}; interior of the two circles
For instance, if you want to fill the two circles with two different materials, you will have to write :
Physical Surface("M1") = {10}; surrounding medium
Physical Surface("M2") = {11}; interior of the big circle
Physical Surface("M3") = {12}; interior of the small circle
and, consequently, you will have to define a new medium numbered 3in the Par_file.
Then, a 2D mesh can be created and saved after selecting the appropriate options in Gmsh : All quads in
Subdivision algorithm and 1or 2in Element order whether you want a 4 or 9 node mesh. This operation
will generate a SqrCirc.msh file which must be processed to get all the files required by SPECFEM2D when using
an external mesh (see previous section). This is done by running a python script called LibGmsh2Specfem.py,
located in directory utils/Gmsh:
python LibGmsh2Specfem.py SqrCirc -t A -b A -r A -l A
Where the options -t,-b,-r and -l represent the different sides of the model (top, bottom, right and left) and can
take the values Aor Fif the corresponding side is respectively absorbing or free. All boundaries are absorbing by
default. The connections of the generated filenames to the filenames indicated in the previous section are :
•Mesh_SqrCirc is the mesh_file
1freely available at the following address : http://www.geuz.org/gmsh/
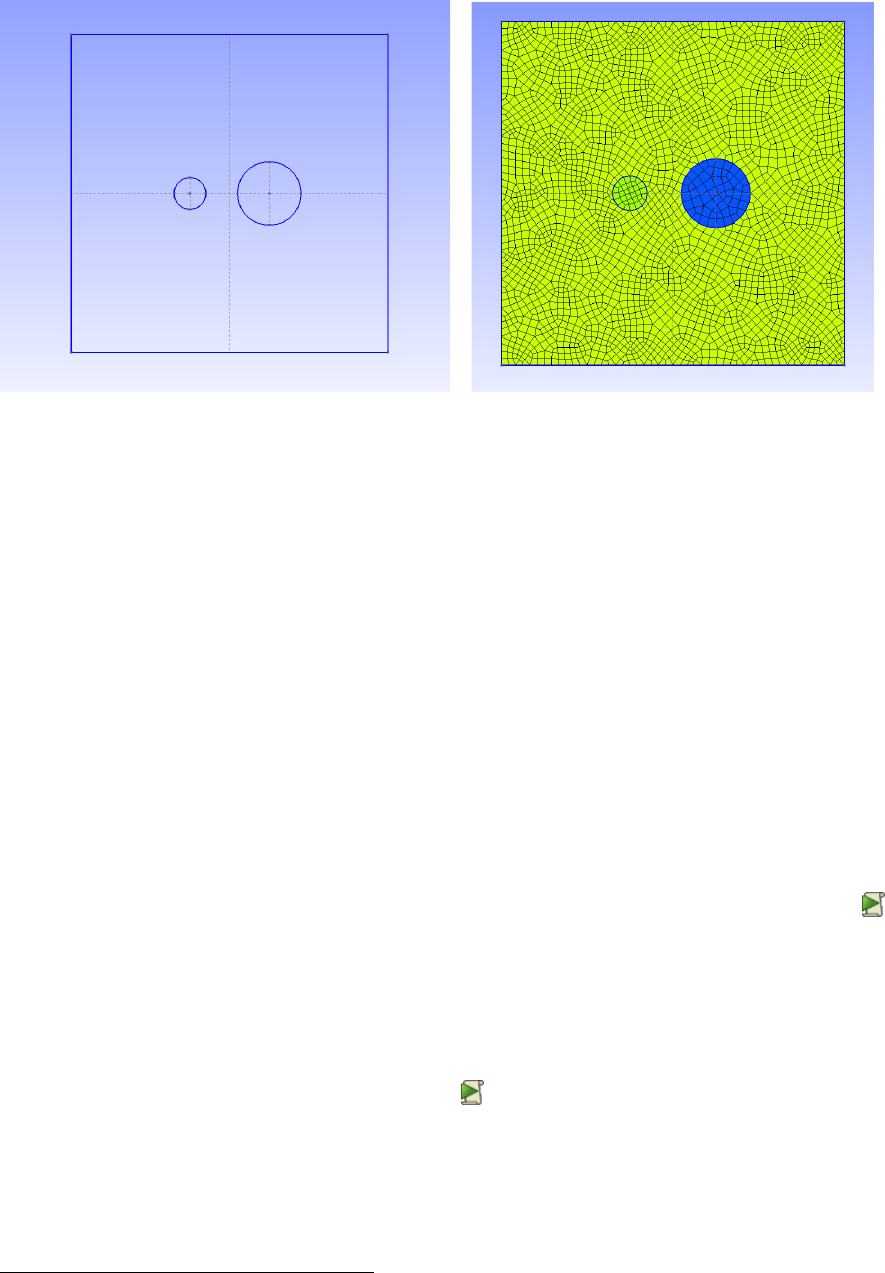
CHAPTER 3. MESH GENERATION 14
Figure 3.3: Geometry and mesh of the two circle model generated with Gmsh
•Material_SqrCirc is the material_file
•Nodes_SqrCirc is the nodes_coords_file
•Surf_abs_SqrCirc is the absorbing_surface_file
•Surf_free_SqrCirc is the free_surface_file
In addition, four files like free_surface_file corresponding to the sides of the model are generated.
3.3 How to use Cubit/Trelis to generate an external mesh
Trelis (that was known as Cubit)2is a 2D/3D finite element grid generator distributed by Csimsoft which can be used
for the generation of quadrangle and hexahedral meshes. Trelis has a convenient interface with Python (module cubit)
which allows to create meshes from Python scripts. To get started with Cubit/Trelis we recommend you the step-
by-step tutorials available at: http://www.csimsoft.com/tutorials.jsp Many powerful graphical tools
are available, and very useful, but we will focus here on the command line functionalities and especially the Python
interface which is the real force of Cubit/Trelis.
To get started we recommend to the inpatients to open Cubit/Trelis and to click on the following symbol: . Then
select the files of type Python Files (*.py) and play the following script:
utils/cubit2specfem2d/simplest2DexampleWithPmls.py
In the case you want to perform an axisymmetric simulation, we recommend you rather to play:
utils/cubit2specfem2d/simpleAxisym2dMesh.py
It will create a simple mesh with PMLs. Then re-click on and play:
utils/cubit2specfem2d/cubit2specfem2d.py
This script will create (in current directory) all the mesh files necessary for a SPECFEM2D simulation. Other com-
mented examples are available. We particularly recommend you to look at the folder
EXAMPLES/paper_axisymmetry_example beginning by reading the README available there. Read care-
fully the comments in these scripts, they are helpful. Another way to use Python together with Cubit/Trelis is to use
2available at http://www.csimsoft.com/

CHAPTER 3. MESH GENERATION 15
the script tab. This tab is a real Python terminal that can be used to pass command line python instruction to Cu-
bit/Trelis through the cubit module. In the case of the Script tab is not visible in the command line panel (at the bottom
of the screen) do:
Tools -> Options... -> Layout [-> Cubit Layout] -> Show script tab
This tab will allow you to play the scripts one line after another directly in Cubit/Trelis. With this you should be able
to understand how to create meshes and export them under SPECFEM2D format.
3.3.1 Note about Cubit/Trelis built-in Python
Beware, there are some (annoying) differences between cubit built-in Python and the actual Python langage:
•"aString" + ’anotherString’ can cause problems even after being stored:
a = "aString"
b = a + ’anotherString’
Example which is not working:
pathToMeshDir = pathToSpecfem + ’EXAMPLES/paper_axisymmetry_example/MESH’
cubit.cmd(’cd \"’+pathToMeshDir+’\"’)
• No comments after double dots:
Example which is not working:
if True: # Just a dummy comment
print "Ok!"
This example works without the comment.
•os.makedirs("~/aDirectory/") does not work. It creates a directory named ~
!!!!! To remove that do: rm -R ./~ AND NEVER rm -rf ~ !!!!!
•sys.argv can not be used
• No comments """ """ at the beginning of a script
And probably many others! Think about that before getting mad.
3.4 Notes about absorbing PMLs
If you use CPML, an additional file listing the CPML elements is needed. Its first line is the total number of CPML
elements, and then a list of all the CPML elements, one per line. The format of these lines is: in the first column the
CPML element number, and in the second column a flag as follows:
Table 3.1: Definition of flags for CPML elements
Flag Meaning
1 element belongs to a X CPML layer only (either in Xmin or in Xmax)
2 element belongs to a Y CPML layer only (either in Ymin or in Ymax)
3 element belongs to both a X and a Y CPML layer (i.e., to a CPML corner)
In order to see how to add PML layers to a mesh / model created with an external mesher such as ‘Gmsh’, see the
examples in directory EXAMPLES/CPML_absorbing_layers.
If you use PML, the mesh elements that belong to the PML layers can be acoustic or elastic, but not viscoelastic nor
poroelastic. Then, when defining your model, you should define these absorbing elements as either acoustic or elastic.
If you forget to do that, the code will fix the problem by automatically converting the viscoelastic or poroelastic PML
CHAPTER 3. MESH GENERATION 16
elements to elastic. This means that strictly speaking the PML layer will not be perfectly matched any more, since the
physical model will change from viscoelastic or poroelastic to elastic at the entrance of the PML, but in practice this
is sufficient and produces only tiny / negligible spurious reflections.
If you use PML and an external mesh (created using an external meshing tool such as Gmsh, CUBIT/TRELIS or
similar), try to have elements inside the PML as regular as possible, i.e. ideally non-deformed rectangles obtained by
‘extrusion’ of the edge mesh elements meshing the outer edges of the computational domain without PML; by doing
so, the PMLs obtained will be far more stable in time (PML being weakly unstable from a mathematical point of view,
very deformed mesh elements inside the PMLs can trigger instabilities much more quickly).
If you have an existing CUBIT (or similar) mesh stored in SPECFEM2D format but do not know how to assign
CPML flags to it, we have created a small serial Fortran program that will do that automatically for you. That program
is utils/CPML/convert_external_layers_of_a_given_mesh_to_CPML_layers2D.f90. When you create the PML layers
using that script, you do not need to mark (i.e. assign to physical entities with a specific name) those external layers in
the mesher. However you still need to specify the boundary of the mesh as you where doing in the case of absorbing
conditions. The script will automatically extract the elements on the PML. It will ask you for a thickness for the
PML layers. Suppose that you have created a region with a 1-meter size element, when it will prompt for the PML
thickness you can enter 3.1 and it will create a PML 3 element thick. Always input a slightly larger (5-10%) size
because the element might be slightly skewed, or if you have not created your PML region via extrusion/webcut in
CUBIT/TRELIS.
To stabilize PMLs it also helps to add a transition layer of geometrically-regular non-PML elements, in which
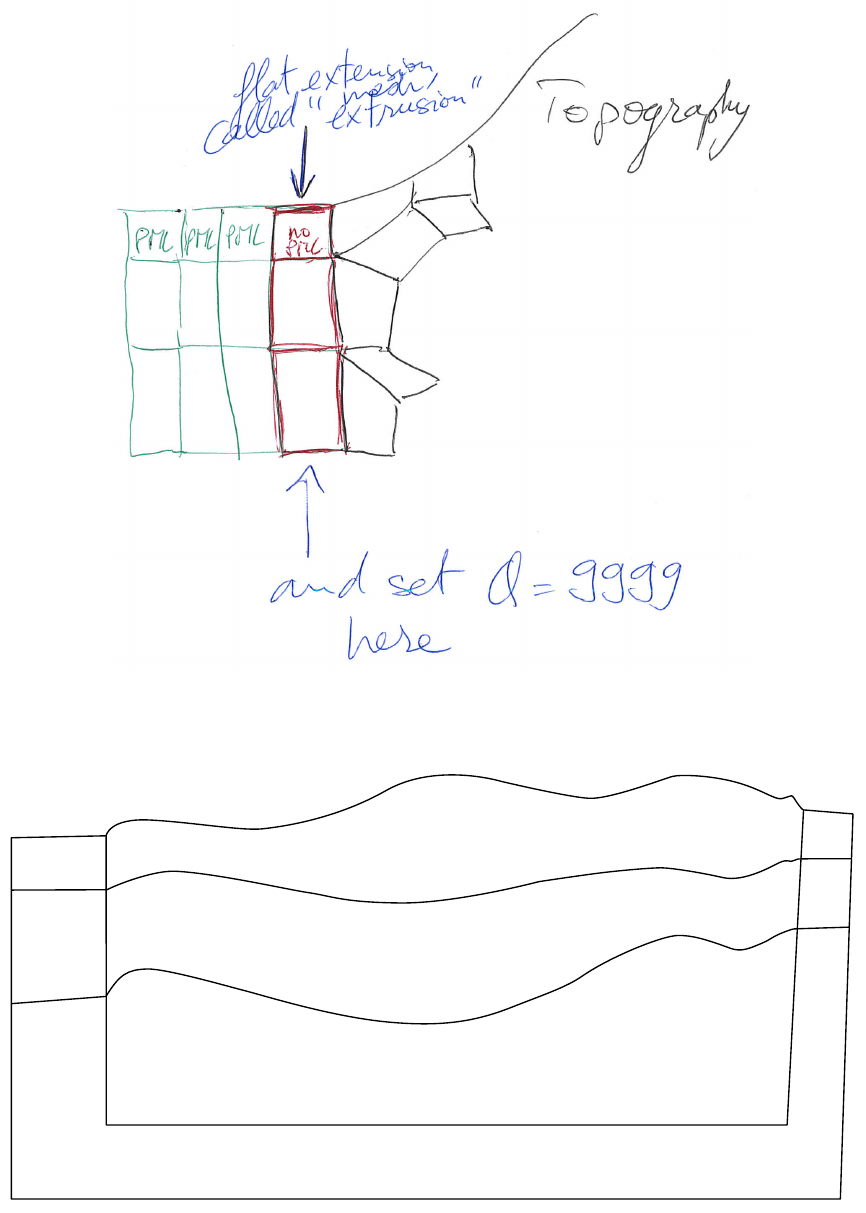
attenuation is also turned off (i.e. Qκ=Qµ= 9999 in that layer), as in the red layer of Figure 3.4. Our tools
in directory in directory utils/CPML should soon (Dimitri: TO DO ONE DAY) implement that transition layer
automatically.
To be more precise:
1/ If one wants to use PML layers, they should NOT mark the layers according to that python script - the reason
is that the xmeshfem2d does not recognize those CPML flags. If whoever developed the script adjusts it to solve this
problem - this might be a great relief for users; as of now no physical identifiers are needed for those layers.
2/ HOWEVER, the "Top", "Bottom", "Left"," and "Right" boundaries of the model, need to be re-assigned to outer
boundaries of the model - that will be the leftmost boundary of the left -bounding PML , rightmost of the right PML,
topmost for the Top PML (if there is one) and the bottom boundary of the bottom layer. Those and only those lines
need to have the mentioned identifiers (opposite to the example with the two-holed square with Stacey conditions).
3/ There is no need to create Top PML in case one wants it to be reflective; as the fortran script that assigns the
flag will ignore the elements that sit within PML-layer thickness distance to the top.
4/ The Fortran program utils/CPML/convert_external_layers_of_a_given_mesh_to_CPML_layers2D.f90 that flags
the PML elements does not create additional elements; it simply takes the elements within chosen distance from the
boundaries, that sit in the interior of model and marks them as absorbing.
If you use PML and an external velocity and density model (e.g., setting flag “MODEL” to tomography), you
should be careful because mathematically a PML cannot handle heterogeneities along the normal to the PML edge
inside the PML layer. This comes from the fact that the damping profile that is defined assumes a constant velocity
and density model along the normal direction. Thus, you need to modify your velocity and density model in order for
it to be 1D inside the PML, as shown in Figure 3.5. This applies to the bottom layer as well; there you should make
sure that your model is 1D and thus constant along the vertical direction. To summarize, only use a 2D velocity and
density model inside the physical region, and in all the PML layers extend it by continuity from its values along the
inner PML edge.
3.5 Controlling the quality of an external mesh
To examine the quality of the elements in your externally build mesh, type
./bin/xcheck_quality_external_mesh
(and answer "3" to the first question asked). This code will tell you which element in the whole mesh has the worst
quality (maximum skewness, i.e. maximum deformation of the element angles) and it should be enough to modify
this element with the external software package used for the meshing, and to repeat the operation until the maximum
CHAPTER 3. MESH GENERATION 17
Figure 3.4: Mesh extrusion for PML (green elements) and a non-PML stabilization layer (red elements).
Use a
horizontally
1D velocity
model here
PML
PML
Use a vertically-1D velocity model here
Figure 3.5: How to modify your external 2D velocity and density model in order to use PML. Such a modification is
not needed when using Stacey absorbing boundary conditions (but such conditions are significantly less efficient).
CHAPTER 3. MESH GENERATION 18
skewness of the whole mesh is less or equal to about 0.75 (above is dangerous: from 0.75 to 0.80 could still work, but
if there is a single element above 0.80 the mesh should be improved).
The code also shows a histogram of 20 classes of skewness which tells how many element are above the skewness
= 0.75, and to which percentage of the total this amounts. To see this histogram, you could type:
gnuplot plot_mesh_quality_histogram.gnu
This tool is useful to estimate the mesh quality and to see it evolve along the successive corrections.
3.6 Controlling how the mesh samples the wave field
To examine (using Gnuplot) how the mesh samples the wave field, type
gnuplot plot_points_per_wavelength_histogram.gnu
and also check the following histogram printed on the screen or in the output file:
histogram of min number of points per S wavelength (P wavelength in
acoustic regions)
(too small: poor resolution of calculations - too big = wasting
memory and CPU time)
(threshold value is around 4.5 points per wavelength in elastic media
and 5.5 in acoustic media)
If you see that you have a significant number of mesh elements below the threshold indicated, then your simulations
will not be accurate and you should create a denser mesh. Conversely, if you have a significant number of mesh
elements above the threshold indicated, the mesh your created is too dense, it will be extremely accurate but the
simulations will be slow; using a coarser mesh would be sufficient and would lead to faster simulations.

Chapter 4
Running the Solver xspecfem2D
To run the solver, type
bin/xspecfem2D
from within the main working directory (use mpirun or equivalent if you compiled with parallel support). This
will output the seismograms and snapshots of the wave fronts at different time steps in directory OUTPUT_FILES/.
To visualize them, type "gs OUTPUT_FILES/vect*.ps" to see the Postscript files (in which the wave field is
represented with small arrows, fluid/solid matching interfaces with a thick pink line, and absorbing edges with a thick
green line) and "gimp OUTPUT_FILES/image*.gif" to see the colour snapshot showing a pixelized image of
one of the two components of the wave field (or pressure, depending on what you have selected for the output in
DATA/Par_file).
Figure 4.1: Wavefield snapshots of the default example generated by xspecfem2D when parameter
output_color_image is set to .true.. To create smaller (subsampled) images you can change double pre-
cision parameter factor_subsample_image = 1.0 to a higher value in file DATA/Par_file. This can be
useful in the case of very large models. The number of pixels of the image in each direction must be smaller than
parameter NX_NZ_IMAGE_MAX defined in file SETUP/constants.h.in, again to avoid creating huge images in
the case of very large models.
Please consider these following points, when running the solver:
• the DATA/Par_file given with the code works fine, you can use it without any modification to test the code
• the seismograms OUTPUT_FILES/*.sem*are simple ASCII files with two columns: time in the first column
and amplitude in the second, therefore they can be visualized with any tool you like, for instance “gnuplot”; if
you prefer to output binary seismograms in Seismic Unix format (which is a simple binary array dump) you can
use parameter SU_FORMAT, in which case all the seismograms will be written to a single file with the extension
*.bin. Depending on your installation of the Seismic Unix package you can use one of these two commands:
19
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 20
surange < Uz_file_single.bin
suoldtonew < Uz_file_single.bin | surange
to see the header info. Replace surange with suxwigb to see wiggle plots for the seismograms.
• if flag MODEL in DATA/Par_file is set to default, the velocity and density model is determined using the
nbmodels and nbregions devices. Otherwise, nbmodels values are ignored and the velocity and density
model is determined from a user supplied file or subroutine.
• when compiling with Intel ifort, use “-assume byterecl” option to create binary PNM images displaying
the wave field
• there are a few useful scripts and Fortran routines in directory utils/.
• you can find a Fortran code to compute the analytical solution for simple media that we use as a reference in
benchmarks in many of our articles at (http://www.spice-rtn.org/library/software/EX2DDIR).
That code is described in: Berg et al. [1994]
Notes about DATA/Par_file parameters
The default DATA/Par_file provided in the root directory of the code contains detailed comments and should
be almost self-explanatory (note that some of the older DATA/Par_file files provided in the EXAMPLES
directory work fine but some of the comments they contain may be obsolete or even wrong; thus refer to the
default DATA/Par_file instead for reliable explanations).
USE_TRICK_FOR_BETTER_PRESSURE This option can only be used so far if all the receivers record pressure and
are in acoustic elements. Use a trick to increase accuracy of pressure seismograms in fluid (acoustic) elements:
use the second derivative of the source for the source time function instead of the source itself, and then record
potential_acoustic() as pressure seismograms instead of potential_dot_dot_acoustic();
this is mathematically equivalent, but numerically significantly more accurate because in the explicit Newmark
time scheme acceleration is accurate at zeroth order while displacement is accurate at second order, thus in fluid
elements potential_dot_dot_acoustic() is accurate at zeroth order while potential_acoustic()
is accurate at second order and thus contains significantly less numerical noise.
READ_VELOCITIES_AT_f0 shift (i.e. change) velocities read from the input file to take average physical disper-
sion into account, i.e. if needed change the reference frequency at which these velocities are defined internally
in the code: by default, the velocity values that are read at the end of this Par_file of the code are supposed to be
the unrelaxed values, i.e. the velocities at infinite frequency. We may want to change this and impose that the
values read are those for a given frequency (here f0_attenuation). (when we do this, velocities will then slightly
decrease and waves will thus slightly slow down)
nbmodels With MODEL = default chosen, a variety of simple velocity and density models can be defined using
the nbmodels device.
I: model_number 1 rho Vp Vs 0 0 QKappa Qmu 0 0 0 0 0 0
II: model_number 2 rho c11 c13 c15 c33 c35 c55 c12 c23 c25 0 0 0
III: model_number 3 rhos rhof phi c kxx kxz kzz Ks Kf Kfr etaf mufr Qmu
IV: model_number -1 0 0 A 0 0 0 0 0 0 0 0 0 0
To make a given region acoustic, use I and make Vs be zero.
To make a given region isotropic elastic, use I and make Vs be nonzero. See Section 4.1 for more details.
To make a given region anisotropic, use II. See Section 4.2 for more details.
To make a given region poroeslatic, use III. See Section 4.3 for more details.
When viscoelasticity is turned on, the Vp and Vs values that are read here are the UNRELAXED ones i.e. the
values at infinite frequency unless the READ_VELOCITIES_AT_f0 parameter above is set to true, in which case
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 21
they are the values at frequency f0. Please also note that Qmu is always equal to Qs, but Qkappa is in general not
equal to Qp. To convert one to the other see doc/note_on_Qkappa_versus_Qp.pdf and utils/attenuation/conversion_from_Qkappa_Qmu_to_Qp_Qs_from_Dahlen_Tromp_959_960.f90.
nbregions With MODEL = default chosen, a variety of simple layered model configurations can be specified
using the nbregions device.
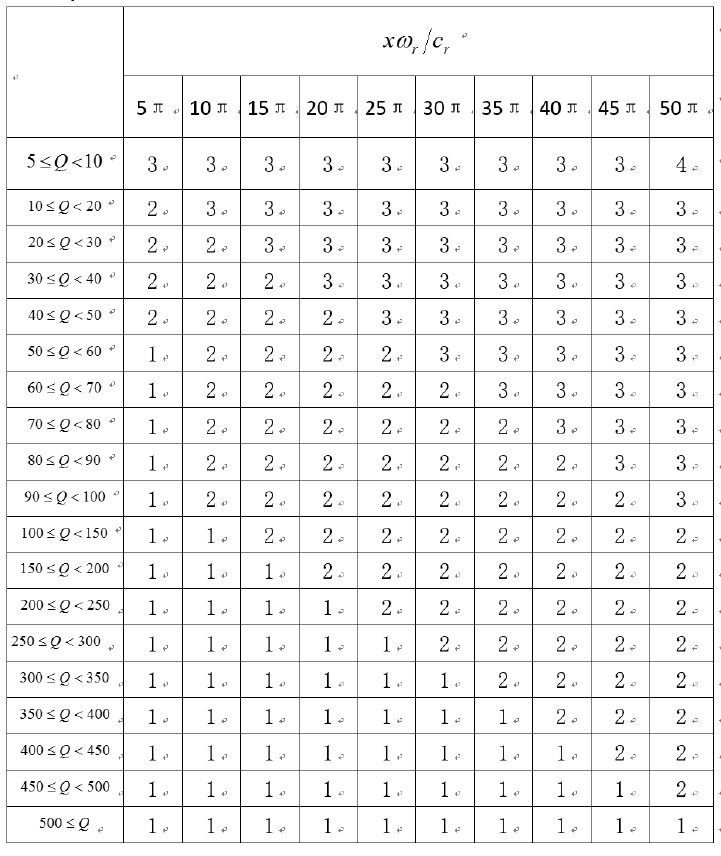
Regarding attenuation (viscoelasticity), in the Par_file you need to select the number of standard linear solids
(N_SLS) to use to mimic a constant Qquality factor. Using N_SLS = 3 is always safe. If (and only if) you know what
you are doing, you can try to reduce that in order to reduce the cost of the simulations. Figure 4.2 shows values that
you can consider using (again, if and only if you know what you are doing). That table has been created by Zhinan
Xie using a comparison between results obtained with a truly-constant Qand results obtained with its approximation
based on N_SLS standard linear solids. The comparison is performed using the time-frequency misfit and goodness-
of-fit criteria proposed by Kristeková et al. [2009]. The table is drawn for a dimensionless parameter representing the
distance of propagation.
Figure 4.2: Table showing how you can select a value of N_SLS smaller than 3, if and only if you know what you are
doing.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 22
Notes about DATA/SOURCE parameters
The SOURCE file located in the DATA/ directory should be edited in the following way:
source_surf Set this flag to .true. to force the source to be located at the surface of the model, otherwise the
sol be placed inside the medium
xs source location xin meters
zs source location zin meters
source_type Set this value equal to 1for elastic forces or acoustic pressure, set this to 2for moment tensor
sources. For a plane wave including converted and reflected waves at the free surface, P wave = 1, S wave = 2,
Rayleigh wave = 3; for a plane wave without converted nor reflected waves at the free surface, i.e. the incident
wave only, P wave = 4, S wave = 5. (incident plane waves are turned on by parameter initialfield in
DATA/Par_file).
time_function_type Choose a source-time function: set this value to 1to use a Ricker, 2the first derivative, 3
a Gaussian, 4a Dirac or 5a Heaviside source-time function.
f0 Set this to the dominant frequency of the source. For point-source simulations using a Heaviside source-time
function (time_function_type = 5), we recommend setting the source frequency parameter f0 equal to
a high value, which corresponds to simulating a step source-time function, i.e., a moment-rate function that is a
delta function.
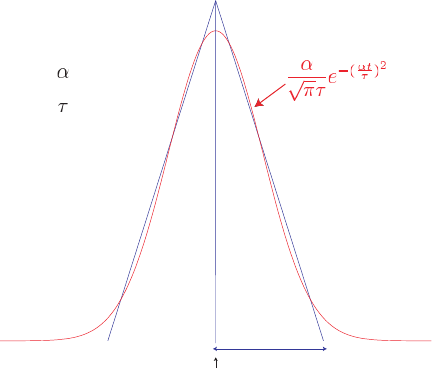
The half duration of a source is obtained by 1/f0. If the code will use a Gaussian source-time function
(time_function_type = 3) (i.e., a signal with a shape similar to a ‘smoothed triangle’, as explained
in Komatitsch and Tromp [2002] and shown in Fig 4.3), the source-time function uses a half-width of half
duration. We prefer to run the solver with half duration set to zero and convolve the resulting synthetic
seismograms in post-processing after the run, because this way it is easy to use a variety of source-time functions.
Komatitsch and Tromp [2002] determined that the noise generated in the simulation by using a step source time
function may be safely filtered out afterward based upon a convolution with the desired source time function
and/or low-pass filtering. Use the serial code convolve_source_timefunction.f90 and the script
convolve_source_timefunction.sh for this purpose, or alternatively use signal-processing software
packages such as SAC (www.llnl.gov/sac). Type
make xconvolve_source_timefunction
to compile the code and then set the parameter hdur in convolve_source_timefunction.sh to the
desired half-duration.
t0 For single sources, we recommend to set the time shift parameter t0 equal to 0.0. The time shift parameter would
simply apply an overall time shift to the synthetics (according to the time shift of the first source), something
that can be done in the post-processing. This time shift parameter can be non-zero when using multiple sources.
anglesource angle of the source (for a force only); for a plane wave, this is the incidence angle. For moment
tensor sources this parameter is unused.
Mxx,Mzz,Mxz Moment tensor components (valid only for moment tensor sources, source_type = 2). Note
that the units for the components of a moment tensor source are different in SPECFEM2D and in SPECFEM3D:
SPECFEM3D: in SPECFEM3D the moment tensor components are in dyne*cm
SPECFEM2D: in SPECFEM2D the moment tensor components are in N*m
To go from strike / dip / slip to CMTSOLUTION moment-tensor format using the classical formulas (of e.g.
Aki and Richards [1980] you can use these two small C programs from SPECFEM3D_GLOBE:
./utils/strike_dip_rake_to_CMTSOLUTION.c
./utils/CMTSOLUTION_to_AkiRichards.c
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 23
half duration
source decay rate
half duration
-
-
tCMT
Figure 4.3: Comparison of the shape of a triangle and the Gaussian function actually used.
but then it is another story to make a good 2D approximation of that, because in plain-strain P-SV what you get
is the equivalent of a line source in the third direction (orthogonal to the plane) rather than a 3D point source
For more details on this see e.g. Section 7.3 "Two-dimensional point sources" of the book of Pilant [1979]. That
book being hard to find, we scanned the related pages in file
discussion_of_2D_sources_and_approximations_from_Pilant_1979.pdf in the same di-
rectory as this users manual. Another very useful reference addressing that is Helmberger and Vidale [1988]
and its recent extension [Li et al.,2014].
factor amplification factor
Note, the zero time of the simulation corresponds to the center of the triangle/Gaussian, or the centroid time of
the earthquake. The start time of the simulation is t=−1.2∗half duration +t0 (the factor 1.2 is to make sure
the moment rate function is very close to zero when starting the simulation; Heaviside functions use a factor 2.0), the
half duration is obtained by 1/f0. If you prefer, you can fix this start time by setting the parameter USER_T0 in the
constants.h file to a positive, non-zero value. The simulation in that case would start at a starting time equal to
-USER_T0.
4.1 How to run elastic wave simulations
For isotropic elastic materials, there are two options:
P-SV: To run a P-SV waves calculation propagating in the x-zplane, set p_sv = .true. in the Par_file.
SH: To run a SH (membrane) waves calculation travelling in the x-zplane with a y-component of motion, set p_sv
= .false.
This feature is only implemented for elastic materials and sensitivity kernels can be calculated (see Tape et al. [2007]
for details on membrane surface waves).
An optional useful Python script called SEM_save_dir.py is provided. It allows one to automatically save all
the parameters and results of a given simulation.
4.2 How to run axisymmetric wave simulations
Axisymmetric simulations are possible in SPECFEM2D. For these simulations the 2D domain simulated is physically
the meridional 2D shape of an axisymmetric 3D domain. We invite you to read our publication [Bottero et al.,2016]
as an introduction. To set the geometry as axisymmetric turn the flag AXISYM to .true. in the Par_file:
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 24
AXISYM = .true.
The left border of the model becomes then a symmetry axis. The wavefield calculated is then physically a 3D wave-
field obtained by revolution of a 2D wavefield around its left border.
Note about the source:
In axisymmetric geometry the whole model is symmetric with respect to this axis, including the source. Hence if the
source is not on the axis it will physically have a circular shape. This is still possible and relevant for some applica-
tions as non destructive testing but is most of the time unwanted. This has to be kept in mind. In acoustic medium, as
an explosion in a fluid is naturally axisymmetric, the wavefield generated has the correct 3D shape. However, if the
source is put in an elastic solid, its 3D radiation pattern will be axisymmetric.
Getting started:
To get started a simple example is available in EXAMPLES/axisymmetric_case_AXISYM_option, we en-
courage you to read the README file you will find there. This example contains an example of the use of AXISYM
option plus a validation using the semi-analytical code OASES (Schmidt [2004]). In this example the domain studied
is a water layer lying above a viscoelastic medium. The source is an explosion in the water and the domain is bounded
with PMLs.
Note about external meshers:
Using external meshers is possible in axisymmetric geometry. An example is available in
EXAMPLES/paper_axisymmetry_example with the mesher Cubit/Trelis (http://www.csimsoft.com/
trelis). We invite you to check this example and read the previous chapter for more details. The only difference
with plane-strain geometry is that SPECFEM2D needs an additional file defining axial elements. The path to this file
has to be given in the Par_file:
axial_elements_file = /path/to/the/axial_elements_file
The axial elements file has the following structure:
48
1 2 8456 8457
2 2 8457 8458
3 2 8458 8459
4 2 8459 8460
623 2 171 204
1053 2 172 9512
1054 2 172 173
1055 2 173 174
...
Which is similar to free surface files. Hence the first line contains the number of axial elements, then the other lines
contain four columns: element id, number of nodes describing an axial element (always 2), first node id, second node
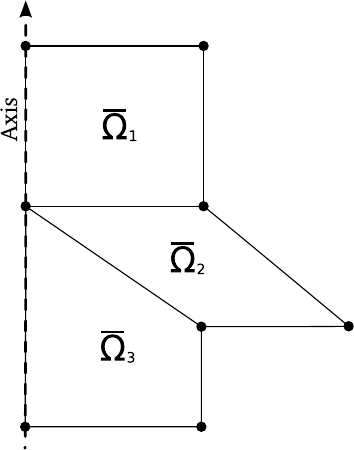
id. Note that the axis elements must include the possible (up and/or down) PMLs elements in contact with the axis. For
simplicity we assume that the mesh elements that are in contact with the symmetry axis are in contact with it by a full
edge rather than by a single point, i.e. we exclude cases as that of Figure 4.4. This amounts to imposing that the left-
most layer of elements in the mesh be structured rather than non structured; The rest of the mesh can be non structured.
Note about the resolution:
In axisymmetry a different quadrature is used in the axial elements making the number of points per wavelength nec-
essary a slightly bigger (≈25%) than in plane-strain.
Note about a small remaining bug:
It has to be noted that a small bug is still hiding somewhere in the code. Indeed the output signals generated are correct
in the whole domain except in the element containing the source. This small bug has not been solved so far but not
prevent to use the code.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 25
Figure 4.4: For simplicity we exclude cases in which the mesh elements that are in contact with the symmetry axis
are in contact with it by a single point instead of by a full edge, such as element ¯
Ω2here. This amounts to imposing
that the leftmost layer of elements in the mesh be structured rather than non structured; The rest of the mesh can be
non structured.
Note about a demo code to learn:
A simplistic demo code is available in
utils/small_SEM_solver_in_Fortran_without_MPI_to_learn. This simple code is useful to learn
how the spectral-element method works in both plane-strain and axisymmetric geometries. Have a look to it if in-
terested. Once in its directory, type ./make_Fortran_2D_axisymmetric.csh and then ./xspecfem2D to
compile and run. The bug discussed above is not present in this small code.
4.3 How to run anisotropic wave simulations
Following Carcione et al. [1988a], we use the classical reduced Voigt notation to represent symmetric tensors [Helbig,
1994,Carcione,2007]:
The constitutive relation of a heterogeneous anisotropic and elastic solid is expressed by the general-
ized Hooke’s law, which can be written as
σij =cijklεkl, i, j, k = 1,...,3,
where tis the time, xis the position vector, σij (x, t)and εij (x, t)are the Cartesian components of the
stress and strain tensors respectively, and cijkl(x)are the components of a fourth-order tensor called the
elasticites of the medium. The Einstein convention for repeated indices is used.
To express the stress-strain relation for a transversely isotropic medium we introduce a shortened
matrix notation commonly used in the literature. With this convention, pairs of subscripts concerning the
elasticities are replaced by a single number according to the following correspondence:
(11) →1,(22) →2,(33) →3,
(23) = (32) →4,(31) = (13) →5,(12) = (21) →6.
Thus in the most general 2D case we have the following convention for the stress-strain relationship:
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 26
! implement anisotropy in 2D
sigma_xx = c11*dux_dx + c13*duz_dz + c15*(duz_dx + dux_dz)
sigma_zz = c13*dux_dx + c33*duz_dz + c35*(duz_dx + dux_dz)
sigma_xz = c15*dux_dx + c35*duz_dz + c55*(duz_dx + dux_dz)
! sigma_yy is not equal to zero in the plane strain formulation
! but is used only in post-processing if needed,
! to compute pressure for display or seismogram recording purposes
sigma_yy = c12*dux_dx + c23*duz_dz + c25*(duz_dx + dux_dz)
where the notations are for instance duz_dx = d(Uz) / dx.
4.4 How to run poroelastic wave simulations
Check the following new inputs in Par_file:
In section "# geometry of model and mesh description":
TURN_VISCATTENUATION_ON,Q0, and FREQ0 deal with viscous damping in a poroelastic medium. Q0 is
the quality factor set at the central frequency FREQ0. For more details see Morency and Tromp [2008].
In section "# time step parameters":
SIMULATION_TYPE defines the type of simulation
(1) forward simulation
(2) UNUSED (purposely, for compatibility with the numbering convention used in our 3D codes)
(3) adjoint method and kernels calculation
In section "# source parameters":
The code now support multiple sources. NSOURCE is the number of sources. Parameters of the sources are
displayed in the file SOURCE, which must be in the directory DATA/. The components of a moment tensor
source must be given in N.m, not in dyne.cm as in the DATA/CMTSOLUTION source file of the 3D version of
the code.
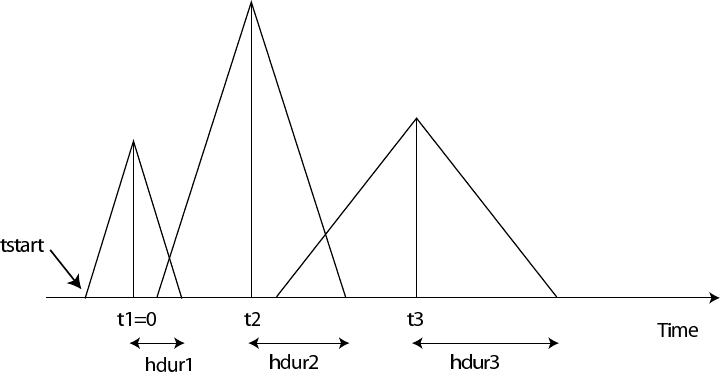
Figure 4.5: Example of timing for three sources. The center of the first source triangle is defined to be time zero. Note
that this is NOT in general the hypocentral time, or the start time of the source (marked as tstart). The time shift
parameter t0 in the SOURCE file would be t1(= 0),t2,t3in this case, and the half-duration parameter, f0, would be
hdur1 = 1/f01,hdur2 = 1/f02,hdur3 = 1/f03for the sources 1, 2, 3 respectively.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 27
In section "# receiver line parameters for seismograms":
SAVE_FORWARD determines if the last frame of a forward simulation is saved (.true.) or not (.false)
In section "# define models....":
There are three possible types of models:
I: (model_number 1 rho Vp Vs 0 0 QKappa Qmu 0 0 0 0 0 0) or
II: (model_number 2 rho c11 c13 c15 c33 c35 c55 c12 c23 c25 0 0 0) or
III: (model_number 3 rhos rhof phi c kxx kxz kzz Ks Kf Kfr etaf mufr Qmu).
For isotropic elastic/acoustic material use Iand set Vs to zero to make a given model acoustic, for anisotropic
elastic use II, and for isotropic poroelastic material use III. The mesh can contain acoustic, elastic, and
poroelastic models simultaneously.
For anisotropic elastic media the last three parameters, c12 c23 c25, are used only when the user asks
the code to compute pressure for display or seismogram recording purposes. Thus, if you do not know these
parameters for your anisotropic material and/or if you do not plan to display or record pressure you can ignore
them and set them to zero. When pressure is used these three parameters are needed because the code needs to
compute σyy, which is not equal to zero in the plane strain formulation.
rho_s = solid density
rho_f = fluid density
phi = porosity
tort = tortuosity
permxx = xx component of permeability tensor
permxz = xz,zx components of permeability tensor
permzz = zz component of permeability tensor
kappa_s = solid bulk modulus
kappa_f = fluid bulk modulus
kappa_fr = frame bulk modulus
eta_f = fluid viscosity
mu_fr = frame shear modulus
Qmu = shear quality factor
Note: for the poroelastic case, mu_s is irrelevant. For details on the poroelastic theory see Morency and Tromp
[2008].
get_poroelastic_velocities.f90 allows to compute cpI, cpII, and cs function of the source dominant
frequency. Notice that for this calculation we use permxx and the dominant frequency of the first source, f0(1).
Caution if you use several sources with different frequencies and if you consider anistropic permeability.
4.5 Coupled simulations
The code supports acoustic/elastic, acoustic/poroelastic, elastic/poroelastic, and acoustic, elastic/poroelastic simula-
tions. Elastic/poroelastic coupling supports anisotropy, but not attenuation for the elastic material.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 28
4.6 How to choose the time step
Three different explicit conditionally-stable time schemes can be used for elastic, acoustic (fluid) or coupled elas-
tic/acoustic media: the Newmark method, the low-dissipation and low-dispersion fourth-order six-stage Runge-Kutta
method (LDDRK4-6) presented in Berland et al. [2006], and the classical fourth-order four-stage Runge-Kutta (RK4)
method. Currently the last two methods are not implemented for poroelastic media. According to De Basabe and Sen
[2010] and Berland et al. [2006], with different degrees N=N GLLX −1of the GLL basis functions the CFL bounds
are given in the following tables. Note that by default the SPECFEM solver uses NGLLX = 5 and thus a degree N=
4, which is thus the value you should use in most cases in the following tables. You can directly compare these values
with the value given in sentence ‘Max stability for P wave velocity’ in file output_solver.txt to see whether you
set the correct ∆tin Par_file or not. For elastic simulation, the CFL value given in output_solver.txt does
not consider the Vp/Vsratio, but the CFL limit slight decreases when Vp/Vsincreases. In viscoelastic simulations the
CFL limit does not change compared to the elastic case because we use a rational approximation of a constant quality
factor Q, which has no attenuation effect on zero-frequency waves. Additionally, if you use C-PML absorbing layers in
your simulations, which are implemented for the Newmark and LDDRK4-6 techniques but not for the classical RK4),
the CFL upper limit decreases to approximately 95% of the limit without absorbing layers in the case of Newmark and
to 85% in the case of LDDRK4-6.
Table 4.1: CFL upper bound for an acoustic (fluid) simulation.
Degree NNewmark LDDRK4-6 RK4
1 0.709 1.349 1.003
2 0.577 1.098 0.816
3 0.593 1.129 0.839
4 0.604 1.150 0.854
5 0.608 1.157 0.860
6 0.608 1.157 0.860
7 0.608 1.157 0.860
8 0.607 1.155 0.858
9 0.607 1.155 0.858
10 0.607 1.155 0.858
Table 4.2: CFL upper bound for an elastic simulation with Vp/Vs=√2.
Degree NNewmark LDDRK4-6 RK4
1 0.816 1.553 1.154
2 0.666 1.268 0.942
3 0.684 1.302 0.967
4 0.697 1.327 0.986
5 0.700 1.332 0.990
6 0.700 1.332 0.990
7 0.700 1.332 0.990
8 0.699 1.330 0.989
9 0.698 1.328 0.987
10 0.698 1.328 0.987
4.7 How to set plane waves as initial conditions
To simulate propagation of incoming plane waves in the simulation domain, initial conditions based on analytical
formulae of plane waves in homogeneous model need to be set. No additional body or boundary forces are required.
To set up this scenario:

CHAPTER 4. RUNNING THE SOLVER XSPECFEM2D 29
Par_file:
• switch on initialfield = .true.
• at this point setting add_bielak_condition does not seem to help with absorbing boundaries, there-
fore, it should be turned off.
SOURCE:
•zs has to be the same as the height of the simulation domain defined in interfacesfile.
•xs is the x-coordinate of the intersection of the initial plane wave front with the free surface.
•source_type = 1 for a plane P wave, 2 for a plane SV wave, 3 for a Rayleigh wave.
•angleforce can be negative to indicate a plane wave incident from the right (instead of the left)
4.8 Note on the viscoelastic model used
The model used is a constant Q, thus with no dependence on frequency (Q(f)= constant). See e.g. Blanc et al. [2016].
However in practice for technical reasons it is approximated based on the sum of different Generalized Zener body
mechanisms and thus the code outputs the band in which the approximation is very good, outside of that range it
can be less accurate. The logarithmic center of that frequency band is the f0 parameter defined (in Hz) in input file
DATA/SOURCE.
4.9 Note on viscoelasticity in the 2D plane strain approximation
In 2D plane strain, one spatial dimension is much greater than the others (see for example: http://www.engineering.
ucsb.edu/~hpscicom/projects/stress/introge.pdf) and thus κ=λ+µin 2D plane strain (in-
stead of κ=λ+2
3µin 3D). See for example Carcione et al. [1988b] equation (A9), and equation 6 in http:
//cherrypit.princeton.edu/papers/paper-99.pdf.
In 2D axisymmetric I think the 2/3 coefficient is OK, but it would be worth doublechecking.
Chapter 5
Adjoint Simulations
5.1 How to obtain finite sensitivity kernels
1. Run a forward simulation:
•SIMULATION_TYPE = 1
•SAVE_FORWARD = .true.
•seismotype = 1 (we need to save the displacement fields to later on derive the adjoint source. Note: if
the user forgets it, the program corrects it when reading the proper SIMULATION_TYPE and SAVE_FORWARD
combination and a warning message appears in the output file)
Important output files (for example, for the elastic case, P-SV waves):
•absorb_elastic_bottom*****.bin
•absorb_elastic_left*****.bin
•absorb_elastic_right*****.bin
•absorb_elastic_top*****.bin
•lastframe_elastic*****.bin
•AA.S****.BXX.semd
•AA.S****.BXZ.semd
2. Define the adjoint source:
• Use adj_seismogram.f90
• Edit to update NSTEP,nrec,t0,deltat, and the position of the cut to pick any given phase if needed
(tstart,tend), add the right number of stations, and put one component of the source to zero if needed.
• The output files of adj_seismogram.f90 are AA.S****.BXX.adj and AA.S****.BXZ.adj,
for P-SV waves (and AA.S****.BXY.adj, for SH (membrane) waves). Note that you will need these
three files (AA.S****.BXX.adj,AA.S****.BXY.adj and AA.S****.BXZ.adj) to be present in
the SEM/ directory together with the absorb_elastic_****.bin and lastframe_elastic.bin
files to be read when running the adjoint simulation.
3. Run the adjoint simulation:
• Make sure that the adjoint source files absorbing boundaries and last frame files are in the OUTPUT_FILES/
directory.
•SIMULATION_TYPE = 3
•SAVE_FORWARD = .false.
30
CHAPTER 5. ADJOINT SIMULATIONS 31
Output files (for example for the elastic case):
•snapshot_rho_kappa_mu*****
•snapshot_rhop_alpha_beta*****
which are the primary moduli kernels and the phase velocities kernels respectively, in ascii format and at the
local level, that is as “kernels(i,j,ispec)”.
5.2 Remarks about adjoint runs and solving inverse problems
SPECFEM2D can produce the gradient of the misfit function for a tomographic inversion, but options for using the
gradient within an iterative inversion are left to the user (e.g., conjugate-gradient, steepest descent). The plan is to
include some examples in the future.
The algorithm is simple:
1. calculate the forward wave field s(x, t)
2. calculate the adjoint wave field s†(x, t)
3. calculate their interaction s(x, t)·s†(x, T −t)(these symbolic, temporal and spatial derivatives should be
included)
4. integrate the interactions, which is summation in the code.
That is all. Step 3 has some tricks in implementation, but which can be skipped by regular users.
If you look into SPECFEM2D, besides “rhop_ac_kl” and “rho_ac_kl”, there are more variables such as
“kappa_ac_kl” and “rho_el_kl” etc. “rho” denotes density ρ(“kappa” for bulk modulus κetc.), “ac”
denotes acoustic (“el” for elastic), “kl” means kernel (and you may find “k” as well, which is the interaction at each
time step, i.e., before doing time integration).
5.3 Caution
Please note that:
• at the moment, adjoint simulations do not support anisotropy, attenuation, and viscous damping.
• you will need AA.S****.BXX.adj,AA.S****.BXY.adj and AA.S****.BXZ.adj to be present in
directory SEM/ even if you are just running an acoustic or poroelastic adjoint simulation.
–AA.S****.BXX.adj is the only relevant component for an acoustic case.
–AA.S****.BXX.adj and AA.S****.BXZ.adj are the only relevant components for a poroelastic
case.
Chapter 6
Doing tomography, i.e., updating the model
based on the sensitivity kernels obtained
The process is described in the same chapter of the manual of SPECFEM3D. Please refer to it.
32

Chapter 7
Oil and gas industry simulations
The SPECFEM2D package provides compatibility with industrial (oil and gas industry) types of simulations. These
features include importing Seismic Unix (SU) format wavespeed models into SPECFEM2D, output of seismograms
in SU format with a few key parameters defined in the trace headers and reading adjoint sources in SU format etc.
There is one example given in EXAMPLES/INDUSTRIAL_FORMAT, which you can follow.
We also changed the relationship between adjoint potential and adjoint displacement in fluid region (the relation-
ship between forward potential and forward displacement remains the same as previously defined). The new definition
is critical when there are adjoint sources (in other words, receivers) in the acoustic domain, and is the direct conse-
quence of the optimization problem.
s≡1
ρ∇φ
p≡ −κ(∇ · s) = −∂2
tφ
∂2
ts†≡ −1
ρ∇φ†
p†≡ −κ∇ · s†=φ†
33
Chapter 8
Information for developers of the code, and
for people who want to learn how the
technique works
You can get a very simple 1D version of a demo code (there is one in Fortran and one in Python):
git clone --recursive https://github.com/geodynamics/specfem1d.git
We also have simple 3D demo source codes that implement the SEM in a single, small program, in directory
utils/small_SEM_solvers_in_Fortran_and_C_without_MPI_to_learn of the specfem3d package. They are useful to
learn how the spectral-element method works, and how to write or modify a code to implement it. Also useful to test
new ideas by modifying these simple codes to run some tests. We also have a similar, even simpler, demo source code
for the 2D case in directory
utils/small_SEM_solver_in_Fortran_without_MPI_to_learn of the specfem2d package.
For information on how to contribute to the code, i.e., for how to make your modifications, additions or improvements
part of the official package, see https://github.com/geodynamics/specfem3d/wiki .
34
Notes & Acknowledgments
The Gauss-Lobatto-Legendre subroutines in gll_library.f90 are based in part on software libraries from the
Massachusetts Institute of Technology, Department of Mechanical Engineering (Cambridge, Massachusetts, USA).
The non-structured global numbering software was provided by Paul F. Fischer (Brown University, Providence, Rhode
Island, USA, now at Argonne National Laboratory, USA).
Please e-mail your feedback, bug reports, questions, comments, and suggestions to the CIG Computational Seis-
mology Mailing List (cig-seismo@geodynamics.org).
35

Copyright
Main historical authors: Dimitri Komatitsch and Jeroen Tromp
CNRS, France and Princeton University, USA
© October 2017
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public
License as published by the Free Software Foundation (see Appendix B).
Please note that by contributing to this code, the developer understands and agrees that this project and contribution
are public and fall under the open source license mentioned above.
Evolution of the code:
version 7.0, Dimitri Komatitsch, Zhinan Xie, Paul Cristini, Roland Martin and Rene Matzen, July 2012:
added support for Convolution PML absorbing layers; added higher-order time schemes (4th order Runge-Kutta and
LDDRK4-6); many small or moderate bug fixes
version 6.2, many developers, April 2011:
restructured package source code into separate src/ directories; added configure & Makefile scripts and a PDF manual
in doc/; added user examples in EXAMPLES/; added a USER_T0 parameter to fix the onset time in simulation
version 6.1, Christina Morency and Pieyre Le Loher, March 2010:
added SH (membrane) waves calculation for elastic media; added support for external fully anisotropic media; fixed
some bugs in acoustic kernels
version 6.0, Christina Morency and Yang Luo, August 2009:
support for poroelastic media; adjoint method for acoustic/elastic/poroelastic
version 5.2, Dimitri Komatitsch, Nicolas Le Goff and Roland Martin, February 2008:
support for CUBIT and GiD meshes; MPI implementation of the code based on domain decomposition with METIS
or SCOTCH; general fluid/solid implementation with any number, shape and orientation of matching edges; fluid po-
tential of density ∗displacement instead of displacement; absorbing edges with any normal vector; general numbering
of absorbing and acoustic free surface edges; cleaned implementation of attenuation as in Carcione (1993); merged
loops in the solver for efficiency; simplified input of external model; added CPU time information; translated many
comments from French to English
version 5.1, Dimitri Komatitsch, January 2005:
more general mesher with any number of curved layers; Dirac and Gaussian time sources and corresponding convo-
lution routine; option for acoustic medium instead of elastic; receivers at any location, not only grid points; moment-
tensor source at any location, not only a grid point; color snapshots; more flexible DATA/Par_file with any number of
comment lines; Xsu scripts for seismograms; subtract t0 from seismograms; seismograms and snapshots in pressure
in addition to vector field
version 5.0, Dimitri Komatitsch, May 2004:
36
CHAPTER 8. INFORMATION FOR DEVELOPERS OF THE CODE, AND FOR PEOPLE WHO WANT TO LEARN HOW THE TECHNIQUE WORKS37
got rid of useless routines, suppressed commons etc.; weak formulation based explicitly on stress tensor; implementa-
tion of full anisotropy; implementation of attenuation based on memory variables
based on SPECFEM2D version 4.2, June 1998
(c) by Dimitri Komatitsch, Harvard University, USA and Jean-Pierre Vilotte, Institut de Physique du Globe de Paris,
France
itself based on SPECFEM2D version 1.0, 1995
(c) by Dimitri Komatitsch and Jean-Pierre Vilotte, Institut de Physique du Globe de Paris, France
Bibliography
C. A. Acosta Minolia and D. A. Kopriva. Discontinuous Galerkin spectral element approximations on moving meshes.
J. Comput. Phys., 230(5):1876–1902, 2011. doi: 10.1016/j.jcp.2010.11.038.
M. Ainsworth and H. Wajid. Dispersive and dissipative behavior of the spectral element method. SIAM Journal on
Numerical Analysis, 47(5):3910–3937, 2009. doi: 10.1137/080724976.
M. Ainsworth and H. Wajid. Optimally blended spectral-finite element scheme for wave propagation and nonstandard
reduced integration. SIAM Journal on Numerical Analysis, 48(1):346–371, 2010. doi: 10.1137/090754017.
M. Ainsworth, P. Monk, and W. Muniz. Dispersive and dissipative properties of discontinuous Galerkin finite element
methods for the second-order wave equation. Journal of Scientific Computing, 27(1):5–40, 2006. doi: 10.1007/
s10915-005-9044-x.
K. Aki and P. G. Richards. Quantitative seismology, theory and methods. W. H. Freeman, San Francisco, USA, 1980.
700 pages.
D. N. Arnold. An interior penalty finite element method with discontinuous elements. SIAM Journal on Numerical
Analysis, 19(4):742–760, 1982. doi: 10.1137/0719052.
M. Benjemaa, N. Glinsky-Olivier, V. M. Cruz-Atienza, J. Virieux, and S. Piperno. Dynamic non-planar crack rupture
by a finite volume method. Geophys. J. Int., 171(1):271–285, 2007. doi: 10.1111/j.1365-246X.2006.03500.x.
M. Benjemaa, N. Glinsky-Olivier, V. M. Cruz-Atienza, and J. Virieux. 3D dynamic rupture simulation by a finite
volume method. Geophys. J. Int., 178(1):541–560, 2009. doi: 10.1111/j.1365-246X.2009.04088.x.
P. Berg, F. If, P. Nielsen, and O. Skovegaard. Analytic reference solutions. In K. Helbig, editor, Modeling the Earth for
oil exploration, Final report of the CEC’s GEOSCIENCE I Program 1990-1993, pages 421–427. Pergamon Press,
Oxford, United Kingdom, 1994.
J. Berland, C. Bogey, and C. Bailly. Low-dissipation and low-dispersion fourth-order Runge-Kutta algorithm. Com-
puters and Fluids, 35:1459–1463, 2006.
M. Bernacki, S. Lanteri, and S. Piperno. Time-domain parallel simulation of heterogeneous wave propagation on
unstructured grids using explicit, nondiffusive, discontinuous Galerkin methods. J. Comput. Acoust., 14(1):57–81,
2006.
C. Bernardi, Y. Maday, and A. T. Patera. A new nonconforming approach to domain decomposition: the Mortar
element method. In H. Brezis and J. L. Lions, editors, Nonlinear partial differential equations and their applications,
Séminaires du Collège de France, pages 13–51, Paris, 1994. Pitman.
E. Blanc, D. Komatitsch, E. Chaljub, B. Lombard, and Z. Xie. Highly accurate stability-preserving optimization of
the Zener viscoelastic model, with application to wave propagation in the presence of strong attenuation. Geophys.
J. Int., 205(1):427–439, 2016. doi: 10.1093/gji/ggw024.
A. Bottero, P. Cristini, D. Komatitsch, and M. Asch. An axisymmetric time-domain spectral-element method for full-
wave simulations: Application to ocean acoustics. J. Acoust. Soc. Am., 140(5):3520–3530, 2016. doi: 10.1121/1.
4965964.
38
BIBLIOGRAPHY 39
F. Bourdel, P.-A. Mazet, and P. Helluy. Resolution of the non-stationary or harmonic Maxwell equations by a discon-
tinuous finite element method: Application to an E.M.I. (electromagnetic impulse) case. In Proceedings of the 10th
international conference on computing methods in applied sciences and engineering, pages 405–422, Commack,
NY, USA, 1991. Nova Science Publishers.
J. M. Carcione. Wave fields in real media: Theory and numerical simulation of wave propagation in anisotropic,
anelastic, porous and electromagnetic media. Elsevier Science, Amsterdam, The Netherlands, second edition,
2007.
J. M. Carcione, D. Kosloff, and R. Kosloff. Wave propagation simulation in an elastic anisotropic (transversely
isotropic) solid. Q. J. Mech. Appl. Math., 41(3):319–345, 1988a.
J. M. Carcione, D. Kosloff, and R. Kosloff. Wave propagation simulation in a linear viscoelastic medium. Geophys. J.
Int., 95:597–611, 1988b.
L. Carrington, D. Komatitsch, M. Laurenzano, M. Tikir, D. Michéa, N. Le Goff, A. Snavely, and J. Tromp. High-
frequency simulations of global seismic wave propagation using SPECFEM3D_GLOBE on 62 thousand processor
cores. In Proceedings of the SC’08 ACM/IEEE conference on Supercomputing, pages 60:1–60:11, Austin, Texas,
USA, Nov. 2008. IEEE Press. doi: 10.1145/1413370.1413432. Article #60, Gordon Bell Prize finalist article.
F. Casadei and E. Gabellini. Implementation of a 3D coupled Spectral Element solver for wave propagation and
soil-structure interaction simulations. Technical report, European Commission Joint Research Center Report
EUR17730EN, Ispra, Italy, 1997.
E. Chaljub. Modélisation numérique de la propagation d’ondes sismiques en géométrie sphérique : application à la
sismologie globale (Numerical modeling of the propagation of seismic waves in spherical geometry: application to
global seismology). PhD thesis, Université Paris VII Denis Diderot, Paris, France, 2000.
E. Chaljub, Y. Capdeville, and J. P. Vilotte. Solving elastodynamics in a fluid-solid heterogeneous sphere: a parallel
spectral-element approximation on non-conforming grids. J. Comput. Phys., 187(2):457–491, 2003.
E. Chaljub, D. Komatitsch, J. P. Vilotte, Y. Capdeville, B. Valette, and G. Festa. Spectral element analysis in seismol-
ogy. In R.-S. Wu and V. Maupin, editors, Advances in wave propagation in heterogeneous media, volume 48 of
Advances in Geophysics, pages 365–419. Elsevier - Academic Press, London, UK, 2007.
B. Cockburn, G. E. Karniadakis, and C.-W. Shu. Discontinuous Galerkin Methods: Theory, Computation and Appli-
cations. Springer-Verlag, Heidelberg, Germany, 2000.
G. Cohen. Higher-order numerical methods for transient wave equations. Springer-Verlag, Berlin, Germany, 2002.
349 pages.
G. Cohen, P. Joly, and N. Tordjman. Construction and analysis of higher-order finite elements with mass lumping for
the wave equation. In R. Kleinman, editor, Proceedings of the second international conference on mathematical
and numerical aspects of wave propagation, pages 152–160. SIAM, Philadelphia, Pennsylvania, USA, 1993.
J. D. De Basabe and M. K. Sen. Grid dispersion and stability criteria of some common finite-element methods for
acoustic and elastic wave equations. Geophysics, 72(6):T81–T95, 2007. doi: 10.1190/1.2785046.
J. D. De Basabe and M. K. Sen. Stability of the high-order finite elements for acoustic or elastic wave propagation
with high-order time stepping. Geophys. J. Int., 181(1):577–590, 2010. doi: 10.1111/j.1365-246X.2010.04536.x.
J. D. De Basabe, M. K. Sen, and M. F. Wheeler. The interior penalty discontinuous Galerkin method for elastic wave
propagation: grid dispersion. Geophys. J. Int., 175(1):83–93, 2008. doi: 10.1111/j.1365-246X.2008.03915.x.
J. de la Puente, J. P. Ampuero, and M. Käser. Dynamic rupture modeling on unstructured meshes using a discontinuous
Galerkin method. J. Geophys. Res., 114:B10302, 2009. doi: 10.1029/2008JB006271.
M. O. Deville, P. F. Fischer, and E. H. Mund. High-Order Methods for Incompressible Fluid Flow. Cambridge
University Press, Cambridge, United Kingdom, 2002. 528 pages.
BIBLIOGRAPHY 40
M. Dumbser and M. Käser. An arbitrary high-order discontinuous Galerkin method for elastic waves on un-
structured meshes-II. The three-dimensional isotropic case. Geophys. J. Int., 167(1):319–336, 2006. doi:
10.1111/j.1365-246X.2006.03120.x.
V. Étienne, E. Chaljub, J. Virieux, and N. Glinsky. An hp-adaptive discontinuous Galerkin finite-element method for
3-D elastic wave modelling. Geophys. J. Int., 183(2):941–962, 2010. doi: 10.1111/j.1365-246X.2010.04764.x.
E. Faccioli, F. Maggio, R. Paolucci, and A. Quarteroni. 2D and 3D elastic wave propagation by a pseudo-spectral
domain decomposition method. J. Seismol., 1:237–251, 1997.
R. S. Falk and G. R. Richter. Explicit finite element methods for symmetric hyperbolic equations. SIAM Journal on
Numerical Analysis, 36(3):935–952, 1999. doi: 10.1137/S0036142997329463.
F. X. Giraldo, J. S. Hesthaven, and T. Warburton. Nodal high-order discontinuous Galerkin methods for the spherical
shallow water equations. J. Comput. Phys., 181(2):499–525, 2002. doi: 10.1006/jcph.2002.7139.
L. Godinho, P. A. Mendes, A. Tadeu, A. Cadena-Isaza, C. Smerzini, F. J. Sánchez-Sesma, R. Madec, and D. Ko-
matitsch. Numerical simulation of ground rotations along 2D topographical profiles under the incidence of elastic
plane waves. Bull. seism. Soc. Am., 99(2B):1147–1161, 2009. doi: 10.1785/0120080096.
W. Gropp, E. Lusk, and A. Skjellum. Using MPI, portable parallel programming with the Message-Passing Interface.
MIT Press, Cambridge, USA, 1994.
M. J. Grote, A. Schneebeli, and D. Schötzau. Discontinuous Galerkin finite element method for the wave equation.
SIAM Journal on Numerical Analysis, 44(6):2408–2431, 2006. doi: 10.1137/05063194X.
K. Helbig. Foundations of anisotropy for exploration seismics. In K. Helbig and S. Treitel, editors, Handbook of
Geophysical exploration, section I: Seismic exploration, volume 22. Pergamon, Oxford, England, 1994.
D. V. Helmberger and J. E. Vidale. Modeling strong motions produced by earthquakes with two-dimensional numerical
codes. Bull. seism. Soc. Am., 78(1):109–121, 1988.
F. Q. Hu, M. Y. Hussaini, and P. Rasetarinera. An analysis of the discontinuous Galerkin method for wave propagation
problems. J. Comput. Phys., 151(2):921–946, 1999. doi: 10.1006/jcph.1999.6227.
F. B. Jensen, W. Kuperman, M. Porter, and H. Schmidt. Computational Ocean Acoustics. Springer-Verlag, Berlin,
Germany, 2nd edition, 2011. 794 pages.
C. Johnson and J. Pitkäranta. An analysis of the discontinuous Galerkin method for a scalar hyperbolic equation.
Math. Comp., 46:1–26, 1986. doi: 10.1090/S0025-5718-1986-0815828-4.
D. Komatitsch. Méthodes spectrales et éléments spectraux pour l’équation de l’élastodynamique 2D et 3D en milieu
hétérogène (Spectral and spectral-element methods for the 2D and 3D elastodynamics equations in heterogeneous
media). PhD thesis, Institut de Physique du Globe, Paris, France, 1997. 187 pages.
D. Komatitsch. Fluid-solid coupling on a cluster of GPU graphics cards for seismic wave propagation. C. R. Acad.
Sci., Ser. IIb Mec., 339:125–135, 2011. doi: 10.1016/j.crme.2010.11.007.
D. Komatitsch and R. Martin. An unsplit convolutional Perfectly Matched Layer improved at grazing incidence for
the seismic wave equation. Geophysics, 72(5):SM155–SM167, 2007. doi: 10.1190/1.2757586.
D. Komatitsch and J. Tromp. Introduction to the spectral-element method for 3-D seismic wave propagation. Geophys.
J. Int., 139(3):806–822, 1999. doi: 10.1046/j.1365-246x.1999.00967.x.
D. Komatitsch and J. Tromp. Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys.
J. Int., 149(2):390–412, 2002. doi: 10.1046/j.1365-246X.2002.01653.x.
D. Komatitsch and J. P. Vilotte. The spectral-element method: an efficient tool to simulate the seismic response of 2D
and 3D geological structures. Bull. seism. Soc. Am., 88(2):368–392, 1998.
BIBLIOGRAPHY 41
D. Komatitsch, R. Martin, J. Tromp, M. A. Taylor, and B. A. Wingate. Wave propagation in 2-D elastic media
using a spectral element method with triangles and quadrangles. J. Comput. Acoust., 9(2):703–718, 2001. doi:
10.1142/S0218396X01000796.
D. Komatitsch, S. Tsuboi, C. Ji, and J. Tromp. A 14.6 billion degrees of freedom, 5 teraflops, 2.5 terabyte earthquake
simulation on the Earth Simulator. In Proceedings of the SC’03 ACM/IEEE conference on Supercomputing, pages
4–11, Phoenix, Arizona, USA, Nov. 2003. ACM. doi: 10.1145/1048935.1050155. Gordon Bell Prize winner article.
D. Komatitsch, Q. Liu, J. Tromp, P. Süss, C. Stidham, and J. H. Shaw. Simulations of ground motion in the Los
Angeles basin based upon the spectral-element method. Bull. seism. Soc. Am., 94(1):187–206, 2004. doi: 10.1785/
0120030077.
D. Komatitsch, J. Labarta, and D. Michéa. A simulation of seismic wave propagation at high resolution in the inner
core of the Earth on 2166 processors of MareNostrum. Lecture Notes in Computer Science, 5336:364–377, 2008.
D. Komatitsch, D. Michéa, and G. Erlebacher. Porting a high-order finite-element earthquake modeling application to
NVIDIA graphics cards using CUDA. Journal of Parallel and Distributed Computing, 69(5):451–460, 2009. doi:
10.1016/j.jpdc.2009.01.006.
D. Komatitsch, G. Erlebacher, D. Göddeke, and D. Michéa. High-order finite-element seismic wave propagation
modeling with MPI on a large GPU cluster. J. Comput. Phys., 229(20):7692–7714, 2010a. doi: 10.1016/j.jcp.2010.
06.024.
D. Komatitsch, L. P. Vinnik, and S. Chevrot. SHdiff/SVdiff splitting in an isotropic Earth. J. Geophys. Res., 115(B7):
B07312, 2010b. doi: 10.1029/2009JB006795.
D. Komatitsch, Z. Xie, E. Bozda˘
g, E. Sales de Andrade, D. Peter, Q. Liu, and J. Tromp. Anelastic sensitivity kernels
with parsimonious storage for adjoint tomography and full waveform inversion. Geophys. J. Int., 206(3):1467–1478,
2016. doi: 10.1093/gji/ggw224.
D. A. Kopriva. Metric identities and the discontinuous spectral element method on curvilinear meshes. Journal of
Scientific Computing, 26(3):301–327, 2006. doi: 10.1007/s10915-005-9070-8.
D. A. Kopriva, S. L. Woodruff, and M. Y. Hussaini. Computation of electromagnetic scattering with a non-conforming
discontinuous spectral element method. Int. J. Numer. Methods Eng., 53(1):105–122, 2002. doi: 10.1002/nme.394.
M. Kristeková, J. Kristek, and P. Moczo. Time-frequency misfit and goodness-of-fit criteria for quantitative compari-
son of time signals. Geophys. J. Int., 178(2):813–825, 2009. doi: 10.1111/j.1365-246X.2009.04177.x.
S. J. Lee, H. W. Chen, Q. Liu, D. Komatitsch, B. S. Huang, and J. Tromp. Three-dimensional simulations of seismic
wave propagation in the Taipei basin with realistic topography based upon the spectral-element method. Bull. seism.
Soc. Am., 98(1):253–264, 2008. doi: 10.1785/0120070033.
S. J. Lee, Y. C. Chan, D. Komatitsch, B. S. Huang, and J. Tromp. Effects of realistic surface topography on seismic
ground motion in the Yangminshan region of Taiwan based upon the spectral-element method and LiDAR DTM.
Bull. seism. Soc. Am., 99(2A):681–693, 2009a. doi: 10.1785/0120080264.
S. J. Lee, D. Komatitsch, B. S. Huang, and J. Tromp. Effects of topography on seismic wave propagation: An example
from northern Taiwan. Bull. seism. Soc. Am., 99(1):314–325, 2009b. doi: 10.1785/0120080020.
A. Legay, H. W. Wang, and T. Belytschko. Strong and weak arbitrary discontinuities in spectral finite elements. Int. J.
Numer. Methods Eng., 64(8):991–1008, 2005. doi: 10.1002/nme.1388.
P. Lesaint and P. A. Raviart. On a finite element method for solving the neutron transport equation (Proc. Symposium,
Mathematical Research Center). In U. of Wisconsin-Madison, editor, Mathematical aspects of finite elements in
partial differential equations, volume 33, pages 89–123, New York, USA, 1974. Academic Press.
D. Li, D. Helmberger, R. W. Clayton, and D. Sun. Global synthetic seismograms using a 2-D finite-difference method.
Geophys. J. Int., 197(2):1166–1183, 2014. doi: 10.1093/gji/ggu050.
BIBLIOGRAPHY 42
Q. Liu and J. Tromp. Finite-frequency kernels based on adjoint methods. Bull. seism. Soc. Am., 96(6):2383–2397,
2006. doi: 10.1785/0120060041.
Q. Liu, J. Polet, D. Komatitsch, and J. Tromp. Spectral-element moment tensor inversions for earthquakes in Southern
California. Bull. seism. Soc. Am., 94(5):1748–1761, 2004. doi: 10.1785/012004038.
Y. Maday and A. T. Patera. Spectral-element methods for the incompressible Navier-Stokes equations. In State of the
art survey in computational mechanics, pages 71–143, 1989. A. K. Noor and J. T. Oden editors.
R. Martin and D. Komatitsch. An unsplit convolutional perfectly matched layer technique improved at grazing inci-
dence for the viscoelastic wave equation. Geophys. J. Int., 179(1):333–344, 2009. doi: 10.1111/j.1365-246X.2009.
04278.x.
R. Martin, D. Komatitsch, C. Blitz, and N. Le Goff. Simulation of seismic wave propagation in an asteroid based upon
an unstructured MPI spectral-element method: blocking and non-blocking communication strategies. Lecture Notes
in Computer Science, 5336:350–363, 2008a.
R. Martin, D. Komatitsch, and A. Ezziani. An unsplit convolutional perfectly matched layer improved at grazing
incidence for seismic wave equation in poroelastic media. Geophysics, 73(4):T51–T61, 2008b. doi: 10.1190/1.
2939484.
R. Martin, D. Komatitsch, and S. D. Gedney. A variational formulation of a stabilized unsplit convolutional perfectly
matched layer for the isotropic or anisotropic seismic wave equation. Comput. Model. Eng. Sci., 37(3):274–304,
2008c. doi: 10.3970/cmes.2008.037.274.
R. Martin, D. Komatitsch, S. D. Gedney, and E. Bruthiaux. A high-order time and space formulation of the unsplit
perfectly matched layer for the seismic wave equation using Auxiliary Differential Equations (ADE-PML). Comput.
Model. Eng. Sci., 56(1):17–42, 2010. doi: 10.3970/cmes.2010.056.017.
T. Melvin, A. Staniforth, and J. Thuburn. Dispersion analysis of the spectral-element method. Quarterly Journal of
the Royal Meteorological Society, 138(668):1934–1947, 2012. doi: 10.1002/qj.1906.
E. D. Mercerat, J. P. Vilotte, and F. J. Sánchez-Sesma. Triangular spectral-element simulation of two-dimensional
elastic wave propagation using unstructured triangular grids. Geophys. J. Int., 166(2):679–698, 2006.
D. Michéa and D. Komatitsch. Accelerating a 3D finite-difference wave propagation code using GPU graphics cards.
Geophys. J. Int., 182(1):389–402, 2010. doi: 10.1111/j.1365-246X.2010.04616.x.
P. Monk and G. R. Richter. A discontinuous Galerkin method for linear symmetric hyperbolic systems in inhomoge-
neous media. Journal of Scientific Computing, 22-23(1-3):443–477, 2005. doi: 10.1007/s10915-004-4132-5.
C. Morency and J. Tromp. Spectral-element simulations of wave propagation in poroelastic media. Geophys. J. Int.,
175:301–345, 2008.
C. Morency, Y. Luo, and J. Tromp. Finite-frequency kernels for wave propagation in porous media based upon adjoint
methods. Geophys. J. Int., 179:1148–1168, 2009. doi: 10.1111/j.1365-246X.2009.04332.
S. P. Oliveira and G. Seriani. Effect of element distortion on the numerical dispersion of spectral-element methods.
Communications in Computational Physics, 9(4):937–958, 2011.
P. S. Pacheco. Parallel programming with MPI. Morgan Kaufmann Press, San Francisco, USA, 1997.
A. T. Patera. A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Phys.,
54:468–488, 1984.
F. Pellegrini and J. Roman. SCOTCH: A software package for static mapping by dual recursive bipartitioning of
process and architecture graphs. Lecture Notes in Computer Science, 1067:493–498, 1996.
D. Peter, D. Komatitsch, Y. Luo, R. Martin, N. Le Goff, E. Casarotti, P. Le Loher, F. Magnoni, Q. Liu, C. Blitz,
T. Nissen-Meyer, P. Basini, and J. Tromp. Forward and adjoint simulations of seismic wave propagation on fully
unstructured hexahedral meshes. Geophys. J. Int., 186(2):721–739, 2011. doi: 10.1111/j.1365-246X.2011.05044.x.
BIBLIOGRAPHY 43
W. L. Pilant. Elastic waves in the Earth, volume 11 of "Developments in Solid Earth Geophysics" Series. Elsevier
Scientific Publishing Company, Amsterdam, The Netherlands, 1979. 506 pages.
E. Priolo, J. M. Carcione, and G. Seriani. Numerical simulation of interface waves by high-order spectral modeling
techniques. J. Acoust. Soc. Am., 95(2):681–693, 1994.
W. H. Reed and T. R. Hill. Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-
479, Los Alamos Scientific Laboratory, Los Alamos, USA, 1973.
B. Rivière and M. F. Wheeler. Discontinuous finite element methods for acoustic and elastic wave problems. Contem-
porary Mathematics, 329:271–282, 2003.
H. Schmidt. OASES Version 3.1 user guide and reference manual. Center for Ocean Engineering, Massachusetts
Institute of Technology, USA, 2004. Available at acoustics.mit.edu/faculty/henrik/oases.html.
G. Seriani and S. P. Oliveira. Optimal blended spectral-element operators for acoustic wave modeling. Geophysics,
72(5):SM95–SM106, 2007. doi: 10.1190/1.2750715.
G. Seriani and S. P. Oliveira. Dispersion analysis of spectral-element methods for elastic wave propagation. Wave
Motion, 45:729–744, 2008. doi: 10.1016/j.wavemoti.2007.11.007.
G. Seriani and E. Priolo. A spectral element method for acoustic wave simulation in heterogeneous media. Finite
Elements in Analysis and Design, 16:337–348, 1994.
G. Seriani, E. Priolo, and A. Pregarz. Modelling waves in anisotropic media by a spectral element method. In
G. Cohen, editor, Proceedings of the third international conference on mathematical and numerical aspects of wave
propagation, pages 289–298. SIAM, Philadephia, PA, 1995.
J. Tago, V. M. Cruz-Atienza, V. Étienne, J. Virieux, M. Benjemaa, and F. J. Sánchez-Sesma. 3D dynamic rupture with
anelastic wave propagation using an hp-adaptive Discontinuous Galerkin method. In Abstract S51A-1915 presented
at 2010 AGU Fall Meeting, San Francisco, California, USA, Dec. 2010.
C. Tape, Q. Liu, and J. Tromp. Finite-frequency tomography using adjoint methods - Methodology and examples using
membrane surface waves. Geophys. J. Int., 168(3):1105–1129, 2007. doi: 10.1111/j.1365-246X.2006.03191.x.
M. A. Taylor and B. A. Wingate. A generalized diagonal mass matrix spectral element method for non-quadrilateral
elements. Appl. Num. Math., 33:259–265, 2000.
S. A. Teukolsky. Short note on the mass matrix for Gauss-Lobatto grid points. J. Comput. Phys., 283:408–413, 2015.
doi: 10.1016/j.jcp.2014.12.012.
J. Tromp, D. Komatitsch, and Q. Liu. Spectral-element and adjoint methods in seismology. Communications in
Computational Physics, 3(1):1–32, 2008.
S. Tsuboi, D. Komatitsch, C. Ji, and J. Tromp. Broadband modeling of the 2002 Denali fault earthquake on the Earth
Simulator. Phys. Earth planet. Inter., 139(3-4):305–313, 2003. doi: 10.1016/j.pepi.2003.09.012.
R. Vai, J. M. Castillo-Covarrubias, F. J. Sánchez-Sesma, D. Komatitsch, and J. P. Vilotte. Elastic wave propagation
in an irregularly layered medium. Soil Dynamics and Earthquake Engineering, 18(1):11–18, 1999. doi: 10.1016/
S0267-7261(98)00027-X.
K. van Wijk, D. Komatitsch, J. A. Scales, and J. Tromp. Analysis of strong scattering at the micro-scale. J. Acoust.
Soc. Am., 115(3):1006–1011, 2004. doi: 10.1121/1.1647480.
L. C. Wilcox, G. Stadler, C. Burstedde, and O. Ghattas. A high-order discontinuous Galerkin method for wave
propagation through coupled elastic-acoustic media. J. Comput. Phys., 229(24):9373–9396, 2010. doi: 10.1016/j.
jcp.2010.09.008.
B. A. Wingate and J. P. Boyd. Spectral element methods on triangles for geophysical fluid dynamics problems. In
A. V. Ilin and L. R. Scott, editors, Proceedings of the Third International Conference on Spectral and High-order
Methods, pages 305–314, Houston, Texas, 1996. Houston J. Mathematics.
BIBLIOGRAPHY 44
Z. Xie, D. Komatitsch, R. Martin, and R. Matzen. Improved forward wave propagation and adjoint-based sensitivity
kernel calculations using a numerically stable finite-element PML. Geophys. J. Int., 198(3):1714–1747, 2014. doi:
10.1093/gji/ggu219.
Z. Xie, R. Matzen, P. Cristini, D. Komatitsch, and R. Martin. A perfectly matched layer for fluid-solid problems:
Application to ocean-acoustics simulations with solid ocean bottoms. J. Acoust. Soc. Am., 140(1):165–175, 2016.
doi: 10.1121/1.4954736.
Appendix A
Troubleshooting
FAQ
Regarding the structure of some of the database files
Question: Can anyone tell me what the columns of the SPECFEM2D boundary condition files in SPECFEM2D/DATA/
Mesh_canyon are?
SPECFEM2D/DATA/Mesh_canyon/canyon_absorbing_surface_file
SPECFEM2D/DATA/Mesh_canyon/canyon_free_surface_file
Answer: canyon_absorbing_surface_file refers to parameters related to the absorbing conditions: The
first number (180) is the number of absorbing elements (nelemabs in the code). Then the columns are:
column 1: the element number
column 2: the number of nodes of this element that form the absorbing surface
column 3: the first node
column 4: the second node
canyon_free_surface_file refers to the elements of the free surface (relevant for enforcing free surface
condition for acoustic media): The first number (160) is the number of elements of the free surface. Then the columns
are (similar to the absorbing case):
column 1: the element number
column 2: the number of nodes of this element that form the absorbing surface
column 3: the first node
column 4: the second node
Concerning the free surface description file, nodes/edges pertaining to elastic elements are discarded when the file
is read (if for whatever reason it was simpler to include all the nodes/edges on one side of a studied area and that there
are among them some elements that are elastic elements, only the nodes/edges of acoustic elements are kept).
These files are opened and read in meshfem2D.F90 using subroutines read_abs_surface() and read_
acoustic_surface(), which are in part_unstruct.F90
45
Appendix B
License
GNU GENERAL PUBLIC LICENSE
Version 3, 29 June 2007
Copyright © 2007 Free Software Foundation, Inc. http://fsf.org/
Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.
Preamble
The GNU General Public License is a free, copyleft license for software and other kinds of works.
The licenses for most software and other practical works are designed to take away your freedom to share and
change the works. By contrast, the GNU General Public License is intended to guarantee your freedom to share
and change all versions of a program–to make sure it remains free software for all its users. We, the Free Software
Foundation, use the GNU General Public License for most of our software; it applies also to any other work released
this way by its authors. You can apply it to your programs, too.
When we speak of free software, we are referring to freedom, not price. Our General Public Licenses are designed
to make sure that you have the freedom to distribute copies of free software (and charge for them if you wish), that
you receive source code or can get it if you want it, that you can change the software or use pieces of it in new free
programs, and that you know you can do these things.
To protect your rights, we need to prevent others from denying you these rights or asking you to surrender the rights.
Therefore, you have certain responsibilities if you distribute copies of the software, or if you modify it: responsibilities
to respect the freedom of others.
For example, if you distribute copies of such a program, whether gratis or for a fee, you must pass on to the
recipients the same freedoms that you received. You must make sure that they, too, receive or can get the source code.
And you must show them these terms so they know their rights.
Developers that use the GNU GPL protect your rights with two steps: (1) assert copyright on the software, and (2)
offer you this License giving you legal permission to copy, distribute and/or modify it.
For the developers’ and authors’ protection, the GPL clearly explains that there is no warranty for this free software.
For both users’ and authors’ sake, the GPL requires that modified versions be marked as changed, so that their problems
will not be attributed erroneously to authors of previous versions.
Some devices are designed to deny users access to install or run modified versions of the software inside them,
although the manufacturer can do so. This is fundamentally incompatible with the aim of protecting users’ freedom to
change the software. The systematic pattern of such abuse occurs in the area of products for individuals to use, which
is precisely where it is most unacceptable. Therefore, we have designed this version of the GPL to prohibit the practice
for those products. If such problems arise substantially in other domains, we stand ready to extend this provision to
those domains in future versions of the GPL, as needed to protect the freedom of users.
Finally, every program is threatened constantly by software patents. States should not allow patents to restrict
development and use of software on general-purpose computers, but in those that do, we wish to avoid the special
46
APPENDIX B. LICENSE 47
danger that patents applied to a free program could make it effectively proprietary. To prevent this, the GPL assures
that patents cannot be used to render the program non-free.
The precise terms and conditions for copying, distribution and modification follow.
TERMS AND CONDITIONS
0. Definitions.
“This License” refers to version 3 of the GNU General Public License.
“Copyright” also means copyright-like laws that apply to other kinds of works, such as semiconductor masks.
“The Program” refers to any copyrightable work licensed under this License. Each licensee is addressed as
“you”. “Licensees” and “recipients” may be individuals or organizations.
To “modify” a work means to copy from or adapt all or part of the work in a fashion requiring copyright
permission, other than the making of an exact copy. The resulting work is called a “modified version” of the
earlier work or a work “based on” the earlier work.
A “covered work” means either the unmodified Program or a work based on the Program.
To “propagate” a work means to do anything with it that, without permission, would make you directly or sec-
ondarily liable for infringement under applicable copyright law, except executing it on a computer or modifying
a private copy. Propagation includes copying, distribution (with or without modification), making available to
the public, and in some countries other activities as well.
To “convey” a work means any kind of propagation that enables other parties to make or receive copies. Mere
interaction with a user through a computer network, with no transfer of a copy, is not conveying.
An interactive user interface displays “Appropriate Legal Notices” to the extent that it includes a convenient and
prominently visible feature that (1) displays an appropriate copyright notice, and (2) tells the user that there is
no warranty for the work (except to the extent that warranties are provided), that licensees may convey the work
under this License, and how to view a copy of this License. If the interface presents a list of user commands or
options, such as a menu, a prominent item in the list meets this criterion.
1. Source Code.
The “source code” for a work means the preferred form of the work for making modifications to it. “Object
code” means any non-source form of a work.
A “Standard Interface” means an interface that either is an official standard defined by a recognized standards
body, or, in the case of interfaces specified for a particular programming language, one that is widely used
among developers working in that language.
The “System Libraries” of an executable work include anything, other than the work as a whole, that (a) is
included in the normal form of packaging a Major Component, but which is not part of that Major Component,
and (b) serves only to enable use of the work with that Major Component, or to implement a Standard Interface
for which an implementation is available to the public in source code form. A “Major Component”, in this
context, means a major essential component (kernel, window system, and so on) of the specific operating system
(if any) on which the executable work runs, or a compiler used to produce the work, or an object code interpreter
used to run it.
The “Corresponding Source” for a work in object code form means all the source code needed to generate,
install, and (for an executable work) run the object code and to modify the work, including scripts to control
those activities. However, it does not include the work’s System Libraries, or general-purpose tools or generally
available free programs which are used unmodified in performing those activities but which are not part of the
work. For example, Corresponding Source includes interface definition files associated with source files for the
work, and the source code for shared libraries and dynamically linked subprograms that the work is specifically
designed to require, such as by intimate data communication or control flow between those subprograms and
other parts of the work.
The Corresponding Source need not include anything that users can regenerate automatically from other parts
of the Corresponding Source.
The Corresponding Source for a work in source code form is that same work.
APPENDIX B. LICENSE 48
2. Basic Permissions.
All rights granted under this License are granted for the term of copyright on the Program, and are irrevocable
provided the stated conditions are met. This License explicitly affirms your unlimited permission to run the un-
modified Program. The output from running a covered work is covered by this License only if the output, given
its content, constitutes a covered work. This License acknowledges your rights of fair use or other equivalent,
as provided by copyright law.
You may make, run and propagate covered works that you do not convey, without conditions so long as your
license otherwise remains in force. You may convey covered works to others for the sole purpose of having
them make modifications exclusively for you, or provide you with facilities for running those works, provided
that you comply with the terms of this License in conveying all material for which you do not control copyright.
Those thus making or running the covered works for you must do so exclusively on your behalf, under your
direction and control, on terms that prohibit them from making any copies of your copyrighted material outside
their relationship with you.
Conveying under any other circumstances is permitted solely under the conditions stated below. Sublicensing is
not allowed; section 10 makes it unnecessary.
3. Protecting Users’ Legal Rights From Anti-Circumvention Law.
No covered work shall be deemed part of an effective technological measure under any applicable law fulfill-
ing obligations under article 11 of the WIPO copyright treaty adopted on 20 December 1996, or similar laws
prohibiting or restricting circumvention of such measures.
When you convey a covered work, you waive any legal power to forbid circumvention of technological measures
to the extent such circumvention is effected by exercising rights under this License with respect to the covered
work, and you disclaim any intention to limit operation or modification of the work as a means of enforcing,
against the work’s users, your or third parties’ legal rights to forbid circumvention of technological measures.
4. Conveying Verbatim Copies.
You may convey verbatim copies of the Program’s source code as you receive it, in any medium, provided
that you conspicuously and appropriately publish on each copy an appropriate copyright notice; keep intact all
notices stating that this License and any non-permissive terms added in accord with section 7 apply to the code;
keep intact all notices of the absence of any warranty; and give all recipients a copy of this License along with
the Program.
You may charge any price or no price for each copy that you convey, and you may offer support or warranty
protection for a fee.
5. Conveying Modified Source Versions.
You may convey a work based on the Program, or the modifications to produce it from the Program, in the form
of source code under the terms of section 4, provided that you also meet all of these conditions:
(a) The work must carry prominent notices stating that you modified it, and giving a relevant date.
(b) The work must carry prominent notices stating that it is released under this License and any conditions
added under section 7. This requirement modifies the requirement in section 4 to “keep intact all notices”.
(c) You must license the entire work, as a whole, under this License to anyone who comes into possession of a
copy. This License will therefore apply, along with any applicable section 7 additional terms, to the whole
of the work, and all its parts, regardless of how they are packaged. This License gives no permission to
license the work in any other way, but it does not invalidate such permission if you have separately received
it.
(d) If the work has interactive user interfaces, each must display Appropriate Legal Notices; however, if the
Program has interactive interfaces that do not display Appropriate Legal Notices, your work need not make
them do so.
A compilation of a covered work with other separate and independent works, which are not by their nature
extensions of the covered work, and which are not combined with it such as to form a larger program, in or
APPENDIX B. LICENSE 49
on a volume of a storage or distribution medium, is called an “aggregate” if the compilation and its resulting
copyright are not used to limit the access or legal rights of the compilation’s users beyond what the individual
works permit. Inclusion of a covered work in an aggregate does not cause this License to apply to the other parts
of the aggregate.
6. Conveying Non-Source Forms.
You may convey a covered work in object code form under the terms of sections 4 and 5, provided that you also
convey the machine-readable Corresponding Source under the terms of this License, in one of these ways:
(a) Convey the object code in, or embodied in, a physical product (including a physical distribution medium),
accompanied by the Corresponding Source fixed on a durable physical medium customarily used for soft-
ware interchange.
(b) Convey the object code in, or embodied in, a physical product (including a physical distribution medium),
accompanied by a written offer, valid for at least three years and valid for as long as you offer spare parts
or customer support for that product model, to give anyone who possesses the object code either (1) a copy
of the Corresponding Source for all the software in the product that is covered by this License, on a durable
physical medium customarily used for software interchange, for a price no more than your reasonable cost
of physically performing this conveying of source, or (2) access to copy the Corresponding Source from a
network server at no charge.
(c) Convey individual copies of the object code with a copy of the written offer to provide the Corresponding
Source. This alternative is allowed only occasionally and noncommercially, and only if you received the
object code with such an offer, in accord with subsection 6b.
(d) Convey the object code by offering access from a designated place (gratis or for a charge), and offer
equivalent access to the Corresponding Source in the same way through the same place at no further
charge. You need not require recipients to copy the Corresponding Source along with the object code. If
the place to copy the object code is a network server, the Corresponding Source may be on a different
server (operated by you or a third party) that supports equivalent copying facilities, provided you maintain
clear directions next to the object code saying where to find the Corresponding Source. Regardless of what
server hosts the Corresponding Source, you remain obligated to ensure that it is available for as long as
needed to satisfy these requirements.
(e) Convey the object code using peer-to-peer transmission, provided you inform other peers where the object
code and Corresponding Source of the work are being offered to the general public at no charge under
subsection 6d.
A separable portion of the object code, whose source code is excluded from the Corresponding Source as a
System Library, need not be included in conveying the object code work.
A “User Product” is either (1) a “consumer product”, which means any tangible personal property which is
normally used for personal, family, or household purposes, or (2) anything designed or sold for incorporation
into a dwelling. In determining whether a product is a consumer product, doubtful cases shall be resolved in
favor of coverage. For a particular product received by a particular user, “normally used” refers to a typical or
common use of that class of product, regardless of the status of the particular user or of the way in which the
particular user actually uses, or expects or is expected to use, the product. A product is a consumer product
regardless of whether the product has substantial commercial, industrial or non-consumer uses, unless such uses
represent the only significant mode of use of the product.
“Installation Information” for a User Product means any methods, procedures, authorization keys, or other
information required to install and execute modified versions of a covered work in that User Product from
a modified version of its Corresponding Source. The information must suffice to ensure that the continued
functioning of the modified object code is in no case prevented or interfered with solely because modification
has been made.
If you convey an object code work under this section in, or with, or specifically for use in, a User Product, and
the conveying occurs as part of a transaction in which the right of possession and use of the User Product is
transferred to the recipient in perpetuity or for a fixed term (regardless of how the transaction is characterized),
the Corresponding Source conveyed under this section must be accompanied by the Installation Information.
APPENDIX B. LICENSE 50
But this requirement does not apply if neither you nor any third party retains the ability to install modified
object code on the User Product (for example, the work has been installed in ROM).
The requirement to provide Installation Information does not include a requirement to continue to provide sup-
port service, warranty, or updates for a work that has been modified or installed by the recipient, or for the User
Product in which it has been modified or installed. Access to a network may be denied when the modifica-
tion itself materially and adversely affects the operation of the network or violates the rules and protocols for
communication across the network.
Corresponding Source conveyed, and Installation Information provided, in accord with this section must be in
a format that is publicly documented (and with an implementation available to the public in source code form),
and must require no special password or key for unpacking, reading or copying.
7. Additional Terms.
“Additional permissions” are terms that supplement the terms of this License by making exceptions from one
or more of its conditions. Additional permissions that are applicable to the entire Program shall be treated as
though they were included in this License, to the extent that they are valid under applicable law. If additional
permissions apply only to part of the Program, that part may be used separately under those permissions, but the
entire Program remains governed by this License without regard to the additional permissions.
When you convey a copy of a covered work, you may at your option remove any additional permissions from
that copy, or from any part of it. (Additional permissions may be written to require their own removal in certain
cases when you modify the work.) You may place additional permissions on material, added by you to a covered
work, for which you have or can give appropriate copyright permission.
Notwithstanding any other provision of this License, for material you add to a covered work, you may (if
authorized by the copyright holders of that material) supplement the terms of this License with terms:
(a) Disclaiming warranty or limiting liability differently from the terms of sections 15 and 16 of this License;
or
(b) Requiring preservation of specified reasonable legal notices or author attributions in that material or in the
Appropriate Legal Notices displayed by works containing it; or
(c) Prohibiting misrepresentation of the origin of that material, or requiring that modified versions of such
material be marked in reasonable ways as different from the original version; or
(d) Limiting the use for publicity purposes of names of licensors or authors of the material; or
(e) Declining to grant rights under trademark law for use of some trade names, trademarks, or service marks;
or
(f) Requiring indemnification of licensors and authors of that material by anyone who conveys the material
(or modified versions of it) with contractual assumptions of liability to the recipient, for any liability that
these contractual assumptions directly impose on those licensors and authors.
All other non-permissive additional terms are considered “further restrictions” within the meaning of section
10. If the Program as you received it, or any part of it, contains a notice stating that it is governed by this
License along with a term that is a further restriction, you may remove that term. If a license document contains
a further restriction but permits relicensing or conveying under this License, you may add to a covered work
material governed by the terms of that license document, provided that the further restriction does not survive
such relicensing or conveying.
If you add terms to a covered work in accord with this section, you must place, in the relevant source files, a
statement of the additional terms that apply to those files, or a notice indicating where to find the applicable
terms.
Additional terms, permissive or non-permissive, may be stated in the form of a separately written license, or
stated as exceptions; the above requirements apply either way.
8. Termination.
APPENDIX B. LICENSE 51
You may not propagate or modify a covered work except as expressly provided under this License. Any attempt
otherwise to propagate or modify it is void, and will automatically terminate your rights under this License
(including any patent licenses granted under the third paragraph of section 11).
However, if you cease all violation of this License, then your license from a particular copyright holder is
reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license,
and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior
to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder
notifies you of the violation by some reasonable means, this is the first time you have received notice of violation
of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your
receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies
or rights from you under this License. If your rights have been terminated and not permanently reinstated, you
do not qualify to receive new licenses for the same material under section 10.
9. Acceptance Not Required for Having Copies.
You are not required to accept this License in order to receive or run a copy of the Program. Ancillary prop-
agation of a covered work occurring solely as a consequence of using peer-to-peer transmission to receive a
copy likewise does not require acceptance. However, nothing other than this License grants you permission
to propagate or modify any covered work. These actions infringe copyright if you do not accept this License.
Therefore, by modifying or propagating a covered work, you indicate your acceptance of this License to do so.
10. Automatic Licensing of Downstream Recipients.
Each time you convey a covered work, the recipient automatically receives a license from the original licensors,
to run, modify and propagate that work, subject to this License. You are not responsible for enforcing compliance
by third parties with this License.
An “entity transaction” is a transaction transferring control of an organization, or substantially all assets of one,
or subdividing an organization, or merging organizations. If propagation of a covered work results from an
entity transaction, each party to that transaction who receives a copy of the work also receives whatever licenses
to the work the party’s predecessor in interest had or could give under the previous paragraph, plus a right to
possession of the Corresponding Source of the work from the predecessor in interest, if the predecessor has it or
can get it with reasonable efforts.
You may not impose any further restrictions on the exercise of the rights granted or affirmed under this License.
For example, you may not impose a license fee, royalty, or other charge for exercise of rights granted under
this License, and you may not initiate litigation (including a cross-claim or counterclaim in a lawsuit) alleging
that any patent claim is infringed by making, using, selling, offering for sale, or importing the Program or any
portion of it.
11. Patents.
A “contributor” is a copyright holder who authorizes use under this License of the Program or a work on which
the Program is based. The work thus licensed is called the contributor’s “contributor version”.
A contributor’s “essential patent claims” are all patent claims owned or controlled by the contributor, whether
already acquired or hereafter acquired, that would be infringed by some manner, permitted by this License,
of making, using, or selling its contributor version, but do not include claims that would be infringed only
as a consequence of further modification of the contributor version. For purposes of this definition, “control”
includes the right to grant patent sublicenses in a manner consistent with the requirements of this License.
Each contributor grants you a non-exclusive, worldwide, royalty-free patent license under the contributor’s
essential patent claims, to make, use, sell, offer for sale, import and otherwise run, modify and propagate the
contents of its contributor version.
In the following three paragraphs, a “patent license” is any express agreement or commitment, however denomi-
nated, not to enforce a patent (such as an express permission to practice a patent or covenant not to sue for patent
APPENDIX B. LICENSE 52
infringement). To “grant” such a patent license to a party means to make such an agreement or commitment not
to enforce a patent against the party.
If you convey a covered work, knowingly relying on a patent license, and the Corresponding Source of the
work is not available for anyone to copy, free of charge and under the terms of this License, through a publicly
available network server or other readily accessible means, then you must either (1) cause the Corresponding
Source to be so available, or (2) arrange to deprive yourself of the benefit of the patent license for this particular
work, or (3) arrange, in a manner consistent with the requirements of this License, to extend the patent license to
downstream recipients. “Knowingly relying” means you have actual knowledge that, but for the patent license,
your conveying the covered work in a country, or your recipient’s use of the covered work in a country, would
infringe one or more identifiable patents in that country that you have reason to believe are valid.
If, pursuant to or in connection with a single transaction or arrangement, you convey, or propagate by procuring
conveyance of, a covered work, and grant a patent license to some of the parties receiving the covered work
authorizing them to use, propagate, modify or convey a specific copy of the covered work, then the patent
license you grant is automatically extended to all recipients of the covered work and works based on it.
A patent license is “discriminatory” if it does not include within the scope of its coverage, prohibits the exercise
of, or is conditioned on the non-exercise of one or more of the rights that are specifically granted under this
License. You may not convey a covered work if you are a party to an arrangement with a third party that is in
the business of distributing software, under which you make payment to the third party based on the extent of
your activity of conveying the work, and under which the third party grants, to any of the parties who would
receive the covered work from you, a discriminatory patent license (a) in connection with copies of the covered
work conveyed by you (or copies made from those copies), or (b) primarily for and in connection with specific
products or compilations that contain the covered work, unless you entered into that arrangement, or that patent
license was granted, prior to 28 March 2007.
Nothing in this License shall be construed as excluding or limiting any implied license or other defenses to
infringement that may otherwise be available to you under applicable patent law.
12. No Surrender of Others’ Freedom.
If conditions are imposed on you (whether by court order, agreement or otherwise) that contradict the conditions
of this License, they do not excuse you from the conditions of this License. If you cannot convey a covered work
so as to satisfy simultaneously your obligations under this License and any other pertinent obligations, then as
a consequence you may not convey it at all. For example, if you agree to terms that obligate you to collect a
royalty for further conveying from those to whom you convey the Program, the only way you could satisfy both
those terms and this License would be to refrain entirely from conveying the Program.
13. Use with the GNU Affero General Public License.
Notwithstanding any other provision of this License, you have permission to link or combine any covered work
with a work licensed under version 3 of the GNU Affero General Public License into a single combined work,
and to convey the resulting work. The terms of this License will continue to apply to the part which is the
covered work, but the special requirements of the GNU Affero General Public License, section 13, concerning
interaction through a network will apply to the combination as such.
14. Revised Versions of this License.
The Free Software Foundation may publish revised and/or new versions of the GNU General Public License
from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to
address new problems or concerns.
Each version is given a distinguishing version number. If the Program specifies that a certain numbered version
of the GNU General Public License “or any later version” applies to it, you have the option of following the
terms and conditions either of that numbered version or of any later version published by the Free Software
Foundation. If the Program does not specify a version number of the GNU General Public License, you may
choose any version ever published by the Free Software Foundation.
If the Program specifies that a proxy can decide which future versions of the GNU General Public License can
be used, that proxy’s public statement of acceptance of a version permanently authorizes you to choose that
version for the Program.
APPENDIX B. LICENSE 53
Later license versions may give you additional or different permissions. However, no additional obligations are
imposed on any author or copyright holder as a result of your choosing to follow a later version.
15. Disclaimer of Warranty.
THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE
LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR
OTHER PARTIES PROVIDE THE PROGRAM “AS IS” WITHOUT WARRANTY OF ANY KIND, EITHER
EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE
QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE
DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
16. Limitation of Liability.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY
COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES AND/OR CONVEYS THE PRO-
GRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL,
SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABIL-
ITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING
RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF
THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR OTHER
PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.
17. Interpretation of Sections 15 and 16.
If the disclaimer of warranty and limitation of liability provided above cannot be given local legal effect accord-
ing to their terms, reviewing courts shall apply local law that most closely approximates an absolute waiver of
all civil liability in connection with the Program, unless a warranty or assumption of liability accompanies a
copy of the Program in return for a fee.
END OF TERMS AND CONDITIONS
How to Apply These Terms to Your New Programs
If you develop a new program, and you want it to be of the greatest possible use to the public, the best way to
achieve this is to make it free software which everyone can redistribute and change under these terms.
To do so, attach the following notices to the program. It is safest to attach them to the start of each source file
to most effectively state the exclusion of warranty; and each file should have at least the “copyright” line and a
pointer to where the full notice is found.
<one line to give the program’s name and a brief idea of what it does.>
Copyright (C) <textyear> <name of author>
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see <http://www.gnu.org/licenses/>.
Also add information on how to contact you by electronic and paper mail.
If the program does terminal interaction, make it output a short notice like this when it starts in an interactive
mode:
APPENDIX B. LICENSE 54
<program> Copyright (C) <year> <name of author>
This program comes with ABSOLUTELY NO WARRANTY; for details type ‘show w’.
This is free software, and you are welcome to redistribute it
under certain conditions; type ‘show c’ for details.
The hypothetical commands show w and show c should show the appropriate parts of the General Public
License. Of course, your program’s commands might be different; for a GUI interface, you would use an “about
box”.
You should also get your employer (if you work as a programmer) or school, if any, to sign a “copyright
disclaimer” for the program, if necessary. For more information on this, and how to apply and follow the GNU
GPL, see http://www.gnu.org/licenses/.
The GNU General Public License does not permit incorporating your program into proprietary programs. If
your program is a subroutine library, you may consider it more useful to permit linking proprietary applications
with the library. If this is what you want to do, use the GNU Lesser General Public License instead of this
License. But first, please read http://www.gnu.org/philosophy/why-not-lgpl.html.