Resolute User Guide
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 14
Resolute User Guide
Peter Feiler Julien Delange
Contents
1 Introduction 2
2 Claim Functions 5
2.1 Resolute Libraries of Claim Functions . . . . . . . . . . . . . . . 6
2.2 Application of Claim Functions . . . . . . . . . . . . . . . . . . . 6
2.3 Uses of Claim Functions . . . . . . . . . . . . . . . . . . . . . . . 7
2.3.1 Claim Functions as Requirements to Be Satised . . . . . 8
2.3.2 Claim Functions as Verication Actions . . . . . . . . . . 9
2.3.3 Verication Assumptions and Preconditions . . . . . . . . 10
2.4 Global Claim Functions . . . . . . . . . . . . . . . . . . . . . . . 11
3 Copyright 13
1

Chapter 1
Introduction
Resolute allows users to dene a set of claim functions and associate them with
an AADL model. You can use these claim functions to represent the require-
ments to be satised, the verication actions used to verify them, and assump-
tions made by a verication action in order to produce a valid result. You will
express the requirements as predicates on subrequirements and verication ac-
tions. Verication actions invoke Boolean computational functions to represent
predicates to be evaluated and general computational functions to compute val-
ues to be compared in predicates. The computational function notation has
its roots in Lute and REAL. You can organize claim functions into a hierarchy
where a claim function is satised only if its subclaim functions are satised
according to the specied predicate logic.
Throughout this document, we use an example of resource budget analysis, in
particular, an analysis of weight. The full example is available on the “OS-
ATE pages at GitHub” (https://github.com/osate/examples/tree/master/core-
examples/resolute).
With the Resolute tool, users dene claim functions and computational functions
in Resolute annex libraries, i.e., Resolute annex clauses placed directly in an
AADL package. The example below shows a claim function called SCSReq1
that represents a requirement and consists of two verication actions. At least
one of them must be satised for the requirement to be satised (expressed by
or). The example also shows a computational function that calculates the sum
of budgets of all direct subcomponents. Finally, the example shows a global
constant denition that a user can reference in a Resolute library or Resolute
subclause. Here, we use it to specify the maximum weight, against which the
verication actions will compare the total.
package BudgetCase
public
2

annex Resolute {**
MaximumWeight : real = 1.2kg
SCSReq1(self : component) <=
** "R1" SCS shall be no heavier than " MaximumWeight%kg **
SCSReq1VA1(self, MaximumWeight) or SCSReq1VA2(self,
MaximumWeight)
AddBudgets(self : component) : real =
sum([WeightBudget(t) for (t: subcomponents(self))])
Listing 1.1: BudgetCase Example
Users then associate the claim functions representing requirements with compo-
nent types or implementations by prove statements declared in Resolute annex
subclauses. The example shows the prove statement for SCSReq1 with the com-
ponent itself passed in as a parameter.
system implementation SCS.Phys
subcomponents
sensor1: device sensor;
sensor2: device sensor;
actuator: device actuator;
annex Resolute {**
prove (SCSReq1(this))
Listing 1.2: Prove Statement for a Claim Function
Users invoke the Resolute command on a component implementation. This
results in an instantiation of the component implementation and the application
of all claim functions associated with all of the components in the instance model
via the prove statements.
The verication results are then displayed in a view labeled Assurance Case.
For each claim function invoked by a prove statement, Resolute evaluates any
claim function called by the claim function expression.
Currently, each prove statement is shown at the top level of the Assurance Case
view. This is the case for dierent prove statements of the top-level component
as well as any subcomponent that has prove statements.
3
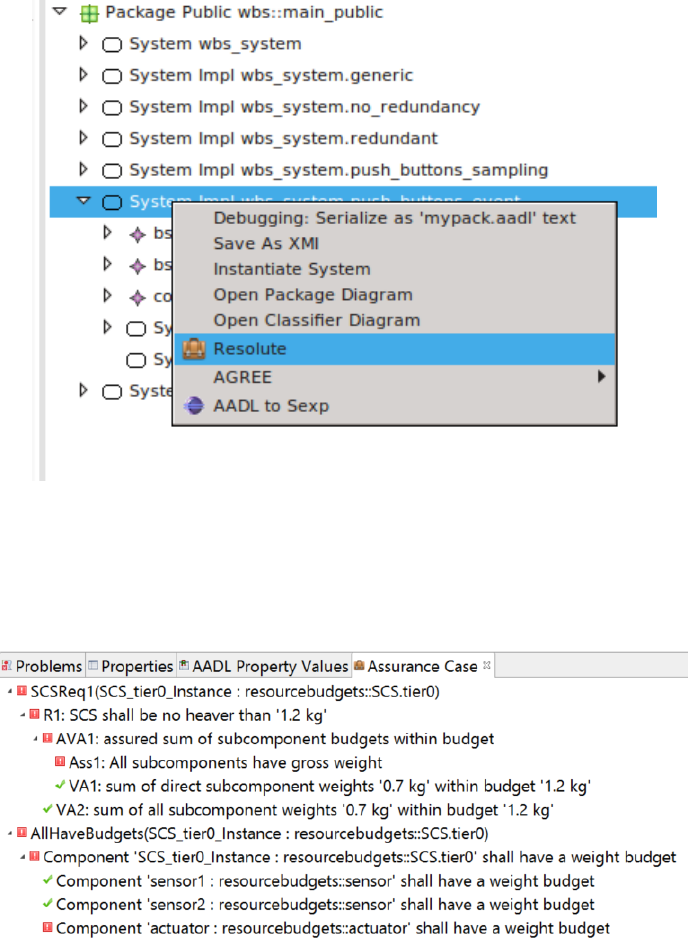
Figure 1.1: Instantiation from OSATE menu
Figure 1.2: Assurance Case Tree View
4

Chapter 2
Claim Functions
Claim functions can represent requirements, verication actions, and assump-
tions. There is currently no syntactic distinction in their use. This section
describes conventions that users should follow to distinguish the dierent uses.
Claim functions have a name, zero or more parameters, a description, and a
predicate expression. The claim function has a return type of Boolean (true to
represent success and false to represent failure). The syntax of a claim function
is as follows:
<Claim_Function> ::=
<name> "(" (<parameter> ("," <parameter) )* )? ")" "<="
"**" <description> "**" <claim_function_expression>
<parameter> ::= <name> ":" <type>
<description> ::= <text> ( <parameter_reference> | <text>)*
Listing 2.1: Claim Function Syntax
Parameters typically represent the model elements to which the claim function
applies and values used in the predicate expression to determine whether the
predicate is satised. The parameter declaration consists of a name and a type
(for more information, see the Resolute Type System section in the Resolute
Language Reference).
The description can be a combination of strings and parameter references; it
explains the role of the claim function and is displayed as part of the result
in the Assurance Case view. The description for a claim function consists of a
sequence of strings and references to claim function parameters, global constants,
or local constants (dened by let statements). If the values are numerical with
a unit, you can specify the unit to be used for display by indicating the desired
5
unit after a %,e.g.,WeightLimit%kg. The units are those dened by Units
property types in AADL property sets and do not have to be qualied by the
Units type.
The evaluation of the predicate determines the success (true return value) or
failure (false return value) of the claim function. The claim function expression
is assumed to be a logical expression (and,forall,or,exists,andthen) to
represent a predicate. In the case of and and forall, all expression elements
are executed and then the result is evaluated and returns true only if all claim
functions return true. Executing all claim functions allows Resolute to inform
the user of all failing claim functions rather than one at a time by not executing
the remaining elements in the and or forall expression. The andthen opera-
tor allows users to specify that the right-hand claim function should only be
executed if the left-hand claim function returns true.
2.1 Resolute Libraries of Claim Functions
Users dene claim functions in Resolute annex libraries. Declare a Resolute
annex library directly in a package through the annex Resolute {** <library
content> **}; statement. You can place this statement in a package by it-
self, combine it with library declarations for other annexes, or combine it with
classier declarations in the same package. A package cannot contain multiple
Resolute annex library declarations; each library must be placed in a separate
package.
Note: Resolute assumes a global name space for the names of claim functions and
computational functions. Therefore, their names must be globally unique. You
can reference them in prove statements, other claim functions, or computational
functions without qualication by a package name.
2.2 Application of Claim Functions
Invoke a claim function on a component by specifying a prove statement in a
Resolute annex subclause of the component implementation. The Resolute sub-
clause of a component implementation can contain multiple prove statements.
This claim function is then executed on every instance of this component imple-
mentation when the Resolute command is invoked.
When you have a system with subsystems, you can associate claim functions
with each component implementation in the system hierarchy. The verication
of this claim will then be performed for each instance of the component im-
plementations with a prove statement. Typically, you have prove statements
for the top-level system that involve verifying the system across multiple layers,
e.g., performing resource budget analysis across the whole system. You may
6

also perform compositional verication by verifying a component with respect
to its direct subcomponents. In this case, you place a prove statement at each
layer, i.e., with each component implementation of components involved in the
system. We illustrate this capability with our resource budget analysis, by an-
alyzing budgets of direct subcomponents against the specied budget limit for
each layer of the architecture.
Note: A prove statement cannot be declared for a component type. A declara-
tion with the component type would mean that it applies to all instances of all
implementations.
The parameter values can be integers, real numbers, strings, Boolean literals,
model elements, references to global constants, and collections of these types.
They must match the specied type for the parameter.
One special model element reference is expressed by the keyword this. It refers
to the instance model object of the model element that contains the prove
statement. The keyword this can only be used in the prove statement — not
in verication action expressions. This constraint means that this must be
passed to a claim function for it to know what model element it operates on —
unless you have a global claim function (see Global Constants).
prove ( Memory_safe ( this ))
You can also identify a subcomponent of this;i.e., associate the verication
action with a component down a path of the architecture hierarchy. This allows
you to specify a verication action for a specic component instance. This
example shows how a prove statement is applied to a subcomponent called
subsystem1:
prove ( Fully_Connected ( this.subsystem1 ))
The prove statement can be associated with the component classier of the
subcomponent. In this case, it applies to all instances of that component. We
recommend that you associate prove statements with a path only if the prove
is intended for that particular instance of a subcomponent.
2.3 Uses of Claim Functions
The compiler does enforce that claim functions can be invoked only in prove
statements, and as operands in and,or,andthen,exists, and forall opera-
tions, and cannot be invoked in computational functions.
7
2.3.1 Claim Functions as Requirements to Be Satised
Users can represent a requirement with a claim function and associated it with
an implementation of a system using the prove statement, as shown in this
example for a system called SCS.
prove (SCSReq1(this))
The description of the claim function representing the requirement may include
a requirement identier as part of the text, as shown in the next example.
Global constants specify values in requirements that users tend to change. This
allows you to localize the change to a single location. In our example, we refer-
ence a Resolute global constant MaximumWeight to indicate the desired limit in
the descriptive text, as parameters to other claim functions and computational
functions, and in predicate expressions.
The expression species the verication actions whose results are used as evi-
dence that the requirement has been met. In the example below, we show a ver-
ication action that assures the subcomponent weight budget totals are within
the limit and a verication action that recursively adds the actual weights.
The rst verication action illustrates compositional verication of weights in
terms of the budgets at the next lower level, while the second always takes into
account all actuals. Note that the rst analysis is not aected by a lower level
change as long as the budget of its enclosing component is not exceeded, while
the second analysis is aected by every change in weights throughout the whole
system.
-- requirement expressed in terms of the Maximum weight constant
SCSReq1(self : component) <=
** "R1: SVS shall be no heavier than " MaximumWeight%kg **
SCSReq1AssureSubcomponentSubtotals(self, MaximumWeight)
and SCSReq1AssureRecursiveTotals(self, MaximumWeight)
Listing 2.2: MaximumWeight Claim Function Example
Because we have already specied the weight limit as a property in the AADL
model, we can reference it to be supplied as a value to the verication action,
as shown below.
SCSReq1AssureSubcomponentTotal(self, property(self,
SEI::WeightLimit))
In addition, we can add a verication action to verify that the property and the
global constant have the same value.
SCSReq1AssureWeightLimitProperty(self, property(self,
SEI::WeightLimit), MaximumWeight)
8
A requirement may be specied vaguely such that it cannot be veried. In
this case, you may need to rene the requirement into subrequirements that are
veriable. Do this by listing claim functions representing the subclaims in the
claim function expression of the original requirement.
The claim function expression in a “requirement” claim function may contain
and,forall,andthen,or, or exists.
The and and forall expressions indicate that all operands are evaluated; the
claim is then true if all operands return true. This means that all claim func-
tions or Boolean computational functions are executed independently of whether
they return true or false. Once all have been executed, the expression returns
true only if all operands are true. This allows Resolute to report to the user
all failing operands rather than aborting after the rst failing one and requiring
the user to correct it before nding out that others fail as well.
• The or and exists indicate alternative sets of verication actions. The
operands are executed and the results are evaluated in order; the rst
returning true determines true for the claim. Eectively the user species
that the right-hand operand is executed only if the left-hand operand fails.
This allows you to specify an alternative way of verifying a claim if one
verication action is not successful. You can also use it to specify a fail
statement as the right-hand operand to provide a special message for a
failing left-hand operand.
• The andthen expression executes the left-hand operand rst. If it fails,
the whole expression is considered as failing (returns false). If the left
returns true, the right-hand side is executed and its result value becomes
the value of the andthen expression. This allows users to specify that
certain claim functions, such as verication actions, should be executed
only if preceding verication actions pass.
Note: Resolute allows computational expressions to be mixed with subclaim
functions in a claim function expression. Unfortunately, the results of their
evaluation are not shown in the Assurance Case view. This leads to the sce-
nario where all subclaims are shown as satised (true), but the claim itself is
shown as failed because the computational constraint expression evaluates to
false. Therefore, we recommend that users not mix subclaims and computa-
tional expressions.
2.3.2 Claim Functions as Verication Actions
Claim functions also represent verication actions, whose execution produces
a verication result as evidence. You can associate verication actions with
a requirement by calling them in the claim function expression of the claim
function representing the requirement, as shown earlier.
9

For a claim function that represents a verication action, the expression rep-
resents the predicate to be evaluated in order for the verication action to
pass. One of the elements of the predicate typically is a constraint value to be
met, and the other is a computational function call or reference to a computa-
tional result to compare. In the next example, the verication action computes
the sum of the subcomponent budgets and compares them to the maximum.
AddSubcomponentWeightBudgets is a computational function that returns a
real value.
Note: The identier VA1 is added into the description text by convention.
If we want to produce a special error message for a failing verication condition,
we can use the or operation with a fail statement as the right-hand side.
Failure of the left-hand side results in the execution of the right-hand side; i.e.,
this operation eectively throws a fail exception with the specied description
text, which is then associated with the enclosing claim function.
SCSReq1VA1VerifySubcomponentTotals(self : component, max : real) <=
** "VA1: sum of direct subcomponent weights " actuals%kg " within
budget " max%kg **
let actuals : real = AddSubcomponentWeightBudgets(self);
(actuals <= max) or fail ** self " weight sum " acutals%kg "over
budget " maxkg **
Listing 2.3: Fail statement example
2.3.3 Verication Assumptions and Preconditions
Verication actions may make
• assumptions that must hold for the verication action result to be accurate
• preconditions that must hold in order for the verication action to be
executed
A use case for a verication action assumption is that the calculation of the
weight totals can be performed even though some components may not yet have
a weight budget. However, it is still useful to evaluate the partial weight total
result as it may already be close to or exceed the limit. This allows Resolute
to inform the user without rst requiring the user to complete the model with
missing weight budget properties. The assumption function will determine how
many components have a weight budget and report the percentage of compo-
nents with a weight budget.
The following example illustrates a verication action with an assumption.
We have a claim function that models the assumption to be evaluated, called
SCSReq1SubcomponentsHaveWeight. It counts the number of components and
those with a GrossWeight property and generates a fail message with the
percentage of components with a weight property.
10

We then use this claim function in a new claim function that executes both
the assumption claim function and the claim function representing the actual
verication by adding the subcomponent weight budgets that we dened ear-
lier (SCSReq1VA1VerifySubcomponentTotals). The and operator allows both
assumption and verication action claim functions to be evaluated.
SCSReq1AssureSubcomponentTotals(self : component, max : real) <=
** "AVA1: assured sum of subcomponent budgets within budget" **
-- we only evaluate the weight total if subcomponents have weight
budget
SCSReq1VA1SubcomponentsHaveWeight(self) and
SCSReq1VA1VerifySubcomponentTotals(self, max)
SCSReq1VA1SubcomponentsHaveWeight(self : component) <=
** "Ass1: All subcomponents have gross weight" **
let ratio : int = SubcomponentWeightBudgetCoveragePercent(self);
forall (sub : subcomponents(self)) . has_property(sub,
SEI::GrossWeight)
or fail ** "Percentage of subcomponents with weight " ratio "
percent" **
A use case for a verication action precondition is that the verication action
cannot perform the analysis until all the data is present; i.e., all components
involved in the computation have appropriate property values. In this case, we
use the andthen operator instead of and.
2.4 Global Claim Functions
Claim functions can be dened without parameter. In this case, the claim
function rst queries the instance model for objects and then applies a claim
function to each element of the query. The query is accomplished by identify-
ing a collection of model elements and then applying a claim function to each
element of the collection using forall or exists. Model element collections
can be identied by category, e.g., by threads for all threads in the instance
model or by set constructors such as instances(classier), which returns all
component instances of the specied classier. Collections and their operations
are discussed in detail in the Resolute Language Reference.
The example shows a global constraint that all threads must have a period
property value.
SystemWideReq1() <= ** "All threads have a period" **
forall (t : thread) . HasPeriod(t)
HasPeriod(t : thread) <= **Thread " t " has a period" **
has_property(t, Timing_Properties::Period)
11
You can include global claim functions as prove statements on any model el-
ement, since they query the whole model independently of a specic model
element. However, you should place them in the top-level component imple-
mentation to which the Resolute command is applied; otherwise, they may be
invoked multiple times.
12
Chapter 3
Copyright
Copyright 2015 Carnegie Mellon University
This material is based upon work funded and supported by the Department of
Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon Univer-
sity for the operation of the Software Engineering Institute, a federally funded
research and development center.
Any opinions, ndings and conclusions or recommendations expressed in this
material are those of the author(s) and do not necessarily reect the views of
the United States Department of Defense.
NO WARRANTY. THIS CARNEGIE MELLON UNIVERSITY AND SOFT-
WARE ENGINEERING INSTITUTE MATERIAL IS FURNISHED ON
AN “AS-IS” BASIS. CARNEGIE MELLON UNIVERSITY MAKES NO
WARRANTIES OF ANY KIND, EITHER EXPRESSED OR IMPLIED, AS
TO ANY MATTER INCLUDING, BUT NOT LIMITED TO, WARRANTY
OF FITNESS FOR PURPOSE OR MERCHANTABILITY, EXCLUSIVITY,
OR RESULTS OBTAINED FROM USE OF THE MATERIAL. CARNEGIE
MELLON UNIVERSITY DOES NOT MAKE ANY WARRANTY OF ANY
KIND WITH RESPECT TO FREEDOM FROM PATENT, TRADEMARK,
OR COPYRIGHT INFRINGEMENT.
This material has been approved for public release and unlimited distribution.
DM-0003006
13