Texas Instruments Calculator Users Manual Ba2plus

BA II PLUS PROFESSIONAL guidebook (English) BAIIPLUSPROGuidebook_EN BA II PLUS™ PROFESSIONAL Guidebook

Calculator to the manual 2a3466f6-c319-4b68-bc05-82502a7f3a4c

2015-02-05

: Texas-Instruments Texas-Instruments-Calculator-Users-Manual-400144 texas-instruments-calculator-users-manual-400144 texas-instruments pdf

Open the PDF directly: View PDF .
Page Count: 116 [warning: Documents this large are best viewed by clicking the View PDF Link!]

BA II PLUS™ PROFESSIONAL Calculator

BA II PLUS™

PROFESSIONAL

Calculator

Important Information

Texas Instruments makes no warranty, either express or implied,

including but not limited to any implied warranties of merchantability

and fitness for a particular purpose, regarding any programs or book

materials and makes such materials available solely on an “as-is” basis.

In no event shall Texas Instruments be liable to anyone for special,

collateral, incidental, or consequential damages in connection with or

arising out of the purchase or use of these materials, and the sole and

exclusive liability of Texas Instruments, regardless of the form of action,

shall not exceed the purchase price of this product. Moreover, Texas

Instruments shall not be liable for any claim of any kind whatsoever

against the use of these materials by any other party.

USA FCC Information Concerning Radio Frequency

Interference

This equipment has been tested and found to comply with the limits for a

Class B digital device, pursuant to Part 15 of the FCC rules. These limits are

designed to provide reasonable protection against harmful interference in

a residential installation. This equipment generates, uses, and can radiate

radio frequency energy and, if not installed and used in accordance with

the instructions, may cause harmful interference to radio communications.

However, there is no guarantee that interference will not occur in a

particular installation.

If this equipment does cause harmful interference to radio or television

reception, which can be determined by turning the equipment off and

on, you can try to correct the interference by one or more of the

following measures:

• Reorient or relocate the receiving antenna.

• Increase the separation between the equipment and receiver.

• Connect the equipment into an outlet on a circuit different from

that to which the receiver is connected.

• Consult the dealer or an experienced radio/television technician for

help.

Caution: Any changes or modifications to this equipment not

expressly approved by Texas Instruments may void your

authority to operate the equipment.

Table of Contents

Table of Contents iii

1 Overview of Calculator Operations..................................1

Turning On the Calculator ............................................................. 1

Turning Off the Calculator............................................................. 1

Selecting 2nd Functions ................................................................. 2

Reading the Display ....................................................................... 2

Setting Calculator Formats ........................................................... 4

Resetting the Calculator ................................................................ 6

Clearing Calculator Entries and Memories ................................... 6

Correcting Entry Errors................................................................... 7

Math Operations ............................................................................ 8

Memory Operations ..................................................................... 12

Calculations Using Constants....................................................... 13

Last Answer Feature..................................................................... 14

Using Worksheets: Tools for Financial Solutions ........................ 15

....................................................................................................... 19

2 Time-Value-of-Money and Amortization Worksheets...21

TVM and Amortization Worksheet Variables............................. 22

Entering Cash Inflows and Outflows........................................... 25

Generating an Amortization Schedule ....................................... 25

Example: Computing Basic Loan Interest.................................... 26

Examples: Computing Basic Loan Payments ............................... 27

Examples: Computing Value in Savings ...................................... 28

Example: Computing Present Value in Annuities....................... 29

Example: Computing Perpetual Annuities.................................. 30

Example: Computing Present Value of Variable Cash Flows ..... 31

Example: Computing Present Value of a Lease With Residual

Value........................................................................................ 33

Example: Computing Other Monthly Payments......................... 34

Example: Saving With Monthly Deposits.................................... 35

Example: Computing Amount to Borrow and Down Payment . 36

Example: Computing Regular Deposits for a Specified Future

Amount ................................................................................... 37

Example: Computing Payments and Generating an

Amortization Schedule........................................................... 38

Example: Computing Payment, Interest, and Loan Balance

After a Specified Payment ..................................................... 39

3 Cash Flow Worksheet......................................................41

Cash Flow Worksheet Variables................................................... 41

Uneven and Grouped Cash Flows................................................ 43

Entering Cash Flows ..................................................................... 43

iv Table of Contents

Deleting Cash Flows......................................................................44

Inserting Cash Flows .....................................................................44

Computing Cash Flows .................................................................45

Example: Solving for Unequal Cash Flows .................................47

Example: Value of a Lease with Uneven Payments ....................49

4 Bond Worksheet ............................................................. 53

Bond Worksheet Variables ...........................................................54

Bond Worksheet Terminology .....................................................56

Entering Bond Data and Computing Results ..............................56

Example: Computing Bond Price, Accrued Interest, and

Modified Duration..................................................................58

5 Depreciation Worksheet ................................................ 59

Depreciation Worksheet Variables ..............................................59

Entering Data and Computing Results ........................................ 61

Example: Computing Straight-Line Depreciation.......................62

6 Statistics Worksheet ....................................................... 65

Statistics Worksheet Variables .....................................................65

Regression Models........................................................................67

Entering Statistical Data...............................................................68

Computing Statistical Results.......................................................69

7 Other Worksheets ........................................................... 71

Percent Change/Compound Interest Worksheet ........................71

Interest Conversion Worksheet....................................................74

Date Worksheet ............................................................................76

Profit Margin Worksheet .............................................................78

Breakeven Worksheet .................................................................. 80

Memory Worksheet ......................................................................82

.......................................................................................................83

A Appendix — Reference Information.............................. 85

Formulas........................................................................................85

Error Messages..............................................................................96

Accuracy Information ...................................................................98

AOS™ (Algebraic Operating System) Calculations .....................98

Battery Information......................................................................99

In Case of Difficulty ....................................................................100

Texas Instruments Support and Service .....................................101

Texas Instruments (TI) Warranty Information ...........................102

Index.............................................................................. 105

Overview of Calculator Operations 1

Overview of Calculator Operations

This chapter describes the basic operation of your BA II PLUS™

PROFESSIONAL calculator, including how to:

• Turn on and turn off the calculator

• Select second functions

• Read the display and set calculator formats

• Clear the calculator and correct entry errors

• Perform math and memory operations

• Use the Last Answer feature

• Use worksheets

Turning On the Calculator

Turning Off the Calculator

Press $.

• The displayed value and any error condition clear.

• Any unfinished standard-calculator operation and worksheet

calculation in progress cancel.

Press $.

• If you turned off the calculator by pressing $, the

calculator returns to the standard-calculator mode

with a displayed value of zero.

All worksheets and formats for numbers, angle units,

dates, separators, and calculation method retain

previous values and configurations.

• If the Automatic Power Down™ (APD™) feature

turned off the calculator, the calculator turns on

exactly as you left it, saving display settings, stored

memory, pending operations, and error conditions.

2 Overview of Calculator Operations

• The Constant Memory™ feature retains all worksheet values and

settings, including the contents of the 10 memories and all format

settings.

Automatic Power Down™ (APD™) Feature

To prolong battery life, the Automatic Power Down (APD) feature turns

off the calculator automatically after about five minutes of inactivity.

The next time you press $, the calculator turns on exactly as you left

it, saving display settings and stored memory and any pending

operations or error conditions.

Selecting 2nd Functions

Reading the Display

The display shows the selected variable labels with values up to 10 digits.

(The calculator displays values exceeding 10 digits in scientific notation.)

The primary function of a key is printed on the key itself.

For example, the primary function of the $ key is to

turn on or turn off the calculator.

Most keys include a second function printed above the key.

To select a second function, press & and the

corresponding key. (When you press &, the 2nd indicator

appears in the upper left corner of the display.)

For example, pressing & U exits the selected

worksheet and returns the calculator to the standard-

calculator mode.

Note: To cancel after pressing &, press & again.

Overview of Calculator Operations 3

The indicators along the top of the display tell you which keys are active

and offer information about the status of the calculator.

Indicator Meaning

2nd Press a key to select its second function.

INV Press a key to select its inverse trigonometric function.

HYP Press a key to select its hyperbolic function.

COMPUTE Press % to compute a value for the displayed variable.

ENTER Press ! to assign the displayed value to the displayed

variable.

SET Press & V to change the setting of the displayed

variable.

# $Press " or # to display the previous or next variable in the

worksheet.

Note: To easily scroll up or down through a range of

variables, press and hold # or ".

DEL Press & W to delete a cash flow or statistical data point.

INS Press & X to insert a cash flow or statistical data point.

BGN TVM calculations use beginning-of-period payments. When

BGN is not displayed, TVM calculations use end-of-period

payments (END).

RAD Angle values appear in radians. When RAD is not displayed,

angle values appear and must be entered in degrees.

The displayed value is entered in the selected worksheet.

The indicator clears following a computation.

The displayed value is computed in the selected worksheet.

When a value changes and invalidates a computed value,

the_indicator clears.

=The displayed variable is assigned the displayed value.

– The displayed value is negative.

4 Overview of Calculator Operations

Setting Calculator Formats

1. To access format options, press & |. The DEC indicator

appears with the selected number of decimal places.

2. To change the number of decimal places displayed, key in a value

and press !.

3. To access another calculator format, press # or " once for each

format.

For example, to access the angle unit format, press #. To access the

number-separator format, press "" "or # # #.

4. To change the selected format, press & V.

5. To change another calculator format, repeat step 3 and step 4.

— or —

To return to the standard-calculator mode, press & U.

— or —

To access a worksheet, press a worksheet key or key sequence.

Choosing the Number of Decimal Places Displayed

The calculator stores numeric values internally to an accuracy of 13 digits,

but you can specify the number of decimal places you want to display.

The calculator displays up to 10 digits with the floating-decimal option.

Results exceeding 10 digits appear in scientific notation.

You can change these calculator formats:

To Select Press Display Default

Number of

decimal

places

& | DEC 0–9 (Press 9 for

floating-decimal)

Angle units #DEG (degrees)

RAD (radians)

DEG

Dates #US (mm-dd-yyyy)

Eur (dd-mm-yyyy)

Number

separators

#US (1,000.00 )

Eur (1.000,00)

Calculation

method

#Chn (chain)

AOSé (algebraic

operating system)

Chn

Overview of Calculator Operations 5

Changing the number of decimal places affects the display only. Except

for amortization and depreciation results, the calculator does not round

internal values. To round the internal value, use the round function. (See

“Rounding & o” on page 10.)

Note: All examples in this guidebook assume a setting of two decimal

places. Other settings might show different results.

Choosing the Angle Units

The angle unit value affects the display of results in trigonometric

calculations. When you select radians, the RAD indicator appears in the

upper right corner of the display. No indicator appears when you select

the default setting of degrees.

Using Dates

The calculator uses dates with the Bond and Date worksheets and the

French depreciation methods. To enter dates, use this convention:

mm.ddyy (US) or dd.mmyy (European). After you key in the date, press

Choosing Calculation Methods

When you choose the chain (Chn) calculation method, the calculator

solves problems in the order that you enter them. (Most financial

calculators use Chn.)

For example, when you enter 3 H 2 < 4 N, the Chn answer is 20 (3 + 2 = 5,

5 * 4 = 20).

Using AOSé (algebraic operating system), the calculator solves problems

according to the standard rules of algebraic hierarchy, computing

multiplication and division operations before addition and subtraction

operations. (Most scientific calculators use AOS.)

For example, when you enter 3 H 2 < 4 N, the AOS answer is 11 (2 Q 4 =

8; 3 + 8 = 11).

Resetting Default Values

To reset default values for all of the calculator formats, press &

z with one of the formats displayed.

6 Overview of Calculator Operations

Resetting the Calculator

Because the calculator includes alternative methods that let you clear

data selectively, use reset carefully to avoid losing data needlessly. (See

“Clearing Calculator Entries and Memories” on page 6.)For example, you

might reset the calculator before using it for the first time, when starting

a new calculation, or when having difficulty operating the calculator and

other possible solutions do not work. (See “In Case of Difficulty” on

page 100.)

Pressing & } !

1. Press & }. The RST ? and ENTER indicators appear.

Note: To cancel reset, press & U. 0.00 appears.

2. Press !. RST and 0.00 appear, confirming that the calculator is

reset.

Note: If an error condition exists, press P to clear the display before

attempting to reset.

Performing a Hard Reset

You can also reset the calculator by gently inserting a pointed object

(such as an unfolded paper clip or similar object) in the hole marked

RESET in back of the calculator.

Clearing Calculator Entries and Memories

Note: To clear variables selectively, see the specific worksheet chapters in

this guidebook.

Resetting the calculator:

• Clears the display, all 10 memories, any unfinished

calculations, and all worksheet data.

• Restores all default settings

• Returns operation to the standard-calculator mode

To clear Press

One character at a time, starting with the last digit

keyed in

An incorrect entry, error condition, or error

message

Overview of Calculator Operations 7

Correcting Entry Errors

Example: You mean to calculate 3 Q 1234.56 but instead enter 1234.86.

The prompted worksheet and reset default values & z

Calculator format settings and reset default values & |

& z

• Out of the prompted worksheet and return to

standard-calculator mode

• All pending operations in standard-calculator

mode

& U

• In a prompted worksheet, the variable value

keyed in but not entered (the previous value

appears)

• Any calculation started but not completed

P P

TVM worksheet variables and reset default values & U

& ^

One of the 10 memories (without affecting the

others)

Q D and a

memory number

key (0–9)

You can correct an entry without clearing a calculation, if

you make the correction before pressing an operation key

(for example, H or 4).

• To clear the last digit displayed, press *.

• To clear the entire number displayed, press P.

Note: Pressing P after you press an operation key clears

the calculation in progress.

To Press Display

Begin the expression. 3 <3.00

Enter a number. 1234.86 1,234.86

Erase the entry error. * * 1,234.

Key in the correct number. 56 1,234.56

Compute the result. N3,703.68

To clear Press

8 Overview of Calculator Operations

Math Operations

When you select the chain (Chn) calculation method, the calculator

evaluates mathematical expressions (for example, 3 + 2 Q 4) in the order

that you enter them.

Examples of Math Operations

These operations require you to press N to complete.

These operations do not require you to press N to complete.

To Press Display

Add 6 + 4 6 H 4 N10.00

Subtract 6 N 4 6 B 4 N2.00

Multiply 6 Q 4 6 < 4 N24.00

Divide 6 P 4 6 6 4 N1.50

Find universal power: 31.25 3 ; 1.25 N3.95

Use parentheses: 7 Q (3 + 5) 7 < 9 3 H 5 : N 56.00

Find percent: 4% of $453 453 < 4 2 N 18.12

Find percent ratio: 14 to 25 14 6 25 2 N 56.00

Find price with percent add-on:

$498 + 7% sales tax

498 H 7 2

34.86

532.86

Find price with percent discount:

$69.99 N 10%

69.99 B 10 2

7.00

62.99

Find number of combinations where:

n = 52, r = 5

52 & s 5 N2,598,960.00

Find number of permutations where:

n = 8, r = 3

8 & m 3 N336.00

To Press Display

Square 6.326.3 439.69

Find square root: 15.5 33.94

Find reciprocal: 1/3.2 3.2 50.31

Find factorial: 5! 5 & g 120.00

Find natural logarithm: ln 203.45 203.45 >5.32

15.5

Overview of Calculator Operations 9

* The random number you generate might be different.

** Angles can be computed in degrees or radians. Examples show

angles in degrees. (See “Choosing the Angle Units” on page 5.)

Universal Power ;

Press ; to raise the displayed positive number to any power (for

example, 2-5 or 2(1/3)).

Note: Because the reciprocal of an even number (such as, 1/2, 1/4, 1/6) is

a complex number, you can only raise a negative number to an integer

power or the reciprocal of an odd number.

Find natural antilogarithm: e.69315 .69315 & i 2.00

Round 2 P 3 to the set decimal format 2 6 3 N & o 0.67

Generate random number* & a 0.86

Store seed value D & a 0.86

Find sine:** sin(11.54°) 11.54 & d 0.20

Find cosine:** cos(120°) 120 & e -0.50

Find tangent:** tan(76°) 76 & f 4.01

Find arcsine:** sin-1(.2) .2 8 d 11.54

Find arccosine:** cos-1(-.5) .5 S 8 e 120.00

Find arctangent:** tan-1(4) 4 8 f 75.96

Find hyperbolic sine: sinh(.5) .5 & c d 0.52

Find hyperbolic cosine: cosh(.5) .5 & c e 1.13

Find hyperbolic tangent: tanh(.5) .5 & c f 0.46

Find hyperbolic arcsine: sinh-1(5) 5 & c 8 d 2.31

Find hyperbolic arccosine: cosh-1(5) 5 & c 8 e 2.29

Find hyperbolic arctangent: tanh-1(.5) .5 & c 8 f 0.55

To Press Display

10 Overview of Calculator Operations

Parentheses 9 :

Use parentheses to control the order in which the calculator evaluates a

numeric expression in division, multiplication, powers, roots, and

logarithm calculations. The calculator includes up to 15 levels of

parentheses and up to 8 pending operations.

Note: You do not have to press : for expressions ending in a series of

closed parentheses. Pressing N closes parentheses automatically,

evaluates the expression, and displays the final result. To view

intermediate results, press : once for each open parenthesis.

Factorial & g

The number for which you compute a factorial must be a positive integer

less than or equal to 69.

Random Numbers & a

The calculator generates a random real number between zero and one

(0<x<1) from a uniform distribution.

You can repeat a sequence of random numbers by storing a seed value in

the random number generator. Seed values help you recreate

experiments by generating the same series of random numbers.

To store a seed value, key in an integer greater than zero and press D

& a.

Combinations & s

The calculator computes the number of combinations of n items taken r

at a time. Both the n and r variables must be greater than or equal to 0.

Permutations & m

The calculator computes the number of permutations of n items taken r

at a time. Both the n and r variables must be greater than or equal to 0.

Rounding & o

The calculator computes using the rounded, displayed form of a number

instead of the internally stored value.

Cr n!

nr)!r!×–(

-----------------------------=

Pr n!

nr)!–(

-------------------=

Overview of Calculator Operations 11

For example, working in the Bond worksheet, you might want to round a

computed selling price to the nearest penny (two decimal places) before

continuing your calculation.

Note: The calculator stores values to an accuracy of up to 13 digits. The

decimal format setting rounds the displayed value but not the

unrounded, internally stored value. (See “Choosing the Number of

Decimal Places Displayed” on page 4.)

Scientific Notation ;

When you compute a value in the standard-decimal format that is either

too large or small to be displayed, the calculator displays it in scientific

notation, that is, a base value (or mantissa), followed by a blank space,

followed by an exponent.

With AOS™ selected, you can press ; to enter a number in scientific

notation. (See “Choosing Calculation Methods” on page 5.)

For example, to enter 3 Q 103, key in 3 < 10 ; 3.

12 Overview of Calculator Operations

Memory Operations

Clearing Memory

Clearing memory before you begin a new calculation is a critical step in

avoiding errors.

• To clear an individual memory, store a zero value in it.

• To clear all 10 calculator memories, press & { & z.

Storing to Memory

To store a displayed value to memory, press D and a numeric key (0–9).

• The displayed value replaces any previous value stored in the

memory.

• The Constant Memory feature retains all stored values when you

turn off the calculator.

Recalling From Memory

To recall a number stored in memory, press J and a numeric key (0–9).

Note: The recalled number remains in memory.

Memory Examples

Memory Arithmetic

Using memory arithmetic, you can perform a calculation with a stored

value and store the result with a single operation.

You can store values in any of 10 memories using the

standard calculator keys.

Note: You can also use the Memory worksheet. (See

“Memory Worksheet” on page 82.)

• You can store in memory any numeric value within the

range of the calculator.

• To access a memory M0 through M9, press a numeric

key (0 through 9).

To Pre s s

Clear memory 4 (by storing a zero value in it) 0 D 4

Store 14.95 in memory 3 (M3)14.95 D 3

Recall a value from memory 7 (M7)J 7

Overview of Calculator Operations 13

• Memory arithmetic changes only the value in the affected memory

and not the displayed value.

• Memory arithmetic does not complete any calculation in progress.

The table lists the available memory arithmetic functions. In each case,

the specified memory stores the result.

Calculations Using Constants

Example: Multiply 3, 7, and 45 by 8

To Pre s s

Add the displayed value to the value stored in memory 9

(M9).

D H 9

Subtract the displayed value from the value stored in

memory 3 (M3).

D B 3

Multiply the value in memory 0 (M0) by the displayed value. D < 0

Divide the value in memory 5 (M5) by the displayed value. D 6 5

Raise the value in memory 4 (M4) to the power of the

displayed value.

D ; 4

To store a constant for use in repetitive calculations, enter

a number and an operation, and then press &`.

To use the stored constant, key in a value and press N.

Note: Pressing a key other than a number or N clears the

constant.

To Press Display

Clear the calculator. & U 0.00

Enter the value for the first calculation. 3 3

Enter the operation and a constant value. < 8 8

Store the operation and value, and then

calculate.

& ` N24.00

Calculate 7 Q 8. 7 N 56.00

Compute 45 Q 8. 45 N 360.00

14 Overview of Calculator Operations

Keystrokes for Constant Calculations

This table shows how to create a constant for various operations.

*The letter c denotes the constant value.

**Repeat constant calculations with n N.

Last Answer Feature

To display the last answer computed, press &x.

Note: The calculator changes the value of the last answer whenever it

calculates a value automatically or whenever you:

• Press ! to enter a value.

• Press % to compute a value.

• Press N to complete a calculation.

Example: Using the Last Answer in a Calculation

To* Press**

Add c to each subsequent entry n H & ` c N

Subtract c from each subsequent entry n B & ` c N

Multiply each subsequent entry by cn < & ` c N

Divide each subsequent entry by cn 6 & ` c N

Raise each subsequent entry to the power of cn ; & ` c N

Add c% of each subsequent entry to that entry n H & ` c 2 N

Subtract c% of each subsequent entry from the

entry

n B & ` c 2 N

Use the Last Answer (ANS) feature with problems that call

repeatedly for the same value or to copy a value:

• From one place to another within the same worksheet

• From one worksheet to another

• From a worksheet to the standard-calculator mode

• From the standard-calculator mode to a worksheet

To Press Display

Key in and complete a calculation 3 H 1 N 4.00

Overview of Calculator Operations 15

Using Worksheets: Tools for Financial Solutions

Each worksheet is independent of the others: operations in a worksheet

do not affect variables in other worksheets. When you exit a worksheet

or turn off the calculator, the calculator retains all worksheet data.

Key in a new calculation 2 ; 2.00

Recall the last answer & x 4.00

Complete the calculation N 16.00

The calculator contains worksheets with embedded

formulas to solve specific problems. You apply settings or

assign known values to worksheet variables and then

compute the unknown value. Changing the values lets you

ask what if questions and compare results.

Except for TVM variables, accessed in the standard-

calculator mode, all variables are prompted.

For example, to assign values to amortization variables, you

must first press & \ to access the Amortization

worksheet.

To select Function Press

TVM worksheet

(Chapter 2)

Analyzes equal cash flows, for

example, annuities, loans,

mortgages, leases, and savings

,, -, .,

/, 0, or

& [

Amortization worksheet

(Chapter 2)

Performs amortization

calculations and generates an

amortization schedule

& \

Cash Flow worksheet

(Chapter 3)

Analyzes unequal cash flows by

calculating net present value

and internal rate of return

& '

Bond worksheet

(Chapter 4)

Computes bond price and yield

to maturity or call

& l

Depreciation worksheet

(Chapter 5)

Generates a depreciation

schedule using one of six

depreciation methods

& p

To Press Display

16 Overview of Calculator Operations

Accessing the TVM Worksheet Variables

Statistics worksheet

(Chapter 6)

Analyzes statistics on one- or

two-variable data using four

regression analysis options

& k

Percent

Change/Compound

Interest worksheet

(Chapter 7)

Computes percent change,

compound interest, and cost-

sell markup

& q

Interest Conversion

worksheet

(Chapter 7)

Converts interest rates

between nominal rate (or

annual percentage rate) and

annual effective rate

& v

Date worksheet

(Chapter 7)

Computes number of days

between two dates, or

date/day of the week a

specified number of days is

from a given date

& u

Profit Margin worksheet

(Chapter 7)

Computes cost, selling price,

and profit margin

& w

Breakeven worksheet

(Chapter 7)

Analyzes relationship between

fixed cost, variable cost, price,

profit, and quantity

& r

Memory worksheet

(Chapter 7)

Accesses storage area for up to

10 values

& {

• To assign values to the TVM worksheet variables, use

the five TVM keys (,, -, ., /, 0).

• To access other TVM worksheet functions, press the &

key, and then press a TVM function key (xP/Y, P/Y,

BGN). (See “TVM and Amortization Worksheet

Variables” on page 22.)

Note: You can assign values to TVM variables while in a

prompted worksheet, but you must return to the

standard-calculator mode to calculate TVM values or

clear the TVM worksheet.

To select Function Press

Overview of Calculator Operations 17

Accessing Prompted-Worksheet Variables

After you access a worksheet, press # or " to select variables. For

example, press & \ to access the Amortization worksheet, and

then press # or " to select the amortization variables (P1, P2, BAL, PRN,

INT).(See “TVM and Amortization Worksheet Variables” on page 22.)

Indicators prompt you to select settings, enter values, or compute results.

For example, the i# $ indicators remind you to press # or " to select

other variables. (See “Reading the Display” on page 2.)

To return to the standard-calculator mode, press & U.

Types of Worksheet Variables

• Enter-only

• Compute-only

• Automatic-compute

• Enter-or-compute

•Settings

Note: The = sign displayed between the variable label and value

indicates that the variable is assigned the value.

Enter-Only Variables

Values for enter-only variables must be entered, cannot be computed,

and are often limited to a specified range, for example, P/Y and C/Y. The

value for an enter-only variable can be:

• Entered directly from the keyboard.

• The result of a math calculation.

• Recalled from memory.

• Obtained from another worksheet using the last answer feature.

When you access an enter-only variable, the calculator displays the

variable label and ENTER indicator. The ENTER indicator reminds you to

press ! after keying in a value to assign the value to the variable.

After you press !, the  indicator confirms that the value is assigned.

Compute-Only Variables

You cannot enter values manually for compute-only variables, for

example, net present value (NPV). To compute a value, display a

compute-only variable and press %. The calculator computes and

displays the value based on the values of other variables.

18 Overview of Calculator Operations

When you display a compute-only variable, the COMPUTE indicator

reminds you to press % to compute its value. After you press %, the 

indicator confirms that the displayed value has been computed.

Automatic-Compute Variables

When you press # or " to display an automatic-compute variable (for

example, the Amortization worksheet INT variable), the calculator

computes and displays the value automatically without you having to

press %.

Enter-or-Compute Variables in the TVM Worksheet

You can either enter or compute values for the TVM worksheet variables

(N, I/Y, PV, PMT, and FV).

Note: Although you do not have to be in the standard-calculator mode

to assign values to these variables, you must be in the standard-calculator

mode to compute their values.

• To assign the value of a TVM variable, key in a number and press a

variable key.

• To compute the value of a TVM variable, press %, and then press the

variable key. The calculator computes and displays the value based

on the values of other variables.

Enter-or-Compute Variables in Prompted Worksheets

You can either enter or compute values for some prompted worksheet

variables (for example, the Bond worksheet YLD and PRI variables).

When you select an enter-or-compute variable, the calculator displays

the variable label with the ENTER and COMPUTE indicators.

•The

ENTER indicator prompts you to press ! to assign the keyed-

in value to the displayed variable.

•The COMPUTE indicator prompts you to press % to compute a

value for the variable.

Selecting Worksheet Settings

Many prompted worksheets contain variables consisting of two or more

options, or settings (for example, the Date worksheet ACT/360 variable).

When you select variables with settings, the calculator displays the SET

indicator and the current setting.

To scroll through the settings of a variable, press & V once for each

setting.

Overview of Calculator Operations 19

Display Indicators

•The  indicator confirms that the calculator entered the displayed

value in the worksheet.

•The  indicator confirms that the calculator computed the displayed

value.

• When a change to the worksheet invalidates either entered or

computed values, the  and  indicators disappear.

20 Overview of Calculator Operations

Time-Value-of-Money and Amortization Worksheets 21

Time-Value-of-Money and Amortization

Worksheets

After solving a TVM problem, you can use the Amortization worksheet to

generate an amortization schedule.

• To access a TVM variable, press a TVM key (,, -, ., /, or 0).

• To access the prompted Amortization worksheet, press & \.

Use the Time-Value-of-Money (TVM) variables to solve

problems with equal and regular cash flows that are either

all inflows or all outflows (for example, annuities, loans,

mortgages, leases, and savings).

For cash-flow problems with unequal cash flows, use the

Cash Flow worksheet.

22 Time-Value-of-Money and Amortization Worksheets

TVM and Amortization Worksheet Variables

Note: This guidebook categorizes calculator variables by the method of

entry. (See “Types of Worksheet Variables” on page 17.)

Using the TVM and Amortization Variables

Because the calculator stores values assigned to the TVM variables until

you clear or change them, you should not have to perform all steps each

time you work a problem.

• To assign a value to a TVM variable, key in a number and press a TVM

key (,, -, ., /, 0).

• To change the number of payments (P/Y), press &[, key in a

number, and press !. To change the compounding periods (C/Y),

press &[ #, key in a number, and press !.

• To change the payment period (END/BGN), press & ], and then

press & V.

• To compute a value for the unknown variable, press %, and then

press the key for the unknown variable.

Variable Key Display Type of Variable

Number of periods ,NEnter-or-compute

Interest rate per year -I/Y Enter-or-compute

Present value .PV Enter-or-compute

Payment /PMT Enter-or-compute

Future value 0FV Enter-or-compute

Number of payments per year & [ P/Y Enter-only

Number of compounding

periods per year

#C/Y Enter-only

End-of-period payments & ] END Setting

Beginning-of-period

payments

& V BGN Setting

Starting payment & \ P1 Enter-only

Ending payment #P2 Enter-only

Balance #BAL Auto-compute

Principal paid #PRN Auto-compute

Interest paid #INT Auto-compute

Time-Value-of-Money and Amortization Worksheets 23

• To generate an amortization schedule, press & \, enter the

first and last payment number in the range (P1 and P2), and press "

or # to compute values for each variable (BAL, PRN, and INT).

Resetting the TVM and Amortization Worksheet Variables

• To reset all calculator variables and formats to default values

(including TVM and amortization variables), press & } !:

• To reset only the TVM variables (N, I/Y, PV, PMT, FV) to default values,

press & ^.

• To reset P/Y and C/Y to default values, press & [ & z.

• To reset the Amortization worksheet variables (P1, P2, BAL, PRN,

INT) to default values, press & z while in the Amortization

worksheet.

• To reset END/BGN to the default value, press & ] & z.

Clearing the Unused Variable

For problems using only four of the five TVM variables, enter a value of

zero for the unused variable.

For example, to determine the present value (PV) of a known future

value (FV) with a known interest rate (I/Y) and no payments, enter 0 and

press PMT.

Entering Positive and Negative Values for Outflows and

Inflows

Enter negative values for outflows (cash paid out) and positive values for

inflows (cash received).

Note: To enter a negative value, press S after entering the number. To

change a negative value to positive, press S.

Variable Default Variable Default

N0END/BGN END

I/Y 0P1 1

PV 0P2 1

PMT 0BAL 0

FV 0PRN 0

P/Y 1INT 0

C/Y 1

24 Time-Value-of-Money and Amortization Worksheets

Entering Values for I/Y, P/Y, and C/Y

•Enter I/Y as the nominal interest rate. The TVM worksheet

automatically converts I/Y to a per period rate based on the values of

P/Y and C/Y.

• Entering a value for P/Y automatically enters the same value for C/Y.

(You can change C/Y.)

Specifying Payments Due With Annuities

Use END/BGN to specify whether the transaction is an ordinary annuity

or an annuity due.

•Set

END for ordinary annuities, in which payments occur at the end

of each payment period. (This category includes most loans.)

•Set BGN for annuities due, in which payments occur at the beginning

of each payment period. (This category includes most leases.)

Note: When you select beginning-of-period payments, the BGN indicator

appears. (No indicator appears for END payments.)

Updating P1 and P2

To update P1 and P2 for a next range of payments, press % with P1 or

P2 displayed.

Different Values for BAL and FV

The computed value for BAL following a specified number of payments

might be different than the computed value for FV following the same

number of payments.

• When solving for BAL, PRN, and INT, the calculator uses the PMT

value rounded to the number of decimal places specified by the

decimal format.

• When solving for FV, the calculator uses the unrounded value for

PMT.

Entering, Recalling, and Computing TVM Values

• To enter a TVM value, key in the value and store it by pressing a TVM

key (,, -, ., /, 0).

• To display a stored TVM value, press J and a TVM key.

You can enter or recall a value for any of the five TVM variables (N, I/Y,

PV, PMT, or FV) in either the standard calculator mode or a worksheet

mode. The information displayed depends on which mode is selected.

• In standard calculator mode, the calculator displays the variable

label, the = sign, and the value entered or recalled.

Time-Value-of-Money and Amortization Worksheets 25

• In worksheet modes the calculator displays only the value you enter

or recall, although any variable label previously displayed remains

displayed.

Note: You can tell that the displayed value is not assigned to the

displayed variable, because the = indicator is not displayed.

To compute a TVM value, press % and a TVM key in standard-calculator

mode.

Using [xP/Y] to Calculate a Value for N

1. Key in the number of years, and then press & Z to multiply by

the stored P/Y value. The total number of payments appears.

2. To assign the displayed value to N for a TVM calculation, press ,.

Entering Cash Inflows and Outflows

The calculator treats cash received (inflows) as a positive value and cash

invested (outflows) as a negative value.

• You must enter cash inflows as positive values and cash outflows as

negative values.

• The calculator displays computed inflows as positive values and

computed outflows as negative values.

Generating an Amortization Schedule

The Amortization worksheet uses TVM values to compute an

amortization schedule either manually or automatically.

Generating an Amortization Schedule Manually

1. Press & \. The current P1 value appears.

2. To specify the first in a range of payments, key in a value for P1 and

press !.

3. Press #. The current P2 value appears.

4. To specify the last payment in the range, key in a value for P2 and

press !.

5. Press # to display each of the automatically computed values:

•BAL— the remaining balance after payment P2

•PRN— the principal

•INT— the interest paid over the specified range

26 Time-Value-of-Money and Amortization Worksheets

6. Press & \.

— or —

If INT is displayed, press # to display P1 again.

7. To generate the amortization schedule, repeat steps 2 through 5 for

each range of payments.

Generating an Amortization Schedule Automatically

After entering the initial values for P1 and P2, you can compute an

amortization schedule automatically.

1. Press & \.

— or —

If INT is displayed, press # to display the current P1 value.

2. Press %. Both P1 and P2 update automatically to represent the

next range of payments.

The calculator computes the next range of payments using the same

number of periods used with the previous range of payments. For

example, if the previous range was 1 through 12 (12 payments),

pressing % updates the range to 13 through 24 (12 payments).

3. Press # to display P2.

• If you press % with P1 displayed, a new value for P2 will be

displayed automatically. (You can still enter a new value for P2.)

• If you did not press % with P1 displayed, you can press %

with P2 displayed to enter values for both P1 and P2 in the next

range of payments.

4. Press # to display each of the automatically computed values for

BAL, PRN, and INT in the next range of payments.

5. Repeat steps 1 through 4 until the schedule is complete.

Example: Computing Basic Loan Interest

If you make a monthly payment of $425.84 on a 30-year mortgage for

$75,000, what is the interest rate on your mortgage?

To Press Display

Set payments per year to 12. & [ 12 !P/Y= 12.00

Return to standard-calculator

mode.

& U 0.00

Enter number of payments

using the payment multiplier.

30 & Z , N= 360.00

Time-Value-of-Money and Amortization Worksheets 27

Answer: The interest rate is 5.5% per year.

Examples: Computing Basic Loan Payments

These examples show you how to compute basic loan payments on a

$75,000 mortgage at 5.5% for 30 years.

Note: After you complete the first example, you should not have to re-

enter the values for loan amount and interest rate. The calculator saves

the values you enter for later use.

Computing Monthly Payments

Answer: The monthly payments are $425.84.

Computing Quarterly Payments

Note: The calculator automatically sets the number of compounding

periods (C/Y) to equal the number of payment periods (P/Y).

Enter loan amount. 75000 .PV= 75,000.00õ

Enter payment amount. 425.84 S / PMT= -425.84

Compute interest rate. % - I/Y= 5.50

To Press Display

Set payments per year to 12. & [ 12 !P/Y= 12.00

Return to standard-calculator

mode.

& U 0.00

Enter number of payments

using payment multiplier.

30 & Z , N= 360.00

Enter interest rate. 5.5 -I/Y= 5.50

Enter loan amount. 75000 .PV= 75,000.00õ

Compute payment. % / PMT= -425.84

To Press Display

Set payments per year to 4. & [ 4 !P/Y= 4.00

Return to standard-calculator

mode.

& U 0.00

Enter number of payments

using payment multiplier.

30 & Z , N= 120.00

To Press Display

28 Time-Value-of-Money and Amortization Worksheets

Answer: The quarterly payments are $1,279.82.

Examples: Computing Value in Savings

These examples show you how to compute the future and present values

of a savings account paying 0.5% compounded at the end of each year

with a 20-year time frame.

Computing Future Value

Example: If you open the account with $5,000, how much will you have

after 20 years?

Answer: The account will be worth $5,524.48 after 20 years.

Computing Present Value

Example: How much money must you deposit to have $10,000 in 20

years?

Answer: You must deposit $9,050.63.

Compute payment. % / PMT= -1,279.82

To Press Display

Set all variables to defaults. & }

RST 0.00

Enter number of payments. 20 ,N= 20.00

Enter interest rate. .5 -I/Y= 0.50

Enter beginning balance. 5000 S . PV= -5,000.00

Compute future value. % 0 FV= 5,524.48

To Press Display

Enter final balance. 10000 0FV= 10,000.00

Compute present value. % . PV= -9,050.63

To Press Display

Time-Value-of-Money and Amortization Worksheets 29

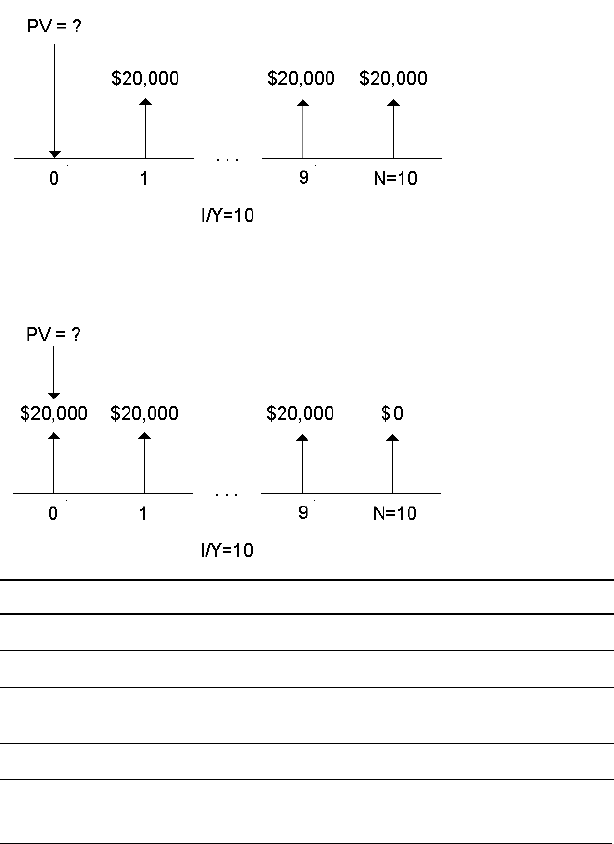
Example: Computing Present Value in Annuities

The Furros Company purchased equipment providing an annual savings

of $20,000 over 10 years. Assuming an annual discount rate of 10%, what

is the present value of the savings using an ordinary annuity and an

annuity due?

Cost Savings for a Present-Value Ordinary Annuity

Cost Savings for a Present-Value Annuity Due in a Leasing

Agreement

To Press Display

Set all variables to defaults. & } ! RST 0.00

Enter number of payments. 10 ,N= 10.00

Enter interest rate per

payment period.

10 -I/Y= 10.00

Enter payment. 20000 S / PMT= -20,000.00

30 Time-Value-of-Money and Amortization Worksheets

Answer: The present value of the savings is $122,891.34 with an ordinary

annuity and $135,180.48 with an annuity due.

Example: Computing Perpetual Annuities

To replace bricks in their highway system, the Land of Oz has issued

perpetual bonds paying $110 per $1000 bond. What price should you pay

for the bonds to earn 15% annually?

Answer: You should pay $733.33 for a perpetual ordinary annuity and

$843.33 for a perpetual annuity due.

A perpetual annuity can be an ordinary annuity or an annuity due

consisting of equal payments continuing indefinitely (for example, a

preferred stock yielding a constant dollar dividend).

Perpetual ordinary annuity

Compute present value

(ordinary annuity).

% . PV= 122,891.34

Set beginning-of-period

payments.

& ] & VBGN

Return to calculator mode. & U 0.00

Compute present value

(annuity due).

% . PV= 135,180.48

To Press Display

Calculate the present value for a

perpetual ordinary annuity.

110 6 15 2 N 733.33

Calculate the present value for a

perpetual annuity due.

H 110 N843.33

To Press Display

Time-Value-of-Money and Amortization Worksheets 31

Perpetual annuity due

Because the term (1 + I/Y / 100)-N in the present value annuity equations

approaches zero as N increases, you can use these equations to solve for

the present value of a perpetual annuity:

• Perpetual ordinary annuity

• Perpetual annuity due

Example: Computing Present Value of Variable

Cash Flows

The ABC Company purchased a machine that will save these end-of-year

amounts:

Year 1234

Amount $5000 $7000 $8000 $10000

PV PMT

I/Y()100÷

----------------------------=

PV PMT PMT

I/Y()100 )⁄

----------------------------+=

32 Time-Value-of-Money and Amortization Worksheets

Given a 10% discount rate, does the present value of the cash flows

exceed the original cost of $23,000?

To Press Display

Set all variables to defaults. & }

RST 0.00

Enter interest rate per cash flow

period.

10 -I/Y= 10.00

Enter 1st cash flow. 5000 S 0 FV= -5,000.00

Enter 1st cash flow period. 1 ,N= 1.00

Compute present value of 1st cash

flow.

% . PV= 4,545.45

Store in M1.D 14,545.45

Enter 2nd cash flow. 7000 S 0 FV= -7,000.00

Enter 2nd cash flow period. 2 ,N= 2.00

Compute present value of 2nd

cash flow.

% . PV= 5,785.12

Sum to memory. D H 15,785.12

Enter 3rd cash flow. 8000 S 0 FV= -8,000.00

Enter period number. 3 ,N= 3.00

Compute present value of 3rd

cash flow.

% . PV= 6,010.52

Sum to memory. D H 16,010.52

Enter 4th cash flow. 10000 S 0 FV= -10,000.00

Enter period number. 4 ,N= 4.00

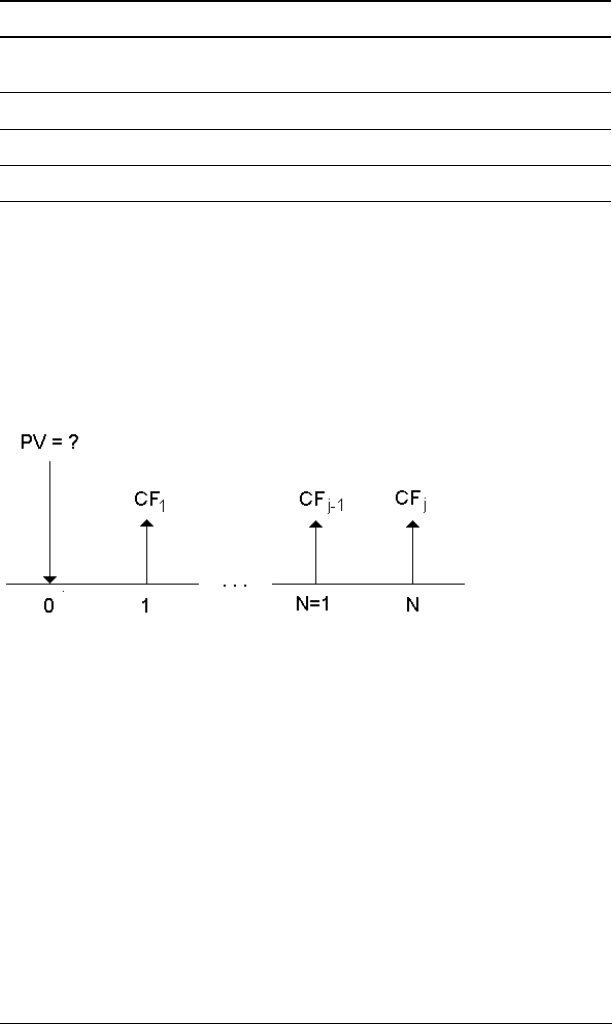
Time-Value-of-Money and Amortization Worksheets 33

Answer: The present value of the cash flows is $23,171.23, which exceeds

the machine’s cost by $171.23. This is a profitable investment.

Note: Although variable cash flow payments are not equal (unlike

annuity payments), you can solve for the present value by treating the

cash flows as a series of compound interest payments.

The present value of variable cash flows is the value of cash flows

occurring at the end of each payment period discounted back to the

beginning of the first cash flow period (time zero).

Example: Computing Present Value of a Lease

With Residual Value

The Peach Bright Company wants to purchase a machine currently leased

from your company. You offer to sell it for the present value of the lease

discounted at an annual interest rate of 22% compounded monthly. The

machine has a residual value of $6500 with 46 monthly payments of

$1200 remaining on the lease. If the payments are due at the beginning

of each month, how much should you charge for the machine?

Compute present value of 4th

cash flow.

% . PV= 6,830.13

Sum to memory. D H 16,830.13

Recall total present value. J 123,171.23

Subtract original cost. B 23000 N171.23

To Press Display

34 Time-Value-of-Money and Amortization Worksheets

The total value of the machine is the present value of the residual value

plus the present value of the lease payments.

Answer: Peach Bright should pay your company $40,573.18 for the

machine.

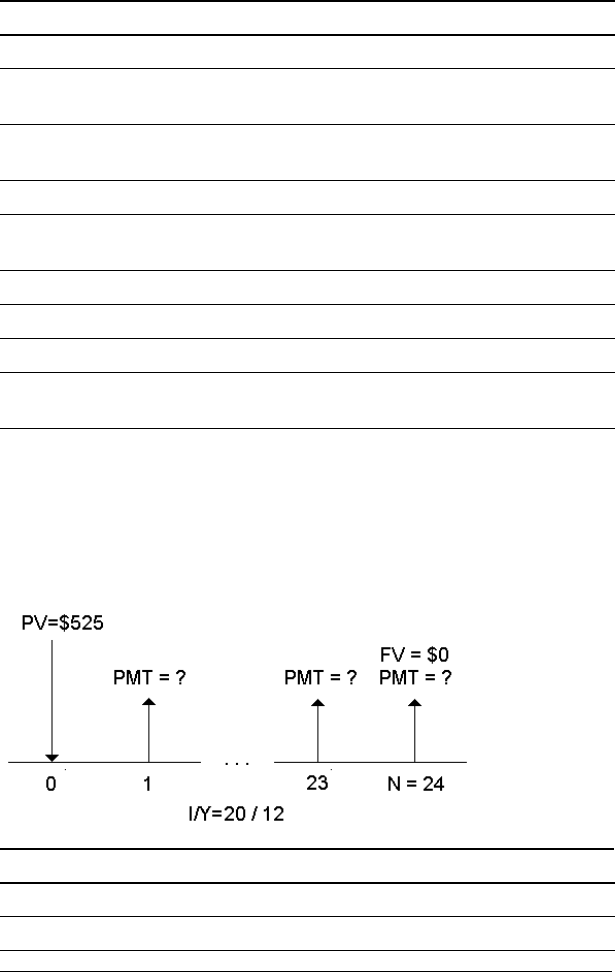
Example: Computing Other Monthly Payments

If you finance the purchase of a new desk and chair for $525 at 20% APR

compounded monthly for two years, how much is the monthly payment?

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set beginning-of-period

payments.

& ] & V BGN

Return to standard-calculator

mode.

& U 0.00

Enter number of payments. 46 ,N= 46.00

Calculate and enter periodic

interest rate.

22 6 12 N - I/Y= 1.83

Enter residual value of asset. 6500 S 0 FV= -6,500.00

Compute residual present value. % . PV= 2,818.22

Enter lease payment amount. 1200 S / PMT= -1,200.00

Compute present value of lease

payments.

% . PV= 40,573.18

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12 !P/Y= 12.00

Time-Value-of-Money and Amortization Worksheets 35

Answer: Your monthly payment is $26.72.

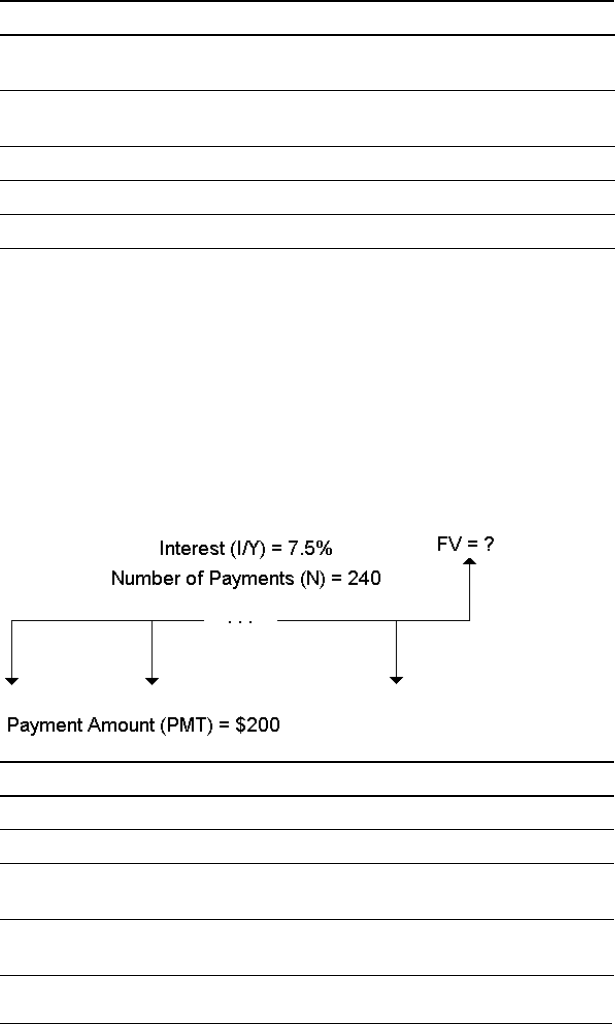
Example: Saving With Monthly Deposits

Note: Accounts with payments made at the beginning of the period are

referred to as annuity due accounts. Interest begins accumulating earlier

and produces slightly higher yields.

You invest $200 at the beginning of each month in a retirement plan.

What will the account balance be at the end of 20 years, if the fund earns

an annual interest of 7.5 % compounded monthly, assuming beginning-

of-period payments?

Return to standard-calculator

mode

& U 0.00

Enter number of payments using

payment multiplier.

2 & Z , N= 24.00

Enter interest rate. 20 -I/Y= 20.00

Enter loan amount. 525 .PV= 525.00

Compute payment. % / PMT= -26.72

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12 !P/Y= 12.00

Set beginning-of-period

payments.

& ] & V BGN

Return to standard-calculator

mode.

& U 0.00

To Press Display

36 Time-Value-of-Money and Amortization Worksheets

Answer: Depositing $200 at the beginning of each month for 20 years

results in a future amount of $111,438.31.

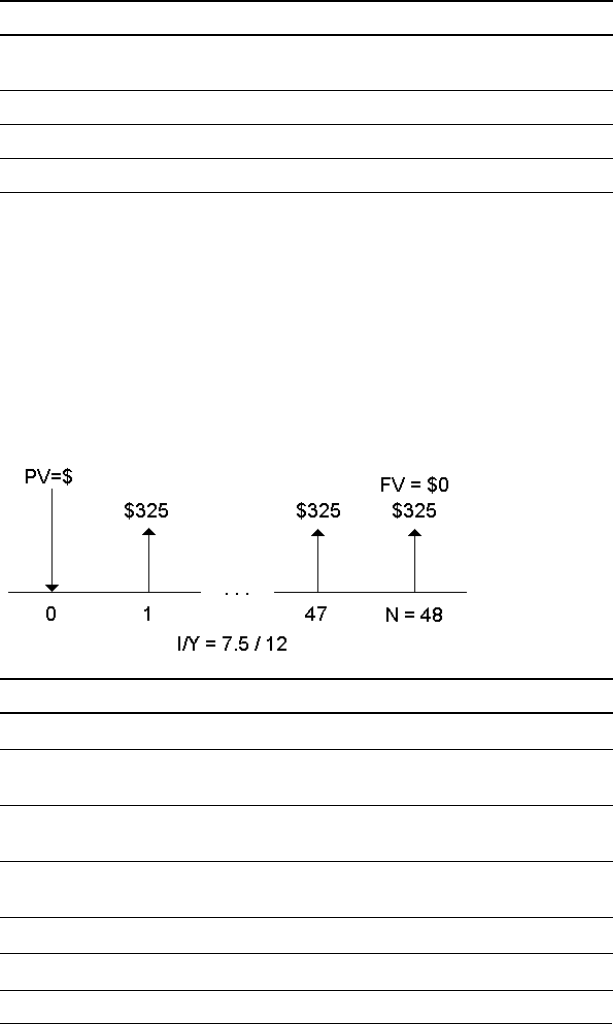
Example: Computing Amount to Borrow and

Down Payment

You consider buying a car for $15,100. The finance company charges

7.5% APR compounded monthly on a 48-month loan. If you can afford a

monthly payment of $325, how much can you borrow? How much do

you need for a down payment?

Enter number of payments

using payment multiplier.

20 & Z , N= 240.00

Enter interest rate. 7.5 -I/Y= 7.50

Enter amount of payment. 200 S / PMT= -200.00

Compute future value. % 0 FV= 111,438.31

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12

!P/Y= 12.00

Return to standard-calculator

mode

& U 0.00

Enter number of payments using

payment multiplier.

4 & Z , N= 48.00

Enter interest rate. 7.5 -I/Y= 7.50

Enter payment. 325 S / PMT= -325.00

To Press Display

Time-Value-of-Money and Amortization Worksheets 37

Answer: You can borrow $13,441.47 with a down payment of $1,658.53.

Example: Computing Regular Deposits for a

Specified Future Amount

You plan to open a savings account and deposit the same amount of

money at the beginning of each month. In 10 years, you want to have

$25,000 in the account.

How much should you deposit if the annual interest rate is 0.5% with

quarterly compounding?

Note: Because C/Y (compounding periods per year) is automatically set

to equal P/Y (payments per year), you must change the C/Y value.

Answer: You must make monthly deposits of $203.13.

Compute loan amount. % . PV= 13,441.47

Compute down payment H 15,100 S N -1,658.53

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12 !P/Y= 12.00

Set compounding periods to 4. # 4 !C/Y= 4.00

Set beginning-of-period

payments.

& ] & V BGN

Return to standard-calculator

mode.

& U 0.00

Enter number of deposits using

payment multiplier.

10 & Z , N= 120.00

Enter interest rate. .5 -I/Y= 0.50

Enter future value. 25,000 0FV= 25,000.00

Compute deposit amount. % / PMT= -203.13

To Press Display

38 Time-Value-of-Money and Amortization Worksheets

Example: Computing Payments and Generating an

Amortization Schedule

This example shows you how to use the TVM and Amortization

worksheets to calculate the monthly payments on a 30-year loan and

generate an amortization schedule for the first three years of the loan.

Computing Mortgage Payments

Calculate the monthly payment with a loan amount of $120,000 and

6.125% APR.

Answer: The computed monthly payment, or outflow, is $729.13.

Generating an Amortization Schedule

Generate an amortization schedule for the first three years of the loan. If

the first payment is in April, the first year has nine payment periods.

(Following years have 12 payment periods each.)

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12 !P/Y= 12.00

Return to standard-calculator

mode.

& U 0.00

Enter number of payments

using payment multiplier.

30 & Z , N= 360.00

Enter interest rate. 6.125 -I/Y= 6.13

Enter loan amount. 120000 .PV= 120,000.00

Compute payment. % / PMT= -729.13*

To Press Display

Select the Amortization worksheet. & \ P1= 0

Set beginning period to 1. 1 !P1= 1.00

Set ending period to 9. # 9 !P2= 9.00

Display 1st year amortization data. #

BAL=

PRN=

INT=

118,928.63*

-1071.37*

-5,490.80*

Change beginning period to 10. # 10 !P1= 10.00

Change ending period to 21. # 21 !P2= 21.00

Time-Value-of-Money and Amortization Worksheets 39

Example: Computing Payment, Interest, and Loan

Balance After a Specified Payment

A group of sellers considers financing the sale price of a property for

$82,000 at 7% annual interest, amortized over a 30-year term with a

balloon payment due after five years. They want to know:

• Amount of the monthly payment

• Amount of interest they will receive

• Remaining balance at the end of the term (balloon payment)

Computing the Monthly Payment

Display 2nd year amortization data. #

BAL=

PRN=

INT=

117,421.60*

_-1,507.03*

-7,242.53*

Move to P1 and press % to enter

next range of payments.

# %P1= 22.00

Display P2.#P2= 33.00

Display 3rd year amortization data. #

BAL=

PRN=

INT=

115,819.62*

-1601.98*

-7,147.58*

To Press Display

Set all variables to defaults. & } ! RST 0.00

Set payments per year to 12. & [ 12 !P/Y= 12.00

Return to standard-calculator

mode.

& U 0.00

Enter number of payments

using payment multiplier.

30 & Z , N= 360.00

Enter interest rate. 7 -I/Y= 7.00

Enter loan amount. 82000 .PV= 82,000.00

Compute payment. % / PMT= -545.55

To Press Display

40 Time-Value-of-Money and Amortization Worksheets

Generating an Amortization Schedule for Interest and

Balloon Payment

If the sellers financed the sale, they would receive:

• Monthly payment: $545.55 for five years

• Interest: $27,790.72 over the five years

• Balloon payment: $77,187.72

To Press Display

Select Amortization worksheet. & \ P1= 1.00

Enter end period (five years). # 5 & Z !P2= 60.00

View balance due after five

years (balloon payment).

#BAL= 77,187.72

View interest paid after five

years.

# #INT= -27,920.72

Cash Flow Worksheet 41

Cash Flow Worksheet

Cash Flow Worksheet Variables

Use the Cash Flow worksheet to solve problems with

unequal cash flows.

To solve problems with equal cash flows, use the TVM

worksheet.

• To access the Cash Flow worksheet and initial cash

flow value (CFo), press '.

• To access the cash flow amount and frequency

variables (Cnn/Fnn), press # or ".

• To access the discount rate variable (I), press (.

• To compute net present value (NPV), press # or " and

% for each variable.

• To compute net present value (NPV), net future value

(NFV), payback (PB), and discounted payback (DPB),

press # or " and % for each variable.

• To compute the internal rate of return (IRR), press ).

• To compute the modified internal rate of return

(MOD), press # to access the reinvestment rate (RI)

variable, key in a value, and press #.

Variable Key Display Variable

Type**

Initial cash flow 'CFo Enter-only

Amount of nth cash flow #Cnn* Enter-only

Frequency of nth cash flow #Fnn* Enter-only

Discount rate (IEnter-only

Net present value # % NPV Compute-only

42 Cash Flow Worksheet

*nn represents the cash flow (C01–C32) or frequency (F01–F32)

number.

** This guidebook categorizes variables by the method of entry. (See

“Types of Worksheet Variables” on page 17.)

Resetting Variables

• To reset CFo, Cnn, and Fnn to default values, press ' and then

&z.

• To reset NPV, NFV, PB, and DPB to default values to the default

value, press ( and then &z.

• To reset IRR, RI, and MOD to default values to the default value,

press ) and then &z.

• To reset all calculator variables and formats to default values,

including all Cash Flow worksheet variables, press &} !.

Entering Cash Flows

• You must enter an initial cash flow (CFo). The calculator accepts up

to 32 additional cash flows (C01–C32). Each cash flow can have a

unique value.

• Enter positive values for cash inflows (cash received) and negative

values for cash outflows (cash paid out). To enter a negative value,

key in a number and press S.

Inserting and Deleting Cash Flows

The calculator displays INS or DEL to confirm that you can press &X

or & W to insert or delete cash flows.

Net future value # % NFV Compute-only

Payback # % PB Compute-only

Discounted payback # % DPB Compute-only

Internal rate of return )% IRR Compute-only

Reinvestment rate #RI Enter-only

Modified Internal rate of return #MOD Auto

Compute

Variable Key Display Variable

Type**

Cash Flow Worksheet 43

Uneven and Grouped Cash Flows

Uneven Cash Flows

The Cash Flow worksheet analyzes unequal cash flows over equal time

periods. Cash-flow values can include both inflows (cash received) and

outflows (cash paid out).

All cash-flow problems start with an initial cash flow labeled CFo. CFo is

always a known, entered value.

Grouped Cash Flows

Cash-flow problems can contain cash flows with unique values as well as

consecutive cash flows of equal value.

Although you must enter unequal cash flows separately, you can enter

groups of consecutive, equal cash flows simultaneously using the Fnn

variable.

Entering Cash Flows

Cash flows consist of an initial cash flow (CFo) and up to 32 additional

cash flows (C01-C32), each of which can have a unique value. You must

enter the number of occurrences (up to 9,999), or frequency (F), for each

additional cash flow (C01-C32).

• The calculator displays positive values for inflows (cash received) and

negative values for outflows (cash paid out).

• To clear the Cash Flow worksheet, press & z.

To enter cash flows:

1. Press '. The initial cash-flow value (CFo) appears.

2. Key in a value for CFo and press !.

3. To select an additional cash-flow variable, press #. The C01 value

appears.

4. To change C01, key in a value and press !.

44 Cash Flow Worksheet

5. To select the cash-flow frequency variable (F01), press #. The F01

value appears.

6. To change F01, key in a value and press !.

7. To select an additional cash-flow variable, press #. The C02 value

appears.

8. Repeat steps 4 through 7 for all remaining cash flows and

frequencies.

9. To review entries, press # or ".

Deleting Cash Flows

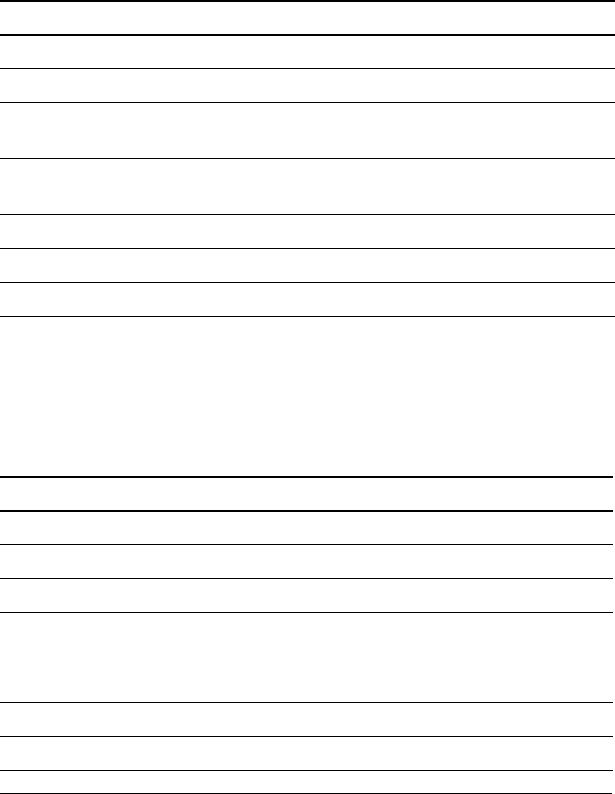
When you delete a cash flow, the calculator decreases the number of

subsequent cash flows automatically.

The DEL indicator confirms that you can delete a cash flow.

1. Press # or " until the cash flow you want to delete appears.

2. Press & W. The cash flow you specified and its frequency is

deleted.

Inserting Cash Flows

When you insert a cash flow, the calculator increases the number of the

following cash flows, up to the maximum of 32.

Note: The INS indicator confirms that you can insert a cash flow.

Cash Flow Worksheet 45

1. Press # or " to select the cash flow where you want to insert the

new one. For example, to insert a new second cash flow, select C02.

2. Press & X.

3. Key in the new cash flow and press !. The new cash flow is

entered at C02.

Computing Cash Flows

The calculator solves for these cash-flow values:

• Net present value (NPV) is the total present value of all cash flows,

including inflows (cash received) and outflows (cash paid out). A

positive NPV value indicates a profitable investment.

• Net future value (NFV) is the total future value of all cash flows. A

positive NFV value also indicates a profitable investment.

• Payback (PB) is the time required to recover the initial cost of an

investment, disregarding the present value of the cash inflows (time

value of money).

• Discounted payback (DPB) is the time required to recover the initial

cost of an investment using the present value of the cash inflows

(time value of money).

• Internal rate of return (IRR) is the interest rate at which the net

present value of the cash flows is equal to 0.

• Modified internal rate of return (MOD) considers the reinvestment

of cash when solving for IRR.

Computing NPV, NFV, PB, and DPB

1. Press ( to display the current discount rate (I).

2. Key in a value and press !.

3. Press # to display the current net present value (NPV).

4. To compute the net present value for the series of cash flows

entered, press %.

5. To compute the net future value (NFV), press #. The NFV value

appears.

6. To compute payback (PB), press #. The PB value appears.

7. To compute the payback discounted over time (DBP), press #. The

DBP value appears.

46 Cash Flow Worksheet

Computing IRR and MOD

1. Press ). The IRR variable and current value are displayed (based on

the current cash-flow values).

2. To compute the internal rate of return, press %. The calculator

displays the IRR value.

3. To select the reinvestment rate (RI), press #.

4. Key in the reinvestment rate value and press !.

5. To compute the modified internal rate of return, press #. The

calculator displays the MOD value.

When solving for IRR, the calculator performs a series of complex,

iterative calculations that can take seconds or even minutes to complete.

The number of possible IRR solutions depends on the number of sign

changes in your cash-flow sequence.

• When a sequence of cash flows has no sign changes, no IRR solution

exists. The calculator displays Error 5.

• When a sequence of cash flows has only one sign change, only one

IRR solution exists, which the calculator displays.

• When a sequence of cash flows has two or more sign changes:

– At least one solution exists.

– As many solutions can exist as there are sign changes.

When more than one solution exists, the calculator displays the one

closest to zero. Because the displayed solution has no financial

meaning, you should use caution in making investment decisions

based on an IRR computed for a cash-flow stream with more than

one sign change.

Cash Flow Worksheet 47

The time line reflects a sequence of cash flows with three sign

changes, indicating that one, two, or three IRR solutions can exist.

• When solving complex cash-flow problems, the calculator might not

find PB, DPB, IRR, and MOD, even if a solution exists. In this case, the

calculator displays Error 7 (iteration limit exceeded).

Example: Solving for Unequal Cash Flows

These examples show you how to enter and edit unequal cash-flow data

to calculate:

• Net present value (NPV)

• Net future value (NFV)

• Payback (PB)

• Discounted payback (DPB)

• Internal rate of return (IRR)

• Modified internal rate of return (MOD)

A company pays $7,000 for a new machine, plans a 20% annual return on

the investment, and expects these annual cash flows over the next six

years:

As the time line shows, the cash flows are a combination of equal and

unequal values. As an outflow, the initial cash flow (CFo) appears as a

negative value.

Year Cash Flow Number Cash Flow Estimate

Purchase CFo -$7,000

1C01 3,000

2–5 C02 5,000 each year

6C03 4,000

48 Cash Flow Worksheet

Entering Cash-Flow Data

Editing Cash-Flow Data

After entering the cash-flow data, you learn that the $4,000 cash-flow

value should occur in the second year instead of the sixth. To edit, delete

the $4,000 value for year 6 and insert it for year 2.

To Press Display

Select Cash Flow worksheet. 'CFo= 0.00

Enter initial cash flow. 7000 S ! CFo= -7,000.00

Enter cash flow for first year. # 3000 !

C01=

F01=

3,000.00

1.00

Enter cash flows for years

two through five.

# 5000 !

# 4 !

C02=

F02=

5,000.00

4.00

Enter cash flow for sixth year. # 4000 !

C03=

F03=

4,000.00

1.00

To Press Display

Move to third cash flow. "C03= 4,000.00

Delete third cash flow. & W C03= 0.00

Move to second cash flow. " " C02= 5,000.00

Insert new second cash flow. & X 4000 !

C02=

F02=

4,000.00

1.00

Move to next cash flow to

verify data.

C03=

F03=

5,000.00

4.00

Cash Flow Worksheet 49

Computing NPV, NFV, PB, and DPB

Use an interest rate per period (I) of 20%.

Answers: NPV is $7,266.44. NFV is $21,697.47. PB is 2.00. DPB is 2.60.

Computing IRR and MOD

Answer: IRR is 52.71%. MOD is 35.12%.

Example: Value of a Lease with Uneven Payments

A lease with an uneven payment schedule usually accommodates

seasonal or other anticipated fluctuations in the lessee’s cash position.

A 36-month lease has the following payment schedule and beginning-of-

period payments.

To Press Display

Access interest rate variable (I= 0.00

Enter interest rate per period. 20 !I= 20.00

Compute net present value. # % NPV= 7,266.44

Compute net future value. # % NFV= 21,697.47

Compute payback. # % PB= 2.00

Compute discounted payback. # % DPB= 2.60

To Press Display

Access IRR.)IRR= 0.00

Compute internal rate of return. #IRR= 52.71

Select reinvestment rate (RI)#RI= 0.00

Enter reinvestment rate. 20 ! RI= 20.0

Compute modified internal rate of return. # % MOD= 35.12

Number of Months Payment Amount

4$0

8 $5000

3$0

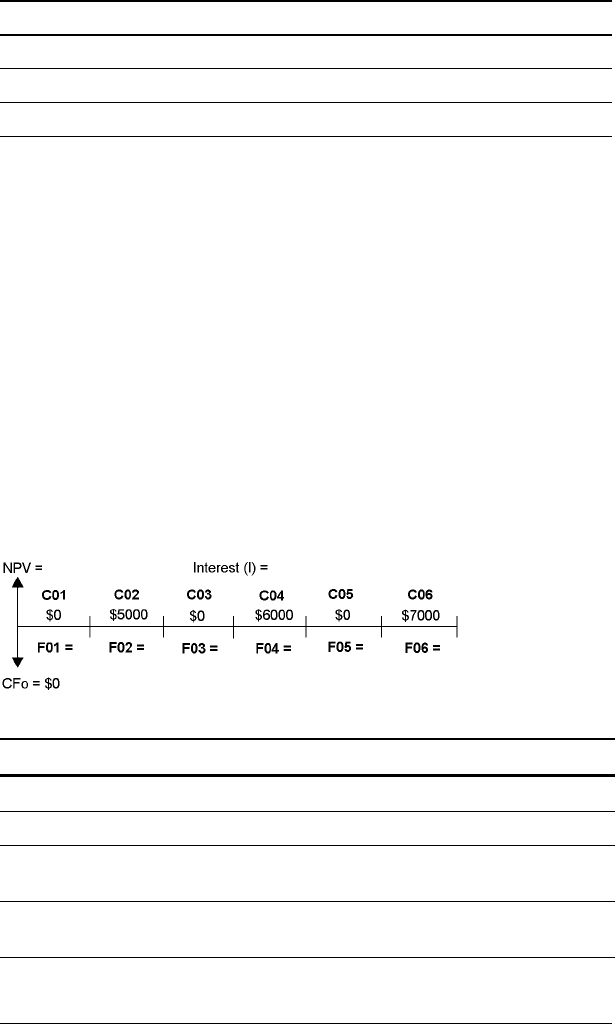
50 Cash Flow Worksheet

If the required earnings rate is 10% per 12-month period with monthly

compounding:

• What is the present value of these lease payments?

• What even payment amount at the beginning of each month would

result in the same present value?

Because the cash flows are uneven, use the Cash Flow worksheet to

determine the net present value of the lease.

Computing NPV

The cash flows for the first four months are stated as a group of four $0

cash flows. Because the lease specifies beginning-of-period payments,

you must treat the first cash flow in this group as the initial investment

(CFo) and enter the remaining three cash flows on the cash flow screens

(C01 and F01).

Note: The BGN/END setting in the TVM worksheet does not affect the

Cash Flow worksheet.

9 $6000

2$0

10 $7000

To Press Display

Set all variables to defaults. & } ! RST 0.00

Select Cash Flow worksheet. 'CFo= 0.00

Enter first group of cash flows. #

# 3 !

C01=

F01=

0.00

3.00

Enter second group of cash

flows.

# 5000 S !

# 8 !

C02=

F02=

-5000.00

8.00

Number of Months Payment Amount

Cash Flow Worksheet 51

Enter third group of cash

flows.

# 3 !

C03=

F03=

0.00

3.00

Enter fourth group of cash

flows.

# 6000 S !

# 9 !

C04=

F04=

-6000.00

9.00

Enter fifth group of cash flows. #

# 2 !

C05=

F05=

0.00

2.00

Enter sixth group of cash flows. # 7000 S !

# 10 !

C06=

F06=

-7000.00

10.00

Select NPV.(I= 0.00

Enter monthly earnings rate. 10 6 12 !I= 0.83

Compute NPV.# % NPV= -138,088.44

To Press Display

52 Cash Flow Worksheet

Bond Worksheet 53

Bond Worksheet

Note: Pressing # or " to navigate through the Bond worksheet before

you enter values causes an error (Error 6). To clear the error, press P.

The Bond worksheet lets you compute bond price, yield to

maturity or call, accrued interest, and modified duration.

You can also use the date functions to price bonds

purchased on dates other than the coupon anniversary.

• To access the Bond worksheet, press & l.

• To access bond variables, press " or #.

• To change the options for day-count methods (ACT

and 360) and coupons per year (2/Y and 1/Y), press &

V once for each option.

54 Bond Worksheet

Bond Worksheet Variables

Resetting Bond Worksheet Variables

• To reset the Bond worksheet variables to default values, press &

z while in the Bond worksheet.

• To reset all calculator variables and formats to default values,

including the Bond worksheet variables, press &}!.

Variable Key Display Variable Type

Settlement date & l SDT Enter only

Annual coupon rate in percent #CPN Enter only

Redemption date #RDT Enter only

Redemption value (percentage of

par value)

#RV Enter only

Actual/actual day-count method #ACT Setting

30/360 day-count method & V 360 Setting

Two coupons per year #2/Y Setting

One coupon per year & V 1/Y Setting

Yield to redemption #YLD Enter/compute

Dollar price #PRI Enter/compute

Accrued interest #AI Auto-compute

Modified duration #DUR Auto-compute

Variable Default Variable Default

SDT 12-31-1990 ACT/360 ACT

CPN 02/Y, 1/Y 2/Y

RDT 12-31-1990 YLD 0

RV 100 PRI 0

DUR 0AI 0

Bond Worksheet 55

Entering Dates

• Use the following convention to key in dates: mm.ddyy or dd.mmyy.

After keying in the date, press !.

Note: You can display dates in either US or European format. (See

“Setting Calculator Formats ” on page 4.)

• You can enter dates from January 1, 1950 through December 31,

2049.

• The calculator assumes that the redemption date (RDT) coincides

with a coupon date:

–To compute to maturity, enter the maturity date for RDT.

–To compute to call, enter the call date for RDT.

Entering CPN

CPN represents the annual coupon rate as a percentage of the bond par

value rather than the dollar amount of the coupon payment.

Entering RV

The redemption value (RV) is a percentage of the bond par value:

•For to maturity analysis, enter 100 for RV.

•For to call analysis, enter the call price for RV.

Setting the Day-Count Method

1. To display the day-count method, press # until ACT or 360 appears.

2. To change the day-count method, press & V.

Setting the Coupon Frequency

1. To display the coupon frequency, press # until 1/Y or 2/Y appears.

2. To change the coupon frequency, press & V.

56 Bond Worksheet

Bond Worksheet Terminology

Entering Bond Data and Computing Results

To compute values for price (PRI), modified duration (DUR), or yield

(YLD) and accrued interest (AI), first enter the four known values for

settlement date (SDT), coupon rate (CPN), redemption date (RDT), and

Term Definition

Call Date A callable bond can be retired by the issuing agency

before the maturity date. The call date for such a

bond is printed in the bond contract.

Coupon

Payment

The periodic payment made to the owner of the

bond as interest.

Coupon Rate The annual interest rate printed on the bond.

Dollar Price Price of the security expressed in terms of dollars per

$100 of par value.

Par (Face) Value The value printed on the bond.

Premium Bond A bond that sells for an amount greater than the par

value.

Discount Bond A bond selling for less than the par value.

Redemption

Date

The date on which the issuing agency retires the

bond. This date can be the date of maturity or, for a

callable bond, the call date.

Redemption

Value

The amount paid to the owner of a bond when

retired. If the bond is redeemed at the maturity

date, the redemption value is the par value printed

on the bond. If the bond is redeemed at a call date,

the redemption value is the bond’s par value plus

any call premium. The calculator treats the

redemption value in terms of dollars per $100 of par

value.

Settlement Date The date on which a bond is exchanged for funds.

Yield to

Maturity

The rate of return earned from payments of

principal and interest, with interest compounded

semiannually at the stated yield rate. The yield to

maturity takes into account the amount of premium

or discount, if any, and the time value of the

investment.

Bond Worksheet 57

redemption value (RV).

If necessary, change the day-count method (ACT or 360) and coupon-

frequency (2/Y or 1/Y). The Bond worksheet stores all values and settings

until you clear the worksheet or change the values and settings.

Note: Dates are not changed when you clear a worksheet.

Entering Known Bond Values

1. Press & l. The current SDT value appears.

2. To clear the worksheet, press & z.

3. If necessary, key in a new SDT value and press !.

4. Repeat step 3 for CPN, RDT, and RV, pressing # once for each

variable.

Note: To enter dates, use this convention: mm.ddyy (US) or dd.mmyy

(European).

Setting the Bond Day-Count Method and Coupon

Frequency

1. To display the day-count method, press # until ACT or 360 appears.

2. To change the day-count method, press &V.

3. To display the coupon frequency, press # until 2/Y or 1/Y appears.

4. To change the coupon frequency, press & V.

Computing the Bond Price (PRI)

1. Press # until YLD appears.

2. Key in a value for YLD and press !.

3. Press # to display PRI, and then press %. The calculator displays the

computed PRI value.

Computing the Bond Yield (YLD)

1. Press # until PRI appears.

2. Key in a value for PRI and press !.

3. Press # to display YLD, and then press %. The calculator displays

the computed YLD value.

Computing Accrued Interest (AI)

To compute accrued interest, press # until the AI variable appears. The

calculator automatically computes AI in terms of dollars per $100 of par

value.

58 Bond Worksheet

Computing Modified Duration (DUR)

To compute modified duration, press # until the DUR variable appears.

The calculator automatically computes DUR.

Example: Computing Bond Price, Accrued Interest,

and Modified Duration

You consider buying a semiannual corporate bond maturing on

December 31, 2007 and settling on June 12, 2006. The bond is based on

the 30/360 day-count method with a coupon rate of 7%, redeemable at

100% of par value. For an 8% yield to maturity, compute the bond’s

price, accrued interest, and modified duration.

Computing Bond Price, Accrued Interest, and Modified

Duration

Answer: The bond price is $98.56 per 100. The accrued interest is $3.15

per 100. Modified duration is 1.44.

To Press Display

Select Bond worksheet. & l SDT = 12-31-1990

Enter settlement date. 6.1206 !SDT = 6-12-2006

Enter coupon rate. # 7 !CPN = 7.00

Enter redemption date. # 12.3107 !RDT = 12-31-2007

Leave redemption value as is. #RV = 100.00

Select 30/360 day-count

method.

# & V 360

Leave two coupon payments

per year.

#2/Y

Enter yield. # 8 !YLD = 8.00

Compute price # % PRI = 98.56

View accrued interest. #AI = 3.15

View modified duration #DUR = 1.44

Depreciation Worksheet 59

Depreciation Worksheet

Depreciation Worksheet Variables

The Depreciation worksheet lets you generate a

depreciation schedule using your choice of depreciation

methods.

• To access the Depreciation worksheet, press & p.

• To change depreciation methods, press &V until

the desired method appears.

• To access other depreciation variables, press # or ".

Note: To easily scroll up or down through a range of

variables, press and hold # or ".

Variable Key Display Variable Type**

Straight-line method & p SL Setting

Sum-of-the-years’-digits

method

& V SYD Setting

Declining-balance method & V DB Setting/Enter

Declining-balance method

with crossover to SL method

& V DBX Setting/Enter

French straight-line method* & V SLF Setting

French declining balance

method*

& V DBF Setting/Enter

Life of the asset in years #LIF Enter only

Starting month #M01 Enter only

Starting date for French

straight-line method**

#DT1 Enter only

Cost of the asset #CST Enter only

Salvage value of the asset #SAL Enter only

60 Depreciation Worksheet

* SLF and DBF are available only if you select the European format for

dates or separators in numbers. (See “Setting Calculator Formats ”

on page 4.)**This guidebook categorizes variables by their method

of entry. (See “Types of Worksheet Variables” on page 17.)

Resetting the Depreciation Worksheet Variables

• To reset all calculator variables and formats to default values,

including the Depreciation worksheet variables, press & }

• To clear only the LIF, YR, CST, and SAL Depreciation worksheet

variables and reset default values without affecting the depreciation

method or other calculator variables and formats, press & z

while in the Depreciation worksheet.

Computing Values for DEP, RBV, and RDV

• The calculator computes one year at a time and rounds the results to

the number of decimal places set. (See “Setting Calculator Formats ”

on page 4.)

• The calculator computes values for DEP, RBV, and RDV automatically

when you press # to display each variable.

Year to compute #YR Enter only

Depreciation for the year #DEP Auto-compute

Remaining book value at the

end of the year

#RBV Auto-compute

Remaining depreciable value #RDV Auto-compute

Variable Default Variable Default

Depreciation

method

SL M01 1

DB 200 YR 1

DBX 200 CST 0

LIF 1 SAL 0

Variable Key Display Variable Type**

Depreciation Worksheet 61

Entering Values for DB and DBX

If you choose either the declining balance (DB) or declining balance with

crossover to SL (DBX) depreciation method, remember to enter a value

representing the percent of declining balance for the DB or DBX

variable.

Note: The declining balance you enter must be a positive number.

Entering Values for LIF

•If SL or SLF is selected, the LIF value must be a positive real number.

•If

SYD, DB, DBX, or DBF is selected, the LIF value must be a positive

integer.

Entering Values for M01

The value you enter for the starting month (M01) has two parts:

• The integer portion represents the month in which the asset is

placed into service.

• The decimal portion represents the fraction of the initial month in

which the asset begins to depreciate.

For example, to specify that the asset will begin to depreciate in the

middle of the first month, enter 1.5. To specify that the asset will begin

to depreciate a quarter of the way through the fourth month, enter 4.25.

Working with YR

• When computing depreciation, the value you enter for the year-to-

compute (YR) variable must be a positive integer.

• If the remaining depreciable value (RDV) variable is displayed, you

can press # to return to the year to compute (YR) variable. To

represent the next depreciation year, press % to increment the

value for YR by one.

• To compute a depreciation schedule, repeatedly return to the year to

compute (YR) variable, press % to increment the value for YR, and

compute values for DEP, RBV, and RDV. The schedule is complete

when RDV equals zero.

Entering Data and Computing Results

Because the Depreciation worksheet stores values and settings until you

either change them or clear the worksheet, you should not have to

perform every step each time you work a problem.

Note: Dates are not changed when you clear a worksheet.

62 Depreciation Worksheet

Selecting a Depreciation Method

1. To access the Depreciation worksheet, press & p. The current

depreciation method is displayed.

2. To clear the worksheet, press & z.

3. Press & V until you display the depreciation method you want

(SL, SLF, SYD, DB, DBX, or DBF).

Note: If you select DB or DBX, you must either key in a value or

accept the default of 200.

Entering Depreciation Data

1. To display LIF, press #.

2. Key in a value for LIF and press !.

3. Repeat steps 1 and 2 for M01, DT1 (if SLF), CST, SAL, and YR.

Note: To select SLF or DBF, you must set either the European date or

European separator format first.

Computing Results for DEP, RBV, and RDV

After entering the data, press # once for each of the DEP, RBV, and RDV

variables to display the computed values.

Note: The _indicator confirms that the displayed value is computed.

Generating a Depreciation Schedule

To generate a depreciation schedule and compute values for other years:

1. To display YR, press #.

2. To increment the value by one, press %.

3. To compute new values for DEP, RBV, and RDV, press # for each

variable.

Example: Computing Straight-Line Depreciation

In mid-March, a company begins depreciation of a commercial building

with a 31½ year life and no salvage value. The building cost $1,000,000.

Use the straight-line depreciation method to compute the depreciation

expense, remaining book value, and remaining depreciable value for the

first two years.

To Press Display

Access Depreciation

worksheet.

& p SL

Depreciation Worksheet 63

Answer: For the first year, the depreciation amount is $25,132.28, the

remaining book value is $974,867.72, and the remaining depreciable

value is $974,867.72.

For the second year, the depreciation amount is $31,746.03, the

remaining book value is $943,121.69, and the remaining depreciable

value is $943,121.69.

Enter life in years. # 31.5 !LIF = 31.50

Enter starting month. # 3.5 !M01 = 3.50

Enter cost. # 1000000 !CST = 1,000,000.00

Leave salvage value as is. #SAL = 0.00

Leave year as is. #YR = 1.00

Display depreciation

amount, remaining book

value, and remaining

depreciable value.

DEP =

RBV =

RDV =

25,132.28*

974,867.72*

View second year. #

YR =

1.00

2.00

Display second year

depreciation data.

DEP =

RBV =

RDV =

31,746.03*

943,121.69*

To Press Display

64 Depreciation Worksheet

Statistics Worksheet 65

Statistics Worksheet

Statistics Worksheet Variables

The Statistics worksheet performs analysis on one-and

two-variable data with four regression analysis models.

• To enter statistical data, press & j.

• To choose a statistics calculation method and compute

the results, press &k.

• To access statistics variables, press # or ".

Variable Key Display Variable Type

Current X value

Current Y value

& j

Xnn*

Ynn*

Enter-only

Standard linear regression

Logarithmic regression

Exponential regression

Power regression

One-variable statistics

& k

& V

LIN

EXP

PWR

1-V

Setting

66 Statistics Worksheet

*nn represents the number of the current X or Y value.

** Not displayed for one-variable statistics.

*** This guidebook categorizes calculator variables by their method of

entry. (See “Types of Worksheet Variables” on page 17.)

Resetting Statistics Worksheet Variables

•To clear all X and Y values as well as all values in the statistics portion

of the worksheet without affecting the statistics calculation method,

press & z while in the data-entry portion of the worksheet

(& j).

• To reset the statistics calculation method to LIN and clear all values

except X and Y, press &z while in the calculation method

and computation portion of the worksheet (&k).

• To reset the statistics calculation method to LIN and clear all values,

including X and Y, press & } !.

Entering Data Points

• You can enter up to 50 (x,y) data points.

• If you press # or " to move through the portion of the worksheet

that displays results without entering data points, the calculator will

display an error.

Number of observations

Mean (average) of X values

Sample standard deviation of X

Population standard deviation of X

Mean (average) of Y values

Sample standard deviation of Y

Population standard deviation of Y

Linear regression y-intercept

Linear regression slope

Correlation coefficient

Predicted X value

Predicted Y value

Sum of X values

Sum of X squared values

Sum of Y values

Sum of Y squared values

Sum of XY products

# (as

needed)

y**

Sy**

sy**

a**

b**

r**

X'**

Y'**

GX2

GY**

GY2**

GXY**

Auto-compute

Enter/compute

Auto-compute

Variable Key Display Variable Type

Statistics Worksheet 67

• When you enter data for one-variable statistics, Xnn represents the

value and Ynn specifies the number of occurrences (frequency).

• When you enter a value for Xnn, the value for Ynn defaults to 1.

Analyzing One-Variable Statistics

To analyze one-variable statistics, select 1-V. Only values for n, v, Sx, sX,

GX, and GX2 are computed and displayed for one-variable statistics.

Analyzing Two-Variable Statistics

You can choose from among these four regression-analysis methods:

•LIN

•Ln

•EXP

•PWR

Computing Values Automatically

Except for the predicted X' and Y' values, the calculator computes and

displays values for statistics variables automatically when you access

them.

Using X' and Y' for Regression Predictions

To use the X' and Y' variables for regression predictions, you either can

enter a value for X' to compute Y' or enter a value for Y' to compute X'.

Regression Models

For two-variable data, the Statistics worksheet uses four regression

models for curve fitting and forecasting.

The calculator interprets the X value as the independent variable and the

Y value as the dependent variable.

The calculator computes the statistical results using these transformed

values:

•LIN uses X and Y.

Model Formula Restrictions

LIN Y = a + b X None

Ln Y = a + b ln(X) All X values > zero

EXP Y = a bxAll Y values > zero

PWR Y = a XbAll X and Y values > zero

68 Statistics Worksheet

•Ln uses ln(X) and Y.

•EXP uses X and ln(Y).

•PWR uses ln(X) and ln(Y).

The calculator determines the values for a and b that create the line or

curve that best fits the data.

Correlation Coefficient

The calculator also determines r, the correlation coefficient, which

measures the goodness of fit of the equation with the data. Generally:

•The closer r is to 1 or -1, the better the fit.

•The closer r is to zero, the worse the fit.

Entering Statistical Data

Because the Statistics worksheet lets you enter and display up to 50 data

points, and then stores the values until you clear the worksheet or

change the values, you probably will not have to perform every step for

each Statistics calculation.

1. To select the data-entry portion of the Statistics worksheet, press &

j. X01 is displayed along with any previous value.

2. To clear the worksheet, press & z.

3. Key in a value for X01 and press !.

• For one-variable data, X01 is the first data point.

• For two-variable data, X01 is the first X value.

4. To display the Y01 variable, press #.

5. Key in a value for Y01 and press !.

• For one-variable data, you can enter the number of times the X

value occurs (frequency).

The default value is 1.

• For two-variable data, enter the first Y value.

6. To display the next X variable, press #.

7. Repeat steps 3 through 5 until you enter all of the data points.

Note: To easily scroll up or down through a range of variables, press and

hold # or ".

Statistics Worksheet 69

Computing Statistical Results

Selecting a Statistics Calculation Method

1. Press & k to select the statistical calculation portion of the

Statistics worksheet.

2. The last selected statistics calculation method is displayed (LIN, Ln,

EXP, PWR, or 1-V).

3. Press & V repeatedly until the statistics calculation method you

want is displayed.

4. If you are analyzing one-variable data, select 1-V.

5. Press # to begin computing results.

Computing Results

To compute results based on the current data set, press # repeatedly

after you have selected the statistics calculation method.

The calculator computes and displays the results of the statistical

calculations (except for X' and Y') automatically when you access them.

For one-variable statistics, the calculator computes and displays only the

values for n, v, Sx, sX, GX, and GX2.

Computing Y'

1. To select the Statistics worksheet, press & k.

2. Press " or # until X' is displayed.

3. Key in a value for X' and press !.

4. Press # to display the Y' variable.

5. Press % to compute a predicted Y' value.

Computing X'

1. To select the Statistics worksheet, press & k.

2. Press " or # until Y' is displayed.

3. Key in a value for Y' and press !.

4. Press " to display the X' variable.

5. Press % to compute an X' value.

70 Statistics Worksheet

Other Worksheets 71

Other Worksheets

The calculator also includes these worksheets:

Percent Change/Compound Interest Worksheet

Percent Change/Compound Interest Worksheet Variables

Note: This guidebook categorizes variables by their method of entry.

(See “Types of Worksheet Variables” on page 17.)

• Percent Change/Compound Interest worksheet

(&q)

• Interest Conversion worksheet (& v)

• Date worksheet (& u)

• Profit Margin worksheet (& w)

• Breakeven worksheet (& r)

• Memory worksheet (& {)

Use the Percent Change/Compound Interest worksheet to

solve percent change, compound interest, and cost-sell-

markup problems.

• To access the Percent Change/Compound Interest

worksheet, press &q.

• To access the Percent Change/Compound Interest

variables, press # or ".

Variable Key Display Variable Type

Old value/Cost &q OLD Enter/compute

New value/Selling price #NEW Enter/compute

Percent change/Percent

markup

#%CH Enter/compute

Number of periods ##PD Enter/compute

72 Other Worksheets

Resetting the Percent Change/Compound Interest

Worksheet Variables

• To reset the Percent Change/Compound Interest variables to default

values, press & z while in the Percent Change/Compound

Interest worksheet.

• To reset default values for all calculator variables and formats, press

& } !.

Entering Values

• For percent-change calculations, enter values for any two of the

three variables (OLD, NEW, and %CH) and compute a value for the

unknown variable (leave #PD=1). A positive percent change

represents a percentage increase; a negative percent change

represents a percentage decrease.

• For compound-interest calculations, enter values for the three

known variables and compute a value for the unknown fourth

variable.

–OLD= present value

–NEW= future value

–%CH= interest rate per period

–#PD= number of periods

• For cost-sell-markup calculations, enter values for two of the three

variables (OLD, NEW, and %CH) and compute a value for the

unknown.

–OLD = cost

–NEW= selling price

–%CH= percent markup

–#PD= 1

Computing Values

1. To select the Percent Change/Compound Interest worksheet, press

& q. The current value for OLD is displayed.

2. To clear the worksheet, press & z.

Variable Default Variable Default

OLD 0%CH 0

NEW 0#PD 1

Other Worksheets 73

3. To enter values for the known variables, press # or " until the

variable you want is displayed, then key in a value, and press !.

(Do not enter a value for the variable you wish to solve.)

•Percent Change — Enter values for two of these three

variables: OLD, NEW, and %CH. Leave #PD set to 1.

•Compound Interest — Enter values for three of these four

variables: OLD, NEW, %CH, and #PD.

•Cost-Sell-Markup — Enter values for two of these three

variables: OLD, NEW, and %CH. Leave #PD set to 1.

4. To compute a value for the unknown variable, press # or " until the

variable you want is displayed and press %. The calculator displays

the value.

Example: Computing Percent Change

First, determine the percentage change from a forecast amount of $658

to an actual amount of $700. Second, determine what the new amount

would be if it were 7% below the original forecast.

Answer: $700 represents a 6.38% increase over the original forecast of

$658. A decrease of 7% would result in a new actual amount of $611.94.

Example: Computing Compound Interest

You purchased stock in 1995 for $500. Five years later, you sell the stock

for $750. What was the annual growth rate?

To Press Display

Select Percent Change/Compound

Interest worksheet.

& q OLD= 0

Enter original forecast amount. 658 !OLD= 658.00

Enter actual amount. # 700 !NEW= 700.00

Compute percent change. # % %CH= 6.38

Enter -7 as percent change. 7 S ! %CH= -7.00

Compute new actual amount. " % NEW= 611.94

To Press Display

Select Percent Change/Compound

Interest worksheet.

& q OLD= 0

Enter stock purchase price. 500 !OLD= 500.00

Enter stock selling price. # 750 !NEW= 750.00

74 Other Worksheets

Answer: The annual growth rate is 8.45%.

Example: Computing Cost-Sell-Markup

The original cost of an item is $100; the selling price is $125. Find the

markup.

Answer: The markup is 25%.

Interest Conversion Worksheet

Note: The calculator categorizes variables by their method of entry.

Enter number of years. # # 5 !#PD= 5.00

Compute annual growth rate. " % %CH= 8.45

To Press Display

Select Percent Change/Compound

Interest worksheet.

& q OLD= 0

Clear worksheet variables. & z OLD= 0.00

Enter original cost. 100 !OLD= 100.00

Enter selling price. # 125 !NEW= 125.00

Compute percent markup. # % %CH= 25.00

The Interest Conversion worksheet converts interest rates

between nominal rate (or annual percentage rate) and

annual effective rate.

• To access the Interest Conversion worksheet, press &

• To select interest conversion variables, press # or ".

Variable Key Display Variable Type

Nominal rate & vNOM Enter/compute

Annual effective rate #EFF Enter/compute

Compounding periods per year #C/Y Enter-only

To Press Display

Other Worksheets 75

Comparing the Nominal Interest Rate of Investments

Comparing the nominal interest rate (annual percentage rate) of

investments is misleading when the investments have the same nominal

rate but different numbers of compounding periods per year.

To make a more valid comparison, convert the nominal interest rate

(NOM) to the annual effective interest rate (EFF) for each investment.

• The nominal interest rate (NOM) is the interest rate per

compounding period multiplied by the number of compounding

periods per year.

• The annual effective interest rate (EFF) is the compound annual

interest rate that you actually earn for the period of time stated.

Resetting Variables

• To reset all calculator variables and formats to default values,

including the Interest Conversion worksheet variables, press &

} !.

• To clear the NOM and EFF variables and reset default values without

affecting C/Y, press & z in the Interest Conversion

worksheet.

Converting Variables

You can convert a nominal rate to an annual effective rate or vice versa.

Entering Values for Nom and EFF

Enter a value for NOM or EFF as an annual rate.

Converting Interest Rates

1. To access the Interest Conversion worksheet, press & v. The

current NOM value appears.

2. To clear the worksheet, press & z.

3. Enter a value for the known interest rate (either NOM or EFF).

4. To enter a value for a known variable, press # or " until NOM or

EFF is displayed, key in a value, and press !.

5. Press # to display C/Y. If necessary, change the value and press !.

Variable Default

NOM 0

EFF 0

C/Y 1

76 Other Worksheets

6. To compute a value for the unknown variable (interest rate), press #

or " until NOM or EFF is displayed, and then press %. The

calculator displays the computed value.

Example: A bank offers a certificate that pays a nominal interest rate of

15% with quarterly compounding. What is the annual effective interest

rate?

Answer: A nominal interest rate of 15% compounded quarterly is

equivalent to an annual effective interest rate of 15.87%.

Date Worksheet

Date Worksheet Variables

To Press Display

Select Interest Conversion

worksheet.

& v NOM= 0

Enter nominal interest rate. 15 !NOM= 15.00

Enter number of compounding

periods per year.

# # 4 !C/Y= 4.00

Compute annual effective

interest rate.

" % EFF= 15.87

Use the Date worksheet to find the number of days

between two dates. You can also compute a date and day

of the week based on a starting date and a specified

number of days.

• To access the Date worksheet, press & u.

• To access the date variables, press # or ".

• To select the day-count method (ACT and 360), press

& V once for each option.

Variable Key Display Variable Type

Date 1 & u DT1 Enter/compute

Date 2 #DT2 Enter/compute

Days between dates #DBD Enter/compute

Actual/actual day-count method #ACT*Setting

30/360 day-count method #360*Setting

Other Worksheets 77

Note: The calculator categorizes variables by their method of entry. (See

“Types of Worksheet Variables” on page 17.)

Resetting the Date Worksheet Variables

• To reset default values for all calculator variables and formats,

including the Date worksheet variables, press & } !.

• To clear Date worksheet variables and reset default values without

affecting the day-count method, press &z while in the Date

worksheet.

Entering Dates

• The calculator assumes that DT1 is earlier than DT2.

• Enter dates for DT1 and DT2 in the selected US or European date

format.

• When you compute a date for DT1 or DT2, the calculator displays a

three-letter abbreviation for the day of the week (for example,

WED).

Selecting the Day-Count Method Affects Calculations

• When you select ACT as the day-count method, the calculator uses

the actual number of days in each month and each year, including

adjustments for leap years.

• When you select 360 as the day-count method, the calculator

assumes 30 days per month (360 days per year). You can compute

DBD using this day-count method, but not DT1 or DT2.

Computing Dates

1. To select the Date worksheet, press & u. The DT1 value is

displayed.

2. To clear the worksheet, press & z.

3. Enter values for two of the three variables: DT1, DT2, and DBD.

Note: Do not enter a value for the variable you wish to solve for.

4. To enter a value for a variable, press # or " to display the variable.

5. Key in a value and press !.

Variable Default Variable Default

DT1 12-31-1990 DBD 0

DT2 12-31-1990 Day-count

method

ACT

78 Other Worksheets

6. To change the day-count method setting, press # until ACT or 360 is

displayed.

7. To compute a value for the unknown variable, press # or " to

display the variable, and then press %. The calculator displays the

computed value.

Example: Computing Days between Dates

A loan made on September 4, 2003 defers the first payment until

November 1, 2003. How many days does the loan accrue interest before

the first payment?

Answer: Because there are 58 days between the two dates, the loan

accrues interest for 58 days before the first payment.

Profit Margin Worksheet

Profit Margin Worksheet Variables

To Press Display

Select Date worksheet. & u DT1= 12-31-1990

Enter first date. 9.0403 !DT1= 9-04-2003

Enter second date. # 11.0103 !DT2= 11-01-2003

Select actual/actual day-count

method.

# # ACT

Compute days between dates. " % DBD= 58.00

The Profit Margin worksheet computes cost, selling price,

and gross profit margin.

Note: To perform markup calculations, use the Percent

Change/Compound Interest worksheet.

• To access the Profit Margin worksheet, press &

• To access profit margin variables, press " or #.

• Enter values for the two known variables, and then

compute a value for the unknown variable.

Variable Key Display Variable Type

Cost & w CST Enter/compute

Selling price #SEL Enter/compute

Other Worksheets 79

Note: This guidebook categorizes calculator variables by their method of

entry.

Gross Profit Margin and Markup

The terms margin and markup often are used interchangeably, but each

has a distinct meaning.

•Gross profit margin is the difference between selling price and cost,

expressed as a percentage of the selling price.

•Markup is the difference between selling price and cost, expressed as

a percentage of the cost.

Clearing Profit Margin Worksheet Variables

• To clear the Profit Margin worksheet variables and reset default

values, press & z. All Profit Margin worksheet variables

default to zero.

• To reset default values for all calculator variables and formats,

including the Profit Margin worksheet variables, press & }

Computing Profit Margin

1. To select the Profit Margin worksheet, press & w. The CST value

appears.

2. To enter a value for one of the two known variables, press # or " to

select a variable, then key in a value and press !.

3. Repeat step 2 for the second known variable.

4. To compute a value for the unknown variable, press # or " to select

the variable and press %. The calculator displays the computed

value.

Example: Computing Profit Margin

The selling price of an item is $125. The gross profit margin is 20%. Find

the original cost.

Profit margin #MAR Enter/compute

To Press Display

Select Profit Margin worksheet. &w CST= 0.00

Enter selling price. # 125 !SEL= 125.00

Enter profit margin. # 20 !MAR= 20.00

Variable Key Display Variable Type

80 Other Worksheets

Answer: The original cost is $100.

Breakeven Worksheet

Note: To solve for quantity (Q), enter a value of zero for profit (PFT).

Breakeven Worksheet Variables

Note: This guidebook categorizes calculator variables by their method of

entry.

Resetting the Breakeven Worksheet Variables

• To reset default values for all Breakeven worksheet variables, press

& z. All Breakeven worksheet variables default to zero.

• To clear all calculator variables and formats and reset default values,

including the Breakeven worksheet variables, press & } !.

Compute cost. " " % CST= 100.00

The Breakeven worksheet computes the breakeven point

and sales level needed to earn a given profit by analyzing

relationships between fixed costs, variable costs per unit,

quantity, price, and profit.

You operate at a loss until you reach the breakeven

quantity (that is, total costs = total revenues).

• To access the Breakeven worksheet, press & r.

• To access breakeven variables, press " or #.

• Enter known values for the four known variables, then

compute a value for the fifth, unknown variable.

Variable Key Display Variable Type

Fixed cost & r FC Enter/compute

Variable cost per unit #VC Enter/compute

Unit price #PEnter/compute

Profit #PFT Enter/compute

Quantity #QEnter/compute

To Press Display

Other Worksheets 81

Computing Breakeven

1. To access the Breakeven worksheet, press & r. The FC variable

appears.

2. Press # or " to select a known variable, key in the value, and press

3. Repeat step 3 for each of the remaining known variables.

4. To compute a value for the unknown variable, press # or " until the

variable is displayed, and then press %. The calculator displays the

computed value.

Example: Computing Breakeven Quantity

A canoe company sells paddles for $20 each. The unit variable cost is $15,

and the fixed costs are $3,000. How many paddles must be sold to break

even?

Answer: 600 paddles must be sold to break even.

To Press Display

Access Breakeven worksheet. & r FC= 0

Enter fixed costs. 3000 !FC= 3,000.00

Enter variable cost per unit. # 15 !VC= 15.00

Enter price. # 20 !P= 20.00

Leave profit as is. #PFT= 0.00

Compute quantity. # % Q= 600.00

82 Other Worksheets

Memory Worksheet

Memory Worksheet Variables

Note: This guidebook categorizes calculator variables by their method of

entry. (See “Types of Worksheet Variables” on page 17.)

Clearing the Memory Worksheet Variables

To clear all 10 memories at once, press & z in the Memory

worksheet.

Using the Memory Worksheet

1. To select the Memory worksheet, press & {. M0 apears.

2. Perform any of the following operations:

• To clear all 10 memories at once, press & z.

The Memory worksheet lets you compare and recall stored

values by accessing the calculator’s 10 memories. All

memory variables are enter-only. (See “Types of Worksheet

Variables” on page 17.)

• To access the Memory worksheet, press & {.

• To access memory variables, press " or #.

Note: You can access memories individually using D,

J, and the digit keys. (See “Memory Operations” on

page 12.)

Variables Key Display Variable Type

Memory 0 & { M0 Enter-only

Memory 1 #M1 Enter-only

Memory 2 #M2 Enter-only

Memory 3 #M3 Enter-only

Memory 4 #M4 Enter-only

Memory 5 #M5 Enter-only

Memory 6 #M6 Enter-only

Memory 7 #M7 Enter-only

Memory 8 #M8 Enter-only

Memory 9 #M9 Enter-only

Other Worksheets 83

• To view the contents of the memories, press # or " once for

each memory.

• To store a value, select a memory (M0-M9), key in a value, and

press !.

• Memory arithmetic. (See “Memory Arithmetic” on page 12.)

Examples: Using the Memory Worksheet

To Press Display

Access Memory worksheet & { M0= 0

Select M4.# # # # M4= 0

Clear M4.0 !M4= 0.00

Store 95. 9 5 !M4= 95.00

Add 65. H 6 5 !M4= 160.00

Subtract 30. B 3 0 !M4= 130.00

Multiply by 95. < 9 5 !M4= 12,350.00

Divide by 65. 6 6 5 !M4= 190.00

Raise to 2nd power. ; 2 !M4= 36,100.00

84 Other Worksheets

Appendix — Reference Information 85

Appendix — Reference Information

This appendix includes supplemental information to help you use your

BA II PLUSé and BA II PLUSé PROFESSIONAL calculator:

•Formulas

• Error conditions

• Accuracy information

• IRR (internal-rate-of-return) calculations

• Algebraic operating system (AOS™)

• Battery information

• In case of difficulty

• TI product service and warranty information

Formulas

This section lists formulas used internally by the calculator.

Time Value of Money

where: PMT ƒÄ0

y =C/Y P P/Y

x =(.01 Q I/Y) P C/Y

C/Y =compounding periods per year

P/Y =payment periods per year

I/Y =interest rate per year

where: PMT =0

The iteration used to compute i:

yx1+()ln×()

[]1–=

i–FV PV÷()

1N÷()

1–=

0PV PMT Gi

11i+()

N–

–

------------------------------FV 1i+()

N–

×+×+=

86 Appendix — Reference Information

I/Y =

where: x = i

y =P/Y P C/Y

Gi = 1 + i Q k

where: k =0 for end-of-period payments

k =1 for beginning-of-period payments

where: i ƒ0

N = L(PV + FV) P PMT

where: i =0

where: i ƒ0

PMT = L(PV + FV) P N

where: i =0

where: i ƒ0

PV = L(FV + PMT Q N)

where: i =0

100 CY e

yx1+()ln×()

1–[]×⁄×

PMT GiFV i×–×

PMT GiPV i×+×

----------------------------------------------





1i+()ln

----------------------------------------------------------=

PMT –i

----- PV PV FV+

1i+()

N1–

----------------------------+×=

PV PMT Gi

------------------------ FV–1

1i+()

-------------------PMT Gi

------------------------–×=

Appendix — Reference Information 87

where: i ƒ0

FV = L(PV + PMT Q N)

where: i =0

Amortization

If computing bal(), pmt2 = npmt

Let bal(0) = RND(PV)

Iterate from m = 1 to pmt2

then: bal( ) =bal(pmt2)

GPrn( ) =bal(pmt2) N bal(pmt1)

GInt( ) =(pmt2 N pmt1 +1) Q RND(PMT) N GPrn( )

where: RND =round the display to the number of decimal

places selected

RND12 =round to 12 decimal places

Balance, principal, and interest are dependent on the values of PMT, PV,

I/Y, and pmt1 and pmt2.

Cash Flow

where:

FV PMT Gi

------------------------ 1 i+()

–PV PMT Gi

------------------------+





×=

ImRND RND12 –i bal m 1–()×()[]=

bal m() bal m 1–()Im

–RND PMT() +=







NPV CF0CFj1i+()

-Sj1–11i+()

-nj

–()

----------------------------------

j1=

∑

i1=

∑j1≥

0j0=











88 Appendix — Reference Information

Net present value depends on the values of the initial cash flow (CF0),

subsequent cash flows (CFj), frequency of each cash flow (nj), and the

specified interest rate (i).

where: i is the periodic interest rate used in the calculation of NPV.

where: is the frequency of the kth cash flow.

IRR = 100 × i, where i satisfies npv() = 0

Internal rate of return depends on the values of the initial cash flow

(CF0) and the subsequent cash flows (CFj).

i = I/Y ÷ 100

The calculator uses this formula to compute the modified internal rate of

return:

where: positive = positive values in the cash flows

negative = negative values in the cash flows

N = number of cash flows

rrate = reinvestment rate

frate = finance rate

NPV (values, rate) = Net present value of the values in the rate

described

NFV 1i+()

pNPV×=

k1=

∑

MOD NPV (positive, rrate–

NPV (negative, frate)

-----------------------------------------------------

1N⁄

1rrate+()1–×=

Appendix — Reference Information 89

Bonds1

Price (given yield) with one coupon period or less to redemption:

where: PRI =dollar price per $100 par value

RV =redemption value of the security per $100 par value (RV =

100 except in those cases where call or put features must be

considered)

R =annual interest rate (as a decimal; CPN _ 100)

M =number of coupon periods per year standard for the

particular security involved (set to 1 or 2 in Bond worksheet)

DSR =number of days from settlement date to redemption date

(maturity date, call date, put date, etc.)

E =number of days in coupon period in which the settlement

date falls

Y =annual yield (as a decimal) on investment with security held

to redemption (YLD P 100)

A =number of days from beginning of coupon period to

settlement date (accrued days)

Note: The first term computes present value of the redemption amount,

including interest, based on the yield for the invested period. The second

term computes the accrued interest agreed to be paid to the seller.

Yield (given price) with one coupon period or less to redemption:

1. Source for bond formulas (except duration): Lynch, John J., Jr., and Jan H. Mayle.

Standard Securities Calculation Methods. New York: Securities Industry Association,

1986.

PRI

RV 100 R×

------------------+

1DSR

----------- Y

-----







---------------------------------------A

--- 100 R×

------------------

×–=

100

---------R

-----+





PRI

100

----------A

--- R

-----









–

PRI

100

----------A

--- R

-----





---------------------------------------------------------------------------ME×

DSR

--------------

×=

90 Appendix — Reference Information

Price (given yield) with more than one coupon period to redemption:

where: N =number of coupons payable between settlement date and

redemption date (maturity date, call date, put date, etc.). (If this

number contains a fraction, raise it to the next whole number;

for example, 2.4 = 3)

DSC =number of days from settlement date to next coupon date

K =summation counter

Note: The first term computes present value of the redemption amount,

not including interest. The second term computes the present values for

all future coupon payments. The third term computes the accrued

interest agreed to be paid to the seller.

Yield (given price) with more than one coupon period to redemption:

Yield is found through an iterative search process using the “Price with

more than one coupon period to redemption” formula.

Accrued interest for securities with standard coupons or interest at

maturity:

where: AI =accrued interest

PA R =par value (principal amount to be paid at maturity)

Modified duration:2

2. Source for duration: Strong, Robert A., Portfolio Construction, Management, and

Protection, South-Western College Publishing, Cincinnati, Ohio, 2000.

PRI

-----+





N1–DSC

------------+

-------------------------------------------

100 R

-----A

---

××–

100 R

-----

-----+





K1–DSC

------------+

-------------------------------------------

K1=

∑

AI PAR R

-----A

---

××=

Modified Duration Duration

-----+

------------------------=

Appendix — Reference Information 91

where Duration is calculated using one of the following formulas used to

calculate Macaulay duration:

• For a bond price with one coupon period or less to redemption:

• For a bond price with more than one coupon period to redemption:

Depreciation

RDV = CST N SAL N accumulated depreciation

Values for DEP, RDV, CST, and SAL are rounded to the number of

decimals you choose to be displayed.

In the following formulas, FSTYR = (13 N MO1) P 12.

Straight-line depreciation

First year:

Last year or more: DEP = RDV

Dur 1Y

-----+





Dsr

Rv 100 R×

------------------+

1Dsr Y×

EM×

-------------------





------------------------------------------

EMPri××

----------------------------------------------------------------

⋅=

CST SAL–

LIF

---------------------------

ST SAL–

LIF

-------------------------- FSTYR×

92 Appendix — Reference Information

Sum-of-the-years’-digits depreciation

First year:

Last year or more: DEP = RDV

Declining-balance depreciation

where: RBV is for YR - 1

First year:

Unless ; then use RDV Q FSTYR

If DEP > RDV, use DEP = RDV

If computing last year, DEP = RDV

Statistics

Note: Formulas apply to both x and y.

Standard deviation with n weighting (sx):

LIF 2YR–FSTYR)–+ CST(× SAL)–

LIF(( LIF(1))+×2)÷

----------------------------------------------------------------------------------------------------

LIF CST SAL–()×

LIF(LIF(× 1)+()2)÷

------------------------------------------------------------ FSTYR×

BV DB%×

LIF 100×

-------------------------------

ST DB%×

LIF 100×

------------------------------FSTYR×

ST DB%×

LIF 100×

------------------------------RDV>

12⁄

∑





--------------------–

∑

-----------------------------------------

Appendix — Reference Information 93

Standard deviation with n-1 weighting (sx):

Mean:

Regressions

Formulas apply to all regression models using transformed data.

Interest Rate Conversions

where: x =.01 Q NOM P CˆY

where: x =.01 Q EFF

Percent Change

12⁄

∑





--------------------–

∑

n1–

-----------------------------------------

∑

(

---------------=

nxy)

∑

()x

∑

()–

∑

() x

∑

()

–

---------------------------------------------------------=

∑bx

∑

–()

---------------------------------=

rbδx

δy

--------=

EFF 100 eCY⁄In×x1÷()

(1)–×=

OM 100 CY⁄e1CY In×⁄÷

(x1+()

1)–××=

NEW OLD 1%CH

100

--------------+





#PD

94 Appendix — Reference Information

where: OLD =old value

NEW =new value

%CH =percent change

#PD =number of periods

Profit Margin

Breakeven

PFT = P Q N (FC + VC Q)

where: PFT =profit

P =price

FC =fixed cost

VC =variable cost

Q =quantity

Days between Dates

With the Date worksheet, you can enter or compute a date within the

range January 1, 1950, through December 31, 2049.

Actual/actual day-count method

Note: The method assumes the actual number of days per month and

per year.

DBD (days between dates) = number of days II - number of days I

Number of Days I= (Y1 - YB) Q 365

+ (number of days MB to M1)

+ DT1

Number of Days II=(Y2 - YB) Q 365

+ (number of days MB to M2)

+ DT2

Gross Profit Margin Selling Price Cost–

Selling Price

----------------------------------------------- 100×=

Y1YB–()

------------------------

Y2YB–()

------------------------

Appendix — Reference Information 95

where: M1 =month of first date

DT1 =day of first date

Y1 =year of first date

M2 =month of second date

DT2 =day of second date

Y2 =year of second date

MB =base month (January)

DB =base day (1)

YB =base year (first year after leap year)

30/360 day-count method3

Note: The method assumes 30 days per month and 360 days per year.

where: M1 =month of first date

DT1 =day of first date

Y1 =year of first date

M2 =month of second date

DT2 =day of second date

Y2 =year of second date

Note: If DT1 is 31, change DT1 to 30. If DT2 is 31 and DT1 is 30 or 31,

change DT2 to 30; otherwise, leave it at 31.

3. Source for 30/360 day-count method formula: Lynch, John J., Jr., and Jan H. Mayle.

Standard Securities Calculation Methods. New York: Securities Industry Association,

1986

DBD Y2(Y1)–360×M2(M1)++ 30×DT2(DT1)–+=

96 Appendix — Reference Information

Error Messages

Note: To clear an error message, press P.

Error Possible Causes

Error 1

Overflow

• A result is outside the calculator range

(±9.9999999999999E99).

• Tried to divide by zero (can occur internally).

• Tried to compute 1/x when x is zero.

• Statistics worksheet: a calculation included X or Y

values that are all the same.

Error 2

Invalid

argument

• Tried to compute x! when x is not an integer 0-69.

• Tried to compute LN of x when x is not > 0.

• Tried to compute yx when y < 0 and x is not an

integer or the inverse of an integer.

• Tried to compute when x < 0.

• Amortization worksheet: tried to compute BAL,

PRN, and INT when P2 < P1.

• Depreciation worksheet: a calculation included

SAL > CST.

Error 3

Too many

pending

operations

• More than 15 active levels of parentheses were

tried in a calculation.

• A calculation tried to use more than 8 pending

operations.

Error 4

Out of range

• Amortization worksheet: the value entered for P1

or P2 is outside the range 1-9,999.

• TVM worksheet: the P/Y or C/Y value  0.

• Cash Flow worksheet: the Fnn value is outside the

range 0.5-9,999.

• Bond worksheet: the RV, CPN, or PRI value _0.

• Date worksheet: the computed date is outside the

range January 1, 1950 through December 31, 2049.

• Depreciation worksheet: the value entered for:

declining balance percent  0; LIF  0; YR _ 0; CST <

0; SAL < 0; or M01 1M01 13.

• Interest Conversion worksheet: the C/Y value  0.

•The

DEC value is outside the range 0-9.

Appendix — Reference Information 97

Error 5

No solution

exists

• TVM worksheet: the calculator computed I/Y when

FV, (N Q PMT), and PV all have the same sign.

(Make sure cash inflows are positive and outflows

are negative.)

• TVM, Cash Flow, and Bond worksheets: the LN

(logarithm) input is not > 0 during calculations.

• Cash Flow worksheet: the calculator computed IRR

without at least one sign change in the cash-flow

list.

Error 6

Invalid date

• Bond and Date worksheets: a date is invalid (for

example, January 32) or in the wrong format (for

example, MM.DDYYYY instead of MM.DDYY.

• Bond worksheet: the calculator attempted a

calculation with a redemption date earlier than or

the same as the settlement date.

Error 7

Iteration limit

exceeded

• TVM worksheet: the calculator computed I/Y for a

very complex problem involving many iterations.

• Cash Flow worksheet: the calculator computed IRR

for a complex problem with multiple sign changes

or for the BA II PLUS™ PROFESSIONAL calculator

PB/DPB with no payback period based on input

cash flow values.

• Bond worksheet: the calculator computed YLD for

a very complex problem.

Error 8

Canceled

iterative

calculation

• TVM worksheet: $ was pressed to stop the

evaluation of I/Y.

• Amortization worksheet: $ was pressed to

stop the evaluation of BAL or INT.

• Cash Flow worksheet: $ was pressed to stop

the evaluation of IRR.

• Bond worksheet: $ was pressed to stop the

evaluation of YLD.

• Depreciation worksheet: $ was pressed to stop

the evaluation of DEP or RDV.

Error Possible Causes

98 Appendix — Reference Information

Accuracy Information

The calculator stores results internally as 13-digit numbers but displays

them rounded to 10 digits or fewer, depending on the decimal format.

The internal digits, or guard digits, increase the calculator’s accuracy.

Additional calculations use the internal value, not the value displayed.

Rounding

If a calculation produces a result with 11-digits or more, the calculator

uses the internal guard digits to determine how to display the result. If

the eleventh digit of the result is 5 or greater, the calculator rounds the

result to the next larger value for display.

For example, consider this problem.

1 P 3 Q 3 = ?

Internally, the calculator solves the problem in two steps, as shown

below.

1. 1 P 3 = 0.3333333333333

2. 0.3333333333333 Q 3 = 0.9999999999999

The calculator rounds the result and displays it as 1. This rounding

enables the calculator to display the most accurate result.

Although most calculations are accurate to within ±1 in the last displayed

digit, higher-order mathematical functions use iterative calculations, in

which inaccuracies can accumulate in the guard digits. In most cases, the

cumulative error from these calculations is maintained beyond the 10-

digit display so that no inaccuracy is shown.

AOS™ (Algebraic Operating System) Calculations

When you select the AOS calculation method, the calculator uses the

standard rules of algebraic hierarchy to determine the order in which it

performs operations.

Algebraic Hierarchy

The table shows the order in which the calculator performs operations

using the AOS calculation method.

Priority Operations

1 (highest) x2, x!, 1/x, %, ‡x, LN, e2, HYP, INV, SIN, COS, TAN

2nCr, nPr

3Yx

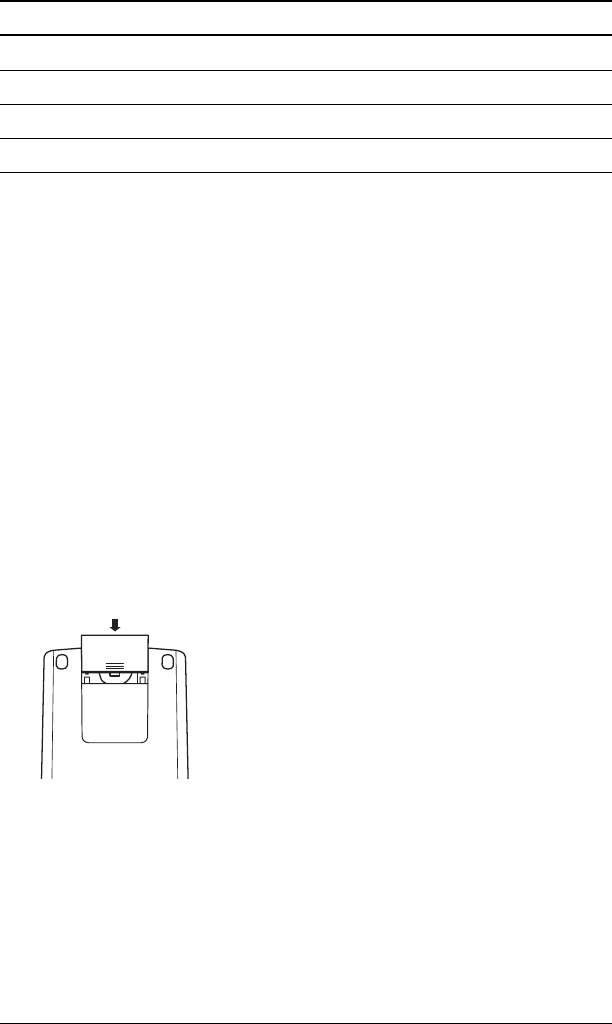
Appendix — Reference Information 99

Battery Information

Replacing the Battery

Replace the battery with a new CR2032 lithium battery.

Caution: Risk of explosion if replaced by an incorrect type. Replace only

with the same or equivalent type recommended by Texas Instruments.

Dispose of used batteries according to local regulations.

Note: The calculator cannot retain data when the battery is removed or

discharged. Replacing the battery has the same effect as resetting the

calculator.

1. Turn off the calculator and turn it over with the back facing you.

2. Slide the battery cover up and remove it from the back case.

3. Remove the battery.

4. Install the new battery with the positive sign (+) sign showing.

5. Replace the battery cover.

Caution: Risk of explosion if replaced by an incorrect type. Replace only

with the same or equivalent type recommended by Texas Instruments.

Dispose of used batteries according to local regulations.

Battery Precautions

• Do not leave battery within the reach of children.

• Do not mix new and used batteries.

• Do not mix rechargeable and non-rechargeable batteries.

4Q, P

5+, -

7 (lowest) =

Priority Operations

100 Appendix — Reference Information

• Install battery according to polarity (+ and - ) diagrams.

• Do not place non-rechargeable batteries in a battery recharger.

• Properly dispose of used batteries immediately.

• Do not incinerate or dismantle batteries.

• Seek Medical Advice immediately if a cell or battery has been

swallowed. (In the USA, contact the National Poison Control Center

collect at 202-625-3333.) Used only for small button cell batteries.

Battery Disposal

• Do not mutilate, or dispose of batteries in fire.

• The batteries can burst or explode, releasing hazardous chemicals.

• Discard used batteries according to local regulations.

In Case of Difficulty

Use this list of possible solutions to difficulties you might encounter with

the calculator to determine if you can correct a problem before having to

return it for service.

Difficulty Solution

The calculator computes

wrong answers.

Check the settings of the current

worksheet to make sure they are

correct for the problem you are

working; for example, in the TVM

worksheet, check END and BGN and be

sure the unused variable is set to zero.

The display is blank; digits do

not appear.

Select the worksheet again. Be sure the

battery is properly installed and

replace, if necessary.

The calculator does not display

the correct worksheet

variables.

Be sure you have selected the correct

worksheet.

The calculator does not display

the correct number of decimal

places.

Press & | to check or adjust the

setting for number of decimal places

displayed.

The calculator does not display

the correct date format.

Press & | # # to check or adjust

the setting for date format.

The calculator does not display

the correct separator format.

Press & | # # # to check or

adjust the setting for separator format.

Appendix — Reference Information 101

If you experience difficulties other than those listed above, press &

} ! to clear the calculator, and then repeat your calculations.

Note: You can also perform a hard reset using the reset hole in back of

the calculator.

Texas Instruments Support and Service

For general information

For technical support

For Product (hardware) Service

Customers in the U.S., Canada, Mexico, Puerto Rico and Virgin

Islands: Always contact Texas Instruments Customer Support before

returning a product for service.

All other customers: Refer to the leaflet enclosed with this product

(hardware) or contact your local Texas Instruments retailer/distributor.

The calculator does not display

the correct result in a math

calculation.

Press & | # # # # to check or

adjust the setting for calculation

method.

An error occurs.

Home Page: education.ti.com

Knowledge Base

and e-mail

inquiries: education.ti.com/support

Phone: (800) TI-CARES / (800) 842-2737

For U.S., Canada, Mexico, Puerto Rico, and

Virgin Islands only

International

Information:

education.ti.com/support

(Click the International Information link.)

Knowledge Base

and support by

e-mail: education.ti.com/support

Phone

(not toll-free): (972) 917-8324

Difficulty Solution

102 Appendix — Reference Information

Texas Instruments (TI) Warranty Information

Customers in the U.S. and Canada Only

One-Year Limited Warranty for Commercial Electronic Product

This Texas Instruments ("TI") electronic product warranty extends only

to the original purchaser and user of the product.

Warranty Duration. This TI electronic product is warranted to the

original purchaser for a period of one (1) year from the original purchase

date.

Warranty Coverage. This TI electronic product is warranted against

defective materials and construction. THIS WARRANTY IS VOID IF THE

PRODUCT HAS BEEN DAMAGED BY ACCIDENT OR UNREASONABLE USE,

NEGLECT, IMPROPER SERVICE, OR OTHER CAUSES NOT ARISING OUT

OF DEFECTS IN MATERIALS OR CONSTRUCTION.

Warranty Disclaimers. ANY IMPLIED WARRANTIES ARISING OUT

OF THIS SALE, INCLUDING BUT NOT LIMITED TO THE IMPLIED WAR-

RANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR

PURPOSE, ARE LIMITED IN DURATION TO THE ABOVE ONE-YEAR

PERIOD. TEXAS INSTRUMENTS SHALL NOT BE LIABLE FOR LOSS OF

USE OF THE PRODUCT OR OTHER INCIDENTAL OR CONSEQUENTIAL

COSTS, EXPENSES, OR DAMAGES INCURRED BY THE CONSUMER

OR ANY OTHER USER.

Some states/provinces do not allow the exclusion or limitation of implied

warranties or consequential damages, so the above limitations or exclu-

sions may not apply to you.

Legal Remedies. This warranty gives you specific legal rights, and you

may also have other rights that vary from state to state or province to

province.

Warranty Performance. During the above one (1) year warranty period,

your defective product will be either repaired or replaced with a recondi-

tioned model of an equivalent quality (at TI's option) when the product is

returned, postage prepaid, to Texas Instruments Service Facility. The

warranty of the repaired or replacement unit will continue for the war-

ranty of the original unit or six (6) months, whichever is longer. Other

than the postage requirement, no charge will be made for such repair

and/or replacement. TI strongly recommends that you insure the product

for value prior to mailing.

Software. Software is licensed, not sold. TI and its licensors do not

warrant that the software will be free from errors or meet your specific

requirements. All software is provided "AS IS."

product are protected by copyright.

Australia & New Zealand Customers only

One-Year Limited Warranty for Commercial Electronic Product

Appendix — Reference Information 103

This Texas Instruments electronic product warranty extends only to

the original purchaser and user of the product.

Warranty Duration. This Texas Instruments electronic product is

warranted to the original purchaser for a period of one (1) year from

the original purchase date.

Warranty Coverage. This Texas Instruments electronic product is

warranted against defective materials and construction. This war-

ranty is void if the product has been damaged by accident or unrea-

sonable use, neglect, improper service, or other causes not arising

out of defects in materials or construction.

Warranty Disclaimers. Any implied warranties arising out of

this sale, including but not limited to the implied warranties of

merchantability and fitness for a particular purpose, are limited

in duration to the above one-year period. Texas Instruments

shall not be liable for loss of use of the product or other inci-

dental or consequential costs, expenses, or damages incurred

by the consumer or any other user.

Except as expressly provided in the One-Year Limited Warranty

for this product, Texas Instruments does not promise that facil-

ities for the repair of this product or parts for the repair of this

product will be available.

Some jurisdictions do not allow the exclusion or limitation of implied

warranties or consequential damages, so the above limitations or

exclusions may not apply to you.

Legal Remedies. This warranty gives you specific legal rights, and

you may also have other rights that vary from jurisdiction to jurisdic-

tion.

Warranty Performance. During the above one (1) year warranty

period, your defective product will be either repaired or replaced with

a new or reconditioned model of an equivalent quality (at TI's option)

when the product is returned to the original point of purchase. The

repaired or replacement unit will continue for the warranty of the

original unit or six (6) months, whichever is longer. Other than your

cost to return the product, no charge will be made for such repair

and/or replacement. TI strongly recommends that you insure the

product for value if you mail it.

Software. Software is licensed, not sold. TI and its licensors do not

warrant that the software will be free from errors or meet your spe-

cific requirements. All software is provided "AS IS."

product are protected by copyright.

All Other Customers

For information about the length and terms of the warranty, refer to

your package and/or to the warranty statement enclosed with this

product, or contact your local Texas Instruments retailer/distributor.

104 Appendix — Reference Information

Index

Index 105

Symbols

#PD (number of periods) 72, 73, 74

#PD (number of periods, Percent

Change/Compound Interest

worksheet) 72

%CH (percent change) 72, 73, 74

(- (negative) indicator 3

(#$ indicator 3

(1 (value entered) indicator 3

(GX (sum of X) 65, 67

(GX² (sum of X²) 65, 67

(GXY (sum of XY products) 65

(GY (sum of Y) 65

(GY² (sum of Y²) 65

(sx (population standard deviation of

X) 65, 67

(sy (population standard deviation of

Y) 65

(v (mean of X) 65, 67

(w (mean of X) 65

* (value computed) indicator 3

= (value assigned) indicator 3

Numerics

1/Y (one coupon per year) 54, 55, 57

1-V (one-variable statistics ) 65, 67

2/Y (two coupons per year) 54, 55, 57

2nd (second)

functions 2

indicator 3

30/360 day-count method (360) 54,

55, 57, 77

360 (30/360 day-count method) 54,

55, 57, 77

a (y-intercept) 65

Accrued interest (AI) 54, 57, 58

Accuracy 98

ACT (actual/actual day-count

method) 54, 55, 57, 77

Actual/actual (ACT) day-count

method 77

Actual/actual day-count method

(ACT) 54, 55, 57

Addition 8

AI (accrued interest) 54, 57, 58

Algebraic Operating System (AOS™)

calculations 4, 5, 98

Amortization

formulas 87

schedule 21, 25, 26, 38

worksheet 21

Amount of nth cash flow (Cnn) 41

Angle units format 5

Annual coupon rate, percent (CPN)

54, 56, 57

Annual effective rate (EFF) 75, 76

annual interest rate 56, 75, 89

Annuities 21

due 24, 29, 30

ordinary 24, 29, 30

perpetual 30

ANS (Last Answer) feature 14

AOS™ (Algebraic Operating System)

calculations 5, 98

APD™ (Automatic Power Down™)

feature 1, 2

Arccosine 9

Arcsine 9

Arctangent 9

Automatic Power Down™ (APD™)

feature 1, 2

b (slope) 65

Backspace key 7

BAL (balance) 22, 24

Balance (BAL) 22, 24

Battery 99

precautions 99

replacing 99

Beginning-of-period (BGN)

indicator 3

payments 22, 24

BGN (beginning-of-period)

indicator 3

106 Index

payments 22, 24

Bond

accrued interest (AI) 54

price (PRI) 58

terminology 56

worksheet 53–58

Breakeven worksheet 80–81

C/Y (compounding periods per year)

22, 24, 76

Calculation method 4, 5

Call date 56

Cash Flow worksheet 41–51

Cash flows

computing 45

deleting 42, 44

editing 48

entering 42

formulas 87

grouped 43

inserting 44

uneven 43

CFo (initial cash flow) 41

Chain (Chn) calculation 4, 5, 8

Chn (chain) calculation 4, 5, 8

Clearing

calculations 6

calculator 6

characters 6

entry errors 6

error messages 6

errors 6

memory 6, 12

worksheets 6

Cnn (amount of nth cash flow) 41

Combinations 8, 10

Compound interest 56, 71, 73, 75

Compounding periods per year (C/Y)

22, 24, 76

COMPUTE indicator 3

Constant Memory™ feature 2

Constants 13

contact information 101

Correcting entry errors 7

Correlation coefficient (r) 65, 68

Cost (CST) 59, 62, 79

Cost-Sell-Markup 73, 74

Coupon payment 56

CPN (annual coupon rate, percent)

54, 55, 56, 57

CST (cost) 59, 62, 79

Curve fitting 67

customer support and service 101

Data points 68

Date 1 and 2 (DT1, DT2) 59, 78

Date worksheet 76

Dates

30/360 day-count method (360)

actual/actual (ACT) day-count

method 77

date 1 and 2 (DT1, DT2) 78

days between dates (DBD) 78

entering 77

Days between dates (DBD) 78

DB (declining balance) 59, 61, 62, 92

DBD (days between dates) 78

DBF (French declining balance) 59,

61, 62

DBX (declining balance with

crossover) 59, 61, 62

DEC (decimal format) 4

Decimal format (DEC) 4

Declining balance (DB) 59, 61, 62, 92

Declining balance with crossover

(DBX) 59, 61, 62

DEG (degrees) 4, 5

Degree angle units 5

Degrees (DEG) 4, 5

DEL (delete) indicator 3

Delete (DEL) indicator 3

DEP (depreciation) 59, 60, 62

Depreciation (DEP) 59, 60, 62

Depreciation worksheet 59–63

Difficulty 100

Discount bond 56

Discount rate (I) 41

Discounted payback (DPB) 41, 45

Display indicators 3

Division 8

Dollar price (PRI) 54, 56, 57

Index 107

DPB (discounted payback) 41, 45

DT1 (starting date) 62

DT1, DT2 (date 1 and 2) 59, 78

DUR (modified duration) 54

EFF (annual effective rate) 75, 76

END (end-of-period)

payments 22, 24

Ending payment (P2) 22, 24

End-of-period (END)

payments 22, 24

ENTER indicator 3

Error

clearing 96

messages 96

Examples

accrued interest 58

amortization schedule 38

amount to borrow 36

annuities 30

balloon payment 40

bond price 58

compound interest 73

computing basic loan payments

constants 13

converting interest 76

correcting an entry error 7

cost-sell-markup 74

days between dates 78

discounted payback 49

down payment 36

editing cash flow data 48

entering cash flow data 48

future value (savings) 28

interest received 40

internal rate of return 49

last answer 14

lease with uneven payments 49

memory 12

Memory worksheet 83

modified duration 58

modified internal rate of return

monthly payments 40

monthly savings deposits 35

mortgage payments 38

net future value 49

net present value 48, 49, 50

other monthly payments 34

payback 49

percent change 73

perpetual annuities 30

present value (annuities) 29

present value (lease with

residual value) 33

present value (savings) 28

present value (variable cash

flow) 33

profit margin 79

regular deposits for specific

goals 37

remaining balance (balloon

payment) 40

residual value 33

saving for future 35

straight-line depreciation 62

EXP (exponential regression) 65, 67

Exponential regression (EXP) 65, 67

Face value 56

Factorial 10

FC (fixed cost) 80, 81

FCC statement ii

Fixed cost (FC) 80, 81

Floating-decimal format 4

Fnn (frequency of nth cash flow) 41

Forecasting 67

Formats

angle units 4, 5

calculation method 5

decimal places 4

number separators 4

setting 4

Formulas

30/360 day-count method 95

accrued interest 90

actual/actual day-count method

amortization 87

108 Index

bond price (more than one

coupon period to

redemption) 90

bond price (one coupon period

or less to redemption) 89

bond yield (more than one

coupon period to

redemption) 90

bond yield (one coupon period

or less to redemption) 89

bonds 89

breakeven 94

cash flow 87

days between dates 94

depreciation 91

depreciation, declining-balance

depreciation, straight-line 91

depreciation, sum-of-the-years’-

digits 92

interest-rate conversions 93

internal rate of return 88

modified duration 90

modified internal rate of return

88, 89

net future value 88

net present value 87

percent change 93

profit margin 94

regressions 93

statistics 92

time-value-of-money 85

French declining balance (DBF) 59,

61, 62

French straight line (SLF) 59, 61, 62

Frequency 44

cash flow 88

coupon 55, 57

one-variable data 68

Y value 65, 67

Frequency of nth cash flow (Fnn) 41

Frequency of X value (Ynn) 67

Future value (FV) 22, 23, 24

FV (future value) 22, 23, 24

Grouped cash flows 43

Hard reset 6

HYP (hyperbolic) indicator 3

Hyperbolic (HYP) indicator 3

I (discount rate) 41

I/Y (interest rate per year) 22, 24

Inflows 21, 23, 25

Initial cash flow (CFo) 41

INS (insert) indicator 3

Insert (IND) indicator 3

INT (interest paid) 22, 24

Interest Conversion worksheet 74

Interest paid (INT) 22, 24

Interest rate per year (I/Y) 22, 24

Internal rate of return (IRR) 41, 45

INV (inverse) indicator 3

Inverse (INV) indicator 3

IRR (internal rate of return) 41, 45

Last Answer (ANS) feature 14

Leases 21

LIF (life of the asset) 59, 61, 62

Life of the asset (LIF) 59, 61, 62

LIN (linear regression) 65, 67

Linear regression (LIN) 65, 67

Ln (logarithmic regression) 65, 67

Loans 21, 24

Logarithmic regression (Ln) 65, 67

M01 (starting month) 59, 61, 62

M0–M9 (memory) 12, 82

MAR (profit margin) 79

Math operations 8

Mean of X (v) 65, 67

Mean of Y (v) 65

Memory

arithmetic 12

clearing 12

examples 12

recalling from 12

storing to 12

Memory worksheet 82–83

Index 109

MOD (modified internal rate of

return) 41, 45

Modified duration (DUR) 54

Modified internal rate of return

(MOD) 41, 45

Mortgages 21

Multiplication 8

n (number of observations) 65, 67

N (number of periods) 24

N (number of periods, TVM

worksheet) 22

Negative (–) indicator 3

Net future value (NFV) 41, 45

Net present value (NPV) 41, 45

NEW (new value) 72, 73, 74

New value (NEW) 72, 73, 74

NFV (net future value) 41, 45

NOM (nominal rate) 76

Nominal rate (NOM) 75, 76

NPV (net present value) 41, 45

Number of observations (n) 65, 67

Number of periods (#PD) 72, 73, 74

Number of periods (#PD), Percent

Change/Compound Interest

worksheet 72

Number of periods (N) 24

Number of periods (N), TVM

worksheet 22

Number separators format 4

OLD (old value) 72, 73, 74

Old value (OLD) 72, 73, 74

One coupon per year (1/Y) 54, 55, 57

One-variable statistics (1-V) 65, 67

Outflows 21, 25

Overview of calculator operation 1–

P (unit price) 80, 81

P/Y (payments per year) 22, 24, 25

P1 (starting payment) 22, 24

P2 (ending payment) 22, 24

Par value 56

Parentheses 8, 10

Payback (PB) 41, 45

Payment (PMT) 22, 23, 24

Payments per year (P/Y) 22, 24, 25

PB (payback) 41, 45

Percent 8

Percent add-on 8

Percent change (%CH) 72, 73, 74

Percent Change/Compound Interest

worksheet 71

Percent discount 8

Percent ratio 8

Permutations 8, 10

PFT (profit) 80, 81

PMT (payment) 22, 23, 24

Population standard deviation of X

((x) 65, 67

Population standard deviation of Y

((y) 65

Power regression (PWR) 65, 67

Predicted X value (X') 65, 67, 69

Predicted Y value (Y') 65, 67, 69

Premium bond 56

Present value (PV) 22, 23, 24

PRI (bond price) 58

PRI (dollar price) 54, 56, 57

Principal paid (PRN) 22, 24

PRN (principal paid) 22, 24

Procedures

computing accrued interest 57

computing basic loan interest 26

computing bond price 57

computing bond yield 57

computing breakeven 81

computing breakeven quantity

computing compound interest

computing cost-sell-markup 72

computing dates 77

computing discounted payback

computing internal rate of

return 46

computing modified duration 58

computing modified internal

rate of return 46

110 Index

computing net future value 45

computing net present value 45

computing payback 45

computing percent change 72

computing profit margin 79

computing statistical results 69

computing X’ 69

computing Y’ 69

constants for various operations

converting interest 75

deleting cash flows 44

entering bond data 57

entering data points 68

entering depreciation data 62

generating a depreciation

schedule 62

generating amortization

schedules 25, 26

inserting cash flows 44

selecting a depreciation method

selecting a statistics calculation

method 69

selecting bond settings 57

using the memory worksheet 82

Profit (PFT) 80, 81

Profit margin (MAR) 79

Profit Margin worksheet 78–80

PV (present value) 22, 23, 24

PWR (power regression) 65, 67

Q (quantity) 80, 81

Quantity (Q) 80, 81

r (correlation coefficient) 65, 68

RAD (radians) 5

RAD (radians) indicator 3

Radians (RAD) 5

Radians (RAD) indicator 3

Random numbers 10

RBV (remaining book value) 59, 60,

RDT (redemption date) 54, 55, 56, 57

RDV (remaining depreciable value)

59, 60, 62

Reading the display 2

Recalling from memory 12

Redemption date (RDT) 54, 55, 56, 57

Redemption value (RV) 54, 55, 56

Regression models

exponential 67

linear 67

logarithmic 67

power 67

Reinvestment rate (RI) 41

Remaining book value (RBV) 59, 60,

Remaining depreciable value (RDV)

59, 60, 62

Resetting

amortization variables 23

bond variables 54

breakeven variables 80

cash flow variables 42

date variables 77

depreciation variables 60

interest conversion variables 75

percent change/compound

interest variables 72

statistics variables 66

TVM variables 23

Resetting calculator 6

hard reset 6

pressing keys 6

RI (reinvestment rate) 41

Rounding 10, 98

RV (redemption value) 54, 55, 56, 57

SAL (salvage value) 59, 62

Salvage value (SAL) 59, 62

Sample standard deviation of X (Sx)

65, 67

Sample standard deviation of Y (Sy)

Savings 21

Scientific notation 11

SDT (settlement date) 54, 56, 57

Second (2nd)

functions 2

Index 111

indicator 3

Quit 2

SEL (selling price) 79

Selling price (SEL) 79

service and support 101

SET (setting) indicator 3

Setting (SET) indicator 3

Settlement date (SDT) 54, 56, 57

SL (straight line) 59, 61, 62

SLF (French straight line) 59, 61, 62

Slope (b) 65

Square 8

Square root 8

Starting date (DT1) 62

Starting month (M01) 59, 61, 62

Starting payment (P1) 22, 24

Statistical data 68

Statistics worksheet 65–69

Storing to memory 12

Straight line (SL) 59, 61, 62

Subtraction 8

Sum of the years’ digits (SYD) 59, 61,

Sum of X (GX) 65, 67

Sum of X² (GX²) 65, 67

Sum of XY products (GXY) 65

Sum of Y (GY) 65

Sum of Y² (GY²) 65

support and service 101

Sx (sample standard deviation of X)

65, 67

Sy (sample standard deviation of Y)

SYD (sum of the years’ digits) 59, 61,

Time-Value-of-Money (TVM)

worksheet 15, 16, 18, 21

Time-Value-of-Money and

Amortization worksheets ??–40

Turning calculator off 1

Turning calculator on 1

TVM (Time-Value-of-Money)

worksheet 15, 16, 18, 21

Two coupons per year (2/Y) 54, 55, 57

Two-variable statistics 67, 69

Uneven cash flows 43

Unit price (P) 80, 81

Universal power 8

Value assigned (=) indicator 3

Value computed (*) indicator 3

Value entered (1) indicator 3

Variable cost per unit (VC) 80, 81

VC (variable cost per unit) 80, 81

warranty 102

What-if calculations 15

Worksheets

Amortization 21

Bond 53

Breakeven 80

Cash Flow 41

Date 76

Depreciation 59

display indicators 19

Interest Conversion 74

Memory 82

Percent Change/Compound

Interest 71

Profit Margin 78

prompted 18

TVM (Time-Value-of-Money) 15,

16, 18, 21

variables 15, 16, 17, 18

X value (Xnn) 65, 67

X' (predicted X value) 65, 67, 69

Xnn (X value) 65, 67

xP/Y key (multiply payments per

year) 25

Y' (predicted Y value) 65, 67

Year to compute (YR) 59, 61, 62

Yield to maturity 56

Yield to redemption (YLD) 54, 57

112 Index

Y-intercept (a) 65

YLD (yield to redemption) 54, 57

Ynn (frequency of X value) 65, 67

YR (year to compute) 59, 61, 62

Texas Instruments Calculator Users Manual Ba2plus

BA II PLUS PROFESSIONAL guidebook (English) BAIIPLUSPROGuidebook_EN BA II PLUS™ PROFESSIONAL Guidebook

Calculator to the manual 2a3466f6-c319-4b68-bc05-82502a7f3a4c

Navigation menu

Versions of this User Manual:

Views

Navigation