700121_Extension_Of_The_PDP 11_Instruction_Set 700121 Extension Of The PDP 11 Instruction Set

User Manual: 700121_Extension_Of_The_PDP-11_Instruction_Set

Open the PDF directly: View PDF .
Page Count: 25

\

PDP-K

Technical

Memoranda

#~

2

-

Thll

drlwlng

end

sneelffeatlonl, h.ereln. are the prop-

erty

of

Dlgltll

Equ'''~en~

Cor-oraton

~nd

s~all

not

be

reproduced

or

cop'e or

u~d

In

W o.e or in part.

as

the basis for the manufacture or

sa:e

of

items without

written permission.

Title:

Extension

of

PDP-ll

Instruction

Set

•

Author

(s)

:

Ad

van

de

Goor

Index

Keys:

Instruction

Sets

Opcode

Space

Modes

Stack

Operations

Distribution

Keys:

K

Revision:

None

Obsolete:

None

Date:

21

January

1970

-1-

0.0

ABSTRACT

Scver~l

methods

of

extending

the

PDP-Il

instruction

sot

ore

di~cussed.

Coding

comparisons

are

made.

Subject

to

the

trivial

weighting

scheme

used,

two

solutions

were

excluded

from

further

analysis

because

of

their

poor

performance.

The

"multiply/

divide"

subsolution

as

discussed

in

sections

4.4

and

5e4

was

the

best

performer.

-2-

1.0

INTRODUCTJON

A

more

elaborate

vers·ion

of

the

PDP-l1/20

is

considered

as

a

possible

candidate-for

the

PDP-K.

It

is

felt

that

if

the

PDP-K

is

a

member

of

the

PDP-Il

family,

sUbstantial

gains

could

be"

obtained

from:

1.1

upw-arda

program

compat.ibili

ty

For

DEC

this

would

mean

a

lower

total

software

investment.,

and new

machin.s

could

be

introduced

mo~e

easily

as

present

PDP-l!

software

would

run

on

PDp-x.

For

customers

this

would

mean

that

they

could

move

to

a

larger

machine

without

the

direct

need

for

reproqramming.

1.2

Peripheral

compatrbility

only

one

line

of

peripheral

devices"

has

to

be

built.

The

introd~ction.

of

a

new

machine

could

be

done

more

easily

for

thi.

reason.

Any

new

peripheral

device

would

b.

available

for

the

whole

f_l~y.

-3-

2.0

PROBLEMS

IN

ADAPTING TIlE

PDP-ll

ARCiITECTURE

TO

Au

BIGGER

MACHINE

~o

important

problems

of

the

PDP-ll

have

to

be

sol

ved

in

order

to

meet

the

PDP-I(

requ:ir

aments.

2.1

Limited

number

of

instructions

and

Itmited

amoUilt

of

opcode

apace

left.

For

the

PDP-K

.

three

more

class..

of

instructions

are

conaidered:

2

.1.1.

BAE

ins

truc:tiona

, i

.•.

,

rotate/

shift

and

multiply/divid~

for

16-bit

word.~

2.1.2

Double

Precision

Integer

Ari~~c

Instruction

••

2.2

Liaited

Address

Spa~

The

total

amount

of

addre.sable

core

....ory

on

the

PDP-ll/20

is

65K

(l~

•

i.

1024)

bytes,

or

32K

16-bit

words.

Por

a

big

32-bi~

version

of

the. PDP-ll·

this

would

only

mean

l6l(

32-bit

word.

could

be

addr

•••

ed,

which

is

certainly

not

adequate

for

auch

•

machill

••

-4-

3.0

PUR~OSE

OF

MEMORANDUM

The

purpose

of

this

memol:;andum

is

to

examine

the

suggested

methods

-of

solving

the

first

problems:

extending

the

basic

PDP-ll

instruction

set.

An

acceptable

solution.

subject

to

several

constraints,

will

be

sought.

3.1

program

compatibility

at

~oa.t

on

the

as.embly

language

level..

•

3.2

S~licity

in

programming

by

.in~1zin9

~.

number

o£

instruction

format.

and

restrictions

imposed

on

inatructions

•

.

3.3

opcode

.pace

left

for

future

tlXpaftuion.

3.4

Opcod

••

of

the

largest

member

of

the

family

have

to

fit

ill

the

added

iD.truction

set.

thus

miniaiziAq

the

Dumber

of

fOrllAta.

and

making

progr~nq

.a.ier.

-5-

4.0

POSSIBLE

SOLUTIONS

If

_

....

Four

possible

solutions

to

the

opcode

space

problem

are

shown

below.

l~ey

are

followed

by

a

discussion

in

se\.~tion

5:

o.

4.1

Implement

new

instructions

as

"pure

stack"

instructions

(i.e

..

,

zero

address).

Each

new"

instrnction

can

l'lOW

be

specified

with

one

combination

out

of

216.

This

allows

for

hundreds

of

new

instructions.

Any

binary

operation

(like

multiply,

diviae,

etc.),

would'take

the

~o

.,:-:

operands

from

t.he

top

of

the

stack,

and

leave

the

result

on

the

top

of

the

stack.

Register

6

would

be

used

as

the

implied

stack

pointer.

4.2

Introduce

a

flag

to

indicate

that

the

remainder

of

the

word

contai.ninqthe

flag

(note:

remainder

can

be

==

0)

and

the

next

word

form

a

new

instruction.

Depending

on

the

length

of

the

flag.

two

cases

exist.

•

Inatruction

",.".,-_._""..,

..

.......

[

......

::

==W~=~d=::~=:]

1

.....

-

_-

_-w=or_d-

_-5

=+

=2

=1

,

...

...,-

L

.....

16-Bit

Flag

Bar

Instruction

4.2~2

Partial

Word

Plaq

...

.....

Flag

~New

Instruction

iJ.'he

advan'tage

of

thl..

technique

ia

that

t!wa 1l.8W'

instn"Lctiona

can

have

the

SUie

aource-dest:ination

forma~

as

the

stand41rd

(i

•••

#

currrent

PDP-ll/20)

#

instructions.

4.3

Modes

-6-

The

disadvantage

.is

that

every

new

instruction

takes

two

words.

The

partial

word

flag

case

offers

the

adva~tage

of

a

greater

number

of

new

instructions

at

the

expense

of

somewhat

more

complicated

hardware.

A mode

is

a

(hardware)

state

of

the

processor

to

allow

instructions

to

be

interpreted

differently.

Basically

two

kinds

of

mod

••

have

to

be

recognized:

4.3.1

~ter

and

leave

modes

only

with

dedicated

commands

(i

..

e.,

only

switch

modes

when

an

instruction

specifi.a

to

do

80).

4.3.2

Enter

mod

••

for

a

specified

number

of

instruction.

after

which

the

mode

is

switched

back

to

the

standard

mode

autOlftatically.

The

advantage

~of

IROde8

i.

that

instructions

in

any

mode

are

only

1

word

long.

The

disadvantage

is

that

.peeial

inatructions

have

to

be

given

to

enter.

and

in

the

ca

••

of

4.3.1.

to

leave

the

mode.

4.4

u

••

R

•••

rved

lIultiply!Divide

Space

'these

two

opeode

apac..

are

not

uaed

in

the

PDP-ll/20.

The

to-be-added

two-operand

instruction.

can

be

implemented

••

aource-

d

••

tiAation

instructions

where

the'

.f:ack

is

one

implied

operand,

and

the

8.econd

operand

is

.pacified

with

the

full

6-bit

dEtstinaticm

field

ot

the

instruction.

One

of

the.e

6

bits

can

be

used

.s

a

direction

bit

such

that

operations

can

have

either

~eir

source

or

destination

as

the

implied

stack.

This

allO\l's

for

32nf'!W

instructions

to

be

specified

..

-7-

5.0

EVALUATION

OF

PROPOS~p

SOLUTIONS

When

e~aluating

the

proposed

solutions,

the

irnplementatio:'l

of

a

32-bit

version

of

t.he

POP-Ii

should

be

included..

Fer

such

a"

machine.

double-preci~ion

floating

point

instruct:i:ons,

together

with

EAE

instructions,

operating

on

32-bit

registers

a.ce

desirable,

(assuming

that

these

instructions

can

operate

on

registers).

This

means

that

opcode

space

for

those

instructions

has

to

be

regerved

to

provide

for

their

efficient

operation.

Simplicity

in

programming

and

machine

organization

dictate

that

the

number

of

instruction

formats

for

the

three

classes

of

new

instructions.

(as

discussed

in

section

2.1),

should

be

minimal.

In

order

to

~ake

the

extended

instruction

set

more

acceptable,

it

is

very

desirable

to

make

the

added

instructions

fit

in

currently

existing

formats,

or

add

at

Most

a

single

new

format.

Several

coding

comparisons

are

done

to

assist

in

the

evaluation,

The

five

problems

below

(Pl-PS),

are

considered

representative"

The

a

••

umptions

made

in

codinq

the

problems

can

be

deduced

frca

the

listed

code

i.n

Appendi.xes

A-D.

The

variable.

A,

B.

C,

D

and

E

are

considered

single

precision

floating

point

(32-bit

numbers).

P]:

A"-B*C

P2:

A f (B+C) * (J>+E)

P3:

A

(i}

.....

a

(i)

*e

(1')

P4:

A(i)

...

B.(i+3)

*C{i*5)

P5:

A

(i,

j)+-A

(i.

j)

+8

(i.Jc.)

*C

(k,

j)

/sillple

case

ltemporary

variable

case

/aubscripted

case

/mixed

arithmetic

(::ase

Imultl-d~en8~onal

array

case

PS

is

an

exaaple

of

the

inner-loop

8tat.eraent

of

the

array

mul

tiplication:

~]...-1)1

*

[cJ.

l·t

is

a.swned

that

the

array

bounds

are

declared

frCD

0

to

u.

For

array

B

this

would

be:

Real

Array

8 (0 -

bul,

0 - bti2)

."

The

first

index

of

IS

90es

t.o

bul.

the

second

to

bu2.

It

will

be

•••

umed

that

the

index

••

are

in

registers

R:L.

Rj.

and

Rk.

Assuming'that

the

index

••

i

and

j

are

in

register

Ri

and

Rj,

the

value

B

(i.

j)

will

be

address

as

follows:

Location

of

B(i.j)

:c

location

of

B

(i.e.,

starting

location

of

aatrix)

+

i*bul+j).

-8--

,;.

5.1

Pure

Stack

Operations

In

order

to

make

the

pure

stack

operations

efficient,

one

of

the

opcode

spaces

reser"ed

for

lrtul

tiply

/d

i

vide

has

to

be

used

for

a

double

move

(MOVD'

instructions.

MOVD:Move

2

words

(32

bit!')

from

S

(OU":cc)

D

(estination)

.

Thia

instruction

is

required

especially

in

a

32-bit

machine.

The

one

bina:cy

op::ode

.pat.;f!

left

can

be

used

to

implement

the

EAE

instructions.

1

The-

instruction

format

would

be

as

foll'Ns:

OPERATION

DESTINATION

wI

3

(6

-:]

3

...."

3

......................

___

-""'f'"

RifGISTER

This

saae

format

1.

uae4

for

t).e

JSR

(IIUbroutine

eall)

instruction.

'!'be

EAE

instruc1.iona

are

made

to

o~rate

on

regiat.er8

only..

The

regist.er

involved

is

•

•

peqifi~

by

the

3 "

reg

iaterr.{

bib.

The

value

of

the

effective

4.id4r

••

a

of

the

ttd

••

t.inat;ion

U

decerain

••

the

number

of

p:isitions

to

be

shifted

or

rotated~

Because

the

aute,·ina_ent

and

auto-

decrement

mod

••

do

not;

apply

to

these

in.t.r1.l.ctions,

one

of

the

2

NOde

bit.

can

b.

u.ed

to

specify

a

.ingle

or

caatbined

operati.on,

(1

....

"

aea

PDP-lO

LSH. LSHC,

etc.).

Ther

....

ining

.p"ea

can

be

used

to

implement

in.truC1l;i0D8

like

EXCHANGE,

REPEAT,

etc.

Appendix

A

give.

the

coding

axaaplea

for

the

fiva

probl....

The

handling

of

ault;.-d~n.ional

arrays

i.

very

cwabersocae

becau..

the

nddre".

computations

have

to

be

done

on

the

stack.

Introducing

a

aec:cm4

Nt

of

16-blt

IlNltiply/divicle

instructions

iapl

...

nted

aa

the

above

EA.B

ir..atructions

will

solve

thi.

preble.

at

t:be

expI:~.Cl

of

a

BlOre

complex

instruction

••

t.

SubcolUBl

Tel'!;

1

MPD

of

Section

6

show.

the

iaprov.aent

gained

b~'

thia

..

lExcept

for

16-bit

mult~ly/divid.

-9-

5.2

Fl199ed

Instructions

Th~~

coding

examples

shown

in

Ap.Pf,-lndix B

are

the

same

for

alternativ£!s

4

..

2.1

and

4.2.2.

4.2.2

Is

proferable

only

if

the

additional

opcode

space

is

neE!ded..

It

is

su99ttsted

that

tl'le EAE

multiply/

divide

instruction

\1i11

be

implel'lented

in

the

space

"reserved"

fo~c

them.

The

EAE

rotate/shift

ins'cructions

have

tfj

be

implemer

ted

as

.t

fla9ged

u

instructions,

the

format

would

}:'.

similar

to

that

dis~~ssed

in

section

5~1.1

eXCGlt

for

the

f~ag.

The

doUble

precision

integer

an,

floating

point

inst.ructi<?lls

would

be

implementEd

as

full

S'.'.)'.Z'

ce-

destination

insUructions.

5.3

Modes

Before

going

into

detail,

propo

••

l

4.3.2

(.'J)t:tinq

the

!lOde.

for

a

specific

nuaber

·,)f

instructions

(N)

),

will

be

examined..

'l'hi.

is

considerer.

less

attractive

because

of

probl_s

aJ:'isinq

in

"-

string

of

Nl

instructions

to

be

focecuted

i:.

tha

n4IW

1DOde.

•

5

()

3.1

Branchiaq

in

teras

of

.ki~\pinCJ

ove.

a

group

of

instructions

in

the

spec!;;ied

striDg

will

cause

problema

becau

•••

i.

not

updatedautaaatically.

5.3.2

Progr

..

ing

will

b.

YeI:Y

difficult

because

whea

branching'

into

•

aequance

of

inauuc:tiofts

their

mode,

(in

which

those

operate),

vill

be

difficult

to

determine.

5.3.3

I~

will

be

diffiealt

lor

a

~pil.r

to

••

t

up

the

right'

-N"

becau..

it

v11l

r.quire

sOIDa

kind

of

"look-ahead".

5.3.4

In

ca.e

of

intarrupt./traPili.

tha

zemainder

of

•

baa

to

be

.avec!

and

r

••

tored

upon

exit:

of

the

interrupt/tzap

nrvlce

rout.ina.

lwbere

N

is

an

arbitrary'

positive

number.

-10-

For

the

reasons

above,

proposal

4.3.~

will

be

dropped.

and

not

considered

further.

The

extended

mode,

(Which

contains

the

floating,

double-precision

integer

instructions,

etc.',

is

entered

by

the

command

Enter

Extended

Mode

(EEM).

The

processor

stays

in

this

mode

until

the

instruction

Leave

Extended

Mode

(LEM)

is

given.

In

regard

to

4.3.1,

subroutine

calls

and

interrrupt/traps

cause

problems

typical

for

modes

in

saving/restoring

the

mode

and

entering

the

routine

(subroutine

or

interrupt/trap

service

routine),

in

the

correct

mode.

The

interrupti

trap

case

is

the

easiest

one~

The

mode.

can

be·

preserved

in

a

dedicated

bit

in

~e

Central

Processor

status

Register(pS).

Entering

the

interrupt/trap

service

routine

in

the

right

mode

can

be

done

similarly

by

storing

the

mode

of

that

routine

in

the

PS

interrupt/trap

vector.

The

correct

mode

will

then

be

entere~

automatically

upon

interrupt.

Entering

a

s·ubroutine

in

the

desired

mode

in

a

p~ogram

cOMpatLble

way

can

be

done

by

taking

the

lowest

bit

(bit

0)

of

the

subroutine

address

as

the

"ode

bit.

In

the

current

PDP-ll/20,

this

bit

has

to

be

equal

zero

because

the

aubroutine

address

is

a

word

address.

By

defining

a

MO"

in

bit

0

of

the

subroutine

addX'e

•••

s

the

st.andard'

MOde,·

program

caapatibility

is

preserved.

Saving/restoring

the

mode

upon

•

subroutine

calli

exit

i.

JIUlch

more

difficult.

The

only

hardware

.olu~ion

found

thu.

far

i.

to

.tore

the

mode

on

the

stack

in

a

separate

word.

The

new

JSR

would

then

store

2

worda

on

the

.tack:

~he

register

to

be

saved

and

the

.ode.

Proqrams

making

use

of

the

knowledge

that

oaly

1

word

gets

stored

on

tht:

stack

by

~

JSl\

have

to

be

modified

.

•

A

program

compatible

software

solution

to

the

mode

problem

is

to

have

the

called

subroutine

take

care

of

the

mode

handling

by

restoring

the

mode

(upon

exit).

which

existed

prior

to

the

call

of

the

subroutine.

A

possible

way

of

dOing

thi~

is

by

having

the

existing

mode.

prior

to

-11-

all

calls

for

a

given

subroutine,

fixed,

such

that

the

subroutine

only

has

to

match

the

mode

upon

exit

to

the

existing

(fixed)

mode

at

call

time.

It

is

suggested

that

the

multiply

and

divide

instructiona,

(opera~in9

on

16-bit

integers)#

·be

~plement.d

in

the

space

reserved

for

th~m~

and

all

other

instructions

be

implemented

in

the

extended

mode.

Appe-,dix

C

shows

the

coding

exaaapl...

They

suggest

that

an

instruction

to

enter

the

ext.ended

mode

for

a

single

instruction

is

very

u8eful.

The

column

EEMl

(Enter

Extended

Mode

for

1

In8truction),

of

Table

1,

Section

6,

shows

this.

5.4

Use

Mutt

iply/Divide

Space

one

of

the

two

binary

opcode

apaces

haa

to

be

used

to

impl..ant

the

EAE

instruction.

.a

d

••

cribed

in

••

etion

5.1.

The

remaining

ins~ctioDS

have

to

implemented

with

the

.tack

••

an

aplied

operand

as

discu

••

ed

in

sect.lOll

4.40

CodinCJ

example.

u.

given

in

Appedix

D.

'1'bey ahO'll,

like

the

"pure

.tack"

case,

that

handl.inq

_lti-dilllenaional

array.

i.

CWlber~.

!'be

imp-mv.-nts

made

by

addift9

a

••

t

of

16-bit

multiply/divide

inatruction

••••

s"99Mted

in

section

5

~

I,

are

shown

in

aubcolQIIID

MJID

of

'hbl.

1,

Section

6.

-12-

6.0

COMPARISON

OF

PROPOS~D

SOLt~IONS

Table

1

'ShO"NS

the

t~esults

of

the

five

problems

for

the

st!ven

J

proposed

solutions.

Four

quantifiers

are

used

for

each

problem

to

measure

the

quality

of

the

solutions.

6el

The

~wnber

of

Instructions

It

is

quite

well

known

that

the

probability

of

making

a

programming

error

increases

more

than

linear

with

the

number

of

instructions,

\apart

from

their

complexity),

thus.

"good"

solution

should

have

a low number

of

instxuctions.

6.2

The

Number

of

words

2

This

is

the

number

of

words

needed

to

core

the

algorithms

given

in

the

appendix...

This

ia

an

import,mt

criteri\Jll,

especially

on

a

small

aachine.

For

a

32-bit

...

chine

the

number.

have

to

be

divided

by

2.

6.

3

The

Number

of

MeMOry

Reference.

The

number

of

memory

references

bot.."t

for

a

16

and

32-bit

machine

a.re

included

in

the

tables

because

they

are

important

indicators

for

the

execution

times

of

the

alqorithatl.

The

numbers

in

Table

1

are

derived

under

the

following

assumptions:

6.

3.1

The.

tack

is

suppaeeel

to

be

in

ccx-e-

aemory.

(Section

6.4

di.cu

••••

the

results

when

this

aS8U11lption

is

not

made)

•

6.3.2

For

the

two

operaad

exteJlde4

iuuuctions

the

arithNetie

unit

i.

8Upposed

to

behave

••

:foll0W8f

1)

read.

both

operands

into

it.

internal

~egi.ter.1

2}

it

performs

t.1le

required

operation

(e.g.

F"MUL,

FADD):

and

J)

it

stor

••

the

results

ba.ck..

In

caa~

of

different

assumptions

the

numbers

in

the

table

can

be

adjusted

accordingly.

lpOUI:

:nain

,.olution_.

f:l'.lr

..

of

which

have

••

'ubeollltion.

2words

are

considered

to

be

16

bit.

long-

-13-

6.4

Number

of

Memory

References

With

A

Hardware

Stack

•

The

idea

is

to

implement.

the

top

Ml

words

of

the

~tack

in

flip-flop

registers.

From

Table

1

it

can

be

seen

that

the

execution

speed

increases

for

almost

all

problems

and

solutions.

Those

solutions

making

hea.V)'

use

of

the

stack

gain

m~st.

lPJ)r

simplicity

M

is

supposed

to

be

such

that

in

Ilona

of

the

problems

the

stack

"overflOW'."

into

cora.

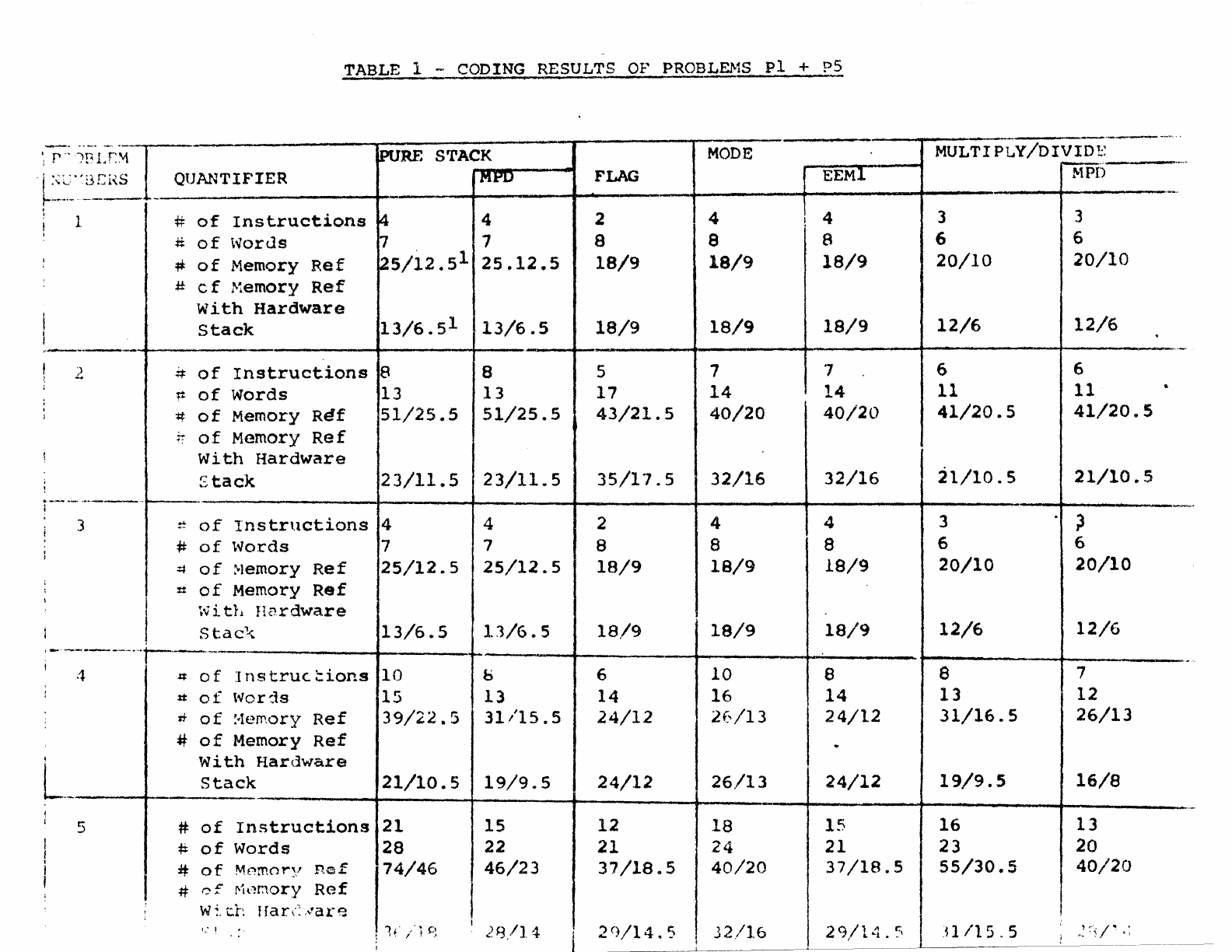
TABLE 1 - CODING RESULTS

OF

PROBLEHS

pl

+ pS

_________

---------r------..,..-----------...----.

------

..

-------

..

1,P-:-:;F·l~r.\1-r

~RE

STACK

MODE

MULTIPLY/DIVIDE

,_

.

~~~~~·.'!~HS

_l_~_AN_'_T_I_F_I_ER--

__

~-,---:M:'-:PD-:--:-

---I:_F_LAG

__

._-t-

____

:~_E~E-M_-~_l-_-:_-_

...

_+_------+-r----l'-t_P_D·=====-,~~'"

: 1 #

of

Instructions

! #

of

\vorc]s

#;

of

~1emory

Ref

#-

c f r-:emory

Ref

with

Hardware

stack

~

4

7.

7

~5/12.51

25.12.5

13/6.5

1

13/6.5

2

8

18/9

18/9

4

a

18/9

18/9

I 4

a

18/9

18/9

3

6

20/10

12/6

3

6

20/10

12/6

--------+-----------+----+------t--------+----4------I-------+----_

..

_.

.2

#

of

Instructions

tt

of

Words

~

of

Memory

Ref

~.

of

Memory

Ref

With

Hardware

stack

8

13

51/25.5

23/11.5

8

13

51/25.5

23/11.5

5

17

43/21.5

35/17.5

7

14

40/20

32/16

7

14

40/20

32/16

6

11

41/20.5

21/10.5

6

11

41/20.5

21/10

..

5

r---·--···---··r--·-------r----;----+----+----t------+---~-.J.-----

3

5

13/6.5

#

of

Instructions

21

#:

of

Words

28

#

of

M0mo

ry

Ref

74/46

#

0f

f\h·1r.10ry

Ref

I

4

7

25/12.5

11/6

..

5

19/9.5

15

22

46/23

2

8

18/9

4

8

18/9

18/9

12

18

21

.24

37/18.5

40/20

4

8

18/9

15

21

37/18.5

3

6

20/10

16

23

55/30.5

~

6

20/10

12/6

7

12

26/13

13

20

40/20

I

28/14

;

'10'

,'j

(:)

2C)/14.

5

32./1.6

29/1

..

1.5

.il

/1

t;.

5

..

?~'.·/~·;

'

..

" I

."

: " I .

,I

~

J }

____________

---.L'

______

~

___

______'__

___

~

___

~

____

~_~

_____

_

-15-

Table

2

gives

a

ratin9

summary

of

Table

1,

the

rating

is

from

1

{lowest"

to

7

(highest).

,When

two

solutions

have

equal

rating,

they

both

get

the

same

number

being

the

average

rating

when

they

would

not

have

been

equal.

The

problems

pl

-

P3

are

very

similar

in

nature,

therefore

a

summarized

rating

is

given

in

the

fir~t

part

of

Table

2.

Similarly_

for

P4 -

PS

in

the

second

part

of

Table

2.

The

third

part

of

Table

2

is

a summary

of

the

previous

~

tables

assuming

equal

weights

for

the

two

previous

groups

of

problems.

Part

4

of

Table

2

is

merely

the

sum

of

the

first

two

quantifiers

of

the

third

part.

1

For

a

small

machine,

the

number

of

-instructions

and

the

number

of

words

are

the

most

important

criteria.

for

selectinq

the

best

solution.

On

a

bigger

machine.

execution

speed

is

beCCIDing

important

..

Part

5

of

Table

2

is

such

an

indicator.

Its

entrie.

are

the

sums

of

the

fir.~#

second,

and

fourth

quantifiers

of

part

3.

It

i.

assumed

that

on

the

bigger

machine

the

top

of

the

stack

"is

impleaent.ed

in

hardware.

lAg.in

here,

foe

.~licity

rea.ons,

equal

weight.

are

assumed.

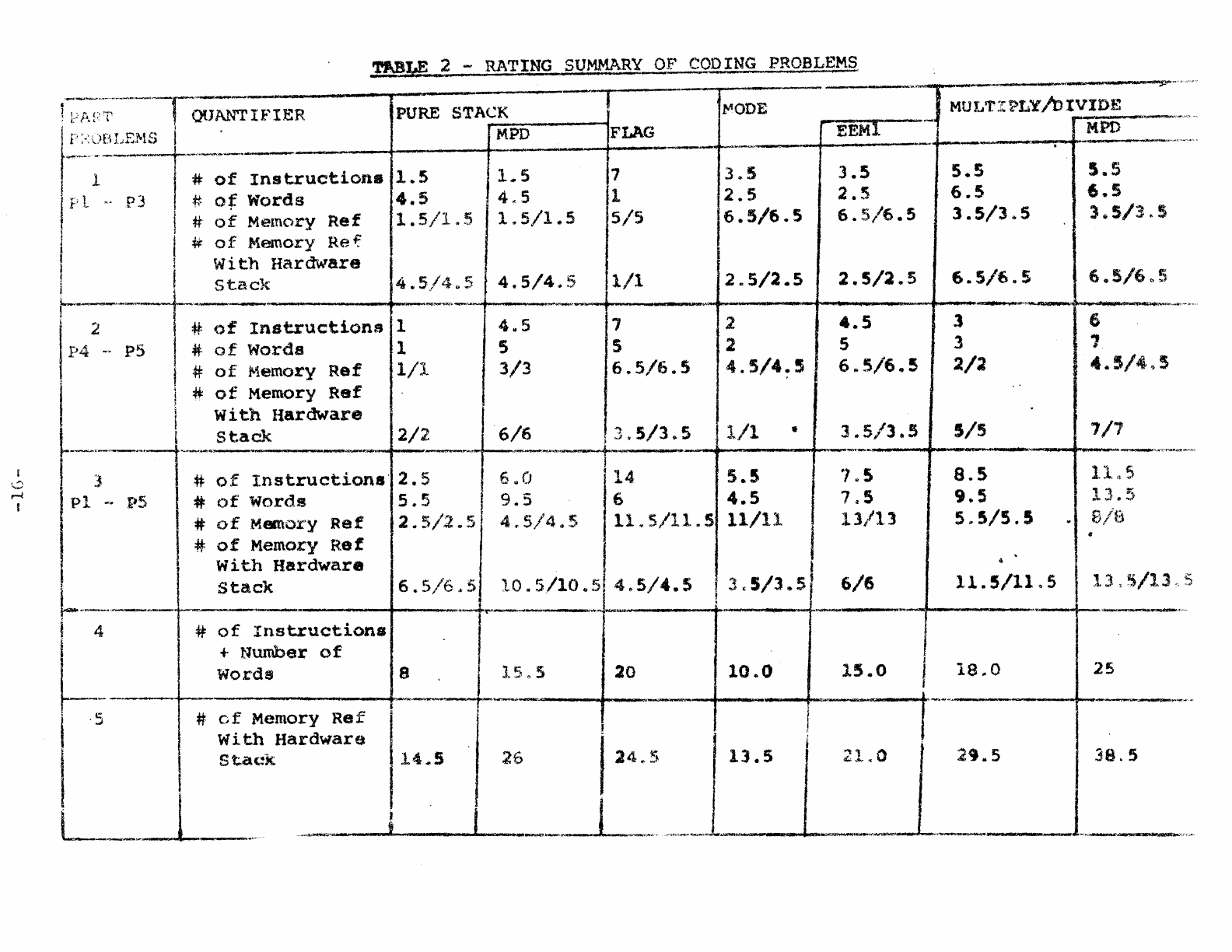
~~.f

-

RATING

SUMMARY

OF

COR.JNG

PROBLEMS

!

~~"

r~~'---'--<~f-OOANT

I F I

ER

T

--

J

M~r~';!PLY~P;"'

"'p

PURE

STACK

MODE

~

___

'''''''''r~

EEMI

MPD

1,:.··

..

,·t~~t:'l\1"

I

It

"\.,)dJ.,;~

.. a

..

} I

.....-'_

,

..

______

.

___

-+-----+---~-+_-----+-.---+-----'i----'--::-+---

MPD

FLAG

. -

--

I

1'/

,.

P3

!:~!

:~!r~C:::n.

1 i #

of

Memory

Ref

I !

with

Hardware

I I

stack

r----.--<....

j.

-------00+---

I

' 2 I #

of

Instructions

P4

~

P5 I #

of

Words

I I #

of

l'-iemory

Ref

l

' 1 #

of

Memory

Ref

1

With

Hardware

/ I .

~

/

I

Stack

2

'2

~

. ..,.5

3.5

1/1

•

I

~~---'I-~

of

Instruct::.

2.;-'

I

!.~"

-'-1

~4

..

5.5 I

I

pl

~""

I~5

#

of'

wo,rds

5.5

.

'.

I

9.5

6

4.5

I #

of

Memox'y

Ref

2.5/2"~5

4~5/445

11

..

5/11

..

5

11/11

#

of

Memory

He!

I

j

with

Hardware,

1.5

145

7

3~5

4.5

4.,5

11

2.5

1.5/1,,5

11.5/1.5

5/5

6.5/6.5

I

4.5/4

..

5

4.5/4~5

1/1

2

..

5/2.5

-..:~r.-

'"

1 4

..

5 1 2

1 5 5 2

1/1

3/3

6.5/6.5

4.5/4.5

3.5

5.5

5

..

5

2.5

6.5

6.5

6.5/6.5

3.5/3,,5

3,,5/3~5

2.5/~.S

6.5/6

..

5

6.5/6,,5

.r-.,

7II!J1

••

5 3 6

5 3

"1

6

..

5/6.5

2/'1.

4.5/4,,5

3

..

5/3.5

5/5

7/7

._-

---t----,-

.........

---..,.-,~-

7,.5

7~5

13/13

8.5

9.5

5,,5/5.5

6/6

11.5/11~5

1)

..

5

..

SIB

13,

S/13

" 5

_.-+

________

,

__

-+

__

~.

___

..

__

o

I 4 #

of

Instructions

l

' +

Number

of

,

Words

e I

15.

5

20

10.0

15.0

I

18.0

I

.~

#

~i~e=~~w:~!

--

r I i ,

___

'''-0_,",_'

.---~&--

...

---~

2S

L_l-=a_Ck___

;

14.5,

26_~~_5

___

._~l.5

.2LJ_.29·_~

__

L.38~_-.

-17-

7

.0

CONCLU§1m!

Lookinq

a'/;

'l'able

2,

part

4

and

5,

it

can

be

conAluded

that

tl~e9uDsolution8,

(i.e~,

MPD

for

"pure

stacks.

and

··multiply/(.~ividet!,

and

EEMl

for

"mod."),

are

a

big

improvemorr;

over

their

umain

t•

solutions.

This,

because

i)f

the

~proved

handling

of

multl-d~en8ional

arrays,

~18

price

paid

for

this.

however.

is

a

more

complex

i~8truction

set

(i

••••

adding

a

duplicate

set

of

iE-bit

multiply/divide

instructions

to

operate

on

reqis·.!er

o~

enter

the

extended

mode

for

a

single

instruction)

. ,

The

rnaj

..

l

solutions

"pure

.t.ack"

and

-mode-

have

the"

low.at

rating

and,

can

therefore

be

excluded

from

furthe:

consideration.

.

In

order

to

make a

definite

commitment 1:0

any

of

the

ramai.ninq

five

solutions,

mo,re

research

should

be

,lone

in

determining

the

weights

of

the

problems

and

~ei9hts

of

the

quantifier

••

Fr(J.m

the

results,

this

far

however,

the

following

can

be

said:

7.1

The

Mmode"

subsolution

haa

to

look

much

better

1

•

in

order

to

be

a

candidate

because

of

the

aode

probl...

in

subroutines.

The

sU99ssted

hardware

solution

i.

such

that

the

price

of

s~ring

the

IIOde

on

the

.tack

haa

to

be

paid

ADiAYS.

Also,

in

prOCJrams

which

do

not

make

u

••

of

the

mode.

(i

••••

all

current

PDP-ll

!Ioftwar.).

For

this

reason

the

sU9gested

.oftware

solution

is

•

better

candidate

because

there,

t.he

price

i.

only

paid

when

mod..

are

uaed.

lWhen

the

proper

weight.

u:e

fouac!.

-18-

7.2

The

at

flag"

3Ql.ution

is

advisable

only

when

it

is

expected

that.

the

use

of

tl'8

'f

flagged

If

instructions

(i.e.

those

of

cl,ss

2.1.2

and

2.1"

3

of

sect.ion

2)

is

low.>

7.3

The.

most

p

remising

solution

thi"i

far

is

the

"multiply/div·id."

subsolution..

It

consistentl~l

scorad

highest

or

second

highest

pl:

P2:

P3~

P4:

-19-

APPENDIX

A

PURE STACK CODING EXAMPLES

'.

now

ItOVD

}'MUL

~OVD

}\.

....

M(\1D

M(lD

F}!)D

MelD

MO'D

FAC

"1,

MOD

c,

-

(SP)

B.

-

(SP)

(SP)

+,A

---(SiC)

*

(D+E)

8.

-.

(SP)

c,

-

(SP)

D,

(SP)

E,

-(SPj

A(.i)

..

~-8

(1)

*c

(1)

MOV)

MOV)

PMtl~

MOV)

A(i,

MOV

AD!>

M'J\'l'

MOV

MOV

lHUL

MOV

MOVD

FMUL

MOVD

C

(Ri)

..

-

(S')

B

(R1),

-

(8P)

(SP)

+,

A

CRi)

~-B

(1+3)

*C

(1*5)

...

Ri.a.

*3.

Ra

8

(Ra).

-

(I.)

Ai.

-

(S.'

.s~

-

(IP)

(SP)+.

RII

C(Ra).

-

(SP)

(SP)+,

A(ai)

. .

/move

C

to

the

stac:k

/fMlve B

to

the

.tack

/floating

.nltiply

B*C

latore

result

in

A

/f19atiog

add

B+C

/float.iDg

add

0+.

/flo&t1ng

lMIltiply

(I>+E).

(:a+e)

/a.~

indeK i

1.

in

register

ai

/110".

C(i)

to

the

.tack

/iadex

1+3

fOftle4

/caapu~e

1*5

.ad

1....

1 word

result

OD

top

of

af:ack

/st:ore

renlt

P5:

-20-

APPEND

IX

A (CONT • )

A(i,

j)......-

A{i,

j)

+8

(i,k)

*C(k,

j)

MOV

MOV

IMUL

MOV

ADD

MOVD

MOV

MOV

lMUL

MOO

ADD

MOVD

FMUL

MOY

MOV

lMUL

MOV

ADD

MOV'D

FADD

MOW

Ri,

-

(SP)

#bul.

-

(SP)

(SP)

+,

Ra

Rk,

Rs

B(Rs),

-

(SP)

Rk.

-

(SP)

#cul,

-

(SP)

(SP)

+,

Rs

R.i,

R8

C(Rs)

I -

(SP)

a'"

-

-,

(SP)

#aul,

-

(SP)

(SP}

+,

Ra

Rj,

Rs

A(R8).

-.

(5P)

(SP)

+,

A(Rs}

IRs

contain.

index

for

array

B

/put

B

(i,k)

on

stack

IRs

contains

index

for

array

C

/R-

contain.

index

for

array

C

I.tore

r

••

ult

-21-

APP~IX

B

FLAGGED

INSTRUCTIONS

CODING

EXAMPLES

PI:

A

~

B*C

MOVD

FMUL

B,A

C,A

p2:

A .....

------(B+C)*

(D+E)

MOVO

FADD

MOVD

FADD

FMUL

B,A

C,A

D,

-

(SP)

c,

(SP)

(SP)

+,A

P3:

A{i}

.......

------B(i).C(i)

MOVD

B(Ri),

A(Ri)

FADD

C(Ri),

A(Ri)

P4:

ACi)

......

------B(i+3)*C(i*5)

NOV

Ri,

as

ADD

*3,

b

MOVD·

B(Ra),

A(Rl)

NO"

Rt,

Rs

MOL

*5,

R.a

FMUL

C(Ra),

A(Ri)

/move

B

to

A

/A

=-

B+C now

/top

of

the

stack

is

C+D

/move.B(i)

to

A(i)

•

IRa

i.

a

acratch

regiater

/index

for

B

(1+3)

exaputed

P5:

A(l,

j)

.......

----A(i.

j)+

8

(l,1tl

*

C(k,

j)

,

MOV

al,

.a

MUL

1IN1,

...

ADO

alt.

..

linda

for

.(i,k)

ccaputed

MOVD

B(R.).

-(SP)

MOV

Jtlc.

•••

KUL

#cul,

Ita

ADD

Rj,

R8

/

index

10%

C

(k,

j)

COIIIp\lted

FMUL C

(Ra),

(SP)·

r«:JlI

Iti.

R8

NUL

kul,

.a

ADD

Rj.

R8

lineSex

PADD

(8P)

+,

A(R8)",

-22-

APPENDIX

C

MODE

CODING

EXPMPLES

pl:

A'"

R*C

EEM

/enter

extended

mode

MOVD

B.A

FMUL

C,A

LEM

/leave

extended

mode

p2:

A

..

(B+C)

* (D+E)

EEM

/enter

extended

mode

MOVD

a,A

FADD

C,A

MOVD

D"

-

(SP)

!'ADD

c,

(SP)

PMUL

(SP)

+,

A

LEM

/leave

extended

1BOd.

P:i:

A(1)

...

&

(1)

*c

(i)

BDI

IIOVD

.(al),

A(Ri)

!'MOt:..

e{ltl),

A

(Ili)

LEN

1*4:

A(i)

...

B

(i+3)

*C(i*S)

MOV

Ri,Ra

ADD

.3,

RtI

£EM

.

J«>VO

•

(as)

,

A(Ri)

LEN

MOV

Ri,

R8

MOL *5"

R8

EEN

FMUL

C(R.),

A(Ril'

LDl

p'; •

,,'

.

A(.i,

j)

..

ACi,

j)

+

Bti,x)

*

C(k,j)

MOY

-Ri,

b

MOL

*bul,

b

ADD

Rk,

••.

lindex

for

B

(i,k)

c01I.pUted

£EM

MOVO

BCRa),

-

(SP)

LEN •

MaV

Rk.

RII

-

MUL

*<:aI,

b

ADD

Itj,

b

/index

for

C

(k,

j)

coaputed

EDt

F'r.1UL

C(RS)~

(SP)

P5:

Cont.

LEM

MOV

MUL

ADD

EEM

FADD

LEM

-23-

AVPENDIX C

MODE

CODING

EX~lPLES

Ri,

Rs

#aul,

Rs

Rj,

Rs

( s

P)

+ , A ( Rs )

/index

for

A(i,j)

computed

pi:

A

.......

-

~10\''D

FMUL

MOVD

p2:

A

.....

MOVD

FADD

MOVl)

FADD

FMUL

MOVD

p3:

A

(i~

.--

MOVD

FMUL

t-10VD

P4:

A{i)

....

MOV

AD;)

MOVV

~'1()V

I~~t;L

~·~C-J

F~~;

rr

.J-,-"

r-tOVD

P5:

A{i,

j)

.....

MOV

11-ruL

Me)V

ADD

MOVD

MOV

lMUL

MOV

ADD

FMUL

MO\t

IMUL

MOV

ADD

FADD

MOV'!)

. T '

. -

~~*C

R,

-

(SP)

c,

(~~P)

(SP)+,A

(B+C)

*

(D+E)

B,-(SP)

c,

(SP)

D,-eSP)

L,

(SP)

(Sr·')

+,

(SP)

(:;p~

+,1\

B

(i)

* C

(i)

B

(Ri)

, -

(SP)

C

(Ri)

,

(SP)

(SP)

+" A

(Ri)

SCi"'3)

+

C(i*

5)

Hi,

Rs

::

3,

Rs

B(Rs),

-

(SP)

Ri,

-

(SP)

;t5,

(SP)

(SP)

+,

Rs

C

(Rs)

,

(SP~

(SP)

+,

A

(Ri)

-

.l\{i,j)

+

B(i,k)

Ri,

-

(SP)

~ibul,

(

SP)

(S

p)

+,

Rs

Rk, Rs

B{Rs),

-

(SP)

Rk.,

-

(SP)

~cul,

{SPj

(SP)-+-,

Rs

Rj,

Ps

C(Rs),

(SP)

Ri,

-

(SP)

~nulk

(SP)

(SP)

+,Rs

Rj,

Rs

A(Rs),

(SP)

(5

P)

4o,

A(Rs)

""~ove

B

to

the

sta·~k

/multiply

c

with

t0P

of

t::e

:~t(L·".

,/move

result

to

A

/index

i+)

in

Rs

/index

i*5

in

Rs

'*

C',k,j)

/index

f.or

B(i,1<)

comput(';!d

/index

for

C(k,j'

computed

,Jindex

for

A

(i.,

j)

computed