AG TRB U1.indb U1 Walch L9Pt2 Examples
User Manual: U1
Open the PDF directly: View PDF ![]() .
.
Page Count: 13

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-565
Introduction
Isosceles triangles can be seen throughout our daily lives in structures, supports, architectural details,
and even bicycle frames. Isosceles triangles are a distinct classification of triangles with unique
characteristics and parts that have specific names. In this lesson, we will explore the qualities of
isosceles triangles.
Key Concepts
• Isosceles triangles have at least two congruent sides, called legs.
• The angle created by the intersection of the legs is called the vertex angle.
• Opposite the vertex angle is the base of the isosceles triangle.
• Each of the remaining angles is referred to as a base angle. The intersection of one leg and the
base of the isosceles triangle creates a base angle.
Prerequisite Skills
This lesson requires the use of the following skills:
• classifying triangles
• identifying and using vertical angles, supplementary angles, and complementary angles to
find unknown angle measures
• applying the Triangle Sum Theorem and the Exterior Angle Theorem to find unknown
measures of triangles
• justifying congruence of triangles
• writing various forms of proofs
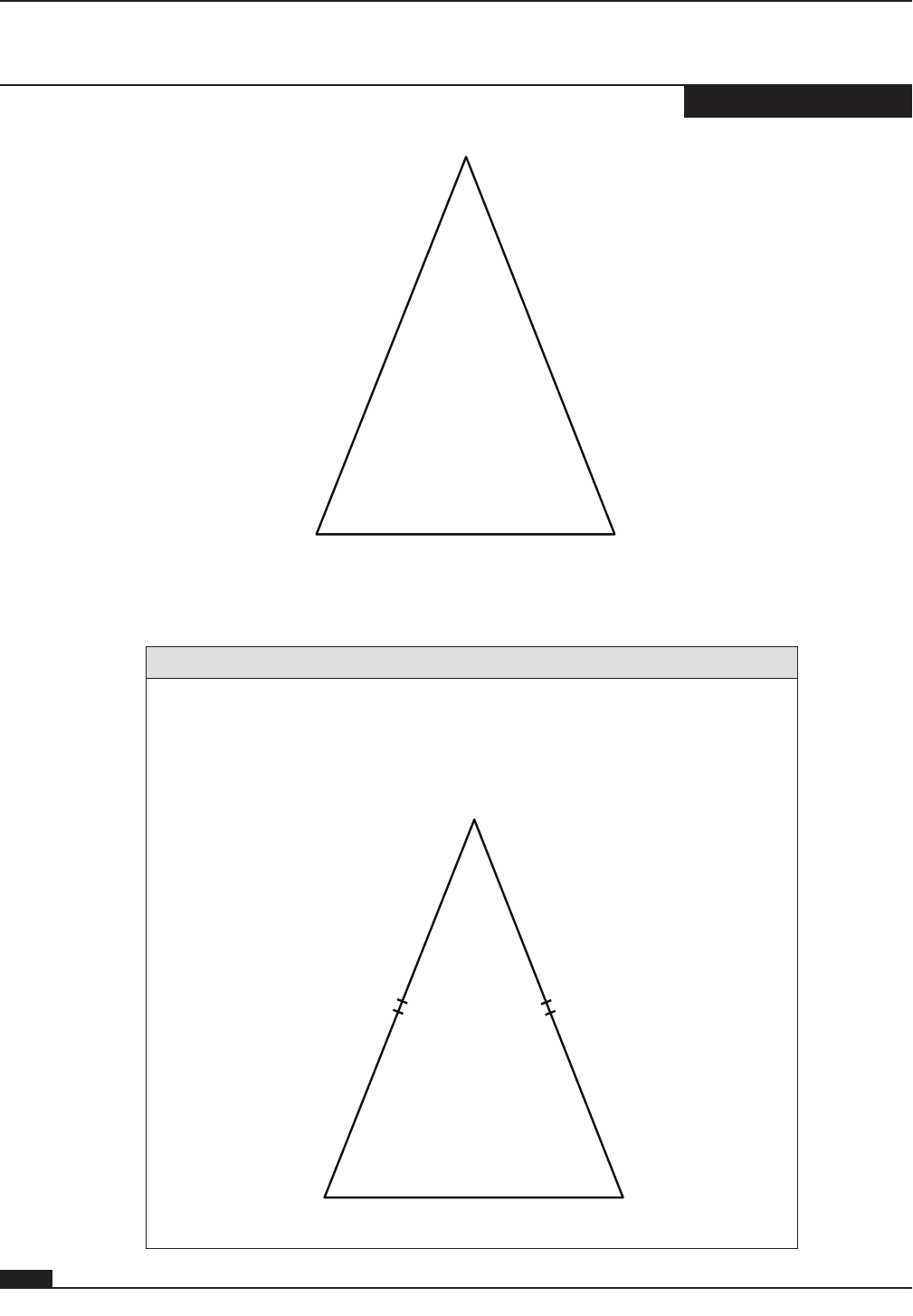
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-566
© Walch Education
Vertex angle
Base angle Base angle
Base
Leg
Leg
• The following theorem is true of every isosceles triangle.
Theorem
Isosceles Triangle Theorem
If two sides of a triangle are congruent, then the angles opposite the
congruent sides are congruent.
A
CB
mBmC∠≅ ∠
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-567
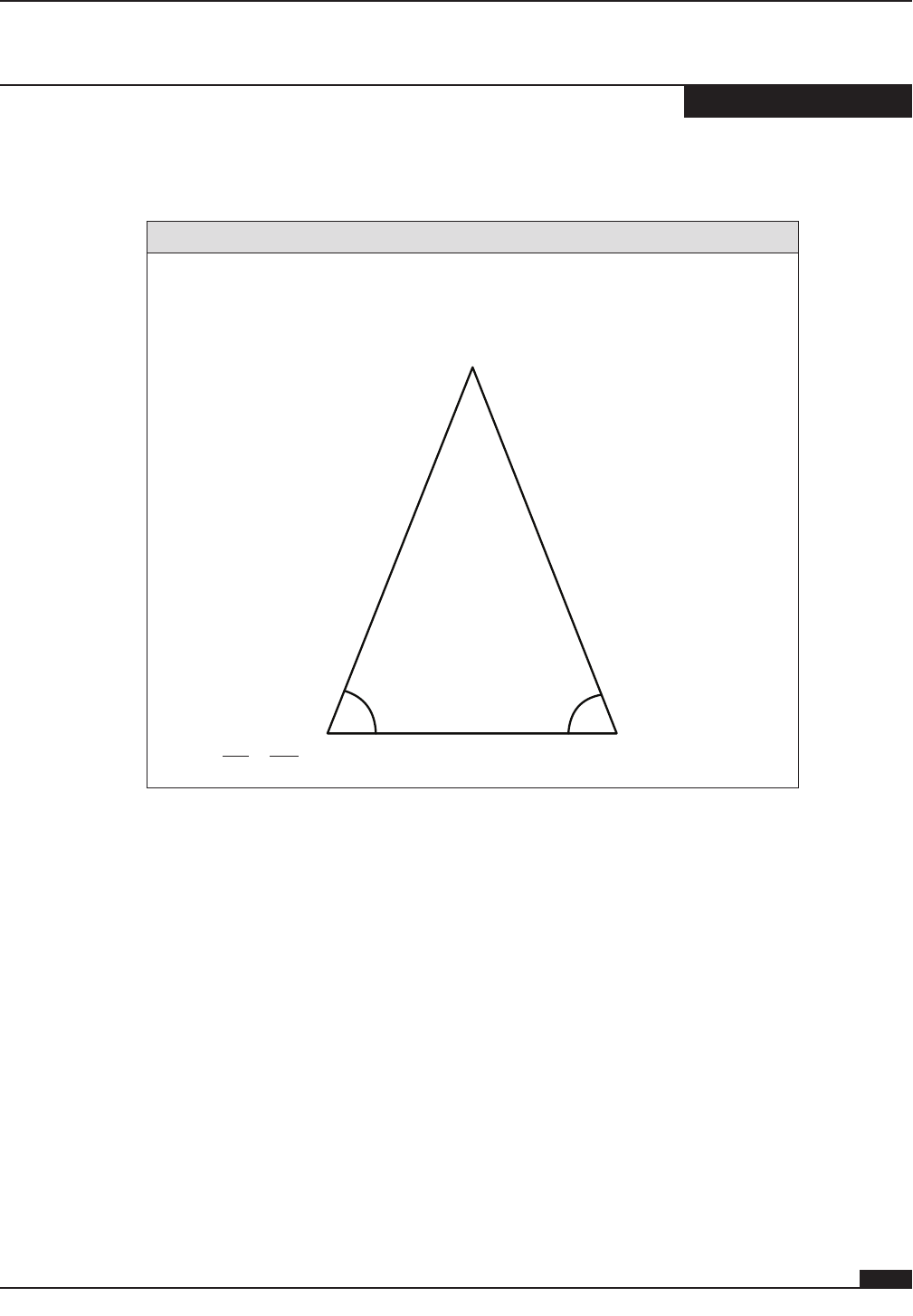
• If the Isosceles Triangle Theorem is reversed, then that statement is also true.
• This is known as the converse of the Isosceles Triangle Theorem.
Theorem
Converse of the Isosceles Triangle Theorem
If two angles of a triangle are congruent, then the sides opposite those
angles are congruent.
A
BC
AB AC≅
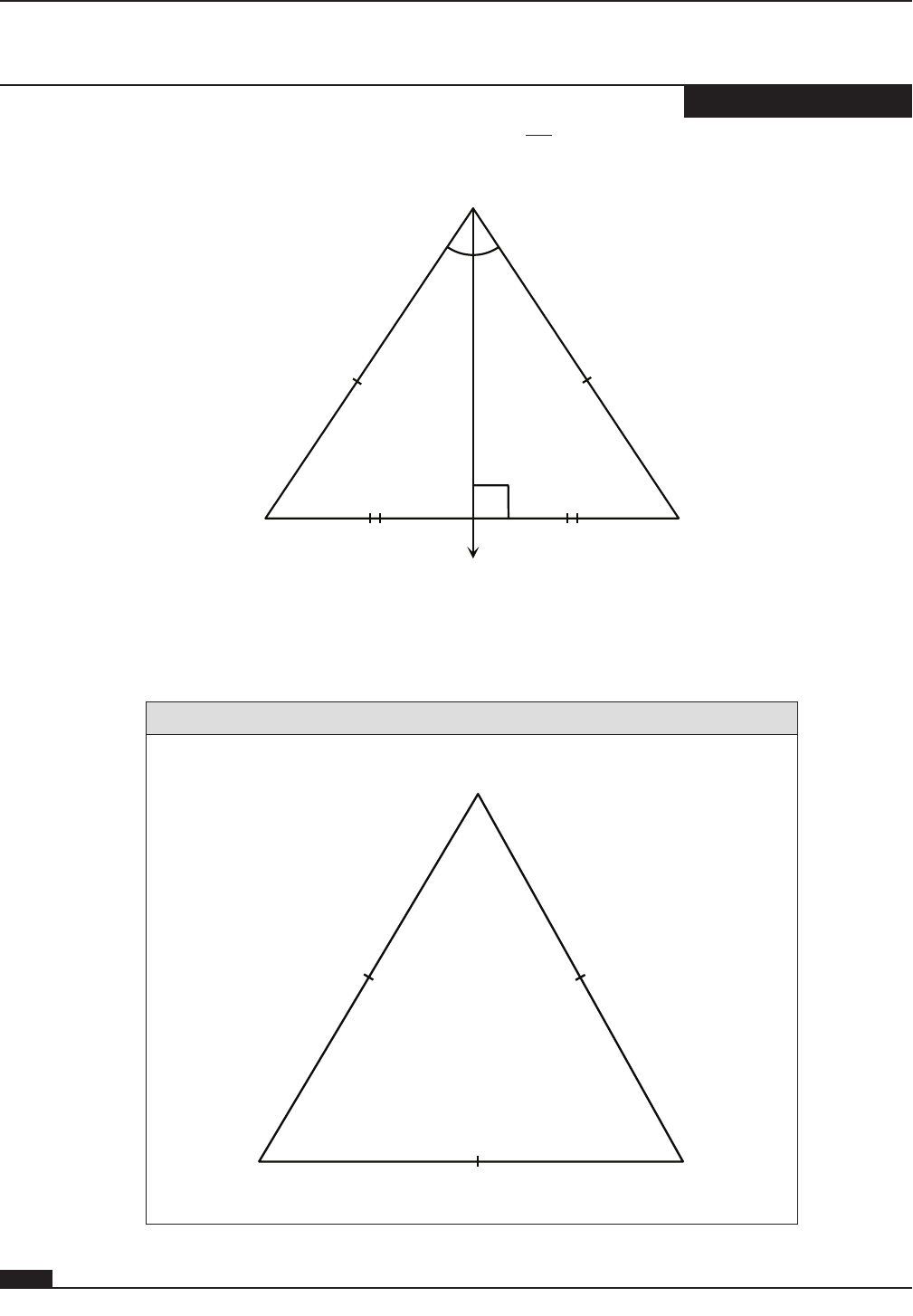
• If the vertex angle of an isosceles triangle is bisected, the bisector is perpendicular to the base,
creating two right triangles.
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-568
© Walch Education
• In the diagram that follows, D is the midpoint of BC .
A
BC
D
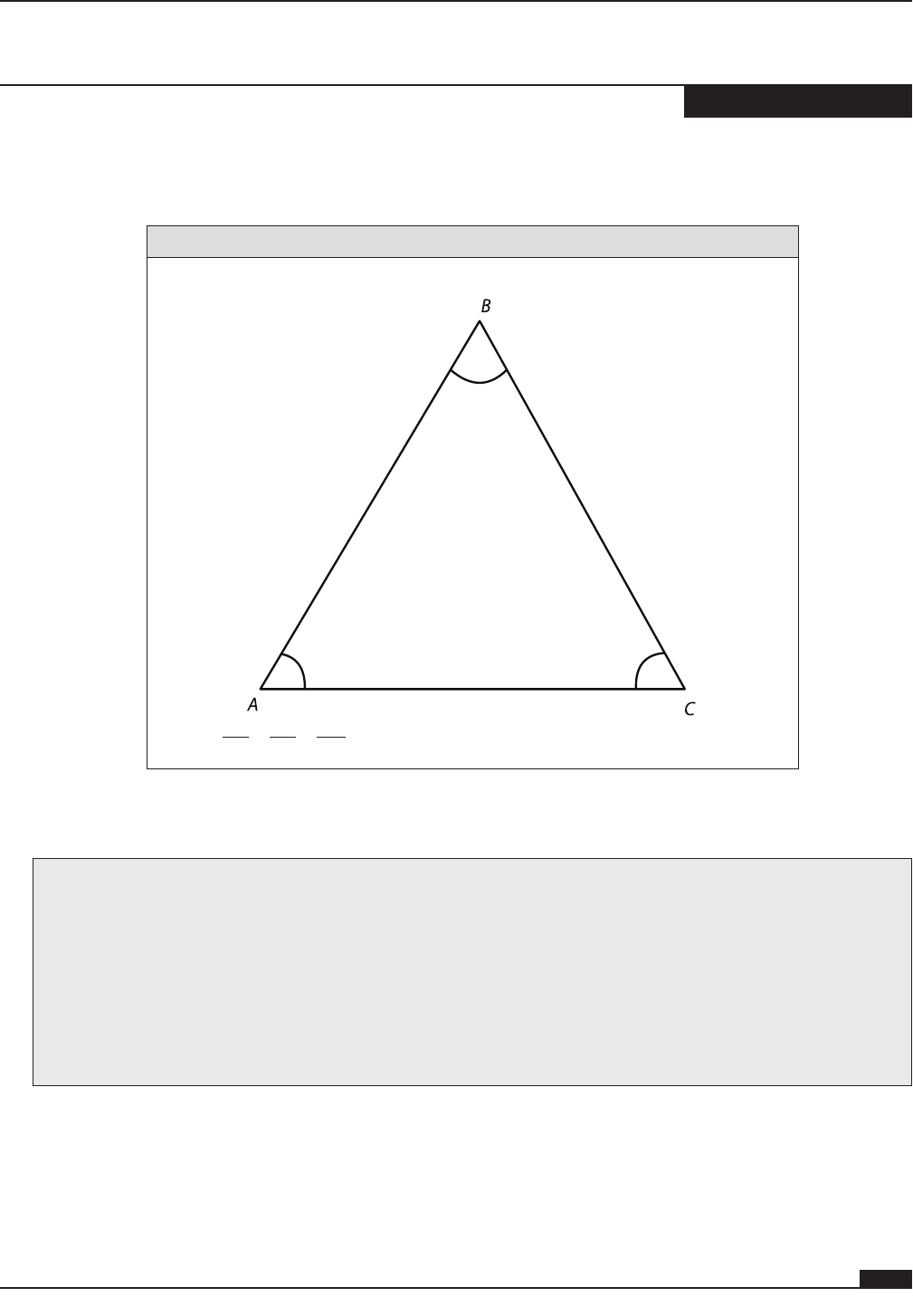
• Equilateral triangles are a special type of isosceles triangle, for which each side of the triangle
is congruent.
• If all sides of a triangle are congruent, then all angles have the same measure.
Theorem
If a triangle is equilateral then it is equiangular, or has equal angles.
B
A C
ABC∠≅∠≅∠
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-569
• Each angle of an equilateral triangle measures 60˚ (
180 360÷=
).
• Conversely, if a triangle has equal angles, it is equilateral.
Theorem
If a triangle is equiangular, then it is equilateral.
AB BC AC≅≅
• These theorems and properties can be used to solve many triangle problems.
Common Errors/Misconceptions
• incorrectly identifying parts of isosceles triangles
• not identifying equilateral triangles as having the same properties of isosceles triangles
• incorrectly setting up and solving equations to find unknown measures of triangles
• misidentifying or leaving out theorems, postulates, or definitions when writing proofs

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-570
© Walch Education
Example 1
Find the measure of each angle of
ABC
.
(4x)˚ (6x – 36)˚
A
BC
1. Identify the congruent angles.
The legs of an isosceles triangle are congruent; therefore, AB AC≅.
The base of
ABC
is BC .
∠B and ∠C are base angles and are congruent.
2. Calculate the value of x.
Congruent angles have the same measure.
Create an equation.
m∠B = m∠CThe measures of base angles of
isosceles triangles are equal.
4x = 6x – 36 Substitute values for m∠B and
m∠C.
–2x = –36 Solve for x.
x = 18
Guided Practice 1.9.2

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-571
3. Calculate each angle measure.
m∠B = 4x = 4(18) = 72 Substitute the value of x into the
expression for m∠B.
m∠C = 6(18) – 36 = 72 Substitute the value of x into the
expression for m∠C.
m∠A + m∠B + m∠C = 180 The sum of the angles of a triangle
is 180˚.
m∠A + 72 + 72 = 180 Substitute the known values.
m∠A = 36 Solve for m∠A.
4. Summarize your findings.
m∠A = 36
m∠B = 72
m∠C = 72

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-572
© Walch Education
Example 2
Determine whether
ABC
with vertices A (–4, 5), B (–1, –4), and C (5, 2) is an isosceles triangle. If it
is isosceles, name a pair of congruent angles.
1. Use the distance formula to calculate the length of each side.
Calculate the length of
AB
.
dxxyy()
()
21
2
21
2
=−+−
AB (1)(4) (4)(5)
22
[]
[]
=−−− +−−
Substitute (–4, 5) and (–1, –4)
for (x1, y1) and (x2, y2).
AB (3)(9)
22
=+−Simplify.
AB 981
=+
AB 90 310==
Calculate the length of BC .
dxxyy()
()
21
2
21
2
=−+−
BC (5)(1) (2)(4)
22
[]
[]
=−−+−−
Substitute (–1, –4) and (5, 2)
for (x1, y1) and (x2, y2).
BC (6)(6)
22
=+
Simplify.
BC 36 36=+
BC 72 62==
Calculate the length of
AC
.
dxxyy()
()
21
2
21
2
=−+−
AC (5)(4) (2)(5)
22
[]
[]
=−−+−
Substitute (–4, 5) and (5, 2)
for (x1, y1) and (x2, y2).
AC (9)(3)
22
=+−Simplify.
AC 81 9=+
AC 90 310==
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-573
2. Determine if the triangle is isosceles.
A triangle with at least two congruent sides is an isosceles triangle.
AB AC≅, so
ABC
is isosceles.
3. Identify congruent angles.
If two sides of a triangle are congruent, then the angles opposite
the sides are congruent.
BC∠≅∠
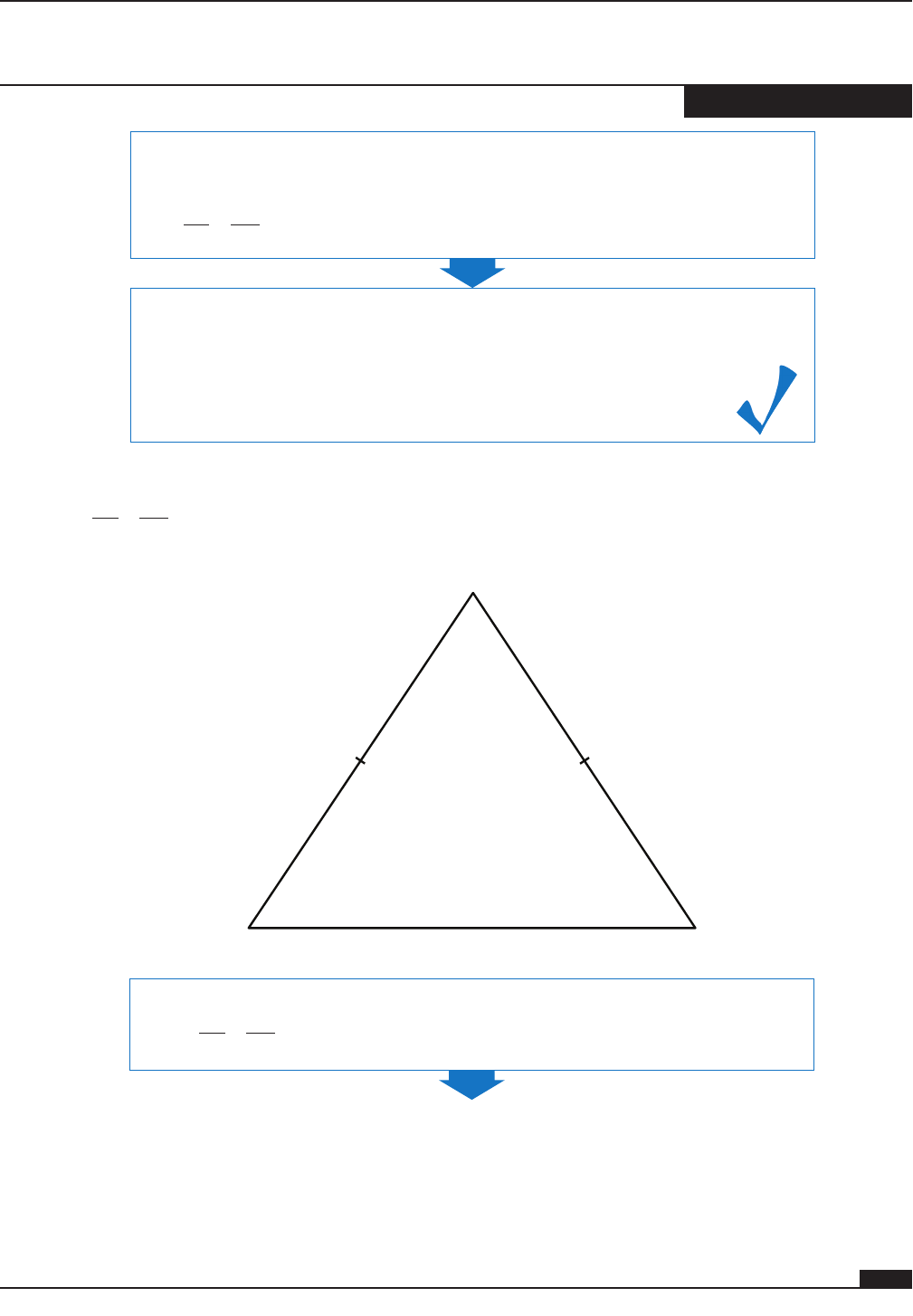
Example 3
Given AB AC≅, prove that
BC∠≅∠
.
A
BC
1. State the given information.
AB AC≅
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-574
© Walch Education
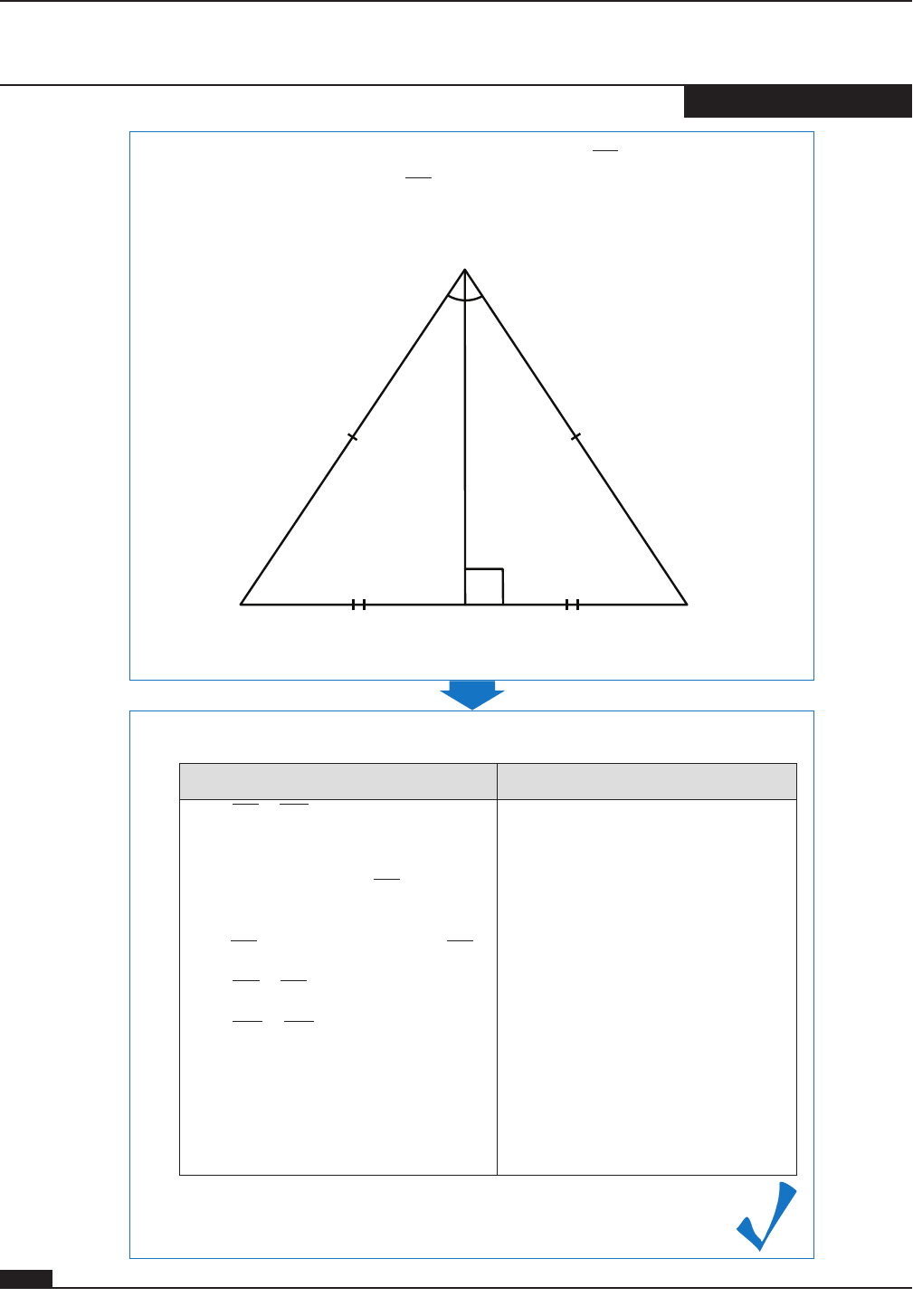
2. Draw the angle bisector of ∠A and extend it to BC , creating the
perpendicular bisector of BC . Label the point of intersection D.
Indicate congruent sides.
A
BC
D
∠B and ∠C are congruent corresponding parts.
3. Write the information in a two-column proof.
Statements Reasons
1. AB AC
≅
2. Draw the angle bisector of ∠A
and extend it to
BC
, creating
a perpendicular bisector of
BC
and the midpoint of
BC
.
3.
BD BC≅
4.
AD AD≅
5.
ABDACD≅
6.
BC∠≅∠
1. Given
2. There is exactly one line
through two points.
3. Definition of midpoint
4. Reflexive Property
5. SSS Congruence Statement
6. Corresponding Parts of
Congruent Triangles are
Congruent
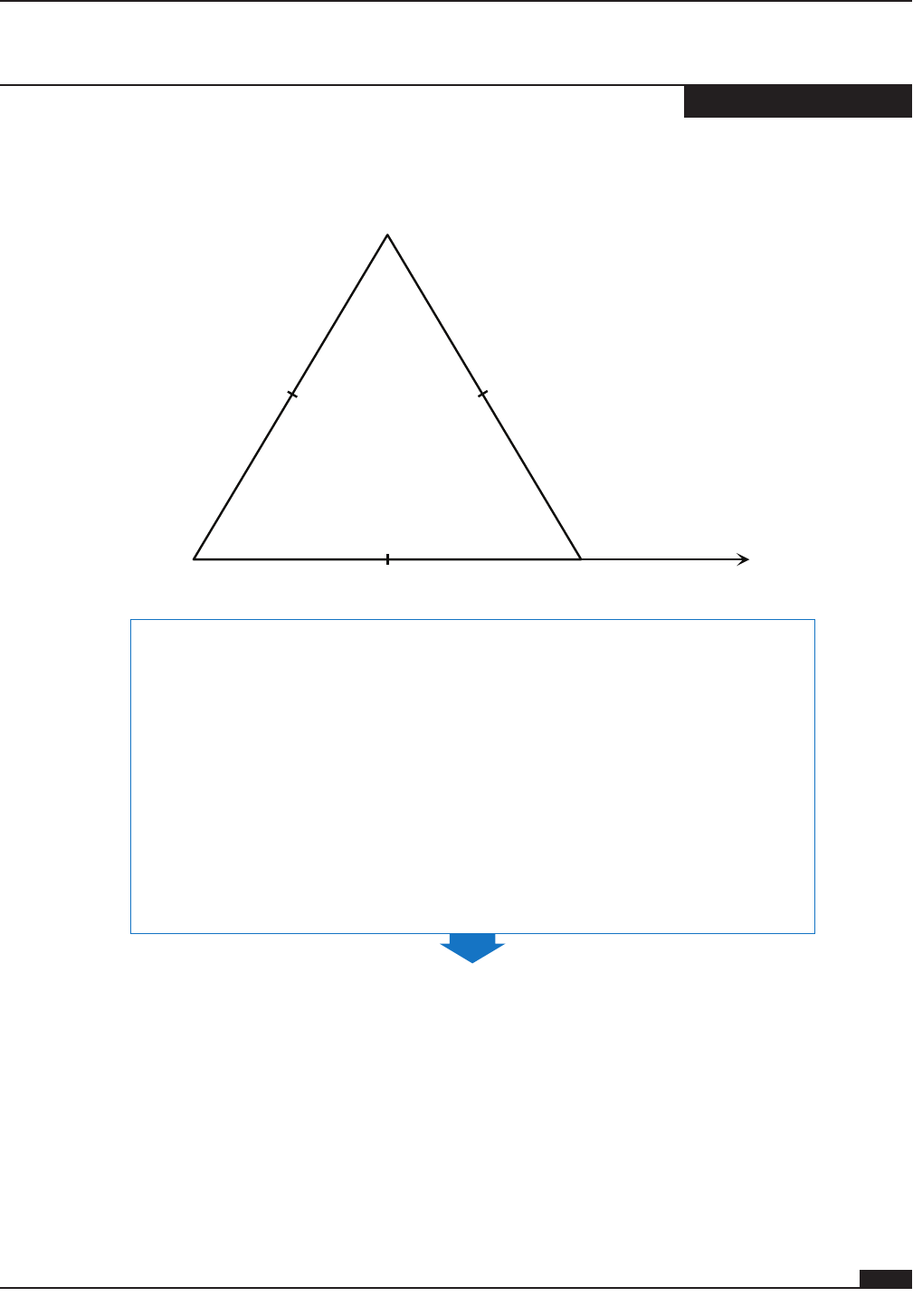
UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-575
Example 4
Find the values of x and y.
(4x + 24)˚ (11y – 23)˚
1. Make observations about the figure.
The triangle in the diagram has three congruent sides.
A triangle with three congruent sides is equilateral.
Equilateral triangles are also equiangular.
The measure of each angle of an equilateral triangle is 60˚.
An exterior angle is also included in the diagram.
The measure of an exterior angle is the supplement of the adjacent
interior angle.

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
U1-576
© Walch Education
2. Determine the value of x.
The measure of each angle of an equilateral triangle is 60˚.
Create and solve an equation for x using this information.
4x + 24 = 60 Equation
4x = 36 Solve for x.
x = 9
The value of x is 9.
3. Determine the value of y.
The exterior angle is the supplement to the interior angle.
The interior angle is 60˚ by the properties of equilateral triangles.
The sum of the measures of an exterior angle and interior angle pair
equals 180.
Create and solve an equation for y using this information.
11y – 23 + 60 = 180 Equation
11y + 37 = 180 Simplify.
11y = 143 Solve for y.
y = 13
The value of y is 13.

UNIT 1 • SIMILARITY, CONGRUENCE, AND PROOFS
Lesson 9: Proving Theorems About Triangles
Instruction
CCGPS Analytic Geometry Teacher Resource
© Walch Education
U1-577
Example 5
ABC
is equilateral. Prove that it is equiangular.
1. State the given information.
ABC
is an equilateral triangle.
2. Plan the proof.
Equilateral triangles are also isosceles triangles.
Isosceles triangles have at least two congruent sides.
AB BC≅
∠A and ∠C are base angles in relation to
AB
and BC .
AC∠≅∠
because of the Isosceles Triangle Theorem.
BC AC≅
∠A and ∠B are base angles in relation to BC and AC .
AB∠≅∠
because of the Isosceles Triangle Theorem.
By the Transitive Property,
ABC∠≅∠≅∠
; therefore,
ABC
is
equiangular.
3. Write the information in a paragraph proof.
Since
ABC
is equilateral, AB BC≅ and BC AC≅. By the Isosceles
Triangle Theorem,
AC∠≅∠
and
AB∠≅∠
. By the Transitive
Property,
ABC∠≅∠≅∠
; therefore,
ABC
is equiangular.