Applied Linear Statistical S:Instructor's Solutions Manual(5th,2005)
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 298 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Contents
- Chapter 1 LINEAR REGRESSION WITH ONE PREDICTOR VARIABLE
- Chapter 2 INFERENCES IN REGRESSION AND CORRELATION ANALYSIS
- Chapter 3 DIAGNOSTICS AND REMEDIAL MEASURES
- Chapter 4 SIMULTANEOUS INFERENCES AND OTHER TOPICS IN REGRESSION ANALYSIS
- Chapter 5 MATRIX APPROACH TO SIMPLE LINEAR REGRESSION ANALYSIS
- Chapter 6 MULTIPLE REGRESSION – I
- Chapter 7 MULTIPLE REGRESSION – II
- Chapter 8 MODELS FOR QUANTITATIVE AND QUALITATIVE PREDICTORS
- Chapter 9 BUILDING THE REGRESSION MODEL I: MODEL SELECTION AND VALIDATION
- Chapter 10 BUILDING THE REGRESSION MODEL II: DIAGNOSTICS
- Chapter 11 BUILDING THE REGRESSION MODEL III: REMEDIAL MEASURES
- Chapter 12 AUTOCORRELATION IN TIME SERIES DATA
- Chapter 13 INTRODUCTION TO NONLINEAR REGRESSION AND NEURAL NETWORKS
- Chapter 14 LOGISTIC REGRESSION, POISSON REGRESSION,AND GENERALIZED LINEAR MODELS
- Chapter 15 INTRODUCTION TO THE DESIGN OF EXPERIMENTAL AND OBSERVATIONAL STUDIES
- Chapter 16 SINGLE-FACTOR STUDIES
Instructor
Solutions Manual
to accompany
Applied Linear
Statistical Models
Fifth Edition
Michael H. Kutner
Emory University
Christopher J. Nachtsheim
University of Minnesota
John Neter
University of Georgia
William Li
University of Minnesota
2005
McGraw-Hill/Irwin
Chicago, IL
Boston, MA
PREFACE
This Solutions Manual gives intermediate and final numerical results for all end-of-chapter
Problems, Exercises, and Projects with computational elements contained in Applied Linear
Statistical Models, 5th edition. This Solutions Manual also contains proofs for all Exercises
that require derivations. No solutions are provided for the Case Studies.
In presenting calculational results we frequently show, for ease in checking, more digits
than are significant for the original data. Students and other users may obtain slightly
different answers than those presented here, because of different rounding procedures. When
a problem requires a percentile (e.g. of the tor Fdistributions) not included in the Appendix
B Tables, users may either interpolate in the table or employ an available computer program
for finding the needed value. Again, slightly different values may be obtained than the ones
shown here.
We have included many more Problems, Exercises, and Projects at the ends of chapters
than can be used in a term, in order to provide choice and flexibility to instructors in assigning
problem material. For all major topics, three or more problem settings are presented, and the
instructor can select different ones from term to term. Another option is to supply students
with a computer printout for one of the problem settings for study and class discussion and to
select one or more of the other problem settings for individual computation and solution. By
drawing on the basic numerical results in this Manual, the instructor also can easily design
additional questions to supplement those given in the text for a given problem setting.
The data sets for all Problems, Exercises, Projects and Case Studies are contained in the
compact disk provided with the text to facilitate data entry. It is expected that the student
will use a computer or have access to computer output for all but the simplest data sets,
where use of a basic calculator would be adequate. For most students, hands-on experience
in obtaining the computations by computer will be an important part of the educational
experience in the course.
While we have checked the solutions very carefully, it is possible that some errors are
still present. We would be most grateful to have any errors called to our attention. Errata
can be reported via the website for the book: http://www.mhhe.com/KutnerALSM5e. We
acknowledge with thanks the assistance of Lexin Li and Yingwen Dong in the checking of
Chapters 1-14 of this manual. We, of course, are responsible for any errors or omissions that
remain.
Michael H. Kutner
Christopher J. Nachtsheim
John Neter
William Li
i
ii
Contents
1 LINEAR REGRESSION WITH ONE PREDICTOR VARIABLE 1-1
2 INFERENCES IN REGRESSION AND CORRELATION ANALYSIS 2-1
3 DIAGNOSTICS AND REMEDIAL MEASURES 3-1
4 SIMULTANEOUS INFERENCES AND OTHER TOPICS IN REGRES-
SION ANALYSIS 4-1
5 MATRIX APPROACH TO SIMPLE LINEAR REGRESSION ANALY-
SIS 5-1
6 MULTIPLE REGRESSION – I 6-1
7 MULTIPLE REGRESSION – II 7-1
8 MODELS FOR QUANTITATIVE AND QUALITATIVE PREDICTORS 8-1
9 BUILDING THE REGRESSION MODEL I: MODEL SELECTION AND
VALIDATION 9-1
10 BUILDING THE REGRESSION MODEL II: DIAGNOSTICS 10-1
11 BUILDING THE REGRESSION MODEL III: REMEDIAL MEASURES11-1
12 AUTOCORRELATION IN TIME SERIES DATA 12-1
13 INTRODUCTION TO NONLINEAR REGRESSION AND NEURAL NET-
WORKS 13-1
14 LOGISTIC REGRESSION, POISSON REGRESSION,AND GENERAL-
IZED LINEAR MODELS 14-1
15 INTRODUCTION TO THE DESIGN OF EXPERIMENTAL AND OB-
SERVATIONAL STUDIES 15-1
16 SINGLE-FACTOR STUDIES 16-1
17 ANALYSIS OF FACTOR LEVEL MEANS 17-1
iii
18 ANOVA DIAGNOSTICS AND REMEDIAL MEASURES 18-1
19 TWO-FACTOR ANALYSIS OF VARIANCE WITH EQUAL SAMPLE
SIZES 19-1
20 TWO-FACTOR STUDIES – ONE CASE PER TREATMENT 20-1
21 RANDOMIZED COMPLETE BLOCK DESIGNS 21-1
22 ANALYSIS OF COVARIANCE 22-1
23 TWO-FACTOR STUDIES WITH UNEQUAL SAMPLE SIZES 23-1
24 MULTIFACTOR STUDIES 24-1
25 RANDOM AND MIXED EFFECTS MODELS 25-1
26 NESTED DESIGNS, SUBSAMPLING, AND PARTIALLY NESTED DE-
SIGNS 26-1
27 REPEATED MEASURES AND RELATED DESIGNS 27-1
28 BALANCED INCOMPLETE BLOCK, LATIN SQUARE, AND RELATED
DESIGNS 28-1
29 EXPLORATORY EXPERIMENTS – TWO-LEVEL FACTORIAL AND
FRACTIONAL FACTORIAL DESIGNS 29-1
30 RESPONSE SURFACE METHODOLOGY 30-1
Appendix D: RULES FOR DEVELOPING ANOVA MODELS AND TABLES
FOR BALANCED DESIGNS D.1
iv
Chapter 1
LINEAR REGRESSION WITH ONE
PREDICTOR VARIABLE
1.1. No
1.2. Y= 300 + 2X, functional
1.5. No
1.7. a. No
b. Yes, .68
1.8. Yes, no
1.10. No
1.12. a. Observational
1.13. a. Observational
1.18. No
1.19. a. β0= 2.11405, β1= 0.03883, ˆ
Y= 2.11405 + .03883X
c. ˆ
Yh= 3.27895
d. β1= 0.03883
1.20. a. ˆ
Y=−0.5802 + 15.0352X
d. ˆ
Yh= 74.5958
1.21. a. ˆ
Y= 10.20 + 4.00X
b. ˆ
Yh= 14.2
c. 4.0
d. ( ¯
X, ¯
Y) = (1,14.2)
1.22. a. ˆ
Y= 168.600000 + 2.034375X
1-1

b. ˆ
Yh= 249.975
c. β1= 2.034375
1.23. a. i: 1 2 . . . 119 120
ei: 0.9676 1.2274 . . . -0.8753 -0.2532
Yes
b. MSE = 0.388, √MSE = 0.623, grade points
1.24. a. i: 1 2 . . . 44 45
ei: -9.4903 0.4392 . . . 1.4392 2.4039
Pe2
i= 3416.377
Min Q=Pe2
i
b. MSE = 79.45063, √MSE = 8.913508, minutes
1.25. a. e1= 1.8000
b. Pe2
i= 17.6000, MSE = 2.2000, σ2
1.26. a.
i: 1 2 3 4 5 6
ei: -2.150 3.850 -5.150 -1.150 .575 2.575
i: 7 8 9 10 11 12
ei: -2.425 5.575 3.300 .300 1.300 -3.700
i: 13 14 15 16
ei: .025 -1.975 3.025 -3.975
Yes
b. MSE = 10.459, √MSE = 3.234, Brinell units
1.27. a. ˆ
Y= 156.35 −1.19X
b. (1) b1=−1.19, (2) ˆ
Yh= 84.95, (3) e8= 4.4433,
(4) MSE = 66.8
1.28. a. ˆ
Y= 20517.6−170.575X
b. (1) b1=−170.575, (2) ˆ
Yh= 6871.6, (3) e10 = 1401.566,
(4) MSE = 5552112
1.31. No, no
1.32. Solving (1.9a) and (1.9b) for b0and equating the results:
PYi−b1PXi
n=PXiYi−b1PX2
i
PXi
1-2

and then solving for b1yields:
b1=nPXiYi−PXiPYi
nPX2
i−(PXi)2=PXiYi−PXiPYi
n
PX2
i−(PXi)2
n
1.33. Q=P(Yi−β0)2
dQ
dβ0
=−2X(Yi−β0)
Setting the derivative equal to zero, simplifying, and substituting the least squares
estimator b0yields:
P(Yi−b0) = 0 or b0=¯
Y
1.34. E{b0}=E{¯
Y}=1
nXE{Yi}=1
nXβ0=β0
1.35. From the first normal equation (1.9a):
PYi=nb0+b1PXi=P(b0+b1Xi) = Pˆ
Yifrom (1.13)
1.36. Pˆ
Yiei=P(b0+b1Xi)ei=b0Pei+b1PXiei= 0 because Pei= 0 from (1.17) and
PXiei= 0 from (1.19).
1.38. (1) 76, yes; (2) 60, yes
1.39. a. Applying (1.10a) and (1.10b) to (5,¯
Y1), (10,¯
Y2) and (15,¯
Y3), we
obtain:
b1=¯
Y3−¯
Y1
10 b0=4¯
Y1+¯
Y2−2¯
Y3
3
Using (1.10a) and (1.10b) with the six original points yields the same results.
b. Yes
1.40. No
1.41. a. Q=P(Yi−β1Xi)2
dQ
dβ1
=−2X(Yi−β1Xi)Xi
Setting the derivative equal to zero, simplifying, and substituting the least squares
estimator b1yields:
b1=PYiXi
PX2
i
b. L=n
Q
i=1
1
(2πσ2)1/2exp ·−1
2σ2(Yi−β1Xi)2¸
1-3
It is more convenient to work with logeL:
logeL=−n
2loge(2πσ2)−1
2σ2X(Yi−β1Xi)2
dlogeL
dβ1
=1
σ2X(Yi−β1Xi)Xi
Setting the derivative equal to zero, simplifying, and substituting the maximum
likelihood estimator b1yields:
P(Yi−b1Xi)Xi= 0 or b1=PYiXi
PX2
i
Yes
c. E{b1}=E(PYiXi
PX2
i)=1
PX2
iXXiE{Yi}
=1
PX2
iXXi(β1Xi) = β1
1.42. a. L(β1) = 6
Q
i=1
1
√32πexp[−1
32(Yi−β1Xi)2]
b. L(17) = 9.45 ×10−30,L(18) = 2.65 ×10−7,L(19) = 3.05 ×10−37
β1= 18
c. b1= 17.928, yes
d. Yes
1.43. a. Total population: ˆ
Y=−110.635 + 0.0027954X
Number of hospital beds: ˆ
Y=−95.9322 + 0.743116X
Total personal income: ˆ
Y=−48.3948 + .131701X
c. Total population: MSE = 372,203.5
Number of hospital beds: MSE = 310,191.9
Total personal income: MSE = 324,539.4
1.44. a. Region 1: ˆ
Y=−1723.0 + 480.0X
Region 2: ˆ
Y= 916.4 + 299.3X
Region 3: ˆ
Y= 401.56 + 272.22X
Region 4: ˆ
Y= 396.1 + 508.0X
c. Region 1: MSE = 64,444,465
Region 2: MSE = 141,479,673
Region 3: MSE = 50,242,464
Region 4: MSE = 514,289,367
1.45. a. Infection risk: ˆ
Y= 6.3368 + .7604X
Facilities: ˆ
Y= 7.7188 + .0447X
1-4

X-ray: ˆ
Y= 6.5664 + .0378X
c. Infection risk: MSE = 2.638
Facilities: MSE = 3.221
X-ray: MSE = 3.147
1.46. a. Region 1: ˆ
Y= 4.5379 + 1.3478X
Region 2: ˆ
Y= 7.5605 + .4832X
Region 3: ˆ
Y= 7.1293 + .5251X
Region 4: ˆ
Y= 8.0381 + .0173X
c. Region 1: MSE = 4.353
Region 2: MSE = 1.038
Region 3: MSE =.940
Region 4: MSE = 1.078
1.47. a. L(β0, β1) = 6
Q
i=1
1
√32πexp[−1
32(Yi−β0−β1Xi)2]
b. b0= 1.5969, b1= 17.8524
c. Yes
1-5
1-6
Chapter 2
INFERENCES IN REGRESSION
AND CORRELATION ANALYSIS
2.1. a. Yes, α=.05
2.2. No
2.4. a. t(.995; 118) = 2.61814, .03883 ±2.61814(.01277), .00540 ≤β1≤.07226
b. H0:β1= 0, Ha:β16= 0. t∗= (.03883 −0)/.01277 = 3.04072. If |t∗| ≤ 2.61814,
conclude H0, otherwise Ha. Conclude Ha.
c. 0.00291
2.5. a. t(.95; 43) = 1.6811, 15.0352 ±1.6811(.4831), 14.2231 ≤β1≤15.8473
b. H0:β1= 0, Ha:β16= 0. t∗= (15.0352 −0)/.4831 = 31.122. If |t∗| ≤ 1.681
conclude H0, otherwise Ha. Conclude Ha.P-value= 0+
c. Yes
d. H0:β1≤14, Ha:β1>14. t∗= (15.0352 −14)/.4831 = 2.1428. If t∗≤1.681
conclude H0, otherwise Ha. Conclude Ha.P-value= .0189
2.6. a. t(.975; 8) = 2.306, b1= 4.0, s{b1}=.469, 4.0±2.306(.469),
2.918 ≤β1≤5.082
b. H0:β1= 0, Ha:β16= 0. t∗= (4.0−0)/.469 = 8.529. If |t∗| ≤ 2.306 conclude H0,
otherwise Ha. Conclude Ha.P-value= .00003
c. b0= 10.20, s{b0}=.663, 10.20 ±2.306(.663), 8.671 ≤β0≤11.729
d. H0:β0≤9, Ha:β0>9. t∗= (10.20 −9)/.663 = 1.810. If t∗≤2.306 conclude H0,
otherwise Ha. Conclude H0.P-value= .053
e. H0:β1= 0: δ=|2−0|/.5 = 4, power = .93
H0:β0≤9: δ=|11 −9|/.75 = 2.67, power = .78
2.7. a. t(.995; 14) = 2.977, b1= 2.0344, s{b1}=.0904, 2.0344 ±2.977(.0904),
1.765 ≤β1≤2.304
2-1
b. H0:β1= 2, Ha:β16= 2. t∗= (2.0344 −2)/.0904 = .381. If |t∗| ≤ 2.977 conclude
H0, otherwise Ha. Conclude H0.P-value= .71
c. δ=|.3|/.1 = 3, power = .50
2.8. a. H0:β1= 3.0, Ha:β16= 3.0. t∗= (3.57 −3.0)/.3470 = 1.643,
t(.975; 23) = 2.069. If |t∗| ≤ 2.069 conclude H0, otherwise Ha. Conclude H0.
b. δ=|.5|/.35 = 1.43, power = .30 (by linear interpolation)
2.10. a. Prediction
b. Mean response
c. Prediction
2.12. No, no
2.13. a. ˆ
Yh= 3.2012, s{ˆ
Yh}=.0706, t(.975; 118) = 1.9803, 3.2012 ±1.9803(.0706),
3.0614 ≤E{Yh} ≤ 3.3410
b. s{pred}=.6271, 3.2012 ±1.9803(.6271), 1.9594 ≤Yh( new) ≤4.4430
c. Yes, yes
d. W2= 2F(.95; 2,118) = 2(3.0731) = 6.1462, W= 2.4792, 3.2012 ±2.4792(.0706),
3.0262 ≤β0+β1Xh≤3.3762, yes, yes
2.14. a. ˆ
Yh= 89.6313, s{ˆ
Yh}= 1.3964, t(.95; 43) = 1.6811, 89.6313 ±1.6811(1.3964),
87.2838 ≤E{Yh} ≤ 91.9788
b. s{pred}= 9.0222, 89.6313 ±1.6811(9.0222), 74.4641 ≤Yh(new) ≤104.7985, yes,
yes
c. 87.2838/6 = 14.5473, 91.9788/6 = 15.3298, 14.5473 ≤Mean time per machine
≤15.3298
d. W2= 2F(.90; 2, 43) = 2(2.4304) = 4.8608, W= 2.2047, 89.6313±2.2047(1.3964),
86.5527 ≤β0+β1Xh≤92.7099, yes, yes
2.15. a. Xh= 2: ˆ
Yh= 18.2, s{ˆ
Yh}=.663, t(.995; 8) = 3.355, 18.2±3.355(.663), 15.976 ≤
E{Yh} ≤ 20.424
Xh= 4: ˆ
Yh= 26.2, s{ˆ
Yh}= 1.483, 26.2±3.355(1.483), 21.225 ≤E{Yh} ≤ 31.175
b. s{pred}= 1.625, 18.2±3.355(1.625), 12.748 ≤Yh(new) ≤23.652
c. s{predmean}= 1.083, 18.2±3.355(1.083), 14.567 ≤¯
Yh(new) ≤21.833, 44 =
3(14.567) ≤Total number of broken ampules ≤3(21.833) = 65
d. W2= 2F(.99; 2,8) = 2(8.649) = 17.298, W= 4.159
Xh= 2: 18.2±4.159(.663), 15.443 ≤β0+β1Xh≤20.957
Xh= 4: 26.2±4.159(1.483), 20.032 ≤β0+β1Xh≤32.368
yes, yes
2.16. a. ˆ
Yh= 229.631, s{ˆ
Yh}=.8285, t(.99; 14) = 2.624, 229.631±2.624(.8285), 227.457 ≤
E{Yh} ≤ 231.805
2-2

b. s{pred}= 3.338, 229.631 ±2.624(3.338), 220.872 ≤Yh(new) ≤238.390
c. s{predmean}= 1.316, 229.631 ±2.624(1.316), 226.178 ≤¯
Yh(new) ≤233.084
d. Yes, yes
e. W2= 2F(.98; 2,14) = 2(5.241) = 10.482, W= 3.238, 229.631 ±3.238(.8285),
226.948 ≤β0+β1Xh≤232.314, yes, yes
2.17. Greater, H0:β1= 0
2.20. No
2.21. No
2.22. Yes, yes
2.23. a.
Source SS df MS
Regression 3.58785 1 3.58785
Error 45.8176 118 0.388285
Total 49.40545 119
b. σ2+β2
1P(Xi−¯
X)2,σ2, when β1= 0
c. H0:β1= 0, Ha:β16= 0. F∗= 3.58785/0.388285 = 9.24, F(.99; 1,118) = 6.855. If
F∗≤6.855 conclude H0, otherwise Ha. Conclude Ha.
d. SSR = 3.58785, 7.26% or 0.0726, coefficient of determination
e. +0.2695
f. R2
2.24. a.
Source SS df MS
Regression 76,960.4 1 76,960.4
Error 3,416.38 43 79.4506
Total 80,376.78 44
Source SS df MS
Regression 76,960.4 1 76,960.4
Error 3,416.38 43 79.4506
Total 80,376.78 44
Correction for mean 261,747.2 1
Total, uncorrected 342,124 45
b. H0:β1= 0, Ha:β16= 0. F∗= 76,960.4/79.4506 = 968.66, F (.90; 1,43) = 2.826.
If F∗≤2.826 conclude H0, otherwise Ha.Conclude Ha.
c. 95.75% or 0.9575, coefficient of determination
d. +.9785
e. R2
2-3
2.25. a.
Source SS df MS
Regression 160.00 1 160.00
Error 17.60 8 2.20
Total 177.60 9
b. H0:β1= 0, Ha:β16= 0. F∗= 160.00/2.20 = 72.727, F(.95; 1,8) = 5.32. If
F∗≤5.32 conclude H0, otherwise Ha. Conclude Ha.
c. t∗= (4.00 −0)/.469 = 8.529, (t∗)2= (8.529)2= 72.7 = F∗
d. R2=.9009, r=.9492, 90.09%
2.26. a.
Source SS df MS
Regression 5,297.5125 1 5,297.5125
Error 146.4250 14 10.4589
Total 5,443.9375 15
b. H0:β1= 0, Ha:β16= 0, F∗= 5,297.5125/10.4589 = 506.51, F (.99; 1,14) =
8.86.If F∗≤8.86 conclude H0, otherwise Ha.Conclude Ha.
c.
i: 1 2 3 4 5 6
Yi−ˆ
Yi: -2.150 3.850 -5.150 -1.150 .575 2.575
ˆ
Yi−¯
Y: -24.4125 -24.4125 -24.4125 -24.4125 -8.1375 -8.1375
i: 7 8 9 10 11 12
Yi−ˆ
Yi: -2.425 5.575 3.300 .300 1.300 -3.700
ˆ
Yi−¯
Y: -8.1375 -8.1375 8.1375 8.1375 8.1375 8.1375
i: 13 14 15 16
Yi−ˆ
Yi: .025 -1.975 3.025 -3.975
ˆ
Yi−¯
Y: 24.4125 24.4125 24.4125 24.4125
d. R2=.9731, r=.9865
2.27. a. H0:β1≥0, Ha:β1<0. s{b1}= 0.090197,
t∗= (−1.19 −0)/.090197 = −13.193, t(.05; 58) = −1.67155.
If t∗≥ −1.67155 conclude H0, otherwise Ha. Conclude Ha.
P-value= 0+
c. t(.975; 58) = 2.00172, −1.19 ±2.00172(.090197), −1.3705 ≤β1≤ −1.0095
2.28. a. ˆ
Yh= 84.9468, s{ˆ
Yh}= 1.05515, t(.975; 58) = 2.00172,
84.9468 ±2.00172(1.05515), 82.835 ≤E{Yh} ≤ 87.059
b. s{Yh(new)}= 8.24101, 84.9468 ±2.00172(8.24101), 68.451 ≤Yh(new) ≤101.443
c. W2= 2F(.95; 2,58) = 2(3.15593) = 6.31186, W= 2.512342,
84.9468 ±2.512342(1.05515), 82.296 ≤β0+β1Xh≤87.598, yes, yes
2.29. a.
2-4

i: 1 2 . . . 59 60
Yi−ˆ
Yi: 0.823243 -1.55675 . . . -0.666887 8.09309
ˆ
Yi−¯
Y: 20.2101 22.5901 . . . -14.2998 -19.0598
b.
Source SS df MS
Regression 11,627.5 1 11,627.5
Error 3,874.45 58 66.8008
Total 15,501.95 59
c. H0:β1= 0, Ha:β16= 0. F∗= 11,627.5/66.8008 = 174.0623,
F(.90; 1,58) = 2.79409. If F∗≤2.79409 conclude H0, otherwise Ha.Conclude
Ha.
d. 24.993% or .24993
e. R2= 0.750067, r=−0.866064
2.30. a. H0:β1= 0, Ha:β16= 0. s{b1}= 41.5743,
t∗= (−170.575 −0)/41.5743 = −4.1029, t(.995; 82) = 2.63712.
If |t∗| ≤ 2.63712 conclude H0, otherwise Ha. Conclude Ha.
P-value = 0.000096
b. −170.575 ±2.63712(41.5743), −280.2114 ≤β1≤ −60.9386
2.31. a.
Source SS df MS
Regression 93,462,942 1 93,462,942
Error 455,273,165 82 5,552,112
Total 548,736,107 83
b. H0:β1= 0, Ha:β16= 0. F∗= 93,462,942/5,552,112 = 16.8338, F(.99; 1,82) =
6.9544. If F∗≤6.9544 conclude H0, otherwise Ha. Conclude Ha. (t∗)2=
(−4.102895)2= 16.8338 = F∗. [t(.995; 82)]2= (2.63712)2= 6.9544 = F(.99; 1,82).
Yes.
c. SSR = 93,462,942, 17.03% or 0.1703
d. -0.4127
2.32. a. Full: Yi=β0+β1Xi+εi, reduced: Yi=β0+εi
b. (1) SSE(F) = 455,273,165, (2) SSE(R) = 548,736,107,
(3) dfF= 82, (4) dfR= 83,
(5) F∗= [(548,736,107 −455,273,165)/1] ÷[455,273,165/82] = 16.83376, (6) If
F∗≤F(.99; 1,82) = 6.95442 conclude H0, otherwise Ha.
c. Yes
2.33. a. H0:β0= 7.5, Ha:β06= 7.5
b. Full: Yi=β0+β1Xi+εi, reduced: Yi−7.5 = β1Xi+εi
c. Yes, dfR−dfF= (n−1) −(n−2) = 1
2-5

2.36 Regression model
2.38. No
2.39. a. Normal, mean µ1= 50, standard deviation σ1= 3
b. Normal, mean E{Y2|Y1= 55}= 105.33, standard deviation σ2|1= 2.40
c. Normal, mean E{Y1|Y2= 95}= 47, standard deviation σ1|2= 1.80
2.40. (1) No, (2) no, (3) yes
2.41. No
2.42. b. .95285, ρ12
c. H0:ρ12 = 0, Ha:ρ12 6= 0. t∗= (.95285√13)/q1−(.95285)2= 11.32194,
t(.995; 13) = 3.012. If |t∗| ≤ 3.012 conclude H0,otherwise Ha. Conclude Ha.
d. No
2.43. a. H0:ρ12 = 0, Ha:ρ12 6= 0. t∗= (.61√82)/q1−(.61)2= 6.9709,
t(.975; 82) = 1.993. If |t∗| ≤ 1.993 conclude H0, otherwise Ha. Conclude Ha.
b. z0=.70892, σ{z0}=.1111, z(.975) = 1.960, .70892 ±1.960(.1111), .49116 ≤ζ≤
.92668, .455 ≤ρ12 ≤.729
c. .207 ≤ρ2
12 ≤.531
2.44. a. H0:ρ12 = 0, Ha:ρ12 6= 0. t∗= (.87√101)/q1−(.87)2= 17.73321, t(.95; 101) =
1.663. If |t∗| ≤ 1.663 conclude H0, otherwise Ha. Conclude Ha.
b. z0= 1.33308, σ{z0}=.1, z(.95) = 1.645, 1.33308 ±1.645(.1), 1.16858 ≤ζ≤
1.49758, .824 ≤ρ12 ≤.905
c. .679 ≤ρ2
12 ≤.819
2.45. a. z0= 1.18814, σ{z0}=.0833, z(.995) = 2.576, 1.18814 ±2.576(.0833),
.97356 ≤ζ≤1.40272, .750 ≤ρ12 ≤.886.
b. .563 ≤ρ2
12 ≤.785
2.46. a. 0.9454874
b. H0: There is no association between Y1and Y2
Ha: There is an association between Y1and Y2
t∗=0.9454874√13
q1−(0.9454874)2= 10.46803. t(0.995,13) = 3.012276. If |t∗| ≤ 3.012276,
conclude H0, otherwise, conclude Ha. Conclude Ha.
2.47. a. -0.866064,
b. H0:ρ12 = 0, Ha:ρ12 6= 0. t∗= (−0.866064√58)/q1−(−0.866064)2=
−13.19326, t(.975; 58) = 2.00172. If |t∗| ≤ 2.00172 conclude H0, otherwise Ha.
Conclude Ha.
2-6
c. -0.8657217
d. H0: There is no association between Xand Y
Ha: There is an association between Xand Y
t∗=−0.8657217√58
q1−(−0.8657217)2=−13.17243. t(0.975,58) = 2.001717. If |t∗| ≤
2.001717, conclude H0, otherwise, conclude Ha. Conclude Ha.
2.48. a. −0.4127033
b. H0:ρ12 = 0, Ha:ρ12 6= 0. t∗= (−0.4127033√82)/q1−(−0.4127033)2=
−4.102897, t(.995; 82) = 2.637123. If |t∗| ≤ 2.637123 conclude H0, otherwise Ha.
Conclude Ha.
2.49. a. -0.4259324
b. H0: There is no association between Xand Y
Ha: There is an association between Xand Y
t∗=−0.4259324√58
q1−(−0.4259324)2=−4.263013. t(0.995,80) = 2.637123. If |t∗| ≤
2.637123, conclude H0, otherwise, conclude Ha. Conclude Ha.
2.50. PkiXi=XÃXi−¯
X
P(Xi−¯
X)2!Xi
=X(Xi−¯
X)(Xi−¯
X)
P(Xi−¯
X)2because X(Xi−¯
X)¯
X
P(Xi−¯
X)2= 0
=P(Xi−¯
X)2
P(Xi−¯
X)2= 1
2.51. E{b0}=E{¯
Y−b1¯
X}
=1
nXE{Yi} − ¯
XE{b1}
=1
nX(β0+β1Xi)−¯
Xβ1
=β0+β1¯
X−¯
Xβ1=β0
2.52. σ2{b0}=σ2{¯
Y−b1¯
X}
=σ2{¯
Y}+¯
X2σ2{b1} − 2¯
Xσ{¯
Y , b1}
=σ2
n+¯
X2σ2
P(Xi−¯
X)2−0
=σ2"1
n+¯
X2
P(Xi−¯
X)2#
2.53. a. L=
n
Y
i=1
1
√2πσ2exp ·−1
2σ2(Yi−β0−β1Xi)2¸g(Xi)
2-7

b. Maximum likelihood estimators can be found more easily by working with logeL:
logeL=−n
2loge(2πσ2)−1
2σ2X(Yi−β0−β1Xi)2+Xlogeg(Xi)
∂logeL
∂β0
=1
σ2X(Yi−β0−β1Xi)
∂logeL
∂β1
=1
σ2X(Yi−β0−β1Xi)(Xi)
∂logeL
∂σ2=−n
2µ1
σ2¶+1
2X(Yi−β0−β1Xi)2µ1
σ4¶
Setting each derivative equal to zero, simplifying, and substituting the maximum
likelihood estimators b0,b1, and ˆσ2yields:
(1) PYi−nb0−b1PXi= 0
(2) PYiXi−b0PXi−b1PX2
i= 0
(3)P(Yi−b0−b1Xi)2
n= ˆσ2
Equations (1) and (2) are the same as the least squares normal equations (1.9),
hence the maximum likelihood estimators b0and b1are the same as those in (1.27).
2.54. Yes, no
2.55. SSR =P(ˆ
Yi−¯
Y)2=P[(b0+b1Xi)−¯
Y]2
=P[( ¯
Y−b1¯
X) + b1Xi−¯
Y]2
=b2
1P(Xi−¯
X)2
2.56. a. E{MSR}= 1,026.36, E{MSE}=.36
b. E{MSR}= 90.36, E{MSE}=.36
2.57. a. Yi−5Xi=β0+εi,n−1
b. Yi−2−5Xi=εi,n
2.58. If ρ12 = 0, (2.74) becomes:
f(Y1,Y2) = 1
2πσ1σ2
exp (−1
2"µY1−µ1
σ1¶2
+µY2−µ2
σ2¶2#)
=1
√2πσ1
exp "−1
2µY1−µ1
σ1¶2#·1
√2πσ2
exp "−1
2µY2−µ2
σ2¶2#
=f1(Y1)·f2(Y2)
2.59. a. L=
n
Y
i=1
1
2πσ1σ2q1−ρ2
12 ×exp{− 1
2(1 −ρ2
12)[(Yi1−µ1
σ1
)2
−2ρ12(Yi1−µ1
σ1
)(Yi2−µ2
σ2
)+(Yi2−µ2
σ2
)2]}
Maximum likelihood estimators can be found more easily by working with logeL:
2-8
logeL=−nloge2π−nlogeσ1−nlogeσ2−n
2loge(1 −ρ2
12)
−1
2(1 −ρ2
12)
n
X
i=1
[(Yi1−µ1
σ1
)2−2ρ12(Yi1−µ1
σ1
)(Yi2−µ2
σ2
)
+(Yi2−µ2
σ2
)2]
∂logeL
∂µ1
=1
σ2
1(1 −ρ2
12)X(Yi1−µ1)−ρ12
σ1σ2(1 −ρ2
12)X(Yi2−µ2)
∂logeL
∂µ2
=1
σ2
2(1 −ρ2
12)X(Yi2−µ2)−ρ12
σ1σ2(1 −ρ2
12)X(Yi1−µ1)
∂logeL
∂σ1
=−n
σ1
+1
(1 −ρ12)2"P(Yi1−µ1)2
σ3
1−ρ12 P(Yi1−µ1)(Yi2−µ2)
σ2
1σ2#
∂logeL
∂σ2
=−n
σ2
+1
(1 −ρ12)2"P(Yi2−µ2)2
σ3
2−ρ12 P(Yi1−µ1)(Yi2−µ2)
σ1σ2
2#
∂logeL
∂ρ12
=nρ12
1−ρ2
12
+1
1−ρ2
12 XµYi1−µ1
σ1¶µYi2−µ2
σ2¶−ρ12
(1 −ρ2
12)2
×P"µYi1−µ1
σ1¶2
−2ρ12 µYi1−µ1
σ1¶µYi2−µ2
σ2¶+µYi2−µ2
σ2¶2#
Setting the derivatives equal to zero, simplifying, and substituting the maximum
likelihood estimators ˆµ1, ˆµ2, ˆσ1, ˆσ2, and ˆρ12 yields:
(1) 1
ˆσ1X(Yi1−ˆµ1)−ˆρ12
ˆσ2X(Yi2−ˆµ2) = 0
(2) 1
ˆσ2X(Yi2−ˆµ2)−ˆρ12
ˆσ1X(Yi1−ˆµ1) = 0
(3) P(Yi1−ˆµ1)2
ˆσ2
1−ˆρ12 P(Yi1−ˆµ1)(Yi2−ˆµ2)
ˆσ1ˆσ2−n(1 −ˆρ2
12) = 0
(4) P(Yi2−ˆµ2)2
ˆσ2
2−ˆρ12 P(Yi1−ˆµ1)(Yi2−ˆµ2)
ˆσ1ˆσ2−n(1 −ˆρ2
12) = 0
(5) nˆρ12(1 −ˆρ2
12) + (1 + ˆρ2
12)PÃYi1−ˆµ1
ˆσ1!ÃYi2−ˆµ2
ˆσ2!
−ˆρ12 P
ÃYi1−ˆµ1
ˆσ1!2
+ÃYi2−ˆµ2
ˆσ2!2
= 0
Solving equations (1) and (2) yields:
ˆµ1=¯
Y1ˆµ2=¯
Y2
Using these results in equations (3), (4), and (5), it will be found that the maxi-
mum likelihood estimators are:
ˆµ1=¯
Y1ˆµ2=¯
Y2ˆσ1=sP(Yi1−¯
Y1)2
n
ˆσ2=sP(Yi2−¯
Y2)2
nˆρ12 =P(Yi1−¯
Y1)(Yi2−¯
Y2)
[P(Yi1−¯
Y1)2]1
2[P(Yi2−¯
Y2)2]1
2
2-9

b. ˆα1|2= ˆµ1−ˆµ2ˆρ12
ˆσ1
ˆσ2
=¯
Y1−¯
Y2"P(Yi1−¯
Y1)(Yi2−¯
Y2)
[P(Yi1−¯
Y1)2]1
2[P(Yi2−¯
Y2)2]1
2#
qP(Yi1−¯
Y1)2/n
qP(Yi2−¯
Y2)2/n
=¯
Y1−¯
Y2"P(Yi1−¯
Y1)(Yi2−¯
Y2)
P(Yi2−¯
Y2)2#
ˆ
β12 = ˆρ12
ˆσ1
ˆσ2
="P(Yi1−¯
Y1)(Yi2−¯
Y2)
[P(Yi1−¯
Y1)2]1
2[P(Yi2−¯
Y2)2]1
2#
qP(Yi1−¯
Y1)2/n
qP(Yi2−¯
Y2)2/n
=P(Yi1−¯
Y1)(Yi2−¯
Y2)
P(Yi2−¯
Y2)2
ˆσ2
1|2= ˆσ2
1(1 −ˆρ2
12)
=P(Yi1−¯
Y1)2
n"1−[P(Yi1−¯
Y1)(Yi2−¯
Y2)]2
P(Yi1−¯
Y1)2P(Yi2−¯
Y2)2#
=P(Yi1−¯
Y1)2
n−[P(Yi1−¯
Y1)(Yi2−¯
Y2)]2
nP(Yi2−¯
Y2)2
c. The equivalence is shown by letting Yi1and Yi2in part (b) be Yiand Xi, respec-
tively.
2.60. Using regression notation and letting
X(Xi−¯
X)2= (n−1)s2
X
and X(Yi−¯
Y)2= (n−1)s2
Y,
we have from (2.84) with Yi1=Yiand Yi2=Xi
b1=r12
sY
sX
since b1="P(Yi−¯
Y)2
P(Xi−¯
X)2#1
2
r12
SSE =P(Yi−¯
Y)2−[P(Xi−¯
X)(Yi−¯
Y)]2
P(Xi−¯
X)2
= (n−1)s2
Y−r2
12(n−1)s2
Y= (n−1)s2
Y(1 −r2
12)
s2{b1}=(n−1)s2
Y(1 −r2
12)
n−2÷(n−1)s2
X=s2
Y(1 −r2
12)
(n−2)s2
X
Hence:
b1
s{b1}=r12
sY
sX÷sYq1−r2
12
³√n−2´sX
=³√n−2´r12
q1−r2
12
=t∗
2-10

2.61. SSR(Y1)
SST O ="Σ(Yi1−¯
Y1)(Yi2−¯
Y2)
Σ(Yi1−¯
Y1)2#2hΣ(Yi1−¯
Y1)2i
Σ(Yi2−¯
Y2)2
=[P(Yi1−¯
Y1)(Yi2−¯
Y2)]2
P(Yi1−¯
Y1)2P(Yi2−¯
Y2)2
SSR(Y2)
SST O ="P(Yi2−¯
Y2)(Yi1−¯
Y1)
P(Yi2−¯
Y2)2#2hP(Yi2−¯
Y2)2i
P(Yi1−¯
Y1)2
=[P(Yi2−¯
Y2)(Yi1−¯
Y1)]2
P(Yi1−¯
Y1)2P(Yi2−¯
Y2)2
2.62. Total population: R2= 0.884067
Number of hospital beds: R2= 0.903383
Total personal income: R2= 0.898914
2.63. Region 1: 480.0±1.66008(110.1), 297.2252 ≤β1≤662.7748
Region 2: 299.3±1.65936(154.2), 43.42669 ≤β1≤555.1733
Region 3: 272.22 ±1.65508(70.34), 155.8017 ≤β1≤388.6383
Region 4: 508.0±1.66543(359.0), −89.88937 ≤β1≤1105.889
2.64. Infection rate: R2=.2846
Facilities: R2=.1264
X-ray: R2=.1463
2.65. Region 1: 1.3478 ±2.056(.316), .6981 ≤β1≤1.9975
Region 2: .4832 ±2.042(.137), .2034 ≤β1≤.7630
Region 3: .5251 ±2.031(.111), .2997 ≤β1≤.7505
Region 4: .0173 ±2.145(.306), −.6391 ≤β1≤.6737
2.66. a. E{Yh}= 36 when Xh= 4, E{Yh}= 52 when Xh= 8, E{Yh}= 68 when Xh= 12,
E{Yh}= 84 when Xh= 16, E{Yh}= 100 when Xh= 20
c. E{b1}= 4, σ{b1}=s25
160 =.3953
d. Expected proportion is .95
2-11

Chapter 3
DIAGNOSTICS AND REMEDIAL
MEASURES
3.3.b.and c.
i: 1 2 3 . . . 118 119 120
ˆ
Yi: 2.92942 2.65763 3.20121 . . . 3.20121 2.73528 3.20121
ei: 0.967581 1.22737 0.57679 . . . 0.71279 -0.87528 -0.25321
d.
Ascending order: 1 2 3 . . . 119 120
Ordered residual: -2.74004 -1.83169 -1.24373 . . . 0.99441 1.22737
Expected value: -1.59670 -1.37781 -1.25706 . . . 1.37781 1.59670
H0: Normal, Ha: not normal. r= 0.97373. If r≥.987 concludeH0, otherwise Ha.
Conclude Ha.
e. n1= 65, ¯
d1= 0.43796, n2= 55, ¯
d2= 0.50652, s= 0.417275, t∗
BF = (0.43796 −
0.50652)/0.417275q(1/65) + (1/55) = −0.89674, t(.995; 18) = 2.61814. If |t∗
BF | ≤
2.61814 conclude error variance constant, otherwise error variance not constant.
Conclude error variance constant.
3.4.c and d.
i: 1 2 . . . 44 45
ˆ
Yi: 29.49034 59.56084 . . . 59.56084 74.59608
ei: -9.49034 0.43916 . . . 1.43916 2.40392
e.
Ascending order: 1 2 . . . 44 45
Ordered residual: -22.77232 -19.70183 . . . 14.40392 15.40392
Expected value: -19.63272 -16.04643 . . . 16.04643 19.63272
H0: Normal, Ha: not normal. r= 0.9891. If r≥.9785 conclude H0, otherwise
Ha. Conclude H0.
g. SSR∗= 15,155, SSE = 3416.38, X2
BP = (15,155/2) ÷(3416.38/45)2= 1.314676,
χ2(.95; 1) = 3.84. If X2
BP ≤3.84 conclude error variance constant, otherwise error
variance not constant. Conclude error variance constant.
3.5. c.
3-1
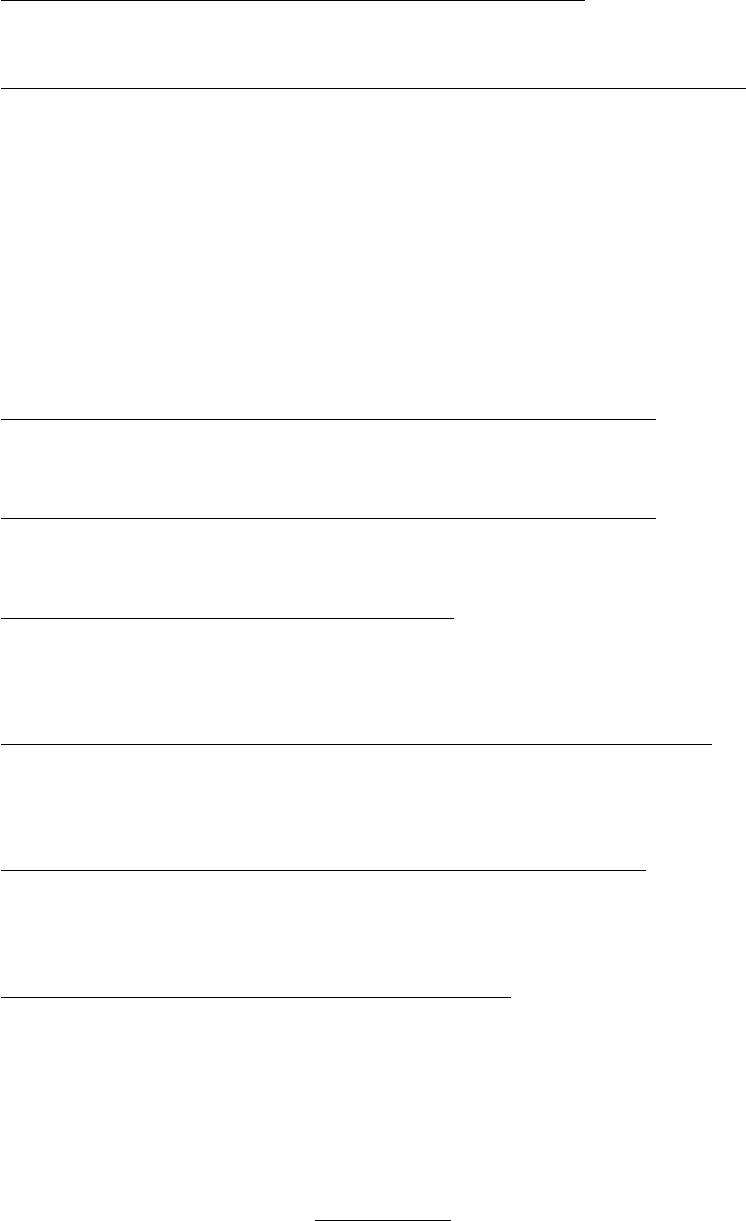
i: 1 2 3 4 5 6 7 8 9 10
ei: 1.8 -1.2 -1.2 1.8 -.2 -1.2 -2.2 .8 .8 .8
e.
Ascending Order: 1 2 3 4 5 6 7 8 9 10
Ordered residual: -2.2 -1.2 -1.2 -1.2 -.2 .8 .8 .8 1.8 1.8
Expected value: -2.3 -1.5 -1.0 -.6 -.2 .2 .6 1.0 1.5 2.3
H0: Normal, Ha: not normal. r=.961. If r≥.879 conclude H0, otherwise Ha.
Conclude H0.
g. SSR∗= 6.4, SSE = 17.6, X2
BP = (6.4/2) ÷(17.6/10)2= 1.03, χ2(.90; 1) = 2.71.
If X2
BP ≤2.71 conclude error variance constant, otherwise error variance not
constant. Conclude error variance constant.
Yes.
3.6.a and b.
i:123456
ei: -2.150 3.850 -5.150 -1.150 .575 2.575
ˆ
Yi: 201.150 201.150 201.150 201.150 217.425 217.425
i: 7 8 9 10 11 12
ei: -2.425 5.575 3.300 .300 1.300 -3.700
ˆ
Yi: 217.425 217.425 233.700 233.700 233.700 233.700
i: 13 14 15 16
ei: .025 -1.975 3.025 -3.975
ˆ
Yi: 249.975 249.975 249.975 249.975
c. and d.
Ascending order: 1 2 3 4 5 6
Ordered residual: -5.150 -3.975 -3.700 -2.425 -2.150 -1.975
Expected value -5.720 -4.145 -3.196 -2.464 -1.841 -1.280
e∗
i: -1.592 -1.229 -1.144 -.750 -.665 -.611
Ascending order: 7 8 9 10 11 12
Ordered residual: -1.150 .025 .300 .575 1.300 2.575
Expected value: -.755 -.250 .250 .755 1.280 1.841
e∗
i: -.356 .008 .093 .178 .402 .796
Ascending order: 13 14 15 16
Ordered residual: 3.025 3.300 3.850 5.575
Expected value: 2.464 3.196 4.145 5.720
e∗
i: .935 1.020 1.190 1.724
H0: Normal, Ha: not normal. r=.992. If r≥.941 conclude H0,otherwise Ha.
Conclude H0. t(.25; 14) = −.692, t(.50; 14) = 0, t(.75; 14) = .692
Actual: 4/16 7/16 11/16
e. n1= 8, ¯
d1= 2.931, n2= 8, ¯
d2= 2.194, s= 1.724,
t∗
BF = (2.931 −2.194)/1.724q(1/8) + (1/8) = .86, t(.975; 14) = 2.145. If |t∗
BF | ≤
2.145 conclude error variance constant, otherwise error variance not constant.
Conclude error variance constant.
3-2

3.7.b and c.
i: 1 2 . . . 59 60
ei: 0.82324 -1.55675 . . . -0.66689 8.09309
ˆ
Yi: 105.17676 107.55675 . . . 70.66689 65.90691
d.
Ascending order: 1 2 . . . 59 60
Ordered residual: -16.13683 -13.80686 . . . 13.95312 23.47309
Expected value: -18.90095 -15.75218 . . . 15.75218 18.90095
H0: Normal, Ha: not normal. r= 0.9897. If r≥0.984 conclude H0, otherwise
Ha. Conclude H0.
e. SSR∗= 31,833.4, SSE = 3,874.45,
X2
BP = (31,833.4/2) ÷(3,874.45/60)2= 3.817116, χ2(.99; 1) = 6.63. If X2
BP ≤
6.63 conclude error variance constant, otherwise error variance not constant. Con-
clude error variance constant. Yes.
3.8.b and c.
i: 1 2 . . . 83 84
ei: 591.964 1648.566 . . . 621.141 28.114
ˆ
Yi: 7895.036 6530.434 . . . 6359.859 7553.886
d.
Ascending order: 1 2 . . . 83 84
Ordered residual: -5278.310 -3285.062 . . . 4623.566 6803.265
Expected value: -5740.725 -4874.426 . . . 4874.426 5740.725
H0: Normal, Ha: not normal. r= 0.98876. If r≥0.9854 conclude H0,otherwise
Ha. Conclude H0.
e. n1= 8, ¯
d1= 1751.872, n2= 76, ¯
d2= 1927.083, s= 1327.772,
t∗
BF = (1751.872 −1927.083)/1327.772q(1/8) + (1/76) = −0.35502, t(.975; 82) =
1.98932. If |t∗
BF | ≤ 1.98932 conclude error variance constant, otherwise error
variance not constant. Conclude error variance constant.
3.10. b. 4, 4
3.11. b. SSR∗= 330.042, SSE = 59.960, X2
BP = (330.042/2) ÷(59.960/9)2= 3.72,
χ2(.95; 1) = 3.84. If X2
BP ≤3.84 conclude error variance constant, otherwise error
variance not constant. Conclude error variance constant.
3.13. a. H0:E{Y}=β0+β1X,Ha:E{Y} 6=β0+β1X
b. SSP E = 2797.66, SSLF = 618.719, F∗= (618.719/8)÷(2797.66/35) = 0.967557,
F(.95; 8,35) = 2.21668. If F∗≤2.21668 conclude H0, otherwise Ha.Conclude
H0.
3.14. a. H0:E{Y}=β0+β1X,Ha:E{Y} 6=β0+β1X.SSP E = 128.750,
SSLF = 17.675, F∗= (17.675/2) ÷(128.750/12) = .824, F(.99; 2,12) = 6.93.If
F∗≤6.93 conclude H0, otherwise Ha. Conclude H0.
3-3

3.15. a. ˆ
Y= 2.57533 −0.32400X
b. H0:E{Y}=β0+β1X,Ha:E{Y} 6=β0+β1X.SSP E =.1575, SSLF =
2.7675, F ∗= (2.7675/3) ÷(.1575/10) = 58.5714, F(.975; 3,10) = 4.83. If F∗≤
4.83 conclude H0, otherwise Ha. Conclude Ha.
3.16. b.
λ: -.2 -.1 0 .1 .2
SSE: .1235 .0651 .0390 .0440 .0813
c. ˆ
Y0=.65488 −.19540X
e.
i: 1 2 3 4 5 6 7 8
ei: -.051 .058 .007 -.083 -.057 .035 .012 .086
ˆ
Y0
i: -1.104 -1.104 -1.104 -.713 -.713 -.713 -.322 -.322
Expected value: -.047 .062 .000 -.086 -.062 .035 .008 .086
i: 9 10 11 12 13 14 15
ei: .046 .018 -.008 -.039 -.006 -.050 .032
ˆ
Y0
i: -.322 .069 .069 .069 .459 .459 .459
Expected value: .047 .017 -.017 -.026 -.008 -.035 .026
f. ˆ
Y=antilog10(.65488 −.19540X) = 4.51731(.63768)X
3.17. b.
λ: .3 .4 .5 .6 .7
SSE: 1099.7 967.9 916.4 942.4 1044.2
c. ˆ
Y0= 10.26093 + 1.07629X
e.
i: 1 2 3 4 5
ei: -.36 .28 .31 -.15 .30
ˆ
Y0
i: 10.26 11.34 12.41 13.49 14.57
Expected value: -.24 .14 .36 -.14 .24
i: 6 7 8 9 10
ei: -.41 .10 -.47 .47 -.07
ˆ
Y0
i: 15.64 16.72 17.79 18.87 19.95
Expected value: -.36 .04 -.56 .56 -.04
f. ˆ
Y= (10.26093 + 1.07629X)2
3.18. b. ˆ
Y= 1.25470 −3.62352X0
d.
i: 1 2 3 . . . 110 111
ei: -1.00853 -3.32526 1.64837 . . . -0.67526 0.49147
ˆ
Yi: 15.28853 12.12526 10.84163 . . . 12.12526 15.28853
Expected value: -0.97979 -3.10159 1.58857 . . . -0.59149 0.36067
e. ˆ
Y= 1.25470 −3.62352√X
3-4

3.21. PP(Yij −ˆ
Yij)2=PPh(Yij −¯
Yj)+(¯
Yj−ˆ
Yij)i2
=PP(Yij −¯
Yj)2+PP(¯
Yj−ˆ
Yij)2+ 2 PP(Yij −¯
Yj)( ¯
Yj−ˆ
Yij)
Now,PP(Yij −¯
Yj)( ¯
Yj−ˆ
Yij)
=PPYij ¯
Yj−PP¯
Y2
j−PPYij ˆ
Yij +PP¯
Yjˆ
Yij
=P
jnj¯
Y2
j−P
jnj¯
Y2
j−P
j
ˆ
Yijnj¯
Yj+P
jnj¯
Yjˆ
Yij = 0
since ˆ
Yij =b0+b1Xjis independent of i.
3.22. E{MSP E}=E(PP(Yij −¯
Yj)2
n−c)=1
n−cXE{(nj−1)s2
j}
=1
n−cXE{σ2χ2(nj−1)}=σ2
n−cX(nj−1) = σ2
3.23. Full: Yij =µj+εij , reduced: Yij =β1Xj+εij
dfF= 20 −10 = 10, dfR= 20 −1 = 19
3.24. a. ˆ
Y= 48.66667 + 2.33333X
i: 1 2 3 4 5 6 7 8
ei: 2.6667 -.3333 -.3333 -1.0000 -4.0000 -7.6667 13.3333 -2.6667
b. ˆ
Y= 53.06796 + 1.62136X
c. ˆ
Yh= 72.52428, s{pred}= 3.0286, t(.995; 5) = 4.032,72.52428 ±4.032(3.0286),
60.31296 ≤Yh(new) ≤84.73560, yes
3.27. b. ˆ
Y= 6.84922 + .60975X
Xh= 6.5: ˆ
Yh= 10.81260, s{pred}= 1.2583, t(.975; 109) = 1.982,10.81260 ±
1.982(1.2583), 8.31865 ≤Yh(new) ≤13.30655
Xh= 5.9: ˆ
Yh= 10.44675, s{pred}= 1.2512, 10.44675 ±1.982(1.2512), 7.96687 ≤
Yh(new) ≤12.92663
Yes
3.29. a.
Median
Band X Y
1 2 23.5
2 4 57
3 5 81.5
4 7 111
b. F(.90; 2,43) = 2.43041, W= 2.204727
Xh= 2: 29.4903 ±2.204727(2.00609),25.067 ≤E{Yh} ≤ 33.913
Xh= 4: 59.5608 ±2.204727(1.43307),56.401 ≤E{Yh} ≤ 62.720
Xh= 5: 74.5961 ±2.204727(1.32983),71.664 ≤E{Yh} ≤ 77.528
3-5

Xh= 7: 104.667 ±2.204727(1.6119),101.113 ≤E{Yh} ≤ 108.221
No
c.
Neighborhood Xcˆ
Yc
1 2 27.000
2 3 43.969
3 4 60.298
4 5 77.905
5 6 93.285
6 7 107.411
3.30. a.
Median
Band X Y
1 0.5 116.5
2 2.5 170.0
3 4.5 226.5
4 6.5 291.5
5 8.5 384.5
b.
Neighborhood Xcˆ
Yc
1 1 131.67
2 2 158.33
3 3 187.00
4 4 210.33
5 5 245.33
6 6 271.67
7 7 319.00
c. F(.95; 2,8) = 4.46, W= 2.987
Xh= 1: 124.061 ±2.987(7.4756), 101.731 ≤E{Yh} ≤ 146.391
Xh= 2: 156.558 ±2.987(6.2872), 137.778 ≤E{Yh} ≤ 175.338
Xh= 3: 189.055 ±2.987(5.3501), 173.074 ≤E{Yh} ≤ 205.036
Xh= 4: 221.552 ±2.987(4.8137), 207.174 ≤E{Yh} ≤ 235.931
Xh= 5: 254.049 ±2.987(4.8137), 239.671 ≤E{Yh} ≤ 268.428
Xh= 6: 286.546 ±2.987(5.3501), 270.565 ≤E{Yh} ≤ 302.527
Xh= 7: 319.043 ±2.987(6.2872), 300.263 ≤E{Yh} ≤ 337.823
Yes
3-6
Chapter 4
SIMULTANEOUS INFERENCES
AND OTHER TOPICS IN
REGRESSION ANALYSIS
4.1. No, no
4.2. 90 percent
4.3. a. Opposite directions, negative tilt
b. B=t(.9875; 43) = 2.32262, b0=−0.580157, s{b0}= 2.80394, b1= 15.0352, s{b1}=
0.483087
−0.580157 ±2.32262(2.80394) −7.093 ≤β0≤5.932
15.0352 ±2.32262(0.483087) 13.913 ≤β1≤16.157
c. Yes
4.4. a. Opposite directions, negative tilt
b. B=t(.9975; 8) = 3.833, b0= 10.2000, s{b0}=.6633, b1= 4.0000, s{b1}=.4690
10.2000 ±3.833(.6633) 7.658 ≤β0≤12.742
4.0000 ±3.833(.4690) 2.202 ≤β1≤5.798
4.5. a. B=t(.975; 14) = 2.145, b0= 168.6000, s{b0}= 2.6570, b1= 2.0344, s{b1}=
.0904
168.6000 ±2.145(2.6570) 162.901 ≤β0≤174.299
2.0344 ±2.145(.0904) 1.840 ≤β1≤2.228
b. Negatively, no
4.6. a. B=t(.9975; 14) = 2.91839, b0= 156.347, s{b0}= 5.51226, b1=−1.190,s{b1}=
0.0901973
156.347 ±2.91839(5.51226) 140.260 ≤β0≤172.434
−1.190 ±2.91839(0.0901973) −1.453 ≤β1≤ −0.927
b. Opposite directions
4-1
c. No
4.7. a. F(.90; 2,43) = 2.43041, W= 2.204727
Xh= 3: 44.5256 ±2.204727(1.67501) 40.833 ≤E{Yh} ≤ 48.219
Xh= 5: 74.5961 ±2.204727(1.32983) 71.664 ≤E{Yh} ≤ 77.528
Xh= 7: 104.667 ±2.204727(1.6119) 101.113 ≤E{Yh} ≤ 108.221
b. F(.90; 2,43) = 2.43041, S= 2.204727; B=t(.975; 43) = 2.01669; Bonferroni
c. Xh= 4: 59.5608 ±2.01669(9.02797) 41.354 ≤Yh(new) ≤77.767
Xh= 7: 104.667 ±2.01669(9.05808) 86.3997 ≤Yh(new) ≤122.934
4.8. a. F(.95; 2,8) = 4.46, W= 2.987
Xh= 0: 10.2000 ±2.987(.6633) 8.219 ≤E{Yh} ≤ 12.181
Xh= 1: 14.2000 ±2.987(.4690) 12.799 ≤E{Yh} ≤ 15.601
Xh= 2: 18.2000 ±2.987(.6633) 16.219 ≤E{Yh} ≤ 20.181
b. B=t(.99167; 8) = 3.016, yes
c. F(.95; 3,8) = 4.07, S= 3.494
Xh= 0: 10.2000 ±3.494(1.6248) 4.523 ≤Yh(new) ≤15.877
Xh= 1: 14.2000 ±3.494(1.5556) 8.765 ≤Yh(new) ≤19.635
Xh= 2: 18.2000 ±3.494(1.6248) 12.523 ≤Yh(new) ≤23.877
d. B= 3.016, yes
4.9. a. B=t(.9833; 14) = 2.360
Xh= 20: 209.2875 ±2.360(1.0847) 206.727 ≤E{Yh} ≤ 211.847
Xh= 30: 229.6312 ±2.360(0.8285) 227.676 ≤E{Yh} ≤ 231.586
Xh= 40: 249.9750 ±2.360(1.3529) 246.782 ≤E{Yh} ≤ 253.168
b. F(.90; 2,14) = 2.737, W= 2.340, no
c. F(.90; 2,14) = 2.737, S= 2.340, B=t(.975; 14) = 2.145
Xh= 30: 229.6312 ±2.145(3.3385) 222.470 ≤Yh(new) ≤236.792
Xh= 40: 249.9750 ±2.145(3.5056) 242.455 ≤Yh(new) ≤257.495
4.10. a. F(.95; 2,58) = 3.15593, W= 2.512342
Xh= 45: 102.797 ±2.512342(1.71458) 98.489 ≤E{Yh} ≤ 107.105
Xh= 55: 90.8968 ±2.512342(1.1469) 88.015 ≤E{Yh} ≤ 93.778
Xh= 65: 78.9969 ±2.512342(1.14808) 76.113 ≤E{Yh} ≤ 81.881
b. B=t(.99167; 58) = 2.46556, no
c. B= 2.46556
Xh= 48: 99.2268 ±2.46556(8.31158) 78.734 ≤Yh(new) ≤119.720
Xh= 59: 86.1368 ±2.46556(8.24148) 65.817 ≤Yh(new) ≤106.457
4-2

Xh= 74: 68.2869 ±2.46556(8.33742) 47.730 ≤Yh(new) ≤88.843
d. Yes, yes
4.12. a. ˆ
Y= 18.0283X
c. H0:β1= 17.50, Ha:β16= 17.50. MSE = 20.3113, s{b1}=.07948, t∗= (18.0283−
17.50)/.07948 = 6.65, t(.99; 11) = 2.718. If |t∗| ≤ 2.718 conclude H0, otherwise
Ha. Conclude Ha.
d. ˆ
Yh= 180.283, s{pred}= 4.576, 180.283 ±2.718(4.576),167.845 ≤Yh(new) ≤
192.721
4.13. a.
i: 1 2 3 4 5 6
ei: 1.802 -3.340 10.717 -2.283 -2.396 -4.708
i: 7 8 9 10 11 12
ei: -.849 6.292 -.510 -3.283 2.887 -1.170
No
b. H0:E{Y}=β1X,Ha:E{Y} 6=β1X.SSLF = 40.924, SSP E = 182.500,
F∗= (40.924/8) ÷(182.500/3) = .084, F(.99; 8,3) = 27.5. If F∗≤27.5 conclude
H0, otherwise Ha. Conclude H0.P-value = .997
4.14. a. ˆ
Y= 0.121643X
b. s{b1}= 0.00263691, t(.975; 19) = 1.9801, 0.121643 ±1.9801(0.00263691),0.116 ≤
β1≤0.127
c. ˆ
Yh= 3.64929, s{ˆ
Yh}= 0.0791074, 3.64929 ±1.9801(0.0791074),3.493 ≤E{Yh} ≤
3.806
4.15. b.
i: 1 2 . . . 119 120
ei: 1.3425 2.1820 . . . -0.0863 -0.4580
No
c. H0:E{Y}=β1X,Ha:E{Y} 6=β1X.SSLF = 23.3378, SSP E = 39.3319,
F∗= (23.3378/20) ÷(39.3319/99) = 2.93711, F(.995; 20,99) = 2.22939. If F∗≤
2.22939 conclude H0, otherwise Ha. Conclude Ha.P-value = 0.0002
4.16. a. ˆ
Y= 14.9472X
b. s{b1}= 0.226424, t(.95; 44) = 1.68023, 14.9472 ±1.68023(0.226424),14.567 ≤
β1≤15.328
c. ˆ
Yh= 89.6834, s{pred}= 8.92008, 89.6834 ±1.68023(8.92008),74.696 ≤Yh(new) ≤
104.671
4.17. b.
i: 1 2 . . . 44 45
ei: -9.89445 0.21108 . . . 1.2111 2.2639
No
4-3
c. H0:E{Y}=β1X,Ha:E{Y} 6=β1X.SSLF = 622.12, SSP E = 2797.66, F ∗=
(622.12/9) ÷(2797.66/35) = 0.8647783, F(.99; 9,35) = 2.96301.If F∗≤2.96301
conclude H0, otherwise Ha. Conclude H0.P-value = 0.564
4.18. No
4.19. a. ˆ
Xh(new) = 33.11991, t(.95; 118) = 1.657870, s{predX}= 16.35037,
33.11991 ±1.657870(16.35037), 6.013 ≤Xh(new))≤60.227
b. No, 0.297453 > .1
4.20. a. ˆ
Xh(new) = 34.1137, t(.995; 14) = 2.977, s{predX}= 1.6610,
34.1137 ±2.977(1.6610), 29.169 ≤Xh(new) ≤39.058
b. Yes, .0175 < .1
4.21. Yes, no
4.22. Let ¯
A3denote the event that statement 3 is correct and ¯
Bthe event ¯
A1∩¯
A2. Then by
(4.2a):
P(¯
B∩¯
A3) = P(¯
A1∩¯
A2∩¯
A3)≥1−2α−α= 1 −3α
4.23. From (4.13) it follows at once that:
PXi(Yi−b1Xi) = PXiei= 0
4.24. From Exercise 1.41c, we have that E{b1}=β1. Hence:
E{ˆ
Y}=E{b1X}=XE{b1}=β1X=E{Y}.
4.25. σ2{ˆ
Yh}=σ2{b1Xh}=X2
hσ2{b1}=X2
h(σ2/PX2
i); hence,
s2{ˆ
Yh}=X2
h(MSE/ PX2
i).
4.26. a. B=t(.9875; 438) = 2.24913, b0=−110.635, s{b0}= 34.7460,
b1= 0.00279542, s{b1}= 0.0000483694
−110.635 ±2.24913(34.7460) −188.783 ≤β0≤ −32.487
0.00279542 ±2.24913(0.00004837) 0.00269 ≤β1≤0.0029
b. Yes
c. F(.90; 2,438) = 2.31473, W= 2.151618;
B=t(.9833; 438) = 2.13397;
Bonferroni
d. Xh= 500: −109.237 ±2.13397(34.7328) −183.356 ≤E{Yh} ≤ −35.118
Xh= 1,000: −107.839 ±2.13397(34.7196) −181.930 ≤E{Yh} ≤ −33.748
Xh= 5,000: −96.6577 ±2.13397(34.6143) −170.524 ≤E{Yh} ≤ −22.792
4.27. a. B=t(.975; 111) = 1.982, b0= 6.3368, s{b0}=.5213, b1=.7604, s{b1}=.1144
4-4
6.3368 ±1.982(.5213) 5.304 ≤β0≤7.370
0.7604 ±1.982(.1144) 0.534 ≤β1≤0.987
b. No
c. F(.95; 2,111) = 3.08, W= 2.482; B=t(.99375; 111) = 2.539; Working-Hotelling
d. Xh= 2: 7.858 ±2.482(.3098) 7.089 ≤E{Yh} ≤ 8.627
Xh= 3: 8.618 ±2.482(.2177) 8.078 ≤E{Yh} ≤ 9.158
Xh= 4: 9.378 ±2.482(.1581) 8.986 ≤E{Yh} ≤ 9.770
Xh= 5: 10.139 ±2.482(.1697) 9.718 ≤E{Yh} ≤ 10.560
4-5
Chapter 5
MATRIX APPROACH TO SIMPLE
LINEAR REGRESSION ANALYSIS
5.1. (1)
2 7
3 10
5 13
(2)
0 1
1 2
1 3
(3)
23 24 1
36 40 2
49 56 3
(4)
13 17 22
20 26 34
27 35 46
(5) "9 26
26 76 #
5.2. (1)
5 9
11 11
10 8
6 12
(2)
−1−7
−5−1
0 6
2 4
(3) h58 80 i
(4)
14 22 11 8
49 54 20 26
71 82 32 38
76 80 28 40
(5) "63 94
55 73 #
5.3. (1)
Y1
Y2
Y3
Y4
−
ˆ
Y1
ˆ
Y2
ˆ
Y3
ˆ
Y4
=
e1
e2
e3
e4
(2) hX1X2X3X4i
e1
e2
e3
e4
=h0i
5.4. (1) 503.77 (2) "5 0
0 160 #(3) "49.7
−39.2#
5.5. (1) 1,259 (2) "6 17
17 55 #(3) "81
261 #
5.6. (1) 2,194 (2) "10 10
10 20 #(3) "142
182 #
5-1
5.7. (1) 819,499 (2) "16 448
448 13,824 #(3) "3,609
103,656 #
5.8. a. Yes
b. 2
c. 0
5.9. a. Yes
b. Yes
c. 2
d. 0
5.10. A−1="−.1.4
.3−.2#B−1=
.10870 −.08696 .10870
.34783 .02174 −.15217
−.23913 .14130 .01087
5.11.
.33088 −.15441 −.03676
.13971 −.19853 .09559
−.26471 .32353 .02941
5.12. ".2 0
0.00625 #
5.13. "1.34146 −.41463
−.41463 .14634 #
5.14. a. "4 7
2 3 #" y1
y2#="25
12 #
b. "y1
y2#="4.5
1#
5.15. a. "5 2
23 7 #" y1
y2#="8
28 #
b. "y1
y2#="0
4#
5.16.
ˆ
Y1
ˆ
Y2
ˆ
Y3
ˆ
Y4
ˆ
Y5
=¯
Y
1
1
1
1
1
+b1
X1−¯
X
X2−¯
X
X3−¯
X
X4−¯
X
X5−¯
X
5.17. a.
W1
W2
W3
=
111
1−1 0
1−1−1
Y1
Y2
Y3
5-2
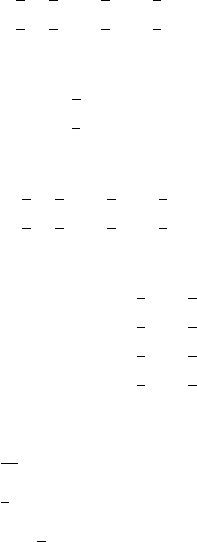
b. E
W1
W2
W3
=
111
1−1 0
1−1−1
E{Y1}
E{Y2}
E{Y3}
=
E{Y1}+E{Y2}+E{Y3}
E{Y1} − E{Y2}
E{Y1} − E{Y2} − E{Y3}
c. σ2{W}=
1 1 1
1−1 0
1−1−1
σ2{Y1}σ{Y1, Y2}σ{Y1, Y3}
σ{Y2, Y1}σ2{Y2}σ{Y2, Y3}
σ{Y3, Y1}σ{Y3, Y2}σ2{Y3}
×
111
1−1−1
1 0 −1
Using the notation σ2
1for σ2{Y1},σ12 for σ{Y1, Y2}, etc., we obtain:
σ2{W1}=σ2
1+σ2
2+σ2
3+ 2σ12 + 2σ13 + 2σ23
σ2{W2}=σ2
1+σ2
2−2σ12
σ2{W3}=σ2
1+σ2
2+σ2
3−2σ12 −2σ13 + 2σ23
σ{W1,W2}=σ2
1−σ2
2+σ13 −σ23
σ{W1,W3}=σ2
1−σ2
2−σ2
3−2σ23
σ{W2,W3}=σ2
1+σ2
2−2σ12 −σ13 +σ23
5.18. a. "W1
W2#="1
4
1
4
1
4
1
4
1
2
1
2−1
2−1
2#
Y1
Y2
Y3
Y4
b. E(" W1
W2#)="1
4[E{Y1}+E{Y2}+E{Y3}+E{Y4}]
1
2[E{Y1}+E{Y2} − E{Y3} − E{Y4}]#
c. σ2{W}="1
4
1
4
1
4
1
4
1
2
1
2−1
2−1
2#
σ2{Y1}σ{Y1, Y2}σ{Y1, Y3}σ{Y1, Y4}
σ{Y2, Y1}σ2{Y2}σ{Y2, Y3}σ{Y2, Y4}
σ{Y3, Y1}σ{Y3, Y2}σ2{Y3}σ{Y3, Y4}
σ{Y4, Y1}σ{Y4, Y2}σ{Y4, Y3}σ2{Y4}
×
1
4
1
2
1
4
1
2
1
4−1
2
1
4−1
2
Using the notation σ2
1for σ2{Y1}, σ12 for σ{Y1, Y2}, etc., we obtain:
σ2{W1}=1
16 (σ2
1+ +σ2
2+σ2
3+σ2
4+ 2σ12 + 2σ13 + 2σ14 + 2σ23 + 2σ24 + 2σ34)
σ2{W2}=1
4(σ2
1+σ2
2+σ2
3+σ2
4+ 2σ12 −2σ13 −2σ14 −2σ23 −2σ24 + 2σ34)
σ{W1,W2}=1
8(σ2
1+σ2
2−σ2
3−σ2
4+ 2σ12 −2σ34)
5.19. "3 5
5 17 #
5.20. "7−4
−4 8 #
5-3
5.21. 5Y2
1+ 4Y1Y2+Y2
2
5.22. Y2
1+ 3Y2
2+ 9Y2
3+ 8Y1Y3
5.23. a. (1) "9.940
−.245 #(2)
−.18
.04
.26
.08
−.20
(3) 9.604 (4) .148
(5) ".00987 0
0.000308 #(6) 11.41 (7) .02097
c.
.6.4.2 0 −.2
.4.3.2.1 0
.2.2.2.2.2
0.1.2.3.4
−.2 0 .2.4.6
d.
.01973 −.01973 −.00987 .00000 .00987
−.01973 .03453 −.00987 −.00493 .00000
−.00987 −.00987 .03947 −.00987 −.00987
.00000 −.00493 −.00987 .03453 −.01973
.00987 .00000 −.00987 −.01973 .01973
5.24. a. (1) ".43902
4.60976 #(2)
−2.8781
−.0488
.3415
.7317
−1.2683
3.1219
(3) 145.2073 (4) 20.2927
(5) "6.8055 −2.1035
−2.1035 .7424 #(6) 18.878 (7) 6.9290
b. (1) −2.1035 (2) 6.8055 (3) .8616
c.
.366 −.146 .024 .195 .195 .366
−.146 .658 .390 .122 .122 −.146
.024 .390 .268 .146 .146 .024
.195 .122 .146 .171 .171 .195
.195 .122 .146 .171 .171 .195
.366 −.146 .024 .195 .195 .366
d.
3.217 .742 −.124 −.990 −.990 −1.856
.742 1.732 −1.980 −.619 −.619 .742
−.124 −1.980 3.712 −.742 −.742 −.124
−.990 −.619 −.742 4.207 −.866 −.990
−.990 −.619 −.742 −.866 4.207 −.990
−1.856 .742 −.124 −.990 −.990 3.127
5-4
5.25. a. (1) ".2−.1
−.1.1#(2) "10.2
4.0#(3)
1.8
−1.2
−1.2
1.8
−.2
−1.2
−2.2
.8
.8
.8
(4)
.1.1.1.1.1.1.1.1.1.1
.1.2 0 .2−.1.1.2.1 0 .2
.1 0 .2 0 .3.1 0 .1.2 0
.1.2 0 .2−.1.1.2.1 0 .2
.1−.1.3−.1.5.1−.1.1.3−.1
.1.1.1.1.1.1.1.1.1.1
.1.2 0 .2−.1.1.2.1 0 .2
.1.1.1.1.1.1.1.1.1.1
.1.0.2 0 .3.1 0 .1.2 0
.1.2 0 .2−.1.1.2.1.0.2
(5) 17.60 (6) ".44 −.22
−.22 .22 #(7) 18.2 (8) .44
b. (1) .22 (2) −.22 (3) .663
c.
0 0 0 0 0 0 0 0 0 0
0.1−.1.1−.2 0 .1 0 −.1.1
0−.1.1−.1.2 0 −.1 0 .1−.1
0.1−.1.1−.2 0 .1 0 −.1.1
0−.2.2−.2.4 0 −.2 0 .2−.2
0 0 0 0 0 0 0 0 0 0
0.1−.1.1−.2 0 .1 0 −.1.1
0 0 0 0 0 0 0 0 0 0
0−.1.1−.1.2 0 −.1 0 .1−.1
0.1−.1.1−.2 0 .1 0 −.1.1
5.26. a. (1) ".675000 −.021875
−.021875 .00078125 #(2) "168.600000
2.034375 #
5-5
(3)
201.150
201.150
201.150
201.150
217.425
217.425
217.425
217.425
233.700
233.700
233.700
233.700
249.975
249.975
249.975
249.975
(4)
.175 .175 .175 ··· −.050 −.050 −.050
.175 .175 .175 ··· −.050 −.050 −.050
.175 .175 .175 ··· −.050 −.050 −.050
.
.
..
.
..
.
..
.
..
.
..
.
.
−.050 −.050 −.050 ··· .175 .175 .175
−.050 −.050 −.050 ··· .175 .175 .175
−.050 −.050 −.050 ··· .175 .175 .175
(5) 146.425 (6) "7.0598 −.2288
−.2288 .008171 #(7) 11.1453
b. (1) 7.0598 (2) −.2288 (3) .0904
c.
.825 −.175 −.175 ··· .050 .050 .050
−.175 .825 −.175 ··· .050 .050 .050
−.175 −.175 .825 ··· .050 .050 .050
.
.
..
.
..
.
..
.
..
.
..
.
.
.050 .050 .050 ··· .825 −.175 −.175
.050 .050 .050 ··· −.175 .825 −.175
.050 .050 .050 ··· −.175 −.175 .825
5.27. E
ε1
ε2
ε3
ε4
=
0
0
0
0
=0
5.28. Let
X=
X1
X2
.
.
.
Xn
5-6
Then by (5.60) b= (X0X)−1X0Y=PXiYi/PX2
i.
5.29 E{b}=E{(X0X)−1X0Y}= (X0X)−1X0E{Y}
= (X0X)−1X0Xβ=β
5.30. ˆ
Yh=X0
hbis a scalar, hence it equals its transpose. By (5.32) then,
X0
hb= (X0
hb)0=b0Xh.
5.31. σ2{ˆ
Y}=Hσ2{Y}H0[by (5.46)]
=Hσ2IH (since His symmetric)
=σ2H(since HH =H)
5-7
5-8

Chapter 6
MULTIPLE REGRESSION – I
6.1. a. X=
1X11 X11X12
1X21 X21X22
1X31 X31X32
1X41 X41X42
β=
β0
β1
β2
b. X=
1X11 X12
1X21 X22
1X31 X32
1X41 X42
β=
β0
β1
β2
6.2. a. X=
X11 X12 X2
11
X21 X22 X2
21
X31 X32 X2
31
X41 X42 X2
41
X51 X52 X2
51
β=
β1
β2
β3
b. X=
1X11 log10 X12
1X21 log10 X22
1X31 log10 X32
1X41 log10 X42
1X51 log10 X52
β=
β0
β1
β2
6.5. a.
Y
X1
X2
1.000 .892 .395
1.000 .000
1.000
b. b0= 37.650, b1= 4.425, b2= 4.375, ˆ
Y= 37.650 + 4.425X1+ 4.375X2
c&d.
i: 1 2 3 4 5 6 7 8
ei:−.10 .15 −3.10 3.15 −.95 −1.70 −1.95 1.30
Expected Val.: −.208 .208 −3.452 2.661 −.629 −1.533 −2.052 1.533
i: 9 10 11 12 13 14 15 16
ei: 1.20 −1.55 4.20 2.45 −2.65 −4.40 3.35 .60
Expected Val.: 1.066 −1.066 4.764 2.052 −2.661 −4.764 3.452 .629
6-1

e. SSR∗= 72.41, SSE = 94.30, X2
BP = (72.41/2) ÷(94.30/16)2= 1.04, χ2(.99; 2) =
9.21. If X2
BP ≤9.21 conclude error variance constant, otherwise error variance
not constant. Conclude error variance constant.
f. H0:E{Y}=β0+β1X1+β2X2,Ha:E{Y} 6=β0+β1X1+β2X2.MSLF = 7.46,
MSP E = 7.125, F∗= 7.46/7.125 = 1.047, F(.99; 5,8) = 6.63. If F∗≤6.63
conclude H0, otherwise Ha. Conclude H0.
6.6. a. H0:β1=β2= 0, Ha: not all βk= 0 (k= 1,2). MSR = 936.350, MSE = 7.254,
F∗= 936.350/7.254 = 129.083, F(.99; 2,13) = 6.70. If F∗≤6.70 conclude H0,
otherwise Ha. Conclude Ha.
b. P-value = 0+
c. s{b1}=.301, s{b2}=.673, B=t(.9975; 13) = 3.372
4.425 ±3.372(.301) 3.410 ≤β1≤5.440
4.375 ±3.372(.673) 2.106 ≤β2≤6.644
6.7. a. SSR = 1,872.7, SST O = 1,967.0, R2=.952
b. .952, yes.
6.8. a. ˆ
Yh= 77.275, s{ˆ
Yh}= 1.127, t(.995; 13) = 3.012, 77.275 ±3.012(1.127),
73.880 ≤E{Yh} ≤ 80.670
b. s{pred}= 2.919, 77.275 ±3.012(2.919), 68.483 ≤Yh(new) ≤86.067
6.9. c.
Y
X1
X2
X3
1.0000 .2077 .0600 .8106
1.0000 .0849 .0457
1.0000 .1134
1.0000
6.10. a. ˆ
Y= 4149.89 + 0.000787X1−13.166X2+ 623.554X3
b&c.
i: 1 2 . . . 51 52
ei:−32.0635 169.2051 ... −184.8776 64.5168
Expected Val.: −24.1737 151.0325 ... −212.1315 75.5358
e. n1= 26, ¯
d1= 145.0, n2= 26, ¯
d2= 77.4, s= 81.7,
t∗
BF = (145.0−77.4)/[81.7q(1/26) + (1/26)] = 2.99, t(.995; 50) = 2.67779.If
|t∗
BF | ≤ 2.67779 conclude error variance constant, otherwise error variance not
constant. Conclude error variance not constant.
6.11. a. H0:β1=β2=β3= 0, Ha: not all βk= 0 (k= 1, 2,3). MSR = 725,535,
MSE = 20,531.9, F∗= 725,535/20,531.9 = 35.337, F(.95; 3,48) = 2.79806. If
F∗≤2.79806 conclude H0, otherwise Ha. Conclude Ha. P -value = 0+.
b. s{b1}=.000365, s{b3}= 62.6409, B=t(.9875; 48) = 2.3139
0.000787 ±2.3139(.000365) −.000058 ≤β1≤0.00163
623.554 ±2.3139(62.6409) 478.6092 ≤β3≤768.4988
6-2

c. SSR = 2,176,606, SST O = 3,162,136, R2=.6883
6.12. a. F(.95; 4,48) = 2.56524, W= 3.2033; B=t(.995; 48) = 2.6822
Xh1Xh2Xh3
302,000 7.2 0:
245,000 7.4 0:
280,000 6.9 0:
350,000 7.0 0:
295,000 6.7 1:
4292.79 ±2.6822(21.3567)
4245.29 ±2.6822(29.7021)
4279.42 ±2.6822(24.4444)
4333.20 ±2.6822(28.9293)
4917.42 ±2.6822(62.4998)
4235.507 ≤E{Yh} ≤ 4350.073
4165.623 ≤E{Yh} ≤ 4324.957
4213.855 ≤E{Yh} ≤ 4344.985
4255.606 ≤E{Yh} ≤ 4410.794
4749.783 ≤E{Yh} ≤ 5085.057
b.Yes, no
6.13. F(.95; 4,48) = 2.5652, S= 3.2033; B=t(.99375; 48) = 2.5953
Xh1Xh2Xh3
230,000 7.5 0:
250,000 7.3 0:
280,000 7.1 0:
340,000 6.9 0:
4232.17 ±2.5953(147.288)
4250.55 ±2.5953(146.058)
4276.79 ±2.5953(145.134)
4326.65 ±2.5953(145.930)
3849.913 ≤Yh(new) ≤4614.427
3871.486 ≤Yh(new) ≤4629.614
3900.124 ≤Yh(new) ≤4653.456
3947.918 ≤Yh(new) ≤4705.382
6.14. a. ˆ
Yh= 4278.37, s{predmean}= 85.82262, t(.975; 48) = 2.01063,
4278.37 ±2.01063(85.82262), 4105.812 ≤¯
Yh(new) ≤4450.928
b. 12317.44 ≤Total labor hours≤13352.78
6.15. b.
Y
X1
X2
X3
1.000 −.7868 −.6029 −.6446
1.000 .5680 .5697
1.000 .6705
1.000
c. ˆ
Y= 158.491 −1.1416X1−0.4420X2−13.4702X3
d&e.
i: 1 2 . . . 45 46
ei:.1129 −9.0797 . . . −5.5380 10.0524
Expected Val.: −0.8186 −8.1772 . . . −5.4314 8.1772
f. No
g. SSR∗= 21,355.5, SSE = 4,248.8, X2
BP = (21,355.5/2) ÷(4,248.8/46)2=
1.2516, χ2(.99; 3) = 11.3449. If X2
BP ≤11.3449 conclude error variance constant,
otherwise error variance not constant. Conclude error variance constant.
6.16. a. H0:β1=β2=β3= 0, Ha: not all βk= 0 (k= 1,2,3).
MSR = 3,040.2, MSE = 101.2, F∗= 3,040.2/101.2 = 30.05, F (.90; 3,42) =
2.2191. If F∗≤2.2191 conclude H0, otherwise Ha.Conclude Ha.P-value =
0.4878
b. s{b1}=.2148, s{b2}=.4920, s{b3}= 7.0997, B=t(.9833; 42) = 2.1995
−1.1416 ±2.1995(.2148) −1.6141 ≤β1≤ −0.6691
−.4420 ±2.1995(.4920) −1.5242 ≤β2≤0.6402
−13.4702 ±2.1995(7.0997) −29.0860 ≤β3≤2.1456
6-3
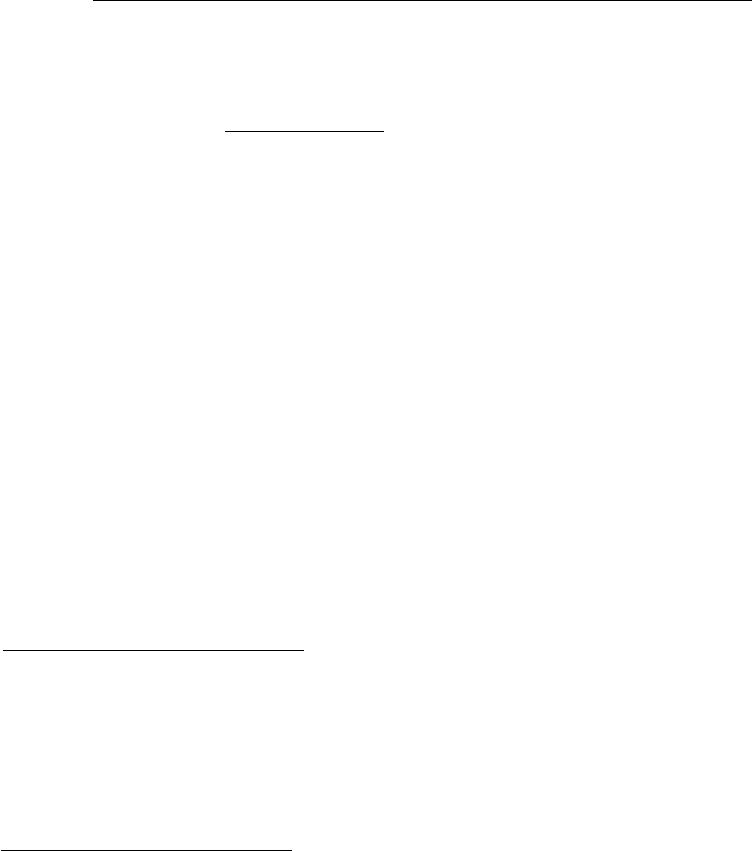
c. SSR = 9,120.46, SST O = 13,369.3, R=.8260
6.17. a. ˆ
Yh= 69.0103, s{ˆ
Yh}= 2.6646, t(.95; 42) = 1.6820, 69.0103 ±1.6820(2.6646),
64.5284 ≤E{Yh} ≤ 73.4922
b. s{pred}= 10.405, 69.0103 ±1.6820(10.405), 51.5091 ≤Yh(new) ≤86.5115
6.18. b.
Y
X1
X2
X3
X4
1.0000 −.2503 .4138 .0665 .5353
1.0000 .3888 −.2527 .2886
1.0000 −.3798 .4407
1.0000 .0806
1.0000
c. ˆ
Y= 12.2006 −.1420X1+.2820X2+ 0.6193X3+ 0.0000079X4
d&e.
i: 1 2 . . . 80 81
ei:−1.0357 −1.5138 . . . −2.0302 −.9068
Expected Val.: −1.1524 −1.5857 . . . −1.9321 −1.0407
f. No
g. n1= 40, ¯
d1= 0.8696, n2= 41, ¯
d2= 0.7793, s= 0.7357, t∗
BF = (0.8696 −
0.7793)/0.7357q(1/40) + (1/41) = 0.5523, t(.975; 79) = 1.9905. If |t∗
BF | ≤ 1.9905
conclude error variance constant, otherwise error variance not constant. Conclude
error variance constant.
6.19. a. H0:β1=β2=β3=β4= 0, Ha: not all βk= 0 (k= 1,2,3,4). MSR = 34.5817
MSE = 1.2925, F∗= 34.5817/1.2925 = 26.7557, F(.95; 4,76) = 2.4920. If
F∗≤2.4920 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
b. s{b1}=.02134, s{b2}=.06317, s{b3}= 1.08681, s{b4}=.00000138, B=
t(.99375; 76) = 2.5585
−.1420 ±2.5585(.02134) −.1966 ≤β1≤ −.0874
.2820 ±2.5585(.06317) .1204 ≤β2≤.4436
.6193 ±2.5585(1.08681) −2.1613 ≤β3≤3.3999
.0000079 ±2.5585(.00000138) .0000044 ≤β1≤.0000114
c. SSR = 138.327, SST O = 236.5576, R2=.5847
6.20. F(.95; 5,76) = 2.3349, W= 3.4168; B=t(.99375; 76) = 2.5585
Xh1Xh2Xh3Xh4
5 8.25 0 250,000:
6 8.50 .23 270,000:
14 11.50 .11 300,000:
12 10.25 0 310,000:
15.7981 ±2.5585(.2781) 15.087 ≤E{Yh} ≤ 16.510
16.0275 ±2.5585(.2359) 15.424 ≤E{Yh} ≤ 16.631
15.9007 ±2.5585(.2222) 15.332 ≤E{Yh} ≤ 16.469
15.8434 ±2.5585(.2591) 15.180 ≤E{Yh} ≤ 16.506
6.21. t(.975; 76) = 1.9917
Xh1Xh2Xh3Xh4
4 10.0 0.10 80,000: 15.1485 ±1.9917(1.1528) 12.852 ≤Yh(new) ≤17.445
6 11.5 0 120,000: 15.5425 ±1.9917(1.1535) 13.245 ≤Yh(new) ≤17.840
12 12.5.32 340,000: 16.9138 ±1.9917(1.1946) 14.535 ≤Yh(new) ≤19.293
6-4

85 percent
6.22. a. Yes
b. No, yes, Y0
i= logeYi=β0+β1Xi1+β2X2
i2+ε0
i, where ε0
i= logeεi
c. Yes
d. No, no
e. No, yes, Y0
i= loge(Y−1
i−1) = β0+β1Xi1+εi
6.23. a. Q=P(Yi−β1Xi1−β2Xi2)2
∂Q
∂β1
=−2X(Yi−β1Xi1−β2Xi2)Xi1
∂Q
∂β2
=−2X(Yi−β1Xi1−β2Xi2)Xi2
Setting the derivatives equal to zero, simplifying, and substituting the least squares
estimators b1and b2yields:
PYiXi1−b1PX2
i1−b2PXi1Xi2= 0
PYiXi2−b1PXi1Xi2−b2PX2
i2= 0
and:
b1=PYiXi2PXi1Xi2−PYiXi1PX2
i2
(PXi1Xi2)2−PX2
i1PX2
i2
b2=PYiXi1PXi1Xi2−PYiXi2PX2
i1
(PXi1Xi2)2−PX2
i1PX2
i2
b. L=n
Q
i=1
1
√2πσ2exp ·−1
2σ2(Yi−β1Xi1−β2Xi2)2¸
It is more convenient to work with logeL:
logeL=−n
2loge(2πσ2)−1
2σ2X(Yi−β1Xi1−β2Xi2)2
∂logeL
∂β1
=1
σ2X(Yi−β1Xi1−β2Xi2)Xi1
∂logeL
∂β2
=1
σ2X(Yi−β1Xi1−β2Xi2)Xi2
Setting the derivatives equal to zero, simplifying, and substituting the maximum
likelihood estimators b1and b2yields the same normal equations as in part (a),
and hence the same estimators.
6.24. a. Q=P(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)2
∂Q
∂β0
=−2X(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)
∂Q
∂β1
=−2X(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)Xi1
∂Q
∂β2
=−2X(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)X2
i1
6-5

∂Q
∂β3
=−2X(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)Xi2
Setting the derivatives equal to zero, simplifying, and substituting the least squares
estimators b0,b1,b2, and b3yields the normal equations:
PYi−nb0−b1PXi1−b2PX2
i1−b3PXi2= 0
PYiXi1−b0PXi1−b1PX2
i1−b2PX3
i1−b3PXi1Xi2= 0
PYiX2
i1−b0PX2
i1−b1PX3
i1−b2PX4
i1−b3PX2
i1Xi2= 0
PYiXi2−b0PXi2−b1PXi1Xi2−b2PX2
i1Xi2−b3PX2
i2= 0
b. L=n
Q
i=1
1
√2πσ2exp[−1
2σ2(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)2]
or
logeL=−n
2loge(2πσ2)−1
2σ2X(Yi−β0−β1Xi1−β2X2
i1−β3Xi2)2
6.25. Fit Y0
i=β0+β1Xi1+β3Xi3+εi, where Y0
i=Yi−4Xi2
6.26. For regression model (6.1), R2= 1 −SSE(X1, X2)
SST O
When regressing Yion ˆ
Yi,SST O remains unchanged and the fitted
regression equation:
ˆ
Y∗
i=b∗
0+b∗
1ˆ
Yi
has coefficients b∗
0= 0, b∗
1= 1 because:
b∗
1=P(ˆ
Yi−¯
Y)(Yi−¯
Y)
P(ˆ
Yi−¯
Y)2=P(ˆ
Yi−¯
Y)[(Yi−ˆ
Yi) + ( ˆ
Yi−¯
Y)]
P(ˆ
Yi−¯
Y)2
=P(ˆ
Yi−¯
Y)[ei+ ( ˆ
Yi−¯
Y)]
P(ˆ
Yi−¯
Y)2= 1
since Peiˆ
Yi= 0 and Pei¯
Y= 0 by (1.20) and (1.17).
b∗
0=¯
Y−b∗
1¯
Y= 0
Hence ˆ
Y∗
i=ˆ
Yiand SSE(ˆ
Y) = P(Yi−ˆ
Y∗
i)2=P(Yi−ˆ
Yi)2=SSE(X1, X2), and:
r2= 1 −SSE(ˆ
Y)
SST O = 1 −SSE(X1, X2)
SST O =R2
6.27. a.
33.93210
2.78476
−.26442
6-6

b.
−2.6996
−1.2300
−1.6374
−1.3299
−.0900
6.9868
c.
.2314 .2517 .2118 .1489 −.0548 .2110
.2517 .3124 .0944 .2663 −.1479 .2231
.2118 .0944 .7044 −.3192 .1045 .2041
.1489 .2663 −.3192 .6143 .1414 .1483
−.0548 −.1479 .1045 .1414 .9404 .0163
.2110 .2231 .2041 .1483 .0163 .1971
d. 3,009.926
e.
715.4711 −34.1589 −13.5949
−34.1589 1.6617 .6441
−13.5949 .6441 .2625
f. 53.8471
g. 5.4247
6.28. b. Model I:
Y
X1
X2
X3
1.0000 0.9402 0.0781 0.9481
1.0000 0.1731 0.9867
1.0000 0.1271
1.0000
Model II:
Y
X1
X2
X3
1.0000 0.4064 −0.0031 0.9481
1.0000 0.0292 0.3162
1.0000 −0.0227
1.0000
c. Model I: ˆ
Y=−13.3162 + 0.000836618X1−0.065523X2+ 0.094132X3
Model II: ˆ
Y=−170.574 + 0.0961589X1+ 6.33984X2+ 0.126566X3
d. Model I: 0.902643
Model II: 0.911749
6.29. a. Region 1: ˆ
Y=−26,140 + 16.34X1+ 0.3834X2+ 291.1X3
Region 2: ˆ
Y= 63,104.1209 + 2.5883X1+ 3.6022X2−854.5493X3
Region 3: ˆ
Y= 56,929.3851 + 0.3065X1+ 4.8955X2−800.3958X3
Region 4: ˆ
Y= 37,720 −0.9915X1+ 3.627X2−489.0X3
c.
MSE R2
Region 1: 8.0728 ×1080.831
Region 2: 1.4017 ×1080.9392
Region 3: 1.9707 ×1080.8692
Region 4: 2.1042 ×1080.9713
6-7

6.30. b. Model I:
Y
X1
X2
X3
1.000 .189 .533 .356
1.000 .001 −.040
1.000 .413
1.000
Model II:
Y
X1
X2
X3
1.000 .409 .533 .356
1.000 .360 .795
1.000 .413
1.000
c. Model I: ˆ
Y= 1.38646 + .08371X1+.65845X2+.02174X3
Model II: ˆ
Y= 6.46738 + .00302X1+.64771X2−.00929X3
d. Model I: .3448
Model II: .3407
6.31. a. Region 1: ˆ
Y=−3.34958 + .11695X1+.05824X2+.00151X3+.00661X4
Region 2: ˆ
Y= 2.29154 + .00474X1+.05803X2+.00117X3+.01502X4
Region 3: ˆ
Y=−.14386 + .03085X1+.10228X2+.00411X3+.00804X4
Region 4: ˆ
Y= 1.56655 + .03524X1+.04033X2−.00066X3+.01279X4
MSE R2
Region 1: 1.022 .4613
Region 2: 1.212 .4115
Region 3: .937 .6088
Region 4: .954 .0896
6-8
Chapter 7
MULTIPLE REGRESSION – II
7.1. (1) 1 (2) 1 (3) 2 (4) 3
7.3. a. SSR(X1) = 1,566.45, SSR(X2|X1) = 306.25, SSE(X1, X2) = 94.30, df: 1, 1, 13.
b. H0:β2= 0, Ha:β26= 0. SSR(X2|X1) = 306.25, SSE(X1, X2) = 94.30, F∗=
(306.25/1) ÷(94.30/13) = 42.219, F(.99; 1,13) = 9.07.If F∗≤9.07 conclude H0,
otherwise Ha. Conclude Ha.P-value = 0+.
7.4. a. SSR(X1) = 136,366, SSR(X3|X1) = 2,033,566, SSR(X2|X1, X3) = 6,674,
SSE(X1, X2, X3) = 985,530, df: 1, 1, 1,48.
b. H0:β2= 0, Ha:β26= 0. SSR(X2|X1, X3) = 6,674, SSE(X1, X2, X3) = 985,530,
F∗= (6,674/1) ÷(985,530/48) = 0.32491, F(.95; 1,17) = 4.04265.If F∗≤
4.04265 conclude H0, otherwise Ha. Conclude H0.P-value = 0.5713.
c. Yes, SSR(X1)+SSR(X2|X1) = 136,366+5,726 = 142,092, SSR(X2)+SSR(X1|X2) =
11,394.9 + 130,697.1 = 142,092.
Yes.
7.5. a. SSR(X2) = 4,860.26, SSR(X1|X2) = 3,896.04, SSR(X3|X2, X1) = 364.16,
SSE(X1, X2, X3) = 4,248.84, df: 1, 1, 1, 42
b. H0:β3= 0, Ha:β36= 0. SSR(X3|X1, X2) = 364.16, SSE(X1, X2, X3) =4,248.84,
F∗= (364.16/1)÷(4,248.84/42) = 3.5997, F(.975; 1,42) = 5.4039. If F∗≤5.4039
conclude H0, otherwise Ha. Conclude H0. P -value = 0.065.
7.6. H0:β2=β3= 0, Ha: not both β2and β3= 0. SSR(X2, X3|X1) = 845.07,
SSE(X1, X2, X3) = 4,248.84, F∗= (845.07/2)÷(4,248.84/42) = 4.1768, F (.975; 2,42) =
4.0327. If F∗≤4.0327 conclude H0, otherwise Ha.Conclude Ha.P-value = 0.022.
7.7. a. SSR(X4) = 40.5033, SSR(X1|X4) = 42.2746, SSR(X2|X1, X4) = 27.8575,
SSR(X3|X1, X2, X4) = 0.4195, SSE(X1, X2, X3, X4) = 98.2306, df: 1, 1, 1, 1, 76.
b. H0:β3= 0, Ha:β36= 0. F∗= (0.42/1) ÷(98.2306/76) = 0.3249, F(.99; 1,76) =
6.9806. If F∗≤6.9806 conclude H0,otherwise Ha. Conclude H0.P-value
=.5704.
7-1
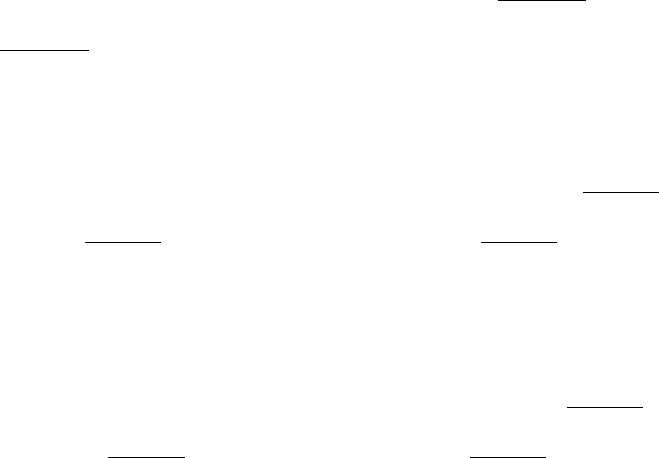
7.8. H0:β2=β3= 0, Ha: not both β2and β3= 0. SSR(X2, X3|X1, X4) = 28.277,
SSE(X1, X2, X3, X4) = 98.2306, F∗= (28.277/2)÷(98.2306/76) = 10.9388, F (.99; 2,20) =
4.8958. If F∗≤4.8958 conclude H0, otherwise Ha. Conclude Ha. P -value = 0+.
7.9. H0:β1=−1.0, β2= 0; Ha: not both equalities hold. Full model: Yi=β0+β1Xi1+
β2Xi2+β3Xi3+εi, reduced model: Yi+Xi1=β0+β3Xi3+εi.SSE(F)=4,248.84,
dfF= 42, SSE(R) = 4,427.7, dfR= 44, F∗= [(4427.7−4248.84)/2]÷(4,248.84/42) =
.8840, F(.975; 2,42) = 4.0327. If F∗≤4.0327 conclude H0, otherwise Ha. Conclude
H0.
7.10. H0:β1=−.1, β2=.4; Ha: not both equalities hold. Full model: Yi=β0+β1Xi1+
β2Xi2+β3Xi3+β4Xi4+εi, reduced model: Yi+.1Xi1−.4Xi2=β0+β3Xi3+β4Xi4+εi.
SSE(F) = 98.2306, dfF= 76, SSE(R) = 110.141, dfR= 78, F∗= [(110.141 −
98.2306)/2] ÷(98.2306/76) = 4.607, F(.99; 2,76) = 4.89584. If F∗≤4.89584 conclude
H0, otherwise Ha. Conclude H0.
7.11. a. R2
Y1=.550, R2
Y2=.408, R2
12 = 0, R2
Y1|2=.929, R2
Y2|1=.907, R2=.958
7.12. R2
Y1=.796, R2
Y2=.156, R2
12 = 0, R2
Y1|2=.943, R2
Y2|1=.765, R2=.952
7.13. R2
Y1=.0431, R2
Y2=.0036, R2
12 =.0072, R2
Y1|2= 0.0415, R2
Y2|1= 0.0019, R2
Y2|13 =
.0067 R2=.6883
7.14. a. R2
Y1=.6190, R2
Y1|2=.4579, R2
Y1|23 =.4021
b. R2
Y2=.3635, R2
Y2|1=.0944, R2
Y2|13 =.0189
7.15. R2
Y4=.2865, R2
Y1=.0626, R2
Y1|4=.2505, R2
14 =.4652, R2
Y2|14 =.2202, R2
Y3|124 =
.0043, R2=.5848
7.16. a. ˆ
Y∗=.89239X∗
1+.39458X∗
2
c. sY= 11.45135, s1= 2.30940, s2= 1.03280, b1=11.45135
2.30940 (.89239) = 4.425,
b2=11.45135
1.03280 (.39458) = 4.375, b0= 81.7500 −4.425(7) −4.375(3) = 37.650.
7.17. a. ˆ
Y∗=.17472X∗
1−.04639X∗
2+.80786X∗
3
b. R2
12 =.0072, R2
13 =.0021,R2
23 =.0129
c. sY= 249.003, s1= 55274.6, s2=.87738, s3=.32260 b1=249.003
55274.6(.17472) =
.00079, b2=249.003
.87738 (−.04639) = −13.16562, b3=249.003
5.32260(.80786) = 623.5572,
b0= 4363.04−.00079(302,693) +13.16562(7.37058)−623.5572(0.115385) = 4149.002.
7.18. a. ˆ
Y∗=−.59067X∗
1−.11062X∗
2−.23393X∗
3
b. R2
12 =.32262, R2
13 =.32456, R2
23 =.44957
c. sY= 17.2365, s1= 8.91809, s2= 4.31356, s3=.29934, b1=17.2365
8.91809(−.59067) =
−1.14162, b2=17.2365
4.31356(−.11062) = −.44203, b3=17.2365
.29934 (−.23393) = −13.47008,
b0= 61.5652+1.14162(38.3913) +.44203(50.4348)+13.47008(2.28696) = 158.4927
7-2

7.19. a. ˆ
Y∗=−.547853X∗
1+.423647X∗
2+.0484614X∗
3+.502757X∗
4
c. sY= 1.71958, s1= 6.63278, s2= 2.58317, s3=.13455,s4= 109099, b1=
1.71958
6.63278(−.547853) = −.14203, b2=1.71958
2.58317(.423647) = .28202,
b3=1.71958
.13455 (.0484614) = .61934, b4=1.71958
109099 (.502757) = 7.9243 ×10−6,
b0= 15.1389 + .14203(7.8642) −.28202(9.68815) −.61934(.08099) −7.9243 ×
10−6(160633) = 12.20054.
7.21. b. The line of fitted values when .5X1−X2=−5.
7.24. a. ˆ
Y= 50.775 + 4.425X1
c. Yes, SSR(X1) = 1,566.45, SSR(X1|X2) = 1,566.45
d. r12 = 0
7.25. a. ˆ
Y= 4079.87 + 0.000935X2
c. No, SSR(X1) = 136,366, SSR(X1|X2) = 130,697
d. r12 =.0849
7.26. a. ˆ
Y= 156.672 −1.26765X1−0.920788X2
c. No, SSR(X1) = 8,275.3, SSR(X1|X3) = 3,483.89
No, SSR(X2) = 4,860.26, SSR(X2|X3) = 708
d. r12 =.5680, r13 =.5697, r23 =.6705
7.27. a. ˆ
Y= 14.3613 −.11447X1+.00001X4
c. No, SSR(X4) = 67.7751, SSR(X4|X3) = 66.8582
No, SSR(X1) = 14.8185, SSR(X1|X3) = 13.7744
d. r12 =.4670, r13 =.3228, r23 =.2538
7.28. a. (1) SSR(X1, X5)−SSR(X1) or SSE(X1)−SSE(X1, X5)
(2) SSR(X1, X3, X4)−SSR(X1) or SSE(X1)−SSE(X1, X3, X4)
(3) SSR(X1, X2, X3, X4)−SSR(X1, X2, X3)
or SSE(X1, X2, X3)−SSE(X1, X2, X3, X4)
b. SSR(X5|X1, X2, X3, X4), SSR(X2, X4|X1, X3, X5)
7.29. a. SSR(X1) + SSR(X2, X3|X1) + SSR(X4|X1, X2, X3)
=SSR(X1) + [SSR(X1, X2, X3)−SSR(X1)]
+[SSR(X1, X2, X3, X4)−SSR(X1, X2, X3)]
=SSR(X1, X2, X3, X4)
b. SSR(X2, X3) + SSR(X1|X2, X3) + SSR(X4|X1, X2, X3)
=SSR(X2, X3)+[SSR(X1, X2, X3)−SSR(X2, X3)]
+[SSR(X1, X2, X3, X4)−SSR(X1, X2, X3)] = SSR(X1, X2, X3, X4)
7-3

7.30. a. ˆ
Y= 68.625 + 4.375X2
i: 1 2 3 4 5 6
ei: -13.3750 -13.1250 -16.3750 -10.1250 -5.3750 -6.1250
i: 7 8 9 10 11 12
ei: -6.3750 -3.1250 5.6250 2.8750 8.6250 6.8750
i: 13 14 15 16
ei: 10.6250 8.8750 16.6250 13.8750
b. ˆ
X1= 7
i:12345678
ei: -3 -3 -3 -3 -1 -1 -1 -1
i: 9 10 11 12 13 14 15 16
ei: 1 1 1 1 3 3 3 3
c. r=.971 = rY1|2
7.31. (1) Yi=β0+β1Xi1+β2Xi2+εi
(2) Yi=β0+β1Xi1+β2Xi2+β4√Xi3+εi
(3) Y0
i=Yi−5(Xi1+Xi2) = β0+β3Xi1Xi2+β4√Xi3+εi
(4) Y0
i=Yi−7√Xi3=β0+β1Xi1+β2Xi2+β3Xi1Xi2+εi
7.32. (1) Yi=β0+β2Xi2+εi
(2) Yi=β1Xi1+β2Xi2+β3X2
i1+εi
(3) Y0
i=Yi−5X2
i1=β0+β1Xi1+β2Xi2+εi
(4) Y0
i=Yi−10 = β1Xi1+β2Xi2+β3X2
i1+εi
(5) Yi=β0+βc(Xi1+Xi2) + β3X2
i1+εi, where βc=β1=β2
7.33. Let:yi=Yi−¯
Y
xi1=Xi1−¯
X1
xi2=Xi2−¯
X2
Then: SSR(X1) = (Pxi1yi)2
Px2
i1
=Xy2
ir2
Y1by (1.10a), (2.51) and (2.84)
SSE(X1) = Py2
i−(Pxi1yi)2
Px2
i1
=Xy2
i(1 −r2
Y1)
SSR(X1,X2) = b1Pxi1yi+b2Pxi2yiby (2.43) and Pyi= 0
Further:
b1=Pxi1yi
Px2
i1−"Py2
i
Px2
i1#1/2
rY2r12
1−r2
12
by (7.56)
7-4
and similarly:
b2=Pxi2yi
Px2
i2−"Py2
i
Px2
i2#1/2
rY1r12
1−r2
12
Substituting these expressions for b1and b2into SSR(X1,X2), we obtain after some
simplification:
SSR(X1,X2) = 1
1−r2
12 hXy2
ir2
Y1+Xy2
ir2
Y2−2Xy2
irY1rY2r12i
Now by (7.36) and (7.2b), we have:
r2
Y2|1=SSR(X1,X2)−SSR(X1)
SSE(X1)
Substituting the earlier expressions into the above, we obtain after some simplifying:
r2
Y2|1=1
Py2
i(1 −r2
Y1)(1 −r2
12)[Xy2
ir2
Y1+Xy2
ir2
Y2−2Xy2
irY1rY2r12
−(1 −r2
12)Py2
ir2
Y1]
After some further simplifying, we obtain:
r2
Y2|1=(rY2−r12rY1)2
(1 −r2
Y1)(1 −r2
12)
7.34. a. (1) "1 0
0 1 #(2) ".7420
.6385 #
(3) ".7420
.6385 #(4) ".0083 0
0.0083 #
b. From (7.53), b∗
1=1.069
7.745(5.375) = .742
b∗
2=.5345
7.745(9.250) = .638
7.35. From (7.45), we have:
Y∗
i=β∗
1X∗
i1+β∗
2X∗
i2+ε∗
i
1
√n−1ÃYi−¯
Y
sY!=β∗
1
1
√n−1ÃXi1−¯
X1
s1!+β∗
2
1
√n−1ÃXi2−¯
X2
s2!+ε∗
i
Simplifying, we obtain:
Yi= ( ¯
Y−β∗
1
sY
s1
¯
X1−β∗
2
sY
s2
¯
X2) + β∗
1
sY
s1
Xi1+β∗
2
sY
s2
Xi2+√n−1sYε∗
i
7-5

Hence:
β∗
1
sY
s1
=β1β∗
2
sY
s2
=β2
7.36. X∗Y="ΣX∗
i1Y∗
i
ΣX∗
i2Y∗
i#=
Σ(Xi1−¯
X1)(Yi−¯
Y)
(n−1)s1sY
Σ(Xi2−¯
X2)(Yi−¯
Y)
(n−1)s2sY
="rY1
rY2#
7.37. a. R2
Y3|12 =.02883, R2
Y4|12 =.00384, R2
Y5|12 =.55382, R2
Y6|12 =.00732
b. X5, yes.
c. Full model: Yi=β0+β1Xi1+β2Xi2+β5Xi5+εi.H0:β5= 0, Ha:β56= 0.
SSR(X5|X1, X2) = 78,070,132, SSE(X1, X2, X5) = 62,896,949,
F∗= (78,070,132/1) ÷(62,896,949/436) = 541.1801, F(.99; 1,137) = 6.69336.
If F∗≤6.69336 conclude H0,otherwise Ha. Conclude Ha. No.
7.38. a. R2
Y3|12 =.01167, R2
Y4|12 =.13620, R2
Y5|12 =.03737, R2
Y6|12 =.03639
b. X4, yes.
c. Full model: Yi=β0+β1Xi1+β2Xi2+β4Xi4+εi.H0:β4= 0, Ha:β46= 0.
SSR(X4|X1, X2) = 37.89858, SSE(X1, X2, X4) = 240.35163, F∗= (37.89858/1)÷
(240.35163/109) = 17.187, F(.95; 1,109) = 3.93. If F∗≤3.93 conclude H0, oth-
erwise Ha. Conclude Ha. No.
7-6

Chapter 8
MODELS FOR QUANTITATIVE
AND QUALITATIVE PREDICTORS
8.4. a. ˆ
Y= 82.9357 −1.18396x+.0148405x2,R2=.76317
b. H0:β1=β11 = 0, Ha: not both β1and β11 = 0. MSR = 5915.31, MSE = 64.409,
F∗= 5915.31/64.409 = 91.8398, F(.95; 2,57) = 3.15884.If F∗≤3.15884 conclude
H0, otherwise Ha. Conclude Ha.
c. ˆ
Yh= 99.2546, s{ˆ
Yh}= 1.4833, t(.975; 57) = 2.00247, 99.2546 ±2.00247(1.4833),
96.2843 ≤E{Yh} ≤ 102.2249
d. s{pred}= 8.16144, 99.2546 ±2.00247(8.16144), 82.91156 ≤Yh(new) ≤115.5976
e. H0:β11 = 0, Ha:β11 6= 0. s{b11}=.00836, t∗=.0148405/.00836 = 1.7759,
t(.975; 57) = 2.00247. If |t∗| ≤ 2.00247 conclude H0, otherwise Ha.Conclude
H0. Alternatively, SSR(x2|x) = 203.1, SSE(x, x2) = 3671.31, F∗= (203.1/1) ÷
(3671.31/57) = 3.15329, F(.95; 1,57) = 4.00987. If F∗≤4.00987 conclude H0,
otherwise Ha. Conclude H0.
f. ˆ
Y= 207.350 −2.96432X+.0148405X2
g. rX,X2=.9961, rx,x2=−.0384
8.5. a. i: 1 2 3 . . . 58 59 60
ei: -1.3238 -4.7592 -3.8091 . . . -11.7798 -.8515 6.22023
b. H0:E{Y}=β0+β1x+β11x2,Ha:E{Y} 6=β0+β1x+β11x2. MSLF = 62.8154,
MSP E = 66.0595, F∗= 62.8154/66.0595 = 0.95, F (.95; 29,28) = 1.87519. If
F∗≤1.87519 conclude H0, otherwise Ha.Conclude H0.
c. ˆ
Y= 82.92730 −1.26789x+.01504x2+.000337x3
H0:β111 = 0, Ha:β111 6= 0. s{b111}=.000933, t∗=.000337/.000933 = .3612,
t(.975; 56) = 2.00324. If |t∗| ≤ 2.00324 conclude H0, otherwise Ha. Con-
clude H0. Yes. Alternatively, SSR(x3|x, x2)=8.6, SSE(x, x2, x3) = 3662.78,
F∗= (8.6/1) ÷(3662.78/56) = .13148, F (.95; 1,56) = 4.01297. If F∗≤4.01297
conclude H0, otherwise Ha.Conclude H0. Yes.
8.6. a. ˆ
Y= 21.0942 + 1.13736x−.118401x2,R2=.81434
8-1

b. H0:β1=β11 = 0, Ha: not all βk= 0 (k= 1,11). MSR = 523.133, MSE =
9.9392, F∗= 523.133/9.9392 = 52.6333,F(.99; 2,24) = 5.6136. If F∗≤5.6136
conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
c. F(.99; 3,24) = 5.04, W= 3.7622; B=t(.99833; 24) = 3.25756
X
10: 20.6276 ±3.25756(1.8945) 14.45615 ≤E{Yh} ≤ 26.79905
15: 11.5142 ±3.25756(4.56694) −3.36288 ≤E{Yh} ≤ 26.39128
20: −3.5192 ±3.25756(8.50084) −31.2112 ≤E{Yh} ≤ 24.1728
d. s{pred}= 5.54942, t(.995; 24) = 2.79694, 11.5142 ±2.79694(5.54942),−4.0072 ≤
Yh(new) ≤27.0356
e. H0:β11 = 0, Ha:β11 6= 0. s{b11}=.02347, t∗=−.118401/.02347 = −5.04478,
t(.995; 24) = 2.79694. If |t∗| ≤ 2.79694 conclude H0, otherwise Ha.Conclude Ha.
Alternatively, SSR(x2|x) = 252.989, SSE(x, x2) = 238.541, F∗= (252.989/1) ÷
(238.541/24) = 25.4536, F(.99; 1,24) = 7.82287. If F∗≤7.82287 conclude H0,
otherwise Ha. Conclude Ha.
f. ˆ
Y=−26.3254 + 4.87357X−.118401X2
8.7. a. i: 1 2 . . . 26 27
ei: 3.96746 -1.42965 . . . 2.10202 -2.43692
b. H0:E{Y}=β0+β1x+β11x2,Ha:E{Y} 6=β0+β1x+β11x2. MSLF = 6.65396,
MSP E = 13.2244, F∗= 6.65396/13.2244 = 0.50316, F(.99; 12,12) = 4.15526. If
F∗≤4.15526 conclude H0, otherwise Ha.Conclude H0.
8.8. a. ˆ
Y= 10.1893 −.181775x1+.0141477x2
1+.314031X2+.000008X4
b. .5927
c. H0:β11 = 0, Ha:β11 6= 0. s{b11}=.005821, t∗=.0141477/.005821 = 2.43046,
t(.975; 76) = 1.99167. If |t∗| ≤ 1.99167 conclude H0, otherwise Ha. Conclude Ha.
d. ˆ
Yh= 17.2009, s{ˆ
Yh}=.37345, t(.975; 76) = 1.99167, 17.2009 ±1.99167(.37345),
16.45711 ≤E{Yh} ≤ 17.94469
e. ˆ
Y= 12.4938 −.404296x1+.0141477x2
1+.314031X2+.000008X4
8.9. a. X2= 3: E{Y}= 37 + 7.5X1
X2= 6: E{Y}= 49 + 12X1
8.10. a. X1= 1: E{Y}= 21 + X2
X1= 4: E{Y}= 42 −11X2
8.11. a. ˆ
Y= 27.150 + 5.925X1+ 7.875X2−.500X1X2
b. H0:β3= 0, Ha:β36= 0. MSR(X1X2|X1, X2) = 20.0000, MSE = 6.1917,
F∗= 20.0000/6.1917 = 3.23, F(.95; 1,12) = 4.75.If F∗≤4.75 conclude H0,
otherwise Ha. Conclude H0.
8.13. E{Y}= 25.3 + .20X1for mutual firms,
8-2
E{Y}= 13.2 + .20X1for stock firms.
8.15. b. ˆ
Y=−0.92247 + 15.0461X1+.75872X2
c. s{b2}= 2.77986, t(.975; 42) = 2.01808, .75872 ±2.01808(2.77986), −4.85126 ≤
β2≤6.3687
e.
i: 1 2 . . . 44 45
Xi1Xi2: 2 0 . . . 0 0
ei: -9.92854 .73790 . . . 1.73790 2.69176
8.16. b. ˆ
Y= 2.19842 + .03789X1−.09430X2
c. H0:β2= 0, Ha:β26= 0. s{b2}=.11997, t∗=−.09430/.11997 = −.786,
t(.995; 117) = 2.6185. If |t∗| ≤ 2.6185 conclude H0, otherwise Ha. Conclude H0.
d.
i: 1 2 . . . 119 120
Xi1Xi2: 0 14 . . . 16 0
ei: .90281 1.25037 . . . -.85042 -.31145
8.17. No
8.18. E{Y}= 25 + .30X1for mutual firms,
E{Y}= 12.5 + .35X1for stock firms.
8.19. a. ˆ
Y= 2.81311 + 14.3394X1−8.14120X2+ 1.77739X1X2
b. H0:β3= 0, Ha:β36= 0. s{b3}=.97459, t∗= 1.77739/.97459 = 1.8237,
t(.95; 41) = 1.68288. If |t∗| ≤ 1.68288 conclude H0, otherwise Ha. Conclude Ha.
Alternatively, SSR(X1X2|X1, X2) = 255.9, SSE(X1, X2, X1X2) = 3154.44, F∗=
(255.9/1)÷(3154.44/41) = 3.32607, F(.90; 1,41) = 2.83208. If F∗≤2.83208
conclude H0, otherwise Ha. Conclude Ha.
8.20. a. ˆ
Y= 3.22632 −.00276X1−1.64958X2+.06224X1X2
b. H0:β3= 0, Ha:β36= 0. s{b3}=.02649, t∗=.06224/.02649 = 2.3496,
t(.975; 116) = 1.9806. If |t∗| ≤ 1.9806 conclude H0, otherwise Ha. Conclude Ha.
Alternatively, SSR(X1X2|X1, X2) = 2.07126, SSE(X1, X2, X1X2) = 45.5769,
F∗= (2.07126/1) ÷(45.5769/116) = 5.271665, F(.95; 1,116) = 3.9229. If F∗≤
3.9229 conclude H0, otherwise Ha. Conclude Ha.
8.21. a. Hard hat: E{Y}= (β0+β2) + β1X1
Bump cap: E{Y}= (β0+β3) + β1X1
None: E{Y}=β0+β1X1
b. (1) H0:β3≥0, Ha:β3<0; (2) H0:β2=β3,Ha:β26=β3
8.22. E{Y}=β0+β1X1Tool models M1
E{Y}= (β0+β2) + (β1+β5)X1Tool models M2
8-3

E{Y}= (β0+β3) + (β1+β6)X1Tool models M3
E{Y}= (β0+β4) + (β1+β7)X1Tool models M4
8.24. b. ˆ
Y=−126.905 + 2.7759X1+ 76.0215X2−1.10748X1X2,
H0:β2=β3= 0, Ha: not both β2= 0 and β3= 0. SSR(X2, X1X2|X1) = 566.15,
SSE(X1, X2, X1X2) = 909.105, F∗= (369.85/2) ÷(909.105/60) = 12.2049,
F(.95; 2,60) = 3.15041. If F∗≤3.15041 conclude H0, otherwise Ha. Conclude
Ha.
c. ˆ
Y=−126.9052 + 2.7759X1for noncorner lots
ˆ
Y=−50.8836 + 1.6684X1for corner lots
8.25. a. ˆ
Y= 4295.72+.000903x1−(1.5767×10−9)x2
1+614.393X3−.000188x1X3+(1.8076×
10−9)x2
1X3
b. H0:β2=β4=β5= 0, Ha: not all β2= 0,β4= 0 and β5= 0.
SSR(x2
1, x1X3, x2
1X3|x1, X3) = 1442, SSE(x1, x2
1, X3, x1X3, x2
1X3) = 990762, F∗=
(1442/3) ÷(990762/46) = .02232, F(.95; 3,46) = 2.8068. If F∗≤2.80681 con-
clude H0, otherwise Ha. Conclude H0.
8.29.
Set 1
X
X2
X3
1.990 .966
1−
1
x
x2
x3
1.379 .904
1−
1
Set 2
X
X2
X3
1.970 .929
1−
1
x
x2
x3
1.846 .89
1−
1
8.30. dE{Y}
dx =β1+ 2β11x
d2E{Y}
dx2= 2β11
8.31. a. ˆ
Y=b0+b1x+b11x2
=b0+b1(X−¯
X) + b11(X−¯
X)2
=b0+b1X−b1¯
X+b11X2+b11 ¯
X2−2b11X¯
X
= (b0−b1¯
X+b11 ¯
X2)+(b1−2b11 ¯
X)X+b11X2
Hence:
b0
0=b0−b1¯
X+b11 ¯
X2
b0
1=b1−2b11 ¯
X
b0
11 =b11
8-4
b. A=
1−¯
X¯
X2
0 1 −2¯
X
0 0 1
σ2{b}=
σ2
0σ01 σ02
σ01 σ2
1σ12
σ02 σ12 σ2
2
where σ2
0=σ2{b0},σ01 =σ{b0, b1}, etc. for the regression coefficients in the
transformed xvariables.
The variance-covariance matrix of the regression coefficients in the original X
variables, A[σ2{b}]A0, then yields:
σ2{b0
0}=σ2
0−2¯
Xσ01 + 2 ¯
X2σ02 +¯
X2σ2
1−2¯
X3σ12 +¯
X4σ2
2
σ2{b0
1}=σ2
1−4¯
Xσ12 + 4 ¯
X2σ2
2
σ2{b0
2}=σ2
2
σ{b0
0,b0
1}=σ01 −2¯
Xσ02 + 3 ¯
X2σ12 −¯
Xσ2
1−2¯
X3σ2
2
σ{b0
0,b0
2}=σ02 −¯
Xσ12 +¯
X2σ2
2
σ{b0
1,b0
2}=σ12 −2¯
Xσ2
2
8.32. When Xiare equally spaced, Px3
i= 0; hence (8.4) becomes:
PYi=nb0+b11 Px2
i
PxiYi=b1Px2
i
Px2
iYi=b0Px2
i+b11 Px4
i
8.33. a. Yi=β0+β1xi1+β2x2
i1+β3Xi2+β4xi1Xi2+β5x2
i1Xi2+β6Xi3+β7xi1Xi3+β8x2
i1Xi3+εi
b. (1) H0:β3=β4=β5=β6=β7=β8= 0
Ha: not all βk= 0 (k= 3, ..., 8)
SSE(R) = SSE(x1, x2
1)
F∗=SSE(R)−SSE(F)
6÷SSE(F)
n−9
If F∗≤F(.99; 6, n −9) conclude H0, otherwise Ha.
(2) H0:β3=β6= 0, Ha: not both β3= 0 and β6= 0
SSE(R) = SSE(x1, x2
1, x1X2, x2
1X2, x1X3, x2
1X3)
F∗=SSE(R)−SSE(F)
2÷SSE(F)
n−9
If F∗≤F(.99; 2, n −9) conclude H0, otherwise Ha.
(3) H0:β4=β5=β7=β8= 0, Ha: not all βk= 0 (k= 4,5,7,8)
SSE(R) = SSE(x1, x2
1, X2, X3)
F∗=SSE(R)−SSE(F)
4÷SSE(F)
n−9
If F∗≤F(.99; 4, n −9) conclude H0, otherwise Ha.
8.34. a. Yi=β0+β1Xi1+β2Xi2+β3Xi3+εi
b. Commercial: E{Y}= (β0+β2) + β1X1
8-5
Mutual savings: E{Y}= (β0+β3) + β1X1
Savings and loan: E{Y}= (β0−β2−β3) + β1X1
8.35. a. Let n2=n−n1and define:
X=
1 0
.
.
..
.
.
1 0
1 1
.
.
..
.
.
1 1
←n1
←n2
Y=
Y11
.
.
.
Yn11
Y12
.
.
.
Yn22
¯
Y1=PYi1
n1
¯
Y2=PYi2
n2
¯
Y=PPYij
n1+n2
Then:
X0X="n n2
n2n2#X0Y="n¯
Y
n2¯
Y2#
(X0X)−1="1
n1−1
n1
−1
n1
1
n1+1
n2#
b. b="¯
Y1
¯
Y2−¯
Y1#
c. SSR =n1¯
Y2
1+n2¯
Y2
2−n¯
Y2
SSE =PPY2
ij −n1¯
Y2
1−n2¯
Y2
2
8.36. a. ˆ
Y= 999.912 + .00296x−3.29518 ×10−11x2
b. R2=.8855 for second-order model; R2=.6711 for first-order model.
c. H0:β11 = 0, Ha:β11 6= 0. s{b11}= 1.400396 ×10−11,t∗=−3.29518 ×
10−11/1.400396 ×10−11 =−2.353, t(.975; 437) = 1.9654. If |t∗| ≤ 1.9654 con-
clude H0,otherwise Ha. Conclude Ha. Alternatively, SSR(x2|x)=2,039,681,
SSE(x, x2) = 160,985,454, F∗= (2,039,681/1) ÷(160,985,454/437) = 5.5368,
F(.95; 1,437) = 3.8628. If F∗≤3.8628 conclude H0, otherwise Ha. Conclude Ha.
8.37. a. ˆ
Y=.056288 + 0.000004585x1−.000088x3+ 2.6982 ×10−12x2
1+.00016293x2
3+
8.3337 ×10−7x1x3,R2=.2485
b. H0:β11 =β33 =β13 = 0, Ha: not all βk= 0 (k= 11,33,13).
SSR(x2
1, x2
3, x1x3|x1, x3) = .005477, SSE(x1, x3, x2
1, x2
3, x1x3) = .246385, F∗=
(.005477/3) ÷(.246385/437) = 3.2381, F(.99; 1,437) = 3.8267. If F∗≤3.8267
conclude H0, otherwise Ha. Conclude H0.
c. ˆ
Y=.0584998+2.9419×10−8x1−5.5765×10−7x2+.00068244x3−3.3559×10−15x2
1,
R2=.1444
8.38. a. ˆ
Y= 150.07921 + 7.06617x+.10116x2
b. R2=.6569 for second-order model; R2=.6139 for first-order model.
8-6
c. H0:β11 = 0, Ha:β11 6= 0. s{b11}=.02722, t∗=.10116/.02722 = 3.716,
t(.995; 110) = 2.621. If |t∗| ≤ 2.621 conclude H0,otherwise Ha. Conclude Ha.
Alternatively, SSR(x2|x) = 93,533.252, SSE(x, x2) = 745,203.642,
F∗= (93,533.252/1) ÷(745,203.642/110) = 13.807, F(.99; 1,110) = 6.871. If
F∗≤6.871 conclude H0,otherwise Ha. Conclude Ha.
8.39. a. ˆ
Y=−207.5 + .0005515X1+.107X2+ 149.0X3+ 145.5X4+ 191.2X5
b. b3−b4= 3.5, s{b3−b4}= 1.68, t(.95; 434) = 1.6484, 3.5±1.6484(1.68), 0.730688 ≤
β3−β4≤6.2693
c. H0:β3=β4=β5= 0, Ha: not all βk= 0 (k= 3,4,5). SSR(X3, X4, X5|X1, X2) =
1,873,626, SSE(X1, X2, X3, X4, X5) = 139,093,455,
F∗= (1,873,626/3) ÷(139,093,455/434) = 1.9487, F(.90; 3,434) = 2.09645. If
F∗≤2.09645 conclude H0, otherwise Ha. Conclude H0.P−value=.121.
8.40. a. ˆ
Y=.85738 + .28882X1−.01805X2+.01995X3+.28782X4
b. s{b4}=.30668, t(.99; 108) = 2.361, .28782 ±2.361(.30668),−.476 ≤β4≤1.012
c. ˆ
Y=.99413 + .26414X1−.02283X2+.02429X3−5.69520X4+.15576X2X4−
.02406X3X4
H0:β5=β6= 0, Ha: not both β5= 0 and β6= 0. SSR(X2X4, X3X4
|X1, X2, X3, X4)=5.1964, SSE(X1, X2, X3, X4, X2X4, X3X4) = 122.0468, F∗=
(5.1964/2) ÷(122.0468/106) = 2.257, F(.90; 2,106) = 2.353. If F∗≤2.353 con-
clude H0, otherwise Ha. Conclude H0.
8.41. a. ˆ
Y= 2.0478+.10369X1+.04030X2+.00660X3−.020761X4+2.14999X5+1.19033X6+
.63348X7
b. H0:β2= 0, Ha:β26= 0. s{b2}=.01430, t∗=.04030/.01430 = 2.818,
t(.975; 105) = 1.983. If |t∗| ≤ 1.983 conclude H0, otherwise Ha. Conclude Ha.
Alternatively, SSR(X2|X1, X3, X4, X5, X6, X7) = 15.52782,
SSE(X1, X2, X3, X4, X5, X6, X7) = 205.3634, F∗= (15.52782/1)÷(205.3634/105) =
7.9392, F(.95; 1,105) = 3.932. If F∗≤3.932 conclude H0, otherwise Ha. Con-
clude Ha.
c. s{b5}=.46152, s{b6}=.43706, s{b7}=.42755, B=t(.99167; 105) = 2.433
2.14999 ±2.443(.46152) 1.0225 ≤β5≤3.2775
1.19033 ±2.443(.43706) .1226 ≤β6≤2.2581
.63348 ±2.443(.42755) −.4110 ≤β7≤1.6780
8.42. a. ˆ
Y= 3.0211−.247X1−.000097X2+.4093X3+.124X4−.01324X5{1999} −.1088X5{2001}−
.08306X5{2002}
b. ˆ
Y= 2.38 −0.453x1−0.000144x2+ 0.00016x1x2+ 0.92x2
1+ 0.000001x2
2+ 0.394X3+
0.115X4+ 0.012X5{1999} − 0.101X5{2001} − 0.0581X5{2002}
H0:β3=β4=β5= 0, Ha: not all βk= 0 (k= 3,4,5). SSE(R) = .65424, dfR=
28, SSE(F) = .62614, dfF= 25, MSE(F) = .02505 F∗=.37392, F(.95; 3,30) =
2.9223. If F∗≤2.9223 conclude H0, otherwise Ha. Conclude H0.
8-7
c. H0:β2=β5=β6=β7= 0, Ha: not all βk= 0 (k= 2,5,6,7). SSE(R) =
.71795, dfR= 32, SSE(F) = .65424, dfF= 28, MSE(F) = .02337, F∗=.68154,
F(.95; 4,28) = 2.71408. If F∗≤2.71408 conclude H0, otherwise Ha. Conclude
H0.
8-8

Chapter 9
BUILDING THE REGRESSION
MODEL I: MODEL SELECTION
AND VALIDATION
9.9.
Variables in Model R2
pAICpCpP RESSp
None 0 262.916 88.16 13,970.10
X1.6190 220.529 8.35 5,569.56
X2.3635 244.131 42.11 9,254.49
X3.4155 240.214 35.25 8,451.43
X1, X2.6550 217.968 5.60 5,235.19
X1, X3.6761 215.061 2.81 4,902.75
X2, X3.4685 237.845 30.25 8,115.91
X1, X2, X3.6822 216.185 4.00 5,057.886
9.10. b.
X1
X2
X3
X4
1.102 .181 .327
1.519 .397
1.782
1
c. ˆ
Y=−124.3820 + .2957X1+.0483X2+ 1.3060X3+.5198X4
9.11. a.
Subset R2
a,p
X1, X3, X4.9560
X1, X2, X3, X4.9555
X1, X3.9269
X1, X2, X3.9247
9.12.
Subset SBCp
X3, X5, X6−126.601
X5−124.970
X3, X5, X6, X8= 2001 −124.969
Note: Variable numbers for predictors are those in the appendix.
9-1

9.13. b.
X1
X2
X3
1.653 −.046
1−.423
1
c. ˆ
Y= 87.1875 −.5645X1−.5132X2−.0720X3
9.14. a.
Subset R2
a,p
x1, x2, x2
1, x2
2.75067
x1, x2, x1x2.75066
x1, x2, x1x2, x2
2.74156
9.15. b.
X1
X2
X3
1.468 −.089
1.068
1
c. ˆ
Y= 120.0473 −39.9393X1−.7368X2+.7764X3
9.16. a.
Subset R2
a,p
x1, x2, x3, x2
3, x1x2.8668
x1, x2, x3, x2
2,x2
3,x1x2.8652
x1, x2, x3,x2
3, x1x2, x1x3.8638
9.17. a. X1,X3
b. .10
c. X1,X3
d. X1,X3
9.18. a. X1,X3,X4
9.19 a. x1,x2,x3,x1x2
b. R2
a,p =.8615
9.20. X3,X5,X6in appendix.
9.21. P RESS = 760.974, SSE = 660.657
9.22. a.
X1
X2
X3
X4
1.011 .177 .320
1.344 .221
1.871
1
b.
9-2
Model-building Validation
data set data set
b0:−127.596 −130.652
s{b0}: 12.685 12.189
b1:.348 .347
s{b1}:.054 .048
b3: 1.823 1.848
s{b3}:.123 .122
MSE: 27.575 21.446
R2:.933 .937
c. MSP R = 486.519/25 = 19.461
d. ˆ
Y=−129.664 + .349X1+ 1.840X3,s{b0}= 8.445, s{b1}=.035, s{b3}=.084
9.23. a. P RESS = 5,102.494, SSE = 1,680.465
9.24. Xi= 10: [E{ˆ
Y} − E{Y}]2= (−55)2, [ ˆ
Y−E{ˆ
Y}]2= (−47)2
Xi= 20: [E{ˆ
Y} − E{Y}]2= (−705)2, [ ˆ
Y−E{ˆ
Y}]2= (−97)2
9.25. b.
X3
X4
X5
X6
X7
X10
X11
X12
1.025 −.101 .161 −.198 −.172 −.236 −.164
1.448 .334 .490 .501 .530 .453
1.195 .168 .204 .239 .240
1.067 .086 .060 .128
1.990 .909 .764
1.904 .729
1.707
1
Note: Variable numbers for predictor variables are those in the data set description.
c.
Subset Cp
X3, X6, X10 3.81
X3, X6, X10, X11 3.86
X3, X6, X7, X10 4.27
9.26. b.
X4
X6
X7
X8
X9
X11
X12
X13
X14
X15
X16
1−.063 .016 .040 .021 −.113 −.145 .169 .181 −.190 .078
1−.599 .174 .113 .245 .486 −.025 −.222 .078 .116
1−.023 .054 −.240 −.359 −.003 .189 −.028 −.023
1.921 .056 .264 .033 −.056 .312 .934
1−.100 .059 .173 .034 .145 .891
1.722 −.753 −.671 .585 .087
1−.466 −.551 .748 .238
1.513 −.649 −.052
1−.379 −.023
1.347
1
Note: Variable numbers for predictor variables are those in the data set description.
9-3

c.
Subset SBCp
X6, X9, X13, X14 3407.16
X6, X8, X9, X13, X14, X15 3407.41
X6, X9, X13, X14, X15 3408.09
9.27. a.
Model-building Validation
data set data set
b0: .6104 .6189
s{b0}: .0888 .1248
b3: .00388 .00399
s{b3}: .00163 .00211
b6: .00117 .00152
s{b6}: .000419 .000437
b10: .000293 .000157
s{b10}: .0000456 .0000622
MSE: .00305 .00423
R2: .519 .293
b. MSP R =.258271/56 = .00461
c. ˆ
Y0=.6272 + .00353X3+.00143X6+.000236X10,s{b0}=.0738, s{b3}=.00129,
s{b6}=.000297, s{b10}=.0000374, where Y0= log10 Y.
9.28. a.
Model-building Validation
data set data set
b0: 243.680 3015.63
s{b0}: 1322.82 1189.63
b6: 122.507 34.3137
s{b6}: 41.1906 34.2984
b9: .578662 .221509
s{b9}: .075844 .057344
b13: 296.117 269.557
s{b13}: 34.3417 39.0049
b14: -224.020 -128.343
s{b14}: 77.1406 70.4556
MSE: 4,816,124 4,484,316
R2: .463 .284
b. MSP R =2,259,424,814
220 = 10,270,113
9-4

Chapter 10
BUILDING THE REGRESSION
MODEL II: DIAGNOSTICS
10.5. a.
i: 1 2 3 . . . 6 7 8
e(Y|X1): −4.475 4.525 −7.475 . . . 2.675 −6.325 5.675
e(X2|X1): −1 1 −1 . . . 1 −1 1
e(Y|X2): −13.38 −13.13 −16.38 . . . −6.125 −6.375 −3.125
e(X1|X2y): −3−3−3 . . . −1−1−1
i: 9 10 11 . . . 14 15 16
e(Y|X1): −3.175 2.825 −.175 . . . −.025 −1.025 4.975
e(X2|X1): −1 1 −1 . . . 1 −1 1
e(Y|X2): 5.625 2.875 8.625 . . . 8.875 16.625 13.875
e(X1|X2): 1 1 1 . . . 3 3 3
c. ˆ
Y(X1) = 50.775 + 4.425X1,ˆ
X2(X1) = 3
[Y−ˆ
Y(X1)] = 4.375[X2−ˆ
X2(X1)], ˆ
Y= 37.650 + 4.425X1+ 4.375X2
10.6. a. ˆ
Y= 3995.48 + .00091916X1+ 12.1205X2
b.
i: 1 2 . . . 51 52
e(Y|X1): −101.811 108.842 . . . −279.061 −11.1165
e(X2|X1): −.205 −1.205 . . . .312 .414
e(Y|X2): −95.621 152.904 . . . −184.865 −27.843
e(X1|X2): 4,036.66 32,043.7 . . . 106,600 −12,742.4
d. ˆ
Y(X1) = 4079.87 + .000935X1,ˆ
X2(X1) = 6.96268 + .00000135X1
[Y−ˆ
Y(X1)] = 12.1205[X2−ˆ
X2(X1)], ˆ
Y= 3995.48 + .000919X1+ 12.1205X2
10.7. a.
i: 1 2 . . . 45 46
e(Y|X1, X2): 1.671 −11.680 . . . −1.967 13.179
e(X3|X1, X2): −.116 .193 . . . −.265 −.232
e(Y|X1, X3): .589 −7.218 . . . −7.365 9.808
e(X2|X1, X3): −1.077 −4.213 . . . 4.134 .554
e(Y|X2, X3): −12.537 −9.734 . . . −4.086 12.696
e(X1|X2, X3): 11.081 .573 . . . −1.272 −2.316
10-1
10.8. a.
i: 1 2 . . . 80 81
e(Y|X1, X2): −.630 −1.768 . . . −.129 −1.068
e(X3|X1, X2): −.039 .179 . . . −.016 .016
e(Y|X1, X3): −2.085 −2.75065 . . . .316 −.240
e(X2|X1, X3): −3.491 −1.155 . . . .905 1.950
e(Y|X2, X3): −.242 −3.259 . . . −.259 −1.490
e(X1|X2, X3): −2.405 8.596 . . . 1.437 3.198
10.9. a&g.
i: 1 2 3 4 5 6
ti:−.041 .061 −1.361 1.386 −.367 −.665
Di:.0002 .0004 .1804 .1863 .0077 .0245
i: 7 8 9 10 11 12
ti:−.767 .505 .465 −.604 1.823 .978
Di:.0323 .0144 .0122 .0204 .1498 .0510
i: 13 14 15 16
ti:−1.140 −2.103 1.490 .246
Di:.1318 .3634 .2107 .0068
t(.9969; 12) = 3.31. If |ti| ≤ 3.31 conclude no outliers, otherwise outliers. Con-
clude no outliers.
c. 2p/n = 2(3)/16 = .375, no
d. X0
new =h1 10 3 i
(X0X)−1=
1.2375 −.0875 −.1875
.0125 0
0.0625
hnew,new =.175, no extrapolation
e.
DF BET AS
DF F IT S b0b1b2D
Case 14: −1.174 .839 −.808 −.602 .3634
f. .68%
10.10. a&f.
i: 1 2 . . . 51 52
ti:−.224 1.225 . . . −1.375 .453
Di:.0003 .0245 . . . .0531 .0015
t(.9995192; 47) = 3.523. If |ti| ≤ 3.523 conclude no outliers, otherwise outliers.
Conclude no outliers.
b. 2p/n = 2(4)/52 = .15385. Cases 3, 5, 16, 21, 22, 43, 44, and 48.
c. X0
new = [ 1 300,000 7.2 0 ]
10-2

(X0X)−1=
1.8628 −.0000 −.1806 .0473
.0000 −.0000 −.0000
.0260 −.0078
.1911
hnew, new =.01829, no extrapolation
d.
DF BET AS
DF F IT S b0b1b2b3D
Case 16: −.554 −.2477 −.0598 .3248 −.4521 .0769
Case 22: .055 .0304 −.0253 −.0107 .0446 .0008
Case 43: .562 −.3578 .1338 .3262 .3566 .0792
Case 48: −.147 .0450 −.0938 .0090 −.1022 .0055
Case 10: .459 .3641 −.1044 −.3142 −.0633 .0494
Case 32: −.651 .4095 .0913 −.5708 .1652 .0998
Case 38: .386 −.0996 −.0827 .2084 −.1270 .0346
Case 40: .397 .0738 −.2121 .0933 −.1110 .0365
e. Case 16: .161%, case 22: .015%, case 43: .164%, case 48: .042%,
case 10: .167%, case 32: .227%, case 38: .152%, case 40: .157%.
10.11. a&f.
i: 1 2 . . . 45 46
ti:.0116 −.9332 . . . −.5671 1.0449
Di:.000003 .015699 . . . .006400 .024702
t(.998913; 41) = 3.27. If |ti| ≤ 3.27 conclude no outliers, otherwise outliers.
Conclude no outliers.
b. 2p/n = 2(4)/46 = .1739. Cases 9, 28, and 39.
c. X0
new = [ 1 30 58 2.0]
(X0X)−1=
3.24771 .00922 −.06793 −.06730
.00046 −.00032 −.00466
.00239 −.01771
.49826
hnew, new =.3267, extrapolation
d.
DF BET AS
DF F IT S b0b1b2b3D
Case 11: .5688 .0991 −.3631 −.1900 .3900 .0766
Case 17: .6657 −.4491 −.4711 .4432 .0893 .1051
Case 27: −.6087 −.0172 .4172 −.2499 .1614 .0867
e. Case 11: 1.10%, case 17: 1.32% , case 27: 1.12%.
10.12. a&f.
i: 1 2 . . . 80 81
ti:−.9399 −1.3926 . . . −1.9232 −.8095
Di:.0117 .0308 . . . .0858 .0046
t(.999938; 75) = 4.05. If |ti| ≤ 4.05 conclude no outliers, otherwise outliers.
Conclude no outliers.
10-3

b. 2p/n = 2(5)/81 = .1235. Cases 3, 8, 53, 61, and 65.
c. X0
new = [ 1 10 12 .05 350,000 ]
(X0X)−1=
.2584 −.0003 −.0251 −.2508 .0000
.0004 −.0002 .0031 −.0000
.0031 .0219 −.0000
.9139 −.0000
.0000
hnew, new =.0402, no extrapolation
d.
DF BET AS
DF F IT S b0b1b2b3b4D
Case 61: .639 −.0554 .0242 −.0076 .5457 .0038 .082
Case 8: .116 −.0142 −.0072 .0030 .0955 .0126 .003
Case 3: −.284 −.2318 −.1553 .2364 .1008 −.0115 .016
Case 53: .525 −.0196 −.0240 −.0243 .4180 .0490 .055
Case 6: −.873 .1951 −.5649 −.1767 −.6182 .4482 .137
Case 62: .690 .2758 −.3335 −.2595 .0627 .4051 .088
e. Case 61: .300%, case 8: .054%, case 3: .192%, case 53: .235%,
case 6: .556%, case 62: .417%.
10.13. a. ˆ
Y= 1.02325 + .96569X1+.62916X2+.67603X3
b. H0:β1=β2=β3= 0, Ha: not all βk= 0 (k= 1,2,3). MSR = 127.553,
MSE = 3.33216, F∗= 127.553/3.33216 = 38.28, F (.95; 3,10) = 2.84. If F∗≤
2.84 conclude H0, otherwise Ha.Conclude Ha.
c. H0:βk= 0, Ha:βk6= 0. t(.975; 10) = 2.021. If |t∗| ≤ 2.021 conclude H0,
otherwise Ha.
b1=.96569, s{b1}=.70922, t∗
1= 1.362, conclude H0
b2=.62916, s{b2}=.77830, t∗
2=.808, conclude H0
b3=.67603, s{b3}=.35574, t∗
3= 1.900, conclude H0
No
d.
X1
X2
X3
1.9744 .3760
1.4099
1
10.14. a. (V IF )1= (1 −.950179)−1= 20.072
(V IF )2= (1 −.951728)−1= 20.716
(V IF )3= (1 −.178964)−1= 1.218
b. ˆ
Y= 3.16277 + 1.65806X1
10.15. b. (V IF )1= 1, (V IF )2= 1
10.16. b. (V IF )1= 1.0086, (V IF )2= 1.0196, (V IF )3= 1.0144.
10-4
10.17. b. (V IF )1= 1.6323, (V IF )2= 2.0032, (V IF )3= 2.0091
10.18. b.
(V IF )1= (1 −.193775)−1= 1.2403
(V IF )2= (1 −.393287)−1= 1.6482
(V IF )3= (1 −.244458)−1= 1.3236
(V IF )4= (1 −.292147)−1= 1.4127
10.19.a,b&c.
i: 1 2 3 ··· 23 24 25
ei: 3.308 5.494 −2.525 ··· −.202 .172 2.035
e(Y|X1): 4.35 8.16 .53 ··· −14.52 27.41 −3.12
e(X3|X1): .57 1.46 1.68 ··· −7.85 14.94 −2.83
e(Y|X3): −2.63 −8.66 −.53 ··· 1.15 −5.14 −1.72
e(X1|X3): −17.03 −40.61 5.73 ··· 3.87 −15.24 −10.79
Exp. value: 4.744 5.590 −2.724 ··· .522 1.050 2.724
H0: normal, Ha: not normal. r=.983. If r≥.939 conclude H0, otherwise
Ha. Conclude H0.
d and e.
i: 1 2 3 ··· 23 24 25
hii:.071 .214 .046 ··· .074 .171 .060
ti:.645 1.191 −.484 ··· −.039 .035 .392
t(.999; 21) = 3.53. If |ti| ≤ 3.53 conclude no outliers, otherwise outliers.
Conclude no outliers.
f.
DF BET AS
Case DF F IT S b0b1b3D
7−.340 −.240 −.151 .303 .040
16 .603 −.069 .152 .051 .092
18 1.000 −.464 .878 .115 .308
g. (V IF )1= (V IF )2= 1.034
10.20.a&b. ˆ
Y= 134.400 −2.133X1−1.699X2+.0333X1X2
i: 1 2 3 ··· 17 18 19
ei: 17.740 4.161 −4.616 ··· −7.061 −.582 −8.256
Exp. value: 14.564 5.789 −2.788 ··· −7.467 .000 −11.609
r=.963
c. (V IF )1= 5.431, (V IF )2= 11.640, (V IF )3= 22.474
d&e.
i: 1 2 3 ··· 17 18 19
hii:.276 .083 .539 ··· .144 .139 .077
ti: 2.210 .399 −.629 ··· −.709 −.057 −.802
10-5

t(.9987; 14) = 3.65. If |ti| ≤ 3.65 conclude no outliers, otherwise outliers. Con-
clude no outliers.
f.
DF BET AS
Case DF F IT S b0b1b2b3D
3−.680 −.652 .592 .433 −.482 .121
7 1.749 1.454 −1.278 −.742 .848 .459
8−4.780 −1.547 1.187 3.162 −3.286 4.991
15 .175 −.016 −.035 .077 −.016 .008
10.21. a. (V IF )1= 1.305, (V IF )2= 1.300, (V IF )3= 1.024
b&c.
i: 1 2 3 ··· 32 33
ei: 13.181 −4.042 3.060 ··· 14.335 1.396
e(Y|X2, X3): 26.368 −2.038 −31.111 ··· 6.310 5.845
e(X1|X2, X3): −.330 −.050 .856 ··· .201 .111
e(Y|X1, X3): 18.734 −17.470 8.212 ··· 12.566 −8.099
e(X2|X1, X3): −7.537 18.226 −6.993 ··· 2.401 12.888
e(Y|X1, X2): 11.542 −7.756 15.022 ··· 6.732 −15.100
e(X3|X1, X2): −2.111 −4.784 15.406 ··· −9.793 −21.247
Exp. value: 11.926 −4.812 1.886 ··· 17.591 −.940
10.22. a. ˆ
Y0=−2.0427 −.7120X0
1+.7474X0
2+.7574X0
3, where Y0= logeY,X0
1= logeX1,
X0
2= loge(140 −X2), X0
3= logeX3
b.
i: 1 2 3 ··· 31 32 33
ei:−.0036 .0005 −.0316 ··· −.1487 .2863 .1208
Exp. value: .0238 .0358 −.0481 ··· −.1703 .2601 .1164
c. (V IF )1= 1.339, (V IF )2= 1.330, (V IF )3= 1.016
d&e.
i: 1 2 3 ··· 31 32 33
hii:.101 .092 .176 ··· .058 .069 .149
ti:−.024 .003 −.218 ··· −.975 1.983 .829
t(.9985; 28) = 3.25. If |ti| ≤ 3.25 conclude no outliers, otherwise outliers. Con-
clude no outliers.
f.
DF BET AS
Case DF F IT S b0b1b2b3D
28 .739 .530 −.151 −.577 −.187 .120
29 −.719 −.197 −.310 −.133 .420 .109
10.23. ˆ
Y=Xb,ˆ
Y(i)=Xb(i). From (10.33a), we obtain:
Di=(Xb −Xb(i))0(Xb −Xb(i))
pMSE =(b−b(i))0X0X(b−b(i))
pMSE
10-6
10.24. H=X(X0X)−1X0=XX−1(X0)−1X0=II =I
hii = 1, ˆ
Yi=Yi
10.25. MSE(i)="(n−p)SSE
n−p−e2
i
1−hii #÷(n−p−1) from (10.25)
Substitution into (10.24a) yields (10.26):
ti=ei"n−p−1
SSE(1 −hii)−e2
i#1/2
10.26. From Exercise 5.31, σ2{ˆ
Y}=Hσ2or σ2{ˆ
Yi}=σ2hii ; hence
Pσ2{ˆ
Yi}=σ2Phii =σ2pby (10.27)
10.27.a&b.
i: 57 58 59 ··· 111 112 113
ei:−.086 −.064 −.004 ··· −.049 .086 .019
Exp. value: −.077 −.057 −.005 ··· −.043 .084 .010
H0: normal, Ha: not normal. r=.990. If r≥.980 conclude H0, otherwise Ha.
Conclude H0.
c. (V IF )3= 1.065, (V IF )6= 1.041, (V IF )10 = 1.045
X3
X6
X10
1.161 −.172
1.086
1
Note: Variable numbers for predictor variables are those in the data set descrip-
tion.
d&e.
i: 57 58 59 ··· 111 112 113
hii:.055 .055 .069 ··· .042 .288 .067
ti:−1.617 −1.201 −.079 ··· −.911 1.889 .348
t(.9999; 52) = 4.00. If |ti| ≤ 4.00 conclude no outliers, otherwise outliers. Con-
clude no outliers.
f.
DF BET AS
Case DF F IT S b0b3b6b10 D
62 .116 .010 .007 −.061 .094 .003
75 .254 .222 −.242 .069 −.066 .016
87 −.411 .025 −.031 .022 −.291 .040
106 .757 −.437 .626 −.400 −.032 .138
112 1.200 −.464 .372 .051 1.132 .343
10.28.a&b.
10-7
i: 2 4 6 ··· 436 438 440
ei:−.794 .323 4.615 ··· .078 .007 −.008
Exp. value: −1.011 .644 1.011 ··· .249 .052 −.010
H0: normal, Ha: not normal. r=.636. If r≥.982 conclude H0, otherwise Ha.
Conclude Ha.
c. (V IF )6= 1.0093, (V IF )8= 4.5906,(V IF )9= 4.2859, (V IF )13 = 1.4728,(V IF )14 =
1.1056, (V IF )15 = 1.4357,
X6
X8
X9
X13
X14
X15
1.174 .113 −.025 −.222 .078
1.921 .033 −.056 .312
1.173 .034 .145
1.513 −.649
1−.379
Note: Variable numbers for predictor variables are those in the data set descrip-
tion.
d&e.
i: 2 4 6 ··· 436 438 440
hii:.514 .090 .095 ··· .063 .041 .007
ti:−3.182 .926 31.797 ··· .219 .020 −.021
t(.99989; 212) = 3.759. If |ti| ≤ 3.759 conclude no outliers, otherwise outliers.
Conclude case 6 is an outlier.
f.
DF BET AS
Case DF F IT S b0b6b8b9b13 b14 b15 D
2−3.27 −2745.72 .403 −.479 −.815 1.184 −.825 1.188 1.467
8−.60 595.06 −.052 .456 −.548 .006 −.488 −.178 .052
48 .31 134.34 −.079 .290 −.271 .088 −.215 .030 .014
128 −.10 170.25 −.003 −.014 .023 −.093 −.222 −.038 .001
206 .20 −399.49 −.056 .030 .0005 .157 −.142 −.275 .006
404 −.12 220.73 −.019 −.011 .018 −.001 −.654 −.028 .002
6 10.29 −8536.94 .274 −4.236 6.678 2.729 5.196 2.110 2.634
10-8

Chapter 11
BUILDING THE REGRESSION
MODEL III: REMEDIAL
MEASURES
11.6. a. ˆ
Y= 19.4727 + 3.2689X
i: 1 2 3 4 5 6
ei: 5.225 4.763 -6.389 -2.162 -3.237 -5.044
i: 7 8 9 10 11 12
ei: 2.838 1.032 6.418 -1.700 2.687 -4.431
b. n1= 6, ¯
d1= 2.821, n2= 6, ¯
d2= 4.833, s= 1.572,
t∗
BF = (2.821 −4.833)/³1.572q1/6+1/6´=−2.218,
t(.975; 10) = 2.228. If |t∗
BF | ≤ 2.228 conclude error variance constant, otherwise
error variance not constant. Conclude error variance constant.
d. ˆs=−.905 + .3226X; smallest weight = .02607, case 3; largest weight = .18556,
cases 4 and 7.
e. ˆ
Y= 17.3006 + 3.4211X
f.
s{b0}:
s{b1}:
Unweighted Weighted
5.5162 4.8277
.3651 .3703
g. ˆ
Y= 17.2697 + 3.4234X
11.7. a. ˆ
Y=−5.750 + .1875X
i: 1 2 3 4 5 6
ei: -3.75 5.75 -13.50 -16.25 -9.75 7.50
i: 7 8 9 10 11 12
ei: -10.50 26.75 14.25 -17.25 -1.75 18.50
b. SSR∗= 123,753.125, SSE = 2,316.500,
11-1

X2
BP = (123,753.125/2)/(2,316.500/12)2= 1.66, χ2(.90; 1) = 2.71. If X2
BP ≤2.71
conclude error variance constant, otherwise error variance not constant. Conclude
error variance constant.
d. ˆv=−180.1 + 1.2437X
i:123456
weight: .01456 .00315 .00518 .00315 .01456 .00518
i: 7 8 9 10 11 12
weight: .00518 .00315 .01456 .00315 .01456 .00518
e. ˆ
Y=−6.2332 + .1891X
f.
s{b0}:
s{b1}:
Unweighted Weighted
16.7305 13.1672
.0538 .0506
g. ˆ
Y=−6.2335 + .1891X
11.8. b. ˆ
Y= 31.4714 + 10.8120X1+ 22.6307X2+ 1.2581X3+ 1.8523X4
i: 1 2 3 ··· 63 64 65
ei: -3.2892 -3.2812 -.3274 ··· 36.9093 -18.6811 -5.3643
c. n1= 33, ¯
d1= 2.7595, n2= 32, ¯
d2= 10.1166, s= 6.3643,
t∗
BF = (2.7595 −10.1166)/³6.3643q1/33 + 1/32´=−4.659,
t(.995; 63) = 2.656. If |t∗
BF | ≤ 2.656 conclude error variance constant, otherwise
error variance not constant. Conclude error variance not constant.
e. ˆs= 2.420 + .3996X3+.2695X4
i: 1 2 3 ··· 63 64 65
weight: .0563 .0777 .0015 ··· .1484 .0941 .0035
f. ˆ
Y= 29.4255 + 10.8996X1+ 26.6849X2+ 1.4253X3+ 1.7239X4
g.
s{b0}:
s{b1}:
s{b2}:
s{b3}:
s{b4}:
Unweighted Weighted
2.8691 1.3617
3.2183 1.4918
3.4846 1.6686
.2273 .2002
.2276 .3206
h. ˆ
Y= 29.0832 + 11.0075X1+ 26.8142X2+ 1.4904X3+ 1.6922X4
11.9. b. c=.06
c. ˆ
Y∗=.410X∗
1+.354X∗
2+.165X∗
3
ˆ
Y= 21.7290 + 1.7380X1+.1727X2+.6929X3
11.10. a. ˆ
Y= 3.32429 + 3.76811X1+ 5.07959X2
11-2

d. c=.07
e. ˆ
Y= 6.06599 + 3.84335X1+ 4.68044X2
11.11. a. ˆ
Y= 1.88602 + 15.1094X(47 cases)
ˆ
Y=−.58016 + 15.0352X(45 cases)
b. i: 1 2 . . . 46 47
ui: -1.4123 -.2711 . . . 4.6045 10.3331
smallest weights: .13016 (case 47), .29217 (case 46)
c. ˆ
Y=−.9235 + 15.13552X
d. 2nd iteration: ˆ
Y=−1.535 + 15.425X
3rd iteration: ˆ
Y=−1.678 + 15.444X
smallest weights: .12629 (case 47), .27858 (case 46)
11.12. a. ˆ
Y=−193.924 + 5.248X
b. smallest weight: .5582 (case 2)
c. ˆ
Y=−236.259 + 5.838X
d. 2nd iteration: ˆ
Y=−241.577 + 5.914X
3rd iteration: ˆ
Y=−242.606 + 5.928X
smallest weight: .5025 (case 2)
11.13. Qw=P1
kXi
(Yi−β0−β1Xi)2
∂Qw
∂β0
=−2X1
kXi
(Yi−β0−β1Xi)
∂Qw
∂β1
=−2X1
k(Yi−β0−β1Xi)
Setting the derivatives equal to zero, simplifying, and substituting the least squares
estimators b0and b1yields:
PYi
Xi−b0X1
Xi−nb1= 0
PYi−nb0−b1PXi= 0
11.14. bw1=Pwi(Xi−¯
Xw)(Yi−¯
Yw)
Pwi(Xi−¯
Xw)2
since Pwi(Xi−¯
Xw)(Yi−¯
Yw) = PwiXiYi−(Pwi)¯
Xw¯
Yw
=PwiXiYi−PwiXiPwiYi
Pwi
and Pwi(Xi−¯
Xw)2=PwiX2
i−(Pwi)¯
X2
w
11-3

=PwiX2
i−(PwiXi)2
Pwi
11.17.
X1/.3 0 0 0
0X2/.3 0 0
0 0 X3/.3 0
0 0 0 X4/.3
11.18. bw= (X0WX)−1X0WY
σ2{bw}= [(X0WX)−1X0W](kW−1)[(X0WX)−1X0W]0
=k(X0WX)−1X0WW−1[W0X(X0WX)−1]
(since (X0WX)−1is symmetric)
=k(X0WX)−1X0IWX(X0WX)−1
(since Wis symmetric)
=k(X0WX)−1
11.19. E{bR−β}2=E{bR−E{bR}+E{bR} − β}2
=E{bR−E{bR}}2+ 2E{bR−E{bR}}[E{bR} − β] + E{E{bR} − β}2
=σ2{bR}+0+[E{bR} − β]2
11.20. a. 38.3666
b. 38.5822, yes.
11.21. a. Xh: 10 20 30 40 50
E{Yh}: 120 220 320 420 520
c. Ordinary least squares: E{b1}= 10, σ2{b1}=.024
Weighted least squares: E{b1}= 10, σ2{b1}=.01975
11.22. a.
c(V IF )1(V IF )2(V IF )3R2
.000 1.6323 2.0032 2.0091 .68219
.005 1.6000 1.9506 1.9561 .68218
.010 1.5687 1.9002 1.9054 .68215
.020 1.5089 1.8054 1.8101 .68204
.030 1.4527 1.7181 1.7222 .68185
.040 1.3997 1.6374 1.6411 .68160
.050 1.3497 1.5626 1.5659 .68129
11-4
c bR
1bR
2bR
3
.000 −.5907 −.1106 −.2339
.005 −.5868 −.1123 −.2338
.010 −.5831 −.1140 −.2337
.020 −.5758 −.1171 −.2334
.030 −.5687 −.1200 −.2331
.040 −.5619 −.1228 −.2329
.050 −.5553 −.1253 −.2326
11.23. a. ˆ
Y= 62.4054 + 1.5511X1+.5102X2+.1019X3−.1441X4
b.
c(V IF )1(V IF )2(V IF )3(V IF )4R2
.000 38.496 254.423 46.868 282.513 .9824
.002 9.844 51.695 11.346 57.092 .9823
.004 5.592 21.903 6.089 23.971 .9822
.006 4.183 12.253 4.359 13.248 .9822
.008 3.530 7.957 3.566 8.478 .9821
.020 2.456 2.108 2.323 2.015 .9819
.040 1.967 .986 1.833 .820 .9813
.060 1.674 .715 1.560 .560 .9805
.080 1.455 .591 1.360 .454 .9794
.010 1.284 .516 1.204 .396 .9783
c bR
1bR
2bR
3bR
4
.000 .6065 .5277 .0434 −.1603
.002 .5524 .3909 −.0159 −.3043
.004 .5351 .3519 −.0343 −.3452
.006 .5257 .3337 −.0439 −.3641
.008 .5193 .3233 −.0502 −.3748
.020 .4975 .3033 −.0694 −.3942
.040 .4751 .2986 −.0864 −.3958
.060 .4577 .2986 −.0984 −.3920
.080 .4429 .2992 −.1079 −.3873
.100 .4300 .2998 −.1157 −.3824
11.24. a. ˆ
Y= 12.2138 −0.1462X1+.2893X2+ 1.4277X3+ 0.0000X4
b. P|Yi−ˆ
Yi|= 64.8315
c. 66.9736, yes.
11.25. a. ˆ
Y= 50.3840 −.7620x1−.5300x2−.2929x2
1
11.26. a. t(.975; 10) = 2.228, bw1= 3.4211, s{bw1}=.3703,
3.4211 ±2.228(.3703), 2.5961 ≤β1≤4.2461
11.27. a. t(.95; 10) = 1.8125, bw1=.18911, s{bw1}=.05056,
.18911 ±1.8125(.05056), .0975 ≤β1≤.2808
11-5
11.28. a. ˆ
Y= 38.64062 + .33143x−.09107x2,R2=.9474
b. ¯
X= 47.5, b1=.331429, b11 =−.091071,
ˆ
Xmax = 47.5−[.5(.331429)]/(−.091071) = 49.3196
ˆ
Yh= 38.640625 + .331429( ˆ
Xmax −47.5) −.091071( ˆ
Xmax −47.5)2= 38.942
11.29 a. First split point at X= 57, SSE = 5108.14
b. Second split point at X= 66, SSE = 4148.78
c. Third split point at X= 47, SSE = 3511.66
11.30 a. First split point at X1= 37, SSE = 6753.62
b. Second split point at X1= 47, SSE = 5276.25
c. Third split point at X1= 30, SSE = 3948.85
d. Fourth split point at X2= 49, for the region defined by X1<30. SSE = 3563.79
11-6

Chapter 12
AUTOCORRELATION IN TIME
SERIES DATA
12.1. a.
t: 1 2 3 4 5 6 7 8 9 10
εt: 3.5 2.8 3.1 3.1.8−1.1−.9−1.2−1.0−1.1
εt−1: 3.0 3.5 2.8 3.1 3.1.8−1.1−.9−1.2−1.0
b.
t: 1 2 3 4 5 6 7 8 9 10
ut:.5−.7.3 0 −2.3−1.9.2−.3.2−.1
εt−1: 3.0 3.5 2.8 3.1 3.1.8−1.1−.9−1.2−1.0
12.2. Yes.
12.5. (1) H0:ρ= 0, Ha:ρ6= 0. dL= 1.12, dU= 1.45. If D > 1.45 and 4 −D > 1.45,
conclude H0, if D < 1.12 or 4 −D < 1.12 conclude Ha, otherwise the test is
inconclusive.
(2) H0:ρ= 0, Ha:ρ < 0. dL= 1.32, dU= 1.66. If 4 −D > 1.66 conclude H0, if
4−D < 1.32 conclude Ha, otherwise the test is inconclusive.
(3) H0:ρ= 0, Ha:ρ > 0. dL= 1.12, dU= 1.45. If D > 1.45 conclude H0, if
D < 1.12 conclude Ha, otherwise the test is inconclusive.
12.6. H0:ρ= 0, Ha:ρ > 0. D= 2.4015, dL= 1.29, dU= 1.38. If D > 1.38 conclude H0, if
D < 1.29 conclude Ha, otherwise the test is inconclusive. Conclude H0.
12.7 H0:ρ= 0, Ha:ρ > 0. D= 2.2984, dL= 1.51, dU= 1.59. If D > 1.59 conclude H0, if
D < 1.51 conclude Ha, otherwise the test is inconclusive. Conclude H0.
12.8. H0:ρ= 0, Ha:ρ > 0. D= 2.652, dL=.83, dU= 1.52. If D > 1.52 conclude H0, if
D < .83 conclude Ha, otherwise the test is inconclusive. Conclude H0.
12.9. a. ˆ
Y=−7.7385 + 53.9533X,s{b0}= 7.1746, s{b1}= 3.5197
t: 1 2 3 4 5 6 7 8
et:−.0737 −.0709 .5240 .5835 .2612 −.5714 −1.9127 −.8276
12-1
t: 9 10 11 12 13 14 15 16
et:−.6714 .9352 1.803 .4947 .9435 .3156 −.6714 −1.0611
c. H0:ρ= 0, Ha:ρ > 0. D=.857, dL= 1.10, dU= 1.37. If D > 1.37 conclude H0,
if D < 1.10 conclude Ha, otherwise the test is inconclusive. Conclude Ha.
12.10. a. r=.5784, 2(1 −.5784) = .8432, D=.857
b. b0
0=−.69434, b0
1= 50.93322
ˆ
Y0=−.69434 + 50.93322X0
s{b0
0}= 3.75590, s{b0
1}= 4.34890
c. H0:ρ= 0, Ha:ρ > 0. D= 1.476, dL= 1.08, dU= 1.36. If D > 1.36 conclude
H0, if D < 1.08 conclude Ha, otherwise the test is inconclusive. Conclude H0.
d. ˆ
Y=−1.64692 + 50.93322X
s{b0}= 8.90868, s{b1}= 4.34890
f. F17 =−1.64692 + 50.93322(2.210) + .5784(−.6595) = 110.534, s{pred}=.9508,
t(.975; 13) = 2.160, 110.534 ±2.160(.9508), 108.48 ≤Y17(new) ≤112.59
g. t(.975; 13) = 2.160, 50.93322 ±2.160(4.349), 41.539 ≤β1≤60.327.
12.11. a. ρ:.1.2.3.4.5
SSE: 11.5073 10.4819 9.6665 9.0616 8.6710
ρ:.6.7.8.9 1.0
SSE: 8.5032 8.5718 8.8932 9.4811 10.3408
ρ=.6
b. ˆ
Y0=−.5574 + 50.8065X0,s{b0
0}= 3.5967, s{b0
1}= 4.3871
c. H0:ρ= 0, Ha:ρ > 0. D= 1.499, dL= 1.08, dU= 1.36. If D > 1.36 conclude
H0, if D < 1.08 conclude Ha, otherwise test is inconclusive. Conclude H0.
d. ˆ
Y=−1.3935 + 50.8065X,s{b0}= 8.9918, s{b1}= 4.3871
f. F17 =−1.3935+50.8065(2.210)+.6(−.6405) = 110.505, s{pred}=.9467, t(.975; 13) =
2.160, 110.505 ±2.160(.9467),108.46 ≤Y17(new) ≤112.55
12.12. a. b1= 49.80564, s{b1}= 4.77891
b. H0:ρ= 0, Ha:ρ6= 0. D= 1.75 (based on regression with intercept term),
dL= 1.08, dU= 1.36. If D > 1.36 and 4 −D > 1.36 conclude H0, if D < 1.08 or
4−D < 1.08 conclude Ha, otherwise the test is inconclusive. Conclude H0.
c. ˆ
Y=.71172 + 49.80564X,s{b1}= 4.77891
e. F17 =.71172 + 49.80564(2.210) −.5938 = 110.188, s{pred}=.9078, t(.975; 14) =
2.145, 110.188 ±2.145(.9078),108.24 ≤Y17(new) ≤112.14
f. t(.975; 14) = 2.145, 49.80564 ±2.145(4.77891), 39.555 ≤β1≤60.056
12.13. a. ˆ
Y= 93.6865 + 50.8801X,s{b0}=.8229, s{b1}=.2634
t: 1 2 3 4 5 6 7
et:−1.5552 −.2471 −.1526 −.2078 .3349 .6431 .2557
12-2

t: 8 9 10 11 12 13 14
et:.5610 −.4949 −.6824 .0747 −.0817 −.2336 −1.0425
t: 15 16 17 18 19 20
et:−.0299 .5671 .8066 .1203 .5750 .7294
c. H0:ρ= 0, Ha:ρ > 0. D=.974, dL=.95, dU= 1.15. If D > 1.15 conclude H0, if
D < .95 conclude Ha, otherwise the test is inconclusive. The test is inconclusive.
12.14. a. r=.3319, 2(1 −.3319) = 1.3362, D=.974
b. b0
0= 63.3840, b0
1= 50.5470
ˆ
Y0= 63.3840 + 50.5470X0
s{b0
0}=.5592, s{b0
1}=.2622
c. H0:ρ= 0, Ha:ρ > 0. D= 1.76, dL=.93, dU= 1.13. If D > 1.13 conclude H0,
if D < .93 conclude Ha, otherwise the test is inconclusive. Conclude H0.
d. ˆ
Y= 94.8720 + 50.5470X
s{b0}=.8370, s{b1}=.2622
f. F21 = 94.8720 + 50.5470(3.625) + .3319(.7490) = 278.3535, s{pred}=.4743,
t(.995; 17) = 2.898, 278.3535 ±2.898(.4743),276.98 ≤Y21(new) ≤279.73
g. t(.995; 17) = 2.898, 50.5470 ±2.898(.2622), 49.787 ≤β1≤51.307
12.15. a. ρ:.1.2.3.4.5
SSE: 4.0450 3.7414 3.5511 3.4685 3.4889
ρ:.6.7.8.9 1.0
SSE: 3.6126 3.8511 4.2292 4.7772 5.5140
ρ=.4
b. ˆ
Y0= 57.04056 + 50.49249X0,s{b0
0}=.53287, s{b0
1}=.27697
c. H0:ρ= 0, Ha:ρ > 0. D= 1.905, dL=.93, dU= 1.13. If D > 1.13 conclude H0,
if D < .93 conclude Ha, otherwise test is inconclusive. Conclude H0.
d. ˆ
Y= 95.0676 + 50.49249X,s{b0}=.88812, s{b1}=.27697
f. F21 = 95.0676+50.49249(3.625)+.4(.7506) = 278.403, s{pred}=.4703, t(.995; 17) =
2.898, 278.403 ±2.898(.4703),277.04 ≤Y21(new) ≤279.77
g. t(.995; 17) = 2.898, 50.49249 ±2.898(.27697), 49.690 ≤β1≤51.295
12.16. a. b0
1= 50.16414, s{b0
1}=.42496, ˆ
Y0= 50.16414X0
b. H0:ρ= 0, Ha:ρ6= 0. D= 2.425 (based on regression with intercept term),
dL=.93, dU= 1.13. If D > 1.13 and 4 −D > 1.13 conclude H0, if D < .93 or
4−D < .93 conclude Ha, otherwise test is inconclusive. Conclude H0.
c. ˆ
Y= 95.88984 + 50.16414X,s{b1}=.42496
e. F21 = 95.88984+50.16414(3.625)+1.116 = 278.851, s{pred}=.5787, t(.995; 18) =
2.878, 278.851 ±2.878(.5787),277.19 ≤Y21(new) ≤280.52
f. t(.995; 18) = 2.878, 50.16416 ±2.878(.42496), 48.941 ≤β1≤51.387
12-3

12.17. a. Positive
b. ˆ
Y=−1.43484 + .17616X,s{b0}=.24196, s{b1}=.0016322
c. t: 1 2 3 4 5 6 7
et:−.0307 −.0664 .0180 .1593 .0428 .0429 .0582
t: 8 9 10 11 12 13 14
et:−.0613 −.0969 −.1517 −.1501 −.0754 −.0249 .1043
t: 15 16 17 18 19 20
et:.1844 .1054 .0289 .0422 −.0439 −.0852
d. H0:ρ= 0, Ha:ρ > 0. D=.663, dL=.95, dU= 1.15. If D > 1.15 conclude H0,
if D < .95 conclude Ha, otherwise the test is inconclusive. Conclude Ha.
12.18. a. r=.67296, 2(1 −.67296) = .65408, D=.663
b. ˆ
Y=−.29235 + .17261X0,s{b0
0}=.17709, s{b0
1}=.00351.
c. H0:ρ= 0, Ha:ρ > 0. D= 1.364, dL=.93, dU= 1.13. If D > 1.13 conclude H0,
if D < .93 conclude Ha, otherwise test is inconclusive. Conclude H0.
d. ˆ
Y=−.89390 + .17261X,s{b0}=.54149, s{b1}=.00351
f. F21 =−.89390 + .17261(181.0) + .67296(−.015405) = 30.338, s{pred}=.09155,
t(.95; 17) = 1.740, 30.338 ±1.740(.09155), 30.179 ≤Y21(new) ≤30.497.
g. t(.95; 17) = 1.740, .17261 ±1.740(.00351), .1665 ≤β1≤.1787.
12.19. a. ρ:.1.2.3.4.5
SSE:.1492 .1318 .1176 .1064 .09817
ρ:.6.7.8.9 1.0
SSE:.09275 .08978 .08857 .08855 .09433
ρ=.9
b. ˆ
Y0=.04644 + .16484X0,s{b0
0}=.11230, s{b0
1}=.006538
c. H0:ρ= 0, Ha:ρ > 0. D= 1.453, dL=.93, dU= 1.13. If D > 1.13 conclude H0,
if D < .93 conclude Ha, otherwise test is inconclusive. Conclude H0.
d. ˆ
Y=.4644 + .16484X,s{b0}= 1.1230, s{b1}=.006538.
f. F21 =.4644+.16484(181.0)+.9(−.03688) = 30.267, s{pred}=.09545, t(.95; 17) =
1.740, 30.267 ±1.740(.09545),30.101 ≤Y21(new) ≤30.433
g. t(.95; 17) = 1.740, .16484 ±1.740(.006538), .1535 ≤β1≤.1762.
12.20. a. b0
1=.16883, s{b0
1}=.0055426, ˆ
Y0=.16883X0
b. H0:ρ= 0, Ha:ρ > 0. D= 1.480 (based on regression with intercept term),
dL=.93, dU= 1.13. If D > 1.13 conclude H0, if D < .93 conclude Ha, otherwise
test is inconclusive. Conclude H0.
c. ˆ
Y=−.35222 + .16883X,s{b1}=.0055426
e. F21 =−.35222 + .16883(181.0) + .0942 = 30.300, s{pred}=.0907, t(.95; 18) =
1.734, 30.300 ±1.734(.0907), 30.143 ≤Y21(new) ≤30.457
12-4

f. t(.95; 18) = 1.734, .16883 ±1.734(.0055426), .1592 ≤β1≤.1784
12.22.
σ{εt, εt−2}=E{εtεt−2}
=E{[ut+ρut−1+ρ2ut−2+ρ3ut−3+···]
×[ut−2+ρut−3+ρ2ut−4+···]}
=E{[(ut+ρut−1) + ρ2(ut−2+ρut−3+···)]
×[ut−2+ρut−3+ρ2ut−4+···]}
=E{(ut+ρut−1)(ut−2+ρut−3+ρ2ut−4+···)}
+E{ρ2(ut−2+ρut−3+ρ2ut−4+· · ·)2}
=ρ2E{ut−2+ρut−3+ρ2ut−4+· · ·}2=ρ2E{ε2
t−2}
=ρ2σ2{εt−2}=ρ2σ2{εt}=ρ2Ãσ2
1−ρ2!
12.23. a. E{Y}= 100 −.35X
t:123456
Yt: 67.2058 61.5825 58.8570 67.2065 68.9889 73.4943
t: 7 8 9 10
Yt: 74.8076 66.7686 62.9622 61.3573
ˆ
Y= 96.08317 −.30839X
b.
t:123456
Yt: 65.7640 60.2590 57.7580 66.6920 69.7650 74.2510
t: 7 8 9 10
Yt: 74.9610 67.1840 62.9510 61.5300
ˆ
Y= 98.94338 −.34023X
c.
t:123456
Yt: 64.0819 60.9017 56.9518 67.4257 70.5170 74.0641
t: 7 8 9 10
Yt: 74.7411 67.7152 62.2754 62.2122
ˆ
Y= 99.45434 −.34576X
εt−εt−1:
t: 1 2 3 4 5
ρ=.6: −.1972 −.3733 −.9750 −2.1510 .0324
ρ= 0: −1.6390 −.2550 −.7510 −1.5660 1.3230
ρ=−.7: −3.3211 2.0698 −2.1999 −.0261 1.3413
t: 6 7 8 9 10
ρ=.6: 1.0054 −.4367 .7110 −.3064 .1451
ρ= 0: .9860 −1.0400 .9730 −.7330 .3290
ρ=−.7: .0471 −1.0730 1.7241 −1.9398 1.6868
12-5

d.
ρΣ(εt−εt−1)2
.6 7.579
0 11.164
-.7 32.687
12.24. Y0
t=Yt−ρYt−1
=β0+β1Xt1+β2Xt2+εt−ρ(β0+β1Xt−1,1+β2Xt−1,2+εt−1)
=β0(1 −ρ) + β1(Xt1−ρXt−1,1) + β2(Xt2−ρXt−1,2)+(εt−ρεt−1)
Since εt−ρεt−1=ut, we have:
Y0
t=β0
0+β0
1X0
t1+β0
2X0
t2+ut
where β0
0=β0(1 −ρ), β0
1=β1,β0
2=β2,X0
t1=Xt1−ρXt−1,1, and
X0
t2=Xt2−ρXt−1,2
12.25. a. Y0
t=Yt−ρ1Yt−1−ρ2Yt−2
X0
t=Xt−ρ1Xt−1−ρ2Xt−2
b. By regressing the residuals etagainst the two independent variables et−1and et−2
with no intercept term in the regression model and obtaining the two regression
coefficients. The answer to Exercise 6.23a provides the explicit formulas, with Y,
X1, and X2replaced by et,et−1, and et−2, respectively.
c. By minimizing SSE =P(Y0
t−b0
0−b0
1X0
t)2with respect to ρ1and ρ2.
12.26. Yn+1 =β0+β1Xn+1 +ρ1εn+ρ2εn−1+un+1
since εn+1 =ρ1εn+ρ2εn−1+un+1. Therefore:
Fn+1 =ˆ
Yn+1 +r1en+r2en−1
where r1and r2are point estimates of ρ1and ρ2, respectively, obtained by either the
Cochrane-Orcutt procedure or the Hildreth-Lu procedure.
12.27. c. E{b1}= 24 even in presence of positive autocorrelation.
12-6

Chapter 13
INTRODUCTION TO NONLINEAR
REGRESSION AND NEURAL
NETWORKS
13.1. a. Intrinsically linear
logef(X,γ) = γ0+γ1X
b. Nonlinear
c. Nonlinear
13.2. a. Intrinsically linear
logef(X,γ) = γ0+γ1logeX
b. Intrinsically linear
logef(X,γ) = logeγ0+γ1logeX1+γ2logeX2
c. Nonlinear
13.3. b. 300, 3.7323
13.4. b. 49, 2.2774
13.5. a. b0=−.5072512, b1=−0.0006934571, g(0)
0= 0, g(0)
1=.0006934571, g(0)
2=.6021485
b. g0=.04823, g1=.00112, g2=.71341
13.6. a. ˆ
Y=.04823 + .71341exp(−.00112X)
City A
i: 1 2 3 4 5
ˆ
Yi:.61877 .50451 .34006 .23488 .16760
ei:.03123 −.04451 −.00006 .02512 .00240
Exp. value: .04125 −.04125 −.00180 .02304 .00180
i: 6 7 8
ˆ
Yi:.12458 .07320 .05640
ei:.02542 −.01320 −.01640
Exp. value: .02989 −.01777 −.02304
13-1

City B
i: 9 10 11 12 13
ˆ
Yi:.61877 .50451 .34006 .23488 .16760
ei:.01123 −.00451 −.04006 .00512 .02240
Exp. value: .01327 −.00545 −.02989 .00545 .01777
i: 14 15 16
ˆ
Yi:.12458 .07320 .05640
ei:−.00458 .00680 −.00640
Exp. value: −.00923 .00923 −.01327
13.7. H0:E{Y}=γ0+γ2exp(−γ1X), Ha:E{Y} 6=γ0+γ2exp(−γ1X).
SSP E =.00290, SSE =.00707, MSP E =.00290/8 = .0003625,
MSLF = (.00707 −.00290)/5 = .000834, F∗=.000834/.0003625 = 2.30069,
F(.99; 5,8) = 6.6318. If F∗≤6.6318 conclude H0, otherwise Ha. Conclude H0.
13.8. s{g0}=.01456, s{g1}=.000092, s{g2}=.02277, z(.9833) = 2.128
.04823 ±2.128(.01456) .01725 ≤γ0≤.07921
.00112 ±2.128(.000092) .00092 ≤γ1≤.00132
.71341 ±2.128(.02277) .66496 ≤γ2≤.76186
13.9. a. g0=.04948, g1=.00112, g2=.71341, g3=−.00250
b. z(.975) = 1.96, s{g3}=.01211, −.00250 ±1.96(.01211), −.02624 ≤γ3≤.02124,
yes, no.
13.10. a. b0=.03376, b1=.454, g(0)
0= 29.6209, g(0)
1= 13.4479
b. g0= 28.13705, g1= 12.57445
13.11. a. ˆ
Y= 28.13705X/(12.57445 + X)
b.
i: 1 2 3 4 5 6
ˆ
Yi: 2.0728 2.9987 3.8611 5.4198 6.7905 8.0051
ei:.0272 −.4987 1.0389 .0802 .2095 .3949
Exp. value: −.1076 −.5513 .9447 .1076 .2597 .3442
i: 7 8 9 10 11 12
ˆ
Yi: 9.0890 10.5123 11.3486 12.4641 14.0268 15.3060
ei:.5110 −.3123 .0514 .0359 −.9268 −.7060
Exp. value: .4390 −.3442 .0356 −.0356 −.9447 −.6983
i: 13 14 15 16 17 18
ˆ
Yi: 16.3726 17.2755 18.7209 19.8267 20.7001 21.4074
ei:.6274 −.4755 −.1209 −.1267 .5999 .1926
Exp. value: .6983 −.4390 −.1817 −.2597 .5513 .1817
c. No
13-2

13.12. s{g0}=.72798, s{g1}=.76305, z(.975) = 1.960
(1) 28.13705 ±1.960(.72798), 26.7102 ≤γ0≤29.5639
(2) H0:γ1= 20, Ha:γ16= 20. z∗= (12.57445 −20)/.76305 = −9.731.
If |z∗| ≤ 1.960 conclude H0, otherwise Ha. Conclude Ha.
13.13. g0= 100.3401, g1= 6.4802, g2= 4.8155
13.14. a. ˆ
Y= 100.3401 −100.3401/[1 + (X/4.8155)6.4802]
b.
i: 1 2 3 4 5 6 7
ˆ
Yi:.0038 .3366 4.4654 11.2653 11.2653 23.1829 23.1829
ei:.4962 1.9634 −1.0654 .2347 −.3653 .8171 2.1171
Expected Val.: .3928 1.6354 −1.0519 −.1947 −.5981 .8155 2.0516
i: 8 9 10 11 12 13 14
ˆ
Yi: 39.3272 39.3272 56.2506 56.2506 70.5308 70.5308 80.8876
ei:.2728 −1.4272 −1.5506 .5494 .2692 −2.1308 1.2124
Expected Val.: .1947 −1.3183 −1.6354 .5981 .0000 −2.0516 1.0519
i: 15 16 17 18 19
ˆ
Yi: 80.8876 87.7742 92.1765 96.7340 98.6263
ei:−.2876 1.4258 2.6235 −.5340 −2.2263
Expected Val.: −.3928 1.3183 2.7520 −.8155 −2.7520
13.15. H0:E{Y}=γ0−γ0/[1 + (X/γ2)γ1], Ha:E{Y} 6=γ0−γ0/[1 + (X/γ2)γ1].
SSP E = 8.67999, SSE = 35.71488, MSP E = 8.67999/6=1.4467, MSLF =
(35.71488 −8.67999)/10 = 2.7035, F∗= 2.7035/1.4467 = 1.869,F(.99; 10,6) = 7.87. If
F∗≤7.87 conclude H0, otherwise Ha. Conclude H0.
13.16. s{g0}= 1.1741, s{g1}=.1943, s{g2}=.02802, z(.985) = 2.17
100.3401 ±2.17(1.1741) 97.7923 ≤γ0≤102.8879
6.4802 ±2.17(.1943) 6.0586 ≤γ1≤6.9018
4.8155 ±2.17(.02802) 4.7547 ≤γ2≤4.8763
13.17. a. b0=.98187, b1=.51485, b2=.29845, g(0)
0= 9.5911, g(0)
1=.51485, g(0)
2=.29845
b. g0= 10.0797, g1=.49871, g2=.30199
13.18. a. ˆ
Y= 10.0797X.49871
1X.30199
2
b.
i: 1 2 3 4 5 6
ˆ
Yi: 10.0797 31.7801 100.1987 20.2039 63.7005 200.8399
ei: 1.9203 .2199 2.8013 −.2039 −2.7005 −2.8399
Exp.val: 1.4685 .2880 2.7817 −.2880 −2.7817 −3.5476
13-3

i: 7 8 9 10 11 12
ˆ
Yi: 40.4970 127.6823 402.5668 10.0797 31.7801 100.1987
ei:−2.4970 5.3177 3.4332 −2.0797 6.2199 −2.1987
Exp.val: −2.0992 5.6437 3.5476 −.8696 7.6346 −1.4685
i: 13 14 15 16 17 18
ˆ
Yi: 20.2039 63.7005 200.8399 40.4970 127.6823 402.5668
ei:−6.2039 −7.7005 4.1601 2.5030 .3177 −4.5668
Exp.val: −5.6437 −7.6346 4.4559 2.0992 .8696 −4.4559
13.19. H0:E{Y}=γ0Xγ1
1Xγ2
2,Ha:E{Y} 6=γ0Xγ1
1Xγ2
2.F(.95; 6,9) = 3.37, SSP E = 150.5,
SSE = 263.443, SSLF = 112.943, F∗= [112.943/(15 −9)] ÷(150.5/9) = 1.126. If
F∗≤3.37 conclude H0, otherwise Ha. Conclude H0.
13.20. a. H0:γ1=γ2,Ha:γ16=γ2.F(.95; 1,15) = 4.54, SSP E = 263.443, SSE =
9,331.62, MSP E = 263.443/15 = 17.563, MSLF = (9,331.62 −263.443)/1 =
9,068.177, F∗= 9,068.177/17.563 = 516.327.If F∗≤4.54 conclude H0, otherwise
Ha. Conclude Ha.
b. s{g1}=.00781, s{g2}=.00485, z(.9875) = 2.24
.49871 ±2.24(.00781) .4812 ≤γ1≤.5162
.30199 ±2.24(.00485) .2911 ≤γ2≤.3129
c. γ16=γ2
13.21. a. Q=P{Yi−[γ0+γ2exp(−γ1Xi)]}2
∂Q
∂γ0
=−2X[Yi−γ0−γ2exp(−γ1Xi)]
∂Q
∂γ1
= 2 X[Yi−γ0−γ2exp(−γ1Xi)][γ2Xiexp(−γ1Xi)]
∂Q
∂γ2
=−2X[Yi−γ0−γ2exp(−γ1Xi)][exp(−γ1Xi)]
Setting each derivative equal to zero, simplifying, and substituting the least squares
estimators g0,g1, and g2yields:
PYi−ng0−g2Pexp(−g1Xi) = 0
g2PYiXiexp(−g1Xi)−g0g2PXiexp(−g1Xi)−g2
2PXiexp(−2g1Xi) = 0
PYiexp(−g1Xi)−g0Pexp(−g1Xi)−g2Pexp(−2g1Xi) = 0
b. L(γ,σ2) = 1
(2πσ2)n/2exp ½−1
2σ2X[Yi−γ0−γ2exp(−γ1Xi)]2¾
13.22. a. Q=PÃYi−γ0Xi
γ1+Xi!2
∂Q
∂γ0
=−2XÃYi−γ0Xi
γ1+Xi!Ã Xi
γ1+Xi!
∂Q
∂γ1
= 2 XÃYi−γ0Xi
γ1+Xi!" γ0Xi
(γ1+Xi)2#
13-4
Setting the derivatives equal to zero, simplifying, and substituting the least squares
estimators g0and g1yields:
PYiXi
g1+Xi−g0XÃXi
g1+Xi!2
= 0
g0PYiXi
(g1+Xi)2−g2
0X"X2
i
(g1+Xi)3#= 0
b. L(γ, σ2) = 1
(2πσ2)n/2exp
−1
2σ2XÃYi−γ0Xi
γ1+Xi!2
13.23. a. Q=P(Yi−γ0Xγ1
i1Xγ2
i2)2
∂Q
∂γ0
=−2X(Yi−γ0Xγ1
i1Xγ2
i2) (Xγ1
i1Xγ2
i2)
∂Q
∂γ1
=−2X(Yi−γ0Xγ1
i1Xγ2
i2) (γ0Xγ1
i1Xγ2
i2logeXi1)
∂Q
∂γ2
=−2X(Yi−γ0Xγ1
i1Xγ2
i2) (γ0Xγ1
i1Xγ2
i2logeXi2)
Setting the derivatives equal to zero, simplifying, and substituting the least squares
estimators g0,g1, and g2yields:
PYiXg1
i1Xg2
i2−g0PX2g1
i1X2g2
i2= 0
g0PYiXg1
i1Xg2
i2logeXi1−g2
0PX2g1
i1X2g2
i2logeXi1= 0
g0PYiXg1
i1Xg2
i2logeXi2−g2
0PX2g1
i1X2g2
i2logeXi2= 0
b. L(γ, σ2) = 1
(2πσ2)n/2exp ·−1
2σ2X(Yi−γ0Xγ1
i1Xγ2
i2)2¸
13.24. a. E{Y}=E(γ0−γ0
1+(X/γ2)γ1+ε)
=γ0−γ0
1+(X/γ2)γ1=γ0"(X/γ2)γ1
1+(X/γ2)γ1#=γ0µA
1 + A¶
since (X/γ2)γ1= exp[γ1(logeX−logeγ2)].
b. E{Y0}= (1/γ0)E{Y0}=A/(1 + A); hence:
E{Y0}
1−E{Y0}=
A
1 + A
1−A
1 + A
=A= exp(β0+β1X0)
c. logeÃY0
1−Y0!= logeÃY
γ0−Y!,X0= logeX
d. Since β0=−γ1logeγ2or γ2= exp(−β0/γ1) and γ1=β1, starting values are
g(0)
1=b1and g(0)
2= exp ³−b0/g(0)
1´.
13.25.
13-5
(5, 5) 1,908.388
(5, 15) 2,285.707
(5, 25) 2,489.092
(5, 35) 2,620.201
(5, 45) 2,712.754
(5, 55) 2,781.925
(5, 65) 2,835.726
(15, 5) 303.526
(15, 15) 838.411
(15, 25) 1,241.451
(15, 35) 1,531.436
(15, 45) 1,748.814
(15, 55) 1,917.745
(15, 65) 2,052.838
(25, 5) 209.013
(25, 15) 105.367
(25, 25) 431.908
(25, 35) 742.980
(25, 45) 1,004.812
(25, 55) 1,222.057
(25, 65) 1,403.365
(35, 5) 1,624.851
(35, 15) 86.575
(35, 25) 60.464
(35, 35) 254.834
(35, 45) 480.747
(35, 55) 694.863
(35, 65) 887.306
(45, 5) 4,551.038
(45, 15) 782.035
(45, 25) 127.119
(45, 35) 66.999
(45, 45) 176.620
(45, 55) 336.160
(45, 65) 504.661
(55, 5) 8,987.574
(55, 15) 2,191.748
(55, 25) 631.873
(55, 35) 179.473
(55, 45) 92.431
(55, 55) 145.951
(55, 65) 255.430
(65, 5) 14,934.461
(65, 15) 4,315.713
(65, 25) 1,574.725
(65, 35) 592.257
(65, 45) 228.178
(65, 55) 124.234
(65, 65) 139.613
13.26.
(1, .2, .1) 459,935
(1, .2, .4) 433,916
(1, .2, .7) 345,157
(1, .5, .1) 429,284
(1, .5, .4) 342,964
(1, .5, .7) 119,656
(1, .8, .1) 322,547
(1, .8, .4) 98,262.9
(1, .8, .7) 728,313
(11, .2, .1) 348,524
(11, .2, .4) 153,117
(11, .2, .7) 494,720
(11, .5, .1) 124,813
(11, .5, .4) 201,515
(11, .5, .7) 12,640,200
(11, .8, .1) 649,132
(11, .8, .4) 13,211,900
(11, .8, .7) 238,296,000
(21, .2, .1) 257,136
(21, .2, .4) 57,435.2
(21, .2, .7) 3,225,660
(21, .5, .1) 46,639.7
(21, .5, .4) 2,152,210
(21, .5, .7) 54,335,000
(21, .8, .1) 4,290,060
(21, .8, .4) 56,967,000
(21, .8, .7) 903,149,000
13-6
Chapter 14
LOGISTIC REGRESSION,
POISSON REGRESSION,AND
GENERALIZED LINEAR MODELS
14.3. No
14.4. a. E{Y}= [1 + exp(25 −.2X)]−1
b. 125
c. X= 150 : π=.993307149, π/(1 −π) = 148.41316
X= 151 : π=.994513701, π/(1 −π) = 181.27224
181.27224/148.41316 = 1.2214 = exp(.2)
14.5. a. E{Y}= [1 + exp(−20 + .2X)]−1
b. 100
c. X= 125 : π=.006692851, π/(1 −π) = .006737947
X= 126 : π=.005486299, π/(1 −π) = .005516565
005516565/.006737947 = .81873 = exp(−.2)
14.6. a. E{Y}= Φ(−25 + .2X)
b. 125
14.7. a. b0=−4.80751, b1=.12508, ˆπ= [1 + exp(4.80751 −.12508X)]−1
c. 1.133
d. .5487
e. 47.22
14.8. a. b0=−2.94964, b1=.07666,
ˆπ= Φ(−2.94964 + .07666X)
b. b0=−3.56532, b1=.08227,
ˆπ= 1 −exp(−exp(−3.56532 + .08227X))
14-1
14.9. a. b0=−10.3089, b1=.01892,
ˆπ= [1 + exp(10.3089 −.01892X)]−1
c. 1.019
d. .5243
e. 589.65
14.10. a. b0=−6.37366, b1=.01169,
ˆπ= Φ(−6.37366 + .01169X)
b. b0=−7.78587, b1=.01344,
ˆπ= 1 −exp(−exp(−7.78587 + .01344X))
14.11. a.
j:123456
pj:.144 .206 .340 .592 .812 .898
b. b0=−2.07656, b1=.13585
ˆπ= [1 + exp(2.07656 −.13585X)]−1
d. 1.1455
e. .4903
f. 23.3726
14.12. a&b.
j:123456
pj:.112 .212 .372 .504 .688 .788
b0=−2.6437, b1=.67399
ˆπ= [1 + exp(2.6437 −.67399X)]−1
d. 1.962
e. .4293
f. 3.922
14.13. a. b0=−4.73931, b1=.067733, b2=.598632,
ˆπ= [1 + exp(4.73931 −.067733X1−.598632X2)]−1
b. 1.070, 1.820
c. .6090
14.14. a. b0=−1.17717, b1=.07279, b2=−.09899, b3=.43397
ˆπ= [1 + exp(1.17717 −.07279X1+.09899X2−.43397X3)]−1
b. exp(b1) = 1.0755, exp(b2) = .9058, exp(b3) = 1.5434
c. .0642
14.15. a. z(.95) = 1.645, s{b1}=.06676, exp[.12508 ±1.645(.06676)],
14-2
1.015 ≤exp(β1)≤1.265
b. H0:β1= 0, Ha:β16= 0. b1=.12508, s{b1}=.06676, z∗=.12508/.06676 =
1.8736. z(.95) = 1.645, |z∗| ≤ 1.645, conclude H0, otherwise conclude Ha. Con-
clude Ha.P-value=.0609.
c. H0:β1= 0, Ha:β16= 0. G2= 3.99, χ2(.90; 1) = 2.7055. If G2≤2.7055,
conclude H0, otherwise conclude Ha. Conclude Ha.P-value=.046
14.16. a. z(.975) = 1.960, s{b1}=.007877, exp[.01892±1.960(.007877)], 1.0035 ≤exp(β1)≤
1.0350
b. H0:β1= 0, Ha:β16= 0. b1=.01892, s{b1}=.007877, z∗=.01892/.007877 =
2.402. z(.975) = 1.960, |z∗| ≤ 1.960, conclude H0, otherwise conclude Ha. Con-
clude Ha.P-value= .0163.
c. H0:β1= 0, Ha:β16= 0. G2= 8.151, χ2(.95; 1) = 3.8415. If G2≤3.8415,
conclude H0, otherwise conclude Ha. Conclude Ha.P-value=.004.
14.17. a. z(.975) = 1.960, s{b1}=.004772, .13585 ±1.960(.004772),
.1265 ≤β1≤.1452,1.1348 ≤exp(β1)≤1.1563.
b. H0:β1= 0, Ha:β16= 0. b1=.13585, s{b1}=.004772, z∗=.13585/.004772 =
28.468. z(.975) = 1.960, |z∗| ≤ 1.960, conclude H0, otherwise conclude Ha.
Conclude Ha.P-value= 0+.
c. H0:β1= 0, Ha:β16= 0. G2= 1095.99, χ2(.95; 1) = 3.8415. If G2≤3.8415,
conclude H0, otherwise conclude Ha. Conclude Ha.P-value= 0+.
14.18. a. z(.995) = 2.576, s{b1}=.03911, .67399 ±2.576(.03911),
.5732 ≤β1≤.7747, 1.774 ≤exp(β1)≤2.170.
b. H0:β1= 0, Ha:β16= 0. b1=.67399, s{b1}=.03911, z∗=.67399/.03911 =
17.23. z(.995) = 2.576, |z∗| ≤ 2.576, conclude H0, otherwise conclude Ha. Con-
clude Ha.P-value= 0+.
c. H0:β1= 0, Ha:β16= 0. G2= 381.62, χ2(.99; 1) = 6.6349. If G2≤6.6349,
conclude H0, otherwise conclude Ha. Conclude Ha.P-value= 0+.
14.19. a. z(1−.1/[2(2)]) = z(.975) = 1.960, s{b1}=.02806, s{b2}=.3901, exp{20[.067733±
1.960(.02806)]}, 1.29 ≤exp(20β1)≤11.64, exp{2[.5986 ±1.960(.3901)]},.72 ≤
exp(2β2)≤15.28.
b. H0:β2= 0, Ha:β26= 0. b2=.5986, s{b2}=.3901, z∗=.5986/.3901 = 1.53.
z(.975) = 1.96, |z∗| ≤ 1.96, conclude H0, otherwise conclude Ha. Conclude H0.
P-value= .125.
c. H0:β2= 0, Ha:β26= 0. G2= 2.614, χ2(.95; 1) = 3.8415. If G2≤3.8415,
conclude H0, otherwise conclude Ha. Conclude H0.P-value= .1059.
d. H0:β3=β4=β5= 0, Ha: not all βk= 0, for k= 3,4,5. G2= 2.438,
χ2(.95; 3) = 7.81. If G2≤7.81, conclude H0, otherwise conclude Ha. Conclude
H0.P-value= .4866.
14-3

14.20. a. z(1−.1/[2(2)]) = z(.975) = 1.960, s{b1}=.03036, s{b2}=.03343, exp{30[.07279±
1.960(.03036)]}, 1.49 ≤exp(30β1)≤52.92, exp{25[−.09899±1.960(.03343)]},.016 ≤
exp(2β2)≤.433.
b. H0:β3= 0, Ha:β36= 0. b3=.43397, s{b3}=.52132, z∗=.43397/.52132 =
.8324. z(.975) = 1.96, |z∗| ≤ 1.96, conclude H0, otherwise conclude Ha. Conclude
H0.P-value= .405.
c. H0:β3= 0, Ha:β36= 0. G2=.702, χ2(.95; 1) = 3.8415. If G2≤3.8415,
conclude H0, otherwise conclude Ha. Conclude H0.
d. H0:β3=β4=β5= 0, Ha: not all βk= 0, for k= 3,4,5. G2= 1.534,
χ2(.95; 3) = 7.81. If G2≤7.81, conclude H0, otherwise conclude Ha. Conclude
H0.
14.21. a. X1enters in step 1;
no variables satisfy criterion for entry in step 2.
b. X22 is deleted in step 1; X11 is deleted in step 2; X12 is deleted in step 3; X2is
deleted in step 4; X1is retained in the model.
c. The best model according to the AICpcriterion is based on X1and X2.AIC3=
42.6896.
d. The best model according to the SBCpcriterion is based on X1.SBC2= 46.2976.
14.22. a. X1enters in step 1; X2enters in step 2;
no variables satisfy criterion for entry in step 3.
b. X11 is deleted in step 1; X12 is deleted in step 2; X3is deleted in step 3; X22 is
deleted in step 4; X1and X2are retained in the model.
c. The best model according to the AICpcriterion is based on X1and X2.AIC3=
111.795.
d. The best model according to the SBCpcriterion is based on X1and X2.SBC3=
121.002.
14.23.
j:123456
Oj1: 72 103 170 296 406 449
Ej1: 71.0 99.5 164.1 327.2 394.2 440.0
Oj0: 428 397 330 204 94 51
Ej0: 429.0 400.5 335.9 172.9 105.8 60.0
H0:E{Y}= [1 + exp(−β0−β1X)]−1,
Ha:E{Y} 6= [1 + exp(−β0−β1X)]−1.
X2= 12.284, χ2(.99; 4) = 13.28. If X2≤13.28 conclude H0, otherwise Ha. Conclude
H0.
14.24.
14-4

j:123456
Oj1: 28 53 93 126 172 197
Ej1: 30.7 53.8 87.4 128.3 168.5 200.5
Oj0: 222 197 157 124 78 53
Ej0: 219.3 196.2 162.6 121.7 81.6 49.5
H0:E{Y}= [1 + exp(−β0−β1X)]−1,
Ha:E{Y} 6= [1 + exp(−β0−β1X)]−1.
X2= 1.452, χ2(.99; 4) = 13.28. If X2≤13.28 conclude H0, otherwise Ha. Conclude
H0.
14.25. a.
Class jˆπ0Interval Midpoint njpj
1−1.1 - under −.4−.75 10 .3
2−.4 - under .6.10 10 .6
3.6 - under 1.5 1.05 10 .7
b.
i: 1 2 3 ··· 28 29 30
rSPi:−.6233 1.7905 −.6233 ··· .6099 .5754 −2.0347
14.26. a.
Class jˆπ0Interval Midpoint njpj
1−2.80 - under −.70 −1.75 9 .222
2−.70 - under .80 .05 9 .556
3.80 - under 2.00 1.40 9 .778
b.
i: 1 2 3 ··· 25 26 27
devi:−.6817 −.4727 −.5692 ··· 1.0433 −.8849 .7770
14.27. a.
Class jˆπ0Interval Midpoint njpj
1−3.00 - under −1.10 −2.050 11 .273
2−1.10 - under .35 −.375 11 .182
3.35 - under 3.00 1.675 11 .818
b.
i: 1 2 3 ··· 31 32 33
rSPi:−.7584 −1.0080 .7622 ··· −.6014 1.3700 −.5532
14.28. a.
j:12345678
Oj1: 0 1 0 2 1 8 2 10
Ej1:.2.5 1.0 1.5 2.4 3.4 4.7 10.3
Oj0: 19 19 20 18 19 12 18 10
Ej0: 18.8 19.5 19.0 18.5 17.6 16.6 15.3 9.7
14-5

b. H0:E{Y}= [1 + exp(−β0−β1X1−β2X2−β3X3)]−1,
Ha:E{Y} 6= [1 + exp(−β0−β1X1−β2X2−β3X3)]−1.
X2= 12.116, χ2(.95; 6) = 12.59. If X2≤12.59, conclude H0, otherwise conclude
Ha. Conclude H0.P-value = .0594.
c.
i: 1 2 3 ··· 157 158 159
devi:−.5460 −.5137 1.1526 ··· .4248 .8679 1.6745
14.29 a.
i: 1 2 3 ··· 28 29 30
hii:.1040 .1040 .1040 ··· .0946 .1017 .1017
b.
i: 1 2 3 ··· 28 29 30
∆X2
i:.3885 3.2058 .3885 ··· 4.1399 .2621 .2621
∆devi:.6379 3.0411 .6379 ··· 3.5071 .4495 .4495
Di:.0225 .1860 .0225 ··· .2162 .0148 .0148
14.30 a.
i: 1 2 3 ··· 25 26 27
hii:.0968 .1048 .1044 ··· .0511 .0744 .0662
b.
i: 1 2 3 ··· 25 26 27
∆X2
i:.2896 .1320 .1963 ··· .7622 .5178 .3774
∆devi:.4928 .2372 .3445 ··· 1.1274 .8216 .6287
Di:.0155 .0077 .0114 ··· .0205 .0208 .0134
14.31 a.
i: 1 2 3 ··· 31 32 33
hii:.0375 .0420 .0780 ··· .0507 .0375 .0570
b.
i: 1 2 3 ··· 31 32 33
∆Xi:.5751 1.0161 .5809 ··· .3617 1.8769 .3061
∆dev2
i:.9027 1.4022 .9031 ··· .6087 2.1343 .5246
Di:.0112 .0223 .0246 ··· .0097 .0366 .0093
14.32 a.
i: 1 2 3 ··· 157 158 159
hii:.0197 .0186 .0992 ··· .0760 .1364 .0273
b.
i: 1 2 3 ··· 157 158 159
∆X2
i:.1340 .1775 1.4352 ··· .0795 .6324 2.7200
∆devi:.2495 .3245 1.8020 ··· .1478 .9578 2.6614
Di:.0007 .0008 .0395 ··· .0016 .0250 .0191
14.33. a. z(.95) = 1.645, ˆπ0
h=.19561, s2{b0}= 7.05306, s2{b1}=.004457, s{b0, b1}=
−.175353, s{ˆπ0
h}=.39428, .389 ≤πh≤.699
14-6

b.
Cutoff Renewers Nonrenewers Total
.40 18.8 50.0 33.3
.45 25.0 50.0 36.7
.50 25.0 35.7 30.0
.55 43.8 28.6 36.7
.60 43.8 21.4 33.3
c. Cutoff = .50. Area = .70089.
14.34. a. z(.975) = 1.960, s2{b0}= 19.1581, s2{b1}=.00006205, s{b0, b1}=−.034293
Xhˆπ0
hs{ˆπ0
h}
550 .0971 .4538 .312 ≤πh≤.728
625 1.5161 .7281 .522 ≤πh≤.950
b.
Cutoff Able Unable Total
.325 14.3 46.2 29.6
.425 14.3 38.5 25.9
.525 21.4 30.8 25.9
.625 42.9 30.8 37.0
c. Cutoff = .525. Area = .79670.
14.35. a. z(.975) = 1.960, ˆπ0
h=−.04281, s2{b0}=.021824, s2{b1}=.000072174, s{b0, b1}=
−.0010644, s{ˆπ0
h}=.0783, .451 ≤πh≤.528
b.
Cutoff Purchasers Nonpurchasers Total
.15 4.81 71.54 76.36
.30 11.70 45.15 56.84
.45 23.06 23.30 46.27
.60 23.06 23.30 46.27
.75 48.85 9.64 52.49
c. Cutoff = .45 (or .60). Area = .82445.
14.36. a. ˆπ0
h=−1.3953, s2{ˆπ0
h}=.1613, s{ˆπ0
h}=.4016, z(.95) = 1.645. L=−1.3953 −
1.645(.4016) = −2.05597, U=−1.3953 + 1.645(.4016) = −.73463.
L∗= [1 + exp(2.05597)]−1=.11345, U∗= [1 + exp(.73463)]−1=.32418.
b.
Cutoff Received Not receive Total
.05 4.35 62.20 66.55
.10 13.04 39.37 52.41
.15 17.39 26.77 44.16
.20 39.13 15.75 54.88
c. Cutoff = .15. Area = .82222.
14.38. a. b0= 2.3529, b1=.2638, s{b0}=.1317, s{b1}=.0792,ˆµ= exp(2.3529 + .2638X).
14-7

b.
i: 1 2 3 ··· 8 9 10
devi:.6074 −.4796 −.1971 ··· .3482 .2752 .1480
c.
Xh:0123
Poisson: 10.5 13.7 17.8 23.2
Linear: 10.2 14.2 18.2 22.2
e. ˆµh= exp(2.3529) = 10.516
P(Y≤10 |Xh= 0) = 10
P
Y=0
(10.516)Yexp(−10.516)
Y!
= 2.7×10−5+··· +.1235 = .5187
f. z(.975) = 1.96, .2638 ±1.96(.0792), .1086 ≤β1≤.4190
14.39. a. b0=.4895, b1=−1.0694, b2=−.0466, b3=.0095, b4=.0086, s{b0}=.3369,
s{b1}=.1332, s{b2}=.1200, s{b3}=.0030, s{b4}=.0043,
ˆµ= exp(.4895 −1.0694X1−.0466X2+.0095X3+.0086X4)
b.
i: 1 2 3 ··· 98 99 100
devi:−.4816 −.6328 .4857 ··· −.3452 .0488 −.9889
c. H0:β2= 0, Ha:β26= 0. G2=.151, χ2(.95; 1) = 3.84. If G2≤3.84 conclude
H0, otherwise Ha. Conclude H0.
d. b1=−1.0778, s{b1}=.1314, z(.975) = 1.96, −1.0778 ±1.96(.1314), −1.335 ≤
β1≤ −.820.
14.40. E{Y}=exp(β0+β1X)
1 + exp(β0+β1X)"exp(−β0−β1X)
exp(−β0−β1X)#=1
1 + exp(−β0−β1X)
= [1 + exp(−β0−β1X)]−1
14.41. Formula (14.26) holds for given observations Y1,Y2,... Yn. Assembling all terms with
a given Xvalue, Xj, we obtain:
y.j(β0+β1Xj)−njloge[1 + exp(β0+β1Xj)]
since there are njcases with Xvalue Xj, of which y.j have value Yi= 1. There are
³nj
y.j ´ways of obtaining these y.j 1sout of nj, all of which are equally likely. Hence,
in the log-likelihood function of the y.j , we must add loge³nj
y.j ´to the above term for
given Xj:
loge³nj
y.j ´+y.j(β0+β1Xj)−njloge[1 + exp(β0+β1Xj)]
Assembling the terms for all Xj, we obtain (14.34).
14.42. From (14.16) and (14.18), we have:
14-8

πi=exp(π0)
1 + exp(π0)
Then:
1−π=1 + exp(π0)−exp(π0)
1 + exp(π0)= [1 + exp(π0)]−1
π
1−π=exp(π0)
1 + exp(π0)×[1 + exp(π0)] = exp(π0)
Solving for π0=F−1
L(π) by taking logarithms of both sides yields the result.
14.43. From (14.26), we obtain:
∂2logeL
∂β2
0
=−
n
X
i=1
exp(β0+β1Xi)
[(1 + exp(β0+β1Xi)]2
∂2logeL
∂β2
1
=−
n
X
i=1
X2
iexp(β0+β1Xi)
[1 + exp(β0+β1Xi)]2
∂2logeL
∂β0∂β1
=−
n
X
i=1
Xiexp(β0+β1Xi)
[1 + exp(β0+β1Xi)]2
Since these partial derivatives only involve the constants Xi,β0, and β1, the expecta-
tions of the partial derivatives are the partial derivatives themselves. Hence:
−E(∂2logeL
∂β2
0)=−g00 −E(∂2logeL
∂β0∂β1)=−g01 =−g10
−E(∂2logeL
∂β2
1)=−g11
and the stated matrix reduces to (14.51).
14.44. "4.1762385 74.574657
74.574657 1,568.4817 #−1
="1.58597 −.075406
−.075406 .0042228 #
14.45. E{Y}=γ0
1 + γ1exp(γ2X)
Consider γ2<0 and γ1>0; as X→ ∞,E{Y}=π→1 so that
1 = limX→∞ "γ0
1 + γ1exp(γ2X)#=γ0
Therefore, letting γ2=−β1and γ1= exp(−β0) we have:
E{Y}=1
1 + exp(−β0−β1X)=exp(β0+β1X)
1 + exp(β0+β1X)
14.46. E{Y}= [1 + exp(−β0−β1X1−β2X2−β3X1X2)]−1
π0(X1+ 1) = β0+β1(X1+ 1) + β2X2+β3(X1+ 1)X2
14-9

π0(X1) = β0+β1X1+β2X2+β3X1X2
π0(X1+ 1) −π0(X1) = loge(odds ratio) = β1+β3X2
Hence the odds ratio for X1is exp(β1+β3X2).No.
14.47. 1 −πi= exp "−exp ÃXi−γ0
γ1!#
−loge(1 −πi) = exp ÃXi−γ0
γ1!
Hence: loge[−loge(1 −πi)] = Xi−γ0
γ1
=−γ0
γ1
+1
γ1
Xi=β0+β1Xi
where β0=−γ0
γ1
and β1=1
γ1
.
14.48. a. X1= age
Socioeconomic
status X2X3
Upper 0 0
Middle 1 0
Lower 0 1
Sector X4
1 0
2 1
b0=.1932, b1=.03476, b2=−1.9092, b3=−2.0940, b4=.9508,
b5=.02633, b6=.007144, b7=−.01721, b8=.004107, b9=.4145,
where X0= (1 X1X2X3X4X1X2X1X3X1X4X2X4X3X4)
b. H0:β5=β6=β7=β8=β9= 0, Ha: not all equalities hold.
G2=.858, χ2(.99; 5) = 15.09. If G2≤15.09 conclude H0, otherwise conclude
Ha. Conclude H0.P-value = .973.
c. Retain socioeconomic status and age.
14.49. a.
j: 1 2 3 4 5
Oj1: 6 4 13 15 16
Ej1: 4.6 7.3 11.7 14.8 15.7
Oj0: 14 16 7 5 2
Ej0: 15.4 12.7 8.3 5.2 2.3
nj: 20 20 20 20 18
H0:E{Y}= [1 + exp(−β0−β1X1−β2X2−β3X3)]−1,
Ha:E{Y} 6= [1 + exp(−β0−β1X1−β2X2−β3X3)]−1.
X2= 3.28, χ2(.95; 3) = 7.81. If X2≤7.81 conclude H0, otherwise Ha. Conclude
H0.P-value = .35.
b.
i: 1 2 3 ··· 96 97 98
devi:.6107 .5905 −1.4368 ··· −.8493 −.7487 −1.0750
14-10

d&e.
i: 1 2 3 ··· 96 97 98
hii .0265 .0265 .0509 ··· .0305 .0316 .0410
∆X2
i:.2106 .1956 1.9041 ··· .4479 .3341 .8156
∆devi:.3785 .3538 2.1613 ··· .7350 .5712 1.1891
Di:.0014 .0013 .0255 ··· .0035 .0027 .0087
f.
Cutoff Savings Account No Savings Account Total
.45 18.5 31.8 24.5
.50 22.2 31.8 26.5
.55 22.2 22.7 22.4
.60 29.6 22.7 26.5
Cutoff = .55. Area = .766.
14.50. a.
Cutoff Savings Account No Savings Account Total
.55 24.5 28.9 26.5
b.
Model Building Combined
Data Set Data Set
b0:.3711 .3896
s{b0}:.5174 .3493
b1:.03678 .03575
s{b1}:.01393 .00961
b2:−1.2555 −1.1572
s{b2}:.5892 .4095
b3:−1.9040 −2.0897
s{b3}:.5552 .3967
c. z(.9833) = 2.128, exp[.03575 ±2.128(.00961)], 1.015 ≤exp(β1)≤1.058,
exp[−1.1572±2.128(.4095)], .132 ≤exp(β2)≤.751, exp [−2.0897 ±2.128(.3967)],
.053 ≤exp(β3)≤.288
14.51. a. X1= age, X2= routine chest X-ray ratio, X3= average daily census, X4=
number of nurses
b0=−8.8416, b1=.02238, b2=.005645, b3=.14721, b4=−.10475, b5=
.0002529, b6=−.001995, b7=.0014375, b8=−.000335, b9=.0003912, b10 =
−.00000519,
where
X0= (1 X1X2X3X4X1X2X1X3X1X4X2X3X2X4X3X4)
b. H0:β5=β6=β7=β8=β9=β10 = 0,
Ha: not all equalities hold. G2= 7.45, χ2(.95; 6) = 12.59. If G2≤12.59 conclude
H0, otherwise Ha. Conclude H0.P-value = .28
c. Retain age and average daily census.
14-11

d. The best subset: X3,X6,X10,AIC4= 59.6852;
The best subset: X10,SBC2= 66.963.
14.52. a.
j:12345
Oj1: 0 0 1 3 13
Ej1:.1.4.9 2.3 13.3
Oj0: 22 23 21 20 10
Ej0: 21.9 22.6 21.1 20.7 9.7
nj: 22 23 22 23 23
H0:E{Y}= [1 + exp(−β0−β1X1−β3X3)]−1,
Ha:E{Y} 6= [1 + exp(−β0−β1X1−β3X3)]−1,
X2=.872, χ2(.95; 3) = 7.81. If X2≤7.81 conclude H0,otherwise Ha. Conclude
H0.P-value = .832
b
i: 1 2 3 ··· 111 112 113
devi:−.3166 −.1039 −.1377 ··· −.1402 .1895 −.0784
d & e.
i: 1 2 3 ··· 111 112 113
hii .0168 .0056 .0074 ··· .0076 .0279 .0041
∆X2
i:.0523 .0054 .0096 ··· .0100 .0186 .0031
∆devi:.1011 .0108 .0190 ··· .0197 .0364 .0062
Di:.00030 .00001 .00002 ··· .00003 .00018 .000004
f.
Cutoff Affiliation No Affiliation Total
.30 29.4 9.4 12.4
.40 29.4 6.3 9.7
.50 41.2 4.2 9.7
.60 52.9 2.1 9.7
Cutoff = .40. Area = .923.
g. z(.95) = 1.645, ˆπ0
h=.6622, s2{b0}= 17.1276, s2{b1}=.006744, s2{b3}=
.000006687, s{b0, b1}=−.33241, s{b0, b3}=.0003495, s{b1, b3}=−.00004731,
s{ˆπ0
h}=.6193, −.35655 ≤π0
h≤1.68095, .70 ≤πh/(1 −πh)≤5.37
14.57. a. b1=
33.249
−1.905
−.046
−.039
.039
−4.513
−.088
.039
−.085
, b2=
12.387
−.838
−.016
−.028
.016
.590
.00008
−.009
−.097
, b3=
13.505
−.562
−.095
−.010
.020
−.595
−.011
−.008
−.044
14-12
b. H0:b13 =b23 =b33 = 0;
Ha: not all bk3= 0, for k= 1,2,3. G2= 2.34, conclude H0.
P-value=.5049.
c. G2= 10.3, conclude H0.P-value=.1126.
d. NE = 1, NC = 0 : b1=
−12.840
.585
.108
.007
−.017
.231
.008
.009
.023
NE = 1, S = 0 : b1=
−14.087
.754
.016
.026
−.025
.567
.010
.010
.113
NE = 1, W = 0 : b1=
−48.020
3.014
.060
.012
−.033
7.415
.079
−.038
.122
e&f. NE = 1, NC = 0 :
i: 1 2 3 ··· 58 59 60
Devi:−1.137 .708 −1.200 ··· −.562 −1.406 .547
∆X2
i: 1.061 .306 1.205 ··· .195 2.260 .347
∆devi: 1.445 .523 1.591 ··· .339 2.550 .485
Di:.020 .003 .019 ··· .003 .085 .044
NE = 1, S = 0 :
i: 1 2 3 ··· 63 64 65
Devi:−.327 .630 −1.153 ··· −.528 .696 −1.080
∆X2
i:.058 .237 1.028 ··· .164 1.189 1.030
∆devi:.110 .415 1.413 ··· .293 1.400 1.404
Di:.0003 .0021 .0103 ··· .002 .441 .035
NE = 1, W = 0 :
14-13

i: 1 2 3 ··· 42 43 44
Devi:−.3762 −.3152 .0177 ··· .0000 −.8576 .0000
∆X2
i:.0936 .0852 .0002 ··· .0000 1.1225 .0000
∆devi:.1618 .1336 .0003 ··· .0000 1.4135 .0000
Di:.0029 .0064 .0000 ··· .0000 .1903 .0000
14.58. a. b1=
−20.8100
−.0016
−.5738
−.2150
142.1400
.3998
.2751
.4516
.2236
−.0005
, b2=
28.7900
−.0013
−.3878
−.1253
147.73
−.2426
.3778
.1510
−.6755
−.0004
, b3=
−18.4800
−.0008
−.0354
−.1897
93.3700
.2884
−.2055
.2979
−.4803
.00008
b.
Row T erm log L(b)G2P-value
1X5/X4−189.129 51.074 .0000
2X6−178.009 28.834 .0000
3X7−166.716 6.248 .1001
4X10/X5−192.499 57.814 .0000
5X11 −197.042 66.900 .0000
6X12 −186.324 45.464 .0000
7X13 −168.769 10.354 .0158
8X14 −183.663 40.142 .0000
9X15 −172.189 17.194 .0006
c. NE = 1, NC = 0 : b1=
7.8100
.0009
.1208
.9224
−107.4200
−.3536
.4683
−.6225
1.0985
−.0002
14-14

NE = 1, S = 0 : b1=
−25.3800
.0015
.2399
−.0852
−172.7000
.2126
−.4522
−.4086
1.7355
.0006
NE = 1, W = 0 : b1=
−48.7700
.0054
1.9580
1.3413
−457.9000
.0917
−.6156
−.7196
−.3703
.0005
d&e. NE = 1, NC = 0 :
i: 1 2 3 ··· 101 102 103
Devi:−1.1205 .6339 −.0909 ··· −.6718 .0464 −.4253
∆X2
i: 1.1715 6.5919 .0042 ··· .3024 .0011 .1067
∆devi: 1.5536 6.7712 .0083 ··· .5006 .0022 .1929
Di:.0400 18.8671 .000 ··· .0059 .0000 .0014
NE = 1, S = 0 :
i: 1 2 3 ··· 122 123 124
Devi:.6801 −.0030 .0542 ··· −.5644 −.4215 −.4334
∆X2
i: 5.5413 .0000 .0015 ··· .2338 .1275 .1091
∆devi: 5.7437 .0000 .0029 ··· .3797 .2123 .1985
Di: 11.2465 .0000 .0000 ··· .0083 .0047 .0012
NE = 1, W = 0 :
i: 1 2 3 ··· 87 88 89
Devi:−.2713 .0000 −.0011 ··· .0713 −.2523 .0004
∆X2
i:.0506 .0000 .0000 ··· .0027 .0795 .0000
∆devi:.0867 .0000 .0000 ··· .0052 .1108 .0000
Di:.0018 .0000 .0000 ··· .0000 .0116 .0000
14-15

14.59. a. b=
4.6970
7.5020
−.0509
−.0359
.0061
−.0710
−.0051
.3531
−.1699
b. X3, orX4, or X6, or X7, or X8can be dropped.
c. Drop X6, then X7, then X3, and then X4, then stop.
d. The result is as follows:
Variable Value Count
Y(1) 1 33 (Event)
0 64
Total 97
Logistic Regression Table
Predictor Coef SE Coef Z P
Constant 3.767 2.208 1.71 0.088
PSA -0.03499 0.02208 -1.59 0.113
age -0.05548 0.03507 -1.58 0.114
Capspen -0.2668 0.1498 -1.78 0.075
Response Information
Variable Value Count
Y(2) 1 76 (Event)
0 21
Total 97
Logistic Regression Table
Predictor Coef SE Coef Z P
Constant 8.704 3.595 2.42 0.015
PSA -0.06045 0.01944 -3.11 0.002
age -0.08484 0.05253 -1.61 0.106
Capspen -0.14496 0.08098 -1.79 0.073
Log-Likelihood = -32.633
Test that all slopes are zero: G = 36.086, DF = 3, P-Value = 0.000
e&f. Y(1)
i: 1 2 ··· 95 96 97
Devi:.8018 −.3651 ··· −.0233 −.0113 −.0012
∆X2
i:.4036 .1476 ··· .0003 .0001 .0000
∆devi:.6673 .1431 ··· .0005 .0001 .0000
Di:.0065 .0026 ··· .0000 .0000 .0000
14-16

Y(2)
i:12··· 95 96 97
Devi:.1545 .3077 ··· −.0297 −.0031 −.0005
∆X2
i:.0122 .0492 ··· .0004 .0000 .0000
∆devi:.0240 .0960 ··· .0009 .0000 .0000
Di:.00004 .00033 ··· .00000 .00000 .00000
14.60. a. b=
−133.0400
−123.4400
.00002
.0014
−.5250
.9014
1.1787
.5412
−.3977
.0585
.0000
.4336
b. X13, or X12, or X8, or X7can be dropped.
c. Drop X12, then X13, then X8, then X7, then stop.
e&f. Y(1)
i:12··· 520 521 522
Devi:−.4904 −.1791 ··· −.0000 −.0143 −.0000
∆X2
i:.1300 .0160 ··· .0000 .0000 .0000
∆devi:.2423 .0322 ··· .0000 .0002 .0000
Di:.0003 .0000 ··· .0000 .0000 .0000
Y(2)
i:12··· 520 521 522
Devi:.0162 .2472 ··· −.2214 −.4205 −.0850
∆X2
i:.0000 .0320 ··· .0250 .0940 .0040
∆devi:.0003 .0616 ··· .0492 .1782 .0072
Di:.00000 .00007 ··· .00003 .00020 .00000
14.61. a. The estimated regression coefficents and their estimated standard deviations are
as follows,
Poisson Regression
Coefficient Estimates
Label Estimate Std. Error
Constant 0.499446 0.176041
Cost 0.0000149508 2.854645E-6
Age 0.00672387 0.00296715
Gender 0.181920 0.0439932
Interventions 0.0100748 0.00380812
Drugs 0.193237 0.0126846
14-17

Complications 0.0612547 0.0599478
Comorbids -0.000899912 0.00368517
Duration 0.000352919 0.000189870
b.
i: 1 2 3 ··· 786 787 788
Devi:.2813 1.7836 −1.0373 ··· .6562 −1.2158 −.0544
c. X3, or X8, or X9or X10 can be dropped.
d. G2= 5.262, conclude X0, the P-value=.1536.
e. We drop X9, then drop X8, then stop.
14-18
Chapter 15
INTRODUCTION TO THE DESIGN
OF EXPERIMENTAL AND
OBSERVATIONAL STUDIES
15.7. Panel.
15.8. a. Mixed. Type of instruction is an experimental factor, and school is an observational
factor.
b. Factor 1: type of instruction, two levels (standard curriculum, computer-based
curriculum).
Factor 2: school, three levels.
Randomized complete blocked design.
d. Section.
15.9. a. Observational.
b. Factor: expenditures for research and development in the past three years.
Factor levels: low, moderate, and high.
c. Cross-sectional study.
d. Firm.
15.10. a. Mixed. Color of paper is experimental factor, and parking lot is an observational
factor.
b. Factor 1: color of paper, three levels (blue, green, orange).
Factor 2: supermarket parking lot, four levels.
c. Randomized complete block design.
d. Car.
15.11. a. Observational.
b. Fitness status, three levels (below average, average, above average).
c. Cross-sectional study.
15-1
d. Person
15.12. a. Mixed. Applicant’s eye contact is an experimental factor, and personnel officer’s
gender is an observational factor.
b. Factor 1: applicant’s eye contact, two levels (yes, no).
Factor 2: personnel officer’s gender (male, female).
c. Randomized complete blocked design.
d. Personnel officer.
15.13. a. Mixed.
b. Wheel.
c. Four rubber compounds.
d. Randomized complete blocked design.
e. Balanced incomplete blocked design.
15.14. a. Experimental.
b. Factor 1: ingredient 1, with three levels (low, medium, high).
Factor 2: ingredient 2, with three levels (low, medium, high).
There are 9 factor-level combinations.
d. Completely randomized design.
e. Volunteer.
15.15. a. Observational.
b. Factor 1: treatment duration, with 2 levels (short, long).
Factor 2: weight gain, with 3 levels (slight, moderate, substantial)
c. Cross-sectional study.
d. Patient.
15.16. a. Mixed.
b. Factor: questionnaire, with 3 levels (A, B, C).
c. Repeated measure design.
d. Subject-time combination (i.e., the different occasions when a treatment is applied
to a subject).
15.17. a. Observational.
b. Factor 1: batch, with 5 levels.
Factor 2: barrel, with 4 levels (nested within batch).
c. Nested design.
d. Barrel.
15-2

15.18. a. Experimental.
b. Factor 1: poly-film thickness, with 2 levels (low, high).
Factor 2: old mixture ratio, with 2 levels (low, high).
Factor 3: operator glove type, with 2 levels (cotton, nylon).
Factor 4: underside oil coating, with 2 levels (no coating, coating).
c. Fractional factorial design.
d. 1000 moldings in a batch.
15.19. a. Randomized complete block design with four blocks and three treatments.
c. Assembler.
15.20. a. 23factorial design with two replicates.
c. Rod.
15.23. a. H0:¯
W= 0, Ha:¯
W6= 0. t∗=−.1915/.0112 = −17.10, t(.975,19) = 2.093. If
|t∗|>2.093 conclude H0, otherwise conclude Ha. Conclude Ha.P-value = 0+.
Agree with results on page 670. They should agree.
b. H0:β2=··· =β20 = 0, Ha: not all βk(k= 2,3, . . . , 20) equal zero. F∗=
[(.23586 −.023828)/(38 −19)] ÷[.023828/19] = 8.90, F(.95; 19,19) = 2.17. If
F∗>2.17 conclude H0, otherwise conclude Ha. Conclude Ha.P-value = 0+.
Not of primary interest because blocking factor was used here to increase the
precision.
15.24. Since ¯
X=n/2
n= 1/2, it follows from the definition of Xithat:
P(Xi−¯
X) = n/2(1 −1/2)2+n/2(0 −1/2)2=n/4.
Then from (15.5a): σ2{b1}= 4σ2/n.
15-3
15-4

Chapter 16
SINGLE-FACTOR STUDIES
16.4. b. E{MST R}= 9 + 25(450)
2= 5,634
E{MSE}= 9
16.5. b. E{MST R}= (2.8)2+100(11)
3= 374.507
E{MSE}= 7.84
c. E{MST R}= (2.8)2+100(15.46)
3= 523.173
16.7. b. ˆ
Y1j=¯
Y1.= 6.87778, ˆ
Y2j=¯
Y2.= 8.13333, ˆ
Y3j=¯
Y3.= 9.20000
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1.772 1.322 −.078 −1.078 .022 −.278
2−1.433 −.033 1.267 .467 −.333 −.433
3−.700 .500 .900 −1.400 .400 .300
i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1−.578 .822 −.878
2.767 −.233 .167 .567 −1.033 .267
Yes
d.
Source SS df MS
Between levels 20.125 2 10.0625
Error 15.362 24 .6401
Total 35.487 26
e. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal. F∗= 10.0625/.6401 =
15.720, F(.95; 2,24) = 3.40. If F∗≤3.40 conclude H0, otherwise Ha. Conclude
Ha.
f. P-value = 0+
16.8. b. ˆ
Y1j=¯
Y1.= 29.4, ˆ
Y2j=¯
Y2.= 29.6, ˆ
Y3j=¯
Y3.= 28.0
16-1

c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−1.4−3.4 1.6−2.4 5.6
2 4.4−.6−4.6 1.4−.6
3 3.0−3.0−1.0 1.0 0.0
d.
Source SS df MS
Between colors 7.60 2 3.80
Error 116.40 12 9.70
Total 124.00 14
e. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal. F∗= 3.80/9.70 = .392,
F(.90; 2,12) = 2.81. If F∗≤2.81 conclude H0, otherwise Ha. Conclude H0.
P-value = .684
16.9. b. ˆ
Y1j=¯
Y1.= 38.0, ˆ
Y2j=¯
Y2.= 32.0, ˆ
Y3j=¯
Y3.= 24.0
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−9.0 4.0 0.0 2.0 5.0
2−2.0 3.0 7.0−4.0−1.0
3 2.0 8.0−3.0−4.0−1.0
i j = 6 j= 7 j= 8 j= 9 j= 10
1 2.0−8.0 4.0
2−1.0−3.0 3.0−3.0 1.0
3−2.0
Yes
d.
Source SS df MS
Between treatments 672.0 2 336.00
Error 416.0 21 19.81
Total 1,088.0 23
e. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal. F∗= 336.00/19.81 =
16.96, F(.99; 2,21) = 5.78. If F∗≤5.78 conclude H0, otherwise Ha. Conclude
Ha. P -value = 0+
16.10. b. ˆ
Y1j=¯
Y1.= 21.500, ˆ
Y2j=¯
Y2.= 27.750, ˆ
Y3j=¯
Y3.= 21.417
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1 1.500 3.500 −.500 .500 −.500 .500
2.250 −.750 −.750 1.250 −1.750 1.250
3 1.583 −1.417 3.583 −.417 .583 1.583
i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1−1.500 1.500 −2.500 .500 −2.500 −.500
2−.750 2.250 .250 −.750 −1.750 1.250
3−.417 −1.417 −2.417 −1.417 .583 −.417
16-2

d.
Source SS df MS
Between ages 316.722 2 158.361
Error 82.167 33 2.490
Total 398.889 35
e. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal. F∗= 158.361/2.490 =
63.599, F(.99; 2,33) = 5.31. If F∗≤5.31 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
16.11. b. ˆ
Y1j=¯
Y1.=.0735, ˆ
Y2j=¯
Y2.=.1905, ˆ
Y3j=¯
Y3.=.4600,ˆ
Y4j=¯
Y4.=.3655,
ˆ
Y5j=¯
Y5.=.1250, ˆ
Y6j=¯
Y6.=.1515
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.2135 .1265 −.0035 .1065 .3065
2.2695 −.0805 −.0705 .2795 .0495
3−.2500 .3200 −.1400 −.0100 −.2400
4.1245 .2145 .1545 −.0755 −.0955
5−.3150 .1450 −.0650 −.0150 .1050
6−.1015 −.2015 .1285 .3185 −.0315
i j = 6 j= 7 j= 8 j= 9 j= 10
1.0265 −.1135 −.3435 .1965 −.2835
2−.1305 −.3105 .1395 −.1305 −.2205
3−.1100 .0800 −.2200 .0100 .1600
4.1845 .0345 −.2255 .1145 −.0255
5.0250 −.1150 .0950 .1650 .0150
6.1185 −.0715 .0185 .2785 −.2215
i j = 11 j= 12 j= 13 j= 14 j= 15
1.3165 −.1435 −.0935 .2065 .0165
2−.1405 .3395 .2295 .0995 .1695
3.0100 .0900 .1300 .2500 −.0100
4−.3555 −.0355 −.1855 −.2355 .1145
5.0750 .1750 −.2350 .1450 −.3250
6.0485 −.1415 −.0515 .0085 −.2115
i j = 16 j= 17 j= 18 j= 19 j= 20
1.0565 .1865 −.0035 −.0835 −.2635
2−.1505 −.0205 −.1705 −.0805 −.0705
3.0200 −.0200 .0400 −.2600 .1500
4.1745 .1445 .0545 .0845 −.1655
5.1150 .0750 .0150 .2250 −.3050
6−.0215 .2785 .1985 −.2415 −.1015
Yes
d.
16-3

Source SS df MS
Between machines 2.28935 5 .45787
Error 3.53060 114 .03097
Total 5.81995 119
e. H0: all µiare equal (i= 1, ..., 6), Ha: not all µiare equal. F∗=.45787/.03097 =
14.78, F(.95; 5,114) = 2.29. If F∗≤2.29 conclude H0, otherwise Ha. Conclude
Ha.
f. P-value = 0+
16.12. b. ˆ
Y1j=¯
Y1.= 24.55, ˆ
Y2j=¯
Y2.= 22.55, ˆ
Y3j=¯
Y3.= 11.75, ˆ
Y4j=¯
Y4.= 14.80,
ˆ
Y5j=¯
Y5.= 30.10
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.55 −.55 4.45 −4.55 −3.55
2−4.55 −2.55 −2.55 1.45 −.55
3−1.75 −.75 −3.75 .25 .25
4.20 −1.80 3.20 1.20 −2.80
5 2.90 −8.10 −2.10 4.90 −1.10
i j = 6 j= 7 j= 8 j= 9 j= 10
1.45 3.45 2.45 −1.55 −3.55
2 6.45 .45 1.45 5.45 −3.55
3−1.75 2.25 −2.75 −3.75 −.75
4 4.20 −4.80 3.20 −3.80 2.20
5−2.10 −.10 .90 −1.10 −2.10
i j = 11 j= 12 j= 13 j= 14 j= 15
1−.55 1.45 −1.55 −.55 3.45
2 1.45 2.45 −1.55 −2.55 1.45
3 4.25 .25 6.25 2.25 1.25
4.20 −2.80 −1.80 −1.80 −.80
5 2.90 −.10 1.90 2.90 −1.10
i j = 16 j= 17 j= 18 j= 19 j= 20
1−1.55 −1.55 2.45 1.45 .45
2−.55 −3.55 3.45 −.55 −1.55
3−.75 2.25 −2.75 −.75 .25
4 2.20 1.20 2.20 −.80 1.20
5 4.90 1.90 −4.10 −.10 −1.10
Yes
d.
Source SS df MS
Between agents 4,430.10 4 1,107.525
Error 714.65 95 7.523
Total 5,144.75 99
16-4
e. H0: all µiare equal (i= 1, ..., 5), Ha: not all µiare equal. F∗= 1,107.525/7.523 =
147.22, F(.90; 4,95) = 2.00. If F∗≤2.00 conclude H0, otherwise Ha. Conclude
Ha.
f. P-value = 0+
16.15. µ.= 80, τ1=−15, τ2= 0, τ3= 15
16.16. µ.= 7.2, τ1=−2.1, τ2=−.9, τ3=.7, τ4= 2.3
16.17. a. ˆµ.= 20.4725
b. H0: all τiequal zero (i= 1, ..., 5), Ha: not all τiequal zero.
No
16.18. a.
Y=
7.6
8.2
6.8
5.8
6.9
6.6
6.3
7.7
6.0
6.7
8.1
9.4
8.6
7.8
7.7
8.9
7.9
8.3
8.7
7.1
8.4
8.5
9.7
10.1
7.8
9.6
9.5
X=
110
110
110
110
110
110
110
110
110
101
101
101
101
101
101
101
101
101
101
101
101
1−1−1
1−1−1
1−1−1
1−1−1
1−1−1
1−1−1
β=
µ.
τ1
τ2
b.
16-5

Xβ=
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
=
µ1
µ1
µ1
µ1
µ1
µ1
µ1
µ1
µ1
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ2
µ3
µ3
µ3
µ3
µ3
µ3
c. ˆ
Y= 8.07037 −1.19259X1+.06296X2,µ.defined in (16.63)
d.
Source SS df MS
Regression 20.125 2 10.0625
Error 15.362 24 .6401
Total 35.487 26
e. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero. F∗= 10.0625/.6401 = 15.720,
F(.95; 2,24) = 3.40. If F∗≤3.40 conclude H0, otherwise Ha. Conclude Ha.
16.19. a.
16-6

Y=
28
26
31
27
35
34
29
25
31
29
31
25
27
29
28
X=
110
110
110
110
110
101
101
101
101
101
1−1−1
1−1−1
1−1−1
1−1−1
1−1−1
β=
µ.
τ1
τ2
b.
Xβ=
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ1
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.+τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
µ.−τ1−τ2
=
µ1
µ1
µ1
µ1
µ1
µ2
µ2
µ2
µ2
µ2
µ3
µ3
µ3
µ3
µ3
c. ˆ
Y= 29.0 + .4X1+.6X2,µ.defined in (16.63)
d.
Source SS df MS
Regression 7.60 2 3.80
Error 116.40 12 9.70
Total 124.00 14
e. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= 3.80/9.70 = .392, F(.90; 2,12) = 2.81. If F∗≤2.81 conclude H0, otherwise
Ha. Conclude H0.
16.20. a.
16-7

Y=
29
.
.
.
42
30
.
.
.
33
26
.
.
.
22
X=
1 1 0
.
.
..
.
..
.
.
1 1 0
1 0 1
.
.
..
.
..
.
.
1 0 1
1−8
6−10
6
.
.
..
.
..
.
.
1−8
6−10
6
β=
µ.
τ1
τ2
b.
Xβ=
µ.+τ1
.
.
.
µ.+τ1
µ.+τ2
.
.
.
µ.+τ2
µ.−8
6τ1−10
6τ2
.
.
.
µ.−8
6τ1−10
6τ2
=
µ1
.
.
.
µ1
µ2
.
.
.
µ2
µ3
.
.
.
µ3
c. ˆ
Y= 32.0+6.0X1+ 0.0X2,µ.defined in (16.80a)
d.
Source SS df MS
Regression 672 2 336.00
Error 416 21 19.81
Total 1088 23
e. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= 336.00/19.81 = 16.96, F(.99; 2,21) = 5.78. If F∗≤5.78 conclude H0,
otherwise Ha. Conclude H0.
16.21. a. ˆ
Y= 23.55556 −2.05556X1+ 4.19444X2,µ.defined in (16.63)
b.
Source SS df MS
Regression 316.722 2 158.361
Error 82.167 33 2.490
Total 398.889 35
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero. F∗= 158.361/2.490 = 63.599,
F(.99; 2,33) = 5.31. If F∗≤5.31 conclude H0, otherwise Ha. Conclude Ha.
16.22. a. ˆ
Y= 38X1+ 32X2+ 24X3
b. ˆ
Y= 32
16-8

c. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal. SSE(F) = 416,
SSE(R) = 1,088, F∗= (672/2) ÷(416/21) = 16.96, F(.99; 2,21) = 5.78. If
F∗≤5.78 conclude H0, otherwise Ha. Conclude Ha.
16.23. 1 −β∼
=.878
16.24. a. µ.= 15.5, φ= 1.58, 1 −β∼
=.47
b. 1 −β∼
=.18
16.25. µ.= 7.889, φ= 2.457, 1 −β∼
=.95
16.26. µ.= 33.917, φ= 2.214, 1 −β∼
=.70
16.27. µ.= 24, φ= 6.12, 1 −β > .99
16.29. a.
4: 10 15 20 30
n: 51 23 14 7
b.
4: 10 15 20 30
n: 39 18 11 6
16.30. a.
σ: 50 25 20
n: 34 10 7
b.
σ: 50 25 20
n: 30 9 6
16.31. a.
λ: 20 10 5
n: 10 38 150
b.
λ: 20 10 5
n: 22 85 337
16.32. a. ∆/σ = 4.5/3.0 = 1.5, n= 13
b. ∆/σ = 6.0/3.0 = 2.0, 1 −β≥.95
c. n= [3.6173(3.0)/1.5]2= 53
16.33. a. ∆/σ = 5.63/4.5 = 1.25, n= 20
b. φ=1
4.5·20
3(40.6667)¸1/2
= 3.659, 1 −β≥.99
c. (2.0√n)/4.5 = 2.2302, n= 26
16.34. a. ∆/σ =.15/.15 = 1.0, n= 22
16-9
b. φ=1
.15 ·22
6(.02968)¸1/2
= 2.199, 1 −β≥.97
c. (.10√n)/.15 = 3.1591, n= 23
16.35. a. ∆/σ = 3.75/3.0 = 1.25, n= 22
b. (1.0√n)/3.0 = 2.5997, n= 61
16.36. L=
3
Y
i=1
2
Y
j=1 µ1
2πσ2¶1/2
exp ·−1
2σ2(Yij −µi)2¸
=1
(2πσ2)3exp
−1
2σ2
3
X
i=1
2
X
j=1
(Yij −µi)2
logeL=−3 loge2π−3 logeσ2−1
2σ2PP(Yij −µi)2
∂(logeL)
∂µi
=−2
2σ2P
j(Yij −µi)(−1)
Setting the partial derivatives equal to zero, simplifying, and substituting the
maximum likelihood estimators yields:
P
j(Yij −ˆµi) = 0
or:
ˆµi=¯
Yi.
Yes
16.37. t∗=¯
Y1.−¯
Y2.
s{¯
Y1.−¯
Y2.}=¯
Y1.−¯
Y2.
snT
n1n2sΣ(Y1j−¯
Y1.)2+ Σ(Y2j−¯
Y2.)2
nT−2
F∗=n1(¯
Y1.−¯
Y..)2+n2(¯
Y2.−¯
Y..)2
ÃΣ(Y1j−¯
Y1.)2+ Σ(Y2j−¯
Y2.)2
nT−2!
Therefore to show (t∗)2=F∗, it suffices to show:
n1n2
nT
(¯
Y1.−¯
Y2.)2=n1(¯
Y1.−¯
Y..)2+n2(¯
Y2.−¯
Y..)2
Now, the right-hand side equals:
n1"¯
Y1.−Ãn1¯
Y1.+n2¯
Y2.
nT!#2
+n2"¯
Y2.−Ãn1¯
Y1.+n2¯
Y2.
nT!#2
=n1ÃnT¯
Y1.−n1¯
Y1.−n2¯
Y2.
nT!2
+n2ÃnT¯
Y2.−n1¯
Y1.−n2¯
Y2.
nT!2
=n1·n2
nT³¯
Y1.−¯
Y2.´¸2
+n2·n1
nT³¯
Y2.−¯
Y1.´¸2
=n1n2
nT³¯
Y1.−¯
Y2.´2
16-10

16.38. Pwiτi=Pwi(µi−µ.) = Pwiµi−µ.Pwi
=µ.−µ.= 0
since Pwi= 1 and µ.=Pwiµi
16.39. a. Using (6.25) and substituting ˆµfor b:
ˆµ= (X0X)−1X0Y
X0X=
n1
n20
··
0·nr
(X0X)−1=
n−1
1
n−1
20
··
0·n−1
r
X0Y=
Y1·
Y2·
·
·
·
Yr·
ˆµ=
¯
Y1·
¯
Y2·
·
·
·
¯
Yr·
SSE(F) = PP(Yij −¯
Yi.)2=SSE
b. X0X=nT, (X0X)−1=1
nT
,X0Y=PPYij
ˆµc=1
nTPPYij =¯
Y..
SSE(R) = PP(Yij −¯
Y..)2=SST O
16.40. a. 90, 15
b. Smallest P-value = .067
16.41. P(µi−µ.)2=µ−µ2+ 1
3¶2
+µ2µ2−1
3¶2
+µ2−µ2
3¶2
Differentiating with respect to µ2yields:
12
9µ2−6
9
Setting this derivative equal to zero and solving yields µ2=.5.
16.42. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
Source SS df MS
Between regions 13.9969 3 4.6656
Error 187.3829 109 1.7191
Total 201.3798 112
F∗= 4.6656/1.7191 = 2.714, F(.95; 3,109) = 2.688. If F∗≤2.688 conclude H0,
otherwise Ha. Conclude Ha.
16.43. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
16-11
Source SS df MS
Between ages 3.0677 3 1.02257
Error 198.3121 109 1.81938
Total 201.3798 112
F∗= 1.02257/1.81938 = .562, F(.90; 3, 109) = 2.135. If F∗≤2.135 conclude H0,
otherwise Ha. Conclude H0.
16.44. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
Source SS df MS
Between regions .059181 3 .019727
Error .268666 436 .000616
Total .327847 439
F∗=.019727/.000616 = 32.01, F(.95; 3, 436) = 2.6254. If F∗≤2.6254 conclude
H0, otherwise Ha. Conclude Ha.
16.45. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
Source SS df MS
Between treatments 1.6613 3 .5538
Error .7850 32 .0245
Total 2.4463 35
F∗=.5538/.0245 = 22.57, F(.95; 3, 32) = 2.9011. If F∗≤2.9011 conclude H0,
otherwise Ha. Conclude Ha.
16.46. c. E{F∗}=ν2
ν2−2= 1.2
d. Expected proportion is .95.
e. E{F∗}= 117.9; E{MST R}= 14,144, E{MSE}= 144
f. φ= 8.05, expected proportion is 1 −β > .99.
16.47. a. 20, 6
b.
F∗:.29 .59 .97 1.06 1.64 2.74
P(F∗) : 4/20 4/20 2/20 4/20 4/20 2/20
P-value = .10
c. P{F(1, 4) ≥2.74}=.17
16.48. a.
F∗: 0 .1.4.98 2.0 3.85 7.71 19.60
P(F∗) : 8/70 18/70 12/70 14/70 8/70 6/70 2/70 2/70
H0:µ1=µ2,Ha:µ16=µ2.F∗= 7.71. P-value = P(F∗≥7.71) = .0571. If
P-value ≥.10 conclude H0, otherwise Ha. Conclude Ha.
b&c.
F(.90; 1,6) = 3.78 F(.95; 1,6) = 5.99 F(.99; 1,6) = 13.7
10/70 = .143 4/70 = .0571 2/70 = .0286
16-12

Chapter 17
ANALYSIS OF FACTOR LEVEL
MEANS
17.3. a. (i) and (iii) are contrasts.
b. (i) ˆ
L=¯
Y1.+ 3 ¯
Y2.−4¯
Y3.,s2{ˆ
L}=26MSE
n
(ii) ˆ
L=.3¯
Y1.+.5¯
Y2.+.1¯
Y3.+.1¯
Y4.,s2{ˆ
L}=.36MSE
n
(iii) ˆ
L=(¯
Y1.+¯
Y2.+¯
Y3.)
3−¯
Y4.,s2{ˆ
L}=4MSE
3n
17.4. a. q(.90; 6,54) = 3.765, F(.90; 5,54) = 1.96
g T S B
2 2.66 3.13 t(.975; 54) = 2.00
5 2.66 3.13 t(.99; 54) = 2.40
15 2.66 3.13 t(.99667; 54) = 2.82
b. Refer to part (a) for Sand Bmultiples.
17.5. a. q(.95; 5, 20) = 4.23, F(.95; 4,20) = 2.87
g T S B
2 2.99 3.39 t(.9875; 20) = 2.42
5 2.99 3.39 t(.995; 20) = 2.845
10 2.99 3.39 t(.9975; 20) = 3.15
b. q(.95; 5,95) = 3.94, F(.95; 4,95) = 2.46
g T S B
2 2.79 3.14 t(.9875; 95) = 2.28
5 2.79 3.14 t(.995; 95) = 2.63
10 2.79 3.14 t(.9975; 95) = 2.87
17.7. q(.99; 2,18) = 4.07, F(.99; 1,18) = 8.29, T=S=B=t(.995; 18) = 2.88
17.8. a. ¯
Y1.= 6.878, ¯
Y2.= 8.133, ¯
Y3.= 9.200
b. s{¯
Y3.}=.327, t(.975; 24) = 2.064, 9.200 ±2.064(.327),8.525 ≤µ3≤9.875
17-1

c. ˆ
D=¯
Y2.−¯
Y1.= 1.255, s{ˆ
D}=.353, t(.975; 24) = 2.064,1.255 ±2.064(.353),
.526 ≤D≤1.984
d. ˆ
D1=¯
Y3.−¯
Y2.= 1.067, ˆ
D2=¯
Y3.−¯
Y1.= 2.322, ˆ
D3=¯
Y2.−¯
Y1.= 1.255, s{ˆ
D1}=
.400, s{ˆ
D2}=.422, s{ˆ
D3}=.353, q(.90; 3,24) = 3.05, T = 2.157
1.067 ±2.157(.400) .204 ≤D1≤1.930
2.322 ±2.157(.422) 1.412 ≤D2≤3.232
1.255 ±2.157(.353) .494 ≤D3≤2.016
e. F(.90; 2,24) = 2.54, S= 2.25
B=t(.9833; 24) = 2.257
Yes
17.9. a. ¯
Y1.= 29.4, ¯
Y2.= 29.6, ¯
Y3.= 28.0, s{¯
Y1.}=s{¯
Y2.}=s{¯
Y3.}=q9.7
5= 1.3928,
t(.975; 12) = 2.179
b. s{¯
Y1.}= 1.393, t(.95; 12) = 1.782, 29.40 ±1.782(1.393),26.92 ≤µ1≤31.88
c. H0:D=µ3−µ2= 0, Ha:D6= 0. ˆ
D=−1.6, s{ˆ
D}= 1.970,
t∗=−1.6/1.970 = −.81, t(.95; 12) = 1.782.
If |t∗| ≤ 1.782 conclude H0, otherwise Ha. Conclude H0. No
17.10. a. ¯
Y1.= 38.00, ¯
Y2.= 32.00, ¯
Y3.= 24.00
b. MSE = 19.81, s{¯
Y2.}= 1.4075, t(.995; 21) = 2.831,32.00±2.831(1.4075), 28.02 ≤
µ2≤35.98
c. ˆ
D1=¯
Y2.−¯
Y3.= 8.00, ˆ
D2=¯
Y1.−¯
Y2.= 6.00, s{ˆ
D1}= 2.298, s{ˆ
D2}= 2.111,
B=t(.9875; 21) = 2.414
8.00 ±2.414(2.298) 2.45 ≤D1≤13.55
6.00 ±2.414(2.111) .90 ≤D2≤11.10
d. q(.95; 3, 21) = 3.57, T= 2.524, no
e. Yes, no
f. q(.95; 3,21) = 3.57
Test Comparison
i Diˆ
Dis{ˆ
Di}q∗
iConclusion
1µ1−µ26.00 2.111 4.02 Ha
2µ1−µ314.00 2.404 8.24 Ha
3µ2−µ38.00 2.298 4.92 Ha
Group 1: Below Average
Group 2: Average
Group 3: Above Average
17.11. a. ¯
Y1.= 21.500, ¯
Y2.= 27.750, ¯
Y3.= 21.417
b. MSE = 2.490, s{¯
Y1.}=.456, t(.995; 33) = 2.733,21.500 ±2.733(.456), 20.254 ≤
µ1≤22.746
17-2
c. ˆ
D=¯
Y3.−¯
Y1.=−.083, s{ˆ
D}=.644, t(.995; 33) = 2.733, −.083 ±2.733(.644),
−1.843 ≤D≤1.677
d. H0: 2µ2−µ1−µ3= 0, Ha: 2µ2−µ1−µ36= 0. F ∗= (12.583)2/1.245 = 127.17,
F(.99; 1,33) = 7.47. If F∗≤7.47 conclude H0,otherwise Ha.Conclude Ha.
e. ˆ
D1=¯
Y3.−¯
Y1.=−.083, ˆ
D2=¯
Y3.−¯
Y2.=−6.333,ˆ
D3=¯
Y2.−¯
Y1.= 6.250,
s{ˆ
Di}=.644 (i= 1,2,3), q(.90; 3,33) = 3.01, T= 2.128
−.083 ±2.128(.644) −1.453 ≤D1≤1.287
−6.333 ±2.128(.644) −7.703 ≤D2≤ −4.963
6.250 ±2.128(.644) 4.880 ≤D3≤7.620
f. B=t(.9833; 33) = 2.220, no
17.12. a. ¯
Y1.=.0735, ¯
Y2.=.1905, ¯
Y3.=.4600,¯
Y4.=.3655, ¯
Y5.=.1250, ¯
Y6.=.1515
b. MSE =.03097, s{¯
Y1.}=.0394, t(.975; 114) = 1.981, .0735 ±1.981(.0394),
−.005 ≤µ1≤.152
c. ˆ
D=¯
Y2.−¯
Y1.=.1170, s{ˆ
D}=.0557, t(.975; 114) = 1.981, .1170 ±1.981(.0557),
.007 ≤D≤.227
e. ˆ
D1=¯
Y1.−¯
Y4.=−.2920, ˆ
D2=¯
Y1.−¯
Y5.=−.0515,ˆ
D3=¯
Y4.−¯
Y5.=.2405,
s{ˆ
Di}=.0557 (i= 1,2,3), B=t(.9833; 114) = 2.178
Test Comparison
i i t∗
iConclusion
1D1−5.242 Ha
2D2−.925 H0
3D34.318 Ha
f. q(.90; 6,114) = 3.71, T= 2.623, no
17.13. a. ¯
Y1.= 24.55, ¯
Y2.= 22.55, ¯
Y3.= 11.75, ¯
Y4.= 14.80, ¯
Y5.= 30.10,
s{¯
Yi.}=q7.52
20 =.6132, (i= 1,2,3,4,5), t(.975; 95) = 1.985
b.
Test 1: H0:µ1−µ2= 0 Test 6: H0:µ2−µ4= 0
Ha:µ1−µ26= 0 Ha:µ2−µ46= 0
Test 2: H0:µ1−µ3= 0 Test 7: H0:µ2−µ5= 0
Ha:µ1−µ36= 0 Ha:µ2−µ56= 0
Test 3: H0:µ1−µ4= 0 Test 8: H0:µ3−µ4= 0
Ha:µ1−µ46= 0 Ha:µ3−µ46= 0
Test 4: H0:µ1−µ5= 0 Test 9: H0:µ3−µ5= 0
Ha:µ1−µ56= 0 Ha:µ3−µ56= 0
Test 5: H0:µ2−µ3= 0 Test 10: H0:µ4−µ5= 0
Ha:µ2−µ36= 0 Ha:µ4−µ56= 0
ˆ
D1= 24.55 −22.55 = 2.00, ˆ
D2= 24.55 −11.75 = 12.80,
ˆ
D3= 24.55 −14.80 = 9.75, ˆ
D4= 24.55 −30.10 = −5.55,
ˆ
D5= 22.55 −11.75 = 10.80, ˆ
D6= 22.55 −14.80 = 7.75,
17-3

ˆ
D7= 22.55 −30.10 = −7.55, ˆ
D8= 11.75 −14.80 = −3.05,
ˆ
D9= 11.75 −30.10 = −18.35, ˆ
D10 = 14.80 −30.10 = −15.30,
s{ˆ
Di}=.8673 (i= 1, ..., 10), q(.90; 5,95) = 3.54.
If |q∗
i| ≤ 3.54 conclude H0, otherwise Ha.
Test
i q∗
iConclusion
1 3.26 Ho
2 20.87 Ha
3 15.90 Ha
4−9.05 Ha
5 17.61 Ha
6 12.64 Ha
7−12.31 Ha
8−4.97 Ha
9−29.92 Ha
10 −24.95 Ha
Group 1 Group 2
Agent 3 ¯
Y3.= 11.75 Agent 4 ¯
Y4.= 14.80
Group 3 Group 4
Agent 1 ¯
Y1.= 24.55 Agent 5 ¯
Y5.= 30.10
Agent 2 ¯
Y2.= 22.55
c. MSE = 7.523, s{¯
Y1.}=.6133, t(.95; 95) = 1.661,24.550 ±1.661(.6133), 23.531 ≤
µ1≤25.569
d. ˆ
D=¯
Y2.−¯
Y1.=−2.000, s{ˆ
D}=.8673, t(.95; 95) = 1.661, −2.000 ±1.661(.8673),
−3.441 ≤D≤ −.559
e. ˆ
D1=¯
Y1.−¯
Y3.= 12.800, ˆ
D2=¯
Y1.−¯
Y5.=−5.550,ˆ
D3=¯
Y3.−¯
Y5.=−18.350,
s{ˆ
Di}=.8673 (i= 1,2,3), B=t(.9833; 95) = 2.158
12.800 ±2.158(.8673) 10.928 ≤D1≤14.672
−5.550 ±2.158(.8673) −7.422 ≤D2≤ −3.678
−18.350 ±2.158(.8673) −20.222 ≤D3≤ −16.478
f. q(.90; 5,95) = 3.54, T= 2.503, no
17.14. a. ˆ
L= ( ¯
Y1.+¯
Y2.)/2−¯
Y3.= (6.8778 + 8.1333)/2−9.200 = −1.6945,
s{ˆ
L}=.3712, t(.975; 24) = 2.064, −1.6945 ±2.064(.3712),−2.461 ≤L≤ −.928
b. ˆ
L= (3/9) ¯
Y1.+ (4/9) ¯
Y2.+ (2/9) ¯
Y3.= 7.9518, s{ˆ
L}=.1540, t(.975; 24) = 2.064,
7.9518 ±2.064(.1540), 7.634 ≤L≤8.270
c. F(.90; 2, 24) = 2.54, S= 2.254; see also part (a) and Problem 17.8.
1.067 ±2.254(.400) .165 ≤D1≤1.969
2.322 ±2.254(.422) 1.371 ≤D2≤3.273
17-4
1.255 ±2.254(.353) .459 ≤D3≤2.051
−1.6945 ±2.254(.3712) −2.531 ≤L1≤ −.858
17.15. a. ˆ
L= ( ¯
Y1.−¯
Y2.)−(¯
Y2.−¯
Y3.) = ¯
Y1.−2¯
Y2.+¯
Y3.= 38.000 −2(32.000)
+24.000 = −2.000, s{ˆ
L}= 3.7016, t(.995; 21) = 2.831,−2.000 ±2.831(3.7016),
−12.479 ≤L≤8.479
b. ˆ
D1=¯
Y1.−¯
Y2.= 6.000, ˆ
D2=¯
Y1.−¯
Y3.= 14.000, ˆ
D3=¯
Y2.−¯
Y3.= 8.000,
ˆ
L1=ˆ
D1−ˆ
D3=−2.000, s{ˆ
D1}= 2.1112, s{ˆ
D2}= 2.4037, s{ˆ
D3}= 2.2984,
s{ˆ
L1}= 3.7016, B=t(.99375; 21) = 2.732
6.000 ±2.732(2.1112) .232 ≤D1≤11.768
14.000 ±2.732(2.4037) 7.433 ≤D2≤20.567
8.000 ±2.732(2.2984) 1.721 ≤D3≤14.279
−2.000 ±2.732(3.7016) −12.113 ≤L1≤8.113
c. F(.95; 2,21) = 3.47, S= 2.634, yes
17.16. a. ˆ
L= ( ¯
Y3.−¯
Y2.)−(¯
Y2.−¯
Y1.) = ¯
Y3.−2¯
Y2.+¯
Y1.= 21.4167−
2(27.7500) + 21.500 = −12.5833, s{ˆ
L}= 1.1158, t(.995; 33) = 2.733,
−12.5833 ±2.733(1.1158), −15.632 ≤L≤ −9.534
b. ˆ
D1=¯
Y2.−¯
Y1.= 6.2500, ˆ
D2=¯
Y3.−¯
Y2.=−6.3333, ˆ
D3=¯
Y3.−¯
Y1.=−.0833,
ˆ
L1=ˆ
D2−ˆ
D1=−12.5833, s{ˆ
Di}=.6442 (i= 1,2,3), s{ˆ
L1}= 1.1158,
F(.90; 2,33) = 2.47, S= 2.223
6.2500 ±2.223(.6442) 4.818 ≤D1≤7.682
−6.3333 ±2.223(.6442) −7.765 ≤D2≤ −4.901
−.0833 ±2.223(.6442) −1.515 ≤D3≤1.349
−12.5833 ±2.223(1.1158) −15.064 ≤L1≤ −10.103
17.17. a. ˆ
L= ( ¯
Y1.+¯
Y2.)/2−(¯
Y3.+¯
Y4.)/2 = (.0735 + .1905)/2−(.4600 + .3655)/2
=−.28075, s{ˆ
L}=.03935, t(.975; 114) = 1.981, −.28075±1.981(.03935), −.3587 ≤
L≤ −.2028
b. ˆ
D1=−.1170, ˆ
D2=.0945, ˆ
D3=−.0265, ˆ
L1=−.28075, ˆ
L2=−.00625,ˆ
L3=
−.2776, ˆ
L4=.1341, s{ˆ
Di}=.0557 (i= 1,2,3), s{ˆ
L1}=s{ˆ
L2}=.03935,
s{ˆ
L3}=s{ˆ
L4}=.03408, B=t(.99286; 114) = 2.488
−.1170 ±2.488(.0557) −.2556 ≤D1≤.0216
.0945 ±2.488(.0557) −.0441 ≤D2≤.2331
−.0265 ±2.488(.0557) −.1651 ≤D3≤.1121
−.28075 ±2.488(.03935) −.3787 ≤L1≤ −.1828
−.00625 ±2.488(.03935) −.1042 ≤L2≤.0917
−.2776 ±2.488(.03408) −.3624 ≤L3≤ −.1928
.1341 ±2.488(.03408) .0493 ≤L4≤.2189
17.18. a. ˆ
L= ( ¯
Y1.+¯
Y2.)/2−(¯
Y3.+¯
Y4.)/2 = (24.55 + 22.55)/2−(11.75 + 14.80)/2
17-5

= 10.275, s{ˆ
L}=.6133, t(.95; 95) = 1.661,10.275 ±1.661(.6133), 9.256 ≤L≤
11.294
b. ˆ
D1= 2.00, ˆ
D2=−3.05, ˆ
L1=−6.55, ˆ
L2=−16.825, ˆ
L3= 10.275, s{ˆ
Di}=.8673
(i= 1,2), s{ˆ
Li}=.7511 (i= 1,2), s{ˆ
L3}=.6133, F (.90; 4,95) = 1.997, S=
2.826
2.00 ±2.826(.8673) −.451 ≤D1≤4.451
−3.05 ±2.826(.8673) −5.501 ≤D2≤ −.599
−6.55 ±2.826(.7511) −8.673 ≤L1≤ −4.427
−16.825 ±2.826(.7511) −18.948 ≤L2≤ −14.702
10.275 ±2.826(.6133) 8.542 ≤L3≤12.008
c. ˆ
L=.25 ¯
Y1.+.20 ¯
Y2.+.20 ¯
Y3.+.20 ¯
Y4.+.15 ¯
Y5.= 20.4725, s{ˆ
L}=.2777, t(.95; 95) =
1.661, 20.4725 ±1.661(.2777),20.011 ≤L≤20.934
17.19. a. L1=µ1−µ.L2=µ2−µ.
L3=µ3−µ.L4=µ4−µ.
L5=µ5−µ.L6=µ6−µ.
ˆ
L1=.0735 −.2277 = −.1542, ˆ
L2=.1905 −.2277 = −.0372
ˆ
L3=.4600 −.2277 = .2323, ˆ
L4=.3655 −.2277 = .1378
ˆ
L5=.1250 −.2277 = −.1027, ˆ
L6=.1515 −.2277 = −.0762
s{ˆ
Li}=s.03097
20 µ25
36¶+.03097
36 µ5
20¶=.0359
B=t(.99583; 114) = 2.685
−.1542 ±2.685(.0359) .2506 ≤L1≤ −.0578
−.0372 ±2.685(.0359) −.1336 ≤L2≤.0592
.2323 ±2.685(.0359) .1359 ≤L3≤.3287
.1378 ±2.685(.0359) .0414 ≤L4≤.2342
−.1027 ±2.685(.0359) −.1991 ≤L5≤ −.0063
−.0762 ±2.685(.0359) −.1726 ≤L6≤.0202
Conclude not all µiare equal.
17.20. a. L1=µ1−µ.L2=µ2−µ.
L3=µ3−µ.L4=µ4−µ.
L5=µ5−µ.
ˆ
L1= 24.55 −20.75 = 3.80, ˆ
L2= 22.55 −20.75 = 1.80
ˆ
L3= 11.75 −20.75 = −9.00, ˆ
L4= 14.80 −20.75 = −5.95
ˆ
L5= 30.10 −20.75 = 9.35
s{ˆ
Li}=s7.5226
20 µ16
25¶+7.5226
25 µ4
20¶=.5485
B=t(.99; 95) = 2.366
17-6

3.80 ±2.366(.5485) 2.502 ≤L1≤5.098
1.80 ±2.366(.5485) .502 ≤L2≤3.098
−9.00 ±2.366(.5485) −10.298 ≤L3≤ −7.702
−5.95 ±2.366(.5485) −7.248 ≤L4≤ −4.652
9.35 ±2.366(.5485) 8.052 ≤L5≤10.648
Conclude not all µiare equal.
17.21. a. Yij =µi+²ij
b.
i: 1 2 3 4 5
¯
Yi.:.0800 .1800 .5333 1.1467 2.8367
c.
Source SS df MS
Treatments 15.3644 4 3.8411
Error .1574 10 .01574
Total 15.5218 14
d. H0: all µiare equal (i= 1, ..., 5), Ha: not all µiare equal. F∗= 3.8411/.01574 =
244.034, F(.975; 4,10) = 4.47. If F∗≤4.47 conclude H0, otherwise Ha. Conclude
Ha.
e. ˆ
D1=¯
Y1.−¯
Y2.=−.1000, ˆ
D2=¯
Y2.−¯
Y3.=−.3533, ˆ
D3=¯
Y3.−¯
Y4.=−.6134.
D4=¯
Y4.−¯
Y5.=−1.6900, s{ˆ
Di}=.1024 (i= 1, ..., 4), B=t(.99375; 10) = 3.038
−.1000 ±3.038(.1024) −.411 ≤D1≤.211
−.3533 ±3.038(.1024) −.664 ≤D2≤ −.042
−.6134 ±3.038(.1024) −.924 ≤D3≤ −.302
−1.6900 ±3.038(.1024) −2.001 ≤D4≤ −1.379
17.23. n= 13
17.24. Bonferroni, n= 24
17.25. Bonferroni, n= 45
17.26. Bonferroni, n= 92
17.27. a. n= 20, 2n= 40, n= 20
b. (1) n= 26, n= 26, n= 26
(2) n= 18, 3n= 54, n= 18
c. b(1)
17.28. a. ˆ
Y= 68.66655 −.36820X
b. eij:
17-7
i j = 1 j= 2 j= 3 j= 4 j= 5
1−9.106 3.894 −.106 1.894 4.894
2−1.847 3.153 7.153 −3.847 −.847
3 1.886 7.886 −3.114 −4.114 −1.114
i j = 6 j= 7 j= 8 j= 9 j= 10
1 1.894 −8.106 3.894
2−.847 −2.847 3.153 −2.847 1.153
3−2.114
c. H0:E{Y}=β0+β1X,Ha:E{Y} 6=β0+β1X.SSP E = 416.0000, SSLF =
.4037, F∗= (.4037/1) ÷(416.0000/21) = .020, F (.95; 1,21) = 4.32. If F∗≤4.32
conclude H0, otherwise Ha. Conclude H0.
d. No
17.29. a. ˆ
Y=.18472 + .06199x+.01016x2
b. eij :
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7
1−.2310 .1090 −.0210 .0890 .2890 .0090 −.1310
2.2393 −.1107 −.1007 .2493 .0193 −.1607 −.3407
3−.2440 .3260 −.1340 −.0040 −.2340 −.1040 .0860
4.1268 .2168 .1568 −.0732 −.0932 .1868 .0368
5−.2969 .1631 −.0469 .0031 .1231 .0431 −.0969
6−.0802 −.1802 .1498 .3398 −.0102 .1398 −.0502
i j = 8 j= 9 j= 10 j= 11 j= 12 j= 13 j= 14
1−.3610 .1790 −.3010 .2990 −.1610 −.1110 .1890
2.1093 −.1607 −.2507 −.1707 .3093 .1993 .0693
3−.2140 .0160 .1660 .0160 .0960 .1360 .2560
4−.2232 .1168 −.0232 −.3532 −.0332 −.1832 −.2332
5.1131 .1831 .0331 .0931 .1931 −.2169 .1631
6.0398 .2998 −.2002 .0698 −.1202 −.0302 .0298
i j = 15 j= 16 j= 17 j= 18 j= 19 j= 20
1−.0010 .0390 .1690 −.0210 −.1010 −.2810
2.1393 −.1807 −.0507 −.2007 −.1107 −.1007
3−.0040 .0260 −.0140 .0460 −.2540 .1560
4.1168 .1768 .1468 .0568 .0868 −.1632
5−.3069 .1331 .0931 .0331 .2431 −.2869
6−.1902 −.0002 .2998 .2198 −.2202 −.0802
c. H0:E{Y}=β0+β1x+β11x2,Ha:E{Y} 6=β0+β1x+β11x2. SSP E = 3.5306,
SSLF =.0408, F∗= (.0408/3) ÷(3.5306/114) = .439, F (.99; 3,114) = 3.96. If
F∗≤3.96 conclude H0, otherwise Ha.Conclude H0.
d. H0:β11 = 0, Ha:β11 6= 0. s{b11}=.00525, t∗=.01016/.00525 = 1.935, t(.995; 117) =
2.619. If |t∗| ≤ 2.619 conclude H0,otherwise Ha.Conclude H0.
17.30. With r= 2 and ni≡n,MSE =s2as defined in (A.63) and
max( ¯
Yi. −µi)−min( ¯
Yi. −µi) = ( ¯
Yi. −µi)−(¯
Yi0.−µi0) =
17-8

= ( ¯
Yi. −¯
Yi0.)−(µi−µi0), i6=i0.
Thus:
q∗=(¯
Yi. −¯
Yi0.)−(µi−µi0)
s/√n=√2|t∗|
17.31. Working within the probability expression, we obtain:
¯¯¯¯¯¯
(¯
Yi. −µi)−(¯
Yi0.−µi0)
qMSE/n ¯¯¯¯¯¯≤q(1 −α;r, nT−r) or
|(¯
Yi. −µi)−(¯
Yi0.−µi0)| ≤ ³qMSE/n´q(1 −α;r, nT−r) or
|(¯
Yi. −µi)−(¯
Yi0.−µi0)| ≤ s{ˆ
D}T
since T=1
√2q(1 −α;r, nT−r) and sMSE
n=s{ˆ
D}
√2or
−s{ˆ
D}T≤(¯
Yi. −¯
Yi0.)−(µi−µi0)≤s{ˆ
D}Tor
(¯
Yi. −¯
Yi0.)−T s{ˆ
D} ≤ µi−µi0≤(¯
Yi. −¯
Yi0.) + T s{ˆ
D}
17.32. When r= 2, S2=F(1 −α; 1, nT−2) which by (A.50b) equals
[t(1 −α/2; nT−2)]2.
17.33.
σ2{ˆ
Li}=σ2{¯
Yi. −
r
X
h=1
¯
Yh./r}
=σ2{¯
Yi.}+σ2{X¯
Yh./r} − 2σ{¯
Yi.,X¯
Yh./r}
=σ2
ni
+1
r2X(σ2/nh)−2σ2
rni
=1
r2σ2
r
X
h6=i
(1/nh) + σ2
ni
+σ2
r2ni−2σ2
rni
=1
r2σ2
r
X
h6=i
(1/nh) + σ2
niµ1 + 1
r2−2
r¶
=1
r2σ2
r
X
h6=i
(1/nh) + σ2
niµr−1
r¶2
Replacing σ2by the estimator MSE leads to (17.49).
17.34. Given n1=n3=nand n2=kn. Let c=kn/nT. Then n1=n3=
(nT−kn)/2 = nT(1 −c)/2 and n2=cnT. Hence:
σ2{¯
Y1.−¯
Y2.}=σ2{¯
Y3.−¯
Y2.}=σ2"2
nT(1 −c)+1
cnT#
Differentiating with respect to cyields:
2σ2
nT
(1 −c)−2+σ2
nT
(−c−2)
17-9
Setting the derivative equal to zero and solving yields c=.4142.
Hence, n2= (.4142)nTand n1=n3= (.2929)nT.
(Note: This derivation treats nas a continuous variable. Since n2must be an
even integer, appropriate rounding of the calculated sample sizes is required. For
example, if nT= 100, the calculated sample sizes are n1= 29.29, n2= 41.42, and
n3= 29.29. The smallest variance is obtained for n1= 29, n2= 42, and n3= 29.)
17.35. ¯
Y1.= 4.86071, ¯
Y2.= 4.39375, ¯
Y3.= 3.92703, ¯
Y4.= 4.38125, MSE = 1.7191,
n1= 28, n2= 32, n3= 37, n4= 16,
ˆ
D1=¯
Y1.−¯
Y2.=.46696,ˆ
D2=¯
Y1.−¯
Y3.=.93368, ˆ
D3=¯
Y1.−¯
Y4.=.47946,
ˆ
D4=¯
Y2.−¯
Y3.=.46667, ˆ
D5=¯
Y2.−¯
Y4.=.01250, ˆ
D6=¯
Y3.−¯
Y4.=−.45422,
s{ˆ
D1}=.3393, s{ˆ
D2}=.3284, s{ˆ
D3}=.4109, s{ˆ
D4}=.3165, s{ˆ
D5}=.4015,
s{ˆ
D6}=.3923, q(.90; 4,109) = 3.28, T= 2.319
.46696 ±2.319(.3393) −.320 ≤D1≤1.254
.93368 ±2.319(.3284) .172 ≤D2≤1.695
.47946 ±2.319(.4109) −.473 ≤D3≤1.432
.46667 ±2.319(.3165) −.267 ≤D4≤1.201
.01250 ±2.319(.4015) −.919 ≤D5≤.944
−.45422 ±2.319(.3923) −1.364 ≤D6≤.456
17.36. ¯
Y1.=.04123, ¯
Y2.=.05111, ¯
Y3.=.07074, ¯
Y4.=.06088, MSE =.000616,
n1= 103, n2= 108, n3= 152, n4= 77,
ˆ
D1=¯
Y1.−¯
Y2.=−.0099, s{ˆ
D1}=.0034
ˆ
D2=¯
Y1.−¯
Y3.=−.0295, s{ˆ
D2}=.0032
ˆ
D3=¯
Y1.−¯
Y4.=−.0196, s{ˆ
D3}=.0037
ˆ
D4=¯
Y2.−¯
Y3.=−.0196, s{ˆ
D4}=.0031
ˆ
D5=¯
Y2.−¯
Y4.=−.0098, s{ˆ
D5}=.0037
ˆ
D6=¯
Y3.−¯
Y4.=.0099, s{ˆ
D6}=.0035, q(.90; 4,137) = 3.24, T= 2.291
−.01771 ≤D1≤ −.00204,−.03677 ≤D2≤ −.02225
−.02822 ≤D3≤ −.01108,−.02679 ≤D4≤ −.01247
−.01825 ≤D5≤ −.00129, .00191 ≤D6≤.01782
17.37. ¯
Y1.= 2.4125, ¯
Y2.= 2.7375, ¯
Y3.= 2.4286, ¯
Y4.= 2.9000, MSE =.0245,
n1= 8, n2= 8, n3= 7, n4= 13,
ˆ
D1=¯
Y1.−¯
Y2.=−.3250, s{ˆ
D1}=.0783
ˆ
D2=¯
Y1.−¯
Y3.=−.0161, s{ˆ
D2}=.0810
ˆ
D3=¯
Y1.−¯
Y4.=−.4875, s{ˆ
D3}=.0703
ˆ
D4=¯
Y2.−¯
Y3.=.3089, s{ˆ
D4}=.0810
ˆ
D5=¯
Y2.−¯
Y4.=−.1625, s{ˆ
D5}=.0703
17-10
ˆ
D6=¯
Y3.−¯
Y4.=−.4714, s{ˆ
D6}=.0734
q(.95; 4,32) = 3.83, T= 2.708
−.5371 ≤D1≤ −.1129,−.2356 ≤D2≤.2035
−.6781 ≤D3≤ −.2969, .0894 ≤D4≤.5285
−.3531 ≤D5≤.0281,−.6703 ≤D6≤ −.2726
17.38. b. Expected proportion is .95.
17-11
17-12

Chapter 18
ANOVA DIAGNOSTICS AND
REMEDIAL MEASURES
18.4. a. See Problem 16.7c.
b. r=.992
c. tij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1.9557 1.8377 −.1010 −1.4623 .0288 −.3615
2−1.9821 −.0426 1.7197 .6011 −.4277 −.5575
3−.9568 .6768 1.2464 −2.0391 .5395 .4035
i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1−.7592 1.0945 −1.1728
2 1.0009 −.2988 .2132 .7326 −1.3737 .3417
H0: no outliers, Ha: at least one outlier. t(.999815; 23) = 4.17.
If |tij |≤ 4.17 conclude H0, otherwise Ha. Conclude H0.
18.5. a. See Problem 16.8c.
b. r=.991
d. tij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.4863 −1.2486 .5576 −.8516 2.3634
2 1.6992 −.2066 −1.7985 .4863 −.2066
3 1.0849 −1.0849 −.3456 .3456 .0000
H0: no outliers, Ha: at least one outlier. t(.99917; 11) = 4.13.
If |tij| ≤ 4.13 conclude H0, otherwise Ha. Conclude H0.
18.6. a. See Problem 16.9c.
b. r=.990
d. tij:
18-1

i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1−2.3926 .9589 .0000 .4714 1.2145 .4714
2−.4647 .7019 1.7354 −.9449 −.2314 −.2314
3.4832 2.1280 −.7301 −.9837 −.2405 −.4832
i j = 7 j= 8 j= 9 j= 10
1−2.0656 .9589
2−.7019 .7019 −.7019 .2314
H0: no outliers, Ha: at least one outlier. t(.99979; 20) = 4.22.
If |tij| ≤ 4.22 conclude H0, otherwise Ha. Conclude H0.
18.7. a. See Problem 16.10c.
b. r=.984
d. tij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1.9927 2.4931 −.3265 .3265 −.3265 .3265
2.1630 −.4907 −.4907 .8234 −1.1646 .8234
3 1.0497 −.9360 2.5645 −.2719 .3811 1.0497
i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1−.9927 .9927 −1.7017 .3265 −1.7017 −.3265
2−.4907 1.5185 .1630 −.4907 −1.1646 .8234
3−.2719 −.9360 −1.6401 −.9360 .3811 −.2719
H0: no outliers, Ha: at least one outlier. t(.99965; 32) = 3.75.
If |tij| ≤ 3.75 conclude H0, otherwise Ha. Conclude H0.
18.8. a. See Problem 16.11c.
b. r=.992
d. tij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7
1−1.2477 .7360 −.0203 .6192 1.8045 .1538 −.6601
2 1.5815 −.4677 −.4095 1.6415 .2874 −.7594 −1.8287
3−1.4648 1.8864 −.8150 −.0580 −1.4052 −.6396 .4648
4.7243 1.2537 .9000 −.4386 −.5551 1.0764 .2003
5−1.8560 .8443 −.3775 −.0871 .6105 .1451 −.6688
6−.5901 −1.1767 .7477 1.8773 −.1829 .6893 −.4153
i j = 8 j= 9 j= 10 j= 11 j= 12 j= 13 j= 14
1−2.0298 1.1472 −1.6656 1.8651 −.8355 −.5434 1.2063
2.8121 −.7594 −1.2892 −.8179 2.0053 1.3427 .5784
3−1.2863 .0580 .9323 .0580 .5230 .7565 1.4648
4−1.3189 .6659 −.1480 −2.1035 −.2061 −1.0823 −1.3784
5.5522 .9616 .0871 .4357 1.0204 −1.3754 .8443
6.1074 1.6355 −1.2952 .2816 −.8238 −.2990 .0493
18-2

i j = 15 j= 16 j= 17 j= 18 j= 19 j= 20
1.0958 .3281 1.0882 −.0203 −.4852 −1.5455
2.9881 −.8765 −.1190 −.9940 −.4677 −.4095
3−.0580 .1161 −.1161 .2322 −1.5246 .8736
4.6659 1.0175 .8414 .3165 .4910 −.9646
5−1.9168 .6688 .4357 .0871 1.3160 −1.7954
6−1.2359 −.1248 1.6355 1.1590 −1.4141 −.5901
H0: no outliers, Ha: at least one outlier. t(.9999417; 113) = 4.08.
If |tij| ≤ 4.08 conclude H0, otherwise Ha. Conclude H0.
18.9. a. See Problem 16.12c.
b. r=.995
d. tij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7
1−.2047 −.2047 1.6805 −1.7195 −1.3334 .1675 1.2951
2−1.7195 −.9534 −.9534 .5404 −.2047 2.4771 .1675
3−.6526 −.2792 −1.4100 .0930 .0930 −.6526 .8404
4.0744 −.6714 1.1998 .4470 −1.0479 1.5835 −1.8172
5 1.0858 −3.1711 −.7840 1.8564 −.4097 −.7840 −.0372
i j = 8 j= 9 j= 10 j= 11 j= 12 j= 13 j= 14
1.9157 −.5778 −1.3334 −.2047 .5404 −.5778 −.2047
2.5404 2.0738 −1.3334 .5404 .9157 −.5778 −.9534
3−1.0290 −1.4100 −.2792 1.6029 .0930 2.3955 .8404
4 1.1998 −1.4293 .8216 .0744 −1.0479 −.6714 −.6714
5.3351 −.4097 −.7840 1.0858 −.0372 .7089 1.0858
i j = 15 j= 16 j= 17 j= 18 j= 19 j= 20
1 1.2951 −.5778 −.5778 .9157 .5404 .1675
2.5404 −.2047 −1.3334 1.2951 −.2047 −.5778
3.4657 −.2792 .8404 −1.0290 −.2792 .0930
4−.2978 .8216 .4470 .8216 −.2978 .4470
5−.4097 1.8564 .7089 −1.5448 −.0372 −.4097
H0: no outliers, Ha: at least one outlier. t(.999875; 94) = 3.81.
If |tij| ≤ 3.81 conclude H0, otherwise Ha. Conclude H0.
18.11. H0: all σ2
iare equal (i= 1,2,3), Ha: not all σ2
iare equal.
˜
Y1= 6.80, ˜
Y2= 8.20, ˜
Y3= 9.55, MST R =.0064815, MSE =.26465,
F∗
BF =.0064815/.26465 = .02, F(.95; 2,24) = 3.40. If F∗
BF ≤3.40 conclude H0,
otherwise Ha. Conclude H0.P-value = .98
18.12. H0: all σ2
iare equal (i= 1,2,3), Ha: not all σ2
iare equal.
˜
Y1= 40.0, ˜
Y2= 31.0, ˜
Y3= 22.5, MST R = 2.96667, MSE = 11.30476,
F∗
BF = 2.96667/11.30476 = .26, F(.90; 2,21) = 2.575. If F∗
BF ≤2.575 conclude
H0, otherwise Ha. Conclude H0.P-value = .77
18-3

18.13. a. H0: all σ2
iare equal (i= 1,2,3), Ha: not all σ2
iare equal.
s1= 1.7321, s2= 1.2881, s3= 1.6765, ni≡12, H∗= (1.7321)2/(1.2881)2= 1.808,
H(.99; 3,11) = 6.75. If H∗≤6.75 conclude H0, otherwise Ha. Conclude H0.
P-value > .05
b. ˜
Y1= 21.5, ˜
Y2= 27.5, ˜
Y3= 21.0, MST R =.19444, MSE =.93434,
F∗
BF =.19444/.93434 = .21, F(.99; 2,33) = 5.31. If F∗
BF ≤5.31 conclude H0,
otherwise Ha. Conclude H0.P-value = .81
18.14. a. H0: all σ2
iare equal (i= 1, ..., 6), Ha: not all σ2
iare equal.
s1=.1925, s2=.1854, s3=.1646, s4=.1654, s5=.1727, s6=.1735, ni≡20,
H∗= (.1925)2/(.1646)2= 1.3677, H(.99; 6, 19) = 5.2. If H∗≤5.2 conclude H0,
otherwise Ha. Conclude H0.P-value > .05
b. ˜
Y1=.08, ˜
Y2=.12, ˜
Y3=.47, ˜
Y4=.41, ˜
Y5=.175, ˜
Y6=.125, MST R =.002336,
MSE =.012336, F∗
BF =.002336/.012336 = .19, F(.99; 5,114) = 3.18. If F∗
BF ≤
3.18 conclude H0, otherwise Ha.Conclude H0.P-value = .97
18.15. a. ¯
Y1.= 3.90, ¯
Y2.= 1.15, ¯
Y3.= 2.00, ¯
Y4.= 3.40
eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7
1.10 −.90 1.10 .10 2.10 −.90 −1.90
2−1.15 .85 −1.15 1.85 .85 −.15 −1.15
3 0.0−1.00 −2.00 1.00 2.00 −1.00 1.00
4 1.60 −1.40 .60 .60 2.60 1.60 −.40
i j = 8 j= 9 j= 10 j= 11 j= 12 j= 13 j= 14
1 1.10 3.10 −2.90 −1.90 1.10 .10 3.10
2 1.85 −.15 −1.15 −1.15 −.15 −.15 −1.15
3 2.00 0.0−2.00 −1.00 1.00 0.0 2.00
4 1.60 3.60 −.40 −2.40 −3.40 −1.40 −.40
i j = 15 j= 16 j= 17 j= 18 j= 19 j= 20
1.10 1.10 −3.90 .10 −2.90 2.10
2−.15 1.85 −.15 .85 .85 −1.15
3−2.00 −1.00 1.00 −2.00 0.0 2.00
4−.40 .60 −2.40 1.60 −1.40 −.40
c. H0: all σ2
iare equal (i= 1, 2, 3, 4), Ha: not all σ2
iare equal.
˜
Y1= 4, ˜
Y2= 1, ˜
Y3= 2, ˜
Y4= 3, M ST R = 1.64583, MSE =.96776,
F∗
BF = 1.64583/.96776 = 1.70, F(.90; 3, 76) = 2.157. If F∗
BF ≤2.157 conclude H0,
otherwise Ha. Conclude H0. P -value = .17
d.
i¯
Yi. si
1 3.9000 1.9708
2 1.1500 1.0894
3 2.0000 1.4510
4 3.4000 1.7889
18-4

e.
λ SSE
−1.0 434.22
−.8 355.23
−.6 297.21
−.4 254.90
−.2 224.59
−.1 213.09
0 203.67
λ SSE
.1 196.14
.2 190.35
.4 183.48
.6 182.41
.8 186.91
1.0 197.15
Yes
18.16. a. ¯
Y0
1.= 1.8714, ¯
Y0
2.=.8427, ¯
Y0
3.= 1.2293, ¯
Y0
4.= 1.7471
e0
ij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7
1.129 −.139 .365 .129 .578 −.139 −.457
2−.843 .572 −.843 .889 .572 .157 −.843
3.185 −.229 −1.229 .503 .771 −.229 .503
4.489 −.333 .253 .253 .702 .489 −.015
i j = 8 j= 9 j= 10 j= 11 j= 12 j= 13 j= 14
1.365 .774 −.871 −.457 .365 .129 .774
2.889 .157 −.843 −.843 .157 .157 −.843
3.771 .185 −1.229 −.229 .503 .185 .771
4.489 .899 −.015 −.747 −1.747 −.333 −.015
i j = 15 j= 16 j= 17 j= 18 j= 19 j= 20
1.129 .365 −1.871 .129 −.871 .578
2.157 .889 .157 .572 .572 −.843
3−1.229 −.229 .503 −1.229 .185 .771
4−.015 .253 −.747 .489 −.333 −.015
b. r=.964
c. H0: all σ2
iare equal (i= 1,2,3,4), Ha: not all σ2
iare equal.
˜
Y1= 2.000, ˜
Y2= 1.000, ˜
Y3= 1.414, ˜
Y4= 1.732, MST R =.07895, MSE =.20441,
F∗
BF =.07895/.20441 = .39, F(.90; 3, 76) = 2.157. If F∗
BF ≤2.157 conclude H0,
otherwise Ha. Conclude H0.
18.17. a. ¯
Y1.= 3.5625, ¯
Y2.= 5.8750, ¯
Y3.= 10.6875, ¯
Y4.= 15.5625
eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1.4375 −.5625 −1.5625 −.5625 .4375 .4375
2 1.1250 .1250 −1.8750 .1250 1.1250 −3.8750
3 1.3125 −4.6875 3.3125 1.3125 −.6875 −1.6875
4.4375 −1.5625 −9.5625 3.4375 −3.5625 −5.5625
18-5

i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1−.5625 2.4375 1.4375 .4375 −1.5625 .4375
2 3.1250 −.8750 −.8750 3.1250 −2.8750 2.1250
3 1.3125 6.3125 −3.6875 −4.6875 1.3125 .3125
4−.5625 8.4375 −5.5625 7.4375 1.4375 4.4375
i j = 13 j= 14 j= 15 j= 16
1.4375 −1.5625 −.5625 .4375
2.1250 −1.8750 1.1250 .1250
3−4.6875 2.3125 −.6875 3.3125
4−.5625 2.4375 −7.5625 6.4375
c. H0: all σ2
iare equal (i= 1,2,3,4), Ha: not all σ2
iare equal.
˜
Y1= 4.0, ˜
Y2= 6.0, ˜
Y3= 11.5, ˜
Y4= 16.5, MST R = 37.1823, MSE = 3.8969,
F∗
BF = 37.1823/3.8969 = 9.54, F(.95; 3, 60) = 2.76. If F∗
BF ≤2.76 conclude H0,
otherwise Ha. Conclude Ha.P-value = 0+
d.
i¯
Yi. si
1 3.5625 1.0935
2 5.8750 1.9958
3 10.6875 3.2397
4 16.5625 5.3786
e.
λ SSE
−1.0 1,038.26
−.8 790.43
−.6 624.41
−.4 516.16
−.2 450.16
−.1 429.84
0 416.84
λ SSE
.1 410.65
.2 410.92
.4 430.49
.6 476.68
.8 553.64
1.0 669.06
Yes
18.18. a. ¯
Y0
1.=.5314, ¯
Y0
2.=.7400, ¯
Y0
3.= 1.0080, ¯
Y0
4.= 1.1943
e0
ij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7 j= 8
1.071 −.054 −.230 −.054 .071 .071 −.054 .247
2.105 .038 −.138 .038 .105 −.439 .214 −.041
3.071 −.230 .138 .071 −.008 −.054 .071 .222
4.036 −.018 −.349 .107 −.080 −.153 .010 .204
i j = 9 j= 10 j= 11 j= 12 j= 13 j= 14 j= 15 j= 16
1.168 .071 −.230 .071 .071 −.230 −.054 .071
2−.041 .214 −.263 .163 .038 −.138 .105 .038
3−.163 −.230 .071 .033 −.230 .106 −.008 .138
4−.153 .186 .061 .128 .010 .085 −.240 .167
18-6

b. r=.971
c. H0: all σ2
iare equal (i= 1,2,3,4), Ha: not all σ2
iare equal.
˜
Y1=.6021, ˜
Y2=.7782, ˜
Y3= 1.0603, ˜
Y4= 1.2173, MST R =.001214,
MSE =.01241, F∗
BF =.001214/.01241 = .10, F(.95; 3, 60) = 2.76.
If F∗
BF ≤2.76 conclude H0, otherwise Ha. Conclude H0.
18.19.
i:1234
si: 1.97084 1.08942 1.45095 1.78885
wi:.25745 .84257 .47500 .31250
H0: all µiare equal (i= 1,2,3,4), Ha: not all µiare equal.
SSEw(F) = 76, dfF= 76, SSEw(R) = 118.54385, dfR= 79,
F∗
w= [(118.54385 −76)/3] ÷(76/76) = 14.18, F(.95; 3,76) = 2.725.
If F∗
w≤2.725 conclude H0, otherwise Ha. Conclude Ha.
18.20.
i:1234
si: 1.09354 1.99583 3.23973 5.37858
wi:.83624 .25105 .09528 .034567
H0: all µiare equal (i= 1,2,3,4), Ha: not all µiare equal.
SSEw(F) = 60, dfF= 60, SSEw(R) = 213.9541, dfR= 63,
F∗
w= [(213.9541 −60)/3] ÷(60/60) = 51.32, F(.99; 3, 60) = 4.13.
If F∗
w≤4.13 conclude H0, otherwise Ha. Conclude Ha.
18.23. a. H0: all µiare equal (i= 1,2,3,4), Ha: not all µiare equal.
MST R = 470.8125, MSE = 28.9740, F∗
R= 470.8125/28.9740 = 16.25,
F(.95; 2,24) = 3.40. If F∗
R≤3.40 conclude H0, otherwise Ha. Conclude Ha.
b. P-value = 0+
e. ¯
R1.= 6.50, ¯
R2.= 15.50, ¯
R3.= 22.25, B=z(.9833) = 2.13
Comparison Testing Limits
1 and 2 −9.00 ±2.13(3.500) −16.455 and −1.545
1 and 3 15.75 ±2.13(4.183) −24.660 and −9.840
2 and 3 −6.75 ±2.13(3.969) −15.204 and 1.704
Group 1
Low Level i= 1
Group 2
Moderate level i= 2
High level i= 3
18.24. a. H0: all µiare equal (i= 1,2,3), Ha: not all µiare equal.
MST R = 1,297.0000, MSE = 37.6667, F∗
R= 1,297.0000/37.6667 = 34.43,
F(.99; 2,33) = 5.31. If F∗
R≤5.31 conclude H0, otherwise Ha. Conclude Ha.
18-7

b. P-value = 0+
e. ¯
R1.= 12.792, ¯
R2.= 30.500, ¯
R3.= 12.208, B=z(.9833) = 2.128
Comparison Testing Limits
1 and 2 −17.708 ±2.128(4.301) −26.861 and −8.555
1 and 3 .584 ±2.128(4.301) −8.569 and 9.737
2 and 3 18.292 ±2.128(4.301) 9.140 and 27.445
Group 1
Young i= 1
Elderly i= 3
Group 2
Middle i= 2
18.25. b. H0: all µiare equal (i= 1, 2, 3), Ha: not all µiare equal.
MST R = 465.6000, MSE = 48.7519, F∗
R= 465.6000/48.7519 = 9.550,
F(.95; 2,27) = 3.354. If F∗
R≤3.354 conclude H0, otherwise Ha. Conclude Ha.
P-value = .0007
c. ¯
R1.= 21.1, ¯
R2.= 7.9, ¯
R3.= 17.5, B=z(.99167) = 2.394
Comparison Testing Limits
1 and 2 13.2±2.394(3.937) 3.775 and 22.625
1 and 3 3.6±2.394(3.937) −5.825 and 13.025
2 and 3 −9.6±2.394(3.937) −19.025 and −.175
Group 1
Production i= 2
Group 2
Sales i= 1
Research i= 3
18.26. Yij =µi+βtj+²ij ,tj= 1, ..., 7
18.27.
nT
X
i=1
i=nT(nT+ 1)
2
nT
X
i=1
i2=nT(nT+ 1)(2nT+ 1)
6
SST O =
nT
X
i=1
i2−ÃnT
X
i=1
i!2
/nT
=nT(nT+ 1)(2nT+ 1)
6−n2
T(nT+ 1)2
4nT
=nT(nT+ 1)(nT−1)
12
SST O/(nT−1) = nT(nT+ 1)/12
18.28. X2
KW =SST R ÷SST O
nT−1
F∗
R=SST R
r−1÷SST O −SST R
nT−r
=ÃX2
KW
r−1!µSST O
nT−1¶÷·SST O −X2
KW µSST O
nT−1¶¸
nT−r
=[(nT−r)X2
KW ]SST O
(r−1)(nT−1) ÷SST O(nT−1−X2
KW )
nT−1
18-8

= [(nT−r)X2
KW ]÷[(r−1)(nT−1−X2
KW )]
18.29. b. r=.994
c. H0: all σ2
iare equal (i= 1, ..., 4), Ha: not all σ2
iare equal.
˜
Y1= 4.85, ˜
Y2= 4.40, ˜
Y3= 4.20, ˜
Y4= 4.45, MST R =.97716, MSE =.70526,
F∗
BF =.97716/.70526 = 1.39, F(.95; 3, 109) = 2.688. If F∗
BF ≤2.688 conclude H0,
otherwise Ha. Conclude H0.
P-value = .25
18.30. b.
i¯
Yi. si
1 11.08893 2.66962
2 9.68344 1.19294
3 9.19135 1.22499
4 8.11375 1.00312
c.
λ SSE
−1.0 206.15
−.8 208.55
−.6 212.09
−.4 216.87
−.2 223.09
−.1 226.79
0 230.93
λ SSE
.1 235.54
.2 240.65
.4 252.56
.6 267.04
.8 284.55
1.0 305.66
Yes
e. r=.995
f. H0: all σ2
iare equal (i= 1, ..., 4), Ha: not all σ2
iare equal.
˜
Y1=.09332, ˜
Y2=.10199, ˜
Y3=.11111, ˜
Y4=.12799, MST R =.00008213,
MSE =.00008472, F∗
BF =.00008213/.00008472 = .97, F (.99; 3,109) = 3.97.
If F∗
BF ≤3.97 conclude H0, otherwise Ha. Conclude H0.P-value = .41
g.
Source SS df MS
Between regions .0103495 3 .0034498
Error .0254284 109 .0002333
Total .0357779 112
H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
F∗=.0034498/.0002333 = 14.787, F(.99; 3,109) = 3.967.
If F∗≤3.967 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
18.31. b. r=.9154
c. H0: all σ2
iare equal (i= 1, ..., 4), Ha: not all σ2
iare equal.
18-9

˜
Y1=.03489, ˜
Y2=.04781, ˜
Y3=.06948, ˜
Y4=.05966, MST R =.001001, MSE =
.000326, F∗
BF =.001001/.000326 = 3.07, F(.99; 3, 436) = 3.83. If F∗
BF ≤3.83
conclude H0, otherwise Ha. Conclude H0.P-value = .028
18.32. b. r=.9902
c. H0: all σ2
iare equal (i= 1, ..., 4), Ha: not all σ2
iare equal.
˜
Y1= 2.415, ˜
Y2= 2.705, ˜
Y3= 2.480, ˜
Y4= 2.880, MST R =.0106, MSE =.0085,
F∗
BF =.0106/.0085 = 1.25, F(.95; 3, 32) = 2.90. If F∗
BF ≤2.90 conclude H0,
otherwise Ha. Conclude H0.P-value = .31
18.33. a. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal. MST R = 2,582.575,
MSE = 1,031.966, F∗
R= 2,582.575/1,031.966 = 2.50, F(.95; 3,109) = 2.69. If
F∗
R≤2.69 conclude H0, otherwise Ha. Conclude H0.P-value = .063
c. ¯
R1.= 69.196, ¯
R2.= 57.797, ¯
R3.= 47.189, ¯
R4.= 56.750, B=z(.99167) = 2.394
Comparison Testing Limits
1 and 2 11.399 ±2.394(8.479) −8.900 and 31.698
1 and 3 22.007 ±2.394(8.207) 2.359 and 41.655
1 and 4 12.446 ±2.394(10.268) −12.136 and 37.028
2 and 3 10.608 ±2.394(7.910) −8.329 and 29.545
2 and 4 1.047 ±2.394(10.032) −22.970 and 25.064
3 and 4 −9.561 ±2.394(9.803) −33.029 and 13.907
Group 1
Region 3
Region 4
Region 2
Group 2
Region 4
Region 2
Region 1
18.34. a. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
MST R = 651,049, MSE = 11,802, F∗
R= 651,049/11,802 = 55.17,
F(.95; 3,436) = 2.6254. If F∗
R≤2.6254 conclude H0, otherwise Ha. Conclude Ha.
P-value = 0+
c. ¯
R1.= 120.4, ¯
R2.= 192.9, ¯
R3.= 290.7,¯
R4.= 254.6,
n1= 103, n2= 108, n3= 152, n4= 77, B=z(.99583) = 2.638
Comparison Testing Limits
1 and 2 −72.5±2.638(17.51) −118.7 and −26.3
1 and 3 −170.3±2.638(16.23) −213.1 and −127.5
1 and 4 −134.2±2.638(19.16) −184.7 and −83.7
2 and 3 −97.8±2.638(16.00) −140.0 and −55.6
2 and 4 −61.7±2.638(18.97) −111.7 and −11.7
3 and 4 36.1±2.638(17.79) −10.8 and 83.0
Group 1
Region 1
Group 2
Region 2
Group 3
Region 3
Region 4
18-10

18.35. a. H0: all µiare equal (i= 1, ..., 4), Ha: not all µiare equal.
MST R = 955.5, MSE = 31.8, F∗
R= 955.5/31.8 = 30.1,
F(.95; 3,32) = 2.90. If F∗
R≤2.90 conclude H0, otherwise Ha. Conclude Ha.
P-value = 0+
c. ¯
R1.= 7.938, ¯
R2.= 22.375, ¯
R3.= 8.571,¯
R4.= 27.962,
n1= 8, n2= 8, n3= 7, n4= 13, B=z(.99583) = 2.638
Comparison Testing Limits
1 and 2 −14.437 ±2.638(5.268) −28.334 and −.541
1 and 3 −.633 ±2.638(5.453) −15.017 and 13.751
1 and 4 −20.024 ±2.638(4.734) −32.513 and −7.535
2 and 3 13.804 ±2.638(5.453) −.580 and 28.188
2 and 4 −5.587 ±2.638(4.734) −18.076 and 6.902
3 and 4 −19.391 ±2.638(4.939) −32.421 and −6.361
Group 1
Region 1
Region 3
Group 2
Region 2
Region 3
Group 3
Region 2
Region 4
18.36. Under H0, each arrangement of the ranks 1, ..., 4 into groups of size 2 are equally
likely and occur with probability 2!2!/4! = 1/6. The values of F∗
Rcomputed for the
six arrangements are 0, .5, and 8, each occurring twice. Therefore the probability
function f(x) is:
x f(x) = P(F∗
R=x)
0 1/3
.5 1/3
8 1/3
18.37. c. For the Fdistribution with ν1= 2 degrees of freedom and ν2= 27 degrees of
freedom, the mean is:
ν2
ν2−2= 1.08
and the standard deviation is:
ν2
ν2−2"2(ν1+ν2−2)
ν1(ν2−4) #1/2
= 1.17.
d. Expect 90% less than 2.51 and 99% less than 5.49.
18-11
18-12

Chapter 19
TWO-FACTOR ANALYSIS OF
VARIANCE WITH EQUAL
SAMPLE SIZES
19.1. a. 8
b. Infection risk
19.3. (αβ)11 =µ11 −(µ.. +α1+β1) = 9 −(12 + 1 −3) = −1
(αβ)12 =µ12 −(µ.. +α1+β2) = 12 −(12 + 1 −1) = 0
(αβ)13 =µ13 −(µ.. +α1+β3) = 18 −(12 + 1 + 4) = 1
(αβ)21 =µ21 −(µ.. +α2+β1) = 9 −(12 −1−3) = 1
(αβ)22 =µ22 −(µ.. +α2+β2) = 10 −(12 −1−1) = 0
(αβ)23 =µ23 −(µ.. +α2+β3) = 14 −(12 −1 + 4) = −1
19.4. a. µ1.= 31, µ2.= 37
b. α1=µ1.−µ.. = 31 −34 = −3, α2=µ2.−µ.. = 37 −34 = 3
19.5. a. µ.j = 269 (j= 1, ..., 4), βj=µ.j −µ..,βj= 0 (j= 1, ..., 4)
c. logeµij :
Factor B
Factor A B1B2B3B4
A15.5215 5.5797 5.5910 5.5947
A25.6630 5.6095 5.5984 5.5947
19.7. a. E{MSE}= 1.96, E{MSA}= 541.96
19.8. a. E{MSE}= 16, E{MSAB}= 952
19.10. a. ¯
Y11.= 21.66667, ¯
Y12.= 21.33333, ¯
Y21.= 27.83333,
¯
Y22.= 27.66667, ¯
Y31.= 22.33333, ¯
Y32.= 20.50000
b. eijk:
19-1
i j = 1 j= 2
1−.66667 −.33333
1.33333 .66667
−2.66667 −1.33333
.33333 −.33333
.33333 −2.33333
1.33333 3.66667
i j = 1 j= 2
2 2.16667 −1.66667
1.16667 1.33333
−1.83333 −.66667
.16667 .33333
−.83333 −.66667
−.83333 1.33333
i j = 1 j= 2
3 2.66667 2.50000
−.33333 −1.50000
.66667 −.50000
−1.33333 .50000
−.33333 −.50000
−1.33333 −.50000
d. r=.986
19.11. b.
Source SS df MS
Treatments 327.222 5 65.444
A(age) 316.722 2 158.361
B(gender) 5.444 1 5.444
AB interactions 5.056 2 2.528
Error 71.667 30 2.389
Total 398.889 35
Yes, factor A(age) accounts for most of the total variability.
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= 2.528/2.389 = 1.06, F(.95; 2,30) = 3.32.
If F∗≤3.32 conclude H0, otherwise Ha. Conclude H0.P-value = .36
d. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= 158.361/2.389 = 66.29, F(.95; 2,30) = 3.32.
If F∗≤3.32 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= 5.444/2.389 = 2.28, F(.95; 1,30) = 4.17.
If F∗≤4.17 conclude H0, otherwise Ha. Conclude H0.P-value = .14
e. α≤.143
g. SSA =SST R,SSB +SSAB +SSE =SSE, yes
19.12. a. ¯
Y11.= 9.2, ¯
Y12.= 13.6, ¯
Y21.= 13.0, ¯
Y22.= 16.4
b. eijk:
i j = 1 j= 2
1 1.8 1.4
−2.2−1.6
2.8.4
−3.2−2.6
.8 2.4
i j = 1 j= 2
2−1.0−2.4
3.0.6
−3.0−3.4
0 3.6
1.0 1.6
d. r=.976
19.13. b.
19-2

Source SS df MS
Treatments 131.75 3 43.917
A(eye contact) 54.45 1 54.45
B(gender) 76.05 1 76.05
AB interactions 1.25 1 1.25
Error 97.20 16 6.075
Total 228.95 19
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 1.25/6.075 = .21,
F(.99; 1,16) = 8.53. If F∗≤8.53 conclude H0, otherwise Ha. Conclude H0.
P-value = .66
d. H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗= 54.45/6.075 = 8.96,
F(.99; 1,16) = 8.53. If F∗≤8.53 conclude H0, otherwise Ha. Conclude Ha.
P-value = .009
H0:β1=β2= 0, Ha: not both β1and β2equal zero. F∗= 76.05/6.075 = 12.52,
F(.99; 1,16) = 8.53. If F∗≤8.53 conclude H0, otherwise Ha. Conclude Ha.
P-value = .003.
e. α≤.030
19.14. a. ¯
Y11.= 2.475, ¯
Y12.= 4.600, ¯
Y13.= 4.575, ¯
Y21.= 5.450, ¯
Y22.= 8.925,
¯
Y23.= 9.125, ¯
Y31.= 5.975, ¯
Y32.= 10.275, ¯
Y33.= 13.250
b. eijk:
i j = 1 j= 2 j= 3
1−.075 0 .225
.225 −.400 −.075
−.175 .300 −.175
.025 .100 .025
i j = 1 j= 2 j= 3
2.350 −.025 −.025
−.250 .175 .175
.050 −.225 −.425
−.150 .075 .275
i j = 1 j= 2 j= 3
3.125 −.375 .250
−.275 .225 −.250
−.075 .325 .050
.225 −.175 −.050
d. r=.988
19.15. b.
Source SS df MS
Treatments 373.105 8 46.638
A(ingredient 1) 220.020 2 110.010
B(ingredient 2) 123.660 2 61.830
AB interactions 29.425 4 7.356
Error 1.625 27 .0602
Total 374.730 35
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 7.356/.0602 =
122.19, F(.95; 4,27) = 2.73. If F∗≤2.73 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
19-3

d. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 110.010/.0602 =
1,827.41, F(.95; 2,27) = 3.35. If F∗≤3.35 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero. F∗= 61.830/.0602 =
1,027.08, F(.95; 2,27) = 3.35. If F∗≤3.35 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
e. α≤.143
19.16. a. ¯
Y11.= 59.8, ¯
Y12.= 47.8, ¯
Y13.= 58.4, ¯
Y21.= 48.4, ¯
Y22.= 61.2,
¯
Y23.= 56.2, ¯
Y31.= 60.2, ¯
Y32.= 60.8, ¯
Y33.= 49.6
b. eijk:
i j = 1 j= 2 j= 3
1 2.2 9.2.6
−11.8−2.8−5.4
3.2−8.8 8.6
−2.8 6.2 7.6
9.2−3.8−11.4
i j = 1 j= 2 j= 3
2 2.6−.2−1.2
8.6−3.2 1.8
−3.4 8.8−6.2
1.6 4.8 12.8
−9.4−10.2−7.2
i j = 1 j= 2 j= 3
3−1.2−2.8−2.6
4.8 2.2 6.4
−5.2 9.2 1.4
−8.2−7.8−5.6
9.8−.8.4
d. r=.989
19.17. b.
Source SS df MS
Treatments 1,268.17778 8 158.52222
A(technician) 24.57778 2 12.28889
B(make) 28.31111 2 14.15556
AB interactions 1,215.28889 4 303.82222
Error 1,872.40000 36 52.01111
Total 3,140.57778 44
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 303.82222/52.01111 =
5.84, F(.99; 4,36) = 3.89. If F∗≤3.89 conclude H0, otherwise Ha. Conclude Ha.
P-value = .001
d. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 12.28889/52.01111 =
.24, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude H0.
P-value = .79
H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero. F∗= 14.15556/52.01111 =
.27, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude H0.
P-value = .76
e. α≤.003
19-4

19.18. a. ¯
Y0
11.=.44348, ¯
Y0
12.=.80997, ¯
Y0
13.= 1.10670,
¯
Y0
21.=.39823, ¯
Y0
22.=.58096, ¯
Y0
23.=.86639
e0
ijk:
i j = 1 j= 2 j= 3
1−.44348 .03364 −.33285 −.11100 .09742 .12375
.03364 −.44348 −.11100 −.20791 −.06531 −.20361
−.14245 .33467 .09312 −.50894 −.15246 .38466
.15858 .40162 .30398 −.03182 −.32855 −.50464
−.44348 .51076 .39415 .51225 .30827 .34046
i j = 1 j= 2 j= 3
2−.39823 .07889 .19719 −.27993 .17500 .33773
−.09720 .50486 .02110 .02110 .08785 −.16742
−.09720 .30074 −.10384 .26413 .24755 .13361
−.39823 −.39823 −.58096 .32213 −.26433 −.02130
.30074 .20383 −.27993 .41904 .03670 −.56536
c. r=.987
19.19. b.
Source SS df MS
Treatments 3.76217 5 .75243
A(duration) .44129 1 .44129
B(weight gain) 3.20098 2 1.60049
AB interactions .11989 2 .05995
Error 5.46770 54 .10125
Total 9.22987 59
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗=.05995/.10125 = .59,
F(.95; 2,54) = 3.17. If F∗≤3.17 conclude H0, otherwise Ha. Conclude H0.P-
value = .56
d. H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗=.44129/.10125 = 4.36,
F(.95; 1,54) = 4.02. If F∗≤4.02 conclude H0, otherwise Ha. Conclude Ha.
P-value = .04
H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero. F∗= 1.60049/.10125 =
15.81, F(.95; 2,54) = 3.17. If F∗≤3.17 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
e. α≤.143
19.20. a. ¯
Y11.= 222.00, ¯
Y12.= 106.50, ¯
Y13.= 60.50, ¯
Y21.= 62.25, ¯
Y22.= 44.75, ¯
Y23.= 38.75
b. eijk:
i j = 1 j= 2 j= 3
1 18 3.5−4.5
−16 11.5−.5
−5−3.5 7.5
3−11.5−2.5
i j = 1 j= 2 j= 3
2 8.75 2.25 −1.75
−9.25 7.25 −5.75
5.75 −13.75 1.25
−5.25 4.25 6.25
19-5

d. r=.994
19.21. b.
Source SS df MS
Treatments 96,024.37500 5 19,204.87500
A(type) 39,447.04167 1 39,447.04167
B(years) 36,412.00000 2 18,206.00000
AB interactions 20,165.33333 2 10,082.66667
Error 1,550.25000 18 86.12500
Total 97,574.62500 23
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 10,082.66667/86.12500 =
117.07, F(.99; 2,18) = 6.01. If F∗≤6.01 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
d. H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗= 39,447.04167/86.12500 =
458.02, F(.99; 1,18) = 8.29. If F∗≤8.29 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero. F∗= 18,206.00000/86.12500 =
211.39, F(.99; 2,18) = 6.01. If F∗≤6.01 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
e. α≤.030
19.27. a. B=t(.9975; 75) = 2.8925, q(.95; 5,75) = 3.96, T= 2.800
b. B=t(.99167; 27) = 2.552, q(.95; 3,27) = 3.51, T= 2.482
19.28. (1) B=t(.9972; 324) = 2.791,
(2) F(.975; 5,324) = 2.606, S= 3.6097
(3) F(.95; 10,324) = 1.86, S= 4.3128
19.30. a. s{¯
Y11.}=.631, t(.975; 30) = 2.042, 21.66667 ±2.042(.631), 20.378 ≤µ11 ≤22.955
b. ¯
Y.1.= 23.94, ¯
Y.2.= 23.17
c. ˆ
D=.77, s{ˆ
D}=.5152, t(.975; 30) = 2.042, .77±2.042(.5152), −.282 ≤D≤1.822
d. ¯
Y1.. = 21.50, ¯
Y2.. = 27.75, ¯
Y3.. = 21.42
e. ˆ
D1=¯
Y1..−¯
Y2.. =−6.25, ˆ
D2=¯
Y1..−¯
Y3.. =.08, ˆ
D3=¯
Y2..−¯
Y3.. = 6.33, s{ˆ
Di}=.631
(i= 1,2,3), q(.90; 3,30) = 3.02, T= 2.1355
−6.25 ±2.1355(.631) −7.598 ≤D1≤ −4.902
.08 ±2.1355(.631) −1.268 ≤D2≤1.428
6.33 ±2.1355(.631) 4.982 ≤D3≤7.678
f. Yes
g. ˆ
L=−6.29, s{ˆ
L}=.5465, t(.976; 30) = 2.042, −6.29 ±2.042(.5465), −7.406 ≤
L≤ −5.174
h. L=.3µ12 +.6µ22 +.1µ32,ˆ
L= 25.05000, s{ˆ
L}=.4280, t(.975; 30) = 2.042,
25.05000 ±2.042(.4280), 24.176 ≤L≤25.924
19-6

19.31. a. s{¯
Y21.}= 1.1023, t(.995; 16) = 2.921, 13.0±2.921(1.1023), 9.780 ≤µ21 ≤16.220
b. s{¯
Y1..}=.7794, t(.995; 16) = 2.921, 11.4±2.921(.7794), 9.123 ≤µ1.≤13.677
c. ¯
Y.1.= 11.1, ¯
Y.2.= 15.0
d. s{¯
Y.1.}=s{¯
Y.2.}=.7794, t(.995; 16) = 2.921
11.1±2.921(.7794) 8.823 ≤µ.1≤13.377
15.0±2.921(.7794) 12.723 ≤µ.2≤17.277
98 percent
e. ¯
Y1.. = 11.4, ¯
Y2.. = 14.7
f. ˆ
D1= 3.3, ˆ
D2= 3.9, s{ˆ
Di}= 1.1023 (i= 1,2), B=t(.9875; 16) = 2.473
3.3±2.473(1.1023) .574 ≤D1≤6.026
3.9±2.473(1.1023) 1.174 ≤D2≤6.626
g. Yes
19.32. a. s{¯
Y23.}=.1227, t(.975; 27) = 2.052, 9.125 ±2.052(.1227), 8.873 ≤µ23 ≤9.377
b. ˆ
D= 2.125, s{ˆ
D}=.1735, t(.975; 27) = 2.052, 2.125 ±2.052(.1735), 1.769 ≤D≤
2.481
c. ˆ
L1= 2.1125, ˆ
L2= 3.5750, ˆ
L3= 5.7875, ˆ
L4= 1.4625, ˆ
L5= 3.6750, ˆ
L6= 2.2125,
s{ˆ
Li}=.1502 (i= 1,2,3), s{ˆ
Li}=.2125 (i= 4,5,6), F(.90; 8,27) = 1.90,
S= 3.899
2.1125 ±3.899(.1502) 1.527 ≤L1≤2.698
3.5750 ±3.899(.1502) 2.989 ≤L2≤4.161
5.7875 ±3.899(.1502) 5.202 ≤L3≤6.373
1.4625 ±3.899(.2125) .634 ≤L4≤2.291
3.6750 ±3.899(.2125) 2.846 ≤L5≤4.504
2.2125 ±3.899(.2125) 1.384 ≤L6≤3.041
d. s{ˆ
Di}=.1735, q(.90; 9,27) = 4.31, T= 3.048, T s{ˆ
Di}=.529, ¯
Y33.= 13.250
e.
i j 1/¯
Yij. q¯
Yij.
1 1 .404 1.573
1 2 .217 2.145
1 3 .219 2.139
2 1 .183 2.335
2 2 .112 2.987
2 3 .110 3.021
3 1 .167 2.444
3 2 .097 3.205
3 3 .075 3.640
19.33. a. s{¯
Y11.}= 3.2252, t(.995; 36) = 2.7195, 59.8±2.7195(3.2252),
51.029 ≤µ11 ≤68.571
b. ˆ
D= 12.8, s{ˆ
D}= 4.5612, t(.995; 36) = 2.7195, 12.8±2.7195(4.5612), .396 ≤D≤
25.204
19-7

c. ˆ
D1=¯
Y11.−¯
Y12.= 12.0, ˆ
D2=¯
Y11.−¯
Y13.= 1.4, ˆ
D3=¯
Y12.−¯
Y13.=−10.6,
ˆ
D4=¯
Y21.−¯
Y22.=−12.8, ˆ
D5=¯
Y21.−¯
Y23.=−7.8, ˆ
D6=¯
Y22.−¯
Y23.= 5.0,
ˆ
D7=¯
Y31.−¯
Y32.=−.6, ˆ
D8=¯
Y31.−¯
Y33.= 10.6, ˆ
D9=¯
Y32.−¯
Y33.= 11.2,
s{ˆ
Di}= 4.5612 (i= 1, ..., 9), B=t(.99167; 36) = 2.511
12.0±2.511(4.5612) .547 ≤D1≤23.453
1.4±2.511(4.5612) −10.053 ≤D2≤12.853
−10.6±2.511(4.5612) −22.053 ≤D3≤.853
−12.8±2.511(4.5612) −24.253 ≤D4≤ −1.347
−7.8±2.511(4.5612) −19.253 ≤D5≤3.653
5.0±2.511(4.5612) −6.453 ≤D6≤16.453
−.6±2.511(4.5612) −12.053 ≤D7≤10.853
10.6±2.511(4.5612) −.853 ≤D8≤22.053
11.2±2.511(4.5612) −.253 ≤D9≤22.653
d. ¯
Y... = 55.8222, 90 ¯
Y... = 5,024, s{90 ¯
Y...}= 96.7574, t(.995; 36) = 2.7195,
5,024 ±2.7195(96.7574), 4,760.87 ≤90µ.. ≤5,287.13
e. L= 10µ11 + 10µ13 + 10µ22 + 10µ23 + 10µ31 + 10µ32 −20µ12 −20µ21 −20µ33,
ˆ
L= 650, s{ˆ
L}= 136.8357, t(.995; 36) = 2.7195,
650 ±2.7195(136.8357), 277.875 ≤L≤1,022.125
f.
i j 1/¯
Yij. log10 ¯
Yij.
1 1 .0167 1.777
1 2 .0209 1.679
1 3 .0171 1.766
2 1 .0207 1.685
2 2 .0163 1.787
2 3 .0178 1.750
3 1 .0166 1.780
3 2 .0164 1.784
3 3 .0202 1.695
19.34. a. s{¯
Y0
22.}=.1006, t(.975; 54) = 2.005,
.58096 ±2.005(.1006), .37926 ≤µ22 ≤.78266
b. ˆ
D=.46816, s{ˆ
D}=.1423, t(.975; 54) = 2.005,
.46816 ±2.005(.1423), .18285 ≤D≤.75347
c. ¯
Y0
1.. =.78672, ¯
Y0
2.. =.61519
¯
Y0
.1.=.42086, ¯
Y0
.2.=.69547, ¯
Y0
.3.=.98655
d. B=t(.9875; 54) = 2.306, q(.95; 2,54) = 2.84, T= 2.008, q(.95; 3,54) = 3.41,
T= 2.411, F(.90; 3,54) = 2.20, S= 2.569
e. ˆ
D1=¯
Y0
1.. −¯
Y0
2.. =.17153, ˆ
D2=¯
Y0
.1.−¯
Y0
.2.=−.27461,
ˆ
D3=¯
Y0
.1.−¯
Y0
.3.=−.56569, ˆ
D4=¯
Y0
.2.−¯
Y0
.3.=−.29108,
s{ˆ
D1}=.0822, s{ˆ
Di}=.1006 (i= 2,3,4), B= 2.306
19-8

.17153 ±2.306(.0822) −.0180 ≤D1≤.3611
−.27461 ±2.306(.1006) −.5066 ≤D2≤ −.0426
−.56569 ±2.306(.1006) −.7977 ≤D3≤ −.3337
−.29108 ±2.306(.1006) −.5231 ≤D4≤ −.0591
f. L=.3µ.1+.4µ.2+.3µ.3,ˆ
L=.70041, s{ˆ
L}=.04149, t(.975; 54) = 2.005,
.70041 ±2.005(.04149), .6172 ≤L≤.7836, (3.142, 5.076), yes
19.35. a. s{¯
Y23.}= 4.6402, t(.995; 18) = 2.878,
38.75 ±2.878(4.6402), 25.3955 ≤µ23 ≤52.1045
b. ˆ
D= 46.00, s{ˆ
D}= 6.5622, t(.995; 18) = 2.878,
46.00 ±2.878(6.5622), 27.114 ≤D≤64.886
c. F(.95; 5,18) = 2.77, S= 3.7216, B=t(.99583; 18) = 2.963
d. ˆ
D1= 159.75, ˆ
D2= 61.75, ˆ
D3= 21.75, ˆ
L1= 98.00, ˆ
L2= 138.00, ˆ
L3= 40.00,
s{ˆ
Di}= 6.5622 (i= 1,2,3), s{ˆ
Li}= 9.2804 (i= 1,2,3), B=t(.99583; 18) =
2.963
159.75 ±2.963(6.5622) 140.31 ≤D1≤179.19
61.75 ±2.963(6.5622) 42.31 ≤D2≤81.19
21.75 ±2.963(6.5622) 2.31 ≤D3≤41.19
98.00 ±2.963(9.2804) 70.50 ≤L1≤125.50
138.00 ±2.963(9.2804) 110.50 ≤L2≤165.50
40.00 ±2.963(9.2804) 12.50 ≤L3≤67.50
e. q(.95; 6,18) = 4.49, T= 3.1749, s{ˆ
D}= 6.5622, T s{ˆ
D}= 20.834, ¯
Y23.= 38.75,
¯
Y22.= 44.75
f. B=t(.9875; 18) = 2.445, s{¯
Yij.}= 4.6402
44.75 ±2.445(4.6402) 33.405 ≤µ22 ≤56.095
38.75 ±2.445(4.6402) 27.405 ≤µ23 ≤50.095
g.
i j 1/¯
Yij. log10 ¯
Yij.
1 1 .00450 2.346
1 2 .00939 2.027
1 3 .01653 1.782
2 1 .01606 1.794
2 2 .02235 1.651
2 3 .02581 1.588
19.36. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk,i= 1, ..., 4; j= 1,2; k= 1,2
b.
Source SS df MS
Treatments 1,910.00 7 272.85714
A(moisture content) 1,581.50 3 527.16667
B(sweetness) 306.25 1 306.25000
AB interactions 22.25 3 7.41667
Error 57.00 8 7.12500
Total 1,967.00 15
19-9
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 7.41667/7.125 =
1.04, F(.99; 3,8) = 7.59. If F∗≤7.59 conclude H0, otherwise Ha. Conclude H0.
d. ˆ
L=−1.500, s{ˆ
L}= 2.669, t(.975; 8) = 2.306,
−1.500 ±2.306(2.669), −7.655 ≤L≤4.655
e. H0:β1=β2= 0, Ha: not both β1and β2equal zero. F∗= 306.25/7.125 = 42.98,
F(.99; 1,8) = 11.3. If F∗≤11.3 conclude H0, otherwise Ha. Conclude Ha.
19.37. n= 21
19.38. ∆/σ = 2, 2n= 8, n= 4
19.39. n= 21
19.40. .5√n/.29 = 4.1999, n= 6
19.41. n= 14
19.42. 8√n/9.1 = 3.1591, n= 13
19.43. Using (19.4) and (19.5), we have:
µij =µ.. +αi+βj
=µ.. + (µi. −µ..)+(µ.j −µ..) = µi. +µ.j −µ..
19.44. P
j(αβ)ij =P
j(µij −µi. −µ.j +µ..)
=bµi. −bµi. −bµ.. +bµ.. = 0
19.45. L=
2
Y
i=1
2
Y
j=1
2
Y
k=1
1
(2πσ2)1/2exp ·−1
2σ2(Yijk −µij )2¸
=1
(2πσ2)4exp ·−1
2σ2PPP(Yijk −µij)2¸
logeL=−4 loge(2πσ2)−1
2σ2PPP(Yijk −µij)2
∂(logeL)
∂µij
=−2
2σ2P
k
(Yijk −µij )(−1)
Setting the derivatives equal to zero, simplifying, and solving for the maximum
likelihood estimators ˆµij yields:
ˆµij =
2
X
k=1
Yijk
2=¯
Yij.
Yes
19.46. Q=PPP(Yijk −µij )2
∂Q
∂µij
= 2 X
k
(Yijk −µij )(−1)
19-10
Setting the derivatives equal to zero, simplifying, and solving for the least squares
estimators yields:
ˆµij =P
k
Yijk
n=¯
Yij.
19.47. PPP(¯
Yij. −¯
Y...)2=PPP[( ¯
Yi.. −¯
Y...)+(¯
Y.j. −¯
Y...)+(¯
Yij. −¯
Yi.. −¯
Y.j. +¯
Y...)]2
=PPP[( ¯
Yi.. −¯
Y...)2+ ( ¯
Y.j. −¯
Y...)2+ ( ¯
Yij. −¯
Yi.. −¯
Y.j. +¯
Y...)2
+2( ¯
Yi.. −¯
Y...)( ¯
Y.j. −¯
Y...) + 2( ¯
Yi.. −¯
Y...)( ¯
Yij. −¯
Yi.. −¯
Y.j. +¯
Y...)
+2( ¯
Y.j. −¯
Y...)( ¯
Yij. −¯
Yi.. −¯
Y.j. +¯
Y...)]
=nb P(¯
Yi..−¯
Y...)2+na P(¯
Y.j.−¯
Y...)2+nPP(¯
Yij.−¯
Yi..−¯
Y.j.+¯
Y...)2
since all summations of cross-product terms equal zero.
19.48. E{ˆ
L}=E{Pcj¯
Y.j.}=PcjE{¯
Y.j.}=Pcjµ.j =L
σ2{ˆ
L}=σ2{Pcj¯
Y.j.}=Pc2
jσ2{¯
Y.j.}because of independence
=Pc2
j
σ2
an =σ2
an Pc2
j
19.49. σ2{PPcij ¯
Yij.}=PPc2
ijσ2{¯
Yij.}because of independence
=PPc2
ij
σ2
n=σ2
nPPc2
ij
19.50. By (19.9a), (αβ)11 + (αβ)21 = 0; hence (αβ)21 =−(αβ)11.
By (19.9b), (αβ)11 + (αβ)12 = 0; hence (αβ)12 =−(αβ)11.
19.51. a. ¯
Y11.= 10.05875, ¯
Y12.= 11.45500, ¯
Y21.= 9.84000, ¯
Y22.= 9.57250,
¯
Y31.= 9.68250, ¯
Y32.= 9.52375, ¯
Y41.= 8.21250, ¯
Y42.= 8.01500
d. r=.996
19.52. b.
Source SS df MS
Treatments 65.08508 7 9.29787
A(region) 56.74396 3 18.91465
B(average age) .59676 1 .59676
AB interactions 7.74436 3 2.58145
Error 76.03013 56 1.35768
Total 141.11521 63
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 2.58145/1.35768 =
1.90, F(.95; 3,56) = 2.77. If F∗≤2.77 conclude H0, otherwise Ha. Conclude H0.
P-value = .14
d. H0: all αiequal zero (i= 1, ..., 4), Ha: not all αiequal zero. F∗= 18.91465/1.35768 =
13.93, F(.95; 3,56) = 2.77. If F∗≤2.77 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
19-11

H0:β1=β2= 0, Ha: not both β1and β2equal zero. F∗=.59676/1.35768 = .44,
F(.95; 1,56) = 4.01. If F∗≤4.01 conclude H0, otherwise Ha. Conclude H0.
P-value = .51
e. α≤.143
19.53. a. ¯
Y11.=.0359, ¯
Y12.=.0454, ¯
Y21.=.0516, ¯
Y22.=.0515,
¯
Y31.=.0758, ¯
Y32.=.1015, ¯
Y41.=.0673, ¯
Y42.=.0766
d. r=.993
19.54. a. ¯
Y1.. =.0406,¯
Y2.. =.0515,¯
Y3.. =.0886,¯
Y4.. =.0719
¯
Y.1.=.0576,¯
Y.2.=.0687
b.
Source SS df MS
A .019171 3 .006390
B.001732 1 .001732
AB .001205 3 .000402
Error .011042 48 .000230
Total .033151 55
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗=.000402/.000230 = 1.75, F(.99; 3,48) = 4.22.
If F∗≤4.22 conclude H0, otherwise Ha. Conclude H0.P-value = .170
d. (i) Test for factor A (region effect)
H0: all αiequal zero (i= 1, ..., 4), Ha: not all αiequal zero.
F∗=.006390/.000230 = 27.79, F(.99; 3,48) = 4.22.
If F∗≤4.22 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
(ii) Test for factor B (% below poverty)
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗=.001732/.000230 = 7.53, F(.99; 1,48) = 7.19.
If F∗≤7.19 conclude H0, otherwise Ha. Conclude Ha.P-value = .009
e. α≤.030
19.55. a. ¯
Y11.= 2.4386, ¯
Y12.= 2.4286, ¯
Y21.= 2.7286, ¯
Y22.= 2.9786,
d. r=.994
19.56. a. ¯
Y1.. = 2.4336,¯
Y2.. = 2.8536
¯
Y.1.= 2.5836,¯
Y.2.= 2.7036
b.
Source SS df MS
A1.2348 1 1.2348
B.1008 1 .1008
AB .1183 1 .1183
Error .5341 24 .0223
Total 1.9880 27
19-12
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗=.1183/.0223 = 5.32, F(.95; 1,24) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha. Conclude Ha.P-value = .030
d. (i) Test for factor A (region effect)
H0:α1=α2= 0, Ha: not both α1and α2equal zero.
F∗= 1.2348/.0223 = 55.48, F(.95; 1,24) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
(ii) Test for factor B (% below poverty)
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗=.1008/.0223 = 4.53, F(.95; 1,24) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha. Conclude Ha.P-value = .044
e. α≤.143
19.57 b. ˆ
D1=¯
Y1.. −¯
Y2.. = 1.0506, ˆ
D2=¯
Y1.. −¯
Y3.. = 1.1538,
ˆ
D3=¯
Y1.. −¯
Y4.. = 2.6431, ˆ
D4=¯
Y2.. −¯
Y3.. =.1032,
ˆ
D5=¯
Y2.. −¯
Y4.. = 1.5925, ˆ
D6=¯
Y3.. −¯
Y4.. = 1.4893,
s{ˆ
Di}=.41196 (i= 1, ..., 6), q(.90; 4,56) = 3.31, T= 2.341
1.0506 ±2.341(.41196) .0862 ≤D1≤2.0150
1.1538 ±2.341(.41196) .1894 ≤D2≤2.1182
2.6431 ±2.341(.41196) 1.6787 ≤D3≤3.6075
.1032 ±2.341(.41196) −.8612 ≤D4≤1.0676
1.5925 ±2.341(.41196) .6281 ≤D5≤2.5569
1.4893 ±2.341(.41196) .5249 ≤D6≤2.4537
19.58. b. ˆ
D1=¯
Y1.. −¯
Y2.. =−.0109, ˆ
D2=¯
Y1.. −¯
Y3.. =−.0480,
ˆ
D3=¯
Y1.. −¯
Y4.. =−.0313, ˆ
D4=¯
Y2.. −¯
Y3.. =−.0371,
ˆ
D5=¯
Y2.. −¯
Y4.. =−.0204, ˆ
D6=¯
Y3.. −¯
Y4.. =.0167,
s{ˆ
Di}=.005732 (i= 1, ..., 6), q(.95; 4,48) = 3.79, T= 2.680
−.0109 ±2.680(.0057) −.0262 ≤D1≤.0043
−.0480 ±2.680(.0057) −.0633 ≤D2≤ −.0328
−.0313 ±2.680(.0057) −.0466 ≤D3≤ −.0161
−.0371 ±2.680(.0057) −.0524 ≤D4≤ −.0219
−.0204 ±2.680(.0057) −.0356 ≤D5≤ −.0052
.0167 ±2.680(.0057) .0015 ≤D6≤.0320
19-13
19-14

Chapter 20
TWO-FACTOR STUDIES – ONE
CASE PER TREATMENT
20.1. 0
20.2. b.
Source SS df MS
Location 37.0050 3 12.3350
Week 47.0450 1 47.0450
Error .3450 3 .1150
Total 84.3950 7
H0: all αiequal zero (i= 1, ..., 4), Ha: not all αiequal zero.
F∗= 12.3350/.1150 = 107.26, F(.95; 3,3) = 9.28. If F∗≤9.28 conclude H0,
otherwise Ha. Conclude Ha.P-value = .0015
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= 47.0450/.1150 = 409.09, F(.95; 1,3) = 10.1. If F∗≤10.1 conclude H0,
otherwise Ha. Conclude Ha.P-value = .0003. α≤.0975
c. ˆ
D1=¯
Y1.−¯
Y2.= 18.95 −14.55 = 4.40, ˆ
D2=¯
Y1.−¯
Y3.= 18.95 −14.60 = 4.35,
ˆ
D3=¯
Y1.−¯
Y4.= 18.95−18.80 = .15, ˆ
D4=¯
Y2.−¯
Y3.=−.05, ˆ
D5=¯
Y2.−¯
Y4.=−4.25,
ˆ
D6=¯
Y3.−¯
Y4.=−4.20, ˆ
D7=¯
Y.1−¯
Y.2= 14.30 −19.15 = −4.85, s{ˆ
Di}=.3391
(i= 1, ..., 6), s{ˆ
D7}=.2398, B=t(.99286; 3) = 5.139
4.40 ±5.139(.3391) 2.66 ≤D1≤6.14
4.35 ±5.139(.3391) 2.61 ≤D2≤6.09
.15 ±5.139(.3391) −1.59 ≤D3≤1.89
−.05 ±5.139(.3391) −1.79 ≤D4≤1.69
−4.25 ±5.139(.3391) −5.99 ≤D5≤ −2.51
−4.20 ±5.139(.3391) −5.94 ≤D6≤ −2.46
−4.85 ±5.139(.2398) −6.08 ≤D7≤ −3.62
20.3. a. ˆµ32 =¯
Y3.+¯
Y.2−¯
Y.. = 14.600 + 19.150 −16.725 = 17.025
b. s2{ˆµ32}=.071875
c. s{ˆµ32}=.2681, t(.975; 3) = 3.182, 17.025 ±3.182(.2681),16.172 ≤µ32 ≤17.878
20-1

20.4. ˆ
D= (−4.13473)/(18.5025)(11.76125) = −.019, SSAB∗=.0786, SSRem∗=
.2664.
H0:D= 0, Ha:D6= 0. F∗= (.0786/1) ÷(.2664/2) = .59, F(.975; 1,2) = 38.5.
If F∗≤38.5 conclude H0, otherwise Ha. Conclude H0.
20.5. b.
Source SS df MS
Type of group 1.125 1 1.125
Size of group 318.375 3 106.125
Error 6.375 3 2.125
Total 325.875 7
H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗= 1.125/2.125 = .53,
F(.99; 1,3) = 34.1. If F∗≤34.1 conclude H0, otherwise Ha. Conclude H0.
P-value = .52
H0: all βjequal zero (j= 1, ..., 4), Ha: not all βjequal zero. F∗= 106.125/2.125 =
49.94, F(.99; 3,3) = 29.5. If F∗≤29.5 conclude H0, otherwise Ha. Conclude Ha.
P-value = .005. α≤.0199
c. ˆ
D1=¯
Y.2−¯
Y.1= 22.5−16.5=6.0, ˆ
D2=¯
Y.3−¯
Y.2= 30.0−22.5=7.5, ˆ
D3=
¯
Y.4−¯
Y.3= 32.5−30.0 = 2.5, s{ˆ
Di}= 1.4577 (i= 1,2,3), B=t(.99167; 3) = 4.857
6.0±4.857(1.4577) −1.08 ≤D1≤13.08
7.5±4.857(1.4577) .42 ≤D2≤14.58
2.5±4.857(1.4577) −4.58 ≤D3≤9.58
d. No, q(.95; 4,3) = 6.82, T= 4.822
20.6. a. ˆµ14 =¯
Y1.+¯
Y.4−¯
Y.. = 25.750 + 32.500 −25.375 = 32.875
b. s2{ˆµ14}= 1.3281
c. s{ˆµ14}= 1.1524, t(.995; 3) = 5.841, 32.875 ±5.841(1.1524),26.144 ≤µ14 ≤39.606
20.7. ˆ
D= (−8.109375)/(.28125)(159.1875) = −.1811, SSAB∗= 1.4688,
SSRem∗= 4.9062. H0:D= 0, Ha:D6= 0. F∗= (1.4688/1) ÷(4.9062/2) = .60,
F(.99; 1,2) = 98.5. If F∗≤98.5 conclude H0, otherwise Ha. Conclude H0.
20.8. b.
Source SS df MS
Humidity 2.12167 2 1.06083
Temperature 202.20000 3 67.40000
Error 6.58500 6 1.09750
Total 210.90667 11
H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= 1.06083/1.09750 = .97, F(.975; 2,6) = 7.26. If F∗≤7.26 conclude H0,
otherwise Ha. Conclude H0.P-value = .43
H0: all βjequal zero (j= 1, ..., 4), Ha: not all βjequal zero.
20-2

F∗= 67.40000/1.09750 = 61.41, F(.975; 3,6) = 6.60. If F∗≤6.60 conclude H0,
otherwise Ha. Conclude Ha.P-value = 0+
c. ˆ
D1=¯
Y.2−¯
Y.1= 15.30 −14.90 = .40, ˆ
D2=¯
Y.3−¯
Y.2= 20.70 −15.30 = 5.40,
ˆ
D3=¯
Y.4−¯
Y.3= 24.83 −20.70 = 4.13, s{ˆ
Di}=.8554 (i= 1,2,3), B=
t(.99167; 6) = 3.2875
.40 ±3.2875(.8554) −2.41 ≤D1≤3.21
5.40 ±3.2875(.8554) 2.59 ≤D2≤8.21
4.13 ±3.2875(.8554) 1.32 ≤D3≤6.94
d. Yes
20.9. a. ˆµ23 =¯
Y2.+¯
Y.3−¯
Y.. = 19.325 + 20.700 −18.933 = 21.092
b. s2{ˆµ23}=.54875
c. s{ˆµ23}=.7408, t(.99; 6) = 3.143, 21.092 ±3.143(.7408),18.764 ≤µ23 ≤23.420,
(2.66%, 4.12%)
20.10. ˆ
D= (−8.27113)/(.5304)(67.4000) = −.2314, SSAB∗= 1.9137, SSRem∗=
4.6713.
H0:D= 0, Ha:D6= 0. F∗= (1.9137/1) ÷(4.6713/5) = 2.05,
F(.995; 1,5) = 22.8. If F∗≤22.8 conclude H0, otherwise Ha. Conclude H0.
20.11. SSA =bP(¯
Yi. −¯
Y..)2,SSB =aP(¯
Y.j −¯
Y..)2
20.12.
(αβ)ij =A+Bαi+Cβj+Dαiβj+Eα2
i+F β2
j(1)
Averaging (1) over iyields:
(αβ).j =A+Cβj+EPα2
i/a +F β2
j= 0 (2)
because Pαi= 0 and P
i(αβ)ij = 0. Similarly:
(αβ)i. =A+Bαi+Eα2
i+FPβ2
j/b (3)
because Pβj= 0 and P
j(αβ)ij = 0. From (2) and (3) we obtain:
Cβj+F β2
j=−A−EPα2
i/a (4)
Bαi+Eα2
i=−A−FPβ2
j/b (5)
Substituting (4) and (5) in (1) yields:
(αβ)ij =−A−EPα2
i/a −FPβ2
j/b +Dαiβj(6)
Averaging (6) over jyields:
(αβ)i. =−A−EPα2
i/a −FPβ2
j/b = 0 (7)
Using (7) in (6) yields:
(αβ)ij =Dαiβj(8)
20-3
20-4

Chapter 21
RANDOMIZED COMPLETE
BLOCK DESIGNS
21.5. b. eij:
i j = 1 j= 2 j= 3
1−2.50000 1.50000 1.00000
2 1.50000 −.50000 −1.00000
3 2.16667 −.83333 −1.33333
4.16667 −.83333 .66667
5 4.16667 −4.83333 .66667
6 1.50000 −.50000 −1.00000
7−1.50000 −1.50000 3.00000
8−2.83333 3.16667 −.33333
9−1.50000 2.50000 −1.00000
10 −1.16667 1.83333 −.66667
r=.984
d. H0:D= 0, Ha:D6= 0. SSBL.T R∗=.13, SSRem∗= 112.20,
F∗= (.13/1) ÷(112.20/17) = .02, F(.99; 1,17) = 8.40. If F∗≤8.40 conclude H0,
otherwise Ha. Conclude H0.P-value = .89
21.6. a.
Source SS df MS
Blocks 433.36667 9 48.15185
Training methods 1,295.00000 2 647.50000
Error 112.33333 18 6.24074
Total 1,840.70000 29
b. ¯
Y.1= 70.6, ¯
Y.2= 74.6, ¯
Y.3= 86.1
c. H0: all τjequal zero (j= 1,2,3), Ha: not all τjequal zero.
F∗= 647.50000/6.24074 = 103.754, F(.95; 2,18) = 3.55. If F∗≤3.55 conclude
H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ˆ
D1=¯
Y.1−¯
Y.2=−4.0, ˆ
D2=¯
Y.1−¯
Y.3=−15.5, ˆ
D3=¯
Y.2−¯
Y.3=−11.5,
s{ˆ
Di}= 1.1172 (i= 1,2,3), q(.90; 3,18) = 3.10, T= 2.192
21-1

−4.0±2.192(1.1172) −6.45 ≤D1≤ −1.55
−15.5±2.192(1.1172) −17.95 ≤D2≤ −13.05
−11.5±2.192(1.1172) −13.95 ≤D3≤ −9.05
e. H0: all ρiequal zero (i= 1, ..., 10), Ha: not all ρiequal zero.
F∗= 48.15185/6.24074 = 7.716, F(.95; 9,18) = 2.46.
If F∗≤2.46 conclude H0, otherwise Ha. Conclude Ha.P-value = .0001
21.7. b. eij:
i j = 1 j= 2 j= 3
1−.05267 .00533 .04733
2−.01267 −.00467 .01733
3.00400 −.00800 .00400
4−.02267 .01533 .00733
5.08400 −.00800 −.07600
r=.956
d. H0:D= 0, Ha:D6= 0. SSBL.T R∗=.0093, SSRem∗=.01002,
F∗= (.0093/1) ÷(.01002/7) = 6.50, F(.99; 1,7) = 12.2.
If F∗≤12.2 conclude H0, otherwise Ha. Conclude H0.P-value = .038
21.8. a.
Source SS df MS
Blocks 1.41896 4 .35474
Fat content 1.32028 2 .66014
Error .01932 8 .002415
Total 2.75856 14
b. ¯
Y.1= 1.110, ¯
Y.2=.992, ¯
Y.3=.430
c. H0: all τjequal zero (j= 1,2,3), Ha: not all τjequal zero.
F∗=.66014/.002415 = 273.35, F(.95; 2,8) = 4.46.
If F∗≤4.46 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ˆ
D1=.118, ˆ
D2=.562, s{ˆ
Di}=.03108 (i= 1,2), B=t(.9875; 8) = 2.7515
.118 ±2.7515(.03108) .032 ≤D1≤.204
.562 ±2.7515(.03108) .476 ≤D2≤.648
e. H0: all ρiequal zero (i= 1, ..., 5), Ha: not all ρiequal zero.
F∗=.35474/.002415 = 146.89, F(.95; 4,8) = 3.84.
If F∗≤3.84 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
21.9. c. ejik:
21-2

k= 1 k= 2
i j = 1 j= 2 i j = 1 j= 2
1−.01875 .01875 1 .00625 −.00625
2.13125 −.03125 2 −.04375 −.05625
3.05625 −.00625 3 −.11875 .06875
4.08125 −.08125 4 .00625 −.00625
5−.09375 −.15625 5 .23125 .01875
6−.09375 −.05625 6 .03125 .11875
7−.09375 .24375 7 .03125 −.18125
8.03125 .06875 8 −.14375 .04375
r=.984
e. H0:D= 0, Ha:D6= 0. SSBL.T R∗=.00503, SSRem∗=.29872,
F∗= (.00503/1) ÷(.29872/20) = .337, F(.99; 1,20) = 8.10.
If F∗≤8.10 conclude H0, otherwise Ha. Conclude H0.P-value = .57
21.10. a.
Source SS df MS
Blocks 5.59875 7 .79982
A2.31125 1 2.31125
B3.38000 1 3.38000
AB interactions .04500 1 .04500
Error .30375 21 .01446
Total 11.63875 31
b. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero.
F∗=.04500/.01446 = 3.112, F(.99; 1,21) = 8.017.
If F∗≤8.017 conclude H0, otherwise Ha. Conclude H0.P-value = .092
c. ¯
Y.1.=.88750, ¯
Y.2.= 1.42500, ¯
Y..1=.83125, ¯
Y..2= 1.42500
d. H0:α1=α2= 0, Ha: not both α1and α2equal zero.
F∗= 2.31125/.01446 = 159.84, F(.99; 1,21) = 8.017.
If F∗≤8.017 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= 3.38000/.01446 = 233.75, F(.99; 1,21) = 8.017.
If F∗≤8.017 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. ˆ
L1=¯
Y.1.−¯
Y.2.=−.53750, ˆ
L2=¯
Y..1−¯
Y..2=−.65000, s{ˆ
L1}=s{ˆ
L2}=.0425,
B=t(.9875; 21) = 2.414
−.53750 ±2.414(.0425) −.640 ≤L1≤ −.435
−.65000 ±2.414(.0425) −.753 ≤L2≤ −.547
f. H0: all ρiequal zero (i= 1, ..., 8), Ha: not all ρiequal zero.
F∗=.79982/.01446 = 55.31, F(.99; 7,21) = 3.64.
If F∗≤3.64 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
21-3

21.12. b. ¯
Y.1.. = 7.25, ¯
Y.2.. = 12.75, ˆ
L=¯
Y.1.. −¯
Y.2.. =−5.50, s{ˆ
L}= 1.25,
t(.995; 8) = 3.355, −5.50 ±3.355(1.25),−9.69 ≤L≤ −1.31
21.13. a. Yijk =µ.. +ρi+τj+ (ρτ )ij +²ijk
b.
Source SS df MS
Blocks 523.20000 4 130.80000
Treatments 1,796.46667 2 898.23333
BL.T R interactions 87.20000 8 10.90000
Error 207.00000 15 13.80000
Total 2,613.86667 29
c. H0: all τjequal zero (j= 1, 2, 3), Ha: not all τjequal zero.
F∗= 898.23333/13.80000 = 65.089, F(.99; 2,15) = 6.36.
If F∗≤6.36 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ¯
Y.1.= 68.9, ¯
Y.2.= 77.1, ¯
Y.3.= 87.8, ˆ
L1=¯
Y.1.−¯
Y.2.=−8.2,ˆ
L2=¯
Y.1.−¯
Y.3.=−18.9,
ˆ
L3=¯
Y.2.−¯
Y.3.=−10.7, s{ˆ
Li}= 1.6613 (i= 1,2,3), q(.95; 3,15) = 3.67,
T= 2.595
−8.2±2.595(1.6613) −12.51 ≤L1≤ −3.89
−18.9±2.595(1.6613) −23.21 ≤L2≤ −14.59
−10.7±2.595(1.6613) −15.01 ≤L3≤ −6.39
e. eijk:
j= 1 j= 2 j= 3
i k = 1 k= 2 k= 1 k= 2 k= 1 k= 2
1 1.5−1.5 3.0−3.0−2.0 2.0
2 2.0−2.0−4.0 4.0−2.5 2.5
3 4.0−4.0 3.5−3.5 1.5−1.5
4−2.5 2.5−2.5 2.5−1.5 1.5
5 1.5−1.5−1.5 1.5 3.5−3.5
r=.956
f. H0: all (ρτ)ij equal zero, Ha: not all (ρτ)ij equal zero.
F∗= 10.90000/13.80000 = .7899, F(.99; 8,15) = 4.00.
If F∗≤4.00 conclude H0, otherwise Ha. Conclude H0.P-value = .62
21.14. φ=1
2.5s10(18)
3= 3.098, ν1= 2, ν2= 27, 1 −β > .99
21.15. φ=1
.04s5(.02)
3= 4.564, ν1= 2, ν2= 12, 1 −β > .99
21.16. nb= 49 blocks
21.17. a. nb= 21 blocks
b. nb= 7 blocks
21-4

21.18. ˆ
E= 3.084
21.19. ˆ
E0= 40.295
21.20. ˆ
E= 13.264
21.21. L=
3
Y
i=1
2
Y
j=1
1
√2πσ2exp ·−1
2σ2(Yij −µ.. −ρi−τj)2¸
logeL=−3 loge2π−3 logeσ2−1
2σ2PP(Yij −µ.. −ρi−τj)2
∂(logeL)
∂µ..
=−2
2σ2PP(Yij −µ.. −ρi−τj)(−1)
∂(logeL)
∂ρi
=−2
2σ2P
j(Yij −µ.. −ρi−τj)(−1)
∂(logeL)
∂τj
=−2
2σ2P
i(Yij −µ.. −ρi−τj)(−1)
Setting each partial derivative equal to zero, utilizing the constraints
Pρi=Pτj= 0, simplifying, and substituting the maximum likelihood
estimators yields:
PPYij =PPˆµ.. or ¯
Y.. = ˆµ..
P
jYij =P
j(ˆµ.. + ˆρi) or ¯
Yi. −ˆµ.. = ˆρi
P
iYij =P
i(ˆµ.. + ˆτj) or ¯
Y.j −ˆµ.. = ˆτj
21.22. E{MST R}=E(nbP(¯
Y.j −¯
Y..)2
r−1)
=nb
r−1E{P(¯
Y.j −¯
Y..)2}
Since:
(¯
Y.j −¯
Y..) = (µ.. +τj+ ¯².j)−(µ.. + ¯²..) = τj+ (¯².j −¯²..)
and:
P(¯
Y.j −¯
Y..)2=Pτ2
j+P(¯².j −¯²..)2+ 2 Pτj(¯².j −¯²..)
we find:
E{Pτ2
j}=Pτ2
j
E{P(¯².j −¯²..)2}= (r−1) Ãσ2
nb!
E{2Pτj(¯².j −¯²..)}= 0
Hence:
E{MST R}=nb
r−1·Pτ2
j+r−1
nb
σ2¸=nb
r−1Pτ2
j+σ2
21.23. From (A.69):
21-5

(t∗)2="¯
W
s{¯
W}#2
=nb(nb−1)( ¯
Y.1−¯
Y.2)2
Σ[(Yi1−Yi2)−(¯
Y.1−¯
Y.2)]2
From (27.6b):
MST R =nb
"¯
Y.1−ï
Y.1+¯
Y.2
2!#2
+"¯
Y.2−ï
Y.1+¯
Y.2
2!#2
=nb
2(¯
Y.1−¯
Y.2)2
From (27.6c):
MSBL.T R =P
i·³Yi1−¯
Yi. −¯
Y.1+¯
Y..´2+ (Yi2−¯
Yi. −¯
Y.2+¯
Y..)2¸
(nb−1)(2 −1)
Using:
¯
Yi. =Yi1+Yi2
2¯
Y.. =¯
Y.1+¯
Y.2
2
we obtain:
MSBL.T R =1
nb−1P
i
1
4h(Yi1−Yi2−¯
Y.1+¯
Y.2)2+ (Yi2−Yi1−¯
Y.2+¯
Y.1)2i
=1
2(nb−1) P
ih(Yi1−Yi2)−(¯
Y.1−¯
Y.2)i2
Therefore:
F∗=nb(nb−1)( ¯
Y.1−¯
Y.2)2
Σ[(Yi1−Yi2)−(¯
Y.1−¯
Y.2)]2= (t∗)2
21.24. When there are no ties:
R2
.. = [nbr(r+ 1)/2]2PR2
i. =nb"r(r+ 1)
2#2
PPR2
ij =nb[r(r+ 1)(2r+ 1)/6]
Then:
nb(r−1)SST R
SST R +SSBL.T R
=
(r−1) ÃΣR2
.j −R2
..
r!
ÃΣR2
.j
nb−R2
..
rnb!+ÃΣΣR2
ij −ΣR2
i.
r−ΣR2
.j
nb
+R2
..
rnb!
=
(r−1) ÃPR2
.j −R2
..
r!
PPR2
ij −ΣR2
i.
r
= (r−1) "PR2
.j −n2
b(r+ 1)2r
4#÷"nbr(r+ 1)(2r+ 1)
6−nbr(r+ 1)2
4#
=12 PR2
.j
nbr(r+ 1) −3nb(r+ 1)
21-6

Chapter 22
ANALYSIS OF COVARIANCE
22.5. a. B=t(.9917; 11) = 2.820
22.6. Yij =µ.+τi+γ1(Xij1−¯
X..1) + γ2(Xij2−¯
X..2) + γ3(Xij1−¯
X..1)2
+γ4(Xij2−¯
X..2)2+²ij,i= 1, ..., 4
22.7. a. eij :
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1−.5281 .4061 .0089 .4573 −.1140 −.1911
2−.2635 −.2005 .3196 .2995 −.1662 .0680
3−.1615 .2586 −.0099 −.3044 .0472 .1700
i j = 7 j= 8 j= 9 j= 10 j= 11 j= 12
1.0660 −.0939 −.0112
2−.0690 −.1776 −.0005 .0653 .0251 .0995
b. r=.988
c. Yij =µ.+τ1Iij1+τ2Iij2+γxij +β1Iij1xij +β2Iij2xij +εij
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
SSE(F) = .9572, SSE(R) = 1.3175,
F∗= (.3603/2) ÷(.9572/21) = 3.95, F(.99; 2,21) = 5.78.
If F∗≤5.78 conclude H0, otherwise Ha. Conclude H0.P-value = .035
d. Yes, 5
22.8. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+γxij +εij, ( ¯
X.. = 9.4).
Reduced model: Yij =µ.+γxij +εij.
c. Full model: ˆ
Y= 7.80627 + 1.65885I1−.17431I2+ 1.11417x,SSE(F) = 1.3175
Reduced model: ˆ
Y= 7.95185 + .54124x,SSE(R) = 5.5134
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (4.1959/2) ÷(1.3175/23) = 36.625, F(.95; 2,23) = 3.42.
If F∗≤3.42 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. MSE(F) = .0573, MSE =.6401
22-1

e. ˆ
Y= ˆµ.+ ˆτ2−.4ˆγ= 7.18629, s2{ˆµ.}=.00258, s2{ˆτ2}=.00412, s2{ˆγ}=.00506,
s{ˆµ.,ˆτ2}=−.00045, s{ˆτ2,ˆγ}=−.00108, s{ˆµ.,ˆγ}=−.00120, s{ˆ
Y}=.09183,
t(.975; 23) = 2.069,7.18629 + 2.069(.09183), 6.996 ≤µ.+τ2−.4γ≤7.376
f. ˆ
D1= ˆτ1−ˆτ2= 1.83316, ˆ
D2= ˆτ1−ˆτ3= 2ˆτ1+ ˆτ2= 3.14339, ˆ
D3= ˆτ2−ˆτ3=
2ˆτ2+ ˆτ1= 1.31023, s2{ˆτ1}=.03759, s{ˆτ1,ˆτ2}=−.00418, s{ˆ
D1}=.22376,
s{ˆ
D2}=.37116, s{ˆ
D3}=.19326, F(.90; 2,23) = 2.55, S= 2.258
1.83316 ±2.258(.22376) 1.328 ≤D1≤2.338
3.14339 ±2.258(.37116) 2.305 ≤D2≤3.981
1.31023 ±2.258(.19326) .874 ≤D3≤1.747
22.9. a. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.5474 −.1325 .2465 −.0567 .4901
2−.2747 .1215 .2655 .0346 −.1468
3−.4225 −.0128 .1090 .5290 −.2027
b. r=.994
c. Yij =µ.+τ1Iij1+τ2Iij2+γxij +β1Iij1xij +β2Iij2xij +εij .
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
SSE(F) = .7682, SSE(R) = 1.3162,
F∗= (.5480/2) ÷(.7682/9) = 3.21, F(.995; 2,9) = 10.1.
If F∗≤10.1 conclude H0, otherwise Ha. Conclude H0.P-value = .089
d. No
22.10. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+γxij +εij , ( ¯
X.. = 280).
Reduced model: Yij =µ.+γxij +εij.
c. Full model: ˆ
Y= 29.00000 + .14361I1+ 1.48842I2−.02981x,SSE(F) = 1.3162
Reduced model: ˆ
Y= 29.00000 −.02697x,SSE(R) = 24.7081
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (23.3919/2) ÷(1.3162/11) = 97.748, F(.90; 2,11) = 2.86.
If F∗≤2.86 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. MSE(F) = .1197, MSE = 9.70
e. ˆ
Y= ˆµ.+ ˆτ1= 29.14361, s2{ˆµ.}=.00798, s2{ˆτ1}=.01602, s{ˆµ.,ˆτ1}= 0, s{ˆ
Y}=
.15492, t(.95; 11) = 1.796,29.14361 ±1.796(.15492), 28.865 ≤µ.+τ1≤29.422
f. ˆ
D1= ˆτ1−ˆτ2=−1.34481, ˆ
D2= ˆτ1−ˆτ3= 2ˆτ1+ ˆτ2= 1.77564, ˆ
D3= ˆτ2−ˆτ3=
2ˆτ2+ ˆτ1= 3.12045, s2{ˆτ2}=.01678, s{ˆτ1,ˆτ2}=−.00822, s{ˆ
D1}=.2219,
s{ˆ
D2}=.2190, s{ˆ
D3}=.2242, F(.90; 2,11) = 2.86, S= 2.392
−1.34481 ±2.392(.2219) −1.876 ≤D1≤ −.814
1.77564 ±2.392(.2190) 1.252 ≤D2≤2.299
3.12045 ±2.392(.2242) 2.584 ≤D3≤3.657
22.11. a. eij:
22-2

i j = 1 j= 2 j= 3 j= 4 j= 5
1.2070 −.4503 −.3648 −.2324 .8999
2.1361 .0001 −.6691 −.9300 .3190
3.7938 −.2099 .2295 .2801 −1.0389
i j = 6 j= 7 j= 8 j= 9 j= 10
1.1178 −.5440 .3668
2−.3813 .4201 .5837 −.1635 .6848
3−.0545
b. r=.995
c. Yij =µ.+τ1Iij1+τ2Iij2+γxij +β1Iij1xij +β2Iij2xij +εij
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
SSE(F) = 5.94391, SSE(R) = 6.16575,
F∗= (.221834/2) ÷(5.94391/18) = .336, F(.95; 2,18) = 3.55.
If F∗≤3.55 conclude H0, otherwise Ha. Conclude H0.P-value = .72
d. No
22.12. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+γxij +εij , ( ¯
X.. = 23.575).
Reduced model: Yij =µ.+γxij +εij.
c. Full model: ˆ
Y= 31.42704 + 3.52342I1+ 1.67605I2+ 1.16729x,SSE(F) = 6.16575
Reduced model: ˆ
Y= 32.00000 + 1.47113x,SSE(R) = 252.24945
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (246.08370/2) ÷(6.16575/20) = 399.114, F(.99; 2,20) = 5.85.
If F∗≤5.85 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. MSE(F) = .30829, MSE = 19.8095
e. ˆ
Y= ˆµ.+ ˆτ2+.425ˆγ= 33.59919, s2{ˆµ.}=.013423, s2{ˆτ2}=.024459, s2{ˆγ}=
.001025, s{ˆµ.,ˆτ2}=−.003069, s{ˆµ.,ˆγ}=.000082, s{ˆτ2,ˆγ}=.000886, s{ˆ
Y}=
.180975, t(.995; 20) = 2.845, 33.59919±2.845(.180975), 33.0843 ≤µ.+τ2+.425γ≤
34.1141
f. ˆ
D1= ˆτ1−ˆτ2= 1.84738, ˆ
D2= ˆτ1−ˆτ3= 2ˆτ1+ ˆτ2= 8.72289, ˆ
D3= ˆτ2−ˆτ3=
2ˆτ2+ ˆτ1= 6.87551, s2{ˆτ1}=.0336934, s{ˆτ1,ˆτ2}=−.0120919, s{ˆ
D1}=.28705,
s{ˆ
D2}=.33296, s{ˆ
D3}=.28838, B=t(.99167; 20) = 2.613
1.84738 ±2.613(.28705) 1.097 ≤D1≤2.597
8.72289 ±2.613(.33296) 7.853 ≤D2≤9.529
6.87551 ±2.613(.28838) 6.122 ≤D3≤7.629
22.13. a. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−1.7973 −6.7636 2.2280 .5922 5.7406
2−3.4017 −4.9059 1.4415 3.9373 2.9288
3−3.0314 −2.5019 .7781 2.6297 2.1255
22-3

b. r=.983
c. Yij =µ.+τ1Iij1+τ2Iij2+γxij +β1Iij1xij +β2Iij2xij +εij
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
SSE(F) = 145.2007, SSE(R) = 176.5300,
F∗= (31.3293/2) ÷(145.2007/9) = .971, F(.95; 2,9) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha. Conclude H0.P-value = .415
d. No
22.14. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+γxij +εij , ( ¯
X.. = 70.46667).
Reduced model: Yij =µ.+γxij +εij.
c. Full model: ˆ
Y= 66.40000−13.57740I1+5.54806I2+.83474x,SSE(F) = 176.5300
Reduced model: ˆ
Y= 66.40000 + .81587x,SSE(R) = 1,573.8109
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1,397.2809/2) ÷(176.5300/11) = 43.53, F(.95; 2,11) = 3.98.
If F∗≤3.98 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. MSE(F) = 16.0482, MSE = 113.9333
e. ˆ
Y= ˆµ.+ ˆτ2+ 4.5333ˆγ= 75.7322, s2{ˆµ.}= 1.06988, s2{ˆτ2}= 2.40689, s2{ˆγ}=
.00939, s{ˆµ.,ˆτ2}=s{ˆµ.,ˆγ}= 0, s{ˆτ2,ˆγ}=−.05009, s{ˆ
Y}= 1.7932, t(.975; 11) =
2.201, 75.7322 ±2.201(1.7932), 71.785 ≤µ.+τ2+ 4.5333γ≤79.679
f. ˆ
D1= ˆτ1−ˆτ2=−19.12546, ˆ
D2= ˆτ1−ˆτ3= 2ˆτ1+ ˆτ2=−21.60674, ˆ
D3= ˆτ2−ˆτ3=
2ˆτ2+ ˆτ1=−2.48128, s2{ˆτ1}= 2.14043, s{ˆτ1,ˆτ2}=−1.08324, s{ˆ
D1}= 2.5911,
s{ˆ
D2}= 2.5760, s{ˆ
D3}= 2.7267, F(.90; 2,11) = 2.86, S= 2.392
−19.12546 ±2.392(2.5911) −25.323 ≤D1≤ −12.928
−21.60674 ±2.392(2.5760) −27.769 ≤D2≤ −15.445
−2.48128 ±2.392(2.7267) −9.004 ≤D3≤4.041
22.15. a. eijk:
i j = 1 j= 2
1−.1184 −.3510
−.3469 −.0939
.0041 .0286
−.6041 .0735
1.2000 −.0163
−.1347 .3592
i j = 1 j= 2
2−.6809 .2082
.8660 −.1877
−.1177 .2531
.2905 −.2327
−.3912 −.2776
.0333 .2367
i j = 1 j= 2
3.9687 .6606
−.0150 .0565
.8789 −.1109
−1.1211 −.0660
.0912 −.4293
−.8027 −.1109
b. r=.974
c. Yijk =µ.. +α1Iijk1+α2Iijk2+β1Iijk3+ (αβ)11Iijk1Iijk3
+(αβ)21Iijk2Iijk3+γxijk +δ1Iijk1xijk +δ2Iijk2xijk
+δ3Iijk3xijk +δ4Iijk1Iijk3xijk +δ5Iijk2Iijk3xijk +²ijk
H0: all δiequal zero (i= 1, ..., 5), Ha: not all δiequal zero.
22-4
SSE(R) = 8.2941, SSE(F) = 6.1765,
F∗= (2.1176/5) ÷(6.1765/24) = 1.646, F(.99; 5,24) = 3.90.
If F∗≤3.90 conclude H0, otherwise Ha. Conclude H0.P-value = .19
22.16. a. Yijk =µ.. +α1Iijk1+α2Iijk2+β1Iijk3+ (αβ)11Iijk1Iijk3
+(αβ)21Iijk2Iijk3+γxijk +²ijk
Iijk1=
1 if case from level 1 for factor A
−1 if case from level 3 for factor A
0 otherwise
Iijk2=
1 if case from level 2 for factor A
−1 if case from level 3 for factor A
0 otherwise
Iijk3=(1 if case from level 1 for factor B
−1 if case from level 2 for factor B
xijk =Xijk −¯
X...(¯
X... = 3.4083)
ˆ
Y= 23.55556−2.15283I1+3.68152I2+.20907I3−.06009I1I3−.04615I2I3+1.06122x
SSE(F) = 8.2941
b. Interactions:
Yijk =µ.. +α1Iijk1+α2Iijk2+β1Iijk3+γxijk +²ijk
ˆ
Y= 23.55556 −2.15400I1+ 3.67538I2+.20692I3+ 1.07393x
SSE(R) = 8.4889
Factor A:
Yijk =µ.. +β1Iijk3+ (αβ)11Iijk1Iijk3+ (αβ)21Iijk2Iijk3+γxijk +²ijk
ˆ
Y= 23.55556 + .12982I3+.01136I1I3+.06818I2I3+ 1.52893x
SSE(R) = 240.7835
Factor B:
Yijk =µ.. +α1Iijk1+α2Iijk2+ (αβ)11Iijk1Iijk3
+(αβ)21Iijk2Iijk3+γxijk +²ijk
ˆ
Y= 23.55556 −2.15487I1+ 3.67076I2−.05669I1I3−.04071I2I3+ 1.08348x
SSE(R) = 9.8393
c. H0: (αβ)11 = (αβ)21 = 0, Ha: not both (αβ)11 and (αβ)21 equal zero.
F∗= (.1948/2) ÷(8.2941/29) = .341, F(.95; 2,29) = 3.33.
If F∗≤3.33 conclude H0, otherwise Ha. Conclude H0.P-value = .714
d. H0:α1=α2= 0, Ha: not both α1and α2equal zero.
F∗= (232.4894/2) ÷(8.2941/29) = 406.445, F(.95; 2,29) = 3.33.
If F∗≤3.33 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
22-5

e. H0:β1= 0, Ha:β16= 0.
F∗= (1.5452/1) ÷(8.2941/29) = 5.403, F(.95; 1,29) = 4.18.
If F∗≤4.18 conclude H0, otherwise Ha. Conclude Ha.P-value = .027
f. ˆ
D1= ˆα1−ˆα2=−5.83435, ˆ
D2= ˆα1−ˆα3= 2ˆα1+ ˆα2=−.62414,
ˆ
D3= ˆα2−ˆα3= 2ˆα2+ ˆα1= 5.21021, ˆ
D4=ˆ
β1−ˆ
β2= 2ˆ
β1=.41814,
s2{ˆα1}=.01593, s2{ˆα2}=.01708, s{ˆα1,ˆα2}=−.00772, s2{ˆ
β1}=.00809,
s{ˆ
D1}=.22011, s{ˆ
D2}=.22343, s{ˆ
D3}=.23102, s{ˆ
D4}=.17989,
B=t(.9875; 29) = 2.364
−5.83435 ±2.364(.22011) −6.355 ≤D1≤ −5.314
−.62414 ±2.364(.22343) −1.152 ≤D2≤ −.096
5.21021 ±2.364(.23102) 4.664 ≤D3≤5.756
.41814 ±2.364(.17989) −.007 ≤D4≤.843
22.17. a. eijk:
i j = 1 j= 2
1.1707 −.8159
.0810 1.3979
−.4586 −.8383
−1.2448 −.5796
1.4517 .8359
i j = 1 j= 2
2.3035 .2069
1.0448 1.5776
−.7190 −2.0965
−.9776 .6672
.3483 −.3552
b. r=.988
c. Yijk =µ.. +α1Iijk1+β1Iijk2+ (αβ)11Iijk1Iijk2+γxijk
+δ1Iijk1xijk +δ2Iijk2xijk +δ3Iijk1Iijk2xijk +²ijk
H0: all δiequal zero (i= 1,2,3), Ha: not all δiequal zero.
SSE(F) = 16.8817, SSE(R) = 18.5364,
F∗= (1.6547/3) ÷(16.8817/12) = .392, F(.995; 3,12) = 7.23.
If F∗≤7.23 conclude H0, otherwise Ha. Conclude H0.P-value = .76
22.18. a. Yijk =µ.+α1Iijk1+β1Iijk2+ (αβ)11Iijk1Iijk2+γxijk +εijk, ( ¯
X... = 44.55).
ˆ
Y= 13.05000 −.36284I1−1.11905I2+.09216I1I2+.32586x
SSE(F) = 18.5364
b. Interactions:
Yijk =µ.. +α1Iijk1+β1Iijk2+γxijk +²ijk
ˆ
Y= 13.05000 −.37286I1−1.12552I2+.32333x
SSE(R) = 18.7014
Factor A:
Yijk =µ.. +β1Iijk2+ (αβ)11Iijk1Iijk2+γxijk +²ijk
ˆ
Y= 13.05000 −1.04962I2+.12074I1I2+.35309x
22-6

SSE(R) = 20.3891
Factor B:
Yijk =µ.. +α1Iijk1+ (αβ)11Iijk1Iijk2+γxijk +²ijk
ˆ
Y= 13.05000 −.10397I1+.16097I1I2+.39140x
SSE(R) = 39.8416
c. H0: (αβ)11 = 0, Ha: (αβ)11 6= 0.
F∗= (.1650/1) ÷(18.5364/15) = .1335, F(.99; 1,15) = 8.68.
If F∗≤8.68 conclude H0, otherwise Ha. Conclude H0.P-value = .72
d. H0:α1= 0, Ha:α16= 0.
F∗= (1.8527/1) ÷(18.5364/15) = 1.499, F(.99; 1,15) = 8.68.
If F∗≤8.68 conclude H0, otherwise Ha. Conclude H0.P-value = .24
e. H0:β1= 0, Ha:β16= 0.
F∗= (21.3052/1) ÷(18.5364/15) = 17.241, F(.99; 1,15) = 8.68.
If F∗≤8.68 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f. ˆ
D=ˆ
β1−ˆ
β2= 2ˆ
β1=−2.2381, s{ˆ
D}=.539, t(.995; 15) = 2.947,
−2.2381 ±2.947(.539), −3.8265 ≤D≤ −.6497
g. ˆ
Y= ˆµ.. + ˆα1−ˆ
β1−(d
αβ)11 −4.55ˆγ= 12.2314, s2{ˆµ..}=.06179, s2{ˆα1}=.08782,
s2{ˆ
β1}=.07264, s2{ˆγ}=.00167, s2{(d
αβ)11}=.06363, s{ˆα1,ˆ
β1}=.01680,
s{ˆα1,(d
αβ)11}=.00692, s{ˆ
β1,(d
αβ)11}=.00447, s{ˆα1,ˆγ}=.00659, s{ˆ
β1,ˆγ}=
.00425, s{ˆγ, (d
αβ)11}=.00175, s{ˆµ..,ˆα1}=s{ˆµ..,ˆ
β1}=s{ˆµ..,(d
αβ)11}=s{ˆµ..,ˆγ}=
0, s{ˆ
Y}=.5259, t(.995; 15) = 2.947,
12.2314 ±2.947(.5259), 10.682 ≤µ.. +α1−β1−(αβ)11 −4.55γ≤13.781
22.19. b. Yij =µ.. +ρ1Iij1+ρ2Iij2+ρ3Iij3+ρ4Iij4+ρ5Iij5+ρ6Iij6
+ρ7Iij7+ρ8Iij8+ρ9Iij9+τ1Iij10 +τ2Iij11 +γxij +²ij
Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 10
0 otherwise
Iij2, . . . , Iij9are defined similarly
Iij10 =
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij11 =
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
xij =Xij −¯
X..(¯
X.. = 80.033333)
c. ˆ
Y= 77.10000 + 4.87199I1+ 3.87266I2+ 2.21201I3+ 3.22003I4
+1.23474I5+.90876I6−1.09124I7−3.74253I8−4.08322I9
22-7
−6.50033I10 −2.49993I11 +.00201x
SSE(F) = 112.3327
d. Yij =µ.. +ρ1Iij1+ρ2Iij2+ρ3Iij3+ρ4Iij4+ρ5Iij5+ρ6Iij6
+ρ7Iij7+ρ8Iij8+ρ9Iij9+γxij +²ij
ˆ
Y= 77.10000 + 6.71567I1+ 5.67233I2+ 3.61567I3+ 4.09567I4
+1.14233I5+.33233I6−1.66767I7−5.33100I8−5.18767I9−.13000x
SSE(R) = 1,404.5167
e. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1,292.18/2) ÷(112.3327/17) = 97.777, F(.95; 2,17) = 3.59.
If F∗≤3.59 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f. ˆτ1=−6.50033, ˆτ2=−2.49993, ˆ
L=−4.0004, L2{ˆτ1}=.44162, s2{ˆτ2}=.44056,
s{ˆτ1, ˆτ2}=−.22048, s{ˆ
L}= 1.1503, t(.975; 17) = 2.11,
−4.0004 ±2.11(1.1503), −6.43 ≤L≤ −1.57
22.20. a. Yij =µ.. +ρ1Iij1+ρ2Iij2+ρ3Iij3+ρ4Iij4+τ1Iij5+τ2Iij6+γxij +²ij
Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 5
0 otherwise
Iij2, . . . , Iij4are defined similarly
Iij5=
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij6=
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
xij =Xij −¯
X..(¯
X.. = 104.46667)
b. ˆ
Y=.84400 −.25726I1−.18916I2−.16649I3+.27012I4+.26663I5
+.15238I6+.009385x
SSE(F) = .007389
c. Yij =µ.. +ρ1Iij1+ρ2Iij2+ρ3Iij3+ρ4Iij4+γxij +²ij
ˆ
Y=.84400 −.34176I1−.24725I2−.17555I3+.32143I4−.00193x
SSE(R) = 1.339085
d. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1.331696/2) ÷(.007389/7) = 630.79, F(.95; 2,7) = 4.737.
If F∗≤4.737 conclude H0, otherwise Ha. Conclude Ha. P -value = 0+
e. ˆτ1=.26663, ˆτ2=.15238, ˆ
L1= ˆτ1−ˆτ2=.11425, ˆ
L2= ˆτ1+ 2ˆτ2=.57139,
s2{ˆτ1}=.0001408, s2{ˆτ2}=.0001424, s{ˆτ1,ˆτ2}=−.0000701, s{ˆ
L1}=.02058,
s{ˆ
L2}=.02074, B=t(.9875; 7) = 2.841
22-8

.11425 ±2.841(.02058) .0558 ≤L1≤.1727
.57139 ±2.841(.02074) .5125 ≤L2≤.6303
22.21. a.
Source SS df MS
Between treatments 25.5824 2 12.7912
Error 1.4650 24 .0610
Total 27.0474 26
b. Covariance: MSE =.0573, ˆγ= 1.11417
22.22. a.
Source SS df MS
Between treatments 1,417.7333 2 708.8667
Error 223.2000 12 18.6000
Total 1,640.9333 14
b. Covariance: MSE = 16.048, ˆγ=.83474
22.23. Yij =µ.+τi+γ(Xij −¯
X..) + ²ij = ∆i+γ(Xij −¯
X..) + ²ij
Q=PP[Yij −∆i−γ(Xij −¯
X..)]2
∂Q
∂∆i
= 2 P
j[Yij −∆i−γ(Xij −¯
X..)](−1)
∂Q
∂γ = 2 PP[Yij −∆i−γ(Xij −¯
X..)][−(Xij −¯
X..)]
Setting the partial derivatives equal to zero, simplifying, and substituting the least
squares estimators yields:
P
jYij −ˆγP
j(Xij −¯
X..) = niˆ
∆i
or:
ˆ
∆i=¯
Yi. −ˆγ(¯
Xi. −¯
X..)
and:
PP[Yij −ˆ
∆i−ˆγ(Xij −¯
X..)](Xij −¯
X..) = 0
or:
PPYij (Xij −¯
X..)−PP[¯
Yi. −ˆγ(¯
Xi. −¯
X..)](Xij −¯
X..) = ˆγPP(Xij −¯
X..)2
or:
ˆγ=PP(Yij −¯
Yi.)(Xij −¯
Xi.)
PP(Xij −¯
Xi.)2
It needs to be recognized in the development that:
PP(Yij −¯
Yi.)(Xij −¯
X..) = PP(Yij −¯
Yi.)(Xij −¯
Xi.)
PP(Xij −¯
X..)(Xij −¯
Xi.) = PP(Xij −¯
Xi.)2
22.24. b. r=.907
c. Yij =µ.+τ1Iij1+τ2Iij2+τ3Iij3+γxij +β1Iij1xij +β2Iij2xij +β3Iij3xij +²ij
22-9

H0:β1=β2=β3= 0, Ha: not all βiequal zero.
SSE(F) = 147.8129, SSE(R) = 151.3719,
F∗= (3.5590/3) ÷(147.8129/56) = .449, F(.995; 3,56) = 4.76.
If F∗≤4.76 conclude H0, otherwise Ha. Conclude H0.P-value = .72
22.25. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+τ3Iij3+γxij +²ij
Iij1=
1 if case from region NE
−1 if case from region W
0 otherwise
Iij2=
1 if case from region NC
−1 if case from region W
0 otherwise
Iij3=
1 if case from region S
−1 if case from region W
0 otherwise
xij =Xij −¯
X.. (¯
X.. = 42.75625)
Reduced model: Yij =µ.+γxij +²ij
c. Full model: ˆ
Y= 9.58406 + 1.60061I1+.05250I2−.26776I3+.02579x,
SSE(F) = 151.3719
Reduced model: ˆ
Y= 9.58406 + .04013x,
SSE(R) = 221.2543
H0: all τiequal zero (i= 1,2,3), Ha: not all τiequal zero.
F∗= (69.8824/3) ÷(151.3719/59) = 9.079, F(.95; 3,59) = 2.76.
If F∗≤2.76 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ˆ
D1= ˆτ1−ˆτ2= 1.54811, ˆ
D2= ˆτ1−ˆτ3= 1.86837, ˆ
D3= ˆτ1−ˆτ4= 2ˆτ1+ ˆτ2+ ˆτ3=
2.98596, ˆ
D4= ˆτ2−ˆτ3=.32026, ˆ
D5= ˆτ2−ˆτ4= 2ˆτ2+ ˆτ1+ ˆτ3= 1.43785,
ˆ
D6= ˆτ3−ˆτ4= 2ˆτ3+ ˆτ1+ ˆτ2= 1.11759, s2{ˆτ1}=.12412, s2{ˆτ2}=.12188,
s2{ˆτ3}=.12355, s{ˆτ1,ˆτ2}=−.03759, s{ˆτ1,ˆτ3}=−.04365, s{ˆτ2,ˆτ3}=−.04240,
s{ˆ
D1}=.56673, s{ˆ
D2}=.57877, s{ˆ
D3}=.57632, s{ˆ
D4}=.57466, s{ˆ
D5}=
.57265, s{ˆ
D6}=.56641, B=t(.99167; 59) = 2.464
1.54811 ±2.464(.56673) .1517 ≤D1≤2.9445
1.86837 ±2.464(.57877) .4423 ≤D2≤3.2945
2.98596 ±2.464(.57632) 1.5659 ≤D3≤4.4060
.32026 ±2.464(.57466) −1.0957 ≤D4≤1.7362
1.43785 ±2.464(.57265) .0268 ≤D5≤2.8489
1.11759 ±2.464(.56641) −.2780 ≤D6≤2.5132
22.26. b. r=.9914
c. Yij =µ.+τ1Iij1+τ2Iij2+τ3Iij3+γxij +β1Iij1xij +β2Iij2xij +β3Iij3xij +²ij
H0:β1=β2=β3= 0, Ha: not all βiequal zero.
22-10
SSE(F) = .6521, SSE(R) = .6778,
F∗= (.0257/3) ÷(.6521/28) = .37, F(.95; 3,28) = 2.95.
If F∗≤2.95 conclude H0, otherwise Ha. Conclude H0.P-value = .78
22.27. b. Full model: Yij =µ.+τ1Iij1+τ2Iij2+τ3Iij3+γxij +²ij
Iij1=
1 if case from (Var5 Var6)=(0,0)
−1 if case from (Var5 Var6)=(1,1)
0 otherwise
Iij2=
1 if case from (Var5 Var6)=(1,0)
−1 if case from (Var5 Var6)=(1,1)
0 otherwise
Iij3=
1 if case from (Var5 Var6)=(0,1)
−1 if case from (Var5 Var6)=(1,1)
0 otherwise
xij =Xij −¯
X.. (¯
X.. = 2.3244)
Reduced model: Yij =µ.+γxij +²ij
c. Full model: ˆ
Y= 2.619 −.217I1+.109I2−.178I3−.344x,SSE(F) = .6778
Reduced model: ˆ
Y= 2.664 −.306x,SSE(R) = 2.3593
H0:τ1=τ2=τ3= 0, Ha: not all τiequal zero.
F∗= (1.6815/3) ÷(.6778/31) = 25.64, F(.99; 3,31) = 4.51.
If F∗≤4.51 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. In Project 16.45, SSE =.7850.
No, almost none.
e. (2.5005, 2.8353)
f. ˆ
D1= ˆτ1−ˆτ2=−.326, ˆ
D2= ˆτ1−ˆτ3=−.039,
ˆ
D3= ˆτ1−ˆτ4= 2ˆτ1+ ˆτ2+ ˆτ3=−.503, ˆ
D4= ˆτ2−ˆτ3=.287,
ˆ
D5= ˆτ2−ˆτ4= 2ˆτ2+ ˆτ1+ ˆτ3=−.177, ˆ
D6= ˆτ3−ˆτ4= 2ˆτ3+ ˆτ1+ ˆτ2=−.464,
s2{ˆτ1}=.002028, s2{ˆτ2}=.002024, s2{ˆτ3}=.002239,
s{ˆτ1,ˆτ2}=−.00071, s{ˆτ1,ˆτ3}=−.00085, s{ˆτ2,ˆτ3}=−.00085,
s{ˆ
D1}=.073927, s{ˆ
D2}=.077232, s{ˆ
D3}=.066790,
s{ˆ
D4}=.077165, s{ˆ
D5}=.066743, s{ˆ
D6}=.069400,
B=t(.99583; 31) = 2.818 (S2= 3F(.95; 3,31) = 3(2.9113), S= 2.955)
−.326 ±2.818(.073927) −.534 ≤D1≤ −.118
−.039 ±2.818(.077232) −.257 ≤D2≤.179
−.503 ±2.818(.066790) −.691 ≤D3≤ −.315
.287 ±2.818(.077165) .070 ≤D4≤.504
−.177 ±2.818(.066743) −.365 ≤D5≤.011
−.464 ±2.818(.069400) −.660 ≤D6≤ −.268
22-11
22.28. b. r=.991
c. Yijk =µ.. +α1Iijk1+α2Iijk2+α3Iijk3+β1Iijk4
+(αβ)11Iijk1Iijk4+ (αβ)21Iijk2Iijk4+ (αβ)31Iijk3Iijk4
+γxijk +δ1Iijk1xijk +δ2Iijk2xijk +δ3Iijk3xijk
+δ4Iijk4xijk +δ5Iijk1Iijk4xijk +δ6Iijk2Iijk4xijk +δ7Iijk3Iijk4xijk +²ijk
H0: all δiequal zero (i= 1, ..., 7), Ha: not all δiequal zero.
SSE(F) = .0093126, SSE(R) = .0108089,
F∗= (.0014963/7) ÷(.0093126/40) = .92, F(.999; 7,40) = 4.436.
If F∗≤4.436 conclude H0, otherwise Ha. Conclude H0.P-value = .46
22.29. a. Yijk =µ.. +α1Iijk1+α2Iijk2+α3Iijk3+β1Iijk4+ (αβ)11Iijk1Iijk4
+(αβ)21Iijk2Iijk4+ (αβ)31Iijk3Iijk4+γxijk +²ijk
Iijk1=
1 if case from region NE
−1 if case from region W
0 otherwise
Iijk2=
1 if case from region NC
−1 if case from region W
0 otherwise
Iijk3=
1 if case from region S
−1 if case from region W
0 otherwise
Iijk4=(1 if percent of poverty less than 8.0 percent
−1 if percent of poverty 8.0 percent or more
xijk =Xijk −¯
X...(¯
X... = 12.521)
ˆ
Y=.0632 −.0239I1−.0115I2+.0254I3−.00548I4
+.00149I1I4+.00643I2I4−.00904I3I4+.000627x
SSE(F) = .0108089
b. Interactions:
Yijk =µ.. +α1Iijk1+α2Iijk2+α3Iijk3+β1Iijk4+γxijk +²ijk
ˆ
Y=.0632 −.0224I1−.0117I2+.0255I3−.00557I4−.000061x
SSE(R) = .0122362
Factor A:
Yijk =µ.. +β1Iijk4+ (αβ)11Iijk1Iijk4+ (αβ)21Iijk2Iijk4
+(αβ)31Iijk3Iijk4+γxijk +²ijk
ˆ
Y=.0632 −.00565I4+.00001I1I4+.00463I2I4−.00532I3I4−.000719x
SSE(R) = .0298356
Factor B:
22-12

Yijk =µ.. +α1Iijk1+α2Iijk2+α3Iijk3+ (αβ)11Iijk1Iijk4
+(αβ)21Iijk2Iijk4+ (αβ)31Iijk3Iijk4+γxijk +²ijk
ˆ
Y=.0632 −.0241I1−.0115I2+.0254I3+.00157I1I4
+.00652I2I4−.00923I3I4+.000695x
SSE(R) = .012488
c. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (.0014273/3) ÷(.0108089/47) = 2.069, F(.99; 3,47) = 4.23.
If F∗≤4.23 conclude H0, otherwise Ha. Conclude H0.P-value = .12
d. H0:α1=α2=α3= 0, Ha: not all αiequal zero.
F∗= (.0190267/3) ÷(.0108089/47) = 27.57, F(.99; 3,47) = 4.23.
If F∗≤4.23 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. H0:β1= 0, Ha:β16= 0.
F∗= (.0016791/1) ÷(.0108089/47) = 7.30, F(.99; 1,47) = 7.21.
If F∗≤7.21 conclude H0, otherwise Ha. Conclude Ha.P-value = .0096
22.30. b. r=.983
c. Yijk =µ.. +α1Iijk1+β1Iijk2+ (αβ)11Iijk1Iijk4+γxijk
+δ1Iijk1xijk +δ2Iijk2xijk +δ3Iijk1Iijk2xijk +²ijk
H0:δ1=δ2=δ3= 0, Ha: not all δiequal zero.
SSE(F) = .48044, SSE(R) = .51032,
F∗= (.02988/3) ÷(.48044/20) = .41, F(.95; 3,20) = 3.10.
If F∗≤3.10 conclude H0, otherwise Ha. Conclude H0.P-value = .75
22.31. a. Yijk =µ.. +α1Iijk1+β1Iijk2+ (αβ)11Iijk1Iijk2+²ijk
Iijk1=(1 no discount price
−1 discount price
Iijk2=(1 no package promotion
−1 package promotion
xijk =Xijk −¯
X...(¯
X... = 2.2716)
ˆ
Y= 2.644 −.197I1−.0605I2+.0533I1I2−.276x
SSE(F) = .51032
b. Interactions:
Yijk =µ.. +α1Iijk1+β1Iijk2+γxijk +²ijk
ˆ
Y= 2.644 −.189I1−.0608I2−.451x
SSE(R) = .57864
Factor A:
22-13

Yijk =µ.. +β1Iijk2+ (αβ)11Iijk1Iijk2+γxijk +²ijk
ˆ
Y= 2.644 −.0616I2+.0241I1I2−.962x
SSE(R) = 1.42545
Factor B:
Yijk =µ.. +α1Iijk1+ (αβ)11Iijk1Iijk2+γxijk +²ijk
ˆ
Y= 2.644 −.198I1+.0536I1I2−.267x
SSE(R) = .61269
c. H0: (αβ)11 = 0, Ha: (αβ)11 6= 0
F∗= (.06832/1) ÷(.51032/23) = 3.08, F(.99; 1,23) = 7.88.
If F∗≤7.88 conclude H0, otherwise Ha. Conclude H0.P-value = .09
d. H0:α1= 0, Ha:α16= 0
F∗= (.91513/1) ÷(.51032/23) = 41.24, F(.99; 1,23) = 7.88.
If F∗≤7.88 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. H0:β1= 0, Ha:β16= 0.
F∗= (.10237/1) ÷(.51032/23) = 4.61, F(.99; 1,23) = 7.88.
If F∗≤7.88 conclude H0, otherwise Ha. Conclude H0.P-value = .04
22-14

Chapter 23
TWO-FACTOR STUDIES WITH
UNEQUAL SAMPLE SIZES
23.3. a. Yijk =µ.. +α1Xijk1+β1Xijk2+ (αβ)11Xijk1Xijk2+²ijk
Xijk1=(1 if case from level 1 for factor A
−1 if case from level 2 for factor A
Xijk2=(1 if case from level 1 for factor B
−1 if case from level 2 for factor B
b. Yentries: in order Y111, ..., Y115,Y121, ..., Y125,Y211, ...
βentries: µ..,α1,β1, (αβ)11
Xentries:
A B Freq. X1X2X1X2
1 1 5 1 1 1 1
1 2 5 1 1 −1−1
2 1 5 1 −1 1 −1
2 2 5 1 −1−1 1
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1−β1−(αβ)11 =µ.. +α1+β2+ (αβ)12
2 1 µ.. −α1+β1−(αβ)11 =µ.. +α2+β1+ (αβ)21
2 2 µ.. −α1−β1+ (αβ)11 =µ.. +α2+β2+ (αβ)22
d. ˆ
Y= 13.05 −1.65X1−1.95X2−.25X1X2
µ..
e.
Source SS df
Regression 131.75 3
X154.45 1] A
X2|X176.05 1] B
X1X2|X1,X21.25 1] AB
Error 97.20 16
Total 228.95 19
23-1

Yes.
f. See Problem 19.13c and d.
23.4. a. Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+β2Xijk4+ (αβ)11Xijk1Xijk3
+(αβ)12Xijk1Xijk4+ (αβ)21Xijk2Xijk3+ (αβ)22Xijk2Xijk4+²ijk
Xijk1=
1 if case from level 1 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk2=
1 if case from level 2 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk3=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijk4=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
b. Yentries: in order Y111, ..., Y114,Y121, ..., Y124,Y131, ..., Y134,Y211, ...
βentries: µ..,α1,α2,β1,β2, (αβ)11, (αβ)12, (αβ)21, (αβ)22
Xentries:
A B Freq. X1X2X3X4X1X3X1X4X2X3X2X4
1 1 4 1 1 0 1 0 1 0 0 0
1 2 4 1 1 0 0 1 0 1 0 0
1 3 4 1 1 0 −1−1−1−100
2 1 4 1 0 1 1 0 0 0 1 0
2 2 4 1 0 1 0 1 0 0 0 1
2 3 4 1 0 1 −1−1 0 0 −1−1
3 1 4 1 −1−1 1 0 −1 0 −1 0
3 2 4 1 −1−1 0 1 0 −1 0 −1
3 3 4 1 −1−1−1−11111
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1+β2+ (αβ)12
1 3 µ.. +α1−β1−β2−(αβ)11 −(αβ)12 =µ.. +α1+β3+ (αβ)13
2 1 µ.. +α2+β1+ (αβ)21
2 2 µ.. +α2+β2+ (αβ)22
2 3 µ.. +α2−β1−β2−(αβ)21 −(αβ)22 =µ.. +α2+β3+ (αβ)23
3 1 µ.. −α1−α2+β1−(αβ)11 −(αβ)21 =µ.. +α3+β1+ (αβ)31
3 2 µ.. −α1−α2+β2−(αβ)12 −(αβ)22 =µ.. +α3+β2+ (αβ)32
3 3 µ.. −α1−α2−β1−β2+ (αβ)11 + (αβ)12 + (αβ)21 + (αβ)22
=µ.. +α3+β3+ (αβ)33
23-2

d. ˆ
Y= 7.18333 −3.30000X1+.65000X2−2.55000X3+.75000X4
+1.14167X1X3−.03333X1X4+.16667X2X3+.34167X2X4
α1=µ1.−µ..
e.
Source SS df
Regression 373.125 8
X1212.415 1] A
X2|X17.605 1] A
X3|X1,X2113.535 1] B
X4|X1,X2,X310.125 1] B
X1X3|X1,X2,X3,X426.7806 1] AB
X1X4|X1,X2,X3,X4,X1X3.2269 1] AB
X2X3|X1,X2,X3,X4,X1X3,X1X41.3669 1] AB
X2X4|X1,X2,X3,X4,X1X3,X1X4,X2X31.0506 1] AB
Error 1.625 27
Total 374.730 35
Yes.
f. See Problem 19.15c and d.
23.5. a. See Problem 23.4a.
b. ˆ
Y= 55.82222 −.48889X1−.55556X2+.31111X3+.77778X4
+4.15556X1X3−8.31111X1X4−7.17778X2X3+ 5.15556X2X4
β1=µ.1−µ..
c.
Source SS df
Regression 1,268.17778 8
X117.63333 1] A
X2|X16.94445 1] A
X3|X1,X214.70000 1] B
X4|X1,X2,X313.61111 1] B
X1X3|X1,X2,X3,X4105.80000 1] AB
X1X4|X1,X2,X3,X4,X1X3493.06667 1] AB
X2X3|X1,X2,X3,X4,X1X3,X1X4317.40000 1] AB
X2X4|X1,X2,X3,X4,X1X3,X1X4,X2X3299.02222 1] AB
Error 1,872.40000 36
Total 3,140.57778 44
Yes.
d. See Problem 19.17c and d.
23.6. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+ (αβ)11Xijk1Xijk3
+(αβ)21Xijk2Xijk3+²ijk
23-3

Xijk1=
1 if case from level 1 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk2=
1 if case from level 2 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk3=(1 if case from level 1 for factor B
−1 if case from level 2 for factor B
b. βentries: µ..,α1,α2,β1, (αβ)11, (αβ)21
Xentries:
A B Freq. X1X2X3X1X3X2X3
1 1 6 1 1 0 1 1 0
1 2 6 1 1 0 −1−1 0
2 1 5 1 0 1 1 0 1
2 2 6 1 0 1 −1 0 −1
3 1 6 1 −1−1 1 −1−1
3 2 5 1 −1−1−111
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1−β1−(αβ)11 =µ.. +α1+β2+ (αβ)12
2 1 µ.. +α2+β1+ (αβ)21
2 2 µ.. +α2−β1−(αβ)21 =µ.. +α2+β2+ (αβ)22
3 1 µ.. −α1−α2+β1−(αβ)11 −(αβ)21 =µ.. +α3+β1+ (αβ)31
3 2 µ.. −α1−α2−β1+ (αβ)11 + (αβ)21 =µ.. +α3+β2+ (αβ)32
d. Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+²ijk
e. Full model:
ˆ
Y= 23.56667 −2.06667X1+ 4.16667X2+.36667X3−.20000X1X3−.30000X2X3,
SSE(F) = 71.3333
Reduced model:
ˆ
Y= 23.59091 −2.09091X1+ 4.16911X2+.36022X3,
SSE(R) = 75.5210
H0: (αβ)11 = (αβ)21 = 0, Ha: not both (αβ)11 and (αβ)21 equal zero.
F∗= (4.1877/2) ÷(71.3333/28) = .82, F(.95; 2,28) = 3.34.
If F∗≤3.34 conclude H0, otherwise Ha. Conclude H0.P-value = .45
f. Aeffects:
ˆ
Y= 23.50000 + .17677X3−.01010X1X3−.49495X2X3,
SSE(R) = 359.9394
H0:α1=α2= 0, Ha: not both α1and α2equal zero.
23-4

F∗= (288.6061/2) ÷(71.3333/28) = 56.64, F(.95; 2,28) = 3.34.
If F∗≤3.34 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
Beffects:
ˆ
Y= 23.56667 −2.06667X1+ 4.13229X2−.17708X1X3−.31146X2X3,
SSE(R) = 75.8708
H0:β1= 0, Ha:β16= 0.
F∗= (4.5375/1) ÷(71.3333/28) = 1.78, F(.95; 1,28) = 4.20.
If F∗≤4.20 conclude H0, otherwise Ha. Conclude H0.P-value = .19
g. ˆ
D1= ˆα1−ˆα2=−6.23334, ˆ
D2= ˆα1−ˆα3= 2ˆα1+ ˆα2=.03333,ˆ
D3= ˆα2−ˆα3=
2ˆα2+ ˆα1= 6.26667, s2{ˆα1}=.14625, s2{ˆα2}=.15333, s{ˆα1,ˆα2}=−.07313,
s{ˆ
D1}=.6677, s{ˆ
D2}=.6677, s{ˆ
D3}=.6834, q(.90; 3,28) = 3.026, T= 2.140
−6.23334 ±2.140(.6677) −7.662 ≤D1≤ −4.804
.03333 ±2.140(.6677) −1.396 ≤D2≤1.462
6.26667 ±2.140(.6834) 4.804 ≤D3≤7.729
h. ˆ
L=.3¯
Y12.+.6¯
Y22.+.1¯
Y32.=.3(21.33333)+.6(27.66667)+.1(20.60000) = 25.06000,
s{ˆ
L}=.4429, t(.975; 28) = 2.048,25.06000 ±2.048(.4429), 24.153 ≤L≤25.967
23.7. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+β2Xijk4
+ (αβ)11Xijk1Xijk3+ (αβ)12Xijk1Xijk4+ (αβ)21Xijk2Xijk3
+ (αβ)22Xijk2Xijk4+²ijk
Xijk1=
1 if case from level 1 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk2=
1 if case from level 2 for factor A
−1 if case from level 3 for factor A
0 otherwise
Xijk3=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijk4=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
b. βentries: µ..,α1,α2,β1,β2, (αβ)11, (αβ)12, (αβ)21, (αβ)22
Xentries:
23-5
A B Freq. X1X2X3X4X1X3X1X4X2X3X2X4
1 1 3 1 1 0 1 0 1 0 0 0
1 2 4 1 1 0 0 1 0 1 0 0
1 3 4 1 1 0 −1−1−1−1 0 0
2 1 4 1 0 1 1 0 0 0 1 0
2 2 2 1 0 1 0 1 0 0 0 1
2 3 4 1 0 1 −1−100−1−1
3 1 4 1 −1−1 1 0 −1 0 −1 0
3 2 4 1 −1−1 0 1 0 −1 0 −1
3 3 4 1 −1−1 1 −11111
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1+β2+ (αβ)12
1 3 µ.. +α1−β1−β2−(αβ)11 −(αβ)12 =µ.. +α1+β3+ (αβ)13
2 1 µ.. +α2+β1+ (αβ)21
2 2 µ.. +α2+β2+ (αβ)22
2 3 µ.. +α2−β1−β2−(αβ)21 −(αβ)22 =µ.. +α2+β3+ (αβ)23
3 1 µ.. −α1−α2+β1−(αβ)11 −(αβ)21 =µ.. +α3+β1+ (αβ)31
3 2 µ.. −α1−α2+β2−(αβ)12 −(αβ)22 =µ.. +α3+β2+ (αβ)32
3 3 µ.. −α1−α2−β1−β2+ (αβ)11 + (αβ)12 + (αβ)21 + (αβ)22
=µ.. +α3+β3+ (αβ)33
d. Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+β2Xijk4+²ijk
e. Full model:
ˆ
Y= 7.18704 −3.28426X1+.63796X2−2.53426X3+.73796X4
+1.16481X1X3−.04074X1X4+.15926X2X3+.33704X2X4,
SSE(F) = 1.5767
Reduced model:
ˆ
Y= 7.12711 −3.33483X1+.62861X2−2.58483X3+.72861X4,
SSE(R) = 29.6474
H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (28.0707/4) ÷(1.5767/24) = 106.82, F(.95; 4,24) = 2.78.
If F∗≤2.78 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f. ¯
Y11.= 2.5333, ¯
Y12.= 4.6000, ¯
Y13.= 4.57500, ¯
Y21.= 5.45000, ¯
Y22.= 8.90000,
¯
Y23.= 9.12500, ¯
Y31.= 5.97500, ¯
Y32.= 10.27500, ¯
Y33.= 13.25000, ˆ
L1= 2.0542,
ˆ
L2= 3.5625, ˆ
L3= 5.7875, ˆ
L4= 1.5083, ˆ
L5= 3.7333, ˆ
L6= 2.2250, s{ˆ
L1}=.1613,
s{ˆ
L2}=.1695, s{ˆ
L3}=.1570, s{ˆ
L4}=.2340, s{ˆ
L5}=.2251, s{ˆ
L6}=.2310,
F(.90; 8,24) = 1.94, S= 3.9395
23-6

2.0542 ±3.9395(.1613) 1.419 ≤L1≤2.690
3.5625 ±3.9395(.1695) 2.895 ≤L2≤4.230
5.7875 ±3.9395(.1570) 5.169 ≤L3≤6.406
1.5083 ±3.9395(.2340) .586 ≤L4≤2.430
3.7333 ±3.9395(.2251) 2.846 ≤L5≤4.620
2.2250 ±3.9395(.2310) 1.315 ≤L6≤3.135
23.8. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Regression model: see (22.4).
b. βentries: µ..,α1,β1,β2, (αβ)11, (αβ)12
Xentries:
A B Freq. X1X2X3X1X2X1X3
1 1 10 1 1 1 0 1 0
1 2 9 1 1 0 1 0 1
1 3 10 1 1 −1−1−1−1
2 1 9 1 −1 1 0 −1 0
2 2 10 1 −1 0 1 0 −1
2 3 9 1 −1−1−111
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1+β2+ (αβ)12
1 3 µ.. +α1−β1−β2−(αβ)11 −(αβ)12 =µ.. +α1+β3+ (αβ)13
2 1 µ.. −α1+β1−(αβ)11 =µ.. +α2+β1+ (αβ)21
2 2 µ.. −α1+β2−(αβ)12 =µ.. +α2+β2+ (αβ)22
2 3 µ.. −α1−β1−β2+ (αβ)11 + (αβ)12 =µ.. +α2+β3+ (αβ)23
d. Yijk =µ.. +α1Xijk1+β1Xijk2+β2Xijk3+²ijk
e. Full model:
ˆ
Y=.69139 + .08407X1−.27492X2−.01281X3−.05706X1X2+.01355X1X3,
SSE(F) = 5.3383
Reduced model:
ˆ
Y=.69092 + .08407X1−.27745X2−.01305X3,
SSE(R) = 5.4393
H0: (αβ)11 = (αβ)12 = 0, Ha: not both (αβ)11 and (αβ)12 equal zero.
F∗= (.1010/2) ÷(5.3383/51) = .48, F(.95; 2,51) = 3.179.
If F∗≤3.179 conclude H0, otherwise Ha. Conclude H0.P-value = .62
f. Duration:
Yijk =µ.. +β1Xijk2+β2Xijk3+ (αβ)11Xijk1Xijk2+ (αβ)12Xijk1Xijk3+²ijk
ˆ
Y=.69287 −.27197X2−.01871X3−.05706X1X2+.01355X1X3,
SSE(R) = 5.7400
23-7

H0:α1= 0, Ha:α16= 0.
F∗= (.4017/1) ÷(5.3383/51) = 3.84, F(.95; 1,51) = 4.03.
If F∗≤4.03 conclude H0, otherwise Ha. Conclude H0.P-value = .06
Weight gain:
Yijk =µ.. +α1Xijk1+ (αβ)11Xijk1Xijk2+ (αβ)12Xijk1Xijk3+²ijk
ˆ
Y=.69139 + .08452X1−.07198X1X2+.01377X1X3,
SSE(R) = 8.3421
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (3.0038/2) ÷(5.3383/51) = 14.35, F(.95; 2,51) = 3.179.
If F∗≤3.179 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
g. H0:µ.1≤.5, Ha:µ.1> .5. ˆµ.1= ( ¯
Y11.+¯
Y21.)/2=(.44348 + .38946)/2 = .41647,
s{ˆµ.1}=.0743, t∗=−.08353/.0743 = −1.12, t(.95; 51) = 1.675. If t∗≤1.675
conclude H0, otherwise Ha. Conclude H0.P-value = .87
h. ¯
Y11.=.44348, ¯
Y12.=.77619, ¯
Y13.= 1.10670, ¯
Y21.=.38946, ¯
Y22.=.58096, ¯
Y23.=
.85155, ˆ
D1=.16813, ˆ
D2=.26211, ˆ
D3=.56266, ˆ
D4=.30055, s{ˆ
D1}=.08582,
s{ˆ
Di}=.10511 (i= 2,3,4), B=t(.9875; 51) = 2.3096
.16813 ±2.3096(.08582) −.0301 ≤D1≤.3663
.26211 ±2.3096(.10511) .0193 ≤D2≤.5049
.56266 ±2.3096(.10511) .3199 ≤D3≤.8054
.30055 ±2.3096(.10511) 0578 ≤D4≤.5433
23.9. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5
+(αβ)11Xijk1Xijk4+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4
+(αβ)22Xijk2Xijk5+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
a. Yijk =µ.. +α1Xijk1+α2Xijk2+β1Xijk3+β2Xijk4+ (αβ)11Xijk1Xijk3
+(αβ)12Xijk1Xijk4+ (αβ)21Xijk2Xijk3+ (αβ)22Xijk2Xijk4+²ijk
Xijk1=
1 if case from level 1 for factor A
−1 if case from level 4 for factor A
0 otherwise
Xijk2and Xijk3are defined similarly
Xijk4=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijk5=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
b. βentries: µ..,α1,α2,α3,β1,β2, (αβ)11, (αβ)12, (αβ)21,
(αβ)22, (αβ)31, (αβ)32
23-8
Xentries:
A B Freq. X1X2X3X4X5X1X4
1 1 2 1 1 0 0 1 0 1
1 2 2 1 1 0 0 0 1 0
1 3 8 1 1 0 0 −1−1−1
2 1 4 1 0 1 0 1 0 0
2 2 5 1 0 1 0 0 1 0
2 3 4 1 0 1 0 −1−1 0
3 1 2 1 0 0 1 1 0 0
3 2 4 1 0 0 1 0 1 0
3 3 5 1 0 0 1 −1−1 0
4 1 2 1 −1−1−1 1 0 −1
4 2 2 1 −1−1−1 0 1 0
4 3 5 1 −1−1−1−1−1 1
A B X1X5X2X4X2X5X3X4X3X5
1 1 0 0 0 0 0
1 2 1 0 0 0 0
1 3 −10000
2 1 0 1 0 0 0
2 2 0 0 1 0 0
2 3 0 −1−100
3 1 0 0 0 1 0
3 2 0 0 0 0 1
3 3 0 0 0 −1−1
4 1 0 −1 0 −1 0
4 2 −1 0 −1 0 −1
4 3 1 1 1 1 1
c. Xβentries:
A B
1 1 µ.. +α1+β1+ (αβ)11
1 2 µ.. +α1+β2+ (αβ)12
1 3 µ.. +α1−β1−β2−(αβ)11 −(αβ)12 =µ.. +α1+β3+ (αβ)13
2 1 µ.. +α2+β1+ (αβ)21
2 2 µ.. +α2+β2+ (αβ)22
2 3 µ.. +α2−β1−β2−(αβ)21 −(αβ)22 =µ.. +α2+β3+ (αβ)23
3 1 µ.. +α3+β1+ (αβ)31
3 2 µ.. +α3+β2+ (αβ)32
3 3 µ.. +α3−β1−β2−(αβ)31 −(αβ)32 =µ.. +α3+β3+ (αβ)33
4 1 µ.. −α1−α2−α3+β1−(αβ)11 −(αβ)21 −(αβ)31
=µ.. +α4+β1+ (αβ)41
4 2 µ.. −α1−α2−α3+β2−(αβ)12 −(αβ)22 −(αβ)32
=µ.. +α4+β2+ (αβ)42
4 3 µ.. −α1−α2−α3−β1−β2+ (αβ)11 + (αβ)12 + (αβ)21 + (αβ)22
+(αβ)31 + (αβ)32 =µ.. +α4+β3+ (αβ)43
d. See Problem 23.10c for fitted model.
23-9

eijk:
i= 1
k j = 1 j= 2 j= 3
1−.10 −.15 −.20
2.10 .15 .00
3.20
4−.20
5−.10
6.10
7.00
8.20
i= 2
k j = 1 j= 2 j= 3
1.05 .18 .05
2−.15 −.12 −.15
3.15 .08 .15
4.05 −.12 −.05
5−.02
i= 3
k j = 1 j= 2 j= 3
1−.05 .05 −.04
2.05 .15 −.14
3−.05 −.04
4−.15 .06
5.16
i= 4
k j = 1 j= 2 j= 3
1−.05 −.25 −.12
2.05 .25 −.02
3−.12
4.08
5.18
e. r=.986
23.10. a. ¯
Y11.= 1.80, ¯
Y12.= 1.95, ¯
Y13.= 2.70, ¯
Y21.= 2.45, ¯
Y22.= 2.52,
¯
Y23.= 3.45, ¯
Y31.= 2.75, ¯
Y32.= 2.85, ¯
Y33.= 3.74, ¯
Y41.= 2.55,
¯
Y42.= 2.55, ¯
Y43.= 3.42
b. Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5+²ijk
c. Full model:
ˆ
Y= 2.72750 −.57750X1+.07917X2−.38583X3−.34000X4−.26000X5
−.01000X1X4+.06000X1X5−.01667X2X4−.02667X2X5
−.02333X3X4−.00333X3X5,
SSE(F) = .7180
Reduced Model:
ˆ
Y= 2.72074 −.59611X1+.08412X2+.39964X3−.33756X4−.26317X5,
SSE(R) = .7624
H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (.0444/6) ÷(.7180/33) = .34, F(.99; 6,33) = 3.41.
If F∗≤3.41 conclude H0, otherwise Ha. Conclude H0.P-value = .91
d. Subject matter:
Yijk =µ.. +β1Xijk4+β2Xijk5+ (αβ)11Xijk1Xijk4+ (αβ)12Xijk1Xijk5
+(αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5+ (αβ)31Xijk3Xijk4
+(αβ)32Xijk3Xijk5+²ijk
23-10

ˆ
Y= 2.75121 −.34885X4−.19441X5+.19925X1X4+.19481X1X5
−.01178X2X4−.08433X2X5−.22413X3X4+.00731X3X5,
SSE(R) = 4.9506
H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= (4.2326/3) ÷(.7180/33) = 64.845, F(.99; 3,33) = 4.437.
If F∗≤4.437 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
Degree:
Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+ (αβ)11Xijk1Xijk4
+(αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5
+(αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
ˆ
Y= 2.88451 −.44871X1−.09702X2+.36160X3−.06779X1X4+.08939X1X5
−.05349X2X4−.03742X2X5+.07190X3X4−.10851X3X5,
SSE(R) = 8.9467
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (8.2287/2) ÷(.7180/33) = 189.10, F(.99; 2,33) = 5.321.
If F∗≤5.321 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. ˆ
D1= ˆµ1.−ˆµ2.= 2.1500 −2.8067 = −.6567, ˆ
D2= ˆµ1.−ˆµ3.= 2.1500 −3.1133 =
−.9633, ˆ
D3= ˆµ1.−ˆµ4.= 2.1500 −2.8400 = −.6900, ˆ
D4= ˆµ2.−ˆµ3.=−.3066,
ˆ
D5= ˆµ2.−ˆµ4.=−.0333, ˆ
D6= ˆµ3.−ˆµ4.=.2733, s{ˆ
D1}=.06642, s{ˆ
D2}=
.07083, s{ˆ
D3}=.07497, s{ˆ
D4}=.06316, s{ˆ
D5}=.06777, s{ˆ
D6}=.07209,
q(.95; 4,33) = 3.825, T= 2.705
−.6567 ±2.705(.06642) −.836 ≤D1≤ −.477
−.9633 ±2.705(.07083) −1.155 ≤D2≤ −.772
−.6900 ±2.705(.07497) −.893 ≤D3≤ −.487
−.3066 ±2.705(.06316) −.477 ≤D4≤ −.136
−.0333 ±2.705(.06777) −.217 ≤D5≤.150
.2733 ±2.705(.07209) .078 ≤D6≤.468
f. ˆ
D1= ˆµ.1−ˆµ.2= 2.3875 −2.4675 = −.0800, ˆ
D2= ˆµ.1−ˆµ.3= 2.3875 −3.3350 =
−.9475, ˆ
D3= ˆµ.2−ˆµ.3=−.8675, s{ˆ
D1}=.06597, s{ˆ
D2}=.05860, s{ˆ
D3}=
.05501, q(.95; 3,33) = 3.470, T= 2.4537
−.0800 ±2.4537(.06597) −.242 ≤D1≤.082
−.9475 ±2.4537(.05860) −1.091 ≤D2≤ −.804
−.8675 ±2.4537(.05501) −1.002 ≤D3≤ −.733
23.11. a. Full model:
Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5+²ijk
Xijk1,Xijk2Xijk3,Xijk4,Xijk5defined same as in Problem 23.9a
Reduced models:
Factor A:Yijk =µ.. +β1Xijk4+β2Xijk5+²ijk
23-11

Factor B:Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+²ijk
b. Full model:
ˆ
Y= 2.72074 −.59611X1+.08412X2+.33964X3−.33756X4−.26317X5,
SSE(F) = .762425, dfF= 39
Reduced models:
Factor A:
ˆ
Y= 2.72494 −.32494X4−.18648X5,SSE(R) = 6.741678, dfR= 42
H0:α1=α2=α3= 0, Ha: not all αiequal zero.
F∗= (5.979253/3) ÷(.762425/39) = 101.95, F(.95; 3,39) = 2.845.
If F∗≤2.845 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
Factor B:
ˆ
Y= 2.86983 −.44483X1−.08521X2+.36654X3,SSE(R) = 9.144878, dfR= 41
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (8.382453/2) ÷(.762425/39) = 214.39, F(.95; 2,39) = 3.238.
If F∗≤3.238 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23.12. a. See Problem 19.14a. ˆ
D1=¯
Y13.−¯
Y11.= 2.100, ˆ
D2=¯
Y23.−¯
Y21.= 3.675,
ˆ
D3=¯
Y33.−¯
Y31.= 7.275, ˆ
L1=ˆ
D1−ˆ
D2=−1.575, ˆ
L2=ˆ
D1−ˆ
D3=−5.175,
MSE =.06406, s{ˆ
Di}=.1790 (i= 1,2,3), s{ˆ
Li}=.2531 (i= 1,2), B=
t(.99; 24) = 2.492
2.100 ±2.492(.1790) 1.654 ≤D1≤2.546
3.675 ±2.492(.1790) 3.229 ≤D2≤4.121
7.275 ±2.492(.1790) 6.829 ≤D3≤7.721
−1.575 ±2.492(.2531) −2.206 ≤L1≤ −.944
−5.175 ±2.492(.2531) −5.806 ≤L2≤ −4.544
b. H0:µ12 −µ13 = 0, Ha:µ12 −µ13 6= 0. ˆ
D=¯
Y12.−¯
Y13.=.025, s{ˆ
D}=.1790,
t∗=.025/.1790 = .14, t(.99; 24) = 2.492. If |t∗| ≤ 2.492 conclude H0, otherwise
Ha. Conclude H0.
H0:µ32 −µ33 = 0, Ha:µ32 −µ33 6= 0. ˆ
D=¯
Y32.−¯
Y33.=−2.975, s{ˆ
D}=.1790,
t∗=−2.975/.1790 = −16.62, t(.99; 24) = 2.492. If |t∗| ≤ 2.492 conclude H0,
otherwise Ha. Conclude Ha.α≤.04
23.13. a. Yijk =µ.. +α1Xijk1+β1Xijk2+β2Xijk3+²ijk
Xijk1=(1 if case from level 1 for factor A
−1 if case from level 2 for factor A
Xijk2=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijk3=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
23-12

ˆ
Y=.66939 + .11733X1−.34323X2+.02608X3,SSE(F) = 4.4898
Factor A:
Yijk =µ.. +β1Xijk2+β2Xijk3+²ijk
ˆ
Y=.70850 −.26502X2−.01303X3,SSE(R) = 5.0404
Factor B:
Yijk =µ.. +α1Xijk1+²ijk
ˆ
Y=.77520 + .03152X1,SSE(R) = 7.1043
b. H0:α1= 0, Ha:α16= 0.
F∗= (.5506/1) ÷(4.4898/46) = 5.641, F(.95; 1,46) = 4.05.
If F∗≤4.05 conclude H0, otherwise Ha. Conclude Ha.P-value = .022
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (2.6145/2) ÷(4.4898/46) = 13.393, F(.95; 2,46) = 3.20.
If F∗≤3.20 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23.14. a. See Problem 19.20a. ˆ
D1=¯
Y12.−¯
Y13.= 46.0, ˆ
D2=¯
Y22.−¯
Y23.= 6.0,
ˆ
L1=ˆ
D1−ˆ
D2= 40.0, MSE = 88.50, s{ˆ
D1}=s{ˆ
D2}= 6.652, s{ˆ
L1}= 9.407,
B=t(.99167; 15) = 2.694
46.0±2.694(6.652) 28.080 ≤D1≤63.920
6.0±2.694(6.652) −11.920 ≤D2≤23.920
40.0±2.694(9.407) 14.658 ≤L1≤65.342
b. H0:µ22 −µ23 ≤0, Ha:µ22 −µ23 >0. ˆ
D=¯
Y22.−¯
Y23.= 6.0, s{ˆ
D}= 6.652,
t∗= 6.0/6.652 = .90, t(.95; 15) = 1.753. If t∗≤1.753 conclude H0otherwise Ha.
Conclude H0.P-value = .19
23.15. a. Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5+²ijk
Xijk1=
1 if case from level 1 for factor A
−1 if case from level 4 for factor A
0 otherwise
Xijk2and Xijk3are defined similarly
Xijk4=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijk5=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
ˆ
Y= 2.71932 −.59897X1+.08546X2+.40036X3−.34043X4−.26218X5,
SSE(F) = .7419
Factor A:
23-13

Yijk =µ.. +β1Xijk4+β2Xijk5+²ijk
ˆ
Y= 2.77494 −.22494X4−.23648X5,SSE(R) = 5.8217
Factor B:
Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+²ijk
ˆ
Y= 2.90108 −.35108X1−.11646X2+.33529X3,SSE(R) = 8.1874
b. H0:α1=α2=α3= 0, Ha: not all αiequal zero.
F∗= (5.0798/3) ÷(.7419/37) = 84.45, F(.99; 3,37) = 4.360.
If F∗≤4.360 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (7.4455/2) ÷(.7419/37) = 185.66, F(.99; 2,37) = 5.229.
If F∗≤5.229 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23.16. a. Yij =µ..+ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+ρ5Xij5+ρ6Xij6
+ρ7Xij7+ρ8Xij8+ρ9Xij9+τ1Xij10 +τ2Xij11 +²ij
Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 10
0 otherwise
Iij2, . . . , Iij9are defined similarly
Iij10 =
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij11 =
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
b. ˆ
Y= 77.10000 + 4.90000X1+ 3.90000X2+ 2.23333X3+ 3.23333X4+ 1.23333X5
+.90000X6−1.10000X7−3.76667X8−4.10000X9−6.50000X10 −2.50000X11
c.
Source SS df MS
Regression 1,728.3667 1 157.1242
X1, X2, X3, X4, X5, X6,X7, X8,X9433.3667 9 48.1519
X10, X11|X1, X2, X3, X4, X5, X6,X7, X8,X91,295.0000 2 647.5000
Error 112.3333 18 6.2407
Total 1,840.7000 29
d. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1,295.0000/2÷(112.3333/18) = 103.754, F(.95; 2,18) = 3.55.
If F∗≤3.55 conclude H0, otherwise Ha. Conclude Ha.
23.17. a. Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+τ1Xij5+τ2Xij6+²ij
23-14

Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 5
0 otherwise
Iij2, . . . , Iij4are defined similarly
Iij5=
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij6=
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
b. ˆ
Y=.84400 −.32733X1−.23733X2−.17400X3+.31267X4+.26600X5+.14800X6
c.
Source SS df MS
Regression 2.7392 6 .4565
X1, X2, X3, X41.4190 4 .35475
X5, X6,|X1, X2, X3, X41.3203 2 .6602
Error .0193 8 .0024
Total 2.7585 14
d. H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1.3203/2) ÷(.0193/8) = 273.637, F(.95; 2,8) = 4.46.
If F∗≤4.46 conclude H0, otherwise Ha. Conclude Ha.
23.18. a. Yij =µ.. +ρi+τj+²ij
Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+ρ5Xij5+ρ6Xij6
+ρ7Xij7+ρ8Xij8+ρ9Xij9+τ1Xij10 +τ2Xij11 +²ij
Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 10
0 otherwise
Iij2, . . . , Iij9are defined similarly
Iij10 =
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij11 =
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
b. Yij =µ.. +ρ1Xij1+ρ2Xij2+ +ρ3Xij3+ρ4Xij4+ρ5Xij5+ρ6Xij6
+ρ7Xij7+ρ8Xij8+ρ9Xij9+²ij
c. Full model: ˆ
Y= 77.15556 + 4.84444X1+ 4.40000X2+ 2.17778X3
+3.17778X4+ 1.17778X5+.84444X6−1.15556X7
−3.82222X8−4.15556X9−6.55556X10 −2.55556X11
23-15

SSE(F) = 110.6667
Reduced model: ˆ
Y= 76.70000 + 5.30000X1+.30000X2+ 2.63333X3
+3.63333X4+ 1.63333X5+ 1.30000X6−.70000X7
−3.36667X8−3.70000X9
SSE(R) = 1,311.3333
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (1,200.6666/2) ÷(110.6667/17) = 92.22, F (.95; 2,17) = 3.59.
If F∗≤3.59 conclude H0, otherwise Ha.Conclude Ha.
d. ˆ
L= ˆτ2−ˆτ3= 2ˆτ2+ ˆτ1=−11.66667, s2{ˆτi}=.44604 (i= 1,2), s{ˆτ1,ˆτ2}=
−.20494, s{ˆ
L}= 1.1876, t(.975; 17) = 2.11,
−11.66667 ±2.11(1.1876), −14.17 ≤L≤ −9.16
23.19. a. Yij =µ.. +ρi+τj+²ij
Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+τ1Xij5+τ2Xij6+²ij
Iij1=
1 if experimental unit from block 1
−1 if experimental unit from block 5
0 otherwise
Iij2, . . . , Iij4are defined similarly
Iij5=
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 3
0 otherwise
Iij6=
1 if experimental unit received treatment 2
−1 if experimental unit received treatment 3
0 otherwise
b. Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+²ij
c. Full model: ˆ
Y=.82941 −.33613X1−.22274X2−.15941X3+.32726X4
+.25085X5+.16259X6
SSE(F) = .0035
Reduced model: ˆ
Y=.84567 −14567X1−.23900X2−.17567X3+.31100X4
SSE(R) = .9542
H0:τ1=τ2= 0, Ha: not both τ1and τ2equal zero.
F∗= (.9507/2) ÷(.0035/6) = 814.89, F(.95; 2,6) = 5.14.
If F∗≤5.14 conclude H0, otherwise Ha. Conclude Ha.
d. ˆ
L= ˆτ1−ˆτ3= 2ˆτ1+ ˆτ2=.66429, s2{ˆτ1}=.000105, s2{ˆτ2}=.000087, s{ˆτ1,ˆτ2}=
−.000043, s{ˆ
L}=.0183, t(.99; 6) = 3.143,
.66429 ±3.143(.0183), .607 ≤L≤.722
23.20. See Problem 19.10a. L1=.3µ11 +.6µ21 +.1µ31,L2=.3µ12 +.6µ22 +.1µ32.
23-16

H0:L1=L2,Ha:L16=L2.
ˆ
L1−ˆ
L2= 25.43332 −25.05001 = .38331, MSE = 2.3889, s{ˆ
L1−ˆ
L2}=.6052,
t∗=.38331/.6052 = .63, t(.975; 30) = 2.042.
If |t∗| ≤ 2.042 conclude H0, otherwise Ha. Conclude H0.P-value = .53
23.21. a.
H0:L1=3µ11 +µ21
4−3µ12 +µ22
4= 0
L2=3µ11 +µ21
4−3µ13 +µ23
4= 0
Ha: not both L1and L2equal zero
b. Regression model equivalent to (19.15) using 1, 0 indicator variables:
Full model:
Yijk =µ11Xijk1+µ12Xijk2+µ13Xijk3+µ21Xijk4+µ22Xijk5
+µ23Xijk6+²ijk
Xijk1=(1 if case from level 1 for factor Aand level 1 for factor B
0 otherwise
Xijk2=(1 if case from level 1 for factor Aand level 2 for factor B
0 otherwise
Xijk3=(1 if case from level 1 for factor Aand level 3 for factor B
0 otherwise
Xijk4=(1 if case from level 2 for factor Aand level 1 for factor B
0 otherwise
Xijk5=(1 if case from level 2 for factor Aand level 2 for factor B
0 otherwise
Xijk6=(1 if case from level 2 for factor Aand level 3 for factor B
0 otherwise
c. Reduced model:
µ11 =µ12 +µ22/3−µ21/3
µ13 =µ12 +µ22/3−µ23/3
Yijk = (µ12 +µ22/3−µ21/3)Xijk1+µ12Xijk2+ (µ12 +µ22/3−µ23/3)Xijk3
+µ21Xijk4+µ22Xijk5+µ23Xijk6+²ijk
or
Yijk =µ12Zijk1+µ21Zijk2+µ22Zijk3+µ23Zijk4+²ijk
where:
Zijk1=Xijk1+Xijk2+Xijk3
Zijk2=−Xijk1/3 + Xijk4
Zijk3= (Xijk1+Xijk3)/3 + Xijk5
Zijk4= (−Xijk3/3) + Xijk6
23-17

d. SSE(F) = 5.468, dfF= 54, SSE(R) = 8.490, dfR= 56,
F∗= [(8.490 −5.468)/2] ÷(5.468/54) = 14.92, F (.95; 2,54) = 3.17.
If F∗≤3.17 conclude H0,otherwise Ha. Conclude Ha.P-value = 0+
e. See Problem 19.18a. ˆ
L2= (.75 ¯
Y11.+.25 ¯
Y21.)−(.75 ¯
Y13.+.25 ¯
Y23.) = −.61446,
s{ˆ
L2}=.1125, t(.975; 54) = 2.005, −.61446 ±2.005(.1125), −.840 ≤L2≤ −.389
23.22. a.
L1=µ11 + 2µ12 + 7µ13
10 −µ21 + 2µ22 + 7µ23
10 = 0
H0:L2=µ11 + 2µ12 + 7µ13
10 −µ31 + 2µ32 + 7µ33
10 = 0
L3=µ11 + 2µ12 + 7µ13
10 −µ41 + 2µ42 + 7µ43
10 = 0
Ha: not all Liequal zero (i= 1,2,3)
b. βentries: µ11,µ12,µ13,µ21,µ22,µ23,µ31,µ32,µ33, µ41,µ42,µ43
Xentries:
A B Freq.
1 1 2 100000000000
1 2 2 010000000000
1 3 8 001000000000
2 1 4 000100000000
2 2 5 000010000000
2 3 4 000001000000
3 1 2 000000100000
3 2 4 000000010000
3 3 5 000000001000
4 1 2 000000000100
4 2 2 000000000010
4 3 5 000000000001
c.
C=
.1.2.7−.1−.2−.7000000
.1.2.7000−.1−.2−.7 0 0 0
.1.2.7000000−.1−.2−.7
h=
0
0
0
d. SSE(R)−SSE(F) = 5.6821
e. SSE(F) = .7180, F∗= (5.6821/3) ÷(.7180/33) = 87.05, F(.99; 3,33) = 4.437.
If F∗≤4.437 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f. See Problem 23.10a. ˆ
L2= (.1¯
Y11.+.2¯
Y12.+.7¯
Y13.)−(.1¯
Y31.+.2¯
Y32.+.7¯
Y33.) =
−1.003, s{ˆ
L2}=.0658, t(.995; 33) = 2.733,
−1.003 ±2.733(.0658), −1.183 ≤L2≤ −.823
23.23. H0:4µ11+4µ12 +2µ13
10 =4µ21+4µ22 +3µ23
11 ,Ha: equality does not hold.
¯
Y... = 93.714, ¯
Y1.. = 143, ¯
Y2.. = 48.91
SSA = 10(143 −93.714)2+ 11(48.91 −93.714)2= 46,372
23-18

F∗= (46,372/1) ÷(1,423.1667/15) = 488.8, F(.99; 1,15) = 8.68.
If F∗≤8.68 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23.24. H0:2
12 µ11 +2
12 µ12 +8
12 µ13 =4
13 µ21 +5
13 µ22 +4
13 µ23 =2
11 µ31 +4
11 µ32 +5
11 µ33 =
2
9µ41 +2
9µ42 +5
9µ43,
Ha: not all equalities hold.
¯
Y... = 2.849, ¯
Y1.. = 2.425, ¯
Y2.. = 2.785, ¯
Y3.. = 3.236, ¯
Y4.. = 3.033
SSA = 12(2.425 −2.849)2+ 13(2.785 −2.849)2+ 11(3.236 −2.849)2+ 9(3.033 −
2.849)2= 4.163
F∗= (4.163/3) ÷(.718/33) = 63.78, F(.95; 3,33) = 2.89.
If F∗≤2.89 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23.25. σ2{ˆ
L}=σ2{Pciˆµi.}=Pc2
iσ2{ˆµi.}=P
ic2
iσ2
P
j
¯
Yij.
b
=1
b2P
ic2
iP
j
σ2
nij
=σ2
b2P
ic2
iP
j
1
nij
because of independence of ¯
Yij..
23.26. Ens2{ˆ
L}o=E(MSE PPc2
ij
nij )=PPc2
ij
nij
E{MSE}=σ2PPc2
ij
nij
=σ2{ˆ
L}
23.27. a.
X=
11010
11001
11000
10110
10101
10100
10010
10001
10000
b.
Xβ=
β0+β1+β3
β0+β1+β4
β0+β1
β0+β2+β3
β0+β2+β4
β0+β2
β0+β3
β0+β4
β0
=
µ.. +ρ1+τ1
µ.. +ρ1+τ2
µ.. +ρ1+τ3
µ.. +ρ2+τ1
µ.. +ρ2+τ2
µ.. +ρ2+τ3
µ.. +ρ3+τ1
µ.. +ρ3+τ2
µ.. +ρ3+τ3
β0=µ.. +ρ3+τ3β2=ρ2−ρ3
β4=τ2−τ3β1=ρ1−ρ3
β3=τ1−τ3
23-19

23.28.
Y=
Y111
Y112
Y121
Y122
Y211
Y212
Y221
X=
1000
1000
0100
0100
0010
0010
0001
β=
µ11
µ12
µ21
µ22
bF=
¯
Y11.
¯
Y12.
¯
Y21.
¯
Y22.
Cβ=h1−1−1 1 i
µ11
µ12
µ21
µ22
=µ11 −µ12 −µ21 +µ22 = 0
From (23.46):
bR=
¯
Y11.
¯
Y12.
¯
Y21.
¯
Y22.
−
1/2 0 0 0
0 1/2 0 0
0 0 1/2 0
0 0 0 1
1
−1
−1
1
µ5
2¶−1³¯
Y11.−¯
Y12.−¯
Y21.+¯
Y22.−0´
=
¯
Y11.
¯
Y12.
¯
Y21.
¯
Y22.
−2
5³¯
Y11.−¯
Y12.−¯
Y21.+¯
Y22.´
1/2
−1/2
−1/2
1
ˆµ22 =¯
Y22.−2
5(¯
Y11.−¯
Y12.−¯
Y21.+¯
Y22.)
23.29. a. βentries: µ11,µ12,µ13,µ22
Xentries:
A B Freq.
1 1 10 1 0 0 0
1 2 10 0 1 0 0
1 3 10 0 0 1 0
2 2 10 0 0 0 1
2 3 10 0 −1 1 1
b. C= [0 1 0 −1] h= 0
23.30. a. Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5
+(αβ)11Xijk1Xijk4+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4
+(αβ)22Xijk2Xijk5+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk4+²ijk
Iijk1=
1 if case from NE
−1 if case from W
0 otherwise
Iijk2=
1 if case from NC
−1 if case from W
0 otherwise
23-20
Iijk3=
1 if case from S
−1 if case from W
0 otherwise
Iijk4=
1 if average age under 52.0
−1 if average age 55.0 or more
0 otherwise
Iijk5=
1 if average age 52.0 - under 55.0
−1 if average age 55.0 or more
0 otherwise
b. ˆ
Y= 9.40661 + 1.45009X1+.23601X2−.24406X3−.38373X4
+.19446X5−.76296X1X4−.57198X1X5+.44674X2X4
+.17515X2X5+.35707X3X4−.38986X3X5,SSE(F) = 261.2341
c. r=.959
23.31. a. ¯
Y11.= 9.71000, ¯
Y12.= 10.47917, ¯
Y13.= 12.38091, ¯
Y21.= 9.70563,
¯
Y22.= 10.01222, ¯
Y23.= 9.21000, ¯
Y31.= 9.13588, ¯
Y32.= 8.96714,
¯
Y33.= 9.38462, ¯
Y41.= 7.54000, ¯
Y42.= 8.94571, ¯
Y43.= 7.40800
b. Yijk =µ.. +α1Xijk1+α1Xijk2+α3Xijk3+β1Xijk4+β2Xijk5+²ijk
c. ˆ
Y= 9.52688 + 1.50561X1+.23119X2−.30781X3−.26423X4−.00518X5,
SSE(R) = 300.4100
H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (39.1759/6) ÷(261.2341/101) = 2.524, F(.99; 6,101) = 2.99.
If F∗≤2.99 conclude H0, otherwise Ha. Conclude H0.P-value = .026
d. Yijk =µ.. +β1Xijk4+β2Xijk5+ (αβ)11Xijk1Xijk4
+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5
+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
ˆ
Y= 9.52473 −.50240X4+.24409X5−1.44778X1X4−.17942X1X5
+.61345X2X4+.11924X2X5+.34296X3X4−.24453X3X5,
SSE(R) = 345.4833
H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= (84.2492/3) ÷(261.2341/101) = 10.858, F(.99; 3,101) = 3.98.
If F∗≤3.98 conclude H0, otherwise Ha. Conclude Ha.P-value 0+
e. Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+ (αβ)11Xijk1Xijk4
+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5
+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
ˆ
Y= 9.42456 + 1.53811X1+.15829X2−.31129X3−.69021X1X4
−.60603X1X5+.29855X2X4+.26600X2X5+.18805X3X4−.35618X3X5,
23-21
SSE(R) = 267.7103
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (6.4762/2) ÷(261.2341/101) = 1.252, F(.99; 2,101) = 4.82.
If F∗≤4.82 conclude H0, otherwise Ha. Conclude H0.P-value = .29
f. n11 = 5, n12 = 12, n13 = 11, n21 = 16, n22 = 9, n23 = 7,
n31 = 17, n32 = 7, n33 = 13, n41 = 4, n42 = 7, n43 = 5,
ˆ
D1= ˆµ1.−ˆµ2.= 10.85669 −9.64262 = 1.21407,
ˆ
D2= ˆµ1.−ˆµ3.= 10.85669 −9.16255 = 1.69414,
ˆ
D3= ˆµ1.−ˆµ4.= 10.85669 −7.96457 = 2.89212,
ˆ
D4= ˆµ2.−ˆµ3.=.48007, ˆ
D5= ˆµ2.−ˆµ4.= 1.67805,
ˆ
D6= ˆµ3.−ˆµ4.= 1.19798, MSE = 2.5865, s{ˆ
D1}=.4455, s{ˆ
D2}=.4332,
s{ˆ
D3}=.5272, s{ˆ
D4}=.4135, s{ˆ
D5}=.5112, s{ˆ
D6}=.5004,
q(.95; 4,101) = 3.694, T= 2.612
1.21407 ±2.612(.4455) .050 ≤D1≤2.378
1.69414 ±2.612(.4332) .563 ≤D2≤2.826
2.89212 ±2.612(.5272) 1.515 ≤D3≤4.269
.48007 ±2.612(.4135) −.600 ≤D4≤1.560
1.67805 ±2.612(.5112) .343 ≤D5≤3.013
1.19798 ±2.612(.5004) −.109 ≤D6≤2.505
23.32. a. ANOVA model: Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Regression: Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5
+ (αβ)11Xijk1Xijk4+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4
+ (αβ)22Xijk2Xijk5+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
Iijk1=
1 if case from NE
−1 if case from W
0 otherwise
Iijk2=
1 if case from NC
−1 if case from W
0 otherwise
Iijk3=
1 if case from S
−1 if case from W
0 otherwise
Iijk4=
1 if poverty level below 6.0 percent
−1 if poverty level is 10 percent or more
0 otherwise
Iijk5=
1 if poverty level between 6.0 and under 10.0 percent
−1 if poverty level is 10 percent or more
0 otherwise
23-22
b. ˆ
Y=.0568 −.00852X1−.00475X2+.00983X3−.0114X4−.00173X5−.00206X1X4
−.00629X1X5−.00106X2X4+.00069X2X5−.00102X3X4+.00133X3X5,
SSE(F) = .23111
c. r=.932
23.33. a. ¯
Y11.=.0348, ¯
Y12.=.0402, ¯
Y13.=.0697, ¯
Y21.=.0396, ¯
Y22.=.0510, ¯
Y23.=.0655,
¯
Y31.=.0542,¯
Y32.=.0662, ¯
Y33.=.0794, ¯
Y41.=.0530,¯
Y42.=.0627, ¯
Y43.=.0649
b. Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+β2Xijk5+²ijk
c. ˆ
Y=.0563 −.0105X1−.0043X2+.0106X3−.0111X4−.0013X5,
SSE(R) = .23589
H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (.00478/6) ÷(.23111/428) = 1.476. F(.995; 6,428) = 3.14.
If F∗≤3.14 conclude H0, otherwise Ha. Conclude H0.P-value = .18
d. Yijk =µ.. +β1Xijk4+β2Xijk5+ (αβ)11Xijk1Xijk4
+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5
+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
ˆ
Y=.0578 −.0141X4−.0024X5−.0043X1X4−.0090X1X5+.0020X2X4
−.0005X2X5−.0040X3X4+.0039X3X5,
SSE(R) = .25118
H0:α1=α2=α3,Ha: not all αiequal zero.
F∗= (.02007/3) ÷(.23111/428) = 12.39, F(.995; 3,428) = 4.34.
If F∗≤4.34 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. Yijk =µ.. +α1Xijk1+α2Xijk2+α3Xijk3+ (αβ)11Xijk1Xijk4
+ (αβ)12Xijk1Xijk5+ (αβ)21Xijk2Xijk4+ (αβ)22Xijk2Xijk5
+ (αβ)31Xijk3Xijk4+ (αβ)32Xijk3Xijk5+²ijk
ˆ
Y=.0558 −.0138X1−.0047X2+.0135X3−.0015X1X4−.0009X1X5
+3.15459X2X4−.23458X2X5−.0032X3X4−.0025X3X5,
SSE(R) = .26209
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (.03098/2) ÷(.23111/428) = 28.69, F(.995; 2,428) = 5.36.
If F∗≤5.36 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f. n11 = 52, n12 = 38, n13 = 13, n21 = 32, n22 = 50, n23 = 26,
n31 = 25, n32 = 52, n33 = 75, n41 = 20, n42 = 33, n43 = 24,
ˆ
D1= ˆµ1.−ˆµ2.=−.0038, ˆ
D2= ˆµ1.−ˆµ3.=−.0184, ˆ
D3= ˆµ1.−ˆµ4.=−.0120,
ˆ
D4= ˆµ2.−ˆµ3.=−.0146, ˆ
D5= ˆµ2.−ˆµ4.=−.0082, ˆ
D6= ˆµ3.−ˆµ4.=.0064,
23-23

MSE =.00054, q(.95; 4,428) = 3.63, T= 2.567
s{ˆ
D1}=.00357, s{ˆ
D2}=.00342, s{ˆ
D3}=.00383,
s{ˆ
D4}=.00312, s{ˆ
D5}=.00356, s{ˆ
D6}=.00342,
−.0038 ±2.567(.00357) −.0130 ≤D1≤.0054
−.0184 ±2.567(.00342) −.0271 ≤D2≤ −.0096
−.0120 ±2.567(.00383) −.0218 ≤D3≤ −.0021
−.0146 ±2.567(.00312) −.0226 ≤D4≤ −.0066
−.0082 ±2.567(.00356) −.0173 ≤D5≤.0010
.0064 ±2.567(.00342) −.0024 ≤D6≤.0152
23.34. a. ANOVA model: Yijk =µ.. +αi+βj+ (αβ)ij +²ijk
Regression: Yijk =µ.. +α1Xijk1+β1Xijk2+ (αβ)11Xijk1Xijk2+²ijk
Xijk1=(1 if no discount price (level 0 of variable 5)
−1 if discount price (level 1 of variable 5)
Xijk2=(1 if no package promotion (level 0 of variable 6)
−1 if package promotion (level 1 of variable 6)
b. ˆ
Y= 2.620 −.199X1−.0446X2+.0366X1X2
SSE(F) = .7850
c. r=.990
23.35. a. ¯
Y00.= 2.4125, ¯
Y01.= 2.4286, ¯
Y10.= 2.7375, ¯
Y11.= 2.9000,
b. Yijk =µ.. +α1Xijk1+β1Xijk2+²ijk
c. ˆ
Y= 2.625 −.201X1−.0498X2,SSE(R) = .8306
H0: (αβ)11 = 0, Ha: (αβ)11 6= 0.
F∗= (.0456/1) ÷(.7850/32) = 1.86. F(.95; 1,32) = 4.15.
If F∗≤4.15 conclude H0, otherwise Ha. Conclude H0.P-value = .18
d. Yijk =µ.. +β1Xijk2+ (αβ)11Xijk1Xijk2+²ijk
ˆ
Y= 2.648 −.0726X2+.0494X1X2,SSE(R) = 2.1352
H0:α1= 0, Ha:α16= 0.
F∗= (1.3502/1) ÷(.7850/32) = 55.04, F(.95; 1,32) = 4.15.
If F∗≤4.15 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. Yijk =µ.. +α1Xijk1+ (αβ)11Xijk1Xijk2+²ijk
ˆ
Y= 2.623 −.205X1+.0429X1X2,SSE(R) = .8529
H0:β1= 0, Ha:β16= 0
F∗= (.0679/1) ÷(.7850/32) = 2.77, F(.95; 1,32) = 4.15.
If F∗≤4.15 conclude H0, otherwise Ha. Conclude H0.P-value = .11
23.36. a. H0:5µ11+12µ12 +11µ13
28 =16µ21+9µ22 +7µ23
32 =17µ31+7µ32 +13µ33
37 =4µ41+7µ42 +5µ43
16 ,
23-24

Ha: not all equalities hold.
F∗= (103.55418/3) ÷(261.23406/101) = 13.346, F(.99; 3,101) = 3.98.
If F∗≤3.98 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
b. H0:5µ11+16µ21 +17µ31 +4µ41
42 =12µ12+9µ22 +7µ32 +7µ42
35 =11µ13+7µ23 +13µ33 +5µ43
36 ,
Ha: not all equalities hold.
F∗= (10.63980/2) ÷(261.23406/101) = 2.057, F(.99; 2,101) = 4.82.
If F∗≤4.82 conclude H0, otherwise Ha. Conclude H0.P-value = .13
23.37. a. H0:52µ11+38µ12 +13µ13
103 =32µ21+50µ22 +26µ23
108 =25µ31+52µ32 +75µ33
152 =20µ41+33µ42 +24µ43
77 ,
Ha: not all equalities hold.
¯
Y... =.05729, ¯
Y1.. =.04123, ¯
Y2.. =.05111, ¯
Y3.. =.07074, ¯
Y4.. =.06088
F∗= (.0592/3) ÷(.23111/428) = 36.54, F(.995; 3,428) = 4.34.
If F∗≤4.34 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
b. H0:52µ11+32µ21 +25µ31 +20µ41
129 =38µ12+50µ22 +52µ32 +33µ42
173 =13µ13+26µ23 +75µ33 +24µ43
138 ,
Ha: not all equalities hold.
¯
Y... =.05729, ¯
Y.1.=.04259, ¯
Y.2.=.05544, ¯
Y.3.=.07334,
F∗= (.0640/2) ÷(.23111/428) = 59.26, F(.995; 2,428) = 5.36.
If F∗≤5.36 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
23-25
23-26

Chapter 24
MULTIFACTOR STUDIES
24.1. a. β1=µ.1.−µ... =−2, β2=µ.2.−µ... =−.5, β3=µ.3.−µ... = 2.5
b. (βγ)12 =µ.12 −µ.1.−µ..2+µ... = 1
c. (αβγ)212 =µ212 −µ21.−µ.12 −µ2.2+µ2.. +µ.1.+µ..2−µ... =−.5
24.4. a. α1=µ1.. −µ... = 138 −131.5 = 6.5, α2=µ2.. −µ... = 131.5−131.5 = 0
α3=µ3.. −µ... = 125 −131.5 = −6.5
b. β2=µ.2.−µ... = 134 −131.5 = 2.5, γ1=µ..1−µ... = 128.5−131.5 = −3
c. (αβ)12 =µ12.−µ1.. −µ.2.+µ... = 141 −138 −134 + 131.5 = .5
(αγ)21 =µ2.1−µ2.. −µ..1+µ... = 128 −131.5−128.5 + 131.5 = −.5
(βγ)12 =µ.12 −µ.1.−µ..2+µ... = 132 −129 −134.5 + 131.5 = 0
d. (αβγ)111 =µ111 −µ.11 −µ1.1−µ11.+µ1.. +µ.1.+µ..1−µ...
= 130 −126 −134 −135 + 138 + 129 + 128.5−131.5 = −1
(αβγ)322 =µ322 −µ32.−µ3.2−µ.22 +µ3.. +µ.2.+µ..2−µ...
= 131 −128 −126.5−137 + 125 + 134 + 134.5−131.5 = 1.5
24.6. a. eijkm:
k= 1
i j = 1 j= 2
1 3.7667 1.1667
−3.9333 −1.6333
.1667 .4667
2−1.7000 −.8333
1.1000 1.3667
.6000 −.5333
k= 2
i j = 1 j= 2
1−.5000 −1.0333
.4000 1.3667
.1000 −.3333
2 1.1333 −.5667
−1.6667 1.7333
.5333 −1.1667
b. r=.973
24.7. a. ¯
Y111.= 36.1333, ¯
Y112.= 56.5000, ¯
Y121.= 52.3333, ¯
Y122.= 71.9333,
¯
Y211.= 46.9000, ¯
Y212.= 68.2667, ¯
Y221.= 64.1333, ¯
Y222.= 83.4667
24-1

b.
Source SS df MS
Between treatments 4,772.25835 7 681.75119
A(chemical) 788.90667 1 788.90667
B(temperature) 1,539.20167 1 1,539.20167
C(time) 2,440.16667 1 2,440.16667
AB interactions .24000 1 .24000
AC interactions .20167 1 .20167
BC interactions 2.94000 1 2.94000
ABC interactions .60167 1 .60167
Error 53.74000 16 3.35875
Total 4,825.99835 23
c. H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero. F∗=.60167/3.35875 =
.18, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude H0.
P-value = .68
d. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗=.24000/3.35875 =
.07, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude H0.
P-value = .79
H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero. F∗=.20167/3.35875 =
.06, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude H0.
P-value = .81
H0: all (βγ)jk equal zero, Ha: not all (βγ)jk equal zero. F∗= 2.94000/3.35875 =
.875, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude
H0.P-value = .36
e. H0: all αiequal zero (i= 1,2), Ha: not all αiequal zero. F∗= 788.90667/3.35875 =
234.88, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all βjequal zero (j= 1,2), Ha: not all βjequal zero. F∗= 1,539.20167/3.35875 =
458.27, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all γkequal zero (k= 1,2), Ha: not all γkequal zero. F∗= 2,440.1667/3.35875 =
726.51, F(.975; 1,16) = 6.12. If F∗≤6.12 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
f. α≤.1624
24.8. a. ˆ
D1= 65.69167 −54.22500 = 11.46667, ˆ
D2= 67.96667 −51.95000 = 16.01667,
ˆ
D3= 70.04167 −49.87500 = 20.16667, MSE = 3.35875,
s{ˆ
Di}=.7482 (i= 1,2,3), B=t(.99167; 16) = 2.673
11.46667 ±2.673(.7482) 9.467 ≤D1≤13.467
16.01667 ±2.673(.7482) 14.017 ≤D2≤18.017
20.16667 ±2.673(.7482) 18.167 ≤D3≤22.167
b. ¯
Y222.= 83.46667, s{¯
Y222.}= 1.0581, t(.975; 16) = 2.120,
24-2

83.46667 ±2.120(1.0581), 81.2235 ≤µ222 ≤85.7098
24.9. a. eijkm:
k= 1
i j = 1 j= 2
1 2.250 −1.825
−1.450 2.975
−1.350 −1.525
.550 .375
2−1.925 .950
−2.325 −1.850
4.075 −2.850
.175 3.750
3−.850 4.375
3.550 −2.525
−2.950 .975
.250 −2.825
k= 2
i j = 1 j= 2
1 1.450 −4.475
−1.050 3.325
2.250 3.725
−2.650 −2.575
2 2.625 2.100
−1.875 .500
−2.075 .100
1.325 −2.700
3−1.350 −2.450
.650 2.450
3.550 −1.250
−2.850 1.250
b. r=.974
24.10. a. ¯
Y111.= 122.050, ¯
Y112.= 111.250, ¯
Y121.= 116.925, ¯
Y122.= 92.675,
¯
Y211.= 121.225, ¯
Y212.= 110.975, ¯
Y221.= 116.250, ¯
Y222.= 90.600,
¯
Y311.= 91.750, ¯
Y312.= 79.950, ¯
Y321.= 85.525, ¯
Y322.= 61.050
b. ¯
Y1... = 110.7250, ¯
Y2... = 109.7625, ¯
Y3... = 79.5688
c.
Source SS df MS
Between treatments 16,291.75564 11 1,481.06870
A(fee) 10,044.27125 2 5,022.13563
B(scope) 1,833.97688 1 1,833.97688
C(supervision) 3,832.40021 1 3,832.40021
AB interactions 1.60125 2 .80062
AC interactions .78792 2 .39396
BC interactions 574.77521 1 574.77521
ABC interactions 3.94292 2 1.97146
Error 266.13750 36 7.39271
Total 16,557.89314 47
d. H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero. F∗= 1.97146/7.39271 =
.27, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude H0.
P-value = .77
e. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗=.80062/7.39271 =
.11, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude H0.
P-value = .90
24-3
H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero. F∗=.39396/7.39271 =
.05, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude H0.
P-value = .95
H0: all (βγ)jk equal zero, Ha: not all (βγ)jk equal zero. F∗= 574.77521/7.39271 =
77.75, F(.99; 1,36) = 7.40. If F∗≤7.40 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
f. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 5,022.13563/7.39271 =
679.34, F(.99; 2,36) = 5.25. If F∗≤5.25 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
g. α≤.049
24.11. a. ˆ
D1=.9625, ˆ
D2= 30.1937, ˆ
D3= 31.1562, ˆ
D4= 111.6750 −100.7250 = 10.9500
ˆ
D5= 106.2333 −81.4417 = 24.7916, ˆ
L1=−13.8416,
s{ˆ
Di}=.9613 (i= 1,2,3), s{ˆ
D4}=s{ˆ
D5}= 1.1100, s{ˆ
L1}= 1.5698,
B=t(.99167; 36) = 2.511
.9625 ±2.511(.9613) −1.451 ≤D1≤3.376
30.1937 ±2.511(.9613) 27.780 ≤D2≤32.608
31.1562 ±2.511(.9613) 28.742 ≤D3≤33.570
10.9500 ±2.511(1.1100) 8.163 ≤D4≤13.737
24.7916 ±2.511(1.1100) 22.004 ≤D5≤27.579
−13.8416 ±2.511(1.5698) −17.783 ≤L1≤ −9.900
b. ˆ
D= 116.925 −116.250 = .675, s{ˆ
D}= 1.9226, t(.975; 36) = 2.028,
.675 ±2.028(1.9226), −3.224 ≤D≤4.574
c. s{ˆ
D}= 1.9226, q(.90; 12, 36) = 4.52, T= 3.196, T s{ˆ
D}= 6.14,
¯
Y111.= 122.050, ¯
Y211.= 121.225, ¯
Y121.= 116.925, ¯
Y221.= 116.250
24.12. a. eijkm:
k= 1
i j = 1 j= 2 j= 3
1 31.4 44.8−1.2
−43.6−23.2−28.2
17.4−33.2−17.2
20.4 20.8 13.8
−25.6−9.2 32.8
k= 2
i j = 1 j= 2 j= 3
1−30.0−3.4−18.2
48.0−12.4 15.8
18.0.6 5.8
−55.0−25.4 25.8
19.0 40.6−29.2
k= 1
i j = 1 j= 2 j= 3
2 29.6 27.6.6
39.6−34.4−.4
−32.4−26.4 14.6
−34.4 50.6−20.4
−2.4−17.4 5.6
k= 2
i j = 1 j= 2 j= 3
2−6.6−4.6−19.4
−22.6 12.4 4.6
10.4 25.4−43.4
21.4−34.6 50.6
−2.6 1.4 7.6
b. r=.992
24-4

24.13. a. ¯
Y111.= 1,218.6, ¯
Y112.= 1,051.0, ¯
Y121.= 1,274.2, ¯
Y122.= 1,122.4,
¯
Y131.= 1,218.2, ¯
Y132.= 1,051.2, ¯
Y211.= 1,036.4, ¯
Y212.= 870.6,
¯
Y221.= 1,077.4, ¯
Y222.= 931.6, ¯
Y231.= 1,020.4, ¯
Y232.= 860.4
b.
Source SS df MS
Between treatments 973,645.933 11 88,513.267
A(gender) 540,360.600 1 540,360.600
B(sequence) 49,319.633 2 24,659.817
C(experience) 382,401.667 1 382,401.667
AB interactions 542.500 2 271.250
AC interactions 91.267 1 91.267
BC interactions 911.233 2 455.617
ABC interactions 19.033 2 9.517
Error 41,186.000 48 858.042
Total 1,014,831.933 59
c. H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero. F∗= 9.517/858.042 =
.01, F(.95; 2,48) = 3.19. If F∗≤3.19 conclude H0, otherwise Ha. Conclude H0.
P-value = .99
d. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗= 271.250/858.042 =
.32, F(.95; 2,48) = 3.19. If F∗≤3.19 conclude H0, otherwise Ha. Conclude H0.
P-value = .73
H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero. F∗= 91.267/858.042 =
.11, F(.95; 1,48) = 4.04. If F∗≤4.04 conclude H0, otherwise Ha. Conclude H0.
P-value = .75
H0: all (βγ)jk equal zero, Ha: not all (βγ)jk equal zero. F∗= 455.617/858.042 =
.53, F(.95; 2,48) = 3.19. If F∗≤3.19 conclude H0, otherwise Ha. Conclude H0.
P-value = .59
e. H0: all αiequal zero (i= 1,2), Ha: not all αiequal zero. F∗= 540,360.600/858.042 =
629.76, F(.95; 1,48) = 4.04. If F∗≤4.04 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero. F∗= 24,659.817/858.042 =
28.74, F(.95; 2,48) = 3.19. If F∗≤3.19 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all γkequal zero (k= 1,2), Ha: not all γkequal zero. F∗= 382,401.667/858.042 =
445.67, F(.95; 1,48) = 4.04. If F∗≤4.04 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
f. α≤.302
24.14. a. ¯
Y1... = 1,155.933, ¯
Y2... = 966.133, ¯
Y.1.. = 1,044.150,¯
Y.2.. = 1,101.400,
¯
Y.3.. = 1,037.550, ¯
Y..1.= 1,140.867,¯
Y..2.= 981.200
ˆ
D1= 189.800, ˆ
D2=−57.250, ˆ
D3= 6.600, ˆ
D4= 63.850, ˆ
D5= 159.667,
MSE = 858.042, s{ˆ
D1}= 7.5633, s{ˆ
Di}= 9.2631 (i= 2,3,4),
24-5
s{ˆ
D5}= 7.5633, B=t(.99; 48) = 2.406
189.800 ±2.406(7.5633) 171.603 ≤D1≤207.997
−57.250 ±2.406(9.2631) −79.537 ≤D2≤ −34.963
6.600 ±2.406(9.2631) −15.687 ≤D3≤28.887
63.850 ±2.406(9.2631) 41.563 ≤D4≤86.137
159.667 ±2.406(7.5633) 141.470 ≤D5≤177.864
b. ¯
Y231.= 1,020.4, s{¯
Y231.}= 13.0999, t(.975; 48) = 2.011,
1,020.4±2.011(13.0999), 994.056 ≤µ231 ≤1,046.744
24.15. a. Yijkm =µ...+α1Xijkm1+β1Xijkm2+γ1Xijkm3+(αβ)11Xijkm1Xijkm2+(αγ)11Xijkm1Xijkm3
+(βγ)11Xijkm2Xijkm3+ (αβγ)111Xijkm1Xijkm2Xijkm3+²ijkm
Xijk1=(1 if case from level 1 for factor A
−1 if case from level 2 for factor A
Xijk2=(1 if case from level 1 for factor B
−1 if case from level 2 for factor B
Xijk3=(1 if case from level 1 for factor C
−1 if case from level 2 for factor C
b. Yijkm =µ... +β1Xijkm2+γ1Xijkm3+ (αβ)11Xijkm1Xijkm2+ (αγ)11Xijkm1Xijkm3
+(βγ)11Xijkm2Xijkm3+ (αβγ)111Xijkm1Xijkm2Xijkm3+²ijkm
c. Full model:
ˆ
Y= 60.01667 −5.67500X1−8.06667X2−10.02500X3+.04167X1X2
+.15000X1X3−.40833X2X3+.10000X1X2X3,
SSE(F) = 49.4933
Reduced model:
ˆ
Y= 61.15167 −9.20167X2−8.89000X3−1.09333X1X2+ 1.28500X1X3
−1.54333X2X3−1.03500X1X2X3,
SSE(R) = 667.8413
H0:α1= 0, Ha:α16= 0.
F∗= (618.348/1) ÷(49.4933/14) = 174.91, F (.975; 1,14) = 6.298.
If F∗≤6.298 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
d. ˆ
D= ˆµ2.. −ˆµ1.. = ˆα2−ˆα1=−2ˆα1= 11.35000, s2{ˆα1}=.18413, s{ˆ
D}=.8582,
t(.975; 14) = 2.145,
11.35000 ±2.145(.8582),9.509 ≤D≤13.191
24.16. a. Yijkm =µ... +α1Xijkm1+β1Xijkm2+β2Xijkm3+γ1Xijkm4
+(αβ)11Xijkm1Xijkm2+ (αβ)12Xijkm1Xijkm3+ (αγ)11Xijkm1Xijkm4
+(βγ)11Xijkm2Xijkm4+ (βγ)21Xijkm3Xijkm4
+(αβγ)111Xijkm1Xijkm2Xijkm4+ (αβγ)121Xijkm1Xijkm3Xijkm4+²ijkm
24-6

Xijkm1=(1 if case from level 1 for factor A
−1 if case from level 2 for factor A
Xijkm2=
1 if case from level 1 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijkm3=
1 if case from level 2 for factor B
−1 if case from level 3 for factor B
0 otherwise
Xijkm4=(1 if case from level 1 for factor C
−1 if case from level 2 for factor C
b. Yijkm =µ... +α1Xijkm1+β1Xijkm2+β2Xijkm3+ (αβ)11Xijkm1Xijkm2
+(αβ)12Xijkm1Xijkm3+ (αγ)11Xijkm1Xijkm4+ (βγ)11Xijkm2Xijkm4
+(βγ)21Xijkm3Xijkm4+ (αβγ)111Xijkm1Xijkm2Xijkm4
+(αβγ)121Xijkm1Xijkm3Xijkm4+²ijkm
c. Full model:
ˆ
Y= 1,062.16667 + 94.82500X1−17.85417X2+ 42.47083X3+ 79.80000X4
−4.33750X1X2+ 2.01250X1X3+.20833X1X4+ 3.38750X2X4
−5.33750X3X4+.40417X1X2X4−1.94583X1X3X4,
SSE(F) = 39,499.9000
Reduced model:
ˆ
Y= 1,063.73137 + 96.38971X1−14.72475X2+ 40.90613X3−10.59632X1X2
+9.83603X1X3+ 1.77304X1X4+ 3.38750X2X4−10.03162X3X4
+3.53358X1X2X4−3.51054X1X3X4,
SSE(R) = 399,106.8647
H0:γ1= 0, Ha:γ16= 0.
F∗= (359,606.9647/1) ÷(39,499.9000/45) = 409.68, F(.95; 1,45) = 4.06.
If F∗≤4.06 conclude H0,otherwise Ha. Conclude Ha.P-value = 0+
d. ˆ
D= ˆµ..1−ˆµ..2= ˆγ1−ˆγ2= 2ˆγ1= 159.60000, s2{ˆγ1}= 15.54394, s{ˆ
D}= 7.8852,
t(.975; 45) = 2.014,
159.60000 ±2.014(7.8852),143.719 ≤D≤175.481
24.17. 2√n
1.8= 4.1475, n= 14
24.18. t[.99; 12(n−1)]q(29)2/2n=±20, n= 6
24.19. P
i(αβγ)ijk =P
i(µijk −µij. −µi.k −µ.jk +µi.. +µ.j. +µ..k −µ...)
=aµ.jk −aµ.j. −aµ..k −aµ.jk +aµ... +aµ.j. +aµ..k −aµ...= 0
24-7

24.20. Yijk =µ... +αi+βj+γk+ (αβ)ij + (αγ)ik + (βγ)jk +²ijk
Source SS df MS
A SSA a −1MSA
B SSB b −1MSB
C SSC c −1MSC
AB SSAB (a−1)(b−1) MSAB
AC SSAC (a−1)(c−1) MSAC
BC SSBC (b−1)(c−1) MSBC
Error SSE (a−1)(b−1)(c−1) MSE
Total SST O abc −1
24.21. σ2{ˆ
L}=σ2{PPcij ¯
Yij..}=PPc2
ijσ2{¯
Yij..}(because of independence)
=PPc2
ij
σ2
cn =σ2
cn PPc2
ij
24.22. c. r=.992
24.23. a. ¯
Y111.= 8.80000, ¯
Y112.= 9.68667, ¯
Y113.= 8.33000, ¯
Y114.= 7.50333,
¯
Y121.= 10.07667, ¯
Y122.= 9.56333, ¯
Y123.= 10.02667, ¯
Y124.= 8.16000,
¯
Y211.= 10.55333, ¯
Y212.= 8.79000, ¯
Y213.= 8.77333, ¯
Y214.= 8.00667,
¯
Y221.= 12.48000, ¯
Y222.= 10.01667, ¯
Y223.= 10.20000, ¯
Y224.= 8.33000
b.
Source SS df MS
Between treatments 69.63346 15 4.64223
A(age) 4.69375 1 4.69375
B(facilities) 13.26152 1 13.26152
C(region) 37.43491 3 12.47830
AB interactions .36575 1 .36575
AC interactions 9.03731 3 3.01244
BC interactions 3.38421 3 1.12807
ABC interactions 1.45601 3 .48534
Error 34.18440 32 1.06826
Total 103.81786 47
c. H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero. F∗=.48534/1.06826 =
.45, F(.99; 3,32) = 4.46. If F∗≤4.46 conclude H0, otherwise Ha. Conclude H0.
P-value = .72
d. H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero. F∗=.36575/1.06826 =
.34, F(.99; 1,32) = 7.50. If F∗≤7.50 conclude H0, otherwise Ha. Conclude H0.
P-value = .56
H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero. F∗= 3.01244/1.06826 =
2.82, F(.99; 3,32) = 4.46. If F∗≤4.46 conclude H0,otherwise Ha. Conclude H0.
P-value = .055
H0: all (βγ)jk equal zero, Ha: not all (βγ)jk equal zero. F∗= 1.12807/1.06826 =
1.06, F(.99; 3,32) = 4.46. If F∗≤4.46 conclude H0, otherwise Ha. Conclude H0.
P-value = .38
24-8
e. H0: all αiequal zero (i= 1,2), Ha: not all αiequal zero. F∗= 4.69375/1.06826 =
4.39, F(.99; 1,32) = 7.50. If F∗≤7.50 conclude H0, otherwise Ha. Conclude H0.
P-value = .044
H0: all βjequal zero (j= 1,2), Ha: not all βjequal zero. F∗= 13.26152/1.06826 =
12.41, F(.99; 1,32) = 7.50. If F∗≤7.50 conclude H0, otherwise Ha. Conclude
Ha.P-value = .0013
H0: all γkequal zero (k= 1, ..., 4), Ha: not all γkequal zero. F∗= 12.47830/1.06826 =
11.68, F(.99; 3,32) = 4.46. If F∗≤4.46 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
f. ¯
Y1... = 9.01833, ¯
Y2... = 9.64375, ¯
Y.1.. = 8.80542, ¯
Y.2.. = 9.85667,
¯
Y..1.= 10.47750, ¯
Y..2.= 9.51417, ¯
Y..3.= 9.33250, ¯
Y..4.= 8.00000
ˆ
D1=¯
Y.1.. −¯
Y.2.. =−1.05125, ˆ
D2=¯
Y..1.−¯
Y..2.=.96333,ˆ
D3=¯
Y..1.−¯
Y..3.= 1.14500,
ˆ
D4=¯
Y..1.−¯
Y..4.= 2.47750,ˆ
D5=¯
Y..2.−¯
Y..3.=.18167, ˆ
D6=¯
Y..2.−¯
Y..4.= 1.51417,
ˆ
D7=¯
Y..3.−¯
Y..4.= 1.33250, MSE = 1.06826,
s{ˆ
D1}=.29836, s{ˆ
Di}=.42195 (i= 2, ..., 7), B=t(.99286; 32) = 2.5915
−1.05125 ±2.5915(.29836) −1.824 ≤D1≤ −.278
.96333 ±2.5915(.42195) −.130 ≤D2≤2.057
1.14500 ±2.5915(.42195) .052 ≤D3≤2.238
2.47750 ±2.5915(.42195) 1.384 ≤D4≤3.571
.18167 ±2.5915(.42195) −.912 ≤D5≤1.275
1.51417 ±2.5915(.42195) .421 ≤D6≤2.608
1.33250 ±2.5915(.42195) .239 ≤D7≤2.426
24.24. c. r=.920
24.25. a. ¯
Y111.=.03303, ¯
Y112.=.03886, ¯
Y121.=.03553, ¯
Y122.=.05415,
¯
Y211.=.04076, ¯
Y212.=.05128, ¯
Y221.=.05516, ¯
Y222.=.06056,
¯
Y311.=.05841, ¯
Y312.=.05997, ¯
Y321.=.07738, ¯
Y322.=.07915,
¯
Y411.=.05655, ¯
Y412.=.04688, ¯
Y421.=.06755, ¯
Y422.=.06442
b. Yijkm =µ... +α1Xijk1+α2Xijk2+α3Xijk3+β1Xijk4+γ1Xijk5
+(αβ)11Xijk1Xijk4+ (αβ)21Xijk2Xijk4+ (αβ)31Xijk3Xijk4
+(αγ)11Xijk1Xijk5+ (αγ)21Xijk2Xijk5+ (αγ)31Xijk3Xijk5
+(βγ)11Xijk4Xijk5+ (αβγ)111Xijk1Xijk4Xijk5
+(αβγ)211Xijk2Xijk4Xijk5+ (αβγ)311Xijk3Xijk4Xijk5+²ijkm
Xijk1=
1 if case from NE
−1 if case from W
0 otherwise
Xijk2=
1 if case from NC
−1 if case from W
0 otherwise
24-9
Xijk3=
1 if case from S
−1 if case from W
0 otherwise
Xijk4=(1 if poverty level below 8 percent
−1 if poverty level 8 percent or higher
Xijk5=(1 if percent of population 65 or older <12.0%
−1 if percent of population 65 or older ≥12.0%
ˆ
Y=.05498 −.0146X1−.00303X2+.0137X3−.00676X4
−.00193X5+.00231X1X4+.00084X2X4−.00278X3X4−.00418X1X5
−.00205X2X5+.00110X3X5+.00090X4X5+.00230X1X4X5
−.00218X2X4X5−.00085X3X4X5,
SSE(F) = .23779
c. ABC interactions;
ˆ
Y=.0552 −.0133X1−.00412X2+.0135X3−.00712X4
−.00157X5+.00085X1X4+.00128X2X4−.00254X3X4
−.00278X1X5−.00251X2X5+.00083X3X5+.00046X4X5,
SSE(R) = .23849
H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero.
F∗= (.0007/3) ÷(.23779/424) = .42, F(.975; 3,424) = 3.147.
If F∗≤3.147 conclude H0, otherwise Ha. Conclude H0.P-value = .74
AB interactions:
ˆ
Y= 0.0556 −0.0133X1−0.00355X2+ 0.0136X3−0.00743X4
−0.00135X5−0.00315X1X5−0.00190X2X5+0.00040X3X5+0.00026X4X5
+0.00095X1X4X5−0.00161X2X4X5−0.00081X3X4X5,
SSE(R) = .23897
H0: all (αβ)ij equal zero, Ha: not all (αβ)ij equal zero.
F∗= (.00118/3) ÷(.23779/424) = .70, F(.975; 3,424) = 3.147.
If F∗≤3.147 conclude H0, otherwise Ha. Conclude H0.P-value = .55
AC interactions:
ˆ
Y= 0.0562 −0.0129X1−0.00419X2+ 0.0127X3−0.00727X4
−0.00161X5+ 0.00038X1X4+ 0.00021X2X4−0.00222X3X4
−0.00023X4X5+ 0.00052X1X4X5−0.00119X2X4X5+ 0.00011X3X4X5,
SSE(R) = .24070
H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero.
F∗= (.00291/3) ÷(.23779/424) = 1.73, F(.975; 3,424) = 3.147.
If F∗≤3.147 conclude H0, otherwise Ha. Conclude H0.P-value = .16
24-10

BC interactions:
ˆ
Y= 0.0553 −0.0142X1−0.00303X2+ 0.0134X3−0.00687X4−0.00179X5
+0.00152X1X4+0.00092X2X4−0.00253X3X4−0.00344X1X5−0.00214X2X5
+0.00085X3X5+ 0.00183X1X4X5−0.00204X2X4X5−0.00042X3X4X5,
SSE(R) = .23801
H0: all (βγ)jk equal zero, Ha: not all (βγ)jk equal zero.
F∗= (.00022/1) ÷(.23779/424) = .39, F(.975; 1,424) = 5.06.
If F∗≤5.06 conclude H0, otherwise Ha. Conclude H0.P-value = .53
d. Aeffects:
ˆ
Y= 0.0585 −0.0104X4+ 0.00191X5−0.00575X1X4+ 0.00409X2X4
−0.00150X3X4+ 0.00401X1X5−0.00558X2X5+ 0.00016X3X5
−0.00218X4X5−0.00445X1X4X5−0.00227X2X4X5+ 0.00280X3X4X5,
SSE(R) = .27011
H0: all αiequal zero (i= 1, ..., 4), Ha: not all αiequal zero.
F∗= (.03232/3) ÷(.23779/424) = 19.21, F(.975; 3,424) = 3.147.
If F∗≤3.147 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
Beffects:
ˆ
Y= 0.0539 −0.0202X1−0.00235X2+ 0.0156X3−0.00465X5
+0.00583X1X4−0.00024X2X4−0.00598X3X4−0.00705X1X5
−0.00208X2X5+ 0.00362X3X5+ 0.00174X4X5+ 0.00828X1X4X5
−0.00275X2X4X5−0.00270X3X4X5,
SSE(R) = .25047
H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= (.01268/1) ÷(.23779/424) = 22.61, F(.975; 1,424) = 5.06.
If F∗≤5.06 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
Ceffects:
ˆ
Y= 0.0552 −0.0129X1−0.00320X2+ 0.0132X3−0.00754X4
+0.00150X1X4+ 0.00083X2X4−0.00206X3X4−0.00318X1X5
−0.00236X2X5+ 0.00018X3X5+ 0.00061X4X5+ 0.00069X1X4X5
−0.00198X2X4X5−0.00032X3X4X5,
SSE(R) = .23882
H0:γ1=γ2= 0, Ha: not both γ1and γ2equal zero.
F∗= (.00103/1) ÷(.23779/424) = 1.84, F(.975; 1,424) = 5.06.
If F∗≤5.06 conclude H0, otherwise Ha. Conclude H0.P-value = .175
e. ˆ
D1= ˆµ1.. −ˆµ2.. = ˆα1−ˆα2=−.01155, ˆ
D2= ˆµ1.. −ˆµ3.. = ˆα1−ˆα3=−.02834,
24-11
ˆ
D3= ˆµ1.. −ˆµ4.. =−.01846, ˆ
D4= ˆµ2.. −ˆµ3.. =−.016784,
ˆ
D5= ˆµ2.. −ˆµ4.. =−.006907, ˆ
D6= ˆµ3.. −ˆµ4.. =.009877,
−.02276 ≤D1≤ −.00034
−.03878 ≤D2≤ −.01790
−.03030 ≤D3≤ −.00662
−.02531 ≤D4≤ −.00826
−.01711 ≤D5≤.00329
.00053 ≤D6≤.01922
24-12

Chapter 25
RANDOM AND MIXED EFFECTS
MODELS
25.3. (1) I, (2) II, (3) I, (4) II
25.5. b. H0:σ2
µ= 0, Ha:σ2
µ>0. F∗=.45787/.03097 = 14.78, F (.95; 5,114) = 2.29.
If F∗≤2.29 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. ¯
Y.. =.22767, nT= 120, s{¯
Y..}=.06177, t(.975; 5) = 2.571,
.22767 ±2.571(.06177), .0689 ≤µ.≤.3865
25.6. a. F(.025; 5,114) = .1646, F(.975; 5,114) = 2.680, L=.22583, U = 4.44098
.1842 ≤σ2
µ
σ2
µ+σ2≤.8162
b. χ2(.025; 114) = 90.351, χ2(.975; 114) = 145.441, .02427 ≤σ2≤.03908
c. s2
µ=.02135
d. Satterthwaite:
df = (ns2
µ)2÷[(MST R)2/(r−1) + (MSE)2/r(n−1)]
= [20(.02135)]2÷[(.45787)2/5+(.03907)2/6(19)] = 4.35,
χ2(.025; 4) = .484, χ2(.975; 4) = 11.143
.0083 = 4.35(.02135)
11.143 ≤σ2
µ≤4.35(.02135)
.484 =.192
MLS:c1=.05, c2=−.05, MS1=.45787, MS2=.03907, df1= 5, df2= 114,
F1=F(.975; 5,∞) = 2.57, F2=F(.975; 114,∞) = 1.28, F3=F(.975; ∞,5) =
6.02, F4=F(.975; ∞,114) = 1.32, F5=F(.975; 5,114) = 2.68, F6=F(.975; 114,5) =
6.07, G1=.6109, G2=.2188, G3=.0147, G4=−.2076, HL=.014, HU=.115,
.02135 −.014, .02135 + .115, .0074 ≤σ2
µ≤.1364
25.7. a.
Source SS df MS
Between brands 854.52917 5 170.90583
Error 30.07000 42 .71595
Total 884.59917 47
25-1

H0:σ2
µ= 0, Ha:σ2
µ>0. F∗= 170.90583/.71595 = 238.71, F (.99; 5,42) = 3.49.
If F∗≤3.49 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
b. ¯
Y.. = 17.62917, nT= 48, s{¯
Y..}= 1.8869, t(.995; 5) = 4.032,
17.62917 ±4.032(1.8869), 10.021 ≤µ.≤25.237
25.8. a. F(.005; 5,42) = .0795, F(.995; 5,42) = 3.95, L= 7.4292, U = 375.20828
.8814 ≤σ2
µ
σ2
µ+σ2≤.9973
b. MSE =.71595, s2
µ= 21.27374
c. χ2(.005; 42) = 22.138, χ2(.995; 42) = 69.336, .4337 ≤σ2≤1.3583
d. H0:σ2
µ≤2σ2,Ha:σ2
µ>2σ2.F∗= [MST R/(2n+ 1)] ÷MSE = 14.042,
F(.99; 5,42) = 3.49. If F∗≤3.49 conclude H0, otherwise Ha. Conclude Ha.
e. c1=.125, c2=−.125, df1= 5, df2= 42, F1=F(.995; 5,∞) = 3.35, F2=
F(.995; 42,∞) = 1.66, F3=F(.995; ∞,5) = 12.1, F4=F(.995; ∞,42) = 1.91,
F5=F(.995; 5,42) = 3.95, F6=F(.995; 42,5) = 12.51, G1=.7015, G2=.3976,
G3=.0497, G4=−1.2371, HL= 14.990, HU= 237.127,21.2737 −14.990,
21.2737 + 237.127, 6.284 ≤σ2
µ≤258.401
25.9. a.
Source SS df MS
Between machines 602.5000 3 200.8333
Error 257.4000 36 7.1500
Total 859.9000 39
H0:σ2
µ= 0, Ha:σ2
µ>0. F∗= 200.8333/7.1500 = 28.09, F (.90; 3,36) = 2.25.
If F∗≤2.25 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
b. ¯
Y.. = 205.05, nT= 40, s{¯
Y..}= 2.2407, t(.95; 3) = 2.353,
205.05 ±2.353(2.2407), 199.778 ≤µ.≤210.322
25.10. a. F(.05; 3,36) = .117, F(.95; 3,36) = 2.87, L=.8787, U = 23.9073
.4677 ≤σ2
µ
σ2
µ+σ2≤.9599
b. H0:σ2
µ=σ2,Ha:σ2
µ6=σ2.
F∗= [MST R/(n+ 1)] ÷MSE = 2.554, F(.05; 3,36) = .117, F(.95; 3,36) = 2.87.
If .117 ≤F∗≤2.87 conclude H0, otherwise Ha. Conclude H0.
c. χ2(.05; 36) = 23.269, χ2(.95; 36) = 50.998, 5.047 ≤σ2≤11.062
d. s2
µ= 19.3683
e. Satterthwaite:
df = [10(19.3683)]2÷[(200.8333)2/3 + (7.1500)2/36] = 2.79,
χ2(.05; 3) = .352, χ2(.95; 3) = 7.815,
25-2

6.915 = 2.79(19.3683)
7.815 ≤σ2
µ≤2.79(19.3683)
.352 = 153.516
MLS:c1=.10, c2=−.10, df1= 3, df2= 36, F1=F(.95; 3,∞) = 2.60,
F2=F(.95; 36,∞)=1.42, F3=F(.95; ∞,3) = 8.53, F4=F(.95; ∞,36) = 1.55,
F5=F(.95; 3,36) = 2.87, F6=F(.95; 36,3) = 8.60, G1=.6154, G2=.2958,
G3=.0261, G4=−.6286, HL= 12.381, HU= 151.198,19.3683 −12.381,
19.3683 + 151.198, 6.987 ≤σ2
µ≤170.566
25.13. a. E{MSA}= 115, E{MSB}= 185, E{MSAB}= 35
b. E{MSA}= 85, E{MSB}= 155, E{MSAB}= 5
25.15. a.
Source SS df MS
Factor A(driver) 280.28475 3 93.42825
Factor B(car) 94.71350 4 23.67838
AB interactions 2.44650 12 .20388
Error 3.51500 20 .17575
Total 380.95975 39
H0:σ2
αβ = 0, Ha:σ2
αβ >0. F∗=.20388/.17575 = 1.16, F (.95; 12,20) = 2.28.
If F∗≤2.28 conclude H0, otherwise Ha.Conclude H0.P-value = .37
b. H0:σ2
α= 0, Ha:σ2
α>0. F∗= 93.42825/.20388 = 458.25, F (.95; 3,12) = 3.49.
If F∗≤3.49 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
H0:σ2
β= 0, Ha:σ2
β>0. F∗= 23.67838/.20388 = 116.14, F (.95; 4,12) = 3.26.
If F∗≤3.26 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
c. s2
α= 9.3224, s2
β= 2.9343
d. c1=.10, c2=−.10, MS1= 93.42825, MS2=.203875, df1= 3, df2= 12, F1=
F(.975; 3,∞) = 3.12, F2=F(.975; 12,∞) = 1.94, F3=F(.975; ∞,3) = 13.9,
F4=F(.975; ∞,12) = 2.72, F5=F(.975; 3,12) = 4.47, F6=F(.975; 12,3) =
14.3, G1=.6795, G2=.4845, G3=−.0320, G4=−2.6241, HL= 6.348,
HU= 120.525,9.3244 −6.348, 9.3224 + 120.525, 2.974 ≤σ2
α≤129.847
e. df = [8(2.9343)]2÷[(23.678375)2/4+(.203875)2/12] = 3.93
χ2(.025; 4) = .484, χ2(.975; 4) = 11.143,
1.03 = 3.93(2.9343)
11.143 ≤σ2
β≤3.93(2.9343)
.484 = 23.83
25.16. a. H0:σ2
αβ = 0, Ha:σ2
αβ >0. F∗= 303.822/52.011 = 5.84, F (.99; 4,36) = 3.89.
If F∗≤3.89 conclude H0, otherwise Ha.Conclude Ha.P-value = .001
b. s2
αβ = 50.362
c. H0:σ2
α= 0, Ha:σ2
α>0. F∗= 12.289/52.011 = .24, F (.99; 2,36) = 5.25.
If F∗≤5.25 conclude H0, otherwise Ha.Conclude H0.
d. H0: all βjequal zero (j= 1,2,3), Ha: not all βjequal zero.
25-3

F∗= 14.156/303.822 = .047, F(.99; 2,4) = 18.0.
If F∗≤18.0 conclude H0, otherwise Ha. Conclude H0.
e. ¯
Y.1.= 56.133, ¯
Y.2.= 56.600, ¯
Y.3.= 54.733, ˆ
D1=¯
Y.1.−¯
Y.2. =−.467, ˆ
D2=
¯
Y.1.−¯
Y.3.=−1.400, ˆ
D3=¯
Y.2.−¯
Y.3.= 1.867, s{ˆ
Di}= 6.3647 (i= 1,2,3),
q(.95; 3,4) = 5.04, T= 3.5638
−.467 ±3.5638(6.3647) −23.150 ≤D1≤22.216
−1.400 ±3.5638(6.3647) −24.083 ≤D2≤21.283
1.867 ±3.5638(6.3647) −20.816 ≤D3≤24.550
f. ˆµ.1= 56.1333, MSA = 12.28889, MSAB = 303.82222, s2{ˆµ.1}= (2/45)(303.82222)+
(1/45)(12.28889) = 13.7763, s{ˆu.1}= 3.712, df = (13.7763)2÷{[(2/45)(303.82222)]2/4+
[(1/45)(12.28889)]2/2}= 4.16, t(.995; 4) = 4.60,
56.1333 ±4.60(3.712), 39.06 ≤µ.1≤73.21
g. MSA = 12.28889, MSE = 52.01111, s2
α= (MSA −MSE)/nb =−2.648,
c1= 1/15, c2=−1/15, df1= 2, df2= 36, F1=F(.995; 2,∞)=5.30, F2=
F(.995; 36,∞) = 1.71, F3=F(.995; ∞,2) = 200, F4=F(.995; ∞,36) = 2.01,
F5=F(.995; 2,36) = 6.16, F6=F(.995; 36,2) = 199.5, G1=.8113, G2=.4152,
G3=.1022, G4=−35.3895, HL= 3.605, HU= 162.730,−2.648 −3.605,
−2.648 + 162.730, −6.253 ≤σ2
α≤160.082
25.17. a.
Source SS df MS
Factor A(coats) 150.3879 2 75.1940
Factor B(batch) 152.8517 3 50.9506
AB interactions 1.8521 6 .3087
Error 173.6250 36 4.8229
Total 478.7167 47
H0:σ2
αβ = 0, Ha:σ2
αβ >0. F∗=.3087/4.8229 = .06, F (.95; 6,36) = 2.36.
If F∗≤2.36 conclude H0, otherwise Ha.Conclude H0.P-value = .999
b. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 75.1940/.3087 =
243.58, F(.95; 2,6) = 5.14. If F∗≤5.14 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0:σ2
β= 0, Ha:σ2
β>0. F∗= 50.9506/4.8229 = 10.56, F (.95; 3,36) = 2.87. If
F∗≤2.87 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
c. ¯
Y1.. = 73.10625, ¯
Y2.. = 76.79375, ¯
Y3.. = 76.92500, ˆ
D1=¯
Y2.. −¯
Y1.. = 3.68750,
ˆ
D2=¯
Y3.. −¯
Y2.. =.13125, s{ˆ
Di}=.1964 (i= 1,2), B=t(.975; 6) = 2.447
3.68750 ±2.447(.1964) 3.2069 ≤D1≤4.1681
.13125 ±2.447(.1964) −.3493 ≤D2≤.6118
d. ˆµ2.= 76.79375, s2{ˆµ2.}= (2/48)(.30868) + (1/48)(50.95056) = 1.0743, s{ˆµ2.}=
1.0365, df = (1.0743)2÷ {[(2/48)(.30868)]2/6 + [(1/48)(50.95056)]2/3}= 3.07,
t(.975; 3) = 3.182, 76.79375 ±3.182(1.0365), 73.496 ≤µ2.≤80.092
e. s2
β= (MSB −MSE)/na = 3.844, c1= 1/12, c2=−1/12, df1= 3, df2= 36,
F1=F(.95; 3,∞) = 2.60, F2=F(.95; 36,∞)=1.42, F3=F(.95; ∞,3) = 8.53,
25-4

F4=F(.95; ∞,36) = 1.55, F5=F(.95; 3,36) = 2.87, F6=F(.95; 36,3) = 8.60,
G1=.6154, G2=.2958, G3=.0261, G4=−.6286, HL= 2.631, HU= 31.989,
3.844 −2.631, 3.844 + 31.989, 1.213 ≤σ2
β≤35.833
25.18. a. H0:β1=β2= 0, Ha: not both β1and β2equal zero.
F∗= 47.0450/.1150 = 409.09, F(.95; 1,3) = 10.1.
If F∗≤10.1 conclude H0, otherwise Ha. Conclude Ha.P-value = .0003
25.19. a. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.175 −1.300 .325 −2.050 3.200
2.025 4.900 −3.475 1.150 −2.600
3−.575 −1.700 .925 −1.450 2.800
4.025 1.900 −1.475 2.150 −2.600
5.025 −1.100 .525 −.850 1.400
6.025 −1.100 2.525 −.850 −.600
7−.175 −.300 −.675 2.950 −1.800
8.825 −1.300 1.325 −1.050 .200
r=.985
c. H0:D= 0, Ha:D6= 0. SSBL.T R∗= 27.729, SSRem∗= 94.521,
F∗= (27.729/1) ÷(94.521/27) = 7.921, F (.995; 1,27) = 9.34.
If F∗≤9.34 conclude H0, otherwise Ha. Conclude H0.
25.20. a.
Source SS df MS
Blocks 4,826.375 7 689.48214
Paint type 531.350 4 132.83750
Error 122.250 28 4.36607
Total 5,479.975 39
b. H0: all τjequal zero (j= 1, ..., 5), Ha: not all τjequal zero.
F∗= 132.83750/4.36607 = 30.425, F(.95; 4,28) = 2.71.
If F∗≤2.71 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. ¯
Y.1= 20.500, ¯
Y.2= 23.625, ¯
Y.3= 19.000, ¯
Y.4= 29.375, ¯
Y.5= 21.125, ˆ
L1=
¯
Y.1−¯
Y.2=−3.125, ˆ
L2=¯
Y.1−¯
Y.3= 1.500, ˆ
L3=¯
Y.1−¯
Y.4=−8.875, ˆ
L4=
¯
Y.1−¯
Y.5=−.625, s{ˆ
Li}= 1.0448 (i= 1, ..., 4), B=t(.9875; 28) = 2.369
−3.125 ±2.369(1.0448) −5.60 ≤L1≤ −.65
1.500 ±2.369(1.0448) −.98 ≤L2≤3.98
−8.875 ±2.369(1.0448) −11.35 ≤L3≤ −6.40
−.625 ±2.369(1.0448) −3.10 ≤L4≤1.85
d. ˆ
L=1
3(¯
Y.1+¯
Y.3+¯
Y.5)−1
2(¯
Y.2+¯
Y.4) = −6.29167, s{ˆ
L}=.6744, t(.975; 28) = 2.048,
−6.29167 ±2.048(.6744), −7.67 ≤L≤ −4.91
25.21. a. eij:
25-5

i j = 1 j= 2 j= 3
1−.1333 .4667 −.3333
2−.1333 −.5333 .6667
3−.4667 1.1333 −.6667
4.8667 −.5333 −.3333
5−.4667 1.1333 −.6667
6 1.2000 −1.2000 .0000
7−.1333 1.4667 −1.3333
8.8667 −1.5333 .6667
9−2.1333 −.5333 2.6667
10 .5333 .1333 −.6667
r=.985
c. H0:D= 0, Ha:D6= 0. SSBL.T R∗= 4.5365, SSRem∗= 24.6635,
F∗= (4.5365/1) ÷(24.6635/17) = 3.127, F(.975; 1,17) = 6.042.
If F∗≤6.042 conclude H0,otherwise Ha. Conclude H0.P-value = .095
25.22. a.
Source SS df MS
Blocks 1,195.5000 9 132.8333
Reagents 123.4667 2 61.7333
Error 29.2000 18 1.6222
Total 1,348.1667 29
b. H0: all τjequal zero (j= 1,2,3), Ha: not all τjequal zero.
F∗= 61.7333/1.6222 = 38.055, F(.975; 2,18) = 4.56.
If F∗≤4.56 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. ¯
Y.1= 15.3, ¯
Y.2= 19.7, ¯
Y.3= 19.5, B=t(.9875; 18) = 2.445,ˆ
L1=.2, ˆ
L2= 4.3,
s{ˆ
L1}=.5696, s{ˆ
L2}=.4933
.2±2.445(.5696) −1.193 ≤L1≤1.593
4.3±2.445(.4933) 3.094 ≤L2≤5.506
d. H0:σ2
ρ= 0, Ha:σ2
ρ>0. F∗= 132.8333/1.6222 = 81.885, F (.975; 9,18) = 2.929.
If F∗≤2.929 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
25.23. a. H0:σ2
αβγ = 0, Ha:σ2
αβγ >0. F∗=MSABC/MSE = 1.49/2.30 = .648,
F(.975; 8,60) = 2.41. If F∗≤2.41 conclude H0, otherwise Ha.Conclude H0.
P-value=.27.
b. H0:σ2
αβ = 0, Ha:σ2
αβ >0. F∗=MSAB/MSABC = 2.40/1.49 = 1.611,
F(.99; 2,8) = 8.65. If F∗≤8.65 conclude H0, otherwise Ha.Conclude H0.
c. H0:σ2
β= 0, Ha:σ2
β>0. F∗∗ =MSB/(MSAB +MSBC −MSABC) =
4.20/(2.40+3.13−1.49) = 1.04, df = 16.32161/5.6067 = 2.91, F(.99; 1,3) = 34.1.
If F∗∗ ≤34.1 conclude H0, otherwise Ha. Conclude H0.
d. s2
α= (MSA −MSAB −MSAC +MSABC)/nbc =.126,
df = [(8.650/30) −(2.40/30) −(3.96/30) + (1.49/30)]2
25-6

÷"(8.65/30)2
2+(2.40/30)2
2+(3.96/30)2
8+(1.49/30)2
8#=.336
χ2(.025; 1) = .001, χ2(.975; 1) = 5.02
.008 = .336(.126)
5.02 ≤σ2
α≤.336(.126)
.001 = 42.336
25.24. a. F∗=MSAC/MSABC,F∗=MSB/MSE
b. H0: all (αγ)ik equal zero, Ha: not all (αγ)ik equal zero. F∗= 91.267/9.517 = 9.59,
F(.95; 1,2) = 18.5. If F∗≤18.5 conclude H0, otherwise Ha. Conclude H0.
c. H0:σ2
β= 0, Ha:σ2
β>0. F∗= 24,659.817/858.042 = 28.74, F (.95; 2,48) = 3.19.
If F∗≤3.19 conclude H0, otherwise Ha. Conclude Ha.
d. s2
β= (MSB −MSE)/acn = (24,659.817 −858.042)/20 = 1,190.09, c1=.05, c2=
−.05, df1= 2, df2= 48, F1=F(.975; 2,∞) = 3.69, F2=F(.975; 48,∞)=1.44,
F3=F(.975; ∞,2) = 39.5, F4=F(.975; ∞,48) = 1.56, F5=F(.975; 2,48) =
3.99, F6=F(.975; 48,2) = 39.5, G1=.7290, G2=.3056, G3=.0416, G4=
−3.6890, HL= 900.39, HU= 47,468.09, 1,190.09 −900.39, 1,190.09 + 47,468.09,
289.70 ≤σ2
β≤48,658.18
25.25. F∗∗ =MSA/(MSAB +MSAC −MSABC)
df = (MSAB +MSAC −MSABC)2÷Ã(MSAB)2
dfAB
+(MSAC)2
dfAC
+(MSABC)2
dfABC !
25.26. a. ˆµ.. = 55.593, ˆ
β1=.641, ˆ
β2=.218, ˆσ2
α= 5.222, ˆσ2
αβ = 15.666,ˆσ2= 55.265, no
(Note: Unrestricted estimators are same except that variance component for
random effect A is zero.)
b. Estimates remain the same.
c. H0:σ2
αβ = 0, Ha:σ2
αβ >0. z(.99) = 2.326, s{ˆσ2
αβ}= 13.333, z∗= 15.666/13.333 =
1.175. If z∗≤2.326 conclude H0, otherwise Ha. Conclude H0.P-value = .12.
d. H0:β1=β2=β3= 0, Ha: not all βj= 0 (j= 1,2,3). −2logeL(R) = 295.385,
−2logeL(F) = 295.253, X2= 295.385 −295.253 = .132, χ2(.99; 2) = 9.21. If
X2≤9.21 conclude H0, otherwise Ha. Conclude H0.P-value = .94.
e. z(.995) = 2.576, 15.666 ±2.576(13.333), −18.680 ≤α2
αβ ≤50.012
25.27. a. ˆµ.. = 75.817, ˆα1=−2.398, ˆα2=.977, ˆσ2
β= 2.994, ˆσ2
αβ = 0, ˆσ2= 3.103, yes
b. Estimates remain the same.
c. H0:σ2
β= 0, Ha:σ2
β>0. −2logeL(R) = 214.034, −2logeL(F) = 192.599, X2=
214.034−192.599 = 21.435, χ2(.95; 1) = 3.84. If X2≤3.84 conclude H0, otherwise
Ha. Conclude Ha.P-value = 0+
d. H0:α1=α2=α3= 0, Ha: not all αi= 0 (i= 1,2,3). −2logeL(R) = 221.722,
−2logeL(F) = 192.599, X2= 221.722 −192.599 = 29.123, χ2(.95; 2) = 5.99. If
X2≤5.99 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. s{ˆσ2
β}= 2.309, z(.975) = 1.96, 2.994 ±1.96(2.309), −1.532 ≤σ2
β≤7.520
25-7
(Note: Answers to parts (c) and (e) are not consistent; may be due to
large-sample approximation not being appropriate here.)
25.28. n0=1
r−1"(Pni)−Pn2
i
Pni#=1
r−1(rn −rn2/rn) = 1
r−1(rn −n) = n
25.29. From (25.12), σ2{¯
Y..}= (σ2
µ/r)+(σ2/nT). When nTis fixed, σ2{¯
Y..}
is minimized by making ras large as possible, i.e.,r=nT.
In that case, n= 1 since rn =nT.
25.30. L≤σ2
µ
σ2≤Uor 1
L≥σ2
σ2
µ≥1
Uor 1
L+ 1 ≥σ2
σ2
µ
+ 1 ≥1
U+ 1 or
1 + L
L≥σ2+σ2
µ
σ2
µ≥1 + U
Uor L∗=L
1 + L≤σ2
µ
σ2+σ2
µ≤U
1 + U=U∗
25.31. σ2{¯
Yi..}=σ2{µ.. +αi+¯
β.+ (αβ)i. + ¯²i..}
=σ2
α+σ2
β
b+σ2
σβ
b+σ2
bn because of independence.
25.32. σ2{Yij}=σ2{µ.. +ρi+τj+²ij }=σ2
τ+σ2
σ2{¯
Y.j}=σ2{µ.. +Pρi
nb
+τj+ ¯².j}=σ2
τ+σ2
nb
25.33. a. Yijk =µ... +ρi+αj+βk+ (αβ)jk +²ijk
b. F∗=MSAB/MSBL.T R,F∗=MSA/MSBL.T R,F∗=MSB/MSBL.T R
25.34. σ{Yij, Yij0}=E{(Yij −E{Yij})(Yij0−E{Yij0})}
=E{[(µ.. +ρi+τj+²ij)−(µ.. +τj)][(µ.. +ρi+τj0+²ij0)−(µ.. +τj0)]}
=E{(ρi+²ij)(ρi+²ij0)}
=E{ρ2
i}+E{ρi²ij}+E{ρi²ij0}+E{²ij²ij0}=σ2
ρ
since ρi,²ij, and ²ij0are pairwise independent and have expectations equal to zero.
25.35. σ2{¯
Yi...}=σ2{µ... +αi+¯
β.+ ¯γ.+ (αβ)i. + (αγ)i. + (βγ).. + (αβγ)i.. + ¯²i...}
=σ2
α+σ2
β
b+σ2
γ
c+σ2
αβ
b+σ2
αγ
c+σ2
βγ
bc +σ2
αβγ
bc +σ2
nbc
25.36. e. E{MSA}= 248.5, E{MSAB}= 8.5
25.37. a.
1
2
3
4
5
137.4286 145.3571 131.2857 156.6429 117.2143
158.5536 135.4286 167.1607 121.6250
128.5714 148.4286 113.8571
179.4107 133.2321
102.9821
25.38. a.
25-8
1
2
3
37.5667 42.9889 40.8333
51.1222 47.3889
47.3889
25.39. a. ˆµ.. = 30.051, ˆσ2
α= 7.439, ˆσ2
β= 2.757, ˆσ2
αβ =.011, ˆσ2=.183,
s{ˆσ2
α}= 5.570, s{ˆσ2
β}= 1.958, s{ˆσ2
αβ}=.053, s{ˆσ2}=.059.
25-9
25-10

Chapter 26
NESTED DESIGNS,
SUBSAMPLING, AND PARTIALLY
NESTED DESIGNS
26.4. a. eijk :
i= 1
k j = 1 j= 2 j= 3 j= 4
1 3.2.2−6.6−7.6
2−3.8−5.8 2.4 3.4
3 1.2 7.2−4.6 1.4
4−4.8−3.8 7.4−4.6
5 4.2 2.2 1.4 7.4
i= 2
k j = 1 j= 2 j= 3 j= 4
1−1.8−6.2−3.8−4.0
2 5.2.8.2 1.0
3.2 4.8 6.2 6.0
4 4.2 2.8 2.2−2.0
5−7.8−2.2−4.8−1.0
i= 3
k j = 1 j= 2 j= 3 j= 4
1−7.8−6.6 6.6−6.4
2 6.2.4−2.4 5.6
3−2.8 2.4−1.4−.4
4 1.2−1.6 1.6 3.6
5 3.2 5.4−4.4−2.4
r=.986
26.5. a. No
b. ¯
Yij.:
i j = 1 j= 2 j= 3 j= 4
1 61.8 67.8 62.6 52.6
2 75.8 75.2 55.8 77.0
3 76.8 69.6 74.4 73.4
c.
26-1

Source SS df MS
Machines (A) 1,695.63 2 847.817
Operators, within mahcines [B(A)] 2,272.30 9 252.478
Error (E) 1,132.80 48 23.600
Total 5,100.73 59
d. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= 847.817/23.600 = 35.924, F(.99; 2,48) = 5.075.
If F∗≤5.075 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
e. H0: all βj(i)equal zero, Ha: not all βj(i)equal zero.
F∗= 252.478/23.600 = 10.698, F(.99; 9,48) = 2.802.
If F∗≤2.802 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
f.
i SSB(Ai)
1 599.20
2 1,538.55
3 134.55
H0: all βj(1) equal zero, Ha: not all βj(1) equal zero.
F∗= (599.20/3) ÷23.600 = 8.46, F(.99; 3,48) = 4.22.
If F∗≤4.22 conclude H0, otherwise Ha. Conclude Ha.
H0: all βj(2) equal zero, Ha: not all βj(2) equal zero.
F∗= (1,538.55/3) ÷23.600 = 21.73, F(.99; 3,48) = 4.22.
If F∗≤4.22 conclude H0, otherwise Ha. Conclude Ha.
H0: all βj(3) equal zero, Ha: not all βj(3) equal zero.
F∗= (134.55/3) ÷23.600 = 1.90, F(.99; 3,48) = 4.22.
If F∗≤4.22 conclude H0, otherwise Ha. Conclude H0.
g. α≤.05
26.6. a. ¯
Y1.. = 61.20, ¯
Y2.. = 70.95, ¯
Y3.. = 73.55, ˆ
L1=¯
Y1.. −¯
Y2.. =−9.75,
ˆ
L2=¯
Y1.. −¯
Y3.. =−12.35, ˆ
L3=¯
Y2.. −¯
Y3.. =−2.60, s{ˆ
Li}= 1.536 (i= 1,2,3),
q(.95; 3,48) = 3.42, T= 2.418
−9.75 ±2.418(1.536) −13.46 ≤L1≤ −6.04
−12.35 ±2.418(1.536) −16.06 ≤L2≤ −8.64
−2.60 ±2.418(1.536) −6.31 ≤L3≤1.11
b. ¯
Y11.= 61.8, ¯
Y12.= 67.8, ¯
Y13.= 62.6, ¯
Y14.= 52.6, ˆ
L1=¯
Y11.−¯
Y12.=−6.0,
ˆ
L2=¯
Y11.−¯
Y13.=−.8, ˆ
L3=¯
Y11.−¯
Y14.= 9.2, ˆ
L4=¯
Y12.−¯
Y13.= 5.2, ˆ
L5=
¯
Y12.−¯
Y14.= 15.2, ˆ
L6=¯
Y13.−¯
Y14.= 10.0, s{ˆ
Li}= 3.0725 (i= 1, ..., 6), B=
t(.99583; 48) = 2.753
26-2
−6.0±3.0725(2.753) −14.46 ≤L1≤2.46
−.8±3.0725(2.753) −9.26 ≤L2≤7.66
9.2±3.0725(2.753) .74 ≤L3≤17.66
5.2±3.0725(2.753) −3.26 ≤L4≤13.66
15.2±3.0725(2.753) 6.74 ≤L5≤23.66
10.0±3.0725(2.753) 1.54 ≤L6≤18.46
c. ˆ
L= 11.467, s{ˆ
L}= 2.5087, t(.995; 48) = 2.682,
11.467 ±2.682(2.5087), 4.74 ≤L≤18.20
26.7. a. βj(i)are independent N(0, σ2
β); βj(i)are independent of ²k(ij).
b. ˆσ2
β= 45.7756
c. H0:σ2
β= 0, Ha:σ2
β>0. F∗= 252.478/23.600 = 10.698, F (.90; 9,48) = 1.765.
If F∗≤1.765 conclude H0, otherwise Ha.Conclude Ha.P-value = 0+
d. c1=.2, c2=−.2, MS1= 252.478, MS2= 23.600, df1= 9, df2= 48,
F1=F(.95; 9,∞) = 1.88, F2=F(.95; 48,∞) = 1.36, F3=F(.95; ∞,9) = 2.71,
F4=F(.95; ∞,48) = 1.45, F5=F(.95; 9,48) = 2.08, F6=F(.95; 48,9) = 2.81,
G1=.4681, G2=.2647, G3=.00765, G4=−.07162, HL= 23.771, HU= 86.258,
45.7756 −23.771, 45.7756 + 86.258, 22.005 ≤σ2
β≤132.034
e. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero.
F∗= 847.817/252.478 = 3.358, F(.90; 2,9) = 3.01.
If F∗≤3.01 conclude H0, otherwise Ha. Conclude Ha.P-value = .081
f. See Problem 26.6a. s{ˆ
Li}= 5.025 (i= 1,2,3), q(.90; 3,9) = 3.32, T= 2.348
−9.75 ±2.348(5.025) −21.55 ≤L1≤2.05
−12.35 ±2.348(5.025) −21.15 ≤L2≤ −.55
−2.60 ±2.348(5.025) −14.40 ≤L3≤9.20
g. H0: all σ2{βj(i)}are equal (i= 1,2,3), Ha: not all σ2{βj(i)}are equal. e
Y1=
62.2, e
Y2= 75.5, e
Y3= 73.9, MST R = 11.6433, MSE = 38.0156, F∗
BF =
11.6433/38.0156 = .31, F(.99; 2,9) = 8.02. If F∗
BF ≤8.02 conclude H0, otherwise
Ha. Conclude H0.
26.8. a. αiare independent N(0, σ2
α); βj(i)are independent N(0, σ2
β);
αi,βj(i), and ²k(ij)are independent.
b. ˆσ2
β= 45.7756, ˆσ2
α= 29.7669
c. H0:σ2
α= 0, Ha:σ2
α>0. F∗= 847.817/252.478 = 3.358, F (.95; 2,9) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha.Conclude H0.P-value = .081
d. c1=.2, c2=−.2, MS1= 252.478, MS2= 23.600, df1= 9, df2= 48,
F1=F(.975; 9,∞) = 2.11, F2=F(.975; 48,∞) = 1.44, F3= (.975; ∞,9) = 3.33,
F4=F(.975; ∞,48) = 1.56, F5=F(.975; 9,48) = 2.39, F6=F(.975; 48,9) =
3.48,
26-3

G1=.5261, G2=.3056, G3=.01577, G4=−.1176, HL= 26.766, HU= 117.544,
45.7756 −26.766, 45.7756 + 117.544, 19.01 ≤σ2
β≤163.32
e. ¯
Y... = 68.56667, s{¯
Y...}= 3.759, t(.975; 2) = 4.303, 68.56667 ±4.303(3.759),
52.392 ≤µ.. ≤84.742
26.9. a. eijk:
i= 1
k j = 1 j= 2 j= 3
1 1.8−12.8−9.6
2 15.8−.8 7.4
3−5.2 3.2 16.4
4−.2−3.8−14.6
5−12.2 14.2.4
i= 2
k j = 1 j= 2 j= 3
1−7.2−2.6 8.8
2 3.8−15.6−8.2
3−15.2 6.4−10.2
4 7.8 11.4 11.8
5 10.8.4−2.2
i= 3
k j = 1 j= 2 j= 3
1−5.8−9.8−12.0
2 11.2 12.2 0.0
3−.8−.8 17.0
4−12.8 3.2 2.0
5 8.2−4.8−7.0
r=.987
26.10. a.
Source SS df MS
States (A) 6,976.84 2 3,488.422
Cities within states [B(A)] 167.60 6 27.933
Error (E) 3,893.20 36 108.144
Total 11,037.64 44
b. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 3,488.422/108.144 =
32.257, F(.95; 2,36) = 3.26. If F∗≤3.26 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
c. H0: all βj(i)equal zero, Ha: not all βj(i)equal zero. F∗= 27.933/108.144 = .258,
F(.95; 6,36) = 2.36. If F∗≤2.36 conclude H0, otherwise Ha. Conclude H0.
P-value = .95
d. α≤.10
26.11. a. ¯
Y11.= 40.2, s{¯
Y11.}= 4.6507, t(.975; 36) = 2.0281,
40.2±2.0281(4.6507), 30.77 ≤µ11 ≤49.63
b. ¯
Y1.. = 40.8667, ¯
Y2.. = 57.3333, ¯
Y3.. = 26.8667, s{¯
Yi..}= 2.6851 (i= 1,2,3),
t(.995; 36) = 2.7195
40.8667 ±2.7195(2.6851) 33.565 ≤µ1.≤48.169
57.3333 ±2.7195(2.6851) 50.031 ≤µ2.≤64.635
26.8667 ±2.7195(2.6851) 19.565 ≤µ3.≤34.169
26-4
c. ˆ
L1=¯
Y1.. −¯
Y2.. =−16.4666, ˆ
L2=¯
Y1.. −¯
Y3.. = 14.0000, ˆ
L3=¯
Y2.. −¯
Y3.. = 30.4666,
s{ˆ
Li}= 3.7973 (i= 1,2,3), q(.90; 3,36) = 2.998, T= 2.120
−16.4666 ±2.120(3.7973) −24.52 ≤L1≤ −8.42
14.0000 ±2.120(3.7973) 5.95 ≤L2≤22.05
30.4666 ±2.120(3.7973) 22.42 ≤L3≤38.52
d. ˆ
L= 12.4, s{ˆ
L}= 6.5771, t(.975; 36) = 2.0281, 12.4±2.0281(6.5771), −.94 ≤L≤
25.74
26.12. a. βj(i)are independent N(0, σ2
β); βj(i)are independent of ²k(j).
b. ˆσ2
β= 0, yes.
c. H0:σ2
β= 0, Ha:σ2
β>0. F∗= 27.933/108.144 = .258, F(.90; 6,36) = 1.94.
If F∗≤1.94 conclude H0, otherwise Ha. Conclude H0.P-value = .95
d. H0: all αiequal zero (i= 1,2,3), Ha: not all αiequal zero. F∗= 3,488.422/27.933 =
124.885, F(.90; 2,6) = 3.46. If F∗≤3.46 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
e. See Problem 26.11c. s{ˆ
Li}= 1.9299 (i= 1,2,3), q(.90; 3,6) = 3.56, T= 2.5173
−16.4666 ±2.5173(1.9299) −21.32 ≤L1≤ −11.61
14.0000 ±2.5173(1.9299) 9.14 ≤L2≤18.86
30.4666 ±2.5173(1.9299) 25.61 ≤L3≤35.32
f. H0: all σ2{βj(i)}are equal (i= 1,2,3), Ha: not all σ2{βj(i)}are equal.
H∗= 37.27/16.07 = 2.32, H(.95; 3,2) = 87.5.
If H∗≤87.5 conclude H0, otherwise Ha. Conclude H0.
26.13. a. αiare independent N(0, σ2
α); βj(i)are independent N(0, σ2
β);
αi,βj(i), and ²k(ij)are independent.
b. ˆσ2
β= 0, ˆσ2
α= 230.699
c. H0:σ2
α= 0, Ha:σ2
α>0. F∗= 3,488.422/27.933 = 124.885, F(.99; 2,6) = 10.9.
If F∗≤10.9 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. c1= 1/15, c2=−1/15, MS1= 3488.422, MS2= 27.933, df1= 2, df2= 6,
F1=F(.995; 2,∞) = 5.30, F2=F(.995; 6,∞) = 3.09, F3=F(.995; ∞,2) = 200,
F4=F(.995; ∞,6) = 8.88, F5=F(.995; 2,6) = 14.5, F6=F(.995; 6,2) = 199,
G1=.8113, G2=.6764, G3=−1.2574, G4=−93.0375, HL= 187.803, HU=
46,279.30, 230.699 −187.803, 230.699 + 46,279.30,42.90 ≤σ2
α≤46,510.00
e. ¯
Y... = 41.6889, s{¯
Y...}= 8.8046, t(.995; 2) = 9.925, 41.6889 ±9.925(8.8046),
−45.70 ≤µ.. ≤129.07
26.14. a. Yijk =µ.. +α1Xijk1+α2Xijk2+β1(1)Xijk3+β2(1)Xijk4+β1(2)Xijk5+β1(3)Xijk6+²ijk
Xijk1=
1 if case from region 1
−1 if case from region 3
0 otherwise
26-5

Xijk2=
1 if case from region 2
−1 if case from region 3
0 otherwise
Xijk3=
1 if case for team 1 from region 1
−1 if case for team 3 from region 1
0 otherwise
Xijk4=
1 if case for team 2 from region 1
−1 if case for team 3 from region 1
0 otherwise
Xijk5=
1 if case for team 1 from region 2
−1 if case for team 2 from region 2
0 otherwise
Xijk6=
1 if case for team 1 from region 3
−1 if case for team 2 from region 3
0 otherwise
b. Full model: ˆ
Y= 150.01667 −9.21667X1+ 5.28333X2+ 6.60000X3
+.50000X4+ 3.70000X5−1.85000X6
eijk:
i= 1 i= 2 i= 3
k j = 1 j= 2 j= 3 j= 1 j= 2 j= 1 j= 2
1 4.20 1.90 −2.30 4.80 0.00 4.90 4.20
2−6.20 −1.90 2.30 −4.80 −4.90 −4.20
3 2.00
r=.962
26.15. a. SSE(F) = 207.2600
Reduced model: ˆ
Y= 147.60248+4.89938X3+1.35031X4+6.26584X5−1.85000X6
SSE(R) = 838.7766
H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗= (631.5166/2) ÷
(207.2600/7) = 10.664, F(.975; 2,7) = 6.54. If F∗≤6.54 conclude H0, otherwise
Ha. Conclude Ha.P-value = .0075
b. Reduced model: ˆ
Y= 150.74206 −8.99921X1+ 5.79127X2
SSE(R) = 483.2338
H0:β1(1) =β2(1) =β1(2) =β1(3) = 0, Ha: not all βj(i)equal zero. F∗=
(275.9738/4) ÷(207.26/7) = 2.33, F(.975; 4,7) = 5.52. If F∗≤5.52 conclude
H0, otherwise Ha. Conclude H0.
c. ˆ
L= ˆα1−ˆα2=−14.5, s2{ˆα1}= 4.0057, s2{ˆα2}= 6.2446, s{ˆα1,ˆα2}=−2.6197,
s{ˆ
L}= 3.9357, t(.99; 7) = 2.998, −14.5±2.998(3.9357), −26.30 ≤L≤ −2.70
26.17. a. eijk:
26-6

i= 1
k j = 1 j= 2 j= 3 j= 4 j= 5
1−2.0 1.5 1.0 1.5−1.0
2 2.0−1.5−1.0−1.5 1.0
i= 2
k j = 1 j= 2 j= 3 j= 4 j= 5
1.5 1.0 1.5−1.5 2.0
2−.5−1.0−1.5 1.5−2.0
i= 3
k j = 1 j= 2 j= 3 j= 4 j= 5
1−2.0−1.5 1.0 2.0−1.5
2 2.0 1.5−1.0−2.0 1.5
r=.957
b. H0: all σ2{²j(i)}are equal (i= 1,2,3), Ha: not all σ2{²j(i)}are equal. e
Y1= 30,
e
Y2= 28, e
Y3= 27, MST R = 2.2167, MSE = 6.8750, F∗
BF = 2.2167/6.8750 = .32,
F(.99; 2,12) = 6.93. If F∗
BF ≤6.93 conclude H0, otherwise Ha. Conclude H0.
26.18. a.
Source SS df MS
Treatments (colors) 3.2667 2 1.63335
Experimental error 369.4000 12 30.78333
Observational error 67.5000 15 4.50000
Total 440.1667 29
b. H0:τ1=τ2=τ3= 0, Ha: not all τiequal zero.
F∗= 1.63335/30.78333 = .053, F(.95; 2,12) = 3.89.
If F∗≤3.89 conclude H0, otherwise Ha. Conclude H0.P-value = .95
c. H0:σ2= 0, Ha:σ2>0. F∗= 30.78333/4.50000 = 6.841, F(.95; 12,15) = 2.48.
If F∗≤2.48 conclude H0, otherwise Ha. Conclude Ha.P-value = .0004
d. ¯
Y1.. = 29.2, s{¯
Y1..}= 1.7545, t(.975; 12) = 2.179,
29.2±2.179(1.7545), 25.38 ≤µ1.≤33.02
e. ˆσ2= 13.1417, ˆσ2
η= 4.5
f. For σ2:c1=.5, c2=−.5, MS1= 30.7833, MS2= 4.5000, df1= 12, df2= 15,
F1=F(.975; 12,∞)=1.94, F2=F(.975; 15,∞)=1.83, F3=F(.975; ∞,12) =
2.72, F4=F(.975; ∞,15) = 2.40, F5=F(.975; 12,15) = 2.96, F6=F(.975; 15,12) =
3.18, G1=.4845, G2=.4536, G3=−.05916, G4=−.0906, HL= 7.968,
HU= 26.434, 13.1417 −7.968, 13.1417 + 26.434, 5.174 ≤σ2≤39.576
For σ2
η:df = 15, χ2(.025; 15) = 6.26, χ2(.975; 15) = 27.49,
2.455 = 15(4.5)
27.49 ≤σ2
η≤15(4.5)
6.26 = 10.783
26.19. eijk:
i= 1
k j = 1 j= 2 j= 3
1−.4000 .0333 −.3667
2.0000 .3333 .0333
3.4000 −.3667 .3333
i= 2
k j = 1 j= 2 j= 3
1.0667 .4333 −.2000
2−.2333 .0667 .3000
3.1667 −.3667 −.1000
26-7

i= 3
k j = 1 j= 2 j= 3
1−.4333 −.1333 −.3667
2.1667 .4667 .3333
3.2667 −.3333 −.0667
i= 4
k j = 1 j= 2 j= 3
1−.0667 −.3000 .4000
2.4333 .2000 .0000
3−.3667 .1000 −.4000
r=.972
26.20. a.
Source SS df MS
Plants 343.1789 3 114.3930
Leaves, within plants 187.4533 8 23.4317
Observations, within leaves 3.0333 24 .1264
Total 533.6655 35
b. H0:σ2
τ= 0, Ha:σ2
τ>0. F∗= 114.3930/23.4317 = 4.88, F(.95; 3,8) = 4.07.
If F∗≤4.07 conclude H0, otherwise Ha. Conclude Ha.P-value = .03
c. H0:σ2= 0, Ha:σ2>0. F∗= 23.4317/.1264 = 185.38, F(.95; 8,24) = 2.36.
If F∗≤2.36 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ¯
Y... = 14.26111, s{¯
Y...}= 1.7826, t(.975; 3) = 3.182,
14.26111 ±3.182(1.7826), 8.59 ≤µ.. ≤19.93
e. ˆσ2
τ= 10.1068, ˆσ2= 7.7684, ˆσ2
η=.1264
f. c1= 1/9 = .1111, c2=−1/9 = −.1111, MS1= 114.3930, MS2= 23.4317,
df1= 3, df2= 8, F1=F(.95; 3,∞)=2.60, F2=F(.95; 8,∞)=1.94, F3=
F(.95; ∞,3) = 8.53, F4=F(.95; ∞,8) = 2.93, F5=F(.95; 3,8) = 4.07, F6=
F(.95; 8,3) = 8.85, G1=.6154, G2=.4845, G3=−.1409, G4=−1.5134,
HL= 9.042, HU= 95.444, 10.1068−9.042, 10.1068+95.444, 1.065 ≤σ2
τ≤105.551
26.21. a. eijk:
i= 1
k j = 1 j= 2 j= 3 j= 4
1.1667 .0667 .0333 −.0333
2−.0333 −.1333 −.1667 .1667
3−.1333 .0667 .1333 −.1333
i= 2
k j = 1 j= 2 j= 3 j= 4
1.0333 .0333 −.0667 −.2000
2.1333 −.1667 −.0667 .2000
3−.1667 .1333 .1333 .0000
i= 3
k j = 1 j= 2 j= 3 j= 4
1.0000 .1667 −.1333 .0667
2.1000 .0667 −.0333 −.2333
3−.1000 −.2333 .1667 .1667
i= 4
k j = 1 j= 2 j= 3 j= 4
1−.1333 −.0333 .1667 −.0333
2.1667 .1667 −.1333 .1667
3−.0333 −.1333 −.0333 −.1333
i= 5
k j = 1 j= 2 j= 3 j= 4
1.0333 .1000 .1333 .2000
2.1333 .1000 −.0667 −.2000
3−.1667 −.2000 −.0667 .0000
26-8

r=.981
b. H0: all σ2{²j(i)}are equal (i= 1, ..., 5), Ha: not all σ2{²j(i)}are equal.
H∗=.100833/.014167 = 7.117, H(.99; 5,3) = 151.
If H∗≤151 conclude H0, otherwise Ha. Conclude H0.
26.22. a.
Source SS df MS
Batches 10.6843 4 2.67108
Barrels, within batches .6508 15 .04339
Determinations, within barrels 1.0067 40 .02517
Total 12.3418 59
b. H0:σ2
τ= 0, Ha:σ2
τ>0. F∗= 2.67108/.04339 = 61.56, F (.99; 4,15) = 4.89.
If F∗≤4.89 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. H0:σ2= 0, Ha:σ2>0. F∗=.04339/.02517 = 1.724, F (.99; 15,40) = 2.52.
If F∗≤2.52 conclude H0, otherwise Ha. Conclude H0.P-value = .085
d. ¯
Y... = 2.9117, s{¯
Y...}=.21099, t(.995; 4) = 4.604,
2.9117 ±4.604(.21099), 1.94 ≤µ.. ≤3.88
e. ˆσ2
τ=.2190, ˆσ2=.0061, ˆσ2
η=.0252
f. c1=.08333, c2=−.08333, MS1= 2.67108, MS2=.04339, df1= 4, df2= 15,
F1=F(.975; 4,∞) = 2.79, F2=F(.975; 15,∞) = 1.83, F3=F(.975; ∞,4) =
8.26, F4=F(.975; ∞,15) = 2.40, F5=F(.975; 4,15) = 3.80, F6=F(.975; 15,4) =
8.66, G1=.6416, G2=.4536, G3=.1082, G4=−1.0925, HL=.1432,
HU= 1.6157, .2190 −.1432, .2190 + 1.6157, .076 ≤σ2
τ≤1.835
26.23. PPP(Yijk −¯
Y...)2=PPP[( ¯
Yi.. −¯
Y...)+(¯
Yij. −¯
Yi..)+(Yijk −¯
Yij.)]2
=PPP[( ¯
Yi.. −¯
Y...)2+ ( ¯
Yij. −¯
Yi..)2+ (Yijk −¯
Yij.)2+ 2( ¯
Yi.. −¯
Y...)( ¯
Yij. −¯
Yi..)
+2( ¯
Yi.. −¯
Y...)(Yijk −¯
Yij.) + 2( ¯
Yij. −¯
Yi..)(Yijk −¯
Yij.)]
=bn P(¯
Yi.. −¯
Y...)2+nPP(¯
Yij. −¯
Yi..)2+PPP(Yijk −¯
Yij.)2
All cross products equal zero by arguments similar to that given in Section 16.8.
26.24. SSB +SSAB =PY2
.j.
na −Y2
...
nab +PPY2
ij.
n−PY2
i..
nb −PY2
.j.
na +Y2
...
nab
=PPY2
ij.
n−PY2
i..
nb =SSB(A)
26.25. a. σ2{¯
Yi..}=σ2{µ.. +αi+¯
β.(i)+ ¯².(i.)}=σ2
β
b+σ2
bn
σ2{¯
Y...}=σ2{µ.. +¯
β.(.)+ ¯².(..)}=σ2
β
ab +σ2
abn
b. [MSB(A)−MSE]/n
26.26. σ2{¯
Yi..}=σ2{µ.. +τi+ ¯².(i)+ ¯η.(i.)}
26-9

=σ2
n+σ2
η
mn =mσ2+σ2
η
mn
26.27. σ2{¯
Y...}=σ2{µ.. + ¯τ.+ ¯².(.)+ ¯η.(..)}
=σ2
τ
r+σ2
rn +σ2
η
rnm
Ens2{¯
Y...}o=E½M ST R
rnm ¾=σ2
η+mσ2+nmσ2
τ
rnm =σ2{¯
Y...}
26.28. σ2{¯
Y1j.. −¯
Y2j..}=2
cÃσ2
βγ +σ2
n+σ2
γ!
df =[bMSBC(A) + MSC(A)−MSE]2
[bMSBC(A)]2
a(b−1)(c−1) +[MSC(A)]2
a(c−1) +(MSE)2
abc(n−1)
26.29. a. Yijk =µ.. +αi+βj(i)+²k(ij),βj(i)and ²k(ij)random
b. eijk:
i= 1
k j = 1 j= 2 j= 3 j= 4
1−.040 .045 .020 −.035
2.040 −.045 −.020 .035
i= 2
k j = 1 j= 2 j= 3 j= 4
1.035 −.045 −.025 .040
2−.035 .045 .025 −.040
i= 3
k j = 1 j= 2 j= 3 j= 4
1.025 .040 −.035 −.060
2−.025 −.040 .035 .060
r=.938
26.30. a.
Source SS df MS
A(lever press rate) .89306 2 .44653
D(A) (rats within A).12019 9 .01335
Error .03555 12 .00296
Total 1.04880 23
b. H0:α1=α2=α3= 0, Ha: not all αiequal zero.
F∗=.44653/.01335 = 33.448, F(.95; 2,9) = 4.26.
If F∗≤4.26 conclude H0, otherwise Ha. Conclude Ha.P-value = .0001
c. H0:σ2
β= 0, Ha:σ2
β>0. F∗=.01335/.00296 = 4.510, F(.95; 9,12) = 2.80.
If F∗≤2.80 conclude H0, otherwise Ha. Conclude Ha.P-value = .009
d. ¯
Y1.. =.53500, ¯
Y2.. =.77375, ¯
Y3.. = 1.00750, ˆ
L1=¯
Y1.. −¯
Y2.. =−.23875, ˆ
L2=
¯
Y1.. −¯
Y3.. =−.47250, ˆ
L3=¯
Y2.. −¯
Y3.. =−.23375, s{ˆ
Li}=.0578 (i= 1,2,3),
q(.90; 3,9) = 3.32, T= 2.3476
−.23875 ±2.3476(.0578) −.374 ≤L1≤ −.103
−.47250 ±2.3476(.0578) −.608 ≤L2≤ −.337
−.23375 ±2.3476(.0578) −.369 ≤L3≤ −.098
26-10
e. ˆσ2
β=.005195, c1=.5, c2=−.5, MS1=.013354, MS2=.002963, df1= 9, df2=
12, F1=F(.95; 9,∞) = 1.88, F2=F(.95; 12,∞) = 1.75, F3=F(.95; ∞,9) =
2.71, F4=F(.95; ∞,12) = 2.30, F5=F(.95; 9,12) = 2.80, F6=F(.95; 12,9) =
3.07, G1=.4681, G2=.4286, G3=−.05996, G4=−.1210, HL=.003589,
HU=.01138, .005195 −.003589, .005195 + .01138, .00161 ≤σ2
β≤.0166
26.31. a. Yijk =µ.. +τi+²j(i)+ηk(ij),²j(i)and ηk(ij)random
b. eijk:
i= 1
k j = 1 j= 2 j= 3 j= 4
1−.035 −.030 −.030 −.025
2.035 .030 .030 .025
i= 2
k j = 1 j= 2 j= 3 j= 4
1.020 .030 −.035 −.020
2−.020 −.030 .035 .020
i= 3
k j = 1 j= 2 j= 3 j= 4
1−.050 −.025 −.035 .045
2.050 .025 .035 −.045
r=.940
c. H0: all σ2{²j(i)}are equal (i= 1,2,3), Ha: not all σ2{²j(i)}are equal.
e
Y1= 1.9075, e
Y2= 2.2200, e
Y3= 2.4075, M ST R =.001431, MSE =.004204,
F∗
BF =.001431/.004204 = .34, F (.99; 2,9) = 8.02.
If F∗
BF ≤8.02 conclude H0, otherwise Ha. Conclude H0.
26.32. a.
Source SS df MS
Treatments (lever press rates) 1.013125 2 .50656
Experimental error .182025 9 .02023
Observational error .025900 12 .00216
Total 1.221050 23
b. H0: all τ1=τ2=τ3= 0, Ha: not all τiequal zero.
F∗=.50656/.02023 = 25.040, F(.99; 2,9) = 8.02.
If F∗≤8.02 conclude H0, otherwise Ha. Conclude Ha.P-value = .0002
c. H0:σ2= 0, Ha:σ2>0. F∗=.02023/.00216 = 9.366, F (.99; 9,12) = 4.39.
If F∗≤4.39 conclude H0, otherwise Ha.Conclude Ha.P-value = .0003
d. ¯
Y1.. = 1.88750, ¯
Y2.. = 2.21875, ¯
Y3.. = 2.38125, ˆ
L1=¯
Y1.. −¯
Y2.. =−.33125, ˆ
L2=
¯
Y1.. −¯
Y3.. =−.49375, ˆ
L3=¯
Y2.. −¯
Y3.. =−.16250, s{ˆ
Li}=.071116 (i= 1,2,3),
q(.95; 3,9) = 3.95, T= 2.793
−.33125 ±2.793(.071116) −.530 ≤L1≤ −.133
−.49375 ±2.793(.071116) −.692 ≤L2≤ −.295
−.16250 ±2.793(.071116) −.361 ≤L3≤.036
f. For σ2: ˆσ2=.00904, c1=.5, c2=−.5, MS1=.020225, MS2=.0021583,
df1= 9, df2= 12, F1=F(.95; 9,∞)=1.88, F2=F(.95; 12,∞) = 1.75, F3=
26-11

F(.95; ∞,9) = 2.71, F4=F(.95; ∞,12) = 2.30, F5=F(.95; 9,12) = 2.80, F6=
F(.95; 12,9) = 3.07, G1=.4681, G2=.4286, G3=−.05996, G4=−.1210,
HL=.00487, HU=.0173, .00904 −.00487, .00904 + .0173, .0042 ≤σ2≤.0263
For σ2
η: ˆσ2
η=.00216, df = 12, χ2(.05; 12) = 5.23, χ2(.95; 12) = 21.03,
.0012 = 12(.00216)
21.03 ≤σ2
η≤12(.00216)
5.23 =.0050
26-12

Chapter 27
REPEATED MEASURES AND
RELATED DESIGNS
27.3. a. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1 2.5556 −1.9444 −3.7778 2.4722 −2.7778 3.4722
2−.1111 .3889 −.4444 2.8056 −3.4444 .8056
3−2.9444 5.5556 3.7222 −3.0278 −2.2778 −1.0278
4−2.7778 .7222 −2.1111 1.1389 1.8889 1.1389
5−2.4444 −3.9444 1.2222 1.4722 1.2222 2.4722
6−.1111 3.3889 −.4444 −3.9944 .5556 −.1944
7−.9444 −2.4444 −1.2778 −2.0278 2.7222 3.9722
8 2.3889 −2.1111 4.0556 −1.6944 .0556 −2.6944
9−.6111 −5.1111 .0556 −1.6944 3.0556 4.3056
10 1.5556 1.0556 −3.7778 3.4722 −.7778 −1.5278
11 1.3889 .8889 .0556 1.3056 1.0556 −4.6944
12 2.0556 3.5556 2.7222 −1.0278 −1.2778 −6.0278
r=.995
d. H0:D= 0, Ha:D6= 0. SST R.S = 467.3889, SST R.S∗= 8.7643, SSRem∗=
458.6246, F∗= (8.7643/1) ÷(458.6246/54) = 1.032, F(.995; 1,54) = 8.567. If
F∗≤8.567 conclude H0, otherwise Ha. Conclude H0.P-value = .31
27.4. a.
Source SS df MS
Subjects 1,197.4444 11 108.8586
Doses 5,826.2778 5 1,165.2556
Error 467.3889 55 8.4980
Total 7,491.1111 71
b. H0: all τjequal zero (j= 1, ..., 6), Ha: not all τjequal zero. F∗= 1,165.2556/8.4980 =
137.12, F(.99; 5,55) = 3.37. If F∗≤3.37 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
c. ¯
Y.1= 14.6667, ¯
Y.2= 19.1667, ¯
Y.3= 23.0000, ¯
Y.4= 28.7500, ¯
Y.5= 35.0000, ¯
Y.6=
40.7500, ˆ
L1=¯
Y.1−¯
Y.2=−4.5000, ˆ
L2=¯
Y.2−¯
Y.3=−3.8333, ˆ
L3=¯
Y.3−¯
Y.4=
27-1

−5.7500, ˆ
L4=¯
Y.4−¯
Y.5=−6.2500, ˆ
L5=¯
Y.5−¯
Y.6=−5.7500, s{ˆ
Li}= 1.1901
(i= 1, ..., 5), B=t(.995; 55) = 2.668
−4.5000 ±2.668(1.1901) −7.6752 ≤L1≤ −1.3248
−3.8333 ±2.668(1.1901) −7.0085 ≤L2≤ −.6581
−5.7500 ±2.668(1.1901) −8.9252 ≤L3≤ −2.5748
−6.2500 ±2.668(1.1901) −9.4252 ≤L4≤ −3.0748
−5.7500 ±2.668(1.1901) −8.9252 ≤L5≤ −2.5748
d. ˆ
E= 2.83
27.5. a. Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+ρ5Xij5+ρ6Xij6+ρ7Xij7
+ρ8Xij8+ρ9Xij9+ρ10Xij10 +ρ11Xij11 +γ1xij +γ2x2
ij +γ3x3
ij +²ij
Xij1=
1 if experimental unit from block 1
−1 if experimental unit from block 12
0 otherwise
Xij2, ..., Xij11 are defined similarly
xij =
−.97 if experimental unit received treatment 1
−.77 if experimental unit received treatment 2
−.57 if experimental unit received treatment 3
−.07 if experimental unit received treatment 4
.43 if experimental unit received treatment 5
1.93 if experimental unit received treatment 6
b. ˆ
Y= 30.3903 + 3.7778X1+ 4.4444X2+.2778X3−2.8889X4−5.2222X5
+3.4444X6−4.7222X7+ 2.9444X8+ 3.9444X9−8.2222X10
+1.9444X11 + 11.5329x−4.0297x2+.4353x3
c. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6
1 2.2076 −1.6998 −3.2045 1.6591 −2.4167 3.4543
2−.4591 .6335 .1288 1.9925 −3.0834 .7877
3−3.2924 5.8002 4.2955 −3.8409 −1.9167 −1.0457
4−3.1257 .9668 −1.5378 .3258 2.2499 1.1210
5−2.7924 −3.6998 1.7955 .6591 1.5833 2.4543
6−.4591 3.6335 .1288 −4.0075 .9166 −.2123
7−1.2934 −2.1998 −.7045 −2.8409 3.0833 3.9543
8 2.0409 −1.8665 4.6288 −2.5075 .4166 −2.7123
9−.9591 −4.8665 .6288 −2.5075 3.4166 4.2877
10 1.2076 1.3002 −3.2045 2.6591 −.4167 −1.5457
11 1.0409 1.1335 .6288 .4925 1.4166 −4.7123
12 1.7076 3.8002 3.2955 −1.8409 −.9167 −6.0457
d. H0:γ3= 0, Ha:γ36= 0. SSE(F) = 483.0053, SSE(R) = 484.8980,
F∗= (1.8927/1) ÷(483.0053/57) = .223, F(.95; 1,57) = 4.01.
If F∗≤4.01 conclude H0, otherwise Ha. Conclude H0.P-value = .64
27-2

27.6. a. eij:
i j = 1 j= 2 j= 3
1−1.2792 −.2417 1.5208
2−.8458 .6917 .1542
3.6208 .0583 −.6792
4.5542 .1917 −.7458
5.5208 −.3417 −.1792
6−.1458 .3917 −.2458
7.9875 −.7750 −.2125
8−.4125 .0250 .3875
r=.992
d. H0:D= 0, Ha:D6= 0. SST R.S = 9.5725, SST R.S∗= 2.9410, SSRem∗=
6.6315, F∗= (2.9410/1) ÷(6.6315/13) = 5.765, F(.99; 1,13) = 9.07. If F∗≤9.07
conclude H0, otherwise Ha. Conclude H0.P-value = .032
27.7. a.
Source SS df MS
Stores 745.1850 7 106.4550
Prices 67.4808 2 33.7404
Error 9.5725 14 .68375
Total 822.2383 23
b. H0: all τjequal zero (j= 1, 2, 3), Ha: not all τjequal zero. F∗= 33.7404/.68375 =
49.346, F(.95; 2,14) = 3.739. If F∗≤3.739 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
c. ¯
Y.1= 55.4375, ¯
Y.2= 53.6000, ¯
Y.3= 51.3375, ˆ
L1=¯
Y.1−¯
Y.2= 1.8375, ˆ
L2=
¯
Y.1−¯
Y.3= 4.1000, ˆ
L3=¯
Y.2−¯
Y.3= 2.2625, s{ˆ
Li}=.413446 (i= 1,2,3),
q(.95; 3,14) = 3.70, T= 2.616
1.8375 ±2.616(.413446) .756 ≤L1≤2.919
4.1000 ±2.616(.413446) 3.018 ≤L2≤5.182
2.2625 ±2.616(.413446) 1.181 ≤L3≤3.344
d. ˆ
E= 48.08
27.8. H0: all τjequal zero (j= 1, ..., 6), Ha: not all τjequal zero.
MST R = 39.8583, M ST R.S =.2883, F∗
R= 39.8583/.2883 = 138.24,
F(.99; 5,25) = 3.855. If F∗
R≤3.855 conclude H0, otherwise Ha. Conclude Ha.
27.9. H0: all τjequal zero (j= 1,2,3), Ha: not all τjequal zero. MST R = 8,
MST R.S = 0, F∗
R= 8/0. Note: Nonparametric Ftest results in SST R.S = 0
and therefore should not be used.
27.10. a. H0: all τjequal zero (j= 1, ..., 5), Ha: not all τjequal zero.
MST R = 15.8500, MST R.S = 1.0167, F∗
R= 15.8500/1.0167 = 15.59, F(.95; 4,36) =
2.63. If F∗
R≤2.63 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
27-3

b. ¯
R.1= 4.0, ¯
R.2= 1.4, ¯
R.3= 2.1, ¯
R.4= 3.1, ¯
R.5= 4.4, B=z(.995) = 2.576,
B[r(r+ 1)/6n]1/2= 1.82
Group 1: B,C,D
Group 2: A,D,E
c. W=.634
27.11. a. eijk:
j= 1 j= 2
i k = 1 k= 2 k= 1 k= 2
1−1.9167 1.9167 −2.3333 2.3333
2−.4167 .4167 .6667 −.6667
3 1.5833 −1.5833 −.3333 .3333
4.0833 −.0833 .6667 −.6667
5 1.0833 −1.0833 −.3333 .3333
6−.4167 .4167 1.6667 −1.6667
r=.994
27.12. a.
Source SS df MS
A(incentive stimulus) 975.38 1 975.38
S(A) 148.75 10 14.875
B(problem type) 513.37 1 513.37
AB interactions 155.04 1 155.04
B.S(A)(Error) 34.08 10 3.408
Total 1826.63 23
b. ¯
Y.11 = 12.667, ¯
Y.12 = 16.833, ¯
Y.21 = 20.333, ¯
Y.22 = 34.667
c. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero.
F∗= 155.04/3.408 = 45.49, F(.95; 1,10) = 4.96.
If F∗≤4.96 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. T=q(.95; 2,10)/√2 = 2.227, s2{ˆ
D}= 2(3.408)/6 = 1.136, s{ˆ
D}= 1.0658
−4.17 ±2.227(1.0658) −6.54 ≤L1≤ −1.80
−14.33 ±2.227(1.0658) −16.70 ≤L2≤ −11.96
e. dfadj =[34.08 + 148.75]2
34.082/10 + 148.752/10 = 14.35, T=q(.95; 2,14)/√2 = 2.143
MS(Within Treatments)=(34.08+148.75)/20=9.1415
s2{ˆ
D}= 2(9.1415)/6 = 3.0472, s{ˆ
D}= 1.7456
−7.67 ±2.143(1.7456) −11.41 ≤L1≤ −3.93
−17.83 ±2.143(1.7456) −21.57 ≤L2≤ −14.09
27.13. a. eijk:
27-4

k= 1 k= 2 k= 3 k= 4
i= 1 9.250 −8.750 1.250 −1.750
i= 2 −11.750 −2.750 15.250 −.750
j= 1 i= 3 7.750 −5.250 5.750 −8.250
i= 4 −5.250 16.750 −22.250 10.750
i= 1 3.625 −3.125 −13.875 13.375
j= 2 i= 2 15.375 6.625 7.875 −29.875
i= 3 −8.375 −3.125 −3.875 15.375
i= 4 −10.625 −.375 9.875 1.125
r=.981
27.14. a. H0:σ2{ρi(1)}=σ2{ρi(2)},Ha:σ2{ρi(1)} 6=σ2{ρi(2)}.
SSS(A1) = 1,478,757.00, SSS(A2) = 1,525,262.25,
H∗= (1,525,262.25/3) ÷(1,478,757.00/3) = 1.03, H(.99; 2,3) = 47.5.
If H∗≤47.5 conclude H0, otherwise Ha. Conclude H0.
b. H0:σ2{²1jk}=σ2{²2jk},Ha:σ2{²1jk} 6=σ2{²2jk}.
SSB.S(A1) = 1,653.00, SSB.S(A2) = 2,172.25,
H∗= (2,172.25/9) ÷(1,653.00/9) = 1.31, H(.99; 2,9) = 6.54.
If H∗≤6.54 conclude H0, otherwise Ha. Conclude H0.
27.15. a.
Source SS df MS
A(type display) 266,085.1250 1 266,085.1250
S(A) 3,004,019.2500 6 500,669.8750
B(time) 53,321.6250 3 17,773.8750
AB interactions 690.6250 3 230.2083
Error 3,825.2500 18 212.5139
Total 3,327,941.8750 31
b. ¯
Y.11 = 681.500, ¯
Y.12 = 696.500, ¯
Y.13 = 671.500, ¯
Y.14 = 785.500,
¯
Y.21 = 508.500, ¯
Y.22 = 512.250, ¯
Y.23 = 496.000, ¯
Y.24 = 588.750
c. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero.
F∗= 230.2083/212.5139 = 1.08, F(.975; 3,18) = 3.95.
If F∗≤3.95 conclude H0, otherwise Ha. Conclude H0.P-value = .38
d. H0:α1=α2= 0, Ha: not both αjequal zero.
F∗= 266,085.1250/500,669.8750 = .53, F(.975; 1,6) = 8.81.
If F∗≤8.81 conclude H0, otherwise Ha. Conclude H0.P-value = .49
H0: all βkequal zero (k= 1, ..., 4), Ha: not all βkequal zero.
F∗= 17,773.8750/212.5139 = 83.636, F(.975; 3,18) = 3.95.
If F∗≤3.95 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
27-5

e. ¯
Y.1.= 708.750, ¯
Y.2.= 526.375, ¯
Y..1= 595.000, ¯
Y..2= 604.375, ¯
Y..3= 583.750,
¯
Y..4= 687.125, ˆ
L1= 182.375, ˆ
L2=−9.375, ˆ
L3= 20.625, ˆ
L4=−103.375,
s{ˆ
L1}= 250.1674, s{ˆ
Li}= 7.2889 (i= 2,3,4), B1=t(.9875; 6) = 2.969, Bi=
t(.9875; 18) = 2.445 (i= 2,3,4)
182.375 ±2.969(250.1674) −560.372 ≤L1≤925.122
−9.375 ±2.445(7.2889) −27.196 ≤L2≤8.446
20.625 ±2.445(7.2889) 2.804 ≤L3≤38.446
−103.375 ±2.445(7.2889) −121.196 ≤L4≤ −85.554
27.16. a. eijk:
j= 1 j= 2
i k = 1 k= 2 k= 1 k= 2
1−.05833 .05833 .05833 −.05833
2−.05833 .05833 .05833 −.05833
3−.03333 .03333 .03333 −.03333
4−.00833 .00833 .00833 −.00833
5.21667 −.21667 −.21667 .21667
6−.05833 .05833 .05833 −.05833
r=.9685
27.17. a.
Source SS df MS
Subjects 1.0533 5 .2107
A(problem) 16.6667 1 16.6667
B(model) 72.1067 1 72.1067
AB 3.6817 1 3.6817
AS .5983 5 .1197
BS .1783 5 .0357
ABS .2333 5 .0467
Total 94.5183 23
b. ¯
Y.11 = 3.367, ¯
Y.12 = 7.617, ¯
Y.21 = 2.483, ¯
Y.22 = 5.167
c. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero.
F∗= 3.6817/.0467 = 78.84, F(.99; 1,5) = 16.3.
If F∗≤16.3 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
d. ˆ
L1= 4.250, ˆ
L2= 2.684, ˆ
L3=−1.566,
s{ˆ
Li}=.1248 (i= 1,2), s{ˆ
L3}=.1765, B=t(.9917; 5) = 3.538
4.250 ±3.538(.1248) 3.808 ≤L1≤4.692
2.684 ±3.538(.1248) 2.242 ≤L2≤3.126
−1.566 ±3.538(.1765) −2.190 ≤L3≤ −.942
27.18. a. eijk:
27-6

j= 1 j= 2
i k = 1 k= 2 k= 1 k= 2
1−.045 .045 .045 −.045
2−.120 .120 .120 −.120
3.080 −.080 −.080 .080
4−.045 .045 .045 −.045
5.080 −.080 −.080 .080
6.055 −.055 −.055 .055
7.030 −.030 −.030 .030
8−.045 .045 .045 −.045
9.055 −.055 −.055 .055
10 −.045 .045 .045 −.045
r=.973
27.19. a.
Source SS df MS
Subjects 154.579 9 17.175
A3.025 1 3.025
B14.449 1 11.449
AB .001 1 .001
AS 2.035 9 .226
BS 5.061 9 .562
ABS .169 9 .019
Total 176.319 39
b. ¯
Y.11 = 3.93, ¯
Y.12 = 5.01, ¯
Y.21 = 4.49, ¯
Y.22 = 5.55
c. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero.
F∗=.001/.019 = .05, F(.995; 1,9) = 13.6.
If F∗≤13.6 conclude H0, otherwise Ha. Conclude H0.P-value = .82
d. H0:α1=α2= 0, Ha: not both αjequal zero.
F∗= 3.025/.226 = 13.38, F(.95; 1,9) = 5.12.
If F∗≤13.6 conclude H0, otherwise Ha. Conclude Ha.P-value = .005
H0:β1=β2= 0, Ha: not both βkequal zero.
F∗= 11.449/.562 = 20.36, F(.95; 1,9) = 5.12.
If F∗≤13.6 conclude H0, otherwise Ha. Conclude Ha.P-value = .001
e. ˆ
L1=.56, ˆ
L2= 1.08, ˆ
L3=−.52, ˆ
L4= 1.62,
s{ˆ
Li}=.0613 (i= 1, ..., 4), B=t(.99375; 9) = 3.11
.56 ±3.11(.0613) .37 ≤L1≤.75
1.08 ±3.11(.0613) .89 ≤L2≤1.27
−.52 ±3.11(.0613) −.71 ≤L3≤ −.33
1.62 ±3.11(.0613) 1.43 ≤L4≤1.81
27.20. a. eijk:
27-7

i j k = 1 k= 2
1 1 −.6.6
2−1.7 1.7
2 1 .4−.4
2 1.3−1.3
3 1 −.6.6
2.3−.3
4 1 .4−.4
2−.2.2
5 1 .4−.4
2.3−.3
r=.981
27.21. a.
Source SS df MS
Whole plots
Irrigation method (A) 1,394.45 1 1,394.45
Whole-plot error 837.60 8 104.70
Split plots
Fertilizer (B) 68.45 1 68.45
AB Interactions .05 1 .05
Split-plot error 12.00 8 1.50
Total 2,312.55 19
b. ¯
Y.11 = 35.4, ¯
Y.21 = 52.2, ¯
Y.12 = 39.2, ¯
Y.22 = 55.8
c. H0: all (αβ)jk equal zero, Ha: not all (αβ)jk equal zero. F∗=.05/1.50 = .033,
F(.95; 1,8) = 5.32. If F∗≤5.32 conclude H0, otherwise Ha. Conclude H0.
P-value = .86
d. H0:α1=α2= 0, Ha: not both αjequal zero. F∗= 1,394.45/104.70 = 13.32,
F(.95; 1,8) = 5.32. If F∗≤5.32 conclude H0, otherwise Ha. Conclude Ha.
P-value = .006
H0:β1=β2= 0, Ha: not both βkequal zero. F∗= 68.45/1.50 = 45.63,
F(.95; 1,8) = 5.32. If F∗≤5.32 conclude H0, otherwise Ha. Conclude Ha.
P-value = .0001
e. ¯
Y.1.= 37.3, ¯
Y.2.= 54.0, ¯
Y..1= 43.8, ¯
Y..2= 47.5, ˆ
L1=−16.7, ˆ
L2=−3.7, s{ˆ
L1}=
4.5760, s{ˆ
L2}=.5477, B1=t(.975; 8) = 2.306, B2=t(.975; 8) = 2.306
−16.7±2.306(4.5760) −27.252 ≤L1≤ −6.148
−3.7±2.306(.5477) −4.963 ≤L2≤ −2.437
27.22.
XX(Yij −¯
Y..)2=XX[(Yij −¯
Yi.)+(¯
Yi. −¯
Y..)]2
=XX(Yij −¯
Yi.)2+XX(¯
Yi. −¯
Y..)2+ 2 XX(Yij −¯
Yi.)( ¯
Yi. −¯
Y..)
=XX(Yij −¯
Yi.)2+rX(¯
Yi. −¯
Y..)2
27-8

Cross-product term equals zero by argument similar to that given in Section 16.5.
27.23. j0
j
1
2
3
4
5
6
27.3333 20.8788 23.0909 19.1818 16.7273 17.0909
29.4242 23.4545 14.3182 12.6364 11.0455
30.9091 14.7273 18.2727 16.4545
18.3864 11.1818 15.0227
17.4545 16.8182
27.8409
27.24. j0
1
j2
3
29.6084 33.0114 34.0598
37.5886 38.7000
40.6255
27.25. a. Yij =µ.. +ρi+τj+²(ij)
b. eij:
i j = 1 j= 2 j= 3 j= 4
1.02083 −.00917 .00833 −.02000
2.00083 −.00917 −.00167 .01000
3.00083 .00083 .00833 −.01000
4.04083 .02083 −.02167 −.04000
5−.03167 .04833 −.04417 .02750
6.01833 −.03167 .05583 −.04250
7−.00167 −.00167 −.02417 .02750
8−.00167 .00833 −.01417 .00750
9−.02417 −.00417 .02333 .00500
10 −.00417 −.04417 .02333 .02500
11 .03333 −.01667 −.03917 .02250
12 −.05167 .03833 .02583 −.01250
r=.994
27.26. a.
Source SS df MS
Subjects 1.80012 11 .163647
Dosage .72615 3 .242050
Error .03220 33 .000976
Total 2.55847 47
b. H0: all τjequal zero (j= 1, ..., 4), Ha: not all τjequal zero.
F∗=.242050/.000976 = 248.0, F(.95; 3,33) = 2.89.
If F∗≤2.89 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. ¯
Y.1= 1.03833, ¯
Y.2= 1.05833, ¯
Y.3= 1.06083, ¯
Y.4=.76917, ˆ
L1=¯
Y.1−¯
Y.2=
−.02000, ˆ
L2=¯
Y.2−¯
Y.3=−.00250, ˆ
L3=¯
Y.3−¯
Y.4=.29166, s{ˆ
Li}=.01275
(i= 1,2,3), B=t(.983; 33) = 2.22
27-9

−.02000 ±2.22(.01275) −.048 ≤L1≤.008
−.00250 ±2.22(.01275) −.031 ≤L2≤.026
.29166 ±2.22(.01275) .263 ≤L3≤.320
d. Yij =µ.. +ρ1Xij1+ρ2Xij2+ρ3Xij3+ρ4Xij4+ρ5Xij5+ρ6Xij6
+ρ7Xij7+ρ8Xij8+ρ9Xij9+ρ10Xij10 +ρ11Xij11 +γ1xij +γ2x2
ij +²ij
Xij1=
1 if experimental unit from subject 1
−1 if experimental unit from subject 12
0 otherwise
Xij2, ..., Xij11 are defined similarly
xij =
−.825 if experimental unit received treatment 1
−.325 if experimental unit received treatment 2
.175 if experimental unit received treatment 3
.975 if experimental unit received treatment 4
ˆ
Y= 1.06647−.24917X1−.26917X2−.23917X3−.12917X4+.02333X5−.09667X6
−.05667X7+.13333X8+.18583X9+.21583X10+.15833X11−.11341x−.19192x2
e. eij:
i j = 1 j= 2 j= 3 j= 4
1.02976 −.03389 .02842 −.02429
2.00976 −.03389 .01842 .00571
3.00976 −.02389 .02842 −.01429
4.04976 −.00389 −.00158 −.04429
5−.02274 .02361 −.02408 .02321
6.02726 −.05639 .07592 −.04679
7.00726 −.02639 −.00408 .02321
8.00726 −.01639 .00592 .00321
9−.01524 −.02889 .04342 .00071
10 .00476 −.06889 .04342 .02071
11 .04226 −.04139 −.01908 .01821
12 −.04274 .01361 .04592 −.01679
f. H0:γ2= 0, Ha:γ26= 0. SSE(F) = .0456, SSE(R) = .2816,
F∗= (.2360/1) ÷(.0456/34) = 175.96, F(.99; 1,34) = 7.44.
If F∗≤7.44 conclude H0, otherwise Ha. Conclude Ha.
27.27. Note: The subscript for subjects here is linstead of the usual iand the subscripts
for factors A,B, and Care i,j, and k, respectively.
a. Yijklm =µ.... +αi+βj+γk+ρl(ik)+ (αβ)ij + (αγ)ik + (βγ)jk + (αβγ)ijk +²m(ijkl)
b. r=.990
27.28. a.
27-10

Source SS df MS
A(initial lever press rate) 7.99586 2 3.99793
B(dosage level) 25.90210 3 8.63403
C(reinforcement schedule) 59.74172 1 59.74172
AB interactions .35167 6 .05861
AC interactions .09465 2 .04733
BC interactions 12.36104 3 4.12035
ABC interactions .37040 6 .06173
S(AC) (rats, within AC) 1.64179 18 .09121
Error .36711 150 .00245
Total 108.82634 191
E{MSA}= 64 Pα2
i/2+8σ2
ρ+σ2
E{MSB}= 48 Pβ2
j/3 + σ2
E{MSC}= 96 Pγ2
k/1+8σ2
ρ+σ2
E{MSS(AC)}= 8σ2
ρ+σ2
E{MSAB}= 16 PP(αβ)2
ij/6 + σ2
E{MSAC}= 32 PP(αγ)2
ik/2+8σ2
ρ+σ2
E{MSBC}= 24 PP(βγ)2
jk/3 + σ2
E{MSABC}= 8 PPP(αβγ)2
ijk/6 + σ2
E{MSE}=σ2
b. H0: all (αβγ)ijk equal zero, Ha: not all (αβγ)ijk equal zero.
F∗=.06173/.00245 = 25.196, F(.99; 6,150) = 2.92.
If F∗≤2.92 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. ¯
Yijk..:
k i j = 1 j= 2 j= 3 j= 4
1 1 .81375 .82375 .83625 .53500
2 1.05375 1.06625 1.05625 .77375
3 1.25500 1.25625 1.27125 1.00750
2 1 2.15125 2.33625 1.88750 .88125
2 2.59250 2.58375 2.21875 1.01250
3 3.04750 2.75125 2.38125 1.29250
27.29. a.
F∗
RP(F∗
R)
0 12/216
.25 90/216
1.00 36/216
1.60 36/216
7.00 36/216
Undefined 6/216
b. F(.90; 2,4) = 4.32, P(F∗
R≤7.00) = .972, P(F∗
R≤1.60) = .806
27-11
27-12

Chapter 28
BALANCED INCOMPLETE
BLOCK, LATIN SQUARE, AND
RELATED DESIGNS
28.3. One such design, for which nb= 3, n= 2, and np= 1:
1 2
1 3
2 3
28.4. For r= 7, rb= 5, a BIBD exists for nb=7!
5!(7 −5)! = 21.
Since nbrb=nr,n= 21(5)/7 = 15.
Since np(r−1) = n(rb−1), np= 15(5 −1)/(7 −1) = 10.
28.5. For r= 8, rb= 3, a BIBD exists for nb=8!
3!(8 −3)! = 56.
Since nbrb=nr,n= 56(3)/8 = 21.
Since np(r−1) = n(rb−1), np= 21(3 −1)/(8 −1) = 6.
28.6. eij:
i j = 1 j= 2 j= 3 j= 4 j= 5 j= 6 j= 7 j= 8 j= 9
1−.704 .185 .519
2 .222 −.111 −.111
3 .556 −1.000 .444
4−.481 −.259 .741
5−.926 .296 .630
6−.519 .481 .037
7 .815 .259 −1.074
8 .222 .444 −.667
9−.111 .667 −.556
10 −.222 .444 −.222
11 1.444 −.667 −.778
12 .370 .926 −1.296
28-1
r=.990
28.7. a. ˆµ.. = 19.36, ˆτ1=.33, ˆτ2=−2.22, ˆτ3=−6.00, ˆτ4=−12.89, ˆτ5= 6.11, ˆτ6= 3.56,
ˆτ7= 1.22, ˆτ8=−.22, ˆτ9= 10.11.
ˆµ.1= 19.69, ˆµ.2= 17.14, ˆµ.3= 13.36, ˆµ.4= 6.47, ˆµ.5= 25.47, ˆµ.6= 22.92,
ˆµ.7= 20.58, ˆµ.8= 19.14, ˆµ.9= 29.47.
b. H0: all τjequal zero (j= 1,2,...,8), Ha: not all τjequal zero. SSE(F) = 14.519,
SSE(R) = 1097.33, F∗= (1082.811/8) ÷(14.519/16) = 149.2, F(.95; 8,16) =
2.59. If F∗≤2.59 conclude H0, otherwise Ha. Conclude Ha.P-value = 0+
c. H0: all ρiequal zero (j= 1,2, . . . , 11), Ha: not all ρiequal zero. SSE(F) = 14.519,
SSE(R) = 25.25, F∗= (10.731/11) ÷(14.519/16) = 1.08, F(.95; 11,16) = 2.46.
If F∗≤2.46 conclude H0, otherwise Ha. Conclude H0.P-value = .43
d. ˆµ.5= 25.47, s2(ˆµ.5) = s2(ˆµ..) + s2( ˆτ5)=(.02778 + .29630).907 = .2939, B=
t(.975; 16) = 2.120, 25.47 ±2.120(.542), 24.32 ≤µ.5≤26.62
e.
28-2

95% C.I. lower center upper
µ.1−µ.2−.21 2.56 5.32
µ.1−µ.33.57 6.33 9.10
µ.1−µ.410.46 13.22 15.99
µ.1−µ.5−8.54 −5.78 −3.01
µ.1−µ.6−5.99 −3.22 −.46
µ.1−µ.7−3.66 −.89 1.88
µ.1−µ.8−2.21 .56 3.32
µ.1−µ.9−12.54 −9.78 −7.01
µ.2−µ.31.01 3.78 6.54
µ.2−µ.47.90 10.67 13.43
µ.2−µ.5−11.10 −8.33 −5.57
µ.2−µ.6−8.54 −5.78 −3.01
µ.2−µ.7−6.21 −3.44 −.68
µ.2−µ.8−4.77 −2.00 .77
µ.2−µ.9−15.10 −12.33 −9.57
µ.3−µ.44.12 6.89 9.66
µ.3−µ.5−14.88 −12.11 −9.35
µ.3−µ.6−12.32 −9.56 −6.79
µ.3−µ.7−9.99 −7.22 −4.46
µ.3−µ.8−8.54 −5.78 −3.01
µ.3−µ.9−18.88 −16.11 −13.35
µ.4−µ.5−21.77 −19.00 −16.23
µ.4−µ.6−19.21 −16.44 −13.68
µ.4−µ.7−16.88 −14.11 −11.35
µ.4−µ.8−15.43 −12.67 −9.90
µ.4−µ.9−25.77 −23.00 −20.23
µ.5−µ.6−.21 2.56 5.32
µ.5−µ.72.12 4.89 7.66
µ.5−µ.83.57 6.33 9.10
µ.5−µ.9−6.77 −4.00 −1.23
µ.6−µ.7−.43 2.33 5.10
µ.6−µ.81.01 3.78 6.54
µ.6−µ.9−9.32 −6.56 −3.79
µ.7−µ.8−1.32 1.44 4.21
µ.7−µ.9−11.66 −8.89 −6.12
µ.8−µ.9−13.10 −10.33 −7.57
28.8. a. eij:
i j = 1 j= 2 j= 3 j= 4
1 13.2083 8.8333 −22.0417
2−7.9167 4.7083 3.2083
3−5.2917 −1.5417 6.8333
4−13.5417 23.5833 −10.0417
r=.995
28-3
28.9. a. ˆµ.. = 297.667, ˆτ1=−45.375, ˆτ2=−41.000, ˆτ3= 30.875, ˆτ4= 55.500
ˆµ.1= 252.292, ˆµ.2= 256.667, ˆµ.3= 328.542, ˆµ.4= 353.167
b. H0:τ1=τ2=τ3= 0, Ha: not all τjequal zero. SSE(F) = 1750.9, SSE(R) =
22480, F∗= (20729.1/3) ÷(1750.9/5) = 19.73, F(.95; 3,5) = 5.41. If F∗≤5.41
conclude H0, otherwise Ha. Conclude Ha.P-value = .003
c. H0:ρ1=ρ2=ρ3= 0, Ha: not all ρiequal zero. SSE(F) = 14.519, SSE(R) =
22789, F∗= (21038.1/3) ÷(1750.9/5) = 20.03, F(.95; 3,5) = 5.41. If F∗≤5.41
conclude H0, otherwise Ha. Conclude Ha.P-value = .003
d. ˆµ.1= 252.292, s2(ˆµ.1) = s2(ˆµ..) + s2( ˆτ1) = (.08333 + .28125)350.2 = 127.68,
B=t(.975; 5) = 2.571, 252.292 ±2.571(11.30), 223.240 ≤µ.1≤281.344
e.
95% C.I. lower center upper
µ.1−µ.2−64.19 −4.375 55.44
µ.1−µ.3−136.07 −76.250 −16.43
µ.1−µ.4−160.69 −100.875 −41.06
µ.2−µ.3−131.70 −71.87 −12.06
µ.2−µ.4−156.30 −96.50 −36.68
µ.3−µ.4−84.44 −24.63 35.19
28.10. r= 4, and rb= 3, dfe= 4n−4−4n/3 + 1 = 8n/3−3.
Since np=n(3 −1)/(4 −1) = 2n/3, σ2{ˆ
Dj}= 2σ2(3)/(4np) = 9σ2/(4n)
T σ{ˆ
Dj}=1
√2q[.95; 4,8n/3−3]s9σ2
4n
For σ2= 2.0 and T σ{ˆ
Dj} ≤ 1.5, so we need to iterate to find nso that
n≥q2[.95; 4,8n/3−3]
We iteratively find n≥15. Since design 2 in Table 28.1 has n= 3, we require
that design 2 be repeated 5 times. Thus, n= 15, and nb= 20.
28.11. r= 5, and rb= 4, dfe= 5n−5−5n/4 + 1 = 15n/4−4.
Since np=n(4 −1)/(5 −1) = 3n/4, σ2{ˆ
Dj}= 2σ2(4)/(5np) = 32σ2/(15n)
T σ{ˆ
Dj}=1
√2q[.90; 5,15n/4−4]s32σ2
15n
For σ2= 1.5 and T σ{ˆ
Dj} ≤ 1.25, so we need to iterate to find nso that
n≥1.024q2[.90; 5,15n/4−4]
We iteratively find n≥14. Since design 5 in Table 28.1 has n= 4, we require
that design 2 be repeated 4 times. Thus, n= 16, and nb= 20.
28.14. eijk:
i j = 1 j= 2 j= 3 j= 4
1−.1375 .0875 −.0125 .0625
2−.0125 −.0125 .1625 −.1375
3.1375 −.0875 −.0625 .0125
4.0125 .0125 −.0875 .0625
28-4

r=.986
28.15. a. ¯
Y..1= 1.725, ¯
Y..2= 1.900, ¯
Y..3= 2.175, ¯
Y..4= 2.425
b.
Source SS df MS
Rows (sales volumes) 5.98187 3 1.99396
Columns (locations) .12188 3 .04062
Treatments (prices) 1.13688 3 .37896
Error .11875 6 .01979
Total 7.35938 15
H0: all τkequal zero (k= 1, ..., 4), Ha: not all τkequal zero. F∗=.37896/.01979 =
19.149, F(.95; 3,6) = 4.76. If F∗≤4.76 conclude H0, otherwise Ha. Conclude
Ha.P-value = .002
c. ˆ
L1=¯
Y..1−¯
Y..2=−.175, ˆ
L2=¯
Y..1−¯
Y..3=−.450, ˆ
L3=¯
Y..1−¯
Y..4=−.700,
ˆ
L4=¯
Y..2−¯
Y..3=−.275, ˆ
L5=¯
Y..2−¯
Y..4=−.525,ˆ
L6=¯
Y..3−¯
Y..4=−.250,
s{ˆ
Li}=.09947 (i= 1, ..., 6), q(.90; 4,6) = 4.07, T= 2.8779
−.175 ±2.8779(.09947) −.461 ≤L1≤.111
−.450 ±2.8779(.09947) −.736 ≤L2≤ −.164
−.700 ±2.8779(.09947) −.986 ≤L3≤ −.414
−.275 ±2.8779(.09947) −.561 ≤L4≤.011
−.525 ±2.8779(.09947) −.811 ≤L5≤ −.239
−.250 ±2.8779(.09947) −.536 ≤L6≤.036
28.16. a. ˆ
E1= 21.1617, ˆ
E2= 1.2631, ˆ
E3= 25.9390
28.17. eijk:
i j = 1 j= 2 j= 3 j= 4 j= 5
1−.88 −.68 .92 .32 .32
2.32 .12 −.28 .92 −1.08
3.52 −.68 −1.08 .12 1.12
4−.68 1.92 .52 −.08 −1.68
5.72 −.68 −.08 −1.28 1.32
r=.993
28.18. a. ¯
Y..1= 7.0, ¯
Y..2= 7.4, ¯
Y..3= 15.0, ¯
Y..4= 19.0, ¯
Y..5= 13.4
b.
Source SS df MS
Rows (executives) 220.16 4 55.040
Columns (months) 10.96 4 2.740
Treatments (reports) 527.36 4 131.840
Error 19.28 12 1.607
Total 777.76 24
H0: all τkequal zero (k= 1, ..., 5), Ha: not all τkequal zero. F∗= 131.840/1.607 =
82.04, F(.99; 4,12) = 5.41. If F∗≤5.41 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
28-5

c. ˆ
L1=¯
Y..1−¯
Y..2=−.4, ˆ
L2=¯
Y..1−¯
Y..3=−8.0, ˆ
L3=¯
Y..1−¯
Y..4=−12.0,
ˆ
L4=¯
Y..1−¯
Y..5=−6.4, ˆ
L5=¯
Y..2−¯
Y..3=−7.6, ˆ
L6=¯
Y..2−¯
Y..4=−11.6,
ˆ
L7=¯
Y..2−¯
Y..5=−6.0, ˆ
L8=¯
Y..3−¯
Y..4=−4.0, ˆ
L9=¯
Y..3−¯
Y..5= 1.6, ˆ
L10 =
¯
Y..4−¯
Y..5= 5.6, s{ˆ
Li}=.8017 (i= 1, ..., 10), q(.95; 5,12) = 4.51, T= 3.189
−.4±3.189(.8017) −2.96 ≤L1≤2.16
−8.0±3.189(.8017) −10.56 ≤L2≤ −5.44
−12.0±3.189(.8017) −14.56 ≤L3≤ −9.44
−6.4±3.189(.8017) −8.96 ≤L4≤ −3.84
−7.6±3.189(.8017) −10.16 ≤L5≤ −5.04
−11.6±3.189(.8017) −14.16 ≤L6≤ −9.04
−6.0±3.189(.8017) −8.56 ≤L7≤ −3.44
−4.0±3.189(.8017) −6.56 ≤L8≤ −1.44
1.6±3.189(.8017) −.96 ≤L9≤4.16
5.6±3.189(.8017) 3.04 ≤L10 ≤8.16
28.19. a. ˆ
E1= 6.66, ˆ
E2= 1.14, ˆ
E3= 7.65
28.20. φ= 3.399, 1 −β∼
=.99
28.21. φ= 2.202, 1 −β∼
=.69
28.22. eijkl:
i j = 1 j= 2 j= 3 j= 4
1.01625 −.01875 .01625 −.01375
2.00625 .01875 −.05375 .02875
3−.00875 −.03125 .03375 .00625
4−.01375 .03125 .00375 −.02125
r=.980
28.23. a. Yijkl =µ... +ρi+κj+αk+βl+ (αβ)kl +²(ijkl)
b.
Source SS df MS
Rows (subjects) .03462 3 .01154
Columns (periods) .00592 3 .00197
Treatments .43333 3 .14444
X .22801 1 .22801
Y .19581 1 .19581
XY interactions .00951 1 .00951
Error .00904 6 .00151
Total .48291 15
H0: all (αβ)kl equal zero, Ha: not all (αβ)kl equal zero. F∗=.00951/.00151 =
6.298, F(.90; 1,6) = 3.78. If F∗≤3.78 conclude H0, otherwise Ha. Conclude Ha.
P-value = .046
c. ¯
Y..1=.0050, ¯
Y..2=.1950, ¯
Y..3=.1775, ¯
Y..4=.4650, ˆ
L=−.0975, s{ˆ
L}=.03886,
t(.95; 6) = 1.943, −.0975 ±1.943(.03886),−.1730 ≤L≤ −.0220
28-6

28.24. a. Yijk =µ... +ρ1Xijk1+ρ2Xijk2+ρ3Xijk3+κ1Xijk4+κ2Xijk5
+κ3Xijk6+τ1Xijk7+τ2Xijk8+τ3Xijk9+²(ijk)
Xijk1=
1 if experimental unit from row blocking class 1
−1 if experimental unit from row blocking class 4
0 otherwise
Xijk2and Xijk3are defined similarly
Xijk4=
1 if experimental unit from column blocking class 1
−1 if experimental unit from column blocking class 4
0 otherwise
Xijk5and Xijk6are defined similarly
Xijk7=
1 if experimental unit received treatment 1
−1 if experimental unit received treatment 4
0 otherwise
Xijk8and Xijk9are defined similarly
b. Full model:
ˆ
Y= 2.05625 −.70625X1−.45625X2+.34375X3+.14375X4
−.05625X5−.00625X6−.33125X7−.15625X8+.11875X9
SSE(F) = .1188
Reduced model:
ˆ
Y= 2.05625−.70625X1−.45625X2+.34375X3+.14375X4−.05625X5−.00625X6
SSE(R) = 1.2556
H0: all τkequal zero (k= 1,2,3), Ha: not all τkequal zero. F∗= (1.1368/3) ÷
(.1188/6) = 19.138, F(.95; 3,6) = 4.76.If F∗≤4.76 conclude H0, otherwise Ha.
Conclude Ha.
c. ˆ
L= ˆτ3−(−ˆτ1−ˆτ2−ˆτ3) = 2ˆτ3+ ˆτ1+ ˆτ2=−.250, s2{ˆτi}=.00371 (i= 1,2,3),
s{ˆτ1,ˆτ2}=s{ˆτ1,ˆτ3}=s{ˆτ2,ˆτ3}=−.00124, s{ˆ
L}=.09930, t(.975; 6) = 2.447,
−.250 ±2.447(.09930),−.493 ≤L≤ −.007
d. (i) Full model:
ˆ
Y= 2.02917 −.67917X1−.53750X2+.37083X3+.17083X4−.02917X5
−.08750X6−.30417X7−.23750X8+.14583X9
SSE(F) = .0483
Reduced model:
ˆ
Y= 2.05556−.70556X1−.45833X2+.34444X3+.14444X4−.05556X5−.00833X6
SSE(R) = 1.2556
H0: all τkequal zero (k= 1,2,3), Ha: not all τkequal zero. F∗= (1.2073/3) ÷
(.0483/5) = 41.66, F(.95; 3,5) = 5.41. If F∗≤5.41 conclude H0, otherwise Ha.
Conclude Ha.
28-7

(ii) ˆ
L= ˆτ1−ˆτ2=−.06667, s2{ˆτ1}=.00191, s2{ˆτ2}=.00272, s{ˆτ1,ˆτ2}=
−.00091, s{ˆ
L}=.0803, t(.975; 5) = 2.571,−.06667 ±2.571(.0803), −.273 ≤L≤
.140
28.25. a. Full model:
ˆ
Y= 12.54286 + 1.91429X1−3.54286X2+ 3.25714X3−3.28571X4+ 1.11429X5
−.34286X6−.94286X7−.74286X8−5.54286X9
−5.14286X10 + 3.11329X11 + 6.71429X12
SSE(F) = 12.6286
Reduced model:
ˆ
Y= 11.96471 + .44706X1−2.96471X2+ 3.83529X3−3.55294X4−.35294X5
+.23529X6−.36471X7−.16471X8
SSE(R) = 494.2353
H0: all τkequal zero (k= 1, ..., 4), Ha: not all τkequal zero. F∗= (481.6067/4) ÷
(12.6286/10) = 95.340, F(.99; 4,10) = 5.99. If F∗≤5.99 conclude H0, otherwise
Ha. Conclude Ha.
b. ˆ
L= ˆτ4−ˆτ1= 12.25715, s2{ˆτ1}=.20927, s2{ˆτ4}=.28144, s{ˆτ1,ˆτ4}=−.06134,
s{ˆ
L}=.7832, t(.995; 10) = 3.169, 12.25715 ±3.169(.7832), 9.775 ≤L≤14.739
28.26. eijkm:
i m j = 1 j= 2 j= 3 j= 4
1 1 −1.9375 −1.5625 .6875 1.3125
2 1.0625 3.4375 −2.3125 −.6875
2 1 −3.6875 6.0625 −1.1875 3.8125
2 2.3125 .0625 −5.1875 −2.1875
3 1 −4.0625 1.1875 −.6875 4.0625
2 2.9375 −4.8125 4.3125 −2.9375
4 1 −.3125 .3125 .1875 −2.6875
2 3.6875 −4.6875 4.1875 −.6875
r=.990
28.27. a. Yijklm =µ... +ρi+κj+αk+βl+ (αβ)kl +²m(ijkl)
b.
Source SS df MS
Rows (ages) 658.09375 3 219.36458
Columns (education levels) 18.34375 3 6.11458
Treatments 1,251.34375 3 417.11458
Volumes 399.03125 1 399.03125
Products 850.78125 1 850.78125
Volume-product interactions 1.53125 1 1.53125
Error 285.43750 22 12.97443
Total 2,213.21875 31
28-8

H0: all (αβ)kl equal zero, Ha: not all (αβ)kl equal zero. F∗= 1.53125/12.97443 =
.118, F(.99; 1,22) = 7.95. If F∗≤7.95 conclude H0, otherwise Ha. Conclude H0.
P-value = .73
c. H0:α1=α2= 0, Ha: not both α1and α2equal zero. F∗= 399.03125/12.97443 =
30.755, F(.99; 1,22) = 7.95.If F∗≤7.95 conclude H0, otherwise Ha. Conclude
Ha. P -value = 0+
H0:β1=β2= 0, Ha: not both β1and β2equal zero. F∗= 850.78125/12.97443 =
65.574, F(.99; 1,22) = 7.95.If F∗≤7.95 conclude H0, otherwise Ha. Conclude
Ha. P -value = 0+
d. ¯
Y..1.= 61.750, ¯
Y..2.= 69.250, ¯
Y..3.= 72.500, ¯
Y..4.= 79.125,
L1=µ..1+µ..3
2−µ..2+µ..4
2
L2=µ..1+µ..2
2−µ..3+µ..4
2
ˆ
L1=−7.0625, ˆ
L2=−10.3125, s{ˆ
L1}=s{ˆ
L2}= 1.2735,
B=t(.9875; 22) = 2.4055
−7.0625 ±2.4055(1.2735) −10.126 ≤L1≤ −3.999
−10.3125 ±2.4055(1.2735) −13.376 ≤L2≤ −7.249
28.28. eijkm:
j= 1 j= 2 j= 3
m= 1 4.3704 −2.7407 −1.6296
i= 1 m= 2 −3.6296 1.2593 2.3704
m= 3 −2.2963 3.5926 −1.2963
m= 1 −.9630 −1.1852 2.1481
i= 2 m= 2 1.0370 −1.1852 .1481
m= 3 2.0370 1.8148 −3.8519
m= 1 −3.5185 −.8519 4.3704
i= 3 m= 2 .1481 3.8148 −3.9630
m= 3 2.8148 −4.5185 1.7037
r=.986
28.29. a.
Source SS df MS
Patterns 14.2963 2 7.1481
Order positions 1,803.6296 2 901.8148
Questionnaires 3,472.0741 2 1,736.0370
Subjects (within patterns) 159.5556 6 26.5926
Error 194.9630 14 13.9259
Total 5,644.5185 26
H0: all ρiequal zero (i= 1, 2, 3), Ha: not all ρiequal zero. F∗= 7.1481/26.5926 =
.269, F(.95; 2,6) = 5.14. If F∗≤5.14 conclude H0, otherwise Ha. Conclude H0.
P-value = .77
28-9
H0: all κjequal zero (j= 1,2,3), Ha: not all κjequal zero. F∗= 901.8148/13.9259 =
64.758, F(.95; 2,14) = 3.74. If F∗≤3.74 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
H0: all τkequal zero (k= 1,2,3), Ha: not all τkequal zero. F∗= 1,736.0370/13.9259 =
126.66, F(.95; 2,14) = 3.74.If F∗≤3.74 conclude H0, otherwise Ha. Conclude
Ha.P-value = 0+
b. ¯
Y..1.= 22.3333, ¯
Y..2.= 22.4444, ¯
Y..3.= 46.4444,ˆ
L1=¯
Y..1.−¯
Y..2.=−.1111,
ˆ
L2=¯
Y..1.−¯
Y..3.=−24.1111,ˆ
L3=¯
Y..2.−¯
Y..3.=−24.0000, s{ˆ
Li}= 1.75916
(i= 1,2,3), q(.90; 3,14) = 3.16, T= 2.234
−.1111 ±2.234(1.75916) −4.0411 ≤µ..1−µ..2≤3.8189
−24.1111 ±2.234(1.75916) −28.0411 ≤µ..1−µ..3≤ −20.1811
−24.0000 ±2.234(1.75916) −27.9300 ≤µ..2−µ..3≤ −20.0700
28-10

Chapter 29
EXPLORATORY EXPERIMENTS –
TWO-LEVEL FACTORIAL AND
FRACTIONAL FACTORIAL
DESIGNS
29.1. Yi=β0Xi0+β1Xil +β2Xi2+β3Xi3+β4Xi4+β12Xi12 +β13Xi13
+β14Xi14 +β23Xi23 +β24Xi24 +β34Xi34 +β123Xi123
+β124Xi124 +β134Xi134 +β234Xi234 +β1234Xi1234 +²i
6, 4, 1
29.2. Fractional factorial designs can be used.
29.3. a. Six factors, two levels, 64 trials
b. No
29.4. a. Seven factors, two levels, 8 trials; no
b. Yes, no
29.5.
X0X1X2X3X12 X13 X23 X123
1−1−1−1111−1
1 1 −1−1−1−1 1 1
1−1 1 −1−1 1 −1 1
1 1 1 −1 1 −1−1−1
1−1−1 1 1 −1−1 1
1 1 −1 1 −1 1 −1−1
1−1 1 1 −1−1 1 −1
1 1 1 1 1 1 1 1
29-1

X0X=
80000000
08000000
00800000
00080000
00008000
00000800
00000080
00000008
= 8I=nTI
29.6. a. σ2{b1}=σ2/nT= 52/64 = .391. Yes, yes
b. z(.975) = 1.96, nT= [1.96(5)/(.5)]2= 384.16, 384.16/64 = 6 replicates
29.7. a. Yi=β0Xi0+β1Xi1+· · · +β5Xi5+β12Xi12 +···+β45Xi45 +β123Xi123
+···+β345Xi345 +β1234Xi1234 +· · · +β2345Xi2345 +β12345Xi12345 +²i
Coef. bq
b06.853
b11.606
b2−.099
b31.258
b4−1.151
b5−1.338
b12 −.033
b13 .455
Coef. bq
b14 −.239
b15 .611
b23 −.134
b24 −.127
b25 −.045
b34 −.311
b35 .912
b45 −.198
Coef. bq
b123 .070
b124 .020
b125 −.118
b134 −.378
b135 −.138
b145 −.183
b234 .233
b235 .055
Coef. bq
b245 .076
b345 −.576
b1234 .062
b1235 .323
b1245 .357
b1345 −.122
b2345 −.292
b12345 .043
29.8. a. Yi=β0Xi0+β1Xi1+· · · +β5Xi5+β12Xi12 +···+β45Xi45 +²i
Coef. bqP-value
b06.853
b11.606 .000
b2−.099 .689
b31.258 .000
b4−1.151 .000
b5−1.338 .000
b12 −.033 .892
b13 .455 .080
Coef. bqP-value
b14 −.239 .340
b15 .611 .023
b23 −.134 .589
b24 −.127 .610
b25 −.045 .855
b34 −.311 .219
b35 .912 .002
b45 −.198 .426
b. H0: Normal, Ha: not normal. r=.983. If r≥.9656 conclude H0, otherwise Ha.
Conclude H0.
c. H0:βq= 0, Ha:βq6= 0. s{bq}=.2432. If P-value ≥.0034 conclude H0, otherwise
Ha. Active effects (see part a): β1,β3,β4,β5,β35
29.9. a. Yi=β0+β1Xi1+···+β4Xi4+β12Xi12 +···+β34Xi34 +β123Xi123
+···+β234Xi234 +β1234Xi1234 +²i
29-2

Coef. bqP-value
b03.7784
b1−.3113 .020
b2−.0062 .903
b3−.1463 .083
b4.0837 .204
b12 .0050 .922
b13 .0400 .468
b14 .0025 .961
Coef. bqP-value
b23 −.0925 .176
b24 .0125 .807
b34 −.2175 .040
b123 −.0087 .865
b124 .0538 .354
b134 −.0363 .505
b234 −.0138 .788
b1234 .0050 .922
(Note: P-values based on MSP E; see part d.)
d. H0:βq= 0, Ha:βq6= 0. MSP E =.0324, s{bq}=q.0324/16 = .0450. If P-value
≥.05 conclude H0, otherwise Ha. Active effects (see part a): β1,β34
29.10. a.
Coef. bqP-value
b03.778
b1−.3112 .000
b3−.1462 .006
b4.0838 .084
b34 −.2175 .000
b. H0: Normal, Ha: not normal. r=.970. If r≥.9485 conclude H0, otherwise Ha.
Conclude H0.
c. H0:βq= 0, Ha:βq6= 0. s{bq}=.0449. If P-value ≥.01 conclude H0, otherwise
Ha. Active effects (see part a): β1,β3,β34.
d. H0: No lack of fit, Ha: lack of fit. SSLF =SSE −SSP E =.45248 −.25617 =
.19631. F∗= [.19631/4] ÷(.25617/10) = 1.92, F(.95; 4,10) = 3.48. If F∗≤3.48
conclude H0, otherwise Ha. Conclude H0.
e. Set X1,X3,X4at high levels to minimize failure rate.
29.11. a. 0 = −234, resolution = III
b. 0 = −234, 1 = −1234, 2 = −34, 3 = −24, 4 = −23, 12 = −134,
13 = −124, 14 = −123
29.12. a.
X1X2X3X4
−1−1−1−1
1−1−1 1
−1 1 −1 1
1 1 −1−1
−1−1 1 1
1−1 1 −1
−1 1 1 −1
1 1 1 1
Resolution = IV
29-3

b. For example, dropping X1and arranging in standard order:
X2X3X4
−1−1−1
1−1−1
−1 1 −1
1 1 −1
−1−1 1
1−1 1
−1 1 1
1 1 1
29.13. No
29.14.
X1X2X3X4
1−1−1−1
−1 1 −1−1
−1−1 1 −1
1 1 1 −1
1−1−1 1
−1 1 −1 1
−1−1 1 1
1 1 1 1
Yes; use 0 = 1234 for resolution IV.
29.15. Defining relation: 0 = 123 = 245 = 1345
Confounding scheme:
0 = 123 = 245 = 1345
1 = 23 = 1245 = 345
2 = 13 = 45 = 12345
3 = 12 = 2345 = 145
4 = 1234 = 25 = 135
5 = 1235 = 24 = 134
14 = 234 = 125 = 35
15 = 235 = 124 = 34
Resolution = III, no
29.16. Defining relation: 0 = −145 = −234 = 1235
Confounding scheme:
0 = −145 = −234 = 1235
1 = −45 = −1234 = 235
2 = −1245 = −34 = 135
3 = −1345 = −24 = 125
4 = −15 = −23 = 12345
5 = −14 = −2345 = 123
12 = −245 = −134 = 35
13 = −345 = −124 = 25
29-4

No
29.17. Defining relation: 0 = 124 = 135 = 2345 = 236 = 1346 = 1256 = 456
X1X2X3X4X5X6
−1−1−1 1 1 1
1−1−1−1−1 1
−1 1 −1−1 1 −1
1 1 −1 1 −1−1
−1−1 1 1 −1−1
1−1 1 −1 1 −1
−1 1 1 −1−1 1
1 1 1 1 1 1
Resolution = III
29.18. a. Defining relation: 0 = 1235 = 2346 = 1247 = 1456 = 3457 = 1367 = 2567,
resolution = IV, no
b. Omitting four-factor and higher-order interactions:
1 = 235 = 247 = 367 = 456
2 = 135 = 147 = 346 = 567
3 = 125 = 167 = 246 = 457
4 = 127 = 156 = 236 = 357
5 = 123 = 146 = 267 = 347
6 = 137 = 145 = 234 = 257
7 = 124 = 136 = 256 = 345
12 = 35 = 47
13 = 25 = 67
14 = 27 = 56
15 = 23 = 46
16 = 37 = 45
17 = 24 = 36
26 = 34 = 57
c. Yi=β0Xi0+β1Xi1+· · · +β7Xi7+β12Xi12 +β13Xi13 +β14Xi14
+β15Xi15 +β16Xi16 +β17Xi17 +β26Xi26 +²i
Coef. bq
b08.028
b1.127
b2.003
b3.021
b4−2.077
Coef. bq
b5.724
b6−.467
b7−.766
b12 .354
b13 −.066
Coef. bq
b14 −.316
b15 .318
b16 .117
b17 .021
b26 −.182
e. H0:β12 =···=β17 =β26 = 0, Ha: not all βq= 0. F∗= (6.046/7) ÷(.1958/1) =
4.41, F(.99; 7,1) = 5,928. If F∗≤5,928 conclude H0, otherwise Ha. Conclude
H0.
29.19. a.
29-5
Coef. bqP-value
b08.028
b1.127 .581
b2.003 .989
b3.021 .928
Coef. bqP-value
b4−2.077 .000
b5.724 .011
b6−.467 .067
b7−.766 .008
b. H0: Case inot an outlier, Ha: case ian outlier (i= 3,14). t3= 2.70, t14 =−4.09,
t(.99844; 7) = 4.41. If |ti|≤ 4.41 conclude H0, otherwise Ha. Conclude H0for
both cases.
c. H0: Normal, Ha: not normal. r=.938. If r≥.929 conclude H0, otherwise Ha.
Conclude H0.
d. H0:βq= 0, Ha:βq6= 0. s{bq}=.2208. If P-value ≥.02 conclude H0, otherwise
Ha. Active effects (see part a): β4,β5,β7
e. Set X4=−1, X5= 1, X7=−1 to maximize extraction.
29.20. a. Yi=β0Xi0+β1Xi1+· · · +β9Xi9+²i
Coef. bqP-value
b070.11
b113.52 .060
b2−.99 .870
b31.32 .829
b42.36 .701
Coef. bqP-value
b513.49 .060
b6.12 .984
b7−21.58 .010
b8−4.07 .512
b93.07 .618
d. H0:βq= 0, Ha:βq6= 0. s{bq}= 5.841. If P-value ≥.10 conclude H0, otherwise
Ha. Active effects (see part a): β1,β5,β7.
29.21. a. b0= 70.11, b1= 13.52, b5= 13.49, b7=−21.58
b. H0: Normal, Ha: not normal. r=.951. If r≥.941 conclude H0, otherwise Ha.
Conclude H0.
c. H0: No lack of fit, Ha: lack of fit. SSLF =SSE−SSP E = 3,824−1,068 = 2,756,
F∗= (2,756/4) ÷(1,068/8) = 5.16, F(.95; 4,8) = 3.84. If F∗≤3.84 conclude
H0, otherwise Ha. Conclude Ha.
29.22. a. Yi=β0Xi0+β1Xi1+β5Xi5+β7Xi7+β15Xi15 +β17Xi17
+β57Xi57 +β157Xi157 +²i
Coef. bqP-value
b070.11
b113.52 .000
b513.49 .000
b7−21.58 .000
Coef. bqP-value
b15 11.68 .004
b17 −1.32 .660
b57 5.83 .078
b157 .12 .968
H0:βq= 0, Ha:βq6= 0. s{bq}= 2.889. If P-value ≥.01 conclude H0, otherwise
Ha. Active effects: β1,β5,β7,β15
29.23. a. Defining relation: 0 = 134
Confounding scheme:
29-6

0 = 134
1 = 34
2 = 1234
3 = 14
4 = 13
12 = 234
23 = 124
24 = 123
Yes. Defining relation 0 = 1234 would yield a resolution IV design.
b. Yi=β0Xi0+β1Xi1+β2Xi2+β3Xi3+β4Xi4+β12Xi12
+β23Xi23 +β24Xi24 +²i
Coef. bq
b0747.50
b1−207.25
b2−17.00
b3108.00
Coef. bq
b488.25
b12 −24.75
b23 −29.00
b24 −18.75
29.24. a.
Coef. bqP-value
b0747.50
b1−207.25 .003
b2−17.00 .538
b3108.00 .022
b488.25 .037
H0:βq= 0, Ha:βq6= 0. s{bq}= 24.53. If P-value ≥.05 conclude H0, otherwise
Ha. Active effects: β1,β3,β4
b. Set X1=−1, X3= 1, X4= 1 to maximize defect-free moldings.
29.25. Confounding scheme for design:
0 = 124 = 135 = 2345
1 = 24 = 35 = 12345
2 = 14 = 1235 = 345
3 = 1234 = 15 = 245
4 = 12 = 1345 = 235
5 = 1245 = 13 = 234
23 = 134 = 125 = 45 = Block effect
25 = 145 = 123 = 34
Design:
Block X1X2X3X4X5
1−1 1 −1−1 1
1 1 1 −1 1 −1
1−1−1 1 1 −1
1 1 −1 1 −1 1
2−1−1−1 1 1
2 1 −1−1−1−1
2−1 1 1 −1−1
2 1 1 1 1 1
29-7

29.26. b. The seven block effects are confounded with the following interaction terms: β135,
β146,β236,β245,β1234,β1256,β3456
No, no
c. Yi=β0Xi0+β1Xi1+· · · +β6Xi6+β12Xi12 +···+β56Xi56 +β123Xi123
+···+β456Xi456 +β1235Xi1235 +· · · +β2456Xi2456 +β12345Xi12345
+···+β23456Xi23456 +β123456Xi123456 +α1Zi1+···+α7Zi7+²i
where α1, ..., α7are the block effects
Coef. bq
b063.922
b12.297
b25.797
b32.172
b42.359
b52.828
b62.922
b12 .547
b13 −.266
b14 −.203
b15 −.797
b16 −.141
b23 −.641
b24 −1.141
b25 .891
b26 .047
Coef. bq
b34 .297
b35 .266
b36 .984
b45 −.422
b46 −.141
b56 .516
b123 .422
b124 .172
b125 1.391
b126 .984
b134 .297
b136 −.641
b145 −.109
b156 −.547
b234 .234
b235 .266
Coef. bq
b246 −.391
b256 .078
b345 −.672
b346 .734
b356 −.734
b456 −.234
b1235 .578
b1236 .922
b1245 .453
b1246 .109
b1345 −.797
b1346 .547
b1356 −1.109
b1456 −.109
b2345 .328
b2346 −.578
Coef. bq
b2356 .766
b2456 .203
b12345 −.297
b12346 −.391
b12356 −.734
b12456 −.422
b13456 −.109
b23456 .203
b123456 .016
Block 1 −4.172
Block 2 −.422
Block 3 1.203
Block 4 6.703
Block 5 −.797
Block 6 −1.047
Block 7 −9.547
29.27. a.
Coef. bqP-value
b063.922
b12.297 .000
b25.797 .000
b32.172 .001
b42.359 .000
b52.828 .000
b62.922 .000
b12 .547 .346
b13 −.266 .645
b14 −.203 .725
b15 −.797 .172
b16 −.141 .807
b23 −.641 .270
b24 −1.141 .054
b25 .891 .128
Coef. bqP-value
b26 .047 .935
b34 .297 .607
b35 .266 .645
b36 .984 .094
b45 −.422 .466
b46 −.141 .807
b56 .516 .373
Block 1 −4.172 .009
Block 2 −.422 .782
Block 3 1.203 .432
Block 4 6.703 .000
Block 5 −.797 .602
Block 6 −1.047 .494
Block 7 −9.547 .000
b. H0: Normal, Ha: not normal. r=.989. If r≥.9812 conclude H0, otherwise Ha.
Conclude H0.
29-8

c. H0:βq= 0, Ha:βq6= 0. s{ˆαi}= 1.513 for block effects, s{bq}=.5719 for factor
effects. If P-value ≥.01 conclude H0, otherwise Ha. Active effects (see part a):
Block effects 1, 4, 7, all main effects
29.28. a. See Problem 29.27a for estimated factor and block effects. (These do not change
with subset model.)
b. Maximum team effectiveness is accomplished by setting each factor at its high
level.
c. ˆ
Yh= 82.297, s{pred}= 4.857, t(.975; 50) = 2.009, 82.297 ±2.009(4.857), 72.54 ≤
Yh(new)≤92.05
29.29. a. Defining relation: 0 = 12345, resolution = V
b. Yi=β0Xi0+β1Xi1+· · · +β5Xi5+β12Xi12 +···+β35Xi35 +α1Zi1+²i
where α1is the block effect
Coef. bq
b0113.18
b126.69
b2−10.94
b35.69
b44.44
b514.69
b12 21.94
b13 .56
Coef. bq
b14 −1.44
b15 −2.94
b23 1.44
b24 5.19
b25 2.94
b34 −3.44
b35 −.94
Block effect 2.27
d. H0:α1= 0, Ha:α16= 0. s{ˆα1}= 3.673, t∗= 2.27/3.673 = .62, (.975; 6) = 2.447.
If |t∗|≤ 2.447 conclude H0, otherwise Ha. Conclude H0.
e.
Coef. bqP-value
b0113.18
b126.69 .000
b2−10.94 .011
b35.69 .094
b44.44 .169
b514.69 .003
b12 21.94 .001
b13 .56 .847
Coef. bqP-value
b14 −1.44 .625
b15 −2.94 .336
b23 1.44 .625
b24 5.19 .119
b25 2.94 .336
b34 −3.44 .268
b35 −.94 .748
(Note: P-values based on MSP E; see part f.)
H0: No lack of fit, Ha: lack of fit. SSLF =SSE −SSP E = 1,894.4−609.5 =
1,284.9, F∗= (1,284.9/2)÷(609.5/5) = 5.270, F(.95; 2,5) = 5.786. If F∗≤5.786
conclude H0, otherwise Ha. Conclude H0.
f. H0:βq= 0, Ha:βq6= 0. M SP E = 121.90, s{bq}=q121.90/16 = 2.760. If
P-value ≥.025 conclude H0, otherwise Ha. Active effects (see part a): β1,β2,β5,
β12
29.30. a.
29-9

Coef. bq
b0113.18
b126.69
b2−10.94
Coef. bq
b514.69
b12 21.94
b. H0: Normal, Ha: not normal. r=.961. If r≥.954 conclude H0, otherwise Ha.
Conclude H0
c. Set factors 1, 2, 5 at their high levels to maximize whippability.
d. ˆ
Yh= 165.56, s{ˆ
Yh}= 8.03, t(.975; 17) = 2.110, 165.56 ±2.110(8.03), 148.62 ≤
E{Yh} ≤ 182.50
29.31. a.
i1 2 3 4 5 6 7 8
s2
i1.244 1.299 1.103 .992 1.966 1.916 1.589 1.576
loges2
i.218 .261 .098 −.008 .676 .650 .463 .455
i9 10 11 12 13 14 15 16
s2
i2.201 1.818 1.901 1.547 1.681 1.020 1.033 1.151
loges2
i.789 .598 .642 .437 .520 .020 .033 .141
b. d
loges2
i=.3746−.0553Xi1−.0919Xi2−.0048Xi3+.0229Xi4+.0289Xi12+.0021Xi13−
.0432Xi14−.0048Xi23+.0077Xi24−.2142Xi34+.0493Xi123+.0453Xi124−.0016Xi134−
.0024Xi234 +.0284Xi1234
X34 appears to be active.
c. ˆvi= 1.17395 (for i= 1,2,3,4,13,14,15,16)
ˆvi= 1.80173 (for i= 5, . . . , 12)
d. ˆ
Yi= 3.7082 −.3754Xi1
e. From location model: X1= +1; and from location model: (X3, X4) = (−1,−1) or
(+1,+1)
f. From dispersion model: ˆ
s2= exp(.3746 −.2142) = 1.17395,
and a 95% P.I. is (exp(.0453),exp(.2755)), or (1.0463, 1.3172).
g. d
MSE = 1.17395 + 3.3332= 12.284
29.32. a.
i1 2 3 4 5 6 7 8
s2
i.0164 .0173 .0804 .1100 .0010 .0079 .0953 .1134
loges2
i−4.109 −4.058 −2.521 −2.207 −6.949 −4.838 −2.351 −2.176
b. d
loges2
i=−3.651 + .331Xi1+ 1.337Xi2−.427Xi3−.275Xi4−.209Xi12 +.240Xi13 +
.477Xi14.
X2appears to be active.
c. ˆvi=.00682 (for i= 1,2,5,6)
ˆvi=.0989 (for i= 3,4,7,8)
d. ˆ
Yi= 7.5800 + .0772Xi1
29-10
e. From the location model: X1= +1; from the dispersion model: X2=−1
f. From dispersion model: ˆ
s2= exp(−3.651 + 1.337(−1)) = .006819,
and a 95% P.I. is (exp(−6.169),exp(−3.808)), or (.0021, .0222).
g. d
MSE =.00682 + (8 −7.657)2=.124
29.33. From (2.51), SSR(Xq) = b2
qP(Xiq −¯
Xq)2. For coding in (29.2a), ¯
Xq= 0. Then:
SSR(Xq) = b2
qPX2
iq =b2
q
nT
P
i=1(±1)2=nTb2
q
29.34. a.
E{ˆ
β1}=E{(X0
1X1)−1X0
1Y}
= (X0
1X1)−1X0
1E{Y}
= (X0
1X1)−1X0
1(X1β1+X2β2)
=β1+ (X0
1X1)−1X0
1X2β2=β1+Aβ2
b. Let:
β1=
β0
β1
β2
β3
β2=
β12
β13
β23
Then:
X1=
1 1 −1−1
1−1 1 −1
1−1−1 1
1111
X2=
−1−1 1
−1 1 −1
1−1−1
1 1 1
and:
A=
000
001
010
100
The results follow from E{b1}=β1+Aβ2.
29-11
29-12

Chapter 30
RESPONSE SURFACE
METHODOLOGY
30.2. Second block:
X1X2X3X4
2 0 0 0
−2 0 0 0
0 2 0 0
0−2 0 0
0 0 2 0
0 0 −2 0
0 0 0 2
0 0 0 −2
Any number of center points may be added to the second block.
30.7. a. 21
b. 5, 5, 10
c. 21, 27
30.8.
30-1

X1X2X3X4X5
−1−1−1−1−1
1 1 −1−1−1
1−1 1 −1−1
−1 1 1 −1−1
1−1−1 1 −1
−1 1 −1 1 −1
−1−1 1 1 −1
1 1 1 1 −1
1−1−1−1 1
−1 1 −1−1 1
−1−1 1 −1 1
1 1 1 −1 1
−1−1−1 1 1
1 1 −1 1 1
1−1 1 1 1
−11111
X1X2X3X4X5
2 0 0 0 0
−2 0 0 0 0
0 2 0 0 0
0−2 0 0 0
0 0 2 0 0
0 0 −2 0 0
0 0 0 2 0
0 0 0 −2 0
0 0 0 0 2
0 0 0 0 −2
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
30.9. No, base design is resolution III.
30.10. α= [29−3(1)/(1)]1/4= 2.828
30.11. b.
Coef. bqP-value
b01.868
b1.190 .007
b2.195 .006
b3−.120 .039
b12 .162 .020
Coef. bqP-value
b13 −.038 .471
b23 −.062 .251
b11 .228 .044
b22 −.047 .602
b33 .028 .757
d. H0:βq= 0, Ha:βq6= 0. s{bq}=.0431 (for linear effects), s{bq}=.0481
(for interaction effects), s{bq}=.0849 (for quadratic effects). If P-value ≥.05
conclude H0, otherwise Ha. Active effects (see part b): β1,β2,β3,β12,β11
30.12. a.
Coef. bq
b01.860
b1.190
b2.195
Coef. bq
b3−.120
b12 .162
b11 .220
b. H0: Normal, Ha: not normal. r=.947. If r≥.938 conclude H0, otherwise Ha.
Conclude H0.
30.13. a.
Coef. bq
b0189.750
b128.247
b2−.772
Coef. bq
b12 13.750
b11 −18.128
b22 −6.875
30-2

c. H0: No lack of fit, Ha: lack of fit. SSLF =SSE −SSP E = 978.9−230.75 =
748.15, F∗= (748.15/3) ÷(230.75/3) = 3.24, F(.99; 3,3) = 29.5. If F∗≤29.5
conclude H0, otherwise Ha. Conclude H0.
e. (1.22,1.16)
f. ˆ
Yh= 206.54, s{ˆ
Yh}= 13.70, t(.975; 6) = 2.447, 206.54 ±2.447(13.70), 173.0≤
E{Yh} ≤ 240.1.
30.14. a.
Design Matrix:
X1X2
−.707 −.707
.707 −.707
−.707 .707
.707 .707
−1 0
1 0
0−1
0 1
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
Corner Points:
X1X2
−.707 −.707
.707 −.707
−.707 .707
.707 .707
b.
(X0X)−1=
.125 0 0 −.125 −.125 0
0.250 0 0 0 0
0 0 .250 0 0 0
−.125 0 0 .5 0 0
−.125 0 0 0 .5 0
0 0 0 0 0 1
30.15. a.
X1X2
−1−1
1−1
−1 1
1 1
−1.414 0
1.414 0
0−1.414
0 1.414
X1X2
0 0
0 0
0 0
0 0
0 0
n0= 5
30-3

b. Variance function:
.20 −.075X2
1−.075X2
2+.14375X4
1+.14375X4
2+.2875X2
1X2
2
30.16. a.
b∗="−2.077
.724 #s= 2.200
b.
t X1X2
1.5−1.416 .494
2.5−2.361 .823
3.5−3.304 1.152
30.17. a.
b∗=
13.519
13.494
−21.581
s= 28.820
b.
t X1X2X3
−1−.469 −.468 .749
−2−.938 −.936 1.498
−3−1.407 −1.404 2.246
30.18. a.
Design Variance Function
1.6788 −.5116X+.1710X2−.02264X3+.001029X4
2.5266 −.4048X+.1475X2−.02012X3+.000914X4
3.6615 −.4504X+.1393X2−.01788X3+.0008129X4
b.
Design ¯
V
1.1993
2.2037
3.1869
Design 3 preferred
c.
Comparison EV
Design 1 relative to design 2 1.02
Design 1 relative to design 3 .94
Design 2 relative to design 3 .92
1/.94 = 1.06 times
d.
Design |(X0X)−1|
1 6.35057 x 10−7
2 4.70419 x 10−7
3 5.57533 x 10−7
30-4

Design 2 preferred
e.
Comparison ED
Design 1 relative to design 2 .90
Design 1 relative to design 3 .96
Design 2 relative to design 3 1.06
1/.90 = 1.11 times
30.19. a. Design 2 is D-optimal
b. Design 3 is V-optimal
30.20. a. Irregular
c.
Design ¯
V
1.5235
2.8962
Design 1 preferred
d. EV= 1.712, 1/1.712 = .584 times
e.
Design |(X0X)−1|
1.393
2 1.567
Design 1 preferred
f. ED=.794, 1/.794 = 1.26 times
30.21. a. D-optimal design: |(X0X)−1|=.2998
X1X2Number of Replicates
−1−1 1
−.5−1 1
−.5 0 1
.25 0 1
0 1 2
1 1 1
.5 1 2
No
b. V-optimal design: ¯
V=.4765
X1X2Number of Replicates
−1−1 1
−.5−1 1
−.5 0 1
.25 0 1
0 1 1
.5 1 1
1 1 1
0.25 2
30-5
No
30-6

Appendix D: RULES FOR
DEVELOPING ANOVA MODELS
AND TABLES FOR BALANCED
DESIGNS
D.1.
i j k
RRR E{MSA}E{MSB}E{MSAB}E{MSE}
a b n Variance i j ij (ij)k
αi1b n σ2
αbn 0 0 0
βja1n σ2
β0an 0 0
(αβ)ij 1 1 n σ2
αβ n n n 0
²k(ij)1 1 1 σ21 1 1 1
D.2. a.
Model Coef- Symbolic Term to Degrees of
Term ficient Product be Squared Freedom
αibcn i −1¯
Yi··· −¯
Y···· a−1
βjacn j −1¯
Y·j·· −¯
Y···· b−1
γkabn k −1¯
Y··k·−¯
Y···· c−1
(αβ)ij cn ij −i−j+ 1 ¯
Yij·· −¯
Yi··· −¯
Y·j·· +¯
Y···· (a−1)(b−1)
(αγ)ik bn ik −i−k+ 1 ¯
Yi·k·−¯
Yi··· −¯
Y··k·+¯
Y···· (a−1)(c−1)
(βγ)jk an jk −j−k+ 1 ¯
Y·jk·−¯
Y·j·· −¯
Y··k·+¯
Y···· (b−1)(c−1)
(αβγ)ijk n ijk −ij −ik ¯
Yijk·−¯
Yij·· −¯
Yi·k·−¯
Y·jk·(a−1)(b−1)(c−1)
−jk +i+j+k−1 + ¯
Yi··· +¯
Y·j·· +¯
Y··k·−¯
Y····
²m(ijk)1ijkm −ijk Yijkm −¯
Yijk abc(n−1)
Total Yijkm −¯
Y···· abcn −1
D.1

b.
i j k m
Expected Mean Square of −−
R R R R Vari- A B C AB AC BC ABC E
a b c n ance i j k ij ik jk ijk (ijk)m
αi1b c n σ2
αbcn 0 0 0 0 0 0 0
βja1c n σ2
β0nac 0 0 0 0 0 0
γka b 1n σ2
γ0 0 abn 0 0 0 0 0
(αβ)ij 1 1 c n σ2
αβ nc nc 0nc 0 0 0 0
(αγ)ik 1b1n σ2
αγ nb 0nb 0nb 0 0 0
(βγ)jk a1 1 n σ2
βγ 0na na 0 0 na 0 0
(αβγ)ijk 1 1 1 n σ2
αβγ n n n n n n n 0
²m(ijk)1 1 1 1 σ21 1 1 1 1 1 1 1
D.3. a. See Problem D.2a.
b.
i j k m
Expected Mean Square of −−
F R R R Vari- A B C AB AC BC ABC E
a b c n ance i j k ij ik jk ijk (ijk)m
αi0b c n σ2
αbcn 0 0 0 0 0 0 0
βja1c n σ2
β0nac 0 0 0 0 0 0
γka b 1n σ2
γ0 0 abn 0 0 0 0 0
(αβ)ij 1 1 c n σ2
αβ nc 0 0 nc 0 0 0 0
(αγ)ik 1b1n σ2
αγ nb 0 0 0 nb 0 0 0
(βγ)jk a1 1 n σ2
βγ 0na na 0 0 na 0 0
(αβγ)ijk 1 1 1 n σ2
αβγ n0 0 n n 0n0
²m(ijk)1 1 1 1 σ21 1 1 1 1 1 1 1
D.4. a.
Model Symbolic Degrees of
Term Product Sum of Squares Freedom
βjj−1an P(¯
Y·j·−¯
Y···)2b−1
αi(j)ij −j n PP(¯
Yij·−¯
Y·j·)2b(a−1)
²k(ij)ijk −ij PPP(Yijk −¯
Yij·)2ab(n−1)
Total PPP(Yijk −¯
Y···)2abn −1
b.
j i k
F R R Vari- E{MSB}E{MSA(B)}E{MSE}
b a n ance j i(j) (ij)k
βj0a n σ2
βan 0 0
αi(j)1 1 n σ2
αn n 0
²k(ij)1 1 1 σ21 1 1
D.2

E{MSB}=an Pβ2
j
b−1+nσ2
α+σ2
E{MSE}=σ2
E{MSA(B)}=nσ2
α+σ2
c. MSA(B)
D.5. a.
Model Coef- Symbolic Term to be Degrees of
Term ficient Product Squared Freedom
ρir i −1¯
Yi·−¯
Y·· n−1
τjnbj−1¯
Y·j−¯
Y·· r−1
Error Remainder = Remainder =
Yij −¯
Yi·−¯
Y·j+¯
Y·· (r−1)(nb−1)
Total Yij −¯
Y·· rnb−1
b.
i j
F F Vari- E{MSBL}E{MSTR}E{MSE}
nbrance i j (ij)
ρi0r σ2
ρr0 0
τjnb0σ2
τ0nb0
²(ij)1 1 σ21 1 1
D.6. a. See Problem D.5a.
b.
i j
F R Vari- E{MSBL}E{MSTR}E{MSE}
nbrance i j (ij)
ρi0r σ2
ρr0 0
τjnb1σ2
τ0nb0
²(ij)1 1 σ21 1 1
D.7. a. See Problem D.5a.
b.
i j
R F Vari- E{MSBL}E{MSTR}E{MSE}
nbr ance i j (ij)
ρi1r σ2
ρr0 0
τjnb0σ2
τ0nb0
²(ij)1 1 σ21 1 1
D.3

D.8. a.
Model Coef- Symbolic Degrees of
Term ficient Product Term to be Squared Freedom
ρirm i −1¯
Yi·· −¯
Y··· nb−1
τjnbm j −1¯
Y·j·−¯
Y··· r−1
²(ij)mRemainder = Remainder =
¯
Yij·−¯
Yi·· −¯
Y·j·+¯
Y··· (nb−1)(r−1)
ηk(ij)1ijk −ij Yijk −¯
Yij·nbr(m−1)
Total Yijk −¯
Y··· nbrm −1
SSBL = rm P(¯
Yi·· −¯
Y···)2
SSEE = mPP(¯
Yij·−¯
Yi·· −¯
Y·j·+¯
Y···)2
SSTR = nbmP(¯
Y·j·−¯
Y···)2
SSOE = PPP(Yijk −¯
Yij·)2
b.
i j k
R F R Vari- E{MSBL}E{M ST R}E{MSEE}E{MSOE}
nbr m ance i j (ij) (ij)k
ρi1r m σ2
ρrm 0 0 0
τjnb0m σ2
τ0nbm0 0
²(ij)1 1 m σ2m m m 0
ηk(ij)1 1 1 σ2
η1 1 1 1
E{MSBL}=rmσ2
ρ+mσ2+σ2
ηE{MSEE}=mσ2+σ2
η
E{MSTR}=nbmPτ2
j
r−1+mσ2+σ2
ηE{MSOE}=σ2
η
D.9. a.
Model Symbolic Degrees of
Term Product Sum of Squares Freedom
αii−1bcn P(¯
Yi··· −¯
Y····)2a−1
βj(k)jk −k an PP(¯
Y·jk·−¯
Y··k·)2c(b−1)
γkk−1abn P(¯
Y··k·−¯
Y····)2c−1
(αγ)ik ik −i−k+ 1 bn PP(¯
Yi·k·−¯
Yi··· −¯
Y··k·+¯
Y····)2(a−1)(c−1)
(αβ)ij(k)ijk −ik −jk +k n PPP(¯
Yijk·−¯
Yi·k·−¯
Y·jk·+¯
Y··k·)2(a−1)(b−1)c
²m(ijk)ijkm −ijk PPPP(Yijkm −¯
Yijk·)2abc(n−1)
Total PPPP(Yijkm −¯
Y····)2abcn −1
D.4

b.
i j k m
Expected Mean Square of −−
F R R R Vari- A B(C)C AC AB(C)E
a b c n ance i j(k)k ik ij(k)m(ijk)
αi0b c n σ2
αbcn 0 0 0 0 0
βj(k)a1 1 n σ2
β0an an 0 0 0
γka b 1n σ2
γ0 0 abn 0 0 0
(αγ)ik 0b1n σ2
αγ bn 0 0 bn 0 0
(αβ)ij(k)0 1 1 n σ2
αβ n0 0 n n 0
²m(ijk)1 1 1 1 σ21 1 1 1 1 1
E{MSA}=bcn Pα2
i
a−1+bnσ2
αγ +nσ2
αβ +σ2
E{MSB(C)}=anσ2
β+σ2
E{MSC}=anσ2
β+abnσ2
γ+σE{MSAB(C)}=nσ2
αβ +σ2
E{MSAC}=bnσ2
αγ +nσ2
αβ +σ2E{MSE}=σ2
D.10. eijk :
j= 1 j= 2 j= 3
k= 1 −2.3333 .3333 −1.6667
i= 1 k= 2 1.6667 −1.6667 .3333
k= 3 .6667 1.3333 1.3333
k= 1 −.3333 2.3333 −1.0000
i= 2 k= 2 1.6667 −.6667 .0000
k= 3 −1.3333 −1.6667 1.0000
k= 1 −1.6667 −1.6667 −1.3333
i= 3 k= 2 1.3333 1.3333 .6667
k= 3 .3333 .3333 .6667
r=.981
D.11. a.
Source SS df MS
Blocks 520.963 2 260.4815
Treatments 103.185 2 51.5925
Experimental error 5.259 4 1.3148
Observation error 45.333 18 2.5185
Total 674.741 26
b. H0: all τjequal zero (j= 1,2,3), Ha: not all τjequal zero. F∗= 51.5925/1.3148 =
39.24, F(.95; 2,4) = 6.94.If F∗≤6.94 conclude H0, otherwise Ha. Conclude Ha.
P−value = .002.
c. ¯
Y·1·= 24.77778, ¯
Y·2·= 20.00000, ¯
Y·3·= 22.66667, ˆ
L1=¯
Y·1·−¯
Y·2·= 4.77778,
ˆ
L2=¯
Y·1·−¯
Y·3·= 2.11111, ˆ
L3=¯
Y·2·−¯
Y·3·=−2.66667, s{ˆ
Li}=.5405 (i= 1,2,3),
q(.90; 3,4) = 3.98, T= 2.8143
4.77778 ±2.8143(.5405) 3.257 ≤L1≤6.299
D.5

2.11111 ±2.8143(.5405) .590 ≤L2≤3.632
−2.66667 ±2.8143(.5405) −4.188 ≤L3≤ −1.146
d. ˆσ2= 0, ˆσ2
η= 2.5185
D.12. a.
Model Coef- Symbolic Term to Degrees of
Term ficient Product Be Squared Freedom
ρiab i −1¯
Yi·· −¯
Y··· s−1
αjsb j −1¯
Y·j·−¯
Y··· a−1
βksa k −1¯
Y··k−¯
Y··· b−1
(αβ)jk s jk −j−k+ 1 ¯
Y·jk −¯
Y·j·−¯
Y··k+¯
Y··· (a−1)(b−1)
Error Remainder = Remainder =
Yijk −¯
Yi·· −¯
Y·jk +¯
Y··· (s−1)(ab −1)
Total Yijk −¯
Y··· abs −1
b.
i j k
Expected Mean Square of −−
R F F Vari- S A B AB Rem
s a b ance i j k jk (ijk)
ρi1a b σ2
ρab 0 0 0 0
αjs0b σ2
α0sb 0 0 0
βks a 0σ2
β0 0 sa 0 0
(αβ)jk s0 0 σ2
αβ 0 0 0 s0
²(ijk)1 1 1 σ21 1 1 1 1
D.13. a.
Model Coef- Symbolic Term to Degrees of
Term ficient Product Be Squared Freedom
αjbs j −1¯
Y·j·−¯
Y··· a−1
βkas k −1¯
Y··k−¯
Y··· b−1
(αβ)jk s jk −j−k+ 1 ¯
Y·jk −¯
Y·j·−¯
Y··k+¯
Y··· (a−1)(b−1)
ρi(j)b ij −j¯
Yij·−¯
Y·j·a(s−1)
Error Remainder = Remainder =
Yijk −¯
Y·jk −¯
Yij·+¯
Y·j·a(s−1)(b−1)
Total Yijk −¯
Y··· abs −1
D.6

b.
j k i
Expected Mean Square of −−
FFRVari- A B AB S(A)Rem
a b s ance j k jk i(j) (ijk)
αj0b s σ2
αbs 0 0 0 0
βka0s σ2
β0as 0 0 0
(αβ)jk 0 0 s σ2
αβ 0 0 s0 0
ρi(j)1b1σ2
ρb0 0 b0
²(ijk)1 1 1 σ21 1 1 1 1
D.14. Note: The subscript for subjects here is linstead of the usual iand the subscripts for
factor A,B, and Care i,j, and k, respectively.
a.
Yijklm =µ···· +αi+βj+γk+ρl(ik)+ (αβ)ij + (αγ)ik + (βγ)jk
+(αβγ)ijk +²m(ijkl)
b.
Model Coef- Symbolic Term to Degrees of
Term ficient Product Be Squared Freedom
αibcrn i −1¯
Yi···· −¯
Y····· a−1
βjacrn j −1¯
Y·j··· −¯
Y····· b−1
γkabrn k −1¯
Y··k·· −¯
Y····· c−1
ρl(ik)abcn ikl −ik ¯
Yi·kl·−¯
Yi·k·· ac(r−1)
(αβ)ij crn ij −i−j+ 1 ¯
Yij··· −¯
Yi···· −¯
Y·j··· +¯
Y····· (a−1)(b−1)
(αγ)ik brn ik −i−k+ 1 ¯
Yi·k·· −¯
Yi···· −¯
Y··k·· +¯
Y····· (a−1)(c−1)
(βγ)jk arn jk −j−k+ 1 ¯
Y·jk·· −¯
Y·j··· −¯
Y··k·· +¯
Y····· (b−1)(c−1)
(αβγ)ijk rn ijk −ik −jk ¯
Yijk·· −¯
Yi·k·· −¯
Y·jk·· −¯
Yij··· (a−1)(b−1)(c−1)
−ij +i+j+k−1 + ¯
Yi···· +¯
Y·j··· +¯
Y··k·· −¯
Y·····
Error Remainder = Remainder =
Yijklm −¯
Yi·kl·−¯
Yijk·· +¯
Yi·k·· abcrn −acr −abc +ac
Total Yijklm −¯
Y····· abcrn −1
SSA =bcrn X(¯
Yi···· −¯
Y·····)2
SSB =acrn X(¯
Y·j··· −¯
Y·····)2
SSC =abrn X(¯
Y··k·· −¯
Y·····)2
etc.
D.7

c.
i j k l m
F F F R R
a= 3 b= 4 c= 2 r= 4 n= 2 Variance
αi0b c r n σ2
α
βja0c r n σ2
β
γka b 0r n σ2
γ
ρl(ik)1b1 1 n σ2
ρ
(αβ)ij 0 0 c r n σ2
αβ
(αγ)ik 0b0r n σ2
αγ
(βγ)jk a0 0 r n σ2
βγ
(αβγ)ijk 0 0 0 r n σ2
αβγ
²m(ijkl)1 1 1 1 1 σ2
Expected Mean Square of −−
A B C S(AC)AB AC BC ABC E
i j k l(ik)ij ik jk ijk m(ijkl)
αibcrn 0 0 0 0 0 0 0 0
βj0acrn 0 0 0 0 0 0 0
γk0 0 abrn 0 0 0 0 0 0
ρl(ik)bn 0bn bn 0bn 0 0 0
(αβ)ij 0 0 0 0 crn 0 0 0 0
(αγ)ik 0 0 0 0 0 brn 0 0 0
(βγ)jk 0 0 0 0 0 0 arn 0 0
(αβγ)ijk 0 0 0 0 0 0 0 rn 0
²m(ijkl)1 1 1 1 1 1 1 1 1
E{MSA}= 64 Xα2
i
2+ 8σ2
ρ+σ2
E{MSB}= 48 Xβ2
j
3+σ2
E{MSC}= 96 Xγ2
k
1+ 8σ2
ρ+σ2
E{MSS(AC)}= 8σ2
ρ+σ2
E{MSAB}= 16 XX(αβ)2
ij
6+σ2
E{MSAC}= 32 XX(αγ)2
ik
2+ 8σ2
ρ+σ2
E{MSBC}= 24 XX(βγ)2
jk
3+σ2
E{MSABC}= 8 XXX(αβγ)2
ijk
6+σ2
E{MSE}=σ2
D.8

D.15.
i j k
F F F Vari- E{MSROW}E{MSCOL}E{MSTR}E{MSE}
r r r ance i j k (ijk)
ρi0r r σ2
ρr0 0 0
κjr0r σ2
κ0r0 0
τkr r 0σ2
τ0 0 r0
²(ijk)111 σ21 1 1 1
D.16.
i j k m
F F F R Vari- E{MSROW}E{MSCOL}E{MSTR}E{MSRem}
r r r n ance i j k m(ijk)
ρi0r r n σ2
ρrn 0 0 0
κjr0r n σ2
κ0rn 0 0
τkr r 0n σ2
τ0 0 rn 0
²m(ijk)1 1 1 1 σ21 1 1 1
E{MSROW}=σ2+rn Pρ2
i
r−1E{MSTR}=σ2+rn Pτ2
k
r−1
E{MSCOL}=σ2+rn Pκ2
j
r−1E{MSRem}=σ2
D.17.
i j k m
Expected Mean Square of −−
F F F R Vari- P O T R S(P)Rem
r r r n ance i j k m(i) (ijkm)
ρi0r r n σ2
ρrn 0 0 0 0
κjr0r n σ2
κ0rn 0 0 0
τkr r 0n σ2
τ0 0 rn 0 0
ηm(i)1r r 1σ2
ηr0 0 r0
²(ijkm)1 1 1 1 σ21 1 1 1 1
D.9