S 102 DG4PS 893 04
User Manual: S-102
Open the PDF directly: View PDF ![]() .
.
Page Count: 11
24 CHAPTER 4 Discovering Geometry Practice Your Skills
Lesson 4.1 • Triangle Sum Conjecture
Name Period Date
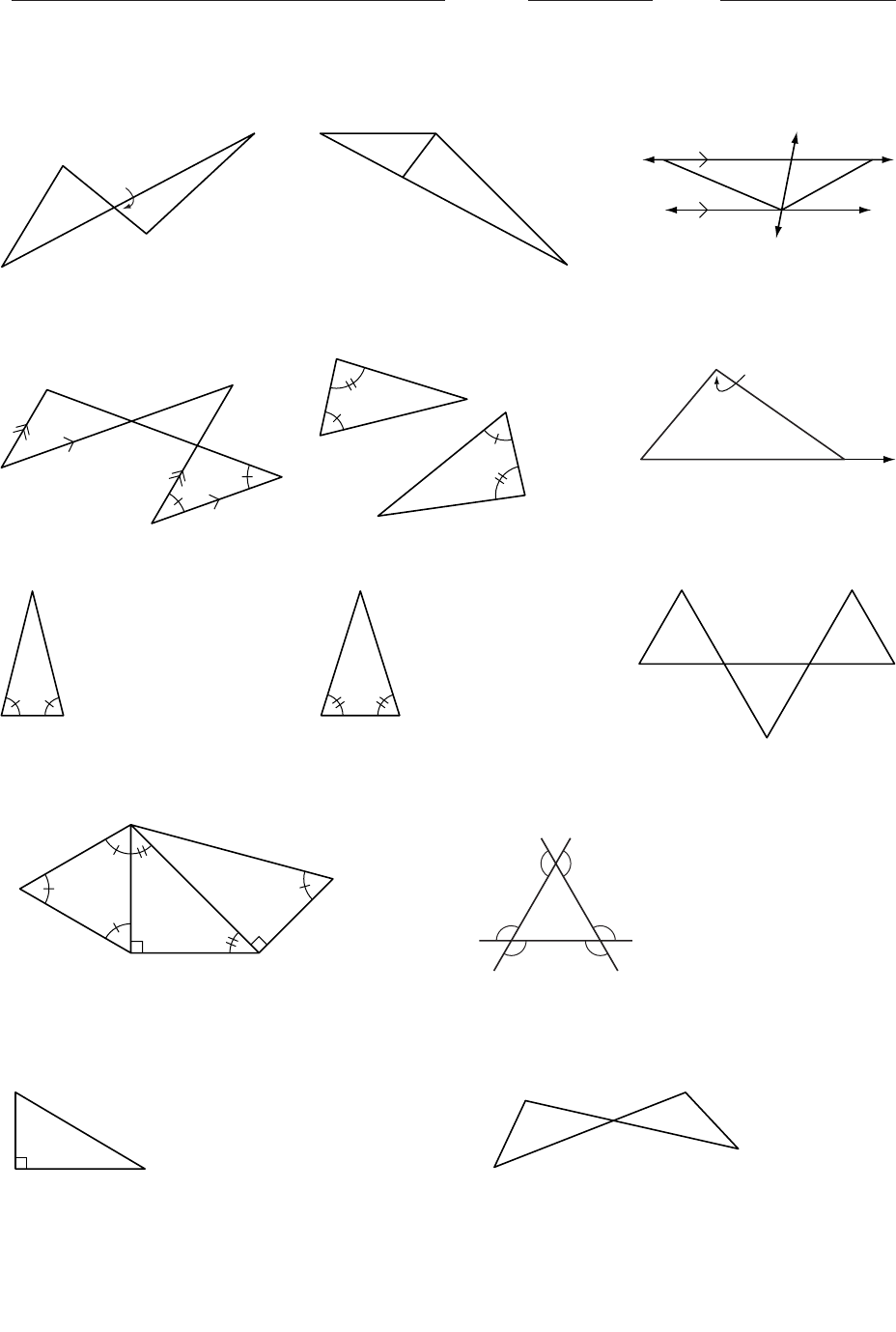
In Exercises 1–9, determine the angle measures.
1. p______, q______ 2. x______, y______ 3. a______, b______
4. r______, s______, 5. x______, y______ 6. y______
t______
7. s______ 8. m______ 9. mP______
10. Find the measure of QPT.11. Find the sum of the measures of
the marked angles.
12. Use the diagram to explain why 13. Use the diagram to explain why
Aand Bare complementary. mAmB mCmD.
A
B
E
D
C
A
CB
P
b
c
c
a
a
m
35⬚
s
76⬚
y
30 ⫹ 4x
100 ⫺ x
7x
85⬚x
31⬚
y
100⬚
s
t
r
79⬚
50⬚
23⬚ab
28⬚
17⬚
53⬚x
y
82⬚
98⬚
q
p
31⬚
Q
RS
P
T
DG4PSA_894_04.qxd 11/1/06 1:24 PM Page 24
©2008 Kendall Hunt Publishing
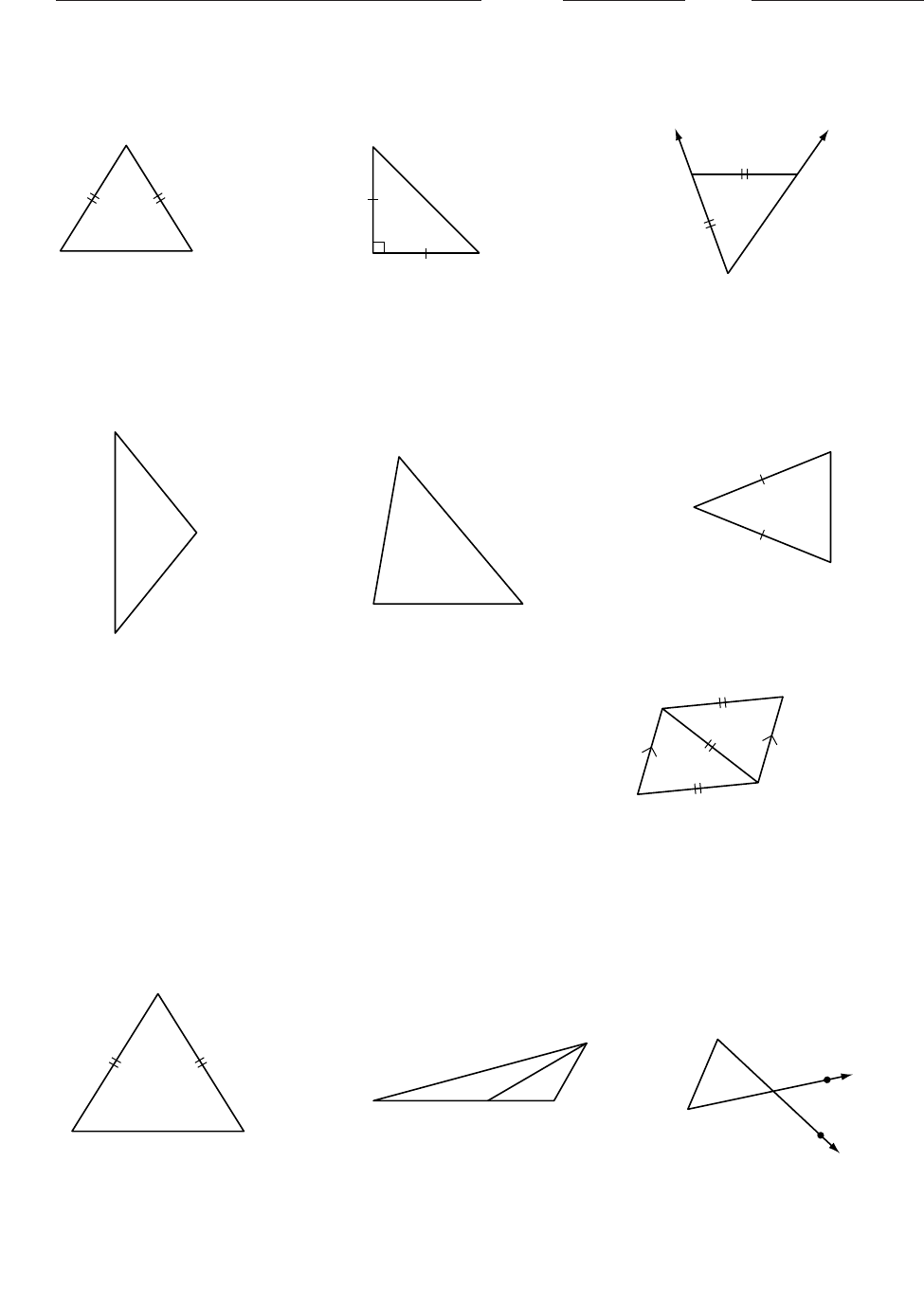
Discovering Geometry Practice Your Skills CHAPTER 4 25
Lesson 4.2 • Properties of Isosceles Triangles
Name Period Date
In Exercises 1–3, find the angle measures.
1. mT______ 2. mG______ 3. x______
In Exercises 4–6, find the measures.
4. mA______, perimeter 5. The perimeter of LMO 6. The perimeter of QRS is
of ABC ______ is 536 m. LM ______, 344 cm. mQ______,
mM______ QR ______
7. a. Name the angle(s) congruent to DAB.
b. Name the angle(s) congruent to ADB.
c. What can you conclude about AD
and BC
?Why?
8. x_____, y_____ 9. PR QR and QS RS.10. Use the diagram to explain
If mRSQ 120°, what is why PQR is isosceles.
mQPR?
P
Q
RT
S
70⬚
55⬚
PRS
Q
4y
2x ⫹ y79⬚ ⫺ x
A
B
C
D
R
S
Qy
y ⫹ 31 cm
68⬚
M
O
Lx ⫹ 30⬚x
163 m
210 m
13 cm
a ⫹ 7 cm
A
a
B
C
39⬚
102⬚
x
110⬚
NG
A
T
RI
58⬚
DG4PSA_894_04.qxd 11/1/06 1:24 PM Page 25
©2008 Kendall Hunt Publishing
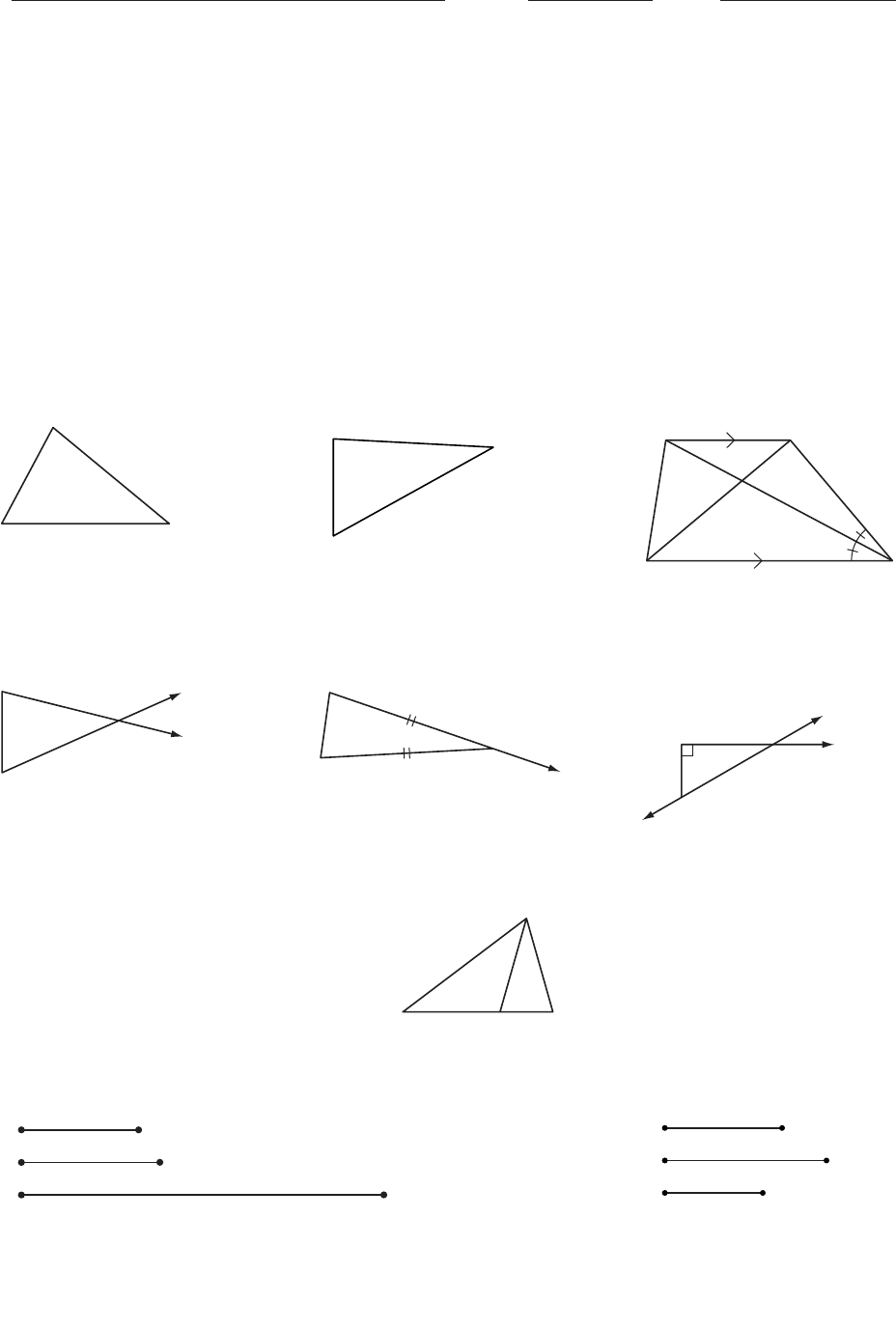
26 CHAPTER 4 Discovering Geometry Practice Your Skills
Lesson 4.3 • Triangle Inequalities
Name Period Date
In Exercises 1 and 2, determine whether it is possible to draw a triangle
with sides of the given measures. If it is possible, write yes. If it is not
possible, write no and make a sketch demonstrating why it is not possible.
1. 16 cm, 30 cm, 45 cm 2. 9 km, 17 km, 28 km
3. If 17 and 36 are the lengths of two sides of a triangle, what is the range
of possible values for the length of the third side?
In Exercises 4–6, arrange the unknown measures in order from greatest
to least.
4. 5. 6.
7. x_____ 8. x_____ 9. What’s wrong with
this picture?
10. Explain why PQS is isosceles.
In Exercises 11 and 12, use a compass and straightedge to construct a
triangle with the given sides. If it is not possible, explain why not.
11. 12. Q
R
R
P
Q
P
B
C
C
A
B
A
x2x
PR
S
Q
120⬚
160⬚
C
A
B
x
158⬚
142⬚
66⬚
x
28⬚40⬚
71⬚
a
c
d
b
61⬚
32⬚
b
c
a
a
b
c
20
18
13
DG4PSA_894_04.qxd 11/1/06 1:24 PM Page 26
©2008 Kendall Hunt Publishing
Discovering Geometry Practice Your Skills CHAPTER 4 27
Lesson 4.4 • Are There Congruence Shortcuts?
Name Period Date
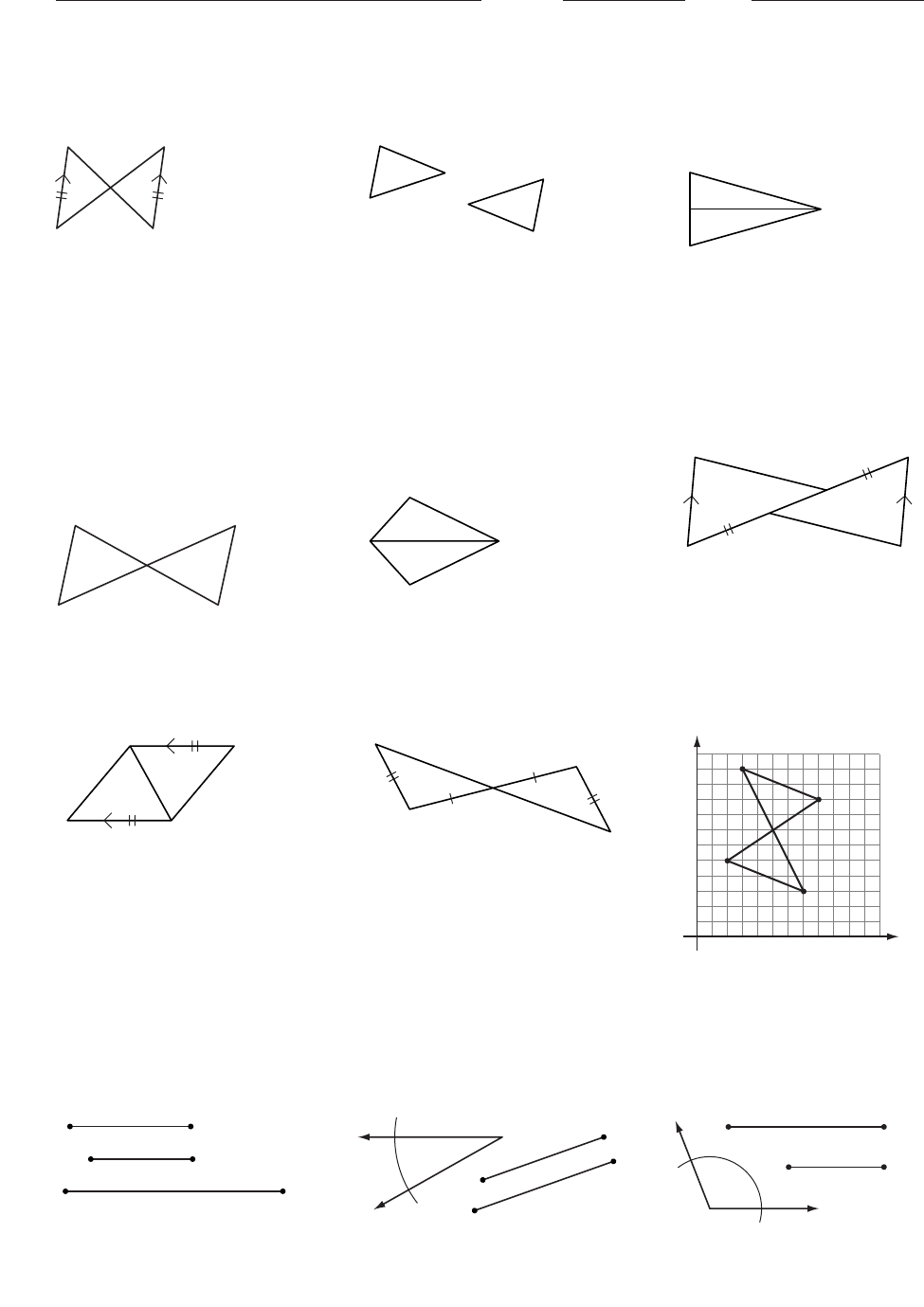
In Exercises 1–3, name the conjecture that leads to each congruence.
1. PAT IMT 2. SID JAN 3. TS
bisects MA
,MT
AT
,
and MST AST
In Exercises 4–9, name a triangle congruent to the given triangle and
state the congruence conjecture. If you cannot show any triangles to be
congruent from the information given, write “cannot be determined” and
redraw the triangles so that they are clearly not congruent.
4. Mis the midpoint of AB
5. KITE is a kite with KI TI.6. ABC _____
and PQ
.
APM _____
KIE _____
7. MON _____ 8. SQR _____ 9. TOP _____
In Exercises 10–12, use a compass and a straightedge or patty paper and a
straightedge to construct a triangle with the given parts. Then, if possible,
construct a different (noncongruent) triangle with the same parts. If it is
not possible, explain why not.
10. 11. 12. XY
XZ
X
B
C
C
A
B
TS
U
T
S
U
y
x
G
D
O
T
P
2
4
6
8
10
246810
Q
T
U
R
S
T
N
O
M
T
I
E
K
P
M
Q
B
A
B
A
X
Z
C
Y
M
T
S
A
6
6
8
8
99
J
I
N
A
D
S
M
IA
T
P
DG4PSA_894_04.qxd 11/1/06 1:24 PM Page 27
©2008 Kendall Hunt Publishing
28 CHAPTER 4 Discovering Geometry Practice Your Skills
Lesson 4.5 • Are There Other Congruence Shortcuts?
Name Period Date
In Exercises 1–6, name a triangle congruent to the given triangle and state
the congruence conjecture. If you cannot show any triangles to be congruent
from the information given, write “cannot be determined” and explain why.
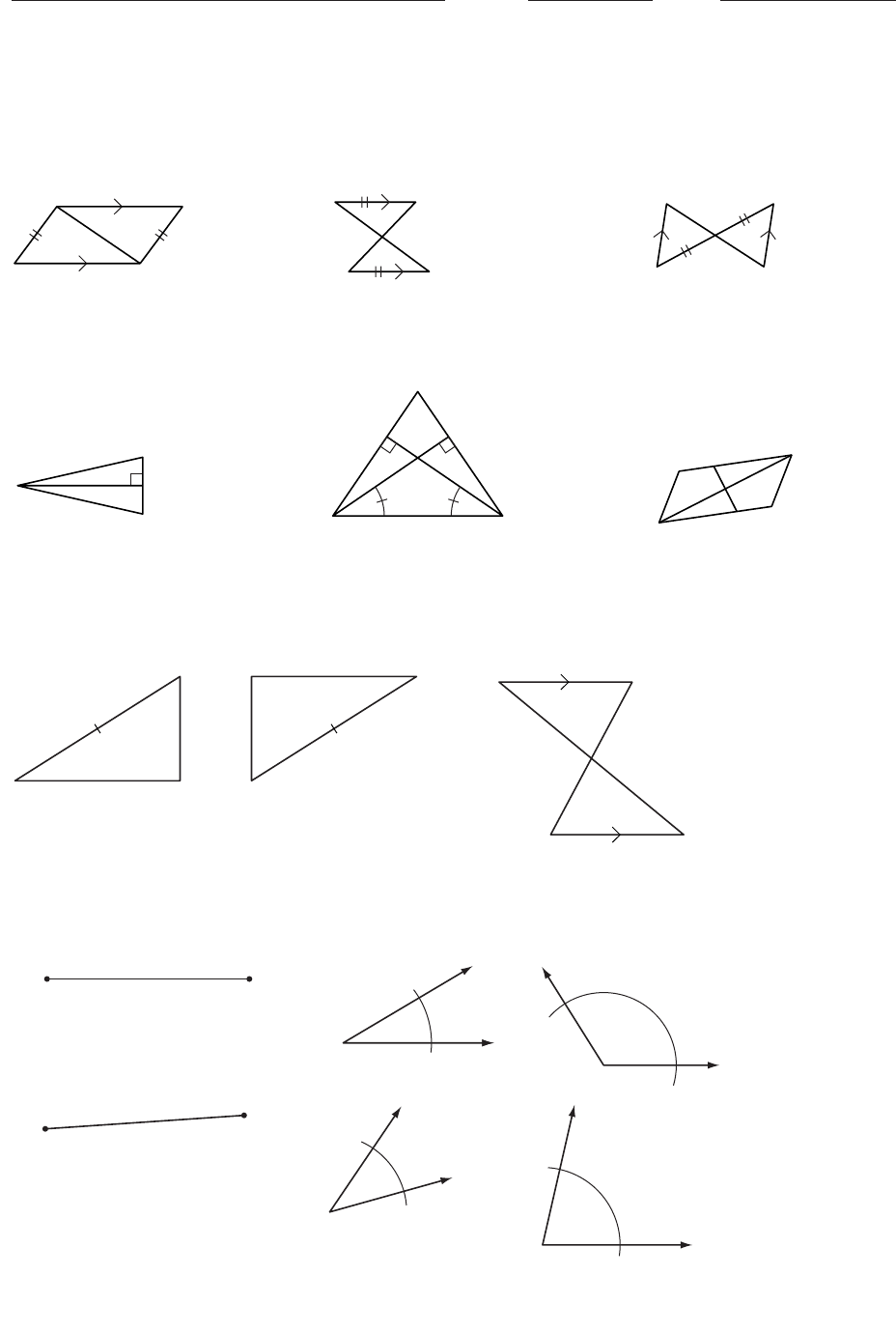
1. PIT _____ 2. XVW _____ 3. ECD _____
4. PS
is the angle bisector 5. ACN _____ 6. EFGH is a parallelogram.
of QPR.GQ EQ.
PQS _____ EQL _____
7. The perimeter of QRS is 350 cm. 8. The perimeter of TUV is 95 cm.
Is QRS MOL? Explain. Is TUV WXV? Explain.
In Exercises 9 and 10, construct a triangle with the given parts. Then, if
possible, construct a different (noncongruent) triangle with the same parts.
If it is not possible, explain why not.
9.
10.
C
A
AB
P
Q
PQ
x
40
x ⫹ 25
2x ⫺ 10
TU
V
X
W
LQ R
S
M
O
x
125
70
x ⫹ 55
2x ⫹ 15
EH
G
Q
K
L
F
P
N
A
RC
SP
Q
R
D
E
B
C
A
Z
Y
X
VW
PO
T
I
DG4PSA_894_04.qxd 11/1/06 1:25 PM Page 28
©2008 Kendall Hunt Publishing
Discovering Geometry Practice Your Skills CHAPTER 4 29
Lesson 4.6 • Corresponding Parts of Congruent Triangles
Name Period Date
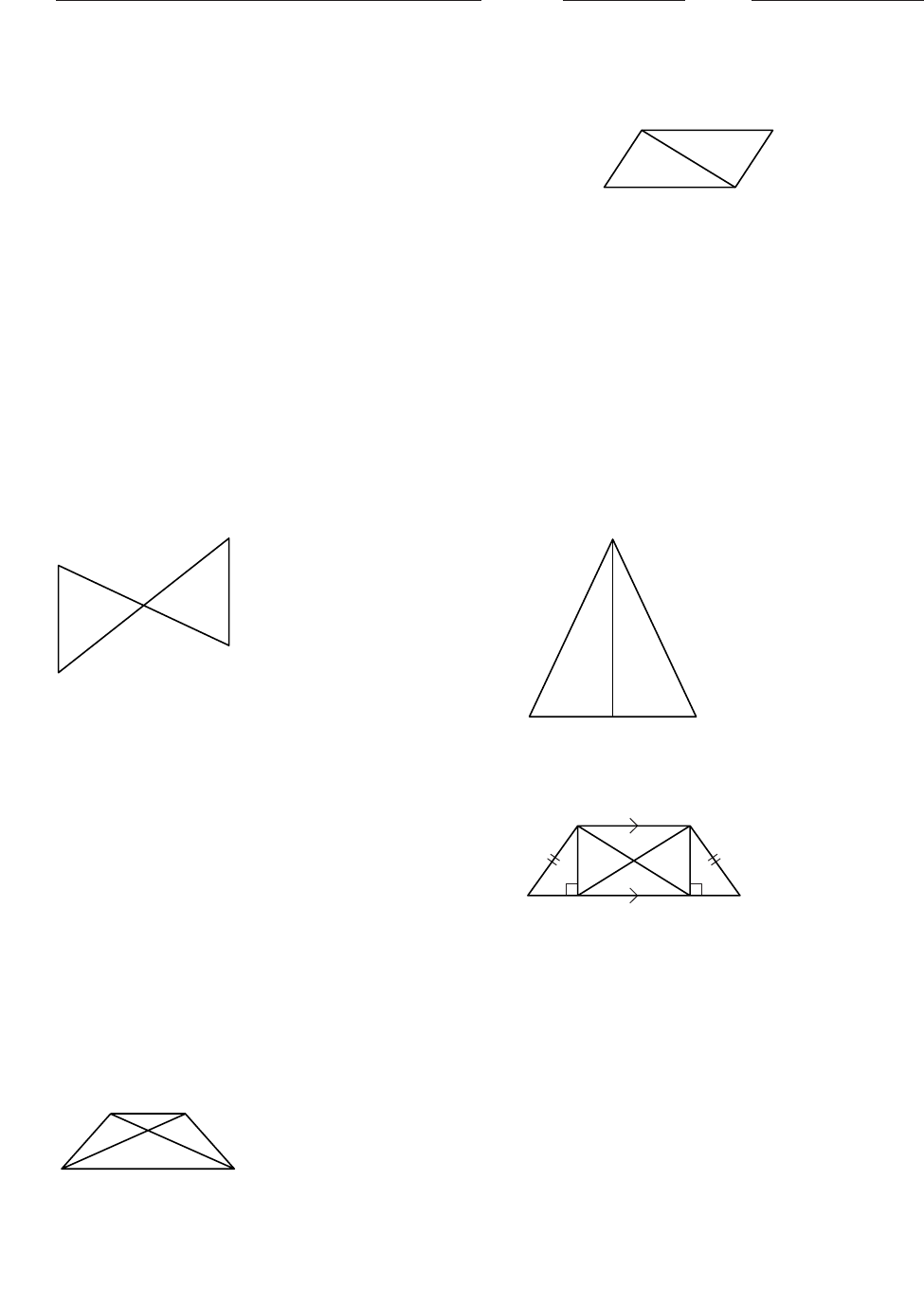
1. Give the shorthand name for each of the four triangle
congruence conjectures.
In Exercises 2–5, use the figure at right to explain why
each congruence is true. WXYZ is a parallelogram.
2. WXZ YZX 3. WZX YXZ
4. WZX YXZ 5. W Y
For Exercises 6 and 7, mark the figures with the given information. To
demonstrate whether the segments or the angles indicated are congruent,
determine that two triangles are congruent. Then state which conjecture
proves them congruent.
6. Mis the midpoint of WX
and 7. ABC is isosceles and CD
is the bisector
YZ
.Is YW
ZX
?Why? of the vertex angle. Is AD
BD
?Why?
In Exercises 8 and 9, use the figure at right to
write a paragraph proof for each statement.
8. DE
CF
9. EC
FD
10. TRAP is an isosceles trapezoid with TP RA and PTR ART.
Write a paragraph proof explaining why TA
RP
.
TR
A
P
DC
BA EF
C
BA D
Y
W
X
Z
M
Z
Y
WX
DG4PSA_894_04.qxd 11/1/06 1:25 PM Page 29
©2008 Kendall Hunt Publishing
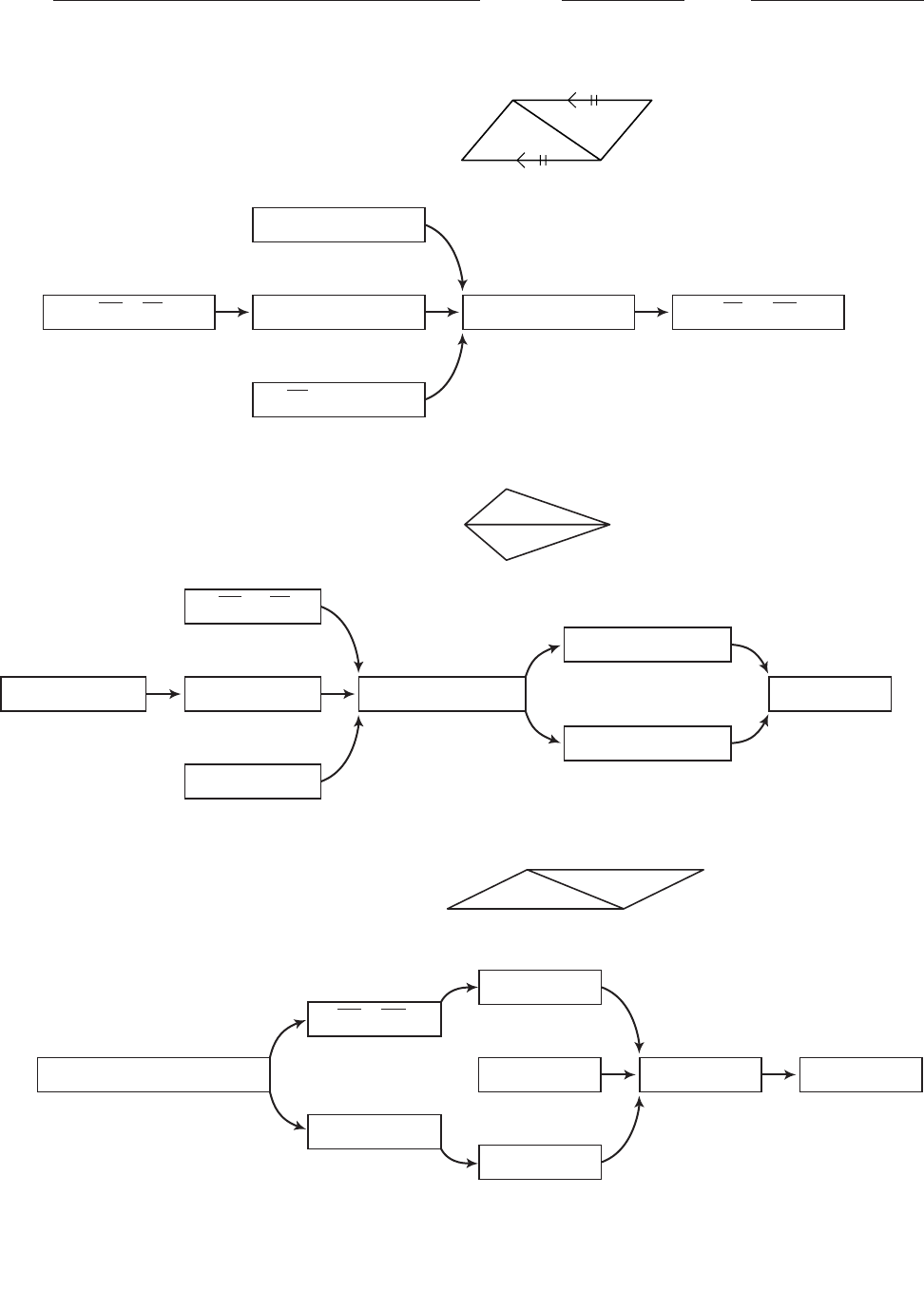
30 CHAPTER 4 Discovering Geometry Practice Your Skills
Lesson 4.7 • Flowchart Thinking
Name Period Date
Complete the flowchart for each proof.
1. Given: PQ
SR
and PQ
SR
Show: SP
QR
Flowchart Proof
2. Given: Kite KITE with KE
KI
Show: KT
bisects EKI and ETI
Flowchart Proof
3. Given: ABCD is a parallelogram
Show: A C
Flowchart Proof
ABCD is a parallelogram
_________________________
AB CD
______________
Definition of
___________
Same segment
_____________
_____________
____________
_____________
A
D
B
C
KET ______
______________
______________
______________
KITE is a kite
_______________
Definition
of bisect
KE KI
________________
ETK ITK
__________________
__________________
TK
I
E
PQS
______
Given
PQ SR
QS
______
SP QR
____________________________________
__________________
_________________ __________________
R
S
Q
P
DG4PSA_894_04.qxd 11/1/06 1:25 PM Page 30
©2008 Kendall Hunt Publishing
Discovering Geometry Practice Your Skills CHAPTER 4 31
Lesson 4.8 • Proving Special Triangle Conjectures
Name Period Date
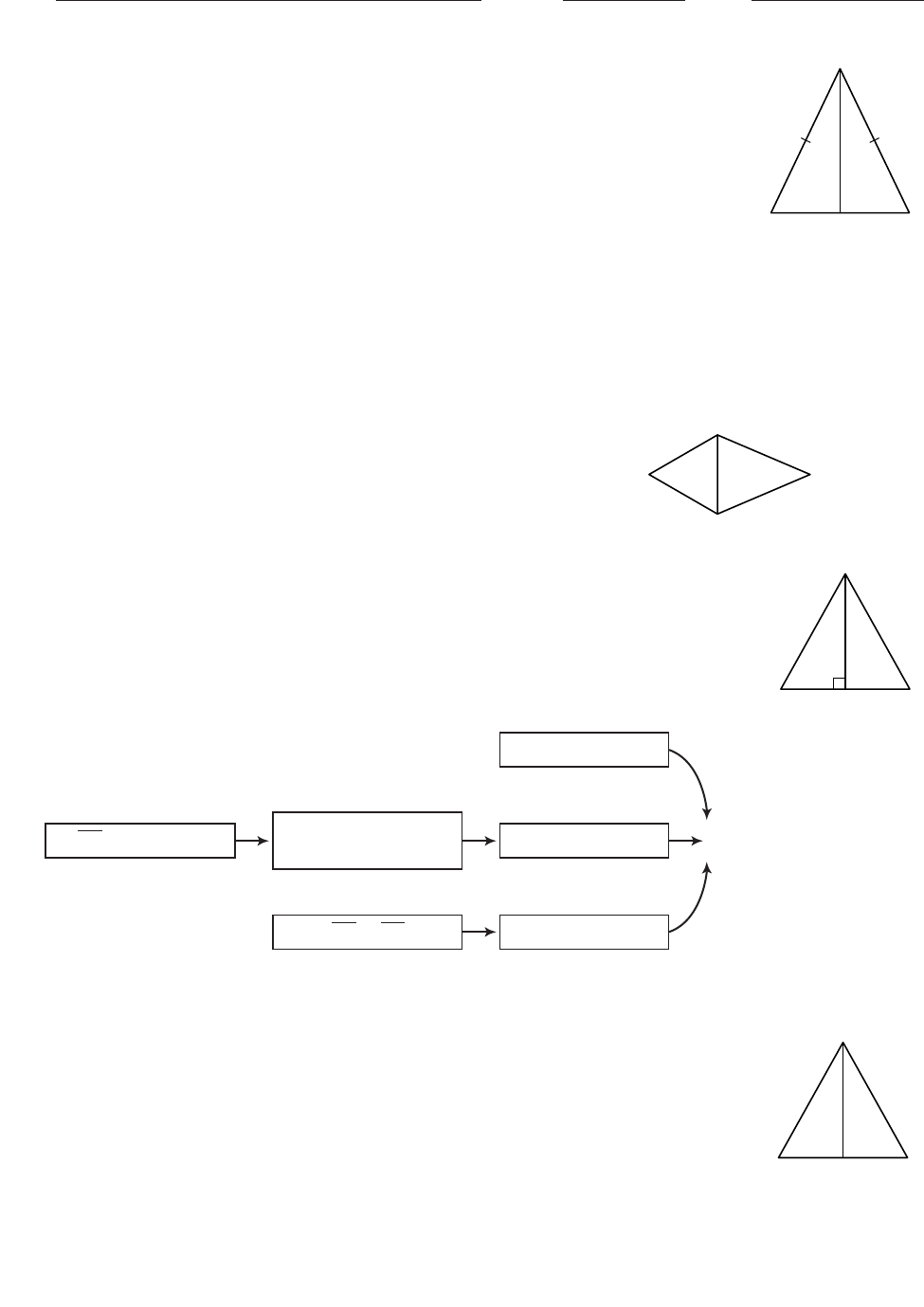
In Exercises 1–3, use the figure at right.
1. CD
is a median, perimeter ABC 60, and AC 22. AD _____
2. CD
is an angle bisector, and mA54°. mACD _____
3. CD
is an altitude, perimeter ABC 42, mACD 38°, and AD 8.
mB_____, CB _____
4. EQU is equilateral. 5. ANG is equiangular
mE_____ and perimeter ANG 51.
AN _____
6. ABC is equilateral, ACD is isosceles with base AC
,
perimeter ABC 66, and perimeter ACD 82.
Perimeter ABCD _____
7. Complete a flowchart proof for this conjecture: In an isosceles triangle,
the altitude from the vertex angle is the median to the base.
Given: Isosceles ABC with AC
BC
and altitude CD
Show: CD
is a median
Flowchart Proof
8. Write a flowchart proof for this conjecture: In an isosceles triangle, the
median to the base is also the angle bisector of the vertex angle.
Given: Isosceles ABC with AC
BC
and median CD
Show: CD
bisects ACB
AB
C
D
• •
•
A ________
ADC BDC
ADC and BDC
are right angles
__________________
____________________ Definition of altitude
Given
__________________
__________________
CD is an altitude
AC BC
AB
C
D
C
D
A
B
AB
C
D
DG4PSA_894_04.qxd 11/1/06 1:25 PM Page 31
©2008 Kendall Hunt Publishing
LESSON 4.2 • Properties of Isosceles Triangles
1. mT64° 2. mG45°
3. x125°
4. mA39°, perimeter of ABC 46 cm
5. LM 163 m, mM50°
6. mQ44°, QR 125
7. a. DAB ABD BDC BCD
b. ADB CBD
c. AD
BC
by the Converse of the AIA Conjecture.
8. x21°, y16° 9. mQPR 15°
10. mPRQ 55° by VA, which makes mP55° by
the Triangle Sum Conjecture. So, PQR is isosceles
by the Converse of the Isosceles Triangle Conjecture.
LESSON 4.3 • Triangle Inequalities
1. Yes
2. No
3. 19 x53 4. bac
5. bca6. acdb
7. x76° 8. x79°
9. The interior angle at Ais 60°. The interior angle at
Bis 20°. But now the sum of the measures of the
triangle is not 180°.
10. By the Exterior Angles Conjecture,
2xxmPQS.So,mPQS x. So, by the
Converse of the Isosceles Triangle Conjecture,
PQS is isosceles.
11. Not possible. AB BC AC
12.
LESSON 4.4 • Are There Congruence Shortcuts?
1. SAA or ASA 2. SSS 3. SSS
4. BQM (SAS) 5. TIE (SSS)
Q
P
R
28 km
17 km 9 km
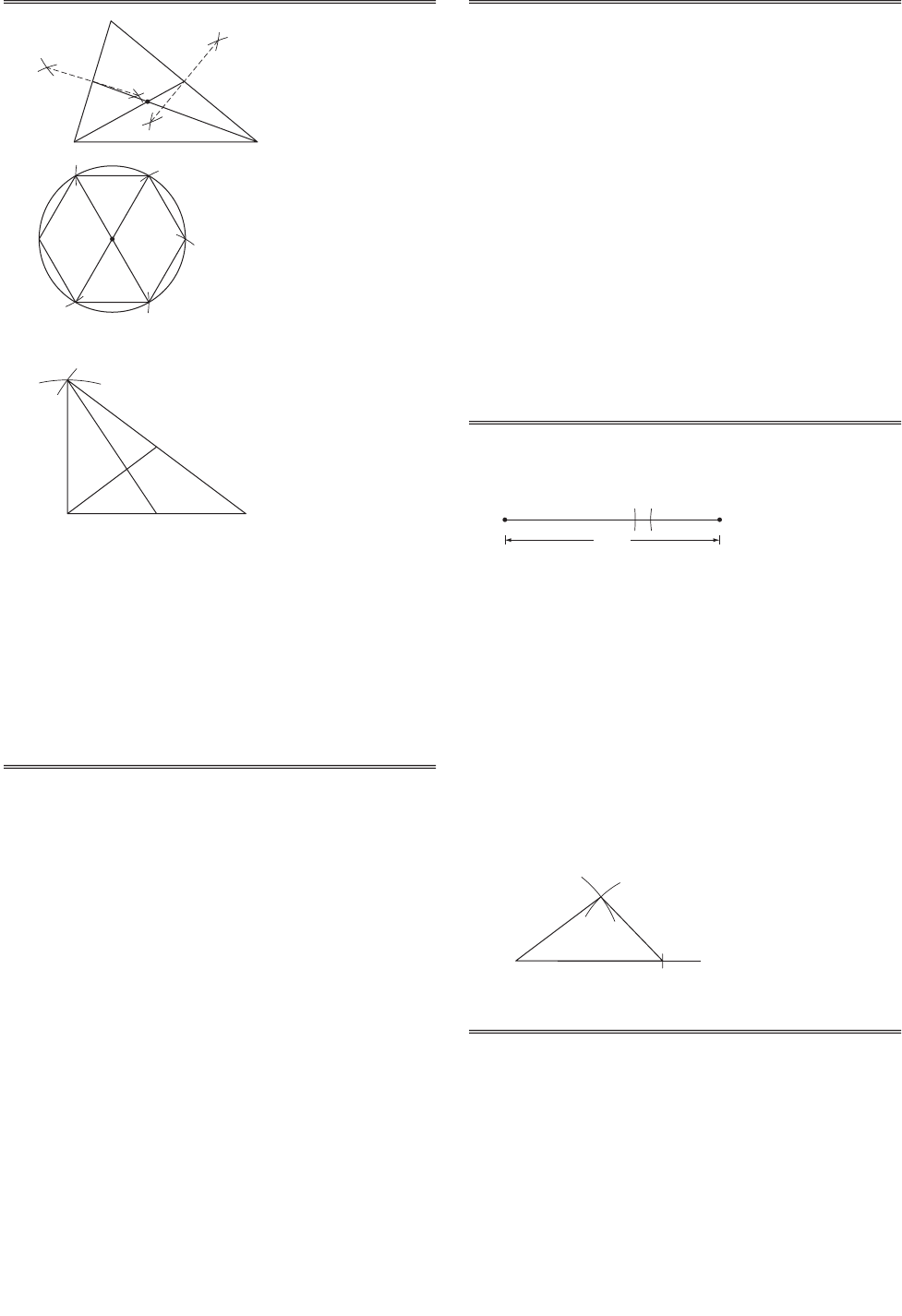
LESSON 3.8 • The Centroid
1.
2.
3. CP 3.3 cm, CQ 5.7 cm, CR 4.8 cm
4. (3, 4)
5. PC 16, CL 8, QM 15, CR 14
6. a. Incenter b. Centroid
c. Circumcenter d. Circumcenter
e. Orthocenter f. Incenter
g. Centroid
LESSON 4.1 • Triangle Sum Conjecture
1. p67°, q15° 2. x82°, y81°
3. a78°, b29°
4. r40°, s40°, t100°
5. x31°, y64° 6. y145°
7. s28° 8. m72
1
2
°
9. mPa10. mQPT 135°
11. 720°
12. The sum of the measures of Aand Bis 90°
because mCis 90° and all three angles must be
180°. So, Aand Bare complementary.
13. mBEA mCED because they are vertical
angles. Because the measures of all three angles in
each triangle add to 180°, if equal measures are
subtracted from each, what remains will be equal.
Q
P
C
R
10 cm
8 cm
6 cm
G
C
Discovering Geometry Practice Your Skills ANSWERS 99
DG4PSA_894_ans.qxd 11/1/06 10:37 AM Page 99
©2008 Kendall Hunt Publishing
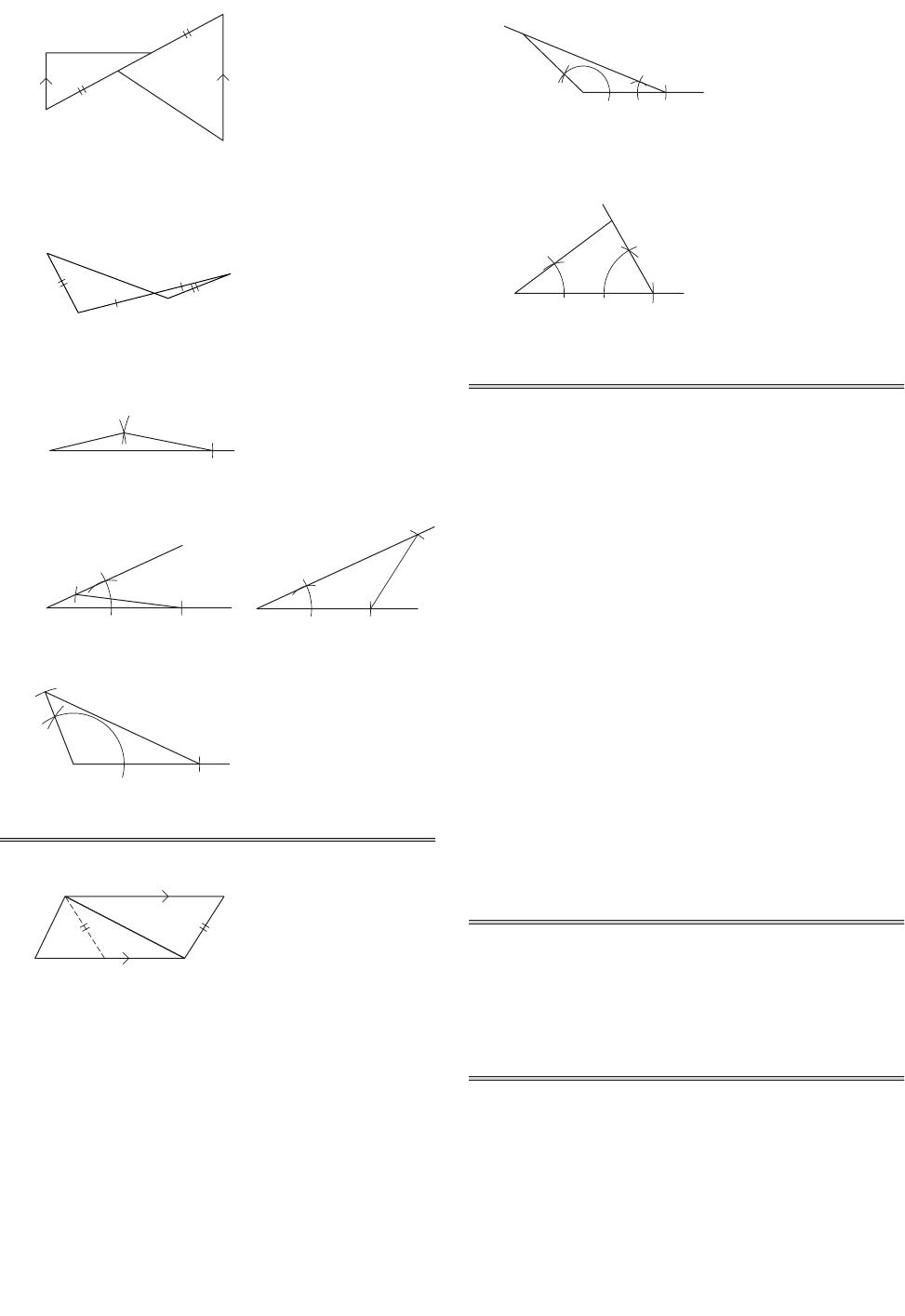
9. All triangles will be congruent by ASA. Possible
triangle:
10. All triangles will be congruent by SAA. Possible
procedure: Use Aand Cto construct Band
then copy Aand Bat the ends of AB
.
LESSON 4.6 • Corresponding Parts of Congruent
Triangles
1. SSS, SAS, ASA, SAA
2. YZ
WX
,AIA Conjecture
3. WZ
XY
,AIA Conjecture
4. ASA 5. CPCTC
6. YWM ZXM by SAS. YW
ZX
by CPCTC.
7. ACD BCD by SAS. AD
BD
by CPCTC.
8. Possible answer: DE and CF are both the distance
between DC
and AB
. Because the lines are parallel,
the distances are equal. So, DE
CF
.
9. Possible answer: DE
CF
(see Exercise 8).
DEF CFE because both are right angles,
EF
FE
because they are the same segment. So,
DEF CFE by SAS. EC
FD
by CPCTC.
10. Possible answer: It is given that TP RA and
PTR ART, and TR
RT
because they
are the same segment. So PTR ART
by SAS and TA
RP
by CPCTC.
LESSON 4.7 • Flowchart Thinking
1. (See flowchart proof at bottom of page 101.)
2. (See flowchart proof at bottom of page 101.)
3. (See flowchart proof at bottom of page 101.)
LESSON 4.8 • Proving Special Triangle Conjectures
1. AD 82. mACD 36°
3. mB52°, CB 13 4. mE60°
5. AN 17 6. Perimeter ABCD 104
C
B
A
Q
P
R
6. Cannot be determined, as shown by the figure.
7. TNO (SAS)
8. Cannot be determined, as shown by the figure.
9. DOG (SAS)
10. Only one triangle because of SSS.
11. Two possible triangles.
12. Only one triangle because of SAS.
LESSON 4.5 • Are There Other Congruence Shortcuts?
1. Cannot be determined
2. XZY (SAA) 3. ACB (ASA or SAA)
4. PRS (ASA) 5. NRA (SAA)
6. GQK (ASA or SAA)
7. Yes , QRS MOL by SSS.
8. No, corresponding sides TV
and WV
are not
congruent.
Z
XY
BC
A
BC
A
U
T
S
Q
T
U
R
S
AC
Y
X
Z
B
100 ANSWERS Discovering Geometry Practice Your Skills
DG4PSA_894_ans.qxd 11/1/06 10:37 AM Page 100
©2008 Kendall Hunt Publishing
3. 170°; 36 sides 4. 15 sides
5. x 105° 6. x 18°
7. mE 150°
LESSON 5.2 • Exterior Angles of a Polygon
1. 12 sides 2. 24 sides 3. 4 sides 4. 6 sides
5. a 64°, b 138
2
3
°6. a 102°, b 9°
7. a 156°, b 132°, c 108°
8. a 135°, b 40°, c 105°, d 135°
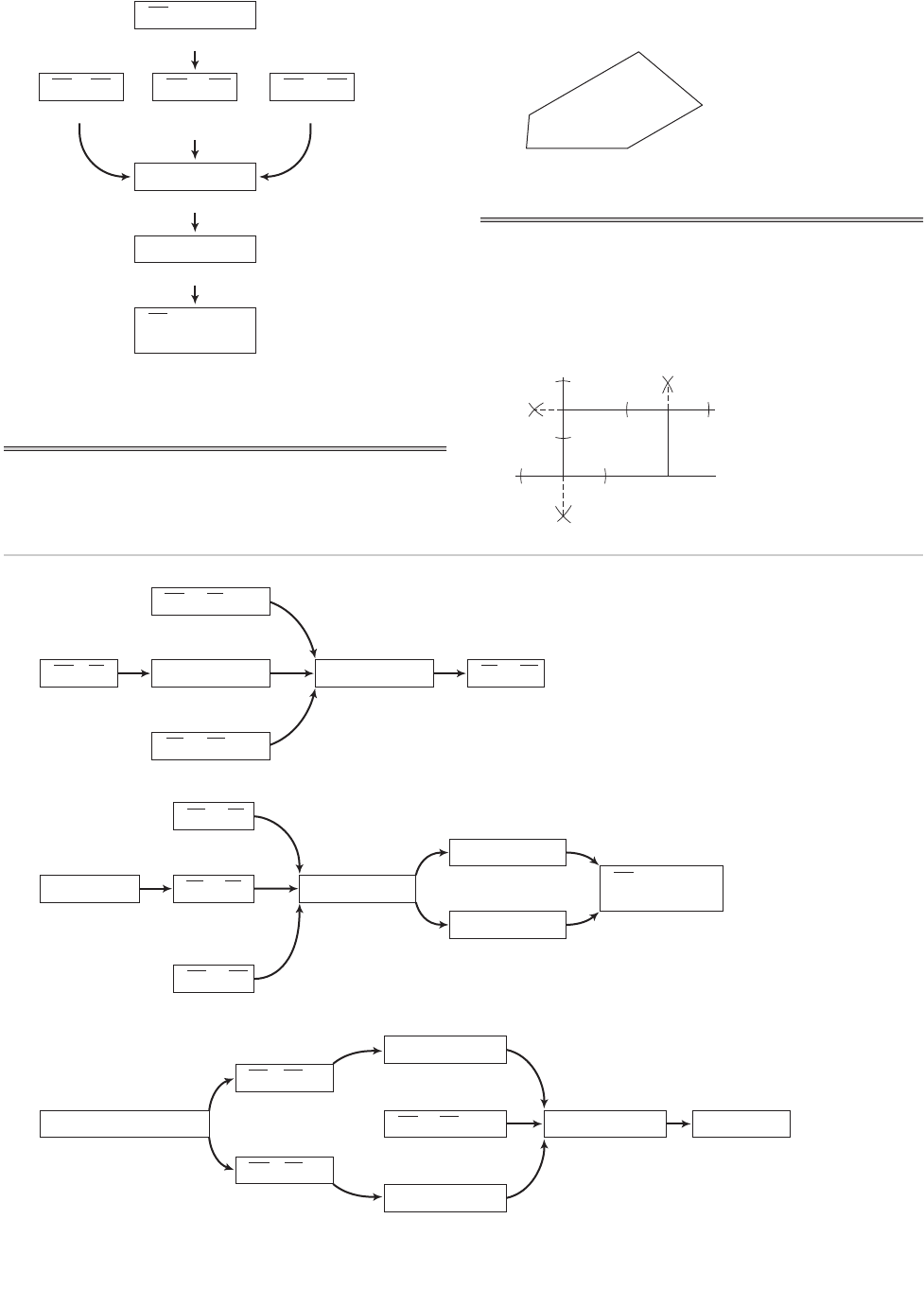
9.
B
A
D
C
E
150°
85°
125°
110°
70°
7. (See flowchart proof at bottom of page 102.)
8. Flowchart Proof
LESSON 5.1 • Polygon Sum Conjecture
1. a 103°, b 103°, c 97°, d 83°, e 154°
2. a 92°, b 44°, c 51°, d 85°, e 44°, f136°
Same segment
AC BC
Given
CD CD
AD BD
Definition of
median
CD is a median
Given
ADC BDC
SSS Conjecture
CD bisects
ACB
Definition of
bisect
ACD BCD
CPCTC
Discovering Geometry Practice Your Skills ANSWERS 101
1.
2.
3.
ABCD is a parallelogram
Given
ABD CDB
AIA Conjecture
ADB CBD
AIA Conjecture
AD CB
Definition of
parallelogram
Definition of
parallelogram
AB CD
BDA DBC
ASA Conjecture
BD DB
Same segment
A C
CPCTC
KE KI
Given
Same segment
KT KT
TE TI
Definition of
kite
KITE is a kite
Given
KET KIT
SSS Conjecture
KT bisects EKI
and ETI
Definition of
bisect
EKT IKT
CPCTC
ETK ITK
CPCTC
PQS RSQ
AIA Conjecture
Same segment
QS QS
PQ SR
Given
PQS RSQ
SAS Conjecture
SP QR
CPCTC
PQ SR
Given
Lesson 4.7, Exercises 1, 2, 3
DG4PSA_894_ans.qxd 11/1/06 10:37 AM Page 101
©2008 Kendall Hunt Publishing