Differential Analyses With DSS Guide

User Manual:

Open the PDF directly: View PDF .
Page Count: 22

1 Introduction
2 Using DSS for differential expression analysis
3 Using DSS for differential methylation analysis
4 Session Info

Diﬀerential analyses with DSS

Hao Wu

[1em]Department of Biostatistics and Bioinformatics

Emory University

Atlanta, GA 303022

[1em] hao.wu@emory.edu

October 30, 2017

Contents

1 Introduction .............................. 2

2 Using DSS for differential expression analysis ........... 3

2.1 Input data preparation ...................... 3

2.2 Single factor experiment ..................... 4

2.3 Multifactor experiment ...................... 6

3 Using DSS for differential methylation analysis........... 7

3.1 Overview ............................. 7

3.2 Input data preparation ...................... 8

3.3 DML/DMR detection from two-group comparison ......... 9

3.4 DML/DMR detection from general experimental design ...... 14

3.4.1 Hypothesis testing in general experimental design ....... 14

3.4.2 Example analysis for data from general experimental design . . . 16

4 Session Info .............................. 21

Abstract

This vignette introduces the use of the Bioconductor package DSS (Dispersion Shrinkage

for Sequencing data), which is designed for diﬀerential analysis based on high-throughput

sequencing data. It performs diﬀerential expression analyses for RNA-seq, and diﬀerential

Diﬀerential analyses with DSS

methylation analyses for bisulﬁte sequencing (BS-seq) data. The core of DSS is a proce-

dure based on Bayesian hierarchical model to estimate and shrink gene- or CpG site-speciﬁc

dispersions, then conduct Wald tests for detecting diﬀerential expression/methylation.

1 Introduction

Recent advances in various high-throughput sequencing technologies have revolutionized ge-

nomics research. Among them, RNA-seq is designed to measure the the abundance of RNA

products, and Bisulﬁte sequencing (BS-seq) is for measuring DNA methylation. A fundamen-

tal question in functional genomics research is whether gene expression or DNA methylation

vary under diﬀerent biological contexts. Thus, identifying diﬀerential expression genes (DEGs)

or diﬀerential methylation loci/regions (DML/DMRs) are key tasks in RNA-seq or BS-seq

data analyses.

The diﬀerential expression (DE) or diﬀerential methylation (DM) analyses are often based on

gene- or CpG-speciﬁc statistical test. A key limitation in RNA- or BS-seq experiments is that

the number of biological replicates is usually limited due to cost constraints. This can lead

to unstable estimation of within group variance, and subsequently undesirable results from

hypothesis testing. Variance shrinkage methods have been widely applied in DE analyses in

microarray data to improve the estimation of gene-speciﬁc within group variances. These

methods are typically based on a Bayesian hierarchical model, with a prior imposed on the

gene-speciﬁc variances to provide a basis for information sharing across all genes.

A distinct feature of RNA-seq or BS-seq data is that the measurements are in the form of

counts and have to be modeld by discrete distributions. Unlike continuous distributions (such

as Gaussian), the variances depend on means in these discrete distributions. This implies

that the sample variances do not account for biological variation, and shrinkage cannot be

applied on variances directly. In DSS, we assume that the count data are from the Gamma-

Poisson (for RNA-seq) or Beta-Binomial (for BS-seq) distribution. We then parameterize

the distributions by a mean and a dispersion parameters. The dispersion parameters, which

represent the biological variation for replicates within a treatment group, play a central role

in the diﬀerential analyses.

DSS implements a series of DE/DM detection algorithms based on the dispersion shrink-

age method followed by Wald statistical test to test each gene/CpG site for diﬀerential

expression/methylation. It provides functions for RNA-seq DE analysis for both two group

comparision and multi-factor design, BS-seq DM analysis for two group comparision, multi-

factor design, and data without biological replicate. Simulation and real data results show

that the methods provides excellent performance compared to existing methods, especially

when the overall dispersion level is high or the number of replicates is small.

Diﬀerential analyses with DSS

For more details of the data model, the shrinkage method, and test procedures, please read

[4] for diﬀerential expression from RNA-seq, [1] for diﬀerential methylation for two-group

comparison from BS-seq, [2] for diﬀerential methylation for data without biological replicate,

and [3] for diﬀerential methylation for general experimental design.

2 Using DSS for differential expression analysis

2.1 Input data preparation

DSS requires a count table (a matrix of integers) for gene expression values (rows are

for genes and columns are for samples). This is diﬀerent from the isoform expression based

analysis such as in cuﬄink/cuﬀdiﬀ, where the gene expressions are represented as non-integers

values. There are a number of ways to obtain the count table from raw sequencing data (fastq

ﬁle), here we provide some example codes using several Bioconductor packages (the codes

require installation of GenomicFeatures,Rsamtools, and GenomicRanges packages).

1. Sequence alignment. There are several RNA-seq aligner, for example, tophat or STAR.

Assume the alignment result is saved in a BAM ﬁle data.bam.

2. Choose a gene annotation. GenomicFeatures package provides a convenient way to

access diﬀerent gene annotations. For example, if one wants to use RefSeq annotation

for human genome build hg19, one can use following codes:

> library(GenomicFeatures)

> txdb = makeTranscriptDbFromUCSC(genom="hg19",tablename="refGene")

> genes = genes(txdb)

3. Obtain count table based on the alignment results and gene annotation. This can be

done in several steps. First read in the BAM ﬁle using the Rsamtools package:

> bam=scanBam("data.bam")

Next, create GRanges object for the aligned sequence reads.

> IRange.reads=GRanges(seqnames=Rle(bam$rname), ranges=IRanges(bam$pos, width=bam$qwidth))

Finally, use the countOverlaps function in GenomicRanges function to obtain the read

counts overlap each gene.

> counts = countOverlaps(genes, IRange.reads)

Diﬀerential analyses with DSS

There are other ways to obtain the counts, for example, using QuasR or easyRNASeq Biocon-

ductor package. Please refer to the package vignettes for more details.

2.2 Single factor experiment

In single factor RNA-seq experiment, DSS also requires a vector representing experimental

designs. The length of the design vector must match the number of columns of the count

table. Optionally, normalization factors or additional annotation for genes can be supplied.

The basic data container in the package is SeqCountSet class, which is directly inherited

from ExpressionSet class deﬁned in Biobase. An object of the class contains all necessary

information for a DE analysis: gene expression values, experimental designs, and additional

annotations.

A typical DE analysis contains the following simple steps.

1. Create a SeqCountSet object using newSeqCountSet.

2. Estimate normalization factor using estNormFactors.

3. Estimate and shrink gene-wise dispersion using estDispersion

4. Two-group comparison using waldTest.

The usage of DSS is demonstrated in the simple simulation below.

1. First load in the library, and make a SeqCountSet object from some counts for 2000

genes and 6 samples.

> library(DSS)

> counts1=matrix(rnbinom(300, mu=10, size=10), ncol=3)

> counts2=matrix(rnbinom(300, mu=50, size=10), ncol=3)

> X1=cbind(counts1, counts2) ## these are 100 DE genes

> X2=matrix(rnbinom(11400, mu=10, size=10), ncol=6)

> X=rbind(X1,X2)

> designs=c(0,0,0,1,1,1)

> seqData=newSeqCountSet(X, designs)

> seqData

SeqCountSet (storageMode: lockedEnvironment)

assayData: 2000 features, 6 samples

element names: exprs

protocolData: none

phenoData

sampleNames: 1 2 ... 6 (6 total)

Diﬀerential analyses with DSS

varLabels: designs

varMetadata: labelDescription

featureData: none

experimentData: use 'experimentData(object)'

Annotation:

2. Estimate normalization factor.

> seqData=estNormFactors(seqData)

3. Estimate and shrink gene-wise dispersions

> seqData=estDispersion(seqData)

4. With the normalization factors and dispersions ready, the two-group comparison can

be conducted via a Wald test:

> result=waldTest(seqData, 0, 1)

> head(result,5)

geneIndex muA muB lfc difExpr stats pval

35 35 6.000000 72.79487 -2.422688 -66.79487 -6.106274 1.019840e-09

60 60 4.333333 59.94872 -2.526259 -55.61538 -6.063770 1.329677e-09

12 12 7.666667 74.92308 -2.223052 -67.25641 -5.965320 2.441553e-09

99 99 7.666667 70.97436 -2.169278 -63.30769 -5.885008 3.980348e-09

52 52 7.333333 62.79487 -2.089416 -55.46154 -5.749004 8.977052e-09

local.fdr fdr

35 1.469796e-05 1.469796e-05

60 1.474650e-05 1.469796e-05

12 2.016697e-05 1.704275e-05

99 2.580658e-05 1.994590e-05

52 3.904835e-05 2.802468e-05

A higher level wrapper function DSS.DE is provided for simple RNA-seq DE analysis in a

two-group comparison. User only needs to provide a count matrix and a vector of 0’s and

1’s representing the design, and get DE test results in one line. A simple example is listed

below:

> counts = matrix(rpois(600, 10), ncol=6)

> designs = c(0,0,0,1,1,1)

> result = DSS.DE(counts, designs)

> head(result)

Diﬀerential analyses with DSS

geneIndex muA muB lfc difExpr stats pval

68 68 6.255892 11.963636 -0.6124003 -5.707744 -2.044332 0.04092073

19 19 5.973064 10.403030 -0.5213912 -4.429966 -1.703204 0.08852996

33 33 8.956229 5.072727 0.5287891 3.883502 1.651242 0.09868912

22 22 7.164983 11.860606 -0.4778522 -4.695623 -1.644890 0.09999251

55 55 7.481481 12.218182 -0.4659086 -4.736700 -1.622868 0.10461760

7 7 7.474747 11.796970 -0.4330729 -4.322222 -1.502718 0.13291190

local.fdr fdr

68 0.3178875 0.3178875

19 0.5192850 0.4198830

33 0.7003377 0.4727321

22 0.5619836 0.4443812

55 0.5788054 0.4572273

7 0.6804533 0.5543755

2.3 Multifactor experiment

DSS provides functionalities for dispersion shrinkage for multifactor experimental designs.

Downstream model ﬁtting (through genearlized linear model) and hypothesis testing can be

performed using other packages such as edgeR, with the dispersions estimated from DSS.

Below is an example, based a simple simulation, to illustrate the DE analysis of a crossed

design.

1. First simulate data for a 2x2 crossed experiments. Note the counts are randomly

generated.

> library(DSS)

> library(edgeR)

> counts=matrix(rpois(800, 10), ncol=8)

> design=data.frame(gender=c(rep("M",4), rep("F",4)), strain=rep(c("WT", "Mutant"),4))

> X=model.matrix(~gender+strain, data=design)

2. make SeqCountSet, then estimate size factors and dispersion

> seqData=newSeqCountSet(counts, as.data.frame(X))

> seqData=estNormFactors(seqData)

> seqData=estDispersion(seqData)

3. Using edgeR’s function to do glm model ﬁtting, but plugging in the estimated size

factors and dispersion from DSS.

Diﬀerential analyses with DSS

> fit.edgeR <- glmFit(counts, X, lib.size=normalizationFactor(seqData),

+ dispersion=dispersion(seqData))

4. Using edgeR’s function to do hypothesis testing on the second parameter of the model

(gender).

> lrt.edgeR <- glmLRT(glmfit=fit.edgeR, coef=2)

> head(lrt.edgeR$table)

logFC logCPM LR PValue

1 -0.2062103 21.32223 0.23420850 0.6284207

2 -0.4818837 21.22234 1.32917575 0.2489519

3 -0.2443803 21.17545 0.32698607 0.5674392

4 0.1101438 21.23479 0.06787492 0.7944564

5 -0.0988723 21.28219 0.04780051 0.8269357

6 -0.2587670 20.97309 0.31941263 0.5719608

3 Using DSS for differential methylation analysis

3.1 Overview

To detect diﬀerential methylation, statistical tests are conducted at each CpG site, and

then the diﬀerential methylation loci (DML) or diﬀerential methylation regions (DMR) are

called based on user speciﬁed threshold. A rigorous statistical tests should account for

biological variations among replicates and the sequencing depth. Most existing methods

for DM analysis are based on ad hoc methods. For example, using Fisher’s exact ignores

the biological variations, using t-test on estimated methylation levels ignores the sequencing

depth. Sometimes arbitrary ﬁltering are implemented: loci with depth lower than an arbitrary

threshold are ﬁltered out, which results in information loss

The DM detection procedure implemented in DSS is based on a rigorous Wald test for beta-

binomial distributions. The test statistics depend on the biological variations (characterized

by dispersion parameter) as well as the sequencing depth. An important part of the algorithm

is the estimation of dispersion parameter, which is achieved through a shrinkage estimator

based on a Bayesian hierarchical model [1]. An advantage of DSS is that the test can be

performed even when there is no biological replicates. That’s because by smoothing, the

neighboring CpG sites can be viewed as “pseudo-replicates", and the dispersion can still be

estimated with reasonable precision.

Diﬀerential analyses with DSS

DSS also works for general experimental design, based on a beta-binomial regression model

with “arcsine” link function. Model ﬁtting is performed on transformed data with generalized

least square method, which achieves much improved computational performance compared

with methods based on generalized linear model.

DSS depends on bsseq Bioconductor package, which has neat deﬁnition of data structures

and many useful utility functions. In order to use the DM detection functionalities, bsseq

needs to be pre-installed.

3.2 Input data preparation

DSS requires data from each BS-seq experiment to be summarized into following information

for each CG position: chromosome number, genomic coordinate, total number of reads, and

number of reads showing methylation. For a sample, this information are saved in a simple

text ﬁle, with each row representing a CpG site. Below shows an example of a small part of

such a ﬁle:

chr pos N X

chr18 3014904 26 2

chr18 3031032 33 12

chr18 3031044 33 13

chr18 3031065 48 24

One can follow below steps to obtain such data from raw sequence ﬁle (fastq ﬁle), using

bismark (version 0.10.0, commands for newer versions could be diﬀerent) for BS-seq align-

ment and count extraction. These steps require installation of bowtie or bowtie2,bismark,

and the fasta ﬁle for reference genome.

1. Prepare Bisulﬁte reference genome. This can be done using the bismark_genome_preparation

function (details in bismark manual). Example command is:

bismark_genome_preparation -path_to_bowtie /usr/local/bowtie/ -verbose /path/to/refgenomes/

2. BS-seq alignment. Example command is:

bismark -q -n 1 -l 50 -path_to_bowtie /path/bowtie/ BS-refGenome reads.fastq

This step will produce two text ﬁles reads.fastq_bismark.sam and reads.fastq_bismark_SE_report.txt.

3. Extract methylation counts using bismark_methylation_extractor function:

bismark_methylation_extractor -s -bedGraph reads.fastq_bismark.sam. This will

create multiple txt ﬁles to summarize methylation call and cytosine context, a bedGraph

ﬁle to display methylation percentage, and a coverage ﬁle containing counts infor-

mation. The count ﬁle contain following columns:chr, start, end, methylation%,

count methylated, count unmethylated. This ﬁle can be modiﬁed to make the input

ﬁle for DSS.

Diﬀerential analyses with DSS

A typical DML detection contains two simple steps. First one conduct DM test at each CpG

site, then DML/DMR are called based on the test result and user speciﬁed threshold.

3.3 DML/DMR detection from two-group comparison

Below are the steps to call DML or DMR for BS-seq data in two-group comparison setting.

1. Load in library. Read in text ﬁles and create an object of BSseq class, which is deﬁned in

bsseq Bioconductor package. This step requires bsseq Bioconductor package. BSseq

class is deﬁned in that package.

> library(DSS)

> require(bsseq)

> path <- file.path(system.file(package="DSS"), "extdata")

> dat1.1 <- read.table(file.path(path, "cond1_1.txt"), header=TRUE)

> dat1.2 <- read.table(file.path(path, "cond1_2.txt"), header=TRUE)

> dat2.1 <- read.table(file.path(path, "cond2_1.txt"), header=TRUE)

> dat2.2 <- read.table(file.path(path, "cond2_2.txt"), header=TRUE)

> BSobj <- makeBSseqData( list(dat1.1, dat1.2, dat2.1, dat2.2),

+ c("C1","C2", "N1", "N2") )[1:1000,]

> BSobj

An object of type 'BSseq' with

1000 methylation loci

4 samples

has not been smoothed

All assays are in-memory

2. Perform statistical test for DML by calling DMLtest function. This function basically

performs following steps: (1) estimate mean methylation levels for all CpG site; (2)

estimate dispersions at each CpG sites; (3) conduct Wald test. For the ﬁrst step, there’s

an option for smoothing or not. Because the methylation levels show strong spatial

correlations, smoothing can help obtain better estimates of mean methylation when

the CpG sites are dense in the data (such as from the whole-genome BS-seq). However

for data with sparse CpG, such as from RRBS or hydroxyl-methylation, smoothing is

not recommended.

To perform DML test without smoothing, do:

> dmlTest <- DMLtest(BSobj, group1=c("C1", "C2"), group2=c("N1", "N2"))

Estimating dispersion for each CpG site, this will take a while ...

Diﬀerential analyses with DSS

> head(dmlTest)

chr pos mu1 mu2 diff diff.se stat

1 chr18 3014904 0.3817233 0.4624549 -0.08073162 0.24997034 -0.3229648

2 chr18 3031032 0.3380579 0.1417008 0.19635711 0.11086362 1.7711592

3 chr18 3031044 0.3432172 0.3298853 0.01333190 0.12203116 0.1092500

4 chr18 3031065 0.4369377 0.3649218 0.07201587 0.10099395 0.7130711

5 chr18 3031069 0.2933572 0.5387464 -0.24538920 0.13178800 -1.8619996

6 chr18 3031082 0.3526311 0.3905718 -0.03794068 0.07847999 -0.4834440

phi1 phi2 pval fdr

1 0.300542998 0.01706260 0.74672190 0.9985094

2 0.008911745 0.04783892 0.07653423 0.6792127

3 0.010409029 0.01994821 0.91300423 0.9985094

4 0.010320888 0.01603200 0.47580174 0.9985094

5 0.012537553 0.02320887 0.06260315 0.6158797

6 0.007665696 0.01145531 0.62878051 0.9985094

To perform statistical test for DML with smoothing, do:

> dmlTest.sm <- DMLtest(BSobj, group1=c("C1", "C2"), group2=c("N1", "N2"), smoothing=TRUE)

Smoothing ...

Estimating dispersion for each CpG site, this will take a while ...

User has the option to smooth the methylation levels or not. For WGBS data, smooth-

ing is recommended so that information from nearby CpG sites can be combined to

improve the estimation of methylation levels. A simple moving average algorithm is

implemented for smoothing. In RRBS since the CpG coverage is sparse, smoothing

might not alter the results much. If smoothing is requested, smoothing span is an

important parameter which has non-trivial impact on DMR calling. We use 500 bp as

default, and think that it performs well in real data tests.

3. With the test results, one can call DML by using callDML function. The results DMLs

are sorted by the signiﬁcance.

> dmls <- callDML(dmlTest, p.threshold=0.001)

> head(dmls)

chr pos mu1 mu2 diff diff.se stat

450 chr18 3976129 0.01027497 0.9390339 -0.9287590 0.06544340 -14.19179

451 chr18 3976138 0.01027497 0.9390339 -0.9287590 0.06544340 -14.19179

638 chr18 4431501 0.01331553 0.9430566 -0.9297411 0.09273779 -10.02548

Diﬀerential analyses with DSS

639 chr18 4431511 0.01327049 0.9430566 -0.9297862 0.09270080 -10.02997

710 chr18 4564237 0.91454619 0.0119300 0.9026162 0.05260037 17.15988

782 chr18 4657576 0.98257334 0.0678355 0.9147378 0.06815000 13.42242

phi1 phi2 pval fdr postprob.overThreshold

450 0.052591567 0.02428826 0 0 1

451 0.052591567 0.02428826 0 0 1

638 0.053172411 0.07746835 0 0 1

639 0.053121697 0.07746835 0 0 1

710 0.009528898 0.04942849 0 0 1

782 0.010424723 0.06755651 0 0 1

By default, the test is based on the null hypothesis that the diﬀerence in methylation

levels is 0. Alternatively, users can specify a threshold for diﬀerence. For example, to

detect loci with diﬀerence greater than 0.1, do:

> dmls2 <- callDML(dmlTest, delta=0.1, p.threshold=0.001)

> head(dmls2)

chr pos mu1 mu2 diff diff.se stat

450 chr18 3976129 0.01027497 0.9390339 -0.9287590 0.06544340 -14.19179

451 chr18 3976138 0.01027497 0.9390339 -0.9287590 0.06544340 -14.19179

638 chr18 4431501 0.01331553 0.9430566 -0.9297411 0.09273779 -10.02548

639 chr18 4431511 0.01327049 0.9430566 -0.9297862 0.09270080 -10.02997

710 chr18 4564237 0.91454619 0.0119300 0.9026162 0.05260037 17.15988

782 chr18 4657576 0.98257334 0.0678355 0.9147378 0.06815000 13.42242

phi1 phi2 pval fdr postprob.overThreshold

450 0.052591567 0.02428826 0 0 1

451 0.052591567 0.02428826 0 0 1

638 0.053172411 0.07746835 0 0 1

639 0.053121697 0.07746835 0 0 1

710 0.009528898 0.04942849 0 0 1

782 0.010424723 0.06755651 0 0 1

When delta is speciﬁed, the function will compute the posterior probability that the

diﬀerence of the means is greater than delta. So technically speaking, the threshold

for p-value here actually refers to the threshold for 1-posterior probability, or the local

FDR. Here we use the same parameter name for the sake of the consistence of function

syntax.

Diﬀerential analyses with DSS

4. DMR detection is also Based on the DML test results, by calling callDMR function.

Regions with many statistically signiﬁcant CpG sites are identiﬁed as DMRs. Some

restrictions are provided by users, including the minimum length, minimum number of

CpG sites, percentage of CpG site being signiﬁcant in the region, etc. There are some

post hoc procedures to merge nearby DMRs into longer ones.

> dmrs <- callDMR(dmlTest, p.threshold=0.01)

> head(dmrs)

chr start end length nCG meanMethy1 meanMethy2 diff.Methy areaStat

27 chr18 4657576 4657639 64 4 0.506453 0.318348 0.188105 14.34236

Here the DMRs are sorted by “areaStat", which is deﬁned in bsseq as the sum of the

test statistics of all CpG sites within the DMR.

Similarly, users can specify a threshold for diﬀerence. For example, to detect regions

with diﬀerence greater than 0.1, do:

> dmrs2 <- callDMR(dmlTest, delta=0.1, p.threshold=0.05)

> head(dmrs2)

chr start end length nCG meanMethy1 meanMethy2 diff.Methy areaStat

31 chr18 4657576 4657639 64 4 0.5064530 0.3183480 0.188105 14.34236

19 chr18 4222533 4222608 76 4 0.7880276 0.3614195 0.426608 12.91667

Note that the distribution of test statistics (and p-values) depends on the diﬀerences in

methylation levels and biological variations, as well as technical factors such as coverage

depth. It is very diﬃculty to select a natural and rigorous threshold for deﬁning DMRs.

We recommend users try diﬀerent thresholds in order to obtain satisfactory results.

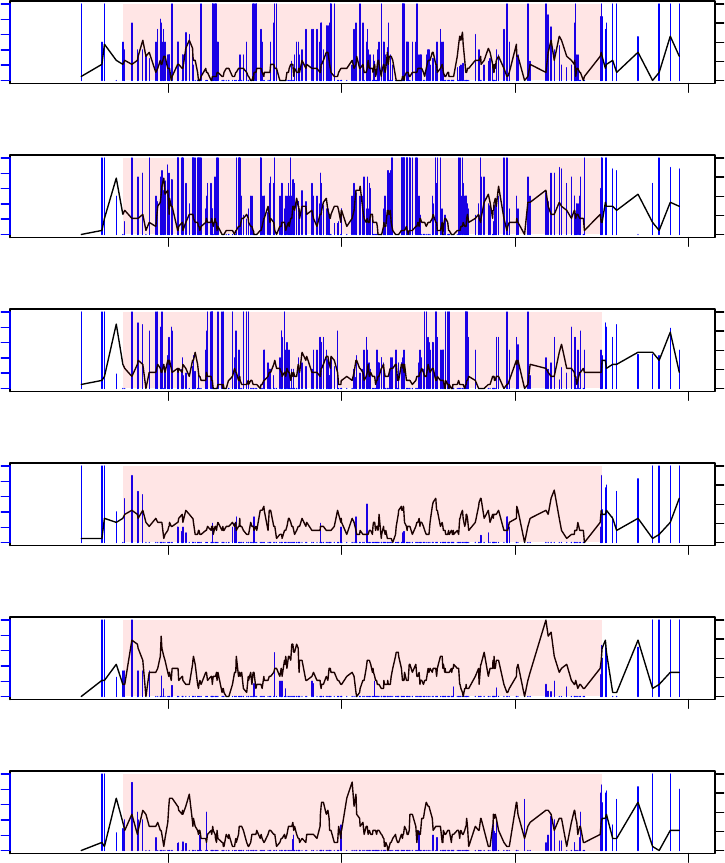
5. The DMRs can be visualized using showOneDMR function, This function provides more

information than the plotRegion function in bsseq. It plots the methylation percent-

ages as well as the coverage depths at each CpG sites, instead of just the smoothed

curve. So the coverage depth information will be available in the ﬁgure.

To use the function, do

> showOneDMR(dmrs[1,], BSobj)

The result ﬁgure looks like the following. Note that the ﬁgure below is not gener-

ated from the above example. The example data are from RRBS experiment

so the DMRs are much shorter.

Diﬀerential analyses with DSS

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

32930000 32931000 32932000 32933000

0.0 0.6

chr21

methyl%

0 10 19

read depth

Diﬀerential analyses with DSS

3.4 DML/DMR detection from general experimental design

In DSS, BS-seq data from a general experimental design (such as crossed experiment, or

experiment with covariates) is modeled through a generalized linear model framework. We

use “arcsine” link function instead of the typical logit link for it better deals with data

at boundaries (methylation levels close to 0 or 1). Linear model ﬁtting is done through

ordinary least square on transformed methylation levels. Variance/covariance matrices for

the estimates are derived with consideration of count data distribution and transformation.

3.4.1 Hypothesis testing in general experimental design

In a general design, the data are modeled through a multiple regression thus there are multiple

regression coeﬃcients. In contrast, there is only one parameter in two-group comparison

which is the diﬀerence between two groups. Under this type of design, hypothesis testing

can be performed for one, multiple, or any linear combination of the parameters.

DSS provides ﬂexible functionalities for hypothesis testing. User can test one parameter in

the model through a Wald test, or any linear combination of the parameters through an

F-test.

The DMLtest.multiFactor function provide interfaces for testing one parameter (through

coef parameter), one term in the model (through term parameter), or linear combinations of

the parameters (through Contrast parameter). We illustrate the usage of these parameters

through a simple example below. Assume we have an experiment from three strains (A, B,

C) and two sexes (M and F), each has 2 biological replicates (so there are 12 datasets in

total).

> Strain = rep(c("A", "B", "C"), 4)

> Sex = rep(c("M", "F"), each=6)

> design = data.frame(Strain,Sex)

> design

Strain Sex

1 A M

2 B M

3 C M

4 A M

5 B M

6 C M

7 A F

8 B F

Diﬀerential analyses with DSS

9 C F

10 A F

11 B F

12 C F

To test the additive eﬀect of Strain and Sex, a design formula is Strain+Sex, and the

corresponding design matrix for the linear model is:

> X = model.matrix(~Strain+ Sex, design)

> X

(Intercept) StrainB StrainC SexM

1 1 0 0 1

2 1 1 0 1

3 1 0 1 1

4 1 0 0 1

5 1 1 0 1

6 1 0 1 1

7 1 0 0 0

8 1 1 0 0

9 1 0 1 0

10 1 0 0 0

11 1 1 0 0

12 1 0 1 0

attr(,"assign")

[1]0112

attr(,"contrasts")

attr(,"contrasts")$Strain

[1] "contr.treatment"

attr(,"contrasts")$Sex

[1] "contr.treatment"

Under this design, we can do diﬀerent tests using the DMLtest.multiFactor function:

•If we want to test the sex eﬀect, we can either specify coef=4,coef="SexM", or

term="Sex". Notice that when using character for coef, the character must match

the column name of the design matrix, cannot do coef="Sex". It is also important to

note that using term="Sex" only tests a single paramter in the model because sex only

has two levels.

Diﬀerential analyses with DSS

•If we want to test the eﬀect of Strain B versus Strain A (this is also testing a single

parameter), we do coef=2 or coef="StrainB".

•If we want to test the whole Strain eﬀect, it becomes a compound test because Strain

has three levels. We do term="Strain", which tests StrainB and StrainC simulta-

neously. We can also make a Contrast matrix L as following. It’s clear that testing

LTβ= 0 is equivalent to testing StrainB=0 and StrainC=0.

> L = cbind(c(0,1,0,0),c(0,0,1,0))

> L

[,1] [,2]

[1,] 0 0

[2,] 1 0

[3,] 0 1

[4,] 0 0

•One can perform more general test, for example, to test StrainB=StrainC, or that

strains B and C has no diﬀerence (but they could be diﬀerent from Strain A). In this

case, we need to make following contrast matrix:

> matrix(c(0,1,-1,0), ncol=1)

[,1]

[1,] 0

[2,] 1

[3,] -1

[4,] 0

3.4.2 Example analysis for data from general experimental design

1. Load in data distributed with DSS. This is a small portion of a set of RRBS experiments.

There are 5000 CpG sites and 16 samples. The experiment is a 2design (2 cases and

2 cell types). There are 4 replicates in each case:cell combination.

> data(RRBS)

> RRBS

An object of type 'BSseq' with

5000 methylation loci

16 samples

has not been smoothed

All assays are in-memory

Diﬀerential analyses with DSS

> design

case cell

1 HC rN

2 HC rN

3 HC rN

4 SLE aN

5 SLE rN

6 SLE aN

7 SLE rN

8 SLE aN

9 SLE rN

10 SLE aN

11 SLE rN

12 HC aN

13 HC aN

14 HC aN

15 HC aN

16 HC rN

2. Fit a linear model using DMLfit.multiFactor function, include case, cell, and case:cell

interaction.

> DMLfit = DMLfit.multiFactor(RRBS, design=design, formula=~case+cell+case:cell)

Fitting DML model for CpG site:

3. Use DMLtest.multiFactor function to test the cell eﬀect. It is important to note that

the coef parameter is the index of the coeﬃcient to be tested for being 0. Because

the model (as speciﬁed by formula in DMLfit.multiFactor) include intercept, the cell

eﬀect is the 3rd column in the design matrix, so we use coef=3 here.

> DMLtest.cell = DMLtest.multiFactor(DMLfit, coef=3)

Alternatively, one can specify the name of the parameter to be tested. In this case, the

input coef is a character, and it must match one of the column names in the design

matrix. The column names of the design matrix can be viewed by

> colnames(DMLfit$X)

[1] "(Intercept)" "caseSLE" "cellrN" "caseSLE:cellrN"

Diﬀerential analyses with DSS

The following line also works. Specifying coef="cellrN" is the same as specifying

coef=3.

> DMLtest.cell = DMLtest.multiFactor(DMLfit, coef="cellrN")

Result from this step is a data frame with chromosome number, CpG site position, test

statistics, p-values (from normal distribution), and FDR. Rows are sorted by chromo-

some/position of the CpG sites. To obtain top ranked CpG sites, one can sort the data

frame using following codes:

> ix=sort(DMLtest.cell[,"pvals"], index.return=TRUE)$ix

> head(DMLtest.cell[ix,])

chr pos stat pvals fdrs

1273 chr1 2930315 5.280301 1.289720e-07 0.0006448599

4706 chr1 3321251 5.037839 4.708164e-07 0.0011770409

3276 chr1 3143987 4.910412 9.088510e-07 0.0015147517

2547 chr1 3069876 4.754812 1.986316e-06 0.0024828953

3061 chr1 3121473 4.675736 2.929010e-06 0.0029290097

527 chr1 2817715 4.441198 8.945925e-06 0.0065858325

Below is a ﬁgure showing the distributions of test statistics and p-values from this

example dataset

> par(mfrow=c(1,2))

> hist(DMLtest.cell$stat, 50, main="test statistics", xlab="")

> hist(DMLtest.cell$pvals, 50, main="P values", xlab="")

test statistics

Frequency

−4 −2 0 2 4

0 100 200 300

P values

Frequency

0.0 0.2 0.4 0.6 0.8 1.0

0 50 150 250 350

4. DMRs for multifactor design can be called using callDMR function:

Diﬀerential analyses with DSS

> callDMR(DMLtest.cell, p.threshold=0.05)

chr start end length nCG areaStat

33 chr1 2793724 2793907 184 5 12.619968

413 chr1 3309867 3310133 267 7 -12.093850

250 chr1 3094266 3094486 221 4 11.691413

262 chr1 3110129 3110394 266 5 11.682579

180 chr1 2999977 3000206 230 4 11.508302

121 chr1 2919111 2919273 163 4 9.421873

298 chr1 3146978 3147236 259 5 8.003469

248 chr1 3090627 3091585 959 5 -7.963547

346 chr1 3200758 3201006 249 4 -4.451691

213 chr1 3042371 3042459 89 5 4.115296

169 chr1 2995532 2996558 1027 4 -2.988665

Note that for results from for multifactor design, delta is NOT supported. This is

because in multifactor design, the estimated coeﬃcients in the regression are based on

a GLM framework (loosely speaking), thus they don’t have clear meaning of methylation

level diﬀerences. So when the input DMLresult is from DMLtest.multiFactor,delta

cannot be speciﬁed.

5. More ﬂexible way to specify a hypothesis test. Following 4 tests should produce the

same results, since ’case’ only has two levels. However the p-values from F-tests (using

term or Contrast) are slightly diﬀerent, due to normal approximation in Wald test.

> ## fit a model with additive effect only

> DMLfit = DMLfit.multiFactor(RRBS, design, ~case+cell)

Fitting DML model for CpG site:

> ## test case effect

> test1 = DMLtest.multiFactor(DMLfit, coef=2)

> test2 = DMLtest.multiFactor(DMLfit, coef="caseSLE")

> test3 = DMLtest.multiFactor(DMLfit, term="case")

> Contrast = matrix(c(0,1,0), ncol=1)

> test4 = DMLtest.multiFactor(DMLfit, Contrast=Contrast)

> cor(cbind(test1$pval, test2$pval, test3$pval, test4$pval))

[,1] [,2] [,3] [,4]

[1,] 1 1 1 1

[2,] 1 1 1 1

[3,] 1 1 1 1

[4,] 1 1 1 1

Diﬀerential analyses with DSS

The model ﬁtting and hypothesis test procedures are computationally very eﬃcient. For

a typical RRBS dataset with 4 million CpG sites, it usually takes less than half hour. In

comparison, other similar software such as RADMeth or BiSeq takes at least 10 times longer.

Diﬀerential analyses with DSS

4 Session Info

> sessionInfo()

R version 3.4.2 (2017-09-28)

Platform: x86_64-pc-linux-gnu (64-bit)

Running under: Ubuntu 16.04.3 LTS

Matrix products: default

BLAS: /home/biocbuild/bbs-3.6-bioc/R/lib/libRblas.so

LAPACK: /home/biocbuild/bbs-3.6-bioc/R/lib/libRlapack.so

locale:

[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C

[3] LC_TIME=en_US.UTF-8 LC_COLLATE=C

[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8

[7] LC_PAPER=en_US.UTF-8 LC_NAME=C

[9] LC_ADDRESS=C LC_TELEPHONE=C

[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C

attached base packages:

[1] splines stats4 parallel stats graphics grDevices utils

[8] datasets methods base

other attached packages:

[1] edgeR_3.20.0 limma_3.34.0

[3] DSS_2.26.0 bsseq_1.14.0

[5] SummarizedExperiment_1.8.0 DelayedArray_0.4.0

[7] matrixStats_0.52.2 GenomicRanges_1.30.0

[9] GenomeInfoDb_1.14.0 IRanges_2.12.0

[11] S4Vectors_0.16.0 Biobase_2.38.0

[13] BiocGenerics_0.24.0

loaded via a namespace (and not attached):

[1] Rcpp_0.12.13 compiler_3.4.2 plyr_1.8.4

[4] XVector_0.18.0 R.methodsS3_1.7.1 bitops_1.0-6

[7] R.utils_2.5.0 tools_3.4.2 zlibbioc_1.24.0

[10] digest_0.6.12 evaluate_0.10.1 lattice_0.20-35

[13] Matrix_1.2-11 yaml_2.1.14 GenomeInfoDbData_0.99.1

Diﬀerential analyses with DSS

[16] stringr_1.2.0 knitr_1.17 gtools_3.5.0

[19] locfit_1.5-9.1 rprojroot_1.2 grid_3.4.2

[22] data.table_1.10.4-3 rmarkdown_1.6 magrittr_1.5

[25] backports_1.1.1 scales_0.5.0 htmltools_0.3.6

[28] permute_0.9-4 BiocStyle_2.6.0 colorspace_1.3-2

[31] stringi_1.1.5 RCurl_1.95-4.8 munsell_0.4.3

[34] R.oo_1.21.0

References

[1] Hao Feng, Karen Conneely and Hao Wu. (2014). A bayesian hierarchical

model to detect diﬀerentially methylated loci from single nucleotide resolution

sequencing data. Nucleic Acids Research. 42(8), e69–e69.

[2] Hao Wu, Tianlei Xu, Hao Feng, Li Chen, Ben Li, Bing Yao, Zhaohui

Qin, Peng Jin and Karen N. Conneely. (2015). Detection of diﬀerentially

methylated regions from whole-genome bisulﬁte sequencing data without replicates.

Nucleic Acids Research. doi: 10.1093/nar/gkv715.

[3] Yongseok Park, Hao Wu. (2016). Diﬀerential methylation analysis for BS-seq

data under general experimental design.

Bioinformatics. doi:10.1093/bioinformatics/btw026.

[4] Hao Wu, Chi Wang and Zhijing Wu. (2013). A new shrinkage estimator for

dispersion improves diﬀerential expression detection in RNA-seq data.

Biostatistics. 14(2), 232–243.

Differential Analyses With DSS Guide

Navigation menu

Versions of this User Manual:

Views

Navigation