Eschgfaeller Mabbs Algoritmi
User Manual: Eschgfaeller-mabbs-algoritmi
Open the PDF directly: View PDF ![]() .
.
Page Count: 47

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 9 gennaio 2005 Indice
Insiemi
La notazione matematica 2
L’assioma della scelta 3
L’insieme delle parti 4
Le funzioni
Le funzioni 2
Uguaglianza di funzioni 3
Composizione di funzioni 3
Associativit`a 3
La funzione identica 3
L’immagine 3
Funzioni iniettive 3
Funzioni suriettive 4
Iniettivit`a categoriale 4
Suriettivit`a categoriale 4
Funzioni biiettive 4
Spazi di funzioni 4
Propriet`a funtoriali 4
Algebra lineare
Equazioni lineari in una incognita 6
Sistemi astratti 7
Due sistemi lineari in due incognite 7
Esempi 8
La forma generale della regola
di Cramer 8
Determinanti 8
L’algoritmo di eliminazione di Gauß 9
Sistemi con pi `u di una soluzione 10
L’insieme delle soluzioni di un
sistema lineare 10
Trigonometria
Trigonometria oggi 11
Un problema di geodesia 11
Il triangolo 12
Il triangolo rettangolo 12
Triple pitagoree 12
Le funzioni trigonometriche 12
La dimostrazione indiana 13
Il triangolo isolatero 13
Angoli sul cerchio 13
Il teorema del coseno 14
Il grafico della funzione seno 14
La periodicit`a di seno e coseno 14
Altre propriet`a di seno e coseno 14
e 14
Geometria
Grafica al calcolatore e geometria 11
Distanze in 15
Il prodotto scalare 15
Ortogonalit`a 15
Coordinate polari nel piano 21
Coordinate cilindriche nello spazio 21
Coordinate polari nello spazio 21
Rotazioni nel piano 21
Disuguaglianze fondamentali 24
Il segno del prodotto scalare 24
Ellissi 29
Iperboli 29
Rette e segmenti 30
Equazione di una retta 30
Proiezione su una retta 30
Riflessione in un punto 36
Riflessione in una retta 36
Numeri complessi
Numeri complessi in R 22
I numeri complessi 23
La formula di Euler 23
Il campo dei numeri complessi 24
La formula di de Moivre 24
Parte reale e parte immaginaria 24
Radici di un polinomio 25
Radici -esime dell’unit`a 25
Radici di un numero complesso 25
Perturbazione dei coefficienti 36
I cammini delle radici 37
Il teorema di Rouch´e 37
Continuit`a delle radici 37
Programmazione in R
R 16
Le funzioni d’aiuto 16
Installazione di R 16
Il libro di Crawley 16
Programmare in R 17
Programmi autonomi 17
Nomi in R 17
Assegnamento 17
Successioni 18
Angoli espressi in gradi 18
I commenti 18
Funzioni in R 22
expression ed eval 29
ifelse 32
NA 32
if ... else 33
identical 33
Operazioni insiemistiche 33
dimnames 33
for, while e repeat 40
Abbreviazioni 45
Options e print(x,n) 45
any e all 46
Ordinamento 46
La libreria 46
Grafica con R
Figure di Lissajous 18
La grafica di R 19
plot e lines 19
Il comando postscript 19
points 22
symbols e rect 22
Grafici di funzioni 26
Curve parametrizzate nel piano 26
Octobrina elegans 26
Octobrinidae I 27
Octobrinidae II 27
abline 28
Parabrinidae 28
Rotazioni 28
Testi matematici 29
Curve di livello 31
31
Una collana 32
33
33
33
34
34
Il foglio di Cartesio 34
La chiocciola di Pascal 34
La lemniscata 34
Una curva trascendente 34
La funzione polygon 35
Il file figure 35
Tratteggi 35
Una modifica in Postscript 36
Parallele 38
Come nasce una forma 38
Vettori e matrici con R
outer 32
Creazione di matrici 38
Matrici in R 39
Esempi per le operazioni matriciali 39
Piccoli operatori 39
Indici vettoriali 40
v[v%%p 0] 40
Assegnazione vettoriale 41
Indici matriciali 41
L’opzione drop 41
rbind e cbind 41
Sistemi lineari con R 42
length e dim 42
det (determinante) e traccia 42
Matrici diagonali 42
abs (valore assoluto) e sign 42
Autovalori 42
Matrici simmetriche 43
eigen (autovalori e autovettori) 43
Matrici reali 43
I cerchi di Gershgorin 43
Analisi
I numeri binomiali 20
La formula di Stirling 21
Funzioni iperboliche 28
Derivazione simbolica 44
La derivata 44
La funzione esponenziale 44
Esempi per l’uso di D 45
La serie di Taylor 45
La professione del matematico
Che cos’`e la matematica? 1
La professione 2
Dall’universit`a all’azienda 2
Geometria applicata 5
La matematica in azienda 5
La statistica matematica 5
La matematica degli ingegneri 5
Matematica e chimica 5
La dinamica dei fluidi 5
Geomatematica 5
Malattie tropicali 5
La matematica del futuro 18
Varia
Il re dei matematici 6
Le basi di Gr¨obner 6
Il sito CRAN di Ferrara 30
Il crivello di Eratostene 40
Strumenti
L’alfabeto greco 1
Esercizi per gli scritti
Esercizi 1-13 10
Esercizi 14-17 15
Esercizi 18-22 18
Esercizi 23-27 22
Esercizi 28-43 25
Esercizi 44-53 30
Esercizi 54-58 34
Esercizi 59-66 38
Esercizi 67-76 43

Corso di laurea in matematica Anno accademico 2004/05 Numero 1
Che cos’`e la matematica?
Dividiamo questa domanda in due sottodomande, cercando di indicare prima i
costituenti elementari della matematica, poi come la matematica deve essere usata.
I componenti elementari del ragionamento matematico sono enunciati della for-
ma ipotesi implica tesi; in questo senso la matematica non conosce affermazioni
assolute, ma soltanto proposizioni che si compongono ogni volta di un preciso elen-
co delle ipotesi che vengono fatte, e poi di una altrettanto precisa specificazione
dell’enunciato che secondo quella proposizione ne consegue. A questo punto non `e
detto che la proposizione sia valida, bisogna ancora dimostrarla, e ci`o significa,
nella matematica, dimostrare che la tesi segue dalle ipotesi unite agli assiomi e ai
risultati gi `a ottenuti e alle regole logiche che dobbiamo applicare. Gli assiomi so-
no enunciati che vengono messi all’inizio di una teoria, senza dimostrazione; ogni
altro enunciato deve essere invece dimostrato.
`
E importante che bisogna sempre dimostrare una proposizione - che `e sempre
nella forma ipotesi implica tesi! - nella sua interezza, cio`e che si tratta di di-
mostrare la validit `a dell’implicazione e non la validit `a della tesi. L’enunciato A
implica B pu`o essere vero, anche se Bnon e vero. Ad esempio in logica si impara
che, se l’ipotesi A`e falsa, allora la proposizione A implica B `e sempre vera. Quin-
di l’affermazione se 3 `e uguale a 3.1, allora io mi chiamo Piero `e sempre vera,
indipendentemente da come mi chiamo io. Nella pratica matematica ci`o significa
che da una premessa errata si pu `o, con un po’ di pazienza, dedurre qualunque
cosa.
La validit `a si riferisce quindi sempre a tutta la proposizione A implica B.
Mentre il matematico puro cerca soprattutto di arricchire l’edificio delle teorie
matematiche con nuovi concetti o con dimostrazioni, talvolta assai difficili, di teo-
remi, il matematico applicato deve anche saper usare la matematica. Nelle scienze
naturali e sociali, le quali pongono problemi molto complessi, uno dei compiti pi `u
importanti `e spesso la separazione degli elementi essenziali di un fenomeno dagli
aspetti marginali. In queste scienze le informazioni disponibili sono quasi sempre
incomplete, cosicch´e possiamo ogni volta descrivere soltanto una piccola parte del-
la realt `a. Anche quando disponiamo di conoscenze dettagliate, queste si presentano
in grande quantit`a, sono complesse e multiformi e richiedono concetti ordinatori
per poterle interpretare. Ci`o significa che bisogna estrarre e semplificare.
Un modello matematico di un fenomeno ha soprattutto lo scopo di permettere di
comprendere meglio quel fenomeno, quindi di metterne in evidenza cause e effetti
e comportamenti quantitativi, di individuarne i tratti essenziali e i meccanismi
fondamentali. In un certo senso la matematica consiste di tautologie, e nel modello
matematico si tenta di evidenziare le tautologie contenute nel fenomeno studiato.
La teoria cerca di comprendere i processi e legami funzionali di un campo del
sapere.
La mente umana pensa in modelli. Anche quando non facciamo matematica
della natura, cerchiamo di comprendere la natura mediante immagini semplifi-
cate. La teoria inizia gi `a nell’istante in cui cominciamo a porci la domanda quali
siano gli aspetti essenziali di un oggetto o di un fenomeno. La matematica non `e
dunque altro che un modo sistematico e controllato di eseguire questi processi di
astrazione e semplificazione costantemente attivi nel nostro intelletto.
Il modello matematico, una volta concepito, se sviluppato correttamente, si mo-
stra poi di una esattezza naturale che spesso impressiona l’utente finale che `e ten-
tato di adottare gli enunciati matematici come se essi corrispondessero precisa-
mente ai fenomeni modellati. Ma ci`o non `e affatto vero: La precisione del modello
matematico `e soltanto una precisione interna, tautologica, e la semplificazione,
quindi verit`a approssimata e parziale, che sta all’inizio del modello, si conserva,
e pi `u avanza lo sviluppo matematico, maggiore `e il pericolo che iterando pi `u volte
l’errore, questo sia cresciuto in misura tale da richiedere un’interpretazione estre-
mamente prudente dei risultati matematici. Proprie le teorie pi `u avanzate, pi `u
belle quindi per il matematico puro, sono spesso quelle pi `u lontane dalla realt `a.
Questo automatismo della matematica pu`o essere per`o anche fonte di nuovi punti
di vista e svelare connessioni nascoste.
Un modello matematico `e perci`o solo un ausilio per la riflessione, per controllare
il contenuto e la consistenza logica di un pensiero o di una ricerca. In altre parole,
modelli sono strumenti intellettuali e non si possono da essi aspettare descrizioni
perfette della realt `a. Essi non forniscono risposte complete, ma indicano piuttosto
quali siano le domande che bisogna porre.
L’astrattezza intrinseca della matematica comporta da un lato che essa rimanga
sempre diversa dalla realt `a, offre per `o dall’altro lato la possibilit `a di generalizzare
i risultati ottenuti nelle ricerche in un particolare campo applicativo o anche uno
strumento della matematica pura a problemi apparentemente completamente di-
versi, se questi hanno propriet `a formali in comune con il primo campo.
In questo numero
1 Che cos’`e la matematica?
L’alfabeto greco
2 La professione
Dall’universit`a all’azienda
La notazione matematica
Le funzioni
3 Uguaglianza di funzioni
Composizione di funzioni
Associativit`a
La funzione identica
L’immagine
Funzioni iniettive
L’assioma della scelta
4 Funzioni suriettive
Iniettivit`a categoriale
Suriettivit`a categoriale
Funzioni biiettive
Spazi di funzioni
Propriet`a funtoriali
L’insieme delle parti
5 Geometria applicata
La matematica in azienda
La statistica matematica
La matematica degli ingegneri
Matematica e chimica
La dinamica dei fluidi
Geomatematica
Malattie tropicali
L’alfabeto greco
alfa
beta
gamma
delta
epsilon
zeta
eta
theta
iota
kappa
lambda
mi
ni
xi
omikron
pi
rho
sigma ,
tau
ypsilon
fi
chi
psi
omega
Sono 24 lettere. La sigma minuscola ha due for-
me: alla fine della parola si scrive , altrimenti
. In matematica si usa solo la .
Mikros ( ) significa piccolo, megas
() grande, quindi la omikron `e la opiccola
e la omega la ogrande.
Le lettere greche vengono usate molto spes-
so nella matematica, ad esempio `e
un’abbreviazione per la somma
e per il prodotto , mentre `e
un oggetto con due indici, per uno dei quali ab-
biamo usato una lettera greca.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 1 2
La professione
\In genere lavoro in un team con in-
gegneri, biologi o bancari. Lavoro auto-
nomo o in team nella programmazione
(chi conosce il C e il Perl pu`o realizzare
le costruzioni e tecniche astratte mate-
matiche imparate nel corso di laurea in
modo creativo e utile per l’azienda).
\Il matematico deve essere in grado di
comprendere e analizzare i problemi
che si pongono nella prassi aziendale,
di tradurli nel linguaggio formale del-
la matematica e di risolverli, spesso con
l’aiuto di tecniche e mezzi informatici.
\Matematica finanziaria e attuariale
(calcolo delle probabilit`a, statistica, se-
rie temporali, previsione dei valori di
borsa, calcolo dei rischi e delle tariffe).
\Matematica aziendale (ottimizzazione,
statistica, teoria dei grafi). Il matema-
tico pu`o lavorare nei reparti di ricerca
operativa in grandi ditte, nello svilup-
po di software aziendale, nel controllo
della produzione, nel servizio statistico,
nelle banche, nelle assicurazioni, nella
pubblica amministrazione.
\Matematica industriale (equazioni dif-
ferenziali, fisica matematica, ma an-
che statistica, serie temporali, ottimiz-
zazione e controllo automatico, analisi
numerica).
\Elaborazione delle immagini (appli-
cazioni nell’industria, nella medicina,
nella robotica). Geometria (discreta e
differenziale) computazionale, grafica
al calcolatore).
\Informatica teorica: algebra, strutture
ordinate, funzioni booleane (metodi
classici di semplificazione, diagrammi
di decisione, propriet`a matematiche-
strutturali), linguaggi formali, automi.
Algoritmi. Analisi formale dei concetti.
\Bioinformatica (confronto di sequenze,
studio dell’espressione genica, reti me-
taboliche). Statistica multivariata di
dati clinici di grandi dimensioni.
\Possibilit`a di posizioni anche supe-
riori (industria farmaceutica, ramo
attuariale-statistico).
Dall’universit `a all’azienda
bPer inserirsi e crescere aziendalmente
nel modo migliore, `e importante capi-
re sin dall’inizio che cosa le imprese vo-
gliono dai laureati appena assunti.
bAllenarsi al lavoro in team vuol
dire l’opposto che vedersi con i
propri simili: vuol dire sviluppare
l’interdisciplinarit`a, la capacit `a di farsi
capire da chi ha una cultura e un
gergo differenti, di trovare soluzioni
a problemi che toccano tutti in modo
diverso.
bL’universit`a spinge invece ad aggregar-
si per omogeneit`a, a verificare di sapere
tutti esattamente le stesse cose.
Purtroppo l’universit`a abitua spesso a
un rapporto passivo, spersonalizzato,
burocratico e disincentiva l’iniziativa
individuale, la capacit`a di costruirsi
sentieri e schemi propri.
Gian Battista Rosa (ed.): Dall’universit`a all’azienda.
ACTL 2002, 350p. Euro 30.
La notazione matematica
Matematica e linguaggi di programmazione
hanno in comune la quasi perfetta precisio-
ne e allo stesso tempo la grande complessit`a
degli enunciati. `
E necessario quindi defini-
re attentamente gli oggetti con cui si vuole
lavorare e le operazioni che si vogliono effet-
tuare. Spesso questi oggetti e queste opera-
zioni vengono utilizzati pi`u volte nello stes-
so ragionamento o in una teoria. `
E quindi
necessario introdurre abbreviazioni e, sic-
come talvolta le stesse operazioni possono
essere effettuate su oggetti diversi, variabi-
li. Ci limitiamo qui ad alcuni dei pi `u comuni
concetti insiemistici.
L’insieme che consiste degli ele-
menti viene denotato con
. `e l’insieme di
tutti gli che godono della propriet `a
o che comunque possono essere descritti
dall’espressione . Se `e elemento di
un insieme , allora si scrive . Il
simbolo significa uguale per definizione.
Alcuni insiemi di numeri:
e
Gli elementi di si chiamano numeri natu-
rali, quelli di numeri interi, gli elementi
di numeri razionali. L’insieme dei numeri
reali viene definito nei corsi di analisi ed `e
denotato con .
Molto importante e versatile `e il concet-
to di prodotto cartesiano di insiemi: dati
due insiemi ed , con si denota
l’insieme delle coppie (ordinate) di elementi
che si possono formare prendendo come pri-
ma componente un elemento di e come
seconda un elemento di :
Si possono anche formare prodotti cartesia-
ni di pi `u di due fattori, in particolare si pu`o
formare l’insieme
volte
.
`e quindi il piano reale, lo spazio
tridimensionale. In statistica una tabella di
righe ed colonne di numeri pu`o essere
considerata come una collezione di punti
nello spazio .
Quando un insieme `e contenuto in un
insieme (ci`o significa, per definizione, che
ogni elemento di `e anche elemento di
), allora si scrive . Cos`ı abbiamo
. Due insiemi si chiamano
uguali se hanno gli stessi elementi. Ci`o si
pu`o formulare anche cos`ı:
se e solo se e .
L’unione di due insiemi e `e
l’insieme di tutti gli elementi che apparten-
gono ad almeno uno dei due insiemi, men-
tre l’intersezione `e l’insieme dei lo-
ro elementi comuni, ci`o degli elementi che
appartengono sia ad che a .
Come in aritmetica `e utile avere un nu-
mero , cos`ı nell’insiemistica si introduce
un insieme vuoto apparentemente artificia-
le definito dalla propriet `a di non avere al-
cun elemento. Esso viene denotato con ed
`e sottoinsieme di ogni altro insieme:
per ogni insieme (infatti ogni elemento di
, cio`e nessuno, appartiene a ).
`e un’abbreviazione per se e solo se.
Le funzioni
Il concetto singolo pi `u importante della ma-
tematica `e certamente quello di funzione.
Mediante funzioni possiamo trasformare in-
formazioni da una forma all’altra, possiamo
semplificare informazioni complesse o im-
mergere informazioni in contesti pi `u gene-
rali. Una funzione del tempo pu`o essere stu-
diata per scoprire propriet `a di periodicit`a,
funzioni complicate possono essere decom-
poste in funzioni pi `u semplici. Se per esem-
pio sappiamo che il prodotto di due funzioni
continue `e ancora continuo e se accettiamo
per certo che la funzione che manda un nu-
mero reale in se stesso `e continua, possia-
mo immediatamente concludere che la fun-
zione che manda un numero reale in `e
anch’essa continua.
Il concetto di funzione in matematica `e
molto generale. Una funzione (o applica-
zione) `e definita da tre componenti: un in-
sieme su cui la funzione `e definita (il do-
minio della funzione), un insieme (il co-
dominio) di valori possibili (ogni valore del-
la funzione deve essere un elemento di ,
ma non necessariamente ogni elemento di
`e valore della funzione), e un sottoinsie-
me (il grafico della funzio-
ne) che deve avere la propriet `a che per ogni
esiste esattamente un tale che
.
La tripla si chiama allo-
ra una funzione da in e si scrive anche
oppure . Per ogni
con si denota quell’unico per cui
.
Se pu`o essere espressa mediante una
formula, per si scrive anche ,
ad esempio .
Quando `e un insieme finito e non troppo
grande, una funzione pu`o essere
rappresentata anche da una tabella:
In questo caso e per
possiamo prendere ad esempio l’insieme
.
Nell’analisi di una variabile reale si stu-
diano funzioni definite su un intervallo di
a valori reali. Il grafo di queste funzioni `e un
sottoinsieme di e pu`o quindi essere rap-
presentato nel piano.
Funzioni di questa forma, rappresentabili
come somme (finite o infinite) di funzioni tri-
gonometriche, vengono studiate nell’analisi
armonica (o analisi di Fourier).
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 1 3
Uguaglianza di funzioni
Quand’`e che due funzioni sono uguali?
Per definizione una funzione `e una tripla.
Due triple di oggetti matematici
e sono uguali, se coincidono in
ogni componente, cio`e se
e . Perci`o due funzioni
e sono
uguali se e solo se e
. Le prime due condizioni significa-
no che le due funzioni hanno lo stesso domi-
nio e lo stesso codominio che a questo punto
possiamo chiamare e ; analizziamo la
terza condizione, cio`e . Ci`o signifi-
ca che, per e si ha
se e solo se e quindi
se e solo se . In altre parole, la ter-
za condizione `e equivalente a
per ogni .
Due funzioni e sono perci`o uguali se
e solo se hanno lo stesso dominio e lo stes-
so codominio e se inoltre
per ogni .
Composizione di funzioni
Se e sono due fun-
zioni, si pu`o definire la funzione composta
ponendo
per ogni . La funzione composta tras-
forma quindi prima in e applica poi
la ad . Questa operazione `e molto im-
portante, sia per costruire nuove funzioni
da funzioni note, sia per studiare funzio-
ni complicate decomponendole in funzioni
pi `u semplici, rappresentando cio `e la funzio-
ne complicata come composizione di funzio-
ni pi `u semplici.
Si usano allora spesso diagrammi com-
mutativi: Un diagramma di funzioni
si chiama commutativo, se . Sic-
come e hanno, per definizione, lo
stesso dominio e lo stesso codominio ,
l’uguaglianza significa che
per ogni . Esempi:
In analisi si dimostra che la composizione
di funzioni continue `e continua; quindi se
sappiamo che e sono con-
tinue, possiamo dedurre che anche la fun-
zione `e continua.
Associativit `a
Assumiamo che siano date tre funzioni
, e . Allora possiamo
formare prima e comporre il risultato
con ottenendo cos`ı , oppure
comporre con , ottenendo la funzione
. Dimostriamo che si ottiene
in entrambi i casi la stessa funzione. In pri-
mo luogo ed hanno lo stesso dominio
e lo stesso codominio . Dobbiamo dimo-
strare che per ogni .
Ma
e quindi . Abbiamo cos`ı otte-
nuto la legge di associativit `a per la compo-
sizone di funzioni:
Possiamo perci`o tralasciare le parentesi e
scrivere semplicemente per una com-
posizione di tre funzioni. In un diagram-
ma commutativo la legge di associativit `a
ci permette di percorrere il diagramma se-
guendo le frecce, il risultato dipender`a so-
lo dall’inizio e dalla fine del cammino. Veri-
ficare questa regola nell’ultimo diagramma
in basso a sinistra!
La legge di associativit `a corrisponde alla
commutativit`a del diagramma
In verit`a, in un diagramma commutativo
non useremo il cerchietto per denotare la
composizione, ma daremo dei nuovi nomi a
tutte le frecce; che nel diagramma che segue
segue proprio dalla commutativit `a.
La funzione identica
Per ogni insieme esiste la funzione iden-
tica (o identit `a) . Per
ogni funzione abbiamo un dia-
gramma commutativo
L’immagine
sia un’applicazione. Allora l’im-
magine di `e l’insieme
esiste con
`e quindi un sottoinsieme di e consi-
ste di quegli che sono immagine sotto
di qualche elemento di .
Funzioni iniettive
Una funzione `e detta iniettiva, se
trasforma elementi distinti di in elementi
distinti di ; quindi la funzione `e inietti-
va se e solo se l’uguaglianza
implica .
Proposizione 3.1. Sia . Allora la fun-
zione `e iniettiva se e solo se esiste
una funzione tale che .
Dimostrazione: (1) sia iniettiva. L’idea
della costruzione di `e di mandare ogni
in quell’ (unico per la inietti-
vit`a di ) per cui . Se ,
abbiamo gi`a finito. Cosa facciamo per`o, in ca-
so generale, con quegli che non appar-
tengono ad ? A questo scopo scegliamo
un elemento qualsiasi (ci`o `e possibile
perch´e per ipotesi ) e mandiamo tutti
gli elementi di in .
In altre parole
se
altrimenti
In verit`a avremmo dovuto definire medi-
ante un grafo. `
E per`o chiaro che basta porre
con , dove
e
.
(2) Molto pi `u semplice, ma in un certo sen-
so anche pi `u interessante `e la seconda di-
rezione della dimostrazione, perch´e d `a un
primo saggio dell’efficacia di questo modo
astratto di ragionare. Assumiamo che esista
una funzione tale che
. Per dimostrare che allora `e iniettiva,
prendiamo due elementi e di per cui
.
Ma, per ipotesi, per ogni
, e quindi .
L’assioma della scelta
Quando si sviluppa assiomaticamente la teo-
ria degli insiemi, si scopre che un enuncia-
to che per molti versi sembrerebbe naturale,
non pu`o essere dedotto dagli altri assiomi.
`
E quindi necessario aggiungerlo al sistema
degli assiomi insiemistici. Questo enunciato
prende il nome di assioma della scelta e pu`o
essere formulato in questo modo:
Sia un insieme e per ogni sia da-
to un insieme non vuoto in modo tale che
per gli insiemi ed non abbiano
elementi in comune. Allora esiste un insieme
contenuto nell’unione degli tale che per
ogni l’intersezione possieda
esattamente un elemento.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 1 4
Funzioni suriettive
Una funzione `e detta suriettiva
se ogni elemento di `e immagine di qual-
che elemento di , cio`e se .
Proposizione 4.1. La funzione
`e suriettiva se e solo se esiste una funzione
tale che .
Dimostrazione: (1) sia suriettiva. Sta-
volta la costruzione di non `e affatto ele-
mentare e richiede l’assioma della scelta.
Per ogni definiamo
Siccome la `e suriettiva, per ogni
. Inoltre ed per non
hanno elementi in comune, come `e evidente
dalla definizione. Per l’assioma della scelta
esiste un insieme contenuto nell’unione
degli (e quindi contenuto in
perch´e per ogni ) tale che
l’intersezione per ogni possie-
da esattamente un elemento.
Quest’ultima condizione significa per`o
per ogni esiste esattamente un
tale che .
Perci`o la tripla `e una fun-
zione ben definita.
Dobbiamo per`o dimostrare che
, cio`e che per ogni .
Ma `e proprio scelto in modo tale che
!
Riassumiamo la dimostrazione di questa
prima parte: L’idea intuitiva `e semplice-
mente che per ogni scegliamo un
tale che (un tale
esiste sempre per l’ipotesi della suriettivit `a
della ). Poi formiamo
. Ma senza l’assioma della scelta non ri-
usciamo a dimostrare che in questo modo
abbiamo veramente definito un insieme .
(2) La seconda direzione `e di nuovo faci-
le e istruttiva. Assumiamo che esista una
funzione tale che .
Ci`o significa che per ogni abbiamo
, per cui .
Iniettivit `a categoriale
L’algebra dei diagrammi commutativi `e cos`ı
importante in alcuni campi avanzati della
matematica, che `e argomento di una disci-
plina apposita, la teoria della categorie. For-
muliamo le proposizioni 3.1 e 4.1 in un mo-
do un po’ pi `u vicino al linguaggio delle cate-
gorie.
Proposizione 4.2. La funzione
`e iniettiva se e solo se per ogni insieme e
ogni coppia di funzioni e
l’uguaglianza im-
plica .
Dimostrazione: Il caso `e banale;
sia quindi . (1) sia iniettiva. Per la
prop. 3.1 esiste una funzione ta-
le che . Allora, usando l’ipotesi e
l’associativit`a della composizione di funzio-
ni, abbiamo
(2) Viceversa siano tali che
. Sia . Definiamo le
funzioni e ponendo
e . `
E chiaro che .
L’ipotesi implica e ci`o a sua volta `e
possibile solo se .
Suriettivit `a categoriale
Proposizione 4.3. La funzione
`e suriettiva se e solo se per ogni insieme e
ogni coppia di funzioni e
l’uguaglianza im-
plica .
Dimostrazione: (1) sia suriettiva. Per la
prop. 4.1 esiste una funzione ta-
le che . Di nuovo, usando l’ipotesi
e l’associativit `a della composizione, abbia-
mo
(2) Viceversa sia . La funzio-
ne sia la funzione costante che
manda ogni in . La funzione
sia definita cos`ı:
se
`
E chiaro che per
ogni , perch´e appartiene sempre
ad . Quindi . Per ipotesi ci`o
implica . Ma questo non sarebbe possi-
bile se . Quindi necessariamente
e ci`o significa che `e suriettiva.
Funzioni biiettive
Un’applicazione si chiama bii-
ettiva se `e allo stesso tempo iniettiva e su-
riettiva. Tralasciamo di nuovo il caso bana-
le (ma un po’ intricato) che sia l’insieme
vuoto e assumiamo quindi che .
(1) sia biiettiva. Per le prop. 3.1 e 4.1
esistono funzioni e
tali che e . Dimo-
striamo prima che . Infatti
Abbiamo quindi un’applicazione
tale che e . Dalle
prop. 4.2 e 4.3 segue inoltre che `e univoca-
mente determinata. Essa si chiama la fun-
zione inversa di e viene denotata con .
(2) Se viceversa esiste una funzione
tale che e ,
allora `e iniettiva e suriettiva, quindi biiet-
tiva, per le prop. 3.1 e 4.1. Abbiamo quindi
il seguente risultato.
Proposizione 4.4. La funzione
`e biiettiva se e solo se esiste una funzione
t.c. e .
`e allora univocamente determinata.
Spazi di funzioni
Per insiemi ed definiamo come
l’insieme di tutte le funzioni . Un
insieme della forma o un suo sottoin-
sieme si chiama uno spazio di funzioni. Sia
una funzione.
(1) Per ogni insieme ed ogni funzione
possiamo formare la composizione
, ottenendo cos`ı una
funzione .
(2) Per ogni insieme ed ogni funzione
possiamo formare la composizione
, ottenendo cos`ı una
funzione .
pu`o essere identificato con .
Propriet `a funtoriali
Proposizione 4.5. Siano date funzioni
e . sia un insieme. Co-
me prima abbiamo applicazioni
e . Allora
Dimostrazione: Sia .
Allora
.
Proposizione 4.6. Siano date funzioni
e . sia un insieme. Abbia-
mo applicazioni e . Al-
lora
Dimostrazione: Sia .
Allora
.
Proposizione 4.7. Sia una fun-
zione. Allora:
`e iniettiva `e iniettiva
per ogni insieme .
`e suriettiva `e iniettiva
per ogni insieme .
Dimostrazione: Ci`o non `e altro che una ri-
formulazione delle prop. 4.2 e 4.3.
L’insieme delle parti
L’insieme delle parti di un insieme `e de-
finito come l’insieme di tutti i sottoinsiemi
di . Ne fanno parte almeno stesso e
l’insieme vuoto che sappiamo essere sot-
toinsieme di ogni insieme. Se `e vuoto e
quindi coincide con , l’insieme delle parti
ha un solo elemento ed `e uguale a ; se
possiede esattamente un elemento,
e non ci sono sottoinsiemi di diversi da
e , quindi l’insieme delle parti `e ugua-
le all’insieme e possiede due elemen-
ti. In genere, se `e un insieme finito con
elementi, l’insieme delle parti consiste di
elementi. L’insieme delle parti di si deno-
ta con .
Una funzione booleana di variabili `e una
funzione o, equivalen-
temente, una funzione ,
dove `e un insieme con elementi.
Il numero delle funzioni booleane `e esor-
bitante. Esistono funzioni booleane di
variabili, quindi 65536 funzioni booleane
con 4 argomenti, pi `u di 4 miliardi con 5 ar-
gomenti, pi `u di 18 miliardi di miliardi con
6 argomenti (ogni volta che si aggiunge una
variabile il numero delle funzioni booleane `e
il quadrato di quello precedente).
Le funzioni booleane appaiono, sotto vesti
distinte, nella matematica pura, nello svi-
luppo di circuiti elettronici, nella ricerca me-
dica. Su Google con boolean gene expression
cancer filetype:pdf si trovano 900 files.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 1 5
Geometria applicata
La geometria viene utilizzata in molti cam-
pi della tecnologia moderna: nella tomogra-
fia computerizzata, nella pianificazione di
edifici, nella creazione di animazioni per
film e pubblicit`a, nell’analisi dei movimenti
di robot e satelliti.
La matematica `e di grande aiuto nella
grafica al calcolatore; conoscere le opera-
zioni fondamentali della geometria (trasla-
zioni, rotazioni, riflessioni, coordinate bari-
centriche, i vari tipi di proiezioni) permet-
te di creare facilmente programmi di grafi-
ca con caratteristiche che talvolta mancano
anche nei programmi di grandi produttori
quando non sono stati sviluppati da mate-
matici.
A livello pi `u avanzato la geometria stu-
dia le varie rappresentazioni di curve, su-
perficie e variet`a geometriche di dimen-
sione superiore, mediante rappresentazioni
parametriche oppure sistemi di equazioni.
Si impara allora come passare da una
rappresentazione parametrica a un siste-
ma di equazioni che descrive la stessa va-
riet`a e viceversa; si studiano le funzioni che
trasformano una variet `a in un’altra.
Nella statistica medica i dati sono spesso
punti in spazi di alta dimensione (se in una
analisi di prove di sangue con la spettrome-
tria di massa vengono rilevate le concentra-
zioni di 80 molecole, ogni prova corrispon-
de a un punto di ). Se adesso vogliamo
suddividere i pazienti in gruppi caratteri-
stici (sani e malati nel caso pi `u semplice)
abbiamo bisogno di metodi geometrici per
definire validi criteri di separazione.
La matematica in azienda
La matematica aziendale comprende
da un lato la ricerca operativa, cio`e
l’ottimizzazione delle risorse di un’azienda
o di un ente, una disciplina che si `e evoluta
dall’ottimizzazione lineare a metodi semp-
re pi `u avanzati (ottimizzazione quadratica,
convessa, dinamica, geometria dei numeri
e ottimizzazione intera, topologia algebri-
ca, programmazione logica), e dall’altro,
soprattutto in campo bancario, la mo-
derna sofisticata matematica finanziaria
che deriva dalla matematica attuariale,
ma utilizza strumenti matematici molto
complicati.
Processi stocastici e serie temporali oltre
che in matematica finanziaria hanno molte
altre applicazioni in economia: osservazioni
del carico elettrico della rete ENEL, cam-
biamenti demografici, andamento di mer-
cati e borse.
La statistica matematica
Lo statistico che lavora in un’azienda,
nell’amministrazione pubblica o nella ricer-
ca clinica, deve comprendere i compiti che
gli vengono posti e deve essere in grado
di interagire con i committenti. Nonostan-
te ci`o la statistica `e di sua natura una dis-
ciplina matematica che si basa sul calcolo
delle probabilit `a e richiede conoscenze tec-
niche in altri campi della matematica come
analisi reale e complessa, analisi armoni-
ca, calcolo combinatorio (ad esempio per la
pianificazione di esperimenti).
La matematica degli ingegneri
Problemi ingegneristici hanno quasi semp-
re una forte componente matematica: dal-
la teoria dei materiali all’elaborazione dei
segnali, dall’interpretazione di misurazio-
ni al controllo di qualit `a, da modelli per
il corpo umano e i suoi movimenti (ad
esempio nell’industria automobilistica, ma
anche nell’industria tessile - in sartoria!)
all’analisi strutturale di edifici e ponti, dai
modelli matematici per i processi fisici e
chimici in un altoforno all’ottimizzazione
dell’illuminazione in impianti industriali,
dallo studio dell’erosione nel letto di un
fiume ai problemi inversi della geofisica
(importanti per esempio anche nell’analisi
strutturale di monumenti e edifici), dapper-
tutto si utilizza la matematica.
Potremmo elencare tanti altri campi di
applicazione: la geometria dei movimenti
(cinematica) in robotica e nella costruzione
di macchine, teoria dei sistemi e controllo
ottimale nell’automazione, modellazione di
reazioni chimiche nella chimica industriale,
ottimizzazione strutturale di componenti di
macchine o della composizione di punte per
trapani da dentista, microstruttura di me-
talli, costruzione di autoveicoli, treni ed ae-
rei, ottimizzazione di orari ferroviari, piani-
ficazione urbanistica, telecomunicazioni.
Matematica e chimica
Il ruolo della matematica in chimica `e in ra-
pida crescita, essa viene applicata ad esem-
pio nel disegno razionale di farmaci, nella
selezione e sintesi di nuovi materiali, come
guida nella ricerca di nuovi catalizzatori,
nello sviluppo di algoritmi per la dinamica
molecolare, nella risoluzione di problemi di
ottimizzazione di conformazioni, per la com-
prensione del ripiegamento delle proteine,
nello studio del trasporto di sostanze attra-
verso le membrane esterne ed interne del-
la cellula (fondamentale per la farmacolo-
gia), nell’analisi del complicato avvolgimen-
to delle molecole di DNA, nello studio della
struttura di cristalli e quasicristalli, nella
chimica quantistica.
La geometria e la topologia possono con-
tribuire alla comprensione della struttura
tridimensionale delle molecole, la teoria dei
grafi permette non solo la visualizzazione
dei legami chimici, ma pu`o essere applicata
alla rappresentazione di reazioni chimiche
oppure nell’organizzazione di banche dati di
molecole o della letteratura chimica; il cal-
colo combinatorio e la teoria dei gruppi in-
tervengono nella chimica combinatoria, una
tecnica sempre pi `u utilizzata dall’industria
farmaceutica. Il matematico pu`o lavorare
nello sviluppo di algoritmi per la trasfor-
mazione di Fourier per le applicazioni nella
spettroscopia molecolare oppure nella chi-
mica quantistica computazionale.
Equazioni differenziali parziali, anali-
si armonica, processi stocastici, statistica,
analisi numerica, teoria combinatoria dei
gruppi finiti, teoria dei grafi, quasiordini,
teoria dei numeri (generazione di numeri
casuali), geometria computazionale e gra-
fica al calcolatore nella modellistica mole-
colare (computer aided molecular design e
computer aided drug design): sono poche le
discipline matematiche che non hanno in-
teressanti applicazioni in chimica.
La dinamica dei fluidi
Uno dei campi pi `u classici e allo stesso tempo
pi `u attuali della fisica matematica `e la dina-
mica dei fluidi e dei gas. Essa richiede un ric-
co bagaglio di tecniche matematiche, soprat-
tutto dall’analisi (equazioni differenziali par-
ziali) e dalla geometria differenziale (calcolo
tensoriale), oltre a solide conoscenze in mec-
canica dei continui e termodinamica (densit `a
e viscosit`a e altre caratteristiche di un flui-
do o di un gas dipendono dalla temperatu-
ra e viceversa – un gas si scalda se viene
compresso). `
E una disciplina molto vasta con
tantissime applicazioni: costruzione di mac-
chine (iniettori, turbine, ventilatori, pompe),
ale di aerei, eliche di aerei e di navi, ruote a
vento, modelli per nuovi materiali, flussi in
medi porosi, raffreddamento di vetri, produ-
zione di fibre plastiche, serbatoi di olio, ot-
timizzazione del caff`e espresso, studio del-
la formazione di vortici e turbolenze, combu-
stione, detonazioni, modelli per il movimen-
to di animali (pesci, serpenti, uccelli), mo-
delli aerodinamici per la meteorologia (circo-
lazioni e turbolenze atmosferiche, moto dei
venti attorno a grandi catene di montagne,
uragani, convezione termica nell’atmosfera)
e l’agricoltura (moto dell’aria in piantagioni
o foreste), aerodinamica di edifici, pianifica-
zione di esperimenti aerodinamici e idrodi-
namici (costruzione di canali aerodinamici),
previsione delle interazioni con l’aria di tre-
ni ad alta velocit`a, stima delle esposizioni al
vento di un ponte. In medicina la fluidodina-
mica del sangue `e un campo importante ma
ancora piuttosto difficile (prevenzione di an-
eurismi e patologie circolatorie).
Geomatematica
Questo `e un campo nuovo, molto bello e diffi-
cile della matematica. Funzioni speciali del-
la geofisica matematica, funzioni armoniche
sulla sfera, operatori pseudodifferenziali del-
la geodesia matematica, metodi di approssi-
mazione multivariata, splines, wavelets, me-
todi degli elementi finiti nella geodesia, de-
terminazione del campo gravitazionale della
Terra, analisi delle deformazioni della super-
ficie terrestre, effetti della rifrazione atmos-
ferica, determinazione del campo magnetico
della Terra mediante l’analisi di dati tras-
messi da satelliti, sono solo alcuni dei temi
di questa interessante disciplina.
Malattie tropicali
`
E tipico per la natura viva che essa pone
dei problemi che difficilmente possono essere
perfettamente modellati con i metodi mate-
matici classici sviluppati in genere per la fi-
sica o l’ingegneria. Ci`o da un lato vale natu-
ralmente anche per le malattie tropicali co-
me malaria, bilharziosi, filariosi, leishmani-
osi, dall’altro lato queste malattie colpisco-
no ogni anno centinaia di milioni di perso-
ne, sono trascurate dalle ditte farmaceutiche
(i pazienti non possono pagare) e richiedo-
no quindi interventi ecologici o politici molto
impegnativi. Alla pianificazione di questi in-
terventi anche i modelli matematici possono
contribuire e sicuramente la medicina tropi-
cale `e attraente per il suo fascino e per il lato
umano.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller

Corso di laurea in matematica Anno accademico 2004/05 Numero 2
Il re dei matematici
Carl Friedrich Gauß (1777-1855) `e conside-
rato il re dei matematici. La lettera ß alla fi-
ne del nome `e una s tedesca antica; il nome
(talvolta scritto Gauss) si pronuncia gaos, si-
mile a caos, ma con la g invece della c e con
la o molto breve e legata alla a in modo che le
due vocali formino un dittongo. Nessun altro
matematico ha creato tanti concetti profondi
ancora oggi importanti nelle discipline mate-
matiche pi `u avanzate (teoria dei numeri, geo-
metria differenziale e geodesia matematica,
teoria degli errori e statistica, analisi com-
plessa). Il ritratto lo mostra a ventisei anni.
`
E stato forse il primo a concepire le geometrie non euclidee, ha dato una
semplice interpretazione dei numeri complessi come punti del piano reale
con l’addizione vettoriale e la moltiplicazione
e ha dimostrato il teorema fondamentale dell’algebra (che afferma che
ogni polinomio con coefficienti complessi possiede, nell’ambito dei nume-
ri complessi, una radice), ha introdotto la distribuzione gaussiana del
calcolo delle probabilit `a, ha conseguito importanti scoperte nella teoria
dell’elettromagnetismo; `e stato direttore dell’osservatorio astronomico di
Gottinga.
L’algoritmo di eliminazione era noto nel 1759 a Lagrange (1736-1813) e
gi `a 2000 anni fa in Cina; Gauß lo ha usato nel suo lavoro sui moti celesti
del 1809, in cui descrisse il metodo dei minimi quadrati, una tecnica di
approssimazione ancora oggi universalmente utilizzata.
Le basi di Gr ¨obner
Se si prova ad imitare l’algoritmo di elimi-
nazione nella soluzione di sistemi polino-
miali di grado maggiore di uno, ad esem-
pio di
si incontrano molte difficolt `a (provare). Il
problema `e stato risolto solo nel 1965 con
l’introduzione delle basi di Gr¨obner (Wolf-
gang Gr¨obner, 1899-1980, era un mate-
matico austriaco)
e dell’algoritmo di
Buchberger (Bru-
no Buchberger, na-
to 1942), molto pi `u
profondo e compli-
cato dell’algoritmo
di eliminazione nel
caso lineare. Siste-
mi di equazioni po-
linomiali appaiono
in molti campi del-
la matematica con Wolfgang Gr¨obner
numerose applicazioni in ingegneria e sta-
tistica. Per questa ragione la geometria al-
gebrica computazionale (compresa la geo-
metria algebrica reale, importantissima
e molto difficile) `e oggi un campo estre-
mamente attivo della matematica, intera-
gendo con la teoria dell’ottimizzazione, la
teoria dei poliedri convessi, la crittogra-
fia, le equazioni differenziali parziali, la
fisica teorica e, se ci si fida, la matematica
finanziaria.
Bruno Buchberger nel 1987 ha fondato
il RISC (Research Institute for Symbolic
Computation, www.risc.uni-linz.ac.at/),
che ha sede nel castello di Hagenberg a 25
km da Linz e di cui `e stato direttore fino
al 2003.
Il RISC `e un istituto dell’universit `a di
Linz e ospita circa 70 collaboratori, tra
cui molti studenti. Le attivit `a, iniziate
con la geometria algebrica algoritmica
nell’intento di sfruttare le possibilit`a offer-
te dall’algoritmo di Buchberger, sono mol-
to varie, ma hanno tutte in qualche modo
da fare con
la risoluzio-
ne di equazio-
ni e disequa-
zioni, talvolta
in senso mol-
to lato confi-
nando con la
logica compu-
tazionale, la
dimostrazio- Il castello di Hagenberg
ne automatica di teoremi, l’inteligenza
artificiale, la robotica e la chimica indu-
striale.
In questo numero
6 Il re dei matematici
Le basi di Gr¨obner
Equazioni lineari in una incognita
7 Sistemi astratti
Due equazioni lineari in due incognite
8 Esempi
La forma generale della regola
di Cramer
Determinanti
9 L’algoritmo di eliminazione di Gauß
10 Sistemi con pi `u di una soluzione
L’insieme delle soluzioni di un
sistema lineare
Esercizi 1-13
Equazioni lineari in una incognita
Siano dati numeri reali e . Cercare di risolve-
re l’equazione nell’incognita significa
cercare tutti i numeri reali per i quali .
Per la soluzione `e unica e data da .
Dimostrazione: `
E chiaro che le seguenti equa-
zioni sono equivalenti, cio`e se soddisfa una di
esse, allora le soddisfa tutte:
`
E evidente che nel nostro ragionamento solo le
propriet`a algebriche formali dei numeri reali so-
no state usate e che rimane quindi valido, cos`ı
come le considerazioni successive, se lavoriamo
con numeri razionali o numeri complessi o al-
tri insiemi di numeri con quelle corrispondenti
propriet`a. Si vede comunque anche che abbiamo
avuto bisogno di poter dividere per un numero
, e quindi il risultato non `e vero nell’ambito
dei numeri naturali o interi.
Un insieme, su cui sono date due operazioni
di addizione e di moltiplicazione che soddisfano
le familiari regole di calcolo e in cui si pu`o semp-
re dividere per un elemento , in matematica
si chiama un campo. Quindi l’algoritmo di eli-
minazione di Gauß rimane valido per sistemi di
equazioni lineari i cui coefficienti appartengono
a un campo qualsiasi.
Elenchiamo le regole che devono valere in un
campo; verranno stabilite e studiate pi `u detta-
gliatamente negli altri corsi.
per

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 2 7
Sistemi astratti
Definizione 7.1. Siano dati un insieme ed una funzione
. Denotiamo con l’insieme degli zeri di :
.
Pi `u in generale, se sono date funzioni
, con
denotiamo l’insieme
degli zeri comuni di queste funzioni. Questa notazione `e
molto usata in calcolo delle probabilit `a.
Osservazione 7.2. sia un insieme. Abbiamo visto a pagi-
na 4 che con si denota l’insieme di tutte le funzioni a va-
lori reali definite su . Possiamo formare somme di funzioni,
moltiplicare funzioni con un numero reale o con un’altra fun-
zione, e costruire combinazioni lineari di funzioni in questo
spazio nel modo seguente.
Siano ed . Allo-
ra:
Teorema 7.3. Siano dati un insieme ed funzioni
. Siano numeri reali con
. Allora gli insiemi
e
coincidono.
Dimostrazione. Per dimostrare l’uguaglianza tra i due in-
siemi, dobbiamo dimostrare che ogni elemento del primo in-
sieme `e anche elemento del secondo, e che ogni elemento del
secondo insieme `e elemento del primo.
Sia quindi un elemento fissato di X
(1) Sia . `
E chiaro che allora anche
(2) Sia viceversa
Dobbiamo dimostrare che . Ma se sostituia-
mo nella prima equazione,
vediamo che
.
Qui possiamo adesso applicare la nostra ipotesi che
. Essa implica .
Attenzione: Il ragionamento non vale pi `u, se non sappiamo
che !
Nota 7.4. Nel seguito avremo oppure, pi `u in gene-
rale, . Nel primo caso scriveremo gli elementi di
nella forma , cosicch´e denoter `a la prima coordinata
di un elemento e non l’elemento stesso.
Gli elementi di saranno scritti nella forma ,
gli elementi di nella forma . Questo
passaggio da una notazione all’altra `e frequente e diventer `a
presto familiare.
Due equazioni lineari in due incognite
Siano dati numeri reali . Risolvere il sistema lineare
significa trovare tutte le coppie di numeri reali che soddisfano entram-
be le equazioni. Per poter applicare il teorema 7.3 introduciamo le funzioni
definite da
cosicch´e l’insieme delle soluzioni cercate coincide con . La-
sciamo come esercizio il caso molto facile che .
Assumiamo quindi che e definiamo la funzione
Per il teorema 7.3 abbiamo
perch´e `e che sicuramente appare con un coefficiente in . Scritta per
esteso l’equazione diventa
cio`e
,
e quindi le soluzioni del sistema originale coincidono con le soluzioni del si-
stema
Il numero si chiama il determinante del sistema; lasciamo
ancora come esercizio il caso che il determinante si annulli; se `e invece ,
allora la seconda equazione significa che
.
Se per numeri reali poniamo , possiamo scrivere
Vediamo che anche il numeratore ha la forma di un determinante; infatti si
ottiene dal denominatore sostituendo per la seconda colonna la colonna che
costituisce il lato destro del sistema.
A questo punto possiamo calcolare anche . Ricordando che , otte-
niamo
Quindi nel caso che il determinante del sistema sia , il sistema possiede
un’unica soluzione data da
Si osservi che il numeratore di si ottiene anch’esso dal determinante del
sistema, sostituendo stavolta la prima colonna con il lato destro del siste-
ma. Questo risultato `e molto importante per l’algebra lineare e pu`o essere
generalizzato a pi `u dimensioni; `e noto come regola di Cramer.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 2 8
Esempi
Risolviamo con la regola di Cramer il sistema
Il determinante del sistema `e , quindi
diverso da , per cui
Esercizio. Risolvere da soli
Esercizio. Perch´e non si pu`o applicare la regola di Cramer al
sistema
Eppure non `e difficile trovare “tutte” le soluzioni. Perch´e ho
messo “tutte” tra virgolette? E perch´e `e anche (quasi) facile tro-
vare tutte le soluzioni di
La forma generale della regola di Cramer
Sia dato un sistema di equazioni lineari in incognite (quindi
il numero delle equazioni `e uguale al numero delle incognite):
Anche in questo caso pi `u generale si pu`o definire il determinan-
te del sistema, un numero che viene denotato con
e si dimostrer `a nel corso di Geometria I che questo determi-
nante `e se e solo se il sistema possiede un’unica soluzione
che in tal caso `e data da
...
`e quindi un quoziente il cui numeratore si ottiene dal deter-
minante del sistema, sostituendo la -esima colonna con il lato
destro del sistema.
Determinanti
Conosciamo gi`a i determinanti : .
Definizione 8.1. Per induzione definiamo i determinanti di ordine supe-
riore:
e cos`ı via. Si noti l’alternanza dei segni. I determinanti hanno molte pro-
priet`a importanti che verranno studiate nel corso di Geometria. Qui ci
limiteremo a determinanti e , per i quali dimostriamo alcune
semplici regole, valide anche per determinanti , se riformulate in
modo naturale.
Lemma 8.2. Se in un determinante scambiamo tra di loro due righe
o due colonne, il determinante si moltiplica con .
Dimostrazione. Immediata.
Lemma 8.3. Un determinante pu`o essere calcolato anche secondo la
regola
Dimostrazione. Le due espansioni si distinguono in
e
che per`o, come vediamo, danno lo stesso risultato.
Lemma 8.4. Se si scambiano due righe o due colonne in una matrice ,
il determinante si moltiplica per .
Dimostrazione. Ci`o, per il lemma 8.2, `e evidente per lo scambio della
seconda e della terza colonna e, per il lemma 8.3, anche per lo scambio
della seconda e della terza riga. Se invece scambiamo la prima e la seconda
colonna, otteniamo il determinante
uguale, come si vede subito, al determinante originale moltiplicato per .
Gli altri casi seguono adesso applicando le regole gi `a dimostrate.
Lemma 8.5. Se in un determinante appaiono due righe o due colonne
uguali, allora il determinante `e uguale a .
Dimostrazione. Ci`o per un determinante `e ovvio, e se ad esempio
sono uguali le ultime due colonne, l’enunciato segue (usando il caso )
dalla formula di espansione anche per i determinanti , e poi dal caso
anche per i determinanti ecc.
Esempio. Verificare con calcoli a mano che
e che
L’ultima uguaglianza `e un caso speciale di un’altra propriet `a fondamenta-
le dei determinanti.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 2 9
L’algoritmo di eliminazione di Gauß
La teoria dei determinanti e la regola di Cramer hanno una
grandissima importanza teorica, ma non possono essere utiliz-
zate se non per sistemi in due o al massimo tre incognite. Inoltre
la regola di Cramer si applica solo al caso di un sistema quadra-
tico. Esiste invece un metodo molto efficiente (anche nel calcolo
a mano) per la risoluzione di sistemi di equazioni lineari, che
viene detto algoritmo di eliminazione di Gauß e che consiste
nella sistematica applicazione del teorema 7.3.
Esempio 9.1. Consideriamo il sistema
In analogia a quanto abbiamo fatto a pagina 7 per il sistema
le funzioni ed sono definite da
Le indichiamo alla destra delle equazioni corrispondenti. Con la
notazione che abbiamo introdotto nell’osservazione 7.2 poniamo
Per il teorema 7.3 allora
perch´e il coefficiente con cui appare in `e diverso da . Es-
plicitamente equivale a
cio`e a
.
Se chiamiamo due sistemi equivalenti quando hanno le stesse
soluzioni, possiamo dire che il sistema originale `e equivalente
al sistema
Nell’ultima equazione la variabile in `e sparita, `e stata eli-
minata. Ripetiamo questa operazione sostituendo la funzione
con
Ci`o `e possibile perch´e in la appare con un coefficiente .
Esplicitamente significa
cio`e
.
Perci`o il sistema originale ha le stesse soluzioni come il sistema
Adesso formiamo che pu`o sostituire sia la
che la . Possiamo togliere la . `e equivalente a
,
cio`e a
.
Otteniamo cos`ı il sistema
che `e ancora equivalente a quello originale. Ma adesso vedia-
mo che nell’ultima equazione `e stata eliminata anche la ed `e
rimasta solo la che possiamo cos`ı calcolare direttamente:
,
poi, usando , otteniamo
,
e infine dal
.
Nella pratica si user `a uno schema in cui vengono scritti,
nell’ordine indicato dall’ordine delle variabili, solo i coefficien-
ti. Nell’esempio appena trattato i conti verrebbero disposti nel
modo seguente:
3
3
3
L’asterisco indica ogni volta l’equazione cancellata in quel pun-
to; l’uncino a destra di un’equazione significa che questa equa-
zione `e stata cancellata. Nei conti a mano spesso si preferir `a
forse cancellare la riga con un tratto orizzontale piuttosto di
usare l’uncino.
Come si vede, nell’algoritmo cerchiamo prima di ottenere un
sistema equivalente all’originale in cui tutti i coefficienti tran-
ne al massimo uno nella prima colonna sono , poi, usando
le equazioni rimaste, applichiamo lo stesso procedimento alla
seconda colonna (non modificando pi `u per `o quella riga a cui
corrisponde quell’eventuale coefficiente nella prima colon-
na), ecc. `
E chiaro che il procedimento termina sempre: alle
equazioni iniziali si aggiungono prima , poi , poi
, ecc.
L’insieme delle soluzioni rimane sempre lo stesso; le equazio-
ni cancellate naturalmente sono superflue e non vengono pi `u
usate. Quindi, se il sistema non ha soluzioni o pi `u di una solu-
zione, riusciamo a scoprire anche questo.
Esempio 9.2. Consideriamo il sistema
Applichiamo il nostro schema:
3
3
3
Il sistema dato `e quindi equivalente al sistema
In particolare siamo arrivati alla contraddizione , quin-
di il sistema non ha soluzione.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 2 10
Sistemi con pi `u di una soluzione
Consideriamo il sistema
Usiamo di nuovo il nostro schema di calcolo:
3
3
3
Stavolta non abbiamo una contraddizione, ma un’ultima equazione
superflua, quindi siamo rimasti con due equazioni per tre incognite:
Per ogni valore di possiamo risolvere
e vediamo che l’insieme delle soluzioni `e una retta nello spazio con la
rappresentazione parametrica
Per ogni numero reale si ottiene un punto che `e una
soluzione del nostro sistema, e viceversa ogni soluzione `e di questa forma.
L’insieme delle soluzioni di un sistema lineare
Negli esempi visti finora abbiamo trovato sistemi che non avevano soluzioni,
oppure un’unica soluzione (descriventi cio`e un unico punto nello spazio),
oppure, nell’ultimo esempio, una retta di soluzioni.
Ci`o vale per ogni sistema di equazioni lineari: l’insieme delle soluzioni `e
sempre o vuoto (nessuna soluzione), oppure un solo punto, oppure una retta,
oppure un piano, oppure uno spazio affine tridimensionale ecc., e viceversa
ogni insieme di questa forma pu`o essere descritto da un sistema di equazio-
ni lineari. La dimostrazione di questo teorema e la definizione precisa del
concetto di spazio affine verranno date nel corso di Geometria I.
Nonostante l’efficienza dell’algoritmo di eliminazione che permette la ri-
soluzione abbastanza agevole di sistemi lineari non troppo grandi (con un
po’ di pazienza si possono risolvere anche sistemi a mano) la pratica
`e pi `u complicata. Nelle applicazioni reali si affrontano sistemi con decine
di migliaia di equazioni e variabili e non solo il tempo di calcolo, ma an-
che l’accumularsi di errori di arrotondamento nei calcoli approssimati che
il software normalmente utilizza possono creare grandi problemi.
Piccoli errori, spesso inevitabili, nei dati in entrata (ad esempio nei co-
efficienti e del nostro sistema) possono provocare in taluni casi, che
bisogna riconoscere e controllare, grandi cambiamenti nelle soluzioni. Cos`ı
il sistema
possiede un’unica soluzione , ma se lo cambiamo di poco,
il determinante si annulla e l’insieme delle soluzioni `e dato da , e
quindi le soluzioni non sono pi `u univocamente determinate e possono essere
arbitrariamente distanti dalla soluzione del primo sistema.
Esercizi per i compiti scritti
1. Sia . Calcolare .
2. Siano e considerate come
funzioni . Calcolare e .
3. Siano e .
Calcolare .
4. Risolvere con la regola di Cramer il sistema
5. Calcolare il determinante
6. Calcolare il determinante
Risolvere i sistemi con l’algoritmo di Gauß usando lo schema.
7.
8.
9.
10.
11.
12.
13.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller
Corso di laurea in matematica Anno accademico 2004/05 Numero 3
Trigonometria oggi
Dai piani di studio, soprattutto nell’universit `a, la trigonometria `e sparita
da molto tempo. Ma questa disciplina, una delle pi`u antiche della mate-
matica, `e ancora oggi una delle pi `u importanti.
Mentre almeno gli elementi della trigonometria pia-
na vengono insegnati nelle scuole, la trigonometria sfe-
rica `e ormai conosciuta pochissimo anche tra i ma-
tematici di professione. Eppure le applicazioni sono
tantissime: nautica, cartografia, geodesia e geoinfor-
matica, astronomia, cristallografia, classificazione dei
movimenti nello spazio, cinematica e quindi robotica e
costruzione di macchine, grafica al calcolatore.
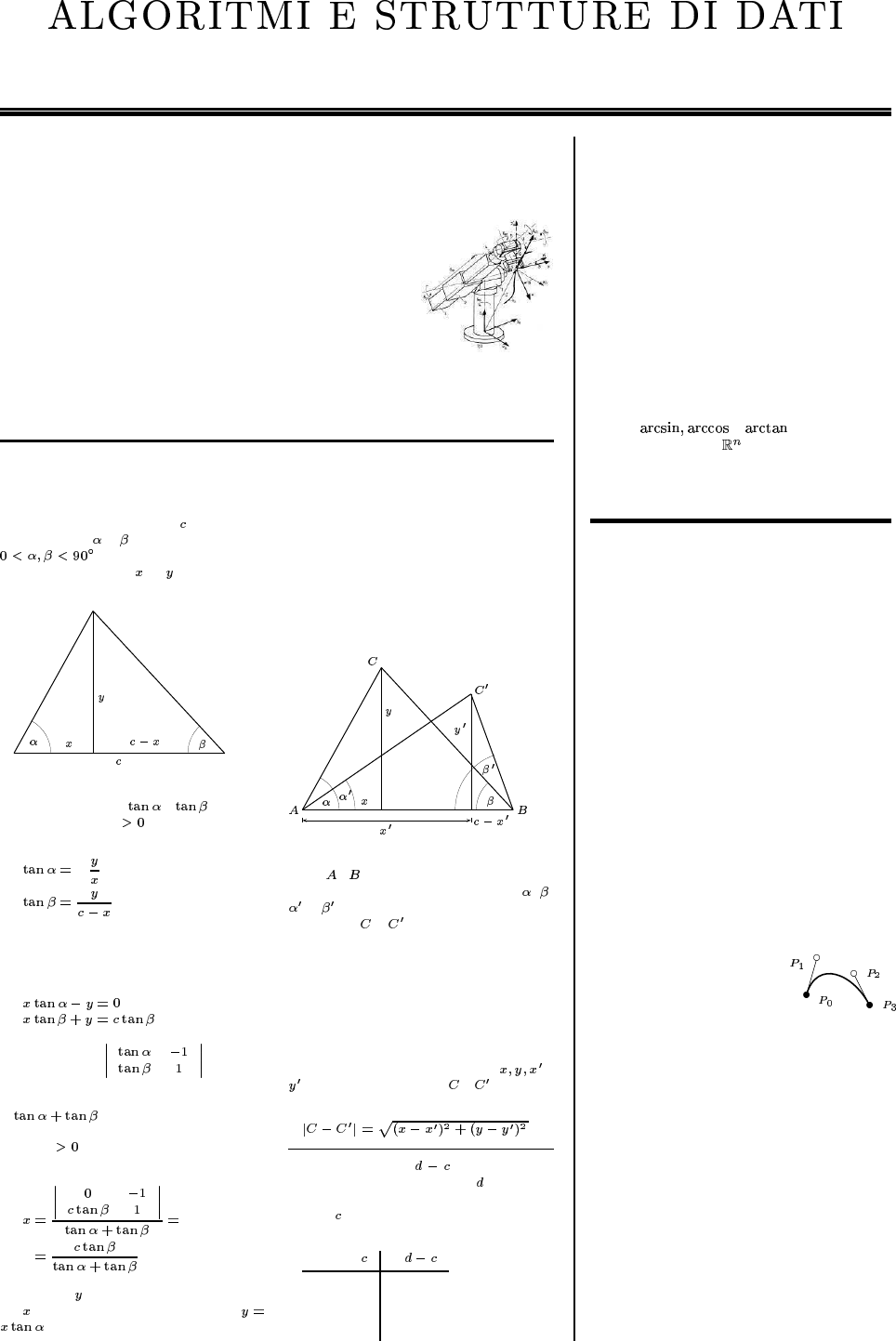
L’immagine rappresenta un robot con i suoi movimenti; trovata su
www.igm.rwth-aachen.de/deutsch/lehre-lehrveranstaltungen/guk/index.php
Un problema di geodesia
Sia dato, come nella figura, un triangolo
con base di lunghezza nota e in cui an-
che gli angoli e siano noti e tali che
.
Vogliamo calcolare ed .
Per le nostre ipotesi e sono nu-
meri ben definiti e (cfr. pag. 13). Inol-
tre abbiamo
Queste equazioni possono essere riscritte
come sistema lineare di due equazioni in
due incognite:
Il determinante di questo
sistema `e uguale a
e quindi . Possiamo perci`o applicare la
regola di Cramer e otteniamo
mentre per possiamo, se calcoliamo pri-
ma , usare direttamente la relazione
.
Esercizio: Prendendo il centimetro come
unit`a di misura e con l’uso di un gonio-
metro verificare le formule con le distanze
nella figura.
Con questo metodo possiamo adesso ri-
solvere un compito elementare ma fre-
quente di geodesia illustrato dalla figura
seguente.
Assumiamo di conoscere la distanza tra i
punti e e, mediante un teodolite, di es-
sere in grado di misurare gli angoli , ,
e . Vorremmo conoscere la distanza
tra i punti e , ai quali per`o non pos-
siamo accedere direttamente, ad esempio
perch´e da essi ci separa un fiume che non
riusciamo ad attraversare o perch´e si tro-
vano in mezzo a una palude. Se le distan-
ze sono molto grandi (maggiore di 50 km),
dovremo appellarci alla trigonometria sfe-
rica, per distanze sufficientemente piccole
invece possiamo utilizzare la tecnica vista
sopra che ci permette di calcolare e
, da cui la distanza tra e si ottiene
come
Calcoliamo l’errore che si commet-
te approssimando la distanza sulla sfera
terrestre tra due punti mediante la lun-
ghezza del segmento di retta che si ottie-
ne utilizzando la trigonometria piana:
50 km 0.13 m
100 km 1 m
500 km 128 m
1000 km 1029 m
In questo numero
11 Trigonometria oggi
Un problema di geodesia
Grafica al calcolatore e geometria
12 Il triangolo
Il triangolo rettangolo
Triple pitagoroee
Le funzioni trigonometriche
13 La dimostrazione indiana
Il triangolo isolatero
Angoli sul cerchio
14 Il teorema del coseno
Il grafico della funzione seno
La periodicit`a di seno e coseno
Altre propriet`a di seno e coseno
e
15 Distanze in
Il prodotto scalare
Ortogonalit`a
Esercizi 14-17
Grafica al calcolatore e geometria
La grafica al calcolatore e le discipline af-
fini come la geometria computazionale e
l’elaborazione delle immagini si basano sulla
matematica. `
E importante separare gli algo-
ritmi dalla loro realizzazione mediante un lin-
guaggio di programmazione. `
E importante sepa-
rare la rappresentazione matematica delle figu-
re nello spazio dalle immagini che creiamo sullo
schermo di un calcolatore.
Il matematico `e molto avvantaggiato in que-
sto. Gi`a semplici nozioni di trigonometria e di
geometria affine e algebra lineare possono ren-
dere facili o immediate costruzioni e formule di
trasformazione (e quindi gli algoritmi che da es-
se derivano) che senza questi strumenti mate-
matici risulterebbero difficoltose o non verreb-
bero nemmeno scoperte.
La geometria proiettiva, apparentemente una
vecchia teoria astratta e filosofica, diventa di
sorpresa una tecnica molto utile per trasfor-
mare compiti di proiezione in semplici calco-
li.
I concetti dell’analisi e della geometria differen-
ziale portano all’introduzione
e allo studio delle curve e su-
perficie di B´ezier, largamente
utilizzate nei programmi di
disegno al calcolatore (CAD,
computer aided design).
Molte figure possono essere descritte median-
te equazioni algebriche; per questa ragione la
geometria algebrica assume notevole importan-
za nella grafica al calcolatore moderna. Curve e
superficie possono essere date in forme parame-
trica oppure mediante un sistema di equazioni;
le basi di Gr¨obner forniscono uno strumento per
passare una rappresentazione all’altra.
La topologia generale, una disciplina tra la
geometria, l’analisi e l’algebra, `e la base della
morfologia matematica, mentre la topologia al-
gebrica e la geometria algebrica reale possiedo-
no applicazioni naturali in robotica.
H. Pottmann/J. Wallner: Computational line geometry.
Springer 1999.
W. B ¨ohm/H. Prautzsch: Geometric concepts for geometric
design. Peters 1994.
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 3 12
Il triangolo
A P’ C’ P C
B’
B
In questa figura i segmenti e sono
paralleli. Nella geometria elementare si di-
mostra che le proporzioni del triangolo pi `u
piccolo sono uguali alle proporzio-
ni del triangolo grande . Cio significa
che, se denota la lunghezza del segmen-
to , allora
Se il valore comune di queste tre frazioni
viene denotato con , abbiamo quindi
Una relazione analoga vale anche per le al-
tezze:
Dati tre punti denotiamo con
l’angolo tra i segmenti e
:
A C
B
Evidentemente .
Con e indichiamo gli altri due angoli
come nella figura; spesso serve solo la gran-
dezza assoluta degli angoli, allora si lascia-
no via le punte di freccia.
Nella prima figura il triangolo piccolo e il
triangolo grande hanno gli stessi angoli,
cio`e
Si pu`o dimostrare ed `e chiaro intuitivamen-
te che, dati due triangoli con gli stessi ango-
li, essi possono essere sovrapposti in manie-
ra tale che si ottenga una figura simile alla
nostra.
Ogni triangolo pu`o essere considerato
(talvolta anche in pi `u modi - quando?) come
unione di due triangoli rettangoli.
A C
B
P
Le formule per i triangoli rettangoli sono
particolarmente semplici; conviene quindi
studiare separatamente i triangoli e
.
Il triangolo rettangolo
Il triangolo sia rettangolo, ad esempio
.
A C
B
b
c
a
Il lato pi `u lungo `e quello opposto all’angolo retto,
cio`e , e si chiama ipotenusa, i due altri lati
sono pi `u brevi e sono detti cateti.
La somma dei tre angoli di un triangolo
`e sempre uguale a :
.
Ci`o implica che un triangolo pu`o avere al massi-
mo un angolo retto (se ce ne fossero due, il terzo
dovrebbe essere zero e non avremmo pi `u un tri-
angolo).
Teorema di Pitagora: Dato un triangolo ret-
tangolo e posto , e
come nella figura, si ha
.
Dimostrazione: Pag. 13.
Il teorema di Pitagora implica che l’ipotenusa `e
veramente pi `u lunga di ciascuno dei due cateti
(perch´e ). La relazione pu`o
essere anche usata per il calcolo di uno dei lati di
un triangolo rettangolo dagli altri due:
Triple pitagoree
Una tripla pitagorea `e una tripla di nu-
meri naturali positivi tali che . La
tripla pitagorea si chiama primitiva, se e
sono relativamente primi tra di loro. Diamo una
tavola delle prime triple pitagoree primitive in
ordine crescente di .
Gli arabi possedevano gi `a nel 972 tavole simili a
questa.
Per non esistono invece soluzioni
dell’equazione
con interi . La dimostrazione di questo
teorema (detto ultimo teorema di Fermat) `e stata
molto difficile; per circa tre secoli i matematici
l’avevano cercata invano e solo intorno al 1995
Andrew Wiles ci `e riuscito, utilizzando strumenti
molto avanzati della geometria algebrica.
Le funzioni trigonometriche
Consideriamo la seguente figura,
A C
B
b
ca
b’
c’ a’
in cui sono come prima i lati del
triangolo rettangolo pi `u grande e
e sono i lati del triangolo pi `u piccolo,
che `e ancora rettangolo. Le proporzioni
nella figura dipendono solo dall’angolo
, si ha cio`e
,
e da ci`o anche
Questi rapporti sono perci`o funzioni
dell’angolo che vengono dette fun-
zioni trigonometriche e denotate come
segue:
seno di
coseno di
tangente di
cotangente di
Dalle definizioni seguono le relazioni
Esercizio. Calcolare , ,
, .
Esercizio. I valori delle funzioni trigo-
nometriche si trovano in tabelle oppure
possono essere calcolati con la calcola-
trice tascabile oppure con una sempli-
ce istruzione in quasi tutti i linguaggi
di programmazione. Ricavare in uno di
questi modi i necessari valori per cal-
colare la distanza e l’altezza nella
seguente figura:
100 m
a
d
Pierre de Fermat (circa 1607-1665) so-
stenne di conoscere una dimostrazione
del teorema che poi port`o il suo nome,
ma non `e mai stata trovata e si dubita
molto che sia esistita.
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 3 13
La dimostrazione indiana
In una fonte indiana del dodicesimo secolo si
trova il seguente disegno, con una sola parola
in sanscrito: guarda!
c
a
b-a
a
Da esso si deduce immediatamente il teorema
di Pitagora:
Il nostro triangolo rettangolo abbia i lati
con . Allora l’area del qua-
drato grande `e uguale a quella del quadrato
piccolo pi `u quattro volte l’area del triangolo,
quindi
,
cio`e
.
Esercizio: Disegnare la figura nel caso che
e convincersi che la dimostrazione ri-
mane ancora valida.
Il triangolo isolatero
Consideriamo adesso un triangolo isolatero di
lato 1. In esso anche gli angoli devono essere
tutti uguali, quindi, dovendo essere la somma
degli angoli , ogni angolo `e uguale a .
1 1
h
Dalla figura otteniamo
Angoli sul cerchio
Siccome le lunghezze assolute non sono importanti,
possiamo assumere che l’ipotenusa del triangolo rettan-
golo considerato sia di lunghezza 1 e studiare le funzio-
ni trigonometriche sulla circonferenza di raggio 1.
Questo ci permette inoltre di estendere la definizione
delle funzioni trigonometriche a valori arbitrari di ,
non necessariamente sottoposti, come finora, alla con-
dizione . Definiamo prima e per
ogni con come nelle seguenti figure:
1
Definiamo poi ogni volta
quando risp. . Si vede subito che questa definizione coincide con quella
data a pag. 12, quando .
Quindi quando entrambi i valori sono definiti.
Se `e infine un numero reale qualsiasi (non necessariamente compreso tra e ),
esiste sempre un numero intero tale che con e possiamo
definire , , , .
In matematica si identifica l’angolo con la lunghez-
za dell’arco descritto sulla circonferenza tra i punti
e della figura a lato, aggiungendo per`o multipli del
perimetro della circonferenza se l’angolo `e immaginato
ottenuto dopo essere girato pi `u volte attorno al centro.
Se il centro del cerchio `e l’origine del piano, pos-
siamo assumere che . Siccome il perimetro
della circonferenza di raggio 1 `e , si ha .
1
E
P
`
E chiaro che un angolo di `e uguale a ,
in altre parole , e viceversa per ogni .
Infatti .

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 3 14
Il teorema del coseno
Dato un triangolo con i vertici po-
niamo ancora , e
. Denotiamo inoltre con la lunghez-
za della proiezione di su misuran-
do a partire da . In modo analogo sono
definite le grandezze , ecc. Se l’angolo
`e ottuso, sar`a negativo. Sono possibili
quattro situazioni:
AC
B
b
c
a
In questo caso .
A C
B
ca
b
A C
B
b
a
c
P
Si osservi che qui `e la lunghezza di tut-
to il segmento .
B
A C
c
b
a
Teorema: In tutti i casi, quindi in ogni tri-
angolo, vale la relazione
.
Per simmetria vale anche
.
Dimostrazione: Quando , la formula
diventa e segue direttamente
dal teorema di Pitagora.
Nei rimanenti tre casi calcoliamo
l’altezza del triangolo con il teorema di
Pitagora in due modi.
Nella seconda figura abbiamo
,
cio`e
,
per cui
.
Similmente nella terza figura
,
la stessa equazione di prima.
Nella quarta figura infine abbiamo
,
che `e ancora la stessa equazione.
Teorema di Pitagora inverso: Un tri-
angolo `e rettangolo con l’ipotenusa se e
solo se
.
Dimostrazione: Dalla figura in alto a de-
stra a pag. 12 si vede che il triangolo `e
rettangolo con ipotenusa se e solo se
(oppure, equivalentemente,
). L’enunciato segue dal teorema prece-
dente.
Teorema del coseno:
Dimostrazione: in tutti e
quattro i casi del precedente teorema (cfr.
le definizioni degli angoli sul cerchio a
pag. 13).
Il grafico della funzione seno
Come si vede dalla figura e come sar `a dimostrato rigorosamente nel corso di Analisi,
la funzione seno `e iniettiva sull’intervallo chiuso e assume su questo inter-
vallo tutti i valori possibili per il seno, cio`e tutti i valori tra -1 e 1. Possiamo quindi
definire una funzione biiettiva . L’inversa di questa fun-
zione viene denotata con . In modo analogo si definiscono l’inversa della
funzione biiettiva e l’inversa della funzione biiettiva
.
La periodicit `a di seno e coseno
Dalle definizioni date a pag. 13 segue che
per ogni numero reale . Invece di possia-
mo anche scrivere , quindi
per ogni numero reale . Le funzioni e
sono quindi funzioni periodiche con periodo .
Facendo percorrere l’asse reale e riportan-
do come ordinata, otteniamo il grafico della
funzione seno rappresentato in basso a sinistra.
Altre propriet `a di seno e coseno
per ogni numero reale , come si vede dai disegni
a pagina 13. Il coseno `e quindi una funzione pari,
il seno una funzione dispari.
Teorema di addizione:
Dimostrazione: Non richiesta. Una dimostrazio-
ne geometrica si trova nei libri scolastici, una di-
mostrazione analitica forse verr `a data nei corsi
di Analisi.
Esercizio: .
Verificare l’enunciato prima nelle illustrazioni
a pag. 13 e utilizzare poi il teorema di addizione
per la dimostrazione.
Esercizio: Calcolare e .
Teorema: .
Ci`o segue direttamente dalle definizioni geo-
metriche. Mentre queste propriet`a algebriche
delle funzioni trigonometriche rimangono vali-
de anche per un argomento complesso, ci`o non
`e pi `u vero per le disuguaglianze e
. Infatti, se dall’analisi complessa an-
ticipiamo le formule
valide per ogni numero complesso , vediamo che
ad esempio , quindi per rea-
le e tendente ad infinito (in questo caso ten-
de a ) si comporta come e tende quindi
fortemente ad infinito.
arcsin, arccos e arctan
Queste funzioni, definite a sinistra, sono deter-
minate dalle seguenti relazioni:
per e
per e
per e
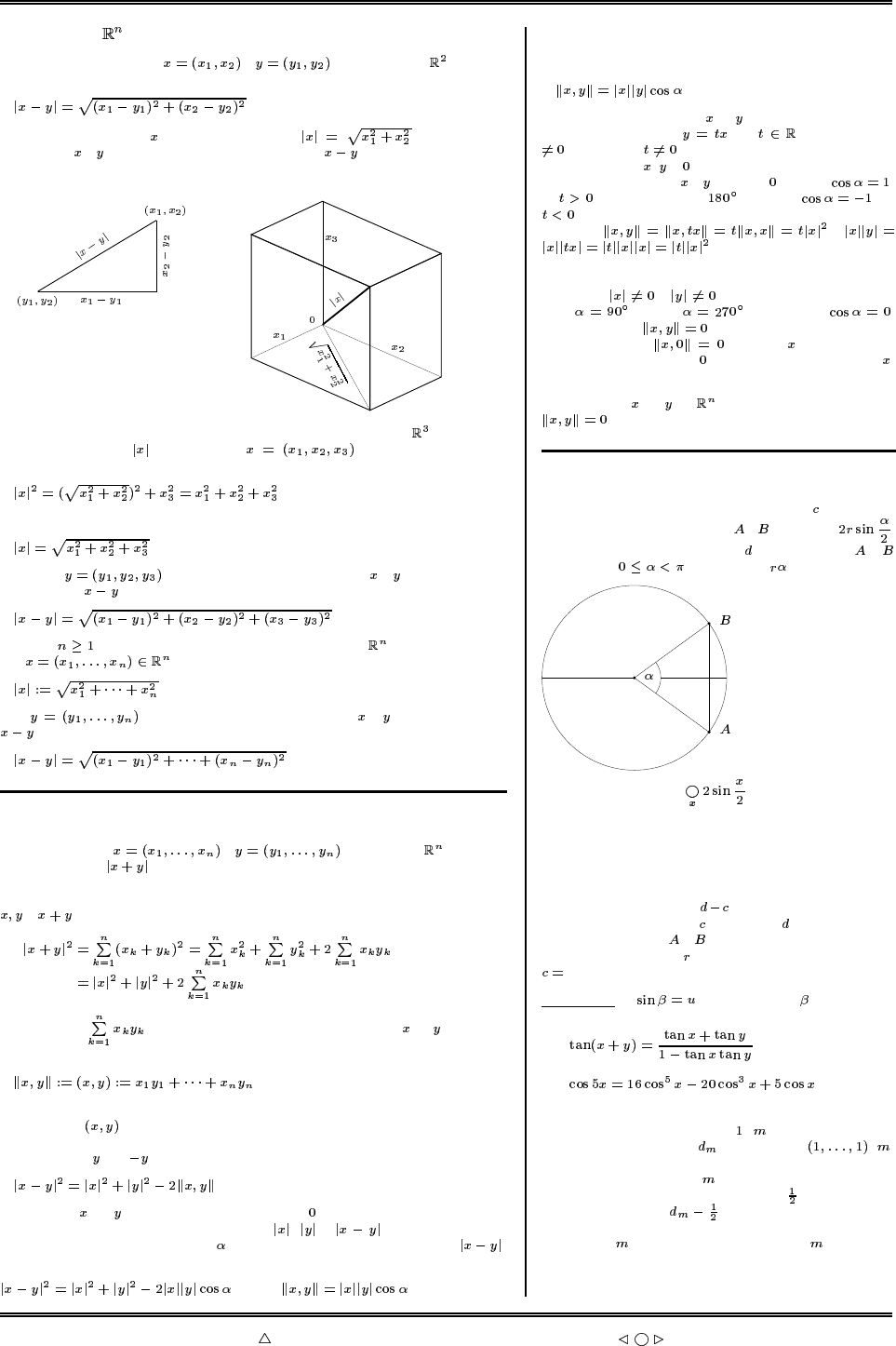
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 3 15
Distanze in
La distanza tra due punti e del piano reale si calcola
secondo il teorema di Pitagora come
.
La distanza del punto dall’origine `e quindi e viceversa la
distanza di e `e proprio la lunghezza del vettore .
Formule del tutto analoghe si hanno nello spazio tridimensionale . Calcoliamo
prima la lunghezza di un vettore utilizzando la figura a
destra, dalla quale si vede che
,
per cui
.
Se adesso `e un altro punto, la distanza tra e sar`a uguale alla
lunghezza di , quindi
.
Per ogni possiamo definire lunghezze e distanze in nello stesso modo.
Per poniamo
,
e se `e un altro punto, la distanza tra e `e la lunghezza di
, cio`e
.
Il prodotto scalare
Siano come sopra e due punti di . Calcolia-
mo la lunghezza della somma dei due vettori; questo `e anche in statistica
il punto di partenza per la definizione del coefficiente di correlazione che, nono-
stante il nome prometta molto di pi `u, non `e altro che un mezzo per confrontare
e !
L’espressione si chiama il prodotto scalare dei vettori ed . Esso `e di
fondamentale importanza per tutta la geometria. Introduciamo le abbreviazioni
La seconda `e pi `u diffusa della prima, comporta per`o il pericolo di confusione
con la coppia che proprio nella statistica multidimensionale appare spesso
contemporaneamente.
Sostituendo con otteniamo
.
I due punti ed formano insieme all’origine un triangolo (eventualmente
degenerato) i cui lati hanno le lunghezze , e . Assumiamo che il
triangolo non sia degenerato e sia l’angolo opposto al lato di lunghezza .
Per il teorema del coseno abbiamo
, da cui .
Ortogonalit `a
La formula fondamentale
rimane valida anche se e sono uno un multiplo
dell’altro, ad esempio per , per`o entrambi
(ci`o implica ). In questo caso infatti il triangolo
determinato da , e `e degenerato, ma `e naturale as-
segnare all’angolo tra e il valore (per cui )
se e invece il valore (cosicch´e ) se
.
Inoltre e
. Dimostrare queste relazioni
e concludere da soli, stando attenti ai segni.
Quindi se i due vettori sono diversi da zero (ci`o implica
che anche e ), allora essi sono ortogonali
(cio`e oppure ) se e solo se ,
cio`e se e solo se .
Siccome infine per ogni , `e naturale in-
cludere anche il vettore tra i vettori ortogonali ad .
Raccogliendo tutto possiamo perci`o dire:
Due vettori ed di sono ortogonali se e solo se
.
Esercizi per gli scritti
14. Dalla figura si vede che la lunghezza della corda
(cio`e del segmento di retta) tra e `e uguale a ,
mentre la distanza (cio`e l’arco) sul cerchio tra e
(nell’ipotesi ) `e uguale ad .
r
La funzione cordale `e probabilmente la pi `u
antica funzione trigonometrica e venne tabulata gi`a da
Ipparco da Nikaia (Nicea) nel secondo secolo prima di
Cristo (tavola delle corde). Gi `a i babilonesi possedevano
per`o una rudimentale trigonometria, di cui erano molto
orgogliosi.
Calcolare la differenza , che corrisponde all’errore
che si commette usando al posto di per misurare la
distanza tra i punti e sulla sfera terrestre, che pos-
siede un raggio medio di 6371 km, per
1 km, 10 km, 50 km, 100 km, 500 km, 1000 km.
Attenzione: Se , come si calcola ?
15. .
16. .
17. Quanto `e lunga la diagonale di un cubo unita-
rio (cio`e di lato uguale a ) -dimensionale , cio`e
qual’`e la distanza del vettore -
dimensionale dall’origine?
Il raggio della sfera -dimensionale iscritta in un
tale cubo `e invece sempre uguale a , quindi la sfera
iscritta dista di dai vertici del cubo e, sicco-
me questa espressione diventa sempre pi `u grande,
il cubo -dimensionale al crescere di assomiglia
sempre di pi `u a un riccio con corpo sferico e aculei
sempre pi `u lunghi.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller

Corso di laurea in matematica Anno accademico 2004/05 Numero 4
R
R `e un linguaggio di programmazione ad altissimo livello orientato so-
prattutto all’uso in statistica. In verit `a lo sbilanciamento verso la stati-
stica non deriva dalla natura del linguaggio, ma dalla disponibilit `a di
grandi raccolte di funzioni statistiche e dagli interessi dei ricercatori che
lo hanno inventato e lo mantengono. R `e gratuito e molto simile a un lin-
guaggio commerciale, S, creato negli anni ’80 e anch’esso molto usato. S
viene commercializzato come sistema S-Plus. Le differenze non sono gran-
dissime se non sul piano della programmazione, dove R aderisce a una
impostazione probabilmente pi `u maneggevole.
R ed S-Plus sono particolarmente popolari nella statistica medica, ma
vengono anche usati nella statistica economica o sociale, in geografia, nel-
la matematica finanziaria. L’alto livello del linguaggio permette di creare
facilmente librerie di funzioni per nuove applicazioni. Il punto debole `e
la velocit `a di esecuzione in calcoli numerici in grandi dimensioni, mentre
sono ricchissime le capacit `a grafiche.
Bench´e cos`ı indirizzato verso la statistica, R non deve essere conside-
rato un pacchetto di statistica. `
E un vero linguaggio di programmazione,
anzi un linguaggio di programmazione molto avanzato, e ci`o permette di
adattarlo ad ogni compito informatico. Nella stessa statistica questa fles-
sibilit `a `e molto importante proprio oggi, dove continuamente si scoprono
nuovi bisogni applicativi, nuove necessit `a di tradurre metodi matema-
tici, ad esempio nella statistica di complessi dati clinici o geografici, in
strumenti informatici.
Le funzioni d’aiuto
R dispone di numerose funzioni d’aiuto.
Da un lato ci sono varie guide disponibi-
li sul sito, dall’altra parte si possono invo-
care gli aiuti mentre si sta lavorando con
il programma. Con
appare una pagina web (mantenuta sul
vostro PC) attraverso la quale si accede
a manuali e informazioni generali. Clic-
cando sulla voce Packages si trovano elen-
chi dei molti pacchetti di base o aggiuntivi
disponibili.
Dopo le informazioni di
aiuto appaiono sullo schermer del brow-
ser; per disattivare questa modalit`a si pu`o
usare dal termi-
nale. Infatti spesso si lavora pi `u veloce-
mente rimanendo sul terminale. Ci sono
diversi modi per ottenere le informazioni
d’aiuto. Il modo pi `u semplice, ma molto ef-
ficiente `e di anteporre un punto interroga-
tivo al comando su cui si desidera sapere
di pi `u; con
vengono fornite i dettagli sull’utilizzo del-
la . R distingue tra il nome di
una funzione e la sua invocazione con ;
naturalmente la parentesi pu`o anche con-
tenere argomenti. Proprio su questi argo-
menti si consulter `a spesso l’aiuto in linea.
Leggendo pi`u attentamente il testo della
guida si osserva che le funzioni di R han-
no spesso argomenti opzionali determina-
ti dal loro nome; ci`o `e tipico dei linguaggi
in qualche modo derivati dal Lisp e verr`a
ancora trattato con pi `u dettaglio.
Per uscire da un file informativo chia-
mato con basta premere il tasto . Da
R si esce con o, equivalentemente, con
. Per saperne di pi `u si pu`o usare il
comando ; le informazioni che ci vengo-
no fornite a questo punto sono pi `u com-
plicate del necessario, come invero acca-
de spesso, d’altra parte il sistema di aiuto
in linea di R `e veramente molto comple-
to anche se non perfettamente organizza-
to, perch´e richiede che si sappia gi `a come
si chiamano i comandi e perch´e i comandi
non sono raggruppati bene secondo le fun-
zionalit `a. Per sapere di pi `u su usare
.
Esiste comunque un’altra funzione che
permette di cercare informazioni su co-
mandi di cui non si conosce il nome o
su gruppi di comandi. Questa funzione `e
; per capire come bisogna uti-
lizzarla battiamo . Assumia-
mo adesso che cerchiamo le funzioni trigo-
nometriche. Proviamo prima con
trovando una breve pagina d’aiuto che ci
rimanda al pacchetto . Se adesso bat-
tiamo , troviamo l’elenco delle fun-
zioni disponibili
con l’indicazione degli argomenti, seguito
da un’esposizione sull’uso.
In questo numero
16 R
Le funzioni d’aiuto
Installazione di R
Il libro di Crawley
17 Programmare in R
Programmi autonomi
Nomi in R
Assegnamento
18 Successioni
Angoli espressi in gradi
Figure di Lissajous
I commenti
La matematica del futuro
Esercizi 18-22
Installazione di R
Per l’uso e l’installazione di R sotto Windows
possiamo dare solo informazioni molto vaghe.
Il sito a cui rivolgersi `e, per ogni sistema ope-
rativo,
www.r-project.org/
dove, per copiare il programma, si sceglie CRAN
e poi uno dei siti depositori; quello che funziona
meglio `e forse cran.r-mirror.de. Nella voce FAQ
esiste invece una guida per Windows.
L’installazione sotto Linux `e molto semplice.
Si ritira il file .rpm adatto per la propria versio-
ne di Linux e poi lo si installa, diventando ,
con
A questo punto, tornati utenti normali, basta
battere dalla tastiera e il programma parte.
Sotto Windows viene consigliato di lanciare
oppure di creare un shortcut a
questo file.
Il libro di Crawley
One of the objectives of statistical analysis is to
distil a long and complicated set of data into
a small number of meaningful descriptive sta-
tistics. Many of the modern computer statistics
packages, however, do exactly the opposite of this.
They generate literally pages of output from the
most meagre sets of data. This copious output
has several major shortcomings: it is open to un-
critical acceptance; it can lead to over interpre-
tation of data; and it encourages the bad habit
of data trawling (dredging through the output
looking for significant results without any prior
notion of a testable hypothesis).
S-Plus, on the other hand, tells you nothing
unless you explicitly ask for it ... The computing
is presented in S-Plus, but all the examples will
also work in the freeware program R, which can
be downloaded from the web, free of charge, any-
where in the world ... S-Plus encourages good
habits of data exploration by providing a superb
range of graphical facilities.
La statistica, in fondo, si sviluppa attorno a
questa domanda: What do we mean when we say
that a result is significant?
M. Crawley: Statistical computing. Wiley 2004.
&www.bio.ic.ac.uk/research/mjcraw/crawley.htm

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 4 17
Programmare in R
Bench´e si tratti di un linguaggio ad alto li-
vello, gli ideatori di R preferiscono presen-
tare R come linguaggio con cui lavorare in
linea e non mediante l’esecuzione di pro-
grammi scritti su files. Oggigiorno ci`o non
`e perfettamente comprensibile ed `e comun-
que possibile scrivere programmi e farli ese-
guire nel modo familiare ai programmatori
con la tecnica che adesso descriviamo.
Prima creiamo una nuova cartella (direc-
tory) in cui vogliamo svolgere un determi-
nato lavoro.
Poi in questa cartella creiamo il file
.Rprofile che contiene solo queste righe:
Le istruzioni contenute in .Rprofile vengo-
no, come vedremo nel prossimo numero,
eseguite alla partenza di R.
Adesso creiamo un file prove in cui scri-
viamo (per il momento) tutto il resto del
programma, ad esempio
La funzione cos`ı definita corrisponde alla
funzione matematica , mentre
`e la funzione elementare di visualizzazione
(un po’ complicata anch’essa come tutte le
funzioni di input/output di R) che qui visua-
lizza per .
`e il carattere di invio che,
nell’output, fa in modo che dopo la vi-
sualizzazione il programma torni su una
nuova riga.
Per eseguire il programma battiamo R
dalla tastiera e poi, una volta in R, diamo
il comando
che, in accordo con la sua definizione, carica
il file prove ed esegue le istruzioni in esso
contenute. Viene visualizzato il risultato:
cio`e , come possiamo verificare aggiun-
gendo la riga
aprove. Cos`ı possiamo continuare a lavora-
re, rimanendo in R, ma scrivendo il pro-
gramma e le sue modifiche in prove, usan-
do il terminale solo per ripetere il comando
(a questo scopo in ambiente Linux `e
sufficiente premere il tasto che utilizza la
storia dei comandi dati in precedenza che si
trova nel file nascosto .Rhistory nella nostra
stessa cartella).
Forse non tutti conoscono il valore del nu-
mero ; esso `e uguale ad , quindi lo pos-
siamo visualizzare aggiungendo
al nostro programma, cio`e al file prove.
Vediamo cos`ı che , se calcolato
sulle prime 6 cifre dopo il punto decimale,
perch´e in verit `a `e un numero trascenden-
te, cio`e non `e radice di un polinomio a co-
efficienti interi, e quindi sicuramente non `e
razionale.
Per scrivere il programma dobbiamo usare
un editor che crea soltanto files in forma-
to testo puro o impostare questa modalit `a
nell’editor che vogliamo usare.
Programmi pi `u grandi verranno scritti su
pi `u files, ad esempio prove,funzioni,grafi-
ca. In tal caso possiamo o modificare la fun-
zione principale nel file .Rprofile,
Bisogna stare un po’ attenti all’ordine in cui
le inclusioni vengono effettuate; infatti un
altro punto debole di R, che deriva dalla fi-
losofia di voler costringere l’utente a pro-
grammare sul terminale, `e che le funzio-
ni possono essere ridefinite, possibilit `a che
compromette notevolmente la trasparenza
dei programmi se il programmatore non `e
abituato ad organizzare bene il proprio la-
voro. Esempio:
Cancelliamo tutto il contenuto del file
prove, scrivendo poi
Se eseguiamo il programma con vie-
ne visualizzato . Ci`o `e comodo nel lavoro
sul terminale, ma piuttosto problematico
quando si vogliono creare programmi pi `u
consistenti o librerie di funzioni.
Programmi autonomi
Dal punto di vista della filosofia Unix, la
tecnica di programmazione che abbiamo
usato nell’articolo precedente, ha un neo
importante. Infatti il programmatore Unix
`e abituato che tutti i programmi possono es-
sere combinati tra di loro, cio`e che possono
essere eseguiti da un altro programma e che
si possono scambiare dati. La nostra tecni-
ca non crea per`o files eseguibili autonoma-
mente perch´e richiede l’esecuzione dal ter-
minale di R.
Praticamente tutti gli altri linguaggi in-
terpretati permettono, sotto Unix, la crea-
zione di programmi eseguibili semplice-
mente mettendo nella prima riga del file il
comando
che fa in modo che il resto del file venga ese-
guito dall’interprete indicato. Per un pro-
gramma in R dovremmo quindi scrivere
Per ragioni misteriose questa possibilit`a per
R non `e mai stata realizzata.
Si pu`o ovviare a questo problema scriven-
do nella prima riga
Bench´e funzioni (almeno in ambiente Unix
o Linux), non `e molto soddisfacente, anche
perch´e in ogni esecuzione R viene caricato
con molte delle sue librerie e quindi l’avvio
`e lento; i tipici programmi Unix si caricano
in genere solo con quanto `e necessario per
poter partire.
Nomi in R
Nomi (detti anche identificatori) in R consi-
stono in una lettera ( ) seguita da una
o pi `u caratteri che possono essere lettere, ci-
fre o punti. Quindi
sono nomi ammissibili, mentre non lo sono
, , . In R (come in C o in Perl)
bisogna distinguere tra minuscole e maius-
cole.
Bisogna anche evitare i nomi riservati di
R. Purtroppo in R anche alcuni caratteri sin-
goli sono riservati:
inoltre ci sono parecchi nomi che consistono
di due lettere, ad esempio e . Questa
scelta sicuramente non `e ottimale. Ad esem-
pio non possiamo usare per il tempo e nem-
meno per le funzioni.
Assegnamento
L’assegnamento di un valore (spesso rappre-
sentato da un’espressione) a una variabile
avviene mediante l’istruzione
Esiste anche la forma tradizionale (legger-
mente pi `u generale)
sicuramente meno leggibile. Per saperne di
pi `u usare .
Pi `u istruzioni sulla stessa riga devono es-
sere separate da un punto e virgola, mentre
il punto e virgola alla fine di una riga `e (a
differenza dal C) facoltativo:
con output

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 4 18
Successioni
Uno dei punti forti di R `e che molte fun-
zioni sono definite direttamente per succes-
sioni finite di valori. Ci`o significa che se
definiamo una funzione in R per la fun-
zione matematica , la possiamo im-
mediatamente applicare a una successio-
ne per ottenere la successione
. In C allo stesso scopo bisogna
lavorare con un ciclo, ad esempio un , e
riflettere sulla struttura di dati che si vo-
gliono utilizzare; in Lisp e Perl si pu`o usa-
re la funzione che, data una funzione ,
trasforma la successione nella successione
. In R `e tutto molto pi `u
semplice e automatico:
con output
Si osservi qui che la successione `e stata
creata utilizzando l’operatore , il cui nome
viene da concatenate e che unisce una se-
quenza di valori in un unico oggetto.
per dettagli.
Anche le operazioni algebriche vengono ese-
guite su tutti gli elementi di una successio-
ne; possiamo ad esempio moltiplicare una
successione con un numero oppure anche
due successioni tra di loro. Esempi:
con output
Un operatore molto utile per generare suc-
cessioni di valori equidistanti `e la funzione
. Il risultato di
`e la successione
che `e continuata fino a quando non si supe-
ra . Il passo di progressione `e quindi se
non viene impostato come terzo argomento:
restituisce la successione
anch’essa continuata fino a quando l’ultimo
valore non supera . Esempi:
Otteniamo
Angoli espressi in gradi
Successioni possono essere valori di una
funzioni. Creiamo ad esempio una funzione
per la risoluzione del problema geo-
detico visto in precedenza. Questa funzione
restituisce una successione i cui compo-
nenti e sono e come a pagina
11. A differenza dal C l’indice delle succes-
sioni parte da . Per il di pagina 11 usia-
mo la variabile , perch´e `e una parola
riservata.
Siccome vogliamo poter indicare gli ango-
li in gradi, definiamo prima tre funzioni che
corrispondono alle funzioni trigonometriche
e per angoli espressi in gradi.
L’argomento va quindi moltiplicato con
come visto a pagina 13.
La base del triangolo era di mm, gli an-
goli di approssimativamente e gradi.
L’output `e
e corrisponde abbastanza bene alle misure
reali.
Useremo da ora in avanti per le funzioni
sempre nomi che iniziano con una maius-
cola, ricordandoci che sono riservati i nomi
.
Figure di Lissajous
Illustreremo nel prossimo numero le capa-
cit`a grafiche di R. Provare intanto questo
esempio che dovrebbe far apparire una fi-
gura di Lissajous, cio`e una curva con una
rappresentazione parametrica tipicamente
della forma per .
I commenti
Se una riga contiene, al di fuori di una
stringa, il carattere , tutto il resto della ri-
ga `e considerato un commento, compreso il
carattere stesso.
Molti altri linguaggi interpretati (Perl, Py-
thon, la shell di Unix) usano questo simbolo
per i commenti. In C una funzione analoga `e
svolta dalla sequenza .
La matematica del futuro
The main scientific challenges of the twenty-
first century may no longer be divided into
the classical disciplines of mathematics, in-
formatics, physics, chemistry, biology, etc. For
example, theoretical biology is currently in
the phase of formulating laws of nature in
terms of mathematical statements; quantum
chemistry has already become an important
research field in applied mathematics; phy-
sics needs more and more input from compu-
ter science and mathematics, including logic
and informatics; and, outside of the natural
sciences, financial mathematics has develo-
ped highly reliable tools for economic market
and stock analysis. But how will researchers
be motivated to do interdisciplinary research
in a university environment, given the cur-
rent system in which academic careers (typi-
cally) advance based upon a record of publi-
cation in a single field?
www.wpi.ac.at/
And the missing ingredient in facing those
problems ... is mathematics.
D. Donoho: High-dimensional data analysis
- the curses and blessings of dimensionality.
Internet 2000, 32p.
Esercizi per gli scritti
18.
19.
Qual’`e la ragione per cui nella seconda
riga del prodotto riappare il secondo fat-
tore?
20.
=
21. =
22. La traccia di una matrice `e la
somma degli elementi nella sua dia-
gonale principale. Una matrice
pu`o (in parte) essere con-
siderata come elemento di .
Possiamo quindi formare il prodotto sca-
lare di due matrici in .
Dimostrare che , dove
denota la matrice trasposta di , cio`e
la matrice che si ottiene da scambian-
do righe e colonne.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller
Corso di laurea in matematica Anno accademico 2004/05 Numero 5
La grafica di R
1 2 34567
8 9 10 11 12 13 14
15 16 17 18
19 20 21 22 23 24 25
R possiede ricche capacit `a grafiche,
per`o anche molti comandi per la
grafica che `e difficile imparare con
tutte le loro opzioni. Da un lato si
pu`o usare l’aiuto in linea (provare
, , , ,
, ), dall’altro lato
per`o `e utile una certa disciplina
nell’impiegare una serie scelta e
ben composta di comandi che si
padroneggia. Cercheremo anche noi
di fare cos`ı, ad esempio utilizzando
il comando in genere solo per
predisporre la finestra grafica su
cui successivamente le immagini verranno create con comandi separati,
anche se molte figure potrebbero essere ottenute con un unico comando
complicato.
In particolare useremo sistematicamente comandi separati dalle
istruzioni di disegno. Infatti il comando permette una perfetta impo-
stazione dei parametri grafici (colore, spessore delle linee, disposizione
degli assi, caratteristiche dei testi che appaiono nelle figure, dimensioni
varie, possibilit `a di linee tratteggiate in vari modi), quindi nonostante
la molteplicit `a delle opzioni andrebbe studiato bene, ma il suo utilizzo
risulta pi `u trasparente se viene usato in modo esplicito al di fuori degli
altri comandi. La figura nell’inserto `e spiegata a pagina 22.
plot e lines
Diamo solo le varianti essenziali di questi
comandi. In particolare useremo solo
per predisporre la finestra grafica, non per
il disegno stesso. Per far apparire la figura
in una finestra sotto Linux in alcune ver-
sioni di R bisogna prima chiamare il dis-
positivo grafico con , ma non sembra
pi `u necessario nelle versioni pi `u recenti.
Per terminare il lavoro del dispositivo gra-
fico si usa .
richiede (nell’uso che ne facciamo)
come primi argomenti l’indicazione dei li-
miti per le coordinate ed , entrambi
nella forma . Se vogliamo disegnare
il coseno, possiamo ad esempio impostare
l’intervallo per con
e l’intervallo per con .
I comandi di base per impostare la fine-
stra grafica sono allora i seguenti:
Se eseguiamo il programma, vedremo per
un istante lampeggiare la finestra grafica
che per`o si chiude subito. Per poterla guar-
dare, inseriamo nella penulti-
ma riga; il parametro indica che il pro-
gramma aspetta che clicchiamo una volta
sull’immagine, prima di chiuderla. Vedia-
mo allora un quadrato nella finestra che
`e stato disegnato a causa dell’indicazione
nel comando .
significa che gli assi delle
coordinate non vengono mostrati; `e
spesso utile per imporre che le coordina-
te ed vengano utilizzate nella stessa
scala ( farebbe in modo che le coor-
dinate appaiono in scala doppia rispetto
alle coordinate ); e riguardano
le scritte che appaiono ai lati del diagram-
ma; infine indica che viene
usato solo per l’impostazione e non per di-
segnare una figura.
A questo punto, far apparire nella fine-
stra il grafico del coseno. `e sufficiente in-
serire la riga
Infatti, l’operazione a cui corresponde
matematicamente pu`o essere de-
scritta in questo modo: Se sono da-
ti due vettori e
, allora
unisce il punto con ,
il punto con , ..., e
con . Quindi se
`e una funzione, con otte-
niamo un’approssimazione poligonale del-
la funzione che, in una figura normale,
per sufficientemente grande (ad esem-
pio maggiore di ) sembrer `a una rap-
presentazione perfetta della funzione.
Possiamo utilizzare la stessa funzione
per aggiungere alla figura (che ve-
diamo nell’inserto a destra) le rette
e . Per fare ci`o uniamo con una ret-
ta i punti e e con una se-
conda retta i punti e :
In questo numero
19 La grafica di R
plot e lines
Il comando postscript
20 I numeri binomiali
21 La formula di Stirling
Coordinate polari nel piano
Coordinate cilindriche nello spazio
Coordinate polari nello spazio
Rotazioni nel piano
22 Numeri complessi in R
Funzioni in R
points
symbols e rect
Esercizi 23-27
Il comando postscript
Per far apparire questa figura sullo schermo
usiamo quindi
Se vogliamo invece conservare l’immagine in
un file in formato PostScript, possiamo usare
il comando come nella seguente se-
quenza di istruzioni, dove abbiamo anche tolto
l’istruzione interattiva :
Abbiamo aggiunto, nei due comandi ,
le specifiche di alcuni parametri grafici:
per azzerare i margini della
figura (la viene da inches, pollici, l’unit `a di
misura utilizzata da R), per usare
uno sfondo (background) giallo, e per
dimezzare lo spessore delle linee (linewidth).
Anche in questo caso non bisogna dimenticare
alla fine.
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 5 20
I numeri binomiali
Situazione 20.1. , un insieme fini-
to con elementi.
Definizione 20.2. Denotiamo con il nu-
mero degli elementi di .
In particolare .
Nota 20.3. Se e sono sottoinsiemi di
tali che (cio`e e
), allora
.
Definizione 20.4. Per denotiamo con
l’insieme di quei sottoinsiemi di
che possiedono esattamente elementi:
Esempio 20.5. Sia .
Quindi . Quanti sottoinsiemi con
esattamente elementi possiede ?
Questi sottoinsiemi sono , ,
, , , , , ,
, . possiede perci`o sot-
toinsiemi con elementi, in altre parole
.
Definizione 20.6. Per sia il nu-
mero dei sottoinsiemi di che possiedono
esattamente elementi. Quindi
I numeri della forma si chiamano co-
efficienti binomiali onumeri binomiali. La
definizione naturalmente non dipende da
, ma solo da .
Osservazione 20.7.
perch´e `e l’unico sottoinsieme di
con elementi.
perch´e `e l’unico sottoinsieme
con elementi.
perch´e i sottoinsiemi con un ele-
mento corrispondono univocamente ag-
li elementi di , e di questi ce ne sono
proprio .
Proposizione 20.8.
per .
Dimostrazione. Ogni sottoinsieme
determina univocamente il suo complemen-
to e viceversa. Se ha elementi,
ne ha . Abbiamo quindi una bi-
iezione tra e .
Corollario 20.9. .
Osservazione 20.10. per .
Dimostrazione. non pu`o possedere sot-
toinsiemi con pi `u di elementi, perch´e si ha
sempre per .
Nota 20.11. sia un elemento esterno che
non appartiene ad . Allora possie-
de elementi. Sia con .
Siccome ogni sottoinsieme di `e anche
un sottoinsieme di , i sottoinsiemi di
con elementi sono o sottoinsiemi
con elementi di , oppure consistono di
e di altri elementi appartenenti ad .
Vediamo cos`ı che `e uguale a
per cui
per . Questa formula vale per`o
anche per :
Infatti per abbiamo a sinistra
e anche a destra
; per abbiamo sia a
destra che a sinistra.
Teorema 20.12.
per ogni ed ogni .
Dimostrazione. Nota 20.11.
Il teorema 20.12 `e equivalente al triango-
lo di Pascal:
Teorema 20.13. Teorema binomiale:
per ogni . Questa formula `e pi `u in
generale valida in ogni anello commutativo
con unit`a.
Dimostrazione. Non richiesta, ma facile.
Corsi di Geometria o Analisi.
Definizione 20.14. Poniamo
per
si pronuncia n fattoriali; si parla anche
del fattoriale di .
Dalla definizione segue direttamente
l’equazione funzionale
Teorema 20.15.
per .
Dimostrazione. Facile per induzione su ,
fissato . Non richiesta.
Nota 20.16. La formula del teorema 20.15
`e molto importante nella teoria, ma, un po’
simile a come accade per il determinante,
pu`o essere utilizzata solo per numeri molto
piccoli.
Infatti per calcolare con il teore-
ma 20.15 dovremmo calcolare e ,
due numeri giganteschi, e formare .
In pratica si usa invece la regola
dove sopra stanno tanti numeri quanti sot-
to, cioe .
Ad esempio
Non `e difficile giustificare questa regola
(esercizio 23).
Definizione 20.17. I numeri
si chiamano binomiali superiori. Anche qui
sia sopra che sotto stanno numeri. Infatti
Basta leggere il numeratore all’indietro nel-
la definizione. Nonostante ci`o, i binomiali
superiori hanno interessanti interpretazioni
combinatoriche.
Nota 20.18. Per calcolare fattoriali e bino-
miali molto grandi al calcolatore conviene
utilizzare il logaritmo. Siccome
e per
abbiamo
e
per
da cui si deduce facilmente un algoritmo.
Quando si usa il logaritmo, si pu`o anche
usare il teorema 20.15 per calcolare i numeri
binomiali:
Quando questi numeri, ad esempio per
, servono spesso, conviene
creare una tabella.
In R comunque tutte queste funzioni sono
gi`a comprese:
Sorprendentemente con non
otteniamo, come magari ci aspetteremmo, lo
stesso risultato come con , cio`e
(perch´e si potrebbe pensare che sempli-
cemente l’argomento venga arrotondato, es-
sendo il fattoriale definito per argomenti che
sono numeri naturali); viene invece restitui-
to il misterioso valore .
La ragione `e molto profonda; infatti la fun-
zione fattoriale `e la restrizione
ad della funzione gamma
una delle pi `u importanti funzioni della ma-
tematica e della statistica. `e quindi de-
finito per ogni numero complesso che non
sia il negativo di un numero naturale, cio`e
per ogni con . Il
fattoriale `e legato alla funzione gamma dalla
relazione
Provare e in R.
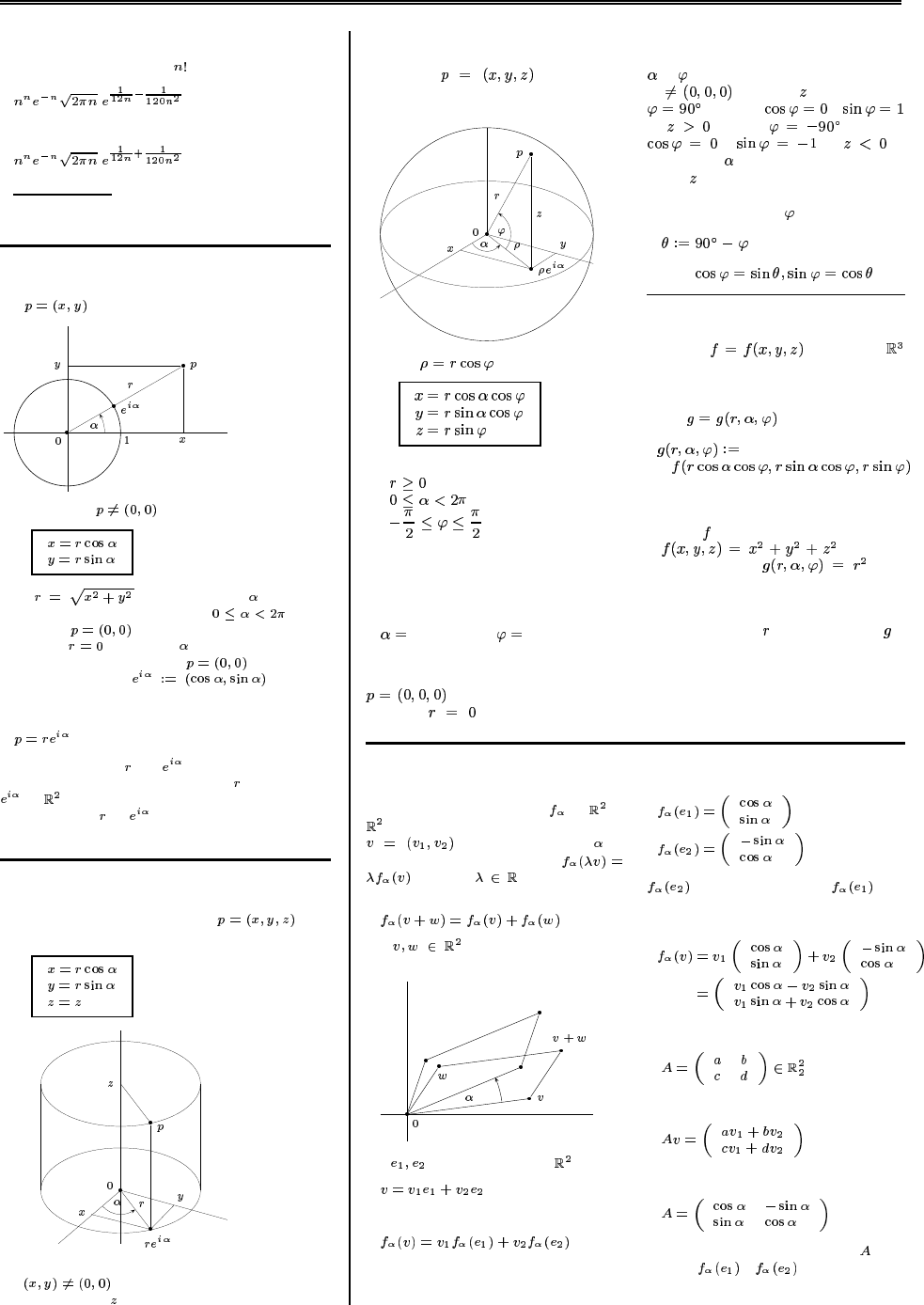
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 5 21
La formula di Stirling
Teorema 21.1. Il valore di `e sempre compreso tra
e
Dimostrazione. Non richiesta. Richiede i potenti
strumenti dell’analisi complessa.
Coordinate polari nel piano
Sia un punto del piano reale.
Si vede che, se , allora
(*)
dove , mentre l’angolo `e univoca-
mente determinato se chiediamo .
Nel caso la rappresentazione (*) rimane
valida con e qualsiasi , la biiettivit `a della (*)
viene quindi meno nel punto .
Scriviamo adesso come ab-
biamo gi`a fatto nel disegno; allora la relazione (*)
pu`o anche essere scritta nella forma
Questo prodotto di con pu`o essere interpreta-
to come prodotto dello scalare reale con il vettore
di ed `e allo stesso tempo il prodotto dei nu-
meri complessi ed come vedremo nel prossimo
numero.
Coordinate cilindriche nello spazio
Dalla figura si vede che un punto dello
spazio pu`o essere rappresentato nella forma
La rappresentazione `e univoca per quei punti per
cui , quindi per tutti i punti che non si
trovano sull’asse .
Coordinate polari (o sferiche) nello spazio
Un punto dello spazio
tridimensionale pu`o anche essere rap-
presentato come nella figura seguente:
Avendo , si vede che
con
Questa rappresentazione `e quella che
si usa nelle coordinate geografiche di
un punto della terra o della sfera cele-
ste:
longitudine, latitudine.
Anche in questo caso la corrisponden-
za non `e biiettiva, perch´e non solo per
la rappresentazione `e va-
lida per e valori arbitrari di
e , ma anche per ogni altro pun-
to dell’asse bisogna porre
e quindi e
se oppure e quindi
e se , e
allora ogni va bene. Quindi su tutta
l’asse le coordinate polari non sono
univocamente determinate.
Spesso al posto di si usa
quindi .
Molte funzioni della matematica e del-
la fisica presentano simmetrie. A una
funzione definita su
(per semplicit `a, ma spesso bisogner `a
studiare bene il pi `u adatto dominio di
definizione) possiamo associare la fun-
zione definita da
che in caso di simmetrie pu`o avere
una forma analitica molto pi `u sempli-
ce della .
ad esem-
pio diventa cos`ı , una
funzione di una sola variabile notevol-
mente pi `u semplice. Altre volte una
funzione dipende solo dalla direzione
e quindi non da ; in questo caso `e
una funzione di sole due variabili e an-
che questa `e una importante semplifi-
cazione. Nello stesso modo si usano le
coordinate cilindriche e le coordinate
polari piane.
Rotazioni nel piano
Consideriamo l’applicazione da in
che consiste nel ruotare un punto
per l’angolo fissato in
senso antiorario. `
E chiaro che
per ogni e dal disegno si
vede che anche
per . Una rotazione `e quindi
un’applicazione lineare.
Sia la base canonica di . Allora
perci`o
Ma
`e il vettore magico di !
Cfr. esercizio 24.
Quindi
Se per una matrice
definiamo
vediamo che possiamo prendere
.
Notiamo anche che le colonne di sono
proprio e .

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 5 22
Numeri complessi in R
Un numero complesso `e un punto
del piano reale. Secondo questa definizione,
i numeri complessi non sono nuovi come og-
getti. Definiremo per`o nel prossimo numero
le due operazioni, addizione e moltiplicazio-
ne, per i numeri complessi, di cui abbiamo
gi`a parlato a pagina 6.
Per stavolta usiamo i numeri complessi so-
lo come la forma pi `u comoda per rappresen-
tare punti del piano in R. In matematica il
numero complesso viene anche
scritto nella forma , ad esem-
pio . In modo quasi identico
vengono rappresentati i numeri complessi in
R, mentre per`o in matematica per si
scrive , in R bisogna scrivere . An-
che da solo non `e ammesso, dobbiamo scri-
vere ; R stesso nell’output utilizza .
Si pu`o usare per il numero complesso
(nell’output ). La parte reale si ottiene
con , la parte immaginaria con .
Molte funzioni grafiche in R sono definite
per successioni di punti. Siccome in statisti-
ca accade spesso che si hanno due serie di
misurazioni, ad esempio
e , molte di queste funzioni
possono essere usate nella forma .
Una coppia di misurazioni (cio`e di vetto-
ri) `e per`o equivalen-
te a una successione
di punti del piano, cio`e a un elemento di
. Questa dualit `a `e onnipresente nella
statistica multivariata. In R dovremmo al-
lora scrivere
che ci costringe a una rappresentazione un
po’ difficoltosa.
Le stesse funzioni grafiche operano cor-
rettamente se diamo i punti come una
successione di numeri complessi, possia-
mo cio`e usarle ad esempio nella forma
. Non dimenticare
l’operatore .
Funzioni in R
Da questi esempi si dovrebbero poter dedur-
re le regole pi `u importanti per la definizione
di funzioni in R. Parametri predefiniti sono
assegnati con . Le funzioni ,
e verranno discusse adesso.
points
Per disegnare punti e simboli in R si pos-
sono usare le funzioni e . Il
primo comando ha il formato
Usiamo qui la seguente convenzione: In pri-
mo luogo gli argomenti possibili nelle fun-
zioni di R sono in genere talmente tan-
ti, che i prototipi che indichiamo corris-
pondono soltanto a un formato scelto per
semplicit`a e funzionalit `a. R permette inol-
tre argomenti riconoscibili per nome, che
quindi non devono necessariamente seguir-
si nell’ordine indicato. Quando nel nostro
prototipo appaiono due segni di uguaglian-
za, ci`o significa che l’ultimo valore `e il valo-
re predefinito in R. Analizziamo in dettaglio
i parametri.
sono le coordinate dei punti, che
possono essere dati sia come elementi
di oppure mediante un vettore di
numeri complessi.
`e il simbolo con cui il punto vie-
ne rappresentato. Questo simbolo pu`o es-
sere una lettera oppure un numero tra 1
e 25. Le forme che corrispondono a questi
numeri sono elencate nella prima figura a
pagina 19.
pu`o omesso oppure scelto tra e
. Se viene omesso, assume il valore pre-
definito , che sta per point e indica che
nel punto indicato viene disegnata la figura
desiderata. fa in modo che i punti ven-
gano uniti con linee (in questo caso `e su-
perfluo), mentre l’interessante opzione
(per both) implica che vengano disegnati sia
i simboli che le linee congiungenti.
`e il colore in cui il simbolo (o il suo
bordo quando `e riempibile) viene disegnato.
Se manca, viene usato il colore di disegno
attualmente impostato.
`e il colore di riempimento per
i simboli con i numeri da 21 a 25. I colori
possono essere indicati per nome (ad esem-
pio , un elenco dei nomi
disponibili lo si ottiene, almeno sotto Linux,
con il comando ) oppure in formato
RGB, ad esempio per il rosso.
`e la scala. `
E normalmente imposta-
ta ad 1, per avere un formato pi `u grande
si pu`o aumentare la scala, ad esempio con
.
La figura a pagina 19 che rappresenta i
simboli e i numeri a cui corrispondono `e sta-
ta ottenuta con questi comandi:
Per ottenere l’output su una finestra grafi-
ca `e sufficiente inserire prima di
.
`e lo stesso come .
symbols e rect
Nella funzione dell’ultimo paragrafo
abbiamo usato la funzione che per-
mette di disegnare simboli pi `u complessi di
quelli che si ottengono con .`
E una
funzione che si usa poco per`o e anche noi la
utilizziamo solo per disegnare cerchi il cui
raggio (in pollici, come tutte le misure di R)
possono essere assegnati. Cerchi si possono
anche ottenere con , dove per`o invece
del raggio si pu`o indicare solo la scala re-
lativa impostando il parametro (o
in ).
Anche rettangoli si possono disegnare sia
con che con ; siccome esiste
per`o una funzione apposita in R, pos-
siamo adattarla definendo una nostra fun-
zione . Usiamo anche qui il plu-
rale perch´e tutte queste figure permettono
di disegnare serie di figure.
L’immagine `e stata ottenuta con
Il semplice ma potente di R viene usato
nella forma
`e la successione con
ripetizioni di .
Esercizi per gli scritti
23. Giustificare la regola della nota 20.16.
24. Per un vettore del piano il
vettore che si ottiene da
per rotazione di 90 gradi in senso an-
tiorario si chiama il vettore magico di
. Usare le matrici di rotazione per ot-
tenere da .
25. Usando le matrici di rotazione dimo-
strare che .
26. Se `e il vettore magico di , allora
`e il vettore magico di .
Usare l’esercizio 25! Riflettere sul caso
.
27. Scrivere una funzione per disegnare
rettangoli in cui il primo argomento
corrisponde al vettore dei centri.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller
Corso di laurea in matematica Anno accademico 2004/05 Numero 6
I numeri complessi
Abbiamo gi `a detto che un numero
complesso `e un punto
del piano reale e che secondo que-
sta definizione i numeri complessi
non sono nuovi come oggetti. De-
finiamo per`o adesso per i numeri
complessi due operazioni, addizio-
ne e moltiplicazione.
Siano e .
Allora
L’addizione `e l’addizione vettoriale
nel piano, la moltiplicazione `e in-
vece motivata nel modo seguente.
L’equazione non ha so-
luzioni reali (perch´e implica
e ). Ci chie-
diamo allora se `e possibile aggiun-
gere ai numeri reali altri numeri,
numeri immaginari, tra cui un nu-
mero ( appunto perch´e immagi-
nario) che soddisfa l’equazione
Naturalmente vorremmo che le
usuali leggi aritmetiche siano con-
servate anche con i nuovi numeri.
Con la nostra definizione tutto fun-
ziona bene:
Chiamiamo il punto del
piano , poniamo cio`e
e identifichiamo il numero reale
con il numero complesso - ci`o
significa geometricamente che con-
sideriamo la retta reale come sotto-
insieme del piano nel solito modo,
identificandola con l’asse delle .
Siano . Allora:
(1) , dove a
sinistra il prodotto `e il nuovo pro-
dotto per i numeri complessi. Infat-
ti, secondo la nostra definizione,
Ci`o significa che `e ugua-
le ad , cio`e al prodotto dello
scalare reale con il vettore
del piano.
(2)
Infatti
(3) Pi `u in generale abbiamo
e quindi anche , e
Osserviamo bene quest’ultima for-
mula. Il risultato `e in accordo con
la nostra definizione per la mol-
tiplicazione di numeri complessi,
ma `e stato raggiunto eseguendo il
calcolo secondo le regole algebriche
usuali, a cui abbiamo aggiunto la
nuova legge .
(4) E infatti per le operazioni e
definite all’inizio valgono le stes-
se leggi algebriche come per i nu-
meri reali (cfr. pagina 6), perch´e,
come si verifica adesso facilmen-
te, l’insieme dei numeri complessi
con queste operazioni `e un anello
commutativo in cui il numero reale
`e l’elemento neutro per la
moltiplicazione. Quest’ultima af-
fermazione segue dal punto (1).
Vedremo a pagina 24 che i nume-
ri complessi formano in verit `a un
campo, cio`e che ogni numero comp-
lesso diverso da zero possiede un
inverso per la moltiplicazione.
Il campo dei numeri complessi
viene denotato con . In pratica
, per`o con le nuove operazio-
ni. Abbiamo gi `a visto che
, e siccome , si pu`o an-
che scrivere .
In questo numero
23 I numeri complessi
La formula di Euler
24 Il campo dei numeri complessi
La formula di de Moivre
Parte reale e parte immaginaria
Disuguaglianze fondamentali
Il segno del prodotto scalare
Poligoni con R
25 Radici di un polinomio
Radici -esime dell’unit`a
Radici di un numero complesso
Esercizi 28-43
La formula di Euler
Abbiamo introdotto gi `a a pagina 21 la notazione
per . Adesso la possiamo riscrivere nella
forma
(formula di Euler). Questa notazione, per il mo-
mento puramente simbolica (perch´e solo nei cor-
si di Analisi si potr`a dimostrare che si tratta
veramente di una potenza), non `e solo molto co-
moda, come vedremo adesso, ma anche estrema-
mente importante nella teoria.
Dal teorema di addizione per le funzioni tri-
gonometriche si deduce immediatamente che
per (esercizio 33). Si vede che nel cam-
po complesso il teorema di addizione assume
una forma molto pi `u semplice.
Per possiamo anche pi `u in generale
definire
Allora
per ogni . La funzione esponenziale `e
quindi un omomorfismo
Leonhard Euler (1707-1783), matematico
svizzero-tedesco, pass`o gran parte della sua
vita a Pietroburgo e a Berlino. `
E stato uno
dei pi `u prolifici matematici di tutti i tempi;
la sua opera riempie 88 volumi. Non era solo
un geniale analista, ma ha inventato anche la
teoria dei grafi, anticipando un campo della
matematica discreta oggi molto studiato per le
numerose applicazioni (ad esempio in ricerca
operativa e in informatica). Ha lavorato su
quasi tutti i campi della matematica pura e
applicata del suo tempo.
C. Boyer. Storia della matematica. Mondadori.
U. Bottazzini. Il flauto di Hilbert. Utet 1990.
C. Berge. The theory of graphs. Dover 2001.
R. Diestel. Graph theory. Springer 1997.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 6 24
Il campo dei numeri complessi
Abbiamo visto a pagina 21 che ogni punto
di pu`o essere scritto nella for-
ma
dove `e univocamente determinato ed
. Abbiamo anche visto che
Se , anche `e univocamente determi-
nato se chiediamo oppure, come
il matematico preferisce dire, univocamente
determinato modulo .
Possiamo quindi scrivere ogni numero
complesso nella forma
anch’essa gi`a anticipata a pagina 21, con
ed come sopra.
Sia adesso anche . Allora
come segue dal teorema di addizione visto
a pagina 24. Il prodotto ha quindi la
stessa lunghezza di ed un angolo aumen-
tato di rispetto a . Ci`o significa che la
moltiplicazione con `e la stessa cosa co-
me una rotazione per l’angolo in senso an-
tiorario.
Prendiamo adesso un numero comples-
so arbitrario. Lo possiamo rappresenta-
re nella forma con . Per il
prodotto otteniamo evidentemente
e quindi vediamo che la moltipli-
cazione con un numero complesso consiste
sempre di una rotazione combinata con un
allungamento (o accorciamento se ).
Definizione 24.1. Sia con
. Allora si chiama il
numero complesso coniugato a.
Geometricamente si ottiene mediante
riflessione di rispetto all’asse reale. `
E
chiaro che .
Lemma 24.2. Sia . Allora
.
Dimostrazione. Immediata. Perch´e `e an-
che un caso speciale dell’esercizio 30?
Nota 24.3. Ogni numero complesso
possiede un inverso rispetto alla moltiplica-
zione, infatti
per cui possiamo porre
o, equivalentemente,
`e quindi un campo. Come in ogni
campo anche in l’inverso `e univocamente
determinato.
La formula di de Moivre
Sia . Per allora, secondo
le formule viste precedentemente, abbiamo
Abraham de Moivre (1667-1754) era un ma-
tematico francese emigrato giovane in In-
ghilterra. Ha scritto un famoso trattato sul
calcolo delle probabilit`a (Doctrines of chan-
ces, 1718).
Parte reale e parte immaginaria
Definizione 24.4. (con rea-
li come sempre) sia un numero complesso.
Definiamo allora
Re
Im
Re si chiama la parte reale di , Im la
parte immaginaria.
Osservazione 24.5. Sia . Allora
Osservazione 24.6. Sia . Allora
Re e Im .
Dimostrazione. Infatti, con ,
Re .
Nello stesso modo per Im .
Osservazione 24.7. Per un numero comp-
lesso la parte reale e la parte immaginaria
di non sono altro che le coordinate di co-
me punto di .`
E quindi chiaro che, se `e
un altro numero complesso, si ha se e
solo se e coincidono sia nelle parti reali
che nelle parti immaginarie.
Usare questa osservazione nella dimo-
strazione degli esercizi 41 e 42.
Disuguaglianze fondamentali
Teorema 24.8. Siano e
due punti di . Allora
Questa `e una delle disuguaglianze pi `u im-
portanti di tutta la matematica e prende
il nome di disuguaglianza di Cauchy-
Schwarz.
Dimostrazione. Possiamo ricondurre que-
sta fondamentale disuguaglianza al caso
. Infatti i due vettori stanno su un
piano e il prodotto scalare si esprime medi-
ante l’angolo che essi formano in questo
piano (pagina 15):
e siccome abbiamo
Proposizione 24.9. Siano ancora
e due
punti di . Allora
Questa seconda disuguaglianza fondamen-
tale `e detta disuguaglianza triangolare.
Dimostrazione. Ci`o `e una facile conse-
guenza della formula
per il prodotto scalare vista a pagina 15 e
della disuguaglianza di Cauchy-Schwarz:
per cui anche
Il segno del prodotto scalare
Nota 24.10. Nella disuguaglianza di
Cauchy-Schwarz anche a sinistra dobbiamo
mettere il segno di valore assoluto, perch´e il
prodotto scalare pu`o essere negativo.
Infatti il segno del prodotto scalare ha una
importantissima interpretazione geometri-
ca: Siano come finora e
due punti di , entrambi
diversi da . Come nella dimostrazione del-
la disuguaglianza di Cauchy-Schwarz sia
l’angolo che i due vettori formano in un pia-
no comune (un tale piano esiste sempre ed
`e univocamente determinato se i due vettori
non sono paralleli). Sappiamo che
Per ipotesi e . Ci`o implica
che e hanno lo stesso segno; in
particolare
e
Fissiamo adesso . Allora i vettori
per i quali sono esattamente i vet-
tori ortogonali ad . Essi formano l’iperpiano
ortogonale ad (una retta ortogonale ad in
, un piano ortogonale ad in ). Come si
vede dalle figure a pagina 13 per il
coseno di `e uguale ad , e se, partendo da
, avviciniamo all’iperpiano ortogona-
le di , il coseno diventa sempre pi `u piccolo,
rimanendo per`o positivo fino a quando non
tocchiamo l’iperpiano ortogonale. Se passa
invece dall’altra parte dell’iperpiano, il cose-
no di diventa negativo.
Avendo e per`o lo stesso segno,
otteniamo il seguente enunciato geometrico,
importante anche in molte applicazioni, ad
esempio nella teoria dell’ottimizzazione:
Teorema 24.11. Siano e
due punti di , entrambi
diversi da zero. Allora se e solo
se si trova dalla stessa parte dell’iperpiano
ortogonale ad come stesso.
Poligoni con R
La semplicit `a delle seguenti costruzioni `e
impressionante - ma richiede la nostra ma-
tematica! Esaminare bene ogni singola riga
del programma e variarlo.
Si ottiene la figura a pagina 25.
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 6 25
Radici di un polinomio
Teorema 25.1. Siano
un polinomio con coefficienti complessi,
e . Allora esistono numeri
complessi , univocamente deter-
minati, tali che
Questa uguaglianza `e intesa come uguag-
lianza di polinomi, cio`e sviluppando il pro-
dotto a destra si ottiene un polinomio con gli
stessi coefficienti di e quindi proprio .
`
E chiaro anche che per ogni e
si pu`o dimostrare che ogni radice di , cio`e
ogni per cui , `e uno degli .
Dimostrazione. Non richiesta. Esistono
molte dimostrazioni, le pi `u semplici utiliz-
zano ancora l’analisi complessa.
Il teorema 25.1 si chiama il teorema fon-
damentale dell’algebra.
In R le radici di un polinomio possono es-
sere ottenute con la funzione che
prende come argomento il vettore dei coef-
ficienti di elencati iniziando con il coeffi-
ciente costante. Per arrotondare i risultati
usiamo la funzione , il cui secondo ar-
gomento `e il numero di cifre decimali a cui
si vuole arrotondare. Esempio:
con output . Infatti
.
Radici -esime dell’unit `a
Sia fissato. Consideriamo il nu-
mero
(che naturalmente dipende da ). Dalla for-
mula di de Moivre segue che elevato al-
la -esima potenza, `e uguale a . `
E anche
chiaro che
per ogni . Consideriamo adesso i nu-
meri .
Dalla formula di Euler vediamo che gli
si trovano tutti sul cerchio unitario, con
ruotato di (cio`e di gradi) rispetto ad
. Essi formano in altre parole (almeno
per ) i vertici del poligono regolare con
vertici iscritto al cerchio unitario con pri-
mo vertice uguale ad . Ci`o implica che gli
per sono tutti distinti
tra di loro e costituiscono un insieme di
radici del polinomio , mentre per al-
tri i valori si ripetono. Dal teorema fonda-
mentale dell’algebra segue che ogni radice
di `e uno degli e che
I numeri si chiamano le
-esime radici dell’unit`a.
Radici di un numero complesso
Siano un numero reale non negativo
ed . Nei corsi di Analisi si impara
che esiste un unico numero tale che
. Denotiamo questo numero con .
Sia adesso un numero complesso
diverso da . Allora con e
. Cerchiamo le radici -esime di , cio`e
le radici del polinomio . Una radice
la troviamo subito; infatti la formula di de
Moivre implica che
soddisfa l’equazione . Se adesso
`e un numero complesso tale che ,
allora anche
Per`o noi conosciamo i per cui ; so-
no le -esime radici dell’unit`a. Quindi cia-
scuno dei numeri
`e una radice di . D’altra parte la mol-
tiplicazione di un numero complesso con
corrisponde alla rotazione di per un
angolo di gradi e, siccome e
quindi anche , tutti gli sono di-
stinti tra di loro. Dal teorema fondamentale
dell’algebra segue che
e che ogni numero complesso che soddisfa
l’equazione `e uno degli .
Troviamo con R le quarte radici di :
L’output `e
Fare un disegno con riga e compasso e veri-
ficare il risultato. Cfr. esercizio 43.
Esercizi per gli scritti
Per vettori si denota
talvolta con non solo la -
pla, ma anche la matrice le cui colonne so-
no i vettori nell’ordine indicato.
In particolare possiamo formare la matrice
per due numeri complessi e , con-
siderati come punti di .
Siano e numeri
complessi con .
28. Il vettore magico di `e .
29. Calcolare e in termini
di .
30. .
Quindi
31. Usiamo il simbolo per indicare l’orto-
gonalit`a tra due vettori.
.
L’insieme si chiama l’asse immagi-
nario, gli elementi di , cio`e i numeri
complessi con parte reale uguale a zero,
si chiamano puramente immaginari.
e sono quindi ortogonali se e solo se
`e puramente immaginario.
32.
.
Nella seconda parte non ripetere i conti!
33.
per ogni .
34. .
35. Calcolare .
36. Calcolare .
37. Calcolare .
38. Calcolare .
39. Calcolare .
40. Calcolare .
41. .
Dimostrare questa formula per
(seno e coseno possono essere definiti
anche su e l’equazione rimane valida,
ma ci`o non pu`o essere dimostrato qui)
usando la formula di de Moivre e con-
frontando le parti reali e immaginarie.
42. .
Questo era l’esercizio 16. Dimostrarlo
adesso con il metodo dell’esercizio 41.
`
E solo un piccolo esempio di quanto il
passaggio per i numeri complessi possa
semplificare anche questioni che appa-
rentemente riguardano soltanto i nume-
ri reali.
43. Siano un numero complesso diverso da
e . Allora le altre radici di
sono .
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller
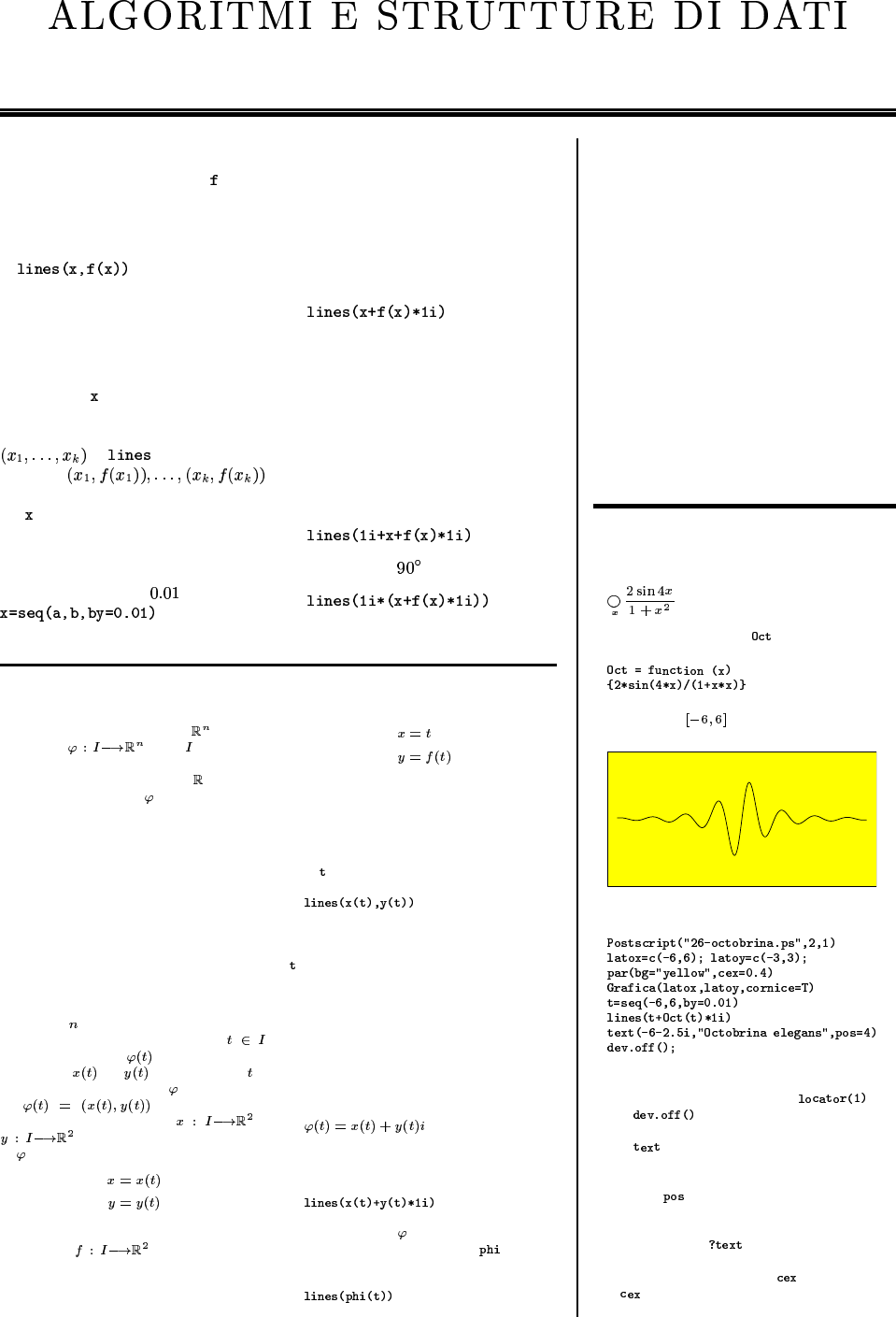
Corso di laurea in matematica Anno accademico 2004/05 Numero 7
Grafici di funzioni
Il grafico di una funzione (di R
o definita da noi) si ottiene, come a
pagina 19 il grafico del coseno, con
la riga
adattando i parametri di am-
biente (dimensioni degli interval-
li per l’ascissa e per l’ordinata,
colori, linee ausiliarie) secondo
le necessit `a. Ricordiamo che il
parametro deve essere un vet-
tore di valori reali che mate-
maticamente siano ad esempio
; congiunge i
punti
con segmenti di rette. Se i punti
di sono sufficientemente vicini,
avremo l’impressione di una curva
continua. In genere, se la funzio-
ne non oscilla troppo, `e sufficiente
una risoluzione di , definendo
.
Mentre la notazione per vettori
e matrici in R non `e particolar-
mente felice, per figure piane pos-
siamo usare con grande vantag-
gio la rappresentazione complessa.
Per un grafico di funzioni possiamo
scrivere
La comodit `a della forma comples-
sa sta soprattutto nel fatto che pos-
siamo cos`ı facilmente eseguire ope-
razioni geometriche, le quali nel
piano, come vedremo in questo nu-
mero, sono tutte esprimibili medi-
ante operazioni algebriche con nu-
meri complessi. Per spostare il gra-
fico di 1 verso l’alto `e sufficiente
per girarlo di `e sufficiente
e cos`ı via.
Curve parametrizzate nel piano
Una curva parametrizzata in `e un’ap-
plicazione , dove `e un inter-
vallo (aperto o chiuso, finito o infinito, ma
pi `u spesso finito e chiuso) di . Normal-
mente si chiede che la sia almeno conti-
nua o anche che sia due volte differenzia-
bile con derivate continue. Lo studio del-
le curve continue rientra nel campo della
topologia e riguarda in primo luogo pro-
priet`a di deformabilit`a di oggetti geome-
trici (ci sono applicazioni in robotica, ad
esempio la questione, se i bracci di un ro-
bot possano o no passare in modo continuo
da una posizione a un’altra, pu`o essere for-
mulata e trattata con gli strumenti della
topologia), lo studio delle curve e superfi-
cie differenziabili fa parte della geometria
differenziale.
Quando `e uguale a 2, si parla di cur-
ve piane. In questo caso, per ogni
abbiamo un punto del piano, le cui
coordinate ed dipendono da e
sono, appunto, legate alla dalla relazio-
ne . In questo modo
sono definite due funzioni e
che a loro volta determinano
la . Spesso si scrive allora
Notiamo subito che il grafico di una fun-
zione reale definita su un in-
tervallo `e un caso speciale di curva para-
metrizzata che pu`o essere rappresentato
nella forma
R si presta particolarmente bene per
la rappresentazione di curve piane pa-
rametrizzate, perch´e, una volta definito
l’intervallo che si vuole usare e che deve
essere rappresentato come successione fi-
nita di punti, `e sufficiente l’istruzione
nel programma per ottenere la curva. Ab-
biamo osservato a pagina 17 che il nome
in R `e riservato (viene utilizzata per for-
mare la trasposta di una matrice), ma lo
possiamo utilizzare per le variabili locali
all’interno di una funzione (naturalmente
solo se non abbiamo contemporaneamente
bisogno della trasposta).
Anche per le curve parametrizzate use-
remo la notazione complessa, quindi ma-
tematicamente
e nel disegno della curva in R useremo
l’istruzione
ma anche, se la `e rappresentata diret-
tamente in R come funzione a valori
complessi, istruzioni della forma
In questo numero
26 Grafici di funzioni
Curve parametrizzate nel piano
Octobrina elegans
27 Octobrinidae I
Octobrinidae II
28 abline
Funzioni iperboliche
Parabrinidae
Rotazioni
29 expression ed eval
Testi matematici
Ellissi
Iperboli
30 Rette e segmenti
Equazione di una retta
Proiezione su una retta
Il sito CRAN di Ferrara
Esercizi 44-53
Octobrina elegans
Rappresentiamo il grafico della funzione
a cui in R diamo il nome :
nell’intervallo .
Octobrina elegans
mediante le istruzioni
Per vedere la figura sullo schermo bisogna eli-
minare la prima riga e inserire pri-
ma di .
Il programma contiene una sola nuova istru-
zione, , che viene usata per aggiungere testi
a una figura. Il primo parametro indica il pun-
to a cui si riferisce la posizione del testo; se il
parametro `e uguale a 4, il testo viene inseri-
to alla destra del punto di riferimento. Quando
questo parametro manca, il testo viene centrato
nel punto. Vedere per le altre possibilit `a.
Per ottenere una scritta piccola abbiamo mo-
dificato il parametro grafico (nella terza ri-
ga); `e un’abbreviazione per character expan-
sion; l’abbiamo gi `a incontrata a pagina 22.
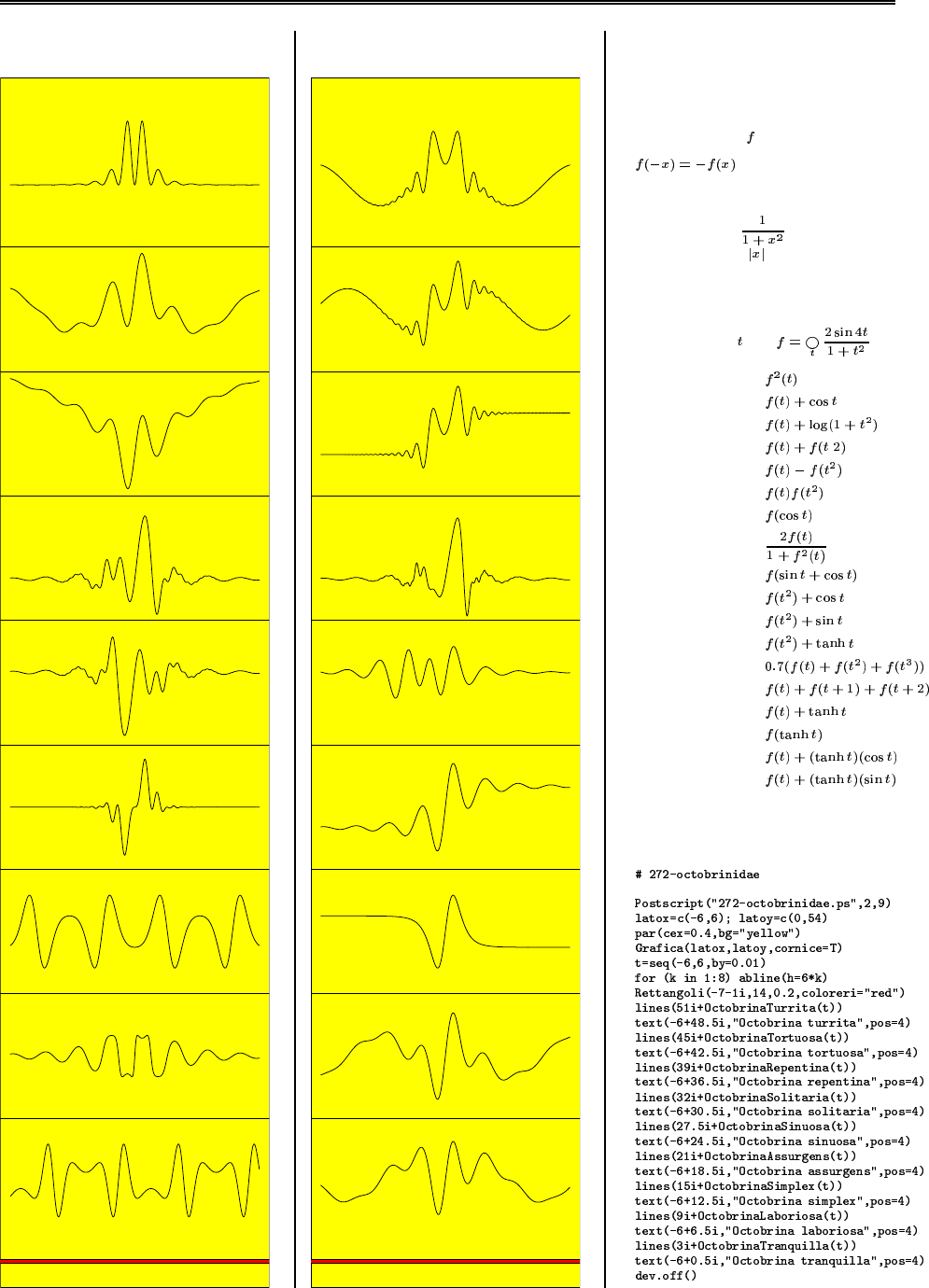
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 7 27
Octobrinidae I
Octobrina geminata
Octobrina montuosa
Octobrina voraginosa
Octobrina irregularis
Octobrina divisa
Octobrina pulcherrima
Octobrina sellulata
Octobrina munita
Octobrina modulata
Octobrinidae II
Octobrina turrita
Octobrina tortuosa
Octobrina repentina
Octobrina solitaria
Octobrina sinuosa
Octobrina assurgens
Octobrina simplex
Octobrina laboriosa
Octobrina tranquilla
Il grafico dell’octobrina `e cos`ı elegante
perch´e presenta una simmetria non perfetta.
Se a prima vista la curva pu`o sembrare sim-
metrica, guardando pi `u attentamente vedia-
mo invece che le due met `a si distinguono nel
segno; infatti la funzione `e una funzione dis-
pari - una funzione si chiama dispari, se
perch´e il seno `e una funzione dispari e il
quadrato una funzione pari; d’altra parte il
fattore smorzante riduce l’ampiezza
della curva quando diventa pi `u grande e
attenua cos`ı la differenza tra le due parti.
Combinando la funzione ad altre funzio-
ni elementari abbiamo ottenuto i grafici su
questa pagina che corrispondono alle se-
guenti funzioni di , con :
O. geminata
O. montuosa
O. voraginosa
O. irregularis
O. divisa
O. pulcherrima
O. sellulata
O. munita
O. modulata
O. turrita
O. tortuosa
O. repentina
O. solitaria
O. sinuosa
O. assurgens
O. simplex
O. laboriosa
O. tranquilla
Il quadro delle figure nella seconda colonna
`e stato ottenuto con il seguente programma
in R:
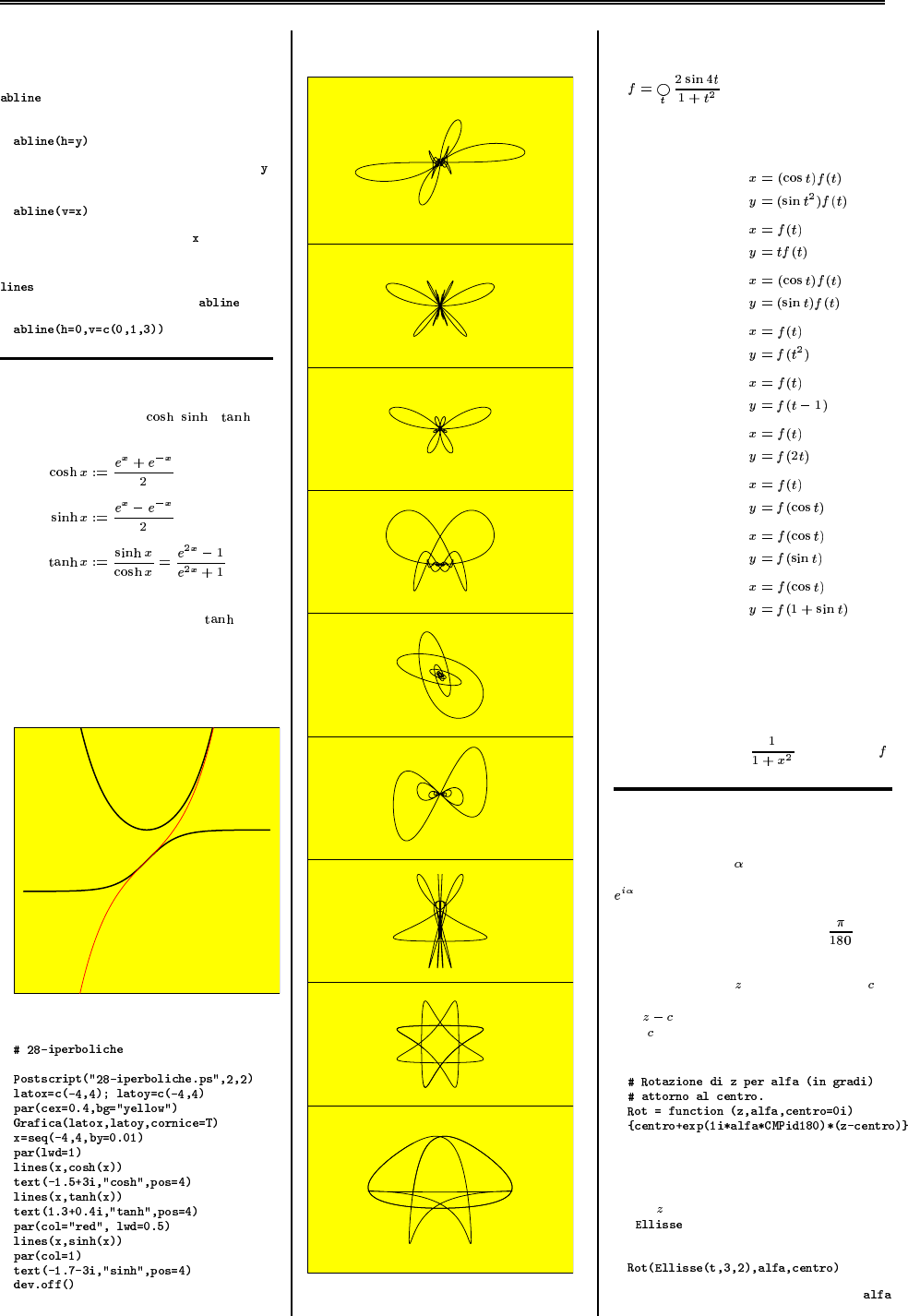
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 7 28
abline
Nel programma a pagina 27 per la suddivi-
sione del quadro abbiamo usato la funzione
di R. Essa pu`o essere utilizzata in
vari modi; con
si ottiene una retta orizzontale all’altezza ,
con
una retta verticale con ascissa . Si possono
anche disegnare altre rette, ma tranne per
questi casi semplici `e forse preferibile usare
. Comoda `e la possibilit`a di disegnare
pi `u linee con un’unico comando :
Funzioni iperboliche
Le funzioni iperboliche , e so-
no definite da
Tutte e tre hanno importanti applicazioni
tecniche; la tangente iperbolica `e an-
che nota sotto il nome di funzione sigmoi-
dea e viene spesso utilizzata per modellare
la crescita di popolazioni (crescita logistica)
o la formazione di impulsi, ad esempio nelle
reti neuronali.
cosh
tanh
sinh
La figura `e stata ottenuta con
Parabrinidae
Parabrina rotans
Parabrina trichoptera
Parabrina muscellaria
Parabrina composita
Parabrina nuclearis
Parabrina rediens
Parabrina faceta
Parabrina octonaria
Parabrina fungina
Le curve della famiglia delle Parabrinidae si
ottengono utilizzando la funzione
dell’octobrina in entrambe le coordinate del-
la parametrizzazione:
P. rotans
P. trichoptera
P. muscellaria
P. composita
P. nuclearis
P. rediens
P. faceta
P. octonaria
P. fungina
Di queste funzioni solo le ultime due sono pe-
riodiche, perci`o, nonostante le apparenze, le
prime sette curve non sono chiuse e ogni al-
largamento dell’intervallo di definizione ne
cambierebbe l’aspetto, anche se i cambia-
menti diventano impercettibili per l’influsso
smorzante del fattore contenuto in .
Rotazioni
Abbiamo visto a pagina 24 che una rotazio-
ne per un angolo attorno all’origine nel
piano corrisponde alla moltiplicazione con
nell’ambito dei numeri complessi. Se vo-
gliamo esprimere l’angolo in gradi, dobbia-
mo moltiplicare l’argomento con come
visto a pagina 13.
Vogliamo inoltre anche rappresentare ro-
tazioni di un punto attorno a un centro . A
questo scopo dobbiamo prima ruotare il vet-
tore attorno all’origine e poi riattaccar-
lo in . Otteniamo cos`ı la seguente funzione
in R:
Come sempre nelle funzioni di R, anche que-
sta pu`o essere applicata usando un vettore
invece di un singolo punto come primo argo-
mento . A pagina 29 definiremo una funzio-
ne che crea un vettore consistente
dei punti di un’ellisse. Con
otteniamo l’ellisse ruotata dell’angolo
attorno al centro.
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 7 29
expression ed eval
R permette di creare espressioni formali con
la funzione . Mentre quindi dopo
`e un’espressione formale il cui va-
lore non viene per`o calcolato (infatti questa
espressione `e lecita anche quando non `e
ancora stato definito), con
ne possiamo calcolare il valore. Esempio:
con output
Testi matematici
Nelle istruzioni , , e ,
che permettono l’aggiunta di testi alle fi-
gure, le espressioni matematiche (nel sen-
so dell’articolo precendente) vengono ela-
borate secondo regole simili a quelle del
Latex per ottenere le formule matemati-
che corrispondenti. I dettagli sono forniti da
e . Esempio:
y=2sin(x) 1+cos(x)
1+x2
La figura `e stata ottenuta con
Per ragioni tipografiche abbiamo suddiviso
alcune istruzioni su due righe. Si possono
anche rappresentare integrali, simboli logi-
ci e insiemistici, indici ecc.
Ellissi
Siano con ed ,
. Allora
quindi il punto si trova su un’ellisse
con gli assi e . Non `e difficile dimostrare
(con le conoscenze sulle funzioni trigonome-
triche e le loro inverse che si imparano nei
corsi di Analisi) che viceversa ogni punto
dell’ellisse pu`o essere rappresentato in que-
sta forma. In altre parole,
con `e una parametrizzazio-
ne dell’ellisse in forma normale. Per
otteniamo un cerchio di raggio . Possiamo
quindi usare la seguente funzione in R:
Questa funzione restituisce un vettore di
punti che, se il vettore dei parametri ha
una risoluzione sufficientemente fine, quan-
do lo disegniamo con apparir`a come
una curva liscia continua.
Pi `u concretamente useremo i punti defi-
niti da
per disegnare un’ellisse intera, ma possia-
mo anche limitarci a una parte del interval-
lo con
per ottenere un arco oppure suddividere
l’intervallo in parti, per ottenere un po-
ligono (regolare per ) ad vertici:
per un esagono (perch´e l’ultimo punto lo ag-
giungiamo per chiudere la curva).
Per spostare il centro `e sufficiente usare
l’addizione in (usando i numeri comples-
si di R), per ruotare la figura possiamo uti-
lizzare la funzione che abbiamo intro-
dotto a pagina 28. Naturalmente traslazio-
ni e rotazioni possono essere applicate an-
che alle altre figure che abbiamo definito.
Nel programma ad ogni figura corrispondo-
no pochissime istruzioni:
Iperboli
Siano con ed ,
. Allora
quindi il punto si trova su un’iperbole
di asse reale e asse immaginaria . Si pu`o
dimostrare che viceversa ogni punto del ra-
mo destro dell’iperbole pu`o essere rappre-
sentato in questa forma. In altre parole,
con `e una parametrizzazione
del ramo destro dell’iperbole in forma nor-
male. Per ottenere il ramo sinistro si pu`o ad
esempio sostituire con . Per otte-
niamo un’iperbole equilatera con equazione
Possiamo quindi usare la seguente funzione
in R:
A parte i soliti comandi di impostazione il
programma contiene le righe
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 7 30
Rette e segmenti
Una retta in pu`o essere rappresentata
nella forma
con e , equivalente alla
rappresentazione parametrica
se e .
In possiamo scrivere
e
se e , oppure, in
forma complessa,
La retta che congiunge due punti e di-
stinti in `e l’insieme ; la
retta che congiunge due punti distinti e
del piano `e quindi . Se
i due punti non sono distinti, questo insie-
me non `e una retta, ma contiene soltanto
l’unico punto dato.
Se come parametri usiamo solo i valori
invece della retta otteniamo il seg-
mento di retta che congiunge i due punti.
Equazione di una retta
Siano e
con . Allora il vettore
`e ortogonale alla retta e un
punto appartiene alla retta se e solo se
`e ortogonale ad . Sia
(cio`e e ). Allora appar-
tiene ad se e solo se ed soddisfano
l’equazione
che pu`o essere scritta anche nella forma
Siccome , anche .
Sia viceversa data un’equazione della for-
ma
con non entrambi uguali a . Allo-
ra possiamo facilmente trovare tali
che e vediamo che l’equazione
descrive la retta con
e .
Per rappresentare rette in R usiamo una
funzione che genera i punti della retta tra
e corrispondenti ai parametri :
Anche in questo caso i punti generati posso-
no essere soggetti a traslazioni o rotazioni
usando l’addizione tra numeri complessi e
la funzione .
Esempio:
Proiezione su una retta
Siano dati una retta in
(con ) e un punto . Vogliamo
calcolare la proiezione ortogonale di su
. Il punto deve essere in primo luogo un
punto della retta e quindi della forma
inoltre il vettore deve essere ortogo-
nale a , cio`e , ossia
Siccome , ci`o `e equivalente a
e quindi abbiamo la formula fondamentale
Da essa otteniamo la proiezione con
Quando (ci`o si pu`o sempre ottenere
sostituendo con ), abbiamo la rappre-
sentazione
Dalla derivazione si vede anche che e con
esso sono univocamente determinati. La
distanza di dalla retta `e uguale a .
Tutto ci`o `e valido in per ogni .
`
E geometricamente chiaro e facile da dimo-
strare che se `e un punto della retta
(esercizio 48).
Definiamo in R una funzione per il calcolo
del prodotto scalare di due punti del piano,
in cui abbiamo usato la relazione
dell’esercizio 30 e la funzione che in R
corrisponde alla formazione del complesso
coniugato, ottenendo cos`ı la funzione per il
calcolo della proiezione di un punto su una
retta nel piano:
Il sito CRAN di Ferrara
A Ferrara opera un gruppo di biologi che la-
vora con R (soprattutto nel campo dei mi-
croarrays) e gestisce anche il deposito italia-
no del CRAN. Gli indirizzi sono
microarrays.unife.it/CRAN
biotecnologie.unife.it/
Esercizi per gli scritti
Quando `e indicato solo una figura, il compi-
to consiste nell’ottenere quella figura con un
programma in R.
44. Octobrina montuosa e Octobrina voragi-
nosa si distinguono apparentemente so-
prattutto nella parte centrale. `
E vero
che per grande hanno un andamento
simile?
45. Trovare l’equazione della retta che con-
giunge i punti e .
46. Trovare, con il metodo indicato su que-
sta pagina, l’equazione della retta che
congiunge i punti e .
47. Rappresentare la retta con equazione
in forma parametrica.
48. sia una retta in e un punto
che appartiene a questa retta. Allora la
proiezione ortogonale di su coincide
con .
49. Calcolare la proiezione ortogonale di
sulla retta con
.
50. Calcolare in la proiezione ortogonale
di sulla retta con
.
51. Calcolare la proiezione ortogonale di
sulla retta che congiunge i punti
e .
52. Usare due .
53. La retta `e e `e .
z
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller

Corso di laurea in matematica Anno accademico 2004/05 Numero 8
Curve di livello
Curve di livello di una funzione in
due variabili non sono altro che
gli insiemi della forma , do-
ve `e una costante. In particolare
per si ottengono gli zeri di ; spes-
so per`o `e interessante guardare co-
me variano queste curve con il va-
riare di e soprattutto in quel ca-
so, cio`e quando si disegnano le cur-
ve (con la notazione della
def. 7.1) contemporaneamente per
pi `u valori di , in modo simile co-
me in un atlante si disegnano cur-
ve di punti con la stessa altezza o
con la stessa quantit `a di precipita-
zioni o con la stessa temperatura
media ecc., si parla di curve di li-
vello.
In R a questo scopo si pu`o usa-
re la funzione che, nella
versione pi `u semplice, si usa come
nella funzione che creiamo
per la nostra libreria:
Il significato dei parametri
e (della matita) `e chiaro.
Il parametro riguarda i
parametri e
della funzione originale, di cui il
primo, se posto uguale a ,
implica che sulle linee di livello
vengono indicati i valori che cor-
rispondono a quei livelli, mentre
indica la grandezza del-
le scritte, di cui abbiamo bisogno
anche noi perch´e il valore pre-
impostato per la visualizzazione
sullo schermo risulta troppo gran-
de per le immagini che otteniamo
con ; per queste ultime
sceglieremo quindi .
Si noti che nella nostra funzio-
ne `e definito attraverso
l’espressione booleana ;
per ottenere una figura senza scrit-
te sulle curve di livello useremo
.
Nella funzione abbia-
mo posto l’argomento uguale
a, perch´e in questo modo pos-
siamo esguire pi `u volte il coman-
do (o ) sulla stessa
grafica senza cancellare il contenu-
to precedente; riguarda la
grandezza delle scritte con cui ven-
gono indicati i valori dei livelli.
(nell’originale ) `e
un singolo numero o un vettore di
numeri che rappresenta l’insieme
dei livelli che vogliamo disegna-
re; con (scelta presta-
bilita in ) viene mostra-
to l’insieme degli zeri di , con
gli insiemi
, e .
La nostra funzione si
basa sulla funzione di R
di cui dobbiamo ancora spiegare
i primi tre parametri. e so-
no vettori di numeri che corris-
pondono matematicamente a due
successioni finite e
. Il terzo argomento (il
nostro ) deve essere una ma-
trice
di righe ed colonne; il coef-
ficiente `e il valore nel punto
della funzione di cui vo-
gliamo disegnare i livelli. Questa
matrice `e il risultato di un co-
mando . La funzione
`e stata predisposta per es-
sere utilizzata in due modi: possia-
mo o indicare la funzione (e allo-
ra viene chiamato all’interno
di ), oppure usare come pa-
rametro una matrice gene-
rata con un precedente; la se-
conda variante verr `a usata quando
vogliamo utilizzare la stessa ma-
trice per pi `u esecuzioni di ,
ad esempio se ogni volta vogliamo
colorare le curve di livello in modo
diverso.
In questo numero
31 Curve di livello
32 outer
ifelse
Una collana
NA
33 if ... else
identical
Operazioni insiemistiche
dimnames
34
Il foglio di Cartesio
La chiocciola di Pascal
La lemniscata
Una curva trascendente
Esercizi 54-58
Come sappiamo per ogni questa equazio-
ne rappresenta un’iperbole equilatera con asse
uguale all’asse delle . Per invece abbia-
mo un’equazione dello stesso tipo con ed in-
vertite, che quindi corrisponde a un’iperbole con
asse uguale all’asse delle .
Per infine l’equazione diventa
e corrisponde alle due rette ed .
Otteniamo la figura su questa pagina che mo-
stra le curve di livello della funzione definita da
con questo programma in R:
L’insieme dei punti su cui avviene l’analisi dei
livelli `e dato dal quadrato sud-
diviso in ogni coordinata con una risoluzione di
, come espresso dall’istruzione
Usiamo la funzione due volte. Infatti la
prima volta disegniamo in nero e con le scritte
tutti i livelli diversi da , la seconda volta solo
le due rette , in rosso e senza scritte.
Nella prima istruzione i livelli scelti corri-
spondono a
Nel programma questo insieme `e definito come
differenza insiemistica (pagina 33)
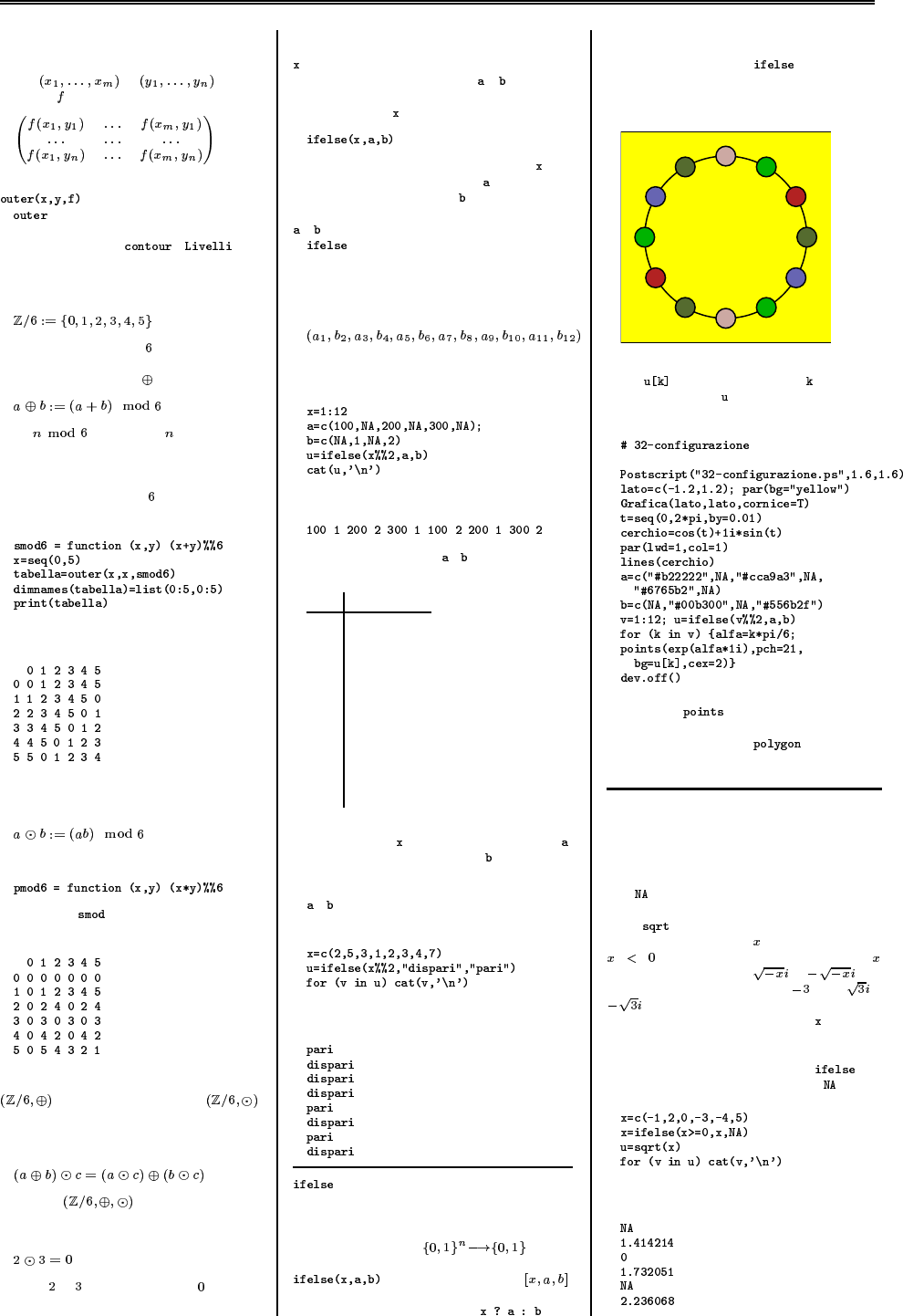
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 8 32
outer
Questa funzione crea da due successioni
finite e e una
funzione la matrice
In R a ci`o corrisponde l’espressione
.
pu`o essere usata in molti modi,
non solo per impostare la matrice dei va-
lori per un comando o , ma
ad esempio anche per creare la tabella di
moltiplicazione per un’operazione binaria.
Consideriamo l’insieme
con l’addizione modulo ; ci`o significa che
introduciamo per gli elementi di questo
insieme un’operazione definita da
dove `e il resto di modulo 6.
Per vedere tutti i risultati che ottenia-
mo in questo modo definiamo la tabella
di moltiplicazione (in questo caso la tabel-
la delle somme modulo ) con le seguenti
istruzioni in R:
con output
Nello stesso modo possiamo definire un
prodotto modulo 6, ponendo
In R allora usiamo la funzione
al posto di . Otteniamo per questa
operazione la tabella di moltiplicazione
Nel corso di Algebra si dimostra che
`e un gruppo abeliano,
`e un semigruppo commutativo con unit `a
e che le due operazioni sono legate dalla
legge distributiva
La tripla `e quindi un anello
commutativo con unit`a. Se guardiamo be-
ne la seconda tabella, vediamo per`o che
bench´e e siano diversi da . Questo
anello possiede perci`o divisori di zero.
ifelse
sia un vettore di valori booleani o di oggetti
convertibili a valori booleani, e due vetto-
ri qualsiasi, non necessariamente della stes-
sa lunghezza di . Allora
`e il vettore che si ottiene sostituendo in ogni
valore vero con un valore di e ogni valo-
re falso con un valore di , percorrendo (in
maniera ciclica, quando necessario) i vettori
e .
`e effettivamente una funzione che
pu`o generare delle configurazioni piuttosto
complicate e matematicamente interessanti.
Assumiamo che vogliamo generare una suc-
cessione della forma
Allora possiamo procedere come in questo es-
empio:
con output
Infatti, siccome i vettori e vengono ripetuti
ciclicamente, abbiamo questa situazione:
xa b
1 100 NA
2NA 1
3200 NA
4NA 2
5300 NA
6NA 1
7100 NA
8NA 2
9200 NA
10 NA 1
11 300 NA
12 NA 2
Secondo il programma, per un valore dispa-
ri nella colonna viene scelto il valore da ,
per un valore pari un valore da . Traducendo
questa idea in una realizzazione geometrica,
otteniamo la collana nella figura.
e possono anche consistere di valori sin-
goli, come in
con output
(nella sua forma non vettoriale) `e una
funzione molto importante anche in informa-
tica teorica e nella teoria dei circuiti digitali,
dove appare nella descrizione di funzioni boo-
leane (cio`e funzioni ) medi-
ante diagrammi binari di decisione. Invece di
si scrive allora spesso .
Questo operatore ternario esiste anche in C
dove viene scritto nella forma .
Una collana
Abbiamo osservato che `e una funzio-
ne da cui si possono far derivare configura-
zioni molto interessanti. Con la stessa idea
vista prima otteniamo questa collana:
Nel seguente programma in R appare il ter-
mine con cui si denota il -esimo ele-
mento del vettore . A differenza dal C in R
si inizia a contare da 1.
La funzione `e stata discussa a pagina
22; per disegnare cerchi pieni colorati si pu`o
usare anche il comando , come vedre-
mo fra poco.
NA
In statistica accade molto spesso che serie
di misurazioni contengano dati non validi o
non disponibili. A questo corrisponde il va-
lore (un’abbreviazione per not available);
l’abbiamo gi`a incontrato a pagina 22. La fun-
zione che calcola la radice quadrata rea-
le di un numero reale non `e definita per
, anche se nel campo complesso
possiede le due radici e (ad
esempio le radici quadrate di sono e
); ci`o `e un caso speciale di quanto visto
a pagina 25. Se `e dato un vettore di nume-
ri reali, non necessariamente tutti positivi,
di cui, se sono positivi, vogliamo calcolare le
radici quadrate, possiamo usare per
convertire tutti i valori negativi in :
con output
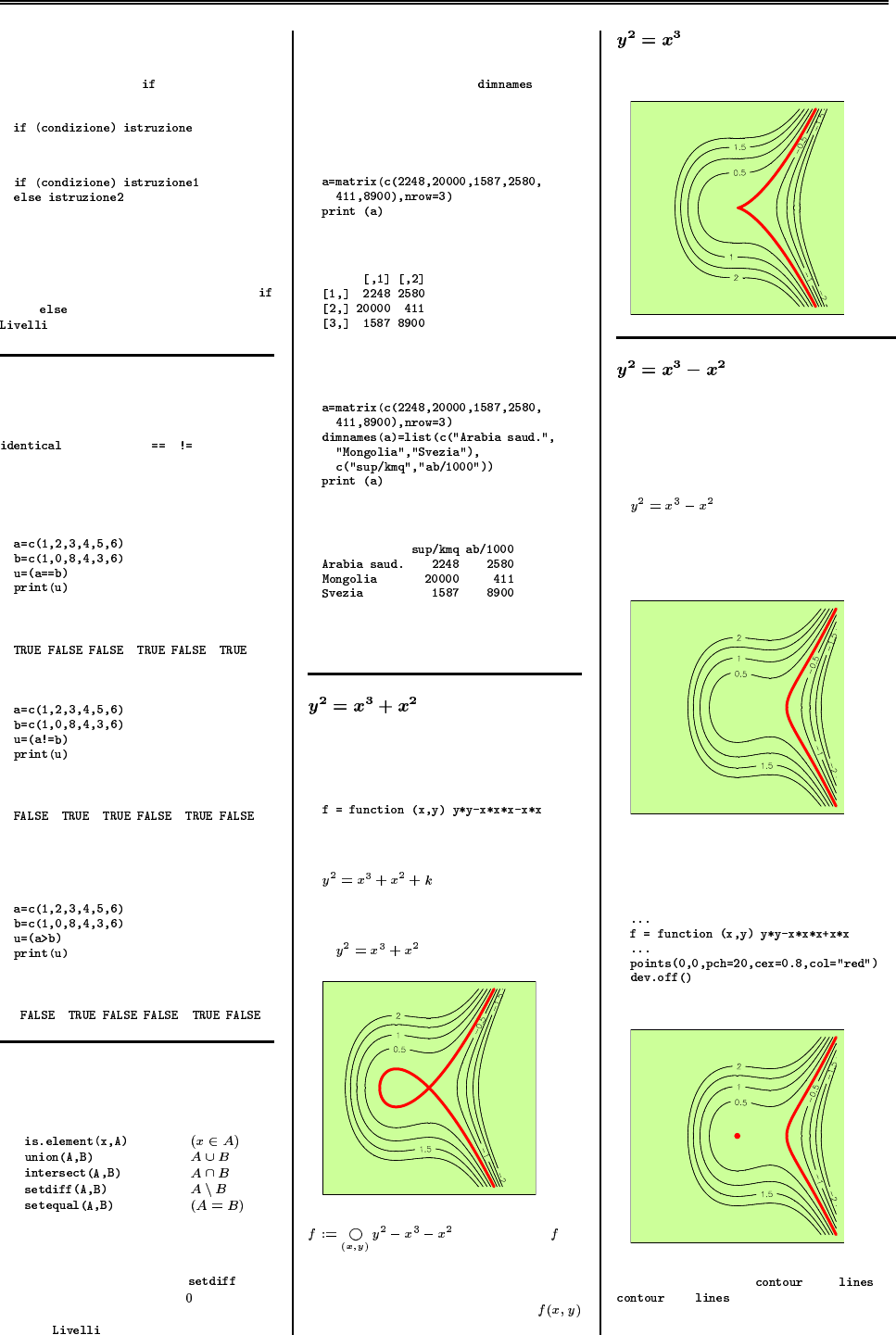
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 8 33
if ... else
All’interno di una funzione o di un blocco
tra parentesi graffe l’ di R viene usato
nelle forme
oppure
Quando il comando complessivamente occu-
pa pi `u righe e non si trova all’interno di un
blocco o di una funzione, bisogna racchiu-
derlo tra parentesi graffe.
Abbiamo usato la prima forma (un
senza ) nella definizione della funzione
a pagina 31.
identical
In R il test per uguaglianza di oggetti
dovrebbe avvenire mediante la funzione
. Gli operatori e sono definiti
in modo un po’ diverso da come uno se lo as-
petterebbe, infatti vengono usati soprattut-
to per il confronto elemento per elemento di
vettori come in
con output
e
con output
Infatti nello stesso modo vettoriale funzio-
nano anche gli operatori per il confronto nu-
merico:
con output
Operazioni insiemistiche
R contiene alcune semplici, ma potenti fun-
zioni insiemistiche:
...
...
...
...
...
Insiemi vengono rappresentati da vettori,
astraendo dall’ordine degli elementi e da
apparizioni molteplici dello stesso valore.
Abbiamo usato la funzione a pa-
gina 31 per togliere il valore dall’insieme
dei livelli da disegnare nella prima esecu-
zione di .
dimnames
Nelle tabelle di moltiplicazione a pagina 32
abbiamo usato la funzione . Essa `e
utile per la visualizzazione di tabelle; altri-
menti nella riga dei titoli e nella colonna dei
nomi delle righe apparirebbero solo gli indi-
ci. Infatti con
otteniamo l’output
che diventa pi `u leggibile se aggiungiamo i
significati dei numeri:
con output
Si noti che nella lista vengono prima indica-
ti i nomi delle righe, poi quelli delle colonne.
Con lo stesso programma che a pagina 31
abbiamo usato per disegnare le iperboli, so-
stituendo solo la riga riguardante la funzio-
ne con
possiamo disegnare la famiglia di curve le
cui equazioni hanno la forma
In questo caso la curva singolare, in rosso, `e
la curva
I livelli indicati sono i livelli della funzione
. Si vede che la as-
sume valori positivi alla destra della curva
singolare e valori negativi alla sua sinistra.
Provare da soli, eventualmente ingran-
dendo la figura, a scoprire il segno di
all’interno del nodo.
Questa curva `e la cuspide o parabola di
Neill:
Purtroppo talvolta il software per la rap-
presentazione di curve pu`o ingannare, e ci`o
non vale solo per R, ma anche per Maple,
Mathematica ecc. In questo caso per esem-
pio `e chiaro che l’origine `e una soluzione
dell’equazione
eppure non appare nella figura (dovrebbe es-
sere un punto rosso nell’origine). Quindi non
ci si pu`o fidare ciecamente dei disegni che si
ottengono con questi programmi.
Non siamo riusciti ad ottenere l’origine co-
me punto della curva mediante il program-
ma; dobbiamo quindi, appellandoci ai risul-
tati della matematica, aggiungerlo a mano:
ottenendo cos`ı
In questo caso potrebbe anche trattarsi di un
difetto della funzione (o di , se
usa ) che non sembra in grado
di disegnare un punto isolato.
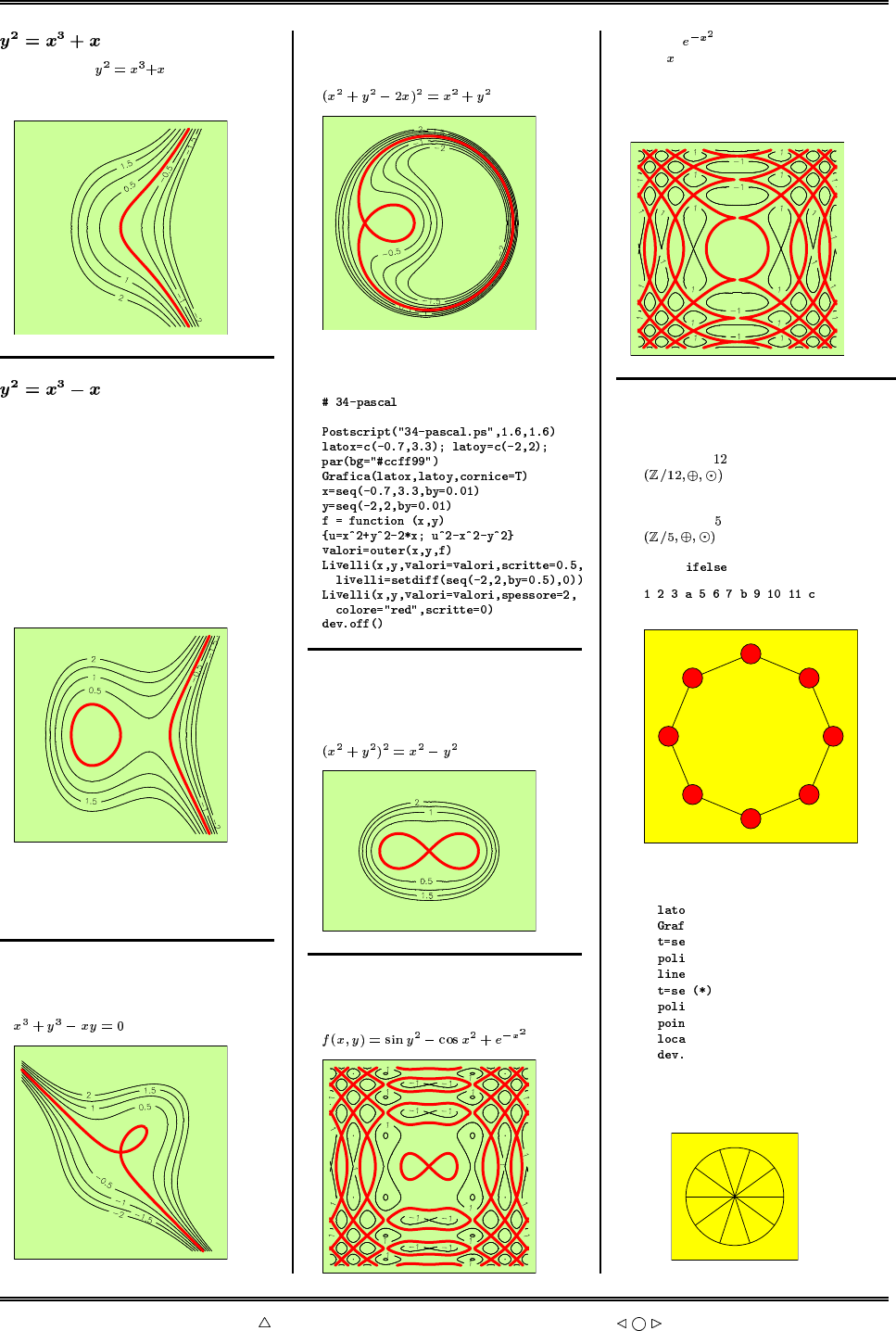
ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 8 34
Anche la curva la possiamo otte-
nere cambiando semplicemente la funzione
nel nostro programma.
Vediamo ancora che una semplice modifi-
cazione dell’equazione implica un cambia-
mento sostanziale nella forma della curva.
Alcune differenze scompaiono comunque se
si considerano queste curve come curve de-
finite sul campo dei numeri complessi. Co-
me una retta complessa corrisponde a un
piano reale, cos`ı una curva complessa cor-
risponde a una superficie reale. Completate
nel senso della geometria proiettiva le cubi-
che finora viste diventano superficie di Rie-
mann, la cui teoria `e ancora oggi un campo
attivo della ricerca.
Nelle applicazioni, ad esempio in statisti-
ca, ancora pi `u importanti sono per `o proprio
le forme reali, la cui classificazione `e molto
difficile.
Il foglio di Cartesio
Questa curva ha l’equazione
La chiocciola di Pascal
La chiocciola di Pascal ha l’equazione
Il programma `e stato leggermente modifica-
to:
La lemniscata
La lemniscata di Bernoulli `e una curva ad
otto con equazione
Una curva trascendente
Consideriamo la funzione
Il termine converge velocemente a zero
quando diventa pi `u grande; la figura espri-
me quindi fortemente la periodicit `a di seno e
coseno.
Se togliamo per`o questo termine, la curva
diventa pi `u regolare, ma forse meno bella:
Esercizi per gli scritti
54. Tabella di addizione e di moltiplicazio-
ne modulo . Ci sono divisori di zero in
?
55. Tabella di addizione e di moltiplicazio-
ne modulo . Ci sono divisori di zero in
?
56. Usare per ottenere l’output
57.
Sono indicate le prime 4 lettere di ogni
riga del programma:
La riga (*) serve per non ridisegnare il
primo dei cerchi piccoli. Come si fa?
58.
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller
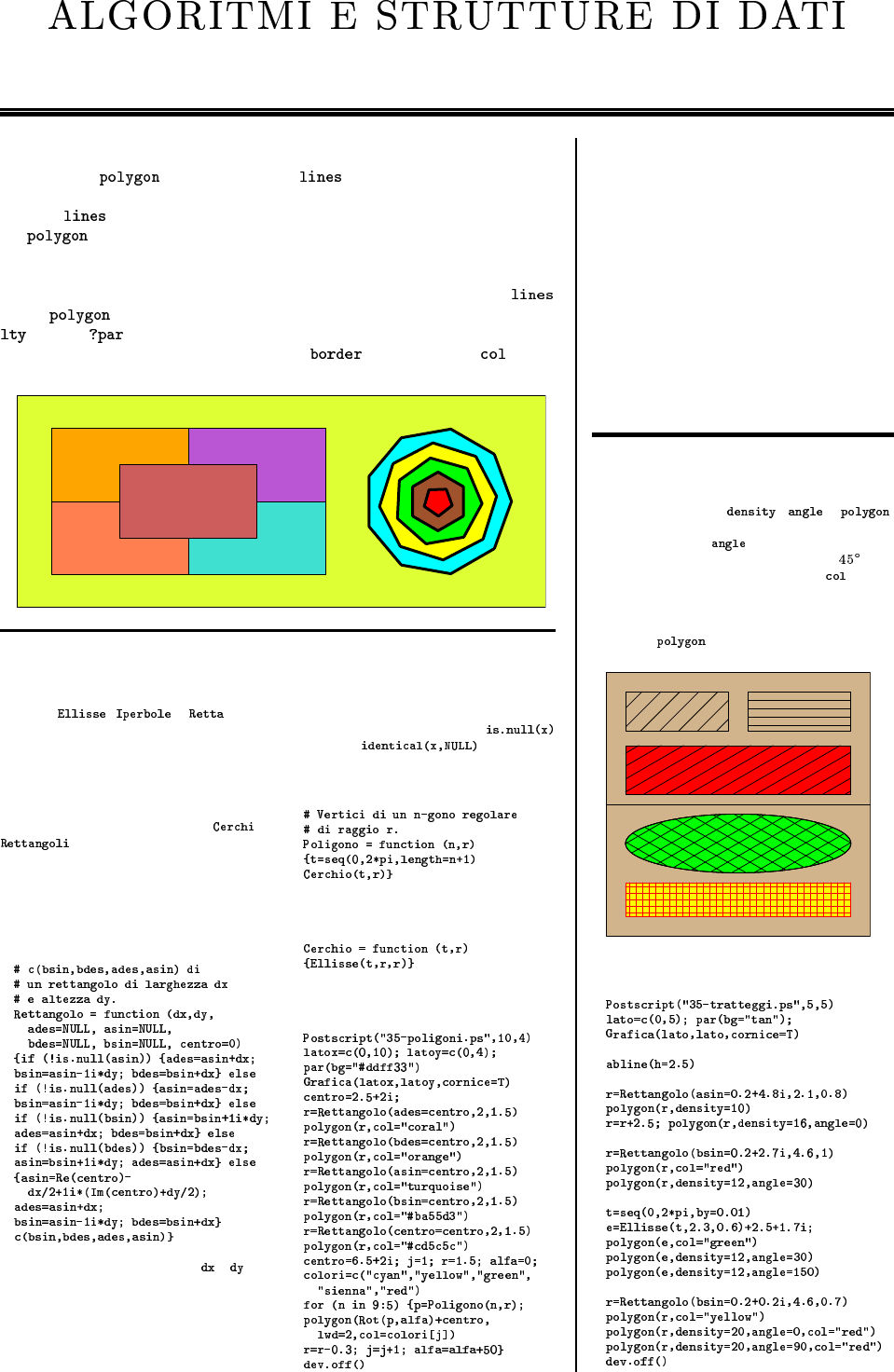
Corso di laurea in matematica Anno accademico 2004/05 Numero 9
La funzione polygon
La funzione `e molto simile a ; anch’essa unisce una suc-
cessione di punti, chiudendola per`o, mentre per ottenere un poligono chi-
uso con dobbiamo aggiungere il punto di partenza alla successio-
ne. permette inoltre di colorare l’interno del poligono (oppure di
tratteggiarlo in vari modi). Useremo soprattutto questa possibilit `a per di-
segnare poligoni colorati, e quindi anche rettangoli, cerchi ed ellissi (che
otteniamo scegliendo successioni di punti molto ravvicinati). Come
anche permette l’uso di linee interrotte impostando il parametro
; vedere .
I parametri per definire i colori sono per il bordo e per il
colore di riempimento.
Il file Figure
Abbiamo visto, quando abbiamo definito le
funzioni , e (pagi-
ne 29-30), che in un approccio matematico
alla grafica una strategia molto efficiente
e versatile `e quella di creare le figure di
base come insiemi di punti e di separare
da esse le operazioni di disegno. Useremo
da ora in avanti questo modo di procede-
re, eliminando quindi le funzioni e
definite a pagina 22 dalla no-
stra libreria; inseriremo le figure di base
in un file Figure della libreria.
Definiamo adesso due funzioni per la
creazione di rettangoli e di poligoni, fun-
zioni che riassumono semplicemente alcu-
ne costruzioni gi `a viste.
In questa funzione i parametri e in-
dicano la larghezza e l’altezza del rettan-
golo; si pu`o inoltre impostare, a scelta, il
centro, il punto in alto a destra o a sini-
stra, il punto in basso a destra o a sinistra.
Il risultato della funzione `e il vettore che
consiste dei quattro vertici del rettangolo
nell’ordine dato dall’ultima riga del lista-
to. Fare un disegno e verificare l’algoritmo.
Abbiamo usato la condizione
al posto di utilizzato a
pagina 31.
Pi `u semplice `e la funzione per i poligoni:
dove abbiamo introdotto la funzione
Otteniamo la figura in alto con
In questo numero
35 La funzione polygon
Il file Figure
Tratteggi
36 Riflessione in un punto
Riflessione in una retta
Perturbazione dei coefficienti
Una modifica in Postscript
37 I cammini delle radici
Il teorema di Rouch ´e
Continuit`a delle radici
38 Creazione di matrici
Parallele
Come nasce una forma
Esercizi 59-66
Tratteggi
Per tratteggiare l’interno di un poligono dobbia-
mo usare i parametri e di .
Una densit `a maggiore corrisponde a un numero
maggiore di linee; imposta l’angolo di in-
clinazione ed `e inizialmente uguale a . Nel
poligono tratteggiato il parametro diven-
ta il colore delle linee di tratteggio. Per trat-
teggi multipli o per colorare allo stesso tempo
l’interno del poligono si possono impiegare pi `u
istruzioni sullo stesso insieme di punti.
Otteniamo la figura con

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 9 36
Riflessione in un punto
Siano ed due punti in . Diciamo che
un punto `e la riflessione di in , se `e
il punto di dimezzamento del segmento tra
e , cio`e se
Ci`o implica che `e univocamente determi-
nato con
Possiamo quindi definire una funzione in R
che realizza questa operazione per punti del
piano:
Nel piano in verit`a la riflessione in coin-
cide con la rotazione per 180 grado attorno
ad , ma la formula `e pi `u sem-
plice e valida in ogni .
Riflessione in una retta
Siano un punto ed una retta in . Di-
ciamo che un punto `e la riflessione di in
, se `e la riflessione di nella proiezione
di sulla retta (cfr. pagina 30).
Nel piano possiamo facilmente combinare
le funzioni e per realizzare
questa operazione in R:
z
z’
m
Possiamo utilizzare questa funzione anche
a un insieme di punti, cio`e a una figura, ad
esempio ai punti di un cerchio o di un poli-
gono:
Otteniamo l’immagine in alto nella colonna
accanto.
Perturbazione dei coefficienti
Abbiamo usato la funzione gi `a a
pagina 25. Il suo unico argomento `e il vetto-
re dei coefficienti (reali o complessi) di un
polinomio, elencati iniziando con il coeffi-
ciente costante. Se i coefficienti delle poten-
ze pi `u alte sono uguali a zero, vengono scar-
tate. Il risultato `e un vettore che rappre-
senta le radici complesse del polinomio con
le loro molteplicit `a. Abbiamo anche usato
la funzione per arrotondare i nume-
ri che otteniamo.
Siccome il risultato di `e un vet-
tore di numeri complessi, `e facile rappre-
sentare le radici di un polinomio con i nostri
strumenti; possiamo ad esempio disegnare
un piccolo cerchio in ogni radice.
Vogliamo adesso studiare il comporta-
mento delle radici quando i coefficienti del
polinomio vengono modificati.
Consideriamo prima il polinomio
Otteniamo le sue radici, se sul terminale di
R battiamo
con output
Ci`o significa che la terza radice `e reale,
mentre le altre due sono l’una la coniugata
complessa dell’altra. Nella rappresentazio-
ne grafica otteniamo
Consideriamo adesso il polinomio
in cui appare anche ; infatti
Se calcoliamo nello stesso modo le radici di
, otteniamo la risposta
Infatti
Dalla rappresentazione grafica, in cui le ra-
dici di corrispondono ai cerchietti verdi, ve-
diamo che esse non sono troppo lontane da
quelle di :
La figura `e stata ottenuta con
Consideriamo il polinomio
Esso possiede una radice doppia, che quin-
di nella rappresentazione grafica corrispon-
der`a a un unico cerchietto rosso nel punto
. Se poi modifichiamo il coefficiente di
con , otteniamo il polinomio
che, come si vede dalla figura, ha due radici
molto vicine alle radici semplici di e due
radici che in un certo senso provengono dalla
radice doppia di anche se sono visibilmente
distanti da essa.
Una modifica in Postscript
Da questo numero abbiamo modificato la
funzione , dividendo i parametri
che indicano larghezza e altezza per 2.54.
Ci`o ci permette di misurare le figure su carta
direttamente in centimetri.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 9 37
I cammini delle radici
Consideriamo il polinomio
e per ogni il polinomio
con
Stavolta le radici di le disegniamo usan-
do in il simbolo con un
:
Otteniamo
Questi grafici possono anche ingannare; in
questo caso ogni ramo si accresce solo in
una direzione dalla radice di partenza; se
usiamo l’intervallo avremo invece
due (mezzi) rami per ogni nuova radice co-
me nel seguente esempio in cui, con le stes-
se notazioni,
e
In questo esempio si vede particolarmente
bene un fenomeno gi `a osservato nell’ultima
figura a pagina 36: Sembra che le nuove ra-
dici non partano direttamente dalla radice
tripla, ma a una certa distanza da essa, con-
tinuando poi su un cammino pi `u continuo.
Infatti tipicamente le radici multiple risen-
tono pi `u fortemente di una perturbazione
dei coefficienti del polinomio di quanto ac-
cada per le radici semplici.
Il teorema di Rouch ´e
Teorema 37.1. ed siano due polinomi
a coefficienti complessi e una circonfe-
renza (cio`e il bordo di un cerchio) nel pia-
no tale che
per ogni .
La disuguaglianza `e quindi richiesta so-
lo sul bordo del cerchio, non al suo inter-
no. Allora i polinomi e possiedono
all’interno del cerchio lo stesso numero di
radici, se queste vengono contate con le lo-
ro molteplicit`a.
Dimostrazione. Questo `e un teorema
molto importante dell’analisi complessa.
Non confondere con .
Il teorema di Rouch´e si usa nel modo se-
guente. Assumiamo che vogliamo studiare
gli zeri di un polinomio . Allora decompo-
niamo nella forma , dove `e un
polinomio sui cui zeri, almeno all’interno
di un cerchio, abbiamo sufficienti informa-
zioni. Consideriamo in altre parole come
perturbazione di mediante . Se riuscia-
mo a dimostrare che sul bordo del cerchio
si ha sempre , allora pos-
siamo concludere che e all’interno del
cerchio possiedono lo stesso numero di ra-
dici, tenuto conto della loro molteplicit `a.
Quindi se nel cerchio possiede una so-
la radice tripla, non possiamo dire che an-
che possiede una radice tripla, possiamo
per`o dire che nel cerchio possiede esat-
tamente tre radici se queste vengono con-
tate con le loro molteplicit `a.
Il teorema di Rouch´e permette una veloce
dimostrazione del teorema fondamentale
dell’algebra (teorema 25.1); naturalmen-
te dovremmo prima, in un corso di ana-
lisi complessa, dimostrare il teorema di
Rouch´e.
Sia quindi dato un polinomio
a coefficienti complessi, con e non
costante, cio`e con .
Per applicare il teorema di Rouch´e con-
sideriamo come perturbazione di
mediante
Per ogni si ha
e si vede facilmente che per sufficien-
temente grande questa -esima potenza
domina largamente le potenze inferiori e
quindi , per quanto grandi siano i
coefficienti di queste potenze inferiori ris-
petto al coefficiente di .
Perci`o esiste certamente un tale
che per ogni che appartiene alla circon-
ferenza di raggio (cio`e tale che )
si ha .
Il teorema di Rouch´e implica allora che
, il nostro polinomio dato, all’interno del
cerchio possiede lo stesso numero
di radici come . Ma in que-
sto cerchio possiede la radice di
molteplicit`a . E quindi anche possiede
all’interno dello stesso cerchio radici e
quindi almeno una radice perch´e per ipo-
tesi .
Continuit `a delle radici
Definizione 37.2. Per un polinomio a coeffi-
cienti complessi sia il massimo dei va-
lori assoluti dei suoi coefficienti.
Osservazione 37.3. sia un polinomio a co-
efficienti complessi di grado . Allora
per ogni .
Osservazione 37.4. Siano e .
Allora
Assumiamo di sapere che . Allora, se
, si ha
Corollario 37.5. Siano e .
Assumiamo di sapere che .
sia un polinomio a coefficienti complessi di
grado . Allora, se , si ha
Teorema 37.6.
con ed sia un polinomio con co-
efficienti complessi. siano le radi-
ci distinte di ; esse possiedano le molteplicit `a
. Possiamo allora scegliere
in modo tale che, per ogni , sia
l’unica radice di nel disco aperto
e inoltre non si annulli sulla circonferenza
e quindi nemmeno sull’unione
di queste circonferenze. Se vogliamo, possiamo
scegliere anche molto piccolo.
Fissato in tal modo , per un teorema ele-
mentare e fondamentale sulle funzioni conti-
nue definite su un insieme compatto (nel nostro
caso ), esiste un numero tale che
per ogni . Sia inoltre
il massimo dei valori assoluti delle radici e sia
Allora per ogni polinomio di grado con
il polinomio possiede per ciascun
esattamente radici all’interno del cerchio
, se queste vengono contate con le
loro molteplicit`a, possiede cio`e lo stesso nu-
mero di radici in questo cerchio come .
Dimostrazione. Abbiamo preparato quasi
tutto per poter applicare il teorema di Rouch´e.
Fissiamo . Sia . Dobbiamo dimo-
strare che .
Ma per il corollario 37.5 abbbiamo

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 9 38
Creazione di matrici
Matrici possono essere definite con il co-
mando che abbiamo gi `a incontrato
a pagina 33. I componenti di una matri-
ce possono essere numeri reali o complessi,
stringhe oppure avere il valore .
ha come argomento obbligatorio
un vettore di dati; inoltre si possono indi-
care con il numero delle righe o con
il numero delle righe. La matrice viene
riempita colonna per colonna, se non si in-
dica . Se `e una matrice, con si
ottiene il vettore dei suoi elementi, elencati
colonna per colonna. Esempi:
con output (senza le dimensioni)
e invece, con gli stessi dati,
con output
Impareremo nel prossimo numero le funzio-
ni di R per l’algebra lineare, in particolare
come risolvere un sistema lineare ;
adesso le useremo per un po’ di grafica.
Parallele
L’istruzione unisce i punti di un
vettore di numeri complessi con segmenti
di rette. Se per`o incontra un valore , inter-
rompe il tracciato e lo riprende con il prossi-
mo valore definito. Usiamo questa caratte-
ristica per creare schemi di rette parallele.
La funzione che adesso defi-
niamo ha come argomento la larghezza e
l’altezza dello schema e il numero di righe
parallele; l’argomento opzionale vie-
ne messo uguale a se vogliamo anche di-
segnare i bordi superiore e inferiore oppure
uguale ad o se vogliamo solo visua-
lizzare il bordo superiore o inferiore.
Il risultato della funzione `e un vettore di
numeri complessi interrotto da valori .
Come nasce una forma
La natura `e molto efficiente a creare una
straordinaria variet `a di forme con elemen-
ti semplicissimi. La ricchezza non sta quin-
di negli ingredienti, ma nella fantasia delle
combinazioni. Uno degli strumenti pi `u effi-
caci `e la ripetizione associata a piccole mo-
difiche negli elementi.
La funzione genera un insie-
me di punti che possiamo sottoporre a tras-
lazioni, rotazioni o altre operazioni geome-
triche e disegnare con , come si vede
nell’esercizio 65 e nelle seguenti figure:
Quanto `e semplice!
Lo schema `e stato centrato.
Esercizi per gli scritti
59.
z
z’
m
60. sia un polinomio a coefficienti reali ed
tale che . Allora anche
.
Non `e difficile, `e sufficiente scrivere
esplicitamente con i suoi coefficienti.
Dall’enunciato di questo esercizio de-
riva facilmente (ma non fa parte del
compito) che le radici non reali di un
polinomio a coefficienti reali appaiono
sempre a coppie coniugate e che un poli-
nomio a coefficienti reali di gradi dispari
possiede sempre una radice reale.
61. Le radici del polinomio
non sono coniugate tra di loro. Perch´e
non `e una contraddizione all’esercizio
precedente?
62. Spiegazione a pagina 37.
63. sia un polinomio a coefficienti com-
plessi di grado . Allora
per ogni .
`
E quindi richiesta la dimostrazione
dell’osservazione 37.2 (molto facile).
64. Spiegare la funzione nella
prima colonna su questa pagina.
Ci`o significa che nel compito pu`o es-
sere dato il listato della funzione e bi-
sogna spiegare, anche e soprattutto con
appositi disegni, il significato delle sin-
gole istruzioni.
65. Prendere le misure con la riga.
66. Riflessione del punto nella retta
che congiunge i punti e .
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller

Corso di laurea in matematica Anno accademico 2004/05 Numero 10
Matrici in R
Conosciamo gi `a il comando
per la creazione di matrici (pagi-
na 38) e vogliamo trattare in que-
sto numero le pi `u importanti ope-
razioni con matrici fornite da R. `
E
spesso utile (in statistica, ma an-
che in matematica pura, cfr. eser-
cizio 22) considerare una matrice
( righe ed colonne) co-
me un unico lungo vettore di
(elencando gli elementi colonna per
colonna come fa R e come sarebbe
in effetti pi `u logico sia in algebra
lineare che in statistica) oppure di
(elencando gli elementi riga
per riga come talvolta `e pi `u intui-
tivo, ma solo perch´e siamo abitua-
ti a leggere riga per riga). A que-
sto punto bisogna distinguere tra
le operazioni definite per vettori da
quelle definite per matrici.
Abbiamo anche, in un altro sen-
so, due operazioni di moltiplicazio-
ne per matrici: da un lato il pro-
dotto elemento per elemento (pro-
dotto di Hadamard), dall’altro la
moltiplicazione matriciale. e
siano due matrici con le appropria-
te dimensioni (cio`e stesso numero
di righe e stesso numero di colonne
per il prodotto di Hadamard, nu-
mero di colonne di uguale al nu-
mero di righe di per il prodot-
to matriciale). Allora i coefficien-
ti del prodotto di Hadamard
sono definiti da
i coefficienti del prodotto matri-
ciale da
.
Possiamo naturalmente anche for-
mare la somma di due matrici
della stessa forma e moltiplicare
una matrice con un numero reale
o complesso:
In R le operazioni matriciali cor-
rispondono ai seguenti comandi:
... addizione
... moltiplicazione di una
... matrice con un numero
... prodotto di Hadamard
... prodotto matriciale
... non , ma !
... trasposta di A
...
Sembra che possiamo senza proble-
ma usare per numeri anche in
uno stesso contesto, non dobbiamo
comunque ridefinire come funzio-
ne se vogliamo usare anche la tras-
posta.
`e anche definito quando e
hanno la stessa lunghezza ( )
totale, ma l’operazione non ha mol-
to senso se le due matrici non han-
no la stessa forma.
L’espressione denota anche il
prodotto di una matrice con un
vettore , in accordo con la nota-
zione matematica; confonde invece
probabilmente che si possa usare
l’operatore anche per il prodot-
to scalare di vettori.
Esempi per le operazioni matriciali
Definiamo prima una nostra funzione per
la creazione di una matrice:
Una matrice `e direttamente convertibile
in un vettore mediante l’operatore , co-
me abbiamo visto a pagina 38, ma anche
in ogni contesto in cui R si aspetta un vet-
tore. Quindi `e corretta la sequenza
con output semplificato
In questo numero
39 Matrici in R
Esempi per le operazioni matriciali
Piccoli operatori
40 Indici vettoriali
Il crivello di Eratostene
for, while e repeat
v[v%%p 0]
41 Assegnazione vettoriale
Indici matriciali
L’opzione drop
rbind e cbind
42 Sistemi lineari con R
length e dim
det (determinante) e traccia
Matrici diagonali
abs (valore assoluto) e sign
Autovalori
43 Matrici simmetriche
eigen (autovalori e autovettori)
Matrici reali
I cerchi di Gershgorin
Esercizi 67-76
Piccoli operatori
`e il prodotto degli elementi del vettore
; anche questa funzione pu`o essere applicata a
matrici, infatti `e uguale a .
Esempi:
e sono la somma e la media del
vettore . Esempi:
Queste funzioni vengono naturalmente usate
molto spesso in statistica.
e sono i vettori delle somme
cumulative e delle differenze del vettore .
L’operatore che forma le differenze `e inverso
all’operatore di sommazione!

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 10 40
Indici vettoriali
R possiede dei meccanismi molto generali e
sofisticati per l’uso degli indici in vettori e
matrici. Consideriamo il vettore
Indicando un singolo indice o un vettore di
indici ne possiamo estrarre singoli elementi
o parti:
con output
Mediante l’uso di indici negativi possiamo
escludere alcuni elementi:
ottenendo
Una caratteristica avanzata di R `e che co-
me indici si possono anche usare vettori di
valori booleani, cio`e vettori i cui componen-
ti sono o o . Se in questo caso il vettore
booleano ha una lunghezza minore di quel-
la del vettore da cui vogliamo estrarre, i va-
lori booleani vengono ciclicamente ripetuti.
Esempi:
con output . Infatti vengono riprodotti
in gli elementi di che corrispondono a po-
sizioni in cui il valore del vettore booleano `e
uguale a .
Con otteniamo ogni secon-
do elemento di , con ogni se-
condo elemento di , saltando il primo:
con output
Possiamo adesso riscrivere in R un famoso
algoritmo che permette di trovare i numeri
primi per un dato numero naturale .
Il crivello di Eratostene
Definizione 40.1. Siano .
Diciamo che divide e scriviamo ,
se esiste tale che .
Quindi se e solo se `e un multiplo
di , cio`e se e solo se . `
E chiaro che
allora anche e viceversa, quindi
se e solo se .
Questa riduzione della relazione di divi-
sibilit`a a una relazione insiemistica `e mol-
to importante e conduce alla teoria degli
ideali, un ramo centrale dell’algebra com-
mutativa.
Definizione 40.2. Un numero naturale
si chiama primo, se e se, per
con si ha .
Osservazione 40.3. sia un nu-
mero naturale fissato. sia un al-
tro numero naturale con che
non sia primo. Allora esiste con
tale che .
In altre parole, se sappiamo che ,
per verificare che sia primo, dobbiamo
solo dimostrare che non possiede divi-
sori tra e .
Nota 40.4. Sia un numero na-
turale fissato. Possiamo creare una
lista di tutti i primi con il seguente pro-
cedimento che prende il nome di crivello
di Eratostene; lo modifichiamo leggermen-
te ai fini del programma in R con cui verr `a
realizzato..
(1) Definiamo due vettori variabili e
e poniamo inizialmente
(2) Calcoliamo la radice .
(3) Poniamo .
(4) Se , andiamo alla fine (F).
(5) Aggiungiamo a , ridefinendo
intendendo con ci`o che viene ag-
giunto come ultimo elemento ad .
(6) Eliminiamo da tutti gli elementi di-
visibili per (compreso stesso).
(7) Torniamo al punto (3).
(F) A questo punto la concatenazione
di e rappresenta la succes-
sione ordinata dei primi .
Dimostrazione. Infatti il numero al
punto (3) `e il pi `u piccolo numero che non
`e stato eliminato da nel passaggio pre-
cedente; esso non `e quindi divisibile da
nessun numero tra e ed `e per-
ci`o primo, cosicch´e lo aggiungiamo ad .
Poi eliminiamo da tutti i multipli di .
Dall’osservazione 40.3 segue che ci possia-
mo fermare quando .
Possiamo trascrivere questo algoritmo di-
rettamente in una funzione in R che con-
serviamo nel file Primi della nostra libre-
ria:
Per provare la funzione usiamo
ottenendo l’output
Abbiamo creato una matrice per una migliore
visualizzazione; per poter riempire la matrice
abbiamo anche aggiunto due zeri che natural-
mente non derivano dall’algoritmo.
for, while e repeat
R possiede tre istruzioni per l’esecuzione di
cicli: (che abbiamo gi `a usato alle pagine
22, 32, 35-37), e (che abbiamo
usato in ); esse vengono utilizzate
con questa sintassi:
dove `e un’istruzione singola oppu-
re una successione di istruzioni che allora de-
ve essere racchiusa tra parentesi graffe.
Per uscire da un ciclo si usa , mentre
interrompe il passaggio corrente di un
ciclo e porta all’immediata esecuzione del pas-
saggio successivo, cosicch´e
stampa sullo schermo i numeri pari compresi
tra 1 e 20.
v[v%%p 0]
Dobbiamo ancora analizzare questa misterio-
sa espressione che abbiamo usato nella funzio-
ne . Intuitivamente `e chiaro che do-
vrebbe rappresentare quegli elementi del vet-
tore il cui resto modulo `e maggiore di zero.
Ma come si inquadra nella sintassi che abbia-
mo visto finora?
La spiegazione `e che in viene pri-
ma calcolato il vettore interno che funge da
filtro, cio`e il vettore booleano che, se-
condo il modo vettoriale delle operazioni di R,
contiene il valore in ogni posizione dove in
si trova un numero non divisibile per , e nelle
altre posizioni contiene il valore .
All’inizio dell’algoritmo, quando e
, `e uguale a ,
nel passaggio successivo, in cui
, `e
uguale a , e cos`ı via.
In modo simile (anche questo esempio `e im-
portante nella teoria dei numeri), se , al-
lora consister`a di tutti i numeri
naturali tra e con resto 1 modulo 4.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 10 41
Assegnazione vettoriale
Le espressioni della forma posso-
no essere anche usate per assegnare va-
lori alla parte del vettore descritta
dall’espressione. Esempi:
Nel penultimo esempio R ci avverte che la
lunghezza della parte dove vogliamo modi-
ficare i valori (in questo caso 5) non `e un
multiplo del vettore che contiene i nuovi va-
lori (in questo caso 3).
Sono operazioni piuttosto potenti.
Indici matriciali
Il coefficiente nella -esima riga e -esima
colonna di una matrice viene denotato con
.
Anche qui possiamo per`o usare espres-
sioni pi `u complesse, cosicch´e ad esempio
con otteniamo la mtrice
2x3 che consiste dei coefficienti nella prima
e terza riga e nella seconda, quarta e sesta
colonna di .
Se e sono vettori di indici, allora
`e la matrice che consiste delle righe di con
indici da , mentre consiste delle co-
lonne con indici da . `e invece la ma-
trice da cui abbiamo tolto le righe con indici
da . Anche vettori booleani di indici posso-
no essere usati per matrici. Esempi:
con output
e, continuando con la stessa matrice ,
con output
con output
con output
con output
con output
Se usiamo un filtro, otteniamo il vettore dei
coefficienti della matrice che soddisfano il
criterio espresso dal filtro, elencati colonna
per colonna:
con output
Anche indici matriciali possono essere usati
per assegnare valori a parti di una matrice:
con output
L’opzione drop
Quando scegliamo solo una riga o una colon-
na di una matrice, queste vengono automa-
ticamente convertite in un vettore. Talvolta
per`o si vorrebbe poter considerare quella ri-
ga o colonna come matrice; per fare ci`o bi-
sogna aggiungere l’opzione all’indice.
Esempio:
con output, stavolta completo, cos`ı come ap-
pare sullo schermo,
rbind e cbind
Possiamo unire pi `u righe con e pi `u co-
lonne con ; le righe o colonne possono
essere date singolarmente o anche come ma-
trici. Esempi:
con output
e, continuando con la stessa matrice ,
con output

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 10 42
Sistemi lineari con R
R permette, per matrici che devono esse-
re quadratiche e invertibili, la risoluzio-
ne di un sistema lineare
mediante l’istruzione
Proviamo prima con il sistema che ab-
biamo risolto a pagina 8:
L’output `e , in accordo con la
soluzione gi`a trovata, infatti
Proviamo con il sistema dell’esempio
9.1:
La risposta `e
in accordo con quanto gi`a trovato.
Se vogliamo le soluzioni come numeri
razionali, nell’ultima riga del program-
ma possiamo usare
La funzione richiede per`o la
libreria MASS, che dobbiamo caricare
con
Otteniamo allora l’output
L’inversa di una matrice non singolare
`e data da
Per verificare se la matrice `e invertibi-
le si pu`o calcolare il determinante con
.
La libreria MASS contiene la funzio-
ne che calcola l’inversa generaliz-
zata nel senso di Penrose di matrici non
necessariamente quadratiche.
length e dim
`e la lunghezza di un vettore o
di una matrice.
Nel caso di una matrice questa viene
considerata come vettore, la lunghezza `e
quindi uguale ad , se la matrice pos-
siede righe ed colonne.
`e allora il vettore .
det (determinante) e traccia
`e il determinante della matrice .
Per la traccia sembra che non ci sia una
apposita funzione che per`o possiamo facil-
mente definire:
Matrici diagonali
La funzione pu`o essere usata in pi `u
modi:
genera una matrice identica ,
genera, per un vettore , una matrica dia-
gonali che contiene i coefficienti di nella
diagonale principale, mentre infine
`e il vettore che consiste degli elementi del-
la diagonale principale di . Esempi:
con output
con output
con output
abs (valore assoluto) e sign
`e il valore assoluto del numero rea-
le o complesso .
Secondo la filosofia di R, se `e un vetto-
re, con si ottiene il vettore dei va-
lori assoluti degli elementi del vettore; lo
stesso vale per una matrice dalla quale ot-
teniamo quindi la matrice dei valori asso-
luti dei suoi coefficienti.
`e il segno di un numero reale
(uguale a zero se `e uguale a zero).
Autovalori
Situazione 42.1. sia un campo e una
matrice quadratica.
Denotiamo con la matrice identica.
Teorema 42.2. Consideriamo l’applicazione
Allora i seguenti enunciati sono equivalenti:
(1) non `e biiettiva.
(2) non `e suriettiva.
(3) non `e iniettiva.
(4) .
`
E chiaro che la condizione (3) si verifica se e solo
se esiste un vettore in tale che .
Dimostrazione. Corsi di Geometria.
Definizione 42.3. Un vettore si chiama
un autovettore di , se e se esiste un ele-
mento tale che .
Ci`o accade se e solo se .
Definizione 42.4. Un elemento si chiama
un autovalore di , se esiste un vettore
con e .
In tal caso diciamo anche che `e un autovettore
di per l’autovalore e che `e un autovalore di
per l’autovettore .
Osservazione 42.5. Sia . Allora `e un
autovettore di se e solo se
.
Dimostrazione. Teorema 42.2.
Nota 42.6. Sviluppando il determinante, non `e
difficile dimostrare che
`e un polinomio di grado in (qui si usa spesso
la stessa lettera sia per un elemento concreto
di che per un’indeterminata) che si chiama il
polinomio caratteristico di .
Consideriamo il caso . Allora
e
quindi
Per una matrice triangolare
il polinomio caratteristico diventa
e quindi i due autovalori in questo caso sono gli
elementi e nella diagonale principale.

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 10 43
Matrici simmetriche
Consideriamo una matrice reale simmetri-
ca
Per la formula vista a pagina 42
Gli autovalori di (nel campo complesso)
sono quindi dati da
con
Perci`o e vediamo che gli autovalori
di una matrice reale simmetrica sono
reali.
Ci`o vale anche per le dimensioni superio-
ri e pu`o essere dimostrato, in modo molto
pi `u semplice, utilizzando il prodotto scalare
e l’ortogonalit`a.
eigen (autovalori e autovettori)
In R gli autovalori di una matrice reale o
complessa si trovano con la funzione .
Essa calcola, se non si pone l’opzione
anche un sistema di autovettori; ci`o pu`o ral-
lentare il calcolo per matrici molto grandi.
Il risultato `e una lista in R, un concetto che
non riusciamo pi `u a trattare, e le compo-
nenti si ottengono con la sintassi e
. Creiamo due funzioni che inseria-
mo nel file Matrici della nostra libreria:
Calcoliamo gli autovalori della matrice
con
trovando e nello stesso modo
quelli di
che, secondo quanto visto prima, dovrebbe-
ro essere reali. Infatti troviamo la risposta
.
Matrici reali
Una matrice reale non possiede ne-
cessariamente autovalori reali; d’altra par-
te pu`o essere anche considerata come una
matrice in e il polinomio caratteristico,
assumendo naturalmente , in pos-
siede sempre radici. Quindi possiede in
ogni caso autovalori e autovettori comples-
si e vediamo di nuovo che lo studio di un
problema formulato in ambito reale ci por-
ta in modo naturale nel regno dell’analisi
complessa.
I cerchi di Gershgorin
Per una matrice reale o complessa
definiamo i cerchi
similmente per una matrice
poniamo
Questi cerchi, che si definiscono in mo-
do analogo per le dimensioni superriori, si
chiamano i cerchi di Gershgorin di .
I centri dei cerchi di Gershgorin sono gli
elementi nella diagonale principale della
matrice; se la matrice `e reale o se almeno
gli elementi nella diagonale sono tutti reali,
i centri dei cerchi di Gershgorin si troveran-
no quindi sull’asse reale.
Teorema di Gershgorin. Gli autovalori di
sono tutti contenuti nell’unione dei suoi
cerchi di Gershgorin.
Dimostrazione. Corsi di Analisi numeri-
ca. Abbastanza facile.
Definiamo una funzione (che far`a parte del
file Matrici nella libreria) che restituisce
il centro e il raggio dell’ -esimo cerchio di
Gershgorin della matrice :
Calcoliamo i cerchi di Gershgorin della ma-
trice dell’esercizio 75:
Esercizi per gli scritti
67. Una matrice di rotazione
possiede autovalori reali se e solo se
. Come `e fatta allora la
matrice e come opera?
68. Gli autovalori di
sono e . Calcolare in questi
esercizi gli autovalori a mano.
69. Gli autovalori di
sono e .
70. Gli autovalori di una matrice reale o
complessa della forma
sono e .
71. Gli autovalori di
sono e . Verificare con R.
72. Gli autovalori di
sono e . Come si trovano queste belle
matrici? Guardare a pagina 12.
73. Sia un autovalore di
Allora .
74. Sia un autovalore di
Allora .
75. Disegnare su sfondo giallo i cerchi di
Gershgorin (in rosso) della matrice
Usare con per i centri.
La funzione viene chiamata
dall’interno del programma.
76. Definire con e come alla
fine della colonna precedente la matri-
ce dell’esercizio 75. Creare, con un unico
comando la matrice che
si ottiene da sostituendo tutti i valori
negativi con 0. Verificare con .
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller

Corso di laurea in matematica Anno accademico 2004/05 Numero 11
Derivazione simbolica
Come vediamo nell’articolo su que-
sta pagina, la formazione della de-
rivata ha molti aspetti puramen-
te formali e algebrici. Per questa
ragione anche R `e in grado di ef-
fettuare la differenziazione di es-
pressioni formali e fornisce a que-
sto scopo la funzione che si usa
come in questo esempio:
con risultato
La derivata
sia una funzione a valori reali
definita su un aperto di (quasi sempre
sar`a un intervallo aperto, anche infini-
to, di oppure un’unione di un numero fi-
nito di intervalli aperti). Sia . Se il
limite
esiste, allora si dice che la funzione `e dif-
ferenziabile in ed si chiama la
derivata di in .
Segue abbastanza direttamente dalla
definizione che, se anche `e una funzio-
ne definita in e se esistono le derivate
e , allora anche
esiste e si ha
Si dimostra inoltre che esiste anche
e che
Qui `e la funzione , da non
confondere con la composizione delle due
funzioni. Se `e l’insieme dei punti in cui
e sono entrambe differenziabili, pos-
siamo considerare e come funzioni
definite su e scrivere pi `u brevemente
Per una funzione costante e
coincidono, e vediamo che la deri-
vata di una funzione costante `e uguale a
zero.
Consideriamo la funzione identica. In
questo caso il limite da studiare `e
perci`o la funzione identica ha derivata
1 in ogni punto.
Assumiamo adesso che la sia differen-
ziabile in e consideriamo le funzioni ,
e . Per la regola del prodotto abbiamo
Intravvediamo la formula generale
che infatti si dimostra facilmente per ogni
con induzione. Se poniamo ugua-
le all’identit `a otteniamo la derivata di un
monomio
che, in modo meno preciso ma pi `u intuiti-
vo, talvolta `e scritta nella forma
Per un numero reale abbiamo
perch´e la derivata della funzione costante
`e uguale a zero, come abbiamo visto.
Ci`o mostra, insieme alla regola per la
somma, che la formazione della derivata
`e un operatore lineare e ci permette di cal-
colare la derivata di una funzione polino-
miale. Sia infatti
Usando la formula per la derivata di un
monomio e la linearit `a otteniamo
Consideriamo adesso il quoziente
di due funzioni differenziabili, dove re-
stringiamo in modo tale che non conten-
ga zeri di . Siccome , dalla regola
del prodotto abbiamo e
quindi
Nei corsi di Analisi si dimostra (e la dimo-
strazione richiede un po’ di attenzione!) la
regola della catena, molto importante, per
la composizione di due funzioni differen-
ziabili:
che in modo astratto pu`o essere scritta an-
che cos`ı (nel dominio dove tutto `e definito):
In questo numero
44 Derivazione simbolica
La derivata
La funzione esponenziale
45 Abbreviazioni
Esempi per l’uso di D
La serie di Taylor
Options e print(x,n)
46 any e all
Ordinamento
La libreria
La funzione esponenziale
Esiste una funzione che `e la derivata di se stes-
sa? Nei corsi di Analisi si impara che una tale
funzione, cio`e una funzione con esi-
ste veramente e che `e unica se chiediamo che
. Questa funzione si chiama la funzio-
ne esponenziale e viene denotata con . Essa
pu`o essere definita per ogni numero reale - in
verit`a pu`o essere estesa su tutto , `e quindi una
funzione
oppure, rivelando allora la sua vera natura e la
profonda parentela con le funzioni trigonometri-
che, una funzione
`e quindi una soluzione dell’equazione diffe-
renziale
e se con denotiamo l’operatore (di cui sappia-
mo che `e lineare) di differenziazione (che `e defi-
nito su un qualche spazio vettoriale di funzioni
di cui la funzione esponenziale fa parte), vedia-
mo che `e soluzione dell’equazione lineare
e quindi un autovettore per l’autovalore 1 (cio`e
un punto fisso) dell’operatore lineare e non
ci sorprende che, come si verifica facilmente,
l’insieme delle soluzioni forma un sottospazio
vettoriale in quello spazio di funzioni. Si dimo-
stra anzi che le soluzioni formano una retta e
che quindi le funzioni che coincidono con la pro-
pria derivata sono esattamente i multipli scala-
ri della funzione esponenziale. Per
otteniamo la funzione costante zero che effetti-
vamente anch’essa `e la derivata di se stessa.
Sia . Allora e vediamo che
ogni soluzione della nostra equazione differen-
ziale pu`o essere scritta nella forma
Si dimostra nei corsi di Analisi che coin-
cide con , dove il numero (detto anche base
del logaritmo naturale) `e definito da
In R la funzione esponenziale corrisponde alla
funzione ; il numero non `e predefinito ma
pu`o essere ottenuto calcolando . Ci`o costa
tempo per`o in esecuzioni ripetute, quindi inse-
riamo il valore nel file Costanti:

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 11 45
Abbreviazioni
Per evitare di dover battere la parola com-
plicata mettiamo la seguente ri-
ga nel file Abbreviazioni della nostra libre-
ria:
Nello stesso modo possiamo rinominare
altre funzioni:
Esempi per l’uso di D
Verifichiamo le formule
con
La serie di Taylor
Molte funzioni reali (ad esempio i polinomi,
le funzioni trigonometriche e iperboliche, la
funzione esponenziale, i quozienti di poli-
nomi) possono, per ogni punto del loro
dominio di definizione ed ogni sufficiente-
mente vicino ad (e spesso per ogni )
essere rappresentate mediante la loro serie
di Taylor:
dove `e la -esima derivata di nel
punto . Questa rappresentazione fornisce
molte informazioni sul comportamento del-
la funzione vicino al punto .
Anche quando `e una funzione polino-
miale la serie di Taylor in `e interessante,
perch´e ci dice come la si esprime in . In
questo caso naturalmente la serie di Taylor
`e formalmente un polinomio in dello
stesso grado di quello di partenza. Abbiamo
ad esempio
e vediamo che le due funzioni coincidono
in , ma vicino ad il secon-
do polinomio si comporta come la funzione
in , il primo invece piut-
tosto come la retta .
(0,0) (1,0)
Creiamo adesso una funzione che re-
stituisce i primi coefficienti di una fun-
zione (rappresentata mediante un’espres-
sione formale) in un punto . Per calcolare
il valore della -esima derivata in usia-
mo che conosciamo dalla pagina 29.
La usiamo per calcolare i coefficienti del pri-
mo dei due polinomi visti sopra; questo po-
linomio ha grado 2 e quindi possiamo impo-
stare uguale a 2:
Otteniamo, correttamente, .
Proviamo adesso con lo sviluppo di Taylor
della funzione esponenziale in :
Vediamo dei numeri che a prima vista non
sembrano dire molto; ma se visualizziamo
invece i coefficienti come frazioni di interi
con
dopo aver caricato, se necessario, la libreria
con (cfr. pagina 42), tro-
viamo
Questi sono i reciproci dei fattoriali! Infatti
la serie di Taylor della funzione esponenziale
nell’origine `e
Abbiamo aumentato il limite superiore del
denominatore in . Proviamo con il
coseno, sostituendo ad , e otteniamo
Infatti
Sostituiamo con per calcolare lo svi-
luppo di Taylor del coseno iperbolico e ritro-
viamo gli stessi coefficienti, ma senza segno.
Quindi
Proviamo infine con :
Infatti ,
ma stavolta la serie di Taylor converge solo
per , bench´e il quoziente sia
definito per ogni .
Options e print(x,n)
Il numero delle cifre significative che vengo-
no visualizzate in un numero reale `e preim-
postato a 7 e pu`o essere modificato mediante
il comando
per avere ad esempio 12 cifre significative.
Il valore massimo `e probabilmente 22, ma
sembra che la precisione arrivi a circa 16 ci-
fre dietro il punto decimale. funzio-
na quindi in modo simile a . Per vedere
anche gli altri parametri provare .
Se si vuole stampare un valore solo una
volta con un certo numero di cifre, si pu`o uti-
lizzare il secondo parametro di .
Esempio:

ALGORITMI E STRUTTURE DI DATI a.a. 2004/05 Numero 11 46
any e all
Se `e un vettore di valori booleani (cio`e
uguali a o ), `e vero se e
solo se almeno uno dei componenti di `e
vero, mentre `e vero se e solo se tut-
ti i componenti di sono veri. Esempi:
Ordinamento
Trattiamo qui le seguenti funzioni:
non `e una vera funzione di ordinamen-
to, ma restituisce semplicemente gli ele-
menti di un vettore in ordine invertito:
La funzione di ordinamento ordi-
na un vettore di numeri reali, in ordi-
ne crescente se non `e indicata l’opzione
. Usiamo lo stesso :
Con si ottiene la posizione di ogni
elemento nella successione ordinata, con
invece successivamente la posizione
dell’elemento pi `u piccolo nella successione
originale, poi quella del secondo e cos`ı via:
La libreria
Elenchiamo qui i singoli files della nostra lib-
reria in ordine alfabetico, tralasciando le Oc-
tobrinidae e Parabrinidae.
Abbreviazioni
Analisi
Costanti
Figure
Geometria
Grafica
Grafica-strumenti
Matrici
Primi
Corso di laurea in matematica Corso di Algoritmi e strutture di dati Docente: Josef Eschgf¨aller