The Comprehensive LaTeX Symbol List Guide

User Manual:

Open the PDF directly: View PDF PDF.
Page Count: 164 [warning: Documents this large are best viewed by clicking the View PDF Link!]

The Comprehensive L
A
T
E
X Symbol List
Scott Pakin <scott+clsl@pakin.org>∗
9 November 2009
Abstract
This document lists 5913 symbols and the corresponding L
A
T
E
X commands that produce them. Some
of these symbols are guaranteed to be available in every L
A
T
E
X 2εsystem; others require fonts and packages
that may not accompany a given distribution and that therefore need to be installed. All of the fonts
and packages used to prepare this document—as well as this document itself—are freely available from the
Comprehensive T
E
X Archive Network (http://www.ctan.org/).
Contents
Contents 1
1 Introduction 8
1.1 DocumentUsage ............................................ 8
1.2 FrequentlyRequestedSymbols .................................... 8
2 Body-text symbols 9
Table 1: L
A
T
E
X 2εEscapable “Special” Characters . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Table 2: Predefined L
A
T
E
X 2εText-modeCommands ......................... 9
Table 3: L
A
T
E
X 2εCommands Defined to Work in Both Math and Text Mode . . . . . . . . . . . 9
Table 4: A
M
SCommands Defined to Work in Both Math and Text Mode . . . . . . . . . . . . . 10
Table 5: Non-ASCII Letters (Excluding Accented Letters) . . . . . . . . . . . . . . . . . . . . . . 10
Table 6: Letters Used to Typeset African Languages . . . . . . . . . . . . . . . . . . . . . . . . . 10
Table 7: Letters Used to Typeset Vietnamese . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Table 8: Punctuation Marks Not Found in OT1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Table 9: pifont Decorative Punctuation Marks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Table 10: tipa PhoneticSymbols ..................................... 11
Table 11: tipx PhoneticSymbols ..................................... 12
Table 12: wsuipa PhoneticSymbols.................................... 13
Table 13: wasysym PhoneticSymbols................................... 13
Table 14: phonetic PhoneticSymbols................................... 13
Table 15: t4phonet PhoneticSymbols................................... 14
Table 16: semtrans TransliterationSymbols ............................... 14
Table17: Text-modeAccents....................................... 14
Table 18: tipa Text-modeAccents .................................... 15
Table 19: extraipa Text-modeAccents .................................. 16
Table 20: wsuipa Text-modeAccents................................... 16
Table 21: phonetic Text-modeAccents .................................. 16
Table 22: metre Text-modeAccents ................................... 17
Table 23: t4phonet Text-modeAccents.................................. 17
Table 24: arcs Text-modeAccents .................................... 17
Table 25: semtrans Accents ........................................ 17
Table 26: ogonek Accents ......................................... 17
Table 27: combelow Accents........................................ 17
∗The original version of this document was written by David Carlisle, with several additional tables provided by Alexander
Holt. See Section 8.8 on page 118 for more information about who did what.
1
Table 28: wsuipa Diacritics ........................................ 18
Table 29: textcomp Diacritics ....................................... 18
Table 30: textcomp CurrencySymbols .................................. 18
Table 31: marvosym CurrencySymbols.................................. 18
Table 32: wasysym CurrencySymbols .................................. 18
Table 33: C
h
in
A2eCurrencySymbols ................................... 19
Table 34: teubner CurrencySymbols ................................... 19
Table 35: eurosym EuroSigns....................................... 19
Table 36: fourier EuroSigns........................................ 19
Table 37: textcomp LegalSymbols .................................... 19
Table 38: cclicenses Creative Commons License Icons . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Table 39: textcomp Old-styleNumerals.................................. 20
Table 40: Miscellaneous textcomp Symbols................................ 20
Table 41: Miscellaneous wasysym Text-modeSymbols ......................... 20
3 Mathematical symbols 21
Table 42: Math-Mode Versions of Text Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Table 43: cmll UnaryOperators...................................... 21
Table44: BinaryOperators........................................ 22
Table 45: A
M
SBinaryOperators .................................... 22
Table 46: stmaryrd BinaryOperators................................... 22
Table 47: wasysym BinaryOperators................................... 23
Table 48: txfonts/pxfonts BinaryOperators ............................... 23
Table 49: mathabx BinaryOperators................................... 23
Table 50: MnSymbol BinaryOperators.................................. 23
Table 51: mathdesign BinaryOperators ................................. 24
Table 52: cmll BinaryOperators ..................................... 24
Table 53: shuffle BinaryOperators .................................... 24
Table 54: ulsy GeometricBinaryOperators ............................... 24
Table 55: mathabx Geometric Binary Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Table 56: MnSymbol Geometric Binary Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Table 57: Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Table 58: A
M
SVariable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Table 59: stmaryrd Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Table 60: wasysym Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Table 61: mathabx Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Table 62: txfonts/pxfonts Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . 27
Table 63: esint Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Table 64: MnSymbol Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Table 65: mathdesign Variable-sized Math Operators . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Table 66: cmll LargeMathOperators .................................. 30
Table67: BinaryRelations ........................................ 30
Table 68: A
M
SBinaryRelations..................................... 30
Table 69: A
M
SNegatedBinaryRelations................................ 31
Table 70: stmaryrd BinaryRelations ................................... 31
Table 71: wasysym BinaryRelations ................................... 31
Table 72: txfonts/pxfonts BinaryRelations................................ 31
Table 73: txfonts/pxfonts NegatedBinaryRelations........................... 31
Table 74: mathabx BinaryRelations ................................... 32
Table 75: mathabx NegatedBinaryRelations .............................. 32
Table 76: MnSymbol BinaryRelations .................................. 32
Table 77: MnSymbol NegatedBinaryRelations ............................. 33
Table 78: mathtools BinaryRelations................................... 34
Table 79: turnstile BinaryRelations.................................... 35
Table 80: trsym BinaryRelations..................................... 36
Table 81: trfsigns BinaryRelations .................................... 36
Table 82: cmll BinaryRelations...................................... 36
Table 83: colonequals BinaryRelations.................................. 36
2
Table 84: fourier BinaryRelations .................................... 36
Table 85: Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Table 86: A
M
SSubset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Table 87: stmaryrd Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Table 88: wasysym Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Table 89: txfonts/pxfonts Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . 37
Table 90: mathabx Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Table 91: MnSymbol Subset and Superset Relations . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Table92: Inequalities ........................................... 37
Table 93: A
M
SInequalities........................................ 38
Table 94: wasysym Inequalities ...................................... 38
Table 95: txfonts/pxfonts Inequalities................................... 38
Table 96: mathabx Inequalities ...................................... 38
Table 97: MnSymbol Inequalities ..................................... 39
Table 98: A
M
STriangleRelations .................................... 39
Table 99: stmaryrd TriangleRelations .................................. 40
Table 100: mathabx TriangleRelations .................................. 40
Table 101: MnSymbol TriangleRelations ................................. 40
Table102: Arrows.............................................. 41
Table103: Harpoons ............................................ 41
Table 104: textcomp Text-modeArrows.................................. 41
Table 105: A
M
SArrows .......................................... 41
Table 106: A
M
SNegatedArrows ..................................... 41
Table 107: A
M
SHarpoons......................................... 41
Table 108: stmaryrd Arrows......................................... 42
Table 109: txfonts/pxfonts Arrows ..................................... 42
Table 110: mathabx Arrows......................................... 42
Table 111: mathabx NegatedArrows.................................... 42
Table 112: mathabx Harpoons ....................................... 43
Table 113: MnSymbol Arrows........................................ 43
Table 114: MnSymbol NegatedArrows................................... 44
Table 115: MnSymbol Harpoons ...................................... 46
Table 116: MnSymbol NegatedHarpoons ................................. 46
Table 117: harpoon ExtensibleHarpoons ................................. 47
Table 118: chemarrow Arrows........................................ 47
Table 119: fge Arrows............................................ 47
Table 120: MnSymbol Spoons........................................ 47
Table 121: MnSymbol Pitchforks...................................... 47
Table 122: MnSymbol SmilesandFrowns ................................. 48
Table 123: ulsy ContradictionSymbols .................................. 48
Table124: ExtensionCharacters...................................... 48
Table 125: stmaryrd ExtensionCharacters................................. 48
Table 126: txfonts/pxfonts ExtensionCharacters ............................. 48
Table 127: mathabx ExtensionCharacters................................. 49
Table128: Log-likeSymbols ........................................ 49
Table 129: A
M
SLog-likeSymbols..................................... 49
Table 130: C
h
in
A2eNumberSets ...................................... 49
Table131: GreekLetters .......................................... 50
Table 132: A
M
SGreekLetters....................................... 50
Table 133: txfonts/pxfonts UprightGreekLetters............................. 50
Table 134: upgreek UprightGreekLetters................................. 51
Table 135: fourier VariantGreekLetters.................................. 51
Table 136: txfonts/pxfonts VariantLatinLetters ............................. 51
Table 137: A
M
SHebrewLetters...................................... 51
Table 138: MnSymbol HebrewLetters................................... 51
Table139: Letter-likeSymbols....................................... 51
Table 140: A
M
SLetter-likeSymbols ................................... 52
3
Table 141: txfonts/pxfonts Letter-likeSymbols .............................. 52
Table 142: mathabx Letter-likeSymbols.................................. 52
Table 143: MnSymbol Letter-likeSymbols................................. 52
Table 144: trfsigns Letter-likeSymbols................................... 52
Table 145: mathdesign Letter-likeSymbols ................................ 52
Table 146: fge Letter-likeSymbols..................................... 53
Table 147: fourier Letter-likeSymbols................................... 53
Table 148: A
M
SDelimiters......................................... 53
Table 149: stmaryrd Delimiters....................................... 53
Table 150: mathabx Delimiters ....................................... 53
Table 151: nath Delimiters ......................................... 53
Table 152: Variable-sized Delimiters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Table 153: Large, Variable-sized Delimiters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Table 154: A
M
SVariable-sizedDelimiters ................................ 54
Table 155: stmaryrd Variable-sizedDelimiters............................... 54
Table 156: mathabx Variable-sizedDelimiters............................... 55
Table 157: MnSymbol Variable-sizedDelimiters.............................. 55
Table 158: mathdesign Variable-sizedDelimiters ............................. 56
Table 159: nath Variable-sized Delimiters (Double) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
Table 160: nath Variable-sized Delimiters (Triple) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Table 161: fourier Variable-sizedDelimiters................................ 57
Table 162: textcomp Text-modeDelimiters ................................ 57
Table 163: metre Text-modeDelimiters .................................. 57
Table164: Math-modeAccents ...................................... 57
Table 165: A
M
SMath-modeAccents ................................... 58
Table 166: MnSymbol Math-modeAccents ................................ 58
Table 167: fge Math-modeAccents .................................... 58
Table 168: yhmath Math-modeAccents .................................. 58
Table169: ExtensibleAccents ....................................... 59
Table 170: overrightarrow ExtensibleAccents ............................... 59
Table 171: yhmath ExtensibleAccents................................... 59
Table 172: A
M
SExtensibleAccents.................................... 59
Table 173: MnSymbol ExtensibleAccents................................. 60
Table 174: mathtools ExtensibleAccents ................................. 60
Table 175: mathabx ExtensibleAccents .................................. 60
Table 176: fourier ExtensibleAccents ................................... 60
Table 177: esvect ExtensibleAccents ................................... 61
Table 178: undertilde ExtensibleAccents ................................. 61
Table 179: ushort ExtensibleAccents ................................... 61
Table 180: A
M
SExtensibleArrows .................................... 61
Table 181: mathtools ExtensibleArrows.................................. 62
Table 182: chemarr ExtensibleArrows................................... 62
Table 183: chemarrow ExtensibleArrows ................................. 62
Table 184: extarrows ExtensibleArrows .................................. 62
Table 185: extpfeil ExtensibleArrows ................................... 63
Table 186: DotArrow ExtensibleArrows.................................. 63
Table 187: trfsigns Extensible Transform Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
Table 188: holtpolt Non-commutative Division Symbols . . . . . . . . . . . . . . . . . . . . . . . . . 63
Table189: Dots ............................................... 63
Table 190: A
M
SDots............................................ 64
Table 191: wasysym Dots .......................................... 64
Table 192: MnSymbol Dots......................................... 64
Table 193: mathdots Dots.......................................... 64
Table 194: yhmath Dots........................................... 64
Table 195: teubner Dots........................................... 64
Table 196: mathcomp MathSymbols.................................... 65
Table 197: marvosym Digits......................................... 65
4
Table 198: fge Digits ............................................ 65
Table 199: dozenal Base-12Digits ..................................... 65
Table 200: mathabx MayanDigits ..................................... 65
Table 201: Miscellaneous L
A
T
E
X 2εMathSymbols ............................ 65
Table 202: Miscellaneous A
M
SMathSymbols .............................. 66
Table 203: Miscellaneous wasysym MathSymbols ............................ 66
Table 204: Miscellaneous txfonts/pxfonts MathSymbols......................... 66
Table 205: Miscellaneous mathabx MathSymbols ............................ 66
Table 206: Miscellaneous MnSymbol MathSymbols ........................... 66
Table 207: Miscellaneous Internal MnSymbol MathSymbols ...................... 67
Table 208: Miscellaneous textcomp Text-mode Math Symbols . . . . . . . . . . . . . . . . . . . . . . 67
Table 209: Miscellaneous marvosym MathSymbols............................ 67
Table 210: Miscellaneous fge MathSymbols ............................... 67
Table 211: Miscellaneous mathdesign MathSymbols ........................... 67
Table 212: Miscellaneous arev MathSymbols............................... 67
Table213: MathAlphabets......................................... 68
4 Science and technology symbols 70
Table 214: gensymb Symbols Defined to Work in Both Math and Text Mode . . . . . . . . . . . . . 70
Table 215: wasysym Electrical and Physical Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
Table 216: ifsym PulseDiagramSymbols ................................. 70
Table 217: ar AspectRatioSymbol .................................... 70
Table 218: textcomp Text-mode Science and Engineering Symbols . . . . . . . . . . . . . . . . . . . 70
Table 219: steinmetz ExtensiblePhasorSymbol ............................. 70
Table 220: wasysym AstronomicalSymbols ................................ 71
Table 221: marvosym AstronomicalSymbols ............................... 71
Table 222: mathabx AstronomicalSymbols ................................ 71
Table 223: wasysym APLSymbols..................................... 71
Table 224: wasysym APLModifiers .................................... 71
Table 225: marvosym Computer Hardware Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
Table 226: keystroke ComputerKeys.................................... 72
Table 227: ascii ControlCharacters(CP437) ............................... 72
Table 228: milstd LogicGates ....................................... 73
Table 229: marvosym CommunicationSymbols .............................. 73
Table 230: marvosym EngineeringSymbols ................................ 73
Table 231: wasysym BiologicalSymbols .................................. 73
Table 232: marvosym BiologicalSymbols ................................. 74
Table 233: marvosym Safety-relatedSymbols ............................... 74
Table 234: feyn FeynmanDiagramSymbols................................ 74
5 Dingbats 75
Table 235: bbding Arrows.......................................... 75
Table 236: pifont Arrows .......................................... 75
Table 237: universal Arrows......................................... 75
Table 238: marvosym Scissors........................................ 75
Table 239: bbding Scissors ......................................... 75
Table 240: pifont Scissors.......................................... 75
Table 241: dingbat Pencils ......................................... 76
Table 242: bbding PencilsandNibs .................................... 76
Table 243: pifont PencilsandNibs..................................... 76
Table 244: dingbat Fists........................................... 76
Table 245: bbding Fists ........................................... 76
Table 246: pifont Fists............................................ 76
Table 247: fourier Fists ........................................... 76
Table 248: bbding CrossesandPlusses................................... 76
Table 249: pifont CrossesandPlusses ................................... 77
Table 250: bbding XsandCheckMarks.................................. 77
Table 251: pifont XsandCheckMarks .................................. 77
5
Table 252: wasysym XsandCheckMarks................................. 77
Table 253: universal Xs ........................................... 77
Table 254: pifont CircledNumbers..................................... 77
Table 255: wasysym Stars.......................................... 77
Table 256: bbding Stars, Flowers, and Similar Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Table 257: pifont Stars, Flowers, and Similar Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Table 258: fourier Ornaments........................................ 78
Table 259: wasysym GeometricShapes................................... 78
Table 260: MnSymbol GeometricShapes ................................. 79
Table 261: ifsym GeometricShapes .................................... 79
Table 262: bbding GeometricShapes.................................... 80
Table 263: pifont GeometricShapes .................................... 80
Table 264: universa GeometricShapes................................... 80
Table 265: universal GeometricShapes................................... 80
Table 266: Miscellaneous dingbat Dingbats ................................ 80
Table 267: Miscellaneous bbding Dingbats................................. 80
Table 268: Miscellaneous pifont Dingbats ................................. 80
6 Ancient languages 81
Table 269: phaistos Symbols from the Phaistos Disk . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
Table 270: protosem Proto-SemiticCharacters .............................. 81
Table 271: hieroglf Hieroglyphics...................................... 82
Table 272: linearA LinearAScript..................................... 82
Table 273: linearb Linear B Basic and Optional Letters . . . . . . . . . . . . . . . . . . . . . . . . . 85
Table 274: linearb LinearBNumerals ................................... 85
Table 275: linearb Linear B Weights and Measures . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
Table 276: linearb LinearBIdeograms................................... 86
Table 277: linearb Unidentified Linear B Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Table 278: cypriot CypriotLetters ..................................... 86
Table 279: sarabian SouthArabianLetters ................................ 87
Table 280: teubner Archaic Greek Letters and Greek Numerals . . . . . . . . . . . . . . . . . . . . . 87
7 Other symbols 88
Table 281: textcomp GenealogicalSymbols ................................ 88
Table 282: wasysym GeneralSymbols ................................... 88
Table 283: wasysym Circles......................................... 88
Table 284: wasysym MusicalSymbols ................................... 88
Table 285: arev MusicalSymbols...................................... 88
Table 286: harmony MusicalSymbols ................................... 89
Table 287: harmony MusicalAccents.................................... 89
Table 288: manfnt DangerousBendSymbols ............................... 89
Table 289: Miscellaneous manfnt Symbols................................. 89
Table 290: marvosym NavigationSymbols................................. 90
Table 291: marvosym LaundrySymbols .................................. 90
Table 292: marvosym InformationSymbols ................................ 90
Table 293: Other marvosym Symbols.................................... 90
Table 294: Miscellaneous universa Symbols ................................ 90
Table 295: Miscellaneous universal Symbols................................ 90
Table 296: Miscellaneous fourier Symbols ................................. 91
Table 297: ifsym WeatherSymbols..................................... 91
Table 298: ifsym AlpineSymbols...................................... 91
Table 299: ifsym Clocks........................................... 91
Table 300: Other ifsym Symbols ...................................... 92
Table 301: clock Clocks........................................... 92
Table 302: epsdice Dice ........................................... 92
Table 303: hhcount Dice........................................... 92
Table 304: hhcount TallyMarkers ..................................... 92
Table 305: skull Symbols .......................................... 93
6
Table 306: Non-Mathematical mathabx Symbols ............................. 93
Table 307: skak ChessInformatorSymbols ................................ 93
Table 308: skak Chess Pieces and Chessboard Squares . . . . . . . . . . . . . . . . . . . . . . . . . . 94
Table 309: igo GoStones .......................................... 94
Table 310: metre MetricalSymbols .................................... 95
Table 311: metre Small and Large Metrical Symbols . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
Table 312: teubner MetricalSymbols.................................... 95
Table 313: dictsym DictionarySymbols .................................. 96
Table 314: simpsons Characters from The Simpsons ........................... 96
Table 315: pmboxdraw Box-DrawingSymbols............................... 97
Table 316: staves MagicalStaves...................................... 97
Table 317: pigpen CipherSymbols..................................... 98
Table 318: C
h
in
A2ePhasesoftheMoon .................................. 98
Table 319: Other C
h
in
A2eSymbols ..................................... 98
Table 320: recycle RecyclingSymbols ................................... 99
8 Additional Information 100
8.1 SymbolNameClashes ......................................... 100
8.2 Resizingsymbols ............................................ 100
8.3 Where can I find the symbol for . . . ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8.4 Math-modespacing........................................... 112
8.5 Boldmathematicalsymbols ...................................... 113
8.6 ASCII and Latin 1 quick reference . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
8.7 Unicodecharacters........................................... 117
8.8 Aboutthisdocument.......................................... 118
8.9 Copyrightandlicense ......................................... 121
References 122
Index 123
7
1 Introduction
Welcome to the Comprehensive L
A
T
E
X Symbol List! This document strives to be your primary source of L
A
T
E
X
symbol information: font samples, L
A
T
E
X commands, packages, usage details, caveats—everything needed to
put thousands of different symbols at your disposal. All of the fonts covered herein meet the following criteria:
1. They are freely available from the Comprehensive T
E
X Archive Network (http://www.ctan.org).
2. All of their symbols have L
A
T
E
X 2εbindings. That is, a user should be able to access a symbol by name,
not just by \charhnumberi.
These are not particularly limiting criteria; the Comprehensive L
A
T
E
X Symbol List contains samples of 5913
symbols—quite a large number. Some of these symbols are guaranteed to be available in every L
A
T
E
X 2εsystem;
others require fonts and packages that may not accompany a given distribution and that therefore need to
be installed. See http://www.tex.ac.uk/cgi-bin/texfaq2html?label=instpackages+wherefiles for help
with installing new fonts and packages.
1.1 Document Usage
Each section of this document contains a number of font tables. Each table shows a set of symbols, with the
corresponding L
A
T
E
X command to the right of each symbol. A table’s caption indicates what package needs to
be loaded in order to access that table’s symbols. For example, the symbols in Table 39, “textcomp Old-Style
Numerals”, are made available by putting “\usepackage{textcomp}” in your document’s preamble. “A
M
S”
means to use the A
M
Spackages, viz. amssymb and/or amsmath. Notes below a table provide additional
information about some or all the symbols in that table.
One note that appears a few times in this document, particularly in Section 2, indicates that certain
symbols do not exist in the OT1 font encoding (Donald Knuth’s original, 7-bit font encoding, which is the
default font encoding for L
A
T
E
X) and that you should use fontenc to select a different encoding, such as T1
(a common 8-bit font encoding). That means that you should put “\usepackage[hencodingi]{fontenc}” in
your document’s preamble, where hencodingiis, e.g., T1 or LY1. To limit the change in font encoding to the
current group, use “\fontencoding{hencodingi}\selectfont”.
Section 8 contains some additional information about the symbols in this document. It discusses how
certain mathematical symbols can vary in height, shows which symbol names are not unique across packages,
gives examples of how to create new symbols out of existing symbols, explains how symbols are spaced in
math mode, compares various schemes for boldfacing symbols, presents L
A
T
E
X ASCII and Latin 1 tables,
shows how to input and output Unicode characters, and provides some information about this document itself.
The Comprehensive L
A
T
E
X Symbol List ends with an index of all the symbols in the document and various
additional useful terms.
1.2 Frequently Requested Symbols
There are a number of symbols that are requested over and over again on comp.text.tex. If you’re looking
for such a symbol the following list will help you find it quickly.
, as in “Spaces are significant.” . . . . . . . . 9
´ı, `ı, ¯ı, ˆı, etc. (versus ´ı, `ı, ¯
i, and ˆı) . . . . . . . . 14
¢............................... 18
e.............................. 18
©,®, and ™...................... 19
‰.............................. 20
.............................. 27
∴............................... 30
Band F......................... 31
.and &......................... 38
................................. 64
°, as in “180°” or “15” .............. 67
L,F,etc. ........................ 68
, , ,etc. ...................... 68
............................... 68
−
R............................... 105
´
¯a, `
ˆe, etc. (i.e., several accents per character) 107
<,>, and |(instead of ¡, ¿, and —) . . . . . . 114
ˆ and ˜ (or ∼) ..................... 115
8
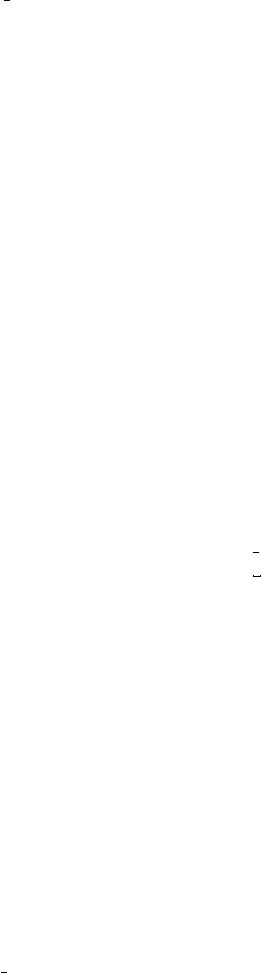
2 Body-text symbols
This section lists symbols that are intended for use in running text, such as punctuation marks, accents,
ligatures, and currency symbols.
Table 1: L
A
T
E
X 2εEscapable “Special” Characters
$\$ %\% \_ ∗}\} &\& #\# {\{
∗The underscore package redefines “_” to produce an underscore in text mode (i.e., it
makes it unnecessary to escape the underscore character).
Table 2: Predefined L
A
T
E
X 2εText-mode Commands
ˆ\textasciicircum∗<\textless
˜\textasciitilde∗aª\textordfeminine
∗\textasteriskcentered oº\textordmasculine
\\textbackslash \textparagraph†
|\textbar ·\textperiodcentered
{\textbraceleft†¿\textquestiondown
}\textbraceright†“\textquotedblleft
•\textbullet ”\textquotedblright
c
©\textcopyright†‘\textquoteleft
†\textdagger†’\textquoteright
‡\textdaggerdbl†r
®\textregistered
$\textdollar†§\textsection†
. . . \textellipsis†£\textsterling†
—\textemdash TM ™\texttrademark
–\textendash \textunderscore†
¡\textexclamdown \textvisiblespace
>\textgreater
Where two symbols are present, the left one is the “faked” symbol that L
A
T
E
X 2ε
provides by default, and the right one is the “true” symbol that textcomp makes
available.
∗\^{} and \~{} can be used instead of \textasciicircum and \textasciitilde.
See the discussion of “˜” on page 115.
†It’s generally preferable to use the corresponding symbol from Table 3 because the
symbols in that table work properly in both text mode and math mode.
Table 3: L
A
T
E
X 2εCommands Defined to Work in Both Math and Text Mode
$\$ \_ ‡\ddag {\{
\P c
©\copyright . . . \dots }\}
§\S †\dag £\pounds
Where two symbols are present, the left one is the “faked” symbol that L
A
T
E
X 2ε
provides by default, and the right one is the “true” symbol that textcomp makes
available.
9
Table 4: A
M
SCommands Defined to Work in Both Math and Text Mode
X\checkmark r\circledR z\maltese
Table 5: Non-ASCII Letters (Excluding Accented Letters)
˚a \aa Ð\DH∗ L \L ø\o ß\ss
˚
A\AA ð\dh∗ l \l Ø\O SS \SS
Æ\AE Ð\DJ∗Ŋ\NG∗Œ\OE Þ\TH∗
æ\ae đ\dj∗ŋ\ng∗œ\oe þ\th∗
∗Not available in the OT1 font encoding. Use the fontenc package to select an
alternate font encoding, such as T1.
Table 6: Letters Used to Typeset African Languages
\B{D} \m{c} \m{f} \m{k} \M{t} \m{Z}
\B{d} \m{D} \m{F} \m{N} \M{T} \T{E}
\B{H} \M{d} \m{G} \m{n} \m{t} \T{e}
\B{h} \M{D} \m{g} \m{o} \m{T} \T{O}
\B{t} \m{d} \m{I} \m{O} \m{u}∗\T{o}
\B{T} \m{E} \m{i} \m{P} \m{U}∗
\m{b} \m{e} \m{J} \m{p} \m{Y}
\m{B} \M{E} \m{j} \m{s} \m{y}
\m{C} \M{e} \m{K} \m{S} \m{z}
These characters all need the T4 font encoding, which is provided by the fc package.
∗\m{v} and \m{V} are synonyms for \m{u} and \m{U}.
Table 7: Letters Used to Typeset Vietnamese
Ơ\OHORN ơ\ohorn Ư\UHORN ư\uhorn
These characters all need the T5 font encoding, which is provided by the vntex
package.
Table 8: Punctuation Marks Not Found in OT1
«\guillemotleft ‹\guilsinglleft „\quotedblbase "\textquotedbl
»\guillemotright ›\guilsinglright ‚\quotesinglbase
To get these symbols, use the fontenc package to select an alternate font encoding,
such as T1.
Table 9: pifont Decorative Punctuation Marks
{\ding{123} }\ding{125} ¡\ding{161} £\ding{163}
|\ding{124} ~\ding{126} ¢\ding{162}
10
Table 10: tipa Phonetic Symbols
È\textbabygamma P\textglotstop ï\textrtailn
b\textbarb ;\texthalflength ó\textrtailr
c\textbarc ż\texthardsign ù\textrtails
d\textbard #\texthooktop ú\textrtailt
é\textbardotlessj á\texthtb ü\textrtailz
g\textbarg ê\texthtbardotlessj $\textrthook
Ü\textbarglotstop Á\texthtc À\textsca
1\textbari â\texthtd à\textscb
ł\textbarl ä\texthtg ď\textsce
8\textbaro H\texthth å\textscg
Ý\textbarrevglotstop Ê\texththeng Ë\textsch
0\textbaru Î\texthtk @\textschwa
ì\textbeltl Ò\texthtp I\textsci
B\textbeta Ó\texthtq ĺ\textscj
ò\textbullseye č\texthtrtaild Ï\textscl
\textceltpal É\texthtscg ð\textscn
\textchi Ö\texthtt Œ\textscoelig
Å\textcloseepsilon ß\texthvlig ś\textscomega
Ñ\textcloseomega Û\textinvglotstop ö\textscr
Æ\textcloserevepsilon K\textinvscr A\textscripta
Þ\textcommatailz Ì\textiota g\textscriptg
^\textcorner ń\textlambda V\textscriptv
ă\textcrb :\textlengthmark Ú\textscu
ą\textcrd ş\textlhookt Y\textscy
g\textcrg ę\textlhtlongi \textsecstress
è\textcrh ű\textlhtlongy ž\textsoftsign
Û\textcrinvglotstop Ô\textlonglegr Â\textstretchc
ň\textcrlambda ¡\textlptr tC \texttctclig
2\textcrtwo M\textltailm Ù\textteshlig
C\textctc ñ\textltailn T\texttheta
ć\textctd ë\textltilde þ\textthorn
ćý \textctdctzlig Ð\textlyoghlig £\texttoneletterstem
š\textctesh Í\textObardotlessj ţ\texttslig
J\textctj ŋ\textOlyoghlig 5\textturna
ő\textctn ř\textomega ŕ\textturncelig
ť\textctt _\textopencorner 4\textturnh
ťC \textcttctclig O\textopeno ľ\textturnk
ÿ\textctyogh %\textpalhook Õ\textturnlonglegr
ý\textctz F\textphi W\textturnm
dý \textdctzlig |\textpipe î\textturnmrleg
S\textdoublebaresh "\textprimstress ô\textturnr
}\textdoublebarpipe ij\textraiseglotstop õ\textturnrrtail
=/ \textdoublebarslash ğ\textraisevibyi 6\textturnscripta
{\textdoublepipe 7\textramshorns Ø\textturnt
Ş\textdoublevertline \\textrevapostrophe 2\textturnv
Ť\textdownstep 9\textreve û\textturnw
Ã\textdyoghlig 3\textrevepsilon L\textturny
dz \textdzlig Q\textrevglotstop U\textupsilon
E\textepsilon ź\textrevyogh Ţ\textupstep
(continued on next page)
11
(continued from previous page)
S\textesh Ç\textrhookrevepsilon Š\textvertline
R\textfishhookr Ä\textrhookschwa ğ\textvibyi
ě\textg ~\textrhoticity ů\textvibyy
G\textgamma ¿\textrptr \textwynn
Ů\textglobfall ã\textrtaild Z\textyogh
Ű\textglobrise í\textrtaill
tipa defines shortcut characters for many of the above. It also defines a command
\tone for denoting tone letters (pitches). See the tipa documentation for more
information.
Table 11: tipx Phonetic Symbols
"\textaolig 3\texthtbardotlessjvar ´\textrthooklong
B\textbenttailyogh ;\textinvomega q\textscaolig
.\textbktailgamma p\textinvsca r\textscdelta
D\textctinvglotstop !\textinvscripta s\textscf
2\textctjvar I\textlfishhookrlig t\textsck
%\textctstretchc #\textlhookfour w\textscm
&\textctstretchcvar <\textlhookp x\textscp
@\textctturnt 1\textlhti y\textscq
)\textdblig >\textlooptoprevesh ˝\textspleftarrow
H\textdoublebarpipevar 6\textnrleg $\textstretchcvar
G\textdoublepipevar 9\textObullseye ˙\textsubdoublearrow
ˇ\textdownfullarrow ˆ\textpalhooklong ¯\textsubrightarrow
7\textfemale ˜\textpalhookvar P\textthornvari
5\textfrbarn F\textpipevar Q\textthornvarii
’\textfrhookd =\textqplig R\textthornvariii
(\textfrhookdvar ¨\textrectangle S\textthornvariv
?\textfrhookt ˚\textretractingvar E\textturnglotstop
-\textfrtailgamma v\textrevscl u\textturnsck
T\textglotstopvari z\textrevscr {\textturnscu
U\textglotstopvarii \textrhooka C\textturnthree
V\textglotstopvariii *\textrhooke A\textturntwo
,\textgrgamma +\textrhookepsilon 8\textuncrfemale
0\textheng :\textrhookopeno ˘\textupfullarrow
4\texthmlig /\textrtailhth
12
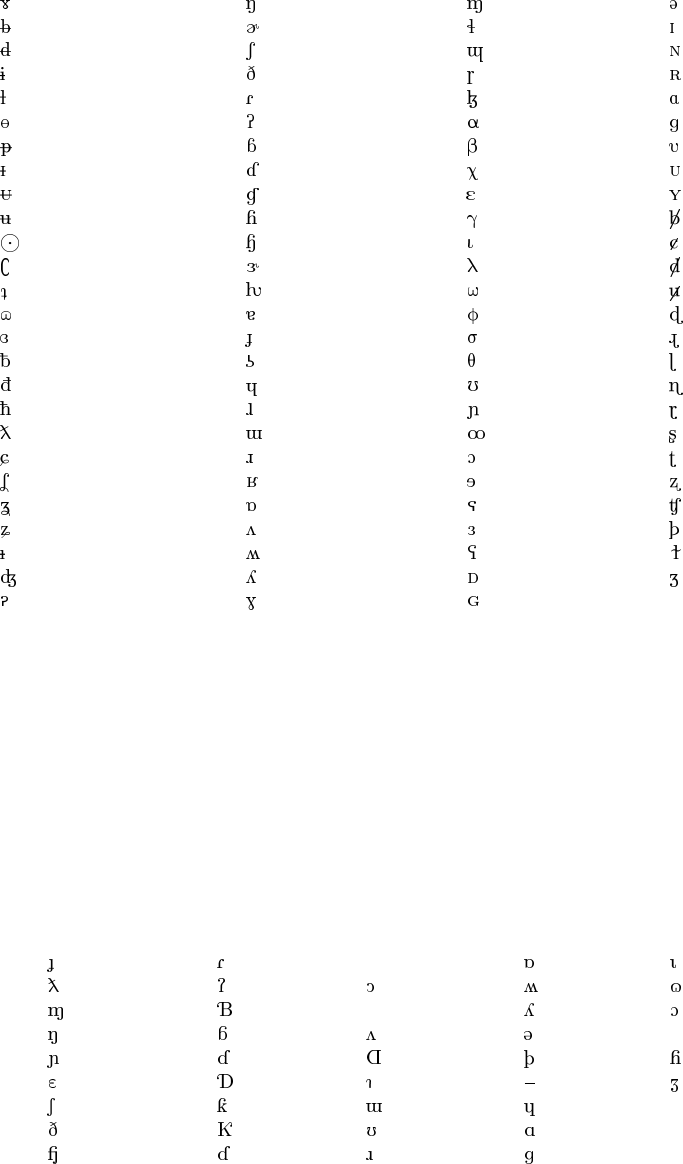
Table 12: wsuipa Phonetic Symbols
\babygamma \eng \labdentalnas \schwa
\barb \er \latfric \sci
\bard \esh \legm \scn
\bari \eth \legr \scr
\barl \flapr \lz \scripta
\baro \glotstop \nialpha \scriptg
\barp \hookb \nibeta \scriptv
\barsci \hookd \nichi \scu
\barscu \hookg \niepsilon \scy
\baru \hookh \nigamma \slashb
\clickb \hookheng \niiota \slashc
\clickc \hookrevepsilon \nilambda \slashd
\clickt \hv \niomega \slashu
\closedniomega \inva \niphi \taild
\closedrevepsilon \invf \nisigma \tailinvr
\crossb \invglotstop \nitheta \taill
\crossd \invh \niupsilon \tailn
\crossh \invlegr \nj \tailr
\crossnilambda \invm \oo \tails
\curlyc \invr \openo \tailt
\curlyesh \invscr \reve \tailz
\curlyyogh \invscripta \reveject \tesh
\curlyz \invv \revepsilon \thorn
\dlbari \invw \revglotstop \tildel
\dz \invy \scd \yogh
\ejective \ipagamma \scg
Table 13: wasysym Phonetic Symbols
D \DH k\dh l\openo
Þ\Thorn U\inve þ\thorn
Table 14: phonetic Phonetic Symbols
\barj \flap i
¯\ibar \rotvara \vari
\barlambda \glottal \openo \rotw \varomega
\emgma \hausaB ¯h \planck \roty \varopeno
\engma \hausab \pwedge \schwa v
˚\vod
\enya \hausad \revD \thorn \voicedh
\epsi \hausaD \riota u\ubar \yogh
\esh \hausak \rotm \udesc
\eth \hausaK \rotOmega \vara
\fj \hookd \rotr \varg
13
Table 15: t4phonet Phonetic Symbols
\textcrd \texthtd \textpipe
\textcrh \texthtk \textrtaild
\textepsilon \texthtp \textrtailt
\textesh \texthtt \textschwa
\textfjlig \textiota \textscriptv
\texthtb \textltailn \textteshlig
\texthtc \textopeno \textyogh
The idea behind the t4phonet package’s phonetic symbols is to provide an interface
to some of the characters in the T4 font encoding (Table 6 on page 10) but using
the same names as the tipa characters presented in Table 10 on page 11.
Table 16: semtrans Transliteration Symbols
\Alif \Ayn
Table 17: Text-mode Accents
¨
A¨a \"{A}\"{a} `
A`a \‘{A}\‘{a} A
.a
.\d{A}\d{a} ˚
A˚a \r{A}\r{a}
´
A´a \’{A}\’{a} \|{A}\|{a}‡\G{A}\G{a}‡
Aa\t{A}\t{a}
˙
A˙a \.{A}\.{a} ˜
A˜a \~{A}\~{a} Ảả \h{A}\h{a}§˘
A˘a \u{A}\u{a}
¯
A¯a \={A}\={a} A
¯a
¯\b{A}\b{a} ˝
A˝a \H{A}\H{a} \U{A}\U{a}‡
ˆ
Aˆa \^{A}\^{a} A¸ ¸a \c{A}\c{a} Ąą \k{A}\k{a}†ˇ
Aˇa \v{A}\v{a}
A
a\newtie{A}\newtie{a}∗A
a
\textcircled{A}\textcircled{a}
∗Requires the textcomp package.
†Not available in the OT1 font encoding. Use the fontenc package to select an
alternate font encoding, such as T1.
‡Requires the T4 font encoding, provided by the fc package.
§Requires the T5 font encoding, provided by the vntex package.
Also note the existence of \i and \j, which produce dotless versions of “i” and “j”
(viz., “ı” and “”). These are useful when the accent is supposed to replace the
dot in encodings that need to composite (i.e., combine) letters and accents. For
example, “na\"{\i}ve” always produces a correct “na¨ıve”, while “na\"{i}ve”
yields the rather odd-looking “na¨
ive” when using the OT1 font encoding and older
versions of L
A
T
E
X. Font encodings other than OT1 and newer versions of L
A
T
E
X
properly typeset “na\"{i}ve” as “na¨ıve”.
14
Table 18: tipa Text-mode Accents
´
¯
A´
¯
a\textacutemacron{A}\textacutemacron{a}
´
ˇ
A´
ˇ
a\textacutewedge{A}\textacutewedge{a}
A
ffia
ffi\textadvancing{A}\textadvancing{a}
A
<a
<\textbottomtiebar{A}\textbottomtiebar{a}
˘
¯
A˘
¯
a\textbrevemacron{A}\textbrevemacron{a}
Ż
AŻa\textcircumacute{A}\textcircumacute{a}
ˆ
˙
Aˆ
˙
a\textcircumdot{A}\textcircumdot{a}
§
A§a\textdotacute{A}\textdotacute{a}
˙
˘
A˙
˘
a\textdotbreve{A}\textdotbreve{a}
‚
A‚a\textdoublegrave{A}\textdoublegrave{a}
İ
Aİa\textdoublevbaraccent{A}\textdoublevbaraccent{a}
Ž
AŽa\textgravecircum{A}\textgravecircum{a}
đ
Ađa\textgravedot{A}\textgravedot{a}
`
¯
A`
¯
a\textgravemacron{A}\textgravemacron{a}
Ź
AŹa\textgravemid{A}\textgravemid{a}
A„a„\textinvsubbridge{A}\textinvsubbridge{a}
A
fla
fl\textlowering{A}\textlowering{a}
Ÿ
AŸa\textmidacute{A}\textmidacute{a}
‰
A‰a\textovercross{A}\textovercross{a}
—
A—
a\textoverw{A}\textoverw{a}
A˛a˛\textpolhook{A}\textpolhook{a}
A
fia
fi\textraising{A}\textraising{a}
A
ffla
ffl\textretracting{A}\textretracting{a}
˚
¯
A˚
¯
a\textringmacron{A}\textringmacron{a}
“
A“a\textroundcap{A}\textroundcap{a}
Aa\textseagull{A}\textseagull{a}
A
›a
›\textsubacute{A}\textsubacute{a}
A
“a
“\textsubarch{A}\textsubarch{a}
A
¯a
¯\textsubbar{A}\textsubbar{a}
A”a”\textsubbridge{A}\textsubbridge{a}
A
ˆa
ˆ\textsubcircum{A}\textsubcircum{a}
A
˙a
˙\textsubdot{A}\textsubdot{a}
A
‹a
‹\textsubgrave{A}\textsubgrave{a}
A
–a
–\textsublhalfring{A}\textsublhalfring{a}
A
ffa
ff\textsubplus{A}\textsubplus{a}
A
»a
»\textsubrhalfring{A}\textsubrhalfring{a}
A
˚a
˚\textsubring{A}\textsubring{a}
A«a«\textsubsquare{A}\textsubsquare{a}
A
˜a
˜\textsubtilde{A}\textsubtilde{a}
A
¨a
¨\textsubumlaut{A}\textsubumlaut{a}
(continued on next page)
15
(continued from previous page)
A—a—\textsubw{A}\textsubw{a}
A
ˇa
ˇ\textsubwedge{A}\textsubwedge{a}
A
&a
&\textsuperimposetilde{A}\textsuperimposetilde{a}
A
"a
"\textsyllabic{A}\textsyllabic{a}
˜
˙
A˜
˙
a\texttildedot{A}\texttildedot{a}
>
A
>
a\texttoptiebar{A}\texttoptiebar{a}
IJ
AIJa\textvbaraccent{A}\textvbaraccent{a}
tipa defines shortcut sequences for many of the above. See the tipa documentation
for more information.
Table 19: extraipa Text-mode Accents
”
A””
a”\bibridge{A}\bibridge{a} A
– »
˚a
– »
˚\partvoiceless{A}\partvoiceless{a}
Ŕ
˜
AŔ
˜
a\crtilde{A}\crtilde{a} A
¯a
¯\sliding{A}\sliding{a}
..
˜
A..
˜
a\dottedtilde{A}\dottedtilde{a} A
˙a
˙\spreadlips{A}\spreadlips{a}
˜
˜
A˜
˜a\doubletilde{A}\doubletilde{a} A
^a
^\subcorner{A}\subcorner{a}
A
»
ˇa
»
ˇ\finpartvoice{A}\finpartvoice{a} A
¯
¯a
¯
¯\subdoublebar{A}\subdoublebar{a}
A
»
˚a
»
˚\finpartvoiceless{A}\finpartvoiceless{a} A
"" a
"" \subdoublevert{A}\subdoublevert{a}
A
–
ˇa
–
ˇ\inipartvoice{A}\inipartvoice{a} A
¡a
¡\sublptr{A}\sublptr{a}
A
–
˚a
–
˚\inipartvoiceless{A}\inipartvoiceless{a} A
¿a
¿\subrptr{A}\subrptr{a}
”
A”
a\overbridge{A}\overbridge{a} A
Ţa
Ţ\whistle{A}\whistle{a}
A
– »
ˇa
– »
ˇ\partvoice{A}\partvoice{a}
Table 20: wsuipa Text-mode Accents
Aa \dental{A}\dental{a}
Aa \underarch{A}\underarch{a}
Table 21: phonetic Text-mode Accents
Aa \hill{A}\hill{a} Aa \rc{A}\rc{a} A
˜a
˜\ut{A}\ut{a}
A
˚a
˚\od{A}\od{a} Aa \syl{A}\syl{a}
Aa \ohill{A}\ohill{a} A
..a
.. \td{A}\td{a}
The phonetic package provides a few additional macros for linguistic accents.
\acbar and \acarc compose characters with multiple accents; for example,
\acbar{\’}{a} produces “´
¯
a” and \acarc{\"}{e} produces “¨
¯
e”. \labvel joins
two characters with an arc: \labvel{mn} →“
mn”. \upbar is intended to go
between characters as in “x\upbar{}y’’ →“x y”. Lastly, \uplett behaves like
\textsuperscript but uses a smaller font. Contrast “p\uplett{h}’’ →“ph”
with “p\textsuperscript{h}’’ →“ph”.
16
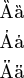
Table 22: metre Text-mode Accents
A
´a´ \acutus{A}\acutus{a}
A
˘a˘ \breve{A}\breve{a}
A
˜a˜ \circumflexus{A}\circumflexus{a}
A
¨a¨ \diaeresis{A}\diaeresis{a}
A
`a` \gravis{A}\gravis{a}
A
¯a¯ \macron{A}\macron{a}
Table 23: t4phonet Text-mode Accents
\textdoublegrave{A}\textdoublegrave{a}
\textvbaraccent{A}\textvbaraccent{a}
\textdoublevbaraccent{A}\textdoublevbaraccent{a}
The idea behind the t4phonet package’s text-mode accents is to provide an interface
to some of the accents in the T4 font encoding (accents marked with “‡” in Table 17
on page 14) but using the same names as the tipa accents presented in Table 18 on
page 15.
Table 24: arcs Text-mode Accents
A
a
_\overarc{A}\overarc{a} A
^a
^\underarc{A}\underarc{a}
The accents shown above scale only to a few characters wide. An optional macro
argument alters the effective width of the accented characters. See the arcs docu-
mentation for more information.
Table 25: semtrans Accents
A
¨a
¨\D{A}\D{a} A
˘a
˘\U{A}\U{a}
A
a
\T{A}\T{a}∗
\T is not actually an accent but a command that rotates its argument 180°using
the graphicx package’s \rotatebox command.
Table 26: ogonek Accents
A
a\k{A}\k{a}
Table 27: combelow Accents
A
,a
,\cb{A}\cb{a}
\cb places a comma above letters with descenders. Hence, while “\cb{s}” produces
“s
,”, “\cb{g}” produces “g
‘”.
17
Table 28: wsuipa Diacritics
\ain \leftp \overring \stress \underwedge
\corner \leftt \polishhook \syllabic \upp
\downp \length \rightp \underdots \upt
\downt \midtilde \rightt \underring
\halflength \open \secstress \undertilde
The wsuipa package defines all of the above as ordinary characters, not as accents.
However, it does provide \diatop and \diaunder commands, which are used to
compose diacritics with other characters. For example, \diatop[\overring|a]
produces “ a ”, and \diaunder[\underdots|a] produces “a”. See the wsuipa doc-
umentation for more information.
Table 29: textcomp Diacritics
\textacutedbl \textasciicaron \textasciimacron
\textasciiacute \textasciidieresis \textgravedbl
\textasciibreve \textasciigrave
The textcomp package defines all of the above as ordinary characters, not as accents.
Table 30: textcomp Currency Symbols
\textbaht $\textdollar∗\textguarani \textwon
¢\textcent \textdollaroldstyle ₤\textlira ¥\textyen
\textcentoldstyle ₫\textdong \textnaira
₡\textcolonmonetary €\texteuro \textpeso
¤\textcurrency ƒ\textflorin £\textsterling∗
∗It’s generally preferable to use the corresponding symbol from Table 3 on page 9
because the symbols in that table work properly in both text mode and math mode.
Table 31: marvosym Currency Symbols
¢\Denarius e\EUR D\EURdig e\EURtm £\Pfund
\Ecommerce d\EURcr c\EURhv ¦\EyesDollar ¡\Shilling
The different euro signs are meant to be visually compatible with different fonts—
Courier (\EURcr), Helvetica (\EURhv), Times Roman (\EURtm), and the marvosym
digits listed in Table 197 (\EURdig). The mathdesign package redefines \texteuro
to be visually compatible with one of three additional fonts: Utopia (€), Char-
ter (€), or Garamond (€).
Table 32: wasysym Currency Symbols
¢\cent ¤\currency
18
Table 33: C
h
in
A2e Currency Symbols
\Euro \Pound
Table 34: teubner Currency Symbols
Ε\denarius Α\hemiobelion Β\tetartemorion
Δ\dracma ῝\stater
Table 35: eurosym Euro Signs
AC\geneuro BC\geneuronarrow CC\geneurowide e\officialeuro
\euro is automatically mapped to one of the above—by default, \officialeuro—
based on a eurosym package option. See the eurosym documentation for more
information. The \geneuro. . . characters are generated from the current body
font’s “C” character and therefore may not appear exactly as shown.
Table 36: fourier Euro Signs
(\eurologo €\texteuro
Table 37: textcomp Legal Symbols
\textcircledP c
©\textcopyright \textservicemark
\textcopyleft r
®\textregistered TM ™\texttrademark
Where two symbols are present, the left one is the “faked” symbol that L
A
T
E
X 2ε
provides by default, and the right one is the “true” symbol that textcomp makes
available.
See http://www.tex.ac.uk/cgi-bin/texfaq2html?label=tradesyms for solu-
tions to common problems that occur when using these symbols (e.g., getting a “ r
”
when you expected to get a “®”).
Table 38: cclicenses Creative Commons License Icons
CC
\cc BY:
\ccby $
\
\ccnc∗=
\ccnd
C
\ccsa∗
∗These symbols utilize the rotating package and therefore display improperly in some
DVI viewers.
19
Table 39: textcomp Old-style Numerals
\textzerooldstyle \textfouroldstyle \texteightoldstyle
\textoneoldstyle \textfiveoldstyle \textnineoldstyle
\texttwooldstyle \textsixoldstyle
\textthreeoldstyle \textsevenoldstyle
Rather than use the bulky \textoneoldstyle,\texttwooldstyle, etc. commands
shown above, consider using \oldstylenums{. . .}to typeset an old-style number.
Table 40: Miscellaneous textcomp Symbols
∗\textasteriskcentered aª\textordfeminine
\textbardbl oº\textordmasculine
○\textbigcircle \textparagraph∗
\textblank ·\textperiodcentered
¦\textbrokenbar \textpertenthousand
•\textbullet ‰\textperthousand
†\textdagger∗\textpilcrow
‡\textdaggerdbl∗'\textquotesingle
\textdblhyphen \textquotestraightbase
\textdblhyphenchar \textquotestraightdblbase
\textdiscount \textrecipe
℮\textestimated \textreferencemark
\textinterrobang §\textsection∗
\textinterrobangdown \textthreequartersemdash
♪\textmusicalnote \texttildelow
№\textnumero \texttwelveudash
◦\textopenbullet
Where two symbols are present, the left one is the “faked” symbol that L
A
T
E
X 2ε
provides by default, and the right one is the “true” symbol that textcomp makes
available.
∗It’s generally preferable to use the corresponding symbol from Table 3 on page 9
because the symbols in that table work properly in both text mode and math mode.
Table 41: Miscellaneous wasysym Text-mode Symbols
h\permil
20
3 Mathematical symbols
Most, but not all, of the symbols in this section are math-mode only. That is, they yield a “Missing $
inserted” error message if not used within $. . .$,\[. . .\], or another math-mode environment. Operators
marked as “variable-sized” are taller in displayed formulas, shorter in in-text formulas, and possibly shorter
still when used in various levels of superscripts or subscripts.
Alphanumeric symbols (e.g., “L” and “”) are usually produced using one of the math alphabets in
Table 213 rather than with an explicit symbol command. Look there first if you need a symbol for a transform,
number set, or some other alphanumeric.
Although there have been many requests on comp.text.tex for a contradiction symbol, the ensuing dis-
cussion invariably reveals innumerable ways to represent contradiction in a proof, including “ ” (\blitza),
“⇒⇐” (\Rightarrow\Leftarrow), “⊥” (\bot), “” (\nleftrightarrow), and “” (\textreferencemark).
Because of the lack of notational consensus, it is probably better to spell out “Contradiction!” than to use a
symbol for this purpose. Similarly, discussions on comp.text.tex have revealed that there are a variety of
ways to indicate the mathematical notion of “is defined as”. Common candidates include “,” (\triangleq),
“≡” (\equiv), “B” (various1), and “def
=” (\stackrel{\text{\tiny def}}{=}). See also the example of
\equalsfill on page 108. Depending upon the context, disjoint union may be represented as “`” (\coprod),
“t” (\sqcup), “ ·
∪” (\dotcup), “⊕” (\oplus), or any of a number of other symbols.2Finally, the average
value of a variable xis written by some people as “x” (\overline{x}), by some people as “hxi” (\langle x
\rangle), and by some people as “x” or “∅x” (\diameter x or \varnothing x). The moral of the story is
that you should be careful always to explain your notation to avoid confusing your readers.
Table 42: Math-Mode Versions of Text Symbols
$\mathdollar \mathparagraph £\mathsterling
. . . \mathellipsis §\mathsection \mathunderscore
It’s generally preferable to use the corresponding symbol from Table 3 on page 9
because the symbols in that table work properly in both text mode and math mode.
Table 43: cmll Unary Operators
!\oc∗ˆ\shneg ?\wn∗
˜\shift ´\shpos
∗\oc and \wn differ from “!” and “?” in terms of their math-mode spacing: $A=!B$
produces “A=!B”, for example, while $A=\oc B$ produces “A= !B”.
1In txfonts,pxfonts, and mathtools the symbol is called \coloneqq. In mathabx and MnSymbol it’s called \coloneq. In
colonequals it’s called \colonequals.
2Bob Tennent listed these and other disjoint-union symbol possibilities in a November 2007 post to comp.text.tex.
21
Table 44: Binary Operators
q\amalg ∪\cup ⊕\oplus ×\times
∗\ast †\dagger \oslash \triangleleft
\bigcirc ‡\ddagger ⊗\otimes \triangleright
5\bigtriangledown \diamond ±\pm E\unlhd∗
4\bigtriangleup ÷\div B\rhd∗D\unrhd∗
•\bullet C\lhd∗\\setminus ]\uplus
∩\cap ∓\mp u\sqcap ∨\vee
·\cdot \odot t\sqcup ∧\wedge
◦\circ \ominus \star o\wr
∗Not predefined in L
A
T
E
X 2ε. Use one of the packages latexsym,amsfonts,amssymb,
txfonts,pxfonts, or wasysym.
Table 45: A
M
SBinary Operators
Z\barwedge }\circledcirc |\intercal∗
\boxdot \circleddash h\leftthreetimes
\boxminus d\Cup \ltimes
\boxplus g\curlyvee i\rightthreetimes
\boxtimes f\curlywedge \rtimes
e\Cap \divideontimes \smallsetminus
\centerdot u\dotplus Y\veebar
~\circledast [\doublebarwedge
∗Some people use a superscripted \intercal for matrix transpose:
“A^\intercal”7→ “A|”. (See the May 2009 comp.text.tex thread, “rais-
ing math symbols”, for suggestions about altering the height of the superscript.)
\top (Table 139 on page 51), T, and \mathsf{T} are other popular choices: “A>”,
“AT”, “AT”.
Table 46: stmaryrd Binary Operators
\baro 9\interleave \varoast
\bbslash 2\leftslice \varobar
N\binampersand !\merge \varobslash
O\bindnasrepma \minuso \varocircle
i\boxast \moo \varodot
k\boxbar `\nplus 5\varogreaterthan
\boxbox :\obar 4\varolessthan
j\boxbslash @\oblong \varominus
\boxcircle ;\obslash \varoplus
\boxdot =\ogreaterthan \varoslash
\boxempty <\olessthan \varotimes
l\boxslash >\ovee 6\varovee
.\curlyveedownarrow ?\owedge 7\varowedge
/\curlyveeuparrow 3\rightslice "\vartimes
'\curlywedgedownarrow \sslash \Ydown
&\curlywedgeuparrow 8\talloblong \Yleft
)\fatbslash ,\varbigcirc \Yright
#\fatsemi \varcurlyvee \Yup
(\fatslash \varcurlywedge
22
Table 47: wasysym Binary Operators
C\lhd #\ocircle \RHD D\unrhd
\LHD B\rhd E\unlhd
Table 48: txfonts/pxfonts Binary Operators
V\circledbar T\circledwedge \medcirc
W\circledbslash M\invamp }\sqcapplus
U\circledvee \medbullet |\sqcupplus
Table 49: mathabx Binary Operators
\ast \curlywedge \sqcap
\Asterisk \divdot \sqcup
\barwedge \divideontimes \sqdoublecap
\bigstar \dotdiv \sqdoublecup
\bigvarstar \dotplus \square
\blackdiamond \dottimes \squplus
\cap \doublebarwedge \udot
\circplus \doublecap \uplus
\coasterisk \doublecup \varstar
\coAsterisk \ltimes \vee
\convolution \pluscirc \veebar
\cup \rtimes \veedoublebar
\curlyvee \sqbullet \wedge
Many of the above glyphs go by multiple names. \centerdot is equivalent to
\sqbullet, and \ast is equivalent to *.\asterisk produces the same glyph as
\ast, but as an ordinary symbol, not a binary operator. Similarly, \bigast pro-
duces a large-operator version of the \Asterisk binary operator, and \bigcoast
produces a large-operator version of the \coAsterisk binary operator.
Table 50: MnSymbol Binary Operators
\amalg \doublesqcup \righttherefore
∗\ast \doublevee \rightthreetimes
\backslashdiv \doublewedge \rightY
\bowtie ∵\downtherefore \rtimes
●\bullet \downY \slashdiv
∩\cap \dtimes \smallprod
\capdot \fivedots \sqcap
\capplus \hbipropto \sqcapdot
⋅\cdot \hdotdot \sqcapplus
○\circ \lefthalfcap \sqcup
(continued on next page)
23
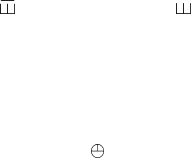
(continued from previous page)
\closedcurlyvee \lefthalfcup \sqcupdot
\closedcurlywedge \lefttherefore \sqcupplus
∪\cup \leftthreetimes ∷\squaredots
\cupdot \leftY ×\times
\cupplus \ltimes \udotdot
⋎\curlyvee \medbackslash ∴\uptherefore
\curlyveedot ◯\medcircle \upY
⋏\curlywedge ∕\medslash \utimes
\curlywedgedot \medvert \vbipropto
\ddotdot \medvertdot ∶\vdotdot
\diamonddots −\minus ∨\vee
÷\div \minusdot \veedot
\dotmedvert ∓\mp \vertbowtie
\dotminus \neswbipropto \vertdiv
\doublecap \nwsebipropto ∧\wedge
\doublecup +\plus \wedgedot
\doublecurlyvee ±\pm \wreath
\doublecurlywedge \righthalfcap
\doublesqcap \righthalfcup
MnSymbol defines \setminus and \smallsetminus as synonyms for
\medbackslash;\Join as a synonym for \bowtie;\wr as a synonym for
\wreath;\shortmid as a synonym for \medvert;\Cap as a synonym for
\doublecap;\Cup as a synonym for \doublecup; and, \uplus as a synonym for
\cupplus.
Table 51: mathdesign Binary Operators
_\dtimes ]\udtimes ^\utimes
The mathdesign package additionally provides versions of each of the binary oper-
ators shown in Table 45 on page 22.
Table 52: cmll Binary Operators
`\parr &\with∗
∗\with differs from “&” in terms of its math-mode spacing: $A \& B$ produces
“A&B”, for example, while $A \with B$ produces “A&B”.
Table 53: shuffle Binary Operators
\cshuffle \shuffle
Table 54: ulsy Geometric Binary Operators
\odplus
24
Table 55: mathabx Geometric Binary Operators
\blacktriangledown \boxright \ominus
\blacktriangleleft \boxslash \oplus
\blacktriangleright \boxtimes \oright
\blacktriangleup \boxtop \oslash
\boxasterisk \boxtriangleup \otimes
\boxbackslash \boxvoid \otop
\boxbot \oasterisk \otriangleup
\boxcirc \obackslash \ovoid
\boxcoasterisk \obot \smalltriangledown
\boxdiv \ocirc \smalltriangleleft
\boxdot \ocoasterisk \smalltriangleright
\boxleft \odiv \smalltriangleup
\boxminus \odot
\boxplus \oleft
Table 56: MnSymbol Geometric Binary Operators
\boxbackslash ▼\filledmedtriangledown \ocirc
\boxbox ◀\filledmedtriangleleft ⊙\odot
\boxdot ▶\filledmedtriangleright ⊖\ominus
\boxminus ▲\filledmedtriangleup ⊕\oplus
\boxplus \filledsquare \oslash
\boxslash ★\filledstar \ostar
\boxtimes \filledtriangledown ⊗\otimes
\boxvert \filledtriangleleft \otriangle
\diamondbackslash \filledtriangleright \overt
\diamonddiamond ▴\filledtriangleup \pentagram
\diamonddot \meddiamond ◇\smalldiamond
\diamondminus \medsquare \smallsquare
\diamondplus \medstar ☆\smallstar
\diamondslash ▽\medtriangledown ▿\smalltriangledown
\diamondtimes ◁\medtriangleleft ◃\smalltriangleleft
\diamondvert ▷\medtriangleright ▹\smalltriangleright
\downslice △\medtriangleup ▵\smalltriangleup
◆\filleddiamond \oast \thinstar
\filledmedsquare \obackslash \upslice
MnSymbol defines \blacksquare as a synonym for \filledmedsquare;\square
and \Box as synonyms for \medsquare;\diamond as a synonym for \smalldiamond;
\Diamond as a synonym for \meddiamond;\star as a synonym for \thinstar;
\circledast as a synonym for \oast;\circledcirc as a synonym for \ocirc;
and, \circleddash as a synonym for \ominus.
Table 57: Variable-sized Math Operators
T\\bigcap NO\bigotimes V^\bigwedge QY\prod
S[\bigcup FG\bigsqcup `a\coprod PX\sum
JK\bigodot U]\biguplus RZ\int
LM\bigoplus W_\bigvee HI\oint
25
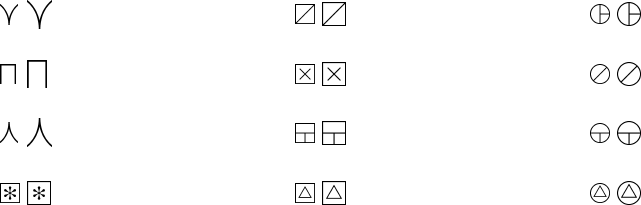
Table 58: A
M
SVariable-sized Math Operators
RR ZZ \iint RRR ZZZ \iiint
RRRRZZZZ \iiiint R···RZ···Z\idotsint
Table 59: stmaryrd Variable-sized Math Operators
em\bigbox go\biginterleave \bigsqcap
bj\bigcurlyvee \bignplus `h\bigtriangledown
ck\bigcurlywedge fn\bigparallel ai\bigtriangleup
Table 60: wasysym Variable-sized Math Operators
rw\int†!"\iint #$\iiint
rw\varint∗uz\varoint∗\oiint
None of the preceding symbols are defined when wasysym is passed the nointegrals
option.
∗Not defined when wasysym is passed the integrals option.
†Defined only when wasysym is passed the integrals option. Otherwise, the default
L
A
T
E
X\int glyph (as shown in Table 57) is used.
Table 61: mathabx Variable-sized Math Operators
\bigcurlyvee \bigboxslash \bigoright
\bigsqcap \bigboxtimes \bigoslash
\bigcurlywedge \bigboxtop \bigotop
\bigboxasterisk \bigboxtriangleup \bigotriangleup
(continued on next page)
26
(continued from previous page)
\bigboxbackslash \bigboxvoid \bigovoid
\bigboxbot \bigcomplementop \bigplus
\bigboxcirc \bigoasterisk \bigsquplus
\bigboxcoasterisk \bigobackslash \bigtimes
\bigboxdiv \bigobot \iiint
\bigboxdot \bigocirc \iint
\bigboxleft \bigocoasterisk \int
\bigboxminus \bigodiv \oiint
\bigboxplus \bigoleft \oint
\bigboxright \bigominus
Table 62: txfonts/pxfonts Variable-sized Math Operators
\bigsqcapplus \ointclockwise
\bigsqcupplus \ointctrclockwise
>?\fint RS\sqiiint
'(\idotsint PQ\sqiint
%&\iiiint \sqint
#$\iiint FG\varoiiintclockwise
(continued on next page)
27
(continued from previous page)
!"\iint NO\varoiiintctrclockwise
LM\oiiintclockwise BC\varoiintclockwise
DE\oiiintctrclockwise JK\varoiintctrclockwise
)*\oiiint -.\varointclockwise
HI\oiintclockwise +,\varointctrclockwise
@A\oiintctrclockwise \varprod
\oiint
Table 63: esint Variable-sized Math Operators
¯˙\dotsint ı\ointclockwise
ffl \fint ‰\ointctrclockwise
ˇ˘\iiiint ”„\sqiint
˝˚\iiint ›“\sqint
˜¨\iint !"\varoiint
%&\landdownint fffi\varointclockwise
#$\landupint flffi\varointctrclockwise
‚‹\oiint
28
Table 64: MnSymbol Variable-sized Math Operators
  \bigcap   \bigominus \complement
  \bigcapdot   \bigoplus   \coprod
  \bigcapplus   \bigoslash   \idotsint
  \bigcircle   \bigostar   \iiiint
  \bigcup   \bigotimes   \iiint
  \bigcupdot   \bigotriangle \iint
  \bigcupplus∗  \bigovert ∫ \int
  \bigcurlyvee   \bigplus \landdownint
  \bigcurlyveedot   \bigsqcap \landupint
  \bigcurlywedge   \bigsqcapdot \lcircleleftint
  \bigcurlywedgedot   \bigsqcapplus \lcirclerightint
  \bigdoublecurlyvee   \bigsqcup   \oiint
  \bigdoublecurlywedge   \bigsqcupdot \oint
  \bigdoublevee   \bigsqcupplus ∏  \prod
  \bigdoublewedge   \bigtimes \rcircleleftint
  \bigoast   \bigvee \rcirclerightint
  \bigobackslash   \bigveedot \strokedint
  \bigocirc   \bigwedge ∑ \sum
  \bigodot   \bigwedgedot \sumint
∗MnSymbol defines \biguplus as a synonym for \bigcupplus.
29
Table 65: mathdesign Variable-sized Math Operators
\intclockwise \ointclockwise
\oiiint \ointctrclockwise
\oiint
The mathdesign package provides three versions of each integral—in fact, of ev-
ery symbol—to accompany different text fonts: Utopia (R), Garamond (R), and
Charter (R).
Table 66: cmll Large Math Operators
˙\bigparr ˘\bigwith
Table 67: Binary Relations
≈\approx ≡\equiv ⊥\perp \smile
\asymp \frown ≺\prec \succ
\bowtie Z\Join∗\preceq \succeq
\cong |\mid†∝\propto `\vdash
a\dashv |=\models ∼\sim
\doteq k\parallel '\simeq
∗Not predefined in L
A
T
E
X 2ε. Use one of the packages latexsym,amsfonts,amssymb,
mathabx,txfonts,pxfonts, or wasysym.
†The difference between \mid and |is that the former is a binary relation while
the latter is a math ordinal. Consequently, L
A
T
E
X typesets the two with different
surrounding spacing. Contrast “P(A | B)”7→ “P(A|B)” with “P(A \mid B)”7→
“P(A|B)”.
Table 68: A
M
SBinary Relations
\approxeq P\eqcirc \succapprox
\backepsilon ;\fallingdotseq <\succcurlyeq
v\backsim (\multimap %\succsim
w\backsimeq t\pitchfork ∴\therefore
∵\because \precapprox ≈\thickapprox
G\between 4\preccurlyeq ∼\thicksim
m\Bumpeq -\precsim ∝\varpropto
l\bumpeq :\risingdotseq \Vdash
$\circeq \shortmid \vDash
2\curlyeqprec \shortparallel \Vvdash
3\curlyeqsucc a\smallfrown
+\doteqdot `\smallsmile
30
Table 69: A
M
SNegated Binary Relations
\ncong \nshortparallel \nVDash
\nmid /\nsim \precnapprox
∦\nparallel \nsucc \precnsim
⊀\nprec \nsucceq \succnapprox
\npreceq \nvDash \succnsim
\nshortmid \nvdash
Table 70: stmaryrd Binary Relations
A\inplus B\niplus
Table 71: wasysym Binary Relations
\invneg {\leadsto \wasypropto
Z\Join \logof
Table 72: txfonts/pxfonts Binary Relations
S\circledgtr X\lJoin ]\opentimes
R\circledless \\lrtimes y\Perp
\colonapprox (\multimap \preceqq
\Colonapprox \multimapboth \precneqq
D\coloneq \multimapbothvert Y\rJoin
H\Coloneq \multimapdot K\strictfi
F\Coloneqq \multimapdotboth J\strictif
B\coloneqq∗\multimapdotbothA L\strictiff
\Colonsim \multimapdotbothAvert \succeqq
\colonsim \multimapdotbothB \succneqq
I\Eqcolon \multimapdotbothBvert ∥\varparallel
E\eqcolon \multimapdotbothvert \varparallelinv
C\eqqcolon \multimapdotinv \VvDash
G\Eqqcolon \multimapinv
\eqsim [\openJoin
∗As an alternative to using txfonts/pxfonts, a “:=” symbol can be constructed with
“\mathrel{\mathop:}=”.
Table 73: txfonts/pxfonts Negated Binary Relations
6\napproxeq $\npreccurlyeq 5\nthickapprox
-\nasymp 9\npreceqq h\ntwoheadleftarrow
*\nbacksim \nprecsim g\ntwoheadrightarrow
+\nbacksimeq ;\nsimeq \nvarparallel
(\nbumpeq 8\nsuccapprox \nvarparallelinv
)\nBumpeq %\nsucccurlyeq \nVdash
.\nequiv :\nsucceqq
7\nprecapprox \nsuccsim
31
Table 74: mathabx Binary Relations
\between \divides \risingdotseq
\botdoteq \dotseq \succapprox
\Bumpedeq \eqbumped \succcurlyeq
\bumpedeq \eqcirc \succdot
\circeq \eqcolon \succsim
\coloneq \fallingdotseq \therefore
\corresponds \ggcurly \topdoteq
\curlyeqprec \llcurly \vDash
\curlyeqsucc \precapprox \Vdash
\DashV \preccurlyeq \VDash
\Dashv \precdot \Vvdash
\dashVv \precsim
Table 75: mathabx Negated Binary Relations
\napprox \notperp \nvDash
\ncong \nprec \nVDash
\ncurlyeqprec \nprecapprox \nVdash
\ncurlyeqsucc \npreccurlyeq \nvdash
\nDashv \npreceq \nVvash
\ndashV \nprecsim \precnapprox
\ndashv \nsim \precneq
\nDashV \nsimeq \precnsim
\ndashVv \nsucc \succnapprox
\neq \nsuccapprox \succneq
\notasymp \nsucccurlyeq \succnsim
\notdivides \nsucceq
\notequiv \nsuccsim
The \changenotsign command toggles the behavior of \not to produce either a
vertical or a diagonal slash through a binary operator. Thus, “$a \not= b$” can
be made to produce either “a=b” or “a=b”.
Table 76: MnSymbol Binary Relations
≈\approx \eqbump }\nwfootline ï\seVdash
\approxeq \eqcirc \nwfree \shortparallel
\backapprox \eqdot å\nwmodels ∼\sim
\backapproxeq \eqsim õ\nwModels \simeq
\backcong =\equal \nwsecrossing \succ
\backeqsim \equalclosed Ó\nwseline \succapprox
\backsim ≡\equiv ×\Nwseline \succcurlyeq
\backsimeq \equivclosed Ý\nwvdash \succeq
\backtriplesim \fallingdotseq í\nwVdash \succsim
\between \hateq \prec ~\swfootline
(continued on next page)
32
(continued from previous page)
\bumpeq \hcrossing \precapprox \swfree
\Bumpeq z\leftfootline \preccurlyeq æ\swmodels
\circeq \leftfree \preceq ö\swModels
\closedequal â\leftmodels \precsim Þ\swvdash
\closedprec ò\leftModels x\rightfootline î\swVdash
\closedsucc ∝\leftpropto \rightfree \triplesim
∶=\coloneq Ð\leftrightline ⊧\rightmodels ∣\updownline
≅\cong Ô\Leftrightline ⊫\rightModels ∥\Updownline
\curlyeqprec \leftslice \rightpropto y\upfootline
\curlyeqsucc ⊣\leftvdash \rightslice \upfree
\doteq ê\leftVdash ⊢\rightvdash á\upmodels
\Doteq |\nefootline ⊩\rightVdash ñ\upModels
{\downfootline \nefree \risingdotseq \uppropto
⫝\downfree ä\nemodels \sefootline ⊥\upvdash
ã\downmodels ô\neModels \sefree ⍊\upVdash
ó\downModels Ò\neswline ç\semodels \vcrossing
\downpropto Ö\Neswline ÷\seModels \Vvdash
⊤\downvdash Ü\nevdash \separated
⍑\downVdash ì\neVdash ß\sevdash
MnSymbol additionally defines synonyms for some of the preceding symbols:
⊣\dashv (same as \leftvdash)
Ó\diagdown (same as \nwseline)
Ò\diagup (same as \neswline)
Ò\divides (same as \updownline)
\doteqdot (same as \Doteq)
⊧\models (same as \rightmodels)
∥\parallel (same as \Updownline)
⊥\perp (same as \upvdash)
∝\propto (same as \leftpropto)
Ð\relbar (same as \leftrightline)
Ô\Relbar (same as \Leftrightline)
∝\varpropto (same as \leftpropto)
⊧\vDash (same as \rightmodels)
⊫\VDash (same as \rightModels)
⊢\vdash (same as \rightvdash)
⊩\Vdash (same as \rightVdash)
Table 77: MnSymbol Negated Binary Relations
\napprox \neqsim \nnwModels \nsucc
\napproxeq ≠\nequal \nnwseline \nsuccapprox
\nbackapprox \nequalclosed \nNwseline \nsucccurlyeq
\nbackapproxeq \nequiv \nnwvdash \nsucceq
\nbackcong \nequivclosed \nnwVdash \nsuccsim
\nbackeqsim \neswcrossing \nprec \nswfootline
\nbacksim \nfallingdotseq \nprecapprox \nswfree
(continued on next page)
33
(continued from previous page)
\nbacksimeq \nhateq \npreccurlyeq \nswmodels
\nbacktriplesim \nleftfootline \npreceq \nswModels
\nbumpeq \nleftfree \nprecsim \nswvdash
\nBumpeq \nleftmodels \nrightfootline \nswVdash
\ncirceq \nleftModels \nrightfree \ntriplesim
\nclosedequal \nleftrightline \nrightmodels \nupdownline
\ncong \nLeftrightline \nrightModels ∦\nUpdownline
\ncurlyeqprec \nleftvdash \nrightvdash \nupfootline
\ncurlyeqsucc \nleftVdash \nrightVdash \nupfree
\ndoteq \nnefootline \nrisingdotseq \nupmodels
\nDoteq \nnefree \nsefootline \nupModels
\ndownfootline \nnemodels \nsefree \nupvdash
\ndownfree \nneModels \nsemodels \nupVdash
\ndownmodels \nneswline \nseModels \precnapprox
\ndownModels \nNeswline \nsevdash \precnsim
\ndownvdash \nnevdash \nseVdash \succnapprox
\ndownVdash \nneVdash \nshortmid \succnsim
\neqbump \nnwfootline \nshortparallel
\neqcirc \nnwfree \nsim
\neqdot \nnwmodels \nsimeq
MnSymbol additionally defines synonyms for some of the preceding symbols:
\ndashv (same as \nleftvdash)
\ndiagdown (same as \nnwseline)
\ndiagup (same as \nneswline)
\ndivides (same as \nupdownline)
≠\ne (same as \nequal)
≠\neq (same as \nequal)
\nmid (same as \nupdownline)
\nmodels (same as \nrightmodels)
∦\nparallel (same as \nUpdownline)
\nperp (same as \nupvdash)
\nrelbar (same as \nleftrightline)
\nRelbar (same as \nLeftrightline)
\nvDash (same as \nrightmodels)
\nvdash (same as \nrightvdash)
\nVdash (same as \nrightVdash)
\nVDash (same as \nrightModels)
Table 78: mathtools Binary Relations
::≈\Colonapprox :−\coloneq −:: \Eqcolon
:≈\colonapprox :∼\colonsim =:\eqqcolon
:=\coloneqq ::∼\Colonsim =:: \Eqqcolon
::=\Coloneqq :: \dblcolon
::−\Coloneq −:\eqcolon
Similar symbols can be defined using mathtools’s \vcentcolon, which produces a
colon centered on the font’s math axis:
=:= vs. =:=
“=:=” “=\vcentcolon=”
34
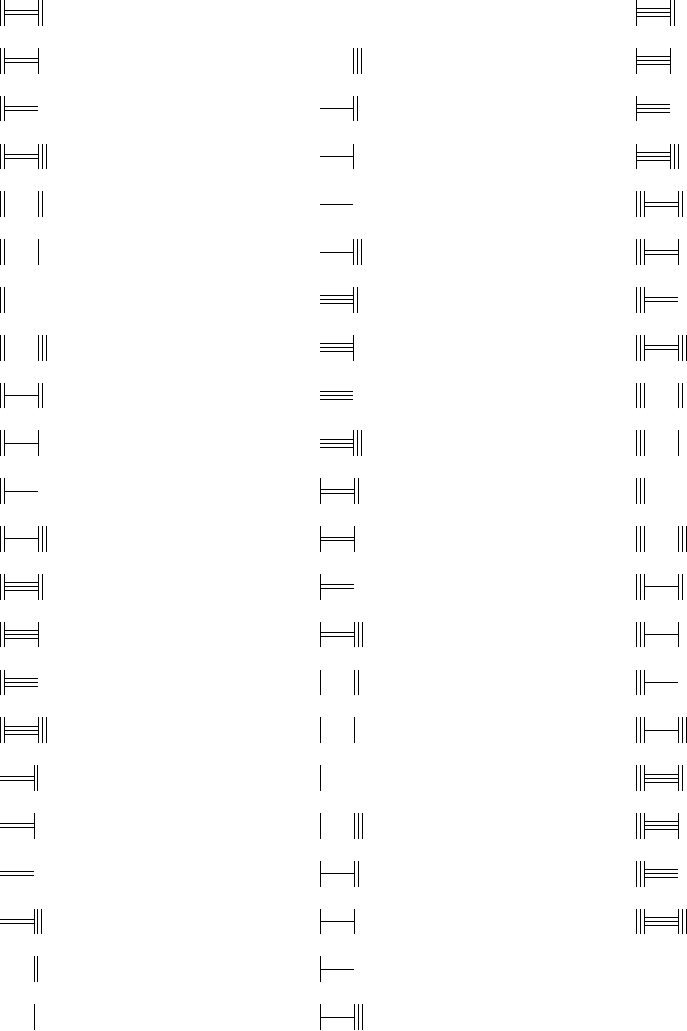
Table 79: turnstile Binary Relations
abc
def \dddtstile{abc}{def} abc
def \nntstile{abc}{def} abc
def
\stdtstile{abc}{def}
abc
def \ddststile{abc}{def} abc
def \nnttstile{abc}{def} abc
def
\stststile{abc}{def}
abc
def \ddtstile{abc}{def} abc
def \nsdtstile{abc}{def} abc
def
\sttstile{abc}{def}
abc
def \ddttstile{abc}{def} abc
def \nsststile{abc}{def} abc
def
\stttstile{abc}{def}
abc
def \dndtstile{abc}{def} abc
def \nststile{abc}{def} abc
def \tddtstile{abc}{def}
abc
def \dnststile{abc}{def} abc
def \nsttstile{abc}{def} abc
def \tdststile{abc}{def}
abc
def \dntstile{abc}{def} abc
def
\ntdtstile{abc}{def} abc
def \tdtstile{abc}{def}
abc
def \dnttstile{abc}{def} abc
def
\ntststile{abc}{def} abc
def \tdttstile{abc}{def}
abc
def \dsdtstile{abc}{def} abc
def
\nttstile{abc}{def} abc
def \tndtstile{abc}{def}
abc
def \dsststile{abc}{def} abc
def
\ntttstile{abc}{def} abc
def \tnststile{abc}{def}
abc
def \dststile{abc}{def} abc
def \sddtstile{abc}{def} abc
def \tntstile{abc}{def}
abc
def \dsttstile{abc}{def} abc
def \sdststile{abc}{def} abc
def \tnttstile{abc}{def}
abc
def
\dtdtstile{abc}{def} abc
def \sdtstile{abc}{def} abc
def \tsdtstile{abc}{def}
abc
def
\dtststile{abc}{def} abc
def \sdttstile{abc}{def} abc
def \tsststile{abc}{def}
abc
def
\dttstile{abc}{def} abc
def \sndtstile{abc}{def} abc
def \tststile{abc}{def}
abc
def
\dtttstile{abc}{def} abc
def \snststile{abc}{def} abc
def \tsttstile{abc}{def}
abc
def \nddtstile{abc}{def} abc
def \sntstile{abc}{def} abc
def
\ttdtstile{abc}{def}
abc
def \ndststile{abc}{def} abc
def \snttstile{abc}{def} abc
def
\ttststile{abc}{def}
abc
def \ndtstile{abc}{def} abc
def \ssdtstile{abc}{def} abc
def
\tttstile{abc}{def}
abc
def \ndttstile{abc}{def} abc
def \ssststile{abc}{def} abc
def
\ttttstile{abc}{def}
abc
def \nndtstile{abc}{def} abc
def \sststile{abc}{def}
abc
def \nnststile{abc}{def} abc
def \ssttstile{abc}{def}
Each of the above takes an optional argument that controls the size of the upper
and lower expressions. See the turnstile documentation for more information.
35
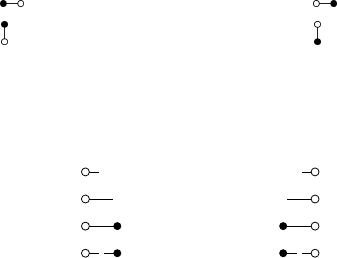
Table 80: trsym Binary Relations
\InversTransformHoriz \TransformHoriz
\InversTransformVert \TransformVert
Table 81: trfsigns Binary Relations
.
.
.
.
.
.
.
.
.
.
.\dfourier .
.
.
.
.
.
.
.
.
.
.\Dfourier
\fourier \Fourier
\laplace \Laplace
.
.
.
.
.
.
.
.
.
.
.\ztransf .
.
.
.
.
.
.
.
.
.
.\Ztransf
Table 82: cmll Binary Relations
¨\coh ˝\scoh
˚\incoh ˇ\sincoh
Table 83: colonequals Binary Relations
≈:\approxcolon ::−\coloncolonminus =:: \equalscoloncolon
≈:: \approxcoloncolon ::∼\coloncolonsim −:\minuscolon
:≈\colonapprox :=\colonequals −:: \minuscoloncolon
:: \coloncolon :−\colonminus :\ratio
::≈\coloncolonapprox :∼\colonsim ∼:\simcolon
::=\coloncolonequals =:\equalscolon ∼:: \simcoloncolon
Table 84: fourier Binary Relations
Ô\nparallelslant Ë\parallelslant
Table 85: Subset and Superset Relations
@\sqsubset∗w\sqsupseteq ⊃\supset
v\sqsubseteq ⊂\subset ⊇\supseteq
A\sqsupset∗⊆\subseteq
∗Not predefined in L
A
T
E
X 2ε. Use one of the packages latexsym,amsfonts,amssymb,
mathabx,txfonts,pxfonts, or wasysym.
Table 86: A
M
SSubset and Superset Relations
\nsubseteq j\subseteqq \supsetneqq
\nsupseteq \subsetneq \varsubsetneq
\nsupseteqq \subsetneqq \varsubsetneqq
@\sqsubset c\Supset \varsupsetneq
A\sqsupset k\supseteqq \varsupsetneqq
b\Subset \supsetneq
36
Table 87: stmaryrd Subset and Superset Relations
D\subsetplus E\supsetplus
F\subsetpluseq G\supsetpluseq
Table 88: wasysym Subset and Superset Relations
@\sqsubset A\sqsupset
Table 89: txfonts/pxfonts Subset and Superset Relations
a\nsqsubset A\nsqsupseteq ?\nSupset
@\nsqsubseteq >\nSubset
b\nsqsupset \nsubseteqq
Table 90: mathabx Subset and Superset Relations
\nsqsubset \nsupset \sqsupseteq \supseteq
\nsqSubset \nSupset \sqsupseteqq \supseteqq
\nsqsubseteq \nsupseteq \sqsupsetneq \supsetneq
\nsqsubseteqq \nsupseteqq \sqsupsetneqq \supsetneqq
\nsqsupset \sqsubset \subset \varsqsubsetneq
\nsqSupset \sqSubset \Subset \varsqsubsetneqq
\nsqsupseteq \sqsubseteq \subseteq \varsqsupsetneq
\nsqsupseteqq \sqsubseteqq \subseteqq \varsqsupsetneqq
\nsubset \sqsubsetneq \subsetneq \varsubsetneq
\nSubset \sqsubsetneqq \subsetneqq \varsubsetneqq
\nsubseteq \sqSupset \supset \varsupsetneq
\nsubseteqq \sqsupset \Supset \varsupsetneqq
Table 91: MnSymbol Subset and Superset Relations
\nSqsubset \nsubseteq \sqsubsetneq ⊆\subseteq
\nsqsubset \nsubseteqq \sqsubsetneqq \subseteqq
\nsqsubseteq \nSupset \Sqsupset \subsetneq
\nsqsubseteqq \nsupset \sqsupset \subsetneqq
\nSqsupset \nsupseteq \sqsupseteq \Supset
\nsqsupset \nsupseteqq \sqsupseteqq ⊃\supset
\nsqsupseteq \Sqsubset \sqsupsetneq ⊇\supseteq
\nsqsupseteqq \sqsubset \sqsupsetneqq \supseteqq
\nSubset \sqsubseteq \Subset \supsetneq
⊄\nsubset \sqsubseteqq ⊂\subset \supsetneqq
MnSymbol additionally defines \varsubsetneq as a synonym for \subsetneq,
\varsubsetneqq as a synonym for \subsetneqq,\varsupsetneq as a synonym
for \supsetneq, and \varsupsetneqq as a synonym for \supsetneqq.
Table 92: Inequalities
≥\geq \gg ≤\leq \ll ,\neq
37
Table 93: A
M
SInequalities
1\eqslantgtr \gtrdot Q\lesseqgtr \ngeq
0\eqslantless R\gtreqless S\lesseqqgtr \ngeqq
=\geqq T\gtreqqless ≶\lessgtr \ngeqslant
>\geqslant ≷\gtrless .\lesssim ≯\ngtr
≫\ggg &\gtrsim ≪\lll \nleq
\gnapprox \gvertneqq \lnapprox \nleqq
\gneq 5\leqq \lneq \nleqslant
\gneqq 6\leqslant \lneqq ≮\nless
\gnsim /\lessapprox \lnsim
'\gtrapprox \lessdot \lvertneqq
Table 94: wasysym Inequalities
?\apprge >\apprle
Table 95: txfonts/pxfonts Inequalities
4\ngg !\ngtrsim \nlesssim
#\ngtrapprox "\nlessapprox 3\nll
&\ngtrless '\nlessgtr
Table 96: mathabx Inequalities
\eqslantgtr \gtreqless \lesssim \ngtr
\eqslantless \gtreqqless \ll \ngtrapprox
\geq \gtrless \lll \ngtrsim
\geqq \gtrsim \lnapprox \nleq
\gg \gvertneqq \lneq \nleqq
\ggg \leq \lneqq \nless
\gnapprox \leqq \lnsim \nlessapprox
\gneq \lessapprox \lvertneqq \nlesssim
\gneqq \lessdot \neqslantgtr \nvargeq
\gnsim \lesseqgtr \neqslantless \nvarleq
\gtrapprox \lesseqqgtr \ngeq \vargeq
\gtrdot \lessgtr \ngeqq \varleq
mathabx defines \leqslant and \le as synonyms for \leq,\geqslant and \ge as
synonyms for \geq,\nleqslant as a synonym for \nleq, and \ngeqslant as a
synonym for \ngeq.
38
Table 97: MnSymbol Inequalities
\eqslantgtr \gtreqqless \lesssim \ngtreqless
\eqslantless \gtrless \ll \ngtreqlessslant
≥\geq \gtrneqqless \lll \ngtreqqless
\geqclosed \gtrsim \lnapprox \ngtrless
\geqdot ≤\leq \lneqq \nleq
\geqq \leqclosed \lnsim \nleqclosed
\geqslant \leqdot \neqslantgtr \nleqdot
\geqslantdot \leqq \neqslantless \nleqq
\gg \leqslant \ngeq \nleqslant
\ggg \leqslantdot \ngeqclosed \nleqslantdot
\gnapprox <\less \ngeqdot \nless
\gneqq \lessapprox \ngeqq \nlessclosed
\gnsim \lessclosed \ngeqslant \nlessdot
>\gtr \lessdot \ngeqslantdot \nlesseqgtr
\gtrapprox \lesseqgtr \ngg \nlesseqgtrslant
\gtrclosed \lesseqgtrslant \nggg \nlesseqqgtr
\gtrdot \lesseqqgtr \ngtr \nlessgtr
\gtreqless \lessgtr \ngtrclosed \nll
\gtreqlessslant \lessneqqgtr \ngtrdot \nlll
MnSymbol additionally defines synonyms for some of the preceding symbols:
\gggtr (same as \ggg)
\gvertneqq (same as \gneqq)
\lhd (same as \lessclosed)
\llless (same as \lll)
\lvertneqq (same as \lneqq)
\ntrianglelefteq (same as \nleqclosed)
\ntriangleleft (same as \nlessclosed)
\ntrianglerighteq (same as \ngeqclosed)
\ntriangleright (same as \ngtrclosed)
\rhd (same as \gtrclosed)
\trianglelefteq (same as \leqclosed)
\trianglerighteq (same as \geqclosed)
\unlhd (same as \leqclosed)
\unrhd (same as \geqclosed)
\vartriangleleft (same as \lessclosed)
\vartriangleright (same as \gtrclosed)
Table 98: A
M
STriangle Relations
J\blacktriangleleft \ntriangleright D\trianglerighteq
I\blacktriangleright \ntrianglerighteq C\vartriangleleft
\ntriangleleft E\trianglelefteq B\vartriangleright
\ntrianglelefteq ,\triangleq
39
Table 99: stmaryrd Triangle Relations
P\trianglelefteqslant Q\trianglerighteqslant
R\ntrianglelefteqslant S\ntrianglerighteqslant
Table 100: mathabx Triangle Relations
\ntriangleleft \ntrianglerighteq \triangleright \vartriangleright
\ntrianglelefteq \triangleleft \trianglerighteq
\ntriangleright \trianglelefteq \vartriangleleft
Table 101: MnSymbol Triangle Relations
▼\filledmedtriangledown \largetriangleup ▿\smalltriangledown
◀\filledmedtriangleleft ▽\medtriangledown ◃\smalltriangleleft
▶\filledmedtriangleright ◁\medtriangleleft ▹\smalltriangleright
▲\filledmedtriangleup ▷\medtriangleright ▵\smalltriangleup
\filledtriangledown △\medtriangleup \triangleeq
\filledtriangleleft \ntriangleeq \trianglelefteq
\filledtriangleright \ntriangleleft \trianglerighteq
▴\filledtriangleup \ntrianglelefteq \vartriangleleft
\largetriangledown \ntriangleright \vartriangleright
\largetriangleleft \ntrianglerighteq
\largetriangleright \otriangle
MnSymbol additionally defines synonyms for many of the preceding sym-
bols: \triangleq is a synonym for \triangleeq;\lhd and \lessclosed
are synonyms for \vartriangleleft;\rhd and \gtrclosed are syn-
onyms for \vartriangleright;\unlhd and \leqclosed are syn-
onyms for \trianglelefteq;\unrhd and \geqclosed are synonyms
for \trianglerighteq;\blacktriangledown,\blacktriangleleft,
\blacktriangleright, and \blacktriangle [sic] are synonyms for,
respectively, \filledmedtriangledown,\filledmedtriangleleft,
\filledmedtriangleright, and \filledmedtriangleup;\triangleright
is a synonym for \medtriangleright;\triangle,\vartriangle, and
\bigtriangleup are synonyms for \medtriangleup;\triangleleft is a
synonym for \medtriangleleft;\triangledown and \bigtriangledown are syn-
onyms for \medtriangledown;\nlessclosed is a synonym for \ntriangleleft;
\ngtrclosed is a synonym for \ntriangleright;\nleqclosed is a synonym for
\ntrianglelefteq; and \ngeqclosed is a synonym for \ntrianglerighteq.
The title “Triangle Relations” is a bit of a misnomer here as only \triangleeq
and \ntriangleeq are defined as T
E
X relations (class 3 symbols). The
\largetriangle. . . symbols are defined as T
E
X “ordinary” characters (class 0)
and all of the remaining characters are defined as T
E
X binary operators (class 2).
40
Table 102: Arrows
⇓\Downarrow ←− \longleftarrow -\nwarrow
↓\downarrow ⇐=\Longleftarrow ⇒\Rightarrow
←\hookleftarrow ←→ \longleftrightarrow →\rightarrow
→\hookrightarrow ⇐⇒ \Longleftrightarrow &\searrow
{\leadsto∗7−→ \longmapsto .\swarrow
←\leftarrow =⇒\Longrightarrow ↑\uparrow
⇐\Leftarrow −→ \longrightarrow ⇑\Uparrow
⇔\Leftrightarrow 7→ \mapsto l\updownarrow
↔\leftrightarrow %\nearrow†m\Updownarrow
∗Not predefined in L
A
T
E
X 2ε. Use one of the packages latexsym,amsfonts,amssymb,
txfonts,pxfonts, or wasysym.
†See the note beneath Table 169 for information about how to put a diagonal arrow
across a mathematical expression (as in “ 0
∇ ·
B”) .
Table 103: Harpoons
\leftharpoondown \rightharpoondown
\rightleftharpoons
\leftharpoonup \rightharpoonup
Table 104: textcomp Text-mode Arrows
↓\textdownarrow →\textrightarrow
←\textleftarrow ↑\textuparrow
Table 105: A
M
SArrows
\circlearrowleft ⇔\leftleftarrows \rightleftarrows
\circlearrowright \leftrightarrows ⇒\rightrightarrows
\curvearrowleft !\leftrightsquigarrow \rightsquigarrow
\curvearrowright W\Lleftarrow \Rsh
c\dashleftarrow "\looparrowleft \twoheadleftarrow
d\dashrightarrow #\looparrowright \twoheadrightarrow
\downdownarrows \Lsh \upuparrows
\leftarrowtail \rightarrowtail
Table 106: A
M
SNegated Arrows
\nLeftarrow \nLeftrightarrow \nRightarrow
\nleftarrow \nleftrightarrow \nrightarrow
Table 107: A
M
SHarpoons
\downharpoonleft \leftrightharpoons \upharpoonleft
\downharpoonright \rightleftharpoons \upharpoonright
41
Table 108: stmaryrd Arrows
^\leftarrowtriangle ⇐\\Mapsfrom \shortleftarrow
-\leftrightarroweq ←[\mapsfrom \shortrightarrow
]\leftrightarrowtriangle ⇒\Mapsto \shortuparrow
\lightning 1\nnearrow %\ssearrow
⇐=\\Longmapsfrom 0\nnwarrow $\sswarrow
←−[\longmapsfrom _\rightarrowtriangle
=⇒\Longmapsto \shortdownarrow
Table 109: txfonts/pxfonts Arrows
\boxdotLeft \circleddotright \Diamondleft
\boxdotleft \circleleft \Diamondright
\boxdotright \circleright \DiamondRight
\boxdotRight e\dashleftrightarrow f\leftsquigarrow
\boxLeft \DiamonddotLeft t\Nearrow
\boxleft \Diamonddotleft v\Nwarrow
\boxright \Diamonddotright V\Rrightarrow
\boxRight \DiamonddotRight u\Searrow
\circleddotleft \DiamondLeft w\Swarrow
Table 110: mathabx Arrows
\circlearrowleft \leftarrow \nwarrow
\circlearrowright \leftleftarrows \restriction
\curvearrowbotleft \leftrightarrow \rightarrow
\curvearrowbotleftright \leftrightarrows \rightleftarrows
\curvearrowbotright \leftrightsquigarrow \rightrightarrows
\curvearrowleft \leftsquigarrow \rightsquigarrow
\curvearrowleftright \lefttorightarrow \righttoleftarrow
\curvearrowright \looparrowdownleft \Rsh
\dlsh \looparrowdownright \searrow
\downdownarrows \looparrowleft \swarrow
\downtouparrow \looparrowright \updownarrows
\downuparrows \Lsh \uptodownarrow
\drsh \nearrow \upuparrows
Table 111: mathabx Negated Arrows
\nLeftarrow \nleftrightarrow \nrightarrow
\nleftarrow \nLeftrightarrow \nRightarrow
42
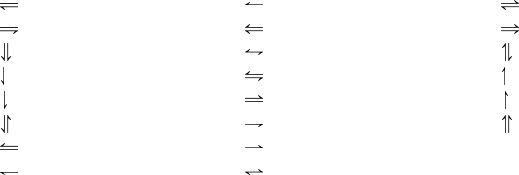
Table 112: mathabx Harpoons
\barleftharpoon \leftharpoonup \rightleftharpoons
\barrightharpoon \leftleftharpoons \rightrightharpoons
\downdownharpoons \leftrightharpoon \updownharpoons
\downharpoonleft \leftrightharpoons \upharpoonleft
\downharpoonright \rightbarharpoon \upharpoonright
\downupharpoons \rightharpoondown \upupharpoons
\leftbarharpoon \rightharpoonup
\leftharpoondown \rightleftharpoon
Table 113: MnSymbol Arrows
Ë\curvearrowdownup ←Ð \longleftarrow ⤦\rhookswarrow
È\curvearrowleftright ⇐Ô \Longleftarrow 9\rhookuparrow
Ì\curvearrownesw ←→ \longleftrightarrow →\rightarrow
Í\curvearrownwse ⇐⇒ \Longleftrightarrow ⇒\Rightarrow
Ê\curvearrowrightleft z→ \longmapsto ↣\rightarrowtail
Ï\curvearrowsenw Ð→ \longrightarrow ⇄\rightleftarrows
Î\curvearrowswne Ô⇒ \Longrightarrow ↝\rightlsquigarrow
É\curvearrowupdown \looparrowleft ↦\rightmapsto
⇣\dasheddownarrow \looparrowright ⇉\rightrightarrows
⇠\dashedleftarrow \Lsh ¨\rightrsquigarrow
d\dashednearrow ↗\nearrow \Rrightarrow
e\dashednwarrow ⇗\Nearrow \Rsh
⇢\dashedrightarrow $\nearrowtail ↘\searrow
g\dashedsearrow ¤\nelsquigarrow ⇘\Searrow
f\dashedswarrow ,\nemapsto '\searrowtail
⇡\dasheduparrow \nenearrows §\selsquigarrow
⇓\Downarrow ¬\nersquigarrow /\semapsto
↓\downarrow ⤡\neswarrow \senwarrows
#\downarrowtail \Neswarrow ¯\sersquigarrow
⇊\downdownarrows \neswarrows \sesearrows
£\downlsquigarrow ↖\nwarrow ³\squigarrowdownup
↧\downmapsto ⇖\Nwarrow ↭\squigarrowleftright
«\downrsquigarrow %\nwarrowtail ´\squigarrownesw
\downuparrows ¥\nwlsquigarrow µ\squigarrownwse
ÿ\lcirclearrowdown -\nwmapsto ²\squigarrowrightleft
⤾\lcirclearrowleft \nwnwarrows ·\squigarrowsenw
⟳\lcirclearrowright \nwrsquigarrow \squigarrowswne
↻\lcirclearrowup ⤢\nwsearrow ±\squigarrowupdown
⤸\lcurvearrowdown \Nwsearrow ↙\swarrow
º\lcurvearrowleft \nwsearrows ⇙\Swarrow
¼\lcurvearrowne \partialvardlcircleleftint∗&\swarrowtail
½\lcurvearrownw \partialvardlcirclerightint∗¦\swlsquigarrow
↷\lcurvearrowright \partialvardrcircleleftint∗.\swmapsto
¿\lcurvearrowse \partialvardrcirclerightint∗\swnearrows
¾\lcurvearrowsw \partialvartlcircleleftint∗®\swrsquigarrow
¹\lcurvearrowup \partialvartlcirclerightint∗\swswarrows
⇐\Leftarrow \partialvartrcircleleftint∗↡\twoheaddownarrow
(continued on next page)
43
(continued from previous page)
←\leftarrow \partialvartrcirclerightint∗↞\twoheadleftarrow
↢\leftarrowtail û\rcirclearrowdown \twoheadnearrow
⇇\leftleftarrows ⟲\rcirclearrowleft \twoheadnwarrow
¢\leftlsquigarrow ⤿\rcirclearrowright ↠\twoheadrightarrow
↤\leftmapsto ↺\rcirclearrowup \twoheadsearrow
↔\leftrightarrow ⤹\rcurvearrowdown \twoheadswarrow
⇔\Leftrightarrow ↶\rcurvearrowleft ↟\twoheaduparrow
⇆\leftrightarrows Ä\rcurvearrowne ↑\uparrow
↜\leftrsquigarrow Å\rcurvearrownw ⇑\Uparrow
3\lhookdownarrow À\rcurvearrowright !\uparrowtail
2\lhookleftarrow Ç\rcurvearrowse ↕\updownarrow
4\lhooknearrow Æ\rcurvearrowsw ⇕\Updownarrow
⤣\lhooknwarrow Á\rcurvearrowup \updownarrows
↪\lhookrightarrow ;\rhookdownarrow ¡\uplsquigarrow
⤥\lhooksearrow ↩\rhookleftarrow ↥\upmapsto
6\lhookswarrow ⤤\rhooknearrow ©\uprsquigarrow
1\lhookuparrow =\rhooknwarrow ⇈\upuparrows
\lightning 8\rhookrightarrow
\Lleftarrow ?\rhooksearrow
MnSymbol additionally defines synonyms for some of the preceding symbols:
↺\circlearrowleft (same as \rcirclearrowup)
↻\circlearrowright (same as \lcirclearrowup)
↶\curvearrowleft (same as \rcurvearrowleft)
↷\curvearrowright (same as \lcurvearrowright)
⇠\dashleftarrow (same as \dashedleftarrow)
⇢\dashrightarrow (same as \dashedrightarrow)
↩\hookleftarrow (same as \rhookleftarrow)
↪\hookrightarrow (same as \lhookrightarrow)
↝\leadsto (same as \rightlsquigarrow)
↭\leftrightsquigarrow (same as \squigarrowleftright)
↦\mapsto (same as \rightmapsto)
↝\rightsquigarrow (same as \rightlsquigarrow)
∗The \partialvar. . . int macros are intended to be used internally by MnSymbol
to produce various types of integrals.
Table 114: MnSymbol Negated Arrows
\ncurvearrowdownup \nlhooknwarrow \nrightleftarrows
\ncurvearrowleftright \nlhookrightarrow \nrightlsquigarrow
\ncurvearrownesw \nlhooksearrow \nrightmapsto
\ncurvearrownwse \nlhookswarrow \nrightrightarrows
\ncurvearrowrightleft \nlhookuparrow \nrightrsquigarrow
\ncurvearrowsenw \nLleftarrow \nRrightarrow
\ncurvearrowswne \nnearrow \nSearrow
\ncurvearrowupdown \nNearrow \nsearrow
(continued on next page)
44
(continued from previous page)
\ndasheddownarrow \nnearrowtail \nsearrowtail
\ndashedleftarrow \nnelsquigarrow \nselsquigarrow
\ndashednearrow \nnemapsto \nsemapsto
\ndashednwarrow \nnenearrows \nsenwarrows
\ndashedrightarrow \nnersquigarrow \nsersquigarrow
\ndashedsearrow \nNeswarrow \nsesearrows
\ndashedswarrow \nneswarrow \nsquigarrowdownup
\ndasheduparrow \nneswarrows \nsquigarrowleftright
\ndownarrow \nNwarrow \nsquigarrownesw
\nDownarrow \nnwarrow \nsquigarrownwse
\ndownarrowtail \nnwarrowtail \nsquigarrowrightleft
\ndowndownarrows \nnwlsquigarrow \nsquigarrowsenw
\ndownlsquigarrow \nnwmapsto \nsquigarrowswne
\ndownmapsto \nnwnwarrows \nsquigarrowupdown
\ndownrsquigarrow \nnwrsquigarrow \nswarrow
\ndownuparrows \nnwsearrow \nSwarrow
\nlcirclearrowdown \nNwsearrow \nswarrowtail
\nlcirclearrowleft \nnwsearrows \nswlsquigarrow
\nlcirclearrowright \nrcirclearrowdown \nswmapsto
\nlcirclearrowup \nrcirclearrowleft \nswnearrows
\nlcurvearrowdown \nrcirclearrowright \nswrsquigarrow
\nlcurvearrowleft \nrcirclearrowup \nswswarrows
\nlcurvearrowne \nrcurvearrowdown \ntwoheaddownarrow
\nlcurvearrownw \nrcurvearrowleft \ntwoheadleftarrow
\nlcurvearrowright \nrcurvearrowne \ntwoheadnearrow
\nlcurvearrowse \nrcurvearrownw \ntwoheadnwarrow
\nlcurvearrowsw \nrcurvearrowright \ntwoheadrightarrow
\nlcurvearrowup \nrcurvearrowse \ntwoheadsearrow
\nLeftarrow \nrcurvearrowsw \ntwoheadswarrow
\nleftarrow \nrcurvearrowup \ntwoheaduparrow
\nleftarrowtail \nrhookdownarrow \nuparrow
\nleftleftarrows \nrhookleftarrow \nUparrow
\nleftlsquigarrow \nrhooknearrow \nuparrowtail
\nleftmapsto \nrhooknwarrow \nupdownarrow
\nleftrightarrow \nrhookrightarrow \nUpdownarrow
\nLeftrightarrow \nrhooksearrow \nupdownarrows
\nleftrightarrows \nrhookswarrow \nuplsquigarrow
\nleftrsquigarrow \nrhookuparrow \nupmapsto
\nlhookdownarrow \nrightarrow \nuprsquigarrow
\nlhookleftarrow ⇏\nRightarrow \nupuparrows
\nlhooknearrow \nrightarrowtail
MnSymbol additionally defines synonyms for some of the preceding symbols:
45
\ncirclearrowleft (same as \nrcirclearrowup)
\ncirclearrowright (same as \nlcirclearrowup)
\ncurvearrowleft (same as \nrcurvearrowleft)
\ncurvearrowright (same as \nlcurvearrowright)
\ndasharrow (same as \ndashedrightarrow)
\ndashleftarrow (same as \ndashedleftarrow)
\ndashrightarrow (same as \ndashedrightarrow)
\ngets (same as \nleftarrow)
\nhookleftarrow (same as \nrhookleftarrow)
\nhookrightarrow (same as \nlhookrightarrow)
\nleadsto (same as \nrightlsquigarrow)
\nleftrightsquigarrow (same as \nsquigarrowleftright)
\nmapsto (same as \nrightmapsto)
\nrightsquigarrow (same as \nrightlsquigarrow)
\nto (same as \nrightarrow)
Table 115: MnSymbol Harpoons
⇂\downharpoonccw∗Z\neswharpoons O\seharpooncw
⇃\downharpooncw∗V\neswharpoonsenw [\senwharpoons
⥯\downupharpoons E\nwharpoonccw F\swharpoonccw
↽\leftharpoonccw∗M\nwharpooncw N\swharpooncw
↼\leftharpooncw∗S\nwseharpoonnesw ^\swneharpoons
⥊\leftrightharpoondownup _\nwseharpoons Q\updownharpoonleftright
⇋\leftrightharpoons W\nwseharpoonswne U\updownharpoonrightleft
⥋\leftrightharpoonupdown ⇀\rightharpoonccw∗⥮\updownharpoons
D\neharpoonccw ⇁\rightharpooncw∗↿\upharpoonccw∗
L\neharpooncw ⇌\rightleftharpoons ↾\upharpooncw∗
R\neswharpoonnwse G\seharpoonccw
∗Where marked, the “ccw” suffix can be replaced with “up” and the “cw” suf-
fix can be replaced with “down”. (In addition, \upharpooncw can be written as
\restriction.)
Table 116: MnSymbol Negated Harpoons
\ndownharpoonccw∗\nneswharpoons \nseharpooncw
\ndownharpooncw∗\nneswharpoonsenw \nsenwharpoons
\ndownupharpoons \nnwharpoonccw \nswharpoonccw
\nleftharpoonccw∗\nnwharpooncw \nswharpooncw
\nleftharpooncw∗\nnwseharpoonnesw \nswneharpoons
\nleftrightharpoondownup \nnwseharpoons \nupdownharpoonleftright
\nleftrightharpoons \nnwseharpoonswne \nupdownharpoonrightleft
\nleftrightharpoonupdown \nrightharpoonccw∗\nupdownharpoons
\nneharpoonccw \nrightharpooncw∗\nupharpoonccw∗
\nneharpooncw \nrightleftharpoons \nupharpooncw∗
\nneswharpoonnwse \nseharpoonccw
∗Where marked, the “ccw” suffix can be replaced with “up” and the “cw” suffix
can be replaced with “down”. (In addition, \nupharpooncw can be written as
\nrestriction.)
46
Table 117: harpoon Extensible Harpoons
abc \overleftharp{abc}
abc \overrightharpdown{abc}
abc \underrightharp{abc}
abc \overleftharpdown{abc}
abc \underleftharp{abc}
abc \underrightharpdown{abc}
abc \overrightharp{abc}
abc \underleftharpdown{abc}
All of the harpoon symbols are implemented using the graphics package (specifically,
graphics’s \resizebox command). Consequently, only T
E
X backends that support
graphical transformations (e.g., not Xdvi) can properly display these symbols.
Table 118: chemarrow Arrows
A\chemarrow
Table 119: fge Arrows
!\fgerightarrow "\fgeuparrow
Table 120: MnSymbol Spoons
s\downfilledspoon \nnespoon u\nwfilledspoon
⫰\downspoon \nnwfilledspoon m\nwspoon
r\leftfilledspoon \nnwspoon p\rightfilledspoon
⟜\leftspoon \nrightfilledspoon ⊸\rightspoon∗
\ndownfilledspoon \nrightspoon∗w\sefilledspoon
\ndownspoon \nsefilledspoon o\sespoon
t\nefilledspoon \nsespoon v\swfilledspoon
l\nespoon \nswfilledspoon n\swspoon
\nleftfilledspoon \nswspoon q\upfilledspoon
\nleftspoon \nupfilledspoon ⫯\upspoon
\nnefilledspoon \nupspoon
∗MnSymbol defines \multimap as a synonym for \rightspoon and \nmultimap as
a synonym for \nrightspoon.
Table 121: MnSymbol Pitchforks
⫛\downpitchfork \nnwpitchfork \rightpitchfork
\leftpitchfork \nrightpitchfork \sepitchfork
\ndownpitchfork \nsepitchfork \swpitchfork
\nepitchfork \nswpitchfork ⋔\uppitchfork
\nleftpitchfork \nuppitchfork
\nnepitchfork \nwpitchfork
∗MnSymbol defines \pitchfork as a synonym for \uppitchfork and \npitchfork
as a synonym for \nuppitchfork.
47
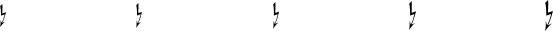
Table 122: MnSymbol Smiles and Frowns
\doublefrown \nsmileeq \smileeq
\doublefrowneq \nsmileeqfrown \smileeqfrown
\doublesmile \nsmilefrown \smilefrown
\doublesmileeq \nsmilefrowneq \smilefrowneq
\eqfrown \nsqdoublefrown \sqdoublefrown
\eqsmile \nsqdoublefrowneq \sqdoublefrowneq
\frown \nsqdoublesmile \sqdoublesmile
\frowneq \nsqdoublesmileeq \sqdoublesmileeq
\frowneqsmile \nsqeqfrown \sqeqfrown
\frownsmile \nsqeqsmile \sqeqsmile
\frownsmileeq \nsqfrown \sqfrown
\ndoublefrown \nsqfrowneq \sqfrowneq
\ndoublefrowneq \nsqfrowneqsmile \sqfrowneqsmile
\ndoublesmile \nsqfrownsmile \sqfrownsmile
\ndoublesmileeq \nsqsmile \sqsmile
\neqfrown \nsqsmileeq \sqsmileeq
\neqsmile \nsqsmileeqfrown \sqsmileeqfrown
\nfrown \nsqsmilefrown \sqsmilefrown
\nfrowneq \nsqtriplefrown \sqtriplefrown
\nfrowneqsmile \nsqtriplesmile \sqtriplesmile
\nfrownsmile \ntriplefrown \triplefrown
\nfrownsmileeq \ntriplesmile \triplesmile
\nsmile \smile
∗MnSymbol defines \smallsmile as a synonym for \smile,\smallfrown as a syn-
onym for \frown,\asymp as a synonym for \smilefrown, and \nasymp as a syn-
onym for \nsmilefrown.
Table 123: ulsy Contradiction Symbols
\blitza \blitzb \blitzc \blitzd \blitze
Table 124: Extension Characters
−\relbar =\Relbar
Table 125: stmaryrd Extension Characters
Y\Arrownot \\Mapsfromchar \Mapstochar
X\arrownot [\mapsfromchar
Table 126: txfonts/pxfonts Extension Characters
\Mappedfromchar \Mmappedfromchar \Mmapstochar
\mappedfromchar \mmappedfromchar \mmapstochar
48
Table 127: mathabx Extension Characters
\mapsfromchar \mapstochar
\Mapsfromchar \Mapstochar
Table 128: Log-like Symbols
\arccos \cos \csc \exp \ker \limsup \min \sinh
\arcsin \cosh \deg \gcd \lg \ln \Pr \sup
\arctan \cot \det \hom \lim \log \sec \tan
\arg \coth \dim \inf \liminf \max \sin \tanh
Calling the above “symbols” may be a bit misleading.3Each log-like symbol merely
produces the eponymous textual equivalent, but with proper surrounding spac-
ing. See Section 8.4 for more information about log-like symbols. As \bmod and
\pmod are arguably not symbols we refer the reader to the Short Math Guide for
L
A
T
E
X [Dow00] for samples.
Table 129: A
M
SLog-like Symbols
inj lim \injlim lim
−→ \varinjlim lim \varlimsup
proj lim \projlim lim \varliminf lim
←− \varprojlim
Load the amsmath package to get these symbols. See Section 8.4 for some additional
comments regarding log-like symbols. As \mod and \pod are arguably not symbols
we refer the reader to the Short Math Guide for L
A
T
E
X [Dow00] for samples.
Table 130: C
h
in
A2e Number Sets
\Complex \Integer \Natural \Rational \Real
\COMPLEX \INTEGER \NATURAL \RATIONAL \REAL
3Michael J. Downes prefers the more general term, “atomic math objects”.
49
Table 131: Greek Letters
α\alpha θ\theta ooτ\tau
β\beta ϑ\vartheta π\pi υ\upsilon
γ\gamma ι\iota \varpi φ\phi
δ\delta κ\kappa ρ\rho ϕ\varphi
\epsilon λ\lambda \varrho χ\chi
ε\varepsilon µ\mu σ\sigma ψ\psi
ζ\zeta ν\nu ς\varsigma ω\omega
η\eta ξ\xi
Γ\Gamma Λ\Lambda Σ\Sigma Ψ\Psi
∆\Delta Ξ\Xi Υ\Upsilon Ω\Omega
Θ\Theta Π\Pi Φ\Phi
The remaining Greek majuscules can be produced with ordinary Latin letters. The
symbol “M”, for instance, is used for both an uppercase “m” and an uppercase “µ”.
See Section 8.5 for examples of how to produce bold Greek letters.
The symbols in this table are intended to be used in mathematical typesetting.
Greek body text can be typeset using the babel package’s greek (or polutonikogreek)
option—and, of course, a font that provides the glyphs for the Greek alphabet.
Table 132: A
M
SGreek Letters
\digamma κ\varkappa
Table 133: txfonts/pxfonts Upright Greek Letters
α\alphaup θ\thetaup π\piup φ\phiup
β\betaup ϑ\varthetaup $\varpiup ϕ\varphiup
γ\gammaup ι\iotaup ρ\rhoup χ\chiup
δ\deltaup κ\kappaup %\varrhoup ψ\psiup
\epsilonup λ\lambdaup σ\sigmaup ω\omegaup
ε\varepsilonup µ\muup ς\varsigmaup
ζ\zetaup ν\nuup τ\tauup
η\etaup ξ\xiup υ\upsilonup
50
Table 134: upgreek Upright Greek Letters
α\upalpha θ\uptheta π\uppi φ\upphi
β\upbeta ϑ\upvartheta ϖ\upvarpi ϕ\upvarphi
γ\upgamma ι\upiota ρ\uprho χ\upchi
δ\updelta κ\upkappa ρ\upvarrho ψ\uppsi
ε\upepsilon λ\uplambda σ\upsigma ω\upomega
ε\upvarepsilon µ\upmu σ\upvarsigma
ζ\upzeta ν\upnu τ\uptau
η\upeta ξ\upxi υ\upupsilon
Γ\Upgamma Λ\Uplambda Σ\Upsigma Ψ\Uppsi
∆\Updelta Ξ\Upxi Υ\Upupsilon Ω\Upomega
Θ\Uptheta Π\Uppi Φ\Upphi
upgreek utilizes upright Greek characters from either the PostScript Symbol font
(depicted above) or Euler Roman. As a result, the glyphs may appear slightly
different from the above. Contrast, for example, “Γ∆Θαβγ” (Symbol) with
“Γ∆Θαβγ” (Euler).
Table 135: fourier Variant Greek Letters
π\pi ρ\rho
$\varpi %\varrho
È\varvarpi Æ\varvarrho
Table 136: txfonts/pxfonts Variant Latin Letters
1\varg 3\varv 4\varw 2\vary
Pass the varg option to txfonts/pxfonts to replace g,v,w, and ywith 1,3,4, and 2
in every mathematical expression in your document.
Table 137: A
M
SHebrew Letters
\beth ג\gimel \daleth
\aleph (ℵ) appears in Table 201 on page 65.
Table 138: MnSymbol Hebrew Letters
ℵ\aleph \beth \gimel \daleth
Table 139: Letter-like Symbols
⊥\bot ∀\forall ı\imath 3\ni >\top
\ell \hbar ∈\in ∂\partial ℘\wp
∃\exists =\Im \jmath <\Re
51
Table 140: A
M
SLetter-like Symbols
k\Bbbk {\complement \hbar
r\circledR \Finv \hslash
s\circledS \Game \nexists
Table 141: txfonts/pxfonts Letter-like Symbols
¢\mathcent £\mathsterling∗<\notin =\notni
∗It’s generally preferable to use the corresponding symbol from Table 3 on page 9
because the symbols in that table work properly in both text mode and math mode.
Table 142: mathabx Letter-like Symbols
\barin \in \nottop \varnotin
\complement \nexists \owns \varnotowner
\exists \notbot \ownsbar
\Finv \notin \partial
\Game \notowner \partialslash
Table 143: MnSymbol Letter-like Symbols
\bot ∈\in \nowns∗\top
∃\exists \nexists ∋\owns ℘\wp
∀\forall ∉\nin∗\powerset
∗MnSymbol provides synonyms \notin for \nin,\ni for \owns, and \intercal for
\top.
Table 144: trfsigns Letter-like Symbols
e\e j\im
Table 145: mathdesign Letter-like Symbols
∈\in 3\owns
6∈ \notin \smallin
\notsmallin \smallowns
\notsmallowns
The mathdesign package additionally provides versions of each of the letter-like
symbols shown in Table 140.
52
Table 146: fge Letter-like Symbols
A\fgeA ı\fgeeszett D\fgeleftB U\fgeU
c\fgec F\fgeF C\fgeleftC
p\fged f\fgef B\fgerightB
e\fgee ”\fgelb∗s\fges
∗The fge package defines \fgeeta,\fgeN, and \fgeoverU as synonyms for \fgelb.
Table 147: fourier Letter-like Symbols
∂\partial
Ç\varpartialdiff
Table 148: A
M
SDelimiters
p\ulcorner q\urcorner
x\llcorner y\lrcorner
Table 149: stmaryrd Delimiters
P\Lbag Q\Rbag N\lbag O\rbag
V\llceil W\rrceil T\llfloor U\rrfloor
L\llparenthesis M\rrparenthesis
Table 150: mathabx Delimiters
\lcorners \rcorners
\ulcorner \urcorner
\llcorner \lrcorner
Table 151: nath Delimiters
\niv \vin
53
Table 152: Variable-sized Delimiters
↓
y\downarrow ⇓w
w
\Downarrow [h[]i]
hD\langle iE\rangle ||k
\|
dl\lceil em\rceil ↑x
\uparrow ⇑~
w
w\Uparrow
bj\lfloor ck\rfloor lx
y\updownarrow m~
w
\Updownarrow
(()){n\{ }o\}
/./\/\backslash
When used with \left and \right, these symbols expand to the height of the
enclosed math expression. Note that \vert is a synonym for |, and \Vert is a
synonym for \|.
ε-T
E
X provides a \middle analogue to \left and \right.\middle can be used, for
example, to make an internal “|” expand to the height of the surrounding \left and
\right symbols. (This capability is commonly needed when typesetting adjacent
bras and kets in Dirac notation: “hφ|ψi”). A similar effect can be achieved in
conventional L
A
T
E
X using the braket package.
Table 153: Large, Variable-sized Delimiters
\lmoustache
\rmoustache
\lgroup
\rgroup
\arrowvert w
ww
w
w
w
w\Arrowvert
\bracevert
These symbols must be used with \left and \right. The mathabx package, how-
ever, redefines \lgroup and \rgroup so that those symbols can work without \left
and \right.
Table 154: A
M
SVariable-sized Delimiters
|\lvert |\rvert
k
\lVert k
\rVert
According to the amsmath documentation [AMS99], the preceding symbols are
intended to be used as delimiters (e.g., as in “|−z|”) while the \vert and \Vert
symbols (Table 152) are intended to be used as operators (e.g., as in “p|q”).
Table 155: stmaryrd Variable-sized Delimiters
~\llbracket \rrbracket
54
Table 156: mathabx Variable-sized Delimiters
\ldbrack \rdbrack
\lfilet \rfilet
\thickvert \vvvert
Table 157: MnSymbol Variable-sized Delimiters
\lceil
\rceil \ulcorner \urcorner
\lfloor
\rfloor \llcorner \lrcorner
\lwavy
\rwavy \langle \rangle
\lWavy
\rWavy \langlebar \ranglebar
( )
\lgroup
\rgroup
\lsem
\rsem \llangle \rrangle
\lmoustache
\rmoustache
\lbrace
\rbrace
/ \backslash < >
[
] \ullcorner \ulrcorner
|
\|
\bracevert
\arrowvert
\Arrowvert
55
\vert is a synonym for |.\Vert is a synonym for \|.\mid and \mvert produce
the same symbol as \vert but designated as math relations instead of ordinals.
\divides produces the same symbol as \vert but designated as a binary operator
instead of an ordinal. \parallel and \mVert produce the same symbol as \Vert
but designated as math relations instead of ordinals.
Table 158: mathdesign Variable-sized Delimiters
Ð
Ð
Ð
Ð
Ð
\leftwave Ð
Ð
Ð
Ð
Ð
\rightwave
Ñ
Ñ
Ñ
Ñ
Ñ
\leftevaw Ñ
Ñ
Ñ
Ñ
Ñ
\rightevaw
The definitions of these symbols include a preceding \left or \right. It is therefore
an error to specify \left or \right explicitly. The internal, “primitive” versions
of these symbols are called \lwave,\rwave,\levaw, and \revaw.
Table 159: nath Variable-sized Delimiters (Double)
hh DD \lAngle ii EE \rAngle
[[ hh \lBrack ]] ii \rBrack
dd ll \lCeil ee mm \rCeil
bb jj \lFloor cc kk \rFloor
|| \lVert∗|| \rVert∗
∗nath redefines all of the above to include implicit \left and \right commands.
Hence, separate \lVert and \rVert commands are needed to disambiguate whether
“|” is a left or right delimiter.
All of the symbols in Table 159 can also be expressed using the \double macro.
See the nath documentation for examples and additional information.
56
Table 160: nath Variable-sized Delimiters (Triple)
hhh DDD \triple< iii EEE \triple>
[[[ hhh \triple[ ]]] iii \triple]
||| \ltriple|∗||| \rtriple|∗
∗Similar to \lVert and \rVert in Table 159, \ltriple and \rtriple must be used
instead of \triple to disambiguate whether “|” is a left or right delimiter.
Note that \triple—and the corresponding \double—is actually a macro that
takes a delimiter as an argument.
Table 161: fourier Variable-sized Delimiters
\llbracket \rrbracket
\VERT
Table 162: textcomp Text-mode Delimiters
〈\textlangle 〉\textrangle
\textlbrackdbl \textrbrackdbl
\textlquill \textrquill
Table 163: metre Text-mode Delimiters
}\alad }\Alad †\crux †\Crux
{\alas {\Alas ]] \quadrad ]] \Quadrad
i\angud i\Angud [[ \quadras [[ \Quadras
h\angus h\Angus
Table 164: Math-mode Accents
´a\acute{a} ˇa\check{a} `a\grave{a} ˜a\tilde{a}
¯a\bar{a} ¨a\ddot{a} ˆa\hat{a} a \vec{a}
˘a\breve{a} ˙a\dot{a} ˚a\mathring{a}
Also note the existence of \imath and \jmath, which produce dotless versions of
“i” and “j”. (See Table 201 on page 65.) These are useful when the accent is
supposed to replace the dot. For example, “\hat{\imath}” produces a correct
“ˆı”, while “\hat{i}” would yield the rather odd-looking “ˆ
i”.
57
Table 165: A
M
SMath-mode Accents
...
a\dddot{a} ....
a\ddddot{a}
These accents are also provided by the mathabx and accents packages and are
redefined by the mathdots package if the amsmath and amssymb packages have pre-
viously been loaded. All of the variations except for the original A
M
Sones tighten
the space between the dots (from ...
ato ˙˙˙
a). The mathabx and mathdots versions also
function properly within subscripts and superscripts (x˙˙˙
ainstead of x...
a) .
Table 166: MnSymbol Math-mode Accents
a\vec{a}
Table 167: fge Math-mode Accents
A
–a
–\spirituslenis{A}\spirituslenis{a}∗
∗When fge is passed the crescent option, \spirituslenis instead uses a crescent
accent as in “ a
—”.
Table 168: yhmath Math-mode Accents
˚a\ring{a}
This symbol is largely obsolete, as standard L
A
T
E
X 2εhas supported \mathring
since June, 1998 [L
A
T98].
58
Table 169: Extensible Accents
›
abc \widetilde{abc}∗”
abc \widehat{abc}∗
←−
abc \overleftarrow{abc}†−→
abc \overrightarrow{abc}†
abc \overline{abc} abc \underline{abc}
z}|{
abc \overbrace{abc} abc
|{z} \underbrace{abc}
√abc \sqrt{abc}‡
As demonstrated in a 1997 TUGboat article about typesetting long-division prob-
lems [Gib97], an extensible long-division sign (“ )abc ”) can be faked by putting a
“\big)” in a tabular environment with an \hline or \cline in the preceding row.
The article also presents a piece of code (uploaded to CTAN as longdiv.tex) that
automatically solves and typesets—by putting an \overline atop “\big)” and
the desired text—long-division problems. See also the polynom package, which au-
tomatically solves and typesets polynomial-division problems in a similar manner.
∗These symbols are made more extensible by the MnSymbol package and even more
extensible by the yhmath package.
†If you’re looking for an extensible diagonal line or arrow to be used for canceling or
reducing mathematical subexpressions (e.g., “x+−x” or “ 5
3 + 2 ”) then consider
using the cancel package.
‡With an optional argument, \sqrt typesets nth roots. For example,
“\sqrt[3]{abc}” produces “ 3
√abc ” and “\sqrt[n]{abc}” produces “ n
√abc ”.
Table 170: overrightarrow Extensible Accents
=⇒
abc \Overrightarrow{abc}
Table 171: yhmath Extensible Accents
ˆ
abc \wideparen{abc} È
abc \widetriangle{abc}
˚
ˆ
abc \widering{abc}
Table 172: A
M
SExtensible Accents
←→
abc \overleftrightarrow{abc} abc
←→ \underleftrightarrow{abc}
abc
←− \underleftarrow{abc} abc
−→ \underrightarrow{abc}
59
Table 173: MnSymbol Extensible Accents
abc \overbrace{abc}
abc \underbrace{abc}

abc \overgroup{abc} abc
 \undergroup{abc}
zx
abc \overlinesegment{abc} abc
zx \underlinesegment{abc}
↼Ð
abc \overleftharpoon{abc} Ð⇀
abc \overrightharpoon{abc}
abc \widehat{abc}
abc \widetilde{abc}
abc \wideparen{abc}
Table 174: mathtools Extensible Accents
z}|{
abc \overbrace{abc} abc
|{z} \underbrace{abc}
abc \overbracket{abc}∗abc \underbracket{abc}∗
∗\overbracket and \underbracket accept optional arguments that specify the
bracket height and thickness. See the mathtools documentation for more infor-
mation.
Table 175: mathabx Extensible Accents
abc \overbrace{abc} abc \widebar{abc}
abc \overgroup{abc} abc \widecheck{abc}
abc \underbrace{abc} abc \wideparen{abc}
abc \undergroup{abc} ˚
abc \widering{abc}
abc \widearrow{abc}
The braces shown for \overbrace and \underbrace appear in their minimum size.
They can expand arbitrarily wide, however.
Table 176: fourier Extensible Accents
Ù
abc \widearc{abc}
abc \wideparen{abc}
å
abc \wideOarc{abc} ˚
abc \widering{abc}
60
Table 177: esvect Extensible Accents
# ”
abc \vv{abc} with package option a
# „
abc \vv{abc} with package option b
# «
abc \vv{abc} with package option c
# »
abc \vv{abc} with package option d
# –
abc \vv{abc} with package option e
# —
abc \vv{abc} with package option f
#
abc \vv{abc} with package option g
# ‰
abc \vv{abc} with package option h
esvect also defines a \vv* macro which is used to typeset arrows over vector vari-
ables with subscripts. See the esvect documentation for more information.
Table 178: undertilde Extensible Accents
abc
›\utilde{abc}
Because \utilde is based on \widetilde it is also made more extensible by the
yhmath package.
Table 179: ushort Extensible Accents
abc \ushortdw{abc} abc \ushortw{abc}
\ushortw and \ushortdw are intended to be used with multi-character argu-
ments (“words”) while \ushortand \ushortd are intended to be used with single-
character arguments.
The underlines produced by the ushort commands are shorter than those pro-
duced by the \underline command. Consider the output from the expres-
sion “\ushort{x}\ushort{y}\underline{x}\underline{y}”, which looks like
“xyxy”.
Table 180: A
M
SExtensible Arrows
abc
←−− \xleftarrow{abc} abc
−−→ \xrightarrow{abc}
61
Table 181: mathtools Extensible Arrows
abc
←−−\xhookleftarrow{abc} abc
−−
−−\xleftrightharpoons{abc}
abc
−−→ \xhookrightarrow{abc} abc
7−−→ \xmapsto{abc}
abc
⇐== \xLeftarrow{abc} abc
==⇒\xRightarrow{abc}
abc
−− \xleftharpoondown{abc} abc
−−\xrightharpoondown{abc}
abc
−− \xleftharpoonup{abc} abc
−−\xrightharpoonup{abc}
abc
←−→ \xleftrightarrow{abc} abc
−−
−− \xrightleftharpoons{abc}
abc
⇐=⇒\xLeftrightarrow{abc}
Table 182: chemarr Extensible Arrows
abc
−−
−− \xrightleftharpoons{abc}
Table 183: chemarrow Extensible Arrows
abc
DGGGGGGG
def
\autoleftarrow{abc}{def}
abc
GGGGGGGA
def
\autorightarrow{abc}{def}
abc
EGGGGGGG
GGGGGGGC
def \autoleftrightharpoons{abc}{def} abc
GGGGGGGB
FGGGGGGG
def \autorightleftharpoons{abc}{def}
In addition to the symbols shown above, chemarrow also provides \larrowfill,
\rarrowfill,\leftrightharpoonsfill, and \rightleftharpoonsfill macros.
Each of these takes a length argument and produces an arrow of the specified
length.
Table 184: extarrows Extensible Arrows
abc
⇐=⇒\xLeftrightarrow{abc} abc
⇐==⇒\xLongleftrightarrow{abc}
abc
←−→ \xleftrightarrow{abc} abc
←−−→ \xlongleftrightarrow{abc}
abc
==== \xlongequal{abc} abc
==⇒\xLongrightarrow{abc}
abc
⇐== \xLongleftarrow{abc} abc
−−→ \xlongrightarrow{abc}
abc
←−− \xlongleftarrow{abc}
62
Table 185: extpfeil Extensible Arrows
abc
==== \xlongequal{abc} abc
7−−→ \xmapsto{abc}
abc
−−−− \xtwoheadleftarrow{abc} abc
−−−−\xtwoheadrightarrow{abc}
The extpfeil package also provides a \newextarrow command to help you define
your own extensible arrow symbols. See the extpfeil documentation for more infor-
mation.
Table 186: DotArrow Extensible Arrows
a\dotarrow{a}
The DotArrow package provides mechanisms for lengthening the arrow, adjusting
the distance between the arrow and its symbol, and altering the arrowhead. See
the DotArrow documentation for more information.
Table 187: trfsigns Extensible Transform Symbols
a\dft{a} a\DFT{a}
Table 188: holtpolt Non-commutative Division Symbols
abc
def \holter{abc}{def} abc
def \polter{abc}{def}
Table 189: Dots
·\cdotp :\colon∗.\ldotp .
.
.\vdots†
··· \cdots ...\ddots†. . . \ldots
∗While “:” is valid in math mode, \colon uses different surrounding spacing. See
Section 8.4 and the Short Math Guide for L
A
T
E
X [Dow00] for more information on
math-mode spacing.
†The mathdots package redefines \ddots and \vdots to make them scale properly
with font size. (They normally scale horizontally but not vertically.) \fixedddots
and \fixedvdots provide the original, fixed-height functionality of L
A
T
E
X 2ε’s
\ddots and \vdots macros.
63
Table 190: A
M
SDots
∵\because∗··· \dotsi ∴\therefore∗
··· \dotsb ··· \dotsm
. . . \dotsc . . . \dotso
∗\because and \therefore are defined as binary relations and therefore also appear
in Table 68 on page 30.
The A
M
S\dots symbols are named according to their intended usage: \dotsb
between pairs of binary operators/relations, \dotsc between pairs of commas,
\dotsi between pairs of integrals, \dotsm between pairs of multiplication signs,
and \dotso between other symbol pairs.
Table 191: wasysym Dots
∴\wasytherefore
Table 192: MnSymbol Dots
⋅\cdot \hdotdot \udots
\ddotdot \hdots ∴\uptherefore
\ddots \lefttherefore ∶\vdotdot
\diamonddots \righttherefore ⋮\vdots
∵\downtherefore ∷\squaredots
\fivedots \udotdot
MnSymbol defines \therefore as \uptherefore and \because as
\downtherefore. Furthermore, \cdotp and \colon produce the same glyphs as
\cdot and \vdotdot respectively but serve as T
E
X math punctuation (class 6
symbols) instead of T
E
X binary operators (class 2).
All of the above except \hdots and \vdots are defined as binary operators and
therefore also appear in Table 50 on page 23. Also, unlike most of the other dot
symbols in this document, MnSymbol’s dots are defined as single characters instead
of as composites of multiple single-dot characters.
Table 193: mathdots Dots
...\iddots
Table 194: yhmath Dots
...\adots
Table 195: teubner Dots
.
.\: .
.
.\; .
.
.
.\? .
..
.\antilabe
64
Table 196: mathcomp Math Symbols
\tccentigrade Ω\tcohm ‰\tcperthousand
µ\tcmu \tcpertenthousand
Table 197: marvosym Digits
0\MVZero 2\MVTwo 4\MVFour 6\MVSix 8\MVEight
1\MVOne 3\MVThree 5\MVFive 7\MVSeven 9\MVNine
Table 198: fge Digits
0\fgestruckzero 1\fgestruckone
Table 199: dozenal Base-12 Digits
\x \e
Table 200: mathabx Mayan Digits
\maya{0} \maya{2} \maya{4}
\maya{1} \maya{3} \maya{5}
Table 201: Miscellaneous L
A
T
E
X 2εMath Symbols
ℵ\aleph ^\Diamond∗∞\infty 0\prime
6\angle ♦\diamondsuit \mho∗\sharp
\\backslash ∅\emptyset‡∇\nabla ♠\spadesuit
\Box∗,†\flat \natural \surd
♣\clubsuit ♥\heartsuit ¬\neg 4\triangle
∗Not predefined in L
A
T
E
X 2ε. Use one of the packages latexsym,amsfonts,amssymb,
txfonts,pxfonts, or wasysym. Note, however, that amsfonts and amssymb define
\Diamond to produce the same glyph as \lozenge (“♦”); the other packages pro-
duce a squarer \Diamond as depicted above.
†To use \Box—or any other symbol—as an end-of-proof (Q.E.D.) marker, consider
using the ntheorem package, which properly juxtaposes a symbol with the end of
the proof text.
‡Many people prefer the look of A
M
S’s \varnothing (“∅”, Table 202) to that of
L
A
T
E
X’s \emptyset.
65
Table 202: Miscellaneous A
M
SMath Symbols
∠\angle H\blacktriangledown \mho
8\backprime \diagdown ^\sphericalangle
F\bigstar \diagup \square
\blacklozenge ð\eth O\triangledown
\blacksquare ♦\lozenge ∅\varnothing
N\blacktriangle ]\measuredangle M\vartriangle
Table 203: Miscellaneous wasysym Math Symbols
2\Box 3\Diamond \mho∗\varangle
∗wasysym also defines an \agemO symbol, which is the same glyph as \mho but is
intended for use in text mode.
Table 204: Miscellaneous txfonts/pxfonts Math Symbols
_\Diamondblack n\lambdaslash r\varheartsuit
\Diamonddot p\varclubsuit s\varspadesuit
o\lambdabar q\vardiamondsuit
Table 205: Miscellaneous mathabx Math Symbols
\degree \fourth \measuredangle \second
\diagdown \hash \pitchfork \sphericalangle
\diagup \infty \propto \third
\diameter \leftthreetimes \rightthreetimes \varhash
Table 206: Miscellaneous MnSymbol Math Symbols
∠\angle ♢\diamondsuit \maltese ♯\sharp
⌐\backneg ♭\flat \measuredangle \smallint
‵\backprime ♡\heartsuit ∇\nabla ♠\spadesuit
✓\checkmark ∞\infty \natural \sphericalangle
♣\clubsuit \invbackneg ¬\neg
\diameter \invneg ′\prime
MnSymbol defines \emptyset and \varnothing as synonyms for \diameter;\lnot
and \minushookdown as synonyms for \neg;\minushookup as a synonym for
\invneg;\hookdownminus as a synonym for \backneg; and, \hookupminus as
a synonym for \invbackneg.
66
Table 207: Miscellaneous Internal MnSymbol Math Symbols
\partialvardint \partialvartint
\partialvardlanddownint \partialvartlanddownint
\partialvardlandupint \partialvartlandupint
\partialvardlcircleleftint \partialvartlcircleleftint
\partialvardlcirclerightint \partialvartlcirclerightint
\partialvardoiint \partialvartoiint
\partialvardoint \partialvartoint
\partialvardrcircleleftint \partialvartrcircleleftint
\partialvardrcirclerightint \partialvartrcirclerightint
\partialvardstrokedint \partialvartstrokedint
\partialvardsumint \partialvartsumint
These symbols are intended to be used internally by MnSymbol to construct the
integrals appearing in Table 64 on page 29 but can nevertheless be used in isolation.
Table 208: Miscellaneous textcomp Text-mode Math Symbols
°\textdegree∗½\textonehalf†¾\textthreequarters†
÷\textdiv ¼\textonequarter†³\textthreesuperior
⁄\textfractionsolidus ¹\textonesuperior ×\texttimes
¬\textlnot ±\textpm ²\texttwosuperior
−\textminus √\textsurd
∗If you prefer a larger degree symbol you might consider defining one as
“\ensuremath{^\circ}” (“◦”).
†nicefrac (part of the units package) or the newer xfrac package can be used to
construct vulgar fractions like “1
/2”, “1
/4”, “3
/4”, and even “c
/o”.
Table 209: Miscellaneous marvosym Math Symbols
W\Anglesign ÷\Squaredot P\Vectorarrowhigh
=\Corresponds p\Vectorarrow
Table 210: Miscellaneous fge Math Symbols
K\fgebackslash S\fgecap R\fgecupacute h\fgelangle
M\fgebaracute Q\fgecapbar P\fgecupbar L\fgeupbracket
O\fgebarcap N\fgecup i\fgeinfty
Table 211: Miscellaneous mathdesign Math Symbols
∟\rightangle
Table 212: Miscellaneous arev Math Symbols
♨\steaming ♦\vardiamond ♤\varspade
♧\varclub ♥\varheart
67
Table 213: Math Alphabets
Font sample Generating command Required package
ABCdef123 \mathrm{ABCdef123} none
ABCdef123 \mathit{ABCdef123} none
ABCdef \mathnormal{ABCdef123} none
ABC \mathcal{ABC} none
ABC \mathscr{ABC} mathrsfs
or \mathcal{ABC} calrsfs
ABC \mathcal{ABC} euscript with the mathcal option
or \mathscr{ABC} euscript with the mathscr option
ABCdef123 \mathpzc{ABCdef123} none; manually defined∗
ABC \mathbb{ABC} amsfonts,§amssymb,txfonts, or pxfonts
 \varmathbb{ABC} txfonts or pxfonts
\mathbb{ABCdef123} bbold or mathbbol†
\mathbb{ABCdef123} mbboard†
\mathbbm{ABCdef12} bbm
\mathbbmss{ABCdef12} bbm
\mathbbmtt{ABCdef12} bbm
ABC1 \mathds{ABC1} dsfont
ABC1 \mathds{ABC1} dsfont with the sans option
\symA\symB\symC china2e‡
ABCdef123 \mathfrak{ABCdef123} eufrak
ABCdef123 \textfrak{ABCdef123} yfonts
ABCdef123 \textswab{ABCdef123} yfonts
ABCˇf123 \textgoth{ABCdef123} yfonts
∗Put “\DeclareMathAlphabet{\mathpzc}{OT1}{pzc}{m}{it}” in your docu-
ment’s preamble to make \mathpzc typeset its argument in Zapf Chancery.
As a similar trick, you can typeset the Calligra font’s script “ ” (or other
calligraphic symbols) in math mode by loading the calligra package and
putting “\DeclareMathAlphabet{\mathcalligra}{T1}{calligra}{m}{n}”
in your document’s preamble to make \mathcalligra typeset its
argument in the Calligra font. (You may also want to specify
“\DeclareFontShape{T1}{calligra}{m}{n}{<->s*[2.2]callig15}{}” to
set Calligra at 2.2 times its design size for a better blend with typical body fonts.)
†The mathbbol package defines some additional blackboard bold characters:
parentheses, square brackets, angle brackets, and—if the bbgreekl option
is passed to mathbbol—Greek letters. For instance, “ ” is pro-
duced by “\mathbb{\Langle\Lbrack\Lparen\bbalpha\bbbeta\bbgamma\Rparen
\Rbrack\Rangle}”.
mbboard extends the blackboard bold symbol set significantly further. It
supports not only the Greek alphabet—including “Greek-like” symbols such
as \bbnabla (“ ”)—but also all punctuation marks, various currency sym-
bols such as \bbdollar (“ ”) and \bbeuro (“ ”), and the Hebrew alpha-
bet (e.g., “\bbfinalnun\bbyod\bbqof\bbpe”→“ ”).
‡The \sym. . . commands provided by the C
h
in
A2e package are actually text-mode
commands. They are included in Table 213 because they resemble the blackboard-
bold symbols that appear in the rest of the table. In addition to the 26 letters
of the English alphabet, C
h
in
A2e provides three umlauted blackboard-bold letters:
\symAE (“ ”), \symOE (“ ”), and \symUE (“ ”). Note that C
h
in
A2e does provide
math-mode commands for the most common number-set symbols. These are pre-
sented in Table 130 on page 49.
68
As their \text. . . names imply, the fonts provided by the yfonts package are
actually text fonts. They are included in Table 213 because they are frequently
used in a mathematical context.
§An older (i.e., prior to 1991) version of the A
M
S’s fonts rendered C,N,R,S,
and Zas C,N,R,S, and Z. As some people prefer the older glyphs—much to
the A
M
S’s surprise—and because those glyphs fail to build under modern versions
of METAFONT, Berthold Horn uploaded PostScript fonts for the older blackboard-
bold glyphs to CTAN, to the fonts/msym10 directory. As of this writing, however,
there are no L
A
T
E
X 2εpackages for utilizing the now-obsolete glyphs.
69
4 Science and technology symbols
This section lists symbols that are employed in various branches of science and engineering.
Table 214: gensymb Symbols Defined to Work in Both Math and Text Mode
\celsius µ\micro ‰\perthousand
°\degree Ω\ohm
Table 215: wasysym Electrical and Physical Symbols
:\AC @\VHF :::: \photon F\HF QPPPPPPR \gluon
Table 216: ifsym Pulse Diagram Symbols
\FallingEdge \LongPulseLow \PulseLow \ShortPulseHigh
\LongPulseHigh \PulseHigh \RaisingEdge \ShortPulseLow
In addition, within \textifsym{. . .}, the following codes are valid:
l m h d < >
L M H D << >>
This enables one to write “\textifsym{mm<DDD>mm}” to get “ ” or
“\textifsym{L|H|L|H|L}” to get “ ”. See also the timing package,
which provides a wide variety of pulse-diagram symbols within an environment
designed specifically for typesetting pulse diagrams.
Finally, \textifsym supports the display of segmented digits, as would appear
on an LCD: “\textifsym{-123.456}” produces “ ”. “\textifsym{b}”
outputs a blank with the same width as an “ ”.
Table 217: ar Aspect Ratio Symbol
\AR
Table 218: textcomp Text-mode Science and Engineering Symbols
\textcelsius \textmho µ\textmu Ω\textohm
Table 219: steinmetz Extensible Phasor Symbol
abc \phase{abc}
The \phase command uses the pict2e package to draw a horizontally and verti-
cally scalable Steinmetz phasor symbol. Consequently, \phase works only with
those T
E
X backends supported by pict2e. See the pict2e documentation for more
information.
70
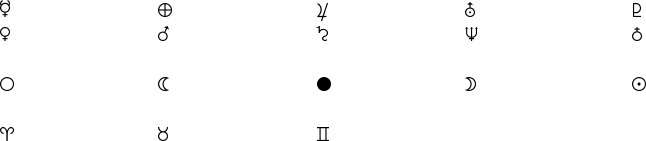
Table 220: wasysym Astronomical Symbols
'\mercury ♁\earth X\jupiter Z\uranus \\pluto
♀\venus ♂\mars Y\saturn [\neptune
\astrosun #\fullmoon $\leftmoon \newmoon %\rightmoon
\aries _\cancer a\libra e\aquarius
]\taurus \leo b\scorpio d\capricornus
^\gemini `\virgo c\sagittarius f\pisces
\ascnode \descnode V\conjunction W\opposition \vernal
Table 221: marvosym Astronomical Symbols
Â\Mercury Ê\Earth Å\Jupiter Ç\Uranus É\Pluto
Ã\Venus Ä\Mars Æ\Saturn È\Neptune
Á\Moon À\Sun
à\Aries ã\Cancer æ\Libra é\Capricorn
á\Taurus ä\Leo ç\Scorpio ê\Aquarius
â\Gemini å\Virgo è\Sagittarius ë\Pisces
Note that \Aries . . . \Pisces can also be specified with \Zodiac{1} . . .
\Zodiac{12}.
Table 222: mathabx Astronomical Symbols
\Mercury \Earth \Jupiter \Uranus \Pluto
\Venus \Mars \Saturn \Neptune \varEarth
\fullmoon \leftmoon \newmoon \rightmoon \Sun
\Aries \Taurus \Gemini
mathabx also defines \girl as an alias for \Venus,\boy as an alias for \Mars, and
\Moon as an alias for \leftmoon.
Table 223: wasysym APL Symbols
~\APLbox ÷~\APLinv E\APLstar
\APLcomment p\APLleftarrowbox \APLup
F\APLdown \APLlog n\APLuparrowbox
o\APLdownarrowbox −\APLminus \− \notbackslash
}\APLinput q\APLrightarrowbox /−\notslash
Table 224: wasysym APL Modifiers
◦\APLcirc{} ∼\APLnot{} |\APLvert{}
71
Table 225: marvosym Computer Hardware Symbols
Í\ComputerMouse Ñ\ParallelPort Î\SerialInterface
Ï\Keyboard Ò\Printer Ð\SerialPort
Table 226: keystroke Computer Keys
Alt \Alt Enter \Enter∗PrtSc \PrtSc∗
AltGr \AltGr Esc \Esc∗→\RArrow
Break \Break∗Home \Home∗←-\Return
7−→
\BSpace†Ins \Ins∗Scroll \Scroll∗
Ctrl \Ctrl∗←\LArrow Shift ⇑\Shift∗
↓\DArrow Num \NumLock \Spacebar
Del \Del∗Page ↓\PgDown∗
−−→
−−→ \Tab†
End \End∗Page ↑\PgUp∗↑\UArrow
∗Changes based on the language option passed to the keystroke package. For exam-
ple, the german option makes \Del produce “ Entf ” instead of “ Del ”.
†These symbols utilize the rotating package and therefore display improperly in most
DVI viewers.
The \keystroke command draws a key with an arbitrary label. For example,
“\keystroke{F7}” produces “ F7 ”.
Table 227: ascii Control Characters (CP437)
␁\SOH ␈\BS ␏\SI ␖\SYN ␝\GS
␂\STX ␉\HT ␐\DLE ␗\ETB ␞\RS
␃\ETX ␊\LF ␑\DCa ␘\CAN ␟\US
␄\EOT ␋\VT ␒\DCb ␙\EM
␅\ENQ ␌\FF ␓\DCc ␚\SUB
␆\ACK ␍\CR ␔\DCd ␛\ESC
␇\BEL ␎\SO ␕\NAK ␜\FS
␡\DEL \NBSP ␀\NUL ¦\splitvert
Code Page 437 (CP437), which was first utilized by the original IBM PC, uses the
symbols \SOH through \US to depict ASCII characters 1–31 and \DEL to depict
ASCII character 127. The \NUL symbol, not part of CP437, represents ASCII
character 0. \NBSP, also not part of CP437, represents a nonbreaking space.
\splitvert is merely the “|” character drawn as it was on the IBM PC.
72
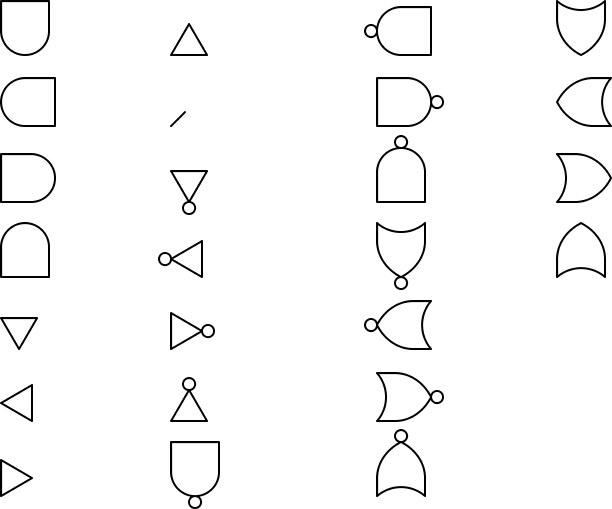
Table 228: milstd Logic Gates
\ANDd \BUFu \NANDl \ORd
\ANDl \BusWidth \NANDr \ORl
\ANDr \INVd \NANDu \ORr
\ANDu \INVl \NORd \ORu
\BUFd \INVr \NORl
\BUFl \INVu \NORr
\BUFr \NANDd \NORu
The milstd package, which provides the digital logic-gate symbols specified by the
U.S. Department of Defense’s MIL-STD-806 standard, was written as a L
A
T
E
X 2.09
.tex file, not as a L
A
T
E
X 2εpackage. Consequently, it must be loaded into a
document with \input milstd, not with the more modern \usepackage{milstd}.
Table 229: marvosym Communication Symbols
k\Email t\fax v\Faxmachine E\Lightning A\Pickup
z\Emailct u\FAX B\Letter H\Mobilefone T\Telefon
Table 230: marvosym Engineering Symbols
"\Beam l\Force ‘\Octosteel \RoundedTTsteel
#\Bearing ’\Hexasteel ˜\Rectpipe —\Squarepipe
›\Circpipe &\Lefttorque ”\Rectsteel “\Squaresteel
•\Circsteel L\Lineload '\Righttorque œ\Tsteel
%\Fixedbearing $\Loosebearing Ÿ\RoundedLsteel∗š\TTsteel
–\Flatsteel ™\Lsteel \RoundedTsteel∗
∗\RoundedLsteel and \RoundedTsteel seem to be swapped, at least in the
2000/05/01 version of marvosym.
Table 231: wasysym Biological Symbols
♀\female ♂\male
73
Table 232: marvosym Biological Symbols
~\Female …\FemaleMale \MALE {\Neutral
\FEMALE }\Hermaphrodite |\Male
„\FemaleFemale \HERMAPHRODITE ƒ\MaleMale
Table 233: marvosym Safety-related Symbols
h\Biohazard C\CEsign `\Explosionsafe j\Radioactivity
n\BSEfree J\Estatically a\Laserbeam !\Stopsign
Table 234: feyn Feynman Diagram Symbols
\bigbosonloop \hfermion \smallbosonloopV
\bigbosonloopA \shfermion \wfermion
\bigbosonloopV \smallbosonloop \whfermion
\gvcropped \smallbosonloopA
\feyn{a} \feyn{fu} \feyn{glS} \feyn{hs}
\feyn{c} \feyn{fv} \feyn{glu} \feyn{hu}
\feyn{f} \feyn{g} \feyn{gu} \feyn{m}
\feyn{fd} \feyn{g1} \feyn{gv} \feyn{ms}
\feyn{fl} \feyn{gd} \feyn{gvs} \feyn{p}
\feyn{flS} \feyn{gl} \feyn{h} \feyn{P}
\feyn{fs} \feyn{glB} \feyn{hd} \feyn{x}
All other arguments to the \feyn command produce a “ ” symbol.
The feyn package provides various commands for composing the preceding symbols
into complete Feynman diagrams. See the feyn documentation for examples and
additional information.
74
5 Dingbats
Dingbats are symbols such as stars, arrows, and geometric shapes. They are commonly used as bullets in
itemized lists or, more generally, as a means to draw attention to the text that follows.
The pifont dingbat package warrants special mention. Among other capabilities, pifont provides a L
A
T
E
X
interface to the Zapf Dingbats font (one of the standard 35 PostScript fonts). However, rather than name each
of the dingbats individually, pifont merely provides a single \ding command, which outputs the character that
lies at a given position in the font. The consequence is that the pifont symbols can’t be listed by name in this
document’s index, so be mindful of that fact when searching for a particular symbol.
Table 235: bbding Arrows
\ArrowBoldDownRight \ArrowBoldRightShort \ArrowBoldUpRight
\ArrowBoldRightCircled \ArrowBoldRightStrobe
Table 236: pifont Arrows
Ô\ding{212} Ý\ding{221} æ\ding{230} ï\ding{239} ù\ding{249}
Õ\ding{213} Þ\ding{222} ç\ding{231} ñ\ding{241} ú\ding{250}
Ö\ding{214} ß\ding{223} è\ding{232} ò\ding{242} û\ding{251}
×\ding{215} à\ding{224} é\ding{233} ó\ding{243} ü\ding{252}
Ø\ding{216} á\ding{225} ê\ding{234} ô\ding{244} ý\ding{253}
Ù\ding{217} â\ding{226} ë\ding{235} õ\ding{245} þ\ding{254}
Ú\ding{218} ã\ding{227} ì\ding{236} ö\ding{246}
Û\ding{219} ä\ding{228} í\ding{237} ÷\ding{247}
Ü\ding{220} å\ding{229} î\ding{238} ø\ding{248}
Table 237: universal Arrows
\bauarrow \bauwhitearrow
Table 238: marvosym Scissors
s\Cutleft q\Cutright S\Leftscissors
r\Cutline R\Kutline Q\Rightscissors
Table 239: bbding Scissors
\ScissorHollowLeft \ScissorLeftBrokenTop
\ScissorHollowRight \ScissorRight
\ScissorLeft \ScissorRightBrokenBottom
\ScissorLeftBrokenBottom \ScissorRightBrokenTop
Table 240: pifont Scissors
!\ding{33} "\ding{34} #\ding{35} $\ding{36}
75
Table 241: dingbat Pencils
\largepencil \smallpencil
Table 242: bbding Pencils and Nibs
\NibLeft \PencilLeft \PencilRightDown
\NibRight \PencilLeftDown \PencilRightUp
\NibSolidLeft \PencilLeftUp
\NibSolidRight \PencilRight
Table 243: pifont Pencils and Nibs
.\ding{46} /\ding{47} 0\ding{48} 1\ding{49} 2\ding{50}
Table 244: dingbat Fists
\leftpointright \rightpointleft \rightpointright
\leftthumbsdown \rightthumbsdown
\leftthumbsup \rightthumbsup
Table 245: bbding Fists
\HandCuffLeft \HandCuffRightUp \HandPencilLeft
\HandCuffLeftUp \HandLeft \HandRight
\HandCuffRight \HandLeftUp \HandRightUp
Table 246: pifont Fists
*\ding{42} +\ding{43} ,\ding{44} -\ding{45}
Table 247: fourier Fists
t\lefthand u\righthand
Table 248: bbding Crosses and Plusses
\Cross \CrossOpenShadow \PlusOutline
\CrossBoldOutline \CrossOutline \PlusThinCenterOpen
\CrossClowerTips \Plus
\CrossMaltese \PlusCenterOpen
76
Table 249: pifont Crosses and Plusses
9\ding{57} ;\ding{59} =\ding{61} ?\ding{63}
:\ding{58} <\ding{60} >\ding{62} @\ding{64}
Table 250: bbding Xs and Check Marks
\Checkmark \XSolid \XSolidBrush
\CheckmarkBold \XSolidBold
Table 251: pifont Xs and Check Marks
3\ding{51} 5\ding{53} 7\ding{55}
4\ding{52} 6\ding{54} 8\ding{56}
Table 252: wasysym Xs and Check Marks
2\CheckedBox \Square 4\XBox
Table 253: universal Xs
\baucross
Table 254: pifont Circled Numbers
¬\ding{172} \ding{182} À\ding{192} Ê\ding{202}
\ding{173} ·\ding{183} Á\ding{193} Ë\ding{203}
®\ding{174} ¸\ding{184} Â\ding{194} Ì\ding{204}
¯\ding{175} ¹\ding{185} Ã\ding{195} Í\ding{205}
°\ding{176} º\ding{186} Ä\ding{196} Î\ding{206}
±\ding{177} »\ding{187} Å\ding{197} Ï\ding{207}
²\ding{178} ¼\ding{188} Æ\ding{198} Ð\ding{208}
³\ding{179} ½\ding{189} Ç\ding{199} Ñ\ding{209}
´\ding{180} ¾\ding{190} È\ding{200} Ò\ding{210}
µ\ding{181} ¿\ding{191} É\ding{201} Ó\ding{211}
pifont (part of the psnfss package) provides a dingautolist environment which
resembles enumerate but uses circled numbers as bullets.4See the psnfss docu-
mentation for more information.
Table 255: wasysym Stars
C\davidsstar A\hexstar B\varhexstar
4In fact, dingautolist can use any set of consecutive Zapf Dingbats symbols.
77
Table 256: bbding Stars, Flowers, and Similar Shapes
\Asterisk \FiveFlowerPetal \JackStar
\AsteriskBold \FiveStar \JackStarBold
\AsteriskCenterOpen \FiveStarCenterOpen \SixFlowerAlternate
\AsteriskRoundedEnds \FiveStarConvex \SixFlowerAltPetal
\AsteriskThin \FiveStarLines \SixFlowerOpenCenter
\AsteriskThinCenterOpen \FiveStarOpen \SixFlowerPetalDotted
\DavidStar \FiveStarOpenCircled \SixFlowerPetalRemoved
\DavidStarSolid \FiveStarOpenDotted \SixFlowerRemovedOpenPetal
\EightAsterisk \FiveStarOutline \SixStar
\EightFlowerPetal \FiveStarOutlineHeavy \SixteenStarLight
\EightFlowerPetalRemoved \FiveStarShadow \Snowflake
\EightStar \FourAsterisk \SnowflakeChevron
\EightStarBold \FourClowerOpen \SnowflakeChevronBold
\EightStarConvex \FourClowerSolid \Sparkle
\EightStarTaper \FourStar \SparkleBold
\FiveFlowerOpen \FourStarOpen \TwelweStar
Table 257: pifont Stars, Flowers, and Similar Shapes
A\ding{65} J\ding{74} S\ding{83} \\ding{92} e\ding{101}
B\ding{66} K\ding{75} T\ding{84} ]\ding{93} f\ding{102}
C\ding{67} L\ding{76} U\ding{85} ^\ding{94} g\ding{103}
D\ding{68} M\ding{77} V\ding{86} _\ding{95} h\ding{104}
E\ding{69} N\ding{78} W\ding{87} `\ding{96} i\ding{105}
F\ding{70} O\ding{79} X\ding{88} a\ding{97} j\ding{106}
G\ding{71} P\ding{80} Y\ding{89} b\ding{98} k\ding{107}
H\ding{72} Q\ding{81} Z\ding{90} c\ding{99}
I\ding{73} R\ding{82} [\ding{91} d\ding{100}
Table 258: fourier Ornaments
o\aldine X\decoone c\floweroneright
m\aldineleft ]\decosix g\leafleft
n\aldineright Y\decothreeleft f\leafNE
j\aldinesmall Z\decothreeright h\leafright
[\decofourleft a\decotwo d\starredbullet
\\decofourright b\floweroneleft
Table 259: wasysym Geometric Shapes
7\hexagon 8\octagon D\pentagon 9\varhexagon
78
Table 260: MnSymbol Geometric Shapes
\filledlargestar \largediamond \largestar ◊\smalllozenge
\filledlozenge \largelozenge \largestarofdavid
\filledmedlozenge \largepentagram \medlozenge
\largecircle \largesquare \medstarofdavid
MnSymbol defines \bigcirc as a synonym for \largecircle;\bigstar as a syn-
onym for \filledlargestar;\lozenge as a synonym for \medlozenge; and,
\blacklozenge as a synonym for \filledmedlozenge.
Table 261: ifsym Geometric Shapes
\BigCircle \FilledBigTriangleRight \SmallCircle
\BigCross \FilledBigTriangleUp \SmallCross
\BigDiamondshape \FilledCircle \SmallDiamondshape
\BigHBar \FilledDiamondShadowA \SmallHBar
\BigLowerDiamond \FilledDiamondShadowC \SmallLowerDiamond
\BigRightDiamond \FilledDiamondshape \SmallRightDiamond
\BigSquare \FilledSmallCircle \SmallSquare
\BigTriangleDown \FilledSmallDiamondshape \SmallTriangleDown
\BigTriangleLeft \FilledSmallSquare \SmallTriangleLeft
\BigTriangleRight \FilledSmallTriangleDown \SmallTriangleRight
\BigTriangleUp \FilledSmallTriangleLeft \SmallTriangleUp
\BigVBar \FilledSmallTriangleRight \SmallVBar
\Circle \FilledSmallTriangleUp \SpinDown
\Cross \FilledSquare \SpinUp
\DiamondShadowA \FilledSquareShadowA \Square
\DiamondShadowB \FilledSquareShadowC \SquareShadowA
\DiamondShadowC \FilledTriangleDown \SquareShadowB
\Diamondshape \FilledTriangleLeft \SquareShadowC
\FilledBigCircle \FilledTriangleRight \TriangleDown
\FilledBigDiamondshape \FilledTriangleUp \TriangleLeft
\FilledBigSquare \HBar \TriangleRight
\FilledBigTriangleDown \LowerDiamond \TriangleUp
\FilledBigTriangleLeft \RightDiamond \VBar
The ifsym documentation points out that one can use \rlap to combine
some of the above into useful, new symbols. For example, \BigCircle and
\FilledSmallCircle combine to give “ ”. Likewise, \Square and \Cross com-
bine to give “ ”. See Section 8.3 for more information about constructing new
symbols out of existing symbols.
79
Table 262: bbding Geometric Shapes
\CircleShadow \Rectangle \SquareShadowTopLeft
\CircleSolid \RectangleBold \SquareShadowTopRight
\DiamondSolid \RectangleThin \SquareSolid
\Ellipse \Square \TriangleDown
\EllipseShadow \SquareCastShadowBottomRight \TriangleUp
\EllipseSolid \SquareCastShadowTopLeft
\HalfCircleLeft \SquareCastShadowTopRight
\HalfCircleRight \SquareShadowBottomRight
Table 263: pifont Geometric Shapes
l\ding{108} o\ding{111} r\ding{114} u\ding{117} y\ding{121}
m\ding{109} p\ding{112} s\ding{115} w\ding{119} z\ding{122}
n\ding{110} q\ding{113} t\ding{116} x\ding{120}
Table 264: universa Geometric Shapes
\baucircle \bausquare \bautriangle
Table 265: universal Geometric Shapes
\baucircle \bauhole \bausquare
\baueclipse \baupunct \bautriangle
Table 266: Miscellaneous dingbat Dingbats
\anchor \eye \Sborder
\carriagereturn \filledsquarewithdots \squarewithdots
\checkmark \satellitedish \Zborder
Table 267: Miscellaneous bbding Dingbats
\Envelope \Peace \PhoneHandset \SunshineOpenCircled
\OrnamentDiamondSolid \Phone \Plane \Tape
Table 268: Miscellaneous pifont Dingbats
%\ding{37} (\ding{40} ¤\ding{164} §\ding{167} «\ding{171}
&\ding{38} )\ding{41} ¥\ding{165} ¨\ding{168} ©\ding{169}
'\ding{39} v\ding{118} ¦\ding{166} ª\ding{170}
80
6 Ancient languages
This section presents letters and ideograms from various ancient scripts. Some of these symbols may also be
useful in other typesetting contexts.
Table 269: phaistos Symbols from the Phaistos Disk
J\PHarrow e\PHeagle B\PHplumedHead
h\PHbee o\PHflute d\PHram
X\PHbeehive H\PHgaunlet l\PHrosette
R\PHboomerang p\PHgrater P\PHsaw
K\PHbow G\PHhelmet L\PHshield
b\PHbullLeg a\PHhide Y\PHship
D\PHcaptive Z\PHhorn V\PHsling
S\PHcarpentryPlane Q\PHlid r\PHsmallAxe
c\PHcat m\PHlily q\PHstrainer
E\PHchild N\PHmanacles C\PHtattooedHead
M\PHclub O\PHmattock I\PHtiara
W\PHcolumn n\PHoxBack g\PHtunny
U\PHcomb k\PHpapyrus j\PHvine
T\PHdolium A\PHpedestrian s\PHwavyBand
f\PHdove i\PHplaneTree F\PHwoman
Table 270: protosem Proto-Semitic Characters
a\Aaleph E\AAhe k\Akaph s\Asamekh R\AAresh
A\AAaleph z\Azayin K\AAkaph p\Ape S\Ashin
b\Abeth w\Avav l\Alamed P\AApe v\Ahelmet
B\AAbeth H\Aheth L\AAlamed x\Asade V\AAhelmet
g\Agimel h\AAheth m\Amem X\AAsade t\Atav
d\Adaleth T\Ateth n\Anun q\Aqoph
D\AAdaleth y\Ayod o\Aayin Q\AAqoph
e\Ahe Y\AAyod O\AAayin r\Aresh
The protosem package defines abbreviated control sequences for each of the above.
In addition, single-letter shortcuts can be used within the argument to the
\textproto command (e.g., “\textproto{Pakyn}” produces “Pakyn”). See
the protosem documentation for more information.
81
Table 271: hieroglf Hieroglyphics
A\HA I\HI n\Hn T\HT
a\Ha i\Hi O\HO t\Ht
B\HB ˝\Hibl o\Ho ˘\Htongue
b\Hb ˆ\Hibp p\Hp U\HU
c\Hc ¨\Hibs P\HP u\Hu
C\HC ˜\Hibw ˙\Hplural V\HV
D\HD J\HJ +\Hplus v\Hv
d\Hd j\Hj Q\HQ |\Hvbar
¸\Hdual k\Hk q\Hq w\Hw
e\He K\HK ?\Hquery W\HW
E\HE L\HL R\HR X\HX
f\Hf l\Hl r\Hr x\Hx
F\HF m\Hm s\Hs Y\HY
G\HG M\HM S\HS y\Hy
g\Hg ˇ\Hman ¯\Hscribe z\Hz
h\Hh ´\Hms /\Hslash Z\HZ
H\HH N\HN ˚\Hsv
|\Hone 3\Hhundred 5\HXthousand 7\Hmillion
2\Hten 4\Hthousand 6\HCthousand
The hieroglf package defines alternate control sequences and single-letter shortcuts
for each of the above which can be used within the argument to the \textpmhg
command (e.g., “\textpmhg{Pakin}” produces “Pakin”). See the hieroglf
documentation for more information.
Table 272: linearA Linear A Script
\LinearAI b\LinearAXCIX \LinearACXCVII t\LinearACCXCV
\LinearAII c\LinearAC \LinearACXCVIII u\LinearACCXCVI
\LinearAIII d\LinearACI \LinearACXCIX v\LinearACCXCVII
\LinearAIV e\LinearACII \LinearACC w\LinearACCXCVIII
\LinearAV f\LinearACIII \LinearACCI x\LinearACCXCIX
\LinearAVI g\LinearACIV \LinearACCII y\LinearACCC
\LinearAVII h\LinearACV \LinearACCIII z\LinearACCCI
\LinearAVIII i\LinearACVI \LinearACCIV {\LinearACCCII
\LinearAIX j\LinearACVII \LinearACCV |\LinearACCCIII
\LinearAX k\LinearACVIII \LinearACCVI }\LinearACCCIV
\LinearAXI l\LinearACIX \LinearACCVII ~\LinearACCCV
\LinearAXII m\LinearACX \LinearACCVIII \LinearACCCVI
\LinearAXIII n\LinearACXI \LinearACCIX \LinearACCCVII
(continued on next page)
82
(continued from previous page)
\LinearAXIV o\LinearACXII \LinearACCX \LinearACCCVIII
\LinearAXV p\LinearACXIII \LinearACCXI \LinearACCCIX
\LinearAXVI q\LinearACXIV !\LinearACCXII \LinearACCCX
\LinearAXVII r\LinearACXV "\LinearACCXIII \LinearACCCXI
\LinearAXVIII s\LinearACXVI #\LinearACCXIV \LinearACCCXII
\LinearAXIX t\LinearACXVII $\LinearACCXV \LinearACCCXIII
\LinearAXX u\LinearACXVIII %\LinearACCXVI \LinearACCCXIV
\LinearAXXI v\LinearACXIX &\LinearACCXVII \LinearACCCXV
\LinearAXXII w\LinearACXX '\LinearACCXVIII \LinearACCCXVI
\LinearAXXIII x\LinearACXXI (\LinearACCXIX \LinearACCCXVII
\LinearAXXIV y\LinearACXXII )\LinearACCXX \LinearACCCXVIII
\LinearAXXV z\LinearACXXIII *\LinearACCXXI \LinearACCCXIX
\LinearAXXVI {\LinearACXXIV +\LinearACCXXII \LinearACCCXX
\LinearAXXVII |\LinearACXXV ,\LinearACCXXIII \LinearACCCXXI
\LinearAXXVIII }\LinearACXXVI -\LinearACCXXIV \LinearACCCXXII
\LinearAXXIX ~\LinearACXXVII .\LinearACCXXV \LinearACCCXXIII
\LinearAXXX \LinearACXXVIII /\LinearACCXXVI \LinearACCCXXIV
\LinearAXXXI \LinearACXXIX 0\LinearACCXXVII \LinearACCCXXV
\LinearAXXXII \LinearACXXX 1\LinearACCXXVIII \LinearACCCXXVI
\LinearAXXXIII \LinearACXXXI 2\LinearACCXXIX \LinearACCCXXVII
!\LinearAXXXIV \LinearACXXXII 3\LinearACCXXX \LinearACCCXXVIII
"\LinearAXXXV \LinearACXXXIII 4\LinearACCXXXI \LinearACCCXXIX
#\LinearAXXXVI \LinearACXXXIV 5\LinearACCXXXII \LinearACCCXXX
$\LinearAXXXVII \LinearACXXXV 6\LinearACCXXXIII \LinearACCCXXXI
%\LinearAXXXVIII \LinearACXXXVI 7\LinearACCXXXIV \LinearACCCXXXII
&\LinearAXXXIX \LinearACXXXVII 8\LinearACCXXXV \LinearACCCXXXIII
'\LinearAXL \LinearACXXXVIII 9\LinearACCXXXVI \LinearACCCXXXIV
(\LinearAXLI \LinearACXXXIX :\LinearACCXXXVII \LinearACCCXXXV
)\LinearAXLII \LinearACXL ;\LinearACCXXXVIII \LinearACCCXXXVI
*\LinearAXLIII \LinearACXLI <\LinearACCXXXIX \LinearACCCXXXVII
+\LinearAXLIV \LinearACXLII =\LinearACCXL \LinearACCCXXXVIII
,\LinearAXLV \LinearACXLIII >\LinearACCXLI \LinearACCCXXXIX
-\LinearAXLVI \LinearACXLIV ?\LinearACCXLII ¡\LinearACCCXL
.\LinearAXLVII \LinearACXLV @\LinearACCXLIII ¢\LinearACCCXLI
/\LinearAXLVIII \LinearACXLVI A\LinearACCXLIV £\LinearACCCXLII
0\LinearAXLIX \LinearACXLVII B\LinearACCXLV ¤\LinearACCCXLIII
1\LinearAL \LinearACXLVIII C\LinearACCXLVI ¥\LinearACCCXLIV
2\LinearALI \LinearACXLIX D\LinearACCXLVII ¦\LinearACCCXLV
3\LinearALII \LinearACL E\LinearACCXLVIII §\LinearACCCXLVI
4\LinearALIII \LinearACLI F\LinearACCXLIX ¨\LinearACCCXLVII
5\LinearALIV \LinearACLII G\LinearACCL ©\LinearACCCXLVIII
6\LinearALV \LinearACLIII H\LinearACCLI ª\LinearACCCXLIX
7\LinearALVI \LinearACLIV I\LinearACCLII «\LinearACCCL
8\LinearALVII \LinearACLV J\LinearACCLIII ¬\LinearACCCLI
9\LinearALVIII \LinearACLVI K\LinearACCLIV \LinearACCCLII
:\LinearALIX \LinearACLVII L\LinearACCLV ®\LinearACCCLIII
;\LinearALX \LinearACLVIII M\LinearACCLVI ¯\LinearACCCLIV
<\LinearALXI \LinearACLIX N\LinearACCLVII °\LinearACCCLV
=\LinearALXII \LinearACLX O\LinearACCLVIII ±\LinearACCCLVI
>\LinearALXIII \LinearACLXI P\LinearACCLIX ²\LinearACCCLVII
?\LinearALXIV ¡\LinearACLXII Q\LinearACCLX ³\LinearACCCLVIII
@\LinearALXV ¢\LinearACLXIII R\LinearACCLXI ´\LinearACCCLIX
(continued on next page)
83
(continued from previous page)
A\LinearALXVI £\LinearACLXIV S\LinearACCLXII µ\LinearACCCLX
B\LinearALXVII ¤\LinearACLXV T\LinearACCLXIII \LinearACCCLXI
C\LinearALXVIII ¥\LinearACLXVI U\LinearACCLXIV ·\LinearACCCLXII
D\LinearALXIX ¦\LinearACLXVII V\LinearACCLXV ¸\LinearACCCLXIII
E\LinearALXX §\LinearACLXVIII W\LinearACCLXVI ¹\LinearACCCLXIV
F\LinearALXXI ¨\LinearACLXIX X\LinearACCLXVII º\LinearACCCLXV
G\LinearALXXII ©\LinearACLXX Y\LinearACCLXVIII »\LinearACCCLXVI
H\LinearALXXIII ª\LinearACLXXI Z\LinearACCLXIX ¼\LinearACCCLXVII
I\LinearALXXIV «\LinearACLXXII [\LinearACCLXX ½\LinearACCCLXVIII
J\LinearALXXV ¬\LinearACLXXIII \\LinearACCLXXI ¾\LinearACCCLXIX
K\LinearALXXVI \LinearACLXXIV ]\LinearACCLXXII ¿\LinearACCCLXX
L\LinearALXXVII ®\LinearACLXXV ^\LinearACCLXXIII À\LinearACCCLXXI
M\LinearALXXVIII ¯\LinearACLXXVI _\LinearACCLXXIV Á\LinearACCCLXXII
N\LinearALXXIX °\LinearACLXXVII `\LinearACCLXXV Â\LinearACCCLXXIII
O\LinearALXXX ±\LinearACLXXVIII a\LinearACCLXXVI Ã\LinearACCCLXXIV
P\LinearALXXXI \LinearACLXXIX b\LinearACCLXXVII Ä\LinearACCCLXXV
Q\LinearALXXXII \LinearACLXXX c\LinearACCLXXVIII Å\LinearACCCLXXVI
R\LinearALXXXIII \LinearACLXXXI d\LinearACCLXXIX Æ\LinearACCCLXXVII
S\LinearALXXXIV \LinearACLXXXII e\LinearACCLXXX Ç\LinearACCCLXXVIII
T\LinearALXXXV \LinearACLXXXIII f\LinearACCLXXXI È\LinearACCCLXXIX
U\LinearALXXXVI \LinearACLXXXIV g\LinearACCLXXXII É\LinearACCCLXXX
V\LinearALXXXVII \LinearACLXXXV h\LinearACCLXXXIII Ê\LinearACCCLXXXI
W\LinearALXXXVIII \LinearACLXXXVI i\LinearACCLXXXIV Ë\LinearACCCLXXXII
X\LinearALXXXIX \LinearACLXXXVII j\LinearACCLXXXV Ì\LinearACCCLXXXIII
Y\LinearALXXXX \LinearACLXXXVIII k\LinearACCLXXXVI Í\LinearACCCLXXXIV
Z\LinearAXCI \LinearACLXXXIX l\LinearACCLXXXVII Î\LinearACCCLXXXV
[\LinearAXCII \LinearACLXXXX m\LinearACCLXXXVIII Ï\LinearACCCLXXXVI
\\LinearAXCIII \LinearACXCI n\LinearACCLXXXIX Ð\LinearACCCLXXXVII
]\LinearAXCIV \LinearACXCII o\LinearACCLXXXX Ñ\LinearACCCLXXXVIII
^\LinearAXCV \LinearACXCIII p\LinearACCXCI Ò\LinearACCCLXXXIX
_\LinearAXCVI \LinearACXCIV q\LinearACCXCII
`\LinearAXCVII \LinearACXCV r\LinearACCXCIII
a\LinearAXCVIII \LinearACXCVI s\LinearACCXCIV
84
Table 273: linearb Linear B Basic and Optional Letters
a\Ba j\Bja B\Bmu ]\Bpte ‘\Broii 4\Bto
;\Baii J\Bje n\Bna I\Bpu V\Bru 5\Btu
<\Baiii b\Bjo N\Bne \\Bpuii s\Bsa ~\Btwo
=\Bau L\Bju C\Bni q\Bqa S\Bse u\Bu
d\Bda k\Bka E\Bno Q\Bqe Y\Bsi w\Bwa
D\Bde K\Bke F\Bnu X\Bqi 1\Bso W\Bwe
f\Bdi c\Bki @\Bnwa 8\Bqo 2\Bsu 6\Bwi
g\Bdo h\Bko o\Bo r\Bra {\Bswa 7\Bwo
x\Bdu v\Bku p\Bpa ^\Braii |\Bswi z\Bza
>\Bdwe m\Bma [\Bpaiii _\Braiii t\Bta Z\Bze
?\Bdwo M\Bme P\Bpe R\Bre }\Btaii 9\Bzo
e\Be y\Bmi G\Bpi O\Bri T\Bte
i\Bi A\Bmo H\Bpo U\Bro 3\Bti
These symbols must appear either within the argument to \textlinb or
following the \linbfamily font-selection command within a scope. Single-
character shortcuts are also supported: Both “\textlinb{\Bpa\Bki\Bna}” and
“\textlinb{pcn}” produce “pcn”, for example. See the linearb documentation
for more information.
Table 274: linearb Linear B Numerals
´\BNi ˇ\BNvii ‚\BNxl «\BNc ı\BNdcc
ˆ\BNii ˘\BNviii ‹\BNl »\BNcc ȷ\BNdccc
˜\BNiii ¯\BNix ›\BNlx –\BNccc ff\BNcm
¨\BNiv ˙\BNx “\BNlxx —\BNcd fi\BNm
˝\BNv ¸\BNxx ”\BNlxxx \BNd
˚\BNvi ˛\BNxxx „\BNxc ‰\BNdc
These symbols must appear either within the argument to \textlinb or following
the \linbfamily font-selection command within a scope.
Table 275: linearb Linear B Weights and Measures
Ď\BPtalent Ľ\BPvolb Ń\BPvolcf Ą\BPwtb Č\BPwtd
Ĺ\BPvola Ł\BPvolcd Ă\BPwta Ć\BPwtc
These symbols must appear either within the argument to \textlinb or following
the \linbfamily font-selection command within a scope.
85
Table 276: linearb Linear B Ideograms
Ž\BPamphora ź\BPchassis ă\BPman Š\BPwheat
ij\BParrow Ř\BPcloth ț\BPnanny ž\BPwheel
Ş\BPbarley ŋ\BPcow Ț\BPolive Ť\BPwine
ť\BPbilly Ÿ\BPcup ń\BPox Ż\BPwineiih
ľ\BPboar š\BPewe ĺ\BPpig IJ\BPwineiiih
Ű\BPbronze ě\BPfoal ś\BPram İ\BPwineivh
ň\BPbull ş\BPgoat ř\BPsheep ą\BPwoman
đ\BPcauldroni Ź\BPgoblet ł\BPsow Ś\BPwool
§\BPcauldronii Ů\BPgold ¡\BPspear
ÿ\BPchariot ď\BPhorse ż\BPsword
These symbols must appear either within the argument to \textlinb or following
the \linbfamily font-selection command within a scope.
Table 277: linearb Unidentified Linear B Symbols
fl\BUi ␣\BUiv #\BUvii &\BUx \Btwe
ffi\BUii !\BUv $\BUviii ’\BUxi
ffl\BUiii "\BUvi %\BUix \BUxii
These symbols must appear either within the argument to \textlinb or following
the \linbfamily font-selection command within a scope.
Table 278: cypriot Cypriot Letters
a\Ca v\Cku B\Cmu H\Cpo 1\Cso 6\Cwi
e\Ce l\Cla n\Cna I\Cpu 2\Csu 7\Cwo
g\Cga L\Cle N\Cne r\Cra t\Cta x\Cxa
i\Ci d\Cli C\Cni R\Cre T\Cte X\Cxe
j\Cja f\Clo E\Cno O\Cri 3\Cti j\Cya
b\Cjo q\Clu F\Cnu U\Cro 4\Cto b\Cyo
k\Cka m\Cma o\Co V\Cru 5\Ctu g\Cza
K\Cke M\Cme p\Cpa s\Csa u\Cu 9\Czo
c\Cki y\Cmi P\Cpe S\Cse w\Cwa
h\Cko A\Cmo G\Cpi Y\Csi W\Cwe
These symbols must appear either within the argument to \textcypr or
following the \cyprfamily font-selection command within a scope. Single-
character shortcuts are also supported: Both “\textcypr{\Cpa\Cki\Cna}” and
“\textcypr{pcn}” produce “pcn”, for example. See the cypriot documentation
for more information.
86
Table 279: sarabian South Arabian Letters
a\SAa z\SAz m\SAm x\SAsd D\SAdb
b\SAb H\SAhd n\SAn q\SAq J\SAtb
g\SAg T\SAtd s\SAs r\SAr G\SAga
d\SAd y\SAy f\SAf S\SAsv Z\SAzd
h\SAh k\SAk ‘\SAlq t\SAt X\SAsa
w\SAw l\SAl o\SAo I\SAhu B\SAdd
These symbols must appear either within the argument to \textsarab or
following the \sarabfamily font-selection command within a scope. Single-
character shortcuts are also supported: Both “\textsarab{\SAb\SAk\SAn}” and
“\textsarab{bkn}” produce “bkn”, for example. See the sarabian documentation
for more information.
Table 280: teubner Archaic Greek Letters and Greek Numerals
\Coppa†\Digamma∗\sampi∗\varstigma
\coppa†\koppa∗\Stigma
\digamma∗,‡\Sampi \stigma∗
∗Technically, these symbols do not require teubner; it is sufficient to load the babel
package with the greek option (upon which teubner depends)—but use \qoppa for
\koppa and \ddigamma for \digamma.
†For compatibility with other naming conventions teubner defines \Koppa as a syn-
onym for \Coppa and \varcoppa as a synonym for \coppa.
‡If both teubner and amssymb are loaded, teubner’s \digamma replaces amssymb’s
\digamma, regardless of package-loading order.
87
7 Other symbols
The following are all the symbols that didn’t fit neatly or unambiguously into any of the previous sections.
(Do weather symbols belong under “Science and technology”? Should dice be considered “mathematics”?)
While some of the tables contain clearly related groups of symbols (e.g., musical notes), others represent motley
assortments of whatever the font designer felt like drawing.
Table 281: textcomp Genealogical Symbols
\textborn \textdivorced \textmarried
\textdied \textleaf
Table 282: wasysym General Symbols
m\ataribox \clock \LEFTarrow ,\smiley
\bell \diameter \lightning ☼\sun
-\blacksmiley L\DOWNarrow \phone K\UParrow
1\Bowtie /\frownie \pointer ◊\wasylozenge
|\brokenvert \invdiameter \recorder
\checked 6\kreuz \RIGHTarrow
Table 283: wasysym Circles
\CIRCLE G# \LEFTcircle H# \RIGHTcircle !\rightturn
#\Circle I\Leftcircle J\Rightcircle
G\LEFTCIRCLE H\RIGHTCIRCLE "\leftturn
Table 284: wasysym Musical Symbols
\eighthnote \halfnote \twonotes \fullnote ♩\quarternote
See also \flat,\sharp, and \natural (Table 201 on page 65).
Table 285: arev Musical Symbols
♩\quarternote ♪\eighthnote ♬\sixteenthnote
See also \flat,\sharp, and \natural (Table 201 on page 65).
88
Table 286: harmony Musical Symbols
ˇ“ˇ“
== \AAcht D
D
/\DDohne ˘“\Halb ˇ“==
== \SechBR >\VM
ˇ“(\Acht D/\Dohne <\HaPa ˇ“==
=\SechBr ˇ“*\Zwdr
ˇ“
== \AchtBL s
s\Ds ‰\Pu @\SePa A\ZwPa
ˇ“== \AchtBR S
S\DS ˇ“)\Sech <\UB
?\AcPa ¯\Ganz ˇ“
==
== \SechBL ˇ“\Vier
D
D\DD <\GaPa ˇ“
==
=\SechBl >\ViPa
The musixtex package must be installed to use harmony.
Table 287: harmony Musical Accents
A
a
.a
a
.\Ferli{A}\Ferli{a}∗A/a/\Ohne{A}\Ohne{a}∗
A
a
.a
a
.\Fermi{A}\Fermi{a} g
Ag
a\Umd{A}\Umd{a}∗
A
l
a
l\Kr{A}\Kr{a}
∗These symbols take an optional argument which shifts the accent either horizontally
or vertically (depending on the command) by the given distance.
In addition to the accents shown above, \HH is a special accent command
which accepts five period-separated characters and typesets them such that
“\HH.X.a.b.c.d.” produces “X
a
b
c
d”. All arguments except the first can be omit-
ted: “\HH.X.....” produces “X”. \Takt takes two arguments and composes them
into a musical time signature. For example, “\Takt{12}{8}” produces “ 8
12”. As
two special cases, “\Takt{c}{0}” produces “S” and “\Takt{c}{1}” produces “R”.
The musixtex package must be installed to use harmony.
Table 288: manfnt Dangerous Bend Symbols
\dbend ~\lhdbend \reversedvideodbend
Note that these symbols descend far beneath the baseline. manfnt also defines non-
descending versions, which it calls, correspondingly, \textdbend,\textlhdbend,
and \textreversedvideodbend.
Table 289: Miscellaneous manfnt Symbols
\manboldkidney \manpenkidney
$\manconcentriccircles &\manquadrifolium
%\manconcentricdiamond \manquartercircle
#\mancone '\manrotatedquadrifolium
\mancube "\manrotatedquartercircle
y\manerrarrow \manstar
!\manfilledquartercircle \mantiltpennib
\manhpennib 7\mantriangledown
\manimpossiblecube x\mantriangleright
\mankidney 6\mantriangleup
\manlhpenkidney \manvpennib
89
Table 290: marvosym Navigation Symbols
·\Forward »\MoveDown ´\RewindToIndex ¼\ToTop
¸\ForwardToEnd º\MoveUp µ\RewindToStart
¹\ForwardToIndex \Rewind ½\ToBottom
Table 291: marvosym Laundry Symbols
Ø\AtForty Ü\Handwash Ô\ShortNinetyFive
Ó\AtNinetyFive ¯\IroningI Ö\ShortSixty
Õ\AtSixty °\IroningII Û\ShortThirty
Ë\Bleech ±\IroningIII Ú\SpecialForty
«\CleaningA Ì\NoBleech \Tumbler
¾\CleaningF ¨\NoChemicalCleaning ‰\WashCotton
¿\CleaningFF ²\NoIroning Š\WashSynthetics
¬\CleaningP \NoTumbler ‹\WashWool
\CleaningPP ×\ShortFifty
Ý\Dontwash Ù\ShortForty
Table 292: marvosym Information Symbols
®\Bicycle o\Football Z\Pointinghand
V\Checkedbox x\Gentsroom w\Wheelchair
U\Clocklogo I\Industry b\Writinghand
K\Coffeecup i\Info
X\Crossedbox y\Ladiesroom
Table 293: Other marvosym Symbols
ˆ\Ankh †\Cross Œ\Heart ©\Smiley
ý\Bat F\FHBOlogo ÿ\MartinVogel þ\Womanface
¥\Bouquet f\FHBOLOGO m\Mundus Y\Yinyang
‡\Celtcross §\Frowny @\MVAt
ª\CircledA \FullFHBO :\MVRightarrow
Table 294: Miscellaneous universa Symbols
\bauforms \bauhead
Table 295: Miscellaneous universal Symbols
\baudash \bauforms \bauquarter \varQ
\bauequal \bauhead \bauquestion
\bauface \bauplus \bauwindow
90
Table 296: Miscellaneous fourier Symbols
L\bomb M\grimace N\textthing∗T\textxswup∗
B\danger A\noway U\textxswdown∗
∗fourier defines math-mode aliases for a few of the preceding symbols:
\thething (“N”), \xswordsup (“T”), and \xswordsdown (“U”).
Table 297: ifsym Weather Symbols
\Cloud \Hail \Sleet \WeakRain
\FilledCloud \HalfSun \Snow \WeakRainCloud
\FilledRainCloud \Lightning \SnowCloud \FilledSnowCloud
\FilledSunCloud \NoSun \Sun
\FilledWeakRainCloud \Rain \SunCloud
\Fog \RainCloud \ThinFog
In addition, \Thermo{0}. . .\Thermo{6} produce thermometers that are between
0/6 and 6/6 full of mercury:
Similarly, \wind{hsuni}{hanglei}{hstrengthi}will draw wind symbols with a given
amount of sun (0–4), a given angle (in degrees), and a given strength in km/h (0–
100). For example, \wind{0}{0}{0} produces “ ”, \wind{2}{0}{0} produces
“ ”, and \wind{4}{0}{100} produces “ ”.
Table 298: ifsym Alpine Symbols
\SummitSign \Summit \SurveySign \HalfFilledHut
\StoneMan \Mountain \Joch \VarSummit
\Hut \IceMountain \Flag
\FilledHut \VarMountain \VarFlag
\Village \VarIceMountain \Tent
Table 299: ifsym Clocks
\Interval \StopWatchStart \VarClock \Wecker
\StopWatchEnd \Taschenuhr \VarTaschenuhr
ifsym also exports a \showclock macro. \showclock{hhoursi}{hminutesi}outputs
a clock displaying the corresponding time. For instance, “\showclock{5}{40}”
produces “ ”. hhoursimust be an integer from 0 to 11, and hminutesimust be an
integer multiple of 5 from 0 to 55.
91
Table 300: Other ifsym Symbols
\FilledSectioningDiamond \Letter \Radiation
\Fire \PaperLandscape \SectioningDiamond
\Irritant \PaperPortrait \Telephone
\Cube{1} \Cube{3} \Cube{5}
\Cube{2} \Cube{4} \Cube{6}
\StrokeOne \StrokeThree \StrokeFive
\StrokeTwo \StrokeFour
Table 301: clock Clocks
\ClockStyle \ClockFramefalse \ClockFrametrue
0
1
2
3
The clock package provides a \clock command to typeset an arbitrary time on
an analog clock (and \clocktime to typeset the document’s build time). For
example, the clocks in the above table were produced with \clock{15}{41}. Clock
symbols are composed from a font of clock-face fragments using one of four values
for \ClockStyle and either \ClockFrametrue or \ClockFrametrue as illustrated
above. See the clock documentation for more information.
Table 302: epsdice Dice
\epsdice{1} \epsdice{3} \epsdice{5}
\epsdice{2} \epsdice{4} \epsdice{6}
Table 303: hhcount Dice
\fcdice{1} \fcdice{3} \fcdice{5}
\fcdice{2} \fcdice{4} \fcdice{6}
The \fcdice command accepts values larger than 6. For example, “\fcdice{47}”
produces “ ”.
Table 304: hhcount Tally Markers
\fcscore{1} \fcscore{3} \fcscore{5}
\fcscore{2} \fcscore{4}
The \fcscore command accepts values larger than 5. For example,
“\fcscore{47}” produces “ ”.
92
Table 305: skull Symbols
\skull
Table 306: Non-Mathematical mathabx Symbols
\rip
Table 307: skak Chess Informator Symbols
g\bbetter d\doublepawns q\seppawns
i\bdecisive L\ending O-O\shortcastling
b\betteris j\equal T\timelimit
a\bishoppair H\file k\unclear
e\bupperhand O\kside u\unitedpawns
X\capturesymbol O-O-O\longcastling R\various
O\castlingchar x\markera f\wbetter
-\castlinghyphen y\markerb h\wdecisive
I\centre m\mate J\weakpt
+\checksymbol S\morepawns v\with
RR \chesscomment U\moreroom A\withattack
P\chessetc N\novelty E\withidea
l\chesssee F\onlymove C\withinit
n\compensation o\opposbishops w\without
V\counterplay r\passedpawn c\wupperhand
t\devadvantage M\qside D\zugzwang
G\diagonal s\samebishops
93
Table 308: skak Chess Pieces and Chessboard Squares
a\BlackBishopOnBlack s\BlackRookOnBlack J\WhiteKingOnBlack
b\BlackBishopOnWhite r\BlackRookOnWhite K\WhiteKingOnWhite
Z\BlackEmptySquare B\symbishop M\WhiteKnightOnBlack
j\BlackKingOnBlack K\symking N\WhiteKnightOnWhite
k\BlackKingOnWhite N\symknight O\WhitePawnOnBlack
m\BlackKnightOnBlack p\sympawn P\WhitePawnOnWhite
n\BlackKnightOnWhite Q\symqueen L\WhiteQueenOnBlack
o\BlackPawnOnBlack R\symrook Q\WhiteQueenOnWhite
p\BlackPawnOnWhite A\WhiteBishopOnBlack S\WhiteRookOnBlack
l\BlackQueenOnBlack B\WhiteBishopOnWhite R\WhiteRookOnWhite
q\BlackQueenOnWhite 0\WhiteEmptySquare
The skak package also provides commands for drawing complete chessboards. See
the skak documentation for more information.
Table 309: igo Go Stones
\blackstone[\igocircle] \whitestone[\igocircle]
\blackstone[\igocross] \whitestone[\igocross]
\blackstone[\igonone] \whitestone[\igonone]
\blackstone[\igosquare] \whitestone[\igosquare]
\blackstone[\igotriangle] \whitestone[\igotriangle]
In addition to the symbols shown above, igo’s \blackstone and \whitestone
commands accept numbers from 1 to 99 and display them circled as , , , . . .
and , , , . . . , respectively.
The igo package is intended to typeset Go boards (goban). See the igo documen-
tation for more information.
94
Table 310: metre Metrical Symbols
×
?
\a ¯
˘
¯
˘
´\bBm \cc ˘
¯
˘
¯
´\Mbb ˙
˙
˙
˙\Pppp ⊗
?
\t
˘
´\B ¯
˘
¯
˘\bbm \Ccc ˘
¯
˘
¯
¯
˘
¯
˘\mbbx ˙
˙
˙
˙\pppp \tsbm
˘\b ¯
˘
¯
˘
´\Bbm ¯\m ◦◦ \oo ˙
˙
˙
˙
˙\Ppppp \tsmb
˘
´
˘\Bb ˘
¯
˘
¯
˘\bbmb ¯
´\M ˙\p ˙
˙
˙
˙
˙\ppppp \tsmm
˘˘
´\BB ¯
˘
¯
˘˘
¯
˘
¯\bbmx ×
¯\ma ¯
˙\pm \ps ¯
˙
˙\vppm
˘˘ \bb ¯
˘\bm ˘
¯
´\Mb ˙
˙\pp ˙
˙\pxp ¯
˙
˙
˙\vpppm
˘˘
´\bB ¯
˘
´\Bm ˘
¯\mb ˙
˙\Pp ˙
˙\Pxp ˙
˙˙
˙\x
×
˘˘ \bba \c ˘
¯
˘
¯
´\mBb ¯
˙˙ \ppm ∼
?
\R
˘
˘˘ \bbb \C ˘
¯
˘
¯
´\mbB ˙
˙
˙\ppp ∼
?
\r
¯
˘
¯
˘
´\BBm \Cc ˘
¯
˘
¯\mbb ˙
˙
˙\Ppp ⊗
?
\T
The preceding symbols are valid only within the argument to the metre command.
Table 311: metre Small and Large Metrical Symbols
÷\anaclasis ÷\Anaclasis
<\antidiple <\Antidiple
<
·
·\antidiple* <
·
·\Antidiple*
⊃\antisigma ⊃\Antisigma
×···
·\asteriscus ×···
·\Asteriscus
∧\catalexis ∧\Catalexis
>\diple >\Diple
>
·
·\diple* >
·
·\Diple*
\obelus \Obelus
·
·\obelus* ·
·\Obelus*
∼\respondens ∼\Respondens
⊗\terminus ⊗\Terminus
⊕\terminus* ⊕\Terminus*
Table 312: teubner Metrical Symbols
Ι\aeolicbii ι\barbrevis η\ipercatal
Θ\aeolicbiii ς\bbrevis λ\longa
Κ\aeolicbiv β\brevis ε\ubarbbrevis
Ξ\anceps γ\catal δ\ubarbrevis
Ζ\ancepsdbrevis \corona φ\ubarsbrevis
Ψ\banceps Ϙ\coronainv κ\ubrevislonga
θ\barbbrevis H\hiatus
The teubner package provides a \newmetrics command that helps users combine
the preceding symbols as well as other teubner symbols. For example, the predefined
\pentam symbol uses \newmetrics to juxtapose six \longas, two \barbbrevises,
four \brevises, and a \dBar into “λθλθλ||λββλββλ”. See the teubner docu-
mentation for more information.
95
Table 313: dictsym Dictionary Symbols
a\dsaeronautical c\dscommercial m\dsmedical
G\dsagricultural H\dsheraldical X\dsmilitary
A\dsarchitectural J\dsjuridical R\dsrailways
B\dsbiological L\dsliterary T\dstechnical
C\dschemical M\dsmathematical
Table 314: simpsons Characters from The Simpsons
\Bart \Homer \Maggie \SNPP
\Burns \Lisa \Marge
The location of the characters’ pupils can be controlled with the \Goofy command.
See AMETAFONT of ‘Simpsons’ characters [Che97] for more information. Also,
each of the above can be prefixed with \Left to make the character face left instead
of right:
\Left\Bart
96
Table 315: pmboxdraw Box-Drawing Symbols
\textblock \textSFli \textSFxli \textSFxxiii
\textdkshade \textSFlii \textSFxlii \textSFxxiv
\textdnblock \textSFliii \textSFxliii \textSFxxv
\textlfblock \textSFliv \textSFxliv \textSFxxvi
\textltshade \textSFv \textSFxlix \textSFxxvii
\textrtblock \textSFvi \textSFxlv \textSFxxviii
\textSFi \textSFvii \textSFxlvi \textSFxxxix
\textSFii \textSFviii \textSFxlvii \textSFxxxvi
\textSFiii \textSFx \textSFxlviii \textSFxxxvii
\textSFiv \textSFxi \textSFxx \textSFxxxviii
\textSFix \textSFxix \textSFxxi \textshade
\textSFl \textSFxl \textSFxxii \textupblock
Code Page 437 (CP437), which was first utilized by the original IBM PC, contains
the set of box-drawing symbols (sides, corners, and intersections of single- and
double-ruled boxes) shown above in character positions 176–223. These symbols
also appear in the Unicode Box Drawing and Block Element tables.
The pmboxdraw package draws the CP437 box-drawing symbols using T
E
X rules
(specifically, \vrule) instead of with a font and thereby provides the ability to
alter both rule width and the separation between rules. See the pmboxdraw docu-
mentation for more information.
Table 316: staves Magical Staves
\staveI \staveXXIV .\staveXLVII
\staveII \staveXXV /\staveXLVIII
\staveIII \staveXXVI 0\staveXLIX
\staveIV \staveXXVII 1\staveL
\staveV \staveXXVIII 2\staveLI
\staveVI \staveXXIX 3\staveLII
\staveVII \staveXXX 4\staveLIII
\staveVIII \staveXXXI 5\staveLIV
\staveIX \staveXXXII 6\staveLV
\staveX \staveXXXIII 7\staveLVI
\staveXI !\staveXXXIV 8\staveLVII
(continued on next page)
97
(continued from previous page)
\staveXII "\staveXXXV 9\staveLVIII
\staveXIII #\staveXXXVI :\staveLIX
\staveXIV $\staveXXXVII ;\staveLX
\staveXV %\staveXXXVIII <\staveLXI
\staveXVI &\staveXXXIX =\staveLXII
\staveXVII '\staveXL >\staveLXIII
\staveXVIII (\staveXLI ?\staveLXIV
\staveXIX )\staveXLII @\staveLXV
\staveXX *\staveXLIII A\staveLXVI
\staveXXI +\staveXLIV B\staveLXVII
\staveXXII ,\staveXLV C\staveLXVIII
\staveXXIII -\staveXLVI
The meanings of these symbols are described on the Web site for the Mu-
seum of Icelandic Sorcery and Witchcraft at http://www.galdrasyning.is/
index.php?option=com content&task=category&sectionid=5&id=18&Itemid=
60 (TinyURL: http://tinyurl.com/25979m). For example, \staveL (“1”) is
intended to ward off ghosts and evil spirits.
Table 317: pigpen Cipher Symbols
A{\pigpenfont A} J{\pigpenfont J} S{\pigpenfont S}
B{\pigpenfont B} K{\pigpenfont K} T{\pigpenfont T}
C{\pigpenfont C} L{\pigpenfont L} U{\pigpenfont U}
D{\pigpenfont D} M{\pigpenfont M} V{\pigpenfont V}
E{\pigpenfont E} N{\pigpenfont N} W{\pigpenfont W}
F{\pigpenfont F} O{\pigpenfont O} X{\pigpenfont X}
G{\pigpenfont G} P{\pigpenfont P} Y{\pigpenfont Y}
H{\pigpenfont H} Q{\pigpenfont Q} Z{\pigpenfont Z}
I{\pigpenfont I} R{\pigpenfont R}
Table 318: C
h
in
A2e Phases of the Moon
\MoonPha{1} \MoonPha{2} \MoonPha{3} \MoonPha{4}
Table 319: Other C
h
in
A2e Symbols
\Greenpoint \Postbox \Telephone
\Info \Request
98
Table 320: recycle Recycling Symbols
A\recycle A\Recycle
A\RECYCLE
The METAFONT code that implements the recycling symbols shown above is,
in the words of its author, “awful code [that] doesn’t even put the logo
in a box (properly)”. Expect to receive “Inconsistent equation (off by
hnumber i)” errors from METAFONT. Fortunately, if you tell METAFONT to pro-
ceed past those errors (e.g., by pressing Enter after each one or by specifying
“-interaction=nonstopmode” on the METAFONT command line) it should pro-
duce a valid font.
The commands listed above should be used within a group (e.g., “{\recycle}”)
because they exhibit the side effect of changing the font to the recycle font.
99
8 Additional Information
Unlike the previous sections of this document, Section 8 does not contain new symbol tables. Rather, it provides
additional help in using the Comprehensive L
A
T
E
X Symbol List. First, it draws attention to symbol names used
by multiple packages. Next, it provides some guidelines for finding symbols and gives some examples regarding
how to construct missing symbols out of existing ones. Then, it comments on the spacing surrounding symbols
in math mode. After that, it presents an ASCII and Latin 1 quick-reference guide, showing how to enter all of
the standard ASCII/Latin 1 symbols in L
A
T
E
X. And finally, it lists some statistics about this document itself.
8.1 Symbol Name Clashes
Unfortunately, a number of symbol names are not unique; they appear in more than one package. Depending
on how the symbols are defined in each package, L
A
T
E
X will either output an error message or replace an
earlier-defined symbol with a later-defined symbol. Table 321 on the following page presents a selection of
name clashes that appear in this document.
Using multiple symbols with the same name in the same document—or even merely loading conflicting
symbol packages—can be tricky but, as evidenced by the existence of Table 321, not impossible. The general
procedure is to load the first package, rename the conflicting symbols, and then load the second package.
Examine the L
A
T
E
X source for this document (symbols.tex) for examples of this and other techniques for
handling symbol conflicts. Note that symbols.tex’s \savesymbol and \restoresymbol macros have been
extracted into the savesym package, which can be downloaded from CTAN.
txfonts and pxfonts redefine a huge number of symbols—essentially, all of the symbols defined by latexsym,
textcomp, the various A
M
Ssymbol sets, and L
A
T
E
X 2εitself. Similarly, mathabx redefines a vast number of
math symbols in an attempt to improve their look. The txfonts,pxfonts, and mathabx conflicts are not listed
in Table 321 because they are designed to be compatible with the symbols they replace. Table 322 on page 102
illustrates what “compatible” means in this context.
To use the new txfonts/pxfonts symbols without altering the document’s main font, merely reset the default
font families back to their original values after loading one of those packages:
\renewcommand\rmdefault{cmr}
\renewcommand\sfdefault{cmss}
\renewcommand\ttdefault{cmtt}
8.2 Resizing symbols
Mathematical symbols listed in this document as “variable-sized” are designed to stretch vertically. Each
variable-sized symbol comes in one or more basic sizes plus a variation comprising both stretchable and
nonstretchable segments. Table 323 on page 102 presents the symbols \} and \uparrow in their default size,
in their \big,\Big,\bigg, and \Bigg sizes, in an even larger size achieved using \left/\right, and—for
contrast—in a large size achieved by changing the font size using L
A
T
E
X 2ε’s \fontsize command. Because
the symbols shown belong to the Computer Modern family, the type1cm package needs to be loaded to support
font sizes larger than 24.88 pt.
Note how \fontsize makes the symbol wider and thicker. (The graphicx package’s \scalebox or
\resizebox commands would produce a similar effect.) Also, the \fontsize-enlarged symbol is vertically
centered relative to correspondingly large text, unlike the symbols enlarged using \big et al. or \left/\right,
which all use the same math axis regardless of symbol size. However, \fontsize is not limited to mathematical
delimiters. Also, \scalebox and \resizebox are more robust to poorly composed symbols (e.g., two symbols
made to overlap by backspacing a fixed distance) but do not work with every T
E
X backend and will produce
jagged symbols when scaling a bitmapped font.
All variable-sized delimiters are defined (by the corresponding .tfm file) in terms of up to five segments, as
illustrated by Figure 1 on page 102. The top, middle, and bottom segments are of a fixed size. The top-middle
and middle-bottom segments (which are constrained to be the same character) are repeated as many times as
necessary to achieve the desired height.
8.3 Where can I find the symbol for . . . ?
If you can’t find some symbol you’re looking for in this document, there are a few possible explanations:
100
Table 321: Symbol Name Clashes
Symbol L
A
T
E
X 2εA
M
Sstmaryrd wasysym mathabx marvosym bbding ifsym dingbat wsuipa
\baro
\bigtriangledown 5`
\bigtriangleup 4a
\checkmark X
\Circle #
\Cross †
\ggg ≫
\Letter B
\lightning
\Lightning E
\lll ≪
\Square
\Sun À
\TriangleDown
\TriangleUp
101
Table 322: Example of a Benign Name Clash
Default txfonts
Symbol (Computer Modern) (Times Roman)
RRR
\textrecipe
Table 323: Sample resized delimiters
Symbol Default size \big \Big \bigg \Bigg \left /\right \fontsize
\} }o™)
}
\uparrow ↑x
x
x
x
x
↑
−→
top
top-middle (extensible)
middle
middle-bottom (extensible)
bottom
Figure 1: Implementation of variable-sized delimiters
102
•The symbol isn’t intuitively named. As a few examples, the ifsym command to draw dice is “\Cube”; a
plus sign with a circle around it (“exclusive or” to computer engineers) is “\oplus”; and lightning bolts
in fonts designed by German speakers may have “blitz” in their names as in the ulsy package. The moral
of the story is to be creative with synonyms when searching the index.
•The symbol is defined by some package that I overlooked (or deemed unimportant). If there’s some
symbol package that you think should be included in the Comprehensive L
A
T
E
X Symbol List, please send
me e-mail at the address listed on the title page.
•The symbol isn’t defined in any package whatsoever.
Even in the last case, all is not lost. Sometimes, a symbol exists in a font, but there is no L
A
T
E
X binding
for it. For example, the PostScript Symbol font contains a “↵” symbol, which may be useful for representing
a carriage return, but there is no package (as far as I know) for accessing that symbol. To produce an
unnamed symbol, you need to switch to the font explicitly with L
A
T
E
X 2ε’s low-level font commands [L
A
T00]
and use T
E
X’s primitive \char command [Knu86a] to request a specific character number in the font.5In fact,
\char is not strictly necesssary; the character can often be entered symbolically. For example, the symbol
for an impulse train or Tate-Shafarevich group (“ ”) is actually an uppercase sha in the Cyrillic alphabet.
(Cyrillic is supported by the OT2 font encoding, for instance). While a sha can be defined numerically as
“{\fontencoding{OT2}\selectfont\char88}” it may be more intuitive to use the OT2 font encoding’s “SH”
ligature: “{\fontencoding{OT2}\selectfont SH}”.
Reflecting and rotating existing symbols
A common request on comp.text.tex is for a reversed or rotated version of an existing symbol.
As a last resort, these effects can be achieved with the graphicx (or graphics) package’s \reflectbox and
\rotatebox macros. For example, \textsuperscript{\reflectbox{?}} produces an irony mark (“
?
”;
cf. http://en.wikipedia.org/wiki/Irony mark), and \rotatebox[origin=c]{180}{$\iota$} produces the
definite-description operator (“
ι
”). The disadvantage of the graphicx/graphics approach is that not every T
E
X
backend handles graphical transformations.6Far better is to find a suitable font that contains the desired
symbol in the correct orientation. For instance, if the phonetic package is available, then \textit{\riota}
will yield a backend-independent “ ”. Similarly, tipa’s \textrevepsilon (“3”) or wsuipa’s \revepsilon (“ ”)
may be used to express the mathematical notion of “such that” in a cleaner manner than with \reflectbox
or \rotatebox.7
Joining and overlapping existing symbols
Symbols that do not exist in any font can sometimes be fabricated out of existing symbols. The L
A
T
E
X 2εsource
file fontdef.dtx contains a number of such definitions. For example, \models (see Table 67 on page 30) is
defined in that file with:
\def\models{\mathrel|\joinrel=}
where \mathrel and \joinrel are used to control the horizontal spacing. \def is the T
E
X primitive upon
which L
A
T
E
X’s \newcommand is based. See The T
E
Xbook [Knu86a] for more information on all three of those
commands.
With some simple pattern-matching, one can easily define a backward \models sign (“=|”):
\def\ismodeledby{=\joinrel\mathrel|}
In general, arrows/harpoons, horizontal lines (“=”, “-”, “\relbar”, and “\Relbar”), and the various math-
extension characters can be combined creatively with miscellaneous other characters to produce a variety of
new symbols. Of course, new symbols can be composed from any set of existing characters. For instance, L
A
T
E
X
defines \hbar (“”) as a “¯” character (\mathchar’26) followed by a backspace of 9 math units (\mkern-9mu),
followed by the letter “h”:
\def\hbar{{\mathchar’26\mkern-9muh}}
5pifont defines a convenient \Pisymbol command for accessing symbols in PostScript fonts by number. For example,
“\Pisymbol{psy}{191}” produces “↵”.
6As an example, Xdvi ignores both \reflectbox and \rotatebox.
7More common symbols for representing “such that” include “|”, “:”, and “s.t.”.
103
We can just as easily define other barred letters:
\def\bbar{{\mathchar’26\mkern-9mu b}}
\def\dbar{{\mathchar’26\mkern-12mu d}}
(The space after the “mu” is optional but is added for clarity.) \bbar and \dbar define “¯b” and “¯d”, respectively.
Note that \dbar requires a greater backward math kern than \bbar; a −9 mu kern would have produced the
less-attractive “¯d” glyph.
The amsmath package provides \overset and \underset commands for placing one symbol respectively
above or below another. For example, \overset{G}{\sim}8produces “G
∼” (sometimes used for “equidecom-
posable with respect to G”).
Sometimes an ordinary tabular environment can be co-opted into juxtaposing existing symbols into a new
symbol. Consider the following definition of \asterism (“ *
**”) from a June 2007 post to comp.text.tex by
Peter Flynn:
\newcommand{\asterism}{\smash{%
\raisebox{-.5ex}{%
\setlength{\tabcolsep}{-.5pt}%
\begin{tabular}{@{}cc@{}}%
\multicolumn2c*\\[-2ex]*&*%
\end{tabular}}}}
Note how the space between columns (\tabcolsep) and rows (\\[. . . ]) is made negative to squeeze the
asterisks closer together.
There is a T
E
X primitive called \mathaccent that centers one mathematical symbol atop another. For
example, one can define \dotcup (“ ·
∪”)—the composition of a \cup and a \cdot—as follows:
\newcommand{\dotcup}{\ensuremath{\mathaccent\cdot\cup}}
The catch is that \mathaccent requires the accent to be a “math character”. That is, it must be a character
in a math font as opposed to a symbol defined in terms of other symbols. See The T
E
Xbook [Knu86a] for more
information.
Another T
E
X primitive that is useful for composing symbols is \vcenter.\vcenter is conceptually similar
to “\begin{tabular}{l}” in L
A
T
E
X but takes a list of vertical material instead of \\-separated rows. Also,
it vertically centers the result on the math axis. (Many operators, such as “+” and “−” are also vertically
centered on the math axis.) Enrico Gregorio posted the following symbol definition to comp.text.tex in
March 2004 in response to a query about an alternate way to denote equivalence:
\newcommand*{\threesim}{%
\mathrel{\vcenter{\offinterlineskip
\hbox{$\sim$}\vskip-.35ex\hbox{$\sim$}\vskip-.35ex\hbox{$\sim$}}}}
The \threesim symbol, which vertically centers three \sim (“∼”) symbols with 0.35 x-heights of space between
them, is rendered as “∼
∼
∼”. \offinterlineskip is a macro that disables implicit interline spacing. Without
it, \threesim would have a full line of vertical spacing between each \sim. Because of \vcenter,\threesim
aligns properly with other math operators: a÷b∼
∼
∼c×d.
A related L
A
T
E
X command, borrowed from Plain T
E
X, is \ooalign.\ooalign vertically overlaps symbols
and works both within and outside of math mode. Essentially, it creates a single-column tabular environment
with zero vertical distance between rows. However, because it is based directly on T
E
X’s \ialign primitive,
\ooalign uses T
E
X’s tabular syntax instead of L
A
T
E
X’s (i.e., with \cr as the row terminator instead of \\). The
following example of \ooalign, a macro that defines a standard-state symbol (\stst, “−◦ ”) as a superscripted
Plimsoll line (\barcirc, “−◦”),9is due to an October 2007 comp.text.tex post by Donald Arseneau:
\makeatletter
\providecommand\barcirc{\mathpalette\@barred\circ}
\def\@barred#1#2{\ooalign{\hfil$#1-$\hfil\cr\hfil$#1#2$\hfil\cr}}
\newcommand\stst{^{\protect\barcirc}}
\makeatother
8L
A
T
E
X’s \stackrel command is similar but is limited to placing a symbol above a binary relation.
9While \barcirc illustrates how to combine symbols using \ooalign, the stmaryrd package’s \minuso command (Table 46 on
page 22) provides a similar glyph (“”) as a single, indivisible symbol.
104
In the preceding code, note the \ooalign call’s use of \hfil to horizontally center a minus sign (“−”) and
a\circ (“◦”).
As another example of \ooalign, consider the following code (due to Enrico Gregorio in a June 2007 post
to comp.text.tex) that overlaps a \ni (“3”) and two minus signs (“−−”) to produce “3−−”, an obscure variation
on the infrequently used “3” symbol for “such that”discussed on page 103:
\newcommand{\suchthat}{%
\mathrel{\ooalign{$\ni$\cr\kern-1pt$-$\kern-6.5pt$-$}}}
The slashed package, although originally designed for producing Feynman slashed-character notation, in
fact facilitates the production of arbitrary overlapped symbols. The default behavior is to overwrite a given
character with “/”. For example, \slashed{D} produces “ /
D”. However, the \declareslashed command
provides the flexibility to specify the mathematical context of the composite character (operator, relation,
punctuation, etc., as will be discussed in Section 8.4), the overlapping symbol, horizontal and vertical adjust-
ments in symbol-relative units, and the character to be overlapped. Consider, for example, the symbol for
reduced quadrupole moment (“-
I”). This can be declared as follows:
\newcommand{\rqm}{{%
\declareslashed{}{\text{-}}{0.04}{0}{I}\slashed{I}}}
\declareslashed{·}{·}{·}{·}{I} affects the meaning of all subsequent \slashed{I} commands in the same
scope. The preceding definition of \rqm therefore uses an extra set of curly braces to limit that scope to
a single \slashed{I}. In addition, \rqm uses amstext’s \text macro (described on the next page) to make
\declareslashed use a text-mode hyphen (“-”) instead of a math-mode minus sign (“−”) and to ensure that
the hyphen scales properly in size in subscripts and superscripts. See slashed’s documentation (located in
slashed.sty itself) for a detailed usage description of the \slashed and \declareslashed commands.
Somewhat simpler than slashed is the centernot package. centernot provides a single command, \centernot,
which, like \not, puts a slash over the subsequent mathematical symbol. However, instead of putting the slash
at a fixed location, \centernot centers the slash over its argument. \centernot might be used, for example,
to create a “does not imply” symbol:
6=⇒\not\Longrightarrow
vs.
6=⇒\centernot\Longrightarrow
See the centernot documentation for more information.
Making new symbols work in superscripts and subscripts
To make composite symbols work properly within subscripts and superscripts, you may need to use T
E
X’s
\mathchoice primitive. \mathchoice evaluates one of four expressions, based on whether the current math
style is display, text, script, or scriptscript. (See The T
E
Xbook [Knu86a] for a more complete descrip-
tion.) For example, the following L
A
T
E
X code—posted to comp.text.tex by Torsten Bronger—composes
a sub/superscriptable “⊥>” symbol out of \top and \bot (“>” and “⊥”):
\def\topbotatom#1{\hbox{\hbox to 0pt{$#1\bot$\hss}$#1\top$}}
\newcommand*{\topbot}{\mathrel{\mathchoice{\topbotatom\displaystyle}
{\topbotatom\textstyle}
{\topbotatom\scriptstyle}
{\topbotatom\scriptscriptstyle}}}
The following is another example that uses \mathchoice to construct symbols in different math modes.
The code defines a principal value integral symbol, which is an integral sign with a line through it.
\def\Xint#1{\mathchoice
{\XXint\displaystyle\textstyle{#1}}%
{\XXint\textstyle\scriptstyle{#1}}%
{\XXint\scriptstyle\scriptscriptstyle{#1}}%
{\XXint\scriptscriptstyle\scriptscriptstyle{#1}}%
105
\!\int}
\def\XXint#1#2#3{{\setbox0=\hbox{$#1{#2#3}{\int}$}
\vcenter{\hbox{$#2#3$}}\kern-.5\wd0}}
\def\ddashint{\Xint=}
\def\dashint{\Xint-}
(The preceding code was taken verbatim from the UK T
E
X Users’ Group FAQ at http://www.tex.ac.uk/
faq.) \dashint produces a single-dashed integral sign (“−
R”), while \ddashint produces a double-dashed
one (“=
R”). The \Xint macro defined above can also be used to generate a wealth of new integrals: “
R”
(\Xint\circlearrowright), “
R” (\Xint\circlearrowleft), “⊂
R” (\Xint\subset), “∞
R” (\Xint\infty), and
so forth.
L
A
T
E
X 2εprovides a simple wrapper for \mathchoice that sometimes helps produce terser symbol def-
initions. The macro is called \mathpalette and it takes two arguments. \mathpalette invokes the first
argument, passing it one of “\displaystyle”, “\textstyle”, “\scriptstyle”, or “\scriptscriptstyle”,
followed by the second argument. \mathpalette is useful when a symbol macro must know which math
style is currently in use (e.g., to set it explicitly within an \mbox). Donald Arseneau posted the following
\mathpalette-based definition of a probabilistic-independence symbol (“⊥⊥”) to comp.text.tex in June 2000:
\newcommand\independent{\protect\mathpalette{\protect\independenT}{\perp}}
\def\independenT#1#2{\mathrel{\rlap{$#1#2$}\mkern2mu{#1#2}}}
The \independent macro uses \mathpalette to pass the \independenT helper macro both the current math
style and the \perp symbol. \independenT typesets \perp in the current math style, moves two math units to
the right, and finally typesets a second—overlapping—copy of \perp, again in the current math style. \rlap,
which enables text overlap, is described later on this page.
Some people like their square-root signs with a trailing “hook” (i.e., “√”) as this helps visually distinguish
expressions like “√3x” from those like “√3x”. In March 2002, Dan Luecking posted a \mathpalette-based
definition of a hooked square-root symbol to comp.text.tex:
\def\hksqrt{\mathpalette\DHLhksqrt}
\def\DHLhksqrt#1#2{\setbox0=\hbox{$#1\sqrt{#2\,}$}\dimen0=\ht0
\advance\dimen0-0.2\ht0
\setbox2=\hbox{\vrule height\ht0 depth -\dimen0}%
{\box0\lower0.4pt\box2}}
Notice how \DHLhksqrt uses \mathpalette to recover the outer math style (argument #1) from within an
\hbox. The rest of the code is simply using T
E
X primitives to position a hook of height 0.2 times the \sqrt
height at the right of the \sqrt. See The T
E
Xbook [Knu86a] for more understanding of T
E
X “boxes” and
“dimens”.
Sometimes, however, amstext’s \text macro is all that is necessary to make composite symbols appear
correctly in subscripts and superscripts, as in the following definitions of \neswarrow (“%.”) and \nwsearrow
(“-&”):10
\newcommand{\neswarrow}{\mathrel{\text{$\nearrow$\llap{$\swarrow$}}}}
\newcommand{\nwsearrow}{\mathrel{\text{$\nwarrow$\llap{$\searrow$}}}}
\text resembles L
A
T
E
X’s \mbox command but shrinks its argument appropriately when used within a subscript
or superscript. \llap (“left overlap”) and its counterpart, \rlap (“right overlap”), appear frequently when
creating composite characters. \llap outputs its argument to the left of the current position, overlapping
whatever text is already there. Similarly, \rlap overlaps whatever text would normally appear to the right
of its argument. For example, “A\llap{B}” and “\rlap{A}B” each produce “AB”. However, the result of the
former is the width of “A”, and the result of the latter is the width of “B”—\llap{. . . }and \rlap{. . . }take
up zero space.
In a June 2002 post to comp.text.tex, Donald Arseneau presented a general macro for aligning an arbitrary
number of symbols on their horizontal centers and vertical baselines:
10Note that if your goal is to typeset commutative diagrams or pushout/pullback diagrams, then you should probably be using
X
Y
-pic.
106
\makeatletter
\def\moverlay{\mathpalette\mov@rlay}
\def\mov@rlay#1#2{\leavevmode\vtop{%
\baselineskip\z@skip \lineskiplimit-\maxdimen
\ialign{\hfil$#1##$\hfil\cr#2\crcr}}}
\makeatother
The \makeatletter and \makeatother commands are needed to coerce L
A
T
E
X into accepting “@” as
part of a macro name. \moverlay takes a list of symbols separated by \cr (T
E
X’s equivalent of
L
A
T
E
X’s \\). For example, the \topbot command defined on page 105 could have been expressed as
“\moverlay{\top\cr\bot}” and the \neswarrow command defined on the previous page could have been
expressed as “\moverlay{\nearrow\cr\swarrow}”.
The basic concept behind \moverlay’s implementation is that \moverlay typesets the given symbols in a
table that utilizes a zero \baselineskip. This causes every row to be typeset at the same vertical position.
See The T
E
Xbook [Knu86a] for explanations of the T
E
X primitives used by \moverlay.
Modifying L
A
T
E
X-generated symbols
Oftentimes, symbols composed in the L
A
T
E
X 2εsource code can be modified with minimal effort to produce
useful variations. For example, fontdef.dtx composes the \ddots symbol (see Table 189 on page 63) out of
three periods, raised 7 pt., 4 pt., and 1 pt., respectively:
\def\ddots{\mathinner{\mkern1mu\raise7\p@
\vbox{\kern7\p@\hbox{.}}\mkern2mu
\raise4\p@\hbox{.}\mkern2mu\raise\p@\hbox{.}\mkern1mu}}
\p@ is a L
A
T
E
X 2εshortcut for “pt” or “1.0pt”. The remaining commands are defined in The
T
E
Xbook [Knu86a]. To draw a version of \ddots with the dots going along the opposite diagonal, we merely
have to reorder the \raise7\p@,\raise4\p@, and \raise\p@:
\makeatletter
\def\revddots{\mathinner{\mkern1mu\raise\p@
\vbox{\kern7\p@\hbox{.}}\mkern2mu
\raise4\p@\hbox{.}\mkern2mu\raise7\p@\hbox{.}\mkern1mu}}
\makeatother
\revddots is essentially identical to the mathdots package’s \iddots command or the yhmath package’s \adots
command.
Producing complex accents
Accents are a special case of combining existing symbols to make new symbols. While various tables in
this document show how to add an accent to an existing symbol, some applications, such as translitera-
tions from non-Latin alphabets, require multiple accents per character. For instance, the creator of pdfT
E
X
writes his name as “H`an Th´
ˆe Th`anh”. The dblaccnt package enables L
A
T
E
X to stack accents, as in “H\‘an
Th\’{\^e} Th\‘anh” (albeit not in the OT1 font encoding). In addition, the wsuipa package defines \diatop
and \diaunder macros for putting one or more diacritics or accents above or below a given character. For
example, \diaunder[{\diatop[\’|\=]}|\textsubdot{r}] produces “´
¯
r
˙”. See the wsuipa documentation for
more information.
The accents package facilitates the fabrication of accents in math mode. Its \accentset command en-
ables any character to be used as an accent. For instance, \accentset{\star}{f} produces “
?
f” and
\accentset{e}{X} produces “
e
X”. \underaccent does the same thing, but places the accent beneath the
character. This enables constructs like \underaccent{\tilde}{V}, which produces “˜
V”. accents provides
other accent-related features as well; see the documentation for more information.
Creating extensible symbols
A relatively simple example of creating extensible symbols stems from a comp.text.tex post by Donald
Arseneau (June 2003). The following code defines an equals sign that extends as far to the right as possible,
just like L
A
T
E
X’s \hrulefill command:
107
\makeatletter
\def\equalsfill{$\m@th\mathord=\mkern-7mu
\cleaders\hbox{$\!\mathord=\!$}\hfill
\mkern-7mu\mathord=$}
\makeatother
T
E
X’s \cleaders and \hfill primitives are the key to understanding \equalsfill’s extensibility. Essen-
tially, \equalsfill repeats a box containing “=” plus some negative space until it fills the maximum avail-
able horizontal space. \equalsfill is intended to be used with L
A
T
E
X’s \stackrel command, which stacks
one mathematical expression (slightly reduced in size) atop another. Hence, “\stackrel{a}{\rightarrow}”
produces “ a
→” and “X \stackrel{\text{definition}}{\hbox{\equalsfill}} Y” produces “Xdefinition
======= Y”.
If all that needs to extend are horizontal and vertical lines—as opposed to repeated symbols such as the
“=” in the previous example—L
A
T
E
X’s array or tabular environments may suffice. Consider the following
code (due to a February 1999 comp.text.tex post by Donald Arseneau and subsequent modifications by Billy
Yu and Scott Pakin) for typesetting annuity and life-insurance symbols:
\DeclareRobustCommand{\actuarial}[2][]{%
\def\arraystretch{0}%
\setlength\arraycolsep{0.5pt}%
\setlength\arrayrulewidth{0.5pt}%
\setbox0=\hbox{$\scriptstyle#1#2$}%
\begin{array}[b]{*2{@{}>{\scriptstyle}c}|}
\cline{2-2}%
\rule[1.25pt]{0pt}{\ht0}%
#1 & #2%
\end{array}%
}
Using the preceding definition, one can type, e.g., “$a_{\actuarial{n}}$” to produce “an” and
“$a_{\actuarial[x:]{n}}$” to produce “ax:n”
A more complex example of composing accents is the following definition of extensible \overbracket,
\underbracket,\overparenthesis, and \underparenthesis symbols, taken from a May 2002
comp.text.tex post by Donald Arseneau:
\makeatletter
\def\overbracket#1{\mathop{\vbox{\ialign{##\crcr\noalign{\kern3\p@}
\downbracketfill\crcr\noalign{\kern3\p@\nointerlineskip}
$\hfil\displaystyle{#1}\hfil$\crcr}}}\limits}
\def\underbracket#1{\mathop{\vtop{\ialign{##\crcr
$\hfil\displaystyle{#1}\hfil$\crcr\noalign{\kern3\p@\nointerlineskip}
\upbracketfill\crcr\noalign{\kern3\p@}}}}\limits}
\def\overparenthesis#1{\mathop{\vbox{\ialign{##\crcr\noalign{\kern3\p@}
\downparenthfill\crcr\noalign{\kern3\p@\nointerlineskip}
$\hfil\displaystyle{#1}\hfil$\crcr}}}\limits}
\def\underparenthesis#1{\mathop{\vtop{\ialign{##\crcr
$\hfil\displaystyle{#1}\hfil$\crcr\noalign{\kern3\p@\nointerlineskip}
\upparenthfill\crcr\noalign{\kern3\p@}}}}\limits}
\def\downparenthfill{$\m@th\braceld\leaders\vrule\hfill\bracerd$}
\def\upparenthfill{$\m@th\bracelu\leaders\vrule\hfill\braceru$}
\def\upbracketfill{$\m@th\makesm@sh{\llap{\vrule\@height3\p@\@width.7\p@}}%
\leaders\vrule\@height.7\p@\hfill
\makesm@sh{\rlap{\vrule\@height3\p@\@width.7\p@}}$}
\def\downbracketfill{$\m@th
\makesm@sh{\llap{\vrule\@height.7\p@\@depth2.3\p@\@width.7\p@}}%
\leaders\vrule\@height.7\p@\hfill
\makesm@sh{\rlap{\vrule\@height.7\p@\@depth2.3\p@\@width.7\p@}}$}
\makeatother
108
Table 324 showcases these accents. The T
E
Xbook [Knu86a] or another book on T
E
X primitives is indispensible
for understanding how the preceding code works. The basic idea is that \downparenthfill,\upparenthfill,
\downbracketfill, and \upbracketfill do all of the work; they output a left symbol (e.g., \braceld [“z”]
for \downparenthfill), a horizontal rule that stretches as wide as possible, and a right symbol (e.g., \bracerd
[“{”] for \downparenthfill). \overbracket,\underbracket,\overparenthesis, and \underparenthesis
merely create a table whose width is determined by the given text, thereby constraining the width of the
horizontal rules.
Table 324: Manually Composed Extensible Accents
abc \overbracket{abc} z {
abc \overparenthesis{abc}
abc \underbracket{abc} abc
| } \underparenthesis{abc}
Note that the simplewick package provides mechanisms for typesetting Wick contractions, which uti-
lize \overbracket- and \underbracket-like brackets of variable width and height (or depth). For ex-
ample, “\acontraction{}{A}{B}{C}\acontraction[2ex]{A}{B}{C}{D}\bcontraction{}{A}{BC}{D}ABCD”
produces
ABCD .
See the simplewick documentation for more information.
Developing new symbols from scratch
Sometimes is it simply not possible to define a new symbol in terms of existing symbols. Fortunately, most, if
not all, T
E
X distributions are shipped with a tool called METAFONT which is designed specifically for creating
fonts to be used with T
E
X. The METAFONTbook [Knu86b] is the authoritative text on METAFONT. If you
plan to design your own symbols with METAFONT, The METAFONTbook is essential reading. You may also
want to read the freely available METAFONT primer located at http://metafont.tutorial.free.fr/. The
following is an extremely brief tutorial on how to create a new L
A
T
E
X symbol using METAFONT. Its primary
purpose is to cover the L
A
T
E
X-specific operations not mentioned in The METAFONTbook and to demonstrate
that symbol-font creation is not necessarily a difficult task.
Suppose we need a symbol to represent a light bulb (“ ”).11 The first step is to draw this in METAFONT.
It is common to separate the font into two files: a size-dependent file, which specifies the design size and
various font-specific parameters that are a function of the design size; and a size-independent file, which draws
characters in the given size. Figure 2 shows the METAFONT code for lightbulb10.mf.lightbulb10.mf
specifies various parameters that produce a 10 pt. light bulb then loads lightbulb.mf. Ideally, one should
produce lightbulbhsizei.mf files for a variety of hsizeis. This is called “optical scaling”. It enables, for
example, the lines that make up the light bulb to retain the same thickness at different font sizes, which looks
much nicer than the alternative—and default—“mechanical scaling”. When a lightbulbhsizei.mf file does
not exist for a given size hsizei, the computer mechanically produces a wider, taller, thicker symbol:
vs. vs. vs. vs. vs. vs.
10 pt. 20 pt. 30 pt. 40 pt. 50 pt. 60 pt. 70 pt.
lightbulb.mf, shown in Figure 3, draws a light bulb using the parameters defined in lightbulb10.mf.
Note that the the filenames “lightbulb10.mf” and “lightbulb.mf” do not follow the Berry font-naming
scheme [Ber01]; the Berry font-naming scheme is largely irrelevant for symbol fonts, which generally lack bold,
italic, small-caps, slanted, and other such variants.
The code in Figures Figure 2 and Figure 3 is heavily commented and should demonstrate some of the
basic concepts behind METAFONT usage: declaring variables, defining points, drawing lines and curves, and
preparing to debug or fine-tune the output. Again, The METAFONTbook [Knu86b] is the definitive reference
on METAFONT programming.
11I’m not a very good artist; you’ll have to pretend that “ ” looks like a light bulb.
109
font identifier := "LightBulb10"; % Name the font.
font size 10pt#; % Specify the design size.
em#:= 10pt#; % “M” width is 10 points.
cap#:= 7pt#; % Capital letter height is 7 points above the baseline.
sb#:= 1
/
4pt#; % Leave this much space on the side of each character.
o#:= 1
/
16pt#; % Amount that curves overshoot borders.
input lightbulb % Load the file that draws the actual glyph.
Figure 2: Sample METAFONT size-specific file (lightbulb10.mf)
mode setup; % Target a given printer.
define pixels(em,cap,sb); % Convert to device-specific units.
define corrected pixels(o); % Same, but add a device-specific fudge factor.
%% Define a light bulb at the character position for “A”
%% with width 1
/
2em#, height cap#, and depth 1pt#.
beginchar("A",1
/
2em#,cap#,1pt#); "A light bulb";
pickup pencircle scaled 1
/
2pt; % Use a pen with a small, circular tip.
%% Define the points we need.
top z1= (w/2, h +o); % z1is at the top of a circle.
rt z2= (w+sb +o−x4, y4); % z2is at the same height as z4but the opposite side.
bot z3= (z1−(0, w −sb −o)); % z3is at the bottom of the circle.
lft z4= (sb −o, 1
/
2[y1, y3]); % z4is on the left of the circle.
path bulb; % Define a path for the bulb itself.
bulb =z1. . z2. . z3. . z4. . cycle; % The bulb is a closed path.
z5=point 2−1
/
3of bulb; % z5lies on the bulb, a little to the right of z3.
z6= (x5,0); % z6is at the bottom, directly under z5.
z7= (x8,0); % z7is at the bottom, directly under z8.
z8=point 2 + 1
/
3of bulb; % z8lies on the bulb, a little to the left of z3.
bot z67 = (1
/
2[x6, x7],pen bot −o−1
/
8pt); % z67 lies halfway between z6and z7but a jot lower.
%% Draw the bulb and the base.
draw bulb; % Draw the bulb proper.
draw z5- - z6. . z67 . . z7- - z8; % Draw the base of the bulb.
%% Display key positions and points to help us debug.
makegrid(0,sb, w/2, w −sb)(0,−1pt, y2, h); % Label “interesting” xand ycoordinates.
penlabels(1,2,3,4,5,6,67,7,8); % Label control points for debugging.
endchar;
end
Figure 3: Sample METAFONT size-independent file (lightbulb.mf)
110
METAFONT can produce “proofs” of fonts—large, labeled versions that showcase the logical structure of
each character. In fact, proof mode is METAFONT’s default mode. To produce a proof of lightbulb10.mf,
issue the following commands at the operating-system prompt:
prompt>mf lightbulb10.mf ⇐Produces lightbulb10.2602gf
prompt>gftodvi lightbulb10.2602gf ⇐Produces lightbulb10.dvi
You can then view lightbulb10.dvi with any DVI viewer. The result is shown in Figure 4. Observe how the
grid defined with makegrid at the bottom of Figure 3 draws vertical lines at positions 0, sb,w/2, and w−sb
and horizontal lines at positions 0, −1pt,y2, and h. Similarly, observe how the penlabels command labels all
of the important coordinates: z1, z2, . . . , z8and z67, which lightbulb.mf defines to lie between z6and z7.
1
2
3
4
5
6
67
7
8
Figure 4: Proof diagram of lightbulb10.mf
Most, if not all, T
E
X distributions include a Plain T
E
X file called testfont.tex which is useful for testing
new fonts in a variety of ways. One useful routine produces a table of all of the characters in the font:
prompt>tex testfont
This is TeX, Version 3.14159 (Web2C 7.3.1)
(/usr/share/texmf/tex/plain/base/testfont.tex
Name of the font to test = lightbulb10
Now type a test command (\help for help):)
*\table
*\bye
[1]
Output written on testfont.dvi (1 page, 1516 bytes).
Transcript written on testfont.log.
The resulting table, stored in testfont.dvi and illustrated in Figure 5, shows every character in the font.
To understand how to read the table, note that the character code for “A”—the only character defined by
lightbulb10.mf—is 41 in hexadecimal (base 16) and 101 in octal (base 8).
The LightBulb10 font is now usable by T
E
X. L
A
T
E
X 2ε, however, needs more information before documents
can use the font. First, we create a font-description file that tells L
A
T
E
X 2εhow to map fonts in a given font
family and encoding to a particular font in a particular font size. For symbol fonts, this mapping is fairly simple.
Symbol fonts almost always use the “U” (“Unknown”) font encoding and frequently occur in only one variant:
normal weight and non-italicized. The filename for a font-description file important; it must be of the form
“hencodingihfamilyi.fd”, where hencodingiis the lowercase version of the encoding name (typically “u” for
symbol fonts) and hfamilyiis the name of the font family. For LightBulb10, let’s call this “bulb”. Figure 6 lists
the contents of ubulb.fd. The document “L
A
T
E
X 2εFont Selection” [L
A
T00] describes \DeclareFontFamily
and \DeclareFontShape in detail, but the gist of ubulb.fd is first to declare a U-encoded version of the bulb
font family and then to specify that a L
A
T
E
X 2εrequest for a U-encoded version of bulb with a (m)edium font
111
Test of lightbulb10 on March 11, 2003 at 1127
´0´1´2´3´4´5´6´7
´10x ˝4x
´11x
˝8˝9˝A˝B˝C˝D˝E˝F
Figure 5: Font table produced by testfont.tex
\DeclareFontFamily{U}{bulb}{}
\DeclareFontShape{U}{bulb}{m}{n}{<-> lightbulb10}{}
Figure 6: L
A
T
E
X 2εfont-description file (ubulb.fd)
series (as opposed to, e.g., bold) and a (n)ormal font shape (as opposed to, e.g., italic) should translate into a
T
E
X request for lightbulb10.tfm mechanically scaled to the current font size.
The final step is to write a L
A
T
E
X 2εstyle file that defines a name for each symbol in the font. Because
we have only one symbol our style file, lightbulb.sty (Figure 7), is rather trivial. Note that instead of
typesetting “A” we could have had \lightbulb typeset “\char65”, “\char"41”, or “\char’101” (respectively,
decimal, hexadecimal, and octal character offsets into the font). For a simple, one-character symbol font
such as LightBulb10 it would be reasonable to merge ubulb.fd into lightbulb.sty instead of maintaining
two separate files. In either case, a document need only include “\usepackage{lightbulb}” to make the
\lightbulb symbol available.
\newcommand{\lightbulb}{{\usefont{U}{bulb}{m}{n}A}}
Figure 7: L
A
T
E
X 2εstyle file (lightbulb.sty)
METAFONT normally produces bitmapped fonts. However, it is also possible, with the help of some
external tools, to produce PostScript Type 1 fonts. These have the advantages of rendering better in Adobe®
Acrobat®(at least in versions prior to 6.0) and of being more memory-efficient when handled by a PostScript
interpreter. See http://www.tex.ac.uk/cgi-bin/texfaq2html?label=textrace for pointers to tools that can
produce Type 1 fonts from METAFONT.
8.4 Math-mode spacing
Terms such as “binary operators”, “relations”, and “punctuation” in Section 3 primarily regard the surrounding
spacing. (See the Short Math Guide for L
A
T
E
X [Dow00] for a nice exposition on the subject.) To use a symbol
for a different purpose, you can use the T
E
X commands \mathord,\mathop,\mathbin,\mathrel,\mathopen,
\mathclose, and \mathpunct. For example, if you want to use \downarrow as a variable (an “ordinary”
symbol) instead of a delimiter, you can write “$3 x + \mathord{\downarrow}$” to get the properly spaced
“3x+↓” rather than the awkward-looking “3x+↓”. Similarly, to create a dotted-union symbol (“ ˙
∪”) that
spaces like the ordinary set-union symbol (\cup) it must be defined with \mathbin, just as \cup is. Contrast
“$A \dot{\cup} B$” (“A˙
∪B”) with “$A \mathbin{\dot{\cup}} B$” (“A˙
∪B”). See The T
E
Xbook [Knu86a]
for the definitive description of math-mode spacing.
The purpose of the “log-like symbols” in Table 128 and Table 129 is to provide the correct amount of
spacing around and within multiletter function names. Table 325 on the following page contrasts the output of
the log-like symbols with various, na¨ıve alternatives. In addition to spacing, the log-like symbols also handle
subscripts properly. For example, “\max_{p \in P}” produces “maxp∈P” in text, but “max
p∈P” as part of a
displayed formula.
The amsmath package makes it straightforward to define new log-like symbols:
\DeclareMathOperator{\atan}{atan}
\DeclareMathOperator*{\lcm}{lcm}
112
Table 325: Spacing Around/Within Log-like Symbols
L
A
T
E
X expression Output
$r \sin \theta$ rsin θ(best)
$r sin \theta$ rsinθ
$r \mbox{sin} \theta$ rsinθ
$r \mathrm{sin} \theta$ rsinθ
The difference between \DeclareMathOperator and \DeclareMathOperator* involves the handling of sub-
scripts. With \DeclareMathOperator*, subscripts are written beneath log-like symbols in display style and
to the right in text style. This is useful for limit operators (e.g., \lim) and functions that tend to map over
a set (e.g., \min). In contrast, \DeclareMathOperator tells T
E
X that subscripts should always be displayed
to the right of the operator, as is common for functions that take a single parameter (e.g., \log and \cos).
Table 326 contrasts symbols declared with \DeclareMathOperator and \DeclareMathOperator* in both text
style ($. . .$) and display style (\[. . .\]).12
Table 326: Defining new log-like symbols
Declaration function $\newlogsym {p \in P}$ \[ \newlogsym {p \in P} \]
\DeclareMathOperator newlogsymp∈Pnewlogsymp∈P
\DeclareMathOperator* newlogsymp∈Pnewlogsym
p∈P
It is common to use a thin space (\,) between the words of a multiword operators, as in
“\DeclareMathOperator*{\argmax}{arg\,max}”. \liminf,\limsup, and all of the log-like symbols shown
in Table 129 utilize this spacing convention.
8.5 Bold mathematical symbols
L
A
T
E
X does not normally use bold symbols when typesetting mathematics. However, bold symbols are occa-
sionally needed, for example when naming vectors. Any of the approaches described at http://www.tex.ac.uk/
cgi-bin/texfaq2html?label=boldgreek can be used to produce bold mathematical symbols. Table 327
contrasts the output produced by these various techniques. As the table illustrates, these techniques exhibit
variation in their formatting of Latin letters (upright vs. italic), formatting of Greek letters (bold vs. normal),
formatting of operators and relations (bold vs. normal), and spacing.
Table 327: Producing bold mathematical symbols
Package Code Output
none $\alpha + b = \Gamma \div D$ α+b= Γ ÷D(no bold)
none $\mathbf{\alpha + b = \Gamma \div D}$ α+b=Γ÷D
none \boldmath$\alpha + b = \Gamma \div D$ α+b= Γ ÷D
amsbsy $\pmb{\alpha + b = \Gamma \div D}$ α+b= Γ ÷D
α+b= Γ ÷D
α+b= Γ ÷D(faked bold)
amsbsy $\boldsymbol{\alpha + b = \Gamma \div D}$ α+b= Γ ÷D
bm $\bm{\alpha + b = \Gamma \div D}$ α+b= Γ ÷D
fixmath $\mathbold{\alpha + b = \Gamma \div D}$ α+b=Γ÷D
12Note that \displaystyle can be used to force display style within $...$and \textstyle can be used to force text style
within \[...\].
113
8.6 ASCII and Latin 1 quick reference
Table 328 amalgamates data from various other tables in this document into a convenient reference for
L
A
T
E
X 2εtypesetting of ASCII characters, i.e., the characters available on a typical U.S. computer keyboard.
The first two columns list the character’s ASCII code in decimal and hexadecimal. The third column shows
what the character looks like. The fourth column lists the L
A
T
E
X 2εcommand to typeset the character as a text
character. And the fourth column lists the L
A
T
E
X 2εcommand to typeset the character within a \texttt{. . .}
command (or, more generally, when \ttfamily is in effect).
Table 328: L
A
T
E
X 2εASCII Table
Dec Hex Char Body text \texttt
33 21 !! !
34 22 "\textquotedbl "
35 23 #\# \#
36 24 $\$ \$
37 25 %\% \%
38 26 &\& \&
39 27 ’’ ’
40 28 (( (
41 29 )) )
42 2A ** *
43 2B ++ +
44 2C ,, ,
45 2D -- -
46 2E .. .
47 2F // /
48 30 00 0
49 31 11 1
50 32 22 2
.
.
..
.
..
.
..
.
..
.
.
57 39 99 9
58 3A :: :
59 3B ;; ;
60 3C <\textless <
61 3D == =
Dec Hex Char Body text \texttt
62 3E >\textgreater >
63 3F ?? ?
64 40 @@ @
65 41 AA A
66 42 BB B
67 43 CC C
.
.
..
.
..
.
..
.
..
.
.
90 5A ZZ Z
91 5B [[ [
92 5C \\textbackslash \char‘\\
93 5D ]] ]
94 5E ˆ\^{} \^{}
95 5F \_ \char‘\_
96 60 ‘‘ ‘
97 61 aa a
98 62 bb b
99 63 cc c
.
.
..
.
..
.
..
.
..
.
.
122 7A zz z
123 7B {\{ \char‘\{
124 7C |\textbar |
125 7D }\} \char‘\}
126 7E ˜\~{} \~{}
The following are some additional notes about the contents of Table 328:
•“"” is not available in the OT1 font encoding.
•Table 328 shows a close quote for character 39 for consistency with the open quote shown for character 96.
A straight quote can be typeset using \textquotesingle (cf. Table 40).
•The characters “<”, “>”, and “|” do work as expected in math mode, although they produce, respectively,
“¡”, “¿”, and “—” in text mode when using the OT1 font encoding.13 The following are some alternatives
for typesetting “<”, “>”, and “|”:
–Specify a document font encoding other than OT1 (as described on page 8).
–Use the appropriate symbol commands from Table 2 on page 9, viz. \textless,\textgreater,
and \textbar.
–Enter the symbols in math mode instead of text mode, i.e., $<$,$>$, and $|$.
Note that for typesetting metavariables many people prefer \textlangle and \textrangle to \textless
and \textgreater; i.e., “hfilenamei” instead of “<filename>”.
13Donald Knuth didn’t think such symbols were important outside of mathematics so he omitted them from his text fonts.
114
•Although “/” does not require any special treatment, L
A
T
E
X additionally defines a \slash command
which outputs the same glyph but permits a line break afterwards. That is, “increase/decrease” is
always typeset as a single entity while “increase\slash{}decrease” may be typeset with “increase/”
on one line and “decrease” on the next.
•\textasciicircum can be used instead of \^{}, and \textasciitilde can be used instead of \~{}.
Note that \textasciitilde and \~{} produce raised, diacritic tildes. “Text” (i.e., vertically centered)
tildes can be generated with either the math-mode \sim command (shown in Table 67 on page 30),
which produces a somewhat wide “∼”, or the textcomp package’s \texttildelow (shown in Table 40
on page 20), which produces a vertically centered “~” in most fonts but a baseline-oriented “” in
Computer Modern, txfonts,pxfonts, and various other fonts originating from the T
E
X world. If your
goal is to typeset tildes in URLs or Unix filenames, your best bet is to use the url package, which has a
number of nice features such as proper line-breaking of such names.
•The various \char commands within \texttt are necessary only in the OT1 font encoding. In other
encodings (e.g., T1), commands such as \{,\},\_, and \textbackslash all work properly.
•The code page 437 (IBM PC) version of ASCII characters 1 to 31 can be typeset using the ascii package.
See Table 227 on page 72.
•To replace “‘” and “’” with the more computer-like (and more visibly distinct) “`” and “'” within
averbatim environment, use the upquote package. Outside of verbatim, you can use \char18 and
\char13 to get the modified quote characters. (The former is actually a grave accent.)
Similar to Table 328, Table 329 on the next page is an amalgamation of data from other tables in this
document. While Table 328 shows how to typeset the 7-bit ASCII character set, Table 329 shows the Latin 1
(Western European) character set, also known as ISO-8859-1.
The following are some additional notes about the contents of Table 329:
•A “(tc)” after a symbol name means that the textcomp package must be loaded to access that symbol.
A “(T1)” means that the symbol requires the T1 font encoding. The fontenc package can change the
font encoding document-wide.
•Many of the \text. . . accents can also be produced using the accent commands shown in Table 17 on
page 14 plus an empty argument. For instance, \={} is essentially the same as \textasciimacron.
•The commands in the “L
A
T
E
X 2ε” columns work both in body text and within a \texttt{. . .}command
(or, more generally, when \ttfamily is in effect).
•The “£” and “$” glyphs occupy the same slot (36) of the OT1 font encoding, with “£” appearing in italic
fonts and “$” appearing in roman fonts. A problem with L
A
T
E
X’s default handling of this double-mapping
is that “{\sffamily\slshape\pounds}” produces “$”, not “£”. Other font encodings use separate slots
for the two characters and are therefore robust to the problem of “£”/”$” conflicts. Authors who use
\pounds should select a font encoding other than OT1 (as explained on page 8) or use the textcomp
package, which redefines \pounds to use the TS1 font encoding.
•Character 173, \-, is shown as “-” but is actually a discretionary hyphen; it appears only at the end of
a line.
Microsoft®Windows®normally uses a superset of Latin 1 called “Code Page 1252” or “CP1252” for
short. CP1252 introduces symbols in the Latin 1 “invalid” range (characters 128–159). Table 330 presents the
characters with which CP1252 augments the standard Latin 1 table.
The following are some additional notes about the contents of Table 330:
•As in Table 329, a “(tc)” after a symbol name means that the textcomp package must be loaded to access
that symbol. A “(T1)” means that the symbol requires the T1 font encoding. The fontenc package can
change the font encoding document-wide.
•Not all characters in the 128–159 range are defined.
•Look up “euro signs” in the index for alternatives to \texteuro.
115
Table 329: L
A
T
E
X 2εLatin 1 Table
Dec Hex Char L
A
T
E
X 2ε
161 A1 ¡!‘
162 A2 ¢\textcent (tc)
163 A3 £\pounds
164 A4 ¤\textcurrency (tc)
165 A5 ¥\textyen (tc)
166 A6 ¦\textbrokenbar (tc)
167 A7 §\S
168 A8 \textasciidieresis (tc)
169 A9 ©\textcopyright
170 AA ª\textordfeminine
171 AB «\guillemotleft (T1)
172 AC ¬\textlnot (tc)
173 AD -\-
174 AE ®\textregistered
175 AF \textasciimacron (tc)
176 B0 °\textdegree (tc)
177 B1 ±\textpm (tc)
178 B2 ²\texttwosuperior (tc)
179 B3 ³\textthreesuperior (tc)
180 B4 \textasciiacute (tc)
181 B5 µ\textmu (tc)
182 B6 \P
183 B7 ·\textperiodcentered
184 B8 ¸\c{}
185 B9 ¹\textonesuperior (tc)
186 BA º\textordmasculine
187 BB »\guillemotright (T1)
188 BC ¼\textonequarter (tc)
189 BD ½\textonehalf (tc)
190 BE ¾\textthreequarters (tc)
191 BF ¿?‘
192 C0 `
A\‘{A}
193 C1 ´
A\’{A}
194 C2 ˆ
A\^{A}
195 C3 ˜
A\~{A}
196 C4 ¨
A\"{A}
197 C5 ˚
A\AA
198 C6 Æ\AE
199 C7 C¸ \c{C}
200 C8 `
E\‘{E}
201 C9 ´
E\’{E}
202 CA ˆ
E\^{E}
203 CB ¨
E\"{E}
204 CC `
I\‘{I}
205 CD ´
I\’{I}
206 CE ˆ
I\^{I}
207 CF ¨
I\"{I}
208 D0 Ð\DH (T1)
Dec Hex Char L
A
T
E
X 2ε
209 D1 ˜
N\~{N}
210 D2 `
O\‘{O}
211 D3 ´
O\’{O}
212 D4 ˆ
O\^{O}
213 D5 ˜
O\~{O}
214 D6 ¨
O\"{O}
215 D7 ×\texttimes (tc)
216 D8 Ø\O
217 D9 `
U\‘{U}
218 DA ´
U\’{U}
219 DB ˆ
U\^{U}
220 DC ¨
U\"{U}
221 DD ´
Y\’{Y}
222 DE Þ\TH (T1)
223 DF ß\ss
224 E0 `a \‘{a}
225 E1 ´a \’{a}
226 E2 ˆa \^{a}
227 E3 ˜a \~{a}
228 E4 ¨a \"{a}
229 E5 ˚a \aa
230 E6 æ\ae
231 E7 ¸c \c{c}
232 E8 `e \‘{e}
233 E9 ´e \’{e}
234 EA ˆe \^{e}
235 EB ¨e \"{e}
236 EC `ı \‘{ı}
237 ED ´ı \’{ı}
238 EE ˆı \^{ı}
239 EF ¨ı \"{ı}
240 F0 ð\dh (T1)
241 F1 ˜n \~{n}
242 F2 `o \‘{o}
243 F3 ´o \’{o}
244 F4 ˆo \^{o}
245 F5 ˜o \~{o}
246 F6 ¨o \"{o}
247 F7 ÷\textdiv (tc)
248 F8 ø\o
249 F9 `u \‘{u}
250 FA ´u \’{u}
251 FB ˆu \^{u}
252 FC ¨u \"{u}
253 FD ´y \’{y}
254 FE þ\th (T1)
255 FF ¨y \"{y}
116
Table 330: L
A
T
E
X 2εCode Page 1252 Table
Dec Hex Char L
A
T
E
X 2ε
128 80 €\texteuro (tc)
130 82 ‚\quotesinglbase (T1)
131 83 f\textit{f}
132 84 „\quotedblbase (T1)
133 85 . . . \dots
134 86 †\dag
135 87 ‡\ddag
136 88 ˆ\textasciicircum
137 89 ‰\textperthousand (tc)
138 8A ˇ
S\v{S}
139 8B ‹\guilsinglleft (T1)
140 8C Œ\OE
142 8E ˇ
Z\v{Z}
Dec Hex Char L
A
T
E
X 2ε
145 91 ‘‘
146 92 ’’
147 93 “‘‘
148 94 ”’’
149 95 •\textbullet
150 96 –--
151 97 —---
152 98 ˜\textasciitilde
153 99 ™\texttrademark
154 9A ˇs \v{s}
155 9B ›\guilsinglright (T1)
156 9C œ\oe
158 9E ˇz \v{z}
159 9F ¨
Y\"{Y}
While too large to incorporate into this document, a listing of ISO 8879:1986 SGML/XML character entities
and their L
A
T
E
X equivalents is available from http://www.bitjungle.com/~isoent/. Some of the characters
presented there make use of isoent, a L
A
T
E
X 2εpackage (available from the same URL) that fakes some of the
missing ISO glyphs using the L
A
T
E
Xpicture environment.14
8.7 Unicode characters
Unicode is a “universal character set”—a standard for encoding (i.e., assigning unique numbers to) the symbols
appearing in many of the world’s languages. While ASCII can represent 128 symbols and Latin 1 can represent
256 symbols, Unicode can represent an astonishing 1,114,112 symbols.
Because T
E
X and L
A
T
E
X predate the Unicode standard and Unicode fonts by almost a decade, support for
Unicode has had to be added to the base T
E
X and L
A
T
E
X systems. Note first that L
A
T
E
X distinguishes between
input encoding—the characters used in the .tex file—and output encoding—the characters that appear in the
generated .dvi,.pdf, etc. file.
Inputting Unicode characters
To include Unicode characters in a .tex file, load the ucs package and load the inputenc package with the utf8x
(“UTF-8 extended”) option.15 These packages enable L
A
T
E
X to translate UTF-8 sequences to L
A
T
E
X commands,
which are subsequently processed as normal. For example, the UTF-8 text “Copyright ©2009”—“©” is not
an ASCII character and therefore cannot be input directly without packages such as ucs/inputenc—is converted
internally by inputenc to “Copyright \textcopyright{} 2009” and therefore typeset as “Copyright ©2009”.
The ucs/inputenc combination supports only a tiny subset of Unicode’s million-plus sym-
bols. Additional symbols can be added manually using the \DeclareUnicodeCharacter command.
\DeclareUnicodeCharacter takes two arguments: a Unicode number and a L
A
T
E
X command to execute
when the corresponding Unicode character is encountered in the input. For example, the Unicode character
“degree celsius” (“ ”) appears at character position U+2103.16 However, “ ℃” is not one of the characters
that ucs and inputenc recognize. The following document shows how to use \DeclareUnicodeCharacter to
tell L
A
T
E
X that the “ ℃” character should be treated as a synonym for \textcelsius:
\documentclass{article}
\usepackage{ucs}
\usepackage[utf8x]{inputenc}
14isoent is not featured in this document, because it is not available from CTAN and because the faked symbols are not “true”
characters; they exist in only one size, regardless of the body text’s font size.
15UTF-8 is the 8-bit Unicode Transformation Format, a popular mechanism for representing Unicode symbol numbers as
sequences of one to four bytes.
16The Unicode convention is to express character positions as “U+hhexadecimal number i”.
117
\usepackage{textcomp}
\DeclareUnicodeCharacter{"2103}{\textcelsius} % Enable direct input of U+2103.
\begin{document}
It was a balmy 21℃.
\end{document}
which produces
It was a balmy 21.
See the ucs documentation for more information and for descriptions of the various options that control
ucs’s behavior.
Outputting Unicode characters
Orthogonal to the ability to include Unicode characters in a L
A
T
E
X input file is the ability to include a given
Unicode character in the corresponding output file. By far the easiest approach is to use X
E
L
A
T
E
X instead of
pdfL
A
T
E
X or ordinary L
A
T
E
X. X
E
L
A
T
E
X handles Unicode input and output natively and can utilize system fonts
directly without having to expose them via .tfm,.fd, and other such files. To output a Unicode character,
a X
E
L
A
T
E
X document can either include that character directly as UTF-8 text or use T
E
X’s \char primitive,
which X
E
L
A
T
E
X extends to accept numbers larger than 255.
Suppose we want to output the symbols for versicle (“ ”) and response (“ ”) in a document. The Unicode
charts list “versicle” at position U+2123 and “response” at position U+211F. We therefore need to install a
font that contains those characters at their proper positions. One such font that is freely available from CTAN
is Junicode Regular (Junicode-Regular.ttf) from the junicode package. The fontspec package makes it easy
for a X
E
L
A
T
E
X document to utilize a system font. The following example defines a \textjuni command that
uses fontspec to typeset its argument in Junicode Regular:
\documentclass{article}
\usepackage{fontspec}
\newcommand{\textjuni}[1]{{\fontspec{Junicode-Regular}#1}}
\begin{document}
We use ‘‘\textjuni{\char"2123}’’ for a versicle
and ‘‘\textjuni{\char"211F}’’ for a response.
\end{document}
which produces
We use “ ” for a versicle and “ ” for a response.
(Typesetting the entire document in Junicode Regular would be even easier. See the fontspec documentation
for more information regarding font selection.) Note how the preceding example uses \char to specify a
Unicode character by number. The double quotes before the number indicate that the number is represented
in hexadecimal instead of decimal.
8.8 About this document
History David Carlisle wrote the first version of this document in October, 1994. It originally contained
all of the native L
A
T
E
X symbols (Table 44, Table 57, Table 67, Table 102, Table 128, Table 131, Table 152,
Table 153, Table 164, Table 169, Table 201, and a few tables that have since been reorganized) and was designed
to be nearly identical to the tables in Chapter 3 of Leslie Lamport’s book [Lam86]. Even the table captions
and the order of the symbols within each table matched! The A
M
Ssymbols (Table 45, Table 68, Table 69,
Table 105, Table 106, Table 132, Table 137, Table 148, and Table 202) and an initial Math Alphabets table
(Table 213) were added thereafter. Later, Alexander Holt provided the stmaryrd tables (Table 46, Table 59,
Table 70, Table 108, Table 125, and Table 149).
In January, 2001, Scott Pakin took responsibility for maintaining the symbol list and has since implemented
a complete overhaul of the document. The result, now called, “The Comprehensive L
A
T
E
X Symbol List”,
includes the following new features:
118
•the addition of a handful of new math alphabets, dozens of new font tables, and thousands of new
symbols
•the categorization of the symbol tables into body-text symbols, mathematical symbols, science and
technology symbols, dingbats, ancient languages, and other symbols, to provide a more user-friendly
document structure
•an index, table of contents, hyperlinks, and a frequently-requested symbol list, to help users quickly
locate symbols
•symbol tables rewritten to list the symbols in alphabetical order
•appendices providing additional information relevant to using symbols in L
A
T
E
X
•tables showing how to typeset all of the characters in the ASCII and Latin 1 font encodings
Furthermore, the internal structure of the document has been completely altered from David Carlisle’s original
version. Most of the changes are geared towards making the document easier to extend, modify, and reformat.
Build characteristics Table 331 lists some of this document’s build characteristics. Most important is the list
of packages that L
A
T
E
X couldn’t find, but that symbols.tex otherwise would have been able to take advantage
of. Complete, prebuilt versions of this document are available from CTAN (http://www.ctan.org/ or one
of its many mirror sites) in the directory tex-archive/info/symbols/comprehensive. Table 332 shows the
package date (specified in the .sty file with \ProvidesPackage) for each package that was used to build this
document and that specifies a package date. Packages are not listed in any particular order in either Table 331
or Table 332.
Table 331: Document Characteristics
Characteristic Value
Source file: symbols.tex
Build date: November 9, 2009
Symbols documented: 5913
Packages included: textcomp latexsym amssymb stmaryrd euscript wasysym
pifont manfnt bbding undertilde ifsym tipa tipx extraipa
wsuipa phonetic ulsy ar metre txfonts mathabx fclfont
skak ascii dingbat skull eurosym esvect yfonts yhmath
esint mathdots trsym universa upgreek overrightarrow
chemarr chemarrow nath trfsigns mathtools phaistos arcs
vietnam t4phonet holtpolt semtrans dictsym extarrows
protosem harmony hieroglf cclicenses mathdesign arev
MnSymbol cmll extpfeil keystroke fge turnstile simpsons
epsdice feyn universal staves igo colonequals shuffle fourier
dozenal pmboxdraw pigpen clock teubner linearA linearb
cypriot sarabian china2e harpoon steinmetz milstd recycle
DotArrow ushort hhcount ogonek combelow accents
nicefrac bm mathrsfs chancery calligra bbold mbboard
dsfont bbm
Packages omitted: none
Table 332: Package versions used in the preparation of this document
Name Date
textcomp 2005/09/27
latexsym 1998/08/17
(continued on next page)
119
(continued from previous page)
Name Date
amssymb 2002/01/22
stmaryrd 1994/03/03
euscript 2001/10/01
wasysym 2003/10/30
pifont 2005/04/12
manfnt 1999/07/01
bbding 1999/04/15
undertilde 2000/08/08
ifsym 2000/04/18
tipa 2002/08/08
tipx 2003/01/01
wsuipa 1994/07/16
metre 2001/12/05
txfonts 2008/01/22
mathabx 2003/07/29
skak 2008/10/09
ascii 2006/05/30
dingbat 2001/04/27
skull 2002/01/23
eurosym 1998/08/06
yfonts 2003/01/08
mathdots 2006/03/16
trsym 2000/06/25
universa 98/08/01
upgreek 2003/02/12
chemarr 2006/02/20
mathtools 2008/08/01
phaistos 2004/04/23
arcs 2004/05/09
t4phonet 2004/06/01
semtrans 1998/02/10
dictsym 2004/07/26
extarrows 2008/05/15
protosem 2005/03/18
harmony 2007/05/03
hieroglf 2000/09/23
cclicenses 2005/05/20
arev 2005/06/14
MnSymbol 2007/01/21
extpfeil 2006/07/27
keystroke 2003/08/15
fge 2007/06/03
turnstile 2007/06/23
epsdice 2007/02/15
feyn 2008/02/29
universal 97/12/24
colonequals 2006/08/01
shuffle 2008/10/27
pmboxdraw 2006/05/03
pigpen 2008/12/07
clock 2001/04/10
teubner 2008/02/10
(continued on next page)
120
(continued from previous page)
Name Date
linearA 2006/03/13
linearb 2005/06/22
cypriot 1999/06/20
sarabian 2005/11/12
china2e 1997/06/01
harpoon 1994/11/02
steinmetz 2009/06/14
DotArrow 2007/02/12
ushort 2001/06/13
hhcount 1995/03/31
ogonek 95/07/17
combelow 2009/08/23
accents 2006/05/12
nicefrac 1998/08/04
bm 2004/02/26
calligra 1996/07/18
8.9 Copyright and license
The Comprehensive L
A
T
E
X Symbol List
Copyright ©2009, Scott Pakin
This work may be distributed and/or modified under the conditions of the L
A
T
E
X Project Public License, either
version 1.3c of this license or (at your option) any later version. The latest version of this license is in
http://www.latex-project.org/lppl.txt
and version 1.3c or later is part of all distributions of L
A
T
E
X version 2006/05/20 or later.
This work has the LPPL maintenance status “maintained”.
The current maintainer of this work is Scott Pakin.
121
References
[AMS99] American Mathematical Society. User’s Guide for the amsmath Package (Version 2.0), December 13,
1999. Available from ftp://ftp.ams.org/pub/tex/doc/amsmath/amsldoc.pdf.
[Ber01] Karl Berry. Fontname: Filenames for T
E
X fonts, June 2001. Available from http://www.ctan.org/
tex-archive/info/fontname.
[Che97] Raymond Chen. A METAFONT of ‘Simpsons’ characters. Baskerville, 4(4):19, September
1997. ISSN 1354-5930. Available from http://tug.ctan.org/usergrps/uktug/baskervi/4 4/
bask4 4.ps.
[Dow00] Michael Downes. Short math guide for L
A
T
E
X, July 19, 2000. Version 1.07. Available from http://
www.ams.org/tex/short-math-guide.html.
[Gib97] Jeremy Gibbons. Hey—it works! TUGboat, 18(2):75–78, June 1997. Available from http://
www.tug.org/TUGboat/Articles/tb18-2/tb55works.pdf.
[Knu86a] Donald E. Knuth. The T
E
Xbook, volume A of Computers and Typesetting. Addison-Wesley, Reading,
MA, USA, 1986.
[Knu86b] Donald E. Knuth. The METAFONTbook, volume C of Computers and Typesetting. Addison-Wesley,
Reading, MA, USA, 1986.
[Lam86] Leslie Lamport. L
A
T
E
X: A document preparation system. Addison-Wesley, Reading, MA, USA, 1986.
[L
A
T98] L
A
T
E
X3 Project Team. A new math accent. L
A
T
E
X News. Issue 9, June 1998. Available from
http://www.ctan.org/tex-archive/macros/latex/doc/ltnews09.pdf (also included in many T
E
X
distributions).
[L
A
T00] L
A
T
E
X3 Project Team. L
A
T
E
X 2εfont selection, January 30, 2000. Available from http://
www.ctan.org/tex-archive/macros/latex/doc/fntguide.ps (also included in many T
E
X distri-
butions).
122
Index
If you’re having trouble locating a symbol, try looking under “T” for “\text. . .”. Many text-mode commands begin
with that prefix. Also, accents are shown over/under a gray box (e.g., “ ´a ” for “\’”).
Some symbol entries appear to be listed repeatedly. This happens when multiple packages define identical (or nearly
identical) glyphs with the same symbol name.17
Symbols
\" (¨a) ................. 14
\# (#) . . . . . . . . . . . . . 9, 114
\$ ($) . . . . . . . . . . . . . . 9, 114
\% (%) . . . . . . . . . . . . . 9, 114
\& (&) . . . . . . . . . . . . . 9, 114
\’ (´a) ................. 14
((() .................. 54
(() .................. 55
)()) .................. 54
)() .................. 55
*(*) .................. 23
\, ................... 113
\- (-) . . . . . . . . . . . . . 115, 116
\. (˙a) ................. 14
/(/) .................. 54
/() ................. 55
\: (.
.) ................. 64
\; (.
.
.) ................. 64
<() .................. 55
\? (.
.
.
.) ................. 64
[([) .................. 54
[(
) ................. 55
\\ ................... 104
](]) .................. 54
](
) ................. 55
\^ (ˆa) ................. 14
\^{} (ˆ) . . . . . . . . . . . . 9, 115
\| (k) ................. 54
\| (k) . . . . . . . . . . . . . . 54, 56
\| ( ) ................. 14
\= (¯a) ................. 14
\={} (¯) .............. 115
|(
) ................. 55
|(|) . . . . . . . . . . 30, 54, 56, 57
\_ ( ) . . . . . . . . . . . . . . 9, 115
\{ ({) . . . . . . . . . . . . 9, 54, 115
\} (}) . . . . . . . . . . . . 9, 54, 115
\‘ (`a) ................. 14
\~ (˜a) ................. 14
\~{} (˜) . . . . . . . . . . . . 9, 115
A
a(esvect package option) . . . 61
\a (×
?
) ................. 95
\AA (˚
A) ................ 10
\aa (˚a) ................ 10
\AAaleph (A) ........... 81
\AAayin (O) ............ 81
\AAbeth (B) ............ 81
\AAcht (ˇ“ˇ“
==) ............. 89
\AAdaleth (D) ........... 81
\AAhe (E) .............. 81
\AAhelmet (V) .......... 81
\AAheth (h) ............ 81
\AAkaph (K) ............ 81
\AAlamed (L) ........... 81
\Aaleph (a) ............ 81
\AApe (P) .............. 81
\AAqoph (Q) ............ 81
\AAresh (R) ............ 81
\AAsade (X) ............ 81
\Aayin (o) ............. 81
\AAyod (Y) ............. 81
\Abeth (b) ............. 81
absolute value . see \lvert and
\rvert
abz¨uglich . . see \textdiscount
\AC (:) ................ 70
\acarc ................ 16
\acbar ................ 16
accents . . 14–18, 57–61, 71, 89,
107–109
acute (´a) . . . . . . 14–18, 57
any character as . . . . . 107
arc (a) . . . . . 14–17, 59, 60
breve (˘a) . . . . . . 14–18, 57
caron (ˇa) . . . 14, 18, 57, 60
cedilla (¸) . . . . . . . . . . 14
circumflex (ˆa) 14–16, 57, 59,
60
comma-below (a
,) . . . . . 17
diæresis (¨a) 14, 17, 18, 57,
68
dot (˙a or .) . . . . 14–16, 57
double acute (˝a) . . . 14, 18
extensible . . . . 59–61, 63,
108–109
grave (`a) . . . . . . 14–18, 57
h´aˇcek . . see accents, caron
hook (ả) ........... 14
Hungarian umlaut . . . see
accents, double acute
krouˇzek . . see accents, ring
macron (¯a) . 14, 17, 18, 57,
59, 60
multiple per character 15–16,
107
ogonek ( ˛) . . . . . . . 14–17
ring (˚a) . 14–16, 18, 57, 58
Romanian comma-belo ac-
cent . . . . . . . see accents,
comma-below
trema see accents, diæresis
umlaut see accents, diæresis
accents (package) . 58, 107, 119,
121
\accentset ............ 107
\Acht (ˇ“() .............. 89
\AchtBL (ˇ“
==) ............ 89
\AchtBR (ˇ“==
) ............ 89
\ACK (␆) ............... 72
\acontraction ......... 109
\AcPa (?) .............. 89
\actuarial ( ) . . . . . . . . . 108
actuarial symbols . . . . . . . 108
\acute (´) ............. 57
acute (´a) . . . . . . . . see accents
\acutus (a´) ............. 17
\Adaleth (d) ........... 81
adeles ( ) . see alphabets, math
adjoint (†) ......... see \dag
Adobe Acrobat . . . . . . . . . 112
\adots (...) . . . . . . . . 64, 107
advancing . see \textadvancing
\AE (Æ) ............... 10
\ae (æ) ................ 10
\aeolicbii (Ι) .......... 95
\aeolicbiii (Θ) ........ 95
\aeolicbiv (Κ) . . . . . . . . 95
\agemO (0) ............. 66
\Agimel (g) ............ 81
\Ahe (e) ............... 81
\Ahelmet (v) ........... 81
\Aheth (H) ............. 81
\ain () ................ 18
\Akaph (k) ............. 81
\Alad (}) .............. 57
\alad (}) .............. 57
\Alamed (l) ............ 81
\Alas ({) .............. 57
\alas ({) .............. 57
\aldine (o) ............ 78
\aldineleft (m) ......... 78
\aldineright (n) . . . . . . . . 78
\aldinesmall (j) . . . . . . . . 78
\aleph (ℵ) . . . . . . . . . . 51, 65
\aleph (ℵ) ............. 51
\Alif () ............... 14
\alpha (α) ............. 50
alphabets
African . . . . . . . . . . . . 10
17This occurs frequently between amssymb and mathabx, for example.
123
Cypriot . . . . . . . . . . . . 86
Cyrillic . . . . . . . . . . . 103
Greek . . . . . 50, 51, 68, 87
Hebrew . . . . . . . . . 51, 68
hieroglyphic . . . . . . . . . 82
Linear A . . . . . . . . . . . 82
Linear B . . . . . . . . . . . 85
math .............. 68
phonetic . . . . . . . . 11–14
proto-Semitic . . . . . . . . 81
South Arabian . . . . . . . 87
Vietnamese . . . . . . . . . 10
\alphaup (α) ............ 50
alpine symbols . . . . . . . . . . . 91
\Alt (Alt ) ............ 72
alternative denial . see \uparrow
and |
\AltGr (AltGr ) ......... 72
\amalg (q) ............. 22
\amalg () ............. 23
\Amem (m) .............. 81
ampersand . . . . . . . . . . see \&
A
M
S. 8, 10, 22, 26, 30, 31, 36,
38, 39, 41, 49–54, 58, 59, 61,
64–66, 69, 100, 118
amsbsy (package) . . . . . . . . 113
amsfonts (package) 22, 30, 36, 41,
65, 68
amsmath (package) . . 8, 49, 58,
104, 112
amssymb (package) 8, 22, 30, 36,
41, 58, 65, 68, 87, 119, 120,
123
amstext (package) . . . . 105, 106
\Anaclasis (÷) .......... 95
\anaclasis (÷) .......... 95
\anceps (Ξ) ............. 95
\ancepsdbrevis (Ζ) . . . . . . . 95
\anchor ( ) ........... 80
ancient-language symbols 81–87
and ............. see \wedge
AND gates . . . . . . . . . . . . . 73
\ANDd ( ) ........... 73
\ANDl ( ) .......... 73
\ANDr ( ) .......... 73
\ANDu ( ) ........... 73
\angle (∠) ............. 66
\angle (6) ............. 65
\angle (∠) ............. 66
angle notation . . . . . . . . . . . 70
angles . . . . . . . . . . . . . . 65–67
\Anglesign (W) .......... 67
˚
Angstr¨om unit
math mode see \mathring
text mode . . . . . . see \AA
\Angud (i) .............. 57
\angud (i) .............. 57
angular minutes . . . . see \prime
angular seconds . . . see \second
\Angus (h) .............. 57
\angus (h) .............. 57
animals . . . . . . . . . . . 81, 82, 86
\Ankh (ˆ) .............. 90
annuity symbols . . . . . . . . 108
\Antidiple (<) .......... 95
\antidiple (<) .......... 95
\Antidiple* (<
·
·) . . . . . . . . . 95
\antidiple* (<
·
·) ......... 95
\antilabe (.
..
. ) . . . . . . . . . . 64
\Antisigma (⊃) .......... 95
\antisigma (⊃) .......... 95
\Anun (n) .............. 81
\Ape (p) ............... 81
APL
modifiers . . . . . . . . . . . 71
symbols . . . . . . . . . . . . 71
\APLbox (~) ............ 71
\APLcirc (◦) ............ 71
\APLcomment () ......... 71
\APLdown (F) ........... 71
\APLdownarrowbox (o) . . . . 71
\APLinput (}) .......... 71
\APLinv (÷~) ............ 71
\APLleftarrowbox (p) . . . . 71
\APLlog () ............ 71
\APLminus (−) .......... 71
\APLnot (∼) ............. 71
\APLrightarrowbox (q) . . . . 71
\APLstar (E) ........... 71
\APLup () ............. 71
\APLuparrowbox (n) . . . . . . 71
\APLvert (|) ............ 71
\apprge (?) ............ 38
\apprle (>) ............ 38
\approx (≈) ............ 30
\approx (≈) ............. 32
\approxcolon (≈:) . . . . . . . 36
\approxcoloncolon (≈::) . . . 36
\approxeq () .......... 30
\approxeq () ........... 32
\Aqoph (q) ............. 81
\Aquarius (ê) .......... 71
\aquarius (e) .......... 71
\AR ( ) ............... 70
ar (package) . . . . . . . . 70, 119
arc (a) ......... see accents
\arccos (arccos) . . . . . . . . . 49
arcminutes . . . . . . . see \prime
arcs (package) . . . . 17, 119, 120
arcseconds . . . . . . . see \second
\arcsin (arcsin) . . . . . . . . . 49
\arctan (arctan) . . . . . . . . . 49
\Aresh (r) ............. 81
arev (package) . 67, 88, 119, 120
\arg (arg) .............. 49
\Aries ( ) ............. 71
\Aries (à) ............. 71
\aries () ............. 71
\ArrowBoldDownRight ( ) . 75
\ArrowBoldRightCircled ( ) 75
\ArrowBoldRightShort ( ) . . 75
\ArrowBoldRightStrobe ( ) 75
\ArrowBoldUpRight ( ) . . . 75
\Arrownot (Y) ............ 48
\arrownot (X) ............ 48
arrows 41–43, 47, 61–63, 72, 75,
81, 86, 90, 103
diagonal, for reducing subex-
pressions . . . . . . . . . . 59
dotted . . . . . . . . . . . . . 63
double-headed, diagonal 106
extensible . . . . . . . 59–63
fletched . . . . . . . . . 47, 75
negated . . . . . . . 41, 42, 44
\Arrowvert (w
w) . . . . . . . . . 54
\Arrowvert (
) ......... 55
\arrowvert (
) .......... 54
\arrowvert (
) .......... 55
Arseneau, Donald 104, 106–108
\Asade (x) ............. 81
\Asamekh (s) ........... 81
ASCII . . 8, 10, 72, 100, 114–115,
117, 119
table . . . . . . . . . . . . . 114
ascii (package) 72, 115, 119, 120
\ascnode () ........... 71
\Ashin (S) ............. 81
aspect ratio . . . . . . . . . . . . . 70
\ast ( ) ............... 23
\ast (∗) ............... 22
\ast (∗) ............... 23
\Asteriscus (
×···
·) ......... 95
\asteriscus (
×···
·) ......... 95
\Asterisk ( ) .......... 23
\Asterisk ( ) .......... 78
\asterisk ( ) ........... 23
\AsteriskBold ( ) . . . . . . . 78
\AsteriskCenterOpen ( ) . . 78
\AsteriskRoundedEnds ( ) . 78
asterisks . . . . . . . . . . . . 23, 78
\AsteriskThin ( ) . . . . . . . 78
\AsteriskThinCenterOpen ( )
......... 78
\asterism (*
**) . . . . . . . . . 104
astrological symbols . . . . . . . 71
astronomical symbols . . . 71, 98
\astrosun () .......... 71
\asymp () ............. 30
\asymp () ............. 48
\atan (atan) . . . . . . . . . . . 113
\ataribox (m) ........... 88
\Atav (t) .............. 81
\Ateth (T) ............. 81
\AtForty (Ø) .......... 90
\AtNinetyFive (Ó) . . . . . . 90
atomic math objects . . 49, 113
\AtSixty (Õ) .......... 90
124
\autoleftarrow (DGGGGG) . . . 62
\autoleftrightharpoons
(EGGGGG
GGGGGC) ........... 62
\autorightarrow (GGGGGA) . . 62
\autorightleftharpoons
(GGGGGB
FGGGGG ) ........... 62
\Avav (w) .............. 81
average . . . . . . . . . . . . . . . . 21
\Ayn () ............... 14
\Ayod (y) .............. 81
\Azayin (z) ............ 81
B
\B .................... 10
\B (
˘
´
) ................. 95
b(esvect package option) . . . 61
\b (a
¯) ................. 14
\b (
˘
) ................. 95
\Ba (a) ............... 85
babel (package) . . . . . . . 50, 87
\babygamma ( ) .......... 13
\backapprox () ......... 32
\backapproxeq () . . . . . . . 32
\backcong () ........... 32
\backepsilon () . . . . . . . . 30
\backeqsim () .......... 32
\backneg (⌐) ............ 66
\backprime (8) .......... 66
\backprime (‵) .......... 66
\backsim (v) ........... 30
\backsim () ............ 32
\backsimeq (w) ......... 30
\backsimeq () .......... 32
\backslash (\) . . . . . . . 54, 65
\backslash () ......... 55
\backslashdiv () . . . . . . . 23
\backtriplesim () . . . . . . . 32
\Baii (;) ............. 85
\Baiii (<) ............ 85
banana brackets . . . . . . . . . . .
.see \llparenthesis and
\rrparenthesis
\banceps (Ψ) ............ 95
\bar (¯) ............... 57
\barb ( ) .............. 13
\barbbrevis (θ) . . . . . . . . 95
\barbrevis (ι) .......... 95
\barcirc (−◦) .......... 104
\bard ( ) .............. 13
\bari () ............... 13
\barin ( ) ............. 52
\barj () ............... 13
\barl () ............... 13
\barlambda ( ) .......... 13
\barleftharpoon ( ) . . . . . 43
\baro () .............. 22
\baro (vs. ) . . . . . . . . . 101
\baro ( ) .............. 13
\barp ( ) .............. 13
barred letters . . . . . . . . . . 104
\barrightharpoon ( ) . . . . 43
\barsci () ............. 13
\barscu ( ) ............ 13
\Bart ( ) ......... 96
\baru ( ) .............. 13
\barwedge ( ) .......... 23
\barwedge (Z) ........... 22
base-twelve digits . . . . . . . . 65
\Bat (ý) ............... 90
\Bau (=) .............. 85
\bauarrow ( ) .......... 75
\baucircle ( ) .......... 80
\baucircle ( ) . . . . . . . . . 80
\baucross ( ) .......... 77
\baudash ( ) ........... 90
\baueclipse ( ) ......... 80
\bauequal ( ) .......... 90
\bauface ( ) ........... 90
\bauforms ( ) .......... 90
\bauforms ( ) ......... 90
\bauhead ( ) ........... 90
\bauhead ( ) . . . . . . . . . . 90
\bauhole ( ) ........... 80
\bauplus ( ) ........... 90
\baupunct ( ) .......... 80
\bauquarter ( ) ......... 90
\bauquestion ( ) . . . . . . . . 90
\bausquare ( ) .......... 80
\bausquare ( ) . . . . . . . . . 80
\bautriangle ( ) . . . . . . . . 80
\bautriangle ( ) . . . . . . . . 80
\bauwhitearrow ( ) . . . . . . 75
\bauwindow ( ) .......... 90
\BB (
˘˘
´) ................ 95
\Bb (
˘
´
˘
) ................ 95
\bB (
˘˘
´
) ................ 95
\bb (
˘˘
) ................ 95
\bba (×
˘˘
) ............... 95
\bbalpha ( ) ............ 68
\bbar (¯b) ............. 104
\bbb (˘
˘˘
) ............... 95
\bbbeta ( ) ............. 68
\Bbbk (k) .............. 52
bbding (package) 75–78, 80, 101,
119, 120
\bbdollar ( ) ........... 68
\bbetter (g) ........... 93
\bbeuro ( ) ............ 68
\bbfinalnun ( ) . . . . . . . . . 68
\bbgamma ( ) ............ 68
bbgreekl (mathbbol package op-
tion) . . . . . . . . . . . . . 68
\BBm (¯
˘
¯
˘
´) .............. 95
\Bbm (¯
˘
¯
˘
´) .............. 95
\bBm (¯
˘
¯
˘
´
) .............. 95
bbm (package) . . . . . . . 68, 119
\bbm (¯
˘
¯
˘) .............. 95
\bbmb (˘
¯
˘
¯
˘) .............. 95
\bbmx (¯
˘
¯
˘˘
¯
˘
¯) ............. 95
\bbnabla ( ) ........... 68
bbold (package) . . . . . . 68, 119
\bbpe ( ) .............. 68
\bbqof ( ) ............. 68
\bbrevis (ς) ........... 95
\bbslash () ........... 22
\bbyod () .............. 68
\bcontraction ......... 109
\Bda (d) ............... 85
\Bde (D) .............. 85
\bdecisive (i) ......... 93
\Bdi (f) ............... 85
\Bdo (g) ............... 85
\Bdu (x) ............... 85
\Bdwe (>) ............. 85
\Bdwo (?) ............. 85
\Be (e) ............... 85
\Beam (") .............. 73
\Bearing (#) ........... 73
\because (∵) . . . . . . . . 30, 64
\because (∵) ............ 64
\BEL (␇) ............... 72
\bell () .............. 88
Berry, Karl . . . . . . . . . . . . 122
\beta (β) .............. 50
\betaup (β) ............. 50
\beth () .............. 51
\beth () .............. 51
\betteris (b) .......... 93
\between ( ) ............ 32
\between (G) ............ 30
\between () ........... 32
\Bi (i) ............... 85
\bibridge (”
a”) ........... 16
biconditional . . . . . . . . . . . . . .
.see \leftrightarrow and
\equiv
\Bicycle (®) ........... 90
\Big .............. 100,102
\big .............. 100,102
big O (O) . see alphabets, math
\bigast ( ) ............ 23
\bigbosonloop () . . . . . . . . 74
\bigbosonloopA () . . . . . . . 74
\bigbosonloopV () . . . . . . . 74
\bigbox (e) ............ 26
\bigboxasterisk ( ) . . . . . 26
\bigboxbackslash ( ) . . . . 27
\bigboxbot ( ) ......... 27
\bigboxcirc ( ) . . . . . . . . 27
\bigboxcoasterisk ( ) . . . 27
\bigboxdiv ( ) ......... 27
\bigboxdot ( ) ......... 27
\bigboxleft ( ) . . . . . . . . 27
\bigboxminus ( ) . . . . . . . 27
\bigboxplus ( ) . . . . . . . . 27
125
\bigboxright ( ) . . . . . . . 27
\bigboxslash ( ) . . . . . . . 26
\bigboxtimes ( ) . . . . . . . 26
\bigboxtop ( ) ......... 26
\bigboxtriangleup ( ) . . . 26
\bigboxvoid ( ) . . . . . . . . 27
\bigcap (T) ............ 25
\bigcap () ............ 29
\bigcapdot () .......... 29
\bigcapplus () ......... 29
\bigcirc () ........... 22
\bigcirc () ........... 79
\BigCircle ( ) ......... 79
\bigcircle () ......... 29
\bigcoast ( ) .......... 23
\bigcomplementop ( ) . . . . . 27
\BigCross ( ) . . . . . . . . . . 79
\bigcup (S) ............ 25
\bigcup () ............ 29
\bigcupdot () .......... 29
\bigcupplus () ........ 29
\bigcupplus () ......... 29
\bigcurlyvee ( ) . . . . . . . . 26
\bigcurlyvee (b) ........ 26
\bigcurlyvee () ........ 29
\bigcurlyveedot () . . . . . 29
\bigcurlywedge ( ) . . . . . . 26
\bigcurlywedge (c) . . . . . . 26
\bigcurlywedge () . . . . . . 29
\bigcurlywedgedot () . . . . 29
\BigDiamondshape ( ) . . . . 79
\bigdoublecurlyvee () . . . 29
\bigdoublecurlywedge () . 29
\bigdoublevee () . . . . . . . 29
\bigdoublewedge () . . . . . 29
\Bigg . . . . . . . . . . . . . 100, 102
\bigg . . . . . . . . . . . . . 100, 102
\BigHBar ( ) ........... 79
\biginterleave (g) . . . . . . 26
\BigLowerDiamond ( ) . . . . 79
\bignplus () .......... 26
\bigoast () ........... 29
\bigoasterisk ( ) . . . . . . . 27
\bigobackslash ( ) . . . . . . 27
\bigobackslash () . . . . . . 29
\bigobot ( ) ........... 27
\bigocirc ( ) .......... 27
\bigocirc () .......... 29
\bigocoasterisk ( ) . . . . . 27
\bigodiv ( ) ........... 27
\bigodot (J) ........... 25
\bigodot () ........... 29
\bigoleft ( ) .......... 27
\bigominus ( ) ......... 27
\bigominus () ......... 29
\bigoplus (L) .......... 25
\bigoplus () .......... 29
\bigoright ( ) ......... 26
\bigoslash ( ) ......... 26
\bigoslash () ......... 29
\bigostar () .......... 29
\bigotimes (N) ......... 25
\bigotimes () ......... 29
\bigotop ( ) ........... 26
\bigotriangle () . . . . . . . 29
\bigotriangleup ( ) . . . . . 26
\bigovert () .......... 29
\bigovoid ( ) .......... 27
\bigparallel (f) ........ 26
\bigparr (˙) ........... 30
\bigplus ( ) ........... 27
\bigplus () ........... 29
\BigRightDiamond ( ) . . . . 79
\bigsqcap ( ) . . . . . . . . . . 26
\bigsqcap () .......... 26
\bigsqcap () ........... 29
\bigsqcapdot () ........ 29
\bigsqcapplus () . . . . . . . 27
\bigsqcapplus () . . . . . . . 29
\bigsqcup (F) .......... 25
\bigsqcup () ........... 29
\bigsqcupdot () ........ 29
\bigsqcupplus () . . . . . . . 27
\bigsqcupplus () . . . . . . . 29
\BigSquare ( ) ......... 79
\bigsquplus ( ) ......... 27
\bigstar ( ) ........... 23
\bigstar (F) ........... 66
\bigstar () ........... 79
\bigtimes ( ) .......... 27
\bigtimes () ........... 29
\BigTriangleDown ( ) . . . . 79
\bigtriangledown (`) . . . . 26
\bigtriangledown (5vs. `) 101
\bigtriangledown (5) . . . . 22
\bigtriangledown (▽) . . . . 40
\BigTriangleLeft ( ) . . . . 79
\BigTriangleRight ( ) . . . 79
\BigTriangleUp ( ) . . . . . . 79
\bigtriangleup (a) . . . . . . 26
\bigtriangleup (4vs. a) 101
\bigtriangleup (4) . . . . . . 22
\bigtriangleup (△) ...... 40
\biguplus (U) .......... 25
\biguplus () .......... 29
\bigvarstar ( ) . . . . . . . . . 23
\BigVBar ( ) ........... 79
\bigvee (W) ............ 25
\bigvee () ............ 29
\bigveedot () .......... 29
\bigwedge (V) .......... 25
\bigwedge () ........... 29
\bigwedgedot () ........ 29
\bigwith (˘) ........... 30
\binampersand (N) . . . . . . . 22
binary operators . . . . . . 22–25
binary relations . . 30–32, 34–39,
47, 48
negated . . . . . . . . . 31–33
\bindnasrepma (O) . . . . . . . 22
\Biohazard (h) ......... 74
biological symbols . . . . . . . . 74
birds .................. 82
bishop ................. 94
\bishoppair (a) ......... 93
\Bja (j) ............... 85
\Bje (J) ............... 85
\Bjo (b) ............... 85
\Bju (L) .............. 85
\Bka (k) .............. 85
\Bke (K) .............. 85
\Bki (c) .............. 85
\Bko (h) ............... 85
\Bku (v) ............... 85
\BlackBishopOnBlack (a) 94
\BlackBishopOnWhite (b) 94
blackboard bold see alphabets,
math
\blackdiamond ( ) . . . . . . . 23
\BlackEmptySquare (Z) . 94
\BlackKingOnBlack (j) . 94
\BlackKingOnWhite (k) . 94
\BlackKnightOnBlack (m) 94
\BlackKnightOnWhite (n) 94
\blacklozenge () . . . . . . . 66
\blacklozenge () . . . . . . . 79
\BlackPawnOnBlack (o) . 94
\BlackPawnOnWhite (p) . 94
\BlackQueenOnBlack (l) 94
\BlackQueenOnWhite (q) 94
\BlackRookOnBlack (s) . 94
\BlackRookOnWhite (r) . 94
\blacksmiley (-) ........ 88
\blacksquare () ........ 66
\blacksquare () . . . . . . . . 25
\blackstone ............ 94
\blacktriangle (N) . . . . . . 66
\blacktriangle (▲) ...... 40
\blacktriangledown ( ) . . . 25
\blacktriangledown (H) . . . 66
\blacktriangledown (▼) . . . 40
\blacktriangleleft ( ) . . . 25
\blacktriangleleft (J) . . . 39
\blacktriangleleft (◀) . . . 40
\blacktriangleright ( ) . . 25
\blacktriangleright (I) . . 39
\blacktriangleright (▶) . . 40
\blacktriangleup ( ) . . . . . 25
126
blank . . . . . . . see \textblank
\Bleech (Ë) ............ 90
\blitza ( ) . . . . . . . . . 21, 48
\blitzb ( ) ............ 48
\blitzc ( ) ............ 48
\blitzd ( ) ............ 48
\blitze ( ) ............ 48
block-element symbols . . . . . 97
\Bm (¯
˘
´) ................ 95
bm (package) . . . . 113, 119, 121
\bm .................. 113
\bm (¯
˘) ................ 95
\Bma (m) .............. 85
\Bme (M) .............. 85
\Bmi (y) .............. 85
\Bmo (A) ............... 85
\bmod ................. 49
\Bmu (B) .............. 85
\Bna (n) ............... 85
\BNc («) ............... 85
\BNcc (») .............. 85
\BNccc (–) ............ 85
\BNcd (—) ............. 85
\BNcm (ff) ........... 85
\BNd () ............. 85
\BNdc (‰) ............ 85
\BNdcc (ı) ........... 85
\BNdccc (ȷ) .......... 85
\Bne (N) .............. 85
\BNi (´) ............... 85
\Bni (C) ............... 85
\BNii (ˆ) .............. 85
\BNiii (˜) ............. 85
\BNiv (¨) .............. 85
\BNix (¯) ............. 85
\BNl (‹) .............. 85
\BNlx (›) ............. 85
\BNlxx (“) ............ 85
\BNlxxx (”) ........... 85
\BNm (fi) .............. 85
\Bno (E) .............. 85
\Bnu (F) ............... 85
\BNv (˝) ............... 85
\BNvi (˚) .............. 85
\BNvii (ˇ) ............. 85
\BNviii (˘) ............ 85
\Bnwa (@) ............. 85
\BNx (˙) ............... 85
\BNxc („) ............. 85
\BNxl (‚) ............. 85
\BNxx (¸) .............. 85
\BNxxx (˛) ............. 85
\Bo (o) ............... 85
body-text symbols . . . . . . 9–20
bold symbols . . . . . . . . . . . 113
\boldmath ............. 113
\boldsymbol ........... 113
\bomb (L) .............. 91
Boolean domain ( ) . . . . . see
alphabets, math
Boolean logic gates . . . . . . . 73
born ......... see \textborn
bosons . . . . . . . . . . . . . . . . 74
\bot (⊥) . . . . . . . . . 21, 51, 105
\bot () ............... 52
\botdoteq ( ) .......... 32
\Bouquet (¥) ........... 90
\Bowtie (1) ............ 88
\bowtie () ............ 30
\bowtie () . . . . . . . . . 23, 24
\Box () ............... 65
\Box (2) ............... 66
\Box () ............... 25
box-drawing symbols . . . . . . 97
\boxast (i) ............ 22
\boxasterisk ( ) . . . . . . . . 25
\boxbackslash ( ) . . . . . . . 25
\boxbackslash () . . . . . . . 25
\boxbar (k) ............ 22
\boxbot ( ) ............ 25
\boxbox () ............ 22
\boxbox () ............ 25
\boxbslash (j) .......... 22
\boxcirc ( ) ........... 25
\boxcircle () .......... 22
\boxcoasterisk ( ) . . . . . . 25
\boxdiv ( ) ............ 25
\boxdot ( ) ............ 25
\boxdot () ............ 22
\boxdot () ............ 25
\boxdotLeft () . . . . . . . . 42
\boxdotleft () . . . . . . . . 42
\boxdotRight () . . . . . . . 42
\boxdotright () . . . . . . . 42
\boxempty () .......... 22
\boxLeft () .......... 42
\boxleft ( ) ........... 25
\boxleft () .......... 42
\boxminus ( ) .......... 25
\boxminus () .......... 22
\boxminus () ........... 25
\boxplus ( ) ........... 25
\boxplus () ........... 22
\boxplus () ............ 25
\boxRight () ......... 42
\boxright ( ) .......... 25
\boxright () ......... 42
\boxslash ( ) .......... 25
\boxslash (l) ........... 22
\boxslash () ........... 25
\boxtimes ( ) .......... 25
\boxtimes () .......... 22
\boxtimes () ........... 25
\boxtop ( ) ............ 25
\boxtriangleup ( ) . . . . . . 25
\boxvert () ............ 25
\boxvoid ( ) ........... 25
\boy ( ) ............... 71
\Bpa (p) ............... 85
\Bpaiii ([) ............ 85
\BPamphora (Ž) .......... 86
\BParrow (ij) ........... 86
\BPbarley (Ş) ........... 86
\BPbilly (ť) ........... 86
\BPboar (ľ) ............ 86
\BPbronze (Ű) .......... 86
\BPbull (ň) ............ 86
\BPcauldroni (đ) . . . . . . . 86
\BPcauldronii (§) . . . . . . 86
\BPchariot (ÿ) . . . . . . . . 86
\BPchassis (ź) . . . . . . . . 86
\BPcloth (Ř) ........... 86
\BPcow (ŋ) ............ 86
\BPcup (Ÿ) ............ 86
\Bpe (P) ............... 85
\BPewe (š) ............ 86
\BPfoal (ě) ........... 86
\BPgoat (ş) ............ 86
\BPgoblet (Ź) .......... 86
\BPgold (Ů) ............ 86
\BPhorse (ď) .......... 86
\Bpi (G) ............... 85
\BPman (ă) ............. 86
\BPnanny (ț) ........... 86
\Bpo (H) ............... 85
\BPolive (Ț) ........... 86
\BPox (ń) ............. 86
\BPpig (ĺ) ............ 86
\BPram (ś) ............ 86
\BPsheep (ř) ........... 86
\BPsow (ł) ............ 86
\BPspear (¡) ........... 86
\BPsword (ż) ............ 86
\BPtalent (Ď) ......... 85
\Bpte (]) ............. 85
\Bpu (I) ............... 85
\Bpuii (\) ............ 85
\BPvola (Ĺ) ........... 85
\BPvolb (Ľ) ............ 85
\BPvolcd (Ł) ........... 85
\BPvolcf (Ń) ........... 85
\BPwheat (Š) ........... 86
\BPwheel (ž) ........... 86
\BPwine (Ť) ............ 86
\BPwineiih (Ż) ......... 86
\BPwineiiih (IJ) . . . . . . . . 86
\BPwineivh (İ) ......... 86
\BPwoman (ą) ........... 86
\BPwool (Ś) ............ 86
127
\BPwta (Ă) ............. 85
\BPwtb (Ą) ............. 85
\BPwtc (Ć) ............ 85
\BPwtd (Č) ............. 85
\Bqa (q) .............. 85
\Bqe (Q) .............. 85
\Bqi (X) .............. 85
\Bqo (8) ............... 85
\Bra (r) ............... 85
bra ................... 54
\braceld (z) ........... 109
\bracerd ({) ........... 109
\bracevert (
) ......... 54
\bracevert (
) ......... 55
brackets . . . . . . . see delimiters
\Braii (^) ............. 85
\Braiii (_) ............ 85
braket (package) . . . . . . . . . 54
\Bre (R) ............... 85
\Break (Break ) ......... 72
\breve (˘) ............. 57
\breve (a˘) ............. 17
breve (˘a) . . . . . . . . see accents
\brevis (β) ............ 95
\Bri (O) ............... 85
\Bro (U) ............... 85
\Broii (‘) ............. 85
\brokenvert (|) .......... 88
Bronger, Torsten . . . . . . . . 105
\Bru (V) ............... 85
\BS (␈) ................ 72
\Bsa (s) ............... 85
\Bse (S) ............... 85
\BSEfree (n) ........... 74
\Bsi (Y) ............... 85
\Bso (1) ............... 85
\BSpace (
7−→
) . . . . . . . . . 72
\Bsu (2) ............... 85
\Bswa ({) .............. 85
\Bswi (|) ............. 85
\Bta (t) ............... 85
\Btaii (}) ............ 85
\Bte (T) ............... 85
\Bti (3) ............... 85
\Bto (4) ............... 85
\Btu (5) ............... 85
\Btwe () .............. 86
\Btwo (~) ............. 85
\Bu (u) ............... 85
\BUFd ( ) ............ 73
buffers ................ 73
\BUFl ( ) ............ 73
\BUFr ( ) ............ 73
\BUFu ( ) ............ 73
\BUi (fl) ............... 86
\BUii (ffi) .............. 86
\BUiii (ffl) ............ 86
\BUiv (␣) .............. 86
\BUix (%) ............. 86
\bullet (•) ............. 22
\bullet (●) ............. 23
bullseye . . . see \textbullseye
\Bumpedeq ( ) .......... 32
\bumpedeq ( ) .......... 32
\Bumpeq (m) ............ 30
\Bumpeq () ............. 33
\bumpeq (l) ............ 30
\bumpeq () ............. 33
\bupperhand (e) ......... 93
\Burns ( ) . . . . . . . . 96
\BusWidth ( ) . . . . . . . . . . 73
\BUv (!) ............... 86
\BUvi (") .............. 86
\BUvii (#) ............ 86
\BUviii ($) ........... 86
\BUx (&) .............. 86
\BUxi (’) ............. 86
\BUxii () ............. 86
\Bwa (w) ............... 85
\Bwe (W) ............... 85
\Bwi (6) ............... 85
\Bwo (7) ............... 85
\Bza (z) .............. 85
\Bze (Z) ............... 85
\Bzo (9) ............... 85
C
\C () ................. 95
c(esvect package option) . . . 61
\c (¸a) . . . . . . . . . . . . . 14, 116
\c ( ) ................ 95
\Ca (a) ............... 86
calligra (package) . . 68, 119, 121
Calligra (font) . . . . . . . . . . . 68
calrsfs (package) . . . . . . . . . 68
\CAN (␘) ............... 72
cancel (package) . . . . . . . . . 59
\Cancer (ã) ............ 71
\cancer (_) ............ 71
\Cap (e) ............... 22
\Cap () ............... 24
\cap ( ) ............... 23
\cap (∩) ............... 22
\cap (∩) ............... 23
\capdot () ............ 23
\capplus () ............ 23
\Capricorn (é) .......... 71
\capricornus (d) ........ 71
\capturesymbol (X) . . . . . . 93
card suits . . . . . . . . . 65–67, 80
cardinality . . . . . . . see \aleph
care of (c
/o) ............. 67
caret ............... see \^
Carlisle, David . . . . 1, 118, 119
caron (ˇa) . . . . . . . . see accents
carriage return . . . . 72, 80, 103
\carriagereturn ( ) . . . . . 80
Cartesian product . . see \times
castle ................. 94
\castlingchar (O) . . . . . . . 93
\castlinghyphen (-) . . . . . . 93
\catal (γ) ............. 95
\Catalexis (∧) .......... 95
\catalexis (∧) .......... 95
catamorphism . . . . . . . . . . . . .
.see \llparenthesis and
\rrparenthesis
\cb (a
,) ................ 17
\Cc () ................ 95
\cc (CC
) ............. 19
\cc ( ) ............... 95
\ccby (BY:
) ........... 19
\Ccc ( ) ............... 95
cclicenses (package) 19, 119, 120
\ccnc ($
\
) ........... 19
\ccnd (=
) ........... 19
\ccsa (
C
) ............. 19
\cdot (·) . . . . . . . . . . . 22, 104
\cdot (⋅) . . . . . . . . . . . . 23, 64
\cdotp (·) .............. 63
\cdotp (⋅) .............. 64
\cdots (···) ............ 63
\Ce (e) ............... 86
Cedi . see \textcolonmonetary
cedilla (¸) . . . . . . . see accents
celestial bodies . . . . . . . 71, 98
\celsius () ........... 70
\Celtcross (‡) .......... 90
\cent (¢) .............. 18
\centerdot ( ) . . . . . . . . . . 23
\centerdot () .......... 22
centernot (package) . . . . . . 105
\centernot ............ 105
centigrade . . . see \textcelsius
\centre (I) ............ 93
cents . . . . . . . . . see \textcent
\CEsign (C) ............ 74
\Cga (g) .............. 86
chancery (package) . . . . . . . 119
\changenotsign ......... 32
\char . . . . 8, 103, 112, 115, 118
Charter (font) . . . . . . . . 18, 30
\check (ˇ) ............. 57
check marks . 10, 66, 77, 80, 88,
90, 101
\checked () ........... 88
\CheckedBox (2) ......... 77
\Checkedbox (V) ......... 90
\Checkmark ( ) ......... 77
128
\checkmark (X) . . . . . . . . . 10
\checkmark (✓) ......... 66
\checkmark (Xvs. ) . . . . 101
\checkmark ( ) ......... 80
\CheckmarkBold ( ) . . . . . . 77
\checksymbol (+) . . . . . . . . 93
chemarr (package) . 62, 119, 120
chemarrow (package) 47, 62, 119
\chemarrow (A) ......... 47
Chen, Raymond . . . . . . . . 122
chess symbols . . . . . . . . 93, 94
\chesscomment (RR) . . . . . . 93
\chessetc (P) ........... 93
\chesssee (l) .......... 93
\chi (χ) ............... 50
china2e (package) 19, 49, 68, 98,
119, 121
\chiup (χ) .............. 50
\Ci (i) ............... 86
cipher symbols . . . . . . . . . . 98
\circ (◦) . . . . . . . . 22, 67, 105
\circ (○) .............. 23
\circeq ( ) ............ 32
\circeq ($) ............ 30
\circeq () ............. 33
\CIRCLE ( ) ............ 88
\Circle ( ) ............ 79
\Circle (#vs. ) . . . . . . 101
\Circle (#) ............ 88
\circlearrowleft ( ) . . . . 42
\circlearrowleft () . . . . 41
\circlearrowleft (↺) . . . . 44
\circlearrowright ( ) . . . . 42
\circlearrowright () . . . 41
\circlearrowright (↻) . . . 44
circled numbers . . . . . . . 77, 94
\CircledA (ª) .......... 90
\circledast (~) ......... 22
\circledast () ......... 25
\circledbar (V) ......... 23
\circledbslash (W) . . . . . . 23
\circledcirc (}) . . . . . . . . 22
\circledcirc () ........ 25
\circleddash () . . . . . . . . 22
\circleddash (⊖) ........ 25
\circleddot ...... see \odot
\circleddotleft () . . . . 42
\circleddotright () . . . . 42
\circledgtr (S) ......... 31
\circledless (R) . . . . . . . . 31
\circledminus ... see \ominus
\circledotleft ........ see
\circleddotleft
\circledotright ....... see
\circleddotright
\circledplus ..... see \oplus
\circledR (r) . . . . . . . 10, 52
\circledS (s) .......... 52
\circledslash ... see \oslash
\circledtimes ... see \otimes
\circledvee (U) ......... 23
\circledwedge (T) . . . . . . . 23
\circleleft () . . . . . . . . 42
\circleright () . . . . . . . 42
circles . . . . . . . . . 79–80, 88, 94
\CircleShadow ( ) . . . . . . . 80
\CircleSolid ( ) . . . . . . . . 80
\Circpipe (›) .......... 73
\circplus ( ) .......... 23
\Circsteel (•) ......... 73
circumflex (ˆa) . . . . see accents
\circumflexus (a˜) . . . . . . . 17
\Cja (j) ............... 86
\Cjo (b) .............. 86
\Cka (k) ............... 86
\Cke (K) .............. 86
\Cki (c) .............. 86
\Cko (h) .............. 86
\Cku (v) .............. 86
\Cla (l) .............. 86
\Cle (L) ............... 86
\CleaningA («) .......... 90
\CleaningF (¾) .......... 90
\CleaningFF (¿) ......... 90
\CleaningP (¬) .......... 90
\CleaningPP () ......... 90
\Cli (d) ............... 86
\clickb ( ) ............ 13
\clickc ( ) ............. 13
\clickt () ............. 13
\Clo (f) ............... 86
clock (package) . . . 92, 119, 120
\clock ( ) ............ 92
\clock () ............. 88
clock symbols . . . . . . 88, 90–92
\ClockFramefalse ........ 92
\ClockFrametrue ........ 92
\Clocklogo (U) .......... 90
\ClockStyle ............ 92
\clocktime ............. 92
\closedcurlyvee () . . . . . . 24
\closedcurlywedge () . . . . 24
\closedequal () . . . . . . . . 33
\closedniomega ( ) . . . . . . 13
\closedprec () ......... 33
\closedrevepsilon ( ) . . . . 13
\closedsucc () ......... 33
\Cloud ( ) ............. 91
clovers ................ 78
\Clu (q) .............. 86
clubs (suit) . . . . . . . . 65–67, 80
\clubsuit (♣) .......... 65
\clubsuit (♣) ........... 66
\Cma (m) .............. 86
\Cme (M) .............. 86
\Cmi (y) .............. 86
cmll (package) 21, 24, 30, 36, 119
\Cmo (A) .............. 86
\Cmu (B) .............. 86
\Cna (n) ............... 86
\Cne (N) ............... 86
\Cni (C) .............. 86
\Cno (E) .............. 86
\Cnu (F) ............... 86
\Co (o) ............... 86
\coAsterisk ( ) ......... 23
\coasterisk ( ) ......... 23
code page 1252 . . . . . . . . . 115
table . . . . . . . . . . . . . 117
code page 437 . . . . . 72, 97, 115
\Coffeecup (K) ......... 90
\coh (¨) ............... 36
coins, ancient . . . . . . . . . . . 19
\colon ................ 63
\colon (:) ............. 63
\colon (∶) .............. 64
\Colonapprox () . . . . . . . 31
\Colonapprox (::≈) . . . . . . . 34
\colonapprox (:≈) . . . . . . . 36
\colonapprox (:≈) ........ 34
\colonapprox () . . . . . . . . 31
\coloncolon (::) ......... 36
\coloncolonapprox (::≈) . . . 36
\coloncolonequals (::=) . . . 36
\coloncolonminus (::−) . . . . 36
\coloncolonsim (::∼) . . . . . 36
\Coloneq (H) ........... 31
\Coloneq (::−) ........... 34
\coloneq ( ) . . . . . . . . 21, 32
\coloneq (:−) ........... 34
\coloneq (D) ........... 31
\coloneq (∶=) ........... 33
\Coloneqq (F) .......... 31
\Coloneqq (::=) .......... 34
\coloneqq (:=) .......... 34
\coloneqq (B) . . . . . . . 21, 31
colonequals (package) 21, 36, 119,
120
\colonequals (:=) . . . . 21, 36
\colonminus (:−) ........ 36
\Colonsim () .......... 31
\Colonsim (::∼) .......... 34
\colonsim (:∼) .......... 36
\colonsim (:∼) .......... 34
\colonsim () .......... 31
combelow (package) 17, 119, 121
combinatorial logic gates . . . 73
comma-below accent (a
,) . . . see
accents
communication symbols . . . . 73
commutative diagrams . . . . 106
comp.text.tex (newsgroup) . 8,
21, 22, 103–108
\compensation (n) . . . . . . . 93
\complement () ......... 52
\complement ({) . . . . . . . . . 52
\complement () ......... 29
complete shuffle product ( ) 24
\COMPLEX ( ) ............ 49
\Complex ( ) ............ 49
129
complex numbers ( ) . . . . see
alphabets, math
composited accents . . . . . . . 14
Comprehensive T
E
X Archive Net-
work . . 1, 8, 59, 69, 100,
117–119
computer hardware symbols . 72
computer keys . . . . . . . . . . . 72
Computer Modern (font) . . 100,
102, 115
\ComputerMouse (Í) . . . . . . . 72
\cong () .............. 30
\cong (≅) .............. 33
congruent . . . . . . . . see \equiv
\conjunction (V) ........ 71
conjunction, logical . see \wedge
and \&
consequence relations . . . . . . 35
contradiction symbols . . 21, 48
control characters . . . . . . . . 72
converse implication . . . . . see
\leftarrow and \subset
converse nonimplication . . . see
\nleftarrow and \nsubset
\convolution ( ) . . . . . . . . 23
\Coppa () ............. 87
\coppa () ............. 87
\coprod (`) . . . . . . . . . 21, 25
\coprod () ............ 29
copyright . . . . . . . . . 9, 19, 116
\copyright (©) .......... 9
\corner () ............. 18
corners, box . . . . . . . . . . . . 97
\corona () ............ 95
\coronainv (Ϙ) .......... 95
\Corresponds (=) . . . . . . . . 67
\corresponds ( ) . . . . . . . . 32
\cos (cos) . . . . . . . . . . 49, 113
\cosh (cosh) . . . . . . . . . . . . 49
\cot (cot) .............. 49
\coth (coth) . . . . . . . . . . . . 49
\counterplay (V) . . . . . . . . 93
Courier (font) . . . . . . . . . . . 18
CP1252 . . . . see code page 1252
CP437 . . . . . see code page 437
\Cpa (p) ............... 86
\Cpe (P) ............... 86
\Cpi (G) .............. 86
\Cpo (H) .............. 86
\Cpu (I) .............. 86
\CR (␍) ................ 72
\cr .................. 104
\Cra (r) ............... 86
\Cre (R) .............. 86
Creative Commons licenses . 19
crescent (fge package option) 58
\Cri (O) .............. 86
\Cro (U) ............... 86
\Cross ( ) ............. 79
\Cross (†vs. vs. ) . . . . 101
\Cross ( ) ............. 76
\Cross (†) ............. 90
cross ratio . . . see \textrecipe
\crossb ( ) ............. 13
\CrossBoldOutline ( ) . . . . 76
\CrossClowerTips ( ) . . . . 76
\crossd ( ) ............. 13
\Crossedbox (X) ......... 90
crosses . . . . . . . . 76, 77, 90, 94
\crossh ( ) ............. 13
\CrossMaltese ( ) . . . . . . . 76
\crossnilambda ( ) . . . . . . 13
\CrossOpenShadow ( ) . . . . . 76
\CrossOutline ( ) . . . . . . . 76
crotchet . . see musical symbols
\crtilde (Ŕ
˜
a) ............ 16
\Cru (V) ............... 86
crucifixes . . . . . . . . . . 76, 77, 90
\Crux (†) .............. 57
\crux (†) .............. 57
\Csa (s) ............... 86
\csc (csc) .............. 49
\Cse (S) ............... 86
\cshuffle ( ) . . . . . . . . . . 24
\Csi (Y) ............... 86
\Cso (1) .............. 86
\Csu (2) .............. 86
\Cta (t) ............... 86
CTAN see Comprehensive T
E
X
Archive Network
\Cte (T) ............... 86
\Cti (3) ............... 86
\Cto (4) ............... 86
\Ctrl (Ctrl ) ........... 72
\Ctu (5) ............... 86
\Cu (u) ............... 86
\Cube ( ) 92, 103
cube root . . . . . . . . see \sqrt
\Cup (d) ............... 22
\Cup () ............... 24
\cup ( ) ............... 23
\cup (∪) . . . . . . . . 22, 104, 112
\cup (∪) ............... 24
\cupdot () ............ 24
\cupplus () ............ 24
\curlyc ( ) ............. 13
\curlyeqprec ( ) . . . . . . . . 32
\curlyeqprec (2) ........ 30
\curlyeqprec () . . . . . . . . 33
\curlyeqsucc ( ) . . . . . . . . 32
\curlyeqsucc (3) ........ 30
\curlyeqsucc () . . . . . . . . 33
\curlyesh ( ) ........... 13
\curlyvee ( ) .......... 23
\curlyvee (g) .......... 22
\curlyvee (⋎) ........... 24
\curlyveedot () . . . . . . . . 24
\curlyveedownarrow (.) . . . 22
\curlyveeuparrow (/) . . . . . 22
\curlywedge ( ) ......... 23
\curlywedge (f) ......... 22
\curlywedge (⋏) ......... 24
\curlywedgedot () . . . . . . 24
\curlywedgedownarrow (') . 22
\curlywedgeuparrow (&) . . . 22
\curlyyogh ( ) .......... 13
\curlyz ( ) ............. 13
\currency (¤) ........... 18
currency symbols . . . . 18, 19, 68
\curvearrowbotleft ( ) . . 42
\curvearrowbotleftright ( )
......... 42
\curvearrowbotright ( ) . . 42
\curvearrowdownup (Ë) . . . . 43
\curvearrowleft ( ) . . . . . 42
\curvearrowleft () . . . . . 41
\curvearrowleft (↶) . . . . . 44
\curvearrowleftright ( ) . 42
\curvearrowleftright (È) . 43
\curvearrownesw (Ì) . . . . . 43
\curvearrownwse (Í) . . . . . 43
\curvearrowright ( ) . . . . 42
\curvearrowright () . . . . 41
\curvearrowright (↷) . . . . 44
\curvearrowrightleft (Ê) . 43
\curvearrowsenw (Ï) . . . . . 43
\curvearrowswne (Î) . . . . . 43
\curvearrowupdown (É) . . . . 43
\Cutleft (s) ........... 75
\Cutline (r) ........... 75
cutoff subtraction . see \dotdiv
\Cutright (q) .......... 75
\Cwa (w) .............. 86
\Cwe (W) ............... 86
\Cwi (6) .............. 86
\Cwo (7) ............... 86
\Cxa (x) ............... 86
\Cxe (X) ............... 86
\Cya (j) ............... 86
\Cyo (b) .............. 86
\cyprfamily ............ 86
Cypriot . . . . . . . . . . . . . . . . 86
cypriot (package) . . 86, 119, 121
\Cza (g) .............. 86
\Czo (9) ............... 86
D
\D (a
¨) ................. 17
d(esvect package option) . . . 61
\d (a
.) ................. 14
\dag (†) . . . . . . . . . . . . 9, 117
\dagger (†) ............. 22
\daleth () ............ 51
\daleth () ............ 51
\danger (B) ............ 91
dangerous bend symbols . . . 89
\DArrow (↓) .......... 72
\dasharrow ............ see
\dashrightarrow
\dasheddownarrow (⇣) . . . . . 43
130
\dashedleftarrow (⇠) . . . . 43
\dashednearrow (d) . . . . . . 43
\dashednwarrow (e) . . . . . . 43
\dashedrightarrow (⇢) . . . . 43
\dashedsearrow (g) . . . . . . 43
\dashedswarrow (f) . . . . . . 43
\dasheduparrow (⇡) . . . . . . . 43
\dashint (−
R) . . . . . . . . . . 106
\dashleftarrow (c) . . . . . . 41
\dashleftarrow (⇠) ...... 44
\dashleftrightarrow (e) . . 42
\dashrightarrow (d) . . . . . 41
\dashrightarrow (⇢) . . . . . 44
\DashV ( ) ............. 32
\Dashv ( ) ............. 32
\dashv (a) ............. 30
\dashv (⊣) ............. 33
\dashVv ( ) ............ 32
\davidsstar (C) ......... 77
\DavidStar ( ) ......... 78
\DavidStarSolid ( ) . . . . . 78
\dBar (||) .............. 95
\dbar (¯d) .............. 104
\dbend () ............ 89
dblaccnt (package) . . . . . . . 107
\dblcolon (::) ........... 34
\DCa (␑) ............... 72
\DCb (␒) ............... 72
\DCc (␓) ............... 72
\DCd (␔) ............... 72
\DD (D
D) ............... 89
\ddag (‡) ........... 9,117
\ddagger (‡) ............ 22
\ddashint (=
R) . . . . . . . . . . 106
\ddddot (....) ............ 58
\dddot (...) ............. 58
\dddtstile ( ) . . . . . . . . . 35
\ddigamma () ........... 87
\DDohne (D
D
/) ............ 89
\ddot (¨) .............. 57
\ddotdot () . . . . . . . . . 24, 64
\ddots (...) . . . . . . . . 63, 107
\ddots () ............. 64
\ddststile ( ) ......... 35
\ddtstile ( ) . . . . . . . . . . 35
\ddttstile ( ) . . . . . . . . 35
\DeclareFontFamily . . . . . 111
\DeclareFontShape . . . . . . 111
\DeclareMathOperator . . . 113
\DeclareMathOperator* . . 113
\declareslashed . . . . . . . 105
\DeclareUnicodeCharacter 117
\decofourleft ([) . . . . . . . 78
\decofourright (\) . . . . . . 78
\decoone (X) ........... 78
\decosix (]) ........... 78
\decothreeleft (Y) . . . . . . 78
\decothreeright (Z) . . . . . 78
\decotwo (a) ........... 78
definite-description operator (
ι
)
........ 103
definition symbols . . . . 21, 108
\deg (deg) . . . . . . . . . . . . . 49
\degree () ............. 66
\degree (°) ............. 70
degrees . . . . . see \textdegree
\DEL (␡) ............... 72
\Del (Del ) ............ 72
\Deleatur ..... see \Denarius
delimiters . . . . . . . . . . . 53–57
text-mode . . . . . . . . . . 57
variable-sized . . . . . 54–57
wavy-line . . . . . . . . 55, 56
\Delta (∆) ............. 50
\delta (δ) ............. 50
\deltaup (δ) ............ 50
demisemiquaver . . . see musical
symbols
\Denarius (¢) .......... 18
\denarius (Ε) .......... 19
\dental (a) ............. 16
derivitive, partial . see \partial
\descnode () .......... 71
\det (det) . . . . . . . . . . . . . . 49
\devadvantage (t) . . . . . . . 93
\Dfourier (.
.
.
.
.
.
.
.
.
.
.) ........ 36
\dfourier (.
.
.
.
.
.
.
.
.
.
.) ........ 36
\DFT ( ) ............. 63
\dft ( ) ............. 63
\DH ( D) ................ 13
\DH (Ð) . . . . . . . . . . . . 10, 116
\dh (k) ................ 13
\dh (ð) . . . . . . . . . . . . 10, 116
diacritics . . . . . . . . see accents
\diaeresis (a¨) . . . . . . . . . . 17
diæresis (¨a) . . . . . . see accents
\diagdown ( ) . . . . . . . . . . 66
\diagdown () .......... 66
\diagdown (Ó) .......... 33
\diagonal (G) .......... 93
\diagup ( ) ............ 66
\diagup () ............ 66
\diagup (Ò) ............ 33
\diameter ( ) .......... 66
\diameter () .......... 21
\diameter () ........... 66
\diameter () .......... 88
\Diamond (^) ........... 65
\Diamond (3) ........... 66
\Diamond () ........... 25
\diamond () ............ 22
\diamond (◇) ............ 25
\diamondbackslash () . . . . 25
\Diamondblack (_) . . . . . . . 66
\diamonddiamond () . . . . . 25
\Diamonddot () ......... 66
\diamonddot () ......... 25
\DiamonddotLeft () . . . . 42
\Diamonddotleft () . . . . 42
\DiamonddotRight () . . . . 42
\Diamonddotright () . . . . 42
\diamonddots () . . . . . 24, 64
\DiamondLeft () . . . . . . . 42
\Diamondleft () . . . . . . . 42
\diamondminus () . . . . . . . 25
\diamondplus () ........ 25
\DiamondRight () . . . . . . 42
\Diamondright () . . . . . . 42
diamonds . . . . . . . . . . . 79–80
diamonds (suit) . . . . . 65–67, 80
\DiamondShadowA ( ) . . . . . 79
\DiamondShadowB ( ) . . . . . 79
\DiamondShadowC ( ) . . . . . 79
\Diamondshape ( ) . . . . . . . 79
\diamondslash () . . . . . . . 25
\DiamondSolid ( ) . . . . . . . 80
\diamondsuit (♦) ........ 65
\diamondsuit (♢) . . . . . . . . 66
\diamondtimes () . . . . . . . 25
\diamondvert () ........ 25
\diatop . . . . . . . . . . . 18, 107
\diaunder . . . . . . . . . . 18, 107
dice . . . . . . . . . . . . . . 92, 103
dictionary symbols . . . 11–14, 96
dictsym (package) . 96, 119, 120
died ......... see \textdied
differential, inexact . see \dbar
\Digamma () ........... 87
\digamma () . . . . . . . . 50, 87
\digamma () ............ 87
digital logic gates . . . . . . . . 73
digits ................. 65
LCD .............. 70
Mayan . . . . . . . . . . . . . 65
old-style . . . . . . . . . . . . 20
segmented . . . . . . . . . . 70
\dim (dim) . . . . . . . . . . . . . 49
\ding . . . . . . . . . 10, 75–78, 80
dingautolist ........... 77
dingbat (package) . . 76, 80, 101,
119, 120
dingbat symbols . . . . . . 75–80
\Diple (>) ............. 95
\diple (>) ............. 95
\Diple* (>
·
·) ............ 95
\diple* (>
·
·) ............ 95
Dirac notation . . . . . . . . . . . 54
discount . . . see \textdiscount
discretionary hyphen . . . . . 115
disjoint union . . . . . . . . . . . 21
disjunction . . . . . . . . see \vee
\displaystyle . . 105, 106, 108,
113
ditto marks . see \textquotedbl
\div (÷) ............... 22
\div (÷) ............... 24
\divdot ( ) ............ 23
\divideontimes ( ) . . . . . . 23
\divideontimes () . . . . . . 22
\divides ( ) ............ 32
\divides (Ò) ........... 33
division . . . . . . . . . . . . . 22, 59
non-commutative . . . . . 63
131
division times . . . . . . . . . . see
\divideontimes
divorced . . . see \textdivorced
\DJ (Ð) ................ 10
\dj (đ) ................ 10
\dlbari () ............. 13
\DLE (␐) ............... 72
\dlsh ( ) .............. 42
\dndtstile ( ) . . . . . . . . . 35
\dnststile ( ) ......... 35
\dntstile ( ) . . . . . . . . . . 35
\dnttstile ( ) . . . . . . . . 35
do not enter . . . . . . see \noway
does not divide . . . . see \nmid
does not exist . . . see \nexists
does not imply . . . . . . . . . 105
\Dohne (D/) ............. 89
dollar . . . . . . see \textdollar
dollar sign . . . . . . . . . . . see \$
\Dontwash (Ý) .......... 90
\dot (˙) ............... 57
dot accent ( ˙a or .) . see accents
dot symbols . . . . 9, 63, 64, 107
DotArrow (package) 63, 119, 121
\dotarrow () ........ 63
\dotcup (·
∪) . . . . . . . . 21, 104
\dotdiv ( ) ............ 23
\Doteq ....... see \doteqdot
\Doteq () ............. 33
\doteq () ............. 30
\doteq () ............. 33
\doteqdot (+) .......... 30
\doteqdot () ........... 33
dotless j()
text mode . . . . . . . . . . 14
dotless i(ı)
math mode . . . . . . 57, 65
text mode . . . . . . . . . . 14
dotless j()
math mode . . . . . . 57, 65
\dotmedvert () ......... 24
\dotminus () ........... 24
\dotplus ( ) ........... 23
\dotplus (u) ........... 22
\dots (. . . ) . . . . . . . . . . 9, 117
dots (ellipses) . . . 9, 63–65, 107
\dotsb (···) ............ 64
\dotsc (. . .) ............ 64
\dotseq ( ) ............ 32
\dotsi (···) ............ 64
\dotsint (¯) .......... 28
\dotsm (···) ............ 64
\dotso (. . .) ............ 64
dotted arrows . . . . . . . . . . . 63
dotted union ( ˙
∪) . . . . . . . . 112
\dottedtilde (..
˜
a) . . . . . . . . 16
\dottimes ( ) .......... 23
\double ............ 56,57
double acute (˝a) . . see accents
\doublebarwedge ( ) . . . . . 23
\doublebarwedge ([) . . . . . 22
\doublecap ........ see \Cap
\doublecap ( ) .......... 23
\doublecap () .......... 24
\doublecup ........ see \Cup
\doublecup ( ) .......... 23
\doublecup () .......... 24
\doublecurlyvee () . . . . . 24
\doublecurlywedge () . . . . 24
\doublefrown () . . . . . . . . 48
\doublefrowneq () . . . . . . . 48
\doublepawns (d) . . . . . . . . 93
\doublesmile () . . . . . . . . 48
\doublesmileeq () . . . . . . . 48
\doublesqcap () ........ 24
\doublesqcup () ........ 23
\doubletilde (˜
˜a) . . . . . . . . 16
\doublevee () .......... 23
\doublewedge () . . . . . . . . 23
\DOWNarrow (L) .......... 88
\Downarrow (⇓) . . . . . . . 41, 54
\Downarrow (⇓) .......... 43
\downarrow ............ 112
\downarrow (↓) . . . . . . . 41, 54
\downarrow (↓) .......... 43
\downarrowtail (#) . . . . . . . 43
\downbracketfill . . . . . . . 109
\downdownarrows ( ) . . . . . 42
\downdownarrows () . . . . . 41
\downdownarrows (⇊) . . . . . 43
\downdownharpoons ( ) . . . . 43
Downes, Michael J. . . . 49, 122
\downfilledspoon (s) . . . . . 47
\downfootline ({) ........ 33
\downfree (⫝) ........... 33
\downharpoonccw (⇂) . . . . . . 46
\downharpooncw (⇃) . . . . . . . 46
\downharpoonleft ( ) . . . . . 43
\downharpoonleft () . . . . . 41
\downharpoonright ( ) . . . . 43
\downharpoonright () . . . . 41
\downlsquigarrow (£) . . . . . 43
\downmapsto (↧) ......... 43
\downModels (ó) ......... 33
\downmodels (ã) . . . . . . . . . 33
\downp ( ) .............. 18
\downparenthfill . . . . . . . 109
\downpitchfork (⫛) . . . . . . . 47
\downpropto () ......... 33
\downrsquigarrow («) . . . . . 43
\downslice () .......... 25
\downspoon (⫰) .......... 47
\downt ( ) .............. 18
\downtherefore (∵) . . . 23, 64
\downtouparrow ( ) . . . . . . 42
\downuparrows ( ) . . . . . . . 42
\downuparrows () . . . . . . . 43
\downupharpoons ( ) . . . . . . 43
\downupharpoons (⥯) . . . . . . 46
\downVdash (⍑) .......... 33
\downvdash (⊤) .......... 33
\downY () ............. 23
dozenal (package) . . . . . 65, 119
dozenal digits . . . . . . . . . . . 65
\dracma (Δ) ............. 19
\drsh ( ) .............. 42
\DS (S
S) ................ 89
\Ds (s
s) ................ 89
\dsaeronautical (a) . . . . . 96
\dsagricultural (G) . . . . . 96
\dsarchitectural (A) . . . . 96
\dsbiological (B) . . . . . . . 96
\dschemical (C) ......... 96
\dscommercial (c) . . . . . . . 96
\dsdtstile ( ) . . . . . . . . . 35
dsfont (package) . . . . . 68, 119
\dsheraldical (H) . . . . . . . 96
\dsjuridical (J) . . . . . . . . 96
\dsliterary (L) ......... 96
\dsmathematical (M) . . . . . . 96
\dsmedical (m) .......... 96
\dsmilitary (X) ......... 96
\dsrailways (R) ......... 96
\dsststile ( ) ......... 35
\dstechnical (T) . . . . . . . . 96
\dststile ( ) . . . . . . . . . . 35
\dsttstile ( ) . . . . . . . . 35
\dtdtstile ( ) . . . . . . . . . 35
\dtimes (_) ............ 24
\dtimes () ............ 23
\dtststile ( ) ......... 35
\dttstile ( ) . . . . . . . . . . 35
\dtttstile ( ) . . . . . . . . 35
duodecimal (base-12) digits . 65
DVI . . . . . . . . . . . . 19, 72, 111
\dz ( ) ............... 13
E
e(esvect package option) . . . 61
\e (e) ................. 52
\e ( ) ................. 65
ε-T
E
X ................. 54
\Earth ( ) ............. 71
\Earth (Ê) ............. 71
\earth (♁) ............. 71
\Ecommerce () ......... 18
\EightAsterisk ( ) . . . . . . 78
\EightFlowerPetal ( ) . . . 78
\EightFlowerPetalRemoved ( )
......... 78
eighth note see musical symbols
\eighthnote (♪) ......... 88
\eighthnote () ......... 88
\EightStar ( ) ......... 78
\EightStarBold ( ) . . . . . . 78
\EightStarConvex ( ) . . . . 78
\EightStarTaper ( ) . . . . . 78
\ejective ( ) ........... 13
electrical symbols . . . . . . . . 70
electromotive force (E) . . . . see
alphabets, math
element of . . . . . . . . . . see \in
132
\ell () ............... 51
\Ellipse ( ) ........... 80
ellipses (dots) . . . 9, 63–65, 107
ellipses (ovals) . . . . . . . . . . . 80
\EllipseShadow ( ) . . . . . . 80
\EllipseSolid ( ) . . . . . . . 80
\EM (␙) ................ 72
\Email (k) ............. 73
\Emailct (z) ........... 73
\emgma ( ) ............. 13
\emptyset (∅) ........... 65
\emptyset () ........... 66
\End (End ) ............ 72
end of proof . . . . . . . . . . . . 65
\ending (L) ............ 93
\eng ( ) ............... 13
engineering symbols . . . . 70, 73
\engma ( ) ............. 13
\ENQ (␅) ............... 72
entails . . . . . . . . . . see \models
\Enter (Enter ) ......... 72
\Envelope ( ) ........... 80
envelopes . . . . . . . . . . . 80, 98
\enya ( ) .............. 13
\EOT (␄) ............... 72
epsdice (package) . . 92, 119, 120
\epsdice ( ) . . . . . 92
\epsi ( ) .............. 13
\epsilon () ............ 50
\epsilonup () .......... 50
\eqbump () ............. 32
\eqbumped ( ) .......... 32
\eqcirc ( ) ............ 32
\eqcirc (P) ............ 30
\eqcirc () ............. 32
\Eqcolon (I) ........... 31
\Eqcolon (−::) ........... 34
\eqcolon ( ) ........... 32
\eqcolon (−:) ........... 34
\eqcolon (E) ........... 31
\eqdot () ............. 32
\eqfrown () ............ 48
\Eqqcolon (G) .......... 31
\Eqqcolon (=::) .......... 34
\eqqcolon (=:) .......... 34
\eqqcolon (C) .......... 31
\eqsim () ............. 31
\eqsim () ............. 32
\eqslantgtr ( ) ......... 38
\eqslantgtr (1) ......... 38
\eqslantgtr () ......... 39
\eqslantless ( ) . . . . . . . . 38
\eqslantless (0) . . . . . . . . 38
\eqslantless () ........ 39
\eqsmile () ............ 48
\equal (=) ............. 32
\equal (j) ............. 93
\equalclosed () ........ 32
\equalscolon (=:) . . . . . . . 36
\equalscoloncolon (=::) . . . 36
\equalsfill . . . . . . . . 21, 108
equidecomposable . . . . . . . 104
equilibrium . . . . . . . . . . . . see
\rightleftharpoons
\equiv (≡) . . . . . . . . . . 21, 30
\equiv (≡) ............. 32
equivalence . . . . . . . . . . . . see
\equiv,\leftrightarrow,
and \threesim
\equivclosed () ........ 32
\er ( ) ................ 13
es-zet ............. see \ss
\ESC (␛) ............... 72
\Esc (Esc ) ............ 72
escapable characters . . . . . . . 9
\esh ( ) ............... 13
\esh () ............... 13
esint (package) . . . . . . . 28, 119
\Estatically (J) . . . . . . . . 74
estimated . see \textestimated
esvect (package) . . . . . . 61, 119
\eta (η) ............... 50
\etaup (η) ............. 50
\ETB (␗) ............... 72
\eth (ð) ............... 66
\eth ( ) ............... 13
\eth ( ) ............... 13
\ETX (␃) ............... 72
eufrak (package) . . . . . . . . . 68
Euler Roman . . . . . . . . . . . . 51
\EUR (e) ............... 18
\EURcr (d) ............. 18
\EURdig (D) ............ 18
\EURhv (c) ............. 18
\Euro ( ) .............. 19
\euro ................. 19
euro signs . . . . . . . . . . . 18, 19
blackboard bold . . . . . . 68
\eurologo (() ........... 19
eurosym (package) . 19, 119, 120
\EURtm (e) ............. 18
euscript (package) . 68, 119, 120
evaluated at . . . . . . see \vert
evil spirits . . . . . . . . . . . . . . 98
exclusive disjunction . . . . . . . .
... see \nleftrightarrow
\nequiv,and \oplus
exclusive or . . . . . . . . . . . . 103
\exists ( ) ............. 52
\exists (∃) ............. 51
\exists (∃) ............. 52
\exp (exp) . . . . . . . . . . . . . 49
\Explosionsafe (`) . . . . . . 74
extarrows (package) 62, 119, 120
extensible accents . . 59–61, 63,
108–109
extensible arrows . . . . . . 59–63
extensible symbols, creating 107–
109
extensible tildes . . . . . . . 59, 61
extension characters . . . 48, 49
extpfeil (package) . . 63, 119, 120
extraipa (package) . . . . 16, 119
\eye ( ) ............. 80
\EyesDollar (¦) ......... 18
F
f(esvect package option) . . . 61
faces . . 72, 81, 88, 90, 91, 96, 98
\fallingdotseq ( ) . . . . . . 32
\fallingdotseq (;) . . . . . . 30
\fallingdotseq () . . . . . . . 32
\FallingEdge ( ) . . . . . . . . 70
\fatbslash ()) .......... 22
\fatsemi (#) ............ 22
\fatslash (() ........... 22
\FAX (u) .............. 73
\fax (t) ............... 73
\Faxmachine (v) . . . . . . . . 73
fc (package) . . . . . . . . . 10, 14
\fcdice () . . . . 92
fclfont (package) . . . . . . . . 119
\fcscore ( ) . . . . . . 92
feet ......... see \prime and
\textquotesingle
\FEMALE () ............ 74
\Female (~) ............ 74
female . . . . . . . . . 12, 71, 73, 74
\female (♀) ............. 73
\FemaleFemale („) . . . . . . . 74
\FemaleMale (…) ......... 74
\Ferli (a
a
.) ............. 89
\Fermi (a
a
.) ............. 89
fermions . . . . . . . . . . . . . . . 74
feyn (package) . . . . 74, 119, 120
Feynman slashed character nota-
tion . . . . . . . . . . . . . 105
Feynman-diagram symbols . . 74
\feyn{a} () ............. 74
\feyn{c} ( ) ........... 74
\feyn{fd} ( ) ........... 74
\feyn{flS} () ........... 74
\feyn{fl} () ............ 74
\feyn{fs} ( ) ........... 74
\feyn{fu} ( ) ........... 74
\feyn{fv} () ............ 74
\feyn{f} ( ) ........... 74
\feyn{g1} () ............ 74
\feyn{gd} ( ) ........... 74
\feyn{glB} () ........... 74
\feyn{glS} () ........... 74
\feyn{glu} () ........... 74
\feyn{gl} () ............ 74
\feyn{gu} ( ) ........... 74
\feyn{gvs} () ........... 74
\feyn{gv} () ............ 74
\feyn{g} ( ) ........... 74
\feyn{hd} ( ) ........... 74
\feyn{hs} ( ) ........... 74
\feyn{hu} ( ) ........... 74
\feyn{h} ( ) ........... 74
\feyn{ms} ( ) ........... 74
\feyn{m} ( ) ........... 74
\feyn{P} ( ) ........... 74
133
\feyn{p} ( ) ........... 74
\feyn{x} () ............. 74
\FF (␌) ................ 72
fge (package) . 47, 53, 58, 65, 67,
119, 120
fge-digits . . . . . . . . . . . . . . . 65
\fgeA (A) .............. 53
\fgebackslash (K) . . . . . . . . 67
\fgebaracute (M) . . . . . . . . 67
\fgebarcap (O) .......... 67
\fgec (c) .............. 53
\fgecap (S) ............ 67
\fgecapbar (Q) .......... 67
\fgecup (N) ............ 67
\fgecupacute (R) . . . . . . . . 67
\fgecupbar (P) .......... 67
\fged (p) .............. 53
\fgee (e) .............. 53
\fgeeszett (ı) .......... 53
\fgeeta (”) ............ 53
\fgeF (F) .............. 53
\fgef (f) .............. 53
\fgeinfty (i) .......... 67
\fgelangle (h) .......... 67
\fgelb ................ 53
\fgelb (”) ............. 53
\fgeleftB (D) ........... 53
\fgeleftC (C) ........... 53
\fgeN (”) .............. 53
\fgeoverU (”) ........... 53
\fgerightarrow (!) . . . . . 47
\fgerightB (B) .......... 53
\fges (s) ............... 53
\fgestruckone (1) . . . . . . . . 65
\fgestruckzero (0) . . . . . . . 65
\fgeU (U) .............. 53
\fgeuparrow (") . . . . . . . . . 47
\fgeupbracket (L) . . . . . . . 67
\FHBOLOGO (f) ........... 90
\FHBOlogo (F) ........... 90
field ( ) . . see alphabets, math
\file (H) .............. 93
\FilledBigCircle ( ) . . . . 79
\FilledBigDiamondshape ( ) 79
\FilledBigSquare ( ) . . . . 79
\FilledBigTriangleDown ( ) 79
\FilledBigTriangleLeft ( ) 79
\FilledBigTriangleRight ( )
......... 79
\FilledBigTriangleUp ( ) . 79
\FilledCircle ( ) . . . . . . . 79
\FilledCloud ( ) . . . . . . . . 91
\filleddiamond (◆) . . . . . . . 25
\FilledDiamondShadowA ( ) 79
\FilledDiamondShadowC ( ) 79
\FilledDiamondshape ( ) . . 79
\FilledHut ( ) .......... 91
\filledlargestar () . . . . 79
\filledlozenge () . . . . . . . 79
\filledmedlozenge () . . . . 79
\filledmedsquare () . . . . . 25
\filledmedtriangledown (▼) 25,
40
\filledmedtriangleleft (◀) 25,
40
\filledmedtriangleright (▶)
. . . . . . . 25, 40
\filledmedtriangleup (▲) 25,
40
\FilledRainCloud ( ) . . . . 91
\FilledSectioningDiamond ( )
......... 92
\FilledSmallCircle ( ) . . 79
\FilledSmallDiamondshape ( )
......... 79
\FilledSmallSquare ( ) . . 79
\FilledSmallTriangleDown ( )
......... 79
\FilledSmallTriangleLeft ( )
......... 79
\FilledSmallTriangleRight
( ) .............. 79
\FilledSmallTriangleUp ( ) 79
\FilledSnowCloud ( ) . . . . 91
\FilledSquare ( ) . . . . . . . 79
\filledsquare () ........ 25
\FilledSquareShadowA ( ) . 79
\FilledSquareShadowC ( ) . 79
\filledsquarewithdots ( ) 80
\filledstar (★) . . . . . . . . . 25
\FilledSunCloud ( ) . . . . . 91
\FilledTriangleDown ( ) . . 79
\filledtriangledown () 25, 40
\FilledTriangleLeft ( ) . . 79
\filledtriangleleft () 25, 40
\FilledTriangleRight ( ) . 79
\filledtriangleright () 25,
40
\FilledTriangleUp ( ) . . . 79
\filledtriangleup (▴) . 25, 40
\FilledWeakRainCloud ( ) . 91
finger, pointing . . . . . . see fists
finite field ( ) . . see alphabets,
math
\finpartvoice (a
»
ˇ) . . . . . . . 16
\finpartvoiceless (a
»
˚) . . . . 16
\fint (>) .............. 27
\fint (ffl) .............. 28
\Finv ( ) .............. 52
\Finv () .............. 52
\Fire ( ) .............. 92
fish hook . . . . . . see \strictif
fists .................. 76
\fivedots () . . . . . . . . 23, 64
\FiveFlowerOpen ( ) . . . . . 78
\FiveFlowerPetal ( ) . . . . 78
\FiveStar ( ) .......... 78
\FiveStarCenterOpen ( ) . . 78
\FiveStarConvex ( ) . . . . . 78
\FiveStarLines ( ) . . . . . . 78
\FiveStarOpen ( ) . . . . . . . 78
\FiveStarOpenCircled ( ) . 78
\FiveStarOpenDotted ( ) . . 78
\FiveStarOutline ( ) . . . . 78
\FiveStarOutlineHeavy ( ) 78
\FiveStarShadow ( ) . . . . . 78
\Fixedbearing (%) . . . . . . . 73
\fixedddots (...) ........ 63
\fixedvdots (.
.
.) .......... 63
fixmath (package) . . . . . . . 113
\fj ( ) ................ 13
\Flag ( ) .............. 91
\flap () .............. 13
\flapr () .............. 13
\flat () ........... 65,88
\flat (♭) ............... 66
\Flatsteel (–) .......... 73
fletched arrows . . . . . . . 47, 75
fleurons . . . . . . . . . . . . . 78, 80
florin . . . . . . see \textflorin
\floweroneleft (b) . . . . . . 78
\floweroneright (c) . . . . . 78
flowers . . . . . . . . . . . . . . . . 78
Flynn, Peter . . . . . . . . . . . 104
\Fog ( ) .............. 91
font encodings
Latin 1 . . . . . . . . . . . 119
font encodings . . . . . 8, 114, 115
7-bit ............... 8
8-bit ............... 8
ASCII . . . . . . . . . . . . 119
document . . . . . . . . . . 115
limiting scope of . . . . . . . 8
LY1 ................ 8
OT1 8, 10, 14, 107, 114, 115
OT2 ............. 103
T1 . . . . . . . . 8, 10, 14, 115
T4 . . . . . . . . . . . 10, 14, 17
T5 . . . . . . . . . . . . . 10, 14
TS1 .............. 115
fontdef.dtx (file) . . . . 103, 107
fontenc (package) . 8, 10, 14, 115
\fontencoding ........... 8
fonts
Calligra . . . . . . . . . . . . 68
Charter . . . . . . . . . 18, 30
Computer Modern 100, 102,
115
Courier . . . . . . . . . . . . 18
Garamond . . . . . . . 18, 30
Helvetica . . . . . . . . . . . 18
Symbol . . . . . . . . 51, 103
Times Roman . . . 18, 102
Type 1 . . . . . . . . . . . 112
Utopia . . . . . . . . . . 18, 30
Zapf Chancery . . . . . . . 68
Zapf Dingbats . . . . 75, 77
134
\fontsize . . . . . . . . . . 100, 102
fontspec (package) . . . . . . . 118
\Football (o) ........... 90
\forall (∀) ............. 51
\forall (∀) ............ 52
\Force (l) ............. 73
\Forward (·) ............ 90
\ForwardToEnd (¸) . . . . . . . 90
\ForwardToIndex (¹) . . . . 90
\FourAsterisk ( ) . . . . . . . 78
\FourClowerOpen ( ) . . . . . 78
\FourClowerSolid ( ) . . . . 78
\Fourier ( ) ......... 36
fourier (package) 19, 36, 51, 53,
57, 60, 76, 78, 91, 119
\fourier ( ) ......... 36
Fourier transform (F) . . . . see
alphabets, math
\FourStar ( ) .......... 78
\FourStarOpen ( ) . . . . . . . 78
\fourth ( ) ............ 66
fractions . . . . . . . . . . . . . . . 67
fraktur . . . see alphabets, math
Freemason’s cipher . . . . . . . 98
Frege logic symbols 47, 53, 65, 67
\frown () ............. 30
\frown () ............. 48
frown symbols . . . . . . . . . . . 48
\frowneq () ............ 48
\frowneqsmile () . . . . . . . 48
\frownie (/) ........... 88
\frownsmile () ......... 48
\frownsmileeq () . . . . . . . 48
\Frowny (§) ............ 90
frowny faces . . . . 72, 88, 90, 91
\FS (␜) ................ 72
\FullFHBO () .......... 90
\fullmoon ( ) .......... 71
\fullmoon (#) .......... 71
\fullnote () ........... 88
G
\G ( ) ................. 14
g(esvect package option) . . . 61
\Game ( ) .............. 52
\Game () .............. 52
\Gamma (Γ) ............. 50
\gamma (γ) ............. 50
\gammaup (γ) ............ 50
\Ganz (¯) .............. 89
\GaPa (<) .............. 89
Garamond (font) . . . . . . 18, 30
\gcd (gcd) . . . . . . . . . . . . . 49
\ge .............. see \geq
\Gemini ( ) ............ 71
\Gemini (â) ............ 71
\gemini (^) ............ 71
genealogical symbols . . . . . . 88
\geneuro (AC) ........... 19
\geneuronarrow (BC) . . . . . . 19
\geneurowide (CC) . . . . . . . . 19
gensymb (package) . . . . . . . . 70
\Gentsroom (x) .......... 90
geometric shapes . . . . 78–80, 94
\geq ( ) ............... 38
\geq (≥) . . . . . . . . . . . . 37, 38
\geq (≥) ............... 39
\geqclosed () . . . . . . . 39, 40
\geqdot () ............. 39
\geqq ( ) .............. 38
\geqq (=) .............. 38
\geqq () .............. 39
\geqslant (>) .......... 38
\geqslant () ........... 39
\geqslantdot () . . . . . . . . 39
german (keystroke package option)
......... 72
\gets ....... see \leftarrow
\gg ( ) ................ 38
\gg () ............... 37
\gg () ............... 39
\ggcurly ( ) ........... 32
\ggg ( ) ............... 38
\ggg (≫) .............. 38
\ggg (≫vs. ) . . . . . . . . 101
\ggg () .............. 39
\gggtr ........... see \ggg
\gggtr () ............ 39
ghosts ................. 98
Gibbons, Jeremy . . . . . . . . 122
\gimel (ג) ............. 51
\gimel () .............. 51
\girl ( ) .............. 71
globe ................. 90
\glotstop ( ) ........... 13
\glottal ( ) ............ 13
\gluon (QPPPPPPR) .......... 70
gluons ................. 74
\gnapprox ( ) .......... 38
\gnapprox () .......... 38
\gnapprox () ........... 39
\gneq ( ) .............. 38
\gneq () .............. 38
\gneqq ( ) ............. 38
\gneqq () ............. 38
\gneqq () ............. 39
\gnsim ( ) ............. 38
\gnsim () ............. 38
\gnsim () ............. 39
Go boards . . . . . . . . . . . . . . 94
Go stones . . . . . . . . . . . . . . 94
goban ................. 94
\Goofy ................ 96
graphics (package) . . . . 47, 103
graphicx (package) . 17, 100, 103
\grave (`) ............. 57
grave (`a) . . . . . . . . see accents
\gravis (a`) ............. 17
greater-than signs . . . . . . . see
inequalities
greatest lower bound see \sqcap
Greek . . . . . . . . . . . . . . 50, 51
blackboard bold . . . . . . 68
bold . . . . . . . . . . 50, 113
polytonic . . . . . . . . . . . 50
upright . . . . . . . . . 50, 51
greek (babel package option) 50,
87
Greek coins . . . . . . . . . . . . . 19
\Greenpoint ( ) ......... 98
Gregorio, Enrico . . . . . 104, 105
\grimace (M) ........... 91
\GS (␝) ................ 72
\gtr (>) ............... 39
\gtrapprox ( ) .......... 38
\gtrapprox (') ......... 38
\gtrapprox () .......... 39
\gtrclosed () . . . . . . . 39, 40
\gtrdot ( ) ............ 38
\gtrdot () ............ 38
\gtrdot () ............. 39
\gtreqless ( ) .......... 38
\gtreqless (R) ......... 38
\gtreqless () .......... 39
\gtreqlessslant () . . . . . . 39
\gtreqqless ( ) ......... 38
\gtreqqless (T) ......... 38
\gtreqqless () ......... 39
\gtrless ( ) ........... 38
\gtrless (≷) ........... 38
\gtrless () ............ 39
\gtrneqqless () ........ 39
\gtrsim ( ) ............ 38
\gtrsim (&) ............ 38
\gtrsim () ............. 39
\guillemotleft («) . . . 10, 116
\guillemotright (») . . 10, 116
\guilsinglleft (‹) . . . 10, 117
\guilsinglright (›) . . 10, 117
\gvcropped ( ) ......... 74
\gvertneqq ( ) .......... 38
\gvertneqq () ......... 38
\gvertneqq () .......... 39
H
\H (˝a) ................. 14
h(esvect package option) . . . 61
\h (ả) ................. 14
\HA (A) .............. 82
\Ha (a) ............... 82
h´aˇcek (ˇa) . . . . . . . see accents
\Hail ( ) .............. 91
\Halb (˘“) .............. 89
half note . . see musical symbols
\HalfCircleLeft ( ) . . . . . . 80
\HalfCircleRight ( ) . . . . . 80
\HalfFilledHut ( ) . . . . . . 91
\halflength () ......... 18
\halfnote () ........... 88
\HalfSun ( ) ........... 91
Hamiltonian (H)see alphabets,
math
\HandCuffLeft ( ) . . . . . . . 76
\HandCuffLeftUp ( ) . . . . . 76
135
\HandCuffRight ( ) . . . . . . 76
\HandCuffRightUp ( ) . . . . 76
\HandLeft ( ) . . . . . . . . . . 76
\HandLeftUp ( ) . . . . . . . . 76
\HandPencilLeft ( ) . . . . . 76
\HandRight ( ) ......... 76
\HandRightUp ( ) . . . . . . . 76
hands ............. see fists
\Handwash (Ü) .......... 90
\HaPa (<) .............. 89
harmony (package) . 89, 119, 120
harpoon (package) . 47, 119, 121
harpoons . . . . . . . 41, 43, 46, 47
\hash ( ) .............. 66
hash mark . . . . . . . . . . . see \#
\hat (ˆ) ............... 57
\hateq () ............. 32
\hausaB ( ) ............ 13
\hausab ( ) ............ 13
\hausaD ( ) ............ 13
\hausad ( ) ............ 13
\hausaK ( ) ............ 13
\hausak ( ) ............ 13
\HB (B) ................ 82
\Hb (b) ............... 82
\HBar ( ) .............. 79
\hbar () . . . . . . . . 51, 52, 103
\hbipropto () ......... 23
\HC (C) ................ 82
\Hc (c) ................ 82
\hcrossing () .......... 33
\HCthousand (6) ........ 82
\HD (D) ............... 82
\Hd (d) ............... 82
\hdotdot () . . . . . . . . . 23, 64
\hdots () ............. 64
\Hdual (¸) ............. 82
\HE (E) ............... 82
\He (e) ............... 82
heads ............ see faces
\Heart (Œ) ............. 90
hearts (suit) . . . . . . . 65–67, 80
\heartsuit (♥) .......... 65
\heartsuit (♡) .......... 66
Hebrew . . . . . . . . . . . . . 51, 68
Helvetica (font) . . . . . . . . . . 18
\hemiobelion (Α) ........ 19
\HERMAPHRODITE () . . . . . . 74
\Hermaphrodite (}) . . . . . . 74
\hexagon (7) ........... 78
\Hexasteel (’) .......... 73
\hexstar (A) ........... 77
\HF (F) ................ 70
\HF (F) .............. 82
\Hf (f) .............. 82
\hfermion ( ) ........... 74
\hfil ................ 105
\HG (G) ................ 82
\Hg (g) ............... 82
\HH ................... 89
\HH (H) ................ 82
\Hh (h) ............... 82
hhcount (package) . 92, 119, 121
\Hhundred (3) ........... 82
\HI (I) ............... 82
\Hi (i) ................ 82
\hiatus (H) ............ 95
\Hibl (˝) ............ 82
\Hibp (ˆ) ............. 82
\Hibs (¨) ............. 82
\Hibw (˜) ............. 82
hieroglf (package) . 82, 119, 120
hieroglyphics . . . . . . . . . . . . 82
Hilbert space (H)see alphabets,
math
\hill (a) .............. 16
\HJ (J) ................ 82
\Hj (j) ............... 82
\HK (K) ................ 82
\Hk (k) ............... 82
\hksqrt (√) . . . . . . . . . . 106
\HL (L) ............... 82
\Hl (l) ............... 82
\HM (M) ............... 82
\Hm (m) ............... 82
\Hman (ˇ) ............. 82
\Hmillion (7) .......... 82
\Hms (´) ............... 82
\HN (N) ............... 82
\Hn (n) ............... 82
\HO (O) ................ 82
\Ho (o) ............... 82
Holt, Alexander . . . . . . . 1, 118
\holter ( ) ........... 63
holtpolt (package) . . . . 63, 119
\hom (hom) . . . . . . . . . . . . . 49
\Home (Home ) ......... 72
\Homer ( ) . . . . . . . . 96
\Hone (|) ............... 82
hook accent (ả) . . . see accents
\hookb ( ) ............. 13
\hookd ( ) ............. 13
\hookd ( ) ............. 13
\hookdownminus (⌐) . . . . . . 66
\hookg ( ) ............. 13
\hookh ( ) ............. 13
\hookheng ( ) ........... 13
\hookleftarrow (←) . . . . . . 41
\hookleftarrow (↩) ...... 44
\hookrevepsilon ( ) . . . . . . 13
\hookrightarrow (→) . . . . . 41
\hookrightarrow (↪) . . . . . 44
\hookupminus () . . . . . . . . 66
Horn, Berthold . . . . . . . . . . 69
\HP (P) .............. 82
\Hp (p) ................ 82
\Hplural (˙) .......... 82
\Hplus (+) ............. 82
\HQ (Q) ............... 82
\Hq (q) ................ 82
\Hquery (?) ............. 82
\HR (R) ............... 82
\Hr (r) .............. 82
\HS (S) ............... 82
\Hs (s) ................ 82
\Hscribe (¯) ........... 82
\Hslash (/) ............. 82
\hslash () ............ 52
\Hsv (˚) .............. 82
\HT (T) ............... 82
\HT (␉) ................ 72
\Ht (t) ............... 82
\Hten (2) .............. 82
\Hthousand (4) .......... 82
\Htongue (˘) .......... 82
\HU (U) ................ 82
\Hu (u) ................ 82
Hungarian umlaut (˝a) see accents
\Hut ( ) ............... 91
\HV (V) ................ 82
\Hv (v) ............... 82
\hv ( ) ................ 13
\Hvbar (|) .............. 82
\HW (W) ................ 82
\Hw (w) ............... 82
\HX (X) ................ 82
\Hx (x) ................ 82
\HXthousand (5) ......... 82
\HY (Y) ............... 82
\Hy (y) ............... 82
hyphen, discretionary . . . . . 115
\HZ (Z) ............... 82
\Hz (z) .............. 82
I
¨
i ..................... 14
\i (ı) ................. 14
\ialign . . . . . . . 104, 106, 108
\ibar (i
¯) .............. 13
IBM PC . . . . . . . . . 72, 97, 115
Icelandic staves . . . . . . . . . . 97
\IceMountain ( ) . . . . . . . . 91
\iddots (...) ............ 64
\iddots () ............ 107
\idotsint (R···R) . . . . . . . 26
\idotsint (') . . . . . . . . 27
\idotsint () .......... 29
\iff .see \Longleftrightarrow
136
ifsym (package) . 70, 79, 91, 92,
101, 103, 119, 120
igo (package) . . . . . . . . 94, 119
\igocircle ( ) ......... 94
\igocircle ( ) ......... 94
\igocross ( ) . . . . . . . . . . 94
\igocross ( ) . . . . . . . . . . 94
\igonone ( ) ........... 94
\igonone ( ) ........... 94
\igosquare ( ) ......... 94
\igosquare ( ) ......... 94
\igotriangle ( ) . . . . . . . . 94
\igotriangle ( ) . . . . . . . . 94
\iiiint (RRRR) ......... 26
\iiiint (%) ........... 27
\iiiint (ˇ) ........... 28
\iiiint () ........... 29
\iiint ( ) ............ 27
\iiint (RRR) ........... 26
\iiint (#) . . . . . . . . . 26, 27
\iiint (˝) ............ 28
\iiint () ............. 29
\iint ( ) .............. 27
\iint (RR) ............. 26
\iint (!) . . . . . . . . . . . 26, 28
\iint (˜) .............. 28
\iint () .............. 29
\Im (=) ................ 51
\im (j) ................ 52
\imath (ı) . . . . . . . . . . . 51, 57
\impliedby see \Longleftarrow
\implies see \Longrightarrow
and \vdash
impulse train . . . . . . . . see sha
\in ( ) ................ 52
\in (∈) ................ 51
\in (∈) ................ 52
\in (∈) ................ 52
inches . . . . . . . see \second and
\textquotedbl
\incoh (˚) ............. 36
independence
probabilistic . . . . . . . . 106
statistical . . . . . . . . . . 106
stochastic . . . . . see \bot
\independent (⊥⊥) . . . . . . . 106
\Industry (I) .......... 90
inequalities . . . . . . . . . 9, 37–39
inexact differential . . see \dbar
\inf (inf) .............. 49
infimum . see \inf and \sqcap
infinity (∞) ....... see \infty
\Info ( ) .............. 98
\Info (i) .............. 90
information symbols . . . . . . 90
informator symbols . . . . . . . 93
\infty ( ) ............. 66
\infty (∞) ............. 65
\infty (∞) ............. 66
\inipartvoice (a
–
ˇ) . . . . . . . 16
\inipartvoiceless (a
–
˚) . . . . 16
\injlim (inj lim) . . . . . . . . . 49
\inplus (A) ............ 31
inputenc (package) . . . . . . . 117
\Ins (Ins ) ............ 72
\int () ............... 27
\int (R) . . . . . . . . . . . . 25, 26
\int (r) ............... 26
\int (∫) ............... 29
\intclockwise () . . . . . . . 30
\INTEGER ( ) ............ 49
\Integer ( ) ............ 49
integers ( ) see alphabets, math
integrals . . . 25–30, 66, 105–106
integrals (wasysym package op-
tion) . . . . . . . . . . . . . 26
\intercal (|) ........... 22
\intercal () ........... 52
\interleave (9) ......... 22
intersection . . . . . . . . see \cap
\Interval ( ) .......... 91
\inva ( ) .............. 13
\invamp (M) ............ 23
\invbackneg () ......... 66
\INVd ( ) ............ 73
\invdiameter () . . . . . . . . 88
\inve (U) .............. 13
inverse limit . see \varprojlim
\InversTransformHoriz ( ) 36
\InversTransformVert ( ) . 36
inverted symbols 11–13, 17, 103
inverters . . . . . . . . . . . . . . . 73
\invf () ............... 13
\invglotstop ( ) . . . . . . . . 13
\invh ( ) .............. 13
\INVl ( ) ............ 73
\invlegr () ............ 13
\invm ( ) .............. 13
\invneg () ............ 31
\invneg () ............ 66
\INVr ( ) ............ 73
\invr () .............. 13
\invscr ( ) ............ 13
\invscripta ( ) ......... 13
\INVu ( ) ............ 73
\invv ( ) .............. 13
\invw ( ) .............. 13
\invy ( ) .............. 13
\iota (ι) ............... 50
iota, upside-down . . . . . . . 103
\iotaup (ι) ............. 50
\ipagamma ( ) ........... 13
\ipercatal (η) .......... 95
\IroningI (¯) .......... 90
\IroningII (°) ......... 90
\IroningIII (±) . . . . . . . . 90
irony mark (
?
) . . . . . . . . . . 103
irrational numbers ( ) . . . . see
alphabets, math
\Irritant ( ) . . . . . . . . . . 92
\ismodeledby (=|) . . . . . . . 103
ISO character entities . . . . 117
isoent (package) . . . . . . . . . 117
J
\j () ................. 14
\JackStar ( ) .......... 78
\JackStarBold ( ) . . . . . . . 78
Jewish star . . . . . . . . . . 77, 78
\jmath () ........... 51,57
\Joch ( ) .............. 91
\Join (Z) . . . . . . . . . . . 30, 31
\Join () .............. 24
\joinrel ............. 103
joint denial . . . see \downarrow
junicode (package) . . . . . . . 118
Junicode-Regular.ttf (file) 118
\Jupiter ( ) ........... 71
\Jupiter (Å) ............ 71
\jupiter (X) ........... 71
K
\k (,
a) ................. 17
\k (˛) ................. 14
\kappa (κ) ............. 50
\kappaup (κ) ............ 50
\ker (ker) .............. 49
ket ................... 54
\Keyboard (Ï) .......... 72
keyboard symbols . . . . . . . . 72
keys, computer . . . . . . . . . . 72
keystroke (package) 72, 119, 120
\keystroke ( ) . . . . . . . . 72
king .................. 94
knight ................. 94
Knuth, Donald E. . . 8, 114, 122
symbols by . . . . . . . . . . 89
\Koppa () ............. 87
\koppa () .............. 87
\Kr (l
) .............. 89
\kreuz (6) ............. 88
Kronecker product . see \otimes
Kronecker sum . . . . see \oplus
krouˇzek (˚a) . . . . . . see accents
\kside (O) ............. 93
\Kutline (R) ........... 75
L
\L ( L) ................. 10
\l ( l) ................. 10
\labdentalnas ( ) . . . . . . . 13
\labvel ............... 16
\Ladiesroom (y) ......... 90
Lagrangian (L) . see alphabets,
math
\Lambda (Λ) ............ 50
\lambda (λ) ............ 50
\lambdabar (o) .......... 66
\lambdaslash (n) . . . . . . . . 66
137
\lambdaup (λ) ........... 50
Lamport, Leslie . . . . . . 118, 122
\land ........... see \wedge
\landdownint (%) ........ 28
\landdownint () ........ 29
\landupint (#) .......... 28
\landupint () .......... 29
\Langle ( ) ............ 68
\lAngle (hh) ............. 56
\langle (h) . . . . . . . . . . 21, 54
\langle () ............. 55
\langlebar () .......... 55
\Laplace ( ) ......... 36
\laplace ( ) ......... 36
Laplace transform (L) . . . . see
alphabets, math
Laplacian (∆) . . . . . see \Delta
Laplacian (∇2) .... see \nabla
\largecircle () ........ 79
\largediamond () . . . . . . 79
\largelozenge () . . . . . . . 79
\largepencil ( ) . . . . . . . 76
\largepentagram () . . . . . 79
\largesquare () ........ 79
\largestar () . . . . . . . . . 79
\largestarofdavid () . . . 79
\largetriangledown () . . 40
\largetriangleleft () . . 40
\largetriangleright () . 40
\largetriangleup () . . . . 40
\LArrow (←) .......... 72
\larrowfill ............ 62
\Laserbeam (a) . . . . . . . . 74
L
A
T
E
X . . 1, 8, 14, 26, 30, 49, 54,
63, 65, 73, 75, 100, 103–109,
112, 113, 115, 117–119, 121,
122
L
A
T
E
X 2ε............. 1,8,
9, 19, 20, 22, 30, 36, 41, 58,
63, 65, 69, 73, 100, 101, 103,
106, 107, 111, 112, 114–117,
122
latexsym (package) 22, 30, 36, 41,
65, 100, 119
\latfric ( ) ............ 13
Latin 1 . . . . . . . . . . 8, 115, 119
table . . . . . . . . . . . . . 116
laundry symbols . . . . . . . . . 90
\Lbag (P) .............. 53
\lbag (N) ............... 53
\lbrace (
) ........... 55
\Lbrack () ............. 68
\lBrack ([[) ............. 56
LCD digits . . . . . . . . . . . . . 70
\lCeil (dd) .............. 56
\lceil (d) .............. 54
\lceil (
) ............. 55
\lcirclearrowdown (ÿ) . . . 43
\lcirclearrowleft (⤾) . . . 43
\lcirclearrowright (⟳) . . 43
\lcirclearrowup (↻) . . . . . 43
\lcircleleftint () . . . . . . 29
\lcirclerightint () . . . . . 29
\lcm (lcm) . . . . . . . . . . . . 113
\lcorners () ........... 53
\lcurvearrowdown (⤸) . . . . . 43
\lcurvearrowleft (º) . . . . 43
\lcurvearrowne (¼) . . . . . . 43
\lcurvearrownw (½) . . . . . . 43
\lcurvearrowright (↷) . . . . 43
\lcurvearrowse (¿) . . . . . . 43
\lcurvearrowsw (¾) . . . . . . 43
\lcurvearrowup (¹) . . . . . . . 43
\ldbrack () ............ 55
\ldotp (.) .............. 63
\ldots (. . .) ............ 63
\le .............. see \leq
\leadsto ({) . . . . . . . . 31, 41
\leadsto (↝) ........... 44
leaf . . . . . . . . . . see \textleaf
\leafleft (g) .......... 78
\leafNE (f) ............ 78
\leafright (h) ......... 78
leaves . . . . . . . . . . . . . . 78, 80
Lefschetz motive (L) . . . . . see
alphabets, math
\Left ................. 96
\left . . . . . . . 54, 56, 100, 102
\LEFTarrow () .......... 88
\Leftarrow (⇐) . . . . . . 21, 41
\Leftarrow (⇐) . . . . . . . . . 43
\leftarrow ( ) ......... 42
\leftarrow (←) ......... 41
\leftarrow (←) .......... 44
\leftarrowtail () . . . . . 41
\leftarrowtail (↢) ...... 44
\leftarrowtriangle (^) . . 42
\leftbarharpoon ( ) . . . . . 43
\LEFTCIRCLE (G) . . . . . . . . . 88
\LEFTcircle (G#) . . . . . . . . . 88
\Leftcircle (I) . . . . . . . . . 88
\leftevaw (Ñ
Ñ
Ñ
Ñ
) .......... 56
\leftfilledspoon (r) . . . . 47
\leftfootline (z) . . . . . . . 33
\leftfree () .......... 33
\lefthalfcap () . . . . . . . . 23
\lefthalfcup () . . . . . . . . 24
\lefthand (t) .......... 76
\leftharpoonccw (↽) . . . . . 46
\leftharpooncw (↼) ...... 46
\leftharpoondown ( ) . . . . 43
\leftharpoondown () . . . . 41
\leftharpoonup ( ) . . . . . . 43
\leftharpoonup () . . . . . . 41
\leftleftarrows ( ) . . . . . 42
\leftleftarrows (⇔) . . . . . 41
\leftleftarrows (⇇) . . . . . 44
\leftleftharpoons ( ) . . . 43
\leftlsquigarrow (¢) . . . . 44
\leftmapsto (↤) ......... 44
\leftModels (ò) ......... 33
\leftmodels (â) ......... 33
\leftmoon ( ) ........... 71
\leftmoon ($) .......... 71
\leftp ( ) .............. 18
\leftpitchfork () ...... 47
\leftpointright ( ) . . . . 76
\leftpropto (∝) ......... 33
\Leftrightarrow (⇔) . . . . . 41
\Leftrightarrow (⇔) . . . . . 44
\leftrightarrow ( ) . . . . . 42
\leftrightarrow (↔) . . . . . 41
\leftrightarrow (↔) . . . . . 44
\leftrightarroweq (-) . . . . 42
\leftrightarrows ( ) . . . . 42
\leftrightarrows () . . . . 41
\leftrightarrows (⇆) . . . . 44
\leftrightarrowtriangle (])
......... 42
\leftrightharpoon ( ) . . . 43
\leftrightharpoondownup (⥊)
......... 46
\leftrightharpoons ( ) . . 43
\leftrightharpoons () . . 41
\leftrightharpoons (⇋) . . . 46
\leftrightharpoonsfill . . . 62
\leftrightharpoonupdown (⥋)
......... 46
\Leftrightline (Ô) . . . . . . 33
\leftrightline (Ð) ...... 33
\leftrightsquigarrow ( ) 42
\leftrightsquigarrow (!) 41
\leftrightsquigarrow (↭) . 44
\leftrsquigarrow (↜) . . . . 44
\Leftscissors (S) . . . . . . . 75
\leftslice (2) .......... 22
\leftslice () .......... 33
\leftspoon (⟜) . . . . . . . . . 47
\leftsquigarrow ( ) . . . . 42
\leftsquigarrow (f) . . . . . 42
\leftt ( ) .............. 18
\lefttherefore () . . . 24, 64
\leftthreetimes ( ) . . . . . 66
\leftthreetimes (h) . . . . . 22
\leftthreetimes () . . . . . . 24
\leftthumbsdown ( ) . . . . 76
\leftthumbsup ( ) . . . . . . 76
\lefttorightarrow ( ) . . . 42
\Lefttorque (&) . . . . . . . . 73
\leftturn (") .......... 88
\leftVdash (ê) .......... 33
\leftvdash (⊣) .......... 33
\leftwave (Ð
Ð
Ð
Ð
) .......... 56
\leftY () ............. 24
legal symbols . . . . . . . 9, 19, 116
\legm ( ) .............. 13
\legr () .............. 13
138
\length () ............. 18
\Leo (ä) ............... 71
\leo () ............... 71
\leq ( ) ............... 38
\leq (≤) . . . . . . . . . . . . 37, 38
\leq (≤) ............... 39
\leqclosed () . . . . . . . 39, 40
\leqdot () ............. 39
\leqq ( ) .............. 38
\leqq (5) .............. 38
\leqq () .............. 39
\leqslant (6) .......... 38
\leqslant () ........... 39
\leqslantdot () ........ 39
\less (<) .............. 39
less-than signs . . see inequalities
\lessapprox ( ) ......... 38
\lessapprox (/) ......... 38
\lessapprox () ......... 39
\lessclosed () . . . . . . 39, 40
\lessdot ( ) ........... 38
\lessdot () ........... 38
\lessdot () ............ 39
\lesseqgtr ( ) .......... 38
\lesseqgtr (Q) ......... 38
\lesseqgtr () .......... 39
\lesseqgtrslant () . . . . . . 39
\lesseqqgtr ( ) . . . . . . . . . 38
\lesseqqgtr (S) ......... 38
\lesseqqgtr () ......... 39
\lessgtr ( ) ........... 38
\lessgtr (≶) ........... 38
\lessgtr () ............ 39
\lessneqqgtr () ........ 39
\lesssim ( ) ........... 38
\lesssim (.) ........... 38
\lesssim () ............ 39
\Letter ( ) ............ 92
\Letter (Bvs. ) . . . . . . 101
\Letter (B) ............ 73
letter-like symbols . . . . . 51–53
letters . . . . . . . . . see alphabets
barred . . . . . . . . . . . . 104
non-ASCII . . . . . . . . . . 10
slashed . . . . . . . . . . . 105
variant Latin . . . . . . . . 51
\levaw (Ñ
Ñ
Ñ
Ñ
) ............. 56
\LF (␊) ................ 72
\lfilet () ............. 55
\lFloor (bb) ............. 56
\lfloor (b) ............. 54
\lfloor (
) ............ 55
\lg (lg) ................ 49
\lgroup (
) ............ 54
\lgroup (
) ........... 55
\LHD () ............... 23
\lhd (C) . . . . . . . . . . . . 22, 23
\lhd () . . . . . . . . . . . . 39, 40
\lhdbend (~) .......... 89
\lhookdownarrow (3) . . . . . . 44
\lhookleftarrow (2) . . . . . 44
\lhooknearrow (4) . . . . . . . 44
\lhooknwarrow (⤣) . . . . . . . 44
\lhookrightarrow (↪) . . . . 44
\lhooksearrow (⤥) . . . . . . . 44
\lhookswarrow (6) . . . . . . . 44
\lhookuparrow (1) ........ 44
\Libra (æ) ............. 71
\libra (a) ............ 71
Lie derivative (L)see alphabets,
math
life-insurance symbols . . . . 108
\lightbulb ( ) . . . . . . . . . 112
lightbulb.mf (file) . . . 109–111
lightbulb.sty (file) . . . . . 112
lightbulb10.2602gf (file) . 111
lightbulb10.dvi (file) . . . 111
lightbulb10.mf (file) . 109–111
lightbulb10.tfm (file) . . . 112
\Lightning (Evs. ) . . . . 101
\Lightning ( ) ......... 91
\Lightning (E) .......... 73
\lightning ( ) .......... 42
\lightning ( vs. ) . . . . . 101
\lightning () .......... 44
\lightning () .......... 88
\lim (lim) . . . . . . . . . . 49, 113
\liminf (lim inf) . . . . . 49, 113
limits ................. 49
\limsup (lim sup) . . . . 49, 113
\linbfamily . . . . . . . . . 85, 86
Linear A . . . . . . . . . . . . . . . 82
Linear B . . . . . . . . . . . . 85, 86
linear implication see \multimap
linear logic symbols . 21–23, 25,
29–30, 36, 51, 52
linearA (package) . . 82, 119, 121
\LinearAC (c) ........... 82
\LinearACC () .......... 82
\LinearACCC (y) ......... 82
\LinearACCCI (z) ......... 82
\LinearACCCII ({) . . . . . . . 82
\LinearACCCIII (|) . . . . . . 82
\LinearACCCIV (}) . . . . . . . 82
\LinearACCCIX () . . . . . . . 83
\LinearACCCL («) . . . . . . . . 83
\LinearACCCLI (¬) . . . . . . . 83
\LinearACCCLII () . . . . . . 83
\LinearACCCLIII (®) . . . . . . 83
\LinearACCCLIV (¯) . . . . . . . 83
\LinearACCCLIX (´) . . . . . . 83
\LinearACCCLV (°) . . . . . . . 83
\LinearACCCLVI (±) . . . . . . 83
\LinearACCCLVII (²) . . . . . 83
\LinearACCCLVIII (³) . . . . . 83
\LinearACCCLX (µ) . . . . . . . 84
\LinearACCCLXI () . . . . . . 84
\LinearACCCLXII (·) . . . . . . 84
\LinearACCCLXIII (¸) . . . . . 84
\LinearACCCLXIV (¹) . . . . . 84
\LinearACCCLXIX (¾) . . . . . . 84
\LinearACCCLXV (º) . . . . . . 84
\LinearACCCLXVI (») . . . . . . 84
\LinearACCCLXVII (¼) . . . . . 84
\LinearACCCLXVIII (½) . . . . 84
\LinearACCCLXX (¿) . . . . . . . 84
\LinearACCCLXXI (À) . . . . . 84
\LinearACCCLXXII (Á) . . . . 84
\LinearACCCLXXIII (Â) . . . 84
\LinearACCCLXXIV (Ã) . . . . . 84
\LinearACCCLXXIX (È) . . . . 84
\LinearACCCLXXV (Ä) . . . . . . 84
\LinearACCCLXXVI (Å) . . . . 84
\LinearACCCLXXVII (Æ) . . . . 84
\LinearACCCLXXVIII (Ç) . . . 84
\LinearACCCLXXX (É) . . . . . . 84
\LinearACCCLXXXI (Ê) . . . . . 84
\LinearACCCLXXXII (Ë) . . . . 84
\LinearACCCLXXXIII (Ì) . . . 84
\LinearACCCLXXXIV (Í) . . . 84
\LinearACCCLXXXIX (Ò) . . . 84
\LinearACCCLXXXV (Î) . . . . . 84
\LinearACCCLXXXVI (Ï) . . . . 84
\LinearACCCLXXXVII (Ð) . . . 84
\LinearACCCLXXXVIII (Ñ) . . 84
\LinearACCCV (~) ......... 82
\LinearACCCVI () . . . . . . . 82
\LinearACCCVII () . . . . . . 82
\LinearACCCVIII () . . . . . 83
\LinearACCCX () . . . . . . . . 83
\LinearACCCXI () . . . . . . . 83
\LinearACCCXII () . . . . . . 83
\LinearACCCXIII () . . . . . 83
\LinearACCCXIV () . . . . . . 83
\LinearACCCXIX () . . . . . . 83
\LinearACCCXL (¡) . . . . . . . 83
\LinearACCCXLI (¢) . . . . . . 83
\LinearACCCXLII (£) . . . . . . 83
\LinearACCCXLIII (¤) . . . . . 83
\LinearACCCXLIV (¥) . . . . . 83
\LinearACCCXLIX (ª) . . . . . . 83
\LinearACCCXLV (¦) . . . . . . 83
\LinearACCCXLVI (§) . . . . . 83
\LinearACCCXLVII (¨) . . . . . 83
\LinearACCCXLVIII (©) . . . . 83
\LinearACCCXV () . . . . . . . 83
\LinearACCCXVI () . . . . . . . 83
\LinearACCCXVII () . . . . . . 83
\LinearACCCXVIII () . . . . 83
\LinearACCCXX () . . . . . . . 83
\LinearACCCXXI () . . . . . . 83
\LinearACCCXXII () . . . . . . 83
\LinearACCCXXIII () . . . . . 83
\LinearACCCXXIV () . . . . . . 83
\LinearACCCXXIX () . . . . . . 83
\LinearACCCXXV () . . . . . . 83
\LinearACCCXXVI () . . . . . . 83
\LinearACCCXXVII () . . . . . 83
\LinearACCCXXVIII () . . . . 83
\LinearACCCXXX () . . . . . . 83
\LinearACCCXXXI () . . . . . . 83
139
\LinearACCCXXXII () . . . . 83
\LinearACCCXXXIII () . . . . 83
\LinearACCCXXXIV () . . . . . 83
\LinearACCCXXXIX () . . . . . 83
\LinearACCCXXXV () . . . . . . 83
\LinearACCCXXXVI () . . . . . 83
\LinearACCCXXXVII () . . . 83
\LinearACCCXXXVIII () . . . 83
\LinearACCI () ......... 82
\LinearACCII () . . . . . . . . 82
\LinearACCIII () . . . . . . . 82
\LinearACCIV () . . . . . . . 82
\LinearACCIX () . . . . . . . . 82
\LinearACCL (G) ......... 83
\LinearACCLI (H) . . . . . . . . 83
\LinearACCLII (I) . . . . . . . 83
\LinearACCLIII (J) . . . . . . . 83
\LinearACCLIV (K) . . . . . . . . 83
\LinearACCLIX (P) . . . . . . . . 83
\LinearACCLV (L) . . . . . . . . 83
\LinearACCLVI (M) . . . . . . . . 83
\LinearACCLVII (N) . . . . . . . 83
\LinearACCLVIII (O) . . . . . 83
\LinearACCLX (Q) . . . . . . . . 83
\LinearACCLXI (R) . . . . . . . . 83
\LinearACCLXII (S) . . . . . . . 84
\LinearACCLXIII (T) . . . . . . 84
\LinearACCLXIV (U) . . . . . . 84
\LinearACCLXIX (Z) . . . . . . 84
\LinearACCLXV (V) . . . . . . . 84
\LinearACCLXVI (W) . . . . . . . 84
\LinearACCLXVII (X) . . . . . . 84
\LinearACCLXVIII (Y) . . . . . 84
\LinearACCLXX ([) . . . . . . . 84
\LinearACCLXXI (\) . . . . . . . 84
\LinearACCLXXII (]) . . . . . . 84
\LinearACCLXXIII (^) . . . . 84
\LinearACCLXXIV (_) . . . . . . 84
\LinearACCLXXIX (d) . . . . . . 84
\LinearACCLXXV (`) . . . . . . 84
\LinearACCLXXVI (a) . . . . . . 84
\LinearACCLXXVII (b) . . . . . 84
\LinearACCLXXVIII (c) . . . . 84
\LinearACCLXXX (e) . . . . . . 84
\LinearACCLXXXI (f) . . . . . . 84
\LinearACCLXXXII (g) . . . . . 84
\LinearACCLXXXIII (h) . . . . 84
\LinearACCLXXXIV (i) . . . . 84
\LinearACCLXXXIX (n) . . . . . 84
\LinearACCLXXXV (j) . . . . . 84
\LinearACCLXXXVI (k) . . . . . 84
\LinearACCLXXXVII (l) . . . . 84
\LinearACCLXXXVIII (m) . . . 84
\LinearACCLXXXX (o) . . . . . 84
\LinearACCV () ......... 82
\LinearACCVI () . . . . . . . . 82
\LinearACCVII () . . . . . . . 82
\LinearACCVIII () . . . . . . . 82
\LinearACCX () ......... 83
\LinearACCXCI (p) . . . . . . . 84
\LinearACCXCII (q) . . . . . . 84
\LinearACCXCIII (r) . . . . . . 84
\LinearACCXCIV (s) . . . . . . 84
\LinearACCXCIX (x) . . . . . . 82
\LinearACCXCV (t) . . . . . . . 82
\LinearACCXCVI (u) . . . . . . 82
\LinearACCXCVII (v) . . . . . . 82
\LinearACCXCVIII (w) . . . . 82
\LinearACCXI ( ) . . . . . . . . 83
\LinearACCXII (!) . . . . . . . 83
\LinearACCXIII (") . . . . . . 83
\LinearACCXIV (#) . . . . . . . 83
\LinearACCXIX (() . . . . . . . 83
\LinearACCXL (=) . . . . . . . . 83
\LinearACCXLI (>) . . . . . . . 83
\LinearACCXLII (?) . . . . . . . 83
\LinearACCXLIII (@) . . . . . 83
\LinearACCXLIV (A) . . . . . . . 83
\LinearACCXLIX (F) . . . . . . 83
\LinearACCXLV (B) . . . . . . . 83
\LinearACCXLVI (C) . . . . . . 83
\LinearACCXLVII (D) . . . . . . 83
\LinearACCXLVIII (E) . . . . . 83
\LinearACCXV ($) . . . . . . . . 83
\LinearACCXVI (%) . . . . . . . . 83
\LinearACCXVII (&) . . . . . . . 83
\LinearACCXVIII (') . . . . . . 83
\LinearACCXX ()) . . . . . . . . 83
\LinearACCXXI (*) . . . . . . . 83
\LinearACCXXII (+) . . . . . . 83
\LinearACCXXIII (,) . . . . . . 83
\LinearACCXXIV (-) . . . . . . . 83
\LinearACCXXIX (2) . . . . . . 83
\LinearACCXXV (.) . . . . . . . 83
\LinearACCXXVI (/) . . . . . . 83
\LinearACCXXVII (0) . . . . . 83
\LinearACCXXVIII (1) . . . . 83
\LinearACCXXX (3) . . . . . . . 83
\LinearACCXXXI (4) . . . . . . . 83
\LinearACCXXXII (5) . . . . . . 83
\LinearACCXXXIII (6) . . . . . 83
\LinearACCXXXIV (7) . . . . . 83
\LinearACCXXXIX (<) . . . . . 83
\LinearACCXXXV (8) . . . . . . . 83
\LinearACCXXXVI (9) . . . . . . 83
\LinearACCXXXVII (:) . . . . 83
\LinearACCXXXVIII (;) . . . . 83
\LinearACI (d) .......... 82
\LinearACII (e) ......... 82
\LinearACIII (f) . . . . . . . . 82
\LinearACIV (g) ......... 82
\LinearACIX (l) ......... 82
\LinearACL () .......... 83
\LinearACLI () ......... 83
\LinearACLII () . . . . . . . . 83
\LinearACLIII () . . . . . . . 83
\LinearACLIV () . . . . . . . . 83
\LinearACLIX () . . . . . . . . 83
\LinearACLV () ......... 83
\LinearACLVI () . . . . . . . . 83
\LinearACLVII () . . . . . . . 83
\LinearACLVIII () . . . . . . 83
\LinearACLX () ......... 83
\LinearACLXI () . . . . . . . . 83
\LinearACLXII (¡) . . . . . . . 83
\LinearACLXIII (¢) . . . . . . . 83
\LinearACLXIV (£) . . . . . . . 84
\LinearACLXIX (¨) . . . . . . . 84
\LinearACLXV (¤) . . . . . . . . 84
\LinearACLXVI (¥) . . . . . . 84
\LinearACLXVII (¦) . . . . . . 84
\LinearACLXVIII (§) . . . . . 84
\LinearACLXX (©) . . . . . . . . 84
\LinearACLXXI (ª) . . . . . . . 84
\LinearACLXXII («) . . . . . . 84
\LinearACLXXIII (¬) . . . . . 84
\LinearACLXXIV () . . . . . . 84
\LinearACLXXIX () . . . . . . . 84
\LinearACLXXV (®) . . . . . . . 84
\LinearACLXXVI (¯) . . . . . . 84
\LinearACLXXVII (°) . . . . . . 84
\LinearACLXXVIII (±) . . . . . 84
\LinearACLXXX () . . . . . . . 84
\LinearACLXXXI () . . . . . . 84
\LinearACLXXXII () . . . . . . 84
\LinearACLXXXIII () . . . . . 84
\LinearACLXXXIV () . . . . . 84
\LinearACLXXXIX () . . . . . . 84
\LinearACLXXXV () . . . . . . . 84
\LinearACLXXXVI () . . . . . 84
\LinearACLXXXVII () . . . . . 84
\LinearACLXXXVIII () . . . . 84
\LinearACLXXXX () . . . . . . 84
\LinearACV (h) .......... 82
\LinearACVI (i) ......... 82
\LinearACVII (j) . . . . . . . . 82
\LinearACVIII (k) . . . . . . . 82
\LinearACX (m) .......... 82
\LinearACXCI () . . . . . . . . 84
\LinearACXCII () . . . . . . . 84
\LinearACXCIII () . . . . . . . 84
\LinearACXCIV () . . . . . . . 84
\LinearACXCIX () . . . . . . . 82
\LinearACXCV () ......... 84
\LinearACXCVI () . . . . . . . 84
\LinearACXCVII () . . . . . . 82
\LinearACXCVIII () . . . . . . 82
\LinearACXI (n) ......... 82
\LinearACXII (o) . . . . . . . . 83
\LinearACXIII (p) . . . . . . . 83
\LinearACXIV (q) . . . . . . . . 83
\LinearACXIX (v) . . . . . . . . 83
\LinearACXL () ......... 83
\LinearACXLI () . . . . . . . . 83
\LinearACXLII () . . . . . . . 83
\LinearACXLIII () . . . . . . 83
\LinearACXLIV () . . . . . . . 83
\LinearACXLIX () . . . . . . . 83
\LinearACXLV () . . . . . . . . 83
\LinearACXLVI () . . . . . . . 83
\LinearACXLVII () . . . . . . 83
\LinearACXLVIII () . . . . . 83
\LinearACXV (r) ......... 83
\LinearACXVI (s) . . . . . . . . 83
\LinearACXVII (t) . . . . . . . 83
\LinearACXVIII (u) . . . . . . . 83
\LinearACXX (w) ......... 83
140
\LinearACXXI (x) . . . . . . . . 83
\LinearACXXII (y) . . . . . . . 83
\LinearACXXIII (z) . . . . . . 83
\LinearACXXIV ({) . . . . . . . 83
\LinearACXXIX () . . . . . . . 83
\LinearACXXV (|) . . . . . . . . 83
\LinearACXXVI (}) . . . . . . . 83
\LinearACXXVII (~) . . . . . . 83
\LinearACXXVIII () . . . . . 83
\LinearACXXX () . . . . . . . . 83
\LinearACXXXI () . . . . . . . 83
\LinearACXXXII () . . . . . . 83
\LinearACXXXIII () . . . . . . 83
\LinearACXXXIV () . . . . . . . 83
\LinearACXXXIX () . . . . . . 83
\LinearACXXXV () . . . . . . . 83
\LinearACXXXVI () . . . . . . 83
\LinearACXXXVII () . . . . . . 83
\LinearACXXXVIII () . . . . 83
\LinearAI () ........... 82
\LinearAII () .......... 82
\LinearAIII () ......... 82
\LinearAIV () .......... 82
\LinearAIX () .......... 82
\LinearAL (1) ........... 83
\LinearALI (2) .......... 83
\LinearALII (3) ......... 83
\LinearALIII (4) . . . . . . . . 83
\LinearALIV (5) ......... 83
\LinearALIX (:) ......... 83
\LinearALV (6) .......... 83
\LinearALVI (7) ......... 83
\LinearALVII (8) . . . . . . . . 83
\LinearALVIII (9) . . . . . . . 83
\LinearALX (;) .......... 83
\LinearALXI (<) ......... 83
\LinearALXII (=) . . . . . . . . 83
\LinearALXIII (>) . . . . . . . 83
\LinearALXIV (?) . . . . . . . . 83
\LinearALXIX (D) . . . . . . . . 84
\LinearALXV (@) ......... 83
\LinearALXVI (A) . . . . . . . . 84
\LinearALXVII (B) . . . . . . . 84
\LinearALXVIII (C) . . . . . . . 84
\LinearALXX (E) ......... 84
\LinearALXXI (F) . . . . . . . . 84
\LinearALXXII (G) . . . . . . . 84
\LinearALXXIII (H) . . . . . . 84
\LinearALXXIV (I) . . . . . . . 84
\LinearALXXIX (N) . . . . . . . 84
\LinearALXXV (J) . . . . . . . . 84
\LinearALXXVI (K) . . . . . . . 84
\LinearALXXVII (L) . . . . . . 84
\LinearALXXVIII (M) . . . . . . 84
\LinearALXXX (O) . . . . . . . . 84
\LinearALXXXI (P) . . . . . . . 84
\LinearALXXXII (Q) . . . . . . . 84
\LinearALXXXIII (R) . . . . . . 84
\LinearALXXXIV (S) . . . . . . 84
\LinearALXXXIX (X) . . . . . . 84
\LinearALXXXV (T) . . . . . . . . 84
\LinearALXXXVI (U) . . . . . . 84
\LinearALXXXVII (V) . . . . . . 84
\LinearALXXXVIII (W) . . . . . 84
\LinearALXXXX (Y) . . . . . . . 84
\LinearAV () ........... 82
\LinearAVI () .......... 82
\LinearAVII () ......... 82
\LinearAVIII () . . . . . . . . 82
\LinearAX () ........... 82
\LinearAXCI (Z) ......... 84
\LinearAXCII ([) . . . . . . . . 84
\LinearAXCIII (\) . . . . . . . 84
\LinearAXCIV (]) . . . . . . . . 84
\LinearAXCIX (b) . . . . . . . . 82
\LinearAXCV (^) ......... 84
\LinearAXCVI (_) . . . . . . . . 84
\LinearAXCVII (`) . . . . . . . . 84
\LinearAXCVIII (a) . . . . . . . 84
\LinearAXI () .......... 82
\LinearAXII () ......... 82
\LinearAXIII () . . . . . . . . 82
\LinearAXIV () ......... 83
\LinearAXIX () ......... 83
\LinearAXL (') .......... 83
\LinearAXLI (() ......... 83
\LinearAXLII ()) . . . . . . . . 83
\LinearAXLIII (*) . . . . . . . 83
\LinearAXLIV (+) . . . . . . . . 83
\LinearAXLIX (0) . . . . . . . . 83
\LinearAXLV (,) ......... 83
\LinearAXLVI (-) . . . . . . . . 83
\LinearAXLVII (.) . . . . . . . 83
\LinearAXLVIII (/) . . . . . . 83
\LinearAXV () .......... 83
\LinearAXVI () ......... 83
\LinearAXVII () . . . . . . . . 83
\LinearAXVIII () . . . . . . . 83
\LinearAXX () .......... 83
\LinearAXXI () ......... 83
\LinearAXXII () . . . . . . . . 83
\LinearAXXIII () . . . . . . . 83
\LinearAXXIV () . . . . . . . . 83
\LinearAXXIX () . . . . . . . . 83
\LinearAXXV () ......... 83
\LinearAXXVI () . . . . . . . . 83
\LinearAXXVII () . . . . . . . 83
\LinearAXXVIII () . . . . . . . 83
\LinearAXXX () ......... 83
\LinearAXXXI () . . . . . . . . 83
\LinearAXXXII () . . . . . . . 83
\LinearAXXXIII ( ) . . . . . . 83
\LinearAXXXIV (!) . . . . . . . 83
\LinearAXXXIX (&) . . . . . . . 83
\LinearAXXXV (") . . . . . . . . 83
\LinearAXXXVI (#) . . . . . . . 83
\LinearAXXXVII ($) . . . . . . 83
\LinearAXXXVIII (%) . . . . . . 83
linearb (package) 85, 86, 119, 121
\Lineload (L) .......... 73
linguistic symbols . . . . . 11–14
\Lisa ( ) ......... 96
\lJoin (X) ............. 31
\ll ( ) ................ 38
\ll () ............... 37
\ll () ............... 39
\llangle () ........... 55
\llap ................ 106
\llbracket (~) .......... 54
\llbracket () .......... 57
\llceil (V) ............. 53
\llcorner () ........... 53
\llcorner (x) ........... 53
\llcorner () ........... 55
\llcurly ( ) ........... 32
\Lleftarrow (W) ........ 41
\Lleftarrow () ........ 44
\llfloor (T) ............ 53
\lll ( ) ............... 38
\lll (≪) .............. 38
\lll (≪vs. ) . . . . . . . . 101
\lll () .............. 39
\llless .......... see \lll
\llless () ........... 39
\llparenthesis (L) . . . . . . . 53
\lmoustache (
) ........ 54
\lmoustache (
) . . . . . . . . 55
\ln (ln) ............... 49
\lnapprox ( ) .......... 38
\lnapprox () .......... 38
\lnapprox () ........... 39
\lneq ( ) .............. 38
\lneq () .............. 38
\lneqq ( ) ............. 38
\lneqq () ............. 38
\lneqq () ............. 39
\lnot ............ see \neg
\lnot (¬) .............. 66
\lnsim ( ) ............. 38
\lnsim () ............. 38
\lnsim () ............. 39
local ring (O) . . see alphabets,
math
\log (log) . . . . . . . . . . 49, 113
log-like symbols . . . . . . 49, 113
logic gates . . . . . . . . . . . . . . 73
logical operators
and . . . . . . . . . see \wedge
not . . . see \neg and \sim
or ........... see \vee
\logof () ............. 31
lollipop . . . . . . . see \multimap
long division . . . . . . . . . . . . 59
\longa (λ) ............. 95
\longcastling (O-O-O) . . . 93
longdiv (package) . . . . . . . . . 59
141
\Longleftarrow (⇐=) . . . . . 41
\Longleftarrow (⇐Ô) . . . . . 43
\longleftarrow (←Ð) . . . . . 43
\longleftarrow (←−) . . . . . 41
\Longleftrightarrow (⇐⇒) 41
\Longleftrightarrow (⇐⇒) 43
\longleftrightarrow (←→) . 43
\longleftrightarrow (←→) 41
\Longmapsfrom (⇐=\) . . . . . . 42
\longmapsfrom (←−[) . . . . . . 42
\Longmapsto (=⇒) . . . . . . . 42
\longmapsto (z→) ........ 43
\longmapsto (7−→) . . . . . . . 41
\LongPulseHigh ( ) . . . . . 70
\LongPulseLow ( ) . . . . . 70
\Longrightarrow (=⇒) . . . . 41
\Longrightarrow (Ô⇒) . . . . 43
\longrightarrow (Ð→) . . . . 43
\longrightarrow (−→) . . . . 41
\looparrowdownleft ( ) . . 42
\looparrowdownright ( ) . . 42
\looparrowleft ( ) . . . . . . 42
\looparrowleft (") . . . . . . 41
\looparrowleft () . . . . . . 43
\looparrowright ( ) . . . . . 42
\looparrowright (#) . . . . . 41
\looparrowright () . . . . . 43
\Loosebearing ($) . . . . . . . 73
\lor ............. see \vee
\LowerDiamond ( ) . . . . . . . 79
lowering . . . see \textlowering
\lozenge (♦) . . . . . . . . 65, 66
\lozenge () ............ 79
\Lparen () ............. 68
\lrcorner () ........... 53
\lrcorner (y) ........... 53
\lrcorner () ........... 55
\lrJoin ......... see \Join
\lrtimes (\) ............ 31
\lsem (
) ............. 55
\lsemantic ..... see \ldbrack
\Lsh ( ) ............... 42
\Lsh () ............... 41
\Lsh () ............... 43
\Lsteel (™) ............ 73
\ltimes ( ) ............ 23
\ltimes () ............ 22
\ltimes () ............ 24
\ltriple .............. 57
Luecking, Dan . . . . . . . . . . 106
\lVert (k) ............. 54
\lVert (||) .............. 56
\lvert (|) .............. 54
\lvertneqq ( ) .......... 38
\lvertneqq () ......... 38
\lvertneqq () .......... 39
\lwave (Ð
Ð
Ð
Ð
) ............. 56
\lWavy (
) ............ 55
\lwavy (
) ............. 55
\lz ( ) ................ 13
M
\M .................... 10
\M (¯
´) ................. 95
\m .................... 10
\m (¯) ................. 95
\ma (×
¯) ................ 95
\macron (a¯) ............. 17
macron (¯a) . . . . . . see accents
\Maggie ( ) . . . . . . . . . 96
magical signs . . . . . . . . . . . . 97
majuscules . . . . . . . . . . . . . 50
\makeatletter ......... 107
\makeatother .......... 107
\MALE () .............. 74
\Male (|) .............. 74
male . . . . . . . . . . . . . 71, 73, 74
\male (♂) .............. 73
\MaleMale (ƒ) .......... 74
\maltese (z) ........... 10
\maltese () ........... 66
man . . . . . . . . . . . . . . . 81, 90
\manboldkidney () . . . . . . . 89
\manconcentriccircles ($) 89
\manconcentricdiamond (%) 89
\mancone (#) ........... 89
\mancube () ........... 89
\manerrarrow (y) . . . . . . . 89
\manfilledquartercircle (!) 89
manfnt (package) . . 89, 119, 120
\manhpennib () ......... 89
\manimpossiblecube () . . . 89
\mankidney () .......... 89
\manlhpenkidney () . . . . . . 89
\manpenkidney () . . . . . . . 89
\manquadrifolium (&) . . . . 89
\manquartercircle ( ) . . . . 89
\manrotatedquadrifolium (')
......... 89
\manrotatedquartercircle (")
......... 89
\manstar () ........... 89
\mantiltpennib () . . . . . . 89
\mantriangledown (7) . . . . . 89
\mantriangleright (x) . . . . 89
\mantriangleup (6) ...... 89
\manvpennib () .......... 89
\Mappedfromchar () . . . . . . . 48
\mappedfromchar () . . . . . . . 48
\Mapsfrom (⇐\) .......... 42
\mapsfrom (←[) .......... 42
\Mapsfromchar () . . . . . . . . 49
\Mapsfromchar (\) . . . . . . . . 48
\mapsfromchar () . . . . . . . . 49
\mapsfromchar ([) . . . . . . . . 48
\Mapsto (⇒) ............ 42
\mapsto (7→) ............ 41
\mapsto (↦) ............ 44
\Mapstochar () . . . . . . . . . . 49
\Mapstochar () .......... 48
\mapstochar () . . . . . . . . . . 49
\Marge ( ) . . . . . . . . . 96
\markera (x) ........... 93
\markerb (y) ........... 93
married . . . . . see \textmarried
\Mars ( ) .............. 71
\Mars (Ä) .............. 71
\mars (♂) .............. 71
\MartinVogel (ÿ) . . . . . . . . 90
marvosym (package) . 18, 65, 67,
71–75, 90, 101
masonic cipher . . . . . . . . . . 98
\mate (m) .............. 93
material biconditional . . . . . . .
.see \leftrightarrow and
\equiv
material conditional . . . . . . see
\rightarrow and \supset
material equivalence . . . . . . . .
.see \leftrightarrow and
\equiv
material implication . . . . . . see
\rightarrow and \supset
material nonimplication . . . . . .
... see \nrightarrow and
\nsupset
math alphabets . . . . . . . . . . 68
mathabx (package) 21, 23, 25, 26,
30, 32, 36–38, 40, 42, 43, 49,
52–55, 58, 60, 65, 66, 71, 93,
100, 101, 119, 120, 123
\mathaccent ........... 104
\mathbb ............... 68
\mathbbm .............. 68
\mathbbmss ............. 68
\mathbbmtt ............. 68
mathbbol (package) . . . . . . . 68
\mathbf .............. 113
\mathbin ............. 112
\mathbold ............. 113
mathcal (euscript package option)
......... 68
\mathcal .............. 68
\mathcent (¢) ........... 52
\mathchoice . . . . . . . . 105, 106
\mathclose ............ 112
mathcomp (package) . . . . . . 65
mathdesign (package) 18, 24, 30,
52, 56, 67, 119
\mathdollar ($) . . . . . . . . . 21
mathdots (package) . 58, 63, 64,
107, 119, 120
\mathds ............... 68
\mathellipsis (. . .) ...... 21
mathematical symbols . . 21–69
\mathfrak .............. 68
142
\mathit ............... 68
\mathnormal ............ 68
\mathop .............. 112
\mathopen ............. 112
\mathord ............. 112
\mathpalette .......... 106
\mathparagraph () ...... 21
\mathpunct ............ 112
\mathpzc .............. 68
\mathrel . . . . . . . . . . 103, 112
\mathring (˚) . . . . . . . . 57, 58
\mathrm ............... 68
mathrsfs (package) . . . . 68, 119
mathscr (euscript package option)
......... 68
\mathscr .............. 68
\mathsection (§) ........ 21
\mathsterling (£) . . . . . . . . 52
\mathsterling (£) . . . . . . . 21
mathtools (package) . 21, 34, 60,
62, 119, 120
\mathunderscore ( ) . . . . . . 21
\max (max) . . . . . . . . . . . . . 49
Maxwell-Stefan diffusion coeffi-
cient ............ see
\DH
\maya ................. 65
\Mb (˘
¯
´) ................ 95
\mb (˘
¯) ................ 95
\Mbb (˘
¯
˘
¯
´) .............. 95
\mBb (˘
¯
˘
¯
´) .............. 95
\mbB (˘
¯
˘
¯
´
) .............. 95
\mbb (˘
¯
˘
¯) .............. 95
mbboard (package) . . . . 68, 119
\mbbx (˘
¯
˘
¯
¯
˘
¯
˘) ............. 95
\mbox ................ 106
\measuredangle ( ) . . . . . . 66
\measuredangle (]) . . . . . . 66
\measuredangle () ...... 66
mechanical scaling . . . . 109, 112
\medbackslash () . . . . . . . 24
\medbullet () .......... 23
\medcirc () ............ 23
\medcircle (◯) .......... 24
\meddiamond () ......... 25
\medlozenge () ......... 79
\medslash (∕) ........... 24
\medsquare () .......... 25
\medstar () ........... 25
\medstarofdavid () . . . . . 79
\medtriangledown (▽) . 25, 40
\medtriangleleft (◁) . 25, 40
\medtriangleright (▷) . 25, 40
\medtriangleup (△) . . . 25, 40
\medvert () ............ 24
\medvertdot () ......... 24
membership . . . . . . . . see \in
\Mercury ( ) ............ 71
\Mercury (Â) ............ 71
\mercury (') ............ 71
\merge (!) ............. 22
METAFONT . . . . . . 69, 109–112
METAFONTbook symbols . . . 89
metre (package) . 17, 57, 95, 119,
120
metre ................. 95
metrical symbols . . . . . . . . . 95
\mho () . . . . . . . . . . . . 65, 66
micro .......... see \textmu
\micro (µ) ............. 70
Microsoft®Windows®. . . 115
\mid (|) ............. 30,56
\middle ............... 54
\midtilde ( ) ........... 18
MIL-STD-806 . . . . . . . . . . . 73
millesimal sign . . . . . . . . . see
\textperthousand
milstd (package) . . . . . . 73, 119
\min (min) . . . . . . . . . 49, 113
minim . . . . see musical symbols
minus . . . . . . . see \textminus
\minus (−) ............. 24
\minuscolon (−:) ........ 36
\minuscoloncolon (−::) . . . . 36
\minusdot () ........... 24
\minushookdown (¬) . . . . . . 66
\minushookup () ........ 66
\minuso () . . . . . . . . 22, 104
minutes, angular . . . see \prime
miscellaneous symbols 65–67, 80,
88–99
“Missing $ inserted” . . . . 21
\Mmappedfromchar () . . . . . . 48
\mmappedfromchar () . . . . . . 48
\Mmapstochar () ......... 48
\mmapstochar () ......... 48
MnSymbol (package) . . . . . 21,
23–25, 29, 32–34, 37, 39, 40,
43–48, 51, 52, 55, 58–60, 64,
66, 67, 79, 119, 120
\Mobilefone (H) ......... 73
\mod .................. 49
\models (|=) . . . . . . . . 30, 103
\models (⊧) ............ 33
moduli space . . . see alphabets,
math
monetary symbols . . . 18, 19, 68
monus . . . . . . . . . . see \dotdiv
\moo () ............... 22
\Moon ( ) .............. 71
\Moon (Á) .............. 71
\MoonPha .............. 98
\morepawns (S) .......... 93
\moreroom (U) .......... 93
\Mountain ( ) . . . . . . . . . . 91
mouse . . . . see \ComputerMouse
\MoveDown (») ........... 90
\moverlay ............. 107
\MoveUp (º) ............ 90
\mp (∓) ................ 22
\mp (∓) ................ 24
\mu (µ) ................ 50
\multimap (() . . . . . . . 30, 31
\multimap (⊸) .......... 47
\multimapboth () . . . . . . 31
\multimapbothvert () . . . . 31
\multimapdot () . . . . . . . . 31
\multimapdotboth () . . . . 31
\multimapdotbothA () . . . 31
\multimapdotbothAvert () . 31
\multimapdotbothB () . . . 31
\multimapdotbothBvert () . 31
\multimapdotbothvert () . . 31
\multimapdotinv () . . . . . 31
\multimapinv () . . . . . . . . 31
multiple accents per character 107
multiplicative disjunction . . . . .
..... see \bindnasrepma,
\invamp, and \parr
\Mundus (m) ............ 90
Museum of Icelandic Sorcery and
Witchcraft . . . . . . . . . 98
musical symbols 20, 65, 66, 88,
89
musixtex (package) . . . . . . . . 89
\muup (µ) .............. 50
\MVAt (@) .............. 90
\MVEight (8) ............ 65
\MVFive (5) ............ 65
\MVFour (4) ............ 65
\MVNine (9) ............ 65
\MVOne (1) ............. 65
\MVRightarrow (:) . . . . . . . 90
\MVSeven (7) ............ 65
\MVSix (6) ............. 65
\MVThree (3) ............ 65
\MVTwo (2) ............. 65
\MVZero (0) ............ 65
N
\nabla (∇) ............. 65
\nabla (∇) ............. 66
\NAK (␕) ............... 72
NAND gates . . . . . . . . . . . . 73
\NANDd ( ) . . . . . . . . . . 73
\NANDl ( ) ......... 73
\NANDr ( ) ......... 73
\NANDu ( ) . . . . . . . . . . 73
\napprox ( ) ........... 32
\napprox () ............ 33
\napproxeq (6) .......... 31
\napproxeq () .......... 33
\nasymp (-) ............ 31
\nasymp () ............. 48
nath (package) . . 53, 56, 57, 119
\NATURAL ( ) ............ 49
\Natural ( ) ............ 49
\natural () . . . . . . . . . 65, 88
\natural () ............ 66
natural numbers ( ) . . . . . see
alphabets, math
143
navigation symbols . . . . . . . 90
\nbackapprox () ........ 33
\nbackapproxeq () . . . . . . . 33
\nbackcong () .......... 33
\nbackeqsim () ......... 33
\nbacksim (*) ........... 31
\nbacksim () ........... 33
\nbacksimeq (+) ......... 31
\nbacksimeq () ......... 34
\nbacktriplesim () . . . . . . 34
\NBSP () .............. 72
\nBumpeq ()) ............ 31
\nBumpeq () ............ 34
\nbumpeq (() ............ 31
\nbumpeq () ............ 34
\ncirceq () ............ 34
\ncirclearrowleft () . . . 46
\ncirclearrowright () . . 46
\nclosedequal () . . . . . . . 34
\ncong ( ) ............. 32
\ncong () ............. 31
\ncong () ............. 34
\ncurlyeqprec ( ) . . . . . . . 32
\ncurlyeqprec () . . . . . . . 34
\ncurlyeqsucc ( ) . . . . . . . 32
\ncurlyeqsucc () . . . . . . . 34
\ncurvearrowdownup () . . . 44
\ncurvearrowleft () . . . . 46
\ncurvearrowleftright () 44
\ncurvearrownesw () . . . . 44
\ncurvearrownwse () . . . . 44
\ncurvearrowright () . . . . 46
\ncurvearrowrightleft () 44
\ncurvearrowsenw () . . . . 44
\ncurvearrowswne () . . . . 44
\ncurvearrowupdown () . . . 44
\ndasharrow () ......... 46
\ndasheddownarrow () . . . . 45
\ndashedleftarrow () . . . . 45
\ndashednearrow () . . . . . 45
\ndashednwarrow () . . . . . 45
\ndashedrightarrow () . . . 45
\ndashedsearrow () . . . . . 45
\ndashedswarrow () . . . . . 45
\ndasheduparrow () . . . . . . 45
\ndashleftarrow () . . . . . 46
\ndashrightarrow () . . . . 46
\nDashV ( ) ............ 32
\nDashv ( ) ............ 32
\ndashV ( ) ............ 32
\ndashv ( ) ............ 32
\ndashv () ............ 34
\ndashVv ( ) ........... 32
\nddtstile ( ) ......... 35
\ndiagdown () ......... 34
\ndiagup () ........... 34
\ndivides () ........... 34
\nDoteq () ............. 34
\ndoteq () ............. 34
\ndoublefrown () . . . . . . . 48
\ndoublefrowneq () . . . . . . 48
\ndoublesmile () . . . . . . . 48
\ndoublesmileeq () . . . . . . 48
\nDownarrow () . . . . . . . . . 45
\ndownarrow () ......... 45
\ndownarrowtail () . . . . . . 45
\ndowndownarrows () . . . . . 45
\ndownfilledspoon () . . . . 47
\ndownfootline () . . . . . . . 34
\ndownfree () .......... 34
\ndownharpoonccw () . . . . . 46
\ndownharpooncw () . . . . . . 46
\ndownlsquigarrow () . . . . 45
\ndownmapsto () ........ 45
\ndownModels () . . . . . . . . 34
\ndownmodels () ........ 34
\ndownpitchfork () . . . . . 47
\ndownrsquigarrow () . . . . 45
\ndownspoon () ......... 47
\ndownuparrows () . . . . . . 45
\ndownupharpoons () . . . . . 46
\ndownVdash () . . . . . . . . . 34
\ndownvdash () ......... 34
\ndststile ( ) . . . . . . . . . 35
\ndtstile ( ) . . . . . . . . . . 35
\ndttstile ( ) . . . . . . . . . 35
\ne .............. see \neq
\ne (≠) ................ 34
\Nearrow (t) ........... 42
\Nearrow (⇗) ........... 43
\nearrow ( ) ........... 42
\nearrow (%) . . . . 41, 106, 107
\nearrow (↗) ........... 43
\nearrowtail ($) ........ 43
\nefilledspoon (t) . . . . . . 47
\nefootline (|) ......... 33
\nefree () ............ 33
\neg (¬) ............... 65
\neg (¬) ............... 66
negation . . . see \neg and \sim
\neharpoonccw (D) . . . . . . . 46
\neharpooncw (L) ........ 46
\nelsquigarrow (¤) . . . . . . 43
\nemapsto (,) .......... 43
\neModels (ô) .......... 33
\nemodels (ä) .......... 33
\nenearrows () . . . . . . . . 43
\nepitchfork () ........ 47
\Neptune ( ) ........... 71
\Neptune (È) ........... 71
\neptune ([) ............ 71
\neq ( ) ............... 32
\neq (,) ............... 37
\neq (≠) ............... 34
\neqbump () ............ 34
\neqcirc () ............ 34
\neqdot () ............. 34
\neqfrown () ........... 48
\neqsim () ............. 33
\neqslantgtr ( ) . . . . . . . . 38
\neqslantgtr () ........ 39
\neqslantless ( ) . . . . . . . 38
\neqslantless () . . . . . . . 39
\neqsmile () ........... 48
\nequal (≠) ............. 33
\nequalclosed () . . . . . . . 33
\nequiv (.) ............ 31
\nequiv () ............. 33
\nequivclosed () . . . . . . . 33
\nersquigarrow (¬) . . . . . . 43
\nespoon (l) ........... 47
\Neswarrow () ......... 43
\neswarrow (%.) . . . . . 106, 107
\neswarrow (⤡) ......... 43
\neswarrows () . . . . . . . . 43
\neswbipropto () . . . . . . . 24
\neswcrossing () . . . . . . . 33
\neswharpoonnwse (R) . . . . 46
\neswharpoons (Z) . . . . . . . 46
\neswharpoonsenw (V) . . . . 46
\Neswline (Ö) .......... 33
\neswline (Ò) .......... 33
\Neutral ({) ........... 74
\neVdash (ì) ........... 33
\nevdash (Ü) ........... 33
\newextarrow ........... 63
\newmetrics ............ 95
\newmoon ( ) ........... 71
\newmoon ( ) ........... 71
\newtie (a) ............. 14
\nexists ( ) ............ 52
\nexists () ............ 52
\nexists () ............ 52
\nfallingdotseq () . . . . . . 33
\nfrown () ............. 48
\nfrowneq () ........... 48
\nfrowneqsmile () . . . . . . . 48
\nfrownsmile () ........ 48
\nfrownsmileeq () . . . . . . . 48
\NG (Ŋ) ................ 10
\ng (ŋ) ................ 10
\ngeq ( ) .............. 38
\ngeq () .............. 38
\ngeq () .............. 39
\ngeqclosed () . . . . . . 39, 40
\ngeqdot () ............ 39
\ngeqq ( ) ............. 38
\ngeqq () ............. 38
\ngeqq () ............. 39
\ngeqslant () ......... 38
\ngeqslant () .......... 39
\ngeqslantdot () . . . . . . . 39
\ngets () ............. 46
\ngg (4) .............. 38
\ngg () ............... 39
\nggg () ............. 39
\ngtr ( ) .............. 38
\ngtr (≯) .............. 38
\ngtr () .............. 39
\ngtrapprox ( ) . . . . . . . . . 38
\ngtrapprox (#) ......... 38
\ngtrclosed () . . . . . . 39, 40
\ngtrdot () ............ 39
\ngtreqless () ......... 39
144
\ngtreqlessslant () . . . . . 39
\ngtreqqless () ........ 39
\ngtrless (&) ........... 38
\ngtrless () ........... 39
\ngtrsim ( ) ........... 38
\ngtrsim (!) ............ 38
\nhateq () ............. 34
\nhookleftarrow () . . . . . 46
\nhookrightarrow () . . . . 46
\ni (3) . . . . . . . . . . . . 51, 105
\ni (∋) ................ 52
\nialpha ( ) ............ 13
\nibar ........ see \ownsbar
\nibeta ( ) ............. 13
\NibLeft ( ) ........... 76
\NibRight ( ) .......... 76
nibs .................. 76
\NibSolidLeft ( ) . . . . . . . 76
\NibSolidRight ( ) . . . . . . 76
nicefrac (package) . 67, 119, 121
\nichi ( ) ............. 13
\niepsilon ( ) .......... 13
\nigamma ( ) ............ 13
\niiota () ............. 13
\nilambda ( ) ........... 13
\nin (∉) ............... 52
\niomega ( ) ............ 13
\niphi ( ) ............. 13
\niplus (B) ............ 31
\nisigma ( ) ............ 13
\nitheta ( ) ............ 13
\niupsilon ( ) .......... 13
\niv ( ) ............... 53
\nj ( ) ................ 13
\nlcirclearrowdown () . . 45
\nlcirclearrowleft () . . 45
\nlcirclearrowright () . 45
\nlcirclearrowup () . . . . 45
\nlcurvearrowdown () . . . . 45
\nlcurvearrowleft () . . . . 45
\nlcurvearrowne () . . . . . 45
\nlcurvearrownw () . . . . . 45
\nlcurvearrowright () . . . 45
\nlcurvearrowse () . . . . . 45
\nlcurvearrowsw () . . . . . 45
\nlcurvearrowup () . . . . . . 45
\nleadsto () .......... 46
\nLeftarrow ( ) . . . . . . . . 42
\nLeftarrow () ........ 41
\nLeftarrow () ........ 45
\nleftarrow ( ) . . . . . . . . 42
\nleftarrow () . . . . . . . . 41
\nleftarrow () ......... 45
\nleftarrowtail () . . . . . 45
\nleftfilledspoon () . . . 47
\nleftfootline () ...... 34
\nleftfree () .......... 34
\nleftharpoonccw () . . . . 46
\nleftharpooncw () . . . . . 46
\nleftleftarrows () . . . . 45
\nleftlsquigarrow () . . . . 45
\nleftmapsto () ........ 45
\nleftModels () ........ 34
\nleftmodels () . . . . . . . . 34
\nleftpitchfork () . . . . . 47
\nLeftrightarrow ( ) . . . . 42
\nLeftrightarrow () . . . . 41
\nLeftrightarrow () . . . . 45
\nleftrightarrow ( ) . . . . 42
\nleftrightarrow () . 21, 41
\nleftrightarrow () . . . . 45
\nleftrightarrows () . . . . 45
\nleftrightharpoondownup ()
......... 46
\nleftrightharpoons () . . 46
\nleftrightharpoonupdown ()
......... 46
\nLeftrightline () . . . . . 34
\nleftrightline () . . . . . 34
\nleftrightsquigarrow () 46
\nleftrsquigarrow () . . . . 45
\nleftspoon () ........ 47
\nleftVdash () ......... 34
\nleftvdash () ......... 34
\nleq ( ) .............. 38
\nleq () .............. 38
\nleq () .............. 39
\nleqclosed () . . . . . . 39, 40
\nleqdot () ............ 39
\nleqq ( ) ............. 38
\nleqq () ............. 38
\nleqq () ............. 39
\nleqslant () ......... 38
\nleqslant () .......... 39
\nleqslantdot () . . . . . . . 39
\nless ( ) ............. 38
\nless (≮) ............. 38
\nless () ............. 39
\nlessapprox ( ) . . . . . . . . 38
\nlessapprox (") . . . . . . . . 38
\nlessclosed () . . . . . 39, 40
\nlessdot () ........... 39
\nlesseqgtr () ......... 39
\nlesseqgtrslant () . . . . . 39
\nlesseqqgtr () ........ 39
\nlessgtr (') ........... 38
\nlessgtr () ........... 39
\nlesssim ( ) .......... 38
\nlesssim ( ) ........... 38
\nlhookdownarrow () . . . . . 45
\nlhookleftarrow () . . . . 45
\nlhooknearrow () . . . . . . 45
\nlhooknwarrow () . . . . . . 44
\nlhookrightarrow () . . . . 44
\nlhooksearrow () . . . . . . 44
\nlhookswarrow () . . . . . . 44
\nlhookuparrow () . . . . . . . 44
\nll (3) .............. 38
\nll () ............... 39
\nLleftarrow () ........ 44
\nlll () ............. 39
\nmapsto () ........... 46
\nmid () ............... 31
\nmid () .............. 34
\nmodels () ............ 34
\nmultimap () . . . . . . . . . 47
\nndtstile () ......... 35
\nNearrow () .......... 44
\nnearrow (1) ........... 42
\nnearrow () .......... 44
\nnearrowtail () . . . . . . . 45
\nnefilledspoon () . . . . . 47
\nnefootline () ........ 34
\nnefree () ........... 34
\nneharpoonccw () . . . . . . 46
\nneharpooncw () . . . . . . . 46
\nnelsquigarrow () . . . . . 45
\nnemapsto () ......... 45
\nneModels () ......... 34
\nnemodels () ......... 34
\nnenearrows () . . . . . . . 45
\nnepitchfork () . . . . . . . 47
\nnersquigarrow () . . . . . 45
\nnespoon () .......... 47
\nNeswarrow () ........ 45
\nneswarrow () ........ 45
\nneswarrows () . . . . . . . 45
\nneswharpoonnwse () . . . 46
\nneswharpoons () . . . . . . 46
\nneswharpoonsenw () . . . 46
\nNeswline () ......... 34
\nneswline () ......... 34
\nneVdash () .......... 34
\nnevdash () .......... 34
\nnststile ( ) . . . . . . . . . 35
\nntstile ( ) . . . . . . . . . . 35
\nnttstile ( ) . . . . . . . . . 35
\nNwarrow () .......... 45
\nnwarrow (0) ........... 42
\nnwarrow () .......... 45
\nnwarrowtail () . . . . . . . 45
\nnwfilledspoon () . . . . . 47
\nnwfootline () ........ 34
\nnwfree () ........... 34
\nnwharpoonccw () . . . . . . 46
\nnwharpooncw () . . . . . . . 46
\nnwlsquigarrow () . . . . . 45
\nnwmapsto () ......... 45
\nnwModels () ......... 33
\nnwmodels () ......... 34
\nnwnwarrows () . . . . . . . 45
\nnwpitchfork () . . . . . . . 47
\nnwrsquigarrow () . . . . . 45
\nNwsearrow () ........ 45
\nnwsearrow () ........ 45
\nnwsearrows () . . . . . . . 45
\nnwseharpoonnesw () . . . 46
\nnwseharpoons () . . . . . . 46
\nnwseharpoonswne () . . . 46
\nNwseline () ......... 33
\nnwseline () ......... 33
\nnwspoon () .......... 47
\nnwVdash () .......... 33
145
\nnwvdash () .......... 33
no entry . . . . . . . . . see \noway
\NoBleech (Ì) .......... 90
\NoChemicalCleaning (¨) . . 90
nointegrals (wasysym package op-
tion) . . . . . . . . . . . . . 26
\NoIroning (²) ......... 90
non-commutative division . . 63
nonbreaking space . . . . . . . . 72
NOR gates . . . . . . . . . . . . . 73
\NORd ( ) ........... 73
\NORl ( ) .......... 73
norm . . see \lVert and \rVert
\NORr ( ) .......... 73
\NORu ( ) ........... 73
\NoSun ( ) ............. 91
not .............. see \neg
\not .............. 32,105
not equal (= vs. =) . . . . . . . 32
\notasymp ( ) .......... 32
\notbackslash (\−) . . . . . . . 71
\notbot ( ) ............ 52
\notdivides ( ) ......... 32
\notequiv ( ) .......... 32
\notin ( ) ............. 52
\notin (<) ............. 52
\notin (6∈) ............. 52
\notin (∉) .............. 52
\notni (=) ............. 52
\notowner ( ) ........... 52
\notowns . . see \notowner and
\notni
\notperp ( ) ........... 32
\notslash (/−) .......... 71
\notsmallin () ......... 52
\notsmallowns () . . . . . . . . 52
\nottop ( ) ............ 52
\NoTumbler () .......... 90
\novelty (N) ........... 93
\noway (A) ............. 91
\nowns () .............. 52
\nparallel (∦) .......... 31
\nparallel (∦) .......... 34
\nparallelslant (Ô) . . . . . 36
\nperp () ............. 34
\npitchfork () . . . . . . . . . 47
\nplus (`) ............. 22
\nprec ( ) ............. 32
\nprec (⊀) ............. 31
\nprec () ............. 33
\nprecapprox ( ) . . . . . . . . 32
\nprecapprox (7) . . . . . . . . 31
\nprecapprox () ........ 33
\npreccurlyeq ( ) . . . . . . . 32
\npreccurlyeq ($) . . . . . . . 31
\npreccurlyeq () . . . . . . . 34
\npreceq ( ) ........... 32
\npreceq () ........... 31
\npreceq () ............ 34
\npreceqq (9) ........... 31
\nprecsim ( ) .......... 32
\nprecsim () ........... 31
\nprecsim () ........... 34
\nrcirclearrowdown () . . 45
\nrcirclearrowleft () . . 45
\nrcirclearrowright () . 45
\nrcirclearrowup () . . . . 45
\nrcurvearrowdown () . . . . 45
\nrcurvearrowleft () . . . . 45
\nrcurvearrowne () . . . . . 45
\nrcurvearrownw () . . . . . 45
\nrcurvearrowright () . . . 45
\nrcurvearrowse () . . . . . 45
\nrcurvearrowsw () . . . . . 45
\nrcurvearrowup () . . . . . . 45
\nRelbar () ........... 34
\nrelbar () ........... 34
\nrestriction () . . . . . . . 46
\nrhookdownarrow () . . . . . 45
\nrhookleftarrow () . . . . 45
\nrhooknearrow () . . . . . . 45
\nrhooknwarrow () . . . . . . 45
\nrhookrightarrow () . . . . 45
\nrhooksearrow () . . . . . . 45
\nrhookswarrow () . . . . . . 45
\nrhookuparrow () . . . . . . . 45
\nRightarrow ( ) . . . . . . . . 42
\nRightarrow () . . . . . . . 41
\nRightarrow (⇏) ........ 45
\nrightarrow ( ) . . . . . . . . 42
\nrightarrow () . . . . . . . 41
\nrightarrow () ........ 45
\nrightarrowtail () . . . . 45
\nrightfilledspoon () . . 47
\nrightfootline () . . . . . 34
\nrightfree () ......... 34
\nrightharpoonccw () . . . . 46
\nrightharpooncw () . . . . 46
\nrightleftarrows () . . . . 44
\nrightleftharpoons () . . 46
\nrightlsquigarrow () . . . 44
\nrightmapsto () . . . . . . . 44
\nrightModels () . . . . . . . 34
\nrightmodels () . . . . . . . 34
\nrightpitchfork () . . . . 47
\nrightrightarrows () . . . 44
\nrightrsquigarrow () . . . 44
\nrightspoon () ........ 47
\nrightsquigarrow () . . . . 46
\nrightVdash () . . . . . . . . 34
\nrightvdash () . . . . . . . . 34
\nrisingdotseq () . . . . . . . 34
\nRrightarrow () . . . . . . . 44
\nsdtstile ( ) ......... 35
\nSearrow () .......... 44
\nsearrow () .......... 44
\nsearrowtail () . . . . . . . 45
\nsefilledspoon () . . . . . 47
\nsefootline () ........ 34
\nsefree () ........... 34
\nseharpoonccw () . . . . . . 46
\nseharpooncw () . . . . . . . 46
\nselsquigarrow () . . . . . 45
\nsemapsto () ......... 45
\nseModels () ......... 34
\nsemodels () ......... 34
\nsenwarrows () . . . . . . . 45
\nsenwharpoons () . . . . . . 46
\nsepitchfork () . . . . . . . 47
\nsersquigarrow () . . . . . 45
\nsesearrows () . . . . . . . 45
\nsespoon () .......... 47
\nseVdash () .......... 34
\nsevdash () .......... 34
\nshortmid () .......... 31
\nshortmid () .......... 34
\nshortparallel () . . . . . . 31
\nshortparallel () . . . . . . 34
\nsim ( ) .............. 32
\nsim (/) .............. 31
\nsim () .............. 34
\nsimeq ( ) ............ 32
\nsimeq (;) ............ 31
\nsimeq () ............. 34
\nsmile () ............. 48
\nsmileeq () ........... 48
\nsmileeqfrown () . . . . . . . 48
\nsmilefrown () ........ 48
\nsmilefrowneq () . . . . . . . 48
\nsqdoublefrown () . . . . . . 48
\nsqdoublefrowneq () . . . . 48
\nsqdoublesmile () . . . . . . 48
\nsqdoublesmileeq () . . . . 48
\nsqeqfrown () ......... 48
\nsqeqsmile () ......... 48
\nsqfrown () ........... 48
\nsqfrowneq () ......... 48
\nsqfrowneqsmile () . . . . . 48
\nsqfrownsmile () . . . . . . . 48
\nsqsmile () ........... 48
\nsqsmileeq () ......... 48
\nsqsmileeqfrown () . . . . . 48
\nsqsmilefrown () . . . . . . . 48
\nSqsubset () .......... 37
\nsqSubset ( ) .......... 37
\nsqsubset ( ) .......... 37
\nsqsubset (a) .......... 37
\nsqsubset () .......... 37
\nsqsubseteq ( ) . . . . . . . . 37
\nsqsubseteq (@) . . . . . . . . 37
\nsqsubseteq () ........ 37
\nsqsubseteqq ( ) . . . . . . . 37
\nsqsubseteqq () . . . . . . . 37
\nSqsupset () .......... 37
\nsqSupset ( ) .......... 37
\nsqsupset ( ) .......... 37
\nsqsupset (b) .......... 37
\nsqsupset () .......... 37
\nsqsupseteq ( ) . . . . . . . . 37
\nsqsupseteq (A) . . . . . . . . 37
\nsqsupseteq () ........ 37
146
\nsqsupseteqq ( ) . . . . . . . 37
\nsqsupseteqq () . . . . . . . 37
\nsqtriplefrown () . . . . . . 48
\nsqtriplesmile () . . . . . . 48
\nsquigarrowdownup () . . 45
\nsquigarrowleftright () 45
\nsquigarrownesw () . . . . 45
\nsquigarrownwse () . . . . . 45
\nsquigarrowrightleft () 45
\nsquigarrowsenw () . . . . 45
\nsquigarrowswne () . . . . 45
\nsquigarrowupdown () . . . 45
\nsststile ( ) . . . . . . . . . 35
\nststile ( ) . . . . . . . . . . 35
\nsttstile ( ) . . . . . . . . . 35
\nSubset ( ) ........... 37
\nSubset (>) ............ 37
\nSubset () ............ 37
\nsubset ( ) ........... 37
\nsubset (⊄) ............ 37
\nsubseteq ( ) .......... 37
\nsubseteq () ......... 36
\nsubseteq () .......... 37
\nsubseteqq ( ) ......... 37
\nsubseteqq () ......... 37
\nsubseteqq () ......... 37
\nsucc ( ) ............. 32
\nsucc () ............. 31
\nsucc () ............. 33
\nsuccapprox ( ) . . . . . . . . 32
\nsuccapprox (8) . . . . . . . . 31
\nsuccapprox () ........ 33
\nsucccurlyeq ( ) . . . . . . . 32
\nsucccurlyeq (%) . . . . . . . 31
\nsucccurlyeq () . . . . . . . 33
\nsucceq ( ) ........... 32
\nsucceq () ........... 31
\nsucceq () ............ 33
\nsucceqq (:) ........... 31
\nsuccsim ( ) .......... 32
\nsuccsim () ........... 31
\nsuccsim () ........... 33
\nSupset ( ) ........... 37
\nSupset (?) ............ 37
\nSupset () ............ 37
\nsupset ( ) ........... 37
\nsupset () ............ 37
\nsupseteq ( ) .......... 37
\nsupseteq () ......... 36
\nsupseteq () .......... 37
\nsupseteqq ( ) . . . . . . . . . 37
\nsupseteqq () ......... 36
\nsupseteqq () ......... 37
\nSwarrow () .......... 45
\nswarrow () .......... 45
\nswarrowtail () . . . . . . . 45
\nswfilledspoon () . . . . . 47
\nswfootline () ........ 33
\nswfree () ........... 33
\nswharpoonccw () . . . . . . 46
\nswharpooncw () . . . . . . . 46
\nswlsquigarrow () . . . . . 45
\nswmapsto () ......... 45
\nswModels () ......... 34
\nswmodels () ......... 34
\nswnearrows () . . . . . . . 45
\nswneharpoons () ...... 46
\nswpitchfork () . . . . . . . 47
\nswrsquigarrow () . . . . . 45
\nswspoon () .......... 47
\nswswarrows () . . . . . . . 45
\nswVdash () .......... 34
\nswvdash () .......... 34
\ntdtstile ( ) ......... 35
ntheorem (package) . . . . . . . 65
\nthickapprox (5) . . . . . . . 31
\nto () ............... 46
\ntriangleeq () . . . . . . . . 40
\ntriangleleft ( ) . . . . . . 40
\ntriangleleft () . . . . . . 39
\ntriangleleft () . . . . 39, 40
\ntrianglelefteq ( ) . . . . 40
\ntrianglelefteq () . . . . 39
\ntrianglelefteq () . . 39, 40
\ntrianglelefteqslant (R) 40
\ntriangleright ( ) . . . . . 40
\ntriangleright () . . . . . 39
\ntriangleright () . . . 39, 40
\ntrianglerighteq ( ) . . . . 40
\ntrianglerighteq () . . . 39
\ntrianglerighteq () . 39, 40
\ntrianglerighteqslant (S) 40
\ntriplefrown () . . . . . . . 48
\ntriplesim () ......... 34
\ntriplesmile () . . . . . . . 48
\ntststile ( ) . . . . . . . . . 35
\nttstile ( ) . . . . . . . . . . 35
\ntttstile ( ) . . . . . . . . . 35
\ntwoheaddownarrow () . . . 45
\ntwoheadleftarrow (h) . . . 31
\ntwoheadleftarrow () . . 45
\ntwoheadnearrow () . . . . 45
\ntwoheadnwarrow () . . . . 45
\ntwoheadrightarrow (g) . . 31
\ntwoheadrightarrow () . . 45
\ntwoheadsearrow () . . . . 45
\ntwoheadswarrow () . . . . 45
\ntwoheaduparrow () . . . . . 45
\nu (ν) ................ 50
nuclear power plant . see \SNPP
\NUL (␀) ............... 72
null infinity see alphabets, math
null set . . . . . . . . . . . . . 65, 66
number sets see alphabets, math
number sign . see \textnumero
numbers . . . . . . . . . . see digits
circled . . . . . . . . . . 77, 94
numerals
Linear B . . . . . . . . . . . 85
old style . . . . . . . . . . . . 20
\NumLock (Num ) . . . . . . . . 72
\nUparrow () ........... 45
\nuparrow () ........... 45
\nuparrowtail () . . . . . . . 45
\nUpdownarrow () . . . . . . . 45
\nupdownarrow () . . . . . . . 45
\nupdownarrows () . . . . . . 45
\nupdownharpoonleftright ()
......... 46
\nupdownharpoonrightleft ()
......... 46
\nupdownharpoons () . . . . . 46
\nUpdownline (∦) ........ 34
\nupdownline () . . . . . . . . 34
\nupfilledspoon () . . . . . . 47
\nupfootline () . . . . . . . . 34
\nupfree () ............ 34
\nupharpoonccw () . . . . . . . 46
\nupharpooncw () . . . . . . . 46
\nuplsquigarrow () . . . . . . 45
\nupmapsto () .......... 45
\nupModels () ......... 34
\nupmodels () .......... 34
\nuppitchfork () . . . . . . . 47
\nuprsquigarrow () . . . . . . 45
\nupspoon () ........... 47
\nupuparrows () . . . . . . . . 45
\nupVdash () .......... 34
\nupvdash () ........... 34
\nuup (ν) .............. 50
\nvargeq ( ) ........... 38
\nvarleq ( ) ........... 38
\nvarparallel () . . . . . . . 31
\nvarparallelinv () . . . . . 31
\nVDash ( ) ............ 32
\nVDash () ............ 31
\nVDash () ............ 34
\nVdash ( ) ............ 32
\nVdash () ............ 31
\nVdash () ............ 34
\nvDash ( ) ............ 32
\nvDash () ............ 31
\nvDash () ............ 34
\nvdash ( ) ............ 32
\nvdash () ............ 31
\nvdash () ............ 34
\nVvash ( ) ............ 32
\Nwarrow (v) ........... 42
\Nwarrow (⇖) ........... 43
\nwarrow ( ) ........... 42
\nwarrow (-) . . . . . . . 41, 106
\nwarrow (↖) ........... 43
\nwarrowtail (%) ........ 43
\nwfilledspoon (u) . . . . . . 47
\nwfootline (}) ......... 32
\nwfree () ............ 32
\nwharpoonccw (E) . . . . . . . 46
\nwharpooncw (M) ........ 46
\nwlsquigarrow (¥) . . . . . . 43
\nwmapsto (-) .......... 43
\nwModels (õ) .......... 32
\nwmodels (å) .......... 32
\nwnwarrows () . . . . . . . . 43
\nwpitchfork () ........ 47
147
\nwrsquigarrow () . . . . . . 43
\Nwsearrow () ......... 43
\nwsearrow (-&) . . . . . . . . 106
\nwsearrow (⤢) ......... 43
\nwsearrows () . . . . . . . . 43
\nwsebipropto () . . . . . . . 24
\nwsecrossing () . . . . . . . 32
\nwseharpoonnesw (S) . . . . 46
\nwseharpoons (_) . . . . . . . 46
\nwseharpoonswne (W) . . . . 46
\Nwseline (×) .......... 32
\nwseline (Ó) .......... 32
\nwspoon (m) ........... 47
\nwVdash (í) ........... 32
\nwvdash (Ý) ........... 32
O
\O (Ø) ................ 10
\o (ø) ................. 10
o(o) .................. 50
\oast () .............. 25
\oasterisk ( ) .......... 25
\obackslash ( ) ......... 25
\obackslash () ......... 25
\obar (:) .............. 22
\Obelus ( ) ........... 95
\obelus ( ) ........... 95
\Obelus* (·
·) ........... 95
\obelus* (·
·) ........... 95
\oblong (@) ............ 22
\obot ( ) .............. 25
\obslash (;) ........... 22
\oc () ................. 21
\ocirc ( ) ............. 25
\ocirc () ............. 25
\ocircle (#) ........... 23
\ocoasterisk ( ) . . . . . . . . 25
\octagon (8) ........... 78
octonions ( ) . . see alphabets,
math
\Octosteel (‘) .......... 73
\od (a
˚
) ................ 16
\odiv ( ) .............. 25
\odot ( ) .............. 25
\odot () .............. 22
\odot (⊙) .............. 25
\odplus ( ) ............ 24
\OE (Œ) . . . . . . . . . . . 10, 117
\oe (œ) . . . . . . . . . . . . 10, 117
\officialeuro (e) . . . . . . . 19
\offinterlineskip . . . . . . 104
ogonek (package) . . 17, 119, 121
ogonek ( ˛) ...... see accents
\ogreaterthan (=) . . . . . . . 22
\ohill (a) ............. 16
ohm .......... see \textohm
\ohm (Ω) ............... 70
\Ohne (a/) .............. 89
\OHORN (Ơ) ............. 10
\ohorn (ơ) ............. 10
\oiiint ()) ........... 28
\oiiint () ........... 30
\oiiintclockwise (L) . . . . 28
\oiiintctrclockwise (D) . 28
\oiint ( ) ............. 27
\oiint () . . . . . . . . . . 26, 28
\oiint (‚) ............. 28
\oiint () ............. 30
\oiint () ............. 29
\oiintclockwise (H) . . . . . 28
\oiintctrclockwise (@) . . 28
\oint () .............. 27
\oint (H) .............. 25
\oint () .............. 29
\ointclockwise () . . . . . . 27
\ointclockwise (ı) . . . . . . . 28
\ointclockwise () . . . . . . . 30
\ointctrclockwise () . . . . 27
\ointctrclockwise () . . . . 28
\ointctrclockwise () . . . . 30
old-style digits . . . . . . . . . . . 20
\oldstylenums .......... 20
\oleft ( ) ............. 25
\olessthan (<) .......... 22
\Omega (Ω) ............. 50
\omega (ω) ............. 50
\omegaup (ω) ........... 50
\ominus ( ) ............ 25
\ominus () ............ 22
\ominus (⊖) ............ 25
\onlymove (F) .......... 93
\oo (◦◦) ............... 95
\oo ( ) ............... 13
\ooalign . . . . . . . . . . 104, 105
\open ( ) .............. 18
open unit disk ( ) . . . . . . see
alphabets, math
\openJoin ([) ........... 31
\openo ( ) .............. 13
\openo ( ) ............. 13
\openo (l) ............. 13
\opentimes (]) .......... 31
operators
binary . . . . . . . . . . 22–25
logical see logical operators
set . . . . . see set operators
unary . . . . . . . . . . . . . 21
\oplus ( ) ............. 25
\oplus (⊕) . . . . . . . 21, 22, 103
\oplus (⊕) ............. 25
\opposbishops (o) . . . . . . . 93
\opposition (W) ........ 71
optical scaling . . . . . . . . . . 109
options . . . see package options
or ............... see \vee
OR gates . . . . . . . . . . . . . . 73
\ORd ( ) ............ 73
\oright ( ) ............ 25
\ORl ( ) ........... 73
\OrnamentDiamondSolid ( ) 80
ornaments . . . . . . . . . . . 78, 80
\ORr ( ) ........... 73
orthogonal to . . . . . . see \bot
\ORu ( ) ............ 73
\oslash ( ) ............ 25
\oslash () ............ 22
\oslash () ............ 25
\ostar () ............. 25
\otimes ( ) ............ 25
\otimes (⊗) ............ 22
\otimes (⊗) ............ 25
\otop ( ) .............. 25
\otriangle () . . . . . . . 25, 40
\otriangleup ( ) . . . . . . . . 25
ovals .................. 80
\ovee (>) .............. 22
\overarc (a
_
) ............ 17
\overbrace ( ) . . . . . . . 60
\overbrace (
) .......... 60
\overbrace (z}|{) ........ 60
\overbrace (z}|{) ........ 59
\overbracket ( ) . . . . . . . . 60
\overbracket ( ) . . . . 108, 109
\overbridge (”
a) ......... 16
\overgroup ( ) . . . . . . . . 60
\overgroup () ......... 60
\overleftarrow (←−) . . . . . . 59
\overleftharp (
) . . . . . . . 47
\overleftharpdown (
) . . . . 47
\overleftharpoon (↼Ð) . . . . 60
\overleftrightarrow (←→) . 59
\overline ( ) . . . . . . . . 21, 59
\overlinesegment (zx) . . . . 60
\overparenthesis (z{) 108, 109
\Overrightarrow (=⇒) . . . . . 59
overrightarrow (package) 59, 119
\overrightarrow (−→) . . . . . 59
\overrightharp (
) . . . . . . . 47
\overrightharpdown (
) . . . 47
\overrightharpoon (Ð⇀) . . . . 60
\overring ( ) . . . . . . . . . . 18
\overset ............. 104
\overt () ............. 25
\ovoid ( ) ............. 25
\owedge (?) ............ 22
\owns ............. see \ni
\owns ( ) .............. 52
\owns (3) .............. 52
\owns (∋) .............. 52
\ownsbar ( ) ............ 52
P
\P () . . . . . . . . . . . . . . 9, 116
\p (˙) ................. 95
\p@ .................. 107
148
package options
a(esvect) ........... 61
b(esvect) ........... 61
bbgreekl (mathbbol) . . . 68
c(esvect) ........... 61
crescent (fge) ........ 58
d(esvect) ........... 61
e(esvect) ........... 61
f(esvect) ........... 61
g(esvect) ........... 61
german (keystroke) . . . . 72
greek (babel) . . . . . 50, 87
h(esvect) ........... 61
integrals (wasysym) . . . . 26
mathcal (euscript) . . . . . 68
mathscr (euscript) . . . . . 68
nointegrals (wasysym) . . 26
polutonikogreek (babel) . 50
sans (dsfont) ......... 68
utf8x (inputenc) . . . . . 117
varg (txfonts/pxfonts) . . 51
packages
longdiv ............. 59
accents . . 58, 107, 119, 121
amsbsy ............ 113
amsfonts 22, 30, 36, 41, 65,
68
amsmath 8, 49, 58, 104, 112
amssymb . 8, 22, 30, 36, 41,
58, 65, 68, 87, 119, 120, 123
amstext . . . . . . . . 105, 106
ar . . . . . . . . . . . . 70, 119
arcs . . . . . . . . 17, 119, 120
arev . . . . . 67, 88, 119, 120
ascii . . . . 72, 115, 119, 120
babel . . . . . . . . . . . 50, 87
bbding 75–78, 80, 101, 119,
120
bbm . . . . . . . . . . . 68, 119
bbold . . . . . . . . . . 68, 119
bm . . . . . . . 113, 119, 121
braket ............. 54
calligra . . . . . . 68, 119, 121
calrsfs ............. 68
cancel ............. 59
cclicenses . . . . 19, 119, 120
centernot .......... 105
chancery ........... 119
chemarr . . . . . 62, 119, 120
chemarrow . . . . 47, 62, 119
china2e 19, 49, 68, 98, 119,
121
clock . . . . . . . 92, 119, 120
cmll . . . 21, 24, 30, 36, 119
colonequals 21, 36, 119, 120
combelow . . . . 17, 119, 121
cypriot . . . . . . 86, 119, 121
dblaccnt ........... 107
dictsym . . . . . 96, 119, 120
dingbat 76, 80, 101, 119, 120
DotArrow . . . . 63, 119, 121
dozenal . . . . . . . . 65, 119
dsfont . . . . . . . . . 68, 119
epsdice . . . . . . 92, 119, 120
esint . . . . . . . . . . 28, 119
esvect . . . . . . . . . 61, 119
eufrak ............. 68
eurosym . . . . . 19, 119, 120
euscript . . . . . 68, 119, 120
extarrows . . . . 62, 119, 120
extpfeil . . . . . . 63, 119, 120
extraipa . . . . . . . . 16, 119
fc ............. 10,14
fclfont ............ 119
feyn . . . . . . . . 74, 119, 120
fge . 47, 53, 58, 65, 67, 119,
120
fixmath ........... 113
fontenc . . . . 8, 10, 14, 115
fontspec ........... 118
fourier 19, 36, 51, 53, 57, 60,
76, 78, 91, 119
gensymb ............ 70
graphics . . . . . . . . 47, 103
graphicx . . . . . 17, 100, 103
harmony . . . . . 89, 119, 120
harpoon . . . . . 47, 119, 121
hhcount . . . . . 92, 119, 121
hieroglf . . . . . 82, 119, 120
holtpolt . . . . . . . . 63, 119
ifsym . . 70, 79, 91, 92, 101,
103, 119, 120
igo . . . . . . . . . . . . 94, 119
inputenc ........... 117
isoent ............. 117
junicode ........... 118
keystroke . . . . 72, 119, 120
latexsym . 22, 30, 36, 41, 65,
100, 119
linearA . . . . . . 82, 119, 121
linearb . . . 85, 86, 119, 121
manfnt . . . . . . 89, 119, 120
marvosym 18, 65, 67, 71–75,
90, 101
mathabx . . . 21, 23, 25, 26,
30, 32, 36–38, 40, 42, 43, 49,
52–55, 58, 60, 65, 66, 71, 93,
100, 101, 119, 120, 123
mathbbol ........... 68
mathcomp .......... 65
mathdesign . 18, 24, 30, 52,
56, 67, 119
mathdots . . 58, 63, 64, 107,
119, 120
mathrsfs . . . . . . . . 68, 119
mathtools . . 21, 34, 60, 62,
119, 120
mbboard . . . . . . . . 68, 119
metre . 17, 57, 95, 119, 120
milstd . . . . . . . . . 73, 119
MnSymbol ......... 21,
23–25, 29, 32–34, 37, 39, 40,
43–48, 51, 52, 55, 58–60, 64,
66, 67, 79, 119, 120
musixtex ............ 89
nath . . . . . . 53, 56, 57, 119
nicefrac . . . . . 67, 119, 121
ntheorem ........... 65
ogonek . . . . . . 17, 119, 121
overrightarrow . . . . 59, 119
phaistos . . . . . 81, 119, 120
phonetic . . 13, 16, 103, 119
pict2e ............. 70
pifont . . 10, 75–78, 80, 103,
119, 120
pigpen . . . . . . 98, 119, 120
pmboxdraw . . . 97, 119, 120
polynom ............ 59
protosem . . . . 81, 119, 120
psnfss ............. 77
pxfonts . . 21–23, 27, 30, 31,
36–38, 41, 42, 48, 50–52, 65,
66, 68, 100, 115
recycle . . . . . . . . . 99, 119
rotating . . . . . . . . . 19, 72
sarabian . . . . . 87, 119, 121
savesym ........... 100
semtrans . 14, 17, 119, 120
shuffle . . . . . . 24, 119, 120
simplewick ......... 109
simpsons . . . . . . . 96, 119
skak . . . . . 93, 94, 119, 120
skull . . . . . . . . 93, 119, 120
slashed ............ 105
staves . . . . . . . . . 97, 119
steinmetz . . . . 70, 119, 121
stmaryrd . . . 22, 26, 31, 37,
40, 42, 48, 53, 54, 101, 104,
118–120
t4phonet . 14, 17, 119, 120
teubner 19, 64, 87, 95, 119,
120
textcomp 8, 9, 14, 18–20, 41,
57, 67, 70, 88, 100, 115, 119
timing ............. 70
tipa 11, 12, 14–17, 103, 119,
120
tipx . . . . . . . . 12, 119, 120
trfsigns . . . . 36, 52, 63, 119
trsym . . . . . . . 36, 119, 120
turnstile . . . . . 35, 119, 120
txfonts . . . . . . . . . . 21–23,
27, 30, 31, 36–38, 41, 42, 48,
50–52, 65, 66, 68, 100, 102,
115, 119, 120
type1cm ........... 100
ucs . . . . . . . . . . . 117, 118
ulsy . . . . . 24, 48, 103, 119
underscore ........... 9
undertilde . . . . 61, 119, 120
units .............. 67
universa . . 80, 90, 119, 120
universal 75, 77, 80, 90, 119,
120
upgreek . . . . . 51, 119, 120
upquote ........... 115
url ............... 115
ushort . . . . . . 61, 119, 121
vietnam ........... 119
149
vntex . . . . . . . . . . . 10, 14
wasysym . . . . . . 13, 18, 20,
22, 23, 26, 30, 31, 36–38, 41,
64–66, 70, 71, 73, 77, 78, 88,
101, 119, 120
wsuipa 13, 16, 18, 101, 103,
107, 119, 120
xfrac .............. 67
yfonts . . . 68, 69, 119, 120
yhmath 58, 59, 61, 64, 107,
119
Pakin, Scott . . . . . . 1, 108, 118
\PaperLandscape ( ) . . . . . 92
\PaperPortrait ( ) . . . . . . 92
par see \bindnasrepma,\invamp,
and \parr
paragraph mark . . . . . . . see \P
\parallel (k) . . . . . . . . 30, 56
\parallel (∥) ........... 33
\ParallelPort (Ñ) . . . . . . . 72
\parallelslant (Ë) . . . . . . . 36
\parr (`) .............. 24
\partial ( ) ............ 52
\partial (∂) ............ 51
\partial (∂) ............ 53
\partialslash ( ) . . . . . . . 52
\partialvardint () . . . . 67
\partialvardlanddownint () 67
\partialvardlandupint () 67
\partialvardlcircleleftint
() .............. 43
\partialvardlcircleleftint
() .............. 67
\partialvardlcirclerightint
() .............. 43
\partialvardlcirclerightint
() .............. 67
\partialvardoiint () . . . 67
\partialvardoint () . . . . . 67
\partialvardrcircleleftint
() .............. 43
\partialvardrcircleleftint
() .............. 67
\partialvardrcirclerightint
() .............. 43
\partialvardrcirclerightint
() .............. 67
\partialvardstrokedint () 67
\partialvardsumint () . . . 67
\partialvartint () . . . . . 67
\partialvartlanddownint () 67
\partialvartlandupint () 67
\partialvartlcircleleftint
() .............. 43
\partialvartlcircleleftint
() .............. 67
\partialvartlcirclerightint
() .............. 43
\partialvartlcirclerightint
() .............. 67
\partialvartoiint () . . . 67
\partialvartoint () . . . . . 67
\partialvartrcircleleftint
() .............. 43
\partialvartrcircleleftint
() .............. 67
\partialvartrcirclerightint
() .............. 44
\partialvartrcirclerightint
() .............. 67
\partialvartstrokedint () 67
\partialvartsumint () . . . 67
particle-physics symbols . . . . 74
parts per thousand . . . . . . see
\textperthousand
\partvoice (a
– »
ˇ) .......... 16
\partvoiceless (a
– »
˚) . . . . . . . 16
\passedpawn (r) ......... 93
pawn ................. 94
pdfL
A
T
E
X ............. 118
\Peace ( ) ............. 80
\PencilLeft ( ) . . . . . . . . 76
\PencilLeftDown ( ) . . . . . 76
\PencilLeftUp ( ) . . . . . . . 76
\PencilRight ( ) . . . . . . . 76
\PencilRightDown ( ) . . . . 76
\PencilRightUp ( ) . . . . . . 76
pencils ................ 76
\pentagon (D) .......... 78
\pentagram () .......... 25
\pentam (λθλθλ||λββλββλ)
......... 95
people . . . . . . . . . . . . see faces
percent sign . . . . . . . . . see \%
\permil (h) ............ 20
\Perp (y) .............. 31
\perp (⊥) . . . . . . . . . . 30, 106
\perp (⊥) .............. 33
\perthousand (‰) . . . . . . . 70
\Pfund (£) ............. 18
\PgDown (Page ↓) . . . . . . . 72
\PgUp (Page ↑) . . . . . . . . . 72
phaistos (package) . 81, 119, 120
Phaistos disk . . . . . . . . . . . . 81
pharmaceutical prescription see
\textrecipe
\PHarrow (J) ............ 81
\phase ( ) ............. 70
phasor ................ 70
\PHbee (h) ............ 81
\PHbeehive (X) . . . . . . . . 81
\PHboomerang (R) . . . . . . . 81
\PHbow (K) .............. 81
\PHbullLeg (b) .......... 81
\PHcaptive (D) ......... 81
\PHcarpentryPlane (S) . . . 81
\PHcat (c) ............ 81
\PHchild (E) ........... 81
\PHclub (M) ............. 81
\PHcolumn (W) ........... 81
\PHcomb (U) ............ 81
\PHdolium (T) .......... 81
\PHdove (f) ........... 81
\PHeagle (e) ........... 81
\PHflute (o) ........... 81
\PHgaunlet (H) ......... 81
\PHgrater (p) .......... 81
\PHhelmet (G) .......... 81
\PHhide (a) ........... 81
\PHhorn (Z) ............. 81
\Phi (Φ) ............... 50
\phi (φ) ............... 50
\phiup (φ) ............. 50
\PHlid (Q) ............. 81
\PHlily (m) ............ 81
\PHmanacles (N) . . . . . . . . 81
\PHmattock (O) ......... 81
\Phone ( ) ............. 80
\phone () ............. 88
\PhoneHandset ( ) . . . . . . . 80
phonetic (package) . 13, 16, 103,
119
phonetic symbols . . . . . . 11–14
\photon (::::) ......... 70
photons . . . . . . . . . . . . . . . 74
\PHoxBack (n) .......... 81
\PHpapyrus (k) .......... 81
\PHpedestrian (A) . . . . . . 81
\PHplaneTree (i) . . . . . . . . 81
\PHplumedHead (B) . . . . . 81
\PHram (d) ............ 81
\PHrosette (l) ......... 81
\PHsaw (P) ............. 81
\PHshield (L) .......... 81
\PHship (Y) ........... 81
\PHsling (V) ........... 81
\PHsmallAxe (r) . . . . . . . . 81
\PHstrainer (q) . . . . . . . 81
\PHtattooedHead (C) . . . . 81
150
\PHtiara (I) ........... 81
\PHtunny (g) .......... 81
\PHvine (j) ............ 81
\PHwavyBand (s) ......... 81
\PHwoman (F) ........... 81
physical symbols . . . . . . . . . 70
\Pi (Π) ................ 50
\pi (π) ................ 50
\pi (π) ................ 51
\Pickup (A) ............ 73
pict2e (package) . . . . . . . . . . 70
pifont (package) . . 10, 75–78, 80,
103, 119, 120
pigpen (package) . . 98, 119, 120
pigpen cipher . . . . . . . . . . . 98
{\pigpenfont A} (A) . . . . . 98
{\pigpenfont B} (B) . . . . . 98
{\pigpenfont C} (C) . . . . . 98
{\pigpenfont D} (D) . . . . . 98
{\pigpenfont E} (E) . . . . . 98
{\pigpenfont F} (F) . . . . . 98
{\pigpenfont G} (G) . . . . . 98
{\pigpenfont H} (H) . . . . . 98
{\pigpenfont I} (I) . . . . . 98
{\pigpenfont J} (J) . . . . . 98
{\pigpenfont K} (K) . . . . . 98
{\pigpenfont L} (L) . . . . . 98
{\pigpenfont M} (M) . . . . . 98
{\pigpenfont N} (N) . . . . . 98
{\pigpenfont O} (O) . . . . . 98
{\pigpenfont P} (P) . . . . . 98
{\pigpenfont Q} (Q) . . . . . 98
{\pigpenfont R} (R) . . . . . 98
{\pigpenfont S} (S) . . . . . 98
{\pigpenfont T} (T) . . . . . 98
{\pigpenfont U} (U) . . . . . 98
{\pigpenfont V} (V) . . . . . 98
{\pigpenfont W} (W) . . . . . 98
{\pigpenfont X} (X) . . . . . 98
{\pigpenfont Y} (Y) . . . . . 98
{\pigpenfont Z} (Z) . . . . . 98
pilcrow . . . . . . . . . . . . . see \P
pipe ......... see \textpipe
\Pisces (ë) ............ 71
\pisces (f) ............ 71
\Pisymbol ............. 103
\pitchfork ( ) .......... 66
\pitchfork (t) .......... 30
\pitchfork (⋔) .......... 47
pitchfork symbols . . . 30, 47, 66
Pitman’s base-12 symbols . . 65
\piup (π) .............. 50
\planck (¯h) . . . . . . . . . . . . 13
\Plane ( ) ............. 80
planets . . . . . . . . . . . . . . . . 71
playing cards . . . . see card suits
Plimsoll line . . . . . . . . . . . 104
\Plus ( ) .............. 76
\plus (+) .............. 24
plus-or-minus sign . . . . see \pm
\PlusCenterOpen ( ) . . . . . 76
\pluscirc ( ) .......... 23
\PlusOutline ( ) . . . . . . . . 76
plusses . . . . . . . . . . . . . 76, 77
\PlusThinCenterOpen ( ) . . 76
\Pluto ( ) ............. 71
\Pluto (É) ............. 71
\pluto (\) ............. 71
\pm (±) ................ 22
\pm (±) ................ 24
\pm (¯
˙) ................ 95
\pmb ................. 113
pmboxdraw (package) . . 97, 119,
120
\pmod ................. 49
\pod .................. 49
\pointer () ............ 88
pointing finger . . . . . . . see fists
\Pointinghand (Z) . . . . . . . 90
\polishhook ( ) ......... 18
\polter () ........... 63
polutonikogreek (babel package op-
tion) . . . . . . . . . . . . . 50
polygons . . . . . . . . . . . . 78, 79
polynom (package) . . . . . . . . 59
polynomial division . . . . . . . 59
polytonic Greek . . . . . . . . . . 50
\Postbox ( ) ........... 98
PostScript . 51, 69, 75, 103, 112
PostScript fonts . . . . . . 75, 103
\Pound ( ) ............. 19
\pounds (£) . . . . . . 9, 115, 116
power set . see alphabets, math
\powerset () ........... 52
\Pp (˙
˙) ................ 95
\pp (˙
˙) ............... 95
\ppm (¯
˙˙) ............... 95
\Ppp (˙
˙
˙) ............... 95
\ppp (˙
˙
˙) .............. 95
\Pppp (˙
˙
˙
˙) ............... 95
\pppp (˙
˙
˙
˙) ............. 95
\Ppppp (˙
˙
˙
˙
˙) .............. 95
\ppppp (˙
˙
˙
˙
˙) ............. 95
\Pr (Pr) ............... 49
\prec (≺) .............. 30
\prec () .............. 32
\precapprox ( ) . . . . . . . . . 32
\precapprox () ......... 30
\precapprox () ......... 33
\preccurlyeq ( ) . . . . . . . . 32
\preccurlyeq (4) . . . . . . . . 30
\preccurlyeq () ........ 33
\precdot ( ) ........... 32
\preceq () ............ 30
\preceq () ............. 33
\preceqq () ............ 31
\precnapprox ( ) . . . . . . . . 32
\precnapprox () ........ 31
\precnapprox () ........ 34
\precneq ( ) ........... 32
\precneqq () .......... 31
\precnsim ( ) .......... 32
\precnsim () .......... 31
\precnsim () ........... 34
\precsim ( ) ........... 32
\precsim (-) ........... 30
\precsim () ............ 33
prescription . . see \textrecipe
present-value symbols . . . . 108
\prime (0) .............. 65
\prime (′) .............. 66
\Printer (Ò) ........... 72
printer’s fist . . . . . . . . see fists
probabilistic independence . 106
\prod (Q) ............. 25
\prod (∏) .............. 29
projective space ( ) . . . . . see
alphabets, math
\projlim (proj lim) . . . . . . . 49
pronunciation symbols . . . . see
phonetic symbols
proof, end of . . . . . . . . . . . . 65
proper subset/superset . . . . see
\subsetneq/\supsetneq
proper vertices . . . . . . . . . . 74
\propto ( ) ............ 66
\propto (∝) ............ 30
\propto (∝) ............ 33
proto-Semitic symbols . . . . . 81
protosem (package) 81, 119, 120
\ProvidesPackage . . . . . . . 119
\PrtSc (PrtSc ) ......... 72
\ps ( ) ............... 95
pseudographics . . . . . . . . . . 97
\Psi (Ψ) ............... 50
\psi (ψ) ............... 50
\psiup (ψ) ............. 50
psnfss (package) . . . . . . . . . . 77
\Pu (‰) ................ 89
pullback diagrams . . . . . . . 106
pulse diagram symbols . . . . . 70
\PulseHigh ( ) ......... 70
\PulseLow ( ) ......... 70
punctuation . . . . . . . . . . . . 10
pushout diagrams . . . . . . . 106
\pwedge ( ) ............ 13
pxfonts (package) . 21–23, 27, 30,
31, 36–38, 41, 42, 48, 50–52,
65, 66, 68, 100, 115
\Pxp (˙
˙) ............... 95
\pxp (˙
˙) .............. 95
Q
Q.E.D. ................ 65
\qoppa () .............. 87
\qside (M) ............. 93
\Quadrad (]]) . . . . . . . . . . . . 57
151
\quadrad (]]) ............ 57
\Quadras ([[) ............ 57
\quadras ([[) ............ 57
quarter note see musical symbols
\quarternote (♩) . . . . . . . . 88
\quarternote (♩) ......... 88
quaternions ( ) see alphabets,
math
quaver . . . see musical symbols
queen ................. 94
\quotedblbase („) . . . . 10, 117
\quotesinglbase (‚) . . 10, 117
R
\R (∼
?
) ................ 95
\r (˚a) ................. 14
\r (∼
?
) ................. 95
\Radiation ( ) ......... 92
radicals . . see \sqrt and \surd
\Radioactivity (j) . . . . . . 74
\Rain ( ) .............. 91
\RainCloud ( ) ......... 91
raising . . . . . see \textraising
\RaisingEdge ( ) . . . . . . . . 70
\Rangle ( ) ............ 68
\rAngle (ii) ............. 56
\rangle (i) . . . . . . . . . . 21, 54
\rangle () ............. 55
\ranglebar () .......... 55
\RArrow (→) .......... 72
\rarrowfill ............ 62
\ratio (:) .............. 36
\RATIONAL ( ) ........... 49
\Rational ( ) ........... 49
rational numbers ( ) . . . . . see
alphabets, math
rationalized Planck constant see
\hbar
\Rbag (Q) .............. 53
\rbag (O) ............... 53
\rbrace (
) ........... 55
\Rbrack () ............. 68
\rBrack (]]) ............. 56
\rc (a) ................ 16
\rCeil (ee) .............. 56
\rceil (e) .............. 54
\rceil (
) ............. 55
\rcirclearrowdown (û) . . . 44
\rcirclearrowleft (⟲) . . . 44
\rcirclearrowright (⤿) . . 44
\rcirclearrowup (↺) . . . . . 44
\rcircleleftint () . . . . . . 29
\rcirclerightint () . . . . . 29
\rcorners () ........... 53
\rcurvearrowdown (⤹) . . . . . 44
\rcurvearrowleft (↶) . . . . 44
\rcurvearrowne (Ä) ...... 44
\rcurvearrownw (Å) ...... 44
\rcurvearrowright (À) . . . . 44
\rcurvearrowse (Ç) ...... 44
\rcurvearrowsw (Æ) ...... 44
\rcurvearrowup (Á) . . . . . . . 44
\rdbrack () ............ 55
\Re (<) ................ 51
\REAL ( ) .............. 49
\Real ( ) .............. 49
real numbers ( ) see alphabets,
math
recipe . . . . . . see \textrecipe
\recorder () ........... 88
\Rectangle ( ) . . . . . . . . . . 80
\RectangleBold ( ) . . . . . . . 80
rectangles . . . . . . . . . . . . . . 80
\RectangleThin ( ) . . . . . . . 80
\Rectpipe (˜) ........... 73
\Rectsteel (”) .......... 73
recycle (package) . . . . . 99, 119
\recycle (A) . . . . . . 99
recycling symbols . . . . . 98, 99
reduced quadrupole moment see
\rqm
\reflectbox ........... 103
registered trademark . . . . . see
\textregistered
relational symbols . . . . . . . . 30
binary 30–32, 34–39, 47, 48
negated binary . . . . 31–33
triangle . . . . . . . . . 39, 40
\Relbar (=) . . . . . . . . 48, 103
\Relbar (Ô) ............ 33
\relbar (−) . . . . . . . . 48, 103
\relbar (Ð) ............ 33
\Request ( ) ........... 98
\resizebox . . . . . . . . . 47, 100
\Respondens (∼) . . . . . . . . . 95
\respondens (∼) ......... 95
response ( ) . . . . . . . . . . . 118
\restoresymbol ........ 100
\restriction .......... see
\upharpoonright
\restriction ( ) . . . . . . . . 42
\restriction (↾) ........ 46
retracting see \textretracting
\Return (←-) .......... 72
return . . . . . see carriage return
\revaw (Ñ
Ñ
Ñ
Ñ
) ............. 56
\revD ( ) .............. 13
\revddots (...) ......... 107
\reve () .............. 13
\reveject ( ) ........... 13
\revepsilon ( ) . . . . . 13, 103
reverse solidus . . . . . . . . . . see
\textbackslash
reversed symbols . . . . . . . . 103
\reversedvideodbend () . 89
\revglotstop ( ) . . . . . . . . 13
\Rewind () ............ 90
\RewindToIndex (´) . . . . . 90
\RewindToStart (µ) . . . . . . 90
\rfilet () ............. 55
\rFloor (cc) ............. 56
\rfloor (c) ............. 54
\rfloor (
) ............ 55
\rgroup (
) ............ 54
\rgroup (
) ........... 55
\RHD () ............... 23
\rhd (B) . . . . . . . . . . . . 22, 23
\rhd () . . . . . . . . . . . . 39, 40
\rho (ρ) ............... 50
\rho (ρ) ............... 51
\rhookdownarrow (;) . . . . . . 44
\rhookleftarrow (↩) . . . . . 44
\rhooknearrow (⤤) . . . . . . . 44
\rhooknwarrow (=) . . . . . . . 44
\rhookrightarrow (8) . . . . 44
\rhooksearrow (?) . . . . . . . 44
\rhookswarrow (⤦) . . . . . . . 43
\rhookuparrow (9) ........ 43
\rhoup (ρ) ............. 50
\right . . . . . . 54, 56, 100, 102
\rightangle (∟) ......... 67
\RIGHTarrow () . . . . . . . . . 88
\Rightarrow (⇒) . . . . . 21, 41
\Rightarrow (⇒) ........ 43
\rightarrow ( ) . . . . . . . . 42
\rightarrow (→) ........ 41
\rightarrow (→) ......... 43
\rightarrowtail () . . . . . 41
\rightarrowtail (↣) . . . . . 43
\rightarrowtriangle (_) . . 42
\rightbarharpoon ( ) . . . . 43
\RIGHTCIRCLE (H) ........ 88
\RIGHTcircle (H#) ........ 88
\Rightcircle (J) ........ 88
\RightDiamond ( ) . . . . . . . 79
\rightevaw (Ñ
Ñ
Ñ
Ñ
) .......... 56
\rightfilledspoon (p) . . . 47
\rightfootline (x) ...... 33
\rightfree () .......... 33
\righthalfcap () . . . . . . . 24
\righthalfcup () . . . . . . . 24
\righthand (u) ......... 76
\rightharpoonccw (⇀) . . . . 46
\rightharpooncw (⇁) . . . . . 46
\rightharpoondown ( ) . . . 43
\rightharpoondown () . . . 41
\rightharpoonup ( ) . . . . . 43
\rightharpoonup () . . . . . 41
\rightleftarrows ( ) . . . . 42
\rightleftarrows () . . . . 41
\rightleftarrows (⇄) . . . . 43
\rightleftharpoon ( ) . . . 43
152
\rightleftharpoons ( ) . . 43
\rightleftharpoons () . . 41
\rightleftharpoons (
) . . 41
\rightleftharpoons (⇌) . . . 46
\rightleftharpoonsfill . . . 62
\rightlsquigarrow (↝) . . . . 43
\rightmapsto (↦) ........ 43
\rightModels (⊫) ........ 33
\rightmodels (⊧) . . . . . . . . 33
\rightmoon ( ) . . . . . . . . . . 71
\rightmoon (%) .......... 71
\rightp ( ) ............. 18
\rightpitchfork () . . . . . 47
\rightpointleft ( ) . . . . 76
\rightpointright ( ) . . . 76
\rightpropto () ........ 33
\rightrightarrows ( ) . . . 42
\rightrightarrows (⇒) . . . 41
\rightrightarrows (⇉) . . . . 43
\rightrightharpoons ( ) . . 43
\rightrsquigarrow (¨) . . . . 43
\Rightscissors (Q) . . . . . . 75
\rightslice (3) . . . . . . . . . 22
\rightslice () ......... 33
\rightspoon (⊸) ........ 47
\rightsquigarrow ( ) . . . 42
\rightsquigarrow ( ) . . . . 41
\rightsquigarrow (↝) . . . . 44
\rightt ( ) ............. 18
\righttherefore () . . . 23, 64
\rightthreetimes ( ) . . . . 66
\rightthreetimes (i) . . . . 22
\rightthreetimes () . . . . . 23
\rightthumbsdown ( ) . . . 76
\rightthumbsup ( ) . . . . . 76
\righttoleftarrow ( ) . . . 42
\Righttorque (') . . . . . . . . 73
\rightturn (!) ......... 88
\rightVdash (⊩) ......... 33
\rightvdash (⊢) ......... 33
\rightwave (Ð
Ð
Ð
Ð
) .......... 56
\rightY () ............ 23
\ring (˚) .............. 58
ring (˚a) . . . . . . . . . see accents
ring equal to . . . . . see \circeq
ring in equal to . . . see \eqcirc
\riota () .............. 13
\rip ( ) ............... 93
\risingdotseq ( ) . . . . . . . 32
\risingdotseq (:) . . . . . . . 30
\risingdotseq () . . . . . . . 33
\rJoin (Y) ............. 31
\rlap ............. 79,106
\rmoustache (
) ........ 54
\rmoustache (
) . . . . . . . . 55
Roman coins . . . . . . . . . . . . 19
Romanian comma-belo accent (a
,)
..... see accents
rook .................. 94
roots ............ see \sqrt
\rotatebox . . . . . . . . . 17, 103
rotated symbols . 11–13, 17, 103
rotating (package) . . . . . 19, 72
\rotm ( ) .............. 13
\rotOmega ( ) ........... 13
\rotr () .............. 13
\rotvara ( ) ............ 13
\rotw ( ) .............. 13
\roty ( ) .............. 13
\RoundedLsteel (Ÿ) . . . . . . 73
\RoundedTsteel () . . . . . . . 73
\RoundedTTsteel () . . . . . . 73
\Rparen () ............. 68
\rqm (-
I) .............. 105
\rrangle () ........... 55
\rrbracket () .......... 54
\rrbracket () .......... 57
\rrceil (W) ............. 53
\rrfloor (U) ............ 53
\Rrightarrow (V) . . . . . . . 42
\Rrightarrow () ........ 43
\rrparenthesis (M) . . . . . . . 53
\RS (␞) ................ 72
\rsem (
) ............. 55
\rsemantic ..... see \rdbrack
\Rsh ( ) ............... 42
\Rsh () ............... 41
\Rsh () ............... 43
\rtimes ( ) ............ 23
\rtimes () ............ 22
\rtimes () ............ 23
\rtriple .............. 57
\rVert (||) .............. 56
\rVert (k) ............. 54
\rvert (|) .............. 54
\rwave (Ð
Ð
Ð
Ð
) ............. 56
\rWavy (
) ............ 55
\rwavy (
) ............. 55
S
\S (§) .............. 9,116
\SAa (a) ............... 87
\SAb (b) ............... 87
\SAd (d) ............... 87
\SAdb (D) .............. 87
\SAdd (B) .............. 87
\SAf (f) ............... 87
safety-related symbols . . . . . 74
\SAg (g) ............... 87
\SAga (G) .............. 87
\Sagittarius (è) . . . . . . . . 71
\sagittarius (c) ........ 71
\SAh (h) ............... 87
\SAhd (H) .............. 87
\SAhu (I) .............. 87
\SAk (k) ............... 87
\SAl (l) ............... 87
\SAlq (‘) .............. 87
\SAm (m) ............... 87
\samebishops (s) . . . . . . . . 93
\Sampi () ............. 87
\sampi () ............. 87
\SAn (n) ............... 87
sans (dsfont package option) . 68
\SAo (o) ............... 87
\SAq (q) ............... 87
\SAr (r) ............... 87
\sarabfamily ........... 87
sarabian (package) . 87, 119, 121
\SAs (s) ............... 87
\SAsa (X) .............. 87
\SAsd (x) .............. 87
\SAsv (S) .............. 87
\SAt (t) ............... 87
\SAtb (J) .............. 87
\SAtd (T) .............. 87
\satellitedish ( ) . . . . . . 80
satisfies . . . . . . . . . see \models
\Saturn ( ) ............ 71
\Saturn (Æ) ............ 71
\saturn (Y) ............ 71
savesym (package) . . . . . . . 100
\savesymbol ........... 100
\SAw (w) ............... 87
\SAy (y) ............... 87
\SAz (z) ............... 87
\SAzd (Z) .............. 87
\Sborder ( ) ........... 80
\scalebox ............. 100
scaling
mechanical . . . . . . 109, 112
optical . . . . . . . . . . . . 109
\scd ( ) ............... 13
\scg ( ) ............... 13
\schwa ( ) .............. 13
\schwa ( ) ............. 13
Schwartz distribution spaces see
alphabets, math
\sci () ............... 13
scientific symbols . . . . . . 70–74
\ScissorHollowLeft ( ) . . 75
\ScissorHollowRight ( ) . 75
\ScissorLeft ( ) . . . . . . . 75
\ScissorLeftBrokenBottom ( )
......... 75
\ScissorLeftBrokenTop ( ) 75
\ScissorRight ( ) . . . . . . . 75
\ScissorRightBrokenBottom
( ) .............. 75
\ScissorRightBrokenTop ( ) 75
scissors . . . . . . . . . . . . . . . . 75
\scn ( ) ............... 13
\scoh (˝) .............. 36
\Scorpio (ç) ........... 71
\scorpio (b) ........... 71
\scr ( ) ............... 13
153
script letters see alphabets, math
\scripta ( ) ............ 13
\scriptg ( ) ............ 13
\scriptscriptstyle . . 105, 106
\scriptstyle . . . . . . . 105, 106
\scriptv ( ) ............ 13
\Scroll (Scroll ) ........ 72
\scu ( ) ............... 13
\scy ( ) ............... 13
\sddtstile ( ) ......... 35
\sdststile ( ) ......... 35
\sdtstile ( ) .......... 35
\sdttstile ( ) . . . . . . . . . 35
seagull . . . . . see \textseagull
\Searrow (u) ........... 42
\Searrow (⇘) ........... 43
\searrow ( ) ........... 42
\searrow (&) . . . . . . . 41, 106
\searrow (↘) ........... 43
\searrowtail (') ........ 43
\sec (sec) .............. 49
\Sech (ˇ“)) .............. 89
\SechBL (ˇ“
==
==) ............ 89
\SechBl (ˇ“
==
=) ............ 89
\SechBR (ˇ“==
==
) ............ 89
\SechBr (ˇ“==
=
) ............ 89
\second ( ) ............. 66
seconds, angular . . see \second
\secstress () ........... 18
section mark . . . . . . . . . see \S
\SectioningDiamond ( ) . . 92
sedenions ( ) . . see alphabets,
math
\sefilledspoon (w) . . . . . . 47
\sefootline () ......... 33
\sefree () ............ 33
segmented digits . . . . . . . . . 70
\seharpoonccw (G) . . . . . . . 46
\seharpooncw (O) ........ 46
\selectfont ............. 8
\selsquigarrow (§) . . . . . . 43
semantic valuation . . . . . 54–57
\semapsto (/) .......... 43
semibreve . see musical symbols
semidirect products . . 22, 23, 66
semiquaver see musical symbols
semitic transliteration . . 14, 17
\seModels (÷) .......... 33
\semodels (ç) .......... 33
semtrans (package) . 14, 17, 119,
120
\senwarrows () . . . . . . . . 43
\senwharpoons ([) . . . . . . . 46
\SePa (@) .............. 89
\separated () .......... 33
\sepitchfork () ........ 47
\seppawns (q) .......... 93
\SerialInterface (Î) . . . . 72
\SerialPort (Ð) ......... 72
\sersquigarrow (¯) . . . . . . 43
\sesearrows () . . . . . . . . 43
\sespoon (o) ........... 47
set operators
intersection . . . . see \cap
membership . . . . . see \in
union . . . . . . . . . see \cup
\setminus (\) ........... 22
\setminus () ........... 24
\seVdash (ï) ........... 32
\sevdash (ß) ........... 33
SGML ............... 117
sha ( ) . . . . . . . . . . . . . . 103
\sharp () ........... 65,88
\sharp (♯) .............. 66
\shfermion () ........... 74
\Shift (Shift ⇑) ........ 72
\shift (˜) ............. 21
\Shilling (¡) ........... 18
\shneg (ˆ) ............. 21
\shortcastling (O-O) . . . . 93
\shortdownarrow () . . . . . . 42
\ShortFifty (×) . . . . . . . . 90
\ShortForty (Ù) . . . . . . . . 90
\shortleftarrow () . . . . . 42
\shortmid () ........... 30
\shortmid () ........... 24
\ShortNinetyFive (Ô) . . . . 90
\shortparallel () . . . . . . . 30
\shortparallel () . . . . . . 32
\ShortPulseHigh ( ) . . . . . 70
\ShortPulseLow ( ) . . . . . . 70
\shortrightarrow () . . . . 42
\ShortSixty (Ö) . . . . . . . . 90
\ShortThirty (Û) . . . . . . . 90
\shortuparrow () . . . . . . . 42
\showclock ............. 91
\shpos (´) ............. 21
shuffle (package) . . 24, 119, 120
\shuffle ( ) ........... 24
shuffle product ( ) . . . . . . . 24
\SI (␏) ................ 72
\Sigma (Σ) ............. 50
\sigma (σ) ............. 50
\sigmaup (σ) ............ 50
\sim (∼) . . . . . . . . 30, 104, 115
\sim (∼) ............... 32
\simcolon (∼:) .......... 36
\simcoloncolon (∼::) . . . . . 36
\simeq (') ............. 30
\simeq () ............. 32
simplewick (package) . . . . . 109
simpsons (package) . . . . 96, 119
Simpsons characters . . . . . . . 96
\sin (sin) . . . . . . . . . . . . . . 49
\sincoh (ˇ) ............ 36
\sinh (sinh) . . . . . . . . . . . . 49
\SixFlowerAlternate ( ) . . 78
\SixFlowerAltPetal ( ) . . 78
\SixFlowerOpenCenter ( ) . 78
\SixFlowerPetalDotted ( ) 78
\SixFlowerPetalRemoved ( ) 78
\SixFlowerRemovedOpenPetal
( ) .............. 78
\SixStar ( ) ........... 78
\SixteenStarLight ( ) . . . 78
sixteenth note . . . . see musical
symbols
\sixteenthnote (♬) . . . . . . 88
skak (package) . 93, 94, 119, 120
skull (package) . . . . 93, 119, 120
\skull ( ) ............. 93
\slash (/) . . . . . . . . . . . . 115
\slashb ( ) ............. 13
\slashc ( ) ............. 13
\slashd ( ) ............. 13
\slashdiv () ........... 23
slashed (package) . . . . . . . . 105
\slashed ............. 105
slashed letters . . . . . . . . . . 105
slashed.sty (file) . . . . . . . 105
\slashu ( ) ............. 13
\Sleet ( ) ............. 91
\sliding (a
¯
) ............ 16
\smallbosonloop () . . . . . . . 74
\smallbosonloopA () . . . . . . 74
\smallbosonloopV () . . . . . . 74
\SmallCircle ( ) . . . . . . . . 79
\SmallCross ( ) . . . . . . . . 79
\smalldiamond (◇) . . . . . . . 25
\SmallDiamondshape ( ) . . 79
\smallfrown (a) ......... 30
\smallfrown () ......... 48
\SmallHBar ( ) ......... 79
\smallin () ............ 52
\smallint () ........... 66
\SmallLowerDiamond ( ) . . 79
\smalllozenge (◊) ........ 79
\smallowns () .......... 52
\smallpencil ( ) . . . . . . 76
\smallprod () .......... 23
\SmallRightDiamond ( ) . . 79
\smallsetminus () . . . . . . 22
\smallsetminus () . . . . . . 24
\smallsmile (`) ......... 30
\smallsmile () ......... 48
\SmallSquare ( ) . . . . . . . . 79
\smallsquare () ........ 25
\smallstar (☆) .......... 25
\SmallTriangleDown ( ) . . 79
\smalltriangledown ( ) . . . 25
\smalltriangledown (▿) 25, 40
\SmallTriangleLeft ( ) . . 79
\smalltriangleleft ( ) . . . 25
\smalltriangleleft (◃) 25, 40
\SmallTriangleRight ( ) . . 79
\smalltriangleright ( ) . . 25
\smalltriangleright (▹) 25, 40
\SmallTriangleUp ( ) . . . . 79
\smalltriangleup ( ) . . . . . 25
154
\smalltriangleup (▵) . . 25, 40
\SmallVBar ( ) ......... 79
\smile () ............. 30
\smile () ............. 48
smile symbols . . . . . . . . . . . 48
\smileeq () ............ 48
\smileeqfrown () . . . . . . . 48
\smilefrown () ......... 48
\smilefrowneq () . . . . . . . 48
\Smiley (©) ............ 90
\smiley (,) ............ 88
smiley faces . . . . . 72, 88, 90, 98
\sndtstile ( ) ......... 35
\Snow ( ) .............. 91
\SnowCloud ( ) ......... 91
\Snowflake ( ) ......... 78
\SnowflakeChevron ( ) . . . 78
\SnowflakeChevronBold ( ) 78
snowflakes . . . . . . . . . . . . . . 78
\SNPP ( ) ............. 96
\snststile ( ) ......... 35
\sntstile ( ) .......... 35
\snttstile ( ) . . . . . . . . . 35
\SO (␎) ................ 72
\SOH (␁) ............... 72
South Arabian alphabet . . . . 87
space
thin .............. 113
visible . . . . . . . . . . . . see
\textvisiblespace
\Spacebar ( ) . . . . 72
spades (suit) . . . . . . . 65–67, 80
\spadesuit (♠) .......... 65
\spadesuit (♠) .......... 66
\Sparkle ( ) ........... 78
\SparkleBold ( ) . . . . . . . . 78
sparkles . . . . . . . . . . . . . . . 78
“special” characters . . . . . . . . 9
\SpecialForty (Ú) . . . . . . 90
\sphericalangle ( ) . . . . . 66
\sphericalangle (^) . . . . . 66
\sphericalangle () . . . . . 66
\SpinDown () ............ 79
\SpinUp () ............. 79
\spirituslenis (a
–) . . . . . . . 58
\spirituslenis (—) . . . . . . . 58
\splitvert (¦) .......... 72
spoon symbols . . . . . . . . . . . 47
\spreadlips (a
˙) ......... 16
\sqbullet ( ) ........... 23
\sqcap ( ) ............. 23
\sqcap (u) ............. 22
\sqcap () ............. 23
\sqcapdot () ........... 23
\sqcapplus (}) .......... 23
\sqcapplus () .......... 23
\sqcup ( ) ............. 23
\sqcup (t) . . . . . . . . . . 21, 22
\sqcup () ............. 23
\sqcupdot () ........... 24
\sqcupplus (|) .......... 23
\sqcupplus () .......... 24
\sqdoublecap ( ) . . . . . . . . 23
\sqdoublecup ( ) . . . . . . . . 23
\sqdoublefrown () . . . . . . . 48
\sqdoublefrowneq () . . . . . 48
\sqdoublesmile () . . . . . . . 48
\sqdoublesmileeq () . . . . . 48
\sqeqfrown () .......... 48
\sqeqsmile () .......... 48
\sqfrown () ............ 48
\sqfrowneq () .......... 48
\sqfrowneqsmile () . . . . . . 48
\sqfrownsmile () . . . . . . . 48
\sqiiint (R) .......... 27
\sqiint (P) ............ 27
\sqiint (”) ............ 28
\sqint () ............. 27
\sqint (›) .............. 28
\sqrt (√) . . . . . . . . . 59, 106
\sqsmile () ............ 48
\sqsmileeq () .......... 48
\sqsmileeqfrown () . . . . . . 48
\sqsmilefrown () . . . . . . . 48
\Sqsubset () ........... 37
\sqSubset ( ) .......... 37
\sqsubset ( ) .......... 37
\sqsubset (@) . . . . . . . 36, 37
\sqsubset () ........... 37
\sqsubseteq ( ) . . . . . . . . . 37
\sqsubseteq (v) . . . . . . . . . 36
\sqsubseteq () ......... 37
\sqsubseteqq ( ) . . . . . . . . 37
\sqsubseteqq () ........ 37
\sqsubsetneq ( ) . . . . . . . . 37
\sqsubsetneq () ........ 37
\sqsubsetneqq ( ) . . . . . . . 37
\sqsubsetneqq () . . . . . . . 37
\Sqsupset () ........... 37
\sqSupset ( ) .......... 37
\sqsupset ( ) .......... 37
\sqsupset (A) . . . . . . . 36, 37
\sqsupset () ........... 37
\sqsupseteq ( ) . . . . . . . . . 37
\sqsupseteq (w) . . . . . . . . . 36
\sqsupseteq () ......... 37
\sqsupseteqq ( ) . . . . . . . . 37
\sqsupseteqq () ........ 37
\sqsupsetneq ( ) . . . . . . . . 37
\sqsupsetneq () ........ 37
\sqsupsetneqq ( ) . . . . . . . 37
\sqsupsetneqq () . . . . . . . 37
\sqtriplefrown () . . . . . . . 48
\sqtriplesmile () . . . . . . . 48
\Square ( ) ............ 79
\Square (vs. vs. ) . . 101
\Square () ............ 77
\Square ( ) ............ 80
\square ( ) ............. 23
\square () ............ 66
\square () ............ 25
square root . . . . . . . see \sqrt
hooked . . . . . see \hksqrt
\SquareCastShadowBottomRight
( ) .............. 80
\SquareCastShadowTopLeft ( )
......... 80
\SquareCastShadowTopRight
( ) .............. 80
\Squaredot (÷) .......... 67
\squaredots (∷) . . . . . . 24, 64
\Squarepipe (—) ......... 73
squares . . . . . . . . . . . 79–80, 94
\SquareShadowA ( ) . . . . . . 79
\SquareShadowB ( ) . . . . . . 79
\SquareShadowBottomRight ( )
......... 80
\SquareShadowC ( ) . . . . . . 79
\SquareShadowTopLeft ( ) . 80
\SquareShadowTopRight ( ) 80
\SquareSolid ( ) . . . . . . . . 80
\Squaresteel (“) . . . . . . . . 73
\squarewithdots ( ) . . . . . 80
\squigarrowdownup (³) . . . 43
\squigarrowleftright (↭) . 43
\squigarrownesw (´) . . . . . 43
\squigarrownwse (µ) . . . . . . 43
\squigarrowrightleft (²) . 43
\squigarrowsenw (·) . . . . . 43
\squigarrowswne () . . . . . 43
\squigarrowupdown (±) . . . . 43
\squplus ( ) ........... 23
\SS (SS) ............... 10
\ss (ß) ................ 10
\ssdtstile ( ) ......... 35
\ssearrow (%) ........... 42
\sslash () ............ 22
\ssststile ( ) . . . . . . . . . 35
\sststile ( ) .......... 35
\ssttstile ( ) . . . . . . . . . 35
\sswarrow ($) ........... 42
\stackrel . . . . . . . 21, 104, 108
standard state . . . . . . . . . . 104
\star () . . . . . . . . . . 22, 107
\star () .............. 25
Star of David . . . . . . . . 77, 78
\starredbullet (d) . . . . . . . 78
stars . . . . . . . . . . . . . 66, 77–79
\stater (῝) ............. 19
statistical independence . . . 106
\staveI () .......... 97
\staveII () .......... 97
\staveIII () . . . . . . . . 97
\staveIV () ......... 97
\staveIX () .......... 97
\staveL (1) . . . . . . . 97, 98
155
\staveLI (2) ......... 97
\staveLII (3) . . . . . . . . 97
\staveLIII (4) ........ 97
\staveLIV (5) . . . . . . . . 97
\staveLIX (:) . . . . . . . . 98
\staveLV (6) .......... 97
\staveLVI (7) ......... 97
\staveLVII (8) . . . . . . . . 97
\staveLVIII (9) . . . . . . . 98
\staveLX (;) . . . . . . . 98
\staveLXI (<) ......... 98
\staveLXII (=) . . . . . . . . 98
\staveLXIII (>) . . . . . . . 98
\staveLXIV (?) ......... 98
\staveLXV (@) ......... 98
\staveLXVI (A) . . . . . . . . 98
\staveLXVII (B) . . . . . . . . 98
\staveLXVIII (C) . . . . . . . 98
staves ................. 97
staves (package) . . . . . . 97, 119
\staveV () .......... 97
\staveVI () ......... 97
\staveVII () . . . . . . . . 97
\staveVIII () . . . . . . . 97
\staveX () .......... 97
\staveXI () .......... 97
\staveXII () ......... 98
\staveXIII () . . . . . . . . 98
\staveXIV () ........ 98
\staveXIX () . . . . . . . . 98
\staveXL (') .......... 98
\staveXLI (() ......... 98
\staveXLII ()) . . . . . . . 98
\staveXLIII (*) . . . . . . . . 98
\staveXLIV (+) . . . . . . . 98
\staveXLIX (0) . . . . . . . . 97
\staveXLV (,) . . . . . . . . 98
\staveXLVI (-) . . . . . . . . 98
\staveXLVII (.) . . . . . . . 97
\staveXLVIII (/) . . . . . 97
\staveXV () ......... 98
\staveXVI () ......... 98
\staveXVII () ........ 98
\staveXVIII () . . . . . . . 98
\staveXX () ......... 98
\staveXXI () . . . . . . . . 98
\staveXXII () . . . . . . . . 98
\staveXXIII () . . . . . 98
\staveXXIV () . . . . . . . . 97
\staveXXIX () . . . . . . . 97
\staveXXV () ........ 97
\staveXXVI () . . . . . . . 97
\staveXXVII () . . . . . . . 97
\staveXXVIII () . . . . . . 97
\staveXXX () . . . . . . . . 97
\staveXXXI () . . . . . . . . 97
\staveXXXII () . . . . . . 97
\staveXXXIII ( ) . . . . . . . 97
\staveXXXIV (!) . . . . . . 97
\staveXXXIX (&) . . . . . . 98
\staveXXXV (") . . . . . . . 98
\staveXXXVI (#) . . . . . . 98
\staveXXXVII ($) . . . . . 98
\staveXXXVIII (%) . . . . 98
\stdtstile ( ) ......... 35
\steaming (♨) .......... 67
steinmetz (package) 70, 119, 121
Steinmetz phasor notation . . 70
sterling . . . . . . . . . see \pounds
stick figures . . . . . . . . . . . . . 81
\Stigma () ............ 87
\stigma () ............. 87
stmaryrd (package) 22, 26, 31, 37,
40, 42, 48, 53, 54, 101, 104,
118–120
stochastic independence see \bot
\StoneMan ( ) ........... 91
\Stopsign (!) .......... 74
\StopWatchEnd ( ) . . . . . . . 91
\StopWatchStart ( ) . . . . . 91
\stress () ............. 18
\strictfi (K) .......... 31
\strictif (J) .......... 31
\strictiff (L) ......... 31
\strokedint () ......... 29
\StrokeFive ( ) . . . . . . . . 92
\StrokeFour ( ) ......... 92
\StrokeOne () ........... 92
\StrokeThree ( ) . . . . . . . . 92
\StrokeTwo ( ) . . . . . . . . . . 92
\stst (−◦ ) ............. 104
\stststile ( ) . . . . . . . . . 35
\sttstile ( ) .......... 35
\stttstile ( ) . . . . . . . . . 35
\STX (␂) ............... 72
\SUB (␚) ............... 72
subatomic particles . . . . . . . 74
\subcorner (a
^) .......... 16
\subdoublebar (a
¯
¯) . . . . . . . 16
\subdoublevert (a
"") . . . . . . . 16
\sublptr (a
¡) ............ 16
\subrptr (a
¿) ............ 16
subscripts
new symbols used in . . 105
\Subset ( ) ............ 37
\Subset (b) ............ 36
\Subset () ............. 37
\subset ( ) ............ 37
\subset (⊂) ............ 36
\subset (⊂) ............. 37
\subseteq ( ) .......... 37
\subseteq (⊆) .......... 36
\subseteq (⊆) ........... 37
\subseteqq ( ) .......... 37
\subseteqq (j) ......... 36
\subseteqq () .......... 37
\subsetneq ( ) .......... 37
\subsetneq () ......... 36
\subsetneq () .......... 37
\subsetneqq ( ) ......... 37
\subsetneqq () ......... 36
\subsetneqq () ......... 37
\subsetplus (D) . . . . . . . . . 37
\subsetpluseq (F) . . . . . . . 37
subsets . . . . . . . . . . . . . 36, 37
\succ () .............. 30
\succ () .............. 32
\succapprox ( ) . . . . . . . . . 32
\succapprox () ......... 30
\succapprox () ......... 32
\succcurlyeq ( ) . . . . . . . . 32
\succcurlyeq (<) . . . . . . . . 30
\succcurlyeq () ........ 32
\succdot ( ) ........... 32
\succeq () ............ 30
\succeq () ............. 32
\succeqq () ............ 31
\succnapprox ( ) . . . . . . . . 32
\succnapprox () ........ 31
\succnapprox () ........ 34
\succneq ( ) ........... 32
\succneqq () .......... 31
\succnsim ( ) .......... 32
\succnsim () .......... 31
\succnsim () ........... 34
\succsim ( ) ........... 32
\succsim (%) ........... 30
156
\succsim () ............ 32
such that . . . . . . . . . . 103, 105
\suchthat (3−−) ......... 105
\sum (P) .............. 25
\sum (∑) ............... 29
\sumint () ............. 29
\Summit ( ) ............ 91
\SummitSign ( ) ......... 91
\Sun ( ) ............... 71
\Sun (Àvs. vs. ) . . . . 101
\Sun ( ) .............. 91
\Sun (À) ............... 71
\sun (☼) ............... 88
\SunCloud ( ) . . . . . . . . . . 91
\SunshineOpenCircled ( ) . 80
\sup (sup) . . . . . . . . . . . . . 49
superscripts
new symbols used in . . 105
supersets . . . . . . . . . . . . 36, 37
supremum . . . . . . . . . see \sup
\Supset ( ) ............ 37
\Supset (c) ............ 36
\Supset () ............. 37
\supset ( ) ............ 37
\supset (⊃) ............ 36
\supset (⊃) ............. 37
\supseteq ( ) .......... 37
\supseteq (⊇) .......... 36
\supseteq (⊇) ........... 37
\supseteqq ( ) .......... 37
\supseteqq (k) ......... 36
\supseteqq () .......... 37
\supsetneq ( ) .......... 37
\supsetneq () ......... 36
\supsetneq () .......... 37
\supsetneqq ( ) ......... 37
\supsetneqq () ......... 36
\supsetneqq () ......... 37
\supsetplus (E) . . . . . . . . . 37
\supsetpluseq (G) . . . . . . . 37
\surd ( ) .............. 65
\SurveySign ( ) ......... 91
\Swarrow (w) ........... 42
\Swarrow (⇙) ........... 43
\swarrow ( ) ........... 42
\swarrow (.) . . . . 41, 106, 107
\swarrow (↙) ........... 43
\swarrowtail (&) ........ 43
\swfilledspoon (v) . . . . . . 47
\swfootline (~) ......... 32
\swfree () ............ 33
\swharpoonccw (F) . . . . . . . 46
\swharpooncw (N) ........ 46
\swlsquigarrow (¦) . . . . . . 43
\swmapsto (.) .......... 43
\swModels (ö) .......... 33
\swmodels (æ) .......... 33
\swnearrows () . . . . . . . . 43
\swneharpoons (^) . . . . . . . 46
swords ................ 91
\swpitchfork () ........ 47
\swrsquigarrow (®) . . . . . . 43
\swspoon (n) ........... 47
\swswarrows () . . . . . . . . 43
swung dash . . . . . . . . see \sim
\swVdash (î) ........... 33
\swvdash (Þ) ........... 33
\syl (a) ............... 16
\syllabic () ........... 18
\symA ( ) .............. 68
\symAE ( ) ............. 68
\symB ( ) .............. 68
\symbishop (B) ......... 94
Symbol (font) . . . . . . . 51, 103
symbols
actuarial . . . . . . . . . . 108
alpine . . . . . . . . . . . . . 91
ancient language . . 81–87
annuity . . . . . . . . . . . 108
APL .............. 71
astrological . . . . . . . . . 71
astronomical . . . . . 71, 98
biological . . . . . . . . . . . 74
block-element . . . . . . . . 97
body-text . . . . . . . . . 9–20
bold . . . . . . . . . . . . . 113
box-drawing . . . . . . . . . 97
chess . . . . . . . . . . . 93, 94
cipher . . . . . . . . . . . . . 98
clock . . . . . . . . . 88, 90–92
communication . . . . . . . 73
computer hardware . . . . 72
contradiction . . . . . 21, 48
currency . . . . . . 18, 19, 68
dangerous bend . . . . . . 89
definition . . . . . . . 21, 108
dictionary . . . . . 11–14, 96
dingbat . . . . . . . . . 75–80
dot . . . . . . . 9, 63, 64, 107
electrical . . . . . . . . . . . 70
engineering . . . . . . 70, 73
extensible . . 47, 59–63, 70,
102, 107–109
Feynman diagram . . . . . 74
Frege logic . . 47, 53, 65, 67
frown .............. 48
gates, digital logic . . . . 73
genealogical . . . . . . . . . 88
general . . . . . . . . . . . . 88
Go stones . . . . . . . . . . 94
information . . . . . . . . . 90
informator . . . . . . . . . . 93
inverted . . . 11–13, 17, 103
keyboard . . . . . . . . . . . 72
Knuth’s . . . . . . . . . . . . 89
laundry . . . . . . . . . . . . 90
legal . . . . . . . . . 9, 19, 116
letter-like . . . . . . . . 51–53
life insurance . . . . . . . 108
linear logic . . . . 21–23, 25,
29–30, 36, 51, 52
linguistic . . . . . . . . 11–14
log-like . . . . . . . . 49, 113
logic . . . . . . . . . . . . . . 73
magical signs . . . . . . . . 97
mathematical . . . . . 21–69
METAFONTbook . . . . . 89
metrical . . . . . . . . . . . . 95
miscellaneous . . 65–67, 80,
88–99
monetary . . . . . . 18, 19, 68
musical . 20, 65, 66, 88, 89
navigation . . . . . . . . . . 90
non-commutative division 63
particle physics . . . . . . 74
Phaistos disk . . . . . . . . 81
phonetic . . . . . . . . 11–14
physical . . . . . . . . . . . . 70
pitchfork . . . . . . 30, 47, 66
Pitman’s base-12 . . . . . 65
present value . . . . . . . 108
proto-Semitic . . . . . . . . 81
pulse diagram . . . . . . . 70
recycling . . . . . . . . 98, 99
relational . . . . . . . . . . . 30
reversed . . . . . . . . . . . 103
rotated . . . 11–13, 17, 103
safety-related . . . . . . . . 74
scientific . . . . . . . . 70–74
Simpsons characters . . . 96
smile .............. 48
spoon . . . . . . . . . . . . . 47
staves . . . . . . . . . . . . . 97
subset and superset 36, 37
technological . . . . . 70–74
T
E
Xbook . . . . . . . . . . . 89
transliteration . . . . . . . 14
upside-down 11–13, 17, 103,
114
variable-sized . 25–30, 100,
102
weather . . . . . . . . . . . . 91
zodiacal . . . . . . . . . . . . 71
symbols.tex (file) . . . . 100, 119
\symC ( ) .............. 68
\symking (K) ........... 94
\symknight (N) ......... 94
\symOE ( ) ............. 68
\sympawn (p) ........... 94
\symqueen (Q) .......... 94
\symrook (R) ........... 94
\symUE ( ) ............. 68
\SYN (␖) ............... 72
T
\T .................... 10
\T (
a
) ................. 17
\T (⊗
?
) ................ 95
\t (a) ................. 14
\t (⊗
?
) ................. 95
t4phonet (package) . 14, 17, 119,
120
\Tab (
−−→
−−→ ) ........... 72
\tabcolsep ............ 104
tacks . . . . . . . . . . . . . . . 30, 51
157
\taild ( ) ............. 13
\tailinvr ( ) ........... 13
\taill () .............. 13
\tailn ( ) ............. 13
\tailr () .............. 13
\tails () .............. 13
\tailt () .............. 13
\tailz ( ) ............. 13
\Takt ................. 89
\talloblong (8) ......... 22
tally markers . . . . . . . . . 85, 92
\tan (tan) .............. 49
\tanh (tanh) . . . . . . . . . . . . 49
\Tape ( ) .............. 80
\Taschenuhr ( ) . . . . . . . . 91
Tate-Shafarevich group see sha
\tau (τ) ............... 50
\Taurus ( ) ............ 71
\Taurus (á) ............ 71
\taurus (]) ............ 71
tautology . . . . . . . . . see \top
\tauup (τ) .............. 50
\tccentigrade () . . . . . . . 65
\tcmu (µ) .............. 65
\tcohm (Ω) ............. 65
\tcpertenthousand () . . 65
\tcperthousand (‰) . . . . . . 65
\td (a
..) ................ 16
\tddtstile ( ) . . . . . . . . 35
\tdststile ( ) . . . . . . . . . 35
\tdtstile ( ) . . . . . . . . . 35
\tdttstile ( ) . . . . . . . . 35
technological symbols . . 70–74
\Telefon (T) ........... 73
\Telephone ( ) . . . . . . . . 92
\Telephone ( ) ......... 98
Tennent, Bob . . . . . . . . . . . 21
\Tent ( ) .............. 91
\Terminus (⊗) .......... 95
\terminus (⊗) ........... 95
\Terminus* (⊕) .......... 95
\terminus* (⊕) .......... 95
\tesh ( ) .............. 13
testfont.dvi (file) . . . . . . 111
testfont.tex (file) . . . 111, 112
\tetartemorion (Β) . . . . . . . 19
teubner (package) 19, 64, 87, 95,
119, 120
T
E
X . . . 40, 47, 64, 70, 97, 100,
103–109, 111–113, 115, 117,
118, 122
T
E
Xbook, The 103–107, 109, 112
symbols from . . . . . . . . 89
\text . . . . . . . . . . 21, 105, 106
\textacutedbl () . . . . . . . 18
\textacutemacron (´
¯
a) . . . . . 15
\textacutewedge (´
ˇ
a) . . . . . . 15
\textadvancing (a
ffi) . . . . . . . 15
\textaolig (") .......... 12
\textasciiacute () . . 18, 116
\textasciibreve () . . . . . . 18
\textasciicaron () . . . . . . 18
\textasciicircum (ˆ) . . 9, 115,
117
\textasciidieresis () 18, 116
\textasciigrave () . . . . . . 18
\textasciimacron . . . . . . . 115
\textasciimacron () 18, 116
\textasciitilde (˜) 9, 115, 117
\textasteriskcentered (∗) . 9,
20
\textbabygamma (È) . . . . . . . 11
\textbackslash (\) . 9, 114, 115
\textbaht () ........... 18
\textbar (|) . . . . . . . . . 9, 114
\textbarb (b) ........... 11
\textbarc (c) ........... 11
\textbard (d) ........... 11
\textbardbl () ......... 20
\textbardotlessj (é) . . . . . 11
\textbarg (g) ........... 11
\textbarglotstop (Ü) . . . . . 11
\textbari (1) ........... 11
\textbarl (ł) ........... 11
\textbaro (8) ........... 11
\textbarrevglotstop (Ý) . . 11
\textbaru (0) ........... 11
\textbeltl (ì) .......... 11
\textbenttailyogh (B) . . . . 12
\textbeta (B) ........... 11
\textbigcircle (○) . . . . . . 20
\textbktailgamma (.) . . . . . 12
\textblank () .......... 20
\textblock ( ) . . . . . . . . . . 97
\textborn () ........... 88
\textbottomtiebar (a
<
) . . . . 15
\textbraceleft ({) ........ 9
\textbraceright (}) ....... 9
\textbrevemacron (˘
¯
a) . . . . . 15
\textbrokenbar (¦) . . . 20, 116
\textbullet (•) . . . . 9, 20, 117
\textbullseye (ò) . . . . . . . 11
\textcelsius () . . . . 70, 117
\textceltpal ( ) ......... 11
\textcent (¢) . . . . . . . 18, 116
\textcentoldstyle () . . . . 18
\textchi ( ............. 11
\textcircled () ........ 14
\textcircledP () . . . . . . 19
\textcircumacute (Ża) . . . . . 15
\textcircumdot (ˆ
˙
a) . . . . . . . 15
\textcloseepsilon (Å) . . . . 11
\textcloseomega (Ñ) ...... 11
\textcloserevepsilon (Æ) . . 11
\textcolonmonetary (₡) . . . 18
\textcommatailz (Þ) . . . . . . 11
textcomp (package) . . . . . . . 8,
9, 14, 18–20, 41, 57, 67, 70,
88, 100, 115, 119
\textcopyleft () . . . . . . 19
\textcopyright (©) . 9, 19, 116
\textcorner (^) .......... 11
\textcrb (ă) ............ 11
\textcrd (ą) ............ 11
\textcrd ( ) ............ 14
\textcrg (g) ............ 11
\textcrh (è) ............ 11
\textcrh ( ) ............ 14
\textcrinvglotstop (Û) . . . 11
\textcrlambda (ň) . . . . . . . 11
\textcrtwo (2) .......... 11
\textctc (C) ............ 11
\textctd (ć) ............ 11
\textctdctzlig (ćý) ...... 11
\textctesh (š) .......... 11
\textctinvglotstop (D) . . . 12
\textctj (J) ............ 11
\textctjvar (2) ......... 12
\textctn (ő) ............ 11
\textctstretchc (%) . . . . . . 12
\textctstretchcvar (&) . . . 12
\textctt (ť) ............ 11
\textcttctclig (ťC) ...... 11
\textctturnt (@) ......... 12
\textctyogh (ÿ) ......... 11
\textctz (ý) ............ 11
\textcurrency (¤) . . . 18, 116
\textcypr .............. 86
\textdagger (†) . . . . . . . 9, 20
\textdaggerdbl (‡) . . . . . 9, 20
\textdbend () ......... 89
\textdblhyphen () . . . . . . . 20
\textdblhyphenchar () . . . . 20
\textdblig ()) . . . . . . . . . 12
\textdctzlig (dý) ........ 11
\textdegree (°) . . . . . 67, 116
\textdied () ........... 88
\textdiscount () . . . . . . . 20
\textdiv (÷) ........... 67
\textdivorced () . . . . . . . 88
\textdkshade ( ) . . . . . . . . 97
\textdnblock ( ) . . . . . . . . 97
\textdollar ($) . . . . . . . 9, 18
\textdollaroldstyle () . . 18
\textdong (₫) ........... 18
\textdotacute (§a) . . . . . . . 15
\textdotbreve (˙
˘
a) . . . . . . . 15
\textdoublebaresh (S) . . . . 11
\textdoublebarpipe (}) . . . 11
\textdoublebarpipevar (H) . 12
\textdoublebarslash (=/ ) . . 11
\textdoublegrave (‚a) . . . . . 15
\textdoublegrave ( ) . . . . . 17
\textdoublepipe ({) . . . . . . 11
\textdoublepipevar (G) . . . 12
\textdoublevbaraccent (İa) . 15
\textdoublevbaraccent ( ) . 17
\textdoublevertline (Ş) . . 11
\textdownarrow (↓) . . . . . . . 41
\textdownfullarrow (ˇ) . . . 12
\textdownstep (Ť) ........ 11
\textdyoghlig (Ã) . . . . . . . 11
\textdzlig (dz) .......... 11
\texteightoldstyle () . . . 20
158
\textellipsis (. . . ) . . . . . . . 9
\textemdash (—) ......... 9
\textendash (–) .......... 9
\textepsilon (E) ........ 11
\textepsilon ( ) . . . . . . . . 14
\textesh (S) ............ 12
\textesh () ............ 14
\textestimated (℮) ...... 20
\texteuro (€) ........... 19
\texteuro (€) ........... 18
\texteuro (€) . . . 18, 115, 117
\textexclamdown (¡) . . . . . . . 9
\textfemale (7) ......... 12
\textfishhookr (R) . . . . . . . 12
\textfiveoldstyle () . . . . 20
\textfjlig ( ) . . . . . . . . . . 14
\textflorin (ƒ) .......... 18
\textfouroldstyle () . . . . 20
\textfractionsolidus (⁄) . . 67
\textfrak .............. 68
\textfrbarn (5) ......... 12
\textfrhookd (’) ........ 12
\textfrhookdvar (() ...... 12
\textfrhookt (?) . . . . . . . . 12
\textfrtailgamma (-) . . . . . 12
\textg (ě) ............. 12
\textgamma (G) .......... 12
\textglobfall (Ů) . . . . . . . 12
\textglobrise (Ű) . . . . . . . 12
\textglotstop (P) . . . . . . . 11
\textglotstopvari (T) . . . . 12
\textglotstopvarii (U) . . . 12
\textglotstopvariii (V) . . 12
\textgoth .............. 68
\textgravecircum (Ža) . . . . . 15
\textgravedbl () . . . . . . . 18
\textgravedot (đa) . . . . . . . 15
\textgravemacron (`
¯
a) . . . . . 15
\textgravemid (Źa) . . . . . . . 15
\textgreater (>) . . . . . 9, 114
\textgrgamma (,) . . . . . . . . 12
\textguarani () ........ 18
\texthalflength (;) . . . . . . 11
\texthardsign (ż) . . . . . . . 11
\textheng (0) ........... 12
\texthmlig (4) . . . . . . . . . 12
\texthooktop (#) . . . . . . . . . 11
\texthtb (á) ............ 11
\texthtb ( ) ............ 14
\texthtbardotlessj (ê) . . . . 11
\texthtbardotlessjvar (3) . 12
\texthtc (Á) ............ 11
\texthtc ( ) ............ 14
\texthtd (â) ............ 11
\texthtd ( ) ........... 14
\texthtg (ä) ............ 11
\texthth (H) ............ 11
\texththeng (Ê) . . . . . . . . . 11
\texthtk (Î) ............ 11
\texthtk ( ) ............ 14
\texthtp (Ò) ............ 11
\texthtp ( ) ............ 14
\texthtq (Ó) ............ 11
\texthtrtaild (č) . . . . . . . 11
\texthtscg (É) .......... 11
\texthtt (Ö) ............ 11
\texthtt () ............ 14
\texthvlig (ß) .......... 11
\textifsym ............. 70
\textinterrobang () . . . . . 20
\textinterrobangdown () . . 20
\textinvglotstop (Û) . . . . . 11
\textinvomega (;) . . . . . . . 12
\textinvsca (p) ......... 12
\textinvscr (K) ......... 11
\textinvscripta (!) . . . . . . 12
\textinvsubbridge (a„) . . . . 15
\textiota (Ì) ........... 11
\textiota () ........... 14
\textlambda (ń) . . . . . . . . . 11
\textlangle (〈) . . . . . 57, 114
\textlbrackdbl () . . . . . . . 57
\textleaf () .......... 88
\textleftarrow (←) . . . . . . 41
\textlengthmark (:) . . . . . . 11
\textless (<) . . . . . . . 9, 114
\textlfblock ( ) . . . . . . . . 97
\textlfishhookrlig (I) . . . 12
\textlhdbend (~) . . . . . . . 89
\textlhookfour (#) . . . . . . . 12
\textlhookp (<) ......... 12
\textlhookt (ş) . . . . . . . . . 11
\textlhti (1) ........... 12
\textlhtlongi (ę) ........ 11
\textlhtlongy (ű) . . . . . . . 11
\textlinb . . . . . . . . . . . 85, 86
\textlira (₤) ........... 18
\textlnot (¬) . . . . . . . 67, 116
\textlonglegr (Ô) . . . . . . . . 11
\textlooptoprevesh (>) . . . . 12
\textlowering (a
fl) . . . . . . . 15
\textlptr (¡) ........... 11
\textlquill () ......... 57
\textltailm (M) ......... 11
\textltailn (ñ) ......... 11
\textltailn ( ) ......... 14
\textltilde (ë) ......... 11
\textltshade ( ) . . . . . . . . 97
\textlyoghlig (Ð) . . . . . . . 11
\textmarried () ........ 88
\textmho () ........... 70
\textmidacute (Ÿa) . . . . . . . 15
\textminus (−) .......... 67
\textmu (µ) . . . . . . . . . 70, 116
\textmusicalnote (♪) . . . . . 20
\textnaira () .......... 18
\textnineoldstyle () . . . . 20
\textnrleg (6) .......... 12
\textnumero (№) ......... 20
\textObardotlessj (Í) . . . . 11
\textObullseye (9) . . . . . . 12
\textohm (Ω) ........... 70
\textOlyoghlig (ŋ) . . . . . . . 11
\textomega (ř) .......... 11
\textonehalf (½) . . . . 67, 116
\textoneoldstyle ........ 20
\textoneoldstyle () . . . . . 20
\textonequarter (¼) . . 67, 116
\textonesuperior (¹) . 67, 116
\textopenbullet (◦) . . . . . . 20
\textopencorner (_) . . . . . . 11
\textopeno (O) .......... 11
\textopeno ( ) . . . . . . . . . . 14
\textordfeminine (ª) 9, 20, 116
\textordmasculine (º) . . 9, 20,
116
\textovercross (‰a) . . . . . . . 15
\textoverw (—
a) . . . . . . . . . . 15
\textpalhook (%) . . . . . . . . . 11
\textpalhooklong (ˆ) . . . . . 12
\textpalhookvar (˜) . . . . . . 12
\textparagraph () . . . . 9, 20
\textperiodcentered (·) . 9, 20,
116
\textpertenthousand () . 20
\textperthousand (‰) 20, 117
\textpeso () ........... 18
\textphi (F) ............ 11
\textpilcrow () ........ 20
\textpipe (|) ........... 11
\textpipe () ........... 14
\textpipevar (F) . . . . . . . . . 12
\textpm (±) . . . . . . . . 67, 116
\textpmhg .............. 82
\textpolhook (a˛) ........ 15
\textprimstress (") . . . . . . 11
\textproto ............. 81
\textqplig (=) . . . . . . . . . 12
\textquestiondown (¿) . . . . . 9
\textquotedbl (") . . . 10, 114
\textquotedblleft (“) . . . . . 9
\textquotedblright (”) . . . . 9
\textquoteleft (‘) . . . . . . . . 9
\textquoteright (’) . . . . . . . 9
\textquotesingle (') . 20, 114
\textquotestraightbase () 20
\textquotestraightdblbase ()
......... 20
\textraiseglotstop (ij) . . . 11
\textraisevibyi (ğ) . . . . . . 11
\textraising (a
fi) ........ 15
\textramshorns (7) . . . . . . . 11
\textrangle (〉) . . . . . 57, 114
\textrbrackdbl () . . . . . . . 57
\textrecipe () . . . . . 20, 102
\textrectangle (¨) . . . . . . . 12
\textreferencemark () 20, 21
\textregistered (®) 9, 19, 116
\textretracting (a
ffl) . . . . . . 15
\textretractingvar (˚) . . . 12
\textrevapostrophe (\) . . . . 11
\textreve (9) ........... 11
\textrevepsilon (3) . . 11, 103
\textreversedvideodbend ()
......... 89
\textrevglotstop (Q) . . . . . 11
\textrevscl (v) ......... 12
159
\textrevscr (z) ......... 12
\textrevyogh (ź) ........ 11
\textrhooka ( ) ......... 12
\textrhooke (*) . . . . . . . . . 12
\textrhookepsilon (+) . . . . 12
\textrhookopeno (:) . . . . . . 12
\textrhookrevepsilon (Ç) . 12
\textrhookschwa (Ä) . . . . . . 12
\textrhoticity (~) . . . . . . . 12
\textrightarrow (→) . . . . . 41
\textringmacron (
˚
¯
a) . . . . . . 15
\textroundcap (“a) . . . . . . . 15
\textrptr (¿) ........... 12
\textrquill () ......... 57
\textrtaild (ã) ......... 12
\textrtaild ( ) ......... 14
\textrtailhth (/) . . . . . . . 12
\textrtaill (í) .......... 12
\textrtailn (ï) ......... 11
\textrtailr (ó) ......... 11
\textrtails (ù) . . . . . . . . . 11
\textrtailt (ú) ......... 11
\textrtailt () ......... 14
\textrtailz (ü) ......... 11
\textrtblock ( ) . . . . . . . . 97
\textrthook ($) .......... 11
\textrthooklong (´) . . . . . . 12
\textsarab ............. 87
\textsca (À) ............ 11
\textscaolig (q) ........ 12
\textscb (à) ............ 11
\textscdelta (r) ........ 12
\textsce (ď) ............ 11
\textscf (s) ............ 12
\textscg (å) ............ 11
\textsch (Ë) ............ 11
\textschwa (@) .......... 11
\textschwa ( ) .......... 14
\textsci (I) ............ 11
\textscj (ĺ) ............ 11
\textsck (t) ............ 12
\textscl (Ï) ............ 11
\textscm (w) ........... 12
\textscn (ð) ............ 11
\textscoelig (Œ) ........ 11
\textscomega (ś) ........ 11
\textscp (x) ............ 12
\textscq (y) ............ 12
\textscr (ö) ............ 11
\textscripta (A) . . . . . . . . 11
\textscriptg (g) ........ 11
\textscriptv (V) ........ 11
\textscriptv () ......... 14
\textscu (Ú) ............ 11
\textscy (Y) ............ 11
\textseagull (a) ........ 15
\textsecstress () . . . . . . . 11
\textsection (§) . . . . . . 9, 20
\textservicemark () . . . . . 19
\textsevenoldstyle () . . . 20
\textSFi ( ) ............ 97
\textSFii ( ) ........... 97
\textSFiii ( ) . . . . . . . . . . 97
\textSFiv ( ) ........... 97
\textSFix ( ) ........... 97
\textSFl ( ) ............ 97
\textSFli ( ) ........... 97
\textSFlii ( ) . . . . . . . . . . 97
\textSFliii ( ) ......... 97
\textSFliv ( ) . . . . . . . . . . 97
\textSFv ( ) ............ 97
\textSFvi ( ) ........... 97
\textSFvii ( ) . . . . . . . . . . 97
\textSFviii ( ) ......... 97
\textSFx ( ) ............ 97
\textSFxi ( ) ........... 97
\textSFxix ( ) . . . . . . . . . . 97
\textSFxl ( ) ........... 97
\textSFxli ( ) . . . . . . . . . . 97
\textSFxlii ( ) ......... 97
\textSFxliii ( ) . . . . . . . . 97
\textSFxliv ( ) ......... 97
\textSFxlix ( ) ......... 97
\textSFxlv ( ) . . . . . . . . . . 97
\textSFxlvi ( ) ......... 97
\textSFxlvii ( ) . . . . . . . . 97
\textSFxlviii ( ) . . . . . . . 97
\textSFxx ( ) ........... 97
\textSFxxi ( ) . . . . . . . . . . 97
\textSFxxii ( ) ......... 97
\textSFxxiii ( ) . . . . . . . . 97
\textSFxxiv ( ) ......... 97
\textSFxxv ( ) . . . . . . . . . . 97
\textSFxxvi ( ) ......... 97
\textSFxxvii ( ) . . . . . . . . 97
\textSFxxviii ( ) . . . . . . . 97
\textSFxxxix ( ) . . . . . . . . 97
\textSFxxxvi ( ) . . . . . . . . 97
\textSFxxxvii ( ) . . . . . . . 97
\textSFxxxviii ( ) . . . . . . . 97
\textshade ( ) . . . . . . . . . . 97
\textsixoldstyle () . . . . . 20
\textsoftsign (ž) ........ 11
\textspleftarrow (˝) . . . . . 12
\textsterling (£) . . . . . 9, 18
\textstretchc (Â) . . . . . . . 11
\textstretchcvar ($) . . . . . 12
\textstyle . . . . . 105, 106, 113
\textsubacute (a
›) . . . . . . . 15
\textsubarch (a
“) . . . . . . . . 15
\textsubbar (a
¯) ......... 15
\textsubbridge (a”) . . . . . . . 15
\textsubcircum (a
ˆ) . . . . . . . 15
\textsubdot (a
˙) ......... 15
\textsubdoublearrow (˙) . . 12
\textsubgrave (a
‹) . . . . . . . 15
\textsublhalfring (a
–) . . . . 15
\textsubplus (a
ff) . . . . . . . . 15
\textsubrhalfring (a
») . . . . 15
\textsubrightarrow (¯) . . . 12
\textsubring (a
˚) . . . . . . . . 15
\textsubsquare (a«) . . . . . . . 15
\textsubtilde (a
˜) . . . . . . . 15
\textsubumlaut (a
¨) . . . . . . . 15
\textsubw (a—) ........... 16
\textsubwedge (a
ˇ) . . . . . . . 16
\textsuperimposetilde (a
&) . 16
\textsuperscript ........ 16
\textsurd (√) ........... 67
\textswab .............. 68
\textsyllabic (a
") . . . . . . . 16
\texttctclig (tC) ........ 11
\textteshlig (Ù) . . . . . . . . 11
\textteshlig ( ) . . . . . . . . 14
\texttheta (T) .......... 11
\textthing (N) .......... 91
\textthorn (þ) .......... 11
\textthornvari (P) . . . . . . . 12
\textthornvarii (Q) . . . . . . 12
\textthornvariii (R) . . . . . 12
\textthornvariv (S) . . . . . . 12
\textthreeoldstyle () . . . 20
\textthreequarters (¾) 67, 116
\textthreequartersemdash ()
......... 20
\textthreesuperior (³) 67, 116
\texttildedot (˜
˙
a) . . . . . . . 16
\texttildelow () . . . 20, 115
\texttimes (×) .......... 67
\texttoneletterstem (£) . . . 11
\texttoptiebar (
>
a) . . . . . . . 16
\texttrademark (™) . 9, 19, 117
\texttslig (ţ) .......... 11
\textturna (5) .......... 11
\textturncelig (ŕ) . . . . . . 11
\textturnglotstop (E) . . . . 12
\textturnh (4) .......... 11
\textturnk (ľ) .......... 11
\textturnlonglegr (Õ) . . . . 11
\textturnm (W) . . . . . . . . . 11
\textturnmrleg (î) . . . . . . 11
\textturnr (ô) .......... 11
\textturnrrtail (õ) . . . . . . 11
\textturnsck (u) ........ 12
\textturnscripta (6) . . . . . 11
\textturnscu ({) ........ 12
\textturnt (Ø) .......... 11
\textturnthree (C) . . . . . . . 12
\textturntwo (A) . . . . . . . . 12
\textturnv (2) .......... 11
\textturnw (û) .......... 11
\textturny (L) .......... 11
\texttwelveudash () . . . . . 20
\texttwooldstyle ........ 20
\texttwooldstyle () . . . . . 20
\texttwosuperior (²) . 67, 116
\textuncrfemale (8) . . . . . . 12
\textunderscore ( ) . . . . . . . 9
\textuparrow (↑) ........ 41
\textupblock ( ) . . . . . . . . 97
\textupfullarrow (˘) . . . . . 12
\textupsilon (U) . . . . . . . . 11
\textupstep (Ţ) ......... 11
\textvbaraccent (IJa) . . . . . . 16
\textvbaraccent ( ) . . . . . . 17
\textvertline (Š) ........ 12
\textvibyi (ğ) .......... 12
\textvibyy (ů) .......... 12
160
\textvisiblespace ( ) . . . . . 9
\textwon () ........... 18
\textwynn () ........... 12
\textxswdown (U) . . . . . . . . 91
\textxswup (T) ......... 91
\textyen (¥) . . . . . . . 18, 116
\textyogh (Z) ........... 12
\textyogh ( ) ........... 14
\textzerooldstyle () . . . . 20
\TH (Þ) . . . . . . . . . . . . 10, 116
\th (þ) . . . . . . . . . . . . 10, 116
Th`anh, H`an Th´
ˆe . . . . . . . . 107
\therefore ( ) .......... 32
\therefore (∴) . . . . . . . 30, 64
\therefore (∴) .......... 64
\Thermo ............... 91
\Theta (Θ) ............. 50
\theta (θ) ............. 50
\thetaup (θ) ............ 50
\thething (N) .......... 91
\thickapprox (≈) . . . . . . . . 30
\thicksim (∼) .......... 30
\thickvert () .......... 55
thin space . . . . . . . . . . . . . 113
\ThinFog ( ) ........... 91
\thinstar () ........... 25
\third ( ) ............. 66
thirty-second note . see musical
symbols
\Thorn (Þ) ............. 13
\thorn ( ) ............. 13
\thorn ( ) ............. 13
\thorn (þ) ............. 13
thousandths . . . . . . . . . . . see
\textperthousand
\threesim (∼
∼
∼) ......... 104
tick ......... see check marks
tilde 9, 11, 13, 15–16, 18, 20, 57,
59, 61, 107, 115
extensible . . . . . . . 59, 61
vertically centered . . . 115
\tilde (˜) . . . . . . . . . 57, 107
\tildel ( ) ............ 13
time of day . . . . . . . . . . 91, 92
\timelimit (T) ......... 93
\times (×) ............. 22
\times (×) ............. 24
Times Roman (font) . . 18, 102
timing (package) . . . . . . . . . 70
tipa (package) 11, 12, 14–17, 103,
119, 120
tipx (package) . . . . 12, 119, 120
\tndtstile ( ) . . . . . . . . 35
\tnststile ( ) . . . . . . . . . 35
\tntstile ( ) . . . . . . . . . 35
\tnttstile ( ) . . . . . . . . 35
\to ........ see \rightarrow
\ToBottom (½) ........... 90
\tone ................. 12
\top (>) . . . . . . . . . 22, 51, 105
\top () ............... 52
\topbot (⊥>) . . . . . . . . 105, 107
\topdoteq ( ) .......... 32
torus ( ) . see alphabets, math
\ToTop (¼) ............. 90
trademark . see \texttrademark
\TransformHoriz ( ) . . . . 36
transforms . . . . . . . . . . 36, 63
\TransformVert ( ) . . . . . . 36
transliteration
semitic . . . . . . . . . . 14, 17
transliteration symbols . . . . 14
transpose . . . . . . . . . . . . . . 22
transversal intersection . . . see
\pitchfork
trema (¨a) . . . . . . . see accents
trfsigns (package) 36, 52, 63, 119
\triangle (4) .......... 65
\triangle (△) .......... 40
triangle relations . . . . . . 39, 40
\TriangleDown ( ) . . . . . . . 79
\TriangleDown ( vs. ) . 101
\TriangleDown ( ) . . . . . . . 80
\triangledown (O) . . . . . . . 66
\triangledown (▽) . . . . . . . 40
\triangleeq () ......... 40
\TriangleLeft ( ) . . . . . . . 79
\triangleleft ( ) . . . . . . . 40
\triangleleft () . . . . . . . 22
\triangleleft (◁) . . . . . . . 40
\trianglelefteq ( ) . . . . . 40
\trianglelefteq (E) . . . . . 39
\trianglelefteq () . . . 39, 40
\trianglelefteqslant (P) . 40
\triangleq (,) . . . . . . 21, 39
\triangleq () .......... 40
\TriangleRight ( ) . . . . . . 79
\triangleright ( ) . . . . . . 40
\triangleright () . . . . . . . 22
\triangleright (▷) ...... 40
\trianglerighteq ( ) . . . . 40
\trianglerighteq (D) . . . . 39
\trianglerighteq () . . 39, 40
\trianglerighteqslant (Q) 40
triangles . . . . 66, 73, 79–80, 94
\TriangleUp ( ) . . . . . . . . 79
\TriangleUp ( vs. ) . . . 101
\TriangleUp ( ) . . . . . . . . 80
\triple ............... 57
\triplefrown () . . . . . . . . 48
\triplesim () .......... 33
\triplesmile () . . . . . . . . 48
trsym (package) . . . 36, 119, 120
\tsbm ( ) .............. 95
\tsdtstile ( ) . . . . . . . . 35
\tsmb ( ) .............. 95
\tsmm ( ) .............. 95
\tsststile ( ) ......... 35
\Tsteel (œ) ............ 73
\tststile ( ) . . . . . . . . . 35
\tsttstile ( ) . . . . . . . . 35
\ttdtstile ( ) . . . . . . . . 35
\TTsteel (š) ........... 73
\ttststile ( ) . . . . . . . . . 35
\tttstile ( ) . . . . . . . . . 35
\ttttstile ( ) . . . . . . . . 35
TUGboat . . . . . . . . . . . . . . 59
\Tumbler () ........... 90
turnstile (package) . 35, 119, 120
\TwelweStar ( ) . . . . . . . . 78
twiddle . . . . . . . . . . . see tilde
\twoheaddownarrow (↡) . . . . 43
\twoheadleftarrow () . . . 41
\twoheadleftarrow (↞) . . . 44
\twoheadnearrow () . . . . . 44
\twoheadnwarrow () . . . . . 44
\twoheadrightarrow () . . 41
\twoheadrightarrow (↠) . . 44
\twoheadsearrow () . . . . . 44
\twoheadswarrow () . . . . . 44
\twoheaduparrow (↟) . . . . . . 44
\twonotes () ........... 88
txfonts (package) . . . . . . 21–23,
27, 30, 31, 36–38, 41, 42, 48,
50–52, 65, 66, 68, 100, 102,
115, 119, 120
type1cm (package) . . . . . . . 100
Type 1 (font) . . . . . . . . . . 112
U
\U (a
˘) ................. 17
\U ( ) ................. 14
\u (˘a) ................. 14
\UArrow (↑) .......... 72
\UB (<
) ................ 89
\ubar (u) .............. 13
\ubarbbrevis (ε) . . . . . . . 95
\ubarbrevis (δ) ......... 95
\ubarsbrevis (φ) . . . . . . . 95
\ubrevislonga (κ) . . . . . . . 95
ubulb.fd (file) . . . . . . 111, 112
ucs (package) . . . . . . . . 117, 118
\udesc ( ) ............. 13
\udot () ............... 23
\udotdot () . . . . . . . . . 24, 64
\udots () ............. 64
\udtimes (]) ........... 24
\UHORN (Ư) ............. 10
\uhorn (ư) ............. 10
\ulcorner () ........... 53
\ulcorner (p) ........... 53
\ulcorner () ........... 55
\ullcorner () .......... 55
\ulrcorner () .......... 55
ulsy (package) . 24, 48, 103, 119
\Umd (g
a) .............. 89
umlaut (¨a) . . . . . . see accents
161
unary operators . . . . . . . . . . 21
\unclear (k) ........... 93
\underaccent .......... 107
\underarc (a
^
) ........... 17
\underarch (a) . . . . . . . . . . 16
\underbrace ( ) . . . . . . 60
\underbrace (
) ......... 60
\underbrace (|{z}) . . . . . . . 60
\underbrace (|{z}) . . . . . . . 59
\underbracket ( ) . . . . . . . 60
\underbracket ( ) . . . 108, 109
\underdots ( ) . . . . . . . . . . 18
\undergroup ( ) . . . . . . . 60
\undergroup () ........ 60
\underleftarrow (←−) . . . . . 59
\underleftharp (
) . . . . . . . 47
\underleftharpdown (
) . . . 47
\underleftrightarrow (←→) 59
underline . . . . . . . 9, 21, 59, 61
\underline ( ) .......... 59
\underlinesegment (zx) . . . . 60
\underparenthesis (|}) 108, 109
\underrightarrow (−→) . . . . 59
\underrightharp (
) . . . . . . 47
\underrightharpdown (
) . . 47
\underring ( ) . . . . . . . . . . 18
underscore . . . . . see underline
underscore (package) . . . . . . . 9
\underset ............. 104
undertilde (package) 61, 119, 120
\undertilde ( ) ......... 18
\underwedge ( ) ......... 18
Unicode . . . . . . 8, 97, 117–118
union ............ see \cup
unit disk ( ) . . . see alphabets,
math
\unitedpawns (u) . . . . . . . . 93
units (package) . . . . . . . . . . 67
unity ( ) . . see alphabets, math
universa (package) . 80, 90, 119,
120
universal (package) 75, 77, 80, 90,
119, 120
\unlhd (E) . . . . . . . . . . 22, 23
\unlhd () . . . . . . . . . . 39, 40
\unrhd (D) . . . . . . . . . . 22, 23
\unrhd () . . . . . . . . . . 39, 40
\upalpha (α) ............ 51
\UParrow (K) ............ 88
\Uparrow (⇑) . . . . . . . . . 41, 54
\Uparrow (⇑) ............ 44
\uparrow (↑) . . . . . . 41, 54, 100
\uparrow (↑) ............ 44
\uparrowtail (!) ........ 44
\upbar ................ 16
\upbeta (β) ............. 51
\upbracketfill ........ 109
\upchi (χ) ............. 51
\Updelta (∆) ............ 51
\updelta (δ) ............ 51
\Updownarrow (m) . . . . . 41, 54
\Updownarrow (⇕) ........ 44
\updownarrow (l) . . . . . 41, 54
\updownarrow (↕) ........ 44
\updownarrows ( ) . . . . . . . 42
\updownarrows () . . . . . . . 44
\updownharpoonleftright (Q) 46
\updownharpoonrightleft (U) 46
\updownharpoons ( ) . . . . . . 43
\updownharpoons (⥮) . . . . . . 46
\Updownline (∥) ......... 33
\updownline (∣) ......... 33
\upepsilon (ε) .......... 51
\upeta (η) ............. 51
\upfilledspoon (q) . . . . . . . 47
\upfootline (y) ......... 33
\upfree () ............ 33
\Upgamma (Γ) ............ 51
\upgamma (γ) ............ 51
upgreek (package) . 51, 119, 120
\upharpoonccw (↿) ........ 46
\upharpooncw (↾) ........ 46
\upharpoonleft ( ) . . . . . . . 43
\upharpoonleft () . . . . . . . 41
\upharpoonright ( ) . . . . . . 43
\upharpoonright () ...... 41
\upiota (ι) ............. 51
\upkappa (κ) ............ 51
\Uplambda (Λ) ........... 51
\uplambda (λ) ........... 51
\uplett ............... 16
\uplsquigarrow (¡) . . . . . . . 44
\uplus ( ) ............. 23
\uplus (]) ............. 22
\uplus () ............. 24
\upmapsto (↥) ........... 44
\upModels (ñ) ........... 33
\upmodels (á) ........... 33
\upmu (µ) .............. 51
\upnu (ν) .............. 51
\Upomega (Ω) ........... 51
\upomega (ω) ........... 51
\upp ( ) ............... 18
\upparenthfill ........ 109
\Upphi (Φ) ............. 51
\upphi (φ) ............. 51
\Uppi (Π) .............. 51
\uppi (π) .............. 51
\uppitchfork (⋔) ........ 47
\uppropto () ........... 33
\Uppsi (Ψ) ............. 51
\uppsi (ψ) ............. 51
upquote (package) . . . . . . . 115
\uprho (ρ) ............. 51
upright Greek letters . . . 50, 51
\uprsquigarrow (©) . . . . . . . 44
upside-down symbols . . . . . 114
upside-down symbols 11–13, 17,
103
\Upsigma (Σ) ............ 51
\upsigma (σ) ............ 51
\Upsilon (Υ) . . . . . . . . . . . 50
\upsilon (υ) ............ 50
\upsilonup (υ) .......... 50
\upslice () ........... 25
\upspoon (⫯) ............ 47
\upt ( ) ............... 18
\uptau (τ) .............. 51
\uptherefore (∴) . . . . . 24, 64
\Uptheta (Θ) ........... 51
\uptheta (θ) ............ 51
\uptodownarrow ( ) . . . . . . 42
\upuparrows ( ) . . . . . . . . . 42
\upuparrows () ........ 41
\upuparrows (⇈) ......... 44
\upupharpoons ( ) . . . . . . . 43
\Upupsilon (Υ) .......... 51
\upupsilon (υ) .......... 51
\upvarepsilon (ε) . . . . . . . . 51
\upvarphi (ϕ) ........... 51
\upvarpi (ϖ) ........... 51
\upvarrho (ρ) ........... 51
\upvarsigma (σ) ......... 51
\upvartheta (ϑ) ......... 51
\upVdash (⍊) ........... 33
\upvdash (⊥) ............ 33
\Upxi (Ξ) .............. 51
\upxi (ξ) .............. 51
\upY () ............... 24
\upzeta (ζ) ............. 51
\Uranus ( ) ............ 71
\Uranus (Ç) ............. 71
\uranus (Z) ............. 71
\urcorner () ........... 53
\urcorner (q) ........... 53
\urcorner () ........... 55
url (package) . . . . . . . . . . . 115
\US (␟) ................ 72
\usepackage ............. 8
ushort (package) . . 61, 119, 121
\ushort ( ) ............. 61
\ushortdw ( ) ........... 61
\ushortw ( ) ............ 61
\ut (a
˜) ................ 16
UTF-8 . . . . . . . . . . . . 117, 118
utf8x (inputenc package option) .
........ 117
\utilde (e) ............. 61
\utimes (^) ............ 24
\utimes () ............ 24
Utopia (font) . . . . . . . . . 18, 30
V
\v (ˇa) ................. 14
\vara ( ) .............. 13
\varangle () .......... 66
\varbigcirc (,) ........ 22
\VarClock ( ) . . . . . . . . . . 91
\varclub (♧) ........... 67
\varclubsuit (p) . . . . . . . . 66
\varcoppa () ........... 87
\varcurlyvee () ........ 22
162
\varcurlywedge () ...... 22
\vardiamond (♦) ......... 67
\vardiamondsuit (q) . . . . . . 66
\varEarth ( ) ........... 71
\varepsilon (ε) ......... 50
\varepsilonup (ε) . . . . . . . . 50
\VarFlag ( ) ........... 91
varg (txfonts/pxfonts package op-
tion) . . . . . . . . . . . . . 51
\varg (1) .............. 51
\varg ( ) .............. 13
\vargeq ( ) ............ 38
\varhash ( ) ........... 66
\varheart (♥) .......... 67
\varheartsuit (r) . . . . . . . 66
\varhexagon (9) . . . . . . . . . 78
\varhexstar (B) ......... 77
\vari () ............... 13
variable-sized symbols . . 25–30,
100, 102
\VarIceMountain ( ) . . . . . 91
\varinjlim (lim
−→) . . . . . . . . . 49
\varint (r) ............ 26
\various (R) ........... 93
\varkappa (κ) .......... 50
\varleq ( ) ............ 38
\varliminf (lim) . . . . . . . . . 49
\varlimsup (lim) . . . . . . . . . 49
\varmathbb ............. 68
\VarMountain ( ) . . . . . . . . 91
\varnothing (∅) . . . . 21, 65, 66
\varnothing () ......... 66
\varnotin ( ) ........... 52
\varnotowner ( ) . . . . . . . . 52
\varoast () ........... 22
\varobar () ........... 22
\varobslash () . . . . . . . . . 22
\varocircle () . . . . . . . . . 22
\varodot () ........... 22
\varogreaterthan (5) . . . . 22
\varoiiintclockwise (F) . 27
\varoiiintctrclockwise (N)
......... 28
\varoiint (!) .......... 28
\varoiintclockwise (B) . . 28
\varoiintctrclockwise (J) 28
\varoint (u) ........... 26
\varointclockwise (-) . . . . 28
\varointclockwise (ff) . . . . 28
\varointctrclockwise (+) . 28
\varointctrclockwise (fl) . . 28
\varolessthan (4) . . . . . . . 22
\varomega ( ) ........... 13
\varominus () .......... 22
\varopeno ( ) ........... 13
\varoplus () .......... 22
\varoslash () .......... 22
\varotimes () .......... 22
\varovee (6) ........... 22
\varowedge (7) .......... 22
\varparallel (∥) . . . . . . . . 31
\varparallelinv () . . . . . . 31
\varpartialdiff (Ç) . . . . . . 53
\varphi (ϕ) ............ 50
\varphiup (ϕ) ........... 50
\varpi () ............. 50
\varpi ($) ............. 51
\varpiup ($) ........... 50
\varprod () ........... 28
\varprojlim (lim
←−) ........ 49
\varpropto (∝) ......... 30
\varpropto (∝) .......... 33
\varQ ( ) .............. 90
\varrho () ............. 50
\varrho (%) ............. 51
\varrhoup (%) ........... 50
\varsigma (ς) ........... 50
\varsigmaup (ς) ......... 50
\varspade (♤) .......... 67
\varspadesuit (s) . . . . . . . 66
\varsqsubsetneq ( ) . . . . . 37
\varsqsubsetneqq ( ) . . . . 37
\varsqsupsetneq ( ) . . . . . 37
\varsqsupsetneqq ( ) . . . . 37
\varstar ( ) ............ 23
\varstigma () .......... 87
\varsubsetneq ( ) . . . . . . . 37
\varsubsetneq () . . . . . . . 36
\varsubsetneq () . . . . . . . 37
\varsubsetneqq ( ) . . . . . . 37
\varsubsetneqq () . . . . . . 36
\varsubsetneqq () . . . . . . . 37
\VarSummit ( ) ......... 91
\varsupsetneq ( ) . . . . . . . 37
\varsupsetneq () . . . . . . . 36
\varsupsetneq () . . . . . . . 37
\varsupsetneqq ( ) . . . . . . 37
\varsupsetneqq () . . . . . . 36
\varsupsetneqq () . . . . . . . 37
\VarTaschenuhr ( ) . . . . . . 91
\vartheta (ϑ) ........... 50
\varthetaup (ϑ) ......... 50
\vartimes (") ........... 22
\vartriangle (M) ........ 66
\vartriangle (△) ........ 40
\vartriangleleft ( ) . . . . 40
\vartriangleleft (C) . . . . 39
\vartriangleleft () . . 39, 40
\vartriangleright ( ) . . . . 40
\vartriangleright (B) . . . 39
\vartriangleright () . 39, 40
\varv (3) .............. 51
\varvarpi (È) .......... 51
\varvarrho (Æ) .......... 51
\varw (4) .............. 51
\vary (2) .............. 51
\VBar ( ) .............. 79
\vbipropto () .......... 24
\vcentcolon (:) .......... 34
\vcenter ............. 104
\vcrossing () .......... 33
\VDash ( ) ............. 32
\VDash (⊫) ............. 33
\Vdash ( ) ............. 32
\Vdash () ............. 30
\Vdash (⊩) ............. 33
\vDash ( ) ............. 32
\vDash () ............. 30
\vDash (⊧) ............. 33
\vdash (`) ............. 30
\vdash (⊢) ............. 33
\vdotdot (∶) . . . . . . . . . 24, 64
\vdots (.
.
.) .............. 63
\vdots (⋮) .............. 64
\vec () ............... 58
\vec () ............... 57
\Vectorarrow (p) ......... 67
\Vectorarrowhigh (P) . . . . . . 67
\vee ( ) ............... 23
\vee (∨) ............... 22
\vee (∨) ............... 24
\veebar ( ) ............ 23
\veebar (Y) ............ 22
\veedot () ............ 24
\veedoublebar ( ) . . . . . . . 23
\Venus ( ) ............. 71
\Venus (Ã) ............. 71
\venus (♀) ............. 71
\vernal () ............ 71
versicle ( ) . . . . . . . . . . . . 118
\VERT (
) .............. 57
\Vert (k) . . . . . . . . . . . 54, 56
\vert (|) . . . . . . . . . . . . 54, 56
\vertbowtie () ......... 24
\vertdiv () ............ 24
\VHF (@) ............... 70
\Vier (ˇ“) .............. 89
vietnam (package) . . . . . . . 119
\Village ( ) . . . . . . . . 91
\vin ( ) ............... 53
vinculum . . . . . . see \overline
\ViPa (>) .............. 89
\Virgo (å) ............. 71
\virgo (`) ............ 71
\VM (>
) ................ 89
vntex (package) . . . . . . . 10, 14
\vod (v
˚) ............... 13
\voicedh ( ) ............ 13
\vppm (¯
˙
˙) .............. 95
\vpppm (¯
˙
˙
˙) ............. 95
\vrule ................ 97
\VT (␋) ................ 72
\vv (#») ............... 61
\VvDash () ............ 31
\Vvdash ( ) ............ 32
\Vvdash () ............ 30
\Vvdash () ............ 33
\vvvert ( ) ............ 55
W
\WashCotton (‰) . . . . . . . . 90
\WashSynthetics (Š) . . . . 90
163
\WashWool (‹) .......... 90
\wasylozenge (◊) ........ 88
\wasypropto () . . . . . . . . . 31
wasysym (package) . . 13, 18, 20,
22, 23, 26, 30, 31, 36–38, 41,
64–66, 70, 71, 73, 77, 78, 88,
101, 119, 120
\wasytherefore (∴) ...... 64
wavy-line delimiters . . . . 55, 56
\wbetter (f) ........... 93
\wdecisive (h) ......... 93
\weakpt (J) ............ 93
\WeakRain ( ) . . . . . . . . . . 91
\WeakRainCloud ( ) . . . . . . 91
weather symbols . . . . . . . . . 91
\Wecker ( ) ........... 91
\wedge ( ) ............. 23
\wedge (∧) ............. 22
\wedge (∧) ............. 24
\wedgedot () ........... 24
Weierstrass ℘function . see \wp
\wfermion ( ) ........... 74
\Wheelchair (w) ......... 90
\whfermion ( ) ......... 74
\whistle (a
Ţ) ............ 16
\WhiteBishopOnBlack (A) 94
\WhiteBishopOnWhite (B) 94
\WhiteEmptySquare (0) . 94
\WhiteKingOnBlack (J) . 94
\WhiteKingOnWhite (K) . 94
\WhiteKnightOnBlack (M) 94
\WhiteKnightOnWhite (N) 94
\WhitePawnOnBlack (O) . 94
\WhitePawnOnWhite (P) . 94
\WhiteQueenOnBlack (L) 94
\WhiteQueenOnWhite (Q) 94
\WhiteRookOnBlack (S) . 94
\WhiteRookOnWhite (R) . 94
\whitestone ............ 94
whole note see musical symbols
Wick contractions . . . . . . . 109
\widearc (Ø) ............ 60
\widearrow ( ) .......... 60
\widebar ( ) ............ 60
\widecheck ( ) .......... 60
\widehat (̂) ............ 60
\widehat (b) ............ 59
\wideOarc (ä) ........... 60
\wideparen ( ) .......... 60
\wideparen () .......... 60
\wideparen () .......... 60
\wideparen (Û) .......... 59
\widering (˚) ........... 60
\widering (˚
) ........... 60
\widering (˚
Û) ........... 59
\widetilde (̃) .......... 60
\widetilde (e) . . . . . . . 59, 61
\widetriangle (Ê) . . . . . . . 59
\wind ................. 91
window ................ 90
Windows®............ 115
\with (&) .............. 24
\with (v) .............. 93
\withattack (A) ......... 93
\withidea (E) .......... 93
\withinit (C) ........... 93
\without (w) ........... 93
\wn (?) ................ 21
woman . . . . . . . . . . . . . 81, 90
\Womanface (þ) ......... 90
won .......... see \textwon
world ................. 90
\wp (℘) ................ 51
\wp (℘) ................ 52
\wr (o) ................ 22
\wr () ................ 24
\wreath () ............. 24
wreath product . . . . . . see \wr
\Writinghand (b) . . . . . . . . 90
wsuipa (package) 13, 16, 18, 101,
103, 107, 119, 120
\wupperhand (c) ......... 93
X
\x ( ) ................. 65
\x (˙
˙˙
˙) ................. 95
\XBox (4) .............. 77
Xdvi . . . . . . . . . . . . . . 47, 103
X
E
L
A
T
E
X .............. 118
xfrac (package) . . . . . . . . . . 67
\xhookleftarrow (←−) . . . . . 62
\xhookrightarrow (−→) . . . . 62
\Xi (Ξ) ................ 50
\xi (ξ) ................ 50
\xiup (ξ) .............. 50
\xLeftarrow (⇐=) . . . . . . . . 62
\xleftarrow (←−) ........ 61
\xleftharpoondown (−) . . . 62
\xleftharpoonup (−) . . . . . 62
\xLeftrightarrow (⇐⇒) . . . 62
\xLeftrightarrow (⇐⇒) . . . 62
\xleftrightarrow (←→) . . . 62
\xleftrightarrow (←→) . . . 62
\xleftrightharpoons (−
−) . 62
\xlongequal (===) . . . . . . . . 63
\xlongequal (===) . . . . . . . . 62
\xLongleftarrow (⇐==) . . . . 62
\xlongleftarrow (←−−) . . . . 62
\xLongleftrightarrow (⇐==⇒)
......... 62
\xlongleftrightarrow (←−−→)
......... 62
\xLongrightarrow (==⇒) . . . 62
\xlongrightarrow (−−→) . . . 62
\xmapsto (7−→) .......... 62
\xmapsto (7−→) .......... 63
XML ................ 117
\xRightarrow (=⇒) ........ 62
\xrightarrow (−→) . . . . . . . 61
\xrightharpoondown (−) . . 62
\xrightharpoonup (−) . . . . 62
\xrightleftharpoons (−
−) . 62
\xrightleftharpoons (−
−) . 62
Xs ................ 77,90
\XSolid ( ) ............ 77
\XSolidBold ( ) . . . . . . . . 77
\XSolidBrush ( ) . . . . . . . . 77
\xswordsdown (U) . . . . . . . . 91
\xswordsup (T) ......... 91
\xtwoheadleftarrow (−−−) 63
\xtwoheadrightarrow (−−−) 63
X
Y
-pic ................ 106
Y
\Ydown () ............. 22
yen ........... see \textyen
yfonts (package) 68, 69, 119, 120
yhmath (package) 58, 59, 61, 64,
107, 119
\Yinyang (Y) ........... 90
\Yleft () ............. 22
\yogh ( ) .............. 13
\yogh ( ) .............. 13
\Yright () ............ 22
Yu, Billy . . . . . . . . . . . . . . 108
\Yup () ............... 22
Z
Zapf Chancery (font) . . . . . . 68
Zapf Dingbats (font) . . . 75, 77
\Zborder ( ) ........... 80
\zeta (ζ) .............. 50
\zetaup (ζ) ............. 50
\Zodiac ............... 71
zodiacal symbols . . . . . . . . . 71
\Ztransf (.
.
.
.
.
.
.
.
.
.
.) ......... 36
\ztransf (.
.
.
.
.
.
.
.
.
.
.) ......... 36
\zugzwang (D) .......... 93
\Zwdr (ˇ“*) .............. 89
\ZwPa (A) .............. 89
164

Navigation menu