Manual De R
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 224 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Índice de cuadros
- Índice de figuras
- Prefacio
- Sobre los autores
- Introducción
- Tipos de objetos
- Guía de estilo
- Funciones básicas de
- Instrucciones de control
- Creación de funciones en
- Lectura de bases de datos
- Tablas de frecuencia
- Medidas de tendencia central
- Medidas de variabilidad
- Medidas de posición
- Medidas de correlación
- Distribuciones discretas
- Distribuciones continuas
- Verosimilitud
- Estudiando la normalidad
- Intervalos de confianza
- Función t.test
- Intervalo de confianza bilateral para la media \mu
- Intervalo de confianza bilateral para la diferencia de medias (\mu_1-\mu_2) de muestras independientes
- Intervalo de confianza bilateral para la diferencia de medias (\mu_1-\mu_2) de muestras dependientes o pareadas
- Intervalo de confianza unilateral para la media \mu
- Función Var.test
- Función var.test
- Función prop.test
- Función t.test
- Prueba de hipótesis
- Prueba de hipótesis para \mu de una población normal
- Prueba de hipótesis para \mu con muestras grandes
- Prueba de hipótesis para la proporción p
- Prueba de hipótesis para la varianza \sigma^2 de una población normal
- Prueba de hipótesis para el cociente de varianzas \sigma_1^2 / \sigma_2^2
- Prueba de hipótesis para la diferencia de medias \mu_1-\mu_2 con varianzas iguales
- Prueba de hipótesis para la diferencia de medias \mu_1-\mu_2 con varianzas diferentes
- Prueba de hipótesis para la diferencia de proporciones p_1 - p_2
- Prueba de hipótesis para la diferencia de medias pareadas
- Aproximación de integrales
- Curiosidades
- Bibliografía
- Índice alfabético

Freddy Hernández Barajas
Olga Cecilia Usuga Manco
Manual de R

Gracias a Dios por todo lo que me ha dado.

Índice general
Índice de cuadros VII
Índice de guras IX
Prefacio XIII
Sobre los autores XVII
1. Introducción 1
1.1. Orígenes ............................. 1
1.2. Descarga e instalación . . . . . . . . . . . . . . . . . . . . . . 2
1.3. Apariencia del programa . . . . . . . . . . . . . . . . . . . . 4
2. Tipos de objetos 7
2.1. Vectores ............................. 7
2.1.1. ¿Cómo extraer elementos de un vector? . . . . . . . . 8
2.2. Matrices ............................. 9
2.2.1. ¿Cómo extraer elementos de una matriz? . . . . . . . 10
2.3. Arreglos ............................. 11
2.3.1. ¿Cómo extraer elementos de un arreglo? . . . . . . . . 12
2.4. Marcodedatos ......................... 13
2.4.1. ¿Cómo extraer elementos de un marco de datos? . . . 13
2.4.2. ¿Cómo extraer subconjuntos de un marco de datos? . 14
2.5. Listas .............................. 16
2.5.1. ¿Cómo extraer elementos de una lista? . . . . . . . . . 17
3. Guía de estilo 21
3.1. Nombres de los archivos . . . . . . . . . . . . . . . . . . . . . 21
3.2. Nombres de los objetos . . . . . . . . . . . . . . . . . . . . . 21
3.3. Longitud de una línea de código . . . . . . . . . . . . . . . . 22
3.4. Espacios ............................. 22
3.5. Asignación ............................ 24
3.6. Puntoycoma .......................... 25
4. Funciones básicas de R27
4.1. ¿Qué es una función de R? ................... 27
4.2. Operadores de asignación . . . . . . . . . . . . . . . . . . . 29
iii

iv Contents
4.3. Operaciones básicas . . . . . . . . . . . . . . . . . . . . . . . 29
4.4. Pruebaslógicas ......................... 31
4.5. Operadores lógicos . . . . . . . . . . . . . . . . . . . . . . . 33
4.6. Funciones sobre vectores . . . . . . . . . . . . . . . . . . . . 35
4.7. Funciones matemáticas . . . . . . . . . . . . . . . . . . . . . 37
4.8. Función seq ........................... 38
4.9. Función rep ........................... 40
4.10. Funciones round,ceiling,floor ytrunc .......... 42
4.11. Funciones sort yrank ..................... 43
5. Instrucciones de control 47
5.1. Instrucción if .......................... 47
5.2. Instrucción if else ....................... 48
5.3. Instrucción ifelse ....................... 48
5.4. Instrucción for ......................... 49
5.5. Instrucción while ........................ 50
5.6. Instrucción repeat ....................... 51
6. Creación de funciones en R53
6.1. Función en R.......................... 53
6.2. Partes de una función en R.................. 53
7. Lectura de bases de datos 63
7.1. ¿En qué formato almacenar una base de datos? . . . . . . . 63
7.1.1. Almacenamiento de información en Excel . . . . . . . 63
7.1.2. Almacenamiento de información en bloc de notas . . 64
7.2. Función read.table ...................... 66
7.3. Lectura de bases de datos en Excel . . . . . . . . . . . . . . 68
8. Tablas de frecuencia 71
8.1. Tabla de contingencia con table ............... 71
Ejemplo: tabla de frecuencia de una vía . . . . . . . . . . . . 71
Ejemplo: tabla de frecuencia de dos vías . . . . . . . . . . . . 73
8.2. Función prop.table ...................... 73
Ejemplo: tabla de frecuencia relativa de una vía . . . . . . . . 74
Ejemplo: tabla de frecuencia relativa de dos vías . . . . . . . 74
8.3. Función addmargins ...................... 75
8.4. Función hist .......................... 76
9. Medidas de tendencia central 81
9.1. Media .............................. 82
9.2. Mediana ............................. 83
9.3. Moda ............................... 84
10.Medidas de variabilidad 87
10.1.Rango .............................. 88

Contents v
10.2. Desviación estándar muestral (S) ............... 89
10.3. Varianza muestral (S2) ..................... 91
10.4. Coeciente de variación (CV ) ................. 93
11.Medidas de posición 95
11.1.Cuantiles ............................. 96
12.Medidas de correlación 97
12.1. Función cor ........................... 97
13.Distribuciones discretas 103
13.1. Funciones disponibles para distribuciones discretas . . . . . 103
13.2. Distribuciones discretas generales . . . . . . . . . . . . . . . 109
14.Distribuciones continuas 115
14.1. Funciones disponibles para distribuciones continuas . . . . . 115
14.2. Distribuciones continuas generales . . . . . . . . . . . . . . . 122
15.Verosimilitud 127
15.1. Función de verosimilitud . . . . . . . . . . . . . . . . . . . . 127
15.2. Función de log-verosimilitud . . . . . . . . . . . . . . . . . . 127
15.3. Método de máxima verosimilitud para estimar parámetros . 128
15.4. Método de máxima verosimilitud para estimar parámetros en
modelos de regresión ...................... 140
16.Estudiando la normalidad 145
16.1. Consideraciones iniciales . . . . . . . . . . . . . . . . . . . . 145
16.2. Histograma y densidad . . . . . . . . . . . . . . . . . . . . . 146
16.3. Grácos cuantil cuantil . . . . . . . . . . . . . . . . . . . . . 149
16.4. Pruebas de normalidad . . . . . . . . . . . . . . . . . . . . . 156
17.Intervalos de conanza 161
17.1. Función t.test ......................... 161
17.1.1. Intervalo de conanza bilateral para la media µ. . . . 161
17.1.2. Intervalo de conanza bilateral para la diferencia de me-
dias (µ1−µ2) de muestras independientes . . . . . . . 163
17.1.3. Intervalo de conanza bilateral para la diferencia de me-
dias (µ1−µ2) de muestras dependientes o pareadas . 166
17.1.4. Intervalo de conanza unilateral para la media µ. . . 168
17.2. Función Var.test ........................ 169
17.2.1. Intervalo de conanza bilateral para la varianza σ2. . 169
17.3. Función var.test ........................ 170
17.3.1. Intervalo de conanza bilateral para la razón de varian-
zas σ2
1/σ2
2......................... 170
17.4. Función prop.test ....................... 171
17.4.1. Intervalo de conanza bilateral para la proporción p. 171
vi Contents
17.4.2. Intervalo de conanza bilateral para la diferencia de pro-
porciones p1−p2..................... 172
18.Prueba de hipótesis 173
18.1. Prueba de hipótesis para µde una población normal . . . . . 173
18.2. Prueba de hipótesis para µcon muestras grandes . . . . . . 175
18.3. Prueba de hipótesis para la proporción p........... 176
18.3.1. Prueba de Wald . . . . . . . . . . . . . . . . . . . . . 176
18.3.2. Prueba X2dePearson.................. 178
18.3.3. Prueba binomial exacta . . . . . . . . . . . . . . . . . 179
18.4. Prueba de hipótesis para la varianza σ2de una población nor-
mal ................................ 181
18.5. Prueba de hipótesis para el cociente de varianzas σ2
1/σ2
2. . . 182
18.6. Prueba de hipótesis para la diferencia de medias µ1−µ2con
varianzasiguales ......................... 188
18.7. Prueba de hipótesis para la diferencia de medias µ1−µ2con
varianzas diferentes . . . . . . . . . . . . . . . . . . . . . . . 190
18.8. Prueba de hipótesis para la diferencia de proporciones p1−p2192
18.9. Prueba de hipótesis para la diferencia de medias pareadas . . 193
19.Aproximación de integrales 197
19.1. Aproximación de Laplace unidimensional . . . . . . . . . . . 197
20.Curiosidades 201
20.1. ¿Cómo vericar si un paquete no está instalado para instalarlo
de forma automática? . . . . . . . . . . . . . . . . . . . . . . 201
Bibliografía 203
Índice alfabético 205


Índice de guras
1.1. Robert Gentleman (izquierda) y Ross Ihaka (derecha) creadores
de R. ................................ 2
1.2. Página del Cran. ......................... 3
1.3. Página de instalación para la primera ocasión. ......... 3
1.4. Página de descarga. ....................... 3
1.5. Apariencia del acceso directo para ingresar a R. ........ 4
1.6. Apariencia de R. ......................... 5
4.1. Ilustración de una función, tomada de www.mathinsight.org. 28
6.1. Ilustración de una función, tomada de www.mathinsight.org . 54
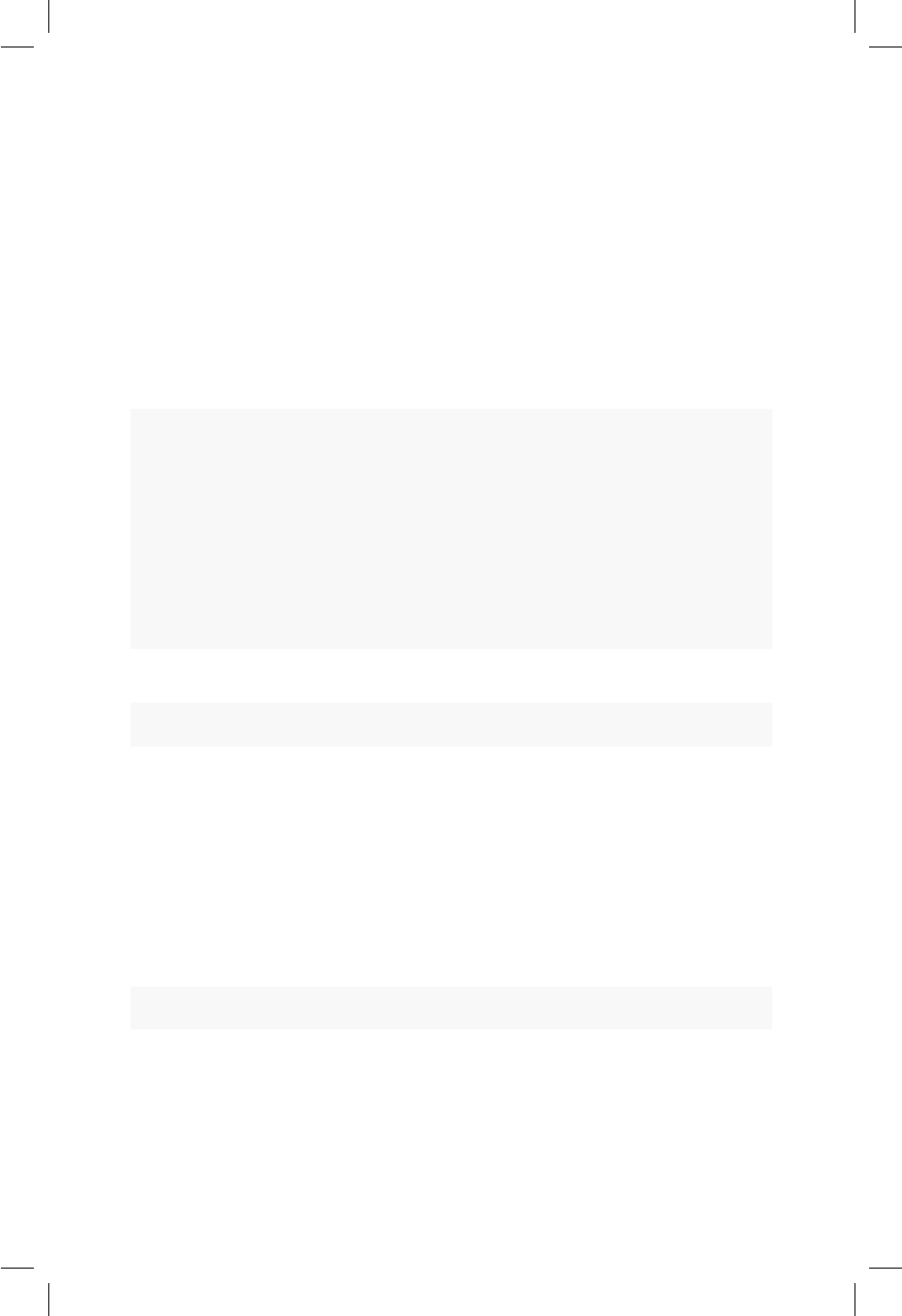
6.2. Ilustración del punto medio entre dos puntos, tomada de
https://www.slideshare.net/bigpassy/midpoint-between-two-
points ............................... 61
7.1. Forma de almacenar los datos en Excel. ............ 64
7.2. Almacenamiento de los datos en bloc de notas usando la barra
espaciadora ............................ 65
7.3. Almacenamiento de los datos en bloc de notas usando la barra
tabuladora ............................. 65
8.1. Ubicación de los puntos del ejemplo con límites en color azul. 78
10.1. Boxplot para el precio de los apartamentos dada la ubicación. 92
12.1. Diagrama de dispersión para precio versus área de los aparta-
mentos usados. .......................... 98
12.2. Matriz de coecientes de correlación. .............. 101
13.1. Función de masa de probabilidad para una Binomial(n=
18, p = 0.1)............................. 105
13.2. Fotografía del cangrejo de herradura, tomada de
http://sccoastalresources.com/home/2016/6/21/a-night-of-
horseshoe-crab-tagging ...................... 110
13.3. Función de masa de probabilidad para el número de satélites
por hembra. ............................ 111
ix

xÍndice de guras
13.4. Función de distribución acumulada para el número de satélites
por hembra. ............................ 112
13.5. Función de distribución acumulada para el número de satélites
por hembra diferenciando por grupo. .............. 114
14.1. Función de densidad para una Beta(2,5)............ 116
14.2. Área sombreada para los ejemplos. ............... 119
14.3. Área sombreada para el ejemplo de los tornillos. . . . . . . . 121
14.4. Función de densidad f(x)para el peso de los cangrejos. . . . 123
14.5. Función acumulada F(x)para el peso de los cangrejos. . . . . 124
14.6. Función de densidad f(x)para el peso del cangrejo diferencian-
do por el color. .......................... 125
14.7. Función de densidad f(x)para el peso del cangrejo diferencian-
do por el color y usando ggplot2. ................ 126
15.1. Función de log-verosimilitud para el ejemplo sobre binomial. . 130
15.2. Gráco de niveles para la función de log-verosimilitud para el
ejemplo sobre normal. ...................... 132
15.3. Gráco cuantil cuantil normal y gamma para la muestra simu-
lada. ................................ 136
15.4. Histograma para la muestra simulada con la densidad de una
Gamma(mu=4.308, sigma=0.6682). ............... 140
16.1. Densidad para 4 muestras de una N(0, 1) con diferente tamaño
de muestra. ............................ 147
16.2. Densidad para el peso corporal de hombres y mujeres. . . . . 149
16.3. Ejemplo de un QQplot. ..................... 150
16.4. QQplot para 4 muestras de una N(0, 1) con diferente tamaño
de muestra. ............................ 151
16.5. QQplot para muestras generadas de poblaciones Poisson, Bino-
mial Negativa, Gamma y Weibull. ............... 153
16.6. QQplot para el peso corporal de hombres y mujeres. . . . . . 155
16.7. QQplot con bandas de conanza para el peso corporal de hom-
bres y mujeres. .......................... 156
17.1. QQplot e histograma para la altura de los hombres. . . . . . 163
17.2. QQplot e histograma para la altura de hombres y mujeres. . . 165
17.3. QQplot y densidad para Diferencias. .............. 168
18.1. Representación del Valor-P para la prueba Wald. . . . . . . . 178
18.2. QQplot para los tiempos de cocción. .............. 184
18.3. QQplot para las concentraciones de arsénico. ......... 186
18.4. Boxplot para los tiempos de cocción dado el tratamiento. . . 189
18.5. Boxplot para las concentaciones de arsénico dada la zona. . . 191
18.6. QQplot para las diferencias de peso. .............. 194

Prefacio
Este libro fue creado con la intención de apoyar el aprendizaje del lenguaje de
programación Ren estudiantes de pregrado, especialización, maestría e investi-
gadores, que necesiten realizar análisis estadísticos. En este libro se explica de
una forma sencilla la utilidad de la principales funciones para realizar análisis
estadístico.
El presente material está en proceso de elaboración, si el lector desea tener
la última versión del libro recomendamos consultar la versión alojada en el
repositorio de GitHub diponible en el siguiente enlace: https://github.com/
fhernanb/Manual-de-R/blob/master/_book/Manual_de_R.pdf
Estructura del libro
El libro está estructurado de la siguiente manera.
En el capítulo 1se presenta una breve introducción sobre el lenguaje de pro-
gramación R; en el capítulo 2se explican los tipos de objetos más comunes
en R; en el capítulo 3se muestran las normas de estilo sugeridas para escribir
código en R; el capítulo 4presenta las funciones básicas que todo usuario debe
conocer para usar con éxito R; el capítulo 6trata sobre cómo crear funciones;
el capítulo 7muestra como leer bases de datos desde R; en el capítulo 8se
ilustra la forma para construir tablas de frecuencia; en el capítulo 9se muestra
como obtener las diversas medidas de tendencial central para variables cuan-
titativas, el capítulo 10 muestra como calcular las medidas de variabilidad, en
el capítulo 11 se ilustra cómo usar las funciones para obtener medidas de posi-
ción; en el capítulo 12 se muestra como obtener medidas de correlación entre
pares de variables; en los capítulos 13 y14 se tratan los temas de distribucio-
nes discretas y continuas; en el capítulo 15 se aborda el tema de verosimilitud;
en el capítulo 19 se muestra el tema de aproximación de integrales.
xiii

xiv Prefacio
Información del software y convenciones
Para realizar este libro se usaron los paquetes de Rknitr (Xie,2015) y book-
down (Xie,2018), estos paquetes permiten construir todo el libro desde Ry
sirven para incluir código que se ejecute de forma automática incluyendo las
salidas y grácos.
En todo el libro se presentarán códigos que el lector puede copiar y pegar
en su consola de Rpara obtener los mismos resultados aquí presentados. Los
códigos se destacan en una caja de color beis (o beige) similar a la mostrada
a continuación.
4+6
a <- c(1,5,6)
5*a
1:10
Los resultados o salidas obtenidos de cualquier código se destacan con dos
símbolos de númeral (##) al inicio de cada línea o renglón, esto quiere decir
que todo lo que inicie con ## son resultados obtenidos y el usuario NO los
debe copiar. Abajo se muestran los resultados obtenidos luego de correr el
código anterior.
## [1] 10
## [1] 5 25 30
##[1]12345678910
Bloques informativos
En varias partes del libro usaremos bloques informativos para resaltar algún
aspecto importante. Abajo se encuentra un ejemplo de los bloques y su signi-
cado.
Nota aclaratoria.
Sugerencia.

Prefacio xv
Advertencia.
Agradecimientos
Agradecemos enormemente a todos los estudiantes, profesores e investigadores
que han leído este libro y nos han retroalimentado con comentarios valiosos
para mejorar el documento.
Freddy Hernández Barajas
Olga Cecilia Usuga Manco


Sobre los autores
Freddy Hernández Barajas es profesor asistente de la Universidad Nacional de
Colombia adscrito a la Escuela de Estadística de la Facultad de Ciencias.
Olga Cecilia Usuga Manco es profesora asociada de la Universidad de An-
tioquia adscrita al Departamento de Ingeniería Industrial de la Facultad de
Ingeniería.
xvii


1
Introducción
1.1. Orígenes
Res un lenguaje de programación usado para realizar procedimientos estadísti-
cos y grácos de alto nivel, este lenguaje fue creado en 1993 por los profesores
e investigadores Robert Gentleman y Ross Ihaka. Inicialmente el lenguaje se
usó para apoyar los cursos que tenían a su cargo los profesores, pero luego de
ver la utilidad de la herramienta desarrollada, decidieron colocar copias de R
en StatLib. A partir de 1995 el código fuente de Restá disponible bajo licen-
cia GNU GPL para sistemas operativos Windows, Macintosh y distribuciones
Unix/Linux. La comunidad de usuarios de Ren el mundo es muy grande y los
usuarios cuentan con diferentes espacios para interactuar, a continuación una
lista no exhaustiva de los sitios más populares relacionados con R:
Rbloggers1.
Comunidad hispana de R2.
Nabble3.
Foro en portugués4.
Stackoverow5.
Cross Validated6.
R-Help Mailing List7.
Revolutions8.
R-statistics blog9.
RDataMining10.
1https://www.r-bloggers.com/
2http://r-es.org/
3http://r.789695.n4.nabble.com/
4http://r-br.2285057.n4.nabble.com/
5http://stackoverflow.com/questions/tagged/r
6http://stats.stackexchange.com/questions/tagged/r
7https://stat.ethz.ch/mailman/listinfo/r-help
8http://blog.revolutionanalytics.com/
9https://www.r-statistics.com/
10https://rdatamining.wordpress.com/
1

21 Introducción
Figura 1.1: Robert Gentleman (izquierda) y Ross Ihaka (derecha) creadores
de R.
1.2. Descarga e instalación
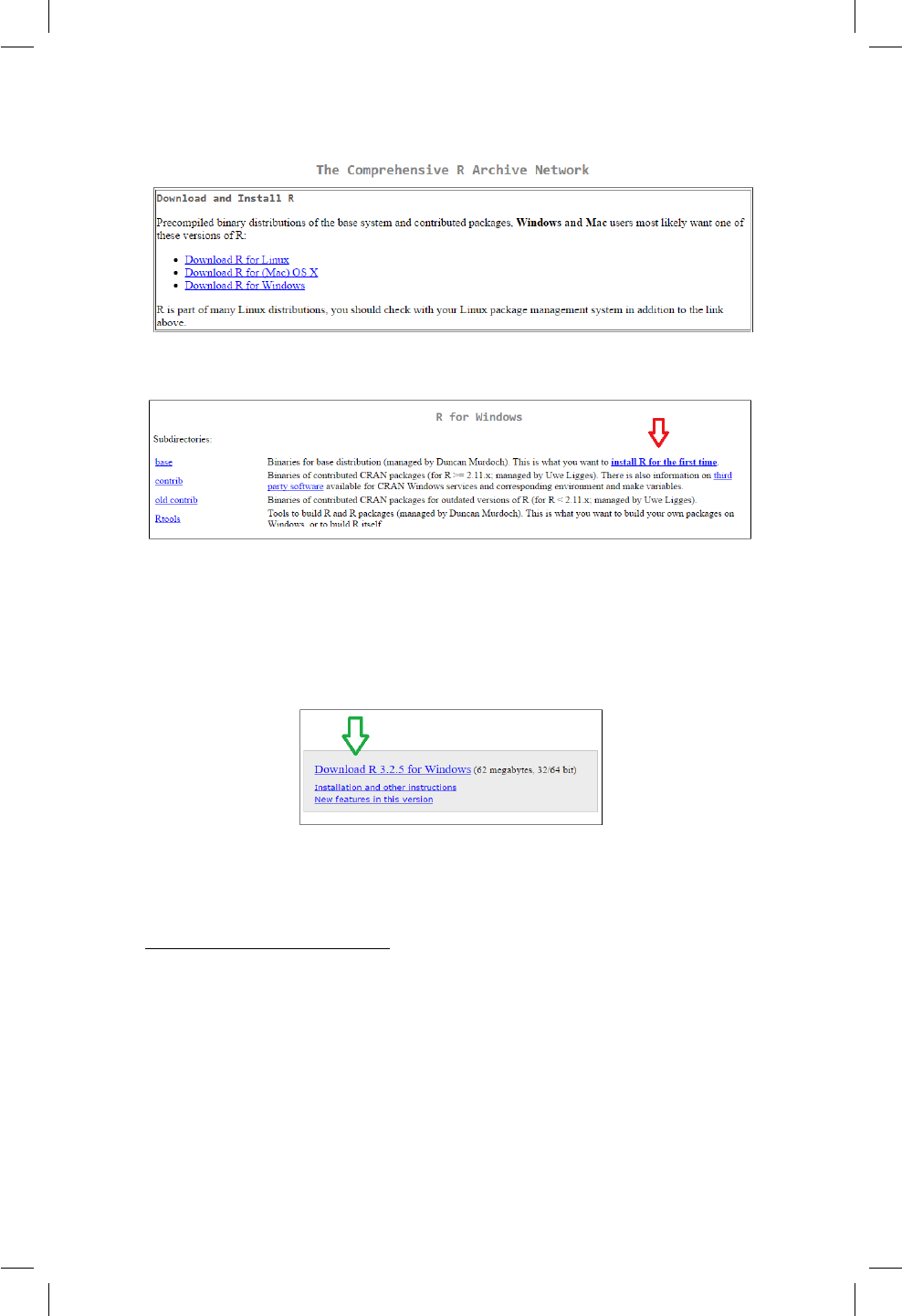
Para realizar la instalación de Rusted debe visitar la página del CRAN (Com-
prehensive R Archive Network) disponible en este enlace11 . Una vez ingrese
a la página encontrará un cuadro similar al mostrado en la Figura 1.2 donde
aparecen los enlaces de la instalación para los sistemas operativos Linux, Mac
y Windows.
Supongamos que se desea instalar Ren Windows, para esto se debe dar clic
sobre el hiperenlace Download R for Windows de la Figura 1.2. Una vez hecho
esto se abrirá una página con el contenido mostrado en la Figura 1.3. Una vez
ingrese a esa nueva página usted debe dar clic sobre el hiperenlace install R
for the rst time como es señalado por la echa roja en la Figura 1.3.
Luego de esto se abrirá otra página con un encabezado similar al mostrado en
la Figura 1.4, al momento de capturar la gura la versión actual de Rera 3.2.5
pero seguramente en este momento usted tendrá disponible una versión actua-
lizada. Una vez allí uste debe dar clic sobre Download R 3.2.5 for Windows
11https://cran.r-project.org/
1.3 Descarga e instalación 3
Figura 1.2: Página del Cran.
Figura 1.3: Página de instalación para la primera ocasión.
como es señalado por la echa verde. Luego de esto se descargará el instalador
Ren el computador el cual deberá ser instalado con las opciones que vienen
por defecto.
Figura 1.4: Página de descarga.
Se recomienda observar el siguiente video didáctico de instalación de Rdispo-
nible en este enlace12 para facilitar la tarea de instalación.
12http://tinyurl.com/jd7b9ks

41 Introducción
1.3. Apariencia del programa
Una vez que esté instalado Ren su computador, usted podrá acceder a él por
la lista de programas o por medio del acceso directo que quedó en el escritorio,
en la Figura 1.5 se muestra la apariencia del acceso directo para ingresar a R.
Figura 1.5: Apariencia del acceso directo para ingresar a R.
Al abrir Raparecerá en la pantalla de su computador algo similar a lo que está
en la Figura 1.6. La ventana izquierda se llama consola y es donde se ingresan
las instrucciones, una vez que se construye un gráco se activa otra ventana
llamada ventana gráca. Cualquier usuario puede modicar la posición y ta-
maños de estas ventanas, puede cambiar el tipo y tamaño de las letras en la
consola, para hacer esto se deben explorar las opciones de editar en la barra
de herramientas.

1.3 Apariencia del programa 5
Figura 1.6: Apariencia de R.


2
Tipos de objetos
En Rexisten varios tipos de objectos que permiten que el usuario pueda al-
macenar la información para realizar procedimientos estadísticos y grácos.
Los principales objetos en Rson vectores, matrices, arreglos, marcos de datos
y listas. A continuación se presentan las características de estos objetos y la
forma para crearlos.
2.1. Vectores
Los vectores vectores son arreglos ordenados en los cuales se puede almacenar
información de tipo numérico (variable cuantitativa), alfanumérico (variable
cualitativa) o lógico (TRUE oFALSE), pero no mezclas de éstos. La función de R
para crear un vector es c() y que signica concatenar; dentro de los paréntesis
de esta función se ubica la información a almacenar. Una vez construído el
vector se acostumbra a etiquetarlo con un nombre corto y representativo de
la información que almacena, la asignación se hace por medio del operador <-
entre el nombre y el vector.
A continuación se presenta un ejemplo de cómo crear tres vectores que con-
tienen las respuestas de cinco personas a tres preguntas que se les realizaron.
edad <- c(15,19,13,NA,20)
deporte <- c(TRUE,TRUE,NA,FALSE,TRUE)
comic.fav <- c(NA,'Superman','Batman',NA,'Batman')
El vector edad es un vector cuantitativo y contiene las edades de las 5 perso-
nas. En la cuarta posición del vector se colocó el símbolo NA que signica Not
Available debido a que no se registró la edad para esa persona. Al hacer una
asignación se acostumbra a dejar un espacio antes y después del operador <-
de asignación. El segundo vector es llamado deporte y es un vector lógico que
almacena las respuestas a la pregunta de si la persona practica deporte, nue-
vamente aquí hay un NA para la tercera persona. El último vector comic.fav
7
82 Tipos de objetos
contiene la información del cómic favorito de cada persona, como esta variable
es cualitativa es necesario usar las comillas ' ' para encerrar las respuestas.
Cuando se usa NA para representar una información Not Available no se
deben usar comillas.
Es posible usar comillas sencillas 'foo' o comillas dobles "foo" para in-
gresar valores de una variable cualitativa.
Si se desea ver lo que está almacenado en cada uno de estos vectores, se debe
escribir en la consola de Rel nombre de uno de los objetos y luego se presiona la
tecla enter ointro, al realizar esto lo que se obtiene se muestra a continuación.
edad
## [1] 15 19 13 NA 20
deporte
## [1] TRUE TRUE NA FALSE TRUE
comic.fav
## [1] NA "Superman" "Batman" NA
## [5] "Batman"
2.1.1. ¿Cómo extraer elementos de un vector?
Para extraer un elemento almacenado dentro un vector se usan los corchetes
[] y dentro de ellos la posición o posiciones que interesan.
Ejemplo
Si queremos extraer la edad de la tercera persona escribimos el nombre del
vector y luego [3] para indicar la tercera posición de edad, a continuación el
código.
edad[3]
## [1] 13

2.2 Matrices 9
Si queremos conocer el cómic favorito de la segunda y quinta persona, escri-
bimos el nombre del vector y luego, dentro de los corchetes, escribimos otro
vector con las posiciones 2 y 5 que nos interesan así [c(2, 5)], a continuación
el código.
comic.fav[c(2,5)]
## [1] "Superman" "Batman"
Si nos interesan las respuestas de la práctica de deporte, excepto la de la
persona 3, usamos [-3] luego del nombre del vector para obtener todo, excepto
la tercera posición.
deporte[-3]
## [1] TRUE TRUE FALSE TRUE
Si desea extraer varios posiciones de un vector NUNCA escriba esto:
mivector[2, 5, 7]. Tiene que crear un vector con las posiciones y luego
colocarlo dentro de los corchetes así: mivector[c(2, 5, 7)]
2.2. Matrices
Las matrices son arreglos rectangulares de las y columnas con información
numérica, alfanumérica o lógica. Para construir una matriz se usa la función
matrix( ). Por ejemplo, para crear una matriz de 4 las y 5 columnas (de
dimensión 4×5) con los primeros 20 números positivos se escribe el código
siguiente en la consola.
mimatriz <- matrix(data=1:20,nrow=4,ncol=5,byrow=FALSE)
El argumento data de la función sirve para indicar los datos que se van a
almacenar en la matriz, los argumentos nrow yncol sirven para denir la
dimensión de la matriz y por último el argumento byrow sirve para indicar si
la información contenida en data se debe ingresar por las o no. Para observar
lo que quedó almacenado en el objeto mimatriz se escribe en la consola el
nombre del objeto seguido de la tecla enter ointro.
10 2 Tipos de objetos
mimatriz
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 5 9 13 17
## [2,] 2 6 10 14 18
## [3,] 3 7 11 15 19
## [4,] 4 8 12 16 20
2.2.1. ¿Cómo extraer elementos de una matriz?
Al igual que en el caso de los vectores, para extraer elementos almacenados
dentro de una matriz se usan los corchetes [,]y dentro, separado por una
coma, el número de la(s) y el número de columna(s) que nos interesan.
Ejemplo
Si queremos extraer el valor almacenado en la la 3 y columna 4 usamos el
siguiente código.
mimatriz[3,4]
## [1] 15
Si queremos recuperar toda la la 2 usamos el siguiente código.
mimatriz[2, ] # No se escribe nada luego de la coma
## [1] 2 6 10 14 18
Si queremos recuperar toda la columna 5 usamos el siguiente código.
mimatriz[, 5]# No se escribe nada antes de la coma
## [1] 17 18 19 20
Si queremos recuperar la matriz original sin las columnas 2 y 4 usamos el
siguiente código.
mimatriz[, -c(2,4)] # Las columnas como vector
## [,1] [,2] [,3]
2.3 Arreglos 11
## [1,] 1 9 17
## [2,] 2 10 18
## [3,] 3 11 19
## [4,] 4 12 20
Si queremos recuperar la matriz original sin la la 1 ni columna 3 usamos el
siguiente código.
mimatriz[-1,-3]# Signo de menos para eliminar
## [,1] [,2] [,3] [,4]
## [1,] 2 6 14 18
## [2,] 3 7 15 19
## [3,] 4 8 16 20
2.3. Arreglos
Un arreglo es una matriz de varias dimensiones con información numérica,
alfanumérica o lógica. Para construir una arreglo se usa la función array( ).
Por ejemplo, para crear un arreglo de 3×4×2con las primeras 24 letras
minúsculas del alfabeto se escribe el siguiente código.
miarray <- array(data=letters[1:24], dim=c(3,4,2))
El argumento data de la función sirve para indicar los datos que se van a
almacenar en el arreglo y el argumento dim sirve para indicar las dimensiones
del arreglo. Para observar lo que quedó almacenado en el objeto miarray se
escribe en la consola lo siguiente.
miarray
##,,1
##
## [,1] [,2] [,3] [,4]
## [1,] "a" "d" "g" "j"
## [2,] "b" "e" "h" "k"
## [3,] "c" "f" "i" "l"
##
##,,2
##
12 2 Tipos de objetos
## [,1] [,2] [,3] [,4]
## [1,] "m" "p" "s" "v"
## [2,] "n" "q" "t" "w"
## [3,] "o" "r" "u" "x"
2.3.1. ¿Cómo extraer elementos de un arreglo?
Para recuperar elementos almacenados en un arreglo se usan también corche-
tes, y dentro de los corchetes, las coordenadas del objeto de interés.
Ejemplo
Si queremos extraer la letra almacenada en la la 1 y columna 3 de la segunda
capa de miarray usamos el siguiente código.
miarray[1,3,2]# El orden es importante
## [1] "s"
Si queremos extraer la segunda capa completa usamos el siguiente código.
miarray[,, 2]# No se coloca nada en las primeras posiciones
## [,1] [,2] [,3] [,4]
## [1,] "m" "p" "s" "v"
## [2,] "n" "q" "t" "w"
## [3,] "o" "r" "u" "x"
Si queremos extraer la tercera columna de todas las capas usamos el siguiente
código.
miarray[, 3,] # No se coloca nada en las primeras posiciones
## [,1] [,2]
## [1,] "g" "s"
## [2,] "h" "t"
## [3,] "i" "u"
2.4 Marco de datos 13
2.4. Marco de datos
El marco de datos marco de datos o data frame es uno de los objetos más
utilizados porque permite agrupar vectores con información de diferente tipo
(numérica, alfanumérica o lógica) en un mismo objeto, la única restricción es
que los vectores deben tener la misma longitud. Para crear un marco de datos
se usa la función data.frame( ), como ejemplo vamos a crear un marco de
datos con los vectores edad,deporte ycomic.fav denidos anteriormente.
mimarco <- data.frame(edad, deporte, comic.fav)
Una vez creado el objeto mimarco podemos ver el objeto escribiendo su nombre
en la consola, a continuación se muestra lo que se obtiene.
mimarco
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 3 13 NA Batman
## 4 NA FALSE <NA>
## 5 20 TRUE Batman
De la salida anterior vemos que el marco de datos tiene 3 variables (columnas)
cuyos nombres coinciden con los nombres de los vectores creados anteriormen-
te, los números consecutivos al lado izquierdo son sólo de referencia y permiten
identicar la información para cada persona en la base de datos.
2.4.1. ¿Cómo extraer elementos de un marco de datos?
Para recuperar las variables (columnas) almacenadas en un marco de datos
se puede usar el operador $o también corchetes []. A continuación algunos
ejemplos para entender el uso del operador $.
Ejemplo
Si queremos extraer la variable deporte del marco de datos mimarco usamos
el siguiente código.
14 2 Tipos de objetos
mimarco$deporte # Se recomienda si el nombre es corto
## [1] TRUE TRUE NA FALSE TRUE
Otra forma de recuperar la variable deporte es indicando la columna donde
se encuentra la variable
mimarco[, 2]# Se recomienda si recordamos su ubicacion
## [1] TRUE TRUE NA FALSE TRUE
Si queremos la edad de las personas que están en las posiciones 2 hasta 4
usamos el siguiente código.
mimarco[2:4,1]
## [1] 19 13 NA
2.4.2. ¿Cómo extraer subconjuntos de un marco de datos?
Para extraer partes de un marco de datos se puede utilizar la función
subset(x, subset, select). El parámetro xsirve para indicar el marco
de datos original, el parámetro subset sirve para colocar la condición y el
parámetro select sirve para quedarnos sólo con algunas de las variables del
marco de datos. A continuación varios ejemplos de la función subset para ver
su utilidad.
Ejemplos
Si queremos el marco de datos mimarco sólo con las personas que SI practican
deporte usamos el siguiente código.
subset(mimarco, subset=deporte == TRUE)
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 5 20 TRUE Batman
Si queremos el marco de datos mimarco sólo con las personas mayores o iguales
a 17 años usamos el siguiente código.
2.4 Marco de datos 15
subset(mimarco, subset=edad >= 17)
## edad deporte comic.fav
## 2 19 TRUE Superman
## 5 20 TRUE Batman
Si queremos el submarco con deporte y comic de las personas menores de 20
años usamos el siguiente código.
subset(mimarco, subset=edad <20,select=c('deporte','comic.fav'))
## deporte comic.fav
## 1 TRUE <NA>
## 2 TRUE Superman
## 3 NA Batman
Si queremos el marco de datos mimarco sólo con las personas menores de 20
años y que SI practican deporte usamos el siguiente código.
subset(mimarco, subset=edad <20 &deporte == TRUE)
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
Ejemplo
Leer la base de datos medidas del cuerpo disponible en este enlace https://
raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo.
Extraer de esta base de datos una sub-base o subconjunto que contenga sólo
la edad, peso, altura y sexo de aquellos que miden más de 185 cm y pesan
más de 80 kg.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
dt1 <- read.table(url, header=T)
dim(dt1) # Para conocer la dimensión de la base original
## [1] 36 6
dt2 <- subset(x=dt1, subset=altura >185 &peso >80,
select=c('sexo','edad','peso','altura'))
dt2 # Para mostrar la base de datos final
16 2 Tipos de objetos
## sexo edad peso altura
## 1 Hombre 43 87.3 188.0
## 6 Hombre 33 85.9 188.0
## 15 Hombre 30 98.2 190.5
Al almacenar la nueva base de datos en el objeto dt2 se puede manipular este
nuevo objeto para realizar los análisis de interés.
2.5. Listas
Las listas son otro tipo de objeto muy usado para almacenar objetos de di-
ferente tipo. La instrucción para crear una lista es list( ). A continuación
vamos a crear una lista que contiene tres objetos: un vector con 5 números
aleatorios llamado mivector, una matriz de dimensión 6×2con los prime-
ros doce números enteros positivos llamada matriz2 y el tercer objeto será
el marco de datos mimarco creado en el apartado anterior. Las instrucciones
para crear la lista requerida se muestran a continuación.
set.seed(12345)
mivector <- runif(n=5)
matriz2 <- matrix(data=1:12,ncol=6)
milista <- list(E1=mivector, E2=matriz2, E3=mimarco)
La función set.seed de la línea número 1 sirve para jar la semilla de tal ma-
nera que los números aleatorios generados en la segunda línea con la función
runif sean siempre los mismos. En la última línea del código anterior se cons-
truye la lista, dentro de la función list se colocan los tres objetos mivector,
matriz2 ymimarco. Es posible colocarle un nombre especial a cada uno de
los elementos de la lista, en este ejemplo se colocaron los nombres E1,E2 y
E3 para cada uno de los tres elementos. Para observar lo que quedó almace-
nado en la lista se escribe milista en la consola y el resultado se muestra a
continuación.
milista
## $E1
## [1] 0.7209 0.8758 0.7610 0.8861 0.4565
##
2.5 Listas 17
## $E2
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 3 5 7 9 11
## [2,] 2 4 6 8 10 12
##
## $E3
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 3 13 NA Batman
## 4 NA FALSE <NA>
## 5 20 TRUE Batman
2.5.1. ¿Cómo extraer elementos de una lista?
Para recuperar los elementos almacenadas en una lista se usa el operador $,
corchetes dobles [[]] o corchetes sencillos []. A continuación unos ejemplos
para entender cómo extraer elementos de una lista.
Ejemplos
Si queremos la matriz almacenada con el nombre de E2 dentro del objeto
milista se puede usar el siguiente código.
milista$E2
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 3 5 7 9 11
## [2,] 2 4 6 8 10 12
Es posible indicar la posición del objeto en lugar del nombre, para eso se usan
los corchetes dobles.
milista[[2]]
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 3 5 7 9 11
## [2,] 2 4 6 8 10 12
El resultado obtenido con milista$E2 ymilista[[2]] es exactamente el
mismo. Vamos ahora a solicitar la posición 2 pero usando corchetes sencillos.

18 2 Tipos de objetos
milista[2]
## $E2
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1 3 5 7 9 11
## [2,] 2 4 6 8 10 12
La apariencia de este último resultado es similar, no igual, al encontrado al
usar $y[[]]. Para ver la diferencia vamos a pedir la clase a la que pertenecen
los tres últimos objetos usando la función class. A continuación el código
usado.
class(milista$E2)
## [1] "matrix"
class(milista[[2]])
## [1] "matrix"
class(milista[2])
## [1] "list"
De lo anterior se observa claramente que cuando usamos $o[[]] el resultado
es el objeto almacenado, una matriz. Cuando usamos [] el resultado es una
lista cuyo contenido es el objeto almacendado.
Al manipular listas con $y[[]] se obtienen los objetos ahí almacenados,
al manipular listas con [] se obtiene una lista.
EJERCICIOS
Use funciones o procedimientos (varias líneas) de Rpara responder cada una
de las siguientes preguntas.
1. Construya un vector con la primeras 20 letras MAYÚSCULAS usan-
do la función LETTERS.

2.5 Listas 19
2. Construya una matriz de 10 ×10 con los primeros 100 números
positivos pares.
3. Construya una matriz identidad de dimension 3×3. Recuerde que
una matriz identidad tiene sólo unos en la diagonal principal y los
demás elementos son cero.
4. Construya una lista con los anteriores tres objetos creados.
5. Construya un marco de datos o data frame con las respuestas de 3
personas a las preguntas: (a) ¿Cuál es su edad en años? (b) ¿Tipo
de música que más le gusta? (c) ¿Tiene usted pareja sentimental
estable?
6. ¿Cuál es el error al correr el siguiente código? ¿A qué se debe?
edad <- c(15,19,13,NA,20)
deporte <- c(TRUE,TRUE,NA,FALSE,TRUE)
comic.fav <- c(NA,'Superman','Batman',NA,'Batman')
matrix(edad, deporte, comic.fav)


3
Guía de estilo
Así como en el español existen reglas ortográcas, la escritura de códigos en
Rtambién tiene unas reglas que se recomienda seguir para evitar confusiones.
Tener una buena guía de estilo es importante para que el código creado por
usted sea fácilmente entendido por sus lectores Wickham (2015). No existe
una única y mejor guía de estilo para escritura en R, sin embargo aquí vamos
a mostrar unas sugerencias basadas en la guía llamada Google’s R style guide1.
3.1. Nombres de los archivos
Se sugiere que el nombre usado para nombrar un archivo tenga sentido y que
termine con extensión .R. A continuación dos ejemplos de como nombrar mal
y bien un archivo.
Bien: hola.R
Mal: analisis_icfes.R
3.2. Nombres de los objetos
Se recomienda no usar los símbolos _y-dentro de los nombres de objetos.
Para las variables es preferible usar letras minúsculas y separar las palabras
con puntos (peso.maiz) o utilizar la notación camello iniciando en minús-
cula (pesoMaiz). Para las funciones se recomienda usar la notación camello
iniciando todas la palabras en mayúscula (PlotRes). Para los nombres de las
constantes se recomienda que inicien con la letra k (kPrecioBus). A continua-
ción ejemplos de buenas y malas prácticas.
Para variables:
1https://google.github.io/styleguide/Rguide.xml
21

22 3 Guía de estilo
Bien: avg.clicks
Aceptable: avgClicks
Mal: avg_Clicks
Para funciones:
Bien: CalculateAvgClicks
Mal: calculate_avg_clicks ,calculateAvgClicks
3.3. Longitud de una línea de código
Se recomienda que cada línea tenga como máximo 80 caracteres. Si una línea
es muy larga se debe cortar siempre por una coma.
3.4. Espacios
Use espacios alrededor de todos los operadores binarios (=, +, -, <-, etc.).
Los espacios alrededor del símbolo “=” son opcionales cuando se usan para
ingresar valores dentro de una función. Así como en español, nunca coloque
espacio antes de una coma, pero siempre use espacio luego de una coma. A
continuación ejemplos de buenas y malas prácticas.
tab <- table(df[df$days <0,2]) # Bien
tot <- sum(x[, 1]) # Bien
tot <- sum(x[1, ]) # Bien
tab <- table(df[df$days<0,2]) # Faltan espacios alrededor '<'
tab <- table(df[df$days <0,2]) # Falta espacio luego de coma
tab <- table(df[df$days <0,2]) # Sobra espacio antes de coma
tab<- table(df[df$days <0,2]) # Falta espacio antes de '<-'
tab<-table(df[df$days <0,2]) # Falta espacio alrededor de '<-'
tot <- sum(x[,1]) # Falta espacio luego de coma
tot <- sum(x[1,]) # Falta espacio luego de coma
Otra buena práctica es colocar espacio antes de un paréntesis excepto cuando
se llama una función.
3.4 Espacios 23
if (debug) # Correcto
if(debug) # Funciona pero no se recomienda
colMeans (x) # Funciona pero no se recomienda
Espacios extras pueden ser usados si con esto se mejora la apariencia del
código, ver el ejemplo siguiente.
plot(x = x.coord,
y = data.mat[, MakeColName(metric, ptiles[1], "roiOpt")],
ylim = ylim,
xlab = "dates",
ylab = metric,
main = (paste(metric, " for 3 samples ",sep = "")))
No coloque espacios alrededor del código que esté dentro de paréntesis ( )
o corchetes [ ], la única excepción es luego de una coma, ver el ejemplo
siguiente.
if (condicion) # Correcto
x[1, ] # Correcto
if ( condicion ) # Sobran espacios alrededor de condicion
x[1,] # Se necesita espacio luego de coma
Los signos de agrupación llaves { } se utilizan para agrupar bloques de código
y se recomienda que nunca una llave abierta {esté sola en una línea; una llave
cerrada }si debe ir sola en su propia línea. Se pueden omitir las llaves cuando
el bloque de instrucciones esté formado por una sola línea pero esa línea de
código NO debe ir en la misma línea de la condición. A continuación dos
ejemplos de lo que se recomienda.
if (is.null(ylim)) { # Correcto
ylim <- c(0,0.06)
}
if (is.null(ylim)) # Correcto
ylim <- c(0,0.06)
if (is.null(ylim)) ylim <- c(0,0.06)# Aceptable
if (is.null(ylim)) # No se recomienda
{
ylim <- c(0,0.06)
24 3 Guía de estilo
}
if (is.null(ylim)) {ylim <- c(0,0.06)}
# Frente a la llave { no debe ir nada
# la llave de cierre } debe ir sola
La sentencia else debe ir siempre entre llaves } {, ver el siguiente ejemplo.
if (condition) {
one or more lines
}else {# Correcto
one or more lines
}
if (condition) {
one or more lines
}
else {# Incorrecto
one or more lines
}
if (condition)
one line
else # Incorrecto
one line
3.5. Asignación
Para realizar asignaciones se recomienda usar el símbolo <-, el símbolo de
igualdad =no se recomienda usarlo para asignaciones.

3.6 Punto y coma 25
x <- 5# Correcto
x = 5# No recomendado
Para una explicación más detallada sobre el símbolo de asignación se reco-
mienda visitar este enlace2.
3.6. Punto y coma
No se recomienda colocar varias instrucciones separadas por ;en la misma
línea, aunque funciona diculta la revisión del código.
n <- 100; y <- rnorm(n, mean=5); hist(y) # No se recomienda
n <- 100 # Correcto
y <- rnorm(n, mean=5)
hist(y)
A pesar de la anterior advertencia es posible que en este libro usemos el ;en
algunas ocasiones, si lo hacemos es para ahorrar espacio en la presentación del
código.
2http://www.win-vector.com/blog/2016/12/the-case-for-using-in-r/


4
Funciones básicas de R
En este capítulo se presentará lo que es una función y se mostrarán varias
funciones básicas que son útiles para realizar diversas tareas.
4.1. ¿Qué es una función de R?
En la Figura 4.1 se muestra una ilustración de lo que es una función o máquina
general. Hay unas entradas (inputs) que luego son procesadas dentro de la caja
para generar unas salidas (outputs). Un ejemplo de una función o máquina muy
común en nuestras casas es la licuadora. Si a una licuadora le ingresamos leche,
fresas, azúcar y hielo, el resultado será un delicioso jugo de fresa.
Las funciones en Rse caracterizan por un nombre corto y que dé una idea
de lo que hace la función. Los elementos que pueden ingresar (inputs) a la
función se llaman parámetros y se ubican dentro de paréntesis, el cuerpo
de la función se ubica dentro de llaves y es ahí donde se procesan los inputs
para convertirlos en outputs, a continuación se muestra la estructura general
de una función.
nombre_de_funcion(parametro1, parametro2, ...) {
tareas internas
tareas internas
tareas internas
salida
}
Cuando usamos una función sólo debemos escribir bien el nombre e ingresar
correctamente los parámetros de la función, el cuerpo de la función ni lo vemos
ni lo debemos modicar. A continuación se presenta un ejemplo de cómo usar
la función mean para calcular un promedio.
27
28 4 Funciones básicas de R
Figura 4.1: Ilustración de una función, tomada de www.mathinsight.org.
notas <- c(4.0,1.3,3.8,2.0)# Notas de un estudiante
mean(notas)
## [1] 2.775

4.3 Operadores de asignación 29
4.2. Operadores de asignación
En Rse pueden hacer asignación de varias formas, a continuación se presentan
los operadores disponibles para tal n.
<- este es el operador de asignación a izquierda, es el más usado y recomen-
dado.
-> este es el operador de asignación a derecha, no es frecuente su uso.
=el símbolo igual sirve para hacer asignaciones pero NO se recomienda
usarlo.
<<- este es un operador de asignación global y sólo debe ser usado por
usuarios avanzados.
Ejemplo
Almacene los valores 5.3, 4.6 y 25 en los objetos a,byage respectivamente,
use diferentes símbolos de asignación.
Para hacer lo solicitado se podría usar el siguiente código.
a <- 5.3 # Recomended
4.6 -> b # It is not usual
age = 25 # Not recomended
Aunque una asignación se puede hacer de tres formas diferentes, se reco-
mienda sólo usar el símbolo <-.
4.3. Operaciones básicas
En Rse pueden hacer diversas operaciones usando operadores binarios. Este
tipo de operadores se denomina binarios porque actuan entre dos objetos, a
continuación el listado.
+operador binario para sumar.
-operador binario para restar.
*operador binario para multiplicar.
/operador binario para dividir.

30 4 Funciones básicas de R
ˆoperador binario para potencia.
%/ % operador binario para obtener el cociente en una división (número
entero).
% % operador binario para obtener el residuo en una división.
A continuación se presentan ejemplos de cómo usar las anteriores funciones.
6+4# Para sumar dos números
## [1] 10
a <- c(1,3,2)
b <- c(2,0,1)# a y b de la misma dimensión
a+b# Para sumar los vectores a y b miembro a miembro
## [1] 3 3 3
a-b# Para restar dos vectores a y b miembro a miembro
## [1] -1 3 1
a*b# Para multiplicar
## [1] 2 0 2
a/b# Para dividir
## [1] 0.5 Inf 2.0
a^b# Para potencia
## [1] 1 1 2
7%/% 3# Para saber las veces que cabe 3 en 7
## [1] 2
7%% 3# Para saber el residuo al dividir 7 entre 3
## [1] 1

4.4 Pruebas lógicas 31
4.4. Pruebas lógicas
En Rse puede vericar si un objeto cumple una condición dada, a continuación
el listado de las pruebas usuales.
<para saber si un número es menor que otro.
>para saber si un número es mayor que otro.
== para saber si un número es igual que otro.
<= para saber si un número es menor o igual que otro.
>= para saber si un número es mayor o igual que otro.
A continuación se presentan ejemplos de cómo usar las anteriores funciones.
5<12 # ¿Será 5 menor que 12?
## [1] TRUE
# Comparando objetos
x <- 5
y <- 20 /4
x== y# ¿Será x igual a y?
## [1] TRUE
# Usando vectores
a <- c(1,3,2)
b <- c(2,0,1)
a>b# Comparación término a término
## [1] FALSE TRUE TRUE
a== b# Comparación de igualdad término a término
## [1] FALSE FALSE FALSE
Ejemplo
Crear un vector con los números de 1 a 17 y extrater los números que son
mayores o iguales a 12.
Primero se crear el vector xcon los elementos del 1 al 17. La prueba lógica x >=
32 4 Funciones básicas de R
12 se usa para evaluar la condición, el resultado es un vector de 17 posiciones
con valores de TRUE oFALSE dependiendo de si la condición se cumple o no.
Este vector lógico se coloca dentro de x[ ] para que al evaluar x[x >= 12]
sólo aparezcan los valores del vector original que SI cumplen la condición. El
código necesario se muestra a continuación.
x <- 1:17 # Se crea el vector
x[x >= 12]# Se solicitan los valores que cumplen la condición
## [1] 12 13 14 15 16 17
Ejemplo
Retome el marco de datos mimarco construído en la sección 2.4 y use una
prueba lógica para extraer la información de las personas que tienen una edad
superior o igual a 15 años.
Inicialmente vamos a construir nuevamente el objeto mimarco de la sección
2.4 usando el siguiente código.
mimarco <- data.frame(edad = c(15,19,13,NA,20),
deporte = c(TRUE,TRUE,NA,FALSE,TRUE),
comic.fav = c(NA,'Superman','Batman',
NA,'Batman'))
mimarco # Para ver el contenido de mimarco
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 3 13 NA Batman
## 4 NA FALSE <NA>
## 5 20 TRUE Batman
Para extraer de mimarco la información de las personas que tienen una
edad superior o igual a 15 años se coloca dentro de corchetes la condición
mimarco$edad >= 15, esto servirá para chequear cuáles de las edades del vec-
tor mimarco$ead cumplen la condición. El resultado de evaluar mimarco$edad
>= 15 será un vector lógico (TRUE oFALSE), que al ser colocado dentro de
mimarco[,], entregará la información de las personas que cumplen la condi-
ción. A continuación el código para extraer la información solicitada.
4.5 Operadores lógicos 33
mimarco[mimarco$edad >= 15, ]
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## NA NA NA <NA>
## 5 20 TRUE Batman
De la salida anterior se observa que 4 personas de las 5 cumplean la condición.
Note que la condición mimarco$edad >= 15 se debe ubicar antes de la coma
para obtener todos individuos que cumplen con la condición.
4.5. Operadores lógicos
En Restán disponibles los operadores lógicos negación, conjunción y disyun-
ción. A continuación el listado de los operadores entre los elementos xey.
!x# Negación de x
x&y# Conjunción entre x e y
x&& y
x|y# Disyunción entre x e y
x|| y
xor(x, y)
A continuación se presentan ejemplos de cómo usar el símbolo de negación !.
ans <- c(TRUE,FALSE,TRUE)
!ans # Negando las respuestas almacenadas en ans
## [1] FALSE TRUE FALSE
x <- c(5,1.5,2,3,2)
!(x <2.5)# Negando los resultados de una prueba
## [1] TRUE FALSE FALSE TRUE FALSE
A continuación se presentan ejemplos de cómo aplicar la conjunción &y&&.
34 4 Funciones básicas de R
x <- c(5,1.5,2)# Se construyen dos vectores para la prueba
y <- c(4,6,3)
x<4# ¿Serán los elementos de x menores que 4?
## [1] FALSE TRUE TRUE
y>5# ¿Serán los elementos de y mayores que 5?
## [1] FALSE TRUE FALSE
x<4&y>5# Conjunción entre las pruebas anteriores.
## [1] FALSE TRUE FALSE
x<4&& y>5# Conjunción vectorial
## [1] FALSE
Note las diferencias entre los dos últimos ejemplos, cuando se usa &se hace
una prueba término a término y el resultado es un vector, cuando se usa &&
se aplica la conjunción al vector de resultados obtenido con &.
Ejemplo
Retome el marco de datos mimarco construído en la sección 2.4 y use una
prueba lógica para extraer la información de las personas que tienen una edad
superior o igual a 15 años y que practican deporte.
Aquí interesa extraer la información de los individuos que cumplen dos condi-
ciones simultáneamente, aquellos con edad ≥15 y que SI practiquen deporte.
El código necesario para obtener la información solicitada es el siguiente.
mimarco[mimarco$edad >= 15 &mimarco$deporte == TRUE, ]
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 5 20 TRUE Batman
De la anterior salida se observa que sólo 3 de las 5 personas cumplen ambas
condiciones.

4.6 Funciones sobre vectores 35
La función with es útil porque nos permite realizar algún procedimiento en
relación de un objeto, escribiendo menos y de una forma más natural.
Una forma alternativa para escribir lo anterior usando la función with es la
siguiente.
with(mimarco, mimarco[edad >= 15 &deporte == TRUE, ])
## edad deporte comic.fav
## 1 15 TRUE <NA>
## 2 19 TRUE Superman
## 5 20 TRUE Batman
Al usar with sólo se tuvo que escribir el objeto mimarco dos veces. Cuando hay
muchas condiciones o cuando el objeto tiene un nombre largo es aconsejable
usar with.
4.6. Funciones sobre vectores
En Rpodemos destacar las siguientes funciones básicas sobre vectores numé-
ricos.
min: para obtener el mínimo de un vector.
max: para obtener el máximo de un vector.
length: para determinar la longitud de un vector.
range: para obtener el rango de valores de un vector, entrega el mínimo y
máximo.
sum: entrega la suma de todos los elementos del vector.
prod: multiplica todos los elementos del vector.
which.min: nos entrega la posición en donde está el valor mínimo del vector.
which.max: nos da la posición del valor máximo del vector.
rev: invierte un vector.
Ejemplo
Construir en vector llamado myvec con los siguientes elementos: 5, 3, 2, 1, 2,
0, NA, 0, 9, 6. Luego aplicar todas las funciones anteriores para vericar el
funcionamiento de las mismas.
36 4 Funciones básicas de R
myvec <- c(5,3,2,1,2,0,NA,0,9,6)
myvec
##[1]532120NA096
min(myvec) # Opss, no aparece el mínimo que es Cero.
## [1] NA
min(myvec, na.rm=TRUE)# Usamos na.rm = TRUE para remover el NA
## [1] 0
max(myvec, na.rm=T) # Para obtener el valor máximo
## [1] 9
range(myvec, na.rm=T) # Genera min y max simultáneamente
## [1] 0 9
sum(myvec, na.rm=T) # La suma de los valores internos
## [1] 28
prod(myvec, na.rm=T) # El productor de los valores internos
## [1] 0
which.min(myvec) # Posición del valor mínimo 0 en el vector
## [1] 6
which.max(myvec) # Posición del valor máximo 9 en el vector
## [1] 9
De las dos últimas líneas podemos destacar lo siguiente:

4.7 Funciones matemáticas 37
1. NO es necesario usar na.rm = TRUE para remover el NA dentro
de las funciones which.min ni which.max.
2. El valor mínimo 0 aparece en las posiciones 6 y 8 pero la función
which.min sólo entrega la posición del primer valor mínimo dentro
del vector.
4.7. Funciones matemáticas
Otras funciones básicas muy utilizadas en estadística son: sin, cos, tan,
asin, acos, atan, atan2, log, logb, log10, exp, sqrt, abs. A
continuación algunos ejemplos de las anteriores funciones.
Ejemplos de medidas trigonométricas
angulos <- c(0, pi/2, pi)
sin(angulos)
## [1] 0.000e+00 1.000e+00 1.225e-16
tan(angulos)
## [1] 0.000e+00 1.633e+16 -1.225e-16
Ejemplos de logaritmos
log(100)
## [1] 4.605
log10(100)
## [1] 2
logb(125,base=5)
## [1] 3
Ejemplos de exponencial

38 4 Funciones básicas de R
exp(1)
## [1] 2.718
exp(2)
## [1] 7.389
exp(1:3)
## [1] 2.718 7.389 20.086
Ejemplos de raices
sqrt(49)# Raiz cuadrada de 49
## [1] 7
27 ^(1/3)# Raiz cúbica de 27
## [1] 3
Ejemplos de valor absoluto
abs(2.5)
## [1] 2.5
abs(-3.6)
## [1] 3.6
4.8. Función seq
En Rpodemos crear secuencias de números de una forma sencilla usando la
función seq, la estructura de esta función es:
4.8 Función seq 39
seq(from=1,to=1, by, length.out)
Los argumentos de esta función son:
from: valor de inicio de la secuencia.
to: valor de n de la secuencia, no siempre se alcanza.
by: incremento de la secuencia.
length.out: longitud deseado de la secuencia.
Ejemplo
Construya las siguientes tres secuencias usando la función seq.
Once valores igualmente espaciados desde 0 hasta 1.
Una secuencia de dos en dos comenzando en 1.
Una secuencia desde 1 con un salto de πy sin pasar del número 9.
El código necesario para obtener las secuencias se muestra a continuación.
seq(from=0,to=1,length.out = 11)
## [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
seq(from=1,to=9,by=2)# matches 'end'
##[1]13579
seq(from=1,to=9,by=pi) # stays below 'end'
## [1] 1.000 4.142 7.283
En Rexiste el operador binario :que sirve para construir secuencias de uno
en uno fácilmente.
Revise los siguientes ejemplos para entender el funcionamiento del operador
:.
2:8
##[1]2345678
40 4 Funciones básicas de R
3:-5
## [1] 3 2 1 0 -1 -2 -3 -4 -5
pi:6# real sequence
## [1] 3.142 4.142 5.142
6:pi # integer sequence
## [1] 6 5 4
4.9. Función rep
En Rpodemos crear repeticiones usando la función rep, la estructura de esta
función es:
rep(x, times=1,length.out=NA,each=1)
Los argumentos de esta función son:
x: vector con los elementos a repetir.
times: número de veces que el vector xse debe repetir.
length.out: longitud deseada para el vector resultante.
each: número de veces que cada elemento de xse debe repetir.
Ejemplo
Construya las siguientes repeticiones usando la función rep, no lo haga ingre-
sando número por número.
12341234
11223344
1 1 2 3 3 4
11223344
La clave para construir una repetición es descrubir la semilla o elemento que
se repite. Las instrucciones para obtener las repeticiones anteriores se muestra
a continuación.
4.10 Función rep 41
rep(x=1:4,times=2)
##[1]12341234
rep(x=1:4,times=c(2,2,2,2))
##[1]11223344
rep(x=1:4,times=c(2,1,2,1))
##[1]112334
rep(x=1:4,each=2)
##[1]11223344
Ejemplo
La función rep es muy versátil, observe los siguientes 4 ejemplos y saque una
conclusión de cada uno de ellos.
rep(x=1:4,each=2)
##[1]11223344
rep(x=1:4,each=2,len=4)# first 4 only.
##[1]1122
rep(x=1:4,each=2,len=10)# 8 integers plus two recycled 1's.
## [1]1122334411
rep(x=1:4,each=2,times=3)# length 24, 3 complete replications
## [1]112233441122334411223344

42 4 Funciones básicas de R
4.10. Funciones round,ceiling,floor ytrunc
Existen 4 funciones útiles para modicar u obtener información de un número,
estas funciones son round,ceiling,floor ytrunc.
round(x, digits): sirve para redondear un número según los dígitos indi-
cados.
ceiling(x): entrega el mínimo entero mayor o igual que x.
floor(x): entrega el máximo entero menor o igual que x.
trunc(x): entrega la parte entera de un número x.
Ejemplo
Aplique las funciones round,ceiling,floor ytrunc a un valor positivo y a
un valor negativo para inspeccionar los resultados.
A continuación el código de prueba para un número positivo cualquiera.
x <- 5.34896 # Número positivo elegido
round(x, digits=3)
## [1] 5.349
ceiling(x)
## [1] 6
floor(x)
## [1] 5
trunc(x)
## [1] 5
A continuación las pruebas con un número negativo cualquiera.
x <- -4.26589 # Número negativo elegido
round(x, digits=3)
## [1] -4.266

4.11 Funciones sort yrank 43
ceiling(x)
## [1] -4
floor(x)
## [1] -5
trunc(x)
## [1] -4
4.11. Funciones sort yrank
Las funciones sort yrank son útiles para ordenar los elementos de un vector
o para saber las posiciones que ocuarían los elementos de un vector al ser
ordenado. La estructura de las dos funciones es la siguiente.
sort(x, decreasing = FALSE)
rank(x)
En el parámetro xse ingresa el vector y el parámetro decreasing sirva para
indicar si el ordenamiento es de menor a mayor (por defecto es este) o de
mayor a menor.
Ejemplo
Considere el vector xque tiene los siguientes elementos: 2, 3, 6, 4, 9 y 5.
Ordene el vector de menor a mayor, de mayor a menor y por último encuentre
la posición que ocupan los elementos de xsi se ordenaran de menor a mayor.
x <- c(2,3,6,4,9,5)
sort(x)
##[1]234569
44 4 Funciones básicas de R
sort(x, decreasing=TRUE)
##[1]965432
rank(x)
##[1]125364
EJERCICIOS
Use funciones o procedimientos (varias líneas) de Rpara responder cada una
de las siguientes preguntas.
1. ¿Qué cantidad de dinero sobra al repartir 10000$ entre 3 personas?
2. ¿Es el número 4560 divisible por 3?
3. Construya un vector con los números enteros del 2 al 87. ¿Cuáles
de esos números son divisibles por 7?
4. Construya dos vectores, el primero con los números enteros desde 7
hasta 3, el segundo vector con los primeros cinco números positivos
divisibles por 5. Sea A la condición de ser par en el primer vector.
Sea B la condición de ser mayor que 10 en el segundo vector. ¿En
cuál de las 5 posiciones se cumple A y B simultáneamente?
5. Consulte el siguiente enlace sobre una anéctoda de Gauss cuando
tenía 10 años de edad http://tinyurl.com/hk2l8h2. Use R para
obtener el resultado de la suma solicitada por el profesor del niño
Gauss.
6. Construya un vector con los siguientes elementos: 1, -4, 5, 9, -4.
Escriba un procedimiento para extraer las posiciones donde está
el valor mínimo en el vector.
7. Calcular 8!
8. Evaluar la siguiente suma i=7
i=3 ei
9. Evaluar la siguiente productoria i=10
i=1 log √i
10. Construya un vector cualquiera e inviertalo, es decir, que el primer
elemento quede de último, el segundo de penúltimo y así sucesiva-
mente. Compare su resultado con el de la función rev.
11. Create the vector: 1,2,3, . . . , 19,20.
12. Create the vector: 20,19, . . . , 2,1.
13. Create the vector: 1,−2,3,−4,5,−6, . . . , 19,−20.
14. Create the vector: 0.13,0.21,0.16,0.24, ..., 0.136,0.234.

4.11 Funciones sort yrank 45
15. Calculate the following: 100
i=10(i3+ 4i2)and 25
i=1 2i
i+3i
i2.
16. Read the data set available in: http://tinyurl.com/hcusrdc
17. Use a code to obtain the number of variables of the data set.
18. Use a code to obtain the number of countries in the data set.
19. Which is the country with the higher population?
20. Which is the country with the lowest literacy rate?
21. ¿Qué valor de verdad tiene la siguiente armación? “Los resultados
de la función floor ytrunc son siempre los mismos”.
En Rhay unas bases de datos incluídas, una de ellas es la base de datos
llamada mtcars. Para conocer las variables que están en mtcars usted puede
escribir en la consola ?mtcars o también help(mtcars). De la base mtcars
obtenga bases de datos que cumplan las siguientes condiciones.
22. Autos que tengan un rendimiento menor a 18 millas por galón de
combustible.
23. Autos que tengan 4 cilindros.
24. Autos que pesen más de 2500 libras y tengan transmisión manual.


5
Instrucciones de control
En Rse disponen de varias instrucciones de control para facilitar los pro-
cedimientos que un usuario debe realizar. A continuación se explican esas
instrucciones de control.
5.1. Instrucción if
Esta instrucción sirve para realizar un conjunto de operaciones si se cumple
cierta condición. A continuación se muestra la estructura básica de uso.
if (condicion) {
operación 1
operación 2
...
operación final
}
Ejemplo
Una secretaria recibe la información del salario básico semanal de un empleado
y las horas trabajadas durante la semana por ese empleado. El salario básico
es la remuneración por 40 horas de labor por semana, las horas extra son
pagadas a ciencuenta mil pesos. Escriba el procedimiento en Rque debe usar
la secretaria para calcular el salario semanal de un empleado que trabajó 45
horas y tiene salario básico de un millon de pesos.
El código para calcular el salario nal del empleado es el siguiente:
sal <- 1# Salario básico por semana
hlab <- 45 # Horas laboradas por semana
47

48 5 Instrucciones de control
if(hlab >40) {
hext <- hlab -40
salext <- hext *0.05
sal <- sal +salext
}
sal # Salario semanal
## [1] 1.25
5.2. Instrucción if else
Esta instrucción sirve para realizar un conjunto de operaciones cuando NO
se cumple cierta condición evaluada por un if. A continuación se muestra la
estructura básica de uso.
if (condicion) {
operación 1
operación 2
...
operación final
}
else {
operación 1
operación 2
...
operación final
}
5.3. Instrucción ifelse
Se recomienda usar la instrucción ifelse cuando hay una sola instrucción
para el caso if y para el caso else. A continuación se muestra la estructura
básica de uso.
5.4 Instrucción for 49
ifelse(condición, operación SI cumple, operación NO cumple)
Ejemplo
Suponga que usted recibe un vector de números enteros, escriba un procedi-
miento que diga si cada elemento del vector es par o impar.
x <- c(5,3,2,8,-4,1)
ifelse(x %% 2== 0,'Es par','Es impar')
## [1] "Es impar" "Es impar" "Es par" "Es par"
## [5] "Es par" "Es impar"
5.4. Instrucción for
La instrucción for es muy útil para repetir un procedimiento cierta cantidad
de veces. A continuación se muestra la estructura básica de uso.
for (i in secuencia) {
operación 1
operación 2
...
operación final
}
Ejemplo
Escriba un procedimiento para crear 10 muestras de tamaño 100 de una dis-
tribución uniforme entre uno y tres. Para cada una de las muestra, se debe
contar el número de elementos de la muestra que fueron mayores o iguales a
2.5.
nrep <- 10 # Número de repeticiones
n <- 100 # Tamaño de la muestra
50 5 Instrucciones de control
conteo <- numeric(nrep) # Vector para almacenar el conteo
for (i in 1:nrep) {
x <- runif(n=n, min=1,max=3)
conteo[i] <- sum(x >= 2.5)
}
conteo # Para obtener el conteo
## [1] 24 37 28 26 30 18 29 23 19 19
5.5. Instrucción while
La instrucción while es muy útil para repetir un procedimiento siempre que
se cumple una condición. A continuación se muestra la estructura básica de
uso.
while (condición) {
operación 1
operación 2
...
operación final
}
Ejemplo
Suponga que se lanza una moneda en la cual el resultado es cara o sello. Escri-
bir un procedimiento que simule lanzamientos hasta que el número de caras
obtenidas sea 5. El procedimiento debe entregar el historial de lanzamientos.
Para simular el lanzamiento de una moneda se puede usar la función sample
y deniendo el vector resultados con size=1 para simular un lanzamiento,
a continuación el código y tres pruebas ilustrativas.
resultados <- c('Cara','Sello')
sample(x=resultados, size=1)# Prueba 1
## [1] "Cara"

5.6 Instrucción repeat 51
Una vez seamos capaces de simular un lanzamiento podemos escribir el proce-
dimiento para generar tantos lanzamientos hasta que se cumpla la condición.
El código mostrado abajo permite hacer lo solicitado.
num.lanza <- 0# Contador de lanzamientos
num.caras <- 0# Contados de caras obtenidas
historial <- NULL # Vector vacío para almacenar
while (num.caras <5) {
res <- sample(x=resultados, size=1)
num.lanza <- num.lanza +1
historial[num.lanza] <- res
if (res == 'Cara') {
num.caras <- num.caras +1
}
}
historial
## [1] "Cara" "Sello" "Sello" "Sello" "Cara" "Sello"
## [7] "Sello" "Cara" "Sello" "Sello" "Cara" "Sello"
## [13] "Cara"
num.lanza
## [1] 13
La instrucción for se usa cuando sabemos el número de veces que se debe
repetir el procedimiento, mientras que la instrucción while se usa cuando
debemos repetir un procedimiento cuando se cumpla una condición.
5.6. Instrucción repeat
La instrucción while es muy útil para repetir un procedimiento siempre que
se cumple una condición. A continuación se muestra la estructura básica de
uso.
repeat {
operación 1
52 5 Instrucciones de control
operación 2
...
operación final
if (condición) break
}
Ejemplo
Escribir un procedimiento para ir aumentando de uno en uno el valor de x
hasta que xsea igual a siete El procedimiento debe imprimir por pantalla la
secuencia de valores de x.
x <- 3# Valor de inicio
repeat {
print(x)
x <- x +1
if (x == 8) {
break
}
}
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
La instrucción break sirve para salir de un procedimiento iterativo.

6
Creación de funciones en R
En este capítulo se explica cómo crear funciones en Rpara realizar tareas
especícas.
6.1. Función en R
Una función es un conjunto de instrucciones que convierten las entradas (in-
puts) en resultados (outputs) deseados. En la Figura 6.1 se muestra una ilus-
tración de lo que es una función o máquina general.
6.2. Partes de una función en R
Las partes de una función son:
Entradas: o llamadas también argumentos, sirven para ingresar informa-
ción necesaria para realizar el procedimiento de la función. Los argumentos
pueden estar vacíos y a la espera de que el usuario ingrese valores, o pue-
den tener valores por defecto, esto signica que si el usuario no ingresa una
valor al función usará el valor por defecto. Una función puede tener o no
argumentos de entrada, en los ejemplos se mostrarán estos casos.
Cuerpo: el cuerpo de la función está formado por un conjunto de instruccio-
nes que transforman las entradas en las salidas deseadas. Si el cuerpo de la
función está formado por varias instrucciones éstas deben ir entre llaves.
Salidas: son los resultados de la función. Toda función debe tener al menos un
resultado, si una función no genera un resultado entonces no sirve para nada.
Si una función entrega varios tipos de objetos se acostumbra a organizarlos
en una lista que puede manejar los diferentes tipos de objetos.
53
54 6 Creación de funciones en R
Figura 6.1: Ilustración de una función, tomada de www.mathinsight.org
nombre_de_funcion <- function(par1, par2, ...) {
cuerpo
cuerpo
cuerpo
cuerpo
return(resultado)
}
A continuación se mostrarán varios ejemplos sencillos para que el lector apren-
da a construir funciones.
6.2 Partes de una función en R55
Ejemplo
Construir una función que reciba dos números y que entregue la suma de estos
números.
Lo primero es elegir un nombre apropiado para la función, aquí se usó el
nombre suma porque así se tiene una idea clara de lo que hace la función. La
función suma recibe dos parámetros, xrepresenta el primer valor ingresado
mientras que yrepresenta el segundo. El cuerpo de la función está formado por
dos líneas, en la primera se crea el objeto resultado en el cual se almanacena
el valor de la suma, en la segunda línea se le indica a Rque queremos que
retorne el valor de la suma almacenada en el objeto resultado. A continuación
se muestra el código para crear la función solicitada.
suma <- function(x, y) {
resultado <- x +y
return(resultado)
}
Para usar la función creada sólo se debe ejecutar, vamos a obtener la suma de
los valores 4 y 6 usando la función suma, a continuación el código necesario.
suma(x=4,y=6)
## [1] 10
Para funciones simples como la anterior es posible escribirlas en forma más
compacta. Es posible reducir el cuerpo de la función de 2 líneas a sólo una
línea solicitándole a Rque retorne directamente la suma sin almacenarla en
ningún objeto. A continuación la función suma modicada.
suma <- function(x, y) {
return(x +y)
}
suma(x=4,y=6)# Probando la función
## [1] 10
Debido a que la función suma tiene un cuerpo muy reducido es posible escri-
birla en forma más compacta, en una sola línea. A continuación se muestra el
código para reescribir la función.
56 6 Creación de funciones en R
suma <- function(x, y) x +y
suma(x=4,y=6)# Probando la función
## [1] 10
Ejemplo
Construir una función que genere números aleatorios entre cero y uno hasta
que la suma de éstos números supere por primera vez el valor de 3. La función
debe entregar la cantidad de números aleatorios generados para que se cumpla
la condición.
Vamos a llamar la función solicitada con el nombre fun1, esta función NO
necesita ningún parámetro de entrada. El valor de 3 que está en la condición
puede ir dentro del cuerpo y por eso no se necesitan parámetros para esta
función. En el cuerpo de la función se genera un vector con un número aleatorio
y luego se chequea si la suma de sus elementos es menor de 3, si se cumple que
la suma es menor que 3 se siguen generando números que se almacenan en el
vector num. Una vez que la suma exceda el valor de 3 NO se ingresa al while
y se pide la longitud del vector o el valor de veces solicitado. A continuación
el código de la función.
fun1 <- function() {
num <- runif(1)
veces <- 1
while (sum(num) <3) {
veces <- veces +1
num[veces] <- runif(1)
}
return(veces)
}
fun1() # primera prueba
## [1] 8
Ejemplo
Construir una función que, dado un número entero positivo (cota) ingresado
por el usuario, genere números aleatorios entre cero y uno hasta que la suma
6.2 Partes de una función en R57
de los números generados exceda por primera vez la cota. La función debe en-
tregar un vector con los números aleatorios, la suma y la cantidad de números
aleatorios. Si el usuario no ingresa el valor de la cota, se debe asumir igual a
1.
La función aquí solicitada es similar a la construída en el ejemplo anterior. La
función fun2 tiene un sólo parámetro con el valor por defecto, si el usuario
no ingresa valor a este parámetro, se asumirá el valor de uno. El cuerpo de
la función es similar al anterior. Como la función debe entregar un vector y
dos números, se construye la lista resultado que almacena los tres objetos
solicitados. A continuación el código para función solicitada.
fun2 <- function(cota=1) {
num <- runif(1)
while (sum(num) <cota) {
num <- c(num, runif(1))
}
resultado <- list(vector=num,
suma=sum(num),
cantidad=length(num))
return(resultado)
}
Probando la función con cota de uno.
fun2()
## $vector
## [1] 0.7704 0.6568
##
## $suma
## [1] 1.427
##
## $cantidad
## [1] 2
Probando la función con cota de tres.
fun2(cota=3)
## $vector
## [1] 0.5174 0.7786 0.6926 0.8071 0.2143
##
## $suma
## [1] 3.01

58 6 Creación de funciones en R
##
## $cantidad
## [1] 5
Ejemplo
Construya una función que reciba dos números de la recta real y que entre-
gue el punto médio de estos números. El resultado debe ser un mensaje por
pantalla.
El punto médio entre dos valores es la suma de los números divido entre dos.
La función cat sirve para concatenar objetos y presentarlos por pantalla. A
continuación el código para la función requerida.
medio <- function(a, b) {
medio <- (a +b) /2
cat("El punto medio de los valores",
a, "y", b,
"ingresados es", medio)
}
medio(a=-3,b=-1)# Probando la función
## El punto medio de los valores -3 y -1 ingresados es -2
La función cat es muy útil para presentar resultados por pantalla. Consulte
la ayuda de la función para ver otros ejemplos.
EJERCICIOS
Construir funciones en Rque realicen lo solicitado.
1. Construya una función que reciba dos números reales ayb, la fun-
ción debe decir cuál es el mayor de ellos.
2. Escriba una función llamada media que calcule la media muestral
de un vector numérico xingresado a la función. A continuación la
fórmula para calcular la media muestral.

6.2 Partes de una función en R59
¯x=n
i=1 xi
n
Nota: no puede usar la función mean( ).
3. Construya una función que encuentre las raíces de una ecuación de
segundo grado. El usuario debe suministrar los coecientes a,byc
de la ecuación ax2+bx +c= 0 y la función debe entregar las raíces.
4. Escribir una función que calcule la velocidad de un proyectil dado
que el usuario ingresa la distancia recorrida en Km y el tiempo
necesario en minutos. Expresar el resultado se debe entregar en
metros/segundo, recuerde que
velocidad =espacio
tiempo
5. Escribir una función que reciba dos valores ayby que los intercambie. Es
decir, si ingresa a= 4 yb= 9 que la función entregue a= 9 yb= 4.
6. Construya una función a la cual le ingrese el salario por hora y el
número de horas trabajadas durante una semana por un trabajador.
La función debe calcular el salario neto.
7. Construya una función llamada precio que calcule el precio total de
sacar A fotocopias y B impresiones, sabiendo que los precios son 50
y 100 pesos para A y B respectivamente si el cliente es un estudiante,
y de 75 y 150 para A y B si el cliente es un profesor. La función
debe tener dos argumentos cuantitativos (AyB) y el argumento
lógico estudiante que por defecto tenga el valor de TRUE. Use la
estructura mostrada abajo.
precio <- function(A, B, estudiante=TRUE) {
...
...
...
return(precio.total)
}
8. Construya una función llamada salario que le ingrese el salario
por hora y el número de horas trabajadas durante una semana por
un trabajador. La función debe calcular el salario neto semanal,
teniendo en cuenta que si el número de horas trabajadas durante
la semana es mayor de 48, esas horas de demás se consideran horas

60 6 Creación de funciones en R
extras y tienen un 35 % de recargo. Imprima el salario neto. Use la
estructura mostrada abajo.
salario <- function(num.horas, valor.hora) {
...
...
...
return(salario.neto)
}
9. Construya una función llamada nota que calcule la nota obtenida
por un alumno en una evaluación de tres puntos cuya ponderación
o importancia son 20 %, 30 % y 50 % para los puntos I, II y III res-
pectivamente. Adicionalmente la función debe generar un mensaje
sobre si el estudiante aprobó la evaluación o no. El usuario debe
ingresar las notas individuales de los tres puntos y la función debe
entregar la nota nal de la evaluación. Use la estructura mostrada
abajo.
nota <- function(p1, p2, p3) {
...
...
...
}
10. Escriba una función llamada minimo que permita obtener el valor
mínimo de un vector numérico. No puede usar ninguna de las funcio-
nes básicas de R como which.min(),which.max(),order(),min(
),max( ),sort( ) uorder( ). Use la estructura mostrada abajo.
minimo <- function(x) {
...
...
return(minimo)
}
11. Construya una función que calcule las coordenadas del punto medio
Mentre dos puntos AyB. Vea la Figura 6.2 para una ilustración.
¿Cuáles cree usted que deben ser los parámetros de entrada de la
función?
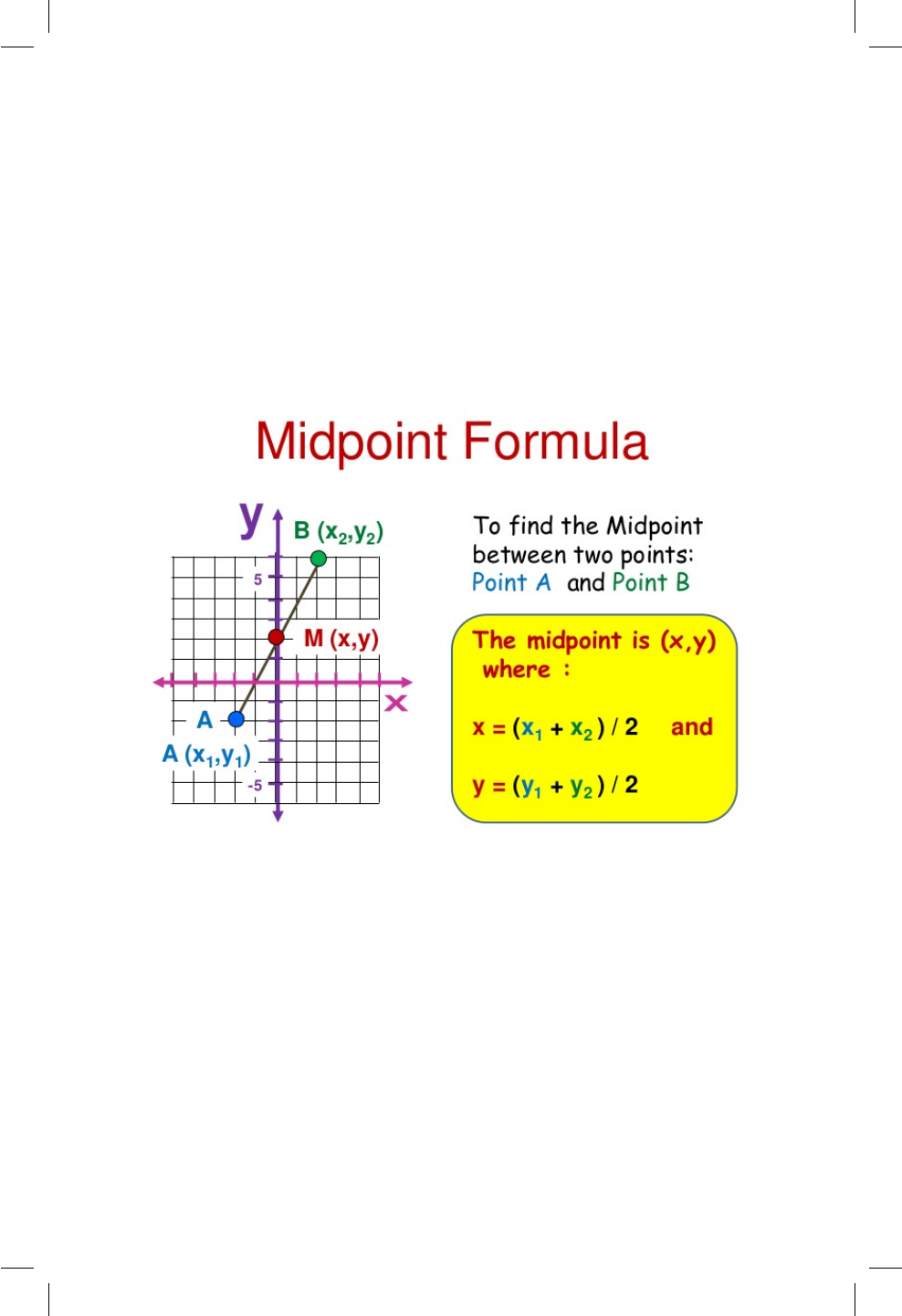
6.2 Partes de una función en R61
Figura 6.2: Ilustración del punto medio entre dos puntos, tomada de
https://www.slideshare.net/bigpassy/midpoint-between-two-points


7
Lectura de bases de datos
En este capítulo se mostrará cómo leer una base de datos externa hacia R.
7.1. ¿En qué formato almacenar una base de datos?
Usualmente los archivos con la información para ser leídos por Rse pueden
almacenar en formato:
plano con extensión .txt o,
Excel con extensión .csv.
En las secciones siguientes se mostrará cómo almacenar datos en los dos for-
matos para ser leídos en R. En el Cuadro 7.1 se presenta una base de datos
pequeña, tres observaciones y tres variables, que nos servirá como ejemplo
para mostrar cómo se debe almacenar la información.
7.1.1. Almacenamiento de información en Excel
Para almacenar la información del Cuadro 7.1 en Excel, abrimos un archivo
nuevo archivo de Excel y copiamos la información tal como se muestra en la
Figura 7.1. Se debe iniciar en la parte superior izquierda, no se deben dejar
las vacías, no se debe colorear, no se deben colocar bordes ni nada, se ingresa
la información sin embellecer el contenido. Por último se guarda el archivo en
Cuadro 7.1: Ejemplo de una base de datos simple.
Edad Fuma Pais
35 TRUE Colombia
46 TRUE Francia
23 FALSE Malta
63
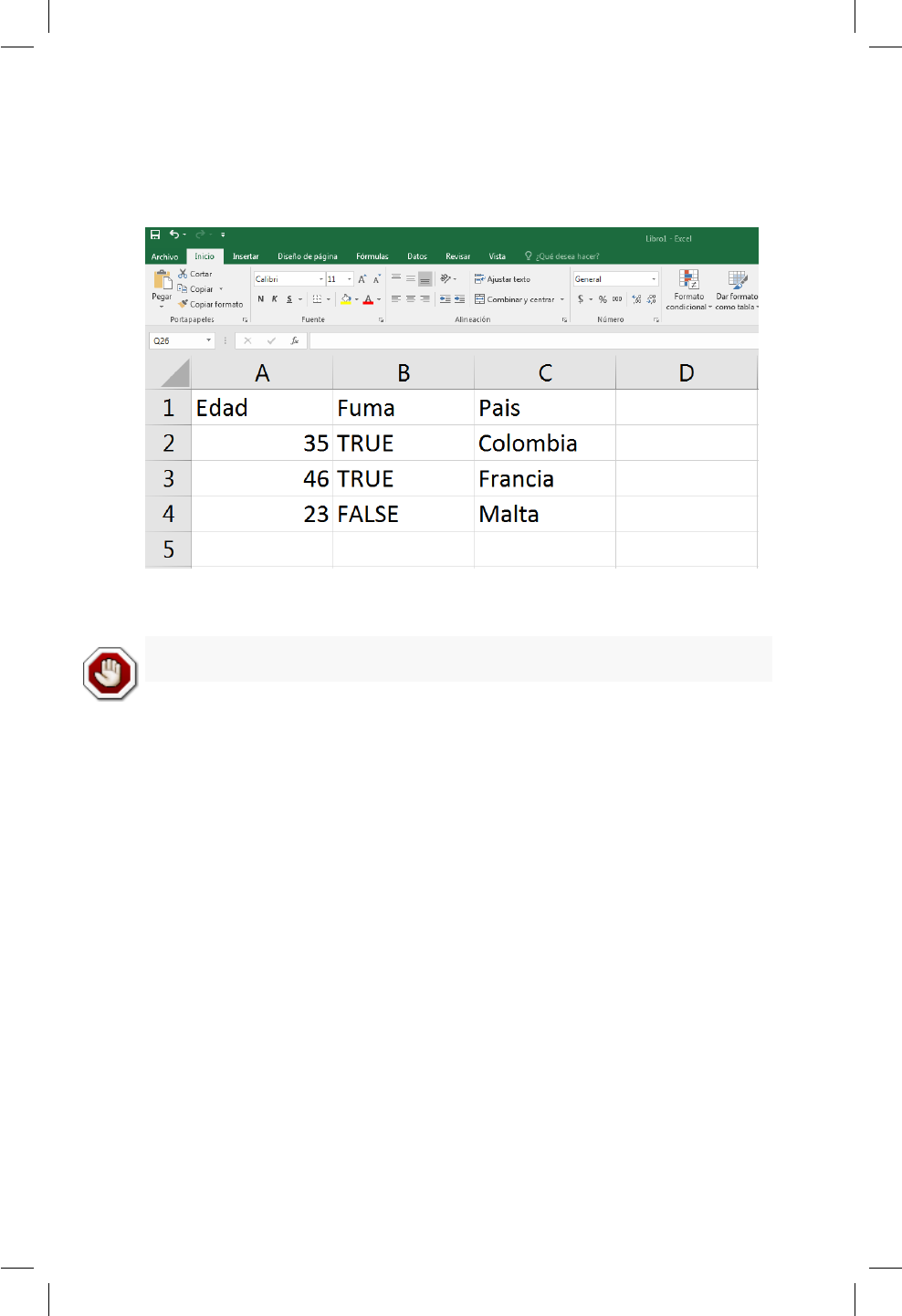
64 7 Lectura de bases de datos
la carpeta deseada y al momento de nombrar el archivo se debe modicar la
opción tipo de archivo a csv (delimitado por comas).
Figura 7.1: Forma de almacenar los datos en Excel.
Recuerde que el archivo de Excel se debe guardar con extensión .csv.
7.1.2. Almacenamiento de información en bloc de notas
Para almacenar la información del Cuadro 7.1 en bloc de notas, abrimos un
archivo nuevo de bloc de notas y copiamos la información tal como se muestra
en la Figura 7.2. Se copian los nombres de las variables o los datos separados
por un espacio obtenido con la tecla tabuladora, cada línea se naliza con un
enter. Se recomienda al guardar el archivo que el cursor al inicio de una línea
vacía, en la Figura 7.2 se señala la posición del cursor con la echa roja, a
pesar de que no éxiste línea número 5, el curso debe quedar al inicio de esa
línea número 5.
Es posible mejorar la apariencia de la información almacenada en el bloc de
notas si, en lugar de usar espacios con la barra espaciadora, se colocan los
espacios con la barra tabuladora, así la información se ve más organizada y
se puede chequear fácilmente la información ingresada. En la Figura 7.3 se
muestra la información para el ejemplo, claramente se nota la organización de
la información.
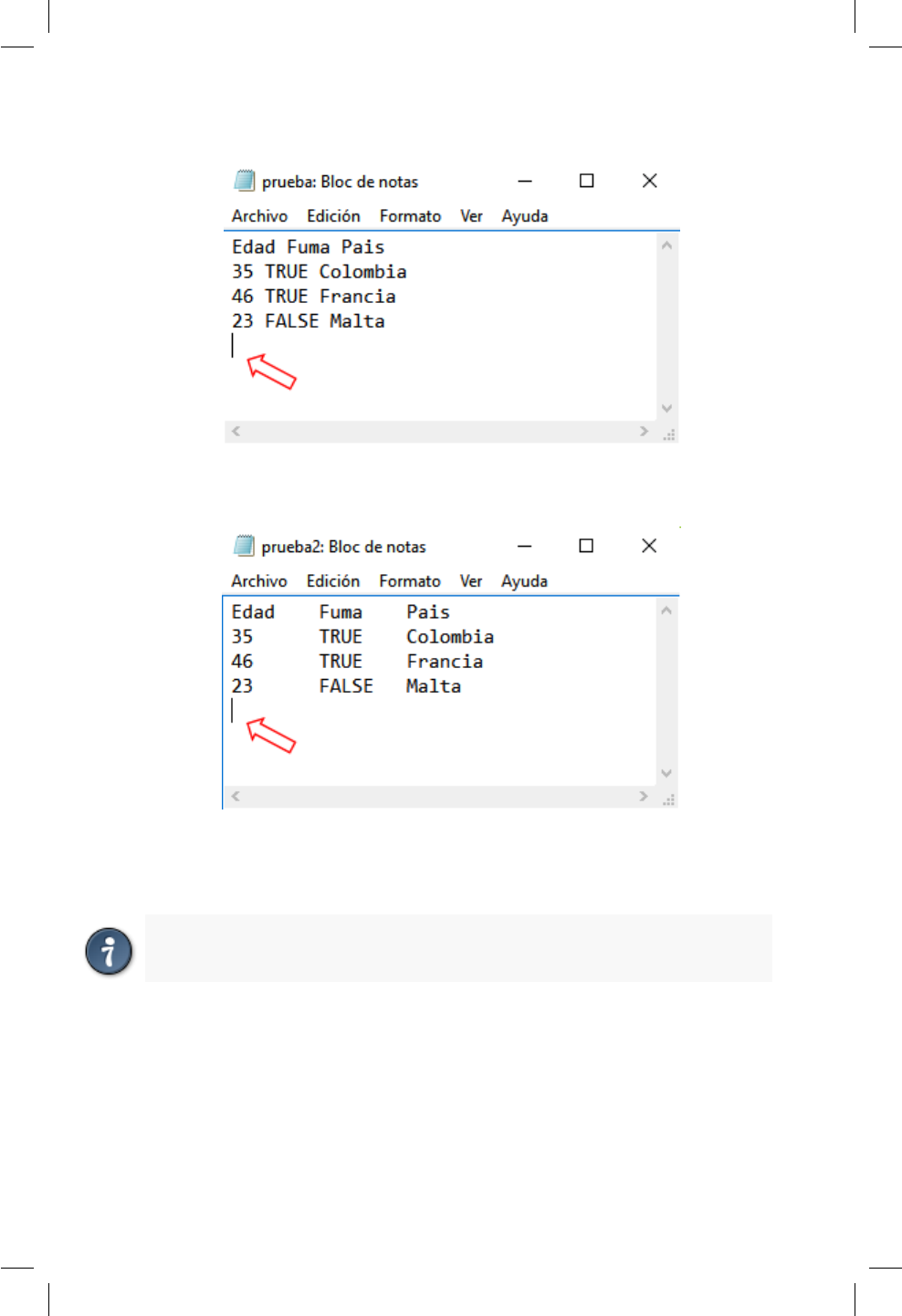
7.2 ¿En qué formato almacenar una base de datos? 65
Figura 7.2: Almacenamiento de los datos en bloc de notas usando la barra
espaciadora
Figura 7.3: Almacenamiento de los datos en bloc de notas usando la barra
tabuladora
Una buena práctica es usar la barra tabuladora para separar, eso permite
que la información se vea ordenada.

66 7 Lectura de bases de datos
7.2. Función read.table
La función read.table se puede usar para leer bases de datos hacia R. La
estructura de la función con los parámetros más comunes de uso es la siguiente.
read.table(file, header, sep, dec)
Los argumentos de la función read.table son:
file: nombre o ruta donde están alojados los datos. Puede ser un url o una
dirección del computador. Es también posible usar file.choose() para que
se abra un ventana y adjuntar el archivo deseado manualmente.
header: valor lógico, se usa TRUE si la primera línea de la base de datos tiene
los nombres de las variables, caso contrario se usa FALSE.
sep: tipo de separación interna para los datos dentro del archivo. Los valores
usuales para este parámetros son:
•sep=',' si el archivo tiene extensión .csv.
•sep='' si el archivo es bloc de notas con espacios por la barra espa-
ciadora.
•sep='\t' si el archivo es bloc de notas con espacios por la barra ta-
buladora.
dec: símbolo con el cual están indicados los decimales.
Ejemplo
Crear la base de datos del Cuadro 7.1 en Excel y bloc de notas para practicar
la lectura de base de datos desde R.
Lo primero que se debe hacer para realizar lo solicitado es construir tres
archivos (uno de Excel y dos bloc de notas) igual a los mostrados en las
guras 7.1,7.2 y7.3, vamos a suponer que los nombres para cada uno de ellos
son base1.csv,base2.txt ybase3.txt respectivamente.
Para Excel
Para leer el archivo de Excel llamado base1.csv podemos usar el siguiente
código.
datos <- read.table(file='C:/Users/Hernandez/Desktop/base1.csv',
header=TRUE,sep=',')
datos
7.2 Función read.table 67
La dirección file='C:/Users/Hernandez/Desktop/base1.csv' le indica a R
en qué lugar del computador debe buscar el archivo, note que se debe usar el
símbolo /para que sea un dirección válida. Substituya la dirección del código
anterior con la dirección donde se encuentra su archivo para que pueda leer
la base de datos.
Si no se conoce la ubicación del archivo a leer o si la dirección es muy extensa,
se puede usar file.choose() para que se abra una ventana y así adjuntar
manualmente el archivo. A continuación se muestra el código para hacerlo de
esta manera.
datos <- read.table(file.choose(), header=TRUE,sep=',')
datos
Para bloc de notas con barra espaciadora
Para leer el archivo de Excel llamado base2.txt podemos usar el siguiente
código.
datos <- read.table(file='C:/Users/Hernandez/Desktop/base2.txt',
header=TRUE,sep='')
datos
Para bloc de notas con barra tabuladora
Para leer el archivo de Excel llamado base3.txt podemos usar el siguiente
código.
datos <- read.table(file='C:/Users/Hernandez/Desktop/base3.txt',
header=TRUE,sep='\t')
datos
El usuario puede usar indiferentemente file='C:/Users/bla/bla' o
file.choose() para ingresar el archivo, con la práctica se aprende a de-
cidir cuando conviene una u otra forma.
Un error frecuente es escribir la dirección o ubicación del archivo usando \,
lo correcto es usar /.

68 7 Lectura de bases de datos
Ejemplo
Leer la base de datos sobre apartamentos usados en la ciudad de Me-
dellín que está disponible en la página web cuya url es: https://raw.
githubusercontent.com/fhernanb/datos/master/aptos2015
Para leer la base de datos desde una url usamos el siguiente código.
enlace <- 'https://raw.githubusercontent.com/fhernanb/datos/master/aptos2015'
datos <- read.table(file=enlace, header=TRUE)
La base de datos ingresada queda en el marco de datos llamado datos y ya
está disponible para usarla.
7.3. Lectura de bases de datos en Excel
Algunas veces los datos están disponibles en un archivo estándar de Excel, y
dentro de cada archivo hojas con la información a utilizar. En estos casos se
recomienda usar el paquete readxl (Wickham and Bryan,2018) y en particu-
lar la función readxl. A continuación un ejemplo de cómo proceder en estos
casos.
Ejemplo
En este enlace1está disponible un archivo de Excel llamado BD_Excel.xlxs,
una vez se ha abierto la página donde está alojado el archivo, se debe descargar
y guardar en alguna carpeta. El archivo contiene dos bases de datos muy
pequeñas, en la primera hoja llamada Hijos está la información de un grupo
de niños y en la segunda hoja llamada Padres está la información de los
padres. ¿Cómo se pueden leer las dos bases de datos?
Lo primero que se debe hacer es instalar el paquete readxl, la instalación
de cualquier paquete en un computador se hace una sola vez y éste quedará
instalado para ser usado las veces que se requiera. La función para instalar un
paquete cualquiera es install.packages, a continuación se muestra el código
necesario para instalar el paquete readxl.
1https://github.com/fhernanb/datos/blob/master/BD_Excel.xlsx
7.3 Lectura de bases de datos en Excel 69
install.packages("readxl")
Una vez instalado el paquete es necesario cargarlo, la función para cargar el
paquete en la sesión actual de Res library. La instrucción para cargar el
paquete es la siguiente:
library(readxl)
La instalación de un paquete con install.packages se hace sólo una vez
y no más. Cargar el paquete con library en la sesión actual se debe hacer
siempre que se vaya a usar el paquete.
Luego de haber cargado el paquete readxl se puede usar la función read_xl
para leer la información contenida en las hojas. A continuación el código para
crear la base de datos hijos contenida en el archivo BD_Excel.xlsx.
hijos <- read_excel(file.choose(), sheet='Hijos')
as.data.frame(hijos) # Para ver el contenido
## Edad Grado ComicFav
## 1 8 2 Superman
## 2 6 1 Batman
## 3 9 3 Batman
## 4 10 5 Bob Esponja
## 5 8 4 Batman
## 6 9 4 Bob Esponja
A continuación el código para crear la base de datos padres contenida en el
archivo BD_Excel.xlsx.
padres <- read_excel('BD_Excel.xlsx',sheet='Padres')
as.data.frame(padres) # Para ver el contenido
## Edad EstCivil NumHijos
## 1 45 Soltero 1
## 2 50 Casado 0
## 3 35 Casado 3
## 4 65 Divorciado 1
La función read_excel tiene otros parámetros adicionales útiles para leer
bases de datos, se recomienda consultar la ayuda de la función escribiendo en
la consola help(read_excel).

70 7 Lectura de bases de datos
Cuadro 7.2: Base de datos para practicar lectura.
Fuma Pasatiempo Num_hermanos Mesada
Si Lectura 0 4500
Si NA 2 2600
No Correr 4 1000
No Correr NA 3990
Si TV 3 2570
No TV 1 2371
Si Correr 1 1389
NA Correr 0 4589
Si Lectura 2 NA
EJERCICIOS
Realice los siguiente ejercicios propuestos.
1. En el Cuadro 7.2 se presenta una base de datos sencilla. Almacene
la información del cuadro en dos archivos diferentes, en Excel y en
bloc de notas. Lea los dos archivos con la función read.table y
compare los resultados obtenidos con la del Cuadro 7.2 fuente.
2. En la url https://raw.githubusercontent.com/fhernanb/
datos/master/medidas_cuerpo están disponibles los datos sobre
medidas corporales para un grupo de estudiante de la universidad,
use la función read.table para leer la base de datos.
8
Tablas de frecuencia
Las tablas de frecuencia son muy utilizadas en estadística y Rpermite crear
tablas de una forma sencilla. En este capítulo se explican las principales fun-
ciones para la elaboración de tablas.
8.1. Tabla de contingencia con table
La función table sirve para construir tablas de frecuencia de una vía, a con-
tinuación la estrctura de la función.
table(..., exclude, useNA)
Los parámetros de la función son:
... espacio para ubicar los nombres de los objetos (variables o vectores)
para los cuales se quiere construir la tabla.
exclude: vector con los niveles a remover de la tabla. Si exclude=NULL
implica que se desean ver los NA, lo que equivale a useNA = 'always'.
useNA: instrucción de lo que se desea con los NA. Hay tres posibles valores
para este parámetro: 'no' si no se desean usar, 'ifany' y'always' si se
desean incluir.
Ejemplo: tabla de frecuencia de una vía
Considere el vector fuma mostrado a continuación y construya una tabla de
frecuencias absolutas para los niveles de la variable frecuencia de fumar.
fuma <- c('Frecuente','Nunca','A veces','A veces','A veces',
'Nunca','Frecuente',NA,'Frecuente',NA,'hola',
'Nunca','Hola','Frecuente','Nunca')
71

72 8 Tablas de frecuencia
A continuación se muestra el código para crear la tabla de frecuencias para la
variable fuma.
table(fuma)
## fuma
## A veces Frecuente hola Hola Nunca
##34114
De la tabla anterior vemos que NO aparece el conteo de los NA, para obtenerlo
usamos lo siguiente.
table(fuma, useNA='always')
## fuma
## A veces Frecuente hola Hola Nunca
##34114
## <NA>
## 2
Vemos que hay dos niveles errados en la tabla anterior, Hola yhola. Para
construir la tabla sin esos niveles errados usamos lo siguiente.
table(fuma, exclude=c('Hola','hola'))
## fuma
## A veces Frecuente Nunca <NA>
## 3 4 4 2
Por último construyamos la tabla sin los niveles errados y los NA, a esta última
tabla la llamaremos tabla1 para luego poder usarla. Las instrucciones para
hacer esto son las siguientes.
tabla1 <- table(fuma, exclude=c('Hola','hola',NA))
tabla1
## fuma
## A veces Frecuente Nunca
## 3 4 4
Al crear una tabla con la instrucción table(var1, var2), la variable 1
quedará por las mientras que la variable 2 estará en las columnas.
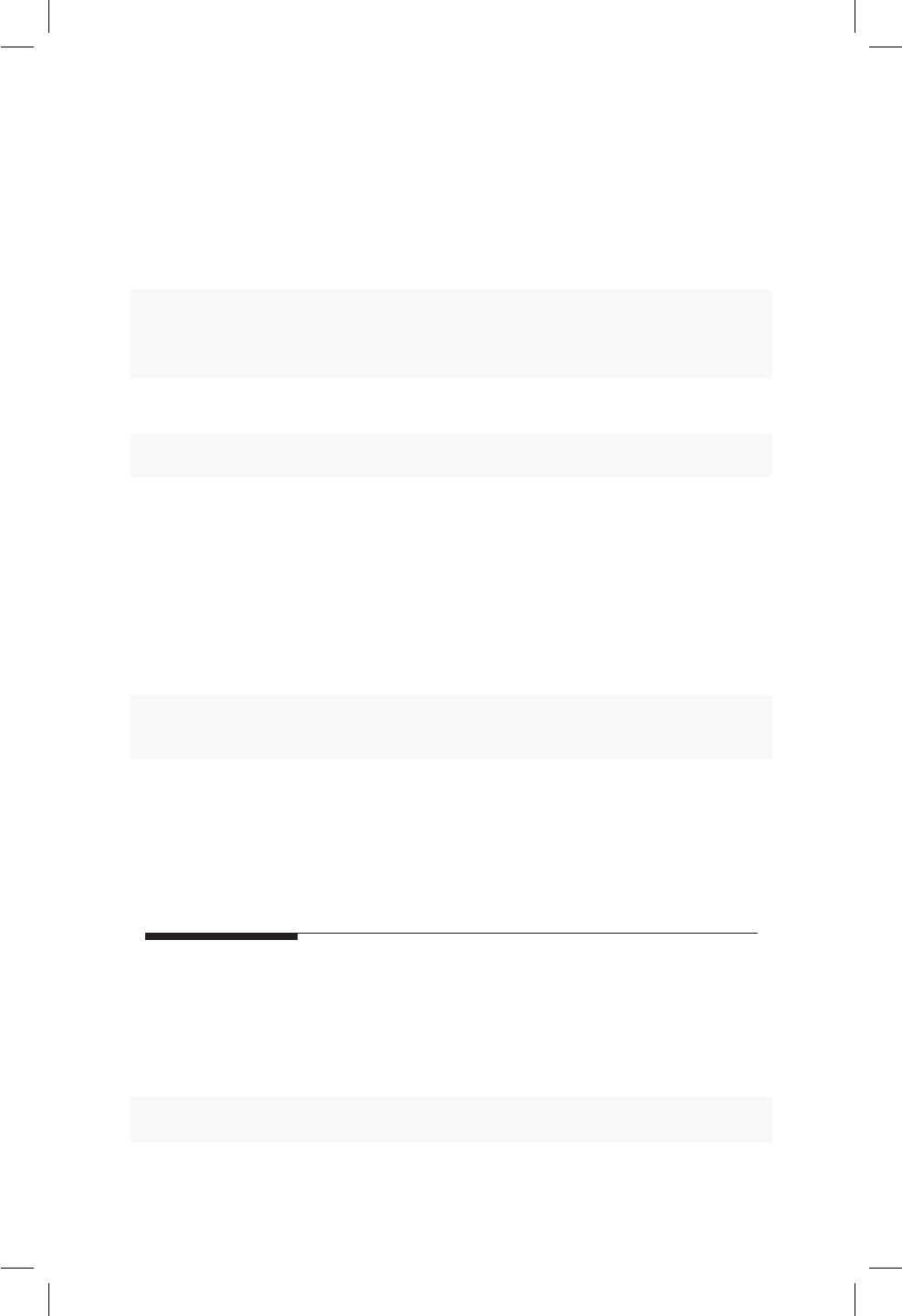
8.2 Función prop.table 73
Ejemplo: tabla de frecuencia de dos vías
Considere otro vector sexo mostrado a continuación y construya una tabla de
frecuencias absolutas para ver cómo se relaciona el sexo con fumar del ejemplo
anterior.
sexo <- c('Hombre','Hombre','Hombre',NA,'Mujer',
'Casa','Mujer','Mujer','Mujer','Hombre','Mujer',
'Hombre',NA,'Mujer','Mujer')
Para construir la tabla solicitada usamos el siguiente código.
table(sexo, fuma)
## fuma
## sexo A veces Frecuente hola Hola Nunca
## Casa 0 0 0 0 1
## Hombre 1 1 0 0 2
## Mujer 1 3 1 0 1
De la tabla anterior vemos que aparecen niveles errados en fuma y en sexo,
para retirarlos usamos el siguiente código incluyendo en el parámetro exclude
un vector con los niveles que NO deseamos en la tabla.
tabla2 <- table(sexo, fuma, exclude=c('Hola','hola','Casa',NA))
tabla2
## fuma
## sexo A veces Frecuente Nunca
## Hombre 1 1 2
## Mujer 1 3 1
8.2. Función prop.table
La función prop.table se utiliza para crear tablas de frecuencia relativa a
partir de tablas de frecuencia absoluta, la estructura de la función se muestra
a continuación.
prop.table(x, margin=NULL)
74 8 Tablas de frecuencia
x: tabla de frecuencia.
margin: valor de 1 si se desean proporciones por las, 2 si se desean por
columnas, NULL si se desean frecuencias globales.
Ejemplo: tabla de frecuencia relativa de una vía
Obtener la tabla de frencuencia relativa para la tabla1.
Para obtener la tabla solicitada se usa el siguiente código.
prop.table(x=tabla1)
## fuma
## A veces Frecuente Nunca
## 0.2727 0.3636 0.3636
Ejemplo: tabla de frecuencia relativa de dos vías
Obtener la tabla de frencuencia relativa para la tabla2.
Si se desea la tabla de frecuencias relativas global se usa el siguiente código.
El resultado se almacena en el objeto tabla3 para ser usado luego.
tabla3 <- prop.table(x=tabla2)
tabla3
## fuma
## sexo A veces Frecuente Nunca
## Hombre 0.1111 0.1111 0.2222
## Mujer 0.1111 0.3333 0.1111
Si se desea la tabla de frecuencias relativas marginal por columnas se usa el
siguiente código.
tabla4 <- prop.table(x=tabla2, margin=2)
tabla4
## fuma
## sexo A veces Frecuente Nunca
## Hombre 0.5000 0.2500 0.6667
## Mujer 0.5000 0.7500 0.3333
8.4 Función addmargins 75
8.3. Función addmargins
Esta función se puede utilizar para agregar los totales por las o por columnas
a una tabla de frecuencia absoluta o relativa. La estructura de la función es
la siguiente.
addmargins(A, margin)
A: tabla de frecuencia.
margin: valor de 1 si se desean proporciones por columnas, 2 si se desean
por las, NULL si se desean frecuencias globales.
Ejemplo
Obtener las tablas tabla3 ytabla4 con los totales margines global y por
columnas respectivamente.
Para hacer lo solicitado usamos las siguientes instrucciones.
addmargins(tabla3)
## fuma
## sexo A veces Frecuente Nunca Sum
## Hombre 0.1111 0.1111 0.2222 0.4444
## Mujer 0.1111 0.3333 0.1111 0.5556
## Sum 0.2222 0.4444 0.3333 1.0000
addmargins(tabla4, margin=1)
## fuma
## sexo A veces Frecuente Nunca
## Hombre 0.5000 0.2500 0.6667
## Mujer 0.5000 0.7500 0.3333
## Sum 1.0000 1.0000 1.0000
Note que los valores de 1 y 2 en el parámetro margin de las funciones
prop.table yaddmargins signican lo contrario.

76 8 Tablas de frecuencia
8.4. Función hist
Construir tablas de frecuencias para variables cuantitativas es necesario en
muchos procedimientos estadísticos, la función hist sirve para obtener este
tipo de tablas. La estructura de la función es la siguiente.
hist(x, breaks='Sturges',include.lowest=TRUE,right=TRUE,
plot=FALSE)
Los parámetros de la función son:
x: vector numérico.
breaks: vector con los límites de los intervalos. Si no se especica se usar la
regla de Sturges para denir el número de intervalos y el ancho.
include.lowest: valor lógico, si TRUE una observación xique coincida con
un límite de intervalo será ubicada en el intervalo izquierdo, si FALSE será
incluída en el intervalo a la derecha.
right: valor lógico, si TRUE los intervalos serán cerrados a derecha de la
forma (liminf , limsup], si es FALSE serán abiertos a derecha.
plot: valor lógico, si FALSE sólo se obtiene la tabla de frecuencias mientras
que con TRUE se obtiene la representación gráca llamada histograma.
Ejemplo
Genere 200 observaciones aleatorias de una distribución normal con media
µ= 170 y desviación σ= 5, luego construya una tabla de frecuencias para
la muestra obtenida usando (a) la regla de Sturges y (b) tres intervalos con
límites 150, 170, 180 y 190.
Primero se construye el vector xcon las observaciones de la distribución nor-
mal por medio de la función rnorm y se especica la media y desviación soli-
citada. Luego se aplica la función hist con el parámetro breaks='Sturges',
a continuación el código utilizado.
x <- rnorm(n=200,mean=170,sd=5)
res1 <- hist(x=x, breaks='Sturges',plot=FALSE)
res1
## $breaks
## [1] 155 160 165 170 175 180 185
##

8.4 Función hist 77
## $counts
## [1] 4 31 61 70 26 8
##
## $density
## [1] 0.004 0.031 0.061 0.070 0.026 0.008
##
## $mids
## [1] 157.5 162.5 167.5 172.5 177.5 182.5
##
## $xname
## [1] "x"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"
El objeto res1 es una lista donde se encuentra la información de la tabla de
frecuencias para x. Esa lista tiene en el elemento breaks los límites inferior
y superior de los intervalos y en el elemento counts están las frecuencias de
cada uno de los intervalos.
Para obtener las frecuencias de tres intervalos con límites 150, 170, 180 y 190
se especica en el parámetros breaks los límites. El código para obtener la
segunda tabla de frecuencias se muestra a continuación.
res2 <- hist(x=x, plot=FALSE,
breaks=c(150,170,180,190))
res2
## $breaks
## [1] 150 170 180 190
##
## $counts
## [1] 96 96 8
##
## $density
## [1] 0.024 0.048 0.004
##
## $mids
## [1] 160 175 185
##
## $xname
## [1] "x"
##
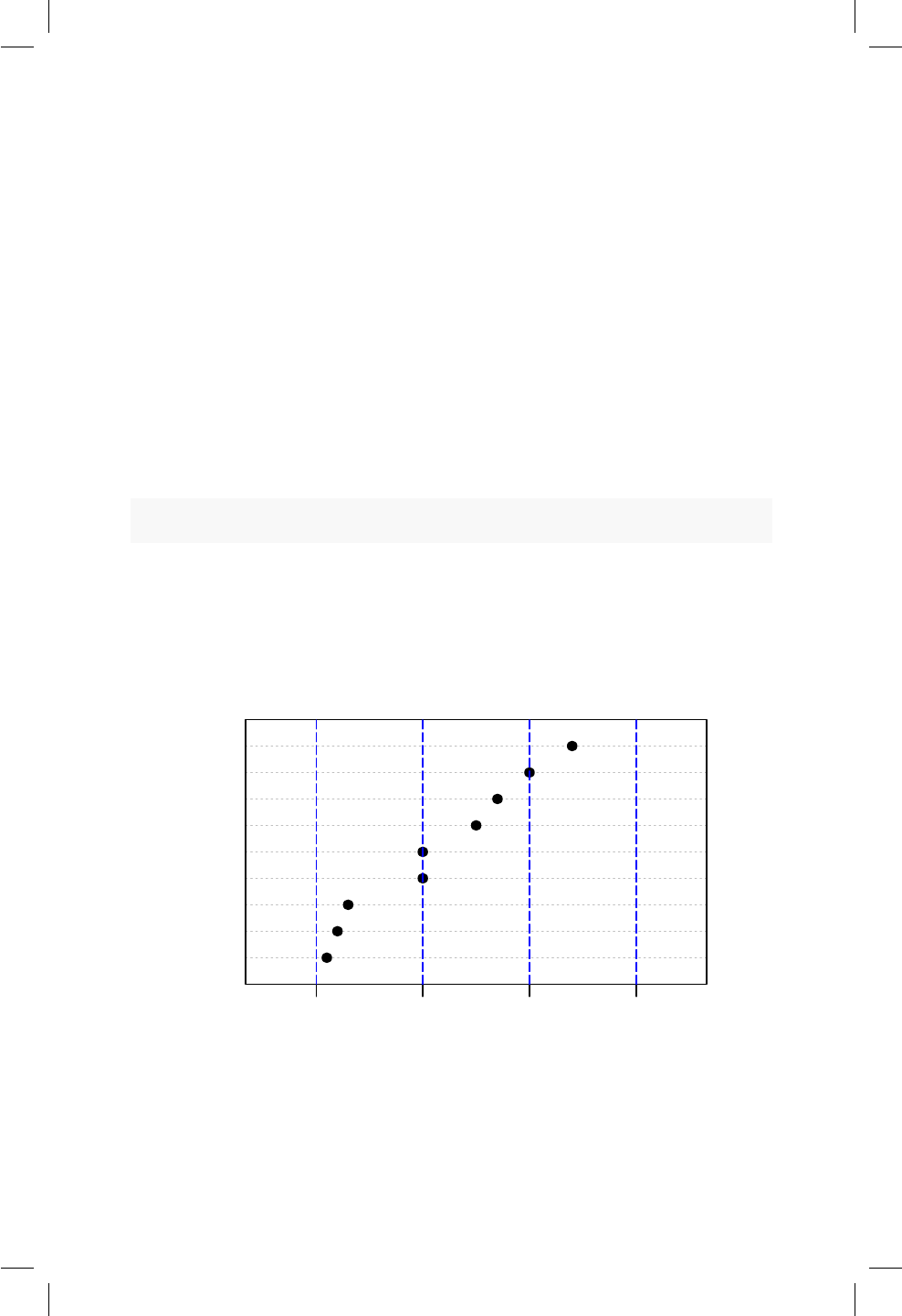
78 8 Tablas de frecuencia
## $equidist
## [1] FALSE
##
## attr(,"class")
## [1] "histogram"
Ejemplo
Construya el vector xcon los siguientes elementos: 1.0, 1.2, 1.3, 2.0, 2.5, 2.7,
3.0 y 3.4. Obtenga varias tablas de frecuencia con la función hist variando
los parámetros include.lowest yright. Use como límite de los intervalos
los valores 1, 2, 3 y 4.
Lo primero que debemos hacer es crear el vector xsolicitado así:
x <- c(1.1,1.2,1.3,2.0,2.0,2.5,2.7,3.0,3.4)
En la Figura 8.1 se muestran los 9 puntos y con color azul se representan los
límites de los intervalos.
1 2 3 4
Valores de x
Figura 8.1: Ubicación de los puntos del ejemplo con límites en color azul.
8.4 Función hist 79
A continuación se presenta el código para obtener la tabla de frecuencia usando
rigth=TRUE, los resultados se almacenan en el objeto res3 y se solicitan sólo
los dos primeros elementos que corresponden a los límites y frecuencias.
res3 <- hist(x, breaks=c(1,2,3,4), right=TRUE,plot=FALSE)
res3[1:2]
## $breaks
##[1]1234
##
## $counts
## [1] 5 3 1
Ahora vamos a repetir la tabla pero usando rigth=FALSE para ver la diferencia,
en res4 están los resultados.
res4 <- hist(x, breaks=c(1,2,3,4), right=FALSE,plot=FALSE)
res4[1:2]
## $breaks
##[1]1234
##
## $counts
## [1] 3 4 2
Al comparar los últimos dos resultados vemos que la primera frecuencia es 5
cuando right=TRUE porque los intervalos se consideran cerrados a la derecha.
Ahora vamos a construir una tabla de frecuencia usando FALSE para los pará-
metros include.lowest yright.
res5 <- hist(x, breaks=c(1,2,3,4),
include.lowest=FALSE,right=FALSE,
plot=FALSE)
res5[1:2]
## $breaks
##[1]1234
##
## $counts
## [1] 3 4 2
De este último resultado se ve claramente el efecto de los parámetros
include.lowest yright en la construcción de tablas de frecuencia.

80 8 Tablas de frecuencia
EJERCICIOS
Use funciones o procedimientos (varias líneas) de Rpara responder cada una
de las siguientes preguntas.
En el Cuadro 7.2 se presenta una base de datos sencilla. Lea la base de datos
usando la funcion read.table y construya lo que se solicita a continuación.
1. Construya una tabla de frecuencia absoluta para la variable pasa-
tiempo.
2. Construya una tabla de frecuencia relativa para la variable fuma.
3. Construya una tabla de frecuencia relativa para las variables pasa-
tiempo y fuma.
4. ¿Qué porcentaje de de los que no fuman tienen como pasatiempo
la lectura.
5. ¿Qué porcentaje de los que corren no fuman?
9
Medidas de tendencia central
En este capítulo se mostrará cómo obtener las diferentes medidas de tendencia
central con R.
Para ilustrar el uso de las funciones se utilizará una base de datos llamada
medidas del cuerpo, esta base de datos cuenta con 6 variables registradas
a un grupo de 36 estudiantes de la universidad. Las variables son:
1. edad del estudiante (años),
2. peso del estudiante (kilogramos),
3. altura del estudiante (centímetros),
4. sexo del estudiante (Hombre, Mujer),
5. muneca: perímetro de la muñeca derecha (centímetros),
6. biceps: perímetro del biceps derecho (centímetros).
A continuación se presenta el código para denir la url donde están los datos,
para cargar la base de datos en R y para mostrar por pantalla un encabezado
(usando head) de la base de datos.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
head(datos) # Para ver el encabezado de la base de datos
## edad peso altura sexo muneca biceps
## 1 43 87.3 188.0 Hombre 12.2 35.8
## 2 65 80.0 174.0 Hombre 12.0 35.0
## 3 45 82.3 176.5 Hombre 11.2 38.5
## 4 37 73.6 180.3 Hombre 11.2 32.2
## 5 55 74.1 167.6 Hombre 11.8 32.9
## 6 33 85.9 188.0 Hombre 12.4 38.5
81
82 9 Medidas de tendencia central
9.1. Media
Para calcular la media de una variable cuantitativa se usa la función mean. Los
argumentos básicos de la función mean son dos y se muestran a continuación.
mean(x, na.rm = FALSE)
En el parámetro xse indica la variable de interés para la cual se quiere calcular
la media, el parámetro na.rm es un valor lógico que en caso de ser TRUE,
signica que se deben remover las observaciones con NA, el valor por defecto
para este parámetro es FALSE.
Ejemplo
Suponga que queremos obtener la altura media del grupo de estudiantes.
Para encontrar la media general se usa la función mean sobre el vector númerico
datos$altura.
mean(x=datos$altura)
## [1] 171.6
Del anterior resultado podemos decir que la estatura media o promedio de los
estudiantes es 171.5556 centímetros.
Ejemplo
Suponga que ahora queremos la altura media pero diferenciando por sexo.
Para hacer esto se debe primero dividir o partir el vector de altura según los
niveles de la variable sexo, esto se consigue por medio de la función split y
el resultado será una lista con tantos elementos como niveles tenga la variable
sexo. Luego a cada uno de los elementos de la lista se le aplica la función mean
con la ayuda de sapply otapply. A continuación el código completo para
obtener las alturas medias para hombres y mujeres.
sapply(split(x=datos$altura, f=datos$sexo), mean)
## Hombre Mujer
## 179.1 164.0
9.2 Mediana 83
El resultado es un vector con dos elementos, vemos que la altura media pa-
ra hombres es 179.0778 centímetros y que para las mujeres es de 164.0333
centímetros.
¿Qué sucede si se usa tapply en lugar de sapply? Substituya en el código
anterior la función sapply por tapply y observe la diferencia entre los resul-
tados.
Ejemplo
Suponga que se tiene el vector edad con las edades de siete personas y su-
póngase que para el individuo cinco no se tiene información de su edad, eso
signica que el vector tendrá un NA en la quinta posición.
¿Cuál será la edad promedio del grupo de personas?
edad <- c(18,23,26,32,NA,32,29)
mean(x=edad)
## [1] NA
Al correr el código anterior se obtiene un error y es debido al símbolo NA en
la quinta posición. Para calcular la media sólo con los datos de los cuales se
tiene información, se incluye el argumento na.rm = TRUE para que R remueva
los NA. El código correcto a usar en este caso es:
mean(x=edad, na.rm=TRUE)
## [1] 26.67
De este último resultado se obtiene que la edad promedio de los individuos es
26.67 años.
9.2. Mediana
Para calcular la mediana de una variable cantitativa se usa la función median.
Los argumentos básicos de la función median son dos y se muestran a conti-
nuación.
median(x, na.rm = FALSE)

84 9 Medidas de tendencia central
En el parámetro xse indica la variable de interés para la cual se quiere calcular
la mediana, el parámetro na.rm es un valor lógico que en caso de ser TRUE,
signica que se deben remover las observaciones con NA, el valor por defecto
para este parámetro es FALSE.
Ejemplo
Calcular la edad mediana para los estudiantes de la base de datos.
Para obtener la mediana usamos el siguiente código:
median(x=datos$edad)
## [1] 28
y obtenemos que la mitad de los estudiantes tienen edades mayores o iguales
a 28 años.
El resultado anterior se pudo haber obtenido con la función quantile e indi-
cando que se desea el cuantil 50 así:
quantile(x=datos$edad, probs=0.5)
## 50%
## 28
9.3. Moda
La moda de una variable cuantitativa corresponde a valor o valores que más
se repiten, una forma sencilla de encontrar la moda es construir una tabla de
frecuencias y observar los valores con mayor frecuencia.
Ejemplo
Calcular la moda para la variable edad de la base de datos de estudiantes.
Se construye la tabla con la función table y se crea el objeto tabla para
almacenarla.

9.3 Moda 85
tabla <- table(datos$edad)
tabla
##
## 19 20 21 22 23 24 25 26 28 29 30 32 33 35 37 40 43 45
##111321532121123121
## 51 55 65
##111
Al mirar con detalle la tabla anterior se observa que el valor que más se repite
es la edad de 25 años en 5 ocasiones. Si la tabla hubiese sido mayor, la ins-
pección visual nos podría tomar unos segundos o hasta minutos y podríamos
equivocarnos, por esa razón es mejor ordenar los resultados de la tabla.
Para observar los valores con mayor frecuencia de la tabla se puede ordenar
la tabla usando la función sort de la siguiente manera:
sort(tabla, decreasing=TRUE)
##
## 25 22 26 37 23 28 30 35 43 19 20 21 24 29 32 33 40 45
##533322222111111111
## 51 55 65
##111
De esta manera se ve fácilmente que la variable edad es unimodal con valor
de 25 años.

10
Medidas de variabilidad
En este capítulo se mostrará cómo obtener las diferentes medidas de variabi-
lidad con R.
Para ilustrar el uso de las funciones se utilizará la base de datos llamada
aptos2015, esta base de datos cuenta con 11 variables registradas a aparta-
mentos usados en la ciudad de Medellín. Las variables de la base de datos
son:
1. precio: precio de venta del apartamento (millones de pesos),
2. mt2: área del apartamento (m2),
3. ubicacion: lugar de ubicación del aparamentos en la ciudad (cua-
litativa),
4. estrato: nivel socioeconómico donde está el apartamento (2 a 6),
5. alcobas: número de alcobas del apartamento,
6. banos: número de baños del apartamento,
7. balcon: si el apartamento tiene balcón (si o no),
8. parqueadero: si el apartamento tiene parqueadero (si o no),
9. administracion: valor mensual del servicio de administración (mi-
llones de pesos),
10. avaluo: valor del apartamento en escrituras (millones de pesos),
11. terminado: si el apartamento se encuentra terminado (si o no).
A continuación se presenta el código para denir la url donde están los datos,
para cargar la base de datos en R y para mostrar por pantalla un encabezado
(usando head) de la base de datos.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/aptos2015'
datos <- read.table(file=url, header=T)
head(datos) # Para ver el encabezado de la base de datos
## precio mt2 ubicacion estrato alcobas banos balcon
## 1 79 43.16 norte 3 3 1 si
## 2 93 56.92 norte 2 2 1 si
## 3 100 66.40 norte 3 2 2 no
## 4 123 61.85 norte 2 3 2 si
## 5 135 89.80 norte 4 3 2 si
87

88 10 Medidas de variabilidad
## 6 140 71.00 norte 3 3 2 no
## parqueadero administracion avaluo terminado
## 1 si 0.050 14.92 no
## 2 si 0.069 27.00 si
## 3 no 0.000 15.74 no
## 4 si 0.130 27.00 no
## 5 no 0.000 39.57 si
## 6 si 0.120 31.15 si
10.1. Rango
Para calcular el rango de una variable cuantitativa se usa la función range.
Los argumentos básicos de la función range son dos y se muestran abajo.
range(x, na.rm = FALSE)
En el parámetro xse indica la variable de interés para la cual se quiere calcular
el rango, el parámetro na.rm es un valor lógico que en caso de ser TRUE,
signica que se deben remover las observaciones con NA, el valor por defecto
para este parámetro es FALSE.
La función range entrega el valor mínimo y máximo de la variable ingresada y
el valor de rango se puede obtener restando del valor máximo el valor mínimo.
Ejemplo
Suponga que queremos obtener el rango para la variable precio de los aparta-
mentos.
Para obtener el rango usamos el siguiente código.
range(datos$precio)
## [1] 25 1700
max(datos$precio) -min(datos$precio)
## [1] 1675

10.2 Desviación estándar muestral (S)89
Del resultado anterior podemos ver que los precios de todos los apartamentos
van desde 25 hasta 1700 millones de pesos, es decir, el rango de la variable
precio es 1675 millones de pesos.
Ejemplo
Suponga que queremos obtener nuevamente el rango para la variable precio
de los apartamentos pero diferenciando por el estrato.
Primero vamos a crear una función auxiliar llamada myrange que calculará
el rango directamente (max −min). Luego vamos a partir la información de
los precios por cada estrato usando split, la partición se almacenará en la
lista precios. Finalmente se aplicará la función myrange a la lista precios
para obtener los rangos del precio por estrato socioeconómico. El código para
realizar esto se muestra a continuación.
myrange <- function(x) max(x) -min(x)
precios <- split(datos$precio, f=datos$estrato)
sapply(precios, myrange)
##23456
## 103 225 610 1325 1560
De los resultados podemos ver claramente que a medida que aumenta de estra-
to el rango (variabilidad) del precio de los apartamentos aumenta. Apartamen-
tos de estrato bajo tienden a tener precios similares mientras que los precios
de venta para apartamentos de estratos altos tienden a ser muy diferentes
entre si.
10.2. Desviación estándar muestral (S)
Para calcular la desviación muestral de una variable cuantitativa se usa la
función sd. Los argumentos básicos de la función sd son dos y se muestran
abajo.
sd(x, na.rm = FALSE)
En el parámetro xse indica la variable de interés para la cual se quiere calcular
la desviación estándar muestral, el parámetro na.rm es un valor lógico que en
90 10 Medidas de variabilidad
caso de ser TRUE, signica que se deben remover las observaciones con NA, el
valor por defecto para este parámetro es FALSE.
Ejemplo
Suponga que queremos obtener la desviación estándar muestral para la varia-
ble precio de los apartamentos.
Para obtener la desviación solicitada usamos el siguiente código:
sd(x=datos$precio)
## [1] 247.6
Ejemplo
Calcular la desviación estándar poblacional (σ) para el siguiente conjunto
de 5 observaciones: 12, 25, 32, 15, 26.
Recordemos que las expresiones matemáticas para obtener Syσson muy
similares, la diferencia está en el denominador, para Sel denominador es
n−1mientras que para σes n. Teniendo esto en cuenta podemos calcular
la desviación poblacional apoyándonos en la función sd, para esto podemos
construir una función llamada Sigma que calcule la desviación poblacional, a
continuación el código necesario.
Sigma <- function(x) {
n <- length(x)
sd(x) *(n-1)/n
}
Ahora para obtener la desviación estándar poblacional de los datos usamos
el siguiente código.
y <- c(12,25,32,15,26)
Sigma(y)
## [1] 6.621

10.3 Varianza muestral (S2)91
10.3. Varianza muestral (S2)
Para calcular la varianza muestral de una variable cuantitativa se usa la fun-
ción var. Los argumentos básicos de la función var son dos y se muestran
abajo.
var(x, na.rm = FALSE)
En el parámetro xse indica la variable de interés para la cual se quiere calcular
la varianza muestral, el parámetro na.rm es un valor lógico que en caso de
ser TRUE, signica que se deben remover las observaciones con NA, el valor por
defecto para este parámetro es FALSE.
Ejemplo
Suponga que queremos determinar cuál región en la ciudad presenta mayor
varianza en los precios de los apartamentos.
Para realizar esto debemos usar en conjunto la función split,sapply yvar
ya que se quiere la varianza de una variable (precio) dado los valores de otra
variable (ubicacion). El código para obtener las varianzas es el siguiente.
precios <- split(datos$precio, f=datos$ubicacion)
sapply(precios, var)
## aburra sur belen guayabal centro
## 4169 2528 2588
## laureles norte occidente
## 25351 1009 3596
## poblado
## 84497
De los resultados anteriores se nota que los apartamentos ubicados en el Po-
blado tienen la mayor variabilidad en el precio, este resultado se conrma al
dibujar un boxplot para la variable precio dada la ubicación, en la Figura 10.1
se muestra el boxplot y se ve claramente la dispersión de los precios en el Po-
blado. El código usado para generar la Figura 10.1 se presenta a continuación.
with(datos, boxplot(precio ~ubicacion, ylab='Precio (millones)'))

92 10 Medidas de variabilidad
aburra sur belen guayabal centro laureles norte occidente poblado
0 500 1000 1500
Precio (millones)
Figura 10.1: Boxplot para el precio de los apartamentos dada la ubicación.
Ejemplo
¿Son los resultados de la función var los mismos que los resultados de la
función sd elevados al cuadrado?
La respuesta es NO. La función sd se aplica sólo a vectores mientras que la
función var de puede aplicar tanto a vectores como a marcos de datos. Al
ser aplicada a marcos de datos numéricos se obtiene una matriz en que la
diagonal representa las varianzas de las de cada una de las variables mientras
que arriba y abajo de la diagonal se encuentran las covarianzas entre pares de
variables.
Por ejemplo, si aplicamos la función var al marco de datos sólo con las va-
riables precio, área y avaluo se obtiene una matriz de dimensión 3×3, a
continuación el código usado.
var(datos[, c('precio','mt2','avaluo')])
## precio mt2 avaluo
## precio 61313 15874 33056
## mt2 15874 5579 9508
## avaluo 33056 9508 28589
Del anterior resultado se observa la matriz de varianzas y covarianzas de di-
mensión 3×3.
10.4 Coeciente de variación (CV )93
10.4. Coeciente de variación (CV )
El coeciente de variación se dene como CV =s/¯xy es muy sencillo de
obtenerlo, la función CV mostrada abajo permite calcularlo.
CV <- function(x, na.rm = FALSE) {
sd(x, na.rm=na.rm) /mean(x, na.rm=na.rm)
}
Ejemplo
Calcular el CV para el vector wdenido a continuación.
w <- c(5,-3,NA,8,8,7)
Vemos que el vector wtiene 6 observaciones y la tercera de ellas es un NA.
Lo correcto aquí es usar la función CV denida antes pero indicándole que
remueva los valores faltantes, para eso se usa el siguiente código.
CV(x=w, na.rm=T)
## [1] 0.9274

11
Medidas de posición
En este capítulo se mostrará cómo obtener las diferentes medidas de posición
con R.
Para ilustrar el uso de las funciones se utilizará una base de datos llamada
medidas del cuerpo, esta base de datos cuenta con 6 variables registradas
a un grupo de 36 estudiantes de la universidad. Las variables son:
1. edad del estudiante (años),
2. peso del estudiante (kilogramos),
3. altura del estudiante (centímetros),
4. sexo del estudiante (Hombre, Mujer),
5. muneca: perímetro de la muñeca derecha (centímetros),
6. biceps: perímetro del biceps derecho (centímetros).
A continuación se presenta el código para denir la url donde están los datos,
para cargar la base de datos en R y para mostrar por pantalla un encabezado
(usando head) de la base de datos.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
head(datos) # Para ver el encabezado de la base de datos
## edad peso altura sexo muneca biceps
## 1 43 87.3 188.0 Hombre 12.2 35.8
## 2 65 80.0 174.0 Hombre 12.0 35.0
## 3 45 82.3 176.5 Hombre 11.2 38.5
## 4 37 73.6 180.3 Hombre 11.2 32.2
## 5 55 74.1 167.6 Hombre 11.8 32.9
## 6 33 85.9 188.0 Hombre 12.4 38.5
95
96 11 Medidas de posición
11.1. Cuantiles
Para obtener cualquier cuantil (cuartiles, deciles y percentiles) se usa la fun-
ción quantile. Los argumentos básicos de la función quantile son tres y se
muestran a continuación.
quantile(x, probs, na.rm = FALSE)
En el parámetro xse indica la variable de interés para la cual se quieren
calcular los cuantiles, el parámetro probs sirve para denir los cuantiles de
interés y el parámetro na.rm es un valor lógico que en caso de ser TRUE,
signica que se deben remover las observaciones con NA, el valor por defecto
para este parámetro es FALSE.
Ejemplo
Suponga que queremos obtener el percentil 5, la mediana y el decil 8 pa la
altura del grupo de estudiantes.
Se solicita el percentil 5, la mediana que es el percentil 50 y el decil 8 que
corresponde al percentil 80, por lo tanto es necesario indicarle a la función
quantile que calcule los cuantiles para las ubicaciones 0.05, 0.5 y 0.8, el
código para obtener las tres medidas solicitadas es el siguiente.
quantile(x=datos$altura, probs=c(0.05,0.5,0.8))
## 5% 50% 80%
## 155.2 172.7 180.3

12
Medidas de correlación
En este capítulo se mostrará cómo obtener el coeciente de correlación lineal
para variables cuantitativas.
12.1. Función cor
La función cor permite calcular el coeciente de correlación de Pearson, Ken-
dall o Spearman para dos variables cuantitativas. La estructura de la función
es la siguiente.
cor(x, y, use="everything",
method=c("pearson","kendall","spearman"))
Los parámetos de la función son:
x, y: vectores cuantitativos.
use: parámetro que indica lo que se debe hacer cuando se presenten registros
NA en alguno de los vectores. Las diferentes posibilidades son: everything,
all.obs,complete.obs,na.or.complete ypairwise.complete.obs, el
valor por defecto es everything.
method: tipo de coeciente de correlación a calcular, por defecto es pearson,
otros valores posibles son kendall yspearman.
Ejemplo
Calcular el coeciente de correlación de Pearson para las variables área y
precio de la base de datos sobre apartamentos usados.
Lo primero que se debe hacer es cargar la base de datos usando la url apro-
piada. Luego de esto se usa la función cor sobre las variables de interés. A
continuación se muestra el código necesario.
97
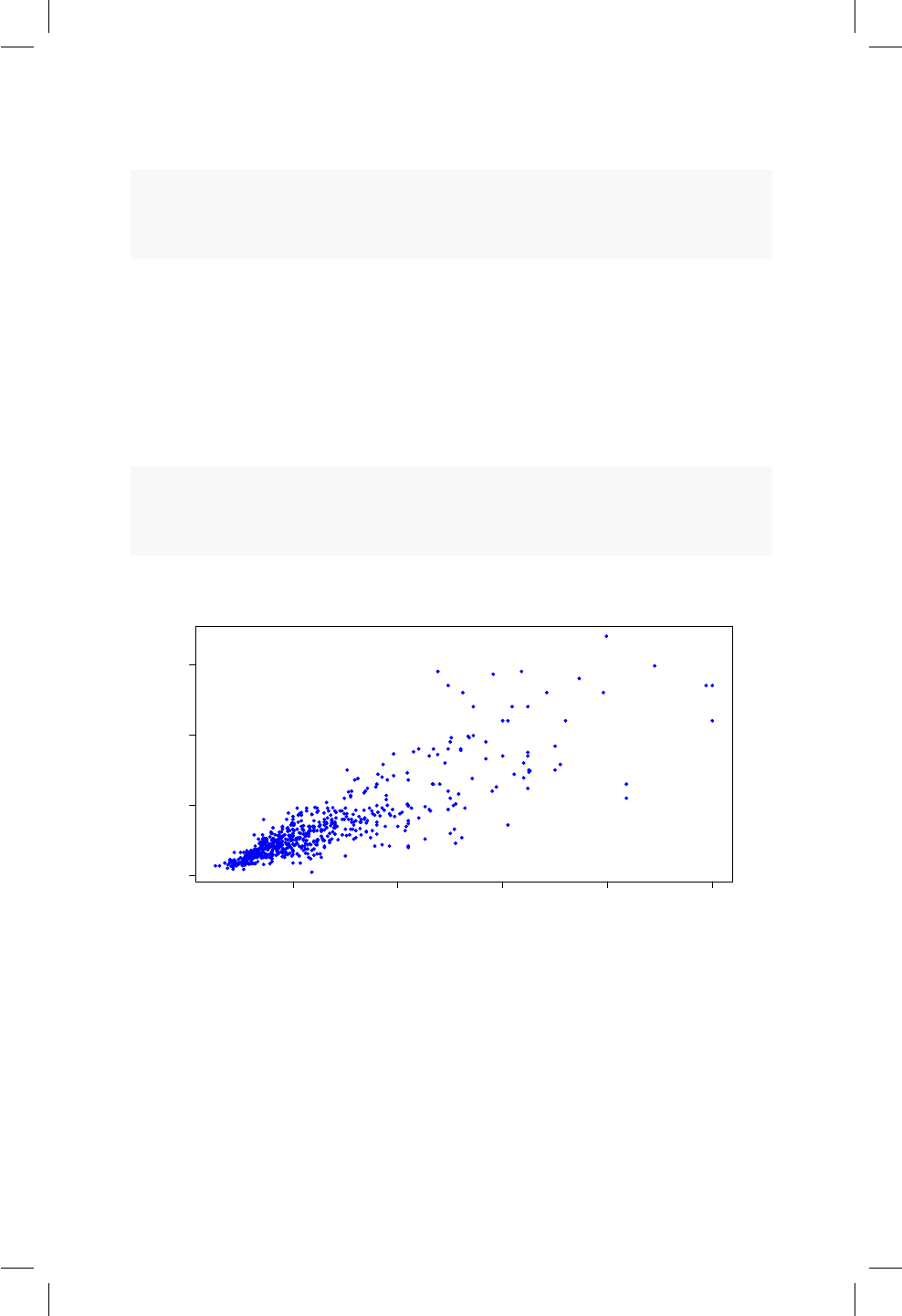
98 12 Medidas de correlación
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/aptos2015'
datos <- read.table(file=url, header=T)
cor(x=datos$mt2, y=datos$precio)
## [1] 0.8583
Del resultado anterior vemos que existe una correlación de 0.8583 entre las
dos variables, eso signica que apartamentos de mayor área tienden a tener
precios de venta más alto. Este resultado se ilustra en la Figura 12.1, se nota
claramente que la nube de puntos tiene un pendiente positiva y por eso el
signo del coeciente de correlación.
A continuación el código para generar la Figura 12.1.
with(datos, plot(x=mt2, y=precio, pch=20,col='blue',
xlab='Área del apartamento',las=1,
ylab='Precio del apartamento (millones COP)'))
100 200 300 400 500
0
500
1000
1500
Área del apartamento
Precio del apartamento (millones COP)
Figura 12.1: Diagrama de dispersión para precio versus área de los aparta-
mentos usados.
Ejemplo
Para las mismas variables del ejemplo anterior calcular los coecientes de
correlación Kendall y Spearman.
12.1 Función cor 99
A continuación el código para obtener lo solicitado.
cor(x=datos$mt2, y=datos$precio, method='pearson')
## [1] 0.8583
cor(x=datos$mt2, y=datos$precio, method='kendall')
## [1] 0.6911
cor(x=datos$mt2, y=datos$precio, method='spearman')
## [1] 0.8603
Ejemplo
Para la base de datos de apartamentos usados, ¿cuáles de las variables cuan-
titativas tienen mayor correlación?
Lo primero que debemos hacer es determinar cuáles son las cuantitativas de
la base de datos. Para obtener información de las variables que están almace-
nadas en el marco de datos llamado datos usamos la función str que muestra
la estructura interna de objeto.
str(datos)
## 'data.frame': 694 obs. of 11 variables:
## $ precio : num 79 93 100 123 135 140 145 160 160 175 ...
## $ mt2 : num 43.2 56.9 66.4 61.9 89.8 ...
## $ ubicacion : Factor w/ 7 levels "aburra sur","belen guayabal",..: 5 5 5 5 5 5 5 5 5 5 ...
## $ estrato : int 3 2 3 2 4 3 3 3 4 4 ...
## $ alcobas : int 3 2 2 3 3 3 2 3 4 3 ...
## $ banos : int 1 1 2 2 2 2 2 2 2 2 ...
## $ balcon : Factor w/ 2 levels "no","si": 2 2 1 2 2 1 2 2 2 2 ...
## $ parqueadero : Factor w/ 2 levels "no","si": 2 2 1 2 1 2 2 2 1 2 ...
## $ administracion: num 0.05 0.069 0 0.13 0 0.12 0.14 0.127 0 0.123 ...
## $ avaluo : num 14.9 27 15.7 27 39.6 ...
## $ terminado : Factor w/ 2 levels "no","si": 1 2 1 1 2 2 2 2 2 2 ...
Del anterior resultado vemos que las variables precio, mt2, alcobas, banos,
administracion y avaluo son las variables cuantitativas, las restantes son cua-
litativas (nominal u ordinal). Las posiciones de las variables cuantitativas en
100 12 Medidas de correlación
el objeto datos son 1, 2, 5, 6, 9, 10, así podemos construir un marco de datos
sólo con la información cuantitativa, a continuación el código usado.
datos.cuanti <- datos[, c(1,2,5,6,9,10)]
# La siguiente instrucción para editar los nombres de la variables
colnames(datos.cuanti) <- c('Precio','Área','Alcobas',
'Baños','Admon','Avaluo')
M <- round(cor(datos.cuanti), digits=2)
M
## Precio Área Alcobas Baños Admon Avaluo
## Precio 1.00 0.86 0.19 0.63 0.75 0.79
## Área 0.86 1.00 0.31 0.67 0.77 0.75
## Alcobas 0.19 0.31 1.00 0.35 0.16 0.15
## Baños 0.63 0.67 0.35 1.00 0.55 0.53
## Admon 0.75 0.77 0.16 0.55 1.00 0.70
## Avaluo 0.79 0.75 0.15 0.53 0.70 1.00
El anterior resultado representa la matriz de correlaciones entre las variables
cuantitativas, se observa que la mayor correlación es entre las variables precio
y área del apartamento.
Es posible representar grácamente la matriz de correlaciones Mpor medio de
la función corrplot del paquete corrplot (Wei and Simko,2017), a continua-
ción el código para obtener su representación gráca.
library('corrplot')# Para cargar el paquete corrplot
## corrplot 0.84 loaded
corrplot.mixed(M)
En la Figura 12.2 se muestra la matriz con los coecientes de correlación. En la
diagonal de la Figura 12.2 están las variables, por encima están unos círculos
de colores, entre más intensidad del color, ya sea azul o rojo, mayor es la
correlación, colores ténues signican correlación baja; el tamaño de los círculos
está asociado al valor absoluto de correlación. Por debajo de la diagonal se
observan los valores exactos de correlación en colores.
La función corrplot es muy versátil, se pueden obtener diferentes represen-
taciones grácas de la matriz de correlaciones, para conocer las diferentes po-
sibilidades recomendamos consultar este enlace: https://cran.r-project.
org/web/packages/corrplot/vignettes/corrplot-intro.html.

12.1 Función cor 101
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Precio
Área
Alcobas
Baños
Admon
Avaluo
0.86
0.19
0.63
0.75
0.79
0.31
0.67
0.77
0.75
0.35
0.16
0.15
0.55
0.53 0.7
Figura 12.2: Matriz de coecientes de correlación.
Ejemplo
Construya dos vectores hipotéticos con el gasto y ahorro de un grupo de 7
familias, incluya dos NA. Calcule el coeciente de correlación entre ahorro y
gasto, use el parámetro use para manejar los NA.
A continuación se presenta el código para crear los objetos ahorro ygasto con
datos cticios. Observe que en el primer caso donde se calcula la correlación no
es posible obtener un resultado debido a que por defecto use='everything'
y por lo tanto usa todas las observaciones incluyendo los NA. En el segun-
do caso si se obtiene un valor para la correlación debido a que se usó
use='complete.obs'.
gasto <- c(170,230,120,156,256,NA,352)
ahorro <- c(45,30,NA,35,15,65,15)
cor(gasto, ahorro)
## [1] NA
cor(gasto, ahorro, use='complete.obs')
## [1] -0.8465

102 12 Medidas de correlación
EJERCICIOS
Use funciones o procedimientos (varias líneas) de Rpara responder cada una
de las siguientes preguntas.
1. Para cada uno de los estratos socioeconómicos, calcular el coecien-
te de correlación lineal de Pearson para las variables precio y área
de la base de datos de los apartamentos usados.
2. Calcular los coecientes de correlación Pearson, Kendall y Spear-
man para las variables cuantitativas de la base de datos sobre medi-
das del cuerpo explicada en el Capítulo 9. La url con la información
es la siguiente: https://raw.githubusercontent.com/fhernanb/
datos/master/medidas_cuerpo
3. Represente grácamente las matrices de correlación obtenidas en el
ejercicio anterior.

13
Distribuciones discretas
En este capítulo se mostrarán las funciones de Rpara distribuciones discretas.
13.1. Funciones disponibles para distribuciones discretas
Para cada distribución discreta se tienen 4 funciones, a continuación el listado
de funciones y su utilidad.
dxxx(x, ...) # Función de masa de probabilidad, f(x)
pxxx(q, ...) # Función de distribución acumulada hasta q, F(x)
qxxx(p, ...) # Cuantil para el cual P(X <= q) = p
rxxx(n, ...) # Generador de números aleatorios.
En el lugar de las letras xxx se de debe colocar el nombre de la distribución en
R, a continuación el listado de nombres disponibles para las 6 distribuciones
discretas básicas.
binom # Binomial
geo # Geométrica
nbinom # Binomial negativa
hyper # Hipergeométrica
pois # Poisson
multinom # Multinomial
Combinando las funciones y los nombres se tiene un total de 24 funciones,
por ejemplo, para obtener la función de masa de probabilidad f(x)de una
binomial se usa la función dbinom( ) y para obtener la función acumulada
F(x)de una Poisson se usa la función ppois( ).
103
104 13 Distribuciones discretas
Ejemplo binomial
Suponga que un grupo de agentes de tránsito sale a una vía principal para
revisar el estado de los buses de transporte intermunicipal. De datos históricos
se sabe que un 10 % de los buses generan una mayor cantidad de humo de la
permitida. En cada jornada los agentes revisan siempre 18 buses, asuma que
el estado de un bus es independiente del estado de los otros buses.
1) Calcular la probabilidad de que se encuentren exactamente 2 buses
que generan una mayor cantidad de humo de la permitida.
Aquí se tiene una distribucion Binomial(n= 18, p = 0.1) y se desea calcular
P(X= 2). Para obtener esta probabilidad se usa la siguiente instrucción.
dbinom(x=2,size=18,prob=0.10)
## [1] 0.2835
Así P(X= 2) = 0.2835.
2) Calcular la probabilidad de que el número de buses que sobrepasan
el límite de generación de gases sea al menos 4.
En este caso interesa calcular P(X≥4), para obtener esta probabilidad se
usa la siguiente instrucción.
sum(dbinom(x=4:18,size=18,prob=0.10))
## [1] 0.0982
Así P(X≥4) = 0.0982
3) Calcular la probabilidad de que tres o menos buses emitan gases
por encima de lo permitido en la norma.
En este caso interesa P(X≤3) lo cual es F(x= 3), por lo tanto, la instrucción
para obtener esta probabilidad es
pbinom(q=3,size=18,prob=0.10)
## [1] 0.9018
Así P(X≤3) = F(x= 3) = 0.9018
4) Dibujar la función de masa de probabilidad.

13.1 Funciones disponibles para distribuciones discretas 105
Para dibujar la función de masa de probabilidad para una Binomial(n=
18, p = 0.1) se usa el siguiente código.
x <- 0:18 # Soporte (dominio) de la variable
Probabilidad <- dbinom(x=x, size=18,prob=0.1)
plot(x=x, y=Probabilidad,
type='h',las=1,lwd=6)
0 5 10 15
0.00
0.05
0.10
0.15
0.20
0.25
0.30
x
Probabilidad
Figura 13.1: Función de masa de probabilidad para una Binomial(n=
18, p = 0.1).
En la Figura 13.1 se muestra la función de masa de probabilidad para la
Binomial(n= 18, p = 0.1), de esta gura se observa claramente que la mayor
parte de la probabilidad está concentrada para valores pequeños de Xdebido
a que la probabilidad de éxito individual es p= 0.10. Valores de X≥7tienen
una probabilidad muy pequeña y es por eso que las longitudes de sus barras
son muy cortas.
5) Generar con 100 de una distribución Binomial(n= 18, p = 0.1)
y luego calcular las frecuencias muestrales y compararlas con las
probabilidades teóricas.
La muestra aleatoria se obtiene con la función rbinom y los resultados se
106 13 Distribuciones discretas
almacenan en el objeto m, por último se construye la tabla de frecuencias
relativas, a continuación el código usado.
m <- rbinom(n=100,size=18,prob=0.1)
m# Para ver lo que hay dentro de m
## [1]4134231032141113050353231
## [26]1241322322323022211311111
## [51]1113124472401211232131123
## [76]5150121411212022330113230
prop.table(table(m)) # Tabla de frecuencia relativa
## m
##0123457
## 0.09 0.34 0.24 0.20 0.08 0.04 0.01
A pesar de ser una muestra aleatoria de sólo 100 observaciones, se observa
que las frecuencias relativas obtenidas son muy cercanas a las mostradas en
la Figura 13.1.
Ejemplo geométrica
En una línea de producción de bombillos se sabe que sólo el 1 % de los bombi-
llos son defectuosos. Una máquina automática toma un bombillo y lo prueba,
si el bombillo enciende, se siguen probando los bombillos hasta que se encuen-
tre un bombillo defectuoso, ahí se para la línea de producción y se toman los
correctivos necesarios para mejorar el proceso.
1) Calcular la probabilidad de que se necesiten probar 125 bombillos
para encontrar el primer bombillo defectuoso.
En la distribución geométrica, la variable Xrepresenta el número de fracasos
antes de encontrar el único éxito, por lo tanto, en este caso el interés es calcular
P(X= 124). La instrucción para obtener esta probabiliad es la siguiente.
dgeom(x=124,prob=0.01)
## [1] 0.002876
2) Calcular P(X≤8).
13.1 Funciones disponibles para distribuciones discretas 107
En este caso interesa P(X≤50) lo que equivale a F(8), la instrucción para
obtener la probabilidad es la siguiente.
pgeom(q=50,prob=0.01)
## [1] 0.401
3) Encontrar el cuantil qtal que P(X≤q) = 0.40.
En este caso interesa encontrar el cuantil qque cumpla la condición de que
hasta qesté el 40 % de las observaciones, por esa razón se usa la función qgeom
como se muestra a continuación.
qgeom(p=0.4,prob=0.01)
## [1] 50
Note que las funciones pxxx yqxxx están relacionadas, pxxx entrega la
probabilidad hasta el cuantil qmientras qxxx entrega el cuantil en el que se
acumula pprobabilidad.
Ejemplo binomial negativa
Una familia desea tener hijos hasta conseguir 2 niñas, la probabilidad indi-
vidual de obtener una niña es 0.5 y se supone que todos los nacimientos son
individuales, es decir, un sólo bebé.
1) Calcular la probabilidad de que se necesiten 4 hijos, es decir, 4
nacimientos para consguir las dos niñas.
En este problema se tiene una distribución binomial negativa con r= 2 niñas,
los éxitos deseados por la familia. La variable Xrepresenta los fracasos, es
decir los niños, hasta que se obtienen los éxitos r= 2 deseados.
En este caso lo que interesa es P(familia tenga 4), en otras palabras interesa
P(X= 2), la instrucción para calcular la probabilidad es la siguiente.
dnbinom(x=2,size=2,prob=0.5)
## [1] 0.1875
2) Calcular P(familia tenga al menos 4 hijos).
108 13 Distribuciones discretas
Aquí interesa calcular P(X≥2) = P(X= 2) + P(X= 3) + . . ., como esta
probabilidad va hasta innito, se debe usar el complemento así:
P(X≥2) = 1 −[P(X= 0) + P(X= 1)]
y para obtener la probabilidad solicitada se puede usar la función dnbinom de
la siguiente manera.
1-sum(dnbinom(x=0:1,size=2,prob=0.5))
## [1] 0.5
Otra forma para obtener la probabilidad solicitada es por medio de la función
pnbinom de la siguiente manera.
1-pnbinom(q=1,size=2,prob=0.5)
## [1] 0.5
Ejemplo hipergeométrica
Un lote de partes para ensamblar en una empresa está formado por 100 ele-
mentos del proveedor A y 200 elementos del proveedor B. Se selecciona una
muestra de 4 partes al azar sin reemplazo de las 300 para una revisión de
calidad.
1) Calcular la probabilidad de que todas las 4 partes de la muestra
sean del proveedor A.
Aquí se tiene una situación que se puede modelar por medio de una distribu-
ción hipergeométrica con m= 100 éxitos en la población, n= 200 fracasos en
la población y k= 4 el tamaño de la muestra. El objetivo es calcular P(X= 4),
para obtener esta probabilidad se usa la siguiente instrucción.
dhyper(x=4,m=100,k=4,n=200)
## [1] 0.01185
2) Calcular la probabilidad de que dos o más de las partes sean del
proveedor A.
Aquí interesa P(X≥2), la instrucción para obtener esta probabilidad es.
13.2 Distribuciones discretas generales 109
sum(dhyper(x=2:4,m=100,k=4,n=200))
## [1] 0.4074
Ejemplo Poisson
En una editorial se asume que todo libro de 250 páginas tiene en promedio 50
errores.
1) Encuentre la probabilidad de que en una página cualquiera no se
encuentren errores.
Este es un problema de distribución Poisson con tasa promedio de éxitos dada
por:
λ=50 errores
libro =0.2errores
pagina
El objetivo es calcular P(X= 0), para obtener esta probabilidad de usa la
siguiente instrucción.
dpois(x=0,lambda=0.2)
## [1] 0.8187
Así P(X= 0) = 0.8187.
13.2. Distribuciones discretas generales
En la práctica nos podemos encontramos con variables aleatorias discretas que
no se ajustan a una de las distribuciones mostradas anteriormente, en esos
casos, es posible manejar ese tipo de variables por medio de unas funciones
básicas de Rcomo se muestra en el siguiente ejemplo.
Ejemplo
El cangrejo de herradura hembra se caracteriza porque su caparazón se adhie-
ren los machos de la misma especie, en la Figura 13.2 se muestra una fotografía
de este cangrejo. Los investigadores están interesado en determinar cual es el

110 13 Distribuciones discretas
patrón de variación del número de machos sobre cada hembra, para esto, se
recolectó una muestra de hembras a las cuales se les observó el color, la condi-
ción de la espina, el peso en kilogramos, el ancho del caparazón en centímetros
y el número de satélites o machos sobre el caparazón, la base de datos está
disponible en el siguiente enlace1.
Figura 13.2: Fotografía del cangrejo de herradura, tomada de
http://sccoastalresources.com/home/2016/6/21/a-night-of-horseshoe-crab-
tagging
1) Encontrar la distribución de probabilidad para la variable Sa que
corresponde al número de machos sobre el caparazón de cada hem-
bra.
Primero se debe leer la base de datos usando la url suministrada y luego se
construye la tabla de frecuencia relativa y se almacena en el objeto t1.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/crab'
crab <- read.table(file=url, header=T)
t1 <- prop.table(table(crab$Sa))
t1
1https://raw.githubusercontent.com/fhernanb/datos/master/crab
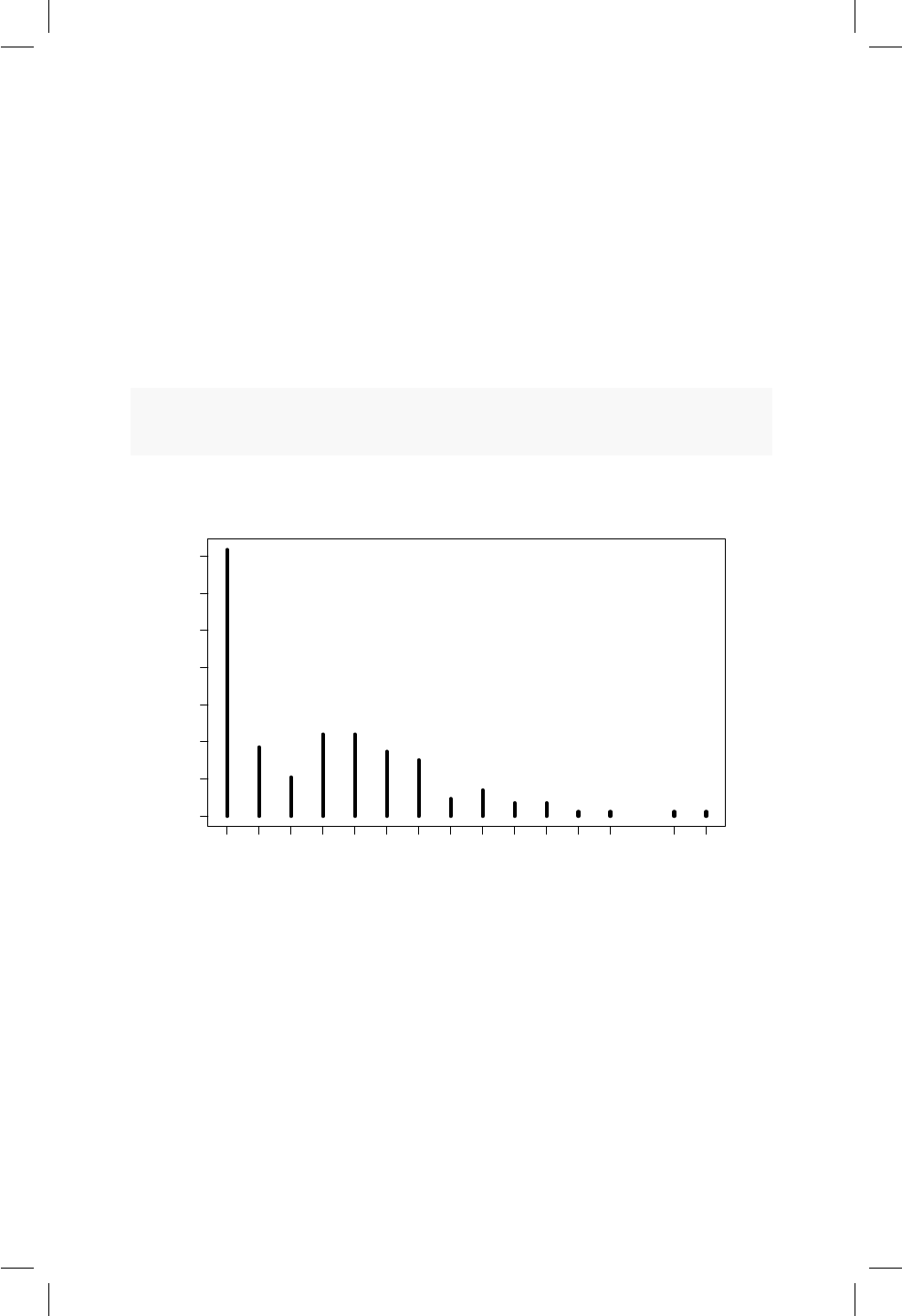
13.2 Distribuciones discretas generales 111
##
##012345
## 0.35838 0.09249 0.05202 0.10983 0.10983 0.08671
## 6 7 8 9 10 11
## 0.07514 0.02312 0.03468 0.01734 0.01734 0.00578
## 12 14 15
## 0.00578 0.00578 0.00578
La anterior tabla de frecuencias relativas se puede representar grácamente
usando el siguiente código.
plot(t1, las=1,lwd=5,xlab='Número de satélites',
ylab='Proporción')
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
Número de satélites
Proporción
0 1 2 3 4 5 6 7 8 9 10 11 12 14 15
Figura 13.3: Función de masa de probabilidad para el número de satélites
por hembra.
2) Sea Xla variable número de satélites por hembra, construir la fun-
ción F(x).
Para construir F(x)se utiliza la función ecdf oempirical cumulative density
function, a esta función le debe ingresar el vector con la información de la
variable cuantitativa, a continuación del código usado. En la Figura 13.4 se
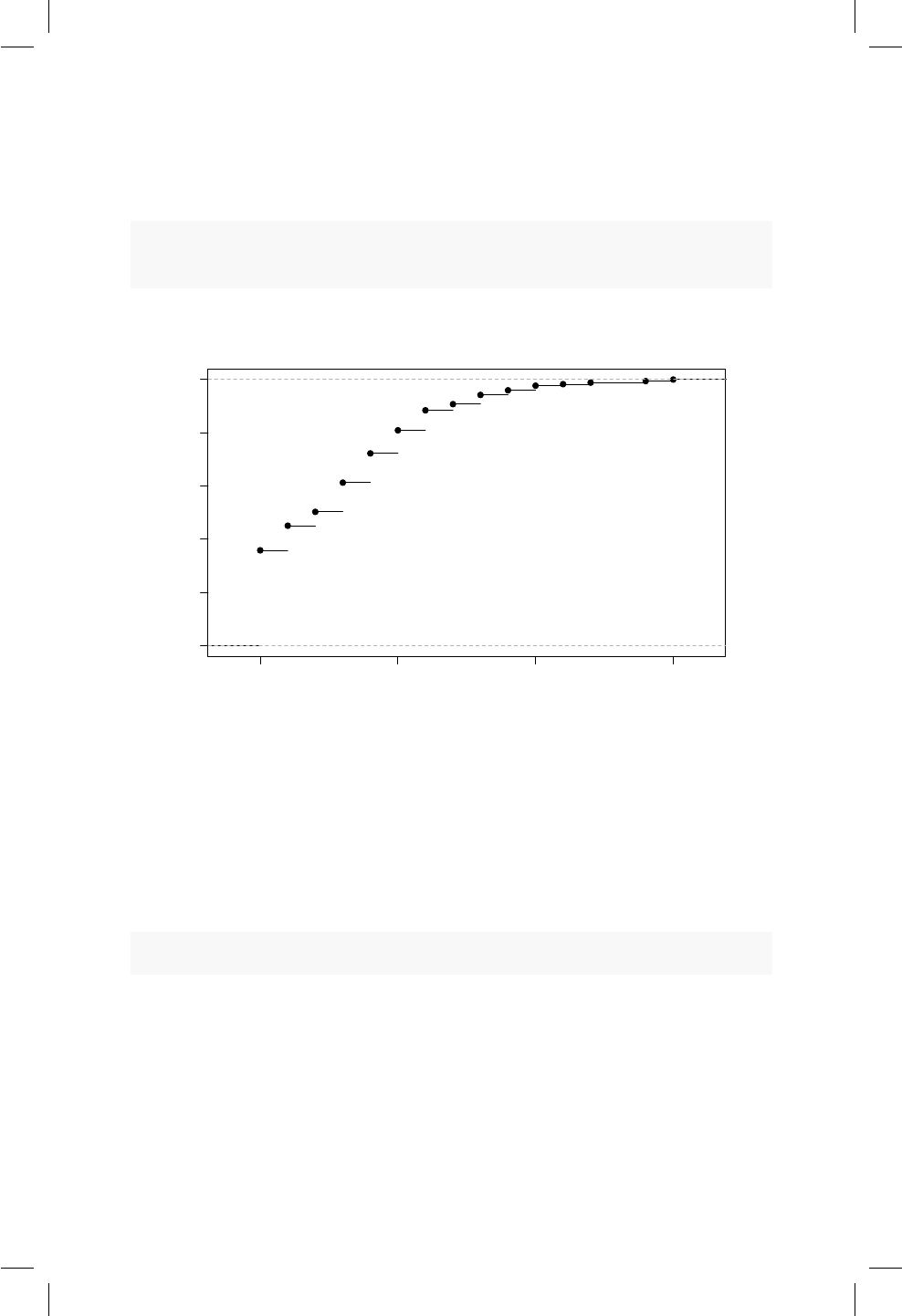
112 13 Distribuciones discretas
muestra la función de distribución acumulada para para el número de satélites
por hembra.
F <- ecdf(crab$Sa)
plot(F, las=1,main='')
0 5 10 15
0.0
0.2
0.4
0.6
0.8
1.0
x
Fn(x)
Figura 13.4: Función de distribución acumulada para el número de satélites
por hembra.
3) Calcular P(X≤9).
Para obtener esta probabilidad se usa el objeto Fque es en realidad una
función, a continuación la instrucción usada.
F(9)
## [1] 0.9595
Así P(X≤9) = 0.9595.
4) Calcular P(X > 4).
Para obtener esta probabilidad se usa el hecho de que P(X > 4) = 1−P(X≤
4), así la instrucción a usar es.
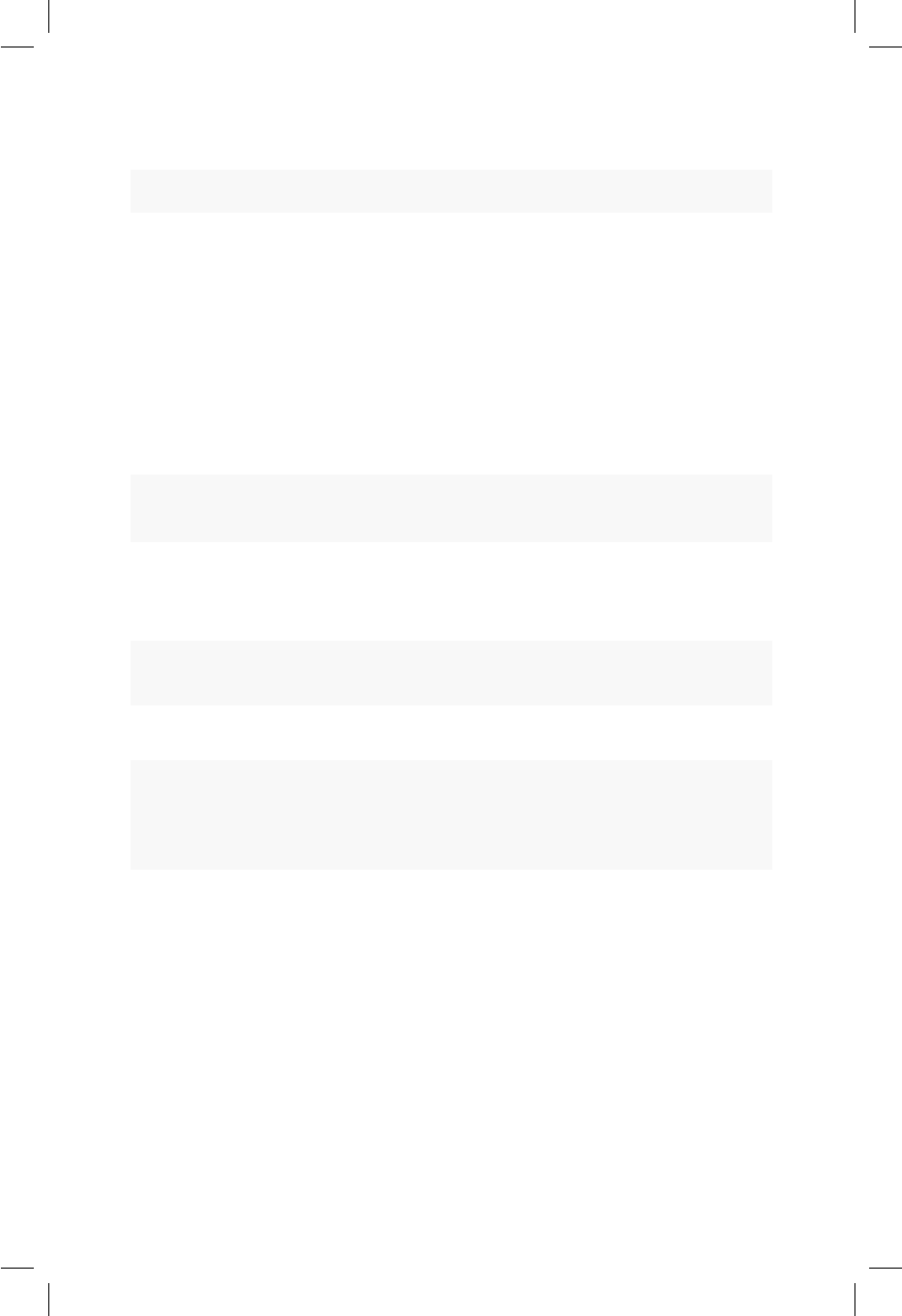
13.2 Distribuciones discretas generales 113
1-F(4)
## [1] 0.2775
Por lo tanto P(X > 4) = 0.2775.
5) Suponga que el grupo 1 está formado por las hembras cuyo ancho
de caparazón es menor o igual al ancho mediano, el grupo 2 está
formado por las demás hembras. ¿Será F(x)diferente para los dos
grupos?
Para realizar esto vamos a particionar el vector Sa en los dos grupos de acuerdo
a la nueva variable grupo creada como se muestra a continuacion.
grupo <- ifelse(crab$Wt <= median(crab$Wt), 'Grupo 1','Grupo 2')
x <- split(x=crab$Sa, f=grupo)
El objeto xes una lista y para acceder a los vectores allí almacenados usamos
dos corchetes [[]], uno dentro del otro. Luego para calcular F(x)para los
dos grupos se procede así:
F1 <- ecdf(x[[1]])
F2 <- ecdf(x[[2]])
Para obtener las dos F(x)en la misma gura se usa el código siguiente.
plot(F1, col='blue',main='',las=1)
plot(F2, col='red',add=T)
legend('bottomright',legend=c('Grupo 1','Grupo 2'),
col=c('blue','red'), lwd=1)
En la Figura 13.5 se muestran las dos F(x), en color azul para el grupo 1 y en
color rojo para el grupo 2. Se observa claramente que las curvas son diferentes
antes de x= 9. El hecho de que la curva azul esté por encima de la roja
para valores menores de 9, es decir, F1(x)≥F2(x), indica que las hembras del
grupo 1 tienden a tener menos satélites que las del grupo 2, esto es coherente
ya que las del grupo 2 son más grandes en su caparazón.
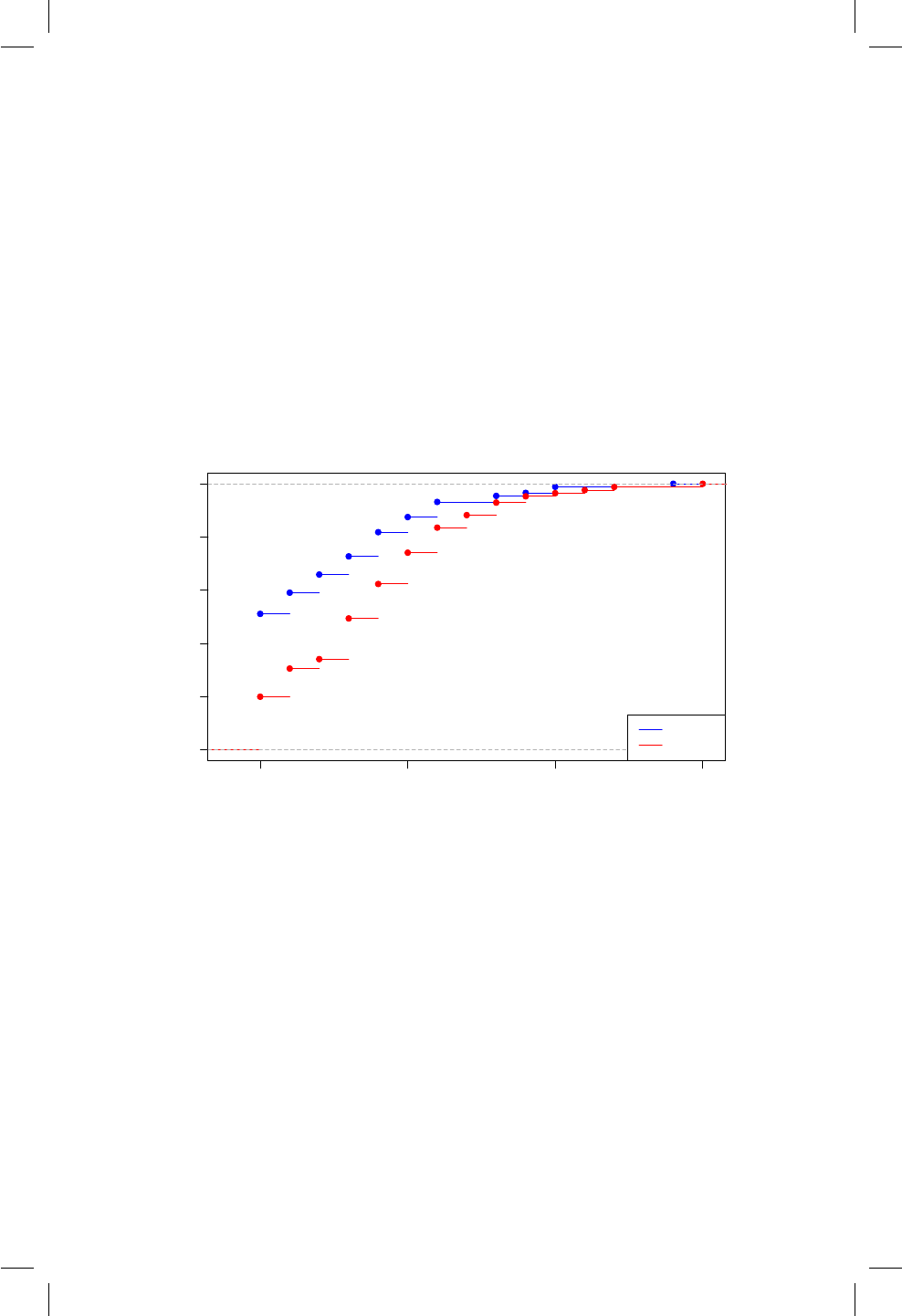
114 13 Distribuciones discretas
0 5 10 15
0.0
0.2
0.4
0.6
0.8
1.0
x
Fn(x)
Grupo 1
Grupo 2
Figura 13.5: Función de distribución acumulada para el número de satélites
por hembra diferenciando por grupo.
14
Distribuciones continuas
En este capítulo se mostrarán las funciones de Rpara distribuciones continuas.
14.1. Funciones disponibles para distribuciones conti-
nuas
Para cada distribución continua se tienen 4 funciones, a continuación el listado
de las funciones y su utilidad.
dxxx(x, ...) # Función de densidad de probabilidad, f(x)
pxxx(q, ...) # Función de distribución acumulada hasta q, F(x)
qxxx(p, ...) # Cuantil para el cual P(X <= q) = p
rxxx(n, ...) # Generador de números aleatorios.
En el lugar de las letras xxx se de debe colocar el nombre de la distribución en
R, a continuación el listado de nombres disponibles para las 11 distribuciones
continuas básicas.
beta # Beta
cauchy # Cauchy
chisq # Chi-cuadrada
exp # Exponencial
f# F
gamma # Gama
lnorm # log-normal
norm # normal
t# t-student
unif # Uniforme
weibull # Weibull
Combinando las funciones y los nombres se tiene un total de 44 funciones,
por ejemplo, para obtener la función de densidad de probabilidad f(x)de una
115
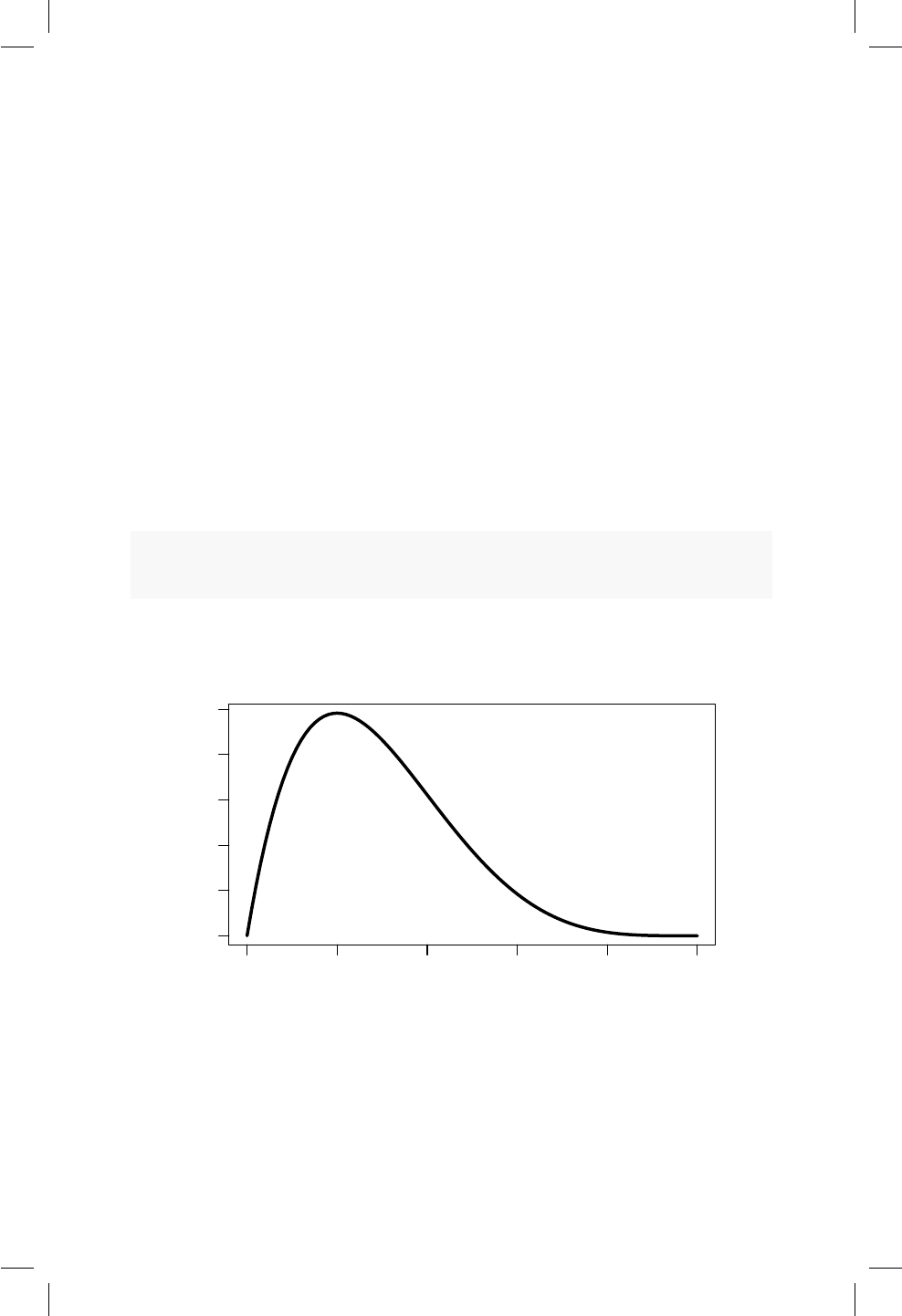
116 14 Distribuciones continuas
normal se usa la función dnorm( ) y para obtener la función acumulada F(x)
de una Beta se usa la función pbeta( ).
Ejemplo beta
Considere que una variable aleatoria Xse distribuye beta con parámetros
a= 2 yb= 5.
1) Dibuje la densidad de la distribución.
La función dbeta sirve para obtener la altura de la curva de una distribu-
ción beta y combinándola con la función curve se puede dibujar la densidad
solicitada. En la Figura 14.1 se presenta la densidad, observe que para la
combinación de parámetros a= 2 yb= 5 la distribución es sesgada a la
derecha.
curve(dbeta(x, shape1=2,shape2=5), lwd=3,las=1,
ylab='Densidad')
0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.5
1.0
1.5
2.0
2.5
x
Densidad
Figura 14.1: Función de densidad para una Beta(2,5).
2) Calcular P(0.3≤X≤0.7).
14.1 Funciones disponibles para distribuciones continuas 117
Para obtener la probabilidad o área bajo la densidad se puede usar la función
integrate, los límites de la integral se ingresan por medio de los parámetros
lower yupper. Si la función a integrar tiene parámetros adicionales como en
este caso, éstos parámetros se ingresan luego de los límites de la integral. A
continuación el código necesario para obtener la probabiliad solicitada.
integrate(f=dbeta, lower=0.3,upper=0.7,
shape1=2,shape2=5)
## 0.4092 with absolute error < 4.5e-15
Otra forma de obtener la probabilidad solicitada es restando de F(xmax)la
probabilidad F(xmin). Las probabilidades acumuladas hasta un valor dado se
obtienen con la función pbeta, a continuación el código necesario.
pbeta(q=0.7,shape1=2,shape2=5)-pbeta(q=0.3,shape1=2,shape2=5)
## [1] 0.4092
De ambas formas se obtiene que P(0.3≤X≤0.7) = 0.4092.
Recuerde que para distribuciones continuas
P(a < X < b) = P(a≤X < b) = P(a < X ≤b) = P(a≤X≤b)
Ejemplo normal estándar
Suponga que la variable aleatoria Zse distribuye normal estándar, es decir,
Z∼N(0,1).
1) Calcular P(Z < 1.45).
Para calcular la probabilidad acumulada hasta un punto dado se usa la función
pnorm y se evalúa en el cuantil indicado, a continuación el código usado.
pnorm(q=1.45)
## [1] 0.9265
En la Figura 14.2 se muestra el área sombreada correspondiente a P(Z <
1.45).
2) Calcular P(Z > −0.37).
118 14 Distribuciones continuas
Para calcular la probabilidad solicitada se usa nuevamente la función pnorm
evaluada en el cuantil dado. Como el evento de interés es Z > −0.37, la
probabilidad solicitada se obtiene como 1 - pnorm(q=-0.37), esto debido a
que por defecto las probabilidades entregadas por la función pxxx son siempre
a izquierda. A continuación el código usado.
1-pnorm(q=-0.37)
## [1] 0.6443
En la Figura 14.2 se muestra el área sombreada correspondiente a P(Z >
−0.37).
Otra forma para obtener la probabilidad solicitada sin hacer la resta es usar el
parámetro lower.tail para indicar que interesa la probabilidad a la derecha
del cuantil dado, a continuación un código alternativo para obtener la misma
probabilidad.
pnorm(q=-0.37,lower.tail=FALSE)
## [1] 0.6443
3) Calcular P(−1.56 < Z < 2.58).
Para calcular la probabilidad solicitada se obtiene la probabilidad acumulada
hasta 2.58 y de ella se resta lo acumulado hasta -1.56, a continuación el código
usado.
pnorm(q=2.58)-pnorm(-1.56)
## [1] 0.9357
En la Figura 14.2 se muestra el área sombreada correspondiente a P(−1.56 <
Z < 2.58).
4) Calcular el cuantil qpara el cual se cumple que P(Z < q) = 0.95.
Para calcular el cuantil en el cual se cumple que P(Z < q) = 0.95 se usa la
función qnorm, a continuación el código usado.
qnorm(p=0.95)
## [1] 1.645
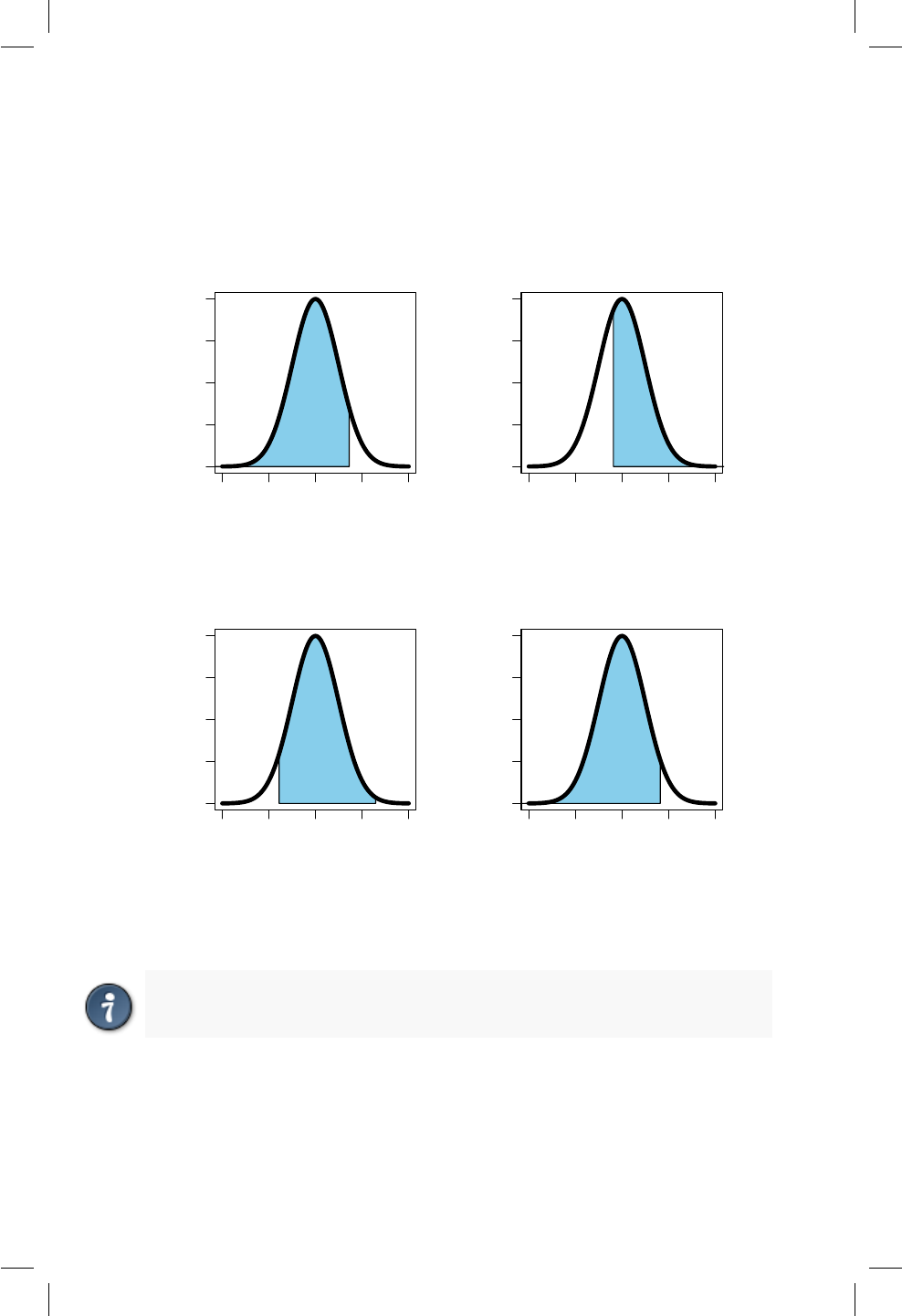
14.1 Funciones disponibles para distribuciones continuas 119
En la Figura 14.2 se muestra el área sombreada correspondiente a P(Z < q) =
0.95.
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
P(Z < 1.45)
Z
Densidad
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
P(Z > -0.37)
Z
Densidad
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
P(-1.56 < Z < 2.58)
Z
Densidad
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
P(Z<q)=0.95
Z
Densidad
Figura 14.2: Área sombreada para los ejemplos.
El parámetro lower.tail es muy útil para indicar si estamos trabajando
una cola a izquierda o una cola a derecha.
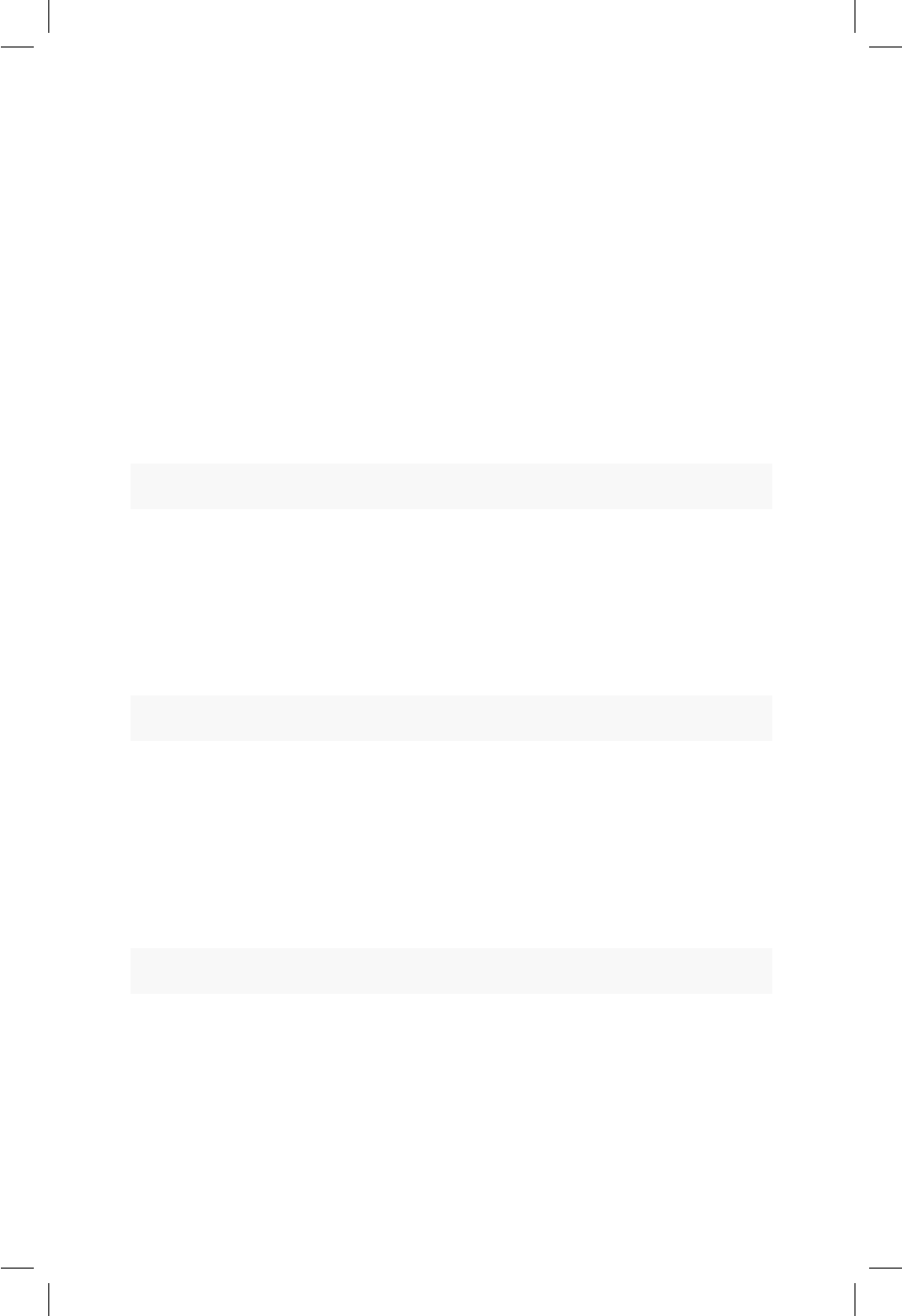
120 14 Distribuciones continuas
Ejemplo normal general
Considere un proceso de elaboración de tornillos en una empresa y suponga
que el diámetro de los tornillos sigue una distribución normal con media de
10 mm y varianza de 4 mm2.
1) Un tornillo se considera que cumple las especicaciones si su diáme-
tro está entre 9 y 11 mm. ¿Qué porcentaje de los tornillos cumplen
las especicaciones?
Como se solicita probabilidad se debe usar pnorm indicando que la media es
µ= 10 y la desviación de la distribución es σ= 2. A continuación el código
usado.
pnorm(q=11,mean=10,sd=2)-pnorm(q=9,mean=10,sd=2)
## [1] 0.3829
2) Un tornillo con un diámetro mayor a 11 mm se puede reprocesar y
recuperar. ¿Cuál es el porcentaje de reprocesos en la empresa?
Como se solicita una probabilidad a derecha se usa lower.tail=FALSE dentro
de la función pnorm. A continuación el código usado.
pnorm(q=11,mean=10,sd=2,lower.tail=FALSE)
## [1] 0.3085
3) El 5 % de los tornillos más delgados no se pueden reprocesar y por
lo tanto son desperdicio. ¿Qué diámetro debe tener un tornillo para
ser clasicado como desperdicio?
Aquí interesa encontrar el cuantil tal que P(Diametro < q) = 0.05, por lo
tanto se usa la función qnorm. A continuación el código usado.
qnorm(p=0.05,mean=10,sd=2)
## [1] 6.71
4) El 10 % de los tornillos más gruesos son considerados como sobredi-
mensionados. ¿cuál es el diámetro mínimo de un tornillo para que
sea considerado como sobredimensionado?
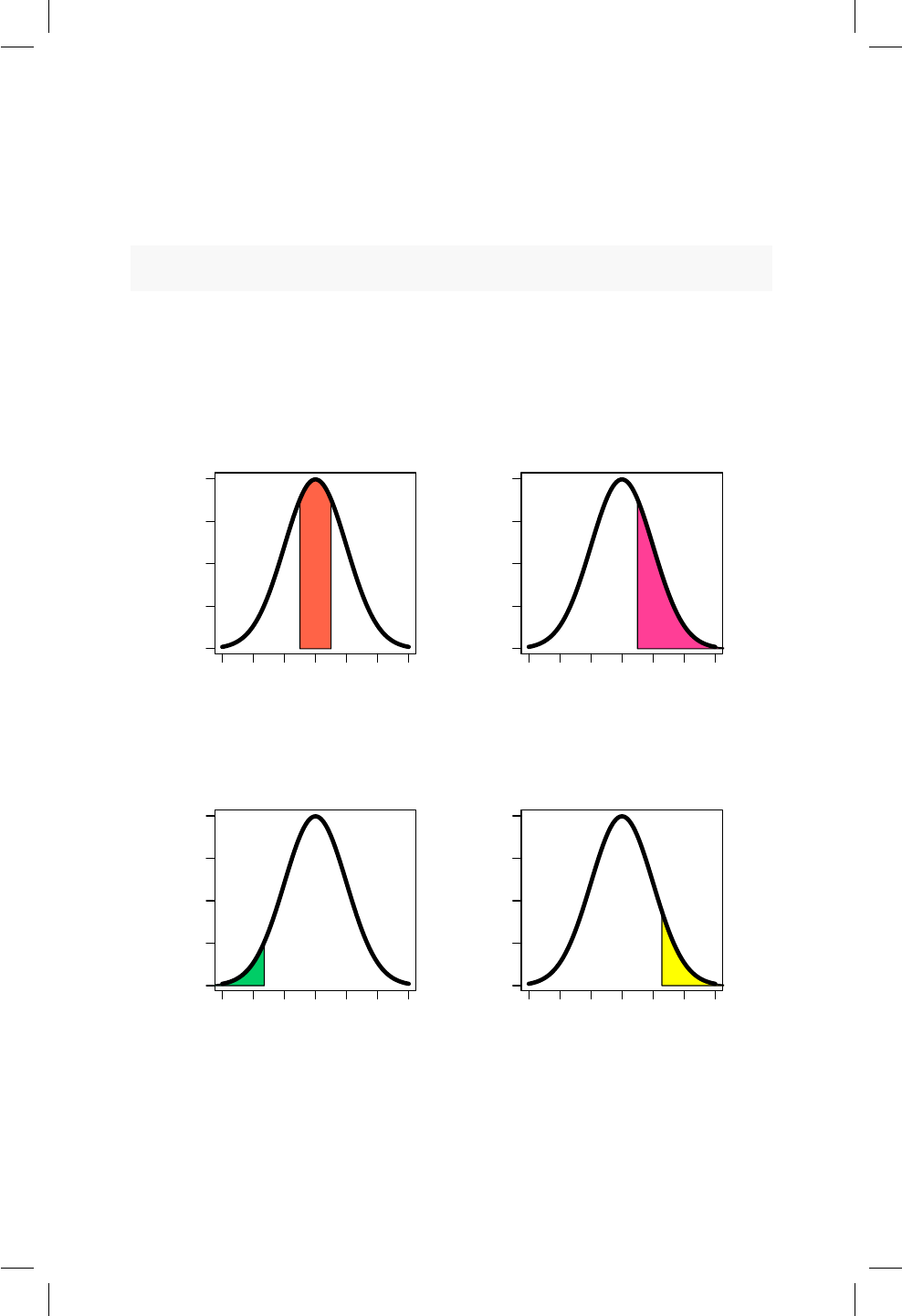
14.2 Funciones disponibles para distribuciones continuas 121
Aquí interesa encontrar el cuantil tal que P(Diametro > q) = 0.10, por lo
tanto se usa la función qnorm pero incluyendo lower.tail=FALSE por ser una
cola a derecha. A continuación el código usado.
qnorm(p=0.10,mean=10,sd=2,lower.tail=FALSE)
## [1] 12.56
En la Figura 14.3 se muestran las áreas sombreadas para cada de las anteriores
preguntas.
4 6 8 10 12 14 16
0.00
0.05
0.10
0.15
0.20
P(9 < Diámetro < 11)
Diámetro
Densidad
4 6 8 10 12 14 16
0.00
0.05
0.10
0.15
0.20
P(Diámetro > 11)
Diámetro
Densidad
4 6 8 10 12 14 16
0.00
0.05
0.10
0.15
0.20
P(Diámetro < q) = 5%
Diámetro
Densidad
4 6 8 10 12 14 16
0.00
0.05
0.10
0.15
0.20
P(Diámetro > q) = 10%
Diámetro
Densidad
Figura 14.3: Área sombreada para el ejemplo de los tornillos.

122 14 Distribuciones continuas
14.2. Distribuciones continuas generales
En la práctica nos podemos encontramos con variables aleatorias continuas
que no se ajustan a una de las distribuciones mostradas anteriormente, en esos
casos, es posible manejar ese tipo de variables por medio de unas funciones
básicas de Rcomo se muestra en el siguiente ejemplo.
Ejemplo
En este ejemplo se retomará la base de datos crab sobre el cangrejo de he-
rradura hembra presentado en el capítulo anterior. La base de datos crab
contiene las siguientes variables: el color del caparazón, la condición de la es-
pina, el peso en kilogramos, el ancho del caparazón en centímetros y el número
de satélites o machos sobre el caparazón, la base de datos está disponible en
el siguiente enlace1.
1) Sea Xla variable peso del cangrejo, dibuje la densidad para X.
Para obtener la densidad muestral de un vector cuantitativo se usa la función
density, y para dibujar la densidad se usa la función plot aplicada a un
objeto obtenido con density, a continuación el código necesario para dibujar
la densidad.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/crab'
crab <- read.table(file=url, header=T)
plot(density(crab$W), main='',lwd=5,las=1,
xlab='Peso (Kg)',ylab='Densidad')
En la Figura 14.4 se muestra la densidad para la variable peso de los cangrejos,
esta densidad es bastante simétrica y el intervalo de mayor densidad está entre
22 y 30 kilogramos.
2) Dibujar F(x)para el peso del cangrejo.
Para dibujar la función F(x)se usa la función ecdf y se almacena el resultado
en el objeto F, luego se dibuja la función deseada usando plot. A continuación
el código utilizado. En la Figura 14.5 se presenta el dibujo para F(x).
1https://raw.githubusercontent.com/fhernanb/datos/master/crab
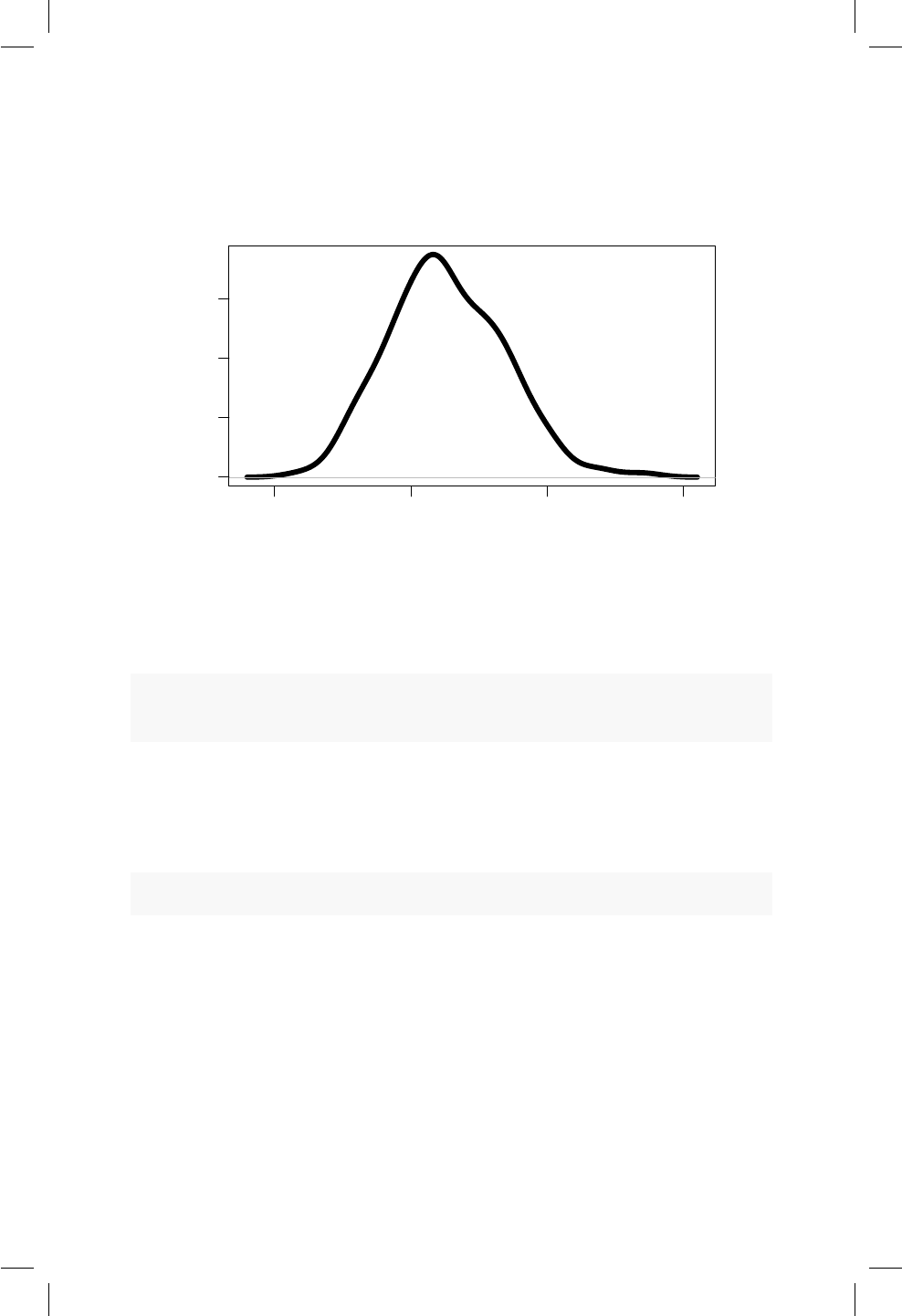
14.2 Distribuciones continuas generales 123
20 25 30 35
0.00
0.05
0.10
0.15
Peso (Kg)
Densidad
Figura 14.4: Función de densidad f(x)para el peso de los cangrejos.
F <- ecdf(crab$W)
plot(F, main='',xlab='Peso (Kg)',ylab='F(x)',cex=0.5,las=1)
3) Calcular la probabilidad de que un cangrejo hembra tenga un peso
inferior o igual a 28 kilogramos.
Para obtener P(X≤28) se evalua en la función F(x)el cuantil 28 así.
F(28)
## [1] 0.7919
Por lo tanto P(X≤28) = 0.7919.
4) Dibujar la función de densidad para el peso de los cangrejos hembra
diferenciando por el color del caparazón.
Como son 4 los colores de los caparazones se deben construir 4 funciones de
densidad. Usando la función split se puede partir el vector de peso de los
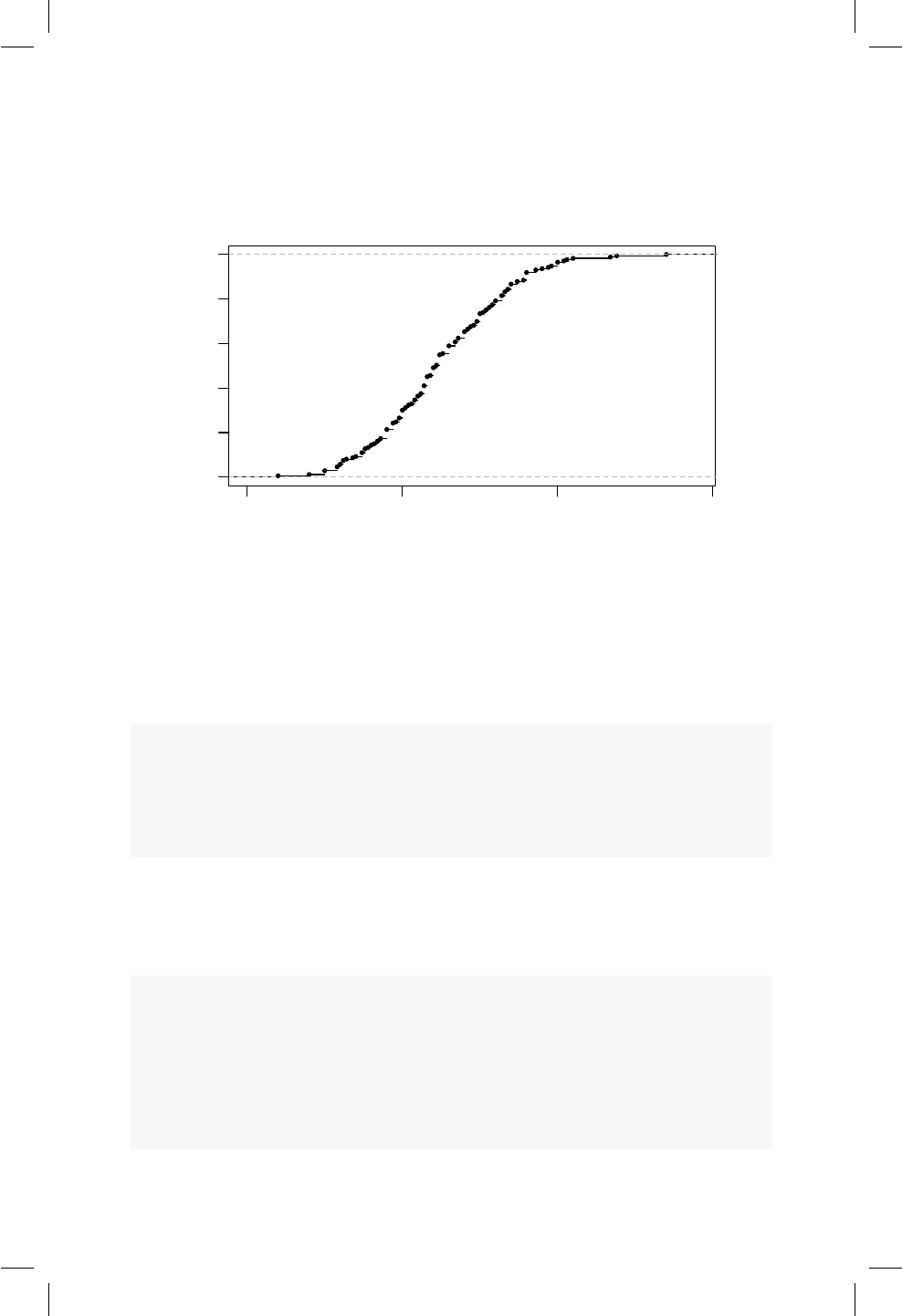
124 14 Distribuciones continuas
20 25 30 35
0.0
0.2
0.4
0.6
0.8
1.0
Peso (Kg)
F(x)
Figura 14.5: Función acumulada F(x)para el peso de los cangrejos.
cangrejos según su color. Luego se construyen las cuatro densidades usando la
función density aplicada a cada uno de los pesos, a continuación el código.
pesos <- split(x=crab$W, f=crab$C)
f1 <- density(pesos[[1]])
f2 <- density(pesos[[2]])
f3 <- density(pesos[[3]])
f4 <- density(pesos[[4]])
Luego de tener las densidades muestrales se procede a dibujar la primera
densidad con plot, luego se usa la funció lines para agregar a la densidad
inicial las restantes densidades. En la Figura 14.6 se muestran las 4 densidades,
una por cada color de caparazón.
plot(f1, main='',las=1,lwd=4,
xlim=c(18,34),
xlab='Peso (Kg)',ylab='Densidad')
lines(f2, lwd=4,col='red')
lines(f3, lwd=4,col='blue')
lines(f4, lwd=4,col='orange')
legend('topright',lwd=4,bty='n',
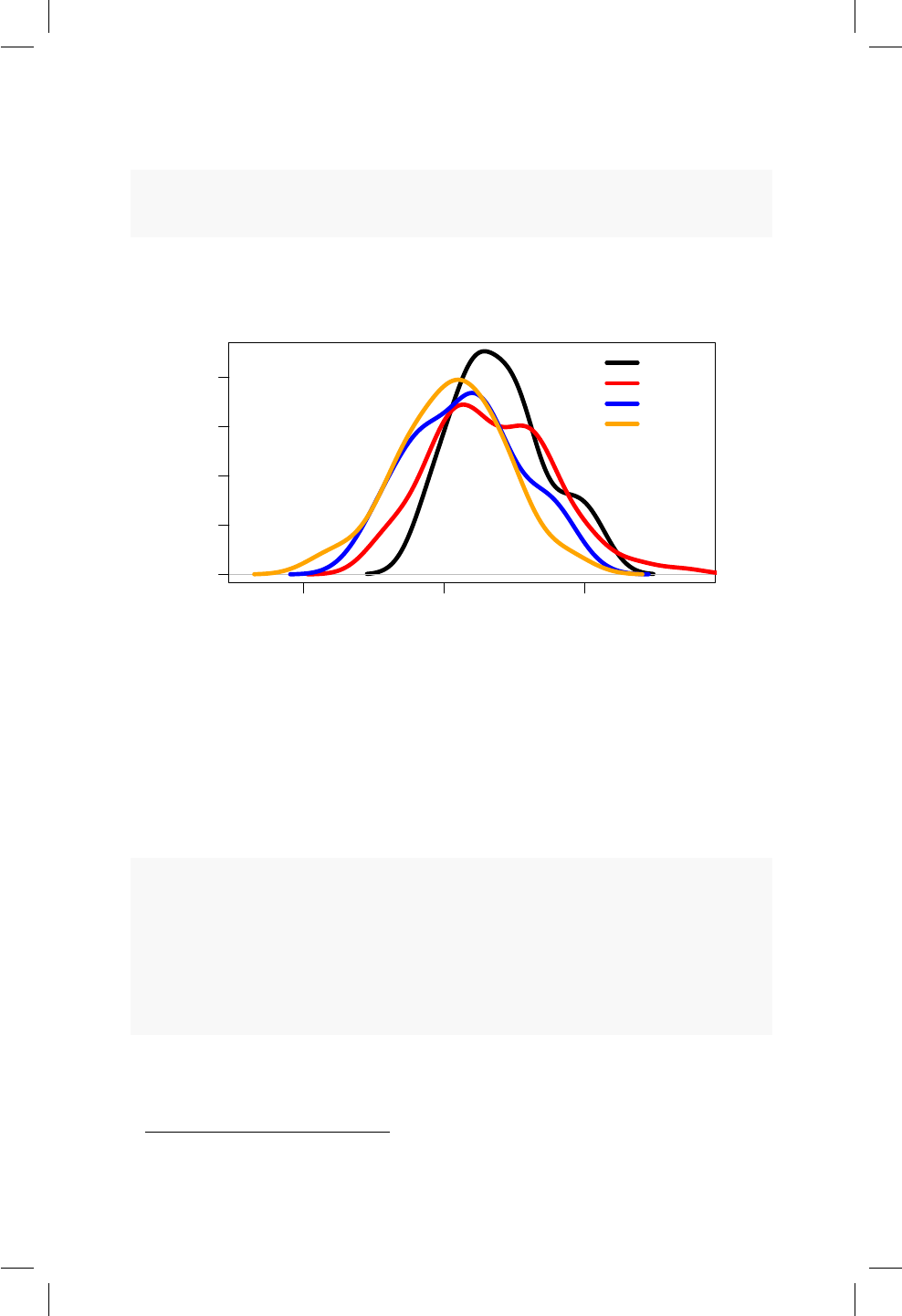
14.2 Distribuciones continuas generales 125
col=c('black','red','blue','orange'),
legend=c('Color 1','Color 2','Color 3','Color 4'))
20 25 30
0.00
0.05
0.10
0.15
0.20
Peso (Kg)
Densidad
Color 1
Color 2
Color 3
Color 4
Figura 14.6: Función de densidad f(x)para el peso del cangrejo diferencian-
do por el color.
Otra forma para dibujar las densidades es usar el paquete ggplot2 (Wickham
et al.,2018). En la Figura 14.7 se muestra el resultado obtenido de correr el
siguiente código.
require(ggplot2) # Recuerde que primero debe instalarlo
crab$Color <- as.factor(crab$C) # Para convertir en factor
ggplot(crab, aes(x=W)) +
geom_density(aes(group=Color, fill=Color), alpha=0.3)+
xlim(18,34)+xlab("Peso (Kg)")+ylab("Densidad")
Para aprender más sobre el paquete ggplot2 se recomienda consultar este
enlace2.
2http://tutorials.iq.harvard.edu/R/Rgraphics/Rgraphics.html
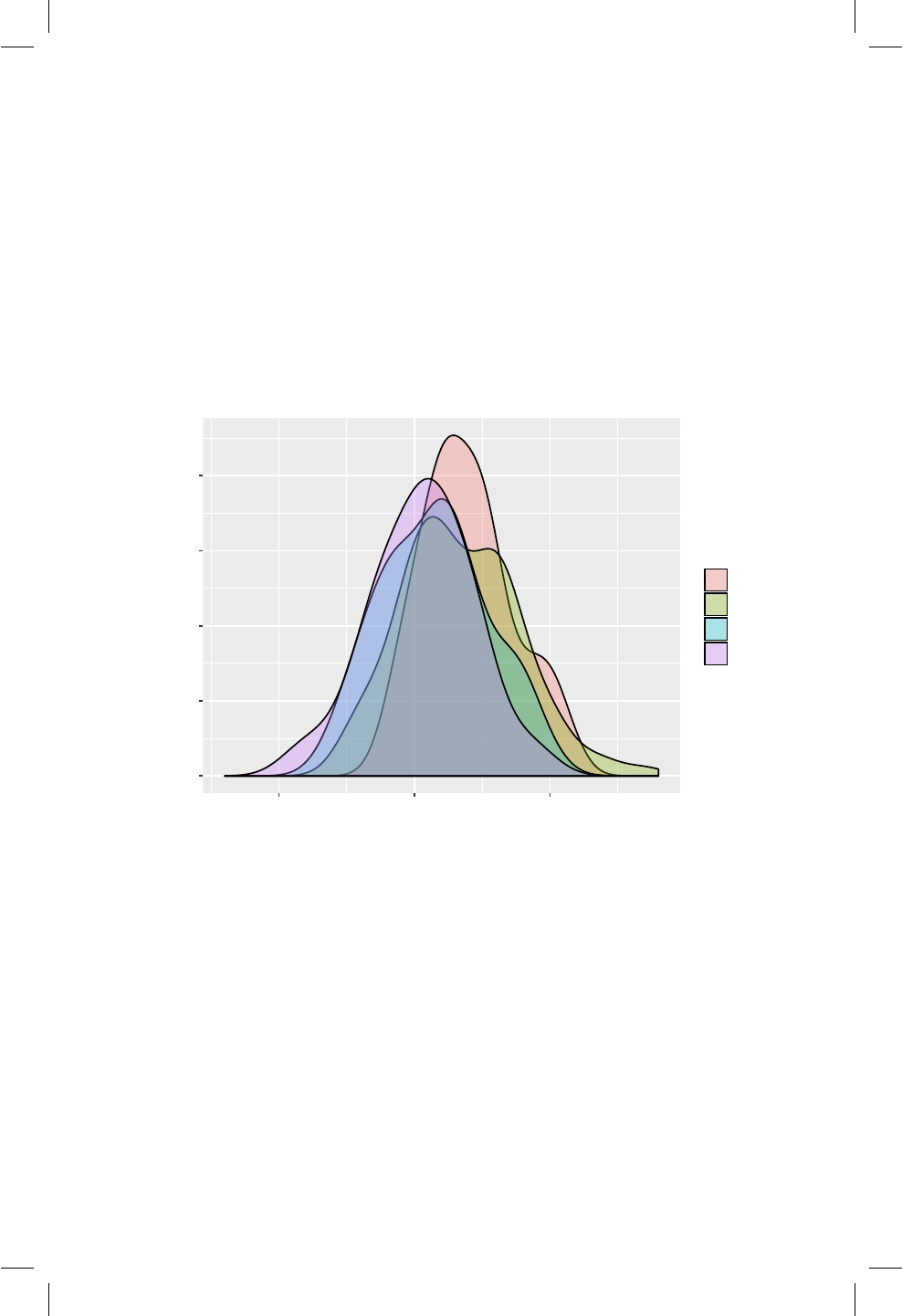
126 14 Distribuciones continuas
0.00
0.05
0.10
0.15
0.20
20 25 30
Peso (Kg)
Densidad
Color
1
2
3
4
Figura 14.7: Función de densidad f(x)para el peso del cangrejo diferencian-
do por el color y usando ggplot2.

15
Verosimilitud
En este capítulo se mostrará como usar Rpara obtener la función de log-
verosimilitud y estimadores por el método de máxima verosimilitud.
15.1. Función de verosimilitud
La función de verosimilitud para un vector de parámetros Θdada una muestra
aleatoria xcon una distribución asumida se dene como:
L(Θ|x) =
n
i=1
f(xi|Θ),(15.1)
donde xirepresenta uno de los elementos de la muestra aleatoria y fes la
función de masa/densidad de la distribución de la cual se obtuvo x.
15.2. Función de log-verosimilitud
La función de log-verosimilitud lse dene como el logaritmo de la función de
verosimilitud L, es decir
l(Θ|x) = log L(Θ|x) =
n
i=1
log f(xi|Θ)(15.2)
127
128 15 Verosimilitud
15.3. Método de máxima verosimilitud para estimar pa-
rámetros
El método de máxima verosimilitud se usa para estimar los parámetros de
una distribución. El objetivo de este método es encontrar los valores de Θque
maximizan Loly valores encontrados se representan por ˆ
Θ.
Ejemplo
En este ejemplo vamos a considerar la distribución binomial cuya función de
masa de probabilidad está dada por:
f(x) = P(X=x) = n
xpx(1−p)n−x,0< p < 1, n ≤1,2, . . . , 0≤x≤n
Suponga que se tiene el vector rta que corresponde a una muestra aleatoria
de una distribución binomial con parámetro n= 5 conocido.
rta <- c(2,2,1,1,1,1,0,2,1,2,
1,0,1,2,1,0,0,2,2,1)
1) Calcular el valor de log-verosimilitud lsi asumiendo que p= 0.30
en la distribución binomial.
Para obtener el valor de len el punto p= 0.30 se aplica la denición dada en
la expresión (15.2). Como el problema trata de una binomial se usa entonces
la función de masa dbinom evaluada en la muestra rta, el parámetro size
como es conocido se reemplaza por el valor de cinco y en el parámetro prob se
cambia por 0.3. Como interesa la función de log-verosimilitud se debe incluir
log=TRUE. A continuación el código necesario.
sum(dbinom(x=rta, size=5,prob=0.3,log=TRUE))
## [1] -24.55
Por lo tanto l(θ) = −24.55
2) Construir una función llamada ll a la cual le ingrese valores del
parámetro pde la binomial y que la función entregue el valor de
log-verosimilitud.
15.3 Método de máxima verosimilitud para estimar parámetros 129
La función solicitada tiene un cuerpo igual al usado en el numeral anterior, a
continuación el código necesario para crearla.
ll <- function(prob) sum(dbinom(x=rta, size=5,prob=prob, log=T))
Vamos a probar la función en dos valores arbitrarios p= 0.15 yp= 0.80 que
pertenezcan al dominio del parámetro pde la distribución binomial.
ll(prob=0.15)# Individual para p=0.15
## [1] -25.54
ll(prob=0.80)# Individual para p=0.80
## [1] -98.46
El valor de log-verosimilitud para p= 0.15 fue de -25.54 mientras que para
p= 0.80 fue de -98.46.
Vamos ahora a chequear si la función ll está vectorizada y para esto usamos
el código mostrado a continuación y deberíamos obtener un vector con los
valores c(-25.54, -98.56).
ll(prob=c(0.15,0.80))
## [1] -57.32
No obtuvimos el resultado esperado, eso signica que nuestra función no está
vectorizada. Ese problema lo podemos solucionar así:
ll <- Vectorize(ll)
ll(prob=c(0.15,0.80))
## [1] -25.54 -98.46
Vemos que ahora que cuando se ingresa un vector a la función ll se obtiene
un vector.
Necesitamos que la función ll esté vectorizada para poder dibujarla y para
poder optimizarla.
3) Dibujar la curva log-verosimilitud l, en el eje X debe estar el pará-
metro pdel cual depende la función de log-verosimilitud.
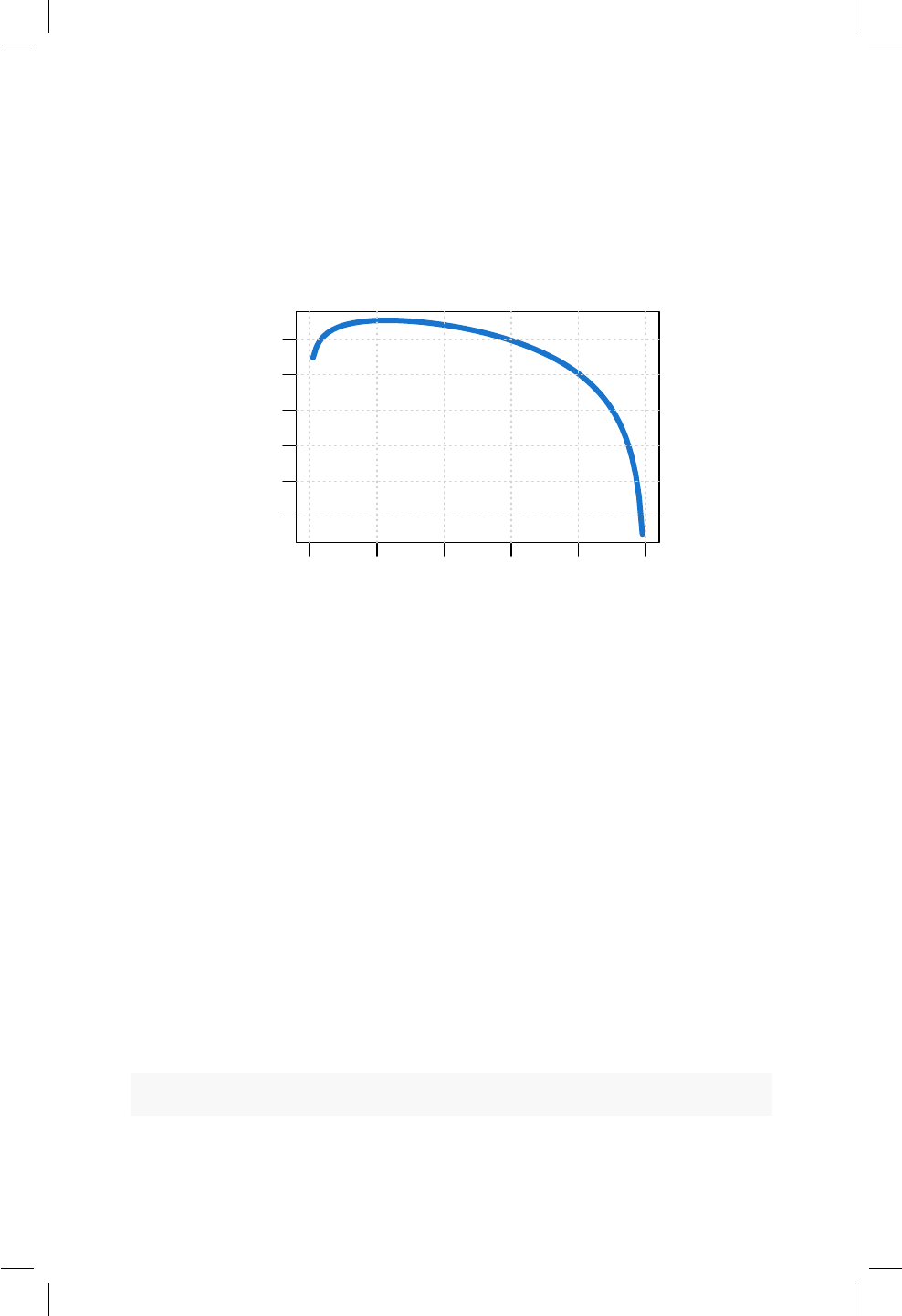
130 15 Verosimilitud
En la Figura 15.1 se presenta la curva solicitada.
0.0 0.2 0.4 0.6 0.8 1.0
-300
-250
-200
-150
-100
-50
Probabilidad de éxito (p)
l(q)
Figura 15.1: Función de log-verosimilitud para el ejemplo sobre binomial.
4) Observando la Figura 15.1, ¿cuál esl el valor de pque maximiza la
función de log-verosimilitud?
Al observar la Figura 15.1 se nota que el valor de pque maximiza la función
log-verosimilitud está muy cerca de 0.2.
5) ¿Cuál es el valor exacto de pque maximiza la función log-
verosimilitud?
En Rexiste la función optimize que sirve para encontrar el valor que mi-
nimiza una función uniparamétrica en un intervalo dado, sin embargo, aquí
interesa es maximimizar la función de log-verosimilitud, por esa razón se cons-
truye la función minusll que es el negativo de la función ll para así poder
usar optimize. A continuación el código usado.
minusll <- function(x) -ll(x)
15.3 Método de máxima verosimilitud para estimar parámetros 131
optimize(f=minusll, interval=c(0,1))
## $minimum
## [1] 0.23
##
## $objective
## [1] 23.32
Del resultado anterior se observa que cuando p= 0.23 el valor máximo de
log-verosimilitud es 23.32.
Ejemplo
Suponga que la estatura de una población se puede asumir como una normal
N(170,25). Suponga también que se genera una muestra aleatoria de 50 ob-
servaciones de la población con el objetivo de recuperar los valores de la media
y varianza poblacionales a partir de la muestra aleatoria.
La muestra se va a generar con la función rnorm pero antes se jará una
semilla con la intención de que el lector pueda replicar el ejemplo y obtener la
misma muestra aleatoria aquí generada, el código para hacerlo es el siguiente.
set.seed(1235)# La semilla es 1235
y <- rnorm(n=50,mean=170,sd=5)
1) Construya la función de log-verosimilitud para los parámetros de la
normal dada la muestra aleatoria y.
ll <- function(param) {
media <- param[1]# param es el vector de parámetros
desvi <- param[2]
sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}
Siempre que el interés sea encontrar los valores que maximizan una función
de log-verosimilitud, los parámetros de la distribución deben ingresar a la
función ll como un vector. Esto se debe hacer para poder usar las funciones
de búsqueda optim ynlminb.
2) Dibujar la función de log-verosimilitud.
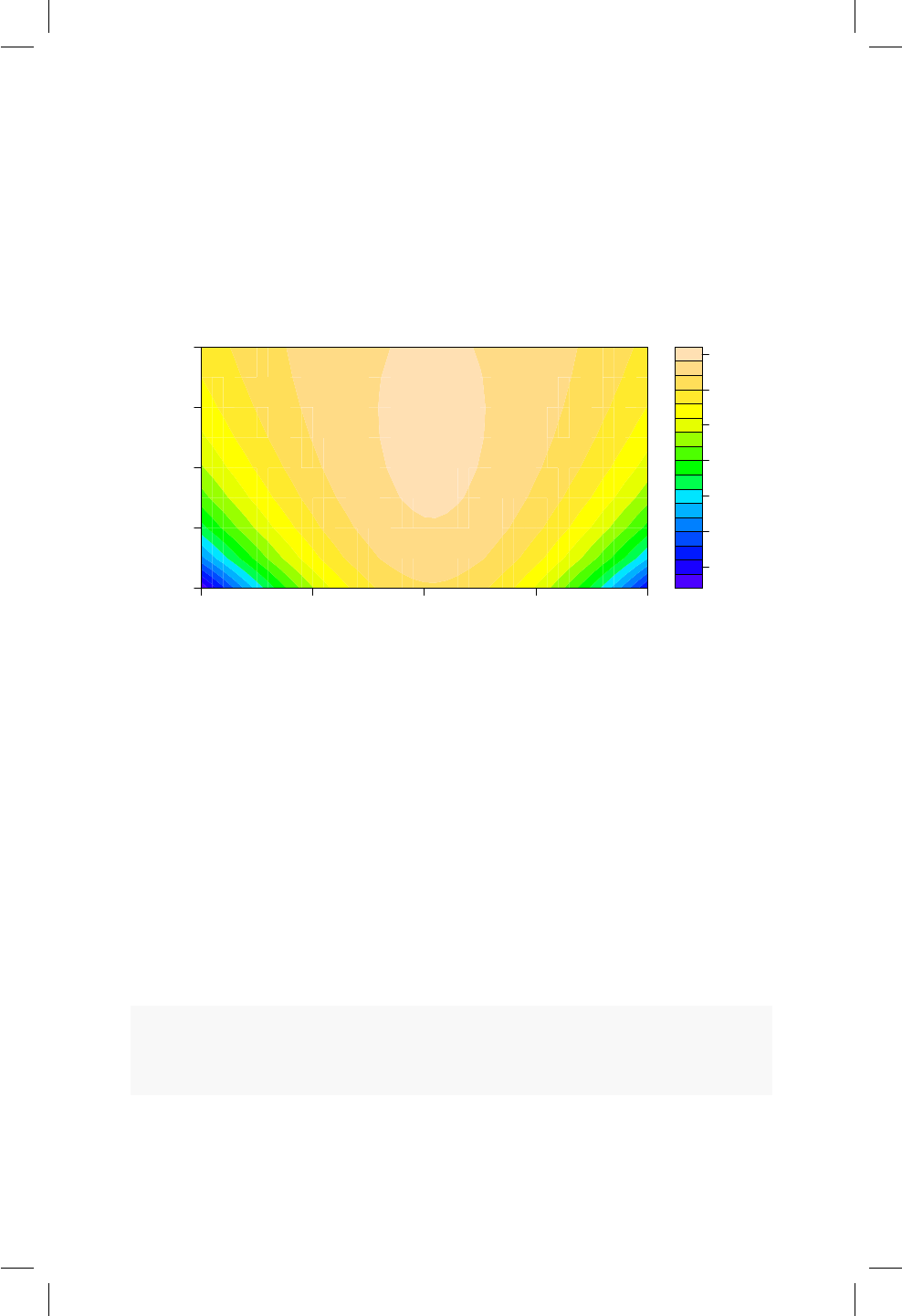
132 15 Verosimilitud
En la Figura 15.2 se muestra el gráco de niveles para la supercie de log-
verosimilitud. De esta gura se nota claramente que los valores que maximizan
la supercie están alrededor de µ= 170 yσ= 5. Para ver el código usado en
la creación de la Figura 15.2 se recomienda consultar la sección sobre contour
en Hernández (2018).
-450
-400
-350
-300
-250
-200
-150
160 165 170 175 180
3
4
5
6
7
m
s
Figura 15.2: Gráco de niveles para la función de log-verosimilitud para el
ejemplo sobre normal.
3) Obtenga los valores de µyσque maximizan la función de log-
verosimilitud.
Para obtener los valores solicitados vamos a usar la función nlminb que es un
optimizador. A la función nlminb se le debe indicar por medio del paráme-
tro objective la función que queremos optimizar (minimizar); el parámetro
start es un vector con los valores iniciales para comenzar la búsqueda de µ
yσ; los parámetros lower yupper sirven para delimitar el espacio de bús-
queda. A continuación se muestra el código usado para obtener los valores
que minimizan a minusll, es decir, los valores que maximizan la función de
log-verosimilitud.
minusll <- function(x) -ll(x)
nlminb(objective=minusll, start=c(163,3.4),
lower=c(160,3), upper=c(180,7))
## $par
## [1] 170.338 5.424
15.3 Método de máxima verosimilitud para estimar parámetros 133
##
## $objective
## [1] 155.5
##
## $convergence
## [1] 0
##
## $iterations
## [1] 13
##
## $evaluations
## function gradient
## 16 35
##
## $message
## [1] "relative convergence (4)"
De la salida anterior podemos observar que los valores óptimos de µyσ
son 170.338 y 5.424 respectivamente, esto coincide con lo observado en la
15.2 y con los valores reales de simulación de la muestra. Esto indica que el
procedimiento de estimación de parámetros por máxima verosimilitud entrega
valores insesgados de los parámetros a estimar.
Un resultado interesante de la salida anterior es que se reporta el valor mínimo
que alcanza la función minusll, este valor fue de 155.5, por lo tanto, se puede
armar que el valor máximo de log-verosimilitud es -155.5.
Otros resultados importantes de la salida anterior son el valor de
convergence=0 que indica que la búsqueda fue exitosa; iterations=13 indica
que se realizaron 13 pasos desde el punto inicial start hasta las coordenadas
de optimización.
En Rse tienen dos funciones básicas para optimizar funciones, es decir, para
encontrar los valores que minimizan una función dada. Esas dos funciones
son nliminb yoptim. Para optimizar en una sola dimensión se usa la función
optimize.
4) ¿Hay alguna función para obtener directamente el valor que maxi-
miza la función log-verosimilitud?
La respuesta es si. Si la distribución estudiada es una de las distribuciones bá-
sicas se puede usar la función fitdistr del paquete básico MASS. La función
fitdistr requiere de los datos que se ingresan por medio del parámetro x, y
de la distribución de los datos que se ingresa por medio del parámetro densfun.
La función fitdistr admite 15 distribuciones diferentes para hacer la búsque-
134 15 Verosimilitud
da de los parámetros que caracterizan una distribución, se sugiere consultar
la ayuda de la función fitdistr escribiendo en la consola help(fitdistr).
A continuación el código usado.
require(MASS) # El paquete ya está instalado, solo se debe cargar
res <- fitdistr(x=y, densfun='normal')
res
## mean sd
## 170.3384 5.4235
## ( 0.7670) ( 0.5424)
El objeto res contiene los resultados de usar fitdistr. En la primer lí-
nea están los valores de los parámetros que maximizan la función de log-
verosimilitud, en la parte de abajo, dentro de paréntesis, están los errores
estándar o desviaciones de éstos estimadores.
Al objeto res es de la clase tdistr y por lo tanto se le puede aplicar la función
genérica logLik para obtener el valor de la log-verosimilitud. Se sugiere con-
sultar la ayuda de la función logLik escribiendo en la consola help(logLik).
A continuación el código para usar logLik sobre el objeto res.
logLik(res)
## 'log Lik.' -155.5 (df=2)
De esta última salida se observa que el valor coincide con el obtenido cuando
se usó nlminb.
Ejemplo
Generar n= 100 observaciones de una gamma con parámetro de forma igual
a 2 y parámetro de tasa igual a 0.5 y luego responder las preguntas.
Para generar la muestra aleatoria ma solicitada se jó la semilla con el objetivo
de que el lector pueda obtener los mismos resultados de este ejemplo.
n <- 100
set.seed(12345)
ma <- rgamma(n=n, shape=2,rate=0.5)
1) Asumiendo que la muestra aleatoria proviene de una normal (lo cual
es incorrecto) estime los parámetros de la distribución normal.
15.3 Método de máxima verosimilitud para estimar parámetros 135
fit1 <- fitdistr(x=ma, densfun='normal')
fit1
## mean sd
## 4.3083 2.8085
## (0.2808) (0.1986)
2) Asumiendo que la muestra aleatoria proviene de una gamma estime
los parámetros de la distribución.
fit2 <- fitdistr(x=ma, densfun='gamma')
fit2
## shape rate
## 2.23978 0.51988
## (0.29620) (0.07703)
En la salida anterior están los valores estimados de los parámetros de la dis-
tribución por el método de máxima verosimilitud, observe la cercanía de éstos
con los verdaderos valores de 2 y 0.5 para forma y tasa respectivamente.
3) Dibuje dos qqplot, uno asumiendo distribución normal y el otro
distribución gamma. ¿Cuál distribución se ajusta mejor a los datos
simulados?
Para dibujar el qqplot se usa la función genérica qqplot, recomendamos con-
sultar Hernández (2018) para los detalles de cómo usar esta función. Al usar
qqplot para obtener el qqplot normal y gamma es necesario indicar los valo-
res ˆ
Θobtenidos en el numeral anterior, por eso es que en el código mostra-
do a continuación aparece mean=4.3083, sd=2.8085 en el qqplot normal y
shape=2.23978, rate=0.51988 en el qqplot gamma.
par(mfrow=c(1,2))
qqplot(y=ma, pch=19,
x=qnorm(ppoints(n), mean=4.3083,sd=2.8085),
main='Normal Q-Q Plot',
xlab='Theoretical Quantiles',
ylab='Sample Quantiles')
qqplot(y=ma, pch=19,
x=qgamma(ppoints(n), shape=2.23978,rate=0.51988),
main='Gamma Q-Q Plot',
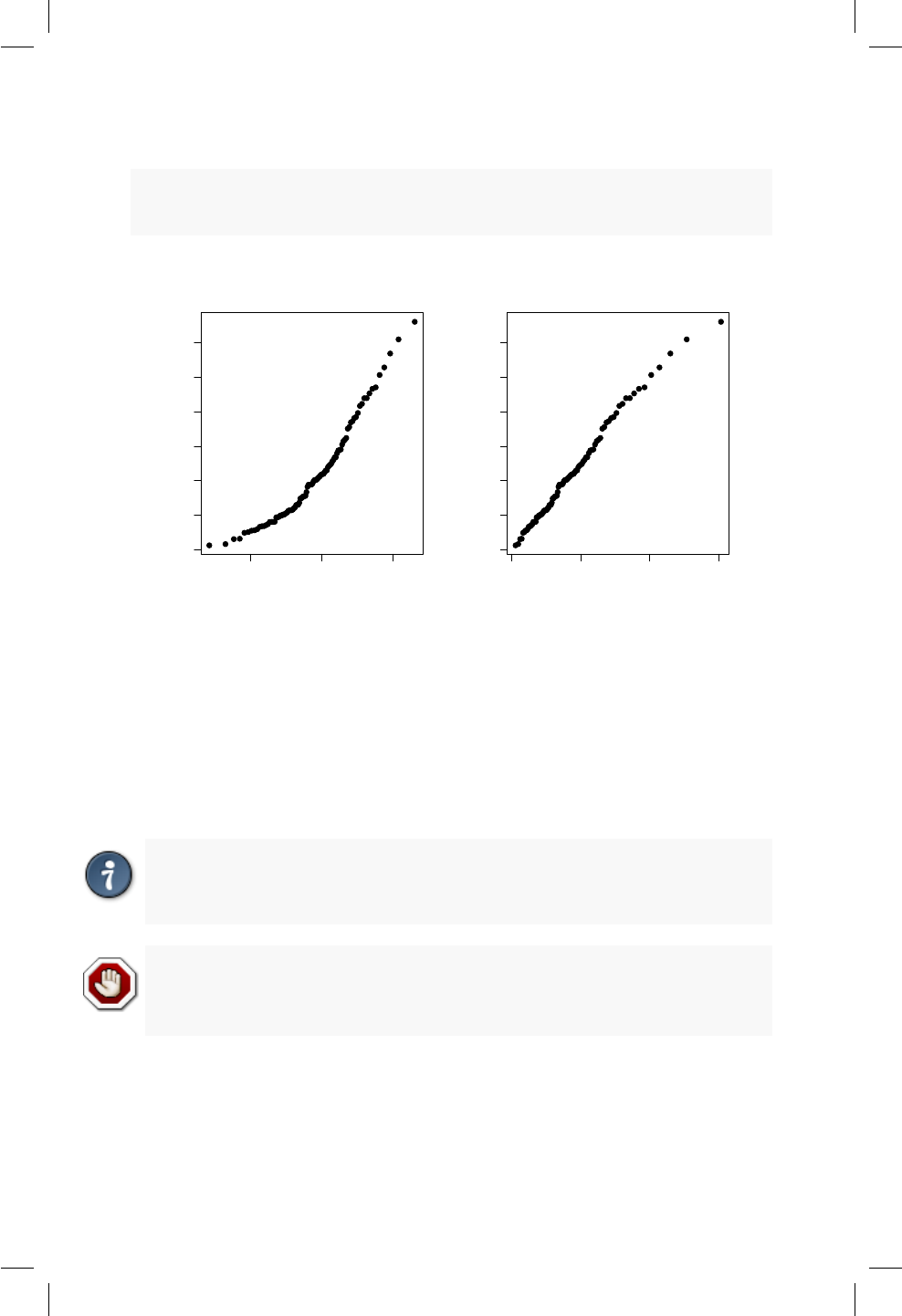
136 15 Verosimilitud
xlab='Theoretical Quantiles',
ylab='Sample Quantiles')
0 5 10
0 2 4 6 8 10 12
Normal Q-Q Plot
Theoretical Quantiles
Sample Quantiles
0 5 10 15
0 2 4 6 8 10 12
Gamma Q-Q Plot
Theoretical Quantiles
Sample Quantiles
Figura 15.3: Gráco cuantil cuantil normal y gamma para la muestra simu-
lada.
En la Figura 15.3 se muestran los qqplot solicitados. Se observa claramente
que al asumir normalidad (lo cual es incorrecto), los puntos del qqplot no están
alineados, mientras que al asumir distribución gamma (lo cual es correcto), los
puntos si están alineados. De esta gura se concluye que la muestra ma puede
provenir de una Gamma(2.23978,0.51988).
Para obtener el gráco cuantil cuantil bajo normalidad se puede usar di-
rectamente la función qqnorm, consultar Hernández (2018) para mayores
detalles.
En este ejemplo se eligió la mejor distribución entre dos candidatas usando
una herramienta gráca, lo que se recomienda usar algún método menos
subjetivo (cuantitativo) para tomar decisiones.
4) Para comparar modelos se puede utilizar el Akaike information cri-
terion (AIC) propuesto por Akaike (1974) que sirve para medir la
calidad relativa de los modelos estadísticos, la expresión para calcu-
lar el indicador es AIC =−2ˆ
l+ 2 df, donde ˆ
lcorresponde al valor
15.3 Método de máxima verosimilitud para estimar parámetros 137
de log-verosimilitud y df corresponde al número de parámetros es-
timados del modelo. Siempre el modelo elegido es aquel modelo con
el menor valor de AIC. Calcular el AIC para los modelos asumidos
normal y gamma.
-2*logLik(fit1) +2*2# AIC para modelo normal
## 'log Lik.' 494.3 (df=2)
-2*logLik(fit2) +2*2# AIC para modelo gamma
## 'log Lik.' 466 (df=2)
De los resultados anteriores se concluye que entre los dos modelos, el mejor es
el gamma porque su AIC = 466 es el menor de toos los AIC.
Modelos anidados pueden ser comparados por medio del global deviance
(GD) dado por GD =−2ˆ
ly modelos no anidados por medio del Genera-
lized Akaike information criterion (GAIC) propuesto por Akaike (1983) y
dado por GAIC =−2ˆ
l+ # df siendo #el valor de penalidad por cada
parámetro adicional en el modelo; cuando # = 2, el GAIC coincide con el
AIC y el Schwarz Bayesian criterion (SBC) propuesto por Schwarz (1978)
se dá cuando el valor de penalidad es # = log(n)donde nes el número de
observaciones del modelo; siempre el modelo elegido es aquel modelo con el
menor valor de cualquiera de los criterios de información anteriores.
Ejemplo
¿Será posible explorar entre muchas distribuciones estadísticas aquella que
mejor explica una variable de interés?
La respuesta es si, se puede usar la función fitDist del paquete gamlss .
Esta función tiene la siguiente estructura:
fitDist(y, k = 2,
type = c("realAll","realline","realplus",
"real0to1","counts","binom"))
El parámetro ysirve para ingresar el vector con la información; k=2 es la
penalización por cada parámetro estimado para calcular el GAIC, por defecto
es 2; y el parámetro type sirve para indicar el tipo de distribución, los posibles
valores son:

138 15 Verosimilitud
realAll: para hacer la búsqueda en todas las distribuciones disponibles en
gamlss.
realline: para variables en ℜ.
realplus: para variables en ℜ+.
real0to1: para variables en el intervalo (0,1).
counts: para variables de conteo.
binom: para variables de tipo binomial.
1) Usar la función fitDist para elegir la distribución que mejor se
ajusta a los datos simulados en el ejemplo anterior, usar una pena-
lizacion de k= 2 para calcular el AIC.
Se usa la función fitDist con type='realplus' porque se sabe que la mues-
tra aleatoria tiene valores sólo en ℜ+, los resultados de almacenan en el objeto
modelos. Para obtener la lista de los mejores modelos con su respectivo BAIC
se escribe en la consola modelos$fits. Abajo el código usado.
require(gamlss)
modelos <- fitDist(y=ma, type='realplus',k=2)
modelos$fits
## GA WEI3 WEI2 WEI GG GIG
## 466.0 466.8 466.8 466.8 468.0 468.0
## BCCGo BCCG BCPE BCPEo GB2 BCTo
## 468.4 468.4 469.4 469.4 470.0 470.4
## BCT exGAUS LOGNO2 LOGNO IG EXP
## 470.4 471.2 474.6 474.6 483.9 494.1
## PARETO2o GP PARETO2 IGAMMA
## 496.1 496.1 496.1 504.2
De la lista anterior se observa que la función gamma está en el primer lugar
con un BAIC = 466, valor que coincide con el AIC obtenido en el ejercicio
anterior. Esto signica que como la gamma tiene el menor BAIC, es la dis-
tribución que mejor se ajusta a los datos de la muestra, esto coincide con la
realidad, ya que la muestra fue generada de una distribución gamma.
¿Por queé AIC yBAIC coinciden en este ejemplo?
2) ¿Cuáles son los valores estimados de los parámetros para la distri-
bución gamma identicada en el paso anterior?
En gamlss los parámetros de las distribuciones se nombran de una forma
especial, el parámetro de posición se denomina µ, el de dispersión se denomina
σy los de simetría y curtosis con νyτ. La distribución gamma sólo tiene 2
parámetros y para obtener sus valores estimados se usa el siguiente código.
15.3 Método de máxima verosimilitud para estimar parámetros 139
modelos$mu
## [1] 4.308
modelos$sigma
## [1] 0.6682
Si comparamos los anteriores resultados, ˆµ= 4.308 yˆσ= 0.6682, con los
encontrados al usar la función fitdist,\
shape = 2.23978 y
rate = 0.51988,
vemos que no coinciden, esto se debe a que la parametrización de la gamma
usada por gamlss es diferente a la parametrización usada por la base de R. Lo
anterior no es motivo de preocupación, lo que se recomienda es que el usuario
elija una de las parametrizaciones y trabaje con ella, no debe mezclarlas.
3) Dibujar el histograma para la muestra aleatoria y agregar la densi-
dad de la distribución gamma identicada como la distribución que
mejor explica el comportamiento de la variable.
Para hacer lo solicitado se usa la función histDist del paquete gamlss, sólo es
necesario ingresar los datos y la familia o distribución de la densidad requerida.
Abajo el código usado.
histDist(y=ma, family=GA, main='',xlab='x',ylab='Densidad',
line.col='blue',line.wd=4)
##
## Family: c("GA", "Gamma")
## Fitting method: "nlminb"
##
## Call:
## gamlssML(formula = ma, family = "GA", data = sys.parent())
##
##
## Mu Coefficients:
## [1] 1.46
## Sigma Coefficients:
## [1] -0.403
##
## Degrees of Freedom for the fit: 2 Residual Deg. of Freedom 98
## Global Deviance: 462
## AIC: 466
## SBC: 471.3
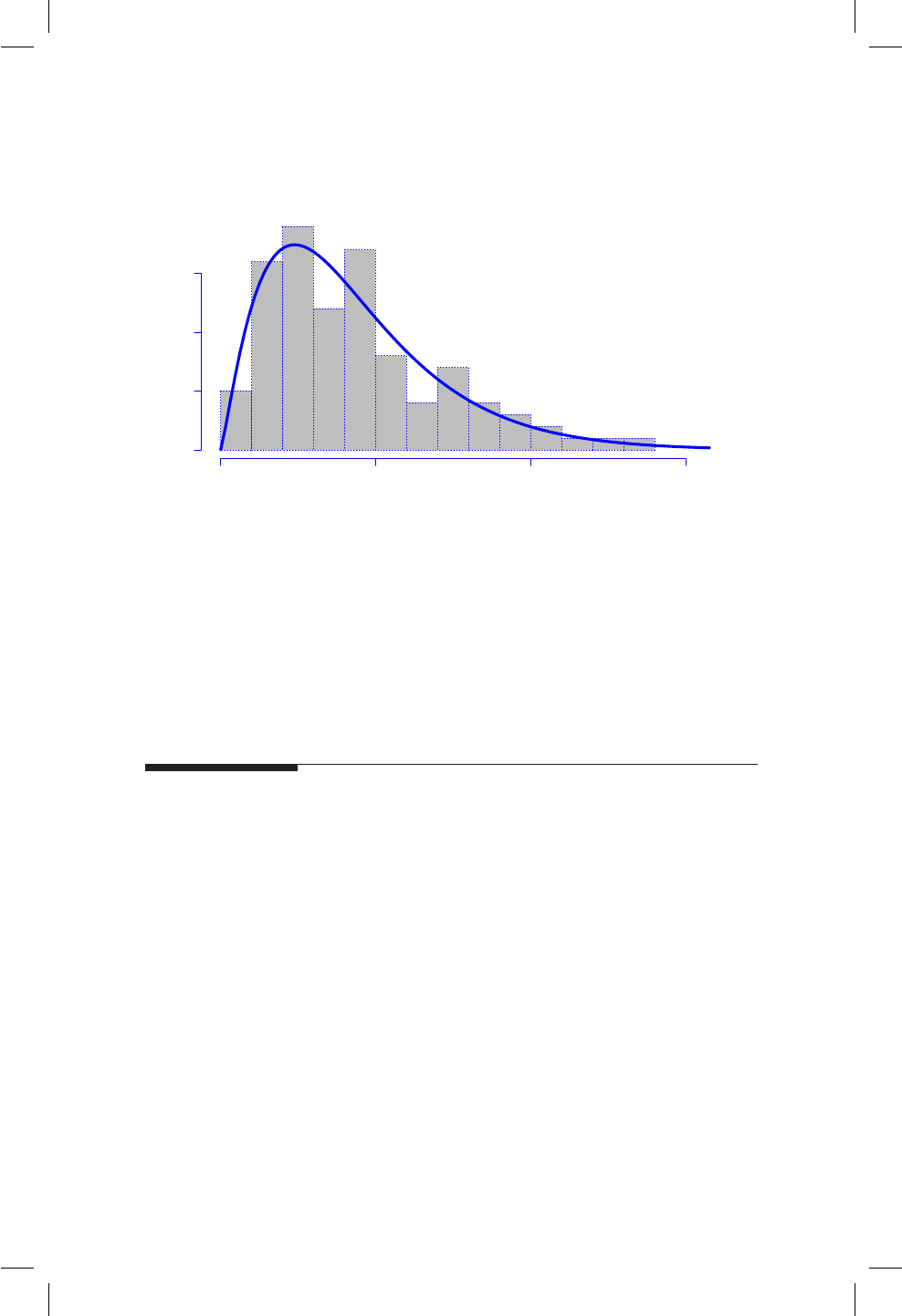
140 15 Verosimilitud
0 5 10 15
0.00 0.05 0.10 0.15
x
Densidad
Figura 15.4: Histograma para la muestra simulada con la densidad de una
Gamma(mu=4.308, sigma=0.6682).
En la Figura 15.4 se presenta el histograma para muestra aleatoria y la den-
sidad de la gamma que mejor explica estos datos. Se observa claramente que
la curva de densidad azul acompaña el patrón de los datos.
15.4. Método de máxima verosimilitud para estimar pa-
rámetros en modelos de regresión
En la sección anterior se estudió cómo estimar los parámetros de una distri-
bución, en este capítulo se aprenderá a estimar los parámetros de un modelo
de regresión general.
Ejemplo
Considere el modelo de regresión mostrado abajo. Simule 1000 observaciones
del modelo y use la función optim para estimar los parámetros del modelo.

15.4 Método de máxima verosimilitud para estimar parámetros en modelos de regresión 141
yi∼N(µi, σ2),
µi=−2+3x1,
σ= 5,
x1∼U(−5,6).
El código mostrado a continuación permite simular un conjunto de valores
con la estructura anteior.
n <- 1000
x1 <- runif(n=n, -5,6)
y <- rnorm(n=n, mean=-2+3*x1, sd=5)
El vector de parámetros del modelo anterior es Θ= (β0, β1, σ)⊤= (−2,3,5)⊤,
el primer elemento corresponde al intercepto, el segundo a la pendiente y el
último a la desviación.
A continuación se dene la función de menos log-verosimilitud para el modelo
anterior. A pesar de que nos interesa maximizar la función de log-verosimilitud
hemos creado su negativo, esto porque la mayoría de las funciones de optimi-
zación minimizan y no maximizan; maximizar f(x)es equivalente a minimizar
−f(x).
minusll <- function(theta, y, x1) {
media <- theta[1]+theta[2]*x1 # Se define la media
desvi <- theta[3]# Se define la desviación.
-sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}
Ahora vamos a usar la función optim para encontrar los valores que maxi-
mizan la función de log-verosimilitud, el código para hacer eso se muestra a
continuación. En el parámetro par se coloca un vector de posibles valores de
Θpara iniciar la búsqueda, en fn se coloca la función de interés, en lower y
upper se colocan vectores que indican los límites de búsqueda de cada pará-
metro, los βkpueden variar entre −∞ y∞mientras que el parámetro σtoma
valores en el intervalo (0,∞). Como la función minusll tiene argumentos adi-
cionales yex1, estos pasan a la función optim al nal como se muestra en el
código.
res1 <- optim(par=c(0,0,1), fn=minusll,
method='L-BFGS-B',
lower=c(-Inf,-Inf,0),
upper=c(Inf,Inf,Inf), y=y, x1=x1)
142 15 Verosimilitud
En el objeto res1 está el resultado de la optimización, para explorar los resul-
tados usamos
res1
## $par
## [1] -1.905 3.080 5.014
##
## $value
## [1] 3031
##
## $counts
## function gradient
## 19 19
##
## $convergence
## [1] 0
##
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"
De la salida anterior se observa que el vector de parámetros estimado es -
1.9046, 3.0796, 5.0142 y que el valor de la máxima log-verosimilitud fue de
3031.2092. Vemos entonces que el vector estimado está muy cerca del verda-
dero Θ= (β0, β1, σ)⊤= (−2,3,5)⊤.
En algunas ocasiones es mejor hacer la búsqueda de los parámetros en el inter-
valo (−∞,∞)que en una región limitada como por ejemplo (0,∞)o(−1,1),
ya que las funciones de búsqueda podrían tener problemas en los límites numé-
ricos. Una estrategia usual en este tipo de casos es aplicar una transformación
apropiada al parámetro que tiene el dominio limitado. En el presente ejemplo
σsólo puede tomar valores mayores que cero y una transformación de tipo
log podría ser muy útil ya que log relaciona los reales positivos con todos los
reales. La transformación para este problema sería log(σ) = β3o escrita de
forma inversa σ= exp(β3). El nuevo parámetro β3puede variar en (−∞,∞)
pero al ser transformado por la función exponencial este se volvería un valor
apropiado para σ. Para implementar esta variación lo único que se debe hacer
es modicar la línea 3 de la función minusll como se muestra a continuación:
minusll <- function(theta, y, x1) {
media <- theta[1]+theta[2]*x1
desvi <- exp(theta[3]) # <<<<<---- El cambio fue aquí
-sum(dnorm(x=y, mean=media, sd=desvi, log=TRUE))
}

15.4 Método de máxima verosimilitud para estimar parámetros en modelos de regresión 143
Para hacer la búsqueda se procede de forma similar, abajo el código necesario.
res2 <- optim(par=c(0,0,0), fn=minusll, y=y, x1=x1)
Para obtener los valores ajustados y almacenados en el objeto res2 usamos el
siguiente código.
c(res2$par[1:2], exp(res2$par[3]))
## [1] -1.905 3.079 5.015
De la salida anterior se observa que el vector estimado está muy cerca del
verdadero Θ= (β0, β1, σ)⊤= (−2,3,5)⊤.
EJERCICIOS
1) Al inicio del Capítulo 9se presentó la base de datos sobre medidas
del cuerpo, consulte la explicación sobre la base de datos y responda
lo siguiente.
Si se asume que la edad tiene distribución normal, ¿cuáles son los estimado-
res de máxima verosimilitud para µyσ?
Como el histograma para la edad muestra un sesgo a la derecha se podría
pensar que la distribución gamma sería una buena candidata para explicar
las edades observadas. Asumiendo una distribución gamma, ¿cuáles son los
estimadores de máxima verosimilitud para los parámetros?
¿Cuál de los dos modelos es más apropiado para explicar la variable de
interés? Calcule el AIC para decidir.
2) En la sección 13.2 se presentó la base de datos sobre cangrejos hem-
bra, consulte la explicación sobre la base de datos y responda lo
siguiente.
Suponga que el número de satélites sobre cada hembra es una variable que se
distribuye Poisson. Construya en Rla función de log-verosimilitud l, dibuje
la función ly encuentre el estimador de máxima verosimilitud de λ.
Repita el ejercicio anterior asumiendo que el número de satélites se distribuye
binomial negativo.
¿Cuál de los dos modelos es más apropiado para explicar la variable de
interés? Calcule el AIC para decidir.

144 15 Verosimilitud
3) Al inicio del Capítulo 10 se presentó la base de datos sobre aparta-
mentos usados en Medellín, consulte la explicación sobre la base de
datos y responda lo siguiente.
Dibuje una densidad para la variable área del apartamento.
Describa lo encontrado en esa densidad.
¿Qué distribuciones de 2 parámetros podrían explicar el comportamiento
del área de los apartamentos? Mencione al menos 3.
Para cada una de las distribuciones anteriores dibuje un gráco de contornos
o calor para la función de log-verosimilitud y estime los parámetros de la
distribución elegida.
¿Cuál de los dos modelos es más apropiado para explicar la variable de
interés? Calcule el AIC para decidir.
4) Considere el siguiente modelo de regresión.
yi∼Gamma(shapei, scalei),
log(shapei) = 3 −7x1,
log(scalei) = 3 −1x2,
x1∼U(0,1),
x2∼P oisson(λ= 3)
Simule 100 observaciones del modelo anterior.
Escriba el vector de parámetros del problema.
Construya la función minusll para el problema.
Use la función optim para estimar los parámetros del problema.

16
Estudiando la normalidad
En este capítulo se mostrará cómo utilizar las herramientas de Rpara estudiar
la normalidad univariada de un conjunto de datos.
16.1. Consideraciones iniciales
En estadística hay una gran cantidad de modelos, pruebas y procedimientos
que tienen como supuesto la normalidad, por lo tanto, se hace necesario contar
con herramientas que nos guíen para responder si se cumple o no el supuesto
de normalidad.
Para estudiar si una muestra aleatoria proviene de una población con distri-
bución normal se disponen de tres herramientas que se listan a continuación.
1. Histograma y/o densidad.
2. Grácos cuantil cuantil (QQplot).
3. Pruebas de hipótesis.
Al construir un histograma y/o densidad para la variable de interés se puede
evaluar visualmente la simetría de la distribución de los datos. Si se observa
una violación clara de la simetría (sesgo a uno de los lados) o si se observa
una distribución con más de una moda, eso sería indicio de que la muestra no
proviene de una población normal. Por otra parte, si se observa simetría en
los datos, esto NO garantiza que la muestra aleatoria proviene de una pobla-
ción normal y se hace necesario recurrir a otras herramientas especícas para
estudiar normalidad como lo son los grácos QQplot y pruebas de hipótesis.
A continuación se presentan varias secciones donde se profundiza sobre el
uso de cada de las tres herramientas anteriormente listadas para estudiar la
normalidad.
145

146 16 Estudiando la normalidad
16.2. Histograma y densidad
El histograma y el gráco de densidad son herramientas muy útiles porque
sirven para mostrar la distribución, la simetría, el sesgo, variabilidad, moda,
mediana y observaciones atípicas de un conjunto de datos. Para explorar la
normalidad de un conjunto de datos lo que se busca es que el histograma o
gráco de densidad presenten un patrón más o menos simétrico. Para obtener
detalles de la construcción de histogramas y grácos de densidad se recomienda
consultar Hernández (2018).
A continuación se presentan dos ejemplos, uno con datos simulados y otro con
datos reales, con los cuales se muestra la utilidad del histograma y gráco de
densidad al explorar la normalidad.
Ejemplo densidad con datos simulados
Simular 4 muestra aleatorias de una N(0,1) con tamaños de muestra n=10,
100, 1000 y 10000; para cada una de las muestras construir los grácos de
densidad y analizar si son simétricos.
Lo primero que se debe hacer es denir el vector ncon los valores de los
tamaños de muestra, luego dentro de una sentencia for se simula cada muestra
y se dibuja su densidad.
par(mfrow=c(2,2))
n <- c(10,100,1000,10000)
for (i in n) {
x <- rnorm(i)
plot(density(x), main=bquote(~n== .(i)),
ylab='Densidad',col='blue3',xlab='x',las=1,lwd=4)
}
En la Figura 16.1 se muestran las cuatro densidades, de esta gura se observa
que, a pesar de haber generado las muestras de una normal estándar, las
densidades no son perfectamente simétricas, sólo para el caso de tamaño de
muestra n= 10000 la densidad muestral fue bastante simétrica. Esto signica
que el gráco de densidad se debe usar con precaución para decidir sobre
la normalidad de un conjunto de datos, como regla práctica se aconseja lo
siguiente:
Si la densidad muestral es muy pero muy asimétrica se debe desconar de
la normalidad de los datos.
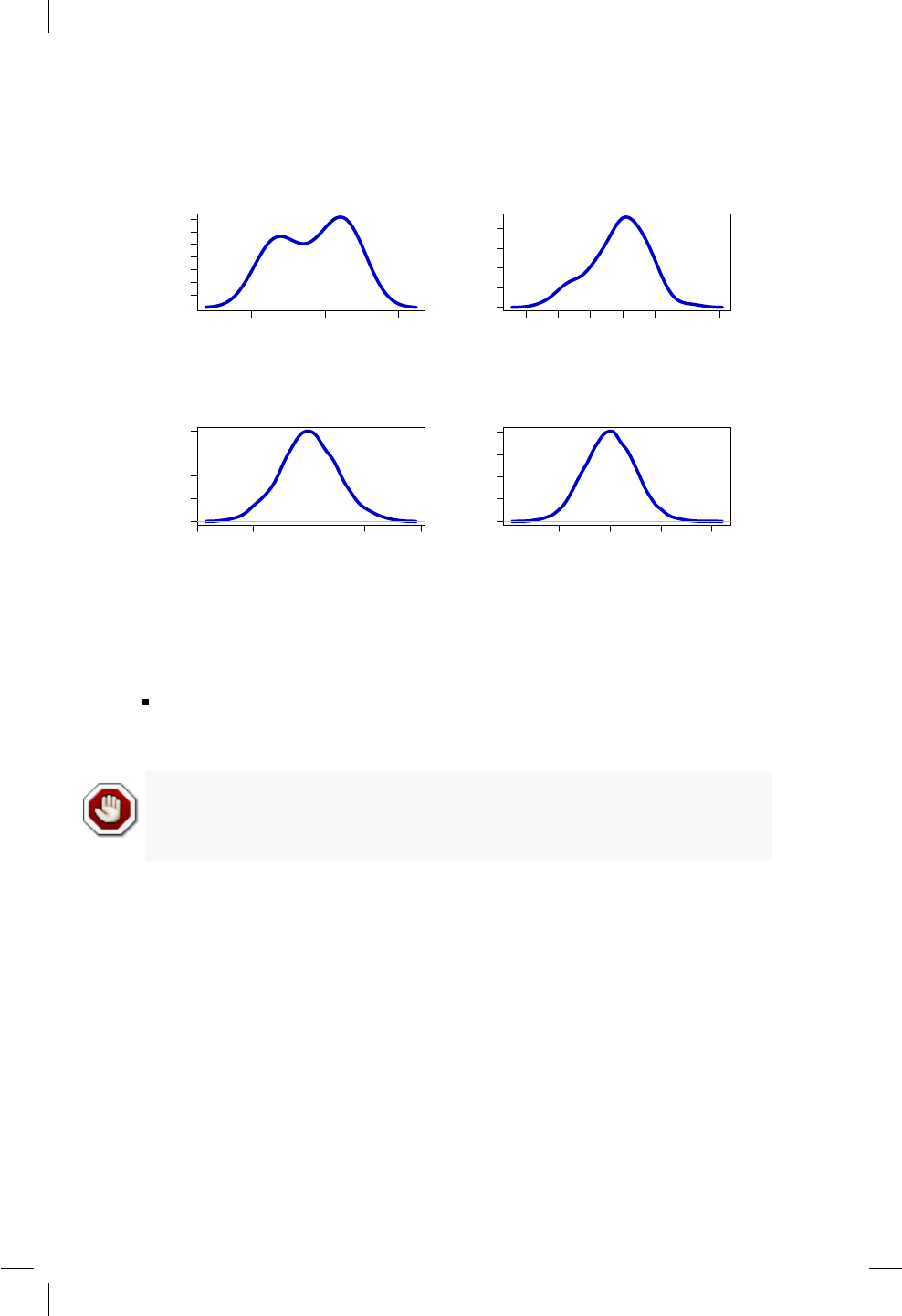
16.2 Histograma y densidad 147
-3 -2 -1 0 1 2
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
n=10
x
Densidad
-3 -2 -1 0 1 2 3
0.0
0.1
0.2
0.3
0.4
n=100
x
Densidad
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
n=1000
x
Densidad
-4 -2 0 2 4
0.0
0.1
0.2
0.3
0.4
n=10000
x
Densidad
Figura 16.1: Densidad para 4 muestras de una N(0, 1) con diferente tamaño
de muestra.
Si la densidad muestral es más o menos simétrica, se deben usar otras he-
rramientas como QQplot o pruebas de hipótesis para obtener una mejor
conclusión.
Si un histograma o densidad es muy asimétrico o sesgado, es evidencia en
contra de la normalidad de los datos. Si el histograma o densidad presentan
simetría, esto no es garantía de la normalidad de los datos.
Ejemplo densidad del peso corporal
Considerando la base de datos medidas del cuerpo presentada en el Capí-
tulo 9, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene
una distribución normal.
Para hacer la exploración lo primero es cargar la base de datos usando el
siguiente código.
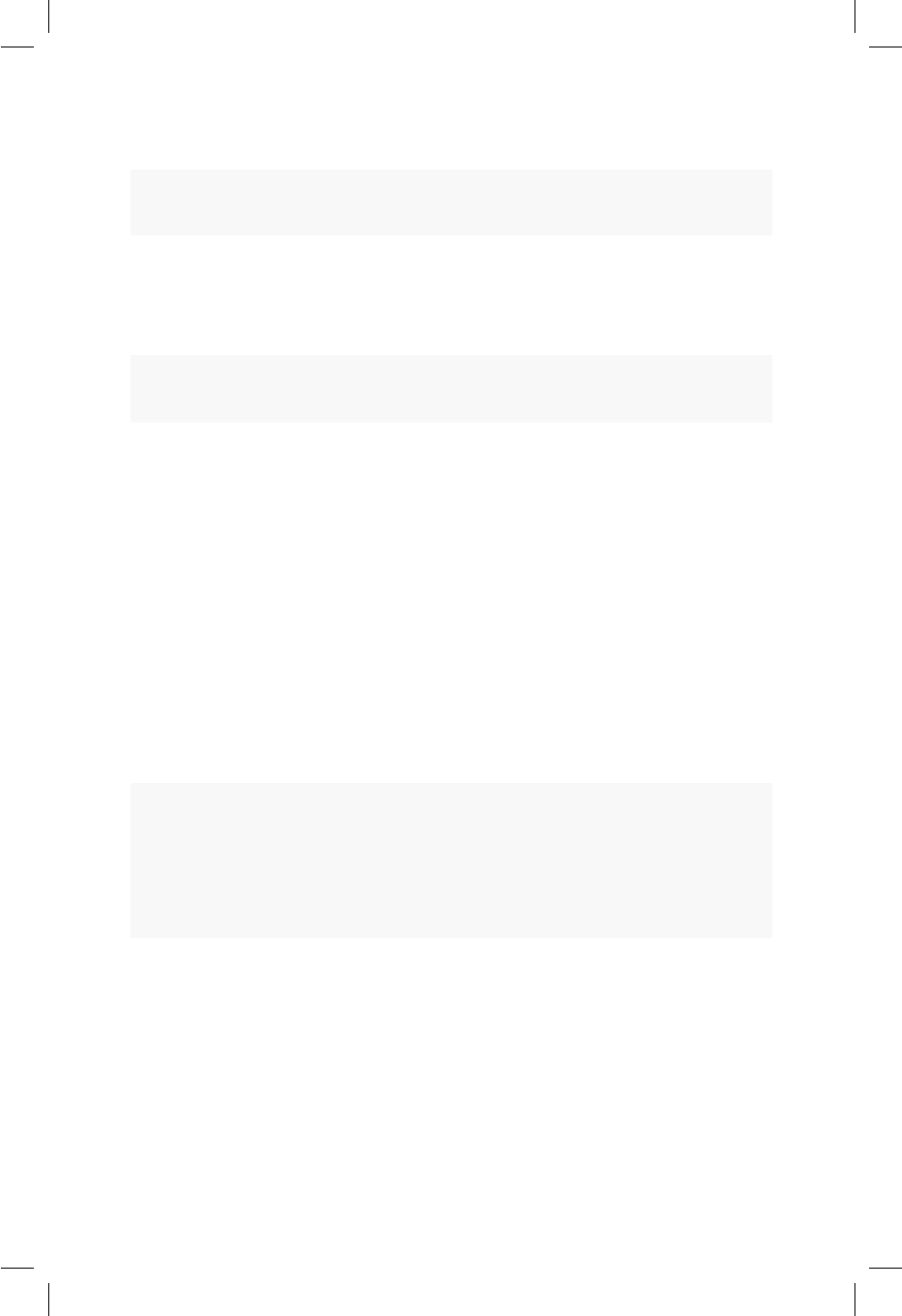
148 16 Estudiando la normalidad
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
La variable peso del objeto datos contiene la información sobre el peso cor-
poral de ambos sexos, debemos entonces partir o dividir esta información
diferenciando entre hombres y mujeres, para esto usamos la función split de
la siguiente forma.
pesos <- split(datos$peso, datos$sexo)
pesos # Para ver los elementos de la lista pesos
## $Hombre
## [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9
## [11] 89.1 62.3 82.7 79.1 98.2 84.1 83.2 83.2
##
## $Mujer
## [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2
## [11] 55.2 54.2 62.5 42.0 50.0 49.8 49.2 73.2
El objeto pesos es una lista con dos elementos, el primero contiene los pesos
de los hombres mientras que el segundo contiene los pesos de las mujeres. Note
que pesos es un objeto mientras que peso es el nombre usado para la variable
peso corporal en la base de datos.
Para explorar la normalidad de los pesos se dibujan dos densidades, una para
el peso de hombres y otra para el peso de las mujeres, a continuación el código
utilizado.
plot(density(pesos$Hombre), lwd=3,col='blue',
xlim=c(30,110), main='',las=1,
xlab='Peso (kg)',ylab='Densidad')
lines(density(pesos$Mujer), lwd=3,col='deeppink')
legend('topleft',legend=c('Hombres','Mujeres'),
lwd=3,col=c('blue','deeppink'), bty='n')
En la Figura 16.2 se muestran las dos densidades, en la gura no se observa
una evidencia clara de sesgo, lo que se observa es que la densidad para los
hombres es un poco más simétrica que la densidad para las mujeres. De estos
resultados no se puede rechazar la premisa de que pesos corporales provienen
de una distribución normal, lo recomendable es construir QQplot y aplicar
prueba de hipótesis.
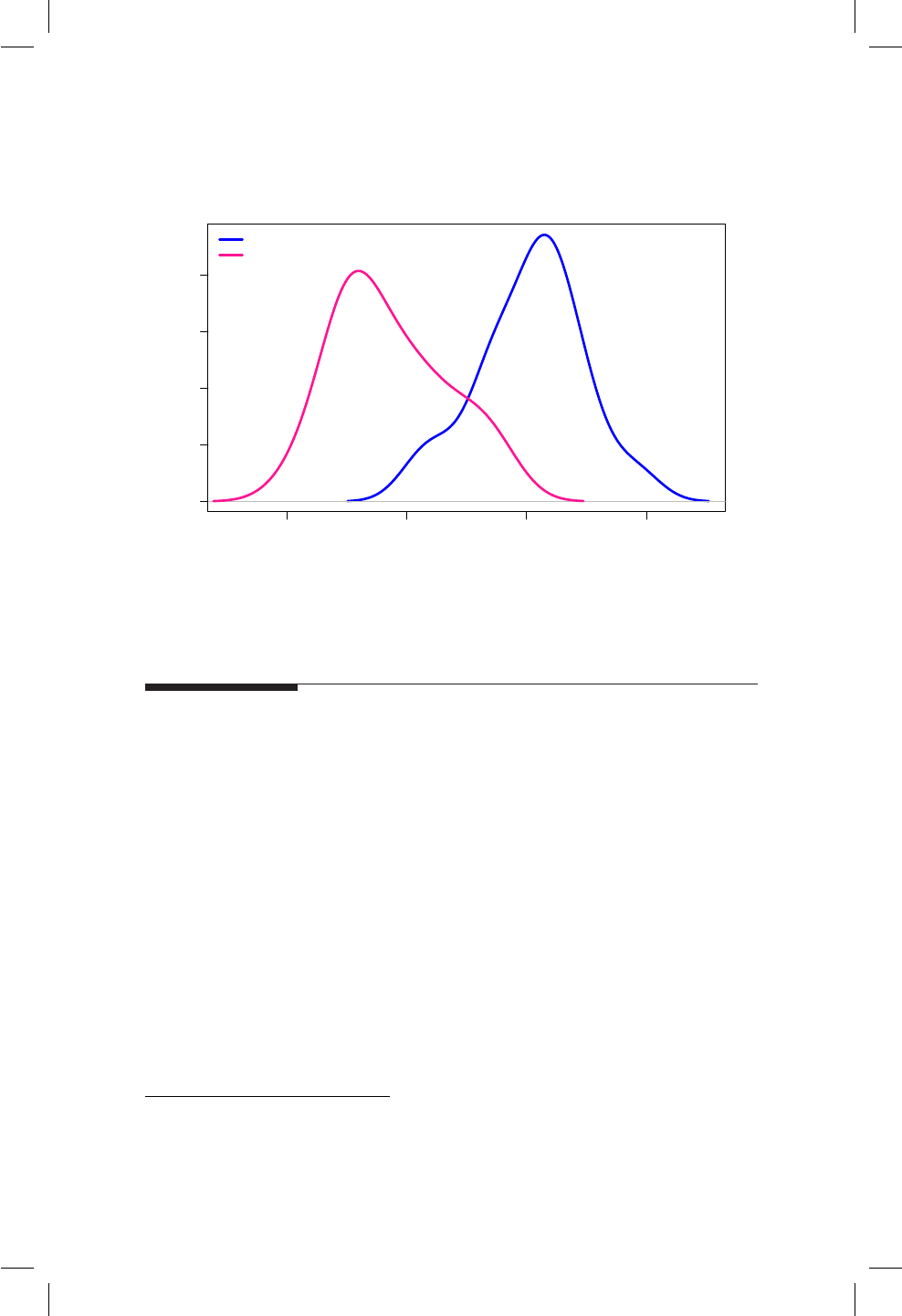
16.3 Grácos cuantil cuantil 149
40 60 80 100
0.00
0.01
0.02
0.03
0.04
Peso (kg)
Densidad
Hombres
Mujeres
Figura 16.2: Densidad para el peso corporal de hombres y mujeres.
16.3. Grácos cuantil cuantil
Los grácos cuantil cuantil (QQplot) son una herramienta gráca para explo-
rar si un conjunto de datos o muestra proviene de una población con cierta
distribución, en particular aquí nos interesan para estudiar la normalidad de
un conjunto de datos. La función qqnorm sirve para construir el QQplot y
la función qqline agrega una línea de referencia que ayuda a interpretar el
gráco QQplot, para obtener una explicación de cómo construir este gráco
se recomienda ver el video disponible en este enlace1.
En la Figura 16.3 se muestra un ejemplo de un QQplot y de sus partes, los
puntos y la línea de referencia. Si se tuviese una muestra distribuída perfecta-
mente normal, se esperaría que los puntos estuviesen perfectamente alineados
con la línea de referencia, sin embargo, las muestran con las que se trabajan en
la práctica casi nunca presentan este comportamiento aún si fueron obtenidas
de una población normal. En la práctica se aceptan alejamientos del patrón
lineal para aceptar que los datos si provienen de una población normal.
1https://www.youtube.com/watch?v=kx_o9rnI4DE
150 16 Estudiando la normalidad
-1 0 1
-1
0
1
Theoretical Quantiles
Sample Quantiles
Figura 16.3: Ejemplo de un QQplot.
A continuación se presentan cuatro ejemplos, dos con datos simulados y otro
con datos reales para mostrar la utilidad del qqplot al explorar la normalidad.
Ejemplo 1 QQplot con datos simulados
Simular 4 muestra aleatorias de una N(0,1) con tamaños de muestra n=10,
30, 50 y 100, para cada una de ellas construir el QQplot.
Lo primero que se debe hacer es denir el vector ncon los valores del tamaño
de muestra, luego dentro de una sentencia for se simula cada muestra xy
por último se dibuja el QQplot para cada muestra, a continuación el código
utilizado.
par(mfrow=c(2,2))
n <- c(10,30,50,100)
for (i in n) {
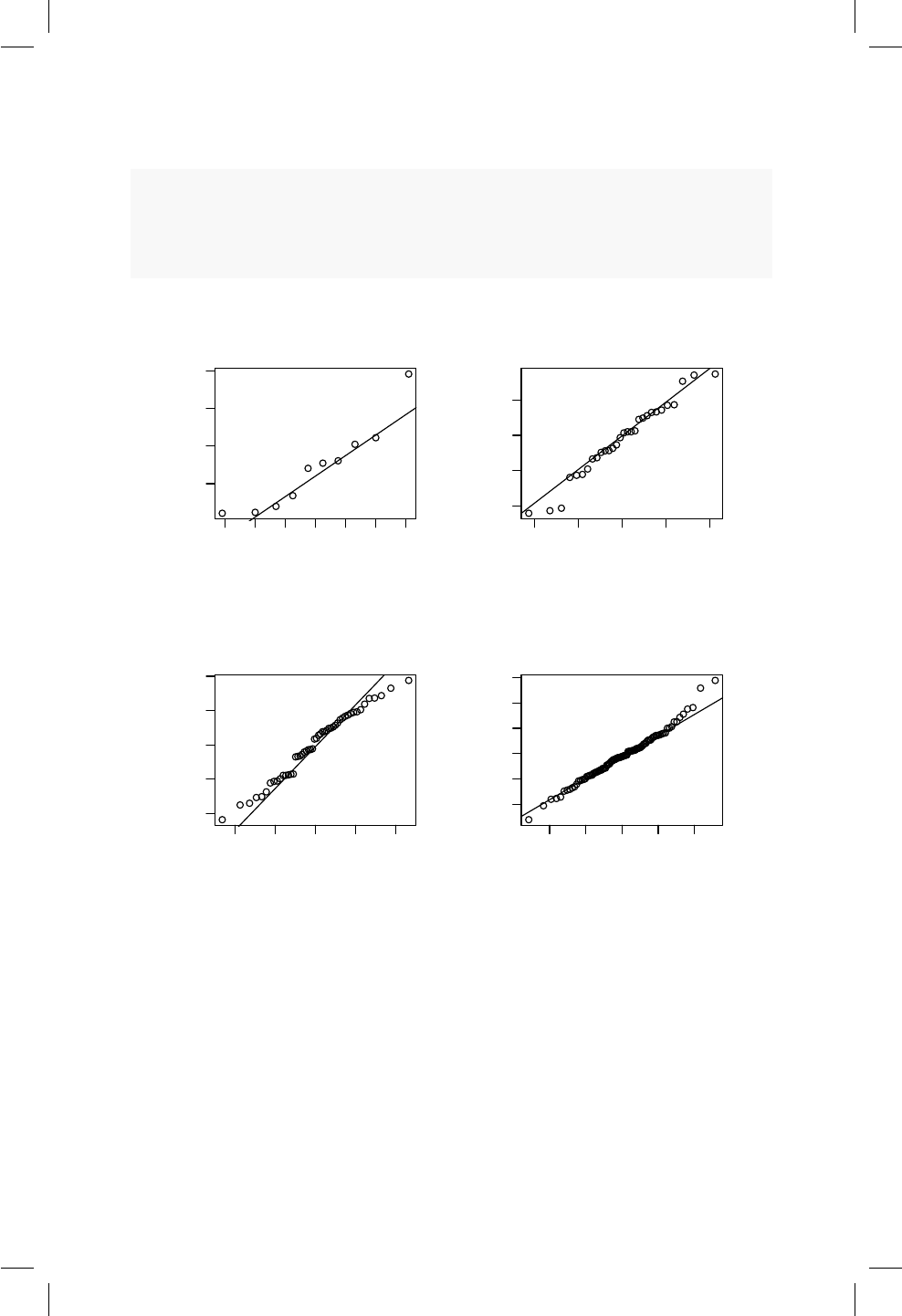
16.3 Grácos cuantil cuantil 151
x <- rnorm(i)
qqnorm(x, main=bquote(~n== .(i)))
qqline(x) # Para agregar la linea de referencia
}
-1.5 -0.5 0.5 1.5
-0.5 0.0 0.5 1.0
n=10
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
-2 -1 0 1
n=30
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
-2 -1 0 1 2
n=50
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
-2 -1 0 1 2 3
n=100
Theoretical Quantiles
Sample Quantiles
Figura 16.4: QQplot para 4 muestras de una N(0, 1) con diferente tamaño
de muestra.
La Figura 16.4 muestra que, a pesar de haber simulado cada muestra xde
una N(0,1), los puntos no se alinean de forma perfecta, esto signica que
en la práctica se debe ser prudente con la interpretación de un QQplot, un
alejamiento del patrón lineal NO signica que la muestra no provenga de una
población normal.
152 16 Estudiando la normalidad
Ejemplo 2 QQplot con datos simulados
Simular 1 muestra aleatoria con n= 50 de cada una de las siguientes pobla-
ciones Poisson(5), NBinom(5, 0.5), Gamma(2, 3) y Weibull(1, 3), para cada
una de las muestras construir el QQplot para explorar la normalidad de las
muestras.
Las muestras de cada una de las poblaciones se generan con las funciones
rpois,rnbinom,rgamma yrweibull especicando los parámetros. A conti-
nuación el código necesario para obtener los QQplot solicitados.
m1 <- rpois(n=50,lambda=5)
m2 <- rnbinom(n=50,size=5,prob=0.35)
m3 <- rgamma(n=50,shape=2,scale=3)
m4 <- rweibull(n=50,shape=1,scale=3)
par(mfrow=c(2,2))
qqnorm(m1, main='Poisson(5)')
qqline(m1)
qqnorm(m2, main='NBinom(5, 0.35)')
qqline(m1)
qqnorm(m3, main='Gamma(2, 3)')
qqline(m1)
qqnorm(m4, main='Weibull(1, 3)')
qqline(m1)
En la Figura 16.5 se muestran los cuatro QQplot para cada una de las mues-
tras generadas de las distribuciones indicadas. Se observa claramente que los
puntos del QQplot no está alineados, esto es una clara evidencia de que las
muestras NO provienen de poblaciones normales. Otro aspecto interesante a
resaltar es el patrón de escalera que se observa para las muestras generadas
de poblaciones discretas (Poisson y Binomial Negativa).
Se debe tener cuidado al concluir con un QQplot, lo que para una persona
puede estar alineado, para otra puede no estarlo. El QQplot es un gráco
exploratorio de normalidad.
Ejemplo QQplot para peso corporal
Retomando la base de datos medidas del cuerpo presentada en el Capítulo
9, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene una
distribución normal usando QQplots.
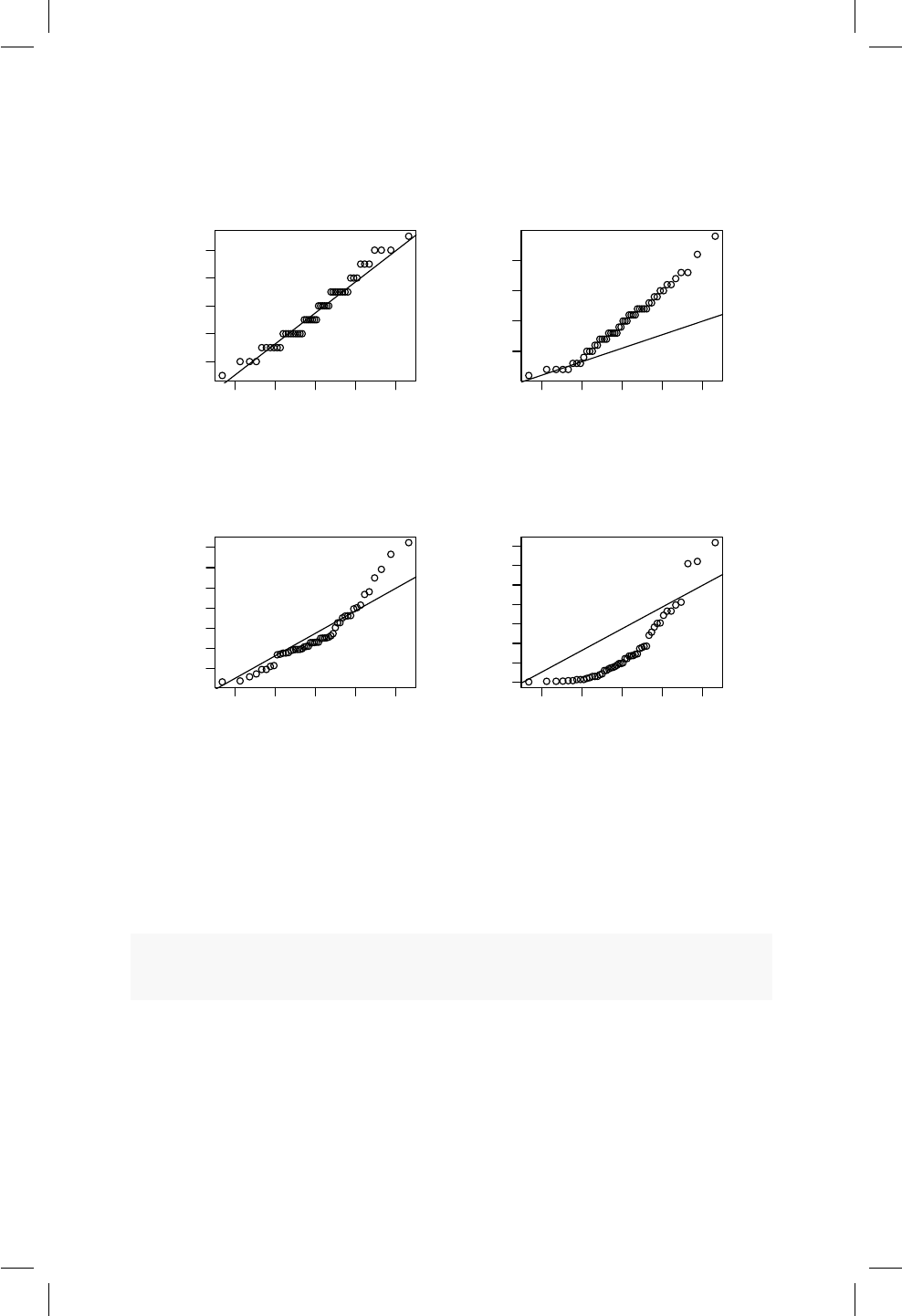
16.3 Grácos cuantil cuantil 153
-2 -1 0 1 2
2 4 6 8 10
Poisson(5)
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
5 10 15 20
NBinom(5, 0.35)
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
2 4 6 8 12
Gamma(2, 3)
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
0 4 8 12
Weibull(1, 3)
Theoretical Quantiles
Sample Quantiles
Figura 16.5: QQplot para muestras generadas de poblaciones Poisson, Bino-
mial Negativa, Gamma y Weibull.
Para hacer la exploración lo primero es cargar la base de datos si aún no se
ha cargado.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
La variable peso del objeto datos contiene la información sobre el peso cor-
poral de ambos sexos, debemos entonces partir o dividir esta información
diferenciando entre hombres y mujeres, para esto usamos la función split de
la siguiente forma.
154 16 Estudiando la normalidad
pesos <- split(datos$peso, datos$sexo)
pesos
## $Hombre
## [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9
## [11] 89.1 62.3 82.7 79.1 98.2 84.1 83.2 83.2
##
## $Mujer
## [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2
## [11] 55.2 54.2 62.5 42.0 50.0 49.8 49.2 73.2
El objeto pesos es una lista con dos elementos, el primero contiene los pesos
de los hombres mientras que el segundo contiene los pesos de las mujeres. Note
que pesos es un objeto mientras que peso es el nombre usado para la variable
peso corporal en la base de datos.
Para explorar la normalidad de los pesos se dibujan dos densidades, una para
el peso de hombres y otra para el peso de las mujeres, a continuación el código
utilizado.
par(mfrow=c(1,2))
qqnorm(pesos$Hombre, pch=20,
main='QQplot para peso de hombres')
qqline(pesos$Hombre)
qqnorm(pesos$Mujer, pch=20,
main='QQplot para peso de mujeres')
qqline(pesos$Mujer)
La Figura 16.6 muestra el QQplot para el peso corporal de hombres y mujeres,
de la gura se observa que los puntos no están tan desalineados, lo cual cual
nos lleva a no rechazar la hipótesis de normalidad.
Se debe interpretar con precaución el QQplot, del ejemplo con datos simu-
lados se vió que a pesar de haber generado las muestras de una N(0,1) los
QQplot no siempre están perfectamente alineados.
Ejemplo QQplot con bandas
Construir QQplot con bandas de conanza para el peso corporal de hombres
y mujeres con los datos del ejemplo anterior. ¿Se puede arma que los pesos
corporales provienen de una distribución normal?
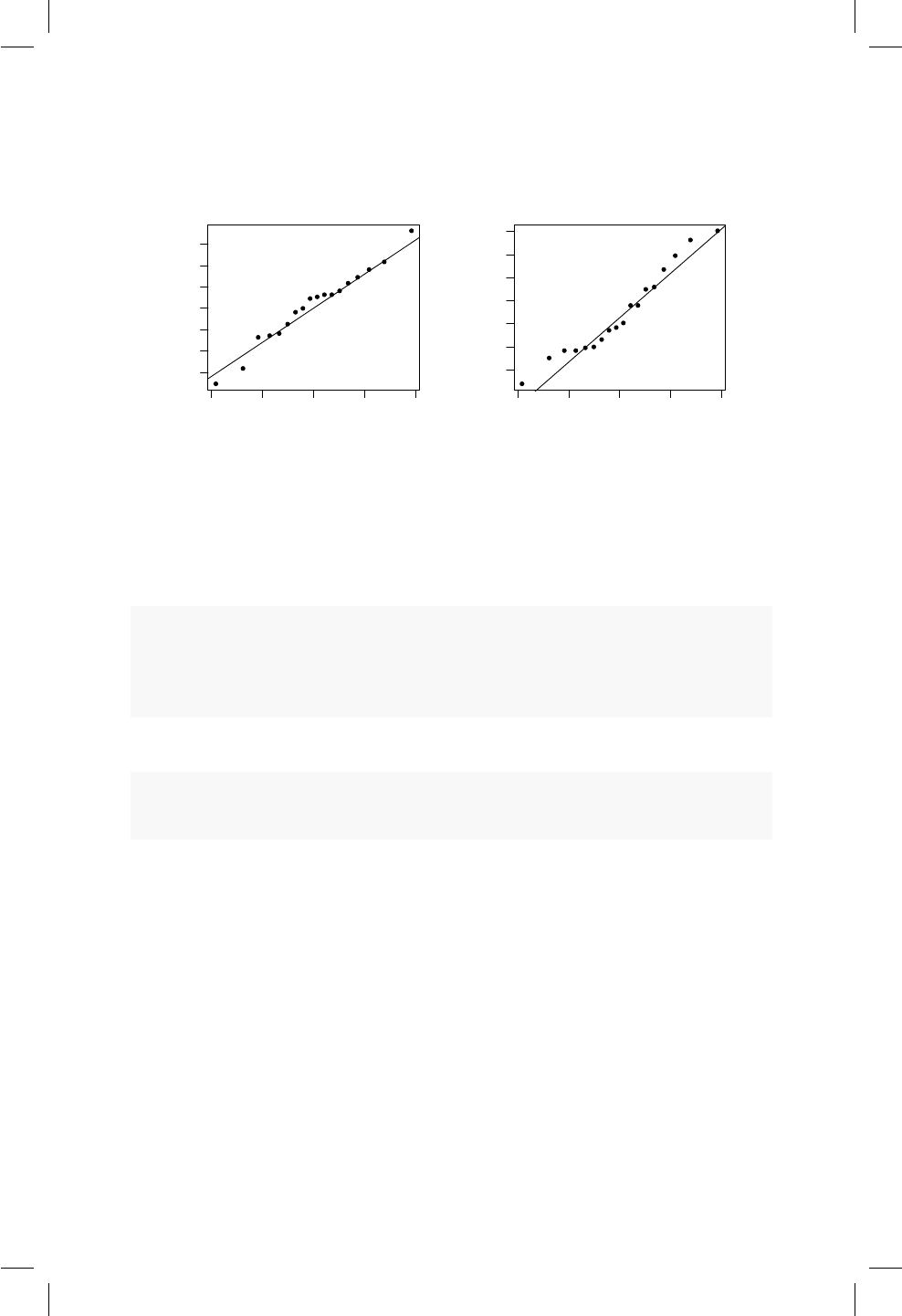
16.4 Grácos cuantil cuantil 155
-2 -1 0 1 2
65 75 85 95
QQplot para peso de hombres
Theoretical Quantiles
Sample Quantiles
-2 -1 0 1 2
45 55 65 75
QQplot para peso de mujeres
Theoretical Quantiles
Sample Quantiles
Figura 16.6: QQplot para el peso corporal de hombres y mujeres.
Para construir este tipo de QQplot se usa la función qqplot del paquete car.
A continuación el código para construir el gráco solicitado.
require(car)
par(mfrow=c(1,2))
qqPlot(pesos$Hombre, pch=20,ylab='Peso (Kg)',
main='QQplot para peso de hombres')
## [1] 12 15
qqPlot(pesos$Mujer, pch=20,ylab='Peso (Kg)',
main='QQplot para peso de mujeres')
## [1] 10 18
En la Figura 16.7 se muestra el QQplot solicitado, como los puntos del QQplot
están dentro de las bandas se puede aceptar que los pesos corporales provienen
de una población normal.
La función qqPlot tiene varios parámetros adicionales que recomendamos
consultar en la ayuda de la función help(qqPlot).
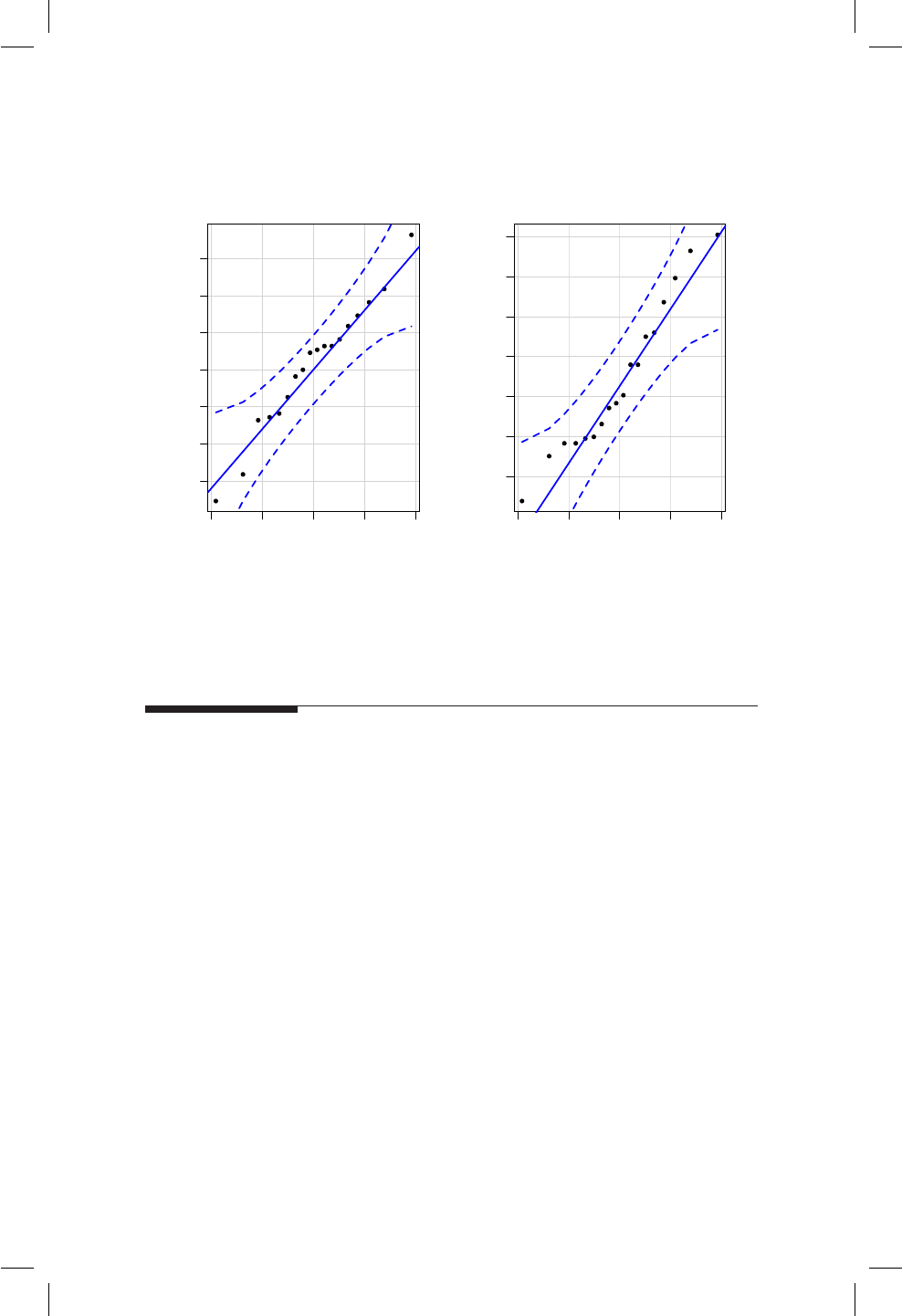
156 16 Estudiando la normalidad
-2 -1 0 1 2
65 70 75 80 85 90 95
QQplot para peso de hombres
norm quantiles
Peso (Kg)
12
15
-2 -1 0 1 2
45 50 55 60 65 70 75
QQplot para peso de mujeres
norm quantiles
Peso (Kg)
10
18
Figura 16.7: QQplot con bandas de conanza para el peso corporal de hom-
bres y mujeres.
16.4. Pruebas de normalidad
Una forma menos subjetiva de explorar la normalidad de un conjunto de datos
es por medio de las pruebas de normalidad. Las hipótesis para este tipo de
pruebas son:
H0:la muestra proviene de una población normal.
HA:la muestra NO proviene de una población normal. (16.1)
En la literatura estadística se reportan varias pruebas, algunas de ellas se
listan a continuación.
1. Prueba Shapiro-Wilk con la función shapiro.test.
2. Prueba Anderson-Darling con la función ad.test del paquete nor-
test.
3. Prueba Cramer-von Mises con la función cvm.test del paquete nor-
test.
16.4 Pruebas de normalidad 157
4. Prueba Lilliefors (Kolmogorov-Smirnov) con la función
lillie.test del paquete nortest.
5. Prueba Pearson chi-square con la función pearson.test del paque-
te nortest.
6. Prueba Shapiro-Francia con la función sf.test del paquete nor-
test).
Ejemplo con datos simulados
Generar una muestra aleatoria con n= 100 de una N(150,25) y aplicar las
pruebas de normalidad Shapiro-Wilk y Anderson-Darling con un nivel de sig-
nicancia del 3 %.
Lo primero es generar la muestra aleatoria xasí:
x <- rnorm(n=100,mean=150,sd=5)
Para aplicar la prueba Shapiro-Wilk se usa la función shapiro.test al vector
xasí:
shapiro.test(x)
##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.99, p-value = 0.9
De la salida anterior se tiene que el valor-P para la prueba fue de 0.9 y que es
mayor al nivel de signicancia 3 %, lo cual indica que no hay evidencias para
rechazar la hipótesis nula de normalidad.
Para aplicar la prueba Anderson-Darling se usa la función ad.test al vector
xasí:
require(nortest) # Se debe haber instalado nortest
ad.test(x)
##
## Anderson-Darling normality test
##
## data: x
## A = 0.2, p-value = 0.9
158 16 Estudiando la normalidad
De la salida anterior se tiene que el valor-P para la prueba fue de 0.9 y que
es mayor al nivel de signicancia 3 %, esto indica que no hay evidencias para
rechazar la hipótesis nula de normalidad.
Ejemplo normalidad para peso corporal
Retomando la base de datos medidas del cuerpo presentada en el Capítulo
9, se desea saber si el peso corporal, tanto de hombres y mujeres, tiene una
distribución normal usando las pruebas normalidad Shapiro-Wilks y Anderson-
Darling con un nivel de signicancia del 5 %.
Lo primero es cargar la base de datos si aún no se ha cargado.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
La variable peso del objeto datos contiene la información sobre el peso cor-
poral de ambos sexos, debemos entonces partir o dividir esta información
diferenciando entre hombres y mujeres, para esto usamos la función split de
la siguiente forma.
pesos <- split(datos$peso, datos$sexo)
pesos
## $Hombre
## [1] 87.3 80.0 82.3 73.6 74.1 85.9 73.2 76.3 65.9 90.9
## [11] 89.1 62.3 82.7 79.1 98.2 84.1 83.2 83.2
##
## $Mujer
## [1] 51.6 59.0 49.2 63.0 53.6 59.0 47.6 69.8 66.8 75.2
## [11] 55.2 54.2 62.5 42.0 50.0 49.8 49.2 73.2
Para aplicar la prueba Shapiro-Wilk se usa la función shapiro.test. Co-
mo el objeto pesos es una lista se debe usar la función lapply para aplicar
shapiro.test a la lista, a continuación el código usado.
lapply(pesos, shapiro.test)
## $Hombre
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
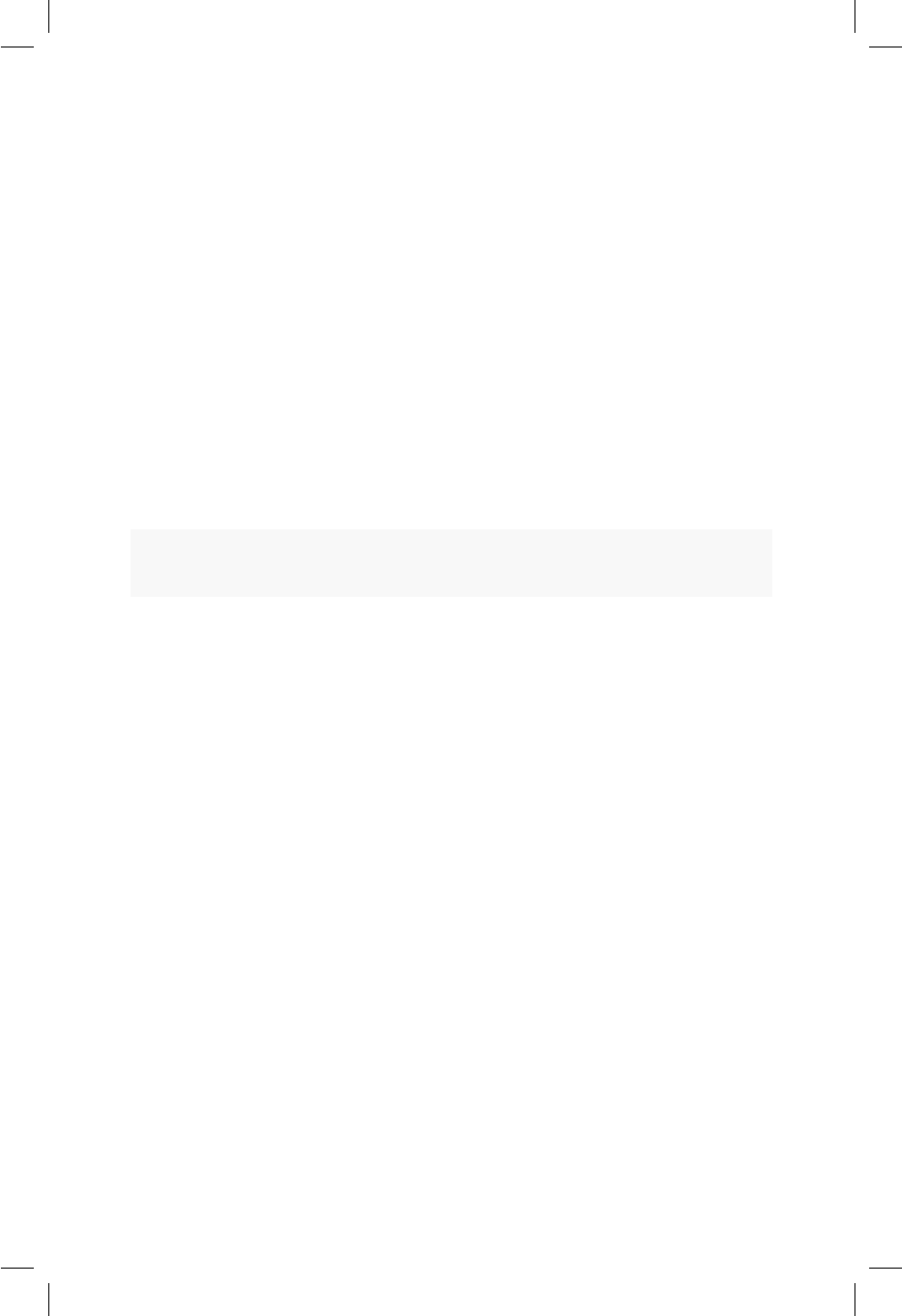
16.4 Pruebas de normalidad 159
## W = 0.98, p-value = 0.9
##
##
## $Mujer
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.95, p-value = 0.4
De la salida anterior se observa que ambos valores-P fueron mayores al nivel de
signicancia 5 %, por lo tanto, se puede concluir que ambas muestras provienen
de poblaciones con distribución normal.
Para aplicar la prueba Anderson-Darling se usa la función ad.test del paquete
nortest. Como el objeto pesos es una lista se debe usar la función lapply
para aplicar ad.test a la lista, a continuación el código usado.
require(nortest) # Se debe haber instalado nortest
lapply(pesos, shapiro.test)
## $Hombre
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.98, p-value = 0.9
##
##
## $Mujer
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.95, p-value = 0.4
De la salida anterior se observa que ambos valores-P fueron mayores al nivel de
signicancia 5 %, por lo tanto, se puede concluir que ambas muestras provienen
de poblaciones con distribución normal.
Al usar las pruebas Shapiro-Wilks y Anderson-Darling se concluye que no
hay evidencias para pensar que los pesos corporales de hombres y mujeres no
provienen de una población normal.

17
Intervalos de conanza
En este capítulo se muestran las funciones que hay disponibles en Rpara
construir intervalos de conanza para:
1. la media µ,
2. la proporción p,
3. la varianza σ2,
4. la diferencia de medias µ1−µ2para muestras independientes y
dependientes (o pareadas),
5. la diferencia de proporciones p1−p2, y
6. la razón de varianzas σ2
1/σ2
2.
Para ilustrar el uso de las funciones se utilizará la base de datos medidas del
cuerpo presentada en el Capítulo 9.
17.1. Función t.test
La función t.test se usa para calcular intervalos de conanza para la me-
dia y diferencia de medias, con muestras independientes y dependientes (o
pareadas). La función y sus argumentos son los siguientes:
t.test(x, y = NULL,
alternative = c("two.sided","less","greater"),
mu = 0,paired = FALSE,var.equal = FALSE,
conf.level = 0.95, ...)
17.1.1. Intervalo de conanza bilateral para la media µ
Para calcular intervalos de conanza bilaterales para la media a partir de la
función t.test es necesario denir 2 argumentos:
161

162 17 Intervalos de conanza
x: vector numérico con los datos.
conf.level: nivel de conanza a usar, por defecto es 0.95.
Los demás argumentos se usan cuando se desea obtener intervalos de conan-
za para diferencia de media con muestras independientes y dependientes (o
pareadas).
Ejemplo
Suponga que se quiere obtener un intervalo de conanza bilateral del 90 %
para la altura promedio de los hombres de la base de datos medidas del
cuerpo.
Para calcular el intervalo de conanza, primero se carga la base de datos
usando la url apropiada, luego se crea un subconjunto de datos y se aloja en
el objeto hombres como sigue a continuación:
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
Una vez leídos los datos, se analiza la normalidad de la variable altura de los
hombres, a partir de un QQplot y un histograma
par(mfrow=c(1,2))
require(car) # Debe instalar antes el paquete car
qqPlot(hombres$altura, pch=19,
main='QQplot para la altura de hombres',
xlab='Cuantiles teóricos',
ylab='Cuantiles muestrales')
## [1] 5 8
hist(hombres$altura, freq=TRUE,
main='Histograma para la altura de hombres',
xlab='Altura (cm)',
ylab='Frecuencia')
En la Figura 17.1 se muestra el QQplot e histograma para la variable altura,
de estas guras no se observa un claro patrón normal, sin embargo, al aplicar
la prueba Shapiro-Wilk a la muestra de alturas de los hombres se obtuvo un
valor-P de 0.3599, por lo tanto, se asume que la muestra de alturas provienen
de una población normal.
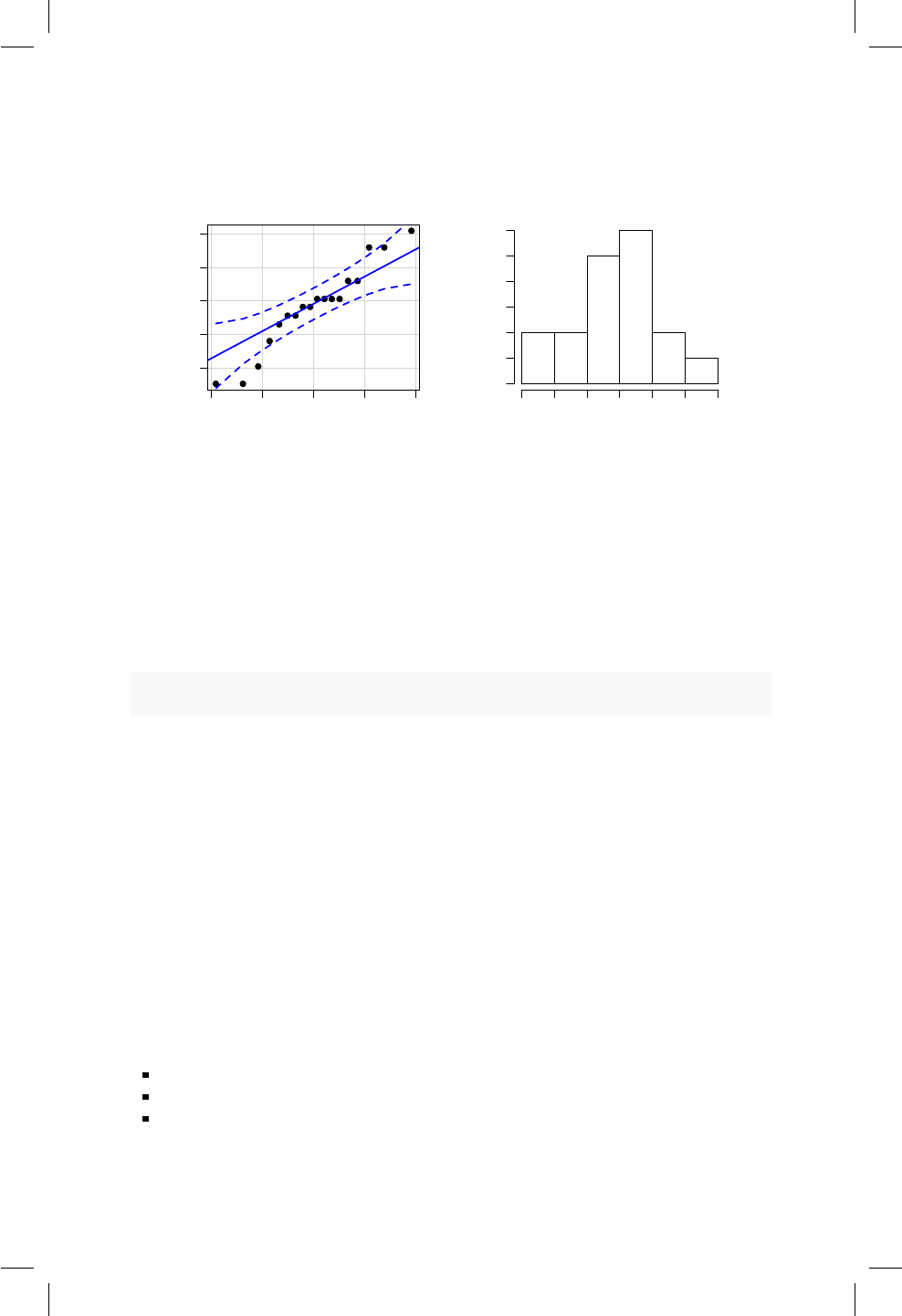
17.1 Función t.test 163
-2 -1 0 1 2
170 175 180 185 190
QQplot para la altura de hombres
Cuantiles teóricos
Cuantiles muestrales
5 8
Histograma para la altura de hombres
Altura (cm)
Frecuencia
165 170 175 180 185 190 195
0123456
Figura 17.1: QQplot e histograma para la altura de los hombres.
Una vez chequeado el supuesto de normalidad se puede usar la función t.test
sobre la variable de interés para construir el intervalo de conanza. El resulta-
do de usar t.test es una lista, uno de los elementos de esa lista es justamente
el intevalo de conanza y para extraerlo es que se usa $conf.int al nal de
la instrucción. A continuación se muestra el código utilizado.
t.test(x=hombres$altura, conf.level=0.90)$conf.int
## [1] 176.4 181.7
## attr(,"conf.level")
## [1] 0.9
A partir del resultado obtenido se puede concluir, con un nivel de conanza
del 90 %, que la altura promedio de los estudiantes hombres se encuentra entre
176.4 cm y 181.7 cm.
17.1.2. Intervalo de conanza bilateral para la diferencia de
medias (µ1−µ2) de muestras independientes
Para construir intervalos de conanza bilaterales para la diferencia de medias
(µ1−µ2) de muestras independientes se usa la función t.test y es necesario
denir 5 argumentos:
x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2,
paired=FALSE: indica que el intervalo de conanza se hará para muestras

164 17 Intervalos de conanza
independientes, en el caso de que sean dependientes (o pareadas) este argu-
mento será paired=TRUE,
var.equal=FALSE: indica que las varianzas son desconocidas y diferentes, si
la varianzas se pueden considerar iguales se coloca var.equal=TRUE.
conf.level: nivel de conanza.
Ejemplo
Se quiere saber si existe diferencia estadísticamente signicativa entre las al-
turas de los hombres y las mujeres. Para responder esto se va a construir un
intervalo de conanza del 95 % para la diferencia de las altura promedio de
los hombres y de las mujeres (µhombres −µmujeres).
Para construir el intervalo de conanza, primero se carga la base de datos
usando la url apropiada, luego se crean dos subconjuntos de datos y se alojan
en los objetos hombres ymujeres como sigue a continuación:
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
mujeres <- datos[datos$sexo=="Mujer", ]
Una vez leídos los datos, se analiza la normalidad de la variable altura de los
hombres y las mujeres, a partir de un QQplot y un histograma
par(mfrow=c(2,2))
require(car) # Debe instalar antes el paquete car
qqPlot(hombres$altura, pch=19,las=1,main='QQplot',
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')
## [1] 5 8
hist(hombres$altura, las=1,xlab='Altura',ylab='Frecuencia',
main='Histograma para la altura de hombres')
qqPlot(mujeres$altura, pch=19,las=1,main='QQplot',
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')
## [1] 16 9
hist(mujeres$altura, las=1,xlab='Altura',ylab='Frecuencia',
main='Histograma para la altura de mujeres')
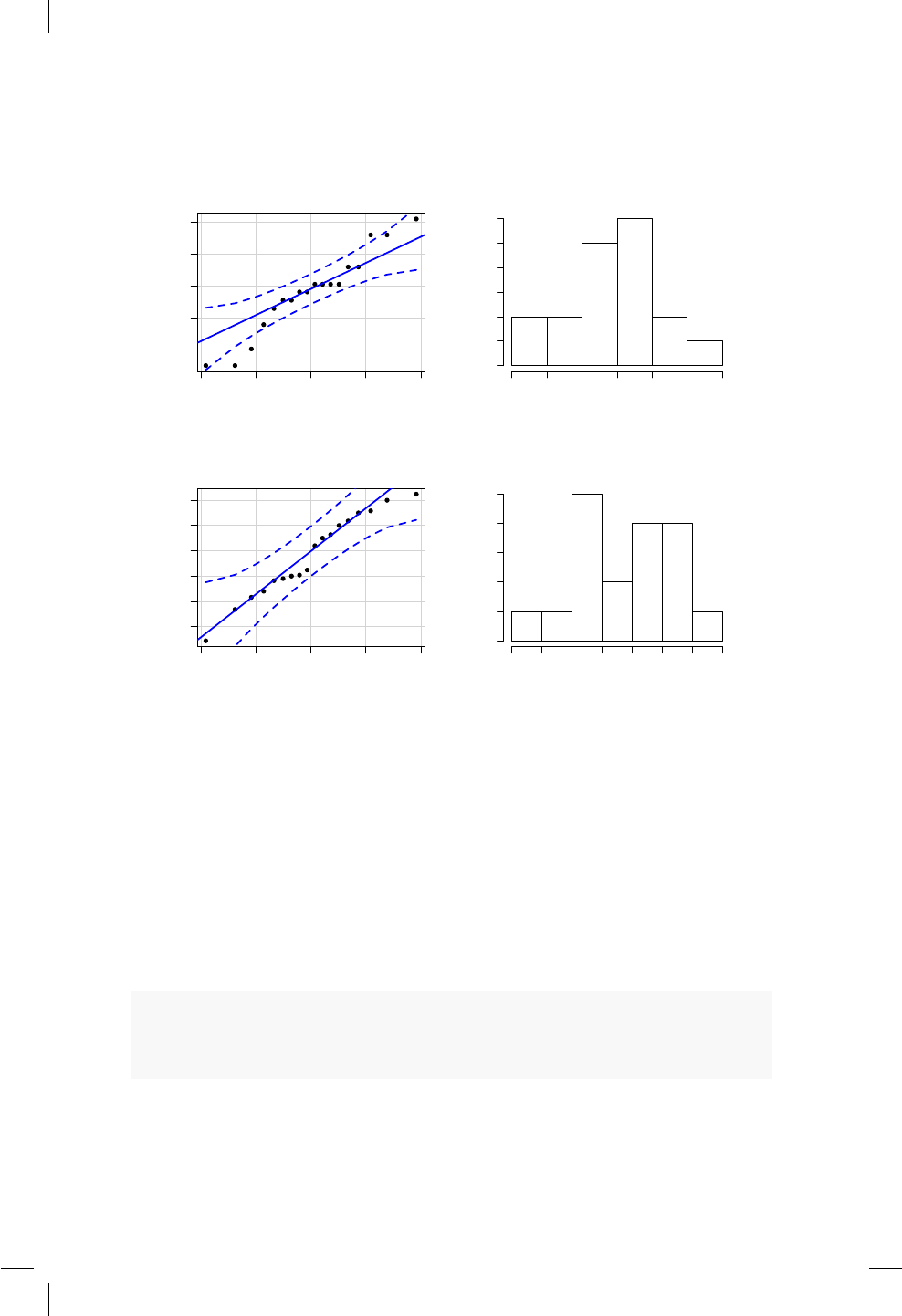
17.1 Función t.test 165
-2 -1 0 1 2
170
175
180
185
190
QQplot
Cuantiles teóricos
Cuantiles muestrales
5 8
Histograma para la altura de hombres
Altura
Frecuencia
165 170 175 180 185 190 195
0
1
2
3
4
5
6
-2 -1 0 1 2
150
155
160
165
170
175
QQplot
Cuantiles teóricos
Cuantiles muestrales
16
9
Histograma para la altura de mujeres
Altura
Frecuencia
145 150 155 160 165 170 175 180
0
1
2
3
4
5
Figura 17.2: QQplot e histograma para la altura de hombres y mujeres.
De la Figura 17.2 se puede concluir que las alturas de los estudiantes hombres
y mujeres siguen una distribución normal. Al aplicar la prueba Shapiro-Wilk
para estudiar la normalidad de la altura se encontró un valor-P de 0.3599 para
el grupo de hombres y un valor-P de 0.5921 para el grupo de mujeres, esto
conrma que se cumple el supuesto de normalidad.
Como se cumple el supuesto de normalidad se puede usar la función t.test
para construir el intervalo de conanza requerido. A continuación se muestra
el código
t.test(x=hombres$altura, y=mujeres$altura,
paired=FALSE,var.equal=FALSE,
conf.level = 0.95)$conf.int
## [1] 10.06 20.03
## attr(,"conf.level")

166 17 Intervalos de conanza
## [1] 0.95
A partir del intervalo de conanza anterior se puede concluir, con un nivel
de conanza del 95 %, que la altura promedio de los hombres es superior a la
altura promedio de las mujeres, ya que el intervalo de conanza NO incluye el
cero y por ser positivos sus limites se puede armar con un nivel de conanza
del 95 % que µhombres > µmujeres.
17.1.3. Intervalo de conanza bilateral para la diferencia de
medias (µ1−µ2) de muestras dependientes o pareadas
Para construir intervalos de conanza bilaterales para la diferencia de medias
de muestras dependientes a partir de la función t.test es necesario denir 4
argumentos:
x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2, paired=TRUE indica
que el intervalo de conanza se hará para muestras dependientes o pareadas.
conf.level: nivel de conanza.
Ejemplo
Los desórdenes musculoesqueléticos del cuello y hombro son comunes entre
empleados de ocina que realizan tareas repetitivas mediante pantallas de
visualización. Se reportaron los datos de un estudio para determinar si condi-
ciones de trabajo más variadas habrían tenido algún impacto en el movimiento
del brazo. Los datos que siguen se obtuvieron de una muestra de n= 16 sujetos.
Cada observación es la cantidad de tiempo, expresada como una proporción
de tiempo total observado, durante el cual la elevación del brazo fue de menos
de 30 grados. Las dos mediciones de cada sujeto se obtuvieron con una separa-
ción de 18 meses. Durante este período, las condiciones de trabajo cambiaron
y se permitió que los sujetos realizaran una variedad más amplia de tareas.
¿Sugieren los datos que el tiempo promedio verdadero durante el cual la ele-
vación es de menos de 30 grados luego del cambio diere de lo que era antes?
Calcular un intervalo de conanza del 95 % para responder la pregunta.
Sujeto 1 2 3 4 5 6 7 8
Antes 81 87 86 82 90 86 96 73
Después 78 91 78 78 84 67 92 70
Diferencia 3 -4 8 4 6 19 4 3

17.1 Función t.test 167
Sujeto 9 10 11 12 13 14 15 16
Antes 74 75 72 80 66 72 56 82
Después 58 62 70 58 66 60 65 73
Diferencia 16 13 2 22 0 12 -9 9
Para construir el intervalo de conanza primero se crean dos vectores con los
datos y se nombran Antes yDespues, luego se calcula la diferencia y se aloja
en el vector Diferencia, como sigue a continuación:
Antes <- c(81,87,86,82,90,86,96,73,
74,75,72,80,66,72,56,82)
Despues <- c(78,91,78,78,84,67,92,70,
58,62,70,58,66,60,65,73)
Diferencia <- Antes -Despues
En seguida se analiza la normalidad de la variable Diferencia de los cambios
en las condiciones de trabajo, a partir de un qqplot y una densidad.
par(mfrow=c(1,2))
require(car)
qqPlot(Diferencia, pch=19,main='QQplot para Diferencias',las=1,
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')
## [1] 15 12
plot(density(Diferencia), main='Densidad para Diferencias',las=1,
xlab='Diferencia de tiempo',ylab='Densidad')
De la Figura 17.3 se observa que la diferencia de los tiempos sigue una dis-
tribución normal, debido a que en el QQplot se observa un patron lineal y la
densidad muestra una forma cercana a la simétrica.
Luego de chequear la normalidad de la variable Diferencia se usa la fun-
ción t.test para construir el intervalo. A continuación se muestra el código
utilizado.
t.test(x=Antes, y=Despues, paired=TRUE,conf.level=0.95)$conf.int
## [1] 2.362 11.138
## attr(,"conf.level")
## [1] 0.95
168 17 Intervalos de conanza
-2 -1 0 1 2
-10
-5
0
5
10
15
20
QQplot para Diferencias
Cuantiles teóricos
Cuantiles muestrales
15
12
-20 -10 0 10 20 30
0.00
0.01
0.02
0.03
0.04
0.05
Densidad para Diferencias
Diferencia de tiempo
Densidad
Figura 17.3: QQplot y densidad para Diferencias.
A partir del resultado obtenido se puede concluir con un nivel de conanza
del 95 %, que el tiempo promedio verdadero durante el cual la elevación es de
menos de 30 grados luego del cambio diere de lo que era antes del mismo.
Como el intervalo de conanza es 2.362 < µD<11.138, esto indica que
µantes −µdespues >0y por lo tanto µantes > µdespues.
17.1.4. Intervalo de conanza unilateral para la media µ
Para construir intervalos de conanza unilaterales se usa el argumento
alternative = 'less' oalternative='greater', a continuación un ejem-
plo.
Ejemplo
Simule una muestra aleatoria de una N(18,3) y calcule un intervalo de con-
anza unilateral superior del 90 % para la media
x <- rnorm(50,mean = 18,sd =3)
t.test(x, alternative = "greater",conf.level = 0.90)$conf.int
## [1] 17 Inf
## attr(,"conf.level")
## [1] 0.9
En el resultado anterior se muestra el intervalo de conanza unilateral.

17.3 Función Var.test 169
17.2. Función Var.test
Para construir intervalos de conanza para la varianza se usa la función
Var.test del paquete usefultools (Hernandez,2018) disponible en el reposi-
torio GitHub1.
Para instalar el paquete usefultools desde GitHub se debe copiar el siguiente
código en la consola de R:
if (!require('devtools')) install.packages('devtools')
devtools::install_github('fhernanb/usefultools',force=TRUE)
Una vez instalado usefultools se puede usar la función Var.test.
17.2.1. Intervalo de conanza bilateral para la varianza σ2
Para calcular intervalos de conanza bilaterales para la varianza σ2a partir
de la función Var.test es necesario denir 2 argumentos:
x: vector numérico con la información de la muestra,
conf.level: nivel de conanza.
Ejemplo
Considerando la información del ejemplo de Intervalos de conanza bilaterales
para la media, construir un intervalo de conanza del 98 % para la varianza
de la altura de los estudiantes hombres.
require(usefultools) # Para cargar el paquete
res <- Var.test(x=hombres$altura, conf.level=0.98)
res$conf.int
## [1] 21.08 109.93
## attr(,"conf.level")
## [1] 0.98
El intervalo de conanza del 98 % indica que la varianza de la estatura de los
estudiantes hombres se encuentra entre 21.08 y 109.93 cm2.
1https://github.com/
170 17 Intervalos de conanza
17.3. Función var.test
La función var.test se usa para calcular intervalos de conanza para la razón
de varianzas. La función y sus argumentos son los siguientes:
var.test(x, y, ratio=1,conf.level=0.95,
alternative=c("two.sided","less","greater"))
17.3.1. Intervalo de conanza bilateral para la razón de va-
rianzas σ2
1/σ2
2
Para calcular intervalos de conanza bilaterales para la razón de varianzas a
partir de la función var.test es necesario denir 3 argumentos:
x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2,
conf.level: nivel de conanza.
Ejemplo
Usando la información del ejemplo de diferencia de medias para muestras
independientes se quiere obtener un intervalo de conanza del 95 % para la
razón de las varianzas de las alturas de los estudiantes hombres y mujeres.
var.test(x=hombres$altura, y=mujeres$altura,
conf.level=0.95)$conf.int
## [1] 0.2327 1.6633
## attr(,"conf.level")
## [1] 0.95
El intervalo de conanza del 95 % indica que la razón de varianzas se encuentra
entre 0.2327 y 1.6633. Puesto que el intervalo de conanza incluye el 1 se
concluye que las varianzas de las alturas de los hombres y las mujeres son
iguales.
¿Notó que las funciones Var.test yvar.test son diferentes?
Var.test sirve para construir IC para σ2.
17.4 Función prop.test 171
var.test sirve para construir IC para σ2
1/σ2
2.
17.4. Función prop.test
La función prop.test se usa para calcular intervalos de conanza para la
porporción y diferencia de proporciones. La función y sus argumentos son los
siguientes:
prop.test(x, n, p=NULL,
alternative=c("two.sided","less","greater"),
conf.level=0.95,correct=TRUE)
17.4.1. Intervalo de conanza bilateral para la proporción p
Para calcular intervalos de conanza bilaterales para la proporción a partir de
la función prop.test es necesario denir 3 argumentos: xconsidera el conteo
de éxitos, nindica el número de eventos o de forma equivalente corresponde
a la longitud de la variable que se quiere analizar, y conf.level corresponde
al nivel de conanza.
Ejemplo
El gerente de una estación de televisión debe determinar en la ciudad qué
porcentaje de casas tienen más de un televisor. Una muestra aleatoria de 500
casas revela que 275 tienen dos o más televisores. ¿Cuál es el intervalo de
conanza del 90 % para estimar la proporción de todas las casas que tienen
dos o más televisores?
prop.test(x=275,n=500,conf.level=0.90)$conf.int
## [1] 0.5122 0.5872
## attr(,"conf.level")
## [1] 0.9
A partir del resultado obtenido se puede concluir, con un nivel de conanza
172 17 Intervalos de conanza
del 90 %, que la proporción pde casas que tienen dos o más televisores se
encuentra entre 0.5122 y 0.5872.
17.4.2. Intervalo de conanza bilateral para la diferencia de
proporciones p1−p2
Para construir intervalos de conanza bilaterales para la proporción a partir
de la función prop.test es necesario denir 3 argumentos:
x: vector con el conteo de éxitos de las dos muestras,
n: vector con el número de ensayos,
conf.level: nivel de conanza.
Ejemplo
Se quiere determinar si un cambio en el método de fabricación de una piezas
ha sido efectivo o no. Para esta comparación se tomaron 2 muestras, una
antes y otra después del cambio en el proceso y los resultados obtenidos son
los siguientes.
Num piezas Antes Después
Defectuosas 75 80
Analizadas 1500 2000
Construir un intervalo de conanza del 90 % para decidir si el cambio tuvo
efecto positivo o no.
prop.test(x=c(75,80), n=c(1500,2000), conf.level=0.90)$conf.int
## [1] -0.002315 0.022315
## attr(,"conf.level")
## [1] 0.9
A partir del resultado obtenido se puede concluir, con un nivel de conanza
del 90 %, que la diferencia de proporción de defectos (p1−p2) se encuentra
entre -0.002315 y 0.022315. Como el cero está dentro del intervalo se concluye
que el cambio en el método de fabricación no ha disminuído el porcentaje de
defectos.

18
Prueba de hipótesis
En este capítulo se muestran las funciones que hay disponibles en Rpara
realizar prueba de hipótesis para:
1. la media µ,
2. la proporción p,
3. la varianza σ2,
4. la diferencia de medias µ1−µ2para muestras independientes y
dependientes (o pareadas),
5. la diferencia de proporciones p1−p2, y
6. la razón de varianzas σ2
1/σ2
2.
18.1. Prueba de hipótesis para µde una población nor-
mal
Para realizar este tipo de prueba se puede usar la función t.test que tiene
la siguiente estructura.
t.test(x, y = NULL,
alternative = c("two.sided","less","greater"),
mu = 0,paired = FALSE,var.equal = FALSE,
conf.level = 0.95, ...)
Los argumentos a denir dentro de t.test para hacer la prueba son:
x: vector numérico con los datos.
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la hipótesis alterna es ̸=,"less" para el caso <y
"greater" para >.
mu: valor de referencia de la prueba.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
173
174 18 Prueba de hipótesis
Ejemplo
Para vericar si el proceso de llenado de bolsas de café con 500 gramos está
operando correctamente se toman aleatoriamente muestras de tamaño diez
cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes
observaciones: 502, 501, 497, 491, 496, 501, 502, 500, 489, 490.
¿Está el proceso llenando bolsas conforme lo dice la envoltura? Use un nivel
de signicancia del 5 %.
Solución
Lo primero es explorar si la muestra proviene de una distribución normal, para
eso ingresamos los datos y aplicamos la prueba Anderson-Darling por medio
de la función ad.test disponible en el paquete nortest (Gross and Ligges,
2015) como se muestra a continuación.
contenido <- c(510,492,494,498,492,
496,502,491,507,496)
require(nortest) # Se debe haber instalado antes nortest
ad.test(contenido)
##
## Anderson-Darling normality test
##
## data: contenido
## A = 0.49, p-value = 0.2
Como el valor-P de la prueba Anderson-Darling es 20 % y mayor que el nivel
de signicancia del 5 %, se puede asumir que la muestra proviene de una
población normal.
Luego de haber explorado la normalidad retornamos al problema de interés
que se puede resumir así:
H0:µ= 500 gr
H1:µ̸= 500 gr
La prueba de hipótesis se puede realizar usando la función t.test por medio
del siguiente código.
t.test(contenido, alternative='two.sided',
conf.level=0.95,mu=500)
##
## One Sample t-test

18.2 Prueba de hipótesis para µcon muestras grandes 175
##
## data: contenido
## t = -1.1, df = 9, p-value = 0.3
## alternative hypothesis: true mean is not equal to 500
## 95 percent confidence interval:
## 493.1 502.5
## sample estimates:
## mean of x
## 497.8
Como el valor-P es 30 % y mayor que el nivel de signicancia 5 %, no se rechaza
la hipótesis nula, es decir, las evidencias no son sucientes para armar que
el proceso de llenando no está cumpliendo con lo impreso en la envoltura.
18.2. Prueba de hipótesis para µcon muestras grandes
Ejemplo
Se arma que los automóviles recorren en promedio más de 20000 kilómetros
por año pero usted cree que el promedio es en realidad menor. Para probar
tal armación se pide a una muestra de 100 propietarios de automóviles se-
leccionada de manera aleatoria que lleven un registro de los kilómetros que
recorren.
¿Estaría usted de acuerdo con la armación si la muestra aleatoria indicara un
promedio de 19500 kilómetros y una desviación estándar de 3900 kilómetros?
Utilice un valor P en su conclusión y use una signicancia del 3 %.
Solución
En este problema interesa:
H0:µ≥20000 km
H1:µ < 20000 km
Para este tipo de pruebas no hay una función de Rque haga los cálculos, por
esta razón uno mismo debe escribir una líneas de código para obtener los re-
sultados deseados, a continuación las instrucciones para calcular el estadístico
y su valor-P.
xbarra <- 19500 # Datos del problema
desvia <- 3900 # Datos del problema
n <- 100 # Datos del problema
176 18 Prueba de hipótesis
mu <- 20000 # Media de referencia
est <- (xbarra -mu) /(desvia /sqrt(n))
est # Para obtener el valor del estadístico
## [1] -1.282
pnorm(est) # Para obtener el valor-P
## [1] 0.09991
Como el valor-P es mayor que el nivel de signicancia 3 %, no hay evidencias
sucientes para pensar que ha disminuido el recorrido anual promedio de los
autos.
18.3. Prueba de hipótesis para la proporción p
Existen varias pruebas para estudiar la propoción pde una distribución bino-
mial, a continuación el listado de las más comunes.
1. Prueba de Wald1,
2. Prueba X2de Pearson2,
3. Prueba binomial exacta3.
18.3.1. Prueba de Wald
Esta prueba se recomienda usar cuando se tiene un tamaño de muestra n
sucientemente grande para poder usar la distribución normal para aproximar
la distribución binomial.
En esta prueba el estadístico está dado por
z=ˆp−p0
p0(1−p0)
n
,
donde ˆpes la proporción muestral calculada como el cociente entre el número
1https://en.wikipedia.org/wiki/Wald_test
2https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test#Fairness_of_dice
3https://en.wikipedia.org/wiki/Binomial_test
18.3 Prueba de hipótesis para la proporción p177
de éxitos xobservados en los nensayos y p0es el valor de referencia de las
hipótesis. El estadístico ztiene distribución N(0,1) cuando n→ ∞.
Para realizar esta prueba en Rno hay una función y debemos escribir la líneas
de código para obtener el estadístico y el valor-P de la prueba. A continuación
se muestra un ejemplo de cómo proceder para aplicar la prueba de Wald.
Ejemplo
Un fabricante de un quitamanchas arma que su producto quita 90 % de todas
las manchas. Para poner a prueba esta armación se toman 200 camisetas
manchadas de las cuales a solo 174 les desapareció la mancha. Pruebe la
armación del fabricante a un nivel α= 0.05.
Solución
En este problema interesa probar lo siguiente:
H0:p= 0.90
H1:p < 0.90
Del anterior conjunto de hipótesis se observa que el valor de referencia de
la prueba es p0= 0.90. De la información inicial se tiene que de las n=
200 pruebas se observó que en x= 174 la mancha desapareció, con esta
información se puede calcular el estadístico zasí:
z <- (174/200 -0.90)/sqrt(0.90 *(1-0.90)/200)
z# Para obtener el valor del estadístico
## [1] -1.414
Para obtener el valor-P de la prueba debemos tener en cuenta el sentido en la
hipótesis alternativa H1:p < 0.90, por esa razón el valor-P será P(Z < z)y
para obtenerlo usamos el siguiente código
pnorm(q=z, lower.tail=TRUE)# Para obtener el valor-P
## [1] 0.07865
El valor-P obtenido se puede representar grácamente en la Figura 18.1.
Como el valor-P obtenido fue mayor que el nivel de signicancia α= 0.05 se
concluye que no hay evidencias sucientes para rechazar la hipótesis nula.

178 18 Prueba de hipótesis
Z
-4 -2 0 2 4
-1.414
0.0786
Figura 18.1: Representación del Valor-P para la prueba Wald.
18.3.2. Prueba X2de Pearson
Para realizar la prueba X2de Pearson se usa la función prop.test que tiene
la siguiente estructura.
prop.test(x, n, p = NULL,
alternative = c("two.sided","less","greater"),
conf.level = 0.95,correct = TRUE)
Los argumentos a denir dentro de prop.test para hacer la prueba son:
x: número de éxitos en la muestra.
n: número de observaciones en la muestra.
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la alterna es ̸=,"less" para el caso <y"greater"
para >.
p: valor de referencia de la prueba.
correct: valor lógico para indicar si se usa la corrección de Yates.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
18.3 Prueba de hipótesis para la proporción p179
Ejemplo
Un fabricante de un quitamanchas arma que su producto quita 90 % de todas
las manchas. Para poner a prueba esta armación se toman 200 camisetas
manchadas de las cuales a solo 174 les desapareció la mancha. Pruebe la
armación del fabricante a un nivel α= 0.05.
Solución
En este problema interesa probar lo siguiente:
H0:p= 0.90
H1:p < 0.90
La forma de usar la función prop.test para realizar la prueba se muestra a
continuación.
prop.test(x=174,n=200,p=0.9,alternative='less',
conf.level=0.95,correct=FALSE)
##
## 1-sample proportions test without continuity
## correction
##
## data: 174 out of 200, null probability 0.9
## X-squared = 2, df = 1, p-value = 0.08
## alternative hypothesis: true p is less than 0.9
## 95 percent confidence interval:
## 0.0000 0.9042
## sample estimates:
## p
## 0.87
Como el valor-P (con valor de 0.07865 pero repotado en la salida como 0.08)
es mayor que αno se rechaza la hipótesis nula y se concluye que no hay
evidencias sucientes para rechazar la hipótesis nula.
18.3.3. Prueba binomial exacta
Para realizar la prueba binomial exacta se usa la función binom.test que
tiene la siguiente estructura.
binom.test(x, n, p = 0.5,
alternative = c("two.sided","less","greater"),
conf.level = 0.95)

180 18 Prueba de hipótesis
Los argumentos a denir dentro de binom.test para hacer la prueba son:
x: número de éxitos en la muestra.
n: número de observaciones en la muestra.
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la alterna es ̸=,"less" para el caso <y"greater"
para >.
p: valor de referencia de la prueba.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
Ejemplo
Un asadero de pollos asegura que 90 % de sus órdenes se entregan en menos
de 10 minutos. En una muestra de 20 órdenes, 17 se entregaron dentro de ese
lapso. ¿Puede concluirse en el nivel de signicancia 0.05, que menos de 90 %
de las órdenes se entregan en menos de 10 minutos?
Solución
En este problema interesa probar lo siguiente:
H0:p= 0.90
H1:p < 0.90
La forma de usar la función binom.test para realizar la prueba se muestra a
continuación.
binom.test(x=17,n=20,p=0.9,alternative="less")
##
## Exact binomial test
##
## data: 17 and 20
## number of successes = 17, number of trials = 20,
## p-value = 0.3
## alternative hypothesis: true probability of success is less than 0.9
## 95 percent confidence interval:
## 0.0000 0.9578
## sample estimates:
## probability of success
## 0.85
Como el valor-P (reportado como 0.3 pero con valor de 0.3231) es mayor que α
no se rechaza la hipótesis nula y se concluye que no hay evidencias sucientes
para rechazar la hipótesis nula.

18.4 Prueba de hipótesis para la varianza σ2de una población normal 181
18.4. Prueba de hipótesis para la varianza σ2de una po-
blación normal
Para realizar este tipo de prueba se usa la función Var.test del paquete use-
fultools (Hernandez,2018) disponible en el repositorio GitHub4. La función
Var.test tiene la siguiente estructura.
Var.test(x, alternative = "two.sided",
null.value = 1,conf.level = 0.95)
Los argumentos a denir dentro de Var.test para hacer la prueba son:
x: vector numérico con los datos.
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la alterna es ̸=,"less" para el caso <y"greater"
para >.
null.value: valor de referencia de la prueba.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
Para instalar el paquete usefultools desde GitHub se debe copiar el siguiente
código en la consola de R:
if (!require('devtools')) install.packages('devtools')
devtools::install_github('fhernanb/usefultools',force=TRUE)
Ejemplo
Para vericar si el proceso de llenado de bolsas de café está operando con
la variabilidad permitida se toman aleatoriamente muestras de tamaño diez
cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes
observaciones: 502, 501, 497, 491, 496, 501, 502, 500, 489, 490. El proceso
de llenado está bajo control si presenta un varianza de 40 o menos. ¿Está
el proceso llenando bolsas conforme lo dice la envoltura? Use un nivel de
signicancia del 5 %.
Solución
En un ejemplo anterior se comprobó que la muestra proviene de una población
normal así que se puede proceder con la prueba de hipótesis sobre σ2.
4https://github.com/

182 18 Prueba de hipótesis
En este ejemplo nos interesa estudiar el siguiente conjunto de hipótesis
H0:σ2≤40
H1:σ2>40
La prueba de hipótesis se puede realizar usando la función Var.test por medio
del siguiente código.
contenido <- c(510,492,494,498,492,
496,502,491,507,496)
require(usefultools) # Ya debe estar instalado
Var.test(x=contenido, alternative='greater',
null.value=40,conf.level=0.95)
##
## X-squared test for variance
##
## data: varx = 42.8444444444444 and nx = 10
## X-squared = 9.6, df = 9, p-value = 0.4
## alternative hypothesis: true is greater than 40
## 95 percent confidence interval:
## 0 116
## sample estimates:
## variance of x
## 42.84
Como el valor-P es mayor que el nivel de signicancia 5 %, no se rechaza la
hipótesis nula, es decir, las evidencias no son sucientes para armar que la
varianza del proceso de llenado es mayor que 40 unidades.
18.5. Prueba de hipótesis para el cociente de varianzas
σ2
1/σ2
2
Para realizar este tipo de prueba se puede usar la función var.test que tiene
la siguiente estructura.
var.test(x, y, ratio = 1,
alternative = c("two.sided","less","greater"),
conf.level = 0.95, ...)

18.5 Prueba de hipótesis para el cociente de varianzas σ2
1/σ2
2183
Los argumentos a denir dentro de var.test para hacer la prueba son:
x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2,
ratio: valor de referencia de la prueba.
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la hipótesis alterna es ̸=,"less" para el caso <y
"greater" para >.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
Ejemplo
Se realiza un estudio para comparar dos tratamientos que se aplicarán a frijoles
crudos con el objetivo de reducir el tiempo de cocción. El tratamiento T1 es
a base de bicarbonato de sodio, el T2 es a base de cloruro de sodio o sal
común. La variable respuesta es el tiempo de cocción en minutos. Los datos se
muestran abajo. ¿Son las varianzas de los tiempos iguales o diferentes? Usar
α= 0.05.
T1: 76, 85, 74, 78, 82, 75, 82.
T2: 57, 67, 55, 64, 61, 63, 63.
Solución
En este problema interesa probar si las varianzas poblacionales son iguales o
no, por esta razón el cociente de σ2
T1/σ2
T2se iguala al valor de 1 que será el
valor de referencia de la prueba.
H0:σ2
T1/σ2
T2= 1
H1:σ2
T1/σ2
T2̸= 1
Para ingresar los datos se hace lo siguiente:
T1 <- c(76,85,74,78,82,75,82)
T2 <- c(57,67,55,64,61,63,63)
Primero se debe explorar si las muestras provienen de una población normal
y para esto se construyen los QQplot que se muestran en la Figura 18.2, a
continuación el código para generar la Figura 18.2.
q1 <- qqnorm(T1, plot.it=FALSE)
q2 <- qqnorm(T2, plot.it=FALSE)
plot(range(q1$x, q2$x), range(q1$y, q2$y), type="n",las=1,
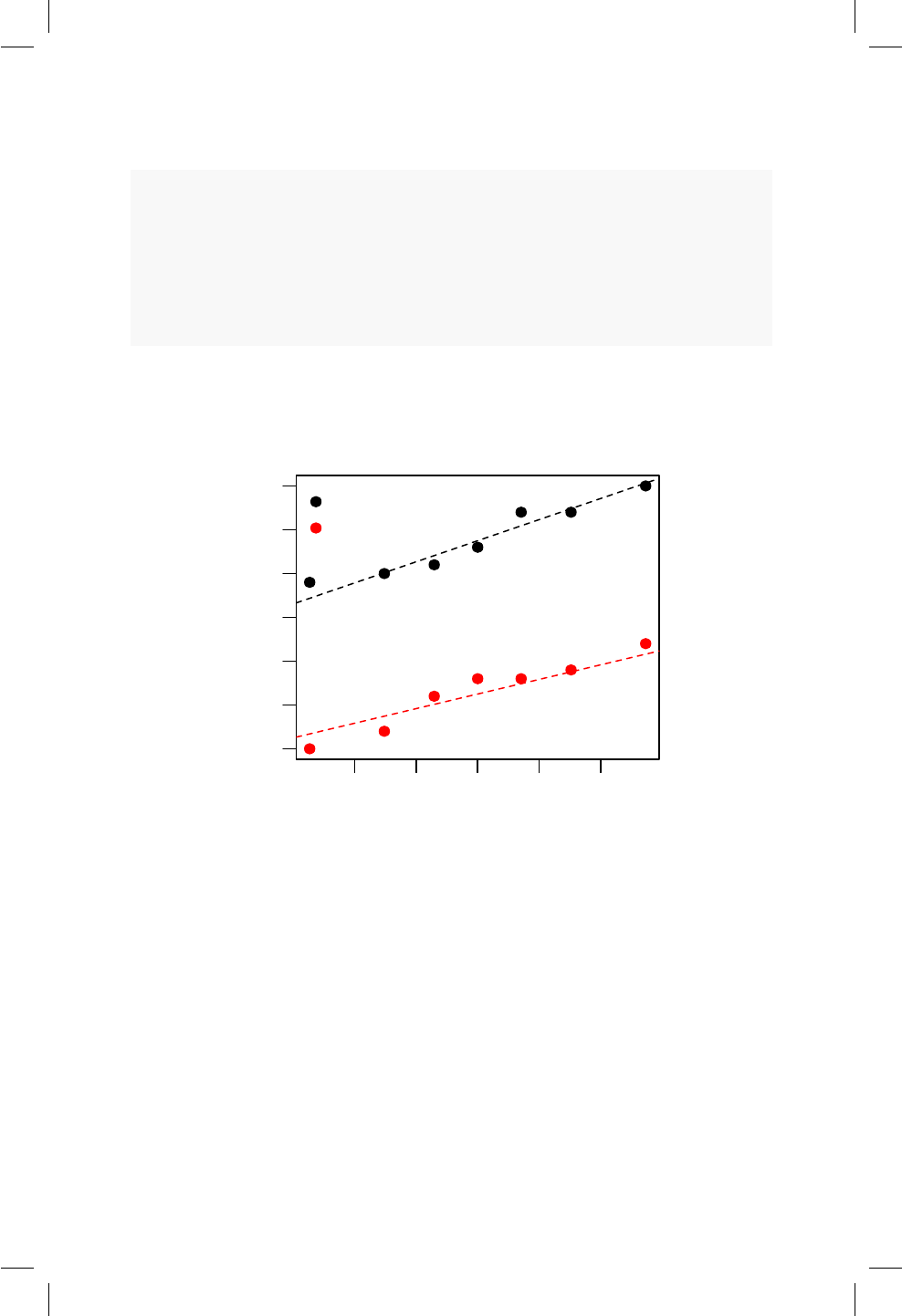
184 18 Prueba de hipótesis
xlab='Theoretical Quantiles',ylab='Sample Quantiles')
points(q1, pch=19)
points(q2, col="red",pch=19)
qqline(T1, lty='dashed')
qqline(T2, col="red",lty="dashed")
legend('topleft',legend=c('T1','T2'), bty='n',
col=c('black','red'), pch=19)
-1.0 -0.5 0.0 0.5 1.0
55
60
65
70
75
80
85
Theoretical Quantiles
Sample Quantiles
T1
T2
Figura 18.2: QQplot para los tiempos de cocción.
De la Figura 18.2 se observa que los puntos están bastante alineados lo cual
nos lleva a pensar que las muestras si provienen de una población normal, para
estar más seguros se aplicará una prueba formal para estudiar la normalidad.
A continuación el código para aplicar la prueba de normalidad Kolmogorov-
Smirnov a cada una de las muestras.
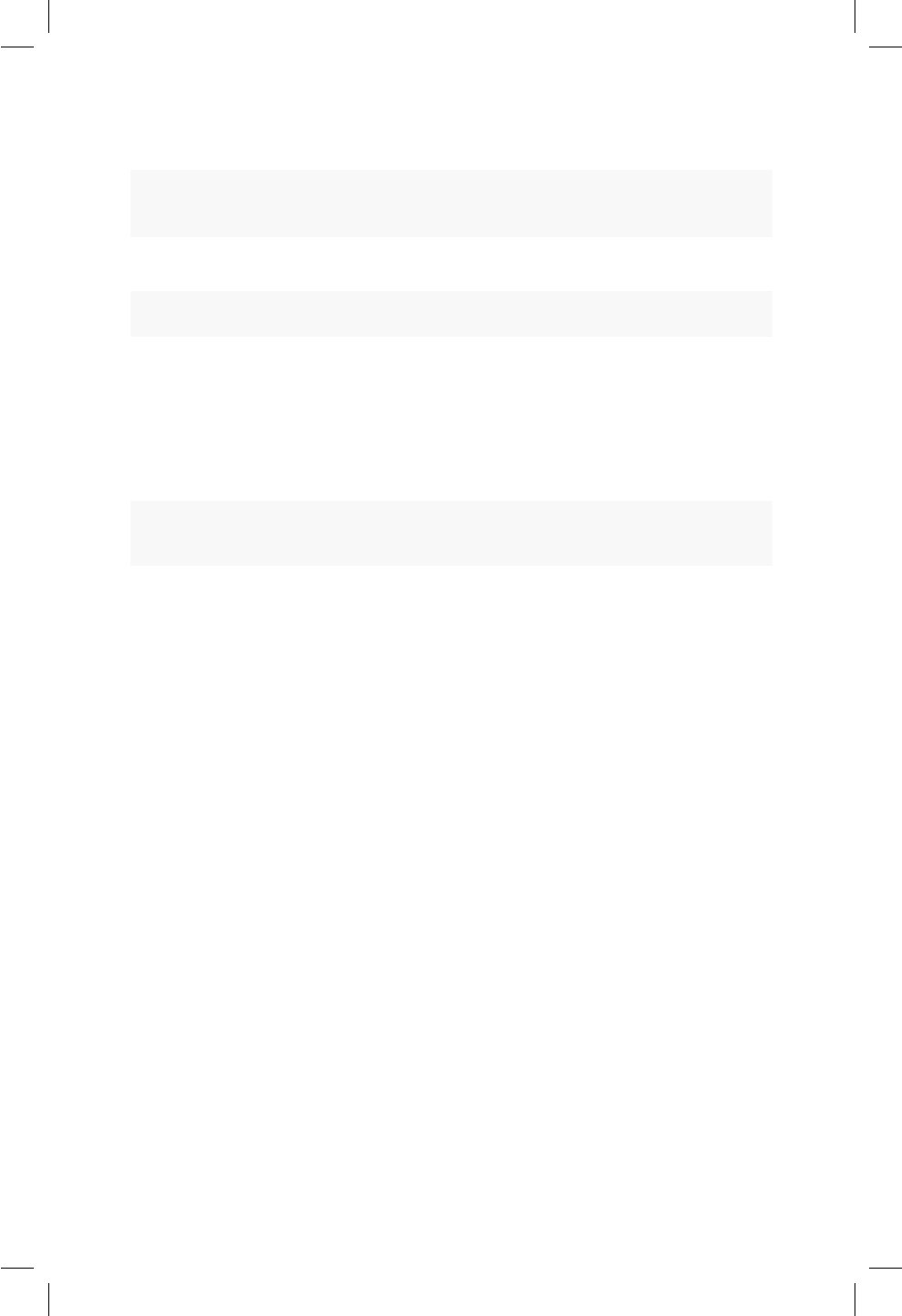
18.5 Prueba de hipótesis para el cociente de varianzas σ2
1/σ2
2185
require(nortest) # Se debe tener instalado
lillie.test(T1)$p.value
## [1] 0.5205
lillie.test(T2)$p.value
## [1] 0.3953
Del QQplot mostrado en la Figura 18.2 y las pruebas de normalidad se observa
que se puede asumir que las poblaciones son normales.
La función var.test se puede usar para probar H0, a continuación el código
para realizar la prueba.
var.test(T1, T2, ratio=1,alternative="two.sided",
conf.level=0.95)
##
## F test to compare two variances
##
## data: T1 and T2
## F = 1, num df = 6, denom df = 6, p-value = 1
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.1737 5.8839
## sample estimates:
## ratio of variances
## 1.011
Como el valor-P es 0.9897 (reportado como 1 en la salida anterior), muy
superior al nivel αde signicancia 5 %, se puede concluir que las varianzas
son similares.
Ejemplo
El arsénico en agua potable es un posible riesgo para la salud. Un artículo
reciente reportó concentraciones de arsénico en agua potable en partes por
billón (ppb) para diez comunidades urbanas y diez comunidades rurales. Los
datos son los siguientes:
Urbana: 3, 7, 25, 10, 15, 6, 12, 25, 15, 7
Rural: 48, 44, 40, 38, 33, 21, 20, 12, 1, 18
186 18 Prueba de hipótesis
Solución
¿Son las varianzas de las concentraciones iguales o diferentes? Usar α= 0.05.
En este problema interesa probar:
H0:σ2
Urb/σ2
Rur = 1
H1:σ2
Urb/σ2
Rur ̸= 1
Para ingresar los datos se hace lo siguiente:
urb <- c(3,7,25,10,15,6,12,25,15,7)
rur <- c(48,44,40,38,33,21,20,12,1,18)
Primero se debe explorar si las muestras provienen de una población normal,
para esto se construyen los QQplot mostrados en la Figura 18.3.
-1.5 -0.5 0.0 0.5 1.0 1.5
0
10
20
30
40
Theoretical Quantiles
Sample Quantiles
Urbana
Rural
Figura 18.3: QQplot para las concentraciones de arsénico.
A continuación el código para aplicar la prueba de normalidad Kolmogorov-
Smirnov, a continuación el código usado.
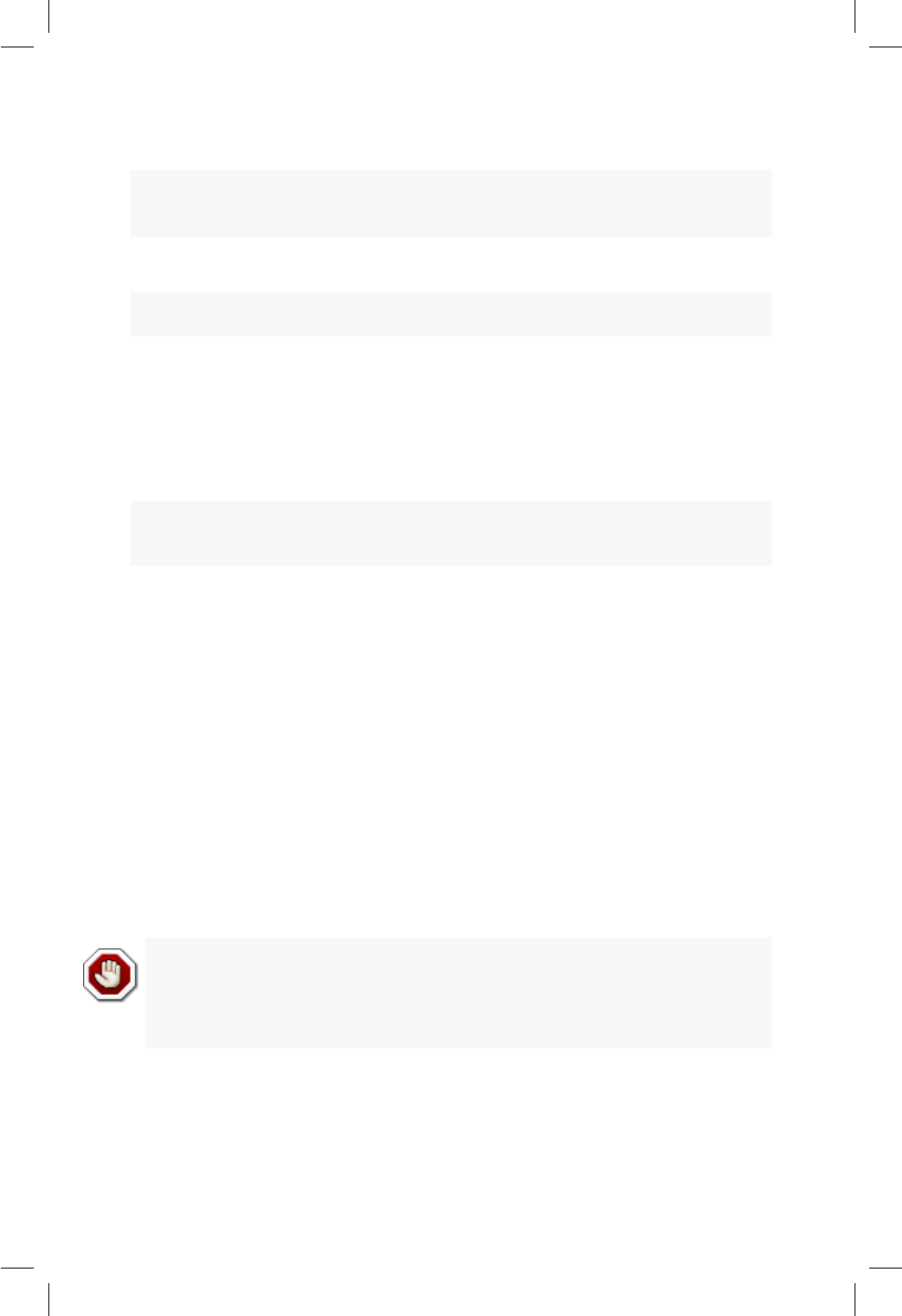
18.6 Prueba de hipótesis para el cociente de varianzas σ2
1/σ2
2187
require(nortest) # Se debe tener instalado
lillie.test(urb)$p.value
## [1] 0.5522
lillie.test(rur)$p.value
## [1] 0.625
Del QQplot mostrado en la Figura 18.3 y las pruebas de normalidad se observa
que se pueden asumir poblaciones normales.
La función var.test se puede usar para probar H0, a continuación el código
para realizar la prueba.
var.test(urb, rur, ratio=1,alternative="two.sided",
conf.level=0.95)
##
## F test to compare two variances
##
## data: urb and rur
## F = 0.25, num df = 9, denom df = 9, p-value =
## 0.05
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.06144 0.99582
## sample estimates:
## ratio of variances
## 0.2473
Como el valor-P es 0.0494 (reportado como 0.05 en la salida anterior) y es
menor que el nivel de signicancia α= 0.05, se puede concluir que las varianzas
no son iguales.
¿Notó que las funciones Var.test yvar.test son diferentes?
Var.test sirve para prueba de hipótesis sobre σ2.
var.test sirve para prueba de hipótesis sobre σ2
1/σ2
2.

188 18 Prueba de hipótesis
18.6. Prueba de hipótesis para la diferencia de medias
µ1−µ2con varianzas iguales
Para realizar este tipo de prueba se puede usar la función t.test que tiene
la siguiente estructura.
t.test(x, y = NULL,
alternative = c("two.sided","less","greater"),
mu = 0,paired = FALSE,var.equal = FALSE,
conf.level = 0.95, ...)
Los argumentos a denir dentro de t.test para hacer la prueba son:
x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2,
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la alterna es ̸=,"less" para el caso <y"greater"
para >.
mu: valor de referencia de la prueba.
var.equal=TRUE: indica que las varianzas son desconocidas pero iguales.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
Ejemplo
Retomando el ejemplo de los fríjoles, ¿existen diferencias entre los tiempos de
cocción de los fríjoles con T1 y T2? Usar un nivel de signicancia del 5 %.
Primero se construirá un boxplot comparativo para los tiempos de cocción
diferenciando por el tratamiento que recibieron. Abajo el código para obtener
en este caso el boxplot. En la Figura 18.4 se muestra el boxplot, de esta gura
se observa que las cajas de los boxplot no se traslapan, esto es un indicio de
que las medias poblacionales, µ1yµ2, son diferentes, se observa también que
el boxplot para el tratamiento T1 está por encima del T2.
datos <- data.frame(tiempo=c(T1, T2), trat=rep(1:2,each=7))
boxplot(tiempo ~trat, data=datos, las=1,
xlab='Tratamiento',ylab='Tiempo (min)')
En este problema interesa estudiar el siguiente conjunto de hipótesis.
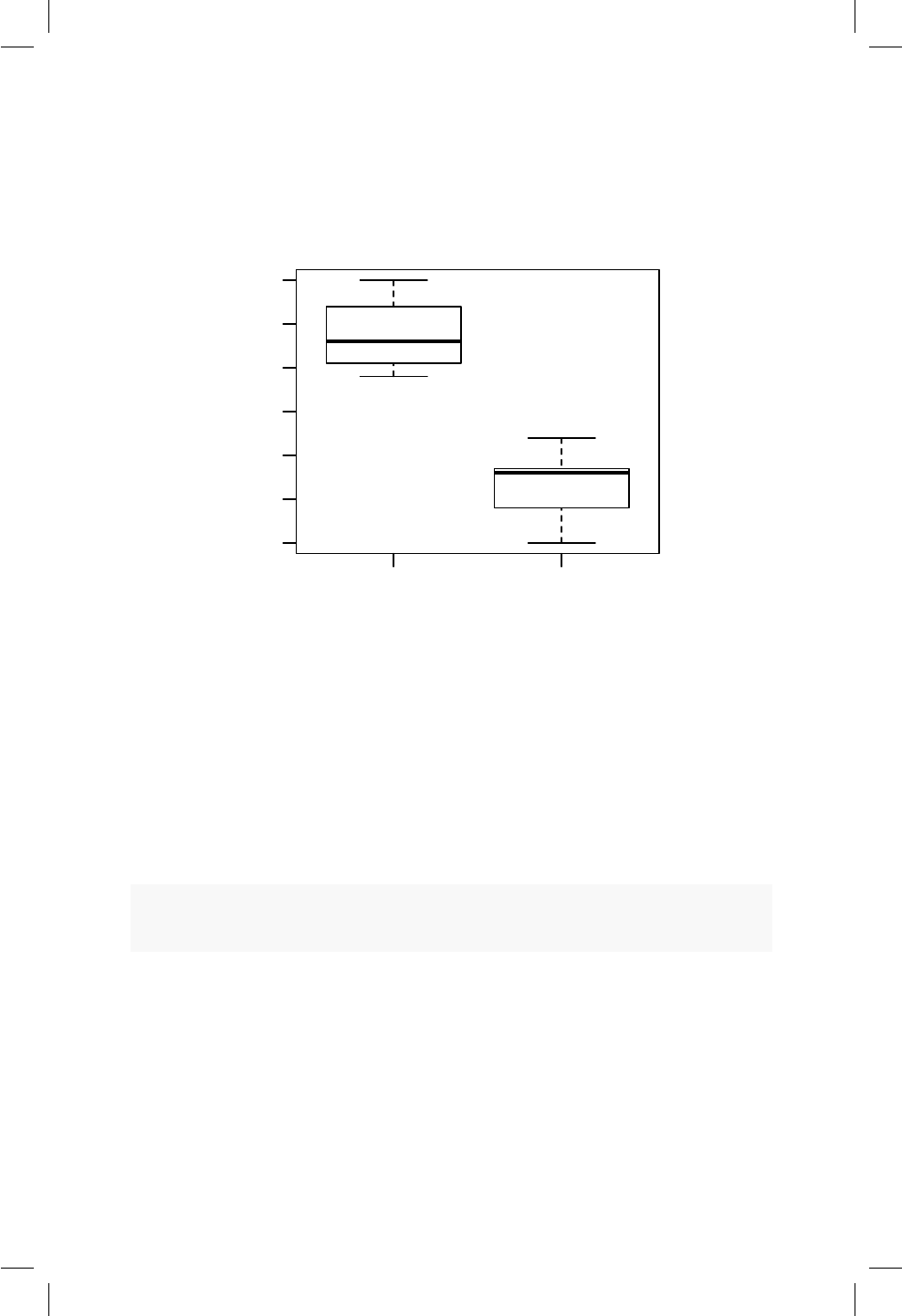
18.6 Prueba de hipótesis para la diferencia de medias µ1−µ2con varianzas iguales 189
1 2
55
60
65
70
75
80
85
Tratamiento
Tiempo (min)
Figura 18.4: Boxplot para los tiempos de cocción dado el tratamiento.
H0:µ1−µ2= 0
H1:µ1−µ2̸= 0
El código para realizar la prueba es el siguiente:
t.test(x=T1, y=T2, alternative="two.sided",mu=0,
paired=FALSE,var.equal=TRUE,conf.level=0.97)
##
## Two Sample t-test
##
## data: T1 and T2
## t = 7.8, df = 12, p-value = 5e-06
## alternative hypothesis: true difference in means is not equal to 0
## 97 percent confidence interval:
## 11.95 22.91

190 18 Prueba de hipótesis
## sample estimates:
## mean of x mean of y
## 78.86 61.43
De la prueba se obtiene un valor-P muy pequeño, por lo tanto, podemos
concluir que si hay diferencias signicativas entre los tiempos promedios de
cocción con T1 y T2, resultado que ya se sospechaba al observar la Figura
18.4.
Si el objetivo fuese elegir el tratamiento que minimice los tiempos de cocción
se recomendaría el tratamiento T2, remojo de fríjoles en agua con sal.
18.7. Prueba de hipótesis para la diferencia de medias
µ1−µ2con varianzas diferentes
Ejemplo
Retomando el ejemplo de la concentración de arsénico en el agua, ¿existen
diferencias entre las concentraciones de arsénico de la zona urbana y rural?
Usar un nivel de signicancia del 5 %.
Primero se construirá un boxplot comparativo para las concentraciones de
arsénico diferenciando por la zona donde se tomaron las muestras. Abajo el
código para obtener en este caso el boxplot. En la Figura 18.5 se muestra el
boxplot, de esta gura se observa que las cajas de los boxplot no se traslapan,
esto es un indicio de que las medias poblacionales, µ1yµ2, son diferentes, se
observa también que el boxplot para la zona rural está por encima del de la
zona urbana.
datos <- data.frame(Concentracion=c(urb, rur),
Zona=rep(c('Urbana','Rural'), each=10))
boxplot(Concentracion ~Zona, data=datos, las=1,
xlab='Zona',ylab='Concentración arsénico (ppb)')
En este problema interesa estudiar el siguiente conjunto de hipótesis.
H0:µ1−µ2= 0
H1:µ1−µ2̸= 0
El código para realizar la prueba es el siguiente:
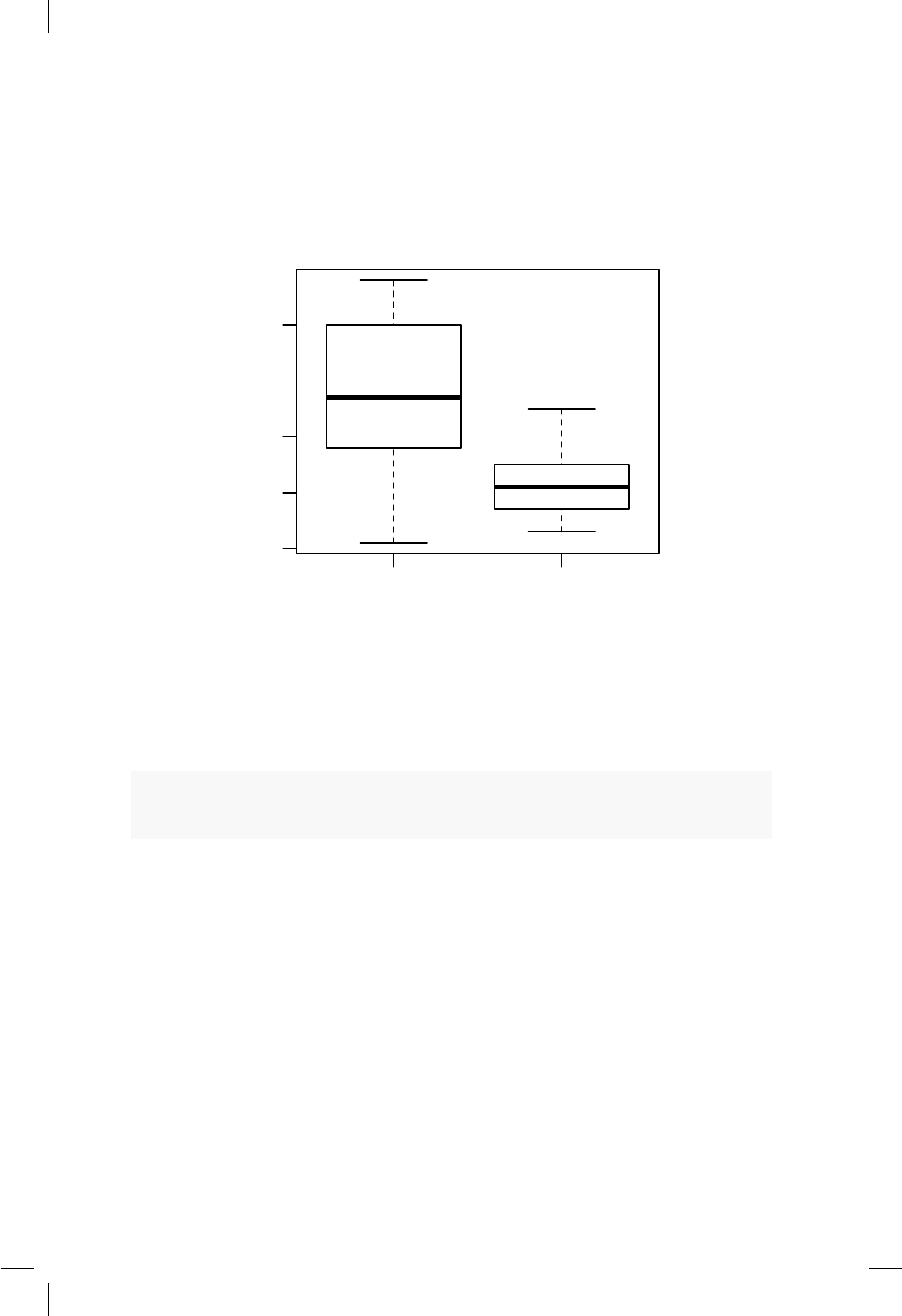
18.7 Prueba de hipótesis para la diferencia de medias µ1−µ2con varianzas diferentes 191
Rural Urbana
0
10
20
30
40
Zona
Concentración arsénico (ppb)
Figura 18.5: Boxplot para las concentaciones de arsénico dada la zona.
t.test(x=urb, y=rur, alternative="two.sided",mu=0,
paired=FALSE,var.equal=FALSE,conf.level=0.95)
##
## Welch Two Sample t-test
##
## data: urb and rur
## t = -2.8, df = 13, p-value = 0.02
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -26.694 -3.306
## sample estimates:
## mean of x mean of y
## 12.5 27.5
De la prueba se obtiene un valor-P pequeño, por lo tanto, podemos concluir
que si hay diferencias signicativas entre las concentraciones de arsénico del

192 18 Prueba de hipótesis
agua entre las dos zonas, resultado que ya se sospechaba al observar la Figura
18.5. La zona que presenta mayor concentración media de arsénico en el agua
es la rural.
Para todas las pruebas se incluyó un intervalo de conanza, revise si la
conclusión obtenida con el IC coincide con la obtenida con PH.
18.8. Prueba de hipótesis para la diferencia de propor-
ciones p1−p2
Para realizar pruebas de hipótesis para la proporción se usa la función
prop.test y es necesario denir los siguientes argumentos:
x: vector con el conteo de éxitos de las dos muestras,
n: vector con el número de ensayos de las dos muestras,
alternative: tipo de hipótesis alterna. Los valores disponibles son
"two.sided" cuando la alterna es ̸=,"less" para el caso <y"greater"
para >.
p: valor de referencia de la prueba.
conf.level: nivel de conanza para reportar el intervalo de conanza aso-
ciado (opcional).
Ejemplo
Se quiere determinar si un cambio en el método de fabricación de una piezas
ha sido efectivo o no. Para esta comparación se tomaron 2 muestras, una
antes y otra después del cambio en el proceso y los resultados obtenidos son
los siguientes.
Num piezas Antes Después
Defectuosas 75 80
Analizadas 1500 2000
Realizar una prueba de hipótesis con un nivel de signicancia del 10 %.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
H0:pantes −pdespues = 0

18.9 Prueba de hipótesis para la diferencia de medias pareadas 193
H1:pantes −pdespues >0
Para realizar la prueba se usa la función prop.test como se muestra a conti-
nuación.
prop.test(x=c(75,80), n=c(1500,2000),
alternative='greater',conf.level=0.90)
##
## 2-sample test for equality of proportions with
## continuity correction
##
## data: c(75, 80) out of c(1500, 2000)
## X-squared = 1.8, df = 1, p-value = 0.09
## alternative hypothesis: greater
## 90 percent confidence interval:
## 0.0002765 1.0000000
## sample estimates:
## prop 1 prop 2
## 0.05 0.04
Del reporte anterior se observa que el Valor-P es 9 %, por lo tanto no hay
evidencias sucientes para pensar que el porcentaje de defectuosos después
del cambio ha disminuído.
18.9. Prueba de hipótesis para la diferencia de medias
pareadas
Ejemplo
Diez individuos participaron de programa para perder peso corporal por medio
de una dieta. Los voluntarios fueron pesados antes y después de haber parti-
cipado del programa y los datos en libras aparecen abajo. ¿Hay evidencia que
soporte la armación de la dieta disminuye el peso medio de los participantes?
Usar nivel de signicancia del 5 %.
Sujeto 001 002 003 004 005 006 007 008 009 010
Antes 195 213 247 201 187 210 215 246 294 310
Después 187 195 221 190 175 197 199 221 278 285
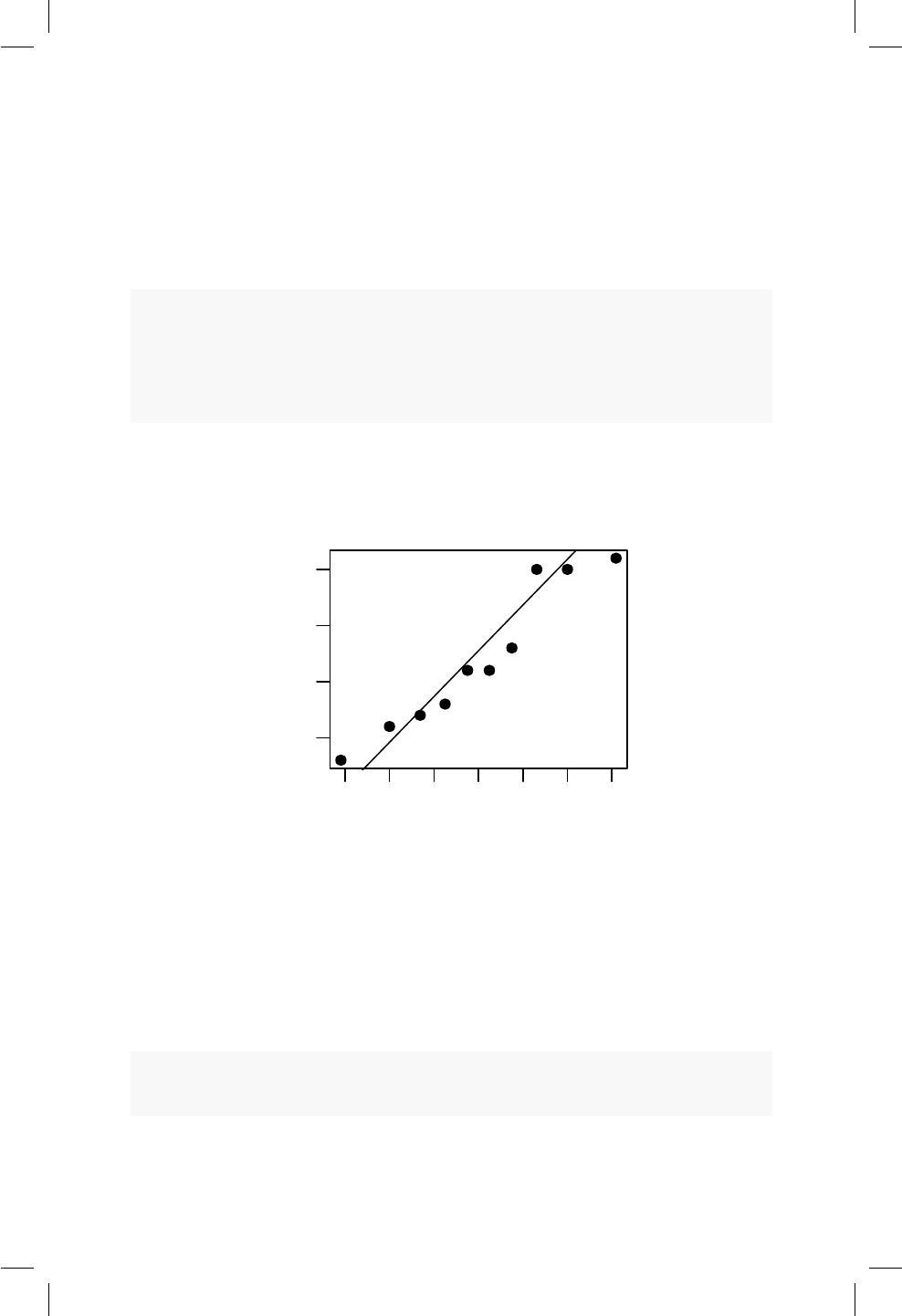
194 18 Prueba de hipótesis
Primero se debe explorar si las diferencias de peso (antes-después) provienen
de una población normal, para esto se construye el QQplot mostrado en la
Figura 18.6. De la gura no se observa un alejamiento serio de la recta de
referencia, por lo tanto se puede asumir que las diferencias se distribuyen en
forma aproximadamente normal.
antes <- c(195,213,247,201,187,210,215,246,294,310)
despu <- c(187,195,221,190,175,197,199,221,278,285)
dif <- antes -despu
qqnorm(dif, pch=19,main='')
qqline(dif)
-1.5 -0.5 0.5 1.5
10 15 20 25
Theoretical Quantiles
Sample Quantiles
Figura 18.6: QQplot para las diferencias de peso.
Se puede aplicar la prueba de normalidad Kolmogorov-Smirnov para estudiar
si las diferencias dif provienen de una población normal, esto se puede realizar
por medio del siguiente código.
require(nortest)
lillie.test(dif)
##
18.9 Prueba de hipótesis para la diferencia de medias pareadas 195
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: dif
## D = 0.19, p-value = 0.4
De la salida anterior se observa que el valor-P de la prueba es grande por lo
tanto se puede asumir que las diferencias se distribuyen en forma aproxima-
damente normal.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
H0:µantes −µdespues = 0
H1:µantes −µdespues >0
El código para realizar la prueba es el siguiente:
t.test(x=antes, y=despu, alternative="greater",mu=0,
paired=TRUE,conf.level=0.95)
##
## Paired t-test
##
## data: antes and despu
## t = 8.4, df = 9, p-value = 8e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## 13.28 Inf
## sample estimates:
## mean of the differences
## 17
De la prueba se obtiene un valor-P pequeño, por lo tanto, podemos concluir
que el peso µantes es mayor que µdespues, en otras palabras, la dieta si ayudó
a disminuir el peso corporal.


19
Aproximación de integrales
En este capítulo se mostrará cómo aproximar integrales en una y varias di-
mensiones.
19.1. Aproximación de Laplace unidimensional
Esta aproximación es útil para obtener el valor de una integral usando la
expansión de Taylor para una función f(x)unimodal en ℜ, en otras palabras
lo que interesa es:
I=∞
−∞
f(x)d(x)
Al hacer una expansión de Taylor de segundo orden para log(f(x)) en su moda
x0el resultado es:
log(f(x)) ≈log(f(x0)) + log(f)′(x0)
1! (x−x0) + log(f)′′(x0)
2! (x−x0)2
El segundo término de la suma se anula porque log(f)′(x0)=0por ser x0el
valor donde está el máximo de log(f(x)). La expresión anterior se simplica
en:
log(f(x)) ≈log(f(x0)) + log(f)′′(x0)
2! (x−x0)2
al aislar f(x)se tiene que
f(x)≈f(x0) exp −c
2(x−x0)2(19.1)
donde c=−d2
dx2log(f(x))x=x0
.
La expresión 19.1 se puede reescribir de manera que aparezca el núcleo de la
función de densidad de la distribución normal con media x0y varianza 1/c, a
continuación la expresión
f(x)≈f(x0)2π/c
2π/c exp −1
2x−x0
1/√c2
197
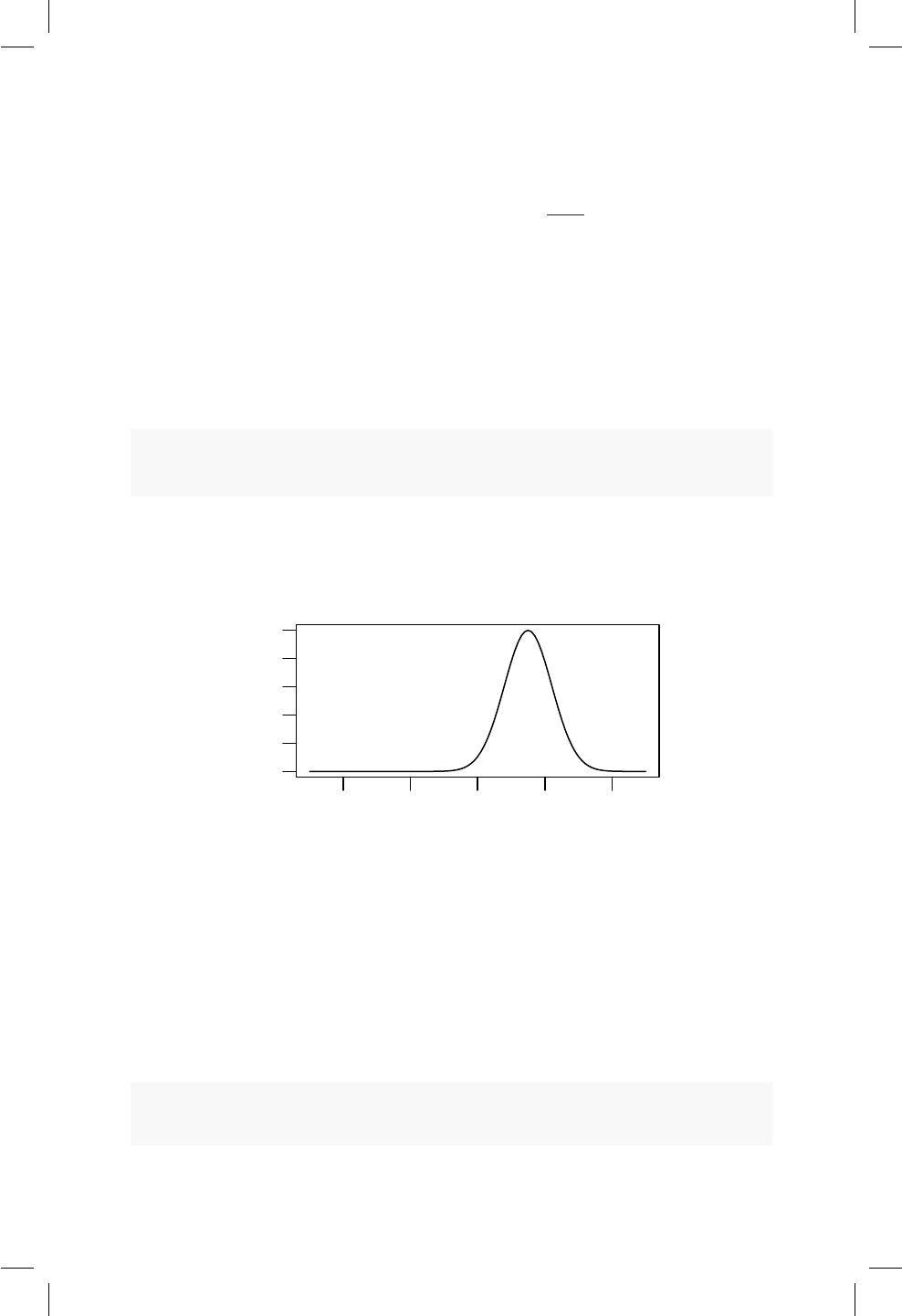
198 19 Aproximación de integrales
Así al calcular la integral de f(x)en ℜse tiene que:
I=∞
−∞
f(x)d(x) = f(x0)2π/c (19.2)
Ejemplo
Calcular la integral de f(x) = exp −(x−1.5)2en ℜutilizando la aproxima-
ción de Laplace.
Primero vamos a dibujar la función f(x)para ver en dónde está su moda x0.
fun <- function(x) exp(-(x-1.5)^2)
curve(fun, from=-5,to=5,ylab='f(x)',las=1)
-4 -2 0 2 4
0.0
0.2
0.4
0.6
0.8
1.0
x
f(x)
Figura 19.1: Perl de la función f(x).
Visualmente se nota que la moda está cerca del valor 1.5 y para determinar nu-
méricamente el valor de la moda x0se usa la función optimize, los resultados
se almacenan en el objeto res. El valor de la moda corresponde al elemento
maximum del objeto res.
res <- optimize(fun, interval=c(-10,10), maximum=TRUE)
res
19.1 Aproximación de Laplace unidimensional 199
## $maximum
## [1] 1.5
##
## $objective
## [1] 1
Para determinar el valor de cde la expresión 19.2 se utiliza el siguiente código.
require("numDeriv")
constant <- -as.numeric(hessian(fun, res$maximum))
Para obtener la aproximación de la integral se usa la expresión 19.2 y pa-
ra tener un punto de comparación se evalua la integral usando la función
integrate, a continuación el código.
fun(res$maximum) *sqrt(2*pi/constant)
## [1] 1.772
integrate(fun, -Inf,Inf)# Para comparar
## 1.772 with absolute error < 1.5e-06
De los anteriores resultados vemos que la aproximación es buena.


20
Curiosidades
En este capítulo se mostrarán algunos procedimientos de Rpara solucionar
problemas frecuentes.
20.1. ¿Cómo vericar si un paquete no está instalado
para instalarlo de forma automática?
Muchas veces compartimos código de Rcon otros colegas y si ellos no tienen
instalados ciertos paquetes el código no funcionará. Para evitar ese problema
podemos colocar al inicio del código unas líneas que chequeen si ciertos pa-
quetes están instalados o no, si están instalados, se cargan esos paquetes y
caso contrario, el código instala los paquetes y luego los carga, todo de forma
automática sin que el usuario tenga que identicar los paquetes que le faltan.
Ejemplo
El código mostrado abajo revisa si los paquetes knitr,png ymarkdown están
instalados e instala los ausentes y luego carga todos los paquetes que estén en
el vector packages.
packages <- c("knitr","png","markdown")
package.check <- lapply(packages, FUN = function(x) {
if (!require(x, character.only = TRUE)) {
install.packages(x, dependencies = TRUE)
library(x, character.only = TRUE)
}
})
201


Bibliografía
Akaike, H. (1974). A new look at the statistical model identication. IEEE
Transactions on Automatic Control, 19(6):716–723.
Akaike, H. (1983). Information measures and model selection. Bulletin of the
International Statistical Institute, 50:277–290.
Gross, J. and Ligges, U. (2015). nortest: Tests for Normality. R package
version 1.0-4.
Hernandez, F. (2018). usefultools: Useful tools for data analysis. R package
version 0.0.0.9000.
Hernández, F. & Correa, J. (2018). Grácos con R. Universidad Nacional de
Colombia, Medellín, Colombia, primera edition. ISBN xxx-xxxxxxxxx.
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics,
6(2):461–464.
Wei, T. and Simko, V. (2017). corrplot: Visualization of a Correlation Matrix.
R package version 0.84.
Wickham, H. (2015). R Packages. O’Reilly Media, Inc.
Wickham, H. and Bryan, J. (2018). readxl: Read Excel Files. R package
version 1.1.0.
Wickham, H., Chang, W., Henry, L., Pedersen, T. L., Takahashi, K., Wil-
ke, C., and Woo, K. (2018). ggplot2: Create Elegant Data Visuali-
sations Using the Grammar of Graphics. http://ggplot2.tidyverse.org,
https://github.com/tidyverse/ggplot2.
Xie, Y. (2015). Dynamic Documents with R and knitr. Chapman and
Hall/CRC, Boca Raton, Florida, 2nd edition. ISBN 978-1498716963.
Xie, Y. (2018). bookdown: Authoring Books and Technical Documents with R
Markdown. R package version 0.7.
203


Índice alfabético
.csv, 63
.txt, 63
addmargins, 75
array, 11
arreglo, 11
asignación, 29
bloc de notas, 64
ceiling, 42
coeciente de variación, 93
cor, 97
correlación, 97
corrplot, 100
cuantiles, 96
cuartiles, 96
data.frame, 13
deciles, 96
desviación, 89
distribucionecs discretas, 103
else, 48
Excel, 63
tdistr, 134
oor, 42
for, 49
función, 27,53
function, 27
gamlss, 137
guía de estilo, 21
hist, 76
if, 47
ifelse, 48
lectura de bases de datos, 63
legth, 35
list, 16
lista, 16
marco de datos, 13
matrices, 9
max, 35
mean, 82
media, 82
median, 83
mediana, 83
min, 35
moda, 84
nlminb, 132
objetos, 7
operaciones básicas, 29
operadores lógicos, 33
optimize, 130
ordenar, 43
partes de función, 53
percentiles, 96
posición, 43
prod, 35
prop.table, 73
prueba de hipótesis, 173
pruebas lógicas, 31
qqline, 149
qqnorm, 149
QQplot, 149
quantile, 96
range, 35,88
rango, 88
205



