ISM_T12_PRE_VII Solution Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 439 [warning: Documents this large are best viewed by clicking the View PDF Link!]

INSTRUCTOR’S
SOLUTIONS MANUAL
MULTIVARIABLE
WILLIAM ARDIS
Collin County Community College
THOMAS’ CALCULUS
TWELFTH EDITION
BASED ON THE ORIGINAL WORK BY
George B. Thomas, Jr.
Massachusetts Institute of Technology
AS REVISED BY
Maurice D. Weir
Naval Postgraduate School
Joel Hass
University of California, Davis

The author and publisher of this book have used their best efforts in preparing this book. These efforts
include the development, research, and testing of the theories and programs to determine their
effectiveness. The author and publisher make no warranty of any kind, expressed or implied, with regard to
these programs or the documentation contained in this book. The author and publisher shall not be liable in
any event for incidental or consequential damages in connection with, or arising out of, the furnishing,
performance, or use of these programs.
Reproduced by Addison-Wesley from electronic files supplied by the author.
Copyright © 2010, 2005, 2001 Pearson Education, Inc.
Publishing as Pearson Addison-Wesley, 75 Arlington Street, Boston, MA 02116.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or
transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise,
without the prior written permission of the publisher. Printed in the United States of America.
ISBN-13: 978-0-321-60072-1
ISBN-10: 0-321-60072-X
1 2 3 4 5 6 BB 14 13 12 11 10
PREFACE TO THE INSTRUCTOR
This Instructor's Solutions Manual contains the solutions to every exercise in the 12th Edition of THOMAS' CALCULUS
by Maurice Weir and Joel Hass, including the Computer Algebra System (CAS) exercises. The corresponding Student's
Solutions Manual omits the solutions to the even-numbered exercises as well as the solutions to the CAS exercises (because
the CAS command templates would give them all away).
In addition to including the solutions to all of the new exercises in this edition of Thomas, we have carefully revised or
rewritten every solution which appeared in previous solutions manuals to ensure that each solution
conforms exactly to the methods, procedures and steps presented in the textì
is mathematically correctì
includes all of the steps necessary so a typical calculus student can follow the logical argument and algebraì
includes a graph or figure whenever called for by the exercise, or if needed to help with the explanationì
is formatted in an appropriate style to aid in its understandingì
Every CAS exercise is solved in both the MAPLE and computer algebra systems. A template showingMATHEMATICA
an example of the CAS commands needed to execute the solution is provided for each exercise type. Similar exercises within
the text grouping require a change only in the input function or other numerical input parameters associated with the problem
(such as the interval endpoints or the number of iterations).
For more information about other resources available with Thomas' Calculus, visit http://pearsonhighered.com.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
TABLE OF CONTENTS
10 Infinite Sequences and Series 569
10.1 Sequences 569
10.2 Infinite Series 577
10.3 The Integral Test 583
10.4 Comparison Tests 590
10.5 The Ratio and Root Tests 597
10.6 Alternating Series, Absolute and Conditional Convergence 602
10.7 Power Series 608
10.8 Taylor and Maclaurin Series 617
10.9 Convergence of Taylor Series 621
10.10 The Binomial Series and Applications of Taylor Series 627
Practice Exercises 634
Additional and Advanced Exercises 642
11 Parametric Equations and Polar Coordinates 647
11.1 Parametrizations of Plane Curves 647
11.2 Calculus with Parametric Curves 654
11.3 Polar Coordinates 662
11.4 Graphing in Polar Coordinates 667
11.5 Areas and Lengths in Polar Coordinates 674
11.6 Conic Sections 679
11.7 Conics in Polar Coordinates 689
Practice Exercises 699
Additional and Advanced Exercises 709
12 Vectors and the Geometry of Space 715
12.1 Three-Dimensional Coordinate Systems 715
12.2 Vectors 718
12.3 The Dot Product 723
12.4 The Cross Product 728
12.5 Lines and Planes in Space 734
12.6 Cylinders and Quadric Surfaces 741
Practice Exercises 746
Additional Exercises 754
13 Vector-Valued Functions and Motion in Space 759
13.1 Curves in Space and Their Tangents 759
13.2 Integrals of Vector Functions; Projectile Motion 764
13.3 Arc Length in Space 770
13.4 Curvature and Normal Vectors of a Curve 773
13.5 Tangential and Normal Components of Acceleration 778
13.6 Velocity and Acceleration in Polar Coordinates 784
Practice Exercises 785
Additional Exercises 791
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
14 Partial Derivatives 795
14.1 Functions of Several Variables 795
14.2 Limits and Continuity in Higher Dimensions 804
14.3 Partial Derivatives 810
14.4 The Chain Rule 816
14.5 Directional Derivatives and Gradient Vectors 824
14.6 Tangent Planes and Differentials 829
14.7 Extreme Values and Saddle Points 836
14.8 Lagrange Multipliers 849
14.9 Taylor's Formula for Two Variables 857
14.10 Partial Derivatives with Constrained Variables 859
Practice Exercises 862
Additional Exercises 876
15 Multiple Integrals 881
15.1 Double and Iterated Integrals over Rectangles 881
15.2 Double Integrals over General Regions 882
15.3 Area by Double Integration 896
15.4 Double Integrals in Polar Form 900
15.5 Triple Integrals in Rectangular Coordinates 904
15.6 Moments and Centers of Mass 909
15.7 Triple Integrals in Cylindrical and Spherical Coordinates 914
15.8 Substitutions in Multiple Integrals 922
Practice Exercises 927
Additional Exercises 933
16 Integration in Vector Fields 939
16.1 Line Integrals 939
16.2 Vector Fields and Line Integrals; Work, Circulation, and Flux 944
16.3 Path Independence, Potential Functions, and Conservative Fields 952
16.4 Green's Theorem in the Plane 957
16.5 Surfaces and Area 963
16.6 Surface Integrals 972
16.7 Stokes's Theorem 980
16.8 The Divergence Theorem and a Unified Theory 984
Practice Exercises 989
Additional Exercises 997
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

CHAPTER 10 INFINITE SEQUENCES AND SERIES
10.1 SEQUENCES
1. a 0, a , a , a
"#$%
""
#
œœ œœ œœ œœ
11 2 13 2 14 3
1 4 39 416
2. a 1, a , a , a
"#$%
""
#
œœ œœ œœ œœ
11111
1! ! 2 3! 6 4! 24
3. a 1, a , a , a
"# $ %
"
#
"" "
œœœœœœ œœ
(1) ( ) (1) (1)
1 413 615 817
4. a 2 ( 1) 1, a 2 ( 1) 3, a 2 ( 1) 1, a 2 ( 1) 3
"#$%
"#$%
œ œ œ œ œ œ œ œ
5. a , a , a , a
"#$%
#####
""""
#
œœ œœ œœ œœ
2222
22
6. a , a , a , a
"#$%
"""
##
œœœœœœœœ
2213217215
24 28 16
2
7. a 1, a 1 , a , a , a , a ,
"# $ % & '
"" " "
## ## # #
œ œœ œ œ œ œ œ œ œ
3 3 7 7 15 15 31 63
4 4 8 8 16 32
a, a, a, a
()*"!
œœœ œ
127 255 511 1023
64 128 256 512
8. a 1, a , a , a , a , a , a , a ,
"# $ % & ' ( )
"" " """"
####
œœœœœœœœœœ œ
ˆ‰ ˆ‰ ˆ‰
3 6 4 4 5 1 0 7 0 5040 40,320
64
a, a
*"!
""
œœ
362,880 3,628,800
9. a 2, a 1, a , a , a ,
"# $ % &
####
"""
œœ œœ œ œ œ œ œ
(1)(2) (1)(1)
248
(1) (1)
ˆ‰ ˆ‰
4
a , a , a , a , a
'( ) * "!
"""""
##
œœœœ œ
16 3 64 1 8 256
10. a 2, a 1, a , a , a , a ,
"#$%&'
##
""
œ œ œ œ œ œ œ œ œ œ
1( 2) 2( 1)
33 4 5 5 3
22
34
††
††
ˆ‰ ˆ‰
2
3
a, a, a, a
()*"!
""
œ œ œ œ
22
749 5
11. a 1, a 1, a 1 1 2, a 2 1 3, a 3 2 5, a 8, a 13, a 21, a 34, a 55
"#$%&'()*"!
œ œ œœ œœ œœ œ œ œ œ œ
12. a 2, a 1, a , a , a 1, a 2, a 2, a 1, a , a
"# $ % & ' () * "!
"" ""
## ##
œ œ œ œ œ œ œ œ œ œ œ œ
ˆ‰ ˆ‰
ˆ‰
1
13. a ( 1) , n 1, 2, 14. a ( 1) , n 1, 2,
n n
n1 n
œ œ á œ œ á
15. a ( 1) n , n 1, 2, 16. a , n 1, 2,
n n
n1 ()
n
œ œ á œ œ á
# " n1
17. a , n 1, 2, 18. a , n 1, 2,
n n
22n 5
3n 2 nn 1
œœá œ œá
n1
ab ab
19. a n 1, n 1, 2, 20. a n 4 , n 1, 2,
n n
œœá œœá
#
21. a 4n 3, n 1, 2, 22. a 4n 2 , n 1, 2,
n n
œ œ á œ œ á
23. a , n 1, 2, 24. a , n 1, 2,
n n
3n 2 n
n! 5
œœá œœá
3
n1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

570 Chapter 10 Infinite Sequences and Series
25. a , n 1, 2, 26. a , n 1, 2,
n n
1(1) n(1) n
œœá œ œÚÛœá
###
n1 nˆ‰
27. lim 2 (0.1) 2 converges (Theorem 5, #4)
nÄ_ œÊ
n
28. lim lim 1 1 converges
nnÄ_ Ä_
n( ) (1)
nn
"
nn
œœÊ
29. lim lim lim 1 converges
nn nÄ_ Ä_ Ä_
"
# #
2n 2
1n
2
2
œœœÊ
ˆ‰
ˆ‰
n
n
30. lim lim diverges
nnÄ_ Ä_
2n
13n
2n
3
"
ÈÈŠ‹
Š‹
œœ_Ê
n
n
31. lim lim 5 converges
nnÄ_ Ä_
"
5n
n8n
5
1
œœÊ
Š‹
ˆ‰
n
8
n
32. lim lim lim 0 converges
nn nÄ_ Ä_ Ä_
n3 n3
n 5n 6 (n 3)(n 2) n
"
#
œœœÊ
33. lim lim lim (n 1) diverges
nn nÄ_ Ä_ Ä_
n2n1
n1 n1
(n 1)(n 1)
œœœ_Ê
34 lim lim diverges
nnÄ_ Ä_
"
n
70 4n
n
4
œœ_Ê
Š‹
Š‹
n
70
n
35. lim 1 ( 1) does not exist diverges 36. lim ( 1) 1 does not exist diverges
nnÄ_ Ä_
ab ˆ‰
Ê Ê
n n "
n
37. lim 1 lim 1 converges
nnÄ_ Ä_
ˆ‰ˆ‰ ˆ ‰ˆ‰
n
nn nn
" " " " " "
####
œ œÊ
38. lim 2 3 6 converges 39. lim 0 converges
nnÄ_ Ä_
ˆ‰ˆ‰
œÊ œÊ
""
## #
"
nn
n1
()
n1
40. lim lim 0 converges
nnÄ_ Ä_
ˆ‰
œ œÊ
"
##
"
n()
n
n
41. lim lim lim 2 converges
nnnÄ_ Ä_ Ä_
ÉÉÊŠ‹
È
2n 2n
n1 n1
œœ œÊ
2
1n
42. lim lim diverges
nnÄ_ Ä_
""
(0.9) 9
0
nœœ_Ê
ˆ‰
n
43. lim sin sin lim sin 1 converges
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹
111
###
""
œ œ œÊ
nn
44. lim n cos (n ) lim (n )( 1) does not exist diverges
nnÄ_ Ä_
11 1œ Ê
n
45. lim 0 because converges by the Sandwich Theorem for sequences
nÄ_
sin n sin n
nnnn
œŸŸÊ
""
46. lim 0 because 0 converges by the Sandwich Theorem for sequences
nÄ_
sin n sin n
###
"
nnn
œŸŸÊ
47. lim lim 0 converges (using l'Hopital's rule)
^
nnÄ_ Ä_
n
ln 2##
"
nn
œœÊ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.1 Sequences 571
48. lim lim lim lim diverges (using l'Hopital's rule)
^
nn n nÄ_ Ä_ Ä_ Ä_
33 ln 3
n3n 6n 6
3(ln 3) 3(ln 3)
nn nn
œœœœ_Ê
49. lim lim lim lim 0 converges
nnnnÄ_ Ä_ Ä_ Ä_
ln (n )
n
2n
n1 1
"
ÈÈŠ‹
Š‹
œœœ œÊ
ˆ‰
Š‹
n1
n
2
n
n
50. lim lim 1 converges
nnÄ_ Ä_
ln n
ln 2n œœÊ
ˆ‰
ˆ‰
n
2
2n
51. lim 8 1 converges (Theorem 5, #3)
nÄ_
1nœÊ
52. lim (0.03) 1 converges (Theorem 5, #3)
nÄ_
1nœÊ
53. lim 1 e converges (Theorem 5, #5)
nÄ_ ˆ‰
œÊ
7
n
n(
54. lim 1 lim 1 e converges (Theorem 5, #5)
nnÄ_ Ä_
ˆ‰ ’“
œ œ Ê
"" "
nn
()
nn
55. lim 10n lim 10 n 1 1 1 converges (Theorem 5, #3 and #2)
nnÄ_ Ä_
È
nœœœÊ
1n 1nÎÎ
††
56. lim n lim n 1 1 converges (Theorem 5, #2)
nnÄ_ Ä_
Ȉ‰
È
nn
###
œœœÊ
57. lim 1 converges (Theorem 5, #3 and #2)
nÄ_ ˆ‰
3
n1
1n lim 3
lim n
Î"
œœœÊ
n
n
1n
1n
58. lim (n 4) lim x 1 converges; (let x n 4, then use Theorem 5, #2)
nx
Ä_ Ä_
œ œÊ œ
1n4 1xÎÐ Ñ Î
59. lim diverges (Theorem 5, #2)
nÄ_
ln n
n lim n
lim ln n
1
1n 1n
œœœ_Ê
n
n
_
60. lim ln n ln (n 1) lim ln ln lim ln 1 0 converges
nnnÄ_ Ä_ Ä_
cd
ˆ‰ Š‹
œ œ œœÊ
nn
n1 n1
61. lim 4 n lim 4 n 4 1 4 converges (Theorem 5, #2)
nnÄ_ Ä_
ÈÈ
nn
nœœœÊ†
62. lim 3 lim 3 lim 3 3 9 1 9 converges (Theorem 5, #3)
nn nÄ_ Ä_ Ä_
È
n2n 1 21n 1n
Î # Î
œœœœÊ
ab ††
63. lim lim lim 0 and 0 lim 0 converges
nn n nÄ_ Ä_ Ä_ Ä_
n! n! n!
n nnn nn n n n
2 3 (n 1)(n)
nnn
œŸœÊœÊ
"â
â
"
††
†† † ˆ‰
64. lim 0 converges (Theorem 5, #6)
nÄ_
(4)
n!
nœÊ
65. lim lim diverges (Theorem 5, #6)
nnÄ_ Ä_
n!
106n (10 )n
n!
œœ_Ê
"
Š‹
66. lim lim diverges (Theorem 5, #6)
nnÄ_ Ä_
n!
23
nn 6n
n!
œœ_Ê
"
ˆ‰
67. lim lim exp ln lim exp e converges
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ ‰ ˆ ‰ˆ‰
"""
ÎÐ Ñ "
nln nnln n
1lnn ln 1 ln n
œœœÊ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

572 Chapter 10 Infinite Sequences and Series
68. lim ln 1 ln lim 1 ln e 1 converges (Theorem 5, #5)
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹
œ œœÊ
""
nn
nn
69. lim lim exp n ln lim exp
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ Š‹
3n 3n
3n 1 3n 1
nln (3n 1) ln (3n 1)
" "
œœ
n
lim exp lim exp exp e convergesœœœœÊ
nnÄ_ Ä_
Š‹
ˆ‰
33
3n 1 3n 1
n
Š‹
6n 6
(3n 1)(3n 1) 9
#Î$
70. lim lim exp n ln lim exp lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ Š‹
nn
n1 n1
nln nln(n1)
œœ œ
ˆ‰ Š‹
n
nn1
n
lim exp e convergesœœÊ
nÄ_ Š‹
n
n(n 1)
"
71. lim lim x x lim exp ln x lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ‰ ˆ ‰ˆ‰ Š‹
x
2n 1 n 1 n n 1 n
1n 1n ln (2n 1)
n
# #
Î"""
Î
œœ œ
x lim exp xe x, x 0 convergesœœœÊ
nÄ_ ˆ‰
!
2
2n 1
72. lim 1 lim exp n ln 1 lim exp lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ – —
œ œ œ
""
nn
nln 1 1
Š‹ ‚
ˆ‰ Š‹Š ‹
Š‹
n
n
2
nn
n
lim exp e 1 convergesœœœÊ
nÄ_ ˆ‰
!
2n
n1
73. lim lim 0 converges (Theorem 5, #6)
nnÄ_ Ä_
36 36
2n! n!
nn n
n
†
†œœÊ
74. lim lim lim 0 converg
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ‰ˆ‰ ˆ ‰
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
10 12 10 120
11 11 11 121
nnnn
9 11 12 9 12 11 108
10 12 11 10 11 12 110
n n nn nn n
œœœÊ
1es
(Theorem 5, #4)
75. lim tanh n lim lim lim lim 1 converges
nn nnnÄ_ Ä_ Ä_ Ä_ Ä_
œœœœ"œÊ
ee e 2e
ee e 1 2e
n n 2n 2n
n n 2n 2n
"
76. lim sinh (ln n) lim lim diverges
nnnÄ_ Ä_ Ä_
œœœ_Ê
ee
2
n
ln n ln n n
#
ˆ‰
77. lim lim lim lim converges
nn n nÄ_ Ä_ Ä_ Ä_
n sin
2n 1
ˆ‰
n
#
"
œœ œœÊ
sin cos
cos
ˆ‰ ˆ‰
Š‹ Š ‹
ˆ‰ˆ‰Š‹ ˆ‰
n n
222
nnnn
nn
2
n
#
78. lim n 1 cos lim lim lim sin 0 converges
nnnnÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ‰
œ œ œ œÊ
" "
n n
ˆ‰
ˆ‰ ‘ˆ‰Š‹
Š‹
"cos sin
n
n
nn
n
79. lim n sin lim lim lim cos cos 0 1 converges
nnn nÄ_ Ä_ Ä_ Ä_
ÈŠ‹ Š‹
1 1
n n
sin cos
È È
Š‹ Š‹Š ‹
œœ œ œœÊ
111
nn
11
n
2n32
2n32
80. lim 3 5 lim exp ln 3 5 lim exp lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ab ab
’“’“–—
nn nn
1n 1n ln3 5
n1
œ œ œ
ÎÎab
nn 3 ln3 5 ln5
nn
35
nn
lim exp lim exp exp ln 5 5œœœœ
nnÄ_ Ä_
’“ ’“
ab
Š‹
ˆ‰ ˆ‰
ˆ‰
3n
5n
33
nn
55
n
3
5
n
ln 3 ln 5
11
ln 3 ln 5
81. lim tan n converges 82. lim tan n 0 0 converges
nnÄ_ Ä_
" "
# #
"
œÊ œ œÊ
1 1
Èn
†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.1 Sequences 573
83. lim lim 0 converges (Theorem 5, #4)
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹Š‹
"" " "
33
nn
22
n
œ œÊ
ÈÈ
n
84. lim n n lim exp lim exp e 1 converges
nn nÄ_ Ä_ Ä_
È’“ ˆ‰
n#
!
œ œ œ œ Ê
ln n n
nnn
2n 1
ab
85. lim lim lim lim 0 converges
nn n nÄ_ Ä_ Ä_ Ä_
(ln n) 200 (ln n) 200 199 (ln n)
nn n n
200!
œœ œáœœÊ
†
86. lim lim lim lim lim 0 converges
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
(ln n) 10(ln n) 80(ln n)
nnnn
3840
ÈÈÈÈ
œ œœœáœœÊ
–—
Š‹
Š‹
5(ln n)
n
n
87. lim n n n lim n n n lim lim
nn nnÄ_ Ä_ Ä_ Ä_
Š‹Š‹Š‹
ÈÈ
œ œ œ
##
"
nnn
nnn nnn
n
11
È
ÈÈ
Én
convergesœÊ
"
#
88. lim lim lim
nn nÄ_ Ä_ Ä_
""
ÈÈÈ
ÈÈÈ
ÈÈ
ÈÈ
n1 nn n1 nn n1 nn
n1 nn n1 nn
1n
œœ
Š‹Š‹
lim 2 convergesœœÊ
nÄ_ ÉÉ
ˆ‰
11
1
nn
n
89. lim dx lim lim 0 converges (Theorem 5, #1)
nnnÄ_ Ä_ Ä_
"" "
nx n n
ln n
'1
nœœœÊ
90. lim dx lim lim 1 if p 1 converges
nn nÄ_ Ä_ Ä_
'1
nn
1
""""""
x1px1pnp1
pp1p1
œœœÊ
’“ ˆ‰
91. Since a converges lim a L lim a lim L L 1 L 72 L L 72 0
nnn1
72 72
1a 1L
2
ÊœÊ œ ʜʜʜ
nnnÄ_ Ä_ Ä_
nab
L 9 or L 8; since a 0 for n 1 L 8Êœ œ Êœ
n
92. Since a converges lim a L lim a lim L L L 2 L 6 L L 6 0
nnn1
a6
a2 L2
L6 2
ÊœÊ œ ʜʜʜ
nnnÄ_ Ä_ Ä_
n
nab
L 3 or L 2; since a 0 for n 2 L 2Êœ œ Êœ
n
93. Since a converges lim a L lim a lim 8 2a L 8 2L L 2L 8 0 L 2
nnn1n 2
ÊœÊ œ ʜʜʜ
nnnÄ_ Ä_ Ä_
ÈÈ
or L 4; since a 0 for n 3 L 4œÊœ
n
94. Since a converges lim a L lim a lim 8 2a L 8 2L L 2L 8 0 L 2
nnn1n 2
ÊœÊ œ ʜʜʜ
nnnÄ_ Ä_ Ä_
ÈÈ
or L 4; since a 0 for n 2 L 4œÊœ
n
95. Since a converges lim a L lim a lim 5a L 5L L 5L 0 L 0 or L 5; since
nnn1n
2
ÊœÊ œ ʜʜʜœ
nnnÄ_ Ä_ Ä_
ÈÈ
a0 for n1L5
nʜ
96. Since a converges lim a L lim a lim 12 a L 12 L L 25L 144 0
nnn1n 2
ÊœÊ œ ʜʜ
nnnÄ_ Ä_ Ä_
ˆ‰
ÈŠ‹
È
L 9 or L 16; since 12 a 12 for n 1 L 9Êœ œ Êœ
Èn
97. a 2 , n 1, a 2. Since a converges lim a L lim a lim 2 L 2
n1 1 n n n1
111
aaL
œ œ Ê œ Ê œ Ê œ
n nnnnÄ_ Ä_ Ä_
Š‹
L 2L 1 0 L 1 2; since a 0 for n 1 L 1 2Ê œÊ œ„ Ê œ
2n
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

574 Chapter 10 Infinite Sequences and Series
98. a 1 a , n 1, a 1. Since a converges lim a L lim a lim 1 a L 1 L
n1 n 1 n n n1 n
œ œ Ê œÊ œ Êœ
È È
ÈÈ
nnnÄ_ Ä_ Ä_
L L 1 0 L ; since a 0 for n 1 LÊ œÊœ Êœ
215 15
22
n
„
ÈÈ
99. 1, 1, 2, 4, 8, 16, 32, 1, 2 , 2 , 2 , 2 , 2 , 2 , x 1 and x 2 for n 2ᜠá Ê œ œ
!"#$%& "nn2
100. (a) 1 2(1) 1, 3 2(2) 1; let f(a b) (a 2b) 2(a b) a 4ab 4b 2a 4ab 2b
## ## # ## ## #
œ œ ßœ œ
2b a ; a 2b 1 f(a b) 2b a 1; a 2b 1 f(a b) 2b a 1œ œÊßœœ œÊßœœ
### # ## # # ##
(b) r 2 2 r 2
# „" "
# #
nn
œ œ œ œ Ê œ „
ˆ‰ ÊŠ‹
a 2b a 4ab 4b 2a 4ab 2b
a b (a b) (a b) y y
a2b
ab
nn
In the first and second fractions, y n. Let represent the (n 1)th fraction where 1 and b n 1
n
aa
bb
for n a positive integer 3. Now the nth fraction is and a b 2b 2n 2 n y n. Thus,Ê
a2b
ab
n
lim r 2.
nÄ_ nœÈ
101. (a) f(x) x 2; the sequence converges to 1.414213562 2œ ¸
#È
(b) f(x) tan (x) 1; the sequence converges to 0.7853981635œ ¸
1
4
(c) f(x) e ; the sequence 1, 0, 1, 2, 3, 4, 5, divergesœ á
x
102. (a) lim nf lim lim f (0), where x
nxx
Ä_ Ä! Ä!
ˆ‰
" "
w
nx x n
f( x) f(0 x) f(0)
œœ œ œ
??
??
?? ?
(b) lim n tan f (0) 1, f(x) tan x
nÄ_
" w "
""
ˆ‰
n10
œœ œ œ
(c) lim n e 1 f (0) e 1, f(x) e 1
nÄ_ ab
1n x
œ œœ œ
w!
(d) lim n ln 1 f (0) 2, f(x) ln (1 2x)
nÄ_ ˆ‰
œ œ œ œ
22
n 1 2(0)
w
103. (a) If a 2n 1, then b 2n 2n 2n 2n, c 2n 2nœ œÚ ÛœÚ ÛœÚ Ûœ œÜ ÝœÜ Ý
a4n4n1 a
## # # #
" "
## #
2n 2n 1 and a b (2n 1) 2n 2n 4n 4n 1 4n 8n 4nœ œ œ
# ## # # # %$#
#
ab
4n 8n 8n 4n 1 2n 2n 1 c .œœ œ
%$# # #
#
ab
(b) lim lim 1 or lim lim sin lim sin 1
aa aa 2
Ä_ Ä_ Ä_ Ä_ ÄÎ
ÚÛ ÚÛ
ÜÝ ÜÝ
aa
aa
œœœœœ
2n 2n
2n 2n 1
))
)1
104. (a) lim (2n ) lim exp lim exp lim exp e 1;
nn n nÄ_ Ä_ Ä_ Ä_
112n ln 2n
2n n
Î !
##
"
ab Š‹
œœ œœœ
ˆ‰ ˆ‰
1
2
2n
n! 2n , Stirlings approximation n! (2n ) for large values of n¸Ê¸¸
ˆ‰ ˆ‰
ÈÈ
nnn
eee
12n
nn
11
Îab
(b) n n!
40 15.76852702 14.71517765
50 19.48325423 18.393
È
nn
e
97206
60 23.19189561 22.07276647
105. (a) lim lim lim 0
nn nÄ_ Ä_ Ä_
ln n
ncn cn
cc1c
œœœ
ˆ‰
n"
(b) For all 0, there exists an N e such that n e ln n ln n ln%œÊÊ
Ð ÑÎ Ð ÑÎ "
ln c ln c c
ln
c
%%
%
%
ˆ‰
n 0 lim 0
n
ÊÊÊ Ê œ
Ä_
c
nn n
"" " "
%cc c
%%
¸¸
106. Let {a } and {b } be sequences both converging to L. Define {c } by c b and c a , where
nn n2nn2n1n
œœ
n 1, 2, 3, . For all 0 there exists N such that when n N then a L and there exists Nχ %%
"" #
kk
n
such that when n N then b L . If n 1 2max{N N }, then c L , so {c } converges to L.ß
#"#
kk kk
nnn
%%
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.1 Sequences 575
107. lim n lim exp ln n lim exp e 1
nn nÄ_ Ä_ Ä_
1n
nn
Î!
""
œœœœ
ˆ‰ ˆ‰
108. lim x lim exp ln x e 1, because x remains fixed while n gets large
nnÄ_ Ä_
1n
n
Î!
"
œœœ
ˆ‰
109. Assume the hypotheses of the theorem and let be a positive number. For all there exists a N such that%%
"
when n N then a L a L L a , and there exists a N such that whenÊÊ
" #
kk
nn n
%% % %
n N then c L c L c L . If n max{N N }, thenÊÊß
#"#
kk
nnn
%% % %
L abcL bL lim bL. Ÿ Ÿ Ê Ê œ%%%
nnn n n
kk nÄ_
110. Let . We have f continuous at L there exists so that x L f(x) f(L) . Also, a L there%$$%! Ê Ê Ä Êkk k k n
exists N so that for n N a L . Thus for n N, f(a ) f(L) f(a ) f(L). Ê Äkk k k
nnn
$%
111. a a 3n 3n 4n 4 3n 6n n 2
n1 n 3(n 1) 1
(n 1) 1 n 1 n n 1
3n 1 3n 4 3n 1
#
##
Ê ÊÊ
4 2; the steps are reversible so the sequence is nondecreasing; 3 3n 1 3n 3Ê Ê
3n
n1
"
1 3; the steps are reversible so the sequence is bounded above by 3Ê
112. a a
n1 n (2(n 1) 3)! (2n 3)! (2n 5)! (2n 3)! (2n 5)! (n 2)!
((n 1) 1)! (n 1)! (n 2)! (n 1)! (2n 3)! (n 1)!
Ê ÊÊ
(2n 5)(2n 4) n 2; the steps are reversible so the sequence is nondecreasing; the sequence is notÊ
bounded since (2n 3)(2n 2) (n 2) can become as large as we please
(2n 3)!
(n 1)!
œ â
113. a a 2 3 n 1 which is true for n 5; the steps are
n1 n 23 23 23
(n 1)! n! 2 3 n!
(n 1)!
ŸÊ Ÿ Ê Ÿ Ê Ÿ
n1n1 nn n1n1
nn †
reversible so the sequence is decreasing after a , but it is not nondecreasing for all its terms; a 6, a 18,
&"#
œœ
a 36, a 54, a 64.8 the sequence is bounded from above by 64.8
$%&
œœœœÊ
324
5
114. a a 2 2 ; the steps are
n1 n 2222 2
n1 n n n1 n(n 1)
# # # # #
"" "" "
Ê Ê Ê
n1 n n1 n n1
reversible so the sequence is nondecreasing; 2 2 the sequence is bounded from above Ÿ Ê
2
n
"
#n
115. a 1 converges because 0 by Example 1; also it is a nondecreasing sequence bounded above by 1
nœ Ä
""
nn
116. a n diverges because n and 0 by Example 1, so the sequence is unbounded
nœ Ä_ Ä
""
nn
117. a 1 and 0 ; since 0 (by Example 1) 0, the sequence converges; also it is
n21
2nn
œœ Ä ÊÄ
n
nn n n
" """ "
## #
a nondecreasing sequence bounded above by 1
118. a ; the sequence converges to by Theorem 5, #4
n21 2
333
n
œœ !
n
nn
"
ˆ‰
119. a ( 1) 1 diverges because a 0 for n odd, while for n even a 2 1 converges to 2; it
nnn
nn1
n n
œ œ œ ab
ˆ‰ ˆ ‰
"
diverges by definition of divergence
120. x max {cos 1 cos 2 cos 3 cos n} and x max {cos 1 cos 2 cos 3 cos (n 1)} x with x 1
nn1 nn
œ ßßßáß œ ßßßáß Ÿ
so the sequence is nondecreasing and bounded above by 1 the sequence converges.Ê
121. a a n 1 2n 2n n 2n 2n n 1 n
nn1 12n
n
2(n 1)
n1
Í Í Í
"
##
ÈÈ
ÈÈ ÈÈ
ÈÈ
ÈÈ
and 2 ; thus the sequence is nonincreasing and bounded below by 2 it converges
12n
n
È
ÈÊ
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

576 Chapter 10 Infinite Sequences and Series
122. a a n 2n 1 n 2n 1 0 and 1; thus the sequence is
nn1 n1 n1
nn1 n
(n 1)
Í ÍÍ
"
##
nonincreasing and bounded below by 1 it convergesÊ
123. 4 so a a 4 4 1 and
43 3 3 3 3 3 3
44 4444 4
nnnnn1
nn1
n1 n
n
"
œ Í Í Í
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
4 4; thus the sequence is nonincreasing and bounded below by 4 it converges Ê
ˆ‰
3
4
n
124. a 1, a 2 3, a 2(2 3) 3 2 2 3, a 2 2 2 3 3 2 2 1 3,
"# $ %
##$$
œ œ œ œ " œ " œ ab a b abab
22
††
a 2 2 2 1 3 3 2 2 1 3, , a 2 2 1 3 2 3 2 3
&$ $ % % " " "
œœáœ œ cdab abab nnn n n1
†
2(13)3 23; a a 23 2 3 2 2 12œ œ Í Í Í Ÿ
n1 n n n1 n n1
nn1
so the sequence is nonincreasing but not bounded below and therefore diverges
125. Let 0 M 1 and let N be an integer greater than . Then n N n n nM M Ê Ê
MM
1M 1M
n M nM n M(n 1) M.Ê Ê Ê
n
n1
126. Since M is a least upper bound and M is an upper bound, M M . Since M is a least upper bound and M
"#"##"
Ÿ
is an upper bound, M M . We conclude that M M so the least upper bound is unique.
#" "#
Ÿœ
127. The sequence a 1 is the sequence , , , , . This sequence is bounded above by ,
n() 33 3
œ á
"
# #### #
""
n
but it clearly does not converge, by definition of convergence.
128. Let L be the limit of the convergent sequence {a }. Then by definition of convergence, for there
n%
#
corresponds an N such that for all m and n, m N a L and n N a L . NowÊ Ê kk kk
mn
%%
##
a a a L L a a L L a whenever m N and n N.kkk kkkkk
mn m n m n
œ Ÿ œ
%%
##%
129. Given an 0, by definition of convergence there corresponds an N such that for all n N,%
La and La . Now LL LaaL La aL 2.kk kk kkk kkkkk
"# #"#"#"
œ Ÿ œ
nn nnnn
%% %%%
L L 2 says that the difference between two fixed values is smaller than any positive number 2 .kk
#"
% %
The only nonnegative number smaller than every positive number is 0, so L L 0 or L L .kk
"# " #
œ œ
130. Let k(n) and i(n) be two order-preserving functions whose domains are the set of positive integers and whose
ranges are a subset of the positive integers. Consider the two subsequences a and a , where a L ,
kn in knÐÑ ÐÑ ÐÑ "
Ä
a L and L L . Thus a a L L 0. So there does not exist N such that for all m, n N
in kn inÐÑ ÐÑ ÐÑ
#"# "#
Ä Á Ä
¸¸
kk
a a . So by Exercise 128, the sequence a is not convergent and hence diverges.Ê Ö×kk
mn n
%
131. a L given an 0 there corresponds an N such that 2k N a L . Similarly,
2k 2k
ÄÍ Ê %%
""
cdkk
a L 2k 1 N a L . Let N max{N N }. Then n N a L whether
2k 1 2k 1 n# "#
ÄÍ Ê œ ß Ê cd kkkk%%
n is even or odd, and hence a L.
nÄ
132. Assume a 0. This implies that given an 0 there corresponds an N such that n N a 0
n n
Ä Ê%%kk
a a a 0 a 0. On the other hand, assume a 0. This implies thatÊÊ Ê Ê Ä Äkk k k k k kk kkkk kk
nn n n n
%% %
given an 0 there corresponds an N such that for n N, a 0 a a%%%%ÊÊkk kk kkkk kk
nnn
a 0 a 0.ÊÊÄkk
nn
%
133. (a) f(x) x a f (x) 2x x x xœÊ œ Ê œ Ê œ œ œ
#w
##
n1 n n1
xa 2x xa xa
x2x2x
x
nnnnn
nnn
na
x
ab ˆ‰
(b) x 2, x 1.75, x 1.732142857, x 1.73205081, x 1.732050808; we are finding the positive
"# $ % &
œœ œ œ œ
number where x 3 0; that is, where x 3, x 0, or where x 3 .
##
œ œ œ
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.2 Infinite Series 577
134. x 1, x 1 cos (1) 1.540302306, x 1.540302306 cos (1 cos (1)) 1.570791601,
"# $
œœ œ œ œ
x 1.570791601 cos (1.570791601) 1.570796327 to 9 decimal places. After a few steps, the
%#
œ œœ
1
arc x and line segment cos x are nearly the same as the quarter circle.ab ab
n1 n1
135-146. Example CAS Commands:
: (sequence functions may vary):Mathematica
Clear[a, n]
a[n_]; = n1 / n
first25= Table[N[a[n]],{n, 1, 25}]
Limit[a[n], n 8]Ä
Mathematica: (sequence functions may vary):
Clear[a, n]
a[n_]; = n1 / n
first25= Table[N[a[n]],{n, 1, 25}]
Limit[a[n], n 8]Ä
The last command (Limit) will not always work in Mathematica. You could also explore the limit by enlarging your table
to more than the first 25 values.
If you know the limit (1 in the above example), to determine how far to go to have all further terms within 0.01 of the
limit, do the following.
Clear[minN, lim]
lim= 1
Do[{diff=Abs[a[n] lim], If[diff < .01, {minN= n, Abort[]}]}, {n, 2, 1000}]
minN
For sequences that are given recursively, the following code is suggested. The portion of the command a[n_]:=a[n] stores
the elements of the sequence and helps to streamline computation.
Clear[a, n]
a[1]= 1;
a[n_]; = a[n]= a[n 1] (1/5) (n 1)
first25= Table[N[a[n]], {n, 1, 25}]
The limit command does not work in this case, but the limit can be observed as 1.25.
Clear[minN, lim]
lim= 1.25
Do[{diff=Abs[a[n] lim], If[diff < .01, {minN= n, Abort[]}]}, {n, 2, 1000}]
minN
10.2 INFINITE SERIES
1. s lim s 3
nn
a1 r
(1 r)
21
1 1
2
œœ Ê œœ
ab ˆ‰ˆ‰
ˆ‰ ˆ‰
n3
n
33
nÄ_
2. s lim s
nn
a1 r
(1 r) 11
1
1 1
œœ Ê œœ
abˆ‰ˆ ‰ ˆ‰ˆ‰
ˆ‰ ˆ‰
"
n99
100 100 100
n
100 100
nÄ_
3. s lim s
nn
a1 r
(1 r) 3
1
1
2
œœ Ê œœ
ab ˆ‰
ˆ‰ ˆ‰
"
nn
3
nÄ_
4. s , a geometric series where r 1 divergence
n1 ( 2)
1 ( 2)
œÊ
nkk
5. s lim s
""" """" """" "
# # # # # # #(n 1)(n ) n 1 n 3 3 4 n 1 n n
n n
œ Êœá œ Ê œ
ˆ‰ˆ‰ ˆ ‰ nÄ_
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

578 Chapter 10 Infinite Sequences and Series
6. s 5 5
5 5 5 5 55 55 5 5 5 5 5
n(n 1) nn 1 2 23 34 n 1n nn 1 n 1
n
œ Êœá œ
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
lim s 5ʜ
nÄ_ n
7. 1 , the sum of this geometric series is á œ œ
"" " " "
41664 5
1 1
4
ˆ‰ ˆ‰
44
8. , the sum of this geometric series is
"" " "
#16 64 256 1
1
á œ
ˆ‰
ˆ‰
16
4
9. , the sum of this geometric series is
77 7 7
41664 3
1
á œ
ˆ‰
ˆ‰
7
4
4
10. 5 , the sum of this geometric series is 4á œ
55 5 5
41664 1
ˆ‰
4
11. (5 1) , is the sum of two geometric series; the sum is á
ˆ‰ˆ‰ˆ‰
555
34987##
"" "
10
5323
1 1
"
##
ˆ‰ ˆ‰
œœ
3
12. (5 1) , is the difference of two geometric series; the sum is á
ˆ‰ˆ‰ˆ‰
555
34987##
"" "
10
5317
1 1
"
##
ˆ‰ ˆ‰
œœ
3
13. (1 1) , is the sum of two geometric series; the sum is á
ˆ‰ˆ‰ˆ ‰
11 1
5425815##
"" "
2
1517
1 1 66
"
ˆ‰ ˆ‰
œœ
5
14. 2 2 1 ; the sum of this geometric series is 2 áœ á œ
48 16 24 8 10
525125 525125 3
1
ˆ‰ Š‹
"
ˆ‰
2
5
15. Series is geometric with r 1 Converges to œÊ Ê œ
22 15
55 3
1
¹¹ 2
5
16. Series is geometric with r 3 3 1 Divergesœ Ê Ê
¹¹
17. Series is geometric with r 1 Converges to œÊ Ê œ
11 1
88 7
1
¹¹ 1
81
8
18. Series is geometric with r 1 Converges to œ Ê Ê œ
22 2
33 5
1
¹¹
2
32
3
ˆ‰
19. 0.23 20. 0.234 œœœ œ œœ
!!
ˆ‰ ˆ‰
_ _
œ œn0 n0
23 23 234 234
100 10 99 1000 10 999
n n
1 1
" "
Š‹ Š‹
ˆ‰ Š‹
23 234
100 1000
1000
100
21. 0.7 22. 0.d œœœ œœœ
!!
ˆ‰ ˆ‰
_ _
œ œn0 n0
77 dd
10 10 9 10 10 9
n n
1 1
" "
Š‹ Š‹
Š‹ Š‹
7 d
10 10
10 10
23. 0.06 œœœœ
!ˆ‰ˆ‰ˆ‰
_
œn0
16 6
10 10 10 90 15
n
1
""
Š‹
Š‹
6
100
10
24. 1.414 1 1 1œ œ œ œ
!ˆ‰
_
œn0
414 414 413
1000 10 999 999
n
1
""
Š‹
Š‹
414
1000
1000
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.2 Infinite Series 579
25. 1.24123 œ œ œ œ œ œ
124 123 124 124 123 124 123
100 10 10 100 100 10 10 100 99,900 99,900 33,300
n
1
123,999 41,333
!ˆ‰
_
œn0
"
Š‹
Š‹
123
10
10
26. 3.142857 3 3 3œ œ œ œ œ
!ˆ‰
_
œn0
142,857 142,857 3,142,854 116,402
10 10 10 1 999,999 37,037
n
1
"
Š‹
Š‹
142,857
10
10
27. 1 0 divergeslim lim
nn
n1
n10 1
Ä_ Ä_
œ œÁÊ
28. 1 0 divergeslim lim lim lim
nnnn
nn 1
n2n3 n 5n6 2n5 2
nn 2n1 2
Ä_ Ä_ Ä_ Ä_
ab
abab
œ œ œ œÁÊ
2
2
29. 0 test inconclusivelim
n
1
n4
Ä_ œÊ
30. 0 test inconclusivelim lim
nn
n1
n3 2n
Ä_ Ä_
2œœÊ
31. cos cos 0 1 0 divergeslim
n
1
n
Ä_ œ œÁÊ
32. 1 0 divergeslim lim lim lim
nnnn
eee1
en e1 e 1
Ä_ Ä_ Ä_ Ä_
nnn
nnn
œ œ œ œÁÊ
33. ln 0 divergeslim
n
1
n
Ä_ œ_Á Ê
34. cos n does not exist divergeslim
nÄ_
1œÊ
35. s 1 1 lim s
k k
22334 k 1kkk 1 k 1
œá œ Ê
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
""""" """" "
kÄ_
lim 1 1, series converges to 1œœ
kÄ_ ˆ‰
"
k 1
36. s 3 lim s
k k
33 33 3 3 3 3 3 3 3
14 49 916 k k
k 1 k 1 k 1
œ á œ Ê
ˆ‰ˆ‰ˆ‰ Š‹Š‹
ab ab ab
22 2 2 2 kÄ_
lim 3 3, series converges to 3œœ
kÄ_ Š‹
3
k 1ab2
37. s ln 2 ln 1 ln 3 ln 2 ln 4 ln 3 ln k ln k 1 ln k 1 ln k
kχ
Š‹Š‹Š‹Š ‹Š ‹
ÈÈ È È
ÈÈ
ÈÈ È
È
ln k 1 ln 1 ln k 1 lim s lim ln k 1 ; series divergesœœÊ œ œ_
ÈÈ È
ÈkkÄ_ Ä_
k
38. s tan 1 tan 0 tan 2 tan 1 tan 3 tan 2 tan k tan k 1 tan k 1 tan k
kχ abababa ba bab ab
tan k 1 tan 0 tan k 1 lim sk lim tan k 1 does not exist; series divergesœœÊ œ œab ab ab
kkÄ_ Ä_
39. s cos cos cos cos cos cos
k11 11 11
11 11 11
23 34 45
χ
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
cos cos cos cos cosœ
ˆ‰ˆ ‰ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰
# #
11 1 1 1
11 1 1 1
kk1 k1k3k
1
lim s lim cos , series converges to Ê œ œœ
kkÄ_ Ä_
k3k326 6
11
’“
ˆ‰
1111 1
#
40. s 5 4 6 5 7 6 k 3 k 2 k 4 k 3
kχ
Š‹Š‹Š‹Š ‹Š ‹
ÈÈÈ
ÈÈÈ
ÈÈ ÈÈ
k 4 2 lim s lim k 4 2 ; series divergesœÊ œ œ_
ÈÈ
’“
kkÄ_ Ä_
k
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

580 Chapter 10 Infinite Sequences and Series
41. s 1
4
(4n 3)(4n 1) 4n 3 4n 1 5 5 9 9 13 4k 7 4k 3
k
" " """"" " "
œ Êœ á
ˆ‰ˆ‰ˆ ‰ ˆ ‰
1 lim s lim 1 1œÊ œ œ
ˆ‰ ˆ‰
"" " "
4k 3 4k 1 4k 1 4k 1
k
kkÄ_ Ä_
42. A(2n 1) B(2n 1) 6 (2A 2B)n (A B) 6
6AB
(2n 1)(2n 1) 2n 1 2n 1 (2n 1)(2n 1)
A(2n 1) B(2n 1)
œœ ʜʜ
2A 6 A 3 and B 3. Hence, 3
2A 2B 0 A B 0
A B6 AB6
ÊÊʜʜœ œ
œ œ
œ œ
œœ !!
ˆ‰
kk
n1 n1œœ
6
(2n 1)(2n 1) n 1 n 1 # #
""
3 3 1 the sum isœ á œ Ê
Š‹
ˆ‰
"""""" " " " "
# # #133557 (k 1) 12k 1 k 1 k 1
lim 3 1 3
kÄ_ ˆ‰
œ
"
#k 1
43. 40n A B C D
(2n 1) (2n 1) (2n 1) (2n 1) (2n 1) (2n 1) (2n 1) (2n 1)
A(2n 1)(2n 1) B(2n 1) C(2n 1)(2n 1) D(2n 1)
œ œ
A(2n 1)(2n 1) B(2n 1) C(2n 1)(2n 1) D(2n 1) 40nÊ œ
## ##
A8n4n2n1B4n4n1C8n4n2n1D4n4n140nÊ œ œabababab
$##$# #
(8A 8C)n (4A 4B 4C 4D)n ( 2A 4B 2C 4D)n ( A B C D) 40nÊ œ
$#
8A 8C 0 8A 8C 0
4A 4B 4C 4D 0 A B C D 0
2A 4B 2C 4D 40 A 2
A B C D 0
ÊÊ
œ œ
œ œ
œ
œ
ÚÚ
ÝÝ
ÝÝ
ÛÛ
ÝÝ
ÝÝ
ÜÜ
BC2D20 2B2D 20
A BC D 0
4B 20 B 5
B D 0
œ œ
œ
Êʜʜ
œ
œ
and D 5 C 0 and A 0. Hence,
A C 0
A5C50
œ Ê Ê œ œ
œ
œ
œ!’“
k
n1œ
40n
(n 1)(2n 1)#
5 5œ œ á
!’“Š ‹
k
n1œ
" " """ " " " " "
# # # # # #( n 1) ( n 1) 1 9 9 5 5 (2(k 1) 1) ( k 1) ( k 1)
5 1 the sum is lim 5 1 5œ Ê œ
Š‹ Š‹
""
(2k 1) (2k 1)
nÄ_
44. s 1
2n 1
n (n 1) n (n 1) 4 4 9 9 16 (k 1) k k (k 1)
k
"" """"" "" ""
œ Ê œ á
ˆ‰ˆ‰ˆ ‰ ’“’“
lim s lim 1 1Êœœ
kkÄ_ Ä_
k(k 1)
’“
"
45. s 1 1
k22 4
33 k 1 k k k 1 k 1
œá œ
Š‹Š‹Š‹Š ‹Š ‹
""""" """" "
ÈÈÈÈÈ ÈÈÈÈ È
lim s lim 1 1Êœœ
kkÄ_ Ä_
kk 1
Š‹
"
È
46. s
kœá œ
ˆ‰ˆ‰ˆ‰ˆ ‰ˆ ‰
"" "" "" " " " " " "
# #
##### # ### #
1k1 1k 1k 1k1 1k1
lim sÊ œœ
kÄ_ k1
"" "
##
47. skln 3 ln ln 4 ln 3 ln 5 ln 4 ln (k 1) ln k ln (k 2) ln (k 1)
χ
ˆ‰ˆ‰ˆ‰Š‹Š ‹
"" "" "" " " " "
#
lim sœ Ê œ
"" "
# #ln ln (k 2) ln
k
kÄ_
48. s tan (1) tan (2) tan (2) tan (3) tan (k 1) tan (k)
kχcdcdc d
" " " " " "
tan (k) tan (k 1) tan (1) tan (k 1) lim s tan (1) œ Ê œ œœcd
" " " " "
##
kÄ_ k44
111 1
49. convergent geometric series with sum 2 2
"
1
2
21
Š‹ È
È
2
œœ
È
50. divergent geometric series with r 2 1 51. convergent geometric series with sum 1kk È
œ œ
Š‹
Š‹
3
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.2 Infinite Series 581
52. lim ( 1) n 0 diverges 53. lim cos (n ) lim ( 1) 0 diverges
nnnÄ_ Ä_ Ä_
ÁÊ œ ÁÊ
n1 n1
54. cos (n ) ( 1) convergent geometric series with sum 1œ Ê œ
n
1
5
6
"
Š‹
5
55. convergent geometric series with sum "
1
e
e1
Š‹
e
œ
56. lim ln 0 diverges
nÄ_
"
3nœ_Á Ê
57. convergent geometric series with sum 2
220182
1 999
Š‹
10
œœ
58. convergent geometric series with sum "
1
x
x 1
Š‹
x
œ
59. difference of two geometric series with sum 3
""
##
1 1
33
Š‹ Š‹
2
33
œœ
60. lim 1 lim 1 e 0 diverges
nnÄ_ Ä_
ˆ‰ ˆ ‰
œ œÁÊ
""
"
nn
nn
61. lim 0 diverges 62. lim lim lim n diverges
nnnnÄ_ Ä_ Ä_ Ä_
n! nnnn
1000 n! 1 n
n
n
œ_Á Ê œ œ_ Ê
†
†
â
#â
63. ; both and are geometric series, and both conve
!!!!! !!
ˆ‰ ˆ‰ ˆ‰ ˆ‰
_____ _ _
œœœœœ œ œn1 n1 n1 n1 n1 n1 n1
23 2 3 1 3 1 3
4442 4 2 4
nn n n
nn n n
nnn
œœ œ rge
since r 1 and r 1, respectivley 1 and 3œÊ œÊ Ê œ œ œ œÊ
11 33 1 3
22 44 2 4
nn
11
¹¹ ¹¹ !!
ˆ‰ ˆ‰
__
œœn1 n1
13
24
13
24
1 3 4 by Theorem 8, part (1)
!
_
œn1
23
4
nn
n
œœ
64. 1 0 diverges by n term test for divergencelim lim lim
nnn
24 1
34 1
th
Ä_ Ä_ Ä_
" "
" "
nn
nn
21
n
42
n
33
nn
44
n
n
œ œ œ œÁÊ
ˆ‰
ˆ‰
65. ln ln (n) ln (n 1) s ln (1) ln (2) ln (2) ln (3) ln (3) ln (4)
!!
ˆ‰ c dcdcdcd
__
œœn1 n1
n
n 1œ Êœá
k
ln (k 1) ln (k) ln (k) ln (k 1) ln (k 1) lim s , divergesœÊ œ_Êcdcd kÄ_ k
66. lim a lim ln ln 0 diverges
nnÄ_ Ä_
nn
2n 1
œœÁÊ
ˆ‰ˆ‰
#
"
67. convergent geometric series with sum "
1 e
ˆ‰
eœ1
1
68. divergent geometric series with r 1kkœ¸
e 23.141
22.459
1e
69. ( 1) x ( x) ; a 1, r x; converges to for x 1
!! kk
__
œœn0 n0
œ œœ œ
nn n ""
1 ( x) 1 x
70. ( 1) x x ; a 1, r x ; converges to for x 1
!!
ab kk
__
œœn0 n0
œ œœ
n2n n
1 x
##
"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

582 Chapter 10 Infinite Sequences and Series
71. a 3, r ; converges to for 1 1 or 1 x 3œœ œ
x 1 3 6 x
1 3 x
"
##
Š‹
x
72. ; a , r ; converges to
!!
ˆ‰ ˆ‰
__
œœn0 n0
(1)
3 sin x 3 sin x 3 sin x
nn
1
# # #
"""""
nœœœ ˆ‰
Š‹
3 sin x
for all x since for all xœœ ŸŸ
3 sin x 3 sin x
2(4 sin x) 8 2 sin x 4 3 sin x
"""
#
ˆ‰
73. a 1, r 2x; converges to for 2x 1 or xœœ
""
#1 2x kk kk
74. a 1, r ; converges to for 1 or x 1.œœ œ
""
xx 1x
1
x1
Š‹
x¸¸ kk
75. a 1, r (x 1) ; converges to for x 1 1 or 2 x 0œ œ œ
n
1 (x 1) x
""
# kk
76. a 1, r ; converges to for 1 or 1 x 5œœ œ
3 x 2 3 x
1 x 1
"
##
Š‹
3 x ¸¸
77. a 1, r sin x; converges to for x (2k 1) , k an integerœœ Á
"
#1 sin x
1
78. a 1, r ln x; converges to for ln x 1 or e x eœœ
"
"
1 ln x kk
79. (a) (b) (c)
!!!
___
œ œ œn 2 n0 n5
"" "
#(n 4)(n 5) (n 2)(n 3) (n 3)(n )
80. (a) (b) (c)
!!!
___
œ œ œn 1 n3 n20
55 5
(n 2)(n 3) (n 2)(n 1) (n 19)(n 18)
81. (a) one example is 1
""" "
#
ᜠœ
4816 1
Š‹
Š‹
(b) one example is 3 ᜠœ
333 3
4816 1
#
Š‹
Š‹
3
(c) one example is 1 1 0. ᜠœ
""" "
#
4816 1
Š‹
Š‹
82. The series k is a geometric series whose sum is k where k can be any positive or negative number.
!ˆ‰
_
œn0
1
2
n1
1
Š‹
Š‹
k
œ
83. Let a b . Then a b 1, while (1) diverges.
nn n n
nn
a
b
œœ œ œ œ œ
ˆ‰ ˆ‰
!!! ! !
Š‹
""
##
__ _ _ _
œœ œ œ œn1 n1 n1 n1 n1
n
n
84. Let a b . Then a b 1, while a b AB.
nn n n nn
nnn
43
œœ œ œ œ œ œÁ
ˆ‰ ˆ‰ ˆ‰
!!! ! !
ab
""""
##
__ _ _ _
œœ œ œ œn1 n1 n1 n1 n1
85. Let a and b . Then A a , B b 1 and 1 .
nn n n
43bB
nn n
aA
œœ œœœœ œœÁ
ˆ‰ ˆ‰ ˆ‰
!!!!
Š‹
"" " "
# #
____
œœœœn1 n1 n1 n1
n
n
86. Yes: diverges. The reasoning: a converges a 0 diverges by the
!! !
Š‹ Š‹
"""
aaa
nn
nnn
Ê Ä Ê Ä_Ê
nth-Term Test.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.3 The Integral Test 583
87. Since the sum of a finite number of terms is finite, adding or subtracting a finite number of terms from a series
that diverges does not change the divergence of the series.
88. Let A a a a and lim A A. Assume a b converges to S. Let
nnnnn
œá œ
"# nÄ_ !ab
S(ab)(ab) (ab) S(aa a)(bb b)
nnnnnn
œá Êœáá
"" ## "# "#
b b b S A lim b b b S A b converges. ThisÊáœ Ê á œÊ
"# "#nnn n n
nÄ_ ab
!
contradicts the assumption that b diverges; therefore, a b diverges.
!!
ab
nnn
89. (a) 5 1 r r ; 2 2 2
22 333
1r 5 5 5 5
#
œÊœÊœ á
ˆ‰ ˆ‰
(b) 5 1 r r ;
Š‹
13
2
1 r 10 10 2 10 10 10
13 3 13 13 3 13 3 13 3
###
#$
œÊœÊœá
ˆ‰ ˆ‰ ˆ‰
90. 1 e e 9 1 e e b ln ᜠœÊœ Ê œ Êœ
b2b b b
1e 999
88""
bˆ‰
91. s 1 2r r 2r r 2r r 2r , n 0, 1,
n2n 2n 1
œ á œ á
#$%&
s 1rr r 2r2r2r 2r lim sÊ œ á á Ê œ
n n
2n 2n 1
1r 1r
2r
aba b
#% $ & "
nÄ_
, if r 1 or r 1œ
12r
1r
#
kk kk
92. L sœ œ
naar
1r 1r 1r
a1 r
ab
nn
93. area 2 2 (1) 4 2 1 8 mœ á œ á œ œ
## #
##
""
#
Š‹ Š‹
ÈÈ2
4
1
94. (a) L 3, L 3 , L 3 , , L 3 lim L lim 3
"# $
#
œœ œ áœ Ê œ œ_
ˆ‰ ˆ‰ ˆ‰ ˆ‰
44 4 4
33 3 3
nn
n1 n1
nnÄ_ Ä_
(b) Using the fact that the area of an equilateral triangle of side length s is s , we see that A ,
ÈÈ
33
44
2"œ
AA3 , AA34 ,
#" $#
""
##
œ œ œ œ
Š‹ Š‹
ˆ‰ ˆ‰
ab
È ÈÈ È ÈÈÈ
3 33 3 333
43 4 1 43 4 12 7
22
2
A A 3 4 , A A 3 4 , . . . ,
%$ ""
œ œab ab
Š‹ Š‹
ˆ‰ ˆ‰
23
33
43 43
22
54
ÈÈ
34
A 34 334 33 .
n
nn n
k2 k2 k2
œ œ œ
ÈÈÈ È
333 3
4434 94
k2 k
k1 k1 4
9
!! !
ab ab
Š‹
ˆ‰ ˆ‰
ÈÈ
Œ
$
""
2
k
k1
lim A lim 3 3 3 3 3 3 1
nnÄ_ Ä_
n
n
k2
œ œ œ œ
ŒŒ
ÈÈÈ
Œ
!ˆ‰ ˆ ‰
ÈÈÈÈ
3333
4442045
413
91
k
k1
1
36 4
9
Aœœ
È3
45 5
88
ˆ‰ "
10.3 THE INTEGRAL TEST
1. f x is positive, continuous, and decreasing for x 1; dx lim dx lim ab ’“
œœœ
1111
xxxx
222
''
11
b
1
b
bbÄ_ Ä_
lim 1 1 dx converges convergesœœÊ Ê
bÄ_ ˆ‰ !
11 1
bx n
n1
'122
œ
_
2. f x is positive, continuous, and decreasing for x 1; dx lim dx lim xab ’“
œœœ
1115
xxx4
0.8
0.2 0.2 0.2
''
11
b
1
b
bbÄ_ Ä_
lim b dx diverges divergesœœ_Ê Ê
bÄ_ ˆ‰ !
55 1 1
44 x n
0.8
n1
'10.2 0.2
œ
_
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

584 Chapter 10 Infinite Sequences and Series
3. f x is positive, continuous, and decreasing for x 1; dx lim dx lim tanab ’“
œœœ
1111x
x4 x4 x4 2 2
1
222
''
11
b
1
b
bbÄ_ Ä_
lim tan tan tan dx converges convergesœœÊ Ê
bÄ_ ˆ‰ !
1b11 11 1 1
2222422 x4 n4
11 1
n1
œ
_
1'122
4. f x is positive, continuous, and decreasing for x 1; dx lim dx lim ln x 4ab ’“
œ œ œ ll
111
x4 x4 x4
''
11
b
1
b
bbÄ_ Ä_
lim ln b 4 ln 5 dx diverges divergesœ ll œ_Ê Ê
bÄ_ ab !
'1
11
x4 n4
n1
œ
_
5. f x e is positive, continuous, and decreasing for x 1; e dx lim e dx lim eab ’“
œœœ
2x 2x 2x 2x
1
2
''
11
b
1
b
bbÄ_ Ä_
lim e dx converges e convergesœœÊ Ê
bÄ_ ˆ‰ !
11 1
2e 2e 2e
2x 2n
n1
2b 22
'1
œ
_
6. f x is positive, continuous, and decreasing for x 2; dx lim dx lim ab ’“
œœœ
1111
xlnx xlnx xlnx ln x
ab ab ab
222
''
22
b
2
b
bbÄ_ Ä_
lim dx converges convergesœœÊ Ê
bÄ_ ˆ‰ !
11 1 1 1
ln b ln 2 ln 2 xlnx nlnn
n2
'2ab ab
22
œ
_
7. f x is positive and continuous for x 1, f x 0 for x 2, thus f is decreasing for x 3;ab abœœ
x4x
x4 x4
2 2
2
2
w
ab
dx lim dx lim ln x 4 lim ln b 4 ln 13 dx
'' '
33 3
b
3
b
xx1 11 x
x4 x4 2 2 2 x4
22
22 2
œœœœ_Ê
bb bÄ_ Ä_ Ä_
’“
ab abab
ˆ‰
diverges diverges divergesÊÊœ
!!!
n3 n1 n3
nn12n
n4 n4 5 8 n4
œœ œ
__ _
22 2
8. f x is positive and continuous for x 2, f x 0 for x e, thus f is decreasing for x 3;ab abœœ
ln x 2 ln x
xx
2 2
2
w
dx lim dx lim 2 ln x lim 2 ln b 2 ln 3 dx
'' '
33 3
b
3
b
ln x ln x ln x
xx x
22 2
œœœœ_Ê
bbbÄ_ Ä_ Ä_
’“
ab a babab
diverges diverges divergesÊÊœ
!!!
n3 n2 n3
ln n ln n ln 4 ln n
nn2n
œœœ
___
222
9. f x is positive and continuous for x 1, f x 0 for x 6, thus f is decreasing for x 7;ab abœœ
x
e3e
xx 6
2
x3 x3
wab
dx lim dx lim lim
''
77
b
7
b
x x 3x 18x 54 3b 18b 54 327
e e eee e e
22 2 2
x3 x3 x3 x3 x3 b3 73
œœœ œ
bb bÄ_ Ä_ Ä_
’“
Š‹
lim lim dx converges convergesœœœÊ Ê
bbÄ_ Ä_
Š‹ ˆ‰ !
36b18
ee eeee e
327 54 327 327 x n
n7
ab
œ
_
b3 73 b3 73 73 x3 n3
22
'7
convergesÊ œ
!!
n1
n 1 4 9 16 25 36 n
eee ee e
ee
n7
œ
__
œ
2 2
n3 13 23 43 53 n3
12
10. f x is continuous for x 2, f is positive for x 4, and f x 0 for x 7, thus f isab abœœ œ
x4 x4 7x
x2x1 x1 x1
w
22 3
ab ab
decreasing for x 8; dx lim dx dx lim dx dxœ œ
''' ''
888 88
bb bb
x4 x1 3 1 3
x1 x1 x1 x1
x1
ab ab ab ab
222 2
bbÄ_ Ä_
”•”•
lim ln x 1 lim ln b 1 ln 7 dx divergesœ ll œ ll œ_Ê
bbÄ_ Ä_
’“
ˆ‰
333x4
x1 b1 7 x1
8
b
8
'ab
2
diverges 2 0 divergesÊ Ê œ
!! !
n8 n2 n8
n4 n4 1 1 2 3 n4
n2n1 n2n1 4 16 25 36 n2n1
œœ œ
__ _
22 2
11. converges; a geometric series with r 1 12. converges; a geometric series with r 1œ œ
" "
10 e
13. diverges; by the nth-Term Test for Divergence, lim 1 0
nÄ_
n
n1œÁ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.3 The Integral Test 585
14. diverges by the Integral Test; dx 5 ln (n 1) 5 ln 2 dx
''
11
n55
x1 x1
œÊ Ä_
15. diverges; 3 , which is a divergent p-series (p )
!!
__
œœn1 n1
3
nn
ÈÈ
œœ
""
#
16. converges; 2 , which is a convergent p-series (p )
!!
__
œœn1 n1
"
#
23
nn n
Èœ œ
17. converges; a geometric series with r 1œ
"
8
18. diverges; 8 and since diverges, 8 diverges
!! ! !
__ _ _
œœ œ œn1 n1 n1 n1
"81 1
nn n n
œ
19. diverges by the Integral Test: dx ln n ln 2 dx
''
22
nln x ln x
xx
œÊ Ä_
"
#
#
ab
20. diverges by the Integral Test: dx; te dt lim 2te 4e
t ln x
dt
dx e dt
''
2ln2
ln x
x
dx
x
t
t2 t2 t2
ÈÔ×
ÕØ ‘
œ
œ
œ
Ĝ
ÎÎÎ
bÄ_
b
ln 2
lim 2e (b 2) 2e (ln 2 2)œœ_
bÄ_ ‘
b2 ln2 2ÎÐÑÎ
21. converges; a geometric series with r 1œ
2
3
22. diverges; lim lim lim 0
nn nÄ_ Ä_ Ä_
55 ln 5ln 55
43 4 ln 4 ln 4 4
n
nn
nn
œœ œ_Á
ˆ‰ˆ‰
23. diverges; 2 , which diverges by the Integral Test
!!
__
œœn0 n0
"
2
n1 n 1
œ
24. diverges by the Integral Test: ln (2n 1) as n
'1
ndx
2x 1#
"
œ Ä_ Ä_
25. diverges; lim a lim lim 0
nn nÄ_ Ä_ Ä_
n22 ln 2
n1 1
œœ œ_Á
nn
26. diverges by the Integral Test: ; ln n 1 ln 2 as n
ux
du
''
12
nn1
dx du
xx1 dx
xu
ÈÈ
ˆ‰ È
–—
Ȉ‰
È
œ"
œÄ œ Ä_ Ä_
27. diverges; lim lim lim 0
nn nÄ_ Ä_ Ä_
ÈÈ
Š‹
Š‹
nn
ln n œœœ_Á
2n
n#
28. diverges; lim a lim 1 e 0
nnÄ_ Ä_
nn
n
œœÁ
ˆ‰
"
29. diverges; a geometric series with r 1.44 1œ¸
"
#ln
30. converges; a geometric series with r 0.91 1œ¸
"
ln 3
31. converges by the Integral Test: dx; du
u ln x
du dx
''
3ln3
Š‹
ÈÈ
x
(ln x) (ln x) 1 xuu 1
""
”•
œ
π
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

586 Chapter 10 Infinite Sequences and Series
lim sec u lim sec b sec (ln 3) lim cos sec (ln 3)œœœ
bb bÄ_ Ä_ Ä_
cd c dkk ‘ˆ‰
" " " " "
"
b
ln 3 b
cos (0) sec (ln 3) sec (ln 3) 1.1439œ œ ¸
" " "
#
1
32. converges by the Integral Test: dx dx; du
u ln x
du dx
'' '
11 0
""
"
x 1 ln x 1 (ln x) 1 u
x
ab Š‹
π
œ
œ
x”•
lim tan u lim tan b tan 0 0œœœœ
bbÄ_ Ä_
cd a b
" " "
##
b
0
11
33. diverges by the nth-Term Test for divergence; lim n sin lim lim 1 0
nn
x0
Ä_ Ä_ Ä
ˆ‰
"
nx
sin x
œœœÁ
sin ˆ‰
ˆ‰
n
n
34. diverges by the nth-Term Test for divergence; lim n tan lim lim
nnnÄ_ Ä_ Ä_
ˆ‰
"
nœœ
tan sec
ˆ‰
ˆ‰ Š‹ˆ‰
Š‹
n
n
nn
n
lim sec sec 0 1 0œœœÁ
nÄ_
##
"
ˆ‰
n
35. converges by the Integral Test: dx; du lim tan u
ue
du e dx
''
1e
x
x
e
1e 1u
x
2x
""
”• cd
œ
œÄœ
nÄ_
b
e
lim tan b tan e tan e 0.35œœ¸
bÄ_ ab
" " "
#
1
36. converges by the Integral Test: dx; du du
ue
du e dx
dx du
'''
1ee
2222
1e u(1u) u u1
x
x
u
"
xÔ×
ÕØ ˆ‰
œ
œ
œ
Ĝ
lim 2 ln lim 2 ln 2 ln 2 ln 1 2 ln 2 ln 0.63œ œ œœ¸
bbÄ_ Ä_
‘ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ube ee
u1 b1 e1 e1 e1
b
e
37. converges by the Integral Test: dx; 8u du 4u 4
utanx
du
''
14
22
4
8 tan x 3
1x 4 16 4
dx
1x
"
#
”• cd Š‹
œ
œÄœœœ
11 1
38. diverges by the Integral Test: dx; lim ln u lim (ln b ln 2)
ux 1
du 2x dx
''
12
xdu
x1 4
###
#"""
”• ‘
œ
œÄœ œ œ_
bbÄ_ Ä_
b
2
39. converges by the Integral Test: sech x dx 2 lim dx 2 lim tan e
''
11
bb
1
œœ
bbÄ_ Ä_
e
1e
x
x
x
"
ab cd
2 lim tan e tan e 2 tan e 0.71œœ¸
bÄ_ ab
" " "b1
40. converges by the Integral Test: sech x dx lim sech x dx lim tanh x lim (tanh b tanh 1)
''
11
bb
1
##
œœœ
bbbÄ_ Ä_ Ä_
cd
1 tanh 1 0.76œ ¸
41. dx lim a ln x 2 ln x 4 lim ln ln ;
'1ˆ‰ ˆ‰
cdkkkk
a 3
x2 x4 b4 5
(b 2)
"
œ œ
bbÄ_ Ä_
b
1
aa
lim a lim (b 2) the series converges to ln if a 1 and diverges to if
, a 1
1, a 1
bbÄ_ Ä_
(b 2)
b4 3
a1 5
aœœ Ê œ _
_
œ
œˆ‰
a 1. If a 1, the terms of the series eventually become negative and the Integral Test does not apply. From
that point on, however, the series behaves like a negative multiple of the harmonic series, and so it diverges.
42. dx lim ln lim ln ln ; lim
'3
b
3
ˆ‰ ˆ‰
’“¹¹
""
x1 x1 (x1) (b1) 4 (b1)
2a x1 b1 2 b
œ œ
bb bÄ_ Ä_ Ä_
2a 2a 2a 2a
lim the series converges to ln ln 2 if a and diverges to if
1, a
, a
œœÊ œœ_
œ
_
bÄ_
" "
# # #
"
#
"
#
a(b 1)
4
2a 1 ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.3 The Integral Test 587
if a . If a , the terms of the series eventually become negative and the Integral Test does not apply.
""
##
From that point on, however, the series behaves like a negative multiple of the harmonic series, and so it diverges.
43. (a)
(b) There are (13)(365)(24)(60)(60) 10 seconds in 13 billion years; by part (a) s 1 ln n whereab
*nŸ
n (13)(365)(24)(60)(60) 10 s 1 ln (13)(365)(24)(60)(60) 10œÊŸab a bab
**
n
1 ln (13) ln (365) ln (24) 2 ln (60) 9 ln (10) 41.55œ ¸
44. No, because and diverges
!!!
___
œœœn1 n1 n1
"" " "
nx x n n
œ
45. Yes. If a is a divergent series of positive numbers, then a also diverges and a .
!!!
ˆ‰ ˆ‰
_ _
œ œn1 n1
nnn
aa
"
## #
_
n1
œ
nn
There is no “smallest" divergent series of positive numbers: for any divergent series a of positive numbers
!
_
œn1
n
has smaller terms and still diverges.
!ˆ‰
_
œn1
an
#
46. No, if is a convergent series of positive numbers, then 2 a 2a also converges, and 2a a .
!!!
___
œœœn1 n1 n1
a
nnn nn
œ
There is no “largest" convergent series of positive numbers.
47. (a) Both integrals can represent the area under the curve f x , and the sum s can be considered anabœ1
x1 50
È
approximation of either integral using rectangles with x 1. The sum s is an overestimate of the?œœ
50 1
n1
!
50
n1œ
È
integral dx. The sum s represents a left-hand sum (that is, the we are choosing the left-hand endpoint of
'1
51 1
x1 50
È
each subinterval for c ) and because f is a decreasing function, the value of f is a maximum at the left-hand endpoint of
i
each sub interval. The area of each rectangle overestimates the true area, thus dx . In a similar
'1
51 11
x1 n1
ÈÈ
!
50
n1œ
manner, s underestimates the integral dx. In this case, the sum s represents a right-hand sum and because
50 50
1
x1
'0
50 È
f is a decreasing function, the value of f is aminimum at the right-hand endpoint of each subinterval. The area of each
rectangle underestimates the true area, thus dx. Evaluating the integrals we find dx
!
50
n1œ
11 1
n1 x1 x1
ÈÈ È
''
0 1
50 51
2 x 1 2 52 2 2 11.6 and dx 2 x 1 2 51 2 1 12.3. Thus,œœ¸ œœ¸
’“ ’“
ÈÈ
ÈÈ
ÈÈ
1 0
51 50
0
50
'1
x1
È
11.6 12.3.
!
50
n1œ
1
n1
È
(b) s 1000 dx 2 x 1 2 n 1 2 2 1000 n 500 2 2 251414.2
n
n1
x1
n2
Ê œ œÊ ¸
'1
1
1
1
È’“
ÈÈ
ÈÈ
Š‹
n 251415.Ê
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
588 Chapter 10 Infinite Sequences and Series
48. (a) Since we are using s to estimate , the error is given by . We can consider this sum as
30 11 1
nn n
œ!! !
30
n1 n1 n31œœ œ
__
44 4 an estimate
of the area under the curve f x when x 30 using rectangles with x 1 and c is the right-hand endpoint ofabœ œ
1
xi
4?
each subinterval. Since f is a decreasing function, the value of f is a minimum at the right-hand endpoint of each
subinterval, thus dx dx 1.23 10 .
!’“ Š‹
_
œn31
11 1 1 11
nx x 3x 3b
bb b
bb
330
5
44 4 3 33
œ œœ¸‚
''
30 30 30
_
Ä_ Ä_ Ä_
lim lim lim ab
Thus the error 1.23 10‚Þ
5
(b) We want S s 0.000001 dx 0.000001 dx dx Ê Êœ œ
n1111
xxx3x
bb
bb
'''
nnn
n
__
Ä_ Ä_
4443
lim lim ’“
0.000001 n 69.336 n 70.œœ Ê ¸ Êlim
b
1 1 1 1000000
3b 3n 3n 3
Ä_ ˆ‰ É
33 3
3
49. We want S s 0.01 dx 0.01 dx dxÊÊœ œœ
n111111
xxx2x2b2n
bbb
bb
'''
nnn n
__
Ä_ Ä_ Ä_
333222
lim lim lim
’“ ˆ‰
0.01 n 50 7.071 n 8 S s 1.195œ Ê ¸ Êʸœ ¸
1 1
2n n
8
2 3
È!
8
n1œ
50. We want S s 0.1 dx 0.1 dx tan Ê Ê œ
n111x
x4 x4 2 2
bb
b1b
''
nn n
_
Ä_ Ä_
22
lim lim ’“
ˆ‰
tan tan tan 0.1 n 2tan 0.2 9.867 n 10 S sœœÊ¸Êʸlim
b
1b1n 1n
2222422 2
11 1 10
Ä_
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ 11
0.57œ¸
!
10
n1œ
1
n4
2
51. S s 0.00001 dx 0.00001 dx dxÊÊœ œœ
n111101010
xxxxbn
bbb
bb
'''
nnn
n
__
Ä_ Ä_ Ä_
1.1 1.1 1.1 0.1 0.1 0.1
lim lim lim
’“ ˆ‰
0.00001 n 1000000 n 10œ Ê Ê
10
n
10 60
0.1
52. S s 0.01 dx 0.01 dx dxÊÊœ œ
n1111
xlnx xlnx xlnx 2lnx
bb
bb
'''
nnn n
__
Ä_ Ä_
ab ab ab ab
3332
lim lim ’“
0.01 n e 1177.405 n 1178œ œÊ¸ Êlim
b
11 1
2lnb 2lnn 2lnn
50
Ä_ Š‹
ab ab ab È
22 2
53. Let A and B 2 a , where {a } is a nonincreasing sequence of positive terms converging to
nkn k
k2
œœ
!!
nn
k1 k1œœ
a ab
k
0. Note that {A } and {B } are nondecreasing sequences of positive terms. Now,
nn
B2a4a8a 2a 2a 2a2a 2a2a2a2a
nn2
œá œ á
#%) # %% ))))
ab
naba b
2a 2a 2a 2a 2a 2a 2a 2a 2a 2a 2a á Ÿ á
ðóóóóóóóóóóóóóóñóóóóóóóóóóóóóóò
ˆ‰
aba b
ab ab ab22 2
nn n "# $% &'()
2 terms
n1
2a 2a 2a 2A 2 a . Therefore if a converges, ᜟ
ˆ‰
!!
ab a b ab ab
221 22 kk
n1 n1 nn
_
œk1
then {B } is bounded above 2 a converges. Conversely,
nÊ!k2k
Aa aa aaaa a a2a4a 2a aB a 2a.
nnn
nk
22
œ á á œ
" #$ %&'( " # % " "
aba b !
ab ab
nk
_
œk1
Therefore, if 2 a converges, then {A } is bounded above and hence converges.
!
_
œk1
k2n
ab
k
54. (a) a 2 a 2 , which diverges
ab ab
ab
22
2 ln 2 2 n(ln 2) n(ln 2) ln n
nn
nn
nn n n
œœ Ê œ œ
"" """
##††
!! !
__ _
œœ œn2 n2 n2
diverges.Ê!
_
œn2
"
n ln n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.3 The Integral Test 589
(b) a 2 a 2 , a geometric series that
ab ab ab
22
nn
2
n
nn
np np p 1 p 1
n
œÊ œ œ œ
""""
###
!!!!
ˆ‰
____
œœœœn1 n1 n1 n1
†
converges if 1 or p 1, but diverges if p 1.
"
#p1 Ÿ
55. (a) ; u du lim lim b (ln 2)
u ln x
du
''
2ln2
pb
ln 2
dx u
x(ln x) p 1 1 p
dx
x
p1 p1
p
p1
”• ’“ Š‹
cd
œ
œÄœ œ
bbÄ_ Ä_
"
the improper integral converges if p 1 and diverges if p 1.
(ln 2) , p 1
, p
œÊ
_"
œ"
p1
p1
For p 1: lim ln (ln x) lim ln (ln b) ln (ln 2) , so the improper integral diverges ifœœ œ œ_
'2
b
2
dx
x ln x bbÄ_ Ä_
cd c d
p1.œ
(b) Since the series and the integral converge or diverge together, converges if and only if p 1.
!
_
œn2
"
n(ln n)p
56. (a) p 1 the series divergesœÊ
(b) p 1.01 the series convergesœÊ
(c) ; p 1 the series diverges
!!
__
œœn2 n2
"" "
n ln n 3 n(ln n)ab
œœÊ
(d) p 3 the series convergesœÊ
57. (a) From Fig. 10.11(a) in the text with f(x) and a , we have dx 1œ œ Ÿá
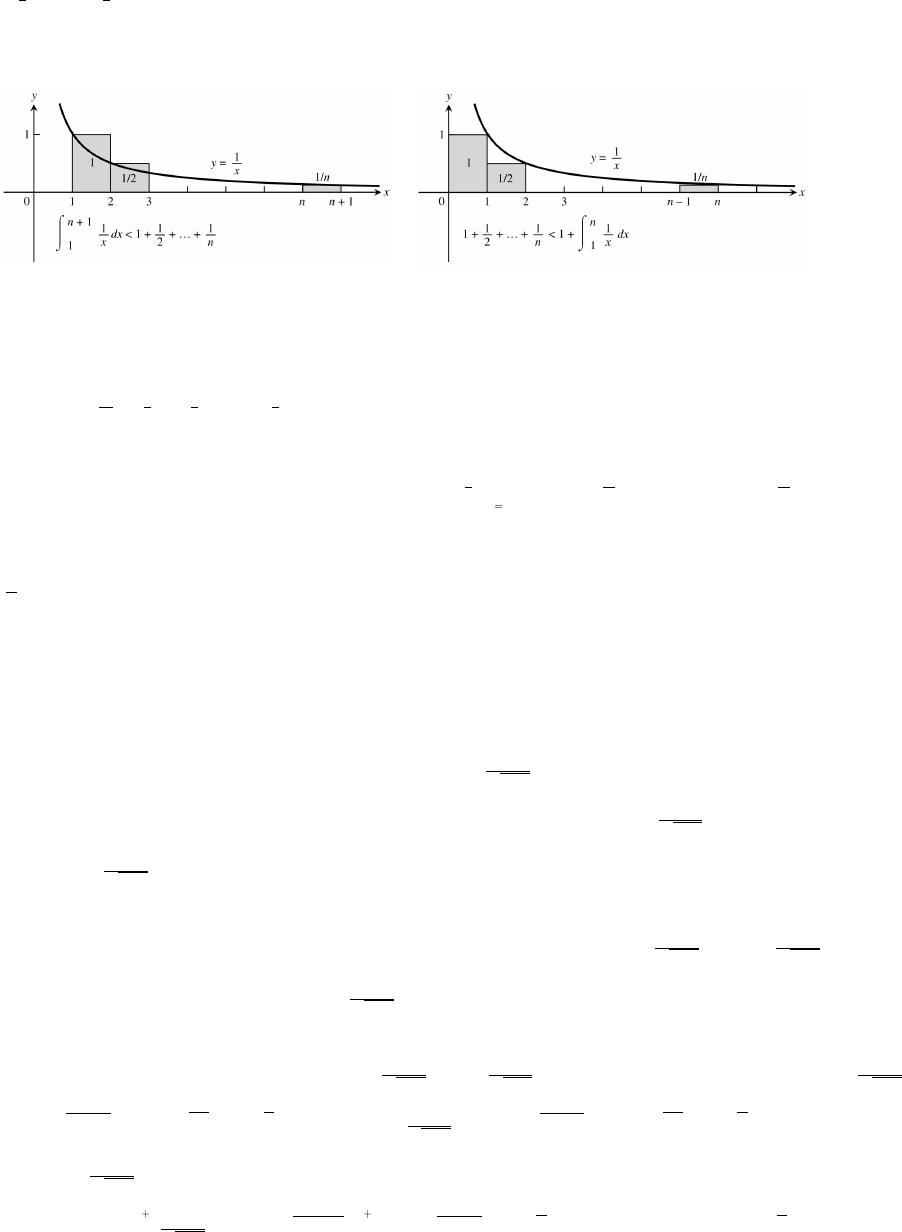
"" " """
#xk x 3n
k'1
n1
1 f(x) dx ln (n 1) 1 1 ln n 0 ln (n 1) ln nŸ Ê ŸáŸ Ê Ÿ
'1
n"" "
#3n
1 ln n 1. Therefore the sequence 1 ln n is bounded above byŸ á Ÿ á
ˆ‰ ˜ ™ˆ‰
"" " "" "
# #3n 3n
1 and below by 0.
(b) From the graph in Fig. 10.11(b) with f(x) , dx ln (n 1) ln nœ œ
"" "
xn1 x
'n
n1
0 ln (n 1) ln n 1 ln (n 1) 1 ln n .Ê œ á á
"""""""
##n1 3 n1 3 n
cd
ˆ‰ˆ‰
If we define a 1 ln n, then 0 a a a a {a } is a decreasing sequence of
nn1nn1nn
3n
œœ Ê Ê
"""
#
nonnegative terms.
58. e e for x 1, and e dx lim e lim e e e e dx converges by
xx x b1
Ÿ œœœÊ
''
1 1
x1x
bbÄ_ Ä_
cd ˆ‰
b
"
the Comparison Test for improper integrals e 1 e converges by the Integral Test.ʜ
!!
__
œœn0 n1
nn
59. (a) s 1.97531986; dx lim x dx lim lim and
10
10
n x 2 2b 242 242
1x111
3
œœ œ œœœ
!’“ ˆ‰
n1
b
11
œ
"
33 2
2
''
11 11
b
bbbÄ_ Ä_ Ä_
dx lim x dx lim lim
''
10 10
b
1x111
x 2 2b 200 200
3
3 2
2
œœœœ
bbbÄ_ Ä_ Ä_
’“ ˆ‰
b
10
1.97531986 s 1.97531986 1.20166 s 1.20253Ê Ê
11
242 200
(b) s 1.202095; error 0.000435œ¸ œ Ÿ œ
!
_"
n1œn2 2
1.20166 1.20253 1.20253 1.20166
3
60. (a) s 1.082036583; dx lim x dx lim lim and
10
10
n x 3 3b 3993 3993
1x111
4
œœ œ œœœ
!’“ ˆ‰
n1
b
11
œ
"
44 3
3
''
11 11
b
bbbÄ_ Ä_ Ä_
dx lim x dx lim lim
''
10 10
b
1x111
x 3 3b 3000 3000
4
4 3
3
œœœœ
bbbÄ_ Ä_ Ä_
’“ ˆ‰
b
10
1.082036583 s 1.082036583 1.08229 s 1.08237Ê Ê
11
3993 3000
(b) s 1.08233; error 0.00004œ¸ œ Ÿ œ
!
_"
n1œn2 2
1.08229 1.08237 1.08237 1.08229
4
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

590 Chapter 10 Infinite Sequences and Series
10.4 COMPARISON TESTS
1. Compare with , which is a convergent p-series, since p 2 1. Both series have nonnegative terms for n 1. For
!
_
œn1
"
n2œ
n 1, we have n n 30 . Then by Comparison Test, converges.ŸÊ
22 11 1
nn30 n30
22 2
!
_
œn1
2. Compare with , which is a convergent p-series, since p 3 1. Both series have nonnegative terms for n 1. For
!
_
œn1
"
n3œ
n 1, we have n n 2 . Then by Comparison Test, ŸÊÊÊ
44 11 nn 1nn1 n1
nn2nn2nn2n2 n2
44 44 34 4 4
!
_
œn1
converges.
3. Compare with , which is a divergent p-series, since p 1. Both series have nonnegative terms for n 2. For
!
_
œn2
""
#
ÈnœŸ
n 2, we have n 1 n . Then by Comparison Test, diverges.ŸÊ
ÈÈ !
11 1
n1 n n1
ÈÈ È
_
œn2
4. Compare with , which is a divergent p-series, since p 1 1. Both series have nonnegative terms for n 2. For
!
_
œn2
"
nœŸ
n 2, we have n n n . Thus diverges. ŸÊ Ê œÊ
22
11 nn1n2n1 n2
nnn nnn n nnnnn nn
2222 22 2
!
_
œn2
5. Compare with , which is a convergent p-series, since p 1. Both series have nonnegative terms for n 1.
!
_
œn1
"
n
3
2
32 œ
For n 1, we have 0 cos n 1 . Then by Comparison Test, converges.ŸŸÊŸ
2cos n 1 cos n
nn n
2 2
32 32 32
!
_
œn1
6. Compare with , which is a convergent geometric series, since r 1. Both series have nonnegative terms for
!¹¹
_
œn1
"
33
1
nllœ
n 1. For n 1, we have n 3 3 . Then by Comparison Test, converges. †ÊŸ
nn 11 1
n3 3 n3††
nn n
!
_
œn1
7. Compare with . The series is a convergent p-series, since p 1, and the series
!! !
__ _
œœ œn1 n1 n1
È È
5 5
nn n
13
2
32 32 32
œ
5 converges by Theorem 8 part 3. Both series have nonnegative terms for n 1. For n 1, we haveœ
È!
_
œn1
1
n32
n n 4n 4n n 4n n 4n 5n n 4n 5n 20 5 n 4 5.
34 3 44344 443 4 4 n4n
n4
ŸÊŸÊŸœÊŸœ Ê Ÿab
43
4
5 Then by Comparison Test, converges.ÊŸÊŸÊ Ÿœ
nn 4
n4 n4 n n4 n n4
n4 5 n4 5 n4
5
n
3
44343 4
32
ab È
ÉÉ
É!
_
œn1
8. Compare with , which is a divergent p-series, since p 1. Both series have nonnegative terms for n 1. For
!
_
œn1
""
#
ÈnœŸ
n 1, we have n 1 2 n 2 2 n 1 3 n 2 n 1 3n 3 2 n n n 3 Ê Ê Ê Ê
ÈÈÈ È È
ˆ‰
n2nnnn3 1Ê Ê Ê Ê Ê
22
nn 2 n 1 n 1 n 1
n3 n3 n n3 n n3 n
n2n 1 11 1
ÈÊÉ
ˆ‰ È ˆ‰ ˆ‰
ÈÈÈ
2222
22
. Then by Comparison Test, diverges.Ê
ÈÈ
ÈÈ È
n1 n1
n3 n3
1
n
2 2
!
_
œn1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.4 Comparison Tests 591
9. Compare with , which is a convergent p-series, since p 2 1. Both series have positive terms for n 1.
!
_
œn1
"
Ä_
n b
n
a
2n
n
œ lim
1 0. Then by Limit Comparison Teœœ œœœœlim lim lim lim lim
nn nnn
1 n n n 3 3n 2n 6n 2 6
n2n 3n4n 6n4 6
Ä_ Ä_ Ä_ Ä_ Ä_
Î
n2
nn3
32
232 2
32 2 st,
converges.
!
_
œn1
n2
nn3
32
10. Compare with , which is a divergent p-series, since p 1. Both series have positive terms for n 1.
!
_
œn1
""
#Ä_
Ènn
a
b
œŸ lim n
n
1 1 0. Then by Limit Comparisonœœœœœœœlim lim lim lim lim
nn n n n
1n
nn nn 2n1 2
n2 n2 2n 2
Ä_ Ä_ Ä_ Ä_ Ä_
Î
ÉÈ
n1
n2
222
22
ÉÉÉÉ
È
Test, diverges.
!É
_
œn1
n1
n2
2
11. Compare with , which is a divergent p-series, since p 1 1. Both series have positive terms for n 2.
!
_
œn2
"
Ä_
n b
n
a
œŸ lim n
n
1 0. Then by Limit Compœœ œ œœœlim lim lim lim lim
nn n nn
1n nnn1 3n2n1 6n2 6
n+n 3n 2n 6n 2 6
Ä_ Ä_ Ä_ Ä_ Ä_
Î
nn 1
n1n1
232 2
32 2 arison
Test, diverges.
!
_
œn2
nn 1
n1n1
ab
abab
2
12. Compare with , which is a convergent geometric series, since r 1. Both series have positive terms for
!¹¹
_
œn1
"
22
1
nllœ
n 1. 1 0. Then by Limit Comparison Test, converœœœœlim lim lim lim
nn n n
a
b12 344ln4 34
44ln4 2
Ä_ Ä_ Ä_ Ä_
Î
n
n
2n
34
n
nnn n
nn n
!
_
œn1
ges.
13. Compare with , which is a divergent p-series, since p 1. Both series have positive terms for n 1.
!
_
œn1
"
Ä_
Èn
1
2b
n
a
œŸ lim n
n
. Then by Limit Comparison Test, diverges.œœœœ_lim lim lim
nnn
1n n4
55 5
44
n
Ä_ Ä_ Ä_
Î †
5n
n4
nn n
nn
È È
ˆ‰ !
_
œn1
14. Compare with , which is a convergent geometric series, since r 1. Both series have positive terms for
!ˆ‰ ¹¹
_
œn1
2 2
5 5
nllœ
n 1. exp ln exp n lnœ œ œ œlim lim lim lim lim
nn n n n
a
b 10n 8 10n 8 10n 8
25
10n 15 10n 15 10n 15
nn
Ä_ Ä_ Ä_ Ä_ Ä_
Î
n
n
2n 3
5n 4
n
n
ˆ‰
ab ˆ‰ ˆ‰ ˆ‰
exp exp exp exp œœ œ œlim lim lim lim
nn n n
ln
1 n 1 n 10n 15 10n 8 100n 230n 120
70n 70n
Ä_ Ä_ Ä_ Ä_
ÎÎ
ˆ‰ abab
10n 15 10 10
10n 8 10n 15 10n 8
2 2
22
exp exp e 0. Then by Limit Comparison Test, converges.œœœlim lim
nn
140n 140 2n 3
200n 230 200 5n 4
710 n
Ä_ Ä_
Î
!ˆ‰
_
œn1
15. Compare with , which is a divergent p-series, since p 1 1. Both series have positive terms for n 2.
!
_
œn2
"
Ä_
n b
n
a
œŸ lim n
n
n . Then by Limit Comparison Test, diverges.œœ œ œœ_lim lim lim lim
nn n n
1n lnn 1n ln n
n1
Ä_ Ä_ Ä_ Ä_
ÎÎ
"
ln n !
_
œn2
16. Compare with , which is a convergent p-series, since p 2 1. Both series have positive terms for n 1.
!
_
œn1
"
Ä_
n b
n
a
2n
n
œ lim
1 0. Then by Limit Comparison Test, ln 1 convergœœ œœ lim lim lim
nn n
ln 1
1n n
1
1
Ä_ Ä_ Ä_
Î
"
Š‹ Š‹
Š‹
n2
2 2
12
1n2n3
2
n3n2!ˆ‰
_
œn1
es.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
592 Chapter 10 Infinite Sequences and Series
17. diverges by the Limit Comparison Test (part 1) when compared with , a divergent p-series:
!
_
œn1
"
Èn
lim lim lim
nnnÄ_ Ä_ Ä_
Œ
Š‹
nn
n
œœ œ
È
ÈÈ
n
2n n n
""
# #
ˆ‰
16
18. diverges by the Direct Comparison Test since n n n n n 0 , which is the nth Ê
È3
nnn
"
È
term of the divergent series or use Limit Comparison Test with b
!
n1
""
nn
nœ
19. converges by the Direct Comparison Test; , which is the nth term of a convergent geometric series
sin n
2nn
Ÿ"
#
20. converges by the Direct Comparison Test; and the p-series converges
1cos n 2
nn n
"
Ÿ!
21. diverges since lim 0
nÄ_
2n 2
3n 1 3œÁ
22. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
nn
n
œœ
ˆ‰
n
n
"
23. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim lim 10
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
Š‹
10n
n(n 1)(n 2)
n
œœœœ
10n n 20n 1 20
n3n2 2n3 2
24. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim lim 5
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
5n 3n
n(n 2) n 5
n
œœœœ
5n 3n 15n 3 30n
n2n5n10 3n4n5 6n4
25. converges by the Direct Comparison Test; , the nth term of a convergent geometric series
ˆ‰ˆ‰ˆ‰
nn
3n13n3
nn
n
"
œ
26. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim 1 1
nnnÄ_ Ä_ Ä_
Š‹
Š‹
n
n2
œœœ
ÉÉ
n2 2
nn
27. diverges by the Direct Comparison Test; n ln n ln n ln ln n and divergesÊ Ê
"" " "
n ln n ln (ln n) n
!
_
œn3
28. converges by the Limit Comparison Test (part 2) when compared with , a convergent p-series:
!
_
œn1
"
n
lim lim lim 2 lim 0
nnn nÄ_ Ä_ Ä_ Ä_
’“
Š‹
(ln n)
n
n
n
œœ œœ
(ln n)
n1 n
2(ln n) ln n
Š‹
29. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim
nnnnÄ_ Ä_ Ä_ Ä_
’“ Š‹
ˆ‰ ˆ‰
1
n ln n 2 n
nn
œœ œœ_
ÈÈ
nn
ln n 2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.4 Comparison Tests 593
30. converges by the Limit Comparison Test (part 2) with , the nth term of a convergent p-series:
"
n
lim lim lim 8 lim 8 lim 32 l
nnn nnÄ_ Ä_ Ä_ Ä_ Ä_
’“
Š‹ Š‹ Š‹
ˆ‰ ˆ‰
(ln n)
n
n4n 4n
2 ln n
nn
œœ œœ œ
(ln n)
nn
ln n im 32 0 0
nÄ_
"
nœœ†
31. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim n
nnnnÄ_ Ä_ Ä_ Ä_
ˆ‰
ˆ‰
1ln n
nn
œœœœ_
n
1ln n
"
Š‹
32. diverges by the Integral Test: dx u du lim u lim b ln 3
''
2ln3
ln (x 1)
x1 2
#
""
###
œœ œ œ_
bbÄ_ Ä_
‘ ab
b
ln 3
33. converges by the Direct Comparison Test with , the nth term of a convergent p-series: n 1 n for
"#
n
n 2 n n 1 n n n 1 n or use Limit Comparison Test with .Ê Ê Ê
# # $ $Î#
#""
ab Ènnn 1
1
n
È
34. converges by the Direct Comparison Test with , the nth term of a convergent p-series: n 1 n
"##
n
n 1 nn n or use Limit Comparison Test with .Ê Ê Ê
# $Î# $Î#
" "
Èn1
n
n
n1 nn
ÈÈ
35. converges because which is the sum of two convergent series:
!!!
___
œœœn1 n1 n1
" " "
#
n
n2 n2
nnn
œ
converges by the Direct Comparison Test since , and is a convergent geometric series
!!
_ _
œ œn1 n1
""""
##n2 n 2
nnn n
36. converges by the Direct Comparison Test: and , the sum of
!!
ˆ‰
__
œœn1 n1
n2
n2 n2 n n2 n n
""""""
#
n
nn nn
œ Ÿ
the nth terms of a convergent geometric series and a convergent p-series
37. converges by the Direct Comparison Test: , which is the nth term of a convergent geometric series
""
313
n1 n1
38. diverges; lim lim 0
nnÄ_ Ä_
Š‹ ˆ‰
3
3333
n1
nn
" " " "
œœÁ
39. converges by Limit Comparison Test: compare with , which is a convergent geometric series with r 1,
!ˆ‰
_
œn1
11
55
nllœ
lim lim lim 0.
nnnÄ_ Ä_ Ä_
Š‹
ab
n1 1
n3n
25n
n2
†
Î
15
n1 1
n3n 2n3
œœœ
40. converges by Limit Comparison Test: compare with , which is a convergent geometric series with r 1,
!ˆ‰
_
œn1
31
45
nllœ
lim lim lim 1 0.
nnnÄ_ Ä_ Ä_
Š‹
ab ˆ‰
ˆ‰
23
nn
34
nn
nn
nn
nn
8
12
n
9
12
34
812 1
912 1
1
1
Î
œœ œœ
41. diverges by Limit Comparison Test: compare with , which is a divergent p-series, lim lim
!
_
œn1
12
n1n
nnÄ_ Ä_
Š‹
2n
n
n2
nn
Îœn
2n
lim lim 1 0.œœœ
nnÄ_ Ä_
2ln2 1
2ln2
2ln2
2ln2
n
n2
n2
n
ab
ab
42. diverges by the definition of an infinite series: ln ln n ln n 1 , s ln 1 ln 2 ln 2 ln 3
!!
ˆ‰ ‘
ababab
__
œœn1 n1
n
n1 k
œ œ
ln k 1 ln k ln k ln k 1 ln k 1 lim s ÞÞÞ œ Ê œ_abababab ab kÄ_ k
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

594 Chapter 10 Infinite Sequences and Series
43. converges by Comparison Test with which converges since , and
!!!
’“
___
œœœn2 n2 n2
1111
nn1 nn1 n1 nab ab
œ
s 1 1 lim s 1; for n 2, n 2 ! 1
k k
111 1 1 11 1
223 k2k1k1k k
œÞÞÞœÊ œ
ˆ‰ˆ‰ ˆ ‰ˆ ‰ ab
kÄ_
nn 1 n 2! nn 1 n! nn 1Ê ÊÊŸababab ab
11
n! n n 1ab
44. converges by Limit Comparison Test: compare with , which is a convergent p-series, lim
!
_
œn1
1
n1n
3 3
n1
n2
nÄ_ Î
lim lim lim lim 1 0œœœœœ
nnnnÄ_ Ä_ Ä_ Ä_
nn 1
n2n1nn1 n 3n2 2n3 2
n2n2
32
2
ab
ababab
x
x
45. diverges by the Limit Comparison Test (part 1) with , the nth term of the divergent harmonic series:
"
n
lim lim 1
nx0
Ä_ Ä
ˆ‰
ˆ‰
sin n
n
œœ
sin x
x
46. diverges by the Limit Comparison Test (part 1) with , the nth term of the divergent harmonic series:
"
n
lim lim lim 1 1 1
nn x0
Ä_ Ä_ Ä
ˆ‰ ˆ‰
ˆ‰ ˆ‰
tan sin
cos
nn
nn
n
œœœœ
Š‹ ˆ‰ˆ‰
""
cos x x
sin x †
47. converges by the Direct Comparison Test: and is the product of a
tan n
nn n n
1.1 1.1 1.1 1.1
œ
!!
__
œœn1 n1
1
#
"
convergent p-series and a nonzero constant
48. converges by the Direct Comparison Test: sec n and is the
"
##
"
Ê œ
11sec n
nn n n
13 13 13 13
ˆ‰ ˆ‰
!!
__
œœn1 n1
product of a convergent p-series and a nonzero constant
49. converges by the Limit Comparison Test (part 1) with : lim lim coth n lim
"
nee
ee
nnnÄ_ Ä_ Ä_
Š‹
Š‹
coth n
n
n
œœ
nn
nn
lim 1œœ
nÄ_
"
e
1e
2n
2n
50. converges by the Limit Comparison Test (part 1) with : lim lim tanh n lim
"
nee
ee
nnnÄ_ Ä_ Ä_
Š‹
Š‹
tanh n
n
n
œœ
nn
nn
lim 1œœ
nÄ_
"
e
1e
2n
2n
51. diverges by the Limit Comparison Test (part 1) with : lim lim 1.
11
nn
nnÄ_ Ä_
Š‹
ˆ‰
1
nn
n
1
n
œœ
È
n
52. converges by the Limit Comparison Test (part 1) with : lim lim n 1
"
nnnÄ_ Ä_
Š‹
Š‹
nn
n
n
n
œœ
È
53. . The series converges by the Limit Comparison Test (part 1) with :
" "
á 123 n n(n1) n
2
œœ
"
ˆ‰
n(n 1)
lim lim lim lim 2.
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
Š‹
2
nn 1
n
œœœœ
2n 4n 4
nn 2n1 2
54. the series converges by the Direct Comparison Test
"
á 12 3 n n(n1)(2n1) n
66
œœ ŸÊ
"
n(n1)(2n1)
6
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.4 Comparison Tests 595
55. (a) If lim 0, then there exists an integer N such that for all n N, 0 1 1 1
nÄ_
aaa
bbb
nnn
nnn
œÊ
¹¹
a b . Thus, if b converges, then a converges by the Direct Comparison Test.Ê
nn n n
!!
(b) If lim , then there exists an integer N such that for all n N, 1 a b . Thus, if
nÄ_
a a
b b nn
n n
n n
œ_ Ê
b diverges, then a diverges by the Direct Comparison Test.
!!
nn
56. Yes, converges by the Direct Comparison Test because a
!
_
œn1
aa
nn
n
n n
57. lim there exists an integer N such that for all n N, 1 a b . If a converges,
nÄ_
a a
b b nn n
n n
n n
œ_ Ê Ê !
then b converges by the Direct Comparison Test
!n
58. a converges lim a 0 there exists an integer N such that for all n N, 0 a 1 a a
!nn nn
n
ÊœÊ ŸÊ
nÄ_
#
a converges by the Direct Comparison TestÊ!#
n
59. Since a 0 and lim a 0, by n term test for divergence, a diverges.
nn n
th
œ_Á
nÄ_ !
60. Since a 0 and lim n a 0, compare a with , which is a convergent p-series; lim
nnn
2
n1n
a
†œ
n nÄ_ Ä_
ab !!
"
Î
n2
lim n a 0 a converges by Limit Comparison Testœ†œÊ
nÄ_ab !
2nn
61. Let q and p 1. If q 0, then , which is a convergent p-series. If q 0, compare with_ _ œ œ Á
!!
__
œœn2 n2
abln n
nn
1
q
pp
where 1 r p, then lim lim , and p r 0. If q 0 q 0 and lim
!
_
œn2
1
n1nn n
ln n ln n
rrpr pr
ln n q
npq q
œ Ê
nn nÄ_ Ä_ Ä_
Îab ab
lim 0. If q 0, lim lim lim . If q 1 0 1 q 0œœœ œ ŸÊ
nnnnÄ_ Ä_ Ä_ Ä_
1
ln n n
ln n q ln n
nprn prn
qlnn
ab ab ab
abˆ‰
ab ab
qpr
qq1
pr pr1 pr
q11
n
and
lim lim 0, otherwise, we apply L'Hopital's Rule again. lim
nn nÄ_ Ä_ Ä_
qlnn
prn
q
prn lnn
qq 1 lnn
ab
ab abab abab
ˆ‰
q1
pr 1q
pr
q21
n
œœ abprn2pr1
lim . If q 2 0 2 q 0 and lim lim 0; otœŸÊ œœ
nnnÄ_ Ä_ Ä_
qq 1 lnn qq 1 lnn qq 1
prn prn prn lnn
abab abab ab
ab ab abab
q2 q2
2222q
pr pr pr herwise, we
apply L'Hopital's Rule again. Since q is finite, there is a positive integer k such that q k 0 k q 0. Thus, after kŸÊ
applications of L'Hopital's Rule we obtain lim lim 0
nnÄ_ Ä_
qq1 qk1lnn qq1 qk1
prn prn lnn
aba bab aba b
ab abab
â â
qk
kkkq
pr pr
œœ. Since the limit is
0 in every case, by Limit Comparison Test, the series converges.
!
n1
ln n
n
œ
_ab
q
p
62. Let q and p 1. If q 0, then , which is a divergent p-series. If q 0, compare with_ _ Ÿ œ œ
!!
__
œœn2 n2
abln n
nn
1
q
pp
, which is a divergent p-series. Then lim lim ln n . If q 0 q 0, compare with ,
! !
ab
_ _
œ œn2 n2
1 1
n1n n
q
p p r
ln n q
np
nnÄ_ Ä_
Îœœ_Ê
where 0 p r 1. lim lim lim since r p 0. Apply L'Hopital's to obtainŸ œ œ
nnnÄ_ Ä_ Ä_
ln n q
np
rpr
qrp
q
1n n
ln n n
ln n
Îab ab
lim lim . If q 1 0 q 1 0 and lim ,
nn nÄ_ Ä_ Ä_
ab ab abab
abab abab
ˆ‰ ab
rpn rpn rpn lnn
qlnn qlnn q
rp1 rp rp
q1 q1
1
n
q1
œŸÊ œ_
otherwise, we apply L'Hopital's Rule again to obtain lim lim
nnÄ_ Ä_
ab ab
aba bab aba bab
ˆ‰
rpn rpn
qq1lnn qq1
22
rp1 rp
q21
n
œln n q2
. If
q 2 0 q 2 0 and lim lim , otherwise, we Ÿ Ê œ œ_
nnÄ_ Ä_
ab abab
aba bab aba b
rpn rpn lnn
qq1lnn qq1
22q2
rp rp
q2
apply L'Hopital's Rule again. Since q is finite, there is a positive integer k such that q k 0 q k 0. Thus, after Ÿ Ê
k applications of L'Hopital's Rule we obtain lim lim
nnÄ_ Ä_
ab abab
aba ba bab aba b
rpn rpn lnn
q q1 qk1lnn qq
â
kkqk
rp rp
qkω1 qk1ab
œ_.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
596 Chapter 10 Infinite Sequences and Series
Since the limit is if q 0 or if q 0 and p 1, by Limit comparison test, the series diverges. Finally if q 0_
!
n1
ln n
n
œ
_ab
q
pr
and p 1 then . Compare with , which is a divergent p-series. For n 3, ln n 1œœ
!! !
__ _
œœ œn2 n2 n2
ab abln n ln n
nn n
1
qq
p
ln n 1 . Thus diverges by Comparison Test. Thus, if q and p 1,ÊÊ __Ÿab !
qlnn lnn
nn n
1
ab ab
qq
_
œn2
the series diverges.
!
n1
ln n
n
œ
_ab
q
pr
63. Converges by Exercise 61 with q 3 and p 4.œœ
64. Diverges by Exercise 62 with q and p .œœ
11
22
65. Converges by Exercise 61 with q 1000 and p 1.001.œœ
66. Diverges by Exercise 62 with q and p 0.99.œœ
1
5
67. Converges by Exercise 61 with q 3 and p 1.1.œ œ
68. Diverges by Exercise 62 with q and p .œ œ
11
22
69. Example CAS commands:
:Maple
a := n -> 1./n^3/sin(n)^2;
s := k -> sum( a(n), n=1..k ); # (a)]
limit( s(k), k=infinity );
pts := [seq( [k,s(k)], k=1..100 )]: # (b)
plot( pts, style=point, title="#69(b) (Section 10.4)" );
pts := [seq( [k,s(k)], k=1..200 )]: # (c)
plot( pts, style=point, title="#69(c) (Section 10.4)" );
pts := [seq( [k,s(k)], k=1..400 )]: # (d)
plot( pts, style=point, title="#69(d) (Section 10.4)" );
evalf( 355/113 );
:Mathematica
Clear[a, n, s, k, p]
a[n_]:= 1 / ( n Sin[n] )
32
s[k_]= Sum[ a[n], {n, 1, k}]
points[p_]:= Table[{k, N[s[k]]}, {k, 1, p}]
points[100]
ListPlot[points[100]]
points[200]
ListPlot[points[200]
points[400]
ListPlot[points[400], PlotRange All]Ä
To investigate what is happening around k = 355, you could do the following.
N[355/113]
N[ 355/113]1
Sin[355]//N
a[355]//N
N[s[354]]
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.5 The Ratio and Root Tests 597
N[s[355]]
N[s[356]]
70. (a) Let S , which is a convergent p-series. By Example 5 in Section 10.2, converges to 1. By Theorem 8,œ!!
_ _
œ œn1 n1
1 1
nnn 1
2ab
S also converges.œœ œ
!! !! ! !
Š‹
__ __ _ _
œœ œœ œ œn1 n1 n1 n1 n1 n1
1 111 1 11
n nn1 n nn1 nn1 n nn1
22 2
ab ab ab ab
(b) Since converges to 1 (from Example 5 in Section 10.2), S 1 1
!!!
Š‹
___
œœœn1 n1 n1
111 1
nn 1 nnn1 nn1ab ab ab
œ œ
22
(c) The new series is comparible to , so it will converge faster because its terms 0 faster than the terms of
!!
_ _
œ œn1 n1
1 1
n3Än2.
(d) The series 1 gives a better approximation. Using Mathematica, 1 1.644933568, whileœ
!!
1000 1000
n1 n1œ œ
1 1
nn 1 nn 1
2 2
ab ab
1.644933067. Note that 1.644934067. The error is 4.99 10 compared with 1 10 .
!
1000000
n1œ
1
n6
76
2
2
œœ ‚‚
1
10.5 THE RATIO AND ROOT TESTS
1. 0 for all n 1; 0 1 converges
222n!22
n! n n! 2 n n!
nn n n1
n n n
2n
n!
2n
n!
n
œ † œ œÊlim lim lim
Ä_ Ä_ Ä_
†
" † " œ
_
Œ Š‹
ˆ‰ !
ab
2. 0 for all n 1; 1 conv
n2 n3 3 n3 1 1 n2
333n23n6333
nn nn n1
Ä_ Ä_ Ä_ Ä_
† œ
_
nn2n n
n1 2
3n1
3n
n
œ †œ œœÊlim lim lim lim
Œ ˆ‰ˆ‰ˆ‰ !erges
3. 0 for all n 1;
ab abab
ab abab
n1! nn1! n
n1 n2
nn n
n1!
n
†"
Ä_ Ä_ Ä_
2 2
n1 1!
n1 1
2
n1!
n1
2
23
œ †œlim lim lim
Œ Š‹Š‹
2n n 3n 4n 1
n4n4 2n4
n
22
2
Ä_
œ lim Š‹
1 divergesœœ_Êlim
n
6n 4
2n1
n1!
n1
Ä_
œ
_
ˆ‰ !ab
ab
2
4. 0 for all n 1;
222n32n
n3 n 1 3 3 2 3
nn n
n1 n1 n1
n1 n1 n1 n1
2n1 1
n13
n1 1
2
n3
n1
†††
Ä_ Ä_ Ä_
††
œ †œlim lim lim
Š‹
ˆ‰
ab n3 3 3
n
22
Ä_
œœ 1lim ˆ‰
convergesÊ!
n1
2
n3
œ
_
†
n1
n1
5. 0 for all n 1;
n 4 n4n6n4n1
444n4n
nn n
n1
4n432
n4n44
n1
4
4n1
n
4n
4
œ †œlim lim lim
Ä_ Ä_ Ä_
†
Œ Š‹Š ‹
ab
1 convergesœœÊlim
n
11311 1 n
4n2n n 4n 4 4
n1
Ä_ œ
_
ˆ‰
!
23 4 n
4
6. 0 for all n 2;
3 3 3 lnn 3lnn
ln n ln n 1 3 ln n 1
nn nn
n2 n2
3n1 2
ln n 1
3n2 n2 1
ln n
3
n
œ †œ œlim lim lim lim
Ä_ Ä_ Ä_ Ä_
†
Œ Š‹Š‹Š‹
ab ab n1
œ lim
n
3n 3
n
Ä_
ˆ‰
3 1 divergesœ œÊlim
n
33
1lnn
n2
Ä_ œ
_
ˆ‰ !n2
7. 0 for all n 1;
nn2! n1n3n2!
n3 n1n33
nn
2
2n 2 2n
n1 n1 2!
2
n13
2n 1
nn 2!
n3
2n
2
ab ababab
ab
x†x †
Ä_ Ä_
œlim lim
Š‹
22 32
2n 3 2
†œ
n3 n5n7n3
n n 2 ! 9n 9n
n
x
Ä_
ab lim Š‹
1 convergesœœœœÊlim lim lim
nnn
3n 15n 7 6n 15 6 1
27n 18n 54n 18 54 9 n 3
n1
nn 2!
Ä_ Ä_ Ä_
x
œ
_
Š‹
ˆ‰ˆ‰ !
2
2 2n
2ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

598 Chapter 10 Infinite Sequences and Series
8. 0 for all n 1;
n5
2n 3 ln n 1 2n 5 ln
nn
n155
†
Ä_ Ä_
††
nn15
n1
2n 1 3 ln n 1 1
n5
n
2n 3 ln n 1
n
abab aba
ab
œlim lim
Œ
Š‹
babab
n2 n5
2n 3 ln n 1
†
†n
œ†œ †œ†lim lim lim lim
nnnn
5n12n3 lnn1 lnn1
n2n5 lnn2 2n 5n lnn2 4n5
10n 25n 15 20n 25
Ä_ Ä_ Ä_ Ä_
†
Š‹Š‹Š‹
ˆ‰
aba bab ab
a b ab ab
2
2lim
nÄ_Š‹
1
n1
1
n2
5 5 1 5 1 divergesœ † œ† œ†œÊlim lim lim
nn n
20 n 2 1 n 5
4n1 1 2n3lnn1
n2
Ä_ Ä_ Ä_
†
œ
_
ˆ‰ ˆ ‰ ˆ‰ !n
abab
9. 0 for all n 1; 0 1 converges
77 7
2n 5 2n 5 2n 5
nn
7
2n 5 n1
ab ab ab
È
Ä_ Ä_ œ
_
nn n
nn
œ œÊlim lim
ÉŠ‹ !
10. 0 for all n 1; 0 1 converges
4444
3n 3n 3n
nn
3n n1
n n
nn n
nn
ab ab ab
œ œÊlim lim
Ä_ Ä_ œ
_
Ɉ‰ !
11. 0 for all n 2; 1 diverges
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
É!
4n 3 4n 3 4n 3 4 4 4n 3
3n 5 3n 5 3n 5 3 3 3n 5
nn n
nnn n1
Ä_ Ä_ Ä_ œ
_
œ œ œÊlim lim lim
n
12. ln e 0 for all n 1; ln e ln e ln e 2 1
’“ Ê’“ ’“
ˆ‰ ˆ‰ ˆ‰ ab
222
111
nnn
n1 n1 11n
nn
2
œ œœ
Î
Ä_ Ä_
lim lim
n
ln e divergesÊ
!’“
ˆ‰
n1
21
n
n1
œ
_
13. 0 for all n 1; 1 converges
8818
3333
nn
8
9n1
ˆ‰ ˆ‰ ˆ‰ ˆ‰
È
Ä_ Ä_ œ
_
1111
nnnn
2n 2n 2 2n
n
n
œ œÊlim lim
Ɍ !
14. sin 0 for all n 1; sin sin sin 0 0 1 sin converges
’“ ’“ ’“
Š‹ Š‹ Š‹ Š‹
Êab !
1111
nnnn
nn n
nn n1
ÈÈÈÈ
œ œ œÊlim lim
Ä_ Ä_ œ
_
n
15. 1 0 for all n 1; 1 1 e 1 1 converges
ˆ‰ ˆ‰ ˆ‰ ˆ‰
É!
œ œÊ
1111
nnnn
nnnn
nn
1
n1
2 2
n2
lim lim
Ä_ Ä_
œ
_
16. 0 for all n 2; 0 1 converges
"" "
Ä_ Ä_ Ä_ œ
_
nn n
nn n
11
nnn n2
1n 1n 1n
nnn
1n 1 n
œ œ œÊlim lim lim
ÉŠ‹ Š‹ !
ÈÈ
È
17. converges by the Ratio Test: lim lim lim lim 1
nn n nÄ_ Ä_ Ä_ Ä_
a
a n
(n 1) 2
n
2
n1
n
2
n1
n
2
œœ œœ
”•
”•
(n 1) 2
2n1
n2
n
###
"""
†ˆ‰ˆ‰
È1
18. converges by the Ratio Test: lim lim lim 1 1
nn n lim
n
Ä_ Ä_ Ä_ œÄ_
a
aennee
(n 1) e
n1
n
2
n1 2
n
œœ œ
Š‹
Š‹
(n 1)2
en1
n
en
"" "
#
†ˆ‰ˆ‰
19. diverges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
aen!e
(n )! en
n1
nn1
n
œœ œœ_
Š‹
ˆ‰
(n 1)!
en1
n!
en
" "
†
20. diverges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
a10n!10
(n )! 10 n
n1
nn1
n
œœ œœ_
Š‹
ˆ‰
(n 1)!
10n1
n!
10n
" †
21. converges by the Ratio Test: lim lim lim lim 1
nn n nÄ_ Ä_ Ä_ Ä_
a
a10nn1
(n ) 10
n1
nn1
n
œœ œ
Š‹
Š‹
(n 1)
10n1
n
10n
" ""
"!
†ˆ‰ˆ‰
010
œ
"1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.5 The Ratio and Root Tests 599
22. diverges; lim a lim lim 1 e 0
nn nÄ_ Ä_ Ä_
nn2 2
nn
nn
œœœÁ
ˆ‰ ˆ ‰
#
23. converges by the Direct Comparison Test: 2 ( 1) (3) which is the n term of a convergent
2(1)
(1.25) 5 5
44
nn
nth
n
nœŸ
ˆ‰ ˆ‰
cd
geometric series
24. converges; a geometric series with r 1kk ¸¸
œ
2
3
25. diverges; lim a lim 1 lim 1 e 0.05 0
nn nÄ_ Ä_ Ä_
n33
nn
nn
œœœ¸Á
ˆ‰ ˆ ‰
$
26. diverges; lim a lim 1 lim 1 e 0.72 0
nn nÄ_ Ä_ Ä_
n3n n
n
n
œœ œ¸Á
ˆ‰
""Î$
Š‹
3
27. converges by the Direct Comparison Test: for n 2, the n term of a convergent p-series.
ln n n
nnn
th
œ
"
28. converges by the nth-Root Test: lim a lim lim lim lim 0
nn n nnÄ_ Ä_ Ä_ Ä_ Ä_
ÈÉ
nnn
n
n1n
n1n
n(ln n)
nn1
(ln n)
n
ln n
œœ œœœ
ab
ab Š‹
n1
29. diverges by the Direct Comparison Test: for n 2 or by the Limit Comparison Test (part 1)
"" ""
#nn n n
n1
œ
ˆ‰
with .
"
n
30. converges by the nth-Root Test: lim a lim lim lim 0 1
nn n nÄ_ Ä_ Ä_ Ä_
ÈɈ‰ ˆ ‰ ˆ‰ˆ‰
nn
nnn nn nn
nn
1n
œœœœ
"" "" ""
Î
31. diverges by the Direct Comparison Test: for n 3
ln n
nn
"
32. converges by the Ratio Test: lim lim 1
nnÄ_ Ä_
a
an ln(n)
(n 1) ln (n 1) 2
n1
nn1
n
œœ
##
"
†
33. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
a (n 1)! (n 1)(n 2)
(n 2)(n 3) n!
n1
nœœ
†
34. converges by the Ratio Test: lim lim 1
nnÄ_ Ä_
a
aene
(n 1) e
n1
nn1
n
œœ
"
†
35. converges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
a 3!(n1)!3 (n3)! 3(n1) 3
(n 4)! 3! n! 3 n 4
n1
nn1
n
œœœ
"
†
36. converges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
a 3 (n 1)! n2 (n 1)! n 3 n 1 3
(n 1)2 (n 2)! 3n! n12n2 2
n1
n
n1
n1 n
n
œœœ
†ˆ‰ˆ‰ˆ‰
37. converges by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
a
a (2n 3)! n! (2n 3)(2n 2)
(n 1)! (2n 1)! n
n1
nœœœ
"
†
38. converges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
a(n1)n!n1
(n 1)! nn
n
n1
nn1
n
œœœ
"
†ˆ‰ ˆ‰
n
n
n
lim 1œœ
nÄ_
""
ˆ‰
1n
ne
39. converges by the Root Test: lim a lim lim lim 0 1
nn nnÄ_ Ä_ Ä_ Ä_
ÈÉ
nnn
n
nn
(ln n) ln n ln n
n
œ œœœ
È"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

600 Chapter 10 Infinite Sequences and Series
40. converges by the Root Test: lim a lim lim 0 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn2
nn
nn
(ln n)
n
ln n lim ln n
lim n
œœœœ
È
ÈÈ
È
n
n
lim n 1
Š‹
È
nÄ_
nœ
41. converges by the Direct Comparison Test: n! ln n ln n n
n(n 2)! n(n 1)(n 2) n(n 1)(n 2) (n 1)(n ) n#
""
œœ
which is the nth-term of a convergent p-series
42. diverges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
a (n1)2 3 (n1)
3n2 n33
n1
n
n1 n 3
n1 n 3
œœœ
##
†ˆ‰
43. converges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
a (2n 2)(2n 1)
n1
2(n 1)
2n n 1
n
n
n1
n
2
2
22
œœœ
‘
ab
‘
ab a b
‘
x
x
x
x
†
2n 1 1
4n 6n 2 4
2œ1
44. converges by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
a
a322n3232n3
2n 5 2 3 32 2n5264233
n1
n
n1
n1 n
nnn
œœ†
ab
ˆ‰
abab
†††
†’n
nnn
†††
6
36 93 22 6“
lim lim 1 1œ† œ†œ
nnÄ_ Ä_
’“ ’ “
2n5 2642336 2 2
2n3 3693226 3 3
† † †
† † †
nnn
nnn
45. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
aa
a
n1
nn
nn
œœ
ˆ‰
1sin n
46. converges by the Ratio Test: lim lim lim 0 since the numerator
nn nÄ_ Ä_ Ä_
a
aa n
atan n
n1
nn
n
œœœ
Š‹
1tan n
n"
approaches 1 while the denominator tends to _
1
#
47. diverges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
aa2n5
a3n 1 3
n 1 2n 5
nn
n
œœœ
ˆ‰
3n 1
#
48. diverges; a a a a a a
n1 n n1 n1 n1 n2
nnn1 nn1n2
n1 n1 n n1 n n1
œÊœ Êœ
ˆ‰ˆ ‰ ˆ‰ˆ‰ˆ ‰
a a a a , which is a constant times theÊœ â ʜʜ
n1 n1 n1
nn1n2 3
n1nn1 n1 n1
a
"
#
"
ˆ‰ˆ‰ˆ‰ˆ‰
general term of the diverging harmonic series
49. converges by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
a
aan
a2
n1
nn
n
œœœ
Š‹
2
n
50. converges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
aa n
a
n1
nn
n
œœœ
Œ
nn
n
Èn"
#
51. converges by the Ratio Test: lim lim lim lim 0 1
nn n nÄ_ Ä_ Ä_ Ä_
a
aa nn
aln n
n1
nn
n
œœœœ
Š‹
1ln n
n" "
52. 0 and a a 0; ln n 10 for n e n ln n n 10 1
nln n nln n
n10 n10
n
"
#
""!
œÊÊÊ
a a a ; thus a a lim a 0, so the series diverges by the nth-Term TestÊœ Ê Á
n1 n n n1 n n
nln n
n10
"
#
nÄ_
53. diverges by the nth-Term Test: a , a , a , a , ,
"# $ %
" " "" ""
œœ œ œ œ œá
3 3 33 33
ÉÉÉ ÉÉ
ÊÊ
Ë
22 2
33
6!
a lim a 1 because is a subsequence of whose limit is 1 by Table 8.1
nn
œÊ œ
ÉÉÉ
š› š›
n! n! n
"""
333
nÄ_
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.5 The Ratio and Root Tests 601
54. converges by the Direct Comparison Test: a , a , a , a ,
"# $ %
"" "" ""
## ## ##
##''#%
$%
œœœœœœá
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
a which is the nth-term of a convergent geometric seriesʜ
n
n! n
ˆ‰ ˆ‰
""
##
55. converges by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
a
a (2n 2)! 2 n! n! (2n
2 (n 1)! (n 1)! (2n)! 2(n 1)(n 1)
n1
n
n1
n
œœ
† )(2n 1)#
lim 1œœ
nÄ_
n
2n 1
" "
#
56. diverges by the Ratio Test: lim lim
nnÄ_ Ä_
a
a (n 1)! (n 2)! (n 3)! (3n)!
(3n 3)! n! (n 1)! (n 2)!
n1
nœ
†
lim lim 3 3 3 3 27 1œœœœ
nnÄ_ Ä_
(3n 3)(3 2)(3n 1)
(n 1)(n 2)(n 3) n n 3
3n 2 3n 1
#
ˆ‰ˆ‰††
57. diverges by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn
n
n(n!)
n
n!
n
´œœ_
ab
58. converges by the Root Test: lim lim lim lim
nnnnÄ_ Ä_ Ä_ Ä_
ÉɈ‰ˆ‰ˆ‰ ˆ ‰ˆ‰
nnn
n
n
nnn
(n!) (n!)
nn
n! 2 3 n 1 n
n nnn n n
œœœ â
ab "
lim 0 1Ÿœ
nÄ_
"
n
59. converges by the Root Test: lim a lim lim lim 0 1
nn nnÄ_ Ä_ Ä_ Ä_
ÈÉ
nnn
nnn
nnn
2 ln 2
œœœœ
##
"
60. diverges by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn
n
nnn
4
œœœ_
ab#
61. converges by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
a
a 4 2 (n 1)! 1 3 (2n 1)
1 3 (2n 1)(2n 1) 42n! 2n
n1
nn1n1
nn
œœ
†† †
†† †
â
â
†
(4 )(n 1) 4
" "
#†œ1
62. converges by the Ratio Test: an13 (2n 1) 1234 (2n 1)(2n) (2n)!
(2 4 n) 3 1 (2 4 2n) 3 1 2n! 3 1
œœ œ
† †††
††
â â
â# â
ab ababa b
nn
nn
lim lim ʜ
nnÄ_ Ä_
(2n 2)!
2 (n 1)! 3 1
2 n! 3 1 (2n )(2n 2) 3 1
(2n)! 2 (n 1) 3 1
"
cdab
abab ab
ab
n1 n1
nn n
n1
†
lim 1 1œœœ
nÄ_ Š‹
4n 6n 2
4n 8n 4 3 3 3 3
1 3
" "
ab
ab
n
n†
63. Ratio: lim lim lim 1 1 no conclusion
nn nÄ_ Ä_ Ä_
a
a (n 1) 1 n 1
nn
p
n1
np
p
œœœœÊ
"
†ˆ‰ p
Root: lim a lim lim 1 no conclusion
nnnÄ_ Ä_ Ä_
ÈÉ
nn
pp
np
nn(1)
n
œœ œœÊ
"""
ˆ‰
È
64. Ratio: lim lim lim lim lim
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
a
a (ln (n 1)) 1 ln (n 1) n
(ln n) ln n n
pp
p
n1
np
p
œœœœ
""
†’“ Š‹
”•
ˆ‰
ˆ‰
n
n1
(1) 1 no conclusionœœÊ
p
Root: lim a lim ; let f(n) (ln n) , then ln f(n)
nnÄ_ Ä_
ÈÉ
nnpp
n(ln n) n
1n ln (ln n)
œœ œ œ
"" Î
Š‹
lim (ln n)
nÄ_
1n
lim ln f(n) lim lim lim 0 lim (ln n)ÊœœœœÊ
nnnn nÄ_ Ä_ Ä_ Ä_ Ä_
ln (ln n)
n1n ln n
1n
ˆ‰
n ln n "Î
lim e e 1; therefore lim a 1 no conclusionœœœ œ œœÊ
nnÄ_ Ä_
ln f n n (1)
ÐÑ ! ""
È
npp
Š‹
lim (ln n)
nÄ_
1n
65. a for every n and the series converges by the Ratio Test since lim 1
nnn 2
22n
(n )
Ÿœ
nn n1
n
!
n1 # #
" "
nÄ_
†
a converges by the Direct Comparison TestÊ!
n1
n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
602 Chapter 10 Infinite Sequences and Series
66. 0 for all n 1;
22n!224
n! n 1 n! n 1 n 1
nn nn
2
nn2n1 2n1 n
2 2
2n1
2
n1!
2nn
22
n!
œ †œ œ œlim lim lim lim
Ä_ Ä_ Ä_ Ä_
†
†
Š‹Š‹
ˆ‰
ab lim
n
24 ln4
1
Ä_
†
ˆ‰
n
1 divergesœ_ Ê!
n1
2
n!
œ
_n2
10.6 ALTERNATING SERIES, ABSOLUTE AND CONDITIONAL CONVERGENCE
1. converges by the Alternating Convergence Test since: u 0 for all n 1; n 1 n 1 n n 1 n
n1
n
œ ÊÊ
ÈÈÈ
u u ; u 0.ÊŸÊŸ œ œ
11 1
n1 nn
n1 n n
nn
ÈÈ È
Ä_ Ä_
lim lim
2. converges absolutely converges by the Alternating Convergence Test since a which is aʜ
!!
kk
__
œœn1 n1
nn
"
convergent p-series
3. converges converges by Alternating Series Test since: u 0 for all n 1; n 1 n 1 n 3 3ÊœÊÊ
n1
n3
n1 n
n
n 1 3 n 3 u u ; u 0.Ê Ê Ÿ Ê Ÿ œ œab
n1 n 11 1
n13 n3 n3
n1 n n
nn
Ä_ Ä_
ab
n1 n n
lim lim
4. converges converges by Alternating Series Test since: u 0 for all n 2; n 2 n 1 nÊœÊ
n4
ln nab
2
ln n 1 ln n ln n 1 ln n u u ;ÊÊÊŸÊŸÊŸab a babab
22
11 44
ln n 1 ln n ln n 1 ln n n1 n
ababababab ab
22 22
u 0.lim lim
nn
n4
ln n
Ä_ Ä_
œœ
ab
2
5. converges converges by Alternating Series Test since: u 0 for all n 1; n 1 2n 2n n n 1ÊœÊ
nn
n1
22
2
n2n2nnnn1nn2n2nnn1nn1 1 n1n1Ê Ê Ê
32 32 2 32 2
2
a b ab a bab
Š‹
u u ; u 0.Ê ÊŸ œ œ
nn1 n
n1 n 1
n1 1 n1 n n
nn
22 2
Ä_ Ä_
ab lim lim
6. diverges diverges by n Term Test for Divergence since: 1 1 does not existʜʜ
th
nn
n5 n5
n4 n4
n1
lim lim
Ä_ Ä_
22
22
ab
7. diverges diverges by n Term Test for Divergence since: 1 does not existʜ_ʜ
th
nn
22
nn
n1
lim lim
Ä_ Ä_
nn
22
ab
8. converges absolutely converges by the Absolute Convergence Test since a , which converges by theʜ
!!
kk
__
œœn1 n1
n10
n1
n
abx
Ratio Test, since 0 1lim lim
nn
a
an2
10
Ä_ Ä_
n1
nœœ
9. diverges by the nth-Term Test since for n 10 1 lim 0 ( 1) diverges Ê Ê ÁÊ
nn n
10 10 10
nn
n1
nÄ_ ˆ‰ ˆ‰
!
_
œn1
10. converges by the Alternating Series Test because f(x) ln x is an increasing function of x is decreasingœÊ
"
ln x
u u for n 1; also u 0 for n 1 and lim 0Ê œ
nn1 n ln n
"
nÄ_
11. converges by the Alternating Series Test since f(x) f (x) 0 when x e f(x) is decreasingœÊ œ Ê
ln x 1 ln x
xx
w
u u ; also u 0 for n 1 and lim u lim lim 0Ê œ œ œ
nn1 n n ln n
n1
nn nÄ_ Ä_ Ä_ Š‹
n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.6 Alternating Series, Absolute and Conditional Convergence 603
12. converges by the Alternating Series Test since f(x) ln 1 x f (x) 0 for x 0 f(x) is decreasingœ Ê œ Êab
" w "
x(x 1)
u u ; also u 0 for n 1 and lim u lim ln 1 ln lim 1 ln 1 0Ê œ œ œ œ
nn1 n n nn
""
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ‰
Š‹
13. converges by the Alternating Series Test since f(x) f (x) 0 f(x) is decreasingœÊœ Ê
ÈÈ
È
x 1x2x
x1 2x(x1)
"
w
u u ; also u 0 for n 1 and lim u lim 0Ê œ œ
nn1 n nnÄ_ Ä_
nn
n1
È"
14. diverges by the nth-Term Test since lim lim 3 0
nnÄ_ Ä_
3n1
n1
31
1
È
ÈÉŠ‹
œœÁ
n
n
15. converges absolutely since a a convergent geometric series
!!
kk ˆ‰
n1 n1
n10
n
œ"
16. converges absolutely by the Direct Comparison Test since which is the nth term
¹¹ ˆ‰
( 1) (0.1)
n (10) n 10
n
""
n1 n
n
œ
of a convergent geometric series
17. converges conditionally since 0 and lim 0 convergence; but a
"" " "
ÈÈ È
nn
n1 nn
œÊ œ
nÄ_ !!
kk
__
œœn1 n1
is a divergent p-series
18. converges conditionally since 0 and lim 0 convergence; but
"" "
1n 1n
1n1
ÈÈ È
œÊ
nÄ_
a is a divergent series since and is a divergent p-series
!! !
kk
__ _
œœ œn1 n1 n1
n1n 1n n n
œ
""""
#
ÈÈÈ
19. converges absolutely since a and which is the nth-term of a converging p-series
!!
kk
__
œœn1 n1
nnn
n1 n1 n
œ
"
20. diverges by the nth-Term Test since lim
nÄ_
n!
#nœ_
21. converges conditionally since 0 and lim 0 convergence; but a
"" "
n3 (n1)3 n3 n
œÊ
nÄ_ !kk
_
œn1
diverges because and is a divergent seriesœ
!!
__
œœn1 n1
""""
n3 n3 4n n
22. converges absolutely because the series converges by the Direct Comparison Test since
!¸¸ ¸¸
_
œn1
sin n sin n
nnn
Ÿ"
23. diverges by the nth-Term Test since lim 1 0
nÄ_
3n
5n
œÁ
24. converges absolutely by the Direct Comparison Test since 2 which is the nth term
¹¹ ˆ‰
(2)
n5 n5 5
22
n
n1
nn
n1
œ
of a convergent geometric series
25. converges conditionally since f(x) f (x) 0 f(x) is decreasing and henceœÊ œ Ê
"" "
w
xx xx
2
ˆ‰
u u 0 for n 1 and lim 0 convergence; but a
nn1 n
œÊ œ
nÄ_ ˆ‰ !!
kk
""
nn n
1n
__
œœn1 n1
is the sum of a convergent and divergent series, and hence divergesœ
!!
__
œœn1 n1
""
nn
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

604 Chapter 10 Infinite Sequences and Series
26. diverges by the nth-Term Test since lim a lim 10 1 0
nnÄ_ Ä_
n1n
œœÁ
Î
27. converges absolutely by the Ratio Test: lim lim 1
nnÄ_ Ä_
Š‹ ”•
u
u3
2
n1
nœœ
(n )
n
" ˆ‰
ˆ‰
2
3
n1
2
3
n
28. converges conditionally since f(x) f (x) 0 f(x) is decreasingœÊœ Ê
"w
x ln x (x ln x)
ln (x) 1cd
u u 0 for n 2 and lim 0 convergence; but by the Integral Test,Ê œÊ
nn1 nÄ_
"
n ln n
lim dx lim ln (ln x) lim ln (ln b) ln (ln 2)
''
22
bb
2
dx
x ln x ln x
œœœœ_
bbbÄ_ Ä_ Ä_
cd c d
Š‹
x
a divergesʜ
!!
kk
__
œœn1 n1
nn ln n
"
29. converges absolutely by the Integral Test since tan x dx lim
'1
b
1
ab
ˆ‰ ’“
" "
#1x
tan x
œbÄ_ ab
lim tan b tan 1œœœ
bÄ_ ’“’“
abab ˆ‰ ˆ‰
" "
##
"
##
##
11 1
432
3
30. converges conditionally since f(x) f (x)œÊœ
ln x
x ln x (x ln x)
(x ln x) (ln x) 1
w
Š‹ Š ‹
xx
0 u u 0 when n e and lim œœÊ
1ln x
(x ln x) (x ln x) n ln n
1 ln x ln n
nn1
Š‹ Š‹
ln x ln x
xx
nÄ_
lim 0 convergence; but n ln n n so thatœœÊ ÊÊ
nÄ_ Š‹
Š‹
n
n
1nln n n nln n n
ln n
"" "
a diverges by the Direct Comparison Test
!!
kk
_
œn1
nln n
nln n
œ
n1
31. diverges by the nth-Term Test since lim 1 0
nÄ_
n
n1œÁ
32. converges absolutely since a is a convergent geometric series
!!
kk ˆ‰
__
œœn1 n1
n5
n
œ"
33. converges absolutely by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
Š‹
u
u (n 1)! (100) n 1
( 00) n! 00
n1
n
n1
n
œœœ
"
"
†
34. converges absolutely by the Direct Comparison Test since a and which is the
!!
kk
__
œœn1 n1
nn2n1 n2n1 n
œ
"""
nth-term of a convergent p-series
35. converges absolutely since a is a convergent p-series
!! !
kk ¹¹
__ _
œœ œn1 n1 n1
n(1)
nn n
œœ
"
n
È
36. converges conditionally since is the convergent alternating harmonic series, but
!!
__
œœn1 n1
cos n
nn
(1)
1œn
a diverges
!!
kk
__
œœn1 n1
nn
œ"
37. converges absolutely by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
Èkk Š‹
nn
n
nœœœ
(n 1)
(2n) n
1n n
Î" "
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.6 Alternating Series, Absolute and Conditional Convergence 605
38. converges absolutely by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
¹¹
a
a ((2n 2)!) (n!) (2n 2)(2n 1)
(n 1)! (2n)! (n 1)
n1
nœœœ
ab
†"
41
39. diverges by the nth-Term Test since lim a lim lim
nn nÄ_ Ä_ Ä_
kk
n(2n)! (n )(n 2) (2n)
2n!n 2n
œœ
n
" â
n
lim lim 0œœ_Á
nnÄ_ Ä_
(n 1)(n 2) (n (n 1)) n1
n1
â
##
n1 ˆ‰
40. converges absolutely by the Ratio Test: lim lim
nnÄ_ Ä_
¹¹
a
a (2n 3)! n! n! 3
(n 1)! (n 1)! 3 (2n 1)!
n1
n
n1
n
œ
†
lim 1œœ
nÄ_
(n 1) 3
(2n 2)(2n 3) 4
3
41. converges conditionally since and is a
ÈÈ
ÈÈ
ÈÈ È
ÈÈ È
n1 n n1 n
1n1 n n1 n n1 n
""
†œš›
decreasing sequence of positive terms which converges to 0 converges; butÊ!
_
œn1
()
n1 n
"
n
ÈÈ
a diverges by the Limit Comparison Test (part 1) with ; a divergent p-series:
!!
kk
__
œœn1 n1
nn1 n n
œ" "
È È
È
lim lim lim
nnnÄ_ Ä_ Ä_
n1 n
n1
n
œœœ
È
ÈÈÉ
n
n1 n
1
11
"
#
42. diverges by the nth-Term Test since lim n n n lim n n n
nnÄ_ Ä_
Š‹Š‹Š‹
ÈÈ
##
œ †È
Ènnn
nnn
lim lim 0œœœÁ
nnÄ_ Ä_
n
nnn 11
ÈÉ
""
#
n
43. diverges by the nth-Term Test since lim n n n lim n n n
nnÄ_ Ä_
Š‹Š‹
ÉÉ
ÈÈ ÈÈ
–—
œ ÉÈÈ
ÉÈÈ
nnn
nnn
lim lim 0œœœÁ
nnÄ_ Ä_
È
ÉÉ
ÈÈ
n
nnn 11
""
#
n
44. converges conditionally since is a decreasing sequence of positive terms converging to 0
š›
"
ÈÈ
nn1
converges; but lim lim lim Êœœœ
!
_
œn1
()
nn1 nn1
n
11
"
""
#
n
n
ÈÈ
ÈÈ
ÈÉ
nnnÄ_ Ä_ Ä_
Š‹
Š‹
nn1
n
so that diverges by the Limit Comparison Test with which is a divergent p-series
!!
_ _
œ œn1 n1
""
ÈÈÈ
nn1 n
45. converges absolutely by the Direct Comparison Test since sech (n) which is theœœœ
22e2e2
ee e 1 e e
n n 2n 2n n
nn
nth term of a convergent geometric series
46. converges absolutely by the Limit Comparison Test (part 1): a
!!
kk
__
œœn1 n1
n2
ee
œnn
Apply the Limit Comparison Test with , the n-th term of a convergent geometric series:
1
en
lim lim lim 2
nnnÄ_ Ä_ Ä_
Œ
2
ee
nn
1
enœœœ
2e 2
ee 1e
n
nn 2n
47. ; converges by Alternating Series Test since: u 0 for all n 1;
111 1 1 1 1
468101214 2n1 2n1
() n
ÞÞÞœ œ
!
_
œn1
"
n1
ab ab
n2n1 2n2 2n1 u u; u 0.Ê Ê Ÿ Ê Ÿ œ œabab 11 1
2n 1 1 2n1 2n1
n1 n n
nn
a b ab abab
Ä_ Ä_
lim lim
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

606 Chapter 10 Infinite Sequences and Series
48. 1 a ; converges by the Absolute Convergence Test since a ÞÞÞœ œ
1111111
491625364964 n
n n
!!!
kk
___
œœœn1 n1 n1
"
which is a convergent p-series
49. error ( 1) 0.2 50. error ( 1) 0.00001kk kk
¸¸ ¸ ¸ˆ‰ ˆ ‰
œ œ
' '
" "
510
51. error ( 1) 2 10 52. error ( 1) t t 1kk kkk k
¹¹
œ‚ œ
' "" % % %
(0.01)
5
53. error 0.001 u 0.001 0.001 n 1 3 1000 n 1 997 30.5753 n 31kk ab È
ÊÊ ÊÊ ¸ Ê
n1 1
n1 3
2
ab
2
54. error 0.001 u 0.001 0.001 n 1 1 1000 n 1 nkk ab abÊÊ Ê Ê
n1 n1
n1 1
2998 998 4 998
2
ab Èab
2
2
998.9999 n 999¸Ê
55. error 0.001 u 0.001 0.001 n 1 3 n 1 1000kk a b
Š‹
È
ÊÊ Ê
n1 1
n1 3n1
3
ˆ‰
ab
È3
n1 3n1100 n1 2n3n4Ê Ê œ œÊœÊ
Š‹
ÈÈ È
23 9 40
2
È
56. error 0.001 u 0.001 0.001 ln ln n 3 1000 n 3 e 5.297 10kk a babÊÊ Ê Ê¸‚
n1 1
ln ln n 3
e 323228467
abab 1000
which is the maximum arbitrary-precision number represented by Mathematica on the particular computer solving this
problem..
57. (2n)! 200,000 n 5 1 0.54030
"""""
#(2n)! 10 5 !4!6!8!
510
Ê œ Êʸ
58. n! n 9 1 1 0.367881944
" """""""
#n! 10 5 ! 3! 4! 5! 6! 7! 8!
510
Ê Êʸ
59. (a) a a fails since
nn1 3
""
#
(b) Since a is the sum of two absolutely convergent
!! ! !
kk ‘ ˆ‰ ˆ‰ˆ‰ ˆ‰
__ _ _
œœ œ œn1 n1 n1 n1
n33
nn n n
œœ
"" " "
##
series, we can rearrange the terms of the original series to find its sum:
1
ˆ‰ˆ‰
"" " """ " "
###
3927 48 11
á ᜠœœ
ˆ‰ ˆ‰
ˆ‰ ˆ‰
3
3
60. s 1 0.6687714032 s 0.692580927
#! #!
""" " " ""
###
œá ¸ Ê ¸
3 4 19 20 1
†
61. The unused terms are ( 1) a ( 1) a a ( 1) a a
!abab
jn1
j1 n1 n3
j n1n2 n3n4
œ á
( 1) a a a a . Each grouped term is positive, so the remainderœ á
n1 n1 n2 n3 n4
cdabab
has the same sign as ( 1) , which is the sign of the first unused term.n1
62. s
n1 2 3 3 4 n(n 1) k(k 1) k k 1
œá œ œ
""" " " ""
#††† !!
ˆ‰
nn
k1 k1œœ
1 which are the first 2n termsχ
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ ‰
""""""" ""
## 33445 nn1
of the first series, hence the two series are the same. Yes, for
s 1 1
nkk1 3 34 45 n1n nn1 n1
œ œá œ
!ˆ ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ ‰ˆ ‰
n
k1œ
"" """"""" """" "
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.6 Alternating Series, Absolute and Conditional Convergence 607
lim s lim 1 1 both series converge to 1. The sum of the first 2n 1 terms of the firstÊœœÊ
nnÄ_ Ä_
nn1
ˆ‰
"
series is 1 1. Their sum is lim s lim 1 1.
ˆ‰ ˆ‰
œ œ œ
"" "
n1 n1 n1
n
nnÄ_ Ä_
63. Theorem 16 states that a converges a converges. But this is equivalent to a diverges a div
!! !!
kk kk
__ __
œœ œœn1 n1 n1 n1
nn nn
ÊÊerges
64. a a a a a a for all n; then a converges a converges and these imply thatk k kk kk kk kk
!!
"# " #
á Ÿ á Ê
nnnn
__
œœn1 n1
a a
ºº
!!
kk
__
œœn1 n1
nn
Ÿ
65. (a) a b converges by the Direct Comparison Test since a b a b and hence
!kk kkkkkk
_
œn1
nn nn n n
Ÿ
a b converges absolutely
!ab
_
œn1
nn
(b) b converges b converges absolutely; since a converges absolutely and
!! !
kk
__ _
œœ œn1 n1 n1
nn n
Ê
b converges absolutely, we have a ( b ) a b converges absolutely by part (a)
!!!
cdab
___
œœœn1 n1 n1
œ
nnnnn
(c) a converges k a ka converges ka converges absolutely
!!!!
kk kk kk k k
____
œœœœn1 n1 n1 n1
nnnn
Êœ Ê
66. If a b ( 1) , then ( 1) converges, but a b diverges
nn nn
nn
nn n
œœ œ
"" "
ÈÈ
!!!
___
œœœn1 n1 n1
67. s , s 1 ,
"#
"""
###
œ œ œ
s 1 0.5099,
$" """"""""""
####
œ¸
468101 141618 02
s s 0.1766,
%$
"
œ¸
3
s s 0.512,
&%
"""""""""""
### #
œ¸
4 6 8303 343638404244
s s 0.312,
'&
"
œ¸
5
s s 0.51106
('
"""""""""""
œ¸
46 48 50 52 54 56 58 60 62 64 66
68. (a) Since a converges, say to M, for 0 there is an integer N such that a M
!!
kk kk
ºº
n n
%
"#
N1
n1
œ
%
a a a a a . Also, aÍ ÍÍ
»»»»
!!! ! ! !
kk kk kk kk kk
N1 N1
n1 n1 nN nN nN
œœœ œ œ
___
nnn n n n
%%%
###
converges to L for 0 there is an integer N (which we can choose greater than or equal to N ) suchÍ%#"
that s L . Therefore, a and s L .kk kk kk
!
NN
%%%
###
_
œnN
n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

608 Chapter 10 Infinite Sequences and Series
(b) The series a converges absolutely, say to M. Thus, there exists N such that a M
!!
kk kk
ºº
_
œ œn1 n1
k
n n"%
whenever k N . Now all of the terms in the sequence b appear in a . Sum together all of the"ef efkk kk
nn
terms in b , in order, until you include all of the terms a , and let N be the largest index in theef efkk kk
nn
N
n1
œ#
sum b so obtained. Then b M as well b converges to M.
!! !
kk kk kk
ºº
NN
n1 n1 n1
œœ œ
_
nn n
Ê%
10.7 POWER SERIES
1. lim 1 lim 1 x 1 1 x 1; when x 1 we have ( 1) , a divergent
nnÄ_ Ä_
¹¹ ¹¹ kk !
u
ux
x
n1
n
n1
n
Ê Ê Ê œ
_
œn1
n
series; when x 1 we have 1, a divergent seriesœ!
_
œn1
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
2. lim 1 lim 1 x 5 1 6 x 4; when x 6 we have
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u(x5)
(x 5)
n1
n
n1
n
Ê Ê Ê œ
( 1) , a divergent series; when x 4 we have 1, a divergent series
!!
_ _
œ œn1 n1
œ
n
(a) the radius is 1; the interval of convergence is 6 x 4
(b) the interval of absolute convergence is 6 x 4
(c) there are no values for which the series converges conditionally
3. lim 1 lim 1 4x 1 1 1 4x 1 1 x 0; when x we
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u (4x 1)
(4x 1)
n1
n
n1
n
Ê Ê Ê Ê œ
##
""
have ( 1) ( 1) ( 1) 1 , a divergent series; when x 0 we have ( 1) (1) ( 1) ,
!!! !!
___ __
œœœ œœn1 n1 n1 n1 n1
œ œ œ œ
nn 2n n nn n
a divergent series
(a) the radius is ; the interval of convergence is x 0
""
#4
(b) the interval of absolute convergence is x 0
"
#
(c) there are no values for which the series converges conditionally
4. lim 1 lim 1 3x 2 lim 1 3x 2 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u n 1 (3x 2) n 1
(3x 2) nn
n1
n
n1
n
Ê Ê Ê
†
1 3x 2 1 x 1; when x we have which is the alternating harmonic series and isÊ Ê œ
""
"
33n
()
!
_
œn1
n
conditionally convergent; when x 1 we have , the divergent harmonic seriesœ!
_
œn1
"
n
(a) the radius is ; the interval of convergence is x 1
""
33
Ÿ
(b) the interval of absolute convergence is x 1
"
3
(c) the series converges conditionally at x œ"
3
5. lim 1 lim 1 1 x 2 10 10 x 2 10
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u10(x2)10
(x 2) 10 x2
n1
n
n1
n1 n
n
Ê Ê Ê Ê
†kk
8 x 12; when x 8 we have ( ) , a divergent series; when x 12 we have 1, a divergent seriesÊ œ " œ
!!
_ _
œ œn1 n1
n
(a) the radius is 0; the interval of convergence is 8 x 12"
(b) the interval of absolute convergence is 8 x 12
(c) there are no values for which the series converges conditionally
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.7 Power Series 609
6. lim 1 lim 1 lim 2x 1 2x 1 x ; when x we have
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (2x)
(2x)
n1
n
n1
n
Ê Ê Ê Ê œ
"" "
## #
( ) , a divergent series; when x we have 1, a divergent series
!!
__
œœn1 n1
" œ
n"
#
(a) the radius is ; the interval of convergence is x
"""
###
(b) the interval of absolute convergence is x
""
##
(c) there are no values for which the series converges conditionally
7. lim 1 lim 1 x lim 1 x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (n3) nx (n3)(n)
(n 1)x (n 2) (n 1)(n 2)
n1
n
n1
n
Ê Ê Ê
†
1 x 1; when x 1 we have ( ) , a divergent series by the nth-term Test; when x weÊ œ " œ"
!
_
œn1
nn
n#
have , a divergent series
!
_
œn1
n
n#
(a) the radius is ; the interval of convergence is x"""
(b) the interval of absolute convergence is x" "
(c) there are no values for which the series converges conditionally
8. lim 1 lim 1 x 2 lim 1 x 2 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
un1(x2) n1
(x 2) nn
n1
n
n1
n
Ê Ê Ê
†
1 x 2 1 3 x 1; when x 3 we have , a divergent series; when x we haveÊ Ê œ œ"
!
_
œn1
"
n
, a convergent series
!
_
œn1
(1)
n
n
(a) the radius is ; the interval of convergence is 3 x"Ÿ"
(b) the interval of absolute convergence is 3 x "
(c) the series converges conditionally at x 1œ
9. lim 1 lim 1 lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
É
u
ux3n1n1
xnn
(n 1) n 1 3
nn3 x
n1
n
n1
n1
n
n
Ê Ê
ÈÈkk
†
(1)(1) 1 x 3 3 x 3; when x 3 we have , an absolutely convergent series;ÊÊÊ œ
kkx
3
()
n
kk !
_
œn1
" n
when x 3 we have , a convergent p-seriesœ!
_
œn1
1
n
(a) the radius is 3; the interval of convergence is 3 x 3Ÿ Ÿ
(b) the interval of absolute convergence is 3 x 3Ÿ Ÿ
(c) there are no values for which the series converges conditionally
10. lim 1 lim 1 x 1 lim 1 x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
u(x1)n1
(x 1)
n1
nn
n1
n
n1
n
Ê Ê Ê
ÈÈ
†
1 x 1 1 0 x 2; when x 0 we have , a conditionally convergent series; when x 2Ê Ê œ œ
!
_
œn1
()
n
" n
we have , a divergent series
!
_
œn1
1
n
(a) the radius is 1; the interval of convergence is 0 x 2Ÿ
(b) the interval of absolute convergence is 0 x 2
(c) the series converges conditionally at x 0œ
11. lim 1 lim 1 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk ˆ‰
u
u(n1)!x n1
xn!
n1
n
n1
n
Ê Ê
"
†
(a) the radius is ; the series converges for all x_
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

610 Chapter 10 Infinite Sequences and Series
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
12. lim 1 lim 1 3 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk ˆ‰
u
u (n1)! 3x n1
3x n!
n1
n
n1 n1
nn
Ê Ê
"
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
13. lim 1 lim 1 x lim 4x 1 x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
un14x n14
4x n 4n 1
n1
n
n12n2
n2n
Ê Ê œ Ê
###
†
x ; when x we have , a divergent p-series; when x we haveÊ œ œ œ
11 1 41 1 1
22 2 n2 n 2
2n
!!
ˆ‰
__
œœn1 n1
n
, a divergent p-series
!!
ˆ‰
__
œœn1 n1
41 1
n2 n
2n
nœ
(a) the radius is ; the interval of convergence is x
111
222
(b) the interval of absolute convergence is x
11
22
(c) there are no values for which the series converges conditionally
14. lim 1 lim 1 x 1 lim x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
u
u(x1) 3
(x 1)
n13 3n1
n3 n 1
n1
n
n1
2n 2
n1
2n 2
Ê Êll œ ll
ab ab
†
2 x 4; when x 2 we have , an absolutely convergent series; when x 4 we haveÊ œ œ œ
!!
__
œœn1 n1
(3) (1)
n3 n
nn
2n 2
, an absolutely convergent series.
!!
__
œœn1 n1
(3)
n3 n
1
n
2n 2
œ
(a) the radius is 3; the interval of convergence is 2 x 4Ÿ Ÿ
(b) the interval of absolute convergence is 2 x 4Ÿ Ÿ
(c) there are no values for which the series converges conditionally
15. lim 1 lim 1 x lim x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn2n4
xn3
(n 1) 3
n3
n1
n
n1
n
Ê Ê "Ê
ÈÈ
†
1 x 1; when x 1 we have , a conditionally convergent series; when x 1 we haveÊ œ œ
!
_
œn1
()
n3
"
n
È
, a divergent series
!
_
œn1
"
Èn3
(a) the radius is 1; the interval of convergence is 1 x 1Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
16. lim 1 lim 1 x lim x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn2n4
xn3
(n 1) 3
n3
n1
n
n1
n
Ê Ê "Ê
ÈÈ
†
1 x 1; when x 1 we have , a divergent series; when x 1 we have ,Ê œ œ
!!
_ _
œ œn1 n1
"
"
ÈÈ
n3 n3
()
n
a conditionally convergent series
(a) the radius is 1; the interval of convergence is 1 x 1 Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.7 Power Series 611
17. lim 1 lim 1 lim 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u5n(x3)5n5
(n 1)(x 3) 5n
x3 x3
n1
n
n1
n1 n
n
Ê Ê Ê
"
†kk kk
x 3 5 5 x 3 5 8 x 2; when x 8 we have ( 1) n, a divergentÊ Ê Ê œ œ kk !!
__
œœn1 n1
n( 5)
5
n
nn
series; when x 2 we have n, a divergent seriesœœ
!!
__
œœn1 n1
n5
5
n
n
(a) the radius is 5; the interval of convergence is 8 x 2
(b) the interval of absolute convergence is 8 x 2
(c) there are no values for which the series converges conditionally
18. lim 1 lim 1 lim 1 x 4
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹ kk
u
u 4 n2n2 nx 4 nn2n2
(n 1)x 4n 1 (n 1)n 1
x
n1
n
n1
n1 n
n
Ê Ê Ê
ab ab
ab ab
kk
†
4 x 4; when x 4 we have , a conditionally convergent series; when x 4 we have ,Ê œ œ
!!
_ _
œ œn1 n1
n( 1)
n1 n1
n
n
a divergent series
(a) the radius is 4; the interval of convergence is 4 x 4Ÿ
(b) the interval of absolute convergence is 4 x 4
(c) the series converges conditionally at x 4œ
19. lim 1 lim 1 lim 1 1 x 3
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Ɉ‰ kk
u
u33n3
n1x x x
3n1
nx
n1
n
n1
n1
n
n
Ê Ê Ê Ê
ÈÈkk kk
†
3 x 3; when x 3 we have ( 1) n , a divergent series; when x 3 we have n, a divergent seriesÊ œ œ
!!
ÈÈ
_ _
œ œn1 n1
n
(a) the radius is 3; the interval of convergence is 3 x 3
(b) the interval of absolute convergence is 3 x 3
(c) there are no values for which the series converges conditionally
20. lim 1 lim 1 2x 5 lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
kk
u
u
n 1 (2x 5) n 1
n (2x 5) n
n1
n
n1 n1
n1
n n
n
Ê Ê
ÈÈ
ÈÈ
2x 5 1 2x 5 1 1 2x 5 1 3 x 2; when x 3 we haveÊ Ê Ê Ê œkk kk
Œ
lim t
lim n
t
n
È
È
t
n
( 1) n, a divergent series since lim n 1; when x 2 we have n, a divergent series
!!
ÈÈÈ
_ _
œ œn1 n1
œœ
nnn
nÄ_
(a) the radius is ; the interval of convergence is 3 x 2
"
#
(b) the interval of absolute convergence is 3 x 2
(c) there are no values for which the series converges conditionally
21. First, rewrite the series as 2 ( 1) x 1 2 x 1 ( 1) x 1 . For the series
!!!
a bab ab ab
___
œœœn1 n1 n1
œ
nn
n1 n1 n1
2 x 1 : lim 1 lim 1 x 1 lim 1 x 1 1 2 x 0; For the
!ab ¹¹ ¹ ¹
_
œn1
Ê Êll œll Ê
n1 2x1
u
u2x 1
nn nÄ_ Ä_ Ä_
n1
n
n
n1
ab
ab
series ( 1) x 1 : lim 1 lim 1 x 1 lim 1 x 1 1
!ab ¹¹ ¹ ¹
_
œn1
Ê Êll œll
nn1 (1) x1
u
u(1)x1
nn nÄ_ Ä_ Ä_
n1
n
n1 n
nn1
ab
ab
2 x 0; when x 2 we have 2 ( 1) 1 , a divergent series; when x 0 we haveÊ œ œ
!abab
_
œn1
nn1
2 ( 1) , a divergent series
!ab
_
œn1
n
(a) the radius is 1; the interval of convergence is 2 x 0
(b) the interval of absolute convergence is 2 x 0
(c) there are no values for which the series converges conditionally
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

612 Chapter 10 Infinite Sequences and Series
22. lim 1 lim 1 x 2 lim 9 x 2 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹
u
u 3n1 n1
(1) 3 x 2 3n 9n
(1)3 x 2
n1
n
n12n2 n1
n2n n
Ê † Êll œll
ab
ab ab
x ; when x we have , a divergent series; when x we haveÊ œ œ œ
17 19 17 1 1 19
99 9 3n93n 9
(1)3 n
!!
ˆ‰
__
œœn1 n1
n2n
, a conditionally convergent series.
!!
ˆ‰
__
œœn1 n1
(1)3 (1)
3n 9 3n
1n
n2n n
œ
(a) the radius is ; the interval of convergence is x
11719
999
Ÿ
(b) the interval of absolute convergence is x
17 19
99
(c) the series converges conditionally at x œ19
9
23. lim 1 lim 1 x 1 x 1 x 1
nnÄ_ Ä_
¹¹ »»
kk kk kk
ˆ‰
u
u e
1 x lim 1
1 x lim 1
e
n1
nn
n1 t
n1
nn
Ê Ê Ê Ê
Š‹ Š‹
Š‹ Š‹
n1 t
nn
t
n
1 x 1; when x 1 we have ( 1) 1 , a divergent series by the nth-Term Test sinceÊ œ
!ˆ‰
_
œn1
n
n
n
"
lim 1 e 0; when x 1 we have 1 , a divergent series
nÄ_ ˆ‰ ˆ‰
!
œÁ œ
""
nn
nn
_
œn1
(a) the radius is ; the interval of convergence is 1 x 1"
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
24. lim 1 lim 1 x lim 1 x lim 1 x 1
nn n nÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ kk kk kk
ºº ˆ‰
u
ux ln n n1
ln (n 1)x n
n1
n
n1
n
Ê Ê Ê Ê
ˆ‰
ˆ‰
n1
n
1 x 1; when x 1 we have ( 1) ln n, a divergent series by the nth-Term Test since lim ln n 0;Ê œ Á
!
_
œn1
n
nÄ_
when x 1 we have ln n, a divergent seriesœ!
_
œn1
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
25. lim 1 lim 1 x lim 1 lim (n 1) 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk ˆ‰
u
unx n
(n 1) x n
n1
n
n1n1
nn
Ê Ê
"
e x lim (n 1) 1 only x 0 satisfies this inequalityÊÊœkknÄ_
(a) the radius is 0; the series converges only for x 0œ
(b) the series converges absolutely only for x 0œ
(c) there are no values for which the series converges conditionally
26. lim 1 lim 1 x 4 lim (n 1) 1 only x 4 satisfies this inequality
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk
u
un!(x4)
(n 1)! (x 4)
n1
n
n1
n
Ê Ê Ê œ
(a) the radius is 0; the series converges only for x 4œ
(b) the series converges absolutely only for x 4œ
(c) there are no values for which the series converges conditionally
27. lim 1 lim 1 lim 1 1 x 2 2
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰ kk
u
u (n1)2 (x2) n1
(x 2) n2 n
x2 x2
n1
n
n1
n1 n
n
Ê Ê Ê Ê
# #
†kk kk
2 x 2 2 4 x 0; when x 4 we have , a divergent series; when x 0 we have ,Ê Ê œ œ
!!
__
œœn1 n1
"
nn
(1)
n1
the alternating harmonic series which converges conditionally
(a) the radius is 2; the interval of convergence is 4 x 0 Ÿ
(b) the interval of absolute convergence is 4 x 0
(c) the series converges conditionally at x 0œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.7 Power Series 613
28. lim 1 lim 1 2 x 1 lim 1 2 x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u ( 2) (n 1)(x 1) n 1
( 2) (n 2)(x 1) n2
n1
n
n1 n1
nn
Ê Ê Ê
x 1 x 1 x ; when x we have (n 1) , a divergent series; when xÊ Ê Ê œ œkk !
"" "" "
## ## # # #
3 3
_
œn1
we have ( 1) (n 1), a divergent series
!
_
œn1
n
(a) the radius is ; the interval of convergence is x
""
###
3
(b) the interval of absolute convergence is x
"
##
3
(c) there are no values for which the series converges conditionally
29. lim 1 lim 1 x lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk
u
uxn1ln(n1)
xnln n
(n 1) ln (n 1)
n(ln n)
n1
n
n1
n
Ê Ê
#
ab
†
x (1) lim 1 x lim 1 x 1 1 x 1; when x 1 we haveÊÊÊÊœkk kk kk
Œ Š‹
nnÄ_ Ä_
ˆ‰
ˆ‰
n
n1
#
#
n1
n
which converges absolutely; when x 1 we have which converges
!!
_ _
œ œn1 n1
(1)
n(ln n) n(ln n)
"
nœ
(a) the radius is ; the interval of convergence is 1 x 1"ŸŸ
(b) the interval of absolute convergence is 1 x 1Ÿ Ÿ
(c) there are no values for which the series converges conditionally
30. lim 1 lim 1 x lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk
u
u (n 1) ln (n 1) x n 1 ln (n 1)
xn
n ln (n) ln (n)
n1
n
n1
n
Ê Ê
†
x (1)(1) 1 x 1 1 x 1; when x 1 we have , a convergent alternating series;ÊÊÊ œkk kk !
_
œn2
(1)
n ln n
n
when x 1 we have which diverges by Exercise 38, Section 9.3œ!
_
œn2
"
n ln n
(a) the radius is ; the interval of convergence is 1 x 1"Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
31. lim 1 lim 1 (4x 5) lim 1 (4x 5) 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
u
u (4x 5) n 1
(4x 5)
(n 1)
nn
n1
n
2n 3
2n 1
Ê Ê Ê
##
$Î#
†
4x 5 1 1 4x 5 1 1 x ; when x 1 we have which isÊÊÊ œ œkk !!
3(1)
nn
#
"
__
œœn1 n1
2n 1
absolutely convergent; when x we have , a convergent p-seriesœ3()
n
#
"
!
_
œn1
2n 1
(a) the radius is ; the interval of convergence is 1 x
"
#4
3
ŸŸ
(b) the interval of absolute convergence is 1 xŸŸ
3
#
(c) there are no values for which the series converges conditionally
32. lim 1 lim 1 3x 1 lim 1 3x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u 2n4 (3x1) 2n4
(3x 1) 2n 2 2n 2
n1
n
n2
n1
Ê Ê Ê
†
1 3x 1 1 x 0; when x we have , a conditionally convergent series;Ê Ê œ
22
332n1
(1)
!
_
œn1
n1
when x 0 we have , a divergent seriesœœ
!!
__
œœn1 n1
()
2n 1 n 1
"
#
"
n1
(a) the radius is ; the interval of convergence is x 0
"
33
2
Ÿ
(b) the interval of absolute convergence is x 0
2
3
(c) the series converges conditionally at x œ2
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

614 Chapter 10 Infinite Sequences and Series
33. lim 1 lim 1 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk ˆ‰
u
u 2 4 6 2n 2 n 1 x 2n 2
x1
246 2n
n1
n
n1
n
Ê Ê
††â
††â
aba bab ab
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
34. lim 1 lim 1 x lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
kk
u
u 357 2n 1x
3 5 7 2n 1 2 n 1 1 x 2n 3 n
n12 2n1
n2
n1
n
n2 2
2n1 2
n1
2n
Ê Ê
††â
††â
aba b abab
ab ab
ab
†Ê only
x 0 satisfies this inequalityœ
(a) the radius is 0; the series converges only for x 0œ
(b) the series converges absolutely only for x 0œ
(c) there are no values for which the series converges conditionally
35. For the series x , recall 1 2 n and 1 2 n so that we can
!
_
œn1
12 n
12 n 2 6
n222
nn 1 nn 1 2n 1
â
â
22 2 ✠⠜
ab aba b
rewrite the series as x x ; then lim 1 lim
!!
Œˆ‰ ¹¹ ¹ ¹
__
œœn1 n1
nn 1
2
nn 1 2n 1
6
n1
n
n1
nn
33x
2n 1 u 2 n 1 1
u2n
œÊ
nnÄ_ Ä_ abab ab
†
1
3xn1
x lim 1 x 1 1 x 1; when x 1 we have 1 , a conditionallyÊÊÊœ kk kk a b
¹¹ !ˆ‰
nÄ_ ab
ab
2n 1 n
2n 3 2n 1
3
_
œn1
convergent series; when x 1 we have , a divergent series.œ!ˆ‰
_
œn1
3
2n 1
(a) the radius is 1; the interval of convergence is 1 x 1Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
36. For the series n 1 n x 3 , note that n 1 n so that we
!Š‹
ÈÈ
ÈÈ
ab
_
œn1
œ † œ
nn1 n n1 n
1n1 n n1 n
1
ÈÈ
ÈÈ
ÈÈ
ÈÈ
can rewrite the series as ; then lim 1 lim 1
!¹¹ ¹ ¹
_
œn1
ab ab
ÈÈÈ
ÈÈÈ
ab
x3 x 3
n1 n n2 n1
u
u
n1 n
x3
nn1
n1
nn
nnÄ_ Ä_
Ê †
x 3 lim 1 x 3 1 2 x 4; when x 2 we have , a conditionallyÊll Êll Ê œ
nÄ_ ÈÈ
ÈÈ Èab
È
n1 n
n2 n1 n1 n
1
!
_
œn1
n
convergent series; when x 4 we have , a divergent series;œ!
_
œn1
1
n1 n
ÈÈ
(a) the radius is 1; the interval of convergence is 2 x 4Ÿ
(b) the interval of absolute convergence is 2 x 4
(c) the series converges conditionally at x 2œ
37. lim 1 lim 1 x lim 1 1 x 3 R 3
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹
u
u 369 3n 3n 1 n x 3 n 1 3
n1x 369 3n n1 x
n1
n
n1
n
Ê Êll Ê ÊllÊ œ
ab ab ab
aba b a bab
x ††â
††â x
ll
†
38. lim 1 lim 1 x lim
nn nÄ_ Ä_ Ä
¹¹ ¹ ¹
u
u
246 2n 2 n 1 x 258 3n 1
258 3n 1 3 n 1 1 246 2n x
n1
n
22
n1
22
n
Ê Êll
abababa b a bab
abababa b abab
††â ††â
††â ††â
†
_ 11
¹¹
ab
ab
2n 2
3n 2
4x
9
ll
2
2Ê
xRÊl l Ê œ
99
44
39. lim 1 lim 1 x lim 1 1 x 8
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹
u
u22n1 22n22n18
n1 x 22n n1
nx
x
n1
n
2 2
n1 n
n1 2n
Ê Êll Ê ÊllÊ
ab ab abab
a b abababab
x x
x
x
ll
†R8œ
40. lim u 1 lim x 1 x lim 1 x e 1 x e R e
nn nÄ_ Ä_ Ä_
ÈɈ ‰ ˆ ‰
nn2
nnn
n1 n1
nn
n1
Ê Êll Êll ÊllÊ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.7 Power Series 615
41. lim 1 lim 1 x lim 3 1 x x ; at x we have
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹
u
u3x 3333
3x 1 1 1 1
n1
n
n1 n1
nn
Ê Êll ÊllÊ œ
3 1 , which diverges; at x we have 3 1 , which diverges. The series 3 x
!! !! !
ˆ‰ ˆ‰
ab
__ __ _
œœ œœ œn0 n0 n0 n0 n0
nnnn
111
333
n n
n
œ œ œ
3x is a convergent geometric series when x and the sum is .œ
!ab
_
œn0
n11 1
33 13x
42. lim 1 lim 1 e 4 lim 1 1 e 4 1 3 e 5 ln 3 x ln 5;
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹
u
u
e4
e4
xxx
n1
n
xn1
xn
Ê Êll ÊllÊ Ê
ab
ab
at x ln 3 we have e 4 1 , which diverges; at x ln 5 we have e 4 1, whichœœ œœ
!! !!
ˆ‰ ˆ‰
ab
__ __
œœ œœn0 n0 n0 n0
ln 3 ln 5
n n
n
diverges. The series e 4 is a convergent geometric series when ln 3 x ln 5 and the sum is .
!ab
_
œn0
xn11
1e4 5e
œ
ab
xx
43. lim 1 lim 1 lim 1 1 (x 1) 4 x 1 2
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk k k
u
u4(x1)4
(x 1) (x 1)
4
n1
n
2n 2
n1 2n
n
Ê Ê Ê Ê
#
†
2 x 1 2 1 x 3; at x 1 we have 1, which diverges; at x 3Ê Ê œ œ œ œ
!!!
___
œœœn0 n0 n0
(2)
44
4
2n
nn
n
we have 1, a divergent series; the interval of convergence is 1 x 3; the series
!!!
___
œœœn0 n0 n0
24
44
2n n
nn
œœ
is a convergent geometric series when 1 x 3 and the sum is
!!
Š‹
ˆ‰
__
œœn0 n0
(x )
4
x1 n
"
#
#
2n
nœ
""
1
44
4 x 2x 1 3 2x x
Š‹ ’“
x4(x )
4
œœ œ
44. lim 1 lim 1 lim 1 1 (x 1) 9 x 1 3
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk k k
u
u9(x1)9
(x 1) (x 1)
9
n1
n
2n 2
n1 2n
n
Ê Ê Ê Ê
#
†
3 x 1 3 4 x 2; when x 4 we have 1 which diverges; at x 2 we haveÊ Ê œ œ œ
!!
__
œœn0 n0
(3)
9
2n
n
which also diverges; the interval of convergence is 4 x 2; the series
!!
__
œœn0 n0
3
9
2n
nœ"
is a convergent geometric series when 4 x 2 and the sum is
!!
Š‹
ˆ‰
__
œœn0 n0
(x 1)
93
x1 n
#
2n
nœ
""
1
99
9 x 2x 1 8 2x x
Š‹ ’“
x1
3
9(x1)
9
œœ œ
45. lim 1 lim 1 x 2 2 2 x 2 2 0 x 4
nnÄ_ Ä_
¹¹ ºº
¸¸
ÈÈÈ
u
u2
x2 2
x2
n1
n
n1
n1
n
n
Ê Ê Ê Ê
ˆ‰
Ȉ‰
È
†
0 x 16; when x 0 we have ( 1) , a divergent series; when x 16 we have (1) , a divergentÊ œ œ
!!
_ _
œ œn0 n0
nn
series; the interval of convergence is 0 x 16; the series is a convergent geometric series when !Š‹
_
œn0
Èx2
#
n
0 x 16 and its sum is œ œ
""
1
2
4x
ŒŒ È
x2 2 x2
46. lim 1 lim 1 ln x 1 1 ln x 1 e x e; when x e or e we
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u(ln x)
(ln x)
n1
n
n1
n
Ê Ê Ê Ê œ
" "
obtain the series 1 and ( 1) which both diverge; the interval of convergence is e x e; (ln x)
!! !
__ _
œœ œn0 n0 n0
nn
1ln x
œ
" "
n
when e x e
"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

616 Chapter 10 Infinite Sequences and Series
47. lim 1 lim 1 lim 1 1 1 x 2
nn nÄ_ Ä_ Ä_
¹¹ Š ‹
ºº
ˆ‰ kk
u
u3x13 3
x1 3 x
n1 nx1
n1
nÊ Ê Ê Ê
"
#
†ab
x 2 2 x 2 ; at x 2 we have (1) which diverges; the interval of convergence isÊ Ê œ„kk ÈÈÈ È !
_
œn0
n
2 x 2 ; the series is a convergent geometric series when 2 x 2 and its sum is
ÈÈ ÈÈ
!Š‹
_
œn0
x1
3
n
""
#
1
3
x
Š‹Š ‹
x1 3x1
33
œœ
48. lim 1 lim 1 x 1 2 3 x 3 ; when x 3 we
nnÄ_ Ä_
¹¹ ¹ ¹ kk ÈÈ È
u
u2
x1 2
x1
n1
n
n1
n1
n
n
Ê Ê Ê œ„
abab
#
†
have 1 , a divergent series; the interval of convergence is 3 x 3 ; the series is a
! !
ÈÈ Š‹
_ _
œ œn0 n0
n x1
2
n
convergent geometric series when 3 x 3 and its sum is œ œ
ÈÈ ""
1
2
3x
Š‹
x1
22x1
49. lim 1 x 3 2 1 x 5; when x 1 we have (1) which diverges;
nÄ_ ¹¹
kk !
(x 3) 2
(x 3)
n
#
n1
n1 n
n
†Ê Ê œ
n1
when x 5 we have ( 1) which also diverges; the interval of convergence is 1 x 5; the sum of thisœ
!
_
œn1
n
convergent geometric series is . If f(x) 1 (x 3) (x 3) (x 3)
""""
# #
#
1
2
x1 4
nn
Š‹
x3 œ œá á
ˆ‰
then f (x) (x 3) n(x 3) is convergent when 1 x 5, and divergesœœáá
2
x1
nn1
## #
w
"" "
ˆ‰
when x 1 or 5. The sum for f (x) is , the derivative of .œw
22
(x 1) x 1
50. If f(x) 1 (x 3) (x 3) (x 3) then f(x) dxœ á áœ
"" "
##
#
4x1
nn2
ˆ‰ '
x . At x 1 the series diverges; at x 5œá á œ œ
(x 3) (x 3) (x 3)
412 n1 n1
n2
"
#
ˆ‰ !
n1 _
œn1
the series converges. Therefore the interval of convergence is 1 x 5 and the sum is
!
_
œn1
(1)2
n1
nŸ
2 ln x 1 (3 ln 4), since dx 2 ln x 1 C, where C 3 ln 4 when x 3.kk kk œ œ œ
'2
x1
51. (a) Differentiate the series for sin x to get cos x 1œ á
3x 5x 7x 9x 11x
3! 5! 7! 9! 11!
1 . The series converges for all values of x sinceœ á
xxxxx
!4!6!8!10!
#
lim x lim 0 1 for all x.
nnÄ_ Ä_
¹¹Š‹
x
(2n 2)! x 2n 1 2n 2
n! 2
2n 2
#"
†ab abab
œœ
(b) sin 2x 2x 2xœ ᜠá
2 x 2 x 2 x 2 x 2 x 8x 32x 128x 512x 2048x
3! 5! 7! 9! 11! 3! 5! 7! 9! 11!
(c) 2 sin x cos x 2 (0 1) (0 0 1 1)x 0 1 0 0 1 x 0 0 1 0 0 1 xœ
ˆ‰ˆ‰
† †† † †† †† ††
" " "
##
#$
3!
0100001x00100 001x
ˆ‰ˆ ‰
††††† ††††††
""" """ "
##
%&
4! 3! 4! 3! 5!
010000001x 2x áœá
‘ˆ‰
’“
†††††††
"""""
#
'
6! 4! 3! 5! 3! 5!
4x 16x
2xœ á
2x 2x 2x 2x 2 x
3! 5! 7! 9! 11!
52. (a) e 1 1 x e ; thus the derivative of e is e itself
d 2x3x4x5x xxx
x 2!3!4!5! !3!4!
xxxx
abœáœáœ
#
(b) e dx e C x C, which is the general antiderivative of e
'xx xxxx
3! 4! 5!
œœá
#
x
(c) e 1 x ; e e 1 1 (1 1 1 1)x 1 1 1 1 x
#
###
""
xxxxx
!3!4!5! ! !
œá œ
xx
† ††† †††
ˆ‰
11 11x11 11x
ˆ‰ˆ ‰
†† †† †† † ††
"""" """"""
## ##
$%
3! ! ! 3! 4! 3! ! ! 3! 4!
1 1 1 1x 100000 áœá
ˆ‰
††††††
" " "" "" " "
##
&
5! 4! ! 3! 3! ! 4! 5!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.8 Taylor and Maclaurin Series 617
53. (a) ln sec x C tan x dx x dxkk Š‹
œ œ á
''
x 2x 17x 62x
3 15 315 2835
C; x 0 C 0 ln sec x ,œ á œÊ œÊ œ á
x x x 17x 31x x x x 17x 31x
1 45 2520 14,175 12 45 2520 14,175
## #
kk
converges when x
11
##
(b) sec x x 1 x , converges
# #
œ œ áœá
d(tan x)
dx dx 3 15 315 2835 3 45 315
d x 2x 17x 62x 2x 17x 62x
Š‹
when x
11
##
(c) sec x (sec x)(sec x) 1 1
#
##
œœáá
Š‹Š‹
x5x61x x5x61x
24 720 24 720
1x x xœ á
ˆ‰ˆ ‰ˆ ‰
"" "
##
#% '
5 5 615561
24 4 24 720 48 48 720
1 x , xχ
#
##
2x 17x 62x
3 45 315
11
54. (a) ln sec x tan x C sec x dx 1 dxkk Š‹
œ œá
''
x5x61x
224720
x C; x 0 C 0 ln sec x tan xœ á œÊ œÊ
x x 61x 277x
6 24 5040 72,576 kk
x , converges when xœ á
x x 61x 277x
6 24 5040 72,576
11
##
(b) sec x tan x 1 x , convergesœœáœá
d(sec x)
dx dx 24 720 6 120 1008
d x 5x 61x 5x 61x 277x
Š‹
#
when x
11
##
(c) (sec x)(tan x) 1 xœ á á
Š‹Š‹
x5x61x x2x17x
24 720 3 15 315
#
xx x xx ,œ ᜠá
ˆ‰ˆ ‰ˆ ‰
"" " "
#
$& (
3 15 6 24 315 15 72 720 6 120 1008
2 5 17 5 61 5x 61x 277x
x
11
##
55. (a) If f(x) a x , then f (x) n(n 1)(n 2) (n (k 1)) a x and f (0) k!aœ œ â œ
!!
__
œœn0 nk
nnk
nk nkkÐÑ ÐÑ
a ; likewise if f(x) b x , then b a b for every nonnegative integer kÊœ œ œ Êœ
knkkk
f(0) f(0)
k! k!
n
k k
!
_
œn0
(b) If f(x) a x 0 for all x, then f (x) 0 for all x from part (a) that a 0 for every nonnegative integer kœœ œ Ê œ
!
_
œn0
n k
nkÐÑ
10.8 TAYLOR AND MACLAURIN SERIES
1. f(x) e , f (x) 2e , f (x) 4e , f (x) 8e ; f(0) e , f (0) 2, f (0) 4, f (0) 8 P (x) 1,œœ œ œ œœ"œœœÊœ
2x 2x 2x 2x 2 0w ww www w ww www !
ab
P (x) 1 2x, P (x) 1 x 2x , P (x) 1 x 2x x
"# $
##
œ œ œ
4
3
3
2. f(x) sin x, f (x) cos x , f (x) sin x , f (x) cos x; f(0) sin 0 0, f (0) 1, f (0) 0, f (0) 1œ œ œ œ œ œ œ œ œ
w ww www w ww www
P (x) 0, P (x) x, P (x) x, P (x) x xÊœœœœ
!"#$ 1
6
3
3. f(x) ln x, f (x) , f (x) , f (x) ; f(1) ln 1 0, f (1) 1, f (1) 1, f (1) 2 P (x) 0,œ œ œ œ œ œ œ œ œ Ê œ
w ww www w ww www
"" !
xxx
2
P (x) (x 1), P (x) (x 1) (x 1) , P (x) (x 1) (x 1) (x 1)
"# $
"""
##
##$
œ œ œ
3
4. f(x) ln (1 x), f (x) (1 x) , f (x) (1 x) , f (x) 2(1 x) ; f(0) ln 1 0,œ œ œ œ œ œœ
w "ww #www $
"
1x
f (0) 1, f (0) (1) 1, f (0) 2(1) 2 P (x) 0, P (x) x, P (x) x , P (x) x
w ww # www $ !"# $
##
œ œ œ œ œ œ Ê œ œ œ œ
1xxx
1 3
5. f(x) x , f (x) x , f (x) 2x , f (x) 6x ; f(2) , f (2) , f (2) , f (x)œ œ œ œ œ œ œ œ œ
""""
" w # ww $ www % w ww www
#x44 8
3
P (x) , P (x) (x 2), P (x) (x 2) (x 2) ,Ê œ œ œ
!" #
""" "" "
## #
#
448
P (x) (x 2) (x 2) (x 2)
$"" " "
#
#$
œ
48 16
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

618 Chapter 10 Infinite Sequences and Series
6. f(x) (x 2) , f (x) (x 2) , f (x) 2(x 2) , f (x) 6(x 2) ; f(0) (2) , f (0) (2)œ œ œ œ œ œ œ
" w # ww $ www % " w #
"
#
, f (0) 2(2) , f (0) 6(2) P (x) , P (x) , P (x) ,œ œ œ œ œ Ê œ œ œ
"" """
ww $ www % !" #
## #44 8 448
3xxx
P(x)
$"
#
œ
xx x
4816
7. f(x) sin x, f (x) cos x, f (x) sin x, f (x) cos x; f sin , f cos ,œ œ œ œ œ œ œ œ
w ww www w
##
ˆ‰ ˆ‰
11 1 1
44 4 4
22
ÈÈ
f sin , f cos P , P (x) x ,
ww www
#####
!"
ˆ‰ ˆ‰ ˆ ‰
11 1 1 1
44 4 4 4
22222
œ œ œ œ Ê œ œ
ÈÈÈÈÈ
P (x) x x , P (x) x x x
#$
## ## #
##$
œ œ
ÈÈ È ÈÈ È È
22 2 22 2 2
44 4 44 4 1 4
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
11 11 1
8. f(x) tan x, f (x) sec x, f (x) 2sec x tan x, f (x) 2sec x 4sec x tan x; f tan 1 ,œœ œ œ œœ
w ww www22 422
44
ˆ‰
11
f sec 2 , f 2sec tan 4 , f 2sec 4sec tan 16 P (x) 1 ,
w ww www !
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 1 11 1 1 11
44 4 44 4 4 44
22 422
œœ œ œ œ œÊœ
P (x) 1 2 x , P (x) 1 2 x 2 x , P (x) 1 2 x 2 x x
"# $
œ œ œ
ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
111 111
444 4434
223
8
9. f(x) x x , f (x) x , f (x) x , f (x) x ; f(4) 4 2,œœ œ œ œ œœ
Ȉ‰ ˆ ‰ ˆ‰ È
"Î# w "Î# ww $Î# www &Î#
""
#48
3
f (4) 4 , f (4) 4 ,f (4) 4 P (x) 2, P (x) 2 (x 4),
w "Î# ww $Î# www &Î#
"" " " "
#!"
œœœœœœÊœœ
ˆ‰ ˆ ‰ ˆ‰
4 4 32 8 256 4
33
P(x)2 (x4) (x4), P(x) 2 (x4) (x4) (x4)
#$
"" "" "
##$
#
œ œ
4 64 4 64 51
10. f(x) (1 x) , f (x) (1 x) , f (x) (1 x) , f (x) (1 x) ; f(0) (1) 1,œ œ œ œ œ œ
"Î# w "Î# ww $Î# www &Î# "Î#
""
#48
3
f (0) (1) , f (0) (1) , f (0) (1) P (x) 1,
w "Î# ww $Î# www &Î#
""" "
## !
œ œ œ œ œ œ Ê œ
4488
33
P (x) 1 x, P (x) 1 x x , P (x) 1 x x x
"# $
""" ""
##$
œ œ œ
228 2816
1
11. f(x) e , f (x) e , f (x) e , f (x) e f (x) 1 e ; f(0) e , f (0) 1,œœœ œÊᜠœœ"œ
w ww www wxxx x x0
k
kab ab
f (0) 1, f (0) 1, f (0) ( 1) e 1 x x x x
ww www #
œ œáß œ Ê œ áœ
kkx3n
11
26 n!
(1)
!
_
œn0
n
12. f(x) x e , f (x) x e e , f (x) x e 2e , f (x) x e 3e f (x) x e k e ; f(0) 0 e 0,œœœ œÊ᜜œ
xxx xx xx xx 0w ww www kabab
f (0) 1, f (0) 2, f (0) 3, f (0) k x x x x
w ww www #
œœ œáßœÊáœ
k11
2n1!
3n
!
_
œn0ab
13. f(x) (1 x) f (x) (1 x) , f (x) 2(1 x) , f (x) 3!(1 x) f (x)œ Ê œ œ œ Êá
" w # ww $ www % k
( 1) k!(1 x) ; f(0) 1, f (0) 1, f (0) 2, f (0) 3!, f (0) ( 1) k!œ œ œ œ œ áß œ
kk1 w ww www kk
1 x x x (x) (1)xÊᜠœ
#$ !!
__
œœn0 n0
nnn
14. f(x) f (x) , f (x) 6(1 x) , f (x) 18(1 x) f (x) 3 k! (1 x) ; f(0) 2,œÊ œ œ œÊá œ œ
2x 3
1x (1x)
w ww $ www % kk1
ab
f (0) 3, f (0) 6, f (0) 18, f (0) 3 k! 2 3x 3x 3x 2 3x
wwwwww #$
œ œ œáß œ Êáœ
kab !
_
œn1
n
15. sin x sin 3x 3xœ Ê œ œ œá
!!!
___
œœœn0 n0 n0
()x ()(3x) ()3 x
(n 1)! (n 1)! (n 1)! 3! 5!
3x 3x
" " "
# # #
n2n1 n 2n1 n2n12n1
16. sin x sin œ Ê œ œ œá
!!!
___
œœœn0 n0 n0
()x ()x
( n 1)! ( n 1)! (2n 1)! 2 3! 2 5!
xxxx
()
" "
# # # # #
"
n2n1 n2n1
nx2n 1
2n 1
ˆ‰
††
17. 7 cos ( x) 7 cos x 7 7 , since the cosine is an even functionœ œ œá
!
_
œn0
()x
(2n)! ! 4! 6!
7x 7x 7x
"
#
n2n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.8 Taylor and Maclaurin Series 619
18. cos x 5 cos x 5 5œ Ê œ œá
!!
__
œœn0 n0
(1)x (1)(x)
(2n)! ( n)! 2! 4! 6!
5x 5x 5x
#
n2n n 2n
11111
19. cosh x 1 x 1 x 1œ œ á á œá
ee xxx xxx xxx
!3!4! !3!4! !4!6!
xx
"
## # # #
#
’“Š‹Š‹
œ!
_
œn0
x
(2n)!
2n
20. sinh x 1 x 1 x xœ œ á á œá
ee xxx xxx xxx
! 3! 4! ! 3! 4! 3! 5! 6!
xx
"
## # #
’“Š‹Š‹
œ!
_
œn0
x
(2n 1)!
2n 1
21. f(x) x 2x 5x 4 f (x) 4x 6x 5, f (x) 12x 12x, f (x) 24x 12, f (x) 24œ Ê œ œ œ œ
% $ w $ # ww # www Ð Ñ4
f (x) 0 if n 5; f(0) 4, f (0) 5, f (0) 0, f (0) 12, f (0) 24, f (0) 0 if n 5Êœœœœ œ œ œ
ÐÑ w ww www ÐÑ ÐÑn4n
x 2x 5x 4 4 5x x x x 2x 5x 4Ê œ œ
%$ $ %%$
12 24
3! 4!
22. f(x) f (x) ; f (x) ; f (x) f (x) ; f(0) 0, f (0) 0, f (0) 2,œÊ œ œ œ Ê œ œ œ œ
x2xx2 6
x1 x1 x1 x1 x1
n1n
w ww www Ð Ñ w ww
x
ab ab ab ab
ab
23 4 n1
n
f(0) 6, f(0) 1n if n2 xxxx 1x
www Ð Ñ #
œ œ x ÊÞÞÞœ
n 345 n
nn
ab ab
!
_
œn2
23. f(x) x 2x 4 f (x) 3x 2, f (x) 6x, f (x) 6 f (x) 0 if n 4; f(2) 8, f (2) 10,œÊ œ œ œÊ œ œ œ
$ w # ww www Ð Ñ wn
f (2) 12, f (2) 6, f (2) 0 if n 4 x 2x 4 8 10(x 2) (x 2) (x 2)
ww www Ð Ñ $ # $
œ œ œ Ê œ
n12 6
2! 3!
8 10(x 2) 6(x 2) (x 2)œ
#$
24. f(x) 2x x 3x 8 f (x) 6x 2x 3, f (x) 12x 2, f (x) 12 f (x) 0 if n 4; f(1) 2,œ Ê œ œ œ Ê œ œ
$ # w # ww www Ð Ñn
f (1) 11, f (1) 14, f (1) 12, f (1) 0 if n 4 2x x 3x 8
wwwwwwÐÑ $#
œœ œ œÊ
n
211(x1) (x1) (x1) 211(x1)7(x1) 2(x1)œ œ
14 12
2! 3!
#$ #$
25. f(x) x x 1 f (x) 4x 2x, f (x) 12x 2, f (x) 24x, f (x) 24, f (x) 0 if n 5;œÊ œ œ œ œ œ
% # w $ ww # www Ð Ñ Ð Ñ4n
f( 2) 21, f ( 2) 36, f ( 2) 50, f ( 2) 48, f ( 2) 24, f ( 2) 0 if n 5 x x 1œ œ œ œ œ œ Ê
w ww www ÐÑ ÐÑ % #4n
21 36(x 2) (x 2) (x 2) (x 2) 21 36(x 2) 25(x 2) 8(x 2) (x 2)œ œ
50 48 24
2! 3! 4!
#$% #$%
26. f(x) 3x x 2x x 2 f (x) 15x 4x 6x 2x, f (x) 60x 12x 12x 2,œÊ œ œ
&% $# w % $ # ww $ #
f (x) 180x 24x 12, f (x) 360x 24, f (x) 360, f (x) 0 if n 6; f( 1) 7,
www # Ð Ñ Ð Ñ Ð Ñ
œœœ œœ
45n
f ( 1) 23, f ( 1) 82, f ( 1) 216, f ( 1) 384, f ( 1) 360, f ( 1) 0 if n 6
w ww www ÐÑ ÐÑ ÐÑ
œ œ œ œ œ œ
45n
3x x 2x x 2 723(x1) (x1) (x1) (x1) (x1)Ê œ
&%$# #$%&
82 216 384 360
2! 3! 4! 5!
7 23(x 1) 41(x 1) 36(x 1) 16(x 1) 3(x 1)œ
#$%&
27. f(x) x f (x) 2x , f (x) 3! x , f (x) 4! x f (x) ( 1) (n 1)! x ;œÊ œ œ œ Ê œ
# w $ ww % www & Ð Ñ nnn2
f(1) 1, f (1) 2, f (1) 3!, f (1) 4!, f (1) ( 1) (n 1)! œœœ œ œÊ
w ww www Ð Ñ "
nn
x
1 2(x 1) 3(x 1) 4(x 1) ( 1) (n 1)(x 1)œáœ
#$
!
_
œn0
nn
28. f(x) f (x) 3(1 x) , f (x) 12(1 x) , f (x) 60 (1 x) f (x) (1 x) ;œÊœ œ œÊ œ
1
1x
45 6n n3
n2!
2
ab ab
w ww www Ð Ñ
3
f 0 1, f 0 3, f 0 12, f 0 60, , f 0 1 3x 6x 10xab ab ab ab abœœ œ œá œÊœá
w ww www Ð Ñ #
n3
n2!
2
1
1x
ab ab
3
xœ!
_
œn0
ababn2n1
2
n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

620 Chapter 10 Infinite Sequences and Series
29. f(x) e f (x) e , f (x) e f (x) e ; f(2) e , f (2) e , f (2) eœÊ œ œÊ œ œ œá œ
xxxnx nwww ÐÑ #w#ÐÑ#
e e e(x2) (x2) (x2) (x2)Êœáœ
x n
ee e
3! n!
## # $
#!
_
œn0
30. f(x) 2 f (x) 2 ln 2, f (x) 2 (ln 2) , f (x) 2 (ln 2) f (x) 2 (ln 2) ; f(1) 2, f (1) 2 ln 2,œÊ œ œ œ Ê œ œ œ
xx x x3nxnw ww # www Ð Ñ w
f (1) 2(ln 2) , f (1) 2(ln 2) , , f (1) 2(ln 2)
ww # www $ Ð Ñ
œœáœ
nn
2 2 (2 ln 2)(x 1) (x 1) (x 1) Êœ áœ
x 3
2(ln 2) 2(ln 2) 2(ln 2) (x 1)
3! n!
#
#
3nn
!
_
œn0
31. f(x) cos 2x , f (x) 2 sin 2x , f (x) 4 cos 2x , f (x) 8 sin 2x ,œ œ œ œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11
22 22
w ww www
f x 2 cos 2x f x 2 sin 2x . . ; f 1, f 0, f 4, f 0, f 2 ,
ab ab ab44 5 5 44
2244444
ab ab
ˆ ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
œßœßœœœœœ
1111111
w ww www
f 0, . . ., f 1 2 cos 2x 1 2 x x . . .
ab52n2n
44 2 434
n24
2
ˆ‰ ˆ‰ ˆ ‰ ˆ ‰ ˆ ‰
ab
11 1 11
œ œ Ê œ
ÐÑ
xœ
!ˆ‰
_
œn0
ab
ab
x
12
2n 4
2n
n2n 1
32. f(x) x 1, f (x) x 1 , f (x) x 1 , f (x) x 1 , f (x) x 1 , . . .;œ œ œ œ œ
Èab ab ab ab
w ww www
Î Î Î Î
113 15
248 16
12 32 52 72
4ab
f(0) 1, f (0) , f (0) , f (0) , f (0) , . . . x 1 1 x x x xœ œ œ œ œ Ê œ ÞÞÞ
w ww www
113 15 1115
2 4 8 16 2816128
4234ab È
33. The Maclaurin series generated by cos x is x which converges on , and the Maclaurin series generated
!ab
_
œn0
ab
ab
x
1
2n
2n
n_ _
by is 2 x which converges on 1, 1 . Thus the Maclaurin series generated by f x cos x is given by
2 2
1x 1x
n
!ab ab
_
œn0
œ
x 2 x 1 2x x which converges on the intersection of , and 1, 1 , so the
!! abab
__
œœn0 n0
ab
ab
x
1
2n 2
2n n 2
5
n œ ÞÞÞÞ _ _
interval of convergence is 1, 1 .ab
34. The Maclaurin series generated by e is which converges on , . The Maclaurin series generated by
xx
n
!ab
_
œn0
n
x_ _
f x 1 x x e is given by 1 x x 1 x x which converges on , abab ab ab
!
œ œ ÞÞÞÞ _ _ Þ
2x 2 2 3
x12
n23
_
œn0
n
x
35. The Maclaurin series generated by sin x is x which converges on , and the Maclaurin series
!ab
_
œn0
ab
ab
x
1
2n 1
2n 1
n_ _
generated by ln 1 x is x which converges on 1, 1 . Thus the Maclaurin series genereated byab ab
!
_
œn1
ab1
n
n
n1
f x sin x ln 1 x is given by x x x x x which converges onab a b ŒŒ
!!
œ † œ ÞÞÞÞ
__
œœn0 n1
ab ab
ab
x
11
2n 1 n 2 6
2n1 n 234
11
nn1
the intersection of , and 1, 1 , so the interval of convergence is 1, 1 .a bab ab_ _
36. The Maclaurin series generated by sin x is x which converges on , . The Maclaurin series
!ab
_
œn0
ab
ab
x
1
2n 1
2n 1
n_ _
genereated by f x x sin x is given by x x x x xab ŒŒŒ
!!!
œœ
2 2n1 2n1 2n1
111
2n 1 2n 1 2n 1
2
___
œœœn0 n0 n0
ab ab ab
ab ab ab
x x x
nnn
x x x . . . which converges on , œ __Þ
35 7
12
345 ab
37. If e (x a) and f(x) e , we have f (a) e f or all n 0, 1, 2, 3,
xœ œ œ œá
!
_
œn0
f(a)
n!
nxna
nÐÑ
e e e 1 (x a) at x aÊœ áœáœ
xa a
(x a) (x a) (x a) (x a)
0! 1! 2! 2!
’“’“
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.9 Convergence of Taylor Series 621
38. f(x) e f (x) e for all n f (1) e for all n 0, 1, 2, œÊ œ Ê œ œ á
xn x nÐÑ ÐÑ
e ee(x1) (x1) (x1) e1(x1)ʜᜠá
xee
!3! 2!3!
(x 1) (x 1)
#
#$
’“
39. f(x) f(a) f (a)(x a) (x a) (x a) f (x)œ áÊ
w#$w
#
f (a) f (a)
3!
f (a) f (a)(x a) 3(x a) f (x) f (a) f (a)(x a) 4 3(x a)œ áÊ œ á
w ww # ww ww www #
f (a) f (a)
3! 4!
4
†
f (x) f (a) f (a)(x a) (x a)Êœ á
ÐÑ ÐÑ ÐÑ #
#
nnn1 f(a)
n2
f(a) f(a) 0, f (a) f (a) 0, , f (a) f (a) 0Êœ œá œ
w w ÐÑ ÐÑnn
40. E(x) f(x) b b (x a) b (x a) b (x a) b (x a)χ
!" # $
#$
nn
0 E(a) f(a) b b f(a); from condition (b),Êœ œ Ê œ
!!
lim 0
xaÄ
f(x) f(a) b (x a) b (x a) b (x a) b (x a)
(x a)
á
nn
nœ
lim 0ʜ
xaÄ
f(x) b 2b(x a) 3b(x a) nb(x a)
n(x a)
á
nn1
n1
b f (a) lim 0Êœ Ê œ
"w á "
xaÄ
f (x) 2b 3! b (x a) n(n )b (x a)
n(n 1)(x a)
nn2
n2
b f (a) lim 0Êœ Ê œ
#"
##
ww á
xaÄ
f (x) 3! b n(n 1)(n 2)b (x a)
n(n 1)(n )(x a)
nn3
n3
b f (a) lim 0 b f (a); therefore,œœ Ê œÊ œ
$""
www Ð Ñ
3! n! n!
f (x) n! b nn
xaÄ
nn
g(x) f(a) f (a)(x a) (x a) (x a) P (x)œ á œ
w#
f (a) f (a)
2! n!
nn
n
41. f(x) ln (cos x) f (x) tan x and f (x) sec x; f(0) 0, f (0) 0, f (0) 1 L(x) 0 and Q(x)œ Ê œ œ œ œ œ Ê œ œ
www#www x
2
42. f(x) e f (x) (cos x)e and f (x) ( sin x)e (cos x) e ; f(0) 1, f (0) 1, f (0) 1œÊœ œ œ œ œ
sin x sin x sin x sin xwww #www
L(x) 1 x and Q(x) 1 xÊœ œ
x
#
43. f(x) 1 x f (x) x 1 x and f (x) 1 x 3x 1 x ; f(0) 1, f (0) 0,œ Ê œ œ œ œab ab ab ab
#w #ww ### w
"Î# $Î# $Î# &Î#
f (0) 1 L(x) 1 and Q(x) 1
ww
#
œÊ œ œ
x
44. f(x) cosh x f (x) sinh x and f (x) cosh x; f(0) 1, f (0) 0, f (0) 1 L(x) 1 and Q(x) 1œÊœ œ œœ œÊœ œ
www www
#
x
45. f(x) sin x f (x) cos x and f (x) sin x; f(0) 0, f (0) 1, f (0) 0 L(x) x and Q(x) xœÊœ œ œ œ œÊœ œ
www www
46. f(x) tan x f (x) sec x and f (x) 2 sec x tan x; f(0) 0, f (0) 1, f 0 L(x) x and Q(x) xœÊœ œ œ œœÊœ œ
w # ww # w ww
10.9 CONVERGENCE OF TAYLOR SERIES
1. e 1 x e 1 ( 5x) 1 5x
x5x
x x 5x 5x
!n! ! !3! n!
( 5x) ( 1) 5 x
œ áœ Ê œ ᜠáœ
###
!!
_ _
œ œn0 n0
nnnn
2. e 1 x e 1 1
xx2
xx x xxx
!n! ! 2!23! 2n!
(1)x
œ áœ Ê œ ᜠáœ
#####
Î
!!
ˆ‰
_ _
œ œn0 n0
nxnn
n
ˆ‰
3. sin x x 5 sin ( x) 5 ( x)œáœ Ê œ áœ
xx
3! 5! ( n 1)! 3! 5! ( n 1)!
( 1) x ( x) ( x) 5( 1) x
!!
’“
_ _
œ œn0 n0
# #
n2n1 n12n1
4. sin x x sin œáœ Ê œáœ
xx x x
3! 5! ( n 1)! 3! 5! 7! 2 ( n 1)!
(1)x (1) x
!!
_ _
œ œn0 n0
# # # #
n2n1 n 2n12n1
xxx
2n 1
11 1
ˆ‰ ˆ‰ ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

622 Chapter 10 Infinite Sequences and Series
5. cos x cos 5x 1œÊœ œ œá
!!!
___
œœœn0 n0 n0
(1)x (1)5x
(2n)! (2n)! (2n)! ! 4! 6!
2(1) 5x 25x 625x 15625x
#
n2n n2n4n
n2
2n 48 12
‘
6. cos x cos cos œÊ œ œ œ
!!!
Š‹ Š‹
Œ
__
œœn0 n0
ab Èab
Œ
Š‹
##
"Î# _
œ
1x
(2n)! ( n)! 2 (2n)!
xx
2
1
n0
(1)x
n2n
nx
2n
n3n
n
1χ
xx x
22! 2 4! 2 6!
†††
7. ln 1 x ln 1 x x . . .ab a b
!!!
œ Ê œ œ œ
___
œœœn1 n1 n1
ab ab
abˆ‰
1x 1 x
n n n 234
22
1x xxx
n1 n1
n 2n
n1 2n468
8. tan x tan 3x 3x 9x x x . . .
1 1 4 4 12 20 28
1x 1 3 x
2n 1 2n 1 n 5 7
13x 243 2187
œÊœ œ œ
!!!
ab
___
œœœn0 n0 n0
ab ab
ab
ˆ‰
n n
2n 1 2n18n4
n42n 1
9. 1 x 1 x 1 x 1 x x x . . .
1 1 3 3 3927
1x 4 4 41664
nnn
n 3 3n 369
1x
nn
œ Ê œ œ œ
!!!
ab ab ab
ˆ‰ ˆ‰
___
œœœn0 n0 n0
3
43
10. x x x x x x . . .
111 111
1x 2x 4 8 16
nn23
1x
nn1
#####
""" " "
œÊœ œ œ œ
!!!
ˆ‰ ˆ‰
___
œœœn0 n0 n0
11. e xe x x x
xx
x x x xxx
n! n! n! ! 3! 4!
n0
œ Ê œ œ œá
!!!
Œ
__
œœn0 n0
nnn1
_
œ
#
#
12. sin x x sin x x xœ Ê œ œ œá
!!!
Œ
___
œœœn0 n0 n0
(1)x (1)x (1)x
(2n 1)! ( n 1)! (2n 1)! 3! 5! 7!
xxx
#
## $
n2n1 n2n1 n2n3
13. cos x 1 cos x 1 1 1œ Ê œ œ á
!!
__
œœn0 n0
(1)x (1)x
(2n)! ( n)! 2 4! 6! 8! 10!
x x x xxxxx
####
n2n n2n
œ áœ
xxxx
4! 6! 8! 10! ( n)!
(1)x
!
_
œn2
#
n2n
14. sin x sin x x xœÊœ
!!
Œ
__
œœn0 n0
(1)x (1)x
(2n 1)! 3! ( n 1)! 3!
xx
#
n2n1 n2n1
xx œ ᜠáœ
Š‹ !
xxxxx x xxxx
3! 5! 7! 9! 11! 3! 5! 7! 9! 11! (2n 1)!
(1)x
_
œn2
n2n1
15. cos x x cos x x xœÊœ œ œá
!!!
___
œœœn0 n0 n0
(1)x (1)(x) ( ) x
(2n)! ( n)! ( n)! 2! 4! 6!
xxx
"
##
n2n n 2n n2n2n1
111
111
16. cos x x cos x x xœ Ê œ œ œá
!!!
ab
___
œœœn0 n0 n0
(1)x ( )x
(2n)! ( n)! ( n)! 2! 4! 6!
(1) x xx x
"
### #
##
n2n n4n2
n2n
ab
17. cos x 1
#""" ""
# # ## ##
œ œ œ á
cos 2x ( 1) (2x) (2x) (2x) (2x) (2x)
(2n)! 2!4!6!8!
!’“
_
œn0
n2n
11 1 œáœ œ
(2x) (2x) (2x) (2x) ( 1) (2x) ( 1) 2 x
2 2! 2 4! 2 6! 2 8! 2 (2n)! (2n)!
†††† †
!!
__
œœn1 n1
n 2n n 2n 1 2n
18. sin x cos 2x 1
#"" ""
### ###
œ œ œ áœá
ˆ‰ Š‹
1 cos 2x (2x) (2x) (2x) (2x) (2x) (2x)
!4!6! 22!24!26!
†††
œœ
!!
__
œœn1 n1
(1) (2x) (1) 2 x
(2n)! (2n)!
#
n1 2n n 2n1 2n
†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.9 Convergence of Taylor Series 623
19. x x (2x) 2 x x 2x 2 x 2 x
x
12x 12x
nnn2
# # # $#%$&
"
œ œ œ œá
ˆ‰ !!
__
œœn0 n0
20. x ln (1 2x) x 2xœ œ œá
!!
__
œœn1 n1
(1) (2x) (1) 2x
nn 45
2x 2x 2x
#
#
n1 n n1nn1
21. x 1 x x x 1 2x 3x nx (n 1)x
"""
#$ # _
œ
1 x dx 1 x (1 x)
nn1 n
d
n0
œ œáÊ œ œ ᜠœ
!!!
ˆ‰
_ _
œ œn0 n1
22. 1 2x 3x 2 6x 12x n(n 1)x
2d d d
1x dx 1 x dx (1 x) dx
n2
ab
""
##
œœ œáœáœ
ˆ‰ Š‹ab !
_
œn2
(n 2)(n 1)xœ
!
_
œn0
n
23. tan x x x x x x tan x x x x x x
1 357 12 2 2 2 2
111 1 1 1
357 3 5 7
357
œÞÞÞÊ œ ÞÞÞ
Š‹
ab ab ab
xxx x œÞÞÞœ
371115
11 1
35 7 2n1
1x
!
_
œn1
ab
n4n 1
24. sin x x sin x cos x sin 2x 2xœáÊ † œ œ á
xxx
3! 5! 7! 3! 5! 7!
2x 2x 2x
357 357
""
##
Š‹
ab ab ab
xx œ áœáœ
4x 16x 64x 2x 2x 4x
3! 5! 7! 3 15 315 ( n 1)!
(1)2 x
357 357 n2n 2n1
!
_
œn0
#
25. e 1 x and 1 x x x e
x23x
xx 1 1
2! 3! 1 x 1 x
œá œáÊ
23
1x 1xx x 2 x x x 1xœ áᜠáœ
Š‹
ab ab
!ˆ‰
xx 3525 1
2! 3! 2 6 24 n!
23 2 3 4 n
n
23 _
œn0
26. sin x x and cos x 1 cos x sin xœá œáÊ
xxx xxx
3! 5! 7! 2! 4! 6!
357 246
1x1xœ á áœá
Š‹Š‹
xxx xxx xxxxxx
2! 4! 6! 3! 5! 7! 2! 3! 4! 5! 6! 7!
246 357 234567
œ
!Š‹
_
œn0
(1)x (1)x
(2n)! ( n 1)!
#
n 2n n 2n 1
27. ln 1 x x x x x ln 1 x x x x xa b a b ab ab ab
Š‹
œáÊ œ á
111 x x 1 1 1
234 3 3 2 3 4
234 2 2 2 2 2
234
xxx x xœ áœ
111 1
36912 3n
357 9 2n1
1
!
_
œn1
ab
n1
28. ln 1 x x x x x and ln 1 x x x x x ln 1 x ln 1 xab ab ababœá œáÊ
111 111
234 234
234 234
xxxx xxxx 2xxx xœááœáœ
ˆ‰ˆ ‰ !
111 111 22 2
234 234 35 2n1
234 234 35 2n1
_
œn0
29. e 1 x and sin x x e sin x
x x
xx xxx
2! 3! 3! 5! 7!
œá œáʆ
23 357
1x x xx x xœ á ᜠÞÞÞÞ
Š‹Š ‹
xx xxx 1 1
2! 3! 3! 5! 7! 3 30
23 5
23 357
30. ln 1 x x x x x and 1 x x x ln 1 xab abœá œáÊ œ †
111
2 3 4 1x 1x 1x
234 ln 1 x
""
#$ ab
xxxx 1xxx xxx xœáᜠÞÞÞÞ
ˆ‰
ab
111 15 7
234 2612
234 23 4#$
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

624 Chapter 10 Infinite Sequences and Series
31. tan x x x x x tan x tan x tan x
1 357 1 1 1
111
357
2
œÞÞÞÊ œababab
xxxx xxxx xxx xœÞÞÞÞÞÞœ ÞÞÞÞ
ˆ‰ˆ‰
111 111 22344
357 357 345105
357 357 246 8
32. sin x x and cos x 1 cos x sin x cos x cos x sin xœá œáÊ † œ † †
xxx xxx
3! 5! 7! 2! 4! 6!
2
357 246
cos x sin 2x 1 2x x x x xœ † œ á ᜠÞÞÞ
""
##
Š‹Š ‹
x x x 7 61 1247
2! 4! 6! 3! 5! 7! 6 120 5040
2x 2x 2x 35 7
246 357
ab ab ab
33. sin x x and e 1 xχ χ
xxx xx
3! 5! 7! 2! 3!
x
357 23
e1x x xÊ œ á á áá
sin x xxx 1 xxx 1 xxx
3! 5! 7! 2 3! 5! 7! 6 3! 5! 7!
23
Š‹Š‹Š‹
357 357 357
1x x xœ ÞÞÞÞ
11
28
24
34. sin x x and tan x x x x x sin tan x x x x xœá œÞÞÞÊ œÞÞÞ
xxx 111 111
3! 5! 7! 3 5 7 3 5 7
1 357 1 357
357
ab
ˆ‰
xxxx xxxx xxxxÞÞÞ ÞÞÞ ÞÞÞá
1111 1 111 1 111
6 3 5 7 120 3 5 7 5040 3 5 7
357 357 357
35 7
ˆ‰ˆ‰ˆ‰
xx x xœ ÞÞÞ
13 5
2816
35 7
35. Since n 3, then f x sin x, f x M on 0, 0.1 sin x 1 on 0, 0.1 M 1. Then R 0.1 1œ œ l lŸ Ò ÓÊl lŸ Ò ÓÊ œ l lŸ
ab ab44 30.1 0
4
ab ab a b ll
x
4
4.2 10 error 4.2 10œ‚ Ê Ÿ‚
66
36. Since n 4, then f x e , f x M on 0, 0.5 e e on 0, 0.5 M 2.7. Thenœ œ l lŸ Ò ÓÊl lŸ Ò ÓÊ œ
ab ab5x5 x
ab ab È
R 0.5 2.7 7.03 10 error 7.03 10llŸ œ‚ÊŸ‚
40.5 0
5
44
ab ll
x
5
37. By the Alternating Series Estimation Theorem, the error is less than x 5! 5 10 x 600 10
kkx
5! Ê ‚ Ê‚kk aba b kk
&&
% %
x 6 10 0.56968Ê ‚ ¸kk È
5#
38. If cos x 1 and x 0.5, then the error is less than 0.0026, by Alternating Series Estimation Theorem;œ œ
x(.5)
24
#kk ¹¹
since the next term in the series is positive, the approximation 1 is too small, by the Alternating Series Estimationx
#
Theorem
39. If sin x x and x 10 , then the error is less than 1.67 10 , by Alternating Series Estimation Theorem;œ ¸‚kk $
ab10
3!
10
The Alternating Series Estimation Theorem says R (x) has the same sign as . Moreover, x sin x
#
x
3!
0 sin x x R (x) x 0 10 x 0.Ê œ ÊÊ
#$
40. 1 x 1 . By the Alternating Series Estimation Theorem the error
Èkk
¹¹
œ á
xx x x
816 88
(0.01)
#
1.25 10œ‚
&
41. R (x) 1.87 10 , where c is between 0 and xkk
¹¹
#
œ ‚
ex
3! 3!
3 (0.1) 4
c01
42. R (x) 1.67 10 , where c is between 0 and xkk
¹¹
#%
œœ‚
ex
3! 3!
(0.1)
c
43. sin x cos 2x 1
#"" ""
### ## #
œ œ œ áœá
ˆ‰ Š‹
1 cos 2x 2x 2x 2x
(2x) (2x) (2x)
2! 4! 6! ! 4! 6!
sin x 2x 2 sin x cos xÊ œ ᜠáÊ
d d 2x 2x 2x
dx dx 2! 4! 6! 3! 5! 7!
(2x) (2x) (2x)
abŠ‹
#
2x sin 2x, which checksœáœ
(2x) (2x) (2x)
3! 5! 7!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.9 Convergence of Taylor Series 625
44. cos x cos 2x sin x 1
##
##
œ œá á
Š‹Š‹
(2x) (2x) (2x) (2x)
!4!6!8! !4!6!8!
2x 2x 2x 2x
11xxxxœáœ á
2x 2x 2x 2
! 4! 6! 3 45 315
#
#% ' )
""
45. A special case of Taylor's Theorem is f(b) f(a) f (c)(b a), where c is between a and b f(b) f(a) f (c)(b a),œ Êœ
w w
the Mean Value Theorem.
46. If f(x) is twice differentiable and at x a there is a point of inflection, then f (a) 0. Therefore,œœ
ww
L(x) Q(x) f(a) f (a)(x a).œœ
w
47. (a) f 0, f (a) 0 and x a interior to the interval I f(x) f(a) (x a) 0 throughout I
ww w #
#
Ÿœ œ ÊœŸ
f(c)
f(x) f(a) throughout I f has a local maximum at x aÊŸ Ê œ
(b) similar reasoning gives f(x) f(a) (x a) 0 throughout I f(x) f(a) throughout I f has aœ Ê Ê
f(c)
#
#
local minimum at x aœ
48. f(x) (1 x) f (x) (1 x) f (x) 2(1 x) f (x) 6(1 x)œ Ê œ Ê œ Ê œ
"w #ww $ÐÑ %3
f (x) 24(1 x) ; therefore 1 x x x . x 0.1 Êœ ¸ÊÊ
ÐÑ & # $
"""
&
4
1x 11 1x 9 (1x) 9
10 10 10
kk ¹¹
ˆ‰
x the error e (0.1) 0.00016935 0.00017, since .Ê Ê Ÿ œ œ
¹¹ ¹ ¹ ¹¹¹¹
ˆ‰ ˆ‰
x10 10
(1 x) 9 4! 9 4! (1 x)
max f (x) x f (x)
%%
&&
$"
4 4
49. (a) f(x) (1 x) f (x) k(1 x) f (x) k(k 1)(1 x) ; f(0) 1, f (0) k, and f (0) k(k 1)œ Ê œ Ê œ œ œ œ
kk1 k2w ww w ww
Q(x) 1 kx xʜ
k(k )"
#
#
(b) R (x) x x 0 x or 0 x .21544kk kk
¸¸
#"" " "
$$
œÊÊ
32
3! 100 100 100
††
50. (a) Let P x x P .5 10 since P approximates accurate to n decimals. Then,œ Ê œ ‚11 1kk k k n
P sin P ( x) sin ( x) ( x) sin x (x sin x) (P sin P) œ œ œ Ê 111 1 1kk
sin x x 10 .5 10 P sin P gives an approximation to correct to 3n decimals.œŸ‚‚ Êkk
kkx
3! 3!
0.125 3n 3n
1
51. If f(x) a x , then f (x) n(n 1)(n 2) (n k 1)a x and f (0) k! aœ œ â œ
!!
__
œœn0 nk
nnk
nk nkkÐÑ ÐÑ
a for k a nonnegative integer. Therefore, the coefficients of f(x) are identical with the correspondingʜ
kf(0)
k!
k
coefficients in the Maclaurin series of f(x) and the statement follows.
52. : f even f( x) f(x) f ( x) f (x) f ( x) f (x) f odd;Note Êœ Êœ Ê œ Ê
www ww
f odd f( x) f(x) f ( x) f (x) f ( x) f (x) f even;Êœ Êœ Ê œ Ê
wwwww
also, f odd f( 0) f(0) 2f(0) 0 f(0) 0Êœ Ê œÊ œ
(a) If f(x) is even, then any odd-order derivative is odd and equal to 0 at x 0. Therefore,œ
a a a 0; that is, the Maclaurin series for f contains only even powers.
"$&
œœœáœ
(b) If f(x) is odd, then any even-order derivative is odd and equal to 0 at x 0. Therefore,œ
a a a 0; that is, the Maclaurin series for f contains only odd powers.
!#%
œœœáœ
53-58. Example CAS commands:
:Maple
f := x -> 1/sqrt(1+x);
x0 := -3/4;
x1 := 3/4;
# Step 1:
plot( f(x), x=x0..x1, title="Step 1: #53 (Section 10.9)" );
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

626 Chapter 10 Infinite Sequences and Series
# Step 2:
P1 := unapply( TaylorApproximation(f(x), x = 0, order=1), x );
P2 := unapply( TaylorApproximation(f(x), x = 0, order=2), x );
P3 := unapply( TaylorApproximation(f(x), x = 0, order=3), x );
# Step 3:
D2f := D(D(f));
D3f := D(D(D(f)));
D4f := D(D(D(D(f))));
plot( [D2f(x),D3f(x),D4f(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green], title="Step 3: #57 (Section 9.9)" );
c1 := x0;
M1 := abs( D2f(c1) );
c2 := x0;
M2 := abs( D3f(c2) );
c3 := x0;
M3 := abs( D4f(c3) );
# Step 4:
R1 := unapply( abs(M1/2!*(x-0)^2), x );
R2 := unapply( abs(M2/3!*(x-0)^3), x );
R3 := unapply( abs(M3/4!*(x-0)^4), x );
plot( [R1(x),R2(x),R3(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green], title="Step 4: #53 (Section 10.9)" );
# Step 5:
E1 := unapply( abs(f(x)-P1(x)), x );
E2 := unapply( abs(f(x)-P2(x)), x );
E3 := unapply( abs(f(x)-P3(x)), x );
plot( [E1(x),E2(x),E3(x),R1(x),R2(x),R3(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green],
linestyle=[1,1,1,3,3,3], title="Step 5: #53 (Section 10.9)" );
# Step 6:
TaylorApproximation( f(x), view=[x0..x1,DEFAULT], x=0, output=animation, order=1..3 );
L1 := fsolve( abs(f(x)-P1(x))=0.01, x=x0/2 ); # (a)
R1 := fsolve( abs(f(x)-P1(x))=0.01, x=x1/2 );
L2 := fsolve( abs(f(x)-P2(x))=0.01, x=x0/2 );
R2 := fsolve( abs(f(x)-P2(x))=0.01, x=x1/2 );
L3 := fsolve( abs(f(x)-P3(x))=0.01, x=x0/2 );
R3 := fsolve( abs(f(x)-P3(x))=0.01, x=x1/2 );
plot( [E1(x),E2(x),E3(x),0.01], x=min(L1,L2,L3)..max(R1,R2,R3), thickness=[0,2,4,0], linestyle=[0,0,0,2],
color=[red,blue,green,black], view=[DEFAULT,0..0.01], title="#53(a) (Section 10.9)" );
abs(`f(x)`-`P`[1](x) ) <= evalf( E1(x0) ); # (b)
abs(`f(x)`-`P`[2](x) ) <= evalf( E2(x0) );
abs(`f(x)`-`P`[3](x) ) <= evalf( E3(x0) );
: (assigned function and values for a, b, c, and n may vary)Mathematica
Clear[x, f, c]
f[x_]= (1 x)3/2
{a, b}= { 1/2, 2};
pf=Plot[ f[x], {x, a, b}];
poly1[x_]=Series[f[x], {x,0,1}]//Normal
poly2[x_]=Series[f[x], {x,0,2}]//Normal
poly3[x_]=Series[f[x], {x,0,3}]//Normal
Plot[{f[x], poly1[x], poly2[x], poly3[x]}, {x, a, b},
PlotStyle {RGBColor[1,0,0], RGBColor[0,1,0], RGBColor[0,0,1], RGBColor[0,.5,.5]}];Ä
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 10.10 The Binomial Series 627
The above defines the approximations. The following analyzes the derivatives to determine their maximum values.
f''[c]
Plot[f''[x], {x, a, b}];
f'''[c]
Plot[f'''[x], {x, a, b}];
f''''[c]
Plot[f''''[x], {x, a, b}];
Noting the upper bound for each of the above derivatives occurs at x = a, the upper bounds m1, m2, and m3 can be defined
and bounds for remainders viewed as functions of x.
m1=f''[a]
m2=-f'''[a]
m3=f''''[a]
r1[x_]=m1 x /2!
2
Plot[r1[x], {x, a, b}];
r2[x_]=m2 x /3!
3
Plot[r2[x], {x, a, b}];
r3[x_]=m3 x /4!
4
Plot[r3[x], {x, a, b}];
A three dimensional look at the error functions, allowing both c and x to vary can also be viewed. Recall that c must be a
value between 0 and x, so some points on the surfaces where c is not in that interval are meaningless.
Plot3D[f''[c] x /2!, {x, a, b}, {c, a, b}, PlotRange All]
2Ä
Plot3D[f'''[c] x /3!, {x, a, b}, {c, a, b}, PlotRange All]
3Ä
Plot3D[f''''[c] x /4!, {x, a, b}, {c, a, b}, PlotRange All]
4Ä
10.10 THE BINOMIAL SERIES
1. (1 x) 1 x 1 x x x œ ᜠá
"Î# #$
""""
## #
ˆ‰ˆ ‰ ˆ‰ˆ ‰ˆ ‰
xx
!3! 816
3
2. (1 x) 1 x 1 x x x œ ᜠá
"Î$ #$
"""
#3 ! 3! 3 9 81
5
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
33 333
225
xx
3. (1 x) 1 ( x) 1 x x x œ á œ á
"Î# #$
" "
## #
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
335
(x) (x)
!3! 816
35
4. (1 2x) 1 ( 2x) 1 x x x œ áœá
"Î# #$
"
##
ˆ‰ˆ ‰
( 2x)
!3! 22
( 2x) 11
Š‹Š ‹Š ‹
3
5. 1 1 1 x x x
ˆ‰ ˆ‰
œ # á œ
xx 3
!3! 4### #
# #$
"
(2)(3) (2)(3)(4)
ˆ‰ ˆ‰
xx
6. 1 1 4 0 1 x x x x
ˆ‰ ˆ‰
œ áœ
xx 42 4 1
33!3! 4! 332781
4234
(4)(3) (4)(3)(2) (4)(3)(2)(1)
ˆ‰ ˆ‰ ˆ‰
xx x
33 3
4
#
7. 1 x 1 x 1 x x xab œ ᜠá
$$ $' *
"Î# " "
## #
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
335
xx
!3! 816
35
8. 1 x 1 x 1 x x xab œ ᜠá
## #% '
"Î$ " "
#3 ! 3! 3 9 81
214
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
33 333
447
xx
9. 1 1 1
ˆ‰ ˆ‰
œ áœá
11 1
x x ! 3! x 8x 16x
"Î# """
## #
ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
131
xx
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

628 Chapter 10 Infinite Sequences and Series
10. x 1 x x 1 x x x x x
x1214
1x
3
! 3! 3981
34
È
3
"Î
#
#
œ œ á œ áab Œ
ˆ‰
c
"
3
xx
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
33 333
447
11. (1 x) 1 4x 1 4x 6x 4x xœ œ
%#$%
#
(4)(3)x (4)(3)(2)x (4)(3)(2)x
!3! 4!
12. 1 x 1 3x 1 3x 3x xab œ œ
## #%'
$
#
(3)(2) x (3)(2)(1) x
!3!
ab ab
13. (1 2x) 1 3( 2x) 1 6x 12x 8xœ œ
$#$
#
(3)(2)( 2x) (3)(2)(1)( 2x)
!3!
14. 1 1 4 1 2x x x x
ˆ‰ ˆ‰
œ œ
xx 3
!3! 4! 216### #
%#$ %
""
(4)(3) (4)(3)(2) (4)(3)(2)(1)
ˆ‰ ˆ‰ ˆ‰
xx x
15. sin x dx x dx 0.00267 with error
''
00
02 02
## !Þ# !Þ#
!!
œáœá¸¸
Š‹’“’“
xx x x x
3! 5! 3 7 3! 3
†
E 0.0000003kkŸ¸
(.2)
73!
†
16. dx 1 x 1 dx 1 dx
'' '
00 0
02 02 02
e xxx xxx
x x !3!4! 6 24
x" "
##
œ á œ á
Š‹Š‹
x 0.19044 with error E 0.00002œ á ¸ Ÿ ¸
’“ kk
xx
418 96
(0.2)
!Þ#
!
17. dx 1 dx x [x] 0.1 with error
''
00
01 01
"
!Þ"
!
!Þ"
!
È1 x
x3x x
28 10
œáœá¸¸
Š‹’“
E 0.000001kkŸœ
(0.1)
10
18. 1 x dx 1 dx x x 0.25174 with error
''
!
!Þ#& $#!Þ#& !Þ#&
!!
ÈŠ‹’“’“
œ á œ á ¸ ¸
0
025 xx xx x
39 945 9
E 0.0000217kkŸ¸
(0.25)
45
19. dx 1 dx x x
''
00
01 01
sin x xxx xxx xx
x 3! 5! 7! 3 3! 5 5! 7 7! 3 3! 5 5!
œ á œ á ¸
Š‹’ “’“
††† ††
!Þ" !Þ"
!!
0.0999444611, E 2.8 10¸Ÿ¸‚kk (0.1)
77!
12
7
†
20. exp x dx 1 x dx x x
''
00
01 01
ab Š‹’“’“
œ á œ á ¸
## !Þ" !Þ"
!!
xxx xx x xxx
2! 3! 4! 3 10 42 3 10 42
0.0996676643, E 4.6 10¸Ÿ¸‚kk (0.1)
216
12
9
21. 1 x (1) (1) x (1) x (1) xa b ab ab abœ
% "Î# "Î# % $Î# % &Î# %
"Î# # $
#
Š‹
1! 3!
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
3
(1) x 1 ᜠá
ˆ‰ˆ‰ˆ‰ˆ‰
35
4! 8 16 128
xxx 5x
(Î# % %
#
ab
1 dx x 0.100001, E 1.39 10Ê á ¸ ¸ Ÿ ¸ ‚
'0
01
Š‹’“
kk
xxx 5x x
8 16 128 10 72
(0.1) 11
#
!Þ"
!
9
22. dx dx
''
00
11
ˆ‰ Š‹’“
1cos x xxx x xx x x x
x 4! 6! 8! 10! 3 4! 5 6! 7 8! 9 10!
"
##
"
!
œ á ¸
††††
0.4863853764, E 1.9 10¸Ÿ¸‚kk 1
11 12!
10
†
23. cos t dt 1 dt t error .00011
''
00
11
#
#
"
!
"
œ á œ á Ê ¸
Š‹’ “
kk
ttt t t t
4! 6! 10 9 4! 13 6! 13 6!
†† †
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.10 The Binomial Series 629
24. cos t dt 1 dt t
''
00
11
ÈŠ‹’ “
œ á œá
tttt t t t t
4! 6! 8! 4 3 4! 4 6! 5 8!#
"
!
†††
error 0.000004960ʸkk"
58!†
25. F(x) t dt œ á œ á ¸
'0
xx
Š‹’ “
#
!
tt t t t t t x x x
3! 5! 7! 3 7 3! 11 5! 15 7! 3 7 3! 11 5!
††† ††
error 0.000013ʸkk"
15 7!†
26. F(x) t t dtœ á œ á
'0
xx
Š‹’ “
#%
!
ttt t tt t t t t
2! 3! 4! 5! 3 5 7 2! 9 3! 11 4! 13 5!
††††
error 0.00064¸ Ê ¸
xx x x x
3 5 7 2! 9 3! 11 4! 13 5!
†† † †
kk"
27. (a) F(x) t dt error .00052œ á œ á ¸ Ê ¸
'0
xx
Š‹’“
kk
ttt t t t xx
357 21 30 1 30
(0.5)
###
!
(b) error .00089 when F(x) ( 1) kk ¸ ¸á
"
#
"&
33 34 3 4 5 6 7 8 31 32
xxxx x
† ††† †
28. (a) F(x) 1 dt t xœ á œá¸
'0
xx
Š‹’ “
ttt tttt xxxx
23 4 22334455 3 4 5
†††† !#
error .00043ʸkk
(0.5)
6
(b) error .00097 when F(x) x ( 1) kk ¸ ¸á
"
#
$"
32 3 4 31
xxx x
29. e (1 x) 1 x 1 x lim
"" "
##
x x 3! 3! 4! x
xxx xx e(1x)
ab
Š‹Š‹
œ á œáÊ
x0Ä
x
lim œáœ
x0ÄŠ‹
""
##
xx
3! 4!
30. e e 1 x 1 x 2x
"" "
##x x !3!4! !3!4! x 3! 5! 7!
xx xxx xxx 2x2x2x
ab
’“Š‹Š‹Š‹
œ á á œ á
2 lim lim 2 2œáÊ œ áœ
2x 2x 2x e e 2x 2x 2x
3! 5! 7! x 3! 5! 7!
x0 x
ÄÄ_
xx
Š‹
31. 1 cos t 1 1 lim
"" "
###
"
tt t
ttttt tt
4! 6! 4! 6! 8!
cos t
Š‹’ “Š‹
œ á œáÊ
t0Ä
Š‹
t
lim œ áœ
t0ÄŠ‹
""
4! 6! 8! 24
tt
32. sin lim
"" "
)) )
) ) )) )) ))
Š‹Š ‹
œ áœáÊ))))
6 6 3! 5! 5! 7! 9!
sin
)Ä0
Š‹
6
lim œ áœ
)Ä0Š‹
""
#5! 7! 9! 1 0
))
33. y tan y y y lim lim
"" " "
"
yy35357 y357
yy yy ytany yy
ab
’“ Š‹Š‹
œ á œáÊ œ á
y0 y0ÄÄ
œ"
3
34. tan y sin y
y cos y y cos y y cos y cos y
yy
áááá
œœœ
ŒŒŒŒ
y y y y y 23y 23y
3 5 3! 5! 6 5! 6 5!
lim lim Êœ œ
y0 y0ÄÄ
tan y sin y
y cos y cos y 6
á "
Œ
65!
23y
35. x 1 e x 1 1 1 lim x e 1
#Î# #Î
"" " " "
##
Š‹ Š‹
ˆ‰
œ áœáÊ
1x 1x
x6x x
x6x
xÄ_
lim 1 1œ áœ
xÄ_ ˆ‰
""
#x6x
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

630 Chapter 10 Infinite Sequences and Series
36. (x 1) sin (x 1) 1 œ áœá
ˆ‰ Š‹
" """ ""
x 1 x 1 3!(x 1) 5!(x 1) 3!(x 1) 5!(x 1)
lim (x 1) sin lim 1 1Ê œ áœ
xxÄ_ Ä_
ˆ‰ Š‹
"""
x 1 3!(x 1) 5!(x 1)
37. lim lim
ln 1 x ln 1 x
1cos x 1cos x
x1 1
11
ab ab
ŒŒ Œ
Š‹
Š‹ Š‹
á á á
á á
œœÊœ
xx xx xx
33 3
xx
!4! !4!
xx0 x0ÄÄ
!4!
x
á œœ2! 2
38. lim
x4 x2 x4
ln (x 1) ln (x 1)
(x 2)(x 2)
(x 2) 1
á á
œœÊ
’“’“
(x 2) (x 2) (x 2)
33
x2 x2Ä
lim 4œœ
x2Ä
x2
1
á
’“
x2 (x 2)
3
39. sin 3x 3x x x . . . and 1 cos 2x 2x x x . . . lim
22610 246
981 2 4 sin3x
2 40 3 45 1 cos 2x
œ œ Ê
x0Ä
2
lim lim œœœ
x0 x0ÄÄ
3x x x . . . 3 x x . . .
2x x x . . . 2 x x . . .
3
2
26 10 4 8
981 981
240 240
24 6 2 4
24 24
345 345
40. ln 1 x x . . . and x sin x x x x x lim ab œ œ ÞÞÞÊ
33 23 7 11 15
xxx 1 1 1
2 3 4 6 120 5040 x sin x
ln 1 x
6912 3
2
x0Ä
ˆ‰
lim lim 1œœœ
x0 x0ÄÄ
x . . . 1 . . .
xx x x 1x x x
3xxx xxx
6912 369
23 4 234
3 7 11 15 4 8 12
11 1 11 1
6 120 5040 6 120 5040
ÞÞÞ ÞÞÞ
41. 1 1 e eÞÞÞœ œ
111
234
1
xxx
42. 1
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
”•
111 1 11 11141
444 4 44 6411464348
345 3 2
ÞÞÞ œ ÞÞÞ œ œ œ
Î
43. 1 1 cosÞÞÞœÞÞÞœ
3 3 3 13 13 13 3
42 44 46 2 4 4 4 6 4 4
246
246
246
xxx x x x
ˆ‰ ˆ‰ ˆ‰ ˆ‰
44. ln 1 ln
1111 1111111 1 3
2223242 2 2 3 4 2 2
234
ÞÞÞœ ÞÞÞœ œ
††† # # #
234 ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰
45. sin
1111 1 1 1 1 1
3 33 35 37 3 33 53 73 3 2
111
357 3
ÞÞÞœÞÞÞœœ
357
357
xxx x x x
ˆ‰ ˆ‰ ˆ‰ ˆ‰ È
46. tan
2222 2121212 2
3333537 3 33 53 73 3
357 1
ÞÞÞœ ÞÞÞœ
357
357
†††
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
47. xxxx x1xxx x
3456 3 23 3
1x
1x 1x
ÞÞÞœ ÞÞÞœ œab
ˆ‰
3
48. 1 1 3x 3x 3x cos 3xÞÞÞœÞÞÞœ
3x 3x 3x 1 1 1
246 2 4 6
246
22 44 66
xxx x x x
ab ab ab ab
49. xxxx x1x x x x
3579 3 2 2 2 3
23 1x
1+x 1+x
ÞÞÞœ ÞÞÞœ œ
Š‹
ab ab ˆ‰
22
3
50. x 2x x 1 2x x e
23 2 22x
2x 2x 2x
234 2 3 4
2x 2x 2x
ÞÞÞœ ÞÞÞœ
24 35 46 234
xxx x x x
Š‹
ab ab ab
51. 1 2x 3x 4x 5x 1 x xxxxÞÞÞœ ÞÞÞœ œ
234 2345
dd11
dx dx 1 x 1x
ab
ˆ‰
ab
2
52. 1 x ln 1 xÞÞœÞÞœ œ
xxxx 1 xxxx 1
2345 x 2345 x x
ln 1 x
234 2345
Š‹
ab ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.10 The Binomial Series 631
53. ln ln (1 x) ln (1 x) x x 2 x
ˆ‰ Š‹Š ‹Š‹
1x xxx xxx xx
1x 34 34 35
##
œ œ áᜠá
54. ln (1 x) x error when x 0.1;œá áÊ œ œ œ
xxx
3 4 n n n10
(1) x ( ) x
#
"
"
n1n n1n
n
kk
¹¹
n10 10 when n 8 7 terms
"" )
n10 10
n
nÊ Ê
55. tan x x error when x 1;
" "
#
"
œá áÊ œ œ œ
xxxx
3579 2n1 2n1 n1
()x (1)x
n12n1 n12n1
kk
¹¹
n 500.5 the first term not used is the 501 we must use 500 terms
""
# #n1 10
1001
Ê œ Ê Ê
st
56. tan x x and lim x lim x
" ##
#
œá á œ œ
xxxx x 2n1 2n1
3579 2n1 2n1x n1
(1) x
n12n1 2n 1
2n 1
nnÄ_ Ä_
¹¹ ¸¸
†
tan x converges for x 1; when x 1 we have which is a convergent series; when x 1Êœ œ
"
kk !
_
œn1
(1)
2n 1
n
we have which is a convergent series the series representing tan x diverges for x 1
!kk
_
œn1
(1)
2n 1
"
n1 Ê
57. tan x x and when the series representing 48 tan has an
" "
"
œá á
xxxx
3579 2n1 18
(1) x
n12n1 ˆ‰
error less than 10 , then the series representing the sum
"'
3†
48 tan 32 tan 20 tan also has an error of magnitude less than 10 ; thus
" " " '
"" "
#
ˆ‰ ˆ‰ ˆ‰
18 57 39
error 48 n 4 using a calculator 4 termskkœÊ Ê
Š‹
18
2n 1
# †
"
n1 310
58. ln (sec x) tan t dt t dtœ œ á ¸á
''
00
xx
Š‹
t2t xxx
315 1245
#
59. (a) 1 x 1 sin x x ; Using the Ratio Test:ab¸Ê ¸
#"
"Î#
#
x3x5x x3x5x
8 16 6 40 112
lim 1 x lim
nnÄ_ Ä_
¹¹¹¹
1 3 5 (2n 1)(2n 1)x 2 4 6 (2n)(2n )
2 4 6 (2n)(2n 2)(2n 3) 1 3 5 (2n 1)x
†† ††
†† ††
â â "
â â
#
2n 3
2n 1
†Ê (2n 1)(2n 1)
(2n 2)
(2n 3)1
x 1 the radius of convergence is 1. See Exercise 69.ÊÊkk
(b) cos x 1 x cos x sin x x x
dx 3x 5x x 3x 5x
dx 6 40 112 6 40 112
abab Š‹
" # " "
"Î#
## #
œ Ê œ ¸ ¸
11 1
60. (a) 1 t (1) (1) tab ab
ˆ‰
¸
# "Î# $Î# #
"Î#
"
##
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
335
(1) t (1) t
!3!
1 sinh x 1 dt xœ Ê ¸ œ
t 3t 3 5t t 3t 5t x 3x 5x
2 2! 2 3! 8 16 6 40 112
##
"
††
†'0
xŠ‹
(b) sinh 0.24746908; the error is less than the absolute value of the first unused
" """
ˆ‰
4 4 384 40,960
3
¸ œ
term, , evaluated at t since the series is alternating error 2.725 10
5x
112 4 112
5
œÊ¸‚
"'
kkˆ‰
4
61. 1 x x x 1 x x x
" " "
#$ #$
1x 1(x) dx 1x 1x dx
d1 d
œ œáÊ œ œ á
ˆ‰ ab
12x3x 4xχ
#$
62. 1 x x x 1 x x x 2x 4x 6x
""
#%' #%' $ &
1x dx1x dx
d2xd
1x
œáÊ œ œ ᜠá
ˆ‰ ab
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

632 Chapter 10 Infinite Sequences and Series
63. Wallis' formula gives the approximation 4 to produce the table1¸’“
244668 (2n 2)(2n)
335577 (2n 1)(2n 1)
††††† †
††††† †
â
â
n µ1
10 3.221088998
20 3.181104886
30 3.167880758
80 3.151425420
90 3.150331383
93 3.150049112
94 3.149959030
95 3.149870848
100 3.149456425
At n 1929 we obtain the first approximation accurate to 3 decimals: 3.141999845. At n 30,000 we still doœ œ
not obtain accuracy to 4 decimals: 3.141617732, so the convergence to is very slow. Here is a CAS1Maple
procedure to produce these approximations:
pie :=
proc(n)
local i,j;
a(2) := evalf(8/9);
for i from 3 to n do a(i) := evalf(2*(2*i 2)*i/(2*i 1)^2*a(i 1)) od;
[[j,4*a(j)] $ (j = n 5 .. n)]
end
64. (a) f x 1 x f x k x 1 x f x 1 x k xab ab a b ab a b
!! !
ˆ‰ ˆ‰ ˆ‰
œ Ê œ Ê † œ
__ _
œœ œ
kk k11 1
mm m
kk k
kk1 k1ww
kx x kx kx kx 1 x kx kxœ†œœ
!!!! !!
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ab
____ __
œœœœ œœ
kkkk kk1111 21
mmmmmmm
kkkk1kk
k1 k1 k1 k 0 k1 k
m k x k x Note that: k x k 1 x .œ œ
!! !!
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
ab
__ _ _
œœ œ œ
kk k k21 2 1
mm m m
kk kk1
k1 k k1 k
Thus, 1 x f x m kx kx m k 1 x kxabab ab
!! ! !
ˆ‰ ˆ‰ ˆ ‰ ˆ‰
† œ œ
w
__ _ _
œœ œ œ
kk k k21 1 1
mm m m
kk k1 k
k1 k k k
m k1x kx m k1 kx.œ œ
!!
’“’“
ˆ‰ ˆ‰ ˆ ‰
ab ab
ˆ‰ ˆ‰
__
œœ
kk11
mm mm
k1 k k1 k
kk k
Note that: k 1 k k 1 k
ˆ‰ ˆ‰
ab ab
mm
k1 k k1! k!
mm m k 1 1 mm m k 1
†"â †"â
œ
aba b aba bab
ab
kmkkmm.œ œ œ œ
mm m k mm m k 1 mm m k 1 mm m k 1
k! k! k! k! k
m
† " â † " â † " â † " â abab aba b aba b aba b
abab ˆ‰
Thus, 1 x f x m k 1 k x m m x m m xabab ab
!!!
’“’“
ˆ‰ˆ‰ˆ‰ˆ ‰ ˆ‰ ˆ‰
† œ œ œ
w
___
œœœ
kkk111
mm m m
k1 k k k
kkk
m1 x mfx fx if x 1.œ œ†Êœ "
Œ
!ˆ‰ ab ab
_
œ
k1
m
k1x
kmfx
w†
ab
ab
(b) Let g x 1 x f x g x m 1 x f x 1 x f xab a b ab ab a b ab a b abœ Ê œ
ww
mm1m
m1x fx 1x m1x fx 1x mfx 0.œ † œ † † œababab ababab ab
†
m1 m mfx m1 m1
1x
ab
ab
(c) g x 0 g x c 1 x f x c f x c 1 x . Since f x 1 x
w
ab ab a b ab ab a b ab !ˆ‰
œÊ œÊ œÊ œ œ œ
mm
c
1x
m
k
k
ab
m
_
œ
k1
f0 1 0 101c10 1c1fx 1x.Ê œ œœÊ œÊœÊ œ ab ab a b ab a b
!ˆ‰
_
œ
k1
m
k
km m
65. 1 x 1 x (1) (1) xab a b abab ˆ‰
œ œ
# # "Î# $Î# #
"Î# "Î# "
##
ˆ‰ˆ‰ ab
3(1) x
!
11 ᜠáœ
ˆ‰ˆ‰ˆ‰ ab
35
(1) x
3! 2 ! 2 3! n!
x 13x 135x 1 3 5 (2n 1)x
## #
â
†††
†† †
††
!
_
œn1
2n
n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 10.10 The Binomial Series 633
sin x 1 t dt 1 dt x ,Êœ œ œ
" # "Î# â â
##â
''
00
xx
ab Œ
!!
__
œœn1 n1
1 3 5 (2n 1)x 1 3 5 (2n 1)x
n! 4 (2n)(2n 1)
†† ††
††
2n 2n 1
n
where x 1kk
66. tan t tan x dt 1 dtcd –— ˆ‰
" "
_
#
""""
xxx x
œ œ œ œ á
1'' '
dt
1t t t t
t
Š‹
Š‹
1
t
t
1
dt lim œ á œ áœá
'x
b
x
ˆ‰ ‘
"""" " " " " " " " "
t t t t 3t 5t x 3x 5x
t7t7x
bÄ_
tan x , x 1; tan t tan x Ê œá œ œ
" " "
##
"" "1 1
x3x 5x 1t
dt
cd
xx
'
lim tan x ,œ áœáÊ œá
bÄ_ ‘
"""" "" " " "" "
"
#t 3t 5t x 3x 5x x 3x 5x
7t 7x
x
b
1
x1
67. (a) e cos ( ) i sin ( ) 1 i(0) 1
i1œ œœ11
(b) e cos i sin (1 i)
i4
44
22 2
i
111
Î""
œ œœ
ˆ‰ ˆ‰ Š‹
ÈÈ È
(c) e cos i sin 0 i( 1) i
Î
##
i2111
œ œœ
ˆ‰ ˆ‰
68. e cos i sin e e cos ( ) i sin ( ) cos i sin ;
iii())))
œ Êœœœ)) ) ) ))
e e cos i sin cos i sin 2 cos cos ;
ii ee
))
œ œ Ê œ
#
)))) ) )
ii
e e cos i sin (cos i sin ) 2i sin sin
ii ee
i
))
œ œ Ê œ
#
)))) ) )
ii
69. e 1 x e 1 i and
xi
xxx
!3!4! 2! 3! 4!
(i ) (i ) (i )
œáÊ œá
#
))))
)
e1i 1i
#
i( i) ( i) ( i) (i) (i) (i)
2! 3! 4! ! 3! 4!
)))) )))
œ áœá))
ʜ
ee
ii
##
Š‹Š‹
1i 1iáá))
(i ) (i ) (i ) (i ) (i ) (i )
!3!4! !3!4!
1 cos ;œáœ
)))
#!4!6! )
ee
ii
ii
##
œŠ‹Š‹
1i 1iáá))
(i ) (i ) (i ) (i ) (i ) (i )
!3!4! !3!4!
sin œáœ))
)))
3! 5! 7!
70. e cos i sin e e cos ( ) i sin ( ) cos i sin
iii)))
œ Êœœœ)) ) )))
ÐÑ
(a) e e (cos i sin ) (cos i sin ) 2 cos cos cosh i
ii ee
))
œ œ Ê œ œ
#
)) )) ) ) )
ii
(b) e e (cos i sin ) (cos i sin ) 2i sin i sin sinh i
ii ee
2
))
œ œ Ê œ œ
)) )) ) ) )
ii
71. e sin x 1 x x
xxxx xxx
!3!4! 3!5!7!
œ á á
Š‹Š‹
#
(1)x (1)x x x x x x x x ;œ ᜠá
#$% &#$&
"" "" " " " " "
####
ˆ‰ˆ‰ˆ ‰
6661014 330
e e e e (cos x i sin x) e cos x i e sin x e sin x is the series of the imaginary part
xix 1ix x x x x
†œœ œ Ê
ÐÑ ab
of e which we calculate next; e 1 (x ix)
ÐÑ ÐÑ
#
1ix 1ix (x ix) (x ix) (x ix) (x ix)
n! !3!4!
œ œá
!
_
œn0
n
1 x ix 2ix 2ix 2x 4x 4x 4ix 8ix the imaginary partœ áÊ
"" " " "
#
#$$%&& '
!3! 4! 5! 6!
ab a b a b a b a b
of e is xxxxx xxxx x in agreement with our
ÐÑ #$&' #$ & '
#
"" "
1ix 2248
!3!5!6! 33090
ᜠá
product calculation. The series for e sin x converges for all values of x.
x
72. e e (cos bx i sin bx) ae (cos bx i sin bx) e ( b sin bx bi cos bx)
dd
dx dx
aib ax ax ax
ˆ‰cd
Ð Ñ œœ
ae (cos bx i sin bx) bie (cos bx i sin bx) ae ibe (a ib)eœ œœ
ax ax aibx aibx aibxÐ Ñ Ð Ñ Ð Ñ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

634 Chapter 10 Infinite Sequences and Series
73. (a) e e (cos i sin )(cos i sin ) (cos cos sin sin ) i(sin cos sin cos )
ii))
œ œ ) ) ) ) )) )) )) ))
" " # # "# "# "# #"
cos( ) i sin( ) eœ œ)) ))
"# "# ÐÑi))
(b) e cos( ) i sin( ) cos i sin (cos i sin )
""
icos i sin
cos i sin cos i sin e
)))
)) ))
œ œ œ œ œ) ))) ))
ˆ‰ i
74. e C iC e (cos bx i sin bx) C iC
abi abi
ab ab
abix ax
Ð Ñ "# "#
œ
ˆ‰
(a cos bx ia sin bx ib cos bx b sin bx) C iCœ
e
ab
ax
"#
[(a cos bx b sin bx) (a sin bx b cos bx)i] C iCœ
e
ab
ax
"#
CiC;œ
e (a cos bx b sin bx) ie (a sin bx b cos bx)
ab ab
ax ax
"#
e e e e (cos bx i sin bx) e cos bx ie sin bx, so that given
Ð Ñabix axibx ax ax ax
œœ œ
e dx e C iC we conclude that e cos bx dx C
''
Ð Ñ Ð Ñ
"# "
abix abix ax
abi
ab ab
e (a cos bx b sin bx)
œ œ
ax
and e sin bx dx C
'ax e (a sin bx b cos bx)
ab
œ
ax
#
CHAPTER 10 PRACTICE EXERCISES
1. converges to 1, since lim a lim 1 1
nnÄ_ Ä_
n(1)
n
œœ
Š‹
n
2. converges to 0, since 0 a , lim 0 0, lim 0 using the Sandwich Theorem for SequencesŸŸ œ œ
n22
nn
ÈÈ
nnÄ_ Ä_
3. converges to 1, since lim a lim lim 1 1œœœ
nn nÄ_ Ä_ Ä_
n12
2
ˆ‰ ˆ ‰
"
#
n
nn
4. converges to 1, since lim a lim 1 (0.9) 1 0 1
nnÄ_ Ä_
nœ œœcd
n
5. diverges, since sin 0 1 0 1 0 1
˜™
ef
n1
#œ ßßßßßßá
6. converges to 0, since {sin n } {0 0 0 }1œ ßßßá
7. converges to 0, since lim a lim 2 lim 0
nn nÄ_ Ä_ Ä_
nln n
n1
œœ œ
Š‹
n
8. converges to 0, since lim a lim lim 0
nn nÄ_ Ä_ Ä_
nln (2n )
n1
œœœ
" Š‹
2
2n 1
9. converges to 1, since lim a lim lim 1
nn nÄ_ Ä_ Ä_
nnln n
n1
1
œœœ
ˆ‰
Š‹
n
10. converges to 0, since lim a lim lim lim lim 0
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
nln 2n 1
n16nn
12n 2
œœœœœ
ab Š‹
6n
2n 1
11. converges to e , since lim a lim lim 1 e by Theorem 5
5 5
n
nn
nn nÄ_ Ä_ Ä_
œœœ
ˆ‰ Š‹
n5
nn
(5)
12. converges to , since lim a lim 1 lim by Theorem 5
""""
ene
n1
nn nÄ_ Ä_ Ä_
œœ œ
ˆ‰
nˆ‰
n
n
13. converges to 3, since lim a lim lim 3 by Theorem 5
nn nÄ_ Ä_ Ä_
n333
n1
1n
n
œœœœ
ˆ‰
n
1n
Î
14. converges to 1, since lim a lim lim 1 by Theorem 5
nn nÄ_ Ä_ Ä_
n331
n1
1n
n
œœœœ
ˆ‰Î1n
1n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Practice Exercises 635
15. converges to ln 2, since lim a lim n 2 1 lim lim lim 2 ln 2
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
n21
œœ œ œab
1n 1n
1n
Š‹
n
2 ln 2
1n
n
n
–—
Š‹
2 ln 2 ln 2œœ
!†
16. converges to 1, since lim a lim 2n 1 lim exp lim exp e 1
nn n nÄ_ Ä_ Ä_ Ä_
nln (2n 1)
n1
œœ œ œœ
ÈŠ‹ Œ
n!
2
2n 1
17. diverges, since lim a lim lim (n 1)
nn nÄ_ Ä_ Ä_
n(n 1)!
n!
œœœ_
18. converges to 0, since lim a lim 0 by Theorem 5
nnÄ_ Ä_
n(4)
n!
œœ
n
19. s
"
# # (2n3)(2n1) n3 2n1 3 5 5 7 n3 2n1 3 2n1
n
œÊœá œ
Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹
–—–—– —
lim s lim Êœœ
nnÄ_ Ä_
n62n1 6
–—
""
Š‹
20. s lim s
# #
222 22 22 22 22
n(n1) n n1 3 3 4 n n1 n1
n n
œ Êœ á œ Ê
ˆ‰ˆ‰ ˆ ‰ nÄ_
lim 1 1œœ
nÄ_ ˆ‰
2
n1
21. s
9 3 3 333333 3 3
(3n1)(3n2) 3n1 3n2 5 5 8 8 11 3n1 3n2
n
#
œ Êœ á
ˆ‰ˆ‰ˆ‰ ˆ ‰
lim s lim œ Ê œ œ
33 3 3 3
3n 3n 2
n
## # #
nnÄ_ Ä_ ˆ‰
22. s
8 22 222222 22
(4n 3)(4n 1) 4n 3 4n 1 9 13 13 17 17 21 4n 3 4n 1
œ Êœ á
nˆ‰ˆ‰ˆ‰ˆ ‰
lim s lim œ Ê œ œ
22 22 2
94n1 94n1 9
nnÄ_ Ä_
nˆ‰
23. e , a convergent geometric series with r and a 1 the sum is
!!
__
œœn0 n0
"""
n
eee1
1
e
œœœÊœ
nŠ‹
e
24. ( 1) a convergent geometric series with r and a the sum is
!!
ˆ‰ˆ‰
__
œœn1 n0
œ œ œÊ
nn
33 3
444 44
n
" "
ˆ‰
ˆ‰
3
4
4
1
3
5
œ
25. diverges, a p-series with p œ"
#
26. 5 , diverges since it is a nonzero multiple of the divergent harmonic series
!!
__
œœn1 n1
"5
nn
œ
27. Since f(x) f (x) 0 f(x) is decreasing a a , and lim a lim 0, the
n
œÊ œÊ Ê œ œ
Ä_
""
w
#
xx n1 n n 1
n
nÄ_ È
series converges by the Alternating Series Test. Since diverges, the given series converges conditional
!!
_ _
œ œn1 n1
()
nn
" "
n
ÈÈ
ly.
28. converges absolutely by the Direct Comparison Test since for n 1, which is the nth term of a convergent
""
#nn
p-series
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

636 Chapter 10 Infinite Sequences and Series
29. The given series does not converge absolutely by the Direct Comparison Test since , which is
""
ln (n 1) n 1
the nth term of a divergent series. Since f(x) f (x) 0 f(x) is decreasingœÊœ Ê
""
w
ln (x 1) (ln (x 1)) (x 1)
a a , and lim a lim 0, the given series converges conditionally by the AlternatingÊ œ œ
n1 n ln (n 1)
"
nnÄ_ Ä_
n
Series Test.
30. dx lim dx lim (ln x) lim the series
''
22
bb
2
"" """
"
#x(ln x) x(ln x) ln b ln 2 ln
œœœœÊ
bb bÄ_ Ä_ Ä_
cd ˆ‰
converges absolutely by the Integral Test
31. converges absolutely by the Direct Comparison Test since , the nth term of a convergent p-series
ln n n
nnn
œ
"
32. diverges by the Direct Comparison Test for e n ln e ln n n ln n ln n ln (ln n)
nn n n
nn
Ê ÊÊ
ˆ‰
n ln n ln (ln n) , the nth term of the divergent harmonic seriesÊ Ê
ln n
ln (ln n) n
"
33. lim lim 1 1 converges absolutely by the Limit Comparison Test
nnÄ_ Ä_
Š‹
Š‹
nn 1
n
œœœÊ
ÉÈ
n
n1
34. Since f(x) f (x) 0 when x 2 a a for n 2 and lim 0, theœÊœ Ê œ
3x 3n
x1 n1
3x 2 x
x1 n1 n
w
ab
ab nÄ_
series converges by the Alternating Series Test. The series does not converge absolutely: By the Limit
Comparison Test, lim lim 3. Therefore the convergence is conditional.
nnÄ_ Ä_
Š‹
ˆ‰
3n
n 1
n
œœ
3n
n1
35. converges absolutely by the Ratio Test since lim lim 0 1
nnÄ_ Ä_
’“
n2 n! n 2
(n 1)! n 1 (n 1)
†œœ
36. diverges since lim a lim does not exist
nnÄ_ Ä_
n()n 1
2n n 1
œ"
nab
37. converges absolutely by the Ratio Test since lim lim 0 1
nnÄ_ Ä_
’“
3n! 3
(n 1)! 3 n 1
n1
n
†œœ
38. converges absolutely by the Root Test since lim a lim lim 0 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnnn
n
nœœœ
23 6
nn
39. converges absolutely by the Limit Comparison Test since lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
n(n 1)(n 2)
œœ
Én(n 1)(n 2)
n
40. converges absolutely by the Limit Comparison Test since lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
nn 1
œœ
Énn 1
n
ab
41. lim 1 lim 1 lim 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u (n 1)3 (x 4) 3 n 1 3
(x 4) n3 n
x4 x4
n1
n
n1
n1 n
n
Ê Ê Ê
†kk kk
x 4 3 3 x 4 3 7 x 1; at x 7 we have , the alternatingÊ Ê Ê œ œkk !!
__
œœn1 n1
(1)3 ( )
n3 n
"
nn n
n
harmonic series, which converges conditionally; at x 1 we have , the divergent harmonic seriesœ œ
!!
__
œœn1 n1
3
n3 n
n
n"
(a) the radius is 3; the interval of convergence is 7 x 1Ÿ
(b) the interval of absolute convergence is 7 x 1
(c) the series converges conditionally at x 7œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Practice Exercises 637
42. lim 1 lim 1 (x 1) lim 0 1, which holds for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹
u
u (2n 1)! (x 1) ( n)(2n 1)
(x 1) (2n 1)!
n1
nÊ Ê œ
#
#"
2n
2n 2
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
43. lim 1 lim 1 3x 1 lim 1 3x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (n 1) (3x 1) (n 1)
(3x 1) nn
n1
n
n1
n
Ê Ê Ê
†
1 3x 1 1 0 3x 2 0 x ; at x 0 we have Ê Ê Ê œ œ
2
3nn
(1) (1) ( )
!!
__
œœn1 n1
"
n1 n 2n1
, a nonzero constant multiple of a convergent p-series, which is absolutely convergent; at x weœ œ
!
_
œn1
"
n 3
2
have , which converges absolutely
!!
__
œœn1 n1
(1) (1) ( )
nn
"
n1 n n1
œ
(a) the radius is ; the interval of convergence is 0 x
"
33
2
ŸŸ
(b) the interval of absolute convergence is 0 xŸŸ
2
3
(c) there are no values for which the series converges conditionally
44. lim 1 lim 1 lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¸¸
u
u 2n3 2 n1 (2x1) 2 2n3 n1
n2 2n1 2 n2 2n
(2x 1) 2x 1
n1
n
n1
n1 n
n
Ê Ê
"
††† †
kk
(1) 1 2x 1 2 2 2x 1 2 3 2x 1 x ; at x we haveÊ Ê Ê Ê Ê œ
kk2x 1 33
### #
"
kk
which diverges by the nth-Term Test for Divergence since
!!
__
œœn1 n1
n1
2n 1 2n 1
(2) ( )(n1)
#
"
†
nn
nœ
lim 0; at x we have , which diverges by the nth-Term Test
nÄ_ ˆ‰ !!
n1 n1 2 n
2n 1 2n 1 2n 1
" " "
# # #
œÁ œ œ
__
œœn1 n1
†
n
n
(a) the radius is 1; the interval of convergence is x
3
##
"
(b) the interval of absolute convergence is x
3
##
"
(c) there are no values for which the series converges conditionally
45. lim 1 lim 1 x lim 1 lim 1
nn n nÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ kk ¸¸ ˆ‰ˆ‰ˆ‰
u
u (n1) x n1 n1 e n1
xn n
nx
n1
n
n1 n
n1 n
Ê Ê Ê
""
†kk
0 1, which holds for all xÊ
kkx
e†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
46. lim 1 lim 1 x lim 1 x 1; when x 1 we have
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn1
xn
n1
n
n1
n
n1
n
Ê Ê Ê œ
ÈÈ
†
, which converges by the Alternating Series Test; when x 1 we have , a divergent p-series
!!
_
œn1
(1)
n n
"
n
È È
œ
n1
(a) the radius is 1; the interval of convergence is 1 x 1Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
47. lim 1 lim 1 lim 1 3 x 3;
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰ ÈÈ
u
u3(n1)x3n1
(n 2)x 3xn2
n1
n
2n 1
n 1 2n 1
n
Ê Ê Ê
†
the series and , obtained with x 3, both diverge
!! È
__
œœn1 n1
œ„
n1 n1
33
ÈÈ
(a) the radius is 3; the interval of convergence is 3 x 3
ÈÈÈ
(b) the interval of absolute convergence is 3 x 3
ÈÈ
(c) there are no values for which the series converges conditionally
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

638 Chapter 10 Infinite Sequences and Series
48. lim 1 lim 1 (x 1) lim 1 (x 1) (1) 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u 2n 3 (x 1) 2n 3
(x 1)x 2n 1 2n 1
n1
n
2n 3
2n 1
Ê Ê Ê
##
†
(x 1) 1 x 1 1 1 x 1 1 0 x 2; at x 0 we have Ê Ê Ê Ê œ
#
#
kk !
_
œn1
(1)(1)
n1
n2n1
which converges conditionally by the Alternating Series Test and the factœœ
!!
__
œœn1 n1
(1) (1)
2n 1 2n 1
3n 1 n1
that diverges; at x 2 we have , which also converges conditionally
!!!
___
œœœn1 n1 n1
"
2n 1 2n 1 2n 1
(1)(1) (1)
œœ
n2n1 n
(a) the radius is 1; the interval of convergence is 0 x 2ŸŸ
(b) the interval of absolute convergence is 0 x 2
(c) the series converges conditionally at x 0 and x 2œœ
49. lim 1 lim 1 x lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk »»
u
ucsch(n)x
csch (n 1)x
n1
n
n1
n
Ê Ê
Š‹
ˆ‰
2
ee
n1 n1
2
ee
nn
x lim 1 1 e x e; the series e csch n, obtained with x e,ÊÊÊ„ œ„kk a b
¹¹ !
nÄ_
ee
1e e
xn
2n 1
2n 2 kk _
œn1
both diverge since lim e) csch n 0
nÄ_ a„Á
n
(a) the radius is e; the interval of convergence is e x e
(b) the interval of absolute convergence is e x e
(c) there are no values for which the series converges conditionally
50. lim 1 lim 1 x lim 1 x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹
kk kk
u
ux coth(n) 1e1e
x coth(n1) 1e 1e
n1
n
n1
n2n22n
2n 2 2n
Ê Ê Ê
†
1 x 1; the series 1 coth n, obtained with x 1, both diverge since lim 1 coth n 0Ê „ œ„ „ Á
!ab ab
_
œn1
n n
nÄ_
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
51. The given series has the form 1 x x x ( x) , where x ; the sum is á ᜠœ œ
#$ "" "
n
1x 4 5
1
4
ˆ‰
4
52. The given series has the form x ( 1) ln (1 x), where x ; the sum isá ᜠœ
xx x 2
3n 3
n1
#
n
ln 0.510825624
ˆ‰
5
3¸
53. The given series has the form x ( 1) sin x, where x ; the sum is sin 0á ᜠœ œ
xx x
3! 5! (2n 1)!
n2n 1
11
54. The given series has the form 1 ( 1) cos x, where x ; the sum is cos á ᜠœ œ
xx x
2! 4! (2n)! 3 3
n2n 11"
#
55. The given series has the form 1 x e , where x ln 2; the sum is e 2áᜠœ œ
xx x
2! 3! n!
xln2
nÐÑ
56. The given series has the form x ( 1) tan x, where x ; the sum isá ᜠœ
xx x
35 (2n1)
n
3
2n 1
" "
È
tan" "
Š‹
È36
œ1
57. Consider as the sum of a convergent geometric series with a 1 and r 2x
" "
12x 12x
œœÊ
1 (2x) (2x) (2x) (2x) 2 x where 2x 1 xœáœ œ Ê
#$ "
#
!! kk kk
__
œœn0 n0
nnn
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Practice Exercises 639
58. Consider as the sum of a convergent geometric series with a 1 and r x
"""
$
1x 1x 1 x
œœÊœ
ab
1 x x x ( 1) x where x 1 x 1 x 1œáœ Ê Êababab kk kk kk
!
$$ $ $ $
#$ _
œn0
n3n
59. sin x sin x œÊœ œ
!!!
___
œœœn0 n0 n0
(1)x (1)(x) (1) x
(2n 1)! (2n 1)! ( n 1)!
#
n2n1 n 2n1 n 2n12n1
111
60. sin x sin œÊœ œ
!!!
___
œœœn0 n0 n0
(1)x (1)2 x
(2n 1)! 3 (2n 1)! 3 ( n 1)!
2x (1)
#
n2n1 n2n12n1
n2n 1
2n 1
Š‹
2x
3
61. cos x cos x œÊœ œ
!!!
ˆ‰
___
œœœn0 n0 n0
(1)x (1)x
(2n)! (2n)! ( n)!
53 (1) x
Î
#
n2n n 10n 3
n53
2n
ˆ‰
62. cos x cos œÊœ œ
!!!
Š‹
___
œœœn0 n0 n0
(1)x (1)x
(2n)! (2n)! 5 ( n)!
x
5
(1)
#
n2n n6n
3nx3
5
2n
n
ÈŠ‹
63. e e
xx2
xx
n! n! n!
n0
œÊœ œ
!!!
__
œœn0 n0
nnn
xn
n
ÐÎÑ _
œ#
11
ˆ‰
64. e e
xx
x
n! n! n!
x(1)x
œÊœ œ
!!!
___
œœœn0 n0 n0
nnn2n
ab
65. f(x) 3 x 3 x f (x) x 3 x f (x) x 3 x 3 xœœ Ê œ Ê œ
Èab ab abab
##w # ww## #
"Î# "Î# $Î# "Î#
f (x) 3x 3 x 3x 3 x ; f( 1) 2, f ( 1) , f ( 1) ,Êœ œœœœ
www $ # # w ww
&Î# $Î# """
##
ab ab 88
3
f ( 1) 3 x 2
www #
œœÊœá
33 9
32 8 32 2 1! 2 2! 2 3!
(x 1) 3(x 1) 9(x 1)
Ȇ† †
66. f(x) (1 x) f (x) (1 x) f (x) 2(1 x) f (x) 6(1 x) ; f(2) 1, f (2) 1,œœÊ œÊ œÊ œ œ œ
"
" w # ww $ www % w
1x
f (2) 2, f (2) 6 1 (x 2) (x 2) (x 2)
ww www # $
"
œ œÊ œ á
1x
67. f(x) (x 1) f (x) (x 1) f (x) 2(x 1) f (x) 6(x 1) ; f(3) ,œœÊ œÊ œÊ œ œ
" "
" w # ww $ www %
x1 4
f (3) , f (3) , f (2) (x 3) (x 3) (x 3)
w ww www # $
""""""
œ œ œÊœá
44 x1444
26
44
68. f(x) x f (x) x f (x) 2x f (x) 6x ; f(a) , f (a) , f (a) ,œœ Ê œ Ê œ Ê œ œ œ œ
"""
" w # ww $ www % w ww
xaaa
2
f (a) (x a) (x a) (x a)
www # $
""" " "
œ Êœ á
6
aa
xaa a
69. exp x dx 1 x dx x
''
00
12 12
ab Š‹’ “
œ á œ á
$$ "Î#
!
xxx x x x x
2! 3! 4! 4 7 2! 10 3! 13 4!
†††
0.484917143¸¸
""""""
###
††† †† †† ††
472!
2 10 3! 2 13 4! 2 16 5!
70. x sin x dx x x dx x dx
'' '
00 0
11 1
ab Š‹Š‹
$$ %
œ á œ á
xxxx xxxx
3! 5! 7! 9! 3! 5! 7! 9!
0.185330149œá¸
’“
xxxxx
5 113! 175! 237! 299!
††††
"
!
71. dx 1 dx x
''
11
12 12
tanx xxxxx xxxx x
x 357911 9254981121
œ á œ á
Š‹’ “
"Î#
!
0.4872223583¸¸
"""""""""""
## ##
##
9 2 5 9 2 11 2 13 2 15 2 19 21
717
†† †††† ††
††
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

640 Chapter 10 Infinite Sequences and Series
72. dx x dx xxxx dx
'' '
00 0
164 164 164
tanx xxx
xx
357 3 5 7
ÈÈ
œ á œ á
" """
"Î# &Î# *Î# "$Î#
Š‹
ˆ‰
x x x x 0.0013020379œ á œ á ¸
‘ˆ‰
22 2 2 2222
3 1 55 105 3 8 55 8 105 8
21 8
$Î# (Î# ""Î# "&Î#
#
"Î'%
!†††
†
73. lim lim lim
x0 x0 x0ÄÄ Ä
7 sin x 7
e1
2x #
œœœ
7x 71
2x 2
Š‹Š‹
Š‹Š‹
á á
á á
xx xx
3! 5! 3! 5!
2x 2x 2x 2x
2! 3! ! 3!
74. lim lim lim
)) )ÄÄ Ä00 0
ee 2
sin
)
))
œœ
Š‹Š‹Š‹
Š‹ Š‹
1122á á á
á
)))
))
! 3! ! 3! 3! 5!
3! 5! 3! 5! á
lim 2œœ
)Ä0
2Š‹
Š‹
3! 5!
3! 5!
á
á
75. lim lim lim lim
t0 t0 t0 t0ÄÄÄ Ä
ˆ‰
""
#
2 cos t t 2t (1 cos t)
t22 cos t t22 2
2t
œ œ œ
ŒŒ
Š‹
1
11
á
á
tt t
4! 4!
tt
4!
á
á
t
6!
2t
4!
Š‹
t
lim œœ
t0Ä
2
1
Š‹
Š‹
4! 6!
t
2t
4!
á
á1
"
#
76. lim lim
h0 h0ÄÄ
Š‹ ŒŒ
sin h
h
hh hh
3! 5! ! 4!
cos h
hh
œ
11á á
lim lim œ œ áœ
h0 h0ÄÄ
Œ
hhhhhh
!3!5!4!6!7!
á
h ! 3! 5! 4! 6! 7! 3
hhhh
Š‹
"" "
#
77. lim lim lim
z0 z0 z0ÄÄ Ä
"
cos z
ln (1 z) sin z
11z z
zz
œœ
Š‹ Š‹
Š‹Š‹Š ‹
zz
33
zz zz z2zz
33!5! 34
á á
áá á
lim 2œœ
z0Ä
Š‹
Š‹
1á
á
z
3
2z z
34
78. lim lim lim
y0 y0 y0ÄÄ Ä
yy y
cos y cosh y 11
œœ
ŒŒŒ
yyy yyy 2y2y
4!6! !4!6! 6!
á á á
lim 1œœ
y0Ä
"
á
Œ
12y
6!
79. lim s lim s lim s 0
x0 x0 x0ÄÄ Ä
ˆ‰
–—
Š‹
sin 3x r r 3 9 81x r
xx x x x 40 x
3x
œ œ á œ
Š‹
á
#
(3x) (3x)
6 120
0 and s 0 r 3 and sÊœ œÊœ œ
r3 9 9
xx ##
80. The approximation sin x is better than sin x x.¸¸
6x
6x
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Practice Exercises 641
81. lim 1 x lim 1 x
nnÄ_ Ä_
¹¹
kk kk
¸¸
2 5 8 (3n 1)(3n 2)x 2 4 6 (2n)
4 6 (2n)(2n 2) 5 8 (3n 1)x 2n 2 3
3n 2 2
†† ††
†† ††
â â
#â #â
n1
n
†Ê Ê
the radius of convergence is Ê2
3
82. lim 1 x lim 1 x
nnÄ_ Ä_
¹¹
kk kk
¸¸
3 5 7 (2n 1)(2n 3)(x 1) 4 9 14 (5n 1)
4 9 14 (5n 1)(5n 4) 3 5 7 (2n 1)x 5n 4 2
2n 3 5
†† ††
†† ††
â â
â â
n1
n
†Ê Ê
the radius of convergence is Ê5
2
83. ln 1 ln 1 ln 1 ln (k 1) ln k ln (k 1) ln k
!! !
ˆ‰ ‘ˆ‰ˆ‰ cd
nn n
k2 k2 k2œœ œ
œ œ
"""
kkk
ln 3 ln 2 ln 1 ln 2 ln 4 ln 3 ln 2 ln 3 ln 5 ln 4 ln 3 ln 4 ln 6 ln 5 ln 4 ln 5œ cdcdcdcd
ln (n 1) ln n ln (n 1) ln n ln 1 ln 2 ln (n 1) ln n after cancellationáœcdcdcd
ln 1 ln ln 1 lim ln ln is the sumÊœ Ê œ œ
!!
ˆ‰ˆ‰ ˆ‰ ˆ‰
n
k2 k2œœ
" " "
#k2n k 2n
n1 n 1
nÄ_
84. -
!!
ˆ ‰ ˆ ‰ˆ ‰ˆ ‰ˆ ‰ ˆ ‰
nn
k2 k2œœ
" " " " " " "" "" "" " "
# # # #k 1 k1 k1 1 3 4 3 5 4 6 n n
1
œ œ á
œ œ œ œ
‘ˆ ‰ˆ ‰ˆ‰ ’“
" " """" " " " " "
# # ## #
n1 n1 1 n n1 n n1 2n(n1) 4n(n1)
33nn2
3n(n 1) 2(n 1) 2n
lim Êœ œ
!ˆ‰
k2œ
""
# k1 2nn1 4
31 1 3
nÄ_
85. (a) lim 1 x lim
nnÄ_ Ä_
¹¹
kk
1 4 7 (3n 2)(3n 1)x (3n)! (3n )
(3n 3)! 1 4 7 (3n 2)x (3n 1)(3n 2)(3n 3)
††
††
â "
â
$
3n 3
3n
†Ê
x 0 1 the radius of convergence is œÊ _kk
$†
(b) y 1 x xœ Ê œ
!!
__
œœn1 n1
147 (3n 2) dy 147 (3n 2)
(3n)! dx (3n 1)!
†† ††â â
3n 3n 1
xx xÊœ œ
dy 147 (3n 2) 147 (3n 5)
dx (3n 2)! (3n 3)!
!!
__
œœn1 n2
†† ††â â
3n 2 3n 2
x 1 x xy 0 a 1 and b 0œ œÊœ œ
Œ
!
_
œn1
147 (3n 2)
(3n)!
††â 3n
86. (a) x x ( x) x ( x) x ( x) xxxx (1)x which
xx
1x 1(x)
nn
## # ## $ #$%&
œ œáœáœ
!
_
œn2
converges absolutely for x 1kk
(b) x 1 ( 1) x ( 1) which divergesœÊ œ
!!
__
œœn2 n2
nn n
87. Yes, the series a b converges as we now show. Since a converges it follows that a 0 a 1
!!
__
œœn1 n1
nn n nn
ÄÊ
for n some index N a b b for n N a b converges by the Direct Comparison Test with bÊÊ
nn n nn n
!!
_ _
œ œn1 n1
88. No, the series a b might diverge (as it would if a and b both equaled n) or it might converge (as it would if
!
_
œn1
nn n n
a and b both equaled ).
nn n
"
89. (x x ) lim (x x ) lim (x x ) lim (x ) x both the series and
!!
__
œœn1 1
n1 n k1 k n1 n1""
œ œ œ Ê
nnnÄ_ Ä_ Ä_
k
sequence must either converge or diverge.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

642 Chapter 10 Infinite Sequences and Series
90. It converges by the Limit Comparison Test since lim lim 1 because a converges
nnÄ_ Ä_
Š‹
an
1a
n
n
aœœ
"
1a n
n!
_
œn1
and so a 0.
nÄ
91. a a a a a
!ˆ‰ ˆ ‰ ˆ ‰
_
œn1
a
n 3 4 34 5678
aaa
nχ
""#%)
##
" "" """"
a (aaaa ) which is a divergent series á á á
ˆ‰
"" " " "
"' #%)"'
#91011 16
92. a for n 2 a a a , and
nln n ln ln 4 ln 8 ln ln 2 3 ln 2
œ Ê á ᜠá
" """ " " "
#$% ###
1 which diverges so that 1 diverges by the Integral Test.œ á
""" "
##ln 3 n ln n
ˆ‰ !
_
œn2
CHAPTER 10 ADDITIONAL AND ADVANCED EXERCISES
1. converges since and converges by the Limit Comparison Test:
"" "
# (3n ) (3n 2) (3n 2)
2n 1 2 !
_
œn1
lim lim 3
nnÄ_ Ä_
Š‹
Š‹
n
(3n 2)
œœ
ˆ‰
3n 2
n
$Î# $Î#
2. converges by the Integral Test: tan x lim lim
'1
b
ab ’“ ’ “
" #
dx
x 1 3 3 192
tan x tan b
œœ
bbÄ_ Ä_
ab ab1
œ œ
Š‹
11 1
24 192 192
7
3. diverges by the nth-Term Test since lim a lim ( 1) tanh n lim ( 1) lim ( 1)
nn n
b
Ä_ Ä_ Ä_
Ä_
nnn n
1e
1e
œ œ œ
Š‹
2n
2n
does not exist
4. converges by the Direct Comparison Test: n! n ln (n!) n ln (n) nÊ Ê
nln (n!)
ln (n)
log (n!) n , which is the nth-term of a convergent p-seriesÊÊ
nlog (n!)
nn
n"
5. converges by the Direct Comparison Test: a 1 , a , a
"# $
œœ œ œ œ
12 12 12 23 12
(1)(3)(2) 3 4 (2)(4)(3) 4 5 3 4
†††
†††
ˆ‰ˆ‰
, a , 1 represents theœœ œáÊ
12 34 23 12 2 12
(3)(5)(4) 5 6 4 5 3 4 (4)(6)(5) (n 1)(n 3)(n 2)
%"
ˆ‰ˆ‰ˆ‰ !
†††
†††
_
œn1
given series and , which is the nth-term of a convergent p-series
12 12
(n 1)(n 3)(n 2) n
6. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
a (n 1)(n 1)
n
n1
nœœ
7. diverges by the nth-Term Test since if a L as n , then L L L 1 0 L 0
n1L
15
ÄÄ_œÊœÊœÁ
"
#
#„
È
8. Split the given series into and ; the first subseries is a convergent geometric series and the
!!
__
œœn1 n1
"
33
2n
2n 1 2n
second converges by the Root Test: lim lim 1
nnÄ_ Ä_
É
n
2n
nn
2n 1
3999
2 n
œœœ
ÈÈ""†
9. f(x) cos x with a f 0.5, f , f 0.5, f , f 0.5;œ œ Ê œ œ œ œ œ
11 1 1 1 1
33 3 3 3 3
33
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
w www
##
ww
ÈÈ
4
cos x x x xœ á
""
## #
#$
ÈÈ
33
34 3 1 3
ˆ‰ˆ‰ ˆ‰
11 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Additional and Advanced Exercises 643
10. f(x) sin x with a 2 f(2 ) 0, f (2 ) 1, f (2 ) 0, f (2 ) 1, f (2 ) 0, f (2 ) 1,œœÊœœœœœœ11 1 1 1 1 1
w www
ww 45
f (2 ) 0, f (2 ) 1; sin x (x 2 )
67
11 1œ œœá
(x 2 ) (x 2 ) (x 2 )
3! 5! 7!
111
11. e 1 x with a 0
xœá œ
xx
!3!
#
12. f(x) ln x with a 1 f(1) 0, f (1) 1, f (1) 1,f (1) 2, f (1) 6;œœÊœœœœœ
w www
ww 4
ln x (x 1)χ
(x 1) (x 1) (x 1)
34
#
13. f(x) cos x with a 22 f(22 ) 1, f (22 ) 0, f (22 ) 1, f (22 ) 0, f (22 ) ,œœÊœœœœœ"11 1 1 1 1
w www
ww 4
f (22 ) 0, f (22 ) 1; cos x 1 (x 22 ) (x 22 ) (x 22 )
56
11 1 1 1œ œ œ á
"" "
#
#%'
4! 6!
14. f(x) tan x with a 1 f(1) , f (1) , f (1) , f (1) ;œœÊœœœœ
" w www
"""
###
ww
1
4
tan x
"
χ
1
42 4 12
(x 1) (x 1) (x 1)
15. Yes, the sequence converges: c a b c b 1 lim c ln b
nœ Êœ Ê œ ab ˆ‰ˆ‰
nn
1n nn
a
bn
n1n
n
ln 1
ÎÎ
Ä_
nÄ_ lim ˆ‰ˆ‰
a
b
n
ln b ln b ln b since 0 a b. Thus, lim c e b.œ œ œ œœlim
n
ln 0 ln
101 nln b
Ä_
†
ˆ‰ ˆ‰ ˆ‰
ˆ‰
aa a
bb b
n
a
b
nnÄ_
16. 1 1 áœ
237237 2 3 7
10 10 10 10 10 10 10 10
10 !!!
__ _
œœ œn1 n1 n1
3n 2 3n 1 3n
1 1œ œ
!!!
__ _
œœ œn0 n0 n0
237
10 10 10 111
3n 1 3n 2 3n 3
2
10
10 10 10
37
10 10
ˆ‰
ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
1œœ œ
200 30 7 999 237 412
999 999 999 999 333
17. s s s
nn n
dx dx dx dx dx
1 x 1x 1x 1x 1x
œÊœáÊœ
!
n1
k0
œ
'''''
k01n10
k1 1 2 n n
lim s lim tan n tan 0Êœ œ
nnÄ_ Ä_
nab
" "
#
1
18. lim lim lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹¸¸
u
u (n2)(2x1) nx 2x1 n(n2) 2x1
(n1)x (n1)(2x1) (n1)
xx
n1
n
n1 n
n1 n
œœœ
††
x 2x 1 ; if x 0, x 2x 1 x 2x 1 x 1; if x 0, x 2x 1Ê ÊÊ kk k k kk k k kk k k
"
#
x 2x 1 3x 1 x ; if x , x 2x 1 x 2x 1 x 1. Therefore,Ê Ê Ê Ê Ê
""
#3kk k k
the series converges absolutely for x 1 and x . "
3
19. (a) No, the limit does not appear to depend on the value of the constant a
(b) Yes, the limit depends on the value of b
(c) s 1 ln s lim ln sœ Ê œ Ê œ
Š‹
cos
n
nln 1
ˆ‰ Œ
ˆ‰
Œ
Š‹
a
n
n
cos a
n
n1cos a
n
n
aa a
nn n
sin cos
n
n
nÄ_
lim 1 lim s e 0.3678794412; similarly,œœœÊœ¸
nnÄ_ Ä_
aa a
nn n
cos a
n
n
sin cos
1
ˆ‰ ˆ‰
01
10
"
lim 1 e
nÄ_ Š‹
œ
cos
bn
n1b
ˆ‰
a
nÎ
20. a converges lim a 0; lim lim
!’“
ˆ‰ ˆ‰
_
œn1
nn
1sin a 1sin a
n1n 1 sin lim a 1sin 0
Êœ œ œ œ
nn nÄ_ Ä_ Ä_
####
Î
nnn
Š‹
n
the series converges by the nth-Root TestœÊ
"
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

644 Chapter 10 Infinite Sequences and Series
21. lim 1 lim 1 bx 1 x 5 b
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
uln(n1)bx bb5
bx ln n
n1
n
n1n1
nn
Ê Ê ÊœÊœ„
"" "
†
22. A polynomial has only a finite number of nonzero terms in its Taylor series, but the functions sin x, ln x and
e have infinitely many nonzero terms in their Taylor expansions.
x
23. lim lim lim x
x0 x0 x0ÄÄ Ä
sin (ax) sin x x
x x x 3!3! 5!5!
ax x x a2 a a
áá " "
#
œœá
Š‹Š‹
ax x
3! 3! ’“Š‹
is finite if a 2 0 a 2; lim œ Ê œ œ œ
x0Ä
sin 2x sin x x 2 7
x3!3!6
"
24. lim 1 lim 1 lim 1
x0 x0 x0ÄÄ Ä
cos ax b ba ax
xx2x448
1b
"
##
á
œ Ê œ Ê á œ
Œ
ax ax
4! Š‹
b 1 and a 2Êœ œ„
25. (a) 1 C 2 1 and converges
u
un nn n
(n 1) 2
n
n1œœÊœ
""
!
_
œn1
(b) 1 C 1 1 and diverges
u
un nn n
n1 1 0
n
n1œœÊœŸ
"
!
_
œn1
26. 1 1 after long division
u
u (2n 1) 4n 4n 1 n 4n 4n 1 n n
2n(2n 1) 4n 2n 5
n
n1œœ œ œ
Š‹ Š‹ –—
63
4
5n
4n 4n 1
C 1 and f(n) 5 u converges by Raabe's TestÊœ œ œ ŸÊ
35n5
4n 4n 1 4n
#
kk !
Š‹
4
nn
_
œn1
27. (a) a L a a a a L a converges by the Direct Comparison Test
!!!
___
œœœn1 n1 n1
nnnn
nn
œÊ Ÿ œ Ê
##
(b) converges by the Limit Comparison Test: lim lim 1 since a converges and
nnÄ_ Ä_
Š‹
an
1a
n
a1a n
nn
œœ
"
!
_
œn1
therefore lim a 0
xÄ_ nœ
28. If 0 a 1 then ln (1 a ) ln (1 a ) a a a a , œ œ á áœ
nnnn n
aa
31a
nn a
kk nn n
n
#
#$
a positive term of a convergent series, by the Limit Comparison Test and Exercise 27b
29. (1 x) 1 x where x 1 (1 x) nx and when x we haveœ Ê œ œ œ
" "
""
#
!!
kk
__
œœn1 n1
nn1
(1 x) dx
d
412 3 4 nœá á
ˆ‰ ˆ‰ ˆ‰ ˆ‰
"" " "
## # #
#$ n1
30. (a) x (n 1)x n(n 1)x n(n 1)x
!! ! !
__ _ _
œœ œ œn1 n1 n1 n1
n1nn1n
x2xx 2 2x
1 x (1 x) (1 x) (1 x)
œÊ œ Ê œ Ê œ
, x 1Êœœ
!kk
_
œn1
n(n 1)
x(x1)
1
2x
n
2
x
x
Š‹
(b) x x x 3x x 1 0 x 1 1 1œ Êœ Ê œÊœ
!Š‹Š‹
_
œn1
n(n )
x(x1) 9 9
2x 57 57
"
$# "Î$ "Î$
nÈÈ
2.769292, using a CAS or calculator¸
31. (a) 1 x x x 1 2x 3x 4x nx
""
#$ # $
(1 x) dx 1 x dx
dd n1
œ œ ᜠáœ
ˆ‰ ab !
_
œn1
(b) from part (a) we have n 6
!ˆ‰ ˆ‰ ˆ‰
’“
_
œn1
5
666
n1
1
2
"""
œœ
ˆ‰
5
6
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 10 Additional and Advanced Exercises 645
(c) from part (a) we have np q
!
_
œn1
n1 qq
(1 p) q q
"
œœœ
32. (a) p 2 1 and E(x) kp k2 k2 2
!! ! ! ! ˆ‰
__ _ _ _
œœ œ œ œk1 k1 k1 k1 k1
kk
kk1k
11
œœœ œœ œ œ œ
"""
##
ˆ‰
ˆ‰ ‘ˆ‰
by Exercise 31(a)
(b) p 1 and E(x) kp k k
!! ! ! ! !
ˆ‰ ˆ‰ ˆ‰
’“
__ _ _ _ _
œœ œ œ œ œk1 k1 k1 k1 k1 k1
k k
55 5 5
6 6
56 5 6 6
kk1
1
œœ œ œ œœ œ
k1 k1
k k
5
65
6
"" "
ˆ‰
ˆ‰
6œœ
ˆ‰
""
61
‘ˆ‰
5
6
(c) p lim 1 1 and E(x) kp k
k
!! ! ! !
ˆ‰ ˆ‰ Š‹
__ _ __
œœ œ œœk1 k1 k1 k1 k1
k k
k(k1) k k1 k1 k(k1)
œ œ œ œ œ œ
Ä_
""" " "
, a divergent series so that E(x) does not existœ!
_
œk1
"
k1
33. (a) R C e C e C e R lim R
n
n n
kt 2kt nkt Ce 1 e
1e 1 e e 1
Ce C
œ á œ Êœ œœ
Ä_
!! !
kt nkt
kt kt kt
kt
ˆ‰
(b) R R e 0.36787944 and R 0.58195028;
ne1e e1e
1e 1e
œÊœ¸ œ¸
1n
ab ab
""!
"
R 0.58197671; R R 0.00002643 0.0001œ¸ ¸ Ê
"
"!
e1 R
RR
(c) R , 4.7541659; R
nn
e1e
1e e1 e1 e1
RR1e
œœ¸Ê
11n
11 11
1n
ˆ‰
## # #
"" " "
ˆ‰ ˆ‰ˆ‰
1 e e ln ln n 6.93 n 7Ê Ê Ê Ê Ê Êœ
Î Î
"" " "
## # #
n10 n10 nn
10 10
ˆ‰ ˆ‰
34. (a) R Re R C C e t lnœÊœœÊœÊœ
C
e1
kt kt
HCC
CkC
kt HH
LL
!!
"Š‹
(b) t ln e 20 hrs
!"
œœ
0.05
(c) Give an initial dose that produces a concentration of 2 mg/ml followed every t ln 69.31 hrs
!"
#
œ¸
0.0 0.5
2
ˆ‰
by a dose that raises the concentration by 1.5 mg/ml
(d) t ln 5 ln 6 hrs
!"
œœ¸
0.2 0.03 3
0.1 10
ˆ‰ ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
646 Chapter 10 Infinite Sequences and Series
NOTES:
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
CHAPTER 11 PARAMETRIC EQUATIONS AND
POLAR COORDINATES
11.1 PARAMETRIZATIONS OF PLANE CURVES
1. x 3t, y 9t , t y x 2. x t , y t, t 0 x yœœ__Êœ œ œÊœ
##
ÈÈ
or y x , x 0œŸ
#
3. x 2t 5, y 4t 7, t 4. x 3 3t, y 2t, 0 t 1 tœ œ__ œ œ ŸŸÊ œ
y
#
x 5 2t 2(x 5) 4t x 3 3 2x 6 3yÊœ Ê œ Êœ Ê œ
ˆ‰
y
#
y 2(x 5) 7 y 2x 3 y 2 x, xÊœ Êœ Êœ !ŸŸ$
2
3
5. x cos 2t, y sin 2t, 0 t 6. x cos ( t), y sin ( t), 0 tœ œ ŸŸ œ œ ŸŸ1111
cos 2t sin 2t 1 x y 1 cos ( t) sin ( t) 1ʜʜ Ê œ
## ## # #
11
x y 1, yʜ !
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
648 Chapter 11 Parametric Equations and Polar Coordinates
7. x 4 cos t, y 2 sin t, 0 t 2 8. x 4 sin t, y 5 cos t, 0 t 2œ œ ŸŸ œ œ ŸŸ11
1 1 1 1Ê œÊ œ Ê œÊ œ
16 cos t 4 sin t x 16 sin t 25 cos t x
16 4 16 4 16 25 16 5
y y
#
9. x sin t, y cos 2t, t 10. x 1 sin t, y cos t 2, 0 tœœŸŸ œœŸŸ
11
22 1
y cos 2t 1 2sin t y 1 2x sin t cos t 1 x 1 y 2 1Êœ œ Êœ Ê œÊ œ
###
##
2abab
11. x t , y t 2t , t 12. x , y , 1 t 1œœ__ œ œ
264 tt2
t1 t1
y t 2 t y x 2x t yʜ ʜ ʜ ʜab ab
22 32
32 x2x
x1 2x1
13. x t, y 1 t , 1 t 0 14. x t 1, y t, t 0œœ ŸŸ œ œ
ÈÈÈ
#
y 1 x y t x y 1, y 0Êœ Ê œÊœ
ÈÈ
# #
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
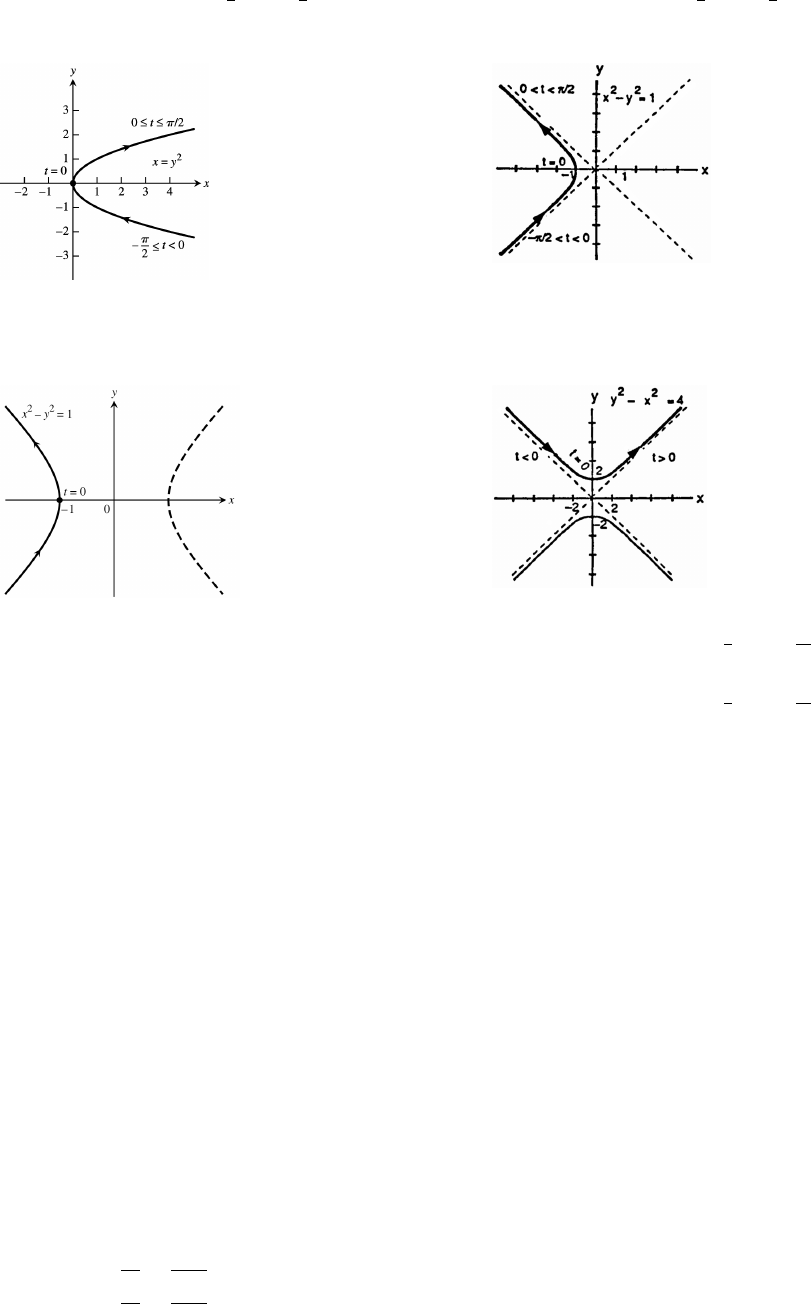
Section 11.1 Parametrizations of Plane Curves 649
15. x sec t 1, y tan t, t 16. x sec t, y tan t, tœœ œ œ
#
## ##
11 11
sec t 1 tan t x y sec t tan t 1 x y 1ʜʜ ʜʜ
## # ## ##
17. x cosh t, y sinh t, 1 18. x 2 sinh t, y 2 cosh t, tœ œ _ _ œ œ _ _
cosh t sinh t 1 x y 1 4 cosh t 4 sinh t 4 y x 4Ê œÊ œ Ê œÊ œ
# # ## # # ##
19. (a) x a cos t, y a sin t, 0 t 2 20. (a) x a sin t, y b cos t, tœœŸŸ œœ ŸŸ111
##
5
(b) x a cos t, y a sin t, 0 t 2 (b) x a cos t, y b sin t, 0 t 2œœŸŸ œœŸŸ11
(c) x a cos t, y a sin t, 0 t 4 (c) x a sin t, y b cos t, tœœŸŸ œœ ŸŸ111
##
9
(d) x a cos t, y a sin t, 0 t 4 (d) x a cos t, y b sin t, 0 t 4œœŸŸ œœŸŸ11
21. Using we create the parametric equations x at and y bt, representing a line which goesab"ß $ œ " œ $
through at t . We determine a and b so that the line goes through when t .ab ab"ß$ œ! %ß" œ"
Since a a . Since b b . Therefore, one possible parameterization is x t,%œ" Ê œ& "œ$ Ê œ% œ"&
y t, 0 t .œ$% Ÿ Ÿ"
22. Using we create the parametric equations x at and y bt, representing a line which goes throughab"ß$ œ" œ$
at t . We determine a and b so that the line goes through when t . Since a a .ab ab"ß $ œ ! $ß # œ " $ œ " Ê œ %
Since b b . Therefore, one possible parameterization is x t, y t, 0 t .#œ$ Ê œ& œ"% œ$& Ÿ Ÿ"
23. The lower half of the parabola is given by x y for y . Substituting t for y, we obtain one possibleœ" Ÿ!
#
parameterization x t , y t, t 0œ"œ ŸÞ
#
24. The vertex of the parabola is at , so the left half of the parabola is given by y x x for x . Substitutingab"ß " œ # Ÿ "
#
t for x, we obtain one possible parametrization: x t, y t t, t .œœ#Ÿ"
#
25. For simplicity, we assume that x and y are linear functions of t and that the point x, y starts at for t and passesab ab#ß $ œ !
through at t . Then x f t , where f and f .a b ab ab ab"ß " œ " œ ! œ # " œ "
Since slope , x f t t t. Also, y g t , where g and g .œ œ œ$ œ œ$ #œ#$ œ ! œ$ " œ"
?
?
x
t
"#
"! ab ab ab ab
Since slope 4. y g t t t.œ œ œ œ œ% $œ$%
?
?
y
t
3"
"! ab
One possible parameterization is: x t, y t, t .œ#$ œ$% !
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

650 Chapter 11 Parametric Equations and Polar Coordinates
26. For simplicity, we assume that x and y are linear functions of t and that the point x, y starts at for t andab a b"ß # œ !
passes through at t . Then x f t , where f and f .a b ab ab ab!ß! œ" œ !œ" "œ!
Since slope , x f t t t. Also, y g t , where g and g .œ œ œ" œ œ" " œ" œ ! œ# " œ!
?
?
x
t
! "
"!
ab ab a b ab ab ab
Since slope . y g t t t.œ œ œ# œ œ# #œ##
?
?
y
t
!#
"! ab
One possible parameterization is: x t, y t, t .œ" œ## !
27. Since we only want the top half of a circle, y 0, so let x 2cos t, y 2 sin t , 0 t 4œœllŸŸ1
28. Since we want x to stay between 3 and 3, let x 3 sin t, then y 3 sin t 9sin t, thus x 3 sin t, y 9sin t,œ œœ œœab
2##
0tŸ_
29. x y a 2x 2y 0 ; let t t x yt. Substitution yields
###
œ Ê œÊ œ œ ʜʜ
dy dy dy
dx dx y dx y
xx
y t y a y and x , t
## # #
œ Êœ œ __
aat
1t 1t
ÈÈ
30. In terms of , parametric equations for the circle are x a cos , y a sin , 0 2 . Since , the arc))))1)œœŸ œ
s
a
length parametrizations are: x a cos , y a sin , and 0 2 0 s 2 a is the interval for s.œœ ŸÊŸŸ
sss
aaa
11
31. Drop a vertical line from the point x, y to the x-axis, then is an angle in a right triangle, and from trigonometry weab )
know that tan y x tan . The equation of the line through 0, 2 and 4, 0 is given by y x 2. Thus))œÊœ œ
y
x 2
1
ab ab
x tan x 2 x and y where 0 .))œ Ê œ œ Ÿ
144tan
22tan12tan1 2))
)1
32. Drop a vertical line from the point x, y to the x-axis, then is an angle in a right triangle, and from trigonometry weab )
know that tan y x tan . Since y x y x x tan x x cot y cot where)) ) ))œÊœ œ Ê œÊ œÊœ Êœ
y
x
22
2
Èab
0.Ÿ)1
2
33. The equation of the circle is given by x 2 y 1. Drop a vertical line from the point x, y on the circle to theab abœ
22
x-axis, then is an angle in a right triangle. So that we can start at 1, 0 and rotate in a clockwise direction, let)ab
x2cos, ysin, 0 2.œ œ ŸŸ)))1
34. Drop a vertical line from the point x, y to the x-axis, then is an angle in a right triangle, whose height is y and whosab )e
base is x 2. By trigonometry we have tan y x 2 tan . The equation of the circle is given byœÊœ))
y
x2ab
x y 1 x x 2 tan 1 x sec 4x tan 4tan 1 0. Solving for x we obtain
22 2 22 2 2
2
œÊ œÊ œabab))))
x 2sin cos cos 3sinœœœ„
„ „
4tan 4tan 4 sec 4tan 1
2sec 2sec
4tan 2 1 3tan 222
2222
2
22
22
))))
))
))
Éab a b È)) ) )
È
2 2cos cos 4cos 3 and y 2 2cos cos 4cos 3 2 tanœ „ œ „
22
22
)) ) )) ) )
ÈÈ
Š‹
2sin cos sin 4cos 3. Since we only need to go from 1, 0 to 0, 1 , letœ„ )) ) )
Èabab
2
x 2 2cos cos 4cos 3, y 2sin cos sin 4cos 3, 0 tan .œ œ Ÿ Ÿ
2 1
22
1
2
)) ) ))) ) )
ÈÈ
ˆ‰
To obtain the upper limit for , note that x 0 and y 1, using y x 2 tan 1 2 tan tan .))))œœ œÊœÊœab ˆ‰
11
2
35. Extend the vertical line through A to the x-axis and let C be the point of intersection. Then OC AQ xœœ
and tan t x 2 cot t; sin t OA ; and (AB)(OA) (AQ) AB xœœÊœ œ œÊ œ œ Ê œ
22 2 2 2 2
OC x tan t OA sin t sin t
##
ˆ‰
AB AB . Next y 2 AB sin t y 2 sin tʜʜ œÊœ œ
ˆ‰ˆ‰ ˆ ‰
2 2 2 sin t 2 sin t
sin t tan t tan t tan t
#
2 2 2 cos t 2 sin t. Therefore let x 2 cot t and y 2 sin t, 0 t .œ œ œ œ
2 sin t
tan t ## # 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
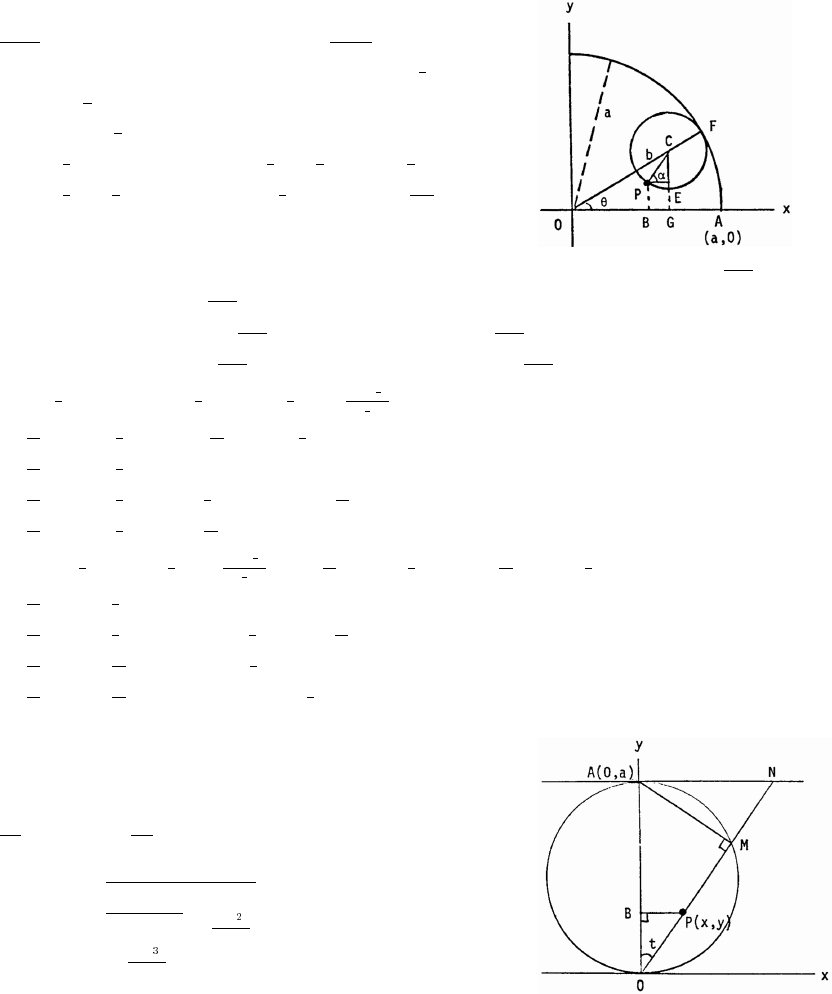
Section 11.1 Parametrizations of Plane Curves 651
36. Arc PF Arc AF since each is the distance rolled andœ
FCP Arc PF b( FCP);
Arc PF Arc AF
ba
œn Ê œ n œ)
Arc AF a a b( FCP) FCP ;ʜʜnÊnœ)) )
a
b
OCG ; OCG OCP PCEnœnœnn
1
#)
OCP . Now OCP FCPœn n œ n
ˆ‰
1
#!1
. Thus OCG œ n œ Ê 1) 1) ! )
aa
bb
11
##
.œ Ê œ œ1) !!1))1 )
aaab
bbb
1
#
ˆ‰
Then x OG BG OG PE (a b) cos b cos (a b) cos b cosœœœ œ )! ) 1)
ˆ‰
ab
b
(a b) cos b cos . Also y EG CG CE (a b) sin b sin œ œ œ œ )) )!
ˆ‰
ab
b
(a b) sin b sin (a b) sin b sin . Thereforeœ œ )1) ) )
ˆ‰ ˆ‰
ab ab
bb
x (a b) cos b cos and y (a b) sin b sin .œ œ )) ))
ˆ‰ ˆ‰
ab ab
bb
If b , then x a cos cosœœ
aaa
444
a
ˆ‰ Š‹
))
ˆ‰
ˆ‰
a
4
a
4
cos cos 3 cos (cos cos 2 sin sin 2 )œ œ
3a a 3a a
44 44
)))))))
cos (cos ) cos sin (sin )(2 sin cos )œ
3a a
44
)))))))abab
##
cos cos cos sin sin cos œ
3a a a 2a
44 4 4
)))) ))
$##
cos cos (cos ) 1 cos a cos ;œ œ
3a a 3a
44 4
)) ) ) )
$#$
ab
y a sin sin sin sin 3 sin (sin cos 2 cos sin 2 )œ œ œ
ˆ‰ Š‹
aa 3aa 3aa
4 4 44 44
a
)))))))))
ˆ‰
ˆ‰
a
4
a
4
sin (sin ) cos sin (cos )(2 sin cos )œ
3a a
44
)))))))abab
##
sin sin cos sin cos sin œ
3a a a 2a
44 4 4
)))) ))
#$ #
sin sin cos sinœ
3a 3a a
44 4
))))
#$
sin (sin ) 1 sin sin a sin .œ œ
3a 3a a
44 4
)) ) ))ab
#$$
37. Draw line AM in the figure and note that AMO is a rightn
angle since it is an inscribed angle which spans the diameter
of a circle. Then AN MN AM . Now, OA a,
###
œ œ
tan t, and sin t. Next MN OP
AN AM
aa
œœ œ
OP AN AM a tan t a sin tÊœœ
#######
OP a tan t a sin tʜ
È## ##
(a sin t) sec t 1 . In triangle BPO,œœ
È#a sin t
cos t
x OP sin t a sin t tan t andœœœ
a sin t
cos t #
y OP cos t a sin t x a sin t tan t and y a sin t.œœÊœ œ
## #
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
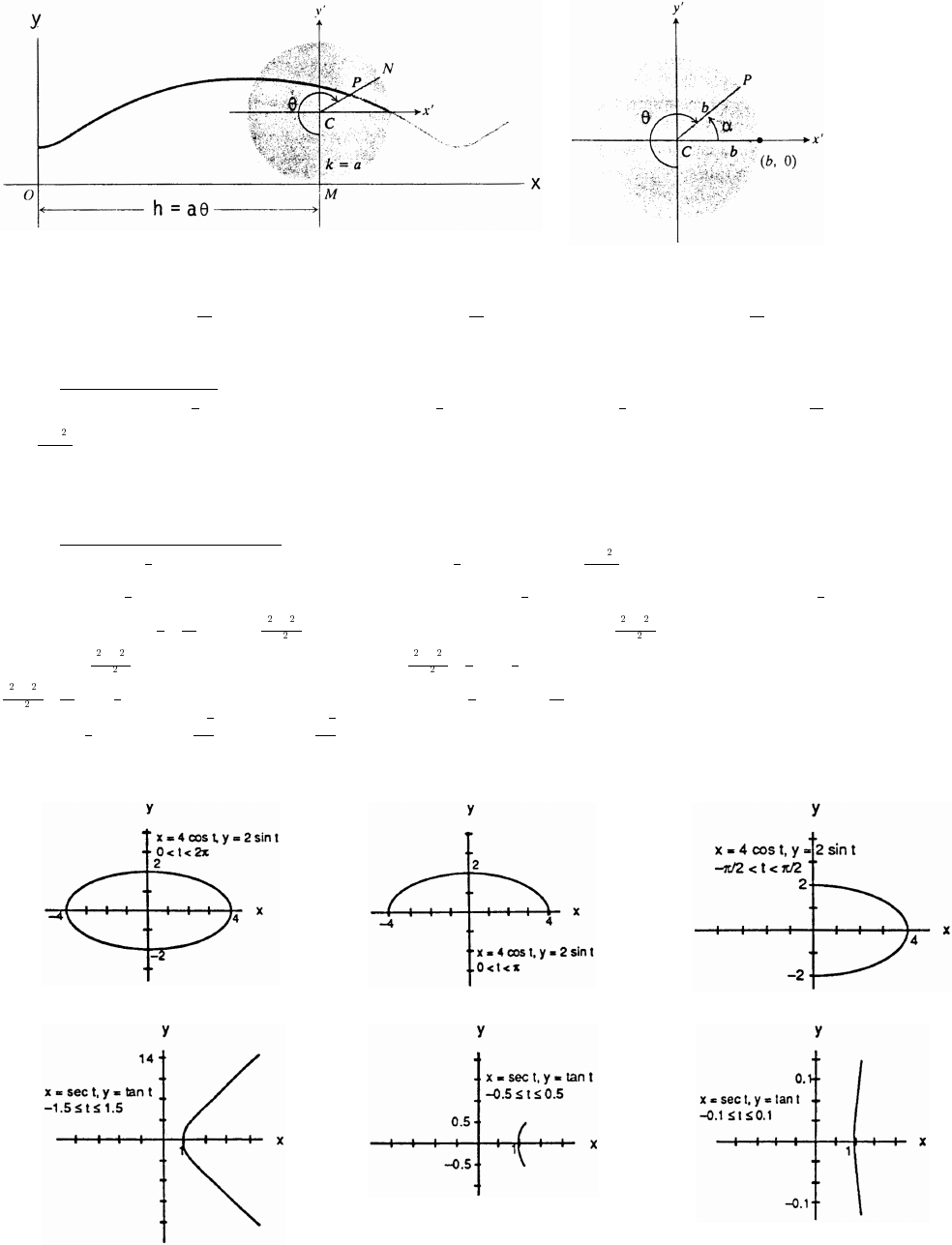
652 Chapter 11 Parametric Equations and Polar Coordinates
38. Let the x-axis be the line the wheel rolls along with the y-axis through a low point of the trochoid
(see the accompanying figure).
Let denote the angle through which the wheel turns. Then h a and k a. Next introduce x y -axes))œœ ww
parallel to the xy-axes and having their origin at the center C of the wheel. Then x b cos and
wœ!
y b sin , where . It follows that x b cos b sin and y b sin
www
## #
œœ œœœ!! ) ) ) )
33 311 1
ˆ‰ ˆ‰
b cos x h x a b sin and y k y a b cos are parametric equations of the trochoid.œ Êœœ œœ))) )
ww
39. D (x 2) y D (x 2) y (t 2) t D t 4tœ Ê œ œ Ê œ
Ɉ‰ ˆ‰ ˆ‰
#"""
###
###
## ## #%
17
4
4t 4 0 t 1. The second derivative is always positive for t 0 t 1 gives a localÊœœÊœ ÁÊœ
dD
dt
ab $
minimum for D (and hence D) which is an absolute minimum since it is the only extremum the closest
#Ê
point on the parabola is (1 1).ß
40. D 2 cos t (sin t 0) D 2 cos t sin t œÊœÊ
Ɉ‰ ˆ‰
33
44dt
dD
##
###
ab
2 2 cos t ( 2 sin t) 2 sin t cos t ( 2 sin t) 3 cos t 0 2 sin t 0 or 3 cos t 0œ œ œÊœ œ
ˆ‰ ˆ‰
333
4##
t 0, or t , . Now 6 cos t 3 cos t 6 sin t so that (0) 3 relativeÊœ œ œ œÊ111
3 3 dt dt
5dD dD
ab ab
##
maximum, ( ) 9 relative maximum, relative minimum, and
dD dD
dt dt 3 2
9
ab ab
1œ Ê œ Ê
ˆ‰
1
relative minimum. Therefore both t and t give points on the ellipse closest to
dD
dt 3 3 3
59 5
ab
ˆ‰
111
œÊ œ œ
#
the point 1 and 1 are the desired points.
ˆ‰ Š‹Š ‹
3
4
33
ß! Ê ß ß
ÈÈ
##
41. (a) (b) (c)
42. (a) (b) (c)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
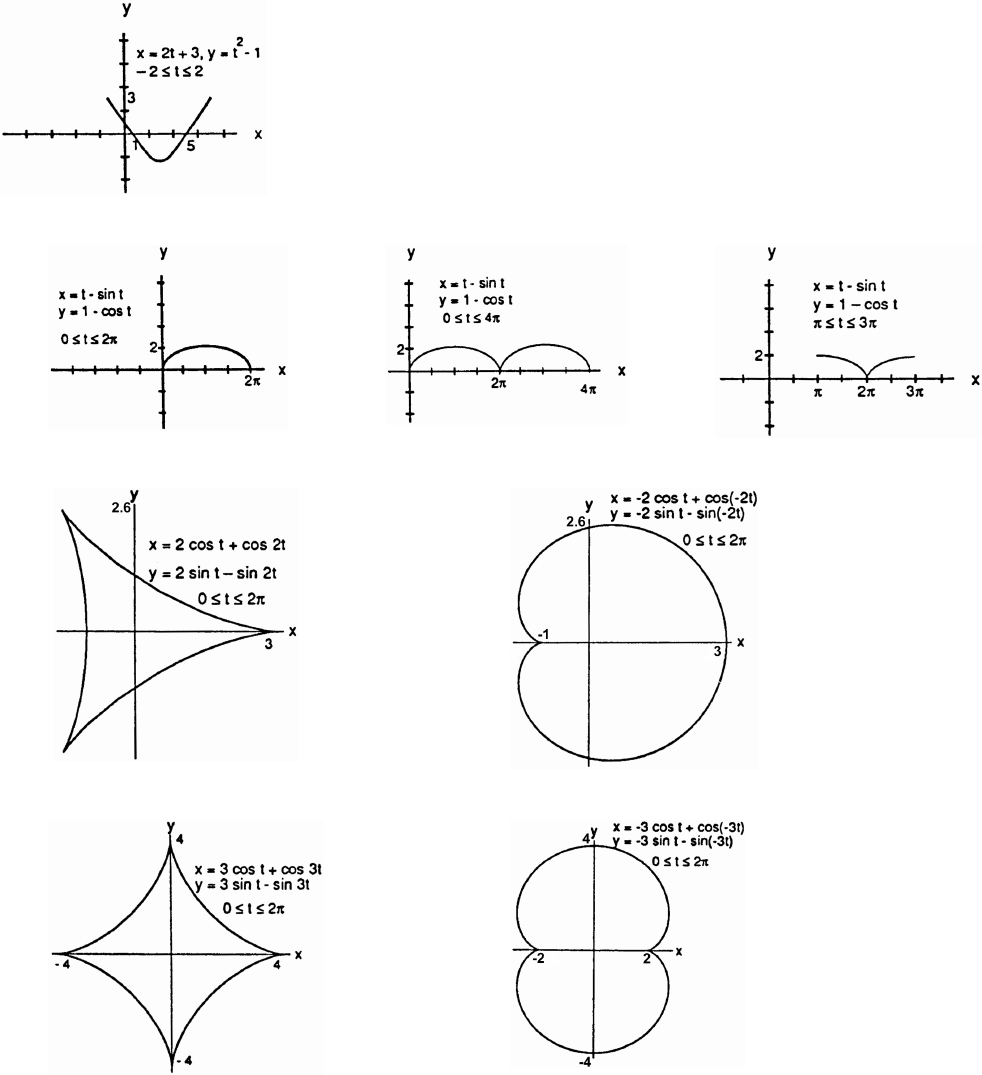
Section 11.1 Parametrizations of Plane Curves 653
43.
44. (a) (b) (c)
45. (a) (b)
46. (a) (b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
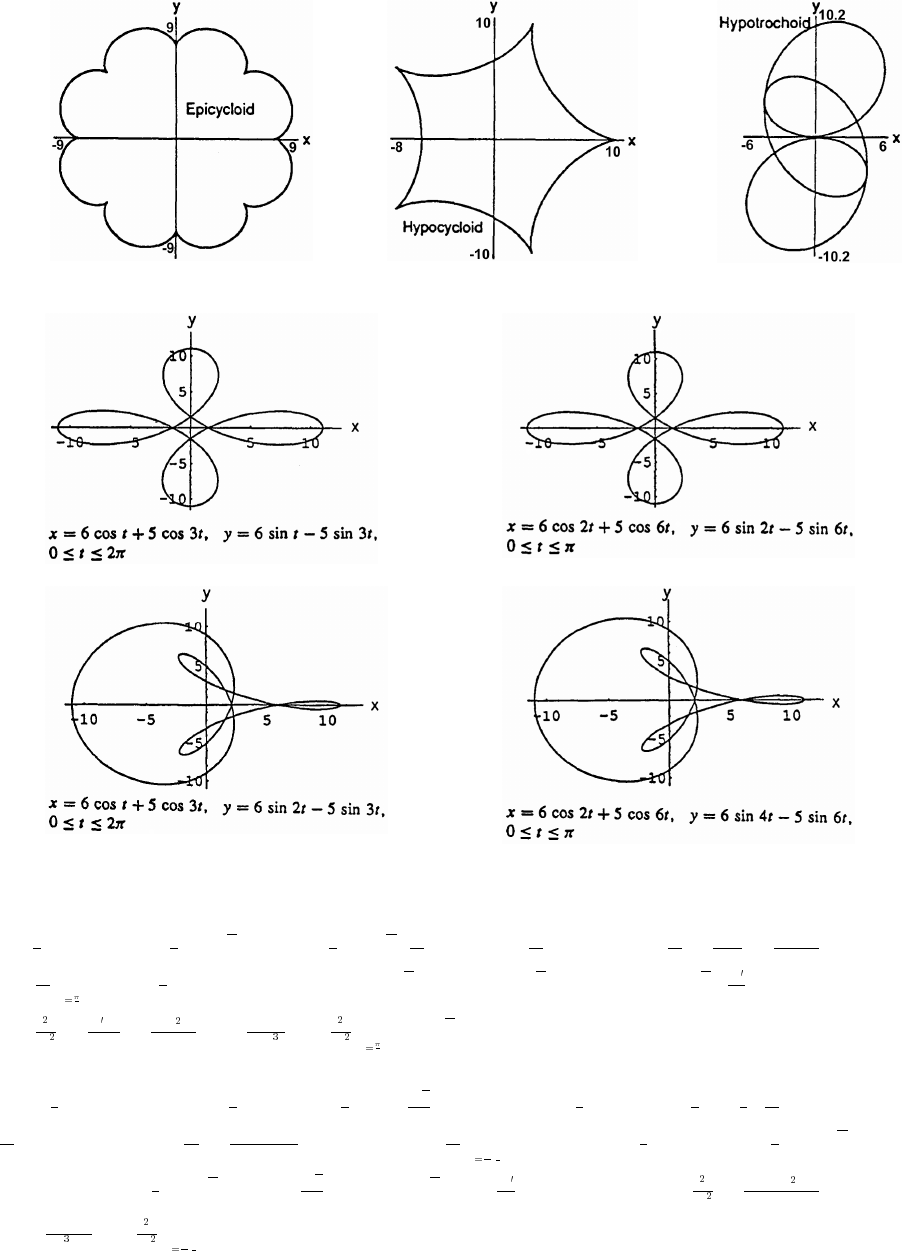
654 Chapter 11 Parametric Equations and Polar Coordinates
47. (a) (b) (c)
48. (a) (b)
(c) (d)
11.2 CALCULUS WITH PARAMETRIC CURVES
1. t x 2 cos 2, y 2 sin 2; 2 sin t, 2 cos t cot tœ Ê œ œ œ œ œ œ Ê œ œ œ
11 1
4 4 4 dt dt dx dx/dt 2 sin t
dx 2 cos t
dy dy dy/dt
ÈÈ
cot 1; tangent line is y 2 1 x 2 or y x 2 2 ; csc tÊœœ œ œ œ
¹Š‹
ÈÈ È
dy dy
dx 4 dt
t4
1#
2Êœ œ œ Ê œ
dy dy/dt dy
dx dx/dt 2 sin t 2 sin t dx
csc t
"¹È
t4
2. t x sin 2 sin , y cos 2 cos ; 2 cos 2 t,œÊœ œœ œ œ œ œ
"" ""
##663 63dt
3dx
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ ˆ‰
1111
11
È
2 sin 2t tan 2t tan2 tan 3;
dy dy dy
dt dx 2 cos 2 t dx 6 3
2 sin 2t
œ Ê œ œ Ê œ œ œ11 1 1
"11 1
11 ¹ˆ‰ˆ‰ˆ‰ È
t1
6
tangent line is y 3 x or y 3x 2; 2 sec 2 t œ œ œ Ê œ
"
##
#
ÈÈ
’“Š‹
È3dy d y
dt dx 2 cos 2 t
2 sec2t
11 11
11
8œ Ê œ
"
cos 2 t dx
dy
1¹t1
6
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.2 Calculus With Parametric Curves 655
3. t x 4 sin 2 2, y 2 cos 2; 4 cos t, 2 sin t œÊœ œ œ œ œ œ Ê œ œ
11 1
4 4 4 dt dt dx dx/dt 4 cos t
dx 2 sin t
dy dy dy/dt
ÈÈ
tan t tan ; tangent line is y 2 x 2 2 or y x 2 2 ;œ Ê œ œ œ œ
""" " "
### # #
¹Š‹
ÈÈ È
dy
dx 4
t4
1
sec t
dy d y dy /dt d y 2
dt dx dx/dt 4 cos t 8 cos t dx 4
sec t
œ Ê œ œ œ Ê œ
""
#
#¹t4
È
4. t x cos , y 3 cos ; sin t, 3 sin t 3œ Ê œ œ œ œ œ œ Ê œ œ
22 2dx
33 3dtdt dxsin t
33 sin t
dy dy
11 1"
##
ÈÈÈ
ÈÈ
3 ; tangent line is y 3 x or y 3 x; 0 0Êœ œ œ œÊœœ
¹Š‹
ÈÈÈ
‘ˆ‰
dy dy d y
dx dt dx sin t
30
t2
3
È
##
"
0ʜ
¹
dy
dx t2
3
5. t x , y ; 1, 1; tangent line isœÊœ œ œ œ Ê œ œ Ê œ œ
11dx 1
4 4 dt dt dx dx/dt dx
dy dy dy/dt dy
t2t
"" "
###
ÈÈ
É
¹t1
44
y 1x or yx ; t t 2œœœÊœœÊœ
"" "" "
#
$Î# $Î#
†ˆ‰ ¹
4 4 dt 4 dx dx/dt 4 dx
dy d y dy /dt d y
t1
4
6. t x sec 1 1, y tan 1; 2 sec t tan t, sec tœ Ê œ œ œ œ œ œ
11 1
44 4dtdt
dx dy
###
ˆ‰ ˆ‰
cot t cot ; tangent line isÊœ œ œ Ê œ œ
dy dy
dx 2 sec t tan t 2 tan t dx 4
sec t "" " "
###
¹ˆ‰
t4
1
y ( 1) (x 1) or y x ; csc t cot t œ œ œ Ê œ œ
"""" "
####
#$
dy d y
dt dx 2 sec t tan t 4
csc t
ʜ
¹
dy
dx 4
t4
"
7. t x sec , y tan ; sec t tan t, sec t œÊœ œ œ œ œ œ Ê œ
11 1
6 6 6 dt dt dx dx/dt
2dx
33
dy dy dy/dt
ÈÈ
"#
csc t csc 2; tangent line is y 2 x or y 2x 3 ;œœÊœœ œ œ
sec t 2
sec t tan t dx 6
dy
33
¹Š‹
È
t6
1"
ÈÈ
csc t cot t cot t 3 3
dy d y dy /dt d y
dt dx dx/dt sec t tan t dx
csc t cot t
œ Ê œ œ œ Ê œ
$¹È
t6
8. t 3 x 3 1 2, y 3(3) 3; (t 1) , (3t) œÊœ œ œ œ œ œ Ê œ
ÈÈdx 3
dt dt dx
dy dy (3t)
(t 1)
"
##
"Î# "Î#
ˆ‰
ˆ‰
3
2; tangent line is y 3 2[x ( 2)] or y 2x 1;œ œ œ œ œ œ
3t1 331
3t
dy
dx 3(3)
ÈÈ
ÈÈ
¹t3
dy d y
dt 3t dx
3t (t 1) 3 t 1 (3t) 33
2t 3t t 1 t 3t
œœÊœœ
È‘‘
ÈÈÈ
ÈŠ‹
Š‹
33 3
2t 3t t 1
1
2t1
ʜ
¹
dy
dx 3
t3
"
9. t 1 x 5, y 1; 4t, 4t t ( 1) 1; tangent line isœ Ê œ œ œ œ Ê œ œ œ Ê œ œ
dx 4t
dt dt dx dx/dt 4t dx
dy dy dy/dt dy
$##
¹t1
y 1 1 (x 5) or y x 4; 2t œ œ œ Ê œ œ œ Ê œ†
dy d y dy /dt d y
dt dx dx/dt 4t dx
2t ""
##
¹t1
10. t 1 x 1, y 2; , t 1; tangent line isœÊœ œ œ œÊ œ œÊ œ
dx
dt t dt t dx dx
dy dy dy
""
ˆ‰
Š‹
t
t¹t1
y ( 2) 1(x 1) or y x 1; 1 t 1 œ œ œ Ê œ œ Ê œ
dy dy dy
dt dx dx
1
#
Š‹
t¹t1
11. t x sin , y 1 cos 1 ; 1 cos t, sin t œ Ê œ œ œ œœ œ œ Ê œ
1111 1
3 3 3 3 3 dt dt dx dx/dt
3dx dy dy dy/dt
È
###
""
3 ; tangent line is y 3 xœÊœ œœ œ
sin t
1cos t dx 3
dy sin
1cos
3
##
"
¹Š‹
ÈÈ
t3
ˆ‰
ˆ‰ Š‹
ˆ‰ È
3
3
3
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

656 Chapter 11 Parametric Equations and Polar Coordinates
y3x 2; Êœ œ œ Ê œ œ
È1Ȉ‰
3
3 dt (1 cos t) 1 cos t dx dx/dt 1 cos t
dy (1 cos t)(cos t) (sin t)(sin t) d y dy /dt
1
1
1 cos t
4œÊœ
1
(1 cos t) dx
dy
¹t3
12. t x cos 0, y 1 sin 2; sin t, cos t cot tœÊœ œ œ œ œ œ Ê œ œ
11 1
22 2dtdtdxsin t
dx cos t
dy dy
cot 0; tangent line is y 2; csc t csc t 1Êœœ œœÊœœÊ œ
¹ ¹
dy dy d y d y
dx dt dx sin t dx
csc t
t t
2 2
1
#
#$
13. t 2 x , y 2; , 9;œÊœœœœ œ œ Êœ Ê œ œ
11 2 dx 1 1
21 3 21 dt dt dx dx
t1 t1 t1 21
dy dy dy
t1 21
ab ab ab ab
ab ab
22 2 2
22
¹t2
tangent line is y 9x 1; 108œ œ Ê œ Ê œ œ
dy dy dy
dt dx dx
4t 1 4t 1 42 1
t1 t1 21
ab ab ab
ab ab ab
33 3
33
¹t2
14. t 0 x 0 e 1, y 1 e 0; 1 e , e ;œÊœ œ œ œ œ œÊ œ Ê œ œ
00 tt
dx e e 1
dt dt dx 1 e dx 1 e 2
dy dy dy
t0
t0
¹t0
tangent line is y x ; œ œ Ê œ Ê œ œ
11 e e e 1
2 2 dt dx dx 8
dy dy dy
1e 1e 1e
tt 0
tt
23 3
0
ab ab ab
¹t0
15. x 2t 9 3x 4t 0 3x 4t ;
32 2
dx dx dx 4t
dt dt dt 3x
œÊ œÊ œÊœ
#2
2y 3t 4 6y 6t 0 ; thus ; t 2
$# #
œÊ œÊœœ œ œ œ œ œ
dy dy dy dy/dt t(3x )
dt dt 6y y dx dx/dt y ( 4t) 4y
6t t 3x
Š‹
Š‹
t
y
4t
3x2
22
x 2(2) 9 x 8 9 x 1 x 1; t 2 2y 3(2) 4Ê œÊ œÊ œÊœ œÊ œ
333#$#
2y 16 y 8 y 2; therefore ʜʜʜ œ œ
$$ "
#
¹
dy
dx 16
3
4
3
t2
ab
ab
2
16. x 5 t 5 t t ; y(t 1) t y (t 1) tœÊœ œ œÊ œ
ÉÈÈ È
ˆ‰ˆ ‰
dx
dt dt
4t 5 t
dy
""" "
## #
"Î# "Î# "Î#
ÈÈ
É
t 1 y ; thus Ê œ Ê œ œ œ œ œ †ab
dy dy dy
dt dt t 1 dx
ttt2t
yyt
"
##
"#
ÈÈÈ
ab È
ttt2t
yt
4t 5 t
dy
dt
dx
dt
"#
#"
"
yt
tt
4t 5 t
È
ÈabÈÈ
É
; t 4 x 5 4 3; t 4 y 3 4 yœœÊœœœÊ†œÊœ
#"# &
"
ˆ‰
ÈÈ
É
yt t
tÉÈÈ
È2
3
therefore, ¹
dy
dx 9
10 3
t4
œœ
22 4 4
4
Š‹
ab
ÈÈ
É
" &
"
2
3È
17. x 2x t t 3x 2t 1 1 3x 2t 1 ; y t 1 2t y 4 œÊ œÊ œÊ œ œ
$Î# # "Î# "Î#
dx dx dx dx 2t 1
dt dt dt dt 13x
ˆ‰ ÈÈ
t1y (t1) 2y2t y 0 t1 2y 0Ê œÊ œ
dy dy dy y dy
dt dt dt y dt
2t1
t
ÈÈ
ˆ‰ ˆ ‰
ÈÈ
Š‹
""
##
"Î# "Î#
ÈÈ
t 1 2 y ; thusÊ œ Êœ œ
Š‹
ÈÈ
t
ydt dt
dy y dy
2t1
ÈÈ
Š‹
È
Š‹
ÈÈÈ
ÈÈ
y
2t1
t
y
2y
t1
yy4yt1
2 y (t 1) 2t t 1
; t 0 x 2x 0 x 1 2x 0 x 0; t 0
dy dy/dt
dx dx/dt
œ œ œÊ œÊ œÊœ œ
Œ
Š‹
yy4yt 1
2 y (t 1) 2t t 1
2t 1
13x
$Î# "Î#
ˆ‰
y 0 1 2(0) y 4 y 4; therefore 6Ê œÊœ œ œ
Èȹ
dy
dx t0
Œ
Œ
444(4)01
2 4(0 1) 2(0) 0 1
2(0) 1
13(0)
18. x sin t 2x t sin t x cos t 2 1 (sin t 2) 1 x cos t ;œÊ œÊ œ Ê œ
dx dx dx dx 1 x cos t
dt dt dt dt sin t 2
t sin t 2t y sin t t cos t 2 ; thus ; t x sin 2xœÊ œ œ œÊ œ
dy dy
dt dx
sin t t cos t 2
ˆ‰
1x cos t
sin t 2
111
x ; therefore 4Êœ œ œ œ
11111
1#
¹
dy
dx 2
sin cos 2 4 8
t–—
1cos
sin 2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
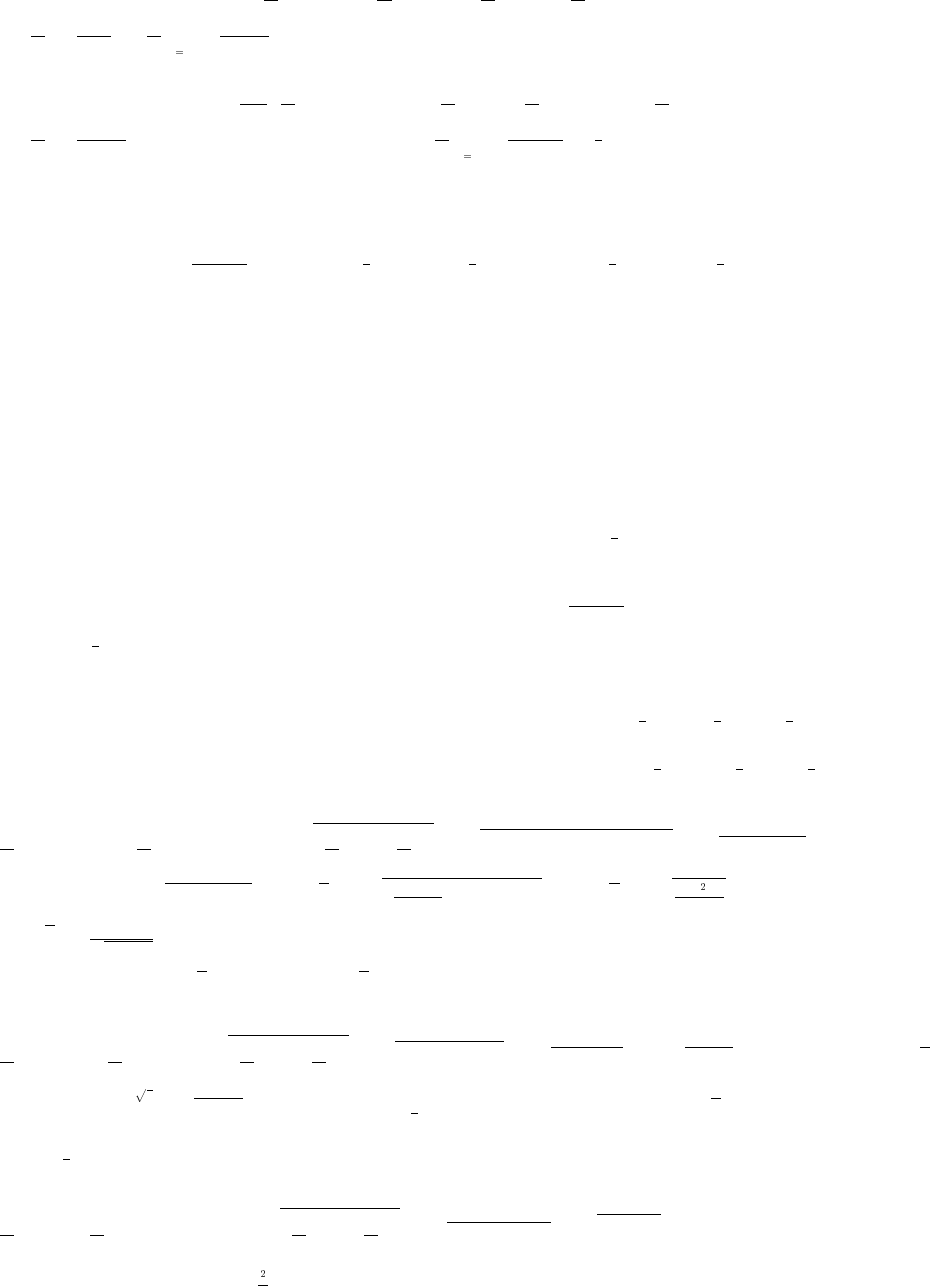
Section 11.2 Calculus With Parametric Curves 657
19. x t t, y 2t 2x t 3t 1, 6t 2 2t 2 3t 1 2t 6t 2t 2œœÊœ œ Êœ œ
332 2 2 2 2
dx dx
dt dt dt dt
dy dy ab
1Êœ Ê œ œ
dy dy
dx 3t 1 dx
2t 2 21 2
31 1
22
¹t1
ab
ab
20. t ln x t , y t e 1 1 x t 1 x t 1, t e e ;œ œ Êœ Êœ Ê œ œ ab ˆ‰
ttt
1dx dx dx
x t dt dt dt dt
dy
; t 0 0 ln x 0 x 1Êœ œÊœ ÊœÊ œ œ
dy dy
dx xt1 dx 101 2
te e 1
0e e
tt 00
ab ¹t0
ab
21. A y dx a 1 cos t a 1 cos t dt a 1 cos t dt a 1 2cos t cos t dtœ œœœ
'' ' '
00 0 0
22 2 2
222
2
11 1 1
abab ab a b
a 1 2cos t dt a 2cos t cos 2t dt a t 2sin t sin 2tœ œ œ
22 2
22
1 cos 2t 3 1 3 1
22224
2
''
00 0
11 1
ˆ‰ˆ‰
”•
a3 0 0 0 3 aœœ
22
ab11
22. A x dy t t e dt u t t du 1 2t dt; dv e dt v eœœ œÊœœÊœ
''
00
11
2t 2 t t
abab a b ab
”•
e t t e 1 2t dt u 1 2t du 2dt; dv e dt v eœ œÊœ œ Êœ
t2 t t t
11
ab a b
º” •
00
'
ett e12t 2edt ett e12t 2eœ œ
t2 t t t2 t t
11 1
1
ab ab abab
º” º •” •º
00 0
0
'
e 0 e 1 2e e0 e1 2e 1 3e 1œœœababab a b ab ab
11 1000 1
3
e
23. A 2 y dx 2 b sin t a sin t dt 2ab sin t dt 2ab dt ab 1 cos 2t dtœœ œ œ œ
'' ' ' '
11
11 100
00 0
21 cos 2t
2
aba b a b
ab t sin 2t ab 0 abœ œ !œ
’“
abab
1
20
1
11
24. (a) x t , y t , 0 t 1 A y dx t 2t dt 2t dt t 0œœŸŸÊœ œ œ œ œœ
26 6 7 8
11 1 111
444
0
1
'' '
00 0
ab ’“
(b) x t , y t , 0 t 1 A y dx t 3t dt 3t dt t 0œœŸŸÊœ œ œ œ œœ
3 9 9 2 11 12
11 1 111
444
0
1
'' '
00 0
ab ’“
25. sin t and 1 cos t sin t 1 cos t 2 2 cos t
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ
ʈ‰ Š‹ Éaba b
È
####
Length 2 2 cos t dt 2 (1 cos t) dt 2 dtÊœ œ œ
'' '
00 0
1cos t sint
1cos t 1cos t
11 1
ÈÈÈ
Ɉ‰ É
2 dt (since sin t 0 on [0 ]); [u 1 cos t du sin t dt; t 0 u 0,œßœÊœœÊœ
È'0
sin t
1cos t
1
È1
t u 2] 2 u du 2 2u 4œÊœ Ä œ œ1ÈÈ
‘
'0
2"Î# "Î# #
!
26. 3t and 3t 3t (3t) 9t 9t 3t t 1 since t 0 on 0 3
dx dx
dt dt dt dt
dy dy
œœÊœœœß
#####%##
#
ʈ‰ Š‹ Š ‹
Éab ÈÈ’“
È
Length 3t t 1 dt; u t 1 du 3t dt; t 0 u 1, t 3 u 4Êœ œÊœœÊœœÊœ
'0
3È’“
È
##
#
3
u du u (81) 7Ä œ œœ
'1
43
#
"Î# $Î# %
"
‘
27. t and (2t 1) t 2t 1 t 1 t 1 t 1 since 0 t 4
dx dx
dt dt dt dt
dy dy
œœÊ œœœœ ŸŸ
"Î# ####
ʈ‰ Š‹ Èa b abkk
É
Length t 1 dt t 8 4 12Ê œ œ œœ
'0
4t
2
ab ab
’“
%
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
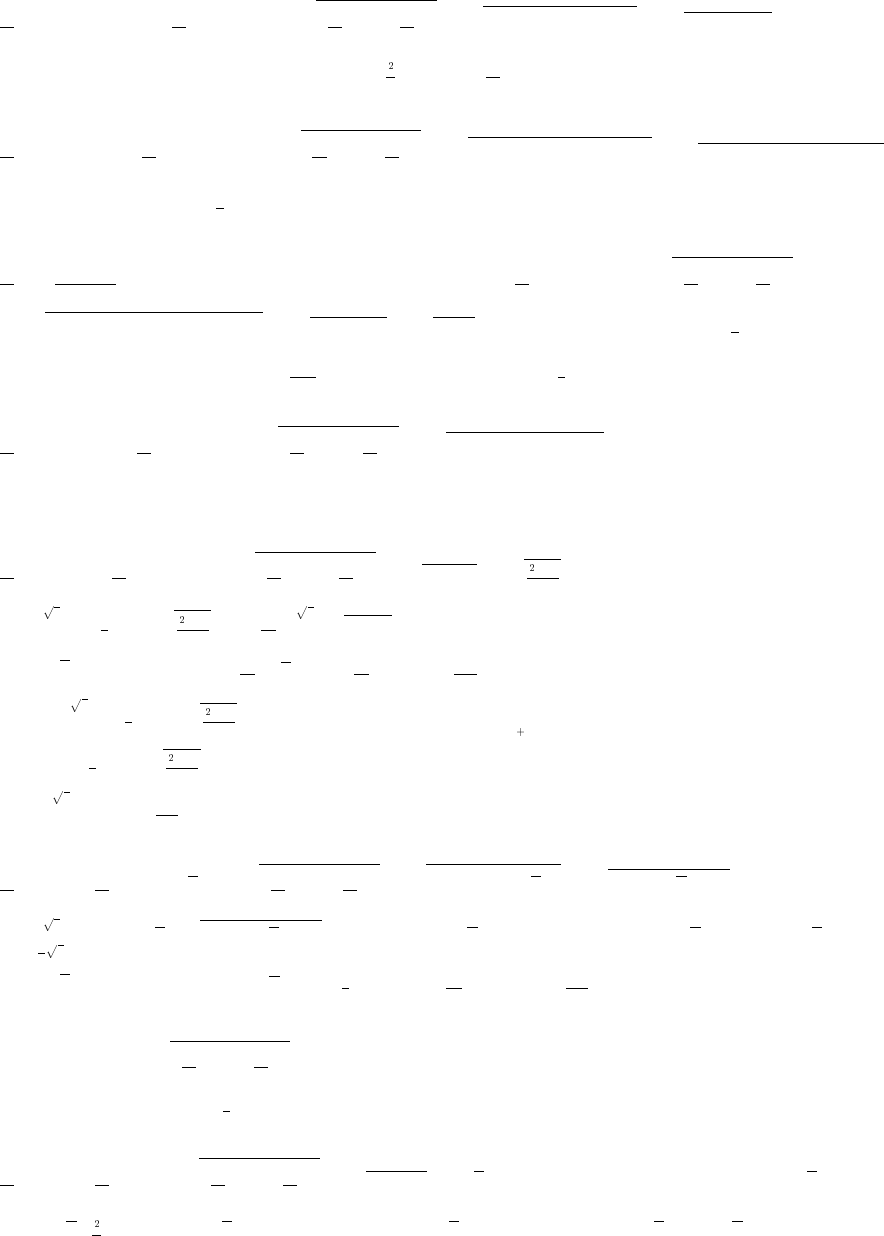
658 Chapter 11 Parametric Equations and Polar Coordinates
28. 2t 3 and 1 t 2t 3 1 t t 4t 4 t 2 t 2
dx dx
dt dt dt dt
dy dy
œ œÊ œ œ œ œab abab kk
ʈ‰ Š‹ ÉÈ
"Î# #
###
since 0 t 3 Length (t 2) dt 2tŸŸ Ê œ œ œ
'0
3t21
2
3
’“
!#
29. 8t cos t and 8t sin t 8t cos t 8t sin t 64t cos t 64t sin t
dx dx
dt dt dt dt
dy dy
œœÊœœ
ʈ‰ Š‹ Éabab
È
####
## ##
8t 8t since 0 t Length 8t dt 4tœœ ŸŸÊ œ œ œkk c d
111
#
Î##
Î#
!
'0
2
1
30. sec t tan t sec t cos t sec t cos t and sin t
dx dx
dt sec t tan t dt dt dt
dy dy
œœœÊ
ˆ‰ ˆ‰
ab ÊŠ‹
"
###
sec t cos t sin t sec t 1 tan t tan t tan t since 0 tœœœœœ ŸŸ
Éabab kk
ÈÈ
##
## 1
3
Length tan t dt dt ln cos t ln ln 1 ln 2Êœ œ œ œœ
''
00
33
sin t
cos t
11 1
ÎÎ Î$
!"
#
cdkk
31. sin t and cos t sin t cos t 1 Area 2 y ds
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ Ê œ
ʈ‰ Š‹ Éabab
#### '1
2 2 sin t 1 dt 2 2t cos t 2 [ 4 1 0 1 ] 8œ œ œ œ
'0
211
1111 1ababc dabab
#
!#
32. t and t t t Area 2 x ds
dx dx t 1
dt dt dt dt t
dy dy
œœÊœœÊœ
"Î# "Î# ##"
ʈ‰ Š‹ ÈÉ'1
2 t dt t t 1 dt; u t 1 du 2t dt; t 0 u 1,œœœÊœœÊœ
''
00
33
1ˆ‰
ÉÈc
2t 4
3t3
$Î# #
" #
1
t 3 u 4 u du u
’“
ÈÈ‘
œÊœÄ œ œ
'1
42428
399
111
$Î# %
"
Note: 2 t dt is an improper integral but lim f t exists and is equal to 0, where
'0
3
1ˆ‰
Éab
2t1
3t
$Î#
tÄ!
f t 2 t . Thus the discontinuity is removable: define F t f t for t 0 and F 0 0ab ab ab ab
ˆ‰
É
œœœ12t
3t
$Î# "
F t dt .ʜ
'0
3ab 28
9
1
33. 1 and t 2 1 t 2 t 2 2 t 3 Area 2 x ds
dx dx
dt dt dt dt
dy dy
œœÊœœÊœ
ÈÈÈ
ÊÊ
ˆ‰ Š‹ Š ‹ É'
###
## 1
2 t 2 t 2 2 t 3 dt; u t 2 2 t 3 du 2t 2 2 dt; t 2 u 1,œœÊœ œÊœ
'2
2
1Š‹ ’ Š ‹
ÈÈ È È È
É##
t 2 u 9 u du u 27 1
’“
ÈÈ‘abœÊœÄ œ œ œ
'1
922 52
33 3
11
$Î# *
"
11
34. From Exercise 30, tan t Area 2 y ds 2 cos t tan t dt 2 sin t dt
ʈ‰ Š‹
dx
dt dt
dy
00
33
##ÎÎ
œÊœ œ œ
'' '
11 1
11
2 cos t 2 ( 1)œ œ œ11 1cd ‘
1Î$
!"
#
35. 2 and 1 2 1 5 Area 2 y ds 2 t 1 5 dt
dx dx
dt dt dt dt
dy dy 1
œœÊœœÊœ œ
ʈ‰ Š‹ ÈÈÈ
ab
#### ''
11
0
2 5 t 3 5. Check: slant height is 5 Area is 1 2 5 3 5 .œœ Ê œ11 11
ÈÈ È ÈÈ
’“ ab
t
2
"
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.2 Calculus With Parametric Curves 659
36. h and r h r Area 2 y ds 2 rt h r dt
dx dx
dt dt dt dt
dy dy 1
œœÊœÊœ œ
ʈ‰ Š‹ ÈÈ
#### ##
''
11
0
2 r h r t dt 2 r h r r h r . Check: slant height is h r Area isœ œœ Ê111
ÈÈÈ È
’“
## ## ## ##
"
!
'0
1t
2
rh r.1È##
37. Let the density be 1. Then x cos t t sin t t cos t, and y sin t t cos t t sin t$œœÊœ œÊœ
dx
dt dt
dy
dm 1 ds dt (t cos t) (t sin t) t dt t dt since 0 t . The curve's mass isÊœ œ œ œ œ ŸŸ†Êˆ‰ Š‹ Èkk
dx
dt dt
dy
#### #
1
M dm t dt . Also M y dm sin t t cos t t dt t sin t dt t cos t dtœœ œ œ œ œ
µ
'' ' ' ' '
0000
2222
8
1111
1
ÎÎÎÎ
#
xab
sin t t cos t t sin t 2 sin t 2t cos t 3 , where we integrated by parts. Therefore,œ œcdc d
111
Î#
!#Î#
!4
y 2. Next, M x dm cos t t sin t t dt t cos t dt t sin t dtœœ œ œ œ œ
µ
M
M
324
000
222
xŠ‹
Š‹
ÎÎÎ
#
4
8
1
111
y'' ' '
ab
cos t t sin t t cos t 2 cos t 2t sin t 3, again integrating by parts. Henceœ œcdc d
111
Î#
!#Î#
!#
3
x . Therefore x y 2 .œ œ œ ßœ ß
M
M
312 24 12 24 24
yˆ‰
Š‹
3
8
11 111
abˆ‰
38. Let the density be 1. Then x e cos t e cos t e sin t, and y e sin t e sin t e cos t$œ œ Êœ œ Êœ
tttttt
dx
dt dt
dy
dm 1 ds dt e cos t e sin t e sin t e cos t dt 2e dt 2 e dt.Êœ œ œ œ œ†Êˆ‰ Š‹ Éabab
ÈÈ
dx
dt dt
dy tt tt 2t t
####
The curve's mass is M dm 2 e dt 2 e 2 . Also M y dm e sin t 2 e dtœœ œ œ œ
µ
'' ' '
00
tt
11
ÈÈÈ È
ab
Š‹
tx
2 e sin t dt 2 (2 sin t cos t) 2 y .œœœÊœœœ
'0
ee e
555M5e1
M2
2e 2
11
ÈÈ È
’“Š‹
2t 2t 2 2
e2
55
!
""
xÈŠ‹
ÈÈ ab
Next M x dm e cos t 2 e dt 2 e cos t dt 2 2 cos t sin t 2
y2t
œœ œ œ œ
µ
'' '
00
tt e2e2
555
11 1
ab a b
Š‹ ’ “ Š ‹
ÈÈ È È
2t 2
!
x . Therefore x y .Êœ œ œ ßœ ß
M
M 5e1 5e15e1
2
2e 2
2e2 2e2e1
y
ÈŠ‹
ÈÈ ab abab
2e 2
2
55 222
abŠ‹
39. Let the density be 1. Then x cos t sin t, and y t sin t 1 cos t$œœÊœ œÊœ
dx
dt dt
dy
dm 1 ds dt sin t 1 cos t dt 2 2 cos t dt. The curve's massÊœ œ œ œ†Êˆ‰ Š‹ Éaba b È
dx
dt dt
dy
####
is M dm 2 2 cos t dt 2 1 cos t dt 2 2 cos dt 2 cos dtœœ œ œ œ
'' ' ' '
0000
tt
1111
ÈÈ
ÈÈ
Ɉ‰ ¸ ¸ˆ‰
###
2 cos dt since 0 t 0 2 2 sin 4. Also M y dmœŸŸÊŸŸœœœ
µ
''
0
ttt
2
111
ˆ‰ ˆ ‰ ‘ˆ‰
###
!
1x
t sin t 2 cos dt 2t cos dt 2 sin t cos dtœ œ
'''
000
tt t
111
ab
ˆ ‰ ˆ‰ ˆ‰
## #
2 4 cos 2t sin 2 cos t cos t 4 y .œœÊœœœ
‘ ‘ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
tt 3 16 4
23 3M43
M4
###
!!
""
111
11
xˆ‰
16
3
Next M x dm cos t 2 cos dt cos t cos dt 2 sin 2
yœœ œ œ œ
µ
'' '
00
ttt2
23 3
sin t
11 1
ab
ˆ ‰ ˆ‰ ˆ‰
’“
## !
ˆ‰
3
x . Therefore x y .œÊœ œ œ ßœß
44
3M43 33
Myˆ‰
4
3""
abˆ‰
1
40. Let the density be 1. Then x t 3t , and y 3t dm 1 ds$œœÊœœÊœÊœ
$#
#
dx 3t
dt dt
dy
†
dt 3t (3t) dt 3 t t 1 dt 3t t 1 dt since 0 t 3. The curve's massœ œœ œ ŸŸ
ʈ‰ Š‹ Éab kk
ÈÈ È
dx
dt dt
dy
#### # #
#
is M dm 3t t 1 dt t 1 7. Also M y dm 3t t 1 dtœœ œ œ œ œ
µ
'' ' '
0 0
3 3
x
ÈÈ
’“ Š‹
ab
# #
#$Î#
!#
È33t
t t 1 dt 17.4 (by computer) y 2.49. Next M x dmœœœ Êœœ¸ œ
µ
9 87 17.4
5M7
M
#
$#
''
0
3
y
Èx
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

660 Chapter 11 Parametric Equations and Polar Coordinates
t 3t t 1 dt 3 t t 1 dt 16.4849 (by computer) x 2.35.œ† œ ¸ Êœœ¸
''
00
33
$%
##
Èab ÈM
M7
16.4849
y
Therefore, x y 2.35 2.49 .aba b߸ ß
41. (a) 2 sin 2t and 2 cos 2t 2 sin 2t 2 cos 2t 2
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ
ʈ‰ Š‹ Éabab
####
Length 2 dt 2tÊœ œœ
'0
211
ÎÎ#
!
cd 1
(b) cos t and sin t cos t sin t
dx dx
dt dt dt dt
dy dy
œœÊœœ11 11 11 11 1
ʈ‰ Š‹ Éaba b
####
Length dt tÊœ œœ
'Î
Î"Î#
"Î#
12
12
11 1cd
42. (a) x g y has the parametrization x g y and y y for c y d g y and 1; thenœœœŸŸÊœœab ab ab
dx
dy dy
dy
w
Length dy 1 dy 1 [g y ] dyœ œ œ
'''
ccc
ddd
dy
dy dy dy
dx dx
ÊÊ
Š‹ Š‹ Š‹ Èab
## # w#
(b) x y , 0 y y L 1 y dy 1 y dy 1 yœŸŸÊœÊœ œœ†
32 12
4dx3 3 9 42 9
3dy2 2 4 93 4
00
43 43
12 32
0
43
ÎÎ
ÎÎ
Î#Î
Î
''
Ɉ‰ ˆ ‰
É”•
41œœ
8856
27 27 27
32 32
ab ab
ÎÎ
(c) x y , 0 y 1 y L 1 y dy 1 dy dyœ ŸŸÊœÊœ œœ
3dx 1
2dy
23 13
00 a
11 1
13 yy
a0
y1
ÎÎ
Î #
Ä
'' '
Éab ÉÉ
23 23
23
lim
y1 ydy y1 2 a1 221œ œ†œœlim lim lim
a0 a0 a0
32 32
23 23
a
123 13 23 23
12 32 32
a
132
ÄÄÄ
ÎÎ Î Î
ÎÎÎ
Î
'ˆ‰ˆ‰ ˆ‰ ˆ‰
”•
Š‹
ab È
43. x 1 2 sin cos , y 1 2 sin sin 2cos sin 1 2 sin , 2cos sin cos 1 2 sinœ œ Êœ œ abab ab ab)) )) ) ) ) )) ) )
dx
dd
2dy
))
Êœ œ œ
dy
dx 2cos sin 1 2 sin 2cos 2sin sin 2 cos 2 sin
2cos sin cos 1 2 sin 4cos sin cos 2 sin 2 cos
)) ) )
)) ) ) )) ))
)) ) ) )
ab
ab
222
(a) x 1 2 sin 0 cos 0 1, y 1 2 sin 0 sin 0 0; œ œ œ œ œ œ œababababab ab º
dy
dx 2 cos 2 0 sin 0 2 0 2
0
2sin20 cos0 01 1
)œ
ab abab
ab abab
(b) x 1 2 sin cos 0, y 1 2 sin sin 3; 0œ œ œ œ œ œ œ
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ º
11 11
)1
## ##
œ
dy
dx 2 1
/2
2sin 2 cos
2cos 2 sin
00
ˆ‰ ˆ‰ˆ‰
ˆ‰ˆ‰ˆ‰
(c) x 1 2 sin cos , y 1 2 sin sin ; œ œ œ œ œ
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ ˆ‰ º
44 44
332 332dx
31 3 3 dy
4/3
2sin 2 cos
2cos 2 sin
11 11
)1
ÈÈ
ˆ‰ˆ‰ˆ‰
ˆ‰ˆ‰ˆ‰
œ
44
33
44
33
433œœœ
ÈÈ
È
3
1
231
32
1
2
3
2Š‹
È
44. x t, y 1 cos t, 0 t 2 1, sin t sin t cos t cos t. Theœœ ŸŸÊœ œ Êœœ Ê œ Êœ œ1dx sin t d cos t
dt dt dx 1 dt dx dx 1
dy dy dy d y
Š‹ 2
2
maximum and minimum slope will occur at points that maximize/minimize , in other words, points where 0
dy d y
dx dx
2
2œ
cos t 0 t or t
232
Ê œ Ê œ œ Ê œ ± ±
ÎÎ
11
22dx
3dy
2
2
11
(a) the maximum slope is sin 1, which occurs at x , y 1 cos 1
dy
dx 2 2 2
t2
ºˆ‰ ˆ‰
œÎ1
111
œœ œœœ
(a) the minimum slope is sin 1, which occurs at x , y 1 cos 1
dy
dx 2 2 2
t3 2
333
ºˆ‰ ˆ‰
œÎ1
111
œœ œœœ
45. cos t and 2 cos 2t ; then 0 0
dx 2 cos 2t
dt dt dx dx/dt cos t cos t dx cos t
dy dy dy/dt dy
22 cost 1 22 cost 1
œœÊœœœ œÊœ
ab ab
2 cos t 1 0 cos t t , , , . In the 1st quadrant: t x sin andʜʜ„Êœ œÊœœ
#"
#
ÈÈ
24444 4 4
357 2
1111 1 1
y sin 2 1 1 is the point where the tangent line is horizontal. At the origin: x 0 and y 0œœÊß œœ
ˆ‰ Š‹
1
4
2
È
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.2 Calculus With Parametric Curves 661
sin t 0 t 0 or t and sin 2t 0 t 0, , , ; thus t 0 and t give the tangent lines atÊ œ Êœ œ œ Êœ œ œ111
11
##
3
the origin. Tangents at origin: 2 y 2x and 2 y 2x
¹¹
dy dy
dx dx
t0 t
œÊœ œÊœ
46. 2 cos 2t and 3 cos 3t
dx 3 cos 3t
dt dt dx dx/dt 2 cos 2t 2 2 cos t 1
dy dy dy/dt 3(cos 2t cos t sin 2t sin t)
œœÊœœœ
ab
œœœ
3 2 cos t 1 (cos t) 2 sin t cos t sin t
2 2 cos t 1 2 2 cos t 1 2 2 cos t
(3 cos t) 2 cos t 1 2 sin t (3 cos t) 4 cos t 3
cdab
ab ab ab
abab
1; then
0 0 3 cos t 0 or 4 cos t 3 0: 3 cos t 0 t , and
dy
dx 2 2 cos t 1
(3 cos t) 4 cos t 3 3
œÊ œÊ œ œ œÊœ
ab
ab
##
#11
4 cos t 3 0 cos t t , , , . In the 1st quadrant: t x sin 2
#
# #
œ Ê œ„ Êœ œ Ê œ œ
È È
3 3
66 6 6 6 6
5711111 1 1 1
ˆ‰
and y sin 3 1 1 is the point where the graph has a horizontal tangent. At the origin: x 0œœÊß œ
ˆ‰ Š‹
1
6
3
È
#
and y 0 sin 2t 0 and sin 3t 0 t 0, , , and t 0, , , , , t 0 and t giveœÊ œ œÊœ œ Êœ œ
1 1 11 11
##
11 1
3245
33 3 3
the tangent lines at the origin. Tangents at the origin: y x, and
¹¹
dy dy
dx 2 cos 0 dx
3 cos 0 3 3
t0 t
œœÊœ
##
yxœœÊœ
3 cos (3 )
2 cos (2 )
33
1
1##
47. (a) x a t sin t , y a 1 cos t , 0 t 2 a 1 cos t , a sin t Lengthœ œ ŸŸÊœ œ Êaba b a b1dx
dt dt
dy
a 1 cos t a sin t dt a 2a cos t a cos t a sin t dtœœ
''
00
2211
Éababab È
## ## ####
a 2 1 cos t dt a 2 2 sin dt 2a sin dt 4a cosœœ œ œ
ÈÈ
ÈɈ‰ ˆ‰ ˆ‰
’“
'''
000
222
2ttt
222
0
2
111 1
4a cos 4a cos 0 8aœ œ1ab
(b) a 1 x t sin t, y 1 cos t, 0 t 2 1 cos t, sin t Surface areaœÊœ œ ŸŸ Ê œ œ Ê œ1dx
dt dt
dy
2 1 cos t 1 cos t sin t dt 2 1 cos t 1 2 cos t cos t sin t dtœ œ
''
00
2211
11ababab ab
ÉÈ
## ##
2 1 cos t 2 2 cos t dt 2 2 1 cos t dt 2 2 1 cos 2 dtœœ œ †111
'''
000
222
32 t
2
32
111
ab ab
ÈÈÈ
ˆ‰ˆ‰
ÎÎ
2 2 2 sin dt 8 sin dtœœ
Ȉ‰ ˆ‰ˆ‰
11
''
00
22
23
tt
22
32
11
Î
u du dt dt 2 du; t 0 u 0, t 2 u
’“
œÊ œ Ê œ œÊœ œ Êœ
t1
22 11
16 sin u du 16 sin u sinudu 16 1 cos u sinudu 16 sinudu 16 cos usinuduœœ œœ11 1 11
'' ' ''
00 0 00
32 2 2
11 1 11
ab
16 cos u cos u 16 16œ œ œ
’“
ˆ‰ˆ ‰
111
16 16 16 64
3333
3
0
1111
1
48. x t sin t, y 1 cos t, 0 t 2 ; Volume y dx 1 cos t 1 cos t dtœ œ ŸŸ œ œ 111
''
00
22
22
11
abab
1 3cos t 3cos t cos t dt 1 3cos t 3 cos t cos t dtœœ 11
''
00
22
23 2
1 cos 2t
2
11
ab
ˆ‰ˆ‰
3cos t cos 2t 1 sin t cos t dt 4cos t cos 2t sin t cos t dtœ œ11
''
00
22
53 53
22 22
22
11
ˆ‰ˆ‰
ab
t 4sin t sin 2t sin t 5 0 0 0 0 5œ œ œ1111
’“
ab
531
243
32
0
21
47-50. Example CAS commands:
:Maple
with( plots );
with( student );
x := t -> t^3/3;
y := t -> t^2/2;
a := 0;
b := 1;
N := [2, 4, 8 ];
for n in N do Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

662 Chapter 11 Parametric Equations and Polar Coordinates
tt := [seq( a+i*(b-a)/n, i=0..n )];
pts := [seq([x(t),y(t)],t=tt)];
L := simplify(add( student[distance](pts[i+1],pts[i]), i=1..n )); # (b)
T := sprintf("#47(a) (Section 11.2)\nn=%3d L=%8.5f\n", n, L );
P[n] := plot( [[x(t),y(t),t=a..b],pts], title=T ): # (a)
end do:
display( [seq(P[n],n=N)], insequence=true );
ds := t ->sqrt( simplify(D(x)(t)^2 + D(y)(t)^2) ): # (c)
L := Int( ds(t), t=a..b ):
L = evalf(L);
11.3 POLAR COORDINATES
1. a, e; b, g; c, h; d, f 2. a, f; b, h; c, g; d, e
3. (a) 2 2n and 2 (2n 1) , n an integer
ˆ‰ˆ ‰
ß ß
11
##
11
(b) ( 2n ) and ( (2n 1) ), n an integer#ß #ß 11
(c) 2 2n and 2 (2n 1) , n an integer
ˆ‰ˆ ‰
ß ß
3311
##
11
(d) ( (2n 1) ) and ( 2n ), n an integer#ß #ß11
4. (a) 3 2n and 3 2n , n an integer
ˆ‰ˆ ‰
ß ß
11
44
5
11
(b) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
5
11
(c) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
3
11
(d) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
3
11
5. (a) x r cos 3 cos 0 3, y r sin 3 sin 0 0 Cartesian coordinates are ( 0)œœ œœœœÊ $ß))
(b) x r cos 3 cos 0 3, y r sin 3 sin 0 0 Cartesian coordinates are ( 0)œœœœœœÊ $ß))
(c) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
22
33
11
ÈÈ
Š‹
(d) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
77
33
11
ÈÈ
Š‹
(e) x r cos 3 cos 3, y r sin 3 sin 0 Cartesian coordinates are (3 0)œœœœœœÊ ß)1 )1
(f) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
11
33
ÈÈ
Š‹
(g) x r cos 3 cos 2 3, y r sin 3 sin 2 0 Cartesian coordinates are ( 3 0)œœ œœœ œÊ ß)1 )1
(h) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœœœœœÊ ß))
ˆ‰ ˆ‰ÈÈ
Š‹
11
33
6. (a) x 2 cos 1, y 2 sin 1 Cartesian coordinates are (1 1)œœœœÊ ß
ÈÈ
11
44
(b) x 1 cos 0 1, y 1 sin 0 0 Cartesian coordinates are (1 0)œœœœÊ ß
(c) x 0 cos 0, y 0 sin 0 Cartesian coordinates are ( 0)œœœœÊ !ß
11
##
(d) x 2 cos 1, y 2 sin 1 Cartesian coordinates are ( 1 1)œ œ œ œ Ê ß
ÈÈ
ˆ‰ ˆ‰
11
44
(e) x 3 cos , y 3 sin Cartesian coordinates are œ œ œ œ Ê ß
553 3
62 6
33 33
11
È È
###
Š‹
(f) x 5 cos tan 3, y 5 sin tan 4 Cartesian coordinates are ( 4)œœœœÊ $ß
ˆ‰ ˆ‰
" "
44
33
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
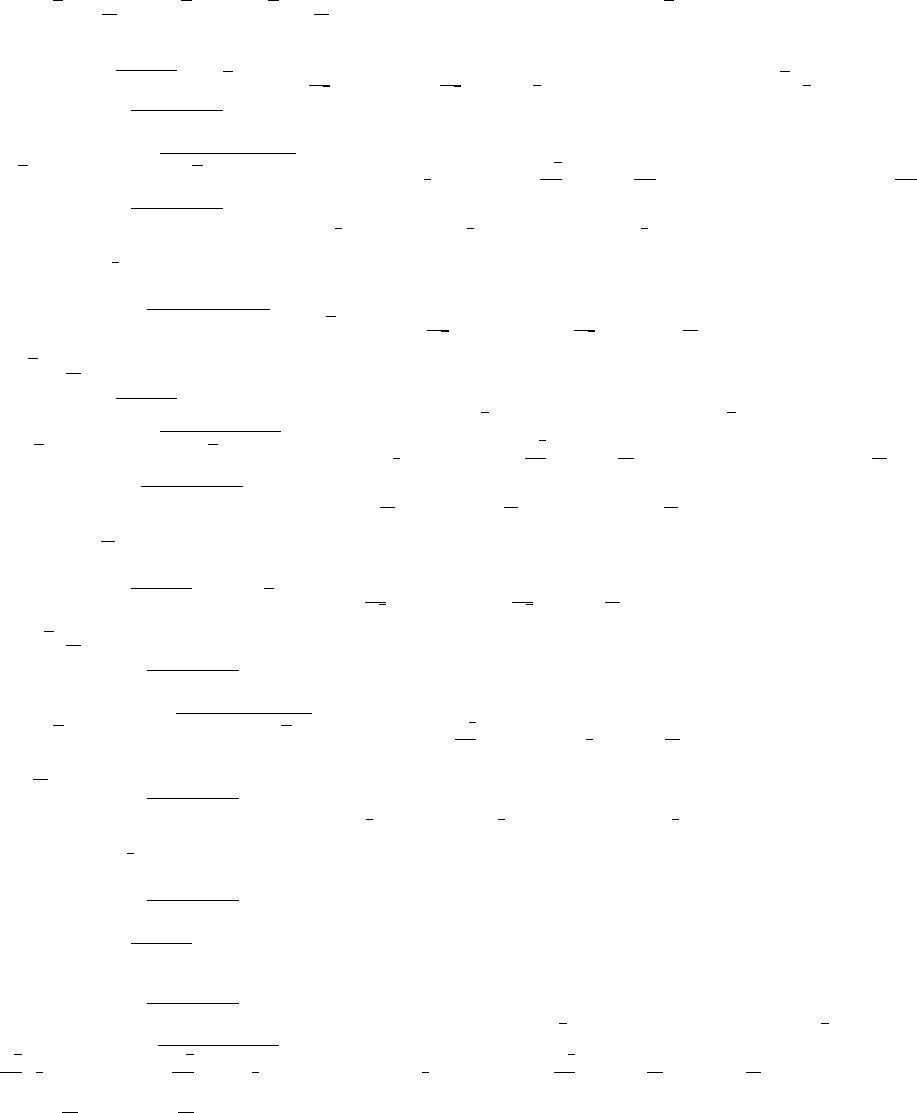
Section 11.3 Polar Coordinates 663
(g) x 1 cos 7 1, y 1 sin 7 0 Cartesian coordinates are (1 0)œ œ œ œ Ê ß11
(h) x 2 3 cos 3, y 2 3 sin 3 Cartesian coordinates are 3 3œœœœÊ ß
ÈÈÈ È
Š‹
22
33
11
7. (a) 1, 1 r 1 1 2, sin and cos Polar coordinates are 2, ab ÈÈÈ
Š‹
Êœ œ œ œ Ê œ Ê
22 11
22
44
)))
ÈÈ
11
(b) 3, 0 r 3 0 3, sin 0 and cos 1 Polar coordinates are 3, ab ab ab
É
Êœœ œ œÊœÊ
22)))1 1
(c) 3, 1 r 3 1 2, sin and cos Polar coordinates are 2,
Š‹ÊŠ‹
ÈÈ
ab ˆ‰
Êœ œ œ œ Êœ Ê
22111 11
226 6
3
)))
È11
(d) 3, 4 r 3 4 5, sin and cos arctan Polar coordinates areab ab
Ɉ‰
Êœœ œ œÊœ Ê
2243 4
55 3
)))1
5, arctan
ˆ‰ˆ‰
14
3
8. (a) 2, 2 r 2 2 2 2, sin and cos Polar coordinates area b ab ab
ÉÈ
Ê œ œ œ œ Ê œ Ê
22 113
22
4
)))
ÈÈ
1
2 2,
Š‹
È3
4
1
(b) 0, 3 r 0 3 3, sin 1 and cos 0 Polar coordinates are 3, ab Ȉ‰
Êœ œ œ œ Ê œ Ê
22 22
)))
11
(c) 3, 1 r 3 1 2, sin and cos Polar coordinates are 2,
Š‹ÊŠ‹
ÈÈ ˆ‰
Êœœœ œÊœÊ
2215 5
226 6
3
)))
È11
(d) 5, 12 r 5 12 13, sin and cos arctan Polar coordinates areab ab
Ɉ‰
Ê œ œ œ œ Ê œ Ê
2212 5 12
13 12 5
)))
13, arctan
ˆ‰ˆ‰
12
5
9. (a) 3, 3 r 3 3 3 2, sin and cos Polar coordinates areab ÈÈ
Ê œ œ œ œ Ê œ Ê
22 115
22
4
)))
ÈÈ
1
3 2,
Š‹
È
5
4
1
(b) 1, 0 r 1 0 1, sin 0 and cos 1 0 Polar coordinates are 1, 0ab ab ab
É
Ê œ œ œ œ Ê œ Ê
22)))
(c) 1, 3 r 1 3 2, sin and cos Polar coordinates are
Š‹ Ê Š‹
ÈÈ
ab Ê œ œ œ œ Ê œ Ê
223
223
15
)))
È1
2,
ˆ‰
5
3
1
(d) 4, 3 r 4 3 5, sin and cos arctan Polar coordinates areab ab
Ɉ‰
Ê œ œ œ œ Ê œ Ê
2234 3
55 4
)))1
5, arctan
ˆ‰ˆ‰
14
3
10. (a) 2, 0 r 2 0 2, sin 0 and cos 1 0 Polar coordinates are 2, 0ab ab ab
É
Ê œ œ œ œ Ê œ Ê
22)))
(b) 1, 0 r 1 0 1, sin 0 and cos 1 or Polar coordinates are 1, orab ab
È
Êœ œ œ œÊ œ œÊ
22 )))1)1 1
1, ab1
(c) 0, 3 r 0 3 3, sin 1 and cos 0 Polar coordinates are 3, ab ab
Ɉ‰
Ê œ œ œ œ Ê œ Ê
22
22
)))
11
(d) , r 1, sin and cos or Polar coordinates
Š‹ ÊŠ‹
ˆ‰
ÈÈ È
33 3
22 2 2 2 2 6 6
111 75
22
Ê œ œ œ œ Ê œ œ Ê))))
11
are 1, or 1,
ˆ‰ˆ ‰
75
66
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
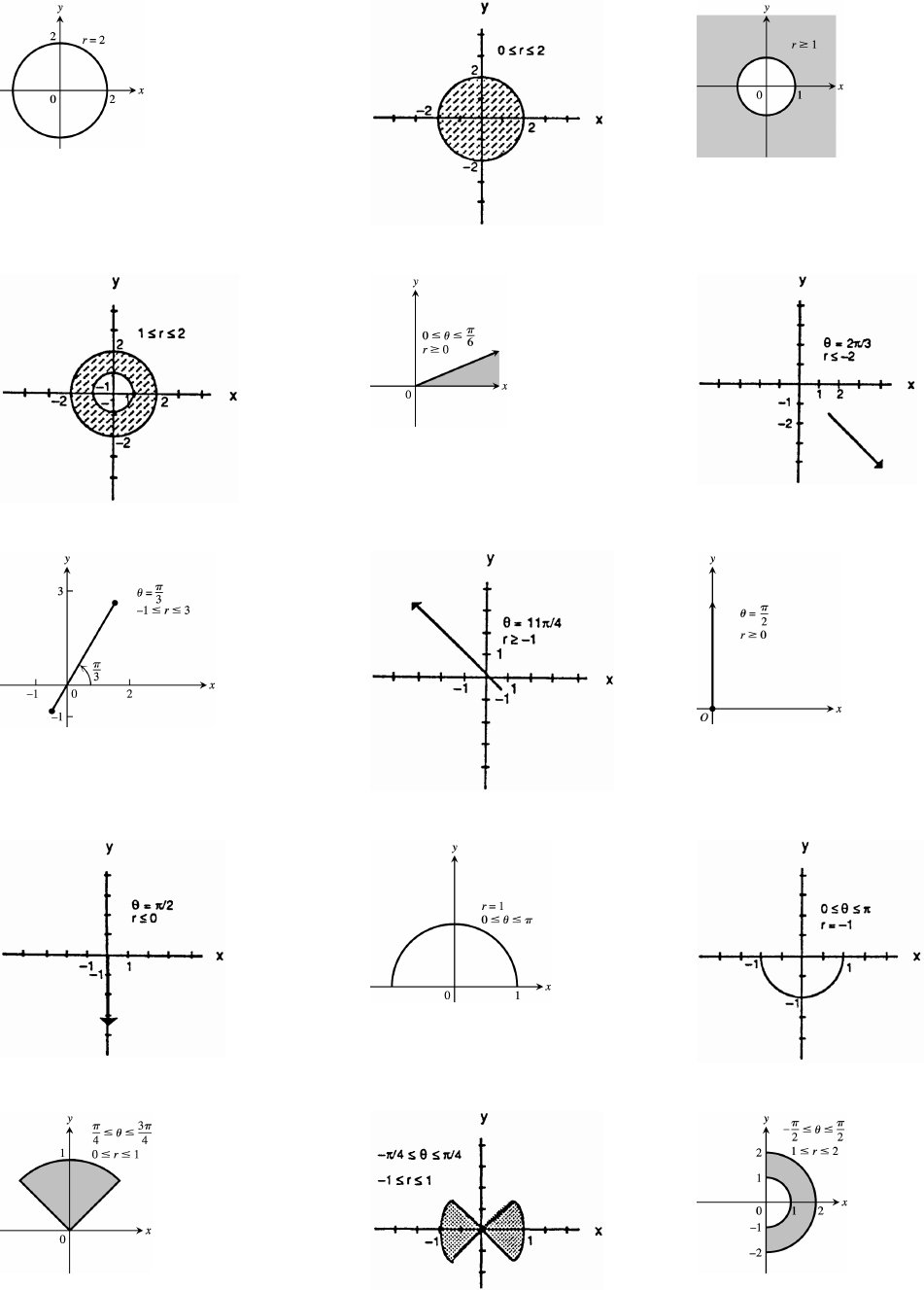
664 Chapter 11 Parametric Equations and Polar Coordinates
11. 12. 13.
14. 15. 16.
17. 18. 19.
20. 21. 22.
23. 24. 25.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.3 Polar Coordinates 665
26.
27. r cos 2 x 2, vertical line through ( 0) 28. r sin 1 y 1, horizontal line through (0 1)))œÊœ #ß œÊœ ß
29. r sin 0 y 0, the x-axis 30. r cos 0 x 0, the y-axis))œÊœ œÊœ
31. r 4 csc r r sin 4 y 4, a horizontal line through (0 4)œÊœÊœÊœ ß))
4
sin )
32. r 3 sec r r cos 3 x 3, a vertical line through ( 3 0)œ Ê œ Ê œ Ê œ ß))
3
cos )
33. r cos r sin 1 x y 1, line with slope m 1 and intercept b 1))œÊœ œ œ
34. r sin r cos y x, line with slope m 1 and intercept b 0))œÊœ œ œ
35. r 1 x y 1, circle with center C ( 0) and radius 1
###
œÊ œ œ!ß
36. r 4r sin x y 4y x y 4y 4 4 x (y 2) 4, circle with center C (0 2) and radius 2
##### ##
œÊœÊœÊœ œß)
37. r r sin 2r cos 5 y 2x 5, line with slope m 2 and intercept b 5œÊœÊœ œ œ
5
sin 2 cos ))))
38. r sin 2 2 2r sin cos 2 (r sin )(r cos ) 1 xy 1, hyperbola with focal axis y x
##
)))))œÊ œÊ œÊ œ œ
39. r cot csc r sin cos r sin r cos y x, parabola with vertex (0 0)œœ ʜʜʜ ß)) ) ) ) )
ˆ‰ˆ‰
cos
sin sin
)
))
"### #
which opens to the right
40. r 4 tan sec r 4 r cos 4 sin r cos 4r sin x 4y, parabola withœÊœÊœÊœÊœ)) ) ) ) )
ˆ‰
sin
cos
)
)
### #
vertex ( 0) which opens upwardœ!ß
41. r (csc ) e r sin e y e , graph of the natural exponential functionœÊœÊœ))
r cos r cos x
42. r sin ln r ln cos ln (r cos ) y ln x, graph of the natural logarithm function)))œ œ Êœ
43. r 2r cos sin 1 x y 2xy 1 x 2xy y 1 (x y) 1 x y 1, two parallel
## ## # # #
œÊ œÊ œÊœÊœ„))
straight lines of slope 1 and y-intercepts b 1œ„
44. cos sin r cos r sin x y x y x y, two perpendicular
########
)) ) )œÊ œ ʜʜʄœkk kk
lines through the origin with slopes 1 and 1, respectively.
45. r 4r cos x y 4x x 4x y 0 x 4x 4 y 4 (x 2) y 4, a circle with
#########
œ ʜʜʜʜ)
center C( 2 0) and radius 2ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

666 Chapter 11 Parametric Equations and Polar Coordinates
46. r 6r sin x y 6y x y 6y 0 x y 6y 9 9 x (y 3) 9, a circle with
####### ##
œ ʜʜʜʜ)
center C(0 3) and radius 3ß
47. r 8 sin r 8r sin x y 8y x y 8y 0 x y 8y 16 16 x (y 4) 16, aœ Ê œ Êœ ʜʜ Ê œ))
####### ##
circle with center C(0 4) and radius 4ß
48. r 3 cos r 3r cos x y 3x x y 3x 0 x 3x yœ Êœ Êœ ʜʜ))
#######
99
44
x y , a circle with center C and radius Ê œ ß!
ˆ‰ ˆ‰
39 3 3
4###
##
49. r 2 cos 2 sin r 2r cos 2r sin x y 2x 2y x 2x y 2y 0œÊœ ʜʜ)) ) )
#####
(x 1) (y 1) 2, a circle with center C(1 1) and radius 2Ê œ ß
## È
50. r 2 cos sin r 2r cos r sin x y 2x y x 2x y y 0œ Ê œ Ê œ Ê œ)) ) )
#####
(x 1) y , a circle with center C 1 and radius Ê œ ß
#""
###
#
ˆ‰ ˆ‰
5
4
5
È
51. r sin 2 r sin cos cos sin 2 r sin r cos 2 y x 2
ˆ‰ ˆ ‰
))) ))œÊ œÊ œÊ œ
111
666
33
ÈÈ
## ##
""
3 y x 4, line with slope m and intercept bÊœ œ œ
È"
ÈÈ
33
4
52. r sin 5 r sin cos cos sin 5 r cos r sin 5 x y 5
ˆ‰ ˆ ‰
222
333
33
111
œÊ œÊ œÊ œ)))))
ÈÈ
## ##
""
3 x y 10, line with slope m 3 and intercept b 10Êœ œ œ
ÈÈ
53. x 7 r cos 7 54. y 1 r sin 1œÊ œ œÊ œ))
55. x y r cos r sin 56. x y 3 r cos r sin 3œÊ œ Êœ œÊ œ))) ))
1
4
57. x y 4 r 4 r 2 or r 2
## #
œÊ œÊœ œ
58. x y 1 r cos r sin 1 r cos sin 1 r cos 2 1
## ## ## # # # #
œÊ œÊ œÊ œ)) )) )ab
59. 1 4x 9y 36 4r cos 9r sin 36
x
94
y
œÊ œ Ê œ
## ## ##
))
60. xy 2 (r cos )(r sin ) 2 r cos sin 2 2r cos sin 4 r sin 2 4œÊ œÊ œÊ œÊ œ) ) )) )) )
###
61. y 4x r sin 4r cos r sin 4 cos
### #
œÊ œ Ê œ)) ))
62. x xy y 1 x y xy 1 r r sin cos 1 r (1 sin cos ) 1
## ## ## #
œÊ œÊ œÊ œ)) ))
63. x (y 2) 4 x y 4y 4 4 x y 4y r 4r sin r 4 sin
# # ## ## #
œÊ œÊ œ Ê œ Êœ))
64. (x 5) y 25 x 10x 25 y 25 x y 10x r 10r cos r 10 cos œ Ê œ Êœ Êœ Êœ
## # # ## # ))
65. (x 3) (y 1) 4 x 6x 9 y 2y 1 4 x y 6x 2y 6 r 6r cos 2r sin 6 œÊ œÊ œÊœ
## # # ## #
))
66. (x 2) (y 5) 16 x 4x 4 y 10y 25 16 x y 4x 10y 13œÊ œÊœ
## # # ##
r 4r cos 10r sin 13ʜ
#))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
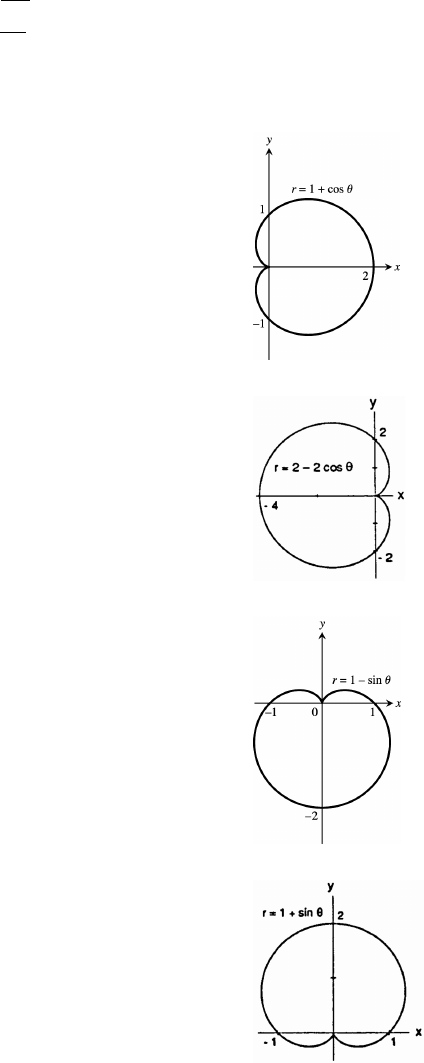
Section 11.4 Graphing in Polar Coordinates 667
67. ( ) where is any angle!ß ))
68. (a) x a r cos a r r a sec œÊ œÊœ Êœ))
a
cos )
(b) y b r sin b r r b csc œÊ œÊœ Êœ))
b
sin )
11.4 GRAPHING IN POLAR COORDINATES
1. 1 cos ( ) 1 cos r symmetric about theœ œÊ))
x-axis; 1 cos ( ) r and 1 cos ( )Á )1)
1 cos r not symmetric about the y-axis;œ ÁÊ)
therefore not symmetric about the origin
2. 2 2 cos ( ) 2 2 cos r symmetric about theœ œÊ))
x-axis; 2 cos ( ) r and 2 2 cos ( )# Á )1)
2 2 cos r not symmetric about the y-axis;œ Á Ê)
therefore not symmetric about the origin
3. 1 sin ( ) 1 sin r and 1 sin ( )œ Á )) 1)
1 sin r not symmetric about the x-axis;œ ÁÊ)
1 sin ( ) 1 sin r symmetric aboutœœÊ1) )
the y-axis; therefore not symmetric about the origin
4. 1 sin ( ) 1 sin r and 1 sin ( )œ Á )) 1)
1 sin r not symmetric about the x-axis;œ ÁÊ)
1 sin ( ) 1 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
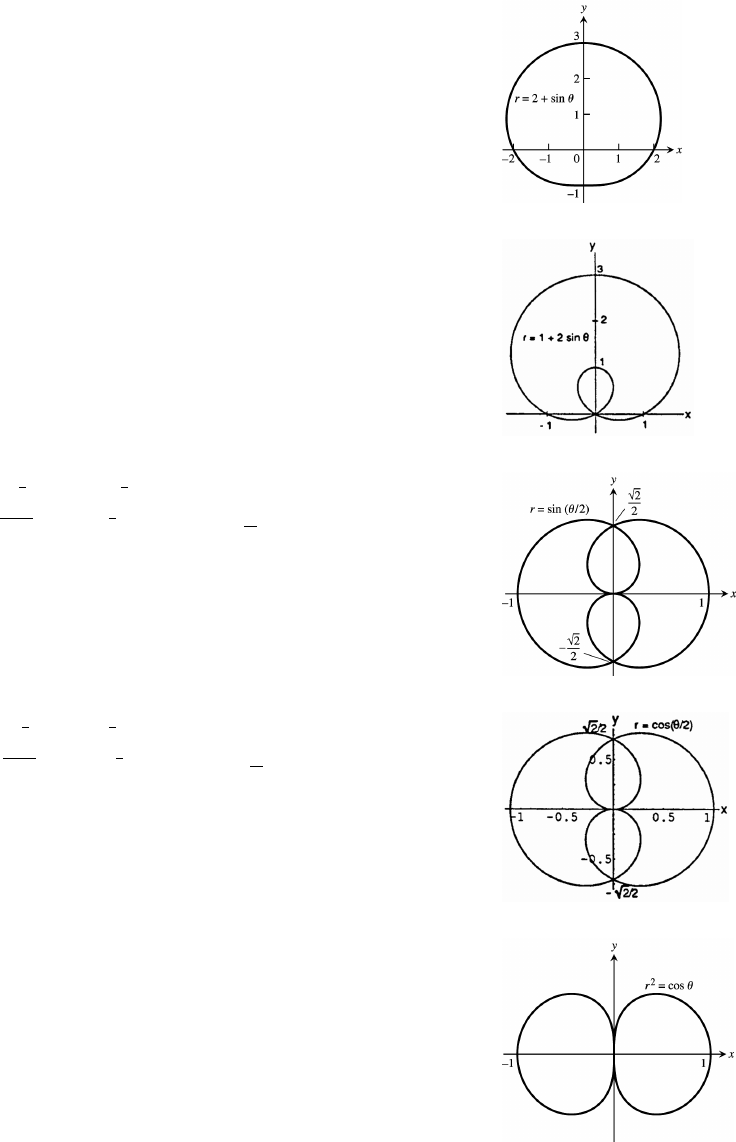
668 Chapter 11 Parametric Equatins and Polar Coordinates
5. 2 sin ( ) 2 sin r and 2 sin ( )œ Á )) 1)
2 sin r not symmetric about the x-axis;œ ÁÊ)
2 sin ( ) 2 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
6. 1 2 sin ( ) 1 2 sin r and 1 2 sin ( )œ Á )) 1)
1 2 sin r not symmetric about the x-axis;œ ÁÊ)
1 2 sin ( ) 1 2 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
7. sin sin r symmetric about the y-axis;
ˆ‰ ˆ‰
œ œÊ
))
##
sin sin , so the graph symmetric about the
ˆ‰ ˆ‰
2
2
1) )
#œis
x-axis, and hence the origin.
8. cos cos r symmetric about the x-axis;
ˆ‰ ˆ‰
œ œÊ
))
##
cos cos , so the graph symmetric about the
ˆ‰ ˆ‰
2
2
1) )
#œis
y-axis, and hence the origin.
9. cos ( ) cos r (r ) and ( r ) are on theœ œ Êß ß)) ) )
#
graph when (r ) is on the graph symmetric about theßÊ)
x-axis and the y-axis; therefore symmetric about the origin
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.4 Graphing in Polar Coordinates 669
10. sin ( ) sin r (r ) and ( r ) are on1) ) 1) 1)œ œ Êß ß
#
the graph when (r ) is on the graph symmetric aboutßÊ)
the y-axis and the x-axis; therefore symmetric about the
origin
11. sin ( ) sin r (r ) and ( r )œœÊß ß1) ) 1) 1)
#
are on the graph when (r ) is on the graph symmetricßÊ)
about the y-axis and the x-axis; therefore symmetric about
the origin
12. cos ( ) cos r (r ) and ( r ) are onœ œÊß ß)) ) )
#
the graph when (r ) is on the graph symmetric aboutßÊ)
the x-axis and the y-axis; therefore symmetric about the
origin
13. Since r are on the graph when (r ) is on the graphab„ß ß))
r 4 cos 2( ) r 4 cos 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the x-axis and the y-axis the graph isÊ
symmetric about the origin
14. Since (r ) on the graph ( r ) is on the graphßÊß))
r 4 sin 2 r 4 sin 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the origin. But 4 sin 2( ) 4 sin 2œ))
r and 4 sin 2( ) 4 sin (2 2 ) 4 sin ( 2 )Áœœ
#1) 1 ) )
4 sin 2 r the graph is not symmetric aboutœ Á Ê)#
the x-axis; therefore the graph is not symmetric about
the y-axis
15. Since (r ) on the graph ( r ) is on the graphßÊß))
r sin 2 r sin 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the origin. But sin 2( ) ( sin 2 )œ))
sin 2 r and sin 2( ) sin (2 2 ))1)1)Á œ
#
sin ( 2 ) ( sin 2 ) sin 2 r the graphœ œ œ Á Ê)))
#
is not symmetric about the x-axis; therefore the graph is
not symmetric about the y-axis
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
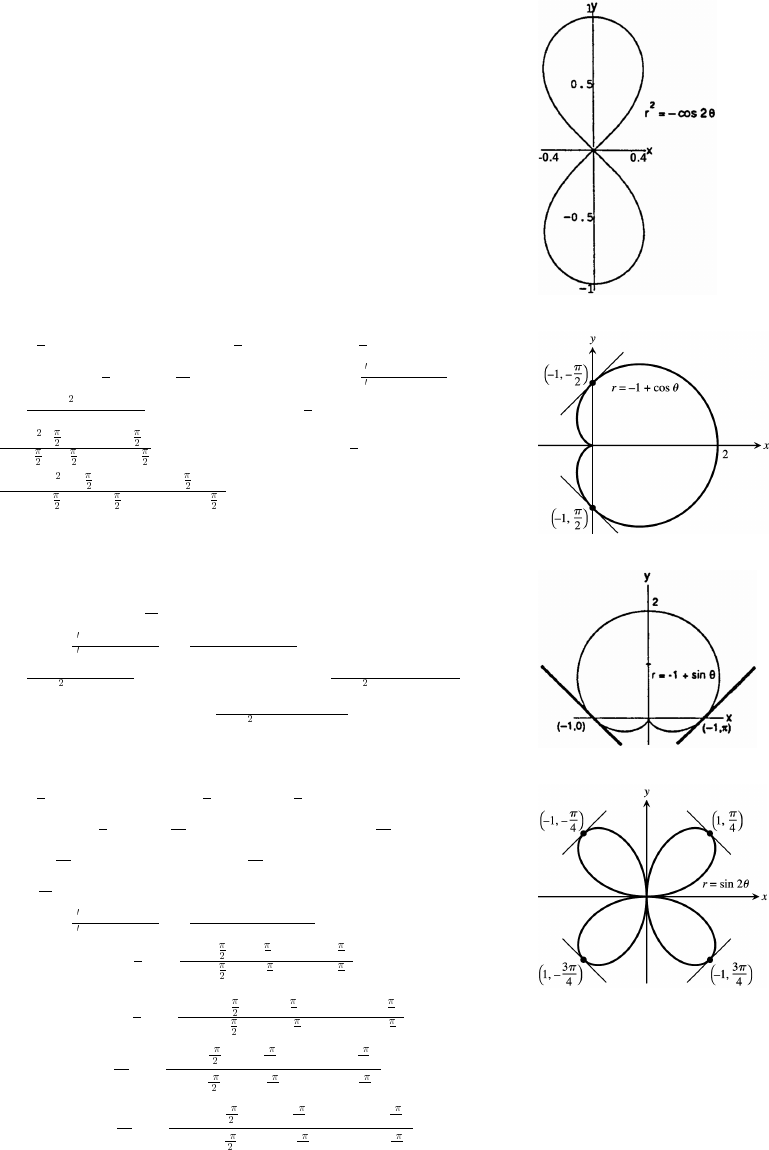
670 Chapter 11 Parametric Equatins and Polar Coordinates
16. Since r are on the graph when (r ) is on theab„ß ß))
graph r cos 2( ) r cos 2 , the
ˆ‰
ab„œ Êœ
##
))
graph is symmetric about the x-axis and the y-axis theÊ
graph is symmetric about the origin.
17. r 1 1 , and r 1))œ Ê œ Ê ß œ Ê œ
111
###
ˆ‰
1 ; r sin ; SlopeÊß œ œ œ
ˆ‰
1))
)))#
wdr r sin r cos
d r cos r sin
)
Slope at 1 isœÊß
#
sin r cos
sin cos r sin
)) 1
)) ) ˆ‰
1; Slope at 1 is
#
sin ( 1) cos
sin cos ( 1) sin
ˆ‰ œ ß
ˆ‰
1
1
sin ( 1) cos
sin cos ( 1) sin
ˆ‰ ˆ‰
ˆ‰ˆ‰ ˆ‰
œ
18. 0 r 1 ( 0), and r 1))1œ Ê œ Ê "ß œ Ê œ
( ); r cos ;Ê"ß œ œ1)
wdr
d)
Slope œœ
r sin r cos cos sin r cos
r cos r sin cos cos r sin
)) )))
)) )))
Slope at ( 0) is œÊ"ß
cos sin r cos
cos r sin cos 0 ( 1) sin 0
cos 0 sin 0 ( 1) cos 0
)) )
))
1; Slope at ( ) is 1œ "ß œ1cos sin ( 1) cos
cos ( 1) sin
11 1
11
19. r 1 ; r 1))œ Ê œ Ê "ß œ Ê œ
111
444
ˆ‰
1; r1 ;Êß œ Ê œÊ"ß
ˆ‰ ˆ‰
11 1
44 4
33
)
r1 1 ;)œ Ê œ Ê ß
33
44
11
ˆ‰
r2 cos 2;
wœœ
dr
d))
Slope œœ
r sin r cos 2 cos 2 sin r cos
r cos r sin 2 cos 2 cos r sin
)) )))
)) )))
Slope at 1 is 1;Êß œ
ˆ‰
1
4
2 cos sin (1) cos
2 cos cos (1) sin
ˆ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
44
44
Slope at 1 is 1;
ˆ‰
ß œ
1
4
2 cos sin ( 1) cos
2 cos cos ( 1) sin
ˆ‰ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
44
44
Slope at 1 is 1;
ˆ‰
ß œ
3
4
2 cos sin ( 1) cos
2 cos cos ( 1) sin
1Š‹ Š‹ Š‹
Š‹ Š‹ Š‹
33 3
44
33 3
44
Slope at 1 is 1
ˆ‰
ß œ
3
4
2 cos sin (1) cos
2 cos cos (1) sin
1Š‹Š‹ Š‹
Š‹Š‹ Š‹
33 3
44
33 3
44
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
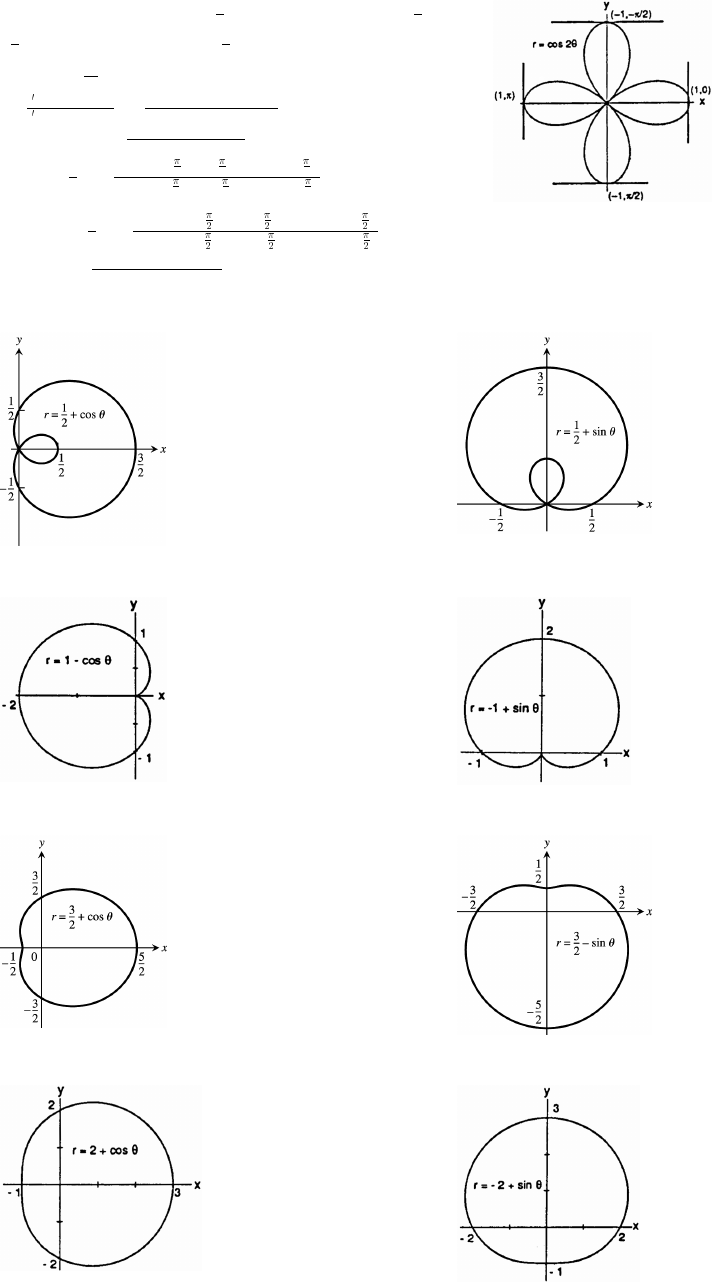
Section 11.4 Graphing in Polar Coordinates 671
20. 0 r 1 (1 0); r 1 1 ;))œÊœÊß œ ÊœÊß
11
22
ˆ‰
r1 ; r1))1œ Ê œ Ê "ß œ Ê œ
11
#ˆ‰
2
(1 ); r 2 sin 2 ;Êß œ œ1)
wdr
d)
Slope œœ
r sin r cos 2 sin 2 sin r cos
r cos r sin 2 sin 2 cos r sin
)) )))
)) )))
Slope at (1 0) is , which is undefined;Êß
2 sin 0 sin 0 cos 0
2 sin 0 cos 0 sin 0
Slope at 1 is 0;
ˆ‰
ß œ
1
2
2 sin 2 sin ( 1) cos
2 sin 2 cos ( 1) sin
ˆ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
22 2
22 2
Slope at 1 is 0;
ˆ‰
ß œ
1
2
2 sin 2 sin ( 1) cos
2 sin 2 cos ( 1) sin
ˆ‰ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
Slope at ( ) is , which is undefined"ß 1
2 sin 2 sin cos
2 sin 2 cos sin
11 1
11 1
21. (a) (b)
22. (a) (b)
23. (a) (b)
24. (a) (b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
672 Chapter 11 Parametric Equatins and Polar Coordinates
25.
26. r 2 sec r r cos 2 x 2œÊœÊœÊœ))
2
cos )
27. 28.
29. Note that (r ) and ( r ) describe the same point in the plane. Then r 1 cos 1 cos ( )ßß œÍ))1 ) )1
1 (cos cos sin sin ) 1 cos (1 cos ) r; therefore (r ) is on the graph ofœ œ œ œ ß)1 )1 ) ) )
r 1 cos ( r ) is on the graph of r 1 cos the answer is (a).œ Íß œ Ê))1 )
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 11.4 Graphing in Polar Coordinates 673
30. Note that (r ) and ( r ) describe the same point in the plane. Then r cos 2 sin 2( ))ßß œÍ ))1 ) )1
ˆ‰
1
#
sin 2 sin (2 ) cos cos (2 ) sin cos 2 r; therefore (r ) is on the graph ofœ œ œ œ ß
ˆ ‰ ˆ‰ ˆ‰
)) ) ) )
555111
###
r sin 2 the answer is (a).œ Ê
ˆ‰
)1
#
31. 32.
33. (a) (b) (c) (d)
34. (a) (b) (c)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
674 Chapter 11 Parametric Equatins and Polar Coordinates
(d) (e)
11.5 AREA AND LENGTHS IN POLAR COORDINATES
1. A dœœœ
'0
1
66
3
111"
#
#
!
)) )
‘ 3
2. A 2 sin d 2 sin d 2 d 1 cos 2 d sin 2œœœœœ
''''
1111
1111
)
1
1
ÎÎÎÎ
ÎÎÎÎ
"
#
#
Î
Î
4444
2222
21cos2 1
22
4
2
ab a b‘
)) )) ) )) ) )
0œœ
ˆ‰ˆ‰
111
24242
11
3. A (4 2 cos ) d 16 16 cos 4 cos d 8 8 cos 2 dœ œ œ
'' '
0
22 2
00
1cos 2
11 1
)""
## #
##
)) ) )) ) )ab
‘ˆ‰
(9 8 cos cos 2 ) d 9 8 sin sin 2 18œ œ œ
'0
2
))))) ) 1
‘
"#
!
2
1
4. A [a(1 cos )] d a 1 2 cos cos d a 1 2 cos dœ œ œ
'' '
00 0
22 2
1cos 2
11 1
)"" "
## ##
## ##
)) ) )) ) )ab
ˆ‰
a 2 cos cos 2 d a 2 sin sin 2 aœ œœ
""""
## # ## #
###
#
!
'0
2333
4
11
ˆ‰ ‘
))) )))1
5. A 2 cos 2 d dœœœœ
''
00
44
1cos 4 sin 4
48
11
))1
1
ÎÎ
""
###
#Î%
!
)) ) )
‘
6. A cos 3 d cos 3 d d 1 cos 6 dœœœœ
''''
Î Î Î
ÎÎÎÎ
"" ""
## #
111
1111
)
666
6666
221cos6
24
ab a b)) )) ) ))
6
sin 6 0 0œ œ œ
"""
Î
Î
46 46 46 12
16
6
‘ˆ‰ˆ‰
))
1
1
111
7. A (4 sin 2 ) d 2 sin 2 d cos 2 2œœœœ
''
00
22
"
#
Î#
!
)) )) )cd
1
8. A (6)(2) (2 sin 3 ) d 12 sin 3 d 12 4œœœœ
''
00
66
"
#
Î'
!
)) )) ‘
cos 3
3
)1
9. r 2 cos and r 2 sin 2 cos 2 sin œœÊœ))))
cos sin ; thereforeʜʜ)))
1
4
A 2 (2 sin ) d 4 sin dœœ
''
00
44
"
#
##
)) ))
4 d (2 2 cos 2 ) dœœ
''
00
44
ˆ‰
1cos 2
#
))))
2sin 2 1œ œcd))
11
Î%
!#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
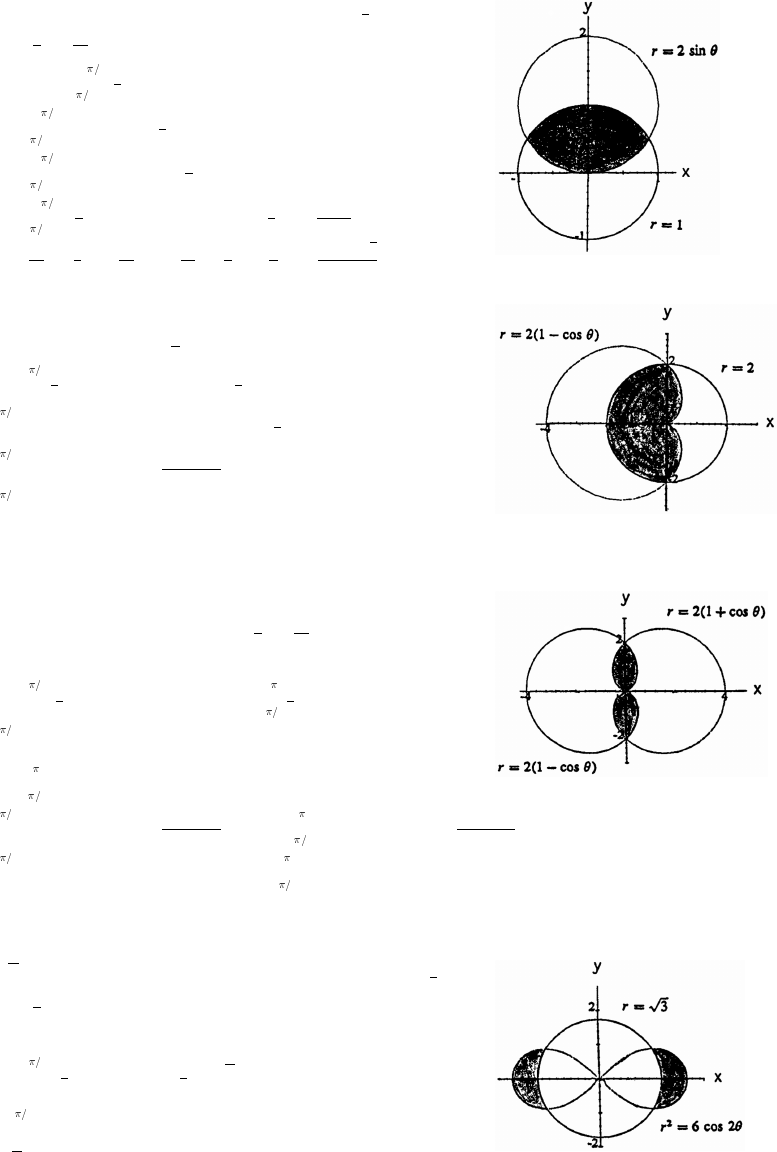
Section 11.5 Area and Lengths in Polar Coordinates 675
10. r 1 and r 2 sin 2 sin 1 sin œœ Ê œÊœ)) )
"
#
or ; thereforeʜ)11
66
5
A (1) (2 sin ) 1 dœ 1))
###
"
#
'6
56 cd
2 sin dœ 1))
'6
56
ˆ‰
#"
#
1 cos 2 dœ 1))
'6
56
ˆ‰
"
#
cos 2 dœ œ 1))1)
'6
56
ˆ‰‘
""
##
&Î'
Î'
2
sin 2)1
1
sin sin œ œ1ˆ‰ˆ‰
55
131236
433
1111
1
## #
""
È
11. r 2 and r 2(1 cos ) 2 2(1 cos )œœÊœ))
cos 0 ; thereforeʜʜ„))
1
#
A 2 [2(1 cos )] d area of the circleœ
'0
2""
##
#
))
4 1 2 cos cos d (2)œ
'0
2ab
ˆ‰
)))1
##
"
#
4 1 2 cos d 2œ
'0
2ˆ‰
))1
1cos 2
#
)
(4 8 cos 2 2 cos 2 ) d 2œ
'0
2
)))1
6 8 sin sin 2 2 5 8œ œcd)))11
1Î#
!
12. r 2(1 cos ) and r 2(1 cos ) 1 cos œ œ Ê)))
1 cos cos 0 or ; the graph alsoœ Ê œ Ê œ)) )
11
##
3
gives the point of intersection (0 0); thereforeß
A 2 [2(1 cos )] d 2 [2(1 cos )] dœ
''
02
2""
##
##
)) ))
4 1 2cos cos dœ
'0
2ab)))
#
4 1 2 cos cos d
'2ab)))
#
4 1 2 cos d 4 1 2 cos dœ
''
02
2ˆ‰ˆ‰
)) ))
1cos 2 1cos 2
##
))
(6 8 cos 2 cos 2 ) d (6 8 cos 2 cos 2 ) dœ
''
02
2
))) )))
6 8 sin sin 2 6 8 sin sin 2 6 16œ œcdcd))) )))1
11
1
Î#
!Î#
13. r 3 and r 6 cos 2 3 6 cos 2 cos 2œœÊœÊœ
È#"
#
)))
(in the 1st quadrant); we use symmetry of theʜ)1
6
graph to find the area, so
A4 (6 cos 2) 3 dœ
'0
6”•
Š‹
È
""
##
#
))
2 (6 cos 2 3) d 2 3 sin 2 3œœ
'0
6
)) ))cd
1Î'
!
33œ
È1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
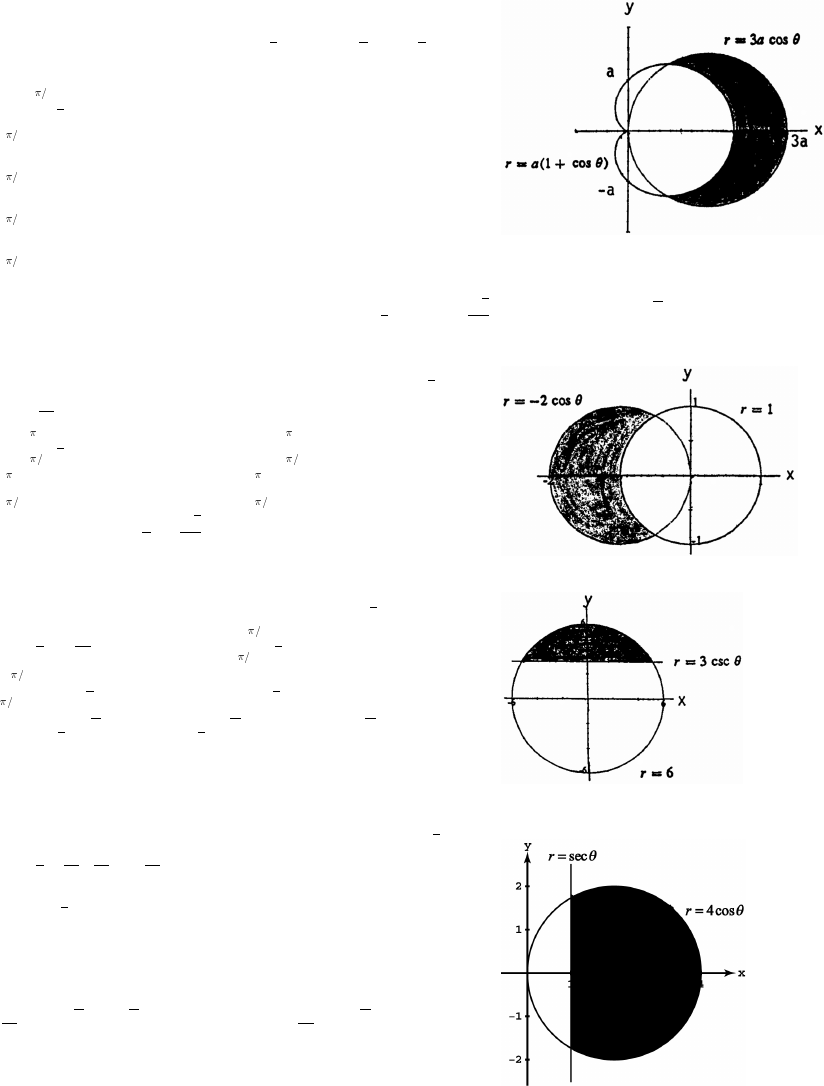
676 Chapter 11 Parametric Equatins and Polar Coordinates
14. r 3a cos and r a(1 cos ) 3a cos a(1 cos )œœÊœ))))
3 cos 1 cos cos or ;ʜʜʜ))))
"
#
11
33
the graph also gives the point of intersection (0 0); thereforeß
A 2 (3a cos ) a (1 cos ) dœ
'0
3"
#
## #
cd)))
9a cos a 2a cos a cos dœ
'0
3ab
## # # ##
))))
8a cos 2a cos a dœ
'0
3ab
## # #
)))
4a (1 cos 2 ) 2a cos a dœ
'0
3cd
###
)))
3a 4a cos 2 2a cos dœ
'0
3ab
## #
)))
3a 2a sin 2 2a sin a 2a 2a a 1 3œ œ œcd
ˆ‰ Š‹ Š ‹
È
## # ## # #
Î$
!"
##
)))1 1
1È3
15. r 1 and r 2 cos 1 2 cos cos œœÊœÊœ)))
"
#
in quadrant II; thereforeʜ)2
3
1
A 2 ( 2 cos ) 1 d 4 cos 1 dœœ
''
23 23
"
#
## #
cdab)) ))
[2(1 cos 2 ) 1] d (1 2 cos 2 ) dœœ
''
23 23
)) ))
sin 2œ œcd))
1
1
1
#Î$ #3
3
È
16. r 6 and r 3 csc 6 sin 3 sin œœ Ê œÊœ)) )
"
#
or ; therefore A 6 9 csc dÊœ œ )))
11
66
5'6
56
"
#
##
ab
18 csc d 18 cot œ œ
'6
56
ˆ‰‘
99
##
#&Î'
Î'
)) ) )
1
1
15 3 3 3 12 9 3œ œ
Š‹Š‹
ÈÈÈ
111
99
##
17. r sec and r 4 cos 4 cos sec cosœœÊœÊœ)))))
21
4
, , , or ; thereforeʜ)111 1
333 3
24 5
A 2 16 cos sec dœ
'0
31Î"
#
##
ab)))
88 cos2 sec dœ
'0
31Î#
ab)))
84sin2tan œ cd)))
0
31Î
23 3 000 3œ œ
Š‹
ÈÈ È
ab
88
33
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
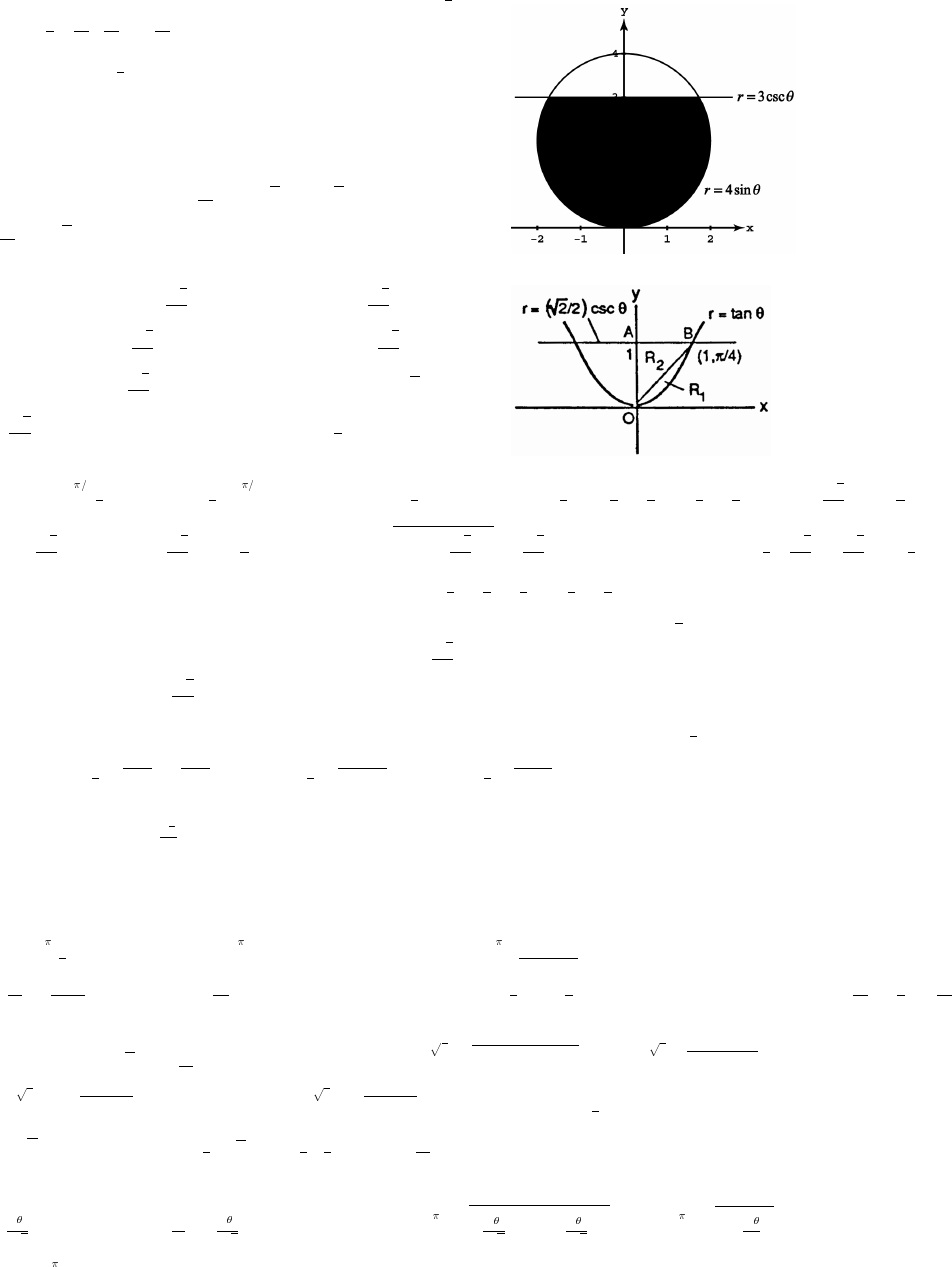
Section 11.5 Area and Lengths in Polar Coordinates 677
18. r 3 csc and r 4 sin 4 sin 3 csc sinœœÊœÊœ)))))
23
4
, , , or ; thereforeʜ)111 1
333 3
24 5
A 4 2 16 sin 9 csc dœ 1)))
'1
1
Î
Î"
#
##
3
2ab
4 8 8 cos 2 9 csc dœ 1)))
'1
1
Î
Î#
3
2ab
4 8 4 sin 2 9 cot œ 1) ) )cd
1
1
Î
Î
3
2
4 4 0 0 23 33œ 11
’“
ab
Š‹
ÈÈ
8
3
1
3œ
8
3
1È
19. (a) r tan and r csc tan csc œœ Êœ))))
Š‹ Š‹
ÈÈ
22
##
sin cos 1 cos cos ʜ ʜ
##
##
))))
Š‹ Š‹
ÈÈ
22
cos cos 1 0 cos 2 orÊ œÊœ
#
#
)) )
Š‹ È
È2
(use the quadratic formula) (the solution
È2
4#ʜ)1
in the first quadrant); therefore the area of R is
"
A tan d sec 1 d tan tan ; AO csc
""" " " "
## # # # ##
## Î%
!
œœœœœœ
''
00
44
)) ) ) ) )abcd
ˆ‰ Š‹
111 1 1
44 8
2
È
and OB csc 1 AB 1 the area of R is A ;œœ œÊœœÊ œ œ
ÈÈ ÈÈ ÈÈ
22 22 22
4 4## ## ###
##
##
""
Š‹ Š‹ Š‹Š‹
Ê
1
therefore the area of the region shaded in the text is 2 . Note: The area must be found this way
ˆ‰
""
##
œ
11
84 4
3
since no common interval generates the region. For example, the interval 0 generates the arc OB of r tan ŸŸ œ))
1
4
but does not generate the segment AB of the liner csc . Instead the interval generates the half-line from B toœÈ2
#)
on the line r csc ._ œ È2
#)
(b) lim tan and the line x 1 is r sec in polar coordinates; then lim (tan sec )
)1 )1ÄÎ ÄÎ2 2
)) ))œ_ œ œ
lim lim lim 0 r tan approachesœœ œ œÊœ
)1 )1 )1ÄÎ ÄÎ ÄÎ222
ˆ‰ ˆ‰ ˆ‰
sin sin 1 cos
cos cos cos sin
)))
)) ) )
"
)
r sec as r sec (or x 1) is a vertical asymptote of r tan . Similarly, r sec (or x 1)œ Ä Ê œ œ œ œ œ)) ) ) )
1
#
is a vertical asymptote of r tan .œ)
20. It is not because the circle is generated twice from 0 to 2 . The area of the cardioid is)1œ
A 2 (cos 1) d cos 2 cos 1 d 2 cos 1 dœœœ
'' '
00 0
"
# #
##
)) ) )) ))ab
ˆ‰
1cos 2)
2 sin . The area of the circle is A the area requested is actuallyœ œ œ œÊ œ
‘ ˆ‰
3sin 2 3 35
24 444
)) 1 1 111
1
)1
!## #
"#
21. r , 0 5 2 ; therefore Length (2 ) d 4 dœŸŸÊœ œ œ )) ) ) )) )))
### %#
#
ÈÉab È
dr
d)''
00
55
4 d (since 0) 4 d ; u 4 du d ; 0 u 4,œ œ œÊœœÊœ
''
00
55
kkÈÈ
)) ) ) )) ) ) )))
##
#"
#
5 u 9 u du u
“
ÈÈ‘
)œÊœÄ œ œ
'4
9""
##
$Î# *
%
219
33
22. r , 0 ; therefore Length d 2 dœŸŸÊœ œ œ
edre ee e
22 22
d
ÈÈ ÈÈ
)1 ) )
)''
00
ÊŠ‹ Š‹ Š‹
Ê
##
#
2
e d e e 1œœœ
'0
))1
1
)‘
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

678 Chapter 11 Parametric Equatins and Polar Coordinates
23. r 1 cos sin ; therefore Length (1 cos ) ( sin ) dœ Ê œ œ )) )))
dr
d)'0
2È##
2 2 2 cos d 2 d 4 d 4 cos d 4 2 sin 8œ œ œ œ œ œ
''''
0000
ÈÉɈ‰ ‘
)) ) ) )
4(1 cos ) 1cos
2
###
!
))))
1
24. r a sin , 0 , a 0 a sin cos ; therefore Length a sin a sin cos dœŸŸÊœ œ
#
### ###
###
))) )))
)
)1 )
dr
d'0Ɉ ‰ ˆ ‰
a sin a sin cos d a sin sin cos d (since 0 ) a sin dœ œ œŸŸ
''
00 0
ÉÉ
¸¸ ˆ‰
'
#% ## # # #
### ### #
))) ))) )
)))1)
2a cos 2aœ œ
‘
)1
2!
25. r , 0 ; therefore Length dœŸŸÊœ œ
6 dr 6 sin 6 6 sin
1cos d (1cos ) 1cos (1cos )#
##
))) ))
1) )
) )
'0
2ʈ‰
Š‹
d6 1 dœœ
''
00
22
ɸ¸
É
36 36 sin sin
(1 cos ) 1 cos (1 cos )
1cos
"
)))
))
)
ab
))
since 0 on 0 6 dœŸŸ
ˆ‰ˆ‰
É
""
#1cos 1cos (1cos )
1 2 cos cos sin
)))
1)))
))
'0
2
6 d 6 2 6 2 3 sec dœœœœ
''''
0000
2222
ˆ‰ ¸¸
ÉÈÈ
"
#
$
1cos (1cos )
22 cos d d
(1 cos ) 2 cos
))
))))
)
))
ˆ‰
3 sec d 6 sec u du (use tables) 6 sec u duœœ œ
'' '
00 0
24 4
$$
# #
Î%
!
")1
)Œ
‘
sec u tan u
2
6 ln sec u tan u 3 2 ln 1 2œ œ
Š‹’“
‘
kk
ÈÈ
Š‹
"" Î%
!
È22
1
26. r , ; therefore Length dœŸŸÊœ œ
2 dr 2 sin 2 2 sin
1cos d (1cos ) 1cos (1cos )#
##
))) ))
1) )
)1 )
'2ʈ‰
Š‹
1 d dœœ
''
22
ÊŠ‹
¸¸
É
4sin 2
(1 cos ) 1 cos (1 cos )
1cos
(1 cos ) sin
)))
)
)
))
ab
))
since 1 cos 0 on 2 dœŸŸ
ˆ‰ˆ‰
É
))1 )
1)))
))#
"
'21cos (1cos )
1 2 cos cos sin
2 d 2 2 2 2 csc dœœœœ
''''
2222
ˆ‰ ¸¸
ÉÈÈ
"
#
$
1cos (1cos )
22 cos d d
(1 cos ) 2 sin
))
))))
)
))
ˆ‰
csc d since csc 0 on 2 csc u du (use tables)œœŸŸ œ
''
2 4
2
$$
###
ˆ‰ ˆ ‰
))1
))1
2 csc u du 2 ln csc u cot u 2 ln 2 1
Œ
‘ ‘
Š‹’“
kk Š‹
È
œœ
csc u cot u
22
22
1
1 1
1
Î#
Î% Î%
""" ""
# #
Î#
'4
2
ÈÈ
2ln1 2œ
ÈÈ
Š‹
27. r cos sin cos ; therefore Length cos sin cos dœÊœ œ
$# $#
##
))) )))
)3d 3 3 3 3 3
dr '0
4Ɉ ‰ ˆ ‰ )
cos sin cos d cos cos sin d cos dœ œ œ
'''
000
444
ÉÉ
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰
'#% ##
##
))) ) )) )
333 3 33 3
)))
d sin œœœ
'0
41cos 32 3
23 88
##
"Î%
!
ˆ‰
2
3))
‘
)1
1
28. r 1 sin 2 , 0 2 (1 sin 2 ) (2 cos 2 ) (cos 2 )(1 sin 2 ) ; thereforeœ ŸŸ Êœ œ
ÈÈ
))1 ) ) ) )
dr
d)
"
#
"Î# "Î#
Length (1 sin 2 ) d dœ œ
''
00
22
ÉÉ
)) )
cos2 12 sin 2sin2cos2
(1 sin 2 ) 1 sin 2
))))
))
d 2 d 2 2œœœœ
''
00
22
ÉÈÈ
’“
22 sin 2
1sin 2
#
!
)
)
1
)))1
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 11.6 Conic Sections 679
29. Let r f( ). Then x f( ) cos f ( ) cos f( ) sin f ( ) cos f( ) sin œœÊœÊœ) ) ) ) )) ) ) )) )
dx dx
dd))
ww
##
ˆ‰ cd
f ( ) cos 2f ( ) f( ) sin cos [f( )] sin ; y f( ) sin f ( ) sin f( ) cos œ œÊœcd
w#w ## w
#
) ) )))) ) ) )) ))) )
dy
d)
f ( ) sin f( ) cos f ( ) sin 2f ( )f( ) sin cos [f( )] cos . ThereforeÊœ œ
Š‹ cdcd
dy
d)
#ww#w##
##
))) ) ) ) )))) ) )
f( ) cos sin [f( )] cos sin f( ) [f( )] r .
ˆ‰ ˆ‰
Š‹ cdababcd
dx dr
dd d
dy
)) )
# #
#w## ###w ##
##
œ œ œ))))))))
Thus, L d r d .œœ
''
ʈ‰ É ˆ‰
Š‹
dx dr
dd d
dy
)) )
##
##
))
30. (a) r a 0; Length a 0 d a d a 2 aœÊ œ œ œ œ œ
dr
d)
1
''
00
22
Èkk c d
## #
!
)))1
(b) r a cos a sin ; Length (a cos ) ( a sin ) d a cos sin dœÊœ œ œ )) ))))))
dr
d)''
00
ÈÈab
#####
a d a aœœœ
'0kk c d)) 1
1
!
(c) r a sin a cos ; Length (a cos ) (a sin ) d a cos sin dœÊœ œ œ )) ))) )))
dr
d)''
00
ÈÈab
## ###
a d a aœœœ
'0kk c d)) 1
1
!
31. (a) r a(1 cos ) d sin a
av 0
2
œœœ
"
#
!
20 2
a
11
1
')) ) )cd
(b) r a d a a
av 0
2
œœœ
""
#
#
!
2011
1
'))cd
(c) r a cos d a sin
av 2
2
œœœ
""
Î#
Î#
ˆ‰ˆ ‰')) )
11
1
1
cd 2a
32. r 2f( ), 2f ( ) r [2f( )] 2f ( ) Length 4[f( )] 4 f ( ) dœŸŸÊœÊœ Êœ )! ) " ) ) ) ) ) )
dr dr
dd))
w# #w
###w
#
ˆ‰ cd cd
É
'
2 [f( )] f ( ) d which is twice the length of the curve r f( ) for .œ œŸŸ
'Écd))) )!)"
#w
#
11.6 CONIC SECTIONS
1. x 4p 8 p 2; focus is (2 0), directrix is x 2œÊ œÊœ ß œ
y
8
2. x 4p 4 p 1; focus is ( 1 0), directrix is x 1œ Ê œ Ê œ ß œ
y
4
3. y 4p 6 p ; focus is , directrix is yœ Ê œ Ê œ !ß œ
x333
6## #
ˆ‰
4. y 4p 2 p ; focus is , directrix is yœÊ œÊœ !ß œ
x111
2## #
ˆ‰
5. 1 c 4 9 13 foci are 13 ; vertices are 2 0 ; asymptotes are y x
x 3
49
y
œÊœ œ Ê „ ß! „ß œ„
ÈÈÈ
Š‹ ab #
6. 1 c 9 4 5 foci are 0 5 ; vertices are 0 3
x
49
y
œÊœ œ Ê ß„ ß„
ÈÈÈ
Š‹ ab
7. y 1 c 2 1 1 foci are 1 0 ; vertices are 2
x
2œÊœ œÊ „ß „ ß!
#ÈÈ
ab Š‹
8. x 1 c 4 1 5 foci are 0 5 ; vertices are 2 ; asymptotes are y 2x
y
4œÊœ œ Ê ß„ !ß„ œ„
#ÈÈÈ
Š‹ ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
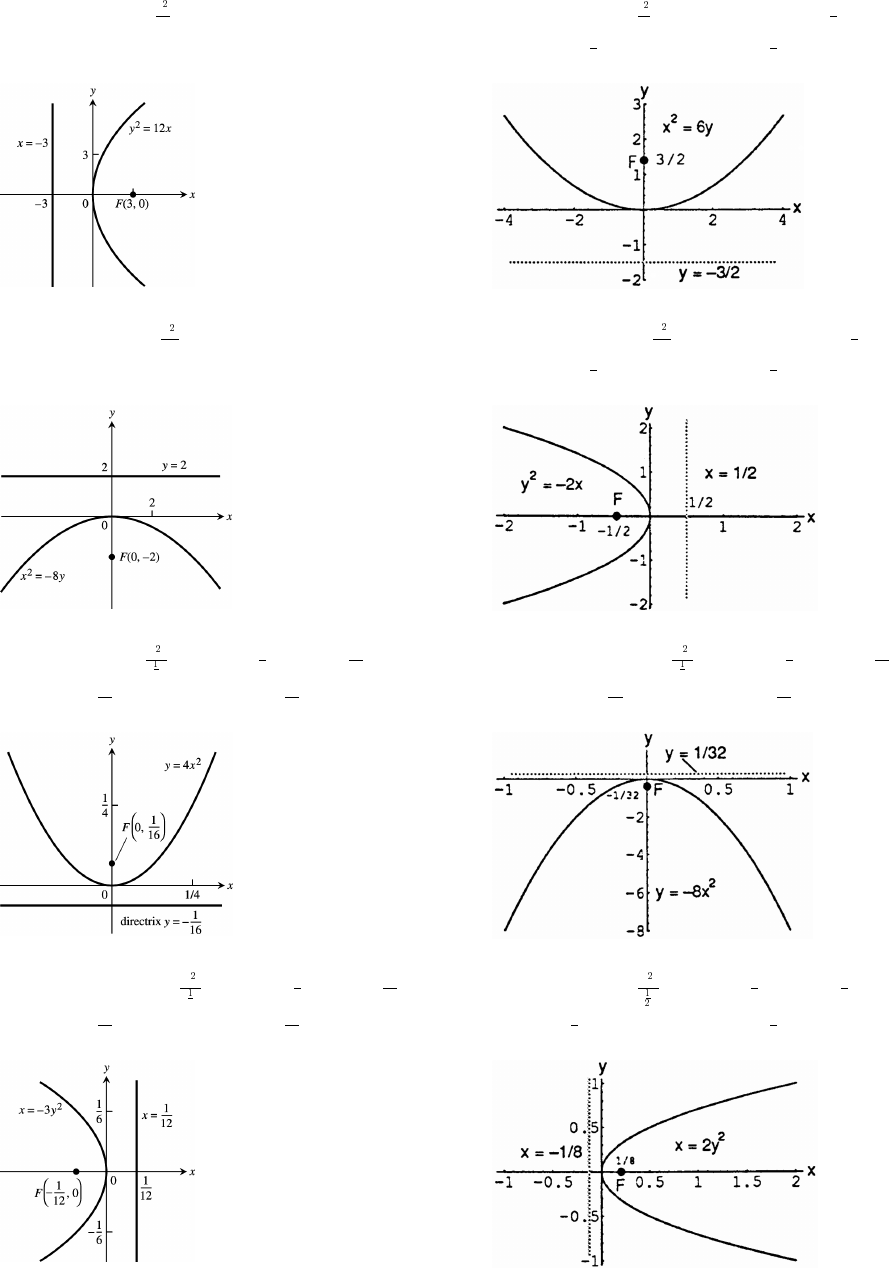
680 Chapter 11 Parametric Equatins and Polar Coordinates
9. y 12x x 4p 12 p 3; 10. x 6y y 4p 6 p ;
# #
# #
œ Êœ Ê œ Êœ œ Êœ Ê œÊœ
y
1 6
x3
focus is ( ), directrix is x 3 focus is , directrix is y$ß ! œ !ß œ
ˆ‰
33
##
11. x 8y y 4p 8 p 2; 12. y 2x x 4p 2 p ;
# #
# #
"
œ Êœ Ê œÊœ œ Êœ Ê œÊœ
x
8
y
focus is ( 2), directrix is y 2 focus is , directrix is x!ß œ ß ! œ
ˆ‰
""
##
13. y 4x y 4p p ; 14. y 8x y 4p p ;œÊœÊœÊœ œÊœÊœÊœ
# #
"" ""x x
416 832
ˆ‰ ˆ‰
4 8
focus is , directrix is y focus is , directrix is y
ˆ‰ ˆ ‰
!ß œ !ß œ
"" ""
#16 16 32 3
15. x 3y x 4p p ; 16. x 2y x 4p p ;œ Êœ Ê œÊœ œ Êœ Ê œÊœ
# #
"" ""
##
y y
31 8
ˆ‰ ˆ‰
3
focus is , directrix is x focus is , directrix is x
ˆ‰ ˆ‰
ß! œ ß! œ
"" " "
##11 8 8
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
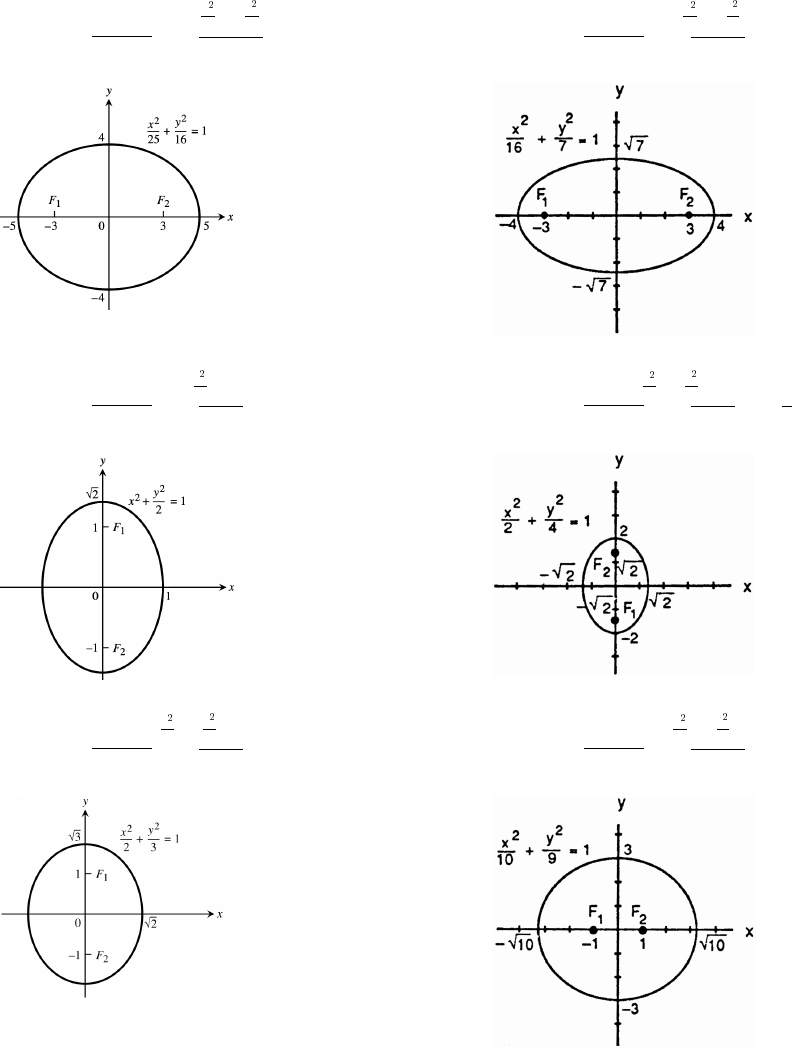
Section 11.6 Conic Sections 681
17. 16x 25y 400 1 18. 7x 16y 112 1
## ##
#
œÊœ œÊœ
x x
516 16 7
y y
cab 25163 cab 1673Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ
## ##
19. 2x y 2 x 1 20. 2x y 4 1
## # ##
##
œÊ œ œÊ œ
y y
x
4
cab 211 cab 422Êœ œ œ Êœ œ œ
ÈÈ
ÈÈÈ
## ##
21. 3x 2y 6 1 22. 9x 10y 90 1
## # #
#
œÊœ œÊœ
x x
y y
310 9
cab 321 cab 1091Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ
## ##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
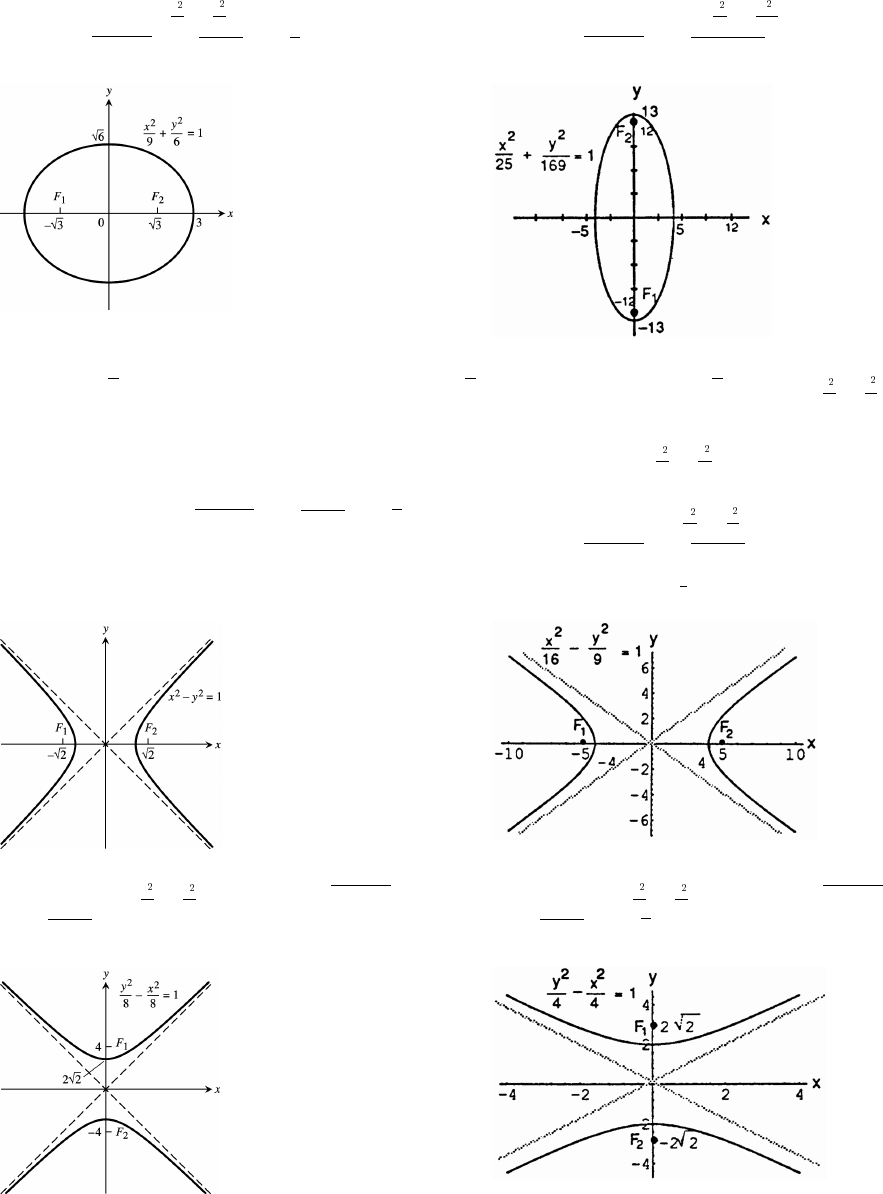
682 Chapter 11 Parametric Equations and Polar Coordinates
23. 6x 9y 54 1 24. 169x 25y 4225 1
## ##
œÊœ œ Êœ
x x
96 25 169
y y
c a b 9 6 3 c a b 169 25 12Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ È
## ##
25. Foci: 2 , Vertices: 2 0 a 2, c 2 b a c 4 2 2 1
Š‹ Š‹
ÈÈÈ
ab„ ß! „ß Êœ œ Ê œœ œÊ œ
### #
#
x
4
y
26. Foci: 4 , Vertices: 0 5 a 5, c 4 b 25 16 9 1ab ab!ß„ ß„ Êœ œÊ œœÊ œ
#
#
x
95
y
27. x y 1 c a b 1 1 2 ; 28. 9x 16y 144 1
## ##
##
œÊœ œ œ œ Ê œ
ÈÈ
Èx
16 9
y
asymptotes are y x c a b 16 9 5;œ„ Ê œ œ œ
ÈÈ
##
asymptotes are y xœ„
3
4
29. y x 8 1 c a b 30. y x 4 1 c a b
## ##
## ##
œÊ œÊœ œÊ œÊœ
y y
88 44
x x
ÈÈ
8 8 4; asymptotes are y x 4 4 2 2; asymptotes are y xœœ œ„ œœ œ„
ÈÈ
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
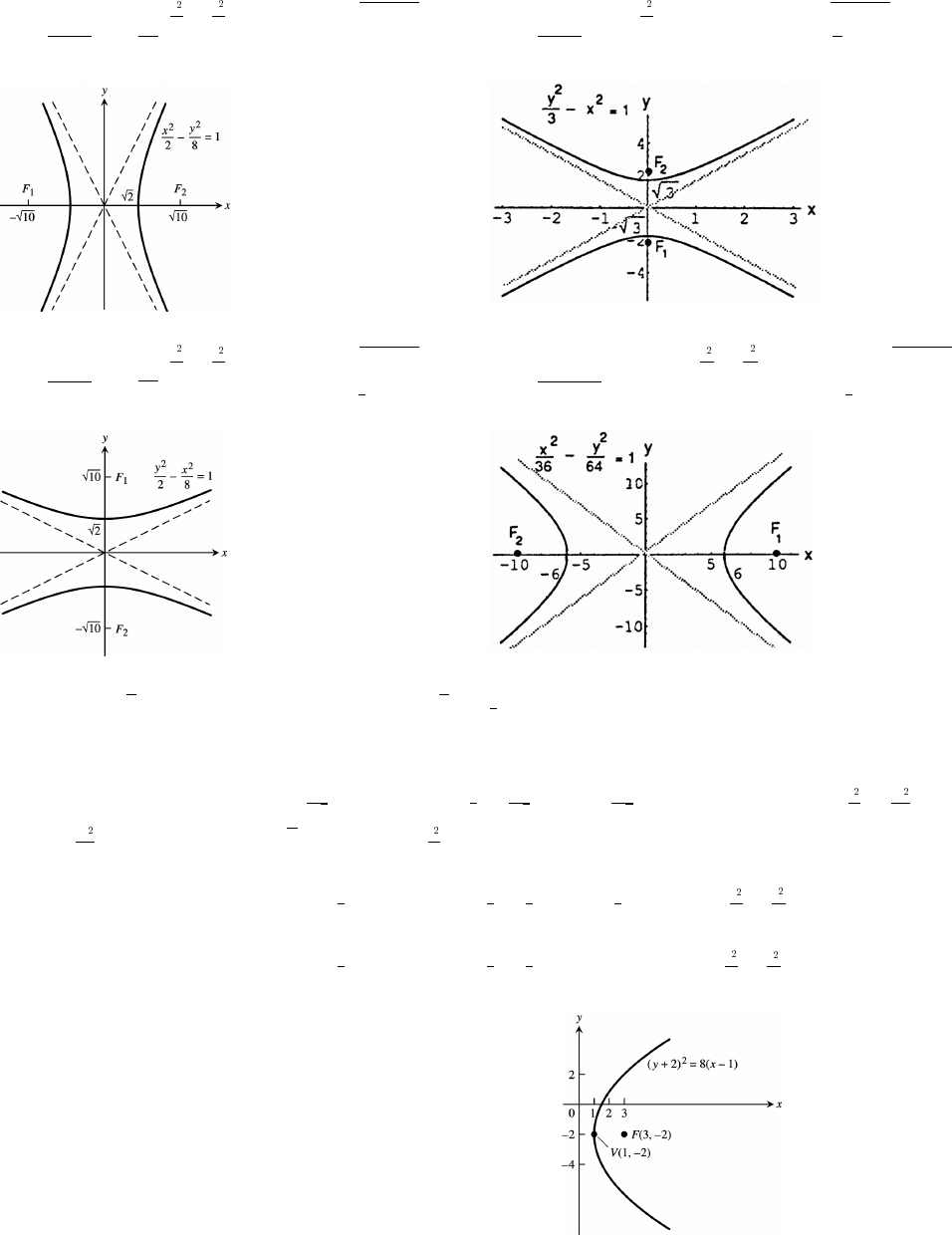
Section 11.6 Conic Sections 683
31. 8x 2y 16 1 c a b 32. y 3x 3 x 1 c a b
## ## #
### ##
œÊœÊœ œÊœÊœ
xyy
83
ÈÈ
2 8 10 ; asymptotes are y 2x 3 1 2; asymptotes are y 3xœœ œ„ œœ œ„
ÈÈ
È È
33. 8y 2x 16 1 c a b 34. 64x 36y 2304 1 c a b
## # #
### ##
œ Ê œÊœ œ Ê œÊœ
y y
x x
836 64
ÈÈ
2 8 10 ; asymptotes are y 36 64 10; asymptotes are yœœ œ„ œ œ œ„
ÈÈ
Èx 4
3#
35. Foci: 2 , Asymptotes: y x c 2 and 1 a b c a b 2a 2 2a
Š‹
ÈÈ
!ß „ œ „ Ê œ œ Ê œ Ê œ œ Ê œ
a
b### # #
a 1 b 1 y x 1ÊœÊœÊ œ
##
36. Foci: 2 , Asymptotes: y x c 2 and b c a b aab„ß! œ„ Ê œ œ Ê œ Ê œ œ œ
""
####
ÈÈÈ
333
ba a4a
a33
4 a 3 a 3 b 1 y 1Êœ Ê œÊœ ÊœÊ œ
4a x
33
##
È
37. Vertices: 3 0 , Asymptotes: y x a 3 and b (3) 4 1ab„ß œ„ Ê œ œ Ê œ œ Ê œ
4b44x
3a33916
y
38. Vertices: 2 , Asymptotes: y x a 2 and b 2(2) 4 1ab!ß „ œ „ Ê œ œ Ê œ œ Ê œ
1a1 x
2b2 416
y
39. (a) y 8x 4p 8 p 2 directrix is x 2,
#œ Ê œÊœÊ œ
focus is ( ), and vertex is ( 0); therefore the new#ß ! !ß
directrix is x 1, the new focus is (3 2), and theœ ß
new vertex is (1 2)ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
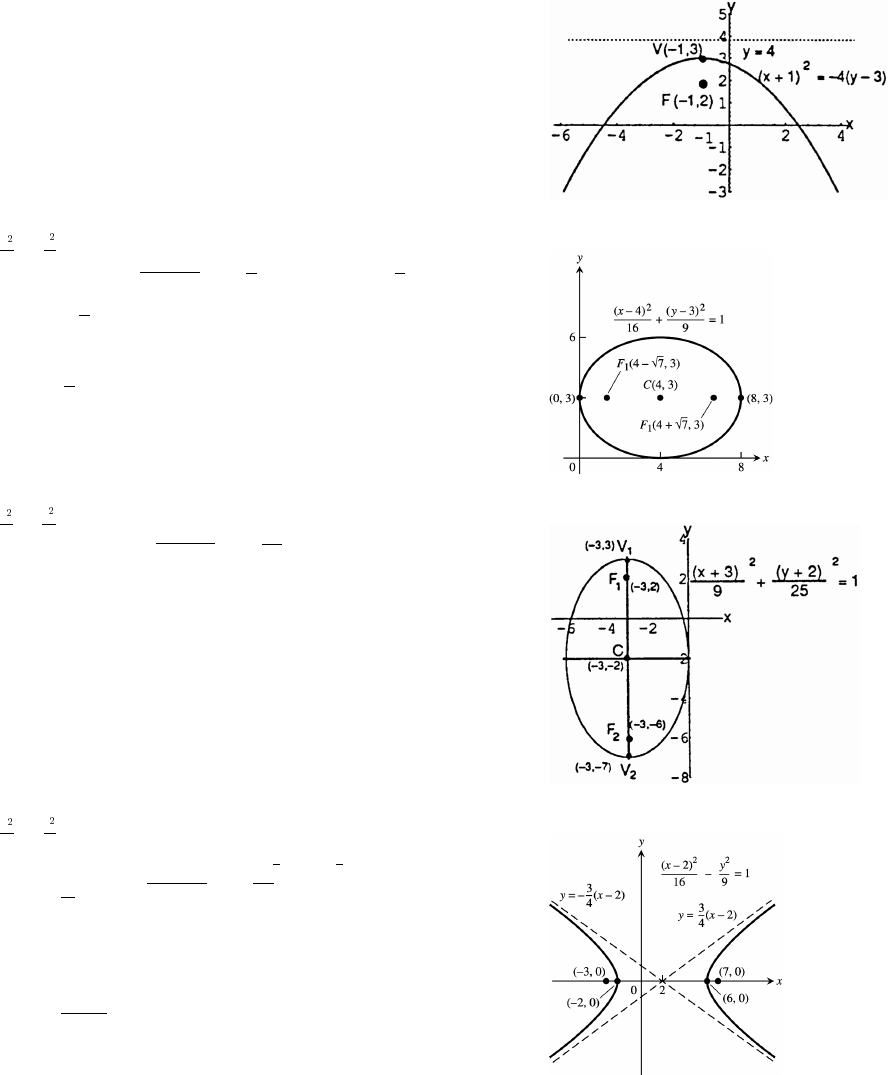
684 Chapter 11 Parametric Equations and Polar Coordinates
40. (a) x 4y 4p 4 p 1 directrix is y 1,
#œ Ê œ Ê œ Ê œ
focus is ( 1), and vertex is ( 0); therefore the new!ß !ß
directrix is y 4, the new focus is ( 1 2), and theϧ
new vertex is ( 1 3)ß
(b)
41. (a) 1 center is ( 0), vertices are ( 4 0)
x
16 9
y
œÊ !ß ß
and ( ); c a b 7 foci are 7 0%ß ! œ œ Ê ß
ÈÈÈ
Š‹
##
and 7 ; therefore the new center is ( ), the
Š‹
È
ß! %ß$
new vertices are ( 3) and (8 3), and the new foci are!ß ß
47
Š‹
È
„ß$
(b)
42. (a) 1 center is ( 0), vertices are (0 5)
x
925
y
œÊ !ß ß
and (0 5); c a b 16 4 foci areß œ œ œ Ê
ÈÈ
##
( 4) and ( 4) ; therefore the new center is ( 3 2),!ß !ß ß
the new vertices are ( 3 3) and ( 3 7), and the newß ß
foci are ( 3 2) and ( 3 6)ß ß
(b)
43. (a) 1 center is ( 0), vertices are ( 4 0)
x
16 9
y
œÊ !ß ß
and (4 0), and the asymptotes are orßœ„
x
43
y
y ; c a b 25 5 foci areœ„ œ œ œ Ê
3x
4ÈÈ
##
( 5 0) and (5 0) ; therefore the new center is (2 0), theß ß ß
new vertices are ( 2 0) and (6 0), the new fociß ß
are ( 3 0) and (7 0), and the new asymptotes areß ß
yœ„
3(x 2)
4
(b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
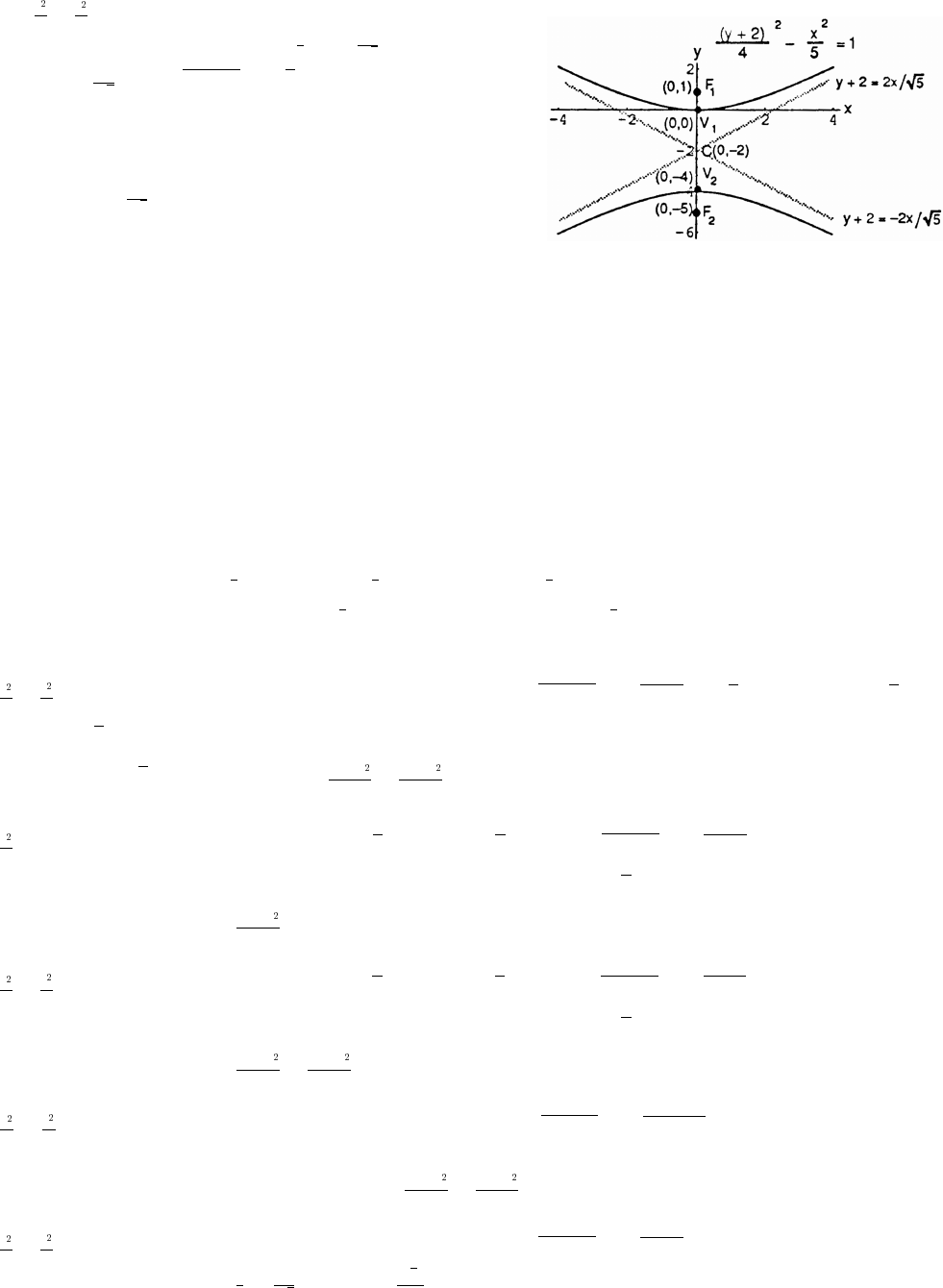
Section 11.6 Conic Sections 685
44. (a) 1 center is ( 0), vertices are (0 2)
y
45
x
œÊ !ß ß
and (0 2), and the asymptotes are orßœ„
y
2
x
5
È
y ; c a b 9 3 foci areœ„ œ œ œ Ê
2x
5
ÈÈÈ
##
(0 3) and (0 3) ; therefore the new center is (0 2),ßß ß
the new vertices are (0 4) and (0 0), the new fociß ß
are (0 1) and (0 5), and the new asymptotes areßß
y2œ„
2x
5
È
(b)
45. y 4x 4p 4 p 1 focus is ( 0), directrix is x 1, and vertex is (0 0); therefore the new
#œ Ê œÊœÊ "ß œ ß
vertex is ( 2 3), the new focus is ( 1 3), and the new directrix is x 3; the new equation isß ß œ
(y 3) 4(x 2)œ
#
46. y 12x 4p 12 p 3 focus is ( 3 0), directrix is x 3, and vertex is (0 0); therefore the new
#œ Ê œ Ê œ Ê ß œ ß
vertex is (4 3), the new focus is (1 3), and the new directrix is x 7; the new equation is (y 3) 12(x 4)ßß œ œ
#
47. x 8y 4p 8 p 2 focus is (0 2), directrix is y 2, and vertex is (0 0); therefore the new
#œ Ê œÊœÊ ß œ ß
vertex is (1 7), the new focus is (1 5), and the new directrix is y 9; the new equation isß ß œ
(x 1) 8(y 7)œ
#
48. x 6y 4p 6 p focus is , directrix is y , and vertex is (0 0); therefore the new
#
## #
œ Ê œ Ê œ Ê !ß œ ß
33 3
ˆ‰
vertex is ( 3 2), the new focus is 3 , and the new directrix is y ; the new equation isß ß œ
ˆ‰
"
##
7
(x 3) 6(y 2)œ
#
49. 1 center is ( 0), vertices are (0 3) and ( 3); c a b 9 6 3 foci are 3
x
69
y
œ Ê !ß ß !ß œ œ œ Ê !ß
ÈÈÈ È
Š‹
##
and 3 ; therefore the new center is ( 1), the new vertices are ( 2 2) and ( 4), and the new foci
Š‹
È
!ß #ß ß #ß
are 1 3 ; the new equation is 1
Š‹
È
#ß „ œ
(x 2) (y 1)
69
50. y 1 center is ( 0), vertices are 2 and 2 ; c a b 2 1 1 foci are
x
2œÊ !ß ß! ß! œ œ œÊ
###
Š‹Š ‹
ÈÈ È
È
( 1 0) and ( ); therefore the new center is (3 4), the new vertices are 3 2 4 , and the new foci are (2 4) ß "ß ! ß „ ß ß
Š‹
È
and (4 4); the new equation is (y 4) 1ߜ
(x 3)
#
#
51. 1 center is ( 0), vertices are 3 and 3 ; c a b 3 2 1 foci are
x
3
y
œÊ !ß ß! ß! œ œ œÊ
###
Š‹Š ‹
ÈÈ È
È
( 1 0) and ( ); therefore the new center is (2 3), the new vertices are 2 3 3 , and the new foci are (1 3) ß "ß ! ß „ ß ß
Š‹
È
and (3 3); the new equation is 1ߜ
(x 2) (y 3)
3
#
52. 1 center is ( 0), vertices are ( ) and ( 5); c a b 25 16 3 foci are
x
16 5
y
œ Ê !ß !ß & !ß œ œ œ Ê
###
ÈÈ
(0 3) and (0 3); therefore the new center is ( 4 5), the new vertices are ( 4 0) and ( 4 10), and the newß ß ß ß ß
foci are ( 4 2) and ( 4 8); the new equation is 1ß ß œ
(x 4) (y 5)
16 5
#
53. 1 center is ( 0), vertices are (2 0) and ( 2 0); c a b 4 5 3 foci are ( ) and
x
45
y
œ Ê !ß ß ß œ œ œ Ê $ß !
ÈÈ
##
( 3 0); the asymptotes are y ; therefore the new center is (2 2), the new vertices areß „ œ Ê œ„ ß
xy
5
5x
##
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
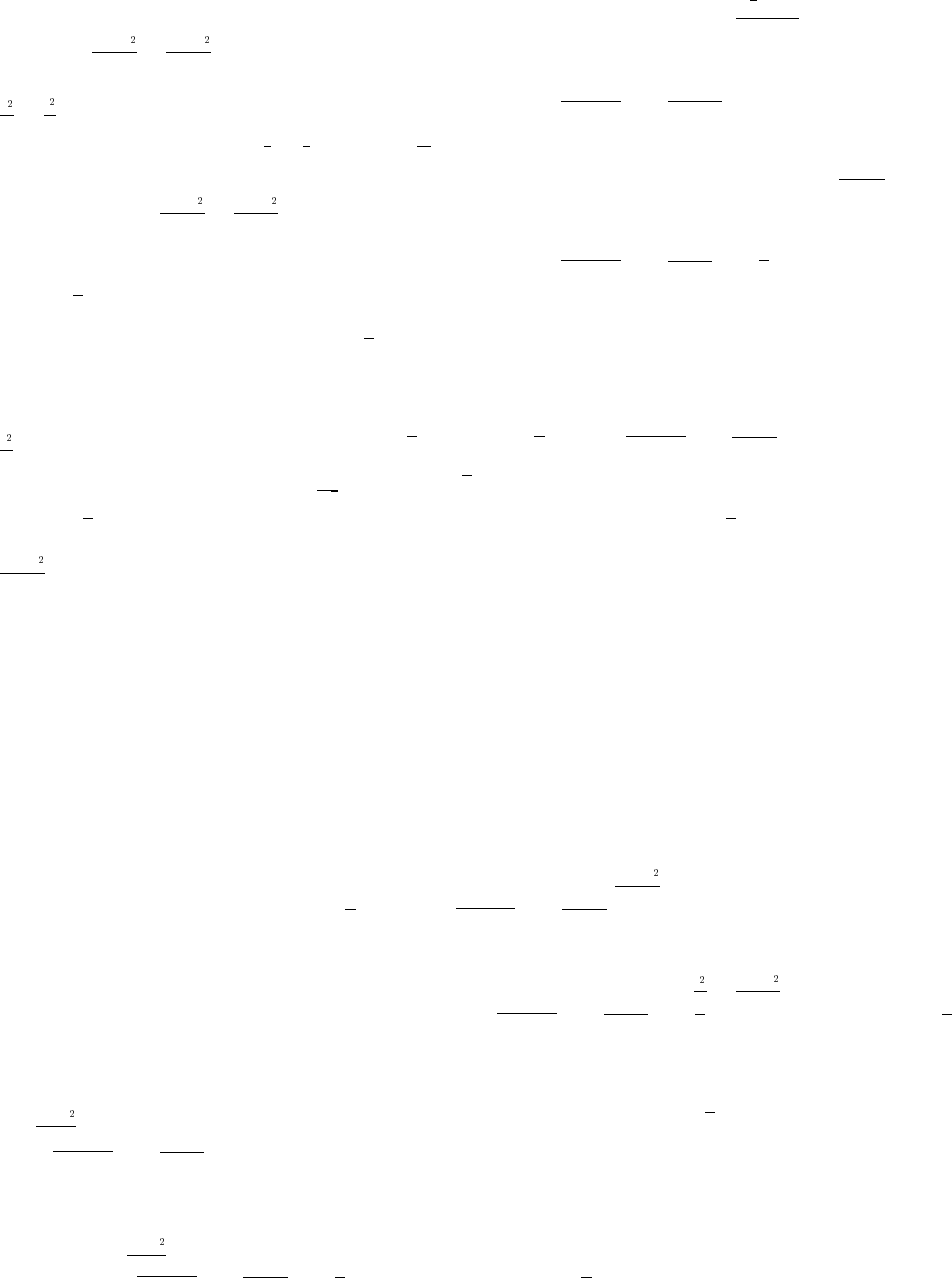
686 Chapter 11 Parametric Equations and Polar Coordinates
(4 2) and (0 2), and the new foci are (5 2) and ( 1 2); the new asymptotes are y 2 ; the newßß ßß œ„
È5(x 2)
#
equation is 1
(x 2) (y 2)
45
œ
54. 1 center is ( 0), vertices are (4 0) and ( 4 0); c a b 16 9 5 foci are ( 5 )
x
16 9
y
œ Ê !ß ß ß œ œ œ Ê ß!
ÈÈ
##
and (5 0); the asymptotes are y ; therefore the new center is ( 5 1), the new vertices areß „ œ Ê œ„ ß
x3x
43 4
y
( 1 1) and ( 9 1), and the new foci are ( 10 1) and (0 1); the new asymptotes are y 1 ;ß ß ß ß œ„
3(x 5)
4
the new equation is 1
(x 5) (y 1)
16 9
œ
55. y x 1 center is ( 0), vertices are (0 1) and (0 1); c a b 1 1 2 foci are
## ##
œÊ !ß ß ß œ œ œ Ê
ÈÈ
È
2 ; the asymptotes are y x; therefore the new center is ( 1 1), the new vertices are ( 1 0) and
Š‹
È
!ß „ œ „ ß ß
( 1 2), and the new foci are 1 1 2 ; the new asymptotes are y 1 (x 1); the new equation isß ß „ œ„
Š‹
È
(y 1) (x 1) 1œ
##
56. x 1 center is ( 0), vertices are 0 3 and 3 ; c a b 3 1 2 foci are ( )
y
3œÊ !ß ß !ß œ œ œÊ !ß#
###
Š‹Š ‹
ÈÈ
ÈÈ
and ( 2); the asymptotes are x y 3x; therefore the new center is (1 3), the new vertices are!ß „ œ Ê œ „ ß
y
3
ÈÈ
3 , and the new foci are ( ) and (1 1); the new asymptotes are y 3 3 (x 1); the new equation is
Š‹
ÈÈ
"ß $ „ "ß & ß œ „
(x 1) 1
(y 3)
3
#
œ
57. x 4x y 12 x 4x 4 y 12 4 (x 2) y 16; this is a circle: center at C( 2 0), a 4
## # # ##
œ Ê œÊ œ ß œ
58. 2x 2y 28x 12y 114 0 x 14x 49 y 6y 9 57 49 9 (x 7) (y 3) 1;
## # # # #
œÊœÊœ
this is a circle: center at C(7 3), a 1ß œ
59. x 2x 4y 3 0 x 2x 1 4y 3 1 (x 1) 4(y 1); this is a parabola: V( 1 1), F( 1 0)
## #
œÊ œÊ œ ß ß
60. y 4y 8x 12 0 y 4y 4 8x 12 4 (y 2) 8(x 2); this is a parabola: V( 2), F( )
## #
œÊ œÊ œ #ß !ß#
61. x 5y 4x 1 x 4x 4 5y 5 (x 2) 5y 5 y 1; this is an ellipse: the
## # # ## #
œÊœÊœÊ œ
(x 2)
5
center is ( 2 0), the vertices are 2 5 0 ; c a b 5 1 2 the foci are ( 4 0) and ( 0)ß „ ß œ œ œ Ê ß !ß
Š‹
ÈÈÈ
##
62. 9x 6y 36y 0 9x 6 y 6y 9 54 9x 6(y 3) 54 1; this is an ellipse:
## # # # #
œÊ œÊ œÊ œab x
69
(y 3)
the center is (0 3), the vertices are ( 0) and ( 6); c a b 9 6 3 the foci are 0 3 3ß !ß !ß œ œ œ Ê ß „
ÈÈÈ È
Š‹
##
63. x 2y 2x 4y 1 x 2x 1 2 y 2y 1 2 (x 1) 2(y 1) 2
## # # # #
œÊ œÊœab
(y 1) 1; this is an ellipse: the center is (1 1), the vertices are 2 ;Ê œ ß "„ß"
(x 1)
2
#Š‹
È
c a b 2 1 1 the foci are (2 1) and (0 1)œœœÊ ß ß
ÈÈ
##
64. 4x y 8x 2y 1 4 x 2x 1 y 2y 1 4 4(x 1) (y 1) 4
## # # # #
œÊ œÊ œab
(x 1) 1; this is an ellipse: the center is ( 1 1), the vertices are ( 1 3) andÊ œ ß ß
#(y 1)
4
( 1 1); c a b 4 1 3 the foci are 1 3ß œ œ œ Ê ß"„
ÈÈÈÈ
Š‹
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
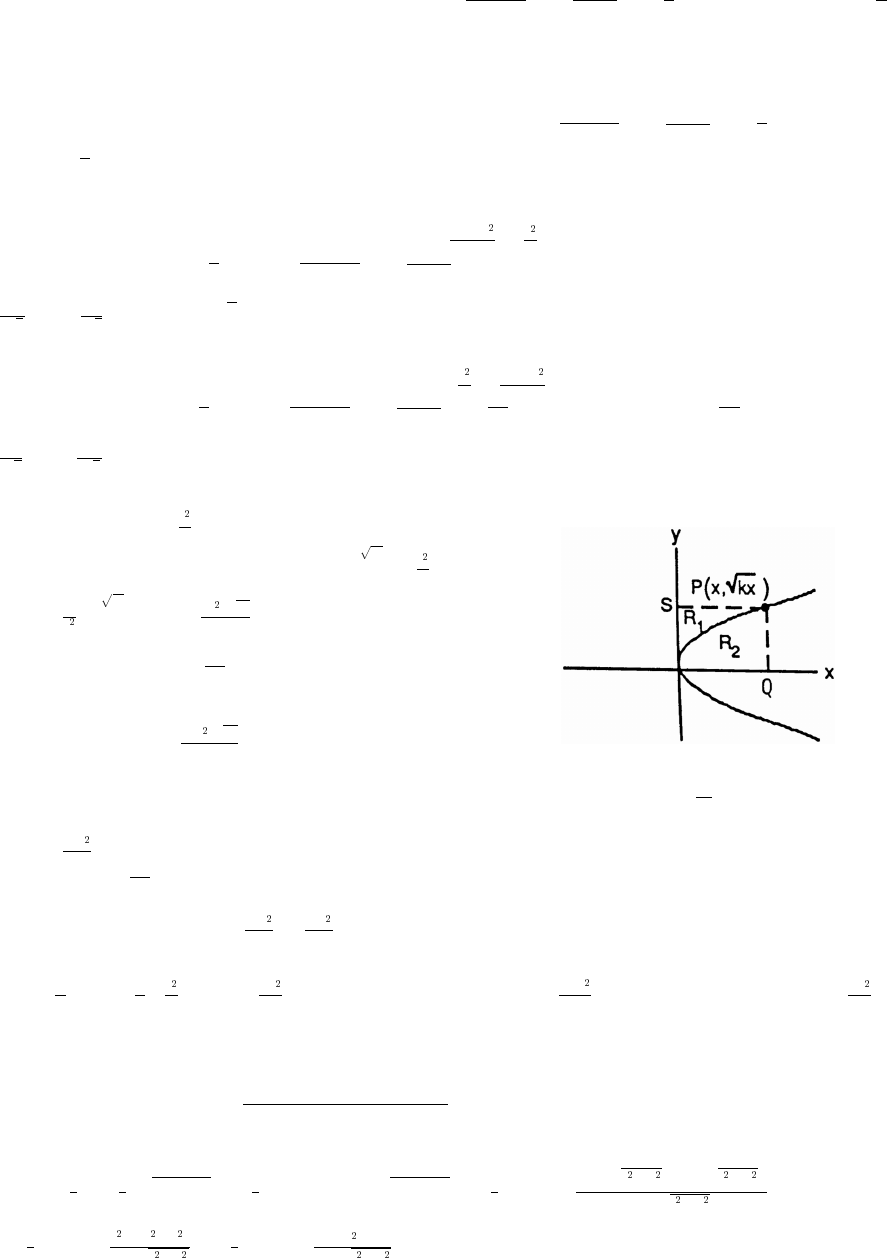
Section 11.6 Conic Sections 687
65. x y 2x 4y 4 x 2x 1 y 4y 4 1 (x 1) (y 2) 1; this is a hyperbola:
## # # # #
œÊ œÊ œab
the center is (1 2), the vertices are (2 2) and ( 2); c a b 1 1 2 the foci are 1 2 ;ß ß !ß œ œ œ Ê „ ß #
ÈÈ È
ÈŠ‹
##
the asymptotes are y 2 (x 1)œ„
66. x y 4x 6y 6 x 4x 4 y 6y 9 1 (x 2) (y 3) 1; this is a hyperbola:
## # # # #
œÊ œÊ œab
the center is ( 2 3), the vertices are ( 1 3) and ( 3 3); c a b 1 1 2 the foci areß ß ß œ œ œ Ê
ÈÈ
È
##
2 2 3 ; the asymptotes are y 3 (x 2)
Š‹
È
„ ß œ„
67. 2x y 6y 3 2x y 6y 9 6 1; this is a hyperbola: the center is ( ),
## # #
œ Ê œ Ê œ !ß $ab(y 3)
63
x
the vertices are 3 6 ; c a b 6 3 3 the foci are (0 6) and ( 0); the asymptotes are
Š‹
ÈÈÈ
!ß „ œ œ œ Ê ß !ß
##
y2x3
y3
63
x
ÈÈ
œ„ Ê œ„
È
68. y 4x 16x 24 y 4 x 4x 4 8 1; this is a hyperbola: the center is (2 0),
## # #
œÊ œÊ œ ßab
y(x2)
82
the vertices are 2 8 ; c a b 8 2 10 the foci are 2 10 ; the asymptotes are
Š‹ Š ‹
ÈÈÈ
ÈÈ
ß„ œ œ œ Ê ß„
##
y 2(x 2)
y
8
x2
2
ÈÈ
œ„ Ê œ„
69. (a) y kx x ; the volume of the solid formed by
#œÊœ
y
k
revolving R about the y-axis is V dy
""
#
œ'0
kx
1Š‹
y
k
y dy ; the volume of the rightœœ
11
k5
xkx
'0
kx %È
circular cylinder formed by revolving PQ about the
y-axis is V x kx the volume of the solid
##
œÊ1È
formed by revolving R about the y-axis is
#
V V V . Therefore we can see the
$#"
œœ
4x kx
5
1È
ratio of V to V is 4:1.
$"
(b) The volume of the solid formed by revolving R about the x-axis is V kt dt k t dt
#"
#
œœ
''
00
xx
11
Š‹
È
. The volume of the right circular cylinder formed by revolving PS about the x-axis isœ1kx
#
V kx x kx the volume of the solid formed by revolving R about the x-axis is
# "
##
œœÊ11
Š‹
È
V V V kx . Therefore the ratio of V to V is 1:1.
$#" $"
#
##
œœ œ111kx kx
70. y x dx C C; y 0 when x 0 0 C C 0; therefore y is theœœœœœÊœÊœ œ
'wwx wx wx
H H 2H 2H 2H
w(0)
Š‹
#
equation of the cable's curve
71. x 4py and y p x 4p x 2p. Therefore the line y p cuts the parabola at points ( 2p p) and
###
œœÊœÊœ„ œ ß
(2p p), and these points are [2p ( 2p)] (p p) 4p units apart.ߜ
È##
72. lim x x a lim x x a lim
xxxÄ_ Ä_ Ä_
Š‹Š‹
ÈÈ
–—
bb b b
aa a a
xxaxxa
xxa
œ œ
## ##
Š‹Š‹
ÈÈ
È
lim lim 0œœœ
bba
aa
xxa
xxa xxa
xxÄ_ Ä_
’“ ’“
ab
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

688 Chapter 11 Parametric Equations and Polar Coordinates
73. Let y 1 on the interval 0 x 2. The area of the inscribed rectangle is given byœ ŸŸ
Éx
4
A(x) 2x 2 1 4x 1 (since the length is 2x and the height is 2y)œœ
Š‹
ÉÉ
xx
44
A (x) 4 1 . Thus A (x) 0 4 1 0 4 1 x 0 x 2Ê œ œÊ œÊ œÊ œ
ww ##
ÉÉ
Š‹
xx xx x
444
11
ÉÉ
x x
4 4
x 2 (only the positive square root lies in the interval). Since A(0) A(2) 0 we have that A 2 4Êœ œ œ œ
È È
Š‹
is the maximum area when the length is 2 2 and the height is 2.
ÈÈ
74. (a) Around the x-axis: 9x 4y 36 y 9 x y 9 x and we use the positive root
## # # #
œÊœ Êœ„
99
44
É
V 2 9 x dx 2 9 x dx 2 9x x 24Êœ œ œ œ
''
00
22
1111
Š‹
Ɉ‰ ‘
993
444
###$
#
!
(b) Around the y-axis: 9x 4y 36 x 4 y x 4 y and we use the positive root
## # # #
œÊœ Êœ„
44
99
É
V 2 4 y dy 2 4 y dy 2 4y y 16Êœ œ œ œ
''
00
33
1111
Š‹
Ɉ‰ ‘
444
9927
###$
$
!
75. 9x 4y 36 y y x 4 on the interval 2 x 4 V x 4 dx
## #
##
##
#
œÊœ Êœ„ ŸŸÊœ
9x 36 3 3
4ÈÈ
Š‹
'2
4
1
x 4 dx 4x 16 8 8 (56 24) 24œœœœœœ
9 9 x 9 64 8 9 56 3
443433434
111 11
'2
4ab ’“‘ˆ‰ˆ‰ˆ‰
#%
#1
76. Let P ( p y ) be any point on x p, and let P(x y) be a point where a tangent intersects y 4px. Now
"" #
ß œ ß œ
y 4px 2y 4p ; then the slope of a tangent line from P is
#"
œÊ œÊœ œœ
dy dy 2p y y dy 2p
dx dx y x ( p) dx y
y yy 2px 2p . Since x , we have y yy 2p 2p y yy y 2pÊ œ œ œ Ê œ
## # ####
"""
"
#
yy
4p 4p
Š‹
y yy 2p 0 y y y 4p . Therefore the slopes of the twoʜʜ œ„
"
##
##
""
„ ##
2y 4y 16p
ÈÈ
tangents from P are m and m m m 1
"" # "#
œœÊœœ
2p 2p 4p
y y 4p y y 4p yy4p
ÈÈ ab
the lines are perpendicularÊ
77. (x 2) (y 1) 5 2(x 2) 2(y 1) 0 ; y 0 (x 2) (0 1) 5 œÊ œÊ œ œÊ œ
## ##
dy dy
dx dx y 1
x2
(x 2) 4 x 4 or x 0 the circle crosses the x-axis at (4 0) and ( 0); x 0Ê œ Ê œ œ Ê ß !ß œ
#
(0 2) (y 1) 5 (y 1) 1 y 2 or y 0 the circle crosses the y-axis at ( 2) and ( ).Ê œ Ê œ Ê œ œ Ê !ß !ß !
## #
At (4 0): 2 the tangent line is y 2(x 4) or y 2x 8ßœœÊ œ œ
dy
dx 0 1
42
At ( ): 2 the tangent line is y 2x!ß ! œ œ Ê œ
dy
dx 0 1
02
At ( ): 2 the tangent line is y 2 2x or y 2x 2!ß # œ œ Ê œ œ
dy
dx 2 1
02
78. x y 1 x 1 y on the interval 3 y 3 V 1 y dy 2 1 y dy
## ###
##
œÊœ„ ŸŸÊ œ œ
ÈÈÈ
ˆ‰ ˆ‰
''
30
33
11
2 1 y dy 2 y 24œœœ111
'0
3ab ’“
#$
!
y
3
79. Let y 16 x on the interval 3 x 3. Since the plate is symmetric about the y-axis, x 0. For aœ ŸŸ œ
É16
9#
vertical strip: x y x , length 16 x , width dx area dA 16 x dxab
ÉÉ
µµ
ßœß œ œÊ œœ
É16 x 16 16
99
###
16
9
mass dm dA 16 x dx. Moment of the strip about the x-axis:Êœœœ $$
É16
9#
y dm 16 x dx 8 x dx so the moment of the plate about the x-axis is
µœœ
É16 x 16 8
99
###
16
9Š‹
Ɉ‰
$$
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
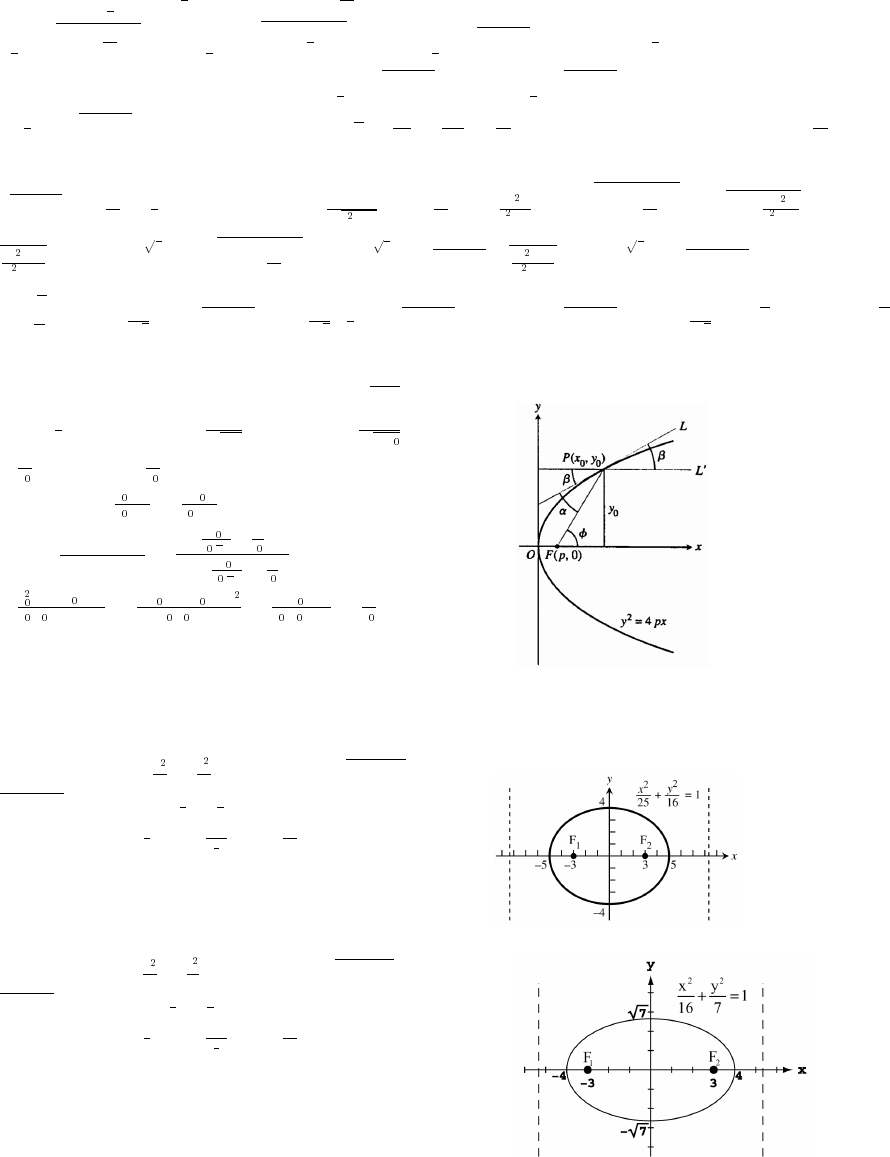
Section 11.7 Conics in Polar Coordinates 689
M y dm 8 x dx 8x x 32 ; also the mass of the plate is
x3
3
œœ œ œ
µ
''$$ $
ˆ‰ ‘
88
927
#$
$
$
M 16 x dx 4 1 x dx 4 3 1 u du where u 3 du dx; x 3œœœ œÊœœ
'' '
33 1
33 1
$$$
ÉɈ‰ È
16 x
93 3
##
"#
u 1 and x 3 u 1. Hence, 4 3 1 u du 12 1 u duÊœ œÊœ œ $$
''
11
11
ÈÈ
##
12 u 1 u sin u 6 y . Therefore the center of mass is .œœÊœœœ !ß$1$
’“Š‹
Ȉ‰
"#" "
"
2M633
M32 16 16
x$
1$ 1 1
80. y x 1 x 1 (2x) 1 1œÊœ œ Ê œ Ê œ
Èab Š‹ Š‹
ÊÉ
#"
#
#"Î#
##
dy dy dy
dx dx x 1 dx x 1
xx x
x1
È
S 2 y 1 dx 2 x 1 dx 2 2x 1 dx ;œÊœ œ œ
ÉÉ
ÊŠ‹ ÈÈ
2x 1 2x 1
x1 dx x1
dy
###
'' '
00 0
22 2
11 1
u1 du uu1lnu u1 25ln2 5
u2x
du 2 dx
–—
È
ÈÈÈÈ
’“’“Š‹Š‹Š‹ÈÈ
œ
œÄ œ œ
22
22 2
2
11 1
ÈÈ È
'0
2###
"#
!
81. (a) tan m tan f (x ) where f(x) 4px ;""œÊ œ œ
Lw!È
f (x) (4px) (4p) f (x )
w "Î# w
"
#!
œœÊœ
2p 2p
4px 4px
ÈÈ
tan .œÊ œ
2p 2p
yy
"
(b) tan m9œœ œ
FP
y0 y
xp xp
(c) tan !œœ
tan tan
1tan tan
9"
9"
Š‹
Š‹Š‹
y
xp y
2p
y
xp y
2p
c
b1
œœ œœ
y 2p(x p)
y (x p 2p) y (x p) y (x p) y
4px 2px 2p 2p(x p) 2p
11.7 CONICS IN POLAR COORDINATES
1. 16x 25y 400 1 c a b
##
###
œÊœÊœ
x
516
yÈ
25 16 3 e ; F 3 0 ;œœÊœœ „ß
Èab
c3
a5
directrices are x 0œ „ œ„ œ„
a525
e3
ˆ‰
3
5
2. 7x 16y 112 1 c a b
## ##
œÊœÊœ
x
16 7
yÈ
16 7 3 e ; F 3 0 ;œœÊœœ „ß
Èab
c3
a4
directrices are x 0œ „ œ„ œ„
a416
e3
ˆ‰
3
4
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
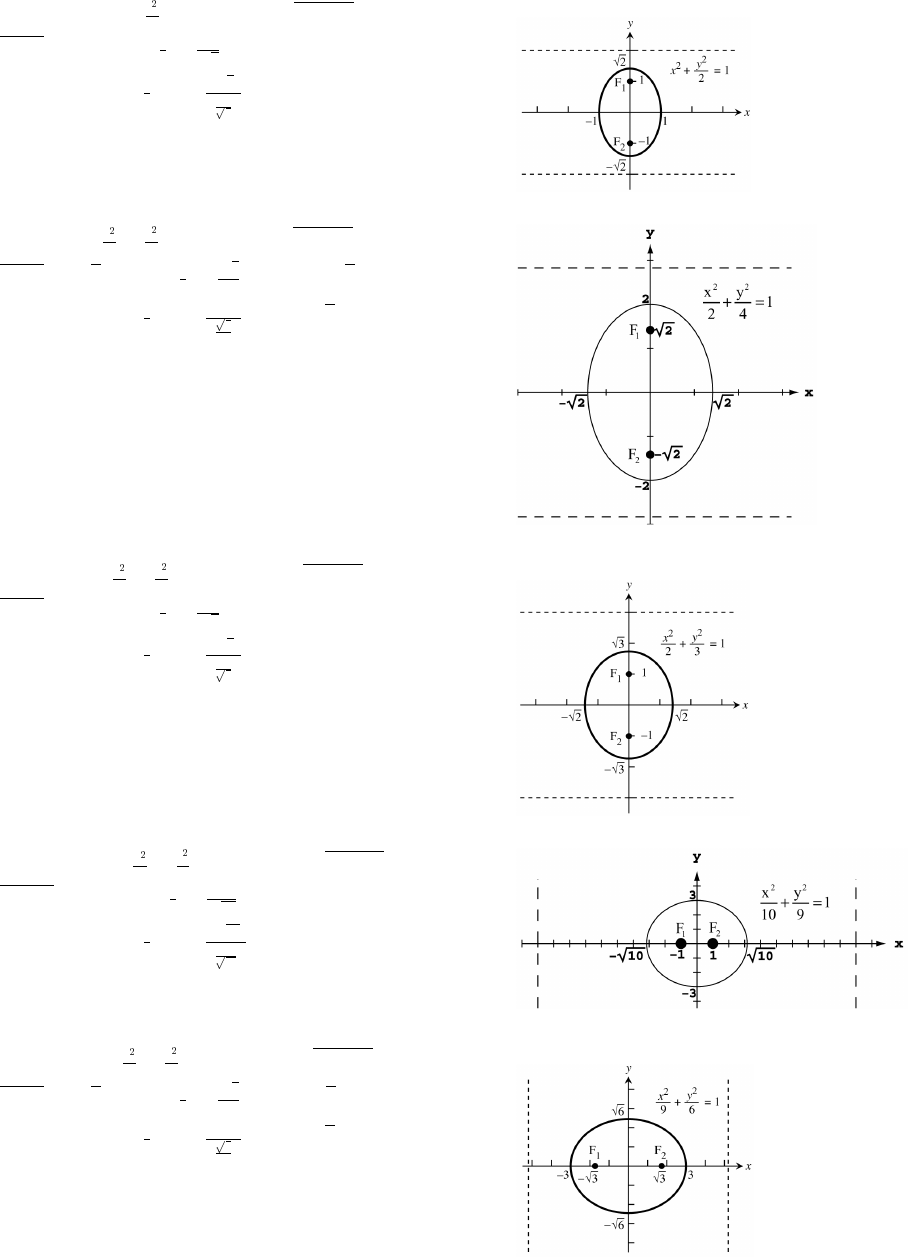
690 Chapter 11 Parametric Equations and Polar Coordinates
3. 2x y 2 x 1 c a b
## # ##
œÊ œÊœ
y
2È
2 1 1 e ; F 0 1 ;œœÊœœ ß„
Èab
c1
a2
È
directrices are y 0 2œ „ œ„ œ„
a
e
2
È
Š‹
1
2
4. 2x y 4 1 c a b
##
###
œÊ œÊœ
xy
4È
4 2 2 e ; F 0 2 ;œœ Êœœ ß„
ÈÈ È
Š‹
c
a2
2
È
directrices are y 0 2 2œ „ œ„ œ„
a2
eŠ‹
2
2È
5. 3x 2y 6 1 c a b
##
###
œÊœÊœ
xy
3È
3 2 1 e ; F 0 1 ;œœÊœœ ß„
Èab
c1
a3
È
directrices are y 0 3œ „ œ„ œ„
a
e
3
È
Š‹
1
3
6. 9x 10y 90 1 c a b
## ##
œÊœÊœ
x
10 9
yÈ
10 9 1 e ; F 1 0 ;œœÊœœ „ß
Èab
c1
a10
È
directrices are x 0 10œ „ œ„ œ„
a
e
10
È
Š‹
1
10
7. 6x 9y 54 1 c a b
## ##
œÊœÊœ
x
96
yÈ
9 6 3 e ; F 3 0 ;œœ Êœœ „ß
ÈÈ È
Š‹
c
a3
3
È
directrices are x 0 3 3œ „ œ„ œ„
a3
eŠ‹
3
3È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
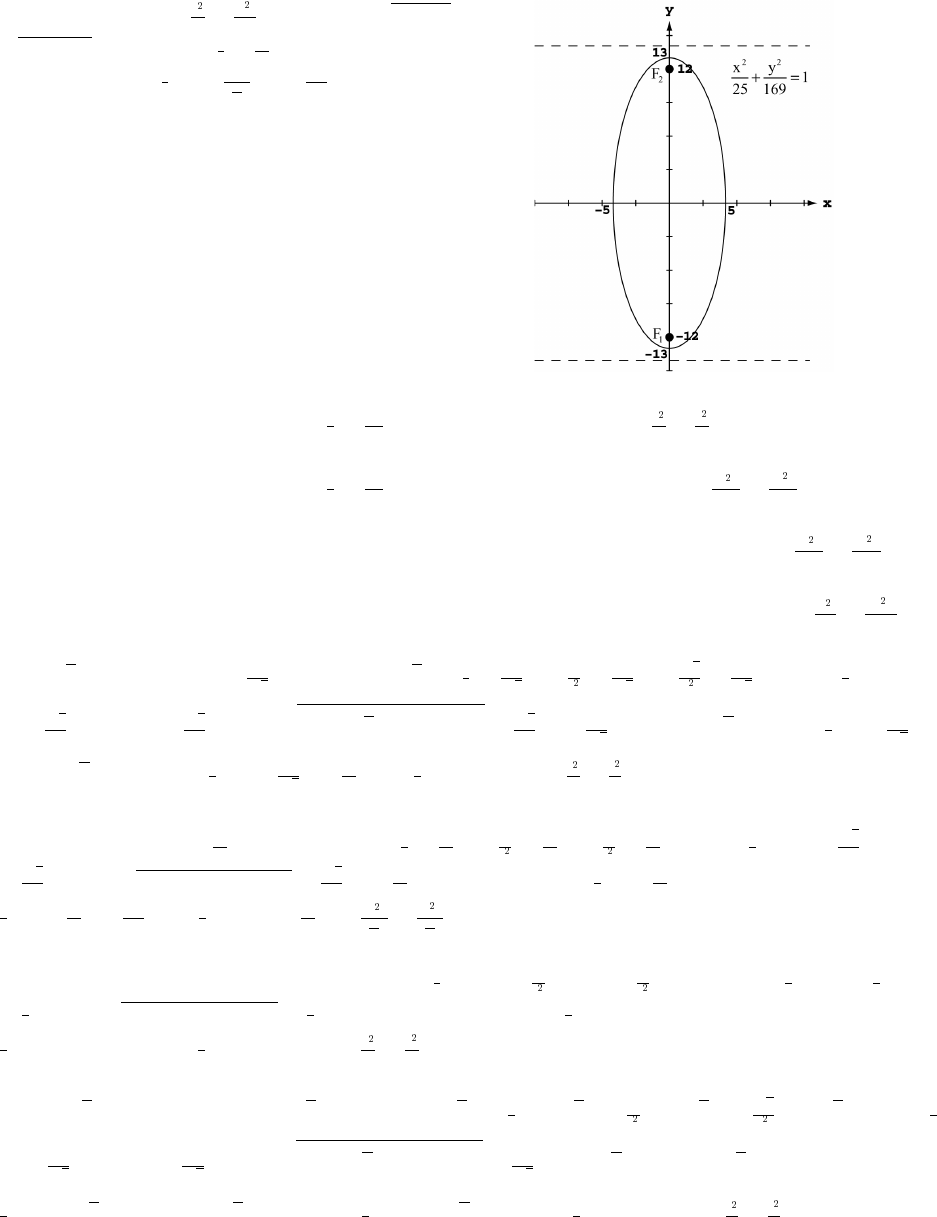
Section 11.7 Conics in Polar Coordinates 691
8. 169x 25y 4225 1 c a b
## ##
œ ʜʜ
x
25 169
yÈ
169 25 12 e ; F 0 12 ;œœÊœœ ß„
Èab
c12
a13
directrices are y 0œ „ œ„ œ„
a 13 169
e12
ˆ‰
12
13
9. Foci: 0 3 , e 0.5 c 3 and a 6 b 36 9 27 1abß„ œ Ê œ œ œ œ Ê œ œ Ê œ
c3 x
e0.5 736
y
#
#
10. Foci: 8 0 , e 0.2 c 8 and a 40 b 1600 64 1536 1ab„ß œ Ê œ œ œ œ Ê œ œ Ê œ
c8 x
e 0. 1600 1536
y
#
#
11. Vertices: 0 70 , e 0.1 a 70 and c ae 70(0.1) 7 b 4900 49 4851 1abß„ œ Ê œ œ œ œ Ê œ œ Ê œ
#x
4851 4900
y
12. Vertices: 10 0 , e 0.24 a 10 and c ae 10(0.24) 2.4 b 100 5.76 94.24 1ab„ß œ Êœ œ œ œ Ê œ œ Ê œ
#x
100 94.24
y
13. Focus: 5 , Directrix: x c ae 5 and e
Š‹
ÈÈ
ß! œÊœœ œÊœÊœÊœ
9a9ae995
5555
ee e 9
5
ÈÈÈÈ
È#
e . Then PF PD x 5 (y 0) x x 5 y xÊœ œ ʜʜ
ÈÈ È
ÈÈ
55 5
33 3 9
959
55
ÊŠ‹ ¹¹Š‹ Š‹
ÈÈ
###
##
x25x5y x x xy 4 1Ê œ Ê œÊœ
### ##
ÈŠ‹
518814 x
959 94
5
y
È
14. Focus: ( 0), Directrix: x c ae 4 and e e . Then%ß œÊœœ œÊœÊœÊœÊœ
16 a16 ae16 4 16 3
3e3e3e34
3
#
#
È
PF PD (x 4) (y 0) x (x 4) y x x 8x 16 yœ Ê œ Êœ Ê
ÈÈ
33
16 3 16
343##
## ## # #
#
ȸ¸ ˆ‰
xx xy 1œÊœÊœ
3 32 256 16 x
4394 3
y
ˆ‰
###
"ˆ‰ ˆ‰
64 16
33
15. Focus: ( 0), Directrix: x 16 c ae 4 and 16 16 16 e e . Then%ß œÊœœ œÊœÊœÊœÊœ
aae 4 1
ee e 4
#"
#
PF PD (x 4) (y 0) x 16 (x 4) y (x 16) x 8x 16 yœ Ê œ Êœ Ê
111
4##
## ## # # #
Èkk
x 32x 256 x y 48 1œÊœÊœ
13x
4 4 64 48
y
ab
###
16. Focus: 2 , Directrix: x 2 2 c ae 2 and 2 2 2 2 2 2 e
Š‹
ÈÈÈÈÈÈ
ß! œÊœœ œÊœÊœÊœ
aae
ee e
2
È#"
#
e . Then PF PD x 2 (y 0) x 2 2 x 2 yÊœ œ Êœ Ê
11 1
22 2
ÈÈ È
ÊŠ‹ ¹ ¹Š‹
ÈÈÈ
##
##
x22 x22x2y x42x8 xy2 1œ Ê œ ʜʜ
"""
####
#### ##
Š‹ Š ‹
ÈÈ È x
4
y
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
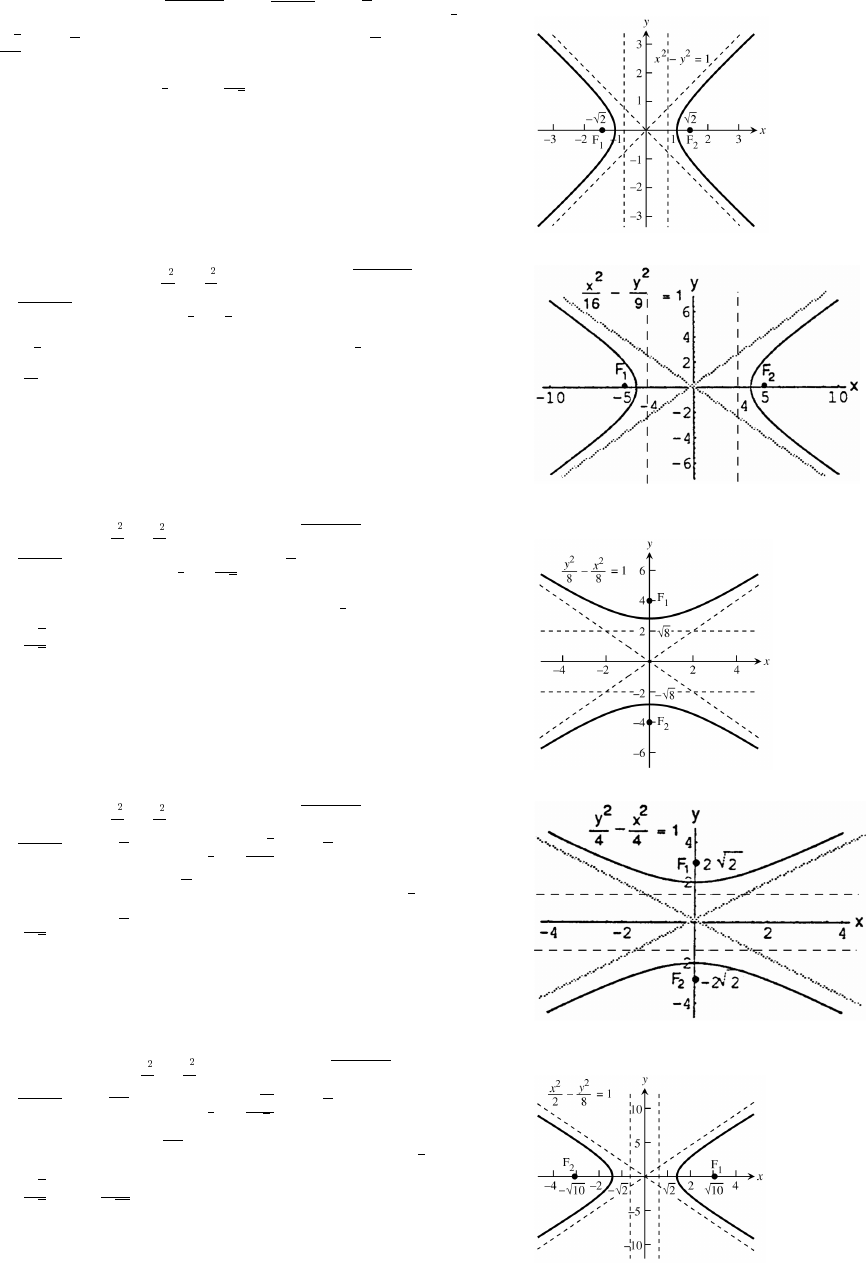
692 Chapter 11 Parametric Equations and Polar Coordinates
17. x y 1 c a b 1 1 2 e
## ##
œÊœ œ œ Êœ
ÈÈ
Èc
a
2 ; asymptotes are y x; F 2 ;œœ œ„ „ß!
È2
1ÈÈ
Š‹
directrices are x 0œ„œ„
a
e2
"
È
18. 9x 16y 144 1 c a b
## ##
œÊœÊœ
x
16 9
yÈ
16 9 5 e ; asymptotes areœœÊœœ
Èc5
a4
y x; F 5 ; directrices are x 0œ„ „ ß! œ „
3a
4e
ab
œ„
"6
5
19. y x 8 1 c a b
## ##
œÊ œÊœ
y
88
xÈ
8 8 4 e 2 ; asymptotes areœœÊœœœ
ÈÈ
c4
a8
È
y x; F 0 4 ; directrices are y 0œ„ ß„ œ „ab a
e
2œ„ œ„
È
È8
2
20. y x 4 1 c a b
## ##
œÊ œÊœ
y
44
xÈ
4 4 2 2 e 2 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a2
22
È
are y x; F 0 2 2 ; directrices are y 0œ„ ß„ œ „
Š‹
Èa
e
2œ„ œ„
2
2
ÈÈ
21. 8x 2y 16 1 c a b
## ##
œÊœÊœ
x
28
yÈ
2 8 10 e 5 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a
10
2
È
È
are y 2x; F 10 ; directrices are x 0œ„ „ ß! œ „
Š‹
Èa
e
œ„ œ„
È
ÈÈ
2
510
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
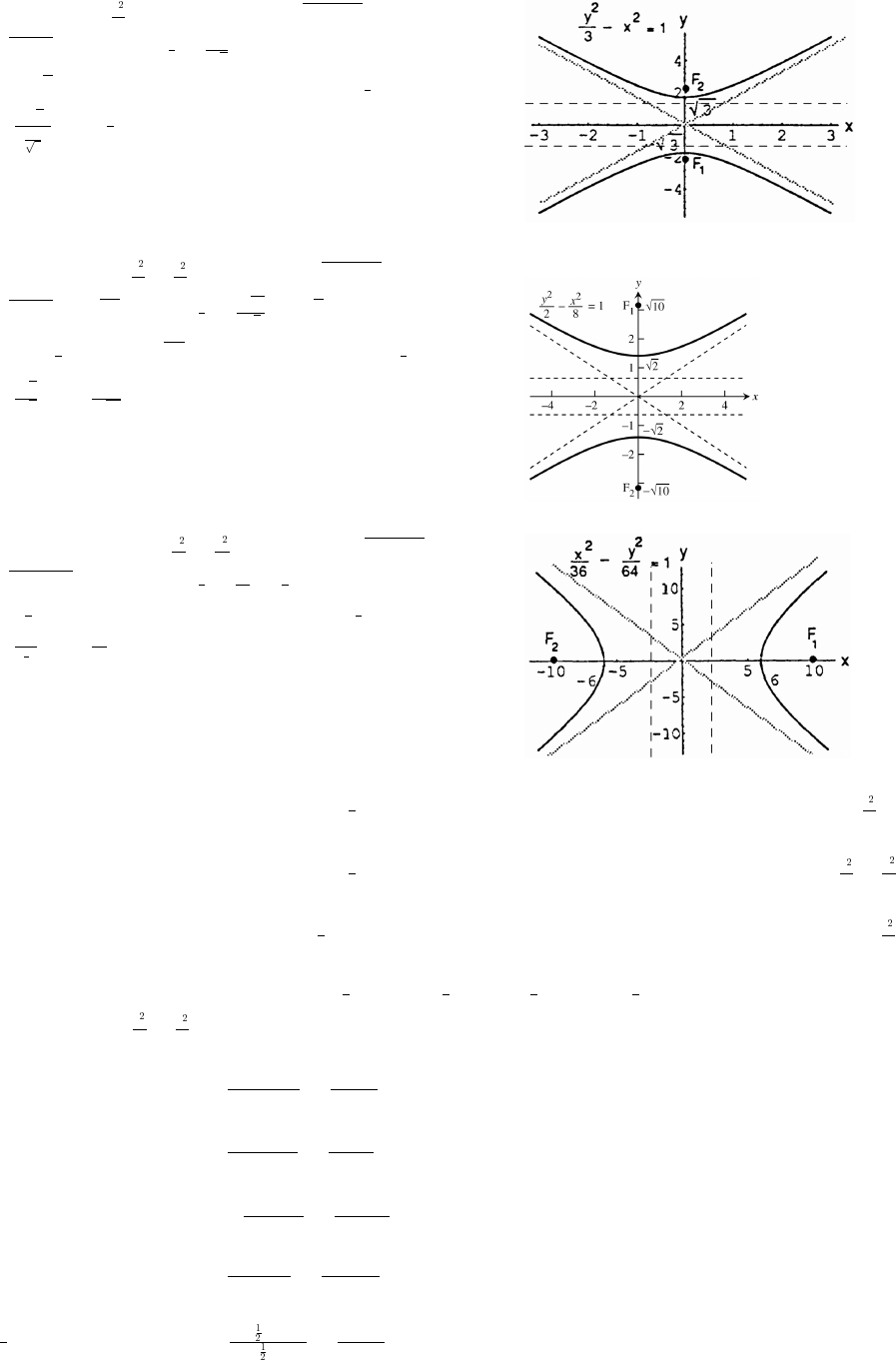
Section 11.7 Conics in Polar Coordinates 693
22. y 3x 3 x 1 c a b
## # ##
œÊœÊœ
y
3È
3 1 2 e ; asymptotes areœœÊœœ
Èc2
a3
È
y 3 x; F 0 2 ; directrices are y 0œ„ ß„ œ „
Èab a
e
œ„ œ„
È
Š‹
33
2
3
#
23. 8y 2x 16 1 c a b
## ##
œÊœÊœ
y
28
xÈ
2 8 10 e 5 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a
10
2
È
È
are y ; F 0 10 ; directrices are y 0œ„ ß„ œ „
xa
e#Š‹
È
œ„ œ„
È
ÈÈ
2
510
2
24. 64x 36y 2304 1 c a b
## ##
œ ʜʜ
x
36 64
yÈ
36 64 10 e ; asymptotes areœœÊœœœ
Èc105
a63
y x; F 10 ; directrices are x 0œ„ „ ß! œ „
4a
3e
ab
œ„ œ„
618
5
ˆ‰
5
3
25. Vertices 1 and e 3 a 1 and e 3 c 3a 3 b c a 9 1 8 y 1ab!ß„ œÊœ œœÊœ œÊ œ œœÊ œ
c x
a 8
### #
26. Vertices 2 and e 2 a 2 and e 2 c 2a 4 b c a 16 4 12 1ab„ß! œÊœ œœÊœ œÊ œœ œ Ê œ
c x
a41
y
###
#
27. Foci 3 and e 3 c 3 and e 3 c 3a a 1 b c a 9 1 8 x 1ab„ß! œÊœ œœÊœ ÊœÊ œœœÊ œ
c
a 8
y
### #
28. Foci 5 and e 1.25 c 5 and e 1.25 c a 5 a a 4 b c aab!ß„ œ Êœ œœ œÊœÊœÊœÊœ
c555
a444 ###
25 16 9 1œœÊ œ
y
16 9
x
29. e 1, x 2 k 2 rœœÊœÊœ œ
2(1)
1 (1) cos 1 cos
2
))
30. e 1, y 2 k 2 rœœÊœÊœ œ
2(1)
1 (1) sin 1 sin
2
))
31. e 5, y 6 k 6 rœœÊœÊœ œ
6(5)
1 5 sin 1 5 sin
30
))
32. e 2, x 4 k 4 rœœÊœÊœ œ
4(2)
1 2 cos 1 2 cos
8
))
33. e , x 1 k 1 rœœÊœÊœ œ
"
#
ˆ‰
ˆ‰
(1)
1 cos
1
2cos
))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
694 Chapter 11 Parametric Equations and Polar Coordinates
34. e , x 2 k 2 rœœÊœÊœ œ
"
44cos
(2)
1 cos
2
ˆ‰
ˆ‰
4
4))
35. e , y 10 k 10 rœœÊœÊœ œ
"
55sin
(10)
1 sin
10
ˆ‰
ˆ‰
5
5))
36. e , y 6 k 6 rœœÊœÊœ œ
"
33sin
(6)
1 sin
6
ˆ‰
ˆ‰
3
3))
37. r e 1, k 1 x 1œÊœœÊœ
"
1cos )
38. r e , k 6 x 6;œœ ÊœœÊœ
63
2cos 1 cos
#
"
))
ˆ‰
a 1 e ke a 1 3 a 3ab ’“
ˆ‰
œÊ œÊ œ
#"
#
#3
4
a 4 ea 2ÊœÊ œ
39. r rœÊœ œ
25
10 5 cos 1 cos 1 cos
)))
ˆ‰ ˆ‰
ˆ‰ ˆ‰
25 5
10
5
10
e , k 5 x 5; a 1 e keÊœ œÊœ œ
"
#
#
ab
a 1 a a eaÊ œÊ œÊœ Ê œ
’“
ˆ‰
"
## #
#535 10 5
433
40. r r e 1, k 2 x 2œÊœÊœœÊœ
42
22 cos 1cos ))
41. r r rœÊœ Êœ
400 25
16 8 sin 1 sin 1 sin
)))
ˆ‰
ˆ‰ ˆ‰
400
16
8
16
e , k 50 y 50; a 1 e keœœÊœ œ
"
#
#
ab
a 1 25 a 25 aÊ œÊ œÊœ
’“
ˆ‰
"
#
#3 100
43
eaʜ
50
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 11.7 Conics in Polar Coordinates 695
42. r r e 1, 43. r r e 1,œÊœÊœ œÊœÊœ
12 4 8 4
33 sin 1sin 22 sin 1sin )) ))
k4 y4 k4 y 4œÊœ œÊœ
44. r r e , k 4œÊœ Êœœ
42
2sin 1 sin
#
"
))
ˆ‰
y 4; a 1 e ke a 1 2Êœ œ Ê œab ’“
ˆ‰
#"
#
#
a2 a eaʜʜʜ
384
433
45. r cos 2 r cos cos sin sin
ˆ‰ ˆ ‰
È
)))œ Ê
111
444
2 r cos r sin 2 x yœÊ œÊ
ÈÈ
"" ""
ÈÈ ÈÈ
22 22
))
2 x y 2 y 2 xœÊœÊœ
È
46. r cos 1 r cos cos sin sin 1
ˆ‰ ˆ ‰
)))œÊ œ
333
444
111
r cos r sin 1 x y 2Ê œ Ê œ
ÈÈ
22
22
)) È
yx 2ʜ
È
47. r cos 3 r cos cos sin sin 3
ˆ‰ ˆ ‰
)))œÊ œ
222
333
111
r cos r sin 3 x y 3Ê œ Ê œ
1
22
33
))
ÈÈ
"
##
x3y6 y x23Ê œ Ê œ
ÈÈ
È3
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
696 Chapter 11 Parametric Equations and Polar Coordinates
48. r cos 2 r cos cos sin sin 2
ˆ‰ ˆ ‰
)))œÊ œ
111
333
r cos r sin 2 x y 2Ê œÊœ
1
22
33
))
ÈÈ
"
##
x3y4 y xÊ œÊœ
ÈÈÈ
343
33
49. 2 x 2 y 6 2 r cos 2 r sin 6 r cos sin 3 r cos cos sin sin
ÈÈ È È Š‹
ˆ‰
œÊ œÊ œÊ )) )) ))
ÈÈ
22
44##
11
3 r cos 3œÊ œ
ˆ‰
)1
4
50. 3 x y 1 3 r cos r sin 1 r cos sin r cos cos sin sin
ÈÈ Š‹
ˆ‰
œ Ê œ Ê œ Ê )) ) ) ) )
È31
66## #
"11
r cosœÊ œ
""
##
ˆ‰
)1
6
51. y 5 r sin 5 r sin 5 r sin ( ) 5 r cos ( ) 5 r cos 5œÊ œÊ œÊ œÊ œÊ œ))) ))
ˆ‰ ˆ‰
11
##
52. x 4 r cos 4 r cos 4 r cos ( ) 4œ Ê œ Ê œ Ê œ)))1
53. 54.
55. 56.
57. (x 6) y 36 C (6 0), a 6 58. (x 2) y 4 C ( 2 0), a 2œ Êœß œ œÊœß œ
## ##
r 12 cos is the polar equation r 4 cos is the polar equationʜ ʜ))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 11.7 Conics in Polar Coordinates 697
59. x (y 5) 25 C ( 5), a 5 60. x (y 7) 49 C ( 7), a 7
## ##
œ Ê œ!ß œ œ Ê œ!ß œ
r 10 sin is the polar equation r 14 sin is the polar equationʜ ʜ))
61. x 2x y 0 (x 1) y 1 62. x 16x y 0 (x 8) y 64
# # ## # # ##
œÊ œ œÊ œ
C ( 1 0), a 1 r 2 cos is C (8 0), a 8 r 16 cos is theÊœß œÊœ Êœß œÊœ))
the polar equation polar equation
63. x y y 0 x y 64. x y y 0 x y
## # ## #
""
#
##
œÊ œ œÊ œ
ˆ‰ ˆ‰
4339
424
C , a r sin is the C 0 , a r sin is theÊ œ !ß œ Ê œ Ê œ ß œ Ê œ
ˆ‰ ˆ‰
""
## ))
22 4
33 3
polar equation polar equation
65. 66.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
698 Chapter 11 Parametric Equations and Polar Coordinates
67. 68.
69. 70.
71. 72.
73. 74.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 11 Practice Exercises 699
75. (a) Perihelion a ae a(1 e), Aphelion ea a a(1 e)œœ œœ
(b) Planet Perihelion Aphelion
Mercury 0.3075 AU 0.4667 AU
Venus 0.7184 AU 0.7282 AU
Earth 0.9833 AU 1.0167 AU
Mars 1.3817 AU 1.6663 AU
Jupiter 4.9512 AU 5.4548 AU
Saturn 9.0210 AU 10.0570 AU
Uranus 18.2977 AU 20.0623 AU
Neptune 29.8135 AU 30.3065 AU
76. Mercury: r œœ
(0.3871) 1 0.2056
1 0.2056 cos 1 0.2056 cos
0.3707
ab
))
Venus: r œœ
(0.7233) 1 0.0068
1 0.0068 cos 1 0.0068 cos
0.7233
ab
))
Earth: r œœ
1 1 0.0167
1 0.0167 cos 1 0.0617 cos
0.9997
ab
))
Mars: r œœ
(1.524) 1 0.0934
1 0.0934 cos 1 0.0934 cos
1.511
ab
))
Jupiter: r œœ
(5.203) 1 0.0484
1 0.0484 cos 1 0.0484 cos
5.191
ab
))
Saturn: r œœ
(9.539) 1 0.0543
1 0.0543 cos 1 0.0543 cos
9.511
ab
))
Uranus: r œœ
(19.18) 1 0.0460
1 0.0460 cos 1 0.0460 cos
19.14
ab
))
Neptune: r œœ
(30.06) 1 0.0082
1 0.0082 cos 1 0.0082 cos
30.06
ab
))
CHAPTER 11 PRACTICE EXERCISES
1. x and y t 1 2x t y 2x 1 2. x t and y 1 t y 1 xœœÊœÊœ œ œÊœ
t
#ÈÈ
3. x tan t and y sec t x tan t 4. x 2 cos t and y 2 sin t x 4 cos t andœœÊœ œœÊœ
"" "
##
## ##
4
and y sec t 4x tan t and y 4 sin t x y 4
#### ####
"
œÊœ œÊœ
4
4y sec t 4x 1 4y 4y 4x 1
## # # ##
œÊœÊœ

700 Chapter 11 Parametric Equations and Polar Coordinates
5. x cos t and y cos t y ( x) x 6. x 4 cos t and y 9 sin t x 6 cos t andœ œ Ê œ œ œ œ Ê œ
### ##
y 81 sin t 1
##
œÊœ
x
16 81
y
7. 16x 9y 144 1 a 3 and b 4 x 3 cos t and y 4 sin t, 0 t 2
##
œ ʜʜ œÊœ œ ŸŸ
x
916
y1
8. x y 4 x 2 cos t and y 2 sin t, 0 t 6
##
œÊœ œ ŸŸ1
9. x tan t, y sec t sin t sin ; tœœÊœœœœÊœœœ
""
## #
dy dy/dt dy
dx dx/dt sec t dx 3 3
sec t tan t
sec t
tan t 3
¹t3
11
È
x tan and y sec 1 y x ; 2 cos t Êœ œ œ œÊœ œ œ œ Ê
"" "
### # œÎ
11
1
3 3 4 dx dx/dt dx
33
dy dy/dt dy
cos t
sec t
3
t3
ÈÈ ¹
2 cosœœ
3
34
ˆ‰
1"
10. x , y t (2) 3; t 2 x 1 andœ" œ" Ê œ œ œ Ê œ œ œ Ê œ œ
" "
##t t dx dx/dt 2 dx 4
333 5
dy dy/dt dy
Š‹
Š‹
3
t
2
t¹t2
y1 y 3x ; t (2) 6œœ Ê œ œ œ œ Ê œ œ
3333
4 dx dx/dt 4 dx 4
dy dy/dt dy
t2
##
""
$$
œ
ˆ‰
Š‹
3
2
t¹
11. (a) x 4t , y t 1 t y 1 1œ œ Ê œ„ Ê œ „ œ„
23 xx
22 8
3x
ÈÈ
Š‹ 32
(b) x cos t, y tan t sec t tan t 1 sec t y 1 yœœÊœÊœÊœœÊœ„
111x
xxxx
222 1x
22
22
È
12. (a) The line through 1, 2 with slope 3 is y 3x 5 x t, y 3t 5, tabœÊœœ__
(b) x1 y2 9 x1 3cost, y2 3sint x13cost, y 23sint, 0t 2ababœÊœ œ Êœ œ ŸŸ
22 1
(c) y4x x xt, y4t t, tœÊœœ__
22
(d) 9x 4y 36 1 x 2 cos t, y 3 sin t, 0 t 2
22 x
49
y
œÊœÊœ œ ŸŸ
221
13. y x x x 2 x L 1 2 x dxœÊœ Ê œ Êœ
"Î# "Î# "Î#
" " "" ""
##
#
x
3dx dx4x 4x
dy dy
Š‹ ˆ‰ ˆ‰
É
'1
4
L 2 x dx x x dx x x dx 2x xÊœ œ œ œ
'' '
11 1
44 4
Ɉ‰ ˆ ‰ ‘
Éab
"" " " "
"Î# "Î# #
##
"Î# "Î# "Î# $Î# %
"
4x 4 3
2
482 2œ œœ
""
##
‘ˆ‰ˆ‰ˆ‰
2 2 14 10
33 33
†
14. x y x L 1 dy 1 dyœÊœ Ê œ Êœ œ
#Î$ "Î$ ##
dx 2 dx 4x dx 4
dy 3 dy 9 dy 9x
Š‹ Š‹
ÊÉ
''
11
88
dx 9x 4 x dx; u 9x 4 du 6y dy; x 1 u 13,œœ œÊœœÊœ
''
11
88
È9x 4
3x 3
"#Î$ "Î$ #Î$ "Î$
Ȉ‰
x 8 u 40 L u du u 40 13 7.634d‘ ‘
œÊœ Äœ œ œ ¸
"""
"Î# $Î# $Î# $Î#
%!
"$ #18 18 3 7
2
'13
40
15. y x x x x x 2 xœÊœ Ê œ
55
12 8 dx dx 4
dy dy
'Î& %Î& "Î& "Î& #Î& #Î&
"" "
##
#
Š‹ ˆ‰
L 1 x 2 x dx L x 2 x dx x x dxÊœ Êœ œ
''
11
32 32 32
1
ÉÉ
ab abab
'É
"""
#Î& #Î& #Î& #Î& "Î& "Î& #
444
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 11 Practice Exercises 701
x x dx x x 2 2œœœœ
'1
32 "" " "
## # #
"Î& "Î& 'Î& %Î& ' %
$#
"
ˆ‰ ‘ ‘ˆ‰ˆ‰ˆ‰
5 5 5 5 5 5 315 75
64 64 64 64
††
(1260 450)œœœ
"
48 48 8
1710 285
16. x y y y L 1 y dyœÊœÊ œÊœ
"" "" """ """
###
$# %
#%
1 y dy 4 y dy 16 16
dx dx
yy
Š‹ Š ‹
Ê
'1
2
y dy y dy y dy yœœ œœ
'''
111
222
ÉÊŠ‹ Š‹’“
""" "" "" ""
%#
# #
##
#$
"
16 4y 4y 1 y
y
1œœœ
ˆ‰ˆ‰
8713
12 1 1 12
"" "
## ##
17. 5 sin t 5 sin 5t and 5 cos t 5 cos 5t
dx dx
dt dt dt dt
dy dy
œ œ Ê
ʈ‰ Š‹
##
5 sin t 5 sin 5t 5 cos t 5 cos 5tœ
Éabab
##
5 sin 5t sin t sin 5t sin t cos t cos t cos 5t cos 5t sin t sin 5t cos t cos 5 tœ##œ&##
ÈÈab
####
5 cos t 5 cos t sin t sin t sin t (since t )œ # " % œ % " % œ "! # œ "!l # l œ "! # ! Ÿ Ÿ
Èab ab
Ɉ‰ È
"
# #
#1
Length sin t dt 5 cos tÊ œ "! # œ # œ&"&"œ"!
'!
ÎÎ#
!
11
2c d abababab
18. 3t 12t and 3t 12t 3t 12t 3t 12t 288t 8t
dx dx
dt dt dt dt
22
dy dy 22 4
œ œÊ œ œ "
ʈ‰ Š‹ Éabab
È
####
#
3 2 t 16 t Length 3 2 t 16 t dt 3 2 t 16 t dt; u 16 t du 2t dtœÊœ œ œÊœ
ÈÈÈ
kk kk
ÈÈÈ
’
222
2
''
!!
""
du t dt; t 0 u 16; t 1 u 17 ; u du u 17 16Êœ œÊœ œÊœ œ œ
"
#
"
“È‘ Š‹
ab ab
32 32 32
223233
16
7222
3/2 17
16
3/2 3/2
ÈÈÈ
'
17 64 2 17 64 8.617.œ† œ ¸
32
23
23/2 3/2
ÈŠ‹Š‹
ab ab
È
19. sin and cos sin cos sin cos
dx dx
dd dd
dy dy
)) ))
œ$ œ$ Ê œ $ $ œ $ œ$)) ))))
ʈ‰ Š‹ Éababa b
È
####
##
Length d dÊœ$œ$ œ$!œ
''
!!
$Î $Î $*
##
11
11
22
))
ˆ‰
20. x t and y t, 3 t 3 2t and t Length 2t t dtœœŸŸÊœ œ"Êœ "
# #
##
#
tdx
3dtdt
dy
3
3
ÈÈ Éab a b
'È
È
t t dt t 2t dt t dt t dt tœ#"œ"œ "œ"œ
'''
%# %# # #
#
ÈÈ È
ÈÈ È
È
ÈÈ
È
33 3
33 3
3
3t
3
3
3
ÈÈÉab ab’“
'3
43œÈ
21. x and y 2t, 0 t 5 t and 2 Surface Area 2 (2t) t 4 dt 2 u duœœŸŸÊœœÊ œ œ
tdx
dt dt
dy
04
59
##"Î#
ÈÈ
''
È11
2 u , where u t 4 du 2t dt; t 0 u 4, t 5 u 9œœ œÊœœÊœœÊœ1‘ È
276
33
$Î# #
*
%
1
22. x t and y 4 t , t 1 2t and œ œ ŸŸ Ê œ œ
#"" "
2t dt 2t dt
2
dx 2
dy
t
ÈÈÈ
Surface Area 2 t 2t dt 2 t 2t dtÊœœ
''
12 12
11
t2t t t
2
t
ÎÎ
##
"" ""
###
##
#
ÈÈ
È
11
ˆ‰ˆ ‰ ˆ‰ˆ ‰
ÊŠ‹ É
2 t 2t dt 2 2t t dt 2 t t tœœ œ111
''
12 12
11
2t 2t 4 2 8
33
ÎÎ
#$$%#
"" " " "
##
"
"Î #
ÈÈ È
ˆ‰ˆ ‰ ˆ ‰ ‘
22œ1Š‹
32
4
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
702 Chapter 11 Parametric Equations and Polar Coordinates
23. r cos 2 3 r cos cos sin sin
ˆ‰ ˆ ‰
È
)))œ Ê
111
333
2 3 r cos r sin 2 3œÊ œ
ÈÈ
"
##
))
È3
r cos 3 r sin 4 3 x 3 y 4 3Ê œÊœ))
ÈÈÈÈ
yx4ʜ
È3
3
24. r cos r cos cos sin sin
ˆ‰ ˆ ‰
)))œ Ê
333
444
2
111
È
#
r cos r sin x y 1œÊ œÊœ
ÈÈ È È
22 2 2
## # #
))
yx1ʜ
25. r 2 sec r r cos 2 x 2œÊœÊœÊœ))
2
cos )
26. r 2 sec r cos 2 x 2œ Ê œ Ê œ
ÈÈÈ
))
27. r csc r sin yœ Ê œ Ê œ
333
###
))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 11 Practice Exercises 703
28. r 3 3 csc r sin 3 3 y 3 3œÊœÊœ
ÈÈÈ
))
29. r 4 sin r 4r sin x y 4y 0œ Ê œ Ê œ))
###
x (y 2) 4; circle with center ( 2) andÊ œ !ß
##
radius 2.
30. r 3 3 sin r 3 3 r sin œÊœ
ÈÈ
))
#
xy33y0 x y ;Ê œÊ œ
## #
#
#
ÈŠ‹
33 27
4
È
circle with center and radius
Š‹
!ß 33 33
ÈÈ
##
31. r 2 2 cos r 2 2 r cos œÊœ
ÈÈ
))
#
xy22x0 x 2 y2;Ê œÊ œ
## #
#
ÈÈ
Š‹
circle with center 2 0 and radius 2
Š‹
ÈÈ
ß
32. r 6 cos r 6r cos x y 6x 0œ Ê œ Ê œ))
###
(x 3) y 9; circle with center ( 3 0) andÊœ ß
##
radius 3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
704 Chapter 11 Parametric Equations and Polar Coordinates
33. x y 5y 0 x y C
## #
##
#
œÊ œ Ê œ!ß
ˆ‰ ˆ‰
525 5
4
and a ; r 5r sin 0 r 5 sin œ œÊœ
5
#
#))
34. x y 2y 0 x (y 1) 1 C ( 1) and
## # #
œÊ œÊ œ!ß
a 1; r 2r sin 0 r 2 sin œ œÊœ
#))
35. x y 3x 0 x y C
## #
##
#
œÊ œÊ œß!
ˆ‰ ˆ‰
39 3
4
and a ; r 3r cos 0 r 3 cos œ œÊœ
3
#
#))
36. x y 4x 0 (x 2) y 4 C ( 2 0)
## ##
œÊ œÊ œß
and a 2; r 4r cos 0 r 4 cos œ œÊœ
#))
37. 38.
39. d 40. e 41. l 42. f
43. k 44. h 45. i 46. j
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 11 Practice Exercises 705
47. A 2 r d (2 cos ) d 4 4 cos cos d 4 4 cos dœœœœ
'' ' '
00 0 0
"
# #
## #
))) ))) ))ab
ˆ‰
1cos 2)
4 cos d 4 sin œ œ œ
'0ˆ‰ ‘
9 cos 2 9 sin 2 9
24## #
!
)))) 1
))
1
48. A sin 3 d d sin 6œœœœ
''
00
33
"""
##
#Î$
!
ab ˆ‰ ‘
)) ) ) )
1cos 6
46 12
)1
1
49. r 1 cos 2 and r 1 1 1 cos 2 0 cos 2 2 ; thereforeœ œ Ê œ Ê œ Ê œ Ê œ)))))
11
#4
A 4 (1 cos 2 ) 1 d 2 1 2 cos 2 cos 2 1 dœœ
''
00
44
"
#
## #
cda b)) )))
2 2 cos 2 d 2 sin 2 2 1 0 2œœœœ
'0
4ˆ‰‘ˆ‰
))))
""
##
Î%
!
cos 4 sin 4
28 8 4
))11
1
50. The circle lies interior to the cardioid. Thus,
A 2 [2(1 sin )] d (the integral is the area of the cardioid minus the area of the circle)œ
'2
2"
#
#
))1
4 1 2 sin sin d (6 8 sin 2 cos 2 ) d 6 8 cos sin 2œ œ œ
''
22
22
ab c d) ))1 ) ))1 ) ) ) 1
#Î#
Î#
1
1
3(3) 5œœcd1 111
51. r 1 cos sin ; Length ( 1 cos ) ( sin ) d 2 2 cos dœ Ê œ œ œ )) ))) ))
dr
d)''
00
22
ÈÈ
##
d 2 sin d 4 cos ( 4)( 1) ( 4)(1) 8œœœœœ
''
00
22
É‘
4(1 cos )
2
##
#
!
)))
1
))
52. r 2 sin 2 cos , 0 2 cos 2 sin ; r (2 sin 2 cos ) (2 cos 2 sin )œ ŸŸÊœ œ ))) )) )) ))
1
))#
###
#
dr dr
dd
ˆ‰
8sin cos 8 L 8 d 2 2 2 2 2œœÊœ œ œ œab È’“
ÈÈÈ
ˆ‰
## Î#
!#
)) ) ) 1
'0
211
53. r 8 sin , 0 8 sin cos ; r 8 sin 8 sin cos œŸŸÊœ œ
$##$#
## #
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ‘ ‘ˆ‰ ˆ‰ ˆ‰
)1 )) ) ))
))34d33d 3 33
dr dr
)
64 sin L 64 sin d 8 sin d 8 dœÊœ œ œ
%#
%
#
ˆ‰ ˆ‰ ˆ‰
É’“
)))
333
1cos
'''
000
444
)) )
ˆ‰
2
3
4 4 cos d 4 6 sin 4 6 sin 0 3œ œ œ œ
'0
4 ‘ ‘ ˆ‰ ˆ‰ˆ‰ ˆ‰
22
3346
))11
1
)) 1
Î%
!
54. r 1 cos 2 (1 cos 2 ) ( 2 sin 2 ) œ Êœ œ Ê œ
Ȉ‰
)))
dr sin 2 dr sin 2
dd1cos 2
1cos 2
)))
))
)
"
#
"Î#
#
È
r1cos 2Ê œ œ œ
##
ˆ‰
dr sin 2 1 2 cos 2 cos 2 sin 2
d 1 cos 2 1 cos 2 1 cos 2
(1 cos 2 ) sin 2
))))
))))
))
)
2 L 2 d 2 2œœÊœ œœ
22 cos 2
1cos 2
##
)11
)'2
2ÈÈ È
‘ˆ‰
)1
55. x 4y y 4p 4 p 1; 56. x 2y y 4p 2 p ;
# #
##
"
œ Êœ Ê œÊœ œ Ê œÊ œÊœ
xx
4
therefore Focus is (0 1), Directrix is y 1 therefore Focus is ; Directrix is yß œ !ß œ
ˆ‰
""
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
706 Chapter 11 Parametric Equations and Polar Coordinates
57. y 3x x 4p 3 p ; 58. y x x 4p p ;
# #
œÊœÊœÊœ œ Êœ ʜʜ
y y
34 3 33
38 82
ˆ‰
8
3
therefore Focus is 0 , Directrix is x therefore Focus is , Directrix is x
ˆ‰ ˆ ‰
33 22
44 33
ßœ ß!œ
59. 16x 7y 112 1 60. x 2y 4 1 c 4 2 2
## ## #
#
œ Ê œ œ Ê œ Ê œœ
xx
716 4
yy
c 16 7 9 c 3; e c 2 ; eÊ œ œÊœ œœ Êœ œœ
#
#
c3 c
a4 a
2
ÈÈ
61. 3x y 3 x 1 c 1 3 4 62. 5y 4x 20 1 c 4 5 9
## # # # # #
œ Ê œ Ê œœ œ Ê œ Ê œœ
y y
345
x
c 2; e 2; the asymptotes are c 3, e ; the asymptotes are y xÊœ œœœ Êœ œœ œ„
c2 c3 2
a1 a5
#È
y3xœ„
È
63. x 12y y 4p 12 p 3 focus is ( 3), directrix is y 3, vertex is (0 0); therefore new
#
#
œ ÊœÊ œ ÊœÊ !ß œ ß
x
1
vertex is (2 3), new focus is (2 0), new directrix is y 6, and the new equation is (x 2) 12(y 3)ßß œ œ
#
64. y 10x x 4p 10 p focus is 0 , directrix is x , vertex is (0 0); therefore new
#
## #
œÊœÊœÊœÊ ß œ ß
y
10
55 5
ˆ‰
vertex is 1 , new focus is (2 1), new directrix is x 3, and the new equation is (y 1) 10 x
ˆ‰ ˆ‰
ß ß œ œ
" "
# #
#
65. 1 a 5 and b 3 c 25 9 4 foci are 4 , vertices are 5 , center is
x
95
y
œÊœ œÊœ œÊ !ß„ !ß„
#Èab ab
(0 0); therefore the new center is ( 5), new foci are ( 3 1) and ( 3 9), new vertices are ( 10) andß $ß ß ß $ß
( 0), and the new equation is 1$ß œ
(x 3) (y 5)
95
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 11 Practice Exercises 707
66. 1 a 13 and b 12 c 169 144 5 foci are 5 0 , vertices are 13 0 , center
x
169 144
y
œÊœ œÊœ œÊ „ß „ß
Èab a b
is (0 0); therefore the new center is (5 12), new foci are (10 12) and (0 12), new vertices are (18 12) andßßßßß
( 8 12), and the new equation is 1ß œ
(x 5) (y 12)
169 144
67. 1 a 2 2 and b 2 c 8 2 10 foci are 0 10 , vertices are
y
82
x
œÊœ œ Êœ œ Ê ß„
ÈÈÈÈÈ
Š‹
0 2 2 , center is (0 0), and the asymptotes are y 2x; therefore the new center is 2 2 2 , new foci are
Š‹ Š‹
È È
ß„ ß œ „ ß
2 2 2 10 , new vertices are 2 4 2 and ( 0), the new asymptotes are y 2x 4 2 2 and
Š‹ Š‹
ÈÈ È
È
ß„ ß #ß œ
y 2x 4 2 2; the new equation is 1œ œ
ÈŠ‹
È
y22
8
(x 2)
#
68. 1 a 6 and b 8 c 36 64 10 foci are 10 0 , vertices are 6 0 , the center
x
36 64
y
œÊœ œÊœ œ Ê „ß „ß
Èab ab
is (0 0) and the asymptotes are or y x; therefore the new center is ( 10 3), the new foci areßœ„œ„ ß
y
86 3
x4
( 20 3) and (0 3), the new vertices are ( 16 3) and ( 4 3), the new asymptotes are y x andß ß ß ß œ
431
33
y x ; the new equation is 1œ œ
449
3 3 36 64
(x 10) (y 3)
69. x 4x 4y 0 x 4x 4 4y 4 (x 2) 4y 4 y 1, a hyperbola; a 2 and
### # ## #
œÊ œÊ œÊ œ œ
(x 2)
4
b 1 c 1 4 5 ; the center is (2 0), the vertices are ( 0) and (4 0); the foci are 2 5 0 andœ Ê œ œ ß !ß ß „ ß
ÈÈÈ
Š‹
the asymptotes are y œ„
x2
#
70. 4x y 4y 8 4x y 4y 4 4 4x (y 2) 4 x 1, a hyperbola; a 1 and
## ## # # #
œÊ œÊ œÊ œ œ
(y 2)
4
b 2 c 1 4 5 ; the center is ( 2), the vertices are (1 2) and ( 2), the foci are 5 2 andœÊœ œ !ß ß "ß „ ß
ÈÈÈ
Š‹
the asymptotes are y 2x 2œ„
71. y 2y 16x 49 y 2y 1 16x 48 (y 1) 16(x 3), a parabola; the vertex is ( 1);
## #
œ Ê œ Ê œ $ß
4p 16 p 4 the focus is ( 7 1) and the directrix is x 1œÊœÊ ß œ
72. x 2x 8y 17 x 2x 1 8y 16 (x 1) 8(y 2), a parabola; the vertex is (1 2);
## #
œ Ê œ Ê œ ß
4p 8 p 2 the focus is (1 4) and the directrix is y 0œÊœÊ ß œ
73. 9x 16y 54x 64y 1 9 x 6x 16 y 4y 1 9 x 6x 9 16 y 4y 4 144
## # # # #
œÊ œÊ œabab a ba b
9(x 3) 16(y 2) 144 1, an ellipse; the center is ( 3 2); a 4 and b 3Ê œ Ê œ ß œ œ
## (x 3) (y 2)
16 9
c 16 9 7 ; the foci are 7 2 ; the vertices are (1 2) and ( 7 2)Êœ œ $„ ß ß ß
ÈÈÈ
Š‹
74. 25x 9y 100x 54y 44 25 x 4x 9 y 6y 44 25 x 4x 4 9 y 6y 9 225
## # # # #
œÊ œÊ œabab a ba b
1, an ellipse; the center is (2 3); a 5 and b 3 c 25 9 4; the foci areÊœ ßœ œÊœœ
(x 2) (y 3)
925
È
(2 1) and (2 7); the vertices are (2 2) and (2 8)ßß ßß
75. x y 2x 2y 0 x 2x 1 y 2y 1 2 (x 1) (y 1) 2, a circle with center (1 1) and
## # # # #
œÊ œÊ œ ß
radius 2œÈ
76. x y 4x 2y 1 x 4x 4 y 2y 1 6 (x 2) (y 1) 6, a circle with center ( 2 1)
## # # # #
œÊ œÊ œ ß
and radius 6œÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
708 Chapter 11 Parametric Equations and Polar Coordinates
77. r e 1 parabola with vertex at (1 0)œÊœÊ ß
2
1cos )
78. r r e ellipse;œÊœ ÊœÊ
84
2cos 1 cos
#
"
))
ˆ‰
ke 4 k 4 k 8; k ea 8 aœÊ œÊœ œÊœ
""
##
aa
eˆ‰
a ea ; therefore the center isÊœ Ê œ œ
16 16 8
333
ˆ‰ˆ ‰
"
#
; vertices are ( ) and 0
ˆ‰ ˆ‰
88
33
ß)ßß11
79. r e 2 hyperbola; ke 6 2k 6œ ÊœÊ œÊ œ
6
12 cos )
k 3 vertices are (2 ) and (6 )ÊœÊ ß ß11
80. r r e ; ke 4œÊœ Êœœ
12 4
3sin 3
1 sin
"
))
ˆ‰
3
k 4 k 12; a 1 e 4 a 1ʜʜ œÊ
""
##
33
ab ’“
ˆ‰
4 a ea ; therefore theœÊœÊ œ œ
993
3###
"
ˆ‰ˆ‰
center is ; vertices are 3 and 6
ˆ‰ ˆ‰ˆ‰
33 3
## # #
ßßß
111
81. e 2 and r cos 2 x 2 is directrix k 2; the conic is a hyperbola; r rœ œÊœ Êœ œ Êœ)ke
1 e cos 1 cos
(2)(2)
#))
rʜ 4
1 cos # )
82. e 1 and r cos 4 x 4 is directrix k 4; the conic is a parabola; r rœœÊœÊœ œÊœ)ke
1e cos 1cos
(4)(1)
))
rʜ 4
1cos )
83. e and r sin 2 y 2 is directrix k 2; the conic is an ellipse; r rœ œÊœ Êœ œ Êœ
"
#
)ke
1e sin
(2)
1 sin
))
ˆ‰
ˆ‰
rʜ 2
2sin )
84. e and r sin 6 y 6 is directrix k 6; the conic is an ellipse; r rœœÊœÊœ œÊœ
"
31e sin
ke (6)
1 sin
)))
ˆ‰
ˆ‰
3
3
rʜ 6
3sin )
85. (a) Around the x-axis: 9x 4y 36 y 9 x y 9 x and we use the positive root:
## # # #
œÊœ Êœ„
99
44
É
V 2 9 x dx 2 9 x dx 2 9x x 24œœœœ
''
00
22
1111
Š‹
Ɉ‰ ‘
993
444
###$
#
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 11 Additional and Advanced Exercises 709
(b) Around the y-axis: 9x 4y 36 x 4 y x 4 y and we use the positive root:
## # # #
œÊœ Êœ„
44
99
É
V 2 4 y dy 2 4 y dy 2 4y y 16œœœœ
''
00
33
1111
Š‹
Ɉ‰ ‘
444
9927
###$
$
!
86. 9x 4y 36, x 4 y y x 4 ; V x 4 dx x 4 dx
## # #
##
##
#
œ œÊœ Êœ œ œ
9x 36 3 3 9
4 4
ÈÈ
Š‹ ab
''
22
44
11
4x 16 8 (32) 24œœ œœ œ
9x 9 64 8 956 24 3
43 4 3 3 43 3 4
11 11
’“‘ˆ‰ˆ‰ˆ‰
%
#1
87. (a) r r er cos k x y ex k x y k ex x yœ Ê œÊœÊœÊ
k
1e cos ## ## ##
))ÈÈ
k 2kex e x x e x y 2kex k 0 1 e x y 2kex k 0œ ÊœÊ œ
######## ####
ab
(b) e 0 x y k 0 x y k circle;œÊ œÊ œ Ê
### ## #
0 e 1 e 1 e 1 0 B 4AC 0 4 1 e (1) 4 e 1 0 ellipse;Ê Ê Ê œ œ Ê
## # # # #
ab ab
e 1 B 4AC 0 4(0)(1) 0 parabola;œÊ œ œÊ
##
e 1 e 1 B 4AC 0 4 1 e (1) 4e 4 0 hyperbolaÊ Ê œ œ Ê
## ###
ab
88. Let (r ) be a point on the graph where r a . Let (r ) be on the graph where r a and
"" " " ## # #
ߜߜ))))
2 . Then r and r lie on the same ray on consecutive turns of the spiral and the distance between)) 1
#" " #
œ
the two points is r r a a a( ) 2 a, which is constant.
#" # " # "
œœ œ)) )) 1
CHAPTER 11 ADDITIONAL AND ADVANCED EXERCISES
1. Directrix x 3 and focus (4 0) vertex is œßÊß!
ˆ‰
7
#
p the equation is xÊœÊ œ
"
###
7y
2. x 6x 12y 9 0 x 6x 9 12y y vertex is (3 0) and p 3 focus is (3 3) and the
##
œ Ê œ Ê œ Ê ß œ Ê ß
(x 3)
12
directrix is y 3œ
3. x 4y vertex is ( 0) and p 1 focus is ( 1); thus the distance from P(x y) to the vertex is x y
###
œ Ê !ß œ Ê !ß ß
È
and the distance from P to the focus is x (y 1) x y 2 x (y 1)
ÈÈÈ
######
Ê œ
x y 4 x (y 1) x y 4x 4y 8y 4 3x 3y 8y 4 0, which is a circleÊœ ÊœÊ œ
## # # ## # # # #
cd
4. Let the segment a b intersect the y-axis in point A and
intersect the x-axis in point B so that PB b and PA aœœ
(see figure). Draw the horizontal line through P and let it
intersect the y-axis in point C. Let PBOnœ)
APC . Then sin and cos Ên œ œ œ)) )
y
ba
x
cos sin 1.Êœ œ
x
ab
y##
))
5. Vertices are 2 a 2; e 0.5 c 1 foci are 0 1ab ab!ß „ Ê œ œ Ê œ Ê œ Ê ß „
cc
a#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
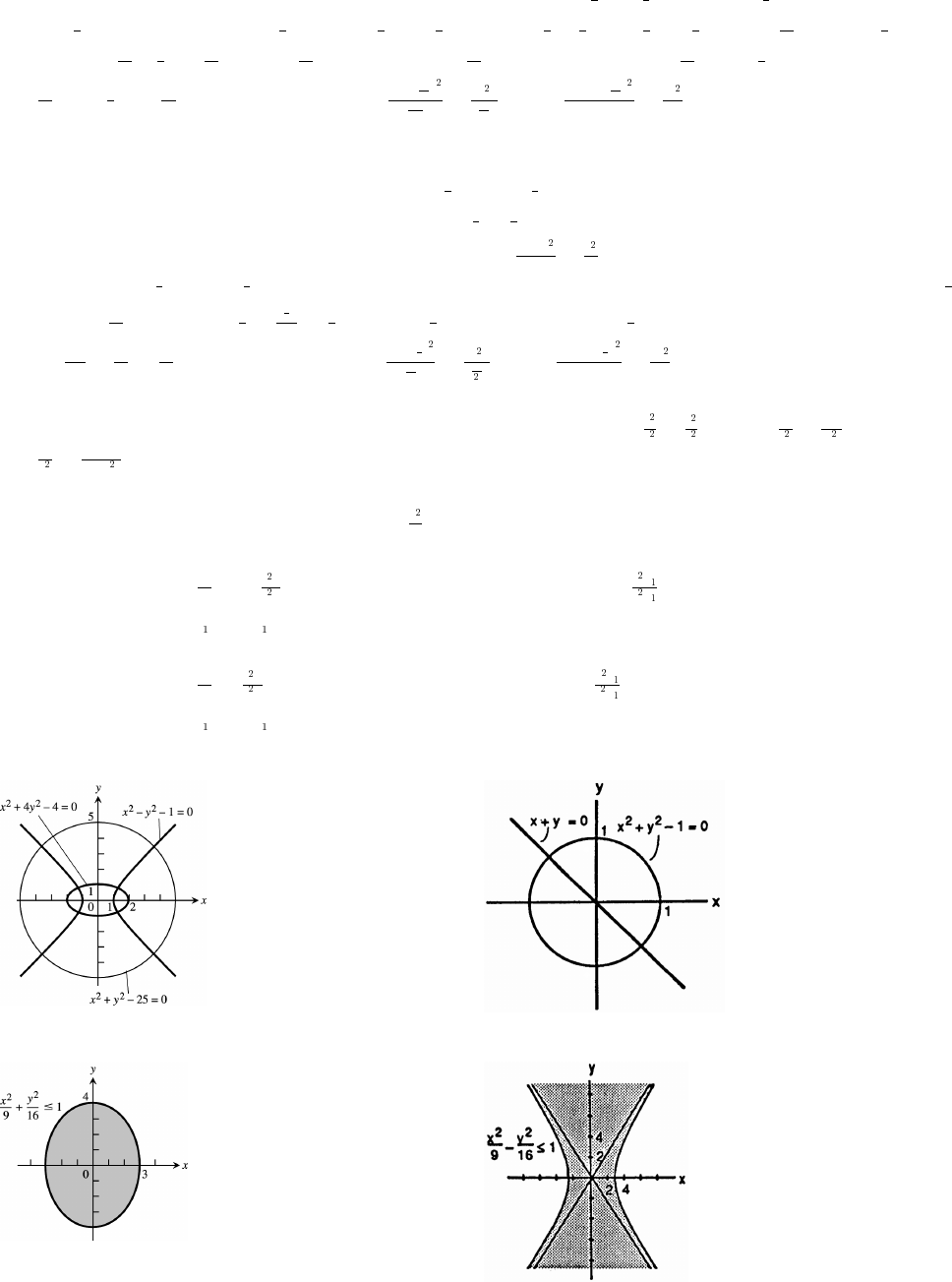
710 Chapter 11 Parametric Equations and Polar Coordinates
6. Let the center of the ellipse be (x 0); directrix x 2, focus (4 0), and e c 2 2 cߜߜʜʜ
2a a
3e e
a (2 c). Also c ae a a 2 a a a a a ; x 2Êœ œ œ Êœ Êœ Ê œ Êœ œ
2222445412a
333339935e
ˆ‰
x 2 x the center is 0 ; x 4 c c 4 so that c a bÊœ œ Êœ Ê ß œÊœ œ œ
ˆ‰ˆ‰ ˆ ‰
12 3 18 28 28 28 8
55 5 5 55#
###
; therefore the equation is 1 or 1œœ œ œ
ˆ‰ ˆ‰
12 8 80
5 5 25 144 16
x25x
y5y
##
ˆ‰ ˆ‰
ˆ‰ ˆ‰
28 28
55
144 80
25 25
7. Let the center of the hyperbola be (0 y).ß
(a) Directrix y 1, focus (0 7) and e 2 c 6 c 6 a 2c 12. Also c ae 2aœ ß œÊœÊœÊœ œœ
aa
ee
a 2(2a) 12 a 4 c 8; y ( 1) 2 y 1 the center is (0 1); c a bÊœ ʜʜ œœœÊœÊ ß œ
a4
e#
###
b c a 64 16 48; therefore the equation is 1Ê œœœ œ
### (y 1)
16 48
x
(b) e 5 c 6 c 6 a 5c 30. Also, c ae 5a a 5(5a) 30 24a 30 aœÊœÊœÊœ œœÊœ Ê œÊœ
aa 5
ee 4
c ; y ( 1) y the center is ; c a b b c aÊœ œœ œ ÊœÊ !ß œ Ê œ
25 a 3 3
4e544 4
ˆ‰
5
4"### ###
ˆ‰
; therefore the equation is 1 or 1œœ œ œ
625 25 75 x 2x
16 16 25 75
y16y
#
ˆ‰ ˆ‰
ˆ‰ ˆ‰
33
44
25
16
75
8. The center is (0 0) and c 2 4 a b b 4 a . The equation is 1 1ߜʜʜ œÊœ
## # # y
ab a b
x 49 144
1 49 4 a 144a a 4 a 196 49a 144a 4a a a 197a 196Ê œÊ œ Ê œ Ê
49 144
a4a
ab
# ### ###%%#
ab ab
0 a 196 a 1 0 a 14 or a 1; a 14 b 4 (14) 0 which is impossible; a 1œÊ œÊœ œ œ Ê œ œabab
## # #
b 4 1 3; therefore the equation is y 1Ê œœ œ
##
x
3
9. b x a y a b ; at (x y ) the tangent line is y y (x x )
## ## ## "" " "
œ Êœ ß œ
dy
dx ay ay
bx bx
Š‹
ayy bxx bx ay ab bxx ayy ab 0ÊœœÊœ
# # ## ## ## # # ##
"" ""
10. b x a y a b ; at (x y ) the tangent line is y y (x x )
## ## ## "" " "
œ Êœ ß œ
dy
dx ay ay
bx bx
Š‹
b xx a yy b x a y a b b xx a yy a b 0ÊœœÊœ
# # ## ## ## # # ##
"" ""
11. 12.
13. 14.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
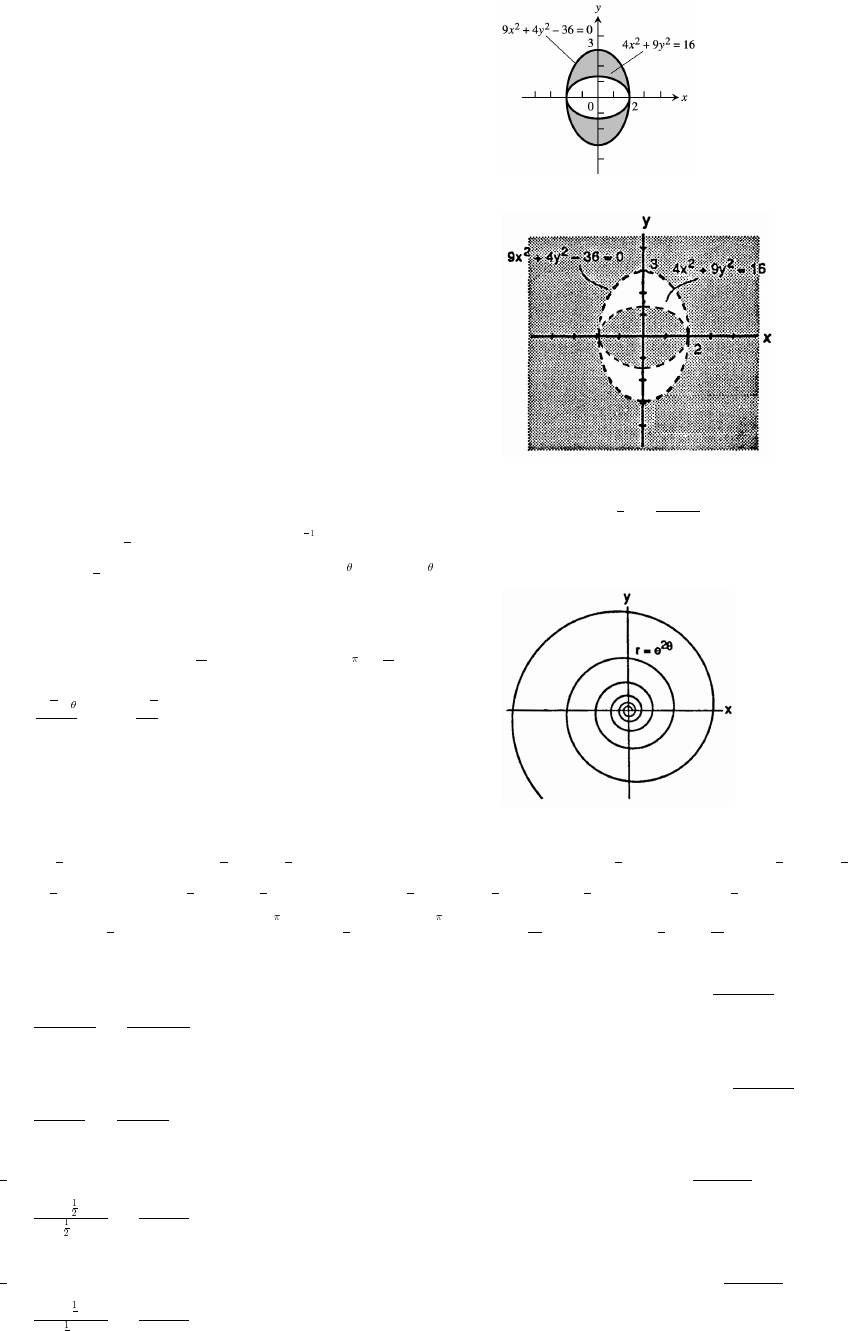
Chapter 11 Additional and Advanced Exercises 711
15. 9x 4y 36 4x 9y 16 0abab
## ##
Ÿ
9x 4y 36 0 and 4x 9y 16 0ÊŸ
## ##
or 9x 4y 36 0 and 4x 9y 16 0
## ##
Ÿ
16. 9x 4y 36 4x 9y 16 0, which is theabab
## ##
complement of the set in Exercise 15
17. (a) x e cos t and y e sin t x y e cos t e sin t e . Also tan tœœÊœœœœ
2t 2t 4t 4t 4t## # # y
xe cos t
e sin t
2t
2t
t tan x y e is the Cartesian equation. Since r x y andÊœ Ê œ œ
" # # # # #
ˆ‰
y
x
%Îtan y xab
tan , the polar equation is r e or r e for r 0)œœœ
" #
ˆ‰
y
x
42
(b) ds r d dr ; r e dr 2e d
### #
œœÊœ))
22))
ds r d 2e d e d 4e dÊœ œ
### # #
##
)) ))
ˆ‰ˆ‰
22 4)) )
5e d ds 5 e d L 5 e dœÊœ Êœ
42 2)) )
)) )
#ÈÈ
'0
2
e1œœ
’“ ab
ÈÈ
5e 5
2
4
2#
!#
11
18. r 2 sin dr 2 sin cos d ds r d dr 2 sin d 2 sin cos dœÊœ Êœœ
$# ####$##
##
ˆ‰ ˆ‰ ˆ‰ ‘ ‘ˆ‰ ˆ‰ ˆ‰
))) )))
333 333
)) ) )
4 sin d 4 sin cos d 4 sin sin cos d 4 sin dœ œ œ
'# % ## % # # # %#
ˆ‰ ˆ‰ ˆ‰ ‘ ‘ ˆ‰ˆ‰ ˆ‰ ˆ‰
))) ))) )
333 333 3
)) ))
ds 2 sin d . Then L 2 sin d 1 cos d sin 3Êœ œ œ œ œ
## $
!
ˆ‰ ˆ‰ ‘ ‘ˆ‰ ˆ‰
))))
1
33323
232
))))1
''
00
33
19. e 2 and r cos 2 x 2 is the directrix k 2; the conic is a hyperbola with rœ œÊœ Êœ œ)ke
1e cos )
rÊœ œ
(2)(2)
12 cos 12 cos
4
))
20. e 1 and r cos 4 x 4 is the directrix k 4; the conic is a parabola with rœœÊœ Êœ œ)ke
1e cos )
rÊœ œ
(4)(1)
1cos 1cos
4
))
21. e and r sin 2 y 2 is the directrix k 2; the conic is an ellipse with rœ œÊœ Êœ œ
"
#
)ke
1e sin )
rÊœ œ
2
1 sin
2
2sin
ˆ‰
ˆ‰
))
22. e and r sin 6 y 6 is the directrix k 6; the conic is an ellipse with rœœÊœ Êœ œ
"
31e sin
ke
))
rÊœ œ
6
1 sin
6
3sin
ˆ‰
ˆ‰
3
3
))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
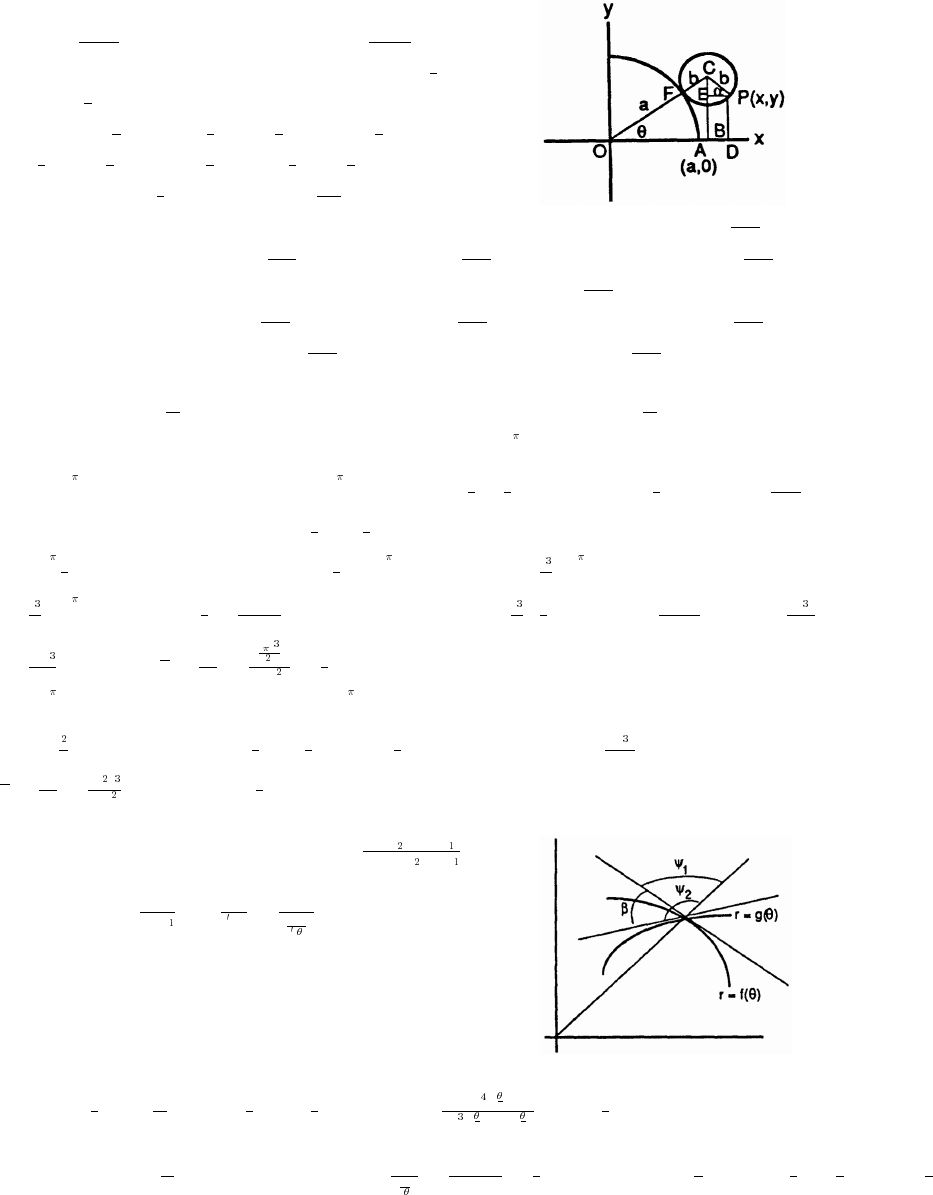
712 Chapter 11 Parametric Equations and Polar Coordinates
23. Arc PF Arc AF since each is the distance rolled;œ
PCF Arc PF b( PCF); nœ Ê œn œ
Arc PF Arc AF
ba
)
Arc AF a a b( PCF) PCF ;ʜʜnÊnœ)) )
ˆ‰
a
b
OCB and OCB PCF PCEnœ nœnn
1
#)
PCF œn œ Ê
ˆ‰ˆ‰ˆ‰
111
###
!)! )
a
b
œÊœ
ˆ‰ ˆ ‰ ˆ‰
aa
bb
)! ))!
11 1
## #
.ʜ ʜ!1) ) !1 )
ˆ‰ ˆ ‰
aab
bb
Now x OB BD OB EP (a b) cos b cos (a b) cos b cosœœœ œ )! ) 1 )
ˆ‰ˆ‰
ab
b
(a b) cos b cos cos b sin sin (a b) cos b cos andœ œ )1 ) 1 ) ) )
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
ab ab ab
bb b
y PD CB CE (a b) sin b sin (a b) sin b sinœœœ œ )! ) )
ˆ‰ˆ‰
ab
b
(a b) sin b sin cos b cos sin (a b) sin b sin ;œ œ )1 ) 1 ) ) )
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
ab ab ab
bb b
therefore x (a b) cos b cos and y (a b) sin b sinœ œ )) ))
ˆ‰ ˆ‰ˆ‰ ˆ‰
ab ab
bb
24. x a(t sin t) a(1 cos t) and let 1 dm dA y dx y dtœ Ê œ œÊ œ œ œ
dx dx
dt dt
$ˆ‰
a(1 cos t) a (1 cos t) dt a (1 cos t) dt; then A a (1 cos t) dtœ œ œ
## ##
'0
2
a 1 2 cos t cos t dt a 1 2 cos t cos 2t dt a t 2 sin tœœ œ
### #
""
##
#
!
''
00
22
ab
ˆ‰‘
3sin 2t
24
1
3 a ; x = x a(t sin t) and y = y a(1 cos t) M y dm y dAœœ œÊœœ
µµ µµ
1 $
#""
## x''
a(1 cos t) a (1 cos t) dt a (1 cos t) dt 1 3 cos t 3 cos t cos t dtœ œ œ
'''
000
222
""
###
##$ $ #$
aab
1 3 cos t 1 sin t (cos t) dt t 3 sin t sin tœ œ
a 3 3 cos 2t a 5 3 sin 2t sin t
243
### #
##
!
'0
2‘
ab ’“
1
. Therefore y a. Also, M x dm x dAœœœœœœ
µµ
5a 5
M
M3a 6 y
1
1
#
x
5a
Š‹ ''
$
a(t sin t) a (1 cos t) dt a t 2t cos t t cos t sin t 2 sin t cos t sin t cos t dtœ œ
''
00
22
##$ # #
ab
a 2 cos t 2t sin t t cos 2t sin 2t cos t sin t 3 a . Thusœ œ
$# ##$
"" #
!
’“
ttcost
2484 3
1
1
x a a a is the center of mass.œœ œ Ê ß
M
M3a 6
3a 5
y1
111
ˆ‰
25. tan tan ( ) ;"< < " < <œ Ê œ œ
#" #"
tan tan
1tan tan
<<
<<
the curves will be orthogonal when tan is undefined, or"
when tan <#" "
œÊœ
tan g ( )
r
<)
’“
r
f()
rf()g()ʜ
#ww
))
26. r sin sin cos tan tanœÊœ Êœ œ
%$
ˆ‰ ˆ‰ ˆ‰ ˆ‰
))) )
)4d 4 4 4
dr sin
sin cos
<ˆ‰
ˆ‰ ˆ‰
4
44
27. r 2a sin 3 6a cos 3 tan tan 3 ; when , tan tan œÊœ Êœœœ œœÊœ))< ))<<
dr r 2a sin 3
d 6a cos 3 3 6 3))
)111
ˆ‰
dr
d
""
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 11 Additional and Advanced Exercises 713
28. (a) (b) r 1 r tan )) )<œÊœ Ê œ Ê
" #
dr
d)k1
lim tan œœÊ œ_
)
)
)<
)Ä_
from the right as the spiral winds inÊÄ<1
#
around the origin.
29. tan cot is at ; tan tan is 3 at ; since the product of<))<))
"#
"
œœœ œœ œ
È
ÈÈ
3 cos
3 sin 3 3cos 3
sin
)
)
1) 1
)È
these slopes is 1, the tangents are perpendicular
30. tan is 1 at <)<œœ œÊœ
ra(1 cos )
a sin 4
ˆ‰
dr
d
#
)
)
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
714 Chapter 11 Parametric Equations and Polar Coordinates
NOTES:
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE
12.1 THREE-DIMENSIONAL COORDINATE SYSTEMS
1. The line through the point 2 3 0 parallel to the z-axisabßß
2. The line through the point 1 0 0 parallel to the y-axisabß ß
3. The x-axis
4. The line through the point 1 0 0 parallel to the z-axisabßß
5. The circle x y 4 in the xy-plane
##
œ
6. The circle x y 4 in the plane z = 2
##
œ
7. The circle x z 4 in the xz-plane
##
œ
8. The circle y z 1 in the yz-plane
##
œ
9. The circle y z 1 in the yz-plane
##
œ
10. The circle x z 9 in the plane y 4
##
œ œ
11. The circle x y 16 in the xy-plane
##
œ
12. The circle x z 3 in the xz-plane
##
œ
13. The ellipse formed by the intersection of the cylinder x y 4 and the plane z y.
##
œ œ
14. The circle formed by the intersection of the sphere x y z 4 and the plane y x.
###
œ œ
15. The parabola y x in the the xy-plane.œ#
16. The parabola z y in the the plane x 1.œœ
#
17. (a) The first quadrant of the xy-plane (b) The fourth quadrant of the xy-plane
18. (a) The slab bounded by the planes x 0 and x 1œœ
(b) The square column bounded by the planes x 0, x 1, y 0, y 1œœœœ
(c) The unit cube in the first octant having one vertex at the origin
19. (a) The solid ball of radius 1 centered at the origin
(b) The exterior of the sphere of radius 1 centered at the origin
20. (a) The circumference and interior of the circle x y 1 in the xy-plane
##
œ
(b) The circumference and interior of the circle x y 1 in the plane z 3
##
œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

716 Chapter 12 Vectors and the Geometry of Space
(c) A solid cylindrical column of radius 1 whose axis is the z-axis
21. (a) The solid enclosed between the sphere of radius 1 and radius 2 centered at the origin
(b) The solid upper hemisphere of radius 1 centered at the origin
22. (a) The line y x in the xy-planeœ
(b) The plane y x consisting of all points of the form (x x z)œßß
23. (a) The region on or inside the parabola y x in the xy-plane and all points above this region.œ#
(b) The region on or to the left of the parabola x y in the xy-plane and all points above it that are 2 units or less awayœ#
from the xy-plane.
24. (a) All the points the lie on the plane z 1 y.œ
(b) All points that lie on the curve z y in the plane x 2.œœ
3
25. (a) x 3 (b) y 1 (c) z 2œœœ
26. (a) x 3 (b) y 1 (c) z 2œœœ
27. (a) z 1 (b) x 3 (c) y 1œœœ
28. (a) x y 4, z 0 (b) y z 4, x 0 (c) x z 4, y 0
## ## ##
œ œ œ œ œ œ
29. (a) x y 2 4, z 0 (b) y 2 z 4, x 0 (c) x z 4, y 2
####
##
œ œ œ œ œ œab ab
30. (a) x 3 y 4 1, z 1 (b) y 4 z 1 1, x 3 abab ababœ œ œ œ
## ##
(c) x 3 z 1 1, y 4ababœ œ
##
31. (a) y 3, z 1 (b) x 1, z 1 (c) x 1, y 3œœ œœ œœ
32. x y z x y 2 z x y z x y 2 z y y 4y 4 y 1
ÈÉab ab
### # #
##
### # # # #
œ Ê œ Ê œÊœ
33. x y z 25, z 3 x y 16 in the plane z 3
### ##
œ œÊœ œ
34. x y z 1 4 and x y z 1 4 x y z 1 x y z 1 z 0, x y 3
## ## ## ## ##
## ##
œ œÊ œ Êœ œab ab ab ab
35. 0 z 1 36. 0 x 2, 0 y 2, 0 z 2ŸŸ ŸŸ ŸŸ ŸŸ
37. z 0 38. z 1 x yŸœ
È##
39. (a) x 1 y 1 z 1 1 (b) x 1 y 1 z 1 1ababab ababab
### ###
40. 1 x y z 4ŸŸ
###
41. P P 3 1 3 1 0 1 9 3kkababab
ÉÈ
"# ###
œ œ œ
42. P P 2 1 5 1 0 5 50 5 2kkababab
ÉÈÈ
"# ###
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
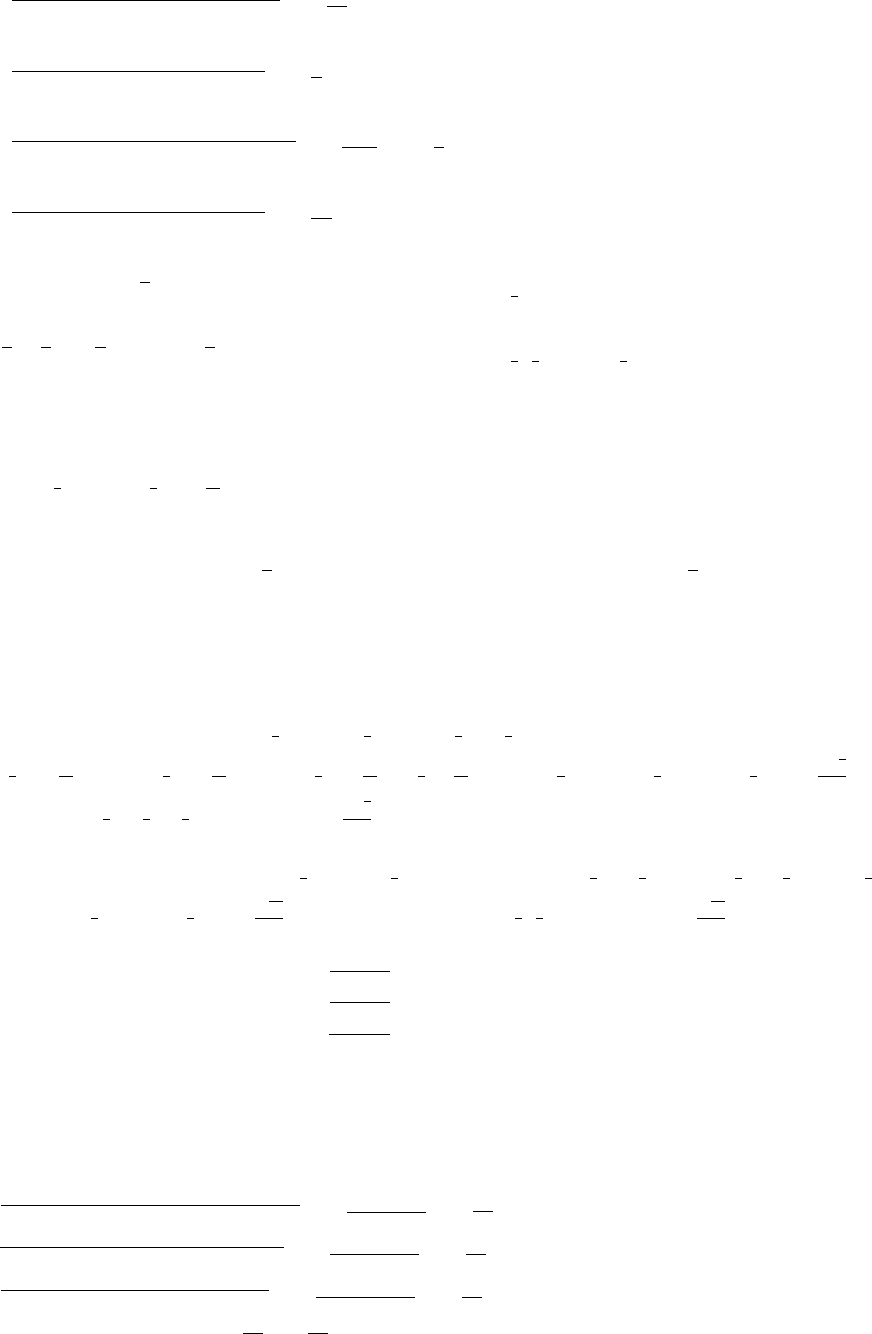
Section 12.1 Three-Dimensional Coordinate Systems 717
43. P P 4 1 2 4 7 5 49 7kkaba bab
ÉÈ
"# ###
œœ œ
44. P P 2 3 3 4 4 5 3kkababab
ÉÈ
"# ###
œ œ
45. P P 2 0 2 0 2 0 3 4 2 3kkababab
ÉÈÈ
"# ###
œœ†œ
46. P P 0 5 0 3 0 2 38kkababab
ÉÈ
"# ###
œ œ
47. center ( 2 0 2), radius 2 2 48. center 1 3 , radius 5ß ß ß ß
Ȉ‰
"
#
49. center 2 2 2 , radius 2 50. center , radius
Š‹
ÈÈ È È ˆ‰
ßß !ßß
""
33 3
4
51. x 1 y 2 z 3 14 52. x y 1 z 5 4ababab ababœ œ
### ##
#
53. x 1 y z 54. x y 7 z 49ab ab
ˆ‰ˆ‰
œ œ
# #
## ##
1216
2381
55. x y z 4x 4z 0 x 4x 4 y z 4z 4 4 4
### # # #
œÊ œabab
x 2 y 0 z 2 8 the center is at 2 0 2 and the radius is 8Ê œ Ê ßßababab a b
Š‹
ÈÈ
###
#
56. x y z 6y 8z 0 x y 6y 9 z 8z 16 9 16 x 0 y 3 z 4 5
### # # # #
###
œÊ œÊ œa ba b ababab
the center is at 0 3 4 and the radius is 5Êßßab
57. 2x 2y 2z x y z 9 x x y y z z
### # # #
"""
####
œ Ê œ
9
xx yy zz x y zÊ œÊœ
ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
Š‹
###
"" "" "" " " "
####
###
#
16 16 16 16 4 4 4 4
93 53
È
the center is at and the radius is Ê ß ß
ˆ‰
"""
444 4
53
È
58. 3x 3y 3z 2y 2z 9 x y y z z 3 x y y z z 3
### ## # ## #
""
œÊœÊ œ
22 2 2 2
33 39 399
ˆ‰ˆ‰
(x 0) y z the center is at 0 and the radius is Ê œ Ê ßß
#"" ""
##
#
ˆ‰ˆ‰ ˆ ‰
Š‹
333 33 3
29 29
ÈÈ
59. (a) the distance between x y z and x 0 0 is y zabab
È
ßß ßß
##
(b) the distance between x y z and 0 y 0 is x zabab
È
ßß ßß
##
(c) the distance between x y z and 0 0 z is x yabab
È
ßß ßß
##
60. (a) the distance between x y z and x y 0 is zababßß ßß
(b) the distance between x y z and 0 y z is xababßß ßß
(c) the distance between x y z and x 0 z is yababßß ßß
61. AB 1 1 1 2 3 1 4 9 4 17kk a ba ba b
Éab ÈÈ
œœœ
###
BC 31 4 1 53 4254 33kkaba bab
Éab ÈÈ
œœœ
###
CA 13 24 15 16416 366kka babab
ÉÈÈ
œœ œ œ
###
Thus the perimeter of triangle ABC is 17 33 6.
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

718 Chapter 12 Vectors and the Geometry of Space
62. PA 2 3 1 1 3 2 1 4 1 6kkaba bab
ÉÈÈ
œœœ
###
PB 43 31 12 141 6kkababab
ÉÈÈ
œ œ œ
###
Thus P is equidistant from A and B.
63. x x y 1 z z x x y 3 z z y 1 y 3 2y 1 6y 9
ÉÉ
aba bab abababababab œ Ê œ Ê œ
########
y1ʜ
64. x 0 y 0 z 2 x x y y z 0 x y z 2 z
ÉÉ
ababab ababab abœ Êœ
### ### #
##2
xy4z40z 1ʜʜ
#2x
44
y2
65. (a) Since the entire sphere is below the xy-plane, the point on the sphere closest to the xy-plane is the point at the top of
the sphere, which occurs when x 0 and y 3 0 3 3 z 5 4 z 5 2 z 3œ œ Ê œÊœ„Êœ
222
abab
0, 3, 3 .Êab
(b) Both the center 0, 3, 5 and the the point 0, 7, 5 lie in the plane z 5, so the point on the sphere closest toab abœ
0, 7, 5 should also be in the same plane. In fact it should lie on the line segment between 0, 3, 5 and 0, 7, 5 ,ab abab
thus the point occurs when x 0 and z 5 0 y 3 5 5 4 y 3 2 y 5œ œÊ œÊœ„Êœ
222
aba b
0, 5, 5 .Êab
66. x 0 y 0 z 0 x 0 y 4 z 0 x 3 y 0 z 0
ÉÉÉ
ababab ababab abababœ œ
### ### ###
x2 y2 z3œ
Éababab
###
xyzxy8y16zx6x9yzx4xy4yz6z17Êœœœ
########22 2 2
Solve: xyzxy8y16z 0 8y16y2
### #
œÊœ Êœ
22
Solve: xyzx6x9yz 0 6x9x
### #
œÊœÊœ
22 3
2
Solve: x y z x 4x y 4y z 6z 17 0 4x 4y 6z 17 0 4 4 2 6z 17
### #
œÊœÊœ
22 3
2
ˆ‰ ab
z , 2, ÊœÊ
13 1
22 2
ˆ‰
12.2 VECTORS
1. (a) 3 3 , 3 2 9, 6 2. (a) 2 2 , 2 5 4, 10
¡¡ ¡¡
abab ab abœ œ
(b) 9 6 117 3 13 (b) 4 10 116 2 29
ÉÉ
ab a b
ÈÈ ÈÈ
2 2
2 2
œ œ œ œ
3. (a) 3 2 , 2 5 1, 3 4. (a) 3 2 , 2 5 5, 7
¡¡ ¡¡
ab ab œ œ
(b) 1 3 10 (b) 5 7 74
ÈÈÈ
Éab
22 2 2
œ œ
5. (a) 2 2 3 , 2 2 6, 4 6. (a) 2 2 3 , 2 2 6, 4uuœœ œœ
¡¡ ¡¡
ab a b ab a b
3 3 2 , 3 5 6, 15 5 5 2 , 5 5 10, 25vvœ œ œ œ
¡¡ ¡¡
abab abab
2 3 6 6 , 4 15 12, 19 2 5 6 10 , 4 25 16, 29uv uvœ œ œ œ
¡¡ ¡¡
ab ab
(b) 12 19 505 (b) 16 29 1097
ÉÉ
ab ab
ÈÈ
2 2
22
œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
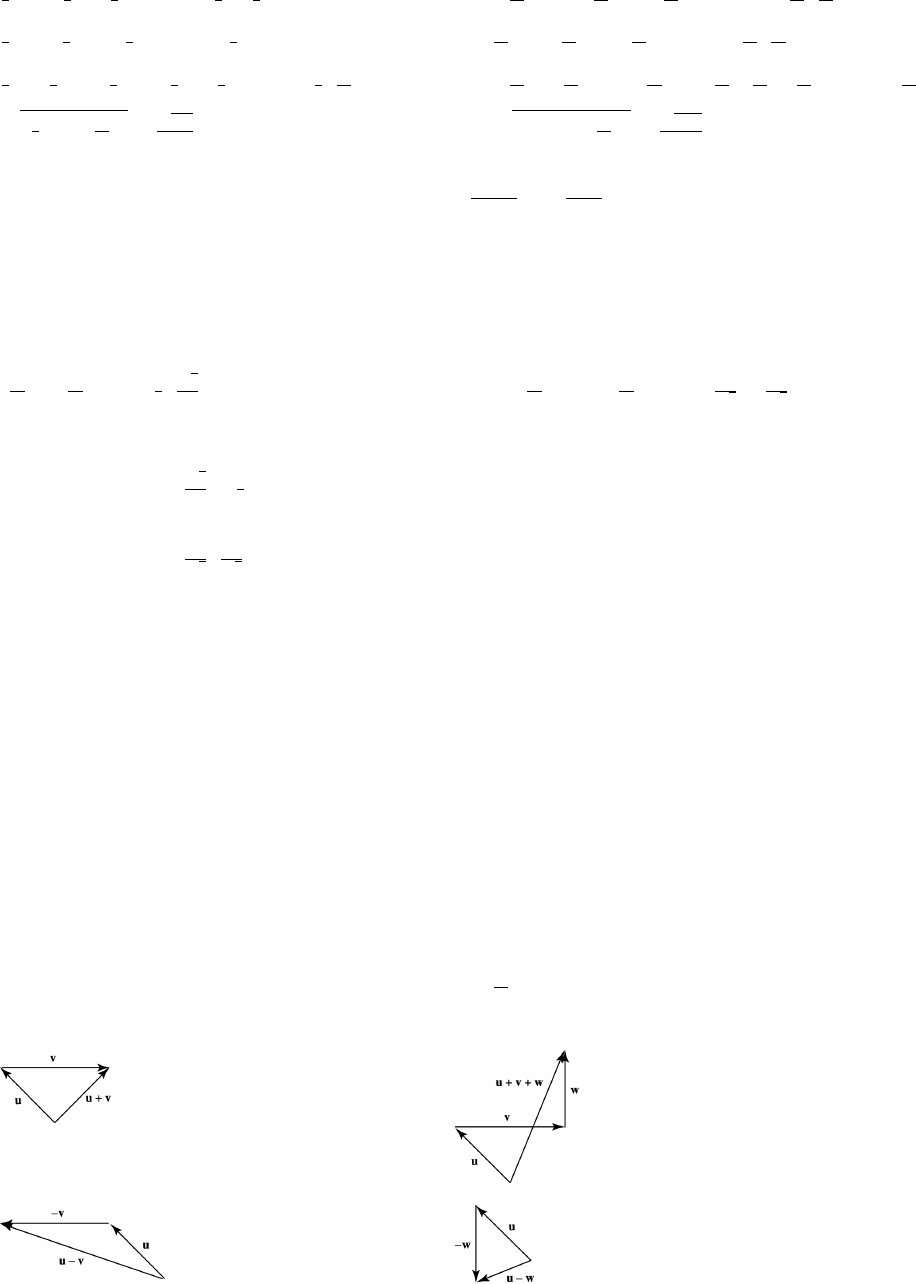
Section 12.2 Vectors 719
7. (a) 3 , 2 , 8. (a) 3 , 2 ,
3 3 3 9 6 5 5 5 15 10
555 55 13 1313 1313
uuœ œ œ œ
¢£¢£ ¢ £¢£
ab a b ab a b
2, 5 , 4 2, 5 ,
4 4 4 8 12 12 12 24 60
5 5 5 5 13 13 13 13 13
vvœ œ œ œ
¢£¢£ ¢ £¢£
abab abab
, 4 , , 3,
34 9 86 114 5 12 15 241060 70
55 5 55 55 1313 13 131313 13
uv u vœ œ œ œ
¢£¢£ ¢ £¢£
ˆ‰ ˆ‰
(b) (b) 3
ÉÉ
ˆ‰ ˆ‰ ˆ‰
ab
114 70
55 5 13 13
22 2
97 6421
2
œ œ
È È
"
9. 2 1, 1 3 1, 4 10. 0, 0 1, 1
¡¡ ¡
¢£
œ œ
24 3
##
"
ab
11. 0 2, 0 3 2, 3
¡¡
œ
12. AB 2 1, 0 1 1, 1 , CD 2 1 , 2 3 1, 1 , AB CD 0, 0
ÄÄ ÄÄ
œ œ œ œ œ
¡¡ ¡ ¡ ¡
ab ab
13. cos , sin , 14. cos , sin ,
¢£¢£ ¢ £¢£
ˆ‰ˆ‰
22 33
33 2 4 4
3
22
11 11
œ œ
"""
#ÈÈÈ
15. This is the unit vector which makes an angle of 120 90 210 with the positive x-axis;
‰‰ ‰
œ
cos 210 , sin 210 ,
¡
¢£
‰‰ "
#
œ
È3
2
16. cos 135 , sin 135 ,
¡
¢£
‰‰ ""
œ
ÈÈ
22
17. P P 2 5 9 7 2 1 3 2
"#
Äœ œ ababa babij kijk
18. P P 3 1 0 2 5 0 4 2 5
"#
Äœ œ a bababijkijk
19. AB 10 7 8 8 1 1 3 16
Äœ œ abababab abijkij
20. AB 1 1 4 0 5 3 2 4 2
Äœ œ a bababijkijk
21. 5 5 1, 1, 1 2, 0, 3 5, 5, 5 2, 0, 3 5 2, 5 0, 5 3 3, 5, 8 3 5 8uv ijkœ œ œœœ
¡¡¡¡ ¡¡
22. 2 3 2 1, 0, 2 3 1, 1, 1 2, 0, 4 3, 3, 3 5, 3, 1 5 3 œ œ œ œuv ijk
¡¡¡¡¡
23. The vector is horizontal and 1 in. long. The vectors and are in. long. is vertical and makes a 45 angle withvuwwu
"‰
1
16
the horizontal. All vectors must be drawn to scale.
(a) (b)
(c) (d)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
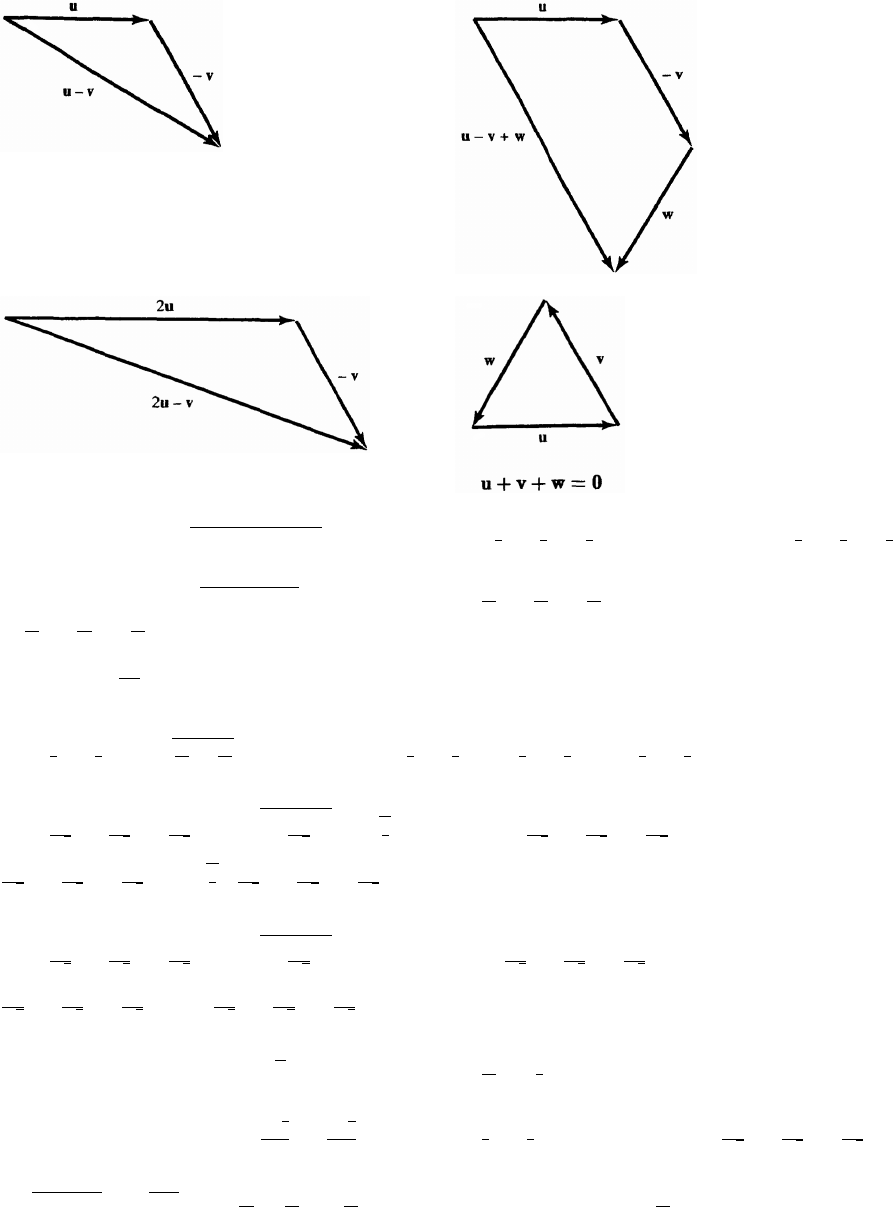
720 Chapter 12 Vectors and the Geometry of Space
24. The angle between the vectors is 120 and vector is horizontal. They are all 1 in. long. Draw to scale.
‰u
(a) (b)
(c) (d)
25. length 2 2 2 1 ( 2) 3, the direction is 2 2 3œ œ œ Êœ kk
Ȉ‰
ij k i j k ij k i j k
## # ""22 22
333 333
26. length 9 2 6 81 4 36 11, the direction is 9 2 6œ œ œ Êkk
È
ijk i j k ijk
926
11 11 11
11œ
ˆ‰
926
11 11 11
ijk
27. length 5 25 5, the direction is 5 5( )œœ œ ÊœkkÈ
kkkk
28. length 1, the direction is 1œ œ œ Êœ
¸¸ ˆ‰
É
34 916 34 34 34
55 2525 55 55 55
ik ik ik ik
29. length 3 , the direction is œ œ œ
¹¹Š‹
ÊÉ
11 11
666 6 333
ÈÈÈ È ÈÈÈ
ijk ijk
""" "
#
#
ʜ
11 11
666 333
ÈÈÈ ÈÈÈ
ijk ijk
"" "
#
ÉŠ‹
30. length 3 1, the direction is œ œ œ
¹¹Š‹
Ê
11 11
333 3 333
ÈÈÈ È ÈÈÈ
ijk ijk
"" "
#
1ʜ
11 11
333 333
ÈÈÈ ÈÈÈ
ijk ijk
""
Š‹
31. (a) 2 (b) 3 (c) (d) 6 2 3ikjkijk
È32
10 5
32. (a) 7 (b) (c) (d) jikijkijk
32 42
55 43
11 a a a
236
ÈÈ ÈÈÈ
33. 12 5 169 13; (12 5 ) the desired vector is (12 5 )kk ÈÈ
v v ik ikœœ œ œœ Ê
## ""v
vkk 13 13 13
7
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.2 Vectors 721
34. ; the desired vector is 3kk ÉŠ‹
vijkijkœœ œ Ê
""" """
#444
3111
333 333
Èkk ÈÈÈ ÈÈÈ
v
v
333œ
ÈÈÈ
ijk
35. (a) 3 4 5 5 2 the direction is ijk i j k i j k œ Ê
ÈŠ‹
34 34
52 52 2 52 52 2
ÈÈÈ ÈÈÈ
""
(b) the midpoint is 3
ˆ‰
"
##
ßß
5
36. (a) 3 6 2 7 the direction is ijk i j k i j k œ Ê
ˆ‰
362 362
777 777
(b) the midpoint is 1 6
ˆ‰
5
#ßß
37. (a) 3 the direction is œ Ê ijk i j k i j k
ÈŠ‹
111 111
333 333
ÈÈÈ ÈÈÈ
(b) the midpoint is ˆ‰
579
###
ßß
38. (a) 2 2 2 2 3 the direction is ijk i j k i j k œ Ê
ÈŠ‹
111 111
333 333
ÈÈÈ ÈÈÈ
(b) the midpoint is ( 1)"ß "ß
39. AB (5 a) (1 b) (3 c) 4 2 5 a 1, 1 b 4, and 3 c 2 a 4, b 3, and
Äœ œ Êœ œ œÊœ œijkijk
c 5 A is the point (4 3 5)œÊ ßß
40. AB (a 2) (b 3) (c 6) 7 3 8 a 2 7, b 3 3, and c 6 8 a 9, b 0,
Äœ œ Êœ œ œÊœ œijkijk
and c 14 B is the point ( 9 0 14)œÊ ßß
41. 2 a( ) b( ) (a b) (a b) a b 2 and a b 1 2a 3 a andij ij ij i jœ œ Ê œ œ Ê œ Ê œ
3
#
baœ"œ
"
#
42. 2 a(2 3 ) b( ) (2a b) (3a b) 2a b 1 and 3a b 2 a 3 andij ij ij i j œ œ Ê œ œÊ œ
b 1 a 7 a(2 3 ) 6 9 and b( ) 7œ#œ Ê œ œ œ œuijijuiji7j
"#
43. 25 west of north is 90 25 115 north of east. 800 cos 115 , sin 115 338.095, 725.046
‰‰‰‰ ‰‰
œ ¸
¡ ¡
44. Let x, y be represent the velocity of the plane alone, 70 cos 60 , 70 sin 60 35, 35 3 , and let theuvœœœ
¡ ¡ ¡
È
‰‰
resultant 500, 0 . Then x, y 35, 35 3 500, 0 x 35, y 35 3 500, 0uvœ œ Ê œ
¡¡ ¡¡ ¡¡
ÈÈ
x 35 500 and y 35 3 0 x 465 and y 35 3 465, 35 3Ê œ œÊœ œ Êœ
ÈÈÈ
¡
u
465 35 3 468.9 mph, and tan 7.4 7.4 south of east.Êl lœ ¸ œ Ê ¸ ÊuÊŠ‹
È
2235 3
465
))
‰‰
È
45. cos 30 , sin 30 , , cos 45 , sin 45 , , andFF F FFFF F FF
11 1 1122 2 22
3
22
111
22
œll ll œ llll œll ll œ ll ll
¢£¢£¢£¢£
‰‰ ‰‰
ÈÈÈ
0, 100 . Since 0, 100 , 0, 100wFF FFFFœ œ Ê ll llll llœ
¡ ¡ ¡
¢£
12 1212
3
22
11 1
22
ÈÈÈ
0 and 100. Solving the first equation for results in: .Ê ll llœ ll llœ ll llœ ll
È È
ÈÈ
3 6
22 2
12 12 2 2 1
111
22
FF FF F F F
Substituting this result into the second equation gives us: 100 73.205 N
1 1 200
22
11 1
2
6
13
ll llœ Êllœ ¸FF F
ÈÈ
È
Š‹
89.658 N 63.397, 36.603 and 63.397, 63.397Êl lœ ¸ Ê ¸ œ ¸FF F
21 2
100 6
13
È
È
¡¡
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
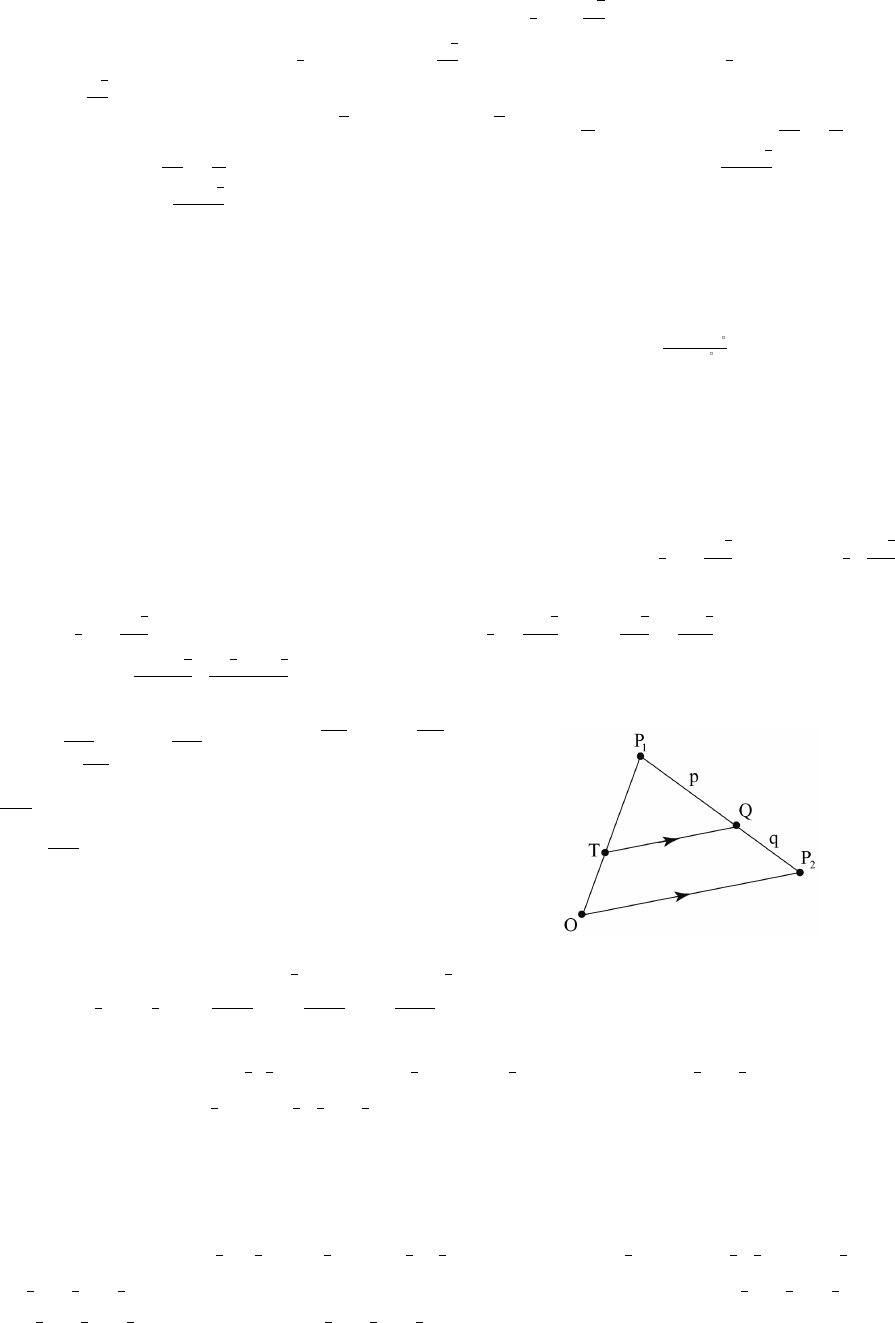
722 Chapter 12 Vectors and the Geometry of Space
46. 35 cos , 35 sin , cos 60 , sin 60 , , and 0, 50 . SinceFFFFFFw
122222
1
22
3
œ œll ll œ ll ll œ
¡ ¡
¢£¢£
!! ‰‰ È
0, 50 35 cos , 35 sin 0, 50 35 cos 0 andFF F F F
12 2 2 2
11
22 2
3
œ Ê ll llœ Ê llœ
¡ ¡¡
!! !
È
35 sin 50. Solving the first equation for results in: 70 cos . Substituting this result into the!! llœ ll llœ
È3
2222
FFF
second equation gives us: 35 sin 35 3 cos 50 3 cos sin 3cos sin sin!! !!! !!œÊœÊœ
ÈÈ
10 100 20
7497
22
3 1 sin sin sin 196 sin 140 sin 47 0 sin . Since 0Ê œ Ê œÊ œ Êab
222
100 20
49 7 14
562
!!!!! ! !
„È
sin 0 sin 74.42 , and 70 cos 18.81 N.!! ! !Ê œ Ê ¸ llœ ¸
562
14 2
‰
ÈF
47. cos 40 , sin 40 , 100 cos 35 , 100 sin 35 , and 0, w . Since 0, wFF F F w FF
11 1 2 12
œll ll œ œ œ
¢£
¡¡¡
‰‰ ‰ ‰
cos 40 100 cos 35 , sin 40 100 sin 35 0, w cos 40 100 cos 35 0 andÊl l l l œ Êl l œ
¢£
¡
FF F
11 1
‰‰‰‰ ‰‰
sin 40 100 sin 35 w. Solving the first equation for results in: 106.933 N. Substituting thisll œ ll llœ ¸FFF
111
100 cos 35
cos 40
‰‰
result into the second equation gives us: w 126.093 N.¸
48. cos , sin 75 cos , 75 sin , cos , sin 75 cos , 75 sin , andFF F FF F
11 1 22 2
œl l l l œ œl l l l œ
¡¡¡¡
! ! !! " " !!
0, 25 . Since 0, 25 75 cos 75 cos , 75 sin 75 sin 0, 25 150 sin 25wFFœ œ Ê œ Ê œ
¡ ¡ ¡¡
12 !!!! !
9.59 .ʸ!‰
49. (a) The tree is located at the tip of the vector OP (5 cos 60°) (5 sin 60°) P
ÄœœÊœßijij
55
53 53
## ##
ÈÈ
Š‹
(b) The telephone pole is located at the point Q, which is the tip of the vector OP PQ
ÄÄ
(10 cos 315°) (10 sin 315°)œ œ
Š‹ Š‹Š ‹
55
2
53 53
10 2 10 2
ij i j i j
ÈÈÈÈ
#####
Q Êœ ß
Š‹
510253102
##
ÈÈ È
50. Let t and s . Choose T on OP so that TQ isœœ
qp
pq pq 1
parallel to OP , so that TP Q is similar to OP P . Then
21 12
˜˜
t OT t OP so that T t x , t y , t z .
kk
kk
OT
OP 1111
1œÊ œ œ
ÄÄ ab
Also, s TQ s OP s x , y , z .
kk
kk
TQ
OP 2222
2œÊ œ œ
ÄÄ
¡
Letting Q x, y, z , we have thatœab
TQ x tx, y ty, z tz sx, y, z
Äœ œ
¡¡
111222
Thus x t x s x , y t y s y , z t z s z .œ œ œ
12 12 12
(Note that if Q is the midpoint, then 1 and t s
p
qœœœ
"
#
so that x x x , y , z so that this result agress with the midpoint formula.)œœ œ œ
""
##
12
xx zz
222
yy
12 12
12
51. (a) the midpoint of AB is M 0 and CM 1 1 ( 3) 3
ˆ‰ ˆ‰ˆ‰
55 5 5 3 3
## # # # #
ßß œ ! œ
Äijkijk
(b) the desired vector is CM 3 2
ˆ‰ ˆ ‰
2233
33
Äœ œ
##
ijkijk
(c) the vector whose sum is the vector from the origin to C and the result of part (b) will terminate
at the center of mass the terminal point of ( 3 ) ( 2 ) 2 2 is the pointÊ œij k ij k i jk
(2 2 1), which is the location of the center of massßß
52. The midpoint of AB is M 0 and CM 1 (0 2) 1 2
ˆ‰ˆ‰ ‘ˆ ‰ˆ‰ ˆ‰
35 2 23 5 25 7
33 3## # # # #
ßß œ œ
Äij kijk
. The vector from the origin to the point of intersection of the medians is OCœ
Ä
547 547
333 333
ijk ijk
ˆ‰
(2) .œ œ
ˆ‰
547 224
333 333
ijk ijk ijk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.3 The Dot Product 723
53. Without loss of generality we identify the vertices of the quadrilateral such that A(0 0 0), B(x 0 0),ßß ßß
b
C(x y 0) and D(x y z ) the midpoint of AB is M 0 0 , the midpoint of BC is
cc ddd AB
x
ßß ßß Ê ßß
ˆ‰
b
#
M 0 , the midpoint of CD is M and the midpoint of AD is
BC CD
xx xx z
yyy
ˆ‰ ˆ ‰
bdd
cc
c c d
## # ##
ßß ß ß
M the midpoint of M M is , which is the same as the midpoint
AD AB CD
xz z
yyy
44
ˆ‰ Œ
dd d
d d
c
### #
ßß Ê ß
xxx
bd
c
b
of M M , .
AD BC yy
44
z
ϧ
Œ
xx x
bd
cb
#
cdd
54. Let V , V , V , , V be the vertices of a regular n-sided polygon and denote the vector from the center to
"#$
áni
v
V for i 1, 2, 3, , n. If and the polygon is rotated through an angle of where i 1, 2, 3, , n,
ii i(2 )
n
œá œ œáSv
!
n
i1œ
1
then would remain the same. Since the vector does not change with these rotations we conclude that .SS S0œ
55. Without loss of generality we can coordinatize the vertices of the triangle such that A(0 0), B(b 0) andßß
C(x y ) a is located at , b is at and c is at 0 . Therefore, Aa ,
cc bx x x
yy y
bb
ßÊ ß ß ß œ
Ä
ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ‰
## ## # ## #
cc c
cc c
ij
Bb b , and Cc x ( y ) Aa Bb Cc .
ÄÄ
œ œ Ê œ
ÄÄÄ
ˆ‰ˆ‰ ˆ‰
xybcc
cc
## #
ij i j 0
56. Let be any unit vector in the plane. If is positioned so that its initial point is at the origin and terminal point is auu t x, y ,ab
then makes an angle with , measured in the counter-clockwise direction. Since 1, we have that x cos andui u) )kkœœ
y sin . Thus cos sin . Since was assumed to be any unit vector in the plane, this holds for unitœœ)))uiju every
vector in the plane.
12.3 THE DOT PRODUCT
NOTE: In Exercises 1-8 below we calculate proj as the vector , so the scalar multiplier of is the number in
vuv v
Š‹
kk
kk
u
v
cos )
column 5 divided by the number in column 2.
cos cos proj vu v u u u†kk kk kk))
v
1. 25 5 5 1 5 2 4 5 ij k
È
2. 3 1 13 3 3
334
13 5 5
ˆ‰
ik
3. 25 15 5 (10 11 2 )
""
339
5ijk
4. 13 15 3 (2 10 11 )
13 13 13
45 15 225 ijk
5. 2 34 3 (5 3 )
ÈÈ 22
334 34 17
ÈÈ È "jk
6. 3 2 2 3 ( )
ÈÈÈ
ÈÈÈ
ÈÈÈ
ÈÈ
32 32 32
32 2
#ij
7. 10 17 26 21 (5 )
ÈÈ È10 17 10 17 10 17
546 26 26
ÈÈÈ
ÈÈ ij
8. ,
""""""
#
6665 5
30 30
30 3
ÈÈ ÈÈÈ
¢£
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

724 Chapter 12 Vectors and the Geometry of Space
9. cos cos cos cos 0.75 rad)œœ œ œ¸
" " " "
Š‹ Š ‹ Š ‹ Š‹
uv
uv
†
kkkk ÈÈÈÈ
È
(2)(1) (1)(2) (0)( 1)
210 12(1)
44
5 6 30
10. cos cos cos cos 0.84 rad)œœ œ œ¸
" " " "
Š‹ Š ‹ Š ‹ ˆ‰
uv
uv
†
kkkk ÈÈÈÈ
3
(2)(3) ( 2)(0) (1)(4)
2(2)1 304
10 2
9 25
11. cos cos cos)œœ œ
" " "
Š‹ Š ‹
ÎÑ
ÏÒ
uv
uv
†
kkkk Š‹Š‹
ÈÈ
ÊŠ ‹ ÊŠ ‹
ÈÈ ÈÈ
3 3 (7)(1) (0)(2)
3(7)0 3(1)(2)
37
52 8
cos 1.77 radœ¸
"
Š‹
1
26
È
12. cos cos cos)œœ œ
" " "
Š‹ Š ‹
ÎÑ
ÏÒ
uv
uv
†
kkkk Š‹ Š ‹
ÈÈ
ÊŠ‹Š‹
ÈÈ
ÈÈÈ
(1)( 1) 2 (1) 2 (1)
(1) 2 2 ( 1) (1) (1)
1
5 3
cos 1.83 radœ¸
"
Š‹
1
15
È
13. AB 3, 1 , BC 1, 3 , and AC 2, 2 . BA 3, 1 , CB 1, 3 , CA 2, 2 .
ÄÄ Ä Ä ÄÄ
œ œ œ œ œ œ
¡¡ ¡¡¡¡
AB BA 10, BC CB 10, AC CA 2 2,
¹¹¹¹ ¹¹¹¹ ¹¹¹¹
ÈÈ È
ÄÄ ÄÄ ÄÄ
œœ œœ œœ
Angle at A cos cos cos 63.435œœ œ¸
" " " ‰
ÄÄ
ÄÄ
Š‹
AB AC 1
AB AC 10 2 2
32 1 2
5
†
¹¹¹¹ Š ‹Š ‹
ab a b
ÈÈÈ
Angle at B cos cos cos 53.130 , andœœ œ¸
" " " ‰
ÄÄ
ÄÄ
ˆ‰
BC BA 3
BC BA 10 10
13 31
5
†
¹¹¹¹ Š‹Š‹
abababab
ÈÈ
Angle at C cos cos cos 63.435œœ œ¸
" " " ‰
ÄÄ
ÄÄ
Š‹
CB CA 1
CB CA 10 2 2
12 32
5
†
¹¹¹¹ Š‹Š‹
ab ab
ÈÈÈ
14. AC 2, 4 and BD 4, 2 . AC BD 2 4 4 2 0, so the angle measures are all 90 .
ÄÄ
œœ†œœ
ÄÄ
¡ ¡ ab a b ‰
15. (a) cos , cos , cos and!"#œœ œœ œ œ
iv kv
iv v jv v kv v
jv
††
†
kkkk kk kkkk kk kkkk kk
ab c
cos cos cos 1
### ###
!"#œœ œœ
Š‹ Š‹ Š‹
abcabc
kk kk kk kkkk kkkk
kkkk
v v v vv vv
vv
(b) 1 cos a, cos b and cos c are the direction cosines of kkv vœÊ œœ œœ œœ!" #
ab c
kk kk kkvv v
16. 10 2 is parallel to the pipe in the north direction and 10 is parallel to the pipe in the eastuik vjkœ œ
direction. The angle between the two pipes is cos cos 1.55 rad 88.88°.)œœ ¸¸
" "
Š‹ Š ‹
uv
uv
†
kkkk ÈÈ
2
104 101
17. The sum of two vectors of equal length is orthogonal to their difference, as we can see from the equationalways
()() 0v v v v vv vv vv vv v v
" # " # "" #" "# ## " #
##
œœœ† ††††kk kk
18. CA CB ( ( )) ( ) 0 because since both equal
ÄÄ
œœœœ œ††††††v u v u vv vu uv uu v u u vkk kk kk kk
##
the radius of the circle. Therefore, CA and CB are orthogonal.
ÄÄ
19. Let and be the sides of a rhombus the diagonals are and uv duvd uvÊœœ
"#
( ) ( ) 0 because , since a rhombusÊ œœœœ œdd uv uv uuuvvuvv v u u v
"# ##
†† ††††kk kk kk kk
has equal sides.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
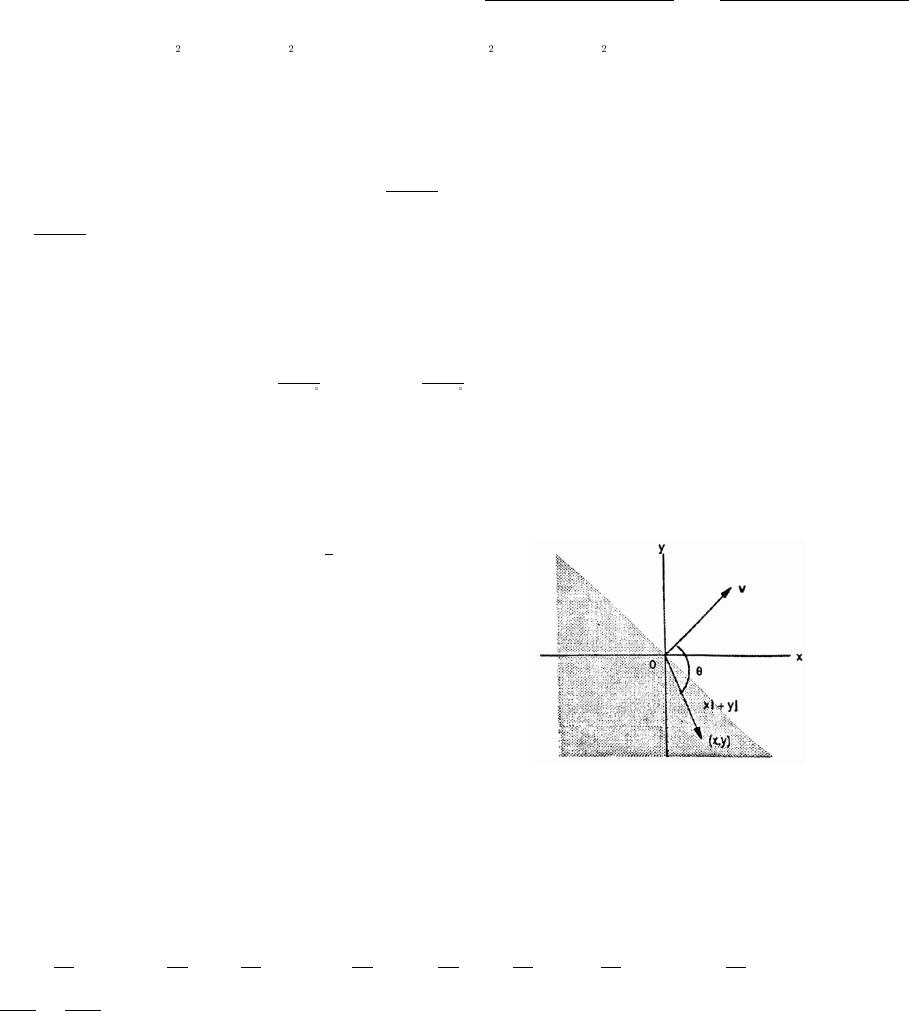
Section 12.3 The Dot Product 725
20. Suppose the diagonals of a rectangle are perpendicular, and let and be the sides of a rectangle the diagonals areuv Ê
and . Since the diagonals are perpendicular we have 0duv d uv dd
"# "#
œ œ œ†
( ) ( ) 0 0 0ÍœœÍœÍ œuv uv uuuvvuvv v u v u v u†††††kkkk ababkk kk kk kk
##
0 which is not possible, or 0 which is equivalent to the rectangle is a square.Íœ œ œÊab ab kkkkkk kk kk kkvu vu v u
21. Clearly the diagonals of a rectangle are equal in length. What is not as obvious is the statement that equal diagonals
happen only in a rectangle. We show this is true by letting the adjacent sides of a parallelogram be the vectors
(v v ) and (u u ). The equal diagonals of the parallelogram are (v v ) (u u ) and
"# "# " "# "#
ij ij d ij ij œ
(v v ) (u u ). Hence (v v ) (u u ) (v v ) (u u )d ijij dd ijij ijij
#"#"# "#"#"# "#"#
œ œœœkk kk k k k k
(v u ) (v u ) (v u ) (v u ) (v u ) (v u ) (v u ) (v u )Ê œ Ê œ kkkk
ÈÈ
"" ## "" ## "" ## "" ##
## ##
ij ij
v 2vu u v 2vu u v 2vu u v 2vu u 2(vu vu)Ê œ Ê
########
"" ## "" ## "" ##
11 11
2(v u v u ) v u v u 0 (v v ) (u u ) 0 the vectors (v v ) and (u u )œ Ê œ Ê œ Ê
"" ## "" ## " # " # " # " #
ij ij ij ij†
are perpendicular and the parallelogram must be a rectangle.
22. If and is the indicated diagonal, then ( )kk kk kk kku v uv uvu uuvu u vu uv vœ œœœ††† ††
##
( ) the angle cos between the diagonal and and the angleœœ Êuv vv u v v u†† † "
Š‹
()
uvu
uvu
†
kkkk
cos between the diagonal and are equal because the inverse cosine function is one-to-one.
"
Š‹
()
uvv
uvv
†
kkkk v
Therefore, the diagonal bisects the angle between and .uv
23. horizontal component: 1200 cos 8 1188 ft/s; vertical component: 1200 sin 8 167 ft/sab ab
‰‰
¸¸
24. cos 33 15 2.5 lb, so . Then cos 33 , sin 33 2.205, 1.432kk a b kk ¡¡
www
‰‰ ‰ ‰
œ œ œ ¸
2.5 lb 2.5 lb
cos 18 cos 18
25. (a) Since cos 1, we have cos (1) .k k k k kkk k kkkk kkkk))ŸŸœuv uv uv uv†œkk
(b) We have equality precisely when cos 1 or when one or both of and is . In the case of nonzerokk)œuv0
vectors, we have equality when 0 or , i.e., when the vectors are parallel.)1œ
26. (x y ) x y cos 0 when . Thisijv ijvœ Ÿ ŸŸ†kkkk))1
1
#
means (x y) has to be a point whose position vector makesß
an angle with that is a right angle or bigger.v
27. (a b ) a b a b( ) a(1) b(0) avu uuuuuuu u uu†††† †
" " # " "" #" " #"
##
œ œ œ œ œkk
28. No, need not equal . For example, 2 but ( ) 1 0 1 andv v ij i j iij iiij
"# Á œ œœ†††
(2) 2 1201.ii j ii ij††††œ œ œ
29. projvuv uv uv uv uv uv uv uv
vvvvvvv v
uvuv vuv v v uv vvœÊ † œ†
††††††† †
ll ll ll ll ll ll ll ll
2222222 2
Š ‹Š‹ Š‹Š‹Š‹Š‹ Š‹
ab ab†œ † †
2
0œllœ
ab abuv uv
vv
††
22
24
ll ll v2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
726 Chapter 12 Vectors and the Geometry of Space
30. 2 3 and 3 proj 3 , is the vector parallel to .Fijk vij F v ij ij vœ œÊ œ œ œ
vFv
v
†
ll "!
22
531
22
Š‹
Èab
proj 2 3 3 is the vector orthogonal to .FFijkijijk v œ œ
vab
ˆ‰
31 13
22 22
31. P(x y ) P x , x and Q(x y ) Q x x are any two points P and Q on the line with b 0
"" " " ## # #
ßœ ßœ ß Á
ˆ‰ ˆ‰
ca ca
bb bb
PQ (x x ) (x x ) PQ (x x ) (x x ) (a b ) a(x x ) b (x x )Êœ Ê œ œ
ÄÄ
#" "# #" "# #" "#
ijvijij
aa a
bb b
††
‘ ˆ‰
0 is perpendicular to PQ for b 0. If b 0, then a is perpendicular to the vertical line ax c.œÊ Á œ œ œ
Ä
vvi
Alternatively, the slope of is and the slope of the line ax by c is , so the slopes are negative reciprocalsvba
ab
œ
the vector and the line are perpendicular.Êv
32. The slope of is and the slope of bx ay c is , provided that a 0. If a 0, then b is parallel tovvj
bb
aa
œ Á œ œ
the vertical line bx c. In either case, the vector is parallel to the line bx ay c.œœv
33. 2 is perpendicular to the line x 2y c;vi jœ œ
P(2 1) on the line 2 2 c x 2y 4ßʜʜ
34. 2 is perpendicular to the line 2x y c;vijœ œ
P( 1 2) on the line ( 2)( 1) 2 cß Ê œ
2x y 0Ê œ
35. 2 is perpendicular to the line 2x y c;vijœ œ
P( 2 7) on the line ( 2)( 2) 7 cß Ê œ
2x y 3Ê œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 12.3 The Dot Product 727
36. 2 3 is perpendicular to the line 2x 3y c;vijœ œ
P(11 10) on the line (2)(11) (3)(10) cßÊœ
2x 3y 8ʜ
37. is parallel to the line x y c;vijœ œ
P( 2 1) on the line 2 1 c x y 1ß Ê œ Ê œab
or x y 1.œ
38. 2 3 is parallel to the line 3x 2y c;vijœ œ
P(0 2) on the line 0 2( 2) c 3x 2y 4ß Ê œ Ê œ
39. 2 is parallel to the line 2x y c;vijœ œ
P(1 2) on the line 2(1) 2 c 2x y 0ßʜʜ
or 2x y 0.œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

728 Chapter 12 Vectors and the Geometry of Space
40. 3 2 is parallel to the line 2x 3y c;vijœ œ
P(1 3) on the line ( 2)(1) (3)(3) cßÊœ
2x 3y 11 or 2x 3y 11Ê œ œ
41. P(0 0), Q(1 1) and 5 PQ and PQ (5 ) ( ) 5 N m 5 Jßß œÊœ œ œ œ œ
ÄÄ
Fj ij WF jij†† †
42. (distance) cos (602,148 N)(605 km)(cos 0) 364,299,540 N km (364,299,540)(1000) N mWFœœ œ œkk )††
3.6429954 10 Jœ‚
""
43. PQ cos (200)(20)(cos 30°) 2000 3 3464.10 N m 3464.10 JWFœœ œœœ
Ä
kk¹¹ È
)†
44. PQ cos (1000)(5280)(cos 60°) 2,640,000 ft lbWFœœ œ
Ä
kk¹¹)†
In Exercises 45-50 we use the fact that a b is normal to the line ax by c.nijœ œ
45. 3 and 2 cos cos cosnijnij
"# " " "
"
œ œÊœ œ œ œ)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈ È
4
61
10 5 2
1
46. 3 and 3 cos cos cosnijnij
"# " " "
"
œ œ Ê œ œ œ œ
ÈÈ Š‹ Š‹ ˆ‰
)nn
nn
†
kkkk ÈÈ
23
31 2
4 4
1
47. 3 and 3 cos cos cosnijnij
"# " " "
œ œ Êœ œ œ œ
ÈÈ
Š‹ Š ‹ Š‹
)nn
nn
†
kkkk ÈÈ È
ÈÈ
26
33 3
4 4
1
48. 3 and 1 3 1 3 cosni j n i j
"# "
œ œ Ê œ
ÈÈÈ
Š‹Š‹ Š‹
)nn
nn
†
kkkk
cos cos cosœœœœ
" " "
"
Š‹ Š‹
1333
13 12331233
4
28 24
ÈÈ
ÈÉÈÈ ÈÈ
1
49. 3 4 and cos cos cos 0.14 radnijnij
"# " " "
œ œÊœ œ œ ¸)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈÈ
34 7
25 2 5 2
50. 12 5 and 2 2 cos cos cos 1.18 radnijnij
"# " " "
œ œÊœ œ œ ¸)Š‹ Š ‹ Š‹
nn
nn
†
kkkk ÈÈ È
24 10 14
169 8 26 2
12.4 THE CROSS PRODUCT
1. 3 length 3 and the direction is ;
22
0
uv i j k i j k
ij k
‚œ œ Ê œ
"
""
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰
22 22
333 333
""
( 3 length 3 and the direction is vu uv) i j k i j k‚œ‚ œ Ê œ
ˆ‰
22 22
333 333
""
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 12.4 The Cross Product 729
2. 5( ) length 5 and the direction is
230
10
uv k k
ijk
‚œ œ Ê œ
"
ââ
ââ
ââ
ââ
ââ
ââ
( 5( ) length 5 and the direction is vu uv) k k‚œ‚ œ Ê œ
3. length 0 and has no direction
224
12
uv 0
ijk
‚œ œ Ê œ
"
ââ
ââ
ââ
ââ
ââ
ââ
( length 0 and has no directionvu uv) 0‚œ‚ œ Ê œ
4. length 0 and has no direction
11 1
00 0
uv 0
ij k
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
( length 0 and has no directionvu uv) 0‚œ‚ œ Ê œ
5. 6( ) length 6 and the direction is
200
030
uv k k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
( 6( ) length 6 and the direction is vu uv) k k‚œ‚ œ Ê œ
6. ( ) ( ) length 1 and the direction is
001
100
uv ij jk ki j j
ijk
‚œ‚‚‚ œ‚œ œÊ œ
ââ
ââ
ââ
ââ
ââ
ââ
( length 1 and the direction is vu uv) j j‚œ‚ œÊ œ
7. 6 12 length 6 5 and the direction is
824
221
uv i k i k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ È"
ÈÈ
55
2
( (6 12 length 6 5 and the direction is vu uv) i k) i k‚œ‚ œ Ê œ
È"
ÈÈ
55
2
8. 1 2 2 2 length 2 3 and the direction is
112
uv i j k i j k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ È
3 1
333
##
"""
ÈÈÈ
( ( 2 2 2 length 2 3 and the direction is vu uv) i j k) i j k‚œ‚ œ Ê œ
È""
ÈÈÈ
333
1
9. 10.
100 10 1
010 01 0
uv k uv ik
ijk ij k
‚œ œ ‚œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
730 Chapter 12 Vectors and the Geometry of Space
11. 12. 5
10 1 2 10
01 1 1 2 0
uv ijk uv k
ij k i j k
‚œ œ ‚œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
13. 2 14. 2
110 012
110 100
uv k uv jk
ijk ijk
‚œ œ ‚œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
15. (a) PQ PR 8 4 4 Area PQ PR 64 16 16 2 6
11 3
13 1
ÄÄ
‚ œ œ Ê œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
ÈÈ
ijk
ijk ""
##
(b) (2 )uijkœœ
PQ PR
PQ PR 6
Ä‚Ä
Ä‚Ä"
¹¹
È
16. (a) PQ PR 4 4 2 Area PQ PR 16 16 4 3
102
220
ÄÄ
‚ œ œ Ê œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ijk
ijk ""
##
(b) (2 2 )uijkœœ
PQ PR
PQ PR 3
Ä‚Ä
Ä‚Ä"
¹¹
17. (a) PQ PR Area PQ PR 1 1
111
110
ÄÄ
‚œ œÊ œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ijk
ij ""
###
È2
(b) ( ) ( )uijijœœœ
PQ PR
PQ PR 22
Ä‚Ä
Ä‚Ä""
¹¹
ÈÈ
18. (a) PQ PR 2 3 Area PQ PR 4 9 1
211
10 2
ÄÄ
‚ œ œÊ œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ij k
ijk ""
## #
È14
(b) (2 3 )uijkœœ
PQ PR
PQ PR 14
Ä‚Ä
Ä‚Ä"
¹¹
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
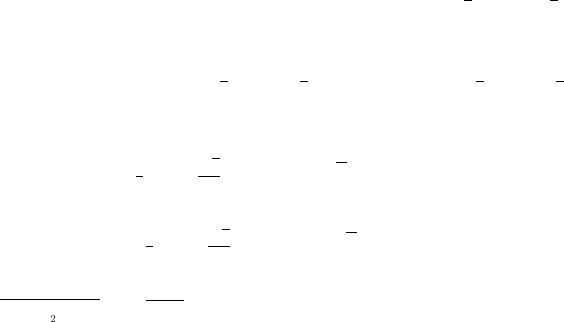
Section 12.4 The Cross Product 731
19. If a a a , b b b , and c c c , then ( ) ,
aaa
bbb
ccc
u ijkv ijk w ijk uvwœ œ œ ‚ œ
"#$ "# $ "#$
"#$
"#$
"#$
†
ââ
ââ
ââ
ââ
ââ
ââ
( ) and ( ) which all have the same absolute value, since
bbb ccc
ccc aaa
aaa bbb
vwu wuv‚œ ‚œ††
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
"#$ "#$
"#$ "#$
"#$ "#$
the
interchanging of two rows in a determinant does not change its absolute value the volume isÊ
() abs 8
200
020
002
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ†
20. ( ) abs 4 (for details about verification, see Exercise 19)
111
21 2
12 1
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ
†
21. ( ) abs 7 7 (for details about verification, see Exercise 19)
210
211
102
kk kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œœ
†
22. ( ) abs 8 (for details about verification, see Exercise 19)
11 2
10 1
24 2
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ
†
23. (a) 6, 81, 18 none are perpendicularuv uw vw†† †œ œ œ Ê
(b) , ,
511 5 11 015
01 5 153 3 153 3
uv 0uw 0vw 0
ij k i j k i jk
‚œ Á ‚ œ œ ‚ œ Á
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
and are parallelÊuw
24. (a) 0, 0, 3 , 0, 0, 0 , , , uv u w ur vw vr wr u vu wv wv r†††††œ‚œ œ œ œ œÊ¼¼¼¼1
and wr¼
(b) , ,
12 1 12 1
11 1 10 1
12 1
uv 0uw 0ur 0
ijk ijk ijk
‚œ Á ‚ œ Á ‚œ œ
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
11
##
1
, ,
111
101
111 1 01
vw 0vr 0wr 0
ijk ijk ijk
‚œ Á ‚œ Á ‚œ Á
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
11 11
## ##
11
and are parallelÊur
25. PQ PQ sin (60°) 30 ft lb 10 3 ft lb
¹¹¹¹
kk È
ÄÄ
‚œ œ œFF 2
3
3
†† † †
È
#
26. PQ PQ sin (135°) 30 ft lb 10 2 ft lb
¹¹¹¹
kk È
ÄÄ
‚œ œ œFF 2
3
2
†† † †
È
#
27. (a) true, a a akk ÈÈ
uuuœœ
##
#
13
†
(b) not always true, uu u†œkk
#
(c) true, 0 0 0 and 0 0 0
uuu 000
000 uuu
u0 ijk0 0u ijk0
ijk ijk
‚œ œ œ ‚œ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
"#$
"#$
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

732 Chapter 12 Vectors and the Geometry of Space
(d) true, ( ) ( uu uu) ( uu uu) ( uu uu)
uuu
uuu
uu i j k0
ijk
‚ œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
"#$
"#$
#$ #$ "$ "$ "# "#
(e) not always true, for exampleij k k ji‚œ Áœ‚
(f) true, distributive property of the cross product
(g) true, ( ) ( ) 0uvv uvv u0‚œ‚œœ†† †
(h) true, the volume of a parallelpiped with , , and along the three edges is the same whether the plane containing uv w u
and or the plane containing and is used as the base plane, and the dot product is commutative.vvw
28. (a) true, u v u v u v v u v u v uuv vu††œœœ
"" ## $$ "" ## $$
(b) true, ( )
uuu vvv
vvv uuu
uv vu
ijk ijk
‚ œ œ œ ‚
ââââ
ââââ
ââââ
ââââ
ââââ
ââââ
"#$ "#$
"#$ "#$
(c) true, ( ) ( )
uuu uuu
vvv vvv
‚œ œ œ‚
uv uv
ijk ijk
ââââ
ââââ
ââââ
ââââ
ââââ
ââââ
"#$ "#$
"#$ "#$
(d) true, (c ) (cu)v (cu)v (cu)v u(cv) u(cv) u(cv) (c) c(uv uv uv)uv u v††œœœœ
"" ## $$ " " # # $ $ "" ## $$
c( )œuv†
(e) true, c( ) c (c ) (c )
u u u cu cu cu u u u
v v v v v v cv cv cv
uv u v u v
ijk i j k i j k
‚œ œ œ ‚œ œ‚
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
"#$ "#$ "#$
"#$ "#$ "#$
(f) true, uuu uuuuu u†œœ œ
### ##
###
13
13
ˆ‰
Èkk
(g) true, ( ) 0uuu 0u‚œœ††
(h) true, and ( ) ( ) 0uv u uv v uvu vuv‚¼ ‚¼ Ê ‚ œ ‚ œ††
29. (a) proj (b) ( ) (c) ( ) (d) ( )
vu v uv uv w uvwœ‚ ‚‚‚
Š‹ ab kk
uv
vv
†
kkkk †
(e) ( ) ( ) (f) uv uw u‚‚‚ kkv
vkk
30. ; . The cross product is not associative.ab abij j kj ii jj i0 0‚‚œ‚œ ‚‚œ‚œ
31. (a) yes, and are both vectors (b) no, is a vector but is a scalaruv w u vw‚†
(c) yes, and are both vectors (d) no, is a vector but is a scalaruuw u vw‚†
32. ( ) is perpendicular to , and is perpendicular to both and ( ) isuv w uv uv u v uv w‚‚ ‚ ‚ Ê ‚‚
parallel to a vector in the plane of and which means it lies in the plane determined by and .uv uv
The situation is degenerate if and are parallel so and the vectors do not determine a plane.uv uv0‚œ
Similar reasoning shows that ( ) lies in the plane of and provided and are nonparallel.uvw v w v w‚‚
33. No, need not equal . For example, , but andv w ij ij i ij iiij 0k kÁ ‚ œ‚‚ œ œab
.iijiiij0kk‚ œ ‚ ‚ œ œabab
34. Yes. If and , then ( ) and ( ) 0. Suppose now that .uv uw uv uw u vw 0 uvw v w‚œ‚ œ ‚ œ œ Á†† †
Then ( ) implies that k for some real number k 0. This in turn implies thatuvw 0 vw u‚ œ œ Á
( ) (k ) k 0, which implies that . Since , it cannot be true that , so .uvw u u u u0 u0 vw vw††œ œ œ œ Á Á œkk
#
35. AB and AD AB AD 2 area AB AD 2
110
110
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.4 The Cross Product 733
36. AB 7 3 and AD 2 5 AB AD 29 area AB AD 29
730
250
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
37. AB 3 2 and AD 5 AB AD 13 area AB AD 13
320
510
Ä Ä ÄÄ ÄÄ
œ œÊ ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
38. AB 7 4 and AD 2 5 AB AD 43 area AB AD 43
740
250
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
39. AB 3 2 4 and DC 3 2 4 AB is parallel to DC; BC 2 and AD 2 BC is parallel to
ÄÄÄÄÄÄÄ
œ œ Ê œ œÊi j k i j k ij ij
AD. AB BC 4 8 7 area AB BC 129
324
210
ÄÄ Ä Ä Ä
‚ œ œ Ê œl ‚ lœ
ââ
ââ
ââ
ââ
ââ
ââ È
ijk
ijk
40. AC 4 and DB 4 AC is parallel to DB; AD 3 3 and CB 3 3 AD is parallel
ÄÄÄÄÄ
œ œ Ê œ œ Ê
ÄÄ
ij ij ijk ijk
to CB. AC AD 12 3 7 area AC AD 202
140
133
ÄÄ Ä Ä Ä
‚œ œÊ œl‚lœ
ââ
ââ
ââ
ââ
ââ
ââ È
ijk
ijk
41. AB 2 3 and AC 3 AB AC 11 area AB AC
230
310
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
11
42. AB 4 4 and AC 3 2 AB AC 4 area AB AC 2
440
320
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
#
43. AB 6 5 and AC 11 5 AB AC 25 area AB AC
650
11 5 0
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
25
44. AB 16 5 and AC 4 4 AB AC 84 area AB AC 42
16 5 0
440
Ä Ä ÄÄ ÄÄ
œ œÊ ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
#
45. AB 2 and AC AB AC 2 2 area AB AC
12 0
10 1
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
i j ik ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
3
46. AB and AC 3 3 AB AC 3 3 area AB AC
11 1
303
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ijk i k i k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
32
È
47. AB 2 and AC 2 AB AC 4 2 area AB AC
12 0
01 2
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij jk ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
È21
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

734 Chapter 12 Vectors and the Geometry of Space
48. AB 2 , AC 3 2 and AD 3 4 5 AB AC AD 5
120
032
345
ÄÄ Ä ÄÄÄ
œ œ œ Ê ‚ † œ œ
ij jk ijkŠ‹
ââ
ââ
ââ
ââ
ââ
ââ
volume AB AC AD 5Êœ‚†œ
ÄÄ Ä
¹¹Š‹
49. If a a and b b , then and the triangle's area is
aa0
bb0
aa
bb
AijBij AB k
ijk
œ œ ‚œ œ
"# "# "#
"#
"#
"#
ââ
ââ
ââ
ââ
ââ
ââ
ºº
. The applicable sign is ( ) if the acute angle from to runs counterclockwise
aa
bb
""
##
"#
"#
kk ºº
AB AB‚œ„
in the xy-plane, and ( ) if it runs clockwise, because the area must be a nonnegative number.
50. If a a , b b , and c c , then the area of the triangle is AB AC . Now,AijBijCijœ œ œ ‚
ÄÄ
"# "# "# "
#¹¹
AB AC AB AC
baba0
caca0
ba ba
ca ca
ÄÄ ÄÄ
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ
ºº
¹¹
ijk
k
""##
""##
"" ##
"" ##
"
#
(b a )(c a ) (c a )(b a ) a (b c ) a (c b ) (b c c b )œ œ
""
##
""## ""## "## #"" "#"#
kkk k
. The applicable sign ensures the area formula gives a nonnegative number.
aa1
bb1
cc1
œ„
"
#
"#
"#
"#
ââ
ââ
ââ
ââ
ââ
ââ
12.5 LINES AND PLANES IN SPACE
1. The direction and P(3 4 1) x 3 t, y 4 t, z 1 tijk ß ß Ê œ œ œ
2. The direction PQ 2 2 2 and P(1 2 1) x 1 2t, y 2 2t, z 1 2t
Äœ ßß Ê œ œ œijk
3. The direction PQ 5 5 5 and P( 2 0 3) x 2 5t, y 5t, z 3 5t
Äœ ßß Êœ œ œijk
4. The direction PQ and P(1 2 0) x 1, y 2 t, z t
Äœ ß ß Ê œ œ œjk
5. The direction 2 and P( ) x 0, y 2t, z tjk !ß!ß! Ê œ œ œ
6. The direction 2 3 and P(3 2 1) x 3 2t, y 2 t, z 1 3tij k ßß Ê œ œ œ
7. The direction and P(1 1 1) x 1, y 1, z 1 tkßß Ê œ œ œ
8. The direction 3 7 5 and P(2 4 5) x 2 3t, y 4 7t, z 5 5tijk ßß Êœ œ œ
9. The direction 2 2 and P(0 7 0) x t, y 7 2t, z 2tijk ßß Êœ œ œ
10. The direction is 2 4 2 and P 2, 3, 0 x 2 2t, y 3 4t, z 2t
123
345
uv i j k
ijk
‚œ œ Ê œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ ab
11. The direction and P(0 0 0) x t, y 0, z 0ißß Ê œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
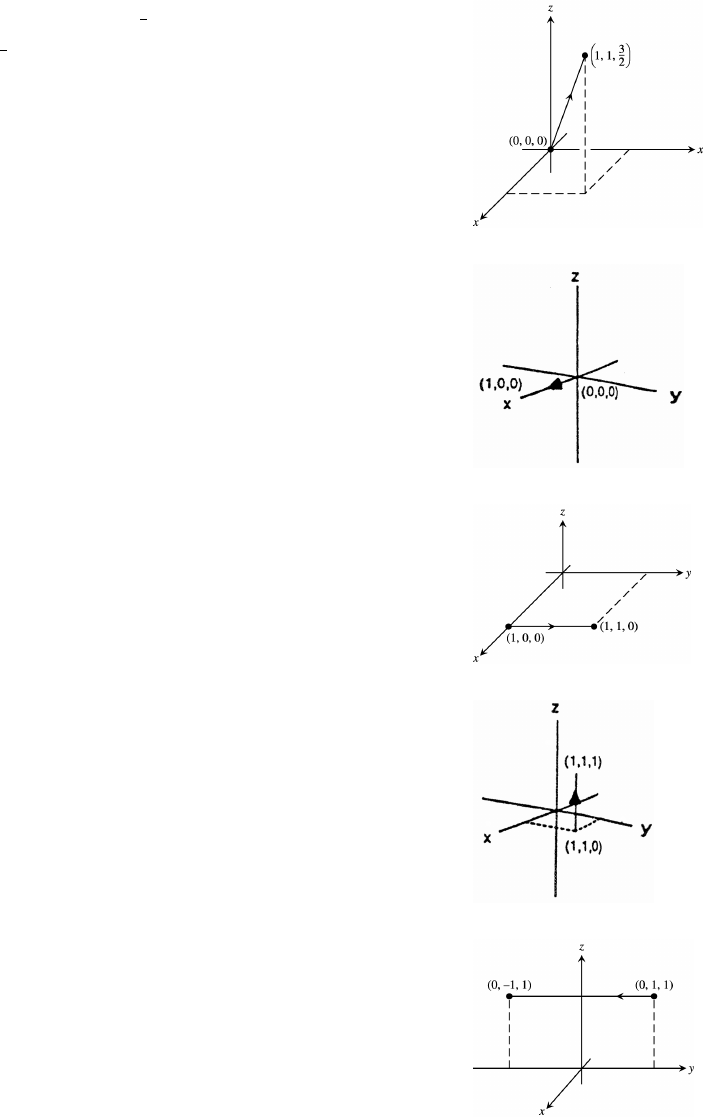
Section 12.5 Lines and Planes in Space 735
12. The direction and P(0 0 0) x 0, y 0, z tkßß Ê œ œ œ
13. The direction PQ and P(0 0 0) x t,
Äœ ßß Ê œij k
3
#
y t, z t, where 0 t 1œœ ŸŸ
3
#
14. The direction PQ and P(0 0 0) x t, y 0, z 0,
ÄœßßÊœœœi
where 0 t 1ŸŸ
15. The direction PQ and P(1 1 0) x 1, y 1 t,
ÄœßßÊœœj
z 0, where 1 t 0œŸŸ
16. The direction PQ and P(1 1 0) x 1, y 1, z t,
ÄœßßÊœœœk
where 0 t 1ŸŸ
17. The direction PQ 2 and P(0 1 1) x 0,
Äœ ß ß Ê œj
y 1 2t, z 1, where 0 t 1œ œ ŸŸ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
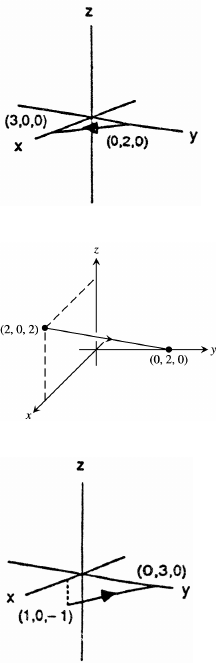
736 Chapter 12 Vectors and the Geometry of Space
18. The direction PQ 2 and P(0 2 0) x 3t,
Äœ$ ß ß Ê œij
y 2 2t, z 0, where 0 t 1œ œ ŸŸ
19. The direction PQ 2 2 2 and P(2 0 2)
Äœ ß ßijk
x 2 2t, y 2t, z 2 2t, where 0 t 1Êœœœ ŸŸ
20. The direction PQ 3 and P(1 0 1)
Äœ ß ßijk
x 1 t, y 3t, z 1 t, where 0 t 1Êœ œ œ ŸŸ
21. 3(x 0) ( 2)(y 2) ( 1)(z 1) 0 3x 2y z 3 œÊ œ
22. 3(x 1) (1)(y 1) (1)(z 3) 0 3x y z 5 œÊ œ
23. PQ 3 , PS 3 2 PQ PS 7 5 4 is normal to the plane
113
132
ÄÄ ÄÄ
œ œ Ê ‚ œ œ
ij k i j k i j k
ijk
ââ
ââ
ââ
ââ
ââ
ââ
7(x 2) ( 5)(y 0) ( 4)(z 2) 0 7x 5y 4z 6Ê œÊ œ
24. PQ 2 , PS 3 2 3 PQ PS 3 is normal to the plane
112
323
ÄÄ ÄÄ
œ œ Ê ‚ œ œ
ij k i j k i jk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
( 1)(x 1) ( 3)(y 5) (1)(z 7) 0 x 3y z 9Ê œ Ê œ
25. 3 4 , P(2 4 5) (1)(x 2) (3)(y 4) (4)(z 5) 0 x 3y 4z 34ni j kœ ßßÊ œÊ œ
26. 2 , P(1 2 1) (1)(x 1) ( 2)(y 2) (1)(z 1) 0 x 2y z 6ni jkœ ßß Ê œ Ê œ
27. t 0 and s 1; then z 4t 3 4s 1
x 2t 1 s 2 2t s 1 4t 2s 2
y 3t 2 2s 4 3t 2s 2 3t 2s 2
œœœ
œœ œ œ
œœ œ œ
ÊÊÊœœœœ
4(0) 3 ( 4)( 1) 1 is satisfied the lines intersect when t 0 and s 1 the point of intersection isÊœ Ê œ œÊ
x 1, y 2, and z 3 or P(1 2 3). A vector normal to the plane determined by these lines isœœ œ ßß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.5 Lines and Planes in Space 737
20 12 , where and are directions of the lines the plane
23 4
12 4
nn i jk n n
ij k
"# " #
‚œ œ Ê
ââ
ââ
ââ
ââ
ââ
ââ
containing the lines is represented by( 20)(x 1) (12)(y 2) (1)(z 3) 0 20x 12y z 7. œÊœ
28. s 1 and t 0; then z t 1 5s 6 0 1 5( 1) 6
x t 2s 2 t 2s 2
yt2 s3 t s1
œœ
œœ œ
œ œ œ
Ê Ê œ œ œœ Ê œ
is satisfied the lines do intersect when s 1 and t 0 the point of intersection is x 0, y 2 and z 1ÊœœÊœœœ
or P(0 2 1). A vector normal to the plane determined by these lines is 6 3 3 ,
11
215
ßß ‚ œ œ
"
nn ijk
ijk
"#
ââ
ââ
ââ
ââ
ââ
ââ
where and are directions of the lines the plane containing the lines is represented bynn
"# Ê
( 6)(x 0) ( 3)(y 2) (3)(z 1) 0 6x 3y 3z 3. œÊ œ
29. The cross product of and 4 2 2 has the same direction as the normal to the planeijk i j k
6 6 . Select a point on either line, such as P( 1 2 1). Since the lines are given
11
42 2
Êœ œ ßß
"
njk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
to intersect, the desired plane is 0(x 1) 6(y 2) 6(z 1) 0 6y 6z 18 y z 3. œÊ œ Êœ
30. The cross product of 3 and has the same direction as the normal to the planeijk ijk
2 2 4 . Select a point on either line, such as P(0 3 2). Since the lines are
131
11 1
nijk
ij k
œœ ßß
ââ
ââ
ââ
ââ
ââ
ââ
given to intersect, the desired plane is ( 2)(x 0) ( 2)(y 3) (4)(z 2) 0 2x 2y 4z 14 œÊœ
xy2z7.Ê œ
31. 3 3 3 is a vector in the direction of the line of intersection of the planes
21 1
12 1
nn ijk
ij k
"#
‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
3(x 2) ( 3)(y 1) 3(z 1) 0 3x 3y 3z 0 x y z 0 is the desired plane containingÊ œÊ œÊœ
P(21 1)
!ßß
32. A vector normal to the desired plane is P P 2 12 2 ; choosing P (1 2 3) as a point on
20 2
412
"# "
Ä‚œ œ ßß
nijk
ij k
ââ
ââ
ââ
ââ
ââ
ââ
the plane ( 2)(x 1) ( 12)(y 2) ( 2)(z 3) 0 2x 12y 2z 32 x 6y z 16 is theÊ œ Ê œ Ê œ
desired plane
33. S(0 0 12), P(0 0 0) and 4 2 2 PS 24 48 24( 2 )
0012
422
ßß ßß œ Ê ‚ œ œ œ
Ä
vijk v i j ij
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 5 24 2 30 is the distance from S to the lineÊœ œ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 24 1 4
1644
24 5
24
Ä‚
v
vÈÈ
†
34. S(0 0 0), P(5 5 3) and 3 4 5 PS 13 16 5
553
34 5
ßß ßß œ Ê ‚ œ œ
Ä
vijk v i jk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 9 3 is the distance from S to the lineÊœ œ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 169 256 25
91625
450
50
Ä‚
v
vÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
738 Chapter 12 Vectors and the Geometry of Space
35. S(2 1 3), P(2 1 3) and 2 6 PS d 0 is the distance from S to the lineßß ßß œ Ê ‚ œ Ê œ œ œ
Ä
vij v0 ¹¹
kk È
PS 0
40
Ä‚v
v
(i.e., the point S lies on the line)
36. S(2 1 1), P(0 1 0) and 2 2 2 PS 2 6 4
20 1
22 2
ßß ßß œ Ê ‚œ œ
Ä
vijk v ijk
ij k
ââ
ââ
ââ
ââ
ââ
ââ
d is the distance from S to the lineÊœ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 43616
444
56
12
14
3
Ä‚
v
vÉ
37. S(3 1 4), P(4 3 5) and 2 3 PS 30 6 6
149
123
ß ß ß ß œ Ê ‚ œ œ
Ä
v ijk v ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d is the distance from S to the lineÊœ œ œœœ œ
¹¹
kk È ÈÈÈ È
ÈÈÈÈ
PS 900 36 36
149
972 486 81 6
14 77
942
7
Ä‚
v
v
†
38. S( 1 4 3), P(10 3 0) and 4 4 PS 28 56 28 28( 2 )
11 7 3
404
ß ß ßß œ Ê ‚ œ œ œ
Ä
vik v i j k ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 7 3 is the distance from S to the lineÊœ œ œ
¹¹
kk È
È
PS 28141
411
Ä‚
v
vÈ
39. S(2 3 4), x 2y 2z 13 and P(13 0 0) is on the plane PS 11 3 4 and 2 2ßß œ ßß Ê œ œ
Äijk nijk
dPS 3Êœ œ œ œ
Ä
¹¹¹ ¹¹¹
†n
nkk ÈÈ
1168 9
144 9
40. S(0 0 0), 3x 2y 6z 6 and P(2 0 0) is on the plane PS 2 and 3 2 6ßß œ ßß Ê œ œ
Äinijk
dPSÊœ œ œ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
666
9436 49 7
41. S(0 1 1), 4y 3z 12 and P(0 3 0) is on the plane PS 4 and 4 3ßß œ ßß Ê œ œ
Äjk n j k
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È
16 3 19
16 9 5
42. S(2 2 3), 2x y 2z 4 and P(2 0 0) is on the plane PS 2 3 and 2 2ßß œ ßß Ê œ œ
Äjk nijk
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È26 8
414 3
43. S(0 1 0), 2x y 2z 4 and P(2 0 0) is on the plane PS 2 and 2 2ß ß œ ß ß Ê œ œ
Äij n ij k
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È
410 5
414 3
44. S(1 0 1), 4x y z 4 and P( 1 0 0) is on the plane PS 2 and 4ßß œ ßß Ê œ œ
Äik n ijk
dPSÊœ œ œ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
È
#
81 9
1611 18
32
45. The point P(1 0 0) is on the first plane and S(10 0 0) is a point on the second plane PS 9 , andßß ßß Ê œ
Äi
2 6 is normal to the first plane the distance from S to the first plane is d PSni j kœ Ê œ Ä
¹¹
†n
nkk
, which is also the distance between the planes.œœ
¹¹
99
1436 41
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.5 Lines and Planes in Space 739
46. The line is parallel to the plane since ( 2 6 ) 1 2 3 0. Also the pointvn i j k i j k††œ œœ
ˆ‰
"
#
S(1 0 0) when t 1 lies on the line, and the point P(10 0 0) lies on the plane PS 9 . The distance fromßß œ ßß Ê œ
Äi
S to the plane is d PS , which is also the distance from the line to the plane.œœ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
99
1436 41
47. and 2 2 cos cos cosnij n ijk
"# " " "
"
œ œ Ê œ œ œ œ)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈ
È
4
21
2 9 2
1
48. 5 and 2 3 cos cos cos (0)nijknijk
"# " " "
#
œ œ Êœ œ œ œ)Š‹ Š ‹
nn
nn
†
kkkk ÈÈ
523
27 14
1
49. 2 2 2 and 2 2 cos cos cos 1.76 radnijknijk
"# " " "
"
œ œÊœ œ œ ¸)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈ
È
442
12 9 33
50. and cos cos 0.96 radnijk nk
"#
" "
œ œ Ê œ œ ¸)Š‹ Š‹
nn
nn
†
kkkk ÈÈ
1
3 1
51. 2 2 and 2 cos cos cos 0.82 radn i jk n i jk
"# " " "
œ œÊœ œ œ ¸)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈ È
241 5
9 6 3 6
52. 4 3 and 3 2 6 cos cos cos 0.73 radnjknijk
"# " " "
œ œ Êœ œ œ ¸)Š‹ Š ‹ ˆ‰
nn
nn
†
kkkk ÈÈ
35
818 26
25 49
53. 2x y 3z 6 2(1 t) (3t) 3(1 t) 6 2t 5 6 t x , y and z œÊ œÊœÊœÊœ œ œ
""
####
33
is the pointÊßß
ˆ‰
33
###
"
54. 6x 3y 4z 12 6(2) 3(3 2t) 4( 2 2t) 12 14t 29 12 t x 2, y 3 , œÊ œ Ê œÊœ Êœ œ
41 41
14 7
and z 2 2 is the pointœ Ê ß ß
41 20 27
777
ˆ‰
55. x y z 2 (1 2t) (1 5t) (3t) 2 10t 2 2 t 0 x 1, y 1 and z 0œÊ œÊ œÊœÊœ œ œ
(1 1 0) is the pointÊßß
56. 2x 3z 7 2( 1 3t) 3(5t) 7 9t 2 7 t 1 x 1 3, y 2 and z 5 œ Ê œ Êœ ÊœÊ œ œ œ
( 4 2 5) is the pointÊ ß ß
57. and , the direction of the desired line; (1 1 1)
111
110
nijk nij nn ij
ijk
"#"#
œ œ Ê ‚ œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
is on both planes the desired line is x 1 t, y 1 t, z 1Êœœœ
58. 3 6 2 and 2 14 2 15 , the direction of the
362
21 2
nijknij2knn ijk
ij k
"#"#
œ œ Ê ‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (1 0 0) is on both planes the desired line is x 1 14t, y 2t, z 15tßß Ê œ œ œ
59. 2 4 and 2 6 3 , the direction of the
124
11 2
nijk nijk nn jk
ij k
"#"#
œ œ Ê ‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (4 3 1) is on both planes the desired line is x 4, y 3 6t, z 1 3tßß Ê œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
740 Chapter 12 Vectors and the Geometry of Space
60. 5 2 and 4 5 10 25 20 , the direction of the
520
04 5
nijnjknn ijk
ij k
"# "#
œ œÊ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (1 3 1) is on both planes the desired line is x 1 10t, y 3 25t, z 1 20tß ß Ê œ œ œ
61. L1 & L2: x 3 2t 1 4s and y 1 4t 1 2s
2t 4s 2 2t 4s 2
4t 2s 2 2t s 1
œ œ œ œ Ê Ê
œ œ
œ œ
œœ
3s 3 s 1 and t 1 on L1, z 1 and on L2, z 1 L1 and L2 intersect at (5 3 1).Ê œ Ê œ œ Ê œ œ Ê ß ß
L2 & L3: The direction of L2 is (4 2 4 ) (2 2 ) which is the same as the direction
""
63
ijk ijk œ
(2 2 ) of L3; hence L2 and L3 are parallel.
"
3ij k
L1 & L3: x 3 2t 3 2r and y 1 4t 2 r 3t 3
2t 2r 0 t r 0
4t r 3 4t r 3
œ œ œ œÊ Ê Ê œ
œ œ
œ œ
œœ
t 1 and r 1 on L1, z 2 while on L3, z 0 L1 and L2 do not intersect. The direction of L1Êœ œ Ê œ œ Ê
is (2 4 ) while the direction of L3 is (2 2 ) and neither is a multiple of the other; hence
""
È21 3
ijk ijk
L1 and L3 are skew.
62. L1 & L2: x 1 2t 2 s and y 1 t 3s 5s 3 s and t on L1,
2t s 1
t3s 1
œ œ œœ Ê Ê œ Ê œ œ Ê
œ
œ
œ34
55
z while on L2, z 1 L1 and L2 do not intersect. The direction of L1 is (2 3 )œœœÊ
12 3 2
555 14
"
Èij k
while the direction of L2 is ( 3 ) and neither is a multiple of the other; hence, L1 and L2 are
"
È11 ijk
skew.
L2 & L3: x 2 s 5 2r and y 3s 1 r 5s 5 s 1 and r 2 on L2,
s2r3
3s r 1
œœ œ œÊ Ê œ Ê œ œÊ
œ
œ
œ
z 2 and on L3, z 2 L2 and L3 intersect at (1 3 2).œœÊ ßß
L1 & L3: L1 and L3 have the same direction (2 3 ); hence L1 and L3 are parallel.
"
È14 ij k
63. x 2 2t, y 4 t, z 7 3t; x 2 t, y 2 t, z 1 tœ œ œ œ œ œ
"
##
3
64. 1(x 4) 2(y 1) 1(z 5) 0 x 4 2y 2 z 5 0 x 2y z 7; œÊ œÊ œ
2 (x 3) 2 2 (y 2) 2 (z 0) 0 2x 2 2y 2z 7 2 œÊ œ
ÈÈÈ ÈÈÈÈ
65. x 0 t , y , z ; y 0 t 1, x 1, z 3 ( 1 0 3); z 0œ Ê œ œ œ Ê !ß ß œ Ê œ œ œ Ê ß ß œ
"" "
### ##
33
ˆ‰
t 0, x 1, y 1 (1 1 0)ÊœœœÊßß
66. The line contains (0 0 3) and 3 1 3 because the projection of the line onto the xy-plane contains the originßß ßß
Š‹
È
and intersects the positive x-axis at a 30° angle. The direction of the line is 3 0 the line in question
Èij k Ê
is x 3t, y t, z 3.œœœ
È
67. With substitution of the line into the plane we have 2(1 2t) (2 5t) ( 3t) 8 2 4t 2 5t 3t 8œÊœ
4t 4 8 t 1 the point ( 1 7 3) is contained in both the line and plane, so they are not parallel.Ê œÊœÊ ßß
68. The planes are parallel when either vector A B C or A B C is a multiple of the other or
""" ###
ijk ijk
when (A B C ) A B C . The planes are perpendicular when their normals are
""" ###
ijk ijk0 ‚ œab
perpendicular, or(A B C ) (A B C ) 0.
""" ###
ijk ijk Ϡ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 12.6 Cylinders and Quadric Surfaces 741
69. There are many possible answers. One is found as follows: eliminate t to get t x 1 2 yœœœ
z3
#
x 1 2 y and 2 y x y 3 and 2y z 7 are two such planes.Ê œ œ Ê œ œ
z3
#
70. Since the plane passes through the origin, its general equation is of the form Ax By Cz 0. Since it meetsœ
the plane M at a right angle, their normal vectors are perpendicular 2A 3B C 0. One choice satisfyingʜ
this equation is A 1, B 1 and C 1 x y z 0. Any plane Ax By Cz 0 with 2A 3B C 0œ œ œÊœ œ œ
will pass through the origin and be perpendicular to M.
71. The points (a 0 0), (0 b 0) and (0 0 c) are the x, y, and z intercepts of the plane. Since a, b, and c are allßß ßß ßß
nonzero, the plane must intersect all three coordinate axes and cannot pass through the origin. Thus,
1 describes all planes except those through the origin or parallel to a coordinate axis.
xz
abc
y
œ
72. Yes. If and are nonzero vectors parallel to the lines, then is perpendicular to the lines.vv vv0
"# "#
‚Á
73. (a) EP cEP x y z c (x x ) y z x c(x x ), y cy and z cz ,
ÄÄ
œÊœÊœœ œ
"! "!"" !"! " "
ijk i j kcd
where c is a positive real number
(b) At x 0 c 1 y y and z z ; at x x x 0, y 0, z 0; lim c lim
""""!!
œÊœÊœ œ œ Ê œ œ œ œ
xxÄ_ Ä_
x
xx
lim 1 c 1 so that y y and z zœœÊÄ ÄÄ
xÄ_
"
""
1
74. The plane which contains the triangular plane is x y z 2. The line containing the endpoints of the lineœ
segment is x 1 t, y 2t, z 2t. The plane and the line intersect at . The visible section of the lineœ œ œ ßß
ˆ‰
222
333
segment is 1 unit in length. The length of the line segment is 1 2 2 3 of
Ɉ‰ ˆ‰ ˆ‰ È
"### ###
333 3
22 2
œ œÊ
the line segment is hidden from view.
12.6 CYLINDERS AND QUADRIC SURFACES
1. d, ellipsoid 2. i, hyperboloid 3. a, cylinder
4. g, cone 5. l, hyperbolic paraboloid 6. e, paraboloid
7. b, cylinder 8. j, hyperboloid 9. k, hyperbolic paraboloid
10. f, paraboloid 11. h, cone 12. c, ellipsoid
13. x y 4 14. z y 1 15. x 4z 16
## # # #
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
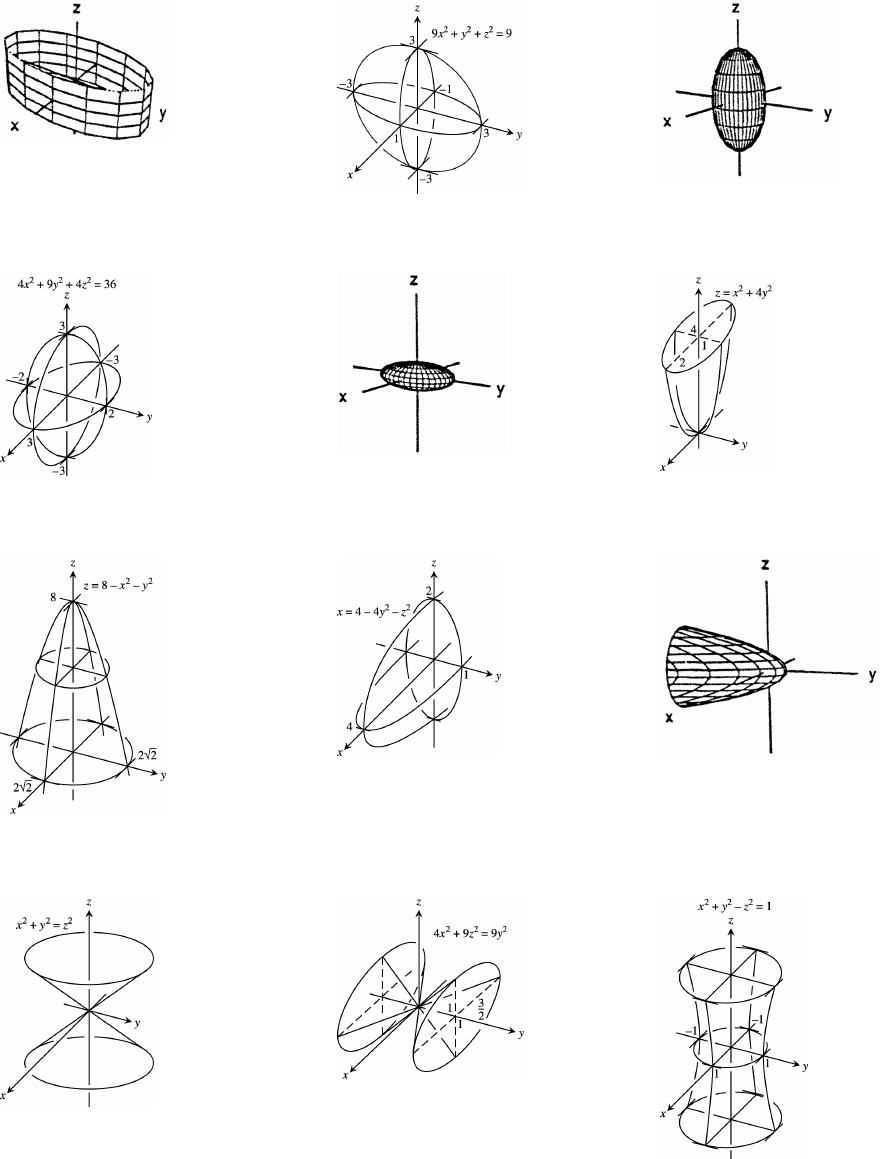
742 Chapter 12 Vectors and the Geometry of Space
16. 4x y 36 17. 9x y z 9 18. 4x 4y z 16
## ### # ##
œ œ œ
19. 4x 9y 4z 36 20. 9x 4y 36z 36 21. x 4y z
### ## # ##
œ œ œ
22. z 8 x y 23. x 4 4y z 24. y 1 x zœ œ œ
## ## ##
25. x y z 26. 4x 9z 9y 27. x y z 1
### # # # ###
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 12.6 Cylinders and Quadric Surfaces 743
28. y z x 1 29. z x y 1 30. z 1
### ### #
œ œ œ
y
44
x
31. y x z 32. x y z 33. z 1 y x
## ## ##
œ œ œ
34. 4x 4y z 35. y x z 36. 16x 4y 1
### ## ##
œ œ œab
37. x y z 4 38. x z y 39. x z 1
### ## ##
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
744 Chapter 12 Vectors and the Geometry of Space
40. 16y 9z 4x 41. z x y 42. y x z 1
## # ## ###
œ œ œab
43. 4y z 4x 4 44. x y z
## # ##
œ œ
45. (a) If x 1 and z c, then x 1 A ab
##
œ œ œ Ê œÊ œ
yyy
49 4 9
z9cx
Š‹’“
9c
9
49 c
9
1
œœ1Š‹Š‹
ÈÈ ab
9c 29c
33 9
29c
1
(b) From part (a), each slice has the area , where 3 z 3. Thus V 2 9 z dz
29z
99
2
11
ab#
Ÿ Ÿ œ
'0
3ab
9 z dz 9z (27 9) 8œœœœ
44z4
9939
111
'0
3ab ’“
#$
!1
(c) 1 1 A
xz x
abc cc
yy
ac z bc z
œÊ œÊ œ
–—–— ÈÈ
ac z bc z
cc
1Š‹Š‹
V 2 c z dz c z c . Note that if r a b c,Êœ œ œ œ œœœ
'0
cc
1111ab 2ab z 2ab 2 4abc
cc3c33
ab ’“ˆ‰
## # $
!
then V , which is the volume of a sphere.œ4r
3
1
46. The ellipsoid has the form 1. To determine c we note that the point (0 r h) lies on the surface
xz
RRc
y
œ ßß
#
of the barrel. Thus, 1 c . We calculate the volume by the disk method:
rh hR
Rc Rr
œÊ œ
#
V y dz. Now, 1 y R 1 R 1 R zœœÊœœœ1'h
h######
y
Rc c hR h
zz Rr
zR r
Š‹’ “ Š‹
ab
V R z dz R z z 2 R h R r h 2Êœ œ œ œ 1111
'h
hh
h
’“’ “ Š‹Š‹ Š‹ ‘
ab
### $###
" "Rr Rr 2Rh rh
h3h 333
R h r h, the volume of the barrel. If r R, then V 2 R h which is the volume of a cylinder ofœ œ œ
42
33
11 1
## #
radius R and height 2h. If r 0 and h R, then V R which is the volume of a sphere.œœ œ
4
31$
47. We calculate the volume by the slicing method, taking slices parallel to the xy-plane. For fixed z, xz
ab c
y
œ
gives the ellipse 1. The area of this ellipse is a b (see Exercise 45a). Hence
xzzabz
y
ccc
Š‹ Š‹
za zb
cc
œ œ1ˆ‰ˆ‰
ÈÈ1
the volume is given by V dz . Now the area of the elliptic base when z h isœœœ œ
'0
hh
111abz abz abh
c2cc
’“
!
A , as determined previously. Thus, V h (base)(altitude), as claimed.œœœœ
111abh abh abh
ccc
""
##
ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
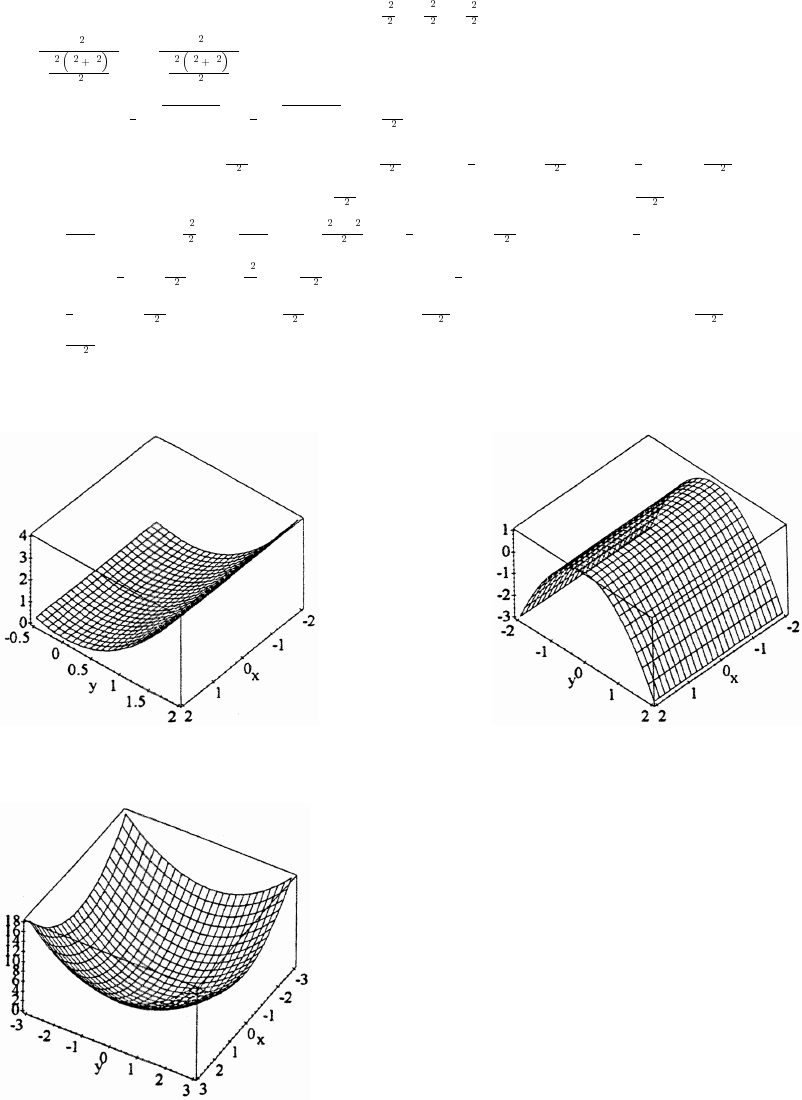
Section 12.6 Cylinders and Quadric Surfaces 745
48. (a) For each fixed value of z, the hyperboloid 1 results in a cross-sectional ellipse
xz
abc
y
œ
1. The area of the cross-sectional ellipse (see Exercise 45a) is
xy
–—–—
ac z bc z
cc
œ
A(z) c z c z c z . The volume of the solid by the method of slices isœ œ1Š‹Š‹
ÈÈ ab
ab ab
cc c
## ## ##
1
V A(z) dz c z dz c z z c h h 3c hœœœœœ
''
00
hh h
11 1 1ab ab ab abh
cc3c33c
ab a b
‘ˆ‰
## # $ # $ ##
""
!
(b) A A(0) ab and A A(h) c h , from part (a) V 3c h
!## ##
œœ œœ Êœ 1h11ab abh
c3c
ab a b
21 2 2ab c h (2A A)œœœ œ
11 1abh h abh c h h ab h
3c3c3c 3
Š‹Š‹
‘
ab
## !
1h
(c) A A c 4c h (A 4A A )
mmh
œœ œ Ê
ˆ‰ Š‹ab
hab h ab h
c44c 6#
###
!
11
ab 4c h c h c 4c h c h 6c 2hœ œ œ
hab ab abh abh
6c c 6c 6c
‘
ababa ba b1111 1
## ## # #### # #
3c h V from part (a)œœ
1abh
3c ab
##
49. z y 50. z 1 yœœ
# #
51. z x yœ
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
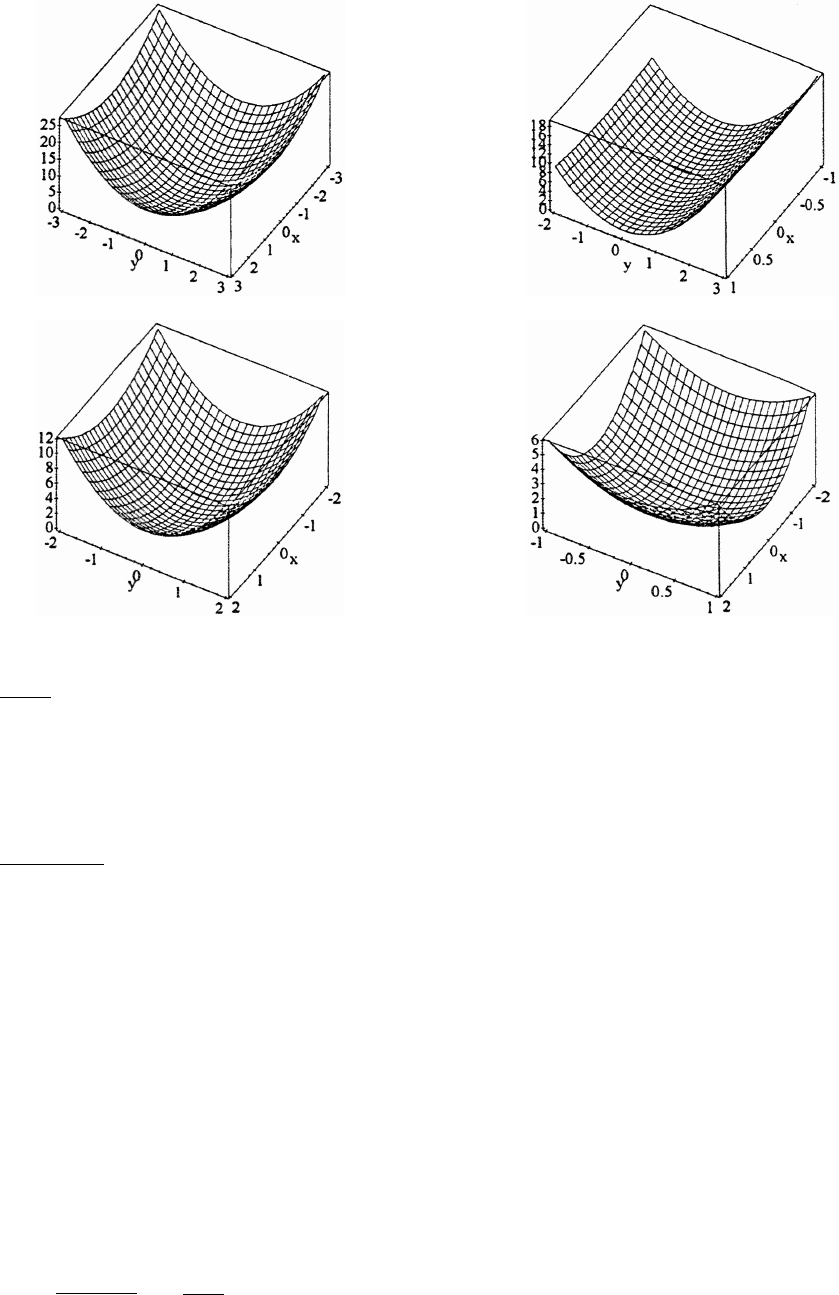
746 Chapter 12 Vectors and the Geometry of Space
52. z x 2yœ
##
(a) (b)
(c) (d)
53-58. Example CAS commands:
:Maple
with( plots );
eq := x^2/9 + y^2/36 = 1 - z^2/25;
implicitplot3d( eq, x=-3..3, y=-6..6, z=-5..5, scaling=constrained,
shading=zhue, axes=boxed, title="#89 (Section 11.6)" );
: (functions and domains may vary):Mathematica
In the following chapter, you will consider contours or level curves for surfaces in three dimensions. For the purposes of
plotting the functions of two variables expressed implicitly in this section, we will call upon the function .ContourPlot3D
To insert the stated function, write all terms on the same side of the equal sign and the default contour equating that
expression to zero will be plotted.
This built-in function requires the loading of a special graphics package.
<<Graphics`ContourPlot3D`
Clear[x, y, z]
ContourPlot3D[x /9 y /16 z /2 1, {x, 9, 9}, {y, 12, 12}, {z, 5, 5},
22 2
Axes True, AxesLabel {x, y, z}, Boxed False,ÄÄÄ
PlotLabel "Elliptic Hyperboloid of Two Sheets"]Ä
Your identification of the plot may or may not be able to be done without considering the graph.
CHAPTER 12 PRACTICE EXERCISES
1. (a) 3 3, 4 4 2, 5 9 8, 12 20 17, 32
¡¡ ¡ ¡
œ œ
(b) 17 32 1313
ÈÈ
22
œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 12 Practice Exercises 747
2. (a) 3 2, 4 5 1, 1 3. (a) 2 3 , 2 4 6, 8
¡¡ ¡¡
ab ab œ œ
(b) 1 1 2 (b) 6 8 10
ÉÉ
abab ab
È
œ œ
22 2
2
4. (a) 5 2 , 5 5 10, 25
¡¡
ab a bœ
(b) 10 25 725 5 29
ÉabÈÈ
22
œ œ
5. radians below the negative x-axis: , [assuming counterclockwise].
1
6
3
¢£
È
##
"
6. ,
¢£
È3
##
"
7. 2 4 8. 5 3 4
Š‹ Š ‹
ab
ˆ‰
182 134
41 17 17 55
ÈÈÈ Éˆ ‰ ˆ ‰
22 34
55
22
ij i j i j i jœ œ
9. length 2 2 2 2 2, 2 2 2 the direction is œœœ œ Ê
¹¹ Š‹
ÈÈ ÈÈ
È
ij ij ij ij
"" ""
ÈÈ ÈÈ
22 22
10. length 1 1 2, 2 the direction is œ œ œ œ Ê kk
ÈÈÈ
Š‹
ij ij i j i j
"" ""
ÈÈ ÈÈ
22 22
11. t ( 2 sin ) 2 cos 2 ; length 2 4 0 2; 2 2 the direction isœÊœ œ œ œ œœÊ
111
222
viji i ii i
ˆ‰ kk ab
È
12. t ln 2 e cos ln 2 e sin ln 2 e sin ln 2 e cos ln 2œÊœ vij
ˆ‰ˆ‰
ab ab ab ab
ln 2 ln 2 ln 2 ln 2
2 cos ln 2 2 sin ln 2 2 sin ln 2 2 cos ln 2 2 cos ln 2 sin ln 2 sin ln 2 cos ln 2
œ œ
ababc dab ab ab ab ababab ab ab ab
ij
ij
length 2 2 cos ln 2 sin ln 2 cos ln 2 sin ln 2
cos ln 2 sin ln 2 sin ln 2 cos ln 2
œœ
k kababc d ab ab ab ab
ababab ab ab ab É
ij 22
2 2cos ln 2 2sin ln 2 2 2;œœ
Èab abÈ
22
222
cos ln 2 sin ln 2 sin ln 2 cos ln 2
cd
ababab ab ab ab ÈŠ‹
œ
ij
ababab ab ab ab
È
cos ln 2 sin ln 2 sin ln 2 cos ln 2
2
ij
directionʜ
ababab ab ab ab
ÈÈ
cos ln 2 sin ln 2 sin ln 2 cos ln 2
22
ij
13. length 2 3 6 4 9 36 7, 2 3 6 7 the direction is œ œ œ œ Ê kk
Ȉ‰
ijk ijk i j k i j k
236 236
777 777
14. length 2 1 4 1 6, 2 6 the direction isœ œ œ œ Êkk
ÈÈÈ
Š‹
ijk ijk i j k
121
666
ÈÈÈ
121
666
ÈÈÈ
ijk
15. 2 2 2
v
v
ij k ij k
kk ÈÈÈÈÈ
œ œ œ††
44 44
4(1)4 33 33 33 33
828
ijk
16. 5 5 5 3 4œ œ œ
v
v
ik ik
kk ˆ‰ ˆ‰ ˆ‰ ˆ‰
Ɉ ‰ ˆ ‰ É
††
34 34
55 55
34
55
916
25 25
ik
17. 1 1 2, 4 1 4 3, 3, 3, 2 2 ,
11 0
21 2
kk kk
ÈÈ
Èââ
ââ
ââ
ââ
ââ
ââ
vu vuuvvu ijk
ij k
œœ œœœœ‚œ œ
††
( ) 2 2 , 4 4 1 3, cos cos ,uv vu i jkvu‚œ‚ œ ‚œ œ œ œ œkk
ÈŠ‹ Š‹
)" " "vu
vu
†
kkkk È
4
2
1
cos , proj ( )kkuuvij)œœ
33
22
Èkkkk
vœŠ‹
vu
vv
†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
748 Chapter 12 Vectors and the Geometry of Space
18. 1 1 2 6, ( 1) ( 1) 2, (1)( 1) (1)(0) (2)( 1) 3,kk kk
ÈÈ
ÈÈ
vu vuœœ œœ œ œ
### # # †
3, , ( ) ,
112
10 1
uv v u i j ku v v u i j k
ijk
†œ ‚ œ œ ‚ œ ‚ œ
ââ
ââ
ââ
ââ
ââ
ââ
( 1) ( 1) 1 3, cos cos coskk
ÈÈŠ‹ Š ‹ Š‹
vu‚œ œ œ œ œ
### " " "
)vu
vu
†
kkkk ÈÈÈ
33
6 2 12
cos , cos 2 , proj ( 2 ) ( )œ œ œ † œ œ œ
"
# #
"
Š‹ Š‹
kk È
ÈÈÈ
kkkk
336
5 3
622 6
1uuvijkijk)vœŠ‹
vu
vv
†
19. proj 2 where 8 and 6
vvu
vv
uvijkvuvvœ††
Š‹
†
kkkk œ œ œ
4
3ab
20. proj 2 where 1 and 3
vvu
vv
u v i j vu vvœ††
Š‹
†
kkkk œ œ œ
1
3ab
21. 100
110
uv k
ijk
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
22. 2
110
110
uv k
ijk
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
23. Let v v v and w w w . Then 2 (v v v ) 2(w w w )vijkw ijk vw ijk ijkœ œ œ
"#$ " # $ "#$ " # $
##
kkk k
(v 2w ) (v 2w ) (v 2w ) (v 2w ) (v 2w ) (v 2w )œ œ kk
ˆ‰
È
"" ## $$ "" ## $$
####
#
ijk
v v v 4(vw vw vw) 4 w w w 4 4 œ œ ab a bkk kk
### # # #
"" ## $$ ##
313
vvww†
4 cos 4 4 4(2)(3) cos 36 40 24 40 12 28 2 28œ œ œ œœ Ê œkk kkkk kk k k
ˆ‰ ˆ‰ È
vvw w vw
## "
#
)1
3
27œÈ
24. and are parallel when (4a 40) (20 2a) (0)
24 5
48a
uv uv0 0 i j k0
ijk
‚œ Ê œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
4a 40 0 and 20 2a 0 a 10Êœ œÊœ
25. (a) area abs 2 3 4 9 1 14
11 1
21 1
œ‚œ œ œ œ
kk k k
ââ
ââ
ââ
ââ
ââ
ââ ÈÈ
uv i jk
ij k
(b) volume 1 3 2 1 6 1 1 4 1 1
11 1
211
123
œ‚ œ œ œ
ab aba ba b
ââ
ââ
ââ
ââ
ââ
ââ abuvw†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 12 Practice Exercises 749
26. (a) area abs 1
110
010
œ‚œ œ œkk kk
ââ
ââ
ââ
ââ
ââ
ââ
uv k
ijk
(b) volume 1 1 0 1 0 0 0 1
110
010
111
œ‚ œ œ œab abab
ââ
ââ
ââ
ââ
ââ
ââ
uvw†
27. The desired vector is or since is perpendicular to both and and, therefore, also parallel tonv vn nv n v‚‚ ‚
the plane.
28. If a 0 and b 0, then the line by c and are parallel. If a 0 and b 0, then the line ax c and areœÁ œ Áœ œij
parallel. If a and b are both 0, then ax by c contains the points and 0 the vectorÁœ ß!ßÊ
ˆ‰ ˆ‰
cc
ab
ab c(b a ) and the line are parallel. Therefore, the vector b a is parallel to the line
ˆ‰
cc
ab
i j ij ijœ
ax by c in every case.œ
29. The line L passes through the point P 0 0 1 parallel to . With PS 2 2 andabßß œ œ
Ä
vijk ijk
PS 2 1 (2 1) 2 2 3 4 , we find the distance
221
111
Ä‚œ œ œ
vijkijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ab ab
d.œœ œœ
¹¹
kk ÈÈÈ
ÈÈ
PS 1916
111
26 78
33
Ä‚
v
v
30. The line L passes through the point P 2 2 0 parallel to . With PS 2 2 andabßß œ œ
Ä
vijk i jk
PS 2 1 2 1 2 2 3 4 , we find the distance
221
111
Ä‚œ œ œ
vijkijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ababab
d.œœ œœ
¹¹
kk ÈÈÈ
ÈÈ
PS 1916
111
26 78
33
Ä‚
v
v
31. Parametric equations for the line are x 1 3t, y 2, z 3 7t.œ œ œ
32. The line is parallel to PQ 0 and contains the point P(1 2 0) parametric equations are
Äœ ßß Êijk
x 1, y 2 t, z t for 0 t 1.œœœ ŸŸ
33. The point P(4 0 0) lies on the plane x y 4, and PS (6 4) 0 ( 6 0) 2 6 with ßß œ œ œ œ
Äij k ik nij
d2.Êœ œ œ œ
¹¹
kk ÈÈ
n
n
†PS 200 2
110 2
Ä
¹¹ È
34. The point P(0 0 2) lies on the plane 2x 3y z 2, and PS (3 0) (0 0) (10 2) 3 8 withßß œ œ œ
Äij kik
2 3 d 14.nijkœ Êœ œ œ œ
¹¹
kk ÈÈ
n
n
†PS 608 14
491 14
Ä
¹¹ È
35. P(3 2 1) and 2 (2)(x 3) (1)(y ( 2)) (1)(z 1) 0 2x y z 5ßß œ Ê œ Ê œnijk
36. P( 1 6 0) and 2 3 (1)(x ( 1)) ( 2)(y 6) (3)(z 0) 0 x 2y 3z 13ßß œ Ê œÊœni j k
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

750 Chapter 12 Vectors and the Geometry of Space
37. P(1 1 2), Q(2 1 3) and R( 1 2 1) PQ 2 , PR 2 3 3 and PQ PRß ß ß ß ß ß Ê œ œ ‚
ÄÄ
ÄÄ
ijk ijk
9 7 is normal to the plane ( 9)(x 1) (1)(y 1) (7)(z 2) 0
121
23 3
œœ Êœ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ij k
9xy7z4Ê œ
38. P(1 0 0), Q(0 1 0) and R(0 0 1) PQ , PR and PQ PRßß ßß ßß Ê œ œ ‚
ÄÄ
ÄÄ
ij ik
is normal to the plane (1)(x 1) (1)(y 0) (1)(z 0) 0
110
101
œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ijk
xyz1Ê œ
39. 0 , since t , y and z when x 0; ( 0 3), since t 1, x 1 and z 3
ˆ‰
ß ß œ œ œ œ "ß ß œ œ œ
"""
## # # #
33
when y 0; (1 1 0), since t 0, x 1 and y 1 when z 0œßß œœ œ œ
40. x 2t, y t, z t represents a line containing the origin and perpendicular to the plane 2x y z 4; thisœ œ œ œ
line intersects the plane 3x 5y 2z 6 when t is the solution of 3(2t) 5( t) 2( t) 6 œ œ
t is the point of intersectionÊœ Ê ßß
2 422
3 333
ˆ‰
41. and 2 the desired angle is cos cosni nij k
"# " " "
#
œ œ Ê œ œ
ÈŠ‹ ˆ‰
nn
nn
†
kkkk 3
1
42. and the desired angle is cos cosnij njk
"# " " "
#
œ œ Ê œ œ
Š‹ ˆ‰
nn
nn
†
kkkk 3
1
43. The direction of the line is 5 3 . Since the point ( 5 3 0) is on
121
112
nn ijk
ijk
"#
‚œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
both planes, the desired line is x 5 5t, y 3 t, z 3t.œ œ œ
44. The direction of the intersection is 6 9 12 3(2 3 4 ) and is the
12 2
521
nn i j k ij k
ij k
"#
‚ œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
same as the direction of the given line.
45. (a) The corresponding normals are 3 and 2 2 and since niknijk nn
"# "#
œ' œ †
(3)(2) (0)(2) (6)( 1) 6 0 6 0, we have that the planes are orthogonalœ œœ
(b) The line of intersection is parallel to 12 15 6 . Now to find a point in
30 6
22 1
nn i jk
ij k
"#
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
the intersection, solve 15x 12y 19 x 0 and y
3x 6z 1 3x 6z 1
2x 2y z 3 12x 12y 6z 18
œœ
œ œ
œ œ
Êʜʜœ
19
12
is a point on the line we seek. Therefore, the line is x 12t, y 15t and z 6t.Ê!ß ß œ œ œ
ˆ‰
19 19
16 12 6#
" "
46. A vector in the direction of the plane's normal is 7 3 5 and P( 2 3) on
231
112
nuv i j k
ijk
œ‚œ œ "ßß
ââ
ââ
ââ
ââ
ââ
ââ
the plane 7(x 1) 3(y 2) 5(z 3) 0 7x 3y 5z 14.Ê œÊ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 12 Practice Exercises 751
47. Yes; (2 4 ) (2 0 ) 2 2 4 1 1 0 0 the vector is orthogonal to the plane's normalvn i j k i j k† † †††œ œ œÊ
is parallel to the planeÊv
48. PP 0 represents the half-space of points lying on one side of the plane in the direction which the normal pointsn n†!
Ä
49. A normal to the plane is AB AC 2 2 the distance is d
20 1
210
nijk
ij k
œ‚œ œÊ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
AP
Ä
†n
n
3œœœ
¹¹
¸¸
(4)( 2 )
144
180
3
ij ijk#
†
È
50. P(0 0 0) lies on the plane 2x 3y 5z 0, and PS 2 2 3 with 2 3 5 ßß œ œ œ Ê
Äijk n ijk
dœœ œ
¹¹¹ ¹
n
n
†PS 4615 25
4925 38
Ä
kk ÈÈ
51. 2 is normal to the plane 0 3 3 3 3 is orthogonal
211
11 1
nijk nv ijk jk
ij k
œ Ê‚œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
to and parallel to the planev
52. The vector is normal to the plane of and ( ) is orthogonal to and parallel to the plane of BC B CABC A B‚Ê‚‚
and :C
5 3 and ( ) 2 3
12 1 2 1 1
11 2 5 3 1
BC i jk A BC i jk
ij k i j k
‚œ œ ‚ ‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
( ) 4 9 1 14 and ( 2 3 ) is the desired unit vector.Ê‚‚œ œ œ kk
ÈÈ
ABC u i jk
"
È14
53. A vector parallel to the line of intersection is 5 3
121
112
vn n ij k
ijk
œ‚œ œ
"#
ââ
ââ
ââ
ââ
ââ
ââ
25 1 9 35 2 (5 3 ) is the desired vector.Êœ œ Ê œ kk ÈÈŠ‹
vijk
v
vkk È2
35
54. The line containing (0 0 0) normal to the plane is represented by x 2t, y t, and z t. This lineßß œ œ œ
intersects the plane 3x 5y 2z 6 when 3(2t) 5( t) 2( t) 6 t the point is . œ œ Êœ Ê ßß
2 422
3 333
ˆ‰
55. The line is represented by x 3 2t, y 2 t, and z 1 2t. It meets the plane 2x y 2z 2 whenœ œ œ œ
2(3 2t) (2 t) 2( 2t) 2 t the point is . " œÊœ Ê ßß
811267
9999
ˆ‰
56. The direction of the intersection is 3 5 cos
21 1
11 2
vn n i jk
ij k
œ‚œ œÊœ
"# "
ââ
ââ
ââ
ââ
ââ
ââ Š‹
)vi
vi
†
kkkk
cos 59.5°œ¸
" Š‹
3
35
È
57. The intersection occurs when (3 2t) 3(2t) t 4 t 1 the point is (1 2 1). The required line œÊœÊ ßß
must be perpendicular to both the given line and to the normal, and hence is parallel to 22 1
13 1
ââ
ââ
ââ
ââ
ââ
ââ
ij k
5 3 4 the line is represented by x 1 5t, y 2 3t, and z 1 4t.œ Ê œ œ œ ijk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
752 Chapter 12 Vectors and the Geometry of Space
58. If P(a b c) is a point on the line of intersection, then P lies in both planes a 2b c 3 0 andßß Ê œ
2a b c 1 0 (a 2b c 3) k(2a b c 1) 0 for all k.œ Ê œ
59. The vector AB CD (2 7 2 ) is normal to the plane and A( 2 0 3) lies on the
324
0
ÄÄ
‚œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
ij k
ijk
26 26
55
26
5
plane 2(x 2) 7(y 0) 2(z ( 3)) 0 2x 7y 2z 10 0 is an equation of the plane.ʜʜ
60. Yes; the line's direction vector is 2 3 5 which is parallel to the line and also parallel to the normalijk
4 6 10 to the plane the line is orthogonal to the plane. Êij k
61. The vector PQ PR 11 3 is normal to the plane.
213
301
Ä‚œ œ
Ä
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ijk
(a) No, the plane is not orthogonal to PQ PR .
Ä‚Ä
(b) No, these equations represent a line, not a plane.
(c) No, the plane (x 2) 11(y 1) 3z 0 has normal 11 3 which is not parallel to PQ PR . œ ‚
ÄÄ
ijk
(d) No, this vector equation is equivalent to the equations 3y 3z 3, 3x 2z 6, and 3x 2y 4œ œ œ
x t, y t, z 1 t, which represents a line, not a plane.Êœ œ œ
42
33
(e) Yes, this is a plane containing the point R( 2 1 0) with normal PQ PR .ß ß ‚
ÄÄ
62. (a) The line through A and B is x 1 t, y t, z 1 5t; the line through C and D must be parallel andœ œ œ
is L : x 1 t, y 2 t, z 3 5t. The line through B and C is x 1, y 2 2s, z 3 4s; the line
"œ œ œ œ œ œ
through A and D must be parallel and is L : x 2, y 1 2s, z 4 4s. The lines L and L intersect
#"#
œœ œ
at D(2 1 8) where t 1 and s 1.ßß œ œ
(b) cos )œœ
(2 4 ) ( 5 )
20 27 15
3
jkijk†
ÈÈ È
(c) BC BC ( 2 ) where BA 5 and BC 2 4
Š‹
BA BC 18 9
BC BC 20 5
ÄÄ
ÄÄ
†
†
ÄÄ Ä Ä
œ œ œ œ jk ijk jk
(d) area (2 4 ) ( 5 ) 14 4 2 6 6œ‚ œœkkkk
È
jk ijk ijk
(e) From part (d), 14 4 2 is normal to the plane 14(x 1) 4(y 0) 2(z 1) 0nijkœ Ê œ
7x 2y z 8.ʜ
(f) From part (d), 14 4 2 the area of the projection on the yz-plane is 14; the area of thenijk niœÊ œkk†
projection on the xy-plane is 4; and the area of the projection on the xy-plane is 2.kk kknj nk††œœ
63. AB 2 , CD 4 and AC 2 5 9 the distance is
21 1
14 1
ÄÄ Ä
œ œ œ Ê œ Ê
ijk i jk, ij n ij k
ijk
œ
ââ
ââ
ââ
ââ
ââ
ââ
dœœ
¹¹
(2 ) ( 5 9 )
25181
11
107
ij ij k
†
ÈÈ
64. AB 2 4 , CD 2 , and AC 3 3 7 3 2 the distance
24 1
112
ÄÄ Ä
œ œ œ Êœ œ Ê
ijk ijk ij n ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
is d œœ
¹¹
(3 3)(7 3 2)
4994
12
62
ijijk†
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
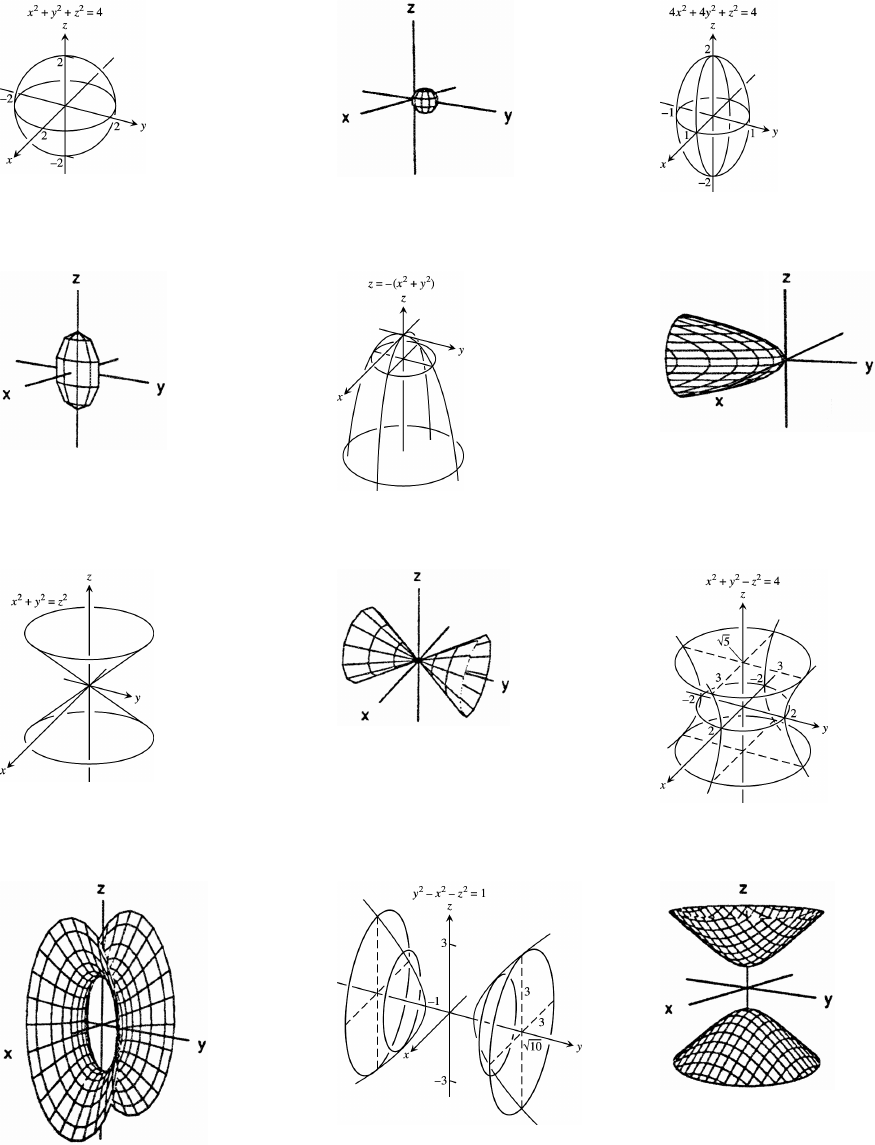
Chapter 12 Practice Exercises 753
65. x y z 4 66. x (y 1) z 1 67. 4x 4y z 4
### # ## # ##
œ œ œ
68. 36x 9y 4z 36 69. z x y 70. y x z
### ## ##
œ œ œab ab
71. x y z 72. x z y 73. x y z 4
### ## # ###
œ œ œ
74. 4y z 4x 4 75. y x z 1 76. z x y 1
## # ### ###
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
754 Chapter 12 Vectors and the Geometry of Space
CHAPTER 12 ADDITIONAL AND ADVANCED EXERCISES
1. Information from ship A indicates the submarine is now on the line L : x 4 2t, y 3t, z t; information from
""
œœœ
3
ship B indicates the submarine is now on the line L : x 18s, y 5 6s, z s. The current position of the sub is
#œœœ
6 3 and occurs when the lines intersect at t 1 and s . The straight line path of the submarine contains both
ˆ‰
ßß œ œ
""
33
points P 2 1 and Q 6 3 ; the line representing this path is L: x 2 4t, y 1 4t, z . The
ˆ‰ˆ‰
ß ß ß ß œ œ œ
"" "
33 3
submarine traveled the distance between P and Q in 4 minutes a speed of 2 thousand ft/min. In 20Êœœ
¹¹ È
PQ
44
32
ÄÈ
minutes the submarine will move 20 2 thousand ft from Q along the line L
È
20 2 (2 4t 6) ( 1 4t 3) 0 800 16(t 1) 16(t 1) 32(t 1) (t 1)Ê œ Ê œ œ Ê œ
ÈÈ### ## ##
800
32
25 t 6 the submarine will be located at 26 23 in 20 minutes.œÊœÊ ßß
ˆ‰
"
3
2. H stops its flight when 6 110t 446 t 4 hours. After 6 hours, H is at P(246 57 9) while H is at (446 13 0).
#"#
œ Êœ ßß ßß
The distance between P and Q is (246 446) (57 13) (9 0) 204.98 miles. At 150 mph, it would take
ȸ
###
about 1.37 hours for H to reach H .
"#
3. Torque PQ 15 ft-lb PQ sin ft 20 lbœ‚Ê œ œ Êœ
ÄÄ
¹¹ ¹¹
kk kk kkFFFF
1
#
3
4†
4. Let be the vector from O to A and 3 2 be the vector from O to B. The vector orthogonal to aijk bi j k v aœ œ
and is parallel to (since the rotation is clockwise). Now 2 ; proj 2 2 2bv ba baij k b a i j kÊ ‚ œ œ œ ‚aab
aa
ˆ‰
†
†
2, 2, 2 is the center of the circular path 1, 3, 2 takes radius 1 1 0 2 arc length perÊÊœœÊab ab ab
ÉÈ
22
2
second covered by the point is 2 units/sec (velocity is constant). A unit vector in the direction of is
3
# ‚
‚
Èkkœvv
ba
bakk
23œ Êœ œ œ
"" ‚ ""
‚#
ÈÈÈ ÈÈÈ
kk ÈÈ
666 666
232
33
22
ijkvv ijk ij kkk
Š‹ Š ‹
ÈÈ
ba
ba
5. (a) By the Law of Cosines we have cos and cos sin and sin!"!"œœ œœÊœ œ
354 3 453 4 4 3
23 5 5 24 5 5 5 5
222 222
abab abab
cos , sin , , cos , sin , , andÊ œll ll œllll œll ll œ llllFF F FFFF F FF
11 1 1122 2 22
34 43
55 55
¢£¢£¢£¢£
!! ""
0, 100 . Since 0, 100 , 0, 100 0wFF FFFF FFœ œ Êllllllllœ Êllllœ
¡ ¡ ¡
¢£
12 1212 12
3443 34
5555 55
and 100. Solving the first equation for results in: . Substituting this result into the
43 3
55 4
12 2 2 1
llllœ ll llœllFF F F F
second equation gives us: 100 80 lb. 60 lb. 48, 64 and
49
520
11 1 2 1
l l l lœ Êl lœ Êl lœ Ê œ FF F F F
¡
48, 36 , and tan and tanF211
43
34
œœœ
¡ ˆ‰ ˆ‰
!"
(b) By the Law of Cosines we have cos and cos sin and sin!"!"œœ œœÊœ œ
51312 5 12135 12 12 5
2 5 13 13 2 12 13 13 13 13
222 222
abab abab
cos , sin , , cos , sin , , andÊ œll ll œll ll œll ll œ ll llFF F FFFF F FF
11 1 1122 2 22
512 125
13 13 13 13
¢£¢£¢£¢£
!! ""
0, 200 . Since 0, 200 , 0, 200wFF FFFFœ œ Êll ll ll llœ
¡ ¡ ¡
¢£
12 1212
512125
13 13 13 13
0 and 200. Solving the first equation for results in: .Êll llœ ll llœ ll llœ ll
512 125 5
13 13 13 13 12
12 12 2 2 1
FF FF F F F
Substituting this result into the second equation gives us: 200 184.615 lb.
12 25 2400
13 156 13
11 1
l l l lœ Êl lœ ¸FF F
76.923 lb. , 71.006, 170.414 and , Êl lœ ¸ Ê œ ¸ œFF F
21 2
1000 12000 28800 12000 5000
13 1169 1169 1169 1169
¢£ ¢£
¡
71.006, 29.586 .¸¡
6. (a) cos , sin , cos , sin , and 0, w . Since 0, wTT T TT T w TT
11 1 22 2 12
œll ll œll ll œ œ Ê
¢£¢£
¡ ¡
!! ""
cos cos , sin sin 0, w cos cos 0 and
¢£
¡
ll ll ll ll œ Êll ll œTTTT TT
1212 12
!"!" !"
sin sin w. Solving the first equation for results in: . Substituting this result intoll ll œ ll llœ llTT T TT
12 2 21
cos
cos
!" !
"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 12 Additional and Advanced Exercises 755
the second equation gives us: sin w andl l l lœ Êl lœ œTTT
111
cos sin wcos wcos
cos sin cos cos sin sin
!!" " "
"!"!"!"ab
llœT2wcos
sin
!
!"ab
(b) ; 0 w cos cos 0 cos 0
dd d
ddsin sin d
11
wcos wcos cos
! ! !" !" !
""!"
ab ab a b a b
Š‹
llœ œ llœÊ œÊ œTT
ab ab
ab
2"!" !"
; ;ʜʜ llœ œ!" ! "
11
! ! !" !"
"!" "!"
22d dsin sin
dd
1wcos cos wcos cos 1
2
22 3
2
ab Š‹
T
ab
ab ab
ˆ‰
ab
w cos 0 local minimum when
d
d 2
1
2
2
2
!
!"
1
ab
º
ll œ Ê œT
œ
"!"
(c) ; 0 w cos cos 0 cos 0
ddwcos d
ddsin sin d
22
wcos cos
" " !" !" "
!!!"
ab ab a b a b
Š‹
llœ œ llœÊ œÊ œTT
ab ab
ab
2!!" !"
; ;ʜʜ llœ œ!" " !
11
" " !" !"
!!" !!"
22d dsin sin
dd
2wcos cos wcos cos 1
2
22 3
2
ab Š‹
T
ab
ab ab
ˆ‰
ab
w cos 0 local minimum when
d
d 2
2
2
2
2
!
"!
1
ab
º
ll œ Ê œT
œ
!"!
7. (a) If P(x y z) is a point in the plane determined by the three points P (x y z ), P (x y z ) andßß ßß ßß
"" "" ## ##
P (x y z ), then the vectors PP , PP and PP all lie in the plane. Thus PP (PP PP ) 0
$$ $$ " # $ " # $
ßß ‚ œ
ÄÄ Ä Ä Ä Ä
†
0 by the determinant formula for the triple scalar product in Section 12.4.
xxyyzz
xxyyzz
xxyyzz
ʜ
ââ
ââ
ââ
ââ
ââ
ââ
"""
###
$$$
(b) Subtract row 1 from rows 2, 3, and 4 and evaluate the resulting determinant (which has the same value
as the given determinant) by cofactor expansion about column 4. This expansion is exactly the
determinant in part (a) so we have all points P(x y z) in the plane determined by P (x y z ),ßß ß ß
"" ""
P(xyz), and P(xyz).
#### $$$$
ßß ßß
8. Let L : x a s b , y a s b , z a s b and L : x c t d , y c t d , z c t d . If L L ,
" " " # # $ $ # "" ## $$ "#
œ œ œ œ œ œ ²
then for some k, a kc , i 1, 2, 3 and the determinant
acb d kccb d
acb d kccb d
acb d
ii
œœ œ
âââ â
âââ â
âââ â
âââ â
âââ â
âââ â
""" " """ "
### # ### #
$$$ $ kccb d
0,
$$$ $
œ
since the first column is a multiple of the second column. The lines L and L intersect if and only if the
"#
system has a nontrivial solution the determinant of the coefficients i
as ct (b d) 0
as ct (b d) 0
as ct (b d) 0
Ú
Û
Ü"" ""
## ##
$$ $$
œ
œ
œ
Ís zero.
9. (a) Place the tetrahedron so that A is at 0, 0, 0 , the point P is on the y-axis, and ABC lies in the xy-plane. Sinceab ˜
ABC is an equilateral triangle, all the angles in the triangle are 60 and since AP bisects BC ABP˜Ê˜
‰
is a 30 - 60 - 90 trinagle. Thus the coordinates of P are 0, 3, 0 , the coordinates of B are 1, 3, 0 , and the
‰‰‰ Š‹ Š‹
ÈÈ
coordinates of C are 1, 3, 0 . Let the coordinates of D be given by a, b, c . Since all of the faces are equilateral
Š‹
Èab
trinagles all the angles in each of the triangles are 60 cos DAB cos 60ÊÊnœœœœ
‰‰
ÄÄ
†
llll
ÄÄ
abab
AD AB 1
AD AB
ab3
22 2
È
abab
a b 3 2 and cos DAC cos 60 a b 3 2. Add the two equationsÊ œ n œ œ œ œ Ê œ
ÈÈ
abab
䀀
†
llll
ÄÄ
AD AC 1
AD AC
ab3
22 2
È
abab
to obtain: 2b 3 4 b . Substituting this value for b in the first equation gives us: a 3 2
È È
Š‹
œÊœ œ
2 2
3 3
È È
a 0. Since AD a b c 2 0 c 4 c . Thus the coordinates of D areÊœ l lœ œÊ œÊœ
ÄÈŠ‹
222 22
2
33
222
ÈÈ
È
0, , . cos cos DAP cos 57.74 .
Š‹ Š‹
ab
2ADAP21
33 23 3
22
AD AP
1
ÈÈ È È
È))œn œ œ Êœ Ê
ÄÄ
†
llll
ÄÄ ‰
(b) Since ABC lies in the xy-plane the normal to the face given by ABC is . The face given by BCD is an˜Ê ˜œ˜nk
1
adjacent face. The vectors DB and DC both lie in the plane containing
Äœ œ
Ä
ij k ij k
11
33 33
22 22
ÈÈ ÈÈ
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

756 Chapter 12 Vectors and the Geometry of Space
BCD. The normal to this plane is given by . The angle between two
1
1
˜œœ
njk
ij k
2
1
33
22
1
33
22
2
33
2
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
È
ÈÈ
ÈÈ
ÈÈ
4)
adjacent faces is given by cos cos DAP cos 70.53 .))œn œ œ Êœ ¸ab ˆ‰
nn
nn
12
12
†
llll
‰
2/ 3
16/3
11
3
È
ab
Š‹
È
10. Extend CD to CG so that CD DG. Then CG t CF CB BG and t CF 3 CE CA, since ACBG is a
ÄÄ ÄÄ Ä ÄÄÄ Ä ÄÄ
œœœœ
parallelogram. If t CF 3 CE CA , then t 3 1 0 t 4, since F, E, and A are collinear.
ÄÄÄ
œ œÊœ0
Therefore, CG 4 CF CD 2 CF F is the midpoint of CD.
ÄÄ ÄÄ
œÊœÊ
11. If Q(x y) is a point on the line ax by c, then P Q (x x ) (y y ) , and a b is normal to theßœœœ
Ä
"""
ijnij
line. The distance is proj P Q
¹¹¹ ¹
n"
Äœœ
[(xx) (yy)](a b)
ab ab
a(x x ) b(y y )
ijij†
ÈÈ
kk
, since c ax by.œœ
kk
È
ax by c
ab
12. (a) Let Q(x y z) be any point on Ax By Cz D 0. Let QP (x x ) (y y ) (z z ) , andßß œ œ
Ä
"" " "
ijk
. The distance is proj QP ((x x ) (y y ) (z z ) )nijkœœ
Ä
ABC ABC
ABC ABC
ijk ijk
""""
È È
¹¹¹ ¹Š‹
n†
.œœ
kkkk
ÈÈ
Ax By Cz (Ax By Cz) Ax By Cz D
ABC ABC
(b) Since both tangent planes are parallel, one-half of the distance between them is equal to the radius of the
sphere, i.e., r 3 (see also Exercise 12a). Clearly, the points (1 2 3) and ( 1 2 3)œ œ ß ß ßß
"
#
kk
È39
111 È
are on the line containing the sphere's center. Hence, the line containing the center is x 1 2t,œ
y 2 4t, z 3 6t. The distance from the plane x y z 3 0 to the center is 3œ œ œ È
3 from part (a) t 0 the center is at (1 2 3). ThereforeʜʜÊßß
kk
È
(1 2t) (2 4t) (3 6t) 3
111
È
an equation of the sphere is (x 1) (y 2) (z 3) 3.œ
###
13. (a) If (x y z ) is on the plane Ax By Cz D , then the distance d between the planes is
""" "
ßß œ
d , since Ax By Cz D , by Exercise 12(a).œœ œ
kkkk
Èkk
Ax By Cz D D D
ABC ABC
""""
ijk
(b) d œœ
kk
ÈÈ
12 6
491
6
14
(c) D 8 or 4 the desired plane is
kkkk
ÈÈ
2(3) ( 1)(2) 2( 1) 4 2(3) ( 1)(2) 2( 1) D
14 14
œÊœÊ
2xy2x8 œ
(d) Choose the point (2 0 1) on the plane. Then 5 D 3 5 6 the desired planes areßß œ Ê œ „ Ê
kk
È
3D
6
È
x2yz 356 and x2yz356.œ œ
ÈÈ
14. Let AB BC and D(x y z) be any point in the plane determined by A, B and C. Then the point D lies innœ‚ ßß
ÄÄ
this plane if and only if AD 0 AD (AB BC ) 0.
ÄÄÄÄ
œÍ ‚ œ††n
15. 2 6 is normal to the plane x 2y 6z 6; 4 5 is parallel to the
111
126
ni j k vn i jk
ijk
œ œ ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
plane and perpendicular to the plane of and ( ) 32 23 13 is a
126
451
vn wnvn i j k
ijk
Êœ‚‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 12 Additional and Advanced Exercises 757
vector parallel to the plane x 2y 6z 6 in the direction of the projection vector proj . Therefore,œ Pv
proj proj
Pv vv w w wwijkœ œ œ œ œ œ œ
wŠ‹Š‹ˆ‰
†ww vw
ww w
kk kk kk
†32 23 13 42 32 23 13
32 23 13 1722 41 41 41 41
"
16. proj proj and proj proj ( proj ) proj ( proj ) proj
zz z z zz zz
wvwwvvwwwwvvwœ œ Ê œ œ
2 proj 2 œ œvvv z
zŠ‹
vz
z
†
kk
17. (a) 2 2 4 ( ) ; ( ) ( ) 0 0 ; 4 ( ) ;uv i j k uv w 0uwv vwu v u 0vw i u vw 0‚œ‚œ Ê ‚‚œ œ œ ‚œÊ‚‚ œ††
()()00uwv uvw v w 0††œœ
(b) 43 ( ) 1026;
111 143
21 2 12 1
uv ijk uvw ijk
ij k ijk
‚œ œ Ê ‚ ‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
( ) ( ) 4(2 2 ) 2( ) 10 2 6 ;uwv vwu i j k i j k i j k†† œœ
vw i j k u vw i j k
ijk ijk
‚œ œ Ê‚‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
21 2 1 11
12 1 3 4 5
345 ( ) 927;
( ) ( ) 4(2 2 ) ( 1)( 2 ) 9 2 7uwv uvw i j k i j k i j k†† œœ
(c) 2 4 ( ) 4 6 2 ;
210 124
211 102
uv ijk uvw ijk
ijk ij k
‚œ œ Ê ‚ ‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
( ) ( ) 2(2 ) 4(2 ) 4 6 2 ;uwv vwu i j k i j i j k††œœ
vw i jk u vw i j k
ijk i jk
‚œ œÊ‚‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
211 210
102 2 31
23 ( ) 24;
( ) ( ) 2(2 ) 3( 2 ) 2 4uwv uvw i j k i k i j k†† œ œ
(d) 3 ( ) 10 10 ;
11 2 131
10 1 2 4 2
uv i jk uv w i k
ijk ijk
‚ œ œ Ê ‚ ‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
( ) ( ) 10( ) 0( 2 ) 10 10 ;uwv vwu ik ij k i k††œœ
vw i j k u vw i j k
ijk ij k
‚œ œ Ê‚‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
10 1 1 1 2
242 444
4 4 4 ( ) 12 4 8 ;
( ) ( ) 10( ) 1(2 4 2 ) 12 4 8uwv uvw i k i j k i j k††œœ
18. (a) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )uvwvwuwuv uwvuvwvuwvwuwvuwuv0‚‚‚‚‚‚œœ†††† ††
(b) [ ( )] [( ( )] [( ( )] [( ) ] [( ) ] [( ) ]uvii uvjj uvkk uvii uvjj uvkk uv†† † †††‚ ‚ ‚ œ‚ ‚ ‚ œ‚
(c) ( ) ( ) [ ( )] [( ) ( ) ] ( )( ) ( )( )
uv wr uv wr u vrw vwr uwvr urvw uw vw
ur vr
‚‚œ‚‚œœœ†† †††††††
††
††
ºº
19. The formula is always true; [ ( )] [( ) ( ) ]uuuvwu uvuuuvw‚‚‚ œ‚ ††††
[( ) ( ) ] œ‚‚œ‚œ‚uvuu uuuvw uuvw uuvw††† ††kk kk
##
20. If (cos B) (sin B) and (cos A) (sin A) , where A B, then sin (A B)uijvij uvuv kœ œ ‚œ cdkkkk
(cos B sin A sin B cos A) sin (A B) cos B sin A sin B cos A, since
cos Bsin B0
cos A sin A 0
œœÊœ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
k
1 and 1.kk kkuvœœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
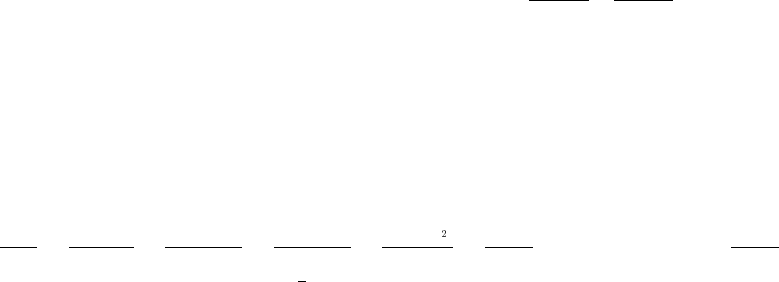
758 Chapter 12 Vectors and the Geometry of Space
21. If a b and c d , then cos ac bd a b c d cos uij vij uvuvœ œ œ Ê œ †kkkk ÈÈ
))
####
(ac bd) a b c d cos (ac bd) a b c d , since cos 1.Ê œ Ê Ÿ Ÿ
###### ##### #
abab abab))
22. If a b c , then a b c 0 and 0 iff a b c 0.u i j k uu uuœ œ œ œœœ††
###
23. ( ) ( ) 2 2 k k kk kkkk kk a b k k kk kkkk kkuv uv uv uu uvvv u uv v u v uv u vœ œ Ÿ œ ÊŸ
####
††††
24. Let denote the angle between and , and the angle between and . Let a and b . Then!"wu wv u vœœkk kk
cos , and likewise, cos ! "œœœœœœ œ
wu vu uv
wu wu wu wu w w w
vuu vuuu vuuu vu
†††
††† †† †
kkkk kkkk kkkk kkkk kk kk kk
ab
a
(a b ) (a b ) (a b ) aba ba ba
.
Since the angle between and is always and cos cos , we have that bisects the angle betweenuv wŸœ œÊ
1
#!" !"
and .uv
25. ( ) ( )kk kk kk kk kk kk kk kk kk kk kk kkuv vu vu uv uv vu vu vu uv uv vu uv œ† ††††
0œ œœkk kk kk kk kk kk kkkk kkkkvu uv v u u u v v vu uv v u u v††††
## ####
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
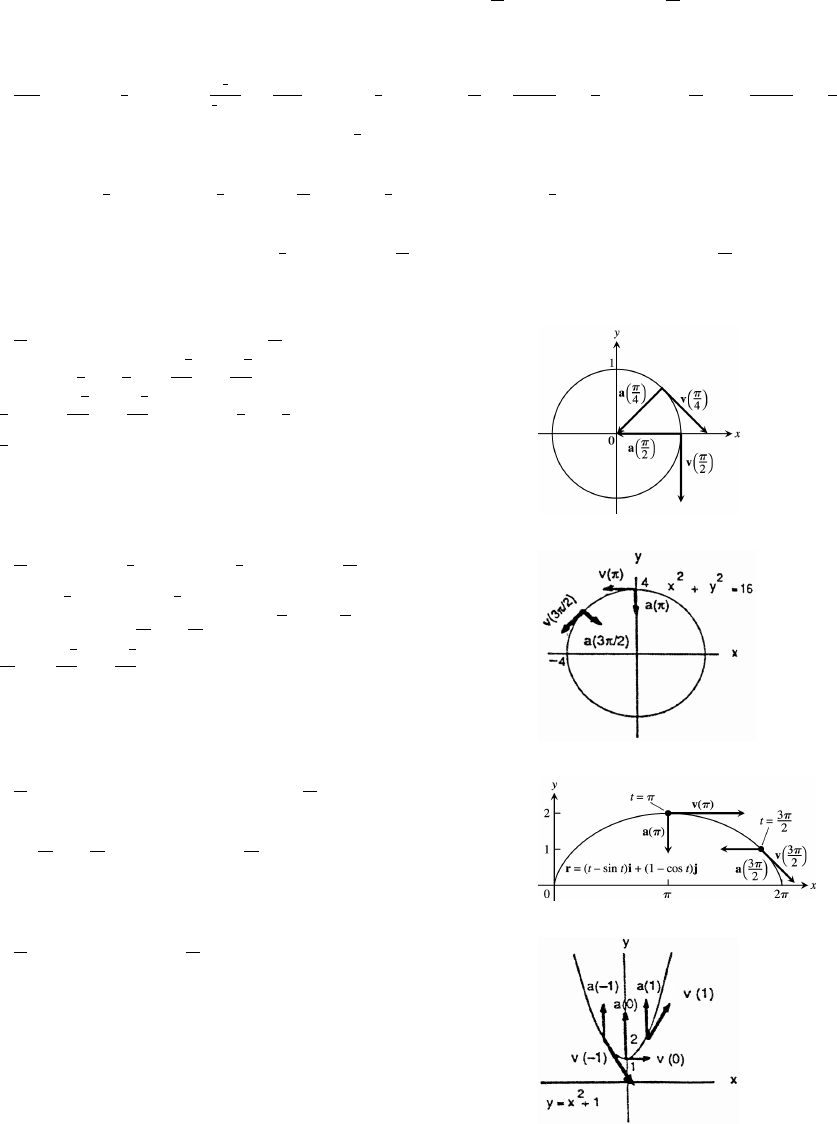
CHAPTER 13 VECTOR-VALUED FUNCTIONS
AND MOTION IN SPACE
13.1 CURVES IN SPACE AND THEIR TANGENTS
1. x t 1 and y t 1 y (x 1) 1 x 2x; 2t 2 2 and 2œ œÊœ œ œ œ Êœ œ Êœ œ
###
vij a jvijaj
dd
dt dt
rv
at t 1œ
2. x and y x y 1; œœÊœœÊœœœÊœœ
t1 11d11d22
t1 t 1y x dt t dt t
1t1 t1
1
y
122 33
y
vija ij
rv
ab ab
4 4 and 16 16 at tÊ œ œ œvija i j
"
#
3. x e and y e y x ; e e e e 3 4 and 3 8 at t ln 3œ œ Êœ œ œ Êœ Êœ œ œ
t2t t2tt2t
22d4 8
99dt9 9
#vijaijvijaij
r
4. x cos 2t and y 3 sin 2t x y 1; ( 2 sin 2t) (6 cos 2t) œœÊœœœÊœ
##
"
9dt dt
dd
vija
rv
( 4 cos 2t) ( 12 sin 2t) 6 and 4 at t 0œ Ê œ œ œijvjai
5. (cos t) (sin t) and (sin t) (cos t)vija ijœœ œœ
dd
dt dt
rv
for t , andÊœ œ
11
44
22
vij
ˆ‰ ÈÈ
##
; for t , andaijvj
ˆ‰ ˆ‰
111
4
22
œ œ œ
ÈÈ
## ##
ai
ˆ‰
1
#œ
6. 2 sin 2 cos and vijaœœ œ
dttd
dt dt
rv
ˆ‰ˆ‰
##
cos sin for t , ( ) 2 andœ Ê œ œ
ˆ‰ˆ‰
tt
##
ij vi11
() ; for t , 2 2 andaj v ij1œ œ œ
3311
##
ˆ‰ ÈÈ
aij
ˆ‰
322
1
###
œ
ÈÈ
7. (1 cos t) (sin t) and vijaœœ œ
dd
dt dt
rv
(sin t) (cos t) for t , ( ) 2 and ( ) ;œ Êœ œ œij viaj11 1
for t , and œœ œ
33 311 1
## #
vija i
ˆ‰ ˆ‰
8. 2t and 2 for t 1,vija jœœ œœ Ê œ
dd
dt dt
rv
( 1) 2 and ( 1) 2 ; for t 0, (0) andvija j viœ œ œ œ
(0) 2 ; for t 1, (1) 2 and (1) 2aj vijajœœœ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

760 Chapter 13 Vector-Valued Functions and Motion in Space
9. (t 1) t 1 2t 2t 2 2 ; Speed: (1) 1 (2(1)) 2 3;ri jkvijka j vœ Ê œ œ Ê œ œ œ œab kk
È
####
dd
dt dt
rr
Direction: (1) 3
vijk
v
(1) 2(1) 2
(1) 3 3 3 3 3 3 3
22 22
kk
œ œ Ê œ
""
ijkv ijk
ˆ‰
10. (1 t) t 2t ; Speed: (1)rijkvijka jk vœ Êœœ Êœ œ
tt d 2t d2
222
3dt dt
ÈÈÈ
rr
#kk
1 (1 ) 2; Direction: (1)œ œ œ œÊ
ÊŠ‹
###
#
## #
"""
2(1) (1)
2 2
(1)
(1 )
È È
kk
v
v
ijk
2(1)
2ijkv
2œ
Š‹
"""
##
ijk
È2
11. (2 cos t) (3 sin t) 4t ( 2 sin t) (3 cos t) 4 ( 2 cos t) (3 sin t) ;rijkv ijka ijœÊœœÊœœ
dd
dt dt
rr
Speed: 2 sin 3 cos 4 2 5; Direction:
¸¸ˆ ‰ˆ ‰ˆ‰ ÉÈ
v111
##
##
#
œ œ
2
v
v
ˆ‰
¸¸ˆ‰
sin cos 2 5œ œ Ê œ
Š‹Š‹ Š ‹
ˆ‰ È
234 2 2
55555 55###
## #
""
ÈÈÈÈÈ ÈÈ
11 1
ijkikv ik
12. (sec t) (tan t) t (sec t tan t) sec t rijkv i jkaœÊœœ Êœ
4d 4d
3dt 3dt
rr
ab
#
sec t tan t sec t 2 sec t tan t ; Speed: sec tan sec 2;œ œ œabab
¸¸ˆ ‰ˆ‰ˆ‰ˆ‰ É
#$ # ##
##
ijv
1111
66663
4
Direction: 2
vijk
v
ˆ‰ ˆ ‰
¸¸ˆ‰
66663
6
4
œ œ Ê œ
sec tan sec
#
""
ˆ‰
333 6 333
22 22
ijkv ijk
ˆ‰ ˆ ‰
1
13. (2 ln (t 1)) t 2t t 2 ;rijkvijka ijkœÊœœ Êœœ
#
td2 d2
2dtt1 dt(t1)
rr
ˆ‰ ’“
Speed: (1) (2(1)) 1 6; Direction: kkɈ‰ È
vœœ œ
2
11 (1)
(1) 2(1) (1)
6
###
v
v
ijk
kk Š‹
È
2
1
(1) 6œ Ê œ
"""
ÈÈÈ ÈÈÈ
666 666
21 2
ijkv ijk
ÈŠ‹
14. e (2 cos 3t) (2 sin 3t) e (6 sin 3t) (6 cos 3t) ri j kv i j kaœ Êœœ Êœab a b
tt
dd
dt dt
rr
e (18 cos 3t) (18 sin 3t) ; Speed: (0) e [ 6 sin 3(0)] [6 cos 3(0)] 37;œ œ œab k k a b
ÉÈ
!##
#
tijkv
Direction: (0) 37
v
v
ij k
(0)
(0)
e 6 sin 3(0) 6 cos 3(0)
37 37 37 37 37
66
kk ab ÈÈÈ ÈÈ
œ œ Êœ
""
ikv ik
ÈŠ‹
15. 3 3 2t and 2 (0) 3 3 and (0) 2 (0) 3 3 0 12 andvi j k ak v i ja k vœ œ Ê œ œ Ê œ œ
ÈÈ È
kkÊŠ‹ È
##
#
(0) 2 2; (0) (0) 0 cos 0 kkÈ
avaœ œ œÊ œÊœ
##
†))
1
16. 32t and 32 (0) and (0) 32 (0)vi ja jv ija jvœ œÊ œ œÊ œ
ÈÈ ÈÈ È È
22 22 2 2
## ## # #
##
Š ‹ Š‹Š‹
kkÊ
1 and (0) ( 32) 32; (0) (0) ( 32) 16 2 cos œ œ œ œ œ Ê œ œ Ê œkkÈŠ‹ È
ava
###
†ÈÈÈ
21622
1(32) 4
3
))
1
17. t t 1 and (0) andvij ka i j kvjœ œ Êœ
ˆ‰ˆ‰ ab ’“’“’ “
2t 1 2t 2 2t
t1 t1 t1 t1 t1
#"Î# "
ab ab ab
(0) 2 (0) 1 and (0) 2 1 5; (0) (0) 0 cos 0 aikv a vaœÊ œ œ œ œÊ œÊœkk kkÈÈ
## †))
1
2
18. (1 t) (1 t) and (1 t) (1 t) (0) andvijka i jvijkœ œ Ê œ
22 22
33 33 3 333
"Î# "Î# "Î# "Î#
"" " "
(0) (0) 1 and (0) ; (0) (0)aijv a vaœ Ê œ œ œ œ œ
"" " " "
##
###
33 3 3 3 3 3 3 99
22 22
2
kk kk
ÉÉ
ˆ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰ Ȇ
0 cos 0 œÊ œÊœ))
1
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 13.1 Curves in Space and Their Tangents 761
19. (t) (sin t) t cos t e (t) (cos t) (2t sin t) e ; t 0 (t ) andr i jk v i jk v ikœÊœ œÊœab
#!
tt
0
(t ) P (0 1 1) x 0 t t, y 1, and z 1 t are parametric equations of the tangent liner0œœßßÊœœ œ œ
!
20. (t) t 2t 1 t (t) 2t 2 3t ; t 2 2 4 2 12 andri jkv ijk v ijkœ Ê œ œÊ œ
23 2
ab !ab
(t ) P 4 3 8 x 4 4t, y 3 2t, and z 8 12t are parametric equations of the tangent liner0œœßßÊœ œ œ
!ab
21. (t) ln t t ln t (t) ln t 1 ; t 1 1 andrijkvij k vijkœ Êœ œÊœab ab a b ab
t1 1 3 1
t2 t 3
t2
!
ab
2
(t ) P 0 0 0 x 0 t t, y 0 t t, and z 0 t t are parametric equations of the tangent liner011
33
œ œ ßß Ê œ œ œ œ œ œ
!ab
22. (t) (cos t) sin t (sin 2t) (t) ( sin t) (cos t) (2 cos 2t) ; t (t ) 2 andrijkv ij k vikœ Êœ œÊœab !#
10
(t ) P (0 1 0) x 0 t t, y 1, and z 0 2t 2t are parametric equations of the tangent liner0œœßßÊœœœ œœ
!
23. (a) (t) (sin t) (cos t) (t) (cos t) (sin t) ;vija ijœ Ê œ
(i) (t) ( sin t) (cos t) 1 constant speed;kkÈ
vœ œÊ
##
(ii) (sin t)(cos t) (cos t)(sin t) 0 yes, orthogonal;va†œœÊ
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
(b) (t) (2 sin 2t) (2 cos 2t) (t) (4 cos 2t) (4 sin 2t) ;vija ijœ Ê œ
(i) (t) 4 sin 2t 4 cos 2t 2 constant speed;kkÈ
vœœÊ
##
(ii) 8 sin 2t cos 2t 8 cos 2t sin 2t 0 yes, orthogonal;va†œœÊ
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
(c) (t) sin t cos t (t) cos t sin t ;vija ijœ Ê œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11
## ##
(i) (t) sin t cos t 1 constant speed;kkɈ‰ ˆ‰
vœœÊ
##
##
11
(ii) sin t cos t cos t sin t 0 yes, orthogonal;va†œ œÊ
ˆ‰ˆ‰ ˆ‰ˆ‰
11 11
## ##
(iii) counterclockwise movement;
(iv) no, (0) 0 instead of 0rij ijœ
(d) (t) (sin t) (cos t) (t) (cos t) (sin t) ;vija ijœ Ê œ
(i) (t) ( sin t) ( cos t) 1 constant speed;kkÈ
vœ œÊ
##
(ii) (sin t)(cos t) (cos t)(sin t) 0 yes, orthogonal;va†œœÊ
(iii) clockwise movement;
(iv) yes, (0) 0rijœ
(e) (t) (2t sin t) (2t cos t) (t) (2 sin t 2t cos t) (2 cos t 2t sin t) ;vija i jœ Ê œ
(i) (t) (2t cos t) 4t sin t cos t 2 t 2t, t 0
2t sin t
kk c d a b kk
Éab È
vœœœœ
#####
variable speed;Ê
(ii) 4 t sin t t sin t cos t 4 t cos t t cos t sin t 4t 0 in general not orthogonal in general;va†œ œÁ Êabab
## ##
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
24. Let 2 2 denote the position vector of the point 2, 2, 1 and let, and .pijk u i j v i j kœ œ œab "" """
ÈÈ ÈÈÈ
22 333
Then (t) (cos t) (sin t) . Note that (2 2 1) is a point on the plane and 2 is normal torp u v nijkœ ßß œ
the plane. Moreover, and are orthogonal unit vectors with 0 and are parallel to theuv unvn uv††œœÊ
plane. Therefore, (t) identifies a point that lies in the plane for each t. Also, for each t, (cos t) (sin t)ruv
is a unit vector. Starting at the point 2 , 2 , 1 the vector t traces out a circle of radius 1 and
Š‹
ab
11
22
ÈÈ r
center (2 2 1) in the plane x y 2z 2.ßß œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
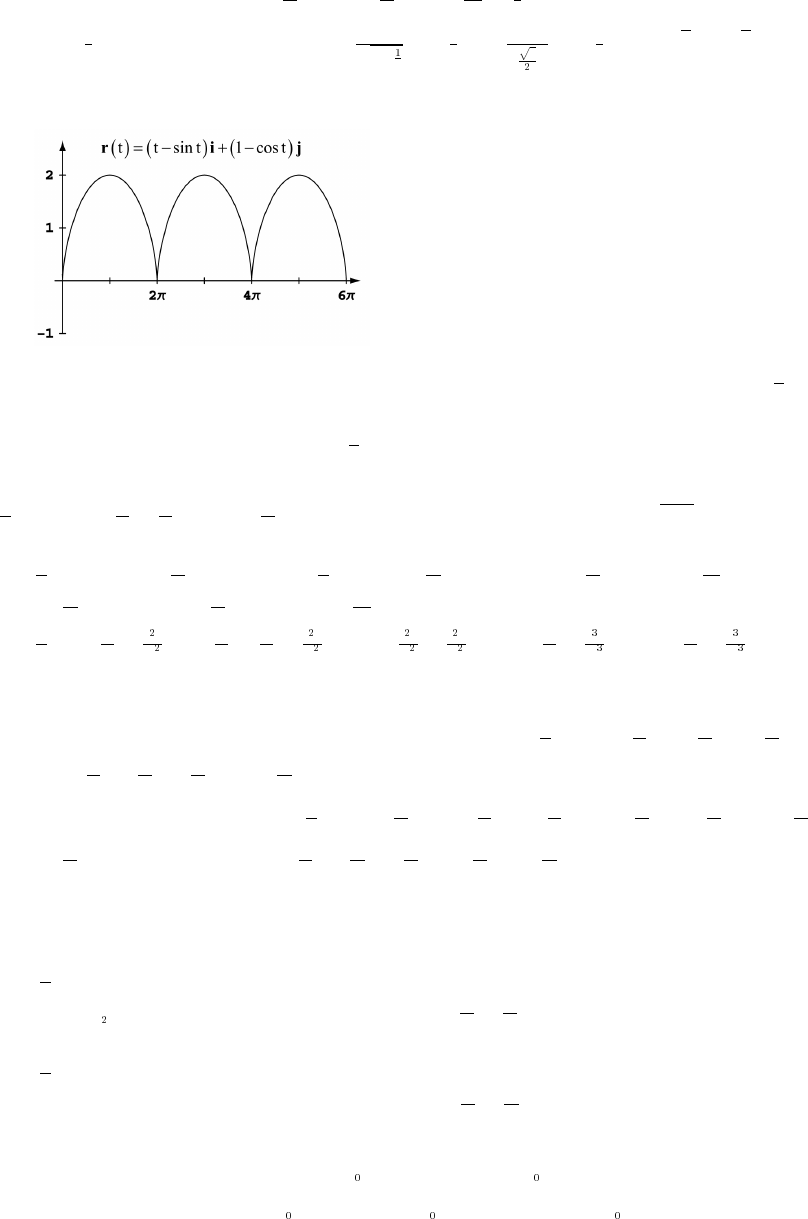
762 Chapter 13 Vector-Valued Functions and Motion in Space
25. The velocity vector is tangent to the graph of y 2x at the point ( ), has length 5, and a positive
#œ#ß# i
component. Now, y 2x 2y 2 the tangent vector lies in the direction of the
#
Ð#ß#Ñ ##
"
œÊ œÊ œœÊ
dy dy
dx dx 2
2
¹†
vector the velocity vector is 2 5 5ij v ij ij i jÊ œ œ œ
"""
###
55
1
Ɍ
45
ˆ‰ ˆ‰
ÈÈ
26. (a)
(b) (1 cos t) (sin t) and (sin t) (cos t) ; (1 cos t) sin t 2 2 cos t is at a maxvijaijv vœ œ œ œ Êkk kk
##
##
when cos t 1 t , 3 , 5 , etc., and at these values of t, 4 max 4 2; is at a minœ Ê œ œ Ê œ œ111 kk kk kk
È
vvv
##
when cos t 1 t 0, 2 , 4 , etc., and at these values of t, 0 min 0; sin t cos t 1œÊœ œÊ œ œ œ11 kk kk kkvva
##
##
for every t max min 1 1Êœœœkk kk È
aa
27. ( ) 2 2 0 0 is a constant is constant
dddd
dt dt dt dt
rr r r r rr r rr†† † † † † †œœ œœÊ Êœ
rr r kk È
28. (a) ( ) ( ) ( ) ( )
dd dd dd
dt dt dt dt dt dt
uvw vw u vw vw u wv††† ††‚œ ‚ ‚œ ‚ ‚‚
uuvw
ˆ‰
()œ‚‚‚
ddd
dt dt dt
uvw
†††vw u wuv
(b) , since ( ) 0
d dd d dd d d dd dd
dt dt dt dt dt dt dt dt dt dt dt dt
’ “Š‹Š‹Š‹Š‹Š‹
rrrrAAB††††† †
rr rrr rr rr rr
‚ œ ‚ ‚ ‚œ ‚ ‚œ
and ( ) 0 for any vectors and AB B A B†‚œ
29. (a) f(t) g(t) h(t) c cf(t) cg(t) ch(t) (c ) c c c uijku i j k u i j kœ Êœ Ê œ
ddf dh
dt dt dt dt
dg
cc œœ
Š‹
df dh d
dt dt dt dt
dg
ijk u
(b) f(t) g(t) h(t) ( ) f(t) g(t) h(t)ff f f f f f fuijk u i j kœÊœ
ddf dh
dt dt dt dt dt dt dt
dddgd
’“’“’“
ff f
[f(t) g(t) h(t) ]œœ
ddgd
dt dt dt dt dt dt
df dh d
ff
ijk ijk uff
’“
u
30. Let f (t) f (t) f (t) and g (t) g (t) g (t) . Thenuijkv ijkœ œ
"#$ " # $
uv i j kœ [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]
"" ## $$
( ) [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]Ê œ
d
dt uv i j k
ww ww ww
"" ## $$
[f (t) f (t) f (t) ] [g (t) g (t) g (t) ] ;œ œ
www w w w
"$"#$
ijk i j k
dd
dt dt
uv
[f (t) g (t)] [f (t) g (t)] [f (t) g (t)]uv i j kœ
"" ## $$
( ) [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]Ê œ
d
dt uv i j k
ww ww ww
"" ## $$
[f (t) f (t) f (t) ] [g (t) g (t) g (t) ]œ œ
www w w w
"#$ " # $
ijk i j k
dd
dt dt
uv
31. Suppose is continuous at t t . Then lim (t) (t ) lim [f(t) g(t) h(t) ]rrrijkœœÍ
!!
tt ttÄÄ
f(t ) g(t ) h(t ) lim f(t) f(t ), lim g(t) g(t ), and lim h(t) h(t ) f, g, and h areœ œ œ œÍ
!!! ! ! !
ijk Ítt tt ttÄÄ Ä
continuous at t t .œ!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 13.1 Curves in Space and Their Tangents 763
32. lim [ (t) (t)] lim f(t) f(t) f(t)
g(t) g(t) g(t)
lim f (t) lim f (t)
tt tt tt tt
ÄÄ
ÄÄ
rr
ijk ijk
"# "#$
"#$
"#
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
lim f (t)
lim g (t) lim g (t) lim g (t)
tt
tt tt tt
Ä
ÄÄÄ
$
"#$
lim (t) lim (t)œ‚œ‚
tt ttÄÄ
rrAB
"#
33. (t ) exists f (t ) g (t ) h (t ) exists f (t ), g (t ), h (t ) all exist f, g, and h are continuous atrijk
w w w w www
! ! ! ! !!!
Ê Ê Ê
t t (t) is continuous at t tœÊ œ
!!
r
34. a b c with a, b, c real constants 0 0 0uCijk i j k ijk0œœ Ê œ œ œ
ddadbdc
dt dt dt dt
u
35-38. Example CAS commands:
:Maple
> with( plots );
r := t -> [sin(t)-t*cos(t),cos(t)+t*sin(t),t^2];
t0 := 3*Pi/2;
lo := 0;
hi := 6*Pi;
P1 := spacecurve( r(t), t=lo..hi, axes=boxed, thickness=3 ):
display( P1, title="#35(a) (Section 13.1)" );
Dr := unapply( diff(r(t),t), t ); # (b)
Dr(t0); # (c)
q1 := expand( r(t0) + Dr(t0)*(t-t0) );
T := unapply( q1, t );
P2 := spacecurve( T(t), t=lo..hi, axes=boxed, thickness=3, color=black ):
display( [P1,P2], title="#35(d) (Section 13.1)" );
39-40. Example CAS commands:
:Maple
a := 'a'; b := 'b';
r := (a,b,t) -> [cos(a*t),sin(a*t),b*t];
Dr := unapply( diff(r(a,b,t),t), (a,b,t) );
t0 := 3*Pi/2;
q1 := expand( r(a,b,t0) + Dr(a,b,t0)*(t-t0) );
T := unapply( q1, (a,b,t) );
lo := 0;
hi := 4*Pi;
P := NULL:
for a in [ 1, 2, 4, 6 ] do
P1 := spacecurve( r(a,1,t), t=lo..hi, thickness=3 ):
P2 := spacecurve( T(a,1,t), t=lo..hi, thickness=3, color=black ):
P := P, display( [P1,P2], axes=boxed, title=sprintf("#39 (Section 13.1)\n a=%a",a) );
end do:
display( [P], insequence=true );
35-40. Example CAS commands:
: (assigned functions, parameters, and intervals will vary)Mathematica
The x-y-z components for the curve are entered as a list of functions of t. The unit vectors , , are not inserted.ijk
If a graph is too small, highlight it and drag out a corner or side to make it larger.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

764 Chapter 13 Vector-Valued Functions and Motion in Space
Only the components of r[t] and values for t0, tmin, and tmax require alteration for each problem.
Clear[r, v, t, x, y, z]
r[t_]={ Sin[t] t Cos[t], Cos[t] t Sin[t], t^2}
t0= 3 / 2; tmin= 0; tmax= 6 ;11
ParametricPlot3D[Evaluate[r[t]], {t, tmin, tmax}, AxesLabel {x, y, z}];Ä
v[t_]= r'[t]
tanline[t_]= v[t0] t r[t0]
ParametricPlot3D[Evaluate[{r[t], tanline[t]}], {t, tmin, tmax}, AxesLabel {x, y, z}];Ä
For 39 and 40, the curve can be defined as a function of t, a, and b. Leave a space between a and t and b and t.
Clear[r, v, t, x, y, z, a, b]
r[t_,a_,b_]:={Cos[a t], Sin[a t], b t}
t0= 3 / 2; tmin= 0; tmax= 4 ;11
v[t_,a_,b_]= D[r[t, a, b], t]
tanline[t_,a_,b_]=v[t0, a, b] t r[t0, a, b]
pa1=ParametricPlot3D[Evaluate[{r[t, 1, 1], tanline[t, 1, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
pa2=ParametricPlot3D[Evaluate[{r[t, 2, 1], tanline[t, 2, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
pa4=ParametricPlot3D[Evaluate[{r[t, 4, 1], tanline[t, 4, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
pa6=ParametricPlot3D[Evaluate[{r[t, 6, 1], tanline[t, 6, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
Show[GraphicsRow[{pa1, pa2, pa4, pa6}]]
13.2 INTEGRALS OF VECTOR FUNCTIONS; PROJECTILE MOTION
1. t 7 (t 1) dt [7t] t 7
'0
1cd
’“ ’ “
$"
""
!!
!"
#
ij k i j k ij k œ œ
tt 3
424
2. (6 6t) 3 t dt 6t 3t 2t 4t 3 4 2 2 2
'1
2‘‘
Ȉ‰ cd cd Š‹
È
œ œ ijk i j ki jk
4
t# $Î# "
#
""
#
"
#
3. (sin t) (1 cos t) sec t dt cos t t sin t tan t 2
'cdcdcdcdab Š‹
ijk i jkjk œ œ
#Î% Î% Î%
Î% Î% Î%
#
111
111
122
È
4. sec t tan t tan t 2 sin t cos t dt [ sec t tan t tan t sin 2t ] dt
''
0 0
3 3
cdabababababa bij k ij k œ
sec t ln cos t cos 2t (ln 2)œ œcd c dab ‘
111
Î$ Î$
!!
"
#
Î$
!
ijkijk
3
4
5. dt ln t ln (5 t) ln t (ln 4) (ln 4) (ln 2)
'1
4ˆ‰ ‘
cd c d
"" " "
# #
%%
""
%
"
t5t t
ijk i j k i j k œœ œ
6. dt 2 sin t 3 tan t
'0
1Š‹ ’“
cd
È
2
1t
33
1t 4
ÈÈÈ
" "
"
!
"
!
ik i kikœ œ11
7. te e dt e e t
'0
1Š‹’“
cd cd
tt t t
1e1e1
22e
22
ijk i j k i ik œ œ
"
!
"
!!
"
8. te e ln t dt te e e t ln t t
'1
ln 3 ln 3 ln 3
11 1
ln 3
abcdcdcd
tt tt t
ij k i j k œ
3 ln3 1 3 e ln3 ln ln3 1 1œ ababa bababii k
9. cos t sin 2t sin t dt cos t sin 2t cos 2t dt
''
00
22
cdababababab ‘ˆ‰
ijk ij k œ œ
211
22
sin t cos t t sin 2tœ œcd ‘ ‘
111
1
Î
!
ÎÎ
!!
2111
224 4
22
ij kijk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 13.2 Integrals of Vector Functions; Projectile Motion 765
10. sec t tan t t sin t dt sec t sec t 1 t sin t dt
''
00
/4 /4
cdc dababab aba babij k i j kœ
22
ln sec t tan t tan t t t cos t sin t ln 1 2 1œ œcdcdcdab Š‹ Š ‹
Ȉ‰
/4 /4 /4
!! !
ij k ij k
11
442 2
1
ÈÈ
11. ( t t t ) dt ; (0) 0 0 0 2 3 2 3r ijk i j kCr ijkCijk Cijkœ œ œ Ê œ
'ttt
### œ
123Ê œ rijk
Š‹Š‹Š‹
ttt
###
12. (180t) 180t 16t dt 90t 90t t ; (0) 90(0) 90(0) (0)r i j i jCr i jCœœœ
'cdab ˆ‰ ‘
###$ ##$
16 16
33
100 100 90t 90t t 100œÊœ ÊœjC j r i j
##$
ˆ‰
16
3
13. (t 1) e dt (t 1) e ln (t 1) ;rijkijkCœ œ
'‘ˆ‰ˆ‰
3
t1#
"Î# $Î#
"
tt
(0) (0 1) e ln (0 1) rijkCkCijkœ œÊ œ
$Î#
(t 1) 1 1 e [1 ln (t 1)]ʜ rijk
‘
ab
$Î# t
14. t 4t t 2t dt 2t ; (0) 2(0)rijk ijkCr ijkCœ œ œ
'cdab Š‹ ’ “
$## #
tt2t 0 0
423 4 23
2(0)
2t 1 1œ Ê œ Ê œ ij C ij r i j k
Š‹Š‹
tt2t
43
#
#
15. ( 32 ) dt 32t ; (0) 8 8 32(0) 8 8 8 8
dd
dt dt
rr
œ œ œÊ œÊ œ
'kkC ij kCijCij
"""
8 8 32t ; (8 8 32t ) dt 8t 8t 16t ; (0) 100Ê œ œ œ œ
d
dt
rij kr ij k i j kCr k
'##
8(0) 8(0) 16(0) 100 100 8t 8t 100 16tÊ œÊœÊœi j kC kC krij k
# #
## ab
16. ( ) dt (t t t ) ; (0) (0 0 0 )
dd
dt dt
rr
œ œ œÊ œÊ œ
'ijk i j k C 0 i j k C 0 C 0
"""
(t t t ) ; (t t t ) dt ; (0) 10 10 10Ê œ œ œ œ
dttt
dt
rijkr ijk i j k Cr i j k
'Š‹
### #
10 10 10 10 10 10Ê œ Ê œ
Š‹
000
### ##
ijkC ijkC ijk
10 10 10Ê œ rijk
Š‹Š‹Š‹
ttt
###
17. 3 (t) 3t t t ; the particle travels in the direction of the vector
d
dt
vœœ Ê œ aijk v ijkC
"
(4 1) (1 2) (4 3) 3 (since it travels in a straight line), and at time t 0 it has speed œ œijkijk
2 (0) (3 ) (t) 3t t tÊœ œÊœœ vijkCv ijk
2d622
911 dt 11 11 11
ÈÈÈÈ
"rŠ ‹Š‹Š‹
(t) t t t t t t ; (0) 2 3Êœ œœrijkCrijkC
Š‹Š‹Š‹
36 2 2
11 11 11
###
###
"" ##
ÈÈÈ
(t) t t1 t t2 t t3Êœrijk
Š‹Š‹Š‹
36 2 2
11 11 11
###
###
""
ÈÈÈ
tt(3 )(23)œ
Š‹
"
#
#2
11
Èijk i j k
18. 2 (t) 2t t t ; the particle travels in the direction of the vector
d
dt
vœœ Ê œ aijk v ijkC
"
(3 1) (0 ( 1)) (3 2) 2 (since it travels in a straight line), and at time t 0 it has speed 2 œ œijkijk
(0) (2 ) (t) 2t t tÊœ œÊœœ vijkCvijk
2d422
411 dt 666
ÈÈÈÈ
"rŠ ‹Š‹Š‹
(t) t t t t t t ; (0) 2Ê œ œ œrijkCrijkC
Š‹Š‹Š‹
###
""
## ##
422
666
ÈÈÈ
(t) t t1 t t1 t t2 t t(2 )( 2)Êœ œ rijkijkijk
Š‹Š‹Š‹Š‹
### #
"" "
## #
422 2
666 6
ÈÈÈ È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

766 Chapter 13 Vector-Valued Functions and Motion in Space
19. x (v cos )t (21 km) (840 m/s)(cos 60°)t t 50 secondsœÊ œ Êœ œ
!!ˆ‰
1000 m
1 km (840 m/s)(cos 60°)
21,000 m
20. R sin 2 and maximum R occurs when 45° 24.5 km (sin 90°)œœÊœ
v v
g9.8 m/s
!!
Š‹
v (9.8)(24,500) m /s 490 m/sÊœ œ
!##
È
21. (a) t 72.2 seconds; R sin 2 (sin 90°) 25,510.2 mœœ ¸ œ œ ¸
2v sin
g 9.8 m/s g 9.8 m/s
2(500 m/s)(sin 45°) (500 m/s)
v
!!
(b) x (v cos )t 5000 m (500 m/s)(cos 45°)t t 14.14 s; thus,œÊœ Êœ ¸
!!5000 m
(500 m/s)(cos 45°)
y (v sin )t gt y (500 m/s)(sin 45°)(14.14 s) 9.8 m/s (14.14 s) 4020 mœÊ¸ ¸
!""
##
###
!ab
(c) y 6378 m
max œœ ¸
(v sin ) ((500 m/s)(sin 45°))
2g 2 9.8 m/s
!ab
22. y y (v sin )t gt y 32 ft (32 ft/sec)(sin 30°)t 32 ft/sec t y 32 16t 16t ;œ Êœ Êœ
!! ""
##
####
!ab
the ball hits the ground when y 0 0 32 16t 16t t 1 or t 2 t 2 sec since t 0; thus,œÊœ Êœ œÊœ
#
x (v cos ) t x (32 ft/sec)(cos 30°)t 32 (2) 55.4 ftœÊœ œ ¸
!#
!Š‹
È3
23. (a) R sin 2 10 m (sin 90°) v 98 m s v 9.9 m/s;œÊœ ʜʸ
vv
g 9.8 m/s
!Š‹ ###
!!
(b) 6m (sin 2 ) sin 2 0.59999 2 36.87° or 143.12° 18.4° or 71.6°¸Ê¸Ê¸ ʸ
(9.9 m/s)
9.8 m/s !! ! !
24. v 5 10 m/s and x 40 cm 0.4 m; thus x (v cos )t 0.4m 5 10 m/s (cos 0°)t
!!
' '
œ‚ œ œ œ Ê œ ‚!ab
t 0.08 10 s 8 10 s; also, y y (v sin )t gtÊœ ‚ œ‚ œ
' ) #
!! "
#
!
y 5 10 m/s (sin 0°) 8 10 s 9.8 m/s 8 10 s 3.136 10 m orÊœ‚ ‚ ‚ œ ‚abababab
' ) # ) "%
"
#
#
3.136 10 cm. Therefore, it drops 3.136 10 cm.‚ ‚
"# "#
25. R sin 2 16,000 m sin 2 sin 2 0.98 2 78.5° or 2 101.5° 39.3°œÊœ ʜʸ ¸Ê¸
v
g 9.8 m/s
(400 m/s)
!!!!!!
or 50.7°
26. (a) R sin 2 sin 2 4 sin or 4 times the original range.œœœ
(2v )
gg g
4v v
!! !
Š‹
(b) Now, let the initial range be R sin 2 . Then we want the factor p so that pv will double the rangeœv
g!!
sin 2 2 sin 2 p 2 p 2 or about 141%. The same percentage will approximatelyʜ ʜʜ
(pv )
gg
v
!!
Š‹ È
#
double the height: p 2 p 2.
ababpv sin 2 v sin
2g 2g
00
22
!!
œÊœÊœ
#È
27. The projectile reaches its maximum height when its vertical component of velocity is zero v sin gt 0Êœ œ
dy
dt 0!
t y v sin g . To find the flight timeʜʜ œœ
vsin vsin vsin
g g g g 2g 2g
max 0
2vsin vsin vsin
000
00 0
22 2
!!!
!! !
ab
Š‹Š‹
!"
#ababab
we find the time when the projectile lands: v sin t g t 0 t v sin g t 0 t 0 or t .ab ˆ‰
00
22v sin
g
!!œÊ œÊœ œ
""
##
0!
t 0 is the time when the projectile is fired, so t is the time when the projectile strikes the ground. The range isœœ
2v sin
g
0!
the value of the horizontal component when t R x v cos 2 sin cos sin 2 .œÊœœ œ œ
2v sin 2v sin
gggg
0vv
0000
22
!!
ab a b
Š‹
!!!!
The range is largest when sin 2 1 45 .!!œÊ œ ‰
28. When marble A is located R units downrange, we have x (v cos )t R (v cos )t t . AtœÊœÊœ
!!
!!
R
v cos !
that time the height of marble A is y y (v sin )t gt (v sin ) gœ œ
!! !
""
##
##
!!
Š‹Š‹
RR
v cos v cos
!!
y R tan g . The height of marble B at the same time t seconds isÊœ œ!"
#Š‹
RR
v cos v cos
!!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
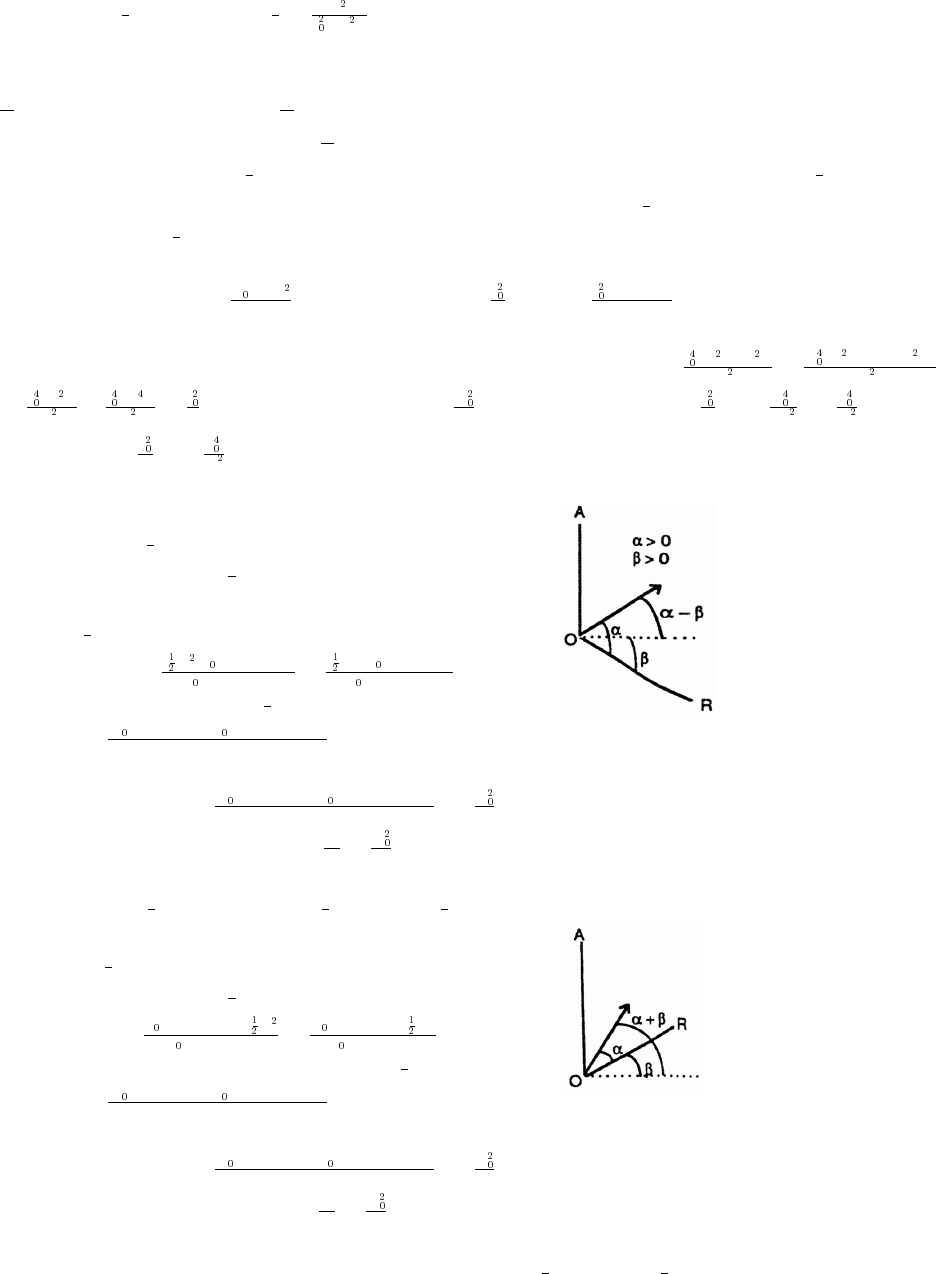
Section 13.2 Integrals of Vector Functions; Projectile Motion 767
h R tan gt R tan g . Since the heights are the same, the marbles collide regardlessœœ!!
""
##
#Š‹
R
v cos !
of the initial velocity v .
!
29. ( g ) dt gt and (0) (v cos ) (v sin ) g(0) (v cos ) (v sin )
dd
dt dt
rr
œ œ œ Ê œ
'jjC i j jC i j
"!! "!!
!! !!
(v cos ) (v sin ) (v cos ) (v sin gt) ; [(v cos ) (v sin gt) ] dtÊœ Êœ œ Cij i jr i j
"! ! ! ! ! !
!! !! !!
d
dt
r'
(v t cos ) v t sin gt and (0) x y [v (0) cos ] v (0) sin g(0)œœÊ
!! #!!! ! #
" "
# #
# #
!! ! !ijCriji jC
ˆ‰ ‘
x y x y (x v t cos ) y v t sin gt x x v t cos andœ Ê œ Êœ Êœ
!! #!! !! !! !!
"
#
#
ijC ijr i j!! !
ˆ‰
y y v t sin gtœ
!! "
#
#
!
30. The maximum height is y and this occurs for x sin 2 . These equations describeœœœ
(v sin )
ggg
v v sin cos
!!!
##
!
parametrically the points on a curve in the xy-plane associated with the maximum heights on the parabolic trajectories in
terms of the parameter (launch angle) . Eliminating the parameter , we have x!!
#
œœ
v sin cos
gg
v sin 1 sin
!! !!
ˆ‰
ab
(2y) (2y) x 4y y 0 x 4 y yœœÊ œÊœ
v sin v sin v 2v v v v
g g g g 2g 16g 4g
!! ### # #
Š‹ ’ “Š‹
x 4 y , where x 0.Ê œ
##
Š‹
vv
4g 4g
31. (a) At the time t when the projectile hits the line OR we
have tan ; x [v cos ( )]t and"!"œœ
y
x!
y [v sin ( )]t gt 0 since R isœ
!"
#
#
!"
below level ground. Therefore let
y gt [v sin ( )]t 0kkœ
"
#
#!!"
so that tan "œœ
‘‘
gt (v sin ( ))t gt v sin ( )
[v cos ( )]t v cos ( )
!" !"
!" !"
v cos ( ) tan gt v sin ( )ʜ
!!
"
#
!" " !"
t , which is the timeʜ
2v sin ( ) 2v cos ( ) tan
g
!" !" "
when the projectile hits the downhill slope. Therefore,
x [v cos ( )] cos ( ) tan sin ( ) cos ( ) . If x isœ œ
! #
!" !" " !" !"
’“
cd
2v sin ( ) 2v cos ( ) tan
gg
2v
!" !" "
maximized, then OR is maximized: [ sin 2( ) tan cos 2( )] 0
dx
dg
2v
!œ œ!" " !"
sin 2( ) tan cos 2( ) 0 tan cot 2( ) 2( ) 90°Ê œÊ œ Ê œ !" " !" " !" !" "
(90° ) (90° ) of AOR.Êœ Êœ œ n!" " ! "
"""
###
(b) At the time t when the projectile hits OR we have
tan ; x [v cos ( )]t and"!"œœ
y
x!
y [v sin ( )]t gtœ
!"
#
#
!"
tan Êœ œ"cd‘
v sin( )t gt v sin( ) gt
[v cos ( )]t v cos ( )
!" !"
!" !"
v cos( ) tan v sin( ) gtʜ
!!
"
#
!" " !"
t , which is the timeʜ
2v sin ( ) 2v cos ( ) tan
g
!" !" "
when the projectile hits the uphill slope. Therefore,
x [v cos ( )] sin ( ) cos ( ) cos ( ) tan . If x isœ œ
! #
!" !" !" !" "
’“
cd
2v sin ( ) 2v cos ( ) tan
gg
2v
!" !" "
maximized, then OR is maximized: [cos 2( ) sin 2( ) tan ] 0
dx
dg
2v
!œœ!" !" "
cos 2( ) sin 2( ) tan 0 cot 2( ) tan cot 2( ) tan Ê œ Ê œ! Ê œ!" !" " !" " !" "
tan ( ) 2( ) 90° ( ) 90° (90° ) of AOR. Therefore v would bisectœÊ œœÊœ œ n"!" " "! "
""
## !
AOR for maximum range uphill.n
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

768 Chapter 13 Vector-Valued Functions and Motion in Space
32. v 116 ft/sec, 45°, and x (v cos )t
!!
œœœ!!
369 (116 cos 45°)t t 4.50 sec;Êœ ʸ
also y (v sin )t gtœ
!"
#
#
!
y (116 sin 45°)(4.50) (32)(4.50)Êœ
"
#
#
45.11 ft. It will take the ball 4.50 sec to travel¸
369 ft. At that time the ball will be 45.11 ft in
the air and will hit the green past the pin.
33. (a) (Assuming that "x" is zero at the point of impact:)
t x t y t ; where x t 35 cos 27 t and y t 4 35 sin 27 t 16t .rijab a b a b ab a b ab a bab abœ œ œ
‰‰2
(b) y 4 4 7.945 feet, which is reached at t 0.497 seconds.
max v sin 35sin 27
2g 64 g 32
vsin 35sin 27
œœ ¸ œœ¸
ab a b
022 0
!!
(c) For the time, solve y 4 35 sin 27 t 16t 0 for t, using the quadratic formulaœ œab
‰2
t 1.201 sec. Then the range is about x 1.201 35 cos 27 1.201 37.453 feet.œ¸ œ¸
35 sin 27 35 sin 27 256
32
‰
Éab
2aba bab
(d) For the time, solve y 4 35 sin 27 t 16t 7 for t, using the quadratic formulaœ œab
‰2
t 0.254 and 0.740 seconds. At those times the ball is aboutœ¸
35 sin 27 35 sin 27 192
32
Éab
2
x 0.254 35 cos 27 0.254 7.921 feet and x 0.740 35 cos 27 0.740 23.077 feet the impact point,aba bab aba babœ¸ œ¸
‰‰
or about 37.453 7.921 29.532 feet and 37.453 23.077 14.376 feet from the landing spot.¸ ¸
(e) Yes. It changes things because the ball won't clear the net (y 7.945).
max ¸
34. x x (v cos )t 0 (v cos 40°)t 0.766 v t and y y (v sin )t gt 6.5 (v sin 40°)t 16tœ œ ¸ œ œ
!! ! ! !! !
"
#
##
!!
6.5 0.643 v t 16t ; now the shot went 73.833 ft 73.833 0.766 v t t sec; the shot lands when y 0¸ Ê œ ʸ œ
! !
#96.383
v
0 6.5 (0.643)(96.383) 16 0 68.474 v 46.6 ft/sec, the shot's initialÊœ ʸ Ê ¸ ¸
Š‹ É
96.383
v 68.474
148,635 148,635
v
#
!
speed
35. Flight time 1 sec and the measure of the angle of elevation is about 64° (using a protractor) so that tœ œ 2v sin
g
!
1 v 17.80 ft/sec. Then y 4.00 ft and R sin 2 R sin 128°Êœ Ê ¸ œ ¸ œ Ê œ
2v sin 64°
32 2(32) g 32
max (17.80 sin 64°) (17.80)
v
!!
7.80 ft the engine traveled about 7.80 ft in 1 sec the engine velocity was about 7.80 ft/sec¸Ê Ê
36. (a) t x t y t ; where x t 145 cos 23 14 t and y t 2.5 145 sin 23 t 16t .rijab a b a b ab a b ab a bab abœ œ œ
‰‰2
(b) y 2.5 2.5 52.655 feet, which is reached at t 1.771 seconds.
max v sin 145sin 23
2g 64 g 32
vsin 145sin 23
œœ ¸ œœ ¸
ab a b
022 0
!!
(c) For the time, solve y 2.5 145 sin 23 t 16t 0 for t, using the quadratic formulaœ œab
‰2
t 3.585 sec. Then the range at t 3.585 is about x 145 cos 23 14 3.585œ¸ ¸œ
145 sin 23 145 sin 23 160
32
‰
Éab
2abab
428.311 feet.¸
(d) For the time, solve y 2.5 145 sin 23 t 16t 20 for t, using the quadratic formulaœ œab
‰2
t 0.342 and 3.199 seconds. At those times the ball is aboutœ¸
145 sin 23 145 sin 23 1120
32
Éab
2
x 0.342 145 cos 23 14 0.342 40.860 feet from home plate and x 3.199 145 cos 23 14 3.199aba bab aba babœ¸ œ
‰ ‰
382.195 feet from home plate.¸
(e) Yes. According to part (d), the ball is still 20 feet above the ground when it is 382 feet from home plate.
37. k g P t k and t g P t dt kt v t e e v t t dt
dd d1
dt dt dt v t
P t dt kt
2
2
rr r
œÊ œ œÊ œ Ê œ œ Ê œjQj Qab ab ab ab ab ab
''
'ab ab
ge e dt ge e , where g ; apply the initial condition:œ œ œ œ
kt kt kt kt
e
k1g
k1
'jjCCC
jC
‘
kt
vcos vsin vcos vsin
d
dt k k
t0 00 0 0
gg
r¹abab ab
ˆ‰
œœœÊœ!! ! !ijjCC i j
v e cos e v sin , dt
v e cos e v sin
Êœ œ
d
dt k k
00
kt kt
gg 00
kt kt
gg
kk
rˆ‰ˆ ‰ˆ‰ˆ‰ˆ ‰ˆ‰
!!
!!
ijr
ij
'cd
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 13.2 Integrals of Vector Functions; Projectile Motion 769
; apply the initial condition:
e cos v sin
œ
ˆ‰ ˆ‰
Š‹
v
kkkk
kt gt g
e02
0kt
!!ij
C
0 cos cos
r0 CC
ij ij
ab ˆ‰ˆ ‰ ˆ‰ˆ ‰
œœ Ê œ
v v sin v v sin
kkk kkk
gg
22
00 00
2 2
!!
!!
t
1e cos 1e sin 1kte
ʜ
rij
ab ˆ‰ˆ ‰ˆ‰ ˆ‰ ˆ ‰
vv
kkk
kt kt kt
g
00
2
!!
38. (a) t x t y t ; where x t 1 e cos 20 andrijababab ab a ba bab ab ˆ‰
œ œ
152
0.12
0.12t‰
y t 3 1 e sin 20 1 0.12t eab a ba b a b
ˆ‰ ˆ‰
œ
152 32
0.12 0.12
0.12t 0.12t‰
2
(b) Solve graphically using a calculator or CAS: At t 1.484 seconds the ball reaches a maximum height of about 40.435¸
feet.
(c) Use a graphing calculator or CAS to find that y 0 when the ball has traveled for 3.126 seconds. The range isœ¸
about x 3.126 1 e cos 20 372.311 feet.ab a b
ˆ‰ˆ ‰
œ ¸
152
0.12
0.12 3.126‰ab
(d) Use a graphing calculator or CAS to find that y 30 for t 0.689 and 2.305 seconds, at which times the ball is aboutœ¸
x 0.689 94.454 feet and x 2.305 287.621 feet from home plate.ab ab¸¸
(e) Yes, the batter has hit a home run since a graph of the trajectory shows that the ball is more than 14 feet above the
ground when it passes over the fence.
39. (a) k (t) dt [kf(t) kg(t) kh(t) ] dt [kf(t)] dt [kg(t)] dt [kh(t)] dt
'' ' ' '
aa a a a
bb b b b
rijk ijkœœ
k f(t) dt g(t) dt h(t) dt k (t) dtœœ
Œ
'' ' '
aa a a
bb b b
ij kr
(b) [ (t) (t)] dt f (t) g (t) h (t) f (t) g (t) h (t) dt
''
aa
bb
rr i j k i j k
"# " " " # # #
„œ „abcdcd
f (t) f (t) [g (t) g (t ] [h (t) h (t)] ) dtœ „ „ „
'a
babcd
"# "# "#
ijk
f (t) f (t) dt g (t) g (t) dt h (t) h (t) dtœ„„ „
'' '
aa a
bb b
cdcdcd
"# "# "#
ij k
f (t) dt f (t) dt g (t) dt g (t) dt h (t) dt h (t) dtœ„„ „
”•”•” •
'' '' ' '
aa aa a a
bb bb b b
"# "# " #
ii jj kk
(t) dt (t) dtœ„
''
aa
bb
rr
"#
(c) Let c c c . Then (t) dt c f(t) c g(t) c h(t) dtCijk Crœ œ
"#$ " # $
''
aa
bb
†cd
c f(t) dt c g(t) dt c h(t) dt = (t) dt;œ
"# $
'' ' '
aa a a
bb b b
Cr†
(t) dt c h(t) c g(t) c f(t) c h(t) c g(t) c f(t) dt
''
aa
bb
Cr i j k‚œ cdcdcd
#$ $" "#
c h(t) dt c g(t) dt c f(t) dt c h(t) dt c g(t) dt c f(t) dtœ
”•”•”•
#$ $" "#
'' '' ''
aa aa aa
bb bb bb
ijk
(t) dtœ‚Cr
'a
b
40. (a) Let u and be continuous on [a b]. Then lim u(t) (t) lim [u(t)f(t) u(t)g(t) u(t)h(t) ]rrijkߜ
tt ttÄÄ
u(t )f(t ) u(t )g(t ) u(t )h(t ) u(t ) (t ) u is continuous for every t in [a b].œ œ Ê ß
!! !! !! !! !
ijkrr
(b) Let u and be differentiable. Then (u ) [u(t)f(t) u(t)g(t) u(t)h(t) ]rrijk
dd
dt dt
œ
f(t) u(t) g(t) u(t) h(t) u(t)œ
ˆ‰ ˆ‰
Š‹
du df du du dh
dt dt dt dt dt dt
dg
ijk
[f(t) g(t) h(t) ] u(t) uœ œijk ijkr
du df dh du d
dt dt dt dt dt dt
dg
Š‹
r
41. (a) If (t) and (t) have identical derivatives on I, then RR ijkijk
"# ddfdhdfdh
dt dt dt dt dt dt dt
dg dg
Rœ œ
, , f (t) f (t) c , g (t) g (t) c , h (t) h (t) cœÊœ œ œÊ œ œ œ
ddfdf dhdh
dt dt dt dt dt dt dt
dg dg
R"#"" ##" #$
f (t) g (t) h (t) [f (t) c ] [g (t) c ] [h (t) c ] (t) (t) , whereÊ œÊ œ
""" #"###$ "#
ijk i j kRRC
ccc.Cijkœ
"#$
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

770 Chapter 13 Vector-Valued Functions and Motion in Space
(b) Let (t) be an antiderivative of (t) on I. Then (t) (t). If (t) is an antiderivative of (t) on I, thenRrRrUr
wœ
(t) (t). Thus (t) (t) on I (t) (t) .Ur UR URC
www
œœÊœ
42. ( ) d [f( ) g( ) h( ) ] d f( ) d g( ) d h( ) d
dd dd d
dt dt dt dt dt
'' '''
aa aaa
tt ttt
rijkijk77 7 7 7 7 77 77 77œœ
f(t) g(t) h(t) (t). Since ( ) d (t), we have that ( ) d is an antiderivative ofœ œ œijkr r r r
d
dt ''
aa
tt
77 77
. If is any antiderivative of , then (t) ( ) d by Exercise 41(b). Then (a) ( ) drR r R r C R r Cœ œ
''
a a
t a
77 77
(a) ( ) d (t) (t) (a) ( ) d (b) (a).œÊ Ê œœ Ê œ 0C C R r R C R R r R Rœ''
aa
tb
77 77
43. (a) t x t y t ; where x t 1 e 152 cos 20 17.6 andrijababab ab a ba bab ab ˆ‰
œ œ
1
0.08
0.08t‰
y t 3 1 e sin 20 1 0.08t eab a ba b a b
ˆ‰ ˆ‰
œ
152 32
0.08 0.08
0.08t 0.08t‰
2
(b) Solve graphically using a calculator or CAS: At t 1.527 seconds the ball reaches a maximum height of about 41.893¸
feet.
(c) Use a graphing calculator or CAS to find that y 0 when the ball has traveled for 3.181 seconds. The range isœ¸
about x 3.181 1 e 152 cos 20 17.6 351.734 feet.ab a b
ˆ‰ˆ ‰
œ ¸
1
0.08
0.08 3.181‰ab
(d) Use a graphing calculator or CAS to find that y 35 for t 0.877 and 2.190 seconds, at which times the ball is aboutœ¸
x 0.877 106.028 feet and x 2.190 251.530 feet from home plate.ab ab¸¸
(e) No; the range is less than 380 feet. To find the wind needed for a home run, first use the method of part (d) to find that
y 20 at t 0.376 and 2.716 seconds. Then define x w 1 e 152 cos 20 w , and solveœ¸ œ ab a b
ˆ‰ˆ ‰
1
0.08
0.08 2.716‰ab
x w 380 to find w 12.846 ft/sec.abœ¸
44. y y and y (v sin )t gt (v sin )t gt
max max
(v sin ) 3(v sin ) 3(v sin )
2g 4 8g 8g
3
œÊœ œ Ê œ
!! !
!!
""
##
##
!!
3(v sin ) (8gv sin )t 4g t 4g t (8gv sin )t 3(v sin ) 0 2gt 3v sin 0 orʜʜʜ
!! !! !
##### #
!! !! !
2gt v sin 0 t or t . Since the time it takes to reach y is t ,œÊœ œ œ
!!3v sin v sin v sin
2g 2g g
max max
!! !
then the time it takes the projectile to reach of y is the shorter time t or half the time it takes
3
42g
max v sin
œ!
to reach the maximum height.
13.3 ARC LENGTH IN SPACE
1. (2 cos t) (2 sin t) 5t ( 2 sin t) (2 cos t) 5rijkv ijkœÊœ
ÈÈ
( 2 sin t) (2 cos t) 5 4 sin t 4 cos t 5 3; Êœ œ œ œkk ÊŠ‹
ÈÈ
vT
## ##
#v
vkk
sin t cos t and Length dt 3 dt 3t 3œ œ œ œ œ
ˆ‰ˆ‰ kk cd
22
33 3
5
ijk v
È''
00
1
!1
2. (6 sin 2t) (6 cos 2t) 5t (12 cos 2t) ( 12 sin 2t) 5rijkv i jkœ Êœ
(12 cos 2t) ( 12 sin 2t) 5 144 cos 2t 144 sin 2t 25 13; Êœ œ œ œkk ÈÈ
v T
##### v
vkk
cos 2t sin 2t and Length dt 13 dt 13t 13œ œœœœ
ˆ‰ˆ‰ kk c d
12 12 5
13 13 13
ijk v
''
00
1
!1
3. t t t 1 t 1 t ; ri k vi k v T i kœ Ê œ Ê œ œ œ œ
2
31t 1t
t
$Î# "Î# # "Î# #"
kk a b
ÉÈv
vkk ÈÈ
È
and Length 1 t dt (1 t)œœœ
'0
8È‘
252
33
$Î# )
!
4. (2 t) (t 1) t 1 ( 1) 1 3 ; rijkvijkv T ijkœ Êœ Ê œ œ œ œ kk ÈÈ
### ""v
vkk ÈÈÈ
333
1
and Length 3 dt 3t 3 3œœœ
'0
3ÈÈÈ
’“
$
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 13.3 Arc Length in Space 771
5. cos t sin t 3 cos t sin t 3 sin t cos t rjkv j kvœ Êœ Êabab a ba b kk
$$ # #
3 cos t sin t 3 sin t cos t 9 cos t sin t cos t sin t 3 cos t sin t ;œ œ œ
Éababababkk
È
## ####
##
( cos t) (sin t) , if 0 t , andTjkjkœœ œ ŸŸ
v
vkkkkkk
#
3 cos t sin t 3 sin t cos t
3 cos t sin t 3 cos t sin t
1
Length 3 cos t sin t dt 3 cos t sin t dt sin 2t dt cos 2tœœœœœ
'''
000
222
kk ‘
333
4##
Î#
!
1
6. 6t 2t 3t 18t 6t 9t 18t 6t 9t 441t 21t ;rijkv ijkvœ Êœ Êœ œ œ
$$$ ### #
### %
###
kk ababab
ÉÈ
and Length 21t dt 7t 49Tijkijkœœ œ œ œ œ
v
vkk "#$
#
"
8t 6t 9t 6 2 3
21t 21t 21t 7 7 7 '1
2cd
7. (t cos t) (t sin t) t (cos t t sin t) (sin t t cos t) 2 trijkv i j kœ Êœ
22
3
È$Î# "Î#
Š‹
È
(cos t t sin t) (sin t t cos t) 2 t 1 t 2t (t 1) t 1 t 1, if t 0;Ê œ œ œ œœ kk kk
ÊŠ‹
ÈÈ È
v## ##
#
and Length (t 1) dt tTijkœœ œœœ
v
vkk È
ˆ‰ˆ‰
Š‹ ’“
cos t t sin t sin t t cos t t
t1 t1 t1 2 2
2t
!
'0
111
8. (t sin t cos t) (t cos t sin t) (sin t t cos t sin t) (cos t t sin t cos t)rijv i jœÊœ
(t cos t) (t sin t) (t cos t) ( t sin t) t t t if 2 t 2; œ Êœ œœœŸŸœijv Tkk kk
ÈÈÈ
### v
vkk
(cos t) (sin t) and Length t dt 1œœ œœœ
ˆ‰ˆ‰ ’“
t cos t t sin t t
tt 2
ijij '2
2#
#
È
9. Let P(t ) denote the point. Then (5 cos t) (5 sin t) 12 and 26 25 cos t 25 sin t 144 dt
!##
vijkœ œ 1'0
tÈ
13 dt 13t t 2 , and the point is P(2 ) (5 sin 2 5 cos 2 24 ) (0 5 24 )œœÊœ œßßœßß
'0
t
!!
111111
10. Let P(t ) denote the point. Then (12 cos t) (12 sin t) 5 and
!vijkœ
13 144 cos t 144 sin t 25 dt 13 dt 13t t , and the point isœ œ œ Êœ11
''
00
tt
È## !!
P( ) (12 sin ( ) 12 cos ( ) 5 ) (0 12 5 ) œ ß ß œ ß ß11111
11. (4 cos t) (4 sin t) 3t ( 4 sin t) (4 cos t) 3 ( 4 sin t) (4 cos t) 3rijkv ijkvœÊœÊœkk È###
25 5 s(t) 5 d 5t Length sœœÊœ œÊ œœ
Ȉ‰
'0
t
711
##
5
12. (cos t t sin t) (sin t t cos t) ( sin t sin t t cos t) (cos t cos t t sin t)rijv i jœ Êœ
(t cos t) (t sin t) (t cos t) (t cos t) t t, since t s(t) dœ Êœ œœœ ŸŸÊœœijvkk ÈÈ
### ##
1177
'0
tt
Length s( ) sÊœœœ1ˆ‰
11 1
###
ˆ‰ 3
8
13. e cos t e sin t e e cos t e sin t e sin t e cos t er i jk v i jkœÊœabababab
ttt ttttt
e cos t e sin t e sin t e cos t e 3e 3 e s(t) 3 e dÊœ œœ œ Ê œkkababab
ÉÈÈÈ
vtt tt t 2t
t
### '0
t77
3 e 3 Length s(0) s( ln 4) 0 3 e 3œÊ œœ œ
ÈÈ È È
Š‹
tln 4
33
4
È
14. (1 2t) (1 3t) (6 6t) 2 3 6 2 3 ( 6) 7 s(t) 7 d 7trij kvijkvœ Êœ Ê œ œÊ œ œkk È## # '0
t
7
Length s(0) s( 1) 0 ( 7) 7Êœœœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
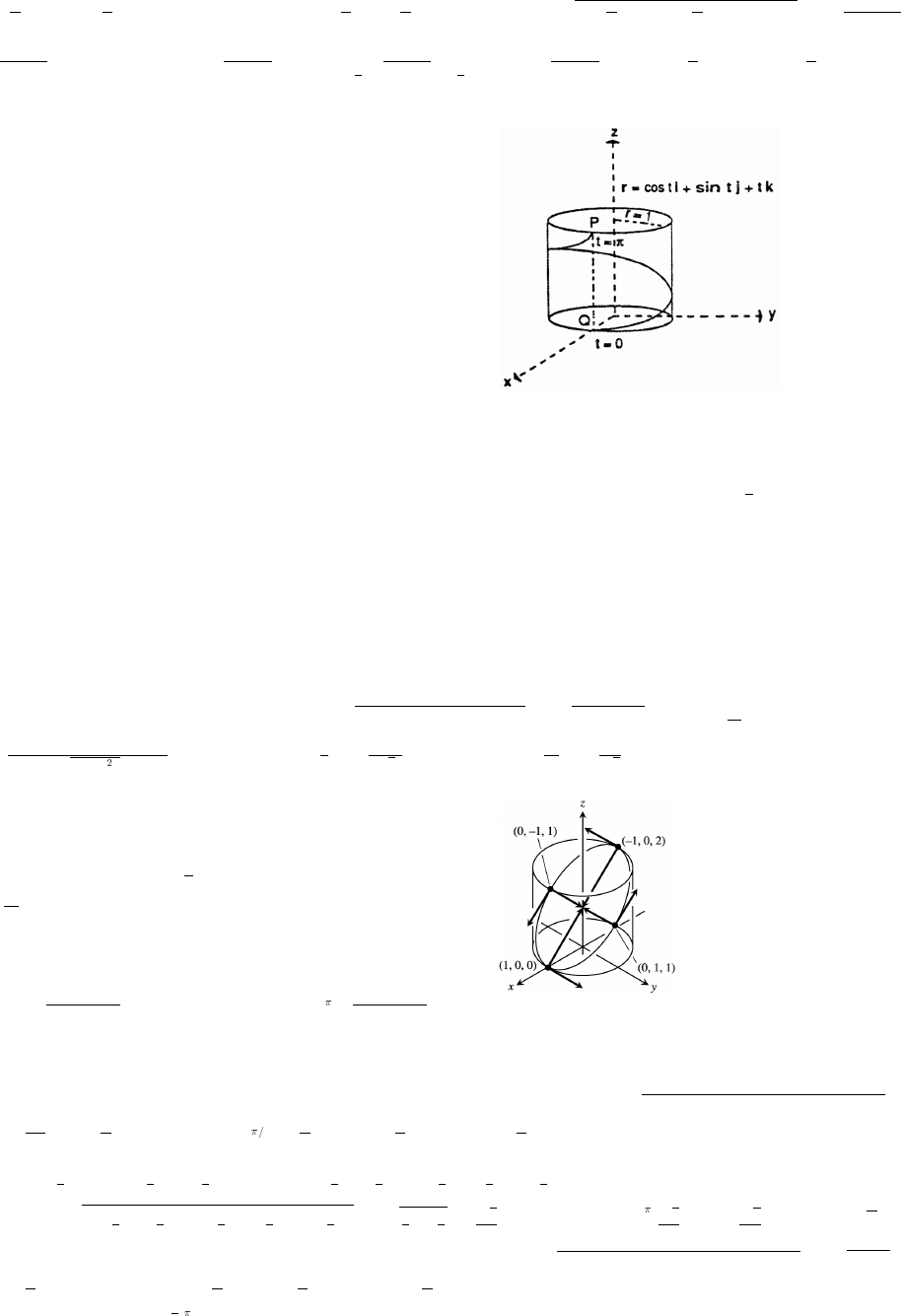
772 Chapter 13 Vector-Valued Functions and Motion in Space
15. 2t 2t 1 t 2 2 2t 2 2 ( 2t) 4 4trij kvijkvœ ʜʜ œ
Š‹Š‹ Š‹Š‹
ÈÈ ÈÈ ÈÈ È
ab kk
Ê
###
##
2 1 t Length 2 1 t dt 2 1 t ln t 1 t 2 ln 1 2œÊ œ œ œ
ÈÈÈÈÈÈ
’“Š‹Š‹Š‹
####
"
#
"
!
'0
1t
2
16. Let the helix make one complete turn from t 0 to t 2 .œœ1
Note that the radius of the cylinder is 1 theÊ
circumference of the base is 2 . When t 2 , the point P is11œ
(cos 2 sin 2 2 ) (1 0 2 ) the cylinder is 2 units111 1 1ßßœßßÊ
high. Cut the cylinder along PQ and flatten. The resulting
rectangle has a width equal to the circumference of the
cylinder 2 and a height equal to 2 , the height of theœ11
cylinder. Therefore, the rectangle is a square and the portion
of the helix from t 0 to t 2 is its diagonal.œœ1
17. (a) (cos t) (sin t) ( cos t) , 0 t 2 x cos t, y sin t, z 1 cos t x yrij kœ" ŸŸÊœœœÊ1##
cos t sin t 1, a right circular cylinder with the z-axis as the axis and radius 1. Thereforeœœ œ
##
P(cos t sin t 1 cos t) lies on the cylinder x y 1; t 0 P(1 0 0) is on the curve; t Q( 1 1)ßß œœÊßß œÊ!ßß
##
#
1
is on the curve; t R( 1 0 2) is on the curve. Then PQ and PR 2 2œ Ê ß ß œ œ
ÄÄ
1ijk i k
ik
ijk
Ê PQ PR 2 2 is a vector normal to the plane of P, Q, and R. Then the
1
202
Ä‚œ œ
Ä""
Ô×
ÕØ
plane containing P, Q, and R has an equation 2x 2z 2(1) 2(0) or x z 1. Any point on the curveœ œ
will satisfy this equation since x z cos t (1 cos t) 1. Therefore, any point on the curve lies on theœ œ
intersection of the cylinder x y 1 and the plane x z 1 the curve is an ellipse.
##
œ œÊ
(b) ( sin t) (cos t) (sin t) sin t cos t sin t 1 sin t vijkv Tœ Ê œ œ Ê œkk ÈÈ
### # v
vkk
(0) , , ( ) , œÊœœœœ
( sin t) (cos t) (sin t)
1sint 2 2
3
##
ijk ik ik
ÈÈÈ
TjT T jT
ˆ‰ ˆ‰
11
1
(c) ( cos t) (sin t) (cos t) ; isaijknikœ œ
normal to the plane x z 1 cos t cos tœÊ œ na†
0 is orthogonal to is parallel to theœÊ Êana
plane; (0) , , ,aika jaikœ œ œ
ˆ‰ ab
1
#1
aj
ˆ‰
31
#œ
(d) 1 sin t (See part (b) L 1 sin t dtkk ÈÈ
vœ Êœ
##
'0
2
(e) L 7.64 (by )¸Mathematica
18. (a) (cos 4t) (sin 4t) 4t ( 4 sin 4t) (4 cos 4t) 4 ( 4 sin 4t) (4 cos 4t) 4rijkv i jkvœÊœ Êœ kk È###
32 4 2 Length 4 2 dt 4 2 t 2 2œœ Ê œ œ œ
ÈÈÈÈÈ
’“
'0
21Î#
!1
(b) cos sin sin cos r i jkv i jkœÊœ
ˆ‰ˆ‰ ˆ ‰ˆ ‰
ttt t t
### #####
"""
sin cos Length dt t 2 2Êœ œ œ Ê œ œ œkk Ɉ‰ˆ‰ˆ‰
É’“ È
v"" """
## # # # # #
### %
!
tt
44 2
222
ÈÈÈ
'0
41
1
(c) (cos t) (sin t) t ( sin t) (cos t) ( sin t) ( cos t) ( 1) 1 1rijkv ijkvœÊœÊœœkk ÈÈ
###
2 Length 2 dt 2 t 2 2œÊ œ œ œ
ÈÈÈÈ
’“
'2
0!
#11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
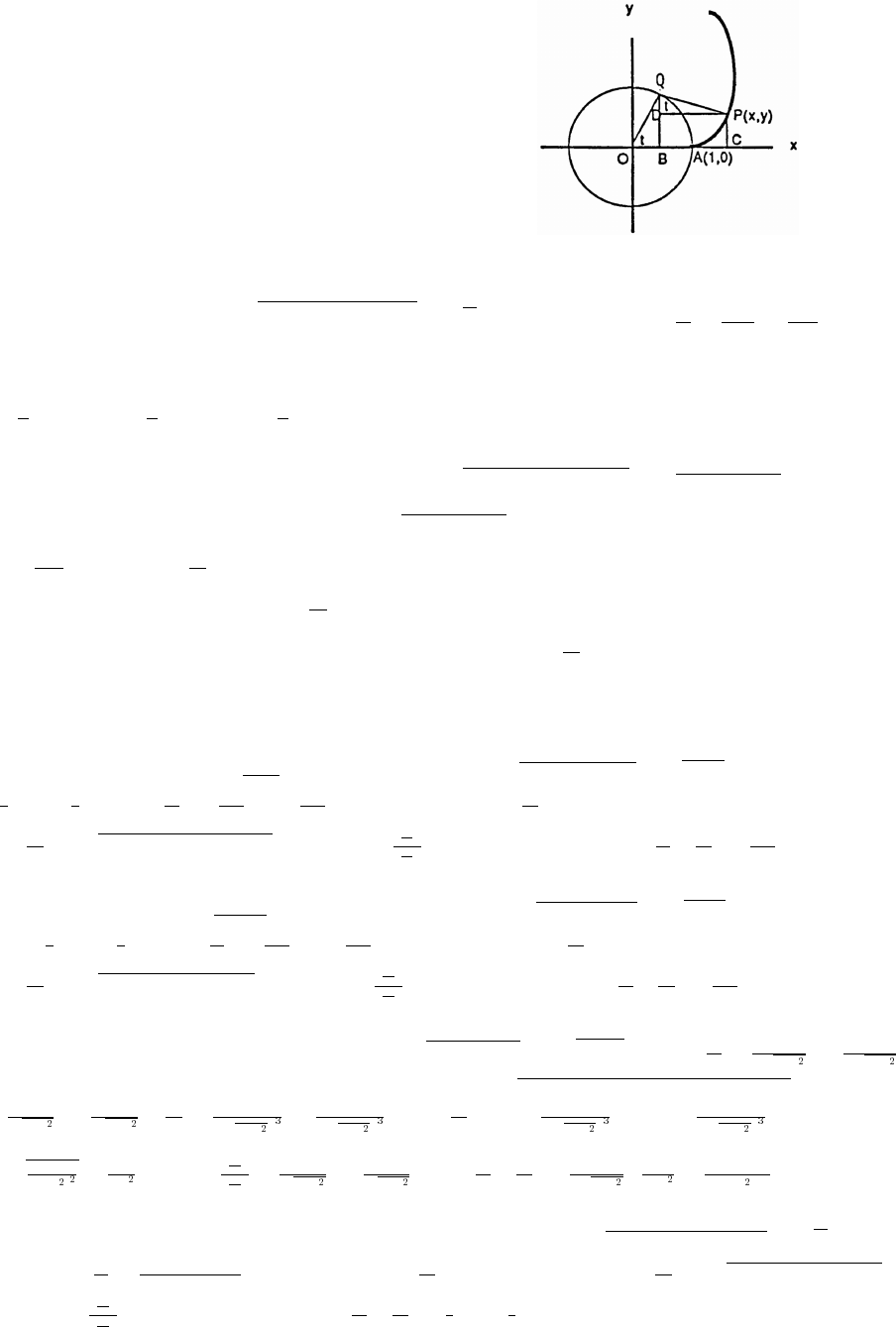
Section 13.4 Curvature and Normal Vectors of a Curve 773
19. PQB QOB t and PQ arc (AQ) t sincenœnœœœ
PQ length of the unwound string length of arc (AQ);œœ
thus x OB BC OB DP cos t t sin t, andœœœ
y PC QB QD sin t t cos tœœ œ
20. cos t t sin t sin t t cos t sin t t cos t sin t cos t t sin t cos trijv i jœ Êœababa ba babab
t cos t t sin t t cos t t sin t t t t, t 0œÊœ œœœÊœœababkkabab kk
ÉÈ
ijv T ij
22
2t cos t t sin t
tt
v
vkk
cos t sin tœij
21. x t u y t u z t u u u u , so s t dt d 1 d tvijkijkuvuœ œ œ œllœllœ œ
ddd
dt dt dt
01 02 03 123
ababab ab
'' '
00 0
tt t
77
22. t t t t t 2t 3t t 1 2t 3t 1 4t 9t . 0, 0, 0 t 0rijkvijkvab ab ab ab a b a b a b
ÉÈ
œ Ê œ Êl lœ œ Êœ
23 2 22
224
2
and 2, 4, 8 t 2. Thus L t dt 1 4t 9t dt. Using Simpson's rule with n 10 andab ab È
Êœ œ l l œ œ
''
00
22
v24
x 0.2 L 0 4 0.2 2 0.4 4 0.6 2 0.8 4 1 2 1.2 4 1.4?œ œ Ê ¸ l ll ll ll ll ll ll ll l
20 0.2
10 3
Šab ab ab ab ab ab ab abvvvvvvvv
2 1.6 4 1.8 2 1 4 1.0837 2 1.3676 4 1.8991 2 2.6919 4 3.7417llllll¸vvvababab ababababab
‹Š
0.2
3
2 5.0421 4 6.5890 2 8.3800 4 10.4134 12.6886 143.5594 9.5706 œ ¸abababa b a b
‹0.2
3
13.4 CURVATURE AND NORMAL VECTORS OF A CURVE
1. t ln (cos t) (tan t) 1 ( tan t) sec t sec t sec t, sinceri j vi ji j vœ Ê œ œ Ê œ œ œ œ
ˆ‰ kk k k
ÈÈ
###
sin t
cos t
t (cos t) (sin t) ; ( sin t) (cos t) Ê œ œ œ œ
11
##
"
Tijij ij
vT
vkk ˆ‰ˆ‰
sec t sec t dt
tan t d
( sin t) ( cos t) 1 ( sin t) (cos t) ; 1 cos t.Êœ œÊœœ œ†œ†œ
¸¸ ¸¸
È
d1d
dt dt sec t
T T
v
## "
Nij
ˆ‰
¸¸ kk
d
dt
d
dt
T
T,
2. ln (sec t) t (tan t) ( tan t) 1 sec t sec t sec t,r i j v ij ij vœÊœ œÊœ œœœ
ˆ‰ kk k k
ÈÈ
sec t tan t
sec t ## #
since t (sin t) (cos t) ; (cos t) (sin t) Ê œ œ œ œ
11
##
Tijijij
vT
vkk ˆ‰ˆ‰
tan t 1 d
sec t sec t dt
(cos t) ( sin t) 1 (cos t) (sin t) ; 1 cos t.Êœ œÊœœ œ†œ†œ
¸¸ ¸¸
È
d1d
dt dt sec t
T T
v
## "
Nij
ˆ‰
¸¸ kk
d
dt
d
dt
T
T,
3. (2t 3) 5 t 2 2t 2 ( 2t) 2 1 t rijvijv T ijœ Êœ Ê œ œ Êœœ ab kk
ÈÈ
### #
v
vkk ÈÈ
22t
21t 21t
; œ œ Êœ
"" "
##
ÈÈ Š‹Š‹ Š‹ Š‹
ÈÈ È È
1t 1t
td t d t
dt dt
1t 1t 1t 1t
ij i j
TT
¸¸Í
Í
Í
Ì
; œœÊœœ œ†œ†œ
ɸ¸
"" " "" "
# #
ab ˆ‰
¸¸ ÈÈ È
kk ab
1t 1t dt 1 t
t1d
1t 1t 1t 1t
Nij
d
dt
d 3/2
dt
T
T,v
T
4. (cos t t sin t) (sin t t cos t) (t cos t) (t sin t) ( t cos t) (t sin t) t t t, sincerijvijvœ Êœ Êœ œœœkk kk
ÈÈ
###
t 0 (cos t) (sin t) ; ( sin t) (cos t) ( sin t) (cos t)Ê œ œ œ œ Ê œ Tijij
vTT
v
ij
kk (t cos t) (t sin t)
tdtdt
dd
##
¸¸È
1 ( sin t) (cos t) ; 1œÊ œ œ œ † œ†œNij
ˆ‰
¸¸ kk
d
dt
d
dt
T
T,1d
dt t tv
T
¸¸ ""
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

774 Chapter 13 Vector-Valued Functions and Motion in Space
5. (a) x . Now, f x x 1 fx
,ab ab k k c d
¹¹ ab Éab
œ† œ Ê œ Êœ
1
xdt
dT x 2
kkab ab
v v
v
vi j v T
wwkk
1 f x 1 . Thus x
fx fx
œŠ‹Š‹
œcd abcd ab
ab ab
ww
ÎÎ
w
22
12 12 d
dt
fxfx fx
11
fx fx
ij ij
Tab ab ab
cd cd
ab ab
Š‹Š‹
22
32 32
Êœ œ œ
¹¹
Í
Í
Í
Ì”•
Ë
dx fx
dt
fxf x
1fx
2
1fx
2
fx fx
1
1fx
fx
1fx
Tab ab
ab ab
cd
ab cd
ab cdcd
ab ab
Š‹
cd
ab kkab
¹¹
cd
ab
Š‹ Š‹ Š‹
232
232
22
232
Thus x,abœ†œ
1
1fx
fx fx
1fx 1fx
ab Š‹
Ò Ó Ò Ó
ab kk kkab ab
kkab cd
ab
212 32
22
(b) y ln (cos x) ( sin x) tan x sec x œÊœœÊœÊœ œ
dy d y
dx cos x dx sec x
sec x
1 ( tan x)
sec x
ˆ‰
"#
,kk
cd
kk
cos x, since xœœ
"
##sec x
11
(c) Note that f (x) 0 at an inflection point.
ww œ
6. (a) f(t) g(t) x y x y x yrijijvijv T i jœ œÊœÊœ Êœœ
ÞÞ Þ Þ ÞÞ
kk È## v
vkk x
xy xy
y
ÈÈ
ÞÞ ÞÞ
dd
dt dt
2
TT
œÊœ
yyx xy xxy yx
xy xy
yyx xy
xy
xxy yx
xy
Þ ÞÞÞ ÞÞÞ Þ ÞÞÞ ÞÞÞ
ÞÞ ÞÞ
ÞÞÞÞ ÞÞÞ
ÞÞ
ÞÞÞÞ ÞÞÞ
ÞÞ
abab
ab ab
ab
ab
ab
ab
3/2 3/2 3/2
ij
¸¸Ê’“’“
3/2
2
3
2
œÊaba b
ab
yxyxxy
xy
ÞÞÞÞÞÞÞÞ
ÞÞ
; .œœ†œ†œ
kk kk
kk kk
Èab
yx xy yx xy xy yx
xy xy
1
xy xy
Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ
ll
ÞÞ ÞÞ
ÞÞ
ÞÞ
,1d
dtkkv
T
¸¸ 3/2
(b) (t) t ln (sin t) , 0 t x t and y ln (sin t) x 1, x 0; y cot t, y csc tri jœ Êœ œ Êœ œ œ œ œ
ÞÞÞÞ ÞÞ
1cos t
sin t #
sin tÊœ œ œ,kk
ab
csc t 0
1cott)
csc t
csc t
(c) (t) tan (sinh t) ln (cosh t) x tan (sinh t) and y ln (cosh t) xrijœÊœ œÊœœ
Þ
" "
"cosh t
1sinht cosh t
sech t, x sech t tanh t; y tanh t, y sech t sech t sech tœœ œœœÊœ œœ
ÞÞ Þ ÞÞ
sinh t
cosh t sech t tanh t
sech t sech t tanh t
#
,kk
ab
kk
7. (a) (t) f(t) g(t) f (t) g (t) is tangent to the curve at the point (f(t) g(t));rijvijœ Êœ ß
ww
g (t) f (t) f (t) g (t) g (t)f (t) f (t)g (t) 0; ( ) 0; thus, and arenv i j i j nv nv n n†† ††œ œ œ œ œ cdcd
ww ww wwww
both normal to the curve at the point
(b) (t) t e 2e 2e points toward the concave side of the curve; andrijvi jn ij Nœ Ê œ Ê œ œ
2t 2t 2t n
nkk
4e 1 kk È
nNijœÊœ
4t 2e
14e 14e
"
2t
4t 4t
ÈÈ
(c) (t) 4 t t points toward the concave side of the curve;rijvijnijœÊœ Êœ
È#
tt
4t 4t
ÈÈ
and 1 4 t tNn N ijœœœÊœ
n
nkk È
kk ÉŠ‹
È
t2
4t 4t
#
"#
8. (a) (t) t t t t points toward the concave side of the curve when t 0 andrijvijnijœ Êœ Êœ
"$##
3
t points toward the concave side when t 0 t for t 0 andœ Ê œ nij N ij
# #
"
È1t
ab
t for t0Nijœ
"
#
È1t
ab
(b) From part (a), 1 t kk ȸ¸É
vTij ijœÊœ Êœ Ê œ
%"
ÈÈ ab ab ab
1t 1t
t d 2t 2t d 4t 4t
dt dt
1t 1t 1t
TT
62
; ; t 0. does not exist at t 0, where tœœœ œ Á œ
2t
1t
1 t 2t 2t t t
2t 1t 1t t1t t1t
kk ˆ‰
¸¸ kk ab ab kk kk
ÈÈ
NijijN
d
dt
d
dt
T
TŠ‹ he
curve has a point of inflection; 0 so the curvature 0 at t 0 is
¸¸¸¸¸
ddddtd
dt ds dt ds ds
TTTT
t0œœœœœœÊœ,†N"
,
undefined. Since x t and y t y x , the curve is the cubic power curve which is concave down forœœÊœ
""
$$
33
x t 0 and concave up for x t 0.œ œ
9. (3 sin t) (3 cos t) 4t (3 cos t) ( 3 sin t) 4 (3 cos t) ( 3 sin t) 4 25rijkv i jkvœ Êœ Êœ œkk ÈÈ
###
5 cos t sin t sin t cos tœÊ œ œ Ê œ Tijk ij
vT
vkk ˆ‰ˆ‰ ˆ ‰ˆ‰
334d33
555dt55
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 13.4 Curvature and Normal Vectors of a Curve 775
sin t cos t ( sin t) (cos t) ; Ê œ œ Ê œ œ œ†œ
¸¸ ˆ ‰ ˆ ‰
É
d3 33 133
dt 5 5 5 5 5 25
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T,
10. (cos t t sin t) (sin t t cos t) 3 (t cos t) (t sin t) (t cos t) (t sin t) trijkvijvœ Êœ Êœ œkk ÈÈ
###
t t, if t 0 (cos t) (sin t) , t 0 ( sin t) (cos t)œœ Êœ œ Ê œ kk Tij ij
vT
vkk d
dt
( sin t) (cos t) 1 ( sin t) (cos t) ; 1Êœ œÊœœ œ†œ
¸¸È
d
dt tt
T## ""
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T,
11. e cos t e sin t 2 e cos t e sin t e sin t e cos t rijkv i jœÊœÊabababab
tt tttt
e cos t e sin t e sin t e cos t 2e e 2 ;kkabab
ÉÈÈ
vœœœ
tt tt 2t
t
##
Tij ijœœ Ê œ
vT
vkk ÈÈ È È
Š‹Š‹ Š ‹Š‹
cos t sin t sin t cos t d sin t cos t cos t sin t
22 2 2
dt
1 ;Êœ œÊœœ
¸¸ÊŠ‹Š‹ Š‹Š‹
d sin t cos t cos t sin t cos t sin t sin t cos t
dt 22 2 2
T
##
ÈÈ È È
ˆ‰
¸¸
Nij
d
dt
d
dt
T
T
1,œ† œ †œ
1d 1 1
dt 22
kk ÈÈ
v
T
¸¸ ee
tt
12. (6 sin 2t) (6 cos 2t) 5t (12 cos 2t) (12 sin 2t) 5 (12 cos 2t) ( 12 sin 2t) 5rijkv i jkvœ Êœ Êœ kk È###
169 13 cos 2t sin 2t sin 2t cos 2tœœÊœœ Êœ
Ȉ‰ˆ‰ ˆ ‰ˆ‰
Tijk ij
vT
vkk 12 12 5 d 24 24
13 13 13 dt 13 13
sin 2t cos 2t ( sin 2t) (cos 2t) ;Êœ œÊœœ
¸¸ ˆ ‰ ˆ ‰
É
d24 24 24
dt 13 13 13
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
.,œ† œ†œ
1d 124 24
dt 13 13 169kkv
T
¸¸
13. , t 0 t t t t t t 1, since t 0 rij vijv Tœ ʜʜœ Êœ
Š‹ Š‹ kk ÈÈ
tt
3#
#%# # v
vkk
œ Êœ Êœ
t1d1 t d t
tt t1 dt dt
t1 t1 t1 t1
ÈÈ ab ab ab ab
"
##
ij i j
TT
¸¸ÊŠ‹Š‹
; .œœÊœœ œ†œ†œ
ɸ¸
1t 1 t 1 d 1 1
t1 t1 dt t1
t1 t1 tt1 tt 1
" "
ab ˆ‰
¸¸ ÈÈ È
kk ab
Nij
d
dt
d
dt
T
T,v
T
14. cos t sin t , 0 t 3 cos t sin t 3 sin t cos trij v i jœ Êœ abab a ba b
$$ # #
#
1
3 cos t sin t 3 sin t cos t 9 cos t sin t 9 sin t cos t 3 cos t sin t, since 0 tÊœ œ œ kk a b a b
ÉÈ
v## %#%#
##
#
1
( cos t) (sin t) (sin t) (cos t) sin t cos t 1 Êœœ Ê œ Ê œ œÊœTijij N
vTT
vkk ˆ‰
¸¸
dd
dt dt
¸¸È## d
dt
d
dt
T
T
(sin t) (cos t) ; 1 .œ œ†œ †œij,1d 1 1
dt 3 cos t sin t 3 cos t sin tkkv
T
¸¸
15. t a cosh , a 0 sinh 1 sinh cosh cosh ri j vi j vœ Ê œ Ê œ œ œ
ˆ ‰ ˆ ‰ ˆ‰ ˆ‰
kk ÉÉ
ttttt
aaaaa
##
sech tanh sech tanh sech Êœœ Ê œ Tij ij
vT
vkk ˆ‰ˆ‰ ˆ ‰ˆ ‰
ttd tt t
aadtaaaaa
""
#
sech tanh sech sech tanh sech ;Êœ œ Êœœ
¸ ¸ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
É
dtttt tt
dt a a a a a a a a a
T"""
## % Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
sech sech .,œ† œ † œ
1d 1 t t
dt a a a a
cosh
kkv
T
¸ ¸ ˆ‰ ˆ‰
t
a
""
#
16. (cosh t) (sinh t) t (sinh t) (cosh t) sinh t ( cosh t) 1 2 cosh trijkvijkvœÊœÊœ œkk ÈÈ
##
tanh t sech t sech t sech t tanh tÊœœ Ê œ Tijk i k
vT
vkk ÈÈÈ È È
Š‹ Š‹ Š‹Š ‹
""" " "
#
222 2 2
d
dt
sech t sech t tanh t sech t (sech t) (tanh t) ;Êœ œ Êœœ
¸¸É
d
dt 2
T"" "
##
%##
Ȉ‰
¸¸
Nik
d
dt
d
dt
T
T
sech t sech t.,œ† œ † œ
1d 1
dt 2 cosh t 2
kk ÈÈ
v
T
¸¸ ""
#
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

776 Chapter 13 Vector-Valued Functions and Motion in Space
17. y ax y 2ax y 2a; from Exercise 5(a), (x) 2a 1 4a xœÊœÊœ œ œ
#w ww ##
$Î#
,kk
ab
2a
14ax kka b
(x) 2a 1 4a x 8a x ; thus, (x) 0 x 0. Now, (x) 0 for x 0 and (x) 0 forÊœ œÊœ ,,,,
w###w w w
#
&Î#
3kka b a b
x 0 so that (x) has an absolute maximum at x 0 which is the vertex of the parabola. Since x 0 is theœ œ,
only critical point for (x), the curvature has no minimum value.,
18. (a cos t) (b sin t) ( a sin t) (b cos t) ( a cos t) (b sin t) r i jv i ja i jvaœ Êœ Êœ Ê‚
ab ab ab, since a b 0; (t)
a sin t b cos t 0
a cos t b sin t 0
œœÊœœœ
ââ
ââ
ââ
ââ
ââ
ââ
kkkk
ijk
kva‚,kk
kk
va
v
‚
ab a sin t b cos t ; (t) (ab) a sin t b cos t 2a sin t cos t 2b sin t cos tœ œ ab aba b
## # # w ## # # # #
$Î# &Î#
#
,3
(ab) a b (sin 2t) a sin t b cos t ; thus, (t) 0 sin 2t 0 t 0, identifyingœ œÊ œÊœ
3
#
## ## ## w
&Î#
aba b ,1
points on the major axis, or t , identifying points on the minor axis. Furthermore, (t) 0 forœ
11
##
w
3,
0 t and for t ; (t) 0 for t and t 2 . Therefore, the points associated
1111
####
w
1, 1 1
33
with t 0 and t on the major axis give absolute maximum curvature and the points associated with tœœ œ11
#
and t on the minor axis give absolute minimum curvature.œ31
#
19. ; 0 a b 0 a b a b since a, b 0. Now, 0 if,œÊœ œÊœÊœ„Êœ
adabd d
a b da da da
ab
##
,, ,
ab
a b and 0 if a b is at a maximum for a b and (b) is the maximum value of .Ê œ œœ
d b
da bb 2b
,,, ,
"
20. (a) From Example 5, the curvature of the helix (t) (a cos t) (a sin t) bt , a, b 0 is ; alsorijkœœ,a
ab
a b . For the helix (t) (3 cos t) (3 sin t) t , 0 t 4 , a 3 and b 1 kk È
vrijkœ œ ŸŸ œ œÊœ œ
##
1,
33
31 10
and 10 K 10 dt tkk ÈÈ
’“
vœÊœ œ œ
'0
43312
10 10 10
ÈÈ
%
!
11
(b) y x x t and y t , t (t) t t 2t 1 4t ;œÊœ œ__Ê œÊœ Ê œ
## # #
rijvijvkk È
; ; . ThusTij i jœ œ œ œ
1 2t d 4t 2 d 16t 4 2
14t 14t dt dt 1 4t
14t 14t 14t
ÈÈ ab ab ab
TT
3/2 3/2
2
3
¸¸É
. Then K 1 4t dt dt,œ†œ œ œ
12 2 2 2
14t 14t 14t
14t 14t
ÈŠ‹
ÈŠ‹
È
#
3''
Š‹
È
lim dt lim dt lim tan 2t lim tan 2tœœ
aa
bb
Ä_ Ä_
Ä_ Ä_
''
a0
0b
a0
b
22
14t 1 4t
" "
!
cd cd
lim tan 2a lim tan 2bœ œœ
ab
Ä_ Ä_
abab
" "
##
111
21. t (sin t) (cos t) 1 (cos t) 1 cos t 1 cos 1; ri j vi j v v Tœ Ê œ Ê œ œ Ê œ œ œkk Èȸ¸ ˆ‰ˆ‰ É
## # #
##
11v
vkk
; œÊœ Êœ œ œœ
ij TTT
œ
cos t
1cost
d sin t cos t sin t d d 1
dt dt 1 cos t dt 1
1cost 1cost
sin t
t
sin
1cos
Èabab kk ¸¸
ˆ‰
222
3/2 3/2 22
2
22
ij
¸¸ ¸¸ 1. Thus 1 1,ˆ‰
1
21
1
œ†œ
1 and the center is 0 x y 1Êœœ ß Ê œ3"
##
##
1ˆ‰ ˆ ‰
11
22. (2 ln t) t 1 1 ;ri jvi jv T ijœÊœÊœœÊœœ
ˆ‰ ˆ‰ˆ‰ ˆ‰
kk É
""
t t t t t t t1 t1
241t12tt1
2
222 22
22
v
vkk
. Thus 1
d4td 21dt22t2
dt dt t 1 dt t 1 t 1 2
2t 1
t1 t1 t1 t1
4 t 1 16t
TT T
v
œ Êœ œ œ†œ†œ Êœ
ˆ‰
ab ab ab ab
ab kk
2
22 2 2
22 42 22 2 2
22
222
ij
¸¸ ¸¸
Êab,,
2. The circle of curvature is tangent to the curve at P(0 2) circle has same tangent as the curveœÊœœ ßÊ
""
#3,
(1) 2 is tangent to the circle the center lies on the y-axis. If t 1 (t 0), then (t 1) 0Êœ Ê Á vi #
t 2t 1 0 t 1 2t 2 since t 0 t 2 t 2 y 2 on bothÊ Ê Ê Ê Ê Ê
##
""t1
ttt
ˆ‰
sides of (0 2) the curve is concave down center of circle of curvature is (0 4) x (y 4) 4ß Ê Ê ß Ê œ
##
is an equation of the circle of curvature
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 13.4 Curvature and Normal Vectors of a Curve 777
23. y x f (x) 2x and f (x) 2œÊ œ œ
#w ww
Êœ œ,kk
abab
2
1(2x) 14x
2
24. y f (x) x and f (x) 3xœÊ œ œ
x
4w$ww #
Êœ œ,kk
Š‹
ab ab
3x
1x
3x
1x
25. y sin x f (x) cos x and f (x) sin xœÊœ œ
www
Êœ œ,kk kk
abab
sin x sin x
1cosx 1cosx
26. y e f (x) e and f (x) eœÊ œ œ
xxxwww
Êœ œ,kk
Š‹
ˆ‰
e
1
e
1
xx
abee
x2x
27-34. Example CAS commands:
:Maple
with( plots );
r := t -> [3*cos(t),5*sin(t)];
lo := 0;
hi := 2*Pi;
t0 := Pi/4;
P1 := plot( [r(t)[], t=lo..hi] ):
display( P1, scaling=constrained, title="#27(a) (Section 13.4)" );
CURVATURE := (x,y,t) ->simplify(abs(diff(x,t)*diff(y,t,t)-diff(y,t)*diff(x,t,t))/(diff(x,t)^2+diff(y,t)^2)^(3/2));
kappa := eval(CURVATURE(r(t)[],t),t=t0);
UnitNormal := (x,y,t) ->expand( [-diff(y,t),diff(x,t)]/sqrt(diff(x,t)^2+diff(y,t)^2) );
N := eval( UnitNormal(r(t)[],t), t=t0 );
C := expand( r(t0) + N/kappa );
OscCircle := (x-C[1])^2+(y-C[2])^2 = 1/kappa^2;
evalf( OscCircle );
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
778 Chapter 13 Vector-Valued Functions and Motion in Space
P2 := implicitplot( (x-C[1])^2+(y-C[2])^2 = 1/kappa^2, x=-7..4, y=-4..6, color=blue ):
display( [P1,P2], scaling=constrained, title="#27(e) (Section 13.4)" );
: (assigned functions and parameters may vary)Mathematica
In Mathematica, the dot product can be applied either with a period "." or with the word, "Dot".
Similarly, the cross product can be applied either with a very small "x" (in the palette next to the arrow) or with the word,
"Cross". However, the Cross command assumes the vectors are in three dimensions
For the purposes of applying the cross product command, we will define the position vector r as a three dimensional vector
with zero for its z-component. For graphing, we will use only the first two components.
Clear[r, t, x, y]
r[t_]={3 Cos[t], 5 Sin[t] }
t0= /4; tmin= 0; tmax= 2 ;11
r2[t_]= {r[t][[1]], r[t][[2]]}
pp=ParametricPlot[r2[t], {t, tmin, tmax}];
mag[v_]=Sqrt[v.v]
vel[t_]= r'[t]
speed[t_]=mag[vel[t]]
acc[t_]= vel'[t]
curv[t_]= mag[Cross[vel[t],acc[t]]]/speed[t] //Simplify
3
unittan[t_]= vel[t]/speed[t]//Simplify
unitnorm[t_]= unittan'[t] / mag[unittan'[t]]
ctr= r[t0] + (1 / curv[t0]) unitnorm[t0] //Simplify
{a,b}= {ctr[[1]], ctr[[2]]}
To plot the osculating circle, load a graphics package and then plot it, and show it together with the original curve.
<<Graphics`ImplicitPlot`
pc=ImplicitPlot[(x a)2 + (y b)2 == 1/curv[t0] , {x, 8, 8},{y, 8, 8}]
2
radius=Graphics[Line[{{a, b}, r2[t0]}]]
Show[pp, pc, radius, AspectRatio 1]Ä
13.5 TANGENTIAL AND NORMAL COMPONENTS OF ACCELERATION
1. (a cos t) (a sin t) bt ( a sin t) (a cos t) b ( a sin t) (a cos t) brijkv ijkvœÊœÊœkk È###
a b a 0; ( a cos t) ( a sin t) ( a cos t) ( a sin t) a aœÊœ œœ Êœ œœ
Èkk kk kk
ÈÈ
## ###
Td
dt va i ja
aa0a (0)aaÊœ œ œœÊœ œ
NT
ÉÉ
kk kk kk kk kk kkaaaaTNN
##
##
2. (1 3t) (t 2) 3t 3 3 3 1 ( 3) 19 a 0; rijkvijkv va0œ Êœ Ê œ œ Ê œ œ œkk kk
ÈÈ
## # Td
dt
a a 0 (0) (0)Êœ œÊœ œ
NT
ÉkkaaTN0
##
3. (t 1) 2t t 2 2t 1 2 (2t) 5 4t a 5 4t (8t)rijkvijkvœ Êœ Ê œ œ Êœ
# #
## # # "
#
"Î#
kk a b
ÈÈT
4t 5 4t a (1) ; 2 (1) 2 (1) 2 a a 2œ Ê œœœÊ œÊ œÊœ œab kk kk
ÉɈ‰
#"Î# ###
#
T N T
44 4
93 3
Èak a k a a
(1)œœÊœ
É20 4
93 3 3
25 25
ÈÈ
aTN
4. (t cos t) (t sin t) t (cos t t sin t) (sin t t cos t) 2trijkv i jkœÊœ
#
(cos t t sin t) (sin t t cos t) (2t) 5t 1 a 5t 1 (10t)Êœ œ Êœ kk a b
ÈÈ
v####
"
#
#"Î#
T
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 13.5 Tangential and Normal Components of Acceleration 779
a (0) 0; ( 2 sin t t cos t) (2 cos t t sin t) 2 (0) 2 2 (0)œÊœœÊœÊ
5t
5t 1
ÈTaijkajkakk
2 2 22 a a 22 0 22 (0) (0) 22 22œœÊœ œ œÊœ œ
ÈÈ È È ÈÈ
Ékk ÊŠ‹
## # #
##
NT
aaTNN
5. t t t t t 2t 1t 1t (2t) 1t 1tri j kvi j k vœ Êœ Ê œ
#$ $ ##
"" ## #
##
ˆ‰ˆ‰ abab kk abab
É
33
2 t 2t 1 2 1 t a 2t 2 a (0) 0; 2 2t 2t (0) 2 (0) 2œœÊœÊœœÊœÊœ
Èabab kk
ÈÈ
%# #TT
ai j k a i a
a a 2 0 2 (0) (0) 2 2Êœ œ œÊ œ œ
NT
Ékk È
aaTNN
####
6. e cos t e sin t 2e e cos t e sin t e sin t e cos t 2er i jkv i jkœÊœabab abab
ÈÈ
tt t tttt t
e cos t e sin t e sin t e cos t 2e 4e 2e a 2e a (0) 2;Êœ œ œ Êœ Ê œkkabab
ÊŠ‹
ÈÈ
vtt tt t 2t
tt
TT
##
#
e cos t e sin t e sin t e cos t e sin t e cos t e cos t e sin t 2eaijkœ abab
È
t ttt tt t t t
2e sin t 2e cos t 2e (0) 2 2 (0) 2 2 6œ Ê œ Ê œ œabab kk
ÈÈ È
ÊŠ‹È
tt t
ijkajka
##
a a 6 2 2 (0) 2 2Êœ œ œ Ê œ
NT
Ékk ÊŠ‹
ÈÈÈ
aaTN
####
7. (cos t) (sin t) ( sin t) (cos t) ( sin t) (cos t) 1 rijkv ijv TœÊœ Êœ œÊœkk È## v
vkk
( sin t) (cos t) ; ( cos t) (sin t) ( cos t) ( sin t)œ Ê œ œ Ê œ ijT ij ij
ˆ‰ ¸ ¸ È
1
4dt dt
22
dd
ÈÈ
## ##
TT
1 ( cos t) (sin t) ; sin t cos t 0
cos t sin t 0
œÊ œ œ Ê œ œ‚œ œ
NijNijBTN k
ijk
ˆ‰
¸¸ ÈÈ
d
dt
d
dt
T
Tˆ‰ ââ
ââ
ââ
ââ
ââ
ââ
1
4
22
##
, the normal to the osculating plane; P 1 lies on theÊ œ œÊœßßBk r ijk
ˆ‰ ˆ‰ Š‹
11
44
22 22
ÈÈ ÈÈ
## ##
osculating plane 0 x 0 y (z ( 1)) 0 z 1 is the osculating plane; is normalʜʜ
Š‹Š‹
ÈÈ
22
## T
to the normal plane x y 0(z ( 1)) 0 x y 0Ê œÊœ
Š‹Š‹Š‹Š‹
ÈÈÈÈ ÈÈ
2222 22
#### ##
x y 0 is the normal plane; is normal to the rectifying planeÊ œ N
x y 0(z ( 1)) 0 x y 1 x y 2 is theÊ œ Ê œÊ œ
Š‹Š ‹Š‹Š ‹ È
ÈÈ ÈÈ ÈÈ
22 22 22
## ## ##
rectifying plane
8. (cos t) (sin t) t ( sin t) (cos t) sin t cos t 1 2 rijkv ijkv TœÊœÊœ œÊœkk ÈÈ
## v
vkk
sin t cos t cos t sin t œ Ê œ Ê
Š‹Š‹ Š‹Š‹
¸¸
""" " "
ÈÈÈ È È
222 2 2
dd
dt dt
ijk i j
TT
cos t sin t ( cos t) (sin t) ; thus (0) and (0)œœÊœœ œ œ
É"" " ""
##
##
ÈÈÈ
ˆ‰
¸¸
222
NijTjkNi
d
dt
d
dt
T
T
(0) , the normal to the osculating plane; (0) P(1 0 0) lies on
0
10 0
Êœ œ œÊßß
Bjk ri
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ââ
"" ""
ÈÈ ÈÈ
22 22
the osculating plane 0(x 1) (y 0) (z 0) 0 y z 0 is the osculating plane; is normalÊ œÊœ
""
ÈÈ
22 T
to the normal plane 0(x 1) (y 0) (z 0) 0 y z 0 is the normal plane; is normal toÊ œÊœ
""
ÈÈ
22 N
the rectifying plane 1(x 1) 0(y 0) 0(z 0) 0 x 1 is the rectifying plane.Ê œÊœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

780 Chapter 13 Vector-Valued Functions and Motion in Space
9. By Exercise 9 in Section 13.4, cos t sin t and ( sin t) (cos t) so that Ti jkNijBTNœ œ œ‚
ˆ‰ˆ ‰
334
555
cos t sin t cos t sin t . Also (3 cos t) ( 3 sin t) 4
sin t cos t 0
œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ‰
ijk
ijkvi jk
3344 4 3
5555 5 5
( 3 sin t) ( 3 cos t) ( 3 cos t) (3 sin t) and 3 cos t 3 sin t 4
3 sin t 3 cos t 0
Êœ Ê œ ‚œ
aij ijva
ijk
d
dt
a
ââ
ââ
ââ
ââ
ââ
ââ
(12 cos t) (12 sin t) 9 12 cos t 12 sin t 9 225. Thusœ Ê ‚ œ œijkvakka ba bab
2###
7œœœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
3 cos t 3 sin t 4
3 sin t 3 sin t 0
3 cos t 3 sin t 0
225 225 225 25
49 sint9 cost 36 4
†
10. By Exercise 10 in Section 13.4, (cos t) (sin t) and ( sin t) (cos t) ; thus TijN ijBTNœ œ œ‚
cos t sin t . Also (t cos t) (t sin t)
cos t sin t 0
sin t cos t 0
œœœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
ijk
kk v i j
##
t sin t cos t t cos t sin t t cos t sin t sin t t sin t cos t cos tÊœ Ê œ aij i jababa ba bab d
dt
a
t cos t 2 sin t 2 cos t t sin t . Thus t cos t t sin t 0
t sin t cos t t cos t sin t 0
œ ‚ œ
ababââ
ââ
ââ
ââ
ââ
ââ
abab
ijva
ijk
[(t cos t)(t cos t sin t) (t sin t)( t sin t cos t)] t t t . ThusœœÊ‚œœkk va
##
#
kkab
24
07œœœ
ââ
ââ
ââ
ââ
ââ
ââ
t cos t t sin t 0
cos t t sin t sin t t cos t 0
2 sin t t cos t 2 cos t t sin t 0
tt
0
44
11. By Exercise 11 in Section 13.4, and ; ThusTijN i jœ œ
Š‹Š‹ Š ‹Š ‹
cos t sin t sin t cos t cos t sin t sin t cos t
22 2 2
ÈÈ È È
0
0
BTN
ijk
œ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
’“Š‹Š‹
cos t sin t sin t cos t
22
cos t sin t sin t cos t
22
cos t 2 cos t sin t sin t sin t 2 sin t
2
ÈÈ
ÈÈ
cos t cos t
2
k
. Also, e cos t e sin t e sin t e cos tœ œœ
’“Š‹Š‹ abab
1sin 2t 1sin 2t
22
tt tt
ab ab kk v i j
= 2e sin t 2e cos t
e sin t cos t e cos t sin t e cos t sin t e sin t cos t
ʜ
aijijcdcdabab
a bababab
tt tt tt
2e cos t sin t 2e sin t cos t . Thus 2e
e cos t sin t e sin t cos t 0
2e sin t 2e cos t 0
Êœ ‚œ œ
d
dt
tt 2t
tt
tt
aaba b ââ
ââ
ââ
ââ
ââ
ââ
abab
ijva k
ijk
2e 4e . Thus Ê‚ œ œ œkkabva
22t 4t
cos t sin t sin t cos t 0
2 sin t 2 cos t 0
2 cos t sin t 2 sin t cos
#
7
ââ
ââ
ââ
ââ
ââ
ââ
abab
aba b
ee
ee
ee
tt
tt
tt
t0
4e4t œ0
12. By Exercise 12 in Section 13.4, cos 2t sin 2t and ( sin 2t) (cos 2t) soTijkNijœœ
ˆ‰ˆ‰
12 12 5
13 13 13
cos 2t sin 2t cos 2t sin 2t . Also,
sin 2t cos 2t 0
BTN i j k
ijk
œ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ ‰ˆ‰ˆ‰
abab
12 12 5 5 5 12
13 13 13 13 13 13
(12 cos 2t) (12 sin 2t) 5 ( 24 sin 2t) (24 cos 2t) and ( 48 cos 2t) (48 sin 2t)vijka ij ijœÊœ œ
d
dt
a
(120 cos 2t) (120 sin 2t) 288
12 cos 2t 12 sin 2t 5
24 sin 2t 24 cos 2t 0
va i j k va
ijk
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ kk
2
(120 cos 2t) ( 120 sin 2t) ( 288) 120 cos 2t sin 2t 288 97344. Thusœœœ
#######
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 13.5 Tangential and Normal Components of Acceleration 781
7œœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
12 cos 2t 12 sin 2t 5
24 sin 2t 24 cos 2t 0
48 cos 2t 48 sin 2t 0
97344 97344 169
52448 10
† †
13. By Exercise 13 in Section 13.4, and so that T i j N i j BTNœ œ œ
t1 1t
t1 t1 t1 t1
ab ab ÈÈ
1/2 1/2 ‚
. Also, t t 2t 2 so that 0 0
0
0
tt0
2t 0
200
œœœÊœÊœœÊœ
"
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
kvijaij i
t1
t1 t1
t1 t1
t
d
dt
ÈÈ
ÈÈ
"
#
#
a7
14. By Exercise 14 in Section 13.4, ( cos t) (sin t) and (sin t) (cos t) so that T i j N i j BTNœ œ œ ‚
. Also, 3 cos t sin t 3 sin t cos t
cos t sin t 0
sin t cos t 0
œœœ
ââ
ââ
ââ
ââ
ââ
ââabab
ijk
kv i j
##
3 cos t sin t 3 sin t cos t 3 cos t sin t 3 sin t cos tÊÊaij i jœ œ
ddddd dd
dt dt dt dt dt dt dt
abab abab
ˆ‰ˆ‰
## # #
a
3 cos t sin t 3 sin t cos t 0
3 cos t sin t 3 sin t cos t 0
3 cos t sin t 3 sin t cos
Ê
ââ
ââ
ââ
ââ
ââ
ââ
ââ
abab
ˆ‰ˆ‰
abab
##
##
##
dd
dt dt
dd dd
dt dt dt dt t0
0 0œÊ œ7
15. By Exercise 15 in Section 13.4, sech tanh and tanh sech so that T i j N i j BTNœœ œ œ
v
vkk ˆ‰ˆ‰ ˆ ‰ˆ‰
tt tt
aa aa ‚
. Also, sinh cosh sinh so that
sech tanh 0
tanh sech 0
œœœÊœÊœ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰
ijk
kvi ja j j
tt
aa
tt
aa
ttdt
aaadtaa
""a
0 0
1sinh 0
0 cosh 0
0 sinh 0
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰
ˆ‰
ˆ‰
t
a
aa
t
aa
t
"
"
œÊ œ7
16. By Exercise 16 in Section 13.4, tanh t sech t and (sech t) (tanh t) so thatTijkNikœ œ
Š‹ Š‹
"""
ÈÈÈ
222
tanh t sech t . Also, (sinh t) (cosh t)
tanh t sech t
sech t 0 tanh t
BTN i j k v i jk
ijk
œœ œ œ
‚
ââ
ââ
ââ
ââ
ââ
ââ
ââ
Š‹ Š‹
""" """
ÈÈÈ ÈÈÈ
222 222
(cosh t) (sinh t) (sinh t) (cosh t) and sinh t cosh t 1
cosh t sinh t 0
aij ijva
ijk
œ Êœ ‚œ
d
dt
a
ââ
ââ
ââ
ââ
ââ
ââ
(sinh t) (cosh t) cosh t sinh t (sinh t) (cosh t) sinh t cosh t 1. Thusœ œ Ê‚œij kijkvaab kk
22 ###
.7œœœ
ââ
ââ
ââ
ââ
ââ
ââ
sinh t cosh t 1
cosh t sinh t 0
sinh t cosh t 0
sinh t cosh t 1 sinh t cosh t 1 cosh t
#
" "
17. Yes. If the car is moving along a curved path, then 0 and a 0 a a .,,ÁœÁÊœÁ
NTN
kkvaTN0
#
18. constant a 0 a is orthogonal to the acceleration is normal to the pathkk kkvvaNTÊœ œÊœ Ê
TN
d
dt
19. a 0 0 is constantav aT v v¼Ê¼ Ê œÊ œÊ
Td
dt kk kk
20. (t) a a , where a (10) 0 and a 100 0 100 . Now, fromaTN v v aT Nœ œ œ œ œ œ Êœ
TN T N
dd
dt dt
kk kk,, ,
#
Exercise 5(a) Section 12.4, we find for y f(x) x that ; also,œœ œ œ œ
#
,kk
‘
ab cdab
f(x)
1f(x)
22
1(2x) 14x
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

782 Chapter 13 Vector-Valued Functions and Motion in Space
(t) t t is the position vector of the moving mass 2t 1 4trij vijvœ Ê œ Ê œ
##
kk È
( 2t ). At (0 0): (0) , (0) and (0) 2 m m(100 ) 200m ;Êœ ß œ œ œÊœ œ œTij TiNj Fa Nj
"
È14t ,,
At 2 2 : 2 2 2 , 2 , and 2 m
Š ‹Š‹ Š ‹ Š‹ Š‹
ÈÈ È È È
ßœœ œ œÊœTijijN ij Fa
"" "
333 33 27
22 22 2
ÈÈ
,
m(100 ) m m mœœœ,Nijij
ˆ‰
Š‹
200 200
27 3 3 81 81
2 2 400 2
ÈÈ
"
21. By a a we have a T N va T T N TT TNœ ‚œ ‚ œ ‚ ‚
TN ds d s ds ds d s ds
dt dt dt dt dt dt
23
ˆ ‰ ˆ‰ ˆ‰
’“
Š‹
ab ab
22
22
,,
. It follows that œ l‚lœ llœ llÊ œ,,,,
ˆ‰ ¹¹
ds ds
dt dt
333
BvaBv
l‚l
ll
va
v3
22. a 0 0 0 (since the particle is moving, we cannot have zero speed) the curvature is zero
NœÊ œÊœ Ê,,kkv#
so the particle is moving along a straight line
23. From Example 1, t and a t so that a , t 0 tkk kkvvœœ œÊœœœÁÊœœ
NN
,, 3
#""
at
tt
N
kkv,
24. (x At) (y Bt) (z Ct) A B C 0. Since the curverijkvijka0va0œ Êœ ʜʂœÊœ
!!! ,
is a plane curve, 0.7œ
25. If a plane curve is sufficiently differentiable the torsion is zero as the following argument shows:
f(t) g(t) f (t) g (t) f (t) g (t) f (t) g (t)rijv i ja i j i jœ Êœ Êœ Êœ
w w ww ww www www
d
dt
a
0Êœ œ7
ââ
ââ
ââ
ââ
ââ
ââ
kk
f (t) g (t) 0
f (t) g (t) 0
f (t) g (t) 0
va‚
26. a sin t a cos t b and a cos t a sin tvijka ijœ œ abab abab
To find the torsion: 7œœœ
ââ
ââ
ââ
ââ
ââ
ââ
Š‹
Ȉ‰ˆ‰
ab
asin tacos tb
a cos t a sin t 0
asin t acos t 0
aa b
bacost asint abcos
aa b
22
2222
22 22 2 2
tsint
aa b a b
bab
ab
w
2
22 2 2 2
ab ab
œÊœ (b) ;7
(b) 0 0 a b 0 b a b a since a, b 0. Also b a 0 and b a7 7
w## w
œÊ œÊœÊœ„Êœ Ê
ab
ab
ab
0 so occurs when b a Ê œÊ œ œ77 7
w
"
max max a
aa 2a
27. (t) f(t) g(t) h(t) f (t) g (t) h (t) ; 0 h (t) 0 h(t) Crijkvijkvkœ Êœ œÊ œÊ œ
www w
†
(t) f(t) g(t) C and (a) f(a) g(a) C f(a) 0, g(a) 0 and C 0 h(t) 0.Êœ œ œÊœ œ œÊœr i jkr i jk0
28. From Exercise 26, (a sin t) (a cos t) b a b vijkv Tœ Ê œ Ê œkk È## v
vkk
(a sin t) (a cos t) b ; (a cos t) (a sin t) œ œ Êœ
""
ÈÈ
ˆ‰
¸¸
ab ab
d
dt
cdcdijk ijN
Td
dt
d
dt
T
T
(cos t) (sin t) ;
cos t sin t 0
œ œ ‚ œ
ijBTN
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ââ
a sin t a cos t b
ab ab ab
ÈÈÈ
(b cos t) (b sin t) œ Êœ Êœ
b sin t b cos t a d d b
ab ab ab ab ab
dt dt
ÈÈÈ È È
"
ijk ijN
BB
cd†
, which is consistent with the result in Exercise 26.Êœ œ œ7""
kk ÈÈ
v
B
ˆ‰
Š‹Š‹
dbb
dt a b
ab ab
†N
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 13.5 Tangential and Normal Components of Acceleration 783
29-32. Example CAS commands:
:Maple
with( LinearAlgebra );
r := < t*cos(t) | t*sin(t) | t >;
t0 := sqrt(3);
rr := eval( r, t=t0 );
v := map( diff, r, t );
vv := eval( v, t=t0 );
a := map( diff, v, t );
aa := eval( a, t=t0 );
s := simplify(Norm( v, 2 )) assuming t::real;
ss := eval( s, t=t0 );
T := v/s;
TT := vv/ss ;
q1 := map( diff, simplify(T), t ):
NN := simplify(eval( q1/Norm(q1,2), t=t0 ));
BB := CrossProduct( TT, NN );
kappa := Norm(CrossProduct(vv,aa),2)/ss^3;
tau := simplify( Determinant(< vv, aa, eval(map(diff,a,t),t=t0) >)/Norm(CrossProduct(vv,aa),2)^3 );
a_t := eval( diff( s, t ), t=t0 );
a_n := evalf[4]( kappa*ss^2 );
: (assigned functions and value for t0 will vary)Mathematica
Clear[t, v, a, t]
mag[vector_]:=Sqrt[vector.vector]
Print["The position vector is ", r[t_]={t Cos[t], t Sin[t], t}]
Print["The velocity vector is ", v[t_]= r'[t]]
Print["The acceleration vector is ", a[t_]= v'[t]]
Print["The speed is ", speed[t_]= mag[v[t]]//Simplify]
Print["The unit tangent vector is ", utan[t_]= v[t]/speed[t] //Simplify]
Print["The curvature is ", curv[t_]= mag[Cross[v[t],a[t]]] / speed[t] //Simplify]
3
Print["The torsion is ", torsion[t_]= Det[{v[t], a[t], a'[t]}] / mag[Cross[v[t],a[t]]] //Simplify]
2
Print["The unit normal vector is ", unorm[t_]= utan'[t] / mag[utan'[t]] //Simplify]
Print["The unit binormal vector is ", ubinorm[t_]= Cross[utan[t],unorm[t]] //Simplify]
Print["The tangential component of the acceleration is ", at[t_]=a[t].utan[t] //Simplify]
Print["The normal component of the acceleration is ", an[t_]=a[t].unorm[t] //Simplify]
You can evaluate any of these functions at a specified value of t.
t0= Sqrt[3]
{utan[t0], unorm[t0], ubinorm[t0]}
N[{utan[t0], unorm[t0], ubinorm[t0]}]
{curv[t0], torsion[t0]}
N[{curv[t0], torsion[t0]}]
{at[t0], an[t0]}
N[{at[t0], an[t0]}]
To verify that the tangential and normal components of the acceleration agree with the formulas in the book:
at[t]== speed'[t] //Simplify
an[t]==curv [t] speed[t] //Simplify
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

784 Chapter 13 Vector-Valued Functions and Motion in Space
13.6 VELOCITY AND ACCELERATION IN POLAR COORDINATES
1. 3 0, r a 1 cos r a sin 3a sin r 3a cos 9a cos
...
ddd
dt dt dt
)))
œœÊœ œ Êœ œ Êœ œ
ÞÞÞ
)) ) ) ) ) )ab
3a sin a 1 cos 3 3a sin 3a 1 cosvu u u uœ œaba bababa bab)) ))
rr))
9a cos a 1 cos 3 a 1 cos 0 2 3a sin 3au uœ †
Š‹
ababa bababab)) ) )
2r)
9a cos 9a 9a cos 18a sin 9a 2 cos 1 18a sinœ œ a baba bab))) ) )uu uu
rr))
2. 2t 2, r a sin 2 r a cos 2 2 4ta cos 2 r 4ta sin 2 2 4a cos 2
...
ddd
dt dt dt
)))
œœÊœ œ Êœ † œ Êœ †
ÞÞÞ
)) ) ) ) ) )
ˆ‰
16t a sin 2 4a cos 2œ
2))
4ta cos 2 a sin 2 2t 4ta cos 2 2ta sin 2vu u uuœ œababababab)) ) )
rr))
16t a sin 2 4a cos 2 a sin 2 2t a sin 2 2 2 4ta cos 2 2tauuœ
’“
a babab ababa bab
‘
22r
))) ) )
)
16t a sin 2 4a cos 2 4t a sin 2 2a sin 2 16t a cos 2œ
’“
‘
22 2
r
)) ) ) )uu
)
20t a sin 2 4a cos 2 2a sin 2 16t a cos 2 4a cos 2 5t sin 2 2a sin 2 8t cos 2œ œ
’“
‘
abab
2222
r r
)) ) ) )) ) )uuuu
))
3. 2 0, r e r e a 2a e r 2a e a 4a e
...
ddd
dt dt dt
aa a a 2a
)))
)) ) ) )
œœÊœ œ Êœ † œ Êœ † œ
ÞÞÞ
))
2a e e 2 2a e 2evu u uuœ œ
ˆ‰ˆ‰ ˆ‰ˆ‰
ab
aa a a
rr
)) ) )
))
4a e e 2 e 0 2 2a e 2 4a e 4e 0 8a eau uuuœ œ
’“’ “’“’“
ˆ ‰ˆ‰ ˆ‰ ˆ ‰
ab ab ab
2a a a a 2a a a
2rr
)) ) ) )) )
))
4e a 1 8a eœ
a2 a
r
))
)
ab
ˆ‰
uu
4. 1 e e e , r a 1 sin t r a cos t r a sin t
...
)))œ Êœ Êœ œ Êœ Êœ
ÞÞÞ
tt t
ab
acost a 1 sint e acost ae 1 sintvu u u uœ œaba babab a bab
rr
tt
))
a sin t a 1 sin t e a 1 sin t e 2 a cos t eau uœ
’“’ “
abababababababab ab
ttt
2r)
asint ae 1 sint ae 1 sint 2ae costœ
’“’ “
ab ab
2t t t
r
uu
)
a sin t e 1 sin t a e 1 sin t 2cos tœ ababab ab
2t t
r
uu
)
a sin t e 1 sin t a e 2cos t 1 sin tœ ababab
2t t
r
uu
)
5. 2t 2 0, r 2 cos 4t r 8 sin 4t r 32 cos 4t
...
)))œÊœÊœ œ Êœ Êœ
ÞÞÞ
8 sin 4t 2 cos 4t 2 8 sin 4t 4 cos 4tvu u uuœ œ ababababab
rr))
32 cos 4t 2 cos 4t 2 2 cos 4t 0 2 8 sin 4t 2au uœ †
Š‹
abababa baba bab
2r)
32 cos 4t 8 cos 4t 0 32sin 4t 40 cos 4t 32 sin 4tœ œ ababababuuuu
rr))
6. e 1 v v ;œ Êœ Êœ
rv
GM r r
GM(e 1) GM(e 1)
#
!
!É
Circle: e 0 vœÊ œ
!ÉGM
r
Ellipse: 0 e 1 v Ê
ÉÉ
GM 2GM
rr
!
Parabola: e 1 vœÊ œ
!É2GM
r
Hyperbola: e 1 vÊ
!É2GM
r
7. r v v which is constant since G, M, and r (the radius of orbit) are constantœÊœÊœ
GM GM GM
vr r
#É
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
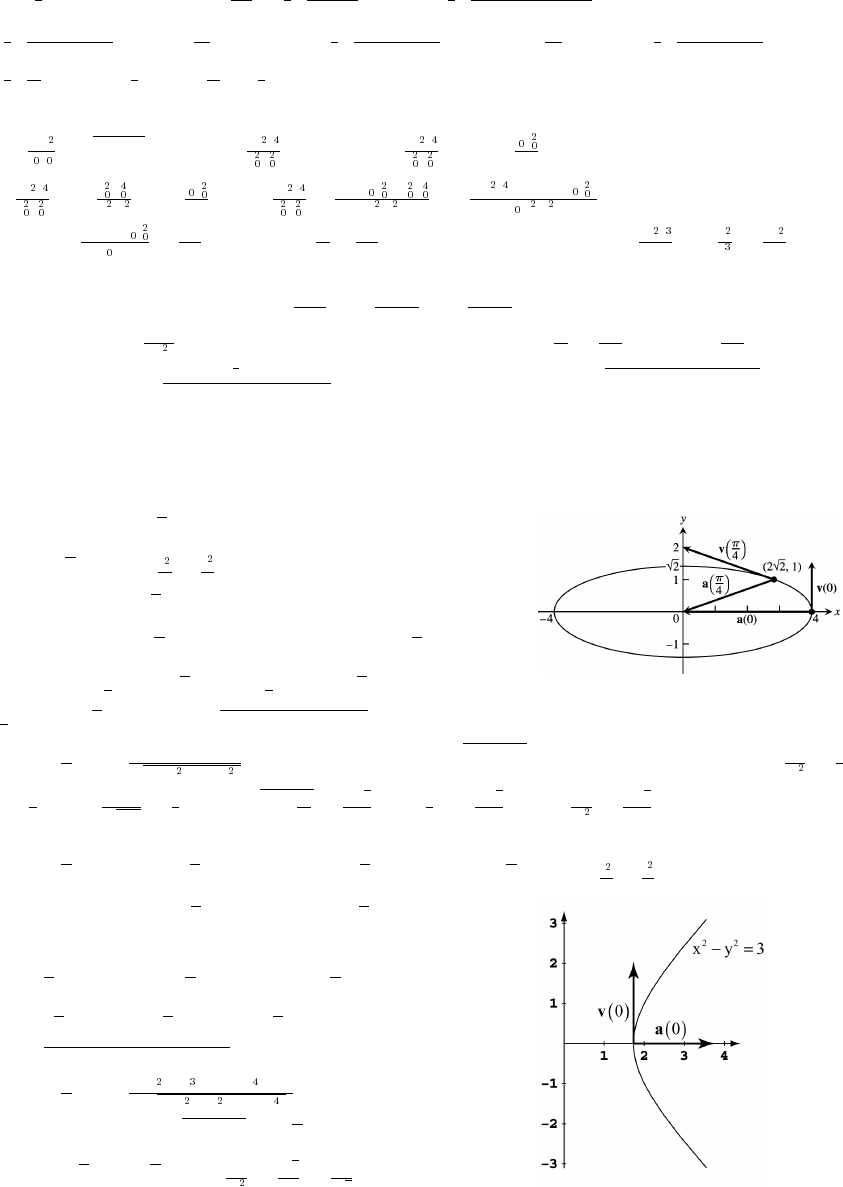
Chapter 13 Practice Exercises 785
8. A (t t) (t) (t) (t)??œ‚Êœ ‚œ ‚
"""
###
kk
¹¹¹ ¹
rr r r
?
?? ?
??
A
tt t
(t t) (t t) (t) (t)rrrr
(t) (t) (t) (t) lim (t)œ‚‚œ‚Êœ ‚
""" "
###
¹ ¹¹¹ ¹¹
rr rr rr(t t) (t) (t t) (t) (t t) (t)
tt t dt t
dA
???
?? ? ?
rrr r r
?t0Ä
(t) (t) œ‚œ ‚œ‚
"""
###
¸¸¸¸
kk
dd
dt dt
rr
rr rr
Þ
9. T 1 e T 1 e 1 1 (from Equation 5)œÊœœ
Š‹ Š‹ Š‹ Š ‹
Èab ”•
2a 4a 4a
rv GM
rv rv
rv
111
### #
2œ œ œ
Š‹’ “Š‹’ “Š‹
4a 4a
rv rv
rv rv 2GMrv rv
GM GM GM rGM
4a 2GMrv
11
1
ˆ‰
ab
4 a 4 a (from Equation 10) T œœ ʜʜab ab
Š‹
ˆ‰ ˆ‰ˆ‰
11
#% #% #
"
2GM r v
2r GM GM 2a GM GM a GM
22 4aT4
11
10. r 365.256 days 365.256 days 24 60 60 31,558,118.4 seconds 3.16 10 ,œœ‚‚‚œ ¸‚
hours minutes seconds
day hour minute
7
G 6.6726 10 , and the mass of the sun M 1.99 10 kg. a Tœ‚ œ‚ œÊœ
†
11 30 3 2
Nm T 4 GM
kg a GM 4
222
32
1
1
a 3.16 10 3.35863335 10 a 3.35863335 10Êœ ‚ ¸ ‚ Êœ ‚
37 33
26.6726 10 1.99 10
433
ab È
ˆ‰ˆ‰
‚‚
11 30
2
3
1
149757138111 m 149.757 billion km¸¸
CHAPTER 13 PRACTICE EXERCISES
1. (t) (4 cos t) 2 sin t x 4 cos tri jœ Êœ
Š‹
È
and y 2 sin t 1;œÊœ
Èx
16
y
#
vi jœ ( 4 sin t) 2 cos t and
Š‹
È
( 4 cos t) 2 sin t ; (0) 4 , (0) 2 ,ai jrivjœ œ œ
Š‹
ÈÈ
(0) 4; 22 , 22 ,air ijv ijœ œ œ
ˆ‰ ˆ‰
ÈÈ
11
44
2 2 ; 16 sin t 2 cos taijv
ˆ‰ ÈÈ
kk
1
4œ œ
##
a ; at t 0: a 0, a 0 4, 0 4 4 , 2;Êœ œ œ œ œ œ œœ œ œœ
TN
d 14 sin t cos t 4
dt 2
16 sin t 2 cos t
a
kk kk
É
vaaTNN
Èkk
#
T,N
v
at t : a , a 9 , , œ œœœœ œ œœ
1
439333 27
77 49 7
81
42 42 42
a
TN
ÈÈÈ È
kk
ÉaT N,N
v
2. (t) 3 sec t 3 tan t x 3 sec t and y 3 tan t sec t tan t 1;rijœ Êœ œÊœœ
Š‹Š‹
ÈÈ È È
x
33
y##
x y 3; 3 sec t tan t 3 sec tÊœ œ
## #
vij
Š‹Š‹
ÈÈ
and
3 sec t tan t 3 sec t 2 3 sec t tan t ;aijœ
Š‹Š‹
ÈÈÈ
#$ #
(0) 3 , (0) 3 , (0) 3 ;rivjaiœœœ
ÈÈÈ
3 sec t tan t 3 sec tkkvœ
È## %
a ;Êœ œ
Td 6 sec t tan t 18 sec t tan t
dt 2 3 sec t tan t 3 sec t
kkv
È
at t 0: a 0, a 0 3,œœœ œ
TNÉkk È
a#
03 3, aT N Nœ œ œ œ œ
ÈÈ
,a3
33
N
kk ÈÈ
v
"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

786 Chapter 13 Vector-Valued Functions and Motion in Space
3. t 1 t 1 t t 1 t 1 trijv i jvœ Êœ Êœ
"
##
$Î# $Î# ##
$Î# $Î#
##
ÈÈ
1t 1t
tab ab kk ab ab
Ê’“’“
. We want to maximize : and 0 0 t 0. For t 0, 0; forœ œ œÊ œÊœ
"
1 t dt dt
d d
2t 2t 2t
1t 1t 1t
kkvkk kk
ab ab ab
vv
t 0, 0 occurs when t 0 1Ê œÊœ
2t
1tab kk kkvv
max max
4. e cos t e sin t e cos t e sin t e sin t e cos trijv i jœ Êœabababab
tt tttt
e cos t e sin t e sin t e cos t e sin t e cos t e cos t e sin tʜ aijabab
t ttt tt t t
2e sin t 2e cos t . Let be the angle between and . Then cosœ œabab Š‹
tt
ij ra))
" ra
ra
†
kkkk
cos cos cos 0 for all tœœœœ
" " "
#
Š‹
2e sin t cos t 2e sin t cos t 0
e cos t e sin t 2e sin t 2e cos t 2e
2t 2t
tt t t 2t
ÉÉ
ababa ba b
1
5. 3 4 and 5 15 25 25; 3 4 5
340
550
vijai j va k va v
ijk
œ œ Ê‚œ œ Ê œ œ œ
"
ââ
ââ
ââ
ââ
ââ
ââ kk kk
È
‚##
Êœ œœ,kk
kk
va
v
‚"
25
55
6. e 1 e e 1 e e 1 e 2e,œœÊœ
kk
‘
ab
y
1y
x2x x2x x 2x 2x
d3
dx
$Î# $Î# &Î#
#
ab ab abab
’“
,
e 1 e 3e 1 e e 1 e 1 e 3e e 1 e 1 2e ;œ œ œ
x 2x 3x 2x x 2x 2x 2x x 2x 2x
ab ab abc daba bab
$Î# &Î# &Î# &Î#
0 1 2e 0 e 2x ln 2 x ln 2 ln 2 y ; therefore is at a
d
dx
2x 2x
2
,œ Ê œ Ê œ Ê œ Ê œ œ Ê œab È
"""
##
È,
maximum at the point ln 2
Š‹
È
ß
"
È2
7. x y and y y. Since the particle moves around the unit circlerij v i jviœ Êœ œÊ œ
dx dx
dt dt dt
dy †
x y 1, 2x 2y 0 (y) x. Since y and x, we have
##
œ œ Ê œ Ê œ œ œ œ
dx x dx x dx
dt dt dt y dt dt y dt dt
dy dy dy dy
y x at (1 0), and the motion is clockwise.vij v jœ Ê ß œ
8. 9y x 9 3x x . If x y , where x and y are differentiable functions of t,œÊ œ Êœ œ
$# #
"
dy dy
dt dt dt 3 dt
dx dx rij
then . Hence 4 4 and x (3) (4) 12 at (3 3). Also,vij vi vjœ œÊœ œœ œ œ ß
dx dx dx
dt dt dt dt 3 dt 3
dy dy
††
""
##
and x x . Hence 2 2 andaij aiœ œ œÊœ
dx 2 dx dx dx
dt dt dt 3 dt 3 dt dt
dy dy ˆ‰ˆ‰ ˆ ‰
#"#†
(3)(4) (3) ( 2) 26 at the point (x y) (3 3).aj†œœ œ ßœß
dy
dt 3 3
2##
"
9. orthogonal to 0 ( ) K, a constant. If x y , where
ddddd
dt dt dt dt dt
rrrr
r r r r rr rr r i jÊœ œ œ Ê œ œ††† ††
"""
###
x and y are differentiable functions of t, then x y x y K, which is the equation of a circlerr†œ Ê œ
## ##
centered at the origin.
10. (a) (b) ( cos t) ( sin t)vijœ 11 1 1 1
sin t cos t ;ʜ aijabab11 1 1
##
(0) and (0) ;v0a jœœ1#
(1) 2 and (1) ;via jœœ11
#
(2) and (2) ;v0a jœœ1#
(3) 2 and (3)via jœœ11
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 13 Practice Exercises 787
(c) Forward speed at the topmost point is (1) (3) 2 ft/sec; since the circle makes revolution perkkkkvvœœ1"
#
second, the center moves ft parallel to the x-axis each second the forward speed of C is ft/sec.11Ê
11. y y (v sin )t gt y 6.5 (44 ft/sec)(sin 45°)(3 sec) 32 ft/sec (3 sec) 6.5 66 2 144œ Êœ œ
!! ""
##
###
!ab È
44.16 ft the shot put is on the ground. Now, y 0 6.5 22 2t 16t 0 t 2.13 sec (the¸ Ê œ Ê œ Ê ¸
È#
positive root) x (44 ft/sec)(cos 45°)(2.13 sec) 66.27 ft or about 66 ft, 3 in. from the stopboardʸ ¸
12. y y 7 ft 57 ft
max œ œ ¸
!#
(v sin ) [(80 ft/sec)(sin 45°)]
g (2) 32 ft/sec
!ab
13. x (v cos )t and y (v sin )t gt tan œœÊœœœ
!!
"
#
#
!!9
y
x (v cos )t v cos
(v sin )t gt (v sin ) gt
!!
!!
v cos tan v sin gt t , which is the time when the golf ballʜʜ
!!
"
#
!9 ! 2v sin 2v cos tan
g
!!9
hits the upward slope. At this time x (v cos ) v sin cos v cos tan .œœ
!###
!!
!!!!9
Š‹Š‹
ab
2v sin 2v cos tan
gg
2
!!9
Now OR ORœÊœ
x2
cos g cos
v sin cos v cos tan
99
!! !9
Š‹Š ‹
œ
Š‹Š ‹
2v cos
gcos cos
sin cos tan
!!
99
!9
œŠ‹Š ‹
2v cos
gcos
sin cos cos sin
!!9 !9
9
[sin ( )]. The distance OR is maximizedœ
Š‹
2v cos
g cos
!
9!9
when x is maximized:
(cos 2 sin 2 tan ) 0
dx
dg
2v
!œœ
Š‹ !!9
(cos 2 sin 2 tan ) 0 cot 2 tan 0 cot 2 tan ( ) 2Ê œÊœÊœÊœÊœ!!9 !9 ! 9!9!
11
9
##4
14. (a) x v (cos 40°)t and y 6.5 v (sin 40°)t gt 6.5 v (sin 40°)t 16t ; x 262 ft and y 0 ftœœœœœ
!! !
"
#
##
5
12
262 v (cos 40°)t or v and 0 6.5 (sin 40°)t 16t t 14.1684Êœ œ œ Êœ
5 262.4167 262.4167
12 (cos 40°)t (cos 40°)t
!! ##
’“
t 3.764 sec. Therefore, 262.4167 v (cos 40°)(3.764 sec) v v 91 ft/secʸ ¸ Ê ¸ Ê ¸
!!!
262.4167
(cos 40°)(3.764 sec)
(b) y y 6.5 60 ft
max œ ¸ ¸
!(v sin )
2g (2)(32)
(91)(sin 40°)
!ab
2
15. (2 cos t) (2 sin t) t ( 2 sin t) (2 cos t) 2t ( 2 sin t) (2 cos t) (2t)rijkv ijkvœÊœÊœ
####
kk È
2 1 t Length 2 1 t dt t 1 t ln t 1 t 1 ln 1œÊ œ œ œ
ÈÈÈÈ
’“Š‹¹¹
ÉÉ
####
Î%
!
'0
4111 1 1
4164 16
16. (3 cos t) (3 sin t) 2t ( 3 sin t) (3 cos t) 3t ( 3 sin t) (3 cos t) 3tr i jkv i jkvœÊœÊœ
$Î# "Î# # # "Î# #
kk a b
É
9 9t 3 1 t Length 3 1 t dt 2(1 t) 14œœ Ê œ œ œ
ÈÈ È‘
'0
3$Î# $
!
17. (1 t) (1 t) t (1 t) (1 t)rijkvijkœ Êœ
44 22
993333
$Î# $Î# "Î# "Î#
""
(1 t) (1 t) 1 (1 t) (1 t)Êœ œÊœ kk É‘ ‘ˆ‰
vTijk
22 22
333333
"Î# "Î#
##
""
#"Î# "Î#
(0) ; (1 t) (1 t) (0) (0)Ê œ œ Ê œ Ê œTijk i j ij
22 d d d
333dt3 3 dt 33 dt 3
2
"" " ""
"Î# "Î#
TTT
¸¸
È
(0) ; (0) (0) (0) ;
0
Êœ œ‚œ œ
NijBTN ijk
ijk
"" " "
"
""
ÈÈ È È È
ÈÈ
2 2 32 32 32
22
333
22
4
ââ
ââ
ââ
ââ
ââ
ââ
ââ
(1 t) (1 t) (0) and (0) (0) (0)aijaijvijk vaœ Ê œ œ Ê ‚
"" "" "
"Î# "Î#
3 3 33 333
22
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

788 Chapter 13 Vector-Valued Functions and Motion in Space
(0) ;
0
œœÊ‚œÊœœœ
ââ
ââ
ââ
ââ
ââ
ââ kk
ijk
ijk va
22
333
33
999 3 1 3
422
"
""
"" ‚
ÈÈ
kk
kk Š‹
,va
v
2
3
(1 t) (1 t) (0) (0)aijaij
ÞÞ
œ Ê œ Ê œ œ œ
"" "" "
$Î# $Î#
‚
66 66 6
0
0
7
ââ
ââ
ââ
ââ
ââ
ââ
ââ
kk ˆ‰ˆ ‰
Š‹
22
333
33
66 318
2
2
3
va
18. e sin 2t e cos 2t 2e e sin 2t 2e cos 2t e cos 2t 2e sin 2t 2er i jkv i jkœ Êœ abababab
tt ttt tt t
e sin 2t 2e cos 2t e cos 2t 2e sin 2t 2e 3e Êœ œ Êkkababab
É
vT
tt t t t
t
###
œv
vkk
sin 2t cos 2t cos 2t sin 2t (0) ;œ Ê œ
ˆ‰ˆ‰
"" "
33 3 3 3 333
22222
ijkTijk
cos 2t sin 2t sin 2t cos 2t (0) (0) 5
d2 4 2 4 d 24 d 2
dt 3 3 3 3 dt 3 3 dt 3
TTT
œ ʜʜ
ˆ‰ˆ ‰ ¸¸
È
ijij
(0) ; (0) (0) (0) ;
0
Êœ œ œ‚œ œ
NijBTN ijk
ijk
ˆ‰
Š‹ ÈÈ È È È
ÈÈ
24
33
25
3
ij"
"
5 5 35 35 35
2425
212
333
55
2
ââ
ââ
ââ
ââ
ââ
ââ
ââ
4e cos 2t 3e sin 2t 3e cos 2t 4e sin 2t 2e (0) 4 3 2 and (0) 2 2a i jkaijkvijkœ Ê œ œaba b
tt tt t
(0) (0) 8 4 10 64 16 100 6 5 and (0) 3
22
432
Ê ‚ œ œ Ê ‚œ œ œ
"
va ijkva v
ijk
ââ
ââ
ââ
ââ
ââ
ââ kk kk
ÈÈ
(0) ;Êœœ,65 25
39
ÈÈ
4e cos 2t 8e sin 2t 3e sin 2t 6e cos 2t 3e cos 2t 6e sin 2t 4e sin 2t 8e cos 2t 2eai jk
ޜ aba b
t ttt t ttt t
2e cos 2t 11e sin 2t 11 e cos 2t 2e sin 2t 2e (0) 2 11 2œ Ê œ
Þ
abab
tt tt t
ijkaijk
(0)Êœ œœ7
ââ
ââ
ââ
ââ
ââ
ââ
kk
212
432
2112 80 4
180 9
‚
va
19. t e e 1 e (ln 2) ;ri j vi j v T i j T i jœ Ê œ Ê œ Ê œ Ê œ
"""
#
2t 2t 4t
11 17 17
4
kk ÈÈÈ ÈÈ
ee
e
4t 4t
2t
(ln 2) (ln 2) ;
d2 2 d 328 4
dt dt
11 17 17 17 17 17 17
TT
œ ʜʜ
"
ee
ee
4t 2t
4t 4t
ˆ‰ ˆ‰ ÈÈ ÈÈ
ij ijN ij
(ln 2) (ln 2) (ln 2) ; 2e (ln 2) 8 and (ln 2) 4
0
0
BTN kaja jvij
ijk
œ‚œ œœÊ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
"
"
ÈÈ
ÈÈ
17 17
4
4
17 17
2t
(ln 2) (ln 2) 8 8 and (ln 2) 17 (ln 2) ; 4e
40
080
Ê‚œ œÊ‚œ œÊ œ œ
"Þ
va kva v aj
ijk
ââ
ââ
ââ
ââ
ââ
ââ kk k k
È,8
17 17
2t
È
(ln 2) 16 (ln 2) 0ʜʜ œ
Þ
aj7
ââ
ââ
ââ
ââ
ââ
ââ
kk
140
080
0160
va‚
20. (3 cosh 2t) (3 sinh 2t) 6t (6 sinh 2t) (6 cosh 2t) 6rijkvijkœÊœ
36 sinh 2t 36 cosh 2t 36 6 2 cosh 2t tanh 2t sech 2tÊœ œ Êœœ kk ÈÈ
Š‹ Š‹
vTijk
## """v
vkk ÈÈÈ
222
(ln 2) ; sech 2t sech 2t tanh 2t (ln 2)Êœ œ ÊTijk i k
15 8 d 2 2 d
17 2 2 17 2 2 2
dt dt
ÈÈ È È È
"#
TT
Š‹Š ‹
(ln 2)œ œÊœœ
Š‹ Š‹ Š ‹Š ‹
ˆ‰ ˆ‰ˆ‰ ¸ ¸ Ê
2 8 2 8 15 128 240 d 128 240
2 2 289 2 289 2 289 2 289 2
17 17 17 dt 17
82
ÈÈ ÈÈ ÈÈ
È
###
ikik
T
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 13 Practice Exercises 789
(ln 2) ; (ln 2) (ln 2) (ln 2) ;
0
Êœ œ‚œ œ
NikBTN ijk
ijk
815 15 8
17 17
15 8
17 2 2 17 2
815
17 17
17 2 2 17 2
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ È ÈÈ È
""
(12 cosh 2t) (12 sinh 2t) (ln 2) 12 12 andaija ijijœ Êœœ
ˆ‰ ˆ‰
17 15 51 45
88##
vijkijkva
ijk
(ln 2) 6 6 6 6 (ln 2) (ln 2) 6
0
œœÊ‚œ
ˆ‰ ˆ‰ ââ
ââ
ââ
ââ
ââ
ââ
15 17 45 51
88 44
45 51
44
51 45
2#
135 153 72 153 2 and (ln 2) 2 (ln 2) ;œ Ê ‚ œ œ Ê œ œijkva vkk k k
ÈÈ
51 32
4 867
153 2
2
,È
Š‹
È
51
4
(24 sinh 2t) (24 cosh 2t) (ln 2) 45 51 (ln 2)aijaij
ÞÞ
œ ʜʜœ7
ââ
ââ
ââ
ââ
ââ
ââ
kk
45 51
44
545
22
6
0
45 51 0 32
867
va‚
21. 2 3t 3t 4t 4t (6 cos t) (3 6t) (4 8t) (6 sin t)rijkvijkœ Êœ abab
##
(3 6t) (4 8t) (6 sin t) 25 100t 100t 36 sin tÊœ œ kk ÈÈ
v### ##
25 100t 100t 36 sin t (100 200t 72 sin t cos t) a (0) (0) 10;Êœ Ê œ œ
d d
dt dt
kk kkv v
"
#
##
"Î#
ab T
6 8 (6 cos t) 6 8 (6 cos t) 100 36 cos t (0) 136aij k a aœ Ê œ œ Ê œkk k k
ÈÈÈ
## # #
a a 136 10 36 6 (0) 10 6Êœ œ œ œÊ œ
NT
Ékk ÈÈ
aaTN
###
22. (2 t) t 2t 1 t (1 4t) 2t 1 (1 4t) (2t)ri j kvi jkvœ Êœ Ê œ abab kk
È
## ###
2 8t 20t 2 8t 20t (8 40t) a (0) 2 2; 4 2œ Ê œ Êœ œ œ
ÈÈ
ab
#"
#
#"Î#
dd
dt dt
kk kkvv
Tajk
4 2 20 a a 20 2 2 12 2 3 (0) 2 2 2 3Êœ œ Êœ œ œ œ Ê œ kk kk
ÈÈÈÈ
ÈÈÈ
ÉÊŠ‹
aa aTN
## #
##
NT
23. (sin t) 2 cos t (sin t) (cos t) 2 sin t (cos t)ri jkv i jkœ Êœ
Š‹ Š‹
ÈÈ
(cos t) 2 sin t (cos t) 2 cos t (sin t) cos t ;Êœ œ Êœœ kk ÊŠ ‹ Š‹ Š‹
ÈÈ
vTijk
##
#""v
vkk ÈÈ
22
sin t (cos t) sin t sin t ( cos t) sin t 1
dd
dt dt
22 2 2
TT
œ Ê œ œ
Š‹ Š‹ Š‹ Š‹
¸¸Ê
"" " "
##
#
ÈÈ È È
ij k
sin t (cos t) sin t ; cos t sin t cos t
sin t cos t sin t
Êœ œ œ‚œ
NijkBTN
ijk
ˆ‰
¸¸ ÈÈ ÈÈ
ÈÈ
d
dt
d
dt
T
TŠ‹ Š‹ ââ
ââ
ââ
ââ
ââ
ââ
ââ
"" ""
""
22 22
22
; ( sin t) 2 cos t (sin t) cos t 2 sin t cos t
sin t 2 cos t sin t
œ œ Ê œ
""
ÈÈ
22
ika i j kva
ijk
Š‹
Èââ
ââ
ââ
ââ
ââ
ââ
È
È
‚
2 2 4 2 ; ( cos t) 2 sin t (cos t)œ Ê‚œœÊœœ œ œ
Þ
ÈÈ È È
kk Š‹
ikva a i j k,kk Š‹
ÈÈ
va
v
‚"
kk
2
22
0Êœ œ œ7
ââ
ââ
ââ
ââ
ââ
ââ
ââ
È
È
È
kk Š‹Š ‹ Š ‹
ÈÈ È
cos t 2 sin t cos t
sin t 2 cos t sin t
cos t 2 sin t cos t (cos t) 2 2 sin t (0) (cos t) 2
4
‚
va
24. (5 cos t) (3 sin t) ( 5 sin t) (3 cos t) ( 5 cos t) (3 sin t)ri jkv j ka jkœ Ê œ Ê œ
25 sin t cos t 9 sin t cos t 16 sin t cos t; 0 16 sin t cos t 0 sin t 0 or cos t 0Ê œ œ œÊ œÊ œ œva va††
t 0, or ʜ 1
#1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
790 Chapter 13 Vector-Valued Functions and Motion in Space
25. 2 4 sin 3 0 ( ) 2(1) 4 sin ( 1) 0 2 4 sin sin ri j k rijœ Êœ œ Êœ Ê œÊœ
ˆ‰ˆ‰ ˆ‰
tt t ttt
6######
"
1
1
†
t (for the first time)ʜ
1
3
26. (t) t t t 2t 3t 1 4t 9t (1) 14rijkvijkv vœ Ê œ Ê œ Ê œ
#$ # #%
kk k k
ÈÈ
(1) , which is normal to the normal planeÊœTijk
"
ÈÈÈ
14 14 14
23
(x 1) (y 1) (z 1) 0 or x 2y 3z 6 is an equation of the normal plane. Next weÊ œ œ
"
ÈÈÈ
14 14 14
23
calculate (1) which is normal to the rectifying plane. Now, 2 6t (1) 2 6 (1) (1)Najkajkvaœ Ê œ Ê ‚
6 6 2 (1) (1) 76 (1) ; (t)
23
026
œ œ Ê ‚ œ Ê œ œ œ Ê
"
ââ
ââ
ââ
ââ
ââ
ââ kk kk
ȹ
ijk
ijk v a v,ÈÈ
Š‹
ÈÈ
76 19
14 714
ds d s
dt dt t1
1 4t 9t 8t 36t , so 2 6œ œ œ Ê
¹
abab ˆ‰
"
#
#% $
"Î# #
t1
22 d s ds
14 dt dt
ÈaT Njk,
14 (x 1) (y 1) (z 1)œ ÊœÊ
22 11 8 9 11 8 9
14 14 7 14
23 14
19
219 777 7 7 7
ÈÈ È È
ÈÈ
Š‹ Š‹
Ȉ‰
ijk #
NN ijk
0 or 11x 8y 9z 10 is an equation of the rectifying plane. Finally, (1) (1) (1)œ œ œ ‚BTN
(3 3 ) 3(x 1) 3(y 1) (z 1) 0 or 3x 3y z
23
11 8 9
œœÊœ
"
Š‹Š‹
ˆ‰ââ
ââ
ââ
ââ
ââ
ââ
È
ÈÈ È
14
219 19
14 7
"" "
ijk
ijk
1 is an equation of the osculating plane.œ
27. e (sin t) ln (1 t) e (cos t) (0) ; (0) (1 0 0) is on the lineri j kvi j kv ijkr iœ Ê œ Ê œ œ Ê ßß
tt
1t
ˆ‰
"
x 1 t, y t, and z t are parametric equations of the lineÊœ œ œ
28. 2 cos t 2 sin t t 2 sin t 2 cos t rijkv ijkvœÊœÊ
Š‹Š‹ Š ‹Š‹
ÈÈ ÈÈ ˆ‰
1
4
2 sin 2 cos is a vector tangent to the helix when t the tangent lineœ œ œ Ê
Š‹Š‹
ÈÈ
11 1
44 4
ijkijk
is parallel to ; also 2 cos 2 sin the point 1 1 is on the linevr i jk
ˆ‰ ˆ‰ ˆ ‰
Š‹Š‹
ÈÈ
11 1 11 1
44 4 44 4
œÊßß
x 1 t, y 1 t, and z t are parametric equations of the lineÊœ œ œ
1
4
29. x v cos t and y gt v sin t x y gt v t
# ### # ### # # ##
!! !
""
##
##
œœÊœab ab
ˆ‰ ˆ‰
!!
30. s x y x y s x y
ÞÞ ÞÞ
œœ Êœ
Þ Þ ÞÞ ÞÞ ÞÞ ÞÞ
d
dt È## ## ##
#
xx yy
xy
xx yy
xy
ÞÞÞ ÞÞÞ
ÞÞ
ÞÞÞ ÞÞÞ
ÞÞ
Èab
œœœ
ababa b a bx y x y xx 2xxyyyy xyyx
xy xy xy
x y y x 2x x y y
ÞÞ ÞÞ Þ Þ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ
ÞÞ ÞÞ ÞÞ
Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ
xys Êœ Ê œ œœ
ÞÞ ÞÞ ÞÞ
È###"
kk ab
ÈÈ kk
xy yx x y
xy
xy
xys xy yx
ÞÞÞ ÞÞÞ Þ Þ
ÞÞ
ÞÞ
ÞÞ ÞÞ
ÞÞ ÞÞÞ ÞÞÞ
,3
31. s a since a 0œÊœÊœÊœÊœœ )) 9 ,
ss
aadsa aa
d
19
#
"""
¸¸
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 13 Additional and Advanced Exercises 791
32. (1) SOT TOD ??¸ÊœÊœ
DO OT 6380
OT SO 6380 6380 437
y
y y 5971 km;ʜ ʸ
!!
6380
6817
(2) VA 2 x 1 dyœ
'5971
6380
1ÊŠ‹
dx
dy
#
2 6380 y dyœ1'5971
6817ÈŠ‹
##
6380
6380 y
È
2 6380 dy 2 6380yœœ11
'5971
6817 cd
')"(
&*("
16,395,469 km 1.639 10 km ;œ¸‚
#(#
(3) percentage visible 3.21%¸¸
16,395,469 km
4 (6380 km)
1
CHAPTER 13 ADDITIONAL AND ADVANCED EXERCISES
1. (a) ( ) (a cos ) (a sin ) b [( a sin ) (a cos ) b ] ; 2gzrijk ijkv)))) ) )œÊœ œœ
ddd
dt dt dt
r r)kk ȸ¸
ab 2œ Êœ œ Ê œ œ
ÈÉÉÉÉ
¸
##
œ#
dd d
dt dt a b a b dt a b a b
2gz 2gb 4 gb gb
)) )
)11
)1
(b) dt 2 t C; t 0 0 C 0
dd
dt a b a b a b
2gb 2gb 2gb
))
)
)
œ Ê œ Ê œ œÊœÊ œ
ÉÉ É
"Î#
È))
2 t ; z b zÊœ Êœ œÊœ)))
"Î#
É2gb gbt gb t
a b 2 a b 2 a b
ab ab
(c) (t) [( a sin ) (a cos ) b ] [( a sin ) (a cos ) b ] , from part (b)vijkijkœœ œ
dd
dt dt a b
gbt
r)) ))
)Š‹
(t) ;Êœ œvT
’“Š‹
( a sin ) (a cos ) b gbt gbt
a b a b a b
))i j k
ÈÈÈ
[( a cos ) (a sin ) ] [( a sin ) (a cos ) b ]
dd d
dt dt dt
rœ )) ) )ij i jk
ˆ‰
))
#
[( a cos ) (a sin ) ] [( a sin ) (a cos ) b ]œ
Š‹ Š‹
gbt gb
a b a b
#)) ) )ij i jk
a [( cos ) (sin ) ]œ
’“Š‹Š‹
( a sin ) (a cos ) b gb gbt
a b a b a b
#
))i j k
ÈÈ ))ij
a (there is no component in the direction of ).œ
gb gbt
a b a b
È
#
TN B
Š‹
2. (a) ( ) (a cos ) (a sin ) b [(a cos a sin ) (a sin a cos ) b ] ;rijk i jk) ) ) )) ) ))) )) )œÊœ
d d
dt dt
r)
2gz a a b kk a b
ȸ¸ ˆ‰
vœœœ Êœ
ddd
dt dt dt
2gb
a a b
r####
"Î#
))) )
)
È
È
(b) s dt a a b dt a a b d a a u b duœœ œ œ
'' ' '
00 0 0
tt t
kkabababv#### #### ####
"Î# "Î# "Î#
)))
d
dt
)
a u du a c u du, where cœœ œ
''
00
ÉÈ
a b
aa
a b
###
Èkk
s a c u ln u c u c c ln c c ln cÊœ œ
’“Š ‹
ÈÈÈÈ
¹¹ ¹¹
uc a
## #
## ## ## ##
!
##
)
)) ) )
3. r ; 0 0 (1 e)r (e sin œÊœ œÊ œÊ
(1 e)r (1 e)r (e sin ) (1 e)r (e sin )
1 e cos d (1 e cos ) d (1 e cos )
dr dr
!
)) )) )
))))0œ
sin 0 0 or . Note that 0 when sin 0 and 0 when sin 0. Since sin 0 onʜʜ ))1 ) ) )
dr dr
dd))
0 and sin 0 on 0 , r is a minimum when 0 and r(0) r œ œ œ1) ) )1 ) (1 e)r
1 e cos 0
!
4. (a) f(x) x 1 sin x 0 f(0) 1 and f(2) 2 1 sin 2 since sin 2 1; since f is continuousœ œ Ê œ œ Ÿ
"""
###
kk
on [0 2], the Intermediate Value Theorem implies there is a root between 0 and 2ß
(b) Root 1.4987011335179¸
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

792 Chapter 13 Vector-Valued Functions and Motion in Space
5. (a) x y and r r r [(cos ) (sin ) ] r [( sin ) (cos ) ] x and
.. .
..
..
vijvu u i j i j viœ œ œ Ê œ
r))))))
)ab ˆ‰ †
r cos r sin x r cos r sin ; y and r sin r cos
.. .
.. .
..
vi vj vj†††œ Êœ œ œ))) ))) )) )
y r sin r cos
...
ʜ )) )
(b) (cos ) (sin ) x cos y sin
..
uijvu
rr
œ Êœ)) ))†
r cos r sin (cos ) r sin r cos (sin ) by part (a),
..
..
œ
ˆ‰ˆ‰
))) ) ))) )
r ; therefore, r x cos y sin ;
..
..
Êœ œ vu†r))
uijvu
))
œ Ê œ (sin ) (cos ) x sin y cos
..
)) ))†
r cos r sin ( sin ) r sin r cos (cos ) by part (a) r ;
..
.. .
œ Êœ
ˆ‰ˆ‰
))) ) ))) ) )vu†)
therefore, r x sin y cos
...
)))œ
6. f( ) f ( ) f ( ) f ( ) ; r rvuuœÊœ Êœ œ)) ))
dr d d r d d dr d
dt dt dt dt dt dt dt
wwww
#
))))
)
ˆ‰ r
cos r sin sin r cos r f f ;œ Êœ œ
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
kk ab
’“’“
)) ) )
dr d dr d dr d d
dt dt dt dt dt dt dt
)) ) )
ijv
##
#w#
"Î# "Î#
#
x y y x , where x r cos and y r sin . Then ( r sin ) (cos ) kkk kva‚œ œ œ œ
ÞÞÞ ÞÞÞ )) ))
dx d dr
dt dt dt
)
( 2 sin ) (r cos ) (r sin ) (cos ) ; (r cos ) (sin ) Êœ œ
dx d dr d d dr d dr
dt dt dt dt dt dt dt dt dt
dy
)))) ))
))) )
ˆ‰
#
(2 cos ) (r sin ) (r cos ) (sin ) . Then Êœ ‚
dy
dt dt dt dt dt dt
ddr d d dr
)) ))
)))
ˆ‰ kk
#va
(after algebra) r r r 2 f f f 2 fœœ†much #ww w
$#$
ˆ‰ ˆ‰ ˆ‰
Š‹
ab
d d dr d d r d dr d
dt dt dt dt dt dt dt dt
22
)))) )
Êœ œ,kk
kk ab
‘
ab
va
v
‚†
f ff 2f
f f
22
7. (a) Let r 2 t and 3t 1 and 3 0. The halfway point is (1 3) t 1;œ œ Ê œ œ Ê œ œ ß Êœ)dr d d r d
dt dt dt dt
))
r (1) 3 ; r r 2 (1) 9 6vu uv uua u ua uuœ Êœ œ Êœ
dr d d r d d dr d
dt dt dt dt dt dt dt
rr r r
))))
)) ) )
’“’ “
ˆ‰
#
(b) It takes the beetle 2 min to crawl to the origin the rod has revolved 6 radiansÊ
L [f( )] f ( ) d 2 d 4 dÊœ œ œ
'' '
00 0
66 6
Écd Ɉ ‰ ˆ ‰ É
))) ) )
#w
##""
#
)))
33 399
4
d ( 6) 1 d ( 6) 1 ln 6 ( 6) 1œ œ œ
''
00
66
ÉÈÈ È
’“
¸¸
37 12
93 3
(6)
" " "
## #
##
'
!
)) )
))) ) ))
37 ln 37 6 6.5 in.œ ¸
ÈÈ
Š‹
"
6
8. (a) x r cos dx cos dr r sin d ; y r sin dy sin dr r cos d ; thusœÊœ œÊœ) ) )) ) ) ))
dx cos dr 2r sin cos dr d r sin d and
### ###
œ ))))))
dy sin dr 2r sin cos dr d r cos d ds dx dy dz dr r d dz
### ### #######
œ Ê œœ )))))) )
2
(c) r e dr e d œÊœ
))
)
L dr r d dzʜ
'0
ln 8 È### #
)
eee dœ
'0
ln 8È###)))
)
3e d 3 eœœ
'0
ln 8 ln 8
0
ÈÈ
’“
))
)
83 3 73œœ
ÈÈ È
(b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 13 Additional and Advanced Exercises 793
9. (a) a right-handed frame of unit vectors
cos sin 0
sin cos 0
uu k
ijk
r‚œ œÊ
)
ââ
ââ
ââ
ââ
ââ
ââ
))
))
(b) ( sin ) (cos ) and ( cos ) (sin )
d
dd
d
uu
r
))
)
œ œ œ œ)) ))iju iju
r
(c) From Eq. (7), r r z r r r r r zvu u k av u u u u u kœ Êœœ
ÞÞÞÞÞ
ÞÞÞÞÞ
ÞÞÞ
ÞÞ Þ
rrr
))))
))))
ab
ˆ‰
rr r 2r zœ
ÞÞ Þ
ÞÞÞÞ
ÞÞ
Š‹
ˆ‰
)))
#uuk
r)
10. (t) (t) m (t) m m ( m ) ( m ) m ; m Lr v vr vvraraFa rœ‚ Êœ‚ ‚ Êœ‚ ‚ œ‚ œ Ê
dd d d c
dt dt dt dt
Lr r L
r
ˆ‰
Š‹ kk
m m ( ) constant vectorœ Ê œ‚ œ‚ œ ‚ œ Ê œararr rr0L
dcc
dt
L
rr
Š‹
kk kk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
794 Chapter 13 Vector-Valued Functions and Motion in Space
NOTES:
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
CHAPTER 14 PARTIAL DERIVATIVES
14.1 FUNCTIONS OF SEVERAL VARIABLES
1. (a) f 0, 0 0 (b) f 1, 1 0 (c) f 2, 3 58ab a b abœœ œ
(d) f 3, 2 33ab œ
2. (a) f 2, (b) f 3, (c) f ,
ˆ‰ ˆ ‰ ˆ‰
11
62 12 4
3111
22
œœ œ
ÈÈÈ
1
(d) f , 7 1
ˆ‰
œ
1
2
3. (a) f 3, 1, 2 (b) f 1, , (c) f 0, , 0 3ab ˆ‰ ˆ‰
œ œ œ
4118 1
5245 3
(d) f 2, 2, 100 0abœ
4. (a) f 0, 0, 0 7 (b) f 2, 3, 6 0 (c) f 1, 2, 3 35ab ab ab
È
œœœ
(d) f , ,
Š‹
É
456 21
222 2
ÈÈÈ œ
5. Domain: all points x y on or above the lineabß
yx2œ
6. Domain: all points x y outside the circleabß
xy4
22
œ
7. Domain: all points x y not liying on the graphabß
of y x or y xœœ
3
8. Domain: all points x y not liying on the graphabß
of x y 25
22
œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
796 Chapter 14 Partial Derivatives
9. Domain: all points x y satisfyingabß
x 1yx 1
22
ŸŸ
10. Domain: all points x y satisfyingabß
x1y1 0abab
11. Domain: all points x y satisfyingabß
x2x2y3y3 0abababab
12. Domain: all points x y inside the circleabß
x y 4 such that x y 3
22 22
œ Á
13. 14.
15. 16.
17. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.1 Functions of Several Variables 797
(c) level curves are straight lines y x c parallel to the line y xœ œ
(d) no boundary points
(e) both open and closed
(f) unbounded
18. (a) Domain: set of all x y so that y x 0 y xabßÊ
(b) Range: z 0
(c) level curves are straight lines of the form y x c where c 0œ
(d) boundary is y x 0 y x, a straight line
Èœ Ê œ
(e) closed
(f) unbounded
19. (a) Domain: all points in the xy-plane
(b) Range: z 0
(c) level curves: for f(x y) 0, the origin; for f x y c 0, ellipses with center 0 0 and major and minorßœ ßœ ßab ab
axes along the x- and y-axes, respectively
(d) no boundary points
(e) both open and closed
(f) unbounded
20. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
(c) level curves: for f x y 0, the union of the lines y x; for f x y c 0, hyperbolas centered atab abßœ œ„ ßœÁ
0 0 with foci on the x-axis if c 0 and on the y-axis if c 0abß
(d) no boundary points
(e) both open and closed
(f) unbounded
21. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
(c) level curves are hyperbolas with the x- and y-axes as asymptotes when f x y 0, and the x- and y-axesabßÁ
when f(x y) 0ߜ
(d) no boundary points
(e) both open and closed
(f) unbounded
22. (a) Domain: all x y 0 yababßÁß
(b) Range: all real numbers
(c) level curves: for f x y 0, the x-axis minus the origin; for f x y c 0, the parabolas y c x minus theab abßœ ßœÁ œ#
origin
(d) boundary is the line x 0œ
(e) open
(f) unbounded
23. (a) Domain: all x y satisfying x y 16abß
##
(b) Range: z "
4
(c) level curves are circles centered at the origin with radii r 4
(d) boundary is the circle x y 16
##
œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

798 Chapter 14 Partial Derivatives
(e) open
(f) bounded
24. (a) Domain: all x y satisfying x y 9abߟ
##
(b) Range: 0 z 3ŸŸ
(c) level curves are circles centered at the origin with radii r 3Ÿ
(d) boundary is the circle x y 9
##
œ
(e) closed
(f) bounded
25. (a) Domain: x y 0 0ababßÁß
(b) Range: all real numbers
(c) level curves are circles with center 0 0 and radii r 0abß
(d) boundary is the single point 0 0abß
(e) open
(f) unbounded
26. (a) Domain: all points in the xy-plane
(b) Range: 0 z 1Ÿ
(c) level curves are the origin itself and the circles with center 0 0 and radii r 0abß
(d) no boundary points
(e) both open and closed
(f) unbounded
27. (a) Domain: all x y satisfying 1 y x 1abß ŸŸ
(b) Range: zŸŸ
11
##
(c) level curves are straight lines of the form y x c where 1 c 1œ ŸŸ
(d) boundary is the two straight lines y 1 x and y 1 xœ œ
(e) closed
(f) unbounded
28. (a) Domain: all x y , x 0abßÁ
(b) Range: z
11
##
(c) level curves are the straight lines of the form y c x, c any real number and x 0œÁ
(d) boundary is the line x 0œ
(e) open
(f) unbounded
29. (a) Domain: all points x y outside the circle x y 1abߜ
##
(b) Range: all reals
(c) Circles centered ar the origin with radii r 1
(d) Boundary: the cricle x y 1
##
œ
(e) open
(f) unbounded
30. (a) Domain: all points x y inside the circle x y 9abߜ
##
(b) Range: z ln 9
(c) Circles centered ar the origin with radii r 9
(d) Boundary: the cricle x y 9
##
œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.1 Functions of Several Variables 799
(e) open
(f) bounded
31. f 32. e 33. a
34. c 35. d 36. b
37. (a) (b)
38. (a) (b)
39. (a) (b)
40. (a) (b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
800 Chapter 14 Partial Derivatives
41. (a) (b)
42. (a) (b)
43. (a) (b)
44. (a) (b)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
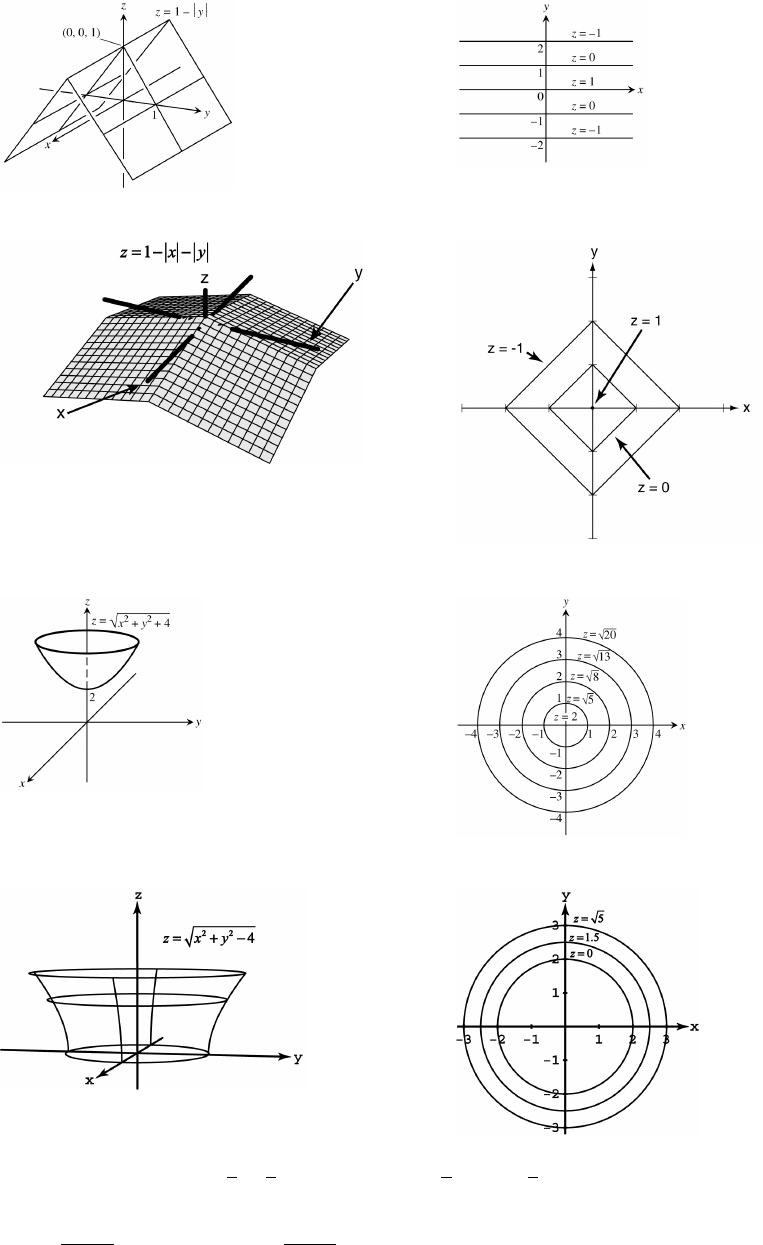
Section 14.1 Functions of Several Variables 801
45. (a) (b)
46. (a) (b)
47. (a) (b)
48. (a) (b)
49. f x y 16 x y and 2 2 2 z 16 2 2 2 6 6 16 x y x y 10ab Š‹ Š‹Š‹
ÈÈ È È
ßœ ß Êœ œÊœ Ê œ
## ## ##
##
50. f x y x 1 and 1 0 z 1 1 0 x 1 0 x 1 or x 1ab ab
ÈÈ
ßœ ßÊœ œÊ œÊœ œ
##
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
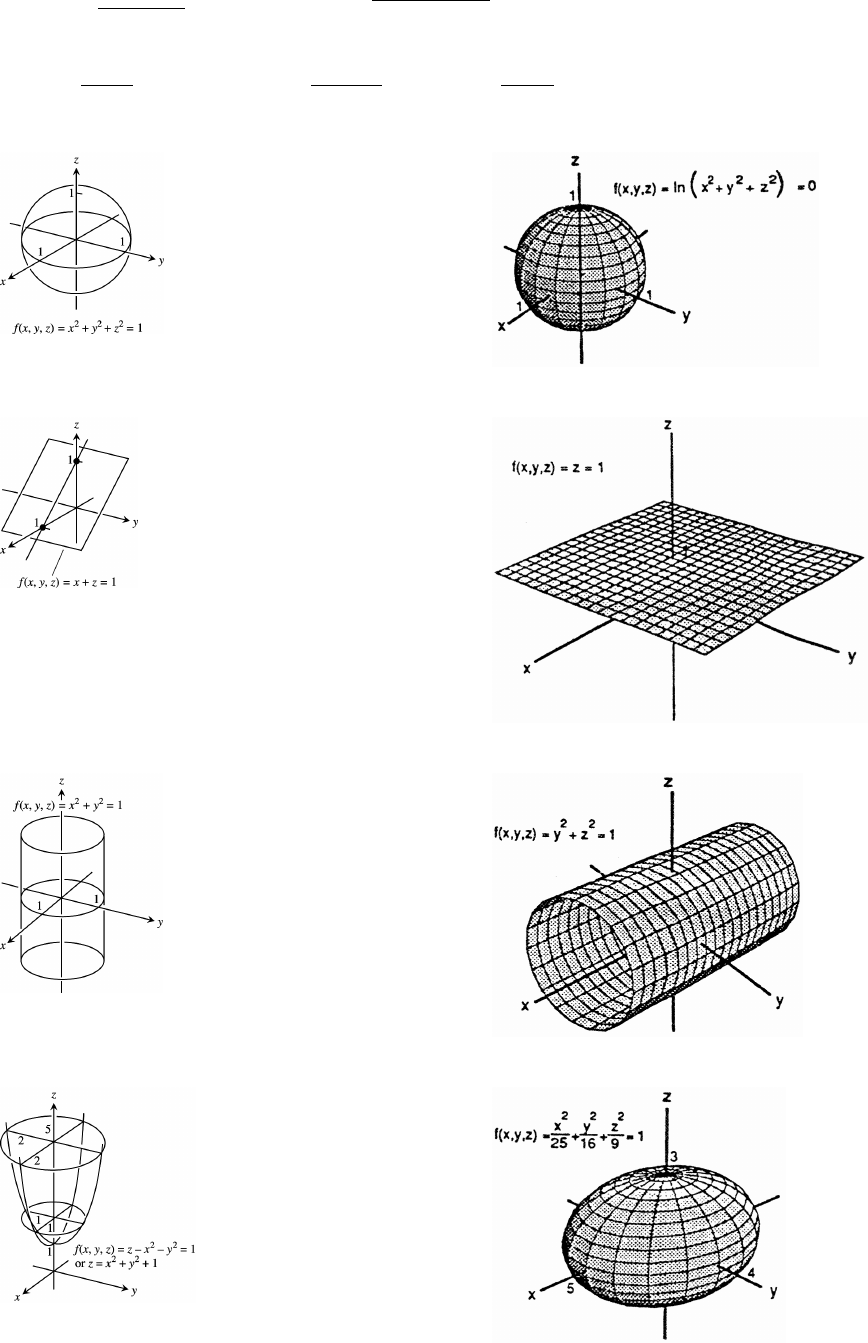
802 Chapter 14 Partial Derivatives
51. f x y x y 3 and 3, 1 z 3 1 3 1 x y 3 1 x y 4ab a b ab
ÈÉ
ßœ Êœ œÊœÊœ
2222
52. f x y and 1 1 z 3 3 y 4x 3ab a bßœ ß Êœ œÊœ Êœ
2y x 2y x
xy1 1 1+1 xy1
11
#ab a b
ab
53. 54.
55. 56.
57. 58.
59. 60.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
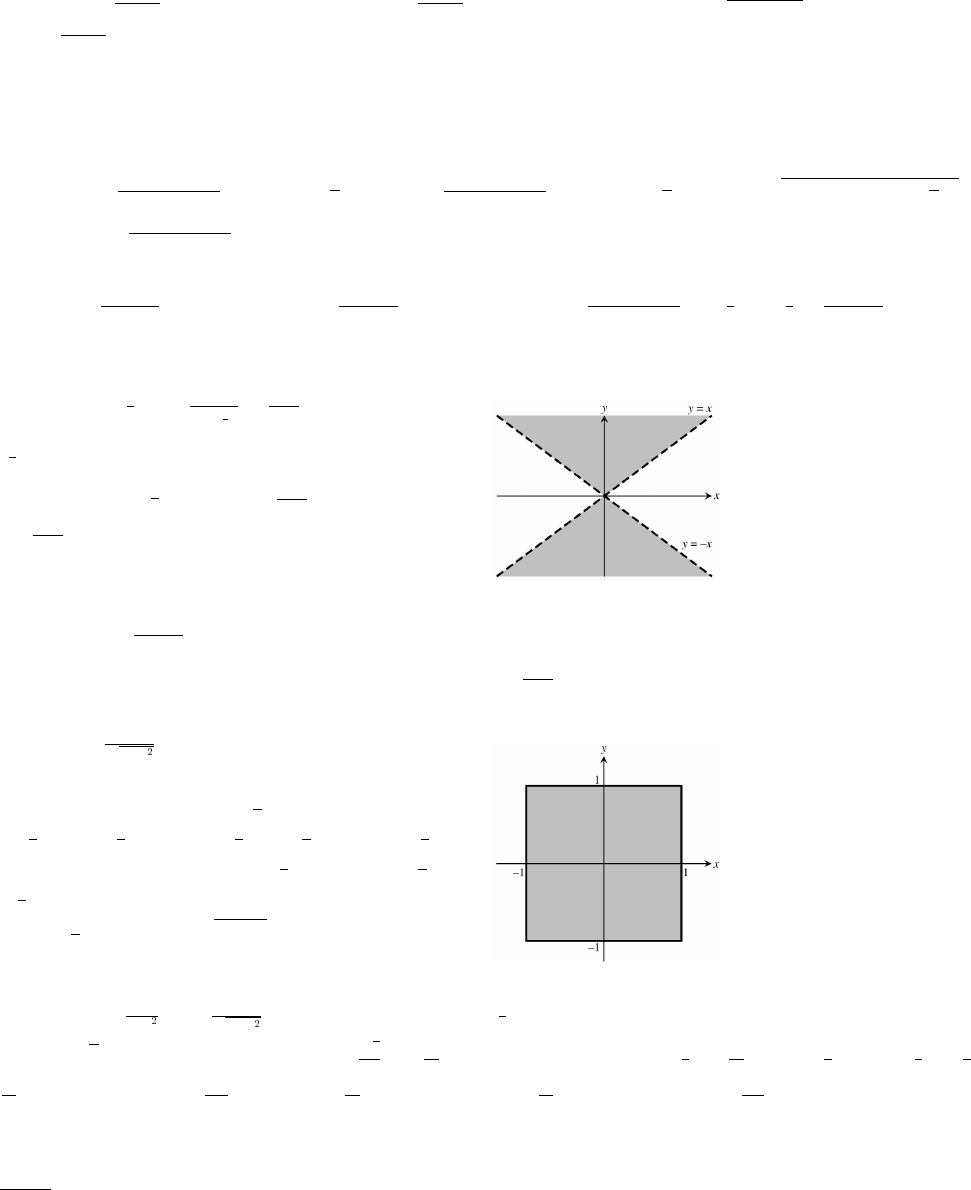
Section 14.1 Functions of Several Variables 803
61. f x y z x y ln z at 3 1 1 w x y ln z; at 3 1 1 w 3 1 ln 1 2ab ab ab ab
ÈÈÈ
ßßœ ßßÊœ ßßÊœœ
xyln z 2ʜ
È
62. f x y z ln x y z at w ln x y z ; at w ln 1 2 1 ln 4ababababababß ß œ "ß #ß " Ê œ "ß #ß " Ê œ œ
## ##
ln 4 ln x y z x y z 4ʜ ʜab
####
63. g x y z x y z at 1 1 2 w x y z ; at 1 1 2 w 1 1 2ab ab
ÈÈ
Š‹ Š‹ Š‹
ÈÈÈ
Ê
ßßœ ßß Êœ ßß Êœ
## ## # #
22 2
2 2 xyz xyz4œÊœ Êœ
È##
##
22
64. g x y z at 1 0 2 w ; at 1 0 2 wab ab abßß œ ßß Ê œ ßß Ê œ œ Ê œ
xyz xyz xyz
2xyz 2xyz 21 0 2 4 4 2xyz
10 2 11
ab
ab a b
2xyz 0Ê œ
65. f x y forab!Š‹
ßœ œ œ
_
œ
n0
x1
yyx
n
1
y
Š‹
x
y
1 Domain: all points x, y satisfying x y ;
¹¹ ab
x
y Ê l ll l
at 1, 2 since z 2ab ¹¹
ÊÊœœ
1
212
21
2y2xʜʜ
y
yx
66. g x y z e Domain: all points x, y, z satisfying z 0; at ln 4 ln 9 2ab ab a b
!
ßß œ œ Ê Á ß ß
_
œn0
(x y)
n! z
bn
nÐÑÎxy z
w e e e 6 6 e ln 6Êœ œ œ œÊœ Ê œ
ÐÑÎ Ð ÑÎ ÐÑÎ
ln4 ln9 2 ln36 2 ln6 x y z xy
z
67. f x y sin y sin x Domain: all pointsabßœ œÊ
'x
yd
1
11
)
)
È
x, y satisfying 1 x 1 and 1 y 1;ab Ÿ Ÿ Ÿ Ÿ
at 0, 1 sin 1 sin 0 sin y sin xabÊœÊ
11 11
2
1
. Since sin y and sin x , inœŸŸŸŸ
11 11 1
22 22 2
11
order for sin y sin x to equal , 0 sin y and
11 1
22
ŸŸ
11
sin x 0; that is 0 y 1 and 1 x 0. ThusŸ Ÿ Ÿ Ÿ Ÿ Ÿ
1
2
1
ysin sinx 1x, x0œ œŸ
ˆ‰
È
1
2
12
68. g x y z tan y tan x sin Domain: all points x, y, z satisfying 2 z 2;ab ab
ˆ‰
ßß œ œ Ê Ÿ Ÿ
''
x0
yz
dt d z
1t 2
4
111
)
)
È
at 0 1 3 tan 1 tan 0 sin tan y tan x sin . Since sin ,
Š‹ Š‹
Ȉ‰ ˆ‰
ßßÊ œÊ œ Ÿ Ÿ
111 111 1
3
212 212 2 22
7z7z
È1111
tan y tan x z 2 sin tan y tan x , tan y tan x
11111
12 12 12 12 12
11 11 11
13 7 13
ŸŸÊœ ŸŸ
ˆ‰
69-72. Example CAS commands:
:Maple
with( plots );
f := (x,y) -> x*sin(y/2) + y*sin(2*x);
xdomain := x=0..5*Pi;
ydomain := y=0..5*Pi;
x0,y0 := 3*Pi,3*Pi;
plot3d( f(x,y), xdomain, ydomain, axes=boxed, style=patch, shading=zhue, title="#69(a) (Section 14.1)" );
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

804 Chapter 14 Partial Derivatives
plot3d( f(x,y), xdomain, ydomain, grid=[50,50], axes=boxed, shading=zhue, style=patchcontour, orientation=[-90,0],
title="#69(b) (Section 14.1)" ); # (b)
L := evalf( f(x0,y0) ); # (c)
plot3d( f(x,y), xdomain, ydomain, grid=[50,50], axes=boxed, shading=zhue, style=patchcontour, contours=[L],
orientation=[-90,0], title="#45(c) (Section 13.1)" );
73-76. Example CAS commands:
:Maple
eq := 4*ln(x^2+y^2+z^2)=1;
implicitplot3d( eq, x=-2..2, y=-2..2, z=-2..2, grid=[30,30,30], axes=boxed, title="#73 (Section 14.1)" );
77-80. Example CAS commands:
:Maple
x := (u,v) -> u*cos(v);
y := (u,v) ->u*sin(v);
z := (u,v) -> u;
plot3d( [x(u,v),y(u,v),z(u,v)], u=0..2, v=0..2*Pi, axes=boxed, style=patchcontour, contours=[($0..4)/2], shading=zhue,
title="#77 (Section 14.1)" );
69-60. Example CAS commands:
: (assigned functions and bounds will vary)Mathematica
For 69 - 72, the command draws 2-dimensional contours that are z-level curves of surfaces z = f(x,y).ContourPlot
Clear[x, y, f]
f[x_, y_]:= x Sin[y/2] y Sin[2x]
xmin= 0; xmax= 5 ; ymin= 0; ymax= 5 ; {x0, y0}={3 , 3 };1111
cp= ContourPlot[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, ContourShading False];Ä
cp0= ContourPlot[[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, Contours {f[x0,y0]}, ContourShading False,ÄÄ
PlotStyle {RGBColor[1,0,0]}];Ä
Show[cp, cp0]
For 73 - 76, the command will be used. Write the function f[x, y, z] so that when it is equated to zero, itContourPlot3D
represents the level surface given.
For 73, the problem associated with Log[0] can be avoided by rewriting the function as x2 + y2 +z2 - e1/4
Clear[x, y, z, f]
f[x_, y_, z_]:= x y z Exp[1/4]
222
ContourPlot3D[f[x, y, z], {x, 5, 5}, {y, 5, 5}, {z, 5, 5}, PlotPoints {7, 7}]; Ä
For 77 - 80, the command ParametricPlot3D will be used. To get the z-level curves here, we solve x and y in terms of z
and either u or v (v here), create a table of level curves, then plot that table.
Clear[x, y, z, u, v]
ParametricPlot3D[{u Cos[v], u Sin[v], u}, {u, 0, 2}, {v, 0, 2p}];
zlevel= Table[{z Cos[v], z sin[v]}, {z, 0, 2, .1}];
ParametricPlot[Evaluate[zlevel],{v, 0, 2 }];1
14.2 LIMITS AND CONTINUITY IN HIGHER DIMENSIONS
1. lim
Ðß ÑÄÐß Ñxy 00
3x y 5 3(0) 0 5
xy2 002
5
#
œœ
2. lim 0
Ðß ÑÄÐß Ñxy 04
x0
y4
ÈÈ
œœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.2 Limits and Continuity in Higher Dimensions 805
3. lim x y 1 3 4 1 24 2 6
Ðß ÑÄÐß Ñxy 34 ÈÈÈ
È
## ##
œ œ œ
4. lim
Ðß ÑÄÐßÑxy 2 3 Š‹
‘ˆ‰ˆ‰
"" " " " "
#
#
##
xy 3 6 36
œ œ œ
5. lim sec x tan y (sec 0) tan (1)(1) 1
Ðß ÑÄ ßxy 0
ˆ‰
4
œœœ
ˆ‰
1
4
6. lim cos cos cos 0 1
Ðß ÑÄÐß Ñxy 00 Š‹Š‹
xy
xy1 001
00
œœœ
7. lim e e e
Ðß ÑÄÐß Ñxy 0ln2
xy 0 ln2 ln "
#
œœœ
ˆ‰
1
2
8. lim ln 1 x y ln 1 (1) (1) ln 2
Ðß ÑÄÐß Ñxy 11 kkk kœ œ
## # #
9. lim lim e e lim 1 1 1
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ä
xy 00 xy 00 x0
e sin x sin x sin x
xxx
y
yœœœœab
ˆ‰ ˆ‰
!††
10. lim cos xy cos cos
Ðß ÑÄÐÎ ß Ñxy 12713ÈɈ‰ ˆ‰
33
œœœ
11
27 3 2
3
11
11. lim
Ðß ÑÄÐß ÎÑxy 1 61
x sin y
x1 11 2 4
1sin 12 1
Î
œœœ
†ˆ‰
6
12. lim 2
Ðß ÑÄ ßxy 0
ˆ‰
2
cos y 1
ysin x 1
cos 0
0sin
11
"
œœœ
ab
ˆ‰
13. lim lim lim (x y) ( 1) 0
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á
xy 11 xy 11 xy 11
xy
x 2xy y (x y)
xy xy
œœœ"œ
14. lim lim lim (x y) (1 1) 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á
xy 11 xy 11 xy 11
xy
x y (x y)(x y)
xy xy
œ œ œœ
15. lim lim lim (y 2) (1 2) 1
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
ÁÁ
xy 11 xy 11 xy 11
x1 x1
xyy2x2 (x1)(y2)
x1 x1
œ œ œœ
16. lim lim lim
Ðß ÑÄÐßÑ Ðß ÑÄÐßÑ Ðß ÑÄÐßÑ
Á Á Á Á Á
xy 2 4 xy 2 4 xy 2 4
y 4, xx y 4, xx xx
y4 y4
x y xy 4x 4x x(x 1)(y 4) x(x 1)
1
#
"
œœœ
(2 1)#
"
œ
17. lim lim lim x y 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
ÁÁ
xy 00 xy 00 xy 00
xy xy
xy2x2y x y x y2
xy xy
ÈÈÈ
ÈÈÈ
ÈÈ
ÈÈ
ˆ‰ˆ ‰
œœ
ˆ‰
ÈÈ
0022œœ
Š‹
ÈÈ
Note: (x y) must approach (0 0) through the first quadrant only with x y.ßß Á
18. lim lim lim x y 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á Á
xy 22 xy 22 xy 22
xy4 xy 4 xy4
xy4
xy2 xy2
xy2 xy2
ÈÈ
ˆ‰ˆ‰
ÈÈ
œœ
ˆ‰
È
222 224œ œœ
Š‹
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

806 Chapter 14 Partial Derivatives
19. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á
xy 20 xy 20 xy 20
2x y 4 2x y 4
ÈÈ
ˆ‰ˆ‰
ÈÈ È
2xy2 2xy2
2xy4 2xy2 2xy2 2xy
#
"
œœ
œœœ
"""
#
È(2)(2) 0 22 4
20. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á
xy 43 xy 43 xy 43
xy1 xy 1
ÈÈ
ÈÈ
ˆ‰ˆ‰
ÈÈ È
ÈÈ È
xy1 xy1
xy1 xy1xy1 xy1
"
œœ
œœœ
"""
ÈÈ
431 22 4
21. lim lim lim lim cos r 1
Ðß ÑÄÐß Ñ ÄÄ Ä
xy 00 r0 r0 r0
sin x y sin r 2r cos r
xy r 2r
a b ab ab†
#
œœ œ œab
22. lim lim lim 0
Ðß ÑÄÐß Ñ ÄÄ
xy 00 u0 u0
1 cos xy
xy u 1
1cosu sinu
ab
œœœ
23. lim lim lim x xy y 1 1 1 1 3
Ðß ÑÄÐß"Ñ Ðß ÑÄÐß"Ñ Ðß ÑÄÐß"Ñxy 1 xy 1 xy 1
xy
xy xy
xyx xyy 222 2
33 22
œœœœ
ab
ˆ‰ a b ababab
Š‹
24. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 22 xy 22 xy 22
xy xy
x y xyxyx y xyx y 222 2 32
111
44 22 22 22
œœœœ
ababa b aba baba b
25. lim
TÄÐßßÑ134 Š‹
""" """
xyz 134 12 12
1243 19
œœ œ
26. lim
TÄÐßßÑ111
2xy yz 2(1)( 1) ( 1)( 1)
xz 1(1) 11
2
#
" "
œœœ
27. lim sin x cos y sec z sin 3 cos 3 sec 0 1 1 2
TÄÐßßÑ330 abab
### ## # #
œ œœ
28. lim tan (xyz) tan 2 tan
TÄ ß ß
ˆ‰
1
42
2
" " "
"
#
œ œ
ˆ‰ˆ‰
44
††
11
29. lim ze cos 2x 3e cos 2 (3)(1)(1) 3
TÄÐßßÑ103
2y 2 0
œœœ1
30. lim ln x y z ln 2 ( 3) 6 ln 49 ln 7
TÄÐßß Ñ236 ÈÈ È
### # ##
œ œ œ
31. (a) All x y (b) All x y except 0 0ab ab abßßß
32. (a) All x y so that x y (b) All x yab abßÁ ß
33. (a) All x y except where x 0 or y 0 (b) All x yab abßœœ ß
34. (a) All x y so that x 3x 2 0 x 2 x 1 0 x 2 and x 1ab ababßÁÊÁÊÁÁ
#
(b) All x y so that y xabßÁ
#
35. (a) All x y z (b) All x y z except the interior of the cylinder x y 1ab abßß ßß œ
##
36. (a) All x y z so that xyz 0 (b) All x y zab abßß ßß
37. (a) All x y z with z 0 (b) All x y z with x z 1ab abßß Á ßß Á
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.2 Limits and Continuity in Higher Dimensions 807
38. (a) All x y z except x 0 0 (b) All x y z except 0 y 0 or x 0 0ab ab ab ababßß ßß ßß ßß ßß
39. (a) All x y z such that z x y 1 (b) All x y z such that z x yab ab È
ßß ßß Á
22 22
40. (a) All x y z such that x y z 4 abßß Ÿ
222
(b) All x y z such that x y z 9 except when x y z 25abßß œ
222 222
41. lim lim lim lim lim ;
Ðß ÑÄÐß Ñ
œ
ÄÄÄÄ
xy 00
along y x
x0
x0 x0 x0 x0
œœœœœ
xxxx
xy xx 2 x 2x 2 2
ÈÈÈÈÈÈ
kk
""
lim lim lim lim
Ðß ÑÄÐß Ñ
œ
ÄÄ Ä
xy 00
along y x
x0
x0 x0 x0
œœœ œ
xxx
xy 2 x 2( x) 2 2
ÈÈÈÈÈ
kk
""
42. lim lim 1; lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
œ
ÄÄÄ
œ
xy 00 xy 00
along y 0
x0 x0 x0
along y x
xx x xx
xy x0 xy 2x
xx
œœ œ œœ
ab "
#
43. lim lim lim different limits for d
Ðß ÑÄÐß Ñ
œ
ÄÄ
xy 00
along y kx
x0 x0
xy
xy xkx
xkx
xkx
xkx 1k
1k
œœœÊ
ab
ab ifferent values of k
44. lim lim lim lim ; if k 0, the limit is 1; but if k
Ðß ÑÄÐß Ñ
œ
Á
ÄÄÄ
xy 00
along y kx
k0
x0 x0 x0
xy x(kx)
xy x(kx) kx k
kx k
kk k k k k kk
œœœ 0, the limit is 1
45. lim lim different limits for different values of k, k 1
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k1
x0
xy
xy xkx 1k
xkx 1k
œœÊ Á
46. lim lim lim different limits for different values of k,
Ðß ÑÄÐß Ñ
œ
Á
ÄÄ
xy 00
along y kx
k1
x0 x0
xy
xy xkx 1k 1k
xkx xk k
22
œœœÊ k1Á
47. lim lim different limits for different values of k, k 0
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k0
x0
xy
ykxk
xkx 1k
œœÊ Á
48. lim lim different limits for different values of k
Ðß ÑÄÐß Ñ
œ
Ä
xy 00
along y kx
x0
xy
xy xkx 1k
kx k
42 424 2
4
œœÊ
49. lim lim lim y 1 2; lim lim li
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
œœ
ÄÄ Ä
xy 11 xy 11
along x 1 along y x
y1 y1 y1
xy1 y1 xy1 y1
y1 y1 y1 y1
22 23
œœœ œœab m y y 1 3
y1Äab
2 œ
50. lim lim lim ; lim lim
Ðß ÑÄÐßÑ Ðß ÑÄÐßÑ
œ
ÄÄ Ä
œ
xy 1 1 xy 1 1
along y 1
x1 x1 x1
along y x
xy 1 xy 1
xy x1 x1 2 xy
x1 1 1
22 2 22
œœœ œ
2
x1 xx1
xx x1x1
32
24 2
œ lim
x1Äaba b
œ3
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

808 Chapter 14 Partial Derivatives
51. f x, y
1if y x
1if y 0
0otherwise
abÚ
Û
Ü
œ
Ÿ
%
(a) lim f x, y 1 since any path through 0, 1 that is close to 0, 1 satisfies y x
Ðß ÑÄÐß Ñxy 01 ab ab abœ
%
(b) lim f x, y 0 since any path through 2, 3 that is close to 2, 3 does not satisfiy either y x or y 0
Ðß ÑÄÐß Ñxy 23 ab ab abœŸ
%
(c) lim f x, y 1 and lim f x, y 0 lim f x, y does not exist
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
œœ
xy 00 xy 00 xy 00
along x 0 along y x
ab ab abœœÊ
2
52. f x, y xif x0
xif x0
abœ
œ
2
3
(a) lim f x, y 3 9 since any path through 3, 2 that is close to 3, 2 satisfies x 0
Ðß ÑÄÐßÑxy 3 2 ab ab abœœ
2
(b) lim f x, y 2 8 since any path through 2, 1 that is close to 2, 1 satisfies x 0
Ðß ÑÄÐß Ñxy 21 abab ab abœ œ
3
(c) lim f x, y 0 since the limit is 0 along any path through 0, 0 with x 0 and the limit is also zero along
Ðß ÑÄÐß Ñxy 00 ab abœ
any path through 0, 0 with x 0ab
53. First consider the vertical line x 0 lim lim lim 0 0. Now consider anœÊ œ œ œ
Ðß ÑÄÐß Ñ
œ
ÄÄ
xy 00
along x 0
y0 y0
2x y
xy
20 y
0y
2
42 4
2
2
ab
ab y nonvertical
through 0, 0 . The equation of any line through 0, 0 is of the form y mx lim f x y lim
ymx
ab ab abœÊ ßœ
œ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00
along alo
ng
ymxœ
2x y
xy
2
42
lim lim lim lim 0. Thus limœœœœœ
x0 x0 x0 x0 xy 00
any line though
ÄÄÄÄ Ðß ÑÄÐß Ñ
2x mx
xmx
2mx 2mx 2mx
xmx xxm xm
2
42422222 22
33
ab
ab ab ab
a b0, 0
2x y
xy
2
42
œ0.
54. If f is continuous at (x y ), then lim f(x y) must equal f(x y ) 3. If f is not continuous at
!! !!
ßßßœ
Ðß ÑÄÐ ß Ñxy x y
(x y ), the limit could have any value different from 3, and need not even exist.
!!
ß
55. lim 1 1 and lim 1 1 lim 1, by the Sandwich Theorem
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
Š‹
œ œÊ œ
xy tan xy
3xy
56. If xy 0, lim lim lim 2 2 andœœœ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
2 xy 2xy
xy xy 6
xy
kkŠ‹ Š‹
kk
xy xy
66
ˆ‰
lim lim 2 2; if xy 0, lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00 xy 00
2 xy
xy xy xy
2 xy 2xy
kk
kk kk
kkŠ‹ Š‹
œœ œ
xy xy
66
lim 2 2 and lim 2 lim 2, by the Sandwich Theoremœœ œÊ œ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
ˆ‰
xy
6xy xy
2 xy 44 cos xy
kk
kk kk
Èkk
57. The limit is 0 since sin 1 1 sin 1 y y sin y for y 0, and y y sin y for
¸ ¸ ˆ‰ ˆ‰ ˆ‰ˆ‰
"" " "
xx x x
Ÿ ÊŸ Ÿ ÊŸ Ÿ
y 0. Thus as (x y) ( ), both y and y approach 0 y sin 0, by the Sandwich Theorem.ŸßÄ!ß! ÊÄ
ˆ‰
"
x
58. The limit is 0 since cos 1 1 cos 1 x x cos x for x 0, and x x cos x
¹ ¹ Š‹ Š‹ Š‹Š‹
"" " "
yy y y
Ÿ ÊŸ Ÿ ÊŸ Ÿ
for x 0. Thus as (x y) ( ), both x and x approach 0 x cos 0, by the Sandwich Theorem.ŸßÄ!ß! ÊÄ
Š‹
"
y
59. (a) f(x y) sin 2 . The value of f(x y) sin 2 varies with , which is the line'skßœœ œ ßœ
ymxœ
2m 2 tan
1m 1tan
)
))))
angle of inclination.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.2 Limits and Continuity in Higher Dimensions 809
(b) Since f(x y) sin 2 and since 1 sin 2 1 for every , lim f(x y) varies from 1 to 1kßœ ŸŸ ß
ymxœ)))
Ðß ÑÄÐß Ñxy 00
along y mx.œ
60. xy x y xy x y x y x y x y x y x y x y x yk kkkkkkkkkkk kk kkab ÈÈÈÈ
## ## ## ## ##
## ####
œ Ÿ œ Ÿ
xy xy xy xyœ Ê Ÿ œÊŸ Ÿab ab ab
¹¹
## ## ## ##
#
xyxy xy xyxy
xy xy xy
abab ab
lim xy 0 by the Sandwich Theorem, since lim x y 0; thus, define f 0 0 0Êœ „œßœ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00
Š‹ ab ab
xy
xy
##
61. lim lim lim 0
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
xxy
xy r cos r sin 1
r cos (r cos ) r sin r cos cos sin
œœœ
))) )))
))
ab a b
62. lim cos lim cos lim cos cos 0 1
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
Š‹ Š ‹ ’ “
xy
xy r cos r sin 1
r cos r sin rcos sin
œœœœ
))
))
))ab
63. lim lim lim sin sin ; the limit does not exist since sin is between
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
y
xy r
r sin
## #
œœ œ
)ab)) )
0 and 1 depending on )
64. lim lim lim ; the limit does not exist for co
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
2x 2r cos 2 cos 2 cos
x x y r r cos r cos cos
œœœ
)))
))) s 0)œ
65. lim tan lim tan lim tan ;
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
" " "
’“ ’ “ ’ “
kk kk k k k k kka bkkkkx y r cos r sin r cos sin
xy r r
œœ
)) ))
if r 0 , then lim tan lim tan ; if r 0 , thenÄœœÄ
" "
#
rrÄ! Ä!
’“ ’“
kka b k k k kkkkkr cos sin cos sin
rr
)) ))1
lim tan lim tan the limit is
rrÄ! Ä!
" "
# #
’“ Š‹
kka b k k k kkkkkr cos sin cos sin
rr
)) )) 11
œœÊ
66. lim lim lim cos sin lim (cos 2 ) which ranges between
Ðß ÑÄÐß Ñ ÄÄ Ä
xy 00 r0 r0 r0
xy
xy r
r cos r sin
##
œœœ
)) ab)) )
1 and 1 depending on the limit does not existÊ)
67. lim ln lim ln
Ðß ÑÄÐß Ñ Ä
xy 00 r0
Š‹Š ‹
3x x y 3y
xy r
3r cos r cos sin 3r sin
œ))) )
lim ln 3 r cos sin ln 3 define f(0 0) ln 3œ œÊßœ
r0Äab
## #
))
68. lim lim lim 3r cos sin 0 define f(0 0) 0
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
3xy
xy r
(3r cos ) r sin
#
œœœÊßœ
))ab ))
69. Let 0.1. Then x y x y 0.1 x y 0.01 x y 0 0.01$$œÊÊÊ
ÈÈ kk
## ## ## ##
f(x y) f( ) 0.01 .Êß!ß! œkk%
70. Let 0.05. Then x and y f x y f 0 0 0 y 0.05 .$$$ %œÊßßœœŸœkk kk k k kkabab¸¸¸¸
yy
x1 x1
71. Let 0.005. Then x and y f x y f 0 0 0 x y x y$$$œ Ê ß ß œ œ Ÿ kk kk k k k k kk kkabab¸¸¸¸
xy xy
x1 x1
0.005 0.005 0.01 .œœ%
72. Let 0.01. Since 1 cos x 1 1 2 cos x 3 1 x y$œŸŸÊŸŸÊŸŸÊŸŸ
""
#
3 cos x 3 2 cos x
xy xy
kk¸¸
kk
x y . Then x and y f x y f 0 0 0 x y 0.01 0.01Ÿ Ê ßßœ œ Ÿ kk kk kk kk k k kk kkabab¸¸¸¸
$$ xy xy
2cos x 2cos x
0.02 .œœ%
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

810 Chapter 14 Partial Derivatives
73. Let 0.04. Since y x y 1 x x x y f x y f 0 0$ $œ Ÿ Ê Ÿ Ê Ÿl lœ Ÿ Ê ß ß
222 y
x y x y
xy 222
2
22 22
2
ll ÈÈkkabab
0 0.04 .œœ
¹¹
xy
xy
2
22
%
74. Let 0.01. If y 1, then y y y x y , so x x x y x y 2 x y . Since$œ l lŸ Ÿl lœ Ÿ l lœ Ÿ Êl l Ÿ
2 2
2 22 2 22 22
ÈÈ È È
È
x x y 1 and y x y 1. Then x y x y 2
222 222 2 2
x x
x y x y x y x y x y
yy
xy
ŸÊ Ÿ ŸÊ Ÿ Ÿ ll Ÿll
2 2
22 22 22 22 22
22
34
ll $
f x y f 0 0 0 2 0.01 0.002 .Êßßœ œ œkk ababab¹¹
xy
x y
34
22
%
75. Let 0.015. Then x y z f(x y z) f( 0 0) x y z 0 x y z$$œ Ê ßß!ßß œ œ
ÈÈkkkkkk
### ### ###
x t x 0.015 0.015 .œ œœ
Š‹Š‹
ÈÈ
## #
##
%
76. Let 0.2. Then x , y , and z f(x y z) f( 0 0) xyz 0 xyz x y z (0.2)$$$$œÊßß!ßßœœœkk kk kk k k k k k k kkkkkk $
0.008 .œœ%
77. Let 0.005. Then x , y , and z f(x y z) f( 0 0) 0$$$$œ Ê ß ß !ß ß œ kk kk kk k k ¹¹
xyz
xyz1
x y z x y z 0.005 0.005 0.005 0.015 .œ ŸŸ œ œ
¹¹
k k kk kk kk
xyz
xyz1
%
78. Let tan (0.1). Then x , y , and z f(x y z) f( 0 0) tan x tan y tan z$$$$œÊßß!ßßœ
" ###
kk kk kk k k k k
tan x tan y tan z tan x tan y tan z tan tan tan 0.01 0.01 0.01 0.03 .Ÿ œ œœœkkkkkk
#########
$$$ %
79. lim f(x y z) lim (x y z) x y z f(x y z ) f is continuous at
Ðß ßÑÄÐ ß ß Ñ Ðß ßÑÄÐ ß ß Ñxyz x y z xyz x y z
ßßœ œœ ßß Ê
!!! !!!
every (x y z )
!!!
ßß
80. lim f(x y z) lim x y z x y z f(x y z ) f is continuous at
Ðß ßÑÄÐ ß ß Ñ Ðß ßÑÄÐ ß ß Ñxyz x y z xyz x y z
ßßœ œœ ßß Êab
### ###
!!! !!!
every point (x y z )
!!!
ßß
14.3 PARTIAL DERIVATIVES
1. 4x, 3 2. 2x y, x 2y
`` ` `
`` ` `
ff f f
xy x y
œœ œœ
3. 2x(y 2), x 1 4. 5y 14x 3, 5x 2y 6
`` ` `
`` ` `
#
ff f f
xy x y
œ œ œ œ
5. 2y(xy 1), 2x(xy 1) 6. 6(2x 3y) , 9(2x 3y)
`` ` `
`` ` `
##
ff f f
xy x y
œœ œ œ
7. , 8. ,
`` ` `"
`` ` `
fxf f2xf
xy x y
xy xy
y
x3x
œœ œ œ
ÈÈ ÉÉ
ˆ‰ ˆ‰
yy
9. (x y) , (x y)
`"` "`"` "
`` ``
ff
x(xy)x (xy)y(xy)y (xy)
œ œ œ œ††
10. ,
``
``
ff
xy
x y (1) x(2x) x y (0) x(2y)
xy xy xy xy
y x 2xy
œœœœ
ab ab
ab ab ab ab
11. ,
``"
``
"
ffx
x (xy 1) (xy 1) y (xy 1) (xy 1)
(xy 1)(1) (x y)(y) y 1 (xy )(1) (x y)(x)
œœ œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.3 Partial Derivatives 811
12. ,
`"` `"`
`` ``
ff1x
xxx xyyyx xy
11
yy y y
x1 x1
œœœœœœ
ˆ‰ ˆ‰
’“ ’“
ˆ‰ ˆ‰
y y
x x
y y
x x
††
ˆ‰ ˆ‰
13. e (x y 1) e , e (x y 1) e
`` ``
`` ``
ÐÑ ÐÑ ÐÑ ÐÑ
ff
xx yy
xy1 xy1 xy1 xy1
œœœœ††
14. e sin (x y) e cos (x y), e cos (x y)
``
``
ff
xy
xx x
œ œ
15. (x y) , (x y)
`"` "`"` "
`` ``
ff
xxyx xyyxyy xy
œœœœ††
16. e (xy) ln y ye ln y, e (xy) ln y e xe ln y
`` `` "
`` ``
ff e
xx yy y y
xy xy xy xy xy
œœœœ†† †† †
xy
17. 2 sin (x 3y) sin (x 3y) 2 sin (x 3y) cos (x 3y) (x 3y) 2 sin (x 3y) cos (x 3y),
`` `
`` `
f
xx x
œ œ œ ††
2 sin (x 3y) sin (x 3y) 2 sin (x 3y) cos (x 3y) (x 3y) 6 sin (x 3y) cos (x 3y)
`` `
`` `
f
yy y
œ œ œ ††
18. 2 cos 3x y cos 3x y 2 cos 3x y sin 3x y 3x y
`` `
`` `
## ###
f
xx x
œ œ ab ab ababab††
6 cos3xy sin3xy,œ abab
##
2 cos 3x y cos 3x y 2 cos 3x y sin 3x y 3x y
`` `
`` `
## ###
f
yy y
œ œ ab ab ababab††
4y cos 3x y sin 3x yœabab
##
19. yx , x ln x 20. f(x y) and
`` `" `
`` ``
ff ln x f f ln x
xy ln y x x ln y y y(ln y)
œœ ߜʜ œ
y1 y
21. g(x), g(y)
``
``
ff
xy
œ œ
22. f(x y) (xy) , xy 1 f(x y) (1 xy) andßœ Ê ßœ Ê œ œ
!
_
œn0
nkk "` "`
` ` 1 xy x (1 xy) x (1 xy)
fy
†
(1 xy)
`"`
``
fx
y (1 xy) y (1 xy)
œ œ†
23. f y , f 2xy, f 4z 24. f y z, f x z, f y x
xyz xyz
œ œ œ œ œ œ
#
25. f 1, f , f
xy z
y
yz yz
z
œœ œ
ÈÈ
26. f x x y z , f y x y z , f z x y z
xyz
œ œ œ ab ab ab
### ### ###
$Î# $Î# $Î#
27. f , f , f
xyz
yz xy
1 xyz 1 xyz 1 xyz
xz
œœœ
ÈÈÈ
28. f , f , f
xy z
xyz (xyz)1 xyz (xyz) 1 xyz (xyz) 1
zy
œœ œ
"
kk kk kk
ÈÈÈ
29. f , f , f
xyz
œœœ
"
x2y3z x2y3z x2y3z
23
30. f yz (xy) , f z ln (xy) yz ln (xy) z ln (xy) (xy) z ln (xy) z,
xy
xy x xy x y xy y
(yz)(y) yz yz
œœœœœœ†† † †
"` ` `
```
f y ln (xy) yz ln (xy) y ln (xy)
zz
œ œ†`
`
31. f 2xe , f 2ye , f 2ze
xyz
xyz xyz xyz
œ œ œ
ab ab ab
32. f yze , f xze , f xye
xyz
xyz xyz xyz
œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

812 Chapter 14 Partial Derivatives
33. f sech (x 2y 3z), f 2 sech (x 2y 3z), f 3 sech (x 2y 3z)
xy z
œœ œ
###
34. f y cosh xy z , f x cosh xy z , f 2z cosh xy z
xyz
œœœ ab ab ab
## #
35. 2 sin (2 t ), sin (2 t )
``
``
ff
tœ œ 11! 1!
!
36. v e 2ve , 2ve v e 2ve 2ue
``
`` ` `
# Ð ÎÑ Ð ÎÑ Ð ÎÑ # Ð ÎÑ Ð ÎÑ Ð ÎÑ
``
gg
uuv v vv
2u v 2u v 2u v 2u v 2u v 2u v
2u 2u
œ œ œ œ††
ˆ‰ ˆ‰
37. sin cos , cos cos , sin sin
`` `
`` `
hh h
39 )
œœ œ9) 39) 39)
38. 1 cos , r sin , 1
```
```
ggg
rz
œ œ œ))
)
39. W V, W P , W , W , W
pv v g
v Vv 2Vv Vv Vv
2g 2g 2g g g
œœ œ œœ œ
$$$$
$#
40. m, , , c,
```` `
``#`` ` #
AAAmAkAkmh
chkqmqqq
q
œœœœœ
41. 1 y, 1 x, 0, 0, 1
``````
` ` ``````
ff ffff
x y xyyxxy
œ œ œ œ œ œ
42. y cos xy, x cos xy, y sin xy, x sin xy, cos xy xy sin xy
``` ` ``
````````
##
ff f f ff
xyxyyxxy
œ œ œ œ œ œ
43. 2xy y cos x, x sin y sin x, 2y y sin x, cos y, 2x cos x
`` ````
` ` ` ` `` ``
#
gg gggg
x y x y yx xy
œ œ œ œ œ œ
44. e , xe 1, 0, xe , e
`` `` ``
` ` ` ` `` ``
hh hh hh
x y x y yx xy
œœœœ œœ
yy y y
45. , , , ,
`"`"` "` "` ` "
``` ` ````
rr r r rr
x xy y xy x (xy) y (xy) yx xy (xy)
œœ œ œ œœ
46. , ,
`"` " `"` "
`` ``
ss1x
xxxxxyyyxxxy
1111
yy y y
œœœœœœ
”• ”• ”• ”•
ˆ‰ ˆ ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰ ˆ‰
yyyy
xxxx
††
, ,
`` ``
` ` `` ``
ss ss
x y yx xy
y(2x) 2xy x(2y) 2xy y x
xy xy xy xy xy xy
x y ( 1) y(2y)
œœ œœ œœ œ
abab ab ab ab ab
ab
47. 2x tan xy x sec xy y 2x tan xy x y sec xy , x sec xy x x sec xy ,
` `
` `
w w
x y
22 2 2 2 2 3 2
œ †œ œ †œab ab ab ab ab ab
2tan xy 2x sec xy y 2xy sec xy x y 2sec xy sec xy tan xy y
`
`
w
x
222
œ † †ab ab ab a babab ab
2tan xy 4xy sec xy 2x y sec xy tan xy , x 2sec xy sec xy tan xy x 2x sec xy tan xyœ œ †œab ab ab ab a b ab ababab ab
2222 3 42
w
y
`
`
3x sec xy x 2sec xy sec xy tan xy y 3x sec xy x y sec xy tan xy
``
`` ``
ww
yx xy
22 3 22 3 2
œœ †œ ab a b ab ab ababab ab
48. ye 2x 2xy e , 1 e ye 1 e 1 y ,
``
``
ww
xy
xy xy xy xy xy
œ†œ œ †œ
22222
ab a b a b
2y e 2xy e 2x 2ye 1 2x , e 1 1 y e 1
` `
` `
w w
x y
xy xy xy 2 xy xy
œ †œ œ†
22 2 2 2
Š‹ Š ‹
a b aba b ab
ey2, e 2x1y2xe1yœœœ†œ
xy xy xy
ww
yx xy
222
``
`` ``
ab ab ab
Š‹
49. sin x y x cos x y 2xy sin x y 2x ycos x y , x cos x y x x cos x y ,
` `
` `
w w
x y
22 222 2232
œ †œ œ †œab ab ab ab ab ab
cos x y 2xy 4xy cos x y 2x y sin x y 2xy 6xy cos x y 4x y sin x y ,
`
`
w
x
2222 2322
œ† †œ ab ab ab ab ab
x sinxy x x sinxy, 3xcosxy xsinxy 2xy 3xcosxy 2xysinxy
```
`````
www
yyxxy
322 52 22 32 22 4 2
œ † œ œ œ † œ ab ab ab ab ab ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.3 Partial Derivatives 813
50. , ,
``
``
wwxx
xy
xy xy2x xy 1 xy
xy xy xy xy
x 2xy y
œœœ œ
ˆ‰ ˆ‰
abab abab
ab ab ab ab
22
22 22
22 22
22
,
`
`
w
x
x y 2x 2y x 2xy y 2 x y 2x 2 x 3x y 3 xy y
xy xy
œœ
ˆ‰ ˆ ‰ˆ‰ ˆ ‰
ab ab
’“
ab ab
222322
2
2223
2
,
```
`````
†† †
w2x2xww
yyxxy
x y 0 x x2x y 1 x y 2x 1 x 2xy y2x y 1
xy xy
xy
œœœœ
ˆ‰ˆ ‰ˆ‰ ˆ‰ ˆ ‰ˆ‰
’“ ’“
ab ab
ab ab
222 2 22
2 2
2 2
2 2
23 2
2
2
œ2x 3x 2xy y
xy
32
23
ab
51. , , , and
` ` ` `
```` ``
w2w3 w 6 w 6
x 2x 3y y 2x 3y y x (2x 3y) x y (2x 3y)
œœ œ œ
52. e ln y , ln x, , and
```""`""
` ` `` ``
wwxw w
x x y y yx y x xy y x
y
œ œ œœ œ
x
53. y 2xy 3x y , 2xy 3x y 4x y , 2y 6xy 12x y , and 2y 6xy 12x y
`` ` `
` ` `` ``
# $ #% ## $$ # #$ # #$
ww w w
x y yx xy
œ œ œ œ
54. sin y y cos x y, x cos y sin x x, cos y cos x 1, and cos y cos x 1
`` ` `
` ` `` ``
ww w w
x y yx xy
œ œ œ œ
55. (a) x first (b) y first (c) x first (d) x first (e) y first (f) y first
56. (a) y first three times (b) y first three times (c) y first twice (d) x first twice
57. f 1 2 lim lim lim
xf(1 h 2) f(1 2)
hh h
1(1h)26(1h) (26) h612hh 6
abßœ œ œ
h0 h0 h0ÄÄ Ä
ß ß
cd ab
lim lim ( 13 6h) 13,œœœ
h0 h0ÄÄ
13h 6h
h
f (1 2) lim lim lim
yf(1 2 h) f(1 2) (2 6 2h) (2 6)
hh h
11(2h)3(2h) (26)
ßœ œ œ
h0 h0 h0ÄÄ Ä
ß ß
cd
lim ( 2) 2œœ
h0Ä
58. f 2 1 lim lim
xf2h1 f21
hh
422h 3 2h 32
abß œ œ
h0 h0ÄÄ
abab cdababab
ß ß
lim lim 1 1,œœœ
h0 h0ÄÄ
ab2h1h 1
h
f 2 1 lim lim
yf21h f21
hh
4431h 21h 32
abß œ œ
h0 h0ÄÄ
abab ‘
ababa b
ß ß
lim lim lim 1 2h 1œœœœ
h0 h0 h0ÄÄÄ
ab
33h24h2h 1
hh
h2h ab
59. f 2 3 lim lim
xf2h3 f23
hh
22h 91 491
abß œ œ
h0 h0ÄÄ
abab Èab È
ß ß
lim lim lim ,œœ œœ
h0 h0 h0ÄÄ Ä
ÈÈÈ
ÈÈ
2h 4 2 2h 4 2 2h 4 2
hh 2
2h 4 2 2h 4 2
21
Š‹
f 2 3 lim lim
yf23h f23
hh
433h 1 491
abß œ œ
h0 h0ÄÄ
abab Èab È
ß ß
lim lim lim œœ œœ
h0 h0 h0ÄÄ Ä
ÈÈÈ
ÈÈ
3h 4 2 3h 4 2 3h 4 2
hh 4
3h 4 2 2h 4 2
33
Š‹
60. f 0 0 lim lim lim 1
xf0 h0 f00
hhh
0sin h
abßœ œ œ œ
h0 h0 h0ÄÄÄ
ababß ß
sin h 0
3
h0
23
3
f 0 0 lim lim lim lim h 0 1 0
yf00 h f00
hhhh
0sin h sin h
ab Š‹
ß œ œ œ œ † œ†œ
h0 h0 h0 h0ÄÄÄÄ
ababß ß
sin 0 h4
0h
244
34
61. (a) In the plane x 2 f x y 3 f 2 1 3 m 3œÊ ß œÊ ßœÊ œ
yy
ab a b
(b) In the plane y 1 f x y 2 f 2 1 2 m 2œÊ ß œÊ ßœÊ œ
xy
ab a b
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

814 Chapter 14 Partial Derivatives
62. (a) In the plane x 1 f x y 3y f 1 1 3 1 3 m 3œ Ê ß œ Ê ß œ œ Ê œ
yy
22
ab a b ab
(b) In the plane y 1 f x y 2x f 1 1 2 1 2 m 2œÊ ßœ ÊßœœÊœ
xy
ab a b ab
63. f x y z lim ;
zfxyz h fx,yz
h
ab
!!! ßß ß
ßß œ
h0Äabab
f 1 2 3 lim lim lim lim 12 2h 12
zf123 h f1,23 23 h 29
hhh
2h 2h
ab a bßß œ œ œ œ œ
h0 h0 h0 h0ÄÄÄÄ
abab ababßß ß "
64. f x y z lim ;
yfx y hz fx,y z
h
ab
!!! ßß ß
ßß œ
h0Äabab
f 1 0 3 lim lim lim 2h 9 9
yf 1h3 f 1,03 2h 9h 0
hh
ab abß ß œ œ œ œ
h0 h0 h0ÄÄÄ
abab a bß ß ß
65. y 3z x z 2y 0 3xz 2y y z at (1 1 1) we have (3 2) 1 1 or 2 œ Ê œ Ê ß ß œ œ
ˆ‰ ab
#$ # $
`` ` ``
`` ` ``
zz z zz
xx x xx
66. z x 2x 0 z 2x x at (1 1 3) we have ( 3 1 2) 1 or
ˆ‰ ˆ‰ ˆ ‰
``` ` ``"
``` ` ``
xxx x xx
zxzz xz zz6
yy
œ Ê œ Ê ß ß œ œ
67. a b c 2bc cos A 2a 2bc sin A ; also 0 2b 2c cos A 2bc sin A
### `` `
`` `
œ Ê œ Ê œ œ ab ab
AAa A
a a bc sin A b
2c cos A 2b 2bc sin A ʜ ʜab
``
``
A A c cos A b
b b bc sin A
68. 0 sin A a cos A 0 ; also
a b a a a cos A
sin A sin B sin A x A sin A
(sin A) a cos A
œÊ œÊ œÊœ
a
A``
``
ab
b csc B cot B b csc B cot B sin A
ˆ‰ ab
"` `
``sin A B B
aa
œ Ê œ
69. Differentiating each equation implicitly gives 1 v ln u u and 0 u ln v v orœ œ
xxxx
vu
uv
ˆ‰ ˆ‰
v
ln u v u 1
v ln v u 0 Ÿ
ab ˆ‰
ˆ‰ ab
xx
v
u
u
vxx
0ln v
ln u
ln v
ln v
ln u ln v 1
œ
œ
Êœ œ
x
ºº
ºº
abab
"
v
u
v
u
u
v
70. Differentiating each equation implicitly gives 1 2x x 2y y and 0 2x x y orœ œab ab ab
uu uu
x and
2x x 2y y 1
2x x y 0
ab ab
ab
uu
uu
2y
01
2x 2y
2x 1
11
2x 4xy 2x 4xy
œ
œ
Êœ œ œ
u
ºº
ºº
"
y ; next s x y 2x 2y
uœœœœ œÊœ
ºº
2x
2x 0
x 4xy 2x 4xy 2x 4xy 1 2y u u u
2x 2x 1 s x y
"
# ` ` `
``
## `
2x 2yœ œœ
Š‹Š‹
"""
#
2x 4xy 1 2y 1 y 1 2y 1 2y
2y 1 2y
71. f x y f x y 0 for all points x, y ; at y 0, f x 0
0if y 0
0if y 0
xx y
h0 h0
f x, 0 h f x, 0 f x, h 0
hh
ab ab ab ab
œ
ßœ Ê ßœ œ ßœ œ
lim lim
ÄÄ
a bab ab
0 because 0 and 0 f x y ;
3y if y 0
2y if y 0
œ œ œœ œœÊßœ
lim lim lim lim lim
h0 h0 h0
f x, h f x, h f x, h
hhhhh
hh
h0 h0 y
2
ÄÄÄ
ÄÄ
ab ab ab
32
abœ
f x y f x y 0 for all points x, y
yx xy
ab ab abߜ ߜ
72. At x 0, f 0 y which does not exist because œßœ œ œ
xh0 h0 h0 h0
f 0 h, y f 0, y f h, y 0 f h, y f h, y
hhh h
ablim lim lim lim
ÄÄÄ Ä
a bab ab ab ab
0 and f x y ;
if x 0
2x if x 0
œœ œœœ_Êßœ
lim lim lim lim
h0
h1
hhh
h0 h0 h0
fh, y h
hx
1
2x
ÄÄÄÄ
2ab ÈÈÈ
ab
f x y f x y 0 for all points x, y ; f x y 0 for all points x, y , while f x y 0 for all
0if x 0
0if x 0
y y yx xy
ab ab abab ab ab
œ
ßœ Ê ßœ ßœ ßœ
points x, y such that x 0.ab Á
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.3 Partial Derivatives 815
73. 2x, 2y, 4z 2, 2, 4 2 2 ( 4) 0
``` ``` ```
``` ``` ```
fff fff fff
xyz xyz xyz
œœœÊœœœÊœœ
74. 6xz, 6yz, 6z 3 x y , 6z, 6z, 12z
``` ``` ```
``` ``` ```
###
fff fff fff
xyz xyz xyz
œ œ œ œ œ œ Ê ab
6z 6z 12z 0œ œ
75. 2e sin 2x, 2e cos 2x, 4e cos 2x, 4e cos 2x
`` ` ` ``
`` ` ` ``
ffff ff
xy x y xy
œ œ œ œ Ê
2y 2y 2y 2y
4e cos 2x 4e cos 2x 0œ œ
2y 2y
76. , , , 0
``` ` ``
``` ` ``
fxf f f ff
xxyyxyx y x y
yyxxy yxxy
xy xy xy xy
œ œ œ œ Êœœ
ab ab abab
77. 3 , 2 , 0 , 0 0 0 0
``` ` ``
``` ` ``
ffff ff
xyx y xy
œœœœÊœœ
78. , , ,
``` `
``` `
ÎÎ
†† ††
ffxf f
xyxyyxx y
1y xy
11
y 2xy
yx0y2x yx0 x2y
yx yx y
œœ œœ œ œ œ
Š‹ Š‹ ab abab
ab ab ab
xx
yy
2
22 xyx
2xy
22
œab
0Êœœ
``
``
ff
xy
2xy 2xy
yx yxabab
22
79. x y z 2x x x y z , x y z 2y
`" `"
`# `#
### ### ###
$Î# $Î# $Î#
f f
x y
œ œ œ ababab abab
yxyz , xyz 2z zxyz ;œ œ œ ab ababab
### ### ###
$Î# $Î# $Î#
`"
`#
f
z
xyz 3xxyz , xyz 3yxyz ,
``
``
### #### ### ####
$Î# &Î# $Î# &Î#
ff
xy
œ œ abab abab
xyz 3zxyz
````
````
### ####
$Î# &Î#
ffff
zxyz
œ Ê abab
xyz 3xxyz xyz 3yxyzœ
’“’“
abababab
### #### ### ####
$Î# &Î# $Î# &Î#
xyz 3zxyz 3xyz 3x3y3zxyz 0 œ œ
’“
abababa bab
### #### ### # # ####
$Î# &Î# $Î# &Î#
80. 3e cos 5z, 4e cos 5z, 5e sin 5z; 9e cos 5z, 16e cos 5z,
``` ` `
``` ` `
fff f f
xyz x y
3x 4y 3x 4y 3x 4y 3x 4y 3x 4y
œœœœ œ
25e cos 5z 9e cos 5z 16e cos 5z 25e cos 5z 0
````
` ```
ffff
z xyz
3x 4y 3x 4y 3x 4y 3x 4y
œ Ê œ œ
81. cos (x ct), c cos (x ct); sin (x ct), c sin (x ct) c [ sin (x ct)] c
`` ` ` ` `
`` ` ` ` `
###
ww w w w w
xt x t t x
œ œ œ œ Êœœ
82. 2 sin (2x 2ct), 2c sin (2x 2ct); 4 cos (2x 2ct), 4c cos (2x 2ct)
`` ` `
`` ` `
#
ww w w
xt x t
œ œ œ œ
c [ 4 cos (2x 2ct)] cÊœ œ
``
``
##
ww
tx
83. cos (x ct) 2 sin (2x 2ct), c cos (x ct) 2c sin (2x 2ct);
``
``
ww
xt
œ œ
sin (x ct) 4 cos (2x 2ct), c sin (x ct) 4c cos (2x 2ct)
``
``
##
ww
xt
œ œ
c [ sin (x ct) 4 cos (2x 2ct)] c Êœ œ
``
``
##
ww
tx
84. , ; , c c
`"` ` ` ` " `
``` ` ` `
##
wwcw1wcw w
x xct t xct x (xct) t (xct) t (xct) x
œœ œ œÊœ œ
’“
85. 2 sec (2x 2ct), 2c sec (2x 2ct); 8 sec (2x 2ct) tan (2x 2ct),
`` `
`` `
###
ww w
xt x
œœ œ
8c sec (2x 2ct) tan (2x 2ct) ux c [8 sec (2x 2ct) tan (2x 2ct)] c
```
```
## # # #
www
ttx
œÊœ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

816 Chapter 14 Partial Derivatives
86. 15 sin (3x 3ct) e , 15c sin (3x 3ct) ce ; 45 cos (3x 3ct) e ,
`` `
`` `
ww w
xt x
œ œ œ
xct xct xct
45c cos (3x 3ct) c e c 45 cos (3x 3ct) e c
`` `
`` `
### #
ww w
tt x
œ Ê œ œ
xct xct
cd
87. (ac) (ac) (ac) a c ; a a a
```` ` ` ````` ` `
```` ` ` `` ``` ` `
##
wfuf w f fwfuf w f
tutu t u uxuxu x u
œœ Êœ œ œœ Êœ
Š‹ Š ‹
††
a ac c a c œÊœ œ œ
######
`` ` ` `
`` ` ` `
fw f f w
ut u u x
Š‹
88. If the first partial derivatives are continuous throughout an open region R, then by Theorem 3 in this section of the text,
f(x y) f(x y ) f (x y ) x f (x y ) y x y, where , 0 as x, y 0. Then asßœßßß Ä Ä
!! !! !! " # "#xy
? ? %? %? % % ? ?
(x y) (x y ), x 0 and y 0 lim f(x y) f(x y ) f is continuous at every point (x y ) in R.ßÄ ß Ä ÄÊ ßœ ß Ê ß
!! !! !!
??
Ðß ÑÄÐ ß Ñxy x y
89. Yes, since f , f , f , and f are all continuous on R, use the same reasoning as in Exercise 76 with
xx yy xy yx
f(xy) f(xy) f(xy) x f(xy) y x y and
x x xx xy
ßœßßß
!! !! !! " #
? ? %? %?
f (x y) f (x y ) f (x y ) x f (x y ) y x y. Then lim f (x y) f (x y )
y y yx yy x x
ßœßßß ßœß
ss
!! !! !! " # !!
? ? %? %? Ðß ÑÄÐ ß Ñxy x y
and lim f (x y) f (x y ).
Ðß ÑÄÐ ß Ñxy x y yy
ßœ ß
!!
90. To find and so that u u u sin x e and u cos x e u sin x e ; then!" "! !! ! !
txx t x xx
tt2t
œ Ê œ œ Ê œab ab ab
"" "
u u sin x e sin x e , thus u u only if
txx txx
t2 t 2
œÊ œ œ œ"! ! ! "!ab ab
""
91. f 0, 0 0; f 0, 0 0;
x y
h0 h0 h0 h0 h0 h0
f0 h0 f00 f00 h f00
hhh hhh
0 0
0 0
ab abœœœœœœœœlim lim lim lim lim lim
ÄÄÄ ÄÄÄ
ßß ßß
abab abab
h0 0h
2 2
h0 0h
24 24
lim f x, y lim lim lim different limits for differ
Ðß ÑÄÐß Ñ
œ
ÄÄÄ
xy 00
along x ky
y0 y0 y0
2abœœœœÊ
ˆ‰
ab
ky y
ky y
ky
ky y k 1 k 1
kk
22
24
224422
4
ent
values of k lim f x, y does not exist f x, y is not continuous at 0, 0 by Theorem 4, f x, y is notÊÊÊ
Ðß ÑÄÐß Ñxy 00 ab ab ab ab
differentiable at 0, 0 .ab
92. f 0, 0 0; f 0, 0 0;
x y
h0 h0 h0 h0 h0 h0
f0 h0 f00 fh0 1 f00 h f00 f0h 1
hhh hhh
11 11
ab abœœœœœœœœlim lim lim lim lim lim
ÄÄÄ ÄÄÄ
ßß ß ßß ß
a bab ab a bab ab
lim f x, y lim 0 0 but lim f x, y lim 1 1 lim f x, y does
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
œœ
ÄÄ
xy 00 xy 00 xy 00
along y x along y 1.5x
y0 y0
22
ab ab abœœ œœÊ not exist
f x, y is not continuous at 0, 0 by Theorem 4, f x, y is not differentiable at 0, 0 .ÊÊab ab ab ab
14.4 THE CHAIN RULE
1. (a) 2x, 2y, sin t, cos t 2x sin t 2y cos t 2 cos t sin t 2 sin t cos t
``
``
w w dx dw
x y dt dt dt
dy
œ œ œ œ Ê œ œ
0; w x y cos t sin t 1 0œ œœ œÊ œ
## # # dw
dt
(b) ( ) 0
dw
dt 1œ
2. (a) 2x, 2y, sin t cos t, sin t cos t
``
``
w w dx dw
x y dt dt dt
dy
œœœ œÊ
(2x)( sin t cos t) (2y)( sin t cos t)œ
2(cos t sin t)(cos t sin t) 2(cos t sin t)(sin t cos t) 2 cos t 2 sin t 2 cos t 2 sin tœ œ abab
## ##
0; w x y (cos t sin t) (cos t sin t) 2 cos t 2 sin t 2 0œ œœ œ œÊ œ
## # # # # dw
dt
(b) (0) 0
dw
dt œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.4 The Chain Rule 817
3. (a) , , , 2 cos t sin t, 2 sin t cos t,
`"`"` "
```
w w w dx dz
x z y z z z dt dt dt t
(x y) dy
œœœ œ œ œ
cos t sin t sin t cos t 1; w t 1Êœ œ œ œœ œÊœ
dw 2 2 cos t sin t x cos t sin t dw
dt z z z t z z dt
xy y
t
Š‹ Š‹ Š‹
ab
ttt
(b) (3) 1
dw
dt œ
4. (a) , , , sin t, cos t, 2t
```
```
"Î#
w2xw w2zdx dz
x xyz y xyz z xyz dt dt dt
2y dy
œœœœœœ
Êœ œ
dw 2x sin t 4zt
dt xyz xyz xyz costsint16t
2y cos t 2 cos t sin t 2 sin t cos t 4 4t t
ˆ‰
; w ln x y z ln cos t sin t 16t ln (1 16t) œœœœÊœ
16 dw 16
1 16t dt 1 16t
### # #
aba b
(b) (3)
dw 16
dt 49
œ
5. (a) 2ye , 2e , , , , e
```" "
```
wwwdx2t dzdw 2ee
x y z z dt t 1 dt t 1 dt dt t 1 t 1 z
xx t
dy 4yte
œœœœœœÊœ
xxt
4t tan t 1; w 2ye ln z 2 tan t t 1 tœœœœ
(4t) tan t t 1 2 t 1
t1 t1 e
ex
a bab ab
" " #
t
tabab
t 1 2 tan t (2t) 1 4t tan t 1Êœ œ
dw 2
dt t 1
ˆ‰
aba b
#" "
(b) (1) (4)(1) 1 1
dw
dt 4
œœ
ˆ‰
11
6. (a) y cos xy, x cos xy, 1, 1, , e y cos xy e
``` "
```
w w w dx dz dw
x y z dt dt t dt dt t
dy x cos xy
œ œ œ œ œ œ Ê œ
t1 t1
(ln t)[cos (t ln t)] e (ln t)[cos (t ln t)] cos (t ln t) e ; w z sin xyœ œ œ
t cos (t ln t)
t
t1 t1
e sin (t ln t) e [cos (t ln t)] ln t t e (1 ln t) cos (t ln t)œ Êœ œ
t1 t1 t1
dw
dt t
‘ˆ‰
"
(b) (1) 1 (1 0)(1) 0
dw
dt œ œ
7. (a) 4e ln y (sin v)
````
`````
`
z z x z cos v 4e 4e sin v
uxuyu u cos v y u y
y4e ln y
x
œœ œ ab
ˆ‰
Š‹
xx
x
(4 cos v) ln (u sin v) 4 cos v;œœ
4(u cos v) ln (u sin v) 4(u cos v)(sin v)
uu sin v
4e ln y (u cos v) 4e ln y (tan v)
````
`````
`
z z x z u sin v 4e 4e u cos v
vxvyv u cos v y y
yxx
œœ œ ab ab
ˆ‰
Š‹
xx
[ 4(u cos v) ln (u sin v)](tan v) ( 4u sin v) ln (u sin v) ;œ œ
4(u cos v)(u cos v)
u sin v sin v
4u cos v
z 4e ln y 4(u cos v) ln (u sin v) (4 cos v) ln (u sin v) 4(u cos v)œœ Êœ
xzsin v
uu sin v
`
`ˆ‰
(4 cos v) ln (u sin v) 4 cos v; also ( 4u sin v) ln (u sin v) 4(u cos v)œœ
`
`
zu cos v
vu sin v
ˆ‰
( 4u sin v) ln (u sin v)œ
4u cos v
sin v
(b) At 2 : 4 cos ln 2 sin 4 cos 2 2 ln 2 2 2 2 (ln 2 2);
ˆ‰ ˆ ‰ ÈÈ ÈÈ
ßœ œ œ
1111
4u 4 4 4
z`
`
( 4)(2) sin ln 2 sin 4 2 ln 2 4 2 2 2 ln 2 4 2
`
`
z
v44
(4)(2) cos
sin
œ œ œ
11
ˆ‰ ÈÈ È È È
ˆ‰
ˆ‰
4
4
8. (a) cos v sin v 0;
`
`
zx sin v
uxyxyu
11
y cos v (u sin v)(cos v) (u cos v)(sin v)
œœœ œ
–— –—
Š‹
Š‹ Š‹
Š‹
y
xx
yy
x
y
( u sin v) u cos v
`
`
zxu cos v
vxyxyu
11
yu sin v (u sin v)(u sin v) (u cos v)(u cos v)
œ œœ
–— –—
Š‹
Š‹ Š‹
Š‹
y
xx
yy
x
y
sin v cos v 1; z tan tan (cot v) 0 and csc vœ œ œ œ Ê œ œ
# # " " #
``"
``
Š‹ ˆ‰
ab
xzz
yuv1cotv
1œœ
"
sin v cos v
(b) At 1.3 : 0 and 1
ˆ‰
ßœ œ
1
6u v
zz``
``
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

818 Chapter 14 Partial Derivatives
9. (a) (y z)(1) (x z)(1) (y x)(v) x y 2z v(y x)
```` ``
```````
`
wwxw wz
uxuyuzu
y
œœœ
(u v) (u v) 2uv v(2u) 2u 4uv; œ œ œ
```` ``
```````
`
wwxw wz
vxvyvzv
y
(y z)(1) (x z)( 1) (y x)(u) y x (y x)u 2v (2u)u 2v 2u ;œ œ œ œ#
w xy yz xz u v u v uv u v uv u v 2u v 2u 4uv andœœ œ Ê œababab
#########`
`
w
u
2v 2u
`
`
#
w
vœ
(b) At 1 : 2 4 (1) 3 and 2(1) 2
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
"` " " ` "
#` # # ` # #
#
ßœ œ œœ
ww3
uv
10. (a) e sin u ue cos u e cos u ue sin u e
`
`
w2x 2z
u xyz xyz xyz
vv v v v
2y
œ
Š‹ Š‹ Š‹
ababab
e sin u ue cos uœ
ˆ‰
ab
2ue sin u
ue sin u ue cos u ue
vv
v
2v 2v 2v
e cos u ue sin u
ˆ‰
ab
2ue cos u
ue sin u ue cos u ue
vv
v
2v 2v 2v
e;œ
ˆ‰
ab
2ue 2
ue sin u ue cos u ue u
v
v
2v 2v 2v
ue sin u ue cos u ue
`
`
w2x 2z
v xyz xyz xyz
vv v
2y
œ
Š‹ Š‹ Š‹
ab ab ab
ue sin uœˆ‰
ab
2ue sin u
ue sin u ue cos u ue
v
v
2v 2v 2v
ue cos uˆ‰
ab
2ue cos u
ue sin u ue cos u ue
v
v
2v 2v 2v
ue 2; w ln u e sin u u e cos u u e ln 2u eœœœ
ˆ‰
ab a b a b
2ue
ue sin u ue cos u ue
v2v2v2v2v
v
2v 2v 2v
### ## #
ln 2 2 ln u 2v and 2œ Êœ œ
``
``
w2 w
uu v
(b) At 2 0 : 1 and 2abß œ œ œ
``
`# `
w2 w
uv
11. (a) 0;
`````"
```````
` `
uuuur
x p x q x r x qr (qr) (qr) (qr)
p q rp pq qrrppq
œœœ œ
`````"
```````
` `
uuuur
y p y q y r y qr (qr) (qr) (qr) (qr)
p q rp pq qrrppq 2p2r
œœœ œ
; œœœ
(2x2y2z)(2x2y2z) p q
(2z 2y) (z y) z p z q z r z
zuuuur
` `
```````
`````
;œ œ œ œ œ
"
q r (q r) (q r) (q r) (q r) (2z 2y) (z y)
rp pq qrrppq 2q2p 4y y
u 0, , and œœ œ Êœ œ œ œ
p q 2y y (z y) y( 1) (z y)(0) y(1)
q r 2z 2y z y x y (z y) (z y) z (z y)
uu z u
` ` `
`` `
œ y
(z y)
(b) At 3 2 1 : 0, 1, and 2
Š‹
Èßß œ œ œ œ œ
``" `
`` `
uu u2
xy(12) z(12)
12. (a) (cos x) re sin p (0) qe sin p (0) y if x ;
`
`##
" "
u e e cos x e cos x
x1p 1p
qr qr z
1sinx
œ œœœ
qr qr z ln y
ÈÈÈ
abab 11
(0) re sin p qe sin p (0) xzy ;
`
`
" "
ue z
yyyy
1p
qr qr z 1
z re sin p zyx
œ œ œœ
qr qr zz
Ȉ‰
abab
Š‹
(0) re sin p (2z ln y) qe sin p 2zre sin p (ln y)
` "
`
" " "
ue
zzz
1p
qr qr qr qe sin p
œ œ
qr qr
Èababa b
ˆ‰
(2z) y x ln y xy ln y; u e sin (sin x) xy if x y ,œœœœŸŸÊœ
ˆ‰
ab
" `
"
##`zz x
zzzlnyz z
z ln y y x u
abab
z11
xzy , and xy ln y from direct calculations
``
``
uu
yz
z1 z
œœœ
(b) At : 2, , ln
ˆ ‰ ˆ‰ ˆ‰ˆ ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
È
111
11
4x y4 4z4 4
uu u
22 ln 2
ßß œ œ œ œ œ œ
""` " ` "" ` " "
##` # ` ## ` # #
"Î# Ð"Î#Ñ" "Î#
ÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
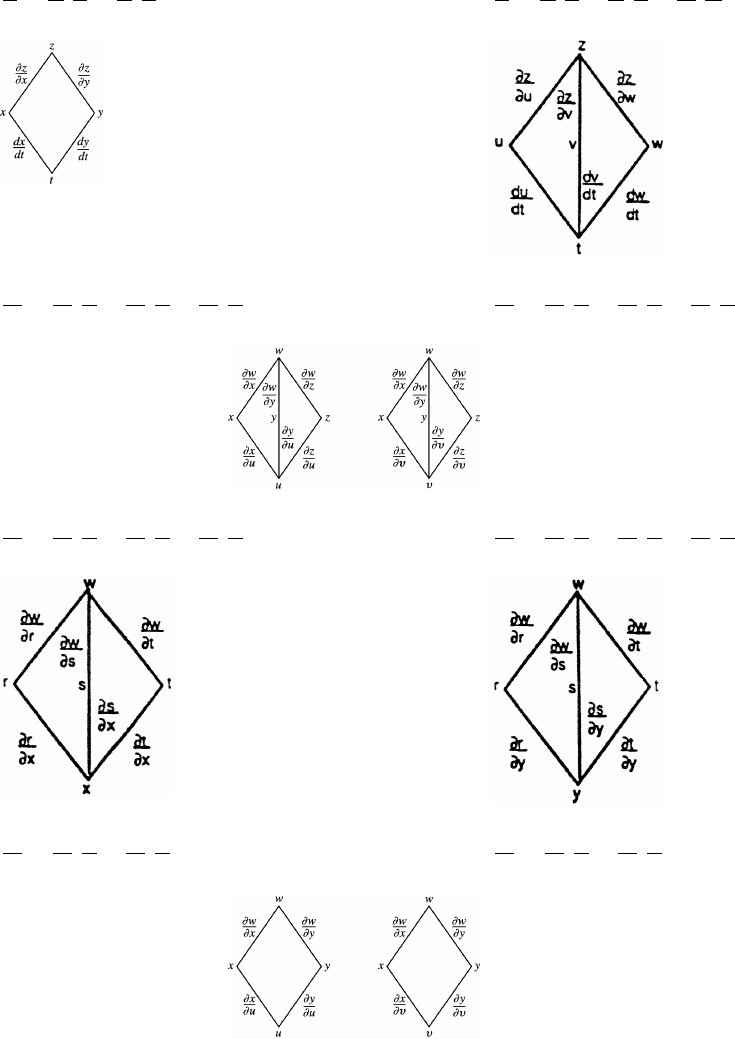
Section 14.4 The Chain Rule 819
13. 14.
dz z dx z dz z du z dv x dw
dt x dt y dt dt u dt v dt w dt
dy
œ œ
`` ```
`` ```
15.
```` `` ```` ``
` `` `` `` ` `` `` ``
` `
wwxw wz wwxw wz
u xu yu zu v xv yv zv
y y
œ œ
16.
``````` ```````
``````` ```````
wwrwswt wwrwswt
xrxsxtx yrysyty
œ œ
17.
```` ````
` `` `` ` `` ``
` `
wwxw wwxw
u xu yu v xv yv
y y
œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
820 Chapter 14 Partial Derivatives
18.
` `` `` ` `` ``
` `` `` ` `` ``
w wu wv w wu wv
x ux vx y uy vy
œ œ
19.
```` ````
` `` `` ` `` ``
` `
zzxz zzxz
t xt yt s xs ys
y y
œ œ
20. 21.
`
`` ````
`````
ydy
rdur s dus t dut
u w dw u w dw u
œœœ
22.
```` ````
` ````````
`
wwxw wzwv
p xpypzpvp
y
œ
23. since 0 since 0
`` ` ` `` ` `
```` ````
w w dx w w dx w w dx w w dx
r x dr y dr x dr dr s x ds y ds y ds ds
dy dy dy dy
œœ œ œœ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.4 The Chain Rule 821
24.
````
`````
`
wwxw
sxsys
y
œ
25. Let F(x y) x 2y xy 0 (x y) 3x yßœ œÊJßœ
$# #
x
and F (x y) 4y x
ydy 3x y
dx F ( 4y x)
F
ßœÊ œœ
x
y
(1 1)Êßœ
dy
dx 3
4
26. Let F(x y) xy y 3x 3 0 F (x y) y 3 and F (x y) x 2y ß œ œ Ê ß œ ß œ Ê œ œ
#
xy dy y 3
dx F x 2y
Fx
y
( 1 1) 2Êßœ
dy
dx
27. Let F(x y) x xy y 7 0 F (x y) 2x y and F (x y) x 2y ßœ œÊ ßœ ßœ Ê œœ
##
xy
dy 2x y
dx F x 2y
Fx
y
(1 2)Êßœ
dy
dx 5
4
28. Let F(x y) xe sin xy y ln 2 0 F (x y) e y cos xy and F (x y) xe x sin xy 1ßœ œÊ ßœ ßœ
yyy
xy
( ln 2) (2 ln 2)Ê œ œ Ê !ß œ
dy e y cos xy dy
dx F xe x sin xy 1 dx
Fx
y
y
y
29. Let F(x y z) z xy yz y 2 0 F (x y z) y, F (x y z) x z 3y , F (x y z) 3z yßßœ œÊ ßßœ ßßœ ßßœ
$$ ##
xy z
(111) ; Ê œ œ œ Ê ß ß œ œ œ œ
``"`
```
zzz
x F 3z y 3z y x 4 y F 3z y 3z y
Fy y xz3y xz3y
F
x
z z
y
(111)Êßßœ
`
`
z3
y4
30. Let F(x y z) 1 0 F (x y z) , F (x y z) , F (x y z)ßß œ œ Ê ßß œ ßß œ ßß œ
""" " " "
xyz x y z
xyz
(236) 9; (236) 4Ê œ œ œ Ê ß ß œ œ œ œ Ê ß ß œ
````
````
zzzzzz
xF xx yF yy
FF
x
z z
x y
z z
y
Š‹ Š‹
Š‹ Š‹
31. Let F(x y z) sin (x y) sin (y z) sin (x z) 0 F (x y z) cos (x y) cos (x z),ßßœœÊßßœ
x
F (x y z) cos (x y) cos (y z), F (x y z) cos (y z) cos (x z)
yz z
xF
F
ßß œ ßß œ Ê œ
`
`
x
z
()1; ()1œ Ê ß ß œ œ œ Ê ß ß œ
cos (x y) cos (x z) cos (x y) cos (y z)
cos (y z) cos (x z) x y F cos (y z) cos (x z) y
zz z
F
` ` `
`` `
111 111
y
z
32. Let F(x y z) xe ye 2 ln x 2 3 ln 2 0 F (x y z) e , F (x y z) xe e , F (x y z) yeßßœ œÊ ßßœ ßßœ ßßœ
yz y yz z
xy z
2
x
(1 ln 2 ln 3) ; (1 ln 2 ln 3)Ê œ œ Ê ß ß œ œ œ Ê ß ß œ
````
````
zz4zxeez5
x F ye x 3 ln 2 y F ye y 3 ln 2
FeF
xx
z z
y2
z z
yyz
ˆ‰
33. 2(x y z)(1) 2(x y z)[ sin (r s)] 2(x y z)[cos (r s)]
```` ``
```````
`
wwxw wz
rxryrzr
y
œ œ
2(x y z)[1 sin (r s) cos (r s)] 2[r s cos (r s) sin (r s)][1 sin (r s) cos (r s)]œ œ
2(3)(2) 12Êœœ
¸
`
`
w
rr1s 1œßœ
34. y x(1) (0) (u v) (1) 8
```` `` " `
``````` `
`
w w x w w z 2v 2v v w 4 4
vxvyvzv u z uu v 1 1
y
œœ œ Ê œ œ
ˆ‰ ˆ‰ ˆ‰ ¸ ˆ‰ˆ‰
u1v2œ ß œ
35. 2x ( 2) (1) 2(u 2v 1) ( 2)
```` " "
`````
`
w w x w 2uv2
v x v y v x x (u2v1) u2v1
yy
œœ œ
ˆ‰ˆ‰
’“
7ʜ
¸
`
`
w
vu0v0œßœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

822 Chapter 14 Partial Derivatives
36. (y cos xy sin y)(2u) (x cos xy x cos y)(v)
````
`````
`
zzxz
uxuyu
y
œœ
uv cos u v uv sin uv (2u) u v cos u v uv u v cos uv (v)œcdc dab ababab
$$ ## $$##
0(cos 0cos 0)(1)2Êœœ
¸
`
`
z
uu0v1œßœ
37. e e (2) 2;
`` `
`` `
zdzx 5 5 z 5
udxu 1x u 1(2)
uu
1eln v
œœ œ Ê œ œ
ˆ‰ ¸
’“ ’“
ab
uuln2v1œßœ
(1) 1
`` " "`
`` `
zdzx 5 5 z 5
vdxv 1xv v v 1(2)
1eln v
œœ œ Ê œ œ
ˆ ‰ˆ‰ ˆ‰ ¸
’“ ’“
ab
uuln2v1œßœ
38. ;
`" " "` "
`` `
`
zdz z2
udqu q 1u 1u tanu1u u tan111
qv3 v3
v3 tanu
œœ œ œ Ê œ œ
Š‹Š‹Š ‹Š‹ ¸
ÈÈ
Èabab abab
u1v 2œßœ 1
`" " "`"
`` #` #
`
z dz tan u tan u z
vdqv q (v3) v
q
2v3 v3 tan u 2v 3
œœ œ œ Ê œ
Š‹Š‹Š ‹Š‹ ¸
ÈÈ È u1v 2œßœ
39. Let x s t w f s t f x f x 3s 3s e , f x 2t 2t eœÊœœÊœ œ†œ œ œ†œ
32 32 2 2st st
wdwx wdwx
sdxs tdxt
a b ab ab ab
`` ``
`` ``
w w
32 32
40. Let x t s and y w f t s f x y f x, y 2t s f x, yœ œÊœ ßœßÊ œ œ † †
22
ss wwxw 1
tt sxsys t
yxy
ˆ‰
ab ab ab
````
`````
`
t s 2t s 2s t ; f x, y s f x, yœ ††œœ œœ † †ab ab ab
ˆ‰
24 2
s1st5stwwxw s
t2t22txtyt t
ts yxy
ˆ‰
2244
2
````
`````
`
ts s sœ††œœab
ˆ‰ ˆ ‰
22 5
ssss
t2t 22
ts
ˆ‰
22
2
55
41. V IR R and I; R I 0.01 volts/secœÊ œ œ œ œ Ê
`` ``
`` ``
V V dV V dI V dR dI dR
I R dt I dt R dt dt dt
(600 ohms) (0.04 amps)(0.5 ohms/sec) 0.00005 amps/secœ Êœ
dI dI
dt dt
42. V abc (bc) (ac) (ab)œÊœœ
dV V da V db V dc da db dc
dt a dt b dt c dt dt dt dt
```
```
(2 m)(3 m)(1 m/sec) (1 m)(3 m)(1 m/sec) (1 m)(2 m)( 3 m/sec) 3 m /secÊœ œ
¸
dV
dt a1b2c3œßœßœ
$
and the volume is increasing; S 2ab 2ac 2bc œ Êœ
dS S da S db S dc
dt a dt b dt c dt
```
```
2(b c) 2(a c) 2(a b) œ Ê
da db dc dS
dt dt dt dt ¸a1b2c3œßœßœ
2(5 m)(1 m/sec) 2(4 m)(1 m/sec) 2(3 m)( 3 m/sec) 0 m /sec and the surface area is not changing;œœ
#
D a b c a b c œÊœœ Ê
Ȉ‰¸
### ``` "
```
dD D da D db D dc da db dc dD
dt a dt b dt c dt dt dt dt dt
abc
Èa1b2c3œßœßœ
[(1 m)(1 m/sec) (2 m)(1 m/sec) (3 m)( 3 m/sec)] m/sec 0 the diagonals areœœÊ
Š‹
"
È È
14 m 14
6
decreasing in length
43. (1) (0) ( 1) ,
``````` ` ` ` ``
` `````` ` ` ` ``
ffufvfwf f f ff
x uxvxwx u v w uw
œ œœ
( 1) (1) (0) , and
``````` ` ` ` ``
` `````` ` ` ` ``
ffufvfwf f f ff
y uyvywy u v w uv
œ œ œ
(0) ( 1) (1) 0
``````` ` ` ` `` ```
``````` ` ` ` `` ```
ffufvfwf f f ff fff
z uzvzwz u v w vw xyz
œ œ œÊœ
44. (a) f f f cos f sin and f ( r sin ) f (r cos ) f sin f cos
`` ` "`
``` ` `
`
wx w w
rrr r
xy x y x y x y
y
œœ œ Ê œ )) ) ) ) )
))
(b) sin f sin cos f sin and f sin cos f cos
``
``
##
wcos w
rr
xy xy
))) ) )) )œ œ
ˆ‰
)
)
f (sin ) ; then f cos (sin ) (sin ) f cos Êœ œ Ê
yx x
wcos w w wcos w
rr r rr
)))))
``` ` `
``` ` `
ˆ‰ ‘ˆ‰
))
))
sin 1 sin f (cos ) œ œ Êœ
`` ` ` ` ``
`` ` ` ` ``
##
w w sin cos w w sin cos w w sin w
rrr rr rr
x
ab a b
ˆ‰ ˆ‰ ˆ‰
)) )
)) )) )
)))
(c) f cos andab a b
ˆ‰ ˆ ‰ˆ ‰ ˆ‰
Š‹
xw 2 sin cos w w sin w
rrrr
##````
````
##
œ ))) )
))
fsin ffab a b ab ab
ˆ‰ ˆ ‰ˆ ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
yxy
w 2 sin cos w w cos w w w
rrr r rr
###
#```` `"`
```` ``
####
œ Êœ))) )
)) )
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.4 The Chain Rule 823
45. w x y w x y
xxx
wwuwv w w w w w
x ux vx u v u xu xv
œœœÊœ
` `` `` ` ` ` `` ``
` `` `` ` ` ` `` ``
ˆ‰ ˆ‰
x y x x y y x yœ œ
` ```` ````` `` ``
`````` `````` ``` ```
w wuwv wuwvw ww ww
uuxvux uvxvxu uvu uvv
Š‹Š‹Š‹Š‹
x 2xy y ; w y x œ œœœ
`` ` ` ````` ``
` ` `` ` ` `` `` ` `
##
ww w w wwuwv ww
u u vu v y uy vy u v
y
wy x ʜ
yy wwuwv wuwv
uuyvuy uvyvy
````` ````
`````` `````
Š‹Š‹
y y x x y x y 2xy x ; thusœ œ
``` ``````
` ` `` `` ` ` ` `` `
##
www wwwwww
u u vu uv v u u vu v
Š‹Š‹
w w xy xy xy(w w)0, since w w 0
xx yy uu vv uu vv
ww
uv
œ œ œ œababab
## ## ##
``
``
46. f (u)(1) g (v)(1) f (u) g (v) w f (u)(1) g (v)(1) f (u) g (v);
`
`
w w w w ww ww ww ww
w
xœœÊœ œ
xx
f (u)(i) g (v)( i) w f (u) i g (v) i f (u) g (v) w w 0
`
`
w w ww # ww # ww ww
w
yœÊœ œÊœ
yy xx yy
ab ab
47. f (x y z) cos t, f (x y z) sin t, and f (x y z) t t 2
xy z df f dx f f dz
dt x dt y dt z dt
dy
ßß œ ßß œ ßß œ Ê œ
#```
```
(cos t)( sin t) (sin t)(cos t) t t 2 (1) t t 2; 0 t t 2 0 t 2œ œœÊœÊœab
## #
df
dt
or t 1; t 2 x cos ( 2), y sin ( 2), z 2 for the point (cos ( 2) sin ( 2) 2); t 1 x cos 1,œ œ Ê œ œ œ ß ß œ Ê œ
y sin 1, z 1 for the point (cos 1 sin 1 1)œœ ßß
48. 2xe cos 3z ( sin t) 2x e cos 3z 3x e sin 3z (1)
dw wdx w wdz
dt x dt y dt z dt t
dy 2y 2y 2y
œœ
``` "
``` #
##
aba ba b
ˆ‰
2xe cos 3z sin t 3x e sin 3z; at the point on the curve z 0 t z 0œ œ Ê œ œ
2y 2y
2x e cos 3z
t
2y
#
#
004Êœœ
¸
dw
dt
2(1) (4)(1)
Ðß ßÑ1ln20 #
49. (a) 8x 4y and 8y 4x (8x 4y)( sin t) (8y 4x)(cos t)
`` ``
`` ``
TTdTTdxT
x y dt x dt y dt
dy
œ œ Ê œ œ
(8 cos t 4 sin t)( sin t) (8 sin t 4 cos t)(cos t) 4 sin t 4 cos t 16 sin t cos t;œ œ Êœ
##
dT
dt
0 4 sin t 4 cos t 0 sin t cos t sin t cos t or sin t cos t t , , , on
dT 537
dt 4444
œÊ œÊ œ Ê œ œ Êœ
## ## 1111
the interval 0 t 2 ;ŸŸ1
16 sin cos 0 T has a minimum at (x y) ;
¹Š‹
dT
dt 4 4
22
tœ4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a maximum at (x y) ;
¹Š‹
dT 3 3
dt 4 4
22
tœ3
4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a minimum at (x y) ;
¹Š‹
dT 5 5
dt 4 4
22
tœ5
4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a maximum at (x y)
¹Š‹
dT 7 7
dt 4 4
22
tœ7
4
œÊ ßœß
11 ÈÈ
##
(b) T 4x 4xy 4y 8x 4y, and 8y 4x so the extreme values occur at the four pointsœ Ê œ œ
##
``
``
TT
xy
found in part (a): T T 4 4 4 6, the maximum and
Š‹Š‹
ˆ‰ ˆ ‰ ˆ‰
ß œ ß œ œ
ÈÈ È È
22 2 2
## # # # # #
"""
T T 4 4 4 2, the minimum
Š‹Š ‹
ˆ‰ ˆ‰ ˆ‰
ÈÈ È È
22 2 2
## ## ###
"""
ߜߜ œ
50. (a) y and x y 2 2 sin t x 2 cos t
`` ``
`` ``
TTdTTdxT
x y dt x dt y dt
dy
œ œÊœœ
Š‹Š‹
ÈÈ
2 sin t 2 2 sin t 2 2 cos t 2 cos t 4 sin t 4 cos t 4 sin t 4 1 sin tœ œœ
Š‹Š ‹Š ‹Š‹
ÈÈÈÈ ab
## # #
4 8 sin t 16 sin t cost t; 0 4 8 sin t 0 sin t sin t t ,œ Ê œ œ Ê œ Ê œ Ê œ„ Êœ
###
""
#
dT dT
dt dt 4
2
È1
, , on the interval 0 t 2 ;
357
444
111 ŸŸ1
8 sin 2 8 T has a maximum at (x y) (2 1);
¹ˆ‰
dT
dt 4
tœ4
œ œ Ê ß œ ß
1
8 sin 2 8 T has a minimum at (x y) ( 2 1);
¹ˆ‰
dT 3
dt 4
tœ3
4
œ œ Ê ß œ ß
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
824 Chapter 14 Partial Derivatives
8 sin 2 8 T has a maximum at (x y) ( 2 1);
¹ˆ‰
dT 5
dt 4
tœ5
4
œ œ Ê ß œ ß
1
8 sin 2 8 T has a minimum at (x y) (2 1)
¹ˆ‰
dT 7
dt 4
tœ7
4
œ œ Ê ß œ ß
1
(b) T xy 2 y and x so the extreme values occur at the four points found in part (a):œÊ œ œ
``
``
TT
xy
T(2 1) T( 2 1) 0, the maximum and T( 2 1) T(2 1) 4, the minimumß œ ß œ ß œ ß œ
51. G(u x) g(t x) dt where u f(x) g(u x)f (x) g (t x) dt; thusßœß œÊœœß ß
''
a a
u u
x
dG G du G dx
dx u dx x dx
``
``
w
F(x) t x dt F (x) x x (2x) t x dt 2x x x dtœÊœ œ
'''
000
xxx
ÈÈ
Éab È
%$ # $ %$ )$
w%`
`
x
3x
2t x
È
52. Using the result in Exercise 51, F(x) t x dt t x dt F (x)œœ Ê
''
x1
1x
ÈÈ
$# $# w
xx x dt
xxx tx dt
œœ
’“
Éab ÈÈ
## $#
$#`
`
#'#
''
1
x
x
1
x
x
tx
È
14.5 DIRECTIONAL DERIVATIVES AND GRADIENT VECTORS
1. 1, 1 f ; f(2 1) 1
``
``
ff
xy
œ œ Ê œ ß œ™ij
1 y x is the level curveÊ œ
2. ( ) 1;
```
` ` `
f2x f f
xxy x yxy
2y
œ Ê "ß " œ œ
( ) 1 f ; f(1 1) ln 2 ln 2Ê"ß"œÊ œ ßœ Ê
`
`
f
y™ij
ln x y 2 x y is the level curveœÊœab
## ##
3. y 2 1 1; 2x y 2 1 4;
`` ` `
`` ` `
gg g g
xx y x
2
œÊ ßœ œ Ê ßœab ab
g 4 ; g 2 1 2 x is the levelÊœ ߜʜ™ijab 2
y
curve
4. x 2 2; y
`` `
`` `
gg g
xx y
œÊ ß"œ œ
Š‹
ÈÈ
21 g2;Êß"œÊœ
`
`
g
yŠ‹
ÈÈ
™ij
g 2 or 1 x y is the level
Š‹
Èß" œ Ê œ œ
""
####
##
xy
curve
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.5 Directional Derivatives and Gradient Vectors 825
5. ( 1 2) ;
```
```
f1 f 1f 3
xx2y
2x 3y 2 2x 3y
œÊßœœ
ÈÈ
( 1 2) ; f ; f( 1 2) 2Ê ßœ Ê œ ßœ
`
`
f3 13
x4 24
™ij
4 2x 3y is the level curveʜ
6. 4 2 ;
``
``
ff1
xx16
y
2y x 2x
œÊßœ
232
Èab
42 f ;
``
``
ff111
y2yx y 4 164
x
œ Ê ß œ Ê œ
È
2ab ™ij
f 4 2 y x is the level curveab È
ß œ Ê œ
1
4
7. 2x (1 1 1) 3; 2y ( ) 2; 4z ln x ( ) 4;
````` `
````` `
fzf f f f f
xxxyyz z
œ Ê ß ß œ œ Ê "ß "ß " œ œ Ê "ß "ß " œ
thus f 3 2 4™œijk
8. 6xz (1 ) ; 6yz ( ) 6; 6z 3 x y
`````
``#`` `
###
fzf11f f f x
xxz1x y y z xz1
œ Ê ß"ß" œ œ Ê "ß"ß" œ œ ab
( ) ; thus f 6Ê "ß"ß" œ œ
`" "
`# ##
f11
z™ij k
9. ( 1 2 2) ; ( 1 2 2) ;
`"` `"`
````
fx f 26f f 23
xxx27yyy54
xyz xyz
y
œ Ê ß ß œ œ Ê ß ß œ
ab ab
( 1 2 2) ; thus f
`"`
``
fz f 23 262323
zzz54275454
xyz
œ Ê ß ß œ œ
ab ™ijk
10. e cos z 1; e cos z sin x 0 0 ;
````
``#``#
"
ffff
xx6yy6
xy xy
y1
1x
33
œÊ!ß!ßœœÊßßœ
ÈÈÈ
ˆ‰ ˆ‰
11
e sin z ; thus f
``" "
``####
ff
zz6
xy 32 3
œ Ê !ß!ß œ œ
ˆ‰ Š‹
1™ÈÈ
ijk
11. ; f (x y) 2y f (5 5) 10; f (x y) 2x 6y f (5 5) 20uijœœ œ ßœÊßœ ßœÊßœ
A
A
ij
kk È
43
43
43
55
xxy y
f10 20 (Df) f 10 20 4ÊœÊ œ œœ™™†ij u
uP43
55
ˆ‰ ˆ‰
12. ; f (x y) 4x f ( 1 1) 4; f (x y) 2y f ( 1 1) 2uijœ œ œ ßœ Ê ßœ ßœ Ê ßœ
A
A
ij
kk È34
3(4)
34
55
xxyy
f42 (Df) f 4ÊœÊ œ œœ™™†ij u
uP12 8
55
13. ; g x y g 1 1 3; g x y g 1 1 3uijœ œ œ ßœ Ê ßœ ßœ Ê ßœ
A
A
ij
kk Èab ab
12 5 y 2
12 5
12 5 x2
13 13 xxy y
xy 2 xy 2
ab a b ab a b
2
22
2
g3 3 Dg gÊ œ Ê œ œœ™™†ij uab
uP36 15 21
13 13 13
14. ; h (x y) h (1 1) ;uijœ œ œ ßœ Ê ßœ
A
A
ij
kk ÈÈÈ Š‹
ˆ‰ ˆ‰
È
ÊŠ‹
32
3(2)
32
13 13 xx
1
3
1
"
#
y
x
y
x
y
xy
4
h (x y) h (1 1) h (D h) h
yy P
1
3
1
33 36
213 213
ßœ Ê ßœÊ œ Ê œ œ
ˆ‰
ˆ‰ ˆ‰
È
ÊŠ‹ ÈÈ
x
y
x
x
xy
4
###
"
™™†ij u
u
œ 3
213
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

826 Chapter 14 Partial Derivatives
15. ; f (x y z) y z f (1 1 2) 1; f (x y z) x zuijkœ œ œ ßßœÊ ßßœ ßßœ
A
A
ijk
kk È36
36(2)
362
777xxy
#
f (1 1 2) 3; f (x y z) y x f (1 1 2) 0 f 3 (D f) f 3Êßßœ ßßœÊßßœÊ œÊ œ œœ
yz z P
318
77
™™†ij u
u
16. ; f (x y z) 2x f (1 1 1) 2; f (x y z) 4yuijkœ œ œ ßß œ Ê ßß œ ßß œ
A
A
ijk
kk ÈÈÈÈ
111
111
333
xxy
f(111) 4; f(xyz) 6z f(111) 6 f 2 4 6 (Df) fÊ ßßœ ßßœ Ê ßßœÊ œ Ê œ
yz z P
™™†ijk u
u
2460œœ
Š‹ Š‹ Š‹
"""
ÈÈÈ
333
17. ; g (x y z) 3e cos yz g (0 0 0) 3; g (x y z) 3ze sin yzuijkœ œ œ ßß œ Ê ßß œ ßß œ
A
A
ij k
kk È22
21(2)
212
333 xxy
xx
g (0 0 0) 0; g (x y z) 3ye sin yz g (0 0 0) 0 g 3 (D g) g 2Ê ßßœ ßßœ Ê ßßœÊ œ Ê œ œ
yz z P
x™™†iu
u
18. ; h (x y z) y sin xy h 1 0 1;uijkœ œ œ ßß œ Ê ßß œ
A
A
ijk
kk È
""
#
22
122
122
333 x
xx
ˆ‰
h (x y z) x sin xy ze h ; h (x y z) ye h 2 h 2
yyzz
yz yz
z
ß ß œ Ê "ß !ß œ ß ß œ Ê "ß !ß œ Ê œ
ˆ‰ ˆ‰
"" " " "
## # #
™ijk
(D h) h 2Ê œ œœ
uP333
4
™†u""
19. f (2x y) (x 2y) f( 1 1) ; f increases™™œ Ê ßœÊœ œ œ ij iju ij
™
™
f
f(1) 1 22
kk ÈÈÈ
""
ij
most rapidly in the direction and decreases most rapidly in the direction ;uij uijœ œ
"" ""
ÈÈ ÈÈ
22 22
(D f) f f 2 and (D f) 2
uuPP
œœœ œ™† ™ukk
ÈÈ
20. f 2xy ye sin y x xe sin y e cos y f(1 0) 2 ; f increases most™™œ Ê ßœÊœœaba b
xy xy xy f
f
ijjuj
#™
™kk
rapidly in the direction and decreases most rapidly in the direction ; (D f) f fuj u j uœœœœ
uP™† ™kk
2 and (D f) 2œœ
uP
21. f z y f(4 ) 5 ;™™œÊ ß"ß"œÊœœ œ
"""
yy f
x 5
f5
1(5)(1) 33 33 33
ijk ijku ijk
Š‹ ™
™kk ÈÈÈÈ
ijk
f increases most rapidly in the direction of and decreases most rapidly in the directionuijkœ
""
33 33 33
5
ÈÈÈ
; (D f) f f 3 3 and (D f) 3 3œ œ œ œ œuijk u
""
33 33 33
5P
ÈÈÈ u™† ™kkÈÈ
uP
22. g e xe 2z g 1 ln 2 2 2 ;™™œ Ê ß ß œÊœ œ œ
yy g
g333
22
221
22
ijk ijku ijk
ˆ‰
" "
#
™
™kk Èijk
g increases most rapidly in the direction and decreases most rapidly in the directionuijkœ
22
333
"
; (D g) g g 3 and (D g) 3œ œ œ œ œuijk u
22
333 PP
"uu
™† ™kk
23. f f( ) 2 2 2 ;™™œ Ê "ß"ß" œ Ê œ œ
ˆ‰ ˆ‰
Š‹
"" "" "" " " "
xx yy zz f
f
333
ijk ijku ijk
™
™kk ÈÈÈ
f increases most rapidly in the direction and decreases most rapidly in the directionuijkœ
"""
ÈÈÈ
333
; (D f) f f 2 3 and (D f) 2 3œ œ œ œ œuijk u
"""
ÈÈÈ
333 PP
™† ™
uu
kkÈÈ
24. h 1 6 h( 0) 2 3 6 ™™œ Ê "ß"ßœ Êœ œ
Š‹Š ‹
2x
xy1 xy1 h
2y 236
h
236
ijk ijku
™
™kk Èijk
; h increases most rapidly in the direction and decreases most rapidly in theœ œ
236 236
777 777
ijk u ijk
direction ; (D h) h h 7 and (D h) 7œ œ œ œ œuijk u
236
777 PPuu
™† ™kk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.5 Directional Derivatives and Gradient Vectors 827
25. f 2x 2y f 2 2 2 2 2 2™™œ Ê ß œ ij i j
Š‹
ÈÈ È È
Tangent line: 2 2 x 2 2 2 y 2 0ʜ
ÈÈÈÈ
Š‹Š‹
2x 2y 4ʜ
ÈÈ
26. f 2x f 2 1 2 2™™œÊ ßœ ij i j
Š‹
ÈÈ
Tangent line: 2 2 x 2 (y 1) 0ʜ
ÈÈ
Š‹
y 2 2x 3ʜ
È
27. f y x f(2 2) 2 2™™œ Ê ßœij ij
Tangent line: 2(x 2) 2(y 2) 0ʜ
yx4ʜ
28. f (2x y) (2y x) f( 1 2) 4 5™™œÊ ßœij ij
Tangent line: 4(x 1) 5(y 2) 0ʜ
4x 5y 14 0Ê œ
29. f 2x y x 2y 1™œaba bij
(a) f 1, 1 3 4 f 1, 1 5 D f 1, 1 5 in the direction of ™™ab ab abœ Êl lœÊ œ œ ij u i j
u34
55
(b) f 1, 1 3 4 f 1, 1 5 D f 1, 1 5 in the direction of œ Êl lœ Ê œ œ ™™ab ab abij u ij
u34
55
(c) D f 1, 1 0 in the direction of or
uabœ œ œuiju ij
43 43
55 55
(d) Let u u u u 1 u u 1; D f 1, 1 f 1, 1 3 4 u uuiju uij ijœÊllœ œÊœ œ †œ†
12 12
12
22 12
22
Èab aba ba b
u™
3u 4u 4 u u 1 u u 1 1 u u 0 u 0 or u ;œ œÊœ Ê œÊ œÊœ œ
12 2 1 1 1 1 1
33 253 24
44 162 25
11
22
2
ˆ‰
u 0 u 1 , or u u
12 1 2
24 7 24 7
25 25 25 25
œÊ œÊœ œ Ê œ Êœ uj u ij
(e) Let u u u u 1 u u 1; D f 1, 1 f 1, 1 3 4 u uuiju uij ijœÊllœ œÊœ œ †œ†
12 12
12
22 12
22
Èab aba ba b
u™
3u 4u 3 u u 1 u 1 u 1 u u 0 u 0 or u ;œœÊœÊ œÊ œÊœ œ
12 1 2 2 2 2 2
44 258 24
33 93 25
2
22
22
ˆ‰
u 0 u 1 , or u u
21 2 2
24 7 7 24
25 25 25 25
œÊ œÊœ œ Ê œ Êœ ui u ij
.
30. f™œ
2y
xy xy
2x
ab ab
22
ij
(a) f , 3 f , 10 D f , 10 in the direction of ™™
ˆ‰ ˆ‰ ˆ‰
ÈÈ
œÊllœ Êœ œ
13 13 13 3 1
22 22 22 10 10
ij u i j
uÈÈ
(b) f , 3 f , 10 D f 1, 1 10 in the direction of œ Êl lœ Ê œ œ ™™
ˆ‰ ˆ‰
ÈÈ
ab
13 13 31
22 22 10 10
ij u i j
uÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

828 Chapter 14 Partial Derivatives
(c) D f , 0 in the direction of or
uˆ‰
œ œ œ
13 13 13
22 10 10 10 10
uiju ij
ÈÈ ÈÈ
(d) Let u u u u 1 u u 1; D f , f , 3 u uuiju uij ijœÊllœ œÊœ œ †œ†
12 12
12
22 12
22 13 13
22 22
Ȉ‰ ˆ‰aba b
u™
3u u 2 u 3u 2 u 3u 2 1 10u 12u 3 0 uœ œÊœÊ œÊ œÊœ
12 2 1 1 1 1
11
22
266
10
ab „
È
u u , or u u
12 12
66 236 66 236 66 236
10 10 10 10 10 10
œÊœ Êœ œÊœ
ÈÈÈÈÈÈ
ui j
ʜ ui j
66 236
10 10
ÈÈ
(e) Let u u u u 1 u u 1; D f , f , 3 u uuiju uij ijœÊllœ œÊœ œ †œ†
12 12
12
22 12
22 13 13
22 22
Ȉ‰ ˆ‰aba b
u™
3u u 1 u 1 3u u 1 3u 1 10u 6u 0 u 0 or u ;œ œÊ œ Ê œÊ œÊ œ œ
12 2 1 1 1 1 1
11
22
23
5
ab
u 0 u 1 , or u u
12 1 2
3434
5555
œÊ œÊœ œÊ œÊœ uj u i j
31. f y (x 2y) f(3 2) 2 7 ; a vector orthogonal to f is 2 ™™ ™œœ Ê ßœ Êœ œi j ij v7ij uv
v
ij
kk È72
7(2)
and are the directions where the derivative is zeroœ œ
72 72
53 53 53 53
ÈÈ ÈÈ
iju ij
32. f f( ) ; a vector orthogonal to f is ™™ ™œ Ê "ß"œ œ
4xy 4x y
xy xy
abab
ij ij vij
and are the directions where the derivative is zeroÊœ œ œ œ uijuij
v
v
ij
kk ÈÈÈ ÈÈ
11 22 22
11 11
33. f (2x 3y) ( 3x 8y) f(1 2) 4 13 f(1 2) ( 4) (13) 185 ; no, the™™™œ Ê ßœ Ê ßœ œij ijkk
ÈÈ
##
maximum rate of change is 185 14
È
34. T 2y (2x z) y T(1 1 1) 2 T(1 1 1) ( 2) 1 1 6 ; no, the™™ ™œ Ê ßßœÊ ßßœœijk ijkkk
ÈÈ
###
minimum rate of change is 6 3
È
35. f f ( ) f ( ) and (D f)(1 2) f (1 2) f (1 2)™œ "ß# "ß# œ œ Ê ß œ ß ß
xy xy
iju ij
"
"" " "
ij
ÈÈÈ È È
11 2 2 2 2
uŠ‹ Š‹
2 2 f (1 2) f (1 2) 4; (D f)(1 2) f (1 2)(0) f (1 2)( 1) 3 f (1 2) 3œ Ê ß ß œ œ Ê ß œ ß ß œ Ê ß œ
Èxy x y y
uj
#u
f (1 2) 3; then f (1 2) 3 4 f (1 2) 1; thus f(1 2) 3 and Êßœ ßœÊßœ ßœ œœ
yx x
™ij uv
v
ij
kk È
2
(1) (2)
(D f) fœ Ê œ œ œ
12 6 7
55 55 5
ÈÈ ÈÈ È
ij u
uP™† "
36. (a) (D f) 2 3 f 2 3; ; thus
uPœ Ê œ œœ œ œ
ÈÈ
kk™uijku
v
v
ijk
kk k k
ÈÈÈÈ
"
11(1)
11
333
f
f
™
™
ff f23 222Ê œ Ê œ œ™™ ™kk ÈŠ‹
uijkijk
"""
ÈÈÈ
333
(b) (D f) f 2 2 2(0) 2 2vij u i j uœÊœœœÊœœœ
v
v
ij
kk ÈÈÈ ÈÈ
"" " "
11 2 2 2 2
uP™† Š‹ Š‹ È
37. The directional derivative is the scalar component. With f evaluated at P , the scalar component of f in the™™
!
direction of is f (D f) .uu™† œuP
38. D f f (f f f ) f ; similarly, D f f f and D f f f
ijk
œœœ œœ œ œ™† † ™† ™†iijki j k
xyz x y z
39. If (x y) is a point on the line, then (x y) (x x ) (y y ) is a vector parallel to the line 0ßßœ ÊœTij TN
!! †
A(x x ) B(y y ) 0, as claimed.ʜ
!!
40. (a) (kf) k k k k k f™ ™œ œ œ œ
```
``` ` ` ` ```
``` ```
(kf) (kf) (kf)
xyz x y z xyz
fff fff
ijk i j k ijk
ˆ‰ ˆ‰
Š‹ Š ‹
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.6 Tangent Planes and Differentials 829
(b) (f g)™œ œ
` ` ` ` ` `
``` ``````
```
(f g) (f g) (f g) g g g
xyz xxyyzz
fff
ijk i j k
Š‹Š‹Š‹
fgœ œ œ
`` ` ```
````` ` ``` ```
`` ` ```
ff f fff
xxyyz z xyz xyz
gg g ggg
iijjkk ijk ijk
Š‹Š‹
™™
(c) (f g) f g (Substitute g for g in part (b) above)™™™œ
(d) (fg) g f g f g f™œ œ
``` ` ` `
``` `` `` ``
```
(fg) (fg) (fg) g g g
xyz xx yy zz
fff
ijk i j k
Š‹Š‹Š‹
gf g f g fœ
ˆ‰ ˆ‰
Š‹Š‹Š‹ Š‹
`` `
``` `` `
```
ff f
xxy yz z
ggg
iijjkk
fgfggfœœ
Š‹Š‹
```
``` ```
```
ggg
xyz xyz
fff
ijk ijk™™
(e) ™Š‹ Š ‹ Š ‹
Œ
f
gx y z g g g
gf gf
gf
œ œ
```
```
Š‹ Š‹ Š‹
fff
ggg
ijk i j k
ff
xx zz
gg
f
yy
g
œœ
ŒŒ
ggg fff
gggg
gf
fff
xyz xyz
ggg fff
xyz xyz
ggg
ijk ijk ijk ijk
Š‹Š‹
œœ
gf fg gffg
gg g
™™ ™™
14.6 TANGENT PLANES AND DIFFERENTIALS
1. (a) f 2x 2y 2z f(1 1 1) 2 2 2 Tangent plane: 2(x 1) 2(y 1) 2(z 1) 0™™œ Ê ßßœ Ê œijk ijk
xyz3;Ê œ
(b) Normal line: x 1 2t, y 1 2t, z 1 2tœ œ œ
2. (a) f 2x 2y 2z f(3 5 4) 6 10 8 Tangent plane: 6(x 3) 10(y 5) 8(z 4) 0™™œ Ê ßßœ Ê œijk ijk
3x 5y 4z 18;Ê œ
(b) Normal line: x 3 6t, y 5 10t, z 4 8tœ œ œ
3. (a) f 2x 2 f(2 0 2) 4 2 Tangent plane: 4(x 2) 2(z 2) 0™™œ Ê ß ß œ Ê œik ik
4x 2z 4 0 2x z 2 0;Ê œÊœ
(b) Normal line: x 2 4t, y 0, z 2 2tœ œ œ
4. (a) f (2x 2y) (2x 2y) 2z f(1 1 3) 4 6 Tangent plane: 4(y 1) 6(z 3) 0™™œ Ê ßßœ Ê œijk jk
2y 3z 7;ʜ
(b) Normal line: x 1, y 1 4t, z 3 6tœœ œ
5. (a) f sin x 2xy ze x z xe y f(0 1 2) 2 2 Tangent plane:™™œ Ê ßßœÊababab11 xz xz
ijk ijk
#
2(x 0) 2(y 1) 1(z 2) 0 2x 2y z 4 0; œÊ œ
(b) Normal line: x 2t, y 1 2t, z 2 tœœœ
6. (a) f (2x y) (x 2y) f(1 1 1) 3 Tangent plane:™™œ Ê ßßœÊijk ijk
1(x 1) 3(y 1) 1(z 1) 0 x 3y z 1; œÊ œ
(b) Normal line: x 1 t, y 1 3t, z 1 tœ œ œ
7. (a) f for all points f(0 1 0) Tangent plane: 1(x 0) 1(y 1) 1(z 0) 0™™œ Ê ßß œ Ê œijk ijk
xyz1 0;ʜ
(b) Normal line: x t, y 1 t, z tœœœ
8. (a) f (2x 2y 1) (2y 2x 3) f(2 3 18) 9 7 Tangent plane:™™œ Ê ßß œÊijk ijk
9(x 2) 7(y 3) 1(z 18) 0 9x 7y z 21; œ Ê œ
(b) Normal line: x 2 9t, y 3 7t, z 18 tœ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

830 Chapter 14 Partial Derivatives
9. z f(x y) ln x y f (x y) and f (x y) f (1 0) 2 and f (1 0) 0 fromœ ßœ Ê ßœ ßœ Ê ßœ ßœÊab
##
xy xy
2x
xy xy
2y
Eq. (4) the tangent plane at (1 0 0) is 2(x 1) z 0 or 2x z 2 0ßß œ œ
10. z f(x y) e f (x y) 2xe and f (x y) 2ye f (0 0) 0 and f ( ) 0œßœ Ê ßœ ßœ Ê ßœ !ß!œ
ab ab abxy xy xy
xy xy
from Eq. (4) the tangent plane at (0 0 1) is z 1 0 or z 1Êßßœœ
11. z f( y) y x f (x y) (y x) and f (x y) (y x) f (1 2) and f ( )œBßœ Ê ßœ ßœ Ê ßœ "ß#œ
Èxyxy
"" ""
## ##
"Î# "Î#
from Eq. (4) the tangent plane at (1 2 1) is (x 1) (y 2) (z 1) 0 x y 2z 1 0Ê ßß œÊ œ
""
##
12. z f( y) 4x y f (x y) 8x and f (x y) y f (1 1) 8 and f ( 1) from Eq. (4) theœBßœ Ê ßœ ßœ#Ê ßœ "ßœ#Ê
## xy xy
tangent plane at (1 1 5) is 8(x 1) 2(y 1) (z 5) 0 or 8x 2y z 5 0ßß œ œ
13. f 2y 2 f(1 1 1) 2 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk i v
2 2 Tangent line: x 1, y 1 2t, z 1 2t
22
00
Ê œ œ Ê œ œ œ
"
"
vjk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
14. f yz xz xy f(1 1 1) ; g 2x 4y 6z g(1 1 1) 2 4 6 ;™™™ ™œ Ê ßßœ œ Ê ßßœijk ijk ijk ijk
f g 2 4 2 Tangent line: x 1 2t, y 1 4t, z 1 2t
11
246
Êœ ‚ Ê œ Ê œ œ œ
"
vijk
ijk
™™
ââ
ââ
ââ
ââ
ââ
ââ
15. f 2x 2 2 f 1 1 2 2 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk j v
ˆ‰
"
#
2 2 Tangent line: x 1 2t, y 1, z 2t
222
010
Êœ œ Ê œ œ œvik
ijk
ââ
ââ
ââ
ââ
ââ
ââ "
#
16. f 2y f 1 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk j v
ˆ‰
""
##
Tangent line: x t, y 1, z t
121
010
Êœ œÊ œ œ œvik
ijk
ââ
ââ
ââ
ââ
ââ
ââ ""
##
17. f 3x 6xy 4y 6x y 3y 4x 2z f(1 1 3) 13 13 6 ; g 2x 2y 2z™™™œ Ê ßßœ œabab
## ##
ijk ijkijk
g( ) 2 2 6 ; f g 90 90 Tangent line:
313 6
22 6
Ê "ß"ß$ œ œ ‚ Ê œ œ Ê
"
™™™ijkv v i j
ijk
ââ
ââ
ââ
ââ
ââ
ââ
x 1 90t, y 1 90t, z 3œ œ œ
18. f 2x 2y f 2 2 4 2 2 2 2 ; g 2x 2y g 2 2 4™™ ™ ™œ Ê ßßœ œÊ ßßij i j ijk
Š‹ Š‹
ÈÈ È È ÈÈ
22 22 ; f g 22 22 Tangent line:
2222 0
2222 1
œœ‚Êœ œ Ê
ÈÈ ÈÈ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
ijkv v i j
ijk
™™
x222t, y222t, z4œ œ œ
ÈÈ ÈÈ
19. f f(3 4 12) ;™™œ Êßßœ
Š‹Š‹Š‹
xz3412
xyz xyz xyz 169 169 169
y
ijk ijk
f and df ( f ) ds (0.1) 0.0008uijkuuœœ œ Ê œ œ œ ¸
v
v
ijk
kk È362
36(2)
362 9 9
7 7 7 1183 1183
™† ™† ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.6 Tangent Planes and Differentials 831
20. f e cos yz ze sin yz ye sin yz f(0 0 0) ; ™™œ Êßßœœœababab
xxx 222
22(2)
ijk iu
v
v
ijk
kk È
f and df ( f ) ds (0.1) 0.0577œ Ê œ œ œ ¸
111 1 1
333 3 3
ÈÈÈ È È
ijk u u™† ™†
21. g (1 cos z) (1 sin z) ( x sin z y cos z) g(2 1 0) 2 ; P P 2 2 2™™œ Ê ßßœ œ œ
Ä
ij k ijkA ijk
!"
g 0 and dg ( g ) ds (0)(0.2) 0Êœ œ œ Ê œ œ œ œuijkuu
v
v
ijk
kk ÈÈÈÈ
222
(2) 2 2
111
333 ™† ™†
22. h y sin ( xy) z x sin ( xy) 2xz h( 1 1 1) ( sin 1) ( sin ) 2™™œ Ê ßß œ cdcd11 11 11 11
#ijk ijk
2 ; P P where P ( ) œ œ œ œ!ß!ß!Ê œ œ œ
Ä
ikv ijk u i j k
!" "
v
v
ijk
kk ÈÈÈÈ
111
111
333
h 3 and dh ( h ) ds 3(0.1) 0.1732Êœœ œ œ¸™† ™†uu
3
3
ÈÈÈ
23. (a) The unit tangent vector at in the direction of motion is ;
Š‹
""
## # #
ߜ
ÈÈ
33
uij
T (sin 2y) (2x cos 2y) T sin 3 cos 3 D T T™™ ™†œ Ê ßœ Êßœij ij u
Š‹Š ‹Š ‹ Š‹
ÈÈ
""
## ##
ÈÈ
33
u
sin 3 cos 3 0.935° C/ftœ¸
È3
##
"
ÈÈ
(b) (t) (sin 2t) (cos 2t) (t) (2 cos 2t) (2 sin 2t) and 2; rijv ijvœ Êœ œœkk dT T dx T
dt x dt y dt
dy
``
``
T T (D T) , where ; at we have from part (a)œœ œ œ ß œ™† ™†vvvu uij
Š‹ Š‹
kk kk
vv
vvkk kk ÈÈ
u""
## # #
33
sin 3 cos 3 2 3 sin 3 cos 3 1.87° C/secÊœ œ ¸
dT
dt
3
Š‹
ÈÈÈÈÈ
È
##
"†
24. (a) T (4x yz) xz xy T(8 6 4) 56 32 48 ; (t) 2t 3t t the particle is™™œ Ê ßßœ œ Êijk ijkr ijk
##
at the point P( 6 4) when t 2; (t) 4t 3 2t (2) 8 3 4 )ßß œ œ Ê œ Êœvijkvijku
v
vkk
D T(8 6 4) T [56 8 32 3 48 ( 4)] ° C/mœ Ê ßßœ œ œ
834 736
89 89 89 89 89
ÈÈÈ È È
ijk u
u™† †††
"
(b) T ( T ) at t 2, D T (2) 89 736° C/sec
dT T dx T dT 736
dt x dt y dt dt
dy
89
œœ œ Êœœ œ œ
``
`` ™† ™†vuv vkk ¸Š‹
È
ut2œÈ
25. (a) f( 0) 1, f (x y) 2x f (0 0) 0, f (x y) 2y f (0 0) 0 L(x y) 1 0(x 0) 0(y 0) 1!ßœ ßœ Ê ßœ ßœ Ê ßœÊ ßœ œ
xxyy
(b) f(1 1) 3, f (1 1) 2, f (1 1) 2 L(x y) 3 2(x 1) 2(y 1) 2x 2y 1ßœ ßœ ßœÊ ßœ œ
xy
26. (a) f( 0) 4, f (x y) 2(x y 2) f (0 0) 4, f (x y) 2(x y 2) f (0 0) 4!ßœ ßœ Ê ßœ ßœ Ê ßœ
xxyy
L(x y) 4 4(x 0) 4(y 0) 4x 4y 4Êßœœ
(b) f(1 2) 25, f (1 2) 10, f (1 2) 10 L(x y) 25 10(x 1) 10(y 2) 10x 10y 5ßœ ßœ ßœ Ê ßœ œ
xy
27. (a) f(0 0) 5, f (x y) 3 for all (x y), f (x y) 4 for all (x y) L(x y) 5 3(x 0) 4(y 0) 3x 4y 5ßœ ßœ ß ßœ ßÊ ßœ œ
xy
(b) f(1 1) 4, f (1 1) 3, f (1 1) 4 L(x y) 4 3(x 1) 4(y 1) 3x 4y 5ßœ ßœ ßœÊ ßœ œ
xy
28. (a) f(1 1) 1, f (x y) 3x y f (1 1) 3, f (x y) 4x y f (1 1) 4ßœ ßœ Ê ßœ ßœ Ê ßœ
xxyy
#% $$
L(x y) 1 3(x 1) 4(y 1) 3x 4y 6Êßœœ
(b) f(0 0) 0, f ( 0) 0, f (0 0) 0 L(x y) 0ßœ !ßœ ßœÊ ßœ
xy
29. (a) f(0 0) 1, f (x y) e cos y f (0 0) 1, f (x y) e sin y f (0 0) 0ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
xx
L(x y) 1 1(x 0) 0(y 0) x 1Êßœœ
(b) f 0 0, f 0 0, f 0 1 L(x y) 0 0(x 0) 1 y y
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
ßœ ßœ ßœÊ ßœ œ
111 11
### ##
xy
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
832 Chapter 14 Partial Derivatives
30. (a) f(0 0) 1, f (x y) e f ( ) 1, f (x y) 2e f (0 0) 2ßœ ßœ Ê !ß!œ ßœ Ê ßœ
xxyy
2y x 2y x
L(xy)11(x0)2(y0) x2y1Êßœœ
(b) f(12) e, f(12) e, f(12) 2e L(xy) e e(x 1) 2e(y 2) ex 2ey 2eßœ ßœ ßœ Ê ßœ œ
$ $ $ $$ $ $$$
xy
31. (a) W 20, 25 11 F; W 30, 10 39 F; W 15, 15 0 Fab a b abœœ œ
‰‰‰
(b) W 10, 40 65.5 F; W 50, 40 88 F; W 60, 30 10.2 F;ab ab abœ œ œ
‰‰‰
(c) W 25, 5 17.4088 F; 25, 5 0.36; 0.6215 0.4275vab abœ œ Ê œ œ
‰```
```
W 5.72 0.0684t W W
Vv v V T
0.16
0.84 0.84
25, 5 1.3370 L V, T 17.4088 0.36 V 25 1.337 T 5 1.337T 0.36V 15.0938ʜʜœ
`
`
W
Tab ab a b ab
(d) i) W 24, 6 L 24, 6 15.7118 15.7 Fabab¸œ¸
‰
ii) W 27, 2 L 27, 2 22.1398 22.1 Fabab¸œ¸
‰
ii) W 5, 10 L 5, 10 30.2638 30.2 F This value is very different because the point 5, 10 is notabab ab¸ œ ¸
‰
close to the point 25, 5 .ab
32. W 50, 20 59.5298 F; 50, 20 0.2651; 0.6215 0.4275vab abœ œ Ê œ œ
‰`` `
`` `
W 5.72 0.0684t W W
Vv v V T
0.16
0.84 0.84
50, 20 1.4209 L V, T 59.5298 0.2651 V 50 1.4209 T 20ÊœÊ œ
`
`
W
Tab ab ab ab
1.4209T 0.2651V 17.8568œ
(a) W 49, 22 L 49, 22 62.1065 62.1 Fabab¸ œ ¸‰
(b) W 53, 19 L 53, 19 58.9042 58.9 Fabab¸ œ ¸‰
(c) W 60, 30 L 60, 30 76.3898 76.4 Fabab¸ œ ¸‰
33. f(2 1) 3, f (x y) 2x 3y f (2 1) 1, f (x y) 3x f (2 1) 6 L(x y) 3 1(x 2) 6(y 1)ßœ ßœ Ê ßœ ßœ Ê ßœÊ ßœ
xxyy
7 x 6y; f (x y) 2, f (x y) 0, f (x y) 3 M 3; thus E(x y) (3) x 2 y 1œ ߜߜߜʜ ߟ
xx yy xy kk a b
ˆ‰ kkkk
"
#
#
(0.1 0.1) 0.06Ÿœ
ˆ‰
3
#
#
34. f(2 2) 11, f (x y) x y 3 f (2 2) 7, f (x y) x 3 f (2 2) 0ßœ ßœÊ ßœ ßœÊ ßœ
xxy y
y
#
L(x y) 11 7(x 2) 0(y 2) 7x 3; f (x y) 1, f (x y) , f (x y) 1Êßœœ ßœ ßœ ßœ
xx yy xy
"
#
M 1; thus E(x y) (1) x 2 y 2 (0.1 0.1) 0.02Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ ˆ‰
kkkk
"
##
##
1
35. f(0 0) 1, f (x y) cos y f (0 0) 1, f (x y) 1 x sin y f (0 0) 1ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
L(x y) 1 1(x 0) 1(y 0) x y 1; f (x y) 0, f (x y) x cos y, f (x y) sin y 1;Ê ßœ œ ßœ ßœ ßœ ÊQœ
xx yy xy
thus E(x y) (1) x y (0.2 0.2) 0.08kk a b
ˆ‰ ˆ‰
kk kkߟ Ÿ œ
"
##
##
1
36. f( ) 6, f (x y) y y sin (x 1) f (1 2) 4, f (x y) 2xy cos (x 1) f (1 2) 5"ß#œ ßœ Ê ßœ ßœ Ê ßœ
xxyy
#
L(x y) 6 4(x 1) 5(y 2) 4x 5y 8; f (x y) y cos (x 1), f (x y) 2x,Ê ßœ œ ßœ ßœ
xx yy
f (x y) 2y sin (x 1); x 1 0.1 0.9 x 1.1 and y 2 0.1 1.9 y 2.1; thus the max of
xy ßœ Ÿ Ê ŸŸ Ÿ Ê ŸŸkk kk
f (x y) on R is 2.1, the max of f (x y) on R is 2.2, and the max of f (x y) on R is 2(2.1) sin (0.9 1)kk kk kk
xx yy xy
ßß ß
4.3 M 4.3; thus E(x y) (4.3) x 1 y 2 (2.15)(0.1 0.1) 0.086Ÿ Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ kkkk
"
#
##
37. f(0 0) 1, f (x y) e cos y f (0 0) 1, f (x y) e sin y f (0 0) 0ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
xx
L(x y) 1 1(x 0) 0(y 0) 1 x; f (x y) e cos y, f (x y) e cos y, f (x y) e sin y;Ê ßœ œ ßœ ßœ ßœ
xx yy xy
xxx
x 0.1 0.1 x 0.1 and y 0.1 0.1 y 0.1; thus the max of f (x y) on R is e cos (0.1)kk kk k kŸÊŸŸ ŸÊŸŸ ß
xx 01Þ
1.11, the max of f (x y) on R is e cos (0.1) 1.11, and the max of f (x y) on R is e sin (0.1)Ÿß Ÿ ßkk kk
yy xy
01 01ÞÞ
0.12 M 1.11; thus E(x y) (1.11) x y (0.555)(0.1 0.1) 0.0222ŸÊœ ߟ Ÿ œkk a b
ˆ‰ kk kk
"
#
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.6 Tangent Planes and Differentials 833
38. f(1 1) 0, f (x y) f (1 1) 1, f (x y) f (1 1) 1 L(x y) 0 1(x 1) 1(y 1)ßœ ßœ Ê ßœ ßœÊ ßœÊ ßœ
xxyy
xy
""
x y 2; f (x y) , f (x y) , f (x y) 0; x 1 0.2 0.98 x 1.2 so the max ofœ ß œ ß œ ß œ Ÿ Ê ŸŸ
xx yy xy
xy
""
kk
f (x y) on R is 1.04; y 1 0.2 0.98 y 1.2 so the max of f (x y) on R iskk kk kk
xx yy
(0.98)
ߟŸÊŸŸ ß
"
1.04 M 1.04; thus E(x y) (1.04) x 1 y 1 (0.52)(0.2 0.2) 0.0832
""
#
##
(0.98) Ÿ Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ kkkk
39. (a) f( ) 3, f (1 1 1) y z 2, f (1 1 1) x z 2, f (1 1 1) y x 2"ß "ß " œ ß ß œ œ ß ß œ œ ß ß œ œkkk
xyz
111 111
111
ÐßßÑ ÐßßÑ
ÐßßÑ
L(x y z) 3 2(x 1) 2(y 1) 2(z 1) 2x 2y 2z 3Ê ßßœœ
(b) f(100) 0, f(100) 0, f(100) 1, f(100) 1 L(xyz) 0 0(x 1) (y 0) (z 0) y zßßœ ßßœ ßßœ ßßœÊ ßßœ œ
xyz
(c) f(000) 0, f(000) 0, f(000) 0, f(000) 0 L(xyz) 0ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
40. (a) f(1 1 1) 3, f (1 1 1) 2x 2, f (1 1 1) 2y 2, f (1 1 1) 2z 2ßßœ ßßœ œ ßßœ œ ßßœ œkkk
xyz
Ð"ß"ß"Ñ Ð"ß"ß"Ñ
Ð"ß"ß"Ñ
L(x y z) 3 2(x 1) 2(y 1) 2(z 1) 2x 2y 2z 3Ê ßßœœ
(b) f(0 1 0) 1, f (0 1 0) 0, f ( 1 0) 2, f (0 1 0) 0 L(x y z) 1 0(x 0) 2(y 1) 0(z 0)ßßœ ßßœ !ßßœ ßßœÊ ßßœ
xyz
2y 1œ
(c) f(1 0 0) 1, f (1 0 0) 2, f (1 0 0) 0, f (1 0 0) 0 L(x y z) 1 2(x 1) 0(y 0) 0(z 0)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
2x 1œ
41. (a) f(1 0 0) 1, f (1 0 0) 1, f (1 0 0) 0,ßßœßßœ œßßœ œ
xy
x
xyz xyz
y
¹¹
ÈÈ
100 100
f (1 0 0) 0 L(x y z) 1 1(x 1) 0(y 0) 0(z 0) x
zz
xyz
ßßœ œÊ ßßœœ
¹
È 100
(b) f(110) 2, f(110) , f(110) , f(110) 0ßß œ ßß œ ßß œ ßß œ
Èxyz
22
""
ÈÈ
L(x y z) 2 (x 1) (y 1) 0(z 0) x yÊßßœœ
È"" ""
ÈÈ ÈÈ
22 22
(c) f(122) 3, f(122) , f(122) , f(122) L(xyz) 3 (x 1) (y 2) (z 2)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
3 3 3 333
22 22""
xyzœ
"
333
22
42. (a) f 1 1 1, f 1 1 0, f 1 1 0,
ˆ‰ ˆ‰ ¸ ˆ‰ ¸
11 1
2z z
xy
y cos xy x cos xy
ßßœßßœ œßßœ œ
##
ß"ß" ß"ß"
ˆ‰ ˆ‰
f 1 1 1 L(x y z) 1 0 x 0(y 1) 1(z 1) 2 z
zsin xy
z
ˆ‰ ˆ‰
¹
1 1
# #
ß"ß"
ßß œ œ Ê ßß œ œ
ˆ‰
(b) f(2 0 1) 0, f (2 0 1) 0, f (2 0 1) 2, f (2 0 1) 0 L(x y z) 0 0(x 2) 2(y 0) 0(z 1) 2yßß œ ßß œ ßß œ ßß œ Ê ßß œ œ
xyz
43. (a) f(0 0 0) 2, f (0 0 0) e 1, f (0 0 0) sin (y z) 0,ßßœßßœ œßßœ œ
xy
xkk
Ð!ß!ß!Ñ Ð!ß!ß!Ñ
f (0 0 0) sin (y z) 0 L(x y z) 2 1(x 0) 0(y 0) 0(z 0) 2 x
zßßœ œÊ ßßœœkÐ!ß!ß!Ñ
(b) f 0 0 1, f 0 0 1, f 0 0 1, f 0 0 1 L(x y z)
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ßß œ ßß œ ßß œ ßß œ Ê ßß
111 1
### #
xy z
11(x0)1y 1(z0)xyz 1œ œ
ˆ‰
11
2#
(c) f 0 1, f 0 1, f 0 1, f 0 1 L(x y z)
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ßß œ ßß œ ßß œ ßß œ Ê ßß
11 11 11 11
44 44 44 44
xy z
11(x0)1y 1z xyz 1œ œ
ˆ‰ˆ‰
11 1
44 #
44. (a) f(1 0 0) 0, f (1 0 0) 0, f (1 0 0) 0,ßßœßßœ œßßœ œ
xy
yz
(xyz) 1 (xyz) 1
xz
¹¹
Ð"ß!ß!Ñ Ð"ß!ß!Ñ
f(100) 0 L(xyz) 0
zxy
(xyz) 1
ßß œ œ Ê ßß œ
¹
Ð"ß!ß!Ñ
(b) f(1 1 0) 0, f (1 1 0) 0, f (1 1 0) 0, f (1 1 0) 1 L(x y z) 0 0(x 1) 0(y 1) 1(z 0) zßß œ ßß œ ßß œ ßß œ Ê ßß œ œ
xyz
(c) f(111) , f(111) , f(111) , f(111) L(xyz) (x 1) (y 1) (z 1)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
1 1
4 4
xyz
" " " """
# # # ###
xyzœ
"""
### #
1
4
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

834 Chapter 14 Partial Derivatives
45. f(x y z) xz 3yz 2 at P (1 1 2) f(1 1 2) 2; f z, f 3z, f x 3y L(x y z)ßß œ ßß Ê ßß œ œ œ œ Ê ßß
!xy z
2 2(x 1) 6(y 1) 2(z 2) 2x 6y 2z 6; f 0, f 0, f 0, f 0, f 3œœ œ œ œ œ œ
xx yy zz xy yz
M 3; thus, E(x y z) (3)(0.01 0.01 0.02) 0.0024Êœ ßߟ œkk
ˆ‰
"
#
#
46. f(x y z) x xy yz z at P (1 1 2) f(1 1 2) 5; f 2x y, f x z, f y zßß œ ßß Ê ßß œ œ œ œ
##
" "
!#4xyz
L(x y z) 5 3(x 1) 3(y 1) 2(z 2) 3x 3y 2z 5; f 2, f 0, f , f 1, f 0,Ê ßßœœ œ œ œ œ œ
xx yy zz xy xz
"
#
f 1 M 2; thus E(x y z) (2)(0.01 0.01 0.08) 0.01
yz œÊ œ ßß Ÿ œkk
ˆ‰
"
#
#
47. f(x y z) xy 2yz 3xz at P (1 1 0) f(1 1 0) 1; f y 3z, f x 2z, f 2y 3xßß œ ßß Ê ßß œ œ œ œ
!xyz
L(x y z) 1 (x 1) (y 1) (z 0) x y z 1; f 0, f 0, f 0, f 1, f 3,Ê ßßœœ œ œ œ œ œ
xx yy zz xy xz
f 2 M 3; thus E(x y z) (3)(0.01 0.01 0.01) 0.00135
yz œÊ œ ßß Ÿ œkk
ˆ‰
"
#
#
48. f(x y z) 2 cos x sin (y z) at P 0 0 f 0 0 1; f 2 sin x sin (y z),ßß œ ßß Ê ßß œ œ
ÈÈ
ˆ‰ˆ‰
!11
44
x
f 2 cos x cos (y z), f 2 cos x cos (y z) L(x y z) 1 0(x 0) (y 0) z
yz 4
œ œ Ê ßßœ
ÈÈ ˆ‰
1
y z 1; f 2 cos x sin (y z), f 2 cos x sin (y z), f 2 cos x sin (y z),œ œ œ œ
1
4xx yy zz
ÈÈÈ
f 2 sin x cos (y z), f 2 sin x cos (y z), f 2 cos x sin (y z). The absolute value of
xy xz yz
œ œ œ
ÈÈÈ
each of these second partial derivatives is bounded above by 2 M 2; thus E(x y z)
ÈÈ
kkÊœ ßß
2 (0.01 0.01 0.01) 0.000636.Ÿœ
ˆ‰
Š‹
È
"
#
#
49. T (x y) e e and T (x y) x e e dT T (x y) dx T (x y) dy
xy xy
yy yy
ßœ ßœ Ê œ ß ß
ab
e e dx x e e dy dT 2.5 dx 3.0 dy. If dx 0.1 and dy 0.02, then theœ Ê œ Ÿ Ÿabab k kk kk
yy yy ln 2
Ð#ß Ñ
maximum possible error in the computed value of T is (2.5)(0.1) (3.0)(0.02) 0.31 in magnitude.œ
50. V 2 rh and V r dV V dr V dh dr dh; now 100 1 and
rh rh
dV 2 rh dr r dh 2 dr
Vrhrh r
œœÊœÊœœ Ÿ11
#"11
1¸¸
†
100 1 100 2 (100) (100) 2 100 100 2(1) 1 3 3%
¸¸ ¸¸¸ ¸¸¸¸¸ˆ‰ ˆ‰
dh dV dr dh dr dh
hVrhrh
†† ††ŸÊ Ÿ Ÿ Ÿ œÊ
51. 0.02, 0.03
dx
xy
dy
ŸŸ
(a) S 2x 4xy dS 4x 4y dx 4x dy 4x 4xy 4xy 4x 4xy 0.02 4xy 0.03œÊœ œ Ÿ
222
dx
xy
dy
ab ab abababab
0.04 2x 0.05 4xy 0.05 2x 0.05 4xy 0.05 2x 4xy 0.05SœŸœ œab ab ab ababa b
22 2
(b) V x y dV 2xy dx x dy 2x y x y 2x y 0.02 x y 0.03 0.07 x y =0.07VœÊœ œ Ÿ œ
2222222
dx
xy
dy abababab ab
52. V r r h dV 4 r 2 rh dr r dh; r 10, h 15, dr and dh 0œ Êœ œ œ œ œÊ
4 1
3 2
32 2 2
11111ab
dV 4 10 2 10 15 10 0 350 cmœ œ
Š‹
ab abab abab
ˆ‰
11 1 1
22
1
2
3
53. V 2 rh and V r dV V dr V dh dV 2 rh dr r dh dV 120 dr 25 dh;
rh rh 512
œœÊœÊœÊœ11 11 11
##
Ðß Ñ
k
dr 0.1 cm and dh 0.1 cm dV (120 )(0.1) (25 )(0.1) 14.5 cm ; V(5 12) 300 cmkk kkŸŸÊŸœßœ11 1 1
$$
maximum percentage error is 100 4.83%Ê„‚œ„
14.5
300
1
1
54. (a) dR dR dR dR dR dR
""" " " "
"# " #
##
RR R R R R
RR
RR
œ Ê œ Ê œ
Š‹ Š‹
(b) dR R dR dR dR R dR dR R will be moreœÊœÊ
##
"" ""
"# "#
ÐÑ
’“’“Š‹ Š‹ k
RR (100) (400)
100 400
sensitive to a variation in R since
"""
(100) (400)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.6 Tangent Planes and Differentials 835
(c) From part (a), dR dR dR so that R changing from 20 to 20.1 ohms dR 0.1 ohmœ Êœ
Š‹ Š‹
RR
RR
##
"#" "
and R changing from 25 to 24.9 ohms dR 0.1 ohms; R ohms
##
"""
Êœ œÊœ
RR R 9
100
dR (0.1) ( 0.1) 0.011 ohms percentage change is 100Êœ ¸ Ê ‚k¸
ÐÑ Ð
20 25 20 25
ˆ‰ ˆ‰
100 100
99
(20) (25) R
dR
100 0.1%œ‚¸
0.011
ˆ‰
100
9
55. A xy dA x dy y dx; if x y then a 1-unit change in y gives a greater change in dA than a 1-unit change in x.œÊ œ
Thus, pay more attention to y which is the smaller of the two dimensions.
56. (a) f (x y) 2x(y 1) f (1 0) 2 and f (x y) x f (1 0) 1 df 2 dx 1 dy df is more
xxyy
ßœ Ê ßœ ßœ Ê ßœÊ œ Ê
#
sensitive to changes in x
(b) df 0 2 dx dy 0 2 1 0 œÊ œÊ œÊ œ
dx dx
dy dy
"
#
57. (a) r x y 2r dr 2x dx 2y dy dr dx dy dr| 0.01 0.01
### Ð$ß%Ñ
œ Ê œ Ê œ Ê œ „ „
x34
rr 5 5
yˆ‰ ˆ‰
abab
0.014 100 100 0.28%; d dx dyœ„ œ„ Ê ‚ œ „ ‚ œ œ
0.07 dr 0.014
5r5 11
¸¸¸ ¸ )Š‹ Š‹
ˆ‰ ˆ‰
y
x
yy
xx
x
dx dy d | 0.01 0.01œ Êœ„„œ
#
Ð$ß%Ñ „
…
y
y x y x 25 25 25 5
x43 0.03
0.04
)ˆ‰ ˆ‰
abab
maximum change in d occurs when dx and dy have opposite signs (dx 0.01 and dy 0.01 or viceÊœœ)
versa) d 0.0028; tan 0.927255218 100 100Êœ ¸„ œ ¸ Ê ‚ œ ‚))
„ „
#
"
0.07 4 d 0.0028
5 3 0.927255218
ˆ‰ ¸ ¸ ¸ ¸
)
)
0.30%¸
(b) the radius r is more sensitive to changes in y, and the angle is more sensitive to changes in x)
58. (a) V r h dV 2 rh dr r dh at r 1 and h 5 we have dV 10 dr dh the volume isœÊœ Êœ œ œ Ê111 11
##
about 10 times more sensitive to a change in r
(b) dV 0 0 2 rh dr r dh 2h dr r dh 10 dr dh dr dh; choose dh 1.5œÊœ œœÊœ œ11
#"
10
dr 0.15 h 6.5 in. and r 0.85 in. is one solution for V dV 0Êœ Êœ œ ¸ œ?
59. f(a b c d) ad bc f d, f c, f b, f a df d da c db b dc a dd; since
ab
cd
ß ß ß œ œ Ê œ œ œ œ Ê œ
ºº ab c d
a is much greater than b , c , and d , the function f is most sensitive to a change in d.kk kkkk kk
60. u e , u xe sin z, u y cos z du e dx xe sin z dy (y cos z) dz
xy z
yy y y
œœ œ Êœ ab
du 3 dx 7 dy 0 dz 3 dx 7 dy magnitude of the maximum possible errorÊ œœ Êk2ln3ßß
2
3(0.2) 7(0.6) 4.8Ÿœ
61. Q , Q , and Q
KM h
œœ œ
"" "
## #
"Î# "Î# "Î#
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ ‰
2KM 2M 2KM 2K 2KM 2KM
hh hh h h
dQ dK dM dhʜ
"" "
## #
"Î# "Î# "Î#
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ ‰
2KM 2M 2KM 2K 2KM 2KM
hh hh h h
dK dM dh dQœÊ
"
#
"Î#
ˆ‰ ‘ k
2KM2M2K 2KM
hhhh 22000.05
dK dM dh (0.0125)(800 dK 80 dM 32,000 dh)œœ
"
#
"Î#
’“’ “
(2)(2)(20) (2)(20) (2)(2) (2)(2)(20)
0.05 0.05 0.05 (0.05)
Q is most sensitive to changes in hÊ
62. A ab sin C A b sin C, A a sin C, A ab cos CœÊœ œ œ
""""
####
abc
dA b sin C da a sin C db ab cos C dC; dC 2° 0.0349 radians, da 0.5 ft,Êœ œœ œ
ˆ‰ˆ‰ˆ ‰ kk k k kk
"""
###
db 0.5 ft; at a 150 ft, b 200 ft, and C 60°, we see that the change is approximatelyœœœ œkk
dA (200)(sin 60°) 0.5 (150)(sin 60°) 0.5 (200)(150)(cos 60°) 0.0349 338 ftœ œ„
"""
###
#
kk kk k k
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

836 Chapter 14 Partial Derivatives
63. z f(x y) g(x y z) f(x y) z 0 g (x y z) f (x y), g (x y z) f (x y) and g (x y z) 1œ ß Ê ßß œ ß œ Ê ßß œ ß ßß œ ß ßß œ
xxyyz
g(x y f(x y)) f(x y), g(x y f(x y)) f(x y) and g(x y f(x y)) 1 the tangentÊ ßßß œ ß ßßß œ ß ßßß œÊ
xxyyz!! !! !! !! !! !! !! !!
plane at the point P is f (x y )(x x ) f (x y )(y y ) [z f(x y )] 0 or
!!! ! !! ! !!xy
ßßßœ
z f (x y )(x x ) f (x y )(y y ) f(x y )œß ß ß
xy!! ! !! ! !!
64. f 2x 2y 2(cos t t sin t) 2(sin t t cos t) and (t cos t) (t sin t) ™œœ œ Êœij i jv i ju
v
vkk
(cos t) (sin t) since t 0 (D f) fœœÊœ
(t cos t) (t sin t)
(t cos t) (t sin t) P
ij u
Èij u™†
2(cos t t sin t)(cos t) 2(sin t t cos t)(sin t) 2œ œ
65. f 2x 2y 2z (2 cos t) (2 sin t) 2t and ( sin t) (cos t) ™œ œ œ Êœijk i jkv i jku
v
vkk
(D f) fœœÊœ
( sin t) (cos t)
(sin t) (cos t) 1
sin t cos t
222 P
"
ijk u
ÈÈÈÈ
Š‹Š‹
ijk u™†
(2 cos t) (2 sin t) (2t) (D f) , (D f)(0) 0 andœœÊœœ
Š‹ Š‹ Š‹ ˆ‰
"sin t cos t 2t
2222 22
4
ÈÈÈÈ È
uu
11
(D f)
uˆ‰
11
422
œÈ
66. r t t (t 3) t t ; t 1 x 1, y 1, z 1 P (1 1 1)œÊœ œÊœœœÊœßß
ÈÈ
ij kv i jk
""""
##
"Î# "Î# !
44
and (1) ; f(x y z) x y z 3 0 f 2x 2yvijk ijkœ ßßœœÊ œ
"""
##
##
4™
f(1 1 1) 2 2 ; therefore ( f) the curve is normal to the surfaceÊ ßßœ œ Ê™™ijk v
"
4
67. r t t (2t 1) t t 2 ; t 1 x 1, y 1, z 1 P (1 1 1) andœ Êœ œÊœ œ œÊ œßß
ÈÈ
ij kv i jk
""
##
"Î# "Î# !
(1) 2 ; f(xyz) x y z 1 0 f 2x 2y f(111) 2 2 ;vijk ijk ijkœ ßßœ œÊ œ Ê ßßœ
""
##
## ™™
now 1 f 1 1 1 0, thus the curve is tangent to the surface when t 1vab a b†™ ßß œ œ
14.7 EXTREME VALUES AND SADDLE POINTS
1. f (x y) 2x y 3 0 and f (x y) x 2y 3 0 x 3 and y 3 critical point is ( 3 3);
xy
ß œ œ ß œ œ Ê œ œ Ê ß
f ( 3 3) 2, f ( 3 3) 2, f ( 3 3) 1 f f f 3 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f( 3 3) 5ß œ
2. f (x y) 2y 10x 4 0 and f (x y) 2x 4y 4 0 x and y critical point is ;
xy 24 24
33 33
ßœ œ ßœ œÊœ œÊ ß
ˆ‰
f 10, f 4, f 2 f f f 36 0 and f 0 local maximum of
xx yy xy xx yy xx
24 24 24
33 33 33 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f0
ˆ‰
24
33
ߜ
3. f (x y) 2x y 3 0 and f (x y) x 2 0 x 2 and y 1 critical point is ( 2 1);
xy
ß œ œ ß œœ Ê œ œ Ê ß
f ( 2 1) 2, f ( 2 1) 0, f ( 2 1) 1 f f f 1 0 saddle point
xx yy xy xx yy xy
ß œ ß œ ß œ Ê œ Ê
#
4. f (x y) 5y 14x 3 0 and f (x y) 5x 6 0 x and y critical point is ;
xy
669 669
55 525
ßœ œ ßœ œÊœ œ Ê ß
#ˆ‰
f 14, f 0, f 5 f f f 25 0 saddle point
xx yy xy xx yy
669 669 669
525 525 525 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œÊ
#
5. f (x y) 2y 2x 3 0 and f (x y) 2x 4y 0 x 3 and y critical point is 3 ;
xy 33
2
ßœœ ßœœÊœ œÊ ß
#ˆ‰
f 3 2, f 3 4, f 3 2 f f f 4 0 and f 0 local maximum of
xx yy xy xx yy xx
333
222 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f3
ˆ‰
ߜ
317
##
6. f (x y) 2x 4y 0 and f (x y) 4x 2y 6 0 x 2 and y 1 critical point is (2 1);
xy
ßœœ ßœœÊœ œÊ ß
f (2 1) 2, f (2 1) 2, f (2 1) 4 f f f 12 0 saddle point
xx yy xy xx yy xy
ßœ ßœ ßœÊ œÊ
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.7 Extreme Values and Saddle Points 837
7. f (x y) 4x 3y 5 0 and f (x y) 3x 8y 2 0 x 2 and y 1 critical point is (2 1);
xy
ßœ œ ßœ œÊœ œÊ ß
f (2 1) 4, f (2 1) 8, f (2 1) 3 f f f 23 0 and f 0 local minimum of f(2 1) 6
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê ß œ
#
8. f (x y) 2x 2y 2 0 and f (x y) 2x 4y 2 0 x 1 and y 0 critical point is (1 0);
xy
ßœœ ßœœÊœ œÊ ß
f (1 0) 2, f (1 0) 4, f (1 0) 2 f f f 4 0 and f 0 local minimum of f(1 0) 0
xx yy xy xx yy xx
xy
ßœ ßœ ßœÊ œ Ê ßœ
#
9. f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and y 2 critical point is (1 2); f (1 2) 2,
xy xx
ßœ œ ßœœÊœ œÊ ß ßœ
f (1 2) 2, f (1 2) 0 f f f 4 0 saddle point
yy xy xx yy xy
ßœ ßœÊ œÊ
#
10. f (x y) 2x 2y 0 and f (x y) 2x 0 x 0 and y 0 critical point is (0 0); f (0 0) 2,
xy xx
ßœ œ ßœ œÊœ œÊ ß ßœ
f (0 0) 0, f (0 0) 2 f f f 4 0 saddle point
yy xy xx yy xy
ßœ ßœÊ œÊ
#
11. f x y 8 0 and f x y 0 critical point is 0 ;
xy
112x 8x 16
56x 8y 16x 31 56x 8y 16x 31
8y
7
ab ab ˆ‰
ßœ œ ßœ œÊ ß
ÈÈ
22 22
f 0 , f 0 , f 0 0 f f f 0 and f 0 local maximum of
xx yy xy xx yy xx
16 8 16 8 16 64
7 15 7 15 7 225
xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f0
ˆ‰
16 16
77
ߜ
12. f x y 0 and f x y 0 there are no solutions to the system f x y 0 and
xy x
2x
3x y 3x y
2y
ab ab abßœ œ ßœ œÊ ßœ
ab ab
22 22
23 23
f x y 0, however, we must also consider where the partials are undefined, and this occurs when x 0 and y 0
yabßœ œœ
critical point is 0 0 . Note that the partial derivatives are defined at every other point other than 0 0 . We cannot useÊß ßab ab
the second derivative test, but this is the only possible local maximum, local minimum, or saddle point. f x y has a localabß
maximum of f 0 0 1 at 0 0 since f x y 1 x y 1 for all x y other than 0 0 .ab ab ab ab ab
È
ßœ ß ßœ Ÿ ß ß
322
13. f (x y) 3x 2y 0 and f (x y) 3y 2x 0 x 0 and y 0, or x and y critical points
xy 22
33
ßœ œ ßœ œÊœ œ œ œ Ê
##
are (0 0) and ; for (0 0): f (0 0) 6x 0, f (0 0) 6y 0, f (0 0) 2ß ß ß ßœ œßœœßœ
ˆ‰ kk
22
33 xx yy xy
00 00
ÐßÑ ÐßÑ
f f f 4 0 saddle point; for : f 4, f 4, f 2Ê œ Ê ß ß œ ß œ ß œ
xx yy xx yy xy
xy 22 22 22 22
33 33 33 33
#ˆ‰ˆ‰ ˆ‰ ˆ‰
f f f 12 0 and f 0 local maximum of fÊœ Ê ßœ
xx yy xx
xy 2 2 170
33 27
#ˆ‰
14. f (x y) 3x 3y 0 and f (x y) 3x 3y 0 x 0 and y 0, or x 1 and y 1 critical points
xy
ßœ œ ßœ œÊœ œ œ œÊ
##
are (0 0) and ( 1 1); for ( ): f (0 0) 6x 0, f (0 0) 6y 0, f (0 0) 3 f f fß ß !ß ! ß œ œ ß œ œ ß œ Ê kk
xx yy xy xx yy
00 00 xy
ÐßÑ ÐßÑ #
9 0 saddle point; for ( 1 1): f ( 1 1) 6, f ( 1 1) 6, f ( 1 1) 3 f f fœ Ê ß ß œ ß œ ß œ Ê
xx yy xy xx yy xy
#
27 0 and f 0 local maximum of f( 1 1) 1œ Ê ßœ
xx
15. f (x y) 12x 6x 6y 0 and f (x y) 6y 6x 0 x 0 and y 0, or x 1 and y 1 critical
xy
ßœ œ ßœœÊœ œ œ œÊ
#
points are (0 0) and (1 1); for ( ): f (0 0) 12 12x 12, f (0 0) 6, f (0 0) 6 f f fß ß !ß! ßœ œ ßœ ßœÊ k
xx yy xy xx yy
00 xy
ÐßÑ #
36 0 and f 0 local minimum of f(0 0) 0; for (1 1): f (1 1) 0, f (1 1) 6,œ Ê ß œ ß ß œ ß œ
xx xx yy
f (1 1) 6 f f f 36 0 saddle point
xy xx yy xy
ß œ Ê œ Ê
#
16. f (x y) 3x 6x 0 x 0 or x 2; f (x y) 3y 6y 0 y 0 or y 2 the critical points are
xy
ßœ œÊœ œ ßœ œÊœ œÊ
##
(0 0), (0 2), ( 2 0), and ( 2 2); for ( ): f (0 0) 6x 6 6, f (0 0) 6y 6 6,ß ß ß ß !ß! ß œ œ ß œ œkk
xx yy
00 00
ÐßÑ ÐßÑ
f (0 0) 0 f f f 36 0 saddle point; for (0 2): f (0 2) 6, f (0 2) 6, f (0 2) 0
xy xx yy xx yy xy
xy
ßœÊœÊ ß ßœßœßœ
#
f f f 36 0 and f 0 local minimum of f(0 2) 12; for ( 2 0): f ( 2 0) 6,Ê œ Ê ßœ ß ßœ
xx yy xx xx
xy
#
f ( 2 0) 6, f ( 2 0) 0 f f f 36 0 and f 0 local maximum of f( 2 0) 4;
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß œ
#
for ( 2 2): f ( 2 2) 6, f ( 2 2) 6, f ( 2 2) 0 f f f 36 0 saddle pointß ß œ ß œ ß œ Ê œ Ê
xx yy xy xx yy xy
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

838 Chapter 14 Partial Derivatives
17. f x y 3x 3y 15 0 and f x y 6x y 3y 15 0 critical points are 2 1 , 2 1 , 0 5 , and
xy
22 2
ab ab aba b
Š‹
È
ßœ œ ßœ œÊ ß ß ß
0 5 ; for 2 1 : f 2 1 6x 12, f 2 1 6x 6y 18, f 2 1 6y 6
Š‹
Èab k k kab aba b abß ß ßœ œ ßœ œ ßœ œ
xx yy xy
21 21 21
ab ab ab
ßßß
f f f 180 0 and f 0 local minimum of f 2 1 30; for 2 1 : f 2 1 6xÊœ Ê ßœ ß ßœ
xx yy xx xx
xy 21
#ß
ab a b kabab
12, f 2 1 6x 6y 18, f 2 1 6y 6 f f f 180 0 andœ ß œ œ ß œ œ Ê œ kkabab ab
yy xy xx yy
21 21 xy
ab abß ß #
f 0 local maximum of f 2 1 30; for 0 5 : f 0 5 6x 0, f 0 5
xx xx yy
05
Ê ß œ ß ß œ œ ßab Š‹ ¹ Š‹
ÈÈ È
Š‹Š‹
È
ß
6x 6y 6 5, f 0 5 6y 6 5 f f f 180 0 saddle pointœ œ ß œ œ Ê œÊ àkab ÈÈ È
¹Š‹
Š‹
ÈŠ‹
È
05 xy xx yy
05 xy
ßß
#
for 0 5 : f 0 5 6x 0, f 0 5 6x 6y 6 5,
Š‹ ¹ Š‹
ÈÈ È È
Š‹ kabß ß œ œ ß œ œ
xx yy
05 05
Š‹
ÈŠ‹
È
ß ß
f 0 5 6y 6 5 f f f 180 0 saddle point.
¹Š‹
ÈÈ
xy xx yy
05 xy
ß œ œ Ê œ Ê
Š‹
È
ß
#
18. f (x y) 6x 18x 0 6x(x 3) 0 x 0 or x 3; f (x y) 6y 6y 12 0 6(y 2)(y 1) 0
x y
ßœ œÊ œÊœ œ ßœ œÊ œ
# #
y 2 or y 1 the critical points are (0 2), (0 1), (3 2), and (3 1); f (x y) 12x 18,Êœ œÊ ß ß ß ß ßœ
xx
f (x y) 12y 6, and f (x y) 0; for ( 2): f (0 2) 18, f (0 2) 18, f (0 2) 0
yy xy xx yy xy
ß œ ß œ !ß ß œ ß œ ß œ
f f f 324 0 and f 0 local maximum of f(0 2) 20; for (0 1): f (0 1) 18,Êœ Ê ßœ ß ßœ
xx yy xx xx
xy
#
f (0 1) 18, f (0 1) 0 f f f 324 0 saddle point; for (3 2): f (3 2) 18,
yy xy xx yy xx
xy
ßœ ßœ Ê œ Ê ß ßœ
#
f (3 2) 18, f (3 2) 0 f f f 324 0 saddle point; for (3 1): f (3 1) 18,
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß ß œ
#
f (3 1) 18, f (3 1) 0 f f f 324 0 and f 0 local minimum of f(3 1) 34
yy xy xx yy xx
xy
ßœ ßœÊ œ Ê ßœ
#
19. f (x y) 4y 4x 0 and f (x y) 4x 4y 0 x y x 1 x 0 x 0, 1, 1 the critical
xy
ßœ œ ßœ œÊœÊ œÊœ Ê
$$ #
ab
points are (0 0), (1 1), and ( 1 1); for ( ): f (0 0) 12x 0, f (0 0) 12y 0,ß ß ß !ß! ßœ œ ßœ œkk
xx yy
00 00
##
ÐßÑ ÐßÑ
f (0 0) 4 f f f 16 0 saddle point; for (1 1): f (1 1) 12, f (1 1) 12, f (1 1) 4
xy xx yy xx yy xy
xy
ß œ Ê œ Ê ß ß œ ß œ ß œ
#
f f f 128 0 and f 0 local maximum of f(1 1) 2; for ( 1 1): f ( 1 1) 12,Êœ Ê ßœ ß ßœ
xx yy xx xx
xy
#
f ( 1 1) 12, f ( 1 1) 4 f f f 128 0 and f 0 local maximum of f( 1 1) 2
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß œ
#
20. f (x y) 4x 4y 0 and f (x y) 4y 4x 0 x y x x 0 x 1 x 0 x 0, 1, 1
xy
ßœ œ ßœ œÊœÊœÊ œÊœ
$$ $#
ab
the critical points are (0 0), (1 1), and ( 1 1); f (x y) 12x , f (x y) 12y , and f (x y) 4;Ê ß ß ß ßœ ßœ ßœ
xx yy xy
##
for ( 0): f (0 0) 0, f (0 0) 0, f (0 0) 4 f f f 16 0 saddle point; for (1 1):!ß ßœ ßœ ßœÊ œÊ ß
xx yy xy xx yy xy
#
f (1 1) 12, f (1 1) 12, f (1 1) 4 f f f 128 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f( 1) 2; for ( 1 1): f ( 1 1) 12, f ( 1 1) 12, f ( 1 1) 4 f f f 128 0 and"ßœßߜߜߜʜ
xx yy xy xx yy xy
#
f 0 local minimum of f( 1 1) 2
xx Ê ßœ
21. f (x y) 0 and f (x y) 0 x 0 and y 0 the critical point is ( 0);
xy
2x
xy1 xy1
2y
ßœ œ ßœ œÊœ œÊ !ß
ab ab
f , f , f ; f ( ) 2, f (0 0) 2, f (0 0) 0
xx yy xy xx yy xy
4x 2y 2 2x 4y 2 8xy
xy1 xy1 xy1
œœ œ!ß!œßœßœ
ab ab ab
f f f 4 0 and f 0 local maximum of f(0 0) 1Êœ Ê ßœ
xx yy xx
xy
#
22. f (x y) y 0 and f (x y) x 0 x 1 and y 1 the critical point is (1 1); f , f ,
xy xx yy
11 22
xy xy
ßœœ ßœœÊœ œÊ ß œ œ
f 1; f (1 1) 2, f (1 1) 2, f (1 1) 1 f f f 3 0 and f 2 local minimum of f(1 1) 3
xy xx yy xy xx yy xx
xy
œßœßœßœÊœ Ê ßœ
#
23. f (x y) y cos x 0 and f (x y) sin x 0 x n , n an integer, and y 0 the critical points are
xy
ßœ œ ßœ œÊœ œÊ1
(n 0), n an integer (Note: cos x and sin x cannot both be 0 for the same x, so sin x must be 0 and y 0);1ß œ
f y sin x, f 0, f cos x; f (n 0) 0, f (n 0) 0, f (n 0) 1 if n is even and f (n 0) 1
xx yy xy xx yy xy xy
œ œ œ ßœ ßœ ßœ ßœ111 1
if n is odd f f f 1 0 saddle point.ÊœÊ
xx yy xy
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.7 Extreme Values and Saddle Points 839
24. f (x y) 2e cos y 0 and f (x y) e sin y 0 no solution since e 0 for any x and the functions
xy
2x 2x 2x
ßœ œ ßœ œÊ Á
cos y and sin y cannot equal 0 for the same y no critical points no extrema and no saddle pointsÊÊ
25. f x y 2x 4 e 0 and f x y 2ye 0 critical point is 2 0 ; f 2 0 , f 2 0 0,
x y xx xy
xy4x xy4x 2
e
aba b ab abab abßœ œ ßœ œÊ ß ßœ ßœ
22 22
4
f 2 0 f f f 0 and f 0 local mimimum of f 2 0
yy xx yy xx
24 1
ee e
xy
ab abßœÊ œ Ê ßœ
48 4
#
26. f x y ye 0 and f x y e e 0 critical point is 0 0 ; f 2 0 0, f 2 0 1, f 2 0 1
x y xx xy yy
xyx
ab ab abab ab abßœ œ ßœœÊ ß ßœ ßœ ßœ
f f f 1 0 saddle pointÊœÊ
xx yy xy
#
27. f x y 2xe 0 and f x y 2ye e x y 0 critical points are 0 0 and 0 2 ; for 0 0 :
xy
yyy22
ab ab a b ab ab abßœœ ßœœÊ ßßß
f 0 0 2e 2, f 0 0 2e 4ye e x y 2, f 0 0 2xe 0kkkab aba b abab
xx yy xy
yyyy22 y
00 00 00
ßœ œßœ œßœ œ
ßßß
ab ab ab
f f f 4 0 and f 0 local mimimum of f 0 0 0; for 0 2 : f 0 2 2e ,Ê œ Ê ß œ ß ß œ œ
xx yy xx xx
xy y02 2
e
# ß
ab ab kab ab 2
f 0 2 2e 4ye e x y , f 0 2 2xe 0 f f f 0kkaba b abab
yy xy xx yy
yyy22 y
02 02
24
ee
xy
ßœ œ ßœ œÊ œ
#
ßßab ab
2 4
saddle pointÊ
28. f x y e x 2x y 0 and f x y 2ye 0 critical points are 0 0 and 2 0 ; for 0 0 :
xy
x2 2 x
ab a b ab ab a b abßœ œ ßœ œÊ ß ß ß
f 0 0 e x 4x 2 y 2, f 0 0 2e 2, f 0 0 2ye 0kk kab a b ab ab
xx yy xy
x2 2 x x
00 00 00
ßœ œ ßœ œ ßœ œ
ab ab ab
ßßß
f f f 4 0 and f 0 saddle point; for 2 0 : f 2 0 e x 4x 2 y ,Êœ Ê ß ßœ œ
xx yy xx xx
xy x2 2 20 2
e
#ß
ab kaba b
ab 2
f 2 0 2e , f 2 0 2ye 0 f f f 0 and f 0 local maximumkkab ab
yy xy xx yy xx
xx
20 20
24
ee
xy
ß œ œ ß œ œ Ê œ Ê
ab abß ß #
2 4
of f 2 0abß œ4
e2
29. f x y 4 0 and f x y 1 0 critical point is , 1 ; f , 1 8, f , 1 1,
x y xx yy
21111
xy222
ab ab ˆ‰ˆ‰ ˆ‰
ßœœ ßœœÊ œ œ
f , 1 0 f f f 8 0 and f 0 local maximum of f , 1 3 2ln 2
xy xx yy xx
1 1
2 2
xy
ˆ‰ ˆ‰
œÊ œ Ê œ
#
30. f x y 2x 0 and f x y 1 0 critical point is , ; f , 1, f , 1,
x y xx yy
1 1 13 13 13
xy xy 22 22 22
ab ab ˆ‰ˆ‰ ˆ‰
ßœ œ ßœ œÊ œ œ
f , 1 f f f 2 0 saddle point
xy xx yy
13
22 xy
ˆ‰
œÊ œÊ
#
31. (i) On OA, f(x y) f(0 y) y 4y 1 on 0 y 2;ßœ ßœ ŸŸ
#
f (0 y) 2y 4 0 y 2;
wßœ œÊœ
f(0 0) 1 and f( ) 3ß œ !ß # œ
(ii) On AB, f(x y) f(x 2) 2x 4x 3 on 0 x 1;ßœ ßœ ŸŸ
#
f (x 2) 4x 4 0 x 1;
wßœ œÊœ
f(0 2) 3 and f(1 ) 5ßœ ß#œ
(iii) On OB, f(x y) f(x 2x) 6x 12x 1 onßœ ß œ
#
0 x 1; endpoint values have been found above;ŸŸ
f (x 2x) 12x 12 0 x 1 and y 2, but ( ) is not an interior point of OB
wßœ œÊœ œ "ß#
(iv) For interior points of the triangular region, f (x y) 4x 4 0 and f (x y) 2y 4 0
xy
ßœ œ ßœ œ
x 1 and y 2, but (1 2) is not an interior point of the region. Therefore, the absolute maximum isÊœ œ ß
1 at (0 0) and the absolute minimum is 5 at ( ).ß "ß #
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
840 Chapter 14 Partial Derivatives
32. (i) On OA, D(x y) D(0 y) y 1 on 0 y 4;ßœ ßœ ŸŸ
#
D(0y)2y0 y0; D()1 and
wßœ œÊœ !ß!œ
D( ) 17!ß % œ
(ii) On AB, D(x y) D(x 4) x 4x 17 onߜ ߜ
#
0 x 4; D (x 4) 2x 4 0 x 2 and (2 4)ŸŸ ß œ œ Ê œ ß
w
is an interior point of AB; D( ) 13 and#ß % œ
D( ) D( ) 17%ß % œ !ß % œ
(iii) On OB, D(x y) D(x x) x 1 on 0 x 4;ßœ ßœ ŸŸ
#
D (x x) 2x 0 x 0 and y 0, which is not an interior point of OB; endpoint values have been found
wßœ œÊœ œ
above
(iv) For interior points of the triangular region, f (x y) 2x y 0 and f (x y) x 2y 0 x 0 and y 0,
xy
ßœ œ ßœ œÊœ œ
which is not an interior point of the region. Therefore, the absolute maximum is 17 at ( ) and ( ), and the!ß % %ß %
absolute minimum is 1 at (0 0).ß
33. (i) On OA, f(x y) f( y) y on 0 y 2;ß œ !ß œ Ÿ Ÿ
#
f (0 y) 2y 0 y 0 and x 0; f(0 0) 0 and
wßœ œÊœ œ ßœ
f(0 ) 4ß# œ
(ii) On OB, f(x y) f(x 0) x on 0 x 1;ßœ ßœ ŸŸ
#
f (x 0) 2x 0 x 0 and y 0; f(0 0) 0 and
wßœ œÊœ œ ßœ
f(1 0) 1ߜ
(iii) On AB, f(x y) f(x 2x 2) 5x 8x 4 onߜ ߜ
#
0x1; f(x2x2)10x80 xŸŸ ß œ œÊœ
w4
5
and y ; f ; endpoint values have been found above.œßœ
242 4
555 5
ˆ‰
(iv) For interior points of the triangular region, f (x y) 2x 0 and f (x y) 2y 0 x 0 and y 0, but ( 0) is
xy
ßœ œ ßœ œÊœ œ !ß
not an interior point of the region. Therefore the absolute maximum is 4 at (0 2) and the absolute minimum is 0 atß
(0 0).ß
34. (i) On AB, T(x y) T( y) y on 3 y 3;ßœ!ßœ ŸŸ
#
T(0y)2y0 y0 and x0; T(00)0,
wßœ œÊœ œ ßœ
T( 3) 9, and T( 3) 9!ß œ !ß œ
(ii) On BC, T(x y) T(x 3) x 3x 9 on 0 x 5;ßœ ßœ ŸŸ
#
T (x 3) 2x 3 0 x and y 3;
w
#
ßœ œÊœ œ
3
T 3 and T(5 3) 19
ˆ‰
327
4#ߜ ߜ
(iii) On CD, T(x y) T(5 y) y 5y 5 onߜ ߜ
#
3 y 3;T (5 y) 2y 5 0 y andŸ Ÿ ß œ œ Ê œ
w
#
5
x 5;T 5 , T( 3) 11 and T(5 3) 19œßœ&ßœ ßœ
ˆ‰
545
4#
(iv) On AD, T(x y) T(x 3) x 9x 9 on 0 x 5; T (x 3) 2x 9 0 x and y 3;ߜߜŸŸßœœÊœ œ
#w
#
9
T 3 , T( 3) 9 and T( 3) 11
ˆ‰
945
4#ß œ !ß œ &ß œ
(v) For interior points of the rectangular region, T (x y) 2x y 6 0 and T (x y) x 2y 0 x 4
xy
ßœ œ ßœ œÊœ
and y 2 (4 2) is an interior critical point with T(4 2) 12. Therefore the absolute maximumœ Ê ß ß œ
is 19 at (5 3) and the absolute minimum is 12 at (4 2).ßß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.7 Extreme Values and Saddle Points 841
35. (i) On OC, T(x y) T(x 0) x 6x 2 onߜ ߜ
#
0x5; T(x0)2x60 x3 andŸŸ ß œ œ Ê œ
w
y 0; T(3 0) 7, T(0 0) 2, and T(5 0) 3œ ßœ ßœ ßœ
(ii) On CB, T(x y) T(5 y) y 5y 3 onߜ ߜ
#
3 y 0; T (5 y) 2y 5 0 y andŸ Ÿ ß œ œ Ê œ
w
#
5
x 5; T 5 and T(5 3) 9œßœ ßœ
ˆ‰
537
4#
(iii) On AB, T(x y) T(x 3) x 9x 11 onߜ ߜ
#
0x 5; T(x3) 2x90 x andŸŸ ßœ œ Ê œ
w
#
9
y 3; T 3 and T( 3) 11œ ß œ !ß œ
ˆ‰
937
4#
(iv) On AO, T(x y) T( y) y 2 on 3 y 0; T (0 y) 2y 0 y 0 and x 0, but (0 0) isßœ!ßœ ŸŸ ßœ œÊœ œ ß
#w
not an interior point of AO
(v) For interior points of the rectangular region, T (x y) 2x y 6 0 and T (x y) x 2y 0 x 4
xy
ßœ œ ßœ œÊœ
and y 2, an interior critical point with T( 2) 10. Therefore the absolute maximum is 11 atœ %ß œ
( 3) and the absolute minimum is 10 at (4 2).!ß ß
36. (i) On OA, f(x y) f( y) 24y on 0 y 1;ßœ!ßœ ŸŸ
#
f (0 y) 48y 0 y 0 and x 0, but (0 0) is
wßœ œÊœ œ ß
not an interior point of OA; f( 0) 0 and!ß œ
f( 1) 24!ß œ
(ii) On AB, f(x y) f(x 1) 48x 32x 24 onߜ ߜ
$
0 x 1; f (x 1) 48 96x 0 x andŸŸ ß œ œ Ê œ
w#
"
È2
y 1, or x and y 1, but 1 is not inœœ œ ß
""
ÈÈ
22
Š‹
the interior of AB; f 1 16 2 24 and f(1 1) 8
Š‹È
"
È2ßœ ßœ
(iii) On BC, f(x y) f( y) 48y 32 24y on 0 y 1; f ( y) 48 48y 0 y 1 and x 1, butßœ"ßœ ŸŸ "ßœ œÊœ œ
#w
( ) is not an interior point of BC; f( 0) 32 and f( ) 8"ß " "ß œ "ß " œ
(iv) On OC, f(x y) f(x 0) 32x on 0 x 1; f (x 0) 96x 0 x 0 and y 0, but (0 0) is not anßœ ßœ ŸŸ ßœ œÊœ œ ß
$w#
interior point of OC; f( 0) 0 and f( 0) 32!ß œ "ß œ
(v) For interior points of the rectangular region, f (x y) 48y 96x 0 and f (x y) 48x 48y 0
xy
ßœ œ ßœ œ
#
x 0 and y 0, or x and y , but (0 0) is not an interior point of the region; f 2.Êœ œ œ œ ß ß œ
"" ""
## ##
ˆ‰
Therefore the absolute maximum is 2 at and the absolute minimum is 32 at (1 0).
ˆ‰
""
##
ßß
37. (i) On AB, f(x y) f(1 y) 3 cos y on y ;ßœ ßœ ŸŸ
11
44
f (1 y) 3 sin y 0 y 0 and x 1;
wßœ œÊœ œ
f( 0) 3, f 1 , and f 1"ߜ ߜ ߜ
ˆ‰ ˆ‰
11
44
32 32
ÈÈ
##
(ii) On CD, f(x y) f( y) 3 cos y on y ;ßœ$ßœ ŸŸ
11
44
f (3 y) 3 sin y 0 y 0 and x 3;
wßœ œÊœ œ
f(3 0) 3, f 3 and f 3ßœ ß œ ß œ
ˆ‰ ˆ‰
11
44
32 32
ÈÈ
##
(iii) On BC, f(x y) f x 4x x onßœ ß œ
ˆ‰ ab
1
4
2
È
#
#
1 x 3; f x 2(2 x) 0 x 2 and y ; f 2 2 2, f 1 , andŸŸ ß œ œ Ê œ œ ß œ ß œ
w
#
ˆ‰ ˆ‰ ˆ‰
ÈÈ
1111
4444
32
È
f3
ˆ‰
ߜ
1
4
32
È
#
(iv) On AD, f(x y) f x 4x x on 1 x 3; f x 2(2 x) 0 x 2 and y ;ß œ ß œ Ÿ Ÿ ß œ œ Ê œ œ
ˆ‰ ˆ‰
ab È
11 1
44 4
2
È
#
#w
f 2 2 2, f 1 , and f 3
ˆ‰ ˆ‰ ˆ‰
È
ß œ ß œ ß œ
11 1
44 4
32 32
ÈÈ
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

842 Chapter 14 Partial Derivatives
(v) For interior points of the region, f (x y) (4 2x) cos y 0 and f (x y) 4x x sin y 0 x 2
xy
ßœ œ ßœ œÊœab
#
and y 0, which is an interior critical point with f(2 0) 4. Therefore the absolute maximum is 4 atœßœ
(2 0) and the absolute minimum is at 3 , 3 , 1 , and 1 .ß ßßß ß
32
44 4 4
È
#ˆ‰ˆ‰ˆ‰ˆ‰
11 1 1
38. (i) On OA, f(x y) f( y) 2y 1 on 0 y 1;ßœ!ßœ ŸŸ
f (0 y) 2 no interior critical points; f(0 0) 1
wßœÊ ßœ
and f(0 1) 3ߜ
(ii) On OB, f(x y) f(x 0) 4x 1 on 0 x 1;ßœ ßœ ŸŸ
f (x 0) 4 no interior critical points; f(1 0) 5
wßœÊ ßœ
(iii) On AB, f(x y) f(x x 1) 8x 6x 3 onߜ ߜ
#
0x1; f(xx1)16x60 xŸŸ ß œ œ Ê œ
w3
8
and y ; f , f(0 1) 3, and f( 0) 5œßœßœ "ßœ
535 15
888 8
ˆ‰
(iv) For interior points of the triangular region, f (x y) 4 8y 0 and f (x y) 8x 2 0
xy
ßœ œ ßœœ
y and x which is an interior critical point with f 2. Therefore the absolute maximum is 5 atÊœ œ ß œ
"" ""
##44
ˆ‰
(1 0) and the absolute minimum is 1 at (0 0).ßß
39. Let F(a b) 6 x x dx where a b. The boundary of the domain of F is the line a b in the ab-plane, andßœ Ÿ œ
'a
bab
#
F(a a) 0, so F is identically 0 on the boundary of its domain. For interior critical points we have:ߜ
6 a a 0 a 3, 2 and 6 b b 0 b 3, 2. Since a b, there is only one
``
``
##
FF
ab
œ œ Ê œ œ œ Ê œ Ÿab ab
interior critical point ( 3 2) and F( 3 2) 6 x x dx gives the area under the parabola y 6 x x that isß ß œ œ
'3
2ab
##
above the x-axis. Therefore, a 3 and b 2.œ œ
40. Let F(a b) 24 2x x dx where a b. The boundary of the domain of F is the line a b and on this line F isßœ Ÿ œ
'a
bab
#"Î$
identically 0. For interior critical points we have: 24 2a a 0 a 4, 6 and
`
`
#"Î$
F
aœ œ Ê œ ab
24 2b b 0 b 4, 6. Since a b, there is only one critical point ( 6 4) and
`
`
#"Î$
F
bœ œÊœ Ÿ ßab
F( 6 4) 24 2x x dx gives the area under the curve y 24 2x x that is above the x-axis.ß œ œ
'6
4ab ab
##
"Î$
Therefore, a 6 and b 4.œ œ
41. T (x y) 2x 1 0 and T (x y) 4y 0 x and y 0 with T 0 ; on the boundary
xy 4
ßœ œ ßœ œÊœ œ ß œ
"""
##
ˆ‰
x y 1: T(x y) x x 2 for 1 x 1 T (x y) 2x 1 0 x and y ;
## # w "
##
œ ßœ ŸŸÊ ßœœÊœ œ„
È3
T , T , T( 1 0) 2, and T( 0) 0 the hottest is 2 ° at and
Š‹Š ‹ Š‹
ß œ ß œ ß œ "ß œ Ê ß
"" ""
## # # ##
ÈÈ È
33 3
99
44 4
; the coldest is ° at 0 .
Š‹ ˆ‰
ß ß
"""
## #
È3
4
42. f (x y) y 2 0 and f (x y) x 0 x and y 2; f 2 8,
xy xx
2 2
xy x
2
ßœœ ßœœÊœ œ ß œ œ
"" "
##
ß
ˆ‰ ¸
ˆ‰
1
2
f 2 , f 2 1 f f f 1 0 and f 0 a local minimum of f 2
¹
ˆ‰ ˆ‰ ˆ‰
yy xy xx yy xx
y4
2xy
"" "" "
## #
ß
#
ßœ œ ßœÊ œ Ê ß
ˆ‰
1
2
2 ln 2 ln 2œ œ
"
#
43. (a) f (x y) 2x 4y 0 and f (x y) 2y 4x 0 x 0 and y 0; f (0 0) 2, f (0 0) 2,
x y xx yy
ßœœ ßœœÊœ œ ßœ ßœ
f (0 0) 4 f f f 12 0 saddle point at (0 0)
xy xx yy xy
ßœÊ œÊ ß
#
(b) f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and y 2; f (1 2) 2, f (1 2) 2,
x y xx yy
ßœ œ ßœ œÊœ œ ßœ ßœ
f (1 2) 0 f f f 4 0 and f 0 local minimum at ( )
xy xx yy xx
xy
ß œ Ê œ Ê "ß #
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.7 Extreme Values and Saddle Points 843
(c) f (x y) 9x 9 0 and f (x y) 2y 4 0 x 1 and y 2; f (1 2) 18x 18,
xy xx
12
ßœ œ ßœ œÊœ„ œ ßœ œ
#ÐßÑ
k
f (1 2) 2, f (1 2) 0 f f f 36 0 and f 0 local minimum at ( );
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê "ß#
#
f ( 1 2) 18, f ( 2) 2, f ( 2) 0 f f f 36 0 saddle point at ( 2)
xx yy xy xx yy xy
ß œ "ß œ "ß œ Ê œ Ê "ß
#
44. (a) Minimum at (0 0) since f(x y) 0 for all other (x y)ßß ß
(b) Maximum of 1 at ( ) since f(x y) 1 for all other (x y)!ß ! ß ß
(c) Neither since f(x y) 0 for x 0 and f(x y) 0 for x 0ß ß
(d) Neither since f(x y) 0 for x 0 and f(x y) 0 for x 0ß ß
(e) Neither since f(x y) 0 for x 0 and y 0, but f(x y) 0 for x 0 and y 0ß ß
(f) Minimum at (0 0) since f(x y) 0 for all other (x y)ßß ß
45. If k 0, then f(x y) x y f (x y) 2x 0 and f (x y) 2y 0 x 0 and y 0 (0 0) is the onlyœ ßœÊ ßœ œ ßœ œÊœ œÊß
## xy
critical point. If k 0, f (x y) 2x ky 0 y x; f (x y) kx 2y 0 kx 2 x 0Á ßœœÊœ ßœœÊ œ
xy
22
kk
ˆ‰
kx 0 k x 0 x 0 or k 2 y (0) 0 or y x; in any case (0 0) is aÊ œÊ œÊœ œ„Êœ œ œ„ ß
4x 4 2
kk k
ˆ‰ ˆ‰
critical point.
46. (See Exercise 45 above): f (x y) 2, f (x y) 2, and f (x y) k f f f 4 k ; f will have a saddle point
xx yy xy xx yy xy
ßœ ßœ ßœÊ œ
##
at (0 0) if 4 k 0 k 2 or k 2; f will have a local minimum at (0 0) if 4 k 0 2 k 2; the test isßÊ ßÊ
# #
inconclusive if 4 k 0 k 2.œÊœ„
#
47. No; for example f(x y) xy has a saddle point at (a b) (0 0) where f f 0.ßœ ßœß œœ
xy
48. If f (a b) and f (a b) differ in sign, then f (a b) f (a b) 0 so f f f 0. The surface must therefore have a
xx yy xx yy xx yy xy
ßß ßß
#
saddle point at (a b) by the second derivative test.ß
49. We want the point on z 10 x y where the tangent plane is parallel to the plane x 2y 3z 0. To find a normalœ œ
##
vector to z 10 x y let w z x y 10. Then w 2x 2y is normal to z 10 x y atœ œ œ œ
## ## ##
™ijk
(x y). The vector w is parallel to 2 3 which is normal to the plane x 2y 3z 0 ifß œ™ijk
6x 6y 3 2 3 or x and y . Thus the point is 10 or .ijkijk œ œ œ ßß ßß
" " "" " " ""
63 633696336
355
ˆ‰ˆ‰
50. We want the point on z x y 10 where the tangent plane is parallel to the plane x 2y z 0. Letœ œ
##
w z x y 10, then w 2x 2y is normal to z x y 10 at (x y). The vector w is parallelœ œ œ ß
## ##
™™ijk
to 2 which is normal to the plane if x and y 1. Thus the point 1 1 10 or 1 is the pointijk œ œ ßß ßß
""""
###
ˆ‰ˆ‰
44
45
on the surface z x y 10 nearest the plane x 2y z 0.œ œ
##
51. d x y z x 0 y 0 z 0 we can minimize d x y z by minimizing D x y z x y z ;abababab ab ab
É
ßß œ Ê ßß ßß œ
222 222
3x 2y z 6 z 6 3x 2y D x y x y 6 3x 2y D x y 2x 6 6 3x 2y 0œÊœÊ ßœ Ê ßœ œab a b ab a b
22 2x
and D x y 2y 4 6 3x 2y 0 critical point is , z ; D , 20, D , 1 10,
yxx yy
96 3 96 1
77 7 77 2
ab a b ˆ‰ ˆ‰ ˆ‰
ßœ œÊ Êœ œ œ
D , 1 12 D D D 56 0 and D 0 local minimum of d , ,
xy xx yy xx
1963
2777 7
xy
314
ˆ‰ ˆ ‰
œÊ œ Ê œ
#È
52. d x y z x 2 y 1 z 1 we can minimize d x y z by minimizinga bababab a b
É
ßß œ Ê ßß
222
Dxyz x2 y1 z1; xyz2 z xy2a babababßß œ œÊœ
222
Dxy x2 y1 xy3 Dxy 2x2 2xy3 0Ê ß œ Ê ß œ œabababa b ababa b
22 2
x
and D x y 2 y 1 2 x y 3 0 critical point is , z ; D , 4, D , 4,
yxx yy
81 1 81 81
33 3 33 33
aba ba b ˆ‰ ˆ‰ ˆ‰
ß œ œÊ Êœ œ œ
D , 2 D D D 12 0 and D 0 local minimum of d , ,
xy xx yy xx
81 811 2
33 333
xy 3
ˆ‰ ˆ ‰
œÊ œ Ê œ
#È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
844 Chapter 14 Partial Derivatives
53. s x y z x y z ; x y z 9 z 9 x y s x y x y 9 x yab ab a bßß œ œÊœÊ ß œ
222 22 2
s x y 2x 2 9 x y 0 and s x y 2y 2 9 x y 0 critical point is 3, 3 z 3;Ê ßœ œ ßœ œÊ Êœ
xy
ab a b ab a b ab
s 3, 3 4, s 3, 3 4, s 3, 3 2 s s s 12 0 and s 0 local minimum of s 3, 3, 3 27
xx yy xy xx yy xx
xy
ab ab ab a bœœœÊœÊ œ
#
54. p x y z xyz; x y z 3 z 3 x y p x y x y 3 x y 3x y x y x yab aba bßß œ œ ÊœÊ ß œ œ
22
p x y 3y 2xy y 0 and p x y 3x x 2xy 0 critical points are 0, 0 , 0, 3 , 3, 0 , andÊßœœ ßœœÊ
xy
22
ab ab ababab
1, 1 ; for 0, 0 z 3; p 0, 0 0, p 0, 0 0, p 0, 0 3 p p p 9 0 saddle point;ab ab ab ab abÊœ œœœÊœÊ
xx yy xy xx yy xy
#
for 0, 3 z 0; p 0, 3 6, p 0, 3 0, p 0, 3 3 p p p 9 0 saddle point;ab ab ab abÊœ œ œ œÊ œÊ
xx yy xy xx yy xy
#
for 3, 0 z 0; p 3, 0 0, p 3, 0 6, p 3, 0 3 p p p 9 0 saddle point;ab ab ab abÊœ œ œ œÊ œÊ
xx yy xy xx yy xy
#
for 1, 1 z 1; p 1, 1 2, p 1, 1 2, p 1, 1 1 p p p 3 0 and p 0 localab ab ab abÊ œ œ œ œ Ê œ Ê
xx yy xy xx yy xx
xy
#
maximum of p 1, 1, 1 1abœ
55. s x y z xy yz xz; x y z 6 z 6 x y s x y xy y 6 x y x 6 x yab abababßß œ œ ÊœÊ ß œ
6x 6y xy x y s x y 6 2x y 0 and s x y 6 x 2y 0 critical point is 2, 2œÊ ßœœ ßœœÊ
22 xy
ab ab ab
z 2; s 2, 2 2, s 2, 2 2, s 2, 2 1 s s s 3 0 and s 0 local maximum ofÊ œ œ œ œ Ê œ Ê
xx yy xy xx yy xx
xy
ab ab ab #
s 2, 2, 2 12abœ
56. d x y z x 6 y 4 z 0 we can minimize d x y z by minimizinga bababab a b
É
ßß œ Ê ßß
222
Dxyz x6 y4 z; z x y Dxy x6 y4 x ya babab ababab
È
ßßœ œ Ê ßœ
22 22
222
22
2x 2y 12x 8y 52 D x y 4x 12 0 and D x y 4y 8 0 critical point is 3, 2œ Ê ßœœ ßœœÊ
22 xy
ab ab a b
z 13; D 3, 2 4, D 3, 2 4, D 3, 2 0 D D D 16 0 and D 0 localÊœ œ œ œÊ œ Ê
Èab ab ab
xx yy xy xx yy xx
xy
#
minimum of d 3, 2, 13 26
Š‹
ÈÈ
œ
57. V x y z 2x 2y 2z 8xyz; x y z 4 z 4 x y V x y 8xy 4 x y ,a bababab a b
ÈÈ
ßßœ œ œÊœ Ê ß œ
222 22 22
x 0 and y 0 V x y 0 and V x y 0 critical points areÊßœ œ ßœ œÊ
xy
32y 16x y 8y 32x 16x y 8x
4x y 4x y
ab ab
23 23
22 22
ÈÈ
0, 0 , , , , , , , and , . Only 0, 0 and , satisfy x 0 and y 0ab ab
Š‹Š‹Š‹Š ‹ Š‹
## # # ## # # ##
ÈÈ È È ÈÈ È È ÈÈ
33 3 3 33 3 3 33
V 0 0 0 and V , ; On x 0, 0 y 2 V 0 y 8 0 y 4 0 y 0, no critical points,ab abab
Š‹ È
ßœ œ œ ŸŸÊ ßœ œ
##
ÈÈ È
33 33
64 22
V 0 0 0, V 0 2 0; On y 0, 0 x 2 V x 0 8x 0 4 x 0 0, no critical points, V 0 0 0,ab ab ab ab ab
È
ßœ ßœ œ ŸŸÊ ßœ œ ßœ
22
V02 0; On y 4x, 0 x2 Vx 4x 8x4x 4x 4x 0ab ÈÈÈÈ
Š‹ ÊŠ‹
ß œ œ ŸŸÊ ß œ œ
22222
2
no critical points, V 0 2 0, V 2 0 0. Thus, there is a maximum volume of if the box is .ab abßœ ßœ ‚ ‚
64
33 333
È ÈÈÈ
###
58. S x y z 2xy 2yz 2xz; xyz 27 z S x y z 2xy 2y 2x 2xy , x 0,ab ab Š‹ Š‹
ßßœ œÊœÊßßœ œ
27 27 27 54 54
xy xy xy x y
y 0; S x y 2y 0 and S x y 2x 0 Critical point is 3, 3 z 3; S 3, 3 4, ßœœ ßœœÊ Êœ œ
xy xx
54 54
xy
ab ab ab ab
22
S 3, 3 4, D 3, 3 2 D D D 12 0 and D 0 local minimum of S 3 3 3 54
yy xy xx yy xx
xy
ab ab a bœœÊœÊ ßßœ
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.7 Extreme Values and Saddle Points 845
59. Let x height of the box, y width, and z length, cut outœœœ
squares of length x from corner of the material See diagram
at right. Fold along the dashed lines to form the box. From
the diagram we see that the length of the material is 2x y
and the width is 2x z. Thus 2x y 2x z 12œabab
z . Since V x, y, z x y zÊœ œ
26 2x xy
2x y
ˆ‰
2ab
V x, y , where x 0, y 0.ʜ ab2x y 6 2 x xy
2x y
ˆ‰
2
V x, y 0 and
x43y4xy4xyxy
2x y
abœœ
ˆ‰
ab
23 223
2
V x, y 0 critical points are 3, 0 , 3, 0 , , ,
y2 12x 4 x 4x y x y
2x y
14
33
ab Š‹Š ‹Š ‹
ÈÈ
œœÊ
ˆ‰
ab ÈÈ
24322
2
and , . Only 3, 0 and , satisfy x 0 and y 0. For 3, 0 : z 0; V 3, 0 0,
Š ‹Š‹Š ‹ Š‹ Š‹
ÈÈÈ
œ œ
14 14
33 33 xx
ÈÈ ÈÈ
V 3, 0 2 3, V 3, 0 4 3 V V V 48 0 saddle point. For , : z ;
yy xy xx yy xy 14 4
33 3
Š‹ Š‹ Š ‹
ÈÈÈÈ
œ œ Ê œ Ê œ
#ÈÈ È
V, , V, , V, VVV 0 and
xx yy xy xx yy
14 80 14 2 14 4 16
33 33 33 33 33 33 xy 3
Š‹ Š‹ Š‹
ÈÈ È ÈÈ È ÈÈ È
œ œ œ Ê œ
#
V 0 local maximum of V , ,
xx 144 16
333 33
Ê œ
Š‹
ÈÈÈ È
60. (a) (i) On x 0, f(x y) f(0 y) y y 1 for 0 y 1; f (0 y) 2y 1 0 y and x 0;œßœßœ ŸŸ ßœœÊœ œ
#w "
#
f 0 , f(0 0) 1, and f(0 1) 1
ˆ‰
ß œ ßœ ßœ
"
#
3
4
(ii) On y 1, f(x y) f(x 1) x x 1 for 0 x 1; f (x 1) 2x 1 0 x and y 1, butœßœßœ ŸŸ ßœœÊœ œ
#w "
#
1 is outside the domain; f(0 1) 1 and f( ) 3
ˆ‰
ß ß œ "ß"œ
"
#
(iii) On x 1, f(x y) f( y) y y 1 for 0 y 1; f (1 y) 2y 1 0 y and x 1, butœ ß œ"ß œ Ÿ Ÿ ß œ œ Ê œ œ
#w "
#
1 is outside the domain; f(1 0) 1 and f( ) 3
ˆ‰
ß ß œ "ß" œ
"
#
(iv) On y 0, f(x y) f(x 0) x x 1 for 0 x 1; f (x 0) 2x 1 0 x and y 0;œßœßœ ŸŸ ßœœÊœ œ
#w "
#
f 0 ; f(0 0) 1, and f( 0) 1
ˆ‰
"
#ß œ ß œ "ß œ
3
4
(v) On the interior of the square, f (x y) 2x 2y 1 0 and f (x y) 2y 2x 1 0 2x 2y 1
xy
ßœ œ ßœ œÊ œ
(xy) . Then f(xy)x y 2xyxy1(xy) (xy)1 is the absoluteÊ œ ß œ œ œ
"
#
## # 3
4
minimum value when 2x 2y 1.œ
(b) The absolute maximum is f( ) 3."ß " œ
61. (a) 2 sin t 2 cos t 0 cos t sin t x y
df f dx f dx
dt x dt y dt dt dt
dy dy
œ œœ œÊ œ Êœ
``
``
(i) On the semicircle x y 4, y 0, we have t and x y 2 f 2 2 2 2. At the
##
œ œ œœ Ê ß œ
1
4ÈÈÈÈ
Š‹
endpoints, f( 2 0) 2 and f( ) 2. Therefore the absolute minimum is f( 2 0) 2 when t ;ß œ #ß! œ ß œ œ1
the absolute maximum is f 2 2 2 2 when t .
Š‹
ÈÈ È
ßœ œ
1
4
(ii) On the quartercircle x y 4, x 0 and y 0, the endpoints give f( 2) 2 and f( 0) 2.
##
œ !ßœ #ßœ
Therefore the absolute minimum is f(2 0) 2 and f( 2) 2 when t 0, respectively; the absoluteßœ !ßœ œ 1
#
maximum is f 2 2 2 2 when t .
Š‹
ÈÈ È
ßœ œ
1
4
(b) y x 4 sin t 4 cos t 0 cos t sin t x y.
dg g g dy dy
dt x dt y dt dt dt
dx dx
œ œœ œÊ œ„ Êœ„
``
``
##
(i) On the semicircle x y 4, y 0, we obtain x y 2 at t and x 2, y 2 at
##
œ œœ œ œ œ
ÈÈÈ
1
4
t . Then g 2 2 2 and g 2 2 2. At the endpoints, g( 2 0) g( 0) 0.œ ß œ ß œ ß œ #ß œ
3
4
1Š‹ Š ‹
ÈÈ ÈÈ
Therefore the absolute minimum is g 2 2 2 when t ; the absolute maximum is
Š‹
ÈÈ
ß œ œ
3
4
1
g22 2 when t .
Š‹
ÈÈ
ßœ œ
1
4
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
846 Chapter 14 Partial Derivatives
(ii) On the quartercircle x y 4, x 0 and y 0, the endpoints give g( 2) 0 and g( 0) 0.
##
œ !ßœ #ßœ
Therefore the absolute minimum is g(2 0) 0 and g( 2) 0 when t 0, respectively; the absoluteßœ !ßœ œ 1
#
maximum is g 2 2 2 when t .
Š‹
ÈÈ
ßœ œ
1
4
(c) 4x 2y (8 cos t)( 2 sin t) (4 sin t)(2 cos t) 8 cos t sin t 0
dh h dx h dx
dt x dt y dt dt dt
dy dy
œœœ œ œ
``
``
t 0, , yielding the points (2 0), (0 2) for 0 t .Êœ ß ß ŸŸ
1
#11
(i) On the semicircle x y 4, y 0 we have h(2 0) 8, h(0 2) 4, and h( 2 0) 8. Therefore,
##
œ ßœ ßœ ßœ
the absolute minimum is h( 2) 4 when t ; the absolute maximum is h(2 0) 8 and h( 2 0) 8!ß œ œ ß œ ß œ
1
#
when t 0, respectively.œ1
(ii) On the quartercircle x y 4, x 0 and y 0 the absolute minimum is h(0 2) 4 when t ; the
##
#
œ ßœ œ
1
absolute maximum is h(2 0) 8 when t 0.ßœ œ
62. (a) 2 3 6 sin t 6 cos t 0 sin t cos t t for 0 t .
df f dx f dx
dt x dt y dt dt dt 4
dy dy
œœœ œÊœÊœ ŸŸ
``
``
11
(i) On the semi-ellipse, 1, y 0, f(x y) 2x 3y 6 cos t 6 sin t 6 6 6 2
x
94
y22
œ ßœœ œ œ
Š‹ Š‹ È
ÈÈ
##
at t . At the endpoints, f( 3 0) 6 and f(3 0) 6. The absolute minimum is f( 3 0) 6 whenœ ßœ ßœ ßœ
1
4
t ; the absolute maximum is f 2 6 2 when t .œßœœ1Š‹
ÈÈ
32
4
È
#
1
(ii) On the quarter ellipse, at the endpoints f(0 2) 6 and f(3 0) 6. The absolute minimum is f(3 0) 6ߜ ߜ ߜ
and f(0 2) 6 when t 0, respectively; the absolute maximum is f 2 6 2 when t .ßœ œ ß œ œ
1 1
##
Š‹
ÈÈ
32
4
È
(b) y x (2 sin t)( 3 sin t) (3 cos t)(2 cos t) 6 cos t sin t 6 cos 2t 0
dg g g dy dy
dt x dt y dt dt dt
dx dx
œ œœ œ œ œ
``
``
##
ab
t , for 0 t .Êœ ŸŸ
11
44
31
(i) On the semi-ellipse, g(x y) xy 6 sin t cos t. Then g 2 3 when t , andßœ œ ß œ œ
Š‹
È
32
4
È
#
1
g 2 3 when t . At the endpoints, g( 3 0) g( 0) 0. The absolute minimum is
Š‹
È
ß œ œ ß œ $ß œ
32 3
4
È
#
1
g 2 3 when t ; the absolute maximum is g 2 3 when t .
Š‹ Š‹
ÈÈ
ß œ œ ß œ œ
32 32
3
4 4
È È
# #
1 1
(ii) On the quarter ellipse, at the endpoints g( 2) 0 and g( 0) 0. The absolute minimum is g(3 0) 0!ߜ $ߜ ߜ
and g(0 2) 0 at t 0, respectively; the absolute maximum is g 2 3 when t .ßœ œ ß œ œ
1 1
##
Š‹
È
32
4
È
(c) 2x 6y (6 cos t)( 3 sin t) (12 sin t)(2 cos t) 6 sin t cos t 0
dh h dx h dx
dt x dt y dt dt dt
dy dy
œœœ œ œ
``
``
t 0, , for 0 t , yielding the points (3 0), (0 2), and ( 3 0).Êœ ŸŸ ß ß ß
1
#11
(i) On the semi-ellipse, y 0 so that h(3 0) 9, h(0 2) 12, and h( 3 0) 9. The absolute minimum isߜߜߜ
h(3 0) 9 and h( 3 0) 9 when t 0, respectively; the absolute maximum is h( 2) 12 when t .ßœ ßœ œ !ßœ œ11
#
(ii) On the quarter ellipse, the absolute minimum is h(3 0) 9 when t 0; the absolute maximum isßœ œ
h( 2) 12 when t .!ß œ œ 1
#
63. y x
df f dx f dx
dt x dt y dt dt dt
dy dy
œœ
``
``
(i) x 2t and y t 1 (t 1)(2) (2t)(1) 4t 2 0 t x 1 and y withœœÊœœœÊœÊœœ
df
dt
""
##
f 1 . The absolute minimum is f 1 when t ; there is no absolute maximum.
ˆ‰ ˆ‰
ß œ ß œ œ
"" "" "
## ## #
(ii) For the endpoints: t 1 x 2 and y 0 with f( 2 0) 0; t 0 x 0 and y 1 withœÊœ œ ßœ œÊœ œ
f( 1) 0. The absolute minimum is f 1 when t ; the absolute maximum is f(0 1) 0!ß œ ß œ œ ß œ
ˆ‰
"" "
## #
and f( 0) 0 when t 1, 0 respectively.#ß œ œ
(iii) There are no interior critical points. For the endpoints: t 0 x 0 and y 1 with f(0 1) 0;œÊœ œ ßœ
t 1 x 2 and y 2 with f(2 2) 4. The absolute minimum is f(0 1) 0 when t 0; the absoluteœÊœ œ ßœ ßœ œ
maximum is f(2 2) 4 when t 1.ßœ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.7 Extreme Values and Saddle Points 847
64. (a) 2x 2y
df f dx f dx
dt x dt y dt dt dt
dy dy
œœ
``
``
(i) x t and y 2 2t (2t)(1) 2(2 2t)( 2) 10t 8 0 t x and y withœœÊœœœÊœÊœ œ
df 4 4 2
dt 5 5 5
f . The absolute minimum is f when t ; there is no absolute
ˆ‰ ˆ‰
42 6 4 4 42 4 4
55 5 25 5 55 5 5
ßœœ ßœ œ
"
#
maximum along the line.
(ii) For the endpoints: t 0 x 0 and y 2 with f(0 2) 4; t 1 x 1 and y 0 with f(1 0) 1.œÊœ œ ßœ œÊœ œ ßœ
The absolute minimum is f at the interior critical point when t ; the absolute maximum is
ˆ‰
42 4 4
55 5 5
ßœ œ
f(0 2) 4 at the endpoint when t 0.ßœ œ
(b)
dg g g dy 2y dy
dt x dt y dt dt dt
dx 2x dx
xy xy
œœ
``
``
’“’“
ab ab
(i) x t and y 2 2t x y 5t 8t 4 5t 8t 4 [( 2t)(1) ( 2)(2 2t)( 2)]œœÊœÊœ
## # # #
dg
dt ab
5t 8t 4 ( 10t 8) 0 t x and y with g . The absoluteœ œ Ê œ Ê œ œ ß œ œab ˆ‰
## "44242 5
55555 4
ˆ‰
4
5
maximum is g when t ; there is no absolute minimum along the line since x and y can be
ˆ‰
42 5 4
55 4 5
ßœ œ
as large as we please.
(ii) For the endpoints: t 0 x 0 and y 2 with g(0 2) ; t 1 x 1 and y 0 with g(1 0) 1.œÊœ œ ßœ œÊœ œ ßœ
"
4
The absolute minimum is g(0 2) when t 0; the absolute maximum is g when t .ßœ œ ß œ œ
"
45545
42 5 4
ˆ‰
65. w m x b y m x b y m x b yωababab
11 22 nn
22 2
2mx b y x 2mx b y x 2mx b y xÊ œ â
`
`
w
m111 222 nnn
a bab a bab a bab
2mx b y 1 2mx b y 1 2mx b y 1Ê œ â
`
`
w
b11 22 nn
a bab a bab a bab
0 2 mx b y x mx b y x mx b y x 0
`
`
w
m111222 nnn
œÊ â œ
‘
a baba bab a bab
mx bx x y mx bx x y mx bx x y 0Êâ œ
22 2
1111 222 nnn
n
#
mx x x bx x x xy xy xy 0Ê â â â œababa b
22 2
1n12 n 1122 nn
#
mx bx xy 0Ê œ
!!!
ab a b
k1 k1 k1
nnn
k
2kkk
œœœ
0 2 mx b y mx b y mx b y 0
`
`
w
b1122 nn
œÊ â œ
‘
ababab
mx b y mx b y mx b y 0Êâœ
1122 nn
mxxxbbbyyy0Ê âââœababab
12 n 12 n
mx b1 y 0 mx bn y 0 b y mx.ʜʜʜ
!!! ! ! !!
Œ
k1 k1 k1 k1 k1 k1 k1
nnn n n n n
kkkk kk
1
n
œœœ œ œ œ œ
Substituting for b in the equation obtained for we get m x y m x x x y 0.
`
`œœœœœ
w1
mn
k1 k1 k1 k1 k1
nnnnn
k
2kkkkk
!!!!!
ab a b
Œ
œ
Multiply both sides by n to obtain m n x y m x x n x y 0
!!!!!
ab a b
Œ
k1 k1 k1 k1 k1
nnnnn
k
2kkk kk
œœœœœ
œ
mn x x y m x n x y 0Ê œ
!!! !!
ab a b
ŒŒŒ
k1 k1 k1 k1 k1
nnn n n
k
2kk k kk
2
œœœ œ œ
mn x m x n x y x yÊ œ
!!!!!
ab a b
Œ ŒŒ
k1 k1 k1 k1 k1
nnn nn
k
2kkkkk
2
œœœ œœ
mn x x n xy x yʜ
–—
!! ! !!
ab a b
Œ ŒŒ
k1 k1 k1 k1 k1
nn n nn
k
2kkkkk
2
œœ œ œœ
mÊœ œ
n xy xy xyn xy
nx x x nx
!!! !!!
ab ab
ŒŒŒŒ
!! ! !
ab ab
Œ Œ
k1 k1 k1 k1 k1 k1
nnn nnn
kk kk kk kk
k1 k1 k1 k1
nn n n
kk
22
kk
22
To show that these values for m and b minimize the sum of the squares of the distances, use second derivative test.
2x 2x 2x 2 x ; 2x 2x 2x 2 x ; 2 2 2 2n
```
````
#œœ
2 2 2
2 2
www
mm bb
22 2 2
1nk1 k1
nn
k12 n k
œâœ œâœ œâœ
!!
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

848 Chapter 14 Partial Derivatives
The discriminant is: 2 x 2 n 2 x 4 n x x .
Š‹Š‹Š ‹”•”•
!!!!
abab ab
–—
Œ
`` `
`` `` œœœœ
#
22 2
22
ww w
mb m b
2
k1 k1 k1 k1
nnnn
kk
22
kk
2
œ œ
Now, n x x n x x x x x x x x x
!!
abababab
Œ
k1 k1
nn
k
222
k12n12n
2
1n
œœ ##
œ â â â
nx nx nx x x x x x x x x x x x x x x xœââââ
22 2 2
11
n n
12 1n 21 2n n1 n2
##
# #
n 1 x n 1 x n 1 x 2xx 2xx 2xx 2xx 2xx 2x xœââââabab ab
22
1n12 13 1n 23 2n n1n
##
x2xxx x2xx x x2xxx x2xx x x2xxxœ â â ababababab
222 22 2 22
1131 3
12 13 1n 23 2n
nn
###
##
x 2 x x xâ ab
2
n1 n1n n
#
xx xx xx xx xx x x 0.œ â â â abab abab ab a b
12 13 1n 23 2n n1n
22 22 2 2
Thus we have : 4 n x x 4 0 0. If x x x then
Š‹Š‹Š ‹ –—
!!
ab ab
Œ
`` `
`` `` œœ
22 2
22
ww w
mb m b
2
k1 k1
nn
k
2k12n
2
œ œ œ œâœ
0. Also, 2 x 0. If x x x 0, then 0.
Š‹Š‹Š ‹ !ab
`` ` ` `
`` `` ` `
œ
22 2 2 2
22 2 2
ww w w w
mb m b m m
2
k1
n
k
212 n
œ œ œ œâœ œ œ
Provided that at least one x is nonzero and different from the rest of x , j i, then 0 and
ij
ww w
mb m b
2
Á
Š‹Š‹Š ‹
`` `
`` ``
22 2
22
0 the values given above for m and b minimize w.
`
`
2
2
w
mÊ
66. m andœœ
(0)(5) 3(6)
(0) 3(8) 4
3
b5(0)œ œ
"
34 3
35
‘
yx; yÊœ œ
35 14
43 3
¸x4œ
k x y x x y
120 4 0
20 2 0 0
32 3 4 6
058 6
kk kk
k
#
D
67. m andœœ
(2)( 1) 3( 4)
(2) 3(10) 13
20
"
b1 (2)œ œ
"
31313
20 9
‘ˆ‰
yx; yÊœ œ
20 9 71
13 13 13
¸x4œ
k x y x x y
112 1 2
20 1 0 0
33 4 9 12
2 1 10 14
kk kk
k
#
D
68. m andœœ
(3)(5) 3(8)
(3) 3(5) 2
3
b5(3)œ œ
"
32 6
31
‘
yx; yÊœ œ
31 37
26 6
¸x4œ
k x y x x y
10 0 0 0
21 2 1 2
32 3 4 6
355 8
kk kk
k
#
D
69-74. Example CAS commands:
:Maple
f := (x,y) -> x^2+y^3-3*x*y;
x0,x1 := -5,5;
y0,y1 := -5,5;
plot3d( f(x,y), x=x0..x1, y=y0..y1, axes=boxed, shading=zhue, title="#69(a) (Section 14.7)" );
plot3d( f(x,y), x=x0..x1, y=y0..y1, grid=[40,40], axes=boxed, shading=zhue, style=patchcontour, title="#69(b)
(Section 14.7)" );
fx := D[1](f); # (c)
fy := D[2](f);
crit_pts := solve( {fx(x,y)=0,fy(x,y)=0}, {x,y} );
fxx := D[1](fx); # (d)
fxy := D[2](fx);
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.8 Lagrange Multipliers 849
fyy := D[2](fy);
discr := unapply( fxx(x,y)*fyy(x,y)-fxy(x,y)^2, (x,y) );
for CP in {crit_pts} do # (e)
eval( [x,y,fxx(x,y),discr(x,y)], CP );
end do;
# (0,0) is a saddle point
# ( 9/4, 3/2) is a local minimum
: (assigned functions and bounds will vary)Mathematica
Clear[x,y,f]
f[x_,y_]:= x y 3x y
23
xmin= 5; xmax= 5; ymin= 5; ymax= 5;
Plot3D[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, AxesLabel {x, y, z}]Ä
ContourPlot[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, ContourShading False, Contours 40]ÄÄ
fx= D[f[x,y], x];
fy= D[f[x,y], y];
critical=Solve[{fx==0, fy==0},{x, y}]
fxx= D[fx, x];
fxy= D[fx, y];
fyy= D[fy, y];
discriminant= fxx fyy fxy2
{{x, y}, f[x, y], discriminant, fxx} /.critical
14.8 LAGRANGE MULTIPLIERS
1. f y x and g 2x 4y so that f g y x (2x 4y ) y 2x and x 4y™™ ™™œ œ œ Ê œ Êœ œij i j ij i j-- --
x 8x or x 0.Êœ Êœ„ œ--
#È2
4
CASE 1: If x 0, then y 0. But (0 0) is not on the ellipse so x 0.œœß Á
CASE 2: x 0 x 2y 2y 2y 1 y .ÁÊœ„ Êœ„ Ê„ œÊœ„-È2
4ÈÈ
Š‹
##"
#
Therefore f takes on its extreme values at and . The extreme values of f on the ellipse
Š‹Š ‹
„ß „ß
ÈÈ
22
22
""
##
are .„È2
#
2. f y x and g 2x 2y so that f g y x (2x 2y ) y 2x and x 2y™™ ™™œ œ œ Ê œ Êœ œij i j ij i j-- --
x 4x x 0 or .Êœ Êœ œ„--
#1
2
CASE 1: If x 0, then y 0. But (0 0) is not on the circle x y 10 0 so x 0.œœß œÁ
##
CASE 2: x 0 y 2x x x x 10 0 x 5 y 5.ÁÊœ„Êœ „ œ„Ê „ œÊœ„ Êœ„-1
2ˆ‰ ab ÈÈ
"
#
##
Therefore f takes on its extreme values at 5 5 and 5 5 . The extreme values of f on the
Š‹Š ‹
ÈÈ È È
„ß „ß
circle are 5 and 5.
3. f 2x 2y and g 3 so that f g 2x 2y ( 3 ) x and y™™™™œ œ œ Ê œ Ê œ œij ij ijij--
--
##
3
3 10 2 x 1 and y 3 f takes on its extreme value at (1 3) on the line.Ê œ Ê œÊ œ œ Ê ß
ˆ‰ˆ‰
--
##
3-
The extreme value is f( ) 49 1 9 39."ß $ œ œ
4. f 2xy x and g so that f g 2xy x ( ) 2xy and x™™™™œ œ œ Ê œÊœ œij ij ij ij
###
----
2xy x x 0 or 2y x.ʜʜ œ
#
CASE 1: If x 0, then x y 3 y 3.œœÊœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
850 Chapter 14 Partial Derivatives
CASE 2: If x 0, then 2y x so that x y 3 2y y 3 y 1 x 2.Á œ œÊ œÊœÊœ
Therefore f takes on its extreme values at ( 3) and (2 ). The extreme values of f are f(0 3) 0 and f(2 1) 4.!ß ß" ßœ ßœ
5. We optimize f(x y) x y , the square of the distance to the origin, subject to the constraintߜ
##
g(x y) xy 54 0. Thus f 2x 2y and g y 2xy so that f g 2x 2yßœ œ œ œ œ Ê
##
™™ ™™ij i j ij-
y 2xy 2x y and 2y 2 xy.œ Êœ œ---ab
##
ij
CASE 1: If y 0, then x 0. But (0 0) does not satisfy the constraint xy 54 so y 0.œœß œÁ
#
CASE 2: If y 0, then 2 2 x x 2 y y . Then xy 54 54ÁœÊœÊœÊœ œÊ œ--
"" "
## #
-- - --
ˆ‰ ˆ‰ˆ‰
22
x 3 and y 18 x 3 and y 3 2.ʜʜʜ œÊœ œ„--
$#
""
27 3 È
Therefore 3 2 are the points on the curve xy 54 nearest the origin (since xy 54 has points increasingly
Š‹
È
$ß „ œ œ
##
far away as y gets close to 0, no points are farthest away).
6. We optimize f(x y) x y , the square of the distance to the origin subject to the constraint g(x y) x y 2 0.ßœ ßœ œ
## #
Thus f 2x 2y and g 2xy x so that f g 2x 2xy and 2y x , since™™ ™™œ œ œ Êœ œ Êœij ij
##
----
2y
x
x 0 y 0 (but g(0 0) 0). Thus x 0 and 2x 2xy x 2y 2y y 2 0 y 1 (sinceœÊœ ßÁ Á œ Ê œ Ê œ Êœ
ˆ‰ ab
2y
x## #
y 0) x 2 . Therefore 2 1 are the points on the curve x y 2 nearest the origin (since x y 2 hasÊœ„ „ß œ œ
ÈÈ
Š‹ ##
points increasingly far away as x gets close to 0, no points are farthest away).
7. (a) f and g y x so that f g (y x ) 1 y and 1 x y and™™ ™™œ œ œ Êœ Ê œ œ Ê œij i j ij i j-- --
"
-
x 16 . Use since x 0 and y 0. Then x 4 and y 4 the minimum value is 8œÊ œ Êœ„ œ œ œÊ
"" " "
-- --
44
at the point (4 4). Now, xy 16, x 0, y 0 is a branch of a hyperbola in the first quadrant with the x-and y-axesߜ
as asymptotes. The equations x y c give a family of parallel lines with m 1. As these lines move away fromœ œ
the origin, the number c increases. Thus the minimum value of c occurs where x y c is tangent to the hyperbola'sœ
branch.
(b) f y x and g so that f g y x ( ) y x y y 16 y 8™™ ™™œ œ œ Ê œ Êœœ œ Êœij ij ij ij---
x 8 f( ) 64 is the maximum value. The equations xy c (x 0 and y 0 or x 0 and y 0ÊœÊ)ß)œ œ
to get a maximum value) give a family of hyperbolas in the first and third quadrants with the x- and y-axes as
asymptotes. The maximum value of c occurs where the hyperbola xy c is tangent to the line x y 16.œœ
8. Let f(x y) x y be the square of the distance from the origin. Then f 2x 2y andßœ œ
## ™ij
g (2x y) (2y x) so that f g 2x (2x y) and 2y (2y x) ™™™œ œ Êœ œÊ œij -- - -
2y
2y x
2x (2x y) x(2y x) y(2x y) x y y x.Ê œ Ê œ Ê œ Êœ„
Š‹
2y
2y x
##
CASE 1: y x x x(x) x 1 0 x and y x.œÊ œÊœ„ œ
## "
È3
CASE 2: y x x x( x) ( x) 1 0 x 1 and y x. Thus fœ Ê œ Ê œ „ œ ß œ
## ""
Š‹
ÈÈ
33
2
3
f and f(1 1) 2 f( 1 1).œ ß ß œ œ ß
Š‹
""
ÈÈ
33
Therefore the points (1 1) and ( 1 1) are the farthest away; and are the closestß ß ß ß
Š‹Š ‹
"" " "
ÈÈ È È
33 3 3
points to the origin.
9. V r h 16 r h 16 r h g(r h) r h 16; S 2 rh 2 r S (2 h 4 r) 2 r andœÊœÊœÊßœœÊ œ111 11 111
### # #
™ij
g 2rh r so that S g (2 rh 4 r) 2 r 2rh r 2 rh 4 r 2rh and 2 r r™™™œ œ Ê œ Ê œ œij i j ij
###
-111- 11-1-ab
r 0 or . But r 0 gives no physical can, so r 0 2 h 4 r 2rh 2r hÊœ œ œ Á Ê œ Ê œ Ê œ--11
222
rrr
111
ˆ‰
16 r (2r) r 2 h 4; thus r 2 cm and h 4 cm give the only extreme surface area of 24 cm . SinceÊœ ʜʜ œ œ
# #
1
r 4 cm and h 1 cm V 16 cm and S 40 cm , which is a larger surface area, then 24 cm must be theœœÊœ œ11 1
$# #
minimum surface area.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.8 Lagrange Multipliers 851
10. For a cylinder of radius r and height h we want to maximize the surface area S 2 rh subject to the constraintœ1
g(r h) r a 0. Thus S 2 h 2 r and g 2r so that S g 2 h 2 r andßœ œ œ œ œ Ê œ
##
# #
#
ˆ‰
h h
™™™™11 - 1-ij ij
2 r and 2 r 4r h h 2r r a 2r a r1-1œ Ê œ œ Ê œÊœÊœÊ œÊœ
-1 1hh hh 4r a
rr 4 2
##
## # # ##
ˆ‰ˆ‰ È
h a 2 S 2 a 2 2 a .Êœ Êœ œ
ÈÈ
Š‹Š ‹
11
a
2
È#
11. A (2x)(2y) 4xy subject to g(x y) 1 0; A 4y 4x and g so that Aœœ ßœœœ œ
xx
16 9 8 9
y2y
™™ ™ij ij
g 4y 4x 4y and 4x and 4xœÊœÊœ œÊœ œ-- ---™ij i j
ˆ ‰ ˆ‰ ˆ‰ ˆ‰ˆ‰
xx
89 8 9 x 9x
2y 2y 32y 2y 32y
y x 1 x 8 x 2 2 . We use x 2 2 since x represents distance.Êœ„ Ê œÊ œÊœ„ œ
3x
4169
x
ˆ‰
3
4#ÈÈ
Then y 2 2 , so the length is 2x 4 2 and the width is 2y 3 2.œœ œ œ
3
4
32
Š‹
ÈÈÈ
È
#
12. P 4x 4y subject to g(x y) 1 0; P 4 4 and g so that P gœ ßœœ œ œ œ
x2x
ab a b
y2y
™™ ™™ij i j -
4 and 4 and 4 y x 1 Êœ œ Êœ œ Êœ Ê œÊ
ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
2x 2a 2a b x x b x
abxbxaaba
2y 2y x
a
--- Š‹
b
a
1 a b x a x , since x 0 y x width 2xœÊ œ Êœ Êœ œ Ê œ œab Š‹
###%
abb2a
ab ab ab
a
ÈÈÈ
and height 2y perimeter is P 4x 4y 4 a bœœ Ê œœ œ
2b 4a 4b
ab ab
ÈÈ
##
È
13. f 2x 2y and g (2x 2) (2y 4) so that f g 2x 2y [(2x 2) (2y 4) ]™™ ™™œ œ œ œ œ ij i j ij i j--
2x (2x 2) and 2y (2y 4) x and y , 1 y 2x x 2x (2x) 4(2x) 0Êœ œ Êœ œ ÁÊœÊ œ-- -
--
--
##
11
2
x 0 and y 0, or x 2 and y 4. Therefore f(0 0) 0 is the minimum value and f(2 4) 20 is the maximumÊœ œ œ œ ß œ ß œ
value. (Note that 1 gives 2x 2x 2 or 2, which is impossible.)-œœ!œ
14. f 3 and g 2x 2y so that f g 3 2 x and 1 2 y and 1 2 y™™ ™™œ œ œ Êœ œ Êœ œij i j ----
33
2x 2x
ˆ‰
y x 4 10x 36 x x and y , or x andÊ œ Ê œ Ê œ Ê œ „ Ê œ œ œ
xx 66 26
33 10 10 10 10
##
#
ˆ‰ ÈÈ È È
y . Therefore f 6 2 10 6 12.325 is the maximum value, and fœ ß œ œ ¸ ß
26220 62
10 10 10 10 10 10
ÈÈÈÈ ÈÈ
Š‹ Š‹
È
2 10 6 0.325 is the minimum value.œ ¸
È
15. T (8x 4y) ( 4x 2y) and g(x y) x y 25 0 g 2x 2y so that T g™™™™œ ßœœÊ œ œij ij
## -
(8x 4y) ( 4x 2y) (2x 2y ) 8x 4y 2 x and 4x 2y 2 y y , 1Êœ Êœ œ Êœ Áijij----
2x
1-
8x 4 2 x x 0, or 0, or 5.Ê œÊœœœ
ˆ‰
2x
1----
CASE 1: x 0 y 0; but (0 0) is not on x y 25 so x 0.œÊœ ß œ Á
##
CASE 2: 0 y 2x x (2x) 25 x 5 and y 2x.-œÊœ Ê œ Êœ„ œ
## È
CASE 3: 5 y x 25 x 2 5 x 2 5 and y 5, or x 2 5-œ Ê œ œ Ê œ Ê œ „ Ê œ œ œ
##
##
2x x x
4ˆ‰ ÈÈ È È
and y 5 .œÈ
Therefore T 5 2 5 0° T 5 2 5 is the minimum value and T 2 5 5 125°
Š‹Š ‹ Š ‹
ÈÈ È È ÈÈ
ß œ œ ß ß œ
T 2 5 5 is the maximum value. (Note: 1 x 0 from the equation 4x 2y 2 y; but weœ ß œÊœ œ
Š‹
ÈÈ --
found x 0 in CASE 1.)Á
16. The surface area is given by S 4 r 2 rh subject to the constraint V(r h) r r h 8000. Thusœ ßœ œ11 11
#$#
4
3
S (8 r 2 h) 2 r and V 4 r 2 rh r so that S V (8 r 2 h) 2 r™™ ™™œ œ œ œ 11 1 1 1 1 - 11 1ij ij ijab
##
4r 2rh r 8r 2h 4r 2rh and 2r r r 0 or 2 r. But r 0œÊœ œÊœœ Á-1 1 1 1 1 -1 1 1 -1 -cdabab
## # #
ij
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

852 Chapter 14 Partial Derivatives
so 2 r 4r h 2r rh h 0 the tank is a sphere (there is no cylindrical part) andœÊœÊœ ÊœÊ--
22
rr
ab
#
r 8000 r 10 .
46
31$"Î$
œÊœ
ˆ‰
1
17. Let f(x y z) (x 1) (y 1) (z 1) be the square of the distance from (1 1 1). Thenßß œ ßß
###
f 2(x 1) 2(y 1) 2(z 1) and g 2 3 so that f g™™™™œ œ œijk ijk -
2(x 1) 2(y 1) 2(z 1) ( 2 3 ) 2(x 1) , 2(y 1) 2 , 2(z 1) 3Ê œ Ê œ œ œijkijk----
2(y 1) 2[2(x 1)] and 2(z 1) 3[2(x 1)] x z 2 3 or z ; thusÊœ œ Êœ Êœ œ
y1 y1 3y1
###
ˆ‰
2y 3 13 0 y 2 x and z . Therefore the point 2 is closest (since no
y1 3y1 35 35
## ## ##
œÊœÊœ œ ßß
ˆ‰ ˆ ‰
point on the plane is farthest from the point (1 1 1)).ßß
18. Let f(x y z) (x 1) (y 1) (z 1) be the square of the distance from (1 1 1). Thenßß œ ßß
###
f 2(x 1) 2(y 1) 2(z 1) and g 2x 2y 2z so that f g x 1 x, y 1 y™™™™œ œ œ Êœ œijk ijk ---
and z 1 z x , y , and z for 1 4œ Ê œ œ œ Á Ê œ--
"" " """
###
1 1 1 111- - - ---
ˆ‰ˆ‰ˆ‰
x , y , z or x , y , z . The largest value of fÊœ„Êœ œ œ œ œ œ
"
"-
2222 222
3333 333
ÈÈÈÈ ÈÈÈ
occurs where x 0, y 0, and z 0 or at the point on the sphere. ßß
Š‹
22 2
33 3
ÈÈ È
19. Let f(x y z) x y z be the square of the distance from the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g 2x 2y 2z so that f g 2x 2y 2z (2x 2y 2z ) 2x 2x , 2y 2y ,™™™œ œ Ê œ Êœ œijk ijk ijk-- --
and 2z 2z x 0 or 1.œ Ê œ œ--
CASE 1: 1 2y 2y y 0; 2z 2z z 0 x 1 0 x 1 0 x 1 and y z 0.-œ Ê œ Ê œ œ Ê œ Ê œ Ê œ Ê œ „ œ œ
##
CASE 2: x 0 y z 1, which has no solution.œÊ œ
##
Therefore the points on the unit circle x y 1, are the points on the surface x y z 1 closest to the origin
## ###
œ œ Þ
The minimum distance is 1.
20. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g y x so that f g 2x 2y 2z (y x ) 2x y, 2y x, and 2z™™™œ œ Ê œ Ê œ œ œijk i j k ijk-----
x 2y y 0 or 2.Êœ Ê œ Êœ œ„
--yy
##
--
Š‹
CASE 1: y 0 x 0 z 1 0 z 1.œÊœÊœÊœ
CASE 2: 2 x y and z 1 x ( 1) 1 0 x 2 0, so no solution.-œÊœ œÊ œÊ œ
##
CASE 3: 2 x y and z 1 ( y)y 1 1 0 y 0, again.-œ Ê œ œ Ê œ Ê œ
Therefore (0 0 1) is the point on the surface closest to the origin since this point gives the only extreme valueßß
and there is no maximum distance from the surface to the origin.
21. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g y x 2z so that f g 2x 2y 2z ( y x 2z ) 2x y , 2y x , and™™™œ œ Ê œ Ê œ œij k i j k ij k-- --
2z 2z 1 or z 0.œÊœ œ--
CASE 1: 1 2x y and 2y x y 0 and x 0 z 4 0 z 2 and x y 0.-œ Ê œ œ Ê œ œ Ê œ Ê œ „ œ œ
#
CASE 2: z 0 xy 4 0 y . Then 2x , and x xœ Ê œ Ê œ œ Ê œ œ Ê œ
44x8 8x
xx x x
-- -
##
Š‹
x 16 x 2. Thus, x 2 and y 2, or x = 2 and y 2.ʜʜ„ œ œ œ
%
Therefore we get four points: ( 2 0), ( 2 2 0), (0 0 2) and ( 0 2). But the points ( 0 2) and ( 2)#ß ß ß ß ß ß !ß ß !ß ß !ß !ß
are closest to the origin since they are 2 units away and the others are 2 2 units away.
È
22. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g yz xz xy so that f g 2x yz, 2y xz, and 2z xy 2x xyz and 2y yxz™™™œ œ Êœ œ œ Ê œ œijk ------
##
x y y x z x x x x 1 x 1 the points are (1 1 1), ( 1 1),Ê œ Êœ„Êœ„Ê „ „œÊœ„Ê ßß "ßß
## abab
( ), and ( 1 1, 1)."ß "ß " ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.8 Lagrange Multipliers 853
23. f 2 5 and g 2x 2y 2z so that f g 2 5 (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Êœ Êœijk i j k ijk i j k-- -
2 2y , and 5 2z x , y 2x, and z 5x x ( 2x) (5x) 30 x 1.œ œ Ê œ œ œ œ œ Ê œ Ê œ„--
""
##
###
-- -
5
Thus, x 1, y 2, z 5 or x 1, y 2, z 5. Therefore f(1 2 5) 30 is the maximum value andœœœ œœœ ßßœ
f( 1 2 5) 30 is the minimum value.ß ß œ
24. f 2 3 and g 2x 2y 2z so that f g 2 3 (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Êœ Êœijk i j k ijk i j k-- -
2 2y , and 3 2z x , y 2x, and z 3x x (2x) (3x) 25 x .œ œ Êœ œœ œ œ Ê œ Êœ„--
""
##
###
-- -
35
14
È
Thus, x , y , z or x , y , z . Therefore fœœœ œœœ ßß
5 10 15 5 10 15 5 10 15
14 14 14 14 14 14 14 14 14
È È È È È È ÈÈÈ
Š‹
5 14 is the maximum value and f , 5 14 is the minimum value.œßœ
ÈÈ
Š‹
51015
14 14 14
ÈÈÈ
25. f(x y z) x y z and g(x y z) x y z 9 0 f 2x 2y 2z and g so thatßßœ ßßœœÊ œ œ
### ™™ijk ijk
f g 2x 2y 2z ( ) 2x , 2y , and 2z x yz xxx9 0™™œ Ê œ Ê œ œ œ Ê œ œÊœ-----ijkijk
x 3, y 3, and z 3.Êœ œ œ
26. f(x y z) xyz and g(x y z) x y z 16 0 f yz xz xy and g 2z so thatßßœ ßßœœÊ œ œ
#™™ijk ijk
f g yz xz xy ( 2z ) yz , xz , and xy 2z yz xz z 0 or y x.™™œÊœÊœœ œÊœÊœœ-----ijkijk
But z 0 so that y x x 2z and xz . Then x 2z(xz) x 0 or x 2z . But x 0 so thatœÊœ œ œÊœœ
## #
--
x 2z y 2z 2z 2z z 16 z . We use z since z 0. Then x and yœÊœÊœÊœ„ œ œ œ
##### 4 4 32 32
55 55
ÈÈ
which yields f .
Š‹
32 32 4 4096
55 5255
ßß œ
ÈÈ
27. V xyz and g(x y z) x y z 1 0 V yz xz xy and g 2x 2y 2z so thatœ ßßœœÊ œ œ
### ™™ijk ijk
V g yz x, xz y, and xy z xyz x and xyz y y x z x™™œÊœœ œÊœ œÊœ„Êœ„------
##
x x x 1 x since x 0 the dimensions of the box are by by for maximumʜʜ Ê
### "
È ÈÈÈ
3 333
111
volume. (Note that there is no minimum volume since the box could be made arbitrarily thin.)
28. V xyz with x y z all positive and 1; thus V xyz and g(x y z) bcx acy abz abc 0œ ßß œ œ ßßœœ
xz
abc
y
V yz xz xy and g bc ac ab so that V g yz bc, xz ac, and xy abÊ œ œ œ Êœ œ œ™™ ™™ijk ijk ----
xyz bcx, xyz acy, and xyz abz 0. Also, bcx acy abz bx ay, cy bz, andÊœ œ œ ÊÁ œ œ Êœ œ-- -- ---
cx az y x and z x. Then 1 x x 1 1 xœ Êœ œ œÊ œÊ œÊœ
bcxcxbc 3x a
aaabzabaca a 3
y""
ˆ‰ ˆ‰
y and z V xyz is the maximum volume. (Note thatÊœ œ œ œÊ œ œ œ
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ba b ca c abc abc
a3 3 a3 3 333 27
there is no minimum volume since the box could be made arbitrarily thin.)
29. T 16x 4z (4y 16) and g 8x 2y 8z so that T g 16x 4z (4y 16)™™™™œ œ œ Ê ij k ijk ij k-
(8x 2y 8z ) 16x 8x , 4z 2y , and 4y 16 8z 2 or x 0.œÊœ œ œÊœ œ-----ijk
CASE 1: 2 4z 2y(2) z y. Then 4z 16 16z z y . Then-œÊ œ Êœ œ ʜʜ
44
33
4x 4 16 x .
###
œ Ê œ„
ˆ‰ ˆ‰
44 4
33 3
CASE 2: x 0 4y 16 8z y 4y 4z 4(0) y y 4y 16 0œÊœ Ê œ Ê œ Ê œ-2z 2z
yy
Š‹ ab
#####
y 2y 8 0 (y 4)(y 2) 0 y 4 or y 2. Now y 4 4z 4 4(4)ÊœÊ œÊœ œ œÊ œ
###
z 0 and y 2 4z ( 2) 4( 2) z 3.Êœ œÊ œ Êœ„
## È
The temperatures are T 642 , T(0 4 0) 600°, T 0 2 3 600 24 3 , and
ˆ‰ Š‹Š ‹
ÈÈ
„ßß œ ßß œ ßß œ
444 2
333 3
°°
T 0 2 3 600 24 3 641.6°. Therefore are the hottest points on the space probe.
Š‹Š‹
ÈÈ ˆ‰
ß ß œ ¸ „ ß ß
°444
333
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

854 Chapter 14 Partial Derivatives
30. T 400yz 400xz 800xyz and g 2x 2y 2z so that T g™™™™œ œ œ
##
ijk ijk -
400yz 400xz 800xyz (2x 2y 2z ) 400yz 2x , 400xz 2y , and 800xyz 2z .Ê œÊœ œ œ
## # #
ijkijk----
Solving this system yields the points 1 0 , 1 0 0 , and . The correspondingabab
Š‹
!ß„ß „ßß „ß„ß„
""
## #
È2
temperatures are T 1 0 0, T 1 0 0 0, and T 50. Therefore 50 is theabab Š‹
!ß „ ß œ „ ß ß œ „ ß „ ß „ œ „
""
## #
È2
maximum temperature at and ; 50 is the minimum temperature at
Š‹Š ‹
"" " "
## # # # #
ßß„ ßß„
ÈÈ
22
and .
Š‹Š‹
"" ""
## # ## #
ßß„ ßß„
ÈÈ
22
31. U (y 2) x and g 2 so that U g (y 2) x (2 ) y 2 and™™™™œ œ œ Ê œ Ê#œij ij ij ij---
x y 2 2x y 2x 2 2x (2x 2) 30 x 8 and y 14. Therefore U(8 14) $128œÊœÊœÊœÊœ œ ßœ-
is the maximum value of U under the constraint.
32. M (6 z) 2y x and g 2x 2y 2z so that M g (6 z) 2y x™™™™œ œ œ Êijk ijk ijk-
(2x 2y 2z ) 6 z 2x , 2y 2y , x 2z 1 or y 0.œÊœœ œÊœœ-----ijk
CASE 1: 1 6 z 2x and x 2z 6 z 2( 2z) z 2 and x 4. Then-œ Ê œ œ Ê œ Ê œ œ
(4)y2360 y 4. œÊœ„
###
CASE 2: y 0, 6 z 2x , and x 2z 6 z 2x 6z z xœœ œ ʜʜ Êœ---
xx
2z 2z
ˆ‰ ##
6z z 0 z 36 z 6 or z 3. Now z 6 x 0 x 0; z 3Ê œ Êœ œ œÊ œÊœ œab
### #
x 27 x 3 3.ʜʜ„
#È
Therefore we have the points 3 3 0 3 , (0 0 6), and 4 4 2 . Then M 3 3 0 3 27 3 60
Š‹ Š‹
ÈÈÈ
ab„ßß ßß ß„ß ßßœ
106.8, M 3 3 0 3 60 27 3 13.2, M(0 0 6) 60, and M( 4 4 2) 12 M( 4 4 2). Therefore,¸ ßß œ ¸ ßß œ ßß œ œ ßß
Š‹
ÈÈ
the weakest field is at 4 4 2 .abß„ ß
33. Let g (x y z) 2x y 0 and g (x y z) y z 0 g 2 , g , and f 2x 2 2z
"# "#
ßß œ œ ßß œ œ Ê œ œ œ ™™ ™ij jk i j k
so that f g g 2x 2 2z (2 ) ( ) 2x 2 2z 2 ( )™™ ™œ ʜʜ-. - . -.-.
"#
ij k ij jk ij k i jk
2x 2 , 2 , and 2z x . Then 2 2z x x 2z 2 so that 2x y 0Ê œ œ œ Ê œ œ Ê œ œ-.- . -
2( 2z 2) y 0 4z 4 y 0. This equation coupled with y z 0 implies z and y . Thenʜʜ œ œ œ
44
33
x so that is the point that gives the maximum value f 2 .œßß ßßœœ
2244 2442444
3333 3333333
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
##
34. Let g (x y z) x 2y 3z 6 0 and g (x y z) x 3y 9z 9 0 g 2 3 ,
"# "
ßß œ œ ßß œ œ Ê œ ™ijk
g 3 9 , and f 2x 2y 2z so that f g g 2x 2y 2z™™ ™™™
#"#
œ œ œ Ê ijk i j k i j k-.
( 2 3 ) ( 3 9 ) 2x , 2y 2 3 , and 2z 3 9 . Then 0 x 2y 3z 6œ Ê œ œ œ œ- . -. -. -.ijk ijk
( ) (2 3 ) 6 7 17 6; 0 x 3y 9z 9œ Êœœ
"
###
-. - . - . - .
ˆ‰
927
( ) 3 9 34 91 18. Solving these two equations for and givesÊ Êœ
"
####
-. - . - . - . - .
ˆ‰ˆ ‰
92781
and x , y , and z . The minimum value is-.œ œÊœœœœ œœ
240 78 81 123 9
59 59 59 59 59
23 39-. -. -.
## #
f . (Note that there is no value of f subject to the constraints because
ˆ‰
81 123 9 369
59 59 59 59 59
21,771
ßß œ œ maximum
at least one of the variables x, y, or z can be made arbitrary and assume a value as large as we please.)
35. Let f(x y z) x y z be the square of the distance from the origin. We want to minimize f(x y z) subject to theßß œ ßß
###
constraints g (x y z) y 2z 12 0 and g (x y z) x y 6 0. Thus f 2x 2y 2z , g 2 ,
"# "
ßß œ œ ßß œœ œ œ™™ijk jk
and g so that f g g 2x , 2y , and 2z 2 . Then 0 y 2z 12™™™™
#"#
œ œ Ê œ œ œ œ ij -. .-. -
2 12 12 5 24; 0 x y 6 6 6œ Ê œ Ê œ œœ Ê œ
ˆ‰ ˆ‰
- -
...
## # # # ## #
" "
--.-. -.
5
12. Solving these two equations for and gives 4 and 4 x 2, y 4, andÊ#œ œ œ Ê œ œ œ œ-. - . - . .-.
##
z 4. The point (2 4 4) on the line of intersection is closest to the origin. (There is no maximum distance from theœœ ßß-
origin since points on the line can be arbitrarily far away.)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.8 Lagrange Multipliers 855
36. The maximum value is f from Exercise 33 above.
ˆ‰
24 4 4
33 3 3
ßß œ
37. Let g (x y z) z 1 0 and g (x y z) x y z 10 0 g , g 2x 2y 2z , and
"# "#
###
ßßœœ ßßœœÊ œ œ™™kijk
f 2xyz x z x y so that f g g 2xyz x z x y ( ) (2x 2y 2z )™™™™œ œ Ê œijk ijkk ijk
## ##
"#
-. -.
2xyz 2x , x z 2y , and x y 2z xyz x x 0 or yz y since z 1.Êœ œ œÊœÊœ œÊœ œ.. .- . ..
##
CASE 1: x 0 and z 1 y 9 0 (from g ) y 3 yielding the points 0 3 1 .œœÊœ Êœ„ ß„ß
##ab
CASE 2: y x z 2y x 2y (since z 1) 2y y 1 10 0 (from g ) 3y 9 0.œÊ œ Ê œ œ Ê œ Ê œ
#### ## #
#
y 3 x 2 3 x 6 yielding the points 6 3 .Êœ„ Ê œ „ Êœ„ „ ß„ ß"
ÈÈÈ ÈÈ
Š‹ Š ‹
##
Now f 3 1 1 and f 6 3 6 3 1 1 6 3. Therefore the maximum of f isab Š‹Š‹
ÈÈ È È
!ß„ß œ „ ß„ ß"œ „ œ„
1 6 3 at 6 3 1 , and the minimum of f is 1 6 3 at 6 3 .„ßß „ßß"
ÈÈÈ ÈÈÈ
Š‹ Š ‹
38. (a) Let g (x y z) x y z 40 0 and g (x y z) x y z 0 g , g , and
"#"#
ßß œ œ ßß œ œ Ê œ œ™™ijk ijk
w yz xz xy so that w g g yz xz xy ( ) ( )™™™™œ œ Ê œijk ijk ijk ijk-. - .
"#
yz , xz , and xy yz xz z 0 or y x.Êœ œ œÊœÊœ œ-. -. -.
CASE 1: z 0 x y 40 and x y 0 no solution.œ Ê œ œ Ê
CASE 2: x y 2x z 40 0 and 2x z 0 z 20 x 10 and y 10 w (10)(10)(20)œÊ œ œÊœ Êœ œ Ê œ
2000œ
(b) 2 2 is parallel to the line of intersection the line is x 2t 10,
nij
ij k
œ œ Ê œ
"" "
"""
ââ
ââ
ââ
ââ
ââ
ââ
y 2t 10, z 20. Since z 20, we see that w xyz ( 2t 10)(2t 10)(20) 4t 100 (20)œ œ œ œ œ œ ab
#
which has its maximum when t 0 x 10, y 10, and z 20.œÊœ œ œ
39. Let g ( y z) y x 0 and g (x y z) x y z 4 0. Then f y x 2z , g , and
"# "
###
Bßß œœ ßß œ œ œ œ™™ij k ij
g 2x2y2z so that f g g yx2z ( ) (2x2y2z)™™™
#"#
œ ™œ Ê œ ijk ijk ij ijk-. - .
y 2x , x 2y , and 2z 2z z 0 or 1.Êœ œ œ Êœ œ-.-. . .
CASE 1: z 0 x y 4 0 2x 4 0 (since x y) x 2 and y 2 yielding the pointsœÊ œÊ œ œ Êœ„ œ„
## # ÈÈ
22.
Š‹
ÈÈ
„ß„ß!
CASE 2: 1 y 2x and x 2y x y 2(x y) 2x 2(2x) since x y x 0 y 0.--œ Ê œ œ Ê œ Ê œ œÊœÊœ
z 4 0 z 2 yielding the points 2 .Ê œ Ê œ „ !ß !ß „
#ab
Now, f 2 4 and f 2 2 2. Therefore the maximum value of f is 4 at 2 and theab ab
Š‹
ÈÈ
!ß !ß „ œ „ ß „ ß ! œ !ß !ß „
minimum value of f is 2 at 2 2 .
Š‹
ÈÈ
„ß„ß!
40. Let f(x y z) x y z be the square of the distance from the origin. We want to minimize f(x y z) subjectßß œ ßß
###
to the constraints g (x y z) 2y 4z 5 0 and g (x y z) 4x 4y z 0. Thus f 2x 2y 2z ,
"#
###
ßß œ œ ßß œ œ œ ™ijk
g 2 4 , and g 8x 8y 2z so that f g g 2x 2y 2z™™ ™™™
"# "#
œ œ œ Ê jk i j k i j k-.
(2 4 ) (8x 8y 2z ) 2x 8x , 2y 2 8y , and 2z 4 2z x 0 or .œ Êœ œ œÊœ œ-. .-.-. .jk i j k "
4
CASE 1: x 0 4(0) 4y z 0 z 2y 2y 4(2y) 5 0 y , or 2y 4( 2y) 5 0œÊ œÊœ„ Ê œÊœ œ
### "
#
y yielding the points and .Êœ !ßß" !ßß
555
663
ˆ‰ˆ ‰
"
#
CASE 2: y y 0 2z 4(0) 2z z 0 2y 4(0) 5 y and.--œÊœÊœÊ œ ÊœÊ œÊœ
""
#44
5
ˆ‰
(0) 4x 4 no solution.
##
#
#
œ Ê
ˆ‰
5
Then f 1 and f 25 the point 1 is closest to the origin.
ˆ‰ ˆ ‰ˆ‰ ˆ‰
!ß ß œ !ß ß œ œ Ê !ß ß
""""
# #
5 5 5 125
46336936
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
856 Chapter 14 Partial Derivatives
41. f and g y x so that f g (y x ) 1 y and 1 x y x™™ ™™œ œ œ Ê œ Ê œ œ Ê œij i j ij i j-- --
y 16 y 4 (4 4) and ( 4) are candidates for the location of extreme values. But as x ,Ê œ Ê œ „ Ê ß %ß Ä _
#
y and f(x y) ; as x , y 0 and f(x y) . Therefore no maximum or minimum valueÄ_ ß Ä_ Ä_ Ä ß Ä_
exists subject to the constraint.
42. Let f(A B C) (Ax By C z ) C (B C 1) (A B C 1) (A C 1) . We wantßß œ œ
!
4
k1œ
kk k
## # # #
to minimize f. Then f (A B C) 4A 2B 4C, f (A B C) 2A 4B 4C 4, and
AB
ßßœ ßßœ
f (A B C) 4A 4B 8C 2. Set each partial derivative equal to 0 and solve the system to get A ,
Cßßœ œ
"
#
B , and C or the critical point of f is .œ œ ßß
33
44###
"""
ˆ‰
43. (a) Maximize f(a b c) a b c subject to a b c r . Thus f 2ab c 2a bc 2a b c andßßœ œ œ
### # # # # ## # # ##
™ijk
g 2a 2b 2c so that f g 2ab c 2a , 2a bc 2b , and 2a b c 2c™™™œ œ Ê œ œ œijk ----
## # # ##
2a b c 2a 2b 2c 0 or a b c .ÊœœœÊœœœ
### # # # # # #
----
CASE 1: 0 a b c 0.-œÊ œ
###
CASE 2: a b c f(abc) aaa and 3a r f(abc) is the maximum value.
# # # ### # # $
œœ Ê ßßœ œÊ ßßœ
Š‹
r
3
(b) The point a b c is on the sphere if a b c r . Moreover, by part (a), abc f a b c
Š‹ Š‹
ÈÈ ÈÈ
È È
ß ß œ œ ß ß
#
(abc) , as claimed.ŸÊ Ÿœ
Š‹
rrabc
333
$"Î$
44. Let f(x x x ) a x a x a x a x and g(x x x ) x x x 1. Then we
" # "" ## " # ## #
ßßáß œ œ á ßßáß œ á
nii nn n n
!
n
i1œ
want f g a (2x ), a (2x ), , a (2x ), 0 x 1™™œÊœ œáœ ÁÊœÊáœ--- --
""##nn i
a
244 4
aa a
i
--- -
n
4 a 2 a f(x x x ) a x a a a isÊœ Êœ Êßßáßœ œ œ œ--
## # ##
"Î# "Î#
"# ##
"
!! !!!!
Œ Œ
ˆ‰
n
i1
ii ii
niii
nnnnn
i1 i1 i1 i1 i1œœœœœ
ai
--
the maximum value.
45-50. Example CAS commands:
:Maple
f := (x,y,z) -> x*y+y*z;
g1 := (x,y,z) -> x^2+y^2-2;
g2 := (x,y,z) -> x^2+z^2-2;
h := unapply( f(x,y,z)-lambda[1]*g1(x,y,z)-lambda[2]*g2(x,y,z), (x,y,z,lambda[1],lambda[2]) ); # (a)
hx := diff( h(x,y,z,lambda[1],lambda[2]), x ); #(b)
hy := diff( h(x,y,z,lambda[1],lambda[2]), y );
hz := diff( h(x,y,z,lambda[1],lambda[2]), z );
hl1 := diff( h(x,y,z,lambda[1],lambda[2]), lambda[1] );
hl2 := diff( h(x,y,z,lambda[1],lambda[2]), lambda[2] );
sys := { hx=0, hy=0, hz=0, hl1=0, hl2=0 };
q1 := solve( sys, {x,y,z,lambda[1],lambda[2]} ); # (c)
q2 := map(allvalues,{q1});
for p in q2 do # (d)
eval( [x,y,z,f(x,y,z)], p );
``=evalf(eval( [x,y,z,f(x,y,z)], p ));
end do;
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.9 Taylor's Formula for Two Variables 857
Mathematica: (assigned functions will vary)
Clear[x, y, z, lambda1, lambda2]
f[x_,y_,z_]:= x y y z
g1[x_,y_,z_]:= x y 2
22
g2[x_,y_,z_]:= x z 2
22
h = f[x, y, z] lambda1 g1[x, y, z] lambda2 g2[x, y, z];
hx= D[h, x]; hy= D[h, y]; hz= D[h,z]; hL1=D[h, lambda1]; hL2= D[h, lambda2];
critical=Solve[{hx==0, hy==0, hz==0, hL1==0, hL2==0, g1[x,y,z]==0, g2[x,y,z]==0},
{x, y, z, lambda1, lambda2}]//N
{{x, y, z}, f[x, y, z]}/.critical
14.9 TAYLOR'S FORMULA FOR TWO VARIABLES
1. f(x y) xe f e , f xe , f 0, f e , f xeßœ Ê œ œ œ œ œ
yyy yy
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 1 y 0 x 0 2xy 1 y 0 x xy quadratic approximation;œ œ†† † † †
"
#
##
ab
f 0, f 0, f e , f xe
xxx xxy xyy yyy
yy
œœœ œ
f(x y) quadratic x f ( ) 3x yf (0 0) 3xy f ( ) y f (0 0)Ê ß ¸ !ß ! ß !ß ! ß
"$# #$
6xxx xxy xyy yyy
cd
x xy x 0 3x y 0 3xy 1 y 0 x xy xy , cubic approximationœ œ
""
$# #$ #
#6ab††††
2. f(x y) e cos y f e cos y, f e sin y, f e cos y, f e sin y, f e cos yßœ Ê œ œ œ œ œ
xxxxxx
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf ( 0) x f ( ) 2xyf ( ) y f (0 0)Ê ß ¸ ß ß !ß !ß ! !ß ! ß
x y xx xy yy
"
#
##
cd
1 x 1 y 0 x 1 2xy 0 y ( 1) 1 x x y , quadratic approximation;œ œ †† † † †
""
##
## ##
cdab
f e cos y, f e sin y, f e cos y, f e sin y
xxx xxy xyy yyy
xxxx
œœœœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1 x x y x 1 3x y 0 3xy ( 1) y 0œ
""
#
## $ # # $
abc d
6††† †
1 x x y x 3xy , cubic approximationœ
""
#
## $ #
aba b
6
3. f(x y) y sin x f y cos x, f sin x, f y sin x, f cos x, f 0ßœ Ê œ œ œ œ œ
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf ( 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê ß¸ ß ß !ß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 0 x 0 2xy 1 y 0 xy, quadratic approximation;œ œ†† † † †
"
#
##
ab
f y cos x, f sin x, f 0, f 0
xxx xxy xyy yyy
œ œ œ œ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
xy x 0 3x y 0 3xy 0 y 0 xy, cubic approximationœ œ
"$# #$
6ab††††
4. f(x y) sin x cos y f cos x cos y, f sin x sin y, f sin x cos y, f cos x sin y,ß œ Ê œ œ œ œ
x y xx xy
f sin x cos y f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
œ Ê߸ßßß ß ß ß
"
#
##
cd
0 x 1 y 0 x 0 2xy 0 y 0 x, quadratic approximation;œ œ†† † † †
"
#
##
ab
f cos x cos y, f sin x sin y, f cos x cos y, f sin x sin y
xxx xxy xyy yyy
œ œ œ œ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
x x ( 1) 3x y 0 3xy ( 1) y 0 x x 3xy , cubic approximationœ œ
""
$##$ $#
66
cdab††††
5. f(x y) e ln (1 y) f e ln (1 y), f , f e ln (1 y), f , fßœ Ê œ œ œ œ œ
xx x
x y xx xy yy
eee
1 y 1 y (1 y)
xxx
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 1 x 0 2xy 1 y ( 1) y 2xy y , quadratic approximation;œ œ †† † † †
""
##
## #
cdab
f e ln (1 y), f , f , f
xxx xxy xyy yyy
xee2e
1 y (1 y) (1 y)
œœ œ œ
xxx
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

858 Chapter 14 Partial Derivatives
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
y 2xy y x 0 3x y 1 3xy ( 1) y 2œ
""
#$ # # $
26
abc d††† †
y 2xy y 3x y 3xy 2y , cubic approximationœ
""
#
###$
aba b
6
6. f(x y) ln (2x y 1) f , f , f , f ,ßœ Ê œ œ œ œ
xyxx xy
242
2x y 1 x y 1 (2x y 1) (2x y 1) #
"
f f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
(2x y 1)
œ Ê ß¸ ß ß ß ß ß ß
" "
#
##
cd
0 x 2 y 1 x ( 4) 2xy ( 2) y ( 1) 2x y 4x 4xy yœ œ †† † † †
""
##
## ##
cdab
(2x y) (2x y) , quadratic approximation;œ
"
#
#
f, f, f, f
xxx xxy xyy yyy
16842
(2x y 1) (2x y 1) (2x y 1) (2x y 1)
œœœœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
(2x y) (2x y) x 16 3x y 8 3xy 4 y 2œ
""
#
#$ # # $
6ab††††
(2x y) (2x y) 8x 12x y 6xy yœ
""
#
#$###
3ab
(2x y) (2x y) (2x y) , cubic approximationœ
""
#
#$
3
7. f(x y) sin x y f 2x cos x y , f 2y cos x y , f 2 cos x y 4x sin x y ,ߜʜœœ ab ab ab ab ab
## ## ## ## # ##
xyxx
f 4xy sin x y , f 2 cos x y 4y sin x y
xy yy
œ œ ab ab ab
## ## # ##
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 0 x 2 2xy 0 y 2 x y , quadratic approximation;œ œ†† † † †
"
#
####
ab
f 12x sin x y 8x cos x y , f 4y sin x y 8x y cos x y ,
xxx xxy
œ œ ab ab ab ab
## $ ## ## # ##
f 4x sin x y 8xy cos x y , f 12y sin x y 8y cos x y
xyy yyy
œ œ ab ab ab ab
## # ## ## $ ##
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
x y x 0 3x y 0 3xy 0 y 0 x y , cubic approximationœ œ
## $ # # $ ##
"
6ab††††
8. f(x y) cos x y f 2x sin x y , f 2y sin x y ,ßœ Ê œ œ ab ab ab
## ## ##
xy
f 2 sin x y 4x cos x y , f 4xy cos x y , f 2 sin x y 4y cos x y
xx xy yy
œ œ œ ab ab ab ab ab
## # ## ## ## # ##
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1 x 0 y 0 x 0 2xy 0 y 0 1, quadratic approximation;œ œ†† † † †
"
#
##
cd
f 12x cos x y 8x sin x y , f 4y cos x y 8x y sin x y ,
xxx xxy
œ œ ab ab ab ab
## $ ## ## # ##
f 4x cos x y 8xy sin x y , f 12y cos x y 8y sin x y
xyy yyy
œ œ ab ab ab ab
## # ## ## $ ##
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1 x 0 3x y 0 3xy 0 y 0 1, cubic approximationœ œ
"$# #$
6ab††††
9. f(x y) f f , f f fßœ Ê œ œ œ œ œ
""
1 x y (1 x y) (1 x y)
x y xx xy yy
2
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1 x 1 y 1 x 2 2xy 2 y 2 1 (x y) x 2xy yœ œ†† † † †
"
#
## ##
abab
1 (x y) (x y) , quadratic approximation; f f f fœ œ œ œ œ
#
xxx xxy xyy yyy
6
(1 x y)
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1(xy)(xy) x63xy63xy6y6œ
#$ # # $
"
6ab††††
1 (x y) (x y) x 3x y 3xy y 1 (x y) (x y) (x y) , cubic approximationœ œ
#$ # #$ # $
ab
10. f(x y) f , f , f ,ßœ Ê œ œ œ
"
"
1 x y xy (1 x y xy) ( x y xy) (1 x y xy)
xyxx
1 y 2(1 y)
1 x
f, f
xy yy
1
( x y xy) (1 x y xy)
2( x)
œœ
"
"
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1x1y1 x22xy1y2 1xyx xyy, quadratic approximation;œ œ†† † † †
"
#
## ##
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 14.10 Partial Derivatives with Constrained Variables 859
f, f ,
xxx xxy
6(1 y) [ 4(1 x y xy) 6(1 y)(1 x)](1 y)
(1 x y xy) (1 x y xy)
œœ
f, f
xyy yyy
[ 4(1 x y xy) 6(1 x)(1 y)](1 x) 6(1 x)
(1 x y xy) (1 x y xy)
œœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1xyx xyy x63xy23xy2y6œ
##$# #$
"
6ab††††
1xyx xyy x xyxy y, cubic approximationœ
# #$# #$
11. f(x y) cos x cos y f sin x cos y, f cos x sin y, f cos x cos y, f sin x sin y,ßœ Ê œ œ œ œ
xyxx xy
f cos x cos y f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
œ Ê߸ßßß ß ß ß
"
#
##
cd
1 x 0 y 0 x ( 1) 2xy 0 y ( 1) 1 , quadratic approximation. Since all partialœ œ†† † † †
"
###
##
cd
xy
derivatives of f are products of sines and cosines, the absolute value of these derivatives is less than or equal
to 1 E(x y) (0.1) 3(0.1) 3(0.1) 0.1) 0.00134.Êߟ Ÿ
"$$$$
6cd
12. f(x y) e sin y f e sin y, f e cos y, f e sin y, f e cos y, f e sin yߜʜœœœœ
xxxxxx
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 1 x 0 2xy 1 y 0 y xy , quadratic approximation. Now, f e sin y,œ œ œ†† † † †
"
#
##
ab xxx x
f e cos y, f e sin y, and f e cos y. Since x 0.1, e sin y e sin 0.1 0.11 and
xxy xyy yyy
xx x x01
œœ œ Ÿ Ÿ¸kk k k k k
Þ
e cos y e cos 0.1 1.11. Therefore,kkk k
x01
Ÿ¸
Þ
E(x y) (0.11)(0.1) 3(1.11)(0.1) 3(0.11)(0.1) (1.11)(0.1) 0.000814.ߟ Ÿ
"$$$$
6cd
14.10 PARTIAL DERIVATIVES WITH CONSTRAINED VARIABLES
1. w x y z and z x y :œ œ
### ##
(a) w ; 0 and 2x 2y
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœœœ
ϧ
œ
œ
```` ``` ` `
```````` ` ``
``
wwxw wzz z x
yxyyyzyy y yy
yy
z
2x 2y 0 2x 2y (2x) (2y)(1) (2z)(0) 2y 2y 0œÊœÊœÊ œœœ
````
````
xxxw
yyyxyx
yy
Š‹ ˆ‰
z
(b) w ; 0 and 2x 2y
x
z
xx
yy(xz)
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœœ
œ
ϧ
œ
```` ``` ` `
```````` ` ` `
``
wwxw wzx z x
zxzyzzzz z z z
yy
x
1 2y (2x)(0) (2y) (2z)(1) 1 2zÊœ Ê œ Ê œ œ
``
``# `
"` "
yy
zzy z 2y
w
ˆ‰ Š‹
x
(c) w ; 0 and 2x 2y
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœœ
ϧ
œ
œ
```` `` ` `
```````` ` ` `
`` `
wwxw wz z x
zxzyzzzz z z z
yy y
y
1 2x (2x) (2y)(0) (2z)(1) 1 2zʜʜʜ œ
`` ` "
`` ` #
xx1 w
zz2x z x
ˆ‰ ˆ‰
y
2. w x y z sin t and x y t:œ œ
#
(a) w ; 0, 0, and
x
y
z
xx
yy
zz
txy
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ Š‹
Ä ÄÊ œ œœ
œ
œ
œ
œ
``````````
```````````
`
wwxwwzwtxz
yxyyyzytyyy
y
xz
1 (2x)(0) (1)(1) ( 1)(0) (cos t)(1) 1 cos t 1 cos (x y)
``
``
tw
yy
œÊ œ œ œ
Š‹
xt
(b) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ Š‹
Ä ÄÊ œ œ œ
œ
œ
œ
œ
````````` `
`````````` `
`
wwxwwzwtz t
yxyyyzytyy y
y
zt
1 (2x)( 1) (1)(1) ( 1)(0) (cos t)(0) 1 2 t y 1 2y 2tÊ œœÊ œ œœ
`` `
``` `
`
xt w
yyy y
yŠ‹ ab
zt
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

860 Chapter 14 Partial Derivatives
(c) w ; 0 and 0
x
y
z
xx
yy
zz
txy
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
`````````
`````````` `
``
wwxwwzwtx
zxzyzzztzz z
yy
xy
(2x)(0) (1)(0) ( 1)(1) (cos t)(0) 1Êœ œ
ˆ‰
`
`
w
zxy
(d) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
```````` `
`````````` `
``
wwxwwzwt t
zxzyzzztzz z
yy
yt
(2x)(0) (1)(0) ( 1)(1) (cos t)(0) 1Êœ œ
ˆ‰
`
`
w
zyt
(e) w ; 0 and 0
x
z
t
xx
ytx
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
` `` ` `` ``` `
`````````` `
`
w wx w wz wt x z
txtytztttt t
y
xz
(2x)(0) (1)(1) ( 1)(0) (cos t)(1) 1 cos tÊœ œ
ˆ‰
`
`
w
txz
(f) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
` `` ` `` `` `
`````````` `
``
w wx w wz wt z
txtytztttt t
yy
yz
(2x)(1) (1)(0) ( 1)(0) (cos t)(1) cos t 2x cos t 2(t y)Ê œ œœ
ˆ‰
`
`
w
tyz
3. U f(P V T) and PV nRTœßß œ
(a) U (0)
P
V
PP
VV
T
Œ ÎÑ
ÏÒ ˆ‰ ˆ‰ ˆ‰ˆ‰
ÄÄÊœœ
œ
œ
œPV
nR
UUPUVUTUU UV
PPPVPTPPV TnR
````````` `
````````` `
V
œ
``
``
UUV
PTnR
ˆ‰ˆ‰
(b) U (0)
V
T
P
VV
TT
Œ ÎÑ
ÏÒ ˆ‰ ˆ‰ˆ‰ˆ‰
ÄÄÊœœ
œ
œ
œ
nRT
VUUPUVUTUnRU U
TPTVTTTPVV T
```````` ` `
```````` ` `
V
œ
ˆ‰ˆ‰
``
``
UnR U
PV T
4. w x y z and y sin z z sin x 0œ œ
###
(a) w ; 0 and
x
y
xx
yy
zz(xy)
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœ
œ
œ
ϧ
```` ``
````````
``
wwxw wz
xxxyxzxx
yy
y
(y cos z) (sin x) z cos x 0 . At (0 1 ),
`` ` `
`` ` `
zz zz cos x z
xx xy cos zsin x x1
œÊœ ßßœœ11
1
(2x)(1) (2y)(0) (2z)( ) 2Êœ œ
ˆ‰ k
`
`
#
w
xk
y(0 1 ) 01
11
(b) w (2x) (2y)(0) (2z)(1)
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœ
ϧ
œ
œ
```` `` `
``````` `
`
wwxw wz x
zxzyzzz z
y
y
(2x) 2z. Now (sin z) y cos z sin x (z cos x) 0 and 0œ œ œ
``
`` ``
``
xx
zz zz
yy
y cos z sin x (z cos x) 0 . At ( ), Ê œ Ê œ !ß "ß œ œ
`` `"
`` `
xx x10
z z z cos x z ( )(1)
y cos z sin x 111
2(0) 2 2Êœœ
ˆ‰ ˆ‰
`"
`C!"ß Ñ
w
z(,
k1111
5. w x y yz z and x y z 6œ œ
## $ # # #
(a) w
x
y
xx
yy
zz(xy)
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœ
œ
œ
ϧ
```` ``
```````
`
wwxw wz
yxyyyzy
y
x
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 14.10 Partial Derivatives with Constrained Variables 861
2xy (0) 2x y z (1) y 3z 2x y z y 3z . Now (2x) 2y (2z) 0 andœœ œaba bab ab
## ## #
````
````
zzxz
yyyy
0 2y (2z) 0 . At (w x y z) (4 2 1 1), 1
``` `"`
``` ``
xzz zw
yyyz y1y
y
œ Ê œ Ê œ ßßß œ ßßß œ œ Ê ¹Š‹
x(421 1)
(2)(2) (1) ( 1) 1 3( 1) (1) 5œœcdcd
##
(b) w
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœ
ϧ
œ
œ
```` ``
```````
`
wwxw wz
yxyyyzy
y
z
2xy 2x y z (1) y 3z (0) 2x y 2x y z. Now (2x) 2y (2z) 0 andœœ œab a b a b ab
## ###
````
````
xxxz
yyyy
0 (2x) 2y 0 . At (w x y z) (4 2 1 1),
`` ` `"`
`` ` ``
zx x xw
y y yx y2 y
y
(
œ Ê œ Ê œ ßßß œ ßßß œ Ê ¹Š‹
z421 1)
(2)(2)(1) (2)(2) (1) ( 1) 5œœ
##
"
#
ˆ‰
6. y uv 1 v u ; x u v and 0 0 2u 2v 1œÊœ œ œÊœ Êœ Ê
`` ` ` ` ` `
`` ` ` ` ` `
##
uv x u v v uu
yy y y y y vy
ˆ‰
v u . At (u v) 2 1 , 1œ œ Êœ ßœ ß œ œ
```` `"
`` `` `
uuuvuuuv u
yvyvyyvu y
12
Š‹Š‹ Š‹
ÈŠ‹
È
1ʜ
Š‹
`
`
u
yx
7. cos ; x y r 2x 2y 2r and 0 2x 2r
rxr cos
y r sin
Œ Œ ˆ‰
))
))ÄÊœœÊœœÊœ
œ
œ
```
`````
### ``
xrr
rxxxx
yy
)
ÊœÊ œ
``
``
rx r x
xr x xy
ˆ‰
yÈ
8. If x, y, and z are independent, then
ˆ‰
````````
`````````
`
wwxwwzwt
xxxyxzxtx
y
yz œ
(2x)(1) ( 2y)(0) (4)(0) (1) 2x . Thus x 2z t 25 1 0 0 1œ œ œÊœÊœ
ˆ‰
`` ``
`` ``
tt tt
xx xx
2x 1. On the other hand, if x, y, and t are independent, then ʜ
ˆ‰ ˆ‰
` `
` `
w w
x x
yz yt
(2x)(1) ( 2y)(0) 4 (1)(0) 2x 4 . Thus, x 2z t 25œœ œ œ
`` ` `` `` ` `
`` `` `` `` ` `
`
wx w wz wt z z
xx yx zx t x x x
y
12 00 2x4 2x2.Ê œÊ œÊ œ œ
``"` "
``#` #
zzw
xxx
ˆ‰ ˆ‰
yt
9. If x is a differentiable function of y and z, then f(x y z) 0 0 0ßßœÊ œÊ œ
`` ` `` ` `
`` `` `` ` ``
``
fx f fz f f
xx yx zx x yx
yy
. Similarly, if y is a differentiable function of x and z, and if z is aÊœ œ
Š‹ Š‹
```
``` ```
`` `
xf/ z
yf/z zf/x
f/ y y
z x
differentiable function of x and y, . Then
ˆ‰ ˆ‰
Š‹Š‹
``` ` `
``` ```
`
zf/x x z
xf/y yzx
y
yy
zx
œ
1.œœ
Š‹ Š‹
ˆ‰
``
`` `` ``
`` ``
f/ y
f/ z f/ x f/ y
f/ z f/ x
10. z z f(u) and u xy 1 1 y ; also 0 x so that x y œ œ Ê œ œ œ œ
`` `` ``
`` `` ``
zdfu dfzdfudf zz
xdux duyduydu xy
x1 y yx xœ œ
ˆ‰ˆ‰
df df
du du
11. If x and y are independent, then g(x y z) 0 0 and 0 0ßß œ Ê œ œ Ê œ
` ``` ``
`` `` `` ` ` ``
``` `
g gyg gg
xy yy zy y y zy
xzx z
, as claimed.ʜ
Š‹
`
```
``
z
yg/z
g/ y
x
12. Let x and y be independent. Then f(x y z w) 0, g(x y z w) 0 and 0ßßß œ ßßß œ œ
`
`
y
x
0 andÊœœ
`` ` `` `` ` `` ``
`` `` `` ` ` ` `` ` `
`
fx f fz f w f fz fw
xx yx zx wx x zx wx
y
0 imply
````` ```
`` `` `` ` ` ` `` ` `
`````
ggygg ggg
xx yx zx wx x zx w x
xzwzw
œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
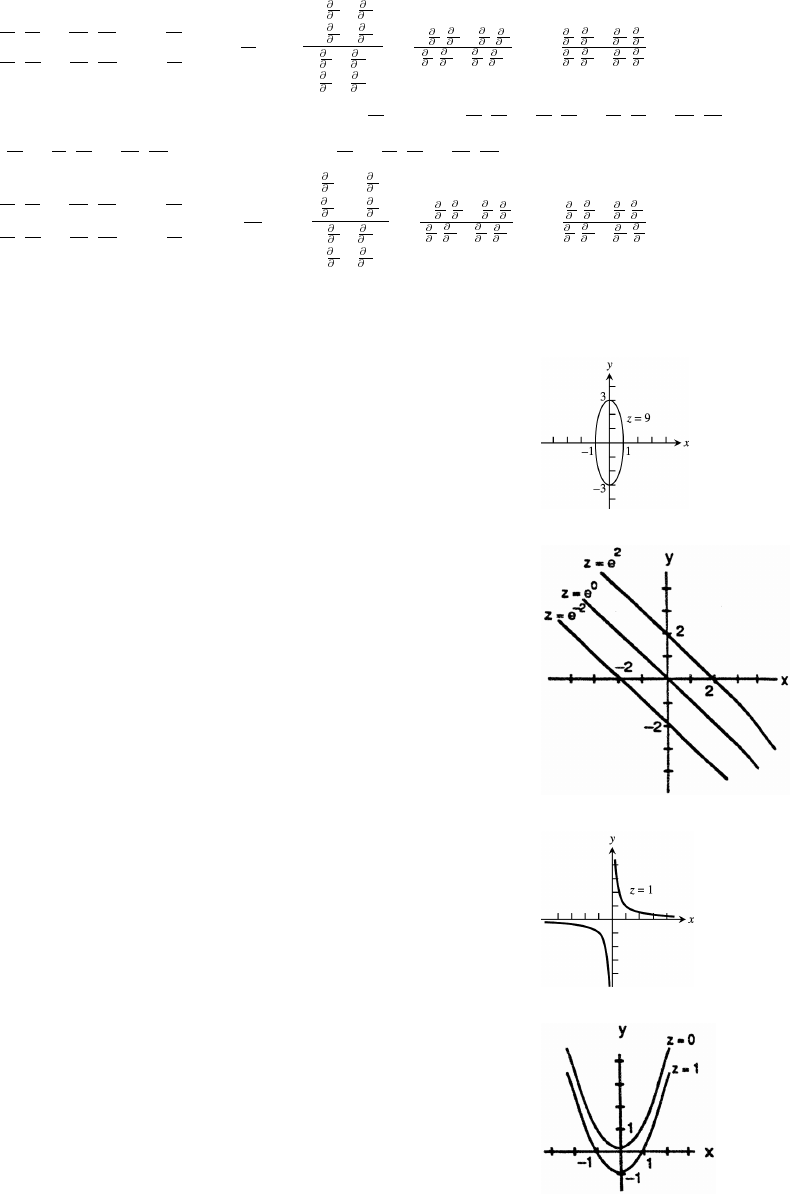
862 Chapter 14 Partial Derivatives
ˆ‰
`` `` `
`` ` ` `
`` `
`` ` ` `
``
`
`
fz fw f
zx wx x
gg g
zx wx x
zw
z
x
œ
œ
Êœ œ
y
»»
»»
c
c
ff
xw
gg
xw
ff
zw
gg
zw
ff
xw xw
gg
f
z
gg g g
wzw zwwz
fff
ff
xw wx
gg
œ , as claimed.
Likewise, f(x y z w) 0, g(x y z w) 0 and 0 ßßß œ ßßß œ œ Ê
````````
` ````````
`
xfxffzfw
y xyyyzywy
y
0 and (similarly) 0 implyœ œ œ
``` `` ` `
````` `````
`` `
ffzfw z w
yzywy yzywy
gg g
Š‹
`` `` `
`` ` ` `
`` `
`` ` ` `
``
`
`
fz fw f
zy wy y
gg g
zy wy y
zw
w
y
œ
œ
Êœ œ
x
»»
»»
ff
zy
gg
zy
ff
zw
gg
zw
c
cff
zy zy
gg
f
z
gg g g
wzw zwwz
fff
ff
zy yz
gg
œ , as claimed.
CHAPTER 14 PRACTICE EXERCISES
1. Domain: All points in the xy-plane
Range: z 0
Level curves are ellipses with major axis along the y-axis
and minor axis along the x-axis.
2. Domain: All points in the xy-plane
Range: 0 z_
Level curves are the straight lines x y ln z withœ
slope 1, and z 0.
3. Domain: All (x y) such that x 0 and y 0ßÁÁ
Range: z 0Á
Level curves are hyperbolas with the x- and y-axes
as asymptotes.
4. Domain: All (x y) so that x y 0ß
#
Range: z 0
Level curves are the parabolas y x c, c 0.œ
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
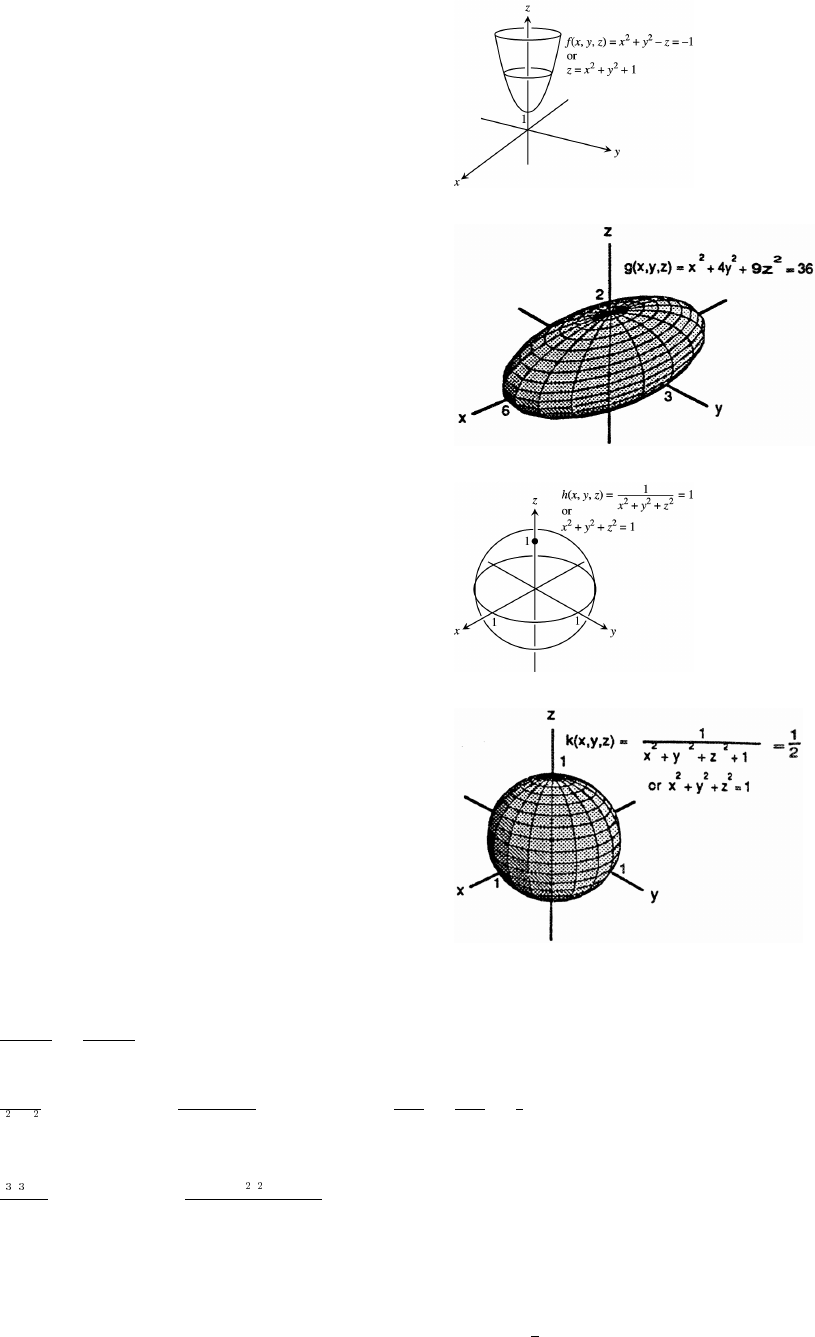
Chapter 14 Practice Exercises 863
5. Domain: All points (x y z) in spaceßß
Range: All real numbers
Level surfaces are paraboloids of revolution with
the z-axis as axis.
6. Domain: All points (x y z) in spaceßß
Range: Nonnegative real numbers
Level surfaces are ellipsoids with center (0 0 0).ßß
7. Domain: All (x y z) such that (x y z) (0 0)ßß ßß Á ß!ß
Range: Positive real numbers
Level surfaces are spheres with center (0 0 0) andßß
radius r 0.
8. Domain: All points (x y z) in spaceßß
Range: (0 1]ß
Level surfaces are spheres with center (0 0 0) andßß
radius r 0.
9. lim e cos x e cos (2)( 1) 2
Ðß ÑÄÐß Ñxy ln21
yln2
œœœ1
10. lim 2
Ðß ÑÄÐß Ñxy 00
2y
xcos y 0cos 0
20
œœ
11. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á„ Á„
xy 11 xy 11 xy 11
xy xy
xy xy
x y (x y)(x y) x y 1 1
1
#
""
œœœœ
12. lim lim lim x y xy 1 1 1 1 1 1 3
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 11 xy 11 xy 11
xy 1
xy 1 xy 1
(xy1)xy xy1
## # #
œœœœ
ab ab††
13. lim ln x y z ln 1 ( 1) e ln e 1
P11eÄÐ ß ß Ñ kkk k œ œ œ
14. lim tan (x y z) tan (1 ( 1) ( 1)) tan ( 1)
P 111Ä Ð ß ß Ñ
" " "
œ œ œ
1
4
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

864 Chapter 14 Partial Derivatives
15. Let y kx , k 1. Then lim lim which gives different limits forœÁ œ œ
#
Ðß ÑÄÐß Ñ
Á
ßÄÐßÑ
xy 00
yx
xkx 00
y
xy xkx 1k
kx k
ab
different values of k the limit does not exist.Ê
16. Let y kx, k 0. Then lim lim which gives different limits forœÁ œ œ
Ðß ÑÄÐß Ñ ß ÑÄÐß Ñ
Á
xy 00 (xkx 00
xy 0
xy x(kx)
xy x(kx) k
1k
different values of k the limit does not exist.Ê
17. Let y kx. Then lim which gives different limits for different valuesœœœ
Ðß ÑÄÐß Ñxy 00
xy
xy xkx 1k
xkx 1k
of k the limit does not exist so f(0 0) cannot be defined in a way that makes f continuous at the origin.Êß
18. Along the x-axis, y 0 and lim lim , so the limit fails to exis
1, x 0
, x 0
œœœ
"
Ðß ÑÄÐß Ñ Ä
xy 00 x0
sin (x y)
xy x
sin x
kkkk kk œt
f is not continuous at (0 0).Êß
19. cos sin , r sin r cos
``
``
gg
rœ œ )) ) )
)
20. ,
`" `"
`# `#
f2x x f x
x xy xy xy xy y xy xy xy xy
11
yxy 2y y xy
œ œœ œ œœ
Š‹ Š‹
Š‹ Š‹
ˆ‰ ˆ‰
y
x
y y
x x
1
x
21. , ,
`"`"`"
```
fff
RRR
RRR
œ œ œ
22. h (x y z) 2 cos (2 x y 3z), h (x y z) cos (2 x y 3z), h (x y z) 3 cos (2 x y 3z)
xyz
ßß œ ßß œ ßß œ 11 1 1
23. , , ,
````
````
P RT P nT P nR P nRT
nVRVTVV V
œœœœ
24. f (r T w) , f (r T w) , f (r T w)
r T
ßjß ß œ ßjß ß œ ßjß ß œ
"""""
j#j#j
j
2r w r w r
TT
w2T
ÉÉ
ˆ‰
Š‹Š‹
11
1
ÈÈ
, f (r T w) wœœ ßjßßœ œ
"" " " " "
jj #j# j
$Î#
4r T w 4r T w r 4r w w
TT T
ÉÉ É É
ˆ‰ ˆ ‰
11 1 1
w
25. , 1 0, ,
`` `` ``
` ` ` ` `` ``
" "
gg gg gg
xyy y x y yyx xy y
x2x
œœÊœœ œœ
26. g (x y) e y cos x, g (x y) sin x g (x y) e y sin x, g (x y) 0, g (x y) g (x y) cos x
x y xx yy xy yx
xx
ßœ ßœ Ê ßœ ßœ ßœ ßœ
27. 1 y 15x , x 30x , 0, 1
``````
````````
#
f2xff22xfff
x x 1 y x y yx xy
x1
œ œ Ê œ œ œ œ
ab
28. f (x y) 3y, f (x y) 2y 3x sin y 7e f (x y) 0, f (x y) 2 cos y 7e , f (x y) f (x y) 3
x y xx yy xy yx
yy
ßœ ßœ Ê ßœ ßœ ßœ ßœ
29. y cos (xy ), x cos (xy ), e ,
`` "
``
wwdx
x y dt dt t 1
dy
œœœœ11
t
[y cos (xy )]e [x cos (xy )] ; t 0 x 1 and y 0Êœ œÊœ œ
dw
dt t 1
11
tˆ‰
"
0 1 [1 ( 1)] 1Êœ œ
¸ˆ‰
dw
dt 0 1
t0œ†† "
30. e , xe sin z, y cos z sin z, t , 1 ,
`` ` "
`` `
"Î#
ww w dx dz
xy z dt dttdt
dy
œœ œ œ œœ
yy 1
e t xe sin z 1 (y cos z sin z) ; t 1 x 2, y 0, and zÊœ œÊœ œ œ
dw
dt t
yy"Î# "
ab
ˆ‰ 11
1 1 (2 1 0)(2) (0 0) 5Êœœ
¸
dw
dt t1œ†† 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 14 Practice Exercises 865
31. 2 cos (2x y), cos (2x y), 1, cos s, s, r
`` ``
`` ````
``
ww xx
xy rsrs
yy
œœœœœœ
[2 cos (2x y)](1) [ cos (2x y)](s); r and s 0 x and y 0Êœ œ œÊœ œ
`
`
w
r11
(2 cos 2 ) (cos 2 )(0) 2; [2 cos (2x y)](cos s) [ cos (2x y)](r)Êœ œœ
¸
``
``
ww
rs
011
(2 cos 2 )(cos 0) (cos 2 )( ) 2Êœ œ
¸
`
`
w
s01111
32. 2e cos v ; u v 0 x 2 (2) ;
`` " ` "
`` `
wdwx x w 2 2
udxu 1xx1 u 55 5
œ œ œœÊœÊ œ œ
ˆ‰ ¸ˆ‰
ab
u
00
2e sin v (0) 0
`` " ` "
`` `
wdwx x w 2
vdxv 1xx1 v 55
œœ Ê œœ
ˆ‰ ¸ˆ‰
ab
u
00
33. y z, x z, y x, sin t, cos t, 2 sin 2t
```
```
fffdx dz
x y z dt dt dt
dy
œ œ œ œ œ œ
(y z)(sin t) (x z)(cos t) 2(y x)(sin 2t); t 1 x cos 1, y sin 1, and z cos 2Êœ œÊœ œ œ
df
dt
(sin 1 cos 2)(sin 1) (cos 1 cos 2)(cos 1) 2(sin 1 cos 1)(sin 2)ʜ
¸
df
dt t1œ
34. (5) and (1) 5 5 5 0
`` `` ``
`` `` ``
w dw s dw w dw s dw dw w w dw dw
x ds x ds y ds y ds ds x y ds ds
œœ œœ œÊœœ
35. F(x y) 1 x y sin xy F 1 y cos xy and F 2y x cos xy ßœ Ê œ œ Ê œœ
#
xy
dy 1 y cos xy
dx F 2y x cos xy
Fx
y
at (x y) ( 1) we have 1œ Ê ß œ !ß œ œ
1 y cos xy dy
2y x cos xy dx 2
1
"
¹ÐßÑ01
36. F(x y) 2xy e 2 F 2y e and F 2x e ß œ Ê œ œ Ê œ œ
xy xy xy
xy
dy 2y e
dx F 2x e
F
x
y
xy
xy
at (x y) ( ln 2) we have (ln 2 1)Êßœ!ß œ œ
¹
dy
dx 0 2
2 ln 2 2
Ðß Ñ0ln2
37. f ( sin x cos y) (cos x sin y) f f ;™™™œ Ê œ Ê œ œ œij ijkkk
Ɉ‰ˆ‰
44
"" " " "
## # # #
##
ÈÈ
2
2
f increases most rapidly in the direction and decreases mostuij uijœœ Ê œ
™
™
f
f
22 22
kk ÈÈ ÈÈ
## ##
rapidly in the direction ; (D f) f and (D f) ;œ œ œ œuij
ÈÈ È È
22 2 2
## # #
uuPP
kk™
(D f) fuiju
""
""
##
œœ œ Ê œ œ œ
v
v
ij
kk È
34
34
34 3 4 7
55 5 5 10
uP™† ˆ‰ˆ‰ˆ‰ˆ‰
38. f 2xe 2x e f f 2 ( 2) 2 2; ™™™œ Ê œ##Êœœ œœ
2y 2y
10
ij ij u ij
###
kkk
ÈÈ™
™
f
f
11
22
kk ÈÈ
f increases most rapidly in the direction and decreases most rapidly in the directionÊœuij
11
22
ÈÈ
; (D f) f 2 2 and (D f) 2 2 ; œ œ œ œ œ œ œ uij u ij
11 11
22 11 2 2
ÈÈ ÈÈÈ
kk
uuPP
kkÈÈ
™"
v
v
ij
(D f) f (2) ( 2) 0Êœ œ œ
uP™†u"""
Š‹ Š‹
ÈÈ
22
39. f f 2 3 6 ;™™œ Êœ
Š‹Š‹Š‹ k
236
2x 3y 6z 2x 3y 6z 2x 3y 6z
ijk ijk
111
f increases most rapidly in the direction andu ijk uijkœ œ œ Ê œ
™
™
f
f777 777
236
236
236 236
kk Èijk
decreases most rapidly in the direction ; (D f) f 7, (D f) 7;œ œ œ œuijk
236
777 uuPP
kk™
(D f) (D f) 7uijk
"œœ Ê œ œ
v
vkk 236
777 uuPP
40. f (2x 3y) (3x 2) (1 2z) f 2 ; f increases most™™œ Ê œ œ œ Êijk jku jkk000
™
™
f
f
2
55
kk ÈÈ
"
rapidly in the direction and decreases most rapidly in the direction ;ujk u jkœ œ
2 2
55 55
ÈÈ ÈÈ
" "
(D f) f 5 and (D f) 5 ;
uuPP
œ œ œ œœ œkk
ÈÈ
™"
"""
uijk
v
v
ijk
kk ÈÈÈÈ
111 333
(D f) f (0) (2) (1) 3Êœœœœ
uP™†u""""
Š‹ Š‹ Š‹ È
ÈÈÈÈ
3333
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
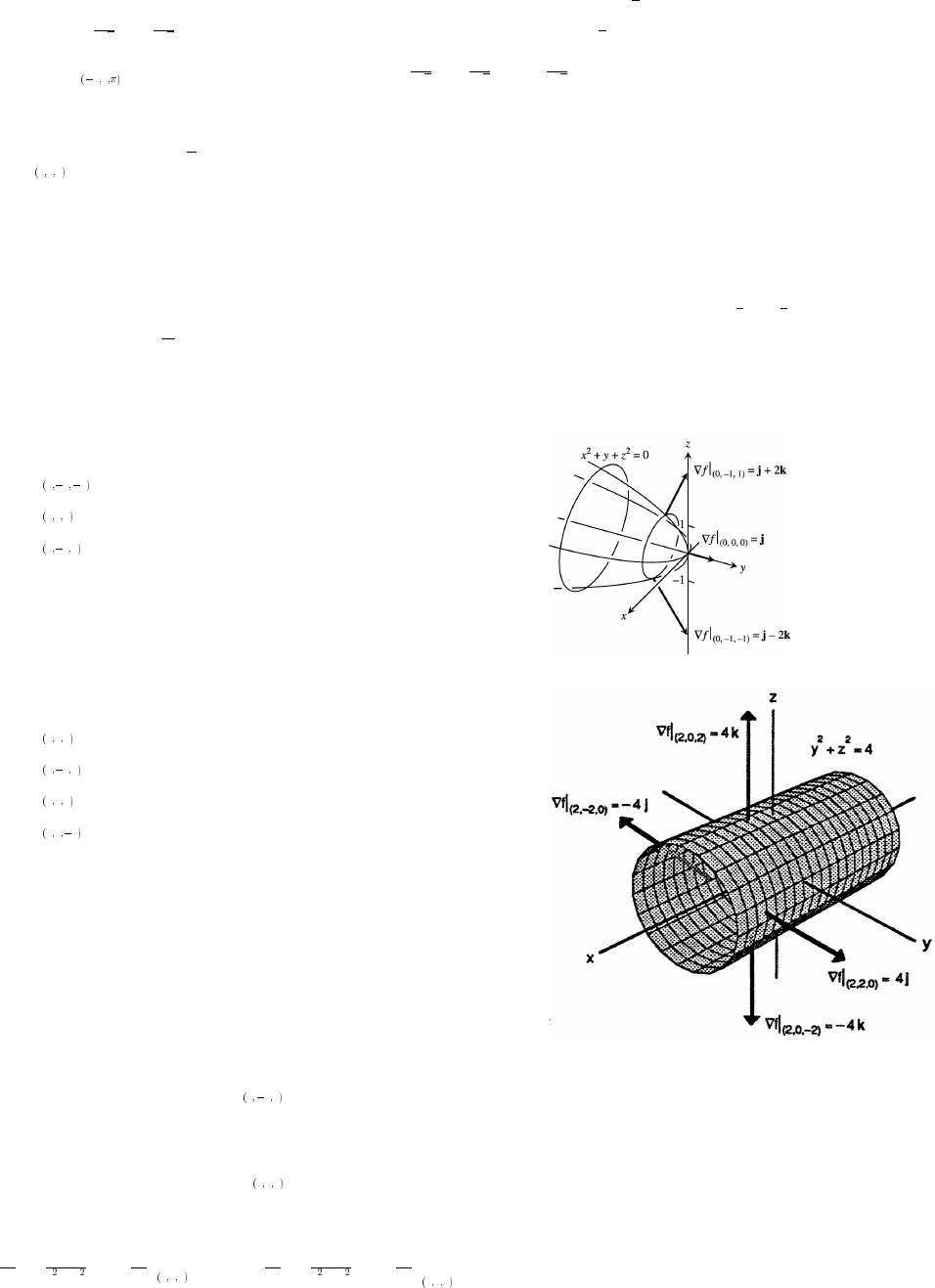
866 Chapter 14 Partial Derivatives
41. (cos 3t) (sin 3t) 3t (t) ( 3 sin 3t) (3 cos 3t) 3 3 3rijkv i jkvjkœÊœ Êœ
ˆ‰
1
3
; f(x y z) xyz f yz xz xy ; t yields the point on the helix ( 1 0 )Ê œ ßß œ Ê œ œ ßßujk ijk
""
ÈÈ
22 3
™11
f f()ʜʜœkŠ‹
™™††
10 11j ujjk
""
ÈÈ È
22 2
1
42. f(x y z) xyz f yz xz xy ; at (1 1 1) we get f the maximum value ofßß œ Ê œ ßß œ Ê™™ijk ijk
Df f 3kkk
È
u111 œœ™
43. (a) Let f a b at (1 2). The direction toward (2 2) is determined by (2 1) (2 2)™œ ß ß œ œœij v i jiu
"
so that f 2 a 2. The direction toward (1 1) is determined by (1 1) (1 2)™†uvijjuœÊœ ß œ œœ
#
so that f 2 b 2 b 2. Therefore f 2 2 ; f 1, 2 f 1, 2 2.™† ™uijœ Ê œ Ê œ œ œ œ
xy
ab ab
(b) The direction toward (4 6) is determined by (4 1) (6 2) 3 4 ßœœÊœvijijuij
$34
55
f.Êœ™†u14
5
44. (a) True (b) False (c) True (d) True
45. f 2x 2z ™œ Êij k
f2,k™011œjk
f,k™000 œj
f2k™011œjk
46. f 2y 2z ™œ Êjk
f4,k™220 œj
f4,k™220œ j
f4,k™202 œk
f4k™20 2 œ k
47. f 2x 5 f 4 5 Tangent Plane: 4(x 2) (y 1) 5(z 1) 0™™œ Ê œ Ê œij k ij kk211
4x y 5z 4; Normal Line: x 2 4t, y 1 t, z 1 5tÊœ œ œœ
48. f 2x 2y f 2 2 Tangent Plane: 2(x 1) 2(y 1) (z 2) 0™™œÊ œÊ œijk ijkk112
2x 2y z 6 0; Normal Line: x 1 2t, y 1 2t, z 2 tÊœ œ œ œ
49. 0 and 2; thus the tangent plane is
`` ``
` ` ` `
z2x z z z
xxy x yxy y
2y
œÊ œ œÊ œ
¸¹
010 010
2(y 1) (z 0) 0 or 2y z 2 0œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
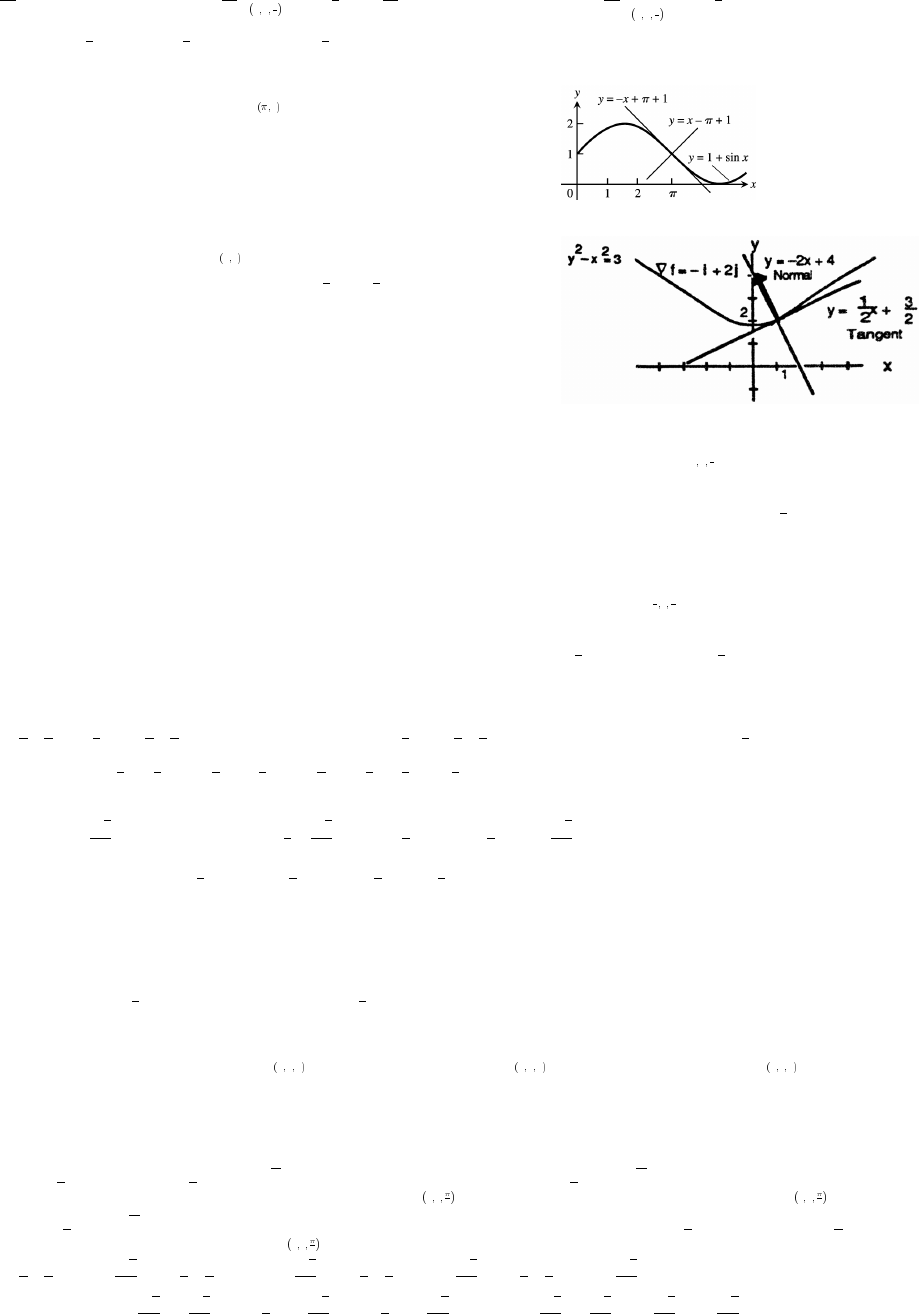
Chapter 14 Practice Exercises 867
50. 2x x y and 2y x y ; thus the tangent
``"``"
``#``#
## ##
# #
zzzz
xxyy
œ Ê œ œ Ê œab ab
¸¹
11 11
1
21
2
plane is (x 1) (y 1) z 0 or x y 2z 3 0œ œ
"" "
## #
ˆ‰
51. f ( cos x) f the tangent™™œ Ê œ Êij ijk1
line is (x ) (y 1) 0 x y 1; theœÊœ11
normal line is y 1 1(x ) y x 1œ Ê œ11
52. f x y f 2 the tangent™™œ Ê œ Êij ijk12
line is (x 1) 2(y 2) 0 y x ; the normal œÊœ
"
##
3
line is y 2 2(x 1) y 2x 4œ Êœ
53. Let f(x y z) x 2y 2z 4 and g(x y z) y 1. Then f 2x 2 2 2 2 2ßß œ ßß œ œ œ
#k™ijk ijk
ab111
2
and g f g 2 2 the line is x 1 2t, y 1, z 2t
222
00
™™™œÊ ‚ œ œ Ê œ œ œ
"
jik
ijk
ââ
ââ
ââ
ââ
ââ
ââ "
#
54. Let f(x y z) x y z 2 and g(x y z) y 1. Then f 2y 2 andßß œ ßß œ œ œ
#k™ijk ijk
ab
11
22
1
g f g the line is x t, y 1, z t
121
00
™™™œÊ ‚ œ œ Ê œ œ œ
"
jik
ijk
ââ
ââ
ââ
ââ
ââ
ââ ""
##
55. f , f cos x cos y , f sin x sin y
ˆ‰ ˆ‰ ˆ‰
kk
11 11 11
11 11
44 44 44
xy
44 44
ßœ ßœ œ ßœ œ
"" "
## #
ÐÎßÎÑ ÐÎßÎÑ
L(x y) x y x y; f (x y) sin x cos y, f (x y) sin x cos y, andÊßœ œ ßœ ßœ
"" " "" "
## # ## #
ˆ‰ˆ‰
11
44 xx yy
f (x y) cos x sin y. Thus an upper bound for E depends on the bound M used for f , f , and f .
xy xx xy yy
ߜ kkkk kk
With M we have E(x y) x y (0.2) 0.0142;œßŸŸŸ
ÈÈ È
22 2
444###
"##
kk
Š‹
ˆ‰¸¸¸¸
11
with M 1, E(x y) (1) x y (0.2) 0.02.œßŸ œ œkk ˆ‰¸¸¸¸
""
##
##
11
44
56. f(1 1) 0, f (1 1) y 1, f (1 1) x 6y 5 L(x y) (x 1) 5(y 1) x 5y 4;ßœ ßœ œ ßœ œÊ ßœ œ kk
xy
11 11
ÐßÑ ÐßÑ
f (x y) 0, f (x y) 6, and f (x y) 1 maximum of f , f , and f is 6 M 6
xx yy xy xx yy xy
ßœ ßœ ßœÊ Ê œkkkk kk
E(x y) (6) x 1 y 1 (6)(0.1 0.2) 0.27Ê ß Ÿ œ œkk a bkkkk
""
##
##
57. f(1 0 0) 0, f (1 0 0) y 3z 0, f (1 0 0) x 2z 1, f (1 0 0) 2y 3x 3ßß œ ßß œ œ ßß œ œ ßß œ œkk k
xyz
100 100
100
L(x y z) 0(x 1) (y 0) 3(z 0) y 3z; f(1 1 0) 1, f (1 1 0) 1, f (1 1 0) 1, f ( ) 1Ê ßßœ œ ßßœ ßßœ ßßœ "ß"ß!œ
xyz
L(x y z) 1 (x 1) (y 1) 1(z 0) x y z 1Ê ßßœ œ
58. f 0 1, f 0 2 sin x sin (y z) 0, f 0 2 cos x cos (y z) 1,
ˆ‰ ˆ‰ ˆ‰
¹¹
ÈÈ
ß!ßœ !ßßœ œ !ßßœ œ
11 1
44 4
x y
00 00
4 4
f 0 2 cos x cos (y z) 1 L(x y z) 1 1(y 0) 1 z 1 y z ;
z00
ˆ‰ ˆ‰
¹
È
!ß ß œ œ Ê ß ß œ œ
111
444
4
f 0 , f 0 , f 0 , f 0
ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11 11 11
44 44 44 44
2222
ßßœ ßßœ ßßœ ßßœ
ÈÈÈÈ
####
xyz
L(xyz) x y (z 0) x y zÊßßœœ
ÈÈÈÈÈÈÈÈ
22222222
44########
ˆ‰ˆ‰
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

868 Chapter 14 Partial Derivatives
59. V r h dV 2 rh dr r dh dV 2 (1.5)(5280) dr (1.5) dh 15,840 dr 2.25 dh.kœÊœ Ê œ œ 111 1 1 11
## #
155280
You should be more careful with the diameter since it has a greater effect on dV.
60. df (2x y) dx ( x 2y) dy df 3 dy f is more sensitive to changes in y; in fact, near the pointkœ Ê œ Ê
12
(1 2) a change in x does not change f.ß
61. dI dV dR dI dV dR dI 0.01 (480)(.0001) 0.038,
¸¸
œ Ê œ Ê œ œ
""
R R 100 100
V24
24 100 dV 1 dR 20œ ß œ
or increases by 0.038 amps; % change in V (100) 4.17%; % change in R (100) 20%;œ ¸ œ œ
ˆ‰ ˆ‰
"
24 100
20
I 0.24 estimated % change in I 100 100 15.83% more sensitive to voltage change.œœ Ê œ‚œ ‚¸ Ê
24 dI 0.038
100 I 0.24
62. A ab dA b da a db dA 16 da 10 db; da 0.1 and db 0.1kœÊœ Ê œ œ„ œ„111 11
10 16
dA 26 (0.1) 2.6 and A (10)(16) 160 100 100 1.625%Êœ„ œ„ œ œ Ê‚œ ‚¸111 1
¸¸¸ ¸
dA 2.6
A 160
1
1
63. (a) y uv dy v du u dv; percentage change in u 2% du 0.02, and percentage change in v 3%œÊœ Ÿ Ê Ÿ Ÿkk
dv 0.03; 100 100 100 100 100ÊŸ œ œÊ‚œ‚‚Ÿ‚‚kk ¹¹
¸ ¸¸¸¸¸
dy dy
yuvuvy u v u v
v du u dv du dv du dv du dv
2% 3% 5%Ÿœ
(b) z u v (since u 0, v 0)œÊœ œŸ
dz du dv du dv du dv
zuvuvuvuv
100 100 100 100Ê ‚ Ÿ‚ ‚ œ‚
¸¸¸ ¸
¹¹
dz du dv
zuvy
dy
64. C C and CœÊœ œ
7
71.84w h 71.84w h 71.84w h
wh
( 0.425)(7) ( 0.725)(7)
0 425 0 725 1 425 0 725 0 425 1 725
dC dw dh; thus when w 70 and h 180 we haveÊœ œ œ
2.975 5.075
71.84w h 71.84w h
1 425 0 725 0 425 1 725
dC (0.00000225) dw (0.00000149) dh 1 kg error in weight has more effectkÐß Ñ70 180 ¸ Ê
65. f (x y) 2x y 2 0 and f (x y) x 2y 2 0 x 2 and y 2 ( 2 2) is the critical point;
xy
ß œ œ ß œ œ Ê œ œ Ê ß
f ( 2 2) 2, f ( 2) 2, f ( 2) 1 f f f 3 0 and f 0 local minimum value
xx yy xy xx yy xx
xy
ßœ #ßœ #ßœÊ œ Ê
#
of f( 2) 8#ß œ
66. f (x y) 10x 4y 4 0 and f (x y) 4x 4y 4 0 x 0 and y 1 (0 1) is the critical point;
xy
ßœ œ ßœ œÊœ œÊß
f (0 1) 10, f (0 1) 4, f (0 1) 4 f f f 56 0 saddle point with f(0 1) 2
xx yy xy xx yy xy
ßœ ßœ ßœ Ê œ Ê ßœ
#
67. f (x y) 6x 3y 0 and f (x y) 3x 6y 0 y 2x and 3x 6 4x 0 x 1 8x 0
xy
ßœ œ ßœ œÊœ œÊ œ
###%$
ab a b
x 0 and y 0, or x and y the critical points are (0 0) and . For ( ):Ê œ œ œ œ Ê ß ß !ß !
"" ""
## ##
ˆ‰
f ( ) 12x 0, f ( ) 12y 0, f ( 0) 3 f f f 9 0 saddle point withkk
xx yy xy xx yy
00 00 xy
!ß ! œ œ !ß ! œ œ !ß œ Ê œ Ê
ÐßÑ ÐßÑ #
f(0 0) 0. For : f 6, f 6, f 3 f f f 27 0 and f 0 local maximumßœ ß œœœÊ œ Ê
ˆ‰
""
##
#
xx yy xy xx yy xx
xy
value of f ˆ‰
ß œ
"" "
## 4
68. f (x y) 3x 3y 0 and f (x y) 3y 3x 0 y x and x x 0 x x 1 0 the critical
xy
ßœ œ ßœ œÊœ œÊ œÊ
###%$
ab
points are (0 0) and (1 1) . For ( ): f ( ) 6x 0, f ( ) 6y 0, f ( 0) 3ß ß !ß ! !ß ! œ œ !ß ! œ œ !ß œ kk
xx yy xy
00 00
ÐßÑ ÐßÑ
f f f 9 0 saddle point with f(0 0) 15. For (1 1): f (1 1) 6, f (1 1) 6, f (1 1) 3Ê œ Ê ß œ ß ß œ ß œ ß œ
xx yy xx yy xy
xy
#
f f f 27 0 and f 0 local minimum value of f(1 1) 14Êœ Ê ßœ
xx yy xx
xy
#
69. f (x y) 3x 6x 0 and f (x y) 3y 6y 0 x(x 2) 0 and y(y 2) 0 x 0 or x 2 and
xy
ßœ œ ßœ œÊ œ œÊœ œ
##
y 0 or y 2 the critical points are (0 0), (0 2), ( 2 0), and ( 2 2) . For ( ): f ( ) 6x 6œ œ Ê ß ß ß ß !ß ! !ß ! œ k
xx 00ÐßÑ
6, f ( ) 6y 6 6, f ( 0) 0 f f f 36 0 saddle point with f(0 0) 0. Forœ !ß ! œ œ !ß œ Ê œ Ê ß œk
yy xy xx yy
00 xy
ÐßÑ #
(0 2): f ( 2) 6, f (0 ) 6, f ( 2) 0 f f f 36 0 and f 0 local minimum value ofß !ßœ ß#œ !ßœÊ œ Ê
xx yy xy xx yy xx
xy
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 14 Practice Exercises 869
f( 2) 4. For ( 0): f ( 2 0) 6, f ( 0) 6, f ( 2 0) 0 f f f 36 0 and f 0!ß œ #ß ß œ #ß œ ß œ Ê œ
xx yy xy xx yy xx
xy
#
local maximum value of f( 2 0) 4. For ( 2 2): f ( 2 2) 6, f ( 2 2) 6, f ( 2 2) 0Ê ß œ ß ß œ ß œ ß œ
xx yy xy
f f f 36 0 saddle point with f( 2 2) 0.ÊœÊ ßœ
xx yy xy
#
70. f (x y) 4x 16x 0 4x x 4 0 x 0, 2, 2; f (x y) 6y 6 0 y 1. Therefore the critical
x y
ßœ œÊ œÊœ ßœ œÊœ
$#
ab
points are (0 1), (2 1), and ( 2 1). For ( 1): f ( 1) 12x 16 16, f ( 1) 6, f ( 1) 0ß ß ß !ß !ß œ œ !ß œ !ß œk
xx yy xy
01
#ÐßÑ
f f f 96 0 saddle point with f(0 1) 3. For (2 1): f (2 1) 32, f (2 1) 6,Ê œÊ ßœ ß ßœ ßœ
xx yy xx yy
xy
#
f (2 1) 0 f f f 192 0 and f 0 local minimum value of f(2 1) 19. For ( 1):
xy xx yy xx
xy
ßœÊ œ Ê ßœ #ß
#
f ( 2 1) 32, f ( 1) 6, f ( 2 1) 0 f f f 192 0 and f 0 local minimum value of
xx yy xy xx yy xx
xy
ß œ #ß œ ß œ Ê œ Ê
#
f( 2 1) 19.ß œ
71. (i) On OA, f(x y) f(0 y) y 3y for 0 y 4ßœ ßœ ŸŸ
#
f ( y) 2y 3 0 y . But Ê!ßœœÊœ !ß
w
##
33
ˆ‰
is not in the region.
Endpoints: f(0 0) 0 and f(0 4) 28.ߜ ߜ
(ii) On AB, f(x y) f(x x 4) x 10x 28ߜ ߜ
#
for 0 x4 f(xx4)2x100ŸŸÊ ßœœ
w
x 5, y 1. But (5 1) is not in the region.Êœ œ ß
Endpoints: f(4 0) 4 and f( 4) 28.ß œ !ß œ
(iii) On OB, f(x y) f(x 0) x 3x for 0 x 4 f (x 0) 2x 3 x and y 0 0 is aßœ ßœ ŸŸ Ê ßœ Êœ œÊ ß
#w
##
33
ˆ‰
critical point with f .
ˆ‰
39
4#ß! œ
Endpoints: f(0 0) 0 and f( 0) 4.ß œ %ß œ
(iv) For the interior of the triangular region, f (x y) 2x y 3 0 and f (x y) x 2y 3 0 x 3
xy
ß œ œ ß œ œ Ê œ
and y 3. But (3 3) is not in the region. Therefore the absolute maximum is 28 at (0 4) and theœ ß ß
absolute minimum is at .ß!
93
4ˆ‰
#
72. (i) On OA, f(x y) f(0 y) y 4y 1 forߜ ߜ
#
0 y 2 f ( y) 2y 4 0 y 2 andŸŸ Ê !ß œ œ Ê œ
w
x 0. But (0 2) is not in the interior of OA.ϧ
Endpoints: f(0 0) 1 and f(0 2) 5.ߜ ߜ
(ii) On AB, f(x y) f(x 2) x 2x 5 for 0 x 4ßœ ßœ ŸŸ
#
f (x 2) 2x 2 0 x 1 and y 2ÊßœœÊœ œ
w
(1 2) is an interior critical point of AB withÊß
f(1 2) 4. Endpoints: f(4 2) 13 and f( 2) 5.ߜ ߜ !ߜ
(iii) On BC, f(x y) f(4 y) y 4y 9 for 0 y 2 f (4 y) 2y 4 0 y and x 4. Butßœ ßœ ŸŸ Ê ßœœÊœ# œ
#w
(4 2) is not in the interior of BC. Endpoints: f(4 0) 9 and f( 2) 13.ßßœ%ßœ
(iv) On OC, f(x y) f(x 0) x 2x 1 for 0 x 4 f (x 0) 2x 2 0 x 1 and y 0 (1 0)ßœ ßœ ŸŸÊ ßœ œÊœ œÊß
#w
is an interior critical point of OC with f(1 0) 0. Endpoints: f(0 0) 1 and f(4 0) 9.ߜ ߜ ߜ
(v) For the interior of the rectangular region, f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and
xy
ßœ œ ßœœÊœ
y 2. But (1 2) is not in the interior of the region. Therefore the absolute maximum is 13 at (4 2)œß ß
and the absolute minimum is 0 at (1 0).ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
870 Chapter 14 Partial Derivatives
73. (i) On AB, f(x y) f( 2 y) y y 4 forߜߜ
#
2y2 f(2y)2y1 y andŸ Ÿ Ê ß œ Ê œ
w"
#
x 2 2 is an interior critical point in ABœ Ê ß
ˆ‰
"
#
with f 2 . Endpoints: f( 2 2) 2 and
ˆ‰
ß œ ß œ
"
#
17
4
f(2 2) 2.ߜ
(ii) On BC, f(x y) f(x 2) 2 for 2 x 2ßœ ßœ ŸŸ
f (x 2) 0 no critical points in the interior ofÊßœÊ
w
BC. Endpoints: f( 2 2) 2 and f(2 2) 2.ß œ ß œ
(iii) On CD, f(x y) f(2 y) y 5y 4 forߜ ߜ
#
2 y 2 f (2 y) 2y 5 0 y and x 2. But is not in the region.Ÿ Ÿ Ê ß œ œ Ê œ œ #ß
w
##
55
ˆ‰
Endpoints: f(2 2) 18 and f(2 2) 2.ß œ ß œ
(iv) On AD, f(x y) f(x 2) 4x 10 for 2 x 2 f (x 2) 4 no critical points in the interiorß œ ß œ Ÿ Ÿ Ê ß œ Ê
w
of AD. Endpoints: f( 2 2) 2 and f(2 2) 18.ß œ ß œ
(v) For the interior of the square, f (x y) y 2 0 and f (x y) 2y x 3 0 y 2 and x 1
xy
ßœœ ßœ œÊœ œ
(1 2) is an interior critical point of the square with f(1 2) 2. Therefore the absolute maximumÊß ßœ
is 18 at (2 2) and the absolute minimum is at .ß #ß
17
4ˆ‰
"
#
74. (i) On OA, f(x y) f(0 y) 2y y for 0 y 2ßœ ßœ ŸŸ
#
f ( y) 2 2y 0 y 1 and x 0 Ê!ßœœÊœ œÊ
w
( 1) is an interior critical point of OA with!ß
f(0 1) 1. Endpoints: f(0 0) 0 and f(0 2) 0.ߜ ߜ ߜ
(ii) On AB, f(x y) f(x 2) 2x x for 0 x 2ßœ ßœ ŸŸ
#
f (x 2) 2 2x 0 x 1 and y 2ÊßœœÊœ œ
w
(1 2) is an interior critical point of AB withÊß
f(1 2) 1. Endpoints: f(0 2) 0 and f(2 2) 0.ߜ ߜ ߜ
(iii) On BC, f(x y) f(2 y) 2y y for 0 y 2ßœ ßœ ŸŸ
#
f (2 y) 2 2y 0 y 1 and x 2ÊßœœÊœ œ
w
(2 1) is an interior critical point of BC with f(2 1) 1. Endpoints: f(2 0) 0 and f(2 2) 0.Êß ßœ ßœ ßœ
(iv) On OC, f(x y) f(x 0) 2x x for 0 x 2 f (x 0) 2 2x 0 x 1 and y 0 (1 0)ßœ ßœ ŸŸÊ ßœ œÊœ œÊß
#w
is an interior critical point of OC with f(1 0) 1. Endpoints: f(0 0) 0 and f(0 2) 0.ߜ ߜ ߜ
(v) For the interior of the rectangular region, f (x y) 2 2x 0 and f (x y) 2 2y 0 x 1 and
xy
ßœ œ ßœ œÊœ
y 1 (1 1) is an interior critical point of the square with f(1 1) 2. Therefore the absolute maximumœÊß ßœ
is 2 at (1 1) and the absolute minimum is 0 at the four corners (0 0), (0 2), (2 2), and (2 0).ß ßßß ß
75. (i) On AB, f(x y) f(x x 2) 2x 4 forߜ ߜ
2 x 2 f (x x 2) 2 0 no criticalŸ Ÿ Ê ß œœ Ê
w
points in the interior of AB. Endpoints: f( 2 0) 8ß œ
and f(2 4) 0.ߜ
(ii) On BC, f(x y) f(2 y) y 4y for 0 y 4ßœ ßœ ŸŸ
#
f (2 y) 2y 4 0 y 2 and x 2ÊßœœÊœ œ
w
(2 2) is an interior critical point of BC withÊß
f(2 2) 4. Endpoints: f(2 0) 0 and f(2 4) 0.ߜ ߜ ߜ
(iii) On AC, f(x y) f(x 0) x 2x for 2 x 2ßœ ßœ ŸŸ
#
f (x 0) 2x 2 x 1 and y 0 (1 0) is an interior critical point of AC with f(1 0) 1.Êߜʜ œÊß ßœ
w
Endpoints: f( 2 0) 8 and f(2 0) 0.ß œ ß œ
(iv) For the interior of the triangular region, f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and
xy
ßœ œ ßœœÊœ
y 2 (1 2) is an interior critical point of the region with f(1 2) 3. Therefore the absolute maximumœÊß ßœ
is 8 at ( 2 0) and the absolute minimum is 1 at (1 0).ß ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 14 Practice Exercises 871
76. (i) On AB, f x y f x x 4x 2x 16 forababߜ ߜ
#%
2x2 fxx 8x8x 0 x0Ÿ Ÿ Ê ß œ œ Ê œ
w$
ab
and y 0, or x 1 and y 1, or x 1 and y 1œœ œœœ
0 0 , 1 1 , 1 1 are all interior points of ABÊß ß ßababa b
with f 0 0 16, f 1 1 18, and f 1 1 18.ab ab a bߜ ߜ ߜ
Endpoints: f 2 2 0 and f 2 2 0.ab abß œ ß œ
(ii) On BC, f x y f 2 y 8y y for 2 y 2ababßœ ßœ ŸŸ
%
f 2 y 8 4y 0 y 2 and x 2ÊßœœÊœ œ
w$
ab È
3
2 2 is an interior critical point of BC withÊß
Š‹
È
3
f 2 2 6 2. Endpoints: f 2 2 32 and f 2 2 0.
Š‹
ÈÈ ab abßœ ßœ ßœ
33
(iii) On AC, f x y f x 2 8x x for 2 x 2 f x 2 8 4x 0 x 2 and y 2abab ab È
ß œ ß œ Ÿ Ÿ Ê ß œ œ Ê œ œ
%w$
3
2 2 is an interior critical point of AC with f 2 2 6 2. Endpoints:Êß ßœ
Š‹ Š‹
ÈÈÈ
333
f 2 2 0 and f 2 2 32.ab abß œ ß œ
(iv) For the interior of the triangular region, f x y 4y 4x 0 and f x y 4x 4y 0 x 0 and
xy
ab abßœ œ ßœ œÊœ
$$
y 0, or x 1 and y 1 or x 1 and y 1. But neither of the points 0 0 and 1 1 , or 1 1 areœœ œœœ ß ßßab aba b
interior to the region. Therefore the absolute maximum is 18 at (1 1) and ( 1 1), and the absolute minimum isßß
32 at 2 2 .ßab
77. (i) On AB, f(x y) f( 1 y) y 3y 2 forߜߜ
$#
1y1 f(1y)3y 6y0 y0ŸŸÊ ß œ œ Ê œ
w#
and x 1, or y 2 and x 1 ( 1 0) is anœ œ œ Ê ß
interior critical point of AB with f( 1 0) 2; ( 1 2)ß œ ß
is outside the boundary. Endpoints: f( 1 1) 2ß œ
and f( 1 1) 0.ß œ
(ii) On BC, f(x y) f(x 1) x 3x 2 forߜ ߜ
$#
1x1 f(x1)3x 6x0 x0Ÿ Ÿ Ê ß œ œ Ê œ
w#
and y 1, or x 2 and y 1 (0 1) is anœœœÊß
interior critical point of BC with f( 1) 2; ( 2 1) is outside the boundary. Endpoints: f( 1) 0 and!ß œ ß "ß œ
f( 1) 2."ß œ
(iii) On CD, f(x y) f( y) y 3y 4 for 1 y 1 f ( y) 3y 6y 0 y 0 and x 1, orßœ"ßœ ŸŸÊ "ßœ œÊœ œ
$# w #
y 2 and x 1 ( 0) is an interior critical point of CD with f( 0) 4; (1 2) is outside the boundary.œœÊ"ß "ßœß
Endpoints: f(1 1) 2 and f( 1) 0.ߜ "ߜ
(iv) On AD, f(x y) f(x 1) x 3x 4 for 1 x 1 f (x 1) 3x 6x 0 x 0 and y 1,ßœ ßœ ŸŸÊ ßœ œÊœ œ
$# w #
or x 2 and y 1 (0 1) is an interior point of AD with f(0 1) 4; ( 1) is outside theœ œ Ê ß ß œ #ß
boundary. Endpoints: f( 1 1) 2 and f( 1) 0.ß œ "ß œ
(v) For the interior of the square, f (x y) 3x 6x 0 and f (x y) 3y 6y 0 x 0 or x 2, and
xy
ßœ œ ßœ œÊœ œ
##
y 0 or y 2 (0 0) is an interior critical point of the square region with f( 0) 0; the points (0 2),œœÊß !ßœ ß
( 2 0), and ( 2 2) are outside the region. Therefore the absolute maximum is 4 at (1 0) and theß ß ß
absolute minimum is 4 at (0 1).ß
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

872 Chapter 14 Partial Derivatives
78. (i) On AB, f(x y) f( 1 y) y 3y for 1 y 1ߜߜ ŸŸ
$
f ( 1 y) 3y 3 0 y 1 and x 1Êßœ œÊœ„ œ
w#
yielding the corner points ( 1 1) and ( 1 1) withß ß
f( 1 1) 2 and f( 1 1) 2.ß œ ß œ
(ii) On BC, f(x y) f(x 1) x 3x 2 forߜ ߜ
$
1 x 1 f (x 1) 3x 3 0 noŸ Ÿ Ê ß œ œ Ê
w#
solution. Endpoints: f( 1) 2 and f( 1) 6."ߜ "ߜ
(iii) On CD, f(x y) f( y) y 3y 2 forß œ "ß œ
$
1 y 1 f ( y) 3y 3 0 noŸŸÊ "ßœ œÊ
w#
solution. Endpoints: f(1 1) 6 and f( 1) 2.ß œ "ß œ
(iv) On AD, f(x y) f(x 1) x 3x for 1 x 1 f (x 1) 3x 3 0 x 1 and y 1ß œ ß œ Ÿ Ÿ Ê ß œ œ Ê œ „ œ
$w#
yielding the corner points ( 1 1) and (1 1) with f( 1 1) 2 and f(1 1) 2ß ß ß œ ß œ
(v) For the interior of the square, f (x y) 3x 3y 0 and f (x y) 3y 3x 0 y x and
xy
ßœ œ ßœ œÊœ
###
x x 0 x 0 or x 1 y 0 or y 1 ( 0) is an interior critical point of the square
%œÊœ œÊœ œÊ!ß
region with f(0 0) 1; ( 1 1) is on the boundary. Therefore the absolute maximum is 6 at ( 1) andßœ ß "ß
the absolute minimum is 2 at (1 1) and ( 1 1).ß ß
79. f 3x 2y and g 2x 2y so that f g 3x 2y (2x 2y ) 3x 2x and™™ ™™œ œ œ Ê œ Êœ
###
ij ij ij ij-- -
2y 2y 1 or y 0.œÊœ œ--
CASE 1: 1 3x 2x x 0 or x ; x 0 y 1 yielding the points (0 1) and ( 1); x-œÊ œ Êœ œ œÊœ„ ß !ß œ
#2 2
3 3
y yielding the points and .Êœ„ ß ß
ÈÈÈ
555
33333
22
Š‹Š ‹
CASE 2: y 0 x 1 0 x 1 yielding the points (1 0) and ( 1 0).œÊ œÊœ„ ß ß
#
Evaluations give f 1 1, f , f( 0) 1, and f( 0) 1. Therefore the absoluteabŠ‹
!ß„œ ß„ œ "ßœ "ßœ
223
33 27
5
È
maximum is 1 at 1 and (1 0), and the absolute minimum is 1 at ( ).ab!ß „ ß "ß !
80. f y x and g 2x 2y so that f g y x (2x 2y ) y 2 x and™™ ™™œ œ œ Ê œ Êœij i j ij i j-- -
xy 2 y x 2 (2 x) 4 x x 0 or 4 1.œÊœ œ Êœ œ---- -
##
CASE 1: x 0 y 0 but (0 0) does not lie on the circle, so no solution.œÊœ ß
CASE 2: 4 1 or . For , y x 1 x y 2x x yielding the--- -
### #
"" " "
## #
œÊœ œ œ œÊœœ ÊœCœ„
È2
points and , . For , y x 1 x y 2x x and
Š‹Š ‹
"" " " " "
#
## #
ÈÈ È È È
22 2 2 2
ß œ œÊœœ Êœ„-
y x yielding the points and , .œ ß
Š‹Š‹
"" " "
ÈÈ È È
22 2 2
Evaluations give the absolute maximum value f f and the absolute minimum
Š‹Š ‹
"" " " "
#
ÈÈ È È
22 2 2
ߜߜ
value f f .
Š‹Š‹
ß œ ß œ
"" " " "
#
ÈÈ È È
22 2 2
81. (i) f(x y) x 3y 2y on x y 1 f 2x (6y 2) and g 2x 2y so that f gßœ œÊ œ œ œ
## ## ™™™™ij ij -
2x (6y 2) (2x 2y ) 2x 2x and 6y 2 2y 1 or x 0.Êœ Êœ œ Êœ œijij----
CASE 1: 1 6y 2 2y y and x yielding the points .-œÊ œ Êœ œ„ „ ß
""
## ##
ÈÈ
33
Š‹
CASE 2: x 0 y 1 y 1 yielding the points 1 .œÊ œÊœ„ !ß„
#ab
Evaluations give f , f(0 1) 5, and f( 1) 1. Therefore and 5 are the extreme
Š‹
„ßœ ßœ !ßœ
È3
### #
"" "
values on the boundary of the disk.
(ii) For the interior of the disk, f (x y) 2x 0 and f (x y) 6y 2 0 x 0 and y
xy
ßœ œ ßœ œÊœ œ
"
3
is an interior critical point with f . Therefore the absolute maximum of f on theÊ !ß !ß œ
ˆ‰ ˆ‰
1
333
""
disk is 5 at (0 1) and the absolute minimum of f on the disk is at .ß !ß
""
33
ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Chapter 14 Practice Exercises 873
82. (i) f(x y) x y 3x xy on x y 9 f (2x 3 y) (2y x) and g 2x 2y so thatßœ œÊ œ œ
## ## ™™ij ij
f g (2x 3 y) (2y x) (2x 2y ) 2x 3 y 2x and 2y x 2y™™œ Ê œ Ê œ œ----ijij
2x( ) y 3 and x 2y(1 ) 0 1 and (2x) y 3 x y 3yÊ"œ œÊœ œÊœ---
xx
2y 2y
Š‹ ##
x y 3y. Thus, 9 x y y 3y y 2y 3y 9 0 (2y 3)(y 3) 0Ê œ œœ Ê œÊ œ
## ### # #
y 3, . For y 3, x y 9 x 0 yielding the point (0 3). For y , x y 9Êœ œ œÊœ ß œ œ
3 3
# #
## ##
x 9 x x . Evaluations give f(0 3) 9, f 9ʜʜʜ„ ßœ ßœ
##
###
927 3
44 4
33 33 273
ÈÈÈ
Š‹
20.691, and f , 9 2.691.¸œ¸
Š‹
33 273
3
4
ÈÈ
##
(ii) For the interior of the disk, f (x y) 2x 3 y 0 and f (x y) 2y x 0 x 2 and y 1
xy
ßœ œ ßœ œÊœ œ
(2 1) is an interior critical point of the disk with f(2 1) 3. Therefore, the absolute maximum of f onÊß ßœ
the disk is 9 at and the absolute minimum of f on the disk is 3 at (2 1).ß ß
27 3 3 3
4
3
ÈÈ
Š‹
##
83. f and g 2x 2y 2z so that f g (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Ê œ Ê œijk i j k ijk i j k-- -
1 2y , 1 2z x y z . Thus x y z 1 3x 1 x yielding the pointsœ œ Êœœœ œÊ œÊœ„-- ""
### #
-È3
, and , , . Evaluations give the absolute maximum value of
Š‹Š ‹
""" """
ÈÈÈ ÈÈÈ
333 333
ß
f 3 and the absolute minimum value of f 3.
Š‹ Š ‹
ÈÈ
""" "" "
ÈÈÈ È ÈÈÈ
333 3 333
3
ßßœœ ßßœ
84. Let f(x y z) x y z be the square of the distance to the origin and g(x y z) x zy 4. Thenßß œ ßß œ
### #
f 2x 2y 2z and g 2x z y so that f g 2x 2 x, 2y z, and™™ ™™œ œ œ Êœ œijk ijk ---
2z y x 0 or 1.œ Ê œ œ--
CASE 1: x 0 zy 4 z and y 2 y and 2 z y andœ Ê œ Ê œ œ Ê œ œ Ê œ
444 4 8
yzy z
Š‹ ˆ‰
--
-
#
z y z y z. But y x z 4 leads to no solution, so y z z 4
8
-œ Ê œ Ê œ „ œ Ê œ œ Ê œ
### # #
z 2 yielding the points (0 2 2) and (0 2 2).Êœ„ ßß ßß
CASE 2: 1 2z y and 2y z 2y 4y y y 0 z 0 x 4 0 -œ Ê œ œ Ê œ Ê œ Ê œ Ê œ Ê œ Ê
ˆ‰
y
#
#
x 2 yielding the points ( 2 0 0) and (2 0).œ„ ß ß ß!ß
Evaluations give f(0 2 2) f(0 2 2) 8 and f( 2 0 0) f(2 0) 4. Thus the points ( 2 0 0) andßßœ ßßœ ßßœ ß!ßœ ßß
(2 0) on the surface are closest to the origin.ß!ß
85. The cost is f(x y z) 2axy 2bxz 2cyz subject to the constraint xyz V. Then f gßß œ œ œ™™-
2ay 2bz yz, 2ax 2cz xz, and 2bx 2cy xy 2axy 2bxz xyz, 2axy 2cyz xyz, andÊœ œ œ Ê œ œ-- - - -
2bxz 2cyz xyz 2axy 2bxz 2axy 2cyz y x. Also 2axy 2bxz 2bxz 2cyz z x.œ Ê œ Êœ œ Êœ-ˆ‰ ˆ‰
ba
cc
Then x x x V x width x , Depth y , and
ˆ‰ˆ‰ ˆ‰
Š‹ Š‹ Š‹
b a cV cV b cV bV
c c ab ab c ab ac
œ Ê œ Ê œœ œœ œ
$"Î$ "Î$ "Î$
Height z .œœ œ
ˆ‰
Š‹ Š‹
acV aV
cab bc
"Î$ "Î$
86. The volume of the pyramid in the first octant formed by the plane is V(a b c) ab c abc. The pointßß œ œ
"" "
#36
ˆ‰
(2 1 2) on the plane 1. We want to minimize V subject to the constraint 2bc ac 2ab abc.ßß Ê œ œ
22
abc
"
Thus, V and g (c 2b bc) (2c 2a ac) (2b a ab) so that V g™™ ™™œ œ œ
bc ac ab
666
ijk i j k -
(c 2b bc), (2c 2a ac), and (2b a ab) (ac 2ab abc),Êœ œ œ Ê œ
bc ac ab abc
66 6 6
-- - -
(2bc 2ab abc), and (2bc ac abc) ac 2 bc and 2 ab 2 bc. Now 0 since
abc abc
66
œ œÊœ œ Á-------
a 0, b 0, and c 0 ac 2bc and ab bc a 2b c. Substituting into the constraint equation givesÁÁ ÁÊœ œÊœœ
1 a 6 b 3 and c 6. Therefore the desired plane is 1 or x 2y z 6.
222 xz
aaa 636
y
œÊœÊœ œ œ œ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
874 Chapter 14 Partial Derivatives
87. f (y z) x x , g 2x 2y , and h z x so that f g h™™™™™™œ œ œ œ ijk i j ik -.
(y z) x x (2x 2y ) (z x ) y z 2 x z, x 2 y, x x x 0 or 1.Êœ Êœ œ œ Êœ œijk i j ik-. -.-. .
CASE 1: x 0 which is impossible since xz 1.œœ
CASE 2: 1 y z 2 x z y 2 x and x 2 y y (2 )(2 y) y 0 or.-----œÊœ Êœ œ Êœ Êœ
4 1. If y 0, then x 1 x 1 so with xz 1 we obtain the points (1 0 1)-##
œœ œÊœ„ œ ßß
and ( 1 0 1). If 4 1, then . For , y x so x y 1 xß ß œ œ„ œ œ œ Ê œ-- -
####
"" "
## #
x with xz 1 z 2, and we obtain the points 2 andÊœ„ œÊœ„ ß ß
"""
ÈÈÈ
222
ÈÈ
Š‹
2 . For , y x x x with xz 1 z 2,
Š‹
ÈÈ
ß ß œ œÊ œÊœ„ œÊœ„
"" " " "
##
#
ÈÈ È
22 2
-
and we obtain the points , 2 and 2 .
Š‹Š ‹
ÈÈ
"" " "
ÈÈ È È
22 2 2
ß ß ß
Evaluations give f(1 0 1) 1, f( 1 0 1) 1, f 2 , f , 2 ,ßß œ ßß œ ß ß œ ß œ
Š‹Š ‹
ÈÈ
"" " "" "
##
ÈÈ ÈÈ
22 22
f 2 , and f 2 . Therefore the absolute maximum is at
Š‹Š ‹
ÈÈ
"" " "
## #
ÈÈ È È
22 2 2
33 3
ß ß œ ß ß œ
2 and 2 , and the absolute minimum is at 2 and
Š‹Š ‹ Š ‹
ÈÈ È
"" " " " ""
#
ÈÈ È È ÈÈ
22 2 2 22
ßß ßß ßß
2.
Š‹
È
""
ÈÈ
22
ß ß
88. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z ,ßßœ œ
### ™ijk
g , and h 4x 4y 2z so that f g h 2x 4x , 2y 4y ,™™ ™™™œ œ œ Ê œ œ ijk i j k - . -. -.
and 2z 2z 2x(1 2 ) 2y(1 2 ) 2z(1 2 ) x y or .œ Êœ œ œ Êœ œ-.- . . . .
"
#
CASE 1: x y z 4x z 2x so that x y z 1 x x 2x 1 or x x 2x 1œ Ê œ Ê œ„ œ Ê œ œ
##
(impossible) x y and z yielding the point .ʜʜ œ ßß
" " " """
##44 44
ˆ‰
CASE 2: 0 0 2z(1 1) z 0 so that 2x 2y 0 x y 0. But the origin.-œÊœÊœ Êœ œÊœœ
"
#
##
( 0 0) fails to satisfy the first constraint x y z 1.!ßß œ
Therefore, the point on the curve of intersection is closest to the origin.
ˆ‰
"""
#44
ßß
89. (a) y, z are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
yxyyyzy
y
2xe zx e (1) yx e (0); z x y 0 2x 2y ; therefore,œ œÊœÊœab ab a b
yz yz yz
```
```
## ##
xxx
yyyx
y
2xe zx e 2y zx e
Š‹ ab a b
ˆ‰
`
`
##
w
yx
y
z
yz yz yz
œœ
(b) z, x are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
zxzyzzz
y
2xe (0) zx e yx e (1); z x y 1 0 2y ; therefore,œ œÊœÊœab ab a b
yz yz yz## ##
```
```#
"
yyy
zzzy
zxe yxe xe y
ˆ‰ ab
Š‹ Š ‹
`
`
###
w1 z
z2y 2y
x
yz yz yz
œœ
(c) z, y are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
zxzyzzz
y
2xe zx e (0) yx e (1); z x y 1 2x 0 ; therefore,œ œÊœÊœab ab a b
yz yz yz
```"
```#
####
xxx
zzzx
2xe yx e 1 x y e
ˆ‰ ˆ‰
ab a b
`
`
##
w1
z2x
y
yz yz yz
œœ
90. (a) T, P are independent with U f(P V T) and PV nRT œßß œ Ê œ
```````
```````
UUPUVUT
TPTVTTT
(0) (1); PV nRT P nR ; therefore,œ œÊœÊœ
ˆ‰ ˆ‰ˆ‰ˆ‰
```` ` `
```` ` `
UUVU V VnR
PVTT T TP
ˆ‰ ˆ‰ˆ‰
`` `
`` `
UUnRU
TVPT
Pœ
(b) V, T are independent with U f(P V T) and PV nRT œßß œ Ê œ
```````
```````
UUPUVUT
VPVVVTV
(1) (0); PV nRT V P (nR) 0 ; therefore,œ œÊœœÊœ
ˆ‰ˆ‰ˆ‰ ˆ‰ ˆ‰
`` ` ` ` ` `
`` ` ` ` ` `
UP U U P T P P
PV V T V V V V
ˆ‰ ˆ‰ˆ ‰
`` `
`` `
UUPU
VPVV
Tœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 14 Practice Exercises 875
91. Note that x r cos and y r sin r x y and tan . Thus,œœÊœœ)) )
Ȉ‰
## " y
x
(cos ) ;
````` ` ` ` `
````` ` ` ` `
wwrw w x w wsin w
xrx x r xy r r
xy
y
œœ œ
)) )
) )
ˆ‰ ˆ‰ ˆ ‰
Š‹ Š‹
È)
(sin )
````` ` ` ` `
```` ` ` ` `
wwrw w w x wcos w
yry y r xy r r
y
xy
œœ œ
)) ) )
) )
ˆ‰ ˆ‰ ˆ ‰
Š‹ Š‹
È)
92. z f f af af , and z f f bf bf
xu v u v yu v u v
œœ œœ
`` ``
`` ``
uv uv
xx yy
93. b and a a and b and
` ` `` `` "` "`
` ` `` `` ` `
u u wdwu dw wdwu dw wdw wdw
y x x du x du y du y du a x du b y du
œœÊœœ œœÊœ œ
b a ʜʜ
"` "` ` `
`` ``ax by x y
ww ww
94. - , ,
`"`
` `#
w2x w rs
x x y 2z (rs) (rs) 4rs 2r 2rss rs y x y 2z (rs) (rs)
2(r s) 2(r s) 2y 2(r s)
œœ œ œœœœ
ab
and (2s)
`"``````""
` ```````
`
w 2 w w x w w z r s 2r 2s
z x y 2z (r s) r x r y r z r r s (r s) (r s) (r s)
y
œœÊœœ œ
’“
and (2r)œœœ œ
2wwxwwz rs 2
rs s x s y s z s rs (rs) (rs) rs
y
` `` `` ``
```` `` " "
`’“
95. e cos v x 0 e cos v e sin v 1; e sin v y 0 e sin v e cos v 0.
uuuuuu
uv u v
xx x x
œ Ê œ œ Ê œabab abab
`` ` `
`` ` `
Solving this system yields e cos v and e sin v. Similarly, e cos v x 0
``
``
uv
xx
uuu
œœ œ
e cos v e sin v 0 and e sin v y 0 e sin v e cos v 1. Solving thisÊœœÊœabab abab
uu u uu
uv u v
yy y y
`` ` `
`` ` `
second system yields e sin v and e cos v. Therefore
` ` `` ``
` ` `` ``
u v uu vv
y y xy xy
uu
œœ
Š‹Š‹
ij ij†
e cos v e sin v e sin v e cos v 0 the vectors are orthogonal the angleœ œÊ Êcdc dababa bab
uu uu
ij i j†
between the vectors is the constant .
1
#
96. ( r sin ) (r cos )
``
````` ` `
`` ` ` `
gy
fx f f f
xy x y)))
œœ ))
( r sin ) (r cos ) (r cos ) (r sin ) ʜ
`` `
` ` ` ``` ` ``` ` ` `
`` ` ` ` ` ` `
gy y
fx f f f x f f
xyx x xyy y))) ))
))))
Š‹ Š‹
( r sin ) (r cos ) (r cos ) (r sin )œ ))))
Š‹ Š‹
``
`` ``
``
xx
yy
)) ))
( r sin r cos )( r sin r cos ) (r cos r sin ) ( 2)( 2) (0 2) 4 2 2 atœ œ œ œ)))) ))
(r ) 2 .ßœß)ˆ‰
1
#
97. (y z) (z x) 16 f 2(z x) 2(y z) 2(y 2z x) ; if the normal line is parallel to theœÊ œ
## ™ij k
yz-plane, then x is constant 0 2(z x) 0 z x (y z) (z z) 16 y z 4.ʜʜʜʜʜ„
`
`
##
f
x
Let x t z t y t 4. Therefore the points are (t t 4 t), t a real number.œÊ œÊ œ„ ß„ß
98. Let f(x y z) xy yz zx x z 0. If the tangent plane is to be parallel to the xy-plane, then f isßßœœ
#™
perpendicular to the xy-plane f 0 and f 0. Now f (y z 1) (x z) (y x 2z)Ê œ œ œ ™† ™† ™ij ijk
so that f y z 1 0 y z 1 y 1 z, and f x z 0 x z. Then™† ™†ijœœ Ê œ Ê œ œœ Ê œ
z(1 z) ( z)z z( z) ( z) z 0 z 2z 0 z or z 0. Now z x and y " œ Ê œ Ê œ œ œ Ê œ œ
##
""""
####
is one desired point; z 0 x 0 and y 1 (0 1 0) is a second desired point.Êßß œ Ê œ œ Ê ßß
ˆ‰
"""
###
99. f (x y z ) x f(x y z) x g(y z) for some function g y™œÊœÊßßœ ß Êœœ--- -ijk `" `
`# ``
#`
f f
xyy
g
g(y z) y h(z) for some function h z h (z) h(z) z C for some arbitraryÊßœ Êœœœ Ê œ
"`"
#``#
#w#
`
-- -
f
zz
g
constant C g(y z) y z C f(x y z) x y z C f(0 0 a) a CÊßœ ÊßßœÊßßœ
" " """ "
# # ### #
## ### #
- - --- -
ˆ‰
and f(0 0 a) ( a) C f(0 0 a) f(0 0 a) for any constant a, as claimed.ßß œ Ê ßß œ ßß
"
#
#
-
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
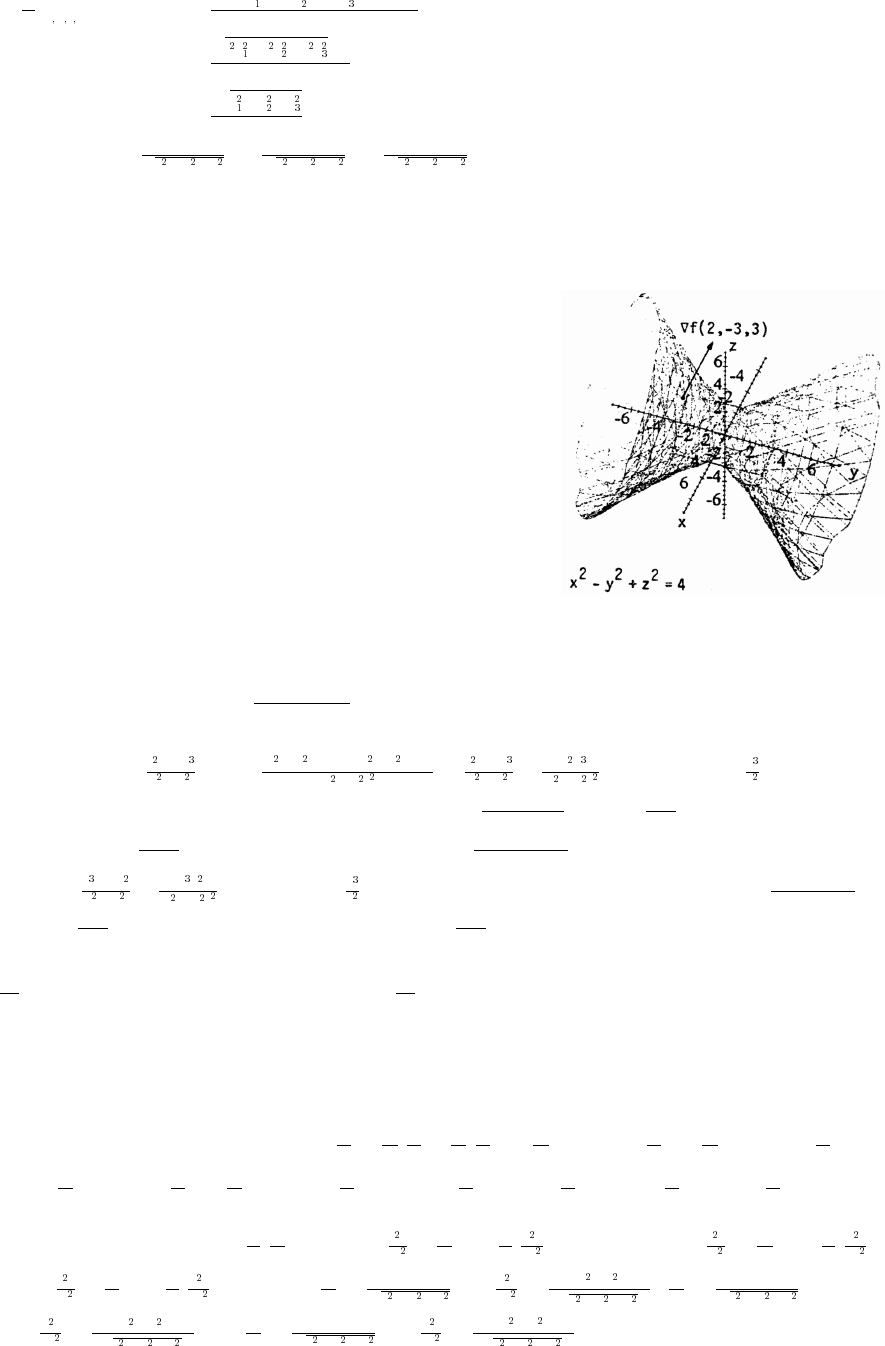
876 Chapter 14 Partial Derivatives
100. lim , s 0
s0
ˆ‰
df
ds
f(0su0su0su)f(000)
u(000) œ
Ä
ßß ßß
s
lim , s 0
s0
œ
Ä
Ésu su su 0
s
lim lim 1;
s0 s0
œœœ
ÄÄ
su u u
É
skku
however, f fails to exist at the origin (0 0 0)™œ ßß
xz
xyz xyz xyz
y
ÈÈÈ
ijk
101. Let f(x y z) xy z 2 f y x . At (1 1 1), we have f the normal line isßß œ Ê œ ßß œ Ê™™ijk ijk
x 1 t, y 1 t, z 1 t, so at t 1 x 0, y 0, z 0 and the normal line passes through the origin.œ œ œ œÊ œ œ œ
102. (b) f(x y z) x y z 4ßßœœ
###
f 2x 2y 2z at (2 3 3)Ê œ Ê ßß™ijk
the gradient is f 4 6 6 which is™œijk
normal to the surface
(c) Tangent plane: 4x 6y 6z 8 orœ
2x 3y 3z 4œ
Normal line: x 2 4t, y 3 6t, z 3 6tœ œ œ
CHAPTER 14 ADDITIONAL AND ADVANCED EXERCISES
1. By definition, f ( 0) lim so we need to calculate the first partial derivatives in the
xy !ß œ h0Ä
f(0h) f(00)
h
xx
ß ß
numerator. For (x y) (0 0) we calculate f (x y) by applying the differentiation rules to the formula forßÁß ß
x
f(x y): f (x y) (xy) f (0 h) h.ß ßœ œ Êßœœ
x x
xy y xy y 4xy
xy xy h
x y (2x) x y (2x)
xy xy
h
abab
ab ab
For (x y) (0 0) we apply the definition: f ( 0) lim lim 0. Then by definitionßœß !ßœ œ œ
xh0 h0ÄÄ
f(h 0) f(0 0)
hh
00
ß ß
f (0 0) lim 1. Similarly, f (0 0) lim , so for (x y) (0 0) we have
xy yx
ßœ œ ßœ ßÁß
h0 h0ÄÄ
ß!ß
h0
hh
f(h0) f( 0)
yy
f (x y) f (h 0) h; for (x y) (0 0) we obtain f (0 0) lim
y y
ßœ Ê ßœ œ ßœß ßœ
xxy 4xy f(0 h) f( 0)
xy h h
xy yh
ß!ß
ab h0Ä
lim 0. Then by definition f (0 0) lim 1. Note that f (0 0) f (0 0) in this case.œœ ßœœ ßÁß
h0 h0ÄÄ
00 h0
hh
xy yx
yx
2. 1 e cos y w x e cos y g(y); e sin y g (y) 2y e sin y g (y) 2y
``
``
ww
ww
xy
xx x x
œ Ê œ œ œ Ê œ
g(y) y C; w ln 2 when x ln 2 and y 0 ln 2 ln 2 e cos 0 0 C 0 2 CÊœœ œ œÊœ Êœ
# #ln 2
C 2. Thus, w x e cos y g(y) x e cos y y 2.Êœ œ œ
xx#
3. Substitution of u u(x) and v v(x) in g(u v) gives g(u(x) v(x)) which is a function of the independentœß ß
variable x. Then, g(u v) f(t) dt f(t) dt f(t) dt ßœ Êœœ
'''
uuu
vvv
dg g g
dx u dx v dx u dx v dx
du dv du dv
``
`` ` `
``
Š‹Š‹
f(t) dt f(t) dt f(u(x)) f(v(x)) f(v(x)) f(u(x)) œ œœ
Š‹Š‹
``
``u dx v dx dx dx dx dx
du dv du dv dv du
''
vu
uv
4. Applying the chain rules, f f . Similarly, f and
xxx yy
œÊœ œ
df r d f r df r d f r df r
dr x dr x dr x dr y dr y
``` ``
``` ``
##
Š‹ Š‹Š‹
ˆ‰
f . Moreover, ;
zz œ œÊœ œ
Š‹
ˆ‰
df r df r r x r r
dr z dr z x x y
xyz xyz
yz y
xyz
`` ` ` `
`` ` ` `
#
ÈÈ
ˆ‰
È3
; and . Next, f f f 0Êœ œ Êœ œ
` ` `
```
rxz r z r
yzz
xyz xyz
xyz
xy xx yy zz
ˆ‰ ˆ‰
ÈÈ
È
3 3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 14 Additional and Advanced Exercises 877
Ê
Š‹Š ‹ Š‹Š ‹
ˆ‰ ˆ‰
Œ Œ
df x df df df x z
dr x y z dr dr x y z dr
yz y
xyz xyz
ˆ‰ ˆ‰
ÈÈ
3 3
0 0 0 œÊœÊœ
Š‹Š ‹ Š ‹
ˆ‰
Œ
df z df df 2 df df 2 df
dr x y z dr dr dr dr r dr
xy
xyz xyz
ˆ‰
ÈÈ
3
(f ) f , where f ln f 2 ln r ln C f Cr , orÊœ œÊœÊœÊœ
d 2 df df 2 dr
dr r dr f r
www w w#
ˆ‰
Cr f(r) b b for some constants a and b (setting a C)
df C a
dr r r
œÊœœ œ
#
5. (a) Let u tx, v ty, and w f(u v) f(u(t x) v(t y)) f(tx ty) t f(x y), where t, x, and y areœ œ œßœßßߜߜß
n
independent variables. Then nt f(x y) x y . Now,
n1 ßœœœ
````` ` `
````` ` `
wwuwv w w
tutvt u v
(t) (0) t . Likewise,
````` ` ` ` ` "`
````` ` ` ` ` `
wwuwv w w w w w
xuxvx u v u utx
œœ œÊœ
ˆ‰ ˆ‰ ˆ‰ˆ‰
(0) (t) . Therefore,
````` ` ` ` "`
````` ` ` ` `
wwuwv w w w w
yuyvy u v vty
œœ Êœ
ˆ‰ ˆ‰ ˆ‰
Š‹
nt f(x y) x y . When t 1, u x, v y, and w f(x y)
n1 ßœœ œœœ œß
`` ` `
`` ` `
wwxw w
uvtxty
y
ˆ‰ˆ ‰ ˆ‰
Š‹
and nf(x y) x y , as claimed.Êœ œÊ ßœ
`` `` ` `
`` `` ` `
wf wf f f
xx yx x y
(b) From part (a), nt f(x y) x y . Differentiating with respect to t again we obtain
n1 ߜ
``
``
ww
uv
n(n 1)t f(x y) x x y y x 2xy y .ßœœ
n2 `` `` `` `` ` ` `
`` ``` ``` `` ` `` `
##
wu wv wu wv w w w
ut vut uvt vt u uv v
Also from part (a), t t t t ,
``` `` ```` ````
``` `` ````` ````
#
ww wwuwvww w
xxx xu uxvux uyyy
œœ œ œ œ
ˆ‰ ˆ ‰ Š‹
t t t t , and t t t œ œ œ œœ œ
`` `` `` ` ` `` `` `` ``
` ` `` ` ` ` ` `` ` ` ` ` ` ` `` `
#
y v uv y v y v yx y x y u u y vu y
wwuwvww w wwuwv
ˆ‰ ˆ‰ ˆ‰
t , , and œÊ œ œ œ
#`"``"`` "``
`` ` ` ` ` `` ``
wwwww ww
vu t x u t y v t yx vu
ˆ‰ ˆ‰ ˆ‰
n(n 1)t f(x y) for t 0. When t 1, w f(x y) andÊ ßœ Á œ œß
n2 Š‹Š ‹ Š ‹Š‹Š ‹
ˆ‰
xw w w
tx tyx ty
2xy y
```
````
we have n(n 1)f(x y) x 2xy y as claimed.ߜ
##
```
````
Š‹ Š ‹ Š‹
fff
xxyy
6. (a) lim lim 1, where t 6r
r0 t0ÄÄ
sin 6r sin t
6r t
œœ œ
(b) f (0 0) lim lim lim lim
rßœ œ œ œ
h0 h0 h0 h0ÄÄÄÄ
f(0 h 0) f(0 0)
h h 6h 12h
1sin 6h 6h 6 cos 6h 6
ß ß
ˆ‰
sin 6h
6h
lim 0 (applying l'Hopital's rule twice)œœ s
h0Ä
36 sin 6h
12
(c) f (r ) lim lim lim 0ßœ œ œ œ)h0 h0 h0ÄÄÄ
f(r h) f(r )
hhh
0
ß ß
)) ˆ‰ˆ‰
sin 6r sin 6r
6r 6r
7. (a) x y z r x y z and rrijk r i j kœ Êœ œ œ œkk È###
™xz
xyz xyz xyz
y
r
ÈÈÈ r
(b) r x y z
nn
œ
ˆ‰
È###
r nxxyz nyxyz nzxyz nrÊ œ œ™abababab
nn2
n2 1 n2 1 n2 1
### ### ###
Ðijkr
(c) Let n 2 in part (b). Then r r x y z is the function.œœÊœÊœ
"""
####
## ###
™™ab a b
ˆ‰
rr
r
(d) d dx dy dz d x dx y dy z dz, and dr r dx r dy r dz dx dy dzrijkrrœ Ê œ œ œ †xyz
xz
rrr
y
r dr x dx y dy z dz dÊœœrr†
(e) a b c ax by cz ( ) a b cA i j k Ar Ar i j k Aœ Ê œ Ê œœ†™†
8. f(g(t) h(t)) c 0 , where is the tangent vectorߜʜœœ
df f dx f f f dx dx
dt x dt y dt x y dt dt dt dt
dy dy dy
`` ``
`` ``
Š‹Š‹
ij ij ij†
f is orthogonal to the tangent vectorÊ™
9. f(x y z) xz yz cos xy 1 f z y sin xy ( z x sin xy) (2xz y) f(0 0 1)ßß œ Ê œ Ê ßß œ
##
™™abijk ij
the tangent plane is x y 0; (ln t) (t ln t) t (ln t 1) ; x y 0, z 1ÊœœÊœœœœri jkri jk
w"
ˆ‰
t
t 1 (1) . Since ( ) ( ) r (1) f 0, is parallel to the plane, andÊ œ Ê œ œ œrijk ijkij r
ww
††™
(1) 0 0 is contained in the plane.rijkrœÊ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

878 Chapter 14 Partial Derivatives
10. Let f(x y z) x y z xyz f 3x yz 3y xz 3z xy f(0 1 1) 3 3ßßœ Ê œ Ê ßßœ
$$$ ###
™™abababijk ijk
the tangent plane is x 3y 3z 0; 2 3 (cos (t 2))Ê œ œ rij k
Š‹
ˆ‰
t4
4t
(sin (t 2)) ; x 0, y 1, z 1 t 2 (2) 3 . SinceÊ œ œ œ œÊœÊ œrij k rij
w w
Š‹ ˆ‰
3t 4
4t
(2) f 0 is parallel to the plane, and (2) is contained in the plane.rr rikr
w†™ œÊ œÊ
11. 3x 9y 0 and 3y 9x 0 y x and 3 x 9x 0 x 9x 0
`` """
``
####%
#
zz
xy 333
œ œ œ œÊœ œÊ œ
ˆ‰
x x 27 0 x 0 or x 3. Now x 0 y 0 or ( 0) and x 3 y 3 or (3 3). NextÊ œÊœ œ œÊœ !ß œÊœ ßab
$
6x, 6y, and 9. For ( 0), 81 no extremum (a saddle point),
`` ` ```
` ` `` ` ` ``
#
zz z zzz
x y xy x y xy
œœ œ!ß œÊ
Š‹
and for (3 3), 243 0 and 18 0 a local minimum.ßœœÊ
`` ` `
`` `` `
#
zz z z
xy xy x
Š‹
12. f(x y) 6xye f (x y) 6y(1 2x)e 0 and f (x y) 6x(1 3y)e 0 x 0 andßœ Êßœ œ ßœ œÊœ
Ð Ñ Ð Ñ Ð Ñ2x 3y 2x 3y 2x 3y
xy
y 0, or x and y . The value f(0 0) 0 is on the boundary, and f . On the positive y-axis,œœ œ ßœ ßœ
"" """
# #33e
ˆ‰2
f(0 y) 0, and on the positive x-axis, f(x 0) 0. As x or y we see that f(x y) 0. Thus the absoluteßœ ßœ Ä_ Ä_ ß Ä
maximum of f in the closed first quadrant is at the point .
"""
#e3
2ˆ‰
ß
13. Let f(x y z) 1 f an equation of the plane tangent at the pointßß œ Ê œ Ê
x z 2x 2z
abc a b c
y2y
™ijk
P (x y y ) is x y z 2 or x y z 1.
!!!!
ßß œ œ œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
2x 2z x z
abcabc abc
2y y
2x 2y 2z
The intercepts of the plane are 0 0 , 0 0 and . The volume of the tetrahedron formed by the
Š‹Š‹Š‹
ab c
xy z
ß ß ß ß !ß !ß
plane and the coordinate planes is V we need to maximize V(x y z) (xyz)œÊ ßßœ
ˆ‰ˆ‰
Š‹Š‹Š‹
""
#
"
3 xyz 6
abc (abc)
subject to the constraint f(x y z) 1. Thus, , ,ßßœœœœ
xz 2x
a b c 6 xyz a 6 xyz b
y (abc) (abc) 2y
’“Š‹ ’“Š‹
""
--
and . Multiply the first equation by a yz, the second by b xz, and the third by c xy. Then equate
’“Š‹
œ
(abc)
6 xyz c
2z
"## #
-
the first and second a y b x y x, x 0; equate the first and third a z c x z x, x 0;ʜʜ ʜʜ
## ## ## ##
b c
a a
substitute into f(x y z) 0 x y z V abc.ßߜʜʜʜʜ
abc
333
3
ÈÈÈ È
#
14. 2(x u) , 2(y v) , 2(x u) , and 2(y v) 2 v x u v y, x u , and œ œ œ œ Ê œ œ-- . . .
#
y v v x u v v or 0. œ Ê œ œ Ê œ œ.. .
.
##
"
CASE 1: 0 x u, y v, and 0; then y x 1 v u 1 and v u v v 1.-œÊœ œ œ œÊœ œÊœ
##
v v 1 0 v no real solution.ʜʜ Ê
#„
#
114
È
CASE 2: v and u v u ; x y and y x 1 x x 2x xœ œ Êœ œ œÊœÊ œÊœ
"""" """"
## #
#44 4 4 8
y . Then f 2 the minimum distance is 2.Ê œ ßßß œ œ Ê
77 73 3
88848488 8
ˆ ‰ˆ ‰ˆ‰ˆ‰ È
""" "" "
##
##
#
(Notice that f has no maximum value.)
15. Let (x y ) be any point in R. We must show lim f(x y) f(x y ) or, equivalently that
!! !!
ßßœß
Ðß ÑÄÐ ß Ñxy x y
lim f(x h y k) f(x y ) 0. Consider f(x h y k) f(x y )
Ðß ÑÄÐß Ñhk 00 kk
!! !! !! !!
ß ß œ ß ß
[f(x h y k) f(x y k)] [f(x y k) f(x y )]. Let F(x) f(x y k) and apply the Mean Valueœ ß ß ß ß œ ß
! ! !! !! !! !
Theorem: there exists with x x h such that F ( )h F(x h) F(x ) hf ( y k)00 0 0
!! ! ! !
w
œ Ê ß
x
f(x h y k) f(x y k). Similarly, k f (x ) f(x y k) f(x y ) for some withœßß ßœßß
!! !! ! !! !!y((
y y k. Then f(x h y k) f(x y ) hf ( y k) kf (x ) . If M, N are positive real
!! !! !! ! !
ß ß Ÿ ß ß(0(kkkkkk
xy
numbers such that f M and f N for all (x y) in the xy-plane, then f(x h y k) f(x y )kk kk k k
xy
ŸŸ ß ßß
!! !!
M h N k . As (h k) 0, f(x h y k) f(x y ) 0 lim f(x h y k) f(x y )Ÿ ßÄ ßßÄÊ ßßkkkkkkkk
!! !! !! !!
Ðß ÑÄÐß Ñhk 00
0 f is continuous at (x y ).œÊ ß
!!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 14 Additional and Advanced Exercises 879
16. At extreme values, f and are orthogonal because f 0 by the First Derivative Theorem for™™†vœœœ
ddfd
dt dt dt
rr
Local Extreme Values.
17. 0 f(x y) h(y) is a function of y only. Also, 0 g(x y) k(x) is a function of x only.
` `
```
`
f f
xyx
g
œÊ ßœ œ œÊ ßœ
Moreover, h (y) k (x) for all x and y. This can happen only if h (y) k (x) c is a constant.
`
``
`ww ww
f
yx
g
œÊ œ œ œ
Integration gives h(y) cy c and k(x) cx c , where c and c are constants. Therefore f(x y) cy cœ œ ßœ
"#"# "
and g(x y) cx c . Then f(1 2) g(1 2) 5 5 2c c c c , and f(0 0) 4 c 4 cßœ ßœ ߜʜ œ ßœÊ œÊœ
#"#"
"
#
c . Thus, f(x y) y 4 and g(x y) x .ʜ ߜ ߜ
### ##
""99
18. Let g(x y) D f(x y) f (x y)a f (x y)b. Then D g(x y) g (x y)a g (x y)bßœ ßœ ß ß ßœ ß ß
uuxy x y
f (x y)a f (x y)ab f (x y)ba f (x y)b f (x y)a 2f (x y)ab f (x y)b .œßß ß ß œß ß ß
xx yx xy yy xx xy yy
####
19. Since the particle is heat-seeking, at each point (x y) it moves in the direction of maximal temperatureß
increase, that is in the direction of T(x y) e sin x 2e cos x . Since T(x y) is parallel to™™ßœ ßaba b
2y 2y
ij
the particle's velocity vector, it is tangent to the path y f(x) of the particle f (x) 2 cot x.œÊœœ
w2e cos x
e sin x
2y
2y
Integration gives f(x) 2 ln sin x C and f 0 0 2 ln sin C C 2 ln lnœ œÊœ Êœœkk ˆ‰ ¸ ¸ Š‹
11
44
22
2
ÈÈ
#
#
ln 2. Therefore, the path of the particle is the graph of y 2 ln sin x ln 2.œœkk
20. The line of travel is x t, y t, z 30 5t, and the bullet hits the surface z 2x 3y whenœœœ œ
##
30 5t 2t 3t t t 6 0 (t 3)(t 2) 0 t 2 (since t 0). Thus the bullet hits theœ Ê œÊ œÊœ
## #
surface at the point (2 2 20). Now, the vector 4x 6y is normal to the surface at any (x y z), so thatßß ßßijk
8 12 is normal to the surface at (2 2 20). If 5 , then the velocity of the particleni jk vijkœ ßß œ
after the ricochet is 2 proj ( 5 )wv vv nv n ij k i j kœ œ œ œ
nŠ‹ ˆ‰ ˆ ‰
2 2 25 400 600 50
209 209 209 209
vn
n
††
kk
.œ
191 391 995
209 209 209
ijk
21. (a) is a vector normal to z 10 x y at the point ( 0 10). So directions tangential to S at ( 0 10) willkœ !ß ß !ß ß
##
be unit vectors a b . Also, T(x y z) (2xy 4) x 2yz 14 y 1uij i j kœ ßßœ ™abab
##
T( 0 10) 4 14 . We seek the unit vector a b such that D T(0 0 10)Ê!ßßœ œ ßß™ijk uij u
(4 14 ) (a b ) (4 14 ) (a b ) is a maximum. The maximum will occur when a bœ œ ijkij ijij ij††
has the same direction as 4 14 , or (2 7 ).iju ijœ
"
È53
(b) A vector normal to S at (1 1 8) is 2 2 . Now, T(1 1 8) 6 31 2 and we seek the unitßß œ ßßœ nijk i jk™
vector such that D T(1 1 8) T has its largest value. Now write T , where is paralleluu vwv
ußß œ œ ™† ™
to T and is orthogonal to T. Then D T T ( ) . Thus™™™†††††w u vwuvuwuwu
uœœœœ
D T(1 1 8) is a maximum when has the same direction as . Now, T
ußß œ uwwn™Š‹
™†Tn
nkk
(6 31 2 ) (2 2 ) 6 31 2œ œ ijk ijk i j k
ˆ‰ ˆ‰ˆ‰ˆ‰
12 62 2 152 152 76
441 9 9 9
(98 127 58 ).œ Ê œ œ
98 127 58
999 29,097
ijku ijk
w
wkk È"
22. Suppose the surface (boundary) of the mineral deposit is the graph of z f(x y) (where the z-axis points up into the air).ϧ
Then is an outer normal to the mineral deposit at (x y) and points in the direction of steepest ß
`` ``
`` ``
ff ff
xy xy
ijk ij
ascent of the mineral deposit. This is in the direction of the vector at (0 0) (the location of the 1st borehole)
``
``
ff
xy
ijß
that the geologists should drill their fourth borehole. To approximate this vector we use the fact that (0 0 1000),ßß
(0 100 950), and (100 1025) lie on the graph of z f(x y). The plane containing these three points is a goodß ß ß !ß œ ß
approximation to the tangent plane to z f(x y) at the point (0 0 0). A normal to this plane is 00050
00 0 25
œß ßß "
"
ââ
ââ
ââ
ââ
ââ
ââ
ijk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

880 Chapter 14 Partial Derivatives
2500 5000 10,000 , or 2 4 . So at (0 0) the vector is approximately 2 . Thus theœ ß ij kijk ij ij
``
``
ff
xy
geologists should drill their fourth borehole in the direction of ( 2 ) from the first borehole.
"
È5ij
23. w e sin x w re sin x and w e cos x w e sin x; w w , where c is theœÊœ œ Êœ œ
rt rt rt rt
t x xx xx t
c
111111
##
"
positive constant determined by the material of the rod e sin x re sin xÊ œ11 1
#"
rt rt
cab
r c e sin x 0 r c w e sin xÊ œÊœ Êœab
## ##
11 1 1
rt c t1
24. w e sin kx w re sin kx and w ke cos kx w k e sin kx; w wœÊœ œ Êœ œ
rt rt rt rt
t x xx xx t
c
#"
k e sin kx re sin kx r c k e sin kx 0 r c k w e sin kx.Ê œ Ê œ Ê œ Ê œ
#####
"
rt rt rt c k t
cabab
Now, w(L t) 0 e sin kL 0 kL n for n an integer k w e sin x .ßœ Ê œ Ê œ Ê œ Ê œ
Îckt cn tL
nn
LL
111
1ˆ‰
As t , w 0 since sin x 1 and e 0.Ä_ Ä Ÿ Ä
¸¸ˆ‰
n
L
cn tL
11Î
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

CHAPTER 15 MULTIPLE INTEGRALS
15.1 DOUBLE AND ITERATED INTEGRALS OVER RECTANGLES
1. 2xy dy dx x y dx 16x dx 8 x 24
'' ' '
10 1 1
24 2 2
42
01
œœœœcd cd
##
2. x y dy dx xy y dx 2x dx x 4
'' ' '
01 0 0
21 2 2 2
0
ab cd
‘
œ œ œœ
1
2##
"
"
3. (x y 1) dx dy yx x dy (2y 2) dy y 2y 1
'' ' '
11 1 1
01 0 0
œ œ œ œ
’“ cd
x
2
"
" "
#!
4. 1 dx dy x dy dy y
'' ' '
00 0 0
11 1 1
Š‹ ’ “Š‹’“
œœœœ
xy xy y y
26262663
x552
33
"
00
1
5. 4 y dy dx 4y dx dx x 16
'' ' '
00 0 0
32 3 3
ab ’“ ‘
œœœœ
#y
333
16 16
#
!
3
0
6. x y 2xy dy dx xy dx 4x 2x dx 2x 0
'' ' '
02 0 0
30 3 3
ab ab
’“ ’“
####
œœœœ
xy
23
2x
!
# !
3
7. dx dy ln 1 x y dy ln 1 y dy y ln 1 y y ln 1 y 2 ln 2 1
'' ' '
00 0 0
11 1 1
y
1xy 0
"
œ l l œ ll œ ll ll œ cd c d
1
0
8. y dx dy x x y dy 4 4 y dy 4y y
'' ' '
10 1 1
44 4 4
4
ˆ‰ ‘ ˆ ‰ ‘
ÈÈ
x1 892
24 33
21/23/2
œœœœ
4
1
9. e dy dx e dx 5e e dx e e 5 e
'' ' '
01 0 0
ln 2 ln 5 ln 2 ln 2 ln 2
2x y 2x y 2x 2x 1 2x 2x 1
53
22
"
#
œœœœcd a b ab
‘
ln 5
0
"
10. x y e dy dx x y e dx x e dx x e e
'' ' '
01 0 0
12 1 1
x2xxxx
3333
2222
œœœœ
‘ ‘
"
#
21
0
"
11. y sin x dx dy y cos x dy y dy y
'' ' '
10 1 1
22 2 2
0
2
1
2
œ œ œ œcd ‘
"
#
23
2
12. sin x cos y dx dy cos x x cos y dy 2 cos y dy 2y sin y 2
'' ' '
222
00
2
abc dabcdœœœœ111
13. 6 y 2 x dA 6 y 2 x dy dx 2 y 2 x y dx 16 4 x dx 16 x 2 x 14
''
Rab ab c dabc d
##
œ œ œœœ
'' ' '
00 0 0
12 1 1
00
21
32
14. dA dy dx dx x dx x
''
R
ÈÈ È
xx x
yy y 33
12 32
18
22
œœœœœ
'' ' '
01 0 0
42 4 4
1
2
0
4
’“ ‘
"
#
ÎÎ
15. x y cos y dA x y cos y dy dx x y sin y x cos y dx 2x dx x 0
''
R
œœœœœ
'' ' '
10 1 1
11 1
01
1
cdabcd
2
16. y sin x y dA y sin x y dy dx y cos x y sin x y dx
''
Rab ab c dababœ œ
'' '
00
00
sin x cos x sin x dx cos x sin x cos x 4œœœ
'00
abc dab ab ab ab11 1 11 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

882 Chapter 15 Multiple Integrals
17. e dA e dy dx e dx e e dx e e
''
R
xy xy xy x x x x
"
#
œœœœœ
'' ' '
00 0 0
ln 2 ln 2 ln 2 ln 2
0 0
ln 2 ln 2 ln 2 ln 2
cd a bc d
18. x y e dA x y e dy dx e dx e dx e x e 3
''
R
xy xy xy x x 2
222
œœœœœ
'' ' '
00 0 0
21 2 2
0
1
0
2
’“ ˆ‰ ‘
ab
""""""
######
19. dA dy dx dx dx 2 ln x 1 2 ln 2
''
R
xy xy xy
x1 x1 4x1 x1
4x 2
33 4
22 22
œœœœllœ
'' ' '
00 0 0
12 1 1
0
2
0
1
’“ cd
ab
20. dA dx dy tan x y dy tan y dy y tan y ln 1 y ln 2
''
R
yy
xy 1 4
xy 1
1112
22 2
##
""
œœœœllœ
'' ' '
00 0 0
11 1 1
0
1
0
1
ab cdab ‘
1
21. dy dx (ln 2 ln 1) dx (ln 2) dx (ln 2)
'' ' '
11 1 1
22 2 2
1
xy x x
œœ œ
""
#
22. y cos xy dx dy sin xy dy sin y dy cos y ( 1 1)
'' ' '
00 0 0
111
œœœœœcd ‘
1
111
!""
"
!
11 2
23. V f x, y dA x y dy dx x y y dx 2 x dx x xœœœœœœ
''
Rab a b ‘ ˆ‰‘
'' ' '
11 1 1
11 1 1
22 2 3 2 3
12228
33333
11
""
24. V f x, y dA 16 x y dy dx 16 y x y y dx 2 x dx x xœœœœœ
''
Rab a b ‘ˆ‰‘
'' ' '
00 0 0
22 2 2
00
22
22 2 3 2 3
188 882
33 33
œ160
3
25 V f x, y dA 2 x y dy dx 2 y x y y dx x dx x x 1Þœ œ œ œ œ œ
''
Rab a b ‘ˆ‰‘
'' ' '
00 0 0
11 1 1
""
##
"
!!
"
22
33
22
26 V f x, y dA dy dx dx 1 dx x 4Þœ œ œ œ œ œ
''
Rab cd
’“
'' ' '
00 0 0
42 4 4
0
2
0
4
yy
24
2
27 V f x,y dA 2sinxcosydydx 2sinxsiny dx 2sinx dx 2cosxÞœ œ œ œ œ
''
Rab c d Š‹’ “
ÈÈ
'' ' '
00 0 0
24 2 2
0
4
0
2
2œÈ
28. V f x, y dA 4 y dy dx 4 y y dx dx xœœœœœœ
''
Rab a b ‘ ˆ‰‘
'' ' '
00 0 0
12 1 1
0
2
23
1161616
3333
"
!
15.2 DOUBLE INTEGRALS OVER GENERAL REGIONS
1. 2.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
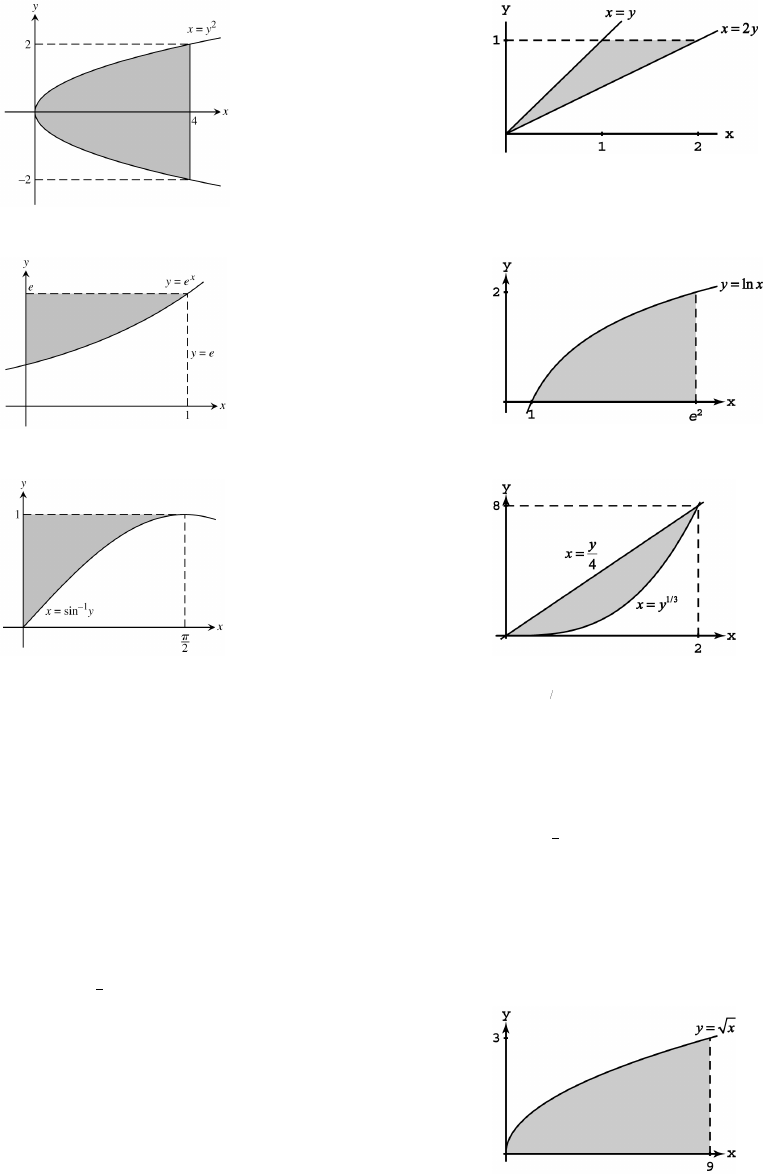
Section 15.2 Double Integrals Over General Regions 883
3. 4.
5. 6.
7. 8.
9. (a) dy dx
''
!
#
x
8
3(b) dx dy
''
!
8y
0
13
10. (a) dy dx
''
!
32x
0(b) dx dy
''
!Î
63
y2
11. (a) dy dx
''
!
33x
x2(b) dx dy
''
!Î
9y
y3
È
12. (a) dy dx
''
!
#
1
ex
(b) dx dy
''
1lny
e2
2
13. (a) dy dx
''
!
9x
0
È
(b) dx dy
''
0y
39
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
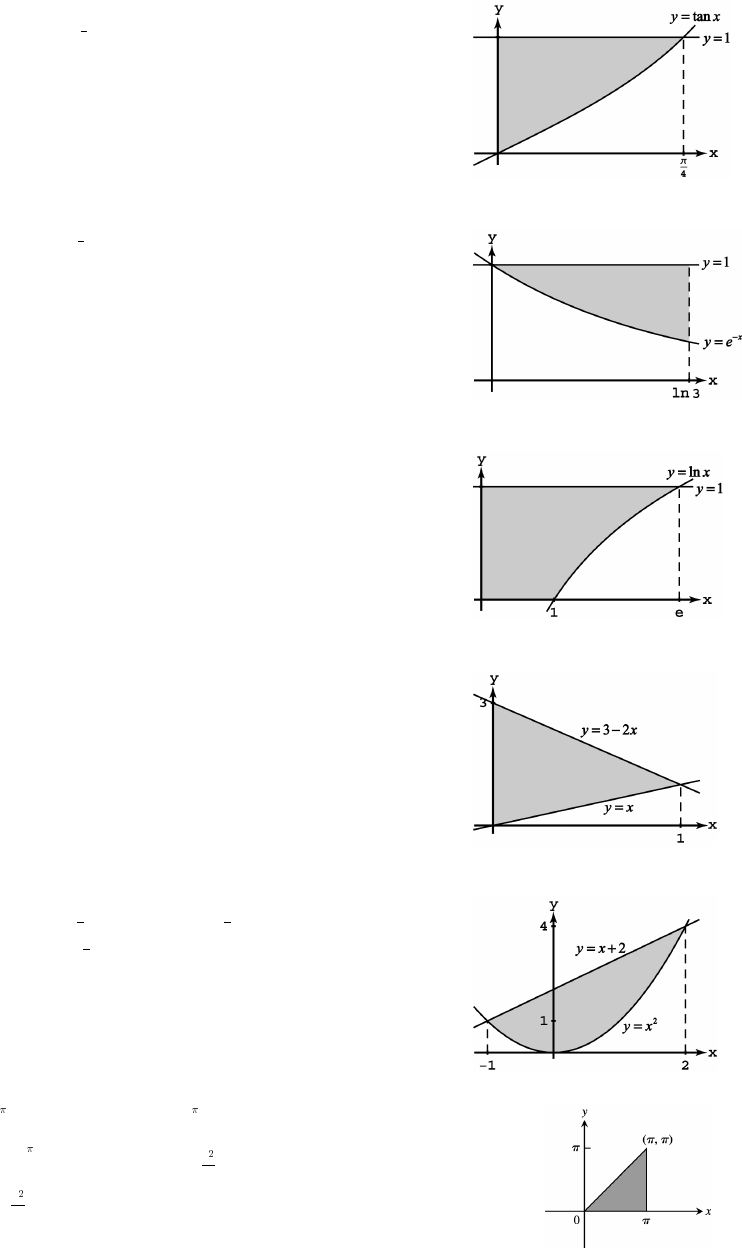
884 Chapter 15 Multiple Integrals
14. (a) dy dx
''
!
Î141
tan x
(b) dx dy
''
00
1tany
1
15. (a) dy dx
''
!
ln 3 1
ex
(b) dx dy
''
13 lny
1ln3
Î
16. (a) dy dx dy dx
'' ''
!
11 e1
01lnx
(b) dx dy
''
00
1e
y
17. (a) dy dx
''
!
132x
x
(b) dx dy dx dy
'' ''
00 10
1y 3 3y2
abÎ
18. (a) dy dx
''
1x
2x2
2
(b) dx dy dx dy
'' ''
0y 1y2
1y 3y
È
ÈÈ
19. (x sin y) dy dx x cos y dx
'' '
00 0
xx
œcd
!
(x x cos x) dx (cos x x sin x)œ œ
'0’“
x
2
1
!
2œ
1
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.2 Double Integrals Over General Regions 885
20. y dy dx dx sin x dx
'' ' '
00 0 0
sin x sin x
œœ
’“
y
2!
"
#
#
(1 cos 2x) dx x sin 2xœ œ œ
"""
!
4424
'0‘
11
21. e dx dy e dy ye e dy
'' ' '
10 1 1
ln 8 ln y ln 8 ln 8
xy xy y y
ln y
œœcd a b
!
(y 1)e e 8(ln 8 1) 8 eœ œ cd
yy
ln 8
1
8 ln 816eœ
22. dx dy y y dy
'' '
1y 1
2y 2
œœab’“
#
#
#
"
yy
3
2œ œœ
ˆ‰ˆ‰
8735
3336
""
##
23. 3y e dx dy 3y e dy
'' '
00 0
11
0
yy
$#xy xy
œcd
3y e 3y dy e y e 2œœœ
'0
1Š‹’“
## $
"
!
yy
24. e dy dx x e dx
'' '
10 1
4x 4
yx yx x
0
33
2#œ‘
ÈÈ
(e 1) x dx (e 1) x 7(e 1)œ œ œ
332
23#
$Î# %
"
'1
4È‘ˆ‰
25. dy dx x ln y dx (ln 2) x dx ln 2
'' ' '
1x 1 1
22x 2 2
2x
x
x3
yœœœcd #
26. x y dy dx x y dx x (1 x) dx x x dx
'' ' ' '
00 0 0 0
11x 1 1 1
x
0
ab ’“ ’ “ ’ “
## # # #$
œœ œ
y (1x) (1x)
333
000œ œ œ
’“
ˆ‰ˆ‰
xx
34 1 34 1 6
(1 x)
##
"
!
"" " "
27. v u dv du v u du u(1 u) du
'' ' '
00 0 0
11u 1 1
u
0
ˆ‰
ÈÈ È
’“ ’ “
œ œ
v12uu
2
#
uuu du uuœ œ œœœ
'0
1Š‹’ “
"""" " "
## # ## #
"Î# $Î# $Î# &Î# "
!
u uuu2 2 22 2
2 6 3 5 635 5 10
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
886 Chapter 15 Multiple Integrals
28. e ln t ds dt e ln t dt (t ln t ln t) dt ln t t ln t t
'' ' '
10 1 1
2lnt 2 2
ln t
0
ss tt
24
œœœcd ’“
#
"
(2 ln 212 ln 22) 1œœ
ˆ‰
""
44
29. 2 dp dv 2 p dv 2 2v dv
'' ' '
2v 2 2
0v 0 0
v
v
œœcd
2v 8œ œcd
#0
2
30. 8t dt ds 4t ds
'' '
00 0
11s 1 1s
0
œcd
#
41 s ds 4sœœœ
'0
1ab ’“
#"
!
s8
33
31. 3 cos t du dt (3 cos t)u
'' '
30 3
3sect 3 sec t
0
œcd
3 dt 2œœ
'3
3
1
32. dv du du
'' '
01 0
32 4 2u 32 42u
1
42u 2u4
vv
œ‘
3 2u du 3u uœœœ
'0
32 2
abc d
#$
!
9
2
33. dx dy
''
20
44y)2
34. dy dx
''
20
0x2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.2 Double Integrals Over General Regions 887
35. dy dx
''
0x
1x
36. dx dy
''
01y
11y
37. dx dy
''
1lny
e1
38. dy dx
''
10
2lnx
39. 16x dx dy
''
00
99y
1
2
40. y dy dx
''
00
44x
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
888 Chapter 15 Multiple Integrals
41. 3y dy dx
''
10
11x
42. 6x dx dy
''
20
24y
43. x y dx dy
''
0e
1e
y
44. x y dx dy
''
00
12 sin y 2
Î1
45. x y dy dx
''
1lnx
e3
3ab
46. x y dy dx
''
0tanx
331ÎÈÈ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
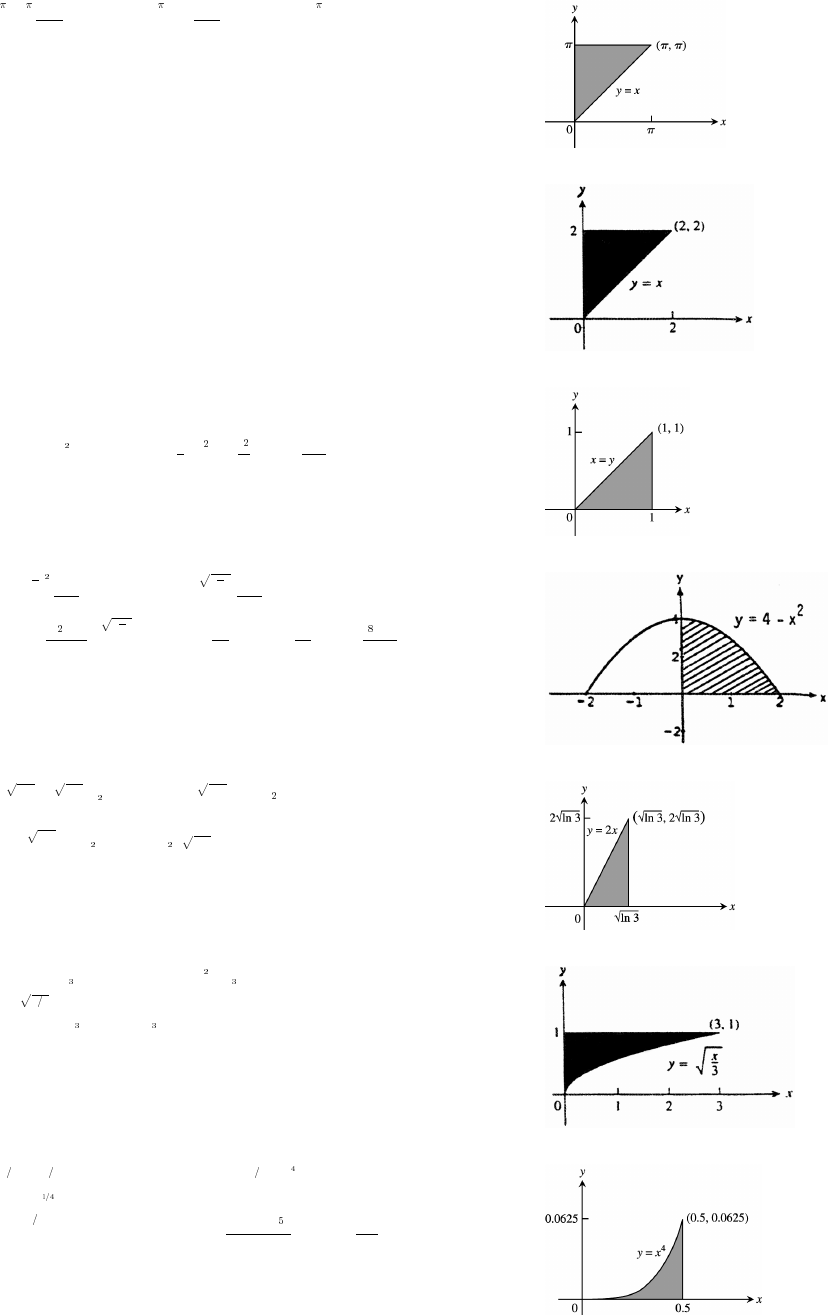
Section 15.2 Double Integrals Over General Regions 889
47. dy dx dx dy sin y dy 2
'' '' '
0x 00 0
y
sin y sin y
yy
œœœ
48. 2y sin xy dy dx 2y sin xy dx dy
'' ''
0x 00
22 2y
##
œ
2y cos xy dy 2y cos y 2y dyœ œ
''
00
22
y
0
cda b
#
sin y y 4 sin 4œ œ cd
##
#
!
49. x e dx dy x e dy dx xe dx
'' '' '
0y 00 0
11 1x 1
xy xy xy x
0
##
œœ cd
xe x dx eœœœ
'0
1xx
ab
’“
"
##
"
!
2
xe2
50. dy dx dx dy
'' ''
00 00
24x 4 4y
xe xe
4y 4y
2y 2y
œ
dy dyœœœœ
''
00
44
4y
0
’“ ’“
xe e e e
(4 y) 4 4
2y 2y 2y
# #
%
!
"
51. e dx dy e dy dx
'' ''
0y/2 00
2 ln 3 ln 3 ln 3 2x
xx
œ
2xe dx e e 1 2œœœœ
'0
ln 3 xx ln3
ln 3
0
cd
52. e dy dx e dx dy
'' ''
0x3 00
31 13y
yy
œ
3y e dy e e 1œœœ
'0
1yy
#"
!
cd
53. cos 16 x dx dy cos 16 x dy dx
'' ''
0y 00
11612 12x
ab ab11
&&
œ
x cos 16 x dxœœœ
'0
12 %& "Î#
!
"
ab’“
1sin 16 x
80 80
ab1
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
890 Chapter 15 Multiple Integrals
54. dy dx dx dy
'' ''
0x 00
82 2y
""
y1 y1
œ
dy ln y 1œœœ
'0
2y
y1 44
ln 17
"%#
!
cdab
55. y 2x dA
''
Rab#
y 2x dy dx y 2x dy dxœ
'' ''
1x1 0x1
0x1 11x
ab ab
##
y 2x y dx y 2x y dxœ
''
10
01
x1x
x1 x1
‘ ‘
""
## ##
22
(x 1) 2x (x 1) ( x 1) 2x ( x 1) dxœ
'1
0‘
""
##
## ##
(1 x) 2x (1 x) (x 1) 2x (x 1) dx
'0
1‘
""
##
## ##
4 x x dx 4 x x dxœ
''
10
01
ab ab
$# $#
444 48œ œ œ œ œ
’“’“’ “
ˆ‰ˆ ‰
xx xx 34 8 2
4 3 4 3 4 3 4 3 12 12 12 3
(1) (1)
0
1
"
!
""
56. xy dA xy dy dx xy dy dx
''
R
œ
'' ''
0x 23x
23 2x 1 2 x
xy dx xy dxœ
''
023
23 1
2x 2 x
xx
‘ ‘
""
##
22
2x x dx x(2 x) x dxœ
''
023
23 1
ˆ‰ ‘
$$ #$
"""
###
x dx 2x x dxœ
''
023
23 1
3
#
$#
ab
xxx 1œœ œœ
‘ ‘ ˆ‰ˆ‰ˆ ‰ ‘ ˆ ‰ˆ‰ˆ ‰
3 2 3 16 2 4 2 8 6 27 36 16 13
8 3 8 81 3 9 3 27 81 81 81 81 81
%#$
"
#Î$
23
0
57. V x y dy dx x y dx 2x dxœœœœ
'' ' '
0x 0 0
12x 1 1
2x
x
ab ’“ ’ “’ “
## # #
"
!
y (2x) (2x)
3 3 3 3 12 12
7x 2x 7x
00œ œ
ˆ‰ˆ‰
27 16 4
31212 12 3
"
58. V x dy dx x y dx 2x x x dx x x xœœœœ
'' ' '
2x 2 2
12x 1 1
2x
x
# # #%$ $ & %
"
#
cd a b ‘
211
354
œœ œœ
ˆ‰ˆ ‰ˆ ‰ˆ ‰
2 16 32 16 40 12 15 320 384 240 189 63
3 5 4 3 5 4 60 60 60 60 60 60 60 20
""
59. V (x 4) dy dx xy 4y dx x 4 x 4 4 x 3x 12x dxœœœ
'' ' '
43x 4 4
14x 1 1
4x
3x
cd c dabab
###
x 7x 8x 16 dx x x 4x 16x 12 64œ œ œœœ
'4
1ab
‘ˆ‰ˆ‰
$# % $# "
%
""1 7 7 64 157 625
43 43 3 3412
60. V (3 y) dy dx 3y dx 3 4 x dxœœœ
'' ' '
00 0 0
24x 2 2
4x
0
’“ ’ “
ÈŠ‹
y
2
4x
#
#
x4 x 6 sin 2x 6 4 3œ œœœ
’“
Ȉ‰ ˆ‰
3xx81698
26663
#"
##
#
!
11
1
61. V 4 y dx dy 4x y x dy 12 3y dy 12y y 24 8 16œ œœœœœ
'' ' '
00 0 0
23 2 2
ab cd abcd
## #$
$
!!
#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.2 Double Integrals Over General Regions 891
62. V 4 x y dy dx 4 x y dx 4 x dx 8 4x dxœœœœ
'' ' ' '
00 0 0 0
24x 2 2 2
4x
a b ab ab
’“ Š‹
## ##
"
##
#
y
2
x
8x x x 16œ œœ œ
‘
4 32 32 480 320 96 128
3 10 3 10 30 15
$&
"
#
!
63. V 12 3y dy dx 12y y dx 24 12x (2 x) dx 24x 6x 20œœœœœ
'' ' '
00 0 0
22x 2 2
ab cd c d
’“
#$ $#
#
!
#
!
x(2 x)
4
64. V (3 3x) dy dx (3 3x) dy dx 6 1 x dx 6 (1 x) dx 4 2 6œ œ œœ
'' '' ' '
1x1 0x1 1 0
0x1 11x 0 1
ab
##
65. V (x 1) dy dx xy y dx 1 1 dx 2 1 dx 2 x ln xœœœœœ
'' ' ' '
11x 1 1 1
21x 2 2 2
1x
1x
cd c d
‘ˆ‰ˆ‰
"" " #
"
xx x
2(1 ln 2)œ
66. V 4 1 y dy dx 4 y dx 4 sec x dxœœœ
'' ' '
00 0 0
3 sec x 3 3
sec x
0
ab ’“ Š ‹
#y
33
sec x
7 ln sec x tan x sec x tan x 7 ln 2 3 2 3œ œ
22
33
cdkk ’“Š‹
ÈÈ
1Î$
!
67.
68.
69. dy dx dx dx lim lim 1 1
'' ' '
1e 1 1
1
e
b
1
xx
"""
"
xy x x x b
ln y x
œœœœœ
’“ ˆ‰ ‘ ˆ ‰
bbÄ_ Ä_
70. (2y 1) dy dx y y dx dx 4 lim sin x
'' ' '
11/1x 1 1
11/1x 1 1
1/ 1 x
1/ 1 x
b
œ œ œcd cd
º
#"
!
1
1
2
1x
Èb1Ä
4 lim sin b 0 2œœ
b1Äcd
" 1
71. -dx dy 2 lim tan b tan 0 dy 2 lim dy
'' ' '
" "
" "
ababx1y1 y1 y1
2
œœ
0 0
b
Š‹Š ‹
bbÄ_ Ä_
1
2 lim tan b tan 0 (2 )œœœ111
Š‹
ˆ‰
bÄ_
" " #
#
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

892 Chapter 15 Multiple Integrals
72. xe dx dy e lim xe e dy e lim be e 1 dy
'' ' '
00 0 0
x2y 2y x x 2y b b
b
0
œœ
bbÄ_ Ä_
cd a b
e dy lim e 1œœœ
'0
2y 2b
""
##
bÄ_ ab
73. f(x y) dA f 0 f(0 0) f 0 0
''
R
߸ßßßœœ
"" " "" """ "
##488448432
3
ˆ‰ ˆ‰ˆ‰ˆ‰
74. f(x y) dA ffff (29313335)8
''
R
ß ¸ ß ß ß ß œ œœ
""
44444444416 16
7 11 9 11 7 13 9 13 128
’“
ˆ‰ˆ‰ˆ‰ˆ‰
75. The ray meets the circle x y 4 at the point 3 1 the ray is represented by the line y . Thus,)œœßÊ œ
1
6
x
3
## Š‹
ÈÈ
f(x y) dA 4 x dy dx 4 x 4 x dx 4x
''
R
ßœ œ œ œ
'' '
0x3 0
34x 3
3
3
0
ÈÈ
’“
ab ”•
##
#
xx
39
4x
33
20 3
ab
ÈÈ
76. dy dx dx dx 6
'' ' ' '
20 2 2 2
22
0
"
ab ab
xx(y1)
3(y 1)
xx xx xx x(x1)
33 dx
œœœ
’“ ˆ‰
6 lim dx 6 lim ln (x 1) ln x 6 lim [ln (b 1) ln b ln 1 ln 2]œ œ œ
bb bÄ_ Ä_ Ä_
'2
bb
2
ˆ‰ cd
""
x1 x
6 lim ln 1 ln 2 6 ln 2œœ
’“
ˆ‰
bÄ_
"
b
77. V x y dy dx x y dxœœ
'' '
0x 0
12x 1 2x
x
ab ’“
## # y
3
2x dxœ œ
'0
1’“’“
#
"
!
7x 2x 7x
33 31212
(2 x) (2 x)
00œ œ
ˆ‰ˆ‰
27 16 4
3121 12 3
"
#
78. tan x tan x dx dy dx dx dy dx dy
'''''''
00x0y2y
22x2y22
ab
" " "" "
1œ œ
1y 1y 1y
dy dy ln 1 y 2 tan y ln 1 yœœ
''
02
22 2
2
ˆ‰ ˆ‰
1y 2
1y 1y 2
#
#
" "
#" #
!
yˆ‰ ‘
cd abab
1
11
ln 5 2 tan 2 ln 1 4 2 tan 2 ln 5œ
ˆ‰ ab
1
11 1
" "
" # "
#
1
22
11
2 tan 2 2 tan 2 ln 1 4œ
" " #
"
#
11
2
ln 5
1ab
79. To maximize the integral, we want the domain to include all points where the integrand is positive and to
exclude all points where the integrand is negative. These criteria are met by the points (x y) such thatß
4 x 2y 0 or x 2y 4, which is the ellipse x 2y 4 together with its interior. Ÿ œ
## ## ##
80. To minimize the integral, we want the domain to include all points where the integrand is negative and to
exclude all points where the integrand is positive. These criteria are met by the points (x y) such thatß
x y 9 0 or x y 9, which is the closed disk of radius 3 centered at the origin.
## ##
Ÿ Ÿ
81. No, it is not possible. By Fubini's theorem, the two orders of integration must give the same result.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.2 Double Integrals Over General Regions 893
82. One way would be to partition R into two triangles with the
line y 1. The integral of f over R could then be writtenœ
as a sum of integrals that could be evaluated by integrating
first with respect to x and then with respect to y:
f(x y) dA
''
R
ß
f(x y) dx dy f(x y) dx dy.œßß
'' ''
022y 1y1
12y2 22y2
Partitioning R with the line x 1 would let us write theœ
integral of f over R as a sum of iterated integrals with
order dy dx.
83. e dx dy e e dx dy e e dx dy e dx e dy
'' '' ' ' ' '
bb bb b b b b
bb bb b b b b
xy y x y x x y
œœ œ
ŒŒŒ
e dx 2 e dx 4 e dx ; taking limits as b gives the stated result.œœ œ Ä_
ŒŒ Œ
'''
b0 0
bbb
xxx
###
84. dy dx dx dy dy
'' '' ' '
00 00 0 0
13 31 3 3
xx x
(y 1) (y 1) (y 1) (y 1)
33
dy
""
"
!
œœœ
’“
lim lim lim (y 1) lim (y 1)œ œ
""
"Î$ "Î$
33
dy dy
(y 1) (y 1)
b1 b1
b1 b1
ÄÄ
ÄÄ
''
0b
b3 b3
0b
‘ ‘
lim (b 1) ( 1) lim (b 1) (2) (0 1) 0 2 1 2œœœ
’“’“Š‹
ÈÈ
b1 b1
ÄÄ
"Î$ "Î$ "Î$ "Î$ 33
85-88. Example CAS commands:
:Maple
f := (x,y) -> 1/x/y;
q1 := Int( Int( f(x,y), y=1..x ), x=1..3 );
evalf( q1 );
value( q1 );
evalf( value(q1) );
89-94. Example CAS commands:
:Maple
f := (x,y) -> exp(x^2);
c,d := 0,1;
g1 := y ->2*y;
g2 := y -> 4;
q5 := Int( Int( f(x,y), x=g1(y)..g2(y) ), y=c..d );
value( q5 );
plot3d( 0, x=g1(y)..g2(y), y=c..d, color=pink, style=patchnogrid, axes=boxed, orientation=[-90,0],
scaling=constrained, title="#89 (Section 15.2)" );
r5 := Int( Int( f(x,y), y=0..x/2 ), x=0..2 ) + Int( Int( f(x,y), y=0..1 ), x=2..4 );
value( r5);
value( q5-r5 );
85-94. Example CAS commands:
: (functions and bounds will vary)Mathematica
You can integrate using the built-in integral signs or with the command . In the command, theIntegrate Integrate
integration begins with the variable on the right. (In this case, y going from 1 to x).
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
894 Chapter 15 Multiple Integrals
Clear[x, y, f]
f[x_, y_]:= 1 / (x y)
Integrate[f[x, y], {x, 1, 3}, {y, 1, x}]
To reverse the order of integration, it is best to first plot the region over which the integration extends. This can be done
with ImplicitPlot and all bounds involving both x and y can be plotted. A graphics package must be loaded. Remember to
use the double equal sign for the equations of the bounding curves.
Clear[x, y, f]
<<Graphics`ImplicitPlot`
ImplicitPlot[{x==2y, x==4, y==0, y==1},{x, 0, 4.1}, {y, 0, 1.1}];
f[x_, y_]:=Exp[x ]
2
Integrate[f[x, y], {x, 0, 2}, {y, 0, x/2}] Integrate[f[x, y], {x, 2, 4}, {y, 0, 1}]
To get a numerical value for the result, use the numerical integrator, . Verify that this equals the original.NIntegrate
Integrate[f[x, y], {x, 0, 2}, {y, 0, x/2}] NIntegrate[f[x, y], {x, 2, 4}, {y, 0, 1}]
NIntegrate[f[x, y], {y, 0, 1},{x, 2y, 4}]
Another way to show a region is with the FilledPlot command. This assumes that functions are given as y = f(x).
Clear[x, y, f]
<<Graphics`FilledPlot`
FilledPlot[{x , 9},{x, 0,3}, AxesLabels {x, y}];
2Ä
f[x_, y_]:= x Cos[y ]
2
Integrate[f[x, y], {y, 0, 9}, {x, 0, Sqrt[y]}]
85. dy dx 0.603 86. e dy dx 0.558
'' ''
11 00
3x 11 xy
"
xy ¸¸
87. tan xy dy dx 0.233 88. 3 1 x y dy dx 3.142
'' ''
00 10
11 11x
" ##
¸¸
È
89. Evaluate the integrals:
e dx dy
''
02y
14
x
e dy dx e dy dxœ
'' ''
00 20
2x/2 41
xx
e 2 erfi 2 2 erfi 4œ
""
44
4
ˆ‰ÈÈ
ab ab11
1.1494 10¸‚
6
The following graph was generated using
Mathematica.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.2 Double Integrals Over General Regions 895
90. Evaluate the integrals:
x cos y dy dx x cos y dx dy
'' ''
0x 00
39 9 y
22
2ab abœ
0.157472œ¸
sin 81
4
ab
The following graph was generated using
Mathematica.
91. Evaluate the integrals:
x y xy dx dy x y xy dy dx
'' ''
0y 0x/32
242y 8 x
22 22
32
3
ab abœ
97.4315œ¸
67,520
693
The following graph was generated using
Mathematica.
92. Evaluate the integrals:
e dx dy e dy dx
'' ''
00 00
24y 4 4x
xy xy
œ
20.5648¸
The following graph was generated using
Mathematica.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
896 Chapter 15 Multiple Integrals
93. Evaluate the integrals:
dy dx
''
10
2x
1
xy
dx dy dx dyœ
'' ''
01 1 y
12 42
11
xy xy
1 ln 0.909543 ¸
ˆ‰
27
4
The following graph was generated using
Mathematica.
94. Evaluate the integrals:
dx dy dy dx
'' ''
1y 11
28 8 x
3
3
11
xy xy
ÈÈ
22 22
œ
0.866649¸
The following graph was generated using
Mathematica.
15.3 AREA BY DOUBLE INTEGRATION
1. dy dx (2 x) dx 2x 2,
'' '
00 0
22x 2
œœœ
’“
x
2
#
!
or dx dy (2 y) dy 2
'' '
00 0
22y 2
œœ
2. dy dx (4 2x) dx 4x x 4,
'' '
02x 0
24 2 2
0
œ œœcd
#
or dx dy dy 4
'' '
00 0
4y2 4
œœ
y
#
3. dx dy y y 2 dy
'' '
2y2 2
1y 1
œab
#
2yœ
’“
yy
3#
"
#
224œ œ
ˆ‰ˆ‰
""
##33
89
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.3 Area by Double Integration 897
4. dx dy 2y y dy y
'' '
0y 0
2yy 2
œœab
’“
##
#
!
y
3
4œœ
84
33
5. dy dx e dx e 2 1 1
'' '
00 0
ln 2 e ln 2 xx
ln 2
0
x
œ œ œœcd
6. dy dx ln x dx x ln x x
'' '
1ln x 1
e2 ln x e e
1
œœcd
(e e) (0 1) 1œœ
7. dx dy 2y 2y dy y y
'' '
0y 0
12yy 1
œ œab
‘
##$
"
!
2
3
œ"
3
8. dx dy y 1 2y 2 dy
'' '
12y2 1
1y1 1
œab
##
1 y dy yœ œœ
'1
1ab’“
#"
"
y
33
4
9. 1 dx dy x dy
'' '
00
23 2 3y
y
y
yœcd
2y dy y 4œœœ
'0
220
2
ab cd
10. 1 dx dy x dy
'' '
11 0
2ln 2
1
ln
y
y
y
y
œcd
ln y 1 y dy y ln y 2yœœ
'1
2y
21
2
ab
’“
2
2ln2œ
1
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
898 Chapter 15 Multiple Integrals
11. 1 dy dx 1 dy dx
'' ''
0x2 1x2
12x 23x
ÎÎ
ydx y dxœ
''
01
12
x2 x2
2x 3 x
cd cd
ÎÎ
xdx 3 xdxœ
''
01
12
33
22
ˆ‰ ˆ ‰
x3xxœœ
‘ ‘
333
442
22
01
12
12. 1 dy dx 1 dy dx
'' ''
0x 1x2
1x 4x
ÈÈ
ydx y dxœ
''
01
14
xx2
xx
cd cd
ÈÈ
xxdx xx2dxœ
''
01
14
ˆ‰ ˆ ‰
ÈÈ
xx xx2xœœ
‘ ‘
21 21 13
32 32 3
32 2 32 2
01
14
ÎÎ
13. dx dy 2y dy y
'' '
0y3 0
62y 6
œœ
Š‹’“
yy
39
#'
!
36 12œ œ
216
9
14. dy dx 3x x dx x x
'' '
0x 0
32xx 3
œœab
‘
##$
"$
!
3
23
9œœ
27 9
##
15. dy dx
''
0sin x
4cos x
(cos x sin x) dx sin x cos xœœ
'0
44
0
cd
(0 1) 2 1œœ
Š‹ È
ÈÈ
22
##
16. dx dy y 2 y dy 2y
'' '
1y 1
2y2 2 2
1
œ œab
’“
#yy
23
24 2 5œœœ
ˆ‰ˆ‰
89
33
"" "
###
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.3 Area by Double Integration 899
17. dy dx dy dx
'' ''
12x 0 x2
01x 21x
(1 x) dx 1 dxœ
''
10
02
ˆ‰
x
#
xx 1(21)œ œœ
’“’“ˆ‰
xx 3
24
02
10
"
##
18. dy dx dy dx
'' ''
0x4 00
20 4 x
4 x dx x dxœ
''
00
24
ab
# "Î#
4x x 8œ œœ
’“
‘ˆ‰
x2 81632
33 333
2
0
4
0
$Î#
19. (a) average sin (x y) dy dx cos (x y) dx [ cos (x ) cos x] dxœœœ
"""
111
'' ' '
00 0 0
0
cd 1
sin (x ) sin x [( sin 2 sin ) ( sin sin 0)] 0œ œ œ
""
11
cd1111
0
(b) average sin (x y) dy dx cos (x y) dx cos x cos x dxœœœ
"Î#
!#
Š‹
'' ' '
00 0 0
222
11
11
cd ‘ˆ‰
sin x sin x sin sin sin sin 0œ œ œ
223 4
11 1
111
‘ ‘ˆ‰ ˆ ‰ˆ ‰
###
01
20. average value over the square xy dy dx dx dx 0.25;œœœœœ
'' ' '
00 0 0
11 1 1
’“
xy
24
x
"
!#
"
average value over the quarter circle xy dy dx dxœœ
"
ˆ‰
4'' '
00 0
11x 1 1x
0
4xy
21’“
x x dx 0.159. The average value over the square is larger.œœœ¸
22xx
24111
'0
1ab ’“
$"
!
"
#
4
21. average height x y dy dx x y dx 2x dxœœœœœ
""""
## # #
##
!!
#44343333
y8x4x8
''''
0000
2222
ab ’“ ’“
ˆ‰
22. average dy dx dxœœ
"""
(ln 2) xy (ln 2) x
ln y
'' '
ln 2 ln 2 ln 2
2 ln 2 2 ln 2 2 ln 2 2 ln 2
ln 2
’“
(ln 2 ln ln 2 ln ln 2) dx ln xœœœ
"" " "
#(ln 2) x ln 2 x ln
dx
''
ln 2 ln 2
2 ln 2 2 ln 2 2 ln 2
ln 2
ˆ‰ ˆ‰
cd
(ln 2 ln ln 2 ln ln 2) 1œœ
ˆ‰
"
#ln
23. dy dx 10,000 1 e 10,000 1 e
'' ' ' '
52 5 5
50 5 5
10,000e
11
dx dx dx
11
y
# #
xx
xx
œ œ ab ab
’“
10,000 1 e 2 ln 1 10,000 1 e 2 ln 1œ ab ab
‘ ‘ˆ‰ ˆ‰
22
xx
##
!&
& !
10,000 1 e 2 ln 1 10,000 1 e 2 ln 1 40,000 1 e ln 43,329œ œ ¸ab ab ab
‘ ‘ ˆ‰ˆ‰ ˆ‰
# # #
##
557
2
24. 100(y 1) dx dy 100(y 1)x dy 100(y 1) 2y 2y dy 200 y y dy
'' ' ' '
0y 0 0 0
12yy 1 1 1
2y y
y
œ œ œ cd ab ab
#$
200 (200) 50œœ œ
’“ ˆ‰
yy
24 4
"
!
"
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

900 Chapter 15 Multiple Integrals
25. Let (x y ) be the location of the weather station in county i for i 1 254. The average temperature
ii
ßœßáß
in Texas at time t is approximately , where T(x y ) is the temperature at time t at the
! !
ß
!
254
i1
T(x y ) A
Aii
ii i
?
ß
weather station in county i, A is the area of county i, and A is the area of Texas.?i
26. Let y f x be a nonnegative, continuous function on a, b , then A dA dy dx y dx f x dxœÒÓœœœœab cd ab
''
R'' ' '
a0 a a
bfx b b
0
fx
15.4 DOUBLE INTEGRALS IN POLAR FORM
1. x y 9 r 9 2 , 0 r 9
22 2
2
œÊœÊŸŸ ŸŸ
1)1
2. x y 1 r 1, x y 4 r 4 , 1 r 4
22 2 22 2
22
œÊœ œÊœÊŸŸ ŸŸ
11
)
3. y x , y x , y 1 r csc , 0 r cscœÊœœÊœœÊœÊŸŸŸŸ)) )) )
11 11
44 44
33
4. x 1 r sec , y 3x 0 , 0 r secœÊœ œ Êœ ÊŸŸ ŸŸ))) )
È11
33
5. x y 1 r 1, x 2 3 r 2 3 sec , y 2 r 2 csc ; 2 3 sec 2 csc
22 2
6
œ Êœ œ Êœ œ Êœ œ Ê œ
ÈÈ È
)))))
1
0 , 1r23sec; , 1r23cscÊŸŸŸŸ ŸŸŸŸ))))
111
662
ÈÈ
6. x y 2 r 2, x 1 r sec ; 2 sec or , sec r 2
22 2
3333
œ Êœ œÊœ œ Êœ œÊŸŸ ŸŸ)))) ) )
1111
7. x y 2x r 2 cos , 0 r 2 cos
22
22
œ Êœ ÊŸŸ ŸŸ)) )
11
8. x y 2y r 2 sin 0 , 0 r 2 sin
22
œ Êœ ÊŸŸ ŸŸ))1 )
9. dy dx r dr d d
'' '' '
10 0 0 0
11x 1
œœœ))
"
##
1
10. x y dx dy r dr d d
'' ' ' '
00 0 0 0
11y 21 2
ab
## $ "
œ œ œ))
48
1
11. x y dx dy r dr d 4 d 2
'' ' ' '
00 0 0 0
24y 22 2
ab
## $
œ œ œ))1
12. dy dx r dr d d a
'' '' '
aax 00 0
aax 2a 2
œœœ))1
a
2#
13. x dx dy r cos dr d 72 cot csc d 36 cot 36
'' ' ' '
00 40 4
6y 26 csc 2 2
4
œœœœ
###
)) ) )) )cd
14. y dy dx r sin dr d tan sec d
'' ' ' '
00 0 0 0
2x 42 sec 4
œœœ
##
)) ) ))
84
33
15. dy dx r dr d sec csc d tan cot 2 3
'' '' '
11
33
31 31
22 22
22
ÈÈ
x4 sec 4
6csc 6
4
6
œœœœ))))))
ˆ‰‘
È
16. dy dx r dr d 2csc 2 d 2 cot 2
'' '' '
ÈÈ
24y
2y 2 21
22
2œœœœ
42 6
2csc 4 2
4
)))))ab
‘
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
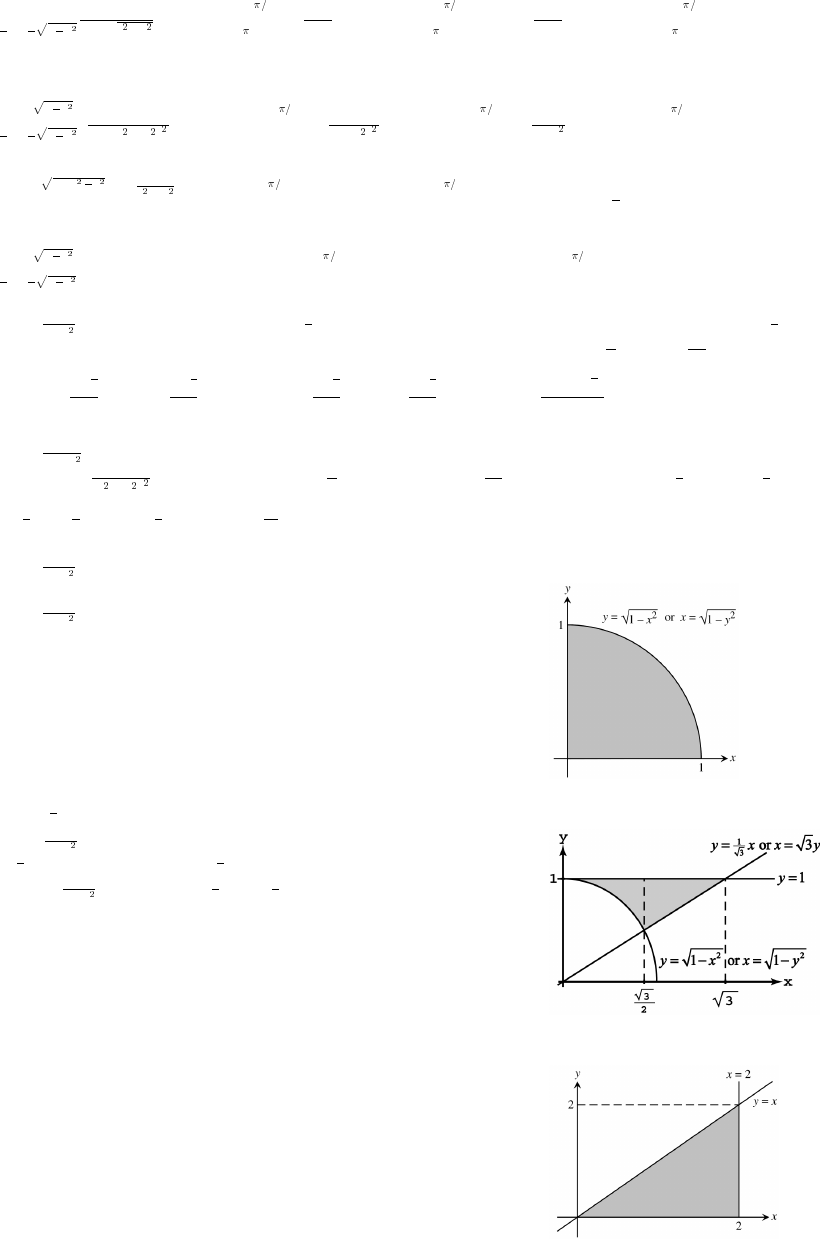
Section 15.4 Double Integrals in Polar Form 901
17. dy dx dr d 2 1 dr d 2 (1 ln 2) d
'' '' '' '
11x 0 0
0 0 32 1 32 1 32
22r
1xy 1r 1r
"
Èœœœ)))
ˆ‰
(1 ln 2)œ 1
18. dy dx 4 dr d 4 d 2 d
'' ' ' ' '
11x 00 0 0
11x 21 2 2
22r
1x y 1r 1r
ab ab
"
"
!
œœœœ)))1
‘
19. e dx dy re dr d 2 ln 2 1 d 2 ln 2 1
'' '' '
00 00 0
ln 2 (ln 2) y 2 ln 2 2
r
Èxy
œœœ))abab
1
#
20. ln x y 1 dx dy 4 ln r 1 r dr d 2 ln 4 1 d ln 4 1
'' ' ' '
11y 00 0
11y 21 2
a b ab abab
## #
œ œ œ ))1
21. x 2y dy dx r cos 2r sin r dr d cos sin d
'' ' ' '
0x 40 4
12x 22 2
0
2
ÈÎ Î
ÎÎ
ab a b ’“
œ œ
11
11
ÈÈ
))) ) ))
r2r
33
33
cos sin d sin cosœœœ
'1
1
1
1
Î
Î
Î
Î
4
222 22
4
22
Š‹’“
24 24
33 33 3
21
ÈÈ ÈÈ ˆ‰
È
))) ) )
22. dy dx r dr d d cos sec d
'' ' ' ' '
10 0 sec 0 0
22xx 42cos 4 4
sec
2cos
ÈÎÎ Î
11111
xy r2r 28
22
ab
œœœœ
1) 1 1
))
)
42
)))))
‘ ˆ ‰
sin2 tanœ œ
‘
11 1
48 8 16
)))
0
41Î1
23. x y dy dx or
''
00
11x
È
xydxdy
''
00
11y
È
24. x dx dy or
''
12 1 y
13y
Î
È
È
x dy dx x dy dx
'' ''
01x 323
32 1 3 1
ÈÈ
ÈÈÈ
Î
Î
xÎ
25. y x y dy dx or
''
00
2x
22 2
ab
yx y dxdy
''
0y
22
22 2
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

902 Chapter 15 Multiple Integrals
26. x y dy dx or
''
00
34
ab
22
3
x y dx dy
''
00
43
ab
22
3
27. r dr d 2 (2 sin 2 ) d 2( 1)
'' '
00 0
222sin 2 2
)))1œ œ
28. A 2 r dr d 2 cos cos dœœœ
'' '
01 0
21cos 2
))))ab
#8
4
1
29. A 2 r dr d 144 cos 3 d 12œœœ
'' '
00 0
6 12 cos 3 6
)))1
#
30. A r dr d dœœœ
'' '
00 0
243 2
)))
864
927
#1
31. A r dr d 2 sin d 1œœœ
'' '
00 0
21sin 2
)))
13 cos 2 3
28
ˆ‰
##
)1
32. A 4 r dr d 2 2 cos d 4œœœ
'' '
00 0
21cos 2
)))
ˆ‰
3cos 23
2##
)1
33. average r a r dr d a dœœœ
442a
a3a311
'' '
00 0
2a 2
È## $
))
34. average r dr d a dœœœ
442a
a3a311
'' '
00 0
2a 2
#$
))
35. average x y dy dx r dr d dœœœœ
""
## #
111aa33
a2a
'' '' '
aax 00 0
aax 2a 2
È))
36. average (1 x) y dy dx (1 r cos ) r sin r dr dœœ
""
## ###
11
''
Rcd c d
''
00
21
)))
r 2r cos r dr d dœœœœ
"""
$#
#111
))
'' '
00 0
21 2 2
0
ab
ˆ‰ ‘
)) ))
3 2 cos 3 2 sin 3
43 4 3
37. r dr d 2 ln r dr d 2 r ln r r d 2 e 1 1 d 2 2 e
'' '' ' '
01 01 0 0
2e 2e 2 2
e
1
Š‹ cd ÈÈ
‘ˆ‰ˆ‰
ln r
r)) ) )1œœœœ
"
#
38. dr d dr d (ln r) d d 2
'' '' ' '
01 01 0 0
2e 2e 2 2
e
1
Š‹ ˆ‰ cd
ln r 2 ln r
rr
))))1œœœœ
#
39. V 2 r cos dr d 3 cos 3 cos cos dœœ
'' '
01 0
21cos 2
##$%
)) ) ) ))
2
3ab
sin 2 3 sin sinœ œ
25 sin 4 4 5
38 32 3 8
‘
"$
))1
))) 2
0
40. V 4 r 2 r dr d (2 2 cos 2 ) 2 dœœ
'' '
00 0
42 cos 2 4
È‘
#$Î# $Î#
)))
4
3
1 cos sin d cos œ œ œ
22 22 6240264
33 333 9
32 32 cos
111
)
ÈÈÈÈ
'0
44
0
ab ’“
#
))) )
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.4 Double Integrals in Polar Form 903
41. (a) I e dx dy e r dr d lim re dr d
#
œœ œ
'' ' ' ' '
00 0 0 0 0
22b
abxy Š‹ ”•
rr
))
bÄ_
lim e 1 d d Iœ œ œ Ê œ
""
###
''
00
22
bÄ_ Š‹
b
4
))
11
È
(b) lim dt e dt 1, from part (a)
xÄ_ ''
00
x2e 2 2
t
t
ÈÈ È
È
11 1
1
œœœ
#
Š‹Š‹
42. dx dy dr d lim dr lim
'' ' ' '
00 0 0 0
2bb
0
" "
#
a b ab ab1x y 1r 1r
rr
41r
œœ œ)11
bbÄ_ Ä_ ‘
lim 1œœ
11
41b4
bÄ_ ˆ‰
"
43. Over the disk x y : dA dr d ln 1 r d
## #
""
Ÿ œ œ
3r
41xy 1r 2
''
R
'' '
00 0
232 2 32
0
))
‘
ab
ln d (ln 2) d ln 4œ œ œ
''
00
22
ˆ‰
""
#4))1
Over the disk x y 1: dA dr d lim dr d
## "
Ÿ œ œ
''
Ra1
1x y 1r 1r
rr
'' ' '
00 0 0
21 2 a
))
’“
Ä
lim ln 1 a d 2 lim ln 1 a 2 , so the integral does not exist overœœœ_
'0
2
a1 a1ÄÄ
‘ ‘
ab ab
""
##
##
)1 1††
xy1
##
Ÿ
44. The area in polar coordinates is given by A r dr d d f ( ) d r d ,œœœœ
'' ' ' '
0
ff
0
)))))
’“
r
2
""
##
##
where r f( )œ)
45. average (r cos h) r sin r dr d r 2r h cos rh dr dœœ
""
### $ # #
11aa
'' ''
00 00
2a 2a
cdab))) ))
d dœœœ
"""
###111
)))))
a43 43 43
a 2a h cos a h a 2ah cos h a 2ah sin h
''
00
22 2
0
Š‹Š‹’“
))
a2hœ
"
#
##
ab
46. A r dr d 4 sin csc dœœ
'' '
4csc 4
3 4 2 sin 3 4
))))
"
#
##
ab
2sin 2cot œ œ
"
##
cd)))
34
4
1
47-50. Example CAS commands:
:Maple
f := (x,y) -> y/(x^2+y^2);
a,b := 0,1;
f1 := x -> x;
f2 := x -> 1;
plot3d( f(x,y), y=f1(x)..f2(x), x=a..b, axes=boxed, style=patchnogrid, shading=zhue, orientation=[0,180], title="#47(a)
(Section 15.4)" ); # (a)
q1 := eval( x=a, [x=r*cos(theta),y=r*sin(theta)] ); # (b)
q2 := eval( x=b, [x=r*cos(theta),y=r*sin(theta)] );
q3 := eval( y=f1(x), [x=r*cos(theta),y=r*sin(theta)] );
q4 := eval( y=f2(x), [x=r*cos(theta),y=r*sin(theta)] );
theta1 := solve( q3, theta );
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

904 Chapter 15 Multiple Integrals
theta2 := solve( q1, theta );
r1 := 0;
r2 := solve( q4, r );
plot3d(0,r=r1..r2, theta=theta1..theta2, axes=boxed, style=patchnogrid, shading=zhue, orientation=[-90,0],
title="#47(c) (Section 15.4)" );
fP := simplify(eval( f(x,y), [x=r*cos(theta),y=r*sin(theta)] )); # (d)
q5 := Int( Int( fP*r, r=r1..r2 ), theta=theta1..theta2 );
value( q5 );
: (functions and bounds will vary)Mathematica
For 47 and 48, begin by drawing the region of integration with the command.FilledPlot
Clear[x, y, r, t]
<<Graphics`FilledPlot`
FilledPlot[{x, 1}, {x, 0, 1}, AspectRatio 1, AxesLabel {x,y}];ÄÄ
The picture demonstrates that r goes from 0 to the line y=1 or r = 1/ Sin[t], while t goes from /4 to /2.11
f:= y / (x y )
22
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, /4, /2}, {r, 0, 1/Sin[t]}]11
For 49 and 50, drawing the region of integration with the ImplicitPlot command.
Clear[x, y]
<<Graphics`ImplicitPlot`
ImplicitPlot[{x==y, x==2 y, y==0, y==1}, {x, 0, 2.1}, {y, 0, 1.1}];
The picture shows that as t goes from 0 to /4, r goes from 0 to the line x=2 y. will find the bound for r.1Solve
bdr=Solve[r Cos[t]==2 r Sin[t], r]//Simplify
f:=Sqrt[x y]
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, 0, /4}, {r, 0, bdr[[1, 1, 2]]}]1
15.5 TRIPLE INTEGRALS IN RECTANGULAR COORDINATES
1. F x, y, z dy dz dx dy dz dx 1 x z dz dx
'' ' '' ' ''
00 xz 00 xz 00
11x1 11x1 11x
ab a bœœ
1x x1x dx dxœ œ œ œ
''
00
11
’“’“
abab
ab ab ab
1x 1x
22 6
1x
60
1
"
22
3
2. dz dy dx 3 dy dx 6 dx 6, dz dx dy, dx dy dz, dx dz dy,
''' '' ' ''' ''' '''
000 00 0 000 000 000
123 12 1 213 321 231
œœœ
dy dx dz, dy dz dx
''' '''
000 000
312 132
3. dz dy dx
'' '
00 0
1 22x 33x3y2
3 3x y dy dxœ
''
00
122x
ˆ‰
3
2
3(1 x) 2(1 x) 4(1 x) dxœ
'0
1‘
††
3
4#
3 (1 x) dx (1 x) 1,œœœ
'0
1#$
"
!
cd
dz dx dy, dy dz dx,
'' ' '' '
00 0 00 0
2 1y2 33x3y2 1 33x 22x2z3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
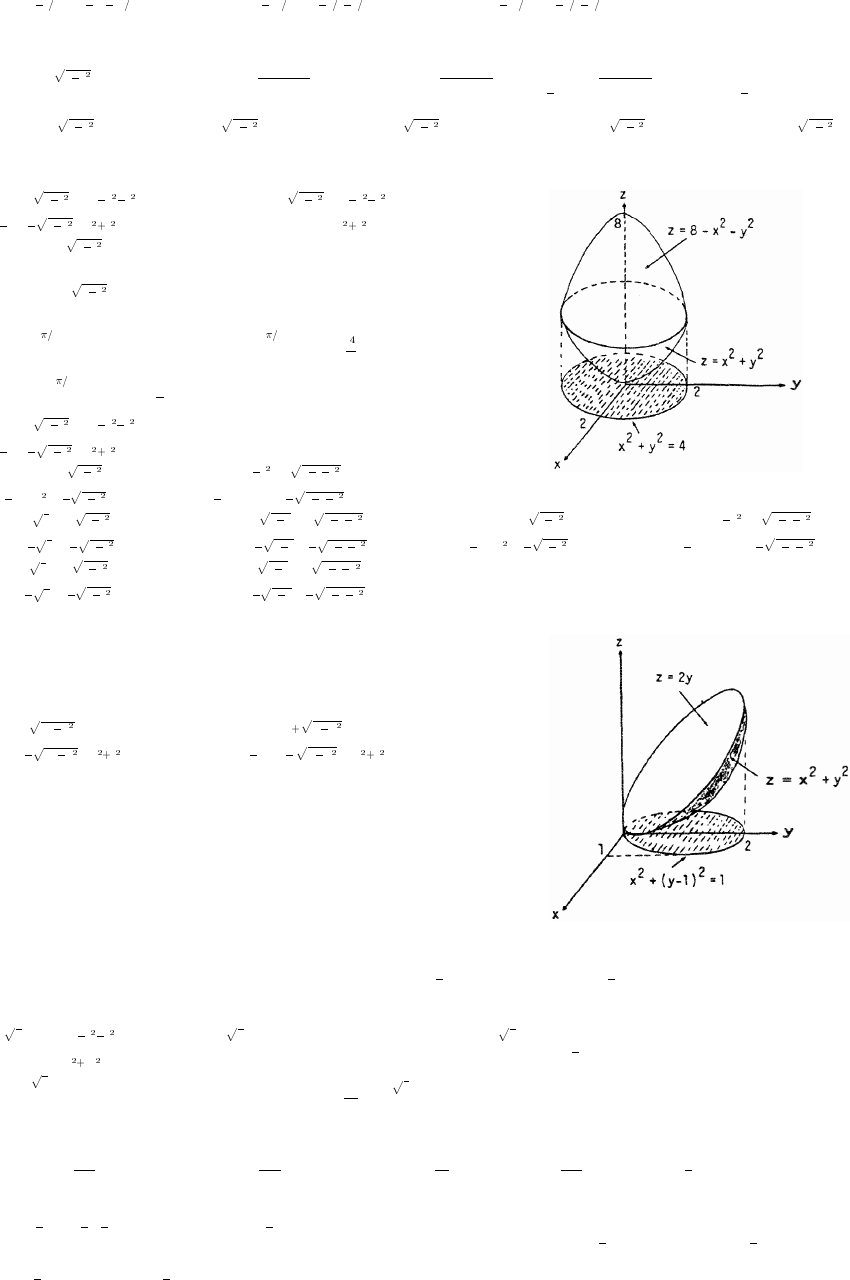
Section 15.5 Triple Integrals in Rectangular Coordinates 905
dy dx dz, dx dz dy, dx dy dz
'' ' '' ' '' '
00 0 00 0 00 0
31z322x2z3 233y21y2z3 322z31y2z3
4. dz dy dx 4 x dy dx 3 4 x dx x 4 x 4 sin 6 sin 1 3 ,
''' '' '
000 00 0
23 4x 23 2 2
0
œœœ œœ
ÈÈÈ
’“
###
##
" "
3x
1
dz dx dy, dy dz dx, dy dx dz, dx dy dz, dx dz dy
''' '' ' '' ' ''' '''
0 00 00 0 00 0 000 000
3 2 4x 2 4x 3 2 4z 3 2 3 4z 3 2 4z
5. dz dy dx 4 dz dy dx
'' ' '' '
24xxy 00 xy
2 4x 8xy 2 4x 8xy
œ
4 8 2 x y dy dxœ
''
00
24x
cdab
##
8 4 x y dy dxœ
''
00
24x
ab
##
8 4 r r dr d 8 2r dœœ
'' '
00 0
22 2
ab ’“
##
#
!
))
r
4
32 d 32 16 ,œœœ
'0
2
)1
ˆ‰
1
#
dz dx dy,
'' '
24yxy
24y8xy
dx dz dy dx dz dy,
''' '' '
2y zy 24 8zy
2 4 zy 2 8y 8zy
dx dy dz dx dy dz, dy dz dx dy dz
'' ' '' ' ''' '' '
0 z zy 4 8z 8zy 2 x zx 2 4 8zx
4 z zy 8 8z 8zy 2 4 zx 2 8x 8zx
dx,
dy dx dz dy dx dz
'' ' '' '
0zzx 48z8zx
4z zx 88z 8zx
6. The projection of D onto the xy-plane has the boundary
x y 2y x (y 1) 1, which is a circle.
## # #
œ Ê œ
Therefore the two integrals are:
dz dx dy and dz dy dx
'' ' '' '
0 2yy xy 11 1x xy
2 2y y 2y 1 1 1 x 2y
7. x y z dz dy dx x y dy dx x dx 1
''' '' '
000 00 0
111 11 1
ab ˆ‰ˆ‰
### ## #
"
œ œ œ
33
2
8. dz dx dy 8 2x 4y dx dy 8x x 4xy dy
''' '' '
00x3y 00 0
23y8xy 23y 2 3y
0
œœab‘
## $ #
2
3
24y 18y 12y dy 12y y 24 30 6œ œ œœ
'0
22
0
ab
‘
$$ # %
"5
2
9. dx dy dz dy dz dy dz dz dz 6
'' ' '' '' ' '
11 1 11 11 1 1
ee e ee ee e e
ee
11
23 2 2
3 2
"
xyz yz yz z z
ln x 3 6
ln y
œœœœœ
’“ ’“
10. dz dy dx (3 3x y) dy dx (3 3x) (3 3x) dx (1 x) dx
'' ' '' ' '
00 0 00 0 0
1 33x 33xy 1 33x 1 1
œœœ
‘
## #
"
##
9
(1 x)œ œ
33
##
$"
!
cd
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

906 Chapter 15 Multiple Integrals
11. y sin z dx dy dz 5y sin z dy dz sin z dz
''' '' '
00 00 0
613 61 6
œœœ
552 3
4#
Š‹
È
12. x y z dy dx dz xy y zy dx dz 2x 2 2z dx dz
''' '' ''
10 0 10 10
112 11 11
0
2
ab a b
‘
œ œ œ
"#
2
x 2x 2zx dz 3 2z dz 3z z 6œ œœœ
''
11
11
1
1
cdabcd
##
"
0
13. dz dy dx 9 x dy dx 9 x dx 9x 18
'' ' '' '
00 0 00 0
39x 9x 39x 3
œœœœ
Èab’“
##$
!
x
3
14. dz dx dy (2x y) dx dy x xy dy 4 y (2y) dy
'' ' '' ' '
04y0 04y 0 0
24y 2xy 24y 2 2
4y
4y
œœœcd ab
##
"Î#
4y (4)œ œ œ
’“
ab
2216
333
# $Î#
$Î# #
!
15. dz dy dx (2 x y) dy dx (2 x) (2 x) dx (2 x) dx
'' ' '' ' '
00 0 00 0 0
12x2xy 12x 1 1
œœœ
‘
## #
""
##
(2 x)œ œ œ
‘
""
$"
!
6666
87
16. x dz dy dx x 1 x y dy dx x 1 x 1 x dx x 1 x dx
'' ' '' ' '
00 3 00 0 0
11x 4xy 11x 1 1
œœœa b abab ab
’“
####
##
""
##
1xœ œ
’“
ab
""
#$"
!
12 12
17. cos (u v w) du dv dw [sin (w v ) sin (w v)] dv dw
''' ''
000 00
œ 1
[( cos (w 2 ) cos (w )) (cos (w ) cos w)] dwœ
'011 1
sin (w 2 ) sin (w ) sin w sin (w ) 0œ œcd11 1
1
!
18. s e ln r dt dr ds s e ln r ln t dr ds ln r dr ds r ln r r ds
'' ' '' '' '
01 1 01 01 0
1ee 1e 1e 1
e
1
e
1
ÈÈ È
ab È
ss
ln t 3
t333
1sese
2ss
œœœabab c d
’“
se ds se eœœœ
2e 2e 2e
66 6
sss
ÈÈ È
'0
11
0
cd
19. e dx dt dv lim e e dt dv e dt dv e dv
'' ' '' '' '
00 00 00 0
4 ln sec v 2t 4 ln sec v 4 ln sec v 4
x 2t b 2t 2 ln sec v
œœœ
bÄ_ ab ˆ‰
""
##
dvœœœ
'0
4Š‹
‘
sec v tan v v
22 8
## #
""
Î%
!
11
20. dp dq dr dq dr 4 q dr dr 8 ln 2
''' '' ' '
000 00 0 0
72 4q 72 7 7
q
r1 r1 3(r1) 3 r1 3
q4q 88 ln 8
""
#$Î# #
!
œœœœœ
È’“
ab
21. (a) dy dz dx (b) dy dx dz (c) dx dy dz
'' ' '' ' '' '
10 x 0 1z x 0 0 y
1 1x 1z 1 1z 1z 1 1z y
(d) dx dz dy (e) dz dx dy
'' ' '' '
00 y 0 y 0
11yy 1y1y
22. (a) dy dz dx (b) dy dx dz (c) dx dy dz
''' ''' ' ' '
00 1 00 1 0 1 0
11 z 11 z 1 z1
(d) dx dz dy (e) dz dx dy
''' '''
10 0 10 0
0y1 01y
23. V dz dy dx y dy dx dxœœœœ
''' '' '
010 01 0
11 y 11 1
#22
33
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.5 Triple Integrals in Rectangular Coordinates 907
24. V dy dz dx (2 2z) dz dx 2z z dx 1 x dx xœœœœœœ
'' ' '' ' '
00 0 00 0 0
11x22z 11x 1 1
1x
0
cd ab
’“
##
"
!
x2
33
25. V dz dy dx (2 y) dy dx 2 4 x dxœœœ
'' ' '' '
00 0 00 0
44x2y 44x 4
’“
Ȉ‰
4x
#
(4 x) (4 x) (4) (16) 4œ œ œ œ
‘
4 4 32 20
34 3433
$Î# # $Î#
""
%
!
26. V 2 dz dy dx 2 y dy dx 1 x dxœœœœ
'' ' ' ' '
01x0 0 1x 0
10 y 1 0 1
ab
#2
3
27. V dz dy dx 3 3x y dy dx 6(1 x) 4(1 x) dxœœœ
'' ' '' '
00 0 00 0
1 22x 33x3y2 1 22x 1
ˆ‰ ‘
33
4#
##
†
3(1 x) dx (1 x) 1œœœ
'0
1#$
"
!
cd
28. V dz dy dx cos dy dx cos (1 x) dxœœœ
'' ' '' '
00 0 00 0
11xcosx2 11x 1
ˆ‰ ˆ ‰
11xx
##
cos dx x cos dx sin u cos u du cos u u sin uœ œ œ
'' '
00 0
11 2 2
0
ˆ‰ ˆ‰ ‘ cd
111
11 11
xx2x4 24
###
"
!
1œ œ
24 4
11 1
1
ˆ‰
#
29. V 8 dz dy dx 8 1 x dy dx 8 1 x dxœœœœ
'' ' '' '
00 0 00 0
11x 1x 11x 1
Èab
##16
3
30. V dz dy dx 4 x y dy dx 4 x 4 x dxœœœ
'' ' '' '
00 0 00 0
24x 4xy 24x 2
a b abab
’“
###
##
"
#
4 x dx 8 4x dxœœœ
"
##
##
#
''
00
22
ab Š‹
x 128
15
31. V dx dz dy (4 y) dz dy (4 y) dyœœœ
'' ' '' '
00 0 00 0
416y24y 416y2 4
È16 y
#
2 16 y dy y 16 y dy y 16 y 16 sin 16 yœ œ
''
00
44
ÈÈÈ
‘
’“
ab
###
""
#
" #
%
!
$Î# %
!
y
46
16 (16) 8œ œ
ˆ‰
1
#
"$Î#
63
32
1
32. V dz dy dx (3 x) dy dx 2 (3 x) 4 x dxœœœ
'' ' '' '
24x0 24x 2
24x3x 24x 2 È#
3 2 4 x dx 2 x 4 x dx 3 x 4 x 4 sin 4 xœœ
''
22
22
ÈÈÈ
’“’“
ab
###
" #
##
# #
$Î#
x2
23
12 sin 1 12 sin ( 1) 12 12 12œœœ
" "
##
ˆ‰ ˆ ‰
11
1
33. dz dy dx 3 dy dx
'' ' ''
0 0 2xy2 0 0
22x42x2y 22x
œ
ˆ‰
3x 3y
##
3 1 (2 x) (2 x) dxœ
'0
2‘ˆ‰
x3
4#
#
66x dxœ
'0
2’“
3x 3(2 x)
4
#
6x3x (121240) 2œ œœ
’“
##
!
x2
24 4
(2 x)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

908 Chapter 15 Multiple Integrals
34. V dx dy dz (8 2z) dy dz (8 2z)( z) dz 64 24z 2z dzœœœ)œ
''' '' ' '
0zz 0z 0 0
488z 48 4 4
ab
#
64z 12z zœ œ
‘
#$
%
!
2 320
33
35. V 2 dz dy dx 2 (x 2) dy dx (x 2) 4 x dxœœœ
'' ' '' '
20 0 20 2
24x2x2 24x2 2 È#
24 x dx x4 x dx x4 x 4 sin 4 xœ œ
''
22
22
ÈÈÈ
’“’“
ab
###
" #
#
##
# #
"$Î#
x
3
44 4œœ
ˆ‰ ˆ ‰
11
##
1
36. V 2 dz dx dy 2 x y dx dy 2 xy dyœœœ
'' ' '' '
00 0 00 0
11y xy 11y 1 1y
0
ab ’“
## #
x
3
2 1 y 1 y y dy 2 1 y y y dy 1 y dyœ œ œ
'''
000
111
abab ab ab
’“ ˆ‰
### ##% '
""""
#
33333
2
yœ œ œ
2264
37 377
y
’“
ˆ‰ˆ‰
"
!
37. average x 9 dz dy dx 2x 18 dy dx 4x 36 dxœœœœ
"""
###
8883
31
''' '' '
000 00 0
222 22 2
ab ab ab
38. average (x y z) dz dy dx (2x 2y 2) dy dx (2x 1) dx 0œœœœ
"""
222
''' '' '
000 00 0
112 11 1
39. average x y z dz dy dx x y dy dx x dx 1œœœœ
''' '' '
000 00 0
111 11 1
ab ˆ‰ˆ‰
### ## #
"
33
2
40. average xyz dz dy dx xy dy dx x dx 1œœœœ
"""
842
''' '' '
000 00 0
222 22 2
41. dx dy dz dy dx dz dx dz z dz
''' ''' '' '
002y 00 0 00 0
412 42 x2 42 4
4 cos x 4 cos x x cos x
2z 2z z
sin 4
ab ab ab
ÈÈÈ
œœœ
ˆ‰
#
"Î#
(sin 4)z 2 sin 4œœ
‘
"Î# %
!
42. 12xz e dy dx dz 12xz e dx dy dz 6yz e dy dz 3e dz
''' ''' '' '
00x 000 00 0
111 11 y 11 1
zy zy zy zy
œœœ
’“
"
!
3ez dz3e1 3e6œœœ
'0
1zz
ab cd
"
!
43. dx dy dz dy dz dz dy
''' '' ''
0z0 0z 00
11 ln 3 11 1y
1 1 11 11e sin y 4 sin y 4 sin y
yyy
2x ab ab ab
œœ
4 y sin y dy 2 cos y 2( 1) 2(1) 4œœœœ
'0
1
11 1ab c dab
##
"
!
44. dy dz dx dz dx x dx dz (4 z) dz
'' ' '' '' '
00 0 00 00 0
24x x 24x 4 4z 4
sin 2z x sin 2z sin 2z sin 2z
4z 4z 4z 4z#
"
œœ œ
ˆ‰ ˆ‰
cos 2z sin zœ œ œ
‘ ‘
"""
%%
!##
#
!
44
sin 4
45. dz dy dx 4 x y a dy dx
'' ' ''
00 a 00
1 4ax 4x y 1 4ax
œÊ œ
44
15 15
ab
#
4 a x 4 a x dx 4 a x dx (4 a) 2x (4 a) x dxÊ œ Ê œ Ê
'''
000
111
’“
abab ab c d
## # ##%
## #
""
##
44
15 15
(4 a) x x (4 a) (4 a) (4 a) 15(4 a) 10(4 a) 5 0œ Ê œ Ê œ Ê œ
82x828
15 3 5 15 3 5 15
’“
#$ # #
"
!
"
3(4 a) 2(4 a) 1 0 [3(4 a) 1][(4 a) 1] 0 4 a or 4 a 1 a or a 3ÊœÊ œÊœ œÊœ œ
#"
33
13
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.6 Moments and Centers of Mass 909
46. The volume of the ellipsoid 1 is so that 8 c 3.
x z 4abc
abc 3 3
y 4(1)(2)(c)
œ œ Êœ
111
47. To minimize the integral, we want the domain to include all points where the integrand is negative and to exclude all
points where it is positive. These criteria are met by the points (x y z) such that 4x 4y z 4 0 orßß Ÿ
###
4x 4y z 4, which is a solid ellipsoid centered at the origin.
###
Ÿ
48. To maximize the integral, we want the domain to include all points where the integrand is positive and to exclude all
points where it is negative. These criteria are met by the points (x y z) such that 1 x y z 0 orßß
###
x y z 1, which is a solid sphere of radius 1 centered at the origin.
###
Ÿ
49-52. Example CAS commands:
:Maple
F := (x,y,z) -> x^2*y^2*z;
q1 := Int( Int( Int( F(x,y,z), y=-sqrt(1-x^2)..sqrt(1-x^2) ), x=-1..1 ), z=0..1 );
value( q1 );
: (functions and bounds will vary)Mathematica
Clear[f, x, y, z];
f:= x y z
22
Integrate[f, {x, 1,1}, {y, Sqrt[1 x ], Sqrt[1 x ]}, {z, 0, 1}]
22
N[%]
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, 0, 2 }, {r, 0, 1},{z, 0, 1}]1
N[%]
15.6 MOMENTS AND CENTERS OF MASS
1. M 3 dy dx 3 2 x x dx ; M 3x dy dx 3 xy dxœœœœ œ
'' ' '' '
0x 0 0x 0
12x 1 12x 1
y
2x
x
ab cd
#
#
7
3 2x x x dx ; M 3y dy dx y dx 4 5x x dxœ œœ œ œ œ
'''''
00x00
112x11
x
2x
x
ab cd ab
$# # #%
##
53319
4 5
x and yÊœ œ
538
14 35
2. M dy dx 3 dx 9 ; I y dy dx dx 27 ;œœœœ œœ$$$$ $ $
'' ' '' '
00 0 00 0
33 3 33 3
x
3
0
#’“
y
3
I x dy dx x y dx 3x dx 27
y00 0 0
33 3 3
œœœœ$$$$
'' ' '
## #
$
!
cd
3. M dx dy 4 y dy ; M x dx dy x dyœœœœ œ
'' ' '' '
0y2 0 0y2 0
24y 2 24y 2
y
4y
y2
Š‹ cd
y14
3
##
"#
16 8y y dy ; M y dx dy 4y y dyœœœ œœ
"
# #
##
''''
00y20
224y2
x
Š‹ Š‹
yy
415 3
128 10
x and yÊœ œ
64 5
35 7
4. M dy dx (3 x) dx ; M x dy dx xy dx 3x x dxœœœœ œœœ
'' ' ' ' ' '
00 0 0 0 0 0
33x 3 3 3x 3 3
y
3x
0
9 9
# #
#
cd a b
x 1 and y 1, by symmetryÊœ œ
5. M dy dx ; M x dy dx xy dx x a x dxœœœ œœœ
'' '' ' '
00 00 0 0
aax aax a a
y
ax
0
1a a
4 3
cd È##
x y , by symmetryÊœœ
4a
31
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

910 Chapter 15 Multiple Integrals
6. M dy dx sin x dx 2; M y dy dx y dx sin x dxœœœœ œ œ
'' ' '' ' '
00 0 00 0 0
sin x sin x
x
sin x
0
""
##
##
cd
(1 cos 2x) dx x and yœ œÊœ œ
"
#448
'0
111
7. I y dy dx dx 4 x dx 4 ; I 4 , by symmetry;
x y
24x 2 2
24x 2 2
4x
4x
œœœœœ
'' ' '
##
$Î#
’“ ab
y
33
211
III8
oxy
œœ1
8. I x dy dx sin x 0 dx (1 cos 2x) dx
y
2sinxx 2 2
0
œœœœ
'' ' '
##
"
##
ab 1
9. M dy dx e dx lim e dx 1 lim e 1; M x dy dx xe dxœœœ œœœ œ
'' ' ' '' '
0e 0 0 0e 0
0b 0
xx b x
y
x x
bbÄ_ Ä_
lim xe dx lim xe e 1 lim be e 1; M y dy dxœœœœœ
bb bÄ_ Ä_ Ä_
'''
b 0
00e
xxx bb
0
bx
cd ab x
e dx lim e dx x 1 and yœœ œÊœœ
"" " "
##
''
00
2x 2x
b
bÄ_ 44
10. M x dy dx lim xe dx lim 1 1
y00 0
eb
x2 b
0
œœ œœ
'' '
x2
x2
bbÄ_ Ä_ ‘
"
e
11. M (x y) dx dy xy dy 2y 2y dy ;œœœœœ
'' ' '
0y 0 0
2yy 2 2
yy
y
’“ Š ‹’ “
x 8
22 10315
yyy2y
$#
#
#
!
I y (x y) dx dy xy dy 2y 2y dy ;
x0y 0 0
2yy 2 2
yy
y
œœœœ
'' ' '
#$&%
’“ Š ‹
xy y
2 2 105
64
12. M 5x dx dy 5 dy 12 4y 16y dy 23 3œœœœ
'' ' '
32 4y 32 32
32 12 4y 32 32
12 4y
4y
’“ ab
È
x5
2#
#%
13. M (6x 3y 3) dy dx 6xy y 3y dx 12 12x dx 8;œœœœ
'' ' '
0x 0 0
12x 1 1
2x
x
‘
ab
3
#
##
M x(6x 3y 3) dy dx 12x 12x dx 3; M y(6x 3y 3) dy dx
y x
0x 0 0x
12x 1 12x
œœœœ
'' ' ''
ab
$
14 6x 6x 2x dx x and yœ œÊœ œ
'0
1ab
#$
#
17 3 17
816
14. M (y 1) dx dy 2y 2y dy ; M y(y 1) dx dy 2y 2y dy ;œœœœ œœ
'' ' '' '
0y 0 0y 0
12yy 1 12yy 1
x
ab a b
$#%
"
#
4
15
M x(y 1) dx dy 2y 2y dy x and y ; I y (y 1) dx dy
y0y 0 0y
12yy 1 12yy
œœœÊœœœ
'' ' ''
ab
#% #
488
15 15 15 x
2 y y dyœœ
'0
1ab
$& "
6
15. M (x y 1) dx dy (6y 24) dy 27; M y(x y 1) dx dy y(6y 24) dy 14;œ œœœ œœ
'' ' '' '
00 0 00 0
16 1 16 1
x
M x(x y 1) dx dy (18y 90) dy 99 x and y ; I x (x y 1) dx dy
y y
00 0 00
16 1 16
œœœÊœœœ
'' ' ''
11 14
327 #
216 dy 432œœ
'0
1ˆ‰
y
36
11
16. M (y 1) dy dx x dx ; M y(y 1) dy dx dxœœœœ œ
'' ' '' '
1x 1 1x 1
11 1 11 1
x
Š‹ Š‹
x332 5xx
15 6 3
## #
#
; M x(y 1) dy dx x dx 0 x 0 and y ; I x (y 1) dy dxœœ œœÊœœœ
48 3x x 9
35 14
y y
1x 1 1x
11 1 11
'' ' ''
Š‹
##
$#
x dxœœ
'1
1Š‹
3x x 16
22 35
%
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.6 Moments and Centers of Mass 911
17. M (7y 1) dy dx x dx ; M y(7y 1) dy dx dx ;œœœœ œœ
'' ' '' '
10 1 10 1
1x 1 1x 1
x
Š‹ Š‹
7x 31 7x x 13
15 3 2 15
#
#
M x(7y 1) dy dx x dx 0 x 0 and y ; I x (7y 1) dy dx
y y
10 1 10
1x 1 1x
œœœÊœœœ
'' ' ''
Š‹
7x 13
31
#
$#
x dxœœ
'1
1Š‹
7x 7
5
#
%
18. M 1 dy dx 2 dx 60; M y 1 dy dx 1 dx 0;œœœœ œ œ
'' ' '' '
01 0 01 0
20 1 20 20 1 20
x
ˆ‰ ˆ‰ ˆ‰ ˆ‰
’“Š‹
xx x x
20 10 20 0
y
##
"
"
M x 1 dy dx 2x dx x and y 0; I y 1 dy dx
y x
01 0 01
20 1 20 20 1
œœœÊœœœ
'' ' ''
ˆ‰ ˆ‰
Š‹
x x 2000 100 x
20 10 3 9 20
#
1 dx 20œœ
2x
320
'0
20ˆ‰
19. M (y 1) dx dy 2y 2y dy ; M y(y 1) dx dy 2 y y dy ;œœœœ œœ
'' ' ''
0y 0 0y
1y 1 1y
x
1
0
ab ab
'
#$#
57
36
M x(y 1) dx dy 0 dy 0 x 0 and y ; I y (y 1) dx dy 2y 2y dy
y x
0y 0 0y 0
1y 1 1y 1
œœœÊœœœ œ
'' ' '' '
7
10 #%$
ab
; I x (y 1) dx dy 2y 2y dy I I Iœœ œ œÊœœ
936
10 3 10 5
yoxy
0y 0
1y 1
'' '
#%$
"ab
20. M 3x 1 dx dy 2y 2y dy ; M y 3x 1 dx dy 2y 2y dy ;œœœœ œœ
'' ' '' '
0y 0 0y 0
1y 1 1y 1
x
ab a b ab a b
#$ # %#
#
316
15
M x 3x 1 dx dy 0 x 0 and y ; I y 3x 1 dx dy 2y 2y dy ;
y x
0y 0y 0
1y 1y 1
œœÊœœœ œœ
'' '' '
ab ab a b
###&$
32 5
45 6
I x 3x 1 dx dy 2 y y dy I I I
yoxy
0y 0
1y 1
œœœÊœœ
'' '
## & $
"
ab ˆ‰
311 6
53 30 5
21. I y z dz dy dx cy dy dx dx
x000 00 0
abc ab a
œœœœ
''' '' '
ab Š‹ Š‹
## #
ccbcb
3333
abc b c
ab
b c where M abc; I a c and I a b , by symmetryœ œ œ œ
MMM
333
ab ab ab
## ## ##
yz
22. The plane z is the top of the wedge I y z dz dy dxœÊœ
42y
3
##
x3243
34 42y3
''' ab
dy dx dx 208; I x z dz dy dxœœœœ
'' ' '''
32 3 3243
34 3 34 42y3
y
’“ ab
8y 2y 8(2 y)
3 3 81 81 3
64 104
##
dy dx 12x dx 280;œœœ
'' '
32 3
34 3
’“
ˆ‰
(4 2y) x (4 2y)
81 3 3 81 3
4x 64 32
#
I x y dz dy dx x y dy dx 12 x 2 dx 360
z3243 32 3
34 42y3 34 3
œœœœ
''' '' '
ab ab ab
ˆ‰
## ## #
8
33
2y
23. M 4 dz dy dx 4 4 4y dy dx 16 dx ; M 4 z dz dy dxœœœœœ
''' '' ' '''
004y 00 0 004y
114 11 1 114
xy
ab
#232
33
2 16 16y dy dx dx z , and x y 0, by symmetry;œœœÊœœœ
'' '
00 0
11 1
ab
%128 128 12
555
I 4 y z dz dy dx 4 4y 4y dy dx 4 dx ;
x004y 00 0
114 11 1
œœœœ
''' '' '
ab ’“
ˆ‰
Š‹
## # %
64 1976 7904
3 3 105 105
64y
I 4 x z dz dy dx 4 4x 4x y dy dx 4 x dx
y004y 00 0
114 11 1
œœœ
''' '' '
ab ’“
ˆ‰ ˆ ‰
Š‹
## # ## #
64 8 128
33 37
64y
; I 4 x y dz dy dx 16 x x y y y dy dxœœ œ
4832
63 z004y 00
114 11
''' ''
ab a b
## ####%
16 dxœœ
'0
1Š‹
2x 2 256
315 45
24. (a) M dz dy dx (2 x) dy dx (2 x) 4 x dx 4 ;œœœœ
'' ' '' '
24x20 24x2 2
24x22x 24x2 2 Š‹
È#1
M x dz dy dx x(2 x) dy dx x(2 x) 4 x dx 2 ;
yz 24x20 24x2 2
24x22x 24x2 2
œœœœ
'' ' '' ' Š‹
È#1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

912 Chapter 15 Multiple Integrals
M y dz dy dx y(2 x) dy dx
xz 24x20 24x2
24x22x 24x2
œœ
'' ' ''
(2 x) dx 0 x and y 0œ œÊœœ
" "
##
'2
2’“
4x 4x
44
(b) M z dz dy dx (2 x) dy dx (2 x) 4 x dx
xy 24x20 24x2 2
24x22x 24x2 2
œœœ
'' ' '' '
""
##
##
#
Š‹
È
5 zœÊœ15
4
25. (a) M 4 dz dy dx 4 r dz dr d 4 4r r dr d 4 4 d 8 ;œœœœœ
'' ' ' '' ' ' '
00 xy 0 0r 0 0 0
2 4x 4 224 22 2
)))1ab
$
M zr dz dr d 16 r dr d d z , and x y 0, by symmetry
xy 00r 00 0
224 22 2
œœœœÊœœœ
''' '' '
)))
r32648
333#
%
ab 1
(b) M 8 4 r dz dr d cr r dr d d c 8 c 2 2,œÊœ œ œ œ ʜʜ11 ) ) )
'' ' '' '
00 r 0 0 0
2cc 2 c 2
ab È
$#
#
cc
4
1
since c 0
26. M 8; M z dz dy dx dy dx 0; M x dz dy dxœœ œ œœ
xy yz
13 1 13 13 1
151 15 151
''' '' '''
’“
z
2
"
"
2 x dy dx 4 x dx 0; M y dz dy dx 2 y dy dx 16 dx 32œœœœ œ œœ
'' ' ''' '' '
13 1 13 1 13 1
15 1 151 15 1
xz
x 0, y 4, z 0; I y z dz dy dx 2y dy dx 100 dx ;Êœ œ œ œ œ œ œ
x13 1 13 1
151 15 1
''' '' '
ab ˆ‰
## #
2 2 400
33 3
I x z dz dy dx 2x dy dx 3x 1 dx ;
y13 1 13 1
151 15 1
œœœœ
''' '' '
ab ab
ˆ‰
## # #
24 16
33 3
I x y dz dy dx 2 x y dy dx 2 2x dx
z13 1 13 1
151 15 1
œœœœ
''' '' '
ab ab ˆ‰
## ## #
98 400
33
27. The plane y 2z 2 is the top of the wedge I (y 6) z dz dy dxœ Êœ
L221
24 2y2
''' cd
##
dy dx; let t 2 y I 4 5t 16t dt 1386;œœÊœœ
'' '
22 2
24 4
L
’“ Š‹
(y 6) (4 y) (2 y)
24 3 24 3
13t 49
#
"#
M (3)(6)(4) 36œœ
"
#
28. The plane y 2z 2 is the top of the wedge I (x 4) y dz dy dxœ Êœ
L221
24 2y2
''' cd
##
x 8x 16 y (4 y) dy dx 9x 72x 162 dx 696; M (3)(6)(4) 36œ œ œ œ œ
" "
# #
## #
'' '
22 2
24 2
ab ab
29. (a) M 2x dz dy dx 4x 2x 2xy dy dx x 4x 4x dxœœœœ
'' ' '' '
00 0 00 0
22x2xy 22x 2
abab
#$#
4
3
(b) M 2xz dz dy dx x(2 x y) dy dx dx ; M by
xy xz
00 0 00 0
22x2xy 22x 2
œœœœœ
'' ' '' '
#x(2 x)
31515
88
symmetry; M 2x dz dy dx 2x (2 x y) dy dx 2x x dx
yz 00 0 00 0
22x2xy 22x 2
œœœœ
'' ' '' '
## #
#
ab16
15
x , and y zÊœ œœ
42
55
30. (a) M kxy dz dy dx k xy 4 x dy dx 4x x dxœœœœ
'' ' '' '
00 0 00 0
2x4x 2x 2
ab a b
##%
#
k 32k
15
(b) M kx y dz dy dx k x y 4 x dy dx 4x x dx
yz 00 0 00 0
2x4x 2x 2
œœœœ
'' ' '' '
###$&
#
ab a b
k8k
3
x ; M kxy dz dy dx k xy 4 x dy dx 4x x dxÊœ œ œ œ
5 k
4 3
xz 00 0 00 0
2x4x 2x 2
'' ' '' '
# # # &Î# *Î#
ab ˆ‰
y ; M kxyz dz dy dx xy 4 x dy dxœÊœ œ œ
256 2k 40 2
231 77
ÈÈ
xy 00 0 00
2x4x 2x
'' ' '' ab
##
16x 8x x dx zœœÊœ
k 256k 8
4 105 7
'0
2ab
#%'
31. (a) M (x y z 1) dz dy dx x y dy dx (x 2) dxœœœœ
''' '' '
000 00 0
111 11 1
ˆ‰
35
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.6 Moments and Centers of Mass 913
(b) M z(x y z 1) dz dy dx x y dy dx x dx
xy 000 00 0
111 11 1
œœœœ
''' '' '
""
##
ˆ‰ ˆ‰
5134
363
M M M , by symmetry x y zÊœœœ Êœœœ
xy yz xz 48
315
(c) I x y (x y z 1) dz dy dx x y x y dy dx
z000 00
111 11
œœ
''' ''
ab ab
ˆ‰
## ##
#
3
x 2x x dx I I I , by symmetryœœÊœœœ
'0
1
xyz
ˆ‰
$#
"
34 6 6
311 11
32. The plane y 2z 2 is the top of the wedge.œ
(a) M (x 1) dz dy dx (x 1) 2 dy dx 18œœœ
''' ''
121 12
14 2y2 14 ˆ‰
y
#
(b) M x(x 1) dz dy dx x(x 1) 2 dy dx 6;
yz 121 12
14 2y2 14
œœœ
''' '' ˆ‰
y
#
M y(x 1) dz dy dx y(x 1) 2 dy dx 0;
xz 121 12
14 2y2 14
œœœ
''' '' ˆ‰
y
#
M z(x 1) dz dy dx (x 1) y dy dx 0 x , and y z 0
xy 121 12
14 2y2 14
œœœÊœœœ
''' ''
"
#Š‹
y
43
1
(c) I (x 1) y z dz dy dx (x 1) 2y dy dx 45;
x121 12
14 2y2 14
œœ"œ
''' ''
ab ’“
ˆ‰
## #
""
#
$
332
yy
I (x 1) x z dz dy dx (x 1) 2x dy dx 15;
y121 12
14 2y2 14
œœ"œ
''' ''
ab ’“
ˆ‰
## #
""
#
$
332
xy y
I (x 1) x y dz dy dx (x 1) 2 x y dy dx 42
z121 12
14 2y2 14
œœœ
''' ''
ab ab
ˆ‰
## ##
#
y
33. M (2y 5) dy dx dz z 5 z dx dz 2 z 5 z (1 z) dzœœœ
'' ' '' '
0z10 0z1 0
11z z 11z 1
ˆ‰ ˆ‰
ÈÈ
2 5z z 5z z dz 2 z z 2z z 2 3œ œ œœ
'0
1ˆ‰ ‘ˆ‰
"Î# $Î# # $Î# # &Î# $
""
##
"
!
10 9 3
333
34. M x y dz dy dx x y 16 4 x y dy dxœœ
'' ' ''
24x2xy 24x
24x162xy 24x
ÈÈ
cdab
## ## ##
4 r 4 r r dr d 4 d 4 dœœœœ
'' ' '
00 0 0
22 2 2
ab ’“
##
!
)))
4r r 64 512
3 5 15 15
1
35. (a) x 0 x (x y z) dx dy dz 0 M 0œœÊ ßß œÊ œ
M
M
yz '''
R
$yz
(b) I h dm (x h) y dm x 2xh h y dm
Lœœ œ
''' ''' '''
DD D
kk k k a bvi ij
##
###
x y dm 2h x dm h dm I 0 h m I h mœ œœ
''' ''' '''
DDD
ab
## # # #
xcm
36. I I mh ma ma ma
Lcm
œ œ œ
####
27
55
37. (a) (x y z) I I abc I Ißß œ ß ß Ê œ Ê œ
ˆ‰ Š‹
É
abc a b
44 4
cm z abc a b
###
#
ÞÞ
zcm ab
; Rœœ œœ
abc a b abc a b abc a b
341 M12
cm Iab
ab ab ab
#ÞÞ
ÉÉ
cm
(b) I I abc 2b
Lcm ab
41241
abc a b abc a 9b abc 4a 28b
œ œ œ
ÞÞ ##
##
Œ
Ɉ ‰ ab a b a b
; Rœœœ
abc a 7b
3M3
LIa7b
ab
ÉÉ
L
38. M dz dy dx (4 y) dy dx 4y dx 12 dx 72;œ œ œœœ
''' '' ' '
3243 32 3 3
34 42y3 34 3 3
22
332
y
’“
%
#
x y z 0 from Exercise 22 I I 72 0 0 I I I 72 16œœœ Ê œ œ Ê œ
xcmL
16
9
cm cmÞÞ ÞÞ
Š‹ Š‹
ÈÉ
##
#
ÞÞ
#
208 72 1488œ œ
ˆ‰
160
9
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
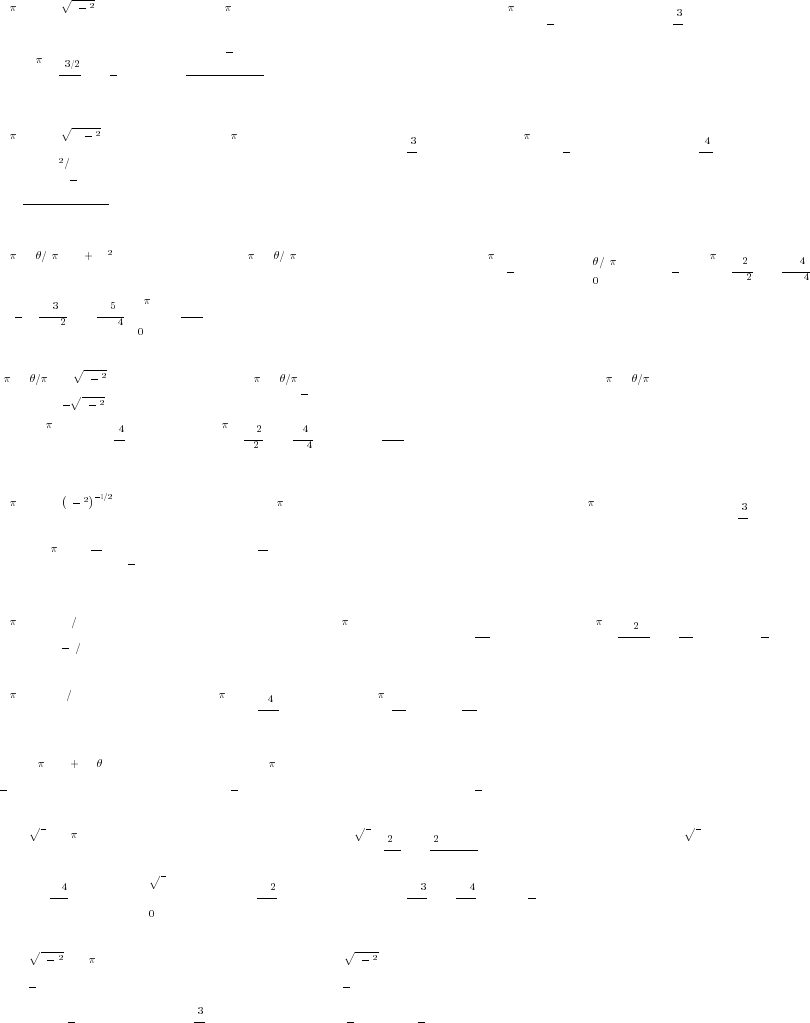
914 Chapter 15 Multiple Integrals
15.7 TRIPLE INTEGRALS IN CYLINDRICAL AND SPHERICAL COORDINATES
1. dz r dr d r 2 r r dr d 2 r d
''' '' '
00r 00 0
21 2r 21 2
)))œœ
’“’ “
ab ab
## #
"Î# $Î#
""
!
33
r
dœœ
'0
2Š‹
22
33 3
42
)1Š‹
È"
2. dz r dr d r 18 r dr d 18 r d
''' '' '
00r3 00 0
23 18r 23 2
)))œœ
’“’ “
ab ab
##
"Î# $Î#
"$
!
rr
3312
œ9827
2
1Š‹
È
3. dz r dr d 3r 24r dr d r 6r d d
'' ' '' ' '
00 0 00 0 0
22324r 22 2 2
2
))))œœœab ‘ Š‹
$#%
#
334
24
16
))
11
œœ
317
12 5
20
#’“
)) 1
11
2
4. z dz r dr d 9 4 r 4 r r dr d 4 4r r dr d
'' ' '' ''
00 4r 00 00
34r
)))œœ
"
#
## $
cdababab
4 2r 4 dœœœ
''
00
’“ Š ‹
#Î
!
r2 37
415
4
)1 )) 1
11)
5. 3 dz r dr d 3 r 2 r r dr d 3 2 r d
''' '' '
00r 00 0
212r 21 2
)))œœ
’“’“
ab ab
## #
"Î# "Î# "
!
r
3
3 2 d 6 2 8œœ
'0
2Š‹Š ‹
ÈÈ
4
3)1
6. r sin z dz r dr d r sin dr d d
''' '' '
00 12 00 0
2112 21 2
ab ˆ‰Š‹
## # $# "
)) )) )œ œœ
rsin
12 4 24 3
)1
7. r dr dz d dz d d
''' '' '
000 00 0
23z3 23 2
$)))œœœ
z33
324 20 10
1
8. 4r dr d dz 2(1 cos ) d dz 6 d 12
''' '' '
10 0 10 1
12 1cos 12 1
)))1)1œ œœ
#
9. r cos z r d dr dz z r dr dz r 2 rz dr dz
'' ' '' ''
00 0 00 00
1z2 1z 1z
ab ab
’“
## # # $ #
#
!
)) ) 11œ œ
rr sin 2
24
)) 1
r z dz z dzœ œ œœ
''
00
11
z
’“Š‹’“
11111rzzz
441243
11
## $ "
!
10. (r sin 1) r d dz dr 2 r dz dr 2 r 4 r r 2r dr
'' ' '' '
0r2 0 0r2 0
24r2 24r 2
)) 1 1œ œ
’“
ab
##
"Î#
24r r2 4(4)8œ œ œ111
’“
ab ‘
""
# # $Î#
$Î# #
!
33 33
r8
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
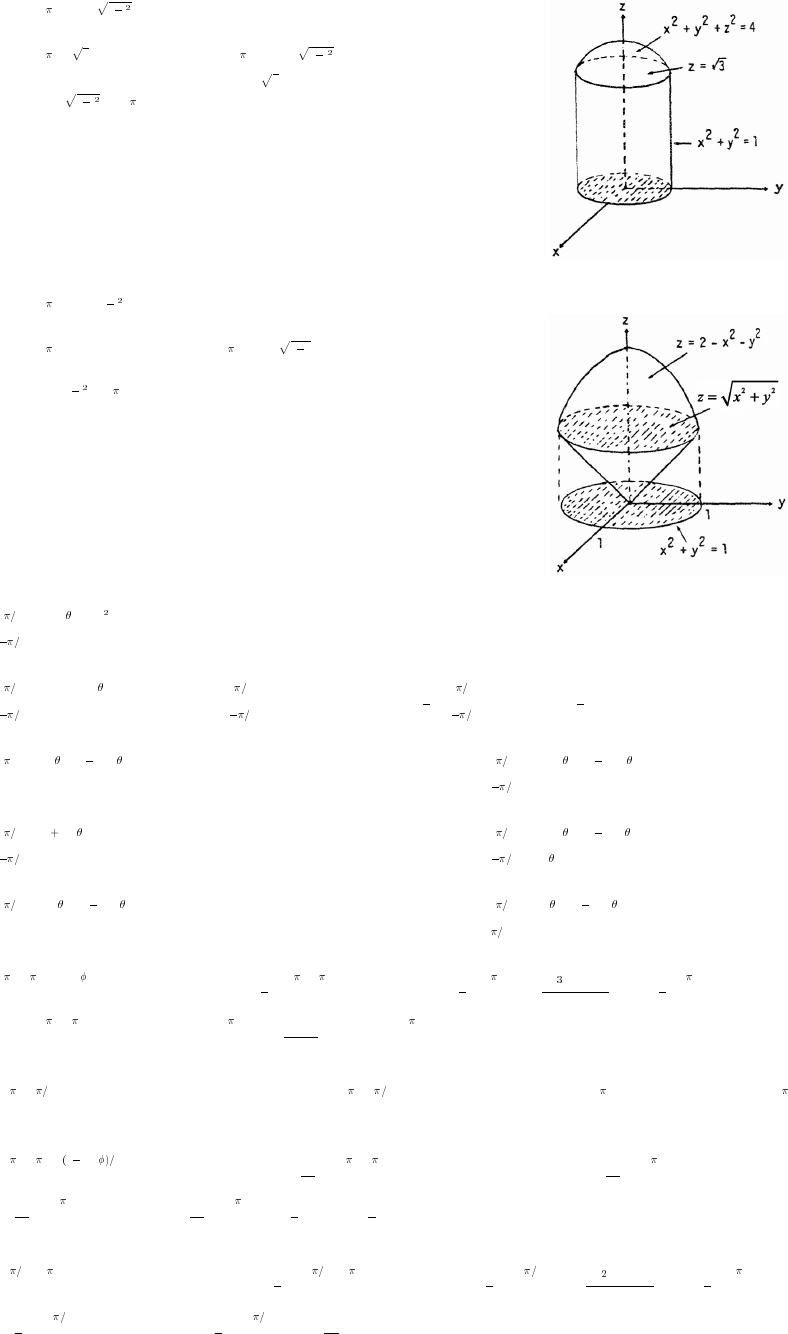
Section 15.7 Triple Integrals in Cylindrical and Spherical Coordinates 915
11. (a) dz r dr d
'''
000
21 4r
)
(b) r dr dz d r dr dz d
'' ' '''
00 0 0 30
231 224z
))
(c) r d dz dr
'' '
00 0
14r2
)
12. (a) dz r dr d
'''
00r
212r
)
(b) r dr dz d r dr dz d
''' '''
000 010
21z 22 2z
))
(c) r d dz dr
'' '
0r 0
12r 2
)
13. f(r z) dz r dr d
'''
20 0
2 cos 3r ßß))
14. r dz dr d r cos dr d cos d
''' '' '
20 0 20 2
21r cos 21 2
$%
"
)))))œœœ
55
2
15. f(r z) dz r dr d 16. f(r z) dz r dr d
'' ' ' ' '
00 0 20 0
2 sin 4 r sin 2 3 cos 5 r cos
ßß ßß)) ))
17. f(r z) dz r dr d 18. f(r z) dz r dr d
'' ' '' '
21 0 2cos 0
21cos 4 2 2 cos 3 r sin
ßß ßß)) ))
19. f(r z) dz r dr d 20. f(r z) dz r dr d
'' ' '' '
00 0 40 0
4 sec 2 r sin 2 csc 2 r sin
ßß ßß)) ))
21. sin d d d sin d d sin d d
''' '' ' '
000 00 0 0
2 sin
3 939) 99) 99 )
#% #
!
œœ
88 3
3344
sin cos
Š‹’“
99
1
2 sin d d d dœœœœ
'' ' '
00 0 0
##
#!
99) ) ) 1) 1
‘
sin 2)1
22. ( cos ) sin d d d 4 cos sin d d 2 sin d d 2
'' ' '' ' '
00 0 00 0 0
242 24 2 2
3 93 939) 9 99) 9 ) ) 1
# # Î%
!
œœœœcd
1
23. sin d d d (1 cos ) sin d d (1 cos ) d
''' '' '
000 00 0
21cos 2 2 2
3 939) 9 99) 9 )
#$%
""
!
œ œ
24 96 cd
1
20 d d (2)œœœœ
""
%
96 96 6 3
16
''
00
22
ab))1
1
24. 5 sin d d d sin d d sin d d
''' '' ' '
000 00 0 0
32 1 32 32
3939) 99) 99)
$$ $
!
œœ
55 2
4433
sin cos
Š‹’“
99
1
cos d dœ œ œ
555
63
''
00
32 32
cd9) )
11
!#
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

916 Chapter 15 Multiple Integrals
25. 3 sin d d d 8 sec sin d d 8 cos sec d
'' ' '' '
00 sec 00 0
232 23 2
3939) 999) 9 9 )
#$ #
"Î$
!
œ œab ‘
2
1
(4 2) 8 d d 5œ œ œ
''
00
22
‘ˆ‰
"
##
))1
5
26. sin cos d d d tan sec d d tan d d
'' ' '' ' '
00 0 00 0 0
24sec 24 2 2
39939) 999) 9 ) )
$##
""""
Î%
!
œœœœ
44284
‘
11
27. sin 2 d d d d d d d d 2
'' ' '' '' '
04 0 0 0
20 2 20 20 2
3 99)3 3 )3 )3 3 1
$$
Î#
Î% ##
#
!
œ œ œœœ
‘ ’“
cos 2
28
91
1
33113
28. sin d d d 2 sin d d sin d
'' ' '' ' '
6 csc 0 6 csc 6 6
3 2 csc 2 3 2 csc 3 2 csc
csc
39)391 3939 39 9
##$
œœœ
214
33
11
cd 3csc d
#99œ28
33
1
È
29. 12 sin d d d 12 8 sin d d d
''' '' '
000 00 0
14 1 4
3 99)3 3 3 99 )3
$Î%
!
œ
Œ
’“
sin cos
3
99
1
8 cos dd 8 dd 8 d 4œ œ œ œ
'' '' '
00 00 0
111
Š ‹ Š‹ Š‹’ “
cd
210105
2222
3333
1
ÈÈÈÈ
39)3 3)313313
Î%
!#"
!
œŠ‹
ÈÈ
425
2
1
30. 5 sin d d d 32 csc sin d d 32 sin csc d d
''' '' ''
62csc 62 62
222 22 22
393)9 99)9 9 9)9
%$ & $ $ #
œ œ ab a b
32 sin csc d sin d cot œœ 19991 9919
''
6 6
2 2
ab cd
’“
$# Î#
Î'
Î#
Î'
32 sin cos
33
64
99
1
1
11
1
cos 3 11 3œ œ œœ1911 1
Š‹ Š‹ Š‹
cd ÈÈ
ˆ‰
32 3 3 3 33 3
24 3 3 3 3
64 64
ÈÈÈÈ
11
1
1
1
Î#
Î' #
31. (a) x y 1 sin 1, and sin 1 csc ; thus
## ##
œÊ œ œÊœ39 39 3 9
sin d d d sin d d d
'' ' '' '
00 0 0 60
262 22csc
3939) 3939)
##
(b) sin d d d sin d d d
''' '''
01 6 000
22sin1 22 6
3993) 3993)
##
32. (a) sin d d d
'' '
00 0
2 4 sec
3939)
#
(b) sin d d d
'''
000
21 4
3993)
#
sin d d d'' '
01 cos
224
3993)
#
33. V sin d d d 8 cos sin d dœœ
'' ' ''
00 cos 00
222 22
3939) 999)
#$
"
3ab
8 cos d 8 d (2 )œ œ œ œ
"""
Î#
!
3434126
cos 31 31
''
00
22
’“
ˆ‰ˆ‰
9) )1
911
34. V sin d d d 3 cos 3 cos cos sin d dœœ
'' ' ''
00 1 00
221cos 22
3939) 9 9 999)
##$
"
3ab
cos cos cos d 1 d d (2 )œ œ œ œ œ
"""
#
#$ %
Î#
!
3432412126
31 3111111
'''
000
222
‘ˆ‰ˆ‰
99 9) ) ) 1
11
35. V sin d d d (1 cos ) sin d d dœœœ
''' '' '
000 00 0
21cos 2 2
3939) 9 99) )
#$
""
"
!
334
(cos )
’“
91
(2) d (2 )œœœ
"%
12 3 3
48
'0
2
)1
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.7 Triple Integrals in Cylindrical and Spherical Coordinates 917
36. V sin d d d (1 cos ) sin d d dœœœ
'' ' '' '
00 0 00 0
221cos 22 2
3939) 9 99) )
#$
""
" Î#
!
334
(cos )
’“
91
d(2)œœœ
""
12 12 6
'0
2
)1
1
37. V sin d d d cos sin d d dœœœ
'' ' '' '
040 04 0
222 cos 22 2
3939) 999) )
#$ Î#
Î%
88
334
cos
’“
91
1
d(2)œœœ
ˆ‰ˆ‰
8
316 6 3
""
'0
2
)1
1
38. V sin d d d sin d d cos d dœœœœœ
'' ' '' ' '
030 03 0 0
222 22 2 2
3939) 99) 9 ) )
#Î#
Î$
8848
3333
cd
1
1
1
39. (a) 8 sin d d d (b) 8 dz r dr d
''' '''
000 000
222 22 4r
3939) )
#
(c) 8 dz dy dx
'' '
00 0
24x 4xy
40. (a) dz r dr d (b) sin d d d
'' ' '''
00 r 000
232 9r 2 43
)3939)
#
(c) sin d d d 9 sin d d 9 1 d
''' '' '
000 00 0
243 24 2
3939) 99) )
#"
œœœ
Š‹
ÈŠ‹
È
2
92 2
4
1
41. (a) V sin d d d (b) V dz r dr dœœ
'' ' '' '
0 0 sec 00 1
232 234r
3939) )
#
(c) V dz dy dxœ'' '
33x1
33x 4xy
(d) V r 4 r r dr d d dœœœ
'' ' '
00 0 0
23 2 2
’“ Š‹
ab ”•
#"Î#
##
$
!
"
)))
ab È
4r
333
r34
dœœ
55
63
'0
2
)1
42. (a) I r dz r dr d
z000
21 1r
œ''' #)
(b) I sin sin d d d , since r x y sin cos sin sin sin
z00 0
221
œ œœ œ
'' 'abab393939) 39)39)39
## # # # # ## # ## # ##
(c) I sin d d sin d d cos d
z00 0 0 0
22 2 2 2
œœœ
'' ' ' '
""
$Î#
!
Î#
!
5533 15
sin cos 22
99) 99 ) 9 )
Œ
’“ cd
99
11
(2 )œœ
24
15 15
11
43. V 4 dz r dr d 4 5r 4r r dr d 4 1 d 4 dœœœœœ
''' '' ' '
00r1 00 0 0
2144r 21 2 2
))))ab ˆ‰
$&
#
"58
63
1
44. V 4 dz r dr d 4 r r r 1 r dr d 4 1 r dœœœ
''' '' '
00 1r 00 0
211r 21 2
)) )
Š‹’ “
Èab
##
#"$Î# "
!
rr
233
4 d2d2œ œ œœ
''
00
22
ˆ‰ ˆ‰
"""
##33
)) 1
1
45. V dz r dr d r sin dr d 9 cos (sin ) d cosœœœœ
'' ' '' '
32 0 0 32 0 32
2 3 cos r sin 2 3 cos 2
)))))))
#$%
#
$Î#
ab ‘
9
4
1
1
0œœ
99
44
46. V 2 dz r dr d 2 r dr d 27 cos dœœœ
'' ' '' '
20 0 20 2
3 cos r 3 cos
))))
#$
2
3
18 cos d 12 sin 12œ œ œ
Œ
’“ cd
cos sin 2
33
))
1
1
1
1
Î# Î#
'2)) )
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
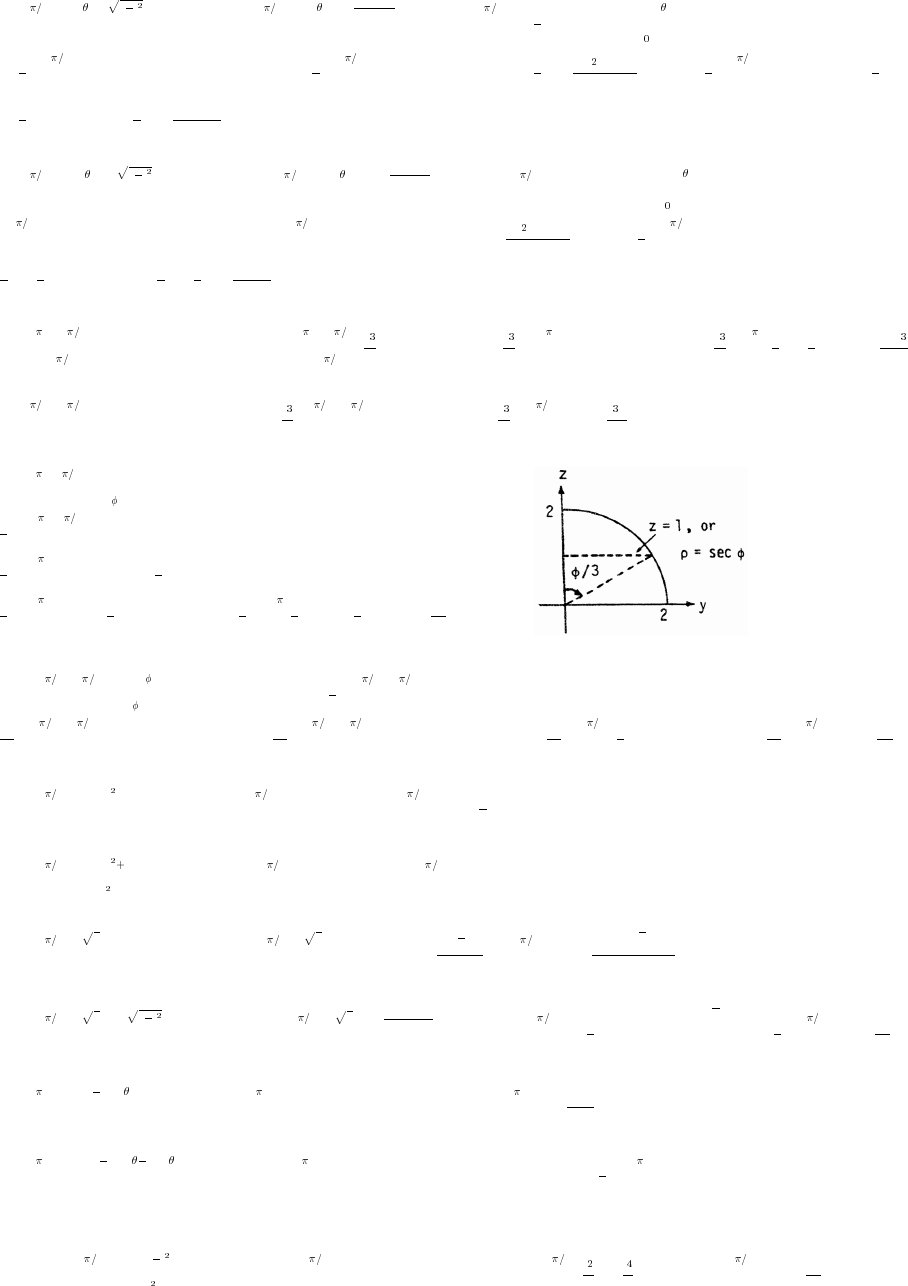
918 Chapter 15 Multiple Integrals
47. V dz r dr d r 1 r dr d 1 r dœœœ
''' '' '
00 0 00 0
2sin 1r 2sin 2 sin
)) )
È’“
ab
#"#$Î#
3
1 sin 1 d cos 1 d cos dœ œ œ
"""
#$
$Î# Î#
!
Î#
!
333333
cos sin 2
'' '
00 0
22 2
’“ ’“
ab abŒ
‘
)) )) ))
)) )
11
sin œ œ
243
9618
cd)111
Î#
!
48. V dz r dr d 3r 1 r dr d 1 r dœœœ
'' ' '' '
00 0 00 0
2cos 1r 2cos 2 cos
3
)) ) È’“
ab
##$Î#
1 cos 1 d 1 sin d sin dœ œ œ
'' '
00 0
22 2
’“ ’“
ab ab
#$
$Î# Î#
!
)) ))) ))
sin cos 2
33
))
1
cos œ œœ
111
1
##
Î#
!2234
336
cd)
49. V sin d d d sin d d cos d dœœœœœ
'' ' '' ' '
030 03 0 0
223a 223 2 2
3939) 99) 9 ) )
##Î$
Î$
""
##
aa a 2a
33 3 3
cd ˆ‰
1
1
1
50. V sin d d d sin d d dœœœœ
''' '' '
000 00 0
62a 62 6
3939) 99) )
#aaa
3318
1
51. V sin d d dœ'' '
0 0 sec
232
3939)
#
8 sin tan sec d dœ
"#
3''
00
23
ab9999)
8 cos tan dœ
""
#Î$
!
32
'0
2‘
99)
1
4 (3) 8 d d (2 )œœ œœ
"" "
##3363
55 5
''
00
22
‘
))1
1
52. V 4 sin d d d 8 sec sec sin d dœœ
''' ''
00sec 00
242 sec 24
3939) 9 999)
#$$
4
3ab
sec sin d d tan sec d d tan d dœœœœœ
28 28 28 14 7
333233
'' '' ' '
00 00 0 0
24 24 2 2
$##
"Î%
!
9 99) 9 99) 9 ) )
‘
11
53. V 4 dz r dr d 4 r dr d dœœœœ
''' '' '
000 00 0
21r 21 2
)))
$
#
1
54. V 4 dz r dr d 4 r dr d 2 dœœœœ
''' '' '
00r 00 0
21r1 21 2
)))1
55. V 8 dz r dr d 8 r dr d 8 dœœœœ
''' '' '
010 01 0
22r 22 2
)) )
#" "
Š‹
22
33
422
ÈŠ‹
È
1
56. V 8 dz r dr d 8 r 2 r dr d 8 2 r d dœœœœœ
'' ' '' ' '
01 0 01 0 0
22 2r 22 2 2
)) ))
È’“
ab
#"#$Î# #
333
1
84
È1
57. V dz r dr d 4r r sin dr d 8 1 d 16œœœœ
''' '' '
000 00 0
224r sin 22 2
))))1ab ˆ‰
#sin
3
)
58. V dz r dr d 4r r (cos sin ) dr d (3 cos sin ) d 16œœœœ
''' '' '
000 00 0
2 2 4 r cos r sin 2 2 2
)))))))1cd
#8
3
59. The paraboloids intersect when 4x 4y 5 x y x y 1 and z 4
# # ## ##
œÊœ œ
V 4 dz r dr d 4 5r 5r dr d 20 d 5 dÊœ œ œ œ œ
''' '' ' '
004r 00 0 0
215r 21 2 2
))))ab ’“
$"
!#
rr 5
24
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.7 Triple Integrals in Cylindrical and Spherical Coordinates 919
60. The paraboloid intersects the xy-plane when 9 x y 0 x y 9 V 4 dz r dr dœÊ œÊ œ
## ## '''
010
23 9r
)
4 9r r dr d 4 d 4 d 64 d 32œœœœœ
'' ' ' '
01 0 0 0
23 2 2 2
ab ’“ ˆ‰
$$
"
))))1
9r r 81 17
24 44
61. V 8 dz r dr d 8 r 4 r dr d 8 4 r dœœœ
''' '' '
000 00 0
21 4r 21 2
)) )ab ab
’“
##
"Î# $Î#
""
!
3
38 dœ œ
8
33
4833
'0
2ˆ‰
$Î#
)1Š‹
È
62. The sphere and paraboloid intersect when x y z 2 and z x y z z 2 0
### ## #
œ œ Ê œ
(z 2)(z 1) 0 z 1 or z 2 z 1 since z 0. Thus, x y 1 and the volume isÊ œÊœ œÊœ œ
##
given by the triple integral V 4 dz r dr d 4 r 2 r r dr dœœ
''' ''
00r 00
21 2r 21
))
’“
ab
#$
"Î#
4 2 r d 4 dœ œ œ
''
00
22
’“Š‹
ab
"#$Î# "
!
34 3126
r7
22 827
))
ÈŠ‹
È
1
63. average r dz dr d 2r dr d dœœœœ
"""
##
##
111
''' '' '
00 1 00 0
211 21 2
)))
33
2
64. average r dz dr d 2r 1 r dr dœœ
"##
#
ˆ‰
4
3''' ''
00 1r 00
21 1r 21
))
3
41È
sin r r 1 r 1 2r d 0 d d (2 )œœœœœ
33333
28 8 16 32 32 1611
11
'''
000
222
’“
Èab ˆ‰ ˆ‰
""
" #
#"
!#
)))1
65. average sin d d d sin d d dœœœœ
"$
ˆ‰
4
3''' '' '
000 00 0
21 2 2
3939) 99) )
333
16 8 411
66. average cos sin d d d cos sin d d dœœœ
"$Î#
!
ˆ‰
2
3'' ' '' '
00 0 00 0
221 22 2
3 9 939) 9 99) )
33
882
sin
11
91
’“
d(2)œœœ
333
16 16 811
'0
2
)1
ˆ‰
67. M 4 dz r dr d 4 r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
21 r 21 2 2 1r
xy
))) )
#42
33
1
r dr d d z , and x y 0, by symmetryœœœÊœœœœœ
"
#
$
'' '
00 0
21 2
))
133
84M428
M
11
1
xy ˆ‰ˆ ‰
68. M dz r dr d r dr d d ; M x dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
22r 22 2 22 r
yz
))) )
#84
33
1
r cos dr d 4 cos d 4; M y dz r dr d r sin dr dœœœœ œ
'' ' ''' ''
00 0 000 00
2 2 2 22r 22
xz
$ $
)) )) ) ))
4 sin d 4; M z dz r dr d r dr d 2 d x ,œœœ œ œœÊœœ
'''''''
0000000
222r222
xy
)) ) ) ) 1
"
#
$M
M
3
yz
1
y , and zœœ œœ
M
MM4
33
M
xz xy
1
69. M ; M z sin d d d cos sin d d d 4 cos sin d dœœ œ œ
8
3
1xy 030 030 03
222 222 22
'' ' '' ' ''
3 939) 3 9 939) 9 99 )
#$
4 d 4 d d z ( ) , and x y 0, by symmetryœœœœÊœœœœœ
'''
000
222
’“ ˆ‰ ˆ‰
sin
28 M88
333
M
91
11
Î#
Î$
""
##
)))11
xy
70. M sin d d d sin d d d ;œœœœ
'' ' '' '
00 0 00 0
24a 24 2
3939) 99) )
#
#
aa
333
22 a2 2
ÈŠ‹
È
1
M sin cos d d d sin cos d d d
xy 00 0 0 0 0
24a 2 4 2
œœœœ
'' ' ' ' '
3 9 939) 9 99) )
$aaa
4168
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

920 Chapter 15 Multiple Integrals
z , and x y 0, by symmetryÊœ œ œ œ œœ
M
M8 8 16
a3 3a
a2 2
22 32 2a
xy Š‹ Š ‹
–—
ˆ‰
1
1Š‹
ÈÈŠ‹
È
#
71. M dz r dr d r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
24 r 24 2 24 r
xy
))) )
$Î# 64 128
55
1
r dr d d z , and x y 0, by symmetryœœœÊœœœœ
"
#
#
'' '
00 0
24 2
))
32 64 5
33M6
M
1xy
72. M dz r dr d 2r 1 r dr d 1 r dœœœ
''' '' '
30 1r 30 3
31 1r 31 3
)) )
È’“
ab
##$Î# "
!
2
3
d ; M r cos dz dr d 2 r 1 r cos dr dœœœœ œ
2224
3339
''''''
3301r30
3311r31
yz
)))))
ˆ‰ˆ ‰ È
11 ##
#
2 sin r r 1 r 1 2r cos d cos d sin 2œœœœœ
''
3 3
3 3 3
3
’“ Š‹
Èab cdˆ‰
1
88 8 8 8 8
33
" #
"#"
!#
)) )) )
111
1
†ÈÈ
x , and y z 0, by symmetryÊœ œ œœ
M
M32
93
yz È
73. We orient the cone with its vertex at the origin and axis along the z-axis . We use the the x-axisʜ91
4
which is through the vertex and parallel to the base of the cone I r sin z dz r dr dʜ
x00r
211
'''
ab
## #
))
r sin r sin dr d dœœœœœ
'' '
00 0
21 2
Š‹Š‹
‘
$# %# "#
!#
)) ) )
rr sin sin 2
3 3 20 10 40 80 10 0 5 4
))))111
1
74. I r dz dr d 2r a r dr d 2 a r d 2 a d
z00 00 0 0
2a 2a 2 2
ar
ar
a
œœœœ
'' '' ' '
'È’“Š‹
ab
$$ ## &
## $Î#
!
)) ))
r2a 2
515 15
œ8a
15
1
75. I x y dz r dr d r dz dr d hr dr d h d
z00 r 00 00 0
2ah 2a h 2a 2
ha
œœ œœ
''' '' ' '' '
hhr
a a
hr
a
ab 'Š‹ ’“
## $ $
!
)) ))
hr r r
a45a
h d dœœ œ
''
00
22
Š‹
a a ha ha
45a 20 10
))
1
76. (a) M z dz r dr d r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
21r 21 2 21r
xy
))) )
""
#
&#
12 6
1
r dr d d z , and x y 0, by symmetry; I zr dz dr dœœœÊœœœ œ
"" "
( $
#32412
'' ' '''
00 0 000
21 2 21r
z
)) )
1
r dr d dœœœ
""
#
(
'' '
00 0
21 2
))
16 8
1
(b) M r dz dr d r dr d d ; M zr dz dr dœœœœœ
''' '' ' '''
000 00 0 000
21r 21 2 21r
xy
#% #
"
))) )
55
21
r dr d d z , and x y 0, by symmetry; I r dz dr dœœœÊœœœ œ
""
' %
214714
5
'' ' '''
00 0 000
21 2 21r
z
)) )
1
r dr d dœœœ
'' '
00 0
21 2
'"
))
77
21
77. (a) M z dz r dr d r r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
00r 00 0 00r
211 21 2 211
xy
))) )
""
#
$#
ab 84
1
r r dr d d z , and x y 0, by symmetry; I zr dz dr dœœœÊœœœ œ
""
% $
31055
4
'' ' '''
00 0 00r
21 2 211
z
ab)) )
1
r r dr d dœœœ
""
#
$&
'' '
00 0
21 2
ab))
24 12
1
(b) M z dz r dr d from part (a); M z dz r dr d r r dr dœœœœ
''' ''' ''
00r 00r 00
211 211 21
xy
#$&
"
)))
1
54
ab
d z , and x y 0, by symmetry; I z r dz dr d r r dr dœœÊœœœ œ œ
" "
#$ $ '
12 6 6 3
5
''''''
000r 00
2211 21
z
)))
1ab
dœœ
"
28 14
'0
2
)1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 15.7 Triple Integrals in Cylindrical and Spherical Coordinates 921
78. (a) M sin d d d sin d d d ; I sin d d dœœœœœ
''' '' ' '''
000 00 0 000
2a 2 2 2a
z
3 939) 99) ) 3 939)
%'$
a2a4a
555
1
1 cos sin d d cos d dœ œœœ
a a 4a 8a
773121
cos
'' ' '
00 0 0
222
ab ’“
#
!#
999) 9 ) )
911
(b) M sin d d d d d d ;œœœœ
''' '' '
000 00 0
2a 2 2
3939) 9) )
$#
#
aaa
484
(1 cos 2 )
911
I sin d d d sin d d
z000 00
2a 2
œœ
''' ''
3939) 99)
&% %
a
6
sin d d d dœœœœ
a3a aa
644 84168
sin cos sin 2
''' '
000 0
222
Š‹’“ ‘
!
#
#!
99 9 9
1111
99 ) ) )
79. M dz r dr d r a r dr d a r dœœœ
''' '' '
000 00 0
2a ar 2a 2
h
a)) )
hh
aa3
a
È’“
ab
## "##
$Î#
!
d ; M z dz r dr d a r r dr dœœœ œ
h a 2ha h
a3 3 2a
'''' ''
0000 00
22a ar2a
xy
)))
1
h
aab
#$
d z h, and x y 0, by symmetryœœÊœ œœœ
haa ah ah33
2a 4 4 4 2ha 8
'0
2Š‹ Š‹
ˆ‰
#)11
1
80. Let the base radius of the cone be a and the height h, and place the cone's axis of symmetry along the z-axis
with the vertex at the origin. Then M and M z dz r dr d h r r dr dœœ œ
1ah h
3 a
xy 00 r 0 0
2ah 2 a
''' ' '
h
a
))
"
#
#$
Š‹
d d d z h, andœœœ œÊœœ œ
h r r h a a ha ha ha 3 3
24a 4 8 4 M 4 ah 4
aM
###
!
'''
000
222
’“ Š‹ Š‹
ˆ‰
)))
11
1
xy
x y 0, by symmetry the centroid is one fourth of the way from the base to the vertexœœ Ê
81. The density distribution function is linear so it has the form ( ) k C, where is the distance from the$3 3 3œ
center of the planet. Now, (R) 0 kR C 0, and ( ) k kR. It remains to determine the constant$$33œÊ œ œ
k: M (k kR) sin d d d k kR sin d dœ œ
''' ''
000 00
2R 2 R
3 3 939) 99)
#’“
33
43
k sin d d R cos d R d kœ œœœÊœ
'' ' '
00 0 0
222
Š‹ cd
RR k k kR 3M
43 1 6 3 R
99) 9 ) )
#
%%
!
11
1
( ) R . At the center of the planet 0 (0) R .Êœ œÊœ œ$3 3 3 $
3M 3M 3M 3M
RR R R
11 1 1
ˆ‰
82. The mass of the plant's atmosphere to an altitude h above the surface of the planet is the triple integral
M(h) e sin d d d e sin d d dœœ
''' '''
00R R00
2h h2
. 3 939) . 3 99)3
!!
Ð Ñ # Ð Ñ #cR cR33
e ( cos ) dd 2 e e dd 4 e e dœœ œ
'' '' '
R0 R0 R
h2 h2 h
‘
.39)3 .3)31. 33
!!!
Ð Ñ # # #
!
cR cRc cR c333
1
4 e (by parts)œ1.!cR e2e
ccc
2e h
R
’“
33
cc
c
4e .œ1.!cR h e 2he 2e R e 2Re 2e
ccc c c c
Š‹
ch ch ch cR cR cR
The mass of the planet's atmosphere is therefore M lim M(h) 4 .œœ
hÄ_ 1.!Š‹
R2R2
ccc
83. (a) A plane perpendicular to the x-axis has the form x a in rectangular coordinates r cos a rœÊœÊœ)a
cos )
r a sec , in cylindrical coordinates.ʜ )
(b) A plane perpendicular to the y-axis has the form y b in rectangular coordinates r sin b rœÊœÊœ)b
sin )
r b csc , in cylindrical coordinates.ʜ )
84. ax by c a r cos b r sin c r a cos b sin c r .œÊ œÊ œÊœabab a b)) )) c
a cos b sin ))
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
922 Chapter 15 Multiple Integrals
85. The equation r f z implies that the point r, , zœab a b)
f z , , z will lie on the surface for all . In particularœabab))
f z , , z lies on the surface whenever f z , , z doesab abab ab)1 )
the surface is symmetric with respect to the z-axis.Ê
86. The equation f implies that the point , , f , , lies on the surface for all . In particular, if39 39) 99) )œœab a b a bab
f , , lies on the surface, then f , , lies on the surface, so the surface is symmetric wiith respect to theab a bab ab99) 99) 1
z-axis.
15.8 SUBSTITUTIONS IN MULTIPLE INTEGRALS
1. (a) x y u and 2x y v 3x u v and y x u x (u v) and y ( 2u v);œ œ Ê œ œ Ê œ œ
""
33
`ß
`ß
""
"
""
(x y)
(u v) 9 9 3
33
2
33
2
œ œœ
»»
(b) The line segment y x from ( 0) to (1 1) is x y 0œ!ßßœ
u 0; the line segment y 2x from (0 0) toÊœ œ ß
(1 2) is 2x y 0 v 0; the line segment x 1ß œ Ê œ œ
from (1 1) to ( 2) is (x y) (2x y) 3ß"ß œ
u v 3. The transformed region is sketched at theʜ
right.
2. (a) x 2y u and x y v 3y u v and x v y y (u v) and x (u 2v);œ œÊœ œÊœ œ
""
33
`ß
`ß
"
"
""
(x y)
(u v) 9 9 3
33
2
1
33
2
œœœ
»»
(b) The triangular region in the xy-plane has vertices (0 0),ß
(2 0), and . The line segment y x from (0 0)ßß œß
ˆ‰
22
33
to is x y 0 v 0; the line segment
ˆ‰
22
33
ߜʜ
y 0 from (0 0) to ( 0) u v; the line segmentœß#ßÊœ
x 2y 2 from to (2 0) u 2. Theœ ß ßÊœ
ˆ‰
22
33
transformed region is sketched at the right.
3. (a) 3x 2y u and x 4y v 5x 2u v and y (u 3x) x (2u v) and y (3v u);œ œÊœ œ Êœ œ
"""
#510
`ß
`ß
"
(x y)
(u v) 50 50 10
21
55
13
10 10
61
œ œœ
»»
(b) The x-axis y 0 u 3v; the y-axis x 0œÊœ œ
v 2u; the line x y 1Êœ œ
(2u v) (3v u) 1ʜ
""
510
2(2u v) (3v u) 10 3u v 10. Theʜʜ
transformed region is sketched at the right.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 15.8 Substitutions in Multiple Integrals 923
4. (a) 2x 3y u and x y v x u 3v and y v x x u 3v and y u 2v;œœÊœœÊœœ
23 1
3
12
`ß
`ß
(x y)
(u v) œ œœ
"
ºº
(b) The line x 3 u 3v 3 or u 3v 3;œ Ê œ œ
x0 u3v0; yx v0; yx1œÊ œ œÊœ œ
v 1. The transformed region is the parallelogramʜ
sketched at the right.
5. x dx dy dy 1 1 y y dy
'' ' '
0y2 0 0
4y21 4 4
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
’“ ’ “
œ œ
yxyyyyy
x
2#######
"##
y
2
y
2
(y 1 y) dy dy (4) 2œœ œœ
"""
###
''
00
44
6. 2x xy y dx dy (x y)(2x y) dx dy
'' ''
RR
ab
##
œ
uv du dv uv du dv;œœ
'' ''
GG
¹¹
`ß
`ß
"
(x y)
(u v) 3
We find the boundaries of G from the boundaries of R,
shown in the accompanying figure:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
y2x4œ "
3(2uv) (uv)4 v4
y 2x7 (2uv) (uv)7 v7
y x 2 ( 2u v) (u v) 2 u 2
y x 1 ( 2u v) (u v) 1 u 1
œ œ
œ œ œ
œ œ œ
œ œ œ
2
3
33
2
33
1
33
1
"
"
"
uv du dv uv dv du u du u du (4 1)Êœ œ œœœœ
"" "
(#
%"
##33 32 244
v 11 11 u 11 33
''
G'' ' '
14 1 1
27 2 2
’“ ’“
ˆ‰ ˆ‰
7. 3x 14xy 8y dx dy
''
Rab
##
(3x 2y)(x 4y) dx dyœ
''
R
uv du dv uv du dv;œœ
'' ''
GG
¹¹
`ß
`ß
"
(x y)
(u v) 10
We find the boundaries of G from the boundaries of R,
shown in the accompanying figure:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
yx1œ
3
#
"
10 10
3
33
10 10
41020
1
41020
1
(3v u) (2u v) 1 u 2
y x 3 (3v u) (2u v) 3 u 6
y x (3v u) (2u v) v 0
y x 1 (3v u) (2u v) 1 v 4
œ œ
œ œ œ
œ œ œ
œ œ œ
#
"
""
""
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
924 Chapter 15 Multiple Integrals
uv du dv uv dv du u du u du (18 2)Êœ œœœœœ
"" "
%'
!#
10 10 10 2 5 5 2 5 5
v4 4u4 64
''
G'' ' '
20 2 2
64 6 6
’“ ’“
ˆ‰ ˆ‰
8. 2(x y) dx dy 2v du dv 2v du dv; the region G is sketched in Exercise 4
'' '' ''
RGG
œ œ
¹¹
`ß
`ß
(x y)
(u v)
2v du dv 2v du dv 2v(3 3v 3v) dv 6v dv 3v 3Ê œ œ œ œ œ
''
G
'' ' '
03v 0 0
133v 1 1 cd
#"
!
9. x and y uv v and xy u ; J(u v) v u v u ;
vuv
vu
œ œÊœ œ œßœ œœ
u2u
vx (uv) v
y(xy)
# # " "
`ß
`ß
" #
ºº
y x uv v 1, and y 4x v 2; xy 1 u 1, and xy 9 u 3; thusœÊ œÊœ œ Êœ œÊœ œÊœ
u
v
xy dx dy (v u) dv du 2u dv du 2uv 2u ln v du
''
RŠ‹ Š‹
ÉȈ‰ cd
y
xvv
2u 2u
œ œœ
'' '' '
11 11 1
32 32 3 ##
"
2u 2u ln 2 du u u ln 2 8 (26)(ln 2) 8 (ln 2)œ œ œ œ
'1
3ab
‘
###
$
"
22 52
33 3
10. (a) J(u v) u, and
0
vu
`ß
`ß
(x y)
(u v) œßœ œ
"
ºº
the region G is sketched at the right
(b) x 1 u 1, and x 2 u 2; y 1 uv 1 v , and y 2 uv 2 v ; thus,œÊœ œÊœ œÊ œÊœ œÊ œÊœ
"
uu
2
dy dx u dv du uv dv du u du u du
'' '' '' ' '
11 11u 11u 1 1
22 22u 22u 2 2
2u
1u
y
xu 2u2u
uv v 2
œœœœ
ˆ‰ ˆ ‰
’“ "
u du ln u ln 2; dy dx dx ln x ln 2œœœ œ†œœœ
333 13dx33
uxx2x
yy
### ###
"# #
" "
'''''
11111
22222
2
1
ˆ‰ cd cd
’“
2
11. x ar cos and y ar sin J(r ) abr cos abr sin abr;
a cos ar sin
b sin br cos
œœÊœßœ œœ
)) ) ))
))
))
`ß
`ß
##
(x y)
(r ))ºº
I x y dA r a cos b sin J(r ) dr d abr a cos b sin dr d
!## ### ## $## ##
œœ ß œ
''
Rababkkab
'' ''
00 00
21 21
)))) )))
a cos b sin dœœœ
ab ab a a sin 2 b b sin 2
4424244
ab a b
'0
22
ab
’“
## ##
!
)))
))))
1ab
12. J(u v) ab; A dy dx ab du dv ab dv du
a0
0b
`ß
`ß
(x y)
(u v) œßœ œ œ œ œ
ºº '' ''
RG''
11u
11u
2ab 1 u du 2ab 1 u sin u ab sin 1 sin ( 1) ab abœœ œœœ
'1
1ÈÈ
’“
cd
‘ˆ‰
##
"
###
" " "
"
"
u
2
11 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
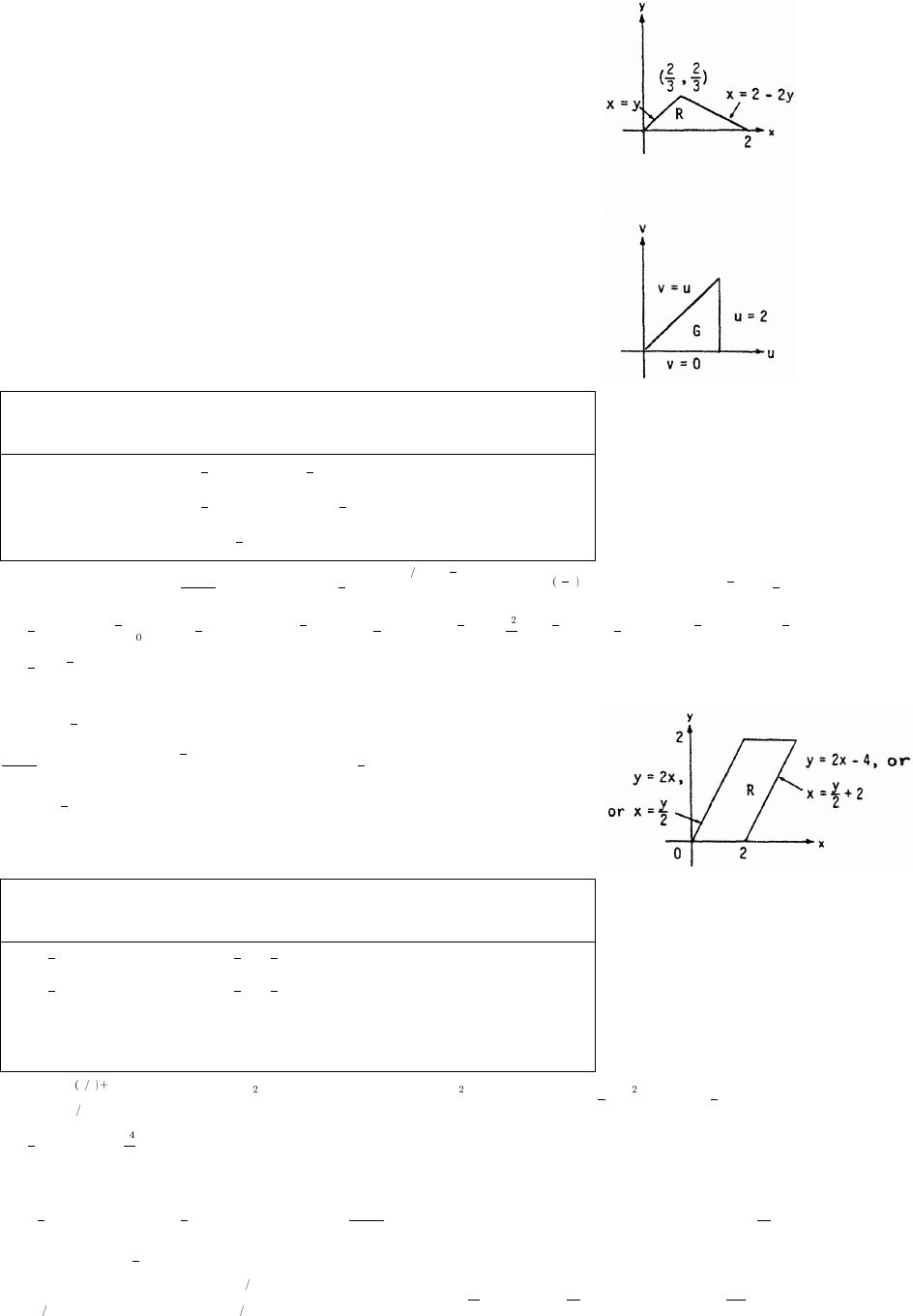
Section 15.8 Substitutions in Multiple Integrals 925
13. The region of integration R in the xy-plane is
sketched in the figure at the right. The
boundaries of the image G are obtained as
follows, with G sketched at the right:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
xy (u2œ
"
3v) (u v) v 0
x 2 2y (u 2v) 2 (u v) u 2
y0 0 (uv) vu
œ œ
œ œ œ
œœ œ
1
3
33
2
1
3
"
Also, from Exercise 2, J(u v) (x 2y) e dx dy ue dv du
`ß
`ß
""
(x y)
(u v) 3 3
œßœÊ œ
'' ''
0y 00
23 2 2y 2 u
yx v
¸¸
u e du u1 e du uu e e 22 e 2 e 1œœ œœ
"" " "
#
#
!
33 3 3
u
''
00
22
vuuu22
u
cd ab ab c d
’“
ab
3e 1 0.4687œ¸
"
3ab
2
14. x u and y v 2x y (2u v) v 2u andœ œ Ê œ œ
v
#
J(u v) 1; next, u x
0
`ß
`ß #
"
#
(x y)
(u v)
v
œßœ œ œ
"
"
ºº
x and v y, so the boundaries of the region ofœ œ
y
#
integration R in the xy-plane are transformed to the
boundaries of G:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
xuœœ
yv
##
v
yvv
#
###
u0
x2 u 2 u2
y0 v0 v0
y2 v2 v2
œ
œ œ œ
œœ œ
œœ œ
y (2x y) e dx dy v (2u) e du dv v e dv v e 1 dvÊœ œ œ
'' '' ' '
0y2 00 0 0
2y22 22 2 2 16
$ÐÑ $ $ $
""
#
!
2x y 4u 4u
44
’“ ab
e1 e1œ œ
"#
!
44
v
ab
’“
16 16
15. x and y uv v and xy u ; J(u v) v u v u ;
vuv
vu
œ œÊœ œ œßœ œœ
u2u
vx (uv) v
y(xy)
# # " "
`ß
`ß
" #
ºº
y x uv v 1, and y 4x v 2; xy 1 u 1, and xy 4 u 2; thusœÊ œÊœ œ Êœ œÊœ œÊœ
u
v
x y dx dy x y dx dy u v du dv 2u v du dv
'' '' '' ''
11y 2y4
2y 44y
11 11
22 22
ab ab Š‹ Š ‹
ˆ‰
22 22 22 3
u2u 2u
vv v
œ œ
23
23
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

926 Chapter 15 Multiple Integrals
u v dv dvœ œœœ
''
11
22
’“ ’“
ˆ‰
u 1 15 15v 15 15v 225
2v 2 2v 2 4v 4 16
42
4 2
332
#
""
16. x u v and y 2uv; J(u v) 4u 4v 4 u v ;
2u 2v
2v 2u
œ œ œßœ œ œ
22 2 2 22
(x y)
(u v)
`ß
`ß ºº ab
y 2 1 x y 4 1 x 2uv 4 1 u v u 1; y 0 2uv 0 u 0 or v 0;œ Ê œ Ê œ Êœ„ œÊ œÊœ œ
Èababa bab
222
2
x 0 u v 0 u v or u v; This gives us four triangular regions, but only the one in the quadrant whereœÊ œÊœ œ
22
both u, v are positive maps into the region R in the xy-plane.
x y dx dy u v 2uv 4 u v dv du 4 u v dv du
'' '' ''
0
1
00 00
1u 1u
0
21x 22 22
2222 22
2
ÈÈÉababab abœ † œ
4 u v u v v du u du uœœ œ œ
''
11
22
0
‘ ‘
4235 5 6
2 1 112 112 1 56
3 5 15 15 6 45
u2
"
17. (a) x u cos v and y u sin v u cos v u sin v u
cos v u sin v
sin v u cos v
œœÊœ œœ
`ß
`ß
##
(x y)
(u v) ºº
(b) x u sin v and y u cos v u sin v u cos v u
sin v u cos v
cos v u sin v
œœÊœ œœ
`ß
`ß
##
(x y)
(u v) ºº
18. (a) x u cos v, y u sin v, z w u cos v u sin v u
cos v u sin v 0
sin v u cos v 0
00
œœœÊœ œœ
"
`ßß
`ßß
##
(xyz)
(uvw)
ââ
ââ
ââ
ââ
ââ
ââ
(b) x 2u 1, y 3v 4, z (w 4) (2)(3) 3
200
030
00
œ œ œ Ê œ œ œ
""
#`ßß #
`ßß
"
#
(xyz)
(uvw)
ââ
ââ
ââ
ââ
ââ
â∉
19.
sin cos cos cos sin sin
sin sin cos sin sin cos
cos sin 0
ââ
ââ
ââ
ââ
ââ
ââ
9)39)39)
9)3 9)39 )
939
(cos ) ( sin )
cos cos sin sin sin cos sin sin
cos sin sin cos sin sin sin cos
œ
939
39)39) 9)39)
39)39) 9)39)
ºººº
cos sin cos cos sin cos sin sin sin cos sin sinœaba baba b3 9 99 ) 99)39 9 ) 9)
########
sin cos sin sin cos sin sin œœ œ3 9 93 93 9 9 93 9
###$# ###
aba b
20. Let u g x J x g x f u du f g x g x dx in accordance with Theorem 7 inœÊœœ Ê œab ab ab ab a babab
du
dx ww
''
aga
bgb
Section 5.6. Note that g x represents the Jacobian of the transformation u g x or x g u .
w"
ab ab abœœ
21. dx dy dz dy dz (y 1) dy dz
''' '' ''
00y2 00 00
341y2 34 34
y2
y2
ˆ‰ ‘
’“
2x y xy y
zxxz z
323 3
####
"Ð "
œ œ
dz dz 2 dz 2z 12œœœœœ
'''
000
333
’“ ’“
ˆ‰ˆ‰
(y 1) y yz
443 434 3 3
94z 4z 2z
% $
! !
"
22. J(u v w) abc; the transformation takes the ellipsoid region 1 in xyz-space
a00
0b0
00c
ßß œ œ Ÿ
ââ
ââ
ââ
ââ
ââ
ââ xz
abc
y
into the spherical region u v w 1 in uvw-space which has volume V
## #
Ÿ œ
ˆ‰
4
31
V dx dy dz abc du dv dwÊœ œ œ
''' '''
RG
4abc
3
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
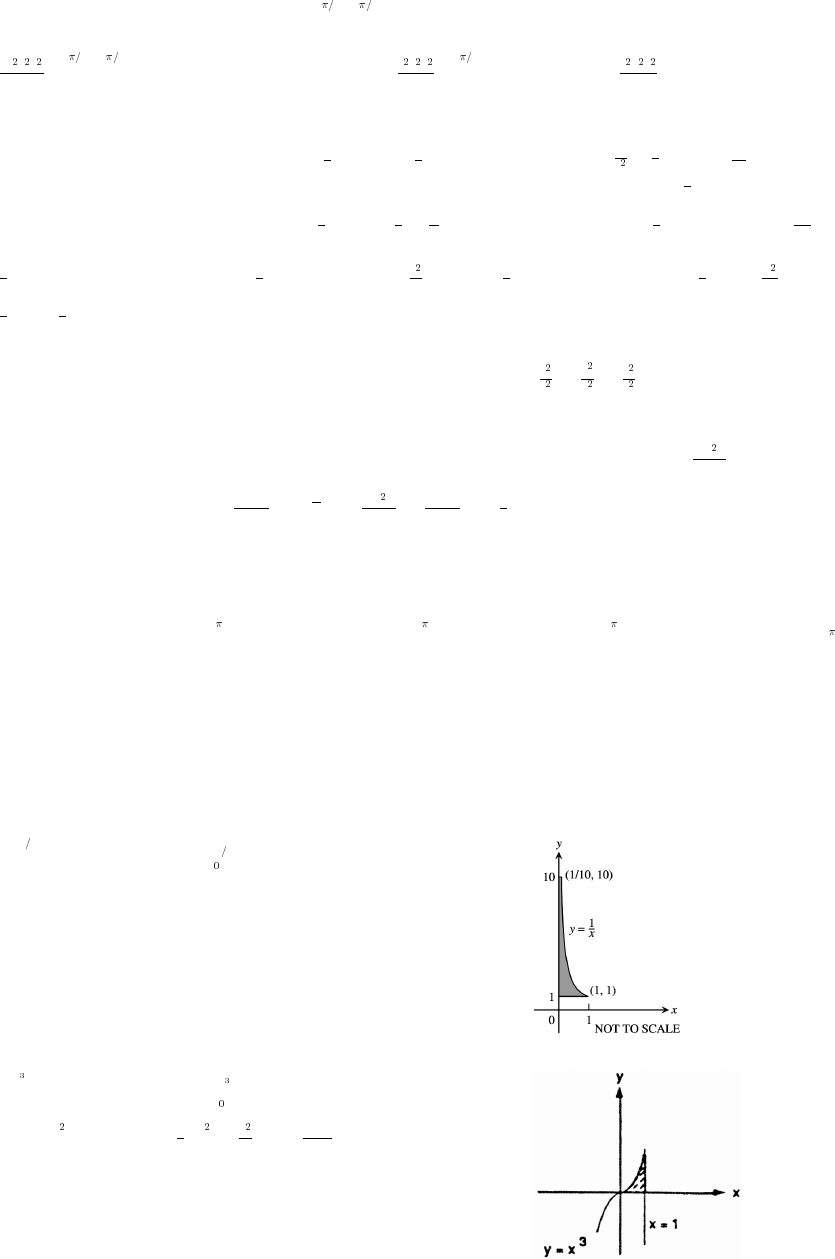
Chapter 15 Practice Exercises 927
23. J(u v w) abc; for R and G as in Exercise 22, xyz dx dy dz
a00
0b0
00c
ßß œ œ
ââ
ââ
ââ
ââ
ââ
ââ kk
'''
R
a b c uvw dw dv du 8a b c ( sin cos )( sin sin )( cos ) sin d d dœœ
'''
G
### ### #
'''
000
221
39 )39)3 93 939)ab
sin cos sin cos d d sin cos dœœœ
4abc abc abc
336
'' '
00 0
22 2
)) 999) )))
$
24. u x, v xy, and w 3z x u, y , and z w J(u v w) ;
100
0
00
œœ œÊœœ œ Êßßœ œ
v
u3 3u
v
uu
3
""
"
"
ââ
ââ
ââ
ââ
ââ
ââ
x y 3xyz dx dy dz u 3u J(u v w) du dv dw v du dv dw
''' '''
DG
ab kk
‘ ˆ‰ˆ‰ ˆ‰ˆ‰
## "
œ ßßœ
vvw vw
uu3 3 u
'''
001
322
(v vw ln 2) dv dw (1 w ln 2) dw (1 w ln 2) dw w ln 2œ œ œ œ
""
#$
!!
332332
v2 2w
'' ' '
00 0 0
32 3 3
’“ ’ “
3 ln 2 2 3 ln 2 2 ln 8œ œ œ
29
3ˆ‰
#
25. The first moment about the xy-coordinate plane for the semi-ellipsoid, 1 using the
xz
abc
y
œ
transformation in Exercise 23 is, M z dz dy dx cw J(u v w) du dv dw
xy œœßß
''' '''
DGkk
abc w du dv dw abc M of the hemisphere x y z 1, z 0 ;œ œ œ œ
## ###
'''
Gaba b†xy abc
4
1
the mass of the semi-ellipsoid is z c
2abc abc 3 3
3 4 2abc 8
11
1
Êœ œ
Š‹
ˆ‰
26. A solid of revolution is symmetric about the axis of revolution, therefore, the height of the solid is solely a function of r.
That is, y f x f r . Using cylindrical coordinates with x r cos , y y and z r sin , we haveœœ œ œ œab ab ))
V r dyddr r dyddr ddr r fr ddr dr
r y r f r
œœ œ œ œ
'''
G
))))
)
'' ' '' '' '
a0 0 a0 a0 a
b2 b2 b2 b 2
fr
00
fr
ab ab
cd ab c d
ab
rf r dr. In the last integral, r is a dummy or stand-in variable and as such it can be replaced by any variable name.
'a
b
21ab
Choosing x instead of r we have V xf x dx, which is the same result obtained using the shell method.œ'a
b
21ab
CHAPTER 15 PRACTICE EXERCISES
1. ye dx dy e dy
'' '
10 1
10 1 y 10 y
xy xy
œcd
"
(e 1) dy 9e 9œœ
'1
10
2. e dy dx x e dx
'' '
00 0
1x 1 x
yx yxÎÎ
œ‘
xe x dx eœœœ
'0
1Š‹’ “
xx
2
xe2
"
##
"
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
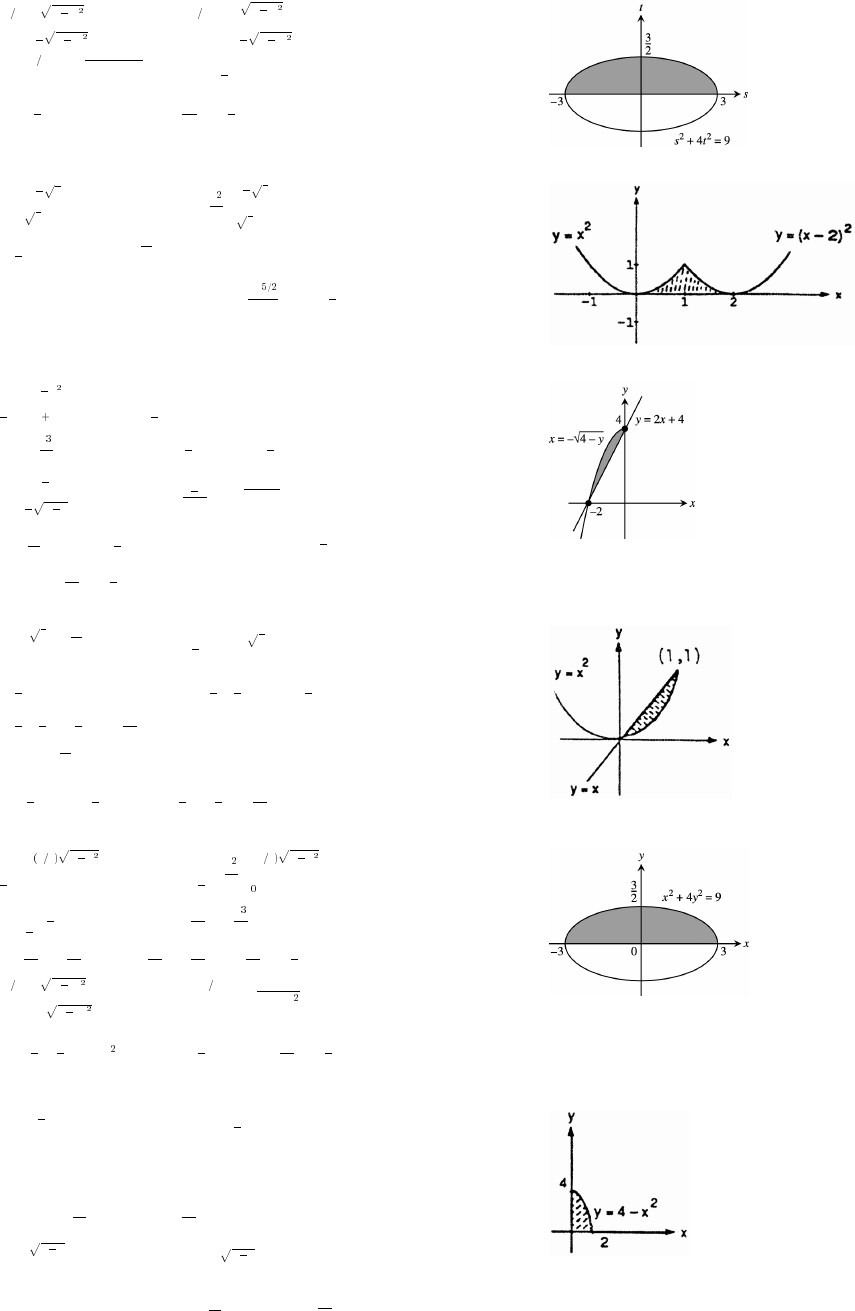
928 Chapter 15 Multiple Integrals
3. t ds dt ts dt
'' '
094t 0
32 9 4t 32 94t
94t
œcd
2t 9 4t dt 9 4tœœ
'0
32 È’“
ab
#"#$Î# $Î#
!
6
09œ œ œ
"$Î# $Î#
#66
27 9
ˆ‰
4. xy dx dy y dy
'' '
0y 0
12y 1 2y
y
œ’“
x
2
y44yyy dyœ
"
#'0
1ˆ‰
È
2y 2y dy yœ œœ
'0
1ˆ‰
’“
$Î# # "
!
"
4y
55
5. dy dx x 2x dx
'' '
22x4 2
04x 0
œab
#
x4œ œ œ
’“
ˆ‰
x84
333
#!
#
dx dy dy
'' '
04y 0
4y4)/2 4
y4
2
(œˆ‰
È4y
48 4
2y 4 y
œœ†
’“
ab
y3/2
23
23/2 4
0
2
3
2
4œ œ
16 4
33
6. x dx dy x dy
'' '
0y 0
1y 1 y
y
È‘
œ2
3$Î#
y y dy y yœœ
2242
3375
'0
1ˆ‰ ‘
$Î% $Î# (Î% &Î# "
!
œœ
24 2 4
37 5 35
ˆ‰
x dy dx x x x dx x x dx
'' ' '
0x 0 0
1x 1 1
2 Èab ˆ‰
œœ
1/2 2 3/2 5/2
xxœ œœ
‘
22 224
57 5735
5/2 7/2
0
1
7. y dy dx dx
'' '
30 3
3129x 3 12 9 x
œ’“
y
2
Ð
9 x dxœœ
'3
3"#$
$
8824
9x x
ab’“
œœœ
ˆ‰ˆ ‰
27 27 27 27 27 9
824 824 6 #
y dx dy 2y dy
'' '
094y 0
32 9 4y 32
œÈ94y
9œ † œ † œ œ
""
#43 6 6
2279
3/2
0
3/2
3/2
ab
º
94y
8. 2x dy dx 2xy dx
'' '
00 0
24x 2 4x
0
22
œcd
2x 4 dx 8x 2 dxœœ
''
00
22
23
abababxx
4168œ œœ
’“
x2
2
x16
22
4
!
2x dx dy x dy
'' '
00 0
44y 4 4y
0
œcd
2
4 y dy 16 8
4y
œœ œœ
'0
4ab’“
y
20
416
2
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 15 Practice Exercises 929
9. 4 cos x dx dy 4 cos x dy dx 2x cos x dx sin x sin 4
'' '' '
02y 00 0
12 2x/2 2
ab ab ab c dab
####
#
!
œœœœ
10. e dx dy e dy dx 2xe dx e e 1
'' '' '
0y2 00 0
21 12x 1
xxxx
œœœœcd
"
!
11. dy dx dx dy dy
'' '' '
0x 00 0
82 2y 2
"""
y1 y1 y1
44
4y ln 17
œœœ
12. dx dy dy dx 2 x sin x dx cos x ( 1) ( 1) 2
'' '' '
0y 00 0
11 1x 1
2 sin x 2 sin x
xx
11 11ab ab
œœœœœ11 1ab c dab
##
"
!
13. A dy dx x 2x dx 14. A dx dy y 2 y dyœœœ œœœ
'' ' '' '
2 2x4 2 1 2y 1
04x 0 4 y 4
ab ˆ‰
È
#437
3 6
15. V x y dy dx x y dx 2x dxœ œ œœ
'' ' '
0x 0 0
12x 1 1
2x
x
ab ’“ ’ “’ “
## # #
"
!
y (2x) (2x)
3 3 3 3 12 12
7x 2x 7x
œ œ
ˆ‰
2724
31212 12 3
"
16. V x dy dx x y dx 6x x x dxœœœœ
'' ' '
3x 3 3
26x 2 2
6x
x
# # #%$
cd a b 125
4
17. average value xy dy dx dx dxœœœœ
'' ' '
00 0 0
11 1 1
’“
xy
224
x
"
!
"
18. average value xy dy dx dx x x dxœœœœ
" "
$
#
ˆ‰
4'' ' '
00 0 0
11x 1 1
1x
42
xy
2111
’“ ab
19. dy dx dr d d d
'' '' ' '
11x 00 0 0
11x 21 2 2
22r
1x y 1r 1r
ab ab
""
#
"
!
2œœœœ)))1
‘
20. ln x y 1 dx dy r ln r 1 dr d ln u du d u ln u u d
'' '' '' '
11y 00 01 0
11y 21 22 2
ab ab cd
## # ""
##
#
"
œ œ œ )) )
(2 ln 2 1) d [ln (4) 1]œœ
"
#'0
2
)1
21. x y x y 0 r r cos 2 0 r cos 2 so the integral is dr dabab
## ## %# #
#
œÊ œÊœ)) )
''
40
4cos 2 r
1rab
1 d 1 dœ œ
'''
444
444
cos 2
’“ ˆ‰ ˆ‰
""""
##2 1 r 1 cos 2 cosab
È d )œ))
))
1 dœœœ
""
###
'4
44
4
Š‹‘
sec tan 2
24
))1
))
22. (a) dx dy dr d d
''
R
""
!
ab ab ab
1x y 1r
r
21 r
œœ
'' '
00 0
3 sec 3 sec
))
’“
d d ;
utan
du sec d
œ œ Ä
œ
œ
'' '
00 0
33 3
’“ ”•
"" " "
## # #
#
ab1sec 1sec 2u
sec du
))
)
))
)
))
tan tan œœ
""
##
" "
$
!
’“ É
ÈÈ
ÈÈ
22
u3
2
4
(b) dx dy dr d lim d
''
Rb
" "
ab ab ab
1x y 1r
r
21 r 0
b
œœ
'' '
00 0
22
))
Ä_ ’“
lim d dœœœ
''
00
22
bÄ_ ’“
"" "
## #ab1b 4
))
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

930 Chapter 15 Multiple Integrals
23. cos (x y z) dx dy dz [sin (z y ) sin (z y)] dy dz
''' ''
000 00
œ 1
[ cos (z 2 ) cos (z ) cos z cos (z )] dz 0œ œ
'011 1
24. e dz dy dx e dy dx e dx 1
''' '' '
ln 6 0 ln 4 ln 6 0 ln 6
ln 7 ln 2 ln 5 ln 7 ln 2 ln 7
ÐÑ ÐÑxyz xy x
œœœ
25. (2x y z) dz dy dx dy dx dx
'' ' '' '
00 0 00 0
1x xy 1x 1
œ œ œ
Š‹ Š‹
3x 3x x 8
3y
35
## ##
26. dy dz dx dz dx ln x dx x ln x x 1
''' '' '
110 11 1
exz ex e e
1
2y
zz
œœœœ
"cd
27. V 2 dz dx dy 2 2x dx dy 2 cos y dy 2œœœœœ
'' ' '' '
0cos y0 0cos y 0
20 2x 20 2 2
#
#
’“
ysin 2y
24
1
28. V 4 dz dy dx 4 4 x dy dx 4 4 x dxœœœ
'' ' '' '
00 0 00 0
24x4x 24x 2
ab ab
##
$Î#
x 4 x 6x 4 x 24 sin 24 sin 1 12œ œ œ
’“
ab È
#""
$Î# ##
!
x
21
29. average 30xz x y dz dy dx 15x x y dy dx 15x x y dx dyœœœ
"""
###
333
''' '' ''
000 00 00
131 13 31
ÈÈÈ
5 x y dy 5(1 y) 5y dy 2(1 y) 2y 2(4) 2(3) 2œœœœ
"" ""
# $Î# $Î# &Î# &Î# &Î# &Î#
$Î# "
!
$
!
33 33
''
00
33
’“
ab ‘‘ ‘
231 3œ
"&Î#
3‘ˆ‰
30. average sin d d d sin d d dœœœœ
33a3a3a
4a 16 8 4111
''' '' '
000 00 0
2a 2 2
3939) 99) )
$
31. (a) 3 dz dx dy
'' '
22yxy
22y 4xy
(b) 3 sin d d d
'' '
00 0
242
3939)
#
(c) 3 dz r dr d 3 r 4 r r dr d 3 4 r d
'' ' '' '
00 r 00 0
224r 22 2
)))œœ
’“’ “
ab ab
## #
"Î# $Î#
"#
!
33
rÈ
224 d842d2842œ œ œ
''
00
22
ˆ‰
Š‹ Š‹
ÈÈ
$Î# $Î# $Î# ))1
32. (a) 21(r cos )(r sin ) dz r dr d 21r cos sin dz r dr d
''' '''
20 r 20 r
21r 21r
)) ) )) )
#$#
œ
(b) 21r cos sin dz r dr d 84 r sin cos dr d 12 sin cos d 4
''' '' '
20 r 0 0 0
21r 21 2
$# '# #
)) ) ))) )))œœœ
33. (a) sin d d d
'' '
00 0
2 4 sec
3939)
#
(b) sin d d d (sec )(sec tan ) d d tan d d
'' ' '' ' '
00 0 00 0 0
24sec 24 2 2
4
3939) 9 999) 9 ) )
# #
""""
Î
œœœœ
33263
‘
11
34. (a) (6 4y) dz dy dx (b) (6 4r sin ) dz r dr d
'' ' ' ''
00 0 000
1 1x xy 21r
))
(c) (6 4 sin sin ) sin d d d
'''
040
2 2 csc 39)3 939)ab
#
(d) (6 4r sin ) dz r dr d 6r 4r sin dr d 2r r sin d
''' '' '
000 00 0
21r 21 2
œœ)) )) ))abcd
#$ $% "
!
(2 sin ) d 2 cos 1œ œ œ
'0
2
)) ) ) 1cd
1Î#
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 15 Practice Exercises 931
35. z yx dz dy dx z yx dz dy dx
'' ' ' ' '
01x1 10 1
13x 4xy 33x 4xy
##
36. (a) Bounded on the top and bottom by the sphere x y z 4, on the right by the right circular
###
œ
cylinder (x 1) y 1, on the left by the plane y 0œ œ
##
(b) dz r dr d
'' '
00 4r
22 cos 4r
)
37. (a) V dz r dr d r 8 r 2r dr d 8 r r dœœœ
''' '' '
002 00 0
22 8r 22 2
)))
Š‹’ “
Èab
#"##
$Î# #
!
3
(4) 4 (8) d 2328 d 425 dœ œ œ œ
'' '
00 0
22 2
‘
Š‹Š‹
ÈÈ
""
$Î# $Î#
33 3 3 3
44
8425
)))
1Š‹
È
(b) V sin d d d 2 2 sin sec sin d dœœ
'' ' ''
00 2 sec 00
248 24
3939) 9 999)
#$
8
3Š‹
È
2 2 sin tan sec d d 2 2 cos tan dœœ
88
33
'' '
00 0
24 2
Š‹’“
ÈÈ
9999) 9 9)
##
"
#
Î%
!
1
222 d dœ œ œ
88
333
542 8425
''
00
22
Š‹Š‹
È
"
##
))
ÈŠ‹
È
1
38. I ( sin ) sin d d d sin d d d
z00 0 00 0
232 232
œœ
'' ' '' '
393 939) 3 939)
## % $
ab
sin cos sin d d cos dœ œœ
32 32 8
5533
cos
'' '
00 0
23 2
ab
’“
9999) 9 )
#Î$
!
911
39. With the centers of the spheres at the origin, I ( sin ) sin d d d
z00a
2b
œ'''$3 9 3 9 3 9 )
##
ab
sin d d sin cos sin d dœœ
$$ab abba ba
55
$#
'' ''
00 00
22
99) 9 9 9 9)ab
cos d dœœ œ
$$1$
91
ab ab abba 4ba 8 ba
5 3 15 15
cos
!
''
00
22
’“
9) )
40. I ( sin ) sin d d d sin d d d
z000 000
21cos 21cos
œœ
''' '''
393 939) 3 939)
## % $
ab
(1 cos ) sin d d (1 cos ) (1 cos ) sin d d ;œ œ
"&$ '
5'' ''
00 00
22
999) 9 999)
u(2u) dud d 2 d
u1cos
du sin d
”• ’“ ˆ‰
œ
œÄœœ
9
99 )))
"""""
' )
#
!
5578578
2u u
'' ' '
00 0 0
22 2 2
d dœœœ
"
556 35 35
2 2 32 64
''
00
22
†))
1
41. M dy dx 2 dx 2 ln 4; M x dy dx x 2 dx 1;œœœœ œœ
'' ' '' '
12x 1 12x 1
22 2 22 2
y
ˆ‰ ˆ‰
22
xx
M y dy dx 2 dx 1 x y
x12x 1
22 2
œœœÊœœ
'' 'ˆ‰
2
xln 4
"
#
42. M dx dy 4y y dy ; M y dx dy 4y y dy ;œ œœ œ œ œœ
'' ' '' '
02y 0 02y 0
42yy 4 42yy 4
x
ab a b
’“
##$
%
!
32 64
3343
4y y
M x dx dy 2y dy x and y 2
y02y 0
42yy 4
œœœœÊœœœœ
'' '’“’“
ab2y y yy
10 2 5 M 5 M
128 12
MM
#
#%
!
yx
43. I x y (3) dy dx 3 4x dx 104
o02x 0
24 2
œ œ œ
'' '
ab Š‹
## #
64 14x
33
44. (a) I x y dy dx 2x dx
o240
33
œœœ
'' '
21 2
21 2
ab ˆ‰
## #
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

932 Chapter 15 Multiple Integrals
(b) I y dy dx dx ; I x dx dy dy I I I
xy oxy
2b 4ab 2a 4a b
33 33
œœœœ œœÊœ
'' ' '' '
ab a ba b
ab a ba b
##
œœ
4ab 4a b
33 3
4ab b a
ab
45. M dy dx dx 3 ; I y dy dx x dx 2œœœœ œœœ$$$$ $
'' ' '' '
00 0 00 0
32x3 3 32x3 3
2x 8 8 3
381814
x#$
$$
ˆ‰
Š‹
46. M (x 1) dy dx x x dx ; M y(x 1) dy dx xxxx dx ;œ œ œ œ œ œ
'' ' '' '
0x 0 0x 0
1x 1 1x 1
ab a b
$$&#%
"""
#4120
x3
M x(x 1) dy dx x x dx x and y ; I y (x 1) dy dx
y x
2813
15 15 30
œœœÊœœœ
'' ' ''
0x 0 0x
1x 1 1x
ab
#% #
xxxx dx R ; I x(x1) dydx xx dxœ œ Ê œ œ œ œ œ
"%($' # $&
3 280 M 70 12
17 17 1
xy
I
''''
00x 0
11x 1
ab ab
ÉÉ
x
47. M x y dy dx 2x dx 4; M y x y dy dx 0 dx 0;œ œœœ œœ
'' ' '' '
11 1 11 1
11 1 11 1
ˆ‰ˆ‰ ˆ‰
## # ##
" "
33 3
4x
M x x y dy dx 2x x dx 0
y33
4
œœœ
'' '
11 1
11 1
ˆ‰ˆ‰
## $
"
48. Place the ABC with its vertices at A(0 0), B(b 0) and C(a h). The line through the points A and C is?ßß ß
y x; the line through the points C and B is y (x b). Thus, M dx dyœœœ
hh
aab''
0ayh
habyhb
$
b 1 dy ; I y dx dy b y dyœœœ œ œ$$$
''''
00ayh0
hhabyhbh
x
ˆ‰ Š‹
y y
hh1
bh bh$ $
# #
##
49. M r dr d d 3 ; M r cos dr d 9 cos d 9 3 x ,œœœœ œ œÊœ
'' ' '' '
30 3 30 3
33 3 33 3
y
))1 )) ))
933
#
#ÈÈ
1
and y 0 by symmetryœ
50. M r dr d 4 d 2 ; M r cos dr d cos d x , andœœœœ œ œÊœ
'' ' '' '
01 0 01 0
23 2 23 2
y
))1 )) ))
#26 26 13
3331
y by symmetryœ13
31
51. (a) M 2 r dr d œ''
01
21cos
)
2 cos d ;œœ
'0
2ˆ‰
))
1cos 2 8
4
#
)1
M (r cos ) r dr d
y21
21cos
œ''
))
cos cos dœ
'2
2Š‹
#$
)) )
cos
3
)
x , andœÊœ
32 15 15 32
24 6 48
11
1
y 0 by symmetryœ
(b)
52. (a) M r dr d d a ; M (r cos ) r dr d dœœœœ œœ
'' ' '' '
00
aa
y
))! )) )
a a cos 2a sin
33
#
#)!
x , and y 0 by symmetry; lim x lim 0Êœ œ œ œ
2a sin 2a sin
33
!!
!!
!1 !1ÄÄ
(b) x and y 0œœ
2a
51
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
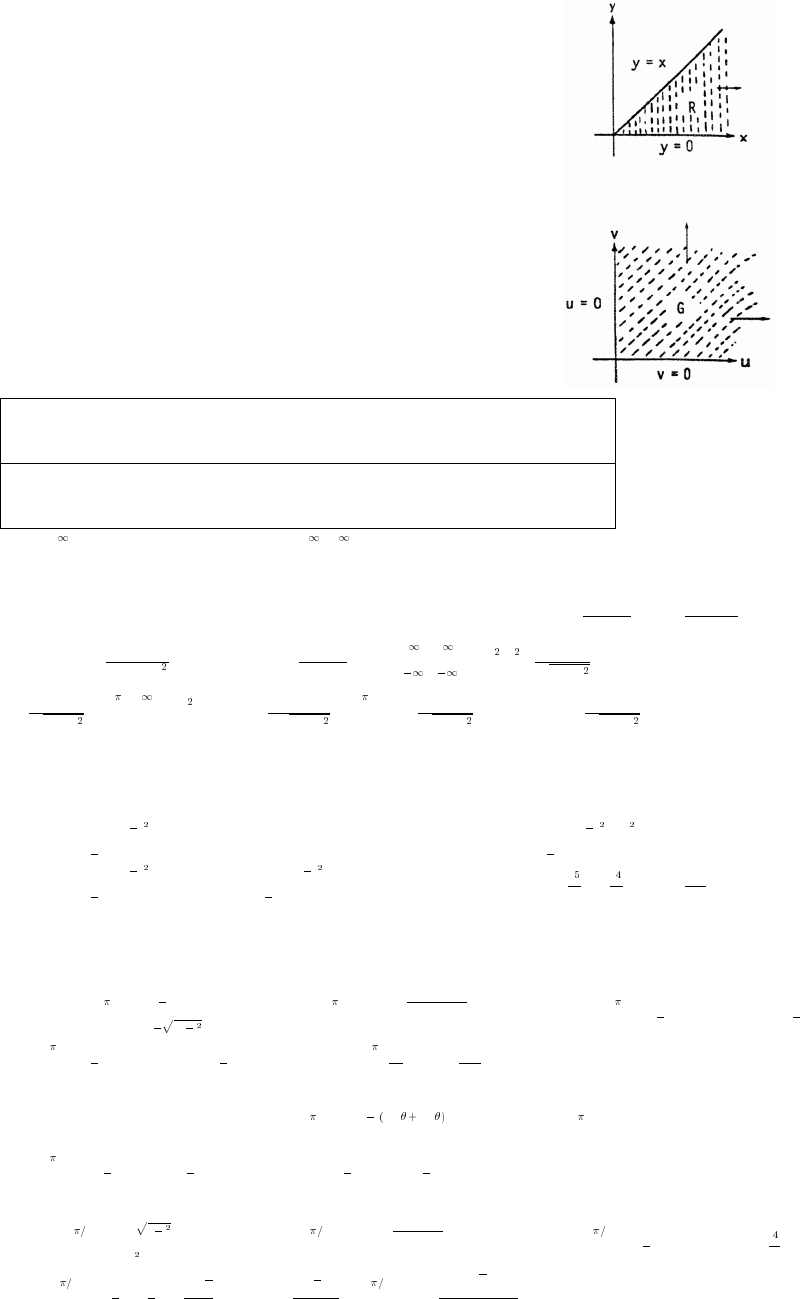
Chapter 15 Additional and Advanced Exercises 933
53. x u y and y v x u v and y vœ œ Ê œ œ
J(u v) 1; the boundary of the
0
Êßœ œ
""
"
ºº
image G is obtained from the boundary of R as
follows:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
yx vuv uœœ œ
œœ œ
0
y0 v0 v0
e f(x y y) dy dx e f(u v) du dvÊßœ ß
'' ''
00 00
xÐÑsx s u v
54. If s x y and t x y where ( ) ac b , then x , y ,œ œ œ œ œ!" #$ !$"#
##
$"
!$ "# !$ "#
#!
st st
and J(s t) e ds dtßœ œ Ê
"" "
()
st
ac b
!$ "# !$ "#
ºº
$"
#! '' ab
È
re dr d d . Therefore, 1 ac b .œœœ œÊœ
""
#
##
ÈÈÈÈ
acb acb acb acb
r
'' '
00 0
22
)) 1
11
CHAPTER 15 ADDITIONAL AND ADVANCED EXERCISES
1. (a) V x dy dx (b) V dz dy dxœœ
'' '' '
3x 3x 0
26x 26xx
#
(c) V x dy dx 6x x x dx 2xœœœœ
'' ''
3x 3x
26x 26x
# #%$ $ #
$
ab
’“
x x 125
54 4
2. Place the sphere's center at the origin with the surface of the water at z 3. Thenœ
9 25 x y x y 16 is the projection of the volume of water onto the xy-planeœ Ê œ
## ##
V dz r dr d r 25 r 3r dr d 25 r r dÊœ œ œ
''' '' '
00 25r 00 0
24 3 24 2
)) )
Š‹’ “
Èab
#"##
$Î#
#
%
!
3
3
(9) 24 (25) d dœ œ œ
''
00
22
‘
""
$Î# $Î#
33 33
26 52
))
1
3. Using cylindrical coordinates, V dz r dr d 2r r cos r sin dr dœœ
''' ''
000 00
2 1 2 r cos sin 2 1
))))ab
##
1 cos sin d sin cos 2œ œ œ
'0
2ˆ‰‘
"" ""
#
!
33 33
))))) )1
1
4. V 4 dz r dr d 4 r 2 r r dr d 4 2 r dœœœ
''' '' '
00r 00 0
21 2r 21 2
)))
Š‹’ “
Èab
#$#
"$Î# "
!
34
r
4 d dœ œ œ
''
00
22
Š‹Š‹
""
34 3 3 6
22 827 82 7
ÈÈ Š‹
È
))
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
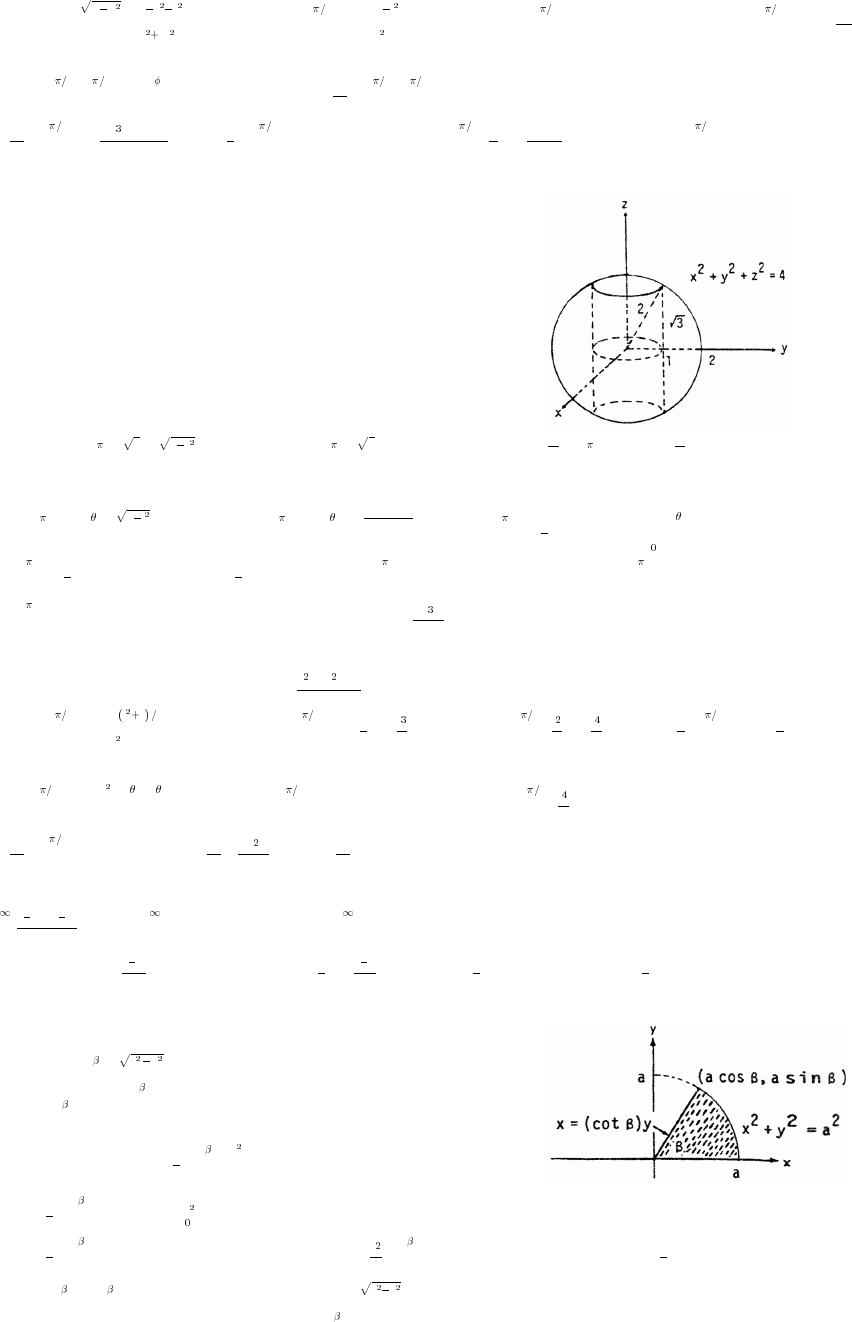
934 Chapter 15 Multiple Integrals
5. The surfaces intersect when 3 x y 2x 2y x y 1. Thus the volume isœ Ê œ
## # # ##
V 4 dz dy dx 4 dz r dr d 4 3r 3r dr d 3 dœœœœœ
'' ' ' '' ' ' '
0 0 2x 2y 0 0 2r 0 0 0
1 1x 3xy 213r 21 2
)))ab
$
#
31
6. V 8 sin d d d sin d dœœ
''' ''
000 00
222 sin 22
3939) 99)
#%
64
3
sin d d 16 d 4 d 2œ œ œ œ
64 3
344 24
sin cos sin 2
''' '
000 0
222 2
”•
¹‘
99 9 9
11
Î#
!
# #
Î#
!
99 ) ) 1 ) 1
7. (a) The radius of the hole is 1, and the
radius of the sphere is 2.
(b) V 2 r dr dz d 3 z dz d 2 3 d 4 3œœœœ
'' ' '' '
00 1 00 0
234z 23 2
)))1ab ÈÈ
#
8. V dz r dr d r 9 r dr d 9 r dœœœ
'' ' '' '
00 0 00 0
3 sin 9 r 3 sin 3 sin
)) )
È’“
ab
#"#$Î#
3
9 9 sin (9) d 9 1 1 sin d 9 1 cos dœ œ œ
'''
000
’“’“
ab ab ab
""
# $Î# # $
$Î# $Î#
33
)) )) ))
1 cos sin cos d 9 sin 9œ œ œ
'0ab
’“
)))))) 1
#
!
sin
3
)1
9. The surfaces intersect when x y x y 1. Thus the volume in cylindrical coordinates is
## ##
#
œ Ê œ
xy1
V 4 dz r dr d 4 dr d 4 d dœ œ œœœ
''' '' ' '
00r 00 0 0
21 r12 21 2 2
))))
Š‹ ’“
rr r r
48 4## #
"
!
"1
10. V dz r dr d r sin cos dr d sin cos dœœœ
''' '' '
010 01 0
22r sin cos 22 2
)))))))
$#
"
’“
r
4
sin cos dœœœ
15 15 sin 15
4428
'0
2
))) ’“
)1Î#
!
11. dx e dy dx e dx dy lim e dx dy
'''''''
00aa0a0
bb bt
ee
x
xy xy xy
ax bx
œœœ
Š‹
tÄ_
lim dy lim dy dy ln y lnœœ œœœ
'' '
aa a
bb b
tb
a
ttÄ_ Ä_
’“ Š ‹ cd ˆ‰
ee b
yyyya
xy yt
!
""
12. (a) The region of integration is sketched at the right
ln x y dx dyÊ
''
0y cot
a sin a y ab
##
r ln r dr d ;œ''
00
aab
#)
ln u du d
ur
du 2r dr
”•
œ
π
#"
#''
00
a
)
[u ln u u] dœ
"
#'0
a)
2a ln a a lim t ln t d (2 ln a 1) d a ln aœ œœ
" "
###
## #
''
00
’“ ˆ‰
t0Ä))"
a
(b) ln x y dy dx ln x y dy dx
'' ''
0 0 a cos 0
a cos (tan )x a a x
ab ab
## ##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
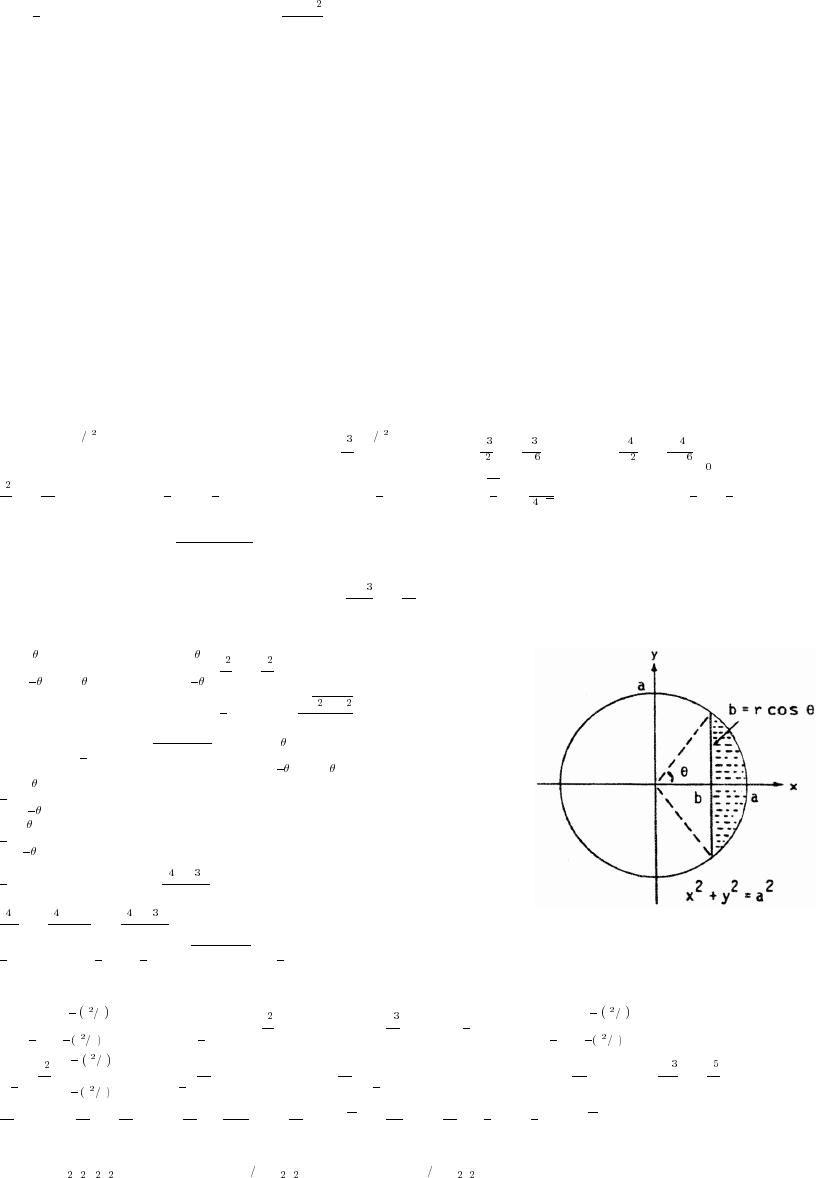
Chapter 15 Additional and Advanced Exercises 935
13. e f(t) dt du e f(t) du dt (x t)e f(t) dt; also
'' '' '
00 0t 0
xu xx x
mx t mx t mx tÐÑ ÐÑ ÐÑ
œœ
e f(t) dt du dv e f(t) du dv dt (v t)e f(t) dv dt
''' ''' ''
000 0t t 0t
xvu xxv xx
mx t mx t mx tÐÑ ÐÑ ÐÑ
œœ
(v t) e f(t) dt e f(t) dtœ œ
''
00
xx
x
t
‘
"#ÐÑ ÐÑ
#2
mx t mx t
(x t)
14. f(x) g(x y)f(y) dy dx g(x y)f(x)f(y) dy dx
'' ''
00 00
1x 1x
Š‹
œ
g(x y)f(x)f(y) dx dy f(y) g(x y)f(x) dx dy;œ œ
'' ' '
0y 0 y
11 1 1
Œ
g x y f(x)f(y) dx dy g(x y)f(x)f(y) dy dx g(y x)f(x)f(y) dy dx
'' '' ''
00 00 0x
11 1x 11
abkkœ
g(x y)f(x)f(y) dx dy g(y x)f(x)f(y) dy dxœ
'' ''
0y 0x
11 11
g(x y)f(x)f(y) dx dy g(x y)f(y)f(x) dx dyœ
'' ''
0y 0y
11 11
ðóóóóóóóóóóóóñóóóóóóóóóóóóò
simply interchange x and y
variable names
2 g(x y)f(x)f(y) dx dy, and the statement now follows.œ
''
0y
11
15. I (a) x y dy dx x y dx dx
o00 0 0
axa a a
xa a
œœœœ
'' ' '
ab ’“ Š‹’ “
## #
!
y
3 a 3a 4a 12a
xx x x
a ; I (a) a a 0 a a . Since I (a) a 0, theœ œ œÊ œÊœ œ œ
a
41 6 3 3 3
""" """ ""
## ##
# w $ % ww %
%
o o
ÉÈ
value of a does provide a for the polar moment of inertia I (a).minimum o
16. I x y (3) dy dx 3 4x dx 104
o02x 0
24 2
œ œ œ
'' '
ab Š‹
## #
14x 64
33
17. M r dr d sec dœœ
'' '
b sec
a
)))
Š‹
ab
##
#
a b tan a cos bœ œ
## #" #
)) ˆ‰ Š‹
b
ab
ab
È
a cos b a b ; I r dr dœœ
#" $
##
ˆ‰ È
b
aob sec
a
'' )
ab sec dœ
"%%%
4'ab))
ab1tan sec dœ
"%% # #
4'cdabab)))
a b tan œ
"%%
43
b tan
’“
))
))
)
œ
a b tan b tan
6
)) )
##
a cos b a b b a bœ
"""
##
%" $ $# #
## $Î#
ˆ‰ Èab
b
a6
18. M dx dy 1 dy y ; M x dx dyœœœœœ
'' ' ''
21y4 2 21y4
22y2 2 22y2
y
Š‹’“
yy
4123
8
#
#
dy 4 y dy 16 8y y dy 16yœœœœ
'' '
22 2
22 2
2y2
1y4
’“ ’ “
ab a b
x33 3
23232 1635
8y y
##% #
!
32 x , and y 0 by symmetryœœ œÊœœ œ œ
36432332848 4836
16 3 5 16 15 15 M 15 8 5
M
ˆ ‰ ˆ‰ˆ ‰ ˆ‰ˆ‰
†y
19. e dy dx e dy dx e dx dy
'' '' ''
00 00 00
ab abxa bayb
max b x a y b x a yabߜ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

936 Chapter 15 Multiple Integrals
x e dx y e dy e e e 1 e 1œœœ
''
00
ab ab
ˆ‰ ˆ‰ ’“’“Š‹Š‹
ba
a b 2ab 2ba ab ab
bx ay bx ay ba ab
""" "
!!
##
e1œ
"
ab
ab
Š‹
20. dx dy dy dx F(x y) F(x y)
'' ' '
yx y y
yx y y
x
x
y
y
`ß `ß `ß `ß
`` ` ` ` "!
F(x y) F(x y) F(x y) F(x y)
xy y y y
œœœßß
’“ ’ “cd
F(x y ) F(x y ) F(x y ) F(x y )œßßßß
"" !" "! !!
21. (a) (i) Fubini's Theorem
(ii) Treating G(y) as a constant
(iii) Algebraic rearrangement
(iv) The definite integral is a constant number
(b) e cos y dy dx e dx cos y dy e e sin sin 0 (1)(1) 1
'' ' '
00 0 0
ln 2 2 ln 2 2
xx ln 20
œœœœ
ŒŒ
ab
ˆ‰
1
#
(c) dx dy dy x dx 1 0
'' ' '
11 1 1
21 2 1
xx
yy y2
œœœœ
ŒŒ
’“’“ ˆ‰ˆ‰
"""""
#"
"" ###
22. (a) f x y D f u x u y; the area of the region of integration is ™œ Ê œ ij u"# "
#
average 2 (u x u y) dy dx 2 u x(1 x) u (1 x) dxÊœ œ
'' '
00 0
11x 1
"# " #
"
#
#
‘
2u u 2 u u (u u)œ œœ
’“Š‹
ˆ‰ ˆ ‰
"# "#"#
""""
#
"
!
xx
23 3 6 6 3
(1 x)
(b) average (u x u y) dA x dA y dA u u u x u yœœ œœ
""# " # "#
area area area M M
uu MM
'' '' ''
RRR
Š‹ ˆ‰
yx
23. (a) I e dx dy e r dr d lim re dr d
#œœœ
'' ' ' ' '
00 0 0 0 0
xy r r
22b
ab ”•
))
bÄ_
lim e 1 d d Iœ œ œ Ê œ
""
###
''
00
22
b
bÄ_ ab))
11
4È
(b) t e dt y e (2y) dy 2 e dy 2 , where y t> 1
ˆ‰ È
ab Š‹ È
"
# #
"Î# #
"Î#
œœ œœœœ
'' '
00 0
tyy
È1
24. Q kr (1 sin ) dr d (1 sin ) d cos œœœœ
'' '
00 0
2R 2
##
!
)) )) ) )
kR kR 2 kR
333
cd
11
25. For a height h in the bowl the volume of water is V dz dy dxœ'' '
hhxxy
hhx h
h x y dy dx h r r dr d d d .œœœœœ
'' '' ' '
hhx 00 0 0
hhx 2 h 2 2
h
ab ab ’“
## #
!#
)))
hr r h h
24 4
È1
Since the top of the bowl has area 10 , then we calibrate the bowl by comparing it to a right circular cylinder1
whose cross sectional area is 10 from z 0 to z 10. If such a cylinder contains cubic inches of water1œœ h1
#
to a depth w then we have 10 w w . So for 1 inch of rain, w 1 and h 20; for 3 inches of1œÊœ œ œ
hh
20
1
#È
rain, w 3 and h 60.œœ
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 15 Additional and Advanced Exercises 937
26. (a) An equation for the satellite dish in standard position
is z x y . Since the axis is tilted 30°, a unitœ
""
##
##
vector 0 a b normal to the plane of thevijkœ
water level satisfies b cosœœ œvk†ˆ‰
1
6
3
È
#
a1b Êœ œÊœ
È#""
###
vjk
È3
(y 1) z 0Ê œ
""
###
È3ˆ‰
zyʜ
"""
#
ÈÈ
33
Š‹
is an equation of the plane of the water level. Therefore
the volume of water is V dz dy dx, where R is the interior of the ellipseœ'''
R
11
22
111
33
2
xy
y
x y y 1 0. When x 0, then y or y , where
##
#
œ œ œ œ œ
22
33
41
ÈÈ ÊŠ‹
!"!
24 2
33
3
and V 1 dz dx dy"œÊœ
24 2
33
3
#
ÊŠ‹
41 '' '
22 11
322
3
22 111
32
333
y1 y x y
y1 y y
(b) x 0 z y and y; y 1 1 the tangent line has slope 1 or a 45° slantœÊœ œ œÊ œÊ
"
#
#dz dz
dy dy
at 45° and thereafter, the dish will not hold water.Ê
27. The cylinder is given by x y 1 from z 1 to z r z dV
## ##
&Î#
œ œ _Ê
'''
Dab
dz r dr d lim dz dr dœœ
''' '''
001 001
21 21a
zrz
rz rzab ab
))
aÄ_
lim dr d lim dr dœ œ
aaÄ_ Ä_
'' ''
00 00
21 21
a
1
’“ ’ “
ˆ‰ ˆ‰ ˆ‰
"""
333
rrr
rz ra r1ab ab ab
))
lim r a r 1 d lim 1 a 2 a dœœ
aaÄ_ Ä_
''
0 0
2 2
’“’ “
ab ab ab ab
ˆ‰
"" """"
# # # # "Î# #
"Î# "Î# "Î# "Î#
"
!
33 3333
))
lim 2 1 a 2 .œœ
aÄ_ 11
’“’“
ab Š‹ ˆ‰ ˆ‰
"""""""
#"Î#
##333a333
22
ÈÈ
28. Let's see?
The length of the "unit" line segment is: L 2 dx 2.œœ
'0
1
The area of the unit circle is: A 4 dy dx .œœ
''
00
11x
2
1
The volume of the unit sphere is: V 8 dz dy dx .œœ
'' '
00 0
11x 1xy
222
4
31
Therefore, the hypervolume of the unit 4-sphere should be:
V 16 dw dz dy dx.
hyper œ'' ' '
00 0 0
11x 1xy 1xyz
222222
Mathematica is able to handle this integral, but we'll use the brute force approach.
V 16 dw dz dy dx 16 dz dy dx
hyper œœ
'' ' ' '' '
00 0 0 00 0
11x 1xy 1xyz 11x 1xy
222
222222 222
È1xyz
16 dz dy dx cos
dz 1 x y sin d
œœ
œ
œ
'' '
00 0
11x 1xy
22 z
1x y
222
2
22
ÈÉ
1x y1 –—
Èz
1x y
22
È
22 )
))
16 1 x y 1 cos sin d dy dx 16 1 x y sin d dy dxœ œ
'' ' '' '
00 /2 00 /2
11x 0 11x 0
2 2
ab ab
È
22 22 2
2))) ))
16 1 x y dy dx 4 1 x x 1 x 1 x dxœ œ
'' '
00 0
11x 1
2
1
4 3
22 2 2
22
3/2
ab ab
Š‹
ÈÈ
1"
4 1 x dx 1 x dx sin d
1x x cos
dx sin d
œ œœ œ
œ
œ
11 1))
)
))
'' '
00 /2
11 0
È‘
ab ab ”•
221x 88
33
24
3/2
$
3
d 1 2 cos 2 cos 2 d 2 cos 2 dœ œ œ œ
81cos 2 2 23 cos 4
32 3 3 22
22
1)1)))1))
'' '
/2 /2 /2
00 0
ˆ‰ ˆ ‰
ab
#
))1
2
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
938 Chapter 15 Multiple Integrals
NOTES:
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

CHAPTER 16 INTEGRATION IN VECTOR FIELDS
16.1 LINE INTEGRALS
1. t t x t and y 1 t y 1 x (c)ri jœ" Ê œ œÊ œÊab
2. t x 1, y 1, and z t (e)rij kœ Ê œ œ œ Ê
3. 2 cos t 2 sin t x 2 cos t and y 2 sin t x y 4 (g)rijœ Êœ œÊœÊabab ##
4. t x t, y 0, and z 0 (a)riœÊœ œ œÊ
5. t t t x t, y t, and z t (d)rijkœ Ê œ œ œÊ
6. t 2 2t y t and z 2 2t z 2 2y (b)rj kœ Ê œ œ Ê œ Êab
7. t 1 2t y t 1 and z 2t y 1 (f)rjkœ Êœ œÊœÊab
## z
4
8. 2 cos t 2 sin t x 2 cos t and z 2 sin t x z 4 (h)rikœ Êœ œÊœÊabab ##
9. t t 1 t , 0 t 1 2 ; x t and y 1 t x y t ( t) 1ri j ij jabœ ŸŸ Ê œÊ œ œ œÊ œ"œab ¸¸ È
dd
dt dt
rr
f x y z ds f t 1 t 0 dt (1) 2 dt 2 t 2Êßßœßß œ œ œ
'' '
C0 0
11
ab a b
¸¸ Š‹ ’ “
ÈÈÈ
d
dt
r"
!
10. (t) t (1 t) , 0 t 1 2; x t, y 1 t, and z 1 x y z 2ri jk ijœ ŸŸ Ê œÊ œ œ œ œ Ê
dd
dt dt
rr
¸¸ È
t (1 t) 1 2 2t 2 f(x y z) ds (2t 2) 2 dt 2 t 2t 2œ œ Ê ßß œ œ œ
''
C0
1ÈÈ È
cd
#"
!
11. (t) 2t t (2 2t) , 0 t 1 2 2 4 1 4 3; xy y zrij k ijkœ ŸŸÊ œ Ê œ œ
dd
dt dt
rr
¸¸ È
(2t)t t (2 2t) f(x y z) ds 2t t 2 3 dt 3 t t 2t 3 2œÊ ßß œ œ œœ
''
C0
1ab
‘ˆ‰
#$#
""
###
"
!
2213
33
12. (t) (4 cos t) (4 sin t) 3t , 2 t 2 ( 4 sin t) (4 cos t) 3rijk ijkœŸŸÊœ11
d
dt
r
16 sin t 16 cos t 9 5; x y 16 cos t 16 sin t 4 f(x y z) ds (4)(5) dtÊœ œ œ œÊ ßßœ
¸¸ ÈÈ
È
d
dt
r## ## ## ''
C2
2
20t 80œœcd
#
#
1
11
13. (t) ( 2 3 ) t( 3 2 ) (1 t) (2 3t) (3 2t) , 0 t 1 3 2r ijk ijk i j k ijkœ œ ŸŸÊ œ
d
dt
r
194 14; xyz(1t)(23t)(32t)66t f(xyz) dsÊ œ œ œ œ Ê ßß
¸¸ ÈÈ
d
dt
r'C
(6 6t) 14 dt 6 14 t 6 14 3 14œ œ œ œ
'0
1ÈÈ È È
’“Š‹
ˆ‰
t
2
"
!
"
#
14. (t) t t t , 1 t 3 ; rijk ijkœ ŸŸ_Ê œ Ê œ œ œ
dd
dt dt x y z t t t 3t
333
rr
¸¸ ÈÈÈÈ
f(x y z) ds 3 dt lim 1 1Êßßœ œœ œ
''
C1
Š‹
È‘ ˆ ‰
È3
3t t b
1_
"
"
bÄ_
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

940 Chapter 16 Integration in Vector Fields
15. C : (t) t t , 0 t 1 2t 1 4t ; x y z t t 0 t t 2t
"# #
##
rij ijœ ŸŸ Ê œ Ê œ œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈkk
since t 0 f(x y z) ds 2t 1 4t dt 4t (5) 5 5 1 ;Ê ßß œ œ " œ œ
''
C0
1È’“ Š‹
ab È
#""""
# $Î#
$Î# "
!
6666
C : (t) t , 0 t 1 1; x y z 1 1 t 2 t
####
rijk kœ ŸŸ Ê œ Ê œ œ œ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds 2 t (1) dt 2t t 2 ; therefore f(x y z) dsÊßßœ œœœ ßß
'' '
C0 C
1ab ‘
#$
""
"
!
333
5
f(x y z) ds f(x y z) ds 5œßßßßœ
''
CC
53
6È#
16. C : (t) t , 0 t 1 1; x y z 0 0 t t
"###
rk kœŸŸÊœÊœœœ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds t (1) dt ;Êßßœ œœ
''
C0
1ab ’“
#"
!
"t
33
C : (t) t , 0 t 1 1; x y z 0 t 1 t 1
##
rjk jœ ŸŸ Ê œ Ê œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈ
f(x y z) ds t 1 (1) dt t t 1 ;Êßßœ œœœ
''
C0
1ˆ‰ ‘
È22
333
$Î# "
!
"
C : (t) t , 0 t 1 1; x y z t 1 1 t
$#
rijk iœ ŸŸÊ œÊ œ œ œ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds (t)(1) dt f(x y z) ds f ds f ds f dsÊ ßßœ œ œÊ ßßœ œ
' ' ' '''
C 0 C CCC
1’“ ˆ‰
t
233
"
!
""""
# #
œ"
6
17. (t) t t t , 0 a t b 3 ; rijk ijkœ ŸŸ Ê œ Ê œ œ œ
d d ttt 1
dt dt x y z t t t t
xyz
rr
¸¸ È
f(x y z) ds 3 dt 3 ln t 3 ln , since 0 a bÊßßœ œ œ Ÿ
''
Ca
bb
a
ˆ‰ ˆ‰
ÈÈ È
’“
kk
1b
ta
18. (t) a cos t a sin t , 0 t 2 ( a sin t) (a cos t) a sin t a cos t a ;rjk jkœ ŸŸÊœ Êœ œabab kk
¸¸ È
1dd
dt dt
rr
## # #
x z 0 a sin t f(x y z) ds a sin t dt a sin t dt
a sin t, 0 t
a sin t, t 2
œ œ Ê ßß œ
ŸŸ
ŸŸ
ÈÈ œkk
kk kk kk
## ## ##
1
11
'' '
C0
2
a cos t a cos t a ( 1) a a a ( 1) 4aœ œ œcdcdc dc d
## #### #
!
#11
1
19. (a) t t t , 0 t 4 x ds t dt t dt t 4 5rij ijabœŸŸÊœÊœÊœœœœ
""
## !
dd
dt dt 2 2 2 4
5555
24
rr
¸¸ ’“È
ÈÈÈÈ
'' '
C0 0
44
(b) t t t , 0 t 2 2t 1 4t x ds t 1 4t dtrij ijabœ ŸŸ Ê œ Ê œ Ê œ
2dd
dt dt 22
rr
¸¸ ÈÈ
''
C0
2
14tœ œ
’“
ab
1
12 12
232 217 17
Î
!
"
È
20. (a) t t 4t , 0 t 1 4 17 x 2y ds t 2 4t 17 dtrij ijabœ ŸŸ Ê œ Ê œ Ê œ
dd
dt dt
rr
¸¸ ÈÈ
ÈÈab
''
C0
1
17 9t dt 3 17 t dt 2 17 t 2 17œœœœ
ÈÈ È È È
È’“
''
00
11
23 1
Î
!
(b) C : t t , 0 t 1 1; C : t t , 0 t 1 1
"ri i rij jab abœ ŸŸÊ œÊ œ œ ŸŸÊ œÊ œ
dd dd
dt dt dt dt
2
rr rr
¸¸ ¸¸
x 2y ds x 2y ds x 2y ds t 2 0 dt 1 2 t dt
''' ' '
CC C 0 0
12
ÈÈÈÈÈ
ab abœ œ
12
t dt 1 2t dt t 1 2tœœœœ
''
00
12
ÈÈ‘
’“Š‹
ab
21 2 1
33 3333
23 123 255 551
Î
!
Î
!
ÈÈ
21. t 4t 3t , 1 t 2 4 3 5 y e ds 3t e 5dtrij ijabœ ŸŸÊœÊ œÊ œ †
dd
dt dt
x4t
rr
¸¸ ab
''
C1
2
22
ab
15 t e dt e e e e eœ œ œ œ
'1
2
1
16t 16t 64 16 16 64
15 15 15 15
32 32 32 32
2
22
’“ ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.1 Line Integrals 941
22. t cos t sin t , 0 t 2 sin t cos t sin t cos t 1 x y 3 dsrij ijabœ ŸŸÊœÊœ œÊabab a bab a b
¸¸ È
1dd
dt dt 22
rr 'C
cos t sin t 3 1 dt sin t cos t 3t 6œ†œœ
'0
2abcd
2
0
11
23. t t t , 1 t 2 2t 3t 2t 3t t 4 9t dsrij ijabœ ŸŸÊœ Ê œ œ Ê
23 2
dd x
dt dt
222
2
y
rr
¸¸ É
ab a b È'C
2
43
t 4 9t dt t 4 9t dt 4 9tœ †œ œ œ
''
11
22
ˆ‰ ÈÈ
ab
t
t
22
1
27 27
232 80 10 13 13
22
343 ÈÈ
’“
ab
Î
2
1
24. t t t , t 1 3t 4t 3t 4t t 9 16t dsrij ijabœ ŸŸÊœ Ê œ œ Ê
34 2 3 2
1d d
2dt dt x
23 2
22 y
rr
¸¸ É
ab ab È'C
È
t 9 16t dt t 9 16t dt 9 16tœ †œ œ œ
''
12 12
11
12
1
È È
t
t4848
22
22
132 125 13 13
4
3ÈÈ
’“
ab
Î
25. C : t t t , 0 t 1 2t 1 4t ; C : t 1 t 1 t , 0 t 1
"rij ij r i jab abœ ŸŸ Ê œ Ê œ œ ŸŸ
2dd
dt dt 22
rr
¸¸ Èabab
2 xyds xyds xydsÊœÊ œ Ê œ
dd
dt dt
rr
ij ¸¸ ˆ‰ ˆ‰ ˆ‰
ÈÈÈÈ
'''
CC C
12
t t 1 4t dt 1 t 1 t 2dt 2t 1 4t dt 1 t 1 t 2dtœ œ
'' ''
00 00
11 11
Š‹ Š ‹ Š ‹
ÈÈÈ
ab
ÈÈ
ÈÈ
22 2
14t 2t t 1tœ œ œ
’“’ “
ab ab
È
12
63666
22
32 32 551 55721
72
Î"
#
Î
11
00
ÈÈÈ
È
26. C : t t , 0 t 1 1; C : t t , 0 t 1 1;
"ri i rij jab abœ ŸŸÊ œÊ œ œ ŸŸÊ œÊ œ
dd dd
dt dt dt dt
2
rr rr
¸¸ ¸¸
C : t 1 t , 0 t 1 1; C : t 1 t , 0 t 1 1;
3 4
dd dd
dt dt dt dt
rij i rj jab abœ ŸŸÊ œÊ œ œ ŸŸÊ œÊ œab ab
¸¸ ¸¸
rr rr
ds ds ds ds dsʜ
'''''
CCCCC
1 1111
xy1 xy1 xy1 xy1 xy1
22 22 22 22 22
1234
œ
''' '
000 0
111 1
dt dt dt dt
t1 t2 1t 2 1t 1
2222
ab ab
tan t tan tan tan 1 t tanœ œcd c d
’“’“ Š‹Š‹ Š‹ ab
11 1 1 1
1t1t1 21
222 2 22
2
1 1
0 0
11
00
ÈÈÈÈ ÈÈ
1
27. (x) x y x , 0 x 2 x 1 x ; f(x y) f x 2x f dsrijij ijœœ ŸŸÊ œ Ê œ ßœ ß œ œ Ê
xdd xx
dx dx
# #
#
rr
¸¸ ÈŠ‹Š‹
x'C
(2x) 1 x dx 1 x 5 1œœœœ
'0
2È’“
ab ˆ‰
## $Î#
$Î# #
!
22
333
10 5 2
È
28. (t) 1 t 1 t , 0 t 1 1 1 t ; f(x y) f 1 t 1 trijœ ŸŸÊ œ ßœ ß œabab ab abab
¸¸ ÉŠ‹
1d 1
2 2
dt
1t 1t
11t
# #
#
rabab
Éab
1
4
4
f ds 1 1 t dt 1 t 1 t dt 1 t 1 tÊœ œœ
'' '
C0 0
11
abab
Éab
1t 1t
11t
11
420
425
#"
#
"
!
1
4
4Éab abab ab ab
Š‹’ “
0œ œ
ˆ‰
""
## #00
11
29. (t) (2 cos t) (2 sin t) , 0 t ( 2 sin t) (2 cos t) 2; f(x y) f(2 cos t 2 sin t)rij ijœ ŸŸÊœ ʜߜß
1
#
dd
dt dt
rr
¸¸
2 cos t 2 sin t f ds (2 cos t 2 sin t)(2) dt 4 sin t 4 cos t 4 ( 4) 8œÊ œ œ œœ
''
C0
2cd
1Î#
!
30. (t) (2 sin t) (2 cos t) , 0 t (2 cos t) ( 2 sin t) 2; f(x y) f(2 sin t 2 cos t)rij ijœ ŸŸÊœ ʜߜß
1
4dt dt
ddrr
¸¸
4 sin t 2 cos t f ds 4 sin t 2 cos t (2) dt 4t 2 sin 2t 4 sin t 2 1 2œ Ê œ œ œ
## Î%
''
C0
4
0
abc d
Š‹
È
11
31. y x , 0 x 2 t t t , 0 t 2 2t 1 4t A f x, y dsœ ŸŸÊ œ ŸŸÊ œ Ê œ Ê œ
22
dd
dt dt 2
rij ijab rr
¸¸ Èab
'C
x y ds t t 1 4t dt 2t 1 4t dt 1 4tœ œ œ œ œ
'' '
C0 0
22
ˆ‰
ÈŠ‹ ’ “
ÈÈÈ
ab
22 2
1
66
232 17 17 1
Î
2
0
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
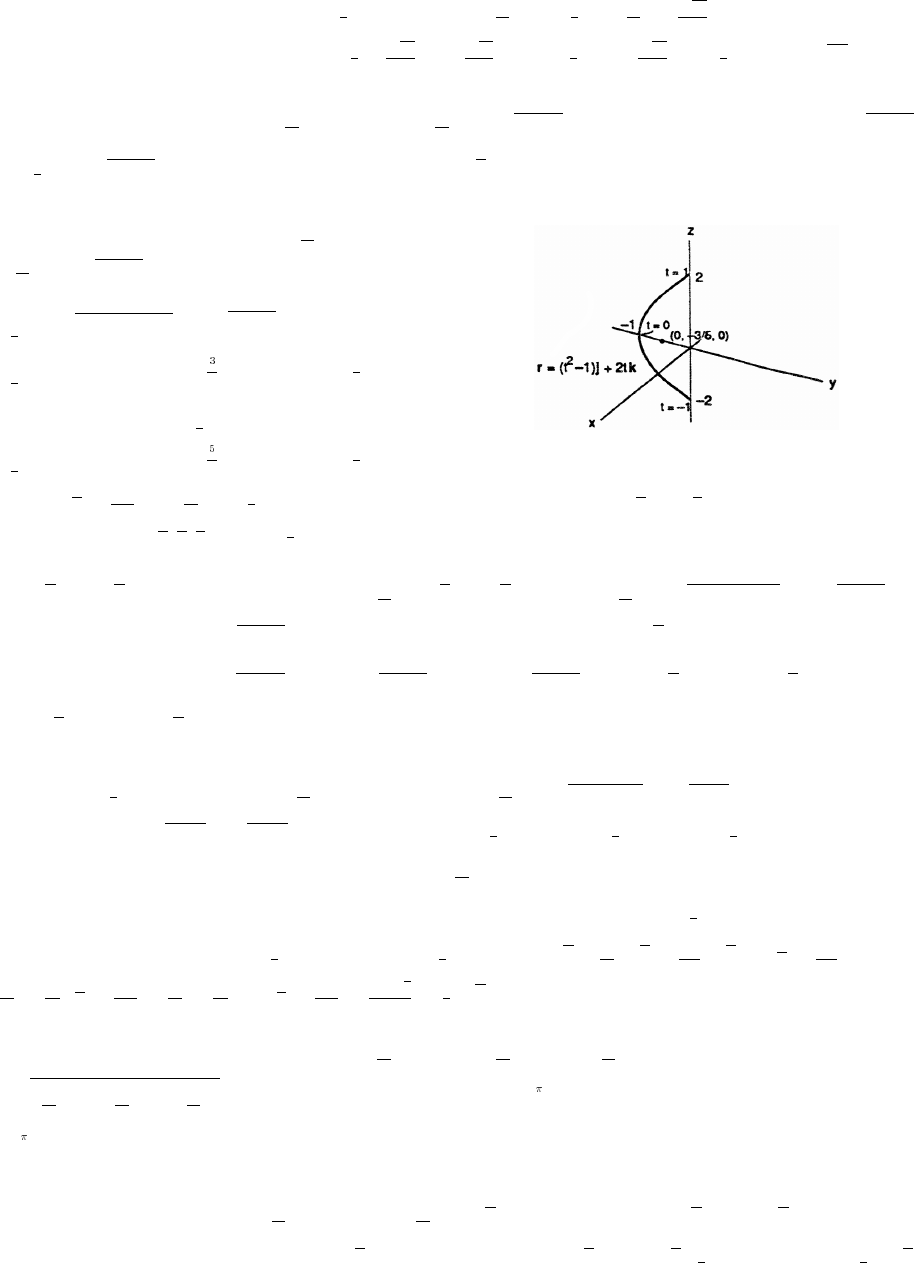
942 Chapter 16 Integration in Vector Fields
32. 2x 3y 6, 0 x 6 t t 2 t , 0 t 6 A f x, y ds œ ŸŸÊ œ ŸŸÊ œ Ê œ Ê œri j ijab ˆ‰ ¸¸ ab
2d2d
3dt3dt3
13
rr
È'C
4 3x 2y ds 4 3t 2 2 t dt 8 t dt 8t t 26 13œœ œ œ œ
'' '
C0 0
66
ab
ˆ‰ˆ‰‘ˆ‰ È
255
33 3 3 3 6
13 13 13 2
ÈÈ È 6
0
33. (t) t 1 2t , 0 t 1 2t 2 2 t 1; M (x y z) ds (t) 2 t 1 dtrjk jkœ ŸŸÊ œÊ œ œ ßß œ ab ¸¸ ÈÈ
Š‹
###
dd
dt dt
rr ''
C0
1
$$
t2t1 dt t1 2 1221œœœœ
'0
1ˆ‰
Š‹’“
ÈÈ
ab
33/2
### $Î#
"
!
34. (t) t 1 2t , 1 t 1 2t 2rjk jkœ ŸŸÊ œab
#d
dt
r
2 t 1; M (x y z) dsÊœ œ ßß
¸¸ È'
d
dt
r#
C
$
15 t 1 2 2 t 1 dtœ
'1
1ˆ‰
ÈabŠ‹
È
##
30 t 1 dt 30 t 60 1 80;œœœœ
'1
1ab’“Š‹ ˆ‰
#"
"
"t
33
M y (x y z) ds t 1 30 t 1 dt
xz C1
1
œßßœ
''
$abc dab
##
30 t 1 dt 30 t 60 1œœœ
'1
1ab’“Š‹ ˆ‰
%"
"
"t
55
48 y ; M x (x y z) ds 0 ds 0 x 0; z 0 by symmetry (since isœ Ê œ œ œ œ ß ß œ œ Ê œ œ
M
M805
48 3 yz
xz ''
CC
$$ $
independent of z) (x y z) 0Êßßœ!ßß
ˆ‰
3
5
35. (t) 2t 2t 4 t , 0 t 1 2 2 2t 2 2 4t 2 1 t ;rij k ijkœ ŸŸÊœÊœœ
ÈÈ ÈÈ È È
ab ¸¸
###
dd
dt dt
rr
(a) M ds (3t) 2 1 t dt 2 1 t 2 2 1 4 2 2œœ œ œœ
''
C0
1
$Š‹’ “
ÈÈ
ab ˆ‰
## $Î#
$Î# "
!
(b) M ds 1 2 1 t dt t 1 t ln t 1 t 2 ln 1 2 0 ln 1œ œ œ œ
''
C0
1
$ab ab
Š‹’ “’ “
ÈÈ ÈÈÈ
Š‹ Š‹
## #
"
!
2ln1 2œ
ÈÈ
Š‹
36. (t) t 2t t , 0 t 2 2 t 1 4 t 5 t;rij k ijkœ ŸŸ Ê œ Ê œ œ
2d d
3dt dt
$Î# "Î#
rr
¸¸ ÈÈ
M ds 3 5 t 5 t dt 3(5 t) dt (5 t) 7 5 (24) 36;œœ œœœœœ
'' '
C0 0
22
$ˆ‰ˆ‰ ‘
ÈÈ ab
333
2###
#
!##
M x ds t[3(5 t)] dt 15t 3t dt t t 30 8 38;
yz 5
2
œœœœœœ
'' '
C0 0
22
$ab
‘
##$
"#
!
M y ds 2t[3(5 t)] dt 2 15t 3t dt 76; M z ds t [3(5 t)] dt
xz xy 2
3
œœ œ œœ œ
'' ' ''
C0 0 C 0
22 2
$$ab
# $Î#
10t 2t dt 4t t 4(2) (2) 16 2 2 2 xœœœœœÊœ
'0
2ˆ‰‘ ÈÈ È
$Î# &Î# &Î# (Î# &Î# (Î#
#
!
4 4 32 144
7777M
Myz
, y , and z 2œœ œ œœ œ œ œ
38 19 76 19 4
36 18 M 36 9 M 7 36 7
MM144 2
xz xy È
†È
37. Let x a cos t and y a sin t, 0 t 2 . Then a sin t, a cos t, 0œœŸŸœœœ1dx dz
dt dt dt
dy
dt a dt; I x y ds a sin t a cos t a dtÊœœœ
ʈ‰ ˆ‰
Š‹ ab a b
dx dz
dt dt dt
dy z
##
### ## ##
''
C0
2
$$
a dt 2 a .œœ
'0
2$$
$1$
38. (t) t (2 2t) , 0 t 1 2 5; M ds 5 dt 5;rj k jkœ ŸŸ Ê œ Ê œ œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈ
''
C0
1
$$ $
I y z ds t (2 2t) 5 dt 5t 8t 4 5 dt 5 t 4t 4t 5 ;
x55
33
œ œ œ œ œ
'' '
C0 0
11
ab c d a b
ÈÈÈÈ
‘
## # # # $ # "
!
$$ $$ $
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.1 Line Integrals 943
I x z ds 0 (2 2t) 5 dt 4t 8t 4 5 dt 5 t 4t 4t 5 ;
y44
33
œ œ œ œ œ
'' '
C0 0
11
ab c d a b
ÈÈÈÈ
‘
## # # # $ # "
!
$$ $$ $
I x y ds 0 t 5 dt 5 5
zC0
1
œ œ œ œ
''
ab ab
ÈÈ È
’“
## ## "
!
"
$$$$
t
33
39. (t) (cos t) (sin t) t , 0 t 2 ( sin t) (cos t) sin t cos t 1 2;rijk ijkœŸŸÊœÊœ œ1dd
dt dt
rr
¸¸ ÈÈ
##
(a) I x y ds cos t sin t 2 dt 2 2
zC0
2
œ œ œ
''
ab a b
ÈÈ
## # #
$$1$
(b) I x y ds 2 dt 4 2
zC0
4
œ œ œ
''
ab ÈÈ
##
$$ 1$
40. (t) (t cos t) (t sin t) t , 0 t 1 (cos t t sin t) (sin t t cos t) 2t rijk i jkœ ŸŸÊœ
22
3dt
d
È$Î# rÈ
(t 1) t 1 for 0 t 1; M ds (t 1) dt (t 1) 2 1 ;Êœœ ŸŸœ œœ œ œ
¸¸ ‘
Èab
d 3
dt 2
r#""
###
"
!##
''
C0
1
$
M z ds t (t 1) dt t t dt t t
xy 22 22 22
33 375
22
œœ œ œ
'' '
C0 0
11
$Š‹ ˆ‰ ‘
ÈÈ È
$Î# &Î# $Î# (Î# &Î# "
!
z ; I x y dsœœ œÊœœ œ œ
22 22 162 162 322
3 7 5 3 35 35 M 35 3 105
22 24 2
Mz
ÈÈÈ ÈÈ
ˆ‰ ˆ‰ ˆ‰
Š‹ ab
xy 'C
##
$
t cos t t sin t (t 1) dt t t dtœ œ œ œœ
''
00
11
abab
’“
## ## $# "
!
""tt 7
43 4312
41. (x y z) 2 z and (t) (cos t) (sin t) , 0 t M 2 2 as found in Example 3 of the text;$11ßß œ œ Ÿ Ÿ Ê œ rjk
also 1; I y z ds cos t sin t (2 sin t) dt (2 sin t) dt 2 2
¸¸ ab a b
d
dt x
rœœ œ œ œ
'' '
C0 0
## # #
$1
42. (t) t t , 0 t 2 2 t t 1 2t t (1 t) 1 t forri jk i jkœ ŸŸ Ê œ Ê œ œ œ
22
3dtdt
td d
È$Î# "Î#
###
rr
ÈÈ
¸¸ È
0 t 2; M ds (1 t) dt dt 2; M x ds t (1 t) dt 2;ŸŸ œ œ œ œ œ œ œ œ
'' ' ' '
C0 0 C 0
22 2
yz
$$
ˆ‰ ˆ‰ ’“
""
#
!
t1 t1 2
t
M y ds t dt t ; M z ds dt x 1,
xz 22 42
31515 63M
32 t t M
œœ œ œœœœœÊœœ
'' ''
C0 C0
2 2
xy
$$
ÈÈ
$Î# &Î# ##
!!
#
%
’“ ’“ yz
y , and z ; I y z ds t t dt t ;œ œ œ œ œ œ œ œœ
M
M15 M3 9 4 9 20 92045
16 8 2 t 32 32 232
Mx
xz xy #"
## $ % % #
!
''
C0
2
ab ˆ‰
’“
$
I x z ds t t dt ; I x y ds
y z
C0 C
2
œ œ œœœœ
'' '
ab ab
ˆ‰
’“
## # % ##
"#
!
$$
432032015
tt 83264
t t dt tœ œœœ
'0
2ˆ‰
’“
#$ %
#
!
8 t 2 8 32 56
939399
43-46. Example CAS commands:
:Maple
f := (x,y,z) -> sqrt(1+30*x^2+10*y);
g := t -> t;
h := t -> t^2;
k := t -> 3*t^2;
a,b := 0,2;
ds := ( D(g)^2 + D(h)^2 + D(k)^2 )^(1/2): # (a)
'ds' = ds(t)*'dt';
F := f(g,h,k): # (b)
'F(t)' = F(t);
Int( f, s=C..NULL ) = Int( simplify(F(t)*ds(t)), t=a..b ); # (c)
`` = value(rhs(%));
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

944 Chapter 16 Integration in Vector Fields
: (functions and domains may vary)Mathematica
Clear[x, y, z, r, t, f]
f[x_,y_,z_]:= Sqrt[1 30x 10y]
2
{a,b}= {0, 2};
x[t_]:= t
y[t_]:= t2
z[t_]:= 3t2
r[t_]:= {x[t], y[t], z[t]}
v[t_]:= D[r[t], t]
mag[vector_]:=Sqrt[vector.vector]
Integrate[f[x[t],y[t],z[t]] mag[v[t]], {t, a, b}]
N[%]
16.2 VECTOR FIELDS, WORK, CIRCULATION, AND FLUX
1. f(xyz)xyz xyz (2x) xxyz ; similarly,ß ß œ Ê œ œ ab ab ab
### ### ###
"Î# $Î# $Î#
`"
`#
f
x
yxyz and zxyz f
``
``
### ###
$Î# $Î#
ff
yz
xyz
xyz
œ œ Ê œab ab™ijk
ab
2. f(x y z) ln x y z ln x y z (2x) ;ßßœ œ Ê œ œ
ÈabŠ‹
###
"`""
#`#
### fx
x xyz x y z
similarly, and f
``
` `
ffz
y xyz z xyz xyz
yxyz
œœÊœ™ijk
3. g(x y z) e ln x y , and eß ß œ Ê œ œ œ
z z
gg2yg
xxyyxy z
2x
ab
## `` `
```
geÊœ™Š‹Š‹
2x
xy xy
2y
ijk
z
4. g(x y z) xy yz xz y z, x z, and y x g (y z) ( z) (x y)ßß œ Ê œ œ œ Ê œ B
`` `
`` `
gg g
xy z ™ijk
5. inversely proportional to the square of the distance from (x y) to the origin (M(x y)) (N(x y))kk È
FßÊßß
##
, k 0; points toward the origin is in the direction of œ Ê œ
k x
xy xy xy
y
FFnij
ÈÈ
a , for some constant a 0. Then M(x y) and N(x y)ʜ ߜ ߜFn
ax
xy xy
ay
ÈÈ
(M(x y)) (N(x y)) a a , for any constant k 0Êßߜʜʜ
È##
kkx
xy xy xy
ky
Fij
ab ab
6. Given x y a b , let x a b cos t and y a b sin t. Then
#### ## ##
œ œ œ
ÈÈ
a b cos t a b sin t traces the circle in a clockwise direction as t goes from 0 to 2rijœ
Š‹Š‹
ÈÈ
## ## 1
a b sin t a b cos t is tangent to the circle in a clockwise direction. Thus, letʜ vij
Š‹Š‹
ÈÈ
## ##
y x and (0 0) .Fv F i j F 0œÊ œ ßœ
7. Substitute the parametric representations for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) 3t 2t 4t and 9t 9t dtFijk ijkFœ œÊ œÊ œ
dd 9
dt dt
rr
†'0
1
#
(b) 3t 2t 4t and 2t 4t 7t 16t 7t 16t dt t 2tFijk ijkFœ œ Ê œ Ê œ
#% $ #(#($)
"
!
dd 7
dt dt 3
rr
†'0
1ab
‘
2œœ
713
33
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.2 Vector Fields, Work, Circulation, and Flux 945
(c) t t and t ; 3t 2t and 5t 5t dt ;r i j r ij kF i j ij F
"# " " #
œ œ œ œ Ê œ Ê œ
dd
dt dt
5
rr
†'0
1
3 2 4t and 4t 4t dt 2 2Fijk kF
##
##
œ œÊ œ Ê œÊœ
dd
dt dt
59
rr
†'0
1
8. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) and dt tan tFjijkFœ œ Ê œ Ê œ œ
ˆ‰ cd
"""
" "
!
t1 dt dt t1 t1 4
ddrr
†'0
11
(b) and 2t 4t dt ln t 1 ln 2FjijkFœœÊœÊœœ
ˆ‰ cdab
"
$#
"
!
t1 dt dt t1 t1
d d 2t 2trr
†'0
1
(c) t t and t ; and ; and rijrijkF j ijF F j k
"# " " #
"""
#
œ œ œ œÊ œ œ œ
ˆ‰
t 1 dt dt t 1 dt
dd d
rr r
†
0 dtÊœÊ œF#"
†d
dt t 1 4
r'0
11
9. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) t 2t t and 2 t 2t 2 t 2t dt t tFijk ijkFœ œ Ê œ Ê œ œ
ÈÈ È È
ˆ‰‘
dd 4
dt dt 3 3
rr
†'0
1$Î# # "
!
"
(b) t 2t t and 2t 4t 4t 3t 4t 3t dt t tFijk ij kFœ œ Ê œ Ê œ œ
# $ %# %# &$
"
!
"dd 4
dt dt 5 5
rr
†'0
1ab
‘
(c) t t and t ; 2t t and 2t 2t dt 1;r i j r ij kF j k ij F
"# " "
œ œ œ œ Ê œ Ê œ
Èdd
dt dt
rr
†'0
1
t 2 and 1 dt 1 1 1 0Fijk kF
##
œ œÊ œÊ œÊœ
Èdd
dt dt
rr
†'0
1
10. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) t t t and 3t 3t dt 1Fijk ijkFœ œÊ œ Ê œ
### # #
dd
dt dt
rr
†'0
1
(b) t t t and 2t 4t t 2t 4t t 2t 4t dtFijk ij kFœ œ Ê œ Ê
$'& $ $() $()
dd
dt dt
rr
†'0
1ab
tœ œ
’“
tt4 17
449 18
*"
!
(c) t t and t ; t and t t dt ;rijrijkF i ijF
"# " "
###
"
œ œ œ œ Ê œ Ê œ
dd
dt dt 3
rr
†'0
1
t t and t t dt Fijk k F
##
"""
##
œ œ Ê œ Ê œ Ê œ
dd
dt dt 3 6
5
rr
†'0
1
11. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) 3t 3t 3t and 3t 1 3t 1 dt t t 2FijkijkFœ œ Ê œ Ê œ œab abcd
###$
"
!
dd
dt dt
rr
†'0
1
(b) 3t 3t 3t and 2t 4t 6t 4t 3t 3tFijkijkFœ œ Ê œab
# % $ &$#
dd
dt dt
rr
†
6t 4t 3t 3t dt t t t tÊ œ œ
'0
1ab
‘
&$# '%$ #
##
"
!
33
(c) t t and t ; 3t 3t and 3t 3tr i j r ij kF ik ij F
"# " "
##
œ œ œ œ Ê œ ab dd
dt dt
rr
†
3t 3t dt t t ; 3t and 1 dt 1Êœœœ œÊ œÊœ
''
0 0
1 1
ab
‘
#$#
"
!
"
###
3
2dtdt
dd
Fjk kF
rr
†
1Ê œ
"
#
1
2
12. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate .FF
'C†d
dt
r
(a) 2t 2t 2t and 6t 6t dt 3t 3Fijk ijkFœ œÊ œÊ œ œ
dd
dt dt
rr
†'0
1cd
#"
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

946 Chapter 16 Integration in Vector Fields
(b) t t t t t t and 2t 4t 6t 5t 3tFijkijkFœ œ Ê œ a babab
#% % # $ &%#
dd
dt dt
rr
†
6t 5t 3t dt t t t 3Êœœ
'0
1abcd
&%# '&$
"
!
(c) t t and t ; t t 2t and 2t 2t dt ;rijrijkFijk ijF
"# " "
œ œ œ œÊ œ Ê œ"
dd
dt dt
rr
†'0
1
(1 t) (t 1) 2 and 2 2 dt 2 2 3FijkkF
##
œ œÊ œÊ œÊ"œ
dd
dt dt
rr
†'0
1
13. x t, y 2t 1, 0 t 3 dx dt x y dx t 2t 1 dt t 1 dt t tœœ ŸŸÊœÊ œ œ œœ
'' '
C0 0
33
ab a b a bab ‘
"
#!
2315
2
14. x t, y t , 1 t 2 dy 2t dt dy 2t dt 2 dt 2t 2œœ ŸŸÊœ Ê œ œ œ œ
2xt
yt
'' '
C1 1
22
1
2
2ab cd
15. C : x t, y 0, 0 t 3 dy 0; C : x 3, y t, 0 t 3 dy dt x y dy
12 22
œ œ ŸŸ Ê œ œ œ ŸŸ Ê œ Ê
'Cab
x y dx x y dx t 0 0 3 t dt 9 t dt 9t t 36œœ†œœœ
'''''
CC 000
333
12
ab ab ab ab ab
‘
22 22 22 22 2 3
1
3
3
!
16. C : x t, y 3t, 0 t 1 dx dt; C : x 1 t, y 3, 0 t 1 dx dt; C : x 0, y 3 t, 0 t 3
12 3
œœ ŸŸÊœ œœŸŸÊœ œœŸŸ
dx 0 x y dx x y dx x y dx x y dxʜʜ
''''
CCCC
ÈÈÈÈ
123
t 3tdt 1 t 3 1 dt 0 3 t 0 2 tdt 4 tdtœ †œ
'' ' ''
00 0 00
11 3 11
ÈÈÈ
abab ab ÈÈ
t4t 23234œœœ
‘’“Š‹
ab ÈÈ
42 4 16
33 3 3
23 123 1
Î
!
Î
!
17. t t t , 0 t 1 dx dt, dy 0, dz 2t dtrijkabœ ŸŸÊ œ œ œ
2
(a) x y z dx t 1 t dt t t t
''
Cabab
‘
œ œ œ
0
11
223
11 5
23 6
!
(b) x y z dy t 1 t 0 0
''
Cabab œ †œ
0
12
(c) x y z dz t 1 t 2t dt 2t 2t 2t dt t t t
'' '
Cabab a b‘
œ œ œœ œ
00
11 1
223324
215
326
!
18. t cos t sin t cos t , 0 t dx sin t dt, dy cos t dt, dz sin t dtrijkabœŸŸÊœœœababab1
(a) x z dx cos t cos t sin t dt cos t sin tdt cos t
'' '
Cœœ œœ
00
11
1
aba ba b ab
’“
212
33
3
!
(b) x z dy cos t cos t cos t dt cos t dt 1 sin t cos t dt sin t sin t 0
'' ' '
Cœ œ œ œ œ
000
111 1
aba bab a b ab
’“
32
1
3
3
!
(c) x y z dz cos t sin t cos t sin t dt cos t sin t dt sin 2t dt dt
'' ' ' '
Cœ œ œ œ
0000
1111
ababa bab 22 2
1 1 1 cos 4t
442
1 cos 4t dt t sin 4tœ œ œ
111
88328
'0
11
ab
‘
!
1
19. t t t , 0 t 1, and xy y yz t t t and 2tri jk F i j k F i j k i jkœ ŸŸ œ Êœ œ
#$#$
d
dt
r
2t work 2t dtʜʜ œF†d
dt
r$$
"
#
'0
1
20. (cos t) (sin t) , 0 t 2 , and 2y 3x (x y)rijk Fij kœ ŸŸ œ
t
61
(2 sin t) (3 cos t) (cos t sin t) and ( sin t) (cos t) Êœ œ ÊFij k ijkF
dd
dt 6 dt
rr"†
3 cos t 2sin t cos t sin t work 3 cos t 2 sin t cos t sin t dtœÊœ
##
"" ""
22
66 66
'0
2ˆ‰
t sin 2t t sin t cos tœ œ
‘
3 3 sin 2t
24 2 6 6
""
#
!
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.2 Vector Fields, Work, Circulation, and Flux 947
21. (sin t) (cos t) t , 0 t 2 , and z x y t (sin t) (cos t) andrijk FijkFijkœ ŸŸ œÊœ1
(cos t) (sin t) t cos t sin t cos t work t cos t sin t cos t dt
dd
dt dt
rr
œÊœÊœ ijkF†##
'0
2ab
cos t t sin t sin tœ œ
‘
tsin 2t
24
#
!
11
22. (sin t) (cos t) , 0 t 2 , and 6z y 12x t cos t (12 sin t) andrijk FijkFi j kœ ŸŸ œÊœ
t
61##
ab
(cos t) (sin t) t cos t sin t cos t 2 sin t
dd
dt 6 dt
rr
œÊœ ijkF
"#
†
work t cos t sin t cos t 2 sin t dt cos t t sin t cos t 2 cos t 0Êœ œ œ
'0
2ab
‘
#$
#
!
1
3
1
23. x t and y x t t t , 1 t 2, and xy (x y) t t t andœœœÊœŸŸ œÊœ
## # $ #
ri j F i j F i jab
2t t 2t 2t 3t 2t xy dx (x y) dy dt 3t 2t dt
dd d
dt dt dt
rr r
œ Ê œ œ Ê œ œ ijF F††
$#$ $# $#
ab ab
'''
CC
tt 12œ œ œœ
‘ˆ‰ˆ‰
3 2 16 3 2 45 18 69
43 3 43434
%$
#
"
24. Along (0 0) to (1 0): t , 0 t 1, and (x y) (x y) t t and t;ßßœŸŸ œÊœ œÊœri F i j Fij i F
dd
dt dt
rr
†
Along (1 0) to (0 1): (1 t) t , 0 t 1, and (x y) (x y) (1 2t) andß ß œ ŸŸ œ Êœ rij F ijF ij
2t;
dd
dt dt
rr
œ Ê œij F†
Along (0 1) to (0 0): (1 t) , 0 t 1, and (x y) (x y) (t 1) (1 t) andß ß œ ŸŸ œ Êœ rj F i jFij
t 1 (x y) dx (x y) dy t dt 2t dt (t 1) dt (4t 1) dt
dd
dt dt
rr
œ Ê œ Ê œ œ jF†'''''
C0000
11 1 1
2t t 2 1 1œ œœcd
#"
!
25. x y y y , 2 y 1, and x y y y 2y and 2y yrij ij F ij ij ij Fœœ œ œ Ê œ œ
##% &
dd
dy dy
rr
†
ds dy 2y y dy y yÊœ œœœœœ
'' '
C2 2
11
FT F††
d64 4 3 63 39
dy 3 3 3 3
rab
‘ˆ‰ˆ‰
&'#
"" ""
#####
"
#
26. (cos t) (sin t) , 0 t , and y x (sin t) (cos t) and ( sin t) (cos t)rij FijFij ijœ ŸŸ œÊœ œ
1
#
d
dt
r
FFrʆ †
d
dt
rœ œ Ê œ œsin t cos t 1 d ( 1) dt
##
#
''
C0
21
27. ( ) t( 2 ) (1 t) (1 2t) , 0 t 1, and xy (y x) 1 3t 2t t andrij ij i j F i j F ijœ œ ŸŸ œ Ê œ ab
#
2 1 5t 2t work dt 1 5t 2t dt t t t
dd d 5225
dt dt dt 2 3 6
rr r
œ Ê œ Ê œ œ œ œij F F††
###$
"
!
''
C0
1ab
‘
28. (2 cos t) (2 sin t) , 0 t 2 , and f 2(x y) 2(x y)rij F ijœ ŸŸ œœ1™
4(cos t sin t) 4(cos t sin t) and ( 2 sin t) (2 cos t) Êœ œ ÊFij ijF
dd
dt dt
rr
†
8 sin t cos t sin t 8 cos t cos t sin t 8 cos t sin t 8 cos 2t work f dœ œ œ Ê œababab
## ## 'C™†r
dt 8 cos 2t dt 4 sin 2t 0œœ œœ
''
C0
2
F†d
dt
rcd
#
!
1
29. (a) (cos t) (sin t) , 0 t 2 , x y , and y x ( sin t) (cos t) ,rij FijFij ijœ ŸŸœ œÊœ1"#d
dt
r
(cos t) (sin t) , and ( sin t) (cos t) 0 and sin t cos t 1FijF ijF F
"# "#
##
œ œ Ê œ œœ††
dd
dt dt
rr
Circ 0 dt 0 and Circ dt 2 ; (cos t) (sin t) cos t sin t 1 andÊœ œ œ œœ Ê œœ
"# "
##
''
00
22
1nijFn†
0 Flux dt 2 and Flux 0 dt 0Fn
#" #
†œÊ œ œ œ œ
''
00
22
1
(b) (cos t) (4 sin t) , 0 t 2 ( sin t) (4 cos t) , (cos t) (4 sin t) , andri j i jF i jœ ŸŸÊœ œ1d
dt
r"
( 4 sin t) (cos t) 15 sin t cos t and 4 Circ 15 sin t cos t dtFijF F
#"#"
œ Ê œ œ Ê œ††
dd
dt dt
rr
'0
2
sin t 0 and Circ 4 dt 8 ; cos t sin t œœœœœ Ê
‘ Š‹Š‹
" "
##
!# "
54
217 17
1'0
2
1nijFn
ÈÈ †
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

948 Chapter 16 Integration in Vector Fields
cos t sin t and sin t cos t Flux ( ) dt 17 dtœ œ Êœ œ
44 15 4
17 17 17 17
ÈÈ È È
##
#""
Fn Fnv††
''
00
22
kk Š‹
È
8 and Flux ( ) dt sin t cos t 17 dt sin t 0œœ œ œœ1## ##
!
''
00
22
Fnv†kk Š‹
È‘
15 15
17 2
È1
30. (a cos t) (a sin t) , 0 t 2 , 2x 3y , and 2x (x y) ( a sin t) (a cos t) ,rij FijFij ijœ ŸŸ œ œ Êœ 1"# d
dt
r
(2a cos t) (3a sin t) , and (2a cos t) (a cos t a sin t) (a cos t) (a sin t) ,FijFi jnvij
"#
œ œÊœkk
2a cos t 3a sin t, and 2a cos t a sin t cos t a sin tFnv Fnv
"#
## ## ## # ##
††kk kkœ œ
Flux 2a cos t 3a sin t dt 2a 3a a , andÊœ œ œ
"## ## # # #
##
!!
'0
2ab
‘‘
tsin 2t tsin 2t
24 24
11
1
Flux 2a cos t a sin t cos t a sin t dt 2a sin t a a
### # ## # # # #
##
!!
#
#
!
œœœ
'0
2abcd
‘ ‘
t sin 2t a t sin 2t
24 24
11
11
31. (a cos t) (a sin t) , ( a sin t) (a cos t) 0 Circ 0; M a cos t,Fij ijF
""""
œ œ ʜʜœ
dd
dt dt
rr
†
N a sin t, dx a sin t dt, dy a cos t dt Flux M dy N dx a cos t a sin t dt
""""
## ##
œœ œÊœœ
''
C0
ab
a dt a ;œœ
'0
##
1
t , t Circ t dt 0; M t, N 0, dx dt, dy 0 FluxFi iF
##### #
œœÊ œÊœ œœœœœÊ
dd
dt dt
rr
†'a
a
M dy N dx 0 dt 0; therefore, Circ Circ Circ 0 and Flux Flux Flux aœ œ œ œœ œ œ
''
Ca
a
## "# "#
#1
32. a cos t a sin t , ( a sin t) (a cos t) a sin t cos t a cos t sin tFij ijF
" "
#### $#$#
œ œÊœ abab
dd
dt dt
rr
†
Circ a sin t cos t a cos t sin t dt ; M a cos t, N a sin t, dy a cos t dt,Êœ œ œ œ œ
"""
$#$# ## ##
'0ab
2a
3
dx a sin t dt Flux M dy N dx a cos t a sin t dt a ;œ Ê œ œ œ
""" $$ $$ $
''
C0
ab
4
3
t , t Circ t dt ; M t , N 0, dy 0, dx dtFi iF
### ##
####
œ œÊ œÊ œ œ œ œœœ
dd
dt dt 3
2a
rr
†'a
a
Flux M dy N dx 0; therefore, Circ Circ Circ 0 and Flux Flux Flux aÊ œ œ œœ œ œ
### "# "#
$
'C
4
3
33. ( a sin t) (a cos t) , ( a sin t) (a cos t) a sin t a cos t aFij ijF
" " ## # # #
œ œ Ê œ œ
dd
dt dt
rr
†
Circ a dt a ; M a sin t, N a cos t, dx a sin t dt, dy a cos t dtÊœ œ œ œ œ œ
"""
##
'01
Flux M dy N dx a sin t cos t a sin t cos t dt 0; t , 0Êœ œ œœœÊ œ
""" # #
##
''
C0
abFj iF
dd
dt dt
rr
†
Circ 0; M 0, N t, dx dt, dy 0 Flux M dy N dx t dt 0; therefore,ÊœœœœœÊœ œœ
### # ##
''
Ca
a
Circ Circ Circ a and Flux Flux Flux 0œœ œ œ
"# " #
#1
34. a sin t a cos t , ( a sin t) (a cos t) a sin t a cos tFij ijF
" "
## # # $$ $ $
œ œ Ê œ abab
dd
dt dt
rr
†
Circ a sin t a cos t dt a ; M a sin t, N a cos t, dy a cos t dt, dx a sin t dtÊ œ œ œ œ œ œ
"""
$$ $ $ $ ## # #
'0ab
4
3
Flux M dy N dx a cos t sin t a sin t cos t dt a ; t , 0Êœ œ œ œ œÊ œ
""" # #
$#$# $#
''
C0
ab
2
3dt dt
dd
Fj iF
rr
†
Circ 0; M 0, N t , dy 0, dx dt Flux M dy N dx t dt a ; therefore,ÊœœœœœÊ œ œœ
### # ##
##$
''
Ca
a2
3
Circ Circ Circ a and Flux Flux Flux 0œœ œ œ
"# " #
$
4
3
35. (a) (cos t) (sin t) , 0 t , and (x y) x y ( sin t) (cos t) andrij F i j ijœ ŸŸ œÊœ1ab
## d
dt
r
(cos t sin t) cos t sin t sin t cos t sin t cos t dsFi jF FTœ Ê œ Êab
## #
††
d
dt
r'C
sin t cos t sin t cos t dt sin t sin tœ œ œ
'0ab
‘
##
"
##
!
24
tsin 2t 11
(b) (1 2t) , 0 t 1, and (x y) x y 2 and (1 2t) (1 2t) ri Fi j iFi jœ ŸŸ œ Ê œ œ Êab
## #
d
dt
r
4t 2 ds (4t 2) dt 2t 2t 0FFT††
d
dt
rœÊ œ œ œ
''
C0
1cd
#"
!
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.2 Vector Fields, Work, Circulation, and Flux 949
(c) (1 t) t , 0 t 1, and (x y) x y and (1 2t) 1 2t 2trij Fi j ijFi j
"## #
œ ŸŸ œ Ê œ œ ab a b
d
dt
r
(2t 1) 1 2t 2t 2t Flow 2t dt ; t (t 1) ,ÊœœÊœ œ œœFFrij††
d d
dt dt 3
2
r r
ab
## #
"#
''
C0
1
0 t 1, and (x y) x y and t t 2t 1ŸŸ œ Ê œ œ Fi j ijFi jab a b
## ##
d
dt
r
2t 2t 1 1 2t 2t 1 2t 2t Flow 2t 2t dtœ Ê œ œ Ê œ œ ijF Fab ab ab
### #
#
††
d d
dt dt
r r
''
C0
1
t t Flow Flow Flow 1œ œ Ê œ œœ
‘
#$
"
!
""
"#
22
33 33
36. From (1 0) to (0 1): (1 t) t , 0 t 1, and (x y) x y ,ß ß œ ŸŸ œ Ê œrij Fi j ij
"##
abd
dt
r
1 2t 2t , and 2t 2t Flux 2t 2t dtFi j nv ij Fnvœ œ Ê œ Ê œ abkk kk ab
###
"" " "
†"'0
1
tt ;œ œ
‘
#$
"
!
"2
33
From (0 1) to ( 1 0): t (1 t) , 0 t 1, and (x y) x y ,ßß œŸŸ œÊœri j F i j ij
###
abd
dt
r
(1 2t) 1 2t 2t , and (2t 1) 1 2t 2t 2 4t 2tFi jnvijFnvœ œ Ê œ œ a b kk kk a b
###
## ##
†
Flux 2 4t 2t dt 2t 2t t ;Êœœœ
###$
"
!
'0
1ab
‘
22
33
From ( 1 0) to (1 0): ( 1 2t) , 0 t 1, and (x y) x y 2 ,ß ß œ Ÿ Ÿ œ Ê œri Fiji
$##
abd
dt
r
( 1 2t) 1 4t 4t , and 2 2 1 4t 4tFi jnvjFnvœ œ Ê œ a b kk kk a b
##
$$ $$
†
Flux 2 1 4t 4t dt 2 t 2t t Flux Flux Flux FluxÊ œ œ œ Ê œ œœ
$"#$
##$
"
!
""
'0
1ab
‘
42 22
3 3 333 3
37. (a) y 2x, 0 x 2 t t 2t , 0 t 2 2t 2t 2 t 2t 2œ ŸŸÊ œ ŸŸÊ œ Ê œ rij ijF i jijab † †
dd
dt dt
2
rr
Š‹
ab abab a b
4t 8t 12t Flow dt 12t dt 4t 32œœ Ê œ œ œ œ
22 2 2 3
d
dt
2
''
C0
2
F†rcd
!
(b) yx, 0x2 t t t, 0t2 2t t 2tt 2tœ ŸŸÊ œ ŸŸÊ œ Ê œ
22 22
dd
dt dt
2
rij ijF i jijab † †
rr
Š‹
ab abab a b
t 4t 5t Flow dt 5t dt t 32œ œ Ê œ œ œ œ
44 4 4 5
d
dt
2
''
C0
2
F†rcd
!
(c) answers will vary, one possible path is y x , 0 x 2 t t t , 0 t 2 3tœ ŸŸÊ œ ŸŸÊ œ
1d
2dt
332
rij ijab
"
#
r
t 2 t t 3t t t t Flow dt t dt tÊ œ œœ Ê œ œ œFijij F†† †
d137d71
dt 4 2 4 dt 4 4
332666 67
22
r r
Š‹
ˆ‰ ˆ‰ ‘
ab a b
""
## ''
C0
2
!
32œ
38. (a) C : t 1 t , 0 t 2 1 1 t 2 1 1;
1dd
dt dt
rij iFi jiabœ ŸŸÊœÊ œ †œab a babab a babab†
rr
C: t 1 t , 0 t 2 1 t 1 21 t 2t 1;
2dd
dt dt
ri j jF i jjabœ Ÿ Ÿ Ê œ Ê œ † œ †ab a bababa bab a b
rr
C : t t 1 , 0 t 2 1 t 1 2 1 1;
3dd
dt dt
rij iF i jiabœ ŸŸÊ œÊ œ † œab a bababa babab†
rr
C: t t 1 , 0 t 2 t 1 1 2t 1 2t 1;
4dd
dt dt
ri j jF i jjabœ ŸŸÊœÊ œ †œ†ab a bababa bab a b
rr
Flow dt dt dt dt dtÊœœ
'''''
CCCCC
F FFFF† ††††
d dddd
dt dt dt dt dt
r rrrr
1234
1 dt 2t 1 dt 1 dt 2t 1 dt t t t t t tœœ
'' ''
00 00
22 22
ab a b ab a b cd c d cd c d
22
22
22
!!!!
22220œœ
(b) x y 4 t 2cos t 2sin t , 0 t 2 2sin t 2cos t
22 d
dt
œÊ œ ŸŸ Êœrij ijab abab a bab1r
2sin t 2cos t 2 2sin t 2sin t 2cos t 4sin t 4cos t 8sin t cos tÊœ † œ Fi jij†
d
dt
22
rabababa ba babab
4cos 2t 4sin 2t Flow dt 4cos 2t 4sin 2t dt 2sin 2t 2cos 2t 0œÊœ œ œ œ
''
C0
2
F†d
dt
2
rabcd
1
!
(c) answers will vary, one possible path is:
C : t t , 0 t 1 0 t 2 1 0;
1dd
dt dt
ri iF i jiabœŸŸÊœÊ œ †œ
rr
†ababab a bab
C : t 1 t t , 0 t 1 t 1 t 2t 1;
2dd
dt dt
rij ijFi jijabœ Ÿ Ÿ Ê œ Ê œ † œab a ba babab†
rr
C: t 1 t , 0 t 1 1 t 0 21 t 2t 1;
3dd
dt dt
rj jF i jjabœ ŸŸÊœÊ œ †œab a bababa bab
rr
†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
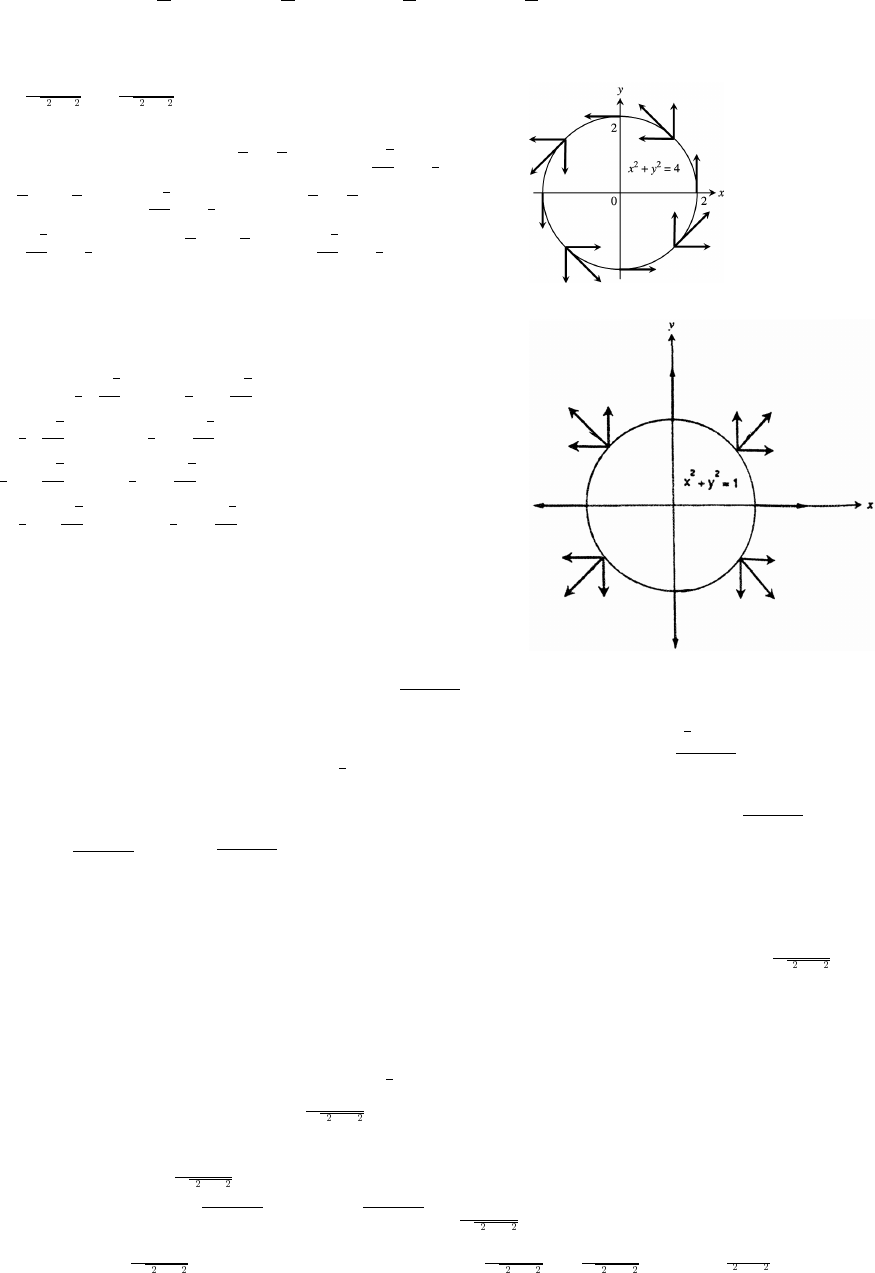
950 Chapter 16 Integration in Vector Fields
Flow dt dt dt dt 0 dt 1 dt 2t 1 dtÊœœœ
'''''''
CCCC 000
111
F FFF† †††
d ddd
dt dt dt dt
r rrr
123 ab ab a b
0t tt 1 1 0œ œ œcd c d a b
121
!!
39. on x y 4;Fijœ œ
y
xy xy
x
ÈÈ
##
at (2 0), ; at (0 2), ; at ( 2 0),ßœ ßœßFj F i
; at ( 2), ; at 2 2 , ;Fj Fi F ijœ !ß œ ß œ
Š‹
ÈÈ È3
##
"
at 2 2 , ; at 2 2 ,
Š‹ Š‹
ÈÈ ÈÈ
ß œ ßFij
È3
##
"
; at 2 2 , Fij Fijœ ß œ
ÈÈ
33
## ##
""
Š‹
ÈÈ
40. x y on x y 1; at (1 0), ;Fij Fiœ œ ß œ
##
at ( 1 0), ; at (0 1), ; at (0 1),ß œ ß œ ßFi Fj
; at , ;Fj Fi jœ ß œ
Š‹
""
## # #
ÈÈ
33
at , ;
Š‹
ß œ
""
## # #
ÈÈ
33
Fij
at , ;
Š‹
""
## # #
ß œ
ÈÈ
33
Fi j
at , .
Š‹
ß œ
""
## # #
ÈÈ
33
Fij
41. (a) P(x y) Q(x y) is to have a magnitude a b and to be tangent to x y a b in aGijœßß œ
È## ####
counterclockwise direction. Thus x y a b 2x 2yy 0 y is the slope of the tangent
#### w w
œ Ê œÊ œ
x
y
line at any point on the circle y at (a b). Let b a a b , with in aÊœ ß œÊ œ
w##
a
bvijv vkk È
counterclockwise direction and tangent to the circle. Then let P(x y) y and Q(x y) xߜ ߜ
y x for (a b) on x y a b we have b a and a b .Ê œ Ê ß œ œ œ Gij GijG
#### ##
kk È
(b) x y a b .GF Fœœ
ˆ‰
ÈŠ‹
È
## ##
42. (a) From Exercise 41, part a, y x is a vector tangent to the circle and pointing in a counterclockwiseij
direction y x is a vector tangent to the circle pointing in a clockwise direction Ê Êœij G y x
x y
i j
È
is a unit vector tangent to the circle and pointing in a clockwise direction.
(b) GFœ
43. The slope of the line through (x y) and the origin is x y is a vector parallel to that line andßÊœ
y
xvij
pointing away from the origin is the unit vector pointing toward the origin.ÊœFx y
x y
i j
È
44. (a) From Exercise 43, is a unit vector through (x y) pointing toward the origin and we wantß
x y
x y
i j
È
to have magnitude x y x y x y .kk ÈÈ
Š‹
FFij
## ##
Êœ œ
x y
x y
i j
È
(b) We want where C 0 is a constant C .kk Š‹Š‹
FFœ Á Êœœ
CC
x y x y x y
x y x y
x y
ÈÈÈ
i j i j
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.2 Vector Fields, Work, Circulation, and Flux 951
45. Yes. The work and area have the same numerical value because work d y dœœ
''
CC
Fr ir††
[f(t) ] dt [On the path, y equals f(t)]œ
'b
a
ii j†‘
df
dt
f(t) dt Area under the curve [because f(t) 0]œœ
'a
b
46. x y x f(x) f (x) ; (x y ) has constant magnitude k and points awayriji j i jF ijœœ Ê œ œ
dk
dx x y
rw
È
from the origin k x [f(x)] , by the chain ruleÊœœ œ F†dkx d
dx dx
x y x y x [f(x)]
k y f (x) kx k f(x) f (x)
rÈÈ È
†† † † ##
È
ds dx k x [f(x)] dx k x [f(x)]Êœ œ œ
'' '
CC a
bb
a
FT F††
dd
dx dx
rÈÈ
‘
## ##
k b [f(b)] a [f(a)] , as claimed.œ
ˆ‰
ÈÈ
####
47. 4t 8t 2 and 2t 12t Flow 12t dt 3t 48Fijk ijFœ œ Ê œ Ê œ œ œ
$# $ $ %
#
!
dd
dt dt
rr
†'0
2cd
48. 12t 9t and 3 4 72t Flow 72t dt 24t 24Fjk jkFœ œÊ œÊ œ œ œ
## # # $
"
!
dd
dt dt
rr
†'0
1cd
49. (cos t sin t) (cos t) and ( sin t) (cos t) sin t cos t 1Fik ikFœ œ Ê œ
dd
dt dt
rr
†
Flow ( sin t cos t 1) dt cos t t 0Êœ œ œœ
'0‘ˆ‰ˆ‰
"""
#
!##2
111
50. ( 2 sin t) (2 cos t) 2 and (2 sin t) (2 cos t) 2 4 sin t 4 cos t 4 0Fijk ijkFœ œ Ê œ œ
dd
dt dt
rr
†##
Flow 0ʜ
51. C : (cos t) (sin t) t , 0 t (2 cos t) 2t (2 sin t) and ( sin t) (cos t)
"#
rijk F ij k ijkœŸŸÊœ œ
1d
dt
r
2 cos t sin t 2t cos t 2 sin t sin 2t 2t cos t 2 sin tÊœ œ F†d
dt
r
Flow ( sin 2t 2t cos t 2 sin t) dt cos 2t 2t sin t 2 cos t 2 cos t 1 ;Êœ œ œ
""Î#
!
'0
2‘
2
11
C : (1 t) , 0 t 1 (1 t) 2 and
## #
rj k F j k k Fœ ŸŸ Ê œ œ Ê œ
1 1
11
dd
dt dt
rr
†
Flow dt t ;Êœœœ
#"
!
'0
1
111cd
C : t (1 t) , 0 t 1 2t 2(1 t) and 2t
$ri j F i k ij Fœ ŸŸ Ê œ œÊ œ
dd
dt dt
rr
†
Flow 2t dt t 1 Circulation ( 1 ) 1 0Êœ œœÊ œœ
$#"
!
'0
1cd 11
52. x y z , where f(x y z) x y x f tFFr† †
d dx dz f dx f f dz d d
dt dt dt dt x dt y dt z dt dt dt
dy dy
r r
œœ ßßœ Ê œ
``` "
``` #
###
ab ababab
by the chain rule Circulation dt f t dt f b f a . Since C is an entire ellipse,Êœœ œ
''
Ca
b
Frrr†dd
dt dt
rabababab ab abab
b a , thus the Circulation 0.rrab abœœ
53. Let x t be the parameter y x t and z x t t t t , 0 t 1 from (0 0 0) to (1 1 1)œ Êœœ œœÊœ ŸŸ ßß ßß
## #
ri jk
2t and xy y yz t t t t 2t t 2t Flow 2t dtÊ œ œ œ Ê œ œ Ê œ
d d
dt dt
r r
ijkF ij kijkF
$#$ $ $$ $ $
†'0
1
œ"
#
54. (a) xy z , where f(x y z) xy z dtFF FœÊœœ ßߜʙ† †ab
#$ #$
```
```
d f dx f z dz df d
dt x dt y dt z dt dt dt
dy
r r
)C
f t dt f b f a 0 since C is an entire ellipse.œœœ
'a
bd
dt abababab ab ababrrr
(b) xy z dt xy z (2)(1) ( 1) (1)(1) (1) 2 1 3
''
C 111
21 1
F†dd
dt dt
rœœœœœabcd
#$ #$ # $ # $
Ð#ß"ß"Ñ
Ð"ß"ß"Ñ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

952 Chapter 16 Integration in Vector Fields
55-60. Example CAS commands:
:Maple
with( LinearAlgebra );#55
F := r -> < r[1]*r[2]^6 | 3*r[1]*(r[1]*r[2]^5+2) >;
r := t -> < 2*cos(t) | sin(t) >;
a,b := 0,2*Pi;
dr := map(diff,r(t),t); # (a)
F(r(t)); # (b)
q1 := simplify( F(r(t)) . dr ) assuming t::real; # (c)
q2 := Int( q1, t=a..b );
value( q2 );
: (functions and bounds will vary):Mathematica
Exercises 55 and 56 use vectors in 2 dimensions
Clear[x, y, t, f, r, v]
f[x_, y_]:= {x y , 3x (x y 2)}
65
{a, b}={0, 2 };1
x[t_]:= 2 Cos[t]
y[t_]:= Sin[t]
r[t_]:={x[t], y[t]}
v[t_]:= r'[t]
integrand= f[x[t], y[t]] . v[t] //Simplify
Integrate[integrand,{t, a, b}]
N[%]
If the integration takes too long or cannot be done, use NIntegrate to integrate numerically. This is suggested for exercises
57 - 60 that use vectors in 3 dimensions. Be certain to leave spaces between variables to be multiplied.
Clear[x, y, z, t, f, r, v]
f[x_, y_, z_]:= {y y z Cos[x y z], x x z Cos[x y z], z x y Cos[x y z]}
2
{a, b}={0, 2 };1
x[t_]:= 2 Cos[t]
y[t_]:= 3 Sin[t]
z[t_]:= 1
r[t_]:={x[t], y[t], z[t]}
v[t_]:= r'[t]
integrand= f[x[t], y[t],z[t]] . v[t] //Simplify
NIntegrate[integrand,{t, a, b}]
16.3 PATH INDEPENDENCE, POTENTIAL FUNCTIONS, AND CONSERVATIVE FIELDS
1. x , y , z Conservative
``` ```
``````
PNMPNM
yzzxxy
œœ œœ œœ Ê
2. x cos z , y cos z , sin z Conservative
``` ```
``````
PNMPNM
yzzxxy
œœ œœœœÊ
3. 1 1 Not Conservative 4. 1 1 Not Conservative
`` ` `
`` ` `
PN NM
yz x y
œ Á œ Ê œ Á œ Ê
5. 0 1 Not Conservative
``
``
NM
xy
œÁœ Ê
6. 0 , 0 , e sin y Conservative
``` `` `
````` `
PNMPN M
yzzxx y
x
œœ œœ œ œ Ê
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.3 Path Independence, Potential Functions, and Conservative Fields 953
7. 2x f(x y z) x g(y z) 3y g(y z) h(z) f(x y z) x h(z)
``
```##
# #
`
ff
xyy
g3y 3y
œÊßßœßÊœœÊßœ Êßßœ
h (z) 4z h(z) 2z C f(x y z) x 2z CÊœ œÊ œÊßßœ
`
` #
w###
f
z
3y
8. y z f(x y z) (y z)x g(y z) x x z z g(y z) zy h(z)
``
````
``
ff
xyyy
gg
œ Ê ßß œ ß Ê œ œ Ê œ Ê ß œ
f(x y z) (y z)x zy h(z) x y h (z) x y h (z) 0 h(z) C f(x y z)Êßßœ Êœ œÊ œÊ œÊßß
`
`
ww
f
z
(yz)xzyCœ
9. e f(x y z) xe g(y z) xe xe 0 f(x y z)
``
````
``
ff
xyyy
y 2z y 2z y 2z y 2z
gg
œÊßßœßÊœœ ÊœÊßß
xe h(z) 2xe h (z) 2xe h (z) 0 h(z) C f(x y z) xe CœÊœ œ ʜʜÊßßœ
y 2z y 2z y 2z y 2z
f
z
ww
`
`
10. y sin z f(x y z) xy sin z g(y z) x sin z x sin z 0 g(y z) h(z)
``
````
``
ff
xyyy
gg
œÊßßœ ßÊœœÊœÊßœ
f(x y z) xy sin z h(z) xy cos z h (z) xy cos z h (z) 0 h(z) C f(x y z)Êßßœ Êœ œ Ê œÊ œÊßß
`
`
ww
f
z
xy sin z Cœ
11. f(x y z) ln y z g(x y) ln x sec (x y) g(x y)
`" `
` # ``
## #
`
fz f
zyz x x
g
œÊßßœ ßÊœœÊßab
(x ln x x) tan (x y) h(y) f(x y z) ln y z (x ln x x) tan (x y) h(y)œ Êßßœ
"
#
##
ab
sec (x y) h (y) sec (x y) h (y) 0 h(y) C f(x y z)Êœ œ Ê œÊ œÊßß
`
`
#w# w
f
yyz yz
yy
ln y z (x ln x x) tan (x y) Cœ
"
#
##
ab
12. f(x y z) tan (xy) g(y z)
``
` ` `
" `
ffxxz
x1xy y1xy y1xy
y g
1yz
œ Êßßœ ßÊœœ
È
g(y z) sin (yz) h(z) f(x y z) tan (xy) sin (yz) h(z)Êœ Êßœ Êßßœ
`
`
" " "
g
y
z
1yz
È
h (z) h (z) h(z) ln z CÊÊœ œ Ê œÊ œ
`""
`
ww
f
zzz
yy
1yz 1yz
ÈÈ kk
f(x y z) tan (xy) sin (yz) ln z CÊßßœ
" " kk
13. Let (x y z) 2x 2y 2z 0 , 0 , 0 M dx N dy P dz isFijkßßœ Êœœ œœ œœ Ê
``` `` `
````` `
PNMPNM
yzzxx y
exact; 2x f(x y z) x g(y z) 2y g(y z) y h(z) f(x y z) x y h(z)
``
```
####
`
ff
xyy
g
œ Ê ßßœ ßÊ œ œ Ê ßœ Ê ßßœœ
h (z) 2z h(z) z C f(x y z) x y z C 2x dx 2y dy 2z dzÊ œ œ Ê œÊ ßßœÊ
`
`
w# ###
f
z'000
23 6
f(2 3 6) f( ) 2 3 ( 6) 49œ ß ß !ß!ß! œ œ
## #
14. Let (x y z) yz xz xy x , y , z M dx N dy P dz isFijkßßœ Ê œœ œœ œœ Ê
``` ```
``````
PNMPNM
yzzxxy
exact; yz f(x y z) xyz g(y z) xz xz 0 g(y z) h(z) f(x y z)
``
````
``
ff
xyyy
gg
œÊßßœ ßÊœœÊœÊßœ Êßß
xyz h(z) xy h (z) xy h (z) 0 h(z) C f(x y z) xyz Cœ Êœ œÊ œÊ œÊßßœ
`
`
ww
f
z
yz dx xz dy xy dz f(3 5 0) f(1 1 2) 0 2 2Ê œ ßß ßß œœ
'112
350
15. Let (x y z) 2xy x z 2yz 2z , 0 , 2xFijkßß œ Ê œ œ œ œ œ œab
## ``````
``````
PNMPNM
yzzxxy
M dx N dy P dz is exact; 2xy f(x y z) x y g(y z) x x z zÊ œÊßßœßÊœœÊœ
``
````
#####
``
ff
xyyy
gg
g(y z) yz h(z) f(x y z) x y yz h(z) 2yz h (z) 2yz h (z) 0 h(z) CÊ ß œ Ê ß ß œ Ê œ œ Ê œ Ê œ
### ww
`
`
f
z
f(x y z) x y yz C 2xy dx x z dy 2yz dz f( ) f( ) 2 2(3) 16Ê ß ß œ Ê œ "ß#ß$ !ß!ß! œ œ
## ## #
'000
123 ab
16. Let (x y z) 2x y 0 , 0 , 0Fijkßß œ Ê œœ œœ œœ
#
``````
``` `` `
ˆ‰
4PNMPNM
1z y z z x x y
M dx N dy P dz is exact; 2x f(x y z) x g(y z) y g(y z) h(z)Ê œ Ê ß ß œ ß Ê œ œ Ê ß œ
``
```
##
`
ff
xyy3
gy
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

954 Chapter 16 Integration in Vector Fields
f(x y z) x h(z) h (z) h(z) 4 tan z C f(x y z)Êßßœ Êœ œ Ê œ Êßß
#w "
`
`
y
3z1z
f4
x 4 tan z C 2x dx y dy dz f(3 3 1) f( )œ Ê œ ß ß !ß!ß!
#" #
y
31z
4
'000
331
94(0)œ !! œ
ˆ‰
27
34
†11
17. Let (x y z) (sin y cos x) (cos y sin x) 0 , 0 , cos y cos xFijkßߜʜœœœœœ
``` `` `
````` `
PNMPN M
yzzxx y
M dx N dy P dz is exact; sin y cos x f(x y z) sin y sin x g(y z) cos y sin xÊ œ Êßßœ ßÊœ
` `
```
`
f f
xyy
g
cos y sin x 0 g(y z) h(z) f(x y z) sin y sin x h(z) h (z) 1 h(z) z Cœ Ê œÊ ßœ Ê ßßœ Ê œ œÊ œ
`
` `
`w
g
y z
f
f(x y z) sin y sin x z C sin y cos x dx cos y sin x dy dz f(0 1 1) f(1 )Ê ßßœ Ê œ ßß ß!ß!
'100
011
(0 1) (0 0) 1œœ
18. Let (x y z) (2 cos y) 2x sin y 0 , 0 , 2 sin yFijkßß œ Ê œ œ œ œ œ œ
Š‹
ˆ‰
""``````
````` `yzyzzxxy
PNMPN M
M dx N dy P dz is exact; 2 cos y f(x y z) 2x cos y g(y z) 2x sin yÊ œ Êßßœ ßÊœ
``
```
`
ff
xyy
g
2x sin y g(y z) ln y h(z) f(x y z) 2x cos y ln y h(z) h (z)œ Ê œ Ê ß œ Ê ßß œ Ê œ œ
"" `"
`
` `
w
yyy zz
gf
kk kk
h(z) ln z C f(x y z) 2x cos y ln y ln z CÊœ Êßßœ kk kk kk
2 cos y dx 2x sin y dy dz f 1 2 f( )Ê œ ß ß !ß #ß "
'021
122 Š‹ ˆ‰
""
#yz
1
2 0 ln ln 2 (0 cos 2 ln 2 ln 1) ln œ œ
ˆ‰
††
11
##
19. Let (x y z) 3x (2z ln y) , 0 , 0Fijkßß œ Ê œ œ œœ œœ
#``````
``````
Š‹
zP2zNMPNM
yyyzzxxy
M dx N dy P dz is exact; 3x f(x y z) x g(y z) g(y z) z ln y h(z)Ê œ Ê ßßœ ß Ê œ œ Ê ßœ
``
```
#$ #
`
ffz
xyyy
g
f(x y z) x z ln y h(z) 2z ln y h (z) 2z ln y h (z) 0 h(z) C f(x y z)Êßßœ Êœ œ Ê œÊ œÊßß
$# w w
`
`
f
z
x z ln y C 3x dx dy 2z ln y dz f(1 2 3) f( )œ Ê œ ß ß "ß "ß "
$# #
'111
123 z
y
(1 9 ln 2 C) (1 0 C) 9 ln 2œ œ
20. Let (x y z) (2x ln y yz) xz (xy) x , y , zFijkßß œ Ê œ œ œ œ œ œ
Š‹
xPNMPN2xM
yyzzxxyy
``` `` `
````` `
M dx N dy P dz is exact; 2x ln y yz f(x y z) x ln y xyz g(y z) xzÊ œ Êßßœ ßÊœ
` `
```
#`
ffx
xyy y
g
xz 0 g(y z) h(z) f(x y z) x ln y xyz h(z) xy h (z) xy h (z) 0œÊ œÊ ßœ Ê ßßœ Ê œ œÊ œ
x f
yy z
g
`
` `
#ww
`
h(z) C f(x y z) x ln y xyz C (2x ln y yz) dx xz dy xy dzÊœÊßßœ Ê
#'121
211 Š‹
x
y
f(2 1 1) f( 2 1) (4 ln 1 2 C) (ln 2 2 C) ln 2œ ß ß "ß ß œ œ
21. Let (x y z) , 0 , Fijkßß œ Ê œ œ œ œ œ œ
Š‹ Š ‹ ˆ‰
"`"`````
````` `yzy z yzzz xxyy
1x P NM PN 1 M
y
M dx N dy P dz is exact; f(x y z) g(y z) Ê œÊßßœßÊœœ
`" ` "
```
`
fxfxx
xy y y y yzy
g
g(y z) h(z) f(x y z) h(z) h (z) h (z) 0 h(z) CÊ œÊ ßœ Ê ßßœ Ê œ œ Ê œÊ œ
`
` `
" ` ww
gy y yy
yz z yz z z z
xf
f(x y z) C dx dy dz f(2 2 2) f( 1 1) C CÊ ßßœÊ œ ßß"ßßœ
x1x 22
yz y zy z 11
yy
'111
222 """
##
Š‹ ˆ‰ˆ‰
0œ
22. Let (x y z) and let x y z , , Fßßœ œÊœœœ
2x 2y 2z y
xyz x y z
xz
ijk
` ` `
#### ```
Š‹
3333
333
, , M dx N dy P dz is exact;Êœœ œœ œœ Ê
``` `` `
````` `
P N M 4xz P N M
yzzxx y
4yz 4xy
333
f(xyz) lnx y z g(yz)
` `
` ``
### `
f2x f
x xyz y xyz y xyz
2y g 2y
œÊßßœßÊœœab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.3 Path Independence, Potential Functions, and Conservative Fields 955
0 g(y z) h(z) f(x y z) ln x y z h(z) h (z)ÊœÊßœ Êßßœ Êœ
`
``
### w
`
g
yz xyz
f2z
ab
h (z) 0 h(z) C f(x y z) ln x y z CœÊœÊœÊßßœ
2z
xyz
w###
ab
f(2 2 2) f( 1 1) ln 12 ln 3 ln 4Êœßß"ßßœœ
'111
222 2x dx 2y dy 2z dz
xyz
23. ( ) t( 2 2 ) (1 t) (1 2t) (1 2t) , 0 t 1 dx dt, dy 2 dt, dz 2 dtrijk ijk i j kœ œ ŸŸÊ œ œ œ
y dx x dy 4 dz (2t 1) dt (t 1)(2 dt) 4( 2) dt (4t 5) dt 2t 5t 3Ê œ œ œœ
'' '
111 0 0
23 1 1 1 cd
#"
!
24. t(3 4 ), 0 t 1 dx 0, dy 3 dt, dz 4 dt x dx yz dy dzrjkœ ŸŸÊœ œ œ Ê
'000
034 #
#
Š‹
y
12t (3 dt) (4 dt) 54t dt 18t 18œœœœ
''
00
11
ab cd
Š‹
###
#
"
!
9t
25. 0 , 2z , 0 M dx N dy P dz is exact is conservative
``` `` `
``` `` `
PNM PNM
yzz xx y
œœ œ œ œœ Ê ÊF
path independenceÊ
26. , ,
``` `` `
````` `
PNMxzPNM
yzzxx y
yz xy
xyz xyz xyz
œ œ œ œ œ œ
ˆ‰ ˆ‰ ˆ‰
ÈÈÈ
M dx N dy P dz is exact is conservative path independenceÊ Ê ÊF
27. 0 , 0 , is conservative there exists an f so that f;
``` `` `
````` `
PNMPN2xM
yzzxxyy
œœ œœ œ œ Ê Ê œFF™
f(x y) g(y) g (y) g (y) g(y) C
``""
``
ww
f2x x f x 1x
xy y y y y y y
œÊßœ Êœ œ Ê œÊ œ
f(x y) C Êߜʜ
xx1
yy y
"
F™Š‹
28. cos z , 0 , is conservative there exists an f so that f;
``````
``````
PNMPNeM
yzzxxyy
œœ œœ œœÊ Ê œ
xFF™
e ln y f(x y z) e ln y g(y z) sin z sin z g(y z)
``
````
``
ffee
xyyyyy
xx gg
œ Ê ßßœ ß Ê œ œ Ê œ Ê ß
xx
y sin z h(z) f(x y z) e ln y y sin z h(z) y cos z h (z) y cos z h (z) 0œÊßߜʜ œ Êœ
xf
z
`
`
ww
h(z) C f(x y z) e ln y y sin z C e ln y y sin zÊœÊßßœ Êœ
xx
F™ab
29. 0 , 0 , 1 is conservative there exists an f so that f;
``` `` `
````` `
PNMPNM
yzzxx y
œœ œœ œœ Ê Ê œFF™
x y f(x y z) x xy g(y z) x y x y g(y z) y h(z)
`"` "
````
#$ ##$
``
ff
x3yyy3
gg
œÊ ßßœ ßÊ œ œÊ œ Ê ßœ
f(x y z) x xy y h(z) h (z) ze h(z) ze e C f(x y z)Êßßœ Êœ œ Ê œÊßß
"" `
$$ w
`33 z
fzzz
xxy yzeeC xxy yzeeœÊœ
"" ""
$$ $$
33 33
zz zz
F™ˆ‰
(a) work dt d x xy y ze e 0 0 e e 0 0 1œ œ œ œ
''
AA
BB
FFr††
d
dt 3 3 3 3
zz
r‘ˆ‰ˆ‰
"" " "
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
1œ
(b) work d x xy y ze e 1œœœ
'A
B
Fr†‘
""
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
33
zz
(c) work d x xy y ze e 1œœœ
'A
B
Fr†‘
""
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
33
zz
: Since is conservative, d is independent of the path from (1 0 0) to (1 0 1).Note FFr
'A
B
†ßß ßß
30. xe xyze cos y , ye , ze is conservative there exists an f so
``````
``````
PNMPNM
yzzxxy
yz yz yz yz
œ œ œœ œœÊ ÊF
that f; e f(x y z) xe g(y z) xze xze z cos y z cos yFœœÊßßœßÊœœÊœ™``
````
``
ff
xyyy
yz yz yz yz
gg
g(y z) z sin y h(z) f(x y z) xe z sin y h(z) xye sin y h (z) xye sin yÊßœ Êßßœ Êœ œ
yz yz yz
f
z
`
`
w
h (z) 0 h(z) C f(x y z) xe z sin y C xe z sin yʜʜÊßßœ Êœ
wyz yz
F™ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

956 Chapter 16 Integration in Vector Fields
(a) work d xe z sin y (1 0) (1 0) 0œ œ œœ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
(b) work d xe z sin y 0œœ œ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
(c) work d xe z sin y 0œœ œ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
: Since is conservative, d is independent of the path from (1 0 1) to 1 0 .Note FFr
'A
B
†ßß ß ß
ˆ‰
1
#
31. (a) x y 3x y 2x y ; let C be the path from ( 1 1) to (0 0) x t 1 andFFijœÊœ ßßÊœ™ab
$# ## $ "
y t 1, 0 t 1 3(t 1) ( t 1) 2(t 1) ( t 1) 3(t 1) 2(t 1)œ Ÿ Ÿ Ê œ œ Fijij
## $ % %
and (t 1) ( t 1) d dt dt d 3(t 1) 2(t 1) dtri jrijFr
"""
%%
œ Ê œ Ê œ
''
C0
1
†cd
5(t 1) dt (t 1) 1; let C be the path from (0 0) to (1 1) x t and y t,œœœ ßßÊœ œ
'0
1%&
"
!#
cd
0 t 1 3t 2t and t t d dt dt d 3t 2t dtŸŸ Ê œ œ Ê œ Ê œ Fijrijr ij Fr
%% %%
## #
''
C0
1
†ab
5t dt 1 d d d 2œœÊœ œ
''''
0CCC
1%"#
Fr Fr Fr†† †
(b) Since f(x y) x y is a potential function for , d f(1 1) f( 1 1) 2ßœ œ ßßœ
$# FFr
'11
11
†
32. 0 , 0 , 2x sin y is conservative there exists an f so that f;
``` `` `
````` `
PNMPN M
yzzxx y
œœ œœ œ œ Ê Ê œFF™
2x cos y f(x y z) x cos y g(y z) x sin y x sin y 0 g(y z) h(z)
``
````
###
``
ff
xyyy
gg
œÊßßœßÊœœÊœÊßœ
f(x y z) x cos y h(z) h (z) 0 h(z) C f(x y z) x cos y C x cos yÊßßœ Êœ œÊ œÊßßœ Êœ
#w # #
`
`
f
zF™ab
(a) 2x cos y dx x sin y dy x cos y 0 1 1
'C œ œœ
##
Ð!ß"Ñ
Ð"ß!Ñ
cd
(b) 2x cos y dx x sin y dy x cos y 1 ( 1) 2
'Cœ œœ
##
Ð"ß!Ñ
Ð"ß Ñ
cd
1
(c) 2x cos y dx x sin y dy x cos y 1 1 0
'C œ œœ
##
Ð"ß!Ñ
Ð"ß!Ñ
cd
(d) 2x cos y dx x sin y dy x cos y 1 1 0
'C œ œœ
##
Ð"ß!Ñ
Ð"ß!Ñ
cd
33. (a) If the differential form is exact, then 2ay cy for all y 2a c, 2cx 2cx for
`` ` `
`` ``
PN MP
yz zx
œÊ œ Êœ œÊ œ
all x, and by 2ay for all y b 2a and c 2a
``
``
NM
xy
œÊœ Êœ œ
(b) f the differential form with a 1 in part (a) is exact b 2 and c 2FœÊ œ Êœ œ™
34. f g(x y z) d f d f(x y z) f(0 0 0) 0, 0, andFFrrœ Ê ßß œ œ œ ßß ßß Ê œ œ ™†™†
''
000 000
xyz xyz ``
`` ``
``
gg
xx yy
ff
0 g f , as claimed
`
``
`
g
zz
f
œÊ œ œ™™F
35. The path will not matter; the work along any path will be the same because the field is conservative.
36. The field is not conservative, for otherwise the work would be the same along C and C .
"#
37. Let the coordinates of points A and B be x , y , z and x , y , z , respectively. The force a b c isabab
AAA BBB Fijkœ
conservative because all the partial derivatives of M, N, and P are zero. Therefore, the potential function is
f x, y, z ax by cz C, and the work done by the force in moving a particle along any path from A to B isabœ
f B f A f x , y , z f x , y , z ax by cz C ax by cz Cab ab a b a b a b a bœ œ
BBB AAA B B B A A A
ax x by y cz z BAœœ†
Ä
ababab
BA BA BAF
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.4 Green's Theorem in the Plane 957
38. (a) Let GmM C CœÊœ Fijk
’“
xz
xyz xyz xyz
y
ababab
, , f forÊœ œ œ œ œ œ Êœ
````` `
````` `
P N M 3xzC P N M
yzz xx y
3yzC 3xyC
xyz xyz xyzab ab ab F™
some f; f(x y z) g(y z)
` `
```
`
fxC C f
xyy
xyz xyz xyz
yC g
œÊßßœßÊœ
ab ab ab
0 g(y z) h(z) h (z)œÊœÊߜʜœ
yC g
xyz xyz xyz
yz
fzC zC
ab ab ab
`
``
`w
h(z) C f(x y z) C . Let C 0 f(x y z) is a potentialÊœÊßßœ œÊßßœ
"""
CGmM
xyz xyzab ab
function for .F
(b) If s is the distance of (x y z) from the origin, then s x y z . The work done by the gravitational fieldßß œ
È###
is work d GmM , as claimed.FFrœ œ œœ
'P
P
†’“ Š‹
GmM GmM GmM
xyz
È
T
T
""
ss ss
16.4 GREEN'S THEOREM IN THE PLANE
1. M y a sin t, N x a cos t, dx a sin t dt, dy a cos t dt 0, 1, 1, andœ œ œ œ œ œ Ê œ œ œ
`` `
`` `
MM N
xy x
0;
`
`
N
yœ
Equation (3): M dy N dx [( a sin t)(a cos t) (a cos t)( a sin t)] dt 0 dt 0;
)' '
C0 0
2 2
œ œ œ
dx dy 0 dx dy 0, Flux
'' ''
RR
Š‹
``
``
MN
xy
œ œ
Equation (4): M dx N dy [( a sin t)( a sin t) (a cos t)(a cos t)] dt a dt 2 a ;
)' '
C0 0
2 2
œ œ œ
##
1
dx dy 2 dy dx 4 a x dx 4 a x sin
''
RŠ‹ ’ “
ÈÈ
``
`` #
## ## "
NM xax
xy 2a
œ œœ
'' '
ac a
aax a a
a
2a 2a , Circulationœœ
##
##
ˆ‰
11 1
2. M y a sin t, N 0, dx a sin t dt, dy a cos t dt 0, 1, 0, and 0;œœ œ œ œ Ê œ œ œ œ
``` `
``` `
MMN N
xyx y
Equation (3): M dy N dx a sin t cos t dt a sin t 0; 0 dx dy 0, Flux
)'
C0
2
œ œ œ œ
###
"#
!
‘
2
1''
R
Equation (4): M dx N dy a sin t dt a a ; dx dy
)'
C0
2
œ œ œ ab‘ Š‹
## # #
#
!
``
``
tsin 2t N M
24 xy
11''
R
1 dx dy r dr d d a , Circulationœ œ œ œ
''
R'' '
00 0
2a 2
))1
a
#
#
3. M 2x 2a cos t, N 3y 3a sin t, dx a sin t dt, dy a cos t dt 2, 0, 0, andœ œ œ œ œ œ Ê œ œ œ
```
```
MMN
xyx
3;
`
`
N
yœ
Equation (3): M dy N dx [(2a cos t)(a cos t) (3a sin t)( a sin t)] dt
)'
C0
2
œ
2a cos t 3a sin t dt 2a 3a 2 a 3 a a ;œ œ œœ
'0
2ab
‘‘
## ## # # # # #
##
!!
tsin 2t tsin 2t
24 24
11
11 1
1 dx dy r dr d d a , Flux
'' ''
RR
Š‹
``
`` #
#
MN a
xy
œ œ œ œ
'' '
00 0
2a 2
))1
Equation (4): M dx N dy [(2a cos t)( a sin t) ( 3a sin t)(a cos t)] dt
)'
C0
2
œ
2a sin t cos t 3a sin t cos t dt 5a sin t 0; 0 dx dy 0, Circulationœ œ œ œ
'0
2ab
‘
## ##
#
!
1
2
1''
R
4. M x y a cos t, N xy a cos t sin t, dx a sin t dt, dy a cos t dtœ œ œ œ œ œ
#$# #$ #
2xy, x , y , and 2xy;Êœ œ œ œ
``` `
``` `
#
MMN N
xyx y
2
Equation (3): M dy N dx a cos t sin t a cos t sin t cos t sin t 0;
)'
C0
2
œ œ œab
’“
%$ % $ % %
#
!
aa
44
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

958 Chapter 16 Integration in Vector Fields
dx dy ( 2xy 2xy) dx dy 0, Flux
'' ''
RR
Š‹
``
``
MN
xy
œœ
Equation (4): M dx N dy a cos t sin t a cos t sin t dt 2a cos t sin t dt
)' '
C0 0
22
œ œabab
%# # %# # %# #
a sin 2t dt sin u du ; dx dy y x dx dyœœœœœ
'' ''
00
24
"``
##``
%# # ##
%
!
aausin 2uaNM
4424 xy
‘ Š‹ ab
11''
RR
r r dr d d , Circulationœœœ
'' '
00 0
2a 2
#
#
†))
aa
4
1
5. M x y, N y x 1, 1, 1, 1 Flux 2 dx dy 2 dx dy 2;œ œ Ê œ œ œ œ Ê œ œ œ
`` ` `
`` ` `
MM N N
xy x y '' ' '
R00
11
Circ [ 1 ( 1)] dx dy 0œ œ
''
R
6. M x 4y, N x y 2x, 4, 1, 2y Flux (2x 2y) dx dyœœÊœ œœœÊœ
##
````
````
MMNN
xyxy ''
R
(2x 2y) dx dy x 2xy dy (1 2y) dy y y 2; Circ (1 4) dx dyœœœœœœ
'' ' ' ''
00 0 0
11 1 1
cd cd
##
""
!!
R
3 dx dy 3œ œ
''
00
11
7. M y x , N x y 2x, 2y, 2x, 2y Flux ( 2x 2y) dx dyœ œ Ê œ œ œ œ Ê œ
## ## ````
````
MMNN
xyxy ''
R
( 2x 2y) dy dx 2x x dx x 9; Circ (2x 2y) dx dyœ œœœœ
'' ' ''
00 0
3x 3
ab
‘
## $
"$
!
3R
(2x 2y) dy dx x dx 9œœœ
'' '
00 0
3x 3
#
8. M x y, N x y 1, 1, 2x, 2y Flux (1 2y) dx dyœ œ Ê œ œ œ œ Ê œ ab
## ``` `
``` `
MMN N
xyx y ''
R
(1 2y) dy dx x x dx ; Circ ( 2x 1) dx dy ( 2x 1) dy dxœ œœœœ
'' ' '' ''
00 0 00
1x 1 1x
ab
#"
6R
2x x dxœ œ
'0
1ab
#7
6
9. M xy y , N x y y, x 2y, 1, 1 Flux y 1 dy dxœ œ Ê œ œ œ œÊ œ
2MM NN
xy xy
`` ``
`` `` ''
Rabab
y 1 dy dx x x x x dx ; Circ 1 x 2y dy dxœœœœ
'' ' ''
00
11
x
x
2
Èab a b
ˆ‰
Èab
""
##
#411
60 R
1 x 2y dy dx x x x x x x dxœ œ œ
'' '
00
11
x
x
2
Èab ˆ‰
È32 3 4 7
60
Î#
10. M x 3y, N 2x y 1, 3, 2, 1 Flux 1 1 dy dx 0œœÊœœœœÊœ œ
````
````
MMNN
xyxy ''
Rabab
Circ 2 3 dy dx 1 dy dx 2 x dx 2œ œ œ œ
'' ' ' '
Rab ab ÈÈ
22
22
2x 2
2x 2
2
2
2
2
2
È1
11. M x y , N x y 3x y , 2x y, 2x y, x Flux 3x y x dy dxœœÊœ œœœÊœ
32 4 22 3 3 4 22 4
MMNN
xyxy
"` ` ` `" "
#` ` ` `# #
''
Rˆ‰
3x y x dy dx 3x x 3x x dx ; Circ 2x y 2x y dy dx 0œœœœœ
'' ' ''
00
22
xx
x
2ˆ‰ˆ ‰ ab
22 4 5 6 7 8 3 3
764
29
"
#R
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.4 Green's Theorem in the Plane 959
12. M , N tan y , , 0, Flux dx dyœœÊœ œ œœÊœ
xM1MNN1 11
1y x 1y y x y 1y 1y 1y
12x y
1y
````
`` ``
222222
2
ab ''
RŠ‹
dx dy dx 4 2 4 ; Circ 0 dy dxœœœœ
'' ' ''
11
11
È
ÈÈab
1y
1y
2
2
2
1y 1y
41y 2x y
1y
22 2
2
2
11
ÈŠ‹Š‹
R
dy dx 0 dx 0œœœ
'' '
11
11
È
Èab
1y
1y
2
2Š‹ ab
2x y
1y
22
13. M x e sin y, N x e cos y 1 e sin y, e cos y, 1 e cos y, e sin yœ œ Ê œ œ œ œ
xx xx xx
MMN N
xyxy
````
````
Flux dx dy r dr d cos 2 d sin 2 ;Êœ œ œ œ œ
''
R'' '
40 4
4cos2 4
))))
ˆ‰‘
"""
##
Î%
Î%
4
1
1
Circ 1 e cos y e cos y dx dy dx dy r dr d cos 2 dœ œ œ œ œ
'' ''
RR
ab ˆ‰
xx '' '
40 4
4cos2 4
)))
""
##
14. M tan , N ln x y , , , œ œÊœœœœ
" # # ````
````
yy 2y
x x xy y xy x xy y xy
MMxN2xN
ab
Flux dx dy r dr d sin d 2;Êœ œ œ œ
''
RŠ‹ ˆ‰
y2y
xy xy r
r sin
'' '
01 0
2))))
Circ dx dy r dr d cos d 0œ œ œ œ
''
RŠ‹ ˆ‰
2x x r cos
xy xy r
'' '
01 0
2))))
15. M xy, N y y, x, 0, 2y Flux (y 2y) dy dx 3y dy dxœœÊœœœœÊœ œ
#````
````
MMNN
xyxy ''
R
''
0x
1x
dx ; Circ x dy dx x dy dx x x dxœ œ œœœœ
''''
00x 0
11x 1
Š‹ ab
3x 3x
5 1
## #
" "
#$
''
R
16. M sin y, N x cos y 0, cos y, cos y, x sin yœ œ Ê œ œ œ œ
`` ` `
`` ` `
MM N N
xy x y
Flux ( x sin y) dx dy ( x sin y) dx dy sin y dy ;Êœœœœ
''
R'' '
00 0
22 2
Š‹
11
88
Circ [cos y ( cos y)] dx dy 2 cos y dx dy cos y dy sin yœ œ œ œ œ
''
R'' '
00 0
22 2
111cd
1Î#
!
17. M 3xy , N e tan y 3y , œ œ Êœ œ
xMN
1y x 1y y 1y
x
``
" `"`"
Flux 3y dx dy 3y dx dy (3r sin ) r dr dÊœ œ œ
'' ''
RR
Š‹
""
1y 1y ''
00
2a1cos
))
a (1 cos ) (sin ) d (1 cos ) 4a 4a 0œ œ œœ
'0
2$$ %$$
#
!
))) )
’“
ab
a
4
1
18. M y e ln y, N 1 , Circ 1 dx dy ( 1) dx dyœ œ Ê œ œ Ê œ œ
xeM eNe e e
yy yxy y y
xxx xx
``
`` '' ''
RR
’“Š‹
dy dx 3 x x 1 dx x x 2 dxœ œ œ œ
'' ' '
1x 1 1 1
13x 1 1
cdababab
#% %# 44
15
19. M 2xy , N 4x y 6xy , 8xy work 2xy dx 4x y dy 8xy 6xy dx dyœœÊœ œÊœ œ
$## # # $## ##
``
``
MN
yx )C''
Rab
2xy dy dx x dxœœœ
'' '
00 0
1x 1
#"!
22
333
20. M 4x 2y, N 2x 4y 2, 2 work (4x 2y) dx (2x 4y) dyœ œ Ê œ œÊ œ
``
``
MN
yx )C
[2 ( 2)] dx dy 4 dx dy 4(Area of the circle) 4( 4) 16œ œ œ œ œ
'' ''
RR
11†
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
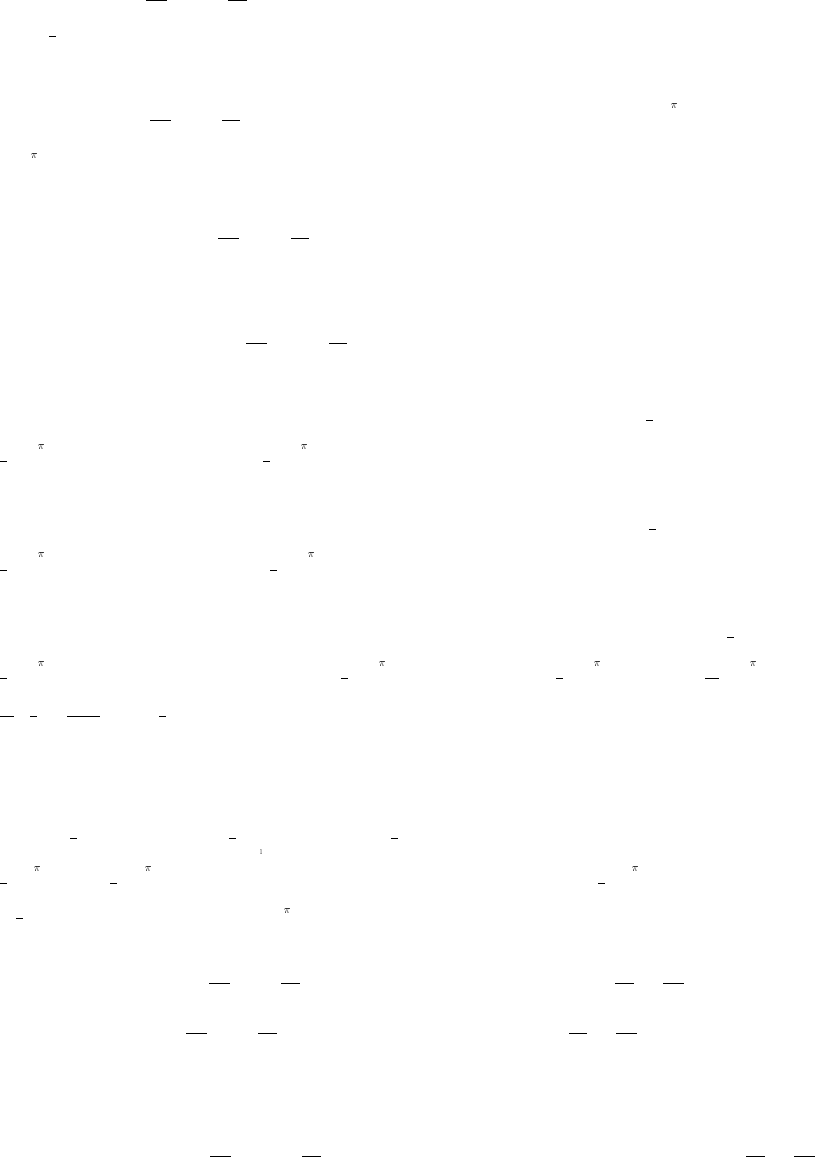
960 Chapter 16 Integration in Vector Fields
21. M y , N x 2y, 2x y dx x dy (2x 2y) dy dxœœÊœ œÊ œ
## ##
``
``
MN
yx )C''
R
(2x 2y) dy dx 3x 4x 1 dx x 2x x 1 2 1 0œœœœœ
'' '
00 0
11x 1
abcd
#$#
"
!
22. M 3y, N 2x 3, 2 3y dx 2x dy 2 3 dx dy 1 dy dxœœÊœœÊ œ œ
``
``
MN
yx )''
C00
sin x
''
Rab ab
sin x dx 2œ œ
'0
23. M 6y x, N y 2x 6, 2 (6y x) dx (y 2x) dy (2 6) dy dxœ œ Ê œ œÊ œ
``
``
MN
yx )C''
R
4(Area of the circle) 16œ œ 1
24. M 2x y , N 2xy 3y 2y, 2y 2x y dx (2xy 3y) dy (2y 2y) dx dy 0œ œ Ê œ œ Ê œ œ
# #
``
``
MN
yx )Cab ''
R
25. M x a cos t, N y a sin t dx a sin t dt, dy a cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
"
#)C
a cos t a sin t dt a dt aœ œœ
""
##
## ## # #
''
00
22
ab 1
26. M x a cos t, N y b sin t dx a sin t dt, dy b cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
"
#)C
ab cos t ab sin t dt ab dt abœ œœ
""
##
##
''
00
22
ab 1
27. M x cos t, N y sin t dx 3 cos t sin t dt, dy 3 sin t cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
$$ # # "
#)C
3 sin t cos t cos t sin t dt 3 sin t cos t dt sin 2t dt sin u duœœœœ
""
##
## # # ## # #
''''
0000
2224
ababab
33
816
œ œ
3 u sin 2u 3
16 2 4 8
‘
%
!
11
28. C : M x t, N y 0 dx dt, dy 0; C : M x 2 t sin 2 t 2 t sin t, N y
12
œœ œœÊ œ œ œœ œ œabab111
1 cos 2 t 1 cos t dx cos t 1 dt, dy sin t dtœ œ Ê œ œab a b1
Area x dy y dx x dy y dx x dy y dxÊœ œ
"" "
## #
)))
CC C
2
0 dt 2 t sin t sin t 1 cos t cos t 1 dt 2 cos t t sin t 2 2 sin t dtœ œ
"" "
## #
'' '
00 0
22 2
ab c d a ba bababab1 1
3 sin t t cos t 2t 2 cos t 3œ œ
1
2
2
cd11
0
29. (a) M f(x), N g(y) 0, 0 f(x) dx g(y) dy dx dy 0 dx dy 0œœÊœœÊ œ œ œ
`` ``
`` ``
MN NM
yx xy
)C'' ''
RR
Š‹
(b) M ky, N hx k, h ky dx hx dy dx dyœœÊœœÊ œ
`` ``
`` ``
MN NM
yx xy
)C''
RŠ‹
(h k) dx dy (h k)(Area of the region)œ œ
''
R
30. M xy , N x y 2x 2xy, 2xy 2 xy dx x y 2x dy dx dyœœÊœ œÊ œ
## # #
`` ``
`` ``
MN NM
yx xy
)Cab Š‹
''
R
(2xy 2 2xy) dx dy 2 dx dy 2 times the area of the squareœ œ œ
'' ''
RR
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.4 Green's Theorem in the Plane 961
31. The integral is 0 for any simple closed plane curve C. The reasoning: By the tangential form of Green's
Theorem, with M 4x y and N x , 4x y dx x dy x 4x y dx dyœœ œ
$%$% %$
``
``
)C''
R’“
ab a b
xy
4x 4x dx dy 0.œ œ
''
Rðóóñóóò
ab
$$
0
32. The integral is 0 for any simple closed curve C. The reasoning: By the normal form of Green's theorem, with
M x and N y , y dy x dx y x dx dy 0.œœœ œ
$$$$ $$
``
``
)C''
R”•
ðñò
ab ab
ï
xy
0 0
33. Let M x and N 0 1 and 0 M dy N dx dx dy x dyœœÊœ œÊ œ Ê
`` ``
`` ``
MN MN
xy xy
))
C C
''
RŠ‹
(1 0) dx dy Area of R dx dy x dy; similarly, M y and N 0 1 andœ Ê œ œ œ œÊœ
'' ''
RR
)C
`
`
M
y
0 M dx N dy dy dx y dx (0 1) dy dx y dx
```
```
NNM
xxy
œÊ œ Ê œ Ê
)))
CCC
'' ''
RR
Š‹
dx dy Area of Rœœ
''
R
34. f(x) dx Area of R y dx, from Exercise 33
')
aC
bœœ
35. Let (x y) 1 x Ax x dA (x 0) dx dy$ߜʜ œ œ œ Ê œ œ
M
MA
x (x y) dA x dA x dA
(x y) dA dA
y
'' '' ''
'' ''
RRR
RR
$
$
ß
ß'' ''
RR
dy, Ax x dA (0 x) dx dy xy dx, and Ax x dA x x dx dyœœœœ œœ
)CC
x 2
33
#
"
'' '' ''
RR R
R
)''
ˆ‰
x dy xy dx x dy xy dx x dy xy dx AxœÊ œœœ
))))
CCCC
"" " "
## #
#33 3
36. If (x y) 1, then I x (x y) dA x dA x 0 dy dx x dy,$$ßœ œ ß œ œ œ
yC
'' '' ''
RRR
### $
"
ab 3)
x dA 0 x dy dx x y dx, and x dA x x dy dx
'' '' '' ''
RR RR
######
"
œ œ œ ab ˆ‰
)C
3
44
x dy x y dx x dy x y dx x dy x y dx x dy x y dx IœœÊ œœœ
)))))
CCCCC
y
"" " " "
$ # $# $ # $#
44 4 3 4
37. M , N , dx dy dx dy 0 for such curves CœœÊœ œÊ œ œ
```````` ``
```````` ``
ffMfNfff ff
yxyyxxyx xy
)C''
RŠ‹
38. M x y y , N x x y , 1 Curl 1 x y 0 in the interior of theœ œÊ œ œÊ œ œ
"" ` ` `` "
# $ ## ##
`` ``43 y4 x xy 4
M1 N N M ˆ‰
ellipse x y 1 work d 1 x y dx dy will be maximized on the region
""
## ##
44
œÊ œ œ
'CFr†''
Rˆ‰
R {(x y) | curl } 0 or over the region enclosed by 1 x yœß œ F"##
4
39. (a) f M , N ; since M, N are discontinuous at (0 0), we™œ Êœœ ß
Š‹Š‹
2x 2x
xy xy xy xy
2y 2y
ij
compute f ds directly since Green's Theorem does not apply. Let x a cos t, y a sin t dx a sin t dt,
'C™†nœœÊœ
dy a cos t dt, M cos t, N sin t, 0 t 2 , so f ds M dy N dxœœœŸŸ œ
22
aa 1''
CC
™†n
cos t a cos t sin t a sin t dt 2 cos t sin t dt 4 . Note that this holds for anyœœœ
''
0 0
2 2
‘ˆ‰ ˆ‰
ab a b a b
22
aa
22 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
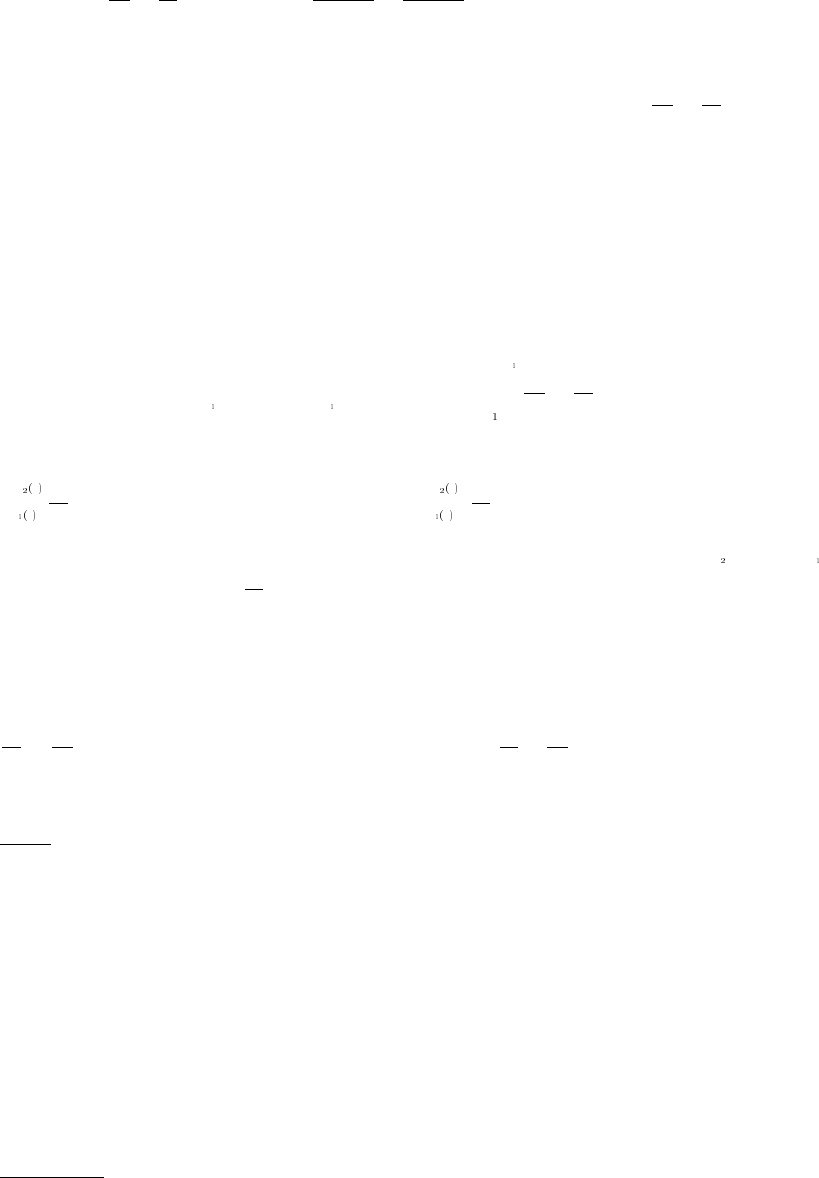
962 Chapter 16 Integration in Vector Fields
a 0, so f ds 4 for any circle C centered at 0, 0 traversed counterclockwise and f ds 4œ œ
''
C C
™† ™†n n1 1ab
if C is traversed clockwise.
(b) If K does not enclose the point (0 0) we may apply Green's Theorem: f ds M dy N dxߜ
''
CC
™†n
dx dy dx dy 0 dx dy 0. If K does enclose the pointœ œ œ œ
'' '' ''
RR R
Š‹ Š ‹
``
``
MN
xy
2y x 2x y
xy xy
ˆ‰ˆ‰
abab
22 22
22 22
22
(0 0) we proceed as follows:ß
Choose a small enough so that the circle C centered at (0 0) of radius a lies entirely within K. Green's Theoremß
applies to the region R that lies between K and C. Thus, as before, 0 dx dy
R
œ
''Š‹
``
``
MN
xy
M dy N dx M dy N dx where K is traversed counterclockwise and C is traversed clockwise.œ
''
KC
Hence by part (a) 0 4 4 f ds. We have shown:
M dy N dx M dy N dx
œÊœœ
’“
''
'
KK
K
11 ™†n
f ds 0 if (0 0) lies inside K
4 if (0 0) lies outside K
'K™†nœß
ß
œ1
40. Assume a particle has a closed trajectory in R and let C be the path C encloses a simply connected region
""
Ê
R C is a simple closed curve. Then the flux over R is ds 0, since the velocity vectors are
"" "
ʜ
)CFn F†
tangent to C . But 0 ds M dy N dx dx dy M N 0, which is a
"``
``
œœœÊœ
))
CC xy
Fn†''
RŠ‹
MN
xy
contradiction. Therefore, C cannot be a closed trajectory.
"
41. dx dy N(g (y) y) N(g (y) y) dx dy [N(g (y) y) N(g (y) y)] dy
''''
gy cgy c
gy dgy d
``
``
#" #"
NN
xx
œßßÊ œ ßß
ˆ‰
N(g (y) y) dy N(g (y) y) dy N(g (y) y) dy N(g (y) y) dy N dy N dyœßßœßßœ
''''''
cc cdCC
dd dc
#" #"
dy N dy dx dy
R
œÊ œ
))
CC
'' `
`
N
x
42. The curl of a conservative two-dimensional field is zero. The reasoning: A two-dimensional field M NFijœ
can be considered to be the restriction to the xy-plane of a three-dimensional field whose k component is zero,
and whose and components are independent of z. For such a field to be conservative, we must haveij
by the component test in Section 16.3 curl 0.
`` ``
`` ``
NM NM
xy xy
œÊœœF
43-46. Example CAS commands:
:Maple
with( plots );#43
M := (x,y) -> 2*x-y;
N := (x,y) -> x+3*y;
C := x^2 + 4*y^2 = 4;
implicitplot( C, x=-2..2, y=-2..2, scaling=constrained, title="#43(a) (Section 16.4)" );
curlF_k := D[1](N) - D[2](M): # (b)
'curlF_k' = curlF_k(x,y);
top,bot := solve( C, y ); # (c)
left,right := -2, 2;
q1 := Int( Int( curlF_k(x,y), y=bot..top ), x=left..right );
value( q1 );
: (functions and bounds will vary)Mathematica
The command will be useful for 43 and 44, but is not needed for 43 and 44. In 44, the equation of the lineImplicitPlot
from (0, 4) to (2, 0) must be determined first.
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.5 Surfaces and Area 963
Clear[x, y, f]
<<Graphics`ImplicitPlot`
f[x_, y_]:= {2x y, x 3y}
curve= x 4y ==4
22
ImplicitPlot[curve, {x, 3, 3},{y, 2, 2}, AspectRatio Automatic, AxesLabel {x, y}]; Ä Ä
ybounds= Solve[curve, y]
{y1, y2}=y/.ybounds;
integrand:=D[f[x,y][[2]], x] D[f[x,y][[1]], y]//Simplify
Integrate[integrand, {x, 2, 2}, {y, y1, y2}]
N[%]
Bounds for y are determined differently in 45 and 46. In 46, note equation of the line from (0, 4) to (2, 0).
Clear[x, y, f]
f[x_, y_]:= {x Exp[y], 4x Log[y]}
2
ybound = 4 2x
Plot[{0, ybound}, {x, 0,2. 1}, AspectRatio Automatic, AxesLabel {x, y}];ÄÄ
integrand:=D[f[x, y][[2]], x] D[f[x, y][[1]], y]//Simplify
Integrate[integrand, {x, 0, 2}, {y, 0, ybound}]
N[%]
16.5 SURFACES AND AREA
1. In cylindrical coordinates, let x r cos , y r sin , z x y r . Then (r ) (r cos ) (r sin ) r ,œœœœ ßœ) ) )))
ˆ‰
È##
###
rijk
0 r 2, 0 2 .ŸŸ Ÿ Ÿ)1
2. In cylindrical coordinates, let x r cos , y r sin , z 9 x y 9 r . Thenœœœœ)) ## #
(r ) (r cos ) (r sin ) 9 r ; z 0 9 r 0 r 9 3 r 3, 0 2 . Butrijkßœ ÊÊ ŸÊŸŸ ŸŸ))) )1ab
###
3 r 0 gives the same points as 0 r 3, so let 0 r 3.ŸŸ Ÿ Ÿ Ÿ Ÿ
3. In cylindrical coordinates, let x r cos , y r sin , z z . Then (r ) (r cos ) (r sin ) .œœœÊœ ßœ) ) )))
Èxy rr
## #
rijk
ˆ‰
For 0 z 3, 0 3 0 r 6; to get only the first octant, let 0 .ŸŸ Ÿ ŸÊŸŸ ŸŸ
r
# #
)1
4. In cylindrical coordinates, let x r cos , y r sin , z 2 x y z 2r. ThenœœœÊœ))
È##
(r ) (r cos ) (r sin ) 2r . For 2 z 4, 2 2r 4 1 r 2, and let 0 2 .rijkßœ ŸŸ Ÿ ŸÊŸŸ ŸŸ))) )1
5. In cylindrical coordinates, let x r cos , y r sin ; since x y r z 9 x y 9 rœœ œÊœœ))
## # ## #2ab
z 9 r , z 0. Then (r ) (r cos ) (r sin ) 9 r . Let 0 2 . For the domainÊœ ßœ ŸŸ
ÈÈ
# #
rijk))) )1
of r: z x y and x y z 9 x y x y 9 2 x y 9 2r 9œ œÊ œÊ œÊ œ
ÈÈ
ˆ‰ ab
## ##
### ## ## #
#
r 0 r .Êœ Ê ŸŸ
33
22
ÈÈ
6. In cylindrical coordinates, (r ) (r cos ) (r sin ) 4 r (see Exercise 5 above with x y z 4,rijkßœ œ)))
È####
instead of x y z 9). For the first octant, let 0 . For the domain of r: z x y and
###
###
œ ŸŸ œ )1È
x y z 4 x y x y 4 2 x y 4 2r 4 r 2. Thus, let 2 r 2
### ## ## #
##
#
œÊ œÊ œÊ œÊœ ŸŸ
ˆ‰
Èab ÈÈ
(to get the portion of the sphere between the cone and the xy-plane).
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

964 Chapter 16 Integration in Vector Fields
7. In spherical coordinates, x sin cos , y sin sin , x y z 3 3œœœÊœÊœ39 ) 39)3 3 3
ÈÈ
### #
z 3 cos for the sphere; z 3 cos cos ; z 3 cos Êœ œ œ Ê œ Ê œ œ Ê œ
ÈÈ È
9999 9
ÈÈÈ
333
3####
"1
cos . Then ( ) 3 sin cos 3 sin sin 3 cos ,ʜʜ ߜ 99 9) 9) 9) 9
"
#
2
3
1rijk
Š‹Š‹Š‹
ÈÈÈ
and 0 2 .
11
33
2
ŸŸ ŸŸ9)1
8. In spherical coordinates, x sin cos , y sin sin , x y z 8 8 2 2œœœÊœÊœœ39 ) 39)3 3 3
ÈÈÈ
### #
x 2 2 sin cos , y 2 2 sin sin , and z 2 2 cos . Thus letÊœ œ œ
ÈÈ È
9) 9) 9
( ) 2 2 sin cos 2 2 sin sin 2 2 cos ; z 2 2 2 2 cos rijk9) 9 ) 9 ) 9 9ßœ œÊœ
Š‹Š‹Š‹
ÈÈÈ È
cos ; z 2 2 2 2 2 2 cos cos 1 0. Thus 0 andʜʜœÊœ ʜʜ ŸŸ99 999 9
"
È2
3 3
4 4
1 1
ÈÈÈ
02.ŸŸ)1
9. Since z 4 y , we can let be a function of x and y (x y) x y 4 y . Then z 0œ Ê ßœ œ
# #
rrijkab
0 4 y y 2. Thus, let 2 y 2 and 0 x 2.Êœ Êœ„ ŸŸ ŸŸ
#
10. Since y x , we can let be a function of x and z (x z) x x z . Then y 2œÊßœœ
# #
rrijk
x 2 x 2. Thus, let 2 x 2 and 0 z 3.ʜʜ„ ŸŸ ŸŸ
#ÈÈÈ
11. When x 0, let y z 9 be the circular section in the yz-plane. Use polar coordinates in the yz-planeœœ
##
y 3 cos and z 3 sin . Thus let x u and v (u,v) u (3 cos v) (3 sin v) whereÊœ œ œ œÊ œ )) )ri j k
0 u 3, and 0 v 2 .ŸŸ ŸŸ1
12. When y 0, let x z 4 be the circular section in the xz-plane. Use polar coordinates in the xz-planeœœ
##
x 2 cos and z 2 sin . Thus let y u and v (u,v) (2 cos v) u (3 sin v) whereÊœ œ œ œÊ œ )) )rijk
2 u 2, and 0 v (since we want the portion the xy-plane).Ÿ Ÿ Ÿ Ÿ1above
13. (a) x y z 1 z 1 x y. In cylindrical coordinates, let x r cos and y r sin œÊœ œ œ))
z 1 r cos r sin (r ) (r cos ) (r sin ) (1 r cos r sin ) , 0 2 andÊœ Ê ß œ ŸŸ))))) )))1rij k
0r3.ŸŸ
(b) In a fashion similar to cylindrical coordinates, but working in the yz-plane instead of the xy-plane, let
y u cos v, z u sin v where u y z and v is the angle formed by (x y z), (x 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with (x 0 0) as vertex. Since x y z 1 x 1 y z x 1 u cos v u sin v, then is aßß œ Ê œ Ê œ r
function of u and v (u v) (1 u cos v u sin v) (u cos v) (u sin v) , 0 u 3 and 0 v 2 .Êßœ ŸŸ ŸŸrijk1
14. (a) In a fashion similar to cylindrical coordinates, but working in the xz-plane instead of the xy-plane, let
x u cos v, z u sin v where u x z and v is the angle formed by (x y z), (y 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with vertex (y 0 0). Since x y 2z 2 y x 2z 2, then (u v)ßß œ Ê œ ßr
(u cos v) (u cos v 2u sin v 2) (u sin v) , 0 u 3 and 0 v 2 .œ ŸŸ ŸŸijk
È1
(b) In a fashion similar to cylindrical coordinates, but working in the yz-plane instead of the xy-plane, let
y u cos v, z u sin v where u y z and v is the angle formed by (x y z), (x 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with vertex (x 0 0). Since x y 2z 2 x y 2z 2, then (u v)ßß œ Ê œ ßr
(u cos v 2u sin v 2) (u cos v) (u sin v) , 0 u 2 and 0 v 2 .œ ŸŸ ŸŸijk
È1
15. Let x w cos v and z w sin v. Then (x 2) z 4 x 4x z 0 w cos v 4w cos v w sin vœ œ œÊ œÊ
## # # ## ##
0 w 4w cos v 0 w 0 or w 4 cos v 0 w 0 or w 4 cos v. Now w 0 x 0 and y 0,œÊ œÊ œ œ Ê œ œ œ Ê œ œ
#
which is a line not a cylinder. Therefore, let w 4 cos v x (4 cos v)(cos v) 4 cos v and z 4 cos v sin v.œÊœ œ œ
#
Finally, let y u. Then (u v) 4 cos v u (4 cos v sin v) , v and 0 u 3.œ ß œ ŸŸ ŸŸrijkab
#
##
11
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.5 Surfaces and Area 965
16. Let y w cos v and z w sin v. Then y (z 5) 25 y z 10z 0œœ œÊœ
## ##
w cos v w sin v 10w sin v 0 w 10w sin v 0 w(w 10 sin v) 0 w 0 orʜʜʜʜ
## ## #
w 10 sin v. Now w 0 y 0 and z 0, which is a line not a cylinder. Therefore, let w 10 sin vœœÊœœ œ
y 10 sin v cos v and z 10 sin v. Finally, let x u. Then (u v) u (10 sin v cos v) 10 sin v ,Êœ œ œ ßœ
# #
ri j kab
0 u 10 and 0 v .ŸŸ ŸŸ1
17. Let x r cos and y r sin . Then (r ) (r cos ) (r sin ) , 0 r 1 and 0 2œœ ßœ ŸŸŸŸ) ) ))) )1rijk
ˆ‰
2r sin
#
)
(cos ) (sin ) and ( r sin ) (r cos )Êœ œ rijkr i jk
rsin r cos
)) ) )
ˆ‰ ˆ ‰
))
)
##
cos sin
r sin r cos
Ê‚œ
rr
ijk
rsin
r cos
)
)
)
ââ
ââ
ââ
ââ
ââ
ââ
))
))
#
#
r cos r sin rœ œ
Š‹Š‹
ab
## ## #
##
r sin cos r sin r cos r
(sin )(r cos )
)) ) )
))
ij kjk))
r A dr d d dÊ‚œ œ Êœ œ œ œkk
É’“
rr
rr
44
5r 5r 5r 5
)1
### #
"
!
ÈÈÈ È
'' ' '
00 0 0
21 2 2
)))
18. Let x r cos and y r sin z x r cos , 0 r 2 and 0 2 . ThenœœÊœœŸŸŸŸ)) ) )1
(r ) (r cos ) (r sin ) (r cos ) (cos ) (sin ) (cos ) andrijkrijkßœ Ê œ ))) ) )))
r
( r sin ) (r cos ) (r sin )rijk
)œ )))
cos sin cos
r sin r cos r sin
Ê‚œ
rr
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ
)) )
)))
r sin r cos (r sin cos r sin cos ) r cos r sin r rœ œab ab
## ##
) ) )) )) ) )ijkik
r r r 2 A r 2 dr d d 2 2 d 4 2Ê‚œ œ Êœ œ œ œkk
ÈÈ È ÈÈ
’“
rr
rr2
2
)## #
!
'' ' '
00 0 0
22 2 2
)))1
È
19. Let x r cos and y r sin z 2 x y 2r, 1 r 3 and 0 2 . ThenœœÊœœŸŸŸŸ)) )1
È##
(r ) (r cos ) (r sin ) 2r (cos ) (sin ) 2 and ( r sin ) (r cos )rijkrijkrijßœ Ê œ œ ))) )) ) )
r)
( 2r cos ) (2r sin ) r cos r sin
cos sin 2
r sin r cos 0
Ê‚œ œ
rr i j k
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ ab
))
))
))))
##
( 2r cos ) (2r sin ) r 4r cos 4r sin r 5r r 5œ Ê ‚ œ œ œ)) ))ijkrrkk
ÈÈÈ
r)## ## # #
A r 5 dr d d 4 5 d 8 5Êœ œ œ œ
'' ' '
01 0 0
23 2 2
ÈÈÈ
’“
)))1
r5
2
È$
"
20. Let x r cos and y r sin z , 3 r 4 and 0 2 . ThenœœÊœœŸŸŸŸ)) )1
Èxy
33
r
(r ) (r cos ) (r sin ) (cos ) (sin ) and ( r sin ) (r cos )r i jkr i jkr i jßœ Ê œ œ ))) )) ) )
ˆ‰ ˆ‰
r
33
r")
cos sin r cos r sin r cos r sin
r sin r cos 0
Ê‚œ œ
rr i j k
ijk
r33 3
)
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ‰
ab)) ) ) ) )
))
"" " ##
r cos r sin r r cos r sin rœ Ê ‚ œ œ œ
ˆ‰ˆ‰kk
ÉÉ
"" ""
## ## #
33 99 93
r10r r10
)) ))ijkrr
)È
A dr d d dÊœ œ œ œ
'' ' '
03 0 0
24 2 2
r 10 r 10 7 10 7 10
3663
ÈÈÈÈ
)))
’“
%
$
1
21. Let x r cos and y r sin r x y 1, 1 z 4 and 0 2 . Thenœ œ Ê œœ ŸŸ ŸŸ)) )1
###
(z ) (cos ) (sin ) z and ( sin ) (cos )rijkrkrijßœ Ê œ œ ))) ) )
z)
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

966 Chapter 16 Integration in Vector Fields
(cos ) (sin ) cos sin 1
sin cos 0
001
Ê‚œ œ Ê‚œ œ
rr i j rr
ijk
) )z z
ââ
ââ
ââ
ââ
ââ
ââ kk
È
)) )) ))
##
A 1 dr d 3 d 6Êœ œ œ
'' '
01 0
24 2
))1
22. Let x u cos v and z u sin v u x z 10, 1 y 1, 0 v 2 . ThenœœÊœœŸŸŸŸ
### 1
(y v) (u cos v) y (u sin v) 10 cos v y 10 sin vrijk ijkßœ œ
Š‹Š‹
ÈÈ
10 sin v 10 cos v and 10 sin v 0 10 cos v
010
Êœ œÊ‚œ
rikrjrr
ijk
vyvy
Š‹Š‹
ÈÈ ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
10 cos v 10 sin v 10 A 10 du dv 10u dvœ Ê ‚ œ Ê œ œ
Š‹Š‹ ’“
ÈÈ È È È
kkikrr
vy 01 0
21 2
'' ' "
"
2 10 dv 4 10œœ
'0
2ÈÈ
1
23. z 2 x y and z x y z 2 z z z 2 0 z 2 or z 1. Since z x y 0,œ œ Ê œ Ê œ Ê œ œ œ
## # #
## ##
ÈÈ
we get z 1 where the cone intersects the paraboloid. When x 0 and y 0, z 2 the vertex of theœœœœÊ
paraboloid is (0 0 2). Therefore, z ranges from 1 to 2 on the “cap" r ranges from 1 (when x y 1) to 0ßß Ê œ
##
(when x 0 and y 0 at the vertex). Let x r cos , y r sin , and z 2 r . Thenœœ œ œ œ)) #
(r ) (r cos ) (r sin ) 2 r , 0 r 1, 0 2 (cos ) (sin ) 2r andrijk rijkßœ ŸŸ ŸŸ Ê œ ))) )1 ))ab
#r
( r sin ) (r cos ) cos sin 2r
r sin r cos 0
rijrr
ijk
))
œ Ê ‚ œ
)) ))
))
r
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r 4r cos 4r sin r r 4r 1œÊ‚œ œabab kk
ÈÈ
## %# %# # #
)) ))ijkrr
r)
A r 4r 1 dr d 4r 1 d d 5 5 1Êœ œ œ œ
'' ' '
00 0 0
21 2 2
È’“Š‹Š‹
ab È
#"#$Î# "
!
"
#
)))
12 1 6
55
È1
24. Let x r cos , y r sin and z x y r . Then (r ) (r cos ) (r sin ) r , 1 r 2,œ œ œœ ßœ ŸŸ) ) )))
### #
rijk
0 2 (cos ) (sin ) 2r and ( r sin ) (r cos )ŸŸ Ê œ œ )1 ) ) ) )rijkr i j
r)
2r cos 2r sin r
cos sin 2r
r sin r cos 0
Ê‚œ œ Ê ‚
rr i jk rr
ijk
r r) )
ââ
ââ
ââ
ââ
ââ
ââ
ababkk
))
))
))
##
4r cos 4r sin r r 4r 1 A r 4r 1 dr d 4r 1 dœœÊœ œ
ÈÈÈ
’“
ab
%# %# # # # "#$Î# #
"
)) ) )
'' '
01 0
22 2
12
d171755œœ
'0
2Š‹Š ‹
ÈÈ
17 17 5 5
16
ÈÈ
#)1
25. Let x sin cos , y sin sin , and z cos x y z 2 on the sphere. Next,œ œ œ Êœ œ39 ) 39) 3 9 3
ÈÈ
###
x y z 2 and z x y z z 2 z 1 z 1 since z 0 . For the lower
### ## #
##
œ œ Ê œÊ œÊœ Êœ
È91
4
portion of the sphere cut by the cone, we get . Then91œ
( ) 2 sin cos 2 sin sin 2 cos , , 0 2rijk9) 9 ) 9 ) 9 9 1 ) 1ßœ ŸŸ ŸŸ
Š‹Š‹Š‹
ÈÈÈ
1
4
2 cos cos 2 cos sin 2 sin and 2 sin sin 2 sin cos Êœ œ rijkr ij
9 )
Š‹Š‹Š‹Š ‹Š‹
ÈÈÈ ÈÈ
9) 9) 9 9) 9)
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ È
ÈÈ
9) 9) 9
9) 9 )
2 sin cos 2 sin sin (2 sin cos )œabab
##
9) 9) 99ijk
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
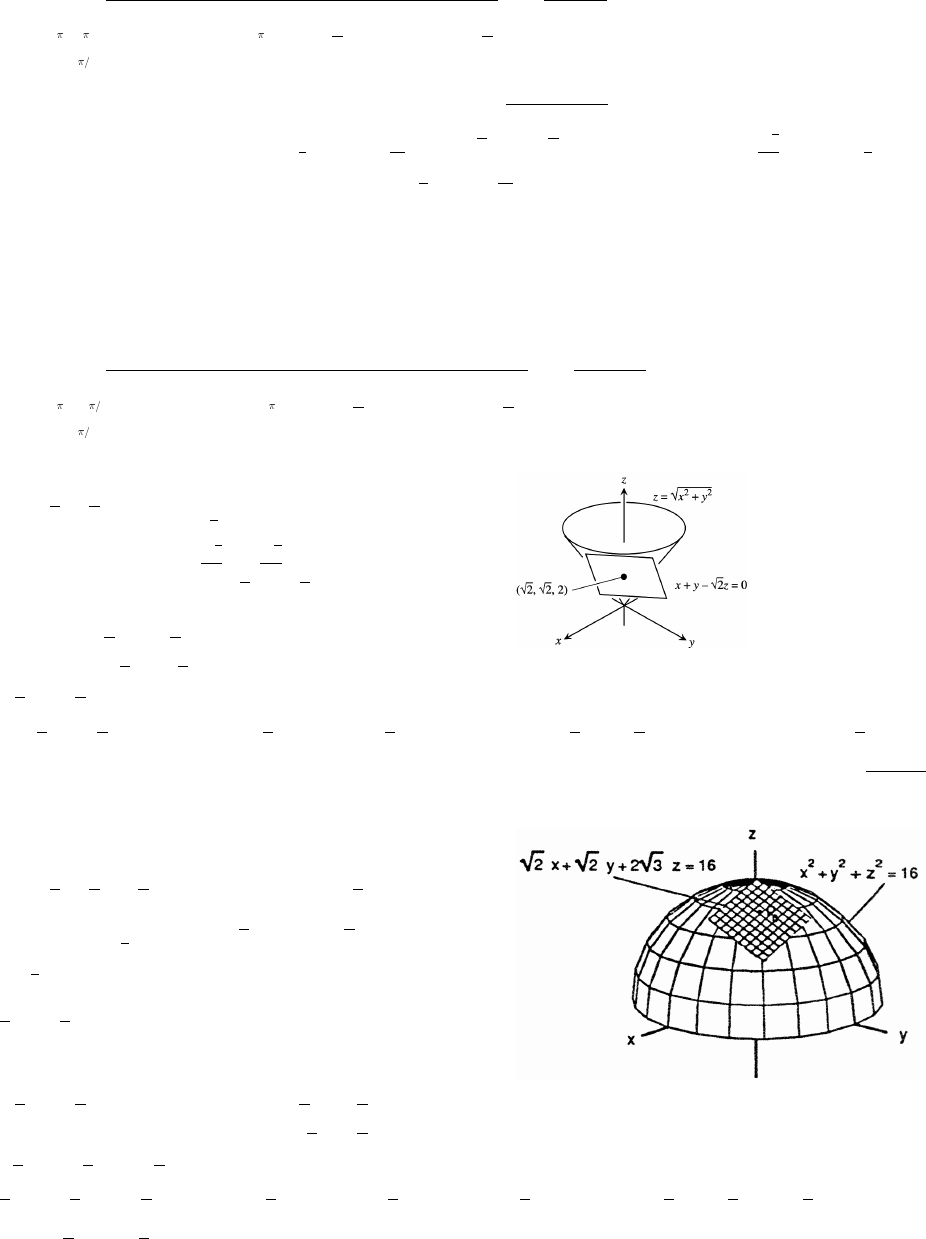
Section 16.5 Surfaces and Area 967
4 sin cos 4 sin sin 4 sin cos 4 sin 2 sin 2 sin Ê‚œ œ œ œkk kk
ÈÈ
rr
9) %# %# ## #
9) 9) 99 9 9 9
A 2 sin d d 2 2 d 4 2 2Êœ œ œ
'' '
04 0
22
99) ) 1
Š‹Š ‹
ÈÈ
26. Let x sin cos , y sin sin , and z cos x y z 2 on the sphere. Next,œ œ œ Êœ œ39 ) 39) 3 9 3
È###
z 1 1 2 cos cos ; z 3 3 2 cos cos . Thenœ Ê œ Ê œ Ê œ œ Ê œ Ê œ Ê œ99 9 99 9
"
# #
2
3 6
3
1 1
ÈÈ È
( ) (2 sin cos ) (2 sin sin ) (2 cos ) , , 0 2rijk9) 9 ) 9 ) 9 9 ) 1ßœ ŸŸ ŸŸ
11
63
2
(2 cos cos ) (2 cos sin ) (2 sin ) andʜ rijk
99) 9) 9
( 2 sin sin ) (2 sin cos )rij
)œ 9) 9 )
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
4 sin cos 4 sin sin (4 sin cos )œabab
##
9) 9) 99ijk
16 sin cos 16 sin sin 16 sin cos 16 sin 4 sin 4 sin Ê‚œ œ œ œkk kk
ÈÈ
rr
9) %# %# ## #
9) 9) 99 9 9 9
A 4 sin d d 2 2 3 d 4 4 3Êœ œ œ
'' '
06 0
223 2
99) ) 1
Š‹Š‹
ÈÈ
27. The parametrization (r ) (r cos ) (r sin ) rrijkߜ )))
at P 2 2 2 , r 2,
!œßßÊœœ
Š‹
ÈÈ )1
4
(cos ) (sin ) andrijkijk
r22
œ œ)) ÈÈ
##
( r sin ) (r cos ) 2 2rijij
)œ œ ))
ÈÈ
2/2 2/2 1
220
Ê‚œ
rr
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
2 2 2 the tangent plane isœ Ê
ÈÈ
ijk
0 2 2 2 x 2 y 2 (z 2) 2x 2y 2z 0, or x y 2z 0.œ Êœ œ
Š‹’ “
ÈÈ È È ÈÈ È
Š‹Š‹
ijk i j k†
The parametrization (r ) x r cos , y r sin and z r x y r z the surface is z x y .rßÊœ œ œÊ œœ Ê œ ))) #### ##
È
28. The parametrization ( )r9)ß
(4 sin cos ) (4 sin sin ) (4 cos )œ9) 9) 9ijk
at P 2 2 2 3 4 and z 2 3
!œßß Êœ œ
Š‹
ÈÈ ÈÈ
3
4 cos ; also x 2 and y 2œÊœ œ œ99
1
6ÈÈ
. Then ʜ)19
4r
(4 cos cos ) (4 cos sin ) (4 sin )œ9) 9) 9ijk
662 andœ
ÈÈ
ijk
( 4 sin sin ) (4 sin cos )rij
)œ 9) 9 )
22 at P 662
220
œ Ê ‚ œ
ÈÈ ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
ij rr
ijk
! 9)
2 2 2 2 4 3 the tangent plane isœ Ê
ÈÈÈ
ijk
22 22 43 x 2 y 2 z 23 0 2x 2y 23z 16,
Š‹’ “
ÈÈ È È ÈÈ
ÈÈÈ
Š‹Š‹Š ‹
ijk i j k œÊ œ†
or x y 6z 8 2. The parametrization x 4 sin cos , y 4 sin sin , z 4 cos œ Ê œ œ œ
ÈÈ9) 9) 9
the surface is x y z 16, z 0.Ê œ
###
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
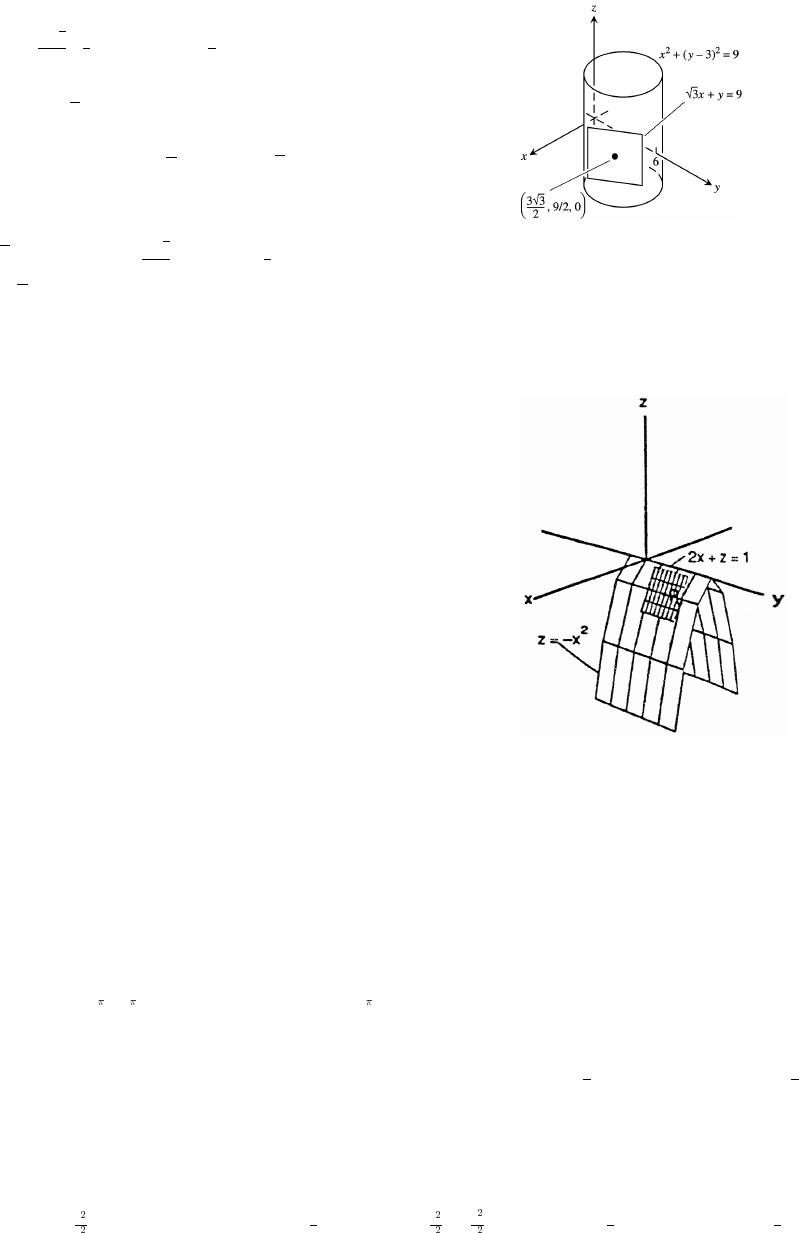
968 Chapter 16 Integration in Vector Fields
29. The parametrization ( z) (3 sin 2 ) 6 sin zrijk)))ߜ ab
#
at P 0 and z 0. Then
!##
œßßÊœ œ
Š‹
33 9
3
È)1
(6 cos 2 ) (12 sin cos )ri j
)œ)))
3 3 3 and at Pœ œijrk
Èz!
33 3
3330
001
Ê‚œ œ
rr ij
ijk
)z
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
the tangent plane isÊ
33 3 x y (z 0) 0
Š‹’ “
ÈŠ‹
ˆ‰
ij i j kϠ33 9
È
##
3x y 9. The parametrization x 3 sin 2ʜ ʜ
È)
and y 6 sin x y 9 sin 2 6 sinœÊœ
#### #
#
)))ab
9 4 sin cos 36 sin 6 6 sin 6y x y 6y 9 9 x (y 3) 9œœœÊœÊœab ab
## % # ## # #
)) ) )
30. The parametrization (x y) x y x atrijkߜ
#
P (1 2 1) 2x 2 and at P
! !
œßß Ê œ œ œri kik rj
xy
2 the tangent plane
10 2
00
Ê‚œ œÊ
"
rr ik
ij k
xy
ââ
ââ
ââ
ââ
ââ
ââ
is (2 ) [(x 1) (y 2) (z 1) ] 0ik i j kϠ
2x z 1. The parametrization x x, y y andÊœ Êœ œ
z x the surface is z xœ Ê œ
##
31. (a) An arbitrary point on the circle C is (x z) (R r cos u, r sin u) (x y z) is on the torus withßœ Ê ßß
x (R r cos u) cos v, y (R r cos u) sin v, and z r sin u, 0 u 2 , 0 v 2œ œ œ ŸŸ ŸŸ11
(b) ( r sin u cos v) (r sin u sin v) (r cos u) and ( (R r cos u) sin v) ((R r cos u) cos v)rijkr i j
uv
œ œ
r sin u cos v r sin u sin v r cos u
(R r cos u) sin v (R r cos u) cos v 0
Ê‚œ
rr
ijk
uv
ââ
ââ
ââ
ââ
ââ
ââ
(R r cos u)(r cos v cos u) (R r cos u)(r sin v cos u) ( r sin u)(R r cos u)œ ijk
(R r cos u) r cos v cos u r sin v cos u r sin u r(R r cos u)Ê‚ œ Ê‚œkk a bkkrr rr
uv uv
### # # # # # # #
A rR r cos u du dv 2 rR dv 4 rRÊœ œ œ
'' '
00 0
22 2
ab
##
11
32. (a) The point (x y z) is on the surface for fixed x f(u) when y g(u) sin v and z g(u) cos vßß œ œ œ
ˆ‰ ˆ‰
11
##
x f(u), y g(u) cos v, and z g(u) sin v (u v) f(u) (g(u) cos v) (g(u) sin v) , 0 v 2 ,Êœ œ œ Ê ßœ ŸŸri j k1
aubŸŸ
(b) Let u y and x u f(u) u and g(u) u (u v) u (u cos v) (u sin v) , 0 v 2 , 0 uœœÊœ œÊßœ ŸŸŸ
## #
ri j k 1
33. (a) Let w 1 where w cos and sin cos cos cos and cos sin
# #
œ œ œ Ê œ Êœ œ
zzxx
ccabab
yy
99 9 9) 9)
x a cos cos , y b sin cos , and z c sin Êœ œ œ)9 )9 9
( ) (a cos cos ) (b sin cos ) (c sin )Êßœ rijk)9 )9 )9 9
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.5 Surfaces and Area 969
(b) ( a sin cos ) (b cos cos ) and ( a cos sin ) (b sin sin ) (c cos )rijrijk
)9
œ œ )9 )9 )9 )9 9
a sin cos b cos cos 0
a cos sin b sin sin c cos
Ê‚œ
rr
ijk
)9
ââ
ââ
ââ
ââ
ââ
ââ
)9 )9
)9 )9 9
bc cos cos ac sin cos (ab sin cos )œabab)9 )9 99
##
ijk
b c cos cos a c sin cos a b sin cos , and the result follows.Ê‚ œ kkrr
)9
### # % ## # % ## # #
)9 )9 99
A d d d d
a b sin cos b c cos cos a c sin cos
Ê‚œ
'' ''
00 00
22 1/2
kk c drr
)9
9) 9)
99 )9 )9
## # # ## # % ## # %
34. (a) ( u) (cosh u cos ) (cosh u sin ) (sinh u)rijk)))ߜ
(b) ( u) (a cosh u cos ) (b cosh u sin ) (c sinh u)rijk)))ߜ
35. ( u) (5 cosh u cos ) (5 cosh u sin ) (5 sinh u) ( 5 cosh u sin ) (5 cosh u cos ) andrijkrij))) ))ßœ Ê œ
)
(5 sinh u cos ) (5 sinh u sin ) (5 cosh u)rijk
uœ))
r 5 cosh u sin 5 cosh u cos 0
5 sinh u cos 5 sinh u sin 5 cosh u
Ê‚œ
)r
ijk
u
ââ
ââ
ââ
ââ
ââ
ââ
))
))
25 cosh u cos 25 cosh u sin (25 cosh u sinh u) . At the point (x y 0), where x y 25œ ßßœabab
## ##
!!
))ijk 00
we have 5 sinh u 0 u 0 and x 25 cos , y 25 sin the tangent plane isœÊœ œ œ Ê
!!
))
5(x y ) [(x x) (y y) z ] 0 xx x yy y 0 xx yy 25
!! ! ! ! ! ! !
##
ij i jkœÊœÊœ†00
36. Let w 1 where cosh u and w sinh u w w cos and w sin
zz xx
cc abab
yy
œ œ œ Ê œÊœ œ
##
))
x a sinh u cos , y b sinh u sin , and z c cosh uÊœ œ œ))
( u) (a sinh u cos ) (b sinh u sin ) (c cosh u) , 0 2 , uÊßœ ŸŸ__rijk))) )1
37. , f 2x 2y f (2x) (2y) ( 1) 4x 4y 1 and f 1;pk i jk pœ œÊ œ œ œ™™ ™†kk k k
ÈÈ
## # ##
z 2 x y 2; thus S dA 4x 4y 1 dx dyœÊ œ œ œ
## ##
'' ''
RR
kk
kk
™
™†
f
fpÈ
4r cos 4r sin 1 r dr d 4r 1 r dr d 4r 1 dœ œ œ
''
RÈÈ
’“
ab
## ## # "#$Î# #
!
))) ) )
'' '
00 0
22 2
12
È
dœœ
'0
213 13
63
)1
38. , f 2x 2y f 4x 4y 1 and f 1; 2 x y 6pk i jk pœ œÊ œ œ ŸŸ™™ ™†kk k k
È## ##
S dA 4x 4y 1 dx dy 4r 1 r dr d 4r 1 r dr dÊœ œ œ œ
'' '' ''
RR R
kk
kk
™
™†
f
fpÈÈÈ
## # #
))
''
02
26
4r 1 d dœ œœ
''
00
22
’“
ab
"#$Î# '
#
12 6 3
49 49
È
È))1
39. , f 2 2 f 3 and f 2; x y and x 2 y intersect at (1 1) and (1 1)pk i j k pœœÊœ œœ œ ß ß™™™†kk k k ##
S dA dx dy dx dy 3 3y dy 4Êœ œ œ œ œ
'' ''
RR
kk
kk
™
™†
f
f
33
p##
#
'' '
1y 1
12y 1
ab
40. , f 2x 2 f 4x 4 2 x 1 and f 2 S dApk i k pœ œÊ œœ œÊœ™™ ™†kk k k
ÈÈ
## ''
R
kk
kk
™
™†
f
fp
dx dy x 1 dy dx x x 1 dx x 1 (4)œœœœœœ
''
R
2x 1
3333
7
ÈÈ
###
"""
# $Î#
$Î# $
!
'' '
00 0
3x 3
ÈÈ
’“
ab
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

970 Chapter 16 Integration in Vector Fields
41. , f 2x 2 2 f (2x) ( 2) ( 2) 4x 8 2 x 2 and f 2pk i j k pœ œ Ê œ œ œ œ™™ ™†kk k k
ÈÈÈ
### # #
S dA dx dy x 2 dy dx 3x x 2 dx x 2Êœ œ œ œ œ
'' ''
RR
kk
kk È
™
™†
f
f
2x 2
p
###
#$Î# #
!
'' '
00 0
23x 2
ÈÈ
’“
ab
66 22œ
ÈÈ
42. , f 2x 2y 2z f 4x 4y 4z 8 2 2 and f 2z; x y z 2 andpk i j k pœ œ Ê œ œ œ œ œ™™ ™†kk k k
ÈÈÈ
### ###
z x y x y 1; thus, S dA dA 2 dAœÊœ œ œ œ
ÈÈ
## ##
#
"
'' '' ''
RR R
kk
kk È
™
™†
f
fz z
22
p
2 dA 2 2 1 2 d 2 2 2œœœœ
ÈÈÈÈÈ
Š‹Š‹
''
R
"
ÈÈ
ab2xy
r dr d
2r
'' '
00 0
21 2
))1
43. , f c f c 1 and f 1 S dA c 1 dx dypk ik pœ œÊ œ œÊœ œ ™™ ™†kk k k
ÈÈ
# #
'' ''
RR
kk
kk
™
™†
f
fp
c 1 r dr d d c 1œœ œ
'' '
00 0
21 2
ÈÈ
##
#
))1
Èc1
44. , f 2x 2z f (2x) (2z) 2 and f 2z for the upper surface, z 0pk i j pœœÊœœ œ ™™ ™†kk k k
È##
S dA dA dy dx 2 dy dx dxÊœ œ œ œ œ
'' '' ''
RRR
kk
kk ÈÈÈ
™
™†
f
fz
21
1x 1x 1x
p#
""
'' '
12 0 12
12 12 12
sin xœœœcd ˆ‰
" "Î#
"Î#
111
663
45. , f 2y 2z f 1 (2y) (2z) 1 4y 4z and f 1; 1 y z 4pi i j k pœ œÊ œœ œŸŸ™™ ™†kk k k
ÈÈ
### ## ##
S dA 1 4y 4z dy dz 1 4r cos 4r sin r dr dÊœ œ œ
'' ''
RR
kk
kk
™
™†
f
fpÈÈ
## ## ##
''
01
22
)))
14r r drd 14r d 171755 d 171755œœ œ œ
'' ' '
01 0 0
22 2 2
È’“Š‹Š‹
ab ÈÈ
ÈÈ
#""
#$Î# #
"#
)) )
12 1 6
1
46. , f 2x 2z f 4x 4z 1 and f 1; y 0 and x y z 2 x z 2;pj ij k pœœÊœ œœ œÊœ™™ ™†kk k k
È## ## ##
thus, S dA 4x 4z 1 dx dz 4r 1 r dr d dœœœ œœ
'' ''
RR
kk
kk
™
™†
f
f63
13 13
pÈÈ
## #
'' '
00 0
22 2
))1
47. , f 2x 15 f 2x 15 ( 1) 4x 8 2xpk i jkœœÊœ œœ™™
ˆ‰ ˆ‰ ˆ‰
ÈÈ
kk
ÊŠ‹ ÉÉ
22 42
xx xx
##
###
2x , on 1 x 2 and f 1 S dA 2x 2x dx dyœ ŸŸ œÊœ œ
2
xf
f
kk a b™†p'' ''
RR
kk
kk
™
™†p
"
2x 2x dx dy x 2 ln x dy (3 2 ln 2) dy 3 2 ln 2œ œ œœ
'' ' '
01 0 0
12 1 1
ab cd
" # #
"
48. , f 3 x 3 y 3 f 9x 9y 9 3 x y 1 and f 3pk i j k pœ œÊ œœ œ™™ ™†
ÈÈkk k k
ÈÈ
S dA x y 1 dx dy x y 1 dx dy (x y 1) dyÊœ œ œ œ
'' ''
RR
kk
kk
™
™†
f
f 3
2
pÈÈ
‘
'' '
00 0
11 1 $Î# "
!
(y 2) (y 1) dy (y 2) (y 1) (3) (2) (2) 1œ œ œ
'0
1‘ ‘‘
22 4 4 4
3 3 15 15 15
$Î# $Î# &Î# &Î# &Î# &Î# &Î#
"
!
93 82 1œ
4
15 Š‹
ÈÈ
49. f (x y) 2x, f (x y) 2y f f 1 4x 4y 1 Area 4x 4y 1 dx dy
xy xy
ßœ ßœ Ê œ Ê œ
ÉÈÈ
## ## ##
''
R
4r 1 r dr d 13 13 1œœ
''
00
23
ÈŠ‹
È
#)1
6
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.5 Surfaces and Area 971
50. f (y z) 2y, f (y z) 2z f f 1 4y 4z 1 Area 4y 4z 1 dy dz
yz yz
ßœ ßœÊ œ Ê œ
ÉÈÈ
## ## ##
''
R
4r 1 r dr d 5 5 1œœ
''
00
21
ÈŠ‹
È
#)1
6
51. f (x y) , f (x y) f f 1 1 2 Area 2 dx dy
xy
xx
xy xy
yy
xy xy xy
ßœ ßœ Ê œ œ Ê œ
ÈÈ
##
ÉÉÈÈ
''
Rxy
2 Area between the ellipse and the circle 2 6 5 2œœœ
ÈÈÈ
abab11 1
52. Over R : z 2 x 2y f (x y) , f (x y) 2 f f 1 4 1
xy x y
22 47
33 93
xy
œ Ê ß œ ß œÊ œ œ
ÉÉ
##
Area dA (Area of the shadow triangle in the xy-plane) .Êœ œ œ œ
''
Rxy
77 737
33 3
ˆ‰ˆ‰
##
Over R : y 1 x z f (x z) , f (x z) f f 1 1
xz x z
11 17
33 946
xz
œ Ê ß œ ß œ Ê œ œ
"""
##
##
ÈÉ
Area dA (Area of the shadow triangle in the xz-plane) (3) .Êœ œ œ œ
''
Rxz
77 7 7
66 6
ˆ‰ #
Over R : x 3 3y z f (y z) 3, f (y z) f f 1 9 1
yz y z
3397
yz 4
œ Ê ß œ ß œ Ê œ œ
## #
##
ÉÉ
Area dA (Area of the shadow triangle in the yz-plane) (1) .Êœ œ œ œ
''
Ryz
77 7 7
22 2
ˆ‰ #
53. y z f (x z) 0, f (x z) z f f 1 z 1 ; y z z 4œ Ê ßœ ßœ Ê œ œ Ê œ Êœ
216 16 2
3333
xz xz
$Î# "Î# $Î#
##
ÈÈ
Area z 1 dx dz z 1 dz 5 5 1Êœ œ œ
'' '
00 0
41 4
ÈÈ
Š‹
È
2
3
54. y 4 z f (x z) 0, f (x z) 1 f f 1 2 Area 2 dA 2 dx dzœ Ê ß œ ß œÊ œ Ê œ œ
xz xz
ÈÈÈÈ
## ''
Rxz
00
24z
''
2 4 z dzœœ
Èab
'0
2#16 2
3
È
55. x, y x y f x, y x, y f x, y , x, y f x, yrijkri krjkab ab ab ab ab abœ Ê œ œ
xxyy
fx,y fx,y
10fx,y
01fx,y
Ê‚œ œ rr i jk
ij k
xy x y
x
y
ââ
ââ
ââ
ââ
ââ
ââ
ab
ab ab ab
fx,y fx,y 1 fx,y fx,y 1Êl‚lœ œ rr
xy x y x y
22 22
2
ÉÉ
abab ababab ab
d f x, y f x, y 1 dAÊœ 5Éab ab
xy
22
56. S is obtained by rotating y f x , a x b about the x-axis where f x 0œŸŸ ab ab
(a) Let x, y, z be a point on S. Consider the cross section when x x , the cross section is a circle with radius r f x .ab abœœ
‡‡
The set of parametric equations for this circle are given by y r cos f x cos and z r sinab a b ab)) )))œœ œ
‡
f x sin where 0 2 . Since x can take on any value between a and b we have x x, x, y x, œŸŸ œab ab ab
‡))1 ))
f x cos , z x, f x sin where a x b and 0 2 . Thus x, x f x cos f x sinœœŸŸŸŸœab a b ab a b ab ab)) ) )1 ) ) )ri j k
(b) x, f x cos f x sin and x, f x sin f x cosri j kr j k
xa b ab ab a b ab ab))))))œ œ
ww )
fx f x fx cos fx sin
1 f x cos f x sin
0fxsinfxcos
Ê‚œ œ †
rr i j k
ij k
x)
ââ
ââ
ââ
ââ
ââ
ââ
ab ab
ab ab ab ab ab ab
ww w
))
))
))
fx f x fx cos fx sin fx 1 f xÊl ‚ lœ † œ rr
x222 2
)ÉÉ
abababababab ab ab ab ab
ww
))
A fx1 fxddx fx1 fx dx 2fx1 fxdxœœ œ
'' ' '
a0 a a
b2 b b
0
2
ab a b ab a b ab a b
ÉÉ É
ab ab ab
”•
Œ
ww w
22 2
))1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

972 Chapter 16 Integration in Vector Fields
16.6 SURFACE INTEGRALS
1. Let the parametrization be (x z) x x z 2x and 12x0
00
rijkrijrkrr
ijk
ßœ Ê œ œ Ê ‚œ
"
#xzxz
ââ
ââ
ââ
ââ
ââ
ââ
2x 4x 1 G(x y z) d x 4x 1 dx dz 4x 1 dzœÊ‚œ Ê ßß œ œ ij r rkk a b
ÈÈ
’“
xz 00 0
32 3
##
"#$Î# #
!
''
S
5'' ' 12
17 17 1 dzœœ
'0
3"
#
"
14
17 17
Š‹
ÈÈ
2. Let the parametrization be (x y) x y 4 y , 2 y 2 and rij k rirj kßœ ŸŸÊ œ œ
È#
xy
y
4y
È
1
10 0
01
Ê‚œ œ Ê ‚œ œ
rr jk rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk
É
y
4y
yy
4y 4y
4y
2
ÈÈÈ
G(x y z) d 4 y dy dx 24Êßßœ œ
''
S
5''
12
42
ÈŠ‹
#
2
4y
È
3. Let the parametrization be ( ) (sin cos ) (sin sin ) (cos ) (spherical coordinates with 1rijk9) 9 ) 9 ) 9 3ßœ œ
on the sphere), 0 , 0 2 (cos cos ) (cos sin ) (sin ) andŸŸ ŸŸ Ê œ 91 ) 1 9 ) 9 ) 9rijk
9
( sin sin ) (sin cos ) cos cos cos sin sin
sin sin sin cos 0
rijrr
ijk
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ââ
ââ
ââ
ââ
ââ
ââ
sin cos sin sin (sin cos ) sin cos sin sin sin cosœÊ‚œ abab kk
È
## %# %# ##
9) 9) 99 9 ) 9 ) 9 9ijkrr
9)
sin ; x sin cos G(x y z) cos sin G(x y z) d cos sin (sin ) d dœœ Êßßœ Êßßœ99) )9 5 )999)
## ##
''
S''
00
2ab
cos 1 cos (sin ) d d ; cos u 1 du d
u cos
du sin d
œ Ä
œ
œ
'' ''
00 01
221
aba b abab
”•
## ##
)999) ) )
9
99
cos u d cos dœœœœ
''
00
22
ab
’“ ‘
##
"
"
#
!
))))
u4 4sin 24
33 3243
)) 1
1
4. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates with a,rijk9) 9 ) 9 ) 9 3ßœ œ
a 0, on the sphere), 0 (since z 0), 0 2 (a cos cos ) (a cos sin ) (a sin ) andŸŸŸŸÊœ9)19)9)9
19
#rijk
( a sin sin ) (a sin cos ) a cos cos a cos sin a sin
a sin sin a sin cos 0
rijrr
ijk
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ââ
ââ
ââ
ââ
ââ
ââ
a sin cos a sin sin (a sin cos )œabab
## ## #
9) 9) 99ijk
a sin cos a sin sin a sin cos a sin ; z a cos Ê‚œ œ œkk
È
rr
9) %% # %% # %# # #
9) 9) 99 9 9
G(x y z) a cos G(x y z) d a cos a sin d d aÊßßœ Ê ßß œ œ
## ## # %
95 999)1
''
S''
00
22
abab 2
3
5. Let the parametrization be (x y) x y (4 x y) and rij krikrjkßœ Ê œ œ
xy
3 F(x y z) d (4 x y) 3 dy dx
10 1
01
Ê ‚ œ œ Ê ‚ œ Ê ßß œ
"
rr ijk rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk
ÈÈ
''
S
5''
00
11
3 4y xy dx 3 x dx 3 x 3 3œœœœ
''
00
11
ÈÈÈÈ
’“ ’“
ˆ‰
y
22
77x
""
!!
##
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.6 Surface Integrals 973
6. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) cos sin
r sin r cos 0
Êœ œ Ê‚œ "
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
( r cos ) (r sin ) r ( r cos ) ( r sin ) r r 2; z r and x r cos œ Ê ‚ œ œ œ œ)) ) ) )ijkrrkk
ÈÈ
r)###
F(x y z) r r cos F(x y z) d (r r cos ) r 2 dr d 2 (1 cos ) r dr dÊßßœ Ê ßß œ œ )5 )) ))
''
S'' ''
00 00
21 21
Š‹
ÈÈ #
œ22
3
1È
7. Let the parametrization be (r ) (r cos ) (r sin ) 1 r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1ab
#
(cos ) (sin ) 2r and ( r sin ) (r cos ) cos sin 2r
r sin r cos 0
Êœ œ Ê‚œ
r i jkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r 2r cos 2r sin r r 1 4r ; z 1 r andœÊ‚œ œœabab kkabab
ÉÈ
## #
####
#
)) ))ijkrr
r)
x r cos H(xyz) r cos 1 4r H(xyz) dœÊßßœ Ê ßß)) 5ab
È
## #''
S
r cos 1 4r r 1 4r dr d r 1 4r cos dr dœœœ
'' ''
00 00
21 21
ab ab
Š‹Š‹
ÈÈ
## $ # #
##
))))
11
12
1
8. Let the parametrization be ( ) (2 sin cos ) (2 sin sin ) (2 cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
2 on the sphere), 0 ; x y z 4 and z x y z z 4 z 2 z 2 (since39œ ŸŸ œ œ Ê œÊ œÊœ
1
4### ## #
##
ÈÈ
z 0) 2 cos 2 cos , 0 2 ; (2 cos cos ) (2 cos sin ) (2 sin )Ê œ Ê œ Êœ ŸŸ œ 999)19)9)9
ÈÈ2
4#
19
rijk
and r ( 2 sin sin ) (2 sin cos ) 2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ijrr
ijk
ââ
ââ
ââ
ââ
ââ
ââ
4 sin cos 4 sin sin (4 sin cos )œabab
##
9) 9) 99ijk
16 sin cos 16 sin sin 16 sin cos 4 sin ; y 2 sin sin andÊ‚œ œ œkk
È
rr
9) %# %# ##
9) 9) 99 9 9)
z 2 cos H(x y z) 4 cos sin sin H(x y z) d (4 cos sin sin )(4 sin ) d dœ Ê ßß œ Ê ßß œ9 99) 5 99) 99)
''
S''
00
24
16 sin cos sin d d 0œœ
''
00
24 #99)9)
9. The bottom face S of the cube is in the xy-plane z 0 G(x y 0) x y and f(x y z) z 0 ÊœÊ ßßœ ßßœœÊœpk
and f f 1 and f 1 d dx dy G d (x y) dx dy™™ ™†œÊ œ œÊ œ Ê œ kpkk k k 55
'' ''
SR
(x y) dx dy ay dy a . Because of symmetry, we also get a over the face of the cubeœœœ
'' '
00 0
aa a
Š‹
a
#
$$
in the xz-plane and a over the face of the cube in the yz-plane. Next, on the top of the cube, G(x y z)
$ßß
G(x y a) x y a and f(x y z) z a and f f 1 and f 1 d dx dyœßßœ ßßœœÊœ œÊ œ œÊœpk k p™™ ™†kk k k 5
G d (x y a) dx dy (x y a) dx dy (x y) dx dy a dx dy 2a .
'' ''
SR
5œ œ œ œ
'' '' ''
00 00 00
aa aa aa $
Because of symmetry, the integral is also 2a over each of the other two faces. Therefore,
$
(xyz) d 3a 2a 9a.
''
cube
œ œ5ab
$$ $
10. On the face S in the xz-plane, we have y 0 f(x y z) y 0 and G(x y z) G(x 0 z) z and fœ Ê ßß œ œ ßß œ ßß œ Ê œ œpj j™
f 1 and f 1 d dx dz G d (y z) d z dx dz 2z dz 1.Êœ œÊœÊ œœ œ œkk k k™™†p555
'' ''
SS '' '
00 0
12 1
On the face in the xy-plane, we have z 0 f(x y z) z 0 and G(x y z) G(x y 0) y and fœ Ê ßß œ œ ßß œ ßß œ Ê œ œpk k™
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

974 Chapter 16 Integration in Vector Fields
f 1 and f 1 d dx dy G d y d y dx dy 1.Êœ œÊœÊ œ œ œkk k k™™†p555
'' ''
SS
''
00
12
On the triangular face in the plane x 2 we have f(x y z) x 2 and G(x y z) G(2 y z) y z andœ ßßœœ ßßœ ßßœÊ œpi
f f 1 and f 1 d dz dy G d (y z) d (y z) dz dy™™ ™†œÊ œ œ Ê œ Ê œ œ ipkk k k 555
'' ''
SS ''
00
11y
1 y dy .œœ
'0
1""
#
#
ab3
On the triangular face in the yz-plane, we have x 0 f(x y z) x 0 and G(x y z) G(0 y z) y zœ Ê ßß œ œ ßß œ ßß œ
and f f 1 and f 1 d dz dy G d (y z) dÊœ œÊ œ œÊ œ Ê œ pi i p™™ ™†kk k k 555
'' ''
SS
(y z) dz dy .œœ
''
00
11y "
3
Finally, on the sloped face, we have y z 1 f(x y z) y z 1 and G(x y z) y z 1 andœ Ê ßß œœ ßß œœ Ê œpk
f f 2 and f 1 d 2 dx dy G d (y z) d™™™†œ Ê œ œ Ê œ Ê œ jk pkk k k
ÈÈ
555
'' ''
SS
2 dx dy 2 2. Therefore, G(x y z) d 1 1 2 2 2 2œ œ ßß œ œ
''
00
12
ÈÈ ÈÈ
''
wedge
5""
33 3
8
11. On the faces in the coordinate planes, G(x y z) 0 the integral over these faces is 0.ßß œ Ê
On the face x a, we have f(x y z) x a and G(x y z) G(a y z) ayz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpi i™™kk
and f 1 d dy dz G d ayz d ayz dy dz .kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
cb ab c
4
On the face y b, we have f(x y z) y b and G(x y z) G(x b z) bxz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpj j™™kk
and f 1 d dx dz G d bxz d bxz dx dz .kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
ca abc
4
On the face z c, we have f(x y z) z c and G(x y z) G(x y c) cxy and f f 1œ ßßœœ ßßœ ßßœ Ê œ œ Ê œpk k™™kk
and f 1 d dy dx G d cxy d cxy dx dy . Therefore,kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
ba abc
4
G(xyz) d .
''
S
ßß œ5abc(ab ac bc)
4
12. On the face x a, we have f(x y z) x a and G(x y z) G(a y z) ayz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpi i™™kk
and f 1 d dz dy G d ayz d ayz dz dy 0. Because of the symmetrykk™†pœÊ œ Ê œ œ œ555
'' ''
SS''
bc
bc
of G on all the other faces, all the integrals are 0, and G(x y z) d 0.
''
S
ßß œ5
13. f(x y z) 2x 2y z 2 f 2 2 and G(x y z) x y (2 2x 2y) 2 x y ,ßßœ œÊ œ ßßœ œÊœ™ijk pk
f 3 and f 1 d 3 dy dx; z 0 2x 2y 2 y 1 x G d (2 x y) dkk k k™™†œ œ Ê œ œ Ê œÊœÊ œ p555
'' ''
SS
3 (2 x y) dy dx 3 (2 x)(1 x) (1 x) dx 3 2x dx 2œœœœ
'' ' '
00 0 0
11x 1 1
‘
Š‹
"
###
#3x
14. f(x y z) y 4z 16 f 2y 4 f 4y 16 2 y 4 and f 4ßß œ œ Ê œ Ê œ œ œ Ê œ
###
™™ ™†jk pk pkk k k
ÈÈ
d dx dy G d x y 4 dx dy dx dyÊœ Ê œ œ55
2y 4 y 4
4
xy 4
ÈÈ
ab
###
''
S'' ''
40 40
41 41
ˆ‰
ÈŠ‹
y 4 dy 4y 16œœœœ
'4
4"""
#
##
%
!
4333
y64 56
ab ’“
ˆ‰
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 16.6 Surface Integrals 975
15. f x, y, z x y z 0 f 2y f 4y 2 2 2y 1 and f 1ab kk k k
ÈÈ
È
œ œÊ œ Ê œ œ œÊ œ
2™™ ™†ijk pk p
##
d dx dy G d x y x 2 2y 1 dx dy 2 y 2y 1 dx dyÊœ Ê œ œ 55
ÈÈ
22y 1
1
22
##
''
S'' ''
00 00
1y 1y
ab
ÈÈ
ÈÈ
2 y 2y 1 dyœœ
ÈÈ
'0
1366 2
30
#
ÈÈ
16. f x, y, z x y z 0 f 2x f 4x 2 2 2x 1 and f 1ab kk k k
ÈÈÈ
œ œ Ê œ Ê œ œ œ Ê œ
2™™ ™†ijk p k p
##
d dx dy G d x 2 2x 1 dx dy 2 x 2x 1 dx dyÊœ Ê œ œ 55
ÈÈ
22x 1
1
##
''
S'' ''
10 10
11 11
ÈÈ È È
dyœœ
36 2 36 2
63
ÈÈ
ÈÈ
'0
1
17. f x, y, z 2x y z 2 f 2 f 6 and f 1 d dy dxab kk k k
È
œ œ Ê œ Ê œ œ Ê œ Ê œ™™ ™†ijk p k p 5È6
1
G d x y 2 2x y 6 dy dx 6 2x y 2x y x y dy dxÊœ œ
''
S
5'' ''
01x 01x
122x 122x
ab a b
ÈÈ 22
6 x 2x 2x x dxœ œ
Ȉ‰
'0
122
3330
23 4 6
È
18. f x, y, z x y f f 2 and f 1ab kk k k
È
œœ"Ê œÊ œ œÊ œ™™ ™†ij p j p
d dz dx G d x 1 x z 2 dz dx 2 2x z 1 dz dxÊ œ Ê œ œ 55
È2
1''
S'' ''
00 00
11 11
ab ababÈÈ
22x dxœœ
Ȉ‰
'0
13
22
2
È
19. Let the parametrization be (x y) x y 4 y , 0 x 1, 2 y 2; z 0 0 4 yrij kßœ ŸŸŸŸ œÊœab
##
y 2; and 2y 2y d
10 0
01 2y
Êœ„ œ œ Ê ‚œ œ Ê
ri rj k rr jk Fn
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ †5
dy dx (2xy 3z) dy dx 2xy 3 4 y dy dx dœ‚œœÊFrr Fn††
rr
rr
xy
xy
‚
‚
#
kk
kk c dab
xy ''
S
5
2xy 3y 12 dy dx xy y 12y dx 32 dx 32œœœœ
'' ' '
02 0 0
12 1 1
abcd
##$
#
#
20. Let the parametrization be (x y) x x z , 1 x 1, 0 z 2 2x and rijk rijrkßœ ŸŸ ŸŸÊ œ œ
#xz
2x d dz dx x dz dx
12x0
001
Ê‚œ œ Ê œ ‚ œrr ij Fn F rr
ijk
xz xz
ââ
ââ
ââ
ââ
ââ
ââ kk††5rr
rr
xz
xz
‚
‚
#
kk
d x dz dxÊœœ
''
S
Fn†5''
10
12 #4
3
21. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
a, a 0, on the sphere), 0 (for the first octant) 0 (for the first octant)39)œ ŸŸ ߟŸ
11
##
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos d d dœ Êœ‚ababab kk
## ## # ‚
‚
9) 9) 99 5 )9ijkFnFrr††
rr
rr
kk
9)
a cos sin d d since z (a cos ) d a cos sin d dœœœÊœ œ
$# $#
99)9 9 5 999)Fk k Fn
''
S
†''
00
22 1a
6
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

976 Chapter 16 Integration in Vector Fields
22. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
a, a 0, on the sphere), 0 , 0 2391)1œ ŸŸ ŸŸ
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos d d dœ Êœ‚ababab kk
## ## # ‚
‚
9) 9) 99 5 )9ijkFnFrr††
rr
rr
kk
9)
a sin cos a sin sin a sin cos d d a sin d d since x y zœ œ œab
$$ # $$ # $ # $
99 9) 99)9 9)9 Fijk
(a sin cos ) (a sin sin ) (a cos ) d a sin d d 4 aœÊœ œ9) 9) 9 5 99)1ijkFn
''
S
†''
00
2$$
23. Let the parametrization be (x y) x y (2a x y) , 0 x a, 0 y a and rij k rikrjkßœ ŸŸ ŸŸÊ œ œ
xy
d dy dx
10 1
01 1
Ê ‚ œ œ Ê œ ‚
rr ijk Fn F rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk††5rr
rr
xy
xy
‚
‚kk
[2xy 2y(2a x y) 2x(2a x y)] dy dx since 2xy 2yz 2xzœ œFijk
2xy 2y(2a x y) 2x(2a x y) dœ ÊijkFn
''
S
†5
[2xy 2y(2a x y) 2x(2a x y)] dy dx 4ay 2y 4ax 2x 2xy dy dxœ œ
'' ''
00 00
aa aa
ab
##
a 3a x 2ax dx aœœœ
'0
aˆ‰ˆ‰
4 432 13a
3336
$# # %
#
24. Let the parametrization be ( z) (cos ) (sin ) z , 0 z a, 0 2 (where r x y 1 onrijk))) )1ßœ ŸŸ ŸŸ œ œ
È##
the cylinder) ( sin ) (cos ) and (cos ) (sin )
sin cos 0
001
Êœ œÊ‚œ œ
rijrkrr ij
ijk
))
)) ))
))
zz
ââ
ââ
ââ
ââ
ââ
ââ
d dz d cos sin dz d dz d , since (cos ) (sin ) zÊœ ‚œ œ œFn F r r F i j k††5)))))))
rr
rr
‚
‚
##
z
z
kk
kk a b
)z
d 1 dz d 2 aÊœ œ
''
S
Fn†5)1
''
00
2a
25. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r d d dr r sin cos r d dr sinceœÊœ ‚œ )) 5 ) )))ijkFnFrr††
rr
rr
‚
‚
$##
r
r
kk
kk a b
)r
FikFnœÊœ œ ab a bˆ‰
r sin cos r d r sin cos r dr d sin cos d
#$###
""
)) 5 ) ) ) ) ) )
''
S
†'' '
00 0
21 2
43
cosœ œ
‘
"$#
!
12 3 3
2
))1
1
26. Let the parametrization be (r ) (r cos ) (r sin ) 2r , 0 r 1 (since 0 z 2) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) 2 and ( r sin ) (r cos ) r sin r cos 0
cos sin 2
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(2r cos ) (2r sin ) r d d drœÊœ ‚)) 5 )ijkFnFrr††
rr
rr
‚
‚
r
r
kk
kk
)r
2r sin cos 4r cos sin r d dr sinceœab
$# $
)) )) )
Fi jkFnœ Ê œ abab a br sin 2r cos d 2r sin cos 4r cos sin r dr d
## # $# $
)) 5 )))))
''
S
†''
00
21
sin cos cos sin d sin sinœœœ
'0
2ˆ‰‘
""""
#$#
#
#
!
2262
1
)) )) ) ) ) ) 1
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 16.6 Surface Integrals 977
27. Let the parametrization be (r ) (r cos ) (r sin ) r , 1 r 2 (since 1 z 2) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r d d dr r cos r sin r d drœÊœ ‚œ)) 5 ) )))ijkFnFrr††
rr
rr
‚
‚
## ## $
r
r
kk
kk a b
)r
r r d dr since ( r cos ) (r sin ) r d r r dr dœ œ Ê œ œab ab
#$ # #$
))) 5 )FijkFn
''
S
†''
01
22 73
6
1
28. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
#
(cos ) (sin ) 2r and ( r sin ) (r cos ) r sin r cos 0
cos sin 2r
Êœ œ Ê‚œ
r i jkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r d d dr 8r cos 8r sin 2r d drœÊœ ‚œabab kka b
## $# $#
‚
‚
)) 5 ) )))ijkFnFrr††
rr
rr
r
r
kk
)r
8r 2r d dr since (4r cos ) (4r sin ) 2 d 8r 2r dr d 2œ œ Ê œ œab ab
$ $
))) 5 )1FijkFn
''
S
†''
00
21
29. g(x y z) z, g g 1 and g 1 Flux d ( ) dAßß œ œ Ê œ Ê œ œ Ê œ œp k k p Fn Fk™™ ™† † †kk k k '' ''
SR
5
3 dy dx 18œœ
''
00
23
30. g(x y z) y, g g 1 and g 1 Flux d ( ) dAßß œ œ Ê œ Ê œ œ Ê œ œ pj j p Fn Fj™™ ™† † †kk k k '' ''
SR
5
2 dz dx 2(7 2) dx 10(2 1) 30œœœœ
'' '
12 1
27 2
31. g 2x 2y 2z g 4x 4y 4z 2a; ;™™ †œ Ê œ œ œ œ Ê œijk n Fnkk
È###
#
2x 2y 2z x y z
xyz aa
z
ijk ijk
È
g 2z d dA Flux dA z dA a x y dx dykk ab
Š‹
ˆ‰ È
™†kœÊ œ Ê œ œ œ 52a z a
2z a z
'' '' ''
RRR
###
a r r dr dœœ
''
00
2a
È## )1a
6
32. g 2x 2y 2z g 4x 4y 4z 2a; ™™ †œ Ê œ œ œ œ Ê œ ijk n Fnkk
È###
#
2x 2y 2z x y z xy xy
xyz aaa
ijk ijk
È
0; g 2z d dA Flux d 0 d 0œœÊœÊœ œœkk™† †kFn555
2a
2z '' ''
SS
33. From Exercise 31, and d dA Flux dAnFnœœÊœœÊœ
xyz xy xy
az aaaa az
azzza
ijk 5†''
Rˆ‰ˆ‰
1 dAœœ
''
R
1a
4
34. From Exercise 31, and d dA z aznFnœœÊœœœ
xyz zy xyz
az aaaa
azxz
ijk
5†Š‹
Flux (za) dx dy a dx dy a (Area of R) aÊœ œ œ œ
'' ''
RR
ˆ‰
a
z4
## %
"1
35. From Exercise 31, and d dA a FluxnFnœœÊœœÊ
xyz y
az aaa
axz
ijk 5†
a dA dA dA r dr dœœœ œ
'' '' ''
RRR
ˆ‰
aa a a
zz
axy ar
ÈÈ
ab
''
00
2a
)
aar dœœ
'0
2a
###
!#
’“
È)1a
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

978 Chapter 16 Integration in Vector Fields
36. From Exercise 31, and d dA 1nFnœœÊœœœ
xyz
az a
a
xyz
ijk
5†Š‹ Š‹
Œ
ÈŠ‹
xz
aaa
ya
a
Flux dx dy dx dy r dr dÊœ œ œ œ
'' ''
RR
aa aa
zaxy ar
ÈÈ
ab
#
''
00
2a
)1
37. g(x y z) y z 4 g 2y g 4y 1 ßß œ œ Ê œ Ê œ Ê œ
##
™™jk nkk
È2y
4y 1
jk
È
; g 1 d 4y 1 dA FluxÊœ œÊ œÊœ ÊFn p k p†™†
2xy 3z
4y 1
#
Èkk È
5
4y 1 dA (2xy 3z) dA; z 0 and z 4 y y 4œœœœÊœ
''
RR
Š‹
È''
2xy 3z
4y 1
###
È
Flux 2xy 3 4 y dA 2xy 12 3y dy dx xy 12y y dxÊœ œ œ
''
Rcdabcdab
###$
#
#
'' '
02 0
12 1
32 dx 32œ œ
'0
1
38. g(x y z) x y z 0 g 2x 2y g 4x 4y 1 4 x y 1ßßœœÊ œÊ œ œ
## ## ##
™™ijkkk a b
ÈÈ
; g 1 d 4 x y 1 dAÊœ Ê œ œÊ œÊ œ nFnpkp
2x 2y 8x 8y 2
4x y 1 4x y 1
ijk
##
ÈÈ
ab ab
†™†kk ab
È
5
Flux 4 x y 1 dA 8x 8y 2 dA; z 1 and x y zÊœ œ œ œ
'' ''
RR
Š‹
Èab a b
8x 8y 2
4x y 1
## ## ##
Èab
x y 1 Flux 8r 2 r dr d 2ÊœÊ œ œ
## #
''
00
21
ab)1
39. g(x y z) y e 0 g e g e 1 ; ßß œ œ Ê œ Ê œ Ê œ Ê œ œ
xx 2x e2e2y
e1 e1
™™ †ij n Fn p ikk
Èxx
2x 2x
ij
ÈÈ
g e d dA Flux dA dAʜʜ Êœ œkk Š‹Š‹
™†pxe1 e 1
eee
2e 2y
e1
2e 2e
5ÈÈ
È
2x 2x
xxx
x
2x
xx
'' ''
RR
4 dA 4 dy dz 4œ œ œ
''
R''
01
12
40. g(x y z) y ln x 0 g g 1 since 1 x eßß œ œ Ê œ Ê œ œ Ÿ Ÿ™™
""
xxx
1x
ij kk
ÉÈ
; g 1 d dAÊœ œ Ê œ œÊ œÊ œnFnpjp
Š‹
Œ
ÈÈ È
x
1x
x
ij ij
x 2xy 1 x
1x 1x x
†™†kk 5
Flux dA 2y dx dz 2 ln x dz dx 2 ln x dxÊœ œ œ œ
''
RŠ‹Š‹
2xy 1 x
1x x
ÈÈ
'' '' '
01 10 1
1e e1 e
2 x ln x x 2(e e) 2(0 1) 2œ œœcd
e
"
41. On the face z a: g(x y z) z g g 1; 2xz 2ax since z a;œßßœÊœÊ œœÊœœ œ™™ †knkFnkk
d dx dy Flux 2ax dx dy 2ax dx dy a .5œÊœ œ œ
''
R''
00
aa %
On the face z 0: g(x y z) z g g 1; 2xz 0 since z 0;œßßœÊœÊ œœÊœœ œ™™ †knkFnkk
d dx dy Flux 0 dx dy 0.5œÊœ œ
''
R
On the face x a: g(x y z) x g g 1; 2xy 2ay since x a;œßßœÊœÊ œœÊœœ œ™™ †iniFnkk
d dy dz Flux 2ay dy dz a .5œÊœ œ
''
00
aa %
On the face x 0: g(x y z) x g g 1; 2xy 0 since x 0œßßœÊœÊ œœÊœœ œ™™ †iniFnkk
Flux 0.ʜ
On the face y a: g(x y z) y g g 1; 2yz 2az since y a;œßßœÊœÊ œœÊœœ œ™™ †jnjFnkk
d dz dx Flux 2az dz dx a .5œÊœ œ
''
00
aa %
On the face y 0: g(x y z) y g g 1; 2yz 0 since y 0œßßœÊœÊ œœÊœœ œ™™ †jnjFnkk
Flux 0. Therefore, Total Flux 3a .Êœ œ
%
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.6 Surface Integrals 979
42. Across the cap: g(x y z) x y z 25 g 2x 2y 2z g 4x 4y 4z 10ßßœœ Ê œ Ê œ œ
### ###
™™ijkkk
È
; g 2z since z 0 d dAÊœ œ Ê œ œÊ œ Ê œnFnpkp
™
™
g
g5 555 2z
xyz yz
xz z 10
kk ijk †™†kk 5
Flux d dA x y 1 dx dy r 1 r dr dÊœ œ œ œ
cap 00
24
'' '' ''
cap RR
Fn†5 )
Š‹
ˆ‰ ab ab
xz z 5
555z
yz ## #
''
72 d 144 .œœ
'0
2
)1
Across the bottom: g(x y z) z 3 g g 1 1; g 1ßß œ œ Ê œ Ê œ Ê œ Ê œ œ Ê œ™™ † ™†knkFnpkpkk k k
d dA Flux d 1 dA 1(Area of the circular region) 16 . Therefore,Ê œ Ê œ œ œ œ55 1
bottom '' ''
bottom R
Fn†
Flux Flux Flux 128œ œ
cap bottom 1
43. f 2x 2y 2z f 4x 4y 4z 2a; f 2z since z 0 d dA™™ ™†œ Ê œ œ œÊ œ Êœijk pk pkk k k
È### 52a
2z
dA; M d (surface area of sphere) ; M z d z dA a dAœœ œ œ œ œ œ
aaa
z8 z
xy
'' '' ''
SS
RR
$5 $5 $ $
$$1
#ˆ‰ ''
a r dr d z . Because of symmetry, x y the centroid isœœÊœœœ œœÊ$)
''
00
2a $1 $1
$1
aa2a a
4M4a 2
Mxy Š‹
ˆ‰#
.
ˆ‰
aaa
###
ßß
44. f 2y 2z f 4y 4z 4 y z 6; f 2z since z 0 d dA™™ ™†œ Ê œ œ œ œÊ œ Êœjk pk kkk a b k k
ÈÈ
## ## 56
2z
dA; M 1 d dx dy dx dy 9 ; M z d z dx dy 54;œœ œ œ œœœ œ
333 3
zz z
9y xy
'' ''
S S
515
'' '' ''
30 30 30
33 33 33
Ȉ‰
M y d y dx dy dx dy 0; M x d dx dy .
xz yz
33x 27
z
3y
9y 9y
œœ œ œœœ œ
'' ''
S S
551
'' '' ''
30 30 30
33 33 33
ˆ‰ ÈÈ
#
Therefore, x , y 0, and zœœœ œœ
Š‹
27 1
11199
3546
#
45. Because of symmetry, x y 0; M d d (Area of S) 3 2 ; f 2x 2y 2zœœœœœ œ œ
'' ''
SS
$5 $ 5 $ 1 $
șijk
f 4x4y4z 2xyz; f 2z d dAÊ œ œ œÊ œÊœkk k k
ÈÈ
™™†
### ###
#
pk p 52xyz
z
È
dA dA M z dA 2 x y dAœœÊœ œ
ÈÈ È
ab ÈÈ
xy xy
zz z
2x y 2x y
xy
##
$$
'' ''
RR
Š‹ ÈÈ
2 r dr d z x y z 0 0 . Next, I x y dœœÊœœÊßßœßßœ$)$ $5
''
01
22
Èab a b
ˆ‰
###
14 2
399
32
14 14 z
1$
1$
Ȍ
È
14 2
3''
S
x y dA 2 x y dA 2 r dr d Rœ œ œ œ Êœœ
'' ''
RR
ab ab
Š‹ÈÈ É
## ## $
##
ÈÈÈÈ
2x y
z M
15 2 I10
$$ $ ) $
''
01
22
z
1z
46. f(x y z) 4x 4y z 0 f 8x 8y 2z f 64x 64y 4zßßœ œÊ œ Ê œ
### ###
™™ijkkk
È
2 16x 16y z 2 4z z 2 5 z since z 0; f 2z d dA 5 dAœ œ œ œÊ œ Ê œ œ
ÈÈÈÈ
kk
### ## pk p™† 525z
2z
È
I x y d 5 x y dx dy 5 r dr dÊœ œ œ œ
z35
'' ''
SR
ab ab
ÈÈ
## ## $
#
$5 $ $ )
''
20
22cos È1$
47. (a) Let the diameter lie on the z-axis and let f(x y z) x y z a , z 0 be the upper hemisphereßßœœ
####
f 2x 2y 2z f 4x 4y 4z 2a, a 0; f 2z since z 0Ê œ Ê œ œ œÊ œ ™™ ™†ijk pk pkk k k
È###
d dA I x y d a dA a r dr dÊœ Êœ œ œ5$5$ $)
aa r
zz
xy
axy ar
z00
2a
'' ab
ˆ‰
SR
##
''ÈÈ
ab ''
a r a r a r d a a d a the moment of inertia is a forœ œ œÊ$)$)$$
''
0 0
2 2
a
’“
Èab
### $% %
## $Î#
!
224 8
333 3
11
the whole sphere
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

980 Chapter 16 Integration in Vector Fields
(b) I I mh , where m is the mass of the body and h is the distance between the parallel lines; now,
Lc.m.
œ
#
I a (from part a) and d dA a dy dx
c.m. 8ma
3z
axy
œœœœ
1%
#
"
$$5$$
'' '' ''
SRR
ˆ‰ Èab
a r dr d a a r d a a d 2 a and h aœœœœœ$)$ )$)1$
'' ' '
00 0 0
2a 2 2
a
"
##
!
#
Èar ’“
È
Ia4aa aÊœ œ
L820
33
11
%##%
$1$ $
48. Let z x y be the cone from z 0 to z h, h 0. Because of symmetry, x 0 and y 0;œ œœ œ œ
h
aÈ##
z x y f(x y z) x y z 0 f 2zœ Êßßœ œÊœ
h h 2xh
aa aa
2yh
Èab
## ## # ™ijk
f 4z 2 xy xy 2 xy 1Êœ œ œ kk abab ab
ÉÉÉ
ˆ‰ ˆ ‰
™4x h h h h h
aa a
4y h
aaa
##### ##
2 z h a since z 0; f 2z d dAœœœÊœÊœ
Ɉ‰ˆ‰
Èkk
###
ha 2z
aa 2z
ha
pk p™† 5ˆ‰
È
2z
a
dA; M d dA a a h a ;œœœ œœ
ÈÈÈ
ha ha ha
aaa
###
'' ''
SR
511ab È
M z d z dA x y dx dy r dr d
xy 00
2a
œœ œ œ
'' '' ''
SRR
5 )
Š‹ È
ÈÈ È
ha ha hha
aaa a
h
## #
''
z the centroid is 0 0œÊœœÊ ßß
2ah h a
3M3 3
M2h 2h
1Èxy ˆ‰
16.7 STOKES' THEOREM
1. curl 0 0 (2 0) 2 and curl 2 d dx dy
x2xz
FF ijkknkFn
ijk
œ ‚œ œ œ œÊ œÊ œ™†
ââ
ââ
ââ
ââ
ââ
ââ
```
```
##
xyz 5
d 2 dA 2(Area of the ellipse) 4Êœ œ œ
)CFr†''
R
1
2. curl 0 0 (3 2) and curl 1 d dx dy
2y 3x z
F F i j kk nk Fn
ij k
œ ‚œ œ œ œÊ œÊ œ
™†
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
#
xy z 5
d dx dy Area of circle 9Êœ œ œ
)CFr†''
R
1
3. curl x 2x (z 1) and curl
yxzx
FF ijkn Fn
ijk
œ‚œ œ œ Ê™†
ââ
ââ
ââ
ââ
ââ
ââ
```
```
#
xyz 3
ijk
È
( x 2x z 1) d dA d ( 3x z 1) 3 dAœÊœ Ê œ
" "
È È
È
3 3
3
1
5)CFr†''
RÈ
[ 3x (1 x y) 1] dy dx ( 4x y) dy dx 4x(1 x) (1 x) dxœ œ œ
'' '' '
00 00 0
11x 11x 1‘
"
#
#
3x x dxœ œ
'0
1ˆ‰
"
##
#
75
6
4. curl (2y 2z) (2z 2x) (2x 2y) and
yzxzxy
FF i j kn
ijk
œ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
######
xyz 3
ijk
È
curl (2y 2z 2z 2x 2x 2y) 0 d 0 d 0Ê œ œÊ œ œFn F r††
"
È3)C''
S
5
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.7 Stoke's Theorem 981
5. curl 2y (2z 2x) (2x 2y) and
yzxyxy
FF i j knk
ijk
œ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
######
xyz
curl 2x 2y d dx dy d (2x 2y) dx dy x 2xy dyʜʜʜ œFn F r††5)'' '
C11 1
11 1
cd
#"
"
4y dy 0œ œ
'1
1
6. curl 0 0 3x y and
xy 1 z
FF ijkn
ijk
œ ‚œ œ œ œ™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
#$
##
xyz
2x 2y 2z x y z
2xyz 4
ijk ijk
È
curl x y z; d dA (Section 16.6, Example 6, with a 4) d x y z dAÊœ œ œÊœFn F r††
34 34
4z 4z
## ##
5)C''
Rˆ‰ˆ‰
3 r cos r sin r dr d 3 (cos sin ) d 32 sin 2 d 4 sin u duœ œ œ œ
'' ' ' '
00 0 0 0
22 2 2 4
abab ’“
## ## # # #
#
!
"
))) ))) ))
r
64
48œ œ
‘
usin 2u
24
%
!
11
7. x 3 cos t and y 2 sin t (2 sin t) 9 cos t 9 cos t 16 sin t sin e at theœœÊœFi j kaba b
##%6 sin t cos t 0
base of the shell; (3 cos t) (2 sin t) d ( 3 sin t) (2 cos t) 6 sin t 18 cos trijr ijFœ Êœ Êœ†d
dt
r#$
d 6 sin t 18 cos t dt 3t sin 2t 6(sin t) cos t 2 6Ê‚œ œ œ
''
S
™†Fn5 1
'0
2ab ab
‘
#$ #
#
!
3
2
1
8. curl 2 ; f(x y z) 4x y z f 8x 2z
ztanyx
FF j ijk
ijk
œ‚œ œ ßßœÊ œ
™ ™
ââ
ââ
ââ
ââ
ââ
ââ
ââ
```
```
""
#
"
##
xyz
x4z
and f 1 d dA f dA; ( 2 f)Êœ œÊ œÊ œ œ ‚ œ œnpjp Fnj
™
™™†™™
™
f
ffff
f2
kk k k kk kk
kk
kk kk™† ™ ™ † †™5p
"
d 2 dA d 2 dA 2(Area of R) 2( 1 2) 4 , where RÊ ‚ œ Ê ‚ œ œ œ œ™† ™† ††Fn Fn55 11
'' ''
SR
is the elliptic region in the xz-plane enclosed by 4x z 4.
##
œ
9. Flux of d d , so let C be parametrized by (a cos t) (a sin t) ,™™† †‚œ ‚ œ œ FFnFr rij
''
S
5)C
0 t 2 ( a sin t) (a cos t) ay sin t ax cos t a sin t a cos t aŸŸ Ê œ Ê œ œ œ1dd
dt dt
rr
ijF†## # # #
Flux of d a dt 2 aÊ‚œœœ™†FFr
)'
C0
2##
1
10. (y ) ; x y z
y00
™‚ œ œ œ œ œikn ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```
xyz
f
f
2x 2y 2z
2xyz
™
™kk È
ijk
(y ) z; d dA (Section 16.6, Example 6, with a 1) (y ) dÊ‚ œ œ œÊ ‚™† ™†in in55
"
z''
S
( z) dA dA , where R is the disk x y 1 in the xy-plane.œ œ œ Ÿ
'' ''
RR
ˆ‰
"##
z1
11. Let S and S be oriented surfaces that span C and that induce the same positive direction on C. Then
"#
d d d
'' ''
SS
™† † ™†‚œœ‚Fn F r Fn
"" ##
55
)C
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
982 Chapter 16 Integration in Vector Fields
12. d d d , and since S and S are joined by the simple
'' '' ''
SSS
™† ™† ™†‚œ‚‚Fn Fn Fn555
"#
closed curve C, each of the above integrals will be equal to a circulation integral on C. But for one surface
the circulation will be counterclockwise, and for the other surface the circulation will be clockwise. Since the
integrands are the same, the sum will be 0 d 0.Ê‚œ
''
S
™†Fn5
13. 5 2 3 ; (cos ) (sin ) 2r and ( r sin ) (r cos )
2z 3x 5y
™‚œ œ œ œ Fijkrijkrij
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```xyz r)) ) )
)
2r cos 2r sin r ; and d dr d
cos sin 2r
r sin r cos 0
Ê‚œ œ œ œ‚
rr i jkn rr
ijk
r r) )
ââ
ââ
ââ
ââ
ââ
ââ
abab kk
))
))
)) 5 )
## ‚
‚
rr
rr
r
r
kk
d ( ) ( ) dr d 10r cos 4r sin 3r dr d dÊ‚ œ‚ ‚ œ Ê ‚™† ™ † ™†Fn F r r Fn5))))5
r)ab
## ''
S
10r cos 4r sin 3r dr d r cos r sin r dœœ
'' '
00 0
22 2
ab
‘
## $ $ #
"
#
#
!
))) ) ) )
043
33
cos sin 6 d 6(2 ) 12œœœ
'0
2ˆ‰
80 32
33
)))11
14. 2 2 ; 2r cos 2r sin r and
yzzxxz
™‚œ œ ‚ œ
Fijkrrijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ abab
```
``` ##
xyz r)))
d ( ) ( ) dr d (see Exercise 13 above) d™† ™ † ™†‚œ‚‚ Ê‚Fn F r r Fn5) 5
r)''
S
2r cos 4r sin 2r dr d r cos r sin r dœ œ
'' '
00 0
23 2
ab
‘
## $ $#
$
!
))) ) ))
24
33
18 cos 36 sin 9 d 9(2 ) 18œ œ œ
'0
2ab)))11
15. 2y 0 x ;
x y 2y z 3z
cos sin 1
r sin r cos 0
™‚œ œ ‚ œ
Fijkrr
ijk ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
```
```
#$
$#
xyz r)))
))
( r cos ) (r sin ) r and d ( ) ( ) dr d (see Exercise 13 above)œ ‚ œ ‚ ‚)) 5 )ijkFn Frr™† ™ †
r)
d 2ry cos rx dr d 2r sin cos r cos dr dÊ‚œ œ
'' ''
SR
™†Fn5)) ))))aba b
$# % $#
''
00
21 3
sin cos cos d sinœœœ
'0
2ˆ‰‘ˆ‰
2sin 2
5410444
34
)) )) )
"""
#
#
#
!
)) 1
1
16. ;
xyyzzx
cos sin 1
r sin r cos 0
™‚ œ œ ‚ œ
Fijkrr
ijk ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
```
```xyz r)))
))
(r cos ) (r sin ) r and d ( ) ( ) dr d (see Exercise 13 above)œ ‚œ‚‚)) 5 )ijkFn Frr™† ™ †
r)
d (r cos r sin r) dr d (cos sin 1) d (2 ) 25Ê‚œ œ œ œ
''
S
™†Fn5))))))11
'' '
00 0
25 2
’“
ˆ‰
r25
##
&
!
17. 0 0 5 ;
3y 5 2x z 2
3 cos cos 3 cos sin 3 sin
3 sin sin
™‚œ œ ‚œ
Fijkrr
ij k ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ÈÈ È
ÈÈ
`` `
`` `
#
xy z 9) 9) 9) 9
9) 3 sin cos 09)
3 sin cos 3 sin sin (3 sin cos ) ; d ( ) ( ) d d (see Exerciseœ ‚œ‚‚abab
##
9) 9) 99 5 9)ijkFnFrr™† ™ †
9)
13 above) d 15 cos sin d d cos d d 15Ê‚œ œ œœ
''
S
™†Fn5999)9))1
'' ' '
00 0 0
2/2 2 2
‘
15 15
2#Î#
!#
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.7 Stoke's Theorem 983
18. 2z 2y ;
yz x
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin
™‚œ œ ‚ œ
Fijkrr
ijk ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
```
```
##
xyz 9) 9) 9) 9
9) 9cos 0)
4 sin cos 4 sin sin (4 sin cos ) ; d ( ) ( ) d d (see Exerciseœ ‚œ‚‚abab
##
9) 9) 99 5 9)ijkFnFrr™† ™ †
9)
13 above) d 8z sin cos 4 sin sin 8y sin cos d dÊ‚œ
'' ''
SR
™†Fn59)9)9)9)ab
##
16 sin cos cos 4 sin sin 16 sin sin cos d dœ
''
00
2/2
ab
###
9 9 ) 9) 9) )9)
sin cos 4 (sin ) 16 (sin cos ) dœ
'0
2‘ˆ‰ ˆ‰
"$
##
Î#
!
6
344
sin 2 sin 2
9) ) )) )
99 99 1
cos sin 4 sin cos d sin cos 2 sin 0œ œ œ
'0
2ˆ‰‘
16 6
33
)1 ) 1 ) )) )1 ) 1 )
"##
!
1
19. (a) 2x 2y 2z curl d d 0 d 0Fijk F0 Fr Fnœ Ê œÊ œ ‚ œ œ
)C†™†
'' ''
SS
55
(b) Let f(x y z) x y z f curl d d 0 dßß œ Ê ‚ œ ‚ œ Ê œ Ê œ ‚ œ
##$ ™™™ † ™†F0F0FrFn
)C'' ''
SS
55
0œ
(c) (x y z ) d d 0 d 0Fijk0F0Fr Fnœ‚œÊ ‚œÊ œ ‚ œ œ™™†™†
)C'' ''
SS
55
(d) f f d d 0 d 0FF0FrFnœÊ‚œ‚œÊ œ ‚ œ œ™™ ™™ † ™†
)C'' ''
SS
55
20. f x y z (2x) x y z (2y) x y z (2z)Fijkœœ ™"""
###
### ### ###
$Î# $Î# $Î#
ab ab ab
xxyz yxyz zxyzœ ababab
### ### ###
$Î# $Î# $Î#
ijk
(a) (a cos t) (a sin t) , 0 t 2 ( a sin t) (a cos t)rij ijœ ŸŸÊœ1d
dt
r
xxyz (a sin t)yxyz (a cos t)Êœ F†d
dt
rab ab
### ###
$Î# $Î#
( a sin t) (a cos t) 0 d 0œ œ Ê œ
ˆ‰ ˆ‰
a cos t a sin t
aa )CFr†
(b) d d f d d 0 d 0
)CFr Fn n 0n†™† ™™† †œ‚ œ‚ œ œ œ
'' '' '' ''
SS SS
5555
21. Let 2y 3z x 3 2 ;
2y 3z x
F i jk F ijkn
ijk
œÊ ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
xy z
22
3
ijk
2 2y dx 3z dy x dz d d 2 dÊ™ † † ™ † Fn F r Fn‚œÊ œ œ ‚ œ
))
CC
'' ''
SS
55
2 d , where d is the area of the region enclosed by C on the plane S: 2x 2y z 2œ œ
'' ''
SS
55
22. 0
xyz
™‚œ œF
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```xyz
23. Suppose M N P exists such that Fijk F i j kœ ‚œ ™Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` `
PN MP NM
yz zx x y
x y z . Then (x) 1. Likewise, (y)œ œ Ê œ œijk `` ` ` ` ` `` ` `
` ` ` ` `` `` ` ` ` `x y z x xy xz y z x y
PN P N MP
Š‹ ˆ‰
1 and (z) 1. Summing the calculated equationsÊœ œ Êœ
`` ``` ` ``
`` `` ` ` ` ` `` ``
MP NM NM
yz yx z x y z zx zy
Š‹
3 or 0 3 (assuming the second mixed partials areÊ œœ
Š‹Š‹Š‹
`` `` ``
`` `` `` `` `` ``
PP NN MM
xy yx zx xz yz zy
equal). This result is a contradiction, so there is no field such that curl x y z .FFijkœ
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

984 Chapter 16 Integration in Vector Fields
24. Yes: If , then the circulation of around the boundary C of any oriented surface S in the domain of™‚œF0 F
is zero. The reason is this: By Stokes's theorem, circulation d d d 0.FFrFn0nœœ‚œ œ
)C†™† †
'' ''
SS
55
25. r x y r x y r 4x x y 4y x y M NœÊœÊœ œ œ
Èab ababab
## % ## % ## ##
#Fijij™
r ds ds M dy N dx dx dyÊœœœ
)))
CCC
™† †ab Š‹
%``
``
nFn ''
R
MN
xy
4 x y 8x 4 x y 8y dA 16 x y dA 16 x dA 16 y dAœœ œ
'' cdabab ab
RRRR
## # ## # ## # #
'' '' ''
16I 16I .œ
yx
26. 0, 0, 0, 0, , curl .
`` ` `` `
`` ``` `
PNMPN M
yz zxx y
yx yx yx yx
xy xy xy xy
œœœœœ œ Ê œ œ
ab ab abab
Fk0
’“
However, x y 1 (cos t) (sin t) ( sin t) (cos t)
##
œÊœ Ê œ rij ij
d
dt
r
sin t cos t sin t cos t 1 d 1 dt 2 which is not zero.Êœ Ê œ œÊ œ œFijF Frabab ††
d
dt
r## ))
C1
16.8 THE DIVERGENCE THEOREM AND A UNIFIED THEORY
1. div 0 2. x y div 1 1 2FF FijFœ Ê œ œ œ Ê œœ
y x xy xy
xy xy
ij
Èab
3. div GMFFœ Ê œ
GM(x y z )
xyz
xyz 3xxyz
xyz
ijk
ab abab
ab
”•
GM GM
”•”•
abab abab
ab ab
xyz 3yxyz xyz 3zxyz
xyz xyz
GM 0œ œ
’“
3xyz 3xyz xyz
xyz
ababab
ab
4. z a r in cylindrical coordinates z a x y a x y div 0œ Êœ Êœ Ê œ
## # ## ###
ab a bvkv
5. (y x) 1, (z y) 1, (y x) 0 2 Flux 2 dx dy dz 2 2 16
```
```
$
xyz
œ œ œ Ê œ Ê œ œ œ™†F'''
111
111 ab
6. x 2x, y 2y, z 2z 2x 2y 2z
```
```
###
xyx
ab ab abœœœÊœ™†F
(a) Flux (2x 2y 2z) dx dy dz x 2x(y z) dy dz (1 2y 2z) dy dzœœœ
''' '' ''
000 00 00
111 11 11
cd
#"
!
y(1 2z) y dz (2 2z) dz 2z z 3œœœœ
''
00
11
cd cd
##
""
!!
(b) Flux (2x 2y 2z) dx dy dz x 2x(y z) dy dz (4y 4z) dy dzœœœ
''' '' ''
111 11 11
111 11 11
cd
#"
"
2y 4yz dz 8z dz 4z 0œ œ œœ
''
11
11
cd cd
##
""
" "
(c) In cylindrical coordinates, Flux (2x 2y 2z) dx dy dzœ
'''
D
(2r cos 2r sin 2z) r dr d dz r cos r sin zr d dzœœ
''' ''
000 00
122 12
)) ) ) ) )
‘
22
33
$$#
#
!
cos sin 4z d dz sin cos 4z dz 8 z dz 4 z 4œœœœœ
'' ' '
00 0 0
12 1 1
ˆ‰ ‘
cd
16 16 6 16
33 33
))) ) )) 111
"#
!
#"
!
1
7. (y) 0, (xy) x, ( z) 1 x 1; z x y z r in cylindrical coordinates
`` `
`` `
## #
xy z
œœœÊœœÊœ™†F
Flux (x 1) dz dy dx (r cos 1) dz r dr d r cos r r dr dÊœ œ œ
'''
D''' ''
000 00
22r 22
)) ))ab
$#
cos d cos 4 d sin 4 8œœ œœ
''
00
22
’“ˆ‰‘
r r 32 32
54 5 5
)) )) )) 1
#
!
#
!
1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
Section 16.8 The Divergence Theorem and a Unified Theory 985
8. x 2x, (xz) 0, (3z) 3 2x 3 Flux (2x 3) dV
```
```
#
xyz
abœœœÊœÊœ™†F'''
D
(2 sin cos 3) sin d d d sin cos sin d dœœ
''' ''
000 00
22 2
3 9 ) 3 9 39) 9 ) 3 99)ab ’“
#$
#
!
3
2
(8 sin cos 8) sin d d 8 cos 8 cos d (4 cos 16) d 32œœœœ
'' ' '
00 0 0
22 2
9) 99) ) 9) 1) ) 1
‘ˆ‰
99 1
24
sin 2
!
9. x 2x, ( 2xy) 2x, (3xz) 3x Flux 3x dx dy dz
`` `
`` `
#
xy z
abœœ œÊœ
'''
D
(3 sin cos ) sin d d d 12 sin cos d d 3 cos d 3œœœœ
''' '' '
000 00 0
222 22 2
3 9 ) 3 9 39) 9 )9) 1 )) 1ab
##
10. 6x 2xy 12x 2y, 2y x z 2, 4x y 0 12x 2y 2
```
```
###$
xyz
ab ababœ œ œÊ œ™†F
Flux (12x 2y 2) dV (12r cos 2r sin 2) r dr d dzÊœ œ
'''
D'' '
00 0
322
)) )
32 cos sin 4 d dz 32 2 dz 112 6œœœ
'' '
00 0
32 3
ˆ‰ˆ‰
))) 1 1
16 16
33
11. (2xz) 2z, ( xy) x, z 2z x Flux x dV
`` `
`` `
#
xy z
œ œ œ Ê œ Ê œ ab ™†F'''
D
x dz dy dx (xy 4x) dy dx x 16 4x 4x 16 4x dxœœœ
'' ' ' ' '
00 0 0 0 0
2 16 4x 4 y 2 16 4x 2’“
ab
È
1
2##
4x x 16 4xœ œ
’“
ab
#% #
"" $Î# #
!
23 3
40
12. x 3x , y 3y , z 3z 3x 3y 3z Flux 3 x y z dV
```
```
$#$#$# ### ###
xyz
ab ab ab a b
'''
œœœÊœÊœ™†F
D
3 sin d d d 3 sin d d 3 dœœœœ
''' '' '
000 00 0
2a 2 2
33 9 39) 99) )
##
ab a2a12a
555
1
13. Let x y z . Then , , ( x) x , ( y) y333333œ œœœÊ œ œ œ
ÈŠ‹ Š‹
### ``` ` `
``` ` ` ` `
``
333 3 3
333 3xyz x x y y
xz x
y
, ( z) z 3 4 , since x y zœ œ œÊ œ œ œ
y xyz
zz
z
333
3
33 3 3 33 3
`
``
` ###
Š‹ È
™†F
Flux 4 dV (4 ) sin d d d 3 sin d d 6 d 12Êœ œ œ œ œ
'''
D
333939)99))1
''' '' '
001 00 0
22 2 2
ab
#
14. Let x y z . Then , , . Similarly,3œ œœœÊ œ œ
ÈŠ‹ Š‹
### ``` `
``` ` `
`"
333 3
333 333 33xyz x x
xzxx1x
y
and
`" `"
``
yz
y y xyz
zz 3 2
Š‹ Š‹
333 333 3 3 3
œ œ Ê œ œ™†F
Flux dV sin d d d 3 sin d d 6 d 12Êœ œ œ œ œ
'''
D
22
33
''' '' '
001 00 0
22 2 2
Š‹
ab3939) 99) ) 1
#
15. 5x 12xy 15x 12y , y e sin z 3y e sin z, 5z e cos z 15z e sin z
`` `
`` `
$###$ # $ #
xy z
yy y y
ab ab a bœ œ œ
15x 15y 15z 15 Flux 15 dV 15 sin d d dÊ œœ Ê œ œ™†F### # # ##
33 33939)
'''
D'''
001
22
aba b
12 2 3 sin d d 24 2 6 d 48 2 12œœœ
'' '
00 0
22
Š‹ Š‹Š ‹
ÈÈÈ
99) ) 1
16. ln x y , tan , z x y x y
`` `
`` `
## "
## ##
xxyyxxx xyz
2x 2z 2z 2z
y
1
cdab ˆ‰ˆ‰ ˆ‰
–— ÈÈ
œ œ œ œ
Š‹
ˆ‰
x
y
x
x y Flux x y dz dy dxʜʜ ™†F2x 2z 2x 2z
xy xy xy xy
## ##
ÈÈ
Š‹
'''
D
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

986 Chapter 16 Integration in Vector Fields
r dz r dr d 6 cos 3r dr dœœ
'' ' ''
01 1 0 1
222 2 2
ˆ‰ ˆ ‰
2r cos 2z 3
rr r
))))
#
6 21 cos 3 ln 2221 d 2 ln 2221œœ
'0
2’“Š‹Š‹
ÈÈÈ È
))1
3
#
17. (a) M N P curl Gijk G G i k k Gœ Ê ‚œ œ Ê ‚™ ™†™
Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` `
PN MP NM
yz zx x y
div(curl )œœG`` ` `` ` `` `
`` ` `` ` `` `xy z yz x zx y
PN MP NM
Š‹ Š‹
ˆ‰
0 if all first and second partial derivatives are continuousœœ
``` ```
`` `` `` `` `` ``
PNMPNM
xy xz yz yx zx zy
(b) By the Divergence Theorem, the outward flux of across a closed surface is zero because™‚G
outward flux of ( ) d™™†‚œ ‚GGn
''
S
5
dV [Divergence Theorem with ]œ‚ œ‚
'''
D
™†™ ™GFG
(0) dV 0 [by part (a)]œœ
'''
D
18. (a) Let M N P and M N P a bFijkFijkFF
"""" #### " #
œ œ Ê
(aM bM ) (aN bN ) (aP bP ) (a b )œ Ê
"# "# "# "#
ijkFF™†
a b a b a bœ
ˆ‰ ˆ‰
Š‹
`` `` ``
`` `` ``
MM NN PP
xx yy zz
aba()b()œœ
Š‹Š‹
``` ```
``` ``` "#
MNP MNP
xyz xyz ™† ™†FF
(b) Define and as in part a (a b )FF FF
"# "#
Ê‚™
ab ab a b abœ
’“Š‹
ˆ‰ ‘ˆ‰ˆ‰
`` ` ` ` ` ``
`` ` ` ` ` ``
PP NN MM PP
yy z z z z xx
ij
ab ab a œ
’“’ “
ˆ‰ ˆ‰
Š‹Š‹ Š‹
`` ` ` `` `` ``
`` ` ` `` `` ``
NN MM PN MP NM
xx y y yz zx xy
kijk
bab œ‚‚
’“Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` ` "#
PN MP NM
yz zx x y
ij kFF™™
(c) (N P P N ) (M P P M ) (M N N M ) ( )
MNP
MNP
FF i j k FF
ijk
" # "# " # "# " # " # " # " #
"""
###
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ ™†
[(N P P N ) (M P P M ) (M N N M ) ]œ™† "# " # "# " # " # " #
ij k
(N P P N ) (M P P M ) (M N N M ) P N N Pœ œ
`` `
`` ` ````
"# " # "# " # " # " # # " # "
````
xy z xxxx
NPPN
ˆ‰
MPPM MNNM
Š‹
ˆ‰
"#"# "#"#
`` ` ` ` ` ` `
`` ` ` ` ` ` `
PMMP NMMN
yy y y z z z z
MNP MNœ
### ""
`` ` ` `` `` ``
`` `` ` ` `` ` `
Š‹ Š‹Š‹
ˆ‰ ˆ‰
PN MP NM NP PM
yz zx x y zy xz
Pœ‚‚
"#""#
``
``
Š‹
MN
yx
FFFF†™ †™
19. (a) div(g ) g (gM) (gN) (gP) g M g N g PFFœœœ™† ``` ` ` `
``` ``````
```
xyz xxyyzz
MNP
ggg
Š‹Š‹Š‹
MNP g g gœœ
Š‹Š‹
```
``` ```
```
ggg
xyz xyz
MNP ™† ™ †FF
(b) (g ) (gP) (gN) (gM) (gP) (gN) (gM)™‚œ Fijk
’“ ’“
‘
`` ` ` ` `
`` ` ` ` `yz z x x y
PgNg Mg Pg Ng Mgœ
Š‹Š‹Š ‹
`` `` ` `
`` `` ` ` `` `` ` `
`` `` ` `
gg gg g g
yy z z z z xx xx y y
PN MP N M
ij k
PN gg MP g g NMœ
Š‹Š‹Š‹ Š‹
ˆ‰
`` `` ` `
`` `` `` `` ` `
`` ` `
gg gg g g
yz yz zx zx x y
PN MP
ii jj k
gg g g œ‚‚
Š‹
``
``
NM
xy
kFF™™
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Section 16.8 The Divergence Theorem and a Unified Theory 987
20. Let M N P and M N P .FijkFijk
"""" ####
œ œ
(a) (N P P N ) (P M M P ) (M N N M ) ( )FF i j k FF
" # "# " # " # "# " # " # " #
‚œ Ê ‚ ‚™
(M N N M ) (P M M P ) (N P P N ) (M N N M )œ
’“
‘
`` ``
`` ``
"# "# "# "# "# "# "# "#
yz zx
ij
(P M M P ) (N P P N )
’“
``
``
" # "# "# " #
xy
k
and consider the -component only: (M N N M ) (P M M P )i``
``
"# "# "# "#
yz
NMMN MP PMœ
#"#"#"#"
````````
````````
MNNMPMMP
yyyyzzzz
NP NP M Mœ
Š‹Š‹Š‹Š‹
## "" " #
`` ```` ``
`` ```` ``
MM MMNP NP
yz yzyz yz
MNP MNP Mœ
Š‹Š‹Š‹
### """ "
``` ``````
``` ``````
MMM MMMMNP
xyz xyzxyz
M . Now, -comp of ( ) M N P M œ
Š‹ Š ‹
```
``` ` ` `
##"###"
```
MNP
xyz x y z
iFF†™
M N P ; likewise, -comp of ( ) M N P ;œ œ
Š‹ Š‹
### "#"""
``` ```
``` ```
MMM MMM
xyz xyz
iFF†™
-comp of ( ) M and -comp of ( ) M .iFF iFF™† ™†
#" " "# #
``` ```
``` ```
œ œ
Š‹ Š‹
MNP MNP
xyz xyz
Similar results hold for the and components of ( ). In summary, since the correspondingjk FF™‚‚
"#
components are equal, we have the result
()()()()()™ †™†™™†™†‚‚œFFFFFF FF FF
"##""# #" "#
(b) Here again we consider only the -component of each expression. Thus, the -comp of ( )iiFF™†
"#
(MM NN PP) M M N N P Pœ œ
`
```````
"# "# "# " # " # " #
``````
xxxxxxx
MMNNPP
ˆ‰
-comp of ( ) M N P ,iFF
"#" " "
```
```
†™ œ
Š‹
MMM
xyz
-comp of ( ) M N P ,iFF
#"# # #
```
```
†™ œ
Š‹
MMM
xyz
-comp of ( ) N P , andiF F
"#" "
`` ` `
`` ``
‚‚œ ™Š‹
ˆ‰
NM MP
xy zx
-comp of ( ) N P .iF F
#"# #
`` ` `
`` ``
‚‚œ ™Š‹
ˆ‰
NM MP
xy zx
Since corresponding components are equal, we see that
( ) ( ) ( ) ( ) ( ), as claimed.™ † †™ †™ ™ ™FFFFFFF FF F
"#"##"" ## "
œ‚‚‚‚
21. The integral's value never exceeds the surface area of S. Since 1, we have (1)(1) 1 andkk k k kkkkFFnFnŸœŸœ†
d d [Divergence Theorem]
''' ''
DS
™† †FFn55œ
d [A property of integrals]Ÿ''
SkkFn†5
(1) d 1ŸŸ
''
S
5cdkkFn†
Area of S.œ
22. Yes, the outward flux through the top is 5. The reason is this: Since (x 2y (z 3) 1 2 1™† ™†Fijkœœ
0, the outward flux across the closed cubelike surface is 0 by the Divergence Theorem. The flux across the top isœ
therefore the negative of the flux across the sides and base. Routine calculations show that the sum of these latter fluxes is
5. (The flux across the sides that lie in the xz-plane and the yz-plane are 0, while the flux across the xy-plane is 3.)
Therefore the flux across the top is 5.
23. (a) (x) 1, (y) 1, (z) 1 3 Flux 3 dV 3 dV 3(Volume of the solid)
```
```xyz
œ œ œÊ œÊ œ œ œ™†F''' '''
DD
(b) If is orthogonal to at every point of S, then 0 everywhere Flux d 0. But the flux isF n Fn Fn††œÊœœ
''
S
5
3 (Volume of the solid) 0, so is not orthogonal to at every point.ÁFn
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

988 Chapter 16 Integration in Vector Fields
24. 2x 4y 6z 12 Flux ( 2x 4y 6z 12) dz dy dx ( 2x 4y 9) dy dx™†FœÊ œ œ
''' ''
000 0 0
ab1 a b
2xb 2b 9b dx a b 2ab 9ab ab( a 2b 9) f(a b); 2ab 2b 9b andœ œ œ œ ß œ
'0
aab
### #
`
`
f
a
a 4ab 9a so that 0 and 0 b( 2a 2b 9) 0 and a( a 4b 9) 0 b 0 or
```
```
#
fff
bab
œ œ œÊœ œÊœ
2a 2b 9 0, and a 0 or a 4b 9 0. Now b 0 or a 0 Flux 0; 2a 2b 9 0 and œ œ œ œ œÊ œ œ
a 4b 9 0 3a 9 0 a 3 b so that f 3 is the maximum flux. œÊ œÊœÊœ ß œ
3327
###
ˆ‰
25. d dV 3 dV d dV Volume of D
'' ''' ''' '' '''
SS
DD D
Fn F Fn†™† †55œœÊœœ
"
3
26. 0 Flux d dV 0 dV 0FC F Fn FœÊ œÊ œ œ œ œ™† † ™†
'' ''' '''
SDD
5
27. (a) From the Divergence Theorem, f d f dV f dV 0 dV 0
'' ''' ''' '''
SDDD
™ † ™†™ ™n5œœœœ
#
(b) From the Divergence Theorem, f f d f f dV. Now,
'' '''
SD
™† ™†™n5œ
ff f f f ff f f f™™†™œ Ê œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹ ’ “ Š‹ ’ “
”•
``` `` `` ``
``` `` `` ``
##
#
fff ff ff ff
xyz xx yy zz
ijk
f f f 0 f since f is harmonic f f d f dV, as claimed.œ œ Ê œ™™ ™ ™† ™
### #
kk kk kk
'' '''
SD
n5
28. From the Divergence Theorem, f d f dV dV. Now,
'' ''' '''
SDD
™ † ™†™n5œœ
Š‹
```
```
fff
xyz
f(x y z) ln x y z ln x y z , , ßßœ œ Ê œ œ œ
Èab
###
"```
#```
### fxf fz
x xyz y xyz z xyz
y
, , , Êœ œ œ Ê
``` ```
``` ```
fff fff
xyz xyz
x y z xyz xyz
xyz xyz xyzab ab ab
f d dddœœÊ œ œ
xyz
xyz xyz xyz
dV sin
"
ab '' '''
SD
™†n539)
'''
000
22a
39
3
a sin d d a cos d a dœœœœ
'' ' '
00 0 0
22 2 2
99) 9 ) )cd
11
Î#
!#
a
29. f g d f g dV f f f dV
'' ''' '''
SDD
™† ™†™ ™†nijk5œœ
Š‹
```
```
ggg
xyz
f f f dVœ
'''
DŠ‹
``````
``` ``` ```
```
gggggg
xxx yyy zzz
fff
f dV f g f g dVœœ
''' '''
D D
’“Š‹Š ‹ab
``` ` ` `
` ` ` ``````
``` #
ggg g g g
x y z xxyyzz
fff ™™†™
30. By Exercise 29, f g d f g f g dV and by interchanging the roles of f and g,
'' '''
SD
™† ™ ™†™n5œab
#
g f d g f g f dV. Subtracting the second equation from the first yields:
'' '''
SD
™† ™ ™ †™n5œab
#
f g g f d f g g f dV since f g g f
'' '''
SD
ab a b™™† ™ ™ ™†™™†™œ œÞn5##
31. (a) The integral p(t x y z) dV represents the mass of the fluid at any time t. The equation says that
'''
D
ßßß
the instantaneous rate of change of mass is flux of the fluid through the surface S enclosing the region D:
the mass decreases if the flux is outward (so the fluid flows out of D), and increases if the flow is inward
(interpreting as the outward pointing unit normal to the surface).n
(b) dV p dV p d p dV p
''' ''' '' '''
DD D
S
`
` `
`
p
tdt t
d
œœœ Êœvn v v†™† ™†53
Since the law is to hold for all regions D, p 0, as claimed™† vœ
`
`
p
t
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Practice Exercises 989
32. (a) T points in the direction of maximum change of the temperature, so if the solid is heating up at the™
point the temperature is greater in a region surrounding the point T points away from the pointÊ™
T points toward the point T points in the direction the heat flows.Ê Ê™™
(b) Assuming the Law of Conservation of Mass (Exercise 31) with k T p and c T p, we haveœ œ™v3
c T dV k T d the continuity equation, ( k T) (c T) 0
d
dt t
''' ''
DS
35 3œ Ê œ™† ™† ™n`
`
c ( k T) k T T K T, as claimedÊœ œ Êœ œ3``
``
###
TTk
ttc
™† ™ ™ ™ ™
3
CHAPTER 16 PRACTICE EXERCISES
1. Path 1: t t t x t, y t, z t, 0 t 1 f(g(t) h(t) k(t)) 3 3t and 1, 1,rijkœ Ê œ œ œ ŸŸ Ê ß ß œ œ œ
#dx
dt dt
dy
1 dt 3 dt f(x y z) ds 3 3 3t dt 2 3
dz dx dz
dt dt dt dt
dy
œÊ œ Ê ßß œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
ab
##
##
''
C0
1
Path 2: t t , 0 t 1 x t, y t, z 0 f(g(t) h(t) k(t)) 2t 3t 3 and 1, 1,rij
"#
œ ŸŸ Ê œ œ œ Ê ß ß œ œ œ
dx
dt dt
dy
0 dt 2 dt f(x y z) ds 2 2t 3t 3 dt 3 2 ;
dz dx dz
dt dt dt dt
dy
œÊ œ Ê ßß œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
'ab
##
##
C0
1
'
t x 1, y 1, z t f(g(t) h(t) k(t)) 2 2t and 0, 0, 1rijk
#œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (2 2t) dt 1ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt
dy
##
#''
C0
1
f(xyz) ds f(xyz) ds f(xyz) 3 2 1Êßßœßßßßœ
'''
CCC
È
2. Path 1: t x t, y 0, z 0 f(g(t) h(t) k(t)) t and 1, 0, 0ri
"#
œÊœ œ œÊ ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds t dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt 3
dy
##
##"
''
C0
1
t x 1, y t, z 0 f(g(t) h(t) k(t)) 1 t and 0, 1, 0rij
#œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (1 t) dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 3
dt dt dt 2
dy
##
#''
C0
1
t x 1, y 1, z t f(g(t) h(t) k(t)) 2 t and 0, 0, 1rijk
$œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (2 t) dtÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 3
dt dt dt 2
dy
##
#''
C0
1
f(xyz) ds f(xyz) ds f(xyz) ds f(xyz) dsÊ ßß œ ßß ßß ßß œ
''''
Path 1 C C C
10
3
Path 2: t t x t, y t, z 0 f(g(t) h(t) k(t)) t t and 1, 1, 0rij
%#
œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt 2 dt f(x y z) ds 2 t t dt 2;ÊœÊßßœ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
ab
dx dz 5
dt dt dt 6
dy
##
##
''
C0
1
t (see above) f(x y z) dsrijk
$œ Ê ßß œ
'C
3
2
f(x y z) ds f(x y z) ds f(x y z) ds 2Ê ßßœ ßß ßßœ œ
'''
Path 2 C C
53
66
529
È#
È
Path 3: t x 0, y 0, z t, 0 t 1 f(g(t) h(t) k(t)) t and 0, 0, 1rk
&œÊœ œ œ ŸŸÊ ßß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds t dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt 2
dy
##
#"
''
C0
1
t x 0, y t, z 1, 0 t 1 f(g(t) h(t) k(t)) t 1 and 0, 1, 0rjk
'œ Ê œ œ œ ŸŸ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (t 1) dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 1
dt dt dt 2
dy
##
#''
C0
1
t x t, y 1, z 1, 0 t 1 f(g(t) h(t) k(t)) t and 1, 0, 0rijk
(#
œÊœ œ œ ŸŸÊ ß ß œ œ œ œ
dx dz
dt dt dt
dy
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
990 Chapter 16 Integration in Vector Fields
dt dt f(x y z) ds t dtÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 1
dt dt dt 3
dy
##
##
''
C0
1
f(xyz) ds f(xyz) ds f(xyz) ds f(xyz) dsÊ ßß œ ßß ßß ßß œ œ
''''
Path 3 C C C
"""
##33
2
3. (a cos t) (a sin t) x 0, y a cos t, z a sin t f g(t) h(t) k(t) a sin t a sin t andrjkœ ÊœœœÊßßœ œab kk
È##
0, a sin t, a cos t dt a dt
dx dz dx dz
dt dt dt dt dt dt
dy dy
œœ œ Ê œ
ʈ‰ ˆ‰
Š‹
##
#
f(x y z) ds a sin t dt a sin t dt a sin t dt 4aÊßßœ œ œ
'' ''
C0 0
22
## ##
kk
4. (cos t t sin t) (sin t t cos t) x cos t t sin t, y sin t t cos t, z 0rijœ Êœ œ œ
f g(t) h(t) k(t) (cos t t sin t) (sin t t cos t) 1 t and sin t sin t t cos tÊßßœ œ œab
ÈÈ
###
dx
dt
t cos t, cos t cos t t sin t t sin t, 0 dtœœœœÊ
dy dy
dt dt dt dt dt
dz dx dz
ʈ‰ ˆ‰
Š‹
##
#
t cos t t sin t dt t dt t dt since 0 t 3 f(x y z) ds t 1 t dtœœœ ŸŸÊßßœœ
È È
kk È
## ## #
''
C0
37
3
5. (xyz) , (xyz) , (xyz)
`" `` " `` " `
`# `` # ``# `
$Î# $Î# $Î#
PNMPNM
yzzxx y
œ œ œ œ œ œ
M dx N dy P dz is exact; f(x y z) 2 x y z g(y z) Ê œ ÊßßœßÊœ
`" `"
```
`
f f
xyy
xyz xyz
g
È È
È
0 g(y z) h(z) f(x y z) 2 x y z h(z) h (z)œ Ê œÊ ßœ Ê ßßœ Ê œ
"`"
`
` `
w
È È
xyz xyz
g
y z
f
È
h (x) 0 h(z) C f(x y z) 2 x y z C œÊœÊœÊßßœÊ
"
w
È È
xyz xyz
dx dy dz
È'111
430
f(4 3 0) f( 1 1 1) 2 1 2 1 0œßßßßœœ
ÈÈ
6. , 0 , 0 M dx N dy dz is exact; 1 f(x y z)
`"`` `` ` `
`# `` `` ` `
PNMPNM f
yyzzz xx y x
œ œ œ œ œ œ Ê T œ Ê ß ß
È
x g(y z) g(y z) 2 yz h(z) f(x y z) x 2 yz h(z)œ ß Ê œ œ Ê ßœ Ê ßßœ
`
``
`
fz
yy y
gÉÈÈ
h (z) h (z) 0 h(z) C f(x y z) x 2 yz CÊœ œ Ê œÊ œÊßßœ
`
`
ww
f
zz z
yy
ÉÉ È
dx dy dz f(10 3 3) f(1 1 1) (10 2 3) (1 2 1) 4 1 5Ê œßßßßœœœ
'111
1033 ÉÉ
z
yz
y††
7. y cos z y cos z is not conservative; 2 cos t 2 sin t , 0 t 2
``
``
MP
zx
œ Á œ Ê œ Ÿ ŸFrijkabab 1
d 2 sin t 2 cos t d 2 cos t sin 1 2 cos t dt
2 sin t sin 1 2 sin t
Êœ Ê œ
rijFrabab c d
abababab aba ba bab
''
C0
2
†
4 sin 1 sin t cos t dt 8 sin 1œœab a b ab
'0
222 1
8. 0 , 0 , 3x is conservative d 0
``` `` `
````` `
#
PNMPN M
yzzxx y
œœ œœ œ œ Ê Ê œFFr
'C†
9. Let M 8x sin y and N 8y cos x 8x cos y and 8y sin x 8x sin y dx 8y cos x dyœœÊœ œÊ
``
``
MN
yx
'C
(8y sin x 8x cos y) dy dx (8y sin x 8x cos y) dy dx sin x 8x dx 0œ œ œœœ
''
R'' '
00 0
/2 /2 /2ab111
###
10. Let M y and N x 2y and 2x y dx x dy (2x 2y) dx dyœœÊœ œÊœ
## ##
``
``
MN
yx
'C''
R
(2r cos 2r sin ) r dr d (cos sin ) d 0œœœ
'' '
00 0
22 2
))) )))
16
3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Practice Exercises 991
11. Let z 1 x y f (x y) 1 and f (x y) 1 f f 1 3 Surface Area 3 dx dyœ Ê ß œ ß œÊ œ Ê œ
xy xy
ÉÈÈ
## ''
R
3(Area of the circular region in the xy-plane) 3œœ
ÈÈ
1
12. f 3 2y 2z , f 9 4y 4z and f 3™™™†œ œ Ê œ œijkpi pkk k k
È##
Surface Area dy dz r dr d 21 d 7 21 9Êœ œ œ œ
''
R
ÈÈ
94y 4z
333446
94r 79
"
'' '
00 0
23 2
))
Š‹Š‹
ÈÈ
1
13. f 2x 2y 2z , f 4x 4y 4z 2 x y z 2 and f 2z 2z since™™ ™†œ œÊ œ œ œ œ œijkpk pkk k kkk
ÈÈ
### ###
z 0 Surface Area dA dA dx dy r dr dÊ œ œ œ œ
'' '' ''
RRR
2
2z z 1x y 1r
"" "
ÈÈ
''
00
212
)
1 r d 1 d 2 1œ œ œ
''
00
22
’ “ Š‹ Š‹
È#"Î #
!
""
ÈÈÈ
))1
22
14. (a) f 2x 2y 2z , f 4x 4y 4z 2 x y z 4 and f 2z since™™ ™†œ œÊ œ œ œ œijkpk pkk k k
ÈÈ
### ###
z 0 Surface Area dA dA 2 r dr d 4 8Ê œ œ œ œ
'' ''
RR
42 2
2z z 4r
''
00
/2 2 cos È)1
(b) 2 cos d 2 sin d ; ds r d dr (Arc length in polar coordinates)rrœÊœ œ))))
### #
ds (2 cos ) d dr 4 cos d 4 sin d 4 d ds 2 d ; the height of theÊœ œ œ Êœ
# ## # ## ## #
) ) )) )) ) )
cylinder is z 4 r 4 4 cos 2 sin 2 sin if 0 Surface Area h dsœœ œ œ ŸŸÊ œ
ÈÈkk
## #
))))
1'2
/2
2 (2 sin )(2 d ) 8œœ
'0
/2
))
15. f(x y z) 1 f f and fßßœœÊ œ Ê œ œÊ œ
xz
abc a b c a b c c
y™™ ™†
ˆ‰ ˆ‰ ˆ‰ kk k k
É
""" """ "
ijk pk p
since c 0 Surface Area dA c dA abc ,Ê œ œ œ
'' ''
RR
ÉŠ‹
abc
c
""" " """
#
ÉÉ
abc abc
since the area of the triangular region R is ab. To check this result, let a c and a b ; the area can be
"
#vik w ijœ œ
found by computing .
"
#kkvw‚
16. (a) f 2y , f 4y 1 and f 1 d 4y 1 dx dy™™™†œœÊ œ œÊœjkp k pkk k k
ÈÈ
##
5
g(x y z) d 4y 1 dx dy y y 1 dx dy y y dx dyÊßßœ œ œ
'' '' ''
SRR
5yz
4y 1
È
##$
Èab ab
''
10
13
3y y dy 3 0œœœ
'1
1ab ’“
$
#
"
"
yy
4
(b) g(x y z) d 4y 1 dx dy y 1 dx dy 3 y 1 dy
'' ''
SR
ßß œ œ œ 5z
4y 1
È
###
Èab ab
'' '
10 1
13 1
3y 4œœ
’“
y
3
"
"
17. f 2y 2z , f 4y 4z 2 y z 10 and f 2z since z 0™™ ™†œ œÊ œœœ œ jkpk pkk k k
ÈÈ
## ##
d dx dy dx dy g(x y z) d x y y z dx dyÊœ œ œ ßß œ 55
10 5 5
2z z z
'' ''
SRaba b
ˆ‰
%##
x y (25) dx dy x dx dy dy 50œœœœ
''
Rab Š‹
%%
5
25 y 25 y 25 y
125y 25y
ÈÈÈ
'' '
00 0
41 4
18. Define the coordinate system so that the origin is at the center of the earth, the z-axis is the earth's axis (north is the
positive z direction), and the xz-plane contains the earth's prime meridian. Let S denote the surface which is Wyoming so
then S is part of the surface z R x y . Let R be the projection of S onto the xy-plane. The surface area ofœab
###
"Î#
xy
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

992 Chapter 16 Integration in Vector Fields
Wyoming is 1 d 1 dA 1 dA dA
''
SRR R
5œ œ œ
'' '' ''
xy xy xy
ʈ‰ Š‹ É
``
``
##
zz x R
xy RxyRxy
y
Rxy
ab
R R r r dr d (where and are the radian equivalent to 104°3 and 111°3 , respectively)œ
''
R sin 45°
R sin 49° ab
## ww
"Î#
"#
)))
R R r R R R sin 45° R R R sin 49° dœ œ
''
¹
ab abab
## # ## # ##
"Î# "Î# "Î#
Rsin 49°
R sin 45°
)
( )R (cos 45° cos 49°) R (cos 45° cos 49°) (3959) (cos 45° cos 49°) 97,751 sq. mi.œ œ œ ¸))
#"
## #
77
180 180
11
19. A possible parametrization is ( ) (6 sin cos ) (6 sin sin ) (6 cos ) (spherical coordinates);rijk9) 9 ) 9 ) 9ߜ
now 6 and z 3 3 6 cos cos and z 3 3 3 3 6 cos 3999 9œœÊœ ʜʜ œÊœ
"
#
2
3
1ÈÈ
cos ; also 0 2ʜʜʟŸ ŸŸ99 9 )1
È3
66 3
2
#
11 1
20. A possible parametrization is (r ) (r cos ) (r sin ) (cylindrical coordinates);rijkߜ )))
Š‹
r
#
now r x y z and 2 z 0 2 0 4 r 0 0 r 2 since r 0;œÊœ ŸŸÊŸŸÊÊŸŸ
È## ##
#
rr
also 0 2ŸŸ)1
21. A possible parametrization is (r ) (r cos ) (r sin ) (1 r) (cylindrical coordinates);rijkߜ )))
now r x y z 1 r and 1 z 3 1 1 r 3 0 r 2; also 0 2œ Êœ ŸŸÊŸŸÊŸŸ ŸŸ
È## )1
22. A possible parametrization is (x y) x y 3 x for 0 x 2 and 0 y 2rij kßœ ŸŸ ŸŸ
ˆ‰
y
#
23. Let x u cos v and z u sin v, where u x z and v is the angle in the xz-plane with the x-axisœœ œ
È##
(u v) (u cos v) 2u (u sin v) is a possible parametrization; 0 y 2 2u 2 u 1Ê ßœ ŸŸÊ ŸÊ Ÿrijk
###
0 u 1 since u 0; also, for just the upper half of the paraboloid, 0 vÊŸŸ ŸŸ1
24. A possible parametrization is 10 sin cos 10 sin sin 10 cos ) , 0 and 0
Š‹Š‹Š
ÈÈÈ
9) 9) 9 9 )ijkŸŸŸŸ
11
2#
25. , 2 6
0
rijrijk rr ijk rr
ijk
u v uv uv
œ œ Ê ‚ œ œ Ê ‚ œ
""
"""
ââ
ââ
ââ
ââ
ââ
ââ kk
È
Surface Area du dv 6 du dv 6Êœ‚œ œ
''
Ruv
00
11
kk ÈÈ
rr
uv ''
26. xy z d (u v)(u v) v 6 du dv 6 u 2v du dv
''
Sab c d a b
ÈÈ
œ œ
####
5'' ''
00 00
11 11
6 2uv dv 6 2v dv 6 v vœ œ œ œ œ
ÈÈÈ
’“ ˆ‰ ‘ É
''
00
11
u22
333333
6
##$
"
!
""
"
!È
27. (cos ) (sin ) , ( r sin ) (r cos ) cos sin 0
r sin r cos
rijr i jkrr
ijk
r r
œ œ Ê‚œ
"
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(sin ) (cos ) r sin cos r 1 r Surface Area dr dœ Ê‚œ œÊ œ ‚)) )) )ijkrr rrkk kk
ÈÈ
r r) )
### # ''
Rr
1 r dr d 1 r ln r 1 r d 2 ln 1 2 dœœœ
'' ' '
00 0 0
21 2 2
ÈÈÈ ÈÈ
’“’“Š‹ Š‹
###
"""
###
"
!
)))
r
2
2ln1 2œ1’“
ÈÈ
Š‹
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Practice Exercises 993
28. x y 1 d r cos r sin 1 1 r dr d 1 r dr d
''
SÈÈÈ
ab
## ## ## # #
œ œ 5))) )
'' ''
00 00
21 21
r d dœ œ œ
''
00
22
’“
r48
333
"
!))1
29. 0 , 0 , 0 Conservative
``` `` `
````` `
PNMPNM
yzzxx y
œœ œœ œœ Ê
30. , , Conservative
````` `
````` `
P N M 3xz P N M
yzzxx y
3zy 3xy
xyz xyz xyz
œœœœœœÊ
ab ab ab
31. 0 ye Not Conservative
``
``
PN
yz
œÁ œ Ê
z
32. , , Conservative
``` ```
` `` `` `
Px NM PN z M
y (xyz) z z (xyz) x x (xyz) y
y
œœ œœœœÊ
33. 2 f(x y z) 2x g(y z) 2y z g(y z) y zy h(z)
``
```
`#
ff
xyy
g
œÊ ßßœ ß Ê œ œ Ê ßœ
f(x y z) 2x y zy h(z) y h (z) y 1 h (z) 1 h(z) z CÊ ßß œ Ê œ œ Ê œ Ê œ
#ww
`
`
f
z
f(xyz) 2x y zy z CÊßßœ
#
34. z cos xz f(x y z) sin xz g(y z) e g(y z) e h(z)
``
```
`
ff
xyy
gyy
œÊßßœßÊœœÊßœ
f(x y z) sin xz e h(z) x cos xz h (z) x cos xz h (z) 0 h(z) CÊßßœ Êœ œ Ê œÊ œ
yf
z
`
`
ww
f(x y z) sin xz e CÊßßœ
y
35. Over Path 1: t t t , 0 t 1 x t, y t, z t and d ( ) dt 2t trijk rijk F ij kœ ŸŸ Ê œ œ œ œ Ê œ
##
d 3t 1 dt Work 3t 1 dt 2;ʜʜ œFr†ab ab
##
'0
1
Over Path 2: t t , 0 t 1 x t, y t, z 0 and d ( ) dt 2t trij rij F ijk
"""
##
œ ŸŸ Ê œ œ œ œ Ê œ
d 2t 1 dt Work 2t 1 dt ; t , 0 t 1 x 1, y 1, z t andÊ œ Ê œ œ œ ŸŸ Ê œ œ œFr rijk
"" " #
##
†ab ab
'0
15
3
d dt 2 d dt Work dt 1 Work Work Work 1rk F ijk Fr
## ## # "#
œÊœÊ œÊ œœÊœœœ†'0
158
33
36. Over Path 1: t t t , 0 t 1 x t, y t, z t and d ( ) dt 2t tr i j k r ijk F i jkœ ŸŸ Ê œ œ œ œ Ê œ
##
d 3t 1 dt Work 3t 1 dt 2;ʜʜ œFr†ab ab
##
'0
1
Over Path 2: Since f is conservative, d 0 around any simple closed curve C. Thus consider
)CFr†œ
d d d , where C is the path from (0 0 0) to (1 1 0) to ( ) and C is the path
'''
curve C C
Fr Fr Fr†††œ ß ß ß ß "ß "ß "
"#
from (1 1 1) to ( ). Now, from Path 1 above, d 2 0 d d ( 2)ß ß !ß !ß ! œ Ê œ œ
'''
C curve C
Fr Fr Fr†††
d2ʜ
'CFr†
37. (a) e cos t e sin t x e cos t, y e sin t from (1 0) to e 0 0 t 2rijœ Êœœ ßßÊŸŸabab ab
tt tt 211
e cos t e sin t e sin t e cos t and Êœ œ œ
d
dt
tt tt xy
xy
e cos t e sin t
e cost e sint
rij ij
ababijF
ab abab
ab
tt
2t 2t
eœ Êœ œ
ˆ‰ˆ‰ Š‹
cos t sin t d cos t sin t cos t sin t sin t cos t
ee dteeee
t
2t 2t t t t t
ijF†r
Work e dt 1 eÊœ œ
'0
2t21
(b) f(x y z) x y g(y z) FœÊœÊßßœßÊœ
xy yg
xy xy xy
fx f
xyy
ij `
` `
```
##
"Î#
ab ab ab
ab
g(y z) C f(x y z) x y is a potential function for dœ Ê ßœ Ê ßßœ Ê
y
xyab
##
"Î#
ab FFr
'C†
fe 0 f(10) 1 eœßßœab
2211
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

994 Chapter 16 Integration in Vector Fields
38. (a) x ze is conservative d 0 for closed path CFF FrœÊ Êœ™†ab
#y)Cany
(b) d x ze d x ze x ze 2 0 2
''
C 100
102
Fr r†™†œœœœab k kab ab
## #
Ð"ß!ß# Ñ Ð"ß!ß!Ñ
yy y
111
39. 2y ; unit normal to the plane is
yy3z
™‚œ œ œ œ
Fk nijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
##
xy z
263
4369
263
777
ijk
È
y; and f(x y z) 2x 6y 3z f 3 d dA dAÊ‚ œ œ ßßœÊ œÊœ œ™† ™†Fn p k p
6 7
7f3
f
kk 5kk
kk
™
™†p
d y d y dA 2y dA 2r sin r dr d sin d 0Êœ œ œ œ œ œ
)'''
C00 0
21 2
Fr†'' '' ''
RR R
667 2
773 3
5))))
ˆ‰ˆ ‰
40. 8y ; the circle lies in the plane f(x y z) y z 0 with unit normal
x y x y 4y z
™‚œ œ ßßœœ
Fi
ijk
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
##
xy z
0 d d 0 d 0njk Fn Fr Fnœ Ê‚ œÊ œ ‚ œ œ
""
ÈÈ
22 ™† † ™†
)C'' ''
RR
55
41. (a) 2t 2t 4 t , 0 t 1 x 2t, y 2t, z 4 t 2, 2, 2trij kœ ŸŸÊœ œ œÊœ œ œ
ÈÈ È È È È
ab
##
dx dz
dt dt dt
dy
dt 4 4t dt M (x y z) ds 3t 4 4t dt (4 4t)ʜʜßßœ œ
ʈ‰ ˆ‰ ‘
Š‹ ÈÈ
dx dz
dt dt dt 4
dy
##
###
"$Î# "
!
''
C0
1
$
42 2œ
È
(b) M (x y z) ds 4 4t dt t 1 t ln t 1 t 2 ln 1 2œßßœœœ
''
C0
1
$ÈÈ ÈÈÈ
’“Š‹Š‹
## #
"
!
42. t 2t t , 0 t 2 x t, y 2t, z t 1, 2, tri j kœ ŸŸ Ê œ œ œ Ê œ œ œ
2 2 dx dz
3 3 dt dt dt
dy
$Î# $Î# "Î#
dt t 5 dt M (x y z) ds 3 5 t t 5 dtʜʜßßœ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
dx dz
dt dt dt
dy
##
#''
C0
2
$
3(t 5) dt 36; M x ds 3t(t 5) dt 38; M y ds 6t(t 5) dt 76;œœœ œœœ œœ
'''''
0C0 C0
22 2
yz xz
$$
M z ds 2t (t 5) dt 2 x , y , z
xy 144 38 19 76 19
7 M 36 18 M 36 9 M 36
MM
M2
œœ œÊœœœœœœœœ
''
C0
2
$$Î# Èyz xy
xz
144
7
Š‹
È
2œ4
7È
43. t t , 0 t 2 x t, y t , z 1, 2 t , tri j kœ ŸŸ Ê œ œ œ Ê œ œ œ
Š‹Š‹ È
22 22 dy
3 3 dt dt dt
t t dx dz
ÈÈ
$Î# $Î# "Î#
##
dt 1 2t t dt (t 1) dt t 1 dt (t 1) dt on the domain given.Êœœœœ
ʈ‰ ˆ‰
Š‹ ÈÈkk
dx dz
dt dt dt
dy
##
###
Then M ds (t 1) dt dt 2; M x ds t (t 1) dt t dt 2;œœ œœœ œ œœ
'' ' ' ' '
C0 0 C 0 0
22 2 2
$$
ˆ‰ ˆ‰
""
t1 t1
yz
M y ds t (t 1) dt t dt ; M z ds
xz xy
22 22
3t1 3 15
32
œœ œ œœ
'' ' '
C0 0 C
22
$$
Š‹
ˆ‰
ÈÈ
$Î# $Î#
"
(t 1) dt dt x 1; y ; zœœœÊœœœœœœœ
''
00
22
Š‹
ˆ‰
tt4216
t1 3 M M 15 M
MM
M
# # # #
"yz xy
xz
32
15
ˆ‰
; I y z ds t dt ; I x z ds t dt ;œœ œ œ œ œ œ œ
ˆ‰
4
3
#
## $ ## #
2 8 t 232 t 64
39445 415
xy
'' ''
C0 C0
2 2
ab ab
Š‹ Š‹
$$
I y x ds t t dt
z856
99
œ œ œ
''
C0
2
ab ˆ‰
## # $
$
44. z 0 because the arch is in the xy-plane, and x 0 because the mass is distributed symmetrically with respectœœ
to the y-axis; (t) (a cos t) (a sin t) , 0 t ds dtrijœ ŸŸÊœ1ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt
dy
##
#
( a sin t) (a cos t) dt a dt, since a 0; M ds (2a y) ds (2a a sin t) a dtœ œ œ œ œ
È## '' '
CC 0
$
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Practice Exercises 995
2a 2a ; M y dt y(2a y) ds (a sin t)(2a a sin t) dt 2a sin t a sin t dtœ œ œ œ œ
21$
####
xz CC 0 0
'' ' '
ab
2a cos t a 4a y x y z 0 0œ œ Ê œ œ Ê ßß œ ß ß
‘ ˆ‰ˆ‰ ab
## #
!#
tsin 2t a 8 8
2 4 2a 2a 4 4 4 4
4a
1111
11 1
Š‹
a
45. (t) e cos t e sin t e , 0 t ln 2 x e cos t, y e sin t, z e e cos t e sin t ,rijkœŸŸÊœœœÊœabab a b
ttt ttt tt
dx
dt
e sin t e cos t , e dt
dy dy
dt dt dt dt dt
tt t
dz dx dz
œ œÊ ab
ʈ‰ ˆ‰
Š‹
##
#
e cos t e sin t e sin t e cos t e dt 3e dt 3 e dt; M ds 3 e dtœœœ œœ
Éababab
ÈÈÈ
tt tt t 2t tt
### ''
C0
ln 2
$
3; M z ds 3 e e dt 3 e dt z ;œœœ œ œÊœœœ
ÈÈÈ
Š‹
ab
xy tt 2t 33 M
M3
3
'' '
C0 0
ln 2 ln 2
$Ȍ
È
##
xy
33
I x y ds e cos t e sin t 3 e dt 3 e dt
z2t 2t t 3t 73
3
œ œ œ œ
'' '
C0 0
ln 2 ln 2
ab a b
Š‹
ÈÈ
## # #
$È
46. (t) (2 sin t) (2 cos t) 3t , 0 t 2 x 2 sin t, y 2 cos t, z 3t 2 cos t, 2 sin t,rijkœ ŸŸÊœœ œÊœ œ1dx
dt dt
dy
3 dt 4 9 dt 13 dt; M ds 13 dt 2 13;
dz dx dz
dt dt dt dt
dy
œÊ œ œ œ œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈÈ
##
#''
C0
2
$$ 1$
M z ds (3t) 13 dt 6 13; M x ds (2 sin t) 13 dt 0;
xy yz
œœ œ œœ œ
'' ''
C0 C0
2 2
$$$1 $ $
Š‹ Š‹
ÈÈ È
#
M y ds (2 cos t) 13 dt 0 x y 0 and z 3 ( 3 ) is the
xz M
M
613
213
œ œ œ Ê œ œ œ œ œ Ê !ß !ß
''
C0
2
$$ 11
Š‹
Èxy $1
$1
È
È
center of mass
47. Because of symmetry x y 0. Let f(x y z) x y z 25 f 2x 2y 2zœœ ßßœœ Ê œ
### ™ijk
f 4x 4y 4z 10 and f 2z, since z 0 M (x y z) dÊ œ œ œÊ œ Êœ ßßkk k k
È
™™†
### pk p ''
R
$5
z dA 5 dA 5(Area of the circular region) 80 ; M z d 5z dAœœœ œœœ
'' '' '' ''
RR RR
ˆ‰
10
zxy
#1$5
5 25 x y dx dy 5 25 r r dr d d zœœ œœÊœœ
''
RÈŠ‹
È
## #
'' '
00 0
24 2
))1
490 980 49
3 3 80 12
Š‹
980
31
1
x y z 0 ; I x y d 5 x y dx dy 5r dr d 320 d 640Êßßœß!ß œ œ œ œ œab ab ab
ˆ‰
49
12 z'' ''
RR
## ## $
$5 ) ) 1
'' '
00 0
24 2
48. On the face z 1: g(x y z) z 1 and g g 1 and g 1 d dAœßßœœ œÊœÊ œ œÊœpk k p™™ ™†kk k k 5
I x y dA 2 r dr d ; On the face z 0: g(x y z) z 0 g and Êœ œ œ œ ßßœœ Ê œ œ
''
Rab
## $
''
00
/4 sec
)2
3™kpk
g 1 g 1 d dA I x y dA ; On the face y 0: g(x y z) y 0ÊœÊ œÊœÊœ œ œßßœœkk k k a b™™†p5''
R
## 2
3
g and g 1 g 1 d dA I x 0 dA x dx dz ;Ê œ œÊ œÊ œÊ œ Êœ œ œ™™™†jpj pkk k k a b5''
R
##
"
''
00
11
3
On the face y 1: g(x y z) y 1 g and g 1 g 1 d dAœßßœœÊœ œÊ œÊ œÊœ™™™†jpj pkk k k 5
I x 1 dA x 1 dx dz ; On the face x 1: g(x y z) x 1 g and Êœ œ œ œ ßßœœ Ê œ œ
''
Rab ab
## #
''
00
11 4
3™ipi
g 1 g 1 d dA I 1 y dA 1 y dy dz ; On the faceÊœÊ œÊœÊœœ œkk k k a b a b™™†p5''
R
## #
''
00
11 4
3
x 0: g(x y z) x 0 g and g 1 g 1 d dAœßßœœÊœ œÊ œÊ œÊœ™™™†ipi pkk k k 5
I 0 y dA y dy dz IÊœ œ œ Ê œœ
''
Rab
## # ""
''
00
11
z
1224414
3 333333 3
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.
996 Chapter 16 Integration in Vector Fields
49. M 2xy x and N xy y 2y 1, 2x, y, x 1 Flux dx dyœ œÊœ œ œ œÊ œ
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
(2y1x1) dydx (2yx) dydx ; Circ dxdyœ œ œ œ
'' ''
R R
''
00
11 3NM
xy#``
``
Š‹
(y 2x) dy dx (y 2x) dy dxœ œ œ
''
R''
00
11 "
#
50. M y 6x and N x y 12x, 1, 1, 2y Flux dx dyœ œ Ê œ œ œ œ Ê œ
##
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
( 12x 2y) dx dy ( 12x 2y) dx dy 4y 2y 6 dy ;œ œ œ œ
''
R'' '
0y 0
11 1
ab
#11
3
Circ dx dy (1 1) dx dy 0œ œœ
'' ''
RR
Š‹
``
``
NM
xy
51. M and N ln x sin y and ln x sin y dy dxœ œ Ê œ œ Ê
cos y sin y sin y cos y
xyxxxx
MN``
``
)C
dx dy dx dy 0œ œ œ
'' ''
RR
Š‹ Š ‹
``
``
NM
xy x x
sin y sin y
52. (a) Let M x and N y 1, 0, 0, 1 Flux dx dyœ œÊœ œœœÊœ
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
(1 1) dx dy 2 dx dy 2(Area of the region)œ œ œ
'' ''
RR
(b) Let C be a closed curve to which Green's Theorem applies and let be the unit normal vector to C. Letn
x y and assume is orthogonal to at every point of C. Then the flux density of at every pointFij F n Fœ
of C is 0 since 0 at every point of C 0 at every point of CFn†œÊœ
``
``
MN
xy
Flux dx dy 0 dx dy 0. But part (a) above states that the flux isÊœ œ œ
'' ''
RR
Š‹
``
``
MN
xy
2(Area of the region) the area of the region would be 0 contradiction. Therefore, cannot beÊÊF
orthogonal to at every point of C.n
53. (2xy) 2y, (2yz) 2z, (2xz) 2x 2y 2z 2x Flux (2x 2y 2z) dV
```
```xyz
œœœÊœÊœ™†F'''
D
(2x 2y 2z) dx dy dz (1 2y 2z) dy dz (2 2z) dz 3œœœœ
''' '' '
000 00 0
111 11 1
54. (xz) z, (yz) z, (1) 0 2z Flux 2z r dr d dz
```
```xyz
œœœÊœÊœ™†F'''
D
)
2z dz r dr d r 16 r dr d 64 d 128œœœœ
''' '' '
003 0 0 0
24 25r 2 4 2
)))1ab
#
55. ( 2x) 2, ( 3y) 3, (z) 1 4; x y z 2 and x y z z 1
```
```
### ##
xyz
œ œ œ Ê œ œ œ Ê œ™†F
x y 1 Flux 4 dV 4 dz r dr d 4 r 2 r r dr dÊ œ Ê œ œ œ
## $
#
'''
D''' ''
00r 00
21 2r 21
))
Š‹
È
42 d782œ œ
'0
2Š‹Š‹
ÈÈ
72 2
12 3 3
)1
56. (6x y) 6, ( x z) 0, (4yz) 4y 6 4y; z x y r
`` `
`` ` ##
xy z
œ œ œ Ê œ œ œ™†FÈ
Flux (6 4y) dV (6 4r sin ) dz r dr d 6r 4r sin dr dÊœ œ œ
'''
D''' ''
000 00
/21r /21
)) ))ab
#$
(2 sin ) d 1œ œ
'0
/2
)) 1
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Additional and Advanced Exercises 997
57. y z x 0 Flux d dV 0Fijk F Fn Fœ Ê œÊ œ œ œ™† † ™†
'' '''
SD
5
58. 3xz y z 3z 1 3z 1 Flux d dVFijk F Fn Fœ Ê œœÊ œ œ
#$ ##
™† † ™†
'' '''
SD
5
1 dz dy dx dx xœœœœ
'' ' '
00 0 0
416x2y2 4
Š‹ ’ “
16 x x 8
16 48 3
%
!
59. xy x y y y x 0 Flux d dVFijk F Fn FœÊ œÊ œ œ
## ##
™† † ™†
'' '''
SD
5
x y dV r dz r dr d 2r dr d dœœ œ œœ
'''
Dab
## # $ "
#
''' '' '
00 1 00 0
211 21 2
)))1
60. (a) (3z 1) 3 Flux across the hemisphere d dV 3 dVFkF Fn Fœ Ê œÊ œ œ œ™† † ™†
'' ''' '''
SDD
5
3a2aœœ
ˆ‰ˆ ‰
"
#
$$
4
311
(b) f(xyz)xyza 0 f2x2y2z f 4x4y4z 4a2a sinceßßœœÊ œ Ê œ œ œ
#### ### #
™™ijkkk
ÈÈ
a0 (3z1) ; f f 2zÊœ œ Ê œ œÊ œ œnFnpkpk
2x 2y 2z x y z
aa a
z
ijk ijk
#†™†™†
ˆ‰
f 2z since z 0 d dA dA d (3z 1) dAʜʜœœÊ œkk ˆ‰ˆ‰
™† †pFn55
kk
kk
™
™†
f
f2z z az
2a a z a
p'' ''
SRxy
(3z 1) dx dy 3 a x y 1 dx dy 3 a r 1 r dr dœ œ œ
'' ''
RR
xy xy
00
2a
ˆ‰
ÈŠ‹
È
### ##
'' )
a d a 2 a , which is the flux across the hemisphere. Across the base we findœœ
'0
2Š‹
a
#
$#$
)1 1
[3(0) 1] since z 0 in the xy-plane (outward normal) 1 Flux across theFkk nk Fnœœ œ Êœ Ê œÊ†
base d 1 dx dy a . Therefore, the total flux across the closed surface isœœœ
'' ''
SR
Fn†51
xy
#
a2a a2a.ab1111
#$# $
œ
CHAPTER 16 ADDITIONAL AND ADVANCED EXERCISES
1. dx ( 2 sin t 2 sin 2t) dt and dy (2 cos t 2 cos 2t) dt; Area x dy y dxœ œ œ
"
#)C
[(2 cos t cos 2t)(2 cos t 2 cos 2t) (2 sin t sin 2t)( 2 sin t 2 sin 2t)] dtœ
"
#'0
2
[6 (6 cos t cos 2t 6 sin t sin 2t)] dt (6 6 cos t) dt 6œ œ œ
""
##
''
0 0
2 2
1
2. dx ( 2 sin t 2 sin 2t) dt and dy (2 cos t 2 cos 2t) dt; Area x dy y dxœ œ œ
"
#)C
[(2 cos t cos 2t)(2 cos t 2 cos 2t) (2 sin t sin 2t)( 2 sin t 2 sin 2t)] dtœ
"
#'0
2
[2 2(cos t cos 2t sin t sin 2t)] dt (2 2 cos 3t) dt 2t sin 3t 2œ œ œ œ
"""
###
#
!
''
0 0
2 2 ‘
2
3
11
3. dx cos 2t dt and dy cos t dt; Area x dy y dx sin 2t cos t sin t cos 2t dtœœœœ
"""
###
)'
C0
ˆ‰
sin t cos t (sin t) 2 cos t 1 dt sin t cos t sin t dt cos t cos t 1œœœœœ
"""""
###
## # $
!
''
0 0
cdabab ‘
333
2
1
4. dx ( 2a sin t 2a cos 2t) dt and dy (b cos t) dt; Area x dy y dxœ œ œ
"
#)C
2ab cos t ab cos t sin 2t 2ab sin t 2ab sin t cos 2t dtœ
"
#
##
'0
2cdaba b
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

998 Chapter 16 Integration in Vector Fields
2ab 2ab cos t sin t 2ab(sin t) 2 cos t 1 dt 2ab 2ab cos t sin t 2ab sin t dtœ œ
" "
# #
## #
''
0 0
2 2
cdabab
2abt ab cos t 2ab cos t 2 abœ œ
"
#
$#
!
‘
2
3
11
5. (a) (x y z) z x y is only at the point (0 0 0), and curl (x y z) is never .Fijk0 Fijk0ßßœ ßß ßßœ
(b) (x y z) z y is only on the line x t, y 0, z 0 and curl (x y z) is never .Fik0 Fij0ßßœ œ œ œ ßßœ
(c) (x y z) z is only when z 0 (the xy-plane) and curl (x y z) is never .Fi0 Fj0ßß œ œ ßß œ
6. yz xz 2xyz and , so is parallel to when yz , xz ,Fij kn F nœ œ œ œ œ
## ##
xyz xyz cy
xyz RRR
cx
ijk ijk
È
and 2xyz 2xy y x y x and z 2x z 2x. Also,œÊ œœ ʜʜ„ œ„œ Êœ„
cz xz c
Rxy R
yz ## # # È
x y z R x x 2x R 4x R x . Thus the points are: ,
#### ## ## ##
####
œ Ê œ Ê œ Êœ„ ßß
RRR
2R
Š‹
È
, , , , ,
Š‹Š ‹Š ‹Š‹Š ‹
RR RR RR RR RR
2R 2R 2R 2R 2R
## # # ## # # # # ## # # #
ß ß ß ß ß ß ß ß ß ß
ÈÈ ÈÈÈ
,
Š‹Š ‹
ßß ßß
RR RR
2R 2R
## # ## #
ÈÈ
7. Set up the coordinate system so that (a b c) (0 R 0) (x y z) x (y R) zßß œ ß ß Ê ßß œ $È###
x y z 2Ry R 2R 2Ry ; let f(x y z) x y z R and œœ ßßœ œ
ÈÈ
### # # ### # pi
f 2x 2y 2z f 2 x y z 2R d dz dy dz dyÊ œ Ê œ œ Ê œ œ™™ijkkkÈ### 5kk
kk
™
™†
f
f2x
2R
i
Mass (x y z) d 2R 2Ry dz dy R dz dyÊœ ßßœ œ
'' '' ''
SRR
$5
yz yz
Ȉ‰
#
R
x
2R 2Ry
Ryz
È
È
4R dz dy 4R 2R 2Ry sin dyœœ
'' '
R0 R
RRy R
0
Ry
È
ÈÈ
2R 2Ry
Ryz
21z
Ry
ÉŠ‹
»
22
2 R 2R 2Ry dy 2 R 2R 2Ryœœœ11
'R
R3/2
R
R
É»
2116R
3R 3
2
ˆ‰
ab
1
8. (r ) (r cos ) (r sin ) , 0 r 1, 0 2 cos sin 0
r sin r cos
rijk rr
ijk
ßœ ŸŸ ŸŸ Ê ‚œ
"
)))) )1 ))
))
r)
ââ
ââ
ââ
ââ
ââ
ââ
(sin ) (cos ) r 1 r ; 2 x y 2 r cos r sin 2rœ Ê‚œœœ œ)) $ ) )ijkrrkk
ÈÈ
È
r)#######
Mass (x y z) d 2r 1 r dr d 1 r d 2 2 1 dÊœ ßßœ œ œ
''
S
$5 ) ) )
'' ' '
00 0 0
21 2 2
ÈÈ
’“ Š‹
ab
##$Î# "
!
22
33
22 1œ
4
3
1Š‹
È
9. M x 4xy and N 6y 2x 4y and 6 Flux (2x 4y 6) dx dyœ œ Ê œ œÊ œ
#``
``
MN
xx ''
00
ba
a 4ay 6a dy a b 2ab 6ab. We want to minimize f(a b) a b 2ab 6ab ab(a 2b 6).œ œ ßœœ
'0
bab
### ##
Thus, f (a b) 2ab 2b 6b 0 and f (a b) a 4ab 6a 0 b(2a 2b 6) 0 b 0 or b a 3.
ab
ßœ œ ßœ œÊ œÊœ œ
##
Now b 0 a 6a 0 a 0 or a 6 (0 0) and (6 0) are critical points. On the other hand, b a 3œÊ œÊœ œÊß ß œ
#
a 4a( a 3) 6a 0 3a 6a 0 a 0 or a 2 (0 3) and ( ) are also critical points. The flux atÊœÊ œÊœ œÊß #ß"
##
(0 0) 0, the flux at (6 0) 0, the flux at (0 3) 0 and the flux at (2 1) 4. Therefore, the flux is minimized at (2 1)ßœ ßœ ßœ ßœ ß
with value 4.
10. A plane through the origin has equation ax by cz 0. Consider first the case when c 0. Assume the plane is givenœ Á
by z ax by and let f(x y z) x y z 4. Let C denote the circle of intersection of the plane with the sphere.œ ßßœœ
###
By Stokes's Theorem, d d , where is a unit normal to the plane. Let
S
)CFr Fn n†™†œ‚
'' 5
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Additional and Advanced Exercises 999
(x y) x y (ax by) be a parametrization of the surface. Then a b
0a
0b
rij k rr ijk
ijk
ßœ ‚œ œ
"
"
xy
ââ
ââ
ââ
ââ
ââ
ââ
d dx dy a b 1 dx dy. Also, and
zxy
Ê œ ‚ œ ‚ œ œ œ5kk Èââ
ââ
ââ
ââ
ââ
ââ
rr F ijk n
ijk
xy xyz
ab
ab1
## ```
```
™ijk
È
d a b 1 dx dy (a b 1) dx dy (a b 1) dx dy. NowÊ‚œ œœ
'' '' '' ''
SRRR
™†Fn5
xy xy xy
ab1
ab1
##
ÈÈ
x y (ax by) 4 x y xy 1 the region R is the interior of the ellipse
## # # #
#
œÊ œÊ
Š‹Š‹ˆ‰
a1 b1 ab
44 xy
Ax Bxy Cy 1 in the xy-plane, where A , B , and C . The area of the ellipse is
##
#
œ œ œ œ
a1 ab b1
44
d h(a b) . Thus we optimize H(a b) :
24
4AC B ab1 ab1
4(a b 1) (a b 1)
ab1
11 1
ÈÈ È
œÊœßœ ßœ
)CFr†
0 and 0 a b 1 0, or b 1 a ab 0
``
``
#
HH
ab
2(ab1)b 1aab 2(ab1)a 1bab
ab1 ab1
œœœœÊœœ
ab ab
ab ab
22
and a 1 b ab 0 a b 1 0, or a b (b a) 0 a b 1 0, or (a b)(a b 1) 0
###
œ Ê œ œ Ê œ œ
a b 1 0 or a b. The critical values a b 1 0 give a saddle. If a b, then 0 b 1 a abÊ œ œ œ œ œ
#
a 1 a a 0 a 1 b 1. Thus, the point (a b) ( 1 1) gives a local extremum for dʜʜʜ ßœß
## )CFr†
z x y x y z 0 is the desired plane, if c 0.ʜʜ Á
: Since h( 1 1) is negative, the circulation about is , so is the correct pointing normal forNote clockwiseß nn
the counterclockwise circulation. Thus ( ) d actually gives the circulation.
''
S
™†‚Fn5maximum
If c 0, one can see that the corresponding problem is equivalent to the calculation above when b 0, which does notœ œ
lead to a local extreme.
11. (a) Partition the string into small pieces. Let s be the length of the i piece. Let (x y ) be a point in the?iii
th ß
i piece. The work done by gravity in moving the i piece to the x-axis is approximately
th th
W (gx y s)y where x y s is approximately the mass of the i piece. The total work done by
i iii i iii th
œ??
gravity in moving the string to the x-axis is W gx y s Work gxy dsDD?
ii
iii
iC
œÊœ
##
'
(b) Work gxy ds g(2 cos t) 4 sin t 4 sin t 4 cos t dt 16g cos t sin t dtœœ œ
'' '
C0 0
/2 /2
## #
##
ab
È
16g gœœ
’“Š‹
sin t 16
33
1Î#
!
(c) x and y ; the mass of the string is xy ds and the weight of the string isœœ
''
''
CC
CC
x(xy) ds y(xy) ds
xy ds xy ds 'C
g xy ds. Therefore, the work done in moving the point mass at x y to the x-axis is
'Cabß
W g xy ds y g xy ds g.œœœ
Š‹
''
CC
#16
3
12. (a) Partition the sheet into small pieces. Let be the area of the i piece and select a point (x y z ) in?5
iiii
th ßß
the i piece. The mass of the i piece is approximately x y . The work done by gravity in moving the
th th ii i
?5
i piece to the xy-plane is approximately (gx y )z gx y z Work gxyz d .
th ii i i iii i
?5 ?5 5œÊœ
''
S
(b) gxyz d g xy(1 x y) 1 ( 1) ( 1) dA 3g xy x y xy dy dx
'' ''
SR
5œœ
xy
00
11x
ÈÈab
## ##
''
3g xy x y xy dx 3g x x x x dxœ œ
ÈÈ
‘ ‘
''
00
11
x
" " " """"
### $ #$%
###
"
!
23 6 6
3gxxx x 3gœ œ œ
ÈÈ
‘ˆ‰
"""" ""
#$% &
"
!#126630 13020
3g
È
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

1000 Chapter 16 Integration in Vector Fields
(c) The center of mass of the sheet is the point x y z where z with M xyz d andabßß œ œ
M
M
xy
xy ''
S
5
M xy d . The work done by gravity in moving the point mass at x y z to the xy-plane isœßß
''
S
5ab
gMz gM gM gxyz d .œœœ œ
Š‹
M
M20
3g
xy
xy ''
S
5È
13. (a) Partition the sphere x y (z 2) 1 into small pieces. Let be the surface area of the i piece and let
## #
œ ?5
ith
(x y z ) be a point on the i piece. The force due to pressure on the i piece is approximately w(4 z ) . The
iii ii
th th
ßß ?5
total force on S is approximately w(4 z ) . This gives the actual force to be w(4 z) d .D?5 5
iS
ii ''
(b) The upward buoyant force is a result of the -component of the force on the ball due to liquid pressure.k
The force on the ball at (x y z) is w(4 z)( ) w(z 4) , where is the outer unit normal at (x y z).ßß œ ßßnnn
Hence the -component of this force is w(z 4) w(z 4) . The (magnitude of the) buoyant forceknkknœ††
on the ball is obtained by adding up all these -components to obtain w(z 4) d .kkn
''
S
†5
(c) The Divergence Theorem says w(z 4) d div(w(z 4) ) dV w dV, where D
'' ''' '''
SDD
œ œkn k†5
is x y (z 2) 1 w(z 4) d w 1 dV w, the weight of the fluid if it
## #
ŸÊ œ œ
'' '''
SD
kn†51
4
3
were to occupy the region D.
14. The surface S is z x y from z 1 to z 2. Partition S into small pieces and let be the area of theœ œ œ
È## ?5
i
i piece. Let (x y z ) be a point on the i piece. Then the magnitude of the force on the i piece due to
th th th
iii
ßß
liquid pressure is approximately F w(2 z ) the total force on S is approximately
iii
œ Ê?5
F w(2 z ) the actual force is w(2 z) d w 2 x y 1 dADD ?5 5
iSR
iii
xy
œ Ê œ
'' '' ˆ‰
ÈÉ
##
x
xy xy
y
2 w 2 x y dA 2w(2 r) r dr d 2w r r d dœœ œœœ
''
Rxy
01 0 0
22 2 2
ÈÈÈ
ˆ‰ ‘
È## #$
"#
"
'' ' '
)))
333
22w 42w
ÈÈ
1
15. Assume that S is a surface to which Stokes's Theorem applies. Then d ( ) d
)CEr En†™†œ‚
''
S
5
d d . Thus the voltage around a loop equals the negative of the rate ofœ œ
'' ''
SS
ˆ‰
``
``
B
tt
††nBn55
change of magnetic flux through the loop.
16. According to Gauss's Law, d 4 GmM for any surface enclosing the origin. But if
''
S
Fn F H†™51œœ‚
then the integral over such a closed surface would have to be 0 by the Divergence Theorem since div 0.Fœ
17. f g d (f g) d (Stokes's Theorem)
)C™† ™ ™ †rnœ‚
''
S
5
(f g f g) d (Section 16.8, Exercise 19b)œ‚‚
''
S
™™ ™ ™†n5
[(f)( ) f g] d (Section 16.7, Equation 8)œ‚
''
S
0n™™†5
( f g) dœ‚
''
S
™™†n5
18. ( ) is conservative f; also, ™ ™ ™ ™ ™† ™†‚œ ‚Ê ‚ œÊ Êœ œFF FF0FF FF FF
" # #" #" #" " #
( ) 0 f 0 (so f is harmonic). Finally, on the surface S, f ( )ʜʜ œ™† ™ ™ † †FF nFFn
#" #"
#
0. Now, (f f) f f f f so the Divergence Theorem givesœœ œ FnFn
#" #
† † ™† ™ ™ †™ ™
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.

Chapter 16 Additional and Advanced Exercises 1001
f dV f f dV (f f) dV f f d 0, and since f 0 we have
''' ''' ''' ''
DDD S
kk™™™†™™† ™
## #
œ œœ œn5
f dV 0 0 dV 0 , as claimed.
''' '''
DD
kk k k™##
#" #" # "
œ Ê œ Ê œ Ê œ FF FF 0 F F
19. False; let y x (y) (x) 0 and 0 0 0
xy0
Fij0 F F ijk0
ijk
œÁÊ œ œ ‚œ œ œ™† ™
``
``
```
```
xy xyz
ââ
ââ
ââ
ââ
ââ
ââ
20. sin 1 cos cos ( )k k kkkk kkkka b kkkk kkkk kkkkrr rr rr rr rr rr rr
uv uv uv uv uv uv uv
‚œ œ œ œ
### ## #### ##
## # #
)) )†
EG F d du dv EG F du dvÊ‚ œÊœ‚ œ kk kk È
rr rr
uv uv
###
5
21. x y z 1 1 1 3 dV 3 dV 3V V dVrijk r r rœ Ê œœÊ œ œ Ê œ™† ™† ™†
''' ''' '''
DD D
"
3
d , by the Divergence Theoremœ"
3''
S
rn†5
Copyright © 2010 Pearson Education Inc. Publishing as Addison-Wesley.