Statistica CSIE ASE Manual De Studiu Undividual 2016 2017 Emilia Gogu
Statistica-CSIE-ASE-Manual-de-studiu-undividual-2016-2017-Emilia-Gogu
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 112 [warning: Documents this large are best viewed by clicking the View PDF Link!]

ACADEMIA DE STUDII ECONOMICE BUCUREȘTI
FACULTATEA DE CIBERNETICĂ, STATIISTICĂ ȘI INFORMATICĂ
ECONOMICĂ
STATISTICA
Manual de studiu individual
Titular disciplină: Emilia GOGU
Anul universitar, 2016-2017

Emilia GOGU Statistica - Manual de studiu individual
Pagina 2 din 112
CUPRINS:
0 INTRODUCERE .................................................................................................................... 6
1 UNITATEA DE STUDIU 1. NOȚIUNI INTRODUCTIVE - OBIECTUL ȘI METODA
STATISTICII ECONOMICO - SOCIALE ................................................................................ 9
1.1 Introducere ......................................................................................................................... 9
1.2 Obiectivele și competențele unității de studiu ................................................................. 9
1.3 Conținutul unității de studiu .......................................................................................... 10
1.3.1 Scurt istoric al apariției și dezvoltării statisticii....................................................... 10
1.3.2 Obiectul și metoda statisticii.................................................................................... 11
1.3.3 Concepte de bază folosite în procesul de cercetare statistică .................................. 12
1.4 Îndrumar pentru autoverificare .................................................................................... 14
1.4.1 Sinteza unității de studiu 1....................................................................................... 14
1.4.2 Concepte și termeni de reținut ................................................................................. 15
1.4.3 Îndrumar pentru autoverificare ................................................................................ 16
1.4.4 Bibliografie obligatorie ............................................................................................ 16
2 UNITATEA DE STUDIU 2 ORGANIZAREA CERCETĂRII STATISTICE ............ 17
2.1 Introducere ....................................................................................................................... 17
2.2 Obiectivele și competențele unității de studiu ............................................................... 17
2.3 Conținutul unității de studiu .......................................................................................... 18
2.3.1 Etapele cercetării statistice ...................................................................................... 18
2.3.2 Observarea (culegerea) datelor statistice ................................................................. 19
2.3.3 Metode de observare statistică ................................................................................. 19
2.3.4 Conceptul de eroare în statistică. Controlul datelor statistice ................................. 21
2.4 Îndrumar pentru autoverificare .................................................................................... 21
2.4.1 Sinteza unității de studiu 2....................................................................................... 21
2.4.2 Concepte și termeni de reținut ................................................................................. 22
2.4.3 Întrebări de control și teme de dezbatere ................................................................. 22
2.4.4 Bibliografie obligatorie ............................................................................................ 23
3 UNITATEA DE STUDIU 3 PRELUCRAREA PRIMARĂ A DATELOR STATISTICE
ȘI PREZENTAREA INFORMAȚIILOR OBȚINUTE ........................................................... 24
3.1 Introducere ....................................................................................................................... 24
3.2 Obiectivele și competențele unității de studiu ............................................................... 24
3.3 Conținutul unității de studiu .......................................................................................... 25
3.3.1 Prelucrarea statistică ................................................................................................ 25
3.3.2 Gruparea și clasificarea datelor statistice ................................................................ 26
3.3.3 Prezentarea datelor statistice ................................................................................... 28
3.4 Îndrumar pentru autoverificare .................................................................................... 30
3.4.1 Sinteza unității de studiu 3....................................................................................... 30
3.4.2 Concepte și termeni de reținut ................................................................................. 30
3.4.3 Întrebări de control și teme de dezbatere ................................................................. 31
4 UNITATEA DE STUDIU 4 INDICATORII STATISTICI .............................................. 33
4.1 Introducere ....................................................................................................................... 33
4.2 Obiectivele și competențele unității de studiu ............................................................... 33

Emilia GOGU Statistica - Manual de studiu individual
Pagina 3 din 112
4.3 Conținutul unității de studiu .......................................................................................... 34
4.3.1 Noțiunea de mărime relativă .................................................................................... 34
4.3.2 Tipuri de mărimi relative ......................................................................................... 34
4.4 Îndrumar pentru autoverificare .................................................................................... 38
4.4.1 Sinteza unității de studiu 4....................................................................................... 38
4.4.2 Concepte și termeni de reținut ................................................................................. 39
4.4.3 Întrebări de control și teme de dezbatere ................................................................. 39
4.4.4 Bibliografie obligatorie ............................................................................................ 40
5 UNITATEA DE STUDIU 5 ANALIZA SERIILOR DE REPARTIȚIE ........................ 41
5.1 Introducere ....................................................................................................................... 41
5.2 Obiectivele și competențele unității de studiu ............................................................... 41
5.3 Conținutul unității de studiu .......................................................................................... 42
5.3.1 Noțiunea de serie de repartiție. Proprietăți .............................................................. 42
5.3.2 Indicatori de nivel și de frecvențe ai seriilor de repartiție ...................................... 44
5.3.3 Indicatorii tendinței centrale .................................................................................... 44
5.3.4 Indicatorii simpli ai variației.................................................................................... 56
5.3.5 Indicatorii sintetici ai variației ................................................................................. 57
5.3.6 Asimetria ................................................................................................................. 61
5.3.7 Aplicație................................................................................................................... 62
5.4 Îndrumar pentru autoverificare .................................................................................... 64
5.4.1 Sinteza unității de studiu 5....................................................................................... 65
5.4.2 Concepte și termeni de reținut ................................................................................. 66
5.4.3 Întrebări de control și teme de dezbatere ................................................................. 66
5.4.4 Bibliografie obligatorie ............................................................................................ 68
6 UNITATEA DE STUDIU 6 ANALIZA SERIILOR INTERDEPENDENTE.
CORELAȚIA ȘI REGRESIA STATISTICĂ ........................................................................... 69
6.1 Introducere ....................................................................................................................... 69
6.2 Obiectivele și competențele unității de studiu ............................................................... 70
6.3 Conținutul unității de studiu .......................................................................................... 70
6.3.1 Noțiunea de corelație. Condiții de aplicare ............................................................. 70
6.3.2 Tipuri de legături între fenomenele social - economice .......................................... 71
6.3.3 Metode de analiză a interdependenței dintre fenomene .......................................... 73
6.3.4 Aplicații ................................................................................................................... 79
6.4 Îndrumar pentru autoverificare .................................................................................... 83
6.4.1 Sinteza unității de studiu 6....................................................................................... 83
6.4.2 Concepte și termeni de reținut ................................................................................. 83
6.4.3 Întrebări de control și teme de dezbatere ................................................................. 84
6.4.4 Bibliografie obligatorie ............................................................................................ 85
7 UNITATEA DE STUDIU 7 ANALIZA SERIILOR CRONOLOGICE ....................... 86
7.1 Introducere ....................................................................................................................... 86
7.2 Obiectivele și competențele unității de studiu ............................................................... 86
7.3 Conținutul unității de studiu .......................................................................................... 87
7.3.1 Serii cronologice – noțiune, proprietăți ................................................................... 87
7.3.2 Seriile cronologice formate din indicatori absoluți ................................................. 89
7.3.3 Serii cronologice formate din indicatori relativi ...................................................... 89
7.3.4 Serii cronologice formate din indicatori medii ........................................................ 90
7.3.5 Serii cronologice de intervale (perioade) de timp și de momente ........................... 91
Emilia GOGU Statistica - Manual de studiu individual
Pagina 4 din 112
7.3.6 Metode analitice de ajustare .................................................................................... 92
7.3.7 Criterii de alegere a procedeelor de ajustare ........................................................... 93
7.3.8 Extrapolarea seriilor cronologice ............................................................................. 94
7.4 Îndrumar pentru autoverificare .................................................................................... 94
7.4.1 Sinteza unității de studiu 7....................................................................................... 94
7.4.2 Concepte și termeni de reținut ................................................................................. 95
7.4.3 Întrebări de control și teme de dezbatere ................................................................. 96
7.4.4 Bibliografie obligatorie ............................................................................................ 97
8 UNITATEA DE STUDIU 8 METODA INDICILOR ....................................................... 98
8.1 Introducere ....................................................................................................................... 98
8.2 Obiectivele și competențele unității de studiu ............................................................... 98
8.3 Conținutul unității de studiu .......................................................................................... 99
8.3.1 Metoda indicilor – noțiune, proprietăți .................................................................... 99
8.3.2 Concepte, criterii de clasificare și sistematizare a indicilor .................................... 99
8.3.3 Sisteme de ponderare folosite la construirea indicilor ........................................... 106
8.3.4 Condiții și limite ale aplicării metodei indicilor .................................................... 108
8.4 Îndrumar pentru autoverificare .................................................................................. 109
8.4.1 Sinteza unității de studiu 8..................................................................................... 109
8.4.2 Concepte și termeni de reținut ............................................................................... 110
8.4.3 Întrebări de control și teme de dezbatere ............................................................... 110
8.4.4 Bibliografie obligatorie .......................................................................................... 111
8.5 Bibliografie generală ..................................................................................................... 112
Precizări privind alcătuirea manualului de studiu individual
Principalele elementele constitutive, care apar în alcătuirea acestui manualul de studiu individual, corespunzătoare
unei unități de studiu proiectată/dezvoltată sunt următoarele:
Titlul unității – corespunde titlului unuia sau mai multor
capitole/subcapitole din programa de studiu
Cuprinsul unității - specifică secțiunile principale, subsecțiunile şi
numărul paginii unde acestea pot fi localizate
Introducere - secțiune (capitol) care va furniza informații în legătură cu:
locul unității de studiu (US) în cadrul disciplinei, obiectivele US formulate
în termeni de competențe generale şi specifice US
Durata medie de studiu individual - 2-4 ore
Emilia GOGU Statistica - Manual de studiu individual
Pagina 5 din 112
Obiectivele unităților de studiu – enunţă competenţele ce urmează a fi
dobândite pe parcursul unităţii de studiu. Dacă, la nivelul programei,
competenţele sunt prea general formulate (în consecinţă neevaluabile), se
redefinesc competenţele programei prin raportare la conţinuturile unităţii
de învăţare. Aceasta se face astfel: fiind dată competenţa Q din programă
şi conţinuturile C ale unităţii de învăţare, se formulează competenţe
specifice pentru unitatea de învăţare astfel încât acestea să fie evaluabile
(pe parcurs şi la sfârşitul unităţii de învăţare). Întrebarea la care trebuie
răspuns este: La ce foloseşte cursantului conţinutul unităţii de învăţare?
Răspunsul se dă în termeni operaţionali/procedurali/contextuali, după caz
şi în funcţie de disciplină.
Conţinutul unităţii de învăţare –(sinteze teoretice, exemple) redactarea
textului propriu-zis va ţine cont de interacţiunea competenţe-conţinuturi.
Textul va fi structurat astfel încât cantitatea de informaţie nouă pe unitatea
de învăţare să fie raţională, echilibrat distribuită şi asimilabilă.
Sinteza unității de studiu - Rezumatul sau Sinteza ideilor, noţiunilor şi
conceptelor dezbătute în cadrul unităţii de învăţare.
Concepte și termeni de reținut - Definiţii şi terminologie
Întrebări de control și teme de dezbatere
Îndrumar pentru autoevaluare sau Testele de autoevaluare reprezintă
exercițiile sau rezolvarea unor probleme. Acestea solicită studentul să
efectueze o activitate mai complexă decât simpla rezolvare a unui test de
autoevaluare. De exemplu, studentului i se poate solicita să scrie un
paragraf prin care descrie opinia personală asupra unui subiect studiat şi
analizat. De asemenea, exercițiile pot solicita practicarea unor deprinderi
necesare formării studentului ca viitor specialist
Bibliografie obligatorie- va enunța o listă minimală pe care cursantul
trebuie să o parcurgă pentru studiul unității de învățare. Bibliografia va fi
prezentată la sfârșitul fiecărei unități de studiu şi va constitui un decupaj
din bibliografia generală de la sfârșitul manualului.
Emilia GOGU Statistica - Manual de studiu individual
Pagina 6 din 112
0 INTRODUCERE
Statistica reprezintă arta și știința
colectării, modelării și înțelegerii datelor/indicatorilor care
analizează și caracterizează fenomenele de masă.
Definiție. Statistica este știința care studiază aspectele cantitative ale determinărilor calitative ale
fenomenelor de masă, fenomene care sunt supuse acțiunii legilor statistice care se manifestă în
condiții concrete, variabile în timp, spațiu și sub aspect organizatoric.
Statistica studiază latura cantitativă a fenomenelor social-economice de masă în strânsă legătură
cu latura calitativă.
Statistica studiază dimensiunea (mărimea) unui fenomen, structura și mutațiile de atribuire
intervenite în timp, dinamica (evoluția în timp) lui și relațiile de interdependență cu alte fenomene.
Cu precădere statistica se ocupă cu studiul fenomenelor de masă care se mai numesc și fenomene
de tip colectiv, incerte nedeterministe sau statistice. Pentru studierea fenomenelor statistice
folosim metode generale (deducția și inducția) și metode proprii. Pornind de la particularitățile
obiectului de studiu statistica și-a elaborat de-a lungul timpului și o metoda proprie de cercetare.
Metoda statisticii constă în totalitatea procedeelor și tehnicilor de culegere a datelor individuale
de masă, de sistematizare și prelucrare a lor și de analiză și interpretare a rezultatelor prelucrării.
Ca disciplină de învățământ statistica se diferențiază în teoria statisticii (statistica generală,
statistica teoretică)care este formată din procedee și metode elaborate de ea și folosită pentru
culegere, prelucrare și analiză a datelor individuale de masă și statistica economică care constă în
aplicarea metodelor statistice la studiul concret al fenomenelor economice și sociale.
Statistica poate fi privită și tratată ca o disciplină metodologică și ea este totalitatea procedeelor și
metodelor utilizate pentru obținerea, sistematizarea și prelucrarea unui număr mare de date
empirice (reale) în scopul obținerii unui număr redus de expresii relevante pentru întregul
ansamblu studiat.
Statistica este importantă pentru economiști și nu numai, deoarece ea permite comprimarea unui
număr mare de date individuale într-un număr mic de indicatori cu ajutorul cărora evidențiem ceea
ce este esențial în nivelul de dezvoltare al fenomenului studiat.
Statistica fiind o disciplină metodologică se poate astfel aplica în diferite domenii de activitate.
indiferent de domeniul de aplicare este necesar ca statistica să opereze cu un sistem unitar de
concepte.
Obiectivele manualului de studiu
Obiectivele principale ale manualului de studiu individual constau în:
Formarea gândirii statistice și însușirea limbajului statistic;
Utilizarea metodelor și tehnicilor de analiză a indicatorilor statistici;
De fundamentare statistică a calculelor de prognoză;
Formarea abilității de a folosi sursele de informații din băncile de date statistice și
din publicațiile oficiale de date statistice;
Folosirea cunoștințelor din manualul de studiu individual, bibliografie și seminarii
pentru elaborarea unui proiect de analiza statistică în domeniul turistic sau comercial.
Competențe conferite
1. Cunoaștere și înțelegere ( cunoașterea și înțelegerea adecvată a noțiunilor specifice
disciplinei)

Emilia GOGU Statistica - Manual de studiu individual
Pagina 7 din 112
Cunoașterea și înțelegerea noțiunilor și conceptelor cu care operează statistica;
Folosirea corectă a termenilor de specialitate din domeniul statistică;
Cunoașterea și însușirea metodologiei de calcul și intrepretare a indicatorilor
statistici economico-sociali
Folosirea competentă a publicațiilor naționale și internaționale de date statistice.
2. Explicare și interpretare (explicarea și interpretarea unor idei, proiecte, procese, precum și
a conținuturilor teoretice și practice ale disciplinei)
Organizarea și funcționarea sistemului informațional statistic;
Organizarea procesului de cercetare statistică într-o viziune sistemică;
Utilizarea cu discernământ a corelațiilor dintre statistică și celelalte științe pentru
analiza cantitativă și calitativă a diferitelor domenii de activitate;
Realizarea unui studiu de caz folosind metodele statistice;
Asigurarea comparabilității datelor statistice pe plan național și internațional.
3. Instrumental aplicative ( proiectarea, conducerea și evaluarea activităților practice
specifice; utilizarea unor metode, tehnici și instrumente de investigare și de aplicare)
Capacitatea de a transpune în practică a cunoștințelor obținute din bibliografie,
seminarii, proiecte și referate ;
Abilități de cercetare, creativitate, competențe în rezolvarea studiilor de caz și a
proiectelor de statistică;
Cunoașterea modului de organizare instituționala a statistici pe plan național și
internațional;
Particularități ale aplicării statistice în comerț și turism.
4. Atitudinale ( manifestarea unei atitudini pozitive și responsabile față de domeniul științific,
cultivarea unui mediu științific centrat pe valori și relații democratice, promovarea unui
sistem de valori culturale, morale și civice, valorificarea optimă și creativă a propriului
potențial în activitățile științifice, implicarea în dezvoltarea instituțională și în promovarea
inovațiilor științifice, angajarea în relații de parteneriat cu alte persoane, instituții cu
responsabilități similare, participarea la propria dezvoltare personală)
Reacții pozitive la disciplina universitară în general și față de exigențele disciplinei de
statistică în particular
Implicarea studenților în activități științifice în legătură cu disciplina statistică pentru
participarea la sesiunile științifice ale universității;
Capacitatea de a avea un comportament etic în relațiile cu colegii și cadrele
didactice;
Capacitatea de a aprecia diversitatea analizei fenomenelor social-economice;
Abilitatea de a colabora cu specialiștii din alte domenii.
Resurse și mijloace de lucru
Disciplina Statistica dispune de un manual de studiu individual pentru studenți, precum și de
material publicat pe site-ul Departamentului ID/IFR sub formă de sinteze, lecții și unități de studiu,
studii de caz și aplicați, necesare întregirii cunoștințelor practice și teoretice în domeniul statistic.
La această materie, în timpul orelor de seminarii sunt folosite echipamente audio-vizuale, metode
interactive și participative de antrenare a studenților pentru conceptualizarea și vizualizarea
practică a noțiunilor predate.
Structura manualului de studiu individual
Unitățile de studiu individual sunt proiectate corespunzător obiectivelor prevăzute în Fișa
disciplinei de Statistică fiind compuse din 8 unități de studiu, astfel:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 8 din 112
Unitatea de studiu
Tematica
Nr. ore
Unitatea de studiu 1.
Obiectul și metoda statisticii economico - sociale
2 ore
Unitatea de studiu 2.
Observarea statistica (culegerea datelor statistice)
3 ore
Unitatea de studiu 3.
Prelucrarea primara a datelor statistice și prezentarea
informațiilor obținute
3 ore
Unitatea de studiu 4.
Indicatori statistici
4 ore
Unitatea de studiu 5.
Analiza seriilor de repartiție
4 ore
Unitatea de studiu 6.
Analiza seriilor interdependente
4 ore
Unitatea de studiu 7.
Analiza seriilor cronologice
4 ore
Unitatea de studiu 8.
Metoda indicilor
4 ore
Teste de control
Desfășurarea testelor de control se va derula conform Calendarului Disciplinei și acestea vor avea
următoarele subiecte:
1. Mărimi relative și reprezentarea grafică
2. Indicatorii tendinței centrale
3. Indicatorii variației și ai asimetriei
4. Corelația și regresia statistică
5. Fundamentarea statistică a calculelor de prognoză
6. Metoda indicilor
Bibliografie obligatorie:
1. Gogu E. - Statistica – Manual de studiu individual CSIE ASE 2016-2017
2. Biji E., Biji. M., Lilea, Anghelache C. Tratat de statistică Editura Economică, 2002
Bibliografie suplimentară:
1. Andrei, T., Stancu, S., - Statistică, Ed. ALL, Bucureşti 1995.
2. Baron,T., Biji, E.,Tovissi, L.,Wagner, P., Isaic-Maniu, A., Korka, M., Porojan, D., - Statistică
teoretică şi economică, Ed. didactică şi pedagogică, Bucureşti, 1996.
3. Biji E.M., Lilea E., Vătui M. Gogu E. Aplicații statistice în studiul fenomenelor economice Editura
Oscar Print, 2007
4. Gogu E. - Statistica în turism și comerț – Teorie și studii de caz Editura Oscar Print, București 2009
5. Isaic-Maniu, A., Mitruţ, C., Voineagu, V., Săvoiu, G., - Statistica afacerilor, Ed. Independenţa
Economică, Piteşti, 2002.
6. Isaic-Maniu, Al. (coord),(2003),Dicţionar de statistică generală, Ed.Economică, Bucureşti
7. Jaba, E., - Statistică, Ed. economică, Bucureşti, 1998.
8. Korka, M.,Tuşa, E., - Statistică pentru afaceri internaţionale, Ed. ASE, Bucureşti, 2004
9. ***Anuarul Statistic al României INS
10. *** Anuarul Statistic al Comerțului Exterior INS
11. *** Statistica teritoriala INS
12. *** www.eurostat.org
13. *** www.unstat.org
14. *** www.ins.ro
15. *** www.tempo-online.ro
Metoda de evaluare:
Examenul final la disciplină Statistica este un examen scris. Subiectele de examinare conțin două
întrebări teoretice deschise și două probleme sub formă de aplicații.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 9 din 112
1 UNITATEA DE STUDIU 1. OBIECTUL ȘI METODA STATISTICII
ECONOMICO - SOCIALE
1.1. Introducere
1.2. Obiectivele și competențele unității de studiu
1.3. Conținutul unității de studiu
1.3.1. Scurt istoric al apariției și dezvoltării statisticii
1.3.2. Obiectul și metoda statisticii
1.3.3. Concepte de bază folosite în procesul de cercetare statistică
1.4. Îndrumar pentru autoverificare
1.1 Introducere
Se poate afirma că statistica a apărut în
necesitatea de a cunoaște, în expresie numerică, o
serie de fenomene, procese și activități social-
economice. Astfel gândirea statistică poate fi
definită ca totalitatea ideilor orientate asupra
căilor de înțelegere, control și reducere a variației.
Obiectul statisticii îl constituie fenomenele de masă care prezintă
proprietatea de a fi variabile ca forma de manifestare individuală în
timp, în spațiu și sub raport organizatoric.
Statistica poate fi privită și tratată ca o disciplină metodologică
și ea este totalitatea procedeelor și metodelor utilizate pentru
obținerea, sistematizarea și prelucrarea unui număr mare de date
empirice(reale) în scopul obținerii unui număr redus de expresii
relevante pentru întregul ansamblu studiat.
Statistica este importantă pentru economiști și nu numai,
deoarece ea permite comprimarea unui număr mare de date
individuale într-un număr mic de indicatori cu ajutorul cărora
evidențiem ceea ce este esențial în nivelul de dezvoltare al
fenomenului studiat.
Statistica fiind o disciplină metodologică se poate astfel aplica în
diferite domenii de activitate. indiferent de domeniul de aplicare este
necesar ca statistica să opereze cu un sistem unitar de concepte.
1.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
identificarea principalelor etape al apariției și dezvoltării
statisticii;
definirea conceptelor de baza cu care operează statistica
în procesul cercetării;
prezentarea obiectului și metodei statisticii.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 10 din 112
Competențele unității de studiu:
studenții vor putea să definească concepte de bază cu care
operează statistica;
studenții vor cunoaște obiectul și metoda statisticii.
Durata medie de studiu individual alocat unității: 2 ore
1.3 Conținutul unității de studiu
1.3.1 Scurt istoric al apariției și dezvoltării statisticii
Cuvântul statistică are o semnificație multiplă pentru cercetători,
specialiști, studenți și populație în general. Pentru cei mai mulți,
statistica înseamnă doar o “descriere numerică” a unor date culese
despre fenomenele de masă.
De-a lungul istoriei, datele au fost permanent colectate. în timpul
civilizației egiptene, grecești și romane datele erau obținute în scopul
primar al taxării și înrolării în armată.
Astfel, în antichitate (cu 4-5 milenii î.e.n.) se întâlnesc forme de
evidență ce pot fi asimilate înțelesului modern de recensăminte
statistice, în special în China, Egipt, Grecia și în Imperiul Roman.
Recensămintele efectuate de romani (din 5 în 5 ani apoi din 10 în 10
ani) erau cunoscute sub denumirea de “cens”. În Dacia, ocupată de
romani, evidențele care se făceau asupra populației, producției și
consumului purtau denumirea de “tabularium”.
Se dezvoltă, de asemenea, evidența cu caracter demografic. În
Evul Mediu, instituțiile bisericești, strângeau adesea și păstrau
informații privind căsătoriile, nașterile, decesele.
Pe măsură ce s-au format statele civilizate statistica s-a diferențiat
față de formele de evidență contabilă.
Modul de gândire statistic ne impune să acceptăm că datele sunt în
mod inerent variabile.
Astfel gândirea statistică poate fi definită ca totalitatea ideilor
orientate asupra căilor de înțelegere, control și reducere a variației.
În procesul istoric de conturare a statisticii moderne pot fi mai
multe momente:
statistica practică
statistica descriptivă - care servea pentru descrierea aspectelor
numerice ale populației și ale statului. Parte a statisticii ce rezumă
datele empirice (intuitive, experimentale, practic, direct) privind
fenomenele de masă investigate.
aritmetica politică – înseamnă elaborarea unor concepte în care
societatea este privită în ansamblul ei. Apar astfel noțiuni de
valoare medie și de tendințe. Cele mai multe studii în această
perioadă, s-au făcut pentru demografie, privind mișcarea
populației. Astfel pe baza unui număr mare de date s-a elaborat

Emilia GOGU Statistica - Manual de studiu individual
Pagina 11 din 112
pentru prima dată o regularitate cu privire la proporția dintre
nașteri și decese, separat pentru populație feminină și cea
masculină.
Ex. Ca tendință generală, la 1000 de fete se nasc 1005 băieți, dar
probabilitatea de supraviețuire este mai mică la băieți, astfel încât
raportul dintre fetițe și băieți este în jurul a 51% de sex feminin și
49% sex masculin, ceea ce însemnă că speranța de viață este mai
mare pentru femei.
calculul probabilităților (statistica matematică) – se ocupă cu
elaborarea unor noțiuni și modele valabile pentru orice domeniu
din natură, societate sau tehnologie.
1.3.2 Obiectul și metoda statisticii
Obiectul statisticii îl constituie studiul fenomenelor și proceselor
social-economice care prezintă următoarele particularități:
Se produc într-un număr suficient de mare de cazuri (sunt
fenomene de masă);
Variază de la un element la altul, de la caz la altul;
Sunt forme individuale de manifestare în timp, în spațiu și ca
formă de organizare.
Rezultă deci că obiectul de studiu al statisticii îl constituie
fenomenele de masa care prezintă proprietatea de a fi variabile ca
forma de manifestare individuală în timp, în spațiu și sub raport
organizatoric.
Spre deosebire de fenomenele simple, fenomenele de masă se
produc sub influența unor factori sistematici sau întâmplători, esențiali
sau neesentiali, de același sens sau de sensuri diferite și au la baza
legile de tip statistic. Pentru a cerceta și verifică o lege statistică este
necesar să fie analizate toate manifestările individuale ale
fenomenului supus cercetării. In acest mod se creează condițiile
necesare pentru manifestarea legii numerelor mari.
Legea numerelor mari este un principiu fundamental al cercetării
statistice care presupune luarea în considerare a unei colectivități
suficient de numeroase de cazuri individuale, astfel încât abaterile
întâmplătoare, într-un sens sau altul, se poate compensa, punându-se
în evidenta o anumita mărime/valoare care este tipica pentru întreaga
colectivitate.
Definiție. "Statistica este știința care studiază aspectele cantitative
ale determinărilor calitative ale fenomenelor de masă, fenomene care
sunt supuse acțiunii legilor statistice care se manifestă în condiții
concrete, variabile în timp și spațiu. "
Fenomenele de masă se mai numesc și :
fenomene de tip colectiv deoarece legea este valabilă pentru
întregul ansamblu și numai întâmplător se verifică în fiecare caz
în parte,
fenomene de tip statistic sau stohastic pentru că ele se supun
legilor statistice1;
1
Legea statistică – lege care acţionează în cadrul unui ansamblu de unităţi, de fenomene sau de procese de aceiaşi
esenţă şi exprimă valoarea medie, predominantă purtată de majoritatea elementelor unui ansamblu distribuit
după o variabilă.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 12 din 112
fenomene aleatoare pentru că între factorii de influență există și
o componență aleatoare,
fenomene atipice pentru că forma lor de manifestare individuală
este diferită;
fenomene nedeterministe ca urmare a faptului că modul de
asociere a factorilor esențiali cu cei neesențiali, a celor sistematici
cu cei aleatori se poate schimba în timp, în spațiu sau ca formă
organizațională,
Principala proprietate a acestor fenomene este variabilitatea în
timp, spațiu și ca formă de organizare, dar care potrivit legii numerelor
mari ea se compensează reciproc față de linia generală de tendință (ce
exprimă esențialitatea fenomenelor legitatea lor de apariție și
dezvoltare).
Fenomenele de masă se întâlnesc în toate comportamentele vieții
economice și sociale și ele nu pot fi studiate decât cu ajutorul
metodelor statistice. Rezultatele cercetării lor se regăsesc în datele
statistice publicate de Institutul Național de Statistică în anuare,
breviare și buletine statistice precum și în diferite studii publicate în
edituri și reviste de specialitate și de Organizațiile Internaționale.
Urmărind etapele oricărui proces de cunoaștere, pentru rezolvarea
problemelor care fac obiectul sau de studiu, statistica, ca orice știința,
și-a elaborat procedee și metode speciale de cercetare.
Metoda statisticii este formată din totalitatea procedeelor și
operațiilor specifici de culegere, prelucrare și analiză statistică a
fenomenelor din realitatea economică și socială în cadrul cărora
activează legile statistice.
Complexitatea și amploarea cercetării statistice fac necesară
perfecționarea continuă a metodelor de observare, prelucrare și
analiză. Dezvoltarea metodelor statisticii este strâns legată de
progresele înregistrate în teoria probabilităților, statistica matematică
și în domeniul informaticii. Necesitatea prelucrării unui volum mare
de date a dus la dezvoltarea mașinilor de calul și implicit la formarea
programelor de calul. (Ex. EXCEL, Eviews, SPSS, SAS.).
1.3.3 Concepte de bază folosite în procesul de cercetare
statistică
În statistică se folosesc o serie de noțiuni (concepte) de bază cu
care se operează în toate etapele cercetării și în toate statisticile
aplicate:
a) Colectivitatea (populația) statistică
b) Unitate statistică:
c) Caracteristici (variabile) statistice
d) Date și indicatori statistici.
e) Măsurarea statistică
f) Estimare statistică.
g) Eroare statistică
a) O primă noțiune de bază din statistică o reprezintă colectivitatea
(denumită și populația) statistică care reprezintă totalitatea

Emilia GOGU Statistica - Manual de studiu individual
Pagina 13 din 112
elementelor de aceeași natură care formează obiectul unui studiu
statistic.
Aceasta poate fi:
concretă (obiectivă și finită), delimitată în timp, spațiu și mod
de organizare cu care operează Statistica social-economică;
infinită și abstractă , cu care operează Statistica matematică;
ipotetică care corespunde unui model de calcul și analiză
statistică în cadrul căreia există relații matematice, strict
determinate,
Statistica abordează de asemenea:
colectivități statice- care exprimă o stare, un nivel la un
moment dat; (ex. Populația Brașovului la 1 dec. 2012)
colectivități dinamice – care caracterizează un proces, o
devenire în timp.(ex. nașterile în București în această lună)
b) Unitatea statistică – reprezintă elementul constitutiv al unei
colectivități statistice.
Unitățile pot fi:
Simple – (Ex. persoana, muncitor etc)
Complexe (Ex. familie, echipă, secție, anul de studiu etc.)
Ca și colectivitățile, unitățile pot fi statice și dinamice.
c) Caracteristicile statistice denumite variabile statistice sau
variabile aliatoare reprezintă proprietățile comune ale unităților care
formează o colectivitate statistică.
În legătură cu acestea se folosesc următoarele noțiuni:
Variabilă –care este orice caracteristică statistică numerică sau
nenumerică care se înregistrează;
Variantă – este forma concretă pe care o variabilă statistică o poate
înregistra la nivelul fiecărei unități prin cuvinte sau expresie
numerică
Variație – proprietatea variabilelor statistice de a-și schimba
nivelul de dezvoltare sau formă concretă de manifestare.
câmp de variație (câmp de împrăștiere) a unităților unei
colectivități în funcție de fiecare variabilă înregistrată. Pentru
variabilele numerice acest câmp se măsoară prin amplitudinea
variației, care este egală cu diferența dintre valoarea maximă și
valoarea minimă înregistrate.
Frecvența – reprezintă numărul de unități la care se înregistrează
aceeași variantă
Ponderea este locul pe care-l ocupă o variantă sau un interval de
variante în cadrul colectivității studiate
Variabilele statistice se pot clasifica:
după conținut în:
Variabile de timp – arată apartenența unităților la un moment
sau perioadă de timp
Variabile de spațiu - situarea în teritoriu al unității;
Variabile atributive – sunt toate celelalte însușiri numerice și
calitative ale unităților.
după modul de exprimare în:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 14 din 112
caracteristici calitative (exprimate prin cuvinte) Ex. profesia
caracteristici cantitative (exprimate numeric) Ex. Vârsta
după natura variației se împart în:
Variație continuă – ex. Vârsta
Variație discontinuă sau discretă Ex. Valoarea capitalului fix
după modul de manifestare în:
alternative – manifestare directă sau opusă ei (Ex Rural Urban)
nealternative - cu variante distincte numerice sau calitative (Ex
Salariu și profesia)
după modul de obținere și folosire a datelor ele pot fi:
primare obținute în procesul de culegerea datelor (Numărul de
cărți din bibliotecă )
derivate - obținute prin aplicarea unui model de calul statistic
(Ex. 90 % din cărți au fot citite)
d) Datele și indicatori statistici reprezintă caracterizări numerice ale
unităților obținute prin observare și prelucrare. în statistică datele
sunt întotdeauna mărimi concrete. Mesajul datelor îl reprezintă
informația statistică.
după modul de utilizare a datelor ele pot fi:
primare - obținute în procesul de observare
derivate - obținute prin prelucrare
O parte din datele statistice se regăsesc sub forma de indicatori
statistici. Deosebirea constă, că datele statistice sunt noțiuni
generalizatoare, în timp ce indicatorii sunt particularizați pe domenii.
e) Măsurare statistică - presupune exprimarea în unități
concrete de măsură.
f) Estimare statistică – presupune și caracterizare statistică
utilizând un model sau o ipoteză statistică.
g) Eroare statistică – înțelegem abaterile care pot să apară între
dimensiunea reală a fenomenelor studiate și cele stabilite printr-
un model de calcul statistic Ele sunt admise într-o proporție de
5%. Acestea sunt reglate prin proprietățile legii numerelor mari și
sunt calculabile, în general, cu ajutorul funcțiilor de probabilitate,
elaborate de statistica matematică.
1.4 Îndrumar pentru autoverificare
1.4.1 Sinteza unității de studiu 1
Se poate afirma că statistica a apărut în necesitatea de a cunoaște, în expresie numerică,
o serie de fenomene, procese și activități social-economice. Astfel gândirea statistică
poate fi definită ca totalitatea ideilor orientate asupra căilor de înțelegere, control și
reducere a variației.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 15 din 112
În procesul istoric de conturare a statisticii moderne pot fi mai multe momente: statistica
practică, statistica descriptivă, aritmetica politică și calculul probabilităților (statistica
matematică).
Obiectul statisticii îl constituie fenomenele de masă care prezintă proprietatea de a fi variabile
ca forma de manifestare individuală în timp, în spațiu și sub raport organizatoric.
Statistica este știința care studiază aspectele cantitative ale determinărilor calitative ale
fenomenelor de masă, fenomene care sunt supuse acțiunii legilor statistice care se manifestă în
condiții concrete, variabile în timp și spațiu.
Metoda statisticii este formată din totalitatea procedeelor și operațiilor specifici de culegere,
prelucrare și analiză statistică a fenomenelor din realitatea economică și socială în cadrul cărora
activează legile statistice.
Complexitatea și amploarea cercetării statistice fac necesară perfecționarea continuă a
metodelor de observare, prelucrare și analiză.
În statistică se folosesc o serie de noțiuni (concepte) de bază cu care se operează în toate
etapele cercetării și în toate statisticile aplicate: colectivitatea (populația) statistică, unitatea
statistică, caracteristici (variabile) statistice, date și indicatori statistici, măsurarea statistică,
estimare statistică și eroare statistică.
1.4.2 Concepte și termeni de reținut
Alternative
Eroare statistică
Nealternative
Anuare statistice
Estimare statistică
Statistica descriptivă
Aritmetica politică
Factori esențiali
Statistica matematică
Breviare statistice
Factori întâmplători
Statistica practică
Buletine statistice
Factori neesențiali
Unitate statistică
Câmp de variație
Factori sistematici
Variabilă
Câmp de împrăștiere
Fenomene aleatoare
Variabile aleatoare
Caracteristici statistice
Fenomene atipice
Variabile atributive
Caracteristici calitative
Fenomene de masă
Variabile de spațiu
Caracteristici cantitative
Fenomene de tip colectiv
Variabile de timp
Colectivitate concretă
Fenomene de tip stohastic
Variabile statistice
Colectivitate infinită și
abstractă
Fenomene nedeterministe
Variantă
Colectivitate ipotetică
Frecvența
Variație
Colectivitatea (populația)
statistică
Gândirea statistică
Variație continuă
Colectivități dinamice
Informația statistică
Variație discretă
Colectivități statice
Ipoteză statistică
Variație discontinuă
Date și indicatori statistici.
Legea numerelor mari
Determinări calitative
Linia generală de tendință

Emilia GOGU Statistica - Manual de studiu individual
Pagina 16 din 112
1.4.3 Îndrumar pentru autoverificare
Întrebări de control și teme de dezbatere
1. Ce este Statistica?
2. Cu ce se ocupă statistica economico-socială?
3. Ce sunt fenomenele de masă? Prin ce se deosebesc de celelalte fenomene din natură,
tehnologie și societate?
4. Care este sfera de cuprindere a fenomenelor de masă care formează obiectul statisticii
economico-sociale?
5. Care sunt etapele procesului de cunoaștere statistică?
6. În ce constă caracterul unitar al acestui proces de cunoaștere?
7. Care sunt noțiunile de bază folosite în statistica economico-socială?
8. Care sunt ramurile statisticii economico-sociale și relațiile dintre ele?
9. Care sunt raporturile statisticii economico-sociale cu celelalte științe?
10. Cum este organizată statistica în țara noastră și pe plan mondial?
11. Care sunt direcțiile de perfecționare ale statisticii în funcție de dotarea economiei
naționale cu tehnică modernă de calcul?
1.4.4 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Gogu E., Statistica în turism și comerț, Editura Oscar Print, București, 2009;
4. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 17 din 112
2 UNITATEA DE STUDIU 2. ORGANIZAREA CERCETĂRII STATISTICE
2.1. Introducere
2.2. Obiectivele și competențele unității de studiu
2.3. Conținutul unității de studiu:
2.3.1. Etapele cercetării statistice
2.3.2. Observarea statistică (culegerea datelor statistice)
2.3.3. Metode de cercetare statistică
2.3.4. Conceptul de eroare în statistică. Controlul datelor statistice
2.4. Îndrumător pentru autoverificare
2.1 Introducere
Ținând seama de particularitățile statisticii ca
știință – studiul fenomenelor de masă și analizarea
aspectelor cantitativ numerice interpretate în
condiții date de timp, de spațiu și de organizare –
statistica trebuie să pornească de la înregistrarea
formelor empirice a fenomenelor și prin abstractizare și generalizare
să ajungă la cunoașterea aspectelor esențiale comune pentru toată masa
de fenomene precum și a legilor care le guvernează.
Procesul de cunoaștere statistică se realizează în trei etape
succesive: Observarea (culegerea) formelor individuale a
fenomenelor de masă;
prelucrarea și obținerea indicatorilor generalizatori și
sintetici
analiza și interpretarea rezultatelor prelucrării.
Urmărind etapele oricărui proces de cunoaștere, pentru
rezolvarea problemelor care fac obiectul sau de studiu, statistica, ca
orice știința, și-a elaborat procedee și metode speciale de cercetare.
Cercetarea statistică este un proces complex care antrenează un
număr mare de specialiști statisticieni, informaticieni și de alte
profesii.
În toate cazurile, în care se organizează un studiu statistic, este
necesar să se înceapă cu observarea (culegerea datelor). În acest scop,
este necesar să se stabilească, în primul rând, sursele de date, metoda
de observare și să se înregistreze datele care vor fi supuse ulterior
prelucrării.
2.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
Identificarea etapelor cercetării statistice;
Emilia GOGU Statistica - Manual de studiu individual
Pagina 18 din 112
Identificarea metodelor de observare statistică;
Culegerea datelor;
Identificarea avantajelor și dezavantajelor metodelor de
observare.
Controlul datelor statistice
Competențele unității de studiu:
studenții vor identifica etapele cercetării statistice;
cursanții vor putea identifica care metodă de observare este
optimă în funcție de domeniul cercetat;
studenții vor putea stabili metoda de control al datelor culese.
Durata medie de studiu individual alocat unității: 2 ore
2.3 Conținutul unității de studiu
2.3.1 Etapele cercetării statistice
Organizarea și desfășurarea unei cercetări statistice concrete se
prezintă astfel:
Deși cercetarea statistică se desfășoară în trei etape succesive ea
reprezintă un proces unitar prin conținutul, scopul și prin metodele
utilizate. În cadrul cercetării statistice rolul cel mai important îi revine
analizei statistice Ea trebuie să asigure nu numai o interpretare
științifică a rezultatelor cercetării, dar mai ales obținerea unui material
documentar real.
Procesul de cercetare statistică se poate realiza în condiții optime
folosind echipamente moderne de calcul. Acesta prezintă un dublu
avantaj:
se pot culege date pentru un număr suficient de mare de
caracteristici;
reduce timpul de prelucrare a datelor culese.
Pe plan național statistica poate fi structurată în statistica oficială
și în statistica academică
De cele mai multe ori ordinea de elaborare a programului de
cercetare este invers procesului de cercetare. Întâi se stabilește ce
anume se va analiza și în ce scop, apoi metodele de prelucrare și în
ultimul rând se aleg caracteristicile ce trebuie înregistrate și forma de
observare. Indiferent de ordinea în care se elaborează programul
acesta se subordonează obiectului și scopului cercetării.
OBSERVAREA
STATISTICĂ
PRELUCRAREA
STATISTICĂ
ANALIZA ȘI
INTERPRETAREA
STATISTICĂ

Emilia GOGU Statistica - Manual de studiu individual
Pagina 19 din 112
2.3.2 Observarea (culegerea) datelor statistice
În toate cazurile, în care se organizează un studiu statistic, este necesar
să se înceapă cu observarea (culegerea datelor). În acest scop, este
necesar să se stabilească, în primul rând, sursele de date, metoda de
observare și să se înregistreze datele care vor fi supuse ulterior
prelucrării.
Prin urmare, observarea statistică este etapă în care se
înregistrează datele primare în mod unitar cu privire la unele
caracteristici în prealabil stabilite, de la unitățile care formează
obiectul supus studiului statistic.
Observarea trebuie să îndeplinească anumite condiții de cantitate
(volum) și calitate.
Principiile organizării și desfășurării observării statistice sunt:
autenticitatea (veridicitatea) datelor culese;
completitudinea datelor;
confidențialitatea datelor înregistrate;
asigurarea credibilității datelor;
Din punct de vedere al planului observării statistice acesta
trebuie să cuprindă:
Obiectul și scopul observării; - se stabilește odată cu programul
întregii cercetări. Acesta trebuie să fie strict precizat deoarece
este necesar să alegem numai acele variabile care răspund direct
cu scopul cercetării;
Timpul observării (la care se referă datele) și timpul înregistrării;
Locul observării;
Programul observării;
Formularele și instrucțiunile de completare trebuie să fie
tipizate;
Măsuri organizatorice.
Unitatea simplă și/sau unitatea complexă de observare;
Unitatea raportoare;
2.3.3 Metode de observare statistică
În procesul de dezvoltare al statistici s-au conturat mai multe metode
de observare. În general metoda de observare a fost și este dependentă
de modul de organizare și funcționare a sistemului informațional
statistic.
Existența mai multor metode de observare, face posibilă
clasificarea lor în funcție de mai multe criterii astfel:
În funcție de gradul de cuprindere a numărului de unități avem:
- observare totală
- observare parțială
În funcție de modul în care este caracterizat fenomenul:
- observări statice (la un moment dat)
- observări dinamice (în timp)
În funcție de modului de organizare:
- observări cu caracter permanent
- observări speciale
Din punct de vedere al timpului de efectuare se pot întâlni:
- observări curente

Emilia GOGU Statistica - Manual de studiu individual
Pagina 20 din 112
- observări periodice
- observări unice
Principalele metode de observare sunt:
1) Recensământul;
2) Rapoartele statistice;
3) Sondajul statistic;
4) Ancheta statistică;
5) Observarea părții principale;
6) Monografia.
1) Recensământul – este o metodă de observare totală, cu caracter
periodic, care surprinde un fenomen în mod static. Este cea mai veche
metodă de observare statistică, apărută încă din antichitate
(recensăminte ale populației a romani care se efectua din 5 în 5 ani).
Acesta în general reprezintă fotografierea fenomenelor la un
moment dat.
Recensământul populației este “un proces de culegere,
prelucrare și publicare a datelor demografice economice și sociale la
un moment specificat”. Aceste date oferă informații despre toate
persoanele din țara respectivă sau de pe un teritoriu delimitat.
La noi în țară acesta se efectuează periodic din 10 în 10 ani.
(Periodicitatea mai mare sau mai mică este în funcție de mutațiile
survenite sau de suportul financiar disponibil).
Momentul critic este ales, uzual, în timpul iernii evitându-se
vacanțele, concediile, astfel ca populația, în prealabil anunțată, să fie
surprinsă. (în România 7 ianuarie 1992; 17 februarie 2002, 20
octombrie 2011).
Din domeniul populației, recensământul s-a extins și asupra altor
domenii: există recensăminte asupra unităților hoteliere, al locuințelor,
al animalelor, al unităților din industrie, comerț, transport agricultură
(prin urmare recensăminte economice).
2) Rapoartele statistice – sau sistemul dărilor de seamă se întocmesc
la nivelul instituțiilor și agenților economici, fie publici sau privați
Acestea sunt obligați (de statul de drept) ca în permanență să furnizeze
informații privind activitatea desfășurată. Prin urmare în aceste dări de
seamă sunt încluși indicatori cu caracter economic social-cultural,
juridic, de sănătate publică și învățământ.
3) Sondajul statistic sau selecția statistică este o metodă parțială de
observare, și a devenit una din cele mai utilizate în prezent. Avantajele
acestei cercetări sunt:
- poate fi aplicabilă în toate cazurile
- economii de resurse bănești
- un program de cercetare amplu
La baza sondajului stă eșantionul extras din colectivitatea totală,
care trebuie să îndeplinească condiția de reprezentativitate. (Mai
amplu vom analiza sondajul statistic în cea de a doua parte a
materiei).
4) Ancheta statistică – este o metodă de observare parțială care constă
în intervievarea unor persoane deja stabilite. Acestea primesc un
chestionar la care răspund benevol.
5) Observarea părții principale – observare parțială special
organizată, care se aplică pentru obținerea informațiilor despre o

Emilia GOGU Statistica - Manual de studiu individual
Pagina 21 din 112
colectivitate împărțită pe grupe de importanță. Se înregistrează datele
numai pentru grupele care au cea mai mare pondere.
6) Monografia - observare parțială care se realizează la o unitate
complexă. Ex. Monografia unui oraș municipiu, întreprindere etc. O
monografie amplă a fost întocmită de Dimitrie Cantemir în
“Descriptio Moldave”. Această lucrare tratează aspecte istorice,
politice, economice, culturale, demografice.
În cadrul oricărei metode se poate opera cu următoarele
procedee de observare: măsurarea directă; interogare;
autoînregistrare; preluare din alți purtători de informație;
corespondența; e-mail; telefon etc.
Din datele înregistrat obținem informația statistică.
2.3.4 Conceptul de eroare în statistică. Controlul datelor
statistice
Eroarea statistică este diferența dintre un indicatorul obținut pe
baza diferitelor calcule și valoarea reală.
Practica a dovedit că în mod curent se pot produce mai multe
feluri de erori:
De observare sau înregistrare
De reprezentativitate
De modelare;
De interpretare.
Toate acestea pot fi sistematice sau întâmplătoare
Pentru a înlătura sau minimiza aceste variații se recurge la
controlul datelor care poate fi:
Cantitativ
Calitativ
Logic
Aplicarea testelor de semnificație pentru indicatorii calculați
Aplicarea metodelor de verificare a ipotezelor pentru validarea
modelului ales.
După ce s-au obținut datele statistice acestea prezintă forme
concrete, individuale de manifestare. Și pentru a le utiliza în analiza și
interpretare statistică este necesar procesul de prelucrare.
2.4 Îndrumar pentru autoverificare
2.4.1 Sinteza unității de studiu 2
Cercetarea statistică se desfășoară în trei etape succesive ea reprezintă un proces
unitar prin conținutul, scopul și prin metodele utilizate. În cadrul cercetării statistice
rolul cel mai important îi revine analizei statistice Ea trebuie să asigure nu numai o
interpretare științifică a rezultatelor cercetării, dar mai ales obținerea unui material
documentar real.
Procesul de cercetare statistică se poate realiza în condiții optime folosind echipamente
moderne de calcul. Prin urmare, observarea statistică este etapă în care se înregistrează datele
primare în mod unitar cu privire la unele caracteristici în prealabil stabilite, de la unitățile care
Emilia GOGU Statistica - Manual de studiu individual
Pagina 22 din 112
formează obiectul supus studiului statistic. Observarea trebuie să îndeplinească anumite condiții
de cantitate (volum) și calitate.
Principiile organizării și desfășurării observării statistice sunt: autenticitatea (veridicitatea)
datelor culese; completitudinea datelor; confidențialitatea datelor înregistrate; asigurarea
credibilității datelor.
În procesul de dezvoltare al statistici s-au conturat mai multe metode de observare. În general
metoda de observare a fost și este dependentă de modul de organizare și funcționare a sistemului
informațional statistic.
Principalele metode de observare sunt:
recensământul,
rapoartele statistice,
sondajul statistic,
ancheta statistică,
observarea părții principale
și monografia.
În cadrul oricărei metode se poate opera cu următoarele procedee de observare: măsurarea
directă, interogare, autoînregistrare, preluare din alți purtători de informație, corespondența,
telefon.
Eroarea statistică este diferența dintre un indicatorul obținut pe baza diferitelor calcule și
valoarea reală.
După ce s-au obținut datele statistice acestea prezintă forme concrete, individuale de
manifestare. Și pentru a le utiliza în analiza și interpretare statistică este necesar procesul de
prelucrare.
2.4.2 Concepte și termeni de reținut
Ancheta statistică,
Modul de funcționare
Asigurarea credibilității datelor.
Modul de organizare
Autenticitatea (veridicitatea) datelor culese;
Monografia
Autoînregistrare,
Observarea părții principale
Completitudinea datelor;
Procedee de observare
Confidențialitatea datelor înregistrate;
Rapoartele statistice,
Directă, interogare,
Recensământul,
Eroarea statistică
Sistemul informațional statistic
Informația statistică
Sistemul dărilor de seamă
Măsurarea statistică
Sondajul statistic
2.4.3 Întrebări de control și teme de dezbatere
1. Care este rolul culegerii datelor (observării) în procesul de cercetare statistică?
2. Ce se înțelege prin observarea statistică?
3. Ce forme de observare statistică se folosește în practică?

Emilia GOGU Statistica - Manual de studiu individual
Pagina 23 din 112
4. Care sunt trăsăturile caracteristice ale recensământului?
5. Care sunt trăsăturile caracteristice ale observării selective?
6. Care sunt trăsăturile caracteristice ale anchetei statistice?
7. Care sunt trăsăturile caracteristice ale monografiei statistice?
8. Ce probleme trebuie să cuprindă planul observării?
9. Ce este timpul observării și timpul înregistrării?
10. Ce este programul observării?
11. Ce se înțelege prin eroare de observare statistică și cum se face controlul datelor?
12. Mărimea de eroare în statistică și cum se face controlul datelor statistice?
2.4.4 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Gogu E., Statistica în turism și comerț, Editura Oscar Print, București, 2009;
4. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 24 din 112
3 UNITATEA DE STUDIU 3 PRELUCRAREA PRIMARĂ A DATELOR
STATISTICE ȘI PREZENTAREA INFORMAȚIILOR OBȚINUTE
3.1. Introducere
3.2. Obiectivele și competențele unității de studiu – timp alocat
3.3. Conținutul unității de studiu:
3.3.1. Prelucrarea statistică
3.3.2. Gruparea și clasificarea statistică
3.3.3. Prezentarea datelor sub formă de tabele, serii și grafice
3.4. Îndrumar pentru autoverificare
3.1 Introducere
Prelucrarea statistica
– este un proces prin care
datele înregistrate sunt sistematizate sunt tratate
statistic în vederea obținerii sistemului de indicatori
statistici. Obținerea indicatorilor statistici este
necesară pentru caracterizarea în expresii numerice
generalizatoare, a ceea ce este esențial pentru un grup de unități sau
pentru întreaga colectivitate, studiate în condiții de timp și de spațiu.
Prelucrarea primară înseamnă în același timp și centralizarea,
sistematizarea și omogenizarea datelor observării în vederea aplicării
modelelor de calcul și analiză statistică.
Sistematizarea datelor înregistrate presupune ordonarea acestora în
funcție de omogenitatea lor.
3.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
cunoașterea etapelor prelucrării statistice;
definirea principalelor elemente ale prelucrării statistice;
centralizarea și gruparea datelor statistice;
metodologia grupării datelor;
prezentarea datelor sub formă grafică (categorii de diagrame).
Competențele unității de studiu:
sistematizarea datelor statistice;
alegerea formei optime de grupare a datelor statistice;
studenții vor putea realiza grupări pe interval egale și neegale;
studenții vor putea stabili și elabora tipul de grafic în vederea
prezentării datelor.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 25 din 112
Durata medie de studiu individual alocat unității: 3 ore
3.3 Conținutul unității de studiu
3.3.1 Prelucrarea statistică
Prelucrarea primară înseamnă în același timp și centralizarea,
sistematizarea și omogenizarea datelor observării în vederea aplicării
modelelor de calcul și analiză satistică
Sistematizarea datelor înregistrate presupune ordonarea acestora
în funcție de omogenitatea lor.
Deci la baza sistematizării se află principiul omogenității. (Ex.
pentru formularea unei idei sau a unei fraze de compliment – cuvintele
trebuiesc alese (grupate), sau (clasificarea studenților după notele
obținute la examenul de statistică).
Principiul omogenității este un principiu de pierdere a
informației pentru a câștiga informație.
Însăși sistematizarea se realizează prin: centralizarea și
gruparea statistica a datelor.
a) centralizarea – presupune totalizarea unităților statistice sau a
valorilor unei caracteristici la nivelul grupelor tipice sau al
colectivității observate. Totalizarea valorilor unei caracteristici se
face prin însumarea directa sau prin folosirea unor coeficienți de
echivalenta (preturi, timpul de munca etc.) În urma centralizării
obținem mult doriții indicatori statistici de nivel (ex, nr. populației
unei localități, valoarea producției)
Centralizarea simplă și obținerea indicatorilor (agregatelor) generali
Tabelul 3.1.
Nr.crt.
al unității
Variabile însumabile direct
X1
X2
Xp
1
x11
x21
xp1
2
x12
x22
xp2
i
x1i
x2i
xpi
n
x1n
x2n
xpn
Total
Pe orizontală se găsește fiecare unitate cu toate variantele
înregistrate la toate caracteristicile (variabilele) înregistrate, iar pe
verticală sunt distribuțiile de valori ale celor p variabile independente
înregistrate.
n
ii
x
11
n
ii
x
12
n
ipi
x
1

Emilia GOGU Statistica - Manual de studiu individual
Pagina 26 din 112
3.3.2 Gruparea și clasificarea datelor statistice
Gruparea statistică – este o centralizare pe grupe a unităților
unei colectivității. Se obține în baza aplicării metodei grupărilor
statistice presupunând principiul omogenității.
Omogenitatea statistică înseamnă ca în grupa (clasa) respectivă să
existe variație minimă între variantele înregistrate – variație care poate
fi explicată ca fiind influența factorilor aleatori.
În forma grupării statistice – rezultă șiruri de date ordonate după
variație, în sens crescător sau descrescător, a caracteristicilor de
grupare.
După conținutul caracteristicii de grupare putem avea:
grupări cronologice în cazul în care sistematizarea datelor se
face după o variabilă de timp;
grupări teritoriale când sistematizarea datelor se face după o
variabilă de spațiu;
grupări atributive se folosesc pentru toate caracteristicile, în
afara caracteristicilor de timp și spațiu.
Caracteristicile atributive pot fi caracteristici cantitative
(numerice) și calitative (nenumerice).
După numărul variabilelor de grupare pot fi: simple și combinate.
Grupările simple (după o singură variabilă) pot fi:
a) gruparea pe variante dacă amplitudinea variației este mică și la
nivelul unităților individuale s-au înregistrat un număr mic de
valori distincte (variante); Tabelul 3.2.
Durata sejurului (zile )
Nr. turiști
5
10
6
15
7
20
8
30
9
35
10
30
11
15
12
10
TOTAL
165
b) gruparea pe intervale de variație egale - dacă amplitudinea
variației este moderată. În acest caz, e necesar, să se stabilească
numărul de grupe și mărimea intervalului de variație.
Tabelul 3.3.
Grupe de studenți după nr.
de prezente
Nr.
studenți
sub 50
50
50-70
80
70-90
60
90-110
120
110-peste
130
Total
440
Emilia GOGU Statistica - Manual de studiu individual
Pagina 27 din 112
c) gruparea pe intervale de variație neegale. Prin gruparea pe
intervale neegale se urmărește să se structureze colectivitatea pe
tipuri calitative, dacă nu se cunosc valorile (pragurile) care
separă tipurile calitative, se procedează mai întâi la gruparea pe
intervale egale și apoi se poate folosi criteriul mediei pentru
formarea tipurilor calitative “mic”, “mediu”, “mare”. In acest
caz se obține o grupare tipologică.
Tabelul 3.3.
Grupe de studenți după nr. de
ore aferente pregătirii pentru
examene
Nr.
studenți
Sub 30
4
30-40
5
40-60
6
60-85
10
85-120
12
120-150
7
150-200
4
200 peste
2
Total
50
Gruparea combinată - presupune sistematizarea datelor după
două sau mai multe caracteristici de grupare (cel mult 4) care pot fi
variabile numerice și/sau calitative. Gruparea combinată impune
stabilirea ordinii de grupare pe baza relației de interdependență dintre
variabile. Grupele formate după prima caracteristică se regrupează după
cea de a doua ș.a.m.d. Tabelul 3.4.
Grupe după
ore lucrate
Repartițiile după veniturile lunare (lei)
Total
Sub
1400
1400-
2500
2500-
3600
3600 și
peste
sub 10
10
10
5
-
25
10 – 20
-
5
10
-
15
20 și peste
-
-
5
15
20
Total
10
15
20
5
60
Clasificarea (gruparea pentru variabile calitative) - se
efectuează după variabile nenumerice (calitative) și presupune
includerea în aceeași grupă (clasă) a tuturor unităților la care s-a
înregistrat aceeași formă de manifestare a caracteristicii. De regulă, are
un caracter oficial (ex. CAEN) și în prealabil trebuie stabilit un
nomenclator al claselor. Tabelul 3.5.
Genul
Nr studenți
feminin
125
masculin
200
Total
325
Metodologia grupării

Emilia GOGU Statistica - Manual de studiu individual
Pagina 28 din 112
Gruparea pe intervale egale implică următoarele etape:
a) calculul amplitudinii absolute de variației (A) care exprimă
împrăștierea maximă a valorilor serei.
Axa = Xmax – Xmin;
b) stabilirea în parametrii într-un anumit număr de grupe (r) se poate
stabili conform relației lui Sturgers,
r = 1+3,322log n, unde n - nr. caracteristicilor.
c) determinarea mărimii intervalului de grupare (h), se calculează ca
raport între amplitudinea absolută a variației și numărul de grupe:
sau
Notă: Mărimea intervalului (h) se rotunjește la întreg în plus (ex.3,254)
Prima grupă se pornește de la xmin adăugându-se succesiv mărimea
intervalului de grupare (h) rezultat din calculul anterior. Valoarea din
stânga intervalului va fi considerată ca limită inferioară, iar valoarea din
dreapta ca limită superioară. Valorile care formează limitele intervalelor
se înregistrează fie numai ca limită superioară fie ca limită inferioară
pentru a evita înregistrări duble a caracteristicilor.
Indiferent de scopul și obiectul grupării, aceasta trebuie să
îndeplinească cel puțin următoarele condiții:
- completitudinea datelor;
- omogenitatea grupelor(claselor) și subgrupelor (subclaselor);
- unicitatea includerii unităților într-o singură grupă (clasă);
- continuitatea variației grupelor în cazul variabilelor numerice,
ceea ce practic înseamnă să nu existe grupe cu frecvențe nule care
ar duce la întreruperea grupării.
Pentru analiza structurii colectivității pe grupe tipice se folosește
gruparea pe intervale neegale.
Gruparea pe intervale neegale presupune regruparea intervalelor egale.
Un prim principiu al grupării pe intervale neegale este trecerea de la
variația liniară (interval de mărime constantă) la variația neuniformă a
unor intervale de grupare din ce în ce mai mari. De exemplu, de la 8
grupe se poate trece la 5,3 grupe obținând calificative
Clasificarea se efectuează după variabile nenumerice (calitative) și are,
de regulă, un caracter oficial (ex. CAEN) și în prealabil trebuie stabilit
un nomenclator al claselor.
3.3.3 Prezentarea datelor statistice
Rezultatul sistematizării necesită o prezentare sub o forma cât mai
comod de manevrat și vizualizat, sub forma de: serii, tabele și grafice.
a) Seriile statistice
Enumerarea datelor statistice într-o anumită ordine se numește
serie statistică. Seria statistică se reprezintă ca două șiruri de date.
r
A
hX
a
n
xx
hlog322,31
minmax

Emilia GOGU Statistica - Manual de studiu individual
Pagina 29 din 112
Primul șir este criteriul de enumerare (valori, variante) al doilea șir
conține datele numerice.
Seriile statistice sunt de următoarele feluri
1. Serii de repartiție sau de distribuție
2. Serii cronologice (ale dinamicii )sau serii de timp.
3. Serii teritoriale sau de spațiu.
4. Serii descriptive sau enumerative (lista candidaților admiși,
facultatea, media de liceu, media examenelor, școala absolvită etc.)
5. Serii unidimensionale și multidimensionale
La rândul lor seriile statistice pot fi atât numerice (cantitative) cât
și nenumerice (calitative).
b) Tabele statistice. Prezentarea datelor sub forma unui tabel statistic
permite atât o bună vizualizare cât și mai ales, efectuarea diverselor
calcule în procesul de prelucrare a datelor.
Pot fi tabele cu o singură intrare și cu două sau mai multe intrări,
tabele de lucru și de prezentare a rezultatelor.
În elaborarea unui tabel se identifică următoarele elemente și reguli
principale:
titlul tabelului
macheta tabelului
subiectul tabelului - colectivitatea și componentele ei
predicatul tabelului - constituie variantele și indicatorii cu care
caracterizăm statistic colectivitatea studiată.
unitatea de măsură
sursa datelor (sub tabel)
numerotarea tabelelor (sus)
c) Reprezentări grafice – Cu ajutorul graficilor se vizualizează
informațiile statistice facilitând perceperea pe ansamblu a datelor,
aspecte privind: variația valorilor observate, repartiția lor, legăturile
existente între ele, a evoluției valorilor în timp ș.a.
Graficul trebuie să cuprindă:
Titlul – (precizându-se și limitele fenomenului)
Legenda
Sistemul axelor rectingulare (ox, oy, oz)
Principalele tipuri de grafice sunt:
grafice de volum
grafice de structură
grafice prin benzi
grafice prin coloane simple sau în aflux
cronogramă (historiogramă) pe scară uniformă sau logaritmică
diagrama polară (radială)
histograma
poligonul frecvențelor
curba cumulativă a frecvențelor
graficul lui Lorentz
cartograma
cartodiagrama

Emilia GOGU Statistica - Manual de studiu individual
Pagina 30 din 112
3.4 Îndrumar pentru autoverificare
3.4.1 Sinteza unității de studiu 3
Prelucrarea statistică este un proces prin care datele înregistrate sunt
sistematizate sunt tratate statistic în vederea obținerii sistemului de indicatori statistici.
Obținerea indicatorilor statistici este necesară pentru caracterizarea în expresii numerice
generalizatoare, a ceea ce este esențial pentru un grup de unități sau pentru întreaga colectivitate,
studiate în condiții de timp și de spațiu.
Deci la baza sistematizării se află principiul omogenității. (Ex. pentru formularea unei idei
sau a unei fraze de compliment – cuvintele trebuiesc alese (grupate), sau (clasificarea studenților
după notele obținute la examenul de statistică). Principiul omogenității este un principiu de
pierdere a informației pentru a câștiga informație.
Însăși sistematizarea se realizează prin: centralizarea și gruparea statistica a datelor.
Centralizarea presupune totalizarea unităților statistice sau a valorilor unei caracteristici
la nivelul grupelor tipice sau al colectivității observate.
Gruparea statistică este o centralizare pe grupe a unităților unei colectivității. Se obține în
baza aplicării metodei grupărilor statistice presupunând principiul omogenității.
Clasificarea se efectuează după variabile nenumerice (calitative) și are, de regulă, un
caracter oficial (ex. CAEN) și în prealabil trebuie stabilit un nomenclator al claselor.
Rezultatul sistematizării necesită o prezentare sub o forma cât mai comod de manevrat și
vizualizat, sub forma de: serii, tabele și grafice.
Enumerarea datelor statistice într-o anumită ordine se numește serie statistică. Seria
statistică se reprezintă ca două șiruri de date.
Prezentarea datelor sub forma unui tabel statistic permite atât o bună vizualizare cât și
mai ales, efectuarea diverselor calcule în procesul de prelucrare a datelor.
Cu ajutorul graficilor se vizualizează informațiile statistice facilitând perceperea pe
ansamblu a datelor, aspecte privind: variația valorilor observate, repartiția lor, legăturile existente
între ele, a evoluției valorilor în timp ș.a.
3.4.2 Concepte și termeni de reținut
Cartodiagrama
Grafice prin benzi
Serie statistică
Cartograma
Grafice prin coloane simple sau în aflux
Sistematizarea datelor
Clasificarea datelor
Graficul lui Lorentz
Sistemul axelor rectingulare
Cronogramă (historiogramă) pe
scară uniformă sau logaritmică
Gruparea statistică
Șiruri de date
Curba cumulativă a frecvențelor
Legăturile existente
Tabele
Diagrama polară (radială)
Legenda
Titlul tabelului
Evoluției valorilor în timp
Poligonul frecvențelor
Titlul graficului
Grafice
Prelucrarea statistică
Variabile nenumerice
Grafice de structură
Principiul omogenității
Variabile numerice
Grafice de volum
Repartiția
Variația valorilor observate

Emilia GOGU Statistica - Manual de studiu individual
Pagina 31 din 112
3.4.3 Întrebări de control și teme de dezbatere
1. În ce constă prelucrarea statistică?
2. De ce este necesară elaborarea planului prelucrării statistice?
3. Care sunt părțile componente ale planului prelucrării statistice?
4. Ce operațiuni comportă prelucrarea statistică?
5. Ce se înțelege prin centralizarea pe grupe și care este rolul ei în sistematizarea datelor
observării de masă?
6. Care este gruparea statistică și scopul său?
7. Care este locul grupării în cunoașterea statistică?
8. Ce probleme ridică aplicarea în practică a grupării statistice?
9. Ce este o caracteristică de grupare?
10. După ce criterii se aleg caracteristicile de grupare?
11. Cum se clasifică grupările statistice?
12. Cum se alege numărul de grupe și cum se stabilește mărimea intervalului de grupare
pentru caracteristicile numerice?
13. Care sunt funcțiile grupărilor statistice?
14. Care este scopul prezentării datelor statistice?
15. Care sunt formele de prezentare a datelor statistice?
16. Care sunt regulile de întocmire a unui tabel statistic? Ce fel de tabele statistice se pot
întâlnim în practică? Exemple.
17. Ce este o serie statistică și de câte feluri sunt seriile statistice? Exemple.
18. Ce este o serie de distribuție (de repartiție)? Exemple.
19. Ce este o serie cronologică (dinamică, de timp)? Exemplu.
20. Ce este o serie de spațiu (teritorială)?
21. Ce este o reprezentare grafică și care sunt elementele unui grafic statistic?
22. Cum se întocmește histograma pentru o serie de distribuție cu intervale egale? Exemple.
23. Cum se întocmește histograma pentru o serie de distribuție cu intervale neegale?
Exemple.
24. Cum se întocmește diagrama prin benzi? Exemple.
25. Cum se întocmește diagrama prin coloane? Exemple.
26. Cum se construiește poligonul frecvențelor pentru o serie de distribuție cu intervale de
variație egale? Exemple.
27. Cum se construiește curba cumulativă a frecvențelor pentru o serie de distribuție cu
intervale egale? Exemple.
28. Cum se construiește curba cumulativă a frecvențelor pentru o serie de distribuție cu
intervale de variație neegale? Exemple.
29. Cum se construiește diagrama polară (radială)?
30. În ce cazuri se folosesc diagramele de suprafață?
31. Cum se întrunește graficul de concentrare ( curba de concentrare Lorentz)
32. Cum se construiește diagrama prin pătrate? Exemple.
33. Cum se construiește diagrama prin cercuri? Exemple.
34. Cum se construiește diagrama prin dreptunghiuri? Exemple.
35. Cum se construiește o cronogramă?

Emilia GOGU Statistica - Manual de studiu individual
Pagina 32 din 112
3.4.4 Teste de evaluare/autoevaluare
Aplicația 1. Se dau datele înregistrate la o societate comercială în luna noiembrie privitor la
salariile brute lunare (lei):
3840; 3340; 4970; 4680; 4850; 3030; 4730; 4840; 3800; 3760; 3340; 3330; 4840; 4690; 3330;
3340; 3540; 4740; 3730; 4840; 4930; 4740; 4930; 3700; 3500; 3340; 3730; 3700; 3580; 3370;
3470; 3090; 3380; 3330; 3030; 4970; 3040; 3840; 3430; 3330; 4730; 4540; 3030; 3490; 4830;
4840; 3450; 3460; 3440; 4550; 4890; 3780; 3500; 4930; 4650; 3880; 3080; 3030; 4730; 4500;
3430; 3340; 3830; 4680; 3040; 3630; 3540; 3570; 3350; 3480; 3680; 4850; 3890; 3030; 4980;
4730; 3080; 3450; 3490; 3340; 3800; 3430; 4770; 3050; 4930; 3300; 3480; 3350; 4730; 3340;
3330; 3850; 3440; 3050; 4890; 3040; 3490; 3530; 3400; 4850; 4930; 3040; 4980; 3360; 3430;
3470; 3450; 3830; 3400; 4830; 4990; 3350; 3300; 3630; 4950; 3440; 3360; 3400; 4790; 4870;
3040; 4930; 3490; 4640; 4990; 3450; 3430; 3340; 3340; 4980; 3340; 3350; 3350; 3450; 3330;
3790; 3650; 4950; 3440; 3300; 3550; 3680; 3600; 3330; 3350; 3450; 3490; 3680; 3330; 3360.
Se cere:
1. să se centralizeze și să se grupeze datele pe 10 intervale egale și pe 5 neegale;
2. să se reprezinte grafic repartițiile obținute.
3.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 33 din 112
4 UNITATEA DE STUDIU 4 INDICATORII STATISTICI
4.1. Introducere
4.2. Obiectivele și competențele unității de studiu – timp alocat
4.3. Conținutul unității de studiu
4.3.1. Noțiune de mărime relativă. Definiri
4.3.2. Tipuri de mărimi relative
4.4. Îndrumar pentru autoverificare
4.1 Introducere
O mărime relativă este rezultatul raportării a doi
indicatori care îndeplinesc condiția de
comparabilitate statistică. Acestea se pot exprima
în coeficienți (forma zecimală), procente (0/0),
promile (0/00), prodecimile (0/000), și procentimile
(0/0000), în cazul în care se raportează doi indicatori cu același conținut.
Mărimile relative sunt numeroase și variate de la un domeniu
la altul și se pot compara direct numai dacă au aceeași bază de
raportare.
4.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
- definirea mărimilor relative;
- caracterizarea tipuri de mărimi relative;
- identificarea relațiilor de calcul;
- prezentarea grafică a mărimilor relative.
Competențele unității de studiu:
- cunoașterea și interpretarea mărimilor relative;
- alegerea adecvată a formei de prezentare tabelară și grafică a
mărimilor relative;
- necesitatea aplicării mărimilor relative în caracterizarea
fenomenelor de masă.
Durata medie de studiu individual alocat unității: 3 ore

Emilia GOGU Statistica - Manual de studiu individual
Pagina 34 din 112
4.3 Conținutul unității de studiu
4.3.1 Noțiunea de mărime relativă
Indicatorii relativi se obțin prin aplicarea unui model de comparație
sub formă de raport. Deci prin mărimi relative înțelegem rezultatul
raportării a doi indicatori absoluți.
Indicatorul din numărătorul raportului se numește indicatorul
raportat, iar cel din numitor, indicatorul bază de raportate. Alegerea
bazei raportate se face în funcție de scopul comparării.
Mărimile relative se pot exprima prin coeficienți, %, promile
00
0
, prodecimile
000
0
cât și procentimile
0000
0
.
Exemple:
Natalitatea (născuți vii la 1000 de locuitori) =
1000
populatiei almediu nr
viinr.nãscuti
Număr medici la 10000 de locuitori =
10000
populatiei almediu nr
nr.medici
Mai rar se întâlnesc exprimării în procentimile, adică cât unități
din indicatorul raportat revin la 100.000 unități bază de raportare.
Alegerea formei de exprimare se face astfel încât mărimile
relative să fie sugestive. Dar forma cea mai obișnuită de exprimare a
lor este cea a procentelor care arata câte unități din indicatorul raportat
revin la 100 unități ale indicatorului baza de raportare.
Forma de exprimare a mărimilor relative se stabilește în raport
cu gradul de variație al fenomenelor, a scopului urmărit, precum si
particularitățile specifice fenomenului cercetat.
Pentru calculul unei mărimi relative, trebuie respectate 3 cerințe:
a) între termenii comparați trebuie să existe o legătură de
condiționalitate sau de cauzalitate;
b) termenii raportați să fie cu adevărat comparabili din punctul de
vedere al sferei de cuprindere, ca metodologie de calcul etc;
c) baza de comparație să aibă o anumită semnificație în evoluția
fenomenului studiat.
În cea mai mare parte mărimile relative în satistică nu prezintă o
dificultate de calcul. Cele mai multe dificultăți apar în comparațiile
internaționale, unde indicatorii provin din diferite surse sau sunt
calculați după metodologii diferite.
4.3.2 Tipuri de mărimi relative
În principal se pot calcula următoarele tipuri de mărimi relative:
a) de structură;
b) de coordonare (corespondență);
c) de intensitate;
d) ale dinamicii;
e) ale planului (planificării).
Emilia GOGU Statistica - Manual de studiu individual
Pagina 35 din 112
a) Mărimea relativă de structură se poate calcula de fiecare dată
când s-a aplicat metoda grupării prin urmare calculul lor este
posibil atunci când colectivitate este separată înde două sau mai
multe grupe. Este un raport dintre o parte la întreg (total).
Dacă se determină pentru frecvența fiecărei grupe se numesc
ponderi iar dacă se determină pentru valorile centralizate ale
diferitelor caracteristici se numesc greutăți specifice care se obțin ca
mărimi relative de structură raportând frecvența fiecărei grupe (ni , fi )
la totalul frecvențelor (
k
i
i
k
i
ifn
11
,
) după relația:
100*
1
(%)
k
i
i
i
i
n
n
n
.
Frecvențele relative permit analiza structurii unei serii de
distribuție în funcție de una sau mai multe variabile (caracteristici) și
compararea repartițiilor empirice cu cele teoretice.
Având caracter de mărimi relative se pot exprima sub formă de
coeficienți sau în procente și fiind “eliberate” de aspectul concret al
exprimării unităților centralizate pe grupe devin comparabile pentru
orice fel de serie și mai ales cu probabilitățile din distribuțiile teoretice.
Proprietăți:
Specifică mărimilor relative de structură este proprietatea de
aditivitate. Fiind calculate față de aceeași bază cu greutăți specifice
corespunzătoare se pot efectua operații de adunare și scădere. Suma
mărimilor relative de structură este egală cu 1 sau 100 în funcție de
forma de exprimare.
Demonstrație:
Sau
Reprezentarea grafică
Mărimile relative de structură se reprezintă grafic printr-o
diagramă de structură care poate fi ilustrată prin:
- cercul sau semicercul de structură;
- dreptunghiul de structură;
100*
1
n
i
i
i
ix
x
x
1
...
... 213
21
i
i
i
n
i
n
iii x
x
x
xxx
x
x
x
x
x
x
x
x
100100*100*
...
100*...100*100*
21
21
i
i
i
n
i
n
ii
x
x
x
xxx
x
x
x
x
x
x

Emilia GOGU Statistica - Manual de studiu individual
Pagina 36 din 112
- pătratul de structură.
b) Mărimile relative de coordonare sau corespondență
caracterizează raportul numeric în care se găsesc doi indicatori cu
același conținut în spații diferite coexistente în timp.
Pentru o colectivitate împărțită în două grupe pentru care
nivelul pe grupe al variabilei studiate este xA și xB :
Forma de prezentare ar fi: :
A
B
AB
B
A
BA X
X
Ksau
X
X
K //
unde:
A și B unități teritoriale.
XA și XB nivelul colectivității de raportate din unitatea A respectiv B
Mărimi relative de coordonare se pot calcula și pornind de la
frecvențe:
n
n
K
B
A
BA
/
sau
n
n
K
A
B
AB
/
De regulă ei se exprimă în coeficienți.
Proprietăți:
Produsul lor este egal cu 1:
1 n
n
n
n
A
B
B
A
, KA/B x KB/A =1
Deci ei corespund testului de reversibilitate.
Dacă sunt mai multe grupe, se alege una ca bază de comparație
și se raportează, pe rând, fiecare grupă la baza aleasă.
De regulă raportul este valoarea cea mai mică, la cel mai mare,
astfel putem obține exprimarea lor în coeficienți supraunitari.
Aceste mărimi se folosesc în studiul variației teritoriale și prin
urmare au caracter de indici teritoriali.
Ex. PIB României cu cel al Greciei
Reprezentarea grafică
Mărimile relative coordonare. se reprezintă grafic prin benzi
sau coloane, stabilind în acest fel relațiile care există între diferitele
părți ale aceleiași colectivități.
c) Mărimile relative ale dinamicii – se obțin ca raport a doi
indicatori ai aceluiași fenomen dar aflate între două momente /
perioade diferite.
Pentru a studia în dinamică recurgem la serii cronologice. În
general o serie statistică este formată din două șiruri de date în care un
șir reprezintă criteriul de sistematizare (factorul e grupare), iar al
doilea șir variabila dependentă de factorul de grupare.
Analiza se face atât în bază fixă cât și mobilă (în lanț).
Indicatorii relativi obținuți prin raportare exprimă indicele de
variație

Emilia GOGU Statistica - Manual de studiu individual
Pagina 37 din 112
- cu bază fixă
100
0
0/ X
X
Kt
t
- cu bază mobilă (în lanț)
100
1
1/
t
t
tt X
X
K
Putem calcula mărimi relative ale dinamicii la nivelul
ansamblului, dacă variabila este aditivă direct:
0
0/ x
x
kt
t
respectiv
1
1/
t
t
tt x
x
k
Ele se exprimă atât sub formă de coeficienți dar mai adesea sub
formă %.
Reprezentarea grafică
Mărimile relative ale dinamicii se reprezintă grafic prin
cronograme (histograme).
d) Mărimile relative ale planului (planificării)
Se calculează la nivelul unităților economice fiind necesar să se
elaboreze programe de aprovizionare, producție și desfacere pe
termene scurte sau mai lungi.
Calculul mărimilor relative ale planului presupune preluarea
din evidențele unității economice analizate a informațiilor referitoare
la:
nivelul fenomenului realizat în perioada de bază (x0);
nivelul planificat (programat) în perioada curentă (xpl)
nivelul realizat în perioada curentă (x1).
Din compararea sub formă de raport a celor trei indicatori
rezultă:
coeficientul sarcinii de plan:
0
0/ x
x
kpl
pl
coeficientul îndeplinirii planului:
x
x
k
pl
pl 1
/1
coeficientul de dinamică:
x
x
k
0
1
0/1
Între cei trei coeficienți există relația:
kkk plpl /10/0/1 .
Interpretarea valorii mărimilor relative ale planului ca și a ratei de
depășire (nerealizare) se face în raport cu conținutul economic al
indicatorului (de creștere sau de reducere obiectivă a fenomenului).
Putem calcula mărimi relative ale planului la nivel de
ansamblu, pentru variabile însumabile direct:
x
x
kpl
pl
0
0/
respectiv
x
x
k
pl
pl
1
/1

Emilia GOGU Statistica - Manual de studiu individual
Pagina 38 din 112
De cele mai multe ori mărimile relative de dinamică și
mărimile relative ale planului se exprimă procentual.
e) Mărimile relative de intensitate se obțin prin raportarea a
doi indicatori absoluți de natura diferita, dar care se află într-un raport
de interdependență.
Relația de calcul este:
la nivel parțial:
Z
Y
X
i
i
Aceste mărimi se pot calcula pentru fiecare grupa de unități în
parte sau pentru întreaga colectivitate.
la nivelul ansamblului:
i
i
iZ
Y
X
sau
Z
ZX
x
i
ii
Ex: Densitatea populației (loc/km2,) Productivitatea muncii
(lei/munc).
Mărimile relative de intensitate au numerose aplicații în:
industrie (coeficientul mecanizării, automatizării, utilizării
intensive etc.)
agricultură (coeficientul chimizări, irigațiilor, recolta
medie la ha);
turism (indicatorii eficienței activității de turism,
productivitatea muncii etc);
demografice (coeficientul mișcării naturale, migratorii a
populației).
4.4 Îndrumar pentru autoverificare
4.4.1 Sinteza unității de studiu 4
Indicatorii relativi se obțin prin aplicarea unui model de comparație sub formă de
raport. Deci prin mărimi relative înțelegem rezultatul raportării a doi indicatori
absoluți.
Indicatorul din numărătorul raportului se numește indicatorul raportat, iar cel din
numitor, indicatorul bază de raportate. Alegerea bazei raportate se face în funcție de scopul
comparării.
Mărimile relative se pot exprima prin coeficienți, %, promile
00
0
, prodecimile
000
0
cât și
procentimile
0000
0
.
Mai rar se întâlnesc exprimării în procentimile, adică cât unități din indicatorul raportat
revin la 100.000 unități bază de raportare.
Alegerea formei de exprimare se face astfel încât mărimile relative să fie sugestive. Dar

Emilia GOGU Statistica - Manual de studiu individual
Pagina 39 din 112
forma cea mai obișnuită de exprimare a lor este cea a procentelor care arata câte unități din
indicatorul raportat revin la 100 unități ale indicatorului baza de raportare.
Forma de exprimare a mărimilor relative se stabilește în raport cu gradul de variație al
fenomenelor, a scopului urmărit, precum si particularitățile specifice fenomenului cercetat.
Pentru calculul unei mărimi relative, trebuie respectate 3 cerințe:
d) între termenii comparați trebuie să existe o legătură de condiționalitate sau de cauzalitate;
e) termenii raportați să fie cu adevărat comparabili din punctul de vedere al sferei de
cuprindere, ca metodologie de calcul etc;
f) baza de comparație să aibă o anumită semnificație în evoluția fenomenului studiat.
În cea mai mare parte mărimile relative în satistică nu prezintă o dificultate de calcul. Cele
mai multe dificultăți apar în comparațiile internaționale, unde indicatorii provin din diferite surse
sau sunt calculați după metodologii diferite.
În practica statisticii se pot calcula următoarele tipuri de mărimi relative:
a) de structură;
b) de coordonare (corespondență);
c) de intensitate
d) ale dinamicii;
e) ale planului (planificării).
Principiile generale care stau la baza oricărui sistem de indicatori statistici, constau în:
unicitatea concepției cu privire la conținutul, metodologia de calcul și mijloacele de
agregare ale acestora;
asigurarea comparabilității;
extinderea sistemului cu noi indicatori.
4.4.2 Concepte și termeni de reținut
Mărimi relative
Mărimi relative de corespondență
Baza de comparație
Mărimi relative de structură
Coeficienți
Procentimile
Densitatea populației
Prodecimile
Forma de exprimare
Productivitatea muncii
Mărimi relative ale dinamicii
Promile
Mărimi relative ale planificării
Rata natalitații
Mărimi relative ale planului
Termenii comparați
Mărimi relative de coordonare
Unitate de mărusă
4.4.3 Întrebări de control și teme de dezbatere
1. De ce este necesară folosirea mărimilor relative în statistică?
2. Ce se înțelege prin mărime relativă?
3. Care sunt condițiile de aplicabilitate a mărimilor relative?
4. Cum se clasifică mărimile relative?
Emilia GOGU Statistica - Manual de studiu individual
Pagina 40 din 112
5. Care sunt domeniile de aplicare a mărimilor relative în practica statistică?
6. Ce sunt mărimile relative de structură și cum se reprezintă grafic?
7. Ce sunt mărimile relative de dinamică și cum se reprezintă grafic?
8. Ce sunt mărimile relative ale planului și cum se reprezintă grafic?
9. Ce sunt mărimile relative de intensitate și cum se reprezintă grafic?
10. Ce este o mărime relativă de coordonare?
4.4.4 Teste de evaluare/autoevaluarea
Aplicația 1
Un agent economic are 3 magazine la care s-au înregistrat datele:
Maga-
zin
Valoarea desfacerilor (mii lei)
Nr. personal
Realizat
oct.
Plan nov.
Realizat
nov.
Realizat
oct.
Plan nov.
Realizat
nov.
I
II
III
68.000
80.000
105.000
75.000
88.000
120.000
80.000
92.000
125.000
30
32
40
32
35
45
33
35
43
Total
253.000
283.000
297.000
102
112
111
Se cere:
1. să se calculeze mărimile relative permise de date;
2. Interpretarea datelor obținute
Aplicația 2
O societate comercială de import export dispune de trei filiale la care se cunosc datele:
Filiale
Structura încasărilor
pentru luna ianuarie
%sarcinii de plan
(ian./dec.)
% îndeplinirii
planului în ianuarie
I
II
III
20%
48%
32%
105,7%
115,0%
110,0%
102%
105%
98%
Total
100,0
…
…
Se cere:
1. să se calculeze valoarea încasărilor realizate și planificate în cele două luni pentru fiecare
filială, știind că pe total încasările din luna ianuarie (perioada curentă) au fost 25.500 mii lei;
2. să se calculeze dinamica încasărilor din ianuarie față de decembrie;
3. Interpretarea datelor obținute
4.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 41 din 112
5 UNITATEA DE STUDIU 5 ANALIZA SERIILOR DE REPARTIȚIE
5.1. Introducere
5.2. Obiectivele și competențele unității de studiu – timp alocat
5.3. Conținutul unității de studiu
5.3.1. Noțiunea de serie de repartiție. Proprietăți
5.3.2. Indicatori de nivel și de frecvențe
5.3.3. Indicatori ai tendinței centrale și ai mediilor de structură (poziție)
5.3.4. Indicatorii simpli ai variației
5.3.5. Indicatorii sintetici ai variației
5.3.6. Coeficientul de asimetrie
5.3.7. Aplicație
5.4. Îndrumător pentru autoverificare
5.1 Introducere
Rezultatul grupării și clasificării unităților
colectivității observate în funcție de caracteristici
atributive cantitative sau calitative se prezintă sub
forma seriilor de repartiție (distribuție) empirică.
Ele se mai numesc simplu repartiții sau distribuții
statistice.
Grupările simple (după o singură caracteristică) conduc la serii
statistice independente sau unidimensionale, iar cele combinate la serii
statistice condiționate sau multidimensionale.
Într-o colectivitate statistică valorile individuale (variantele)
diferă mai mult sau mai puțin unele față de altele. Ele pot fi mai
apropiate sau mai împrăștiate. De aceea, comparația se face, în
principal, cu media aritmetică, considerată ca fiind valoarea cea mai
reprezentativă pentru colectivitatea studiată. De cele mai multe ori
este important de cunoscut cât de departe sunt valorile variantelor
seriei față de această medie, sau cu alte cuvinte care este dispersia
variantelor în cadrul seriei sau câmpul de variație a caracteristicii
înregistrate.
5.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
- definirea seriilor de distribuție;
- definirea proprietărilor seriilor de repartiție;
- identificarea indicatorilor care analizează seriile de
distribuție.
- definirea noțiunii de variație;

Emilia GOGU Statistica - Manual de studiu individual
Pagina 42 din 112
- identificarea formelor de manifestare a seriilor de repartiție;
- prezentarea indicatorilor de variație;
- determinarea și cuantificarea variației;
- cuantificarea coeficientului de variație;
- asimetria seriei.
Competențele unității de studiu:
- studenții vor cunoaște particularitățile seriilor de repartiție;
- studenții vor putea să identifica indicatorii tendinței centrale;
- vor putea calcula indicatorii medii de structura/de poziție ;
- cunoașterea curbei lui Gauss;
- stabilirea formelor de repartiție.
- studenții vor putea defini noțiunea de variație a seriilor de
repartiție;
- vor putea identifica formele de variație a seriilor;
- studenții vor cunoaște indicatorii de determinare a variației ;
- vor putea calcula și interpreta omogenitatea seriei;
- studenții vor putea determina și interpreta asimetria.
Durata medie de studiu individual alocat unității: 4 ore
5.3 Conținutul unității de studiu
5.3.1 Noțiunea de serie de repartiție. Proprietăți
La calculul și analiza indicatorilor (parametrilor) distribuțiilor
empirice trebuie avute în vedere o serie de proprietăți, care se pot
întâlni în toate cazurile, dar cu forme specifice fiecărei serii.
Principalele proprietăți ale unei serii de repartiție sunt:
variabilitatea,
omogenitatea,
independența
concentrarea sau dispersia
Variabilitatea termenilor unei serii statistice de repartiție este
determinată de faptul că fenomenele de masă apar ca rezultat al
acțiunii combinate a mai multor cauze, unele cu caracter esențial,
altele cu caracter întâmplător, care se manifestă, de regulă, în condiții
individuale diferite. Cu cât acțiunea cauzelor aleatoare este mai
puternică, cu atât variabilitatea termenilor este mai mare iar gradul de
omogenitate este mai mic.
Omogenitatea termenilor unei serii de repartiție se explică prin
faptul că toate valorile au același conținut, depinzând de același factor
esențial.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 43 din 112
Dacă în urma analizei statistice se constată că seria nu prezintă
omogenitate, se trage concluzia că această colectivitate este formată
din mai multe tipuri calitative și deci, seria respectivă trebuie separată
în două sau mai multe serii componente. Se vor folosi și în acest scop
indicatori medii de variație și asimetrie parțiali și totali (vor fi
prezentați în subcapitolele următoare).
Independența termenilor unei serii de repartiție de frecvențe
provine din faptul că fiecare valoare individuală se înregistrează pentru
o unitate statistică care reprezintă un element distinct și obiectiv al unei
colectivități statistice. Această independență este relativă deoarece
unitățile statistice aparținând aceleiași colectivități se supun acelorași
legi care se manifestă sub formă de tendință. Față de aceasta tendință
există abateri într-un sens sau altul, care pentru un număr mare de
cazuri, se compensează reciproc. De aceea, este necesar ca prin metode
statistice corespunzătoare, să se afle trăsăturile esențiale și comune
care leagă aceste valori individuale relativ independente, dar care
aparțin aceleași structuri calitative și care în statistică este cunoscută
sub denumirea de ,,legea de repartiție a seriei “.
Concentrarea sau dispersia față de una sau mai multe valori ale
seriei apare ca rezultat al intensității cu care influențează cauzele
(esențiale și întâmplătoare) la nivelul fiecărei unități și care prin
centralizare se determină frecvențele de apariție.
De cele mai multe ori, intensitatea factorilor de influență este
diferită și atunci frecvențele de apariție se concentrează fie către un
singur capăt al seriei (caz în care pe grafic se descriu repartiții în formă
de "j"), fie către valoarea centrală a seriei (caz în care pe grafic se
descrie o repartiție normală (simetrică) [Legea normală a repartiției
este numită și curba normală Gauss-Laplace și graficul ei "clopotul lui
Gauss".], fie către ambele capete ale seriei (caz în care pe grafic se
obține o repartiție în formă de "u".
Multitudinea situațiilor întâlnite în practică demonstrează
necesitatea caracterizării tendințelor de concentrare/diversificare a
valorilor unei serii de repartiție de frecvențe cu ajutorul unor metode
statistice specifice. Aceste metode conduc la obținerea uneia sau a mai
multor valori reprezentative, fie pentru întreaga serie, fie pe intervale
de variație a valorilor individuale.
Sistemul de indicatori al unei repartiții empirice este format din:
1. indicatori de nivel și de frecvențe,
2. indicatori ai tendinței centrale și ai mediilor de structură
(poziție);
3. indicatori de variație;
4. indicatori de asimetrie;
5. indicatori de concentrare.
Acești indicatori se pot stabili în întregime pentru seriile de variabile
cantitative (numerice). În cazul celor cu variabile calitative, numărul
indicatorilor calculați este mai restrâns. În continuare acești indicatori
se vor prezenta pe exemplul seriilor de variabile numerice și în măsura
în care ei se pot aplica și pentru seriile de variabile calitative vor fi
menționați separat.
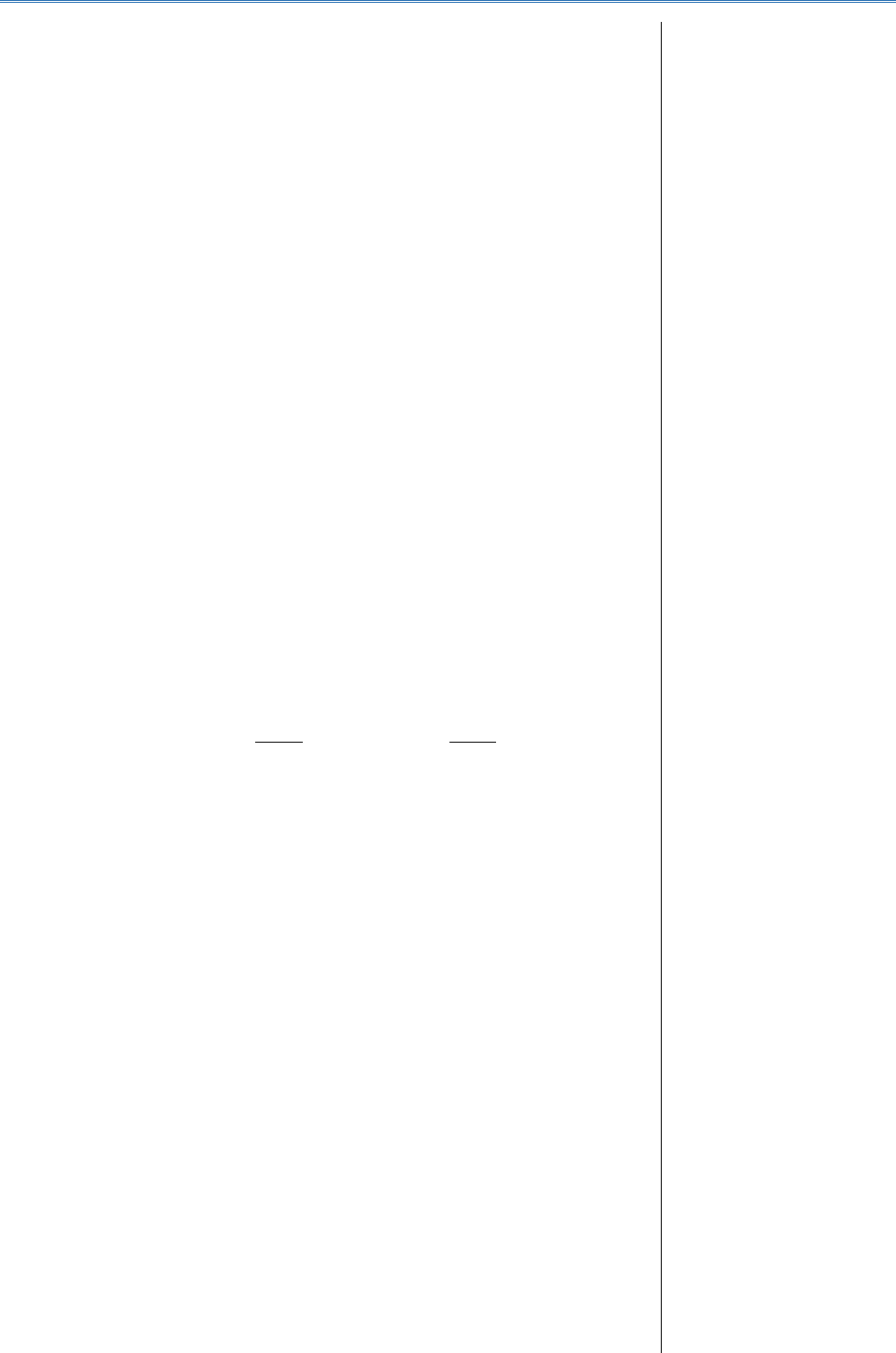
Emilia GOGU Statistica - Manual de studiu individual
Pagina 44 din 112
5.3.2 Indicatori de nivel și de frecvențe ai seriilor de repartiție
Caracterizarea statistică a unui fenomen de masă într-o colectivitate
statistică presupune luarea în considerație atât a valorilor individuale
cât și a frecvențelor de apariție a acestora.
Indicatorii de nivel ai seriei pot fi exprimați în cazul variabilelor
numerice prin variante în cazul grupării pe variante. În cazul
intervalelor de variație se utilizează ca indicator de nivel centrul
(mijlocul) intervalului de grupare.
În grupa indicatorilor de frecvență deosebim: frecvențe absolute,
frecvențe relative și frecvențe cumulate.
Frecvențele absolute notate în unele lucrări cu "fi" sau "ni " în
altele, reprezintă numărul de unități care corespunde grupelor de
unități (variante sau intervale de valori) obținut ca rezultat al
centralizării statistice. Frecvențele absolute se exprimă în unități
concrete (număr de salariați, număr de agenți comerciali, număr de
unități turistice, etc.). Frecvențele absolute stau la baza calculului
frecvențelor relative.
Frecvențele relative permit analiza structurii unei serii de
distribuție în funcție de una sau mai multe variabile (caracteristici) și
compararea repartițiilor empirice cu cele teoretice.
Frecvențele relative notate cu ,, fi* “sau ,, ni * “denumite și
ponderi, greutăți specifice sau probabilități de apariție se obțin ca
mărimi relative de structură raportând frecvența fiecărei grupe (ni , fi )
la totalul frecvențelor (
k
i
i
k
i
ifn
11
,
) după relația:
100**;100**
1
(%)
1
(%)
k
i
i
i
i
k
i
i
i
i
n
n
n
f
f
f
Având caracter de mărimi relative se pot exprima sub formă de
coeficienți sau în procente
În cercetarea statistică calculul frecvențelor relative prezintă
interes la determinarea altor indicatori statistici ce permit aprofundarea
analizei seriilor de repartiție sau când ne interesează structura seriei.
Frecvențele cumulate se notează cu Fi sau F'i în funcție de felul
frecvențelor incluse în calcul (absolute sau relative). Cumularea se
face succesiv pornind de la ambele capete ale seriei, obținând astfel
pentru fiecare valoare a seriei frecvențe cumulate crescător și
descrescător
Frecvențele cumulate sunt comparabile între ele indiferent de
felul de intervalului de grupare. De asemenea ele stau la baza stabilirii
medianei și a celorlalte medii de structură sau poziție – indicatori care
vor fi prezentați într-un subcapitol din acest capitol.
5.3.3 Indicatorii tendinței centrale
Analiza statistică a trăsăturilor esențiale ale fenomenelor de masă,
stabilirea tendințelor ce apar în producerea lor necesită calcularea
anumitor valori sintetice cu conținut de valori tipice, care să fie
reprezentative pentru întreaga serie studiată.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 45 din 112
În funcție de gradul de variabilitate a valorilor individuale, de
sursele de date de care dispunem și de nevoile de cunoaștere, în
teoria și practica statistică se utilizează ca principali indicatori ai
tendinței centrale:
A. mărimile medii;
B. modul (dominanta) seriei
C. mediana;
A. Mărimile medii
Media în statistică reprezintă principalul indicator sintetic cu
care se caracterizează un număr mare de valori individuale diferite ca
forme de manifestare dar având același conținut.
În consecință, mărimile medii sunt utilizate ca instrumente
principale de cunoaștere a fenomenelor de masă, deoarece numai pe
baza lor se poate exprima ceea ce este comun și general în forma de
manifestare a acestor fenomene, în fiecare etapă dată, prin eliminarea
a ceea ce este întâmplător și neesențial în producerea lor.
Media sintetizează deci, într-o singură expresie numerică toate
valorile individuale punând în evidență ceea ce este esențial și comun
tuturor unităților.
De cele mai multe ori, valoarea mediei nu coincide cu nici una
din valorile individuale din care s-a calculat.
Pentru a asigura un conținut cât mai real mediilor calculate este
necesar ca valorile individuale din care se calculează să fie cât mai
apropiate ca mărime ceea ce corespunde conceptului de omogenitate
statistică, semnificând faptul că există o valoare în jurul căreia se
concentrează cele mai multe valori individuale.
Calculul mediei este recomandabil să se bazeze pe folosirea unui
număr mare de cazuri individuale diferite sub care s-a înregistrat
caracteristica, a căror variație să poată fi considerată ca întâmplătoare
în raport cu întreaga masă de valori înregistrate.
În cazurile în care nu dispunem de date dintr-o observare totală,
care ar permite evidențierea tuturor factorilor esențiali și întâmplători
care determină variația caracteristicii studiate, se pot utiliza și date
provenite dintr-o observare parțială. În acest caz, mediile calculate
pot fi considerate semnificative și pentru întregul ansamblu numai
dacă eșantionul îndeplinește condiția de reprezentativitate.
Media este semnificativă numai în cazul unei colectivități cu
grad ridicat de omogenitate. În cazul în care colectivitatea este
eterogenă se va proceda la împărțirea colectivității în grupe folosind și
serii condiționate pentru care se vor calcula mediile parțiale
corespunzătoare iar media pe total colectivitate va fi în același timp și
o sinteză a mediilor de grupe.
Pentru ca mărimea medie să aibă un conținut obiectiv, este
necesar ca alegerea formei de calcul să se facă în funcție de forma de
variație și de sursele de informație cu privire la caracteristica studiată.
In analiza seriilor de repartiție de frecvențe se pot calcula
următoarele tipuri de medii:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 46 din 112
media aritmetică (
a
x
sau media simplă
x
);
media armonica (
h
x
);
media pătratica (
p
x
);
media geometrică (
g
x
).
Fiecare poate fi calculată ca medie simplă și ca medie ponderată.
Mediile simple se folosesc în cazul datelor negrupate sau când
repartițiile au intervale cu frecvențe egale între ele și deci se pot
simplifica.
Mediile ponderate se utilizează pentru repartițiile în care fiecărei
valori a caracteristicii i se atașează o frecvență care diferă de la caz la
caz. În statistica social - economică, cel mai frecvent se folosește
media aritmetică.
A.1. Media aritmetică
Media aritmetică este rezultatul sintetizării într-o singură
expresie numerică a tuturor nivelurilor individuale observate, obținută
prin raportarea valorii totalizate a caracteristicii la numărul total al
unităților.
În sens statistic, media aritmetică calculată pentru colectivitate
statistică este valoarea care s-ar fi înregistrat dacă toți factorii ar fi
influențat în mod constant în toate cazurile înregistrate. În acest sens,
poate fi folosit în statistică termenul de “speranță” matematică către
care tind valorile individuale ale unei variabile statistice înregistrate
într-o observare empirică.
Media aritmetică simplă se calculează ca raport între suma
nivelurilor individuale sub care s-a înregistrat caracteristica și numărul
cazurilor individuale luate în observare. Media se poate calcula
raportând valoarea totalizată a caracteristicii la numărul total al
unităților la care s-a făcut centralizarea. Se folosește relația:
n
x
x
n
i
i
a
1
,
unde:
i
x
reprezintă nivelurile individuale ale variabilei;
n
i
i
x
1
reprezintă nivelul centralizat al variabilei;
n reprezintă numărul unităților observate.
Media aritmetică ponderată cu frecvențe absolute Într-o
colectivitate statistică se întâlnesc foarte rar cazuri în care numărul
variantelor coincide cu numărul unităților. De regulă, fenomenele de
masă sunt numeroase și aceeași valoare individuală (varianta) poate fi
întâlnită de mai multe ori. În acest caz, pentru a putea cuprinde în
calcul toate valorile individuale trebuie sa se țină seama și de frecvența

Emilia GOGU Statistica - Manual de studiu individual
Pagina 47 din 112
1or de apariție iar media se va calcula ca o medie ponderată utilizând
formula:
k
i
i
k
i
ii
n
nx
x
1
1
în care: k reprezintă numărul de grupe deci k < n
Media aritmetică ponderată cu frecvențe relative
100
1
1
1
k
i
ii
k
i
i
k
i
ii nx
n
nx
x
De reținut:
Dacă repartiția de frecvențe se prezintă pe intervale de variație,
xi reprezintă centrul de interval corespunzător.
Media aritmetică are anumite proprietăți care au utilitate practică
pentru calculul și interpretarea valorii ei.
Media este mai exactă când o calculăm direct din valorile sub
care s-a înregistrat caracteristica. Este o medie aproximativă când o
calculăm pentru seriile pe intervale de variație deoarece în acest caz
determinarea ei se bazează pe ipoteza repartizării uniforme a
frecvențelor în cadrul fiecărui interval ceea ce, de regulă nu
corespunde realității.
A.2. Alte tipuri de medii utilizate în analiza seriilor de
repartiție
Una din condițiile de aplicare a valorilor medii este aceea de a
găsi criterii de alegere corectă a tipului de medii folosit.
În general este recomandabil să alegem media aritmetică atunci
când fenomenul supus cercetării înregistrează modificări aproximativ
în progresia aritmetică.
În teoria și practica statistică cel mai frecvent se folosește media
aritmetică.
De aceea când nu se precizează media folosită se presupune că
s-a calculat media aritmetică care este considerat principalul
parametru al tendinței centrale.
Când fenomenul înregistrează modificări în progresia aritmetică,
sau intenționăm să dăm o importanță mai mare termenilor mai mici
sau mai mari ai seriei, calculăm alte tipuri de medii și anume:
media armonică (xh)
media geometrică (xg ),
media pătratică (xp)
Media armonică
Media armonică se definește ca fiind egală cu valoarea inversă
a mediei aritmetice calculată din valorile inverse ale termenilor
aceleiași serii.
Deși derivă din media aritmetică ponderată, în practică se
întâlnesc două variante ale mediei armonice, simplă și ponderată.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 48 din 112
Se folosesc relațiile de calcul:
- pentru o serie simplă:
n
ii
h
x
n
x
1
1
- pentru o serie de repartiție de frecvențe:
k
i
i
i
k
i
i
h
n
x
n
x
1
1
1
Comparând formula mediei armonice cu aceea a mediei
aritmetice se pot stabili anumite relații care pot fi utile în practica
statistică:
1) dacă termenii seriei sunt pozitivi, media armonică este
întotdeauna mai mică decât media aritmetică calculată pe baza
acelorași valori.
2) în cazul în care între două variabile interdependente există un
raport de inversă proporționalitate, acest raport se păstrează și în cazul
mediilor calculate. Astfel, dacă pentru calculul nivelului mediu al
uneia dintre cele două variabile se folosește media aritmetică pentru
cealaltă se folosește obligatoriu media armonică.
3) dacă se folosesc sisteme de ponderare diferite și anume la
media aritmetică frecvențele absolute (ni), iar la media armonică
produsele de frecvențe(xini) se obține aceeași valoare a mediei. Practic
media aritmetică poate fi substituită cu media armonică ponderată cu
produsele de frecvențele (xini).
De cele mai multe ori din evidențe nu rezultă frecvențele
absolute (ni) ci numai variantele caracteristicii (xi) și respectiv
produsele de frecvență (xini). În acest caz vom folosi următoarea
formulă pentru calculul mediei armonice ponderate:
k
i
ii
i
k
i
ii
h
nx
x
nx
x
1
1
1
Se observă că în această formă de ponderare media armonică
este o formă transformată a mediei aritmetice.
În cazul distribuțiilor de frecvențe media armonică este indicat
a fi folosită când predomină valorile mici ale seriei, seria prezentând
deci o asimetrie către valorile minime ale caracteristicii. În acest caz
se folosește formula mediei armonice ponderate clasice.
Media pătratică

Emilia GOGU Statistica - Manual de studiu individual
Pagina 49 din 112
Media pătratică
( )xp
este acea valoare care înlocuind termenii
seriei ridicați la pătrat nu modifică suma pătratelor lor.
Media pătratică este folosită, de obicei, atunci când nivelurile
variabilei aleatoare prezintă creșteri din ce în ce mai mari sau când
într-o repartiție predomină frecvențele valorilor ridicate ale variabilei
și dorim să le dăm acestora o importanță mai mare. Și această medie,
în cazul seriilor de repartiție de frecvențe se folosește complementar
mediei aritmetice care rămâne principalul parametru al tendinței
centrale.
Bazându-se pe ridicarea la pătrat ea se poate folosi și în cazul în
care termenii seriei au valori pozitive și negative.
În cazul unei distribuții de frecvențe se vor efectua mai întâi
produsele dintre fiecare termen ridicat la pătrat și ponderea sa și pe
baza acestora utilizând un raționament analog cu cel descris anterior
se obține formula mediei pătratice ponderate:
k
i
i
i
k
i
i
p
n
nx
x
1
1
2
De reținut faptul ca media pătratică este întotdeauna mai mare
decât media aritmetică a acelorași termeni, indiferent de semnul pe
care îl au, deoarece prin ridicare la pătrat toți termenii devin pozitivi,
iar pătratul crește pe măsură ce cresc valorile termenilor.
Media pătratică stă la baza calculului abaterii medii pătratice
care este unul din cei mai utilizați indicatori de variație.
Media geometrică
Spre deosebire de celelalte medii prezentate până aici, care se
bazează pe relații de însumare între termenii seriei, media geometrică
se bazează pe relația de produs dintre ei.
n
n
i
ig xx
1
unde
este semnul produsului
În cazul unei serii de distribuție de frecvențe, fiecare termen
trebuie să fie luat în funcție de frecvența sa.
k
i
ii
nk
i
n
ig xx 1
1
De reținut faptul că media geometrică devine incalculabilă dacă
cel puțin un termen al seriei este egal cu zero sau negativ.
Media geometrică se folosește cel mai frecvent în cazul seriilor
cronologice, la calculul mediilor din mărimile relative ale dinamicii,
respectiv la determinarea indicelui mediu de dinamică.
În cazul seriilor de distribuție de frecvențe, media geometrică se
folosește mai rar. Este recomandabil să se folosească acest tip de
medie atunci când seria prezintă variații foarte mari între termeni sau
un pronunțat caracter de asimetrie. Prin 1ogaritmare, abaterile dintre

Emilia GOGU Statistica - Manual de studiu individual
Pagina 50 din 112
termenii seriei se micșorează și se obține un grad mai mare de
concentrare a frecvențelor.
De asemenea, când predomină valorile mai mici, folosind media
geometrică, li se acordă acestora o mai mare importanță, media
geometrică fiind mai mică decât media aritmetică a acelorași termeni.
Intre mediile prezentate există următoarea relație de ordine:
pagh xxxx
În concluzie la calculul nivelului mediu al unei repartiții
unidimensionale se folosește pentru măsurarea nivelului mediu media
aritmetică și complementar celelalte tipuri de medii prezentate, dacă
seria prezintă anumite particularități, sau în scopul aprofundării
analizei.
B. Valori medii de poziție sau de structură
Pentru completarea analizei seriilor de distribuție este necesar să
se calculeze anumite valori medii de poziție sau medii de structură,
care să evidențieze și forma de repartiție a frecvențelor. Dintre acestea,
mediana și modul sunt cel mai frecvent utilizate, fiind considerate tot
ca indicatori ai tendinței centrale.
B.1. Mediana (Me) reprezintă valoarea centrală a unei serii
statistice, ordonate crescător sau descrescător, care împarte termenii
seriei în două părți egale.
Indiferent de tipul seriei (simplă sau cu frecvențe) la calculul
medianei se cer rezolvate două aspecte:
- aflarea locului medianei
- calculul valorii medianei
În cazul seriilor simple 1ocul medianei se află după relația: 1ocul
Me =
2
1n
unde n reprezintă numărul termenilor seriei.
Determinarea medianei necesită ordonarea prealabilă
crescătoare sau descrescătoare a termenilor seriei.
Dacă numărul termenilor este impar (n=2p+l), mediana este
termenul de rang p+1 (valoarea termenului central).
Dacă numărul termenilor este par, adică n=2p, orice valoare
cuprinsă între termenul de rang p și termenul de rang p+1 poate fi
considerată ca o mediană, deci mediana se găsește într-un interval de
valori.
Dacă datele sunt grupate pe intervale (clase) de valori ele își
pierd individualitatea și la determinarea medianei trebuie să se țină
seama de relațiile dintre grupele de valori și frecvențele acestora.
Determinarea valorii se poate realiza în două moduri:
prin calcul algebric;
prin calcul grafic.
Calculul algebric al medianei presupune utilizarea următoarei
formule de calcul:
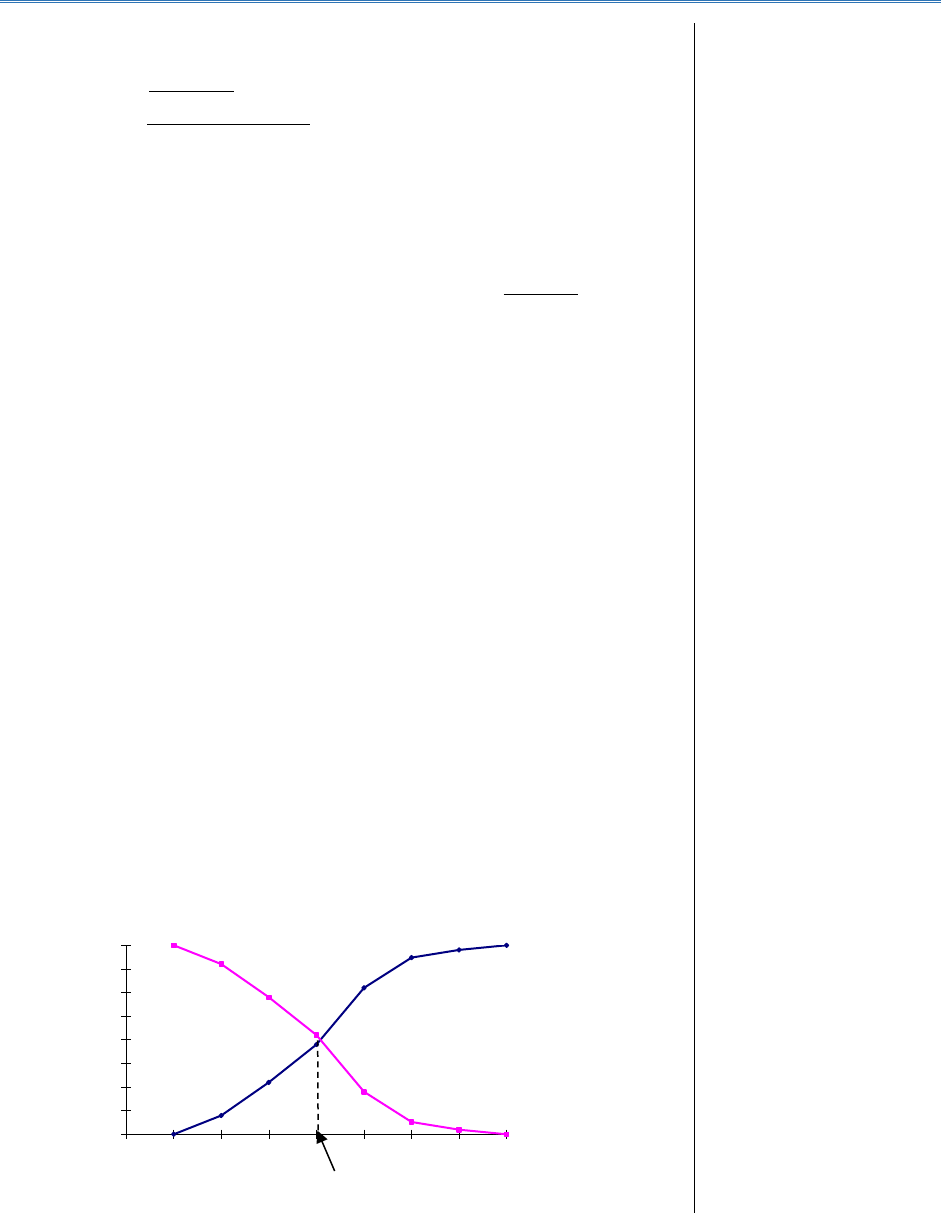
Emilia GOGU Statistica - Manual de studiu individual
Pagina 51 din 112
m
m
i
i
k
i
i
n
n
n
hxMe
1
1
1
0
2
1
unde:
x0 - limita inferioară a intervalului median (primul interval a cărui
frecvență cumulată este mai mare sau egală cu
2
1n
k
1i i
;
h - mărimea intervalului median;
m - indexul intervalului median;
1m
1i i
n
- frecvența cumulată a intervalului care precedă intervalul
median;
nm - frecvența absolută a intervalului median.
Calculul grafic al medianei se poate realiza în două moduri:
1. Se trasează poligonul frecvențelor cumulate crescător și
descrescător. Din punctul de intersecție al celor două curbe se trasează
perpendiculara pe axa absciselor și se citește valoarea medianei pe Ox
(vezi fig. 5.1.); Me=32,375 milioane lei.
2. Se trasează numai poligonul frecvențelor cumulate crescător. De
pe axa ordonatelor din punctul corespunzător locului medianei (în
cazul nostru 100,5) se duce o paralelă la Ox ce întâlnește poligonul în
punctul m. Din acest punct se coboară perpendiculara pe Ox și se
obține astfel valoarea medianei.
Figura 5.1
0
25
50
75
100
125
150
175
200
20 24 28 32 36 40 44 48
Me
Calculul grafic al medianei
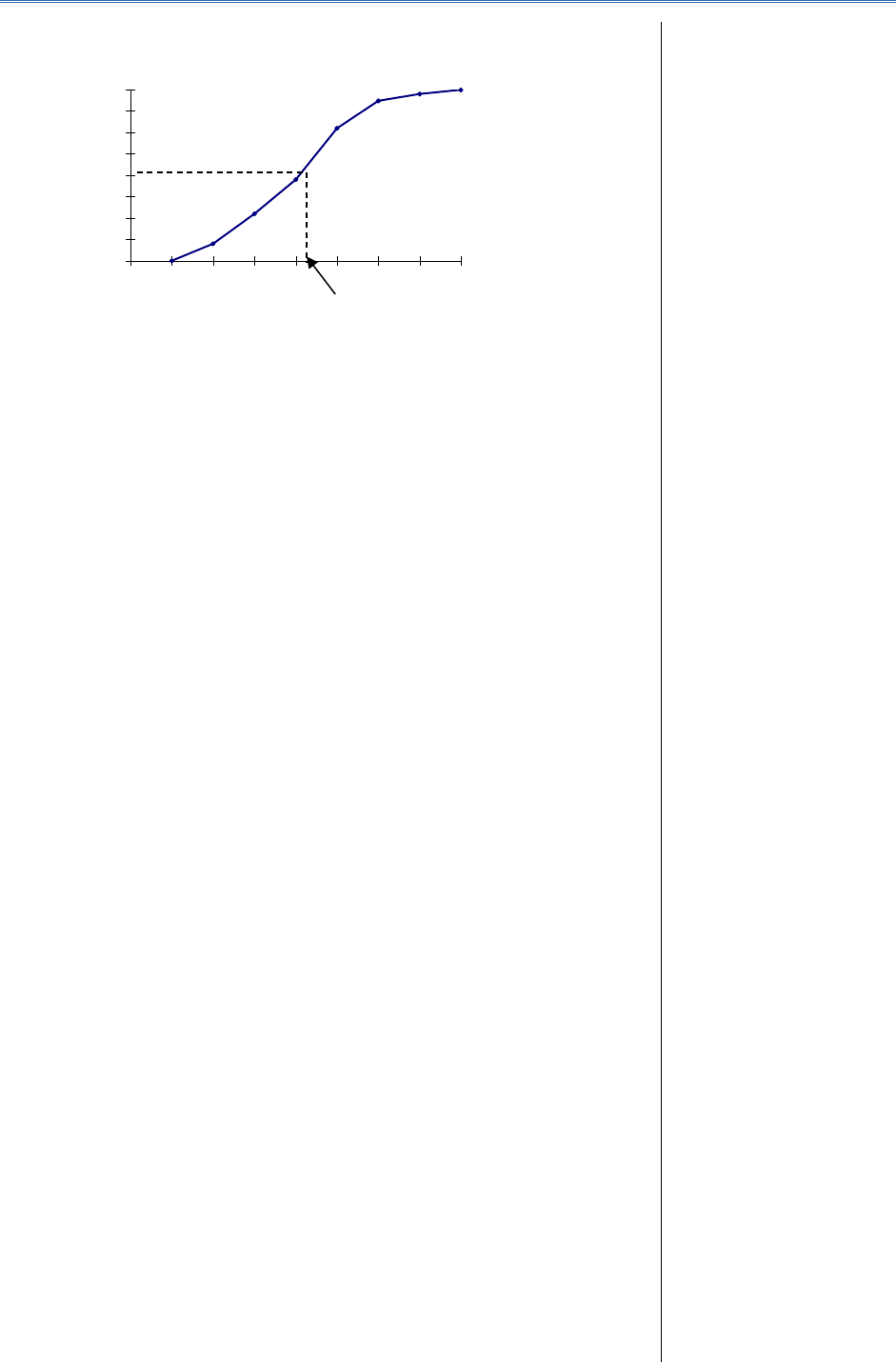
Emilia GOGU Statistica - Manual de studiu individual
Pagina 52 din 112
Figura 5.2
Menționăm în continuare câteva proprietăți ale medianei.
Mediana depinde de locul valorilor în serie, nu de mărimea acestor
valori. În felul acesta ea nu este supusă influenței așa-ziselor valori
aberante (anormal de mari sau anormal de mici) care sunt lăsate în
afara seriei prin deschiderea intervalelor marginale.
Din punct de vedere grafic precizăm că verticala corespunzând
medianei împarte histograma seriei în două parți de aceeași suprafață,
deoarece ariile coloanelor care constituie histograma sunt prin
definiție proporționale ca înălțime cu frecvențele absolute
corespunzătoare, iar ca baze cu mărimea intervalului de grupare.
Dacă sistematizarea datelor s-a făcut pe intervale neegale,
calculele privind locul și valoarea medianei se fac după aceleași
ipoteze și formule.
Mediana are o largă aplicabilitate în practică: la studiul
mortalității, la determinarea duratei medii de viață, etc fiind alături de
media aritmetică și de mod, principalii indicatori ai tendinței centrale.
Când seria empirică analizată prezintă o tendință de repartiție
normală (simetrică), mediana poate să înlocuiască valoarea medie,
fiind mai ușor de calculat.
Cu cât seria este mai apropiată de distribuția normală, cu atât
abaterea dintre media aritmetică și mediana este mai mică, deci
proprietatea de compensare a abaterilor față de medie se realizează și
în cazul medianei, doar pentru o serie perfect simetrică. Se poate
aprecia că mediana este un indicator semnificativ al tendinței centrale
dacă se obține o minimizare a abaterilor tuturor termenilor de la
mediană, adică:
min
1
n
i
iMex
, pentru datele negrupate,
min
i
k
1i inMex
, pentru datele grupate.
B.2. Moda [Mod sau moda vine de la termenul franțuzesc “la mode” cu
sensul de modă ] (modul, dominanta)
0
25
50
75
100
125
150
175
200
20 24 28 32 36 40 44 48
Calculul grafic al medianei
Me
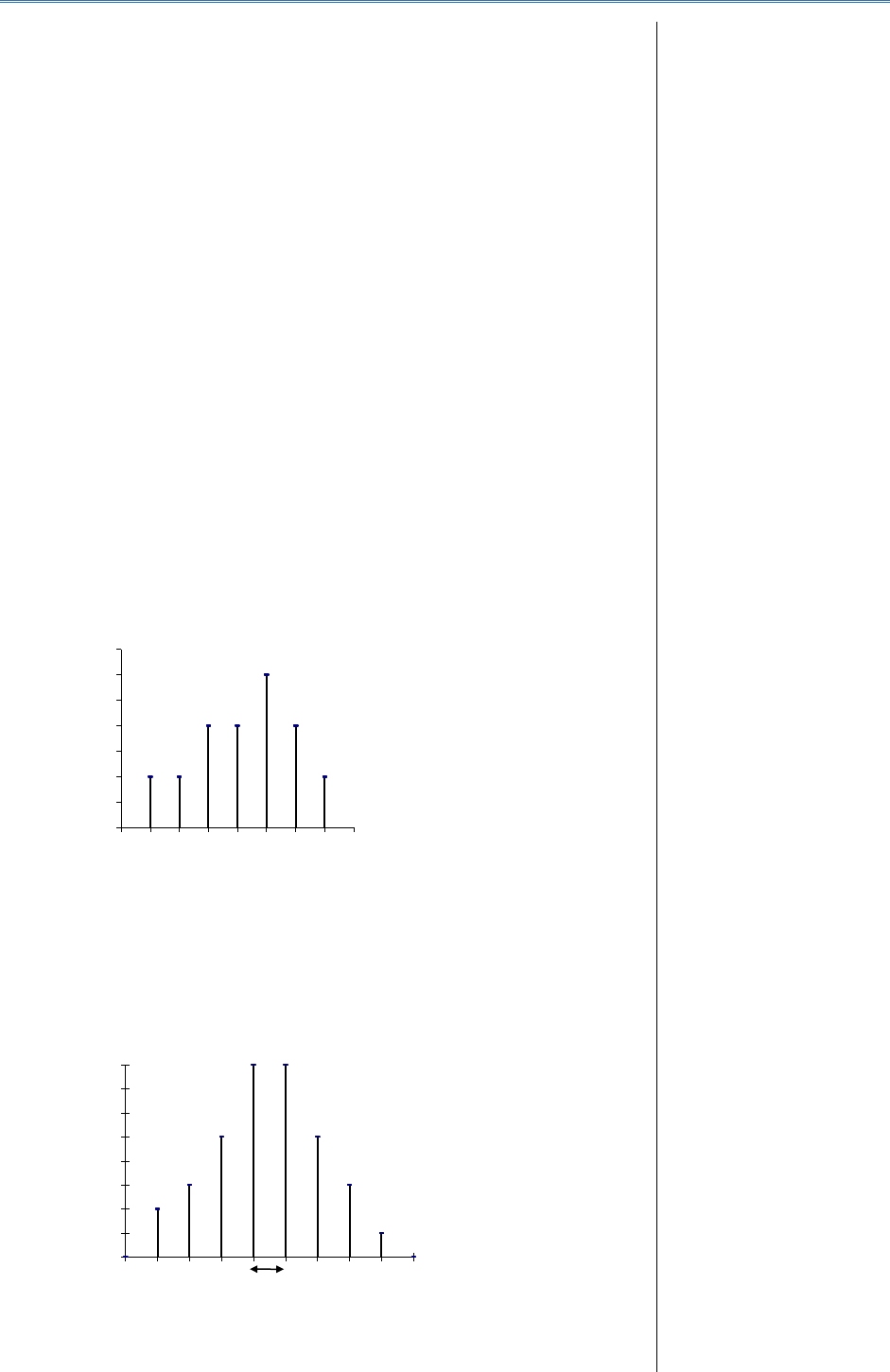
Emilia GOGU Statistica - Manual de studiu individual
Pagina 53 din 112
Modul (Mo) este valoarea cea mai frecvent întâlnită, motiv
pentru care mai este cunoscut în literatura de specialitate și sub
denumirea de dominanta seriei.
Pentru serii simple (date negupate) modul se calculează dacă
întâlnim o valoare a variabilei care se repetă de mai multe ori.
Astfel, în seria (4, 5, 6, 6, 7, 7, 8, 8, 8, 9, 9, 10), valoarea 8 apare
cel mai frecvent; modul este deci Mo=8.
Modul se poate calcula cu certitudine pentru orice serie de
distribuție de frecvență, indiferent de modul ei de prezentare (pe
variante sau pe intervale de variație).
Modul se poate calcula fie pe cale algebrică fie prin metoda
grafică.
În cazul unei serii de distribuție pe variante modul este ușor de
reperat. În tabelul statistic în care este prezentată seria pe variante
analizată, modul este varianta xi corespunzătoare frecvenței maxime.
Determinarea grafică a modului presupune utilizarea diagramei
prin bastoane. În acest caz Mo este acea valoare de pe abscisă care are
ordonata maximă și corespunde frecvenței acelei mărimi (vezi fig.
5.3).
Figura 5. 3
Dacă seria prezintă două frecvențe maxime identice alăturate
se definește un interval modal (vezi fig. 5.3) fără a putea preciza
valoarea exactă a modului.
Figura 5.4.
0
0,5
1
1,5
2
2,5
3
3,5
4 5 6 7 8 9 10
fi
Mo
xi
0
1
2
3
4
5
6
7
8
0123456789
fi
Interval modal
xi

Emilia GOGU Statistica - Manual de studiu individual
Pagina 54 din 112
Pentru o serie de distribuție pe intervale egale valoarea modului
trebuie calculată. Intervalul modal se consideră intervalul care are
frecvența cea mai mare.
În seria prezentată pentru calculul medianei intervalul modal
este cuprins între 32-36 milioane lei profit, deoarece aici frecvența
este maximă (60). Cu aceste precizări se poate proceda la calculul
algebric și grafic.
a) Calculul algebric al modului se bazează pe relația:
21
1
0hxMo
în care:
x0 - reprezintă limita inferioară a intervalului modal;
h - mărimea intervalului modal;
1
- diferența dintre frecvența intervalului modal și a celui precedent
2
- diferența dintre frecvența intervalului modal și a celui următor
b) Pe grafic, valoarea modală se poate determina și cu ajutorul
histogramei formată din dreptunghiurile corespunzătoare fiecărei
grupe (clase) de valori..
Se procedează astfel: se construiește histograma (vezi figura
5.5). Din intersecția segmentelor de dreaptă care unesc vârfurile
superioare ale dreptunghiului aferent modului cu frecvențele de
incidență ale acestuia cu dreptunghiurile adiacente, se coboară o
perpendiculară pe abscisă. Punctul găsit indică valoarea modului. De
pe grafic rezultă o valoare apropiată de cea obținută prin calcul
algebric.
Figura 5.5.
c) În cazul distribuțiilor moderat asimetrice Mo se mai poate
determina și pornind de la condiția care trebuie să fie îndeplinită în
acest caz:
x2Me3Mo
Mex3Mox
)(
De precizat faptul că modul este o valoare foarte instabilă.
Simpla deplasare cu câteva unități (deci reluarea grupării) poate să
modifice sensibil valoarea modului.
0
10
20
30
40
50
60
Nr.ag. ec.
mil. lei
Distribuţia agenţilor economici după
mărimea profitului (mil. lei)
20 24 28 32 36 40 44
Mo

Emilia GOGU Statistica - Manual de studiu individual
Pagina 55 din 112
Dacă seria prezintă două sau mai multe frecvențe maxime
nealăturate și nu ne apărat egale, spunem că seria este bimodală,
trimodală etc.
Mediana și modul se exprimă în aceleași unități de măsură ca și
variabilele pentru care se determină și prezintă avantajul că valoarea
lor nu se modifică dacă se închid în mod convențional intervalele
deschise.
Cu toate inconvenientele, modul are o largă aplicabilitate
practică (mai ales în comerț) și stă la baza calculului și interpretării
gradului de asimetrie a repartiției.
Modul prezintă avantajul că se poate stabili și pentru o variabilă
calitativă. De exemplu, în analizele de marketing se poate stabili
culoarea cea mai frecvent solicitată la articolele de îmbrăcăminte sau
încălțăminte.
La seriile cu un grad mare de variație, unde pot apărea și mai
multe valori modale este necesar să se separe seria pe serii
componente și să se calculeze și valori medii parțiale pe zone de
variație.
Folosirea modului se impune atunci când o valoare domină clar
seria de distribuție față de toate celelalte valori și deci poate fi
substituită celorlalte două valori ale tendinței centrale (media și
valoarea mediană) fără să se producă abateri semnificative.
În același timp utilizarea modului trebuie să se facă cu prudență
În cazul în care frecvențele se distribuie relativ uniform, valoarea
modală este doar mai frecventă decât celelalte valori ale seriei. Dacă
celelalte valori sunt însă aproape tot așa de frecvente ca valoarea
modală, s-ar putea ca o valoare să devină dominantă din întâmplare, și
ea s-ar deplasa, dacă intervalele de grupare s-ar schimba. Deci, modul
este semnificativ ca valoare tipică, numai dacă o valoare domină în
seria de distribuție.
Pentru seriile cu un pronunțat caracter de asimetrie, valoarea
dominantă nu are sens să fie folosită pentru a caracteriza tendința
centrală. În acest caz, se recomandă să se folosească grupări combinate
care să separe colectivitatea înregistrată pe mai multe grupe de
variație, aparținând unor structuri diferite.
Pentru seriile de distribuție cu tendință pronunțată de asimetrie,
caracterizate printr-o amplitudine mare a variației, se calculează și alți
indicatori de poziție cum sunt: cuartilele, decilele, centilele,
percentilele etc.
Cuartilele sunt acele valori ale caracteristicii, care separă seria
în patru părți egale:
cuartila inferioară, notată cu Q1, este mai mare sau
egală de 25% din termenii seriei și mai mică sau egală
de 75% dintre ei;
cuartila a doua Q2 coincide cu Me și separă seria în
două părți egale ca efectiv;

Emilia GOGU Statistica - Manual de studiu individual
Pagina 56 din 112
cuartila superioară Q3 este mai mare sau egală de 75%
din numărul termenilor și mai mică sau egală de 25%
din numărul lor.
Analog cu mediana pentru cuartile obținem:
Locul cuartilei
Valoarea cuartilei
)( 1n
4
1
Qloc i1
1
Q
1
pQi
01 n
n1n
hxQ 4
1
)(
MeQ2
)( 1n
4
3
Qloc i3
3
Q
3
pQi
03 n
n1n
4
3
hxQ
)(
în care:
n 1
pQ
și
3pQ
n
reprezintă suma frecvențelor intervalelor
precedente locului pe care-l ocupă Q1 și Q3
3Q
1
Qnn şi
reprezintă frecvențele intervalelor care conțin cuartilele
respective.
În cazul în care se calculează decilele, seria se divide în zece
părți egale folosind în acest scop nouă decile.
5.3.4 Indicatorii simpli ai variației
Indicatorii simpli ai variației servesc pentru a caracteriza gradul
de împrăștiere a unităților purtătoare ale caracteristicilor înregistrate.
Ei se calculează pentru a măsura amplitudinea variației și abaterile
valorilor individuale de la media lor. Acești indicatori se pot exprima
atât în mărimi absolute - folosind aceleași unități de măsură ca și
pentru caracteristica studiată - cât și în mărimi relative, calculate în
raport cu valoarea medie.
Din această grupă a indicatorilor simpli fac parte:
amplitudinea variației (absolută și relativă)
abaterile individuale (absolute și relative).
a) Amplitudinea absolută (Aa) se calculează ca diferență între
nivelul maxim (xmax) și nivelul minim (xmin) al caracteristicii:
Aa=xmax-xmin
Amplitudinea absolută se exprimă în unitățile de măsură ale
variabilei respective și prin urmare nu poate fi folosită la compararea
a două variabile exprimate în unități de măsură diferite.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 57 din 112
Amplitudinea relativă a variației (A%) se exprimă de regulă în
procente și se calculează ca raport între amplitudinea absolută a
variației și nivelul mediu al caracteristicii:
AA
x
a
% 100
b) Abaterile individuale absolute (di) se calculează ca diferență
între fiecare variantă înregistrată și media aritmetică a acestora după
relația:
n1ixxd ii ,
Abaterile individuale relative (di%) se calculează raportând
abaterile absolute la nivelul mediu al caracteristicii:
n1,i
%
100
x
xx
100
x
d
dii
i
Atât gradul cât și forma de variație a unei caracteristici depind
însă de toate abaterile variantelor înregistrate și de frecvența lor de
apariție și prin urmare indicatorii simpli ai variației nu pot exprima
decât un aspect al variației unei caracteristici înregistrate. Din acest
motiv caracterizarea gradului de variație se face în special cu ajutorul
indicatorilor sintetici ai variației care iau în considerație toate abaterile
caracteristicii.
5.3.5 Indicatorii sintetici ai variației
Indicatorii sintetici ai variației, la fel ca indicatorii tendinței
centrale, trebuie să se bazeze pe toate observațiile, să fie ușor de
înțeles, ușor de calculat, cât mai puțin posibil afectați de fluctuațiile
de selecție și adecvați unui studiu algebric.
Indicatorii sintetici ai variației sunt:
a) abaterea medie liniară
( )d
,
b) abaterea medie pătratică sau abaterea standard
( )
,
c) coeficientul de variație (v);
d) dispersia
( )
2
.
a) Abaterea medie liniară
( )d
se calculează ca medie
aritmetică simplă sau ponderată a abaterilor termenilor seriei de la
media lor, luate în valoare absolută.
Formulele de calcul ale abaterii medii liniare sunt:
pentru o serie simplă:
n
xx
d
n
i
i
1
pentru o serie de frecvențe absolute:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 58 din 112
k
i
i
i
k
i
i
n
nxx
d
1
1
pentru o serie cu frecvențe relative, exprimate în procente:
100
%
*
1
i
k
i
inxx
d
pentru o serie cu frecvențe relative, exprimate în
coeficienți:
*
i
k
1i inxxd
Abaterea medie liniară se exprimă în unitățile de măsură ale
variabilei și deci nu poate fi folosită la comparații.
Abaterea medie liniară prezintă și dezavantajul că nu ține seama
de faptul că abaterile mai mari în valoare absolută măresc semnificativ
gradul de variație a unei caracteristici, în comparație cu abaterile mai
mici. În plus, din punct de vedere algebric nu este indicat să se renunțe,
în mod arbitrar, la semnul valorilor din care se calculează o valoare
medie. Din aceste considerente se folosește ca principal indicator
sintetic al variației abaterea medie pătratică.
b) Abaterea medie pătratică, abaterea tip sau abaterea
standard
( )
se calculează ca medie pătratică a abaterile tuturor
variantelor seriei de la media lor aritmetică.
Relațiile de calcul ale abaterii medii pătratice sunt:
pentru o serie simplă:
n
xx
n
1i
2
i
)(
pentru o serie de frecvențe absolute:
k
1i i
i
k
1i
2
i
n
nxx )(
pentru o serie cu frecvențe relative, exprimate în procente:
100
nxx i
k
1i
2
i%
)(
pentru o serie cu frecvențe relative, exprimate sub formă de
coeficienți:
i
k
1i
2
inxx *
)(
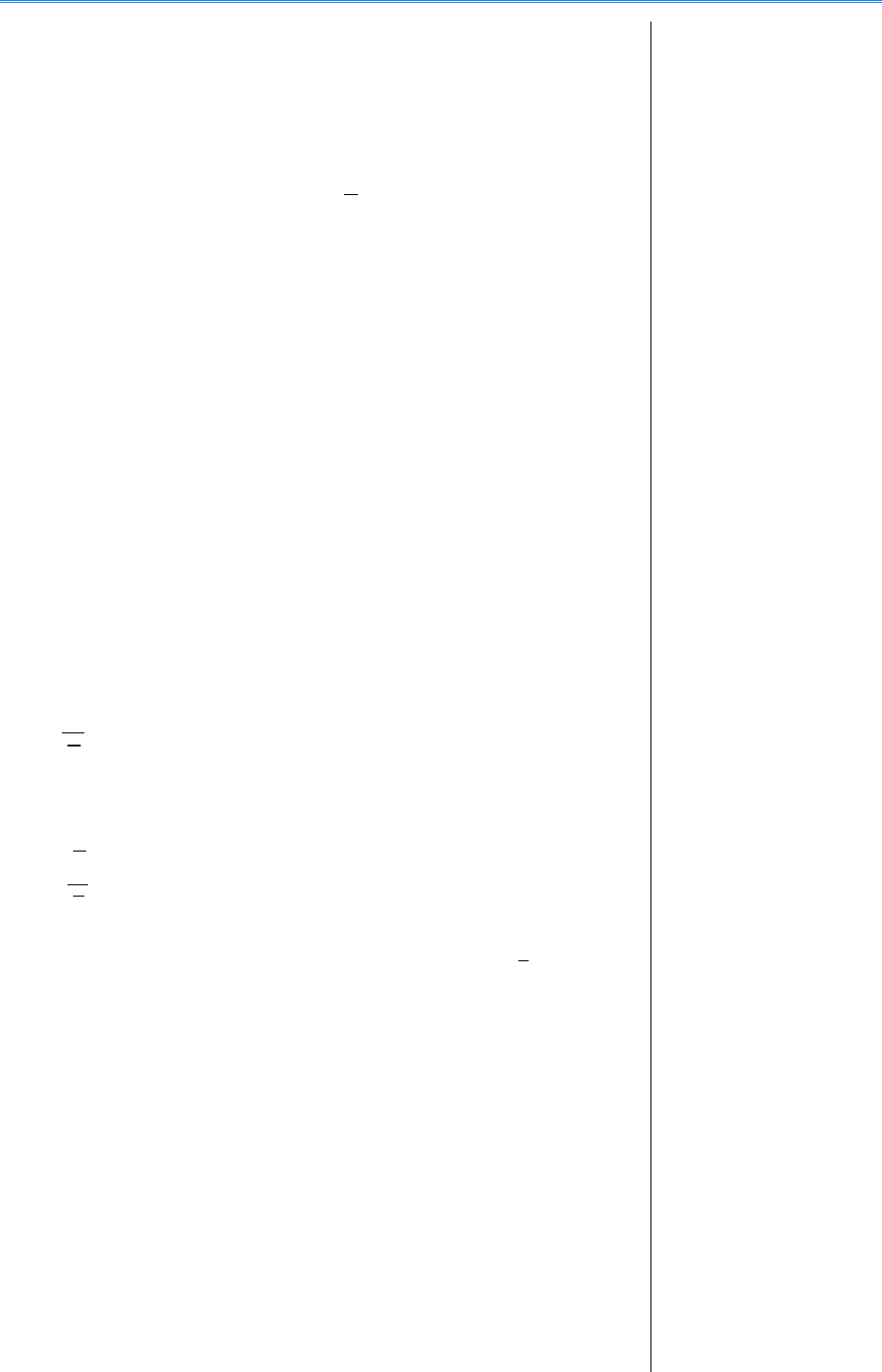
Emilia GOGU Statistica - Manual de studiu individual
Pagina 59 din 112
Indicatorul abatere medie pătratică fiind calculat din pătratul
abaterilor este mai concludent decât abaterea medie liniară. Prin
ridicarea la pătrat se dă o importanță mai mare abaterilor mai mari în
valoare absolută, acestea influențând într-o măsură mai mare gradul
de variație al variabilei analizate. Din acest motiv, calculați pentru
aceeași serie, cei doi indicatori verifică relația:
d
În literatura de specialitate se apreciază că pentru o serie de
distribuție cu tendință clară de normalitate, abaterea medie liniară
este aproximativ egală cu 4/5 din valoarea abaterii medii pătratice.
Abaterea medie pătratică este un indicator de bază, care se
folosește în analiza variației, la estimarea erorilor de selecție, în
calcule de corelație.
La fel ca abaterea medie liniară, abaterea medie pătratică se
exprimă în unitatea de măsură a variabilei a cărei variație o
caracterizează. Prin urmare cei doi indicatori nu se pot folosi pentru
compararea gradului de variație a două sau mai multe variabile diferite
dar aparținând aceleași colectivități și în aceste situații se recurge la un
alt indicator de variație - coeficientul de variație.
c) Coeficientul de variație (v) se calculează ca raport între
abaterea medie pătratică și nivelul mediu al serie, deoarece abaterea
standard se folosește frecvent pentru măsurarea abaterii medii.
Formula de calcul a coeficientului de variație este:
vx
100
Dacă s-a calculat și abaterea medie liniară, coeficientul de
variație se mai poate calcula și după relația:
vd
x100
Coeficientul de variație se exprimă, de regulă, în procente, ceea
ce înseamnă că el este de fapt expresia relativă fie a lui
d
, fie a lui
și evident v`<v. De aceea se preferă care conduce la un coeficient
de variație mai mare.
Cu cât nivelul lui v este mai apropiat de zero, cu atât variația este
mai redusă, colectivitatea este mai omogenă, media având un grad
ridicat de reprezentativitate; cu cât valoarea sa este mai departe de zero
cu atât variația este mai intensă, colectivitatea este mai eterogenă, iar
media are un nivel de semnificație mai scăzut. Se apreciază că, pentru
fenomenele economice și sociale, în cazul unui coeficient de variație
de peste 35-40%, media nu mai este reprezentativă și datele trebuie să
fie separate în serii componente, pe grupe, în funcție de variația unei
alte caracteristici de grupare. Deci se poate afirma că acest indicator
(coeficientul de variație) poate fi folosit ca un test de verificare în
aplicarea metodei grupării care are ca funcție principală omogenizarea
datelor dintr-o observare statistică.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 60 din 112
Deși indicatorul - coeficientul de variație - înlătură dezavantajele
prezentate de
și
d
și acest indicator are limitele lui. Astfel, acest
coeficient este în mod evident neadecvat în cazul în care media
aritmetică este apropiată de zero sau când valorile înregistrate sunt
relativ egale între ele.
Deși în literatura de specialitate coeficientul de variație se
calculează de cele mai multe ori prin relațiile menționate (media fiind
indicatorul care respectă cele mai multe din condițiile impuse de
Yule), acest indicator se poate calcula și înlocuind media cu mediana,
modul sau mediala.
;' ; 100
Me
d
v100
Me
vMeMe
;' ; 100
Mo
d
v100
Mo
vMoMo
Într-o formă explicită, pentru o serie de frecvențe, vom avea
pentru mediană:
100
Me
n
nMex
v100
Me
n
nMex
v
k
1i i
k
1i ii
k
1i i
k
1i i
2
i
` si
În mod analog se pot scrie și celelalte formule înlocuind
mediana prin alt indicator al tendinței centrale.
Un alt indicator sintetic al variației, cu o largă utilizare în analiza
statistică a fenomenelor, este dispersia.
d) Dispersia (varianța) unei caracteristici
( )
2
se calculează
ca medie aritmetică simplă sau ponderată a pătratelor abaterilor
termenilor seriei față de media lor. Se mai numește și pătratul mediu
al abaterilor termenilor față de media lor. Formulele de calcul sunt:
pentru o serie simplă:
2
2
1
( )x x
n
i
i
n
pentru o serie de frecvențe absolute:
k
1i i
i
k
1i
2
i
2
n
nxx )(
pentru o serie cu frecvențe relative, exprimate în procente:
100
nxx i
k
1i
2
i
2(%)
*
)(
pentru o serie cu frecvențe relative, exprimate sub formă de
coeficienți:
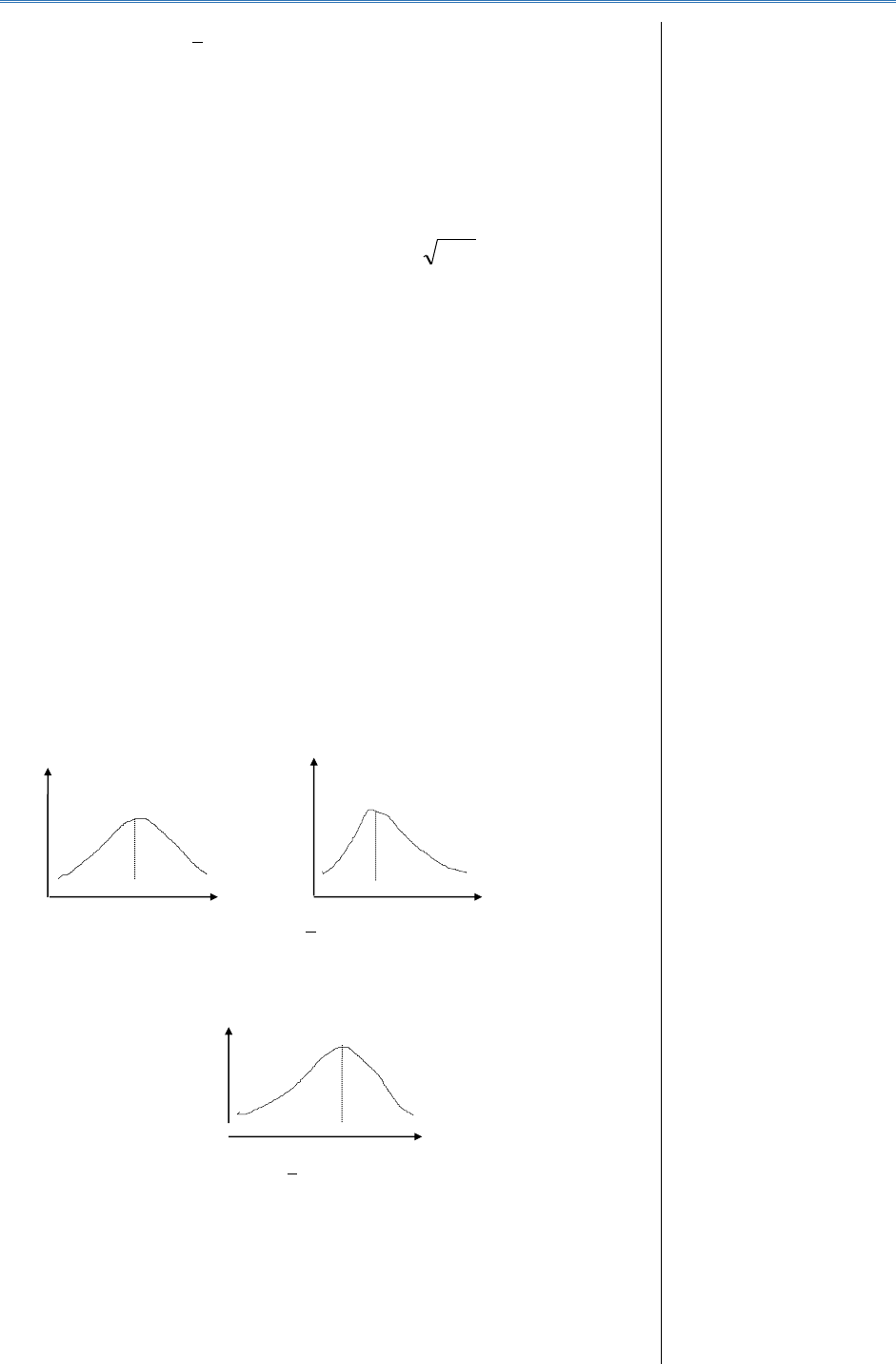
Emilia GOGU Statistica - Manual de studiu individual
Pagina 61 din 112
i
k
1i
2
i
2nxx *
)(
În literatura de specialitate, dispersia este cunoscută și sub
denumirea de momentul centrat de ordinul doi.
Din relațiile de calcul prezentate anterior se observă că abaterea
medie pătratică implică calculul prealabil al dispersiei, din care se
extrage apoi rădăcina pătratică, pentru a ajunge la același grad cu
caracteristica a cărei variație se studiază (=
2
).
Dispersia necesitând calcule destul de dificile (mai ales când
variabila are valori mari) în teoria și practica statistică se folosește
formula de calcul simplificat. Acest calcul simplificat se bazează pe
unele proprietăți ale dispersiei.
5.3.6 Asimetria
Pentru caracterizarea seriilor de distribuție unidimensionale și
unimodale un interes deosebit îl prezintă și cunoașterea gradului de
oblicitate, de îndepărtare a acestor distribuții de la simetrie. În practica
statistică acest aspect este cunoscut sub numele de asimetrie.
La interpretarea gradului de asimetrie se pornește de la poziția și
valorile pe care le au cei trei indicatori ai tendinței centrale: media,
mediana și modul.
Într-o distribuție simetrică cei trei indicatori: mod, mediană și
media aritmetică se confundă ca în diagrama din figura 5.6.
xMM eo
Figura 5.6. Figura 5.7.
x M M
e o
Figura 5.8.
O distribuție nonsimetrică se mai numește și oblică și ea poate
prezenta asimetrie de stânga sau de dreapta (vezi figurile 5.7 și 5.8).
Forma repartiției se poate analiza:
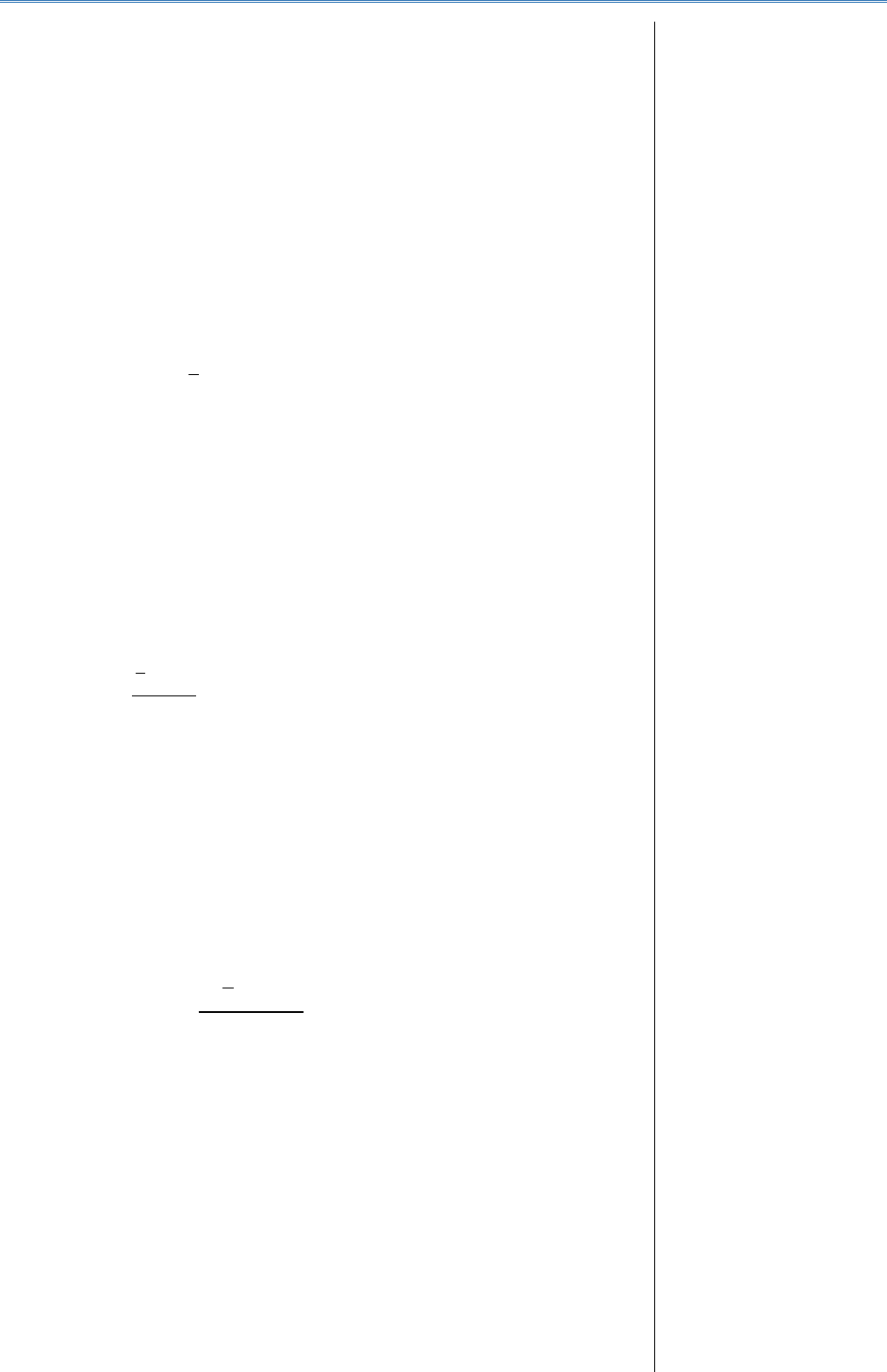
Emilia GOGU Statistica - Manual de studiu individual
Pagina 62 din 112
a) utilizând metoda grafică;
b) calculând indicatorii de asimetrie adecvați.
Asimetria se poate analiza în primul rând cu ajutorul metodei
grafice. În acest scop se folosesc: poligonul frecvențelor și histograma.
După ce s-a construit poligonul frecvențelor interpretarea se face ca
mai sus.
Reprezentarea grafică a seriei oferă o imagine sugestivă asupra
gradului de asimetrie fără însă a-l putea măsura printr-o valoare
numerică. De aceea se calculează și indicatorii de asimetrie, exprimați
în mărimi absolute și relative.
Asimetria absolută se calculează după relația:
As xMo
Se exprimă în unitățile de măsură ale variabilei și nu poate fi
folosit la comparații între serii.
De aceea pentru a măsura gradul de asimetrie recurgem la
indicatorii de asimetrie relativi. Din acest grup reținem un anumit
număr de coeficienți, adică numere fără dimensiune, permițând
comparațiile.
Prezentăm în continuare doi coeficienți de asimetrie ce poartă
numele autorilor lor, Pearson și Yule.
dreaptalaoblicãserie0
stângalaoblicãserie0
simetrie0
as
as
as
as
C
C
C
Mox
c
Acest coeficient poate lua valori cuprinse între -1 și +1; cu cât
este mai mic în valoare absolută cu atât asimetria este mai mică.
De reținut. Acest coeficient este recomandabil a se folosi numai
pentru distribuții ușor asimetrice.
În cazul când se cunoaște mediana seriei, coeficientul de
asimetrie
( )
Cas
se poate calcula utilizând relația:
CxMe
as
3( )
Acest coeficient se folosește când între cei trei indicatori ai
tendinței centrale se verifică relația:
Modul = Media - 3(Media - Mediană)
Acest coeficient poate să ia valori cuprinse între -3 și +3 și va arăta
un grad mai mare de simetrie cu cât se va apropia mai mult de 0.
5.3.7 Aplicație
Pentru exemplificarea calculării indicatorilor sintetici de variație
se va folosi seria de distribuție de frecvență prezentată în tabelul
următor.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 63 din 112
Calculul indicatorilor sintetici de variație
Agenți
ec. după
mărimea
profitului
(mil. lei)
Nr. agenți
economic
i
(ni)
Centrul
de
interval
(xi)
xini
Frecve
nte
cumul
ate
crescat
or
ii nxx
i
2
inxx )(
0
1
2
3
4
5
20 - 24
20
22
480
20
197,20
1944,392
24 - 28
35
26
910
55
205,10
1201,886
28 - 32
40
30
1200
95
74,40
138,384
32 - 36
60
34
2040
155
128,40
274,776
36 - 40
32
38
1216
187
196,48
1206,387
40 - 44
8
42
360
195
81,12
822,557
44 - 48
5
46
230
200
40,40
999,698
TOTAL
200
-
6412
953,40
6588,080
i
n
ii nx
i
inxx
i
2
inxx )(
Profitul mediu pe agent economic:
06,32
200
6412
1
1
k
i
i
k
i
ii
n
nx
x
mil lei /agent ec.
Modul
33,67
32)(6040)(60
40)(60
432
Mo
mil lei profit / agent.ec.
Mediana
Repartitia agentilor economici dupa marimea profitului
20
35
40
60
32
8
5
0
10
20
30
40
50
60
70
20 - 24 24 - 28 28 - 32 32 - 36 36 - 40 40 - 44 44 - 48
mil.lei
pers.
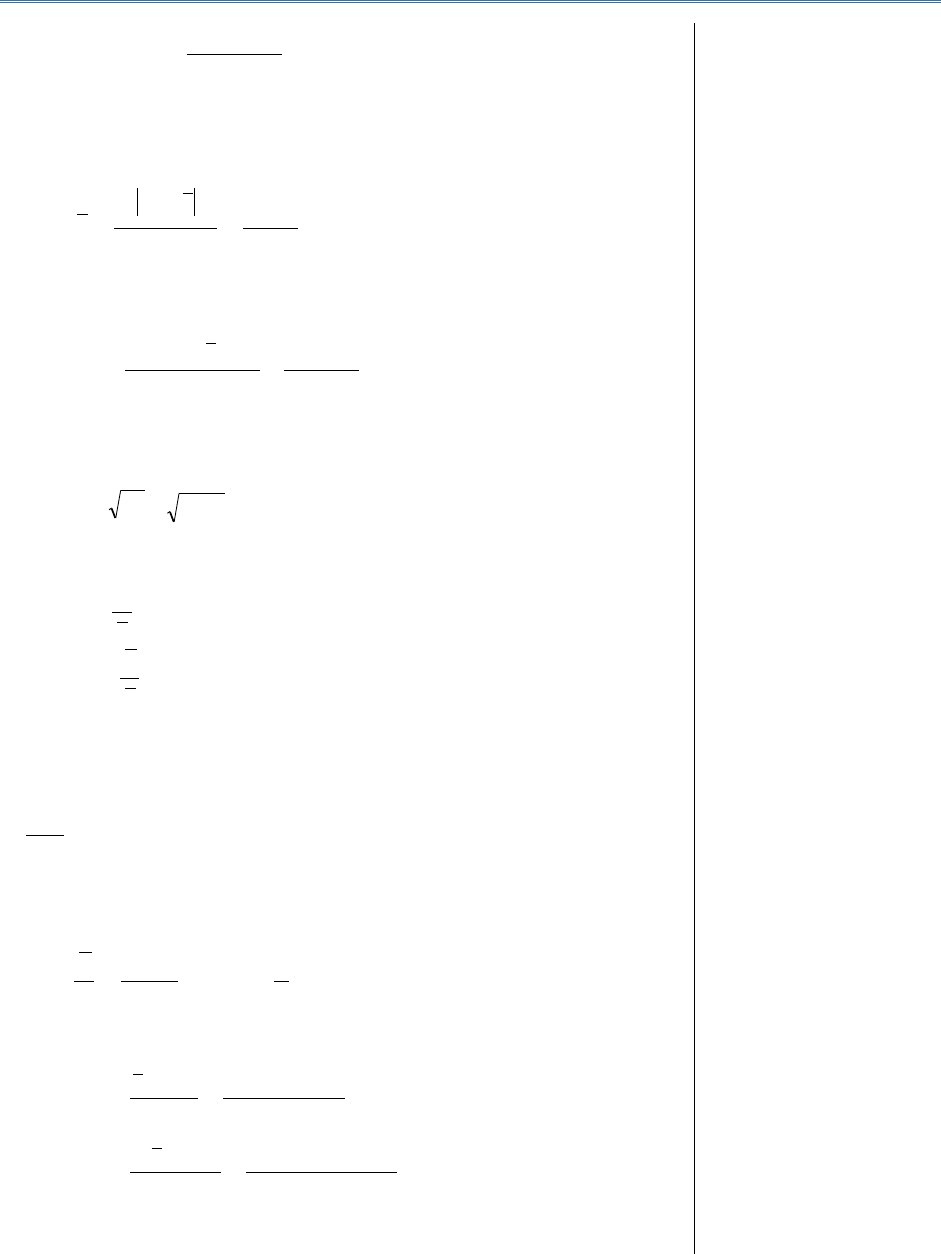
Emilia GOGU Statistica - Manual de studiu individual
Pagina 64 din 112
37,32
60
955,100
432
Me
mil lei profit / agent. ec..
3. Abaterea medie liniară:
7674
200
4953
n
nxx
dk
1i i
k
1i ii ,
,
mil lei profit / agent ec.
Dispersia:
32,94
200
6588,08
)(
1
2
2
k
i
i
i
i
n
nxx
Abaterea medie pătratică:
739,594,32
2
miloane lei profit/agent ec.
Coeficientul de variație:
vx
vd
x
100 18 01%
100 14 96%
,
,
Pe baza rezultatelor obținute se poate afirma că media este
reprezentativă pentru seria din care s-a calculat, deoarece s-a obținut
un coeficient de variație de 18,01% iar cele mai multe valori
(60
200 100 30%)
se concentrează în intervalul 32-36 milioane lei.
Tendința de normalitate a distribuției se poate constata și pe
baza relației dintre abaterea medie liniară și abaterea medie pătratică:
5
4
830
7395
7674d ,
,
,
Coeficienți de asimetrie
315.0
739.5
67,3386,31
Mox
Cas
2665.0
739.5
)37.3286.31(3)(3
Mex
Cas
Rezultă asimetrie negativă moderat.
5.4 Îndrumar pentru autoverificare

Emilia GOGU Statistica - Manual de studiu individual
Pagina 65 din 112
5.4.1 Sinteza unității de studiu 5
Multitudinea situațiilor întâlnite în practică demonstrează necesitatea caracterizării
tendințelor de concentrare (diversificare) a valorilor unei serii de repartiție de frecvențe
cu ajutorul unor metode statistice specifice care să conducă la obținerea uneia sau a mai
multor valori reprezentative, fie pentru întreaga serie, fie pe intervale de variație a valorilor
individuale.
Aceste proprietăți se regăsesc nemijlocit în elaborarea și analiza repartițiilor teoretice de
probabilități și se pot verifica în cazul repartițiilor empirice. În consecință, după cum s-a precizat
într-un capitol anterior repartițiile teoretice sunt elaborate pe baza unei ipoteze de repartiție a
frecvențelor, astfel încât să se poată stabili relații matematice bine determinate între valorile
variabilei studiate și frecvențele lor de apariție, interpretate ca o funcție de probabilități. Pentru
aceste repartiții s-au stabilit o serie de parametri care le definesc și care pot fi folosiți în compararea
repartițiilor empirice cu cele teoretice. Printre repartițiile teoretice mai des utilizate menționăm:
repartiția binomială, repartiția normală și repartiția Poisson. Proprietățile acestor repartiții -
studiate de statistica matematică - sunt folosite și în statistica social-economică la interpretarea
fenomenelor luate independent și interdependent. De asemenea, ele sunt folosite la interpretarea
indicatorilor care caracterizează colectivitate generală atunci când nu se dispune decât de date din
observări parțiale.
Revenind la repartițiile empirice cu studiul cărora ne ocupăm în acest capitol menționăm că
analiza acestora trebuie realizată într-o viziune sistemică.
Sistemul de indicatori al unei repartiții empirice este format din:
indicatori de nivel și frecvențe;
indicatori ai tendinței centrale și ai mediilor de structură (poziție);
indicatori de variație și asimetrie;
indicatori de concentrare.
Acești indicatori se pot stabili în întregime pentru seriile de variabile cantitative
(numerice). În cazul celor cu variabile calitative, numărul indicatorilor calculați este mai
restrâns. În continuare acești indicatori se vor prezenta pe exemplul seriilor de variabile
numerice și în măsura în care ei se pot aplica și pentru seriile de variabile calitative vor fi
menționați separat.
Într-o colectivitate statistică valorile individuale (variantele) diferă mai mult sau mai puțin
unele față de altele. Ele pot fi mai apropiate sau mai împrăștiate. Comparația se face, în mod
practic, cu media seriei, considerată ca fiind valoarea cea mai reprezentativă pentru colectivitatea
studiată. De cele mai multe ori este important de cunoscut cât de departe sunt valorile variantelor
seriei față de această medie, sau cu alte cuvinte care este dispersia variantelor în cadrul seriei.
Se apreciază că dacă variantele au valori mai apropiate de valoarea mediei seriei, deci
prezintă abateri mici, media este reprezentativă.
În practica statistică de cele mai multe ori datele care trebuie să fie analizate sunt extrem de
numeroase și de regulă cu o amplitudine mare a variației. De aceea este necesar să separăm și să
stabilim intensitatea cu care activează cele două grupe de factori esențiali și întâmplători având
drept consecință imediată un anumit grad de variabilitate.
Dacă am limita analiza numai la determinarea și interpretarea mărimii medii nu ar fi posibilă
cunoașterea condițiilor concrete în care apar și se dezvoltă fenomenele și nici depistarea tendințelor
evolutive ale variabilității acestor fenomene.
Cu cât fenomenele sunt mai complexe, deci dependente de mai mulți factori, cu atât variația
este mai mare și utilizarea mărimilor medii devine insuficientă implicând verificări riguroase cu
privire la stabilitatea și reprezentativitatea lor. O medie este reprezentativă numai atunci când se
calculează din valori omogene între ele.
Emilia GOGU Statistica - Manual de studiu individual
Pagina 66 din 112
Analiza statistică a unei repartiții poate fi aprofundată prin calculul indicatorilor de variație.
Acești indicatori trebuie să servească la:
verificarea reprezentativității mediei ca valoare tipică a unei serii de date statistice;
verificarea gradului de omogenitate a seriei;
caracterizarea statistică a formei și gradului de variație a unei caracteristici;
compararea în timp și spațiu a mai multor serii statistice de distribuție pentru
aceeași caracteristică sau pentru caracteristici interdependente;
cunoașterea gradului de influență a factorilor după care s-a făcut gruparea
unităților observate.
Indicatorii variației pot fi calculați ca indicatori simpli și ca indicatori sintetici.
5.4.2 Concepte și termeni de reținut
Abaterea absoluta
Indicatorii medii
Media aritmetică ponderată
Abaterea liniară
Indicatorii variație
Media aritmetică simplă
Abaterea medie patratica
ponderată
Mărimea intervalului
Media armonică ponderată
Abaterea medie patratica simplă
Frecvența intervalului modal
Media armonică simplă
Abaterea standard
Frecvențe absolute
Media geometrică ponderată
Abateri relative individuale
Frecvențe cumulate
Media geometrică simplă
Amplitudine
Frecvente cumulate crescător
Media pătratică ponderată
Asimetrie
Frecvente cumulate descrescător
Media pătratică simplă
Asimetrie negativă moderat
Frecvente relative
Mediana
Coeficient de variatie
Grad de omogenitate
Metoda grafică
Coeficienți de asimetrie
Grad de variație
Modul
Cuartile
Indicatorii asimetriei
Reprezentativitate
Decile
Indicatorii concentrării
Reprezentativitatea mediei
Dispersia
Indicatorii de poziție
Variatie
Frecvența intervalului median
Indicatorii de strucutra
Verificarea reprezentativității
5.4.3 Întrebări de control și teme de dezbatere
1. Care sunt indicatorii cu care se caracterizează o serie de repartiție de frecvențe?
2. De ce este necesară folosirea mărimilor medii?
3. Care sunt condițiile de aplicare a metodei statistice a indicatorilor medii?
4. Ce fel de medii se folosesc frecvent în statistica economico-socială?
5. Când se aplică media aritmetică în statistica economico-socială?
6. Ce procedee se folosesc la calculul mediei aritmetice?
7. Care sunt proprietățile mediei aritmetice?
8. Când se aplică în statistică media armonică? În ce relație se aplică față de celelalte medii?
9. Care sunt indicatorii cu care se caracterizează tendința centrală a unei serii?
10. Ce sunt mediana, cuartilele, decilele, cum se calculează și care este rolul lor în descrierea
statistică a unei serii?
Emilia GOGU Statistica - Manual de studiu individual
Pagina 67 din 112
11. Ce este valoarea modală, cum se calculează și care este rolul ei în descrierea statistică a unei
caracteristici?
12. In ce raport se găsesc indicatorii: media, mediana, modulul și cum se folosește relația dintre ei
în caracterizarea seriei?
13. De ce este necesară studierea variației unei caracteristici?
14. Ce indicatori se folosesc în măsurarea variației unei caracteristici?
15. Ce procedee de calcul se folosesc la determinarea indicatorilor de variație?
16. Care sunt și cum se calculează indicatorii de asimetrie?
17. Cum se calculează media și dispersia unei caracteristici alternative?
18. Cum se studiază variația unei caracteristici atunci când colectivitatea este împărțită pe mai
multe grupe?
19. Care sunt relațiile între indicatorii de variație din fiecare grupă și aceia din colectivitatea totală?
20. Cum se poate determina cu ajutorul indicatorilor de variație dependența dintre caracteristicile
de grupare?
5.4.4 Teste de evaluare/autoevaluare
Aplicația 1 Se dau datele pentru aceiași societate comercială:
Repartiția salariaților Repartiția salariaților
după valoarea desfacerii după salariile lunare.
Grupe după valoarea
desfacerii (mii lei)
Nr.
salariați
Grupe după
salarii (lei)
Structura
salariaților (în
% față de total)
Sub 500
500-600
600-700
700-800
800-900
900-1000
1000 peste
10
15
23
28
18
16
10
Sub 1350
1350-1460
1460-1580
1580-1800
1800-2400
peste 2400
12
15
21
16
18
15
Total
120
Total
100 %
Se cere:
1. să se reprezinte grafic cele două serii;
2. să se prezinte cele două serii cu frecvențe absolute și frecvențe relative;
3. să se calculeze indicatorii tendinței centrale (media mediana și modul);
4. să se calculeze indicatorii variației și ai asimetriei

Emilia GOGU Statistica - Manual de studiu individual
Pagina 68 din 112
5.4.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Gogu E., Statistica în turism și comerț, Editura Oscar Print, București, 2009;
4. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.
Emilia GOGU Statistica - Manual de studiu individual
Pagina 69 din 112
6 UNITATEA DE STUDIU 6 ANALIZA SERIILOR INTERDEPENDENTE.
CORELAȚIA ȘI REGRESIA STATISTICĂ
6.1 Introducere
6.2 Obiectivele și competențele unității de studiu – timp alocat
6.3 Conținutul unității de studiu
6.3.1. Noțiunea de corelație. Condiții de aplicare
6.3.2. Tipuri de legături între fenomenele social - economice
6.3.3. Metode de analiză a interdependenței dintre fenomene
6.3.4. Aplicații
6.4. Îndrumător pentru autoverificare
6.1 Introducere
Teoretic și practic se demonstrează în mod
științific că fenomenele sociale apar și se
dezvoltă ca urmare a unor cauze variate, care
pot acționa m același sens sau în sens opus și
cu grad diferit de intensitate. Complexitatea
interacțiunii dintre fenomene este cu atât mai mare, cu cât ele
aparțin unor colectivități mai numeroase Reiese că fenomenele
sociale nu sunt, de regulă, fenomene univoc determinate, fiind
rezultatul conjugării influenței mai multor fenomene-cauză, iar în
sistemul acesta de legături nu toate raporturile de dependență au
aceeași importanță, acțiunea unora dintre factori compensându-se
reciproc.
De aceea, în analiza statistică a raporturilor de dependență
dintre fenomene, problema care se pune este aceea a măsurării
relației care există între două sau mai multe caracteristici cuprinse
în programul unei cercetări concrete a fenomenelor social-
economice de masă. Aceasta presupune, în primul rând, să se
constate dacă între caracteristica x - denumită caracteristica
factorială sau independentă și caracteristica y caracteristică
rezultativă sau dependentă - există sau nu un raport de dependență
și, în al doilea rând, dacă această relație există să se exprime
printr-un indicator simplu sau sintetic de corelație, măsura în care
caracteristica factorială x contribuie la formarea caracteristicii
rezultative y sub aspectul naturii, direcției și formei de legătură
între ele.
În acest stadiu de cercetare statistică analiza calitativă ce
trebuie să preceadă aplicarea uneia sau a alteia dintre metodele
statistice este deosebit de importantă și are un vădit caracter
interdisciplinar. Aceasta permite ca, din ansamblul de legături
existente în mod obiectiv între fenomenele aceleiași colectivități
statistice, să se desprindă acelea care au caracter permanent și sunt
determinante în formarea nivelurilor concrete de dezvoltare a
caracteristicii rezultative. Acest lucru apare cu atât mai necesar,
cu cât legitatea de apariție și dezvoltare a fenomenelor social-
Emilia GOGU Statistica - Manual de studiu individual
Pagina 70 din 112
economice fiind valabilă pentru întregul ansamblu, nu este
sesizabilă, de obicei, în cadrul cercetării empirice, decât dacă
datele se referă la un număr mare de cazuri individuale concrete,
diferite ca forme de manifestare, aparținând aceleiași colectivități.
Având în vedere toate aceste aspecte, trebuie precizat că
metoda corelației nu poate da rezultate bune decât dacă se
lucrează cu un număr suficient de mare de cazuri individuale în
care distribuția abaterilor este aproximativ normală. Dacă
această condiție nu este satisfăcută, câmpul de acțiune a legii
numerelor mari este limitat, iar concluziile desprinse în urma
obținerii anumitor indicatori de corelație pot, da naștere unei
interpretări eronate, ca urmare a reflectării neveridice a
fenomenelor supuse cercetării statistice. Și cu această ocazie este
necesar ca procesul de analiză să pornească de la simplu la
complex, de la fenomene la esență, de la o esență de un anumit
grad la o esență de grad superior. Aceasta presupune ca, în analiza
legăturilor dintre fenomene, să se folosească metoda
abstractizării succesive a factorilor, prin care să se poată studia
atât legăturile simple, imediate dintre două fenomene legate
printr-o relație de cauzalitate directă, cât și interacțiunea dintre
factori.
6.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
- definirea noțiunii de corelație;
- tipuri de legături;
- identificarea factorilor cauză și rezultativi;
- metode de determinare a interdependențelor.
Competențele unității de studiu:
- studenții vor putea identifica existența legăturilor;
- vor putea prezenta grafic interdependența factorilor;
- studenții vor cunoaște metodele de analiza a corelației/
regresiei;
- vor putea calcula și interpreta intensitatea legăturii.
Durata medie de studiu individual alocat unității: 4 ore
6.3 Conținutul unității de studiu
6.3.1 Noțiunea de corelație. Condiții de aplicare

Emilia GOGU Statistica - Manual de studiu individual
Pagina 71 din 112
În domeniul fenomenelor și proceselor social-economice,
iau naștere o serie de legături, de interdependențe, determinate de
acțiunea unor cauze și condiții diferite, care influențează mai mult
sau mai puțin fenomenele existente.
Complexitatea fenomenelor economice și sociale,
caracterizarea lor cantitativă și calitativă determină folosirea
combinată a diferitelor științe în investigarea relațiilor de
cauzalitate, care stau la baza apariției și dezvoltării lor.
Printre metodele și modelele care s-au impus în studiul
interdependenței cele care se folosesc cel mai frecvent sunt
corelația și regresia statistică
Utilizarea acestor metode este justificată de necesitatea
crescândă a reflectării într-o formă numerică adecvată a
interdependenței obiective dintre fenomenele social-economice în
ceea ce privește natura, direcția și gradul de intensitate a
legăturilor, care se manifestă într-o anumită perioadă de timp sau
în dinamică.
Studiul statistic al interdependenței dintre fenomene
necesită identificarea legăturilor studiate de la cauză la efect,
precum și legăturile realizate prin intermediul unui șir de
cauzalități. în acest sens, este necesar ca relațiile de cauzalitate din
interiorul fenomenelor complexe să fie studiate și prezentate tot
sub o formă de tendință valabilă la nivelul întregului ansamblu și
nu la nivelul unor valori individuale izolate. Aceasta conduce în
mod obligatoriu la folosirea unor metode statistice m care să se
țină seama de formele de distribuție de frecvență ale fenomenelor
pentru care se studiază interdependențele dintre ele și care nu pot
fi interpretate decât pe baza indicatorilor medii și a celor de
variație.
6.3.2 Tipuri de legături între fenomenele social - economice
Formele de manifestare a relațiilor de interdependență sunt
extrem de variate și adesea destul de greu de sesizat. Pentru a le
studia este necesar să fie clasificate în funcție de unele criterii,
după care se pot deosebi unele de altele.
După natura relației de cauzalitate, legăturile dintre
fenomene pot fi legături funcționale și legături statistice sau
stohastice
1. Legăturile funcționale sunt univoce, realizate direct între
un fenomen-cauză și un fenomen-efect. Deci, fenomenul-efect
depinde de o singură cauză, care poate fi identificată de câte ori
se produce, ceea ce înseamnă că, dacă condițiile rămân constante,
atunci unei valori a caracteristicii factoriale îi corespunde o
singură valoare a caracteristicii rezultative. Ele se mai numesc și
legături de tip determinist.
Relația matematică dintre fenomenul-efect și fenomenul-
cauză, pentru legăturile de tip funcțional (determinist) este:
yi=f(xi).
Ex Un exemplu de astfel de legătură funcțională este aceea dintre
nivelul productivității muncii și consumul specific de timp de muncă
pentru produsul respectiv în cadrul unei perioade de timp. Se poate, cu

Emilia GOGU Statistica - Manual de studiu individual
Pagina 72 din 112
ușurință, demonstra că, pe măsură ce scade timpul de producere, cu
atât crește productivitatea muncii pentru produsul respectiv.
2. Legături statistice, denumite și legături stohastice, de
tip nedeterminist descrise prin funcția matematică:
),...,,( 21 kiiii xxxfy
și se referă la fenomene complexe,
influențate de mai multe cauze, care se manifestă în condiții
diferite și se pot clasifica după mai multe criterii astfel:
după numărul variabilelor înregistrate:
legături simple (unifactoriale) când se înregistrează un singur
factor;
legături multiple (bifactoriale și multifactoriale) –
înregistrează cel puțin două variabile factoriale.
după conținutul variabilelor corelate:
legături numerice denumite corelații statistice – când legătura
se stabilește între variabile cantitative
legături în care cel puțin o variabilă este nenumerică, denumite
asocieri statistice – când legătura se stabilește între variabile
calitative
după direcția legăturii:
legături directe - pe măsură ce crește variabila factorială
crește și cea rezultativă.
legături inverse - pe măsură ce crește variabila factorială
descrește cea rezultativă.
Ex. între w și salariu există o legătură directă de tipul unei
corelații statistice. Legătura dintre calificare și salariu este o
asociere statistică, pentru că calificarea este o variabilă
calitativă
după funcția analitică cu care pot fi exprimate corelațiile
statistice:
liniare – a cărei linie de tendință se măsoară cu ecuația
funcției rectiliniare,
curbiliniare, cunoscute sub denumirea generică de legături
neliniare – care pot fi de tipul unei funcții exponențiale, a
funcțiilor hiperbolice și a funcțiilor de tip parabolic.
după timpul în care se produc:
concomitente sau sincrone
cu decalaj sau asincrone este acea în care după o anumită
modificare a factorului începe să apară și modificarea efectului.
În cadrul analizei în timp, a legăturilor, trebuie verificat dacă,
există decalaj până la începerea corelației și necesitatea stabilirii
perioadei de corelare a seriilor după eliminarea decalajului.
Ex. Între înzestrarea tehnică productivitatea poate să
apară legată după un număr de ani necesari procesului de
asimilare sau după o anumită perioadă un produs atinge
performanțele de calitate și poate să apară la export.
Interpretarea rezultatelor, verificarea ipotezelor, aplicarea
testelor de semnificație a funcțiilor și parametrilor lor se face
potrivit particularităților fenomenelor studiate în funcție de timp,
loc și formă de organizare.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 73 din 112
Dacă datele provin dintr-un sondaj statistic trebuie să se
verifice reprezentativitatea ansamblului și să se interpreteze
probabilistic indicatorii calculați.
6.3.3 Metode de analiză a interdependenței dintre
fenomene
Pentru interpretarea legăturilor dintre fenomene se pot folosi
metode de sistematizare și verificare a legăturilor:
A. Metode parametrice simple și analitice,
B. Metode neparametrice
A. Metode parametrice simple
Metodele de sistematizare și verificare a corelației sunt:
a) seriile interdependente,
b) metoda tabelului de corelație
c) metoda grupării,
d) metoda grafică,
e) metoda balanțelor
a) Metoda seriilor interdependente pe baza unor analize
complexe imprimă cu științele care studiază același domeniu să
înregistrăm și să înscriem în datele în funcție de prima variabilă
factorială.
Pentru aceasta se pot folosi serii cronologice, teritoriale,
distribuții statistice referitoare la aceeași perioadă de timp. Dacă
vrem să analizăm într-o companie care este legată de numărul de
ore lucrate și salariu vom nota cu x numărul de ore lucrate și cu y
salariul.
Nr crt
ore lucrate
xi
salariu
yi
1
2
3
.
.
.
n
x1
x2
x3
.
.
.
xn
y1
y2
y3
.
.
.
yn
Dacă există legătură între cele două, și ea este directă, pe
măsură ce crește variabila factorială, descrește și rezultativă.
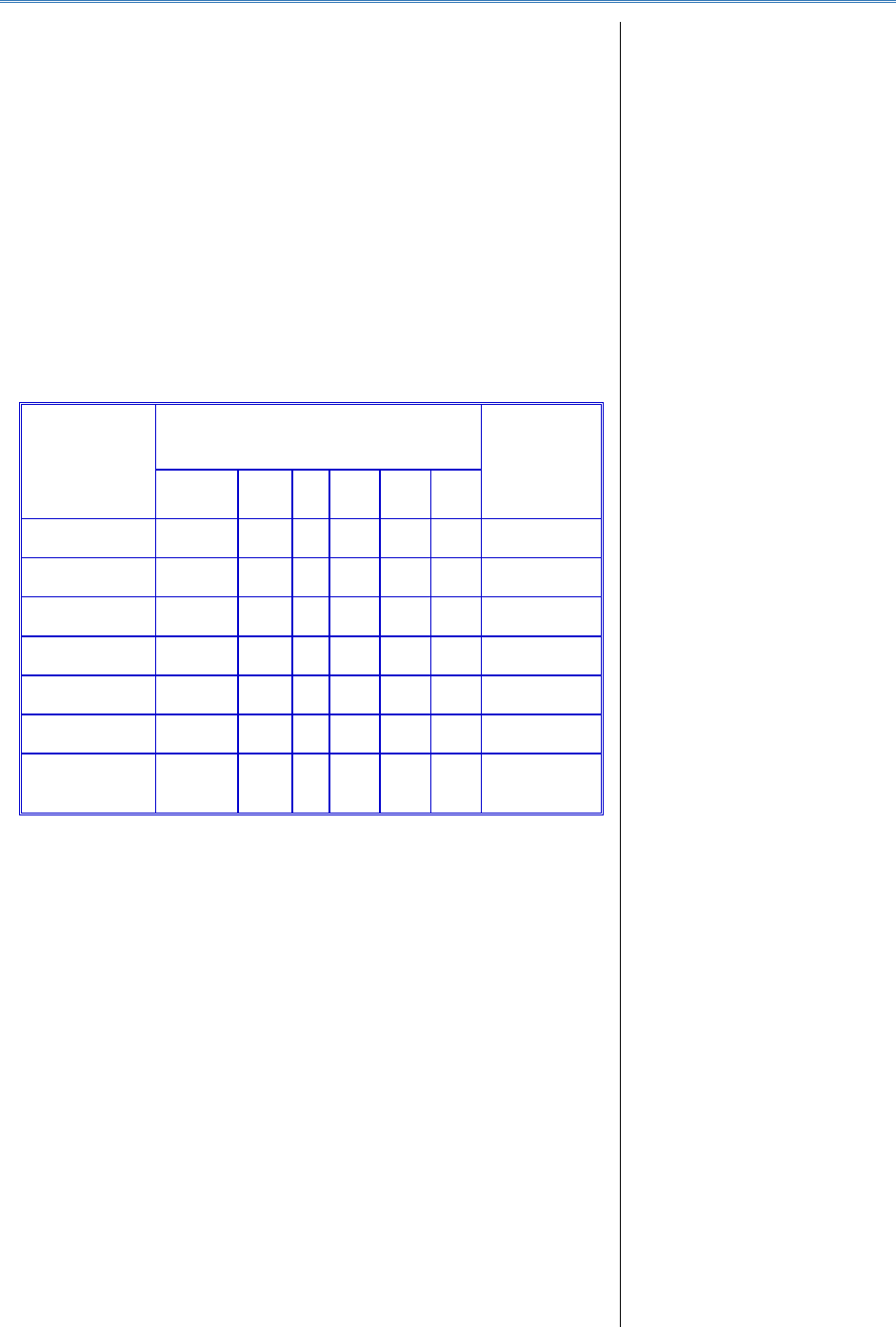
Emilia GOGU Statistica - Manual de studiu individual
Pagina 74 din 112
b) Metoda tabelului de corelație care are la baza tabelul de
corelație, tabel cu dublă intrare reprezentând o formă specială a
unei grupări combinate, în care separarea pe grupe a unităților se
face după variația ambelor caracteristici – factorială și rezultativă.
Cu ajutorul tabelului de corelație în funcție de modul de
distribuție a frecvențelor, în tabel se obțin informații cu privire la
existența și direcția legăturii dintre cele două variabile.
În unele cazuri direcția legăturii este dată de poziția
diagonalei în jurul căreia se grupează frecvențele: când diagonala
leagă unghiul stâng de sus al tabelului cu unghiul drept de jos -
legătura este directa, iar când unește unghiul stâng de jos cu
unghiul drept de sus, se apreciază că între cele două caracteristici
există o legătură în sens invers.
Valorile
caracteristicii
de grupare X
Variantele sau valorile
caracteristicii dependente Y
Volumul
grupei
y1
y2
…
yj
…
ym
x1
n11
n12
...
n1j
…
n1m
n1.
x2
n21
n22
…
n2j
…
n2m
n2.
...
...
...
…
...
…
...
...
xi
ni1
ni2
…
nij
…
nim
ni.
...
...
...
…
...
…
...
...
xr
nr1
nr2
…
nrj
…
nrm
nr.
Total
n.1
n.2
…
n.j
…
nm
m
1j j
r
1i inn .
.
Modul de așezare a frecventelor în jurul diagonalei ne dă
posibilitatea să apreciem intensitatea legăturii: concentrarea
intensă a frecventelor în jurul diagonalelor indică existența unei
legaturi strânse între caracteristici. În alte cazuri, frecventele se
grupează pe diverse curbe. Dacă frecvențele se repartizează pe
întregul tabel fără nici o regularitate, atunci ori nu există legătura,
ori aceasta este foarte slabă.
c) Metoda grupării reprezintă un model de analiză prin
excelență calitativ, capabil să surprindă aspecte esențiale ale
legaturilor dinte variabile. Studiul legaturilor se realizează după
ce unitățile colectivității se grupează în funcție de caracteristica
factorială, iar pentru caracteristica rezultativă se calculează

Emilia GOGU Statistica - Manual de studiu individual
Pagina 75 din 112
indicatorii derivați (mărimile relative sau medii) specifici
fiecărei grupe.
Această metodă de studiere a legăturilor dintre fenomene
necesită calcularea mediilor condiționate ale variabilei
rezultative
xi
y
pentru grupele obținute după variabila factorială.
Pe baza tabelului de corelație se pot calcula următoarele medii
de grupă:
m
1j ij
m
1j ijj
in
ny
y
Metoda grafică
Graficul de corelație denumit și corelogramă sau graficul
norului de puncte, permite să identifice cu ajutorul ajustării care
este funcția analitică corespunzătoare valorilor noastre.
Prin ajustare înțelegim înlocuirea valorilor empirice
obținute pentru o observație statistică cu valori teoretice calculate
după un model statistic. În cazul în care am întocmit un grafic de
corelație putem face o ajustare vizuală și după aceea aplicăm
modelul de calcul și o ajustare numerică. Ajustarea vizuală constă
în trasarea unei linii drepte sau a unei curbe care să treacă cât mai
aproape de valorile empirice înscrise în grafic.
Metoda grafică este utilizată cu bune rezultate pentru
alegerea funcției analitice care se studiază (în cazul regresiei și
corelației).
d) Metoda balanțelor. Această metodă servește pentru
analiza relațiilor care există în cadru unui proces stocastic în care
se pot analiza relațiile de interdependență dintre diferitele
elemente ale procesului, dintre diferitele laturi ale lui sau dintre
diferitele etape sau momente în care el se desfășoară.
A.2. Metode parametrice analitice
Metode și procedee de analiză a legăturilor dintre
fenomene
Analiza dispersională
Analiza dispersională este folosită pentru verificarea
semnificației factorului de grupare ales (înainte de aplicarea
regresiei) și după aplicarea acesteia, pentru calculul și
interpretarea rezultatelor obținute în urma aplicării modelului de
corelație (validarea modelului ales pentru cazuri concrete .
Metoda regresiei

Emilia GOGU Statistica - Manual de studiu individual
Pagina 76 din 112
Metodele de studiere a legaturilor prezentate anterior au ca
deficiență principală faptul că deși permit constatarea legăturii și
caracterulul ei, nu o pot măsura printr-un indicator sintetic. Acest
inconvenient este înlăturat prin utilizarea metodei regresie.
Metoda regresiei constituie o metoda statistică analitică de
cercetare a legăturii dintre variabile cu ajutorul unor funcții
denumite funcții de regresie.
Notând cu Y variabile dependenta și cu x1 , x2 ... xn
variabilele independente obținem ecuația de regresie y = f (x1 , x2
... xn).
După ce am stabilit funcția care devine funcția de ajustare,
trecem la măsurarea corelației cu ajutorul metodei regresiei.
Această metodă presupune să aibă înregistrate datele cu privire la
cele două variabile una factorială și una rezultativă și să
presupunem că legătura dintre cele două este de forma unei ecuații
de tendință, care descrie funcția rectiliniară. Fiind vorba de
legătura de tip statistic care se supune legilor statistice, care
acționează sub forma de tendință cu caracter de medie, ecuația:
ix bxaY i
,
în care:
i
x
Y
- valoarea ecuației de regresie medie;
xi – variabilă factorială
Parametrul “a” reprezintă ordonata la origine și arată la ce
nivel ar fi ajuns valoarea caracteristicii Y dacă toți factorii - mai
puțin cel înregistrat - ar fi avut o acțiune constantă asupra formării
ei.
Parametrul “b” se mai numește și coeficient de regresie și
reprezintă, în sens geometric, panta liniei drepte. Coeficientul de
regresie “b“ arată cu cât se schimbă în medie variabila Y în cazul
în care variabila X se modifică cu o unitate. Acest parametru este
pozitiv în cazul legăturii directe și negativ în cazul legăturii
inverse.
Parametrii “a” și “b” se determină din sistemul de ecuații
normale obținut prin metoda celor mai mici pătrate
minim)( 2
i
xi Yy
.
Dacă modelul ales este corelația liniară simplă corespunde
datelor empirice, atunci ecuația de regresie consideră că valorile
teoretice obținute prin celor mai mici pătrate să prezinte abateri
minime. (
minim)( 2
ii bxay
).
Parametri ecuației în acest caz se determină prin rezolvarea
următorului sistem de ecuații:
iiii
ii
yxxbxa
yxbna
2
Dacă se folosește metoda determinanților se obține:
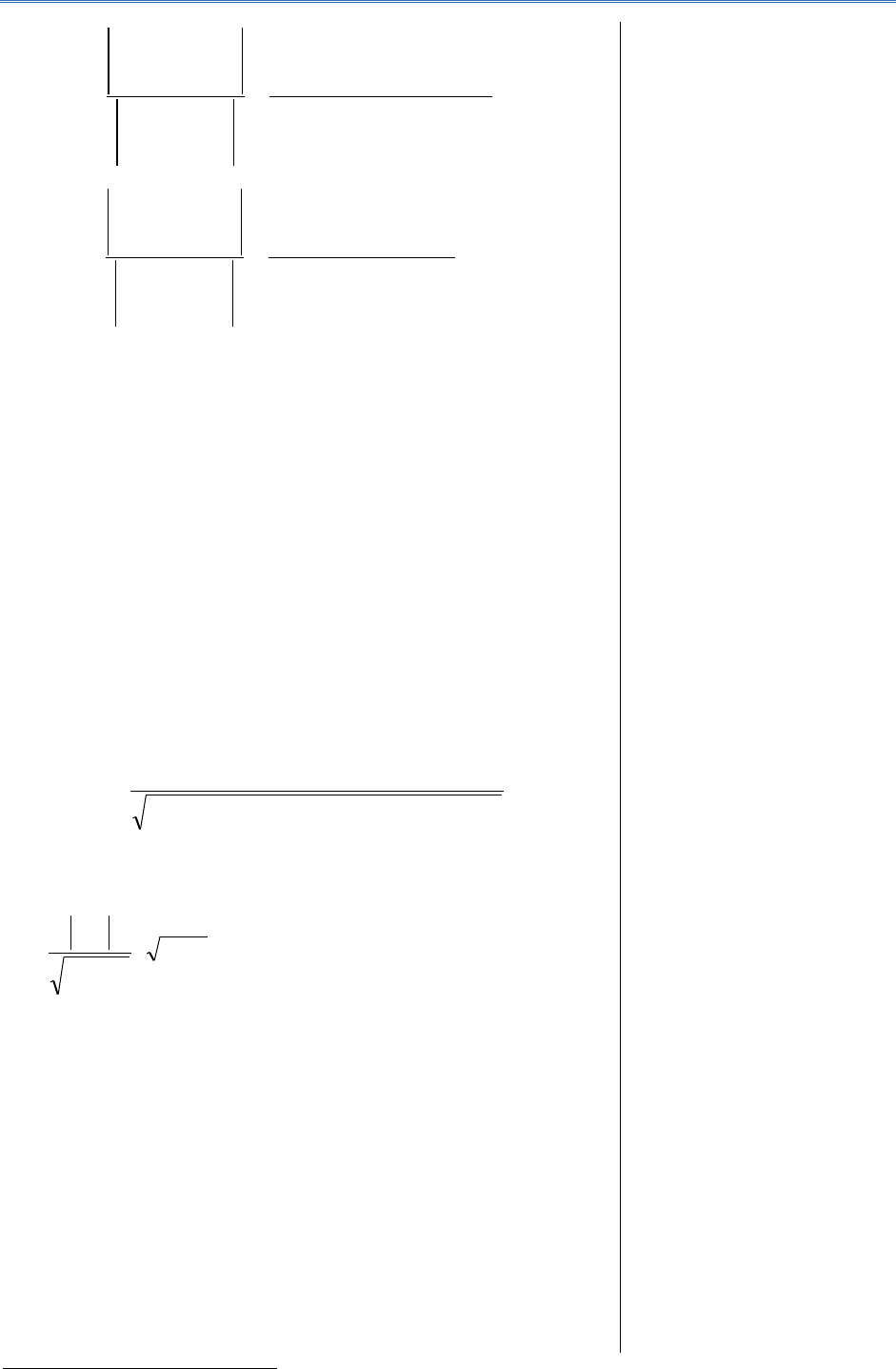
Emilia GOGU Statistica - Manual de studiu individual
Pagina 77 din 112
22
2
2
2
)( ii
iiiii
ii
i
iii
ii
xxn
xyxxy
xx
xn
xyx
xy
a
22
2
)( ii
iiii
ii
i
iii
i
xxn
yxyxn
xx
xn
yxx
yn
b
Celelalte modele de funcții sunt prezentate în “Statistica
aplicată în economie” pag 66-692
Coeficientul de corelație
Coeficientul de corelație liniară simplă poate să ia valori
între -1 și +1.
Între -1 și 0, legătura dintre cele două variabile este de sens
invers și este cu atât mai intensă, cu cât se apropie de –1.
Între 0 și +1, legătura dintre cele două variabile este directă
și este cu atât mai intensă, cu cât se apropie de 1.
Formulă de calcul simplificat pentru seria bidimensională
simplă:
2222
/)()(
))((
iiii
iiii
xy yynxxn
yxyxn
r
Pentru verificarea semnificației coeficientului de corelație
liniară simplă, se aplică, cel mai frecvent, testul t:
2
12/
/
n
r
r
t
xy
xy
, unde, n reprezintă numărul de perechi de
valori.
Valoarea calculată se compară cu cea tabelară stabilită
probabilistic pentru un nivel de semnificație
2/1
P
și cu n-
2 grade de libertate.
Dacă
tabelarcalculat tt
, se verifică ipoteza semnificației
coeficientului de corelație iar dacă
tabelarcalculat tt
, legătura este
nesemnificativă și trebuie căutat un alt factor esențial cu care să
se studieze corelația.
Raportul de corelație
În cazul în care dispunem de un număr mic de perechi de
valori (xi, yi), negrupate:
2
Acest manual studenţii îl vor avea în timpul orelor de curs şi seminar inclusiv la examen.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 78 din 112
pornind de la devianța factorială :
2
2
/)(
)(
yy
yY
R
i
x
xy i
sau
pornind de la devianța reziduală :
2
2
/)(
)(
1yy
Yy
R
i
xi
xy i
unde
i
x
Y
reprezintă valorile ajustate indiferent de modelul
de regresie selectat.
Raportul de corelație poate lua valori de la zero la +1;
interpretarea sensului legăturii se face după funcția de regresie.
Dacă
xyxy rR //
se confirmă ipoteza legăturii liniare și
această relație este considerată un test de verificare a legăturii.
În cazul unei serii bidimensionale avem abaterile:
- abaterea dintre yi și ecuația de regresie;
- abaterea dintre ecuația de regresie și medie;
- abaterea dintre yi și media lor
Coeficientul de determinație
)( 2/xy
R
:
100
2
2/
2/
xy
xy
R
Coeficientul de nedeterminație:
100
2
2/
2/
ry
xy
K
Interpretând cele două dispersii putem avea două variante:
Dacă:
2/xy
R
>
2/xy
K
rezultă legătură între x și y
Dacă:
2/xy
R
<
2/xy
K
tendință spre independență
B. Indicatorii sintetici ai corelației neparametrice
Coeficientul de asociere
Această metodă se utilizează pentru măsurarea intensității
legăturii a două caracteristici alternative prezentate într-un tabel
de asociere de forma:
y
x
y1
y2
Total
x1
a
b
a+b
x2
c
d
c+d
Total
a+c
b+d
a+b+c+d

Emilia GOGU Statistica - Manual de studiu individual
Pagina 79 din 112
Produsul ad arată gradul de realizare a legăturii directe
dintre X și Y, iar produsul bc gradul de legătură inversă între
aceste două caracteristici cercetate.
Pentru stabilirea valorii numerice a coeficientului de
asociere, care să indice existența și intensitatea unei legături,
formula cea mai utilizată este cea propusă de Yule:
bcad
bcad
Q
Acest indicator poate să ia valori între -1 și +1, arătând nu
numai gradul de intensitate al asocierii celor două caracteristici,
dar și sensul ei.
Coeficienul de corelație a rangurilor propus de Spearman
pentru serii paralele fără frecvențe:
nn
d
ri
s
3
2
6
1
în care:
di - reprezintă diferența între rangurile perechii de valori
(xi,yi); di=rxi - ryi
n - numărul de perechi de valori.
Coeficientul de corelație a rangurilor propus de Kendall
pentru serii paralele fără frecvențe:
)1(
2
nn
S
rk
în care
)( ii QPS
unde:
Pi - numărul rangurilor mai mari care urmează rangului
curent pentru variabila dependentă - y
Qi - numărul rangurilor mai mici care urmează rangului
curent pentru variabila dependentă – y
6.3.4 Aplicații
Aplicația 1. Corelația liniară simplă (date negrupate)
Se prezintă următoarele date cu privire la numărul de otre
lucrate și salariu net lunar
Nr. crt
Ore lucrate
(xi)
Salariul net lunar
(lei)
(yi)
1.
140
2200
2.
146
2555
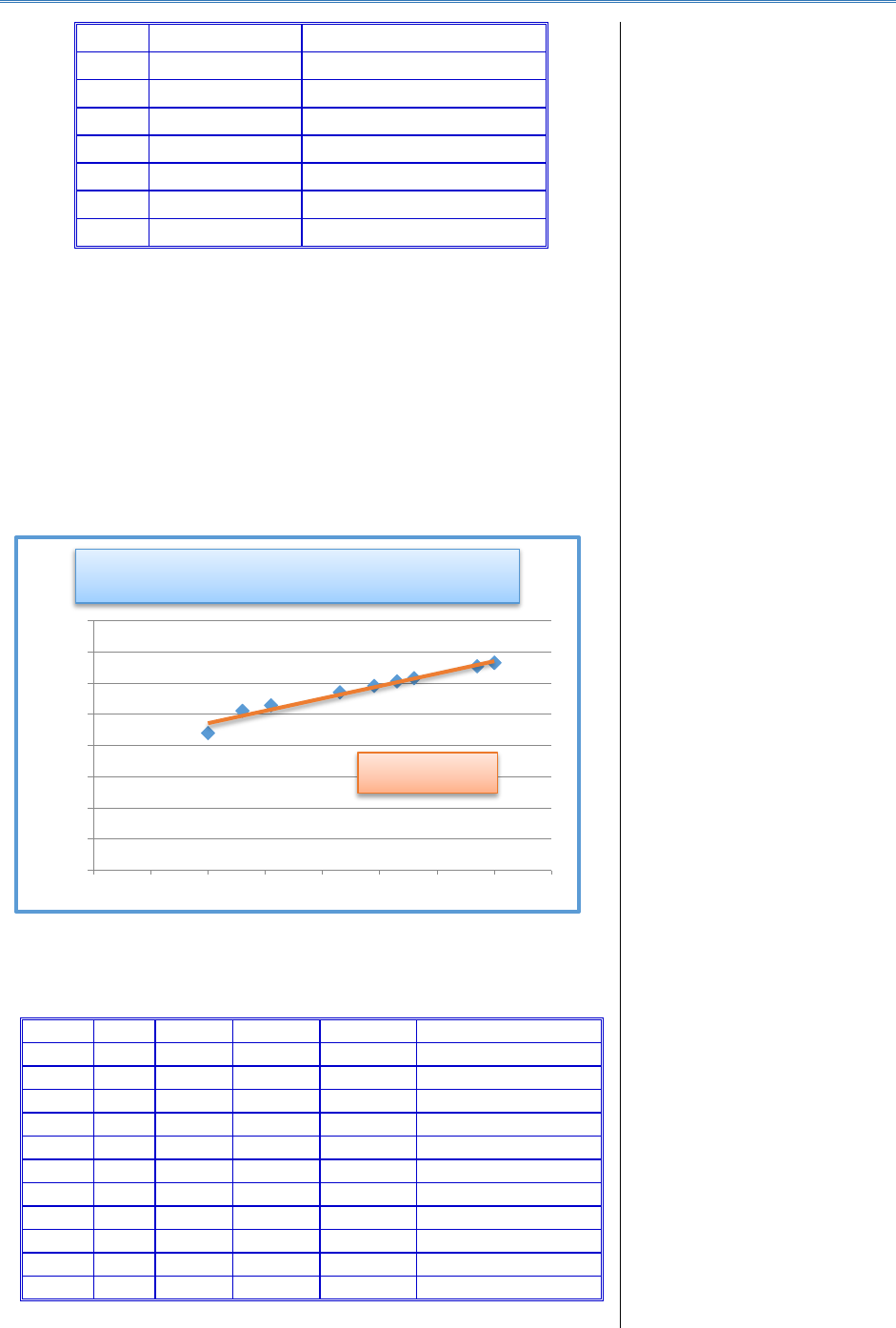
Emilia GOGU Statistica - Manual de studiu individual
Pagina 80 din 112
3.
151
2642
4.
163
2852
5.
169
2957
6.
173
3027
7.
176
3080
8.
187
3272
9.
190
3325
10.
190
3325
Dintre metodele simple de cercetare a legaturilor statistice
recurgem la:
A) Metoda seriilor paralele interdependente
Concluzie: Valorile xi fiind ordonate crescător se poate
observa că și valorile yi cresc în cea mai mare parte, ceea ce
sugerează o legătură directă.
B) Metoda grafică este o altă cale de a stabili legătura
dintre fenomene.
Graficul de asemenea confirmă o legătură directă de formă liniară.
Datele necesare calculării celor doi parametri sunt
prezentate în tabelul de mai jos.
Nr ctr.
xi
yi
x2
xiyi
Yxi=-425,62+19,87xi
1.
140
2200
19600
308000
2357
2.
146
2555
21316
373030
2476
3.
151
2642
22801
398942
2576
4.
163
2852
26569
464876
2814
5.
169
2957
28561
499733
2933
6.
173
3027
29929
523671
3013
7.
176
3080
30976
542080
3073
8.
187
3272
34969
611864
3291
9.
190
3325
36100
631750
3351
10.
190
3325
36100
631750
3351
Total
1685
29235
286921
4985696
29235
y = 19,876x - 425,62
R² = 0,968
0
500
1000
1500
2000
2500
3000
3500
4000
120 130 140 150 160 170 180 190 200
lei
ore
Corelația dintre salariul net lunar si numărul de
ore lucrate
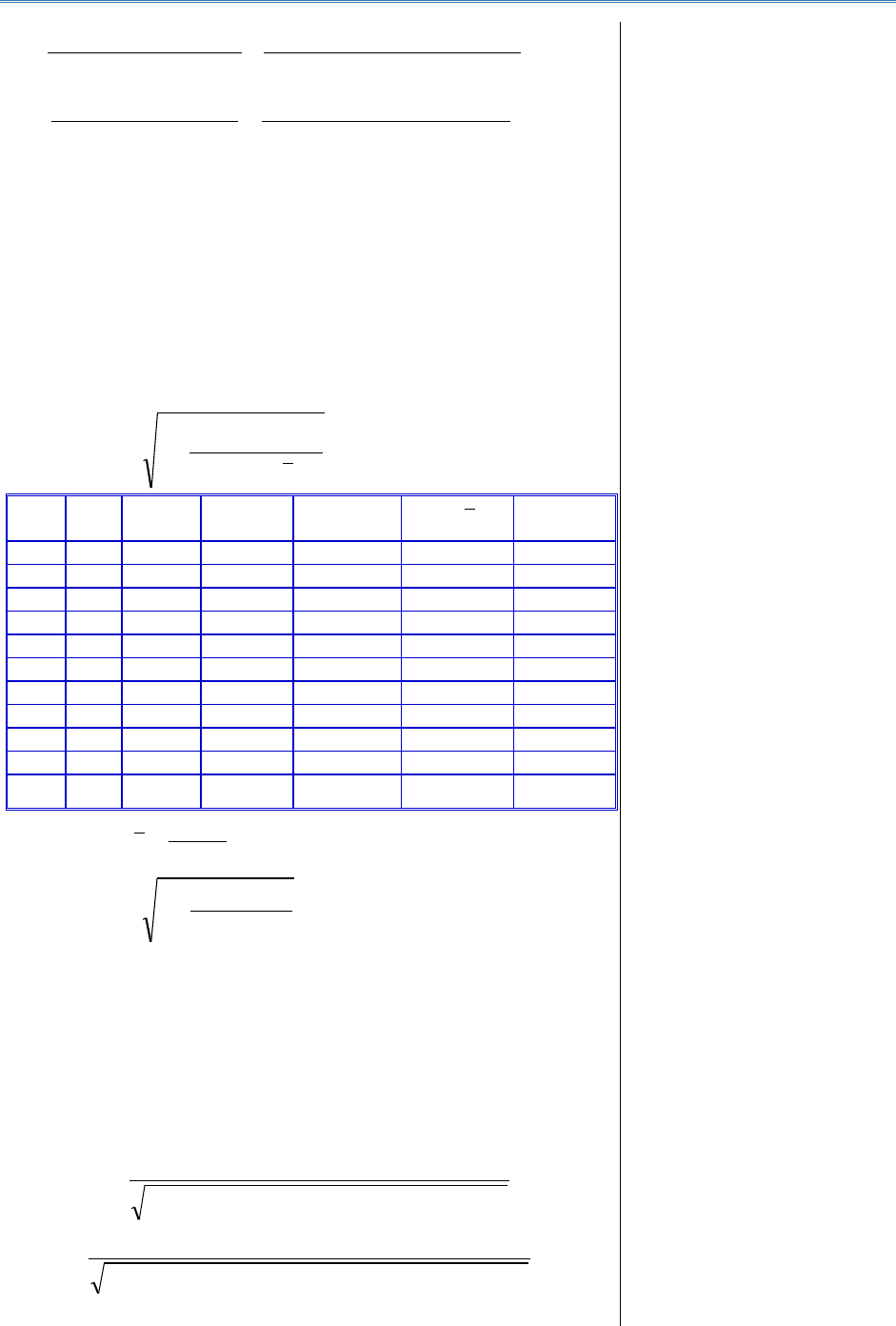
Emilia GOGU Statistica - Manual de studiu individual
Pagina 81 din 112
62,425
168528692110
1685498569628692129235
)( 222
2
ii
iiiii
xxn
xyxxy
a
87,19
)1685(28692110
292351685498569610
)( 222
ii
iiii
xxn
yxyxn
b
Funcția de regresie este: Yxi=-425,62+19,87xi
Valorile funcție de regresie se obțin înlocuind xI cu valorile
empirice.
Parametrul b=19,87 se interpretează astfel: pentru fiecare
ora lucrata salariului net crește , în medie cu 19,87 lei.
a) Raportul de corelație liniară simplă se ca calcula cu
formula:
2
2
/)(
)(
1yy
Yy
R
i
xi
xy i
Nr.
Crt.
xi
yi
Yxi
(yi - Yxi)2
(yi -
y
)2
2
i
y
1.
140
2200
2357
24659.9
523452.3
4840000
2.
146
2555
2476
6195.1
135792.3
6528025
3.
151
2642
2576
4399.4
79242.3
6980164
4.
163
2852
2814
1430.0
5112.3
8133904
5.
169
2957
2933
555.0
1122.3
8743849
9.
173
3027
3013
197.5
10712.3
9162729
7.
176
3080
3073
55.1
24492.3
9486400
8.
187
3272
3291
369.1
121452.3
10705984
9.
190
3325
3351
667.7
161202.3
11055625
10.
190
3325
3351
667.7
161202.3
11055625
1685
29235
29235
39196.5
1223782.5
86692305
Unde:
/vzlei mii 5,2923
10
29235y
9838,0
5,1223782
5,39196
1
/
xy
R
Se poate spune că legătură este strânsă (r/x=0,9838) și
gradul de determinație
22/9838,0
xy
R
este de 0,968 sau de
96,8%.
b) Metoda coeficientului de corelație
Intensitatea legăturii se măsoară prin coeficientul de corelație
(ry/x).
0,9838
29235-8669230510168528692110
292351685498569610
)()(
22
2222
/
iiii
iiii
xy yynxxn
yxyxn
r
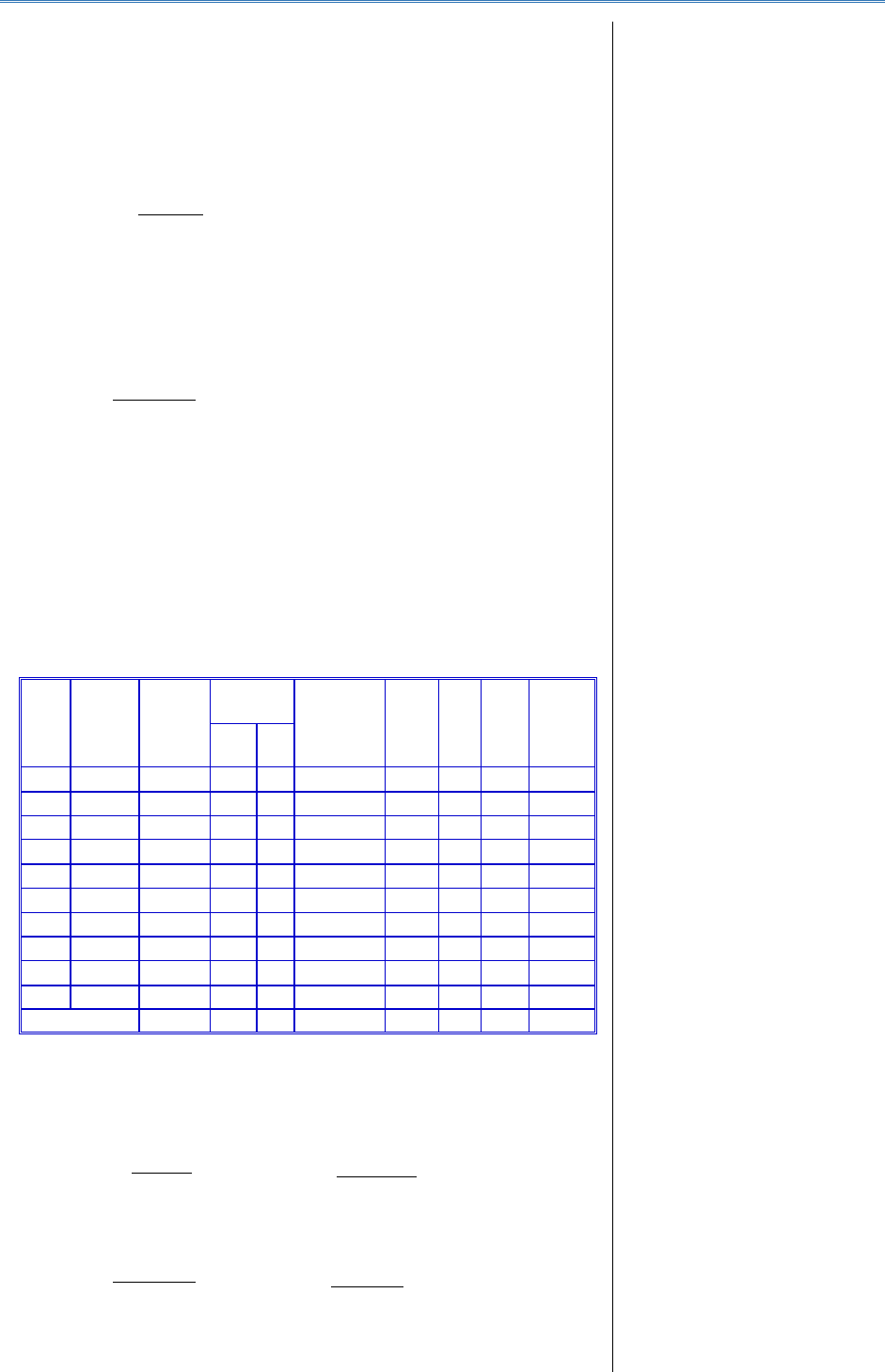
Emilia GOGU Statistica - Manual de studiu individual
Pagina 82 din 112
Rezultă că legătura dintre aceste două variabile este directă
(rz/x>0) și puternică. Există legătură liniară intensă deoarece
ry/x=Ry/x.
c) Calculul coeficientului de corelație a rangurilor
Coeficienul de corelație a rangurilor propus de Spearman:
nn
d
ri
s
3
2
6
1
în care: di - reprezintă diferența între rangurile perechii de
valori (xi,yi);
n - numărul de perechi de valori.
Coeficientul de corelație a rangurilor propus de Kendall
:
)1(
2
nn
S
rk
în care
)( ii QPS
în care: Pi - numărul rangurilor mai mari care urmează
rangului curent pentru variabila dependentă;
Qi - numărul rangurilor mai mici care urmează
rangului curent pentru variabila dependentă.
Aplicația 2. Calculul coeficienților de corelație a
rangurilor
Nr
crt
Ofert
a
xi
Cerer
ea
yi
Rangur
i
di=rxi-ryi
di2
Pi
Qi
Pi-Qi
rxi
ryi
1.
21
13
1
2
-1
1
7
1
6
2.
23
12
2
1
1
1
7
0
7
3.
24
14
3
3
0
0
6
0
6
4.
26
15
4
4
0
0
5
0
5
5.
29
17
5
6
-1
1
3
1
2
9.
30
16
6
5
1
1
3
0
3
7.
31
19
7
7
0
0
2
0
2
8.
40
20
8
8
0
0
1
1
0
9.
42
19
9
7
2
4
1
0
1
10.
45
21
10
9
1
1
0
0
0
Total
9
32
Se cere:
Să se determine coeficienții de corelație a rangurilor
Coeficienul de corelație a rangurilor propus de Spearman:
nn
d
ri
s
3
2
6
1
95,0
)110(10
96
12
s
r
Coeficientul de corelație a rangurilor propus de Kendall:
)1(
2
nn
S
rk
71,0
)110(10
322
k
r
Rezultă o intensitate directă și puternică
Emilia GOGU Statistica - Manual de studiu individual
Pagina 83 din 112
6.4 Îndrumar pentru autoverificare
6.4.1 Sinteza unității de studiu 6
Studiul statistic al interdependenței dintre fenomene necesită identificarea
legăturilor studiate de la cauză la efect, precum și legăturile realizate prin intermediul
unui șir de cauzalități. în acest sens, este necesar ca relațiile de cauzalitate din interiorul
fenomenelor complexe să fie studiate și prezentate tot sub o formă de tendință valabilă la nivelul
întregului ansamblu și nu la nivelul unor valori individuale izolate. Aceasta conduce în mod
obligatoriu la folosirea unor metode statistice m care să se țină seama de formele de distribuție de
frecvență ale fenomenelor pentru care se studiază interdependențele dintre ele și care nu pot fi
interpretate decât pe baza indicatorilor medii și a celor de variație.
Formele de manifestare a relațiilor de interdependență sunt extrem de variate și adesea destul
de greu de sesizat. Pentru a le studia este necesar să fie clasificate în funcție de unele criterii, după
care se pot deosebi unele de altele.
După natura relației de cauzalitate, legăturile dintre fenomene pot fi legături funcționale și
legături statistice sau statistice.
Legăturile funcționale sunt univoce, realizate direct între un fenomen-cauză și un fenomen-
efect. Deci, fenomenul-efect depinde de o singură cauză, care poate fi identificată de câte ori se
produce, ceea ce înseamnă că, dacă condițiile rămân constante, atunci unei valori a caracteristicii
factoriale îi corespunde o singură valoare a caracteristicii rezultative. Ele se mai numesc și legături
de tip determinist.
6.4.2 Concepte și termeni de reținut
Analiza dispersională
Metoda balanțelor
Coeficienții de asociere
Metoda grafică
Coeficienții de corelație a rangurilor
Metoda grupărilor
Coeficienții de corelație multiplă
Metoda seriilor statistice interdependente
Coeficienții de corelație parțială
Metodele
Coeficienții de corelație simplă
Modelele
Corelația
Procedee analitice
Direcția legăturii
Ranguri
Ecuațiile de regresie
Raporturilor de interdependență
Gradul de intensitate
Regresia statistică
Indicatori de corelație
Tabelul de asociere
Intensitatea legăturii
Tabelul de corelație
Interdependenței
Tendinței de manifestare

Emilia GOGU Statistica - Manual de studiu individual
Pagina 84 din 112
6.4.3 Întrebări de control și teme de dezbatere
1. De câte feluri sunt legăturile dintre fenomene?
2. Ce se înțelege prin corelație, dependență și independență statistică?
3. Ce se înțelege prin caracteristică (variabilă) factorială, exogenă sau independentă și
caracteristică rezultativă, endogenă sau dependentă?
4. De ce este necesară analiza teoretică prealabilă a raporturilor de interdependență dintre
fenomene pentru alegerea numărului și ordinii de influență a caracteristicilor factoriale asupra
variației caracteristicii rezultative?
5. Cum se identifică, înregistrează și ierarhizează factorii de influență pentru efectuarea analizei
dispersionale? Care sunt indicatorii utilizați într-un model de analiza dispersională
unifactorial?
6. Care sunt metodele simple de studiere a legăturii dintre fenomenele statistice?
7. Cum se aplică metoda seriilor statistice interdependente la verificarea existenței legăturilor
dintre fenomenele și procesele social-economice de masă?
8. Cum se aplică metoda grupării la verificarea existenței legăturilor dintre fenomenele de masă?
9. Cum se întocmește și se interpretează un tabel de corelație?
10. Cum se întocmește și se interpretează un tabel de asociere?
11. Cum se întocmește și se interpretează un grafic de corelație?
12. Ce se înțelege prin funcție de regresie?
13. Cum se calculează și interpretează funcția de regresie pentru legăturile simple de tip liniar?
14. Cum se calculează și interpretează funcția de regresie liniară pentru legăturile multiple?
15. Cum se calculează și interpretează funcția de regresie pentru studierea legăturilor:
de tip parabolic?
de tip hiperbolic?
de tip exponențial?
16. Cum se calculează și interpretează coeficientul de corelație liniară simplă ry/x?
17. Cum se calculează și interpretează raportul de corelație liniară Ry/x
18. Care este semnificația egalității: ry/x =Ry/x?
19. În ce constă deosebirea dintre ry/x și Ry/x?
20. Ce indicator de corelație se calculează în cazul legăturilor curbilinii?
21. Cum se calculează și interpretează raportul de determinație?
22. Cum se calculează și interpretează coeficientul de corelație multiplă; în ce relație se află cu
coeficientul de corelație liniară simplă?
23. Când se utilizează metodele neparametrice în studierea statistică a legăturilor dintre
fenomenele de masă?
24. Care este metodologia de calcul a coeficienților de corelație a rangurilor: (coeficientul
Spearman și Kendall)?
25. Cu ce indicator statistic se analizează legătura dintre caracteristicile calitative?

Emilia GOGU Statistica - Manual de studiu individual
Pagina 85 din 112
6.4.4 Teste de evaluare/autoevaluare
Aplicația 1. La o societate comercială s-au înregistrat următoarele date:
Nr
crt.
Nr
salariati
Cifra de
afaceri
(mil.lei)
Se cere:
1. să se precizeze care este variabila factorială și care
cea rezultativă;
2. să de ajusteze seria după o funcție analitică pe baza
graficului de corelație;
3. să se măsoare gradul de corelație după cele două
variabile printr-un indicator sintetic de corelație.
1.
44
146
2.
27
137
3.
17
129
4.
33
143
5.
18
132
6.
30
140
7.
24
135
8.
14
128
9.
41
146
10.
26
131
6.4.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Gogu E., Statistica în turism și comerț, Editura Oscar Print, București, 2009;
4. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 86 din 112
7 UNITATEA DE STUDIU 7 ANALIZA SERIILOR CRONOLOGICE
7.1. Introducere
7.2. Obiectivele și competențele unității de studiu – timp alocat
7.3. Conținutul unității de studiu:
7.3.1. Serii cronologice – noțiune, proprietăți
7.3.2. Seriile cronologice formate din indicatori absoluți
7.3.3. Serii cronologice formate din indicatori relative
7.3.4. Serii cronologice formate din indicatori medii
7.3.5. Serii cronologice de intervale (perioade) de timp și de momente
7.3.6. Metode analitice de ajustare
7.3.7. Criterii de alegere a procedeelor de ajustare
7.3.8 Extrapolarea seriilor cronologice
7.4. Îndrumar pentru autoverificare
7.1 Introducere
Una din sarcinile statisticii este aceea de a studia
fenomenele și procesele social-economice de
masă de-a lungul diferitelor perioade de timp
sub aspectul evoluției volumului acestora și al
schimbărilor intervenite în structura lor, a
interdependențelor dintre fenomene de natură diferită etc.
În munca de analiză concretă a dezvoltării fenomenelor în
timp, statistica folosește ca instrument principal de cercetare
indicatorii obținuți din prelucrarea statistică a seriilor cronologice.
Calculul acestor indicatori este precedat de elucidarea noțiunii de
"serie cronologică" și precizarea particularităților acesteia.
7.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
- definirea seriilor cronologice;
- tipuri de serii cronologice
- stabilirea sistemului de indicatori de analiza a seriilor de
timp;
- definirea indicatorilor medii ai seriilor cronologice;
- ajustarea seriilor cronologice;
- estimarea datelor.
Competențele unității de studiu:
- studenții vor putea identifica tipul seriei cronologice;
- vor putea analiza seria utilizând indicatorii absoluți,
relativi și medii;

Emilia GOGU Statistica - Manual de studiu individual
Pagina 87 din 112
- vor putea reprezenta grafic seria de timp stabilind trendul;
- vor putea ajusta și extrapola datele cronologice.
Durata medie de studiu individual alocat unității: 4 ore
7.3 Conținutul unității de studiu
7.3.1 Serii cronologice – noțiune, proprietăți
Seria cronologică este formată din două șiruri de date paralele,
în care primul își arată variația caracteristicii de timp, iar cel de-al
doilea șir variația fenomenului sau caracteristicii cercetate, de la o
unitate de timp la alta. Seriile cronologice se mai numesc și serii de
timp sau serii ale dinamicii.
La analiza seriilor cronologice trebuie avut în vedere unele
proprietăți ale acestora și anume:
- variabilitatea,
- omogenitatea,
- periodicitatea,
- interdependența termenilor prezentați.
Variabilitatea termenilor unei serii cronologice provine din
faptul că fiecare termen se obține prin centralizarea unor date
individuale diferite ca nivel de dezvoltare. Aceste diferențieri apar pe
de o parte ca urmare a acțiunii factorilor întâmplători și pe de altă
parte ca urmare a faptului că în dinamica legile sociale și economice
se manifestă ca tendință imprimând fenomenelor forme diferite de
variație. Cu cât acțiunea comună a acestor factori este mai puternică
cu atât variația în cadrul seriei este mai mare și tendințele de scurtă
și lungă durată mai greu de sesizat.
Având în vedere această trăsătură, este necesar ca analizând o
serie cronologică să se măsoare atât gradul și forma de influență a
factorilor esențiali, care imprimă fenomenului o lege specifică de
evoluție, cât și gradul de abatere de la această tendință generală
rezultată din influența factorilor neesențiali, cu caracter întâmplător.
Omogenitatea termenilor trebuie înțeleasă în sensul că în
aceeași serie nu pot fi înscrise decât fenomene de același gen, care
sunt rezultatul acțiunii acelorași cauze esențiale. Asigurarea
omogenității observațiilor de-a lungul unei perioade de timp
presupune menținerea aceleiași metodologii de calcul și evaluare a
indicatorilor care urmează să fie analizați în dinamică a criteriilor de
clasificare a colectivității studiate și nomenclatoarelor și lungimii
intervalelor de grupare, menținerea unității social-economice sau
administrativ teritoriale asupra căreia s-au făcut observații, cât și a
unității de măsurare a timpului. Practic, înseamnă că de fiecare dată,
când se analizează o serie statistică trebuie să se verifice dacă datele

Emilia GOGU Statistica - Manual de studiu individual
Pagina 88 din 112
provin din aceeași sursă, are același grad de cuprindere a unităților și
au fost folosite aceleași principii și metode de prelucrare, cu alte
cuvinte este asigurată comparabilitatea datelor înscrise în aceeași
serie. O altă trăsătură caracteristică a seriilor cronologice o constituie
periodicitatea termenilor din care este formată seria, ceea ce
înseamnă de fapt asigurarea continuității datelor din punct de vedere
a variabilei de timp și care poate da posibilitatea interpretării seriei
cronologice ca o funcție analitică (yi=f(ti)). Variabila de timp poate
fi înregistrată cu periodicități diferite. De aceea, alegerea unității de
timp la care se referă datele unei serii cronologice trebuie făcută în
raport cu scopul cercetării, al conținutului și posibilităților de
măsurare a fiecărui indicator. De exemplu, producția industrială se
poate urmări atât în unități de timp mici (zilua, decada, luna) cât și în
unități mari de timp (trimestrul, semestrul, anul).
În cazurile când unele caracteristici sunt influențate în variația
lor de schimbare a anotimpurilor, cu alte cuvinte apar fenomene cu
caracter sezonier (lunar sau trimestrial) este obligatoriu să se
folosească o astfel de periodizare a seriei.
În studiul seriilor cronologice, se pune problema atât a alegerii
unităților de timp la care se referă fiecare indicator, cât și a lungimii
etapei pentru care se prezintă datele, cu precizarea anului de bază. Ca
an de bază se alege acel an care prezintă o anumită semnificație în
evoluția fenomenului studiat.
Interdependența termenilor unei serii cronologice apare ca
urmare a respectării principiului unității de timp și spațiu și structurii
organizatorice. Ca atare, indicatorii prezenți sunt valori succesive ale
acelorași fenomene înregistrate la nivelul aceleiași unități teritorial
administrative sau orice unitate statistică complexă care poate fi
înregistrată autonom. Această face ca valoarea fiecărui indicator să
depindă într-o oarecare măsură de valoarea indicatorului precedent,
ca urmare a faptului că relațiile de cauzalitate se manifestă în condiții
asemănătoare de la o unitate de timp la alta.
Luând în considerare toate aceste particularități, analiza
statistica a seriilor cronologice trebuie sa se bazeze pe un sistem de
indicatori, care sa caracterizeze multiplele relații cantitative din
interiorul seriei si pe toata perioada la care se refera datele. Ca atare,
problemele care se pun si trebuie rezolvate la analiza seriilor
cronologice sunt:
alegerea lungimii seriei si elaborarea ei astfel încât, pe cat
posibil, sa îndeplinească condiția legii numerelor mari, adică
să aibă un număr suficient de date pentru orizontul de analiza
statistica cu care sa se fundamenteze corect prognozele de
lunga si scurta durata;
calculul si analiza unui sistem de indicatori statistici absoluți,
relativi si medii necesari caracterizării seriei;
identificarea trendului (tendinței) de evoluție a fenomenelor
din cadrul seriei prin utilizarea metodelor de ajustare statistica
si testelor de verificare a ipotezelor privind forma obiectiva de
evoluție pe perioada luata în calcul;
calculul si analiza sezonalității si a altor forme de evoluție cu
caracter ciclic;

Emilia GOGU Statistica - Manual de studiu individual
Pagina 89 din 112
interpolarea si extrapolarea seriilor cronologice potrivit
scopului cercetării statistice.
Aceste probleme se rezolva diferit de la o serie la alta, în raport
cu felul seriei, lungimea ei si tendințele de lunga si scurta durata ce
pot fi identificate.
Astfel, în prezentarea dinamica a fenomenelor se pot întâlni
mai multe feluri de serii. Clasificarea seriilor cronologice se face în
funcție de modul de exprimare a indicatorilor și după modul de
exprimare a timpului la care se refera datele.
În funcție de modul de exprimare a indicatorilor din care este
formata seria, seriile cronologice pot fi:
1. serii cronologice formate din indicatori absoluți,
2. serii cronologice formate din indicatori relativi,
3. serii cronologice formate din indicatori medii.
7.3.2 Seriile cronologice formate din indicatori absoluți
Reprezintă forma de baza a seriilor dinamice. Pe baza lor se pot
obține indicatorii generalizatori pe întreaga perioada.
Indicatorii de nivel sunt chiar termenii unei serii formate din
indicatori absoluți (y1, ...yt, ..., yt.).
Nivelul totalizat al termenilor
n
t
t
y
1
, numai pentru seriile
de intervale de timp de mărimi absolute.
Modificările absolute
cu bază fixă(t/1):
t/1=yt - y1 unde,
nt ,2
cu bază în lanț (bază mobilă sau variabilă) (t/t-1):
t/t-1=yt - yt-1 unde,
nt ,2
Relații de trecere de la o bază la alta:
de la bază în lanț la bază fixă pentru un termen din
interiorul seriei:
1/m
m
2t
1t/t
unde
nm
și pentru toată seria:
11/
21/ yynn
n
t
tt
de la bază fixă la bază în lanț:
t/1 - t-1/1 = t/t-1 unde
nt ,2
7.3.3 Serii cronologice formate din indicatori relativi
Constituie un mod de prezentare de regula procentual. În
aceasta situație este obligatoriu ca în titlu sau în afara tabelului sa se
specifice care este baza de raportare, pentru ca interpretarea datelor
să se facă corect.
Emilia GOGU Statistica - Manual de studiu individual
Pagina 90 din 112
Indice de dinamică
cu bază fixă (It/1):
1
1/ y
y
It
t
sau
100
1
(%)1/ y
y
It
t
unde
nt ,2
cu bază în lanț (It/t-1) :
1
1/
t
t
tt y
y
I
sau
100
1
(%)1/
t
t
tt y
y
I
unde
nt ,2
Ritmul de dinamică
cu bază fixă (Rt/1) :
%100
(%)1/1/ tt IR
nt ,2
cu bază în lanț (Rt/t-1) :
%100
(%)1/1/ tttt IR
nt ,2
7.3.4 Serii cronologice formate din indicatori medii
Se folosesc ca mijloc de prezentare a evoluției unor
caracteristici calitative ce apar sub forma de categorii medii:
productivitatea muncii, randamentul mediu, recolta medie la ha,
salariul mediu etc. De asemenea, se folosesc astfel de serii si pentru
unele caracteristici cantitative atunci când ele trebuie incluse în
analiza unor fenomene ce se produc în cadrul unui interval de timp,
ca de exemplu: valoarea medie anuala a fondurilor fixe, numărul
mediu al personalului muncitor.
Nivelului mediu
pentru o serie cronologică de intervale de timp
formate din indicatori absoluți:
n
y
y
n
t
t
1
pentru o serie de momente cu intervale egale între
momente (media cronologică simplă ):
12
......
2132
1
n
y
yyyy
y
y
n
ni
cr
pentru o serie de momente cu intervale neegale între
momente (media cronologică ponderată):
1
1
1121
2
1
12
...
2
...
22
n
i
i
n
n
ii
i
cr d
d
y
dd
y
dd
y
d
y
y
Modificarea medie absolută:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 91 din 112
1
1/
n
tt
sau
1
1
n
yyn
Indicele mediu de dinamică
)(I
:
11/
ntt
II
sau
1
1
nn
y
y
I
Dacă dispunem de mai mulți indici medii ce caracterizează
mai multe subperioade succesive de timp, indicele mediu ce
caracterizează întreaga perioadă se calculează astfel:
k
i
i
ki
nn
k
n
i
nn IIIII 121 ......
21
, în care:
I
- indicele mediu general de dinamică;
i
I
- indicii medii parțiali de dinamică;
ni - numărul indicilor cu bază în lanț ce intră în componența
fiecărui indice mediu parțial;
k - numărul subperioadelor, adică al indicilor medii parțiali.
Ritmul mediu de dinamică
%100
(%) IR
7.3.5 Serii cronologice de intervale (perioade) de timp și de
momente
Denumite și serii de fluxuri, sunt seriile statistice în care fiecare
indicator reprezintă rezultatul unui proces social-economic pe fiecare
perioadă de timp folosită în prezentarea datelor. Astfel de serii se pot
întâlni în prezentarea evoluției producției, a cifrei de afaceri, a
mărimii investițiilor, a profitului realizat, a creditului acordat și/sau
rambursat etc. Ele se întocmesc pentru indicatori însumabili pe o
anumită perioadă de timp, care determină periodicitatea cu care se
prezintă termenii seriei. Termenii seriei de intervale pot fi cumulați
obținându-se un indicator totalizator pe întreaga serie sau pe
subperioade.
Serii cronologice de momente (sau de stocuri)
Sunt acelea în care fiecare indicator caracterizează mărimea la
care a ajuns caracteristica urmărită sau volumul colectivității în
momentul de calcul. De exemplu, puterea instalată, exprimată în mii
Kw, la sfârșitul fiecărui an; populația României, la 1 iulie a fiecărui
an; valoarea capitalului fix al întreprinderii x la sfârșitul anului;
valoarea capitalului investit în industrie la sfârșitul fiecărui trimestru
sau an; numărul depunătorilor și depozitelor la sfârșitul fiecărei luni
etc. Pentru seria de elemente este caracteristic faptul că termenii ei
nu se pot cumula în vederea obținerii unui indicator statistic
totalizator cu conținut real pe întreaga perioadă, deoarece seria de
momente cuprinde înregistrări repetate. De exemplu, o parte din

Emilia GOGU Statistica - Manual de studiu individual
Pagina 92 din 112
mărfurile de la 1 I se pot găsi și în stocurile de la 1 II, 1 III etc. Deci,
acești termeni reprezintă mărimi de stoc. Caracterizarea nivelului
atins pe întreaga perioadă nu se poate face, în acest caz, decât pe baza
unui indicator mediu.
Scopul analizei datelor unei scrii cronologice este acela de a
caracteriza modul de dezvoltare a fenomenelor sociale și economice
pe o perioadă expirată, în vederea extrapolării datelor statistice
pentru fundamentarea diferitelor calcule de prognoza. Aceasta
analiza statistică se realizează în mod diferențiat în funcție de felul
seriei (de stocuri sau de fluxuri); de lungimea seriei și de
periodicitatea cu care este înregistrata variabila de timp. Cea mai
cuprinzătoare analiză statistică se realizează pentru seriile
cronologice, în care variația de timp este continuă și pe grafic se
poate descrie sub forma unei cronograme (historiograme) și ca atare
poate fi interpretata ca o funcție analitică de timp.
7.3.6 Metode analitice de ajustare
Metodele analitice au la bază un model matematic, în care
tendința centrală a evoluției se exprimă ca o funcție de timp:
yi = f(ti) numită funcție de ajustare, în care:
ti - reprezintă valorile variabilei independente (timpul);
yi - reprezintă valorile variabilei dependente (fenomenele)
care sunt prezentate în seria cronologică.
Alegerea tipului de funcție care se potrivește cel mai bine
pentru exprimarea trendului se face pe baza următoarelor criterii
aplicabile opțional:
criteriul bazat pe reprezentarea grafică. Se construiește
cronograma și se apreciază forma tendinței de evoluție
criteriul diferențelor. Se procedează la calculul diferențelor
absolute cu bază în lanț de ordinul unu, doi etc. până când
obținem diferențele de ordin i aproximativ constante
ajustarea făcându-se după polinomul de gradul i.
Dacă fenomenul cercetat s-a dezvoltat în progresie
geometrică, adică indicii cu bază în lanț sunt constanți (It/t-1 =
constant), admitem că seria cronologică respectivă prezintă o
tendință exponențială.
În urma alegerii funcției de ajustare după criteriile prezentate
se impune estimarea parametrilor acestor funcții utilizând metoda
celor mai mici pătrate. Această metodă are ca funcție obiectiv
minimizarea sumei pătratelor abaterilor valorilor reale de la cele
ajustate deci:
2
min i
ti Yy
ti= 1, 2, ... ,n timpul
Trend liniar Yti = a + b ti, în care:
Yti - reprezintă valorile ajustate calculate în funcție de valorile
caracteristicii factoriale (ti);

Emilia GOGU Statistica - Manual de studiu individual
Pagina 93 din 112
a - reprezintă parametrul care are sens de mărime medie și arată ce
nivel ar fi atins y dacă influența tuturor factorilor cu excepția
celui înregistrat, ar fi fost constantă pe toată perioada;
b - reprezintă parametrul care sintetizează numai influența
caracteristicii factoriale (t):
ti - reprezintă valorile caracteristicii factoriale care, în cazul seriilor
cronologice, este timpul.
Parametrii a și b se determină prin rezolvarea sistemului de
ecuații normale obținut prin metoda celor mai mici pătrate (
min)( 2
ii btay
):
iiii
ii
yttbta
ytbna
2
Pentru
ti
=0, sistemul de ecuații normale devine:
iii
i
yttb
yna
2
de unde,
2
i
ii
i
t
yt
b
n
y
a
Variația de timp trebuie centrată și pentru seriile impare se
măsoară în unități iar pentru cele pare în jumătăți de interval între
termenii seriei
Înlocuind valorile calculate ale celor doi parametri în ecuația
de regresie și apoi înlocuind succesiv valorile variabilei timp se
obțin valorile ajustate ale caracteristicii rezultative.
Verificarea corectitudinii calculării ecuațiilor de regresie se
face pe baza relației
it yYi
în care
iti tbaY
7.3.7 Criterii de alegere a procedeelor de ajustare
Se calculează suma abaterilor, luate în valoare absolută, dintre
datele empirice și cele ajustate
tt Yy
pentru toate procedeele de
ajustare folosite. Se consideră cel mai potrivit procedeul la care se
obține
.min
tt Yy
Se calculează coeficientul de variație:
100
/
/
y
d
Vty
ty
, în care
t/y
d
reprezintă abaterea medie
liniară a valorilor reale de la valorile ajustate calculată după
formula:
n
Yy
di
tt
ty
/

Emilia GOGU Statistica - Manual de studiu individual
Pagina 94 din 112
Sezonalitatea este variația produsă de influența modificării
succesive a anotimpurilor
Metoda grafică; se prezintă succesiv variația de timp astfel
încât în cronogramă să apară tendințele de variație pe luni, trimestre
sau semestre după cum este alcătuită seria.
Metoda mediilor mobile; se calculează medii mobile
provizorii sau definitive după numărul de termeni – par sau impar
- din care se calculează mediile și se face ajustarea seriei. Numărul
mediilor mobile este mai mic față de numărul termenilor seriilor
Se ajustează și se calculează mediile multi anuale lunare,
trimestriale, sau semestriale calculate din rapoartele dintre valorile
ajustate și cele reale și se calculează indicii de sezonalitate ca raport
între fiecare medie parțială și media generală.
Metoda analitică diferă numai prin faptul că înainte de a
calcula sezonalitatea se ajustează seria de date impirice printr-o
funcție analitică care corespunde, cu tendința obiectivă de
dezvoltate în timp a fenomenului.
7.3.8 Extrapolarea seriilor cronologice
Extrapolarea datelor unei serii statistice are la bază metodele
și procedeele folosite la ajustare.
Pentru a face distincție între termenii ajustați (Yti) și cei
extrapolați - care sunt considerați tot termenii teoretici - se vor nota
termenii extrapolați cu
,
i
t
Y
iar variabila de timp cu ti’.
Deci, formulele de calcul vor fi:
pentru extrapolarea pe baza sporului mediu:
)1(
ˆ1
tyYi
t
pentru extrapolarea pe baza indicelui mediu de creștere:
1
1
t
tIyYi
Aceste formule se aplică atunci când se folosesc valorile
parametrilor
I,
din perioada expirată. În cazul când aceștia se
modifică, formulele se modifică cu un coeficient K, astfel:
'
0it tyY i
în care:
k'
t
tIyY
0
în care:
IkI
7.4 Îndrumar pentru autoverificare
7.4.1 Sinteza unității de studiu 7

Emilia GOGU Statistica - Manual de studiu individual
Pagina 95 din 112
Fiecare proces economic se desfășoară în timp; dezvoltarea și creșterea economică
sunt interpretabile în timp. La fel recesiunile și colapsul economic.
Proiecția variabilelor economice pe axa timpului creează un mijloc de investigație
a dinamicii - seriile de timp. Ele constituie instrumentul de investigație longitudinală al mișcării,
dinamicii, devenirii, progresului, regresului etc., în timp ce analiza transversală se bazează pe
seriile de distribuție. Seriile de timp stau la baza analizei statistice cantitative a schimbărilor.
Studiul variației unei variabile economice ne ajută să clarificăm noțiunea de așteptare
probabilistică. Am înțelege de ce în cazul unei singure serii dinamice, tratată fără legătură cu o altă
serie de observații cantitative, variația nu poate fi calculată față de medie, ci față de o " valoare
așteptată". Or, aceasta este ea însăși o variabilă. Pentru serii de timp (sau serii în timp, cum li se
mai spune) valoarea așteptată este o funcție de timp.
Caracterizarea evoluției în timp a fenomenelor presupune calcularea unor indicatori
specifici, cu ajutorul cărora sunt evidențiate diferite aspecte ale acestui proces complex. astfel,
prelucrarea seriilor dinamice se face utilizând indicatorii absoluți, relativi și medii.
Una din principalele surse de informare statistică o reprezintă înregistrarea unui fenomen
socio-economic în timp. Informațiile statistice sub forma seriilor de timp, capătă o importanță
deosebită în analiza etapelor parcurse în fundamentarea unor decizii cu implicații majore în
funcționarea mecanismului socio-economic al sistemului pe care îl definește. Datele ce
caracterizează un fenomen pot fi obținute în urma unei observări continue sau pe baza unor
înregistrări la anumite momente.
În cadrul activității economice din turism, metodele de analiză statistică a seriilor dinamice
își găsesc o largă utilizare, fiind folosite ori de câte ori este necesar să caracterizăm evoluția în
timp a fenomenelor și proceselor social-economice din această ramură.
Pentru obținerea unei serii dinamice este necesar să se prezinte, în paralel, variația
caracteristicii de timp cu variația caracteristicii analizate, de la o unitate de timp la alta. Astfel,
înregistrarea unui produs comercial pe parcursul unei perioade, arată cel mai bine mersul și starea
lui în acea perioadă.
În vederea unei perceperi mai bune a mesajului adus de o serie de timp, forma tabelară de
prezentare este completată cu prezentarea ei grafică. Aceasta poate îmbrăca cele mai variate forme,
în funcție de scopul urmărit, de natura seriei etc.
Caracterizarea evoluției în timp a fenomenelor presupune calcularea unor indicatori
specifici, cu ajutorul cărora sunt evidențiate diferite aspecte ale acestui proces complex. astfel,
prelucrarea seriilor dinamice se face utilizând indicatorii: absoluți, relativi și medii. Analiza lor
se poate face atât în bază fixă (la o perioadă de referință) cât și în bază mobilă sau în lanț.
7.4.2 Concepte și termeni de reținut
Baza fixa
Indicii de sezonalitate
Perioadă de bază
Baza în lanț
Interdependența
Perioadă de referință
Baza mobilă
Media cronologică
Periodicitatea
Cronogramă
Medii mobile provizorii
Ritmul de dinamica
Extrapolarea seriilor
cronologice
Metoda analitică
Ritmul mediu
Indicatorii absoluți
Metoda grafică
Serie cronologică

Emilia GOGU Statistica - Manual de studiu individual
Pagina 96 din 112
Indicatorii medii
Metoda mediilor mobile
Sezonalitatea
Indicatorii relativi
Modificarea absolută
Sporul mediu
Indicele de dinamica
Modificării succesive
Tendințele de variație
Indicele mediu
Omogenitatea
Variabilitatea
7.4.3 Întrebări de control și teme de dezbatere
1. Ce se înțelege printr-o serie cronologică? De câte feluri sunt?
2. Ce probleme se pun pentru calculul și interpretarea seriilor cronologice?
3. Care sunt și cum se calculează indicatorii absoluți ai seriilor cronologice?
4. Ce relații se pot stabili între indicatorii absoluți cu bază fixă și cu bază în lanț?
5. Care sunt și cum se calculează indicatorii relativi ai seriilor cronologice?
6. Ce relații se pot stabili între indicatorii relativi ai seriilor cronologice?
7. Care sunt și cum se calculează indicatorii medii ai seriilor cronologice?
8. Ce relații se pot stabili între indicatorii absoluți, relativi și medii ai unei serii cronologice?
9. Ce se înțelege prin ajustarea unei serii cronologice și ce procedee cunoașteți?
10. Cum se alege procedeul de ajustare?
11. Ce legătură este între ajustare și extrapolare?
12. Ce procedee se pot folosi pentru fundamentarea statistică a calculelor de prognoză?
13. Care sunt posibilitățile de studiere a variației sezoniere?
14. Care sunt și cum se calculează indicatorii statistici care caracterizează o serie de
momente?
7.4.4 Teste de evaluare/autoevaluare
Aplicația 1. La o unitate hotelieră s-au înregistrat următoarele date:
Luna
Volumul încasărilor
(mil.lei)
Ianuarie
730
Februarie
720
Martie
740
Aprilie
800
Mai
850
Iunie
890
Iulie
910
Se cere:
1. să se reprezinte grafic seria;
2. să se calculeze indicatorii absoluți, relativi și medii care caracterizează seria;
3. să se ajusteze seria valorilor absolute folosind un procedeu mecanic sau analitic, sa se
determine volum încasărilor pentru lunile august și septembrie.
Aplicația 2. Se cunosc următoarele date cu privire la activitatea unei societăți comerciale:

Emilia GOGU Statistica - Manual de studiu individual
Pagina 97 din 112
Ani
Modificarea relativă față
de anul precedent %
2008
+3,8
2009
+2,6
2010
+3,5
2011
+3,2
2012
+3,4
2013
+3,6
2014
+3,0
2015
+3,4
Știind că în anul 2007 valoarea încasărilor a fost de 40 mii euro, se cere:
1. să se reconstitue seria valorilor absolute;
2. să se reprezinte grafic seria reconstiruită;
3. să se calculeze indicatorii medii;
4. Să se ajusteze seria valorilor absolute folosind un procedeu mecanic și unul analitic.
7.4.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Gogu E., Statistica în turism și comerț, Editura Oscar Print, București, 2009;
4. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 98 din 112
8 UNITATEA DE STUDIU 8 METODA INDICILOR
8.1. Introducere
8.2. Obiectivele și competențele unității de studiu – timp alocat
8.3. Conținutul unității de studiu:
8.3.1. Metoda indicilor – noțiune, proprietăți
8.3.2. Concepte, criterii de clasificare și sistematizare a indicilor
8.3.3. Sisteme de ponderare folosite la construirea indicilor
8.3.4. Condiții și limite ale aplicării metodei indicilor
8.4. Îndrumar pentru autoverificare
8.1 Introducere
Cuprinderea unui număr din ce în ce mai mare de
fenomene în sfera de cercetare statistică, ca urmare
a creșterii gradului de complexitate a proceselor
social-economice 1a nivelului întregului ansamblu
și a structurii lor din interiorul acestora, a dus la
lărgirea și perfecționarea permanentă a metodelor sale de studiu.
Necesitatea identificării și cuantificării gradului de influență a
diferiților factori ce determină dimensiunea și structura proceselor
studiate au condus la perfecționarea continuă a metodelor de analiză
factorială, care includ și metoda indicilor statistici.
Metodologia de elaborare a indicilor statistici este extrem de
variată, cuprinzând atât metode elementare de comparație statistică,
cât și metode cu un grad mare de rafinament interpretativ, combinând
mai multe procedee de calcul și analiză statistică.
8.2 Obiectivele și competențele unității de studiu
Obiectivele unității de studiu:
- Prezentarea particularităților metodei indicilor;
- Clasificarea indicilor;
- Demonstrarea proprietăților indicilor individuali și de grup;
- Aplicabilitatea metodei indicilor.
Competențele unității de studiu:
- studenții vor cunoaște metoda indicilor;
- vor putea exemplifica metoda indicilor în domeniul turistic
și comercial;
- vor putea exemplifica metoda indicilor pe exemplu
macroeconomic.
Durata medie de studiu individual alocat unității: 4 ore

Emilia GOGU Statistica - Manual de studiu individual
Pagina 99 din 112
8.3 Conținutul unității de studiu
8.3.1 Metoda indicilor – noțiune, proprietăți
Rezultatele aplicării metodei indicilor se pot concretiza fie sub
forma unui sistem de indici, atunci când se face o analiză complexă în
care operăm cu variabile factoriale și rezultative, fie sub forma unor
variabile independente când fenomenul studiat se analizează izolat,
separat. De exemplu, dacă se studiază indicele productivității muncii,
în prima variantă, în analiză se vor include obligatoriu și indicatorii
producției și consumului total de muncă, în timp ce, în a doua variantă
se vor studia numai probleme legate de nivelul și variația în timp și
spațiu a productivității muncii, chiar dacă și în această situație vom
opera cu o serie de relații numerice.
În cadrul acestui sistem de indicatori primari și derivați fără
îndoială că metoda indicilor, datorită funcțiilor sale cognitive
deosebite, poate răspunde în cea mai mare măsură acestor cerințe
complexe legate de caracterizarea numerică a proceselor sociale și
economice. În acest fel, domeniul de aplicare a indicilor la studiul
fenomenelor social economice s-a lărgit continuu, iar metoda lor și
forme1e specifice pe care le îmbracă în studiul concret al acestora au
format în permanență obiectul unor discuții interesante purtate de un
număr mare de economiști și statisticieni în diferite reviste și studii de
specialitate. In principal, problemele care formează obiectul discuțiilor
se referă la:
volumul, calitatea și sursa datelor statistice necesare elaborării
indicilor;
structurarea informației potrivit unităților de observare utilizate;
verificarea reprezentativității eșantionului, pentru cazul când
datele provin dintr-o observare parțială;
alegerea formulelor de calcul;
alegerea bazei de raportare;
alegerea sistemului de ponderare;
găsirea unor soluții de trecere de la analiza separată a
fenomenelor de indexat la interpretarea diferitelor corelații ce se
pot forma atât în structura orizontală, cât și în structura verticală
a sistemului;
particularități ale metodei indicilor utilizate pentru elaborarea
unei serii de indici in plan teritorial și dinamic.
8.3.2 Concepte, criterii de clasificare și sistematizare a indicilor
Metoda indicilor are o largă aplicabilitate în analiza statistică a
variației fenomenelor sociale și economice complexe în dinamică și pe
plan teritorial. De asemenea, cu o anumită adaptabilitate, indicii
statistici sânt utilizați și în analiza modului de îndeplinire a
programelor elaborate la nivelul agenților economici sau la nivelul

Emilia GOGU Statistica - Manual de studiu individual
Pagina 100 din 112
macroeconomiei. De precizat, că indicele în statistică nu arată
niciodată nivelul atins de un fenomen, deci nu este un măsurător de
mărime sau de nivel, ci măsurător al gradului de variație (schimbare)
a două niveluri coexistente in spațiu sau în unități de timp diferite.
Datorită faptului că această metodă se aplică unor fenomene
complexe, ea face parte din cadrul metodelor de analiză factorială, în
care variația în timp și spațiu a fenomenului complex analizat este
explicată prin variația factorilor determinanți. În acest sens, se folosesc
atât pentru studiul variației fenomenului complex cât și pentru variația
factorilor indici statistici. Aceasta înseamnă că, pe lângă analiza
complexă bazată pe descompunerea pe factori de influență, fiecare
variație a indicatorilor absoluți (de nivel) care intră în calcul poate fi
analizată printr-un indice relativ independent. Deci, în acest caz se
pune problema să se înregistreze în primul rând fenomenul pe care-l
studiem și apoi să se identifice și să se înregistreze, pe o anumită
structură, factorii de care depinde variația acestuia. Astfel, aplicând
metoda indicilor vom putea obține un sistem de relații care să permită
caracterizarea sub raport statistic a modificării colectivității în
ansamblu, a părților sale componente, stabilind și gradul de contribuție
a factorilor.
Rezultă că specific metodei indicilor este faptul că fenomenul
complex supus indexării se bazează pe relația de descompunere într-
un produs al factorilor înregistrați. Utilizând astfel un indice sintetic si
mai mulți indici factoriali. De precizat, că la această descompunere pe
factori trebuie să existe întotdeauna, pe lângă factorii calitativi, și un
factor cantitativ care, de regulă, are conținut de frecvență de apariție
pentru aceștia.
Generalizând în cazul unui fenomen bifactorial putem nota cu
(y) fenomenul complex a cărui variație se studiază în timp și /sau
spațiu, în funcție de un singur factor calitativ (x) și un factor cantitativ
(f), care joacă și rol de frecvență (pondere). Deci, în acest caz
fenomenul de indexat are la bază relația:
iii fxy
Dacă se înregistrează două caracteristici factoriale calitative
(x) și (z), atunci fenomenul complex de indexat se descompune in
produsul dintre frecvențe și valorile perechi ale factorilor înregistrați,
adică:
iiii fzxy
ș.a.m.d.
În consecință, variabila (f) se regăsește întotdeauna ca o
entitate relativ independentă în cadrul unui ansamblu care corespunde
cu unitatea de observare (muncitorul, produsul, județul etc.), în timp
ce variabilele calitative sunt atribute ale acestor unități care, de regulă,
se înregistrează ca mărimi relative de intensitate sau ca medii parțiale
(preț unitar de cost sau de vânzare, salariu mediu, recolta medie la ha.,
nivelul productivității muncii etc.)
Aplicând metoda indicilor trebuie să măsurăm variația în timp
și /sau spațiu a acestor variabile înregistrate.
Indicii se calculează deci ca raport între nivelurile atinse de un
fenomen în două unități diferite de timp sau în două unități diferite de
spațiu sau comparând nivelul realizat cu cel programat. Indicii pot,
astfel, fi considerați ca mărimi relative de dinamică, de coordonare sau
de programare. Când indicii se calculează la nivelul unei grupe sau al

Emilia GOGU Statistica - Manual de studiu individual
Pagina 101 din 112
întregului ansamblu de unități statistice ei au și proprietatea de mărime
medie, sintetizând în valoarea lor toate modificările cantitative și
calitative intervenite în interiorul acestei variații. În consecință, și
interpretarea lor trebuie să se facă ca la orice mărime medie
determinată din mai multe valori individuale diferite.
În aceste condiții, pentru a asigura un conținut veridic indicilor
statistici, este necesar să se țină seama de următoarele aspecte:
a) datele folosite la calculul indicilor să provină dintr-o
observare totală sau, dacă s-a organizat o cercetare parțială, partea
supusă observării să fie reprezentativă în raport cu întreaga
colectivitate;
b) valorile indicatorilor din numărătorul și numitorul raportului
să fie mărimi reale sau, dacă sunt calculate folosind o ipoteză statistică,
ele să fie practic posibile;
c) diferența dintre numărătorul și numitorul indicelui să
corespundă modificării absolute a fenomenului respectiv.
Reiese că, întotdeauna, indicii statistici prezintă și la numărător
și la numitor același fenomen, dar cu valori diferite, ceea ce face ca
indicele folosit să capete denumirea corespunzătoare. De exemplu,
dacă se compară cantitatea de produse: "A" din luna ianuarie a anului
curent cu cantitatea de produse "A" din luna ianuarie a anului
precedent, înseamnă că se măsoară variația în timp a volumului fizic,
deci indicele se va numi "indicele votumului fizic al producției".
În legătură cu folosirea metodei indicilor, mai trebuie adăugat
și faptul că ei se folosesc de regulă sub formă de sistem. De exemplu:
sistemul indicilor valorii, volumul fizic și al prețurilor producției și
circulației de mărfuri sau sistemul indicilor producției, productivității
muncii și ai cheltuielilor totale de timp de muncă, sau sistemul
indicilor recoltei totale, a recoltei medii și ai suprafețelor însămânțate
etc. De remarcat că fiecare sistem de indici poate fi considerat ca un
sistem independent sau ca un subsistem în cadrul unui sistem mai
cuprinzător, fie sub raport organizatoric, fie din punct de vedere al
gradului de cuprindere al caracteristicilor ce se găsesc în relații de
interdependență.
Problemele care se pun cu ocazia calculării unor "numere
indici” sunt variate, și soluționarea lor depinde de conținutul
indicatorilor comparați și de natura datelor de care se dispune.
Varietatea mare a indicilor întâlniți în teoria și practica statică și
problemele diferite care se pun pentru fiecare formă de indice în parte
necesită o sistematizare a acestora sub forma unei clasificări.
1. O primă grupare a indicilor se face după funcția pe care o
au în studiul variației fenomenelor social-economice. După acest
criteriu indicii se împart în trei grupe mari:
- indici ai dinamicii;
- indici teritoriali;
- indici ai planificării (programării).
Indicii dinamicii sunt rezultatul comparării în timp a aceluiași
fenomen (y), deci în acest caz trebuie să existe o perioadă de bază
notată cu yo și una sau mai multe perioade curente care se notează cu
y1 sau cu y1, y2 ,...,yn.
Indicii teritoriali sunt indicii care măsoară variația în spațiu a
aceluiași fenomen (y), în cadrul aceleiași perioade de timp. Ei pot fi

Emilia GOGU Statistica - Manual de studiu individual
Pagina 102 din 112
considerați și ca mărimi relative de coordonare - când se compară două
unități teritoriale, care sunt părți ale aceluiași ansamblu (țară, continent
etc.,) între ele. In acest caz trebuie existe e o valoare statistică
înregistrată în unitatea teritorială A, notată cu yA și o valoare statistică
înregistrată în unitatea teritorială B, notată cu yB.
Indicii planificării sunt rezultatul comparării unei valori
realizate față de valoarea aceluiași fenomen înscrisă într-un plan
(program) sau invers, elaborat la diferite niveluri ale procesului de
conducere. Dacă se compară nivelul realizat cu nivelul planificat
pentru același fenomen din cadrul aceleiași perioade de timp, atunci se
obține un indice a1 îndeplinirii planului. Dacă se compară însă nivelul
planificat în perioada de plan cu nivelul realizat în perioada de bază
pentru același fenomen, atunci se obține un indice a1 sarcinii de plan.
Deci, în acest caz, față de indicii de dinamică intervine în plus nivelul
planificat, notat cu ypl. Ei se folosesc, în special, 1a nivel micro.
În continuare, problemele metodologice comune tuturor
indicilor se vor prezenta pe exemplul indicilor de dinamică și numai
cele specifice vor fi tratate separat și pentru celelalte două grupe mari:
indicii teritoriali și indicii planului. Aceasta se explică prin faptul ca
inițial metodologia utilizată a fost elaborată pentru studii în dinamică
și acești indici de dinamică s-au adaptat la studiul variației teritoriale
sau pentru prognoze și realizarea lor.
2. O altă grupare a indicilor statistici se face după nivelul la
care s-au înregistrat datele. După cum s-a mai arătat, în practica
statistică, la calculul indicilor se folosește unități de observare
complexe; ca de exemplu: echipa, secția, întreprinderea, categoria de
calificare, lotu1 de produse, parcela etc.
Din acest punct de vedere indicii pot fi:
- indici individuali;
- indici de grup;
- indici generali.
Indicii individuali ai unei variabile statistice (y) sa calculează
la nivelul unei unități de observare și se notează cu iy1/0 indicele
individual arată de câte ori s-a modificat fenomenul y în perioada
curentă față de perioada de bază. De obicei, indicii (individuali și de
grup) se exprimă sub formă de coeficienți sau procente, adică:
0
1
0/ y
y
iy
L
sau
100
0
1
0/ y
y
iy
L
Indicii de grup ai unei variabile statistice y se notează cu
y
I0/1
și se calculează la nivelul unei grupe sau pe întreaga colectivitate,
sintetizând variația medie a fenomenului studiat. Deci, indicele de
grup nu este o sumă a indicilor individuali ci o medie a acestora,
exprimând tendința medie de modificare în timp și spațiu a
caracteristicii la care se referă.
În general, elaborarea indicilor de grup ridică cele mai multe
probleme. În principal aceste probleme se referă la:
- posibilitatea de însumare a elementelor componente;
- alegerea bazei de raportare;
- alegerea formulei de calcul în funcție de natura datelor de
care dispunem;

Emilia GOGU Statistica - Manual de studiu individual
Pagina 103 din 112
- alegerea sistemului de ponderare în funcție de conținutul
indicatorului de comparat și a relațiilor din interiorul
sistemului utilizat, astfel încât variația fenomenului
complex să poată fi descompusă în produsul factorilor care
o determină.
Enumerarea acestor probleme arată că ele trebuie să se rezolve
de la caz la caz pe baza analizei calitative care este obligatorie de
fiecare dată când se aplică metoda statistică de studiere a fenomenelor
de tip colectiv.
Rezultă de aici că în teoria și practica statistică se folosesc mai
multe tipuri de indici de grup, care se pot și ei clasifica după diferite
criterii.
1. După modul de calcul, indicii de grup se pot calcula ca indici
agregați, ca indici sub formă de medie (aritmetică sau armonică a
indicilor individuali respectivi) sau sub formă de raport a două medii.
Indicii sub formă de agregat se calculează raportând suma
nivelurilor parțiale ale unui fenomen din perioada curentă la suma
nivelurilor parțiale corespunzătoare din perioada de bază. Ei se
întâlnesc ca indice de grup și ca indice general
De exemplu, dacă se calculează un indice de grup sub formă
de agregat pentru fenomenul y, atunci formula de calcul este:
0
1
10
11
0/ y
y
y
y
Ik
i
i
k
i
i
y
l
; pentru
ki ,1
În practica statistică se pot întâlni indici agregați ale căror
elemente sunt însumabile direct, de exemplu indicele valorii
producției și indicele agregat al unor fenomene neînsumabile direct,
pentru care trebuie găsit un element de echivalență, care în teoria
statistică se mai numește și pondere, cum ar fi indicele volumului fizic
al producției. În acest caz se transformă cantitățile vândute în valori și
apoi se însumează pentru toate produsele. Pentru a nu influența
valoarea indicelui se folosesc aceleași prețuri și la numărătorul și
numitorul indicelui, adică pentru indicele volumului fizic (indicele
factorului cantitativ) pot fi considerate ca ponderi prețurile din
perioada de bază.
k
i
iio
k
i
ii
fy
l
fx
fx
I
10
110
)(0/
Indicele prețurilor (indicele factorului calitativ) se construiește
utilizând ca ponderi cantitățile din perioada curentă:
Deoarece atât la numărător (perioada curentă), cât şi la numitor (perioada de bază)
ki ,1
, în teoria şi practica
statistică frecvent se renunţă la explicitarea nivelurilor de însumare a valorilor individuale.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 104 din 112
k
i
iio
k
i
ii
xy
l
fx
fx
I
11
111
)(0/
Indicii sub formă de medie de indici individuali se aplică
atunci când nu se cunosc toate elementele necesare calculării unui
indice agregat. Pentru aceasta ei trebuie să îndeplinească următoarele
două condiții:
a) să fie o medie a indicilor individuali ai fenomenului de
indexat,
b) să fie egal în valoare cu indicele agregat pe care-l
substituie.
Pentru a respecta aceste condiții trebuie să se folosească fie o
medie aritmetică, fie o medie armonică a indicilor individuali, la care
ponderarea să se facă cu unul din elementele care formează indicele
agregat.
Indicele agregat fiind o mărime relativă generală cu conținut
de mărime medie a unor mărimi relative parțiale, înseamnă că se
poate transforma fie intr-o medie aritmetică a indicilor individuali
ponderați cu valorile din numitorii din care s-au calculat, fie ca o
medie armonică la care ponderarea să se facă cu numărătorii parțiali,
adică:
- indicele de forma unei medii aritmetice:
0
00/1
0/
)(
y
yi
I
y
y
l
- indicele de forma unei medii armonice:
1
1
1
0/
0/1 y
y
I
y
i
y
l
Este ușor de demonstrat că cei doi indicii sub formă de medie
sunt egali cu indicele agregat al variabilei y și deci egali intre ei.
În cazul mediei aritmetice, dacă se înlocuiesc indici individuali
cu formula lor de calcul se obține:
0
00/
0/
)(
y
yi
I
y
l
y
l
=
0
0
1
y
y
y
y
o
0
y
yl
În cazul indicelui de forma mediei armonice se, procedează la
fel, adică:
1
1
1
0/
0/1 y
y
I
y
i
y
l
1
1
1
0
1y
y
y
y
1
1
0
1
y
y
y
y
0
1
y
y
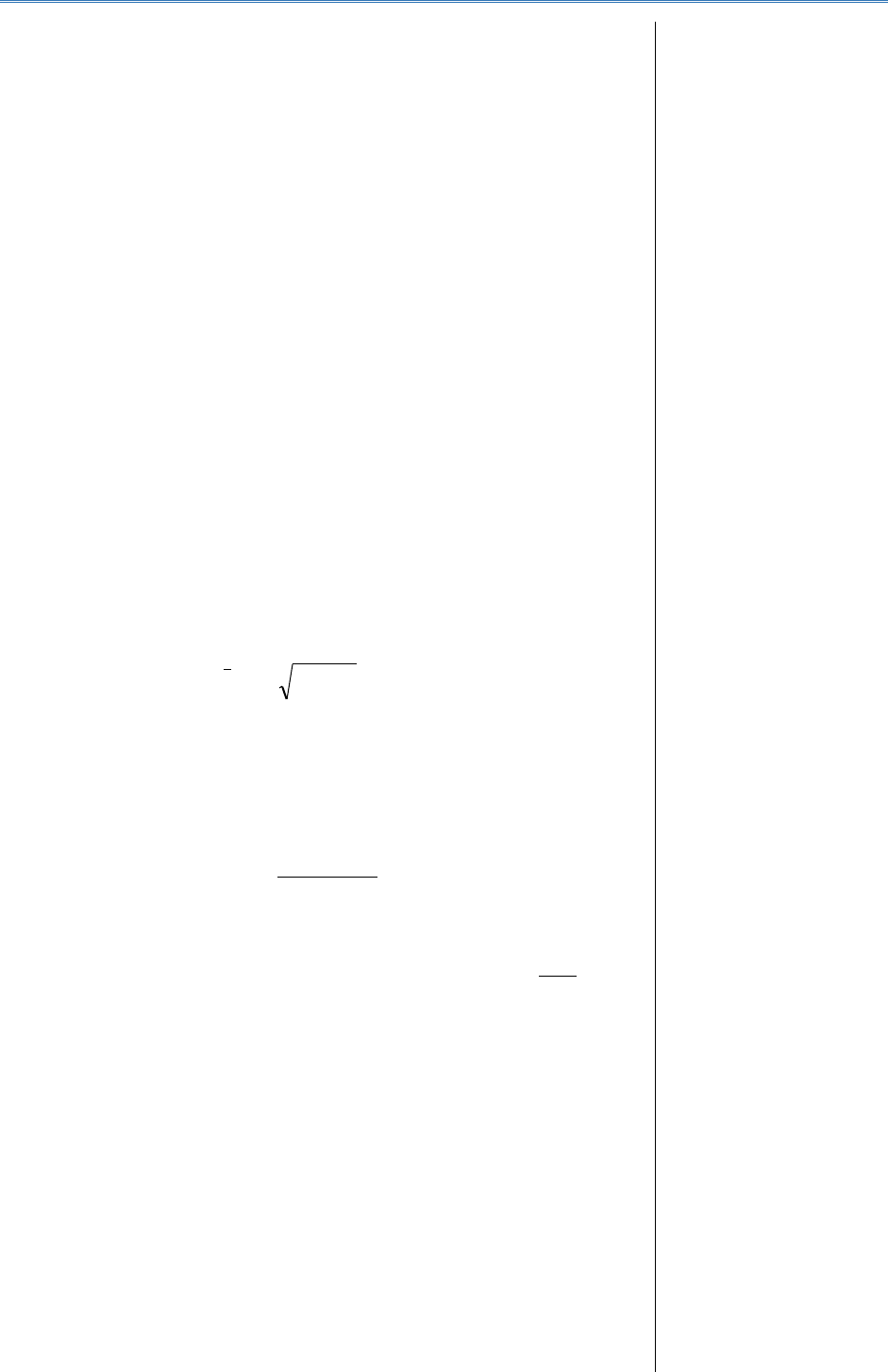
Emilia GOGU Statistica - Manual de studiu individual
Pagina 105 din 112
Dacă se respectă condițiile de folosire a mediei aritmetice și
armonice pentru calculul mediei mărimilor relative parțiale, indicele
aritmetic se folosește când se cunosc indicii individuali și valorile din
numitorii parțiali, iar indicele armonic când se cunosc indicii
individuali și valorile din numărătorii parțiali.
De subliniat, că indicii sub formă de medie aritmetică se
folosesc și în cazu1 când datele provin dintr-o observare selectivă și
se pune problema de a măsura eroarea medie și eroarea limită de
reprezentativitate. În acest sens indicele mediu se folosește ca orice
valoare medie pentru care i se poate calcula dispersia, utilizându-se
în consecința la estimarea indicilor din colectivitatea generală,
folosind eroarea limitată de reprezentativitate corespunzătoare.
La calculul indicilor de grup se mai poate folosi și media
geometrică, care însă nu mai conduce la egalitatea acestuia cu indicele
agregat respectiv. Conform proprietății mediei geometrice acest
indice are o valoare mai mică decât media aritmetică a acelorași indici
individuali, dar prezintă avantajul că reduce sistematic variația dintre
valorile care intră în calcul.
Indicat ar fi să se folosească și în acest caz o medie geometrică
ponderată cu unul din elementele raportului.
Din motive practice se poate calcula media geometrică a
indici1or individuali neponderați, dacă din experiența datelor
anterioare se știe că nu s-au produs mutații semnificative în structura
ansamblului.
nyy iI
0/10/1
Indicele general se calculează la nivelul întregului ansamblu.
Dacă în prealabil s-au calculat indici de grup corespunzători fiecărui
nivel ierarhic de organizare și structurare a fuxului informațional,
atunci în cazul indicelui agregat vom avea:
i
i
n
j
ij
k
i
n
j
ij
k
i
y
l
y
y
I
10
1
11
1
0/
în care (i) reprezintă variația elementelor sistemului (grupelor) de la 1
la k iar (j) reprezintă variația în interiorul fiecărei grupe (
i
n,1
), unde
ni reprezintă volumul grupei i.
În cazul în care sistemul nu este structurat pe grupe, indicele
general este de fapt un indice sintetic pentru toate unitățile componente
ale sistemului. De aici concluzia că, dacă sistemul este structurat pe
grupe, fiecare indice de grup la rândul său este un indice sintetic față
de indicii individuali.
În viziunea sistematică, indicele general al variabilei (y)
însumabilă direct se poate calcula în două variante, în funcție de
sursele de informație de care dispunem și de modul de structurare al
informației.
Se presupune că datele au fost sistematizate în raport cu
unitatea la care au fost înregistrate (vezi tabelul 8.1)
Tabelul 8.1.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 106 din 112
Calculul indicelui general al variabilei y în cazul colectivității
generale negrupată
Nr. crt.
al unității
Perioada de
bază
(yi0)
Perioada
curentă
(yi1)
0
1
0/
i
i
y
ly
y
ii
0
1
2
3
1
y10
y11
10/1
y
i
2
y20
y21
2
0/1
y
i
:
:
:
:
i
yi0
yil
i
y
i0/1
:
:
:
:
n
yn0
yn1
n
y
i0/1
Total
n
i
i
y
10
n
i
i
y
11
n
i
i
n
i
i
y
y
y
I
10
11
0/1
Pe baza tabelului 8.1. se pot calcula n indici individuali, adică
numărul indicatorilor corespunde cu numărul unităților înregistrate și
un indice general sub forma de agregat. Acest indice general poate fi
transformat într-un indice mediu aritmetic.
Deci, avem relația:
n
i
i
n
i
i
y
n
i
i
n
i
i
y
l
y
yi
y
y
I
i
10
100/1
10
11
0/
Această variantă este posibilă numai în cazul unui număr mic
de unități observate. El se întâlnește frecvent la nivelul unei
subcolectivități sau al unei societăți comerciale.
8.3.3 Sisteme de ponderare folosite la construirea indicilor
În practica statistică problemele cele mai dificile apar în
legătură cu alegerea și folosirea ponderilor la elaborarea indicilor de
grup. Alegerea și folosirea sistemelor de ponderare trebuie să se facă
în mod diferențiat, ținând seama de conținutul indicatorului de
comparat, de natura datelor existente în evidența curentă și de
posibilitatea de a stabili o analogie între descompunerea pe factori a
modificării absolute și relative.
În cursul dezvoltării statisticii s-au propus mai multe sisteme
de ponderare care au fost particularizate, de regulă, pe exemplul
indicilor volumului fizic sau ai prețurilor producției și circulației de
mărfuri. Pentru generalizare însă se vor prezenta sistemele de indici
pentru o variabilă complexă (y) dependentă de un factor calitativ (x) și
un factor cantitativ (f).

Emilia GOGU Statistica - Manual de studiu individual
Pagina 107 din 112
Având trei variabile înregistrate la nivelul unităților complexe
care formează în mod permanent colectivitatea supusă observării,
înseamnă că se pot calcula trei indici individuali și trei indici de grup.
Indicii individuali se calculează ca indici simpli folosind datele
înregistrate pentru fiecare variabilă la nivelul unității de observare
folosită.
Indicii de grup calculați la nivelul întregului ansamblu se
calculează ca indici agregați. Pentru prezentarea diferitelor sisteme
de ponderare se presupune că variabila y este însumabilă direct și că
se descompune integral la nivelul fiecărei unități în produsul dintre
variabila x - cu caracter de mărime derivată - și variabila f cu caracter
de variabilă cantitativă neînsumabilă direct. Aceasta înseamnă că
pentru indicii de grup ai celor două variabile-factori se va folosi tot
un indice agregat în care succesiv fenomenul de indexat este variabil,
iar celălalt are caracter de pondere.
1. Un prim sistem de ponderare este cel propus în 1864 de
către statisticianul belgian Laspeyres, la care ponderile folosite sunt
cele din perioada de bază. În acest caz se obține:
- indicele variabilei calitative x de tip Laspeyres, este:
)(0/ xy
l
I
00
01
ii
ii
fx
fx
- indicele variabilei cantitative f de tip Laspeyres, este:
)(0/ fy
l
I
00
10
ii
ii
fx
fx
Acceptarea sau respingerea celor doi indici nu se poate face
decât după ce se analizează conținutul lor și măsura în care ei reflectă
niște proporții reale cu privire la dezvoltarea fenomenelor la care se
referă. În consecință, fiecare indice trebuie analizat separat,
corespunzător cu conținutul indicatorilor absoluți pe care-i conține și
a relațiilor de interdependență dintre fenomenul de indexat și
ponderile folosite.
După cum s-a mai arătat în mod frecvent, în teoria și practica
statistică se întâlnesc indici ai unor caracteristici cantitative care se
obțin prin centralizarea unităților simple la nivelul unităților complexe
de observare și indici ai unor caracteristici calitative, care se exprimă
fie printr-un raport, fie printr-o mărime medie.
În primul caz, valorile calculate la nivelul unităților de
observare folosite sunt independente de valorile corespunzătoare ale
elementelor care se folosesc ca ponderi. De aceea, pentru astfel de
caracteristici cantitative se folosesc de obicei ponderile perioadei de
bază corespunzătoare ipotezei în care s-ar fi modificat numai factorul
cantitativ, iar factorul calitativ care joacă rol de pondere ar fi rămas
același nivel de dezvoltare. În schimb, la măsurarea dinamicii
fenomenului calitativ, dacă se folosesc ponderile perioadei de bază, nu
s-ar ține seama de dependența sa de modificările factorului cantitativ
la care se referă.
În teoria și practica statistică, se apreciază, de regulă, că numai
indicele factorului cantitativ se poate calcula după sistemul de

Emilia GOGU Statistica - Manual de studiu individual
Pagina 108 din 112
ponderare folosit de Laspeyres. Indicele unei caracteristici calitative
de tip Laspeyres nu este suficient de semnificativ și nici nu poate fi
inclus intr-un sistem, care sa permită descompunerea directă pe factori
de influență.
Din considerente practice, însă, se întâlnesc frecvent cazuri
când și pentru variabila calitativă se folosește sistemul de ponderare
Laspeyres, mai ales în cazul când lipsesc sau de obțin cu întârziere
datele pentru ponderile curente. Teoretic este de admis, ca aceasta
substituire se poate face când există o stabilitate a structurii ponderilor.
2. Un alt sistem de ponderare este cel propus în 1874 de câtre
statisticianul german Paasche, la care ponderile utilizate sunt cele din
perioada curentă a indicelui.
- pentru indicele factorului cantitativ, formula va fi:
)(0/ fy
l
I
01
11
ii
ii
fx
fx
- pentru indicele factorului calitativ, formula va fi:
)(0/ xy
l
I
10
11
ii
ii
fx
fx
Și aceste formule trebuie să fie analizate în raport cu conținutul
și scopul analizei. Pe lângă argumentele legate de conținutul
fenomenelor de indexat și care au fost prezentate la interpretarea
indicilor de tip Laspeyres se mai adaugă și unele aspecte legate de
valoarea ponderilor. Acceptarea sau respingerea sistemului de
ponderare trebuie să se facă și în funcție de tendința obiectivă de
modificare a prețurilor. Dacă tendința obiectivă a fenomenului este de
scădere, atunci ponderile perioadei curente utilizate vor influența în
sensul diminuării indicelui - ceea ce este nejustificat pentru cazul în
care variația caracteristicii de indexat este independentă de variația
ponderilor.
8.3.4 Condiții și limite ale aplicării metodei indicilor
Din cele prezentate în acest capitol reiese cu claritate faptul că
la elaborarea și folosirea indicilor la studiul variației în timp și spațiu
a fenomenelor trebuie rezolvate numeroase probleme, atât de conținut,
cât și de formă.
Analizând succint problematica atât de vastă și complexă a
metodei indicilor se constata că, pentru a obține rezultatele corecte,
este necesar să se facă o analiză complexă astfel încât să se evidențieze
condițiile și limitele aplicării lor.
În acest scop trebuie, în primul rând, să se stabilească daca
indicele respectiv se folosește ca indice independent sau în
interdependență cu alți indici care se referă la aceeași colectivitate.
În primul caz metodologia de elaborare a fiecărui indice trebuie
să permită includerea acestuia într-o serie teritorială sau de dinamică.
De exemplu, se poate elabora o serie de indici ai prețurilor, care să
studieze evoluția lor în timp, păstrând constantă variabila de spațiu și
organizatorică sau o serie de indici care să păstreze. constante
variabilele de timp și cea organizatorică. De aici rezultă că este necesar

Emilia GOGU Statistica - Manual de studiu individual
Pagina 109 din 112
să se folosească și in acest caz nu numai indicii individuali, ci și indicii
de grup și sintetici.
Odată cu calculul indicilor individuali trebuie să se rezolve și
sistemul de ponderare al indicilor de grup. În acest caz, nu se alege
întotdeauna sistemul de ponderare care corespunde cel mai bine
rezolvării teoretico-metodologice. Frecvent, aceste sisteme de
ponderare sunt condiționate de sursele de informație existente sau care
pot fi abordate. Indiferent de sistemul de ponderare (însă) la fel de
importantă pentru valoarea indicelui și credibilitatea lui este structura
ponderilor. Aceasta se rezolvă prin elaborarea periodică a unor
nomenclatoare analitice pe grupe și subgrupe de produse.
În sfârșit, calculul unui indice al prețurilor ridică in plus
problema gradului de reprezentativitate în general, acest indice se
obține pe baza unor observări parțiale, ceea ce înseamnă că
interpretarea corectă a sa necesită verificarea gradului de
reprezentativitate a eșantionului. Aceasta înseamnă că, de regulă,
indicii prețurilor trebuie să fie interpretați potrivit principiilor teoriei
probabilităților.
În cel de-ai doilea caz indicii fac parte din metodele de analiza
factorială, deci la elaborarea lor trebuie să se țină seama de relațiile de
sistem. Prima condiție care se pune este aceea a gradului de cuprindere
a unităților colectivității, relația de sistem fiind valabilă numai în cazul
în care ne referim la aceleași elemente componente ale ansamblului.
De pildă, în cazul sistemului de indici ai valorii, ai volumului fizic si
ai prețurilor, relația de sistem este valabilă numai dacă ne referim la o
producție comparabilă. În ipoteza în care folosim un indice al valorii
globale, utilizarea relației de sistem prin care calculăm un indice
factorial ca raport între indicele variabilei complexe și celălalt indice
factorial atunci înseamnă că am considerat că și partea necomparabilă
ar fi supusă aceleași condiții de variabilitate că și partea comparabilă.
De asemenea, când se includ mai mulți indici într-un sistem trebuie să
se verifice în prealabil dacă toți au luat în discuție variația totală sau
pe rând variația fiecărui factor față de aceeași bază de referință.
Această restricție este valabilă și pentru cazul în care, din motive de
surse de informație de care dispunem se înlocuiește un indice agregat
printr-un indice mediu.
Pentru o mai bună înțelegere a relațiilor dintre indici și a
funcțiilor acestora în analiza fenomenelor economico-sociale se poate
utiliza schema privind “clasificarea și legătura între indicii statistici”
8.4 Îndrumar pentru autoverificare
8.4.1 Sinteza unității de studiu 8
Necesitatea identificării și cuantificării gradului de influență a diferiților factori ce
determină dimensiunea și structura proceselor studiate au condus la perfecționarea
continuă a metodelor de analiză factorială, care includ și metoda indicilor statistici.

Emilia GOGU Statistica - Manual de studiu individual
Pagina 110 din 112
Metodologia de elaborare a indicilor statistici este extrem de variată, cuprinzând atât
metode elementare de comparație statistică, cât și metode cu un grad mare de rafinament
interpretativ, combinând mai multe procedee de calcul și analiză statistică
Rezultatele aplicării metodei indicilor se pot concretiza fie sub forma unui sistem de indici,
atunci când se face o analiză complexă în care operăm cu variabile factoriale și rezultative, fie sub
forma unor variabile independente când fenomenul studiat se analizează izolat, separat. De
exemplu, dacă se studiază indicele productivității muncii, în prima variantă, în analiză se vor
include obligatoriu și indicatorii producției și consumului total de muncă, în timp ce, în a doua
variantă se vor studia numai probleme legate de nivelul și variația în timp și spațiu a productivității
muncii, chiar dacă și în această situație vom opera cu o serie de relații numerice.
În cadrul acestui sistem de indicatori primari și derivați fără îndoială că metoda indicilor,
datorită funcțiilor sale cognitive deosebite, poate răspunde în cea mai mare măsură acestor cerințe
complexe legate de caracterizarea numerică a proceselor sociale și economice. În acest fel,
domeniul de aplicare a indicilor la studiul fenomenelor social economice s-a lărgit continuu, iar
metoda lor și formele specifice pe care le îmbracă în studiul concret al acestora au format în perma-
nență obiectul unor discuții interesante purtate de un număr mare de economiști și statisticieni în
diferite reviste și studii de specialitate. In principal, problemele care formează obiectul discuțiilor
se referă la:
volumul, calitatea și sursa datelor statistice necesare elaborării indicilor;
structurarea informației potrivit unităților de observare utilizate;
verificarea reprezentativității eșantionului, pentru cazul când datele provin dintr-o
observare parțială;
alegerea formulelor de calcul;
alegerea bazei de raportare;
alegerea sistemului de ponderare;
găsirea unor soluții de trecere de la analiza separată a fenomenelor de indexat la
interpretarea diferitelor corelații ce se pot forma atât în structura orizontală, cât și în
structura verticală a sistemului;
particularități ale metodei indicilor utilizate pentru elaborarea unei serii de indici in
plan teritorial și dinamic.
8.4.2 Concepte și termeni de reținut
Alegerea bazei de raportare
Fenomenelor de indexat
Indicii agregați
Metoda indicilor
Indicii de grup
Serii de indici in plan dinamic
Indicii individuali
Serii de indici in plan teritorial
Indice general
Sistemul de ponderare Laspeyres
Indici sub formă de medie
Sistemul de ponderare
Indici raport a două medii
Sistemul de ponderare Paasche
8.4.3 Întrebări de control și teme de dezbatere

Emilia GOGU Statistica - Manual de studiu individual
Pagina 111 din 112
1. Ce se înțelege prin noțiunea de indice?
2. Care sunt funcțiile indicilor?
3. Care sunt criteriile de clasificare a indicilor?
4. Cum se calculează un indice individual?
5. Cum se calculează indicele de grup al valorii?
6. Care sunt posibilitățile de calcul al indicelui de grup al volumului fizic?
7. Care sunt posibilitățile de calcul al indicelui de grup al prețurilor?
8. Ce relații există între indicele de grup al valorii, volumul fizic și al prețurilor și cum se
reprezintă grafic?
9. Cum se calculează indicii de grup ca raport de medii și ce relații există între ei?
10. Ce sisteme de ponderare se pot folosi în construirea indicilor?
11. Cum se descompune pe factori variația unui fenomen complex?
12. Cum se calculează indicii individuali și de grup ai productivității muncii?
13. Cum se calculează un indice teritorial?
14. Care sunt particularitățile ce intervin în construirea indicilor teritoriali?
8.4.4 Teste de evaluare/autoevaluare
Aplicația 1.
Pentru trei puncte de desfacere aparținând aceleiași societăți comerciale se cunosc următoarele
date pentru vânzarea a trei produse:
Produs
Cantitate
Prețul unitar (mii lei)
ianuarie
februarie
ianuarie
februarie
A
B
C
830
940
730
820
980
700
1500
1530
1540
1420
1450
1510
Se cere:
1. să se calculeze indicii individuali ai valorii, volumului fizic și ai prețurilor pe fiecare produs;
2. să se determine indicii de grup privind valoarea, volumul fizic și prețurile;
3. modificările absolute corespunzătoare pe total.
8.4.5 Bibliografie obligatorie
1. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
2. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
3. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008

Emilia GOGU Statistica - Manual de studiu individual
Pagina 112 din 112
8.5 Bibliografie generală
1. Andrei, T., Stancu, S., - Statistică, Ed. ALL, Bucureşti 1995.
2. Baron,T., Biji, E.,Tovissi, L.,Wagner, P., Isaic-Maniu, A., Korka, M., Porojan, D., - Statistică
teoretică şi economică, Ed. didactică şi pedagogică, Bucureşti, 1996.
3. Biji E., Biji. M., Lilea, Anghelache C., Tratat de statistică, Editura Economică, București,
2002;
4. Biji E.M., Lilea E., Vătui M. Gogu E. Aplicații statistice în studiul fenomenelor economice
Editura Oscar Print, 2007
5. Biji E.M., Lilea E., Vătui M. Gogu E., Aplicații statistice în studiul fenomenelor economice,
Editura Oscar Print, București, 2007;
6. Gogu E. - Statistica în turism și comerț – Teorie și studii de caz Editura Oscar Print,
București 2009
7. Isaic-Maniu, A., Mitruţ, C., Voineagu, V., Săvoiu, G., - Statistica afacerilor, Ed.
Independenţa Economică, Piteşti, 2002.
8. Isaic-Maniu, Al. (coord),(2003),Dicţionar de statistică generală, Ed.Economică, Bucureşti
9. Jaba, E., - Statistică, Ed. economică, Bucureşti, 1998.
10. Korka, M.,Tuşa, E., - Statistică pentru afaceri internaţionale, Ed. ASE, Bucureşti, 2004
11. Lilea E., Biji E.M., Vătui M. Gogu E., Statistica, Editura ProUniversitaria, București, 2008
12. ***Anuarul Statistic al României INS
13. *** Anuarul Statistic al Comerțului Exterior INS
14. *** Statistica teritoriala INS
15. *** www.eurostat.org
16. *** www.unstat.org