Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 81
軌道最適化による動作生成
リファレンスマニュアル
平成 31 年2月11 日
室岡雅樹
murooka@jsk.t.u-tokyo.ac.jp
目 次
1軌道最適化による動作生成の基礎 1
1.1 タスク関数のノルムを最小にするコンフィギュレーションの探索 ................. 1
1.2 コンフィギュレーション二次形式の正則化項の追加 ........................ 2
1.3 コンフィギュレーション更新量の正則項の追加 ........................... 3
1.4 ソースコードと数式の対応 ...................................... 3
1.5 章の構成 ................................................ 4
2コンフィギュレーションとタスク関数 4
2.1 瞬時コンフィギュレーションと瞬時タスク関数 ........................... 4
2.2 軌道コンフィギュレーションと軌道タスク関数 ........................... 21
3勾配を用いた制約付き非線形最適化 28
3.1 逐次二次計画法 ............................................ 28
3.2 複数解候補を用いた逐次二次計画法 ................................. 30
3.2.1 複数解候補を用いた逐次二次計画法の理論 ......................... 30
3.2.2 複数解候補を用いた逐次二次計画法の実装 ......................... 34
4動作生成の拡張 35
4.1 マニピュレーションの動作生成 ................................... 35
4.2 B スプラインを用いた関節軌道生成 ................................. 46
4.2.1 B スプラインを用いた関節軌道生成の理論 ......................... 46
4.2.2 B スプラインを用いた関節軌道生成の実装 ......................... 55
5補足 67
5.1 既存のロボット基礎クラスの拡張 .................................. 67
5.2 環境と接触するロボットの関節・リンク構造 ............................ 70
5.3 irteus のinverse-kinematics 互換関数 ................................ 72
i
1
1軌道最適化による動作生成の基礎
1.1 タスク関数のノルムを最小にするコンフィギュレーションの探索
q∈Rnqを設計対象のコンフィギュレーションとする.例えば一般の逆運動学計算では,qはある瞬間のロ
ボットの関節角度を表すベクトルで,コンフィギュレーションの次元 nqはロボットの関節自由度数となる.
動作生成問題を,所望のタスクに対応するタスク関数 e(q) : Rnq→Rneについて,次式を満たす qを得る
こととして定義する.
e(q) = 0(1.1)
例えば一般の逆運動学計算では,e(q)はエンドエフェクタの目標位置姿勢と現在位置姿勢の差を表す 6次元
ベクトルである.非線形方程式 (1.1) の解を解析的に得ることは難しく,反復計算による数値解法が採られる.
式(1.1) が解をもたないときでも最善のコンフィギュレーションを得られるように一般化すると,式 (1.1) の
求解は次の最適化問題として表される 1.
min
qF(q) (1.2a)
where F(q)def
=1
2∥e(q)∥2(1.2b)
コンフィギュレーションが最小値 qmin と最大値 qmax の間に含まれる必要があるとき,逆運動学計算は次の制
約付き非線形最適化問題として表される.
min
qF(q) s.t.qmin ≤q≤qmax (1.3)
例えば一般の逆運動学計算では,qmin ,qmax は関節角度の許容範囲の最小値,最大値を表す.以降では,式 (1.3) の
制約を,より一般の形式である線形等式制約,線形不等式制約として次式のように表す 2.
min
qF(q) (1.4a)
s.t.Aq =¯
b(1.4b)
Cq ≥¯
d(1.4c)
制約付き非線形最適化問題の解法のひとつである逐次二次計画法では,次の二次計画問題の最適解として得
られる ∆q∗
kを用いて,qk+1 =qk+ ∆q∗
kとして反復更新することで,式 (1.4) の最適解を導出する 3.
min
∆qk
F(qk) + ∇F(qk)T∆qk+1
2∆qT
k∇2F(qk)∆qk(1.5a)
s.t.A∆qk=¯
b−Aqk(1.5b)
C∆qk≥¯
d−Cqk(1.5c)
1任意の半正定値行列 Wに対して,∥e(q)∥2
W=e(q)TW e(q) = e(q)TSTSe(q) = ∥Se(q)∥2を満たす Sが必ず存在するので,
式(1.2b) は任意の重み付きノルムを表現可能である.
2式(1.3) における関節角度の最小値,最大値に関する制約は次式のように表される.
qmin ≤q≤qmax
⇔(I
−I)q≥(qmin
−qmax )
3式(1.5a) はF(q)をqkの周りでテーラー展開し三次以下の項を省略したものに一致する.逐次二次計画法については,以下の書籍
の18 章で詳しく説明されている.
Numerical optimization, S. Wright and J. Nocedal, Springer Science, vol. 35, 1999, http://www.xn--vjq503akpco3w.top/
literature/Nocedal_Wright_Numerical_optimization_v2.pdf.

2
∇F(qk),∇2F(qk)はそれぞれ,F(qk)の勾配,ヘッセ行列 4で,次式で表される.
∇F(q) = ∂e(q)
∂qT
e(q) (1.6a)
=J(q)Te(q) (1.6b)
∇2F(q) =
m
i=1
ei(q)∇2ei(q) + ∂e(q)
∂qT∂e(q)
∂q(1.6c)
≈∂e(q)
∂qT∂e(q)
∂q(1.6d)
=J(q)TJ(q) (1.6e)
ただし,ei(q) (i= 1,2,··· , m)はe(q)のi番目の要素である.式 (1.6c) から式 (1.6d) への変形では e(q)の
二階微分がゼロであると近似している.J(q)def
=∂e(q)
∂q∈Rne×nqはe(q)のヤコビ行列である.
式(1.6a) , 式(1.6d) から式 (1.5a) の目的関数は次式で表される 5.
1
2eT
kek+eT
kJk∆qk+1
2∆qT
kJT
kJk∆qk(1.7a)
=1
2∥ek+Jk∆qk∥2(1.7b)
ただし,ek
def
=e(qk),Jk
def
=J(qk)とした.
結局,逐次二次計画法で反復的に解かれる二次計画問題 (1.5) は次式で表される.
min
∆qk
1
2∆qT
kJT
kJk∆qk+eT
kJk∆qk(1.8a)
s.t.A∆qk=b(1.8b)
C∆qk≥d(1.8c)
ここで,
b=¯
b−Aqk(1.9)
d=¯
d−Cqk(1.10)
とおいた.
1.2 コンフィギュレーション二次形式の正則化項の追加
式(1.2a) の最適化問題の目的関数を,次式の ˆ
F(q)で置き換える.
ˆ
F(q) = F(q) + Freg (q) (1.11)
where Freg (q) = 1
2qT¯
Wreg q(1.12)
目的関数 ˆ
F(q)の勾配,ヘッセ行列は次式で表される.
∇ˆ
F(q) = ∇F(q) + ∇Freg (q) (1.13a)
=J(q)Te(q) + ¯
Wreg q(1.13b)
∇2ˆ
F(q) = ∇2F(q) + ∇2Freg (q) (1.13c)
≈J(q)TJ(q) + ¯
Wreg (1.13d)
4式(1.5a) の∇2F(qk)の部分は一般にはラグランジュ関数の qkに関するヘッセ行列であるが,等式・不等式制約が線形の場合は
F(qk)のヘッセ行列と等価になる.
5式(1.7b) は,以下の論文で紹介されている二次計画法によってコンフィギュレーション速度を導出する逆運動学解法における目的関
数と一致する.
Feasible pattern generation method for humanoid robots, F. Kanehiro et al., Proceedings of the 2009 IEEE-RAS International
Conference on Humanoid Robots, pp. 542-548, 2009.

3
したがって,式 (1.8) の二次計画問題は次式で表される.
min
∆qk
1
2∆qT
kJT
kJk+¯
Wreg ∆qk+JT
kek+¯
Wreg qkT
∆qk(1.14a)
s.t.A∆qk=b(1.14b)
C∆qk≥d(1.14c)
1.3 コンフィギュレーション更新量の正則項の追加
Gauss-Newton 法と Levenberg-Marquardt 法の比較を参考に,式 (1.14a) の二次形式項の行列に,次式のよ
うに微小な係数をかけた単位行列を加えると,一部の適用例について逐次二次計画法の収束性が改善された 6.
min
∆qk
1
2∆qT
kJT
kJk+¯
Wreg +λI∆qk+JT
kek+¯
Wreg qkT
∆qk(1.15a)
s.t.A∆qk=b(1.15b)
C∆qk≥d(1.15c)
改良誤差減衰最小二乗法 7を参考にすると,λは次式のように決定される.
λ=λrF(qk) + wr(1.16)
λrとwrは正の定数である.
1.4 ソースコードと数式の対応
Wreg
def
=¯
Wreg +λI(1.17a)
vreg
def
=¯
Wreg qk(1.17b)
とすると,式 (1.15) は次式で表される.
min
∆qk
1
2∆qT
kJT
kJk+W∆qk+JT
kek+vreg T
∆qk(1.18a)
s.t.A∆qk=b(1.18b)
C∆qk≥d(1.18c)
第2節や第 4章で説明する***-configuration-task クラスのメソッドは式 (1.18) 中の記号と以下のように対
応している.
:config-vector get q
:set-config set q
:task-value get e(q)
:task-jacobian get J(q)def
=∂e(q)
∂q
:config-equality-constraint-matrix get A
:config-equality-constraint-vector get b
:config-inequality-constraint-matrix get C
:config-inequality-constraint-vector get d
:regular-matrix get Wreg
:regular-vector get vreg
6これは,最適化における信頼領域 (trust region) に関連している.
7Levenberg-Marquardt 法による可解性を問わない逆運動学,杉原 知道,日本ロボット学会誌, vol. 29, no. 3, pp. 269-277, 2011.
4
1.5 章の構成
第2章では,コンフィギュレーション qの取得・更新,タスク関数 e(q)の取得,タスク関数のヤコビ行列
J(q)def
=∂e(q)
∂qの取得,コンフィギュレーションの等式・不等式制約 A,b,C,dの取得のためのクラスを説明
する.第 2.1 節ではコンフィギュレーション qが瞬時の情報,第 2.2 節ではコンフィギュレーション qが時系
列の情報を表す場合をそれぞれ説明する.
第3章では,第 2章で説明されるクラスを用いて逐次二次計画法により最適化を行うためのクラスを説明
する.
第4章では,用途に応じて拡張されたコンフィギュレーションとタスク関数のクラスを説明する.第 4.1 節
では,マニピュレーションのために,ロボットに加えて物体のコンフィギュレーションを計画する場合を説明
する.第 4.2 節では,ロボットの関節位置の軌道を Bスプライン関数でパラメトリックに表現する場合を説明
する.いずれにおいても,最適化では第 3章で説明された逐次二次計画法のクラスが利用される.
第5章では,その他の補足事項を説明する.第 5.1 節では,jskeus で定義されているクラスの拡張について
説明する.第 5.2 節では,環境との接触を有するロボットの問題設定を記述するためのクラスについて説明す
る.第 5.4 節では,関節トルクを関節角度で微分したヤコビ行列を導出するための関数について説明する.
2コンフィギュレーションとタスク関数
2.1 瞬時コンフィギュレーションと瞬時タスク関数
instant-configuration-task [class]
:super propertied-object
:slots ( robot-env robot-environment instance)
( theta-vector θ[rad] [m])
( wrench-vector ˆw[N] [Nm])
( torque-vector τ[Nm])
( phi-vector ϕ[rad] [m])
( num-kin Nkin := |T kin-trg |=|T kin-att |)
( num-contact Ncnt := |T cnt-trg |=|T cnt-att |)
( num-variant-joint Nvar-joint := |Jvar |)
( num-invariant-joint Ninvar -joint := |Jinvar |)
( num-drive-joint Ndrive-joint := |Jdrive |)
( num-posture-joint Nposture-joint := |Jposture |)
( num-external Nex := number of external wrenches)
( num-collision Ncol := number of collision check pairs)
( dim-theta dim(θ) = Nvar-joint )
( dim-wrench dim(ˆw) = 6Ncnt )
( dim-torque dim(τ) = Ndrive-joint )
( dim-phi dim(ϕ) = Ninvar -joint )
( dim-variant-config dim(qvar ))
( dim-invariant-config dim(qinvar ))
( dim-config dim(q))
( dim-task dim(e))
( kin-scale-mat-list Kkin )
( target-posture-scale kposture )
5
( norm-regular-scale-max kmax )
( norm-regular-scale-offset koff )
( torque-regular-scale ktrq )
( variant-joint-list Jvar )
( invariant-joint-list Jinvar )
( drive-joint-list Jdrive )
( kin-target-coords-list Tkin-trg )
( kin-attention-coords-list Tkin-att )
( contact-target-coords-list Tcnt-trg )
( contact-attention-coords-list Tcnt -att )
( variant-joint-angle-margin margin of θ[deg] [mm])
( invariant-joint-angle-margin margin of ϕ[deg] [mm])
( delta-linear-joint trust region of linear joint configuration [mm])
( delta-rotational-joint trust region of rotational joint configuration [deg])
( contact-constraint-list list of contact-constraint instance)
( posture-joint-list Jposture )
( posture-joint-angle-list ¯
θtrg )
( external-wrench-list {wex
1,wex
2,· · · ,wex
Nex })
( external-coords-list {Tex
1, T ex
2,· · · , T ex
Nex })
( collision-pair-list list of bodyset-link or body pair)
( collision-distance-margin-list list of collision distance margin)
( only-kinematics? whether to consider only kinematics or not)
( variant-task-jacobi buffer for ∂e
∂qvar )
( invariant-task-jacobi buffer for ∂e
∂qinvar )
( task-jacobi buffer for ∂e
∂q)
( collision-theta-inequality-constraint-matrix buffer for Ccol ,θ )
( collision-phi-inequality-constraint-matrix buffer for Ccol ,ϕ)
( collision-inequality-constraint-vector buffer for Ccol )
瞬時コンフィギュレーション q(l)と瞬時タスク関数 e(l)(q(l))のクラス.
このクラスの説明で用いる全ての変数は,時間ステップ lを表す添字をつけて x(l)と表されるべきだが,
このクラス内の説明では省略して xと表す.また,以降では,説明文やメソッド名で,“瞬時”や“instant”
を省略する.
コンフィギュレーション qの取得・更新,タスク関数 e(q)の取得,タスク関数のヤコビ行列 ∂e(q)
∂qの取
得,コンフィギュレーションの等式・不等式制約 A,b,C,dの取得のためのメソッドが定義されている.
コンフィギュレーション・タスク関数を定めるために,初期化時に以下を与える
•ロボット・環境
robot-environment ロボット・環境を表す robot-environment クラスのインスタンス
variant-joint-list Jvar 時変関節
invariant-joint-list Jinvar 時不変関節 (与えなければ時不変関節は考慮されない)
drive-joint-list Jdrive 駆動関節 (与えなければ関節駆動トルクは考慮されない)
•幾何拘束
kin-target-coords-list Tkin-trg 幾何到達目標位置姿勢リスト
6
kin-attention-coords-list Tkin-att 幾何到達着目位置姿勢リスト
kin-scale-mat-list Kkin 幾何拘束の座標系,重みを表す変換行列のリスト
•接触拘束
contact-target-coords-list Tcnt-trg 接触目標位置姿勢リスト
contact-attention-coords-list Tcnt-att 接触着目位置姿勢リスト
contact-constraint-list 接触レンチ制約リスト
•コンフィギュレーション拘束 (必要な場合のみ)
posture-joint-list Jposture 着目関節リスト
posture-joint-angle-list ¯
θtrg 着目関節の目標関節角
target-posture-scale kposture コンフィギュレーション拘束の重み
•干渉回避拘束 (必要な場合のみ)
collision-pair-list 干渉回避する bodyset-link もしくは body のペアのリスト
collision-distance-margin 干渉回避の距離マージン (全てのペアで同じ値の場合)
collision-distance-margin-list 干渉回避の距離マージンのリスト (ペアごとに異なる値の場合)
•外レンチ (必要な場合のみ)
external-wrench-list 外レンチのリスト (ワールド座標系で表す)
external-coords-list 外レンチの作用点座標のリスト (位置のみを使用)
•目的関数の重み
norm-regular-scale-max kmax コンフィギュレーション更新量正則化の重み最大値
norm-regular-scale-offset koff コンフィギュレーション更新量正則化の重みオフセット
torque-regular-scale ktrq トルク正則化の重み
コンフィギュレーション qは以下から構成される.
q:= θTˆwTτTϕTT
(2.1)
θ∈RNvar-joint 時変関節角度 [rad] [m]
ˆw∈R6Ncnt 接触レンチ [N] [Nm]
τ∈RNdrive-joint 関節駆動トルク [Nm] [N]
ϕ∈RNinvar-joint 時不変関節角度 [rad] [m]
ˆwは次式のように,全接触部位でのワールド座標系での力・モーメントを並べたベクトルである.
ˆw=wT
1wT
2· · · wT
Ncnt T
(2.2)
=fT
1nT
1fT
2nT
2· · · fT
Ncnt nT
Ncnt T
(2.3)
タスク関数 e(q)は以下から構成される.
e(q) := ekinT(q)eeom-transT(q)eeom-rotT(q)etrqT(q)epostureT(q)T
(2.4)
ekin (q)∈R6Nkin 幾何到達拘束 [rad] [m]
eeom -trans (q)∈R3力の釣り合い [N]
eeom -rot (q)∈R3モーメントの釣り合い [Nm]
etrq (q)∈RNdrive -joint 関節トルクの釣り合い [rad] [m]
7
eposture (q)∈RNposture-joint 関節角目標 [rad] [m]
:init &key (name) [method]
(robot-env)
(variant-joint-list (send robot-env :variant-joint-list))
(invariant-joint-list (send robot-env :invariant-joint-list))
(drive-joint-list (send robot-env :drive-joint-list))
(only-kinematics?)
(kin-target-coords-list)
(kin-attention-coords-list)
(contact-target-coords-list)
(contact-attention-coords-list)
(variant-joint-angle-margin 3.0)
(invariant-joint-angle-margin 3.0)
(delta-linear-joint)
(delta-rotational-joint)
(contact-constraint-list (send-all contact-attention-coords-list :get :contact-constraint))
(posture-joint-list)
(posture-joint-angle-list)
(external-wrench-list)
(external-coords-list)
(collision-pair-list)
(collision-distance-margin 0.01)
(collision-distance-margin-list)
(kin-scale 1.0)
(kin-scale-list)
(kin-scale-mat-list)
(target-posture-scale 0.001)
(norm-regular-scale-max (if only-kinematics? 0.001 1.000000e-05))
(norm-regular-scale-offset 1.000000e-07)
(torque-regular-scale 1.000000e-04)
&allow-other-keys
Initialize instance
:robot-env [method]
return robot-environment instance
:variant-joint-list [method]
return Jvar
:invariant-joint-list [method]
return Jinvar
:drive-joint-list [method]
return Jdrive
:only-kinematics? [method]
return whether to consider only kinematics or not
8
:theta [method]
return θ
:wrench [method]
return ˆw
:torque [method]
return τ
:phi [method]
return ϕ
:num-kin [method]
return Nkin := |T kin-trg |=|T kin-att |
:num-contact [method]
return Ncnt := |T cnt-trg |=|T cnt -att |
:num-variant-joint [method]
return Nvar-joint := |Jvar |
:num-invariant-joint [method]
return Ninvar-joint := |Jinvar |
:num-drive-joint [method]
return Ndrive-joint := |Jdrive |
:num-posture-joint [method]
return Ntarget -joint := |Jtarget |
:num-external [method]
return Nex := number of external wrench
:num-collision [method]
return Ncol := number of collision check pairs
:dim-variant-config [method]
dim(qvar ) := dim(θ) + dim(ˆw) + dim(τ) (2.5)
=Nvar-joint + 6Ncnt +Ndrive-joint (2.6)
return dim(qvar )
:dim-invariant-config [method]
return dim(qinvar ) := dim(ϕ) = Ninvar -joint
:dim-config [method]
return dim(q) := dim(qvar ) + dim(qinvar )
:dim-task [method]
dim(e) := dim(ekin ) + dim(eeom-trans ) + dim(eeom-rot ) + dim(etrq ) + dim(eposture ) (2.7)
= 6Nkin + 3 + 3 + Ndrive-joint +Nposture-joint (2.8)
9
return dim(e)
:variant-config-vector [method]
return qvar :=
θ
ˆw
τ
:invariant-config-vector [method]
return qinvar := ϕ
:config-vector [method]
return q:= qvar
qinvar =
θ
ˆw
τ
ϕ
:set-theta theta-new &key (relative? nil) [method]
(apply-to-robot? t)
Set θ.
:set-wrench wrench-new &key (relative? nil) [method]
Set ˆw.
:set-torque torque-new &key (relative? nil) [method]
Set τ.
:set-phi phi-new &key (relative? nil) [method]
(apply-to-robot? t)
Set ϕ.
:set-variant-config variant-config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set qvar .
:set-invariant-config invariant-config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set qinvar .
:set-config config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set q.
:kin-target-coords-list [method]
Tkin-trg
m={pkin-trg
m,Rkin-trg
m}(m= 1,2,··· , Nkin ) (2.9)
return Tkin-trg := {Tkin-trg
1, T kin-trg
2,· · · , T kin-trg
Nkin }
:kin-attention-coords-list [method]
Tkin-att
m={pkin-att
m,Rkin-att
m}(m= 1,2,··· , Nkin ) (2.10)
10
return Tkin-att := {Tkin-att
1, T kin-att
2,· · · , T kin -att
Nkin }
:contact-target-coords-list [method]
Tcnt-trg
m={pcnt-trg
m,Rcnt-trg
m}(m= 1,2,· · · , Ncnt ) (2.11)
return Tcnt-trg := {Tcnt -trg
1, T cnt-trg
2,··· , T cnt-trg
Ncnt }
:contact-attention-coords-list [method]
Tcnt-att
m={pcnt-att
m,Rcnt-att
m}(m= 1,2,· · · , Ncnt ) (2.12)
return Tcnt-att := {Tcnt-att
1, T cnt-att
2,··· , T cnt-att
Ncnt }
:contact-constraint-list [method]
return list of contact-constraint instance
:wrench-list [method]
return {w1,w2,· · · ,wNcnt }
:force-list [method]
return {f1,f2,· · · ,fNcnt }
:moment-list [method]
return {n1,n2,· · · ,nNcnt }
:external-wrench-list [method]
return {wex
1,wex
2,··· ,wex
Nex }
:external-force-list [method]
return {fex
1,fex
2,· · · ,fex
Nex }
:external-moment-list [method]
return {nex
1,nex
2,· · · ,nex
Nex }
:mg-vec [method]
return mg
:cog &key (update? t) [method]
return pG(q)
:kinematics-task-value &key (update? t) [method]
ekin (q) = ekin (θ,ϕ) (2.13)
=
ekin
1(θ,ϕ)
ekin
2(θ,ϕ)
.
.
.
ekin
Nkin (θ,ϕ)
(2.14)
ekin
m(θ,ϕ) = Kkin pkin-trg
m(θ,ϕ)−pkin-att
m(θ,ϕ)
aRkin-trg
m(θ,ϕ)Rkin-att
m(θ,ϕ)T∈R6(m= 1,2,· · · , Nkin ) (2.15)
11
a(R)は姿勢行列 Rの等価角軸ベクトルを表す.
return ekin (q)∈R6Nkin
:eom-trans-task-value &key (update? t) [method]
eeom -trans (q) = eeom-trans (ˆw) (2.16)
=
Ncnt
m=1
fm−mg+
Nex
m=1
fex
m(2.17)
return eeom -trans (q)∈R3
:eom-rot-task-value &key (update? t) [method]
eeom -rot (q) = eeom-rot (θ,ˆw,ϕ) (2.18)
=
Ncnt
m=1 pcnt-trg
m(θ,ϕ)−pG(θ,ϕ)×fm+nm
+
Nex
m=1
{(pex
m(θ,ϕ)−pG(θ,ϕ)) ×fex
m+nex
m}(2.19)
return eeom -rot (q)∈R3
:torque-task-value &key (update? t) [method]
etrq (q) = etrq (θ,ˆw,τ,ϕ) (2.20)
=τ+
Ncnt
m=1
τcnt
m(θ,ϕ)−τgrav (θ,ϕ) +
Nex
m=1
τex
m(θ,ϕ) (2.21)
=τ+
Ncnt
m=1
Jcnt-att
drive-joint ,m(θ,ϕ)Twm−τgrav (θ,ϕ) +
Nex
m=1
Jex
drive-joint ,m(θ,ϕ)Twex
m(2.22)
τcnt
m(θ,ϕ)はm番目の接触部位にかかる接触レンチ wmによる関節トルク,τgrav
m(θ,ϕ)は自重による関
節トルクを表す.
return etrq (q)∈RNdrive -joint
:posture-task-value &key (update? t) [method]
eposture (q) = eposture (θ) (2.23)
=kposture ¯
θtrg −¯
θ(2.24)
¯
θtrg ,¯
θは着目関節リスト Jposture の目標関節角と現在の関節角.
return eposture (q)∈RNposture-joint
:task-value &key (update? t) [method]
return e(q) :=
ekin (q)
eeom -trans (q)
eeom -rot (q)
etrq (q)
eposture (q)
=
ekin (θ,ϕ)
eeom -trans (ˆw)
eeom -rot (θ,ˆw,ϕ)
etrq (θ,ˆw,τ,ϕ)
eposture (θ)

12
:kinematics-task-jacobian-with-theta [method]
∂ekin
∂θ=
∂ekin
1
∂θ
∂ekin
2
∂θ
.
.
.
∂ekin
Nkin
∂θ
(2.25)
∂ekin
m
∂θ=Kkin Jkin-trg
θ,m (θ,ϕ)−Jkin -att
θ,m (θ,ϕ)(m= 1,2,· · · , Nkin ) (2.26)
return ∂ekin
∂θ∈R6Nkin ×Nvar-joint
:kinematics-task-jacobian-with-phi [method]
∂ekin
∂ϕ=
∂ekin
1
∂ϕ
∂ekin
2
∂ϕ
.
.
.
∂ekin
Nkin
∂ϕ
(2.27)
∂ekin
m
∂ϕ=Kkin Jkin-trg
ϕ,m (θ,ϕ)−Jkin-att
ϕ,m (θ,ϕ)(m= 1,2,· · · , Nkin ) (2.28)
return ∂ekin
∂ϕ∈R6Nkin ×Ninvar-joint
:eom-trans-task-jacobian-with-wrench [method]
∂eeom -trans
∂ˆw=∂eeom-trans
∂f1
∂eeom-trans
∂n1· · · ∂eeom-trans
∂fNcnt
∂eeom-trans
∂nNcnt (2.29)
=I3O3· · · I3O3(2.30)
return ∂eeom-trans
∂ˆw∈R3×6Ncnt
:eom-rot-task-jacobian-with-theta [method]
∂eeom -rot
∂θ=
Ncnt
m=1 −[fm×]Jcnt-trg
θ,m (θ,ϕ)−JGθ (θ,ϕ)
+
Nex
m=1 −[fex
m×]Jex
θ,m(θ,ϕ)−JGθ(θ,ϕ) (2.31)
=Ncnt
m=1
fm+
Nex
m=1
fex
m×JGθ(θ,ϕ)
−
Ncnt
m=1
[fm×]Jcnt-trg
θ,m (θ,ϕ)−
Nex
m=1
[fex
m×]Jex
θ,m(θ,ϕ) (2.32)
Ncnt
m=1 fm+Nex
m=1 fex
m=mgつまり,eom-trans-task が成立すると仮定すると次式が成り立つ.
∂eeom -rot
∂θ= [mg×]JGθ(θ,ϕ)−
Ncnt
m=1
[fm×]Jcnt-trg
θ,m (θ,ϕ)−
Nex
m=1
[fex
m×]Jex
θ,m(θ,ϕ) (2.33)
13
return ∂eeom-rot
∂θ∈R3×Nvar-joint
:eom-rot-task-jacobian-with-wrench [method]
∂eeom -rot
∂ˆw=∂eeom-rot
∂f1
∂eeom-rot
∂n1··· ∂eeom-rot
∂fNcnt
∂eeom-rot
∂nNcnt (2.34)
∂eeom -rot
∂fm
=pcnt-trg
m(θ,ϕ)−pG(θ,ϕ)×(m= 1,2,· · · , Ncnt ) (2.35)
∂eeom -rot
∂nm
=I3(m= 1,2,· · · , Ncnt ) (2.36)
return ∂eeom-rot
∂ˆw∈R3×6Ncnt
:eom-rot-task-jacobian-with-phi [method]
∂eeom -rot
∂ϕ=
Ncnt
m=1 −[fm×]Jcnt-trg
ϕ,m (θ,ϕ)−JGϕ(θ,ϕ)
+
Nex
m=1 −[fex
m×]Jex
ϕ,m(θ,ϕ)−JGϕ(θ,ϕ) (2.37)
=Ncnt
m=1
fm+
Nex
m=1
fex
m×JGϕ(θ,ϕ)
−
Ncnt
m=1
[fm×]Jcnt-trg
ϕ,m (θ,ϕ)−
Nex
m=1
[fex
m×]Jex
ϕ,m(θ,ϕ) (2.38)
Ncnt
m=1 fm+Nex
m=1 fex
m=mgつまり,eom-trans-task が成立すると仮定すると次式が成り立つ.
∂eeom -rot
∂ϕ= [mg×]JGϕ(θ,ϕ)−
Ncnt
m=1
[fm×]Jcnt-trg
ϕ,m (θ,ϕ)−
Nex
m=1
[fex
m×]Jex
ϕ,m(θ,ϕ) (2.39)
return ∂eeom-rot
∂ϕ∈R3×Ninvar-joint
:torque-task-jacobian-with-theta [method]
∂etrq
∂θ=
Ncnt
m=1
∂τcnt
m
∂θ−∂τgrav
∂θ+
Nex
m=1
∂τex
m
∂θ(2.40)
return ∂etrq
∂θ∈RNdrive-joint ×Nvar -joint
:torque-task-jacobian-with-wrench [method]
∂etrq
∂ˆw=∂etrq
∂w1
∂etrq
∂w2· · · ∂etrq
∂wNcnt (2.41)
∂etrq
∂wm
=Jcnt-att
drive-joint ,m(θ,ϕ)T(m= 1,2,· · · , Ncnt ) (2.42)
return ∂etrq
∂ˆw∈RNdrive-joint ×6Ncnt
:torque-task-jacobian-with-phi [method]
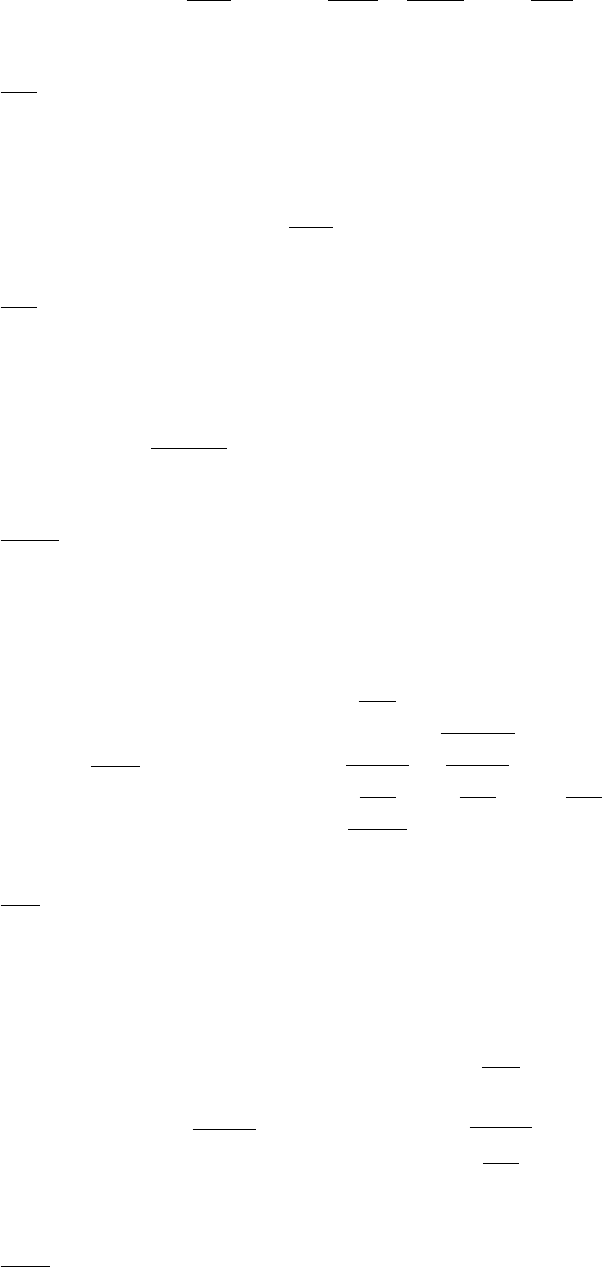
14
∂etrq
∂ϕ=
Ncnt
m=1
∂τcnt
m
∂ϕ−∂τgrav
m
∂ϕ+
Nex
m=1
∂τex
m
∂ϕ(2.43)
return ∂etrq
∂ϕ∈RNdrive-joint ×Ninvar -joint
:torque-task-jacobian-with-torque [method]
∂etrq
∂τ=INdrive-joint (2.44)
return ∂etrq
∂τ∈RNdrive-joint ×Ndrive-joint
:posture-task-jacobian-with-theta &key (update? nil) [method]
∂eposture
∂θi,j
=−kposture (Jposture,i=Jvar ,j)
0 otherwise (2.45)
return ∂eposture
∂θ∈RNposture-joint ×Nvar -joint
:variant-task-jacobian [method]
∂e
∂qvar
=
Nvar-joint 6Ncnt Ndrive-joint
6Nkin ∂ekin
∂θ
3∂eeom-trans
∂ˆw
3∂eeom-rot
∂θ
∂eeom-rot
∂ˆw
Ndrive-joint ∂etrq
∂θ
∂etrq
∂ˆw
∂etrq
∂τ
Nposture-joint ∂eposture
∂θ
(2.46)
return ∂e
∂qvar ∈R(6Nkin +3+3+Ndrive-joint +Nposture-joint )×(Nvar -joint +6Ncnt +Ndrive-joint )
:invariant-task-jacobian [method]
∂e
∂qinvar
=
Ninvar-joint
6Nkin ∂ekin
∂ϕ
3
3∂eeom-rot
∂ϕ
Ndrive-joint ∂etrq
∂ϕ
Nposture-joint
(2.47)
return ∂e
∂qinvar ∈R(6Nkin +3+3+Ndrive-joint +Nposture-joint )×Ninvar -joint
:task-jacobian [method]
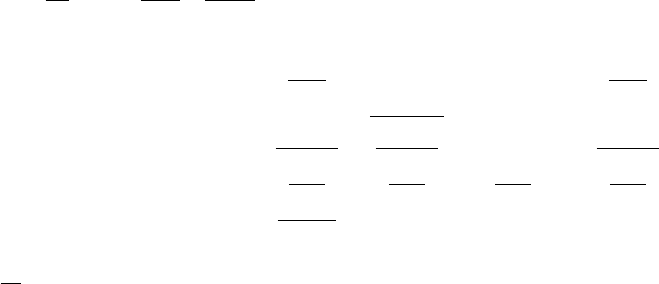
15
∂e
∂q=∂e
∂qvar
∂e
∂qinvar (2.48)
=
Nvar-joint 6Ncnt Ndrive-joint Ninvar -joint
6Nkin ∂ekin
∂θ
∂ekin
∂ϕ
3∂eeom-trans
∂ˆw
3∂eeom-rot
∂θ
∂eeom-rot
∂ˆw
∂eeom-rot
∂ϕ
Ndrive-joint ∂etrq
∂θ
∂etrq
∂ˆw
∂etrq
∂τ∂etrq
∂ϕ
Nposture-joint ∂eposture
∂θ
(2.49)
return ∂e
∂q∈R(6Nkin +3+3+Ndrive-joint +Nposture-joint )×(Nvar -joint +6Ncnt +Ndrive-joint +Ninvar-joint )
:theta-max-vector &key (update? nil) [method]
return θmax ∈RNvar-joint
:theta-min-vector &key (update? nil) [method]
return θmin ∈RNvar-joint
:delta-theta-limit-vector &key (update? nil) [method]
get trust region of θ
return ∆θlimit
:theta-inequality-constraint-matrix &key (update? nil) [method]
θmin ≤θ+ ∆θ≤θmax
−∆θlimit ≤∆θ≤∆θlimit (if ∆θlimit is set) (2.50)
⇔
I
−I
I
−I
∆θ≥
θmin −θ
−(θmax −θ)
−∆θlimit
−∆θlimit
(2.51)
⇔Cθ∆θ≥dθ(2.52)
return Cθ:=
I
−I
I
−I
∈R4Nvar-joint ×Nvar -joint
:theta-inequality-constraint-vector &key (update? t) [method]
return dθ:=
θmin −θ
−(θmax −θ)
−∆θlimit
−∆θlimit
∈R4Nvar-joint
:wrench-inequality-constraint-matrix &key (update? t) [method]
接触レンチ w∈R6が満たすべき制約(非負制約,摩擦制約,圧力中心制約)が次式のように表される
とする.
Cww≥dw(2.53)
16
Ncnt 箇所の接触部位の接触レンチを並べたベクトル ˆwの不等式制約は次式で表される.
Cw,m(wm+ ∆wm)≥dw,m (m= 1,2,· · · , Ncnt ) (2.54)
⇔Cw,m∆wm≥dw,m −Cw,mwm(m= 1,2,· · · , Ncnt ) (2.55)
⇔
Cw,1
Cw,2
...
Cw,Ncnt
∆w1
∆w2
.
.
.
∆wNcnt
≥
dw,1−Cw,1w1
dw,2−Cw,2w2
.
.
.
dw,Ncnt −Cw,Ncnt wNcnt
(2.56)
⇔Cˆw∆ˆw≥dˆw(2.57)
return Cˆw:=
Cw,1
Cw,2
...
Cw,Ncnt
∈RNwrench-ineq ×dim(ˆw)
:wrench-inequality-constraint-vector &key (update? t) [method]
return dˆw:=
dw,1−Cw,1w1
dw,2−Cw,2w2
.
.
.
dw,Ncnt −Cw,Ncnt wNcnt
∈RNwrench-ineq
:torque-max-vector &key (update? nil) [method]
return τmax ∈RNdrive-joint
:torque-min-vector &key (update? nil) [method]
return τmin ∈RNdrive-joint
:torque-inequality-constraint-matrix &key (update? nil) [method]
τmin ≤τ+ ∆τ≤τmax (2.58)
⇔I
−I∆τ≥τmin −τ
−(τmax −τ)(2.59)
⇔Cτ∆τ≥dτ(2.60)
return Cτ:= I
−I∈R2Ndrive-joint ×Ndrive-joint
:torque-inequality-constraint-vector &key (update? t) [method]
return dτ:= τmin −τ
−(τmax −τ)∈R2Ndrive-joint
:phi-max-vector &key (update? nil) [method]
return ϕmax ∈RNinvar-joint
:phi-min-vector &key (update? nil) [method]
return ϕmin ∈RNinvar-joint
:delta-phi-limit-vector &key (update? nil) [method]
get trust region of ϕ
return ∆ϕlimit
17
:phi-inequality-constraint-matrix &key (update? nil) [method]
ϕmin ≤ϕ+ ∆ϕ≤ϕmax
−∆ϕlimit ≤∆ϕ≤∆ϕlimit (if ∆ϕlimit is set) (2.61)
⇔
I
−I
I
−I
∆ϕ≥
ϕmin −ϕ
−(ϕmax −ϕ)
−∆ϕlimit
−∆ϕlimit
(2.62)
⇔Cϕ∆ϕ≥dϕ(2.63)
return Cϕ:=
I
−I
I
−I
∈R4Ninvar-joint ×Ninvar -joint
:phi-inequality-constraint-vector &key (update? t) [method]
return dϕ:=
ϕmin −ϕ
−(ϕmax −ϕ)
−∆ϕlimit
−∆ϕlimit
∈R4Ninvar-joint
:variant-config-inequality-constraint-matrix &key (update? nil) [method]
Cθ∆θ≥dθ
Cˆw∆ˆw≥dˆw
Cτ∆τ≥dτ
(2.64)
⇔
Cθ
Cˆw
Cτ
∆θ
∆ˆw
∆τ
≥
dθ
dˆw
dτ
(2.65)
⇔Cvar ∆qvar ≥dvar (2.66)
return Cvar :=
Cθ
Cˆw
Cτ
∈RNvar-ineq ×dim(qvar )
:variant-config-inequality-constraint-vector &key (update? t) [method]
return dvar :=
dθ
dˆw
dτ
∈RNvar-ineq
:invariant-config-inequality-constraint-matrix &key (update? nil) [method]
Cϕ∆ϕ≥dϕ(2.67)
⇔Cinvar ∆qinvar ≥dinvar (2.68)
return Cinvar := Cϕ∈RNinvar-ineq ×dim(qinvar )
:invariant-config-inequality-constraint-vector &key (update? t) [method]

18
return dinvar := dϕ∈RNinvar-ineq
:config-inequality-constraint-matrix &key (update? nil) [method]
(update-collision? nil)
Cvar ∆qvar ≥dvar
Cinvar ∆qinvar ≥dinvar
Ccol ∆qvar
∆qinvar ≥dcol
(2.69)
⇔
Cvar
Cinvar
Ccol
∆qvar
∆qinvar ≥
dvar
dinvar
dcol
(2.70)
⇔C∆q≥d(2.71)
return C:=
Cvar
Cinvar
Ccol
∈RNineq ×dim(q)
:config-inequality-constraint-vector &key (update? t) [method]
(update-collision? nil)
return d:=
dvar
dinvar
dcol
∈RNineq
:variant-config-equality-constraint-matrix &key (update? nil) [method]
return Avar ∈R0×dim(qvar )(no equality constraint)
:variant-config-equality-constraint-vector &key (update? t) [method]
return bvar ∈R0(no equality constraint)
:invariant-config-equality-constraint-matrix &key (update? nil) [method]
return Ainvar ∈R0×dim(qinvar )(no equality constraint)
:invariant-config-equality-constraint-vector &key (update? t) [method]
return binvar ∈R0(no equality constraint)
:config-equality-constraint-matrix &key (update? nil) [method]
return A∈R0×dim(q)(no equality constraint)
:config-equality-constraint-vector &key (update? t) [method]
return b∈R0(no equality constraint)
:torque-regular-matrix &key (update? nil) [method]
(only-variant? nil)
二次形式の正則化項として次式を考える.
Ftau (q) =
τ
τmax
2
(ベクトルの要素ごとの割り算を表す) (2.72)
=τT¯
Wtrq τ(2.73)

19
ここで,
¯
Wtrq :=
1
τ2
max ,1
1
τ2
max ,2
...
1
τ2
max ,Ndrive-joint
∈Rdim(τ)×dim(τ)(2.74)
only-variant? is true:
Wtrq :=
dim(θ)dim(ˆw)dim(τ)
dim(θ)
dim(ˆw)
dim(τ)¯
Wtrq
∈Rdim(qvar )×dim(qvar )(2.75)
otherwise:
Wtrq :=
dim(θ)dim(ˆw)dim(τ)dim(ϕ)
dim(θ)
dim(ˆw)
dim(τ)¯
Wtrq
dim(ϕ)
∈Rdim(q)×dim(q)(2.76)
return Wtrq
:torque-regular-vector &key (update? t) [method]
(only-variant? nil)
¯vtrq := ¯
Wtrq τ(2.77)
=
τ1
τ2
max ,1
τ2
τ2
max ,2
.
.
.
τdim(τ)
τ2
max ,dim(τ)
∈Rdim(τ)(2.78)
only-variant? is true:
vtrq :=
1
dim(θ)
dim(ˆw)
dim(τ)¯vtrq
∈Rdim(qvar )(2.79)
otherwise:
vtrq :=
1
dim(θ)
dim(ˆw)
dim(τ)¯vtrq
dim(ϕ)
∈Rdim(q)(2.80)
return vtrq

20
:torque-ratio [method]
return τ
τmax :=
τ1
τmax ,1
τ2
τmax ,2
.
.
.
τNdrive-joint
τmax ,Ndrive-joint
:regular-matrix [method]
Wreg := min(kmax ,∥e∥2+koff )I+ktrq Wtrq (2.81)
return Wreg ∈Rdim(q)×dim(q)
:regular-vector [method]
vreg := ktrq vtrq (2.82)
return vreg ∈Rdim(q)
:update-collision-inequality-constraint [method]
リンク 1とリンク 2の最近点を p1,p2とする.リンク 1とリンク 2が干渉しない条件を,最近点 p1,p2
の距離が dmargin 以上である条件に置き換えて考える.これは次式で表される.
dT
12(p1−p2)≥dmargin (2.83)
where d12 =p1−p2(2.84)
コンフィギュレーションが ∆qだけ更新されてもこれが成立するための条件は次式で表される.
dT
12 {(p1+ ∆p1)−(p2+ ∆p2)} ≥ dmargin (2.85)
where ∆p1=Jθ,1∆θ+Jϕ,1∆ϕ(2.86)
∆p2=Jθ,2∆θ+Jϕ,2∆ϕ(2.87)
Jθ,i =∂pi
∂θ,Jϕ,i =∂pi
∂ϕ(i= 1,2) (2.88)
これは以下のように変形される.
dT
12 {(p1+Jθ,1∆θ+Jϕ,1∆ϕ)−(p2+Jθ,2∆θ+Jϕ,2∆ϕ)} ≥ dmargin (2.89)
⇔dT
12(Jθ,1−Jθ,2)∆θ+dT
12(Jϕ,1−Jϕ,2)∆ϕ≥ −(dT
12(p1−p2)−dmargin ) (2.90)
⇔cT
col ,var ∆θ+cT
col ,invar ∆ϕ≥dcol (2.91)
where cT
col ,var =dT
12(Jθ,1−Jθ,2) (2.92)
cT
col ,invar =dT
12(Jϕ,1−Jϕ,2) (2.93)
dcol =−(dT
12(p1−p2)−dmargin ) (2.94)
i番目の干渉回避リンクペアに関する行列,ベクトルをそれぞれ cT
col ,var ,i,cT
col ,invar ,i, dcol,iとする.i=

21
1,2,· · · , Ncol の全てのリンクペアにおいて干渉が生じないための条件は次式で表される.
Ccol ,θ Ccol,ϕ∆θ
∆ϕ≥dcol (2.95)
Ccol ,θ :=
cT
col ,var ,1
.
.
.
cT
col ,var ,Ncol
∈RNcol ×dim(θ)(2.96)
Ccol ,ϕ :=
cT
col ,invar ,1
.
.
.
cT
col ,invar ,Ncol
∈RNcol ×dim(ϕ),(2.97)
dcol :=
dcol ,1
.
.
.
dcol ,Ncol
∈RNcol (2.98)
update inequality matrix Ccol,θ,Ccol ,ϕ and inequality vector dcol for collision avoidance
:collision-theta-inequality-constraint-matrix [method]
return Ccol ,θ ∈RNcol ×dim(θ)
:collision-phi-inequality-constraint-matrix [method]
return Ccol ,ϕ ∈RNcol ×dim(ϕ)
:collision-inequality-constraint-matrix &key (update? nil) [method]
Ccol :=
dim(θ)dim(ˆw)dim(τ)dim(ϕ)
Ncol Ccol,θ O O Ccol ,ϕ (2.99)
return Ccol ∈RNcol ×dim(q)
:collision-inequality-constraint-vector &key (update? nil) [method]
return dcol ∈RNcol
:update-viewer [method]
Update viewer.
:print-status [method]
Print status.
2.2 軌道コンフィギュレーションと軌道タスク関数
trajectory-configuration-task [class]
:super propertied-object
:slots ( instant-config-task-list list of instant-config-task instance)
( num-instant-config-task L)
( dim-variant-config dim(qvar ))
( dim-invariant-config dim(qinvar ))
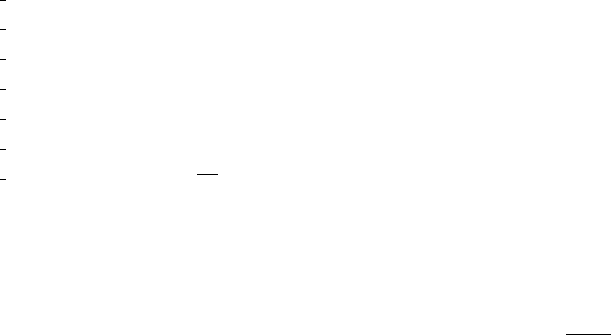
22
( dim-config dim(q))
( dim-task dim(e))
( norm-regular-scale-max kmax )
( norm-regular-scale-offset koff )
( adjacent-regular-scale kadj )
( torque-regular-scale ktrq )
( task-jacobi buffer for ∂e
∂q)
軌道コンフィギュレーション qと軌道タスク関数 e(q)のクラス.
以降では,説明文やメソッド名で,“軌道”や“trajectory” を省略する.
コンフィギュレーション qの取得・更新,タスク関数 e(q)の取得,タスク関数のヤコビ行列 ∂e(q)
∂qの取
得,コンフィギュレーションの等式・不等式制約 A,b,C,dの取得のためのメソッドが定義されている.
コンフィギュレーション・タスク関数を定めるために,初期化時に以下を与える
•瞬時のコンフィギュレーション・タスクのリスト
instant-config-task-list instant-configuration-task のリスト
•目的関数の重み
norm-regular-scale-max kmax コンフィギュレーション更新量正則化の重み最大値
norm-regular-scale-offset koff コンフィギュレーション更新量正則化の重みオフセット
adjacent-regular-scale kadj 隣接コンフィギュレーション正則化の重み
torque-regular-scale ktrq トルク正則化の重み
コンフィギュレーション qは以下から構成される.
q:= q(1)T
var q(2)T
var · · · q(L)T
var qT
invar T
(2.100)
ここで,
qinvar := q(1)
invar =q(2)
invar =· · · =q(L)
invar (2.101)
q(l)
var ,q(l)
invar (l= 1,2,· · · , L)はl番目の瞬時の時変,時不変コンフィギュレーションを表す.
タスク関数 e(q)は以下から構成される.
e(q) := e(1)T(q(1)
var ,qinvar )e(2)T(q(2)
var ,qinvar )··· e(L)T(q(L)
var ,qinvar )T
(2.102)
e(l)(q(l)
var ,qinvar ) (l= 1,2,· · · , L)はl番目の瞬時のタスク関数を表す.
:init &key (name) [method]
(instant-config-task-list)
(norm-regular-scale-max 1.000000e-04)
(norm-regular-scale-offset 1.000000e-07)
(adjacent-regular-scale 0.005)
(torque-regular-scale 0.001)
Initialize instance
:instant-config-task-list [method]
return instant-config-task-list
23
:dim-variant-config [method]
return dim(qvar ) := L
l=1 dim(q(l)
var )
:dim-invariant-config [method]
return dim(qinvar ) := dim(q(l)
invar ) (l= 1,2,· · · , L で同じ)
:dim-config [method]
return dim(q) := dim(qvar ) + dim(qinvar )
:dim-task [method]
return dim(e) := L
l=1 dim(e(l))
:variant-config-vector [method]
return qvar :=
q(1)
var
q(2)
var
.
.
.
q(L)
var
:invariant-config-vector [method]
return qinvar := q(l)
invar (l= 1,2,· · · , L で同じ)
:config-vector [method]
return q:= qvar
qinvar =
q(1)
var
q(2)
var
.
.
.
q(L)
var
qinvar
:set-variant-config variant-config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set qvar .
:set-invariant-config invariant-config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set qinvar .
:set-config config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set q.
:task-value &key (update? t) [method]
return e(q) :=
e(1)(q(1)
var ,qinvar )
e(2)(q(2)
var ,qinvar )
.
.
.
e(L)(q(L)
var ,qinvar )
:variant-task-jacobian [method]
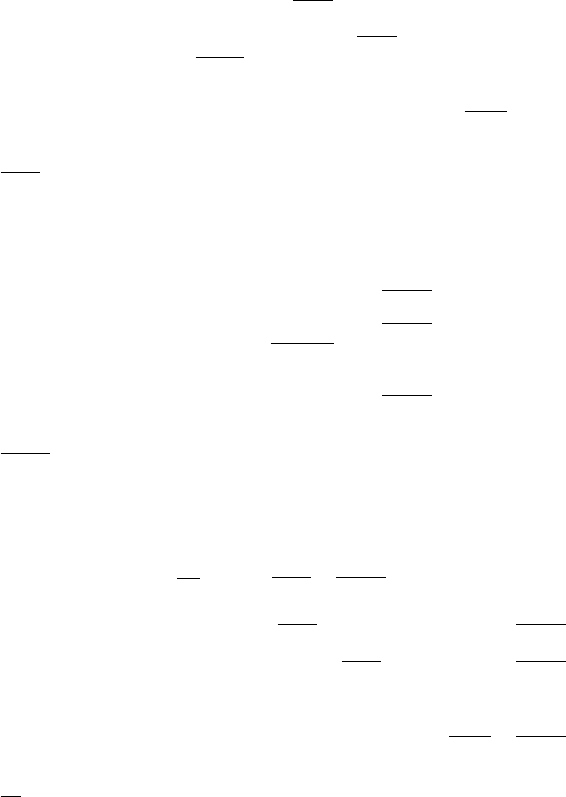
24
∂e
∂qvar
=
∂e(1)
∂q(1)
var
O
∂e(2)
∂q(2)
var
...
O∂e(L)
∂q(L)
var
(2.103)
return ∂e
∂qvar ∈Rdim(e)×dim(qvar )
:invariant-task-jacobian [method]
∂e
∂qinvar
=
∂e(1)
∂qinvar
∂e(2)
∂qinvar
.
.
.
∂e(L)
∂qinvar
(2.104)
return ∂e
∂qinvar ∈Rdim(e)×dim(qinvar )
:task-jacobian [method]
∂e
∂q=∂e
∂qvar
∂e
∂qinvar (2.105)
=
∂e(1)
∂q(1)
var
O∂e(1)
∂qinvar
∂e(2)
∂q(2)
var
∂e(2)
∂qinvar
...
O∂e(L)
∂q(L)
var
∂e(L)
∂qinvar
(2.106)
return ∂e
∂q∈Rdim(e)×dim(q)
:variant-config-inequality-constraint-matrix &key (update? nil) [method]
Cvar :=
C(1)
var O
C(2)
var
...
O C(L)
var
(2.107)
return Cvar ∈RNvar-ineq ×dim(qvar )
:variant-config-inequality-constraint-vector &key (update? t) [method]
dvar :=
d(1)
var
d(2)
var
.
.
.
d(L)
var
(2.108)
return dvar ∈RNvar-ineq

25
:invariant-config-inequality-constraint-matrix &key (update? nil) [method]
Cinvar := C(l)
invar (l= 1,2,· · · , L で同じ) (2.109)
return Cinvar ∈RNinvar-ineq ×dim(qinvar )
:invariant-config-inequality-constraint-vector &key (update? t) [method]
dinvar := d(l)
invar (l= 1,2,· · · , L で同じ) (2.110)
return dinvar ∈RNinvar-ineq
:config-inequality-constraint-matrix &key (update? nil) [method]
(update-collision? nil)
C:=
Cvar
Cinvar
Ccol
∈RNineq ×dim(q)(2.111)
return C∈RNineq ×dim(q)
:config-inequality-constraint-vector &key (update? t) [method]
(update-collision? nil)
d:=
dvar
dinvar
dcol
(2.112)
return d∈RNineq
:variant-config-equality-constraint-matrix &key (update? nil) [method]
Avar :=
A(1)
var O
A(2)
var
...
O A(L)
var
(2.113)
return Avar ∈RNvar-eq ×dim(qvar )
:variant-config-equality-constraint-vector &key (update? t) [method]
bvar :=
b(1)
var
b(2)
var
.
.
.
b(L)
var
(2.114)
return bvar ∈RNvar-eq
26
:invariant-config-equality-constraint-matrix &key (update? nil) [method]
Ainvar := A(l)
invar (l= 1,2,· · · , L で同じ) (2.115)
return Ainvar ∈RNinvar-eq ×dim(qinvar )
:invariant-config-equality-constraint-vector &key (update? t) [method]
binvar := b(l)
invar (l= 1,2,· · · , L で同じ) (2.116)
return binvar ∈RNinvar-eq
:config-equality-constraint-matrix &key (update? nil) [method]
A:= Avar
Ainvar ∈RNeq ×dim(q)(2.117)
return A∈RNeq ×dim(q)
:config-equality-constraint-vector &key (update? t) [method]
b:= bvar
binvar (2.118)
return b∈RNeq
:update-collision-inequality-constraint [method]
update inequality matrix C(l)
col ,θ ,C(l)
col ,ϕ and inequality vector d(l)
col for collision avoidance (l= 1,2,· · · , L)
:collision-inequality-constraint-matrix &key (update? nil) [method]
ˆ
C(l)
col ,θ :=
dim(θ(l))dim(ˆw(l))dim(τ(l))
N(l)
col C(l)
col ,θ O O (2.119)
Ccol :=
ˆ
C(1)
col ,θ C(1)
col ,ϕ
ˆ
C(2)
col ,θ C(2)
col ,ϕ
....
.
.
ˆ
C(L)
col ,θ C(L)
col ,ϕ
(2.120)
return Ccol ∈RNcol ×dim(q)
:collision-inequality-constraint-vector &key (update? nil) [method]
dcol :=
d(1)
col
d(2)
col
.
.
.
d(L)
col
(2.121)
return dcol ∈RNcol
27
:adjacent-regular-matrix &key (update? nil) [method]
二次形式の正則化項として次式を考える.
Fadj (q) =
L−1
l=1
∥θl+1 −θl∥2(2.122)
=qTWadj q(2.123)
ここで,
¯
Iadj :=
dim(θ(l))dim(ˆw(l))dim(τ(l))
dim(θ(l))I
dim(ˆw(l))
dim(τ(l))
∈Rdim(q(l)
var )×dim(q(l)
var )(2.124)
¯
Wadj :=
¯
Iadj −¯
Iadj
−¯
Iadj 2¯
Iadj −¯
Iadj O
...
−¯
Iadj 2¯
Iadj −¯
Iadj
O−¯
Iadj ¯
Iadj
∈Rdim(qvar )×dim(qvar )
(2.125)
Wadj := ¯
Wadj
O(2.126)
return Wadj ∈Rdim(q)×dim(q)
:adjacent-regular-vector &key (update? t) [method]
vadj := Wadj q(2.127)
return vadj ∈Rdim(q)
:torque-regular-matrix &key (update? nil) [method]
¯
Wtrq :=
W(1)
trq O
W(2)
trq
...
O W (L)
trq
∈Rdim(qvar )×dim(qvar )(2.128)
Wtrq := ¯
Wtrq
O(2.129)
return Wtrq ∈Rdim(q)×dim(q)
:torque-regular-vector &key (update? t) [method]
¯vtrq :=
v(1)
trq
v(2)
trq
.
.
.
v(L)
trq
∈Rdim(qvar )(2.130)
vtrq := ¯vtrq
0(2.131)

28
return vtrq ∈Rdim(q)
:regular-matrix [method]
Wreg := min(kmax ,∥e∥2+koff )I+kadj Wadj +ktrq Wtrq (2.132)
return Wreg ∈Rdim(q)×dim(q)
:regular-vector [method]
vreg := kadj vadj +ktrq vtrq (2.133)
return vreg ∈Rdim(q)
:update-viewer [method]
Update viewer.
:print-status [method]
Print status.
:play-animation &key (robot-env) [method]
(loop? t)
(visualize-callback-func)
Play motion.
:generate-robot-state-list &key (robot-env) [method]
(joint-name-list (send-all (send robot-env :robot :joint-list) :name))
(root-link-name (send (car (send robot-env :robot :links)) :name))
(step-time 0.004)
(divide-num 100)
(limb-list (list :rleg :lleg :rarm :larm))
Generate and return robot state list.
3勾配を用いた制約付き非線形最適化
3.1 逐次二次計画法
sqp-optimization [class]
:super propertied-object
:slots ( config-task instance of configuration-task)
( qp-retval buffer for QP return value)
( qp-status buffer for QP status)
( qp-int-status QP status)
( task-value buffer for task value e(q))
( task-jacobian buffer for task jacobian ∂e
∂q)

29
( dim-config-buf-matrix matrix buffer)
( convergence-check-func function to check convergence)
( failure-callback-func callback function of failure)
( pre-process-func pre-process function)
( post-process-func post-process function)
( i buffer for iteration count)
( status status of sqp optimization)
( no-visualize? whether to supress visualization)
( no-print? whether to supress print)
逐次二次計画法のクラス.
instant-configuration-task クラスや trajectory-configuration-task クラスの instance (以降,configuration-
task と呼ぶ)が与えられた時に,configuration-task のタスク関数ノルム二乗 ∥e(q)∥2を最小にするコン
フィギュレーション qを反復計算により求める.
:init &key (config-task) [method]
(convergence-check-func)
(failure-callback-func)
(pre-process-func)
(post-process-func)
(no-visualize?)
(no-print?)
&allow-other-keys
Initialize instance
:config-task [method]
Return configuration-task instance
:optimize &key (loop-num 100) [method]
(loop-num-min)
(update-viewer-interval 1)
(print-status-interval 10)
Optimize
In each iteration, do following:
1. check convergence
2. call pre-process function
3. print status
4. solve QP and update configuration
5. call post-process function

30
Solve following QP:
min
∆q(k)
1
2∆q(k)TW∆q(k)+vT∆q(k)(3.1)
s.t.A∆q(k)=b(3.2)
C∆q(k)≥d(3.3)
where W=∂e(q(k))
∂q(k)T∂e(q(k))
∂q(k)+Wreg (3.4)
v=∂e(q(k))
∂q(k)T
e(q(k)) + vreg (3.5)
and update configuration:
q(k+1) =q(k)+ ∆q(k)∗(3.6)
:iteration [method]
Return iteration index.
:status [method]
Return status of sqp optimization.
3.2 複数解候補を用いた逐次二次計画法
3.2.1 複数解候補を用いた逐次二次計画法の理論
式(1.4a) の最適化問題に逐次二次計画法などの制約付き非線形最適化手法を適用すると,初期値から勾配方
向に進行して至る局所最適解が得られると考えられる.したがって解は初期値に強く依存する.
式(1.4a) の代わりに,以下の最適化問題を考える.
min
ˆq
i∈I F(q(i)) + kmsc Fmsc (ˆq;i)(3.7)
s.t.Aq(i)=¯
bi∈ I (3.8)
Cq(i)≥¯
di∈ I (3.9)
where ˆqdef
=q(1)Tq(2)T· · · q(Nmsc )TT
(3.10)
Idef
={1,2,· · · , Nmsc }(3.11)
Fmsc (ˆq;i)def
=−1
2
j∈I
j̸=i
log ∥d(q(i),q(j))∥2(3.12)
d(q(i),q(j))def
=q(i)−q(j)(3.13)
Nmsc は解候補の個数で,事前に与えるものとする.msc は複数解候補 (multiple solution candidates) を表す.
これは,複数の解候補を同時に探索し,それぞれの解候補 q(i)が本来の目的関数 F(q(i))を小さくして,なお
かつ,解候補どうしの距離が大きくなるように最適化することを表している.これにより,初期値に依存した
唯一の局所解だけでなく,そこから離れた複数の局所解を得ることが可能となり,通常の最適化に比べてより
良い解が得られることが期待される.以降では,解候補どうしの距離のコストを表す項 Fmsc (ˆq;i)を解候補分
散項と呼ぶ 8.
8解分散項の log を無くすことは適切ではない.なぜなら,d=∥d(q(i),q(j))∥として,解分散項の勾配は,
∂
∂d (−1
2log d2)=−1
d→ −∞ (d→+0) ∂
∂d (−1
2log d2)=−1
d→0 (d→ ∞) (3.14)
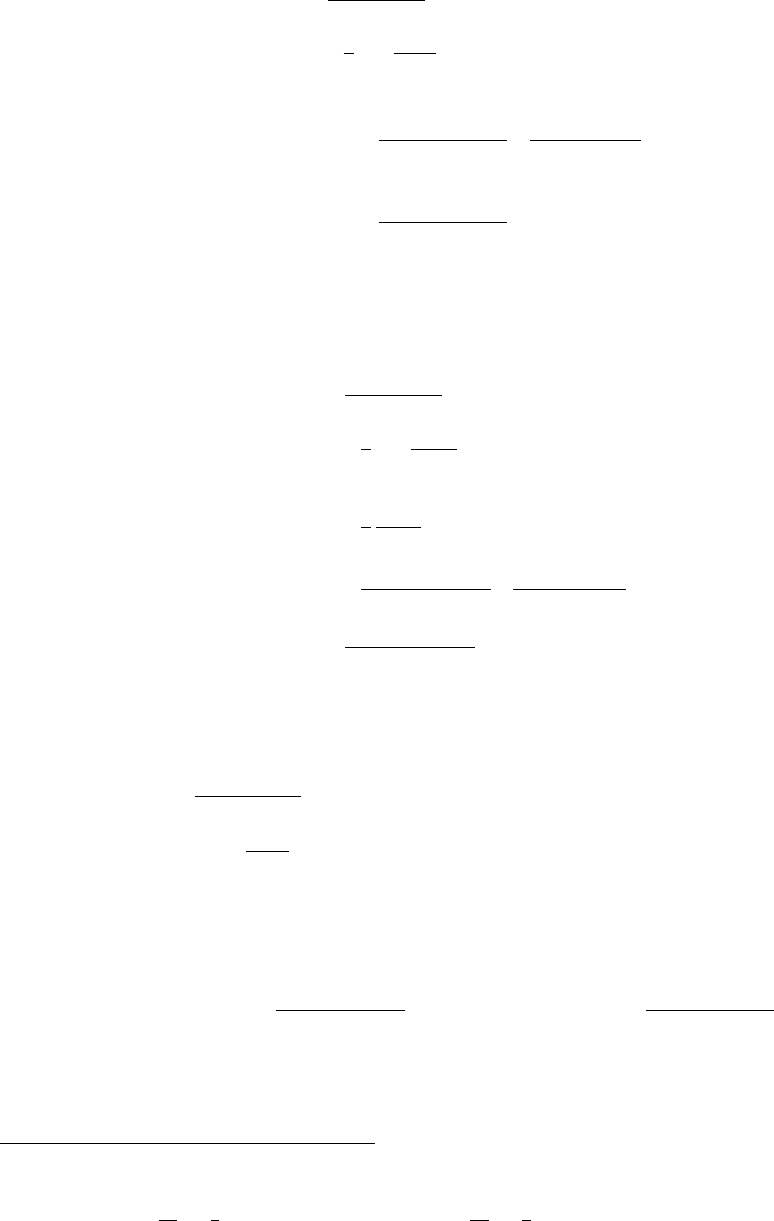
31
解候補分散項のヤコビ行列,ヘッセ行列の各成分は次式で得られる 9.
∇iFmsc (ˆq;i) = ∂Fmsc (ˆq;i)
∂q(i)(3.16a)
=−1
2
j∈I
j̸=i
∂
∂q(i)log ∥d(q(i),q(j))∥2(3.16b)
=−
j∈I
j̸=i
1
∥d(q(i),q(j))∥2∂d(q(i),q(j))
∂q(i)T
d(q(i),q(j)) (3.16c)
=−
j∈I
j̸=i
d(q(i),q(j))
∥d(q(i),q(j))∥2(3.16d)
(3.16e)
∇kFmsc (ˆq;i) = ∂Fmsc (ˆq;i)
∂q(k)k∈ I ∧ k̸=i(3.17a)
=−1
2
j∈I
j̸=i
∂
∂q(k)log ∥d(q(i),q(j))∥2(3.17b)
=−1
2
∂
∂q(k)log ∥d(q(i),q(k))∥2(3.17c)
=−1
∥d(q(i),q(k))∥2∂d(q(i),q(k))
∂q(k)T
d(q(i),q(k)) (3.17d)
=d(q(i),q(k))
∥d(q(i),q(k))∥2(3.17e)
(3.17f)
∇2
iiFmsc (ˆq;i) = ∂2Fmsc (ˆq;i)
∂q(i)2 (3.18a)
=−
j∈I
j̸=i
∂
∂q(i)∥d(q(i),q(j))∥2−1
d(q(i),q(j))(3.18b)
=−
j∈I
j̸=i−2∥d(q(i),q(j))∥2−2
d(q(i),q(j))d(q(i),q(j))T+∥d(q(i),q(j))∥2−1
I
(3.18c)
=−
j∈I
j̸=i−2
∥d(q(i),q(j))∥4d(q(i),q(j))d(q(i),q(j))T+1
∥d(q(i),q(j))∥2I(3.18d)
=−
j∈I
j̸=i
H(q(i),q(j)) (3.18e)
となり,最適化により,コンフィギュレーションが近いときほど離れるように更新し,遠くなるとその影響が小さくなる効果が期待され
る.それに対し,log がない場合の勾配は,
∂
∂d (−1
2d2)=−d→0 (d→+0) ∂
∂d (−1
2d2)=−d→ −∞ (d→ ∞) (3.15)
となり,コンフィギュレーションが遠くなるほど離れるように更新し,近いときはその影響が小さくなる.これは,コンフィギュレーショ
ンが一致する勾配ゼロの点と,無限に離れ発散する最適値をもち,これらは最適化において望まない挙動をもたらす.
9ヘッセ 行 列 の 導 出 は 以 下 を 参 考 に し た .https://math.stackexchange.com/questions/175263/
gradient-and-hessian-of-general-2-norm
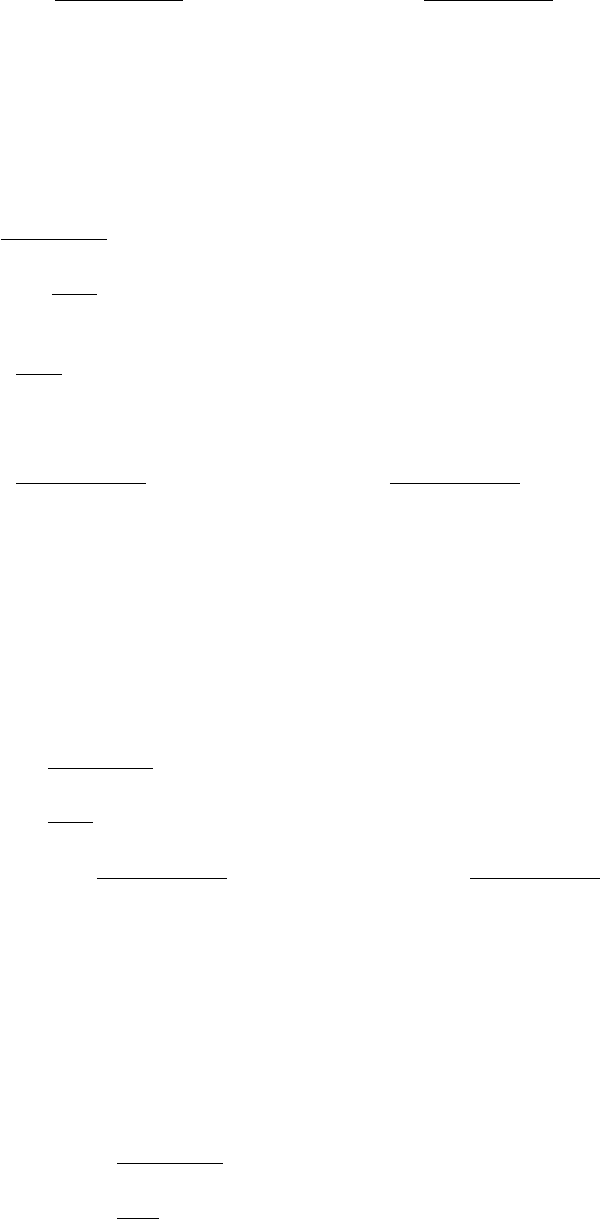
32
ただし,
H(q(i),q(j))def
=−2
∥d(q(i),q(j))∥4d(q(i),q(j))d(q(i),q(j))T+1
∥d(q(i),q(j))∥2I(3.19)
∇2
ikFmsc (ˆq;i) = ∂2Fmsc (ˆq;i)
∂q(i)∂q(k)k∈ I ∧ k̸=i(3.20a)
=−
j∈I
j̸=i
∂
∂q(k)∥d(q(i),q(j))∥2−1
d(q(i),q(j))(3.20b)
=−∂
∂q(k)∥d(q(i),q(k))∥2−1
d(q(i),q(k))(3.20c)
=−2∥d(q(i),q(k))∥2−2
d(q(i),q(k))d(q(i),q(k))T−∥d(q(i),q(k))∥2−1
I
(3.20d)
=−2
∥d(q(i),q(k))∥4d(q(i),q(k))d(q(i),q(k))T+1
∥d(q(i),q(k))∥2I(3.20e)
=H(q(i),q(k)) (3.20f)
∇2
kk Fmsc (ˆq;i) = ∂2Fmsc (ˆq;i)
∂q(k)2 k∈ I ∧ k̸=i(3.21a)
=∂
∂q(k)∥d(q(i),q(k))∥2−1
d(q(i),q(k))(3.21b)
=−−2
∥d(q(i),q(k))∥4d(q(i),q(k))d(q(i),q(k))T+1
∥d(q(i),q(k))∥2I(3.21c)
=−H(q(i),q(k)) (3.21d)
∇2
klFmsc (ˆq;i) = ∂2Fmsc (ˆq;i)
∂q(k)∂q(l)k∈ I ∧ l∈ I ∧ k̸=i∧l̸=i∧k̸=l(3.22a)
=∂
∂q(l)∥d(q(i),q(k))∥2−1
d(q(i),q(k))(3.22b)
=O(3.22c)

33
したがって,解候補分散項のヤコビ行列,ヘッセ行列は次式で表される.
∇Fmsc (ˆq;i) = ∂Fmsc (ˆq;i)
∂ˆq(3.23a)
=
d(q(i),q(1))
∥d(q(i),q(1))∥2
.
.
.
d(q(i),q(i−1))
∥d(q(i),q(i−1))∥2
−j∈I
j̸=i
d(q(i),q(j))
∥d(q(i),q(j))∥2
d(q(i),q(i+1))
∥d(q(i),q(i+1))∥2
.
.
.
d(q(i),q(Nmsc ))
∥d(q(i),q(Nmsc ))∥2
(3.23b)
vmsc
def
=
i∈I
∇Fmsc (ˆq;i) (3.23c)
= 2
−j∈I
j̸=1
d(q(1),q(j))
∥d(q(1),q(j))∥2
.
.
.
−j∈I
j̸=Nmsc
d(q(Nmsc ),q(j))
∥d(q(Nmsc ),q(j))∥2
(3.23d)
∇2Fmsc (ˆq;i) = ∂2Fmsc (ˆq;i)
∂ˆq2(3.24a)
=
1· · · i−1i i + 1 ··· Nmsc
1−Hi,1Hi,1
.
.
.....
.
.
i−1−Hi,i−1Hi,i−1
iHi,1· · · Hi,i−1−j∈I
j̸=i
Hi,j Hi,i+1 ··· Hi,Nmsc
i+ 1 Hi,i+1 −Hi,i+1
.
.
..
.
....
Nmsc Hi,Nmsc −Hi,Nmsc
(3.24b)
Wmsc
def
=
i∈I
∇2Fmsc (ˆq;i) (3.24c)
= 2
−j∈I
j̸=i
H1,j H1,2· · · H1,Nmsc
H2,1−j∈I
j̸=i
H2,j H2,Nmsc
.
.
.....
.
.
HNmsc ,1HNmsc ,2· · · − j∈I
j̸=i
HNmsc ,j
(3.24d)
ただし,H(q(i),q(j))をHi,j と略して記す.また,d(q(i),q(j)) = −d(q(j),q(i)),Hi,j =Hj,i を利用した.
解候補分散項 i∈I Fmsc (ˆq;i)による二次計画問題の目的関数 (式(1.5a) ) は次式で表される.
i∈I Fmsc (ˆqk;i) + ∇Fmsc (ˆqk;i)T∆ˆqk+1
2∆ˆqT
k∇2Fmsc (ˆqk;i)∆ˆqk(3.25)
=
i∈I
Fmsc (ˆqk;i) +
i∈I
∇Fmsc (ˆqk;i)T
∆ˆqk+1
2∆ˆqT
k
i∈I
∇2Fmsc (ˆqk;i)∆ˆqk(3.26)
=
i∈I
Fmsc (ˆqk;i) + vT
msc ∆ˆqk+1
2∆ˆqT
kWmsc ∆ˆqk(3.27)

34
Wmsc が必ずしも半正定値行列ではないことに注意する必要がある.以下のようにして Wmsc に近い正定
値行列を計算し用いることで対処する 10.Wmsc が次式のように固有値分解されるとする.
Wmsc =Vmsc Dmsc V−1
msc (3.28)
ただし,Dmsc は固有値を対角成分にもつ対角行列,Vmsc は固有ベクトルを並べた行列である.このとき Wmsc
に近い正定値行列 ˜
Wmsc は次式で得られる.
˜
Wmsc =Vmsc D+
msc V−1
msc (3.29)
ただし,D+
msc はDmsc の対角成分のうち,負のものを 0で置き換えた対角行列である.
式(3.7) において,解候補を分散させながら,最終的に本来の目的関数を最小にする解を得るために,SQP
のイテレーションごとに,解候補分散項のスケール kmsc を次式のように更新することが有効である.
kmsc ←min(γmsc kmsc , kmsc-min ) (3.30)
γmsc は0< γmsc <1なるスケール減少率,kmsc-min はスケール最小値を表す.
3.2.2 複数解候補を用いた逐次二次計画法の実装
sqp-msc-optimization [class]
:super sqp-optimization
:slots ( num-msc number of multiple solution candidates Nmsc )
( config-task-list list of configuration-task instance)
( dispersion-scale kmsc )
( dispersion-scale-min kmsc-min , minimum of kmsc )
( dispersion-scale-decrease-ratio γmsc , decrease ration of kmsc )
( config-vector-dist2-min minimum squared distance of configuration vector)
( dispersion-matrix buffer for Wmsc )
複数回候補を用いた逐次二次計画法のクラス.
instant-configuration-task クラスや trajectory-configuration-task クラスの instance (以降,configuration-
task と呼ぶ)が与えられた時に,configuration-task のタスク関数ノルム二乗 ∥e(q)∥2を最小にするコン
フィギュレーション qを,複数の解候補を同時に考慮しながら反復計算により求める.
:init &rest args &key (num-msc 3) [method]
(dispersion-scale 0.01)
(dispersion-scale-min 0.0)
(dispersion-scale-decrease-ratio 0.5)
(config-vector-dist2-min 1.000000e-10)
&allow-other-keys
Initialize instance
:config-task-list [method]
Return list of configuration-task instance
10Wmsc が対称行列であることから,以下を参考にした.https://math.stackexchange.com/questions/648809/
how-to-find-closest-positive-definite-matrix-of-non-symmetric-matrix#comment1689831_649522

35
:dispersion-matrix [method]
式(3.23d) 参照.
return Wmsc ∈RNmsc dim(q)×Nmsc dim(q)
:dispersion-vector [method]
式(3.24d) 参照.
return vmsc ∈RNmsc dim(q)
4動作生成の拡張
4.1 マニピュレーションの動作生成
robot-object-environment [class]
:super robot-environment
:slots ( obj O)
( obj-with-root-virtual ˆ
O)
ロボットと物体とロボット・環境間の接触のクラス.
以下を合わせた関節・リンク構造に関するメソッドが定義されている.
1. 浮遊ルートリンクのための仮想関節付きのロボットの関節
2. 物体位置姿勢を表す仮想関節
3. 接触位置を定める仮想関節
関節・リンク構造を定めるために,初期化時に以下を与える
robot Rロボット (cascaded-link クラスのインスタンス).
object O物体 (cascaded-link クラスのインスタンス).関節をもたないことを前提とする.
contact-list {C1,C2,· · · ,CNC}接触 (2d-planar-contact クラスなどのインスタンス)のリスト.
ロボット Rに,浮遊ルートリンクの変位に対応する仮想関節を付加した仮想関節付きロボット ˆ
Rを内部
で保持する.同様に,物体 Oに,物体の変位に対応する仮想関節を付加した仮想関節付き物体 ˆ
Oを内部
で保持する.
:init &key (robot) [method]
(object)
(contact-list)
(root-virtual-mode :6dof)
(root-virtual-joint-class-list)
(root-virtual-joint-axis-list)
Initialize instance
:object &rest args [method]
return O
:object-with-root-virtual &rest args [method]

36
return ˆ
O
instant-manipulation-configuration-task [class]
:super instant-configuration-task
:slots ( robot-obj-env robot-object-environment instance)
( wrench-obj-vector ˆwobj [N] [Nm])
( num-contact-obj Ncnt-obj := |T cnt -trg-obj |)
( num-act-react Nact-react := |Pact -react |)
( dim-wrench-obj dim(ˆwobj ) = 6Ncnt -obj )
( contact-target-coords-obj-list Tcnt-trg-obj )
( contact-constraint-obj-list list of contact-constraint instance for object)
( act-react-pair-list Pact -react )
マニピュレーションにける瞬時コンフィギュレーション q(l)と瞬時タスク関数 e(l)(q(l))のクラス.マニ
ピュレーション対象の物体の瞬時コンフィギュレーションや瞬時タスク関数を含む.
このクラスの説明で用いる全ての変数は,時間ステップ lを表す添字をつけて x(l)と表されるべきだが,
このクラス内の説明では省略して xと表す.また,以降では,説明文やメソッド名で,“瞬時”や“instant”
を省略する.
コンフィギュレーション qの取得・更新,タスク関数 e(q)の取得,タスク関数のヤコビ行列 ∂e(q)
∂qの取
得,コンフィギュレーションの等式・不等式制約 A,b,C,dの取得のためのメソッドが定義されている.
コンフィギュレーション・タスク関数を定めるために,instant-configuration-task の設定に加えて,初期
化時に以下を与える
•ロボット・物体・環境
robot-object-environment ロボット・物体・環境を表す robot-object-environment クラスのイ
ンスタンス
•物体の接触拘束
contact-target-coords-obj-list Tcnt-trg-obj 物体の接触目標位置姿勢リスト
contact-constraint-obj-list 物体の接触レンチ制約リスト
•作用・反作用の拘束
act-react-pair-list Pact-react 作用・反作用の関係にあるロボット・物体の接触目標位置姿勢ペア
のリスト
コンフィギュレーション qは以下から構成される.
θ∈RNvar-joint 時変関節角度 [rad] [m]
ˆw∈R6Ncnt ロボットの接触レンチ [N] [Nm]
ˆwobj ∈R6Ncnt -obj 物体の接触レンチ [N] [Nm]
τ∈RNdrive-joint 関節駆動トルク [Nm] [N]
ϕ∈RNinvar-joint 時不変関節角度 [rad] [m]
ˆwは次式のように,全接触部位でのワールド座標系での力・モーメントを並べたベクトルである.
ˆw=wT
1wT
2· · · wT
Ncnt T
(4.1)
=fT
1nT
1fT
2nT
2· · · fT
Ncnt nT
Ncnt T
(4.2)
37
タスク関数 e(q)は以下から構成される.
ekin (q)∈R6Nkin 幾何到達拘束 [rad] [m]
eeom -trans (q)∈R3ロボットの力の釣り合い [N]
eeom -rot (q)∈R3ロボットのモーメントの釣り合い [Nm]
eeom -trans-obj (q)∈R3物体の力の釣り合い [N]
eeom -rot-obj (q)∈R3物体のモーメントの釣り合い [Nm]
etrq (q)∈RNdrive -joint 関節トルクの釣り合い [rad] [m]
eposture (q)∈RNposture-joint 関節角目標 [rad] [m]
:init &rest args &key (contact-target-coords-obj-list) [method]
(contact-constraint-obj-list)
(act-react-pair-list)
&allow-other-keys
Initialize instance
:robot-obj-env [method]
return robot-object-environment instance
:wrench-obj [method]
return ˆwobj
:num-contact-obj [method]
return Ncnt-obj := |T cnt-trg-obj |
:dim-variant-config [method]
dim(qvar ) := dim(θ) + dim(ˆw) + dim(ˆwobj ) + dim(τ) (4.3)
=Nvar-joint + 6Ncnt + 6Ncnt-obj +Ndrive-joint (4.4)
return dim(qvar )
:dim-task [method]
dim(e) := dim(ekin ) + dim(eeom-trans ) + dim(eeom-rot ) + dim(eeom-trans-obj )
+dim(eeom-rot-obj ) + dim(etrq ) + dim(eposture ) (4.5)
= 6Nkin +3+3+3+3+Ndrive-joint +Nposture-joint (4.6)
return dim(e)
:variant-config-vector [method]
return qvar :=
θ
ˆw
ˆwobj
τ
:config-vector [method]
38
return q:= qvar
qinvar =
θ
ˆw
ˆwobj
τ
ϕ
:set-wrench-obj wrench-obj-new &key (relative? nil) [method]
Set ˆwobj .
:set-variant-config variant-config-new &key (relative? nil) [method]
(apply-to-robot? t)
Set qvar .
:contact-target-coords-obj-list [method]
Tcnt-trg-obj
m={pcnt-trg-obj
m,Rcnt-trg-obj
m}(m= 1,2,··· , Ncnt-obj ) (4.7)
return Tcnt-trg-obj := {Tcnt-trg-obj
1, T cnt-trg-obj
2,· · · , T cnt-trg-obj
Ncnt-obj }
:contact-constraint-obj-list [method]
return list of contact-constraint instance for object
:wrench-obj-list [method]
return {wobj ,1,wobj ,2,· · · ,wobj ,Nobj }
:force-obj-list [method]
return {fobj ,1,fobj ,2,· · · ,fobj ,Ncnt-obj }
:moment-obj-list [method]
return {nobj ,1,nobj ,2,· · · ,nobj ,Ncnt-obj }
:mg-obj-vec [method]
return mobj g
:cog-obj &key (update? t) [method]
return pGobj (q)
:eom-trans-obj-task-value &key (update? t) [method]
eeom -trans-obj (q) = eeom-trans-obj (ˆwobj ) (4.8)
=
Ncnt-obj
m=1
fobj ,m−mobj g(4.9)
return eeom -trans-obj (q)∈R3
:eom-rot-obj-task-value &key (update? t) [method]
eeom -rot-obj (q) = eeom -rot-obj (θ,ˆwobj ,ϕ) (4.10)
=
Ncnt-obj
m=1 pcnt-trg-obj
m(θ,ϕ)−pGobj (θ,ϕ)×fobj ,m+nobj ,m(4.11)
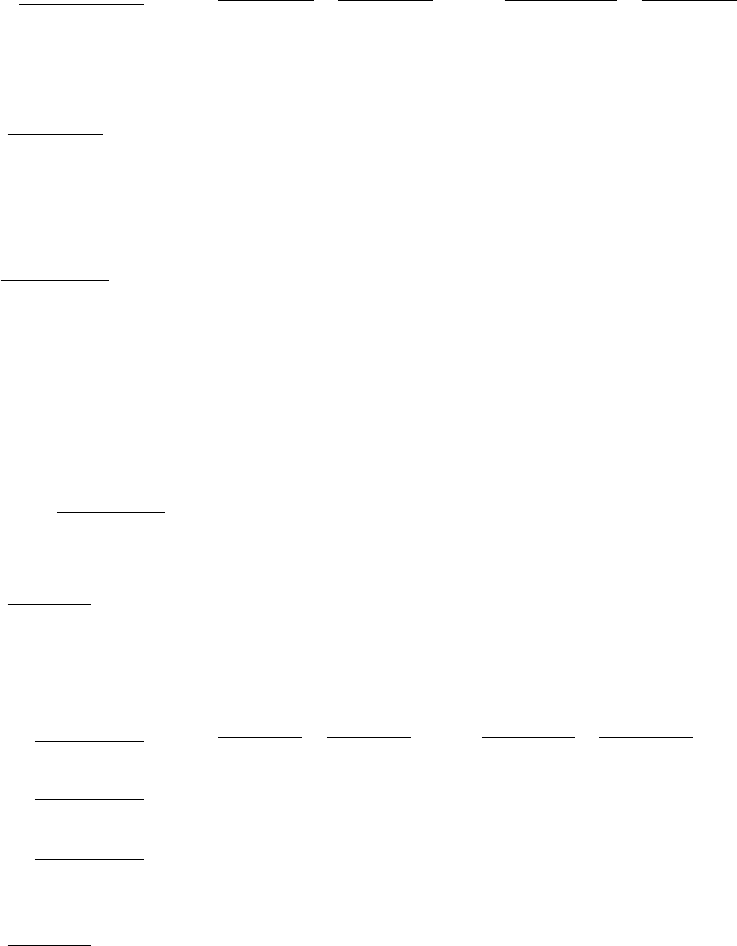
39
return eeom -rot-obj (q)∈R3
:task-value &key (update? t) [method]
return e(q) :=
ekin (q)
eeom -trans (q)
eeom -rot (q)
eeom -trans-obj (q)
eeom -rot-obj (q)
etrq (q)
eposture (q)
=
ekin (θ,ϕ)
eeom -trans (ˆw)
eeom -rot (θ,ˆw,ϕ)
eeom -trans-obj (ˆwobj )
eeom -rot-obj (θ,ˆwobj ,ϕ)
etrq (θ,ˆw,τ,ϕ)
eposture (θ)
:eom-trans-obj-task-jacobian-with-wrench-obj [method]
∂eeom -trans-obj
∂ˆwobj
=∂eeom-trans-obj
∂fobj ,1
∂eeom-trans-obj
∂nobj ,1··· ∂eeom-trans-obj
∂fobj ,Ncnt-obj
∂eeom-trans-obj
∂nobj ,Ncnt-obj (4.12)
=I3O3· · · I3O3(4.13)
return ∂eeom-trans-obj
∂ˆwobj
∈R3×6Ncnt-obj
:eom-rot-obj-task-jacobian-with-theta [method]
∂eeom -rot-obj
∂θ=
Ncnt-obj
m=1 −[fobj ,m×]Jcnt-trg-obj
θ,m (θ,ϕ)−JGobj θ(θ,ϕ) (4.14)
=
Ncnt-obj
m=1
fobj ,m
×
JGobj θ(θ,ϕ)−
Ncnt-obj
m=1
[fobj ,m×]Jcnt-trg-obj
θ,m (θ,ϕ) (4.15)
Ncnt-obj
m=1 fobj ,m=mobj gつまり,eom-trans-obj-task が成立すると仮定すると次式が成り立つ.
∂eeom -rot-obj
∂θ= [mobj g×]JGobj θ(θ,ϕ)−
Ncnt-obj
m=1
[fobj ,m×]Jcnt-trg-obj
θ,m (θ,ϕ) (4.16)
return ∂eeom-rot-obj
∂θ∈R3×Nvar-joint
:eom-rot-obj-task-jacobian-with-wrench-obj [method]
∂eeom -rot-obj
∂ˆwobj
=∂eeom-rot-obj
∂fobj ,1
∂eeom-rot-obj
∂nobj ,1· · · ∂eeom-rot-obj
∂fobj ,Ncnt-obj
∂eeom-rot-obj
∂nobj ,Ncnt-obj (4.17)
∂eeom -rot-obj
∂fobj ,m
=pcnt-trg-obj
m(θ,ϕ)−pGobj (θ,ϕ)×(m= 1,2,··· , Ncnt-obj ) (4.18)
∂eeom -rot-obj
∂nobj ,m
=I3(m= 1,2,· · · , Ncnt-obj ) (4.19)
return ∂eeom-rot-obj
∂ˆwobj ∈R3×6Ncnt-obj
:eom-rot-obj-task-jacobian-with-phi [method]
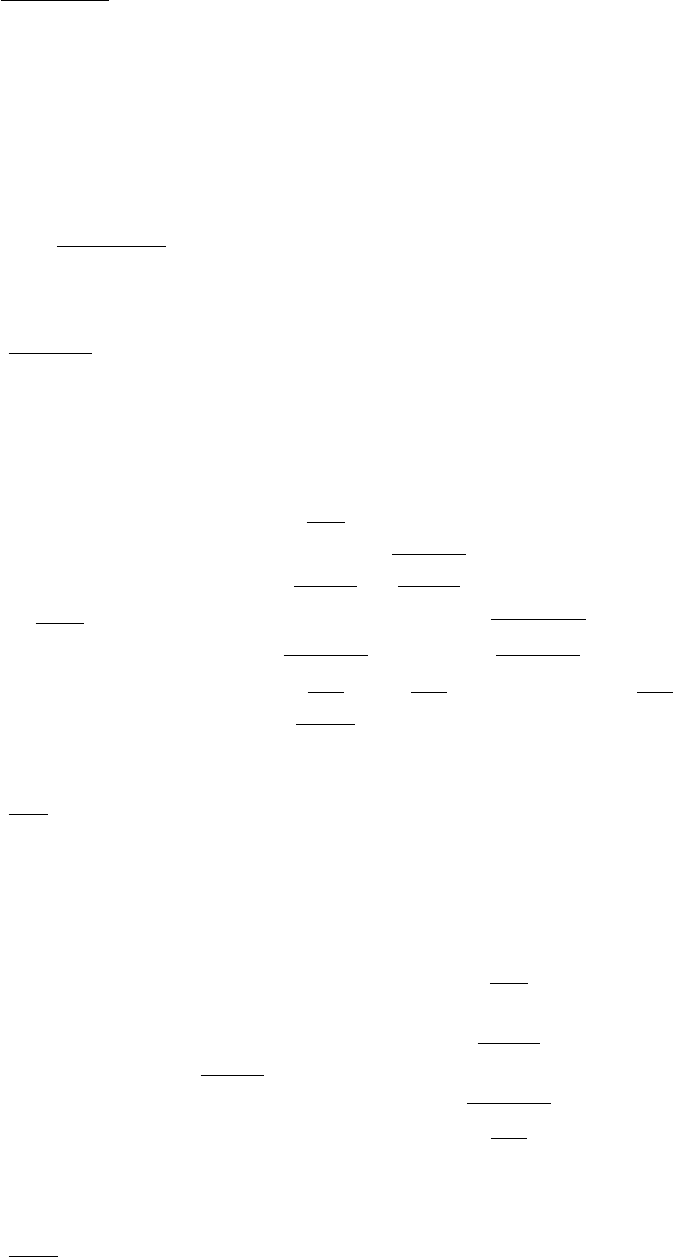
40
∂eeom -rot-obj
∂ϕ=
Ncnt-obj
m=1 −[fobj ,m×]Jcnt-trg-obj
ϕ,m (θ,ϕ)−JGobj ϕ(θ,ϕ) (4.20)
=
Ncnt-obj
m=1
fobj ,m
×
JGobj ϕ(θ,ϕ)−
Ncnt-obj
m=1
[fobj ,m×]Jcnt-trg-obj
ϕ,m (θ,ϕ)(4.21)
Ncnt-obj
m=1 fobj ,m=mobj gつまり,eom-trans-obj-task が成立すると仮定すると次式が成り立つ.
∂eeom -rot-obj
∂ϕ= [mobj g×]JGobj ϕ(θ,ϕ)−
Ncnt-obj
m=1
[fobj ,m×]Jcnt-trg-obj
ϕ,m (θ,ϕ) (4.22)
return ∂eeom-rot-obj
∂ϕ∈R3×Ninvar-joint
:variant-task-jacobian [method]
∂e
∂qvar
=
Nvar-joint 6Ncnt 6Ncnt-obj Ndrive-joint
6Nkin ∂ekin
∂θ
3∂eeom-trans
∂ˆw
3∂eeom-rot
∂θ
∂eeom-rot
∂ˆw
3∂eeom-trans-obj
∂ˆwobj
3∂eeom-rot-obj
∂θ
∂eeom-rot-obj
∂ˆwobj
Ndrive-joint ∂etrq
∂θ
∂etrq
∂ˆw
∂etrq
∂τ
Nposture-joint ∂eposture
∂θ
(4.23)
return ∂e
∂qvar ∈R(6Nkin +3+3+3+3+Ndrive-joint +Nposture-joint )×(Nvar -joint +6Ncnt +6Ncnt-obj +Ndrive-joint )
:invariant-task-jacobian [method]
∂e
∂qinvar
=
Ninvar-joint
6Nkin ∂ekin
∂ϕ
3
3∂eeom-rot
∂ϕ
3
3∂eeom-rot-obj
∂ϕ
Ndrive-joint ∂etrq
∂ϕ
Nposture-joint
(4.24)
return ∂e
∂qinvar ∈R(6Nkin +3+3+3+3+Ndrive-joint +Nposture-joint )×Ninvar -joint
:task-jacobian [method]
41
∂e
∂q=∂e
∂qvar
∂e
∂qinvar (4.25)
=
Nvar-joint 6Ncnt 6Ncnt-obj Ndrive-joint Ninvar -joint
6Nkin ∂ekin
∂θ
∂ekin
∂ϕ
3∂eeom-trans
∂ˆw
3∂eeom-rot
∂θ
∂eeom-rot
∂ˆw
∂eeom-rot
∂ϕ
3∂eeom-trans-obj
∂ˆwobj
3∂eeom-rot-obj
∂θ
∂eeom-rot-obj
∂ˆwobj
∂eeom-rot-obj
∂ϕ
Ndrive-joint ∂etrq
∂θ
∂etrq
∂ˆw
∂etrq
∂τ∂etrq
∂ϕ
Nposture-joint ∂eposture
∂θ
(4.26)
return ∂e
∂q∈R(6Nkin +3+3+3+3+Ndrive-joint +Nposture-joint )×(Nvar -joint +6Ncnt +6Ncnt-obj +Ndrive-joint +Ninvar -joint )
:wrench-obj-inequality-constraint-matrix &key (update? t) [method]
物体の接触レンチ wobj ∈R6が満たすべき制約(非負制約,摩擦制約,圧力中心制約)が次式のように
表されるとする.
Cwobj wobj ≥dwobj (4.27)
Ncnt-obj 箇所の接触部位の接触レンチを並べたベクトル ˆwobj の不等式制約は次式で表される.
Cwobj ,m(wobj ,m+ ∆wobj ,m)≥dwobj ,m (m= 1,2,··· , Ncnt -obj ) (4.28)
⇔Cwobj ,m∆wobj ,m≥dwobj ,m −Cwobj ,mwobj ,m(m= 1,2,··· , Ncnt-obj ) (4.29)
⇔
Cwobj ,1
Cwobj ,2
...
Cwobj ,Ncnt-obj
∆wobj ,1
∆wobj ,2
.
.
.
∆wobj ,Ncnt-obj
≥
dwobj ,1−Cwobj ,1wobj ,1
dwobj ,2−Cwobj ,2wobj ,2
.
.
.
dwobj ,Ncnt-obj −Cwobj ,Ncnt -obj wobj ,Ncnt-obj
(4.30)
⇔Cˆwobj ∆ˆwobj ≥dˆwobj (4.31)
return Cˆwobj :=
Cwobj ,1
Cwobj ,2
...
Cwobj ,Ncnt-obj
∈RNwrench-obj -ineq ×6Ncnt-obj
:wrench-obj-inequality-constraint-vector &key (update? t) [method]
return dˆwobj :=
dwobj ,1−Cwobj ,1wobj ,1
dwobj ,2−Cwobj ,2wobj ,2
.
.
.
dwobj ,Ncnt-obj −Cwobj ,Ncnt -obj wobj ,Ncnt-obj
∈RNwrench-obj -ineq
:variant-config-inequality-constraint-matrix &key (update? nil) [method]
42
Cθ∆θ≥dθ
Cˆw∆ˆw≥dˆw
Cˆwobj ∆ˆwobj ≥dˆwobj
Cτ∆τ≥dτ
(4.32)
⇔
Cθ
Cˆw
Cˆwobj
Cτ
∆θ
∆ˆw
∆ˆwobj
∆τ
≥
dθ
dˆw
dˆwobj
dτ
(4.33)
⇔Cvar ∆qvar ≥dvar (4.34)
return Cvar :=
Cθ
Cˆw
Cˆwobj
Cτ
∈RNvar-ineq ×dim(qvar )
:variant-config-inequality-constraint-vector &key (update? t) [method]
return dvar :=
dθ
dˆw
dˆwobj
dτ
∈RNvar-ineq
:act-react-equality-constraint-matrix &key (update? nil) [method]
43
ロボット・物体間の接触レンチに関する作用・反作用の法則は次式のように表される.
ˆwi(m)+ˆwobj ,j(m)=0(m= 1,2,· · · , Nact -react ) (4.35)
⇔Aact-react,robot ,mˆw+Aact-react,obj ,mˆwobj =0(m= 1,2,· · · , Nact-react ) (4.36)
where Aact-react,robot ,m=
i(m)番目
O6O6· · · I6· · · O6O6∈R6×6Ncnt (4.37)
Aact-react,obj ,m=
j(m)番目
O6O6· · · I6· · · O6O6∈R6×6Ncnt -obj
(4.38)
⇔Aact-react,robot ˆw+Aact-react,obj ˆwobj =0(4.39)
where Aact-react,robot =
Aact-react,robot ,1
.
.
.
Aact-react,robot ,Nact -react
∈R6Nact-react ×6Ncnt (4.40)
Aact-react,obj =
Aact-react,obj ,1
.
.
.
Aact-react,obj ,Nact-react
∈R6Nact-react ×6Ncnt -obj (4.41)
⇔Aact-react ˆw
ˆwobj =0∈R6Nact -react (4.42)
where Aact-react =Aact-react ,robot Aact-react,obj ∈R6Nact-react ×(6Ncnt +6Ncnt-obj )(4.43)
⇔Aact-react ˆw+ ∆ ˆw
ˆwobj + ∆ ˆwobj =0(4.44)
⇔Aact-react ∆ˆw
∆ˆwobj =bact-react (4.45)
where bact-react =−Aact-react ˆw
ˆwobj (4.46)
i(m), j(m)は作用・反作用の関係にある接触レンチの m番目の対におけるロボット,物体の接触レンチ
のインデックスである.
return Aact-react ∈R6Nact-react ×(6Ncnt +6Ncnt-obj )
:act-react-equality-constraint-vector &key (update? t) [method]
return bact-react ∈R6Nact-react
:variant-config-equality-constraint-matrix &key (update? nil) [method]
Aact-react ∆ˆw
∆ˆwobj =bact-react (4.47)
⇔O Aact-react O
∆θ
∆ˆw
∆ˆwobj
∆τ
=bact-react (4.48)
⇔Avar ∆qvar =bvar (4.49)
return Avar := O Aact-react O∈R6Nact-react ×dim(qvar )
44
:variant-config-equality-constraint-vector &key (update? t) [method]
return bvar := bact-react ∈R6Nact-react
:invariant-config-equality-constraint-matrix &key (update? nil) [method]
return Ainvar ∈R0×dim(qinvar )(no equality constraint)
:invariant-config-equality-constraint-vector &key (update? t) [method]
return binvar ∈R0(no equality constraint)
:config-equality-constraint-matrix &key (update? nil) [method]
Avar ∆qvar =bvar (4.50)
⇔Avar O∆qvar
∆qinvar =bvar (4.51)
⇔A∆q=b(4.52)
return A:= Avar O∈RNeq ×dim(q)
:config-equality-constraint-vector &key (update? t) [method]
return b:= bvar ∈RNeq
:torque-regular-matrix &key (update? nil) [method]
(only-variant? nil)
二次形式の正則化項として次式を考える.
Ftau (q) =
τ
τmax
2
(ベクトルの要素ごとの割り算を表す) (4.53)
=τT¯
Wtrq τ(4.54)
ここで,
¯
Wtrq :=
1
τ2
max ,1
1
τ2
max ,2
...
1
τ2
max ,Ndrive-joint
∈Rdim(τ)×dim(τ)(4.55)
only-variant? is true:
Wtrq :=
dim(θ)dim(ˆw)dim(ˆwobj )dim(τ)
dim(θ)
dim(ˆw)
dim(ˆwobj )
dim(τ)¯
Wtrq
∈Rdim(qvar )×dim(qvar )(4.56)
otherwise:
Wtrq :=
dim(θ)dim(ˆw)dim(ˆwobj )dim(τ)dim(ϕ)
dim(θ)
dim(ˆw)
dim(ˆwobj )
dim(τ)¯
Wtrq
dim(ϕ)
∈Rdim(q)×dim(q)(4.57)

45
return Wtrq
:torque-regular-vector &key (update? t) [method]
(only-variant? nil)
¯vtrq := ¯
Wtrq τ(4.58)
=
τ1
τ2
max ,1
τ2
τ2
max ,2
.
.
.
τdim(τ)
τ2
max ,dim(τ)
∈Rdim(τ)(4.59)
only-variant? is true:
vtrq :=
1
dim(θ)
dim(ˆw)
dim(ˆwobj )
dim(τ)¯vtrq
∈Rdim(qvar )(4.60)
otherwise:
vtrq :=
1
dim(θ)
dim(ˆw)
dim(ˆwobj )
dim(τ)¯vtrq
dim(ϕ)
∈Rdim(q)(4.61)
return vtrq
:collision-inequality-constraint-matrix &key (update? nil) [method]
Ccol :=
dim(θ)dim(ˆw)dim(ˆwobj )dim(τ)dim(ϕ)
Ncol Ccol,θ O O O Ccol ,ϕ (4.62)
return Ccol ∈RNcol ×dim(q)
:update-viewer [method]
Update viewer.
:print-status [method]
Print status.

46
4.2 B スプラインを用いた関節軌道生成
4.2.1 B スプラインを用いた関節軌道生成の理論
一般の Bスプライン基底関数の定義
Bスプライン基底関数は以下で定義される.
bi,0(t)def
=1 if ti≤t < ti+1
0 otherwise (4.63)
bi,n(t)def
=t−ti
ti+n−ti
bi,n−1(t) + ti+n+1 −t
ti+n+1 −ti+1
bi+1,n−1(t) (4.64)
tiはノットと呼ばれる.
使用区間を指定してノットを一様とする場合の Bスプライン基底関数
ts, tfをBスプラインの使用区間の初期,終端時刻とする.
n < m とする.
tn=ts(4.65)
tm=tf(4.66)
とする.ti(0 ≤i≤n+m)が等間隔に並ぶとすると,
ti=i−n
m−n(tf−ts) + ts(4.67)
=hi +mts−ntf
m−n(4.68)
ただし,
hdef
=tf−ts
m−n(4.69)
式(4.68) を式 (4.63) , 式(4.64) に代入すると,Bスプライン基底関数は次式で得られる.
bi,0(t) = 1 if ti≤t < ti+1
0 otherwise (4.70)
bi,n(t) = (t−ti)bi,n−1(t)+(ti+n+1 −t)bi+1,n−1(t)
nh (4.71)
以降では,nをBスプラインの次数,mを制御点の個数と呼ぶ.
Bスプラインの凸包性
式(4.70) , 式(4.71) で定義される Bスプライン基底関数 bi,n(t)は次式のように凸包性を持つ.
m−1
i=0
bi,n(t) = 1 (ts≤t≤tf) (4.72)
0≤bi,n(t)≤1 (i= 0,1,· · · , m −1, ts≤t≤tf) (4.73)

47
Bスプラインの微分
Bスプライン基底関数の微分に関して次式が成り立つ 11.
˙
bn(t) = dbn(t)
dt =Dbn−1(t) (4.74)
ただし,
bn(t)def
=
b0,n(t)
b1,n(t)
.
.
.
bm−1,n(t)
∈Rm(4.75)
Ddef
=1
h
1−1O
1−1
......
...−1
O1
∈Rm×m(4.76)
したがって,k階微分に関して次式が成り立つ.
b(k)
n(t) = d(k)bn(t)
dt(k)=Dkbn−k(t) (4.77)
Bスプラインによる関節角軌道の表現
j番目の関節角軌道 θj(t)を次式で表す.
θj(t)def
=
m−1
i=0
pj,ibi,n(t) = pT
jbn(t)∈R(ts≤t≤tf) (4.78)
ただし,
pj=
pj,0
pj,1
.
.
.
pj,m−1
∈Rm,bn(t) =
b0,n(t)
b1,n(t)
.
.
.
bm−1,n(t)
∈Rm(4.79)
以降では,pjを制御点,bn(t)を基底関数と呼ぶ.制御点 pjを決定すると関節角軌道が定まる.制御点 pjを
動作計画の設計変数とする.
j= 1,2,· · · , Njoint 番目の関節角軌道を並べたベクトル関数は,
θ(t)def
=
θ1(t)
θ2(t)
.
.
.
θNjoint (t)
=
pT
1bn(t)
pT
2bn(t)
.
.
.
pT
Njoint bn(t)
=
pT
1
pT
2
.
.
.
pT
Njoint
bn(t) = P bn(t)∈RNjoint (4.80)
ただし,
Pdef
=
pT
1
pT
2
.
.
.
pT
Njoint
∈RNjoint ×m(4.81)
11数学的帰納法で証明できる.http://mat.fsv.cvut.cz/gcg/sbornik/prochazkova.pdf
48
式(4.80) は,制御点を縦に並べたベクトルとして分離して,以下のようにも表現できる.
θ(t) =
θ1(t)
θ2(t)
.
.
.
θNjoint (t)
=
bT
n(t)p1
bT
n(t)p2
.
.
.
bT
n(t)pNjoint
=
bT
n(t)O
bT
n(t)
...
O bT
n(t)
p1
p2
.
.
.
pNjoint
=Bn(t)p∈RNjoint (4.82)
ただし,
Bn(t)def
=
bT
n(t)O
bT
n(t)
...
O bT
n(t)
∈RNjoint ×mNjoint ,pdef
=
p1
p2
.
.
.
pNjoint
∈RmNjoint (4.83)
Bスプラインによる関節角軌道の微分
式(4.80) と式 (4.74) から,関節角速度軌道は次式で得られる.
˙
θ(t) = P˙
bn(t) (4.84)
=P Dbn−1(t) (4.85)
=
pT
1
.
.
.
pT
Njoint
Dbn−1(t) (4.86)
=
pT
1Dbn−1(t)
.
.
.
pT
Njoint Dbn−1(t)
(4.87)
=
bT
n−1(t)DTp1
.
.
.
bT
n−1(t)DTpNjoint
(4.88)
=
bT
n−1(t)DTO
...
O bT
n−1(t)DT
p1
.
.
.
pNjoint
(4.89)
=
bT
n−1(t)O
...
O bT
n−1(t)
DTO
...
O DT
p1
.
.
.
pNjoint
(4.90)
=Bn−1(t)ˆ
D1p(4.91)
ただし,
ˆ
D1=
DTO
DT
...
O DT
∈RmNjoint ×mNjoint (4.92)

49
同様にして,関節角軌道の k階微分は次式で得られる.
θ(k)(t) = d(k)θ(t)
dt(k)(4.93)
=P Dkbn−k(t) (4.94)
=Bn−k(t)ˆ
Dkp(4.95)
ただし,
ˆ
Dk=
(Dk)TO
...
O(Dk)T
= ( ˆ
D1)k∈RmNjoint ×mNjoint (4.96)
計算時間は式 (4.94) のほうが式 (4.95) より速い.
エンドエフェクタ位置姿勢拘束のタスク関数
関節角 θ∈RNjoint からエンドエフェクタ位置姿勢 r∈R6への写像を f(θ)で表す.
r=f(θ) (4.97)
関節角軌道が式 (4.82) で表現されるとき,エンドエフェクタ軌道は次式で表される.
r(t) = f(θ(t)) = f(Bn(t)p) (4.98)
l= 1,2,··· , Ntm について,時刻 tlでエンドエフェクタの位置姿勢が rlであるタスクのタスク関数は次式
で表される.以降では,tlをタイミングと呼ぶ.
e(p,t)def
=
e1(p,t)
e2(p,t)
.
.
.
eNtm (p,t)
=
r1−f(θ(t1))
r2−f(θ(t2))
.
.
.
rNtm −f(θ(tNtm ))
=
r1−f(Bn(t1)p)
r2−f(Bn(t2)p)
.
.
.
rNtm −f(Bn(tNtm )p)
∈R6Ntm (4.99)
ただし,
el(p,t)def
=rl−f(θ(tl)) = rl−f(Bn(tl)p)∈R6(l= 1,2,· · · , Ntm ) (4.100)
tdef
=
t1
t2
.
.
.
tNtm
∈RNtm (4.101)
このタスクを実現する関節角軌道は,次の評価関数を最小にする制御点 p,タイミング tを求めることで導
出することができる.
F(p,t)def
=1
2∥e(p,t)∥2(4.102)
=1
2
Ntm
l=1
∥rl−f(θ(tl))∥2(4.103)
=1
2
Ntm
l=1
∥rl−f(Bn(tl)p)∥2(4.104)

50
また,l番目の幾何拘束の許容誤差を etol,l ≥0∈R6とする場合,タスク関数 ˜el(p,t)は次式で表される.
˜el,i(p,t)def
=
el,i(p,t)−etol ,l,i el,i(p,t)> etol,l,i
el,i(p,t) + etol ,l,i el,i(p,t)<−etol,l,i
0 otherwise
(i= 1,2,· · · ,6) (4.105)
˜el,i(p,t)は˜el(p,t)のi番目の要素である.el,i(p,t)はe(p,t)のi番目の要素である.
タスク関数を制御点で微分したヤコビ行列
式(4.104) を目的関数とする最適化問題を Gauss-Newton 法,Levenberg-Marquardt 法や逐次二次計画法で
解く場合,タスク関数 (4.99) のヤコビ行列が必要となる.
各時刻でのエンドエフェクタ位置姿勢拘束のタスク関数 el(p,t)の制御点 pに対するヤコビ行列は次式で求
められる.
∂el(p,t)
∂p=∂
∂p{rl−f(Bn(tl)p)}(4.106)
=−∂
∂pf(Bn(tl)p) (4.107)
=−∂f
∂θθ=θ(tl)
∂θ
∂p(4.108)
=−J(θ(tl)) ∂
∂p{Bn(tl)p}(4.109)
=−J(θ(tl))Bn(tl) (4.110)
途中の変形で,θ(p;t) = Bn(t)pであることを利用した.ただし,
Jdef
=∂f
∂θ(4.111)
タスク関数をタイミングで微分したヤコビ行列
各時刻でのエンドエフェクタ位置姿勢拘束のタスク関数 el(p,t)のタイミング tに対するヤコビ行列は次式
で求められる.
∂el(p,t)
∂tl
=∂
∂tl
{rl−f(P bn(tl))}(4.112)
=−∂
∂tl
f(P bn(tl)) (4.113)
=−∂f
∂θθ=θ(tl)
∂θ
∂tl
(4.114)
=−J(θ(tl)) ∂
∂tl
{P bn(tl)}(4.115)
=−J(θ(tl))P˙
bn(tl) (4.116)
=−J(θ(tl))P Dbn−1(tl) (4.117)
途中の変形で,θ(p;t) = P bn(t)であることを利用した.

51
初期・終端関節速度・加速度のタスク関数とヤコビ行列
初期,終端時刻の関節速度,加速度はゼロであるべきである.タスク関数は次式となる.
esv(p,t)def
=˙
θ(ts) (4.118)
=Bn−1(ts)ˆ
D1p(4.119)
=P Dbn−1(ts) (4.120)
efv (p,t)def
=˙
θ(tf) (4.121)
=Bn−1(tf)ˆ
D1p(4.122)
=P Dbn−1(tf) (4.123)
esa(p,t)def
=¨
θ(ts) (4.124)
=Bn−2(ts)ˆ
D2p(4.125)
=P D2bn−2(ts) (4.126)
efa(p,t)def
=¨
θ(tf) (4.127)
=Bn−2(tf)ˆ
D2p(4.128)
=P D2bn−2(tf) (4.129)
制御点で微分したヤコビ行列は次式で表される.
∂esv(p,t)
∂p=Bn−1(ts)ˆ
D1(4.130)
∂efv (p,t)
∂p=Bn−1(tf)ˆ
D1(4.131)
∂esa(p,t)
∂p=Bn−2(ts)ˆ
D2(4.132)
∂efa(p,t)
∂p=Bn−2(tf)ˆ
D2(4.133)
初期時刻,終端時刻で微分したヤコビ行列は次式で表される.
∂esv(p,t)
∂ts
=P D ∂bn−1(ts)
∂ts
=P D2bn−2(ts) (4.134)
∂efv (p,t)
∂tf
=P D ∂bn−1(tf)
∂tf
=P D2bn−2(tf) (4.135)
∂esa(p,t)
∂ts
=P D2∂bn−2(ts)
∂ts
=P D3bn−3(ts) (4.136)
∂efa(p,t)
∂tf
=P D2∂bn−2(tf)
∂tf
=P D3bn−3(tf) (4.137)
関節角上下限制約
式(4.78) の関節角軌道定義において,
pj≤θmax,j 1m(4.138)
のとき,Bスプラインの凸包性 (式(4.72) , 式(4.73) ) より次式が成り立つ.ただし,1m∈Rmは全要素が 1
52
のm次元ベクトルである.
θj(t) =
m−1
i=0
pj,ibi,n(t) (4.139)
≤
m−1
i=0
θmax,j bi,n(t) (4.140)
=θmax,j
m−1
i=0
bi,n(t) (4.141)
=θmax,j (4.142)
同様に,θmin,j 1m≤pjとすれば,θmin,j ≤θj(t)が成り立つ.
したがって,j番目の関節角の上下限を θmax,j , θmin,j とすると,次式の制約を制御点に課すことで,関節角
上下限制約を満たす関節角軌道が得られる.
θmin,j 1m≤pj≤θmax,j 1m(j= 1,2,· · · , Njoint ) (4.143)
つまり,
ˆ
Eθmin ≤p≤ˆ
Eθmax (4.144)
⇔I
−Ip≥ˆ
Eθmin
−ˆ
Eθmax(4.145)
ただし,
ˆ
Edef
=
1m0m
1m
...
0m1m
∈RmNjoint ×Njoint (4.146)
これは,逐次二次計画法の中で,次式の不等式制約となる.
I
−I∆p≥ˆ
Eθmin −p
−ˆ
Eθmax +p(4.147)
関節角速度・角加速度上下限制約
式(4.78) と式 (4.74) より,関節角速度軌道,角加速度軌道は次式で表される.
˙
θj(t) = pT
j˙
bn(t) = pT
jDbn−1(t) = (DTpj)Tbn−1(t)∈R(ts≤t≤tf) (4.148)
¨
θj(t) = pT
j¨
bn(t) = pT
jD2bn−2(t) = ((D2)Tpj)Tbn−2(t)∈R(ts≤t≤tf) (4.149)
j番目の関節角速度,角加速度の上限を vmax,j , amax,j とする.関節角上下限制約の導出と同様に考えると,
次式の制約を制御点に課すことで,関節角速度・角加速度上下限制約を満たす関節角軌道が得られる.
−vmax,j 1m≤DTpj≤vmax,j 1m(j= 1,2,· · · , Njoint ) (4.150)
−amax,j 1m≤(D2)Tpj≤amax,j 1m(j= 1,2,· · · , Njoint ) (4.151)
53
つまり,
−ˆ
Evmax ≤ˆ
D1p≤ˆ
Evmax (4.152)
⇔ˆ
D1
−ˆ
D1p≥−ˆ
Evmax
−ˆ
Evmax(4.153)
−ˆ
Eamax ≤ˆ
D2p≤ˆ
Eamax (4.154)
⇔ˆ
D2
−ˆ
D2p≥−ˆ
Eamax
−ˆ
Eamax(4.155)
これは,逐次二次計画法の中で,次式の不等式制約となる.
ˆ
D1
−ˆ
D1∆p≥−ˆ
Evmax −ˆ
D1p
−ˆ
Evmax +ˆ
D1p(4.156)
ˆ
D2
−ˆ
D2∆p≥−ˆ
Eamax −ˆ
D2p
−ˆ
Eamax +ˆ
D2p(4.157)
タイミング上下限制約
タイミングが初期,終端時刻の間に含まれる制約は次式で表される.
ts≤tl≤tf(l= 1,2,··· , Ntm ) (4.158)
⇔ts1≤t≤tf1(4.159)
⇔I
−It≥ts1
−tf1(4.160)
これは,逐次二次計画法の中で,次式の不等式制約となる.
I
−I∆t≥ts1−t
−tf1+t(4.161)
(4.162)
また,タイミングの順序が入れ替わることを許容しない場合,その制約は次式で表される.
tl≤tl+1 (l= 1,2,· · · , Ntm −1) (4.163)
⇔ −tl+tl+1 ≥0 (l= 1,2,· · · , Ntm −1) (4.164)
⇔Dtm t≥0(4.165)
ただし,
Dtm =
−1 1 O
−1 1
...
O−1 1
∈R(Ntm −1)×Ntm (4.166)
これは,逐次二次計画法の中で,次式の不等式制約となる.
Dtm ∆t≥ −Dtm t(4.167)
54
関節角微分二乗積分最小化
関節角微分の二乗積分は次式で得られる.
Fsqr,k(p) = tf
ts
θ(k)(t)
2dt (4.168)
=tf
ts
Bn−k(t)ˆ
Dkp
2dt (4.169)
=tf
tsBn−k(t)ˆ
DkpTBn−k(t)ˆ
Dkpdt (4.170)
=pTtf
tsBn−k(t)ˆ
DkT
Bn−k(t)ˆ
Dkdtp(4.171)
=pTHkp(4.172)
ただし,
Hk=tf
tsBn−k(t)ˆ
DkT
Bn−k(t)ˆ
Dkdt (4.173)
Bn−k(t)ˆ
Dk=
bT
n−k(t)O
...
O bT
n−k(t)
(Dk)TO
...
O(Dk)T
(4.174)
=
bT
n−k(t)(Dk)TO
...
O bT
n−k(t)(Dk)T
(4.175)
=
Dkbn−k(t)T
O
...
ODkbn−k(t)T
(4.176)
Bn−k(t)ˆ
DkT
Bn−k(t) =
Dkbn−k(t)T
O
...
ODkbn−k(t)T
T
Dkbn−k(t)T
O
...
ODkbn−k(t)T
(4.177)
=
Dkbn−k(t)Dkbn−k(t)T
O
...
ODkbn−k(t)Dkbn−k(t)T
(4.178)
これを逐次二次計画問題において,二次形式の正則化項として目的関数に加えることで,滑らかな動作が生成
されることが期待される.
動作期間の最小化
動作期間 (tf−ts)の二乗は次式で表される.
Fduration (t) = |t1−tNtm |2(4.179)
=tT
1−1
−1 1
t(4.180)
55
ただし,初期時刻 ts=t1,終端時刻 tf=tNtm がタイミングベクトル tの最初,最後の要素であるとする.こ
れを逐次二次計画問題において,二次形式の正則化項として目的関数に加えることで,短時間でタスクを実現
する動作が生成されることが期待される.
4.2.2 B スプラインを用いた関節軌道生成の実装
bspline-configuration-task [class]
:super propertied-object
:slots ( robot robot instance)
( control-vector p)
( timing-vector t)
( num-kin Nkin := |T kin-trg |=|T kin-att |)
( num-joint Njoint := |J |)
( num-control-point Nctrl )
( num-timing Ntm )
( bspline-order B-spline order, n)
( dim-control-vector dim(p))
( dim-timing-vector dim(t))
( dim-config dim(q))
( dim-task dim(e))
( num-collision Ncol := number of collision check pairs)
( stationery-start-finish-task-scale kstat )
( first-diff-square-integration-regular-scale ksqr,1)
( second-diff-square-integration-regular-scale ksqr,2)
( third-diff-square-integration-regular-scale ksqr,3)
( motion-duration-regular-scale kduration )
( norm-regular-scale-max kmax ,p)
( norm-regular-scale-offset koff ,p)
( timing-norm-regular-scale-max kmax ,t)
( timing-norm-regular-scale-offset koff ,t)
( joint-list J)
( start-time ts)
( finish-time tf)
( kin-time-list {tkin -tm
1, tkin-tm
2,· · · , tkin-tm
Nkin })
( kin-variable-timing-list list of bool. t for variable timing.)
( kin-target-coords-list Tkin -trg )
( kin-attention-coords-list Tkin -att )
( kin-pos-tolerance-list list of position tolerance etol ,pos [m])
( kin-rot-tolerance-list list of rotation tolerance etol ,rot [rad])
( joint-angle-margin margin of θ[deg] [mm])
( collision-pair-list list of bodyset-link or body pair)
( keep-timing-order? whether to keep order of timing tor not)
( bspline-matrix buffer for Bn(t))
56
( diff-mat buffer for Dk)
( diff-mat-list buffer for {D1,D2,· · · ,DK})
( extended-diff-mat-list buffer for {ˆ
D1,ˆ
D2,· · · ,ˆ
DK})
( task-jacobi buffer for ∂e
∂q)
( regular-mat buffer for Wreg )
( regular-vec buffer for vreg )
Bスプラインを利用した軌道生成のためのコンフィギュレーション qとタスク関数 e(q)のクラス.
コンフィギュレーション qの取得・更新,タスク関数 e(q)の取得,タスク関数のヤコビ行列 ∂e(q)
∂qの取
得,コンフィギュレーションの等式・不等式制約 A,b,C,dの取得のためのメソッドが定義されている.
コンフィギュレーション・タスク関数を定めるために,初期化時に以下を与える
•ロボット
robot ロボットのインスタンス
joint-list J関節
•Bスプラインのパラメータ
start-time tsBスプラインの使用区間の初期時刻
finish-time tfBスプラインの使用区間の終端時刻
num-control-point Nctrl 制御点の個数
bspline-order nBスプラインの次数
•幾何拘束
kin-target-coords-list Tkin-trg 幾何到達目標位置姿勢リスト
kin-attention-coords-list Tkin-att 幾何到達着目位置姿勢リスト
kin-time-list {tkin-tm
1, tkin-tm
2,· · · , tkin-tm
Nkin }幾何到達タイミングリスト
kin-variable-timing-list 幾何到達タイミングが可変か (t),固定か (nil) のリスト.このリスト内
のtの個数がタイミング tの次元 Ntm となる.
コンフィギュレーション qは以下から構成される.
q:= p
t(4.181)
p∈RNctrl Njoint 制御点 (B スプライン基底関数の山の高さ) [rad] [m]
t∈RNtm タイミング (幾何拘束タスクの課される時刻) [sec]
タスク関数 e(q)は以下から構成される.
e(q) := ekin (q)
estat (q)∈R6Nkin +4Njoint (4.182)
ekin (q)∈R6Nkin 幾何到達拘束 [rad] [m]
estat (q)∈R4Njoint 初期,終端時刻静止拘束 [rad][rad/s][rad/s2][m][m/s][m/s2]
57
:init &key (name) [method]
(robot)
(joint-list (send robot :joint-list))
(start-time 0.0)
(finish-time 10.0)
(num-control-point 10)
(bspline-order 3)
(kin-time-list)
(kin-variable-timing-list (make-list (length kin-time-list) :initial-element nil))
(kin-target-coords-list)
(kin-attention-coords-list)
(kin-pos-tolerance-list (make-list (length kin-time-list) :initial-element 0.0))
(kin-rot-tolerance-list (make-list (length kin-time-list) :initial-element 0.0))
(joint-angle-margin 3.0)
(collision-pair-list)
(keep-timing-order? t)
(stationery-start-finish-task-scale 0.0)
(first-diff-square-integration-regular-scale 0.0)
(second-diff-square-integration-regular-scale 0.0)
(third-diff-square-integration-regular-scale 0.0)
(motion-duration-regular-scale 0.0)
(norm-regular-scale-max 1.000000e-05)
(norm-regular-scale-offset 1.000000e-07)
(timing-norm-regular-scale-max 1.000000e-05)
(timing-norm-regular-scale-offset 1.000000e-07)
Initialize instance
:robot [method]
return robot instance
:joint-list [method]
return J
:num-kin [method]
return Nkin := |T kin-trg |=|T kin-att |
:num-joint [method]
return Njoint := |J |
:num-control-point [method]
return Nctrl
:num-timing [method]
return Ntm
:num-collision [method]
return Ncol := number of collision check pairs
:dim-config [method]
return dim(q) := dim(p) + dim(t) = Nctrl Njoint +Ntm

58
:dim-task [method]
return dim(e) := dim(ekin ) + dim(estat ) = 6Nkin + 4Njoint
:control-vector [method]
return control vector p
:timing-vector [method]
return timing vector t
:config-vector [method]
return q:= p
t
:set-control-vector control-vector-new &key (relative? nil) [method]
Set p.
:set-timing-vector timing-vector-new &key (relative? nil) [method]
Set t.
:set-config config-new &key (relative? nil) [method]
Set q.
:bspline-vector tm &key (order-offset 0) [method]
bn(t) :=
b0,n(t)
b1,n(t)
.
.
.
bNctrl −1,n(t)
∈RNctrl (4.183)
return bn(t)
:bspline-matrix tm &key (order-offset 0) [method]
Bn(t) :=
bT
n(t)O
bT
n(t)
...
O bT
n(t)
∈RNjoint ×Nctrl Njoint (4.184)
return Bn(t)
:differential-matrix &key (diff-order 1) [method]
D:= 1
h
1−1O
1−1
......
...−1
O1
∈RNctrl ×Nctrl (4.185)
return Dk

59
:extended-differential-matrix &key (diff-order 1) [method]
ˆ
Dk:=
(Dk)TO
...
O(Dk)T
∈RNctrl Njoint ×Nctrl Njoint (4.186)
return ˆ
Dk
:bspline-differential-matrix tm &key (diff-order 1) [method]
return Bn−k(t)ˆ
Dk∈RNjoint ×Nctrl Njoint
:control-matrix [method]
P:=
pT
1
pT
2
.
.
.
pT
njoint
∈RNjoint ×Nctrl (4.187)
return P
:theta tm [method]
return θ(t) = Bn(t)p[rad][m]
:theta-dot tm &key (diff-order 1) [method]
return θ(k)(t) = d(k)θ(t)
dt(k)=P Dkbn−k(t) [rad/sk][m/sk]
:theta-dot-numerical tm &key (diff-order 1) [method]
(delta-time 0.05)
return θ(k)(t) = d(k)θ(t)
dt(k)=θ(k−1)(t+ ∆t)−θ(k−1)(t)
∆t[rad/sk][m/sk]
:apply-theta-to-robot tm [method]
apply θ(t) to robot.
:kin-target-coords-list [method]
Tkin-trg
m={pkin-trg
l,Rkin-trg
l}(l= 1,2,··· , Nkin ) (4.188)
return Tkin-trg := {Tkin-trg
1, T kin-trg
2,· · · , T kin-trg
Nkin }
:kin-attention-coords-list [method]
Tkin-att
m={pkin-att
l,Rkin-att
l}(l= 1,2,· · · , Nkin ) (4.189)
return Tkin-att := {Tkin-att
1, T kin-att
2,· · · , T kin -att
Nkin }
:kin-start-time [method]
return tkin
s:= tkin-tm
1
60
:kin-finish-time [method]
return tkin
f:= tkin-tm
Nkin
:motion-duration [method]
return (tkin-tm
Nkin −tkin-tm
1)
:kinematics-task-value &key (update? t) [method]
ekin (q) = ekin (p,t) (4.190)
=
ekin
1(p,t)
ekin
2(p,t)
.
.
.
ekin
Nkin (p,t)
(4.191)
ekin
l(p,t) = pkin-trg
l−pkin-att
l(p,t)
aRkin-trg
lRkin-att
l(p,t)T∈R6(l= 1,2,· · · , Nkin ) (4.192)
a(R)は姿勢行列 Rの等価角軸ベクトルを表す.
return ekin (q)∈R6Nkin
:stationery-start-finish-task-value &key (update? t) [method]
estat (q) = estat (p,t) (4.193)
=
estat
sv (p,t)
estat
fv (p,t)
estat
sa (p,t)
estat
fa (p,t)
(4.194)
estat
sv (p,t) := ˙
θ(tkin
s) (4.195)
estat
fv (p,t) := ˙
θ(tkin
f) (4.196)
estat
sa (p,t) := ¨
θ(tkin
s) (4.197)
estat
fa (p,t) := ¨
θ(tkin
f) (4.198)
return estat (q)∈R4Njoint
:task-value &key (update? t) [method]
return e(q) := ekin (q)
kstat estat (q)∈R6Nkin +4Njoint
:kinematics-task-jacobian-with-control-vector [method]
式(4.110) より,タスク関数 ekin を制御点 pで微分したヤコビ行列は次式で得られる.
∂ekin
∂p=
∂ekin
1
∂p
∂ekin
2
∂p
.
.
.
∂ekin
Nkin
∂p
(4.199)
∂ekin
l
∂p=−Jkin-att (θ(tkin-tm
l))Bn(tkin-tm
l) (l= 1,2,· · · , Nkin ) (4.200)
61
return ∂ekin
∂p∈R6Nkin ×Nctrl Njoint
:kinematics-task-jacobian-with-timing-vector [method]
式(4.117) より,タスク関数 ekin をタイミング tで微分したヤコビ行列は次式で得られる.
∂ekin
∂t=
∂ekin
1
∂t
∂ekin
2
∂t
.
.
.
∂ekin
Nkin
∂t
(4.201)
∂ekin
l
∂tのi番目の列ベクトル ∂ekin
l
∂ti∈R6は次式で表される (i= 1,2,· · · , Ntm ).
∂ekin
l
∂ti
=−Jkin-att (θ(tkin-tm
l))P Dbn−1(tkin-tm
l)tkin-tm
land tiis identical
0otherwise (4.202)
return ∂ekin
∂t∈R6Nkin ×Ntm
:stationery-start-finish-task-jacobian-with-control-vector [method]
式(4.130) , 式(4.131) , 式(4.132) , 式(4.133) より,タスク関数 estat を制御点 pで微分したヤコビ行
列は次式で得られる.
∂estat
∂p=
∂estat
sv
∂p
∂estat
f v
∂p
∂estat
sa
∂p
∂estat
f a
∂p
(4.203)
∂estat
sv (p,t)
∂p=Bn−1(tkin
s)ˆ
D1(4.204)
∂estat
fv (p,t)
∂p=Bn−1(tkin
f)ˆ
D1(4.205)
∂estat
sa (p,t)
∂p=Bn−2(tkin
s)ˆ
D2(4.206)
∂estat
fa (p,t)
∂p=Bn−2(tkin
f)ˆ
D2(4.207)
return ∂estat
∂p∈R4Njoint ×Nctrl Njoint
:stationery-start-finish-task-jacobian-with-timing-vector [method]
式(4.134) , 式(4.135) , 式(4.136) , 式(4.137) より,タスク関数 estat をタイミング tで微分したヤコ
ビ行列は次式で得られる.
∂estat
∂t=
∂estat
sv
∂t
∂estat
f v
∂t
∂estat
sa
∂t
∂estat
f a
∂t
(4.208)
62
∂estat
x
∂tのi番目の列ベクトル ∂estat
x
∂ti∈RNjoint は次式で表される (x∈ {sv, fv, sa, fa}, i = 1,2,· · · , Ntm ).
∂estat
sv (p,t)
∂ti
=P D2bn−2(tkin
s)tkin
sand tiis identical
0otherwise (4.209)
∂estat
fv (p,t)
∂ti
=P D2bn−2(tkin
f)tkin
fand tiis identical
0otherwise (4.210)
∂estat
sa (p,t)
∂ti
=P D3bn−3(tkin
s)tkin
sand tiis identical
0otherwise (4.211)
∂estat
fa (p,t)
∂ti
=P D3bn−3(tkin
f)tkin
fand tiis identical
0otherwise (4.212)
return ∂estat
∂t∈R4Njoint ×Ntm
:task-jacobian [method]
∂e
∂q=
Nctrl Njoint Ntm
6Nkin ∂ekin
∂p∂ekin
∂t
4Njoint kstat ∂estat
∂pkstat ∂estat
∂t
(4.213)
return ∂e
∂q=R(6Nkin +4Njoint )×(Nctrl Njoint +Ntm )
:theta-max-vector &key (update? nil) [method]
return θmax ∈RNjoint
:theta-min-vector &key (update? nil) [method]
return θmin ∈RNjoint
:theta-inequality-constraint-matrix &key (update? nil) [method]
式(4.144) より,関節角度上下限制約は次式で表される.
ˆ
Eθmin ≤p+ ∆p≤ˆ
Eθmax (4.214)
⇔I
−I∆p≥ˆ
Eθmin −p
−ˆ
Eθmax +p(4.215)
⇔Cθ∆p≥dθ(4.216)
ただし,
ˆ
E:=
1Nctrl 0Nctrl
1Nctrl
...
0Nctrl 1Nctrl
∈RNctrl Njoint ×Njoint (4.217)
1Nctrl ∈RNctrl は全要素が 1のNctrl 次元ベクトルである.
return Cθ:= I
−I∈R2Nctrl Njoint ×Nctrl Njoint
:theta-inequality-constraint-vector &key (update? t) [method]
return dθ:= ˆ
Eθmin −p
−ˆ
Eθmax +p∈R2Nctrl Njoint
63
:velocity-max-vector &key (update? nil) [method]
return vmax ∈RNjoint
:velocity-inequality-constraint-matrix &key (update? nil) [method]
式(4.152) より,関節速度上下限制約は次式で表される.
−ˆ
Evmax ≤ˆ
D1(p+ ∆p)≤ˆ
Evmax (4.218)
⇔ˆ
D1
−ˆ
D1∆p≥−ˆ
Evmax −ˆ
D1p
−ˆ
Evmax +ˆ
D1p(4.219)
⇔C˙
θ∆p≥d˙
θ(4.220)
return C˙
θ:= ˆ
D1
−ˆ
D1∈R2Nctrl Njoint ×Nctrl Njoint
:velocity-inequality-constraint-vector &key (update? t) [method]
return d˙
θ:= −ˆ
Evmax −ˆ
D1p
−ˆ
Evmax +ˆ
D1p∈R2Nctrl Njoint
:acceleration-max-vector &key (update? nil) [method]
return amax ∈RNjoint
:acceleration-inequality-constraint-matrix &key (update? nil) [method]
式(4.154) より,関節加速度上下限制約は次式で表される.
−ˆ
Eamax ≤ˆ
D2(p+ ∆p)≤ˆ
Eamax (4.221)
⇔ˆ
D2
−ˆ
D2∆p≥−ˆ
Eamax −ˆ
D2p
−ˆ
Eamax +ˆ
D2p(4.222)
⇔C¨
θ∆p≥d¨
θ(4.223)
return C¨
θ:= ˆ
D2
−ˆ
D2∈R2Nctrl Njoint ×Nctrl Njoint
:acceleration-inequality-constraint-vector &key (update? t) [method]
return d¨
θ:= −ˆ
Eamax −ˆ
D2p
−ˆ
Eamax +ˆ
D2p∈R2Nctrl Njoint
:control-vector-inequality-constraint-matrix &key (update? nil) [method]
Cθ∆p≥dθ
C˙
θ∆p≥d˙
θ
C¨
θ∆p≥d¨
θ
(4.224)
⇔
Cθ
C˙
θ
C¨
θ
∆p≥
dθ
d˙
θ
d¨
θ
(4.225)
⇔Cp∆p≥dp(4.226)
return Cp:=
Cθ
C˙
θ
C¨
θ
∈RNp-ineq ×dim(p)
:control-vector-inequality-constraint-vector &key (update? t) [method]
64
return dp:=
dθ
d˙
θ
d¨
θ
∈RNp-ineq
:timing-vector-inequality-constraint-matrix &key (update? nil) [method]
式(4.159) より,タイミングが Bスプラインの初期,終端時刻の間に含まれる制約は次式で表される.
ts1≤t+ ∆t≤tf1(4.227)
⇔I
−I∆t≥ts1−t
−tf1+t(4.228)
また,式 (4.165) より,タイミングの順序が入れ替わることを許容しない場合,その制約は次式で表さ
れる.
Dtm (t+ ∆t)≥0(4.229)
⇔Dtm ∆t≥ −Dtm t(4.230)
ただし,
Dtm =
−1 1 O
−1 1
...
O−1 1
∈R(Ntm −1)×Ntm (4.231)
これらを合わせると,
I
−I
Dtm
∆t≥
ts1−t
−tf1+t
−Dtm t
⇔Ct∆p≥dt(4.232)
return Ct:=
I
−I
Dtm
∈R(3Ntm −1)×dim(t)
:timing-vector-inequality-constraint-vector &key (update? t) [method]
return dt:=
ts1−t
−tf1+t
−Dtm t
∈R(3Ntm −1)
:config-inequality-constraint-matrix &key (update? nil) [method]
(update-collision? nil)
Cp∆p≥dp
Ct∆t≥dt
(4.233)
⇔Cp
Ct∆p
∆t≥dp
dt(4.234)
⇔C∆q≥d(4.235)
return C:= Cp
Ct∈RNineq ×dim(q)

65
:config-inequality-constraint-vector &key (update? t) [method]
(update-collision? nil)
return d:= dp
dt∈RNineq
:config-equality-constraint-matrix &key (update? nil) [method]
return A∈R0×dim(q)(no equality constraint)
:config-equality-constraint-vector &key (update? t) [method]
return b∈R0(no equality constraint)
:square-integration-regular-matrix &key (diff-order 1) [method]
(delta-time (/ (- finish-time start-time) 100.0))
式(4.172) より,関節角微分の二乗積分は次式で得られる.
Fsqr,k(p) = tf
ts
θ(k)(t)
2dt (4.236)
=pTHsqr,kp(4.237)
ただし,
Hsqr,k=tf
tsBn−k(t)ˆ
DkT
Bn−k(t)ˆ
Dkdt (4.238)
=tf
ts
Dkbn−k(t)Dkbn−k(t)T
O
...
ODkbn−k(t)Dkbn−k(t)T
dt(4.239)
これは二次形式の正則化項である.
return Hsqr,k∈Rdim(p)×dim(p)
:first-differential-square-integration-regular-matrix &key (delta-time (/ (- finish-time start-time)
100.0)) [method]
return Hsqr,1∈Rdim(p)×dim(p)
:second-differential-square-integration-regular-matrix &key (delta-time (/ (- finish-time start-time)
100.0)) [method]
return Hsqr,2∈Rdim(p)×dim(p)
:third-differential-square-integration-regular-matrix &key (delta-time (/ (- finish-time start-time)
100.0)) [method]
return Hsqr,3∈Rdim(p)×dim(p)
:control-vector-regular-matrix [method]
Wreg,p:= min(kmax ,p,∥e∥2+koff ,p)I+ksqr ,1Hsqr ,1+ksqr ,2Hsqr ,2+ksqr,3Hsqr ,3(4.240)
return Wreg,p∈Rdim(p)×dim(p)
:control-vector-regular-vector [method]

66
vreg,p:= (ksqr ,1Hsqr ,1+ksqr ,2Hsqr ,2+ksqr,3Hsqr ,3)p(4.241)
return vreg,p∈Rdim(p)
:motion-duration-regular-matrix [method]
式(4.180) より,動作期間の二乗は次式で得られる.
Fduration (t) = |t1−tNtm |2(4.242)
=tT
1−1
−1 1
t(4.243)
=tTHduration t(4.244)
これは二次形式の正則化項である.
return Hduration ∈Rdim (t)×dim(t)
:timing-vector-regular-matrix [method]
Wreg,t:= min(kmax ,t,∥e∥2+koff ,t)I+kduration Hduration (4.245)
return Wreg,t∈Rdim(t)×dim(t)
:timing-vector-regular-vector [method]
vreg,t:= kduration Hduration t(4.246)
return vreg,t∈Rdim(t)
:regular-matrix [method]
Wreg := Wreg,p
Wreg,t(4.247)
return Wreg ∈Rdim(q)×dim(q)
:regular-vector [method]
vreg := vreg,p
vreg,t(4.248)
return vreg ∈Rdim(q)×dim(q)
:update-collision-inequality-constraint [method]
Not implemented yet.
:update-viewer &key (trajectory-delta-time (/ (- finish-time start-time) 10.0)) [method]
Update viewer.
67
:print-status [method]
Print status.
:print-motion-information [method]
Print motion information.
:play-animation &key (robot) [method]
(delta-time (/ (- finish-time start-time) 100.0))
(only-motion-duration? t)
(loop? t)
(visualize-callback-func)
Print motion animation.
:plot-theta-graph &key (joint-id nil) [method]
(divide-num 200)
(plot-numerical? nil)
(only-motion-duration? t)
(dat-filename /tmp/bspline-configuration-task-plot-theta-graph.dat)
(dump-pdf? nil)
(dump-filename (ros::resolve-ros-path package://eus qp/optmotiongen/logs/bspline-configuration-task-graph.pdf))
Plot graph.
:generate-angle-vector-sequence &key (divide-num 100) [method]
Generate angle-vector-sequence.
get-bspline-knot i n m x min x max h [function]
ti=i−n
m−n(tf−ts) + ts(4.249)
=hi +mts−ntf
m−n(4.250)
return knot tifor B-spline function
bspline-basis-func x i n m x min x max &optional (n-orig n) (m-orig m) [function]
bi,0(t) = 1 if ti≤t < ti+1
0 otherwise (4.251)
bi,n(t) = (t−ti)bi,n−1(t) + (ti+n+1 −t)bi+1,n−1(t)
nh (4.252)
return B-spline function value bi,n(t).
5補足
5.1 既存のロボット基礎クラスの拡張
joint [class]
68
:super propertied-object
:slots (parent-link)
(child-link)
(joint-angle)
(min-angle)
(max-angle)
(default-coords)
(joint-velocity)
(joint-acceleration)
(joint-torque)
(max-joint-velocity)
(max-joint-torque)
(joint-min-max-table)
(joint-min-max-target)
:child-link &rest args [method]
Returns child link of this joint. If any arguments is set, it is passed to the child-link.
Override to support the case that child-link is cascaded-link instantiate. Return the root link of child
cascaded-link instantiate in that case.
:axis-vector [method]
Return joint axis vector. Represented in world coordinates.
return ai∈R3
:pos [method]
Return joint position. Represented in world coordinates.
return pi∈R3
bodyset-link [class]
:super bodyset
:slots (rot)
(pos)
(parent)
(descendants)
(worldcoords)
(manager)
(changed)
(geometry::bodies)
(joint)
(parent-link)
(child-links)
(analysis-level)
(default-coords)
(weight)
(acentroid)
69
(inertia-tensor)
(angular-velocity)
(angular-acceleration)
(spacial-velocity)
(spacial-acceleration)
(momentum-velocity)
(angular-momentum-velocity)
(momentum)
(angular-momentum)
(force)
(moment)
(ext-force)
(ext-moment)
:mg [method]
return mg =∥mg∥
:mg-vec [method]
return mg
cascaded-link [class]
:super cascaded-coords
:slots (rot)
(pos)
(parent)
(descendants)
(worldcoords)
(manager)
(changed)
(links)
(joint-list)
(bodies)
(collision-avoidance-links)
(end-coords-list)
:calc-jacobian-from-joint-list &key (union-joint-list) [method]
(move-target)
(joint-list (mapcar #’(lambda (mt) (send-all (send self :link-list (send mt :parent)) :joint)) move-target))
(transform-coords (mapcar #’(lambda (mt) (make-coords)) move-target))
(translation-axis (mapcar #’(lambda (mt) t) move-target))
(rotation-axis (mapcar #’(lambda (mt) t) move-target))
union-joint-list list of all joints considered in jacobian. column num of jacobian is same with length of

70
union-joint-list.
move-target list of move-target.
joint-list list of joint-list which is contained in each chain of move-target.
transform-coords list of transform-coords of each move-target.
translation-axis list of translation-axis of each move-target.
rotation-axis list of rotation-axis of each move-target.
Get jacobian matrix from following two information: (1) union-joint-list and (2) list of move-target.
One recession compared with :calc-jacobian-from-link-list is that child-reverse is not supported. (Only
not implemented yet because I do not need such feature in current application.)
:calc-cog-jacobian-from-joint-list &key (union-joint-list) [method]
(update-mass-properties t)
(translation-axis :z)
union-joint-list list of all joints considered in jacobian. column num of jacobian is same with length of
union-joint-list.
Get CoG jacobian matrix from union-joint-list.
:find-link-route to &optional from [method]
Override to support the case that joint does not exist between links. Change from (send to :parent-link)
to (send to :parent).
5.2 環境と接触するロボットの関節・リンク構造
2d-planar-contact [class]
:super cascaded-link
:slots ( contact-coords Tcnt )
( contact-pre-coords Tcnt -pre )
二次元平面上の長方形領域での接触座標を表す仮想の関節・リンク構造.
:init &key (name contact) [method]
(contact-pre-offset 100)
Initialize instance
:contact-coords &rest args [method]
return Tcnt := {pcnt ,Rcnt }
:contact-pre-coords &rest args [method]
return Tcnt-pre := {pcnt -pre ,Rcnt-pre }
:set-from-face &key (face) [method]
(margin 150.0)
set coords and min/max joint angle from face.
71
robot-environment [class]
:super cascaded-link
:slots ( robot R)
( robot-with-root-virtual ˆ
R)
( root-virtual-joint-list list of root virtual joint)
( contact-list {C1,C2,··· ,CNC})
( variant-joint-list Jvar )
( invariant-joint-list Jinvar )
( drive-joint-list Jdrive )
ロボットとロボット・環境間の接触のクラス.
以下を合わせた関節・リンク構造に関するメソッドが定義されている.
1. 浮遊ルートリンクのための仮想関節付きのロボットの関節
2. 接触位置を定める仮想関節
関節・リンク構造を定めるために,初期化時に以下を与える
robot Rロボット (cascaded-link クラスのインスタンス).
contact-list {C1,C2,· · · ,CNC}接触 (2d-planar-contact クラスなどのインスタンス)のリスト.
ロボット Rに,浮遊ルートリンクの変位に対応する仮想関節を付加した仮想関節付きロボット ˆ
Rを内部
で保持する.
:init &key (robot) [method]
(contact-list)
(root-virtual-mode :6dof)
(root-virtual-joint-class-list)
(root-virtual-joint-axis-list)
Initialize instance
:dissoc-root-virtual [method]
dissoc root virtual parent/child structure.
:init-pose [method]
set zero joint angle.
:robot &rest args [method]
return R
:robot-with-root-virtual &rest args [method]
return ˆ
R
:contact-list &rest args [method]
return {C1,C2,· · · ,CNC}
:contact name &rest args [method]
return Ci
:variant-joint-list &optional (jl :nil) [method]
72
return Jvar
:invariant-joint-list &optional (jl :nil) [method]
return Jinvar
:drive-joint-list &optional (jl :nil) [method]
return Jdrive
:root-virtual-joint-list [method]
return list of root virtual joint
5.3 irteus のinverse-kinematics 互換関数
cascaded-link [class]
:super cascaded-coords
:slots (rot)
(pos)
(parent)
(descendants)
(worldcoords)
(manager)
(changed)
(links)
(joint-list)
(bodies)
(collision-avoidance-links)
(end-coords-list)
:inverse-kinematics-optmotiongen target-coords &key (stop 50) [method]
(link-list)
(move-target)
(debug-view)
(revert-if-fail t)
(transform-coords target-coords)
(translation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t))))
(rotation-axis (cond ((atom move-target) t) (t (make-list (length move-target) :initial-element t))))
(thre (cond ((atom move-target) 1) (t (make-list (length move-target) :initial-element 1))))
(rthre (cond ((atom move-target) (deg2rad 1)) (t (make-list (length move-target) :initial-element (deg2rad 1)))))
(collision-avoidance-link-pair :nil)
(collision-distance-limit 10.0)
(obstacles)
(min-loop)
(root-virtual-mode :fix)
73
(joint-angle-margin 0.0)
(posture-joint-list)
(posture-joint-angle-list)
(target-posture-scale 0.001)
(norm-regular-scale-max 0.01)
(norm-regular-scale-offset 1.000000e-07)
(pre-process-func)
(post-process-func)
&allow-other-keys
Solve inverse kinematics problem with sqp optimization. ;; target-coords, move-target, rotation-axis,
translation-axis ;; -¿ both list and atom OK. target-coords : The coordinate of the target that returns
coordinates. Use a list of targets to solve the IK relative to multiple end links simultaneously. Function
is not available to target-coords. link-list : List of links to control. When the target-coords is list, this
should be a list of lists. move-target : Specify end-effector coordinate. When the target-coords is list,
this should be list too. stop : Maximum number for IK iteration. Default is 50. debug-view : Set t
to show debug message and visualization. Use :no-message to just show the irtview image. Default is
nil. revert-if-fail : Set nil to keep the angle posture of IK solve iteration. Default is t, which return
to original position when IK fails. translation-axis : :x :y :z for constraint along the x, y, z axis. :xy
:yz :zx for plane. Default is t. rotation-axis : Use nil for position only IK. :x, :y, :z for the constraint
around axis with plus direction. When the target-coords is list, this should be list too. Default is t.
thre : Threshold for position error to terminate IK iteration. Default is 1 [mm]. rthre : Threshold for
rotation error to terminate IK iteration. Default is 0.017453 [rad] (1 deg).
cascaded-link [class]
:super cascaded-coords
:slots (rot)
(pos)
(parent)
(descendants)
(worldcoords)
(manager)
(changed)
(links)
(joint-list)
(bodies)
(collision-avoidance-links)
(end-coords-list)
:inverse-kinematics-trajectory-optmotiongen target-coords-list &key (stop 50) [method]
(move-target-list)
(debug-view)
(revert-if-fail t)
(transform-coords-list :nil)
(translation-axis-list :nil)
74
(rotation-axis-list :nil)
(thre 1.0)
(rthre (deg2rad 1))
(thre-list :nil)
(rthre-list :nil)
(collision-avoidance-link-pair :nil)
(collision-distance-limit 10.0)
(obstacles)
(min-loop)
(root-virtual-mode :fix)
(root-virtual-joint-invariant? nil)
(joint-angle-margin 0.0)
(posture-joint-list (make-list (length target-coords-list) :initial-element nil))
(posture-joint-angle-list (make-list (length target-coords-list) :initial-element nil))
(norm-regular-scale-max 0.001)
(norm-regular-scale-offset 1.000000e-07)
(adjacent-regular-scale 0.0)
(pre-process-func)
(post-process-func)
&allow-other-keys
Solve inverse kinematics problem with sqp optimization. target-coords-list : The coordinate of the
target that returns coordinates. Use a list of targets to solve the IK relative to multiple end links
simultaneously. Function is not available to target-coords. move-target-list : Specify end-effector
coordinate. When the target-coords is list, this should be list too. stop : Maximum number for IK
iteration. Default is 50. debug-view : Set t to show debug message and visualization. Use :no-message
to just show the irtview image. Default is nil. revert-if-fail : Set nil to keep the angle posture of IK
solve iteration. Default is t, which return to original position when IK fails. translation-axis-list : :x :y
:z for constraint along the x, y, z axis. :xy :yz :zx for plane. Default is t. rotation-axis-list : Use nil for
position only IK. :x, :y, :z for the constraint around axis with plus direction. When the target-coords is
list, this should be list too. Default is t. thre : Threshold for position error to terminate IK iteration.
Default is 1 [mm]. rthre : Threshold for rotation error to terminate IK iteration. Default is 0.017453
[rad] (1 deg).
robot-model [class]
:super cascaded-link
:slots (rot)
(pos)
(parent)
(descendants)
(worldcoords)
(manager)
(changed)
(links)
(joint-list)
(bodies)
(collision-avoidance-links)

75
(end-coords-list)
(larm-end-coords)
(rarm-end-coords)
(lleg-end-coords)
(rleg-end-coords)
(head-end-coords)
(torso-end-coords)
(larm-root-link)
(rarm-root-link)
(lleg-root-link)
(rleg-root-link)
(head-root-link)
(torso-root-link)
(larm-collision-avoidance-links)
(rarm-collision-avoidance-links)
(larm)
(rarm)
(lleg)
(rleg)
(torso)
(head)
(force-sensors)
(imu-sensors)
(cameras)
(support-polygons)
:limb limb method &rest args [method]
Extend to support to call :inverse-kinematics-optmotiongen.
contact-ik-arg [class]
:super cascaded-link
:slots ( contact-coords Tcnt )
inverse-kinematics-optmotiongen のtarget-coords, translation-axis, rotation-axis, transform-coords 引
数に対応する接触座標を表す仮想の関節・リンク構造.
:init &key (target-coords) [method]
(translation-axis)
(rotation-axis)
(transform-coords target-coords)
(name (send target-coords :name))
Initialize instance
:contact-coords &rest args [method]
76
return Tcnt := {pcnt ,Rcnt }
ik-arg-axis->axis-list ik-arg-axis [function]
Convert translation-axis / rotatoin-axis to axis list.
generate-contact-ik-arg-from-rect-face &key (rect-face) [function]
(name (send rect-face :name))
(margin (or (send rect-face :get :margin) 0))
Generate contact-ik-arg instance from rectangle face.
generate-contact-ik-arg-from-line-segment &key (line-seg) [function]
(name (send line-seg :name))
(margin (or (send line-seg :get :margin) 0))
Generate contact-ik-arg instance from line segment.
axis->index axis [function]
axis->sgn axis [function]
5.4 関節トルク勾配の計算
get-link-jacobian-for-contact-torque &key (robot) [function]
(drive-joint-list)
(contact-coords)
(contact-parent-link)
contact-coords に対応する接触部位の番号を mとする.contact-coords の位置姿勢を rm∈R6,drive-
joint-list の関節角度ベクトルを ψ∈RNdrive-joint として,次式を満たすヤコビ行列 Jmを返す.
˙rm=Jm˙
ψ(5.1)
=
Ndrive-joint
i=1
j(i)
m˙
ψi(5.2)
j(i)
m=aψi×(pm−pψi)
aψi(5.3)
Jm=j(1)
mj(2)
m··· jNdrive-joint
m(5.4)
aψi,pψi∈R3はi番目の関節の回転軸ベクトルと位置である.
return Jm∈R6×Ndrive-joint
get-contact-torque &key (robot) [function]
(drive-joint-list)
(wrench-list)
(contact-target-coords-list)
(contact-attention-coords-list)
ロボットの接触部位に加わる接触レンチによって生じる関節トルク τcnt は,以下で得られる.
τcnt =
Ncnt
m=1
JT
mwm(5.5)
wmはm番目の接触部位で受ける接触レンチである.
return τcnt ∈RNdrive-joint

77
get-contact-torque-jacobian &key (robot) [function]
(joint-list)
(drive-joint-list)
(wrench-list)
(contact-target-coords-list)
(contact-attention-coords-list)
式(5.4) のJmを以下のように分解して利用する.
Jm=
jT
x,m
jT
y,m
jT
z,m
jT
R,m
jT
P,m
jT
Y,m
=
∂rx,m
∂ψT
∂ry,m
∂ψT
∂rz,m
∂ψT
∂rR,m
∂ψT
∂rP,m
∂ψT
∂rY,m
∂ψT
(5.6)
これを式 (5.5) に代入すると,
τcnt =
Ncnt
m=1
JT
mwm(5.7)
=
Ncnt
m=1 jx,m jy,m jz,m jR,m jP,m jY,m
fx,m
fy,m
fz,m
nx,m
ny,m
nz,m
(5.8)
=
Ncnt
m=1 jx,mfx,m +jy,mfy,m +jz,mfz,m +jR,mnx,m +jP,mny,m +jY,mnz,m(5.9)
=
Ncnt
m=1 ∂rx,m
∂ψfx,m +∂ry,m
∂ψfy,m +∂rz,m
∂ψfz,m +∂rR,m
∂ψnx,m +∂rP,m
∂ψny,m +∂rY,m
∂ψnz,m
(5.10)
joint-list の関節角度ベクトルを θ∈RNjoint ,drive-joint-list の関節角度ベクトルを ψ∈RNdrive-joint とす
る.トルク勾配行列 ∂τcnt
∂θは次式で得られる.
∂τcnt
∂θ=
Ncnt
m=1 ∂Jm
∂θT
wm(5.11)
=
Ncnt
m=1 fx,m
∂2rx,m
∂ψ∂θ+fy,m
∂2ry,m
∂ψ∂θ+fz,m
∂2rz,m
∂ψ∂θ+nx,m
∂2rR,m
∂ψ∂θ+ny,m
∂2rP,m
∂ψ∂θ+nz,m
∂2rY,m
∂ψ∂θ
(5.12)
=
M
m=1 fx,m fy,m fz,m nx,m ny,m nz,m
∂2rx,m
∂ψi∂θj
∂2ry,m
∂ψi∂θj
∂2rz,m
∂ψi∂θj
∂2rR,m
∂ψi∂θj
∂2rP,m
∂ψi∂θj
∂2rY,m
∂ψi∂θj
i=1,··· ,Ndrive-joint ,j=1,··· ,Njoint
(5.13)
return ∂τcnt
∂θ∈RNdrive-joint ×Njoint
78
get-link-jacobian-for-gravity-torque &key (robot) [function]
(drive-joint-list)
(gravity-link)
gravity-link のリンク番号を kとする.gravity-link の重心位置を pcog,k∈R3,drive-joint-list の関節角
度ベクトルを ψ∈RNdrive-joint として,次式を満たすヤコビ行列 Jcog,kを返す.
˙pcog ,k=Jcog ,k˙
ψ(5.14)
=
Nk
i=1
j(i)
cog,k˙
ψi(5.15)
j(i)
cog,k=aψi×(pcog ,k−pψi) (1 ≤i≤Nk)
03(Nk+ 1 ≤i≤Ndrive-joint )(5.16)
aψi,pψi∈R3はi番目の関節の回転軸ベクトルと位置である.gravity-link よりもルート側にある関節の
番号を 1,· · · , Nk,gravity-link よりも末端側にある関節の番号を Nk+ 1,· · · , Ndrive-joint とする.リン
クの重心位置と関節角度の依存関係から,ヤコビ行列の右には次式のように零ベクトルが並ぶ.
Jcog,k=j(1)
cog,k· · · j(Nk)
cog,kj(Nk+1)
cog,k· · · jNdrive-joint
cog,k(5.17)
=j(1)
cog,k· · · j(Nk)
cog,k0· · · 0(5.18)
return Jcog,k∈R3×Ndrive -joint
get-gravity-torque &key (robot) [function]
(drive-joint-list)
(gravity-link-list)
ロボットのリンク自重によって生じる関節トルク τgrav は,ロボットモーション P111 式(3.3.22) より以
下で得られる.
τgrav =
Ngravity-link
k=1
mkJT
cog,k
g(5.19)
mkはk番目のリンクの質量である.
return τgrav ∈RNdrive -joint
get-gravity-torque-jacobian &key (robot) [function]
(joint-list)
(drive-joint-list)
(gravity-link-list)
式(5.18) のJcog,kを以下のように分解して利用する.
Jcog,k=
jT
cog,x,k
jT
cog,y,k
jT
cog,z,k
=
∂pcog ,x,k
∂ψT
∂pcog ,y,k
∂ψT
∂pcog ,z,k
∂ψT
(5.20)
79
これを式 (5.19) に代入すると,
τgrav =
Ngravity-link
k=1
mkJT
cog,k
g(5.21)
=
Ngravity-link
k=1
mkjcog,x,kjcog ,y,kjcog,z,k
0
0
g
(5.22)
=
Ngravity-link
k=1
mkgjcog,z,k(5.23)
=
Ngravity-link
k=1
mkg∂pcog,z,k
∂ψ(5.24)
joint-list の関節角度ベクトルを θ∈RNjoint ,drive-joint-list の関節角度ベクトルを ψ∈RNdrive-joint とす
る.トルク勾配行列 ∂τgrav
∂θは次式で得られる.これは対称行列である.
∂τgrav
∂θ=
Ngravity-link
k=1
mkg∂2pcog,z,k
∂ψ∂θ(5.25)
∂2pcog,z,k
∂ψ∂θ=∂2pcog,z,k
∂ψi∂θji=1,··· ,Ndrive-joint ,j=1,··· ,Njoint
(5.26)
つまり
∂τgrav
∂θ=
Ngravity-link
k=1
mkg∂2pcog,z,k
∂ψi∂θj
i=1,··· ,Ndrive-joint ,j=1,··· ,Njoint
(5.27)
return ∂τgrav
∂θ∈RNdrive-joint ×Njoint