Rads4 Data Manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 43

RADS Data Manual

Remko Scharroo

Version 4.3.2

7 November 2018

Laboratory for Satellite Altimetry

NOAA•NESDIS•STAR

NOAA

)

))

This document was typeset with L

EX 2ε.

The layout was designed by Remko Scharroo c

1993–2015

Contents

1 Introduction 1

2 Time and location 3

2.1 Time ........................................... 3

2.2 Latitudeandlongitude................................. 4

2.3 Orbitalaltitude ..................................... 4

2.4 Orbitalaltituderate................................... 6

3 Sea level variables 7

3.1 Sealevelanomaly.................................... 7

3.2 Altimeterrange ..................................... 8

3.3 Altimeter range statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

3.4 Dry tropospheric correction and air tide . . . . . . . . . . . . . . . . . . . . . . . 10

3.5 Wet tropospheric correction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

3.6 Ionosphericcorrection ................................. 13

3.7 Atmospheric (inverse barometer) correction . . . . . . . . . . . . . . . . . . . . . 14

3.8 Solidearthandpoletide................................ 15

3.9 Oceanandloadtide................................... 15

3.10Seastatebias....................................... 17

3.11 Mean sea surface and geoid . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

4 Wind speed and wave height variables 20

4.1 Signiﬁcantwaveheight................................. 20

4.2 Altimeter backscatter coefﬁcient . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.3 Windspeed ....................................... 22

4.4 Otherwavemodeldata................................. 23

5 Radiometer variables 24

5.1 Radiometer brightness temperatures . . . . . . . . . . . . . . . . . . . . . . . . . 24

5.2 Watervapourcontent.................................. 24

5.3 Liquidwatercontent .................................. 24

6 Variables for data editing 25

6.1 Engineering and geophysical ﬂags . . . . . . . . . . . . . . . . . . . . . . . . . . 25

6.2 Bathymetry and topography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

6.3 Distance from coast and coastal proximity parameter . . . . . . . . . . . . . . . 29

6.4 Basincodes........................................ 29

Bibliography 31

iii

iv Contents

Index 37

Chapter 1

Introduction

This manual is intended to explain the details about the many variables available in the RADS

data base. Many of the variables come in different ”ﬂavours”, like one could choose to use

the wet tropospheric correction based on radiometer measurements (wet tropo rad) or one of

the atmospheric models (e.g., wet tropo ecmwf). RADS also provides the option to use more

generic variable names (like wet tropo) that will pick the best available correction depending

on the satellite mission (or period).

The variables are organised various chapters. Consult the table of contents to ﬁnd the

variables you are looking for, or go to the index at the end of the manual, where all variables

are listed.

For each variable, a list of different ﬂavours is presented. For an example, turn to Sec-

tion 3.5. This Section describes the various wet tropospheric corrections. The table in that

Section lists in the ﬁrst column the various variable names, followed by the ﬁeld number as

was used in RADS 3 (and can still be used in RADS 4), a short description, and the units of this

variable. The next column lists for which altimeter missions this variable is available (see Ta-

ble 1.1), where ”all” stands for all missions, and ”other” stands for all missions not mentioned

above it. The second to last column is the default range used for editing (NaN is returned when

Altimeter Abbr. Nr Alternatives References

GEOS 3 g3 1 ge3 geos-3 geos3 (not included in RADS)

Seasat ss 2 sea seasat-a (not included in RADS)

Geosat gs 3 geo geosat

ERS-1 e1 4 er1 ers-1 ers1 [Francis, 1990; Francis et al., 1991]

TOPEX tx 5 top topex [Fu et al., 1994]

Poseidon pn 6 pos poseidon

ERS-2 e2 7 er2 ers-2 ers2 [Francis et al., 1995]

GFO g1 8 gfo gfo-1 gfo1

Jason-1 j1 9 ja1 jason-1 jason1 [M´enard et al., 2003]

Envisat n1 10 en1 envisat

Jason-2 j2 11 ja2 jason-2 jason2 [Lambin et al., 2010]

CryoSat-2 c2 12 cs2 cryosat-2 cryosat2 [Wingham et al., 2006]

SARAL sa 13 sa srl saral altika

Jason-3 j3 14 ja3 jason-3 jason3

HY-2A 2a 15 h2a hy-2a hy2a (not included in RADS)

Sentinel-3A 3a 16 s3a sentinel-3a sentinel3a sntnl-3a

Sentinel-3B 3b 17 s3b sentinel-3b sentinel3b sntnl-3b (limited access in RADS)

Table 1.1 Abbreviation and numbers used for the various altimeter missions.

2 Introduction

the value exceeds this range). When this column is empty, no range limits are set. Finally, the

rightmost column relates to a list of notes provided in that Section.

Near the bottom of each variable table a number of ”aliases” are provided. These are

short-cuts to one (or more) of the ﬂavours of variables. For example, the tables in Section 3.5

shows that for most altimeter missions the alias wet tropo means that radiometer wet tropo-

spheric correction is used (wet tropo), but, when not available, for example during extended

outage, the ECMWF model wet tropospheric correction (wet tropo ecmwf) is used instead.

These ”aliases” make it easier to get the preferred ﬂavour of the variable which may differ

from mission to mission (for example, some do not have a radiometer). This largely simpliﬁes

the construction of sea level anomalies, as described in Section 3.1.

Chapter 2

Time and location

2.1 Time

Time in the RADS data sets is stored as 8-byte ﬂoats in UTC seconds since a given epoch (nor-

mally 1 January 1985 or 1 January 2000). RADS will automatically convert these values into a

few common time scales, depending on which time variable is selected. However, irrespective

of the time scale, the clock references to UTC, rather than an atomic clock, meaning that leap

seconds may result in a duplication of measurement times. No provision has been made to

avoid confusion between measurements made before and after a leap second.

The time corresponds to the moment of reﬂection of the radar pulse on the sea surface and

is corrected for time tag biases.

Variable ﬁeld name units sat range note

time 1985 101 time since 1985-01-01 00:00:00 s all

time 2000 106 time since 2000-01-01 00:00:00 s all

time rel eq 102 time relative to equator crossing s all 1

time local solar 103 local solar time s all 2

time mjd 105 time since 1858-11-17 00:00:00 days all 3

time ymdhms 104 time formatted as ymdhms all 4

time 1alias of time 1985 all 5

Notes:

1. Time is negative prior to equator crossing, positive thereafter.

2. The local solar time is expressed as seconds since the start of the day.

3. Time in Modiﬁed Julian Days.

4. The variable time ymdhms will produce a ﬂoating value of the type 20110908135001.536

for 8 Sep 2011 13:50:01.536 UTC.

5. No time limit is set by default. Can be controlled by the --t or --ymd ﬂags on the com-

mand line.

6. A time tag bias (surplus) of 1.8 ms was removed from the time tags of ERS-1 as they oc-

curred on the ESA OPR (Ocean Product) data product. Likewise, all time tags of ERS-2

were decreased by 1.3 ms. The orbital altitude and location has been adjusted accordingly.

4 Time and location

2.2 Latitude and longitude

The position of the centre of the footprint of the measurement is given by its geographical

longitude and latitude relative the TOPEX reference ellipsoid. Longitude is in degrees relative

to the Greenwich meridian, positive measuring east. Latitude is in degrees relative to the

equator, positive measuring north.

Variable ﬁeld name units sat range note

lat 2, 201 latitude degrees north all -90 90

lon 3, 301 longitude degrees east all -180 180 1

Note:

1. RADS will automatically adjust the values to be within the range speciﬁed. So, by default,

longitudes are kept within the -180 to +180 range.

2.3 Orbital altitude

The orbital altitude is the height of the centre-of-mass of the satellite above the TOPEX ref-

erence ellipsoid (semi-major axis = 6378136.3 m, inverse ﬂattening = 298.257) as computed

by satellite orbit determination. Numerous solutions exist, based on varying combinations of

tracking data or gravity ﬁeld solutions, or computed at shorter or longer latency. Some ”legacy

solutions” (those that were provided on the original data products) are included for reference

even when they have been long replaced by more accurate solutions.

The altitude is that of the centre-of-mass of the spacecraft, so corrections from the tracking

devices (DORIS, GPS, PRARE, SLR) to the centre-of-mass, as well as motion of the centre-of-

mass within the spacecraft are accounted for, and should also be accounted for when later

subtracting the altimeter range referenced to the same point.

If the time tags on the original GDR data include a bias, the orbit has either been

(re)interpolated at the corrected time tag, or a correction proportional to the orbital altitude

rate has been applied.

2.3 Orbital altitude 5

Variable ﬁeld name units sat range note

alt jgm3 401 JGM-3 altitude m gs pn tx 1

alt dgme04 402 DGM-E04 altitude m e1 e2 2

alt cnes 404 CNES altitude m c2 n1 pn tx 3

alt pgs7777 410 PGS7777 altitude m g1 4

alt ggm02c itrf2000 411 GGM02c(ITRF2000) altitude m gs pn tx 5

alt ggm02c itrf2005 413 GGM02c(ITRF2005) altitude m pn tx 5

alt eiggl04s 414 EIGEN-GL04c altitude m j1 6

alt gdrcp 415 GDR-C’ altitude m g1 gs j1 j2 n1 pn tx 7

alt gps 416 GPS altitude m j1 j2 8

alt eig6c 417 EIGEN-6C altitude m c2 n1 9

alt eig6s2 417 EIGEN-6S2 altitude m j1 j2 9

alt gdrd 418 CNES GDR-D altitude m c2 j1 j2 n1 sa 10

alt std1204 419 GSFC/Std1204 altitude m j1 j2 pn tx 11

alt reaper 420 REAPER/COMBI altitude m e1 e2 12

alt reaper deos 421 REAPER/DEOS altitude m e1 e2 12

alt reaper gfz 422 REAPER/GFZ altitude m e1 e2 12

alt reaper esoc 423 REAPER/ESOC altitude m e1 e2 12

alt std1404 424 GSFC/Std1404 altitude m j2 13

alt gdre 425 CNES GDR-E altitude m c2 j2 j3 sa 14

alt slcci 426 GFZ/SLCCI altitude m e1 e2 j1 j2 n1 pn tx 15

alt 4alias of alt gdre alt cnes c2 16

alt 4alias of alt reaper alt gfz e1 e2 16

alt 4alias of alt pgs7777 g1 16

alt 4alias of alt gdrcp gs 16

alt 4alias of alt gdre j1 16

alt 4alias of alt gdre alt gdrd j2 16

alt 4alias of alt gdre j3 sa 16

alt 4alias of alt gdrd alt gdrcp n1 16

alt 4alias of alt gdrcp alt jgm3 pn tx 16

Notes:

1. JGM-3 [Tapley et al., 1996] was the original gravity ﬁeld solutions used by NASA for the

orbit determination of Geosat and TOPEX/Poseidon that featured on the GDR products.

Though the gravity ﬁeld was tailored to the TOPEX orbit, it was generally regarded the

best at the time and was hence also used more widely than just for TOPEX/Poseidon. The

radial orbit accuracy of about 3 cm for TOPEX/Poseidon and 8 cm for Geosat has since

been superseded by more up-to-date orbit solutions.

2. DGM-E04 was a gravity ﬁeld model developed at the Delft University of Technology tai-

lored to the ERS-1 and ERS-2 orbits and derived from the JGM-3 model. The model signiﬁ-

cantly improved the radial orbit accuracy to about 3.5 cm, better than any general purpose

models available at the time [Scharroo and Visser, 1998].

3. CNES produces the operational and precise orbits for a number of satellites. Unfortunately,

in RADS the CNES orbits are based on mix of gravity ﬁeld solutions. The CNES orbits for

the TOPEX/Poseidon mission feature on the GDRs and are based on the JGM-3 gravity

ﬁeld model [Tapley et al., 1996]. The CNES orbits for CryoSat and Envisat are obtained

from their respective GDR products and are based on the EIGEN-GL04c gravity ﬁeld model

[Ablain et al., 2008].

4. PGS7777 is a NASA preliminary gravity ﬁeld solution tailored to the Geosat and GFO

satellite orbits. The NASA PGS7777 orbit solution for GFO [Lemoine et al., 2006] is based on

SLR data only as the GPS tracking system on GFO failed.

6 Time and location

5. Orbit solutions created at NASA using the GGM02c gravity ﬁeld and station coordinates

in the ITRF2000 or ITRF2005 reference frame.

6. Orbits produced with the EIGEN-GL04c or EIGEN-GL04s gravity ﬁelds.

7. Orbits produced under strict Jason GDR-C’ standards.

8. Reduced-dynamic (fast-delivery) orbits based on GPS tracking data only.

9. Orbits provided by ESOC using the EIGEN-6C or EIGEN-6S2 gravity ﬁeld. The orbits are

available for parts of the various altimeter missions only: CryoSat-2 cycles 4-58, Envisat all

cycles, Jason-1 cycles 1-260, Jason-2 cycles 1-220.

10. Orbits produced by CNES under strict Jason GDR-D standards [International DORIS Ser-

vice, 2011]. These orbits are kept on Jason-2 data (until April 2015) and SARAL data (until

June 2015) for comparison, although the GDR-E orbits are now default. Jason-1 data does

not have GDR-E orbits yet.

11. Orbits provided by GSFC using their standards ”Std1204”. They are ”GDR-D compatible”

and use the goce2s ﬁt2 gravity ﬁeld [Lemoine et al., 2013].

12. Orbits produced by the REAPER project. A combined solution and individual solutions

created by DEOS (TU Delft), GFZ and ESOC are available [Rudenko et al., 2011].

13. Orbits provided by GSFC using their standards ”Std1404”. They are ”GDR-E compatible”.

14. Orbits produced by CNES under strict Jason GDR-E standards (baseline for the production

of orbits since April 2015) [International DORIS Service, 2015].

15. Orbits produced by GFZ in the framework of the ESA Sea Level CCI project. RADS initially

included version VER06 of these orbits (based on the EIGEN-6S2A gravity ﬁeld model)

[Rudenko et al., 2014] for ERS-1, ERS-2, Envisat and TOPEX/Poseidon. Any data produced

since 18 May 2016 (which includes Jason-1 and Jason-2) incorporated version VER11 of

these orbits and are based on the EIGEN-6S4 gravity ﬁeld model [Rudenko et al., 2015, 2016].

16. The variable alt refers to the preferred (best) orbit solution for each satellite. If two variable

names are mentioned, RADS picks the ﬁrst one by preference; it that is not available, the

second variable is used.

2.4 Orbital altitude rate

The rate of change of the orbital altitude is relevant for computing the Doppler correction and

for correcting the altitude as a result of a time tag bias. Furthermore, the orbital altitude rate

can be used to estimate time tag biases.

Variable ﬁeld name units sat range note

alt rate 5, 501 orbital altitude rate m/s all

Chapter 3

Sea level variables

3.1 Sea level anomaly

The sea level anomaly (SLA) or sea surface height anomaly (SSHA) is the height for the sea

surface relative to a long term mean. It can be constructed by subtracting from the satellite

orbital altitude the altimeter range, propagation corrections, sea state bias, tides, and a mean

sea surface model.

The sea level anomaly in RADS is always computed on-the-ﬂy. This means that the RADS

software will gather the required variables and their selected ﬂavours from the netCDF data

ﬁles, edit those data based on the user-selected criteria, and then constructs the sea level

anomaly based on those. If any of the variables that make up the sea level anomaly is not

available, marked invalid, or is out of range, then the sea level anomaly is also marked invalid

(set to the NaN value). In addition, variables that do not strictly make up the sea level anomaly

(like wave height or wind speed) can be used as edit criteria, e.g. rejecting data with high sea

states.

The rads.xml conﬁguration ﬁle spells out, in reverse polish notation (RPN), how the sea

level anomaly (sla) is computed. The ’sea level equation’ is written as:

<data>

alt range SUB dry_tropo SUB wet_tropo SUB iono SUB

dac SUB tide_solid SUB tide_ocean SUB tide_load SUB

tide_pole SUB ssb SUB mss SUB ref_frame_offset SUB

</data>

where SUB stands for ’subtract’ and the others are names or aliases of the various variables

that make up the sea level anomaly. If any of these variables is NaN, the result is NaN as well.

The use of aliases comes in handy here. We can, for example, switch out the orbit solution

between one ﬂavour and another simply by directing the alias alt from say alt jgm3 to alt

dgme04. We do not have to change anything to the sea level equation.

The conﬁguration ﬁle also spells out which variables are used as ’quality ﬂag’. That is, if

any of these variables is set to NaN, the sea level anomaly is also set to NaN, even though

these variables are not added or subtracted as part of the ’sea level equation’. For example:

<quality_flag>

swh sig0 range_rms range_numval flags

</quality_flag>

While the sea level anomaly variable sla is computed on-the-ﬂy by the RADS software,

there is a second variable ssha that is already stored on the RADS products. Users can use this

variable directly as well, but then give up the opportunity to edit the results themselves.

8 Sea level variables

Variable ﬁeld name units sat range note

sla 0 sea level anomaly m all -5 5 1

ssha sea level anomaly (precomputed) m all 2

Notes:

1. The limits on the sea level anomaly can be changed in the conﬁguration ﬁle, of by using

the --sla=MIN,MAX option on the command line.

2. The variable ssha is read directly from the RADS products and already is screened by

editing.

3.2 Altimeter range

The range between the satellite and the sea surface is based on the total travel time of the

radar pulse divided by twice the speed of light. This range is then corrected for internal paths

within the instrument (internal calibration), variations in the frequency of the ultra-stable os-

cillator (USO correction), and the distance between the antenna and the satellite centre of mass

(centre-of-mass offset). The range is further corrected for the Doppler effect. As such the range

measures the distance between the satellite centre of mass and the sea surface, except for path

delays in the atmosphere and sea surface interactions.

To compute the height of the sea surface, we subtract the primary range (generally Ku-

band) from the satellite orbital altitude and then further correct for path delays and other

corrections.

Dual-frequency altimeters measure the range also on a secondary frequency (C- and S-

band) which allows for the computation of the ionospheric path delay directly for altimeter

observations rather than models.

Variable ﬁeld name units sat range note

range ka 601 altimeter range (Ka) m sa

range ku 601 altimeter range (Ku) m other

range ku mle3 601 altimeter range (MLE3) m j2 j3 10

range c 602 altimeter range (C) m tx j1 j2 j3

range s 602 altimeter range (S) m n1

range 6alias of range ka sa

range 6alias of range ku other

Notes:

1. A constant bias of -124 mm is added to the Geosat range. An additional internal calibration

and USO correction comes from an external ﬁle [Brian Beckley, priv. comm., 2002].

2. The range of the ERS-1 and ERS-2 altimeters has been corrected for SPTR bias jumps and

USO drift based on ofﬂine tables [Martini and F´em´enias, 2000].

3. A constant bias of 409.2 mm is added to the ERS-1 range [Francis et al., 1993; Stum et al.,

1998].

4. The ERS-2 USO correction appears to be low during the periods 1997-07-26 20:24:04 to

1998-01-07 03:58:09 and 1998-03-17 11:10:48 to 2000-01-08 06:04:13. During both periods

4.77 mm is added to the USO correction (and to range).

5. The USO correction for Envisat is based on external USO correction ﬁles (1-Hz data): http:

//earth.esa.int/pcs/envisat/ra2/auxdata/

3.3 Altimeter range statistics 9

6. Even though the Envisat Ku- and S-band ranges have biases of the order of 45 cm, this is

not corrected for in the range, but in the reference frame offset (ref frame offset). A cor-

rection of 150 mm is added to the S-band range to account for a bias in the dual-frequency

ionosphere correction [Scharroo and Smith, 2010]. During the short operation of the Side B

altimeter, an additional 9 mm was added to both Ku- and S-band ranges.

7. S-band range for Envisat is available only until the loss of the S-band signal.

8. TOPEX Ku- and C-band ranges are corrected for internal path delays and oscillator drifts

based on external correction ﬁles (one value per cycle: http://topex.wff.nasa.gov/) [Hayne

et al., 1994]. An additional -15.4 mm is added to the C-band range to account for a bias in

the dual-frequency ionosphere correction [Scharroo and Smith, 2010].

9. A constant bias of -2.3 mm is added to the Jason-1 C-band range to account for a bias in the

dual-frequency ionosphere correction [Scharroo and Smith, 2010].

10. A separate range based on an MLE3 retracker is available for Jason-2 and -3.

3.3 Altimeter range statistics

The altimeter ranges are provided in RADS as (approximately) 1-second averages based on 10,

20, or 40 ’elementary’ measurements during that second. The altimeter range reported is, in

fact, not the statistical mean, but is generally determined as follows:

Interpolate the orbital altitude at the same time tags as the elementary measurements;

Subtract the orbital altitude from the range;

Fit a linear trend true ‘range minus orbit’;

Remove the linear trend;

Compute the standard deviation of the residuals (using n−2 in the denominator) where n

is the number of elementary measurements during a 1-Hz period;

Evaluate the linear trend at the mid point and add the local orbital altitude back at this

point to obtain the average range.

Hence, technically, range rms is not the standard deviation of the altimeter range, but the stan-

dard deviation of the elementary ‘orbit minus range’ values with a trend ﬁtted and removed

as well, and taking into account the extra degree of freedom. It should also not be confused

with an error estimate for the range measurement.

Variable ﬁeld name units sat range note

range rms ka 2002 std dev of Ka-band range m sa 0.0 0.17

range rms ku 2002 std dev of Ku-band range m g1 gs 0.0 0.25

j1 0.0 0.2

j2 j3 0.0 0.17

tx 0.0 0.15

other 0.0 0.4

range rms c 2004 std dev of C-band range m j1 j2 j3 0.0 0.4

range rms s 2004 std dev of S-band range m n1 0.0 0.4 1

range rms 20 alias of range rms ka sa

range rms 20 alias of range rms ku other

10 Sea level variables

Note:

1. Standard deviation of S-band range for Envisat is available only until the loss of the S-band

signal.

Variable ﬁeld name units sat range note

range numval ku 2101 nr of valid Ka-band measurements sa 33 40

range numval ku 2101 nr of valid Ku-band measurements g1 gs tx 9 10

j1 j2 j3 16 20

other 17 20

range numval c 2102 nr of valid C-band measurements j1 j2 j3 17 20

range numval 21 alias of range numval ka sa

range numval 21 alias of range numval ku other

3.4 Dry tropospheric correction and air tide

The dry tropospheric correction (the negative of the zenith hydrostatic delay, ZHD) accounts

for the delay of the radar signal in the atmosphere, not counting the effect of water vapour.

This effect is non-dispersive, i.e., it is the same on all frequencies, and is proportional to the

surface pressure [Saastamoinen, 1972]. The surface pressure, in turn, is determined by interpo-

lation (in space and time) of model grids of surface (or sea level) pressure (see Notes). Most

altimeter missions provide the ECMWF operational analysis models as baseline.

Generally, the temporal spacing of the model grids is 6 hours, while the spatial resolu-

tion varies. The 6-hourly interval between successive model grids hampers the capturing of

12-hourly and 24-hourly phenomena. Common 24-hourly traveling waves turn into standing

waves, while 12-hourly variations are insufﬁciently described. These phenomena are consid-

ered S1 and S2 air tides [Ponte and Ray, 2002].

To remedy this problem an air tide correction is applied to the sea level pressure, by remov-

ing the air tide from the 6-hourly grids before spatio-temporal interpolation and then adding

the air tide back for the time and location of the measurement. This correction is already

applied to the ECMWF dry tropospheric correction on the Jason-2 GDRs; for all others it is

corrected in the RADS processing.

Variable ﬁeld name units sat range note

dry tropo ecmwf 701 ECWMF dry tropo corr m all but g1 gs -2.4 -2.1 1

dry tropo ncep 702 NCEP dry tropo corr m all -2.4 -2.1 2, 4

dry tropo era 709 ERA Interim dry tropo corr m all -2.4 -2.1 3, 4

dry tropo airtide 4901 air tide corr m c2 e1 j1 pn tx 5

dry tropo 7alias of dry tropo era g1 gs

dry tropo 7alias of dry tropo ecmwf other

Notes:

1. The pressure ﬁelds on which this correction is based are from the ECMWF operational

analysis runs. That means that numerous changes to the models and their resolution create

an unstable reference for long-term studies. Please verify any of the ECMWF model results

against the other models. Because of an unfortunate choice to use surface pressure ﬁelds,

instead of sea level pressure ﬁelds, for this correction, coastal areas may be affected by

“leaking” of the effect of higher terrain over land (thus lower pressure) into the sea and

ocean (where there should be no terrain effect).

3.5 Wet tropospheric correction 11

2. The NCEP reanalysis model used for this correction has not gone through any updates,

so from that point of view the correction should be consistent over time. However, this

older model also is less accurate and has a lower resolution (2.5◦×2.5◦) than the ECMWF

analysis ﬁelds.

3. The ERA (ECMWF ReAnalysis) Interim model provides an excellent long-term consistency.

The data is distributed by ECMWF as Gaussian grids with an approximately uniform spac-

ing of 79 km [Berrisford et al., 2011].

4. NCEP and ERA sea level pressure grids are interpolated and, over land and lakes, the pres-

sure is then corrected for altitude based on a high-resolution terrain model, thus avoiding

the coastal contamination seen in the ECMWF dry tropospheric correction.

5. The air tide correction to the dry tropospheric correction is provided for reference only. It

is already applied to all variations of the dry tropospheric correction (ECMWF, NCEP, ERA

interim).

3.5 Wet tropospheric correction

The wet tropospheric correction (the negative of zenith wet delay, ZWD) accounts for the delay

of the radar signal in the atmosphere due to the presence of water vapour. This effect is non-

dispersive, i.e., it is the same on Ku-, S- and C-band frequencies, and it can be determined by

integrating a function of water vapour density and temperature [e.g., Askne and Nordius, 1987],

which to good approximation simpliﬁes to

ZWD IWVRw(k3/Tm+k0

where IWV is integrated water vapour, Tmis the mean temperature in the atmospheric column,

and Rw,k0

2and k3are constants [Bevis et al., 1994]. The mean temperature can further be

approximated from model data of near-surface air temperature, Ts, by

Tm50.4+0.789Ts

[Mendes et al., 2000]. In this way, the 6-hourly models of integrated water vapour and near-

surface temperature are interpolated in space and time and then converted to a wet tropo-

spheric correction. Generally, the temporal spacing of the model grids is 6 hours, but since the

power of the water vapour content at 12 and 24 hours is low, an air tide correction like in case

of the pressure is not needed.

Because of the large spatial and temporal variability (much more so than pressure), most

altimeter missions are equipped with passive microwave radiometers, collecting brightness

temperatures of the ocean surface at two or three frequencies. Using the three frequencies, or

two frequencies plus the radar altimeter backscatter measurement, a wet tropospheric correc-

tion (and some related variables) can be derived. However, the radiometer measurements are

strongly affected by land in the measurement footprint (extending to a radius of 40 km in some

cases), limiting its use in coastal regions, hence the existence of a radiometer land ﬂag.

The radiometer wet tropospheric correction for ERS-1, ERS-2, and Envisat is based

on the altimeter backscatter coefﬁcient (before correction for atmospheric attenuation) and

the radiometer brightness temperatures at 23.8 GHz and 36.5 GHz, using all the same

neural network algorithm as was developed for Envisat [Labroue and Obligis, 2003]. For

TOPEX/Poseidon, Jason-1 and -2, the radiometer wet tropospheric correction is derived from

their respective 3-channel brightness temperatures using multi-layer parametric algorithms

[Keihm et al., 1995; Dumont et al., 2001]. For GFO, the the 2-channel brightness temperatures are

12 Sea level variables

combined with the altimeter wind speed using a log-linear model [Ruf et al., 1996]. See Sec-

tions 4.2 and 5.1 for information about corrections applied to the backscatter and brightness

temperatures prior to evaluating the models.

Variable ﬁeld name units sat range note

wet tropo rad 801 radiometer wet tropo corr m n1 -0.6 0.05 1

pn tx -0.6 -0.001 2

e2 -0.6 0.0 3

e1 g1 j1 j2 j3 -0.6 0.0

wet tropo ecmwf 802 ECMWF wet tropo corr m all but g1 gs -0.6 0.0 4

wet tropo ncep 803 NCEP wet tropo corr m all -0.6 0.0 5

wet tropo nvap 804 NASA NVAP wet tropo corr m gs -0.6 0.0 6

wet tropo tovs ssmi 805 TOVS/SSMI wet tropo corr m gs -0.6 0.0 7

wet tropo tovs ncep 807 TOVS/NCEP wet tropo corr m gs -0.6 0.0 8

wet tropo era 809 ERA interim wet tropo corr m all -0.6 0.0 9

wet tropo 8alias of wet tropo ecmwf c2 10

wet tropo 8alias of wet tropo era gs 10

wet tropo 8alias of wet tropo rad wet tropo era g1 10

wet tropo 8alias of wet tropo rad wet tropo ecmwf other 10

Notes:

1. Because of model bias and noise, allow positive values.

2. The TOPEX Microwave Radiometer (TMR) measurements values come from the TMR

Replacement Product, version 1.0 (https://podaac.jpl.nasa.gov/dataset/TOPEX L2 OST

TMR Replacement). The upper limit of -0.001 m for the radiometer wet tropospheric cor-

rection is needed to exclude bogus zero values.

3. ERS-2 MWR is not available from 2009-05-04 to 2010-01-15.

4. The ECMWF correction is actually computed by integrating several layers of the atmo-

sphere, rather than using the simpliﬁed form discussed above. The meteorological ﬁelds

on which this correction is based are from the ECMWF operational analysis runs. That

means that numerous changes to the models and their resolution create an unstable ref-

erence for long-term studies. Please verify any of the ECMWF model results against the

other models.

5. NCEP reanalysis model used for this correction has not gone through any updates, so from

that point of view the correction should be consistent over time. However, this older model

also is less accurate and has a lower resolution (2.5◦×2.5◦) than the ECMWF analysis ﬁelds.

6. The NASA NVAP model is an old water vapour model used in the Geosat era.

7. TOVS and SSMI are separate radiometer constellations whose data were used to model the

water vapour content globally.

8. This the result of a merger of the TOVS radiometer data with the NCEP water vapour and

near-surface temperature models.

9. The ERA (ECMWF ReAnalysis) Interim model provides an excellent long-term consistency.

The data is distributed by ECMWF as Gaussian grids with an approximately uniform spac-

ing of 79 km [Berrisford et al., 2011].

10. CryoSat-2 and Geosat have no radiometer, so the wet tropospheric correction is always

based on models. For the other missions we may default to the model if the radiometer

correction is not at all available on the product. This would be the case when the radiometer

3.6 Ionospheric correction 13

is permanently switched off, or off for a long time. The model will not be used during short

outages.

3.6 Ionospheric correction

The radar signal is also delayed by ions and electrons in the upper layers of the atmosphere

(the ionosphere). The delay is inversely proportional to the altimeter radar frequency, and

otherwise proportional to the vertically integrated electron density, known as total electron

content or TEC. This dispersive nature allows dual-frequency altimeters (TOPEX, Envisat,

Jason-1 and -2) to directly determine the ionospheric path delay on either frequency. For sin-

gle frequency altimeters we rely on TEC estimates from models based on other dual-frequency

equipment (GPS, DORIS) or climatologies.

Variable ﬁeld name units sat range note

iono alt 901 dual-frequency iono corr m n1 j1 j2 j3 tx -0.4 0.04 1

iono alt smooth 903 smoothed dual-freq iono corr m n1 j1 j2 j3 tx -0.4 0.04 2

iono bent 902 Bent iono corr m c2 e1 e2 n1 pn tx -0.4 0.04 4

iono doris 904 DORIS iono corr m n1 pn tx -0.4 0.04 5

iono gim 906 JPL GIM iono corr m all but gs e1 pn -0.4 0.04 6

iono iri2007 907 IRI2007 iono corr m all -0.4 0.04 7

iono nic09 908 NIC09 iono corr m all -0.4 0.04 8

iono alt mle3 911 dual-freq iono corr (MLE3) m j2 j3 -0.4 0.04 3

iono alt smooth mle3 913 smoothed d-f iono corr (MLE3) m j2 j3 -0.4 0.04 3

iono 9alias of iono alt smooth

iono gim iono nic09 j1 j2 j3 n1 tx 9

iono 9alias of iono gim iono nic09 c2 e2 g1 sa 9

iono 9alias of iono nic09 e1 gs pn 9

Notes:

1. Positive correction values are allowed to account for noise in the altimeter dual-frequency

ionospheric correction. The values for this correction have been adjusted from the original

GDR products to account for relative C-band and S-band biases (Section 3.2).

2. Because of the relatively large noise in the dual-frequency ionospheric correction, iono alt

is smoothed over 35 seconds along the altimeter track (appoximately 250 km), in contrast

to the 21 seconds suggested by Imel [1994].

3. For Jason-2 and -3, a separate dual-frequency correction based on the MLE3 retracker is

available.

4. The “ancient” Bent TEC climatology [Llewellyn and Bent, 1973] should no longer be used.

5. The TEC model based on DORIS featured for a while on TOPEX/Poseidon and Envisat al-

timeter products but was far behind the accuracy of the (similar in construct) GPS-derived

GIM models.

6. JPL produces, based on the global constellation of GPS satellites and IGS GPS receivers,

2-hourly maps of TEC, known as the JPL GIM model [Komjathy et al., 2000]. The models

have a spatial resolution of 5◦×2.5◦and start in August 1998.

7. The International Reference Ionosphere went through several versions, the latest of which

is IRI2007 [Bilitza and Reinisch, 2008]. Because of its rather coarse spatial and temporal

resolution, it cannot compete with the JPL GIM model, or even the NIC09 climatology.

14 Sea level variables

8. The NIC09 climatology is based on 12 years of JPL GIM maps and can be extended as

far back as the 1950s or extrapolated using predicted solar ﬂux values [Scharroo and Smith,

2010]. This model is particularly useful for the period prior to August 1998 (before the

availability of iono gim).

9. The alias iono with use either the smoothed dual-frequency ionospheric correction or one

of the models in the order as given.

3.7 Atmospheric (inverse barometer) correction

The inverse barometer (IB) correction accounts for the suppression of sea level due to higher

sea level pressure, and its rise during lower sea level pressure. When we assume a linear

relation between pressure and suppression we talk about a ”static” IB correction, and because

the sea level goes down with increasing pressure, opposite to the way we think of a mercury

barometer, we use the term ”inverse”. The simplest form of this correction is:

IB C(p−p0)

where Cis -9.948 mm/mbar, pis the sea level pressure and p0is a reference pressure. Since

the global ocean as a whole is incompressible, p0here stands for the global mean sea level

pressure over oceans.

However, there are also dynamics involved in this. For example, an ocean basin cannot

instantly be suppressed as a whole because of rapidly increasing regional pressure. Also wind

can play a role as well. Hence, the static correction is too simplistic. A more accurate model in-

cludes wind and ocean dynamics and is hence called a dynamic atmospheric correction (DAC).

RADS, AVISO, and other altimeter datasets include the dynamic atmospheric correction pro-

duced by CLS Space Oceanography Division using the MOG2D model from Legos [Carr`ere and

Lyard, 2003; Roblou et al., 2008] and distributed by AVISO, with support from CNES. A more re-

cent update of the MOG2D correction ﬁles is based on forcing by the ERA Interim atmospheric

models. Those have been made available for the period 1991 through 2015 [Carr`ere et al., 2016].

Over inland waters, this correction should not be applied [Cr´etaux and Birkett, 2006].

Variable ﬁeld name units sat range note

inv bar static 1001 static inverse baro corr m all -1 1 1

inv bar global 1002 global mean inv baro corr m all -1 1 2

inv bar mog2d 1003 MOG2D dynamic atmospheric corr m all -1 1 3

inv bar mog2d era 1003 MOG2D DAC from ERA-Int. m all -1 1 4

inv bar mok2d 1004 MOK2D dynamic atmospheric corr m all -1 1 5

inv bar mog2d mean 1005 local mean of MOG2D m all -1 1 6

inv bar 10 alias of inv bar mog2d era inv bar mog2d all 7

dac inv bar mok2d 7

Notes:

1. This correction is the simpliﬁcation explained above.

2. For reference the global mean pressure, converted to an IB correction, Cp0, is provided.

3. The dynamic atmospheric correction model MOG2D includes the ocean dynamic response

to wind and pressure forcing. It also accounts for the aliasing of the air tides as discussed

in Section 3.4. MOG2D also comes with two latencies: (a) a few days, and thus features on

the IGDR-derived products, and (b) a few weeks, and thus features on the GDR-derived

3.9 Ocean and load tide 15

products. For fast-delivery products there is generally no MOG2D correction (so MOK2D

will be used), but the MOG2D ﬁeld will be ﬁlled in as soon as the MOG2D maps have been

distributed.

4. The DAC based on forcing by the ECMWF ERA Interim atmospheric reanalysis model is

available as inv bar mog2d era. When chosing the detail DAC (either dac or inv bar) this

model is used for the years 1991 through 2015. After that inv bar mog2d or inv bar mok2d.

5. Since the MOG2D only start in 1992, we have created a “mock-up” version of MOG2D

(a simple linear variant of inv bar static) to match the mean of MOG2D as to not disturb

continuity of the DAC prior to 1992..

6. For reference, the local long-term mean of the MOG2D correction is provided. This is the

interpolation of a static grid computed as the average of all MOG2D maps over the period

1993-2009.

7. When using the inv bar or dac alias, inv bar mog2d era is used when available (1991-2015),

otherwise inv bar mog2d is used, or automatically defaulting to inv bar mok2d.

3.8 Solid earth and pole tide

The solid earth tide is the variation of the elevation of the crust of the earth surface as a result

of the attraction by the sun and moon (other planets are generally ignored as their inﬂuence is

at least an order of magnitude smaller). As per geodetic convention the ”permanent tide” (the

mean tide resulting from the mere presence of the sun and moon) is excluded from the solid

earth tide but is included in the geoid.

The RADS implementation of the Cartwright-Taylor-Edden solid earth tide model includes

386 second order waves and 99 third order waves [Cartwright and Taylor, 1971; Cartwright and

Edden, 1973].

The pole tide is the vertical deformation of the earth crust as a result of polar motion.

We can visualise this as the ellipsoidal shape of the earth being moved as the rotation axis

of the earth moves away or closer to the mean pole [Munk and MacDonald, 1960]. We use

the IERS(EOP)05C04 earth orientation parameters and their predictions. The motion of the

mean pole, describing the effect of global isostatic adjustment (GIA) is represented by a linear

motion, as suggested by Wahr et al. [2015] following the work of Argus and Gross [2004]. The

implicit effect on pole tide is further discussed by Desai et al. [2015].

Two Love numbers multiply the results of this simple equilibrium model: (1 + k2)= 1.302

for the combination of solid earth and oceans, and h2= 0.609 for the solid earth only (over land

and lakes) [Wahr, 1985].

Variable ﬁeld name units sat range note

tide solid 1101 solid earth tide m all -1 1

tide pole 1401 pole tide m all -0.1 0.1

11 alias of tide solid all

14 alias of tide pole all

3.9 Ocean and load tide

The (pure) ocean tide is the variation of the height of the water column as a result of luni-solar

attraction. Since this is measured relative to a ﬁxed point on the solid earth (like the sea ﬂoor),

the ocean tide compares directly to tide gauge measurements. The load tide is the effect of

16 Sea level variables

the tides weighing on the elastic earth. In general, when the ocean tide goes up, the sea ﬂoor

is going down, hence reducing the sum of the two, the geocentric ocean tide. Consequently,

in order to detide the measurement of the water surface from altimetry, both the ocean tide

(tide ocean) and the load tide (tide load) need to be subtracted over ocean surfaces, while over

lakes only the load tide is subtracted.

Although some altimeter products provide the geocentric ocean tide, we have chosen to

keep ocean and load tide separate, for two reasons: (1) it makes it easier to differentiate tides

over land/lakes and ocean, and (2) it makes it easier to add regional tides which are generally

expressed as pure ocean tides.

Tides are expressed as the sum of a (large) number of waves with different frequencies, each

combinations of the frequencies associated with the rotation and progression of the earth, sun

and moon. A select portion of those waves are expressed as grids of amplitude and phase,

which can be interpolated in space and evaluated at the time of the altimeter measurement.

Then, by a process called admittance, the amplitude and phase of a number of minor tides are

inferred.

Tide models generally only include the diurnal and semi-diurnal waves (those around

a period of 12 and 24 hours). On top of that there are secondary and tertiary waves with

periods of a week or longer. Most of these waves can be expressed by a simple latitude and

time dependent equilibrium model (the long-period equilibrium tide). The FES ocean tide

models also include the non-equilibrium component of the monthly, fortnightly, tri-monthly,

and weekly tides.

Although the FES and GOT models are global, they are limited in scope. Over land, the

ocean tide is not deﬁned and will be set to the NaN value. In some coastal regions, where the

models may likely not be deﬁned, the ocean tide value is set to NaN as well.

For a very elaborate and thorough accuracy assessment of most of these tide models, we

highly recommend reading the work by Stammer et al. [2014].

Variable ﬁeld name units sat range note

tide ocean fes04 1213 FES2004 ocean tide m all -5 5 1

tide load fes04 1313 FES2004 load tide m all -0.5 0.5 1

tide ocean webtide 1215 WebTide ocean tide m all -5 5 2

tide ocean got48 1219 GOT4.8 ocean tide m all -5 5 3

tide load got48 1319 GOT4.8 load tide m all -0.5 0.5 3

tide ocean got410 1222 GOT4.10c ocean tide m all -5 5 4

tide load got410 1322 GOT4.10c load tide m all -0.5 0.5 4

tide ocean fes14 1224 FES2014b ocean tide m all -5 5 5

tide load fes14 1324 FES2014a load tide m all -0.5 0.5 5

tide equil 3901 long-period equilib. tide m all -1 1 6

tide non equil 3902 long-period non-equil. tide m all -1 1 7

tide ocean 12 alias of tide ocean got410 all

tide load 13 alias of tide load got410 all

39 alias of tide equil all

Notes:

1. The Finite Element Solution (FES2004) includes 9 short-period waves (Q1, O1, K1, P1, 2N2,

N2, M2, K2, and S2) plus 24 additional short-period waves determined by admittance, and

4 long-period waves (Mf, Mm, Mtm and MSqm) [Lyard et al., 2006]. Long-period equilib-

rium tides (not yet included in FES2004) are added to these.

2. WebTide is a collection of regional tide models along the Canadian coast, made

available on the web by the Bedford Institute of Oceanography http://www.bio.gc.ca/

3.10 Sea state bias 17

research-recherche/WebTide-MareeWeb/webtide-eng.htm. In RADS, a single value is pre-

sented in tide ocean webtide, determined from (in order of decreasing preference) the re-

gional models for: Scotia/Fundy/Maine, Northeast Paciﬁc, Arctic, Hudson Bay. Each

of these models has a very limited amount of constituents, does not include admittance

to infer others, and also does not include any long-period tides (equilibrium or non-

equilibrium).

3. The Goddard Ocean Tide model GOT 4.8 includes 10 short-period waves (K1, O1, P1, Q1,

S1, K2, M2, N2, S2, and M4) plus 17 additional short-period waves determined by admit-

tance [Ray et al., 2011].

4. The Goddard Ocean Tide model GOT4.10c differs from GOT4.8 in two ways. First,

GOT4.10c is based only on Jason data, whereas 4.8 was from only TOPEX data. Second,

it includes an adjustment for the geocenter. (Hence the ’c’ in the name.) The processing

for 4.8 and 4.10 was largely identical; one exception involved an improvement to P1 alone.

GOT4.10c is an update of Ray [2013]. This model is now the default tide model.

5. FES2014 (Finite Element Solution 2014) takes advantage of longer altimeter time series, im-

proved modelling, and data assimilation techniques, and more accurate and higher reso-

lution ocean bathymetry. A new global ﬁnite element grid (with approx. 1.5 million nodes)

was used to create a ’free’ solution (independent of in situ and remote-sensing data) that

has more than twice the accuracy of the FES2004 version. The ’free’ solution was assim-

ilated with long-term altimetry data from TOPEX/POSEIDON, Jason-1, Jason-2, ERS-1,

ERS-2, and ENVISAT. The FES2014 solution shows particular improvement in coastal and

shelf regions, as well as in overall open ocean statistics, particularly due to a higher grid

resolution (1/16◦). The model is also extended into the coast to improve the data coverage.

As with other FES models tide ocean fes14 includes long-period non-equilibrium tides;

speciﬁcally: Mf, Mm, Mtm, MSf, MSqm, Sa, and Ssa.

6. The equilibrium ocean tide includes 15 tidal spectrum lines from the Cartwright-Tayler-

Edden tables [Cartwright and Taylor, 1971; Cartwright and Edden, 1973] plus an additional

123 second and third order waves [Tamura, 1987].

7. The four long-period non-equlibrium ocean tidal components (Mm, Mf, MSf, Mtm, and

MSqm) from the FES2004 model are represented in tide non equil. The equilibrium parts

of those have been removed to avoid double accounting.

3.10 Sea state bias

Sea state bias (SSB) is the term used for any altimetric range offset as a function of the sea state

(wave height, wind speed, wave age, swell). In fact, there are three components to the sea state

bias:

Electromagnetic (EM) bias is the tendency of a radar to measure towards the wave troughs

since they are better reﬂectors than the wave peaks.

Skewness bias comes from the fact that the sea surface has a skewed height distribution.

While the altimeter measures the median height of the surface in the footprint, what we

want to measure is the mean height, which is lower.

Tracker bias is the any error in the waveform tracker that is a function of the sea state, which

may be either instrumental or algorithmic.

Because of the instrumental part of sea state bias, every altimeter, in principle, requires

a different sea state bias correction model. But also when a new tracker algorithm is imple-

18 Sea level variables

mented, the sea state bias changes. This is one of the reasons for the wide proliferation of SSB

models.

In the earlier days of altimetry the sea state bias was generally considered as a simple frac-

tion, around –3.5%, of signiﬁcant wave height [Chelton, 1994]. Then Gaspar et al. [1994] brought

a major improvement in SSB modelling by expressing SSB as a polynomial function of SWH

and wind speed, recognising that not only the wave height, but also the shape of the waves (al-

tered by wind) has inﬂuence on the altimeter range bias. But this approach still exhibits some

limitations, in that it imposes the type of variations that are allowed as a result of changes in

SWH or wind speed. Currently, SSB models tend to be non-parametric, generally expressed

in the form of a grid with SWH and wind speed as coordinates [e.g., Gaspar and Florens, 1998].

But several more complex multi-dimensional models are currently under development [e.g.,

Feng et al., 2010; Tran et al., 2010].

Variable ﬁeld name units sat range note

ssb bm3 1501 parametric sea state bias m e1 e2 g1 gs pn tx -1 1 1

ssb cls 1502 CLS non-parametric SSB m j1 j2 j3 n1 tx -1 1 2

ssb csr 1503 CSR BM4 sea state bias m tx -1 1 3

ssb hyb 1504 NOAA hybrid sea state bias m g1 gs n1 pn sa -1 1 4

ssb cls c 1505 CLS non-parametric SSB (C-band) m j1 j2 j3 -1 1 2

ssb cls mle3 1512 CLS non-parametric SSB (MLE3) m j2 j3 -1 1 5

ssb tran2012 1513 Tran et al. 2012 non-parametric sea state bias m j2 j3 -1 1 6

ssb 15 alias of ssb bm3 e1 e2 pn

ssb 15 alias of ssb cls j1 j2 j3 n1 tx

ssb 15 alias of ssb hyb c2 g1 gs sa

Notes:

1. One-, three- or four-term polynomials of SWH and wind speed [Gaspar et al., 1994].

2. Non-parametric sea state bias models for Ku-band and C-band by CLS [Gaspar et al., 2002;

Labroue et al., 2004].

3. Four-term sea state bias model for TOPEX (different model for side A and side B altimeters)

[Chambers et al., 2003].

4. Hybrid (mix between parametric and non-parametric techniques) sea state bias models

produced at NOAA [Scharroo and Lillibridge, 2005].

5. For Jason-2 and -3 data retracked by MLE3, a separate non-parametric model is available.

6. The non-parametric SSB model developed by Tran et al. [2012] will be part of the upcoming

GDR-E standards.

3.11 Mean sea surface and geoid

The sea level anomaly (SLA) is expressed as the difference of the instantaneous tide-corrected

sea surface with respect to a well-established mean. Over the years several (more or less)

global mean sea surface models have been developed from the compilation of satellite altime-

ter (and sometimes gravity) data. Generally, the more altimeter data collected, the more precise

the model. But also the resolution of the model counts. Each model has been referenced to the

TOPEX reference ellipsoid, just as the satellite orbits (Section 2.3).

Another reference surface is the geoid (the theoretical mean sea surface in absence of ocean

currents, wind, etc.). Geoid models are generally made from satellite tracking data (for the

3.11 Mean sea surface and geoid 19

longer wave lengths), GRACE and/or GOCE (for the medium wave lengths), and altimetry

and in-situ gravimetry (for the shorter wave lengths).

Variable ﬁeld name units sat range note

mss cnescls11 1614 CNES-CLS11 mean sea surface m all -200 200 1

mss cnescls15 1619 CNES-CLS15 mean sea surface m all -200 200 2

mss dtu13 1616 DTU13 mean sea surface m all -200 200 3

mss dtu15 1618 DTU15 mean sea surface m c2 j2 j3 sa -200 200 4

geoid egm2008 1611 EGM2008 geoid m all -200 200 5

geoid eigen6 1617 EIGEN-6C3stat geoid m all -200 200 6

mss 16 alias of mss dtu13 all

geoid alias of geoid eigen6 all

Notes:

1. Iteration of mean sea surface models at CNES/CLS from 2011, based on altimeter data

from 1993 to 1999 [Schaeffer et al., 2012].

2. Latest iteration of mean sea surface models at CNES/CLS from 2015, based on altimeter

data from 1993 to 2012 [Schaeffer et al., 2012].

3. The DTU13MSS is the penultimate release of the global high-resolution mean sea surface

from DTU Space, which includes two major advances over DTU10MSS. First, the time se-

ries have been extended to 20 years from 17 years. Second, the DTU13MSS ingests Cryosat-

2 SAR lead data in order to map the high latitude parts of the Arctic Ocean. In high-latitude

regions a combination of joint ERS-1/ERS-2/ENVISAT and Cryosat-2 altimetry have been

used. Also, the Jason-1 geodetic mission has been used for the DTU13MSS [Andersen et al.,

2013]. This is the default mean sea surface model and is used as reference for the sea level

anomaly variable (sla).

4. The DTU15MSS is the latest state-of-the-art of the global high-resolution mean sea surface

derived by DTU Space from satellite altimetry. The main improvement over DTU13 is

the inclusion of four years of CryoSat-2 data, with a new treatment of orbit errors and ice

classiﬁcation [Stenseng et al., 2015]. This model is intended to replace in the near future

DTU13 as the default mean sea surface.

5. Combined geoid and mean sea surface solution from the US Defence Mapping

Agency[Pavlis et al., 2012].

6. The EIGEN-6C3stat geoid model has been generated in preparation for the ﬁnal release of

EIGEN-6C4. It was computed from a combination of LAGEOS, GRACE, and GOCE data,

augmented with DTU13 surface gravity data to degree and order 1949 (corresponding to

approximately 10 km spatial resolution). [F¨orste et al., 2013; Shako et al., 2014]. This is the

default geoid model.

Chapter 4

Wind speed and wave height variables

4.1 Signiﬁcant wave height

The signiﬁcant wave height (SWH) is generally deﬁned as the mean wave height (peak to

trough) of the highest one-third of the ocean waves. Another commonly used deﬁnition is

four times the standard deviation of the elevation of the sea surface in the radar footprint.

SWH is determined from the rate of increase of returned power of the radar altimeter pulse

(the waveform slope) and requires no further correction other than some instrument parame-

ters. There is one complexity in this, and that is that SWH is deﬁned as follows:

SWH2α2(σ2

c−σ2

where σcis a measure of the waveform slope and σpis an instrument parameter, and αis a con-

stant. Because of noise in the measurement of σcand a possible bias in σp, SWH2could become

negative. In most GDR products, SWH is then set to zero, which creates a wrongly truncated

measurement, and makes it difﬁcult to correct for any biases in SWH the measurement (which

would raise the zero SWH above zero). Where we can, however, in RADS, this case is tackled

by writing out the negative of the square root of the absolute value of the argument instead.

Hence:

SWH −αqσ2

p−σ2

cwhen σc< σp

SWH αqσ2

c−σ2

pwhen σc≥σp

(See Note 1 below).

The 1-Hz standard deviation of SWH is determined from the individual 10-, 20-, or 40-Hz

elementary measurements. Note that this is the standard deviation of the elementary mea-

surements (denominator is (n−1)), not an estimate of the error of SWH.

4.2 Altimeter backscatter coefﬁcient 21

Variable ﬁeld name units sat range note

swh ka 1701 Ka-band signiﬁcant wave height m sa 0 8

swh ku 1701 Ku-band signiﬁcant wave height m c2 n1 -0.5 8 1,2

other 0 8

swh c 1702 C-band signiﬁcant wave height m j1 j2 j3 tx 0 8

swh s 1702 S-band signiﬁcant wave height m n1 -0.5 8 1,3

swh ku mle3 1711 Ku-band signiﬁcant wave height (MLE3) m j2 j3 0 8 4

swh ww3 1712 WAVEWATCH3 signiﬁcant wave height m c2 j2 j3 sa 5

swh rms ka 2802 std dev of Ku-band SWH m sa 0 2.1

swh rms ku 2802 std dev of Ku-band SWH m g1 0 0.5

j1 j2 j3 0 1.5

tx 0 0.9

other 0 2.1

swh rms c 2804 std dev of C-band SWH m j1 j2 j3 tx 0 2.1

swh rms s 2804 std dev of S-band SWH m n1 0 2.1 3

swh 17 alias of swh ka sa

swh 17 alias of swh ku other

swh rms 28 alias of swh rms ka sa

swh rms 28 alias of swh rms ku other

Notes:

1. The SWH of Envisat and CryoSat will be set to a negative value when σc< σp. For other

missions, the value is set to 0.

2. During the degradation of the TOPEX SWH measurements (cycles 98-235) the SWH values

are corrected according to Queffeulou [2004]. Thereafter 32 mm was added.

3. S-band SWH for Envisat is only until the loss of the S-band signal.

4. For Jason-2 and -3, signiﬁcant wave heights from the MLE3 retracker are available as well.

5. The SWH in this ﬁeld is based on wave hindcasts done by NOAA using the WAVE-

WATCH III model [Tolman, 2009] and GFS analysis winds [Chawla et al., 2011]. The hind-

casts cover the entire globe and are carried out in monthly installments, so they are only

available on delay-time data in RADS. The original resolution of these model grids is 1◦by

1◦by 6 hours. For other WAVEWATCH III ﬁelds see Section 4.4.

4.2 Altimeter backscatter coefﬁcient

The backscatter coefﬁcient is derived from the total returned power of the radar altimeter

pulse. After correction for losses due to water vapour in the atmosphere, it identiﬁes the small

scale ripples on the sea surfaces, and hence becomes a measure for wind speed (Section 4.3).

The correction for atmospheric losses is generally determined from the radiometer mea-

surements. In case the brightness temperatures were corrected with respect to the GDR values

(Section 5.1), so is the wet tropospheric correction, the atmospheric correction to the backscat-

ter and the backscatter coefﬁcient itself.

The 1-Hz standard deviation of backscatter coefﬁcient is determined from the individual

10-, 20- or 40-Hz elementary measurements. Note that this is the standard deviation of the ele-

mentary measurements (denominator is (n−1)), not an estimate of the error of the backscatter

coefﬁcient.

22 Wind speed and wave height variables

Variable ﬁeld name units sat range note

sig0 ka 1801 Ka-band backscatter coefﬁcient dB sa 6 27

sig0 ku 1801 Ku-band backscatter coefﬁcient dB other 6 27 1-6

sig0 c 1802 C-band backscatter coefﬁcient dB j1 j2 j3 tx 6 27 3-6

sig0 s 1802 S-band backscatter coefﬁcient dB n1 6 27 7

sig0 ku mle3 1811 Ku-band backscatter coefﬁcient (MLE3) dB j2 j3 6 27 8

sig0 rms ka 2902 std dev of Ka-band SWH dB sa 0 1

sig0 rms ku 2902 std dev of Ku-band SWH dB all 0 1

sig0 rms c 2904 std dev of C-band SWH dB j1 j2 j3 tx 9

sig0 rms s 2904 std dev of S-band SWH dB n1 7

sig0 18 alias of sig0 ka sa

sig0 18 alias of sig0 ku other

sig0 rms 29 alias of sig0 rms ka sa

sig0 rms 29 alias of sig0 rms ku other

Notes:

1. The ERS-1 backscatter coefﬁcient is corrected for varying biases due to the attitude control.

Between 0 and 0.35 dB was added.

2. The GFO backscatter is corrected for a few deﬁciencies in lookup tables, adding 0.37 dB

before 6 Dec 2000 and between 7 and 9 March 2001.

3. The Jason-1 Ku- and C-band backscatter are aligned with TOPEX values by subtracting

2.40 and 0.725 dB, respectively. For the time being, the same biases are applied to Jason-2.

However, wind speed values are not adjusted.

4. The Jason-2 Ku- and C-band backscatter are reduced in noise based on a correlation with

off-nadir angle [Quartly, 2009]. In addition, biases of 2.40 and 0.725 dB have been removed

from the Ku- and C-band backscatter, respectively.

5. The Jason-3 Ku- and C-band backscatter are adjusted the same way as Jason-2.

6. TOPEX backscatter is corrected following the off-line Wallops correction tables.

7. S-band backscatter for Envisat is only until the loss of the S-band signal.

8. For Jason-2 and -3, the backscatter coefﬁcient from the MLE3 retracker is available as well.

9. For TOPEX, the standard deviation is that of the automatic gain control, not of the backscat-

ter coefﬁcient. That means that the variation of the total volume of the waveform in not

included, only the variation of the gain setting of the instrument.

4.3 Wind speed

Wind speed can be derived from the altimeter backscatter coefﬁcient (Section 4.2). The larger

the backscatter, the lower the wind speed. Several models have been developed to map this

relationship, some depending merely on backscatter, some also taking into account signiﬁcant

wave height. Which models are applied to which satellites is shown in the notes below.

Three-channel radiometers provide the opportunity to estimate wind speed. In essences

this is the reverse side of the fact that one of those channels can be replaced with the altimeter

wind speed to obtain the wet tropospheric correction. This variable is available for all missions

with 3-channel radiometers.

Atmospheric models, like those at ECMWF also provide wind speed and wind directions,

or their vectorial components pointing north and east. Those model values are provided for

some missions as well.

4.4 Other wave model data 23

Variable ﬁeld name units sat range note

wind speed alt 1901 altimeter wind speed m/s all -1 30 1-5

wind speed rad 1902 radiometer wind speed m/s j1 j2 j3 pn tx 0 30

wind speed ecmwf u 1903 ECMWF model wind speed (U) m/s e2 j1 j2 j3 n1 sa 6

wind speed ecmwf v 1904 ECMWF model wind speed (V) m/s e2 j1 j2 j3 n1 sa 6

wind speed ecmwf ECMWF model wind speed m/s e2 j1 j2 j3 n1 sa 6

wind speed gfs u 1903 NOAA/GFS model wind speed (U) m/s sa 7

wind speed gfs v 1904 NOAA/GFS model wind speed (V) m/s sa 7

wind speed gfs NOAA/GFS model wind speed m/s sa 7

wind speed 19 alias of wind speed alt all

Notes:

1. For Geosat, GFO, ERS-1 and ERS-2, the wind speed is based on the Modiﬁed Chelton-

Wentz (MCW) algorithm [Witter and Chelton, 1991]. In case of GFO 0.63 dB was subtracted

from the backscatter coefﬁcient before feeding it into the MCW algorithm.

2. The CryoSat and Envisat wind speed is based on the ECMWF 1-parameter algorithm tai-

lored to Envisat [Abdalla, 2007].

3. The Ka-band altimeter of SARAL required a new 1-parameter algorithm, similar to En-

visat’s, again matching ECWMF wind ﬁelds [Lillibridge et al., 2014].

4. The TOPEX/Poseidon wind speed is based on the 2-parameter model by Gourrion et al.

[2002].

5. For Jason-1 and Jason-2, a variant of the 2-parameter model by Gourrion et al. [2002] tailored

to Jason-1 is used to derive wind speed [Collard, 2005].

6. The U (towards east) and V (towards north) components of the wind speed according to

ECMWF model data. The absolute magnitude can be computed on-the-ﬂy.

7. The U (towards east) and V (towards north) components of the wind speed according to

0.5◦×0.5◦×6h model grids from NOAA’s Global Forecast System. The absolute magnitude

can be computed on-the-ﬂy. The inclusion of these ﬁelds is experimental, and may be removed in

the future.

4.4 Other wave model data

For calibration and validation purposes, and to support further studies that include wind and

wave processes (like swell and their effect on sea state bias) a number of variables from the

WAVEWATCH III model (version 3.14) [Tolman, 2009] as run by the University of New Hamp-

shire. These variables are currently only available during the year 2000 to 2012 (inclusive).

The original resolution of the model grids is 1◦by 1◦by 6 hours, and are restricted to latitudes

lower than 77.5◦.

In addition, SWH from the WAVEWATCH III model is made available as swh ww3 (see

Section 4.1).

Variable ﬁeld name units sat range note

wave m0 4001 WaveWatch3 wave height variance m2all

wave m1 4002 WaveWatch3 ﬁrst moment of wave height m2/s all

wave m2 4003 WaveWatch3 wave velocity variance m2/s2all

wave m4 4004 WaveWatch3 wave slope variance rad2all

wave shs 4005 WaveWatch3 wave swell m all

Chapter 5

Radiometer variables

5.1 Radiometer brightness temperatures

5.2 Water vapour content

5.3 Liquid water content

Chapter 6

Variables for data editing

6.1 Engineering and geophysical ﬂags

The engineering and geophysical ﬂags are historically a number of bits in a 2-byte integer

number that describe either instrument settings, type of surface overﬂow, or warnings about

the quality of the data. In RADS4 there are a number of aliases to help pick out single bits

from this word. The editing, however, is currently still determined by the limits set on the ﬂag

word, where the lower limits indicates which bits of the ﬂag word should not be set, and the

upper limits indicates the bits of the ﬂag word that should be set. In other words, a record will

be rejected if either:

ﬂags AND ﬂags low is not equal to 0.

ﬂags AND ﬂags high is not equal to ﬂags high.

where ﬂags low and ﬂags high are the lower and higher limit of ﬂags speciﬁed, and AND is the

logical bitwise AND operator.

In a future version of the data base the ﬂag word ﬂags will be phased out and only the

more elementary ﬂag variables that are now deﬁned as aliases will be available.

Variable ﬁeld name units sat range note

ﬂags 2601 ﬂag word 3a 3b 65448 0 1

c2 32 0

e1 e2 j1 j2 65512 0

j3 65384 0 1

g1 65384 0

gs 51176 0

n1 36712 0

pn 480 0

tx 49640 0

26 alias of ﬂags

Notes:

1. This is a temporary value, where the radiometer land ﬂag is not considered as an edit

criterion.

The individual bits of the ﬂag word ﬂags are described in the following table. Note that the

limits on these alias are not actually set at this time, but they are a transposition of the editing

26 Variables for data editing

ranges for each individual altimeter as indicated in the table above. In general, 0 means no or

OK, 1 means yes or bad.

6.1 Engineering and geophysical ﬂags 27

Variable ﬁeld name values sat note

ﬂag alt oper mode 2516 bit 0: hardware/software status 0 = nominal, 1 = bad pn tx

2516 bit 0: altimeter operating mode 0 = Side A, 1 = Side B j1 j2 j3 n1

2516 bit 0: altimeter operating mode 0 = LRM, 1 = SAR 3a 3b c2

qual sptr 2516 bit 0: SPTR availability e1

qual attitude 2501 bit 1: quality of attitude 0 = ok, 1 = bad 3a 3b e2 j1 j2 j3 n1 tx sa

bit 1: quality of attitude 0 = ok, 1 = suspect g1 gs pn

qual dh 2502 bit 2: dH status 1 = suspect gs

ﬂag rad oper mode 2502 bit 2: TMP 21 GHz Channel status 0 = A, 1 = B pn tx

ﬂag continental ice 2502 bit 2: continental ice ﬂag 0 = no, 1 = yes 3a 3b c2 j1 j2 j3 n1 sa

qual iono alt 2503 bit 3: quality of dual-frequency iono corr 0 = ok, 1 = bad 3a 3b j1 j2 j3 n1 tx

ﬂag water 2504 bit 4: water/dry ﬂag 0 = open ocean or enclosed sea or lake, 1 = land all

ﬂag ocean 2505 bit 5: ocean/land ﬂag 0 = open ocean, 1 = land or enclosed sea or lake all

surface type rad 2506 bit 6: radiometer land ﬂag 0 = water, 1 = land all but c2 gs

qual alt rain ice 2507 bit 7: altimeter rain/ice ﬂag 0 = no rain/ice, 1 = rain/ice 3a 3b g1 j1 j2 j3 n1 pn sa tx

qual rad rain ice 2508 bit 8: radiometer rain/ice ﬂag 0 = no rain/ice, 1 = rain/ice 3a 3b e1 e2 j1 j2 j3 n1 pn tx

qual rad tb 2509 bit 9/10: radiometer quality ﬂag 0 = ok, 1 = interp. near land, 2 = extrap., 3 = interp. failed pn tx

0 = ok, 1 = bad tb238, 2 = bad tb365, 3 = both bad 3a 3b e1 e2 n1

0 = ok, 1 = bad tb220, 2 = bad tb370, 3 = both bad g1

0 = ok, 1 = bad tb187/tb238, 2 = bad tb340, 3 = both bad j1 j2 j3

0 = ok, 1 = bad tb238, 2 = bad tb370, 3 = both bad sa

qual range 2511 bit 11: quality of range 0 = ok, 1 = some 10Hz invalid gs

0 = ok, 1 = suspect other

qual swh 2512 bit 12: quality of SSB 0 = ok, 1 = suspect gs

bit 12: quality of SWH 0 = ok, 1 = suspect other

qual sig0 2513 bit 13: quality of wind speed 0 = ok, 1 = suspect gs

bit 13: quality of sigma0 0 = ok, 1 = suspect other

ﬂag alt track mode 2514 bit 14: altimeter tracking mode 0 = nominal, 1 = preset e1 e2

0 = nominal, 1 = coarse or acquisition gs tx

0 = nominal, 1 = C-band coarse j1

0 = nominal, 1 = acquisition pn

qual orbit 2515 bit 15: orbital quality ﬂag 0 = ok, 1 = suspect all

surface type surface type 0 = open ocean, 2 = enclosed sea or lake, 3 = land, all 1

4 = continental ice

surface class surface class 0 = open ocean, 1 = land, 2 = continental water, all 2

3 = aquatic vegetation, 4 = continental ice or snow,

5 = ﬂoating ice, 6 = salted basin

28 Variables for data editing

Notes:

1. A new variable surface type has been introduced to combine the original ﬂag bits 2, 4,

and 5 into a single variable. Generally, the ﬂag mask determined by ﬂags low as discussed

above will be set to only allow data over open ocean. Effort is made to get rid of this quirky

method of screening the data and use the individual ﬂags instead.

The values of surface type are based on the GSHHG coastline dataset [Wessel and Smith,

1996] that is distributed with the Generic Mapping Tools (GMT) plotting package [Wessel

et al., 2013]. Version 2.3.4 of this data set was used to create land mask of ocean/land/lake

indicators at 1 arcminute resolution. This grid was than queried to determine whether

the satellite nadir point was over ocean, land, or lakes or enclosed seas. The additional

information about continental ice came for the original GDR data. If this indicator was set

in the GDR, surface type was set to the value 4, and bits 4 and 5 of ﬂags were both set to 1,

irrespective of the aforementioned land mask.

Experience has shown that for Antarctica only the grounded ice is marked as ”continental

ice” (4). The ice sheets are marked ”land” (2) as the GSHHG coastline datasets marks the

(minimum) extent of the ice sheets.

The value of 1 of surface type has been reserved for later use.

2. A more elaborate version of surface type is available as surface class. It fas 7 different

states and is based on a high-resolution mask built from MERIS and GlobCover data.

6.2 Bathymetry and topography

Bathymetry is the depth of the oceans (and seas). It is given as a negative number, and thus

constitutes the elevation of the sea bottom with respect to the geoid. The bathymetry is gener-

ally predicted from altimeter data, by inverting altimeter-derived gravity anomalies into ocean

depth [Smith and Sandwell, 1994, e.g.].

Topography is the elevation of the land (and lakes). It is represented generally by a positive

value and is measured relative to the geoid. Occasionally the values can be negative, like in

large parts of The Netherlands, and around the Dead Sea. By convention, the elevation of the

lake surfaces (not the lake bottom) is stored, except for the Caspian Sea for which generally

the bottom topography is given. The topography models are based on a number of different

sources: altimetry, the SRTM mission, and local leveling.

In RADS the bathymetry and topography are combined into a single ﬁeld. Please use the

surface type variable to distinguish between ocean, land, and lakes.

Variable ﬁeld name units sat range note

topo dtm2000 2202 DTM2000 topography m j1 j2 j3 n1 sa 1

topo srtm30plus 2204 SRTM30PLUS topography m all 2

topo dtu10 2205 DTU10 topography m all 3

topo 22 alias of topo srtm30plus all

Notes:

1. On some of the GDR products, the topography/bathymetry is determined from the

DTM2000.1 model (N. Pavlis and J. Saleh, GSFC) and is copied into the RADS data base.

2. Ocean data are based on the Smith and Sandwell global 1-minute grid between the lat-

itudes 81◦S and 81◦N degrees [Sandwell et al., 2014]. Higher resolution grids have been

added from the LDEO Ridge Multibeam Synthesis Project, the JAMSTEC Data Site for

6.4 Basin codes 29

Research Cruises, and the NGDC Coastal Relief Model. Arctic bathymetry is from the In-

ternational Bathymetric Chart of the Oceans (IBCAO) [Jakobsson et al., 2012].

Land data are based on the 1-km averages of topography derived from the USGS SRTM30

gridded DEM data product created with data from the NASA Shuttle Radar Topography

Mission. GTOPO30 data are used for high latitudes where SRTM data are not available.

V10 of SRTM30 PLUS was released in May 2014. For more information about

SRTM30 PLUS, please see: http://topex.ucsd.edu/WWW html/srtm30 plus.html

3. The DTU10 topography/bathymetry model was derived from altimeter data together with

the DTU10 mean sea surface model [Andersen and Knudsen, 2010] and is an update of the

DNSC08 bathymetry model [Andersen and Knudsen, 2009]. It is not clear where the topo-

graphic (land) data stem from. The model is interpolated to the altimeter ground track

location.

6.3 Distance from coast and coastal proximity parameter

Because the altimeter and radiometer measurements are affected by land in their respective

footprints, it is worthwhile to know what the distance from the satellite nadir to any coastline

is, since it would facilitate editing out of possibly corrupted measurements. RADS contains

two parameters for this purpose, to be used by the user at leisure: the distance from the coast

and the coastal proximity parameter. Both are based on the proximity of the altimeter footprint

to land, but potentially suit different purposes.

The distance to (of from) the coast is measured from the centre of the altimeter footprint

(i.e. the satellite nadir point) to the nearest ocean or lake shoreline. The values in the RADS

data base have been interpolated in a grid with a resolution of 1 arcminute. Positive values are

offshore distances to the nearest shoreline, negative values are inland distances to the nearest

ocean or lake shore. The grid is based on Version 2.3.0 of the GSHHG shoreline dataset [Wessel

and Smith, 1996] that is distributed with the Generic Mapping Tools (GMT) plotting package

[Wessel et al., 2013]. Any islets or lakes of less than 1 square kilometer have been excluded.

The coastal proximity parameter is a dimensionless measure of the effect of land over al-

timetric waveforms, and has values in the range from -1 to +1, where -1 means unaffected by

land (normally offshore, open-ocean points) and 1 means totally affected by land (for instance

points a few km inland). Therefore this parameter can be used for screening purposes in place

of distance from coast. The grid for this parameter was developed by NOC Southampton in

the framework of the ESA Sea Level CCI project and has a resolution of 0.01◦×0.01◦[Cipollini,

2011].

Variable ﬁeld name units sat range note

dist coast 45, 4501 distance to coast km all

prox coast 4502 coastal proximity parameter all

6.4 Basin codes

Eric Leuliette (NOAA) divided the world’s larger water bodies into 39 different ocean basins,

enclosed seas and lakes, giving each of them a separate numerical code. This has been rep-

resented in a grid with a 5’×5’ resolution as shown in Figure 6.1. This grid is queried to the

nearest grid point when creating the RADS data and stored as the variable basin code. For

land areas a default value of NaN is stored.

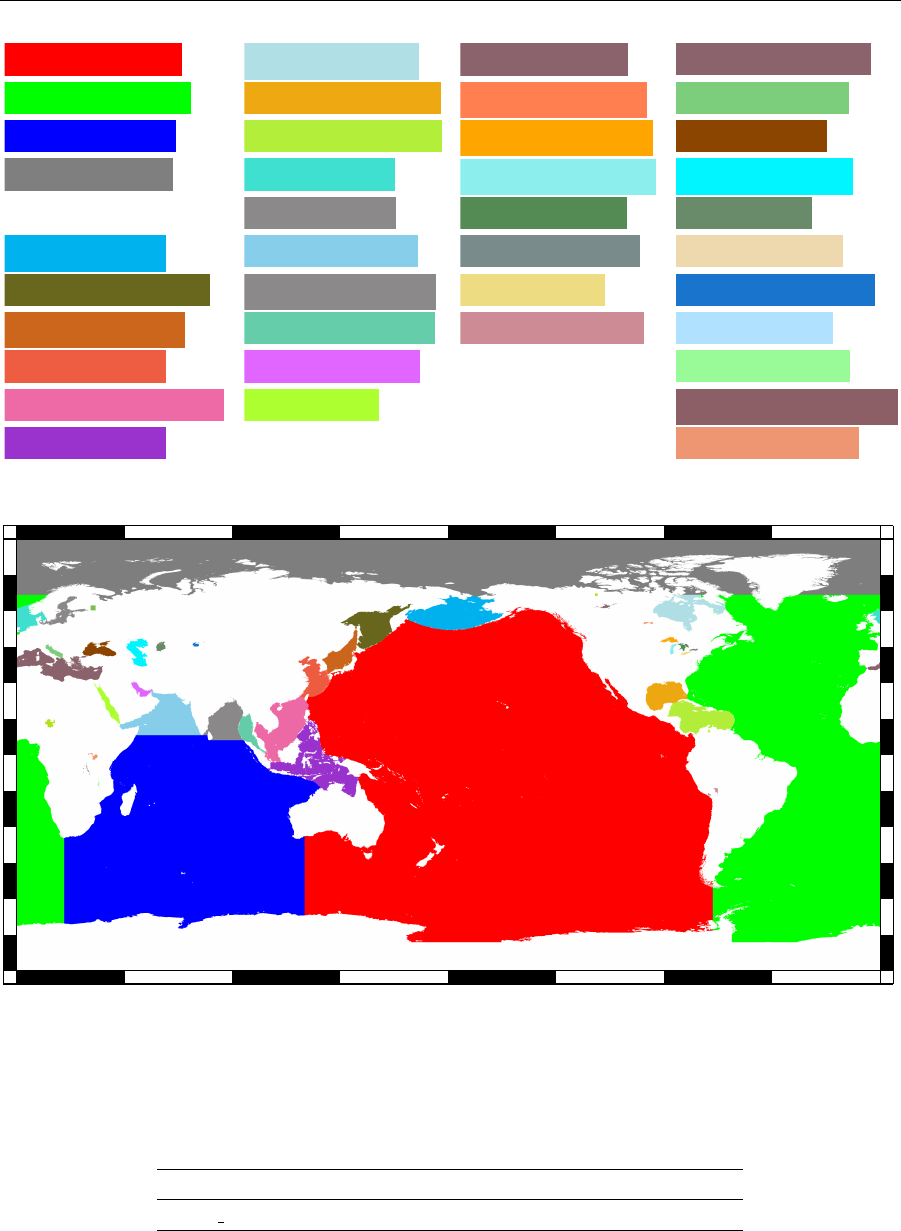
30 Variables for data editing

1 Pacific Ocean

2 Atlantic Ocean

3 Indian Ocean

4 Arctic Ocean

10 Bering Sea

11 Sea of Okhotsk

12 Sea of Japan

13 Yellow Sea

14 South China Sea

15 Indonesian

20 Hudson Bay

21 Gulf of Mexico

22 Caribbean Sea

23 North Sea

24 Baltic Sea

31 Arabian Sea

32 Bay of Bengal

33 Andaman Sea

34 Persian Gulf

35 Red Sea

41 Great Slave

42 Lake Winipeg

43 Lake Superior

44 Lake Michigan

45 Lake Huron

46 Lake Ontario

47 Lake Erie

50 Lake Titicaca

60 Mediterranean

61 Adriatic Sea

70 Black Sea

71 Caspian Sea

72 Aral Sea

73 Lake Baikal

74 Lake Balkhash

80 Lake Chad

81 Lake Malawi

82 Lake Tanganyika

83 Lake Victoria

Figure 6.1 Basin codes. The different colours relate to the various numerical identiﬁers used for

each ocean basin, enclosed sea or lake.

This ﬁeld allows users to separate the selected data by region, or select data from just a

single region. Normally data from all regions is selected.

Variable ﬁeld name units sat range note

basin code 36, 3601 basin code - all

Bibliography

Abdalla, S. (2007), Ku-band radar altimeter surface wind speed algorithm, in Proc. of the 2007

Envisat Symposium, Montreux, Switzerland, 23-27 April 2007, Eur. Space Agency Spec. Publ.,

ESA SP-636.

Ablain, M., M.-I. Pujol, S. Philipps, and N. Picot (2008), Assessment of Jason-2 and Jason-1

orbit quality from SSH analysis, Ocean Science Topography Science Team Meeting, Nice,

France, 10-12 November 2008.

Andersen, O. B., and P. Knudsen (2009), The DNSC08BAT bathymetry developed from satellite

altimetry, Tech. rep., Danish National Spacecenter.

Andersen, O. B., and P. Knudsen (2010), The DTU10 mean sea surface and mean dynamic to-

pography: Improvements in the Arctic and coastal zone, Ocean Science Topography Science

Team Meeting, Lisbon, Portugal, 19-21 October 2010.

Andersen, O. B., P. Knudsen, and L. Stenseng (2013), The DTU13 global mean sea surface from

20 years of satellite altimetry, Ocean Science Topography Science Team Meeting, Boulder,

Colorado, 8-11 October 2013.

Argus, D. F., and R. S. Gross (2004), An estimate of motion between the spin axis and

the hotspots over the past century, Geophys. Res. Lett.,31, L06614, doi:doi:10.1029/

2004GL019657.

Askne, J., and H. Nordius (1987), Estimation of tropospheric delay for microwaves from sur-

face weather data, Radio Sci.,22(3), 379–386, doi:10.1029/RS022i003p00379.

Berrisford, P., et al. (2011), The ERA-interim archive Version 2.0, ERA Report Series 1, ECMWF,

Reading, UK.

Bevis, M., S. Businger, S. Chriswell, T. A. Herring, R. A. Anthes, C. Rocken, and R. H. Ware

(1994), GPS meteorology: Mapping zenith wet delays onto precipitable water, J. Appl. Me-

teor.,33(3), 379–386, doi:10.1175/1520-0450(1994)033$h$0379:GMMZWD$i$2.0.CO;2.

Bilitza, D., and B. W. Reinisch (2008), International Reference Ionosphere 2007: Improvements

and new parameters, Adv. Space Res.,42(4), 599–609, doi:10.1016/j.asr.2007.07.048.

Carr`

ere, L., and F. Lyard (2003), Modeling the barotropic response of the global ocean to at-

mospheric wind and pressure forcing - comparisons with observations, Geophys. Res. Lett.,

30(6), doi:10.1029/2002GL016473.

Carr`

ere, L., Y. Faug`

ere, and M. Ablain (2016), Major improvement of altimetry sea level esti-

mations using pressure derived corrections based on ERA-interim atmospheric reanalysis,

Ocean Sci. Discuss.

Cartwright, D. E., and A. C. Edden (1973), Corrected tables of tidal harmonics, Geophys. J. Roy.

Astron. Soc.,33, 253–264, doi:10.1111/j.1365-246X.1973.tb03420.x.

Cartwright, D. E., and R. J. Taylor (1971), New computations of the tide-generating potential,

Geophys. J. Roy. Astron. Soc.,23, 45–74, doi:10.1111/j.1365-246X.1971.tb01803.x.

32 Bibliography

Chambers, D. P., S. A. Hayes, J. C. Ries, and T. J. Urban (2003), New TOPEX sea state bias

models and their effect on global mean sea level, J. Geophys. Res.,108(C10).

Chawla, A., D. Spindler, and H. L. Tolman (2011), WAVEWATCH III hindcasts with re-analysis

winds: Initial report on model setup, MMAB Contribution No. 291, NOAA National Weather

Service, Camp Springs, Maryland.

Chelton, D. B. (1994), The sea state bias in altimeter estimates of sea lvel from collinear analysis

of TOPEX data, J. Geophys. Res.,99(C12), 24,995–25,008.

Cipollini, P. (2011), A new parameter to facilitate screening of coastal altimetry data and cor-

rections, Ocean Science Topography Science Team Meeting, San Diego, 19-21 October 2011.

Collard, F. (2005), Algorithmes de vent et periode moyenne des vagues JASON a base de re-

seaux de neurons, Rapport BO-021-CLS-0407-RF, Boost Technologies.

Cr´

etaux, J.-F., and C. M. Birkett (2006), Lake studies from satellite radar altimetry, C. R. Geo-

science,338, 1098–1112, doi:10.1016/j.crte.2006.08.002.

Desai, S. D., J. M. Wahr, and B. D. Beckley (2015), Revisiting the pole tide for and from satellite

altimetry, J. Geod.,89(12), 1233–1243, doi:10.1007/s00190-015-0848-7.

Dumont, J.-P., P. Sicard, J. Stum, and O.-Z. Zanif´

e (2001), Algorithm deﬁnition, accuracy and

speciﬁcation volume 4: CMA altimeter level 2 processing, Tech. Rep. SMM-ST-M2-EA-11005-

CN, CNES/SSALTO.

Feng, H., S. Yao, L. Li, N. Tran, D. Vandemark, and S. Labroue (2010), Spline-based nonpara-

metric estimation of the altimeter sea state bias correction, IEEE Geosci. Rem. Sens. Lett.,7(3),

577–581.

F¨

orste, C., et al. (2013), EIGEN-6C3stat – the newest high resolution global combined gravity

ﬁeld model based on the 4th release of the GOCE direct approach, Tech. rep., ICGEM/GFZ

Postdam.

Francis, C. R. (1990), The ERS-1 radar altimeter, paper presented at the 2nd ERS-1 PI meeting,

Noordwijk,The Netherlands.

Francis, C. R., et al. (1993), The Calibration of the ERS-1 Radar Altimeter – The Venice Cali-

bration Campaign, ESA Report ER-RP-ESA-RA-0257 issue 2.0, ESA/ESTEC, Noordwijk,The

Netherlands.

Francis, C. R., et al. (1995), The ERS-2 spacecraft and its payload, ESA Bulletin,83, 13–31.

Francis, C. R., et al. (1991), The ERS-1 spacecraft and its payload, ESA Bulletin,65, 26–48.

Fu, L.-L., E. J. Christensen, C. A. Yamarone, M. Lefebvre, Y. M´

enard, M. Dorrer, and P. Escudier

(1994), TOPEX mission overview, J. Geophys. Res.,99(C12), 24,369–24,382.

Gaspar, P., and J.-P. Florens (1998), Estimation of the sea state bias in radar altimeter mea-

surements of sea level: Results from a new nonparametric method, J. Geophys. Res.,103(C8),

15,803–15,814.

Gaspar, P., F. Ogor, P.-Y. Le Traon, and O.-Z. Zanif´

e (1994), Estimating the sea state bias of

the TOPEX and POSEIDON altimeters from crossover differences, J. Geophys. Res.,99(C12),

24,981–24,994.

Gaspar, P., S. Labroue, F. Ogor, G. Laﬁtte, L. Marchal, and M. Rafanel (2002), Improving non-

parametric estimates of the sea state bias in radar altimeter measurements of sea level, J.

Atmos. Oceanic Technol.,19(10), 1690–1707.

Gourrion, J., D. Vandemark, S. Bailey, B. Chapron, C. P. Gommenginger, P. G. Challenor, and

M. A. Srokosz (2002), A two-parameter wind speed algorithm for Ku-band altimeters, J.

Atmos. Oceanic Technol.,19(12), 2030–2048, doi:10.1175/1520-0426(2002)019h2030:ATPWSAi

2.0.CO;2.

Bibliography 33

Hayne, G. S., D. W. Hancock, III, and C. L. Purdy (1994), TOPEX altimeter range stability

estimates from calibration mode data, TOPEX Research News,3, 18–22.

Imel, D. A. (1994), Evaluation of the TOPEX dual-frequency ionosphere correction, J. Geophys.

Res.,99(C12), 24,895–24,906.

International DORIS Service (2011), New GDR-D orbit standards, ftp://ftp.ids-doris.org/pub/

ids/data/POD conﬁguration GDRD.pdf (retrieved 25 June 2015).

International DORIS Service (2015), New GDR-E orbit standards, ftp://ftp.ids-doris.org/pub/ids/

data/POD conﬁguration GDRE.pdf (retrieved 25 June 2015).

Jakobsson, M., et al. (2012), The International Bathymetric Chart of the Arctic Ocean (IBCAO)

version 3.0, Geophys. Res. Lett.,39, L12609, doi:10.1029/2012GL052219.

Keihm, S. J., M. A. Janssen, and C. S. Ruf (1995), TOPEX microwave radiometer (TMR): III.

Wet troposphere range correction algorithm and pre-launch error budget, IEEE Trans. Geosci.

Rem. Sens.,33(1), 147–161.

Komjathy, A., G. H. Born, and D. N. Anderson (2000), An improved high precision iono-

spheric total electron content modeling using GPS, in Proc. International Geoscience and

Remote Sensing Symposium (IGARSS), Honolulu, Hawaii, 2000, vol. 7, pp. 2858–2860, doi:

10.1109/IGARSS.2000.86027.

Labroue, S., and E. Obligis (2003), Neural network retrieval algorithms for the Envisat/MWR,

Tech. Rep. CLS/DOS/NT/03.848, Collect., Localisation, Satell., Ramonville St. Agne, France.

Labroue, S., P. Gaspar, J. Dorandeu, O.-Z. Zanif´

e, F. Mertz, P. Vincent, and D. Choquet (2004),

Nonparametric estimates of the sea state bias for the Jason-1 radar altimeter, Mar. Geod.,

27(3-4), 453–481, doi:10.1080/01490410490902089.

Lambin, J., et al. (2010), The OSTM/Jason-2 mission, Mar. Geod.,33(S1), 4–25, doi:10.1080/

01490419.2010.491030.

Lemoine, F. G., N. P. Zelensky, D. S. Chinn, B. D. Beckley, and J. L. Lillibridge (2006), Towards

the GEOSAT Follow-On precise orbit determination goals of high accuracy and near-real-

time processing, paper 2006-6402, AIAA/AAS Astrodynamics Specialist Conference, Au-

gust 21–24, 2006, Keystone, Colorado.

Lemoine, F. G., N. P. Zelensky, S. A. Melachroinos, D. S. Chinn, and B. D. Beckley (2013),

Status of the GSFC precise orbit ephemerides for Jason-2, Jason-1 and TOPEX/Poseidon,

Ocean Science Topography Science Team Meeting, Boulder, Colorado, 8-11 October 2013.

Lillibridge, J. L., R. Scharroo, S. Abdalla, and D. C. Vandemark (2014), One- and two-

dimensional wind speed models for Ka-band altimetry, J. Atmos. Oceanic Technol.,31(3), 630–

638, doi:10.1175/JTECH-D-13-00167.1.

Llewellyn, S. K., and R. B. Bent (1973), Documentation and description of the Bent ionospheric

model, Rep. AFCRL-TR-73-0657, Air Force Cambridge Research Laboratory, Hanscom Air

Force Base, Massachusetts.

Lyard, F., F. Lef`

evre, T. Letellier, and O. Francis (2006), Modelling the global ocean

tides: modern insights from FES2004, Ocean Dynamics,56(5-6), 394–415, doi:10.1007/

s10236-006-0086-x.

Martini, A., and P. F´

em´

enias (2000), The ERS SPTR2000 altimeric range correction: Results and

validation, Technical Note ERE-TN-ADQ-GSO-6001, ESA/ESRIN, Frascati, Italy.

M´

enard, Y., L.-L. Fu, P. Escudier, B. J. Haines, G. Kunstmann, F. Parisot, J. Perbos, P. Vincent,

and S. D. Desai (2003), The Jason-1 mission, J. Mar. Geod.,Jason-1.

34 Bibliography

Mendes, V. B., G. Prates, L. Santos, and R. B. Langley (2000), An evaluation of the accuracy of

models for the determination of the weighted mean temperature of the atmosphere, in Proc.

of the 2000 National Technical Meeting of The Institute of Navigation, Anaheim, CA, January 2000,

pp. 433–438.

Munk, W. H., and G. J. F. MacDonald (1960), The Rotation of the Earth: A Geophysical Discussion,

Cambridge University Press, New York.

Pavlis, N. K., S. A. Holmes, S. C. Kenyon, and J. K. Factor (2012), The development and eval-

uation of the Earth Gravitational Model 2008 (EGM2008), J. Geophys. Res.,117, B04406, doi:

10.1029/2011JB008916.

Ponte, R. M., and R. D. Ray (2002), Atmospheric pressure corrections in geodesy and oceanog-

raphy: A strategy for handling air tides, Geophys. Res. Lett.,29(24), 2153–2156, doi:10.1029/

2002GL016340.

Quartly, G. D. (2009), Optimizing σ0information from Jason-2 altimeter, IEEE Geosci. Rem.

Sens. Lett.,6(3), 398–402, doi:10.1109/LGRS.2009.2013973.

Queffeulou, P. (2004), Long-term validation of wave height measurements from altimeters,

Mar. Geod.,27, 495–510, doi:10.1080/01490410490883478.

Ray, R. D. (2013), Precise comparisons of bottom-pressure and altimetric ocean tides, J. Geophys.

Res.,118, 4570–4584, doi:10.1002/jgrc.20336.

Ray, R. D., G. D. Egbert, and S. Y. Erofeeva (2011), Tide predictions in shelf and coastal waters:

status and prospects, in Coastal Altimetry, edited by S. Vignudelli, A. Kostianoy, P. Cipollini,

and J. Benveniste, Springer-Verlag.

Roblou, L., F. Lyard, J. Dorandeu, J. Lamouroux, and J. Bouffard (2008), Dealiasing high fre-

quency ocean response to atmospheric forcing, presented at the Coastal Altimetry Work-

shop, Silver Spring, Maryland, 5-7 Feb 2008.

Rudenko, S., M. Otten, P. N. A. M. Visser, R. Scharroo, and T. Sch¨

one (2011), Improvements

in ERS-1 and ERS-2 precise orbit determination, Poster presentation at EGU 2011 General

Assembly.

Rudenko, S., D. Dettmering, S. Esselborn, T. Sch¨

one, C. F¨

orste, J.-M. Lemoine, M. Ablain,

D. Alexandre, and K.-H. Neumayer (2014), Inﬂuence of time variable geopotential models

on precise orbits of altimetry satellites, global and regional mean sea level trends, Adv. Space

Res.,54(1), 92–118, doi:10.106/j.asr.2014.03.010.

Rudenko, S., K.-H. Neumayer, D. Dettmering, S. Esselborn, T. Sch ¨

one, and J. C. Raimondo

(2015), New orbits of ERS-1, ERS-2, TOPEX/Poseidon, Envisat, Jason-1 and Jason-2 for al-

timetry applications and their validation, Ocean Science Topography Science Team Meeting,

Reston, Virginia, 20-23 October 2015.

Rudenko, S., K.-H. Neumayer, D. Dettmering, S. Esselborn, T. Sch ¨

one, and J. C. Raimondo

(2016), Improvements in precise orbits of altimetry satellites and their altimetry validation,

(under preparation).

Ruf, C. S., R. P. Dewan, and B. Sabramanya (1996), Combined microwave radiometer and

altimeter retrieval of wet path delay for Geosat Follow-On, IEEE Trans. Geosci. Rem. Sens.,

34(4), 991–999.

Saastamoinen, J. (1972), Atmospheric corrections for the troposphere and stratosphere in ra-

dio ranging of satellites, in The Use of Artiﬁcial Satellites for Geodesy,Geophys. Monogr. Ser.,

vol. 15, edited by S. W. Hendriksen, A. Mancini, and B. H. Chovitz, pp. 247–251, American

Geophysical Union, Washington, D.C.

Bibliography 35

Sandwell, D. T., R. D. M ¨

uller, W. H. F. Smith, E. S. Garcia, and C. R. Francis (2014), New global

marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure, Science,

346(6205), 65–67, doi:10.1126/science.1258213.

Schaeffer, P., Y. Faug`

ere, J.-F. Legeais, A. Ollivier, T. Guinle, and N. Picot (2012), The CNES-

CLS11 global mean sea surface computed from 16 years of satellite altimeter data, Mar. Geod.,

35(sup1), 3–19, doi:10.1080/01490419.2012.718231.

Scharroo, R., and J. L. Lillibridge (2005), Non-parametric sea-state bias models and their rele-

vance to sea level change studies, in Proceedings of the 2004 Envisat & ERS Symposium, Eur.

Space Agency Spec. Publ., ESA SP-572, edited by H. Lacoste and L. Ouwehand.

Scharroo, R., and W. H. F. Smith (2010), A global positioning system-based climatology for

the total electron content in the ionosphere, J. Geophys. Res.,115(A10318), doi:10.1029/

2009JA014719.

Scharroo, R., and P. N. A. M. Visser (1998), Precise orbit determination and gravity ﬁeld im-

provement for the ERS satellites, J. Geophys. Res.,103(C4), 8113–8127, doi:10.1029/97JC03179.

Shako, R., C. F¨

orste, O. Abrikosov, S. Bruinsma, J. C. Marty, J.-M. Lemoine, F. Flechtner, K.-

H. Neumayer, and C. Dahle (2014), EIGEN-6C: A high-resolution global gravity combina-

tion model including GOCE data, in Observation of the System Earth from Space - CHAMP,

GRACE, GOCE and future missions, edited by F. Flechtner, N. Sneeuw, and W.-D. Schuh,

Advanced Technologies in Earth Sciences, pp. 155–161, Springer Berlin Heidelberg, doi:

10.1007/978-3-642-32135-1 20.

Smith, W. H. F., and D. T. Sandwell (1994), Bathymetric prediction from dense satellite altime-

try and sparse shipboard bathymetry, J. Geophys. Res.,99(B11), 21,803–21,824.

Stammer, D., et al. (2014), Accuracy assessment of global barotropic ocean tide models, Rev.

Geophys.,52(3), 243–282, doi:10.1002/2014RG000450.

Stenseng, L., G. Piccioni, O. B. Andersen, and P. Knudsen (2015), Sea surface retracking and

classiﬁcation of cryosat-2 altimetry observations in the arctic ocean, presented at AGU 2015

Fall Meeting.

Stum, J., F. Ogor, P.-Y. Le Traon, J. Dorandeu, P. Gaspar, and J.-P. Dumont (1998), An intercal-

ibration study of TOPEX, ERS-1 and ERS-2 altimetric missions: Final report of IFREMER

contract No. 97/2 426 086/C, Tech. Rep. CLS/DOS/NT/98.070, Collect., Localisation, Satell.,

Ramonville St. Agne, France.

Tamura, Y. (1987), A harmonic development of the tide-generating potential, Bull. d’Inform.

Mar´ees Terr.,99, 6813–6855.

Tapley, B. D., M. M. Watkins, J. C. Ries, G. W. Davis, R. J. Eanes, S. R. Poole, H. J. Rim, B. E.

Schutz, and C.-K. Shum (1996), The Joint Gravity Model 3, J. Geophys. Res.,101(B12), 28,029–

28,049.

Tolman, H. L. (2009), User manual and system documentation of WAVEWATCH III version

3.14, Tech. rep., NOAA National Weather Service.

Tran, N., D. Vandemark, S. Labroue, H. Feng, B. Chapron, H. L. Tolman, J. Lambin, and N. Picot

(2010), The sea state bias in altimeter sea level estimates determined by combining wave

model and satellite data, J. Geophys. Res.,115, C03020, doi:10.1029/2009JC005534.

Tran, N., S. Philipps, J. C. Poisson, S. Urien, E. Bronner, and N. Picot (2012), Impact of GDR-

D standards on SSB correction, Ocean Science Topography Science Team Meeting, Venice,

Italy, 27-29 September 2012.

Wahr, J. M. (1985), Deformation of the Earth induced by polar motion, J. Geophys. Res.,90(B11),

9363–9368, doi:10.1029/JB090iB11p09363.

36 Bibliography

Wahr, J. M., R. S. Nerem, and S. V. Bettadpur (2015), The pole tide and its effect on GRACE

time-variable gravity measurements: implications for the estimates of surface mass varia-

tions, J. Geophys. Res.,120, 4597–4615, doi:10.1002/2015JB011986.

Wessel, P., and W. H. F. Smith (1996), A global, self-consistent, hierarchical, high-resolution

shoreline, J. Geophys. Res.,101(B4), 8741–8743.

Wessel, P., W. H. F. Smith, R. Scharroo, J. Luis, and F. Wobbe (2013), Generic Mapping Tools:

Improved version released, Eos Trans. AGU,94(45), 409–410, doi:10.1002/2013EO450001.

Wingham, D. J., et al. (2006), CryoSat: A mission to determine the ﬂuctuations in Earth’s land

and marine ice ﬁelds, Adv. Space Res.,37(4), 841–871, doi:10.1016/j.asr.2005.07.027.

Witter, D. L., and D. B. Chelton (1991), A Geosat altimeter wind speed algorithm and a method

for altimeter wind speed algorithm development, J. Geophys. Res.,96(C5), 8853–8860.

Index

ﬁles

rads.xml, 7

variables

alt, 5–7

alt cnes, 5

alt dgme04, 5, 7

alt eig6c, 5

alt eig6s2, 5

alt eiggl04s, 5

alt gdrcp, 5

alt gdrd, 5

alt gdre, 5

alt gfz, 5

alt ggm02c itrf2000, 5

alt ggm02c itrf2005, 5

alt gps, 5

alt jgm3, 5, 7

alt pgs7777, 5

alt rate, 6

alt reaper, 5

alt reaper deos, 5

alt reaper esoc, 5

alt reaper gfz, 5

alt slcci, 5

alt std1204, 5

alt std1404, 5

basin code, 29, 30

dac, 14, 15

dist coast, 29

dry tropo, 10

dry tropo airtide, 10

dry tropo ecmwf, 10

dry tropo era, 10

dry tropo ncep, 10

ﬂag alt oper mode, 27

ﬂag alt track mode, 27

ﬂag continental ice, 27

ﬂag ocean, 27

ﬂag rad oper mode, 27

ﬂag water, 27

ﬂags, 25, 28

ﬂags high, 25

ﬂags low, 25, 28

geoid, 19

geoid egm2008, 19

geoid eigen6, 19

inv bar, 14, 15

inv bar global, 14

inv bar mog2d, 14, 15

inv bar mog2d era, 14, 15

inv bar mog2d mean, 14

inv bar mok2d, 14, 15

inv bar static, 14, 15

iono, 13, 14

iono alt, 13

iono alt mle3, 13

iono alt smooth, 13

iono alt smooth mle3, 13

iono bent, 13

iono doris, 13

iono gim, 13, 14

iono iri2007, 13

iono nic09, 13

lat, 4

lon, 4

mss, 19

mss cnescls11, 19

mss cnescls15, 19

mss dtu13, 19

mss dtu15, 19

prox coast, 29

qual alt rain ice, 27

qual attitude, 27

qual dh, 27

qual iono alt, 27

qual orbit, 27

qual rad rain ice, 27

qual rad tb, 27

qual range, 27

38 Index

qual sig0, 27

qual sptr, 27

qual swh, 27

range, 8

range c, 8

range ka, 8

range ku, 8

range ku mle3, 8

range numval, 10

range numval c, 10

range numval ka, 10

range numval ku, 10

range rms, 9

range rms c, 9

range rms ka, 9

range rms ku, 9

range rms s, 9

range s, 8

ref frame offset, 9

sig0, 22

sig0 c, 22

sig0 ka, 22

sig0 ku, 22

sig0 ku mle3, 22

sig0 rms, 22

sig0 rms c, 22

sig0 rms ka, 22

sig0 rms ku, 22

sig0 rms s, 22

sig0 s, 22

sla, 7, 8, 19

ssb, 18

ssb bm3, 18

ssb cls, 18

ssb cls c, 18

ssb cls mle3, 18

ssb csr, 18

ssb hyb, 18

ssb tran2012, 18

ssha, 7, 8

surface class, 27, 28

surface type, 27, 28

surface type rad, 27

swh, 21

swh c, 21

swh ka, 21

swh ku, 21

swh ku mle3, 21

swh rms, 21

swh rms c, 21

swh rms ka, 21

swh rms ku, 21

swh rms s, 21

swh s, 21

swh ww3, 21, 23

tide equil, 16

tide load, 16

tide load fes04, 16

tide load fes14, 16

tide load got410, 16

tide load got48, 16

tide non equil, 16, 17

tide ocean, 16

tide ocean fes04, 16

tide ocean fes14, 16, 17

tide ocean got410, 16

tide ocean got48, 16

tide ocean webtide, 16, 17

tide pole, 15

tide solid, 15

time, 3

time 1985, 3

time 2000, 3

time local solar, 3

time mjd, 3

time rel eq, 3

time ymdhms, 3

topo, 28

topo dtm2000, 28

topo dtu10, 28

topo srtm30plus, 28

wave m0, 23

wave m1, 23

wave m2, 23

wave m4, 23

wave shs, 23

wet tropo, 1, 2, 12

wet tropo ecmwf, 1, 2, 12

wet tropo era, 12

wet tropo ncep, 12

wet tropo nvap, 12

wet tropo rad, 1, 12

wet tropo tovs ncep, 12

wet tropo tovs ssmi, 12

wind speed, 23

wind speed alt, 23

wind speed ecmwf, 23

wind speed ecmwf u, 23

wind speed ecmwf v, 23

wind speed gfs, 23

Index 39

wind speed gfs u, 23

wind speed gfs v, 23

wind speed rad, 23

Rads4 Data Manual

Navigation menu

Versions of this User Manual:

Views

Navigation