MAC 2.4 Similar Polygons Mac2
User Manual: MAC 2.4
Open the PDF directly: View PDF ![]() .
.
Page Count: 6
'
%
&
+
-
,
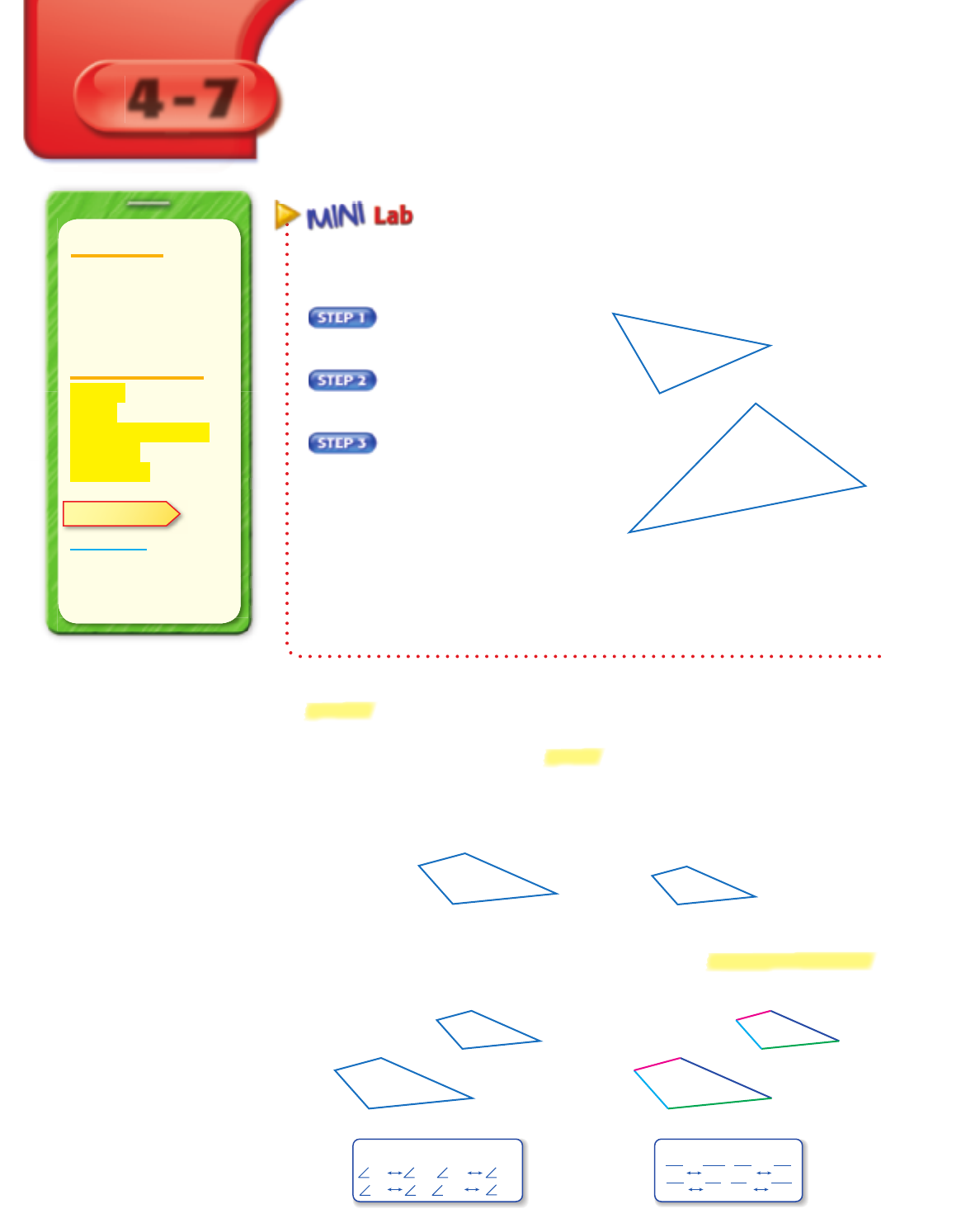
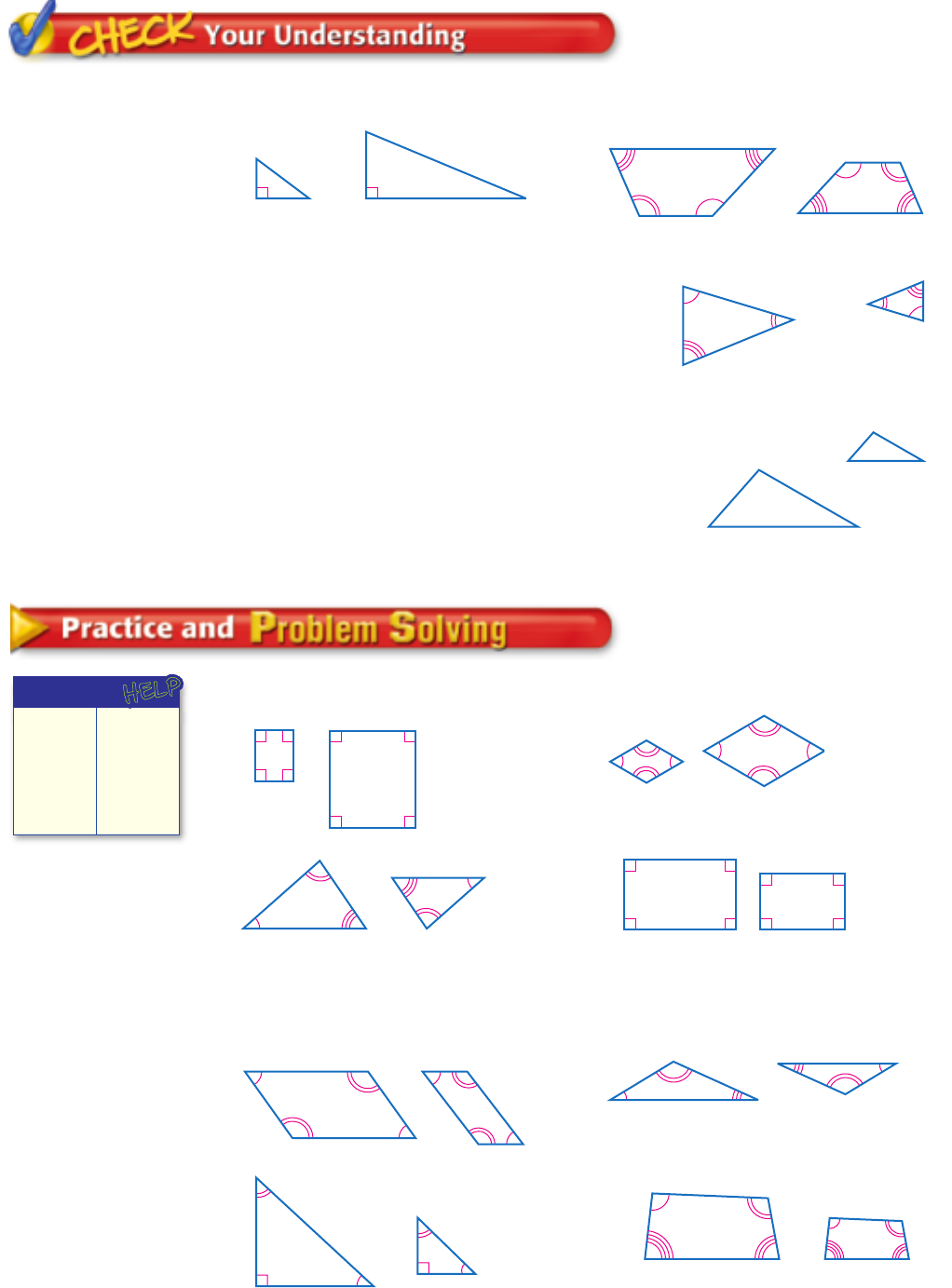
Follow the steps below to discover how the triangles at the right
are related.
Copy both triangles
onto tracing paper.
Measure and record the
sides of each triangle.
Cut out both triangles.
1. Compare the angles of the
triangles by matching them up.
Identify the angle pairs that
have equal measure.
2. Express the ratios
DF
_
LK
,
EF
_
JK
, and
DE
_
LJ
as decimals to the nearest tenth.
3. What do you notice about the ratios of these sides of matching
triangles?
A polygon consists of a sequence of consecutive line segments in a
plane, placed end to end to form a simple closed figure. Polygons that
have the same shape are called similar polygons. In the figure below,
polygon ABCD is similar to polygon WXYZ. This is written as polygon
ABCD ∼ polygon WXYZ.
%;
"
#
$:
9
8
The parts of similar figures that “match” are called corresponding parts.
%
;
"
#
$
:
9
8
%
;
"
#
$
:
9
8
Corresponding Angles
A W,B X,
C Y,D Z
Corresponding Sides
AB WX,BC XY,
CD YZ,DA ZW
Similar Polygons
4-7
218 Chapter 4 Proportions and Similarity
MAIN IDEA
Identify similar polygons
and find missing
measures of similar
polygons.
New Vocabulary
polygon
similar
corresponding parts
congruent
scale factor
Math Online
glencoe.com
• Extra Examples
• Personal Tutor
• Self-Check Quiz
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 218218_223_C04_L07_874050.indd 218 9/18/07 2:47:21 PM9/18/07 2:47:21 PM
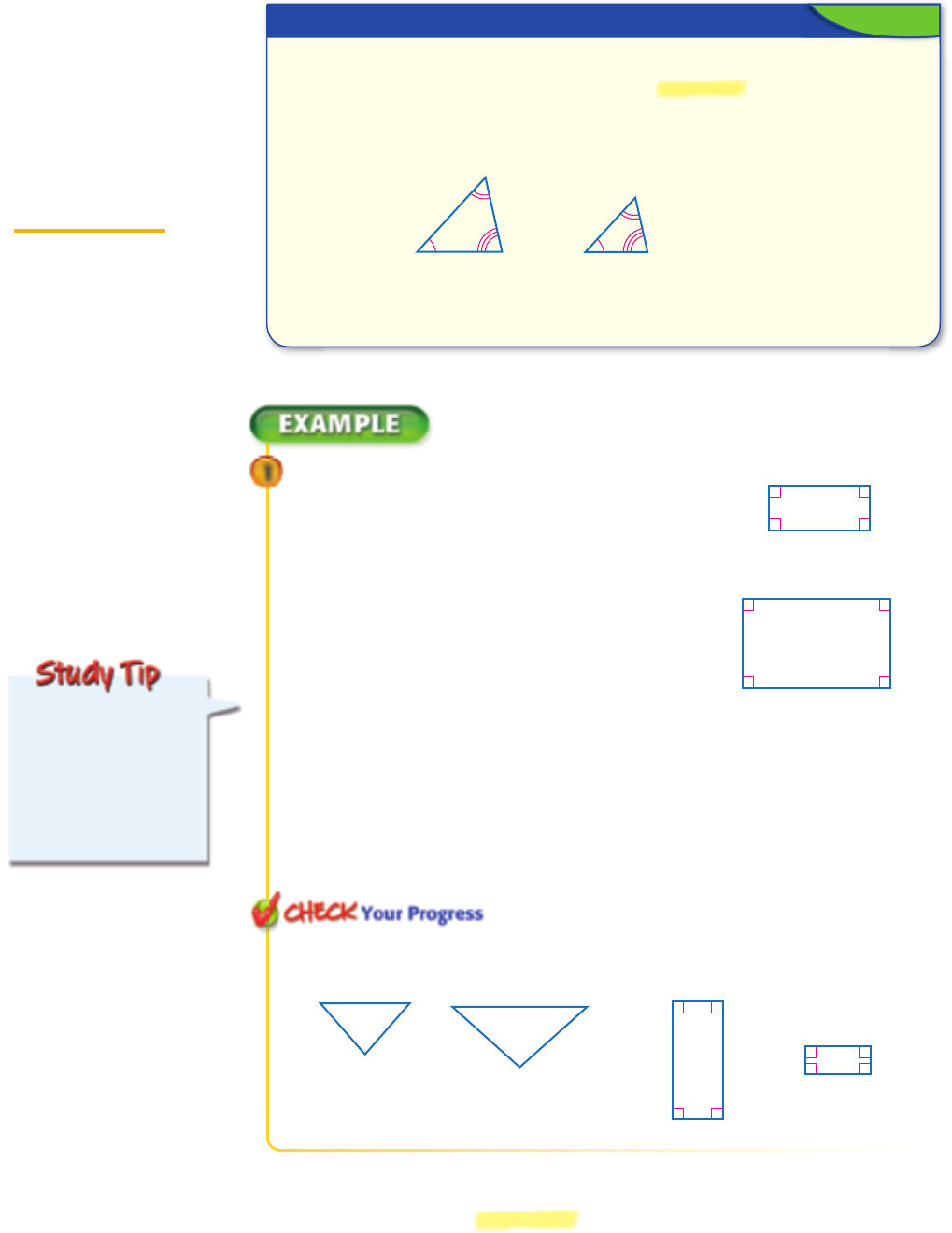
The similar triangles in the Mini Lab suggest the following.
Identify Similar Polygons
1 Determine whether rectangle HJKL is
/
1
.
2
10
10
66
+
,
)
-
7
7
33
similar to rectangle MNPQ. Explain.
First, check to see if corresponding
angles are congruent.
Since the two polygons are rectangles,
all of their angles are right angles.
Therefore, all corresponding angles
are congruent.
Next, check to see if corresponding
sides are proportional.
HJ
_
MN
= 7
_
10
JK
_
NP
=
3
_
6
or
1
_
2
KL
_
PQ
= 7
_
10
LH
_
QM
=
3
_
6
or
1
_
2
Since 7
_
10
and
1
_
2
are not equivalent ratios, rectangle HJKL is not similar
to rectangle MNPQ.
Determine whether these polygons are similar. Explain.
a. 12
8
66
8
8
b.
3.5
1.51.51414
3.5
6
6
"#
$
+,
-.
%
The ratio of the lengths of two corresponding sides of two similar
polygons is called the scale factor. You can use the scale factor of similar
figures or a proportion to find missing measures.
Common ErrorCommon Error
Do not assume that two
polygons are similar
just because their
corresponding angles
are congruent. Their
corresponding sides
must also be proportional.
Reading Math
Congruence The symbol
is read is congruent to. Arcs
are used to show congruent
angles.
Lesson 4-7 Similar Polygons 219
Words If two polygons are similar, then
• their corresponding angles are congruent, or have the
same measure, and
• the measures of their corresponding sides are proportional.
Model #
:
"$9;
ABC ∼ XYZ
Symbols ∠A ∠X, ∠B ∠Y, ∠C ∠Z, and
AB
_
XY
=
BC
_
YZ
=
AC
_
XZ
Key Concept
Similar Polygons
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 219218_223_C04_L07_874050.indd 219 9/18/07 2:47:25 PM9/18/07 2:47:25 PM
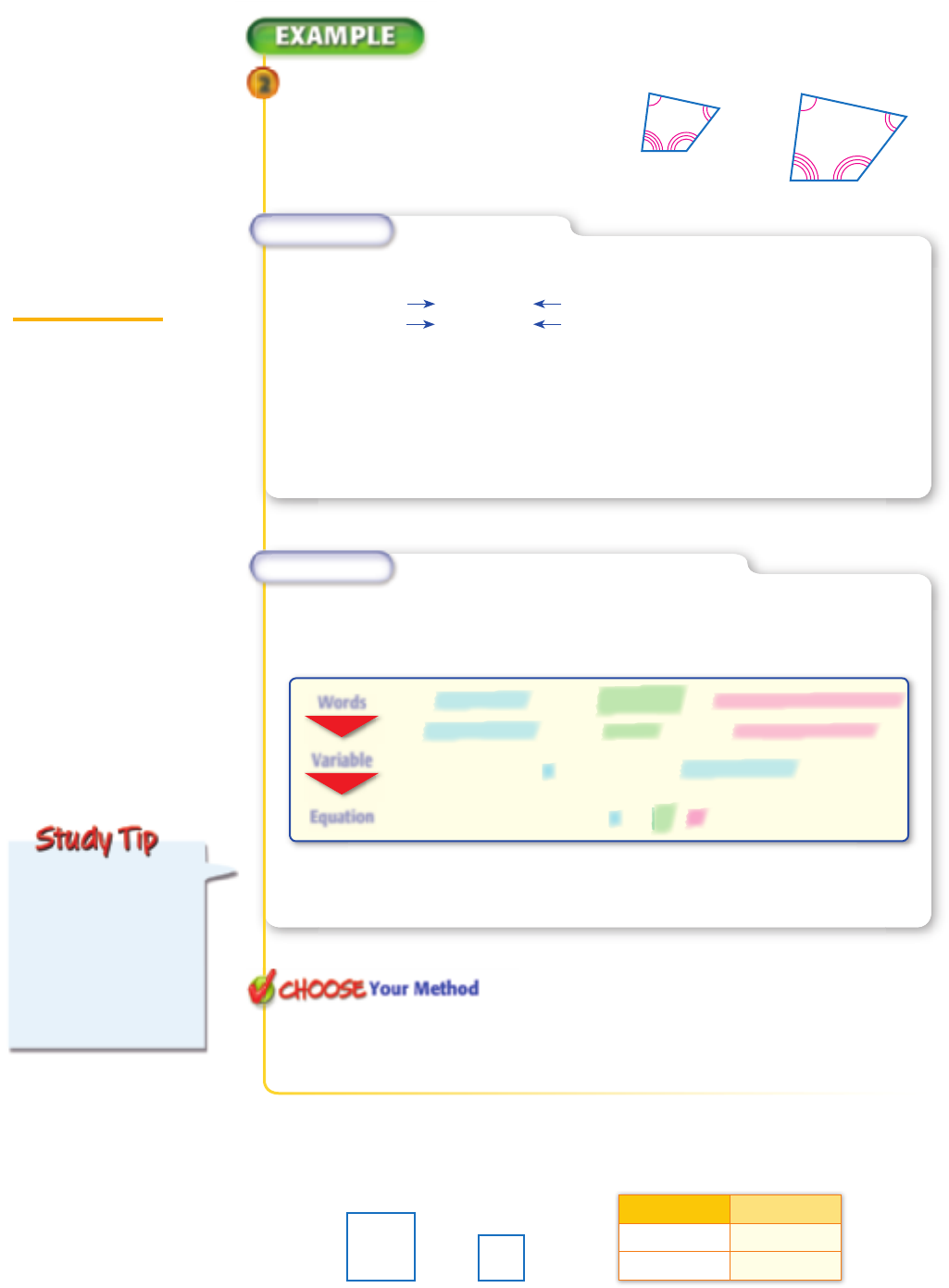
Find Missing Measures
2GEOMETRY Given that polygon
m
15
24
8
9
;:
12
10
13
"
#
%$
WXYZ ∼ polygon ABCD,
find the missing measure.
METHOD 1 Write a proportion.
The missing measure m is the length of
−−
XY . Write a proportion.
polygon WXYZ
polygon ABCD
XY
_
BC
= YZ
_
CD
polygon WXYZ
polygon ABCD
m
_
12
=
15
_
10
XY = m, BC = 12,
YZ = 15, and CD = 10.
m · 10 = 12 · 15 Find the cross products.
10m = 180 Multiply.
m = 18 Divide each side by 10.
METHOD 2 Use the scale factor to write an equation.
Find the scale factor from polygon WXYZ to polygon ABCD.
scale factor: YZ
_
CD
=
15
_
10
or
3
_
2
The scale factor is the
constant of proportionality.
Words
Variable
Equation
A length on
polygon WXYZ
is
3
_
2
times as
long as
a corresponding length
on polygon ABCD.
Let m represent the measure of
−−
XY .
m =
3
_
2
· 12
m =
3
_
2
(12) Write the equation.
m = 18 Multiply.
Find each missing measure above.
c. WZ d. AB
Square A ∼ square B with a scale factor of 3:2. Notice that the ratio
of their perimeters is 12:8 or 3:2.
3 m
Square A Square B
2 m Square Perimeter
A12 m
B8 m
Scale FactorScale Factor
In Example 2, the scale
factor from polygon ABCD
to polygon WXYZ is
2
_
3
,
which means that a length
on polygon ABCD is
2
_
3
as
long as a length on polygon
WXYZ.
Reading Math
Segment Measure The
measure of
−−
XY is written as
XY. It represents a number.
220 Chapter 4 Proportions and Similarity
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 220218_223_C04_L07_874050.indd 220 9/18/07 2:47:26 PM9/18/07 2:47:26 PM
This and other related examples suggest the following.
Similarity
Statements In
naming similar
triangles, the order
of the vertices
indicates the
corresponding parts.
Read the similarity
statement carefully
to be sure that
you compare
corresponding parts.
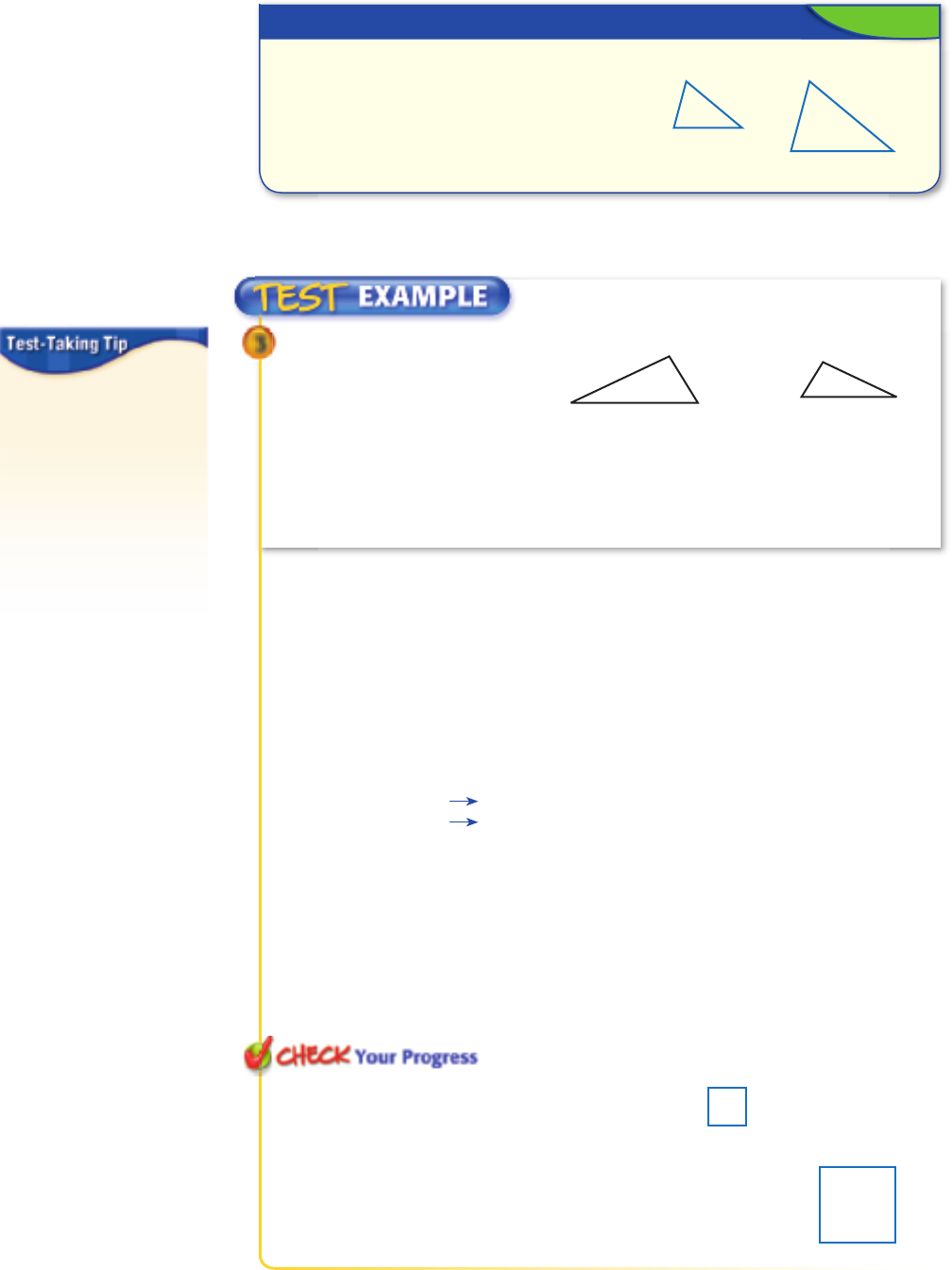
3 Triangle LMN is similar
24 18
./
-
32
1
to triangle PQR. If the
perimeter of LMN is
64 units, what is the
perimeter of PQR?
A 108 units C 48 units
B 96 units D 36 units
Read the Item
You know the measures of two corresponding sides and the
perimeter of LMN. You need to find the perimeter of PQR.
Solve the Item
Triangle LMN ∼ triangle PQR with a scale factor of 24
_
18
or 4
_
3
. The ratio
of the perimeters of LMN to PQR is also 4
_
3
.
perimeter of LMN
perimeter of PQR
64
_
x
=
4
_
3
⎫
⎬
⎭ Scale factor relating LMN to PQR
64 · 3 = 4 · x Find the cross products.
192 = 4x Multiply.
192
_
4
=
4x
_
4
Divide each side by 4.
48 = x Simplify.
The answer is C.
e. Square KLMN is similar to
square TUVW. If the perimeter
of square KLMN is 32 units, what
is the perimeter of square TUVW?
F 128 units H 64 units
G 96 units J 40 units
16
67
85
8
-.
/,
Lesson 4-7 Similar Polygons 221
Words If two figures are similar with
a scale factor of
a
_
b
, then the
perimeters of the figures have
a ratio of
a
_
b
.
Model
a
Figure A
b
Figure B
Key Concept
Ratios of Similar Figures
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 221218_223_C04_L07_874050.indd 221 9/18/07 2:47:28 PM9/18/07 2:47:28 PM
Example 1
(p. 219)
Determine whether each pair of polygons is similar. Explain.
1.
124
5
5
3
13
2.
8
8
18
10
7.5 6
6
13.5
Example 2
(p. 220)
3. In the figure at the right, FGH ∼ KLJ.
6
9
x
(
'
)
y
6
3
+
,
-
Write and solve a proportion to find each
missing side measure.
Example 3
(p. 221)
4. MULTIPLE CHOICE ABC is similar to XYZ.
8
:
;
9
16
#
$
"
If the perimeter of ABC is 40 units, what
is the perimeter of XYZ?
A 10 units C 40 units
B 20 units D 80 units
Determine whether each pair of polygons is similar. Explain.
5.
8
4
73 6. 5
5
33
33
5
5
7.
24
20 16
15
12
18 8.
86
4
5
Each pair of polygons is similar. Write and solve a proportion to find
each missing side measure.
9. 12
12
x
8
8
3
10.
10
4.8
5x
8
4
11.
21
29
x
10.5
10
14.5
12.
26
12 8
14
7.5
22.4
12.8
x
For
Exercises
See
Examples
5–8
9–12
18, 19
1
2
3
HOMEWORK
HELP
HELP
222 Chapter 4 Proportions and Similarity
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 222218_223_C04_L07_874050.indd 222 9/18/07 2:47:30 PM9/18/07 2:47:30 PM
20. ROCK CLIMBING Grace is working her way up a climbing wall. Every
5 minutes she is able to climb 6 feet, but then loses her footing, slips back
1 foot, and decides to rest for 1 minute. If the rock wall is 30 feet tall, how
long will it take her to reach the top? Use the draw a diagram strategy. (Lesson 4-6)
Solve each proportion. (Lesson 4-5)
21. 5
_
4
= y
_
12
22. 120
_
b
=
24
_
60
23.
0.6
_
5
=
1.5
_
n
PREREQUISITE SKILL Graph and connect each pair of ordered pairs. (Lesson 3-6)
24. (-2.5, 1.5), (1.5, -3.5) 25.
(
-2, -1 1
_
2
)
,
(
4, 3
1
_
2
)
26.
(
-2 1
_
3
, 1
)
,
(
2, 3
2
_
3
)
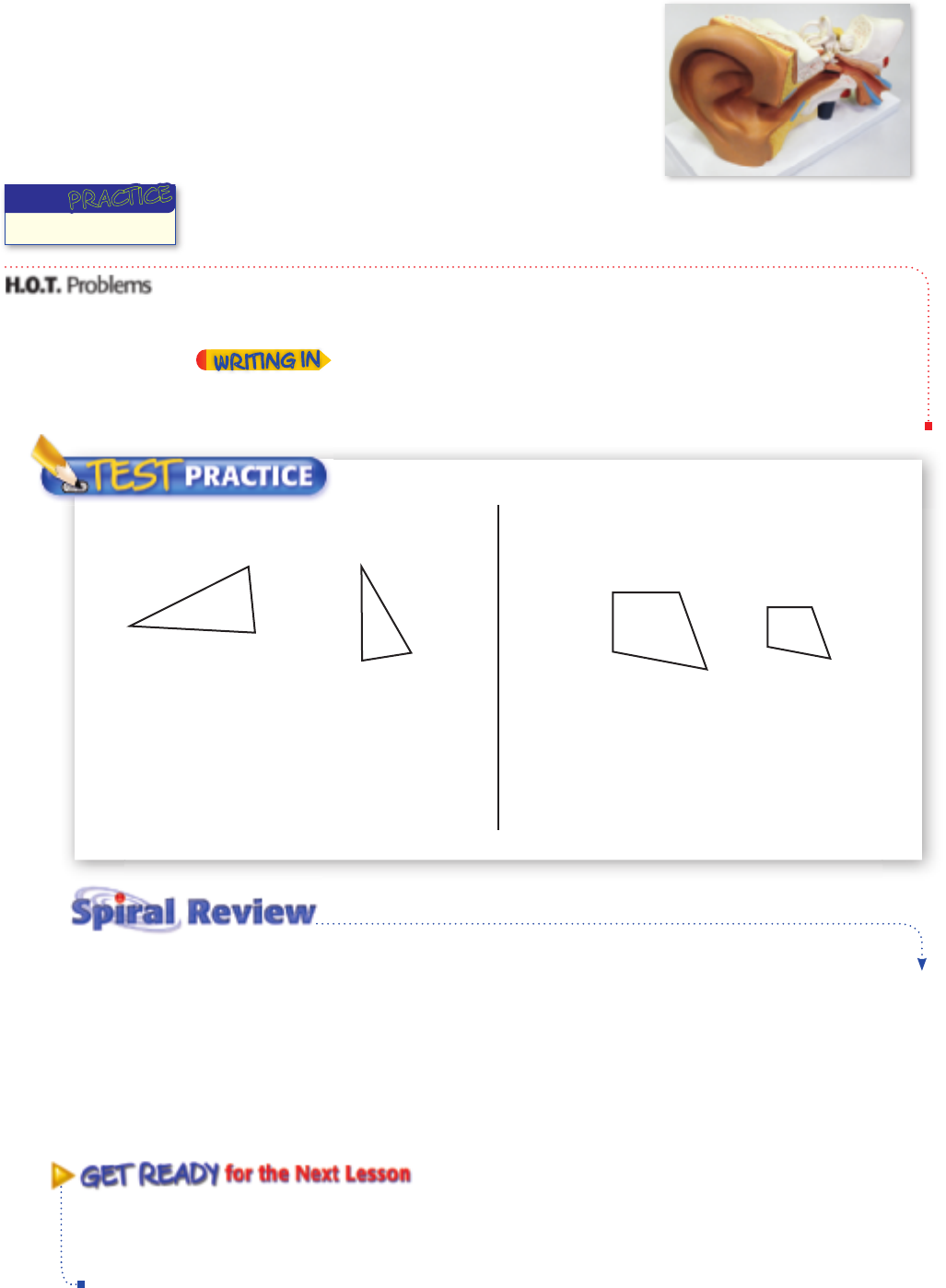
13. LIFE SCIENCE The scale factor from the model
of a human inner ear to the actual ear is
55:2. If one of the bones of the model is
8.25 centimeters long, how long is the actual
bone in a human ear?
14. TELEVISION The ratio of the length of
a wide-screen TV to its width is 16:9. Find
the width of a wide-screen TV if the length
measures 28 inches. Round to the nearest tenth.
H.O.T. Problems
15. CHALLENGE Suppose two rectangles are similar with a scale factor of 2.
What is the ratio of their areas? Explain.
MATH
WRITING IN
Determine whether each statement is always,
sometimes, or never true. Explain your reasoning.
16. Any two rectangles are similar. 17. Any two squares are similar.
Lesson 4-7 Similar Polygons 223
See pages 679, 703.
EXTRA
PRACTICE
PRACTICE
18. Triangle FGH is similar to triangle RST.
36 in.
18 in.
34 in.
?
27 in.
F
G
H
R
TS
What is the length of
−−
TS ?
A 13
1
_
2
inches C 24 inches
B 22
2
_
3
inches D 25
1
_
2
inches
19. Quadrilateral ABCD is similar to
quadrilateral WXYZ.
%
6 in.
"#
$
4 in.
89
:
;
If the perimeter of quadrilateral ABCD
is 54 units, what is the perimeter of
quadrilateral WXYZ?
F 13.5 inches H 27 inches
G 24 inches J 36 inches
Gr8 MS Math SE ©09 - 874050
218_223_C04_L07_874050.indd 223218_223_C04_L07_874050.indd 223 9/18/07 2:47:36 PM9/18/07 2:47:36 PM