Emerson Fisher 249 249B 249Bf 249C 249K And 249L Instruction Manual
2015-03-30
: Emerson Emerson-Fisher-249-249B-249Bf-249C-249K-And-249L-Instruction-Manual-681812 emerson-fisher-249-249b-249bf-249c-249k-and-249l-instruction-manual-681812 emerson pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 12
www.Fisher.com
1. Note that this document does not consider the effects of the thermal expansion of
the moment arm, or the thermal expansion of displacer volume.
Simulation of Process Conditions for Calibration
of Fisherr Level Controllers and
Transmitters—Supplement to 249 Sensor
Instruction Manuals
Displacer / torque tube sensors are transducers that convert a buoyancy change into a shaft rotation. The change in
buoyancy is proportional to the volume of fluid displaced, and the density of the fluid. The change in rotation is
proportional to the change in buoyancy, the moment arm of the displacer about the torque tube, and the torque rate.
The torque rate itself is a function of the torque tube material, the temperature of the material, the wall thickness, and
the length. If the density of the process fluid, process temperature, and torque tube material of the sensor are known,
simulation of process conditions may be accomplished by one of the following means(1):
1. Weight or Force Method:
The interface application is the most general case. The level application can be considered an interface with the upper
fluid SG = 0, and the density application can be considered as a variable SG application with the interface at the top of
the displacer. The buoyancy for a given interface level on the displacer is given by:
FBSGU)Hdisp *]
[
=* VD *
(1)
ρw(SGL - SGU)
Where:
FB= buoyant force
ρw= density of water at 4_C, 1
atmosphere = 1.0000 Kg/liter
(0.03613 lb/in3)
VD= displacer volume
Hdisp = height of interface on displacer,
normalized to displacer length
SGU= specific gravity of upper fluid
(0.0 for Level)
SGL= specific gravity of lower fluid
Figure 1. Cutaway View of Fisher 249 Displacer
Sensor
LIQUID DISPLACER
TORQUE TUBE
W2141-1
SUSPENSION ROD
DRIVER ROD
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014

Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
2
Figure 2. Fisher 2500 or 2503 Level Controller
Transmitter on Caged 249 Sensor
2500 OR 2503
CONTROLLER/
TRANSMITTER
249 SENSOR
W8334
Figure 3. FIELDVUE™ DLC3010 Digital Level
Controller
W7977
For the density application, Hdisp = 1.0, SGu = lowest expected density, and SGL becomes the independent variable, the
actual process density.
The net load on the driver rod is then computed from the equation:
Wnet WD - FB
=
(2)
Where:
Wnet = net load on driver rod
WD= weight of displacer
To simplify equations in the following discussion, let us define a few intermediate terms:
The minimum buoyancy, developed when the interface level is at the bottom of the displacer, is given by:
FBmin ρw *
=
(3)
VD *SGU
The change in buoyant force as the normalized interface level rises on the displacer is:
ΔFBρw *
=
(4)
VD *(SGL - SGU) * Hdisp
The maximum change in buoyancy, developed when the interface level is at the top of the displacer is:
(ΔFB)max ρw *
=(5)
VD *(SGL - SGU)
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
3
Temperature Effect
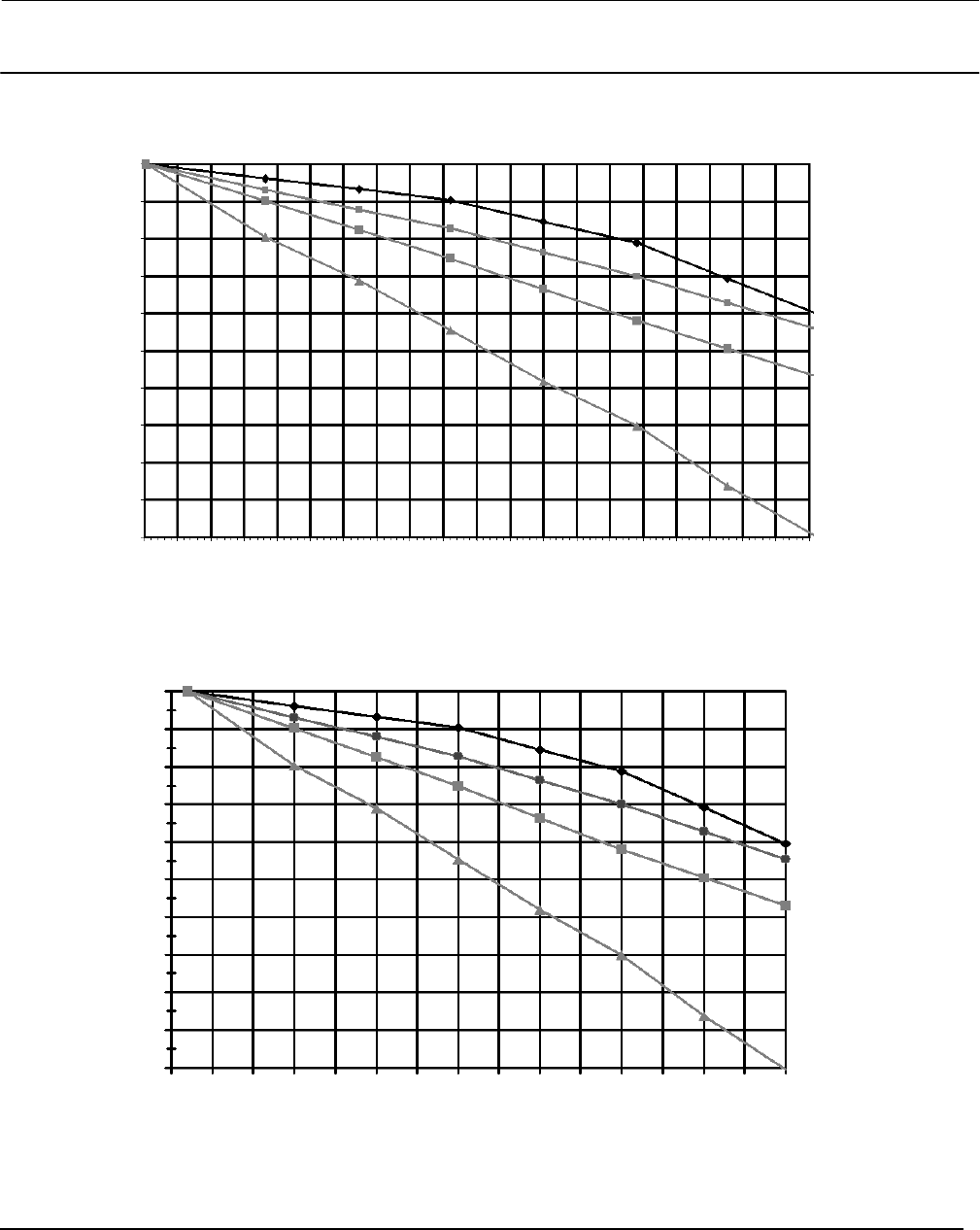
As process temperature increases, the torque rate decreases due to the change in modulus of rigidity. This effect can
be represented by normalizing the modulus vs. temperature curve for a given material to the room temperature value,
and using it as a scale factor on the torque rate. See figure 4 and table 1 or 2.
Because we can simulate the rotation of a more compliant torque tube by increasing the load, the weight value may be
divided by the same scale factor to simulate the process condition:
Wnet_test
WD - FB
=
(6)
Gnorm
Where:
Wnet_test = net load adjusted to simulate
process temperature effect
Gnorm = normalized modulus of torque
tube material, a function of
temperature.
Displacer Rise Effect
Note that equation 6 simulates the process level on the displacer. The actual level in the cage or vessel will be
different, due to the rise of the displacer as the torque tube load is decreased by the increasing buoyancy.
On a 14‐inch displacer, or on a 249VS with a long driver rod, the displacer rise can become a significant fraction of the
span. If the torque tube rate and driver rod length are known, change in rotation can be computed by dividing the
torque change by the rate.
ΔAngle Driver
=*
(7)
π
(
Ramb )
ΔFB/180_
*
Gnorm
*
Where:
ΔAngle = resulting change in torque tube
angle in radians
Driver = driver rod length
Ramb = Torque rate (torque per
_rotation) at ambient
temperature
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
4
Figure 4. “Gnorm”: Theoretical Temperature Effect on Torque Rate for Most Commonly Used Materials
TORQUE RATE REDUCTION
(NORMALIZED MODULUS OF RIGIDITY)
Gnorm
TEMPERATURE (_C)
N05500
N06600
N10276
S31600
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
1.00
0.96
0.92
0.88
0.84
0.82
0.80
0.90
0.86
0.98
0.94
TORQUE RATE REDUCTION
(NORMALIZED MODULUS OF RIGIDITY)
TEMPERATURE (_F)
N05500
N06600
N10276
S31600
50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800
1.00
0.96
0.92
0.88
0.84
0.82
0.80
0.90
0.86
0.98
0.94
Gnorm
NOTE: THIS CHART DEPICTS THE REVERSIBLE CHANGE ONLY. THE IRREVERSIBLE DRIFT IS A FUNCTION OF THE NET LOAD, THE ALLOY, AND THE LEVEL OF STRESS EQUALIZATION
ACHIEVED IN MANUFACTURING. (THE IRREVERSIBLE EFFECT CAN ONLY BE COMPENSATED BY PERIODIC ZERO TRIM.) N05500 IS AN APPROPRIATE SPRING MATERIAL FOR
TEMPERATURES BELOW AMBIENT AND UP TO 232_C (450_F). ABOVE 260_C (500_F), THE INDUSTRY DOES NOT RECOMMEND USING IT AS A SPRING MATERIAL. N06600 IS
CONSIDERED ACCEPTABLE TO APPROXIMATELY 399_C (750_F) WITH PROPER STRESS EQUALIZATION.

Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
5
Recognizing that the displacer rise is the side opposite this changing angle, in a triangle of which the drive rod is the
hypotenuse, the displacer rise can be approximated applying the small‐angle sine approximation to the result of
equation 7.
(8)
ΔRisedisp =
Ramb Gnorm
ΔFB*Driver 2
()
**π
180_
The above expression may be factored to produce an ambient‐temperature displacer‐rise rate.
RiseRateamb
Driver2
=
(9)
π
(
Ramb
)
/180_*
The net rise is then restated with aid of the temperature correction term Gnorm.
ΔRisedisp =
(10)
Gnorm
ΔFB*RiseRateamb
The digital instrument firmware makes an internal correction for the displacer rise, so we must account for it in our
weight calculation to make sure that we get the expected digital value of interface level in the cage. (Analog electronic
and pneumatic devices don't have this correction capability, but the accuracy of the calibration would still be improved
by accounting for the effect during simulation.) The ratio of the level change on the displacer to the level change in the
cage needed to produce it is:
ΔHdisp =
(11)
RiseRateamb
*/
ΔHcage
proc (
LD)Gnorm
LD
)
ΔFB max
Where:
LD= length of displacer
Hcage = interface level in cage, normalized to displacer length.
The above equation is valid only for 0.0 < Hdisp < 1.0 (since interface level excursions above or below the displacer
produce no additional change in buoyancy)
The % span error introduced by neglecting the displacer rise effect becomes smaller as the displacer length increases.
The displacer rise at the initial condition, (displacer completely submerged in the upper fluid), is given by:
Rise0proc =
(12)
Gnorm
RiseRateamb
FBmin_eff *
Where:
FBmin_eff = [ FBmin Max( (Wdisp Wmax), 0.0) ]
Wmax = the load that will cause the linkage to contact the lower travel stop.
Max( (Wdisp Wmax), 0.0 ) = the amount of buoyancy required to lift the displacer off the travel stop so that rise can
actually commence. The maximum available shift below the zero rest position at ambient temperature is also limited
by this travel stop, so the value of Wmax will be a function of temperature. To account for this, replace Wmax by
(Wmax_ambient * Gnorm) in the FBmin_eff equation.
Note that Wmax_ambient would have to be determined by experiment on the specific physical hardware, but for a first
approximation, you could use the ‘maximum unbuoyed displacer weight’ value given in table 5.
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
6
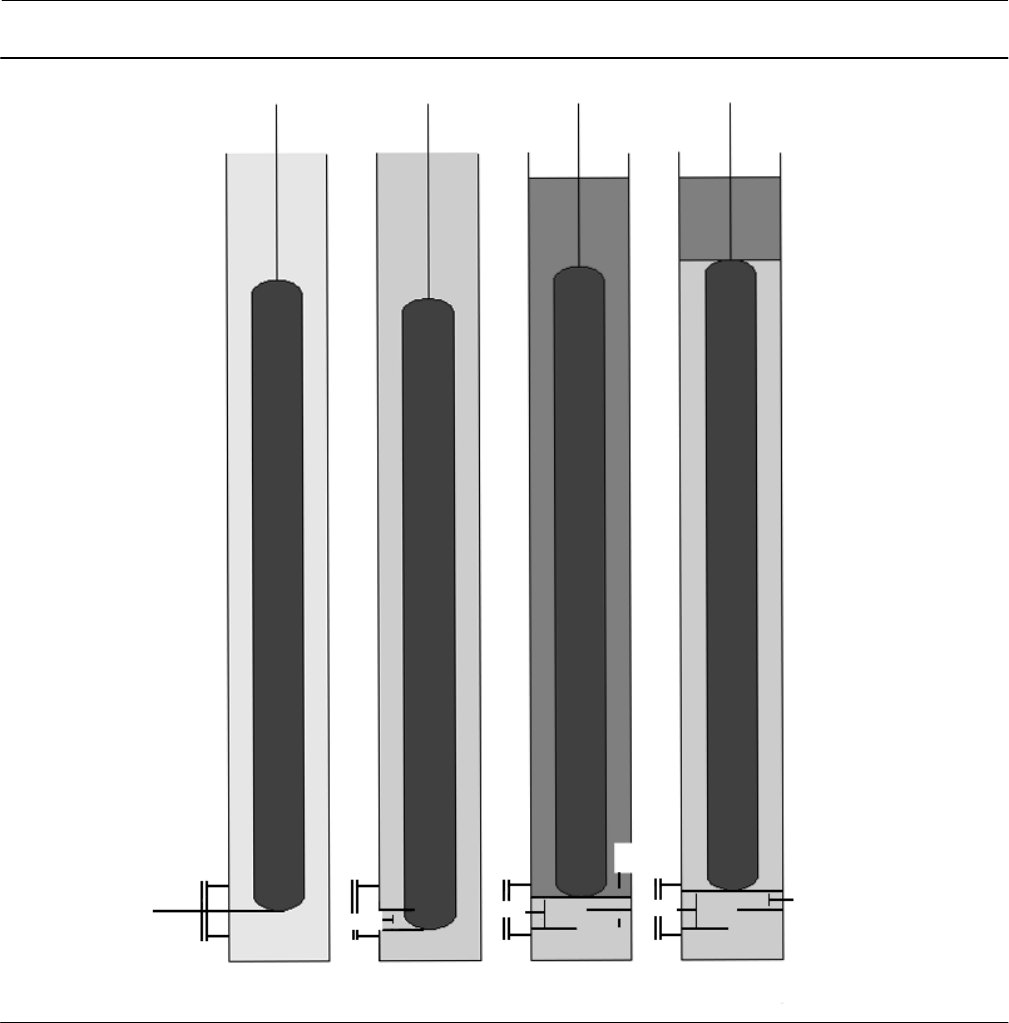
Figure 5. Illustration of Displacer Rise Effect
Final Offset
Initial
Offset
RiseiRisef
Zero Shift
Ref
T = amb
Fb = 0
T = proc
Fb = 0
T = proc
Fb = f(SGU)
T = proc
Fb = f(SGL)
B
B
B
B
Y
Y
Y
Y

Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
7
Temperature‐Induced Zero‐Shift at Zero Buoyancy
If the physical zero reference was established at zero buoyancy and ambient temperature, there is an additional
zero‐shift to take into account. The zero buoyancy position of the bottom of the displacer at process temperature will
be lower, because of the reduction in torque rate.
ZeroShiftproc =
(13)
Gnorm
RiseRateamb
*
WD*Gnorm-1.0 )
(
Note that the combination of:
a. the location of the displacer bottom relative to the external reference at ambient,
b. the zero-shift at process temperature, and
c. the initial displacer rise at process temperature,
will determine the extent of any unobservable region between the external zero reference and the displacer bottom.
We must decide what our process variable (PV) calculation is going to use for a zero reference. Since any interface level
excursion below the bottom of the displacer cannot change the output, it is convenient to call the displacer bottom
“zero” for the test, and this has been standard procedure in pilot mounting. In the digital level controller, Level Offset
is used to adjust the digital output to zero at this condition.
Lowest Observable Cage Interface Level
If it is desired to line up the calculation with the physical external reference, the Level Offset (and range values) can be
adjusted according to the following.
Hcage0 =
(14)
LD
ZeroShiftproc )Rise0proc
Where:
Hcage0 = highest possible value of cage
interface level (normalized to
displacer length), relative to zero
buoyancy, ambient temperature
coupling point, when displacer
interface level is 0.0 (bottom of
displacer).
This is the physical interface level below which a change is unobservable. The range values or alarm values should be
set within the observable range of PV to make sure that over‐ and under‐flow conditions are reported to the control
system.
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
8
Weight Calculation Procedure
To compute the weight required, at room temperature, to simulate a given process‐condition cage interface level:
a. Start with an initial buoyancy based on the SG of the upper fluid,
b. subtract it from the displacer weight, and
c. correct the result for process temperature.
This will give the test weight for the lowest observable process condition.
Wnet_test
i
WD -
=
(15)
JGnorm
FBmin
The change in weight for a process‐temperature, cage (or vessel) interface level condition, one displacer length higher
than the above state, is given by:
ΔW f=
(16)
J*
()
Gnorm
ΔHdisp /ΔHcage proc ΔFB max
)
(
The net weight for the 100% cage process condition is:
Wnet_test =
(17)
JWnet_test −
JJ
ΔW f
f i
Other values of ΔW can be computed from:
ΔW=
(18)
*
()
Gnorm
ΔHdisp /ΔHcage proc
ΔHcage *(ΔFB)max
Where:
ΔHcage =H
cage − Hcage0
Valid for Hcage0 < Hcage < [1/ (ΔHdisp / ΔHcage)proc]
Remember that it is common to arbitrarily set Hcage0 to zero for test purposes when using weights. (For water column
calculations in the next section, it is more important to keep track of the initial process‐condition cage level to
simulate the initial buoyancy correctly.) The resultant net weights for the intermediate levels are given by:
Wnet_test -
=
(19)
J
Wnet_test ΔW
i
This assumes that the net weights do not violate the maximum or minimum load for the torque tube. Refer to table 5.

Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
9
2. Water Column Method:
It is possible to simulate a range of buoyancy adjusted for process temperature effect by using a water column at room
temperature. At the ambient SG = 1.0 level application, the corrections should all cancel out, leaving Hcage = desired
PV.
Cage Water Level Required to Simulate Interface Levels
If we have computed an equivalent weight for a given process condition in section 1, the ambient temperature water
level on the displacer that will produce the same torque tube rotation is:
Hdisp_eq =
(20)
*
Wnet
WD -
ρwVD
For high temperatures and high SG, the range of conditions that can be simulated will contract, since we are limited by
the actual displacer weight and the nominal density of water.
We must next convert this equivalent displacer level into an equivalent cage level using the inverse of the relationship
in equation 11, without the temperature compensation.
ΔHdisp =
(21)
RiseRateamb
*
ΔHcage
amb LD)ρw
LD
VD*
The result is:
(22)
ρwVD
*
()
ΔHdisp /ΔHcage amb
*
Hcage_eq Wnet
WD -
()
=
Process Interface Level Simulated by a Given Cage Water Level
We can also write a generic equation for the process‐condition displacer interface level simulated by a given
room‐temperature displacer water level:
First, convert the ambient cage water level to an ambient displacer water level:
Hdisp_eq =
(23)
Hcage
()
ΔHdisp
/
ΔHcage amb
Next, define an intermediate variable to compute the apparent SG being simulated at process conditions by the
ambient displacer water level:
SGappsim =
*
1- )
ρwVD
Gnorm *WD
)Gnorm *Hdisp_eq
(
(24)
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
10
Now use this apparent SG value to compute the simulated interface level on the displacer:
Hdisp =
(25)
sim
-SGU
SGL-SGU
SGappsim
Finally convert the simulated process‐conditions displacer interface level to simulated process‐condition cage
interface level, by the equation:
=
(26)
/
Hcage0
()
ΔHdisp proc
Hcagesim )
Hdispsim
ΔHcage
Where Hcage0 is either 0.0 or the value computed in equation 14, per the practice being followed for PV reference.
3. Tables of Nominal Values
If the calibration is being run per standard practice the values of the parameters for the above equations are generally
available for observation in the instrument memory. For analog instruments, a table of nominal values may be
consulted to generate good approximations.
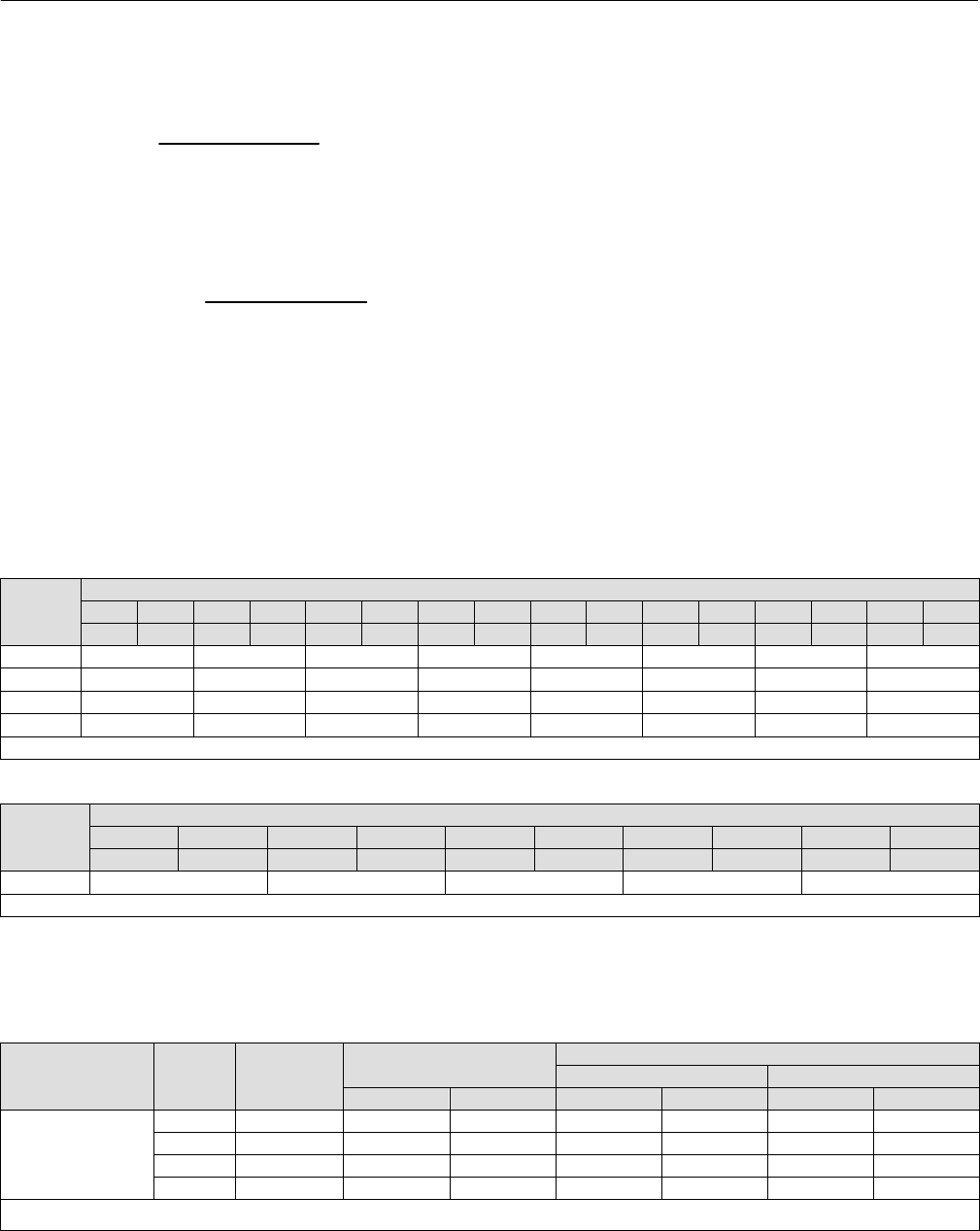
Table 1. Gnorm for Common Torque Tube Materials Above Room Temperature
Material
Gnorm
_C_F_C_F_C_F_C_F_C_F_C_F_C_F_C_F
21 70 93 200 149 300 204 400 260 500 316 600 371 700 427 800
N05500 1 0.9923 0.9866 0.9808 0.9692 0.9577 0.9385 0.9192
N06600 1 0.9861 0.9759 0.9657 0.9529 0.9401 0.9256 0.9111
N10276 1 0.9802 0.9649 0.9497 0.9329 0.9161 0.9010 0.8859
S31600 1 0.9609 0.9378 0.9108 0.8837 0.8597 0.8277 0.7993
These values are approximations derived from various metal-alloy industry publications
Table 2. Gnorm for 316 SST Below Room Temperature
Material
Gnorm
_C_F_C_F_C_F_C_F_C_F
-240 -400 -184 -300 -129 -200 -18 0 21 70
S31600 1.0836 1.0807 1.0635 1.0179 1
Low temperature data for N05500, N06600, and N10276 not available at time of publication.
Table 3 provides the theoretical unloaded rate, and the composite or effective torque rate measured by the digital
level controller at the end of the pilot shaft. The physical rotation at the far end of the torque tube may be a bit greater
than what these tables would predict, due to some wind‐up of the pilot shaft.
Table 3. Theoretical Room Temperature Torque Rates
Family / Wall Material Torque Tube
Part Number
Unloaded Rate(2) Composite Rate
W/O Insulator W/Insulator
Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg
249, 249B,
249BF 249BP, 259B,
249P (CL150-600),
249W
HEAVY
N05500(1) 1K4497X0012 1.48 13.1 1.90 16.8 2.01 17.8
N06600 1P8662X0012 1.66 14.7 2.07 18.3 2.18 19.3
S31600 1K4541000A2 1.76 15.5 2.18 19.3 2.29 20.3
N10276 1K453140152 1.75 15.5 2.16 19.1 2.27 20.1
1. N05500 is the default material.
2. Appropriate for 2500 controllers only.
-continued-
Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
11
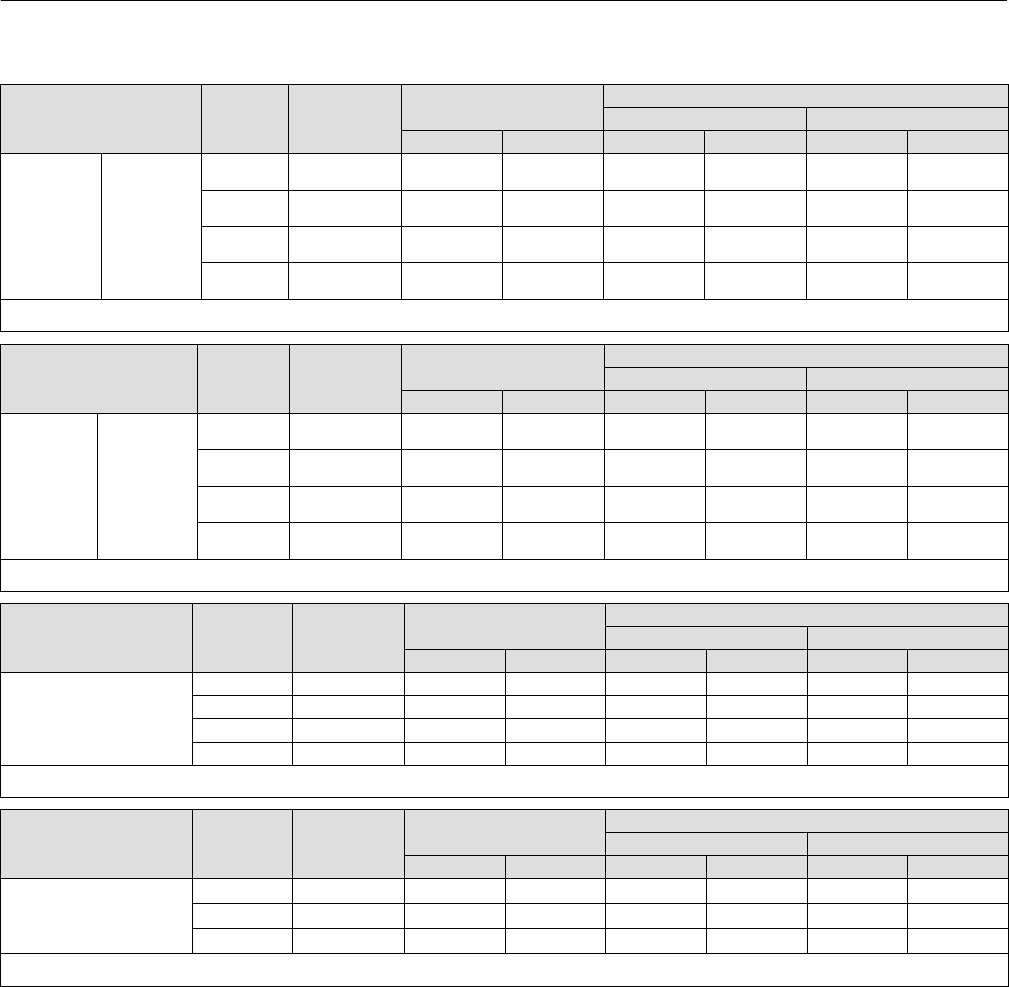
Table 3. Theoretical Room Temperature Torque Rates (continued)
Family / Wall Material Torque Tube
Part Number
Unloaded Rate(2) Composite Rate
W/O Insulator W/Insulator
Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg
249,
249B, 249BF
249BP,
259B,
249P
(CL150-600),
249W
STANDARD
249C
249CP
249PT
249VT
HEAVY
N05500(1) 1K4493X0012 0.764 6.76 0.988 8.75 1.05 9.27
N06600 1K4515000A2 0.758 6.71 0.952 8.42 1.00 8.87
S31600 1K4503000A2 0.848 7.50 1.06 9.36 1.11 9.85
N10276 1K4527000A2 0.799 7.07 0.993 8.79 1.04 9.23
1. N05500 is the default material.
2. Appropriate for 2500 controllers only.
Family / Wall Material Torque Tube
Part Number
Unloaded Rate(2) Composite Rate
W/O Insulator W/Insulator
Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg
249B
249,
249BP,
259B,
249P
(CL150-600),
249W
THIN
249C
249CP
249PT
249VT
STANDARD
N05500(1) 1K4495X0012 0.384 3.40 0.502 4.44 0.532 4.70
N06600 1K4517000A2 0.405 3.58 0.513 4.54 0.540 4.78
S31600 1K4505000A2 0.416 3.68 0.524 4.64 0.551 4.87
N10276 1K4529X0012 0.427 3.78 0.535 4.73 0.562 4.97
1. N05500 is the default material.
2. Appropriate for 2500 controllers only.
Family / Wall Material Torque Tube
Part Number
Unloaded Rate(2) Composite Rate
W/O Insulator W/Insulator
Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg
249K,
249L, 249N, 249VS,
249P (CL900‐2500),
STANDARD
N05500(1) 1K4499X0012 1.06 9.41 1.46 13.0 1.54 13.7
N06600 1K4519000A2 1.20 10.6 1.58 14.0 1.66 14.7
S31600 1K4507000A2 1.26 11.2 1.66 14.7 1.75 15.4
N10276 1K9159X0012 1.26 11.2 1.65 14.6 1.73 15.3
1. N05500 is the default material.
2. Appropriate for 2500 controllers only.
Family / Wall Material Torque Tube
Part Number
Unloaded Rate(2) Composite Rate
W/O Insulator W/Insulator
Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg Nwm/deg lbfwin/deg
249K,
249L, 249N, 249VS,
249P (CL900‐2500)
THIN
N05500(1) 1K4501X0012 0.550 4.87 0.762 6.74 0.804 7.12
N06600 1P747040042 0.546 4.83 0.729 6.45 0.765 6.77
S31600 1K450935072 0.611 5.40 0.809 7.16 0.848 7.51
1. N05500 is the default material.
2. Appropriate for 2500 controllers only.

Instruction Manual Supplement
D103066X012
249 Sensors
March 2014
12
Additional Information
Table 4. Moment Arm (Driver Rod) Length(1)
Sensor Type(2) Moment Arm
mm Inch
249 203 8.01
249B 203 8.01
249BF 203 8.01
249BP 203 8.01
249C 169 6.64
249CP 169 6.64
249K 267 10.5
249L 229 9.01
249N 267 10.5
249P
(CL125-600) 203 8.01
249P
(CL900-2500) 229 9.01
249VS (Special)(1) See serial card See serial card
249VS (Std) 343 13.5
249W 203 8.01
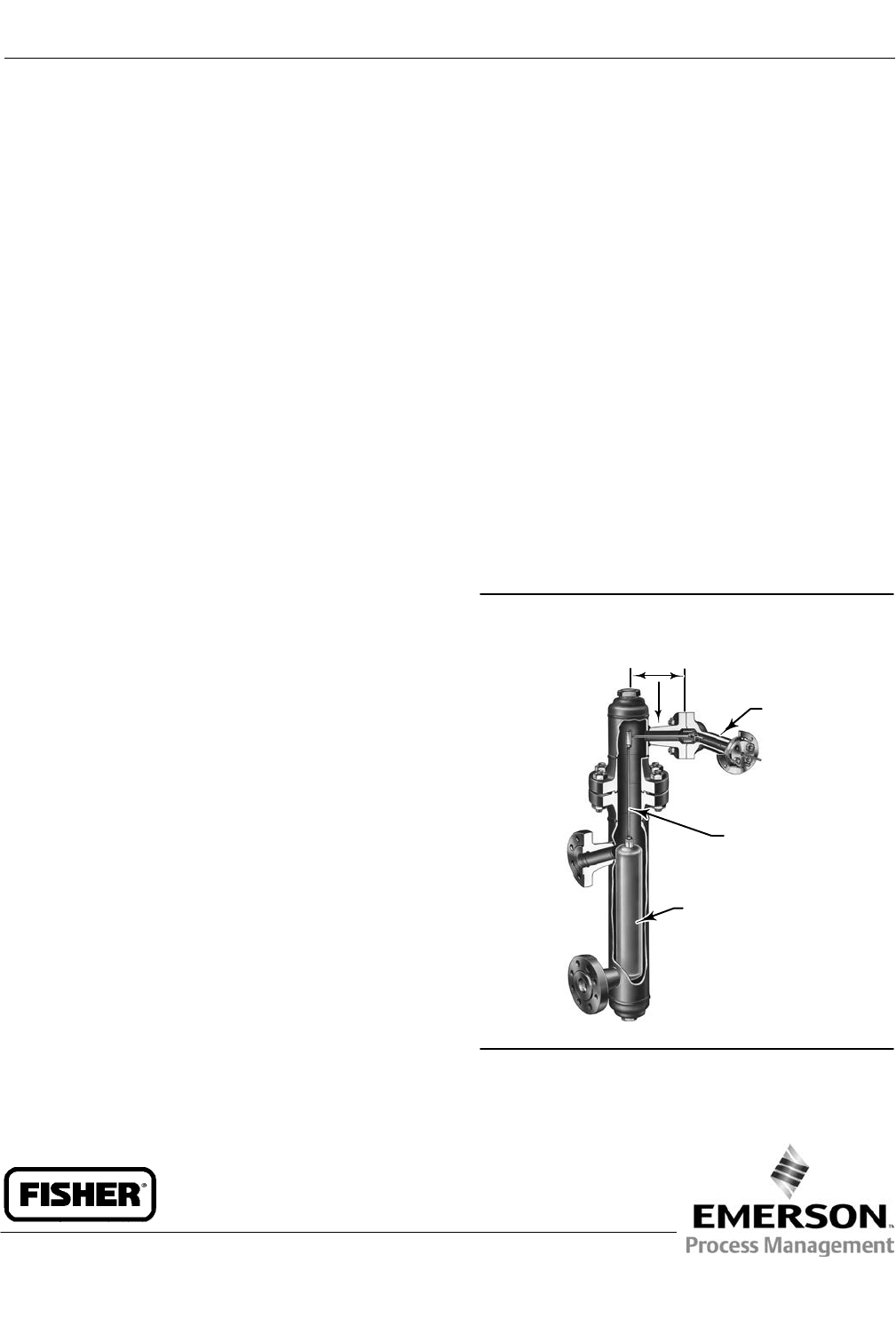
1. Moment arm (driver rod) length is the perpendicular distance between the vertical
centerline of the displacer and the horizontal centerline of the torque tube. See figure
6. If you cannot determine the driver rod length, contact your Emerson Process
Management sales office and provide the serial number of the sensor.
2. This table applies to sensors with vertical displacers only. For sensor types not listed,
or sensors with horizontal displacers, contact your Emerson Process Management sales
office for the driver rod length. For other manufacturers' sensors, see the installation
instructions for that mounting.
Table 5. Maximum Unbuoyed Displacer Weight
Sensor Type Torque Tube Wall
Thickness
Displacer Weight,
WT (lb)
249, 249B, 249BF,
249BP, 249W
Thin
Standard
Heavy
3.3
5.0
9.5
249C, 249CP Standard
Heavy
4.0
6.4
249VS Thin
Standard
3.0
5.5
249L, 249P(1) Thin
Standard
4.5
8.5
249K Thin
Standard
3.8
7.3
1. High pressure CL900 through 2500.
Figure 6. Method of Determining Moment Arm from
External Measurements
E0283
HORIZONTAL CL
OF TORQUE TUBE
VERTICAL CL
OF DISPLACER
MOMENT
ARM
LENGTH
Table 6. Related Documents
Document Part Number
249 Caged Displacer Sensors Instruction Manual D200099X012
249 Cageless Displacer Sensors Instruction Manual D200100X012
249VS Cageless Displacer Sensor Instruction Manual D103288X012
249W Cageless Wafer Style Level Sensor Instruction
Manual D102803X012
2500 and 2503 Level Controllers and Transmitters
Instruction Manual D200124X012
DLC3010 Digital Level Controller Quick Start Guide D103214X012
DLC3010 Digital Level Controller Instruction Manual D102748X012
DLC3020f Digital Level Controller Quick Start Guide D103434X012
DLC3020f Digital Level Controller instruction Manual D103470X012
2502 Level Controller D200126X012
These documents are available from your Emerson Process Management sales office.
Also visit our website at www.Fisher.com.
Emerson Process Management
Marshalltown, Iowa 50158 USA
Sorocaba, 18087 Brazil
Chatham, Kent ME4 4QZ UK
Dubai, United Arab Emirates
Singapore 128461 Singapore
www.Fisher.com
The contents of this publication are presented for informational purposes only, and while every effort has been made to ensure their accuracy, they are not
to be construed as warranties or guarantees, express or implied, regarding the products or services described herein or their use or applicability. All sales are
governed by our terms and conditions, which are available upon request. We reserve the right to modify or improve the designs or specifications of such
products at any time without notice.
E 2003, 2014 Fisher Controls International LLC. All rights reserved.
Fisher and FIELDUVE are marks owned by one of the companies in the Emerson Process Management business unit of Emerson Electric Co. Emerson Process
Management, Emerson, and the Emerson logo are trademarks and service marks of Emerson Electric Co. All other marks are the property of their respective
owners.
Neither Emerson, Emerson Process Management, nor any of their affiliated entities assumes responsibility for the selection, use or maintenance
of any product. Responsibility for proper selection, use, and maintenance of any product remains solely with the purchaser and end user.