Fairchild Semiconductor An 7502 Users Manual Power MOSFET Switching Waveforms

AN-7502 to the manual 261076ed-a383-4dbc-8c1a-dcfb2b7f8b35

2015-02-09

: Fairchild Fairchild-Semiconductor-An-7502-Users-Manual-550603 fairchild-semiconductor-an-7502-users-manual-550603 fairchild pdf

Open the PDF directly: View PDF .
Page Count: 9

AN-7502

Power MOSFET Switching Waveforms:

A New Insight

The examination of power MOSFET voltage and current

waveforms during switching transitions reveals that the

device characterization now practiced by industry is inade-

quate. In this Note, device waveforms are explained by con-

sidering the interaction of a vertical JFET driven in cascode

from a lateral MOSFET in combination with the interelec-

trode capacitances. Particular attention is given to the

drain-voltage waveform and its dual-slope nature. The

three terminal capacitances now published by the industry

are shown to be valid only for zero drain current. For cases

where the gate drive is a voltage step generator with inter-

nal fixed resistance, the drain voltage characteristics are

inferred from the gate current drive behavior and compared

to observed waveforms. The nature of the “asymmetric

switching times” is explained.

A waveform family is proposed as a more descriptive and

accurate method of characterization. This new format is a

plot of drain voltage and gate voltage versus normalized

time. A family of curves is presented for a constant load

resistance with VDS varied. Gate drive during switching

transitions is a constant current with voltage compliance

limits of 0 and 10 volts. Time is normalized by the value of

gate driving current. The normalization shows excellent

agreement with data over five orders of magnitude, and is

bounded on one extreme by gate propagation effects and

on the other by transition time self-heating (typically tens of

nanoseconds to hundreds of microseconds).

Device Models

The keystone of an understanding of power MOSFET

switching performance is the realization that the active

device is bimodal and must be described using a model that

accounts for the dual nature. Buried in today’s power MOS-

FET devices is the equivalent of a depletion layer JFET that

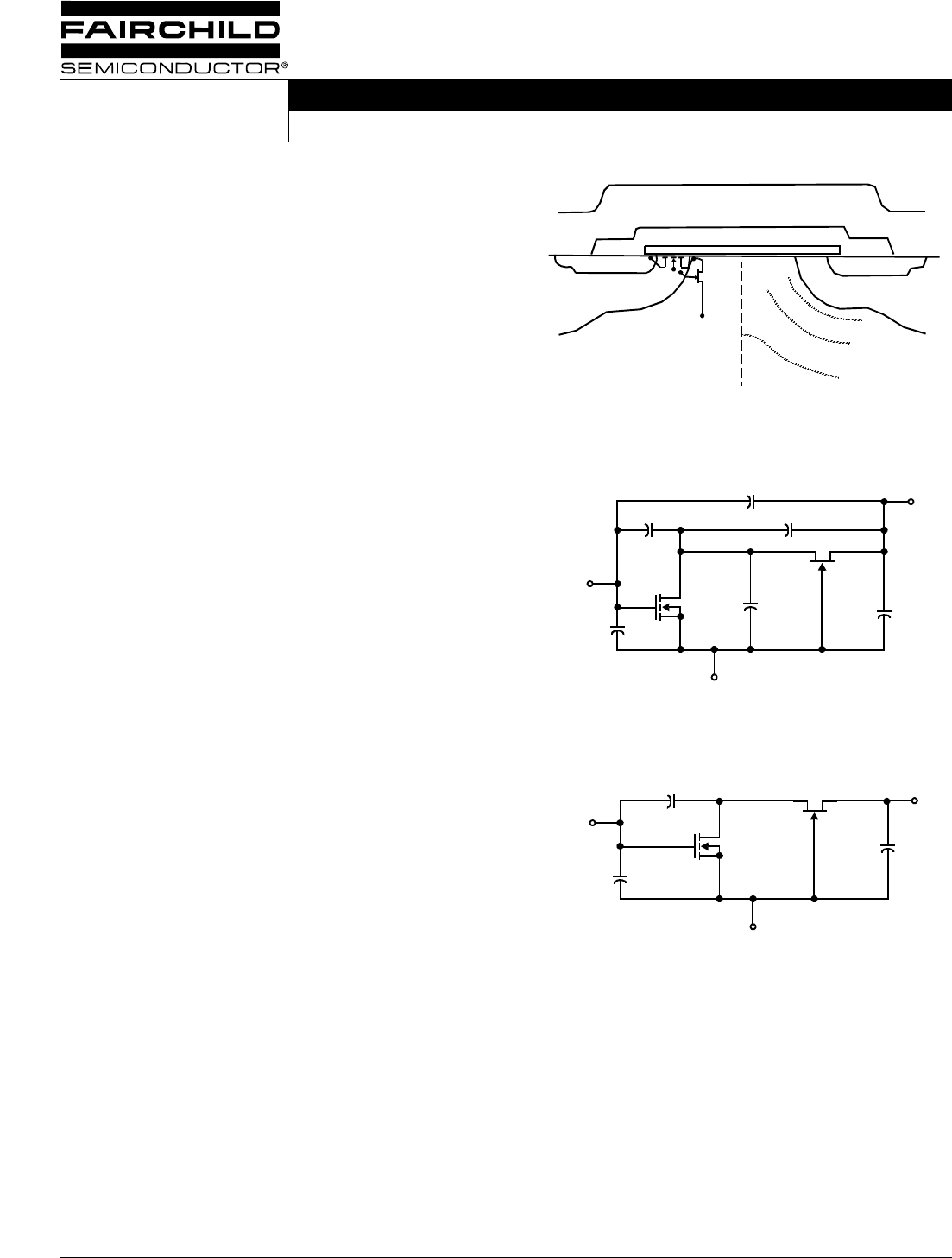
contributes significantly to switching speed. Figure 1 is a

cross-sectional view of a typical power MOSFET, with MOS-

FET/JFET symbols superimposed on the structure.

Figure 2 is obtained by taking the lateral MOS and vertical

JFET from this conception and adding all the possible node-

to-node capacitances. Computed values of the six capaci-

tances for a typical device structure suggest that device

behavior may be adequately modeled using only three

capacitors in the manner of Figure 3. This is the model to be

employed for analysis and study.

FIGURE 1. CROSS-SECTION VIEW OF MOSFET SHOWING

EQUIVALENT MOS TRANSISTOR AND JFET

FIGURE 2. MOS TRANSISTOR WITH CASCODE-CONNECTED

JFET AND ALL CAPACITORS

FIGURE 3. FIGURE 2 SIMPLIFIED

Gate Drive: Constant Voltage or

Constant Current

Before moving on to the study of the equivalent circuit states

of the model, a gate-drive forcing function which is easy to

represent, relates to reality, and best illustrates device

behavior must be chosen. The choice may be immediately

narrowed to two:

(1) An instantaneous step voltage with internal resistance R,

Figure 5.

(2) An instantaneous step current with infinite internal resis-

tance, Figure 6.

SOURCE METAL

POLY GATE GLASS GATE OXIDE

10 VOLTS

DEPLETION EDGE

40 VOLTS

n+ DRAIN

JFET

MOS

n+ SOURCE

p BODY

GATE

SOURCE

DRAIN

GATE

CGS

CDS

SOURCE

DRAIN

Application Note October 1999

itle

ect

wer

S-

itch

ve-

orm

nsi

)

tho

()

Int

er-

po-

ati

on,

tor)

tor

()

ge-

ine

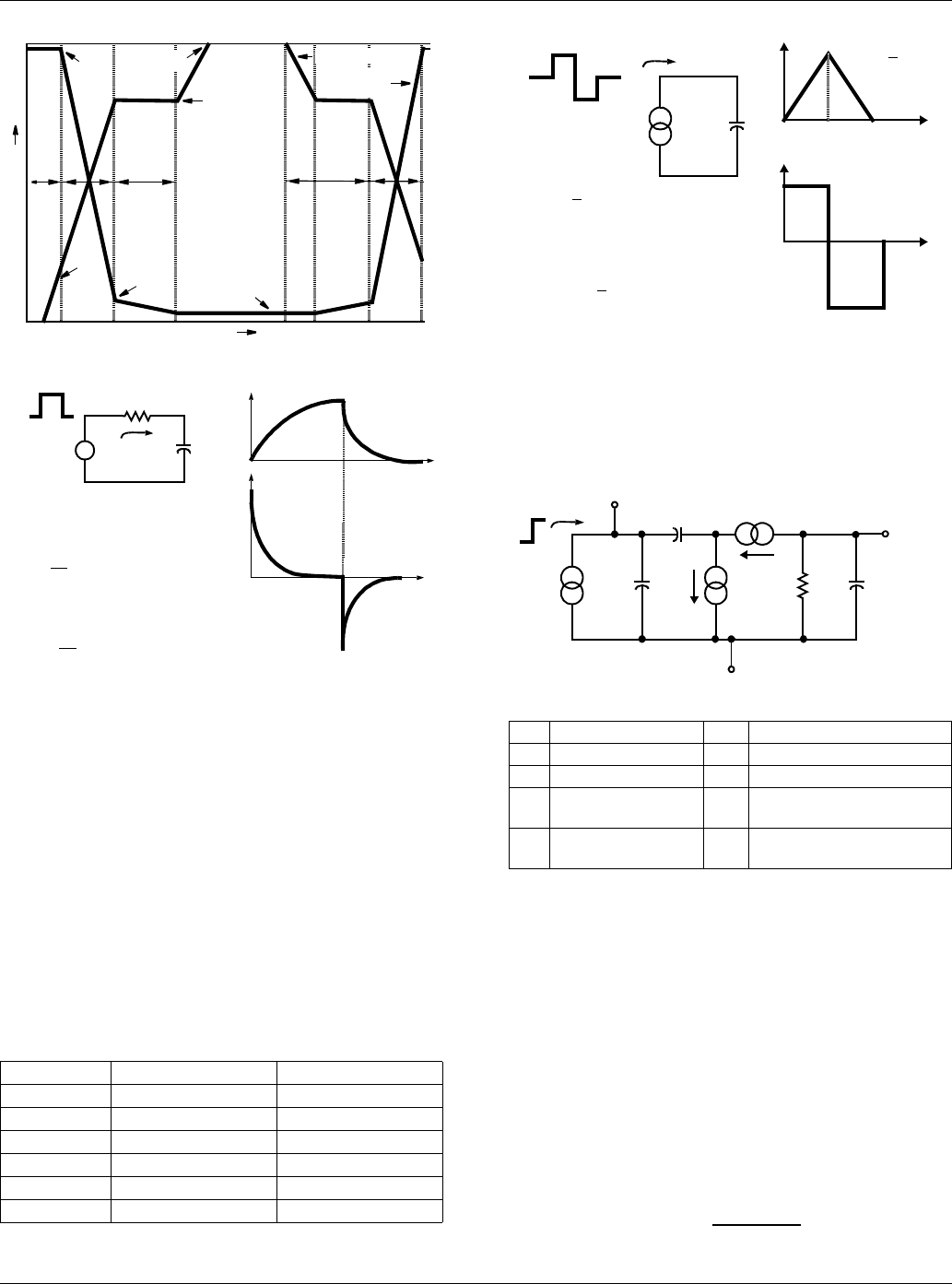
FIGURE 4. IDEALIZED POWER MOSFET WAVEFORMS

FIGURE 5. STEP-VOLTAGE FORCING FUNCTION

Power MOSFET devices are highly capacitive in nature;

hence, simple capacitor responses to the forcing functions

offer a good vehicle for comparison. The advantageous

choice is immediately obvious: Figure 6. Voltage/time

responses dominated by capacitance are straight lines

(when constant current is used). The slope of these lines is

proportional to current and inversely proportional to capaci-

tance. Analytically, then, constant current is most conve-

nient. It is quite another matter, however, to build a

bidirectional current drive that is accurate across the many

decades of both current and time required to establish

experimental verification.

Six States

To completely characterize power MOSFET switching wave-

forms, the six states that a device assumes, Figure 6, must

be addressed:

†The term saturated is taken to mean a constant low-voltage drain-source

condition.

FIGURE 6. STEP CURRENT FORCING FUNCTION

Equivalent Circuit

The lumped-parameter model of Figure 3, with the cascode-

connected JFET, can now be reduced to the linear equiva-

lent circuit of Figure 7, and the six device states investigated

from full off to full on.

FIGURE 7. POWER MOSFET EQUIVALENT CIRCUIT

State 1: MOS Off, JFET Off

In a power-MOSFET device, no drain current will flow until

the device’s gate threshold voltage, Vgs(TH), is reached. Dur-

ing this time, the gate’s current drive is only charging the

gate source capacitance. More accurately, IG is charging

CISS (CISS = CGS + CGD, CDS shorted), the capacitance

designation published by the industry.

The current generators, gMVG and gMJVX are open circuits

for zero drain current, and RL is presumed to be so low as to

represent a short circuit (generally true for practical applica-

tions). This is academic however since CGS is very much

larger that CX. The time to reach threshold, then, is simply:

STATE MOS JFET

Turn-on 1 Off Off

Turn-on 2 Active Active

Turn-on 3 Active Saturated†

Turn-off 4 Saturated Saturated†

Turn-off 5 Active Saturated

Turn-off 6 Active Active

12 3 4 5 6

STATES

IG = CONSTANT

GATE VOLTAGE

DRAIN

VOLTAGE

VG(SAT)

VD(SAT)

VDD VGS

VOLTAGE

VDK

TIME

-VG

i(t) v(t)

-IPK = VG/RO

IPK = VG/RO

v(t)

i(t)

TURN ON

v(t) = VG (1 - e)

i(t) = VG e

TURN OFF

v(t) = VG e

i(t) = - VG e

-t/ROC

LEGEND

VGS - Gate Voltage CDS - Drain Source Capacitance

VX- JFET Driving Voltage gM- MOSFET Transconductance

VD- Drain Voltage gMJ - JFET Transconductance

CGS - Gate Source

Capacitance

RL- Drain Load Resistance

CX- MOSFET Feedback

Capacitance

IG- Constant Current Amplitude

T1 =

CISS

Vgs(TH)

-IG

i(t)

TT t

-IG

i(t) v(t)

v(t)

-VG = C

IGT

TURN ON

v(t) = IGt

i(t) = IG, 0 < t < T

TURN OFF

v(t) = 2VG-IGt

i(t) = IG, T < t < 2T

GATE

CDS

SOURCE

DRAIN

VGS

gMJ VX

CGS gM VG

Application Note 7502

State 2: MOS ActIve, JFET ActIve

This state graphically illustrates the dramatic influence that

the JFET has on the power MOSFET drain-voltage wave-

form. Instead of having to discharge Cx from VDD to ground,

the lateral MOSFET need only swing VX to ground, a much

smaller voltage thanks to the grounded gate JFET. Since the

interaction of RL with the device capacitances has a second-

order effect on the drain voltage, the equivalent circuit of Fig-

ure 7 predicts a drain voltage change of:

dVG/dt = gMRLlG/[CGS + CX(1 + gM/gMJ)]

In all but the smallest power-MOSFET devices, Cx is several

thousand picofarads and gM/gMJ is of the order of 3:1.

Power-MOSFET devices exhibit a high dVD/dt switching rate

because of the cascode-connected JFET, not because

CRSS (CRSS = CGD) is a small value, as zero-drain-current

data sheet capacitance values might lead one to believe. If

CRSS were, in actuality, small, long drain voltage tails would

not exist. The tail response is a direct result of JFET satura-

tion. In order to delineate the transition from state 2 to state

3, a drain voltage at which the transition occurs must be

defined. VDK is the knee voltage at which linear extrapola-

tions of drain-voltage slopes intersect. The time duration of

state 2 is:

t2(t6) = (VDD - VDK)[CGS + CX(1 + gM/gMJ)]/gMRLIG

State 3: MOS Active, JFET Saturated

When the JFET saturates, the gMJVX current generator

becomes a short circuit and the equivalent circuit predicts:

dVD/dt = gMRLIG/[CGS + CX(1 + gMRL)]

This is the Miller effect so often referred to in older texts that

describe the behavior of grounded-cathode vacuum-tube

amplifier circuits. Allowing for the fact that 1 + gMRL is

approximately equal to gMRL and CX(1 + gMRL) is very

much larger than CGS, the expression for drain-voltage tail

time is:

t3(t5) = (VDK - VD(SAT))Cx/lG

State 4: MOS Saturated, JFET Saturated (Turn-Off)

In this state, in addition to gMJVX being shorted, the gMVG cur-

rent generator is shorted, and IG is occupied with charging CX

and CGS, in parallel, from the peak value of VG to VG(SAT). The

time required for this is:

t4 = (VG - VG(SAT))(CGS + Cx)/IG

Since a value for CGS may be measured independently of

switching time, the method described is the simplest way of

determining CX.

On turn-off, the state time equations are equally applicable,

but in reverse order (states 5 and 6); see the idealized wave-

form of Figure 4.

Experimental Verification

The four switching states just analyzed indicate that for a

given device, all four switching state times are inversely pro-

portional to the magnitude of the gate drive current. Figure 8

illustrates the switching performance of a typical power

MOSFET across three decades of gate drive current and

time. In each case the data slope is almost a perfect -1.

A New Device Characterization

Figure 8 could not be a reasonable device data sheet pre-

sentation because it does not give the designer any informa-

tion on a typical value for CX, nor does it convey how VDK,

gM, gM/gMJ, and VG(sat) vary with drain current. What would

be of enormous value to the designer is a plot of VD(t), VG(t)

for selected values of VDD and ID within device ratings.

A reasonable characterization would be as follows:

1. The x axis would be normalized in terms of gate current drive.

2. The y axis would be normalized in terms of percent maximum rated

BVDSS (0 to 100%).

3. RL = BVDSS/ID(max) would define the drain load resistance.

4. Four plots of VD(t), VG(t) at 100%, 75%, 50%, and 25% BVDSS(max)

would be shown.

FIGURE 8. CONSTANT GATE CURRENT SWITCHING TIME

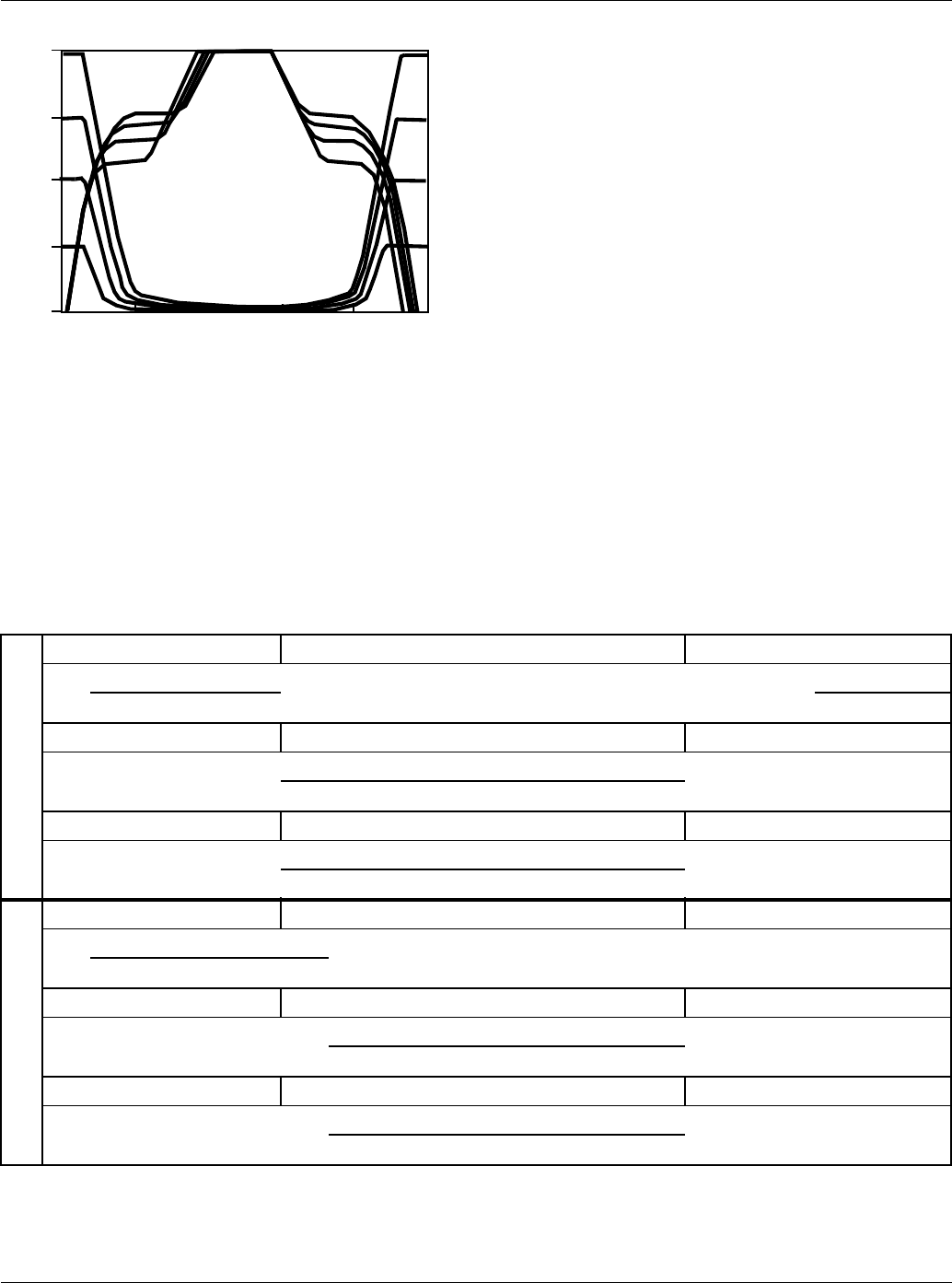
Figure 9 is such a plot for the RFM15N15 power MOSFET.

With such a plot, a designer can estimate device switching

performance under any resistive gate/drain conditions.

0.1

0.01 1 10 100 1000

RFM15N15

VDD = 75V

= 7.5A

= ∞ Ω

= 10V

(t) - MICROSECONDS

(IG) - MILLIAMPERES

DATA

tD(OFF)

tD(ON)

THEORY

Application Note 7502

FIGURE 9. NORMALIZED RFM15N15 SWITCHING WAVE-

FORMS FOR CANSTANT GATE-CURRENT DRIVE.

Step-Voltage Gate Drive

The majority of power MOSFET applications employ a step

gate-voltage input with a finite source resistance RO. Often

RO for turn-on is not the same as RO for turn-off. How can

switching times for these situations be estimated using the

switching characterization curves just described? The analy-

sis for resistive step voltage inputs, which is complex

because the gate current is no longer constrained to be con-

stant, but is a function of device gate-voltage response, is

covered in Appendix A. (A second, shorter appendix, B, has

been added to illustrate the estimation of RO for some practi-

cal gate drive circuits.) Table 1 summarizes the common

switching equations, and indicates the appropriate 1G to be

used in each state for relating step voltage drives to the char-

acterization curves.

Experimental Verification

Since the switching equations for step currents and voltages

differ only by gate-current magnitudes for the same device

type, one would expect a plot of switching time versus 1/RO

to be of the same form as those obtained for a step current

drive. This is exactly the case, as Figure 10 is merely a vari-

ation of Figure 8. Using the relationships of Table 1, the

observed differences between Figures 7 and 9 can be pin-

pointed. The two sets of experimental curves confirm that,

on the basis of the short-circuit drive current VG/RO equal-

ling the constant IG, tD(on), tR, tD(off), and tF will all be

longer, as predicted by the ratios of the gate drive currents of

Table 1. Notice also that tR, tF switching symmetry is dis-

rupted by the use of a step voltage with source resistance

RO. For states 2 and 6 the time ratio is:

100

20IT/IG40IT/IG60IT/IG80IT/IG

RFM15N15

IT = 1mA

VG = 10 VOLTS

RL = VDSS/ID(RMS)

% RATES VDSS

TIME - microseconds

TABLE 1. COMMON SWITCHING EQUATIONS

CONSTANT CURRENT STATE 1: MOS OFF, JFET OFF CONSTANT VOLTAGE

t = CISS VGS(TH) t = RO CISS In [1]

IG[1 - VGS(TH)/VG]

IG = ITSTATE 2: ACTIVE, ACTIVE IG = (VG - VGS(TH))/RO

t = [VDD - VDK] [CGS + Cx (1 + gM/gMJ)]

gMRLIG

IG = ITSTATE 3: ACTIVE, SATURATED IG = (VG - VG(SAT))/RO

t = (VDK - VD(SAT))CX

IG = ITSTATE 4: SATURATED, SATURATED IG = -VG/RO

t = (CGS + CX)(VG - VG(SAT))t = RO(CGS + CX) In (VG/VG(SAT))

IG = ITSTATE 5: ACTIVE, SATURATED IG = (VG - VG(SAT))/RO

t = (VDK - VD(SAT))CX

IG = ITSTATE 6: ACTIVE, ACTIVE IG = (VG - VG(SAT))/RO

t = [VDD - VDK] [CGS + CX (1 + gM/gMJ)]

gMRLIG

Application Note 7502

Experimental Verification

Since the switching equations for step currents and voltages

differ only by gate-current magnitudes for the same device

type, one would expect a plot of switching time versus 1/RO

to be of the same form as those obtained for a step current

drive. This is exactly the case, as Figure 10 is merely a vari-

ation of Figure 8. Using the relationships of Table 1, the

observed differences between Figures 7 and 9 can be pin-

pointed. The two sets of experimental curves confirm that,

on the basis of the short-circuit drive current VG/RO equal-

ling the constant IG, tD(on), tR, tD(off), and tF will all be

longer, as predicted by the ratios of the gate drive currents of

Table 1. Notice also that tR, tF switching symmetry is dis-

rupted by the use of a step voltage with source resistance

RO. For states 2 and 6 the time ratio is:

For states 3 and 5 the time ratio is:

Utilization of available maximum gate drive voltage and cur-

rent can be optimized for fastest power MOSFET switching

speed through the use of constant-current gate drive at the

expense of increased gate-drive circuit complexity.

FIGURE 10. CONSTANT GATE VOLTAGE SWITCHING TIME

Using the Characterization Curve,

Figure 9

To estimate the switching times for an RFM15N15 power

MOSFET under the conditions VG = 10V, VDD = 75V, RO =

100 ohms, and RL = 10 ohms, precedes as follows:

State 1: MOS Off, JFET Off

This time can be estimated without recourse to the curves

State 2 & 6: MOS Active, JFET Active

State 3: MOS Active, JFET Saturated

State 4: MOS Saturated, JFET Saturated

State 5: MOS Active, JFET Saturated

Figure 11 shows RFM15N15 waveforms using the conditions

specified in the example.

FIGURE 11. STEP GATE VOLTAGE INPUT TO AN RFM15N15

tTURN-ON =VG(SAT)

tTURN-OFF VG - VGS(TH)

tTURN-ON =VG(SAT)

tTURN-OFF VG - VG(SAT)

0.1

0.01

10-4 10-3 10-2 10-1

DATA

tD(OFF)

tD(ON)

(t) - MICROSECONDS

THEORY

1/RO

RFM15N15

VDD = 75V

= 7.5A

= 10V

t = 100(1200 x 10-12) ln [1/(1 - 4/10)]

t = 61 ns

IG = (10 - 4)/100 = 60mA

t = (curve divisions) x IT µs=9= 150ns

60 60

IG = (10 - 7)/100 = 30mA

t = (curve divisions) x IT µs=14 = 467ns

30 30

CGS + Cx= (gate voltage slope)(test current)

= (1.5 x 10-6s/5 volts)(10mA)

= 3000pF

t = 100(3000 x 10-12) ln [10/6.6]

t = 125ns

IG = 6.6/100 = 66mA

t = (curve divisions) x IT µs=8= 121ns

66 66

STATE CALCULATED

TIME MEASURED

TIME RATIO

(tC, ns) (tM, ns) (tC/tM)

161 60 1.02

2 + 3 617 670 0.92

4125 137 0.91

5 + 6 271 375 0.72

TIME - MICROSECONDS

DRAIN VOLTAGE - VOLTS

RFM15N15

VDD = 75 VOLTS

RL = 10 OHMS

VG = 10 VOLTS

RO = 100 OHMS

VGS

01.53

Application Note 7502

For peak gate voltages other than 10 volts, and load resis-

tances other than BVDSS/ID(MAX), the equations of Table 1

may be used in conjunction with slope estimates from the

characterization curves for CX and CGS + CX(1 + gM/gMJ) at

the appropriate drain-current level.

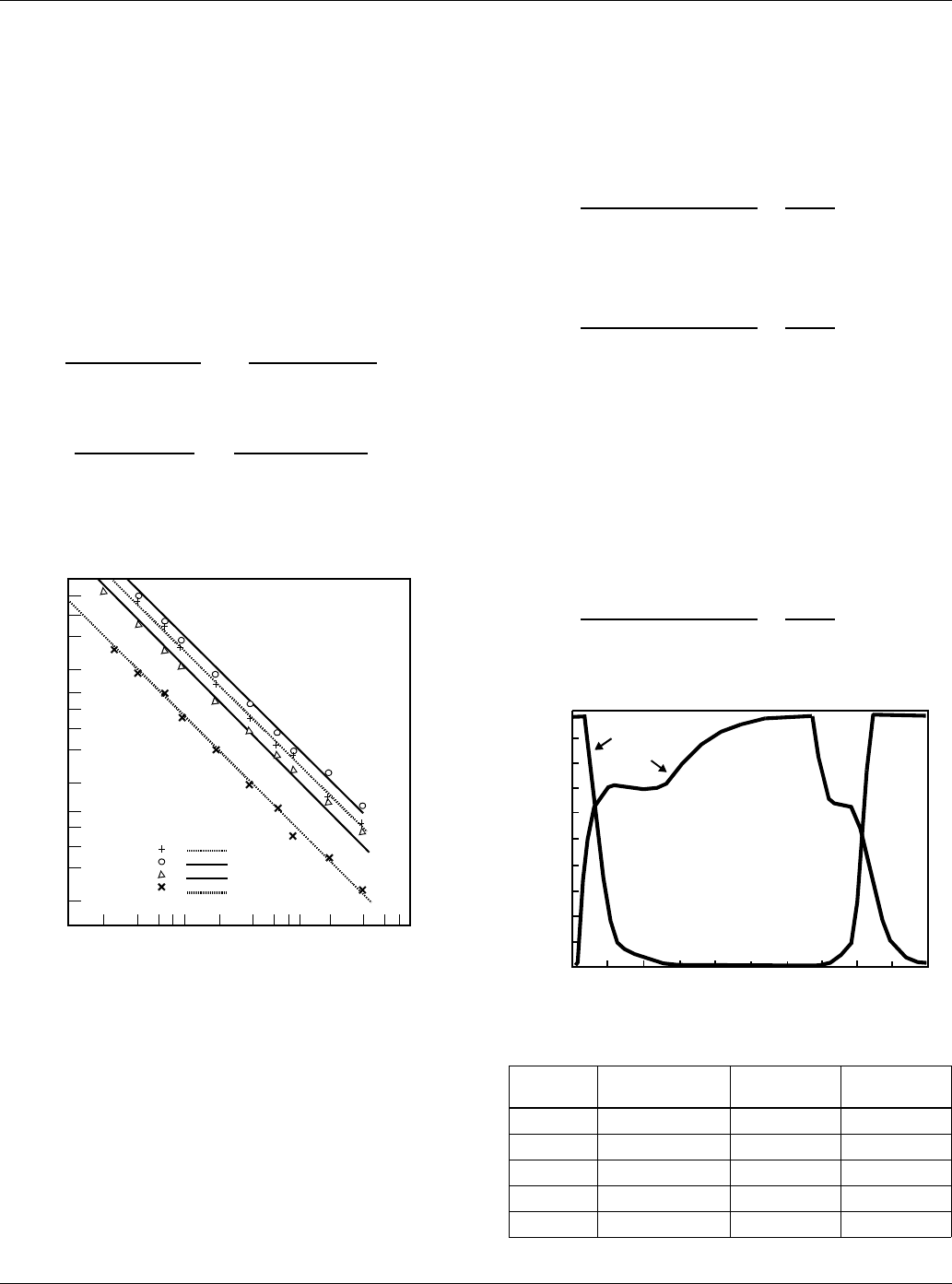
Characterization-Curve Limits

The switching-time range over which the characterization can be

applied is very impressive. For gate currents of the order of

microamperes, device dissipation is the limiting factor. For gate

currents of the order of amperes, the device response will be

slowed by gate propagation delay. This delay, of course,

degrades the linear switching relationship to gate current. How-

ever, as Figure 12 graphically shows, the characterization is valid

across five decades of gate current and switching time, allowing

all but a very few switching applications to be described by the

characterization curves of Figure 9.

FIGURE 12. FIVE DECADES OF LINEAR RESPONSE

Conclusions

The viability of the proposed characterization curves using con-

stant current has been demonstrated and the limits of applica-

tion defined. The existence of a vertical JFET in a power

MOSFET makes data-sheet capacitances of little use for esti-

mating switching times. The classical method of defining

switching time by 10% and 90% is a poor representation for

power MOSFETs because of the dual-slope nature of the drain

waveforms. Switching influences are masked because the 10%

level is controlled by one mechanism and the 90% level by

another. Device comparisons based on the classical switching

definition can be very misleading.

Appendix A - Analysis for Resistive Step

Voltage Inputs

Step Voltage Gate Drive

To obtain the necessary relationships, six device switching

states must be examined using the same device equivalent

circuit as was used for the constant-gate-current case, but

with the forcing function replaced wIth a step voltage with

internal resistance RO, Figure A-1.

FIGURE A-1. POWER MOSFET EQUIVALENT CIRCUIT

State 1: Mos Off, JFET Off

As before, both current generators are open circuits, reducing

the equivalent circuit to simply charging CISS through RO.

State 2: Mos Active, JFET Active

Before proceeding, it is wise to examine an actual device

response and make use of available simplifications. Figure A-2

shows iG(t) and iD(t) for a typical power MOSFET driven by a

step gate voltage. For truly resistive switching, realize that these

waveforms are only mirror images of their voltage counterparts

vG(t) and vD(t). Using Figure A-2, applicable gate currents for

each of the device states may be listed.

FIGURE A-2. iG(t) AND iD(t) FOR A TYPICAL POWER MOSFET

DRIVEN BY A STEP GATE VOLTAGE

104

102

100

10-2

100102104

RFM15N15

tD(OFF)

tD(ON)

GATE CURRENT (IG) - MICROAMPERES

TIME(t) - MICROSECONDS

103

101

10-1

101103105106

LEGEND

VGS - Gate Voltage CDS - Drain Source Capacitance

VX- JFET Driving Voltage gM- MOSFET Transconductance

VD- Drain Voltage gMJ - JFET Transconductance

CGS - Gate Source

Capacitance

RL- Drain Load Resistance

CX- MOSFET Feedback

Capacitance

IG- Constant Current Amplitude

t = ROCISSIn(1/(1 - VGS(TH)/VG)]

GATE

CDS

SOURCE

DRAIN

VGS

gMJ VX

CGS gM VG

IPK1

IPK2

IPK3

IPK4 IPK5

IPK6

CURRENT

TIME

iD(t)

iG(t)

Application Note 7502

Turn-On

State 1: MOS Off, JFET Off

IPK1 = VG/RO

State 2: MOS Active, JFET Active

IPK2 = (VG - VGS(TH))/RO

State 3: MOS Active, JFET Saturated

IPK3 = (VG - VG(SAT))/RO

Turn-Off

State 4: MOS Saturated, JFET Saturated

IPK4 = VG/RO

State 5: MOS Active, JFET Saturated

IPK5 = VG(SAT)/RO

State 6: MOS Active, JFET Active

IPK6 = VG(SAT)/RO

The equivalent circuit of Figure A-1 predicts that:

dVD/dt = (-gMRL(VG - VGS(TH))e-t/T1) /T1

where T1 = ROCGS + (1 + gM/gMJ)ROCX

Note that gMRL(VG - VGS(TH)) is usually an order of magnitude

greater than VDD, indicating that the drain voltage is discharg-

ing toward a very large negative value. The device operation,

then, is on the early, almost linear, portion of the exponential,

where e-t/T1 approximates unity. The drain current of Figure A-

2, and hence the drain voltage, does indeed exhibit a linear

decrease with time.

Thus, for state 2:

where IPK2 = (VG - VGS(TH))/RO

State 3: Mos Active, JFET Saturated

Because of the Miller effect, the gate voltage and, hence, the

gate current, is almost constant during the tail time. The

equivalent circuit then predicts:

State 4: Mos Saturated, JFET Saturated (Turn-off)

Both equivalent-circuit generators are short circuits, and the

gate drive is discharging CX in parallel with CGS through RO.

t = RO(CGS + CX) ln[VG/VG(SAT)]

IPK4 = VG/RO

State 5: Mos Active, JFET Saturated

The JFET current generator VxgmJ, is operative.

IPK5 = VG(SAT)/RO

State 6: Mos Active, JFET Active

The Miller effect is now reduced by the activation of VGgMJ,

and the equivalent circuit predicts:

IPAK6 = VG(SAT)/RO

Appendix B - Estimating RO for Some

Typical Gate-Drive Circuits

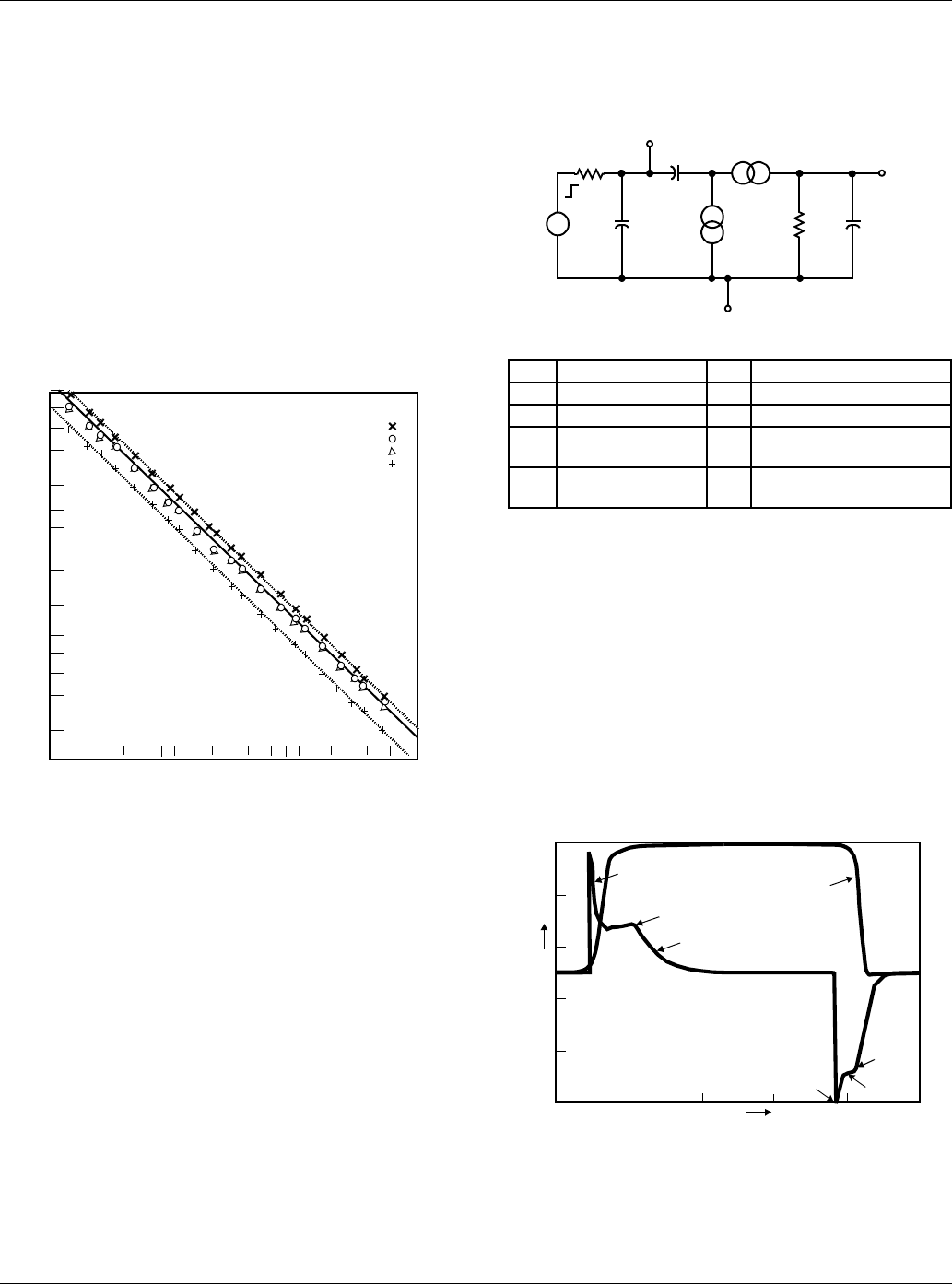
Case 1: Typical Pulse-Generator Drive, Figure B-1

FIGURE B-1. TYPICAL PULSE-GENERATOR DRIVE CIRCUIT

Turn-On and Turn-Off

RO = RGENRGS/(RGEN + RGS)

For the typical case where RGEN = 50Ω, and a coaxial-cable

termination of 50 ohms, RO = 25Ω and VG = VGEN/2.

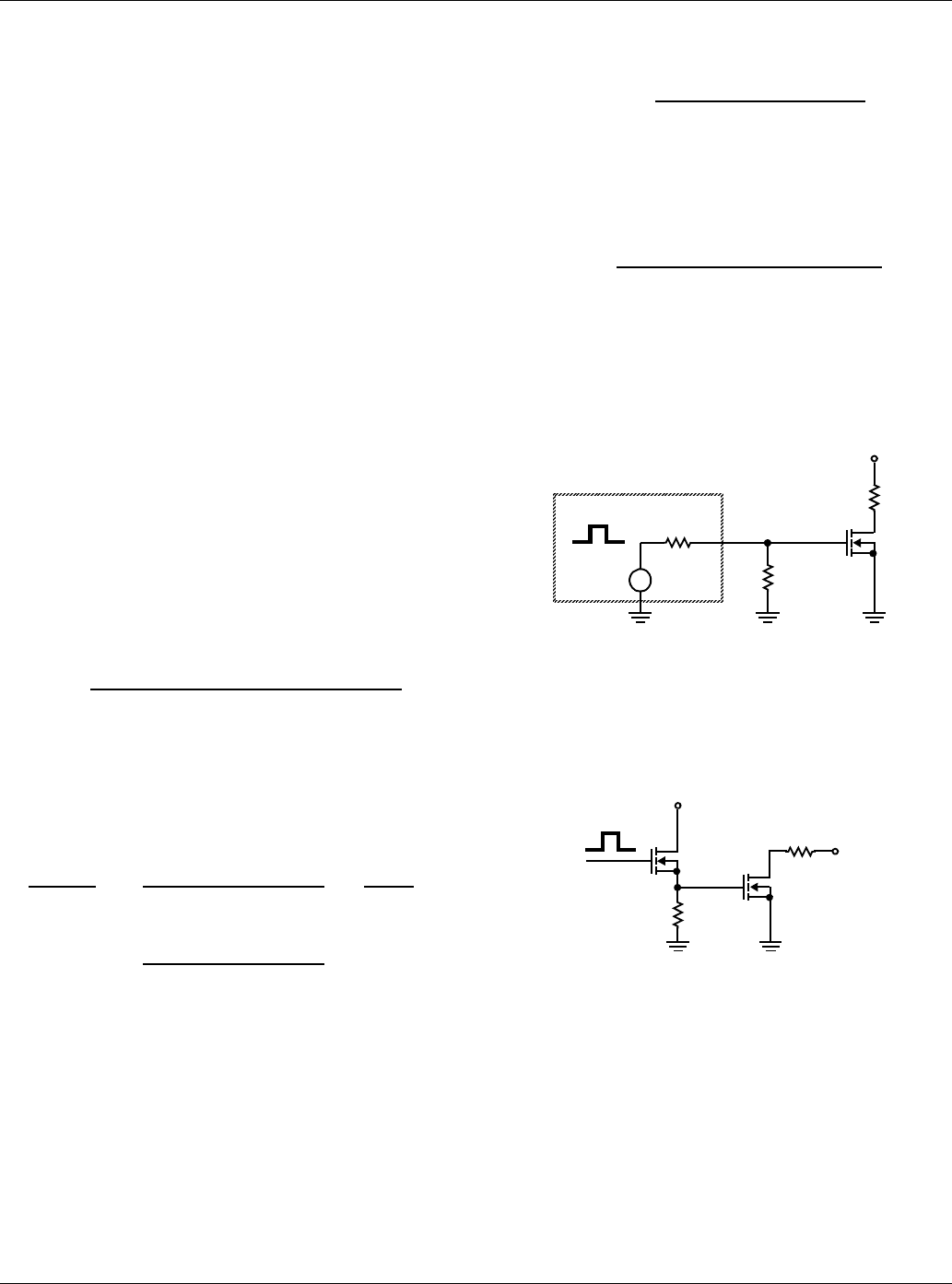
Case 2: Voltage-Follower Gate Drive, Figure B-2

FIGURE B-2. VOLTAGE-FOLLOWER GATE-DRIVE CIRCUIT

Turn-On

RO is approximately equal to 1/gM for RS very much

greater than 1/gM.

gm = transconductance of driving MOSFET transistor.

Turn Off

RO = RS

t = [VDD - VDK][CGS + CX(1 + gM/gMJ)]

gMRL IPK2

dVD=gMRLlG=lG

dt CGS + (1 + gMRL)CXCX

lG = IPK3 = (VG - VG(SAT))/RO

and t = (VDK - VD[SAT])Cx

IPK3

t = [VDK - VD[SAT])CX

IPK5

t = [VDD - VDK][CGS + CX(1 + gM/gMJ)]

gMRL IPAK6

VGEN RGEN VG

VDD

RGS

VDD

Application Note 7502

Case 3 :Common-Source Gate Drive, Figure B-3

FIGURE B-3. COMMON-SOURCE GATE-DRIVE CIRCUIT

Turn-On

RO = RD

(drain-to-ground capacitance of driving device adds to

CGS of driven MOSFET.)

Turn Off

RO = rDS(ON) of driving MOSFET when

RD is very much greater than RDS(ON)

RDVDD

10V

Application Note 7502

DISCLAIMER

FAIRCHILD SEMICONDUCTOR RESERVES THE RIGHT TO MAKE CHANGES WITHOUT FURTHER

NOTICE TO ANY PRODUCTS HEREIN TO IMPROVE RELIABILITY, FUNCTION OR DESIGN. FAIRCHILD

DOES NOT ASSUME ANY LIABILITY ARISING OUT OF THE APPLICATION OR USE OF ANY PRODUCT

OR CIRCUIT DESCRIBED HEREIN; NEITHER DOES IT CONVEY ANY LICENSE UNDER ITS PATENT

RIGHTS, NOR THE RIGHTS OF OTHERS.

TRADEMARKS

The following are registered and unregistered trademarks Fairchild Semiconductor owns or is authorized to use and is

not intended to be an exhaustive list of all such trademarks.

LIFE SUPPORT POLICY

FAIRCHILDS PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT

DEVICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF FAIRCHILD SEMICONDUCTOR CORPORATION.

As used herein:

1. Life support devices or systems are devices or

systems which, (a) are intended for surgical implant into

the body, or (b) support or sustain life, or (c) whose

failure to perform when properly used in accordance

with instructions for use provided in the labeling, can be

reasonably expected to result in significant injury to the

user.

2. A critical component is any component of a life

support device or system whose failure to perform can

be reasonably expected to cause the failure of the life

support device or system, or to affect its safety or

effectiveness.

PRODUCT STATUS DEFINITIONS

Definition of Terms

Datasheet Identification Product Status Definition

Advance Information

Preliminary

No Identification Needed

Obsolete

This datasheet contains the design specifications for

product development. Specifications may change in

any manner without notice.

This datasheet contains preliminary data, and

supplementary data will be published at a later date.

Fairchild Semiconductor reserves the right to make

changes at any time without notice in order to improve

design.

This datasheet contains final specifications. Fairchild

Semiconductor reserves the right to make changes at

any time without notice in order to improve design.

This datasheet contains specifications on a product

that has been discontinued by Fairchild semiconductor.

The datasheet is printed for reference information only.

Formative or

In Design

First Production

Full Production

Not In Production

MICROWIRE

OPTOLOGIC

OPTOPLANAR

PACMAN

POP

Power247

PowerTrench

QFET

QS

QT Optoelectronics

Quiet Series

FAST

FASTr

FRFET

GlobalOptoisolator

GTO

HiSeC

I2C

ISOPLANAR

LittleFET

MicroFET

MicroPak

Rev. H5

ACEx

Bottomless

CoolFET

CROSSVOLT

DenseTrench

DOME

EcoSPARK

E2CMOSTM

EnSignaTM

FACT

FACT Quiet Series

SILENT SWITCHER

SMART START

SPM

STAR*POWER

Stealth

SuperSOT-3

SuperSOT-6

SuperSOT-8

SyncFET

TinyLogic

TruTranslation

ââ

STAR*POWER is used under license

UHC

UltraFET

VCX

Fairchild Semiconductor An 7502 Users Manual Power MOSFET Switching Waveforms

AN-7502 to the manual 261076ed-a383-4dbc-8c1a-dcfb2b7f8b35

Navigation menu

Versions of this User Manual:

Views

Navigation