JBL TI Nspire CAS Referanseguide (Norsk) Reference Guide NO
User Manual: JBL TI-Nspire CAS Referanseguide (Norsk) TI-Nspire™ CAS Reference Guide
Open the PDF directly: View PDF ![]() .
.
Page Count: 265 [warning: Documents this large are best viewed by clicking the View PDF Link!]

2
Viktig Informasjon
Dersom ikke annet er uttrykkelig nevnt i Lisensen som finnes vedlagt programmet, gir ikke
Texas Instruments noen garanti, verken uttrykt eller underforstått, herunder, men ikke
begrenset til noen impliserte garantier for salgbarhet og egnethet for et bestemt formål, med
hensyn tilnoen som helst programmer eller bokmaterialer som kun er tilgjengelig på et ”som
det er”-grunnlag. Ikke i noen tilfeller kan Texas Instruments bli holdt ansvarlig overfor noen
for spesielle, indirekte, tilfeldige eller følgeskader i forbindelse med eller som et resultat av
anskaffelsen eller bruken av disse materialene. Texas Instruments’ eneste og eksklusive
ansvar, uten hensyn til aksjonsformen, kan ikke overstige den summen som er blitt fremsatt i
lisensen for programmet. I tillegg kan ikke Texas Instruments bli holdt ansvarlig for noen krav
av noe slag mot bruken av disse materialene av en annen part.
Lisens
Se fullstendig lisens installert i C:\ProgramFiles\TIEducation\<TI-Nspire™ Product
Name>\license.
© 2006 - 2014 Texas Instruments Incorporated

Innhold
Viktig Informasjon 2
Innhold 3
Uttrykkssjabloner 5
Alfabetisk oversikt 12
A 12
B 21
C 24
D 47
E 58
F 66
G 75
I 80
L 88
M 103
N 110
O 119
P 121
Q 129
R 132
S 145
T 168
U 182
V 182
W 184
X 185
Z 186
Symboler 193
Tomme (åpne) elementer 217
Snarveier/hurtigtaster for å legge inn matematiske uttrykk 219
EOS™ (Ligningsoperativsystem)-hierarkiet 221
3

Uttrykkssjabloner
Med uttrykkssjablonene er det enkelt å skrive inn uttrykk i standardisert, matematisk
fremstilling. Når du setter inn en sjablon, kommer den tilsyne på kommandolinjen med små
blokker i posisjoner der du kan legge inn elementer. En markør viser hvilke elementer du kan
sette inn.
Bruk pilknappene eller trykk på efor å bevege markøren til hvert elements posisjon, og
skrivinn en verdieller et uttrykkfor elementet. Trykk på ·eller /· for å behandle
uttrykket.
Brøk-sjablon /p taster
Merk: Se også / (divider), side 195.
Eksempel:
Eksponent-sjablon ltast
Merk: Skriv inn den første verdien, trykk på log
skriv så inn eksponenten. For å flytte markøren
tilbake til grunnlinjen, trykk på høyre pil (¢).
Merk: Se også ^ (potens), side 196.
Eksempel:
Kvadratrot-sjablon /q taster
Merk: Se også ‡() (kvadratrot), side 205.
Eksempel:
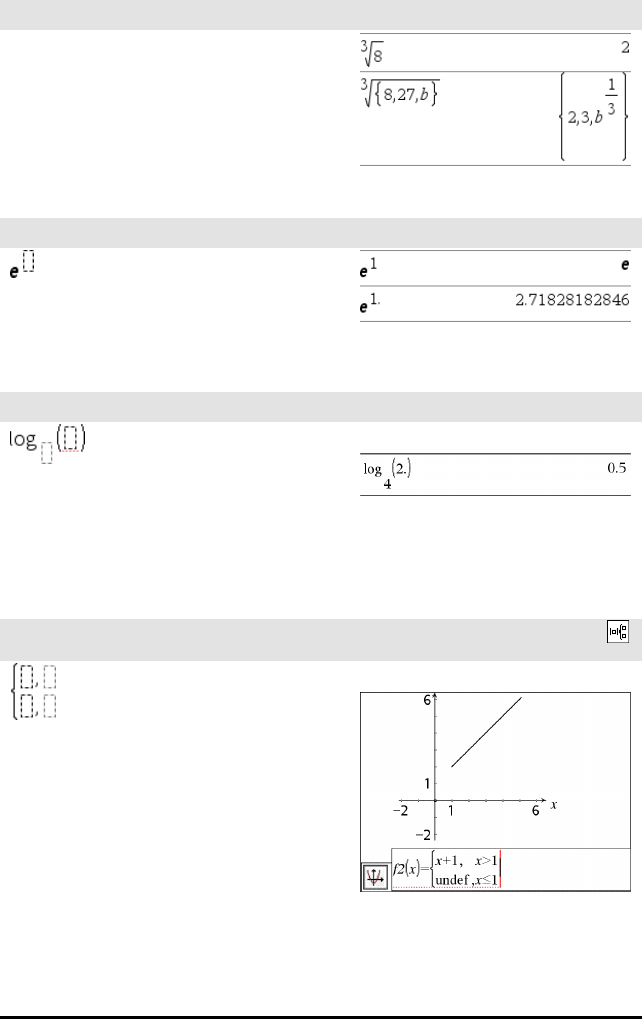
N-te rot-sjablon /l taster
Merk: Se også rot(), side 142.
Eksempel:
Uttrykkssjabloner 5
6 Uttrykkssjabloner
N-te rot-sjablon /l taster
eeksponent-sjablon utast
Naturlig grunntall eopphøyd i en eksponent
Merk: Se også e^(), side 58.
Logaritme-sjablon /s taster
Beregner logaritme til et spesifisert grunntall. Hvis
grunntallet er forhåndsinnstilt på 10, utelates
grunntallet.
Merk: Se også log(), side 98.
Eksempel:
Stykkevis sjablon (2-delers) Katalog >
Lar deg opprette uttrykk og betingelser for en
to-delers stykkevis definert funksjon. For å legge til
en del, klikk på sjablonen og gjenta sjablonen.
Merk: Se også stykkevis(), side 122.
Eksempel:
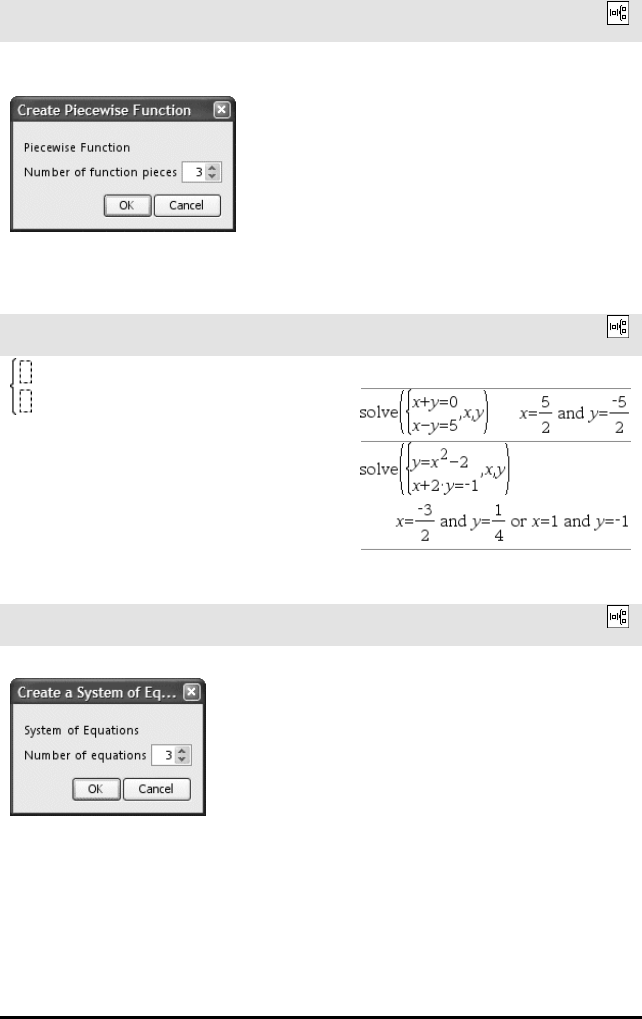
Stykkevis sjablon (N-delers) Katalog >
Lar deg opprette uttrykk og betingelser for en N--delers stykkevis
definert funksjon. Ber om N.
Merk: Se også stykkevis(), side 122.
Eksempel:
Se eksemplet for Stykkevis sjablon (2-
delers).
Sjablon for ligningssystemer med 2 ukjente Katalog >
Oppretter et system av to ligninger. For å legge en rad
til et eksisterende system, klikk inn sjablonen og
gjenta sjablonen.
Merk: Se også system(), side 167.
Eksempel:
Sjablon for ligningssystemer med N ukjente Katalog >
Lar deg opprette et system av Nligninger. Ber om N.
Merk: Se også system(), side 167.
Eksempel:
Se eksemplet for Sjabloner for
ligningssystemer (2 ligninger).
Uttrykkssjabloner 7

8 Uttrykkssjabloner
Sjablon for absoluttverdi Katalog >
Merk: Se også abs(), side 12.
Eksempel:
gg°mm’ss.ss’’ sjablon Katalog >
Lar deg sette inn vinkler i gg°mm’ss.ss’’ -format, der
gg er antallet desimale grader, mm er antallet minutter
og ss.ss er antallet sekunder.
Eksempel:
Matrise-sjablon (2 x 2) Katalog >
Oppretter en 2 x 2-matrise.
Eksempel:
Matrise-sjablon (1 x 2) Katalog >
.
Eksempel:
Matrise-sjablon (2 x 1) Katalog >
Eksempel:
Matrise-sjablon (m x n) Katalog >
Sjablonen kommer til syne etter at du er blitt bedt om
å spesifisere antallet rader og kolonner.
Eksempel:
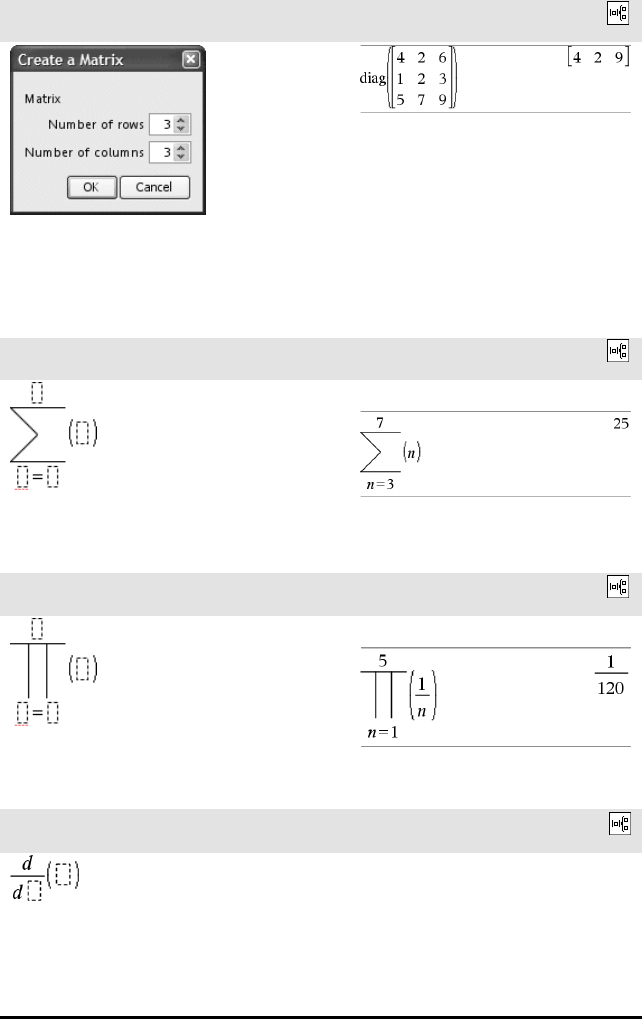
Matrise-sjablon (m x n) Katalog >
Merk: Hvis du oppretter en matrise med et stort antall
rader og kolonner, må du muligens vente en liten
stund før den vises på skjermen.
Sum-sjablon (G)Katalog >
Merk: Se også G() (sumSeq), side 206.
Eksempel:
Produkt-sjablon (Π)Katalog >
Merk: Se også Π() (prodSeq), side 205.
Eksempel:
Første derivert-sjablon Katalog>
Den første deriverte sjablonen kan også brukes for å
beregne førstederiverte i et punkt.
Eksempel:
Uttrykkssjabloner 9

10 Uttrykkssjabloner
Første derivert-sjablon Katalog>
Merk: Se også d() (derivert), side 203.
Andre derivert-sjablon Katalog>
Den andre deriverte sjablonen kan også brukes for å
beregne andrederiverte i et punkt.
Merk: Se også d() (derivert), side 203.
Eksempel:
N-te derivert-sjablon Katalog >
Merk: Se også d() (derivert), side 203.
Eksempel:
Bestemt integral-sjablon Katalog >
Merk: Se også‰() integral(), side 193.
Eksempel:
ubestemt integral-sjablon Katalog >
Eksempel:
12 Alfabetisk oversikt
Alfabetisk oversikt
Elementer med navn som ikke er alfabetiske (som f.eks. +, !, og >) er opplistet på slutten av
dette avsnittet (side 193). Hvis ikke annet er spesifisert, er alle eksemplene idette avsnittet
utført i grunninnstilling-modus, og det antas at ingen av variablene er definert.
A
abs() Katalog >
abs(Uttr1)⇒uttrykk
abs(Liste1)⇒liste
abs(Matrise1)⇒matrise
Returnerer argumentets absoluttverdi.
Merk: Se også Absoluttverdi-sjablon, side 8.
Hvis argumentet er et komplekst tall, returneres
absoluttverdien (modulus).
Merk: Alle ubestemte variabler behandles som reelle
variabler.
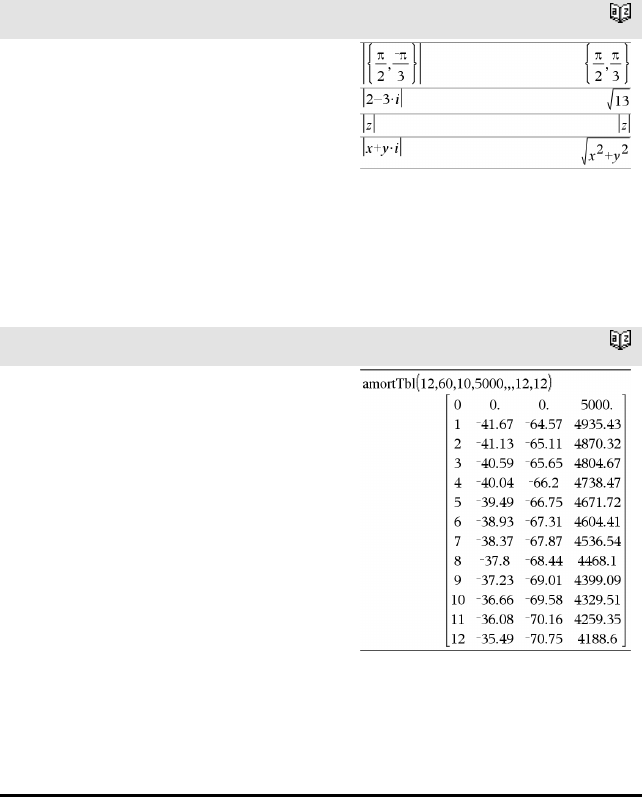
amortTbl() Katalog >
amortTbl(NPmt,N,I,PV,[Pmt],[FV],[PpY],[CpY],
[PmtAt],[avrundVerdi])⇒matrise
Amortiseringsfunksjon som returnerer en matrise
som en amortiseringstabell for et sett med TVM-
argumenter.
NPmt er antallet betalinger som skal inkluderes i
tabellen. Tabellen starter med den første betalingen.
N,I,PV,Pmt,FV,PpY,CpY og PmtAt er beskrevet i
tabellen med TVM-argumenter, side 179.
• Hvis du utelater Pmt, grunninnstilles den til
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Hvis du utelater FV, grunninnstilles den til
FV=0.
• Grunninnstillingene for PpY,CpY og PmtAt er de
samme som for TVM-funksjonene.
avrundVerdi spesifiserer antallet desimalplasser for
amortTbl() Katalog >
avrunding. Grunninnstilling=2.
Kolonnene i resultatmatrisen er i denne rekkefølgen:
Betalingsnummer, betalt rentebeløp, betalt
hovedbeløp og balanse.
Balansen som vises i rad ner balansen etter betaling
n.
Du kan bruke resultatmatrisen som inndata for de
andre amortiseringsfunksjonene GInt() og GPrn(), side
206, og bal(), side 21.
and Katalog >
BoolskUttr1 and BoolskUttr2 ⇒Boolsk uttrykk
Boolsk liste1 and Boolsk liste2⇒Boolsk liste
Boolsk matrise1 and Boolsk matrise2⇒Boolsk
matrise
Returnerer sann eller usann eller en forenklet form av
opprinnelig uttrykk.
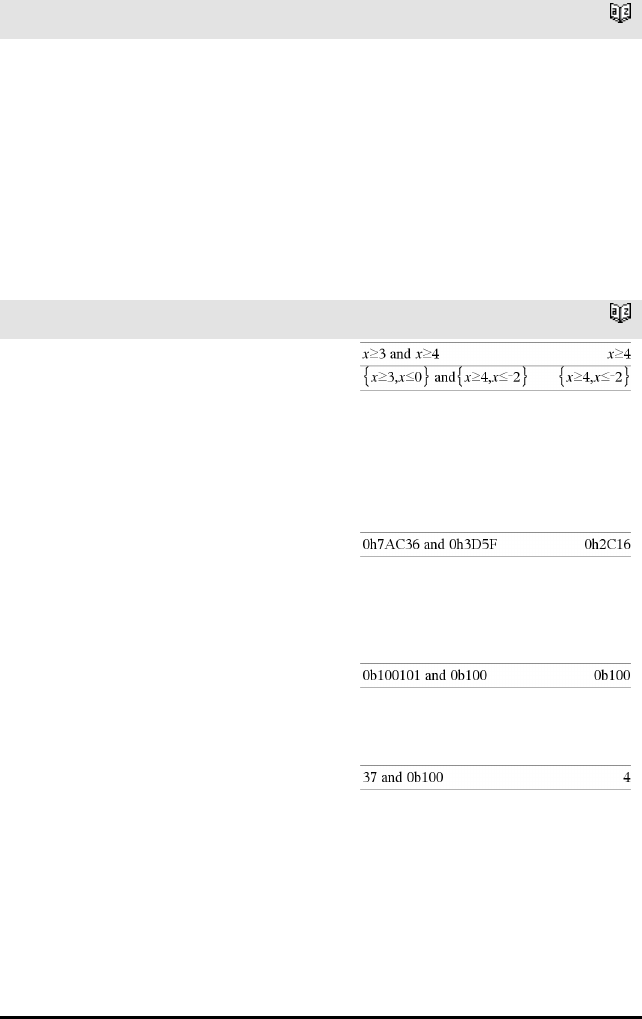
Heltall1andHeltall2⇒heltall
Sammenlikner to reelle heltall bit-for-bit med en and-
handling. Internt er begge heltallene omregnet til 64-
biters binære tall med fortegn. Når tilsvarende biter
sammenliknes, er resultatet 1 hvis en av bitene er 1;
ellers er resultatet 0. Den returnerte verdien
representerer bit-resultatene og vises i
grunntallmodus.
Du kan skrive inn heltallene med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten slik prefiks blir heltall behandlet som
desimalt (grunntall10).
Hvis du skriver inn et desimalt heltall som er for stort
for en 64-biters binær form med fortegn, brukes en
symmetrisk modul-handling for å sette verdien inn i
gyldig område.
I heksades grunntall-modus:
Viktig: Null, ikke bokstaven O.
I binær grunntall-modus:
I desimalt grunntall-modus:
Merk: Et binært innlegg kan bestå av opptil 64 siffer (i
tillegg til prefikset 0b). Et heksadesimalt innlegg kan
bestå av opptil 16 siffer.
Alfabetisk oversikt 13
14 Alfabetisk oversikt
angle() vinkel Katalog >
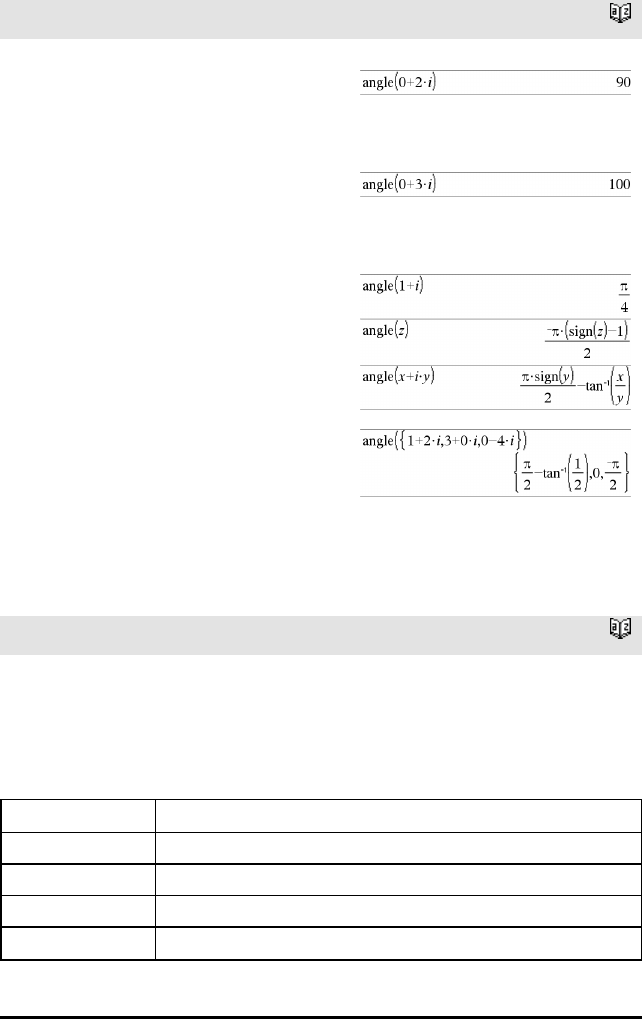
angle(Uttr1)⇒uttrykk
Returnerer vinkelen til argumentet, tolker argumentet
som et komplekst tall.
Merk: Alle ubestemte variabler behandles som reelle
variabler.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
angle(Liste1)⇒liste
angle(Matrise1)⇒matrise
Returnerer en liste eller vinkelmatrise av elementene i
Liste1 eller Matrise1, tolker hvert element som et
komplekst tall som representerer et to-dimensjonalt,
rektangulært koordinatpunkt.
ANOVA Katalog >
ANOVA Liste1,Liste2[,Liste3,...,Liste20][,Merke]
Utfører en enveis analyse av varians for å sammenlikne
gjennomsnitt for mellom 2 og 20 populasjoner. En oversikt over
resultatene lagres i stat.results-variabelen (side 162).
Merke=0 for Data, Merke=1 for Stats
Utdata-variabel Beskrivelse
stat.FVerdi av F-statistikken
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader frihet for gruppene
stat.SS Sum av kvadrater for gruppene

Utdata-variabel Beskrivelse
stat.MS Gjennomsnitt av kvadrater for gruppene
stat.dfError Grader av frihet for feilene
stat.SSError Sum av kvadrater av feilene
stat.MSError Gjennomsnitt av kvadrater av feilene (gjennomsnittlig kvadratavvik)
stat.sp Felles standardavvik
stat.xbarliste Gjennomsnitt av listenes inndata
stat.CLowerList 95% konfidensintervaller for gjennomsnittet av hver inndata-liste
stat.UpperList 95% konfidensintervaller for gjennomsnittet av hver inndata-liste
ANOVA2way Katalog >
ANOVA2way Liste1,Liste2[,…[,Liste10]][,LevRad]
Beregner en toveis analyse av varians for å sammenlikne
gjennomsnitt for mellom 2 og 10 populasjoner. En oversikt over
resultatene lagres i stat.results-variabelen (side 162).
LevRad=0 for Blokk
LevRad=2,3,...,Len-1, for To Faktor, hvor Len=lengde(Liste1)
=lengde(Liste2) = … = lengde(Liste10) og Len/LevRad ∈ {2,3,…}
Utdata: Blokk-oppsett
Utdata-variabel Beskrivelse
stat.F F-statistikk over kolonnefaktoren
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader frihet for kolonnefaktoren
stat.SS Sum av kvadrat for kolonnefaktoren
stat.MS Gjennomsnitt av kvadrater for kolonnefaktor
stat.FBlock F-statistikk for faktor
stat.PValBlock Minste sannsynlighet som null-hypotesen kan forkastes ved
stat.dfBlockstat.dfBlock Grader frihet for faktor
stat.SSBlock Sum av kvadrater for faktor
stat.MSBlock Gjennomsnitt av kvadrater for faktor
stat.dfError Grader av frihet for feilene
Alfabetisk oversikt 15

16 Alfabetisk oversikt
Utdata-variabel Beskrivelse
stat.SSError Sum av kvadrater av feilene
stat.MSError Gjennomsnitt av kvadrater av feilene (gjennomsnittlig kvadratavvik)
stat.s Standardavvik for feilen
KOLONNEFAKTOR Utdata
Utdata-variabel Beskrivelse
stat.Fcol F-statistikk over kolonnefaktoren
stat.PValCol Kolonnefaktorens sannsynlighetsverdi
stat.dfCol Grader frihet for kolonnefaktoren
stat.SSCol Sum av kvadrater av kolonnefaktoren
stat.MSCol Gjennomsnitt av kvadrater for kolonnefaktor
RADFAKTOR Utdata
Utdata-variabel Beskrivelse
stat.Frow F-statistikk over kolonnefaktoren
stat.PValRow Kolonnefaktorens sannsynlighetsverdi
stat.dfRow Grader frihet for radfaktoren
stat.SSRow Sum av kvadrater for radfaktoren
stat.MSRow Gjennomsnitt av kvadrater for radfaktor
INTERAKSJON Utdata
Utdata-variabel Beskrivelse
stat.FInteract F-statistikk over interaksjonen
stat.PValInteract Interaksjonens sannsynlighetsverdi
stat.dfInteract Grader av frihet for interaksjonen
stat.SSInteract Sum av kvadrater for interaksjonen
stat.MSInteract Gjennomsnitt av kvadrater for interaksjon
FEIL Utdata
Utdata-variabel Beskrivelse
stat.dfError Grader av frihet for feilene
stat.SSError Sum av kvadrater av feilene

Utdata-variabel Beskrivelse
stat.MSError Gjennomsnitt av kvadrater av feilene (gjennomsnittlig kvadratavvik)
s Standardavvik for feilen
Ans (svar) /v taster
Ans⇒verdi
Returnerer resultatet av det sist behandlede
uttrykket.
approx() (tilnærm) Katalog >
approx(Uttr1)⇒uttrykk
Returnerer behandlingen av argumentet som et
uttrykk med desimalverdier, hvis mulig, uavhengig av
om modus er Auto eller Tilnærmet.
Dette er det samme som å skrive inn argumentet og
trykke på /·.
approx(Liste1)⇒liste
approx(Matrise1)⇒matrise
Returnerer en liste eller matrise hvor hvert element er
blitt behandlet til en desimalverdi, hvis mulig.
4approxFraction() Katalog >
Uttr 4approxFraction([Tol])⇒uttrykk
Liste 4approxFraction([Tol])⇒liste
Matrise 4approxFraction([Tol])⇒matrise
Returnerer argumentet som en brøk med en toleranse
på Tol. Hvis tol utelates, brukes en toleranse på 5.E-
14.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive
@>approxFraction(...).
Alfabetisk oversikt 17

18 Alfabetisk oversikt
approxRational() Katalog >
approxRational(Uttr[,Tol])⇒uttrykk
approxRational(Liste[,Tol])⇒liste
approxRational(Matrise[,Tol])⇒matrise
Returnerer argumentet som en brøk med en toleranse
på Tol. Hvis Tol utelates, brukes en toleranse på 5.E-
14.
arccos() Se cos/(), side 34.
arccosh() Se cosh/(), side 36.
arccot() Se cot/(), side 36.
arccoth() Se coth/(), side 37.
arccsc() Se csc/(), side 40.
arccsch() Se csch/(), side 41.
arcLen() (bueLen) Katalog >
arcLen(Uttr1,Var,Start,Slutt)⇒uttrykk
Returnerer buelengden for Uttr1 fra Start til Slutt med
hensyn på variabel Var.
Buelengden beregnes som et integral av et uttrykk
definert i funksjonsmodus.

arcLen() (bueLen) Katalog >
arcLen(Liste1,Var,Start,End)⇒liste
Returnerer en liste over buelengdene til hvert element
iListe1 fra Start til Slutt med hensyn til Var.
arcsec() Se sec/(), side 145.
arcsech() Se sech/(), side 146.
arcsin() Se sin/(), side 155.
arcsinh() Se sinh/(), side 156.
arctan() Se tan/(), side 169.
arctanh() Se tanh/(), side 170.
() (utvid/sett sammen) Katalog >
augment(Liste1, Liste2)⇒liste
Returnerer en ny liste som er Liste2 lagt til på slutten
av Liste1.
Alfabetisk oversikt 19

20 Alfabetisk oversikt
() (utvid/sett sammen) Katalog >
augment(Matrise1,Matrise2)⇒matrise
Returnerer en ny matrise som er Matrise2 lagt til på
Matrise1. Når tegnet “,” brukes, må matrisen ha like
raddimensjoner, og Matrise2 er lagt til på Matrise1
som nye kolonner. Endrer ikke Matrise1 eller
Matrise2.
avgRC() (gjsnEH) Katalog >
avgRC(Uttr1,Var [=Verdi] [,Trinn])⇒uttrykk
avgRC(Uttr1,Var [=Verdi] [,Liste1])⇒liste
avgRC(Liste1,Var [=Verdi] [,Trinn])⇒liste
avgRC(Matrise1,Var [=Verdi] [,Trinn])⇒matrise
Returnerer differenskvotienten tatt i positiv retning
(gjennomsnittlig endringshastighet).
Uttr1 kan være et brukerdefinert funksjonsnavn (se
Func).
Hvis verdi er spesifisert, opphever den eventuell
forhåndstildelt verdi eller aktuell “|” erstatning for
variabelen.
Trinn er trinnverdien. Hvis Trinn utelates, brukes
grunninnstilling 0,001.
Merk at den liknende funksjonen centralDiff() bruker
derivasjonskvotienten.

B
bal() Katalog >
bal(NPmt,N,I,PV,[Pmt],[FV],[PpY],[CpY],[PmtAt],
[avrundVerdi])⇒verdi
bal(NPmt,amortTabell)⇒verdi
Amortiseringsfunksjon som beregner planlagt balanse
etter en spesifisert betaling.
N,I,PV,Pmt,FV,PpY,CpY og PmtAt er beskrevet i
tabellen med TVM-argumenter, side 179.
NPmt spesifiserer det betalingsnummeret som du vil
at dataene skal beregnes etter.
N,I,PV,Pmt,FV,PpY,CpY og PmtAt er beskrevet i
tabellen med TVM-argumenter, side 179.
• Hvis du utelater Pmt, grunninnstilles den til
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Hvis du utelater FV, grunninnstilles den til
FV=0.
• Grunninnstillingene for PpY,CpY og PmtAt er de
samme som for TVM-funksjonene.
avrundVerdi spesifiserer antallet desimalplasser for
avrunding. Grunninnstilling=2.
bal(NPmt,amortTabell)beregner balansen etter
betalingsnummer NPmt, basert på
amortiseringstabell amortTabell. Argumentet
amortTabell må være en matrise i den form som er
beskrevet under amortTbl(), side 12.
Merk: Se også GInt() og GPrn(), side 206.
4Base2 (Grunntall2) Katalog >
Heltall1 4Base2⇒heltall
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Base2.
Regner om Heltall1 til et binært tall. Binære eller
heksadesimale tall har alltid et prefiks, hhv. 0b eller
0h. Null, ikke bokstaven O, fulgt av b eller h.
0b binærTall
Alfabetisk oversikt 21

22 Alfabetisk oversikt
4Base2 (Grunntall2) Katalog >
0h heksadesimalTall
Et binært tall kan bestå av opptil 64 siffer. Et
heksadesimaltall kan bestå av opptil 16.
Uten prefiks blir Heltall1 behandlet som et desimalt
tall (grunntall10). Resultatet vises binært, uavhengig
av grunntallets modus.
Negative tall vises på “toerkomplement”-form.
Eksempel:
N1vises som
0hFFFFFFFFFFFFFFFFi heksadesimal modus
0b111...111 (641-ere)i binær modus
N263 vises som
0h8000000000000000i heksadesimal modus
0b100...000 (63 nuller)i binær modus
Hvis du oppgir et desimalt heltall som ligger utenfor
verdiområdet for et 64-bit binært tall med fortegn, vil
en symmetrisk modulusoperasjon bli brukt til å
konvertere tallet inn i gyldig verdiområde. Se følgende
eksempler på verdier utenfor verdiområdet.
263 blir N263 og vises som
0h8000000000000000i heksadesimal modus
0b100...000 (63 nuller)i binær modus
264 blir 0 og vises som
0h0i heksadesimal modus
0b0i binær modus
N263 N1 blir 263 N1 og vises som
0h7FFFFFFFFFFFFFFFi heksadesimal modus
0b111...111 (641-ere)i binær modus
4Base10 (Grunntall10) Katalog >
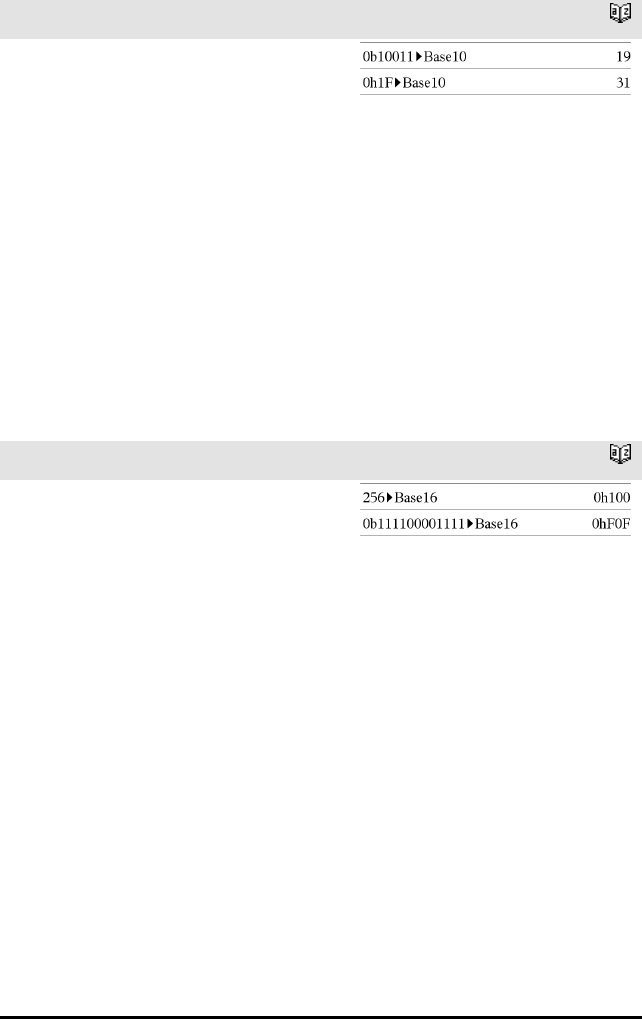
Heltall1 4Base10⇒heltall
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Base10.
Omregner Heltall1 til et desimaltall (grunntall10).
Binært eller heksadesimalt inndata må alltid ha et
prefiks, hhv. 0b eller 0h.
0b binærTall
0h heksadesimalTall
Null, ikke bokstaven O, fulgt av b eller h.
Et binært tall kan bestå av opptil 64 siffer. Et
heksadesimaltall kan bestå av opptil 16.
Uten prefiks behandles Heltall1 som desimaltall.
Resultatet vises i desimaltall, uavhengig av grunntall-
modus.
4Base16 (Grunntall16) Katalog >
Heltall1 4Base16⇒heltall
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Base16.
Omregner Heltall1 til et heksadesimaltall. Binære
eller heksadesimale tall har alltid et prefiks, hhv. 0b
eller 0h.
0b binærTall
0h heksadesimalTall
Null, ikke bokstaven O, fulgt av b eller h.
Et binært tall kan bestå av opptil 64 siffer. Et
heksadesimaltall kan bestå av opptil 16.
Uten prefiks blir Heltall1 behandlet som et desimalt
tall (grunntall10). Resultatet vises i heksadesimal,
uavhengig av grunntallets modus.
Hvis du oppgir et desimalt heltall som er for stort for et
64-bit binært tall med fortegn, vil en symmetrisk
modulusoperasjon bli brukt til å konvertere tallet inn i
gyldig verdiområde. For mer informasjon, se 4Base2,
side 21.
Alfabetisk oversikt 23

24 Alfabetisk oversikt
binomCdf() katalog >
binomCdf(n,p)⇒tall
binomCdf(n,p,nedreGrense,øvreGrense)⇒tall hvis
nedreGrense og øvreGrense er tall, liste hvis nedreGrense og
øvreGrense er lister
binomCdf(n,p,øvreGrense)for P(0{X{øvreGrense)⇒tall hvis
øvreGrense er et tall, liste hvis øvreGrense er en liste
Beregner en kumulativ sannsynlighet for diskret binomisk
fordeling med nantall forsøk og sannsynlighet pfor å finne treff
ved hvert forsøk.
For P(X {øvreGrense), sett nedreGrense=0
binomPdf() Katalog >
binomPdf(n,p)⇒tall
binomPdf(n,p,XVerd)⇒tall hvis XVerd er et tall, liste hvis XVerd
er en liste
Beregner en sannsynlighet ved XVerd for diskret binomisk
fordeling med nantall forsøk og sannsynlighet pfor å finne treff
ved hvert forsøk.
C
ceiling() (øvre) Katalog >
ceiling(Uttr1)⇒heltall
Returnerer det nærmeste heltallet som er |
argumentet.
Argumentet kan være et reelt eller et komplekst tall.
Merk: Se også floor() (nedre).
ceiling(Liste1)⇒liste
ceiling(Matrice1)⇒matrice
Returnerer en liste eller matrise med den øvre i hvert
element.

centralDiff() Katalog >
centralDiff(Uttr1,Var [=Verdi][,Trinn])⇒uttrykk
centralDiff(Uttr1,Var [,Trinn])|Var=Verdi⇒uttrykk
centralDiff(Uttr1,Var [=Verdi][,Liste])⇒liste
centralDiff(Liste1,Var [=Verdi][,Trinn])⇒liste
centralDiff(Matrise1,Var [=Verdi][,Trinn])⇒matrise
Returnererden numeriske deriverte ved hjelp av
derivasjonskvotient-formelen.
Hvis verdi er spesifisert, opphever den eventuell
forhåndstildelt verdi eller aktuell “|” erstatning for
variabelen.
Trinn er trinnverdien. Hvis Trinn utelates, brukes
grunninnstilling 0,001.
Hvis du bruker Liste1 eller Matrise1, blir handlingen
avbildet gjennom verdiene i listen eller gjennom
matriseelementene.
Merk: Se også og d().
cFactor() (kFaktor) Katalog >
cFactor(Uttr1[,Var])⇒uttrykk
cFactor(Liste1[,Var])⇒liste
cFactor(Matrise1[,Var])⇒matrise
cFactor(Uttr1)returnerer Uttr1, faktorisert med
hensyn på alle dets variabler over en felles nevner.
Uttr1 er faktorisert så mye som mulig i lineære
rasjonale faktorer, selv om det innfører nye, ikke-
reelle tall. Med dette alternativet kan du faktorisere
med hensyn på mer enn en variabel.
cFactor(Uttr1,Var)returnerer Uttr1, faktorisert med
hensyn på variabel Var.
Uttr1 er faktorisert så mye som mulig i faktorer som
er lineære i Var, muligens med ikke-reelle konstanter,
selv om det innfører irrasjonale konstanter eller
deluttrykk som er irrasjonale i andre variabler.
Alfabetisk oversikt 25

26 Alfabetisk oversikt
cFactor() (kFaktor) Katalog >
Faktorene og leddene deres er sortert med Var som
hovedvariabel. Liknende potenser av Var er samlet
sammen i hver faktor. Inkluder Var hvis du må
faktorisere med hensyn på bare den ene variabelen og
du er villig til å akseptere irrasjonale uttrykk i en annen
tilfeldig variabel for å øke faktoriseringen med hensyn
på Var. Det kan hende at faktor bestemmes tilfeldig
med hensyn på andre variabler.
Ved Auto-innstilling av modusen Auto eller Tilnærmet
vil en inkludering av Var også gjøre det mulig å
tilnærme med flytende desimalpunkt-koeffisienter der
hvor irrasjonale koeffisienter ikke kan uttrykkes
eksplisitt utfra innebygde funksjoner. Selv dersom det
bare er én variabel, vil man kunne oppnå en mer
komplett faktorisering ved å inkludere Var.
Merk: Se også faktor().
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
char() Katalog >
char(Heltall)⇒tegn
Returnerer en tegnstreng som inneholder det tegnet
som er nummerert med Heltall fra tegnsettet på
grafregneren. Gyldig område for Heltall er 0–65535.
charPoly() katalog >
charPoly(kvadratMatrise,Var)⇒polynomuttrykk
charPoly(kvadratMatrise,Uttr)⇒polynomuttrykk
charPoly(kvadratMatrise1,Matrise2)
⇒polynomuttrykk
Returnerer det karakteristiske polynomet til
kvadratMatrise. Det karakteristiske polynomet til
n×n-matrisen A, angitt som pA(l), er polynomet som
er definert ved
pA(l) = det(l•INA)
der Ier n×nidentitetsmatrisen.
kvadratMatrise1 og kvadratMatrise2 må ha samme
dimensjon.

c22way Katalog >
c22way ObsMatrise
chi22way ObsMatrise
Beregner en c2test for samling av “tellinger” på toveis-tabellen i
den observerte matrisen ObsMatrise. En oversikt over
resultatene lagres i stat.results-variabelen (side 162).
For informasjon om effekten av tomme elementer i en matrise,
se “Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.c2Chi-kvadratstat: sum (observert - forventet)2/forventet
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader av frihet for chi-kvadratstatistikk
stat.UttrMat Matrise av forventet element-telletabell ved antatt nullhypotese
stat.KompMat Matrise av elementbidrag til chi kvadratstatistikk
c2Cdf() Katalog >
c2Cdf(nedreGrense,øvreGrense,df)⇒tall hvis nedreGrense og
øvreGrense er tall, liste hvis nedreGrense og øvreGrense er
lister
chi2Cdf(nedreGrense,øvreGrense,df)⇒tall hvis nedreGrense
og øvreGrense er tall, liste hvis nedreGrense og øvreGrense er
lister
Beregner c2-fordelingens sannsynlighet mellom nedreGrense og
øvreGrense for det angitte antall frihetsgrader df.
For P(X{øvreGrense), sett nedreGrense = 0.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
c2GOF Katalog >
c2GOF obsListe,uttrListe,df
chi2GOF obsListe,uttrListe,df
Utfører en test for å bekrefte at utvalgsdata er fra en populasjon
som er i overensstemmelse med en angitt fordeling. obsListe er
en liste over antall, og må inneholde heltall. En oversikt over
Alfabetisk oversikt 27

28 Alfabetisk oversikt
c2GOF Katalog >
resultatene lagres i stat.resultater-variabelen (side 162).
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.c2Chi-kvadratstat: sum((observert - forventet)2/forventet
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader av frihet for chi-kvadratstatistikk
stat.CompList Elementbidrag til chi kvadratstatistikk
c2Pdf() Katalog >
c2Pdf(XVerd,df)⇒tall hvis XVerd er et tall, liste hvis XVerd er en
liste
chi2Pdf(XVerd,df)⇒tall hvis XVerd er et tall, liste hvis XVerd er
en liste
Beregner sannsynlighetstettheten (pdf) for c2-fordelingen ved en
bestemt XVerd-verdi for det angitte antallet frihetsgrader df.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
ClearAZ (slettAZ) Katalog >
ClearAZ
Sletter alle enkelttegn-variabler i det aktuelle
oppgaveområdet.
Hvis en eller flere av variablene er låst, viser denne
kommandoen en feilmelding og sletter kun de ulåste
variablene. Se unLock, side 182.
ClrErr (SlettFeil) Katalog >
ClrErr
Tømmer feilstatus og stiller systemvariabelen feilKode til null.
Else -leddet i Try...Else...EndTry-blokken bør bruke ClrErr eller
PassErr. Hvis feilen skal bearbeides eller ignoreres, bruk ClrErr.
For et eksempel på ClrErr, se
eksempel 2 under Try -kommandoen,
side 176.

ClrErr (SlettFeil) Katalog >
Hvis det ikke er kjent hva som skal gjøres med feilen, bruk
PassErr for å sende den til den neste feilbehandleren. Hvis det
ikke er flere ventende Try...Else...EndTry feilbehandlere, vises
feil-dialogboksen som normalt.
Merk: Se også PassErr, side 122, og Try, side 176.
Merk for å legge inn eksemplet: For anvisninger om hvordan du
legger inn flerlinjede program- og funksjonsdefinisjoner, se
avsnittet Kalkulator i produkthåndboken.
colAugment() (kolUtvid) Katalog >
colAugment(Matrise1,Matrise2)⇒matrise
Returnerer en ny matrise som er Matrise2 lagt til på
Matrise1. Matrisene må ha like kolonnedimensjoner,
og Matrise2 er lagt til Matrise1 som nye rader. Endrer
ikke Matrise1 eller Matrise2.
colDim() Katalog >
colDim(Matrise)⇒uttrykk
Returnerer antallet kolonner som ligger i Matrise.
Merk: Se også radDim().
colNorm() Katalog >
colNorm(Matrise)⇒uttrykk
Returnerer den største summene av absoluttverdiene
for elementene i kolonnene i Matrise.
Merk: Udefinerte matriseelementer er ikke tillatt. Se
også radNorm().
Alfabetisk oversikt 29

30 Alfabetisk oversikt
comDenom() Katalog >
comDenom(Uttr1[,Var])⇒uttrykk
comDenomListe1[,Var])⇒liste
comDenom(Matrise1[,Var])⇒matrise
comDenom(Uttr1)returnerer en redusert brøk av en
fullt utvidet teller over en fullt utvidet nevner.
comDenom(Uttr1,Var)returnerer en redusert brøk av
teller og nevner som er utvidet med hensyn på Var.
Leddene og faktorene deres er sortert med Var som
hovedvariabel. Liknende potenser av Var er samlet
sammen. Det kan hende at faktor bestemmes tilfeldig
av de innsamlede koeffisienter. Sammenliknet med å
utelate Var sparer dette ofte tid samt plass både i
minnet og på skjermen, samtidig som uttrykket blir
mer forståelig. Det gjør også at etterfølgende
handlinger på resultatet går raskere og at minnet ikke
belastes så mye.
Hvis Var ikke opptrer i Uttrykk1, vil comDenom
(Uttr1,Var) returnere en redusert brøk av en ikke
utvidet teller over en ikke utvidet nevner. Slike
resultater sparer vanligvis både tid og plass i både
minnet og på skjermen. Slike delvis faktoriserte
resultater gjør også at etterfølgende handlinger på
resultatet går mye raskere og at minnet ikke belastes
så mye.
Selv om det ikke foreligger noen nevner, er comDen -
funksjonen ofte en rask måte å oppnå delvis
faktorisering på, hvis factor() er for langsom eller hvis
den tar for stor plass i minnet.
Tips: Legg inn denne comden()-funksjonsdefinisjonen
og prøv den rutinemessig som et alternativ til
comDenom() og factor().
completeSquare () Katalog >
completeSquare(UttrEllerLign,Var)⇒uttrykk eller
ligning
completeSquare(UttrEllerLign,Var^Potens)
⇒uttrykk eller ligning

completeSquare () Katalog >
completeSquare(UttrEller Lign,Var1, Var2 [,...])
⇒uttrykk eller ligning
completeSquare(UttrEllerLign,{Var1, Var2 [,...]})
⇒uttrykk eller ligning
Omregner et kvadratisk polynomuttrykk av formen
a·x2+b·x+c til formen a·(x-h)2+k
- eller -
Omregner en kvadratisk ligning av formen
a·x2+b·x+c=d til formen a·(x-h)2=k
Det første argumentet må være et kvadratisk uttrykk
eller en kvadratisk ligning i standard form med hensyn
på det andre argumentet.
Det andre argumentet må være et enkelt ledd i én
variabel eller et enkelt ledd i én variabel opphøyd i en
rasjonal eksponent, for eksempel x,y2ellerz(1/3).
Den tredje eller fjerde syntaksen forsøker å fullføre
kvadratet med hensyn på variabler Var1,Var2 [,… ]).
conj() Katalog >
conj(Uttr1)⇒uttrykk
conj(Liste1)⇒liste
conj(Matrise1)⇒matrise
Returnerer den komplekse konjugerte av argumentet.
Merk: Alle ubestemte variabler behandles som reelle
variabler.
constructMat() katalog >
constructMat(Uttr,Var1,Var2,antRad,antKol)
⇒matrise
Returnerer en matrise basert på argumentene.
Uttr er et uttrykk i variablene Var1 og Var2.
Elementene i resultatmatrisen dannes ved å beregne
Uttr for hver økte verdi av Var1 og Var2.
Var1 økes automatisk fra 1og opp til antRad. I hver
Alfabetisk oversikt 31
32 Alfabetisk oversikt
constructMat() katalog >
rad øker Var2 fra 1og opp til antKol.
CopyVar (kopiVar) katalog >
CopyVar Var1,Var2
CopyVar Var1., Var2.
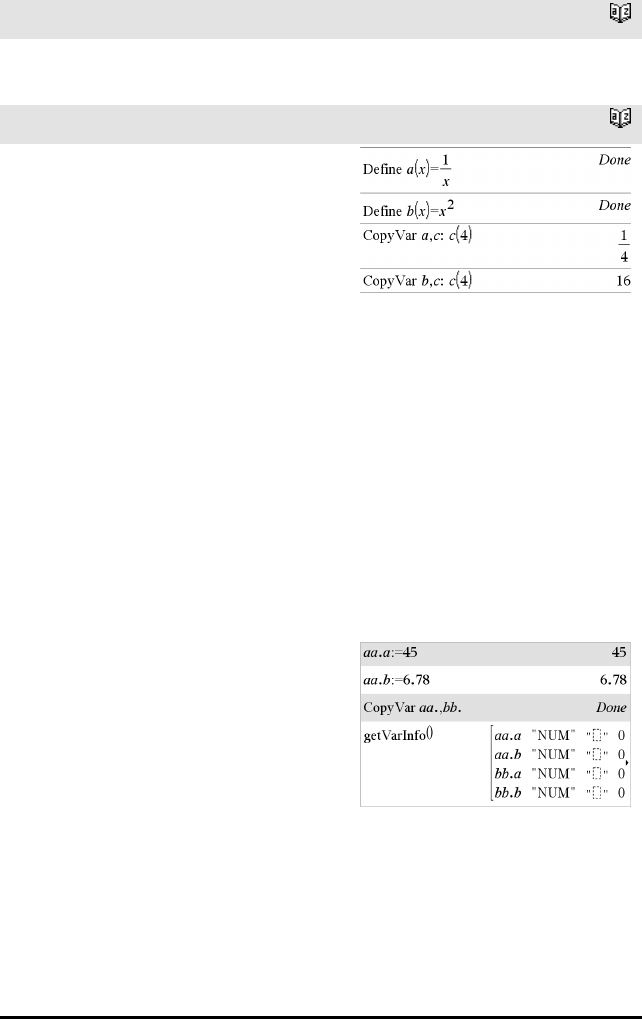
CopyVar Var1,Var2 kopierer verdien av variabelen
Var1 til variabelen Var2, og oppretter Var2 om
nødvendig. Variabel Var1 må ha en verdi.
Hvis Var1 er navnet på en eksisterende
brukerdefinert funksjon, kopieres definisjonen av
denne funksjonen til funksjon Var2. Funksjon Var1
må være definert.
Var1 må følge reglene for variabelnavn eller være et
indirekte uttrykk som kan forenkles til et variabelnavn
som oppfyller reglene.
Var1. må være navnet på en eksisterende
variabelgruppe, for eksempel statistikk stat.nn-
resultater eller variabler som er opprettet med
LibShortcut() -funksjonen). Hvis Var2. allerede
eksisterer, vil denne kommandoen erstatte alle
medlemmer som er felles for begge grupper og legge
til de medlemmene som ikke allerede eksisterer. Hvis
ett eller flere medlemmer av Var2. er låst, blir alle
medlemmer av Var2. værende uendret.
CopyVar Var1.,Var2. kopierer alle medlemmene av
Var1. variabelgruppe til Var2. gruppe, og oppretter
Var2. om nødvendig.
Var1. må være navnet på en eksisterende
variabelgruppe, for eksempel statistikk stat.nn-
resultater, eller variabler som er opprettet med
LibShortcut()-funksjonen. Hvis Var2. allerede finnes,
vil denne kommandoen erstatte alle medlemmer som
er felles for begge gruper, og legge til de medlemmene
som ikke allerede finnes. Hvis en enkel (ikke i gruppe)
variabel med navnet Var2 finnes, oppstår det en feil.

corrMat() Katalog >
corrMat(Liste1,Liste2[,…[,Liste20]])
Beregner korrelasjonsmatrisen for den utvidede matrisen [
Liste1, Liste2, . . ., Liste20 ].
4cos katalog >
Uttr 4cos
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>cos.
Representerer Uttr med cosinus. Dette er en
konverteringsoperator. Den kan bare brukes på
slutten av kommandolinjen.
4cos reduserer alle potenser avsin(...) modulus
1Ncos(...)^2 slik at alle gjenværende potenser av cos
(...) har eksponenter i området (0, 2). Dermed vil
resultatet være uten sin(...) hvis og bare hvis sin(...)
inntreffer i det gitte uttrykket bare med
partallseksponenter.
Merk: Denne konverteringsoperatoren støttes ikke i
vinkelmodusen grader eller gradianer. Før du bruker
den, må du kontrollere at vinkelmodus er satt til
radianer, og at Uttr ikke inneholder eksplisitte
referanser til vinkler i grader eller gradianer.
cos() µtast
cos(Uttr1)⇒uttrykk
cos(Liste1)⇒liste
cos(Uttr1)returnerer cosinus til argumentet som et
uttrykk.
cos(Liste1)returnerer en liste av cosinus til alle
elementer i Liste1.
Merk: Argumentet tolkes som grader, gradian eller
radian av en vinkel, avhengig av aktuell vinkelmodus-
innstilling. Du kan bruke ¡,Geller Rfor å hoppe over
vinkelmodusen midlertidig.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
Alfabetisk oversikt 33

34 Alfabetisk oversikt
cos() µtast
I Radian-vinkelmodus:
cos(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens cosinus til kvadratMatrise1.
Dette er ikke det samme som å beregne cosinus til
hvert element.
Når en skalarfunksjon f(A) virker på kvadratMatrise1
(A), beregnes resultatet av algoritmen:
Beregner egenverdiene (li) og egenvektorene (V i) av
A.
kvadratMatrise1 må kunne diagonaliseres. Den kan
heller ikke ha symbolske variabler som ikke er tildelt
noen verdi.
Utform matrisene:
Da er A = X B X/og f(A) = X f(B) X/. For eksempel,
cos(A) =X cos(B) X/hvor:
cos (B) =
Alle beregningene utføres med flytende desimalpunkt-
aritmetikk.
I Radian-vinkelmodus:
cos/() µtast
cos/(Uttr1)⇒uttrykk
cos/(Liste1)⇒liste
I Grader-vinkelmodus:

cos/() µtast
cos/(Uttr1)returnerer vinkelen som har cosinus lik
Uttr1
som et uttrykk.
cos/(Liste1)returnerer en liste over invers cosinus
for hvert element i Liste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradian eller radian, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccos(...).
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
cos/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse cosinus til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers cosinus til hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I radian-vinkelmodus og rektangulært, kompleks
format:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
cosh() Katalog >
cosh(Uttr1)⇒uttrykk
cosh(Liste1)⇒liste
cosh(Uttr1)returnerer hyperbolsk cosinus til
argumentet som et uttrykk.
cosh(Liste1) returnerer en liste over hyperbolsk
cosinus til hvert element i Liste1.
I Grader-vinkelmodus:
cosh(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens hyperbolske cosinus til
kvadratMatrise1. Detteer ikke det samme som å
beregne hyperbolsk cosinus til hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:
Alfabetisk oversikt 35

36 Alfabetisk oversikt
cosh/() Katalog >
cosh/(Uttr1)⇒uttrykk
cosh/(Liste1)⇒liste
cosh/(Uttr1)returnerer invers hyperbolsk cosinus for
argumentet som et uttrykk.
cosh/(Liste1) returnerer en liste over invers
hyperbolsk cosinus til hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccosh(...).
cosh/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse hyperbolsk cosinus til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers hyperbolsk cosinus til hvert element.
For mer informasjon om beregningsmetode, se under
cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I radian-vinkelmodus og rektangulært, kompleks
format:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
cot() µtast
cot(Uttr1)⇒uttrykk
cot(Liste1)⇒liste
Returnerer cotangens av uttrykk1, eller returnerer en
liste med cotangens til alle elementene i liste1.
Merk: Argumentet tolkes som grader, gradianer eller
radianer av en vinkel, avhengig av aktuell
vinkelmodus-innstilling. Du kan bruke ¡,Geller Rfor å
hoppe over vinkelmodusen midlertidig.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
cot/() µtast
cot /(Uttr1)⇒uttrykk I Grader-vinkelmodus:

cot/() µtast
cot /(Liste1)⇒liste
Returnerer vinkelen som har cotangens lik Uttr1 eller
returnerer en liste som inneholder invers cotangens til
hvert element i Liste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradian eller radian, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccot(...).
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
coth() Katalog >
coth(Uttr1)⇒uttrykk
coth(Liste1)⇒liste
Returnerer hyperbolsk cotangens til uttrykk1, eller
returnerer en liste med hyperbolsk cotangens til alle
elementene i liste1.
coth/() Katalog >
coth/(Uttr1)⇒uttrykk
coth/(Liste1)⇒liste
Returnerer invers hyperbolsk cotangens til Uttr1, eller
returnerer en liste med invers hyperbolisk cotangens
til hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccoth(...).
Alfabetisk oversikt 37
38 Alfabetisk oversikt
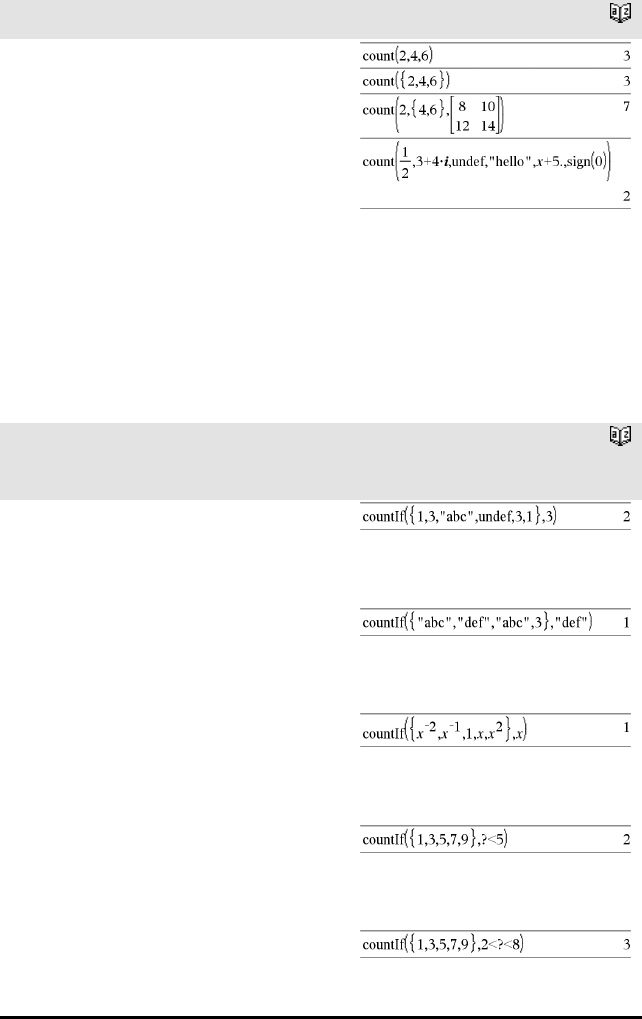
count() (antall) Katalog >
count(Verdi1ellerListe1 [,Verdi2ellerListe2 [,...]])
⇒verdi
Returnerer samlet antall av alle elementer i
argumentene som behandles til numeriske verdier.
Hvert argument kan være et uttrykk. en verdi, liste
eller matrise. Du kan blande datatyper og bruke
argumenter med forskjellige dimensjoner.
For en liste, matrise eller et celleområde blir hver
element behandlet for å bestemme om det bør
inkluderes i antallet.
I applikasjonen Lister og regneark kan du bruke et
celleområde istedenfor et argument.
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.
I det siste eksemplet ble bare 1/2 og 3+4*italt. De
resterende argumentene, dersom xer udefinert,
behandler ikke til numeriske verdier.
countIf() (tellIf)
Katalog >
countIf(Liste,Kriterium)⇒verdi
Returnerer samlet antall av alle argumenter i Liste
som møter de spesifiserte kriterier.
Kriterium kan være:
• En verdi, et uttrykk eller en streng. For
eksempel, 3teller kun de elementene i Liste
som forenkles til verdien 3.
• Et boolsk uttrykk som inneholder symbolet ?
som plassholder for hvert element. For
eksempel, ?<5 teller kun de elementene i Liste
som er mindre enn 5.
I applikasjonen Lister og regneark kan du bruke et
celleområde istedenfor Liste.
Tomme (åpne) elementer i listen ignoreres. For mer
informasjon om tomme elementer, se side 217.
Merk: Se også sumIf(), side 166, og frequency(), side
73.
Teller alle elementer som er lik 3.
Teller alle elementer som er lik “def.”
Teller alle elementer som er lik x; dette eksemplet
antar at variabelen xer udefinert.
Teller 1 og 3.

countIf() (tellIf)
Katalog >
Teller 3, 5 og 7.
Teller 1, 3, 7 og 9.
cPolyRoots() Katalog >
cPolyRoots(Poly,Var)⇒liste
cPolyRoots(KoeffListe)⇒liste
Den første syntaksen, cPolyRoots(Poly,Var),
returnerer en liste over komplekse røtter av polynom
Poly med hensyn på variabel Var.
Poly må være et polynom i én variabel.
Den andre syntaksen, cPolyRoots(KoeffListe),
returnerer en liste over komplekse røtter for
koeffisienter i KoeffListe.
Merk: Se også polyRoots(), side 126.
crossP() (kryssprodukt) Katalog >
crossP(Liste1,Liste2)⇒liste
Returnerer kryssproduktet av Liste1 og Liste2 som
en liste.
Liste1 og Liste2 må ha lik dimensjon, og dimensjonen
må være enten 2 eller 3.
crossP(Vektor1,Vektor2)⇒vektor
Returnerer en rad- eller kolonnevektor (avhengig av
argumentene) som er kryssproduktet av Vektor1 og
Vektor2.
Både Vektor1 og Vektor2 må være radvektorer, eller
begge må være kolonnevektorer. Begge vektorene
må ha lik dimensjon, og dimensjonen må være enten
2eller3.
Alfabetisk oversikt 39

40 Alfabetisk oversikt
csc() µtast
csc(Uttr1)⇒uttrykk
csc(Liste1)⇒liste
Returnerer cosekans til Uttr1, eller returnerer en liste
med cosekans til hvert element i Liste1.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
csc/() µtast
csc/(Uttr1)⇒uttrykk
csc/(Liste1)⇒liste
Returnerer vinkelen som har cosekans lik Uttr1, eller
returnerer en liste med invers cosekans til hvert
element i Liste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradianer eller radianer, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccsc(...).
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
csch() Katalog >
csch(Uttr1)⇒uttrykk
csch(Liste1)⇒liste
Returnerer hyperbolsk cosekans til Uttr1 eller
returnerer en liste med hyperbolsk cosekans til alle
elementene i Liste1.

csch/() Katalog >
csch/(Uttr1)⇒uttrykk
csch/(Liste1)⇒liste
Returnerer invers hyperbolsk cosekans til Uttr1, eller
returnerer en liste med invers hyperbolsk cosekans til
hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive arccsch(...).
cSolve() (kLøs) Katalog >
cSolve (Ligning,Var)⇒Boolsk uttrykk
cSolve(Ligning,Var=Forslag)⇒Boolsk utrykk
cSolve (Ulikhet,Var)⇒Boolsk uttrykk
Returnerer komplekse løsningsalternativer av en
ligning eller ulikhet i Var. Målet er å produsere
alternativer for alle reelle og ikke-reelle løsninger. Selv
omLigning er reell, kan cSolve() returnere ikke-reelle
resultater i Reelt resultat Komplekst format.
Selv om alle udefinerte variabler som ikke slutter med
en senket strek (_) behandles som om de er reelle,
kan cSolve() løse polynomiske ligninger med
komplekse løsninger.
cSolve() setter midlertidig grunnmengde til kompleks i
løpet av løsningsprosessen selv om den aktuelle
grunnmengden er reell. I kompleks grunnmengde
bruker brøkpotens med oddetall i nevneren
hovedforgreining heller enn reell forgreining. Følgelig
er løsninger fra solve() på ligninger som omfatter slike
brøkpotenser ikke nødvendigvis en delmengde av
løsningene fra cSolve().
cSolve() starter med eksakte, symbolske metoder.
Unntatt i Eksakt modus bruke cSolve() også iterativ,
tilnærmet kompleks polynomisk faktorisering, om
nødvendig.
Merk: Se også cZeros(),solve(), og zeros().
Merk: Hvis Ligning er ikke-polynomisk med
funksjoner, som abs(),angle(),conj(),real() eller imag
I Vis siffer-modus av Fast 2:
For å se hele resultatet, trykk på £og bruk så ¡og¢
Alfabetisk oversikt 41

42 Alfabetisk oversikt
cSolve() (kLøs) Katalog >
(), bør du sette en senket strek (trykk på /_) på
slutten av Var. I grunninnstilling behandles variabelen
som en reell verdi.
for å bevege markøren.
Hvis du bruker var _, behandles variabelen som
kompleks.
Du bør også bruke var_ for alle andre variabler i
Ligning som kan ha ikke-reelle verdier. Ellers kan du
få returnert uventede resultater.
cSolve(Lign1and Lign2 [and…],VarElForslag1,
VarElForslag2 [, … ])⇒Boolskuttrykk
cSolve(LignSystem,VarElForslag1,VarElForslag2
[, …])⇒Boolskuttrykk
Returnerer komplekse løsningsalternativer til
simultane, algebraiske ligninger, der hvert
varElForslag spesifiserer en variabel som du vil finne
løsningen til.
Alternativt kan du spesifisere et startforslag for en
variabel. Hvert varElForslag må ha formen:
variabel
– eller –
variabel =reelt eller ikke-reelt tall
For eksempel er x gyldig, og det er også x=3+i.
Hvis alle ligningene er polynomiske og hvis du IKKE
spesifiserer noe startforslag, bruker cSolve()
Gröbner/Buchbergers leksikale eliminasjonsmetode
for å prøve å bestemme alle komplekse løsninger.
Merk: Følgende eksempler bruker en senket strek
(trykk på /_) slik at variablene behandles som
komplekse.
Komplekse løsninger kan inkludere både reelle og
ikke-reelle løsninger, som i eksemplet til høyre.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Simultane, polynomiske ligninger kan ha ekstra
variabler uten verdiparametre, men som
representerer gitte tallverdier som kan settes inn
senere.

cSolve() (kLøs) Katalog >
Du kan også inkludere løsningsvariabler som ikke
forekommer i ligningene. Disse løsningene viser
hvordan løsningsfamilier kan inneholde vilkårlige
konstanter i form av ck, hvor ker et heltall mellom 1
og 255.
For polynomiske systemer kan beregningstiden eller
plassen i minnet sterkt avhenge av hvilken rekkefølge
du setter løsningsvariabler i. Hvis startforslaget
bruker opp minneplassen eller tålmodigheten din, kan
du prøve å flytte om på variablene i ligningene og/eller
varElForslag -listen.
Hvis du ikke inkluderer noen forslag og hvis en ligning
er ikke-polynomisk i en vilkårlig variabel men alle
ligningene er lineære i alle løsningsvariabler, bruker
cSolve() gaussisk eliminasjon for å prøve å
bestemme alle løsninger.
Hvis et system er verken polynomisk i alle variablene
eller lineært i løsningsvariablene, bestemmer cSolve()
som regel en løsning med en tilnærmet iterativ
metode. I så fall må antallet løsningsvariabler være lik
antallet ligninger, og alle andre variabler (parametre) i
ligningene må forenkles til tall.
Et ikke-reelt forslag er ofte nødvendig for å bestemme
en ikke-reell løsning. For konvergens kan det hende at
et forslag må være ganske nært en løsning.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
CubicReg Katalog >
CubicReg X,Y[,[Frekv] [,Kategori,Inkluder]]
Finner den kubiske polynomiske regresjonen y = a·x3+b·
x2+c·x+d for listene Xog Ymed frekvensen Frekv. En oversikt
over resultatene lagres i stat.resultater-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
Alfabetisk oversikt 43

44 Alfabetisk oversikt
CubicReg Katalog >
heltall|0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a·x3+b·x2+c·x+d
stat.a, stat.b,
stat.c, stat.d
Regresjonskoeffisienter
stat.R2Koeffisientbestemmelse
stat.Resid Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste, og Inkludert kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og inkludert kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
cumulativeSum() Katalog >
cumulativeSum(Liste1)⇒liste
Returnerer en liste over de kumulative summene av
elementene i Liste1, og starter med element 1.
cumulativeSum(Matrise1)⇒matrise
Returnerer en matrise av de kumulative summene av
elementene i Matrise1. Hvert element er den
kumulative summen av kolonnen fra topp til bunn.
Et tomt (åpent) element i Liste1 eller Matrise1
produserer et åpent element i den resulterende listen
eller matrisen. For mer informasjon om tomme
elementer, se side 217.
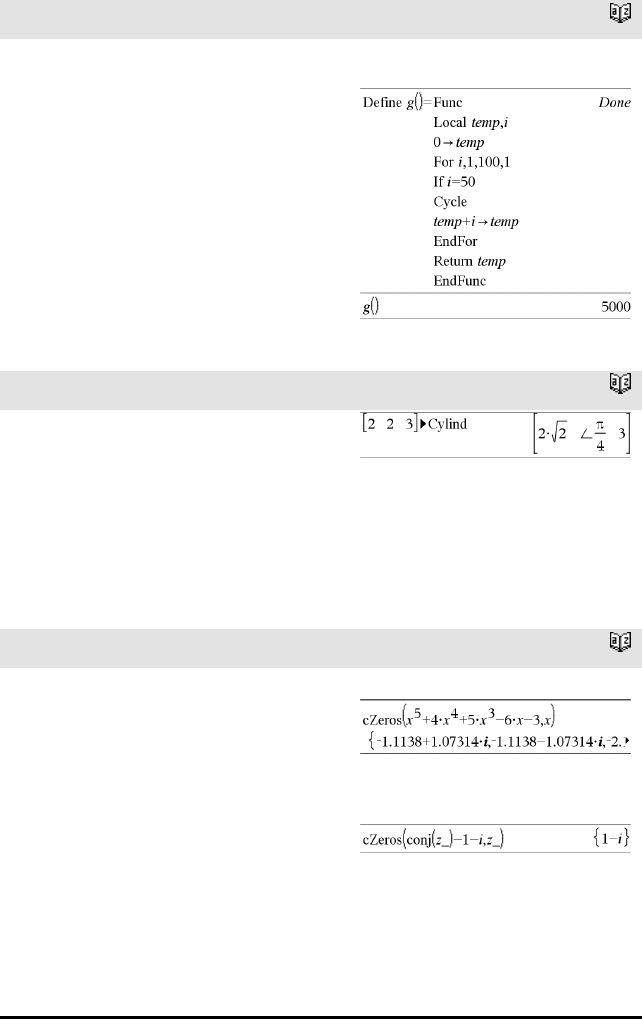
Cycle (Løkke) Katalog >
Cycle (Løkke)
Overfører øyeblikkelig kontroll til den neste
iterasjonen i aktuell løkke (For,While, eller Loop).
Cycle er ikke tillatt utenfor de tre løkkestrukturene
(For,While, eller Loop).
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Funksjonsliste som summerer heltallene fra 1 til 100
og hopper over 50.
4Cylind Katalog >
Vektor 4Cylind
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Cylind.
Viser rad- eller kolonnevektor i sylindrisk form [r, ±q,
z].
Vektor må ha nøyaktig tre elementer. Det kan være
enten en rad eller en kolonne.
cZeros() (kNullp) Katalog >
cZeros (Uttr,Var)⇒liste
Returnerer en liste over alternative reelle eller ikke-
reelle verdier av Var som gir Uttr=0. cZeros() gjør
dette ved å beregne uttr4liste(cSolve
(Uttr=0,Var),Var). Ellers er cZeros() lik zeros().
Merk: Se også cSolve(),solve() og zeros().
I Vis siffer-modus av Fast 3:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Merk: Hvis Uttr er ikke-polynomisk med funksjoner,
som abs(),angle(),conj(),real(), eller imag(), bør du
sette en senket strek (trykk på /_) på slutten av
Var. I grunninnstilling behandles variabelen som en
reell verdi. Hvis du bruker var_, behandles variabelen
som kompleks.
Alfabetisk oversikt 45

46 Alfabetisk oversikt
cZeros() (kNullp) Katalog >
Du bør også bruke var_ for alle andre variabler i Uttr
som kan ha ikke-reelle verdier. Ellers kan du få
returnert uventede resultater.
cZeros({Uttr1,Uttr2 [,… ] },
{VarElForslag1,VarElForslag2 [,… ] })⇒matrise
Returnerer alternative posisjoner der alle uttrykkene
er null samtidig. Hvert VarElForslag spesifiserer en
ukjent som du vil finne verdien til.
Alternativt kan du spesifisere et startforslag for en
variabel. Hvert varElForslag må ha formen:
variabel
– eller –
variabel = reelt eller ikke-reelt tall
For eksempel er x gyldig, og det er også x=3+i.
Hvis alle uttrykkene er polynomiske og hvis du IKKE
spesifiserer noe startforslag, bruker cZeros()
Gröbner/Buchbergers leksikale eliminasjonsmetode
for å prøve å bestemme alle komplekse nullpunkter.
Merk: Følgende eksempler bruker en senket strek _
(trykk på /_) slik at variablene behandles som
komplekse.
Komplekse nullpunkter kan inkludere både reelle og
ikke-reelle nullpunkter, som i eksemplet til høyre.
Hver rad i resultatmatrisen presenterer et alternativt
nullpunkt, med komponentene plassert som i
VarElForslag -listen. For å trekke ut en rad, pek på
matrisen med [rad].
Trekk ut rad 2:
Simultane polynomer kan ha ekstra variabler uten
verdi (parametre), men som representerer gitte
tallverdier som kan settes inn senere.

cZeros() (kNullp) Katalog >
Du kan også inkludere ukjente variabler som ikke
forekommer i uttrykkene. Disse nullpunktene viser
hvordan nullpunkt-familier kan inneholde vilkårlige
konstanter i form av ck, hvor k er et heltall mellom 1
og 255.
For polynomiske systemer kan beregningstiden eller
plassen i minnet sterkt avhenge av hvilken rekkefølge
du setter de ukjente i. Hvis startforslaget bruker opp
minneplassen eller tålmodigheten din, kan du prøve å
flytte om på variablene i uttrykkene og/eller
VarElForslag-listen.
Hvis du ikke inkluderer noen forslag og hvis et uttrykk
er ikke-polynomisk i en vilkårlig variabel men alle
uttrykkene er lineære i alle ukjente, bruker cZeros()
gaussisk eliminasjon for å prøve å bestemme alle
nullpunktene.
Hvis et system er verken polynomisk i alle variablene
eller lineært i de ukjente, bestemmer cZeros() som
regel ett nullpunkt med en tilnærmet iterativ metode. I
så fall må antallet ukjente være lik antallet uttrykk, og
alle andre variabler i uttrykkene må forenkles til tall.
Et ikke-reelt forslag er ofte nødvendig for å bestemme
et ikke-reelt nullpunkt. For konvergens kan det hende
at et forslag må være ganske nært et nullpunkt.
D
dbd() Katalog >
dbd(dato1,dato2)⇒verdi
Returnerer antallet dager mellom dato1 og dato2 ved
hjelp av aktuelt-antall-dager-metoden.
dato1 og dato2 kan være tall eller lister av tall innenfor
datoområdet på en vanlig kalender. Hvis både dato1
og dato2 er lister, må de være like lange.
dato1 og dato2 må ligge mellom årene 1950 og 2049.
Du kan legge inn datoene i ett av to formater. Hvor du
setter desimalkommaet bestemmer hvilket
datoformat du bruker.
Alfabetisk oversikt 47

48 Alfabetisk oversikt
dbd() Katalog >
MM.DDÅÅ (format som vanligvis brukes i USA)
DDMM.ÅÅ (format som vanligvis brukes i Europa)
4DD Katalog >
Verdi 4DD⇒verdi
Liste1 4DD⇒liste
Matrise1 4DD⇒matrise
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>DD.
Returnerer desimalekvivalenten til argumentet uttrykt
i grader. Argumentet er et tall, en liste eller matrise
som tolkes av vinkelmodus-innstillingen i gradianer,
radianer eller grader.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
4Decimal Katalog >
Uttr1 4Decimal⇒Uttrykk
Liste1 4Decimal⇒Uttrykk
Matrise1 4Decimal⇒Uttrykk
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Decimal.
Viser argumentet i desimalform. Denne operatoren
kan kun brukes på slutten av kommandolinjen.
Define (Definer) Katalog >
Define Var =Uttrykk
Define Funksjon(Param1,Param2,...) = Uttrykk
Definerer variabelen Var eller den egendefinerte

Define (Definer) Katalog >
funksjonen Funksjon.
Parametere, som f.eks. Param1, er plassholdere for å
sette argumenter til funksjonen. Når du kaller opp en
egendefinert funksjon, må du legge til argumenter (for
eksempel verdier eller variabler) som samsvarer med
parameterne. Når funksjonen er kalt opp, behandler
den Uttrykk ved hjelp av de argumentene som er lagt
til.
Var og Funksjon kan ikke være navnet på
systemvariabel eller innebygget funksjon eller
kommando.
Merk: Denne type Define er ekvivalent til å utføre
uttrykket: uttrykk &Funksjon(Param1,Param2).
Define Funksjon(Param1,Param2,...) = Funk
Blokk
EndFunk
Define Program(Param1,Param2,...) = Prgm
Blokk
EndPrgm
I denne formen kan egendefinert funksjon eller
program utføre en blokk med flere utsagn.
Blokk kan enten være et enkelt utsagn eller en rekke
med utsagn på separate linjer. Blokk kan også
inkludere uttrykk og instruksjoner (som If,Then,Else
og For).
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Merk: Se også Define BiblPriv, side 49 og Define
BiblOff, side 50.
Define LibPriv (Definer BiblPriv) Katalog >
Define LibPriv Var =Uttrykk
Define LibPriv Funksjon(Param1,Param2,...) = Uttrykk
Alfabetisk oversikt 49
50 Alfabetisk oversikt
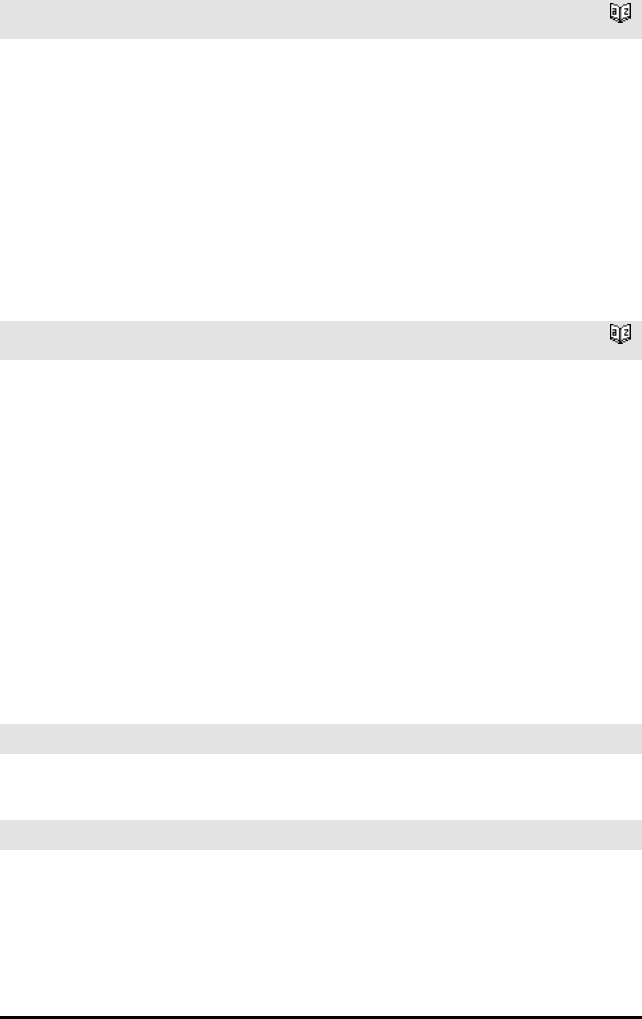
Define LibPriv (Definer BiblPriv) Katalog >
Define LibPriv Funksjon(Param1,Param2,...) = Funk
Blokk
EndFunk
Define LibPriv Program(Param1,Param2,...) = Prgm
Blokk
EndPrgm
Opererer på samme måte som Define, men definerer en privat
biblioteksvariabel, -funksjon eller et -program. Private funksjoner
og programmer forekommer ikke i Katalogen.
Merk: Se også Define, side 48 og Define LibPub, side 50.
Define LibPub (Definer BiblOff) Katalog >
Define LibPub Var =Uttrykk
Define LibPub Funksjon(Param1,Param2,...) = Uttrykk
Define LibPub Funksjon(Param1,Param2,...) = Funk
Blokk
EndFunk
Define LibPub Program(Param1,Param2,...) = Prgm
Blokk
EndPrgm
Opererer på samme måte som Define, men definerer en felles
(offentlig) biblioteksvariabel, -funksjon eller et -program. Felles
(offentlige) funksjoner og programmer forekommer i Katalogen
etter at biblioteket er blitt lagret og oppdatert.
Merk: Se også Define, side 48 og Define LibPriv, side 49.
deltaList() Se @List(), side 95.
deltaTmpCnv() Se @tmpCnv(), side 175.
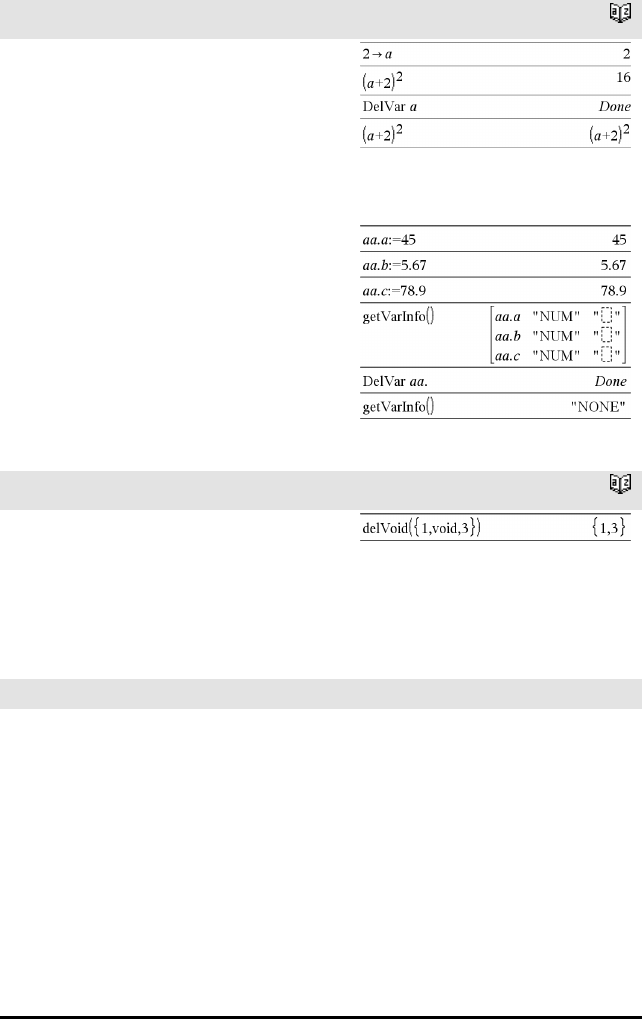
DelVar katalog >
DelVar Var1[,Var2] [,Var3] ...
DelVar Var.
Sletter den angitte variabelen eller variabelgruppen fra
minnet.
Hvis en eller flere av variablene er låst, viser denne
kommandoen en feilmelding og sletter kun de ulåste
variablene. Se unLock, side 182.
DelVar Var. sletter alle medlemmer av Var.
variabelgruppen (for eksempel statistikk stat.nn-
resultater eller variabler som er opprettet med
LibShortcut()-funksjonen).Prikken (.) i denne formen
av DelVar-kommandoen begrenser den til å slette en
variabelgruppe. Enkeltvariabelen Var påvirkes ikke.
delVoid() Katalog >
delVoid(Liste1)⇒liste
Returnerer en liste som har innholdet til Liste1, der
alle tomme (åpne) elementer er fjernet.
For mer informasjon om tomme elementer, se side
217.
derivative() Se d(), side 203.
Alfabetisk oversikt 51

52 Alfabetisk oversikt
deSolve() Katalog >
deSolve(1.el2.ordensODE,Var,avhVar)⇒en
generell løsning
Returnerer en ligning som eksplisitt eller implisitt
spesifiserer en generell løsning til 1.- eller 2.-ordens
ordinær differensialligning (ODE). I ODE:
• Bruk et apostrofsymbol (trykk på º) for å
markere den første deriverte av den avhengige
variabelen med hensyn på den uavhengige
variabelen.
• Bruk to apostrofsymboler for å markere den
tilsvarende andre deriverte.
Symbolet ' brukes bare for deriverte innenfor deSolve
(). I andre tilfeller, brukd().
Den generelle løsningen av en førsteordens ligning
inneholder en vilkårlig kontstant av formen ck, hvor k
er et heltall mellom 1 og 255. Løsningen av en
andreordens ligning inneholder to slike konstanter.
Bruk solve() på en implisitt løsning hvis du vil prøve å
omregne den til en eller flere ekvivalente, eksplisitte
løsninger.
Når du sammenlikner resultatene dine med
løsningene i et oppgavehefte eller i en håndbok, bør du
være klar over at ulike metoder introduserer vilkårlige
konstanter ved forskjellige trinn i beregningen, og
dette kan frembringe ulike, generelle løsninger.
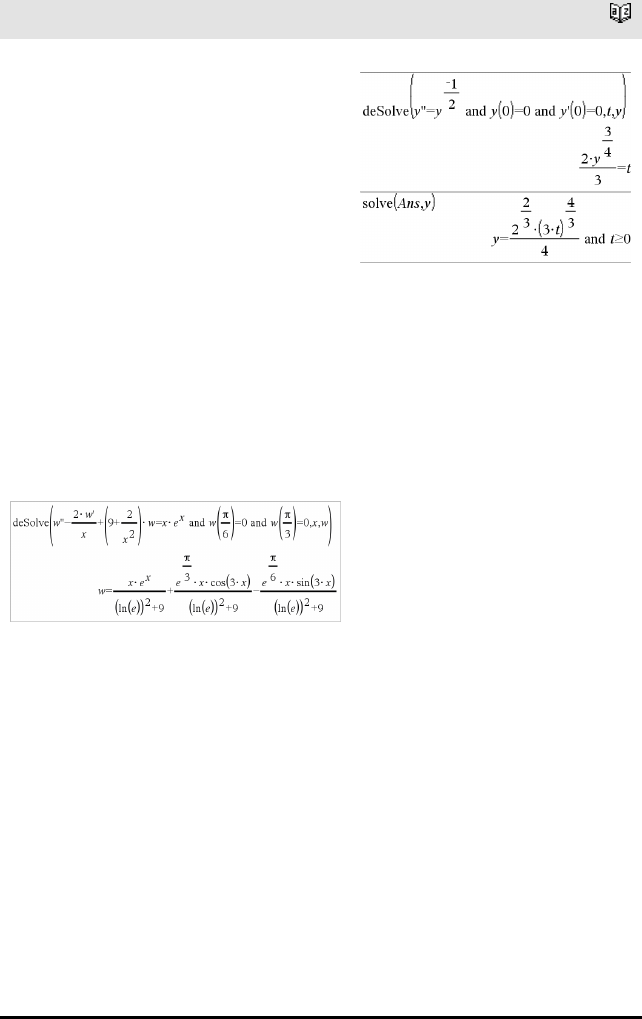
deSolve(1.ordensODEand startBet,Var,avhVar)
⇒en bestemt løsning
Returnerer en bestemt løsning som tilfredsstiller
1.ordensODE og startBet. Dette er vanligvis enklere
enn å bestemme en generell løsning, bytte ut
startverdier, finne løsning for den vilkårlige konstanten
og deretter sette denne verdien inn i den generelle
løsningen.
startBet er en ligning på formen:
avhVar (startUavhengigVerdi) = startAvhengigVerdi
startUavhengigVerdi og startAvhengigVerdi kan
være variabler, f.eks. x0 og y0, som ikke har noen
lagret verdi. Implisitt derivasjon kan være en hjelp til å
deSolve() Katalog >
verifisere implisitte løsninger.
deSolve(2.ordensODEandstartBet1andstartBet2,
Var,avhVar)⇒en bestemt løsning
Returnerer en bestemt løsning som tilfredsstiller 2.
ordens ODE og har en spesifisert verdi av den
avhengige variabelen og dens første deriverte i ett
punkt.
For startBet1 bruker du formen:
avhVar (startUavhengigVerdi) = startAvhengigVerdi
For startBet2 bruker du formen:
avhVar (startUavhengigVerdi) =
start1.DerivertVerdi
deSolve(2.ordensODEand
grenseBet1andgrenseBet2,Var,avhVar)⇒en
bestemt løsning
Returnerer en bestemt løsning som tilfredsstiller
2.ordensODE og har spesifiserte verdier ved to ulike
punkter.
Alfabetisk oversikt 53

54 Alfabetisk oversikt
det() Katalog >
det(kvadratMatrise[,Toleranse])⇒uttrykk
Returnerer determinanten til kvadratMatrise.
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn
Toleranse. Denne toleransen brukes bare hvis
matrisen har elementer med flytende desimalpunkt og
ikke inneholder noen symbolske variabler som ikke er
tildelt noen verdi. Ellers ignoreres Toleranse.
• Hvis du bruker /· eller stiller modusen
Auto eller Tilnærmet på Tilnærmet, utføres
beregningene med flyttallsaritmetikk.
• Hvis Toleranse utelates eller ikke blir brukt,
beregnes standardtoleransen som:
5EM14 ·maks(dim(kvadratMatrise))·
radNorm(kvadratMatrise)
diag() Katalog >
diag(Liste)⇒matrise
diag(radMatrise)⇒matrise
diag(kolonneMatrise)⇒matrise
Returnerer en matrise med verdiene i argumentlisten
eller matrise i hoveddiagonalen.
diag(kvadratMatrise)⇒radMatrise
Returnerer en radmatrise som inneholder elementene
fra hoveddiagonalen til kvadratMatrise.
kvadratMatrise må være kvadrat.
dim() Katalog >
dim(Liste)⇒heltall
Returnerer dimensjonen av Liste.
dim(Matrise)⇒liste
Returnerer matrisens dimensjoner som en to-
elements liste {rader, kolonner}.
dim() Katalog >
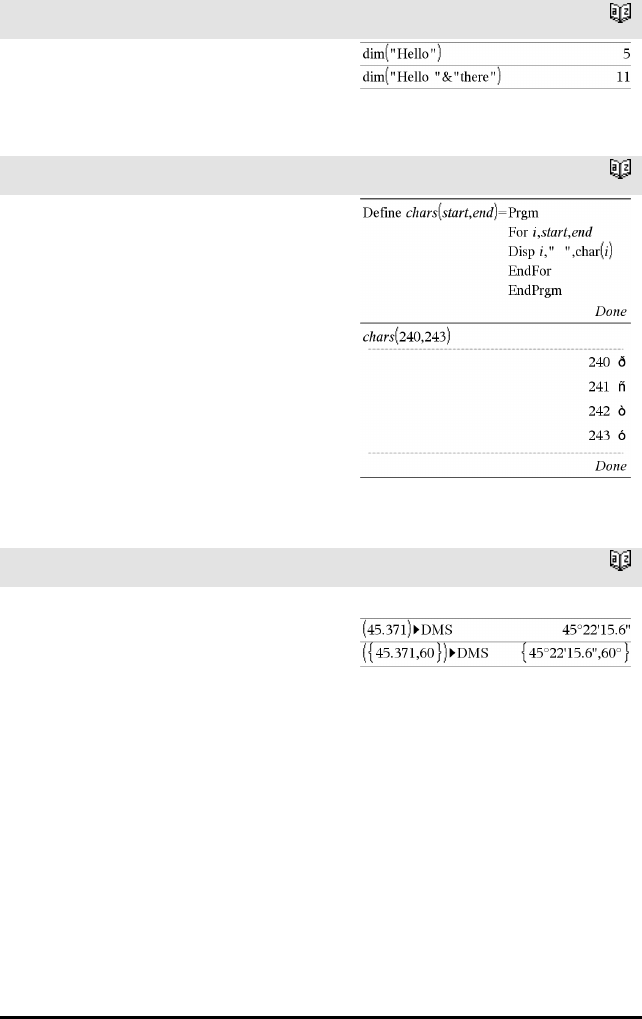
dim(Streng)⇒heltall
Returnerer antallet tegn som er inneholdt i
tegnstrengen Streng.
Disp (Vis) Katalog >
Disp [uttrElStreng1] [,uttrElStreng2] ...
Viser argumentene i Calculator-loggen. Agrumentene
vises suksessivt, med korte avstander som skille.
Hovedsakelig nyttig i programmer og funksjoner for å
sikre visning av mellomregninger.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
4DMS (GMS) Katalog >
Uttr 4DMS
Liste 4DMS
Matrise 4DMS
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>DMS.
Tolker argumentet som en vinkel og viser
ekvivalenten DMS (GGGGGG¡MM ' SS.ss '')-tallet.
Se ¡, ', '' (side 210) for DMS-format (grader, minutter,
sekunder).
Merk: 4DMS vil omregne fra radianer til grader når det
brukes i radian-modus. Hvis inndata blir fulgt av et
grader-symbol ¡, finner det ikke sted noe omregning.
Du kan bare bruke 4DMS på slutten av en
kommandolinje.
I Grader-vinkelmodus:
Alfabetisk oversikt 55

56 Alfabetisk oversikt
domain() (område) Katalog >
domain(Uttr1,Var)⇒uttrykk
Returnerer definisjonsområdet for Uttr1 med hensyn
på Var.
domain() kan brukes til å undersøke
definisjonsområder for funksjoner. Det er begrenset til
ekte og endelig område.
Denne funksjonaliteten har begrensninger grunnet for
svake algebraiske forenklings- og løsningsalgoritmer
på datamaskinen.
Enkelte funksjoner kan ikke brukes som argumenter
for domain(), uavhengig av om de vises eksplisitt eller
i brukerdefinerte variabler og funksjoner. Uttrykket
kan ikke forenkles i det følgende eksemplet, fordi ‰()
er en funksjon som ikke er tillatt.
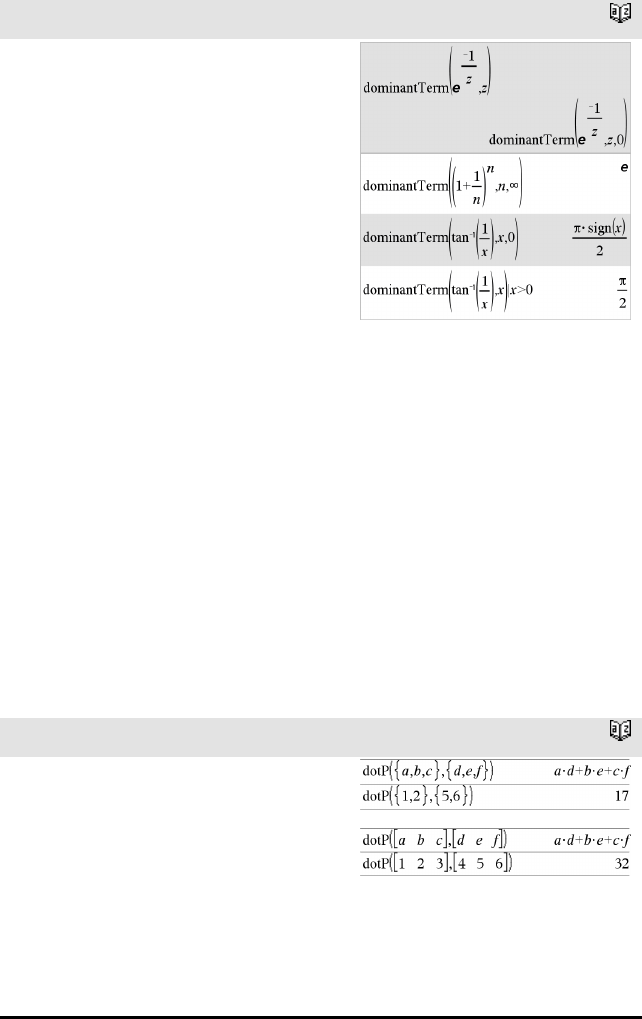
dominantTerm() (dominerende ledd) Katalog >
dominantTerm(Uttr1,Var [,Punkt])⇒uttrykk
dominantTerm(Uttr1,Var [,Punkt]) |
Var>Punkt⇒ uttrykk
dominantTerm(Uttr1,Var [,Punkt]) |
Var<Punkt ⇒uttrykk
Returnerer dominantTerm i en
potensrekkepresentasjon av Uttr1 som er utvidet
rundt Punkt. DominantTerm er det hvis størrelse
vokser raskest i nærheten av Var =Punkt.
Resulterende potens av (Var NPunkt) kan ha en
negativ eksponent og/eller en brøk-eksponent.
Koeffisienten foran denne potensen kan inkludere
logaritmer av (Var NPunkt) og andre funksjoner av
Var som er dominert av alle potensene til (Var N
Point) som har samme eksponenttegn (-sign).
Punkt grunninnstilles til 0. Punkt kan være ˆeller Nˆ,
i så fall vil det dominerende leddet være det leddet
dominantTerm() (dominerende ledd) Katalog >
som har den største eksponenten av Var istedenfor
den minste eksponenten av Var.
dominantTerm(…) returnerer “dominantTerm(…)” hvis
det ikke er i stand til å bestemme en slik
representasjon, som for vesentlige singulærpunkt,
f.eks. sin(1/z)ved z=0, eN1/z ved z=0, eller ezved z =
ˆeller Nˆ.
Dersom rekken eller en av dens deriverte har en
“hopp-diskontinuitet” ved Punkt, er det sannsynlig at
resultatet inneholder deluttrykk av formen tegn(…)
eller abs(…) for en reell utvidelsesvariabel eller (-1)nedre
(…vinkel(…)…) for en sammensatt utvidelsesvariabel, som
er en som ender med “_”. Dersom du vil bruke det
dominerende leddet kun for verdier på en side av
Punkt, så utvider du dominantTerm(...)med det
passende “| Var >Punkt”, “| Var <Punkt”, “| “Var |
Punkt” eller “Var {Punkt” for å oppnå et enklere
resultat.
dominantTerm() fordeler over 1. argument-lister og
matriser.
dominantTerm() er nyttig når du vil vite det enklest
mulige uttrykket som er asymptotisk til et annet
uttrykk som Var "Punkt.dominantTerm() er også
nyttig når det ikke er opplagt hva graden av det første
leddet som ikke er null i en rekke vil bli og du ikke
iterativt vil gjette enten interaktivt eller med en
programmert loop.
Merk: Se også rekke(), side 148.
dotP() (prikkP) Katalog >
dotP(Liste1,Liste2)⇒uttrykk
Returnerer “prikk”produktet av to lister.
dotP(Vektor1,Vektor2)⇒uttrykk
Returnerer “prikk”produktet av to vektorer.
Begge må være radvektorer, eller begge må være
kolonnevektorer.
Alfabetisk oversikt 57

58 Alfabetisk oversikt
E
e^() utast
e^(Uttr1)⇒uttrykk
Returnerer eopphøyd i Uttr1-potens.
Merk: Se også e eksponent-sjablon, side 6.
Merk: Å trykke på ufor å vise e^(er forskjellig fra å
trykke på tegnet Epå tastaturet.
Du kan legge inn et komplekst tall i reiqpolar form.
Men bruk denne formen bare i radian-vinkelmodus;
den forårsaker grunnmengdefeil i grader- eller gradian-
vinkelmodus.
e^(Liste1)⇒liste
Returnerer tallet eopphøyd i potens av hvert element i
Liste1.
e^(kvadratMatrise1)⇒kvadratMatrise
Returnerer kvadratMatrise som er e opphøyd i
kvadratMatrise1. Dette er ikke det samme som å
beregne e opphøyd i potens av hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
eff() Katalog >
eff(nominellRente,CpY)⇒verdi
Finansiell funksjon som omregner den nominelle
renten nominellRente til en årlig effektiv rente, gitt
CpY som antall renteperioder per år.
nominellRente må være et reelt tall, og CpY må være
et reelt tall>0.
Merk: Se også nom(), side 114.
eigVc() (egenvektor) Katalog >
eigVc(kvadratMatrise)⇒matrise
Returnerer en matrise som inneholder egenvektorer
I rektangulært, kompleks format:

eigVc() (egenvektor) Katalog >
for en reell eller kompleks kvadratMatrise, der hver
kolonne i resultatet samsvarer med en egenverdi.
Merk at en egenvektor ikke er entydig; den kan
skaleres av enhver konstant faktor. Egenvektorene er
normalisert, dvs. at if V = [x1, x2, …, xn], then:
x1
2+x2
2+ … +xn
2= 1
kvadratMatrise blir først balansert med
likhetstransformasjoner til normene for rad og kolonne
er så nær den samme verdien som mulig.
KvadratMatrisen blir så redusert til øvre Hessenberg-
form og egenvektorene beregnes via en Schur-
faktorisering.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
eigVl() (egenverdi) Katalog >
eigVl(kvadratMatrise)⇒liste
Returnerer en liste over egenverdiene av en reell eller
kompleks kvadratMatrise.
kvadratMatrise blir først balansert med
likhetstransformasjoner til normene for rad og kolonne
er så nær den samme verdien som mulig.
KvadratMatrisen blir så redusert til øvre Hessenberg-
form og egenverdiene beregnes fra den øvre
Hessenberg-matrisen.
I rektangulær, kompleks format-modus:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Else Se If, side 81.
Alfabetisk oversikt 59
60 Alfabetisk oversikt
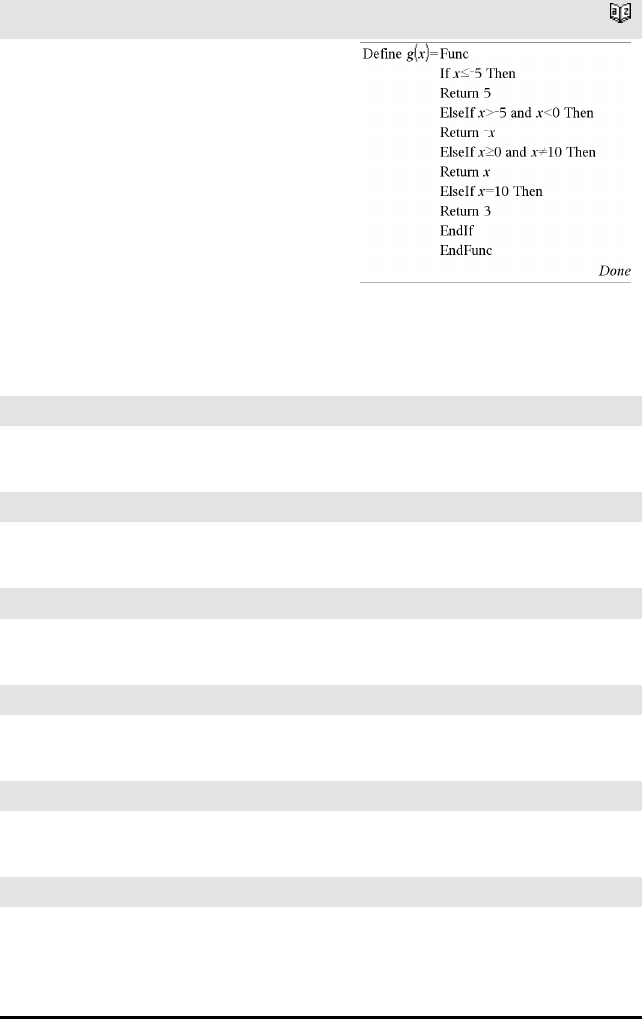
ElseIf Katalog >
IfBoolskUttr1 Then
Blokk1
ElseIf BoolskUttr2 Then
Blokk2
©
ElseIf Boolsk UttrN Then
BlokkN
EndIf
©
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
EndFor Se For, side 71.
EndFunc Se Func, side 74.
EndIf Se If, side 81.
EndLoop Se Loop, side 101.
EndPrgm Se Prgm, side 127.
EndTry Se Try, side 176.

EndWhile Se While, side 185.
euler () Katalog >
euler(Uttr,Var,avhVar,{Var0, VarMaks},avhVar0,
VarTall [,eulersIntervall])⇒matrise
euler(SystemAvUttr,Var,ListeMedAvhVarer,{Var0,
VarMaks},ListeMedAvhVarer0,VarIntervall [,
eulersIntervall])⇒matrise
euler(ListeMedUttr,Var,ListeMedAvhVarer,{Var0,
VarMaks},ListeMedAvhVarer0,VarIntervall [,
eulersIntervall])⇒matrise
Bruker Eulers metode for å løse systemet
med avhVar(Var0)=avhVar0 på intervallet
[Var0,VarMaks]. Returnerer en matrise, hvor den
første raden definerer verdiene i Var -resultatet og
hvor den andre raden definerer verdien av den første
løsningskomponenten ved de tilsvarende Var -
verdiene, og så videre.
Uttr er høyre side, som definerer den ordinære
differensialligningen (ODE).
SystemAvUttr er systemet på høyre side som
definerer systemet av ODE-er (tilsvarer til
rekkefølgen av avhengige variabler i
ListeMedAvhVarer).
ListeMedUttr er en liste på høyre side som definerer
systemet av ODE-er (tilsvarer til rekkefølgen av
avhengige variabler i ListeMedAvhVarer).
Var er den uavhengige variabelen.
ListeMedAvhVarer er en liste over avhengige
variabler.
{Var0,VarMaks} er en liste med to elementer som
forteller funksjonen at den skal integrere fra Var0 til
VarMaks.
ListeMedAvhVarer er en liste over startverdier for
avhengige variabler.
Differensialligning:
y'=0,001*y*(100-y) og y(0)=10
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Sammenlign resultatet over med eksakt løsning i
CAS som ble funnet ved hjelp av deLøs() og sekvGen
():
System av ligninger:
med y1(0)=2 og y2(0)=5
Alfabetisk oversikt 61

62 Alfabetisk oversikt
euler () Katalog >
VarIntervall er et tall som ikke er null, slik at sign
(VarIntervall)=sign(VarMaks-Var0)og løsninger
returneres ved Var0+i·VarIntervall for alle i=0,1,2,…
slik at Var0+i·VarIntervall er i [var0,VarMaks] (det
kan hende at det ikke er noen løsningsverdi ved
VarMaks).
eulersIntervall er et positivt heltall (grunninnstilt på 1)
som definerer antallet euler-intervaller mellom
resultatverdiene. Den faktiske tallstørrelsen som
brukes ved eulers metode, er
VarIntervallàeulersIntervall.
exact() Katalog >
exact(Uttr1 [,Toleranse])⇒uttrykk
exact(Liste1 [,Toleranse])⇒liste
exact(Matrise1 [,Toleranse])⇒matrise
Bruker aritmetisk eksakt-modus til om mulig å
returnere argumentet uttrykt som et rasjonalt tall.
Toleranse spesifiserer toleransen for omregningen.
Standard er 0 (null).
Exit (Avslutt) Katalog >
Exit
Avslutter aktuell For,While, eller Loop-blokk.
Exit er ikke tillatt utenfor de tre løkkestrukturene (For,
While, eller Loop).
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Program:

4exp katalog >
Uttr 4exp
Viser Uttr uttrykt ved det naturlige grunntallet e. Dette
er en konverteringsoperator. Den kan bare brukes på
slutten av kommandolinjen.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>exp.
exp() utast
exp(Uttr1)⇒Uttrykk
Returnerer eopphøyd i Uttr1-potens.
Returnerer eopphøyd i Verdi1-potens.
Merk: Se også eeksponent-sjablon, side 6.
Du kan legge inn et komplekst tall i reiqpolar form.
Men bruk denne formen bare i radian-vinkelmodus;
den forårsaker grunnmengdefeil i grader- eller gradian-
vinkelmodus.
exp(Liste1)⇒liste
Returnerer tallet eopphøyd i potens av hvert element i
Liste1.
exp(kvadratMatrise1)⇒kvadratMatrise
Returnerer kvadratMatrise som er e opphøyd i
kvadratMatrise1. Dette er ikke det samme som å
beregne eopphøyd i potens av hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
exp4list() Katalog >
exp4list(Uttr,Var)⇒liste
UndersøkerUttr for ligninger som er adskilt med ordet
“or,” og returnerer en liste som inneholder de høyre
sidene i ligningen med formen Var=Uttr. Dette gir deg
en enkel måte å trekke ut noen løsningsverdier som er
implementert i resultatene av funksjonene solve
(),cSolve(),fMin() og fMax().
Alfabetisk oversikt 63
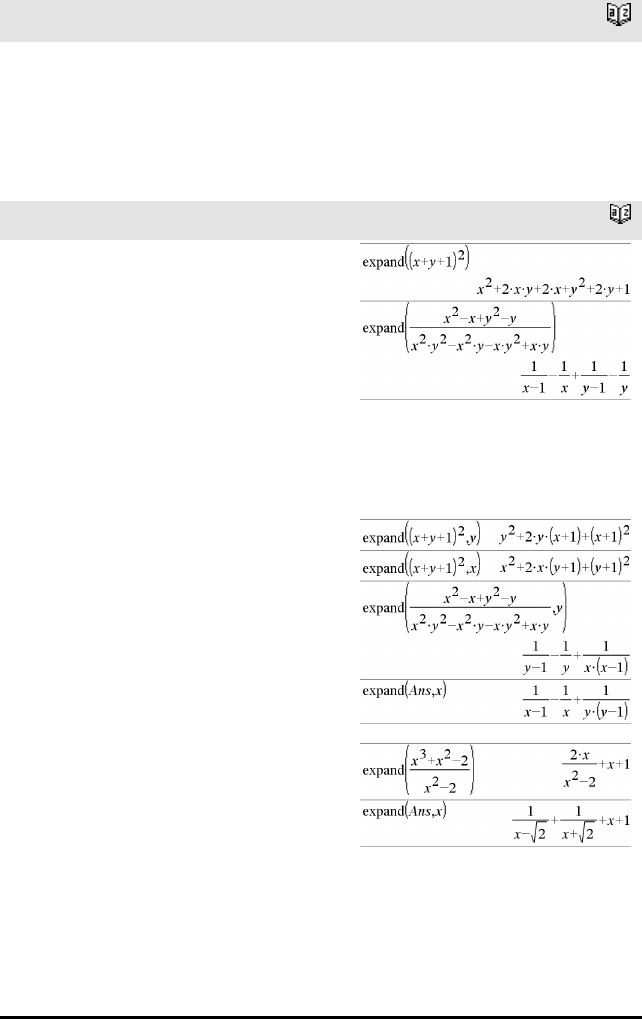
64 Alfabetisk oversikt
exp4list() Katalog >
Merk: exp4list() er ikke nødvendig ved zeros- og
cZeros() -funksjonene, fordi de returnerer en liste av
løsningsverdier direkte.
Du kan sette inn denne funksjonen fra tastaturet ved
å skrive exp@>list(...).
expand() (utvid) Katalog >
expand(Uttr1 [,Var])⇒uttrykk
expand(Liste1 [,Var])⇒liste
expand(Matrise1 [,Var])⇒matrise
expand(Uttr1)returnerer Uttr1 utvidet med hensyn på
alle variablene. Utvidelsen er polynomisk utvidelse for
polynomer og delbrøkoppspalting for rasjonale
uttrykk.
Hensikten med expand() er å omforme Uttr1 til en
sum og/eller differanse av enkle ledd. Derimot er
hensikten med factor() å omforme Uttr1 til et produkt
og/eller koeffisient av enkle faktorer.
expand(Uttr1,Var)returnerer Uttr1 utvidet med
hensyn på Var. Liknende potenser av Var er samlet
sammen. Leddene og faktorene deres er sortert med
Var som hovedvariabel. Det kan forekomme
faktoriseringer eller utvidelser av innsamlede
koeffisienter. Sammenliknet med å utelate Var sparer
dette ofte tid samt plass både i minnet og på
skjermen, samtidig som uttrykket blir mer forståelig.
Hvis du bruker Var, kan dette gjøre faktoriseringen av
nevneren som brukes for å spalte en delbrøk mer
fullstendig, selv om det bare er èn variabel.
Tips: For rasjonale uttrykk er propFrac() et raskere,
men mindre ekstremt alternativ til expand().
Merk: Se også comDenom() for en utvidet teller over
en utvidet nevner.

expand() (utvid) Katalog >
expand(Uttr1,[Var])oppløser også logaritmer og
brøkpotenser uavhengig av Var. For økt oppløsning i
logaritmer og brøkpotenser kan ulikhetsbegrensninger
være nødvendige for å garantere at noen av faktorene
er ikke-negative.
expand(Uttr1, [Var])oppløser også absoluttverdier,
sign() og eksponenter, uavhengig av Var.
Merk: Se også tExpand() for trigonometrisk vinkelsum
og flervinklet utvidelse.
expr() (uttrykk) Katalog >
expr (String)⇒Uttrykk
Returnerer tegnstrengen som ligger i Streng som et
uttrykk og utfører den straks.
ExpReg Katalog >
ExpReg X, Y [,[Frekv] [, Kategori, Inkluder]]
Finner den eksponensielle regresjoneny = a·(b)xfor listene Xog
Ymed frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall|0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
Alfabetisk oversikt 65
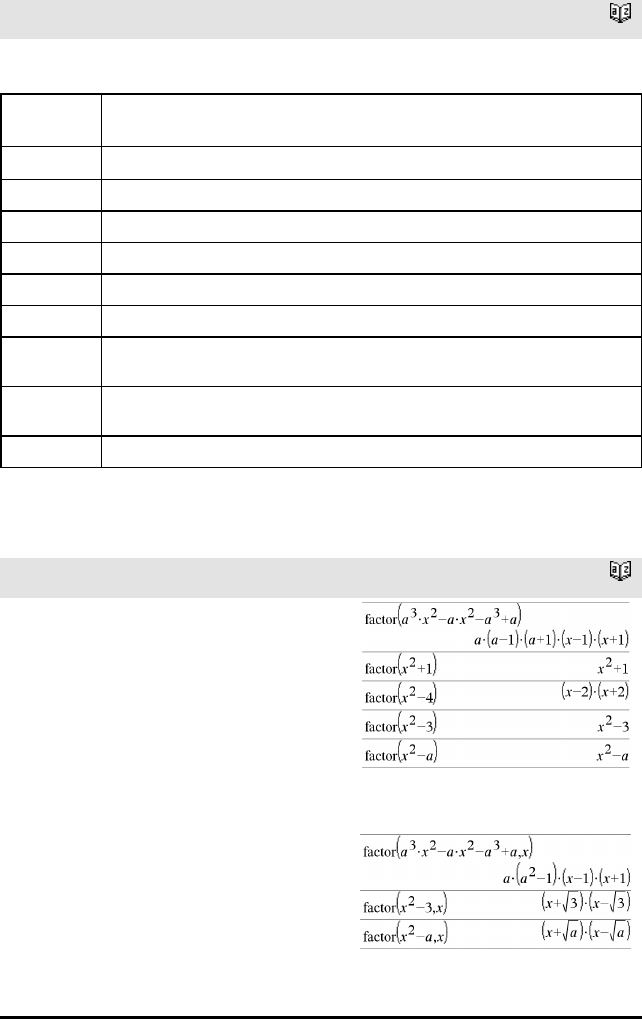
66 Alfabetisk oversikt
ExpReg Katalog >
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a·(b)x
stat.a, stat.b Regresjonskoeffisienter
stat.r2Lineær determinasjonskoeffisient for transformerte data
stat.r Korrelasjonskoeffisient for transformerte data (x, ln(y))
stat.Resid Residualene for den eksponensielle modellen
stat.ResidTrans Rester tilordnet ved lineær tilpasning av transformerte data
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste, og Inkludert kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og inkludert kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
F
factor() (faktor) Katalog >
factor(Uttr1[,Var])⇒Uttrykk
factor(Liste1[,Var])⇒liste
factor(Matrise1[,Var])⇒matrise
factor(Uttr1)returnerer Uttr1 faktorisert med hensyn
på alle dens variabler over en felles nevner.
Uttr1 er faktorisert så mye som mulig i lineære
rasjonale faktorer uten å innføre nye, ikke-reelle
deluttrykk. Med dette alternativet kan du faktorisere
med hensyn på mer enn en variabel.
factor(Uttr1,Var)returnerer Uttr1 faktorisert med
hensyn på variabel Var.
Uttr1 er faktorisert så mye som mulig mot reelle
faktorer som er lineære i Var, selv om det innfører
irrasjonale konstanter eller deluttrykk som er
irrasjonelle i andre variabler.

factor() (faktor) Katalog >
Faktorene og leddene deres er sortert med Var som
hovedvariabel. Liknende potenser av Var er samlet
sammen i hver faktor. Inkluder Var hvis du må
faktorisere med hensyn på bare den ene variabelen og
du er villig til å akseptere irrasjonale uttrykk i en annen
tilfeldig variabel for å øke faktoriseringen med hensyn
på Var. Det kan hende at faktor bestemmes tilfeldig
med hensyn på andre variabler.
For automatisk innstilling av modusen Auto eller
Tilnærmet, vil en inkludering av Var også gjøre det
mulig å tilnærme med flytende desimalpunkt-
koeffisienter der hvor irrasjonelle koeffisienter ikke
kan uttrykkes eksplisitt utfra innebygde funksjoner.
Selv dersom det bare er én variabel, vil man kunne
oppnå en mer komplett faktorisering ved å inkludere
Var.
Merk: Se også comDenom() for en rask måte å oppnå
delvis faktorisering på, hvis factor() er for langsom
eller hvis den tar for stor plass i minnet.
Merk: Se også cFactor() for å faktorisere overalt med
komplekse koeffisienter i letingen etter lineære
faktorer.
factor(rasjonaltTall)returnerer det rasjonale tallet
faktorisert i primtall. For sammensatte tall øker
behandlingstiden eksponensielt med antallet siffer i
den nest største faktoren. For eksempel kan det ta
mer enn en hel dag å faktorisere et heltall med 30
siffer, og å faktorisere et tall med 100 siffer kan ta mer
enn et århundre.
Slik stopper du en beregning manuelt,
•Grafregner: Hold nede tasten c, og trykk på
·flere ganger.
•Windows®: Hold nede tasten F12, og trykk på
Enter flere ganger.
•Macintosh®: Hold nede tasten F5, og trykk på
Enter flere ganger.
•iPad®: Applikasjonen viser en ledetekst. Du
kan fotsette å vente, eller avbryte.
Hvis du bare vil bestemme om et tall er et primtall,
Alfabetisk oversikt 67
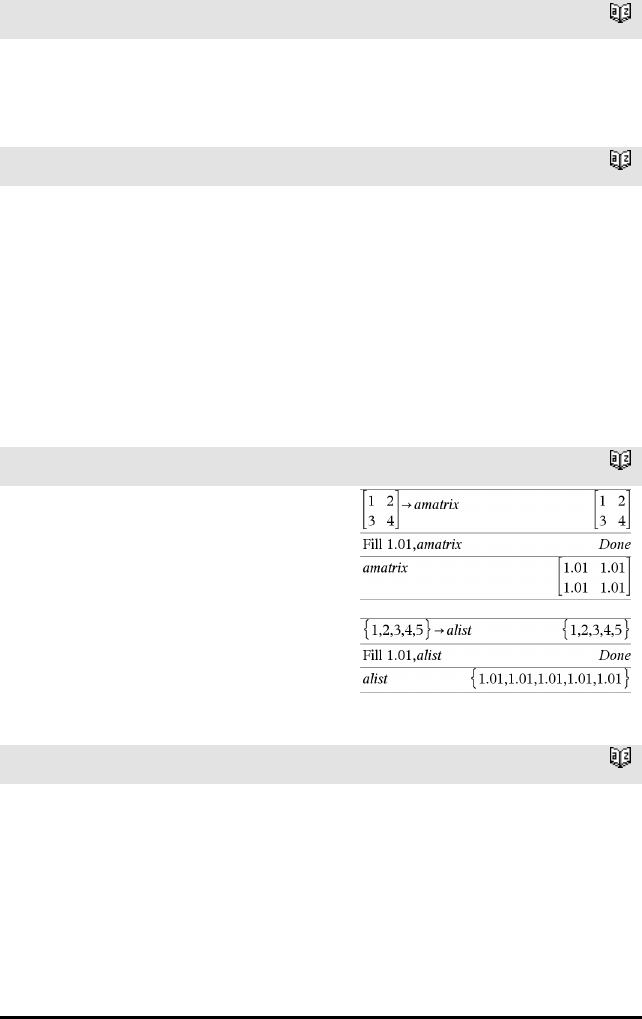
68 Alfabetisk oversikt
factor() (faktor) Katalog >
bruk isPrime() istedenfor. Det er mye raskere, særlig
hvis rasjonaltTall ikke er et primtall og hvis den nest
største faktoren består av mer enn fem siffer.
FCdf() Katalog >
FCdf(nedGrense,øvGrense,dfTeller,dfNevner)⇒tall hvis
nedGrens og øvGrens er tall, liste hvis nedGrens og øvGrens er
lister
FCdf(nedGrense,øvGrense,dfTeller,dfNevner)⇒tall hvis
nedGrens og øvGrens er tall, liste hvis nedGrens og øvGrens er
lister
Beregner Ffordelingssannsynligheten mellom nedGrense og
øvGrense for spesifisert dfTeller (frihetsgrader) og dfNevner.
For P(X{øvGrens), set nedGrens = 0.
Fill (Fyll) Katalog >
Fill Uttr, matriseVar ⇒matrise
Erstatter hvert element i variabel matriseVar med
Uttr.
matriseVar må eksistere allerede.
Fill Uttr, listeVar⇒liste
Erstatter hvert element i variabel listeVar med Uttr.
listeVar må eksistere allerede.
FiveNumSummary katalog >
FiveNumSummary X[,[Frekv][,Kategori,Inkluder]]
Gir en forkortet versjon av den 1-variabels statistiske
observatoren på listen X. Enoversikt over resultatene lagres i
stat.resultater-variabelen (side 162.)
Xrepresenterer en liste med dataene.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hver korresponderende X-verdi

FiveNumSummary katalog >
forekommer. Standardverdien er 1. Alle elementene må være
heltall 0.
Kategori er en liste over kategorikoder for de tilsvarende X-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
Et tomt (åpent) element i enhver av listene X,Frekv eller
Kategori resulterer i et åpent element for det tilsvarende
elementet til alle disse listene. For mer informasjon om tomme
elementer, se side 217.
Utdata-variabel Beskrivelse
stat.MinX Minimum av x-verdiene
stat.Q 1X Første kvartil av x
stat.MedianX Medianen av x
stat.Q 3X Tredje kvartil av x
stat.MaxX Maksimum av x-verdiene
floor() (nedre) Katalog >
floor(Uttr1)⇒heltall
Returnerer det største heltallet som er {argumentet.
Dennefunksjonen er identisk med int().
Argumentet kan være et reelt eller et komplekst tall.
floor(Liste1)⇒liste
floor(Matrise1)⇒matrise
Returnerer en liste eller matrise med nedre verdi for
hvert element.
Merk: Se også ceiling() og int().
Alfabetisk oversikt 69
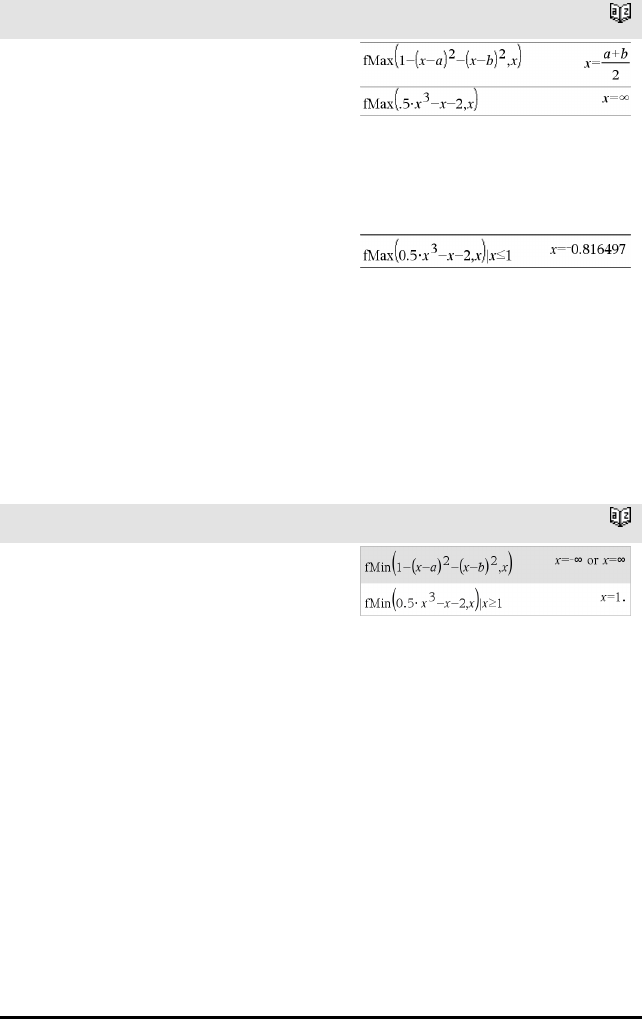
70 Alfabetisk oversikt
fMax() Katalog >
fMax(Uttr, Var)⇒Boolsk uttrykk
fMax(Uttr,Var,nedGrense)
fMax(Uttr,Var,nedGrense,øvGrense)
fMax(Uttr,Var) | nedGrense{Var{øvGrense
Returnerer et Boolsk uttrykk som spesifiserer
alternativverdier av Var som maksimerer Uttr eller
lokaliserer den minste øvre grensen.
Du kan bruke (“|”)-operatoren for å begrense
løsningsintervallene og/eller spesifisere
begrensninger.
For Tilnærmet innstilling av modusen Auto eller
Tilnærmet søker fMax() iterativt etter tilnærmet lokalt
maksimum. Dette er ofte raskere, særlig hvis du
bruker “|” operatoren for å begrense søket til et relativt
lite intervall som inneholder eksakt ett lokalt
maksimum.
Merk: Se også fMin() og max().
fMin() Katalog >
fMin(Uttr, Var)⇒Boolsk uttrykk
fMin(Uttr,Var,nedGrense)
fMin(Uttr,Var,nedGrense,øvGrense)
fMin(Uttr,Var) | nedGrense{Var{øvGrense
Returnerer et Boolsk uttrykk som spesifiserer
alternativverdier av Var som minimerer Uttr eller
lokaliserer den største nedre grensen.
Du kan bruke (“|”)-operatoren for å begrense
løsningsintervallene og/eller spesifisere
begrensninger.
For Tilnærmet innstilling av modusen Auto eller
Tilnærmet, søker fMin() iterativt etter tilnærmet lokalt
minimum. Dette er ofte raskere, særlig hvis du bruker
“|” operatoren for å begrense søket til et relativt lite
intervall som inneholder eksakt ett lokalt minimum.
Merk: Se også fMax() og min().
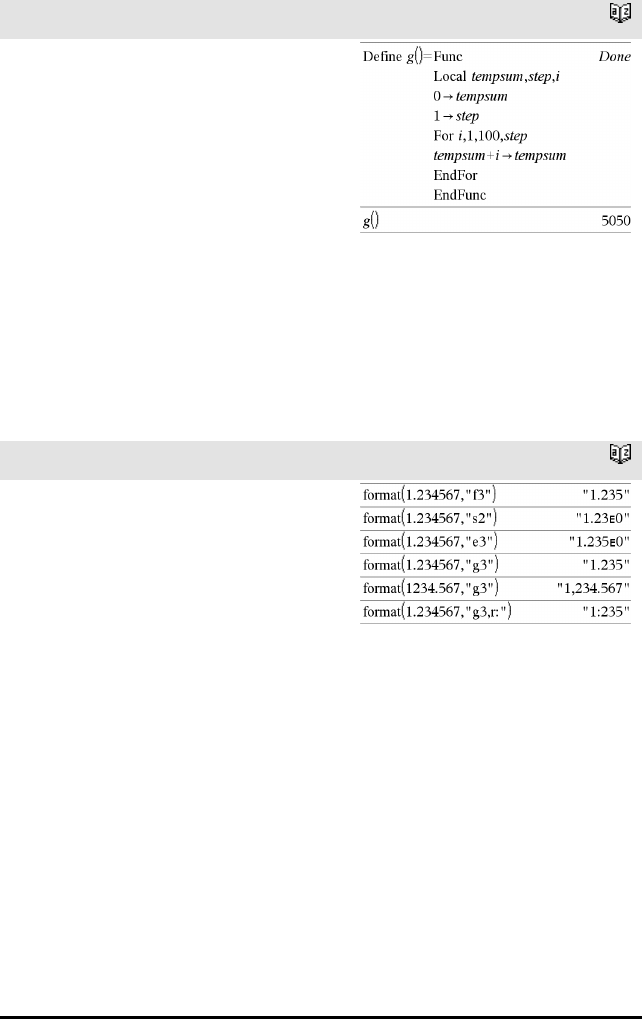
For Katalog >
For Var,Lav,Høy [,Intervall]
Blokk
EndFor
Utfører utsagnene i Blokk iterativt for hver verdi av
Var, fra Lav til Høy, i trinn på Intervall.
Var må ikke være en systemvariabel.
Intervall kan være positiv eller negativ. Grunnverdien
er 1.
Blokk kan enten være et enkelt utsagn eller en
sekvens av utsagn som er adskilt med tegnet “:”.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
format() Katalog >
format(Uttr[, formatStreng])⇒streng
Returnerer uttrykk som en tegnstreng basert på
formatsjablonen.
Uttrykket må forenkles til et tall.
formatStreng er en streng og må være av formen: “F
[n]”, “S[n]”, “E[n]”, “G[n][c]”, hvor [] viser alternative
muligheter.
F[n]: Fast format. n er antallet siffer som vises etter
desimalpunktet.
V[n]: Vitenskapelig format. n er antallet siffer som
vises etter desimalpunktet.
T[n]: Teknisk format. n er antallet siffer etter det
første signifikante sifferet. Eksponenten er tilpasset
til et multiplum av tre, og desimalpunktet er flyttet til
høyre med sifrene null, ett eller to.
G[n][c]: Samme som fast format, men skiller også
sifrene til venstre for basen i grupper på tre. c
spesifiserer gruppens og basens skilletegn som et
komma. Hvis c er en periode, vises basen som et
komma.
Alfabetisk oversikt 71

72 Alfabetisk oversikt
format() Katalog >
[Rk]: Som etterledd bak noen av spesifikantene over
kan basemerket Rc tilføyes, der hvor c er et enkelt
tegn som spesifiserer hva som erstatter komma.
fPart() (funksjonsdel) Katalog >
fPart(Uttr1)⇒uttrykk
fPart(Liste1)⇒liste
fPart(Matrise1)⇒matrise
Returnerer brøk-delen i argumentet.
For en liste eller matrise, returneres brøk-delene i
elementene.
Argumentet kan være et reelt eller et komplekst tall.
FPdf() Katalog >
FPdf(XVerdi,dfTeller,dfNevner)⇒tall hvis XVerdi er et tall,
liste hvis XVerdi er en liste
FPdf(XVerdi,dfTeller,dfNevner)⇒tall hvis XVerdi er et tall,
liste hvis XVerdi er en liste
Beregner Ffordelingssannsynligheten mellom XVerdi for den
spesifiserte dfTeller (grader av frihet) og dfNevner.
freqTable4liste() katalog >
freqTable4liste(Liste1,frekvHeltallListe)⇒liste
Returnerer en liste som inneholder elementene fra
Liste1 utvidet i henhold til frekvensene i
frekvHeltallListe. Denne funksjonen kan brukes til å
generere en frekvenstabell for applikasjonen Data og
statistikk.
Liste1 kan være enhver gyldig liste.
frekvHeltallListe må ha samme dimensjon som
Liste1 og kun inneholde ikke-negative
heltallselementer. Hvert element angir hvor mange
ganger det korresponderende Liste1-elementet skal
gjentas i resultatlisten. En verdi lik null utelater det
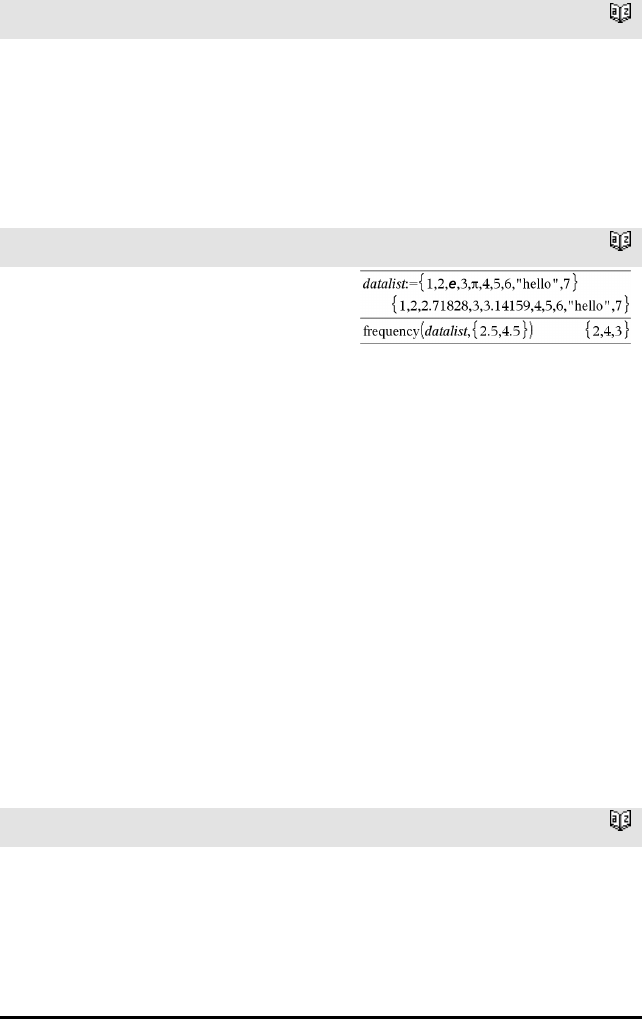
freqTable4liste() katalog >
korresponderende Liste1-elementet.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive
freqTable@>list(...).
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.
frequency() (frekvens) Katalog >
frequency(Liste1,stolperListe)⇒liste
Returnerer en liste som inneholder antallet elementer i
Liste1. Antallet er basert på områder (stolper) som du
definerer i stolperListe.
Hvis stolperListe er {b(1), b(2), …, b(n)}, er de
spesifiserte områdene {?{b(1), b(1)<?{b(2),…,b(n-1)
<?{b(n), b(n)>?}. Den resulterende listen er ett
element lenger enn stolperListe.
Hvert element av resultatet samsvarer med antallet
elementer fra Liste1 som er i området for den stolpen.
Uttrykt med begrep fra countIf()-funksjonen er
resultatet {countIf(liste, ?{b(1)), countIf(liste, b(1)<?
{b(2)), …, countIf(liste, b(n-1)<?{b(n)), countIf(liste, b
(n)>?)}.
Elementer fra Liste1 som ikke kan “plasseres i en
stolpe” ignoreres. Tomme (åpne) elementer ignoreres
også. For mer informasjon om tomme elementer, se
side 217.
I applikasjonen Lister og regneark kan du bruke et
celleområde istedenfor begge arumentene.
Merk: Se også countIf(), side 38.
Forklaring til resultat:
2elementer fra Dataliste er {2,5
4elementer fra Dataliste er >2,5 og {4,5
3elementer fra Dataliste er >4,5
Elementet “hallo” er en streng og kan ikke plasseres i
nopen av de definerte stolpene.
FTest_2Samp (2_utvalg F test) Katalog >
FTest_2SampListe1,Liste2[,Frekv1[,Frekv2[,Hypot]]]
FTest_2Samp Liste1,Liste2[,Frekv1[,Frekv2[,Hypot]]]
(Dataliste inndata)
FTest_2Samp sx1,n1,sx2,n2[,Hypot]
Alfabetisk oversikt 73

74 Alfabetisk oversikt
FTest_2Samp (2_utvalg F test) Katalog >
FTest_2Samp sx1,n1,sx2,n2[,Hypot]
(Summering statistikk inndata)
Utfører en to-utvalgs Ftest. En oversikt over resultatene lagres i
stat.results-variabelen (side 162).
eller Ha:s1 > s2, sett Hypoth>0
For Ha:s1ƒ s2 (standard), sett Hypoth =0
For Ha:s1 < s2, sett Hypoth<0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” på side 217.
Utdata-variabel Beskrivelse
stat.FBeregnet Û -statistikk for datasekvensen
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.dfNumer frihetsgrad for teller = n1-1
stat.dfDenom frihetsgrad for nevner = n2-1
stat.sx1, stat.sx2 Utvalgets standardavvik til datasekvenser i Liste1 og Liste2
stat.x1_bar
stat.x2_bar
Utvalgets gjennomsnitt av datasekvenser i Liste1 og Liste2
stat.n1, stat.n2 Utvalgenes størrelse
Func (Funk) Katalog >
Func
Blokk
EndFunc
Sjablon for oppretting av brukerdefinert funksjon.
Blokk kan være ett enkelt utsagn, en rekke utsagn
adskilt med “:”-tegnet, eller en rekke med utsagn på
separate linjer. Funksjonen kan bruke Returner-
kommandoen for å returnere et spesifikt resultat.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Definere en sammensatt funksjon:
Resultat av grafisk fremstilling g(x)

Func (Funk) Katalog >
G
gcd() (største felles divisor) Katalog >
gcd(Tall1, Tall2)⇒uttrykk
Returnerer største felles divisor for de to
argumentene. gcd av to brøker er gcd av tellerne
dividert med lcm av nevnerne.
I modusen Auto eller Tilnærmet er gcd av brøkens
flytende desimalpunkttall 1,0.
gcd(Liste1, Liste2)⇒liste
Returnerer største felles divisorer av samsvarende
deler i Liste1 og Liste2.
gcd(Matrise1, Matrise2)⇒matrise
Returnerer største felles divisorer av samsvarende
deler i Matrise1og Matrise2.
geomCdf() Katalog >
geomCdf(p,nedreGrense,øvreGrense)⇒tall hvis nedreGrense
og øvreGrense er tall, liste hvis nedreGrense og øvreGrense er
lister
geomCdf(p,øvreGrense)for P(1{X{øvreGrense)⇒tall hvis
øvreGrense er et tall, liste hvis øvreGrense er en liste
Beregner en kumulativ geometrisk sannsynlighet fra
nedreGrense til øvreGrense med den spesifiserte
sannsynligheten for suksess p.
For P(X {øvreGrense), sett nedreGrense = 1.
Alfabetisk oversikt 75

76 Alfabetisk oversikt
geomPdf() Katalog >
geomPdf(p,XVerdi)⇒tall hvis XVerdi er et tall, liste hvis XVerdi
er en liste
Beregner en sannsynlighet ved XVerdi, antall forsøk før første
suksess inntreffer, for diskret geometrisk fordeling med
spesifisert suksess-sannsynligheten p.
getDenom() (lesNevner) Katalog >
getDenom(Uttr1)⇒uttrykk
Omformer argumentet inn til et uttrykk som har en
redusert felles nevner og returnerer så uttrykkets
nevner.
getLangInfo() katalog >
getLangInfo()⇒streng
Returnerer en streng som svarer til kortnavnet på det
aktive språket. Du kan for eksempel bruke den i et
program eller en funksjon for å finne aktivt språk.
Engelsk = “en”
Dansk = “da”
Tysk = “de”
Finsk = “fi”
Fransk = “fr”
Italiensk = “it”
Nederlandsk = “nl”
Belgisk nederlandsk = “nl_BE”
Norsk = “no”
Portugisisk = “pt”
Spansk = “es”
Svensk = “sv”
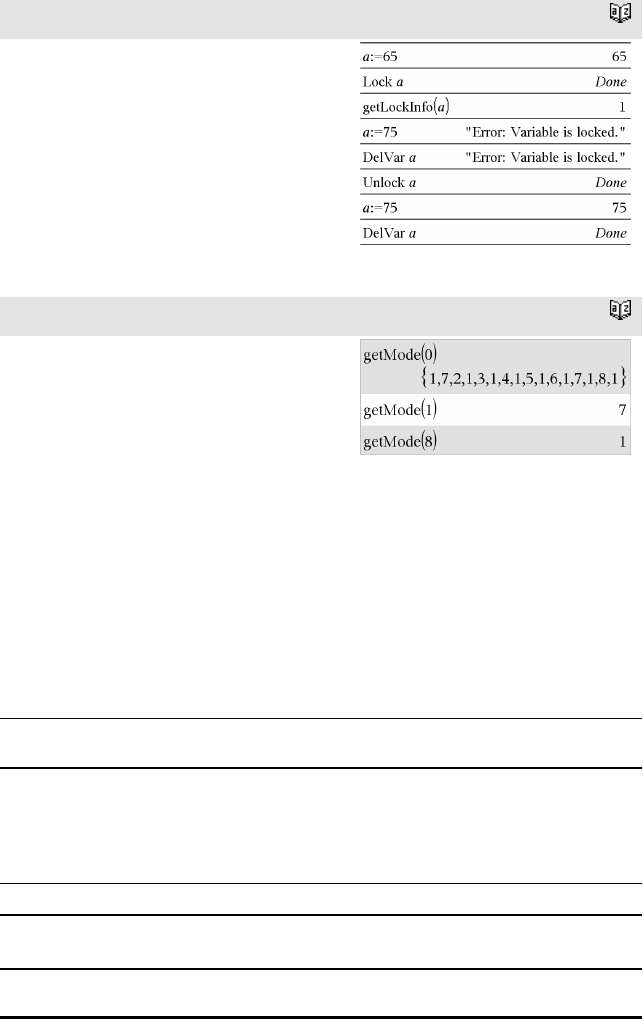
getLockInfo() Katalog >
getLockInfo(Var)⇒verdi
Returnerer aktuell låst/opplåst status for variabel Var.
verdi =0:Var er låst opp eller eksisterer ikke.
verdi =1:Var er låst opp og kan ikke modifiseres eller
slettes.
Se Lock, side 98, og unLock, side 182.
GetMode() (lesModus) Katalog >
GetMode(ModusNavnHeltall)⇒verdi
GetMode(0)⇒liste
GetMode(ModusNavnHeltall)returnerer en verdi
som representerer aktuell innstilling av
ModusNavnHeltall-modus.
GetMode(0) returnerer en liste som inneholder tallpar.
Hvert par består av et modusheltall og et
innstillingsheltall.
For en opplisting av modusene og deres innstillinger,
referer til tabellen under.
Hvis du lagrer innstillingene med GetMode(0) &var,
kan du bruke GetMode(var)i en funksjon eller et
program for midlertidig å gjenopprette innstillingene
kun innenfor utføringen av funksjonen eller
programmet. Se GetMode(), side 149.
Modus Navn Modus
Heltall
Innstille heltall
Vis sifre 1 1=Flytende, 2=Flytende1, 3=Flytende2, 4=Flytende3, 5=Flytende4,
6=Flytende5, 7=Flytende6, 8=Flytende7, 9=Flytende8, 10=Flytende9,
11=Flytende10, 12=Flytende11, 13=Flytende12, 14=Fast0, 15=Fast1,
16=Fast2, 17=Fast3, 18=Fast4, 19=Fast5, 20=Fast6, 21=Fast7,
22=Fast8, 23=Fast9, 24=Fast10, 25=Fast11, 26=Fast12
Vinkel 2 1=Radian, 2=Grader, 3=Gradian
Eksponensielt
format
31=Normal, 2=Vitenskapelig, 3=Teknisk
Alfabetisk oversikt 77
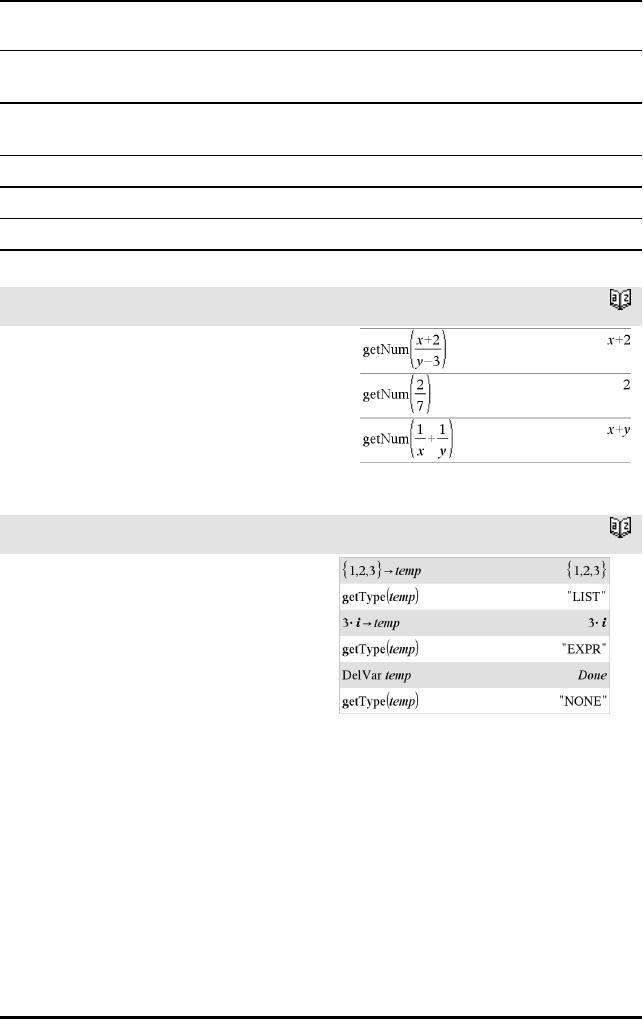
78 Alfabetisk oversikt
Modus Navn Modus
Heltall
Innstille heltall
Reell eller
kompleks
41=Reell, 2=Rektangulær, 3=Polar
Auto eller
tilnærm.
51=Auto, 2=Tilnærmet, 3=Eksakt
Vektorformat 6 1=Rektangulær, 2=Sylindrisk, 3=Sfærisk
Grunntall 7 1=Desimal, 2=Heks, 3=Binær
Måleenheter 8 1=SI, 2=Eng/USA
getNum() (lesTeller) Katalog >
getNum(Uttr1)⇒uttrykk
Omformert argumentet til et uttrykk som har en
redusert felles nevner og returnerer så uttrykkets
teller.
getType() Katalog >
getType(var)⇒streng
Returnerer en streng som angir dataens
typevariabel var.
Hvis var ikke er definert, returnerer strengen
"INGEN".

getVarInfo() katalog >
getVarInfo()⇒matrise eller streng
getVarInfo(BibliotekNavnStreng)⇒matrise eller
streng
getVarInfo() returnerer en matrise med informasjon
(variabelnavn, type, bibliotektilgjengelighet og
låst/opplåst status) for alle variabler og
biblioteksobjekter som er definert i den aktuelle
oppgaven.
Hvis ingen variabler er definert, returnerer getVarInfo
() strengen "INGEN".
getVarInfo(BibliotekNavnStreng)returnerer en
matrise med informasjon for alle bibliotekobjektene
som er definert i biblioteket BibliotekNavnStreng.
BibliotekNavnStreng må være en streng (tekst
omsluttet av anførselstegn) eller en strengvariabel.
Hvis biblioteket BibliotekNavnStreng ikke finnes,
oppstår det en feil.
Se for eksempel til venstre, der resultatet av
getVarInfo() tilordnes variabelen vs. Hvis du forsøker
å vise rad 2 eller 3 av vs, returneres en “Ugyldig liste
eller matrise”-feil, siden minst ett av elementene i de
radene (for eksempel variabel b) reevalueres til en
matrise.
Denne feilen kan også oppstå når du bruker Ans til å
reevaluere et getVarInfo()-resultat.
Systemet viser ovenstående feil fordi den gjeldende
versjonen av programvaren ikke støtter en
generalisert matrisestruktur der et element kan være
enten en matrise eller en liste.
Alfabetisk oversikt 79
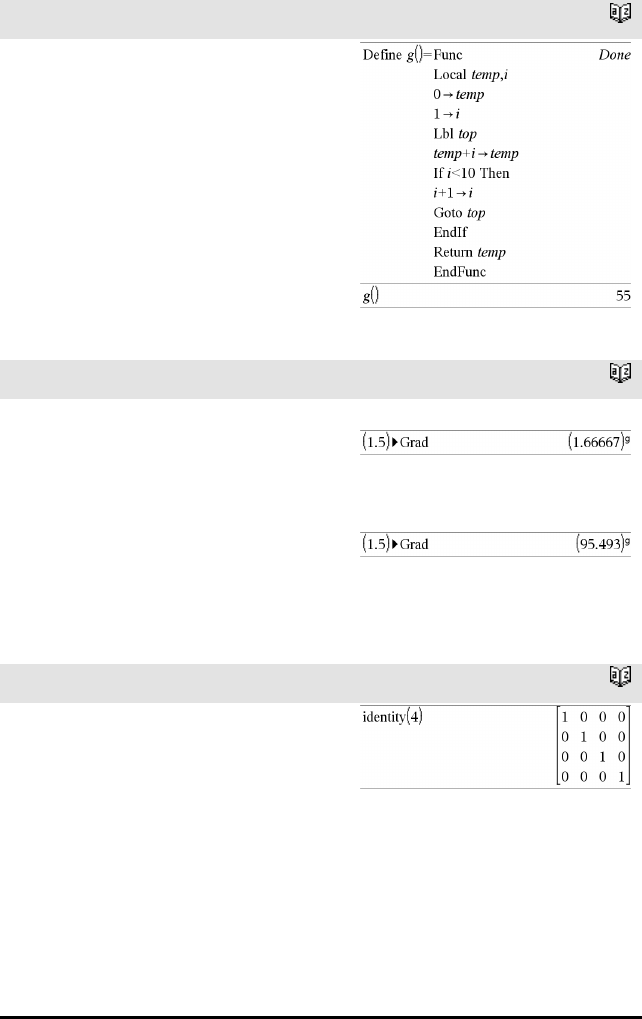
80 Alfabetisk oversikt
Goto (Gåtil) Katalog >
Goto etikettNavn
Overfører kontroll til navnet etikettNavn.
etikettNavn må være definert i samme funksjon med
en Lbl-instruksjon.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
4Grad Katalog >
Uttr1 4Grad ⇒Uttrykk
Omregner Uttr1 til gradian vinkelmåling.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Grad.
I Grader-vinkelmodus:
I Radian-vinkelmodus:
I
identity() (identitetsmatrise) Katalog >
identity(Heltall)⇒matrise
Returnerer identitetsmatrisen med dimensjonen
Heltall.
Heltallet må være et positivt heltall.

If Katalog >
If Boolsk uttrykk
Utsagn
If Boolsk uttrykk Then
Blokk
EndIf
Hvis Boolsk uttrykk behandles som sann, utføres det
enkle utsagnet Utsagn eller blokken av utsagn Blokk
før utførelsen fortsetter.
Hvis Boolsk uttrykk behandles som usann, fortsettes
utførelsen uten å utføre utsagnet eller blokken av
utsagn.
Blokk kan enten være et enkelt utsagn eller en
sekvens av utsagn som er adskilt med tegnet.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
If Boolsk uttrykk Then
Blokk1
Else
Blokk2
EndIf
Hvis Boolsk uttrykk behandles som sann, utføres
Blokk1 og utelater så Blokk2.
Hvis Boolsk uttrykk behandles som usann, utelates
Blokk1 men utfører Blokk2.
Blokk1 og Blokk2 kan være et enkelt utsagn.
Alfabetisk oversikt 81
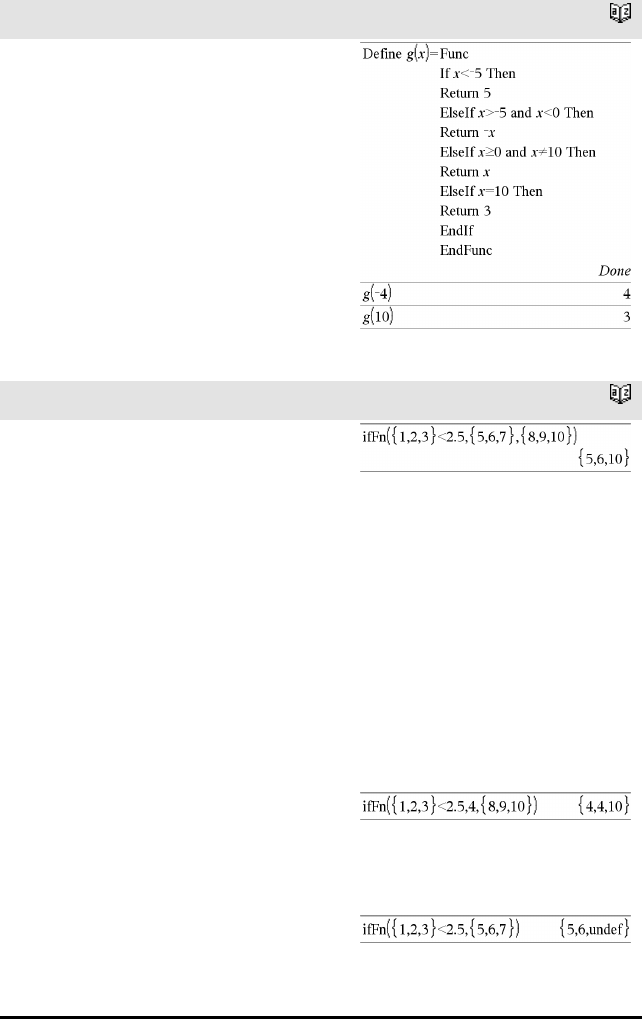
82 Alfabetisk oversikt
If Katalog >
If BoolskUttr1Then
Blokk1
ElseIfBoolskUttr2 Then
Blokk2
©
ElseIfBoolsk uttrykkN Then
BlokkN
EndIf
Tillater forgreining. Hvis BoolskUttr1 behandles som
sann, utføres Blokk1. Hvis BoolskUttr1 behandles
som usann, utføres BoolskUttr2, osv.
ifFn() Katalog >
ifFn(BoolskUttr,Verdi_Hvis_sann [,Verdi_Hvis_
usann [,Verdi_Hvis_ukjent]])⇒uttrykk, liste eller
matrise
Behandler det boolske uttrykket BoolskUttr (eller
hvert element fra BoolskUttr) og produserer et
resultat basert på følgende regler:
•BoolskUttr kan teste en enkelt verdi, en liste
eller en matrise.
• Hvis et element i BoolskUttr behandles som
sant, returneres det tilsvarende elementet fra
Verdi_Hvis_sann.
• Hvis et element i BoolskUttr behandles som
usant, returneres det tilsvarende elementet fra
Verdi_Hvis_usann. Hvis du utelater Verdi_
Hvis_usann, returneres udef.
• Hvis et element i BoolskUttr verken er sant
eller usant, returneres det tilsvarende elementet
Verdi_Hvis_ukjent. Hvis du utelater Verdi_
Hvis_ukjent, returneres udef.
• Hvis det andre, tredje eller fjerde argumentet i
ifFn()-funksjonen et et enkelt uttrykk, brukes
det boolske uttrykket i hver posisjon i
BoolskUttr.
Merk: Hvis det forenklede utsagnet BoolskUttr
involverer en liste eller matrise, må alle andre liste-
Testverdi av 1er mindre enn 2,5, så dens tilsvarende
Verdi_Hvis_Sann-element av 5kopieres til
resultatlisten.
Testverdi av 2er mindre enn 2,5, så dens tilsvarende
Verdi_Hvis_Sann-element av 6kopieres til
resultatlisten.
Testverdi av 3er ikke mindre enn 2,5, så dens
tilsvarende Verdi_Hvis_Usann-element av 10
kopieres til resultatlisten.
Verdi_Hvis_sann er en enkelt verdi og korresponderer
med enhver valgt posisjon.

ifFn() Katalog >
eller matriseargumenter ha de(n) samme
dimensjonen(e), og resultatet vil ha de(n) samme
dimensjonen(e).
Verdi_Hvis_usann er ikke spesifisert. Udef er brukt.
Et element som er valgt fra Verdi_Hvis_sann. Et
element som er valgt fra Verdi_Hvis_ukjent.
imag() (imaginær del) Katalog >
imag(Uttr1)⇒Uttrykk
Returnerer den imaginære delen av argumentet.
Merk: Alle ubestemte variabler behandles som reelle
variabler. Se også real(), side 135
imag(Liste1)⇒liste
Returnerer en liste av de imaginære delene i
elementene.
imag(Matrise1)⇒matrise
Returnerer en matrise over de imaginære delene i
elementene.
impDif() (implisitt derivert) Katalog >
impDif(Ligning,Var,avhengVar[,Ord])⇒uttrykk
der orden Ord har standardverdien 1.
Beregner den implisitte deriverte for ligninger som
inneholder en variabel som er definert implisitt med
hensyn på en annen.
Indirection (Omregning) Se |, side 208.
Alfabetisk oversikt 83

84 Alfabetisk oversikt
inString() (iStreng) Katalog >
inString(srkStreng,delStreng[,Start])⇒heltall
Returnerer tegnposisjonen i streng srkStreng der hvor
strengen delStreng, begynner.
Start, hvis inkludert, spesifiserer tegnposisjonen
innenfor srkStreng hvor søket starter. Grunninnstilling
= 1 (det første tegnet i srkStreng).
Hvis srkStreng ikke inneholder delStreng eller Start er
> lengden av srkStreng, returneres null.
int() (heltall) Katalog >
int(Uttr)⇒heltall
int(Liste1)⇒liste
int(Matrise1)⇒matrise
Returnerer det største heltallet som er mindre enn
eller lik argumentet. Denne funksjonen er identisk
med floor().
Argumentet kan være et reelt eller et komplekst tall.
For en liste eller matrise, returneres det største
heltallet for hvert element.
intDiv() (heltDiv) Katalog >
intDiv(Tall1,Tall2)⇒heltall
intDiv(Liste1,Liste2)⇒liste
intDiv(Matrise1,Matrise2)⇒matrise
Returnerer heltall-del med fortegn av (Tall1/Tall2).
For lister og matriser, returnerer heltall-del med
fortegn av (argument1/argument2) for hvert
elementpar.
integral Se ‰(), side 193.

interpolate () Katalog >
interpolate(xVerdi,xListe,yListe,yPrimListe)⇒liste
Denne funksjonen gjør følgende:
Gitt xListe,yListe=f(xListe), og yPrimListe=f'
(xListe)for en ukjent funksjon f, brukes en kubisk
interpolant for å tilnærme funksjonen fved xVerdi.
Det antas at xListe er en liste over monotont stigende
eller synkende tall, men denne funksjonen kan
returnere en verdi selv om den ikke er det. Denne
funksjonen går gjennom xListe for å søke etter et
intervall [xListe[i], xListe[i+1]] som inneholder
xVerdi. Hvis den finner et slikt intervall, returnerer
den en interpolert verdi for f(xVerdi); ellers returnerer
den undef.
xListe,yListe og yPrimListe må være av lik
dimensjon |2 og inneholde uttrykk som forenkles til
tall.
xVerdi kan være en udefinert variabel, et tall eller en
liste med tall.
Differensialligning:
y'=-3·y+6·t+5 og y(0)=5
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Bruk den interpolerte() funksjonen for å beregne
funksjonens verdier for xverdilisten:
invc2() Katalog >
invc2(Areal,df)
invChi2(Areal,df)
Beregner invers kumulativ c2(chi-kvadrat)
sannsynlighetsfunksjon spesifisert av Grader av frihet, df for et
gitt Areal under kurven.
invF() Katalog >
invF(Areal,dfTeller,dfNevner)
invF(Areal,dfTeller,dfNevner)
Beregner invers kumulativ Ffordelingsfunksjon spesifisert av
dfTeller og dfNevner for et gitt Areal under kurven.
Alfabetisk oversikt 85
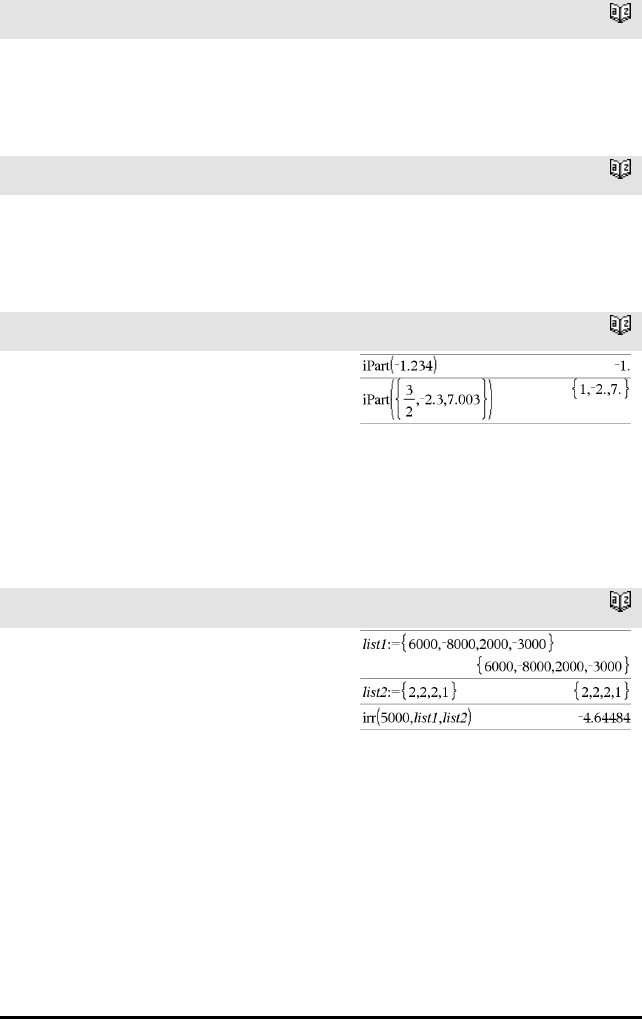
86 Alfabetisk oversikt
invNorm() Katalog >
invNorm(areal[,m[,s]])
Beregner invers kumulativ normalfordelingsfunksjon for et gitt
areal under den normale fordelingskurven spesifisert av mog s.
invt() Katalog >
invt(Areal,df)
Beregner invers kumulativ student-t-sannsynlighetsfunksjon
spesifisert av grader av frihet, df for et gitt Areal under kurven.
iPart() (heltDel) Katalog >
iPart(Tall)⇒heltall
iPart(Liste1)⇒liste
iPart(Matrise1)⇒matrise
Returnerer heltallsdelen av argumentet.
For lister og matriser, returnerer heltallsdelen for hvert
element.
Argumentet kan være et reelt eller et komplekst tall.
irr() Katalog >
irr(CF0,CFListe [,CFFrekv])⇒value
Finansiell funksjon som beregner internrente av retur
av en investering.
CF0 er kontantstrømmen ved start kl. 0; den må være
et reelt tall.
CFListe er en liste over kontantstrømbeløpene etter
den innledende kontanstrømmen CF0.
CFFrekv er en valgfri liste der hvert element
spesifiserer frekvensen av forekomsten for et
gruppert (konsekutivt) kontantstrømbeløp, som er det
tilsvarende elementet til CFListe. Grunninnstilling er
1; hvis du legger inn verdier, må dette være positive
heltall < 10.000.
Merk: Se også mirr(), side 107.
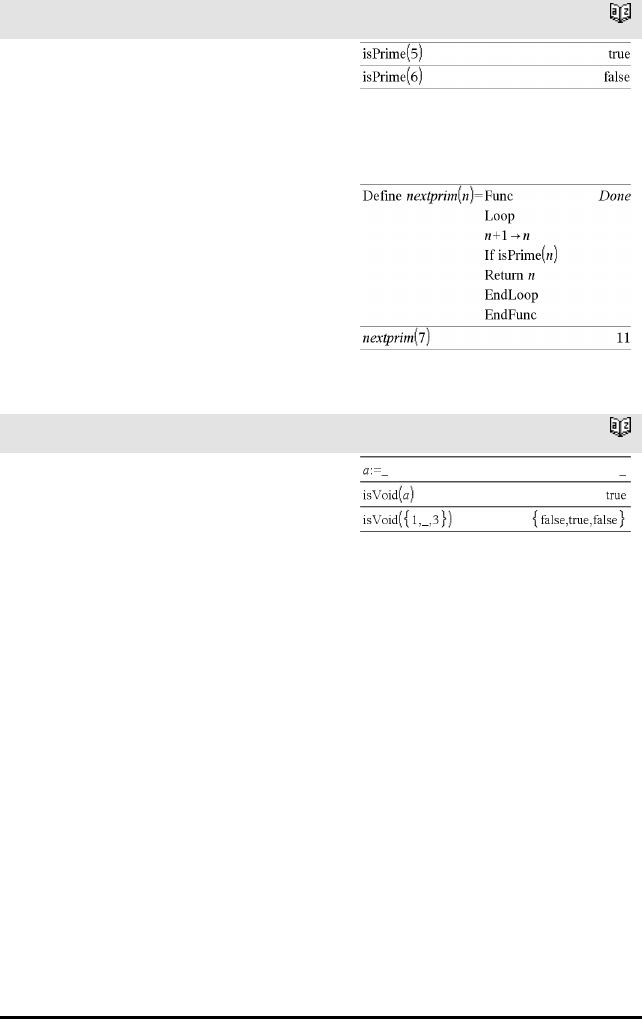
isPrime() (primtallstest) Katalog >
isPrime(Tall)⇒Boolsk konstant uttrykk
Returnerer sann eller usann for å vise om taller et helt
tall |2 som bare er delelig med seg selv og 1.
Hvis Tall består av mer enn 306 siffer og ikke
inneholder noen faktorer {1021, viser isPrime(Tall)
en feilmelding.
Hvis du bare vil bestemme om Tall er et primtall, bruk
isPrime() istedenfor factor(). Det er mye raskere,
særlig hvis Tall ikke er et primtall og hvis den nest
største faktoren består av mer enn fem siffer.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Funksjon for å finne det neste primtallet etter et
spesifisert tall:
isVoid() Katalog >
isVoid(Var)⇒Boolsk konstant uttrykk
isVoid(Uttr)⇒Boolsk konstant uttrykk
isVoid(Liste)⇒liste over Boolske konstante uttrykk
Returnerer sann eller usann for å vise om utsagnet er
en åpen (tom) datatype.
For mer informasjon om åpne (tomme) elementer, se
side 217.
Alfabetisk oversikt 87
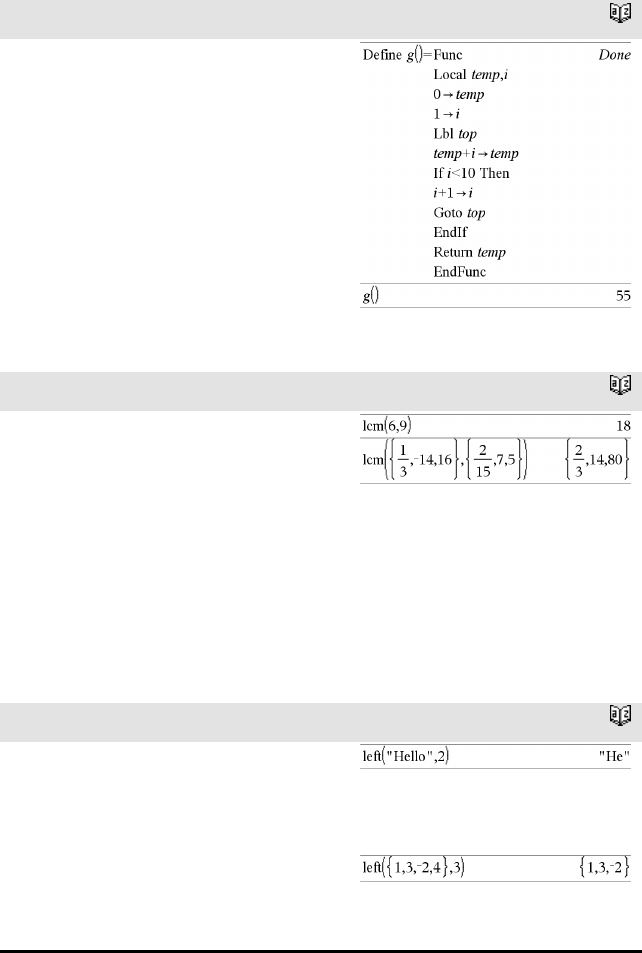
88 Alfabetisk oversikt
L
Lbl (Nvn) Katalog >
Lbl etikettNavn
Definerer en etikett med navnet etikettNavn innenfor
en funksjon.
Du kan bruke en Goto etikettNavn -instruksjon for å
overføre kontroll til den instruksjonen som
umiddelbart følger etter etiketten.
etikettNavn må følge de samme reglene for navn som
gjelder for variabelnavn.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
lcm() (mfm) Katalog >
lcm(Tall1,Tall2)⇒uttrykk
lcm(Liste1,Liste2)⇒liste
lcm(Matrise1,Matrise2)⇒matrise
Returnerer minste felles multiplum av de to
argumentene. lcm av to brøker er lcm av tellerne
dividert med gcd av nevnerne. lcm av brøk som
består av flytende desimalpunkttall er produktet av
teller og nevner.
For to lister eller matriser, returnerer minste felles
multiplum for samsvarende elementer.
left() (venstre) Katalog >
left(kildeStreng[,Num])⇒streng
Returnerer de Num-tegnene som ligger lengst til
venstre i tegnstrengen kildeStreng.
Hvis du utelater Num, returneres alle i kildeStreng.
left(Liste1[,Num])⇒liste
Returnerer de Num-elementene som ligger lengst til

left() (venstre) Katalog >
venstre i Liste1.
Hvis du utelater Num, returneres alle elementer i
Liste1.
left(Sammenlikning)⇒Uttrykk
Returnerer venstre side av en ligning eller ulikhet.
libShortcut() katalog >
libShortcut(BibliotekNavnStreng,
HurtigtastNavnStreng[,BiblPrivMerke])⇒liste av
variabler
Oppretter en variabelgruppe i den gjeldende oppgaven
som inneholder referanser til alle objektene i det
angitte bibliotekdokumentet bibliotekNavnStreng.
Legger også gruppemedlemmene til i Variabler-
menyen. Deretter kan du referere til hvert objekt ved å
bruke dets HurtigtastNavnStreng.
Sett BiblPrivMerke=0hvis du skal ekskludere
private bibliotekobjekter (standard)
Sett BiblPrivMerke=1hvis du skal inkludere private
bibliotekobjekter
Hvis du skal kopiere en variabelgruppe, se CopyVar
(side 32).
Hvis du skal slette en variabelgruppe, se DelVar (side
51).
Dette eksemplet forutsetter et riktig lagret og
oppdatert bibliotekdokument med navnet linalg2 som
inneholder objekter definert som clearmat,gauss1, og
gauss2.
Alfabetisk oversikt 89
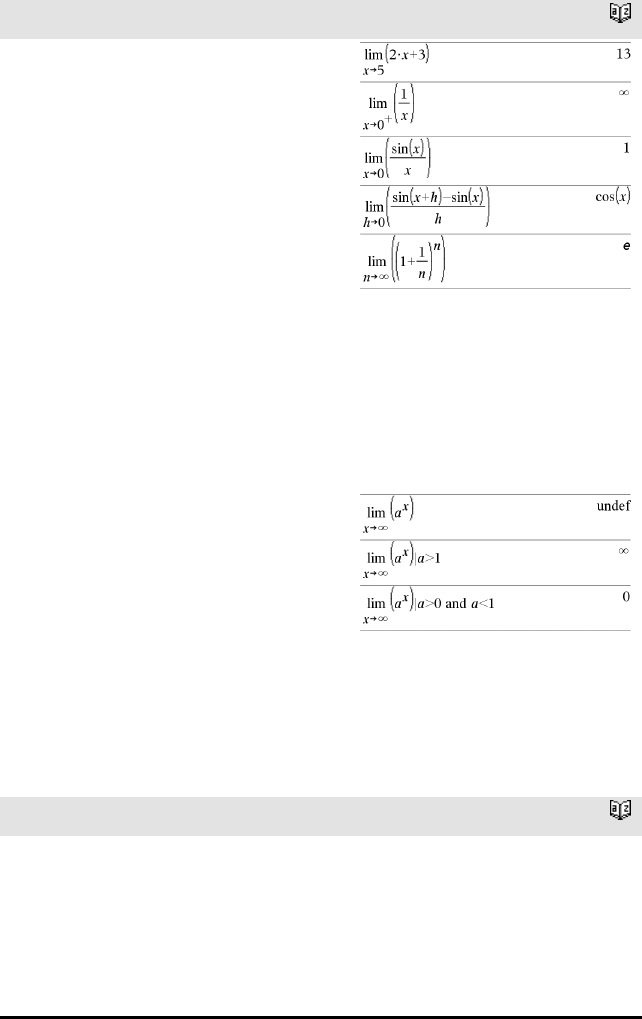
90 Alfabetisk oversikt
limit() eller lim() (grense) Katalog >
limit(Uttr1,Var,Punkt[,Retning])⇒uttrykk
limit(Liste1,Var,Punkt[,Retning])⇒liste
limit(Matrise1,Var,Punkt [,Retning])⇒matrise
Returnerer etterspurt grense.
Merk: Se også Grense-sjablon, side 11.
Retning: negativ=fra venstre, positiv=fra høyre,
ellers=begge. (Hvis utelatt, normeres Retning til
begge.)
Grenser ved positiv ˆog ved negativ ˆomregnes
alltid til ensidige grenser fra den endelige siden.
Avhengig av omstendighetene, returnerer limit() seg
selv eller udef hvis den ikke kan definere en endelig
grense. Dette trenger ikke å bety at det ikke
eksisterer noen endelig grense. udef innebærer at
resultatet enten er et ukjent tall med endelig eller
uendelig størrelse, eller det er et helt sett av slike tall.
limit() bruker metoder, som L’Hopital’s regel, så det
finnes endelige grenser som den ikke kan bestemme.
Hvis Uttr1 inneholder udefinerte variabler utenom
Var, kan det hende at du må begrense dem for å
oppnå et mer nøyaktig resultat.
Grenser kan være svært utsatte for avrundingsfeil.
Hvis mulig, unngå Tilnærm-innstillingen i modusen
Auto eller Tilnærmet og tilnærmede tall når du
beregner grenser. Ellers kan det hende at grenser
som skulle være null eller ha uendelig størrelse
kanskje ikke har dette, og grenser som skulle ha
endelig størrelse forskjellig fra null ikke har det.
LinRegBx (lineær regresjon) katalog >
LinRegBx X,Y[,Frekv[,Kategori,Inkluder]]
Finner den lineære regresjoneny = a+b·xfor listene Xog Ymed
frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen. (Se side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
LinRegBx (lineær regresjon) katalog >
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekvangir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a+b·x
stat.a, stat.b Regresjonskoeffisienter
stat.r2Determinasjonskoeffisient
stat.r Korrelasjonskoeffisient
stat.Rest Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
LinRegMx (lineær regresjon) katalog >
LinRegMx X,Y[,Frekv[,Kategori,Inkuder]]
Finner den lineære regresjonen y = m·x+b for listene Xog Ymed
frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen. (side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
Alfabetisk oversikt 91

92 Alfabetisk oversikt
LinRegMx (lineær regresjon) katalog >
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: m·x+b
stat.m, stat.b Regresjonskoeffisienter
stat.r2Determinasjonskoeffisient
stat.r Korrelasjonskoeffisient
stat.Rest Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
LinRegtIntervals (lineær regresjon) katalog >
LinRegtIntervals X,Y[,F[,0[,CNivå]]]
For stigningstall. Beregner et konfidensintervall med
konfidensnivå C for stigningstallet.
LinRegtIntervals X,Y[,F[,1,Xverd[,CNivå]]]
For respons. Beregner en predikert y-verdi, et
prediksjonsintervall med nivå C for én enkelt observasjon, og et
konfidensintervall med nivå C for den gjennomsnittlige
responsen.
En oversikt over resultatene lagres i stat.resultater-variabelen
(side 162.)
Alle listene må ha samme dimensjon.

LinRegtIntervals (lineær regresjon) katalog >
Xog Yer lister av uavhengige og avhengige variabler.
Fer en valgfri liste over frekvensverdier. Hvert element i F
spesifiserer frekvensen av forekomst for hvert tilsvarende Xog Y
datapunkt. Standardverdien er 1. Alle elementene må være
heltall |0.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.RegEqn Regresjonsligning: a+b·x
stat.a, stat.b Regresjonskoeffisienter
stat.gf Frihetsgrader
stat.r2Determinasjonskoeffisient
stat.r Korrelasjonskoeffisient
stat.Resid Residualene fra regresjonen
Gjelder kun stigningstall
Utdata-variabel Beskrivelse
[stat.CLower, stat.CUpper] Konfidensintervall for stigningstallet
stat.ME Konfidensintervallets feilmargin
stat.SESlope Standardfeil for stigningstallet
stat.s Standardfeil rundt linjen
Gjelder kun responstype
Utdata-variabel Beskrivelse
[stat.CLower, stat.CUpper] Konfidensintervall for gjennomsnittlig respons
stat.ME Konfidensintervallets feilmargin
stat.SE Standardfeil for gjennomsnittlig respons
[stat.LowerPred,
stat.UpperPred]
Prediksjonsintervall for én enkeltobservasjon
stat.MEPred Prediksjonsintervallets feilmargin
stat.SEPred Standardfeil for prediksjonen
stat.ya + b·XVerdi
Alfabetisk oversikt 93
94 Alfabetisk oversikt
LinRegtTest katalog >
LinRegtTest X,Y[,Frekv[,Hypot]]]
Beregner en lineær regresjon på X- og Y-listene og en ttest på
verdien av stigningstallet bog korrelasjonskoeffisienten rfor
ligningen y=a+bx. Den tester null-hypotesenH0:b=0 (tilsvarende,
r=0) mot én av tre alternative hypoteser.
Alle listene må ha samme dimensjon.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekvangir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Hypot er en valgfri verdi som angir en av tre alternative hypoteser
som nullhypotesen (H0:b=r=0) skal testes mot.
For Ha:bƒ0 og rƒ0 (standard), sett Hypot=0
For Ha:b<0 og r<0, sett Hypot<0
For Ha:b>0 og r>0, sett Hypot>0
En oversikt over resultatene lagres i stat.resultater-variabelen
(side 162).
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.RegEqn Regresjonsligning: a + b·x
stat.t t-observator for signifikanstest
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Frihetsgrader
stat.a, stat.b Regresjonskoeffisienter
stat.s Standardfeil rundt linjen
stat.SESlope Standardfeil for stigningstallet
stat.r2Determinasjonskoeffisient
stat.r Korrelasjonskoeffisient
stat.Resid Residualene fra regresjonen

linSolve() Katalog >
linSolve(SystemAvLineæreLign,Var1,Var2,...)
⇒liste
linSolve(LineærLign1 and LineærLign2 and ...,
Var1,Var2,...)⇒liste
linSolve({LineærLign1,LineærLign2,...}, Var1,
Var2,...)⇒liste
linSolve(SystemAvLineæreLign, {Var1,Var2,...})
⇒liste
linSolve(LineærLign1 and LineærLign2 and ...,
{Var1,Var2,...})⇒liste
linSolve({LineærLign1,LineærLign2,...}, {Var1,
Var2,...}) ⇒liste
Returnerer en liste over løsninger for variablene Var1,
Var2,...
Det første argumentet må behandles som et system
av lineære ligninger eller som en lineær ligning. Ellers
oppstår det en argumentfeil.
Ved for eksempel å behandle linSolve(x=1 og x=2,x)
produserer et “Argumentfeil” -resultat.
@list() (liste) Katalog >
@List(Liste1)⇒liste
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive deltaList(...).
Returnerer en liste som inneholder differensene
mellom nabo-elementer i Liste1. Hvert element i
Liste1 subtraheres fra det neste elementet i Liste1.
Resultatlisten er alltid ett element kortere enn
opprinnelige Liste1.
list4mat() Katalog >
list4mat(Liste [,elementerRerRad])⇒matrise
Returnerer en matrise fylt rad-for-rad med
elementene fra Liste.
elementerRerRad, hvis inkludert, spesifiserer antallet
Alfabetisk oversikt 95

96 Alfabetisk oversikt
list4mat() Katalog >
elementer per rad. Grunninnstilling er antallet
elementer i Liste (en rad).
Hvis Liste ikke fyller resultatmatrisen, legges det til
nuller.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive list@>mat
(...).
4ln Katalog >
Uttr1 4ln ⇒Uttrykk
Fører til at inndata Uttr1 omregnes til et uttrykk som
bare inneholder naturlige logaritmer (ln).
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>ln.
ln() /u taster
ln(Uttr1)⇒Uttrykk
ln(Liste1)⇒liste
Returnerer argumentets naturlige logaritme.
For en liste, returneres elementenes naturlige
logaritmer.
Hvis kompleks formatmodus er reell:
Hvis kompleks formatmodus er rektangulær:
ln(kvadratMatrise)⇒kvadratMatrise
Returnerer matrisens naturlige logaritme av
kvadratMatrise1. Dette er ikke det samme som å
beregne naturlig logaritme av hvert element. For mer
informasjon om beregningsmetode, se etter under
cos()
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I radian-vinkelmodus og rektangulært, kompleks
format:
For å se hele resultatet, trykk på £og bruk så ¡og¢
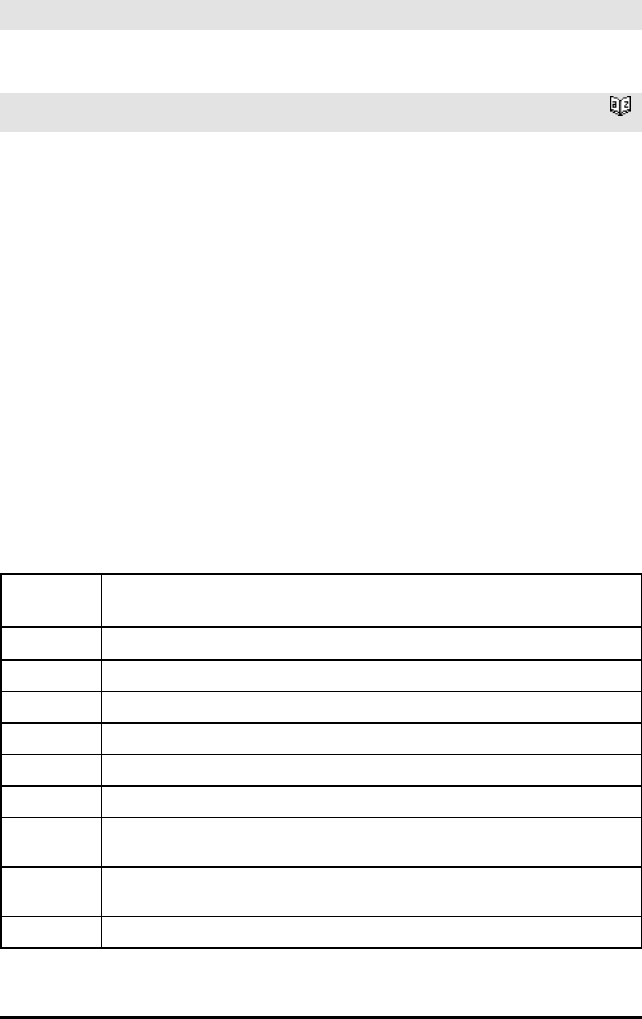
ln() /u taster
for å bevege markøren.
LnReg katalog >
LnReg X,Y[,[Frekv][,Kategori,Inkludert]]
FInner den logaritmiske regresjonen y = a+b·ln(x) for listene Xog
Ymed frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekvangir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a+b·ln(x)
stat.a, stat.b Regresjonskoeffisienter
stat.r2Lineær determinasjonskoeffisient for transformerte data
stat.r Korrelasjonskoeffisient for transformerte data (ln(x), y)
stat.Resid Residualene for den logaritmiske modellen
stat.ResidTrans Residualene for den lineære tilpasningen av de transformerte dataene
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
Alfabetisk oversikt 97
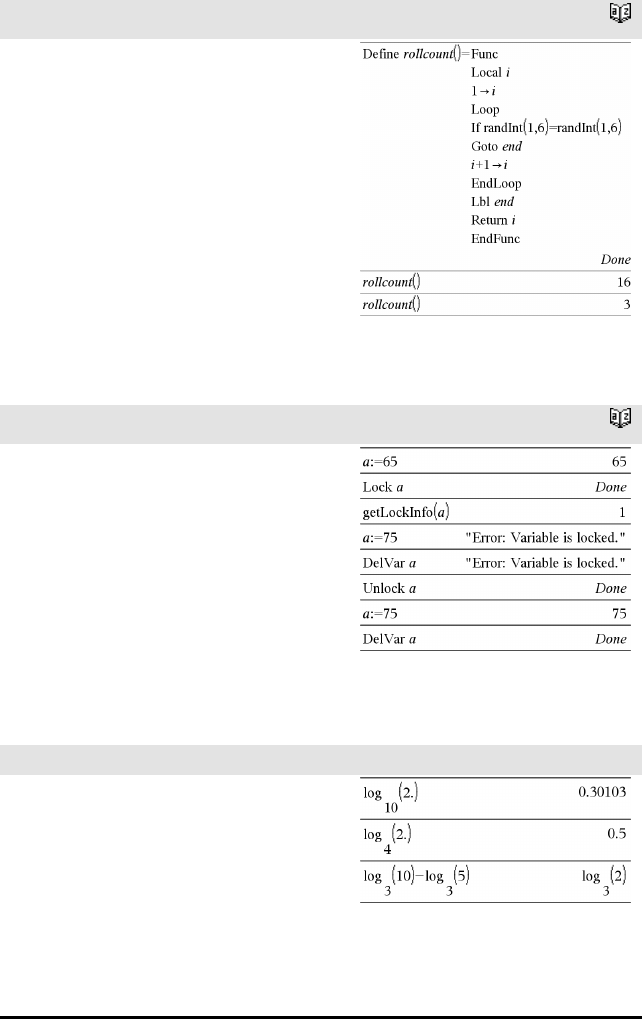
98 Alfabetisk oversikt
Local Katalog >
Local Var1[,Var2] [,Var3] ...
Deklarerer spesifiserte vars som lokale variabler.
Disse variablene eksisterer kun mens en funksjon
utføres og slettes når funksjonen er ferdig utført.
Merk: Lokale variabler sparer plass i minnet, fordi de
bare eksisterer midlertidig. Dessuten forstyrrer de
ingen eksisterende globale variabelverdier. Bruk
lokale variabler for For -stigningstall og for midlertidige
lagringsverdier i en flerlinjet funksjon, siden endringer
på globale variabler ikke er tillatt i en funksjon.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Lock (Lås) Katalog >
LockVar1 [,Var2] [,Var3] ...
LockVar.
Låser spesifiserte variabler eller variabelgruppe.
Låste variabler kan ikke modifiseres eller slettes.
Du kan ikke låse eller låse opp systemvariabelen
Svar, og du kan ikke låse systemvariabelgruppene
stat. eller tvm.
Merk: Kommandoen Lås (Lock) tømmer angre/gjør
om-loggen når den brukes på ulåste variabler.
Se unLock, side 182 og getLockInfo(), side 77.
log() /s taster
log(Uttr1[,Uttr2])⇒Uttrykk
log(Liste1[,Uttr2])⇒liste
Returnerer grunntallet -Uttr2 argumentets logaritme.
Merk: Se også Log-sjablon, side 6.
For en liste, returneres grunntall -Uttr2 for
elementenes logaritme.
Hvis kompleks formatmodus er reell:

log() /s taster
Hvis Uttr2 utelates, brukes 10 som grunntall.
Hvis kompleks formatmodus er rektangulær:
log(kvadratMatrise1[,Uttr2])⇒kvadratMatrise
Returnerer matrisens grunntall- Uttr2 logaritme av
kvadratMatrise1. Dette er ikke det samme som å
beregne grunntallet- Uttr2 logaritme av hvert element.
For mer informasjon om beregningsmetode, se under
cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
Hvis grunntall-argumentet utelates, brukes 10 som
grunntall.
I radian-vinkelmodus og rektangulært, kompleks
format:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
4logbase Katalog >
Uttr1 4logbase(Uttr1)⇒uttrykk
Fører til inndata Uttrykk som skal forenkles til et
uttrykk som bruker grunntall Uttr1.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>logbase
(...).
Logistic katalog >
Logistic X,Y[,[Frekv] [,Kategori,Inkluder]]
Finner den logistiske regresjonen y = (c/(1+a·e-bx)) for listene X
og Ymed frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Alfabetisk oversikt 99
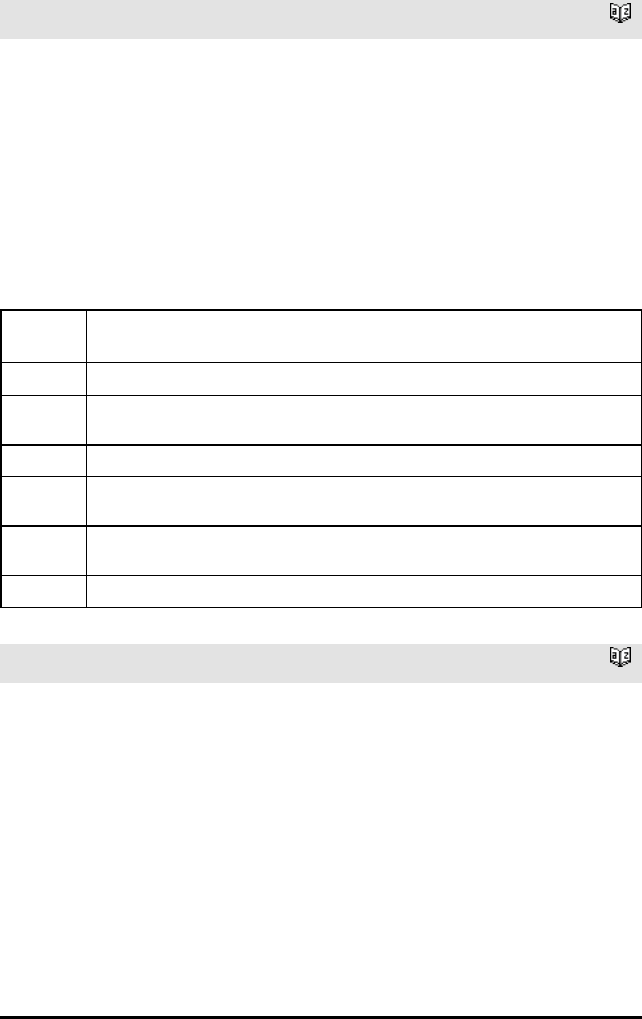
100 Alfabetisk oversikt
Logistic katalog >
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekvangir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: c/(1+a·e-bx)
stat.a, stat.b,
stat.c
Regresjonskoeffisienter
stat.Resid Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
LogisticD katalog >
LogisticD X,Y[,[Iterasjoner],[Frekv] [,Kategori,Inkluder] ]
Finner den logistiske regresjonen y = (c/(1+a·e-bx)+d) for listene
Xog Ymed frekvensen Frekv, ved å bruke et angitt antall
Iterasjoner. En oversikt over resultatene lagres i stat.resultater-
variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Iterasjoner er en valgfri verdi som angir maksimalt antall ganger
det skal gjøres forsøk på å finne en løsning. Hvis utelatt, brukes
64. Vanligvis resulterer større verdier i bedre nøyaktighet men
lengre kjøretid, og omvendt.

LogisticD katalog >
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: c/(1+a·e-bx)+d)
stat.a, stat.b,
stat.c, stat.d
Regresjonskoeffisienter
stat.Resid Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluderte kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluderte kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
Loop (Stigningstall) Katalog >
Loop
Blokk
EndLoop
Utfører utsagnene gjentatte ganger i Blokk. Merk at
stigningstallet utføres uendelig, hvis ikke en Goto eller
Exit instruksjon utføres innenfor Blokk.
Blokk er en sekvens av utsagn som er adskilt med
tegnet.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
Alfabetisk oversikt 101

102 Alfabetisk oversikt
Loop (Stigningstall) Katalog >
produkthåndboken.
LU (= nedre/øvre) Katalog >
LU Matrise,lMatrise,uMatrise,pMatrise[,Tol]
Beregner Doolittle LU (lower-upper=nedre-øvre)
dekomposisjon av en reell eller kompleks matrise.
Den nedre trekantede matrisen lagres i lMatrise, den
øvre trekantede matrisen i uMatrise og
permutasjonsmatrisen (som beskriver radskiftene
som gjøres i løpet av beregningen) i pMatrise.
lMatrise ·uMatrise =pMatrise ·matrise
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn Tol.
Denne toleransen brukes bare hvis matrisen er lagt
inn med flytende desimalpunkt og ikke inneholder
noen symbolske variabler som ikke er tildelt noen
verdi. Ellers ignoreres Tol.
• Hvis du bruker /· eller stiller modusen
Auto eller Tilnærmet på Tilnærmet, utføres
beregningene med flytende
desimalpunktaritmetikk.
• Hvis Tol utelates eller ikke blir brukt, blir
grunninnstillingstoleransen beregnet som:
5EM14 ·maks(dim(Matrise)) ·radNorm
(Matrise)
Faktoriserende algoritme LU bruker delvis pivotering
med radutvekslinger.

M
mat4list() (matrise til liste) Katalog >
mat4list(Matrise)⇒liste
Returnerer en liste fylt med elementene i Matrise.
Elementene kopieres fra Matrise rad for rad.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive mat@>list
(...).
max() Katalog >
max(Uttr1,Uttr2)⇒Uttrykk
max(Liste1,Liste2)⇒liste
max(Matrise1,Matrise2)⇒matrise
Returnerer maksimum (det største) av de to
argumentene. Hvis argumentene er to lister eller
matriser, returneres en liste eller matrise som
inneholder maksimum verdi i hvert par av
samsvarende elementer.
max(Liste)⇒Uttrykk
Returnerer maksimumelementet i liste.
max(Matrise1)⇒matrise
Returnerer en radvektor som inneholder
maksimumselementet av hver kolonne i Matrise1.
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.
Merk: Se også fMax() og min().
mean() (gjennomsnitt) Katalog >
mean(Liste[,frekvListe])⇒uttrykk
Returnerer gjennomsnittet av elementene i Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
mean(Matrise1[,FrekvMatrise])⇒matrise I rektangulært vektorformat:
Alfabetisk oversikt 103

104 Alfabetisk oversikt
mean() (gjennomsnitt) Katalog >
Returnerer en radvektor av gjennomsnittet for alle
kolonnene i Matrise1.
Hvert frekvMatrise element teller antallet
forekomster av det tilsvarende elementet i Matrise1.
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.
median() Katalog >
median(Liste[,frekvListe])⇒uttrykk
Returnerer medianen av elementene i Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
median(Matrise1[,frekvMatrise])⇒matrise
Returnerer en radvektor som inneholder medianer av
kolonnene i Matrise1.
Hvert frekvMatrise element teller antallet
forekomster av det tilsvarende elementet i Matrise1.
Merknader:
• Alle inndata i listen eller matrisen må forenkles
til tall.
• Tomme (åpne) elementer i listen eller matrisen
ignoreres. For mer informasjon om tomme
elementer, se side 217.
MedMed katalog >
MedMed X,Y[,Frekv] [,Kategori,Inkluder]]
Beregner median-median-linjeny = (m·x+b)for listene Xog Ymed
frekvens Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen. (Se side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
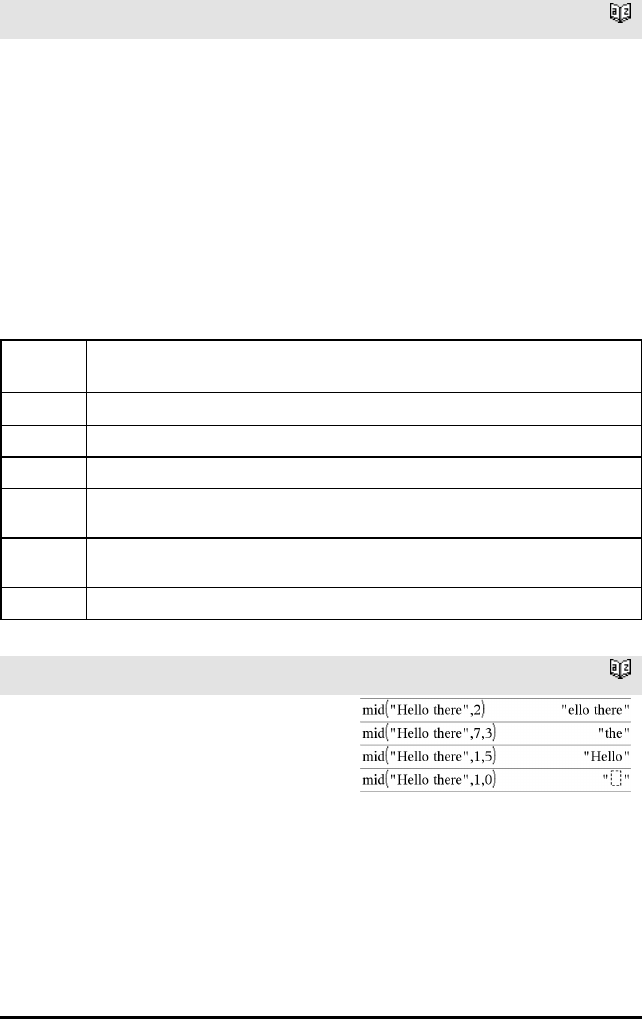
MedMed katalog >
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene. Bare
dataelementene med kategorikode som er i listen blir inkludert i
beregningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Ligning for median-median-linjen: m·x+b
stat.m, stat.b Modellkoeffisienter
stat.Resid Residualene fra median-median-linjen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
mid() (midtstreng) Katalog >
mid(kildeStreng,Start[,Antall])⇒streng
Returnerer Antall tegn fra tegnstreng kildeStreng,
begynnende med tegnnummer Start.
Hvis Antall utelates eller er større enn dimensjonen
på kildeStreng, returneres alle tegnene fra
kildeStreng, begynnende med tegnnummer Start.
Antall må være |0. Hvis Antall = 0, returneres en
tom streng.
Alfabetisk oversikt 105

106 Alfabetisk oversikt
mid() (midtstreng) Katalog >
mid(kildeListe,Start [,Antall])⇒liste
Returnerer Antall elementer fra kildeListe,
begynnende med elementnummer Start.
Hvis Antall utelates eller er større enn dimensjonen
på kildeListe, returneres alle elementer fra
kildeListe, begynnende med elementnummer Start.
Antall må være |0. Hvis Antall = 0, returneres en tom
liste.
mid(kildeStrengListe,Start[,Antall])⇒liste
Returnerer Antall strenger fra listen over strenger
kildeStrengListe, begynnende med elementnummer
Start.
min() (minimum) Katalog >
min(Uttr1,Uttr2)⇒Uttrykk
min(Liste1, Liste2)⇒liste
min(Matrise1, Matrise2)⇒matrise
Returnerer minimum (det minste) av de to
argumentene. Hvis argumentene er to lister eller
matriser, returneres en liste eller matrise som
inneholder minimumsverdien i hvert par av
samsvarende elementer.
min(Liste)⇒Uttrykk
Returnerer minimumselementet av Liste.
min(Matrise!)⇒matrise
Returnerer en radvektor som inneholder
minimumselementet av hver kolonne i Matrise1.
Merk: Se også fMin() og max().

mirr() Katalog >
mirr(finansRente,reinvestRente,CF0,CFListe
[,CFFrekv])
Finansiell funksjon som returnerer modifisert rente av
en investering.
finanseRente er den renten som du betaler på
kontantstrømbeløpene.
reinvestRente er den renten som kontantstrømmen
reinvesteres til.
CF0 er kontantstrømmen ved start kl. 0; den må være
et reelt tall.
CFListe er en liste over kontantstrømbeløpene etter
den innledende kontanstrømmen CF0.
CFFrekv er en valgfri liste der hvert element
spesifiserer frekvensen av forekomsten for et
gruppert (konsekutivt) kontantstrømbeløp, som er det
tilsvarende elementet til CFListe. Grunninnstilling er
1; hvis du legger inn verdier, må dette være positive
heltall < 10.000.
Merk: Se også irr(), side 86.
mod() Katalog >
mod(Uttr1,Uttr2)⇒Uttrykk
mod(Liste1,Liste2)⇒liste
mod(Matrise1,Matrise2)⇒matrise
Returnerer det første argumentet modulo det andre
argumentet slik som definert ved identitetene:
mod(x,0) = x
mod(x,y) = x -y floor(x/y)
Hvis det andre argumentet ikke er null, er resultatet
periodisk i dette argumentet. Resultatet er enten null
eller det har samme fortegn som det andre
argumentet.
Hvis argumentene er to lister eller matriser,
returneres en liste eller matrise som inneholder
modulen av hvert par av samsvarende elementer.
Merk: Se også rest(), side 137
Alfabetisk oversikt 107

108 Alfabetisk oversikt
mRow() (mRad) Katalog >
mRow(Uttr,Matrise1,Indeks)⇒matrise
Returnerer en kopi av Matrise1 med hvert element i
rad Indeks iMatrise1 multiplisert med Uttr.
mRowAdd() (mRadAdd) Katalog >
mRowAdd(Uttr,Matrise1,Indeks1,Indeks2)
⇒matrise
Returnerer en kopi av Matrise1 med hvert element i
rad Indeks2 iMatrise1 erstattet med:
Uttr × rad Indeks1 + rad Indeks2
MultReg katalog >
MultReg Y,X1[,X2[,X3,…[,X10]]]
Beregner multiple lineære regresjoner av liste Yfor listene X2,
X2,…,X10. En oversikt over resultatene lagres i stat.resultater-
variabelen (side 162).
Alle listene må ha samme dimensjon.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.RegEqn Regresjonsligning: b0+b1·x1+b2·x2+ ...
stat.b0, stat.b1, ... Regresjonskoeffisienter
stat.R2Multippel determinasjonskoeffisient
stat.yList yList = b0+b1·x1+ ...
stat.Resid Residualene fra regresjonen
MultRegIntervals katalog >
MultRegIntervals Y,X1[,X2[,X3,…[,X10]]],XVerListe[,CNivå]
Beregner en predikert y-verdi, et prediksjonsintervall med nivå C
for én enkelt observasjon, og et konfidensintervall med nivå C for
den gjennomsnittlige responsen.

MultRegIntervals katalog >
En oversikt over resultatene lagres i stat.resultater-variabelen
(side 162).
Alle listene må ha samme dimensjon.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.RegEqn Regresjonsligning: b0+b1·x1+b2·x2+ ...
stat.yEt punktestimat: y= b0 + b1 ·xl + ... for XVerListe
stat.dfError Feilens frihetsgrader
stat.CLower, stat.CUpper Konfidensintervall for gjennomsnittlig respons
stat.ME Konfidensintervall feilmargin
stat.SE Standardfeil for gjennomsnittlig respons
stat.LowerPred,
stat.UpperPred
Prediksjonsintervall for én enkeltobservasjon
stat.MEPred Prediksjonsintervallets feilmargin
stat.SEPred Standardfeil for prediksjonen
stat.bList Liste over regresjonskoeffisienter, {b0,b1,b2,...}
stat.Resid Residualene fra regresjonen
MultRegTests katalog >
MultRegTests Y,X1[,X2[,X3,…[,X10]]]
Multippel lineær regresjonstest beregner en multippel lineær
regresjon på de angitte dataene og beregner den globale
statistiske F- og t-testobservatoren for koeffisientene.
En oversikt over resultatene lagres i stat.resultater-variabelen
(side 162).
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata
Alfabetisk oversikt 109
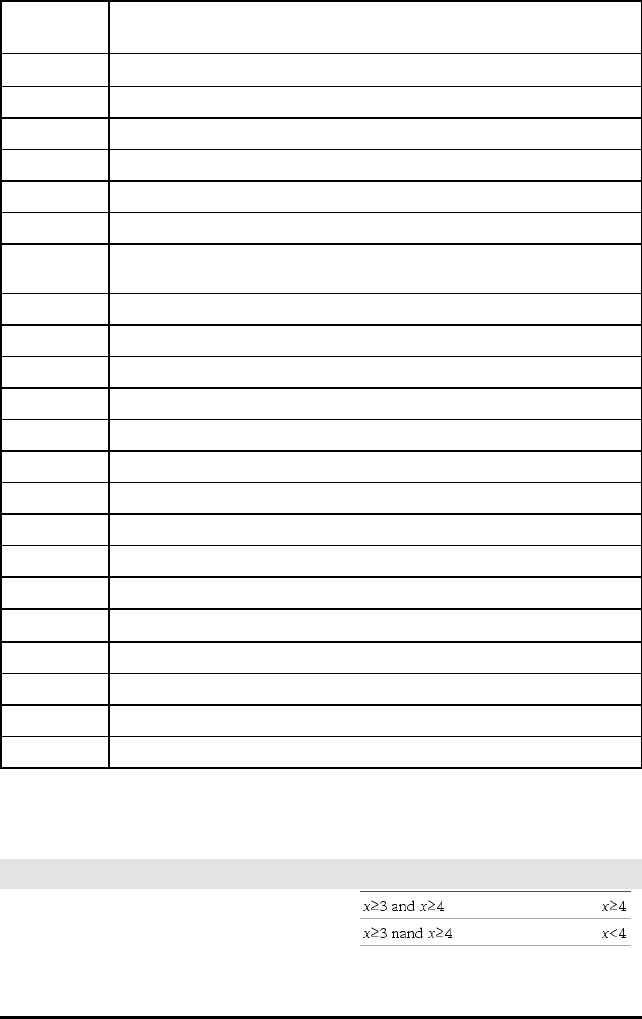
110 Alfabetisk oversikt
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: b0+b1·x1+b2·x2+ ...
stat.F Global statistisk F-testobservator
stat.PVal P-verdi knyttet til global F-observator
stat.R2Multippel determinasjonskoeffisient
stat.AdjR2Justert multippel determinasjonskoeffisient
stat.s Standardavvik for feilen
stat.DW Durbin-Watson-observator. Brukes for å bestemme om første ordens autokorrelasjon er til stede i
modellen
stat.dfReg Regresjonens frihetsgrader
stat.SSReg Regresjonens kvadratsum
stat.MSReg Regresjonens kvadratgjennomsnitt
stat.dfError Feilens frihetsgrader
stat.SKvFeil Feilens kvadratsum
stat.MSError Feilens kvadratgjennomsnitt (gjennomsnittlig kvadratavvik)
stat.bList {b0,b1,...} Liste over koeffisienter
stat.tList Liste over statistiske t-observatorer, én for hver koeffisient i bList
stat.PList Liste over P-verdier for hver t-observator
stat.SEList List over standardfeil for koeffisientene i bList
stat.yList yList = b0+b1·x1+...
stat.Resid Residualene fra regresjonen
stat.sResid Standardiserte residualer. Beregnes ved å dividere en restverdi (residual) med dens standardavvik
stat.CookDist Cooks distanse. Mål for innflytelsen av en observasjon basert på residual og stigning
stat.Leverage Mål for hvor langt verdiene for den uavhengige variabelen er fra gjennomsnittsverdiene
N
nand (ikke både...og) /=-taster
BoolskUttr1nandBoolskUttr2 returnerer Boolsk
uttrykk
BoolskListe1nandBoolskListe2 returnerer Boolsk

nand (ikke både...og) /=-taster
liste
BoolskMatrise1nandBoolskMatrise2 returnerer
Boolsk matrise
Returnerer negasjon av en logisk and-handling på de
to argumentene. Returnerer sann, usann eller en
forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger
element for element.
Heltall1nandHeltall2⇒heltall
Sammenlikner to reelle heltall bit-for-bit med en nand-
handling. Internt er begge heltallene omregnet til 64-
biters binære tall med fortegn. Når tilsvarende biter
sammenliknes, er resultatet 1 hvis begge bitene er 1;
ellers er resultatet 0. Den returnerte verdien
representerer bit-resultatene og vises i
grunntallmodus.
Du kan skrive inn heltallene med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten slik prefiks blir heltall behandlet som
desimalt (grunntall10).
nCr() (antKomb) Katalog >
nCr(Uttr1,Uttr2)⇒uttrykk
For heltall Uttr1 ogUttr2 der Uttr1 |Uttr2 |0, er nCr()
et antall kombinasjoner av Uttr1, som tar Uttr2 om
gangen. (Dette er også kjent som en binomisk
koeffisient.) Begge argumentene kan være heltall eller
symbolske uttrykk.
nCr(Uttr1, 0)⇒1
nCr(Uttr1,negHeltall)⇒0
nCr(Uttr1,posHeltall)⇒Uttr1·(Uttr1N1)...
(Uttr1NposHeltall+1)/ posHeltall!
nCr(Uttr1,ikke-heltall)⇒uttrykk!/
((Uttr1NikkeHeltall)!·ikkeHeltall!)
Alfabetisk oversikt 111
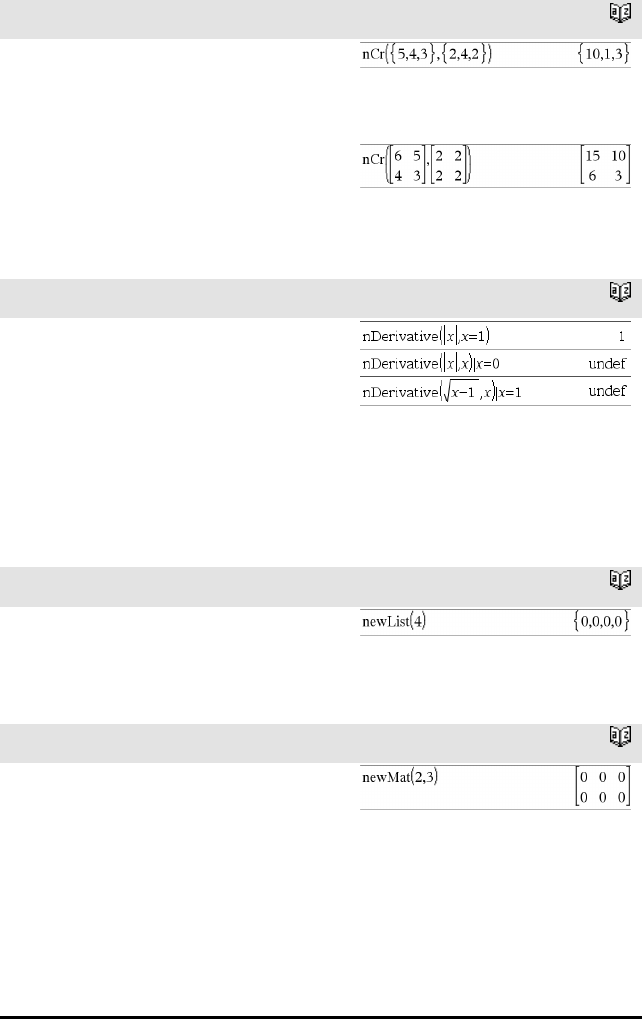
112 Alfabetisk oversikt
nCr() (antKomb) Katalog >
nCr(Liste1,Liste2)⇒liste
Returnerer en liste over kombinasjoner basert på
samsvarende elementpar i de to listene.
Argumentene må ha samme listestørrelse.
nCr(Matrise1,Matrise2)⇒matrise
Returnerer en matrise av kombinasjoner basert på
samsvarende elementpar i de to matrisene.
Argumentene må ha samme matrisestørrelse.
nDerivative() Katalog >
nDerivative(Uttr1,Var=Verdi[,Orden])⇒verdi
nDerivative(Uttr1,Var[,Orden])|Var=Verdi⇒verdi
Returnerer den numeriske deriverte som er beregnet
ved hjelp av automatiske derivasjonsmetoder.
Hvis verdi er spesifisert, opphever den eventuell
forhåndstildelt verdi eller aktuell “|” erstatning for
variabelen.
Den deriverte må være av orden 1eller 2.
newList() (nyListe) Katalog >
newList(numElementer)⇒liste
Returnerer en liste med en dimensjon lik
numElementer. Hvert element er null.
newMat() (nyMat) Katalog >
newMat(numRader,numKolonner)⇒matrise
Returnerer en matrise med bare nuller med
dimensjonen numRader og numKolonner.

nfMax() Katalog >
nfMax(Uttr1,Var)⇒verdi
nfMax(Uttr1,Var,nedGrense)⇒verdi
nfMax(Uttr1,Var,nedGrense,øvGrense)⇒verdi
nfMax(Uttr1, Var) | nedGrense{Var
{øvGrense⇒verdi
Returnerer et forslag til numerisk verdi av variabel
Var, der lokalt maksimum av Uttr1 forekommer.
Hvis du setter nedGrens og øvGrens, ser funksjonen i
det lukkede intervallet [nedGrens,øvGrens] etter
lokalt maksimum.
Merk: Se også fMax() og d().
nfMin() Katalog >
nfMin(Uttr1,Var)⇒verdi
nfMin(Uttr1,Var,nedGrense)⇒verdi
nfMin(Uttr1,Var,nedGrense,øvGrense)⇒verdi
nfMin(Uttr1, Var) | nedGrense{Var
{øvGrense⇒verdi
Returnerer et forslag til numerisk verdi av variabel
Var, der lokalt minimum av Uttr1 forekommer.
Hvis du setter nedGrens og øvGrens, ser funksjonen i
det lukkede intervallet [nedGrens,øvGrens] etter
lokalt minimum.
Merk: Se også fMin() og d().
nInt() Katalog >
nInt(Uttr1, Var, Nedre, Øvre)⇒uttrykk
Hvis integranden Uttr1 ikke inneholder andre verdier
enn Var, og hvis Nedre og Øvre er konstanter, positiv
ˆ, eller negativ ˆ, så returnerer nInt()en tilnærmet av
‰(Uttr1,Var,Nedre,Øvre). Denne tilnærmede er et
veiet gjennomsnitt av noen utvalgsverdier av
integranden i intervallen Nedre<Var<Øvre.
Alfabetisk oversikt 113

114 Alfabetisk oversikt
nInt() Katalog >
Målet er seks signifikante sifre. Den adaptive
algoritmen slutter når det er sannsynlig at målet er
nådd, eller når det er usannsynlig at ekstra utvalg vil gi
nevneverdig forbedring.
Det kommer til syne et varsel (“Tvilsom nøyaktighet”)
når det ser ut til at målet ikke er nådd.
Nest nInt() å utføre multippel numerisk integrasjon.
Integrasjonsgrensene kan avhenge av
integrasjonsvariabler utenfor dem.
Merk: Se også ‰(), side 193.
nom() Katalog >
nom(effektivRente,CpY)⇒verdi
Finansiell funksjon som omregner den årlige effektive
renten effektivRente til en nominell rente, gitt CpY
som antall renteperioder perioder per år.
effektivRente må være et reelt tall, og CpY må være
et reelt tall > 0.
Merk: Se også eff(), side 58.
nor (verken ... eller) /=-taster
BoolskUttr1norBoolskUttr2 returnerer Boolsk uttrykk
BoolskListe1norBoolskListe2 returnerer Boolsk liste
BoolskMatrise1norBoolskMatrise2 returnerer Boolsk
matrise
Returnerer negasjon av en logisk or-handling på de to
argumentene. Returnerer sann, usann eller en
forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger
element for element.

nor (verken ... eller) /=-taster
Heltall1norHeltall2⇒heltall
Sammenlikner to reelle heltall bit-for-bit med en nor-
handling. Internt er begge heltallene omregnet til 64-
biters binære tall med fortegn. Når tilsvarende biter
sammenliknes, er resultatet 1 hvis begge bitene er 1;
ellers er resultatet 0. Den returnerte verdien
representerer bit-resultatene og vises i
grunntallmodus.
Du kan skrive inn heltallene med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten slik prefiks blir heltall behandlet som
desimalt (grunntall10).
norm() katalog >
norm(Matrise)⇒uttrykk
norm(Vektor)⇒uttrykk
Returnerer Frobenius-normen.
normalLine() katalog >
normalLine(Uttr1,Var,Punkt)⇒uttrykk
normalLine(Uttr1,Var=Punkt)⇒uttrykk
Returnerer normallinjen til kurven som er representert
av Uttr1 i punktet angitt av Var=Punkt.
Sørg for at den uavhengige variabelen ikke er definert.
Hvis for eksempel f1(x):=5 og x:=3, vil normalLine(f1
(x),x,2)returnere “false” (“usann”).
normCdf() Katalog >
normCdf(nedreGrense,øvreGrense[,m[,s]])⇒tall hvis
nedreGrense og øvreGrense er tall, liste hvis nedreGrense og
Alfabetisk oversikt 115
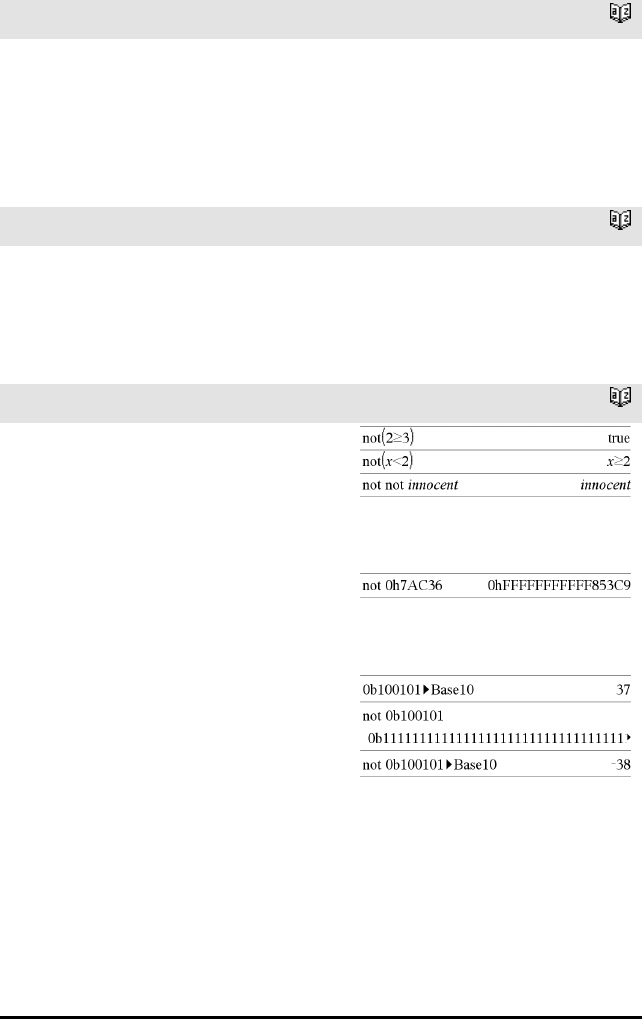
116 Alfabetisk oversikt
normCdf() Katalog >
øvreGrense er lister
Beregner sannsynligheten i normalfordelingen mellom
nedreGrense og øvreGrense for den angitte m(standard=0) og s
(standard=1).
For P(X {øvreGrense), sett nedreGrense =.ˆ.
normPdf() Katalog >
normPdf(XVerdi[[,m[,s]])⇒tall hvis XVerdi er et tall, liste hvis
XVerdi er en liste
Beregner sannsynlighetstetthet for normalfordelingen ved en
spesifisert XVerdi-verdi for spesifisert mog s.
not (ikke) Katalog >
not BoolksUttr1⇒Boolsk uttrykk
Returnerer sann, usann eller en forenklet form av
argumentet.
not Heltall1⇒heltall
Returnerer tallets komplement av et reelt heltall.
Internt er Heltall1 omregnet til et 64-biters binært tall
med fortegn. Verdien av hver bit er forskjøvet (0 blir til
1 og motsatt) for tallets komplement. Resultatene
vises i forhold til grunntall-modusen.
Du kan skrive inn heltallet med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten prefiks blir heltallet behandlet som et
desimalt tall (grunntall10).
Hvis du oppgir et desimalt heltall som er for stort for et
64-bit binært tall med fortegn, vil en symmetrisk
modulusoperasjon bli brukt til å konvertere tallet inn i
gyldig verdiområde. For mer informasjon, se 4Base2,
side 21.
I heksades grunntall-modus:
Viktig: Null, ikke bokstaven O.
I binær grunntall-modus:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Merk: Et binært innlegg kan bestå av opptil 64 siffer (i
tillegg til prefikset 0b). Et heksadesimalt innlegg kan
bestå av opptil 16 siffer.

nPr() (antPerm) Katalog >
nPr(Uttr1,Uttr2)⇒uttrykk
For heltall Uttr1 ogUttr2 der Uttr1 |Uttr2 |0, er nPr()
et antall permutasjoner av Uttr1 som tar Uttr2 om
gangen. Begge argumentene kan være heltall eller
symbolske uttrykk.
nPr(Uttr1, 0)⇒1
nPr(Uttr1,negHeltall)⇒1/((Uttr1+1)·(Uttr1+2)...
(Uttr1NnegHeltall))
nPr(Uttr1,posHeltall)⇒Uttr1·(Uttr1N1)...
(Uttr1posHeltall+1)
nPr(Uttr1,ikkeHeltall)⇒Uttr1! /
(Uttr1NikkeHeltall)!
nPr(Liste1,Liste2)⇒liste
Returnerer en liste over permutasjoner basert på
samsvarende elementpar i de to listene.
Argumentene må ha samme listestørrelse.
nPr(Matrise1,Matrise2)⇒matrise
Returnerer en matrise av permutasjoner basert på
tilsvarende elementpar i de to matrisene.
Argumentene må ha samme matrisestørrelse.
npv() Katalog >
npv(Rentefot,CFO,CFListe[,CFFrekv])
Finansiell funksjon som beregner netto nåverdi;
summen av nåverdier for kontanstrøm inn og ut. Et
positivt resultat for npv forteller at en investering er
lønnsom.
Rentefot er den renten som trekkes fra
kontantstrømmene (pengekostnadene) over en
periode.
CF0 er kontantstrømmen ved start kl. 0; den må være
et reelt tall.
CFListe er en liste med kontantstrømbeløp etter den
innledende kontantstrømmen CF0.
CFFrekv er en liste der hvert element spesifiserer
Alfabetisk oversikt 117
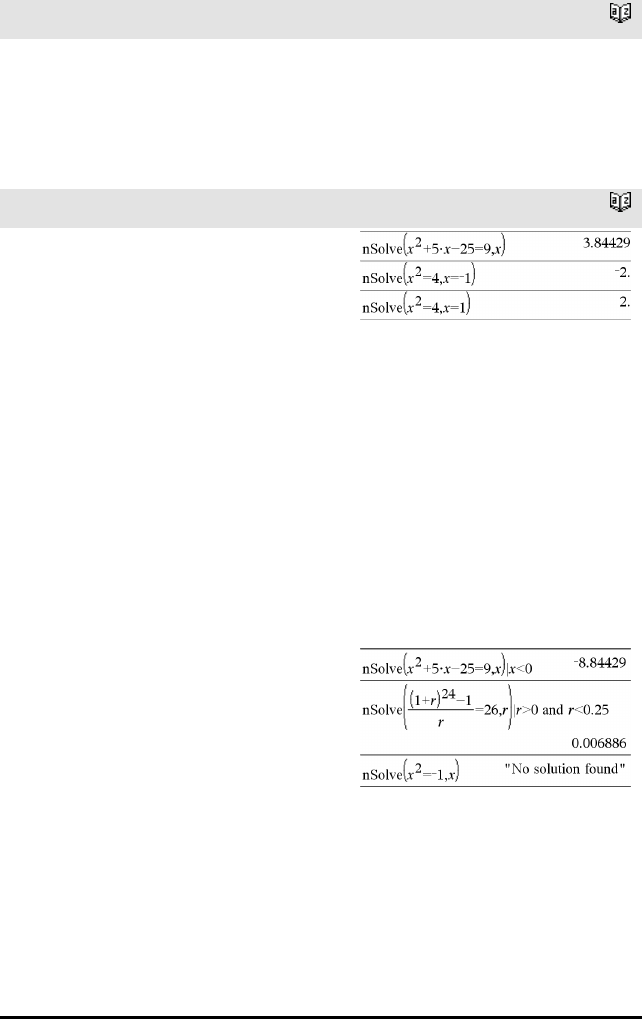
118 Alfabetisk oversikt
npv() Katalog >
frekvensen av forekomsten for et gruppert
(konsekutivt) kontantstrømbeløp, som er det
tilsvarende elementet til CFListe. Grunninnstilling er
1; hvis du legger inn verdier, må dette være positive
heltall < 10.000.
nSolve() (nLøs) Katalog >
nSolve(Ligning,Var[=Forslag])⇒tall eller feil_
streng
nSolve(Ligning,Var[=Forslag],nedGrense)⇒tall
eller feil_streng
nSolve(Ligning,Var
[=Forslag],nedGrense,øvGrense)⇒tall eller feil_
streng
nSolve(Ligning,Var[=Forslag]) | nedGrense{Var
{øvGrense ⇒tall eller feil_streng
Søker iterativt etter en tilnærmet reell numerisk
løsning for Ligning i variabelen. Spesifiser variabelen
som:
variabel
– eller –
variabel =reelt tall
For eksempel er x gyldig, og det er x=3 også.
Merk: Hvis det foreligger flere løsninger, kan du
bruke et forslag som hjelp for å finne en spesiell
løsning.
nSolve() er ofte mye raskere enn solve() eller zeros(),
særlig hvis du bruker “|” operatoren for å begrense
søket til et relativt lite intervall som inneholder en
eksakt eller enkel løsning.
nSolve() prøver å bestemme enten ett punkt der rest
er null, eller to relativt nære punkter, der rest har
motsatte fortegn og størrelsen på resten ikke er for
stor. Hvis den ikke kan oppnå dette med et lite antall
utvalgspunkter, returnerer den strengen “fant ingen
løsning.”
Merk: Se også cSolve(),cZeros(),solve() og zeros().

O
OneVar (EnVar) Katalog >
OneVar [1,]X[,[Frekv][,Kategori,Inkludert]]
OneVar[n,]X1,X2[X3[,…[,X20]]]
Beregner en-variabel-statistikker med opptil 20 lister. En oversikt
over resultatene lagres i stat.results-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
X-argumentene er datalister.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hver korresponderende X-verdi
forekommer. Standardverdien er 1. Alle elementene må være
heltall |0.
Kategori er en liste med numeriske kategorikoder for de
korresponderende X-verdiene.
Inkluder er en liste med én eller flere av kategorikodene. Bare
dataelementene med kategorikode som er i listen blir inkludert i
beregningen.
Et tomt (åpent) element i enhver av listene X,Frekv eller
Kategori resulterer i et åpent (tomt) element for det tilsvarende
elementet til alle disse listene. Et tomt element i enhver av
listene fra X1 til X20 resulterer i et åpent (tomt) element for det
tilsvarende elementet i alle disse listene. For mer informasjon om
tomme elementer, se side 217.
Utdata-variabel Beskrivelse
stat.vGjennomsnitt av x-verdier
stat.Gx Sum av x-verdier
stat.Gx2Sum av x2-verdier
stat.sx Utvalgets standardavvik av x
stat.sx Populasjonens standardavvik av x
stat.n Antall datapunkter
stat.MinX Minimum av x-verdier
stat.Q 1X Første kvartil av x
stat.MedianX Median av x
Alfabetisk oversikt 119
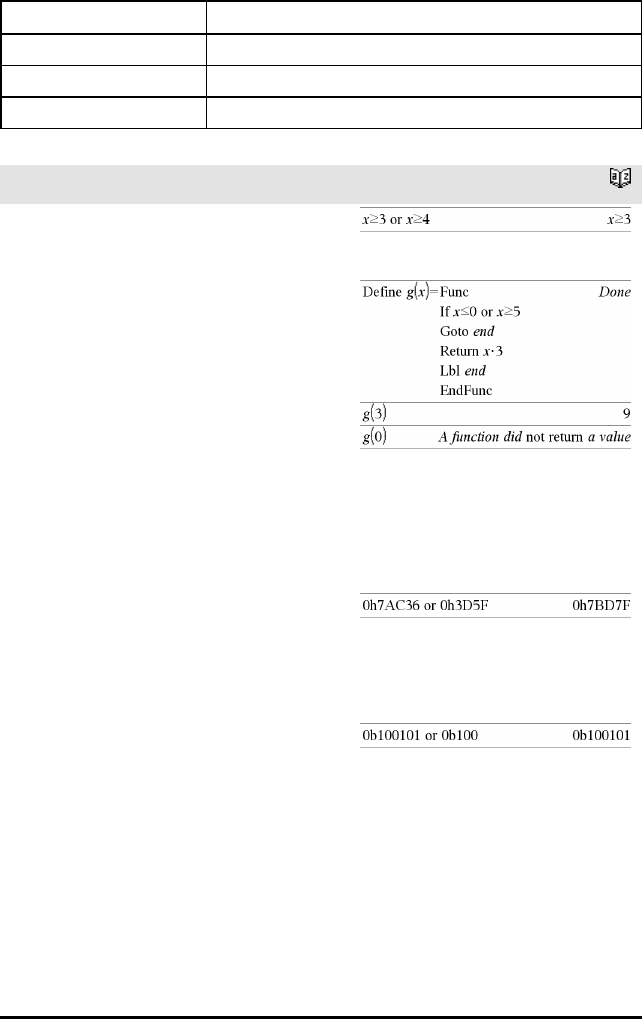
120 Alfabetisk oversikt
Utdata-variabel Beskrivelse
stat.Q 3X Tredje kvartil av x
stat.MaxX Maksimum av x-verdier
stat.SSX Sum av kvadratavvik fra gjennomsnittet av x
or (eller) Katalog >
BoolskUttr1orBoolskUttr2 returnerer Boolsk uttrykk
BoolskListe1orBoolskListe2 returnerer Boolsk liste
BoolskMatrise1orBoolskMatrise2 returnerer Boolsk
matrise
Returnerer sann eller usann eller en forenklet form av
opprinnelig uttrykk.
Returnerer sann hvis ett eller begge uttrykkene er
sanne. Returnerer usann kun hvis begge uttrykkene
behandles som usanne.
Merk: Se xor.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Heltall1 or Heltall2Þheltall
Sammenlikner to reelle heltall bit-for-bit med en or-
handling. Internt er begge heltallene omregnet til 64-
biters binære tall med fortegn. Når tilsvarende biter
sammenliknes, er resultatet 1 hvis minst en av bitene
er 1; resultatet er 0 bare hvis begge bitene er 0. Den
returnerte verdien representerer bit-resultatene og
vises i grunntall-modus.
Du kan skrive inn heltallene med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten slik prefiks blir heltall behandlet som
desimalt (grunntall10).
Hvis du oppgir et desimalt heltall som er for stort for et
64-bit binært tall med fortegn, vil en symmetrisk
modulusoperasjon bli brukt til å konvertere tallet inn i
gyldig verdiområde. For mer informasjon, se 4Base2,
side 21.
I heksades grunntall-modus:
Viktig: Null, ikke bokstaven O.
I binær grunntall-modus:
Merk: Et binært innlegg kan bestå av opptil 64 siffer (i
tillegg til prefikset 0b). Et heksadesimalt innlegg kan
bestå av opptil 16 siffer.

or (eller) Katalog >
Merk: Se xor.
ord() (num. tegnkode) Katalog >
ord(Streng)⇒heltall
ord(Liste1)⇒liste
Returnerer numerisk kode for de første tegnene i
tegnstreng Streng, eller en liste over de første
tegnene i hvert listeelement.
P
P4Rx() Katalog >
P4Rx(rUttr,qUttr)⇒uttrykk
P4Rx(rListe,qListe)⇒liste
P4Rx(rMatrise,qMatrise)⇒matrise
Returnerer ekvivalent x-koordinat av (r,q) paret.
Merk: q-argumentet tolkes enten som grader,
gradianer eller radianer, avhengig av aktuell
vinkelmodus. Hvis argumentet er et uttrykk, kan du
bruke¡,Geller Rfor å hoppe over vinkelmodus-
innstillingen midlertidig.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive P@>Rx(...).
I Radian-vinkelmodus:
P4Ry() Katalog >
P4Ry(rUttr,qUttr)⇒Uttr
P4Ry(rListe,qListe)⇒liste
P4Ry(rMatrise,qMatrise)⇒matrise
Returnerer ekvivalent y-koordinat av (r,q)-paret.
Merk: q-argumentet tolkes enten som grader,
gradianer eller radianer, avhengig av aktuell
vinkelmodus. Hvis argumentet er et uttrykk, kan du
bruke¡,Geller Rfor å hoppe over vinkelmodus-
I Radian-vinkelmodus:
Alfabetisk oversikt 121
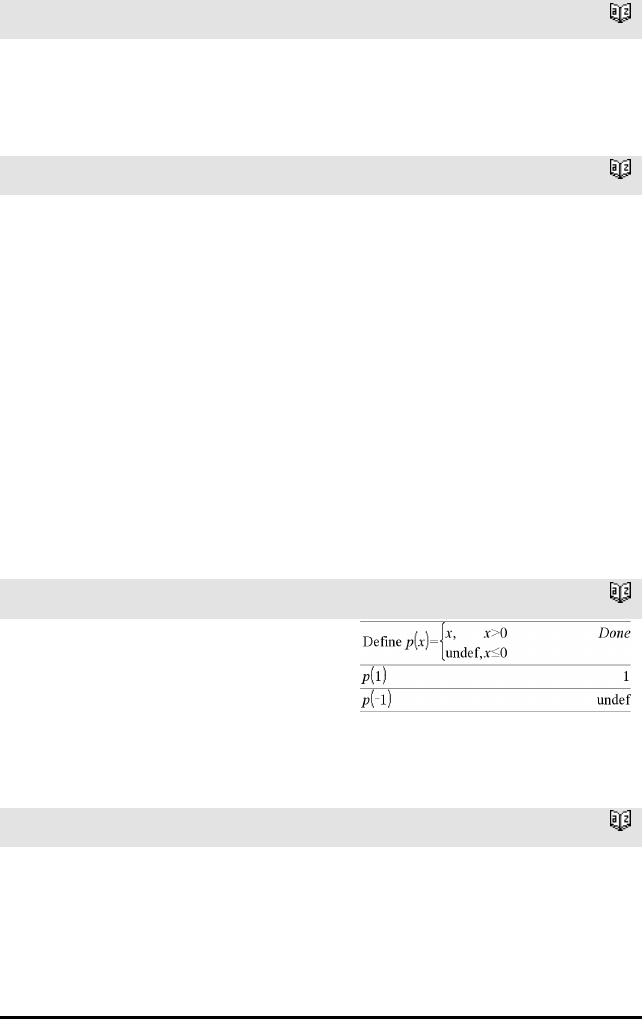
122 Alfabetisk oversikt
P4Ry() Katalog >
innstillingen midlertidig.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive P@>Ry(...).
PassErr (SendFeil) Katalog >
PassErr
Sender en feil til neste nivå.
Hvis systemvariabelen feilKode er null, gjør ikke PassErr
noenting.
Else -leddet i Try...Else...EndTry-blokken bør bruke ClrErr eller
PassErr. Hvis feilen skal bearbeides eller ignoreres, bruk ClrErr.
Hvis det ikke er kjent hva som skal gjøres med feilen, bruk
PassErr for å sende den til den neste feilbehandleren. Hvis det
ikke er flere ventende Try...Else...EndTry feilbehandlere, vises
feil-dialogboksen som normalt.
Merk: Se også ClrErr (SlettFeil), side 28, og Try, side 176.
Merk for å legge inn eksemplet: For anvisninger om hvordan du
legger inn flerlinjede program- og funksjonsdefinisjoner, se
avsnittet Kalkulator i produkthåndboken.
For et eksempel på PassErr, se
eksempel 2 under Try -kommandoen,
side 176.
piecewise() (stykkevis) Katalog >
piecewise(Uttr1 [,Betingelse1[,Uttr2[,Betingelse2
[,…]]]])
Returnerer definisjoner for en stykkevis definert
funksjon i form av en liste. Du kan også opprette
stykkevise definisjoner med en sjablon.
Merk: Se ogsåstykkevis-sjablon, side 7.
poissCdf() Katalog >
poissCdf(l,nedreGrense,øvreGrense)⇒tall hvis nedreGrense
og øvreGrense er tall, liste hvis nedreGrense og øvreGrense er
lister
poissCdf(l,øvreGrense)(for P(0{X{øvreGrense)⇒tall hvis
øvreGrense er et tall, liste hvis øvreGrense er en liste
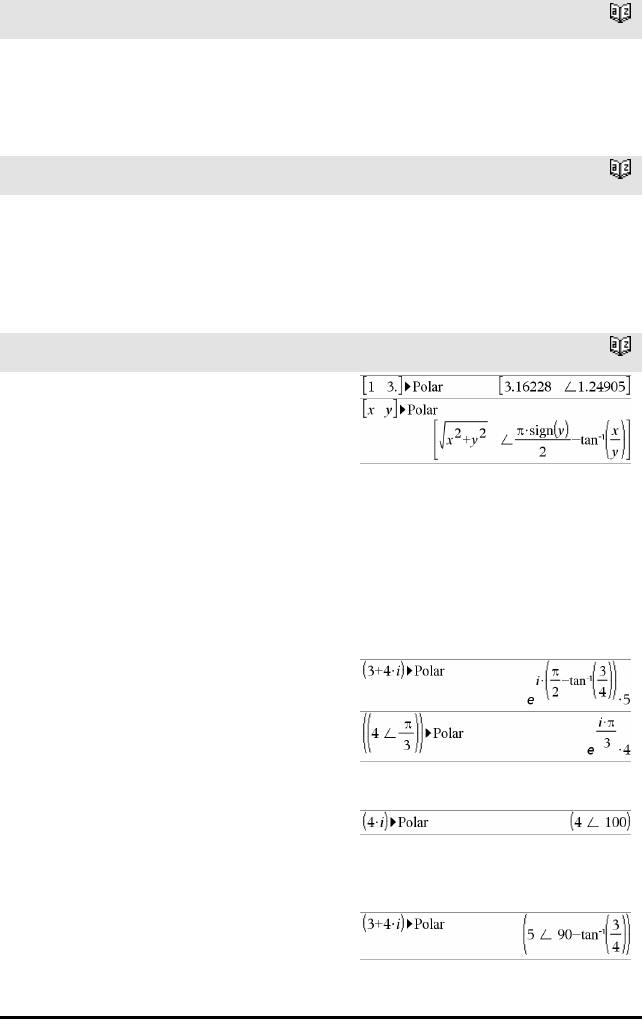
poissCdf() Katalog >
Beregner en kumulativ sannsynlighet for den diskrete Poisson-
fordeling med spesifisert gjennomsnitt l.
For P(X {øvreGrense), sett nedreGrense=0
poissPdf() Katalog >
poissPdf(l,XVerd)⇒tall hvis XVerd er et tall, liste hvis XVerd er
en liste
Beregner en sannsynlighet for diskret Poisson-fordeling med
spesifisert gjennomsnitt l.
4Polar Katalog >
Vektor 4Polar
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Polar.
Viser vektor i polar form [r∠θ]. Vektoren må være av
dimensjon 2 og kan være en rad eller en kolonne.
Merk: 4Polar er en visningsformat-instruksjon, ikke en
omregningsfunksjon. Du kan bare bruke den på
slutten av en kommandolinje, og den oppdaterer ikke
svar.
Merk: Se også 4Rekt, side 135.
kompleksVerdi 4Polar
Viser kompleksVektor i polar form.
• Grader-vinkelmodus returnerer (r∠θ).
• Radian-vinkelmodus returnerer reiθ.
kompleksVerdi kan ha en hvilken som helst kompleks
form. Men hvis du legger inn reiθ, forårsaker dette feil
når vinkelmodus er grader.
Merk: Du må bruke parentes for å legge inn polar
(r∠θ).
I Radian-vinkelmodus:
I Gradian-vinkelmodus:
I Grader-vinkelmodus:
Alfabetisk oversikt 123

124 Alfabetisk oversikt
polyCoeffs() (polyKoeffs) Katalog >
polyCoeffs(Poly [,Var])⇒liste
Returnerer en liste over koeffisienter av polynom Poly
med hensyn på variabel Var.
Poly må være et polynomisk uttrykk i Var. Vi
anbefaler at du ikke utelater Var med mindre Poly er
et uttrykk i en enkel variabel.
Utvider polynomet og velger xfor den utelatte Var.
polyDegree() (polyGrader) Katalog >
polyDegree(Poly [,Var])⇒verdi
Returnerer grader av polynomisk uttrykk Poly med
hensyn på variabel Var. Hvis du utelukker Var, velger
polyDegree() funksjonen en grunninnstilling fra de
variablene som ligger i polynom Poly.
Poly må være et polynomisk uttrykk i Var. Vi
anbefaler at du ikke utelater Var med mindre Poly er
et uttrykk i en enkel variabel.
Konstante polynomer

polyDegree() (polyGrader) Katalog >
Graden kan trekkes ut, selv om koeffisientene ikke
kan det. Dette er fordi graden kan trekkes ut uten å
utvide polynomet.
polyEval() Katalog >
polyEval(Liste1,Uttr1)⇒uttrykk
polyEval(Liste1,Liste2)⇒uttrykk
Tolker det første argumentet som koeffisienter for et
polynom med fallende eksponenter, og returnerer en
utregnet verdi av polynomet, innsatt verdien av det
andre argumentet.
polyGcd() Katalog >
polyGcd(Uttr1,Uttr2)⇒uttrykk
Returnerer største felles divisor for de to
argumentene.
Uttr1 og Uttr2 må være polynomiske uttrykk.
Liste, matrise og boolske argumenter er ikke tillatt.
polyQuotient() (polyKvotient) Katalog >
polyQuotient(Poly1,Poly2 [,Var])⇒uttrykk
Returnerer kvotienten av polynom Poly1 dividert med
polynom Poly2 med hensyn på den spesifiserte
variabelen Var.
Poly1 og Poly2 må være polynomiske uttrykk i Var.
Vi anbefaler at du ikke utelater Var med mindre Poly1
og Poly2 er uttrykk i den samme enkeltvariabelen.
Alfabetisk oversikt 125

126 Alfabetisk oversikt
polyQuotient() (polyKvotient) Katalog >
polyRemainder() (polyRest) Katalog >
polyRemainder(Poly1,Poly2 [,Var])⇒uttrykk
Returnerer rest av polynom Poly1 dividert med
polynom Poly2 med hensyn på den spesifiserte
variabelen Var.
Poly1 og Poly2 må være polynomiske uttrykk i Var.
Vi anbefaler at du ikke utelater Var med mindre Poly1
og Poly2 er uttrykk i den samme enkeltvariabelen.
polyRoots() Katalog >
polyRoots(Poly,Var)⇒liste
polyRoots(KoeffListe)⇒liste
Den første syntaksen, polyRoots(Poly,Var),
returnerer en liste over sanne røtter av polynom Poly
med hensyn på variabel Var. Hvis det ikke eksisterer
noen sanne røtter, returneres en tom liste: {}.
Poly må være et polynom i én variabel.
Den andre syntaksen, polyRoots(KoeffListe),
returnerer en lsite over sanne røtter for koeffisientene
iKoeffListe.
Merk: Se også cPolyRoots(), side 39.
PowerReg (PotensReg) katalog >
PowerReg X,Y[,Frekv] [,Kategori,Inkluder]]
Finner potensregresjoneny = (a·(x)b)for listene Xog Ymed
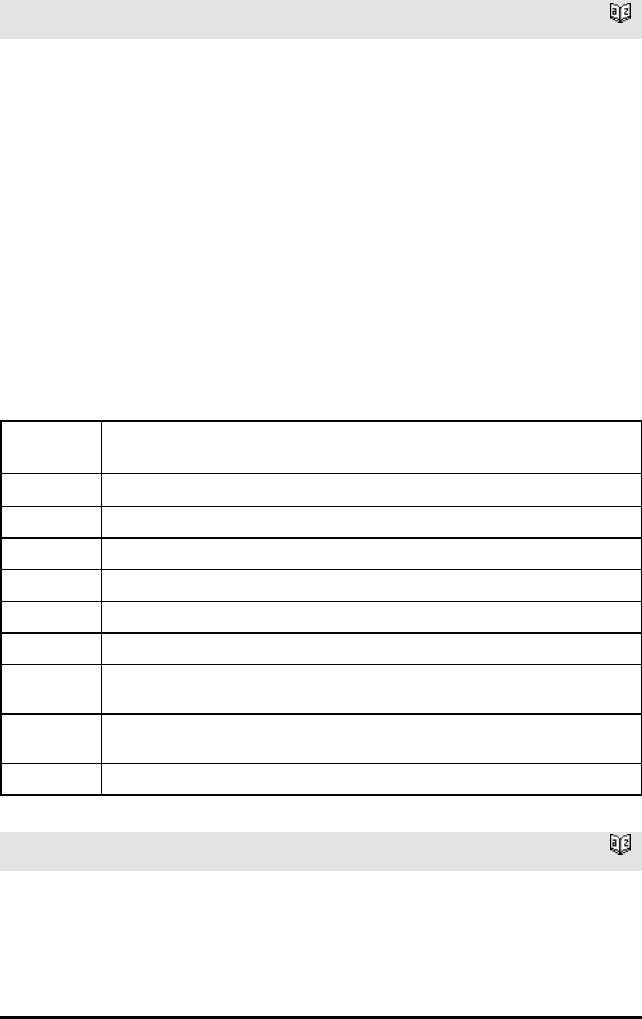
PowerReg (PotensReg) katalog >
frekvensen Frekv. En oversikt over resultatene lagres i
stat.resultater-variabelen (side 162).
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a ·(x) b
stat.a, stat.b Regresjonskoeffisienter
stat.r2Lineær determinasjonskoeffisient for transformerte data
stat.r Korrelasjonskoeffisient for transformerte data (ln(x), ln(y))
stat.Resid Residualene for potensmodellen
stat.ResidTrans Residualene for den lineære tilpasningen av de transformerte dataene
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
Prgm Katalog >
Prgm
Blokk
EndPrgm
Sjablon for å opprette et egendefinert program. Må
Beregn GCD og vis mellomresultater.
Alfabetisk oversikt 127
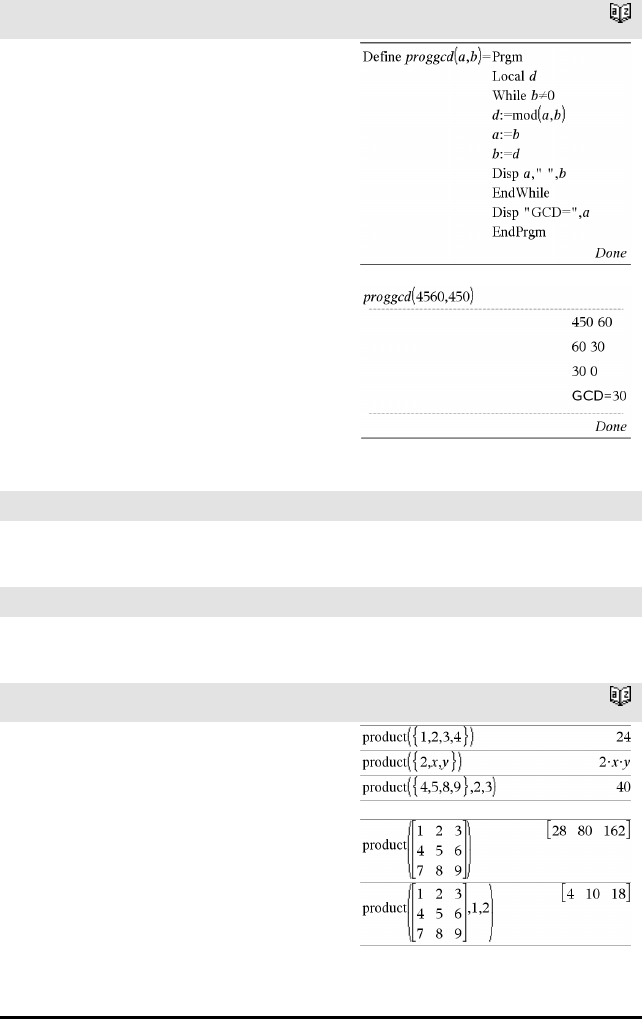
128 Alfabetisk oversikt
Prgm Katalog >
brukes med kommandoen Define,Define LibPub eller
Define LibPriv.
Blokk kan være ett enkelt utsagn, en rekke utsagn
adskilt med “:”-tegnet eller en rekke med utsagn på
separate linjer.
Blokk kan være ett enkelt utsagn, en rekke utsagn
adskilt med “:”-tegnet, eller en rekke med utsagn på
separate linjer.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
prodSeq() Se Π(), side 205.
Produkt (PI) Se Π(), side 205.
Product() Katalog >
product(Liste[,Start[,slutt]])⇒uttrykk
Returnerer produktet av elementene i Liste.Start og
Slutt er valgfrie. De spesifiserer et elementområde.
product(Matrise1[,Start[,slutt]])⇒matrise
Returnerer en radvektor som inneholder produktet av
elementene i kolonnene i Matrise1.Start og slutt er
alternativer. De spesifiserer et radområde.
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.

propFrac() (ekteBrøk) Katalog >
propFrac(Uttr1[,Var])⇒uttrykk
propFrac(rasjonal_tall)returnerer rasjonalt_tall som
summen av et heltall og en brøk som har samme
fortegn og større nevner enn teller.
propFrac(rasjonalt_uttrykk,Var)returnerer summen
av ekte brøk og et polynom med hensyn på Var.
Gradene til Var i nevneren er større enn gradene til
Var i telleren i hver ekte brøk. Liknende potenser av
Var er samlet sammen. Leddene og faktorene deres
er sortert med Var som hovedvariabel.
Hvis Var utelates, utvides den ekte brøken med
hensyn på de fleste hovedvariablene. Koeffisientene
til den polynomiske delen omgjøres så til “ekte” med
hensyn på de fleste hovedvariablene og så videre.
For rasjonale uttrykk er propFrac() et raskere, men
mindre ekstremt alternativ til expand().
Q
QR Katalog >
QR Matrise,qMatNavn,rMatNavn(,Tol]
Beregner den faste QR faktoriseringen av en reell eller
en kompleks matrise. De resulterende matrisene Q
og R lagres til det spesifiserte MatNavn. Q-matrisen
er enhetlig. R-matrisen er øvre trekantet.
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn Tol.
Denne toleransen brukes bare hvis matrisen er lagt
inn med flytende desimalpunkt og ikke inneholder
noen symbolske variabler som ikke er tildelt noen
verdi. Ellers ignoreres Tol.
• Hvis du bruker /· eller stiller modusen
Auto eller Tilnærmet på Tilnærmet, utføres
beregningene med flytende
desimalpunktaritmetikk.
• Hvis Tol utelates eller ikke blir brukt, blir
grunninnstillingstoleransen beregnet som:
5EL14 ·maks(dim(Matrise)) ·radNorm
(Matrise)
Det flytende desimalpunkttallet (9.) i m1 gjør at
resultatene må beregnes i flytende desimalpunkt-
form.
Alfabetisk oversikt 129
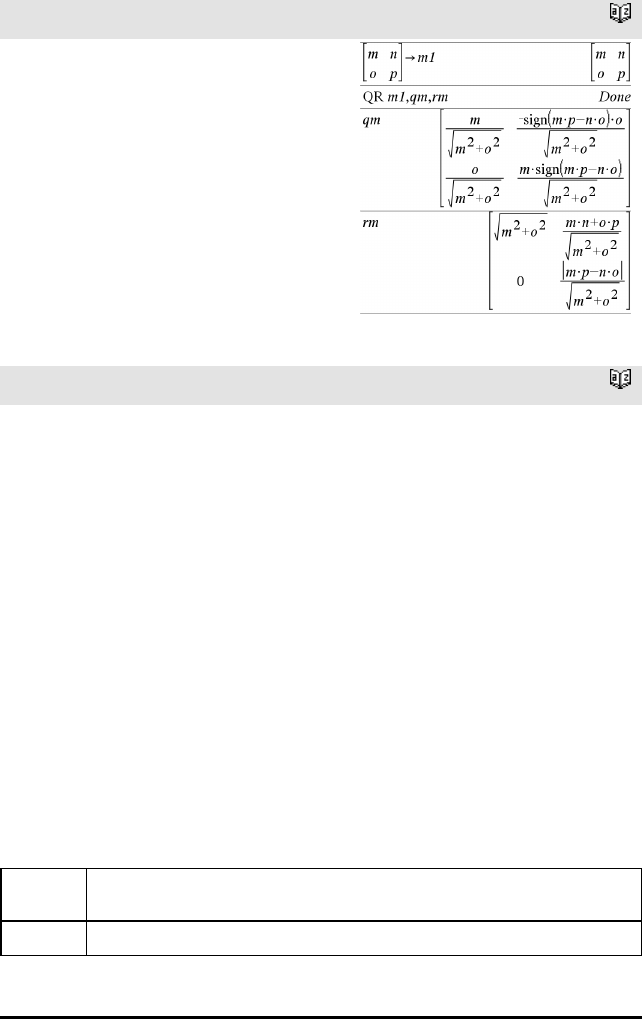
130 Alfabetisk oversikt
QR Katalog >
Faktoriseringen QR beregnes numerisk med faste
transformasjoner. Den symbolske løsningen
beregnes med Gram-Schmidt. Kolonnene i qMatNavn
er ortonormale grunnvektorer som utspenner rommet
som defineres av matrise.
QuadReg (KvadReg) katalog >
QuadReg X,Y[,Frekv] [,Kategori,Inkluder]]
Finner den kvadratiske polynomiske regresjoneny =
a·x2+b·x+cfor listene Xog Ymed frekvens Frekv. En oversikt
over resultatene lagres i stat.resultater-variabelen. (Se side
162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene.
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel
Beskrivelse
stat.RegEqn Regresjonsligning: a·x2+b·x+c

stat.a, stat.b,
stat.c
Regresjonskoeffisienter
stat.R2Determinasjonskoeffisient
stat.Resid Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på begrensninger i
Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
QuartReg Katalog >
QuartReg X,Y[,Frekv] [,Kategori,Inkluder]]
Finner den fjerdegrads polynomiske regresjonen
y = a·x4+b·x3+c·x2+d·x+efor listene Xog Ymed frekvens
Frekv. En oversikt over resultatene lagres i stat.resultater-
variabelen. (Se side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.RegEqn Regresjonsligning: a·x4+b·x3+c·x2+d·x+e
stat.a, stat.b, stat.c,
stat.d, stat.e
Regresjonskoeffisienter
stat.R2Determinasjonskoeffisient
stat.Resid Residualene fra regresjonen
Alfabetisk oversikt 131
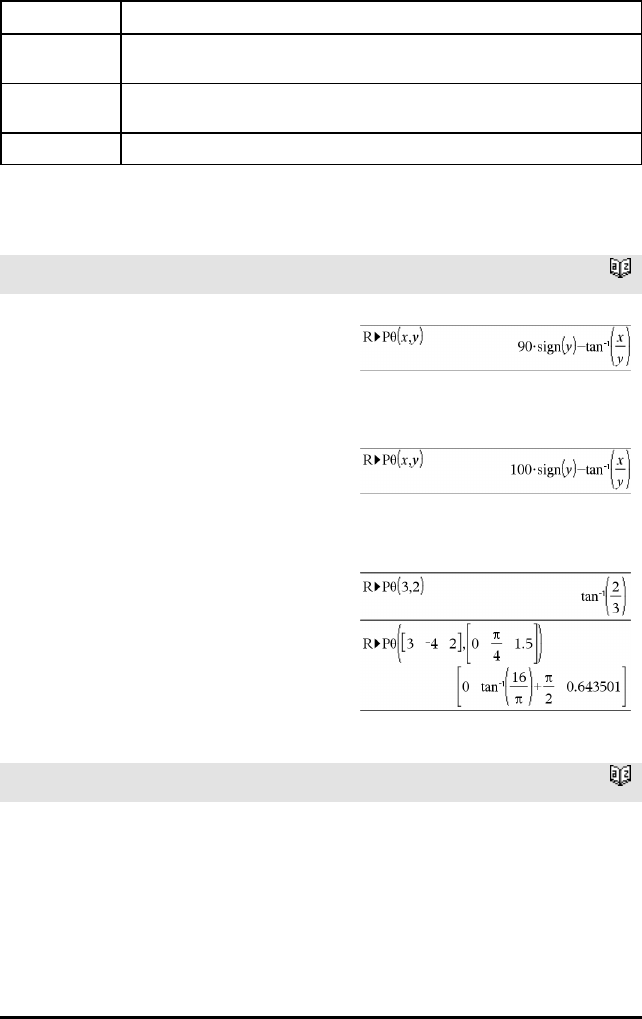
132 Alfabetisk oversikt
Utdata-variabel Beskrivelse
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
R
R4Pq() Katalog >
R4Pq(xUttr,yUttr)⇒Uttrykk
R4Pq(xListe,yListe)⇒liste
R4Pq(xMatrise,yMatrise)⇒matrise
Returnerer ekvivalent q-koordinat av (x,y)
argumentparet.
Merk: Resultatet returneres som en vinkel i enten
grader, gradian eller radian, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
datamaskintastaturet ved å skrive R@>Ptheta
(...).
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
R4Pr() Katalog >
R4Pr (xUttr,yUttr)⇒Uttrykk
R4Pr (xListe,yListe)⇒liste
R4Pr (xMatrise,yMatrise)⇒matrise
Returnerer ekvivalent r-koordinat av (x,y)
argumentparet.
Merk: Du kan sette inn denne funksjonen fra
I Radian-vinkelmodus:
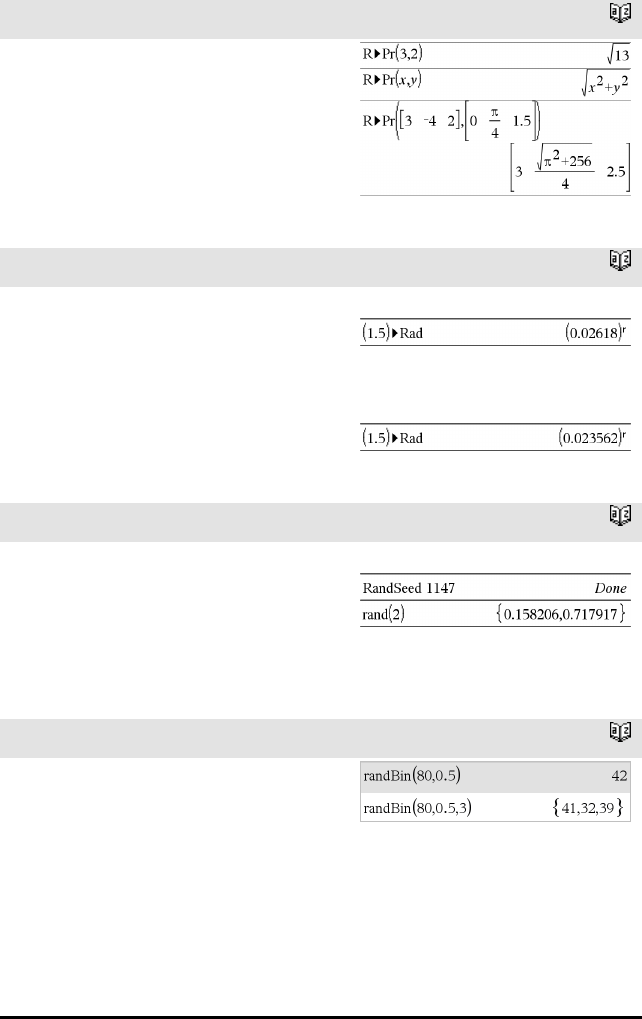
R4Pr() Katalog >
datamaskintastaturet ved å skrive R@>Pr(...).
4Rad Katalog >
Uttr14Rad⇒Uttrykk
Omformer argumentet til radian vinkelmåling.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Rad.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
rand() (tilf) Katalog >
rand()⇒uttrykk
rand(antForsøk)⇒liste
rand() returnerer en tilfeldig verdi mellom 0 og 1.
rand(antForsøk)returnerer en liste som inneholder
antForsøk tilfeldige verdier mellom 0 og 1.
Setter start for tilfeldig tall.
rrandBin() (tilfBin) Katalog >
randBin(n,p)⇒uttrykk
randBin(n,p,antForsøk)⇒liste
randBin(n,p)returnerer et tilfeldig reelt tall fra en
spesifisert binomisk fordeling.
randBin(n,p,antForsøk)returnerer en liste som
inneholder antForsøk tilfeldige relle tall fra en
spesifisert binomisk fordeling.
Alfabetisk oversikt 133
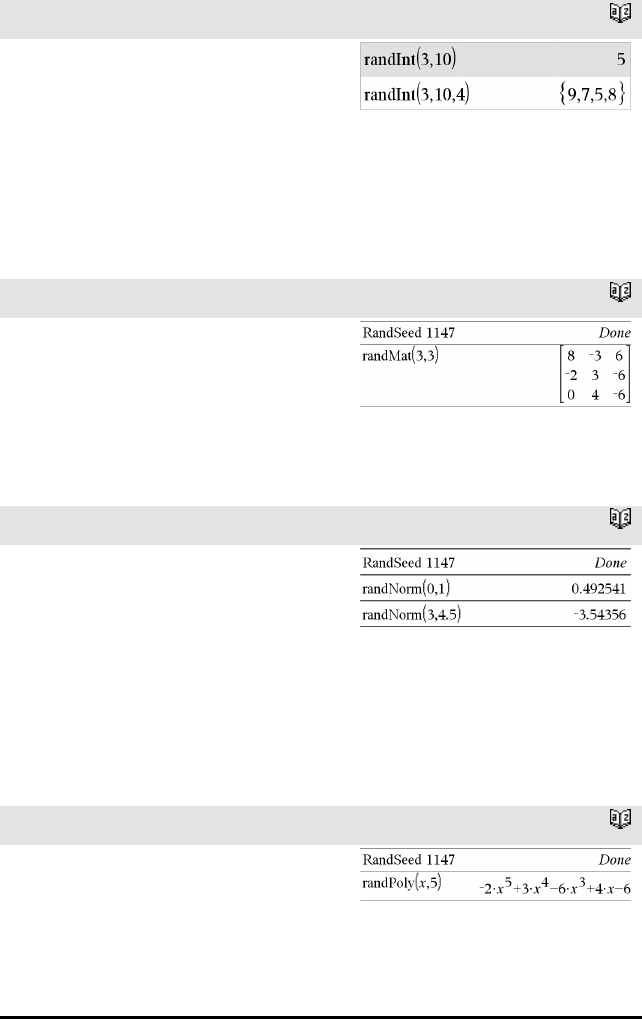
134 Alfabetisk oversikt
randInt() (tilfInt) Katalog >
randInt(nedreGrense,øvreGrense)⇒uttrykk
randInt(nedreGrense,øvreGrense,antForsøk)⇒liste
randInt(nedreGrense,øvreGrense)returnerer et
tilfeldig heltall innenfor et område som spesifiseres av
nedreGrense og øvreGrense heltall-grenser.
randInt(nedreGrense,øvreGrense,antForsøk)
returnerer en liste som inneholder antForsøk tilfeldige
heltall innenfor spesifisert område.
randMat() (tilfMat) Katalog >
randMat(antRader,antKolonner)⇒matrise
Returnerer en matrise av heltall mellom -9 og 9 av
spesifisert dimensjon.
Begge argumentene må forenkles til heltall.
Merk: Verdiene i denne matrisen endres hver gang du
trykker på ·.
randNorm() (tilfNorm) Katalog >
randNorm(m,s)⇒uttrykk
randNorm(m,s,antForsøk)⇒liste
Returnerer et desimaltall fra den spesifiserte
normalfordelingen. Det kan være et hvilket som helst
tall, men vil være sterkt konsentrert i intervallet
[mN3·s,m+3·s].
randNorm(m,s,antForsøk)returnerer en liste med
antForsøk desimaltall fra den angitte
normalfordeligen.
randPoly() (tilfPoly) Katalog >
randPoly(Var,Orden)⇒uttrykk
Returnerer et polynom i Var av spesifisert Orden
(grad). Koeffisientene er tilfeldige heltall i området fra
L9 til 9. Første koeffisient kan ikke være null.
Orden (graden) må være 0–99.

randSamp() (tilfUtv) Katalog >
randSamp(Liste,antForsøk[,ingErst])⇒liste
Returnerer en liste som inneholder et tilfeldig utvalg
av antForsøk forsøk fra Liste med mulighet for å
erstatte utvalget (ingErst=0), eller ingen ertatning av
utvalget (ingErst=1). Grunninnstillingen er med
erstatning av utvalg.
RandSeed Katalog >
RandSeed Tall
Hvis Tall = 0, settes startverdien for tilfeldig tall-
generator til fabrikkinnstilling. Hvis Tall ƒ0, brukes
det for å opprette to startverdier, som lagres i
systemvariablene startverdi1 ogstartverdi2.
real() (reell) Katalog >
real((Uttr1)⇒uttrykk
Returnerer den reelle delen av argumentet.
Merk: Alle ubestemte variabler behandles som reelle
variabler. Se også imag(), side 83.
real(Liste1)⇒liste
Returnerer reelle deler av alle elementer.
real(Matrise1)⇒matrise
Returnerer reelle deler av alle elementer.
4Rect (Rekt) Katalog >
Vektor 4Rect
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Rect.
Viser Vektor i rektangulær form [x, y, z]. Vektoren må
være av dimensjon 2 eller 3 og kan være en rad eller
en kolonne.
Merk: 4Rect er en visningsformat-t-instruksjon, ikke
en omregningsfunksjon. Du kan bare bruke den på
Alfabetisk oversikt 135

136 Alfabetisk oversikt
4Rect (Rekt) Katalog >
slutten av en kommandolinje, og den oppdaterer ikke
svar.
Merk: Se også 4Polar, side 123.
kompleksVerdi 4Rect
Viser kompleksVerdi i rektangulær form a+bi.
kompleksVerdi kan ha en hvilken som helst kompleks
form. Men hvis du legger inn reiθ, forårsaker dette feil
når vinkelmodus er grader.
Merk: Du må bruke parentes for å legge inn polar
(r∠θ).
I Radian-vinkelmodus:
I Gradian-vinkelmodus:
I Grader-vinkelmodus:
Merk: For å skrive ±, velg den fra symbollisten i
Katalogen.
ref() Katalog >
ref((Matrise1(,Tol()⇒matrise
Returnerer eliminasjonsformen av Matrise1.
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn Tol.
Denne toleransen brukes bare hvis matrisen er lagt
inn med flytende desimalpunkt og ikke inneholder
noen symbolske variabler som ikke er tildelt noen
verdi. Ellers ignoreres Tol.
• Hvis du bruker /· eller stiller modusen
Auto eller Tilnærmet på Tilnærmet, utføres
beregningene med flytende
desimalpunktaritmetikk.
• Hvis Tol utelates eller ikke blir brukt, blir
grunninnstillingstoleransen beregnet som:
5EL14 ·max(dim(Matrise1)) ·radNorm
(Matrise1)

ref() Katalog >
Unngå udefinerte elementer i Matrise1. De kan føre til
uventede resultater.
Hvis for eksempel aer udefinert i følgende uttrykk,
vises en varselmelding, og resultatet vises som:
Varselet vises fordi det generaliserte elementet 1/a
ikke ville være gyldig for a=0.
Dette kan du unngå ved å lagre en verdi til apå
forhånd eller ved å bruke begrensningen (“|”), som vist
i følgende eksempel.
Merk: Se også rref(), side 144.
remain() (rest) Katalog >
remain(Uttr1,Uttr2)⇒Uttrykk
remain(Liste1,Liste2)⇒liste
remain(Matrise1,Matrise2)⇒matrise
Returnerer resten av det første argumentet med
hensyn på det andre argumentet som definert av
identitetene:
remain(x,0) x
remain(x,y) xNy·iPart(x/y)
Som en konsekvens, merk at remain(Nx,y)Nremain
(x,y). Resultatet er enten null eller det har samme
fortegn som det første argumentet.
Merk: Se også mod(), side 107.
Alfabetisk oversikt 137
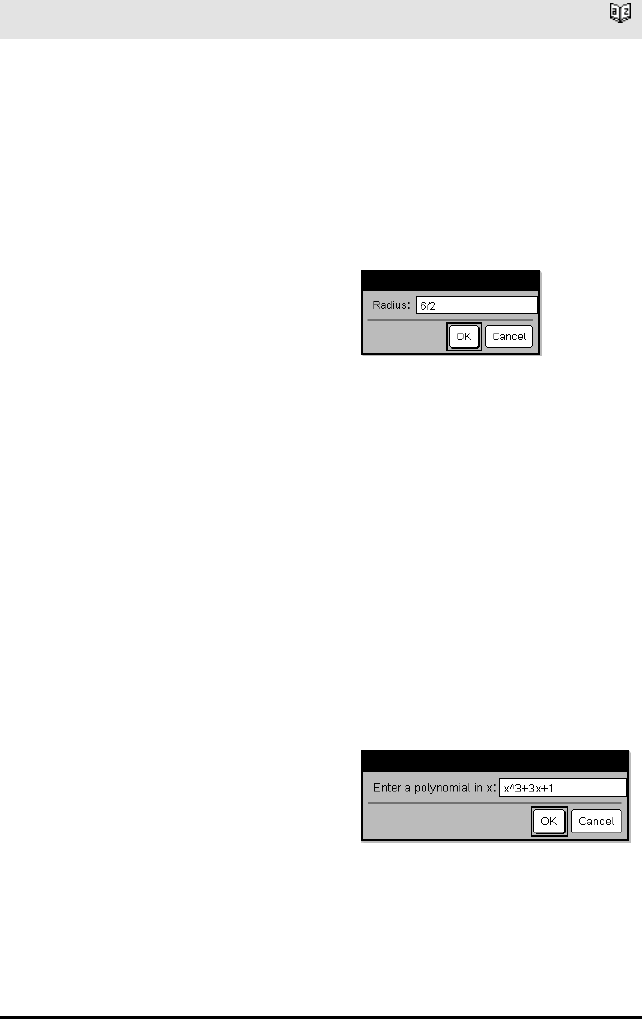
138 Alfabetisk oversikt
Request (Forespør) Katalog >
RequestpromptStreng,var[,DispFlagg [,statusVar]]
RequestpromptStreng,funk(arg1,...argn)
[,DispFlagg [,statusVar]]
Programmeringskommando: Stopper programmet og
viser en dialogboks med meldingen promptStreng og
en inndata-boks for brukerens svar.
Når brukeren skriver inn et svar og klikker på OK, blir
innholdet i inndata-boksen tildelt til variabel var.
Hvis brukeren klikker på Avbryt, fortsetter
programmet uten å akseptere noen innlegg.
Programmet bruker den tidligere verdien av var hvis
var allerede er blitt definert.
Det valgfrie argumentet VisFlagg kan være et hvilket
som helst uttrykk.
• Hvis VisFlagg utelates eller behandles til 1, blir
prompt-meldingen og brukerens svar vist i
Kalkulator-loggen.
• Hvis VisFlagg behandles til 0, blir prompten og
svaret ikke vist i loggen.
Definere et program:
Definer forespør_demo()=Prgm
Forespør “Radius: ”,r
Vis “Areal = “,pi*r2
AvslPrgm
Kjør programmet og skriv inn et svar:
forespør_demo()
Resultat etter trykk på OK:
Radius: 6/2
Area-= 28,2743
Det valgfrie statusVar -argumentet gir programmet en
måte å bestemme hvordan brukeren avviste
dialogboksen. Merk at statusVar krever DispFlag -
argumentet.
• Hvis brukeren har klikket på OK eller trykket på
Enter eller Ctrl+Enter, innstilles variabelen
statusVar til en verdi på 1.
• Ellers innstilles variabelen statusVar til en vedri
på 0.
Argumentet funk() tillater et program å lagre brukerens
svar som en funksjonsdefinisjon. Denne syntaksen
arbeider som om brukeren utførte kommandoen:
Definer funk(arg1, ...argn) = brukers svar
Programmet kan så bruke den definerte funksjonen
funk(). PromptStreng skal veilede brukeren i å legge
inn et passende bruker-svar som fullfører
funksjonsdefinisjonen.
Merk: Du kan bruke Request -kommandoen med et
Definere et program:
Definer polynom()=Prgm
Forespør "Legg inn en polynom i x:",p(x)
Vis "Sanne røtter er:",polyRøtter(p(x),x)
AvslPrgm
Kjør programmet og skriv inn et svar:
polynom()
Resultat etter trykk på OK:
Legg inn en polynom i x: x^3+3x+1
Sanne røtter er: {-0,322185}
Request (Forespør) Katalog >
brukerdefinert program, men ikke med en funksjon.
Slik stopper du et program som inneholder en
Request-kommando inne i en infinit løkke:
•Grafregner: Hold nede tasten c, og trykk på
·flere ganger.
•Windows®: Hold nede tasten F12, og trykk på
Enter flere ganger.
•Macintosh®: Hold nede tasten F5, og trykk på
Enter flere ganger.
•iPad®: Applikasjonen viser en ledetekst. Du kan
fotsette å vente, eller avbryte.
Merk: Se også RequestStr, side 139.
RequestStr (ForespørStr) Katalog >
RequestStrpromptStreng,var[,VisFlagg]
Programmeringskommando: Arbeider identisk med den første
syntaksen i Request -kommandoen, unntatt at brukerens svar
alltid tolkes som en streng. Som kontrast tolker Request -
kommandoen svaret som et uttrykk hvis ikke brukeren setter
det i anførselstegn (““).
Merk: Du kan bruke RequestStr -kommandoen inne i et
brukerdefinert program. men ikke inne i en funksjon.
Slik stopper du et program som inneholder en RequestStr-
kommando inne i en infinitt løkke:
•Grafregner: Hold nede tasten c, og trykk på ·flere
ganger.
•Windows®: Hold nede tasten F12, og trykk på Enter flere
ganger.
•Macintosh®: Hold nede tasten F5, og trykk på Enter flere
ganger.
•iPad®: Applikasjonen viser en ledetekst. Du kan fotsette å
vente, eller avbryte.
Merk: Se også Request, side 138.
Definere et program:
Definer forespørStr_demo()=Prgm
ForespørStr “Navnet ditt:”,navn,0
Vis “Forespør har “,dim(navn),” tegn.”
AvslPrgm
Kjør programmet og skriv inn et svar:
forespørStr_demo()
Resultat etter klikk på OK (Merk at
argumentet VisFlagg av 0utelater
prompten og svaret fra loggen):
forespørStr_demo()
Svaret har 5 tegn.
Alfabetisk oversikt 139
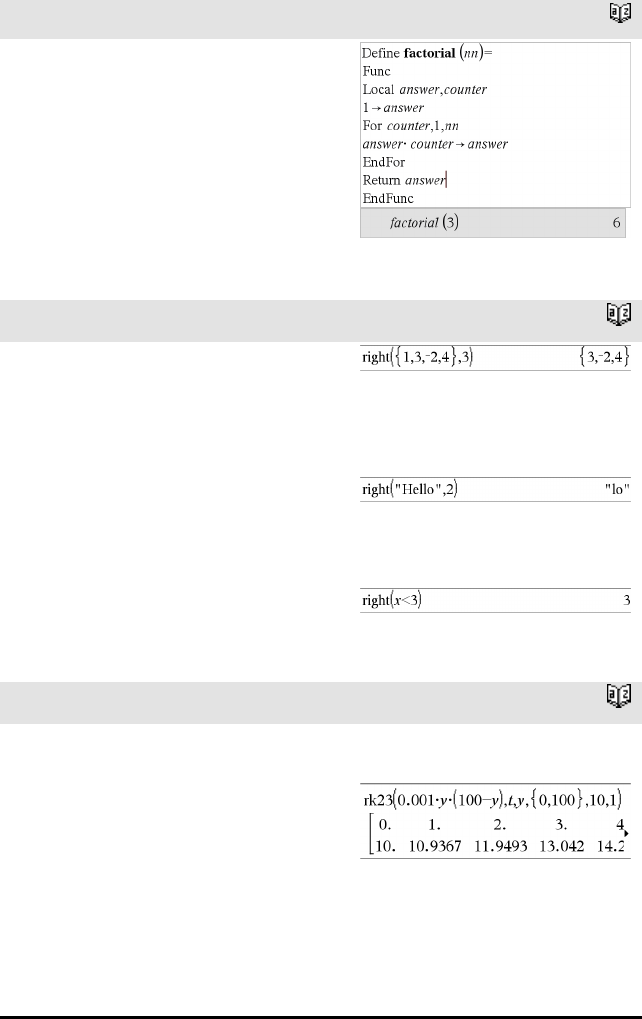
140 Alfabetisk oversikt
Return (Retur) Katalog >
Return [Uttr]
Returnerer Uttr som resultatet av funksjonen. Brukes
innenfor en Func...EndFunc blokk.
Merk: Bruk Returner uten et argument innenfor en
Prgm...EndPrgm-blokk for å avslutte et program.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
right() (høyre) Katalog >
right(Liste1[,Num])⇒liste
Returnerer de Num-elementene som ligger lengst til
høyre i Liste1.
Hvis du utelater Num, returneres alle elementer i
Liste1.
right(kildeStreng[,Num])⇒streng
Returnerer de Num-tegnene som ligger lengst til høyre
i tegnstreng kildeStreng.
Hvis du utelater Num, returneres alle i kildeStreng.
right(Sammenlikning)⇒uttrykk
Returnerer høyre side av en ligning eller ulikhet.
rk23 () Katalog >
rk23(Uttr,Var,avhVar, {Var0,VarMaks}, avhVar0,
VarIntervall [, diftol])⇒matrise
rk23(SystemAvUttr,Var,ListeMedAvhVarer,{Var0,
VarMaks},ListeMedAvhVarer0,VarIntervall [,
diftol])⇒matrise
rk23(ListeMedUttr,Var,ListeMedAvhVarer,{Var0,
VarMaks},ListeMedAvhVarer0,VarIntervall [,
diftol])⇒matrise
Bruker Runge-Kutta-metoden for å løse systemet
Differensialligning:
y'=0,001*y*(100-y) og y(0)=10
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Samme ligning med diftol innstilt på 1.E−6

rk23 () Katalog >
med avhVar(Var0)=avhVar0 på intervallet
[Var0,VarMaks]. Returnerer en matrise, hvis første
rad definerer resultatverdiene av Var som definert av
VarTall. Den andre raden definerer verdien av den
første løsningskomponenten for de tilsvarende Var-
verdiene, og så videre.
Uttr er høyre side, som definerer den ordinære
differensialligningen (ODE).
SystemAvUttr er et system på høyre side som
definerer systemet av ODE-er (tilsvarer til
rekkefølgen av avhengige variabler i
ListeMedAvhVarer).
ListeMedUttr er en liste på høyre side som definerer
systemet av ODE-er (tilsvarer til rekkefølge av
avhengige variabler i ListeMedAvhVarer).
Var er den uavhengige variabelen.
ListeMedAvhVarer er en liste over avhengige
variabler.
{Var0,VarMaks} er en liste med to elementer som
forteller funksjonen at den skal integrere fra Var0 til
VarMaks.
ListeMedAvhVarer er en liste over startverdier for
avhengige variabler.
Hvis VarIntervall beregnes til et tall som ikke er null:
tegn(VarIntervall) = tegn(VarMaks-Var0) og
løsninger returneres ved Var0+i*VarIntervall for alle
i=0,1,2,… slik at Var0+i*VarIntervall er i
[var0,VarMaks] (får kanskje ikke en løsningsverdi
ved VarMaks).
Hvis VarIntervall beregnes til null, returneres
løsningene ved "Runge-Kutta" Var-verdiene.
diftol er feiltoleransen (grunnverdi på 0,001).
Sammenlign resultatet over med nøyaktig løsning i
CAS som ble funnet ved hjelp av deSolve() og
seqGen():
System av ligninger:
med y1(0)=2 og y2(0)=5
Alfabetisk oversikt 141
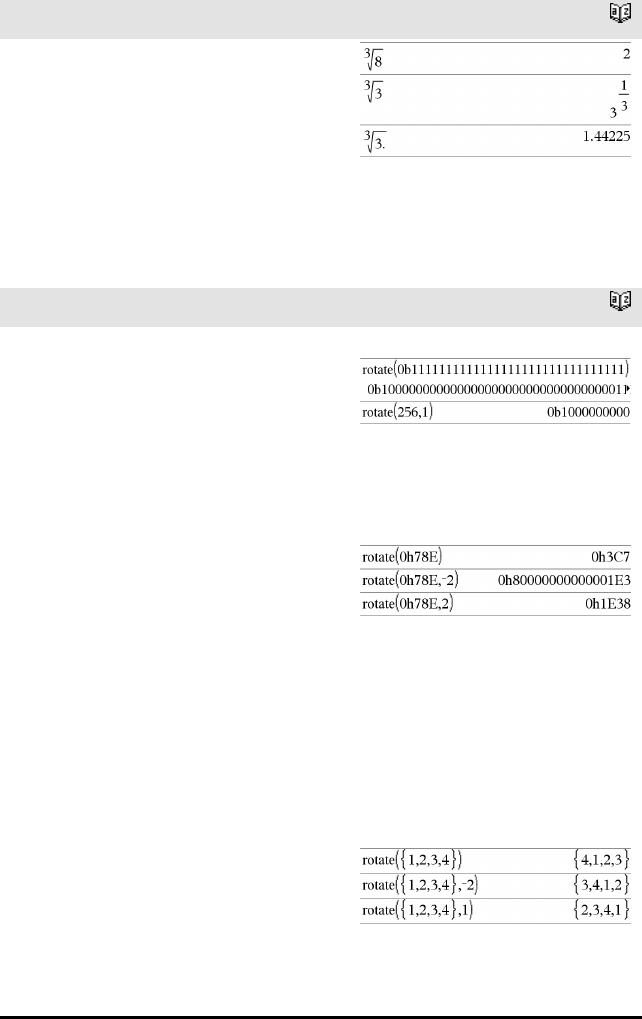
142 Alfabetisk oversikt
root() (rot) Katalog >
root(Uttr)⇒rot
root(Uttr1,Uttr2)⇒rot
root(Uttr)returnerer kvadratroten av Uttr.
root(Uttr1,Uttr2)returnerer Uttr2 rot av Uttr1.Uttr1
kan være en reell eller kompleks flytende
desimalpunktkonstant, et heltall eller en kompleks
rasjonal konstant eller et generelt symbolsk uttrykk.
Merk: Se også N-te rot-sjablon, side 5.
rotate() (rotere) Katalog >
rotate(Heltall1[,#avRotasjoner])⇒heltall
Roterer bitene i et binært heltall. Du kan legge inn
Heltall1 med hvilket som helst grunntall. Det
konverteres automatisk til 64-bit binær form med
fortegn. Hvis Heltall1 er for stort for denne formen, vil
en symmetrisk modulusoperasjon bli brukt til å
konvertere tallet inn i gyldig verdiområde. For mer
informasjon, se 4Base2, side 21.
I binær grunntall-modus:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Hvis #avRotasjoner er positiv, skjer rotasjonen til
venstre. Hvis #avRotasjoner er negativ, skjer
rotasjonen til høyre. Grunninnstilling er L1 (roteres én
bit mot høyre).
For eksempel i en høyre-rotasjon:
I heksades grunntall-modus:
Hver bit roterer mot høyre.
0b00000000000001111010110000110101
Bit til høyre roterer mot venstre.
produserer:
0b10000000000000111101011000011010
Resultatene vises i forhold til grunntall-modusen.
Viktig: Hvis du vil skrive inn et binært eller
heksadesimalt tall, må du alltid bruke prefikset 0b
eller 0h (null, ikke bokstaven O).
rotate(Liste1(,#avRotasjoner))⇒liste
Returnerer en kopi av Liste1 som er rotert mot høyre
eller mot venstre av #avRotasjoner-elementer. Endrer
ikke Liste1.
Hvis #avRotasjoner er positiv, skjer rotasjonen til
venstre. Hvis #avRotasjoner er negativ, skjer
I desimalt grunntall-modus:
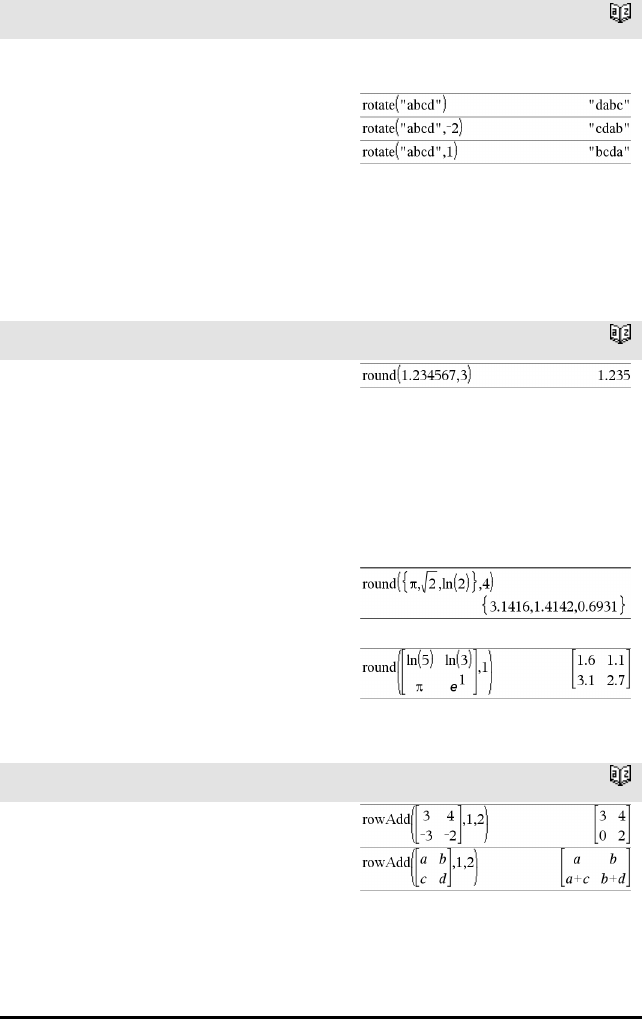
rotate() (rotere) Katalog >
rotasjonen til høyre. Grunninnstilling er L1 (roteres én
bit mot høyre).
rotate(Streng1[,#avRotasjoner])⇒streng
Returnerer en kopi av Streng1 som er rotert mot høyre
eller mot venstre av #avRotasjoner -tegn. Endrer ikke
Streng1.
Hvis #avRotasjoner er positiv, skjer rotasjonen til
venstre. Hvis #avRotasjoner er negativ, skjer
rotasjonen til høyre. Grunninnstillingen er L1 (roteres
ett tegn mot høyre).
round() (avrund) Katalog >
round(Uttr1[,sifre])⇒uttrykk
Returnerer argumentet rundet av til spesifisert antall
sifre etter desimalpunktet.
sifre må være et heltall i området 0–12. Hvis sifre ikke
er inkludert, returneres argumentet avrundet til 12
gjeldende sifre.
Merk: Visning av siffermodus kan ha innvirkning på
hvordan dette vises.
round(Liste1(,sifre))⇒liste
Returnerer en liste over elementer rundet av til
spesifisert antall sifre.
round(Matrise1(,sifre()⇒matrise
Returnerer en matrise av elementene som er rundet
av til spesifisert antall sifre.
rowAdd() (radAdd) Katalog >
rowAdd(Matrise1,rindeks1,rindeks2)⇒matrise
Returnerer en kopi av Matrise1 med rad rIndeks2
erstattet med summen av rader rIndeks1 og
rIndeks2.
Alfabetisk oversikt 143

144 Alfabetisk oversikt
rowDim() (radDim) Katalog >
rowDim(Matrise)⇒uttrykk
Returnerer antallet rader i Matrise.
Merk: Se også colDim(), side 29.
rowNorm() (radNorm) Katalog >
rowNorm(Matrise)⇒uttrykk
Returnerer den største summen av absoluttverdiene
for elementene i radene i Matrise.
Merk: Alle matriseelementene må forenkles til tall. Se
også colNorm(), side 29.
rowSwap() (radSkift) Katalog >
rowSwap(Matrise1,Rindeks1,Rindeks2)⇒matrise
Returnerer Matrise1 med rader rIndeks1 og rIndeks2
ombyttet.
rref() (relform) Katalog >
rref(Matrise1(,Tol))⇒matrise
Returnerer eliminasjonsform av Matrise1.
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn Tol.
Denne toleransen brukes bare hvis matrisen er lagt
inn med flytende desimalpunkt og ikke inneholder
noen symbolske variabler som ikke er tildelt noen
verdi. Ellers ignoreres Tol.
• Hvis du bruker /· eller stiller modusen
Auto eller Tilnærmet på Tilnærmet, utføres

rref() (relform) Katalog >
beregningene med flytende
desimalpunktaritmetikk.
• Hvis Tol utelates eller ikke blir brukt, blir
grunninnstillingstoleransen beregnet som:
5EL14 ·max(dim(Matrise1)) ·radNorm
(Matrise1)
Merk: Se også ref(), side 136.
S
sec() µtast
sec(Uttr1)⇒Uttrykk
sec(Liste1)⇒liste
Returnerer sekans til uttrykk1, eller returnerer en liste
med secant til hvert element i liste1.
Merk: Argumentet tolkes som grader, gradianer eller
radianer, avhengig av aktuell vinkelmodus-innstilling.
Du kan bruke ¡,Geller Rfor å hoppe over
vinkelmodusen midlertidig.
I Grader-vinkelmodus:
sec/() µtast
sec/(Uttr1)⇒Uttrykk
sec/(Liste1)⇒liste
Returnerer vinkelen som har sekans lik uttrykk1, eller
returnerer en liste med invers sekans til hvert element
iliste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradianer eller radianer, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arcsec(...).
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
Alfabetisk oversikt 145

146 Alfabetisk oversikt
sech() Katalog >
sech(Uttr1)⇒Uttrykk
sech(Liste1)⇒liste
Returnerer hyperbolsk secant avuttrykk1, eller
returnerer en liste med hyperbolsk sekans av hvert
element i liste1.
sech/() Katalog >
sech/(Uttr1)⇒Uttrykk
sech/(Liste1)⇒liste
Returnerer invers hyperbolsk sekans til uttrykk1, eller
returnerer en liste med invers hyperbolsk sekans til
hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arcsech(...).
I Radian-vinkelmodus og Rectangular-
kompleksmodus:
seq() (sekv) Katalog >
seq(Uttr,Var,Lav,Høy(,Trinn))⇒liste
Øker Var fra Lav til Høy med trinn på Intervall,
behandler Uttr og returnerer resultatene som en liste.
Det opprinnelige innholdet i Var er fremdeles der etter
at seq() er fullført.
Grunnverdien for Intervall = 1.
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .

seqGen() Katalog >
seqGen(Uttr,Var,avhVar,{Var0,VarMaks}[,
ListeAvInnlLedd [,VarIntervall [,Loftverdi]]])⇒liste
Genererer en liste over ledd for tallfølge avhVar(Var)
=Uttr som følger: Øker uavhengig variabel Var fra
Var0 til VarMaks med VarIntervaller, beregner
avhVar(Var) for tilsvarende verdier av Var ved hjelp
av Uttr-formel og ListeAvInnlLedd, og returnerer
resultatene som en liste.
seqGen(ListeEllerSystemAvUttr,Var,
ListeMedAvhVarer,{Var0,VarMaks} [,
MatriseAvInnlLedd [,VarIntervall [,Loftverdi]]])
⇒matrise
Genererer en matrise av ledd for et system (eller en
liste) av tallfølger ListeMedAvhVarer(Var)
=ListeEllerSystemAvUttr som følger: Øker uavhengig
variabel Var fra Var0 til VarMaks med VarIntervall,
behandler ListeMedAvhVarer(Var) for tilsvarende
verdier av Var ved hjelp av ListeEllerSystemAvUttr -
formel og MatriseAvInnlLedd, og returnerer
resultatene som en matrise.
Opprinnelig innhold i Var er uendret etter at seqGen()
er fullført.
Grunnverdien for VarIntervall =1.
Genererer de første 5 leddene i tallfølgen u(n)=u(n-
1)2/2, med u(1)=2og VarIntervall=1.
Eksempel der Var0=2:
Eksempel der det innledende leddet er
symbolsk:
System av to tallfølger:
Merk: Tomrommet (_) i matrisen med innledende
ledd over brukes for å angi at det innledende leddet for
u1(n) er beregnet ved hjelp av den eksplisitte
tallfølgeformelen u1(n)=1/n.
seqn() Katalog >
seqn(Uttr(u,n[,ListeMedInnlLedd[,nMaks [,
Loftverdi]]])⇒liste
Genererer en liste over ledd for tallfølge u(n)=Uttr(u,
n) som følger: Øker nfra 1 til nMaks med 1, beregner
Genererer de første 6 leddene i tallfølgen u(n)=u(n-
1)/2, med u(1)=2.
Alfabetisk oversikt 147

148 Alfabetisk oversikt
seqn() Katalog >
u(n) for tilsvarende verdier av nved hjelp av formel
Uttr(u,n) og ListeMedInnlLedd, og returnerer
resultatene som en liste.
seqn(uttr(n[,nMaks [,Loftverdi]])⇒liste
Genererer en liste over ledd for en ikke-rekursiv
tallfølge u(n)=Uttr(n) som følger: Øker nfra 1 til
nMaks med 1, beregner u(n) for tilsvarende verdier av
nved hjelp av formelen Uttr(n), og returnerer
resultaten e som en liste.
Hvis nMaks mangler, innstilles nMaks på 2500
Hvis nMax=0, innstilles nMaks på 2500
Merk: seqn() kaller seqGen() med n0=1og nintervall
=1
series() (rekke) Katalog >
series(Uttr1,Var,Orden [,Punkt])⇒uttrykk
series(Uttr1,Var,Orden [,Punkt]) |
Var>Punkt⇒uttrykk
series(Uttr1,Var,Orden [,Punkt]) |
Var<Punkt⇒uttrykk
Returnerer en generalisert kuttet
potensrekkepresentasjon av Uttr1 som er utvidet
rundt Punkt av grad Orden.Orden kan være et
vilkårlig, rasjonelt tall. Resulterende potenser av (Var
NPunkt) kan inkludere negative eksponenter og/eller
brøk-eksponenter. Koeffisientene foran disse
potensene kan inkludere logaritmer av (Var NPunkt)
og andre funksjoner av Var som er dominert av alle
potensene til (Var NPunkt) som har samme
eksponenttegn (-sign).
Punkt grunninnstilles til 0. Punkt kan være ˆeller Nˆ,
i så fall er utvidelsen gjennom grader Orden i 1/(Var N
Punkt).
series(...) returnerer “series(...)” hvis den ikke er i
stand til å bestemme en slik representasjon, som for
vesentlige singulærpunkter, f.eks. sin(1/z)ved z=0,

series() (rekke) Katalog >
eN1/z ved z=0 eller ezved z = ˆeller Nˆ.
Dersom rekken eller en av dens deriverte har en
“hopp-diskontinuitet” ved Punkt, er det sannsynlig at
resultatet inneholder deluttrykk av formen tegn(…)
eller abs(…) for en reell utvidelsesvariabel eller (-1)nedre
(…vinkel(…)…) for en sammensatt utvidelsesvariabel, som
er en som ender med “_”. Dersom du vil bruke rekken
kun for verdier på den ene siden av Punkt, så utvider
du med det som passer av “| Var >Punkt”, “| Var <
Punkt”, “| “Var |Punkt” eller “Var {Punkt” for å oppnå
et enklere resultat.
series() kan gi symbolsk tilnærming til ubestemte
integraler og bestemte integraler som det ellers ikke
kan oppnås symbolske løsninger for.
series() fordeler over 1. argument-lister og matriser.
series() er en generalisert versjon av taylor().
Som vist i det siste eksemplet til høyre kan
visningsrutinene nedover fra resultatet som er
produsert av series(...) arrangere leddene på nytt, slik
at dominantTerm ikke er det som er helt til venstre.
Merk: Se også dominantTerm(), side 56.
SetMode() (lesModus) Katalog >
SetMode(modusNavnHeltall,innstillingHeltall)
⇒heltall
SetMode(liste)⇒heltallsliste
Kun gyldig innenfor en funksjon eller et program.
SetMode(modusNavnHeltall,innstillingHeltall)
setter foreløpig modus modusNavnHeltall til den
nye innstillingen innstillingHeltall, og returnerer
et heltall som samsvarer med den opprinnelige
innstillingen av den modusen. Endringen er
begrenset til hvor lenge det varer å utføre
programmet/funksjonen.
modusNavnHeltall spesifiserer hvilken modus
du vil stille inn. Det må være en av modus-
heltallene fra tabellen nedenfor.
Vis tilnærmet verdi av pved hjelp av grunninnstillingen for
Vis sifre, og vis så pmed en innstilling på Fast2. Kontroller
for å se at grunninnstillingen gjenopprettes etter at
programmet utføres.
Alfabetisk oversikt 149

150 Alfabetisk oversikt
SetMode() (lesModus) Katalog >
innstilleHeltall spesifiserer den nye innstillingen
for modusen. Det må være en av
innstillingsheltallene fra listen nedenfor for den
spesifikke modusen som du stiller inn.
SetMode(liste)lar deg endre flere innstillinger.
liste inneholder tallpar med modusheltall og
innstillingeheltall. SetMode(liste)returnerer en
liknende liste med heltallpar som representerer
de opprinnelige modusene og innstillingene.
Hvis du har lagret alle modusinnstillinger med
SetMode(0) &var, kan du bruke SetMode(var)
for å gjenopprette disse innstillingene til
funksjonen eller programmet lukkes. Se
SetMode(), side 77.
Merk: De aktuelle modusinnstillingene sendes til
påkalte underrutiner. Hvis en underrutine endrer
en modusinnstilling, går modusinnstillingen tapt
når kontrollen går tilbake til påkallingsrutinen.
Merk for å legge inn eksemplet: For anvisninger
om hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Modus Navn Modus
Heltall
Innstille heltall
Vis sifre 1 1=Flytende, 2=Flytende1, 3=Flytende2, 4=Flytende3, 5=Flytende4,
6=Flytende5, 7=Flytende6, 8=Flytende7, 9=Flytende8, 10=Flytende9,
11=Flytende10, 12=Flytende11, 13=Flytende12, 14=Fast0,
15=Fast1, 16=Fast2, 17=Fast3, 18=Fast4, 19=Fast5, 20=Fast6,
21=Fast7, 22=Fast8, 23=Fast9, 24=Fast10, 25=Fast11, 26=Fast12
Vinkel 2 1=Radian, 2=Grader, 3=Gradian
Eksponensielt
format
31=Normal, 2=Vitenskapelig, 3=Teknisk
Reell eller
kompleks
41=Reell, 2=Rektangulær, 3=Polar
Auto eller
tilnærm.
51=Auto, 2=Tilnærmet, 3=Eksakt
Vektorformat 6 1=Rektangulær, 2=Sylindrisk, 3=Sfærisk

Modus Navn Modus
Heltall
Innstille heltall
Grunntall 7 1=Desimal, 2=Heks, 3=Binær
Måleenheter 8 1=SI, 2=Eng/USA
shift() (skift) Katalog >
shift(Heltall1[,#avSkift])⇒heltall
Forskyver (skifter) bitene i et binært heltall. Du kan
legge inn Heltall1 med hvilket som helst grunntall.
Det konverteres automatisk til 64-bit binær form med
fortegn. Hvis Heltall1 er for stort for denne formen, vil
en symmetrisk modulusoperasjon bli brukt til å
konvertere tallet inn i gyldig verdiområde. For mer
informasjon, se 4Base2, side 21.
Hvis #avSkift er positiv, er skift til venstre. Hvis
#avSkift er negativ, er skift til høyre. Grunninnstilling
er L1 (skiftes èn bit mot høyre).
I et høyre-skift er biten helt til høyre droppet og 0 eller
1 lagt inn for å stemme overens med den venstre
biten. I et venstre-skift er biten helt til venstre droppet
og 0 er lagt inn som høyre-bit.
For eksempel i et høyre-skift:
Hver bit skifter mot høyre.
0b0000000000000111101011000011010
Setter inn 0 hvis biten helt til venstre er 0,
eller 1 hvis biten helt til venstre er 1.
produserer:
0b00000000000000111101011000011010
Resultatene vises i forhold til grunntall-modusen.
Ledende nuller vises ikke.
I binær grunntall-modus:
I heksades grunntall-modus:
Viktig: Hvis du vil skrive inn et binært eller
heksadesimalt tall, må du alltid bruke prefikset 0b
eller 0h (null, ikke bokstaven O).
shift(Liste1 [,#avSkift])⇒liste
Returnerer en kopi av Liste1 skiftet til høyre eller til
venstre av #avSkift-elementer. Endrer ikke Liste1.
Hvis #avSkift er positiv, er skift til venstre. Hvis
#avSkift er negativ, er skift til høyre.
Grunninnstillingen er L1 (skiftes et element til høyre).
Elementer som introduseres ved begynnelsen eller
I desimalt grunntall-modus:
Alfabetisk oversikt 151
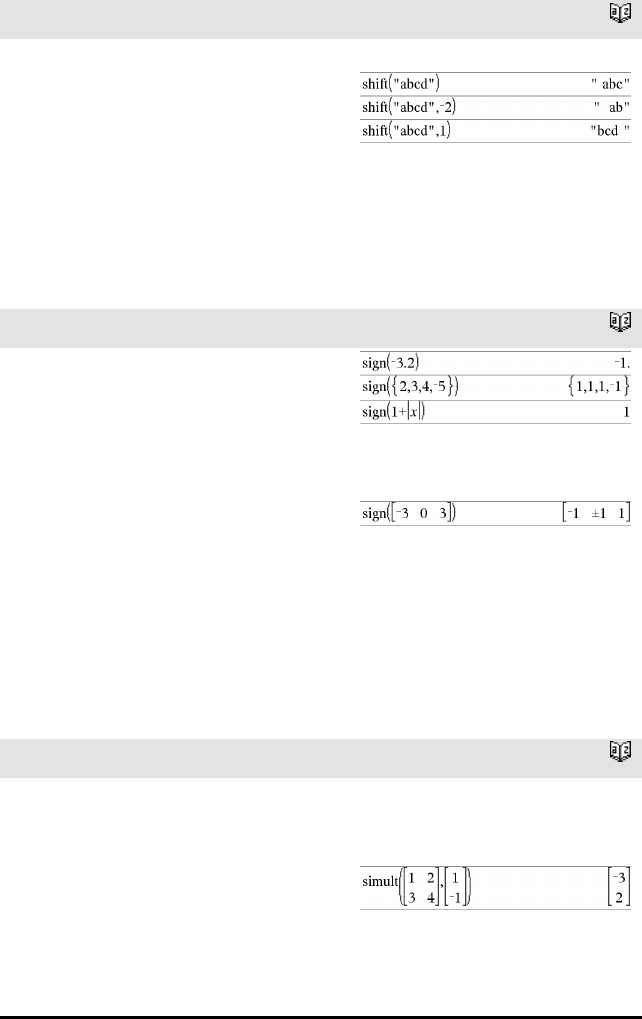
152 Alfabetisk oversikt
shift() (skift) Katalog >
slutten av liste ved skiftet er satt til symbolet “udef”.
shift(Streng1 [,,#avSkift](⇒streng
Returnerer en kopi av Streng1 skiftet mot høyre eller
mot venstre av #ofShifts-tegn. Endrer ikke Streng1.
Hvis #avSkift er positiv, er skift til venstre. Hvis
#avSkift er negativ, er skift til høyre.
Grunninnstillingen er L1 (skiftes et tegn mot høyre).
Tegn som introduseres ved begynnelsen eller slutten
av streng ved skiftet er satt til et mellomrom.
sign() (fortegn) Katalog >
sign(Uttr1)⇒Uttrykk
sign(Liste1)⇒list e
sign(Matrise1)⇒matrise
For reell og komplekst Uttrykk1, returneres
Uttrykk1/abs(Uttrykk1)når Uttrykk1ƒ0.
Returnerer 1 hvis Uttrykk1 er positiv.
Returnerer L1 hvisUttr1 er negativ.
sign(0) returnerer „1 hvis kompleks formatmodus er
Reell; ellers returnerer den seg selv.
sign(0) representerer enhetssirkelen i den komplekse
grunnmengden.
For en liste eller matrise returneres fortegnene for alle
elementene.
Hvis kompleks formatmodus er reell:
simult() Katalog >
simult(koeffMatrise,konstVektor(,Tol))⇒matrise
Returnerer en kolonnevektor som inneholder
løsningene til et system av lineære ligninger.
Merk: Se også linSolve(), side 95.
koeffMatrise må være en kvadratmatrise som
inneholder ligningskoeffisientene.
konstVektor må ha samme antall rader (samme
Løs mhp. x og y:
x + 2y = 1
3x + 4y = L1
Løsningen er x= L3 og y=2.

simult() Katalog >
dimension) som koeffMatrise og inneholde
konstantene.
Alternativt kan ethvert matriseelement behandles
som null hvis absoluttverdien er mindre enn Tol.
Denne toleransen brukes bare hvis matrisen er lagt
inn med flytende desimalpunkt og ikke inneholder
noen symbolske variabler som ikke er tildelt noen
verdi. Ellers ignoreres Tol.
• Hvis du bruker modusen Auto eller Tilnærmet
på Tilnærmet, utføres beregningene med
flytende desimalpunktaritmetikk.
• Hvis Tol utelates eller ikke blir brukt, blir
grunninnstillingstoleransen beregnet som:
5EL14·max(dim(koeffMatrise))
·radNavnkoeffMatrise)
Løs:
ax + by = 1
cx + dy = 2
simult(koeffMatrise,konstMatrise(,Tol))⇒matrise
Løser multiple systemer av lineære ligninger, hvor
hvert system har samme ligningskoeffisienter men
forskjellige konstanter.
Hver kolonne i konstMatrise må inneholde
konstantene for et ligningssystem. Hver kolonne i
resultatmatrisen inneholder løsningen for det
tilsvarende systemet.
Løs:
x + 2y = 1
3x + 4y = L1
x + 2y = 2
3x + 4y = L3
For det første systemet er x=L3 og y=2. For det andre
systemet er x=L7 og y=9/2.
4sin katalog >
Uttr 4sin
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>sin.
Representerer Uttr ved sinus. Dette er en
konverteringsoperator. Denkan bare brukes på
slutten av kommandolinjen.
4sin reduserer alle potenser av cos(...) modulus 1Nsin
(...)^2 slik at alle gjenværende potenser av sin(...) har
eksponenter i området (0, 2). Dermed vil resultatet
Alfabetisk oversikt 153

154 Alfabetisk oversikt
4sin katalog >
være uten cos(...) hvis og bare hvis cos(...) inntreffer i
det gitte uttrykket bare med partallseksponenter.
Merk: Denne konverteringsoperatoren støttes ikke i
vinkelmodusen grader eller gradianer. Før du bruker
den, må du kontrollere at vinkelmodus er satt til
radianer, og at Uttr ikke inneholder eksplisitte
referanser til vinkler i grader eller gradianer.
sin() µtast
sin(Uttr1)⇒Uttrykk
sin(Liste1)⇒liste
sin(Uttr1)returnerer sinus til argumentet som et
uttrykk.
sin(Liste1)returnerer en liste over sinus til alle
elementer i Liste1.
Merk: Argumentet tolkes som grader, gradianer eller
som radianer, avhengig av aktuell vinkelmodus. Du
kan bruke¡,G, eller Rfor å hoppe over vinkelmodusen
midlertidig.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
sin(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens sinus til kvadratMatrise1.
Dette er ikke det samme som å beregne sinus til hvert
element. For mer informasjon om beregningsmetode,
se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:

sin/() µtast
sin/(Uttr1)⇒Uttrykk
verdi
sin/(Liste1)⇒liste
sin/(Uttr1)returnerer vinkelen med sinus likUttr1
som et uttrykk.
sin/(Liste1)returnerer en liste over invers sinus til
hvert element i Liste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradianer eller radianer, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arcsin(...).
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
sin/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse sinus til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers sinus til hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I radian-vinkelmodus og rektangulær, kompleks
modus:
sinh() Katalog >
sinh(Uttr1)⇒Uttrykk
sinh(Liste1)⇒liste
sinh (Uttr1)returnerer hyperbolsk sinus til argumentet
som et uttrykk.
sinh (Liste1)returnerer en liste over hyperbolsk sinus
til hvert element i Liste1.
sinh(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens hyperbolske sinus for
kvadratMatrise1. Dette er ikke det samme som å
beregne hyperbolsk sinus for hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:
Alfabetisk oversikt 155
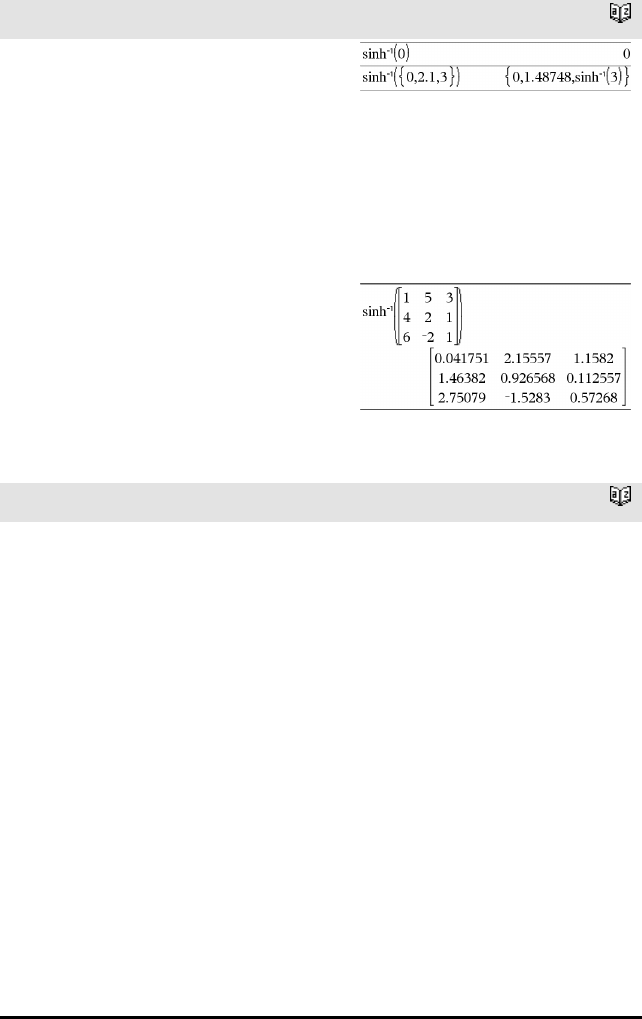
156 Alfabetisk oversikt
sinh/() Katalog >
sinh/(Uttr1)⇒Uttrykk
sinh/(Liste1)⇒liste
sinh(/(Uttr1)returnerer invers hyperbolsk sinus til
argumentet som et uttrykk.
sinh/(Liste1)returnerer en liste over invers
hyperbolsk sinus til hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arcsinh(...).
sinh/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse hyperbolske sinus til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers hyperbolsk sinus til hvert element. For
mer informasjon om beregningsmetode, se under cos
().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:
SinReg katalog >
SinReg X,Y[,[Iterasjoner],[Periode] [,Kategori,Inkluder] ]
Finner sinusregresjonen for listene Xog Y. En oversikt over
resultatene lagres i stat.resultater-variabelen. (Se side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Iterasjoner er en verdi som angir maksimalt antall ganger (1 til
16) det skal gjøres forsøk på å finne en løsning. Hvis utelatt,
brukes 8. Vanligvis resulterer større verdier i bedre nøyaktighet
men lengre kjøretid, og omvendt.
Periode spesifiserer en estimert periode. Hvis utelatt, bør
forskjellen mellom verdiene i Xvære like og i sekvensiell
rekkefølge. Hvis du spesifiserer Periode, kan forskjellene
mellom x-verdiene være ulike.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.

SinReg katalog >
Resultatet av SinReg er alltid i radianer, uavhengig av innstilling
forvinkelmodus.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-
variabel Beskrivelse
stat.RegEqn Regresjonsligning: a·sin(bx+c)+d
stat.a, stat.b,
stat.c, stat.d
Regresjonskoeffisienter
stat.Rest Residualene fra regresjonen
stat.XReg Liste over de datapunkter i den endrede X-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.YReg Liste over de datapunkter i den endrede Y-listen som faktisk brukes i regresjonen basert på
begrensninger i Frekv,Kategoriliste og Inkluder kategorier
stat.FreqReg Liste over frekvenser som samsvarer med stat.XReg og stat.YReg
solve() (løs) Katalog >
solve(Ligning,Var)⇒Boolsk uttrykk
solve(Ligning,Var=Forslag)⇒Boolsk uttrykk
solve(Ulikhet,Var)⇒Boolsk uttrykk
Returnerer reelle løsningskandidater til en ligning eller
ulikhet for Var. Målet er å returnere kandidater for alle
løsninger. Det kan imidlertid forekomme ligninger eller
ulikheter der antall løsninger er uendelig.
Det kan hende at løsningsalternativene ikke er reelle,
endelige tall ved enkelte kombinasjoner av verdier for
udefinerte variabler.
For autoinnstilling av modusen Auto/Tilnærmet er
målet å produsere eksakte løsninger når de er
konsise, samt supplere med iterative søk med
tilnærmet aritmetikk når eksakte løsninger er
upraktiske.
På grunn av forkorting av største felles divisor i teller
og nevner kan det hende at en “løsning” bare er
løsning i den forenklede ligningen eller ulikheten, og
Alfabetisk oversikt 157

158 Alfabetisk oversikt
solve() (løs) Katalog >
ikke i den opprinnelige ligningen/ulikheten.
For ulikheter av typene |,{, <, eller >, er eksplisitte
løsninger ikke sannsynlige hvis ikke ulikheten er
lineær og inneholder kun Var.
Hvis det er valgt Eksakt innstilling i modusen
Auto/Tilnærmet, blir deler som ikke kan løses,
returnert som en implisitt ligning eller ulikhet.
Bruk begrensningsoperatoren (“|”) for å begrense
løsningsintervallet og/eller andre variabler som
forekommer i ligningen eller ulikheten. Når du finner
en løsning i ett intervall, kan du bruke ulikhet-
operatorene for å utelate dette intervallet fra senere
søk.
I Radian-vinkelmodus:
usann returneres hvis ingen reelle løsninger blir
funnet. sann returneres hvis solve() kan bestemme at
enhver endelig reell verdi av Var tilfredsstiller
ligningen eller ulikheten.
Siden solve() alltid returnerer et Boolsk resultat, kan
du bruke “and,” “or,” og “not” for å kombinere
resultatene fra solve() med hverandre eller med andre
Boolske uttrykk.
Løsninger kan inneholde en unik, ny udefinert
konstant av formen nj, der j er et heltall i intervallet 1–
255. Slike variabler betegner et vilkårlig heltall.
I Radian-vinkelmodus:
I reell modus markerer brøkpotenser med
oddetallsnevnere bare reell forgreining. Ellers
markerer multiple forgreinede uttrykk, som
brøkpotens, logaritmer og inverse trigonometriske
funksjoner, bare hovedforgreiningen. Dermed
produserer solve() kun løsninger som samsvarer med
den ene reelle forgreiningen eller med
hovedforgreiningen.
Merk: Se også cSolve(),cZeros(),nSolve() og zeros
().
solve(Lign1and Lign2 [and… ],VarElForslag1,
VarElForslag2 [,… ])⇒Boolskuttrykk
solve(LignSystem,VarElForslag1,VarElForslag2 [,
… ])⇒Boolskuttrykk

solve() (løs) Katalog >
solve({Lign1,Lign2 [,...]} {VarElForslag1,
VarElForslag2 [,… ]})⇒Boolskuttrykk
Returnerer reelle løsningsalternativer til de simultane,
algebraiske ligningene, der hver VarElForslag
spesifiserer en variabel som du vil løse med hensyn
på.
Du kan skille ligningene med and-operatoren, eller du
kan legge inn et LignSystem ved å bruke en sjablon fra
katalogen. Antall argumenter iVarElForslag må
passe til antallet ligninger. Alternativt kan du
spesifisere et startforslag for en variabel. Hver
VarElForslag må være på formen:
variabel
– eller –
variabel =reelt eller ikke-reelt tall
For eksempel er x gyldig, og det er x=3 også.
Hvis alle ligningene er polynomer og hvis du IKKE
spesifiserer noe startforslag, bruker solve()
Gröbner/Buchbergers leksikale eliminasjonsmetode
for å prøve å bestemme alle reelle løsninger.
La oss for eksempel anta at du har en sirkel med
radius r om origo og en annen sirkel med radius r
midtstilt der hvor den første sirkelen krysser den
positive x-aksen. Bruk solve() for å finne
skjæringspunktene.
Som vist med r i eksemplet til høyre, kan simultane
polynomiske ligninger ha ekstra variabler som ikke
har noen verdi, men som representerer gitte
numeriske verdier som kan settes inn senere.
Du kan også (eller istedenfor) inkludere
løsningsvariabler som ikke forekommer i ligningene.
For eksempel kan du inkludere z som en
løsningsvariabel for å utvide det forrige eksemplet til
to parallelle gjennomskjærende sylindre med radius r.
Sylinderløsningene viser hvordan løsningsfamilier kan
inneholde vilkårlige konstanter i form av ck, hvor k er
et heltall fra 1 til 255.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Alfabetisk oversikt 159

160 Alfabetisk oversikt
solve() (løs) Katalog >
For polynomiske systemer kan beregningstiden eller
plassen i minnet sterkt avhenge av hvilken rekkefølge
du setter løsningsvariabler i. Hvis startforslaget
bruker opp minneplassen eller tålmodigheten din, kan
du prøve å flytte om på variablene i ligningene og/eller
varElForslag-listen.
Hvis du ikke inkluderer noen forslag og hvis en ligning
er ikke-polynomisk i en vilkårlig variabel men alle
ligningene er lineære i løsningsvariablene, bruker
solve() gaussisk eliminasjon for å prøve å bestemme
alle reelle løsninger.
Hvis et system verken er polynomisk i alle variablene
eller lineær i løsningsvariablene, bestemmer solve()
som regel en løsning med en tilnærmet iterativ
metode. I så fall må antallet løsningsvariabler være lik
antallet ligninger, og alle andre variabler (parametre) i
ligningene må forenkles til tall.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
Hver løsningsvariabel starter ved foreslått verdi hvis
den er spesifisert; ellers starter den ved 0.0.
Bruk forslagene til å finne andre løsninger en etter en.
For konvergens kan det hende at et forslag må være
ganske nært en løsning.
SortA (SorterSt) Katalog >
SortAListe1[,Liste2] [,Liste3]...
SortAVektor1[,Vektor2] [,Vektor3] ...
Sorterer elementene i det første argument i stigende
rekkefølge.
Hvis du inkluderer andre argumenter, sorteres
elementene av hvert slik at den nye posisjonen deres
stemmer overens med den nye posisjonen til
elementene i det første argumentet.
Alle argumentene må være navn på lister eller
vektorer. Alle argumentene må ha like dimensjoner.
Tomme (åpne) elementer innenfor det første utsagnet
flyttes til bunnen. For mer informasjon om tomme
elementer, se side 217.
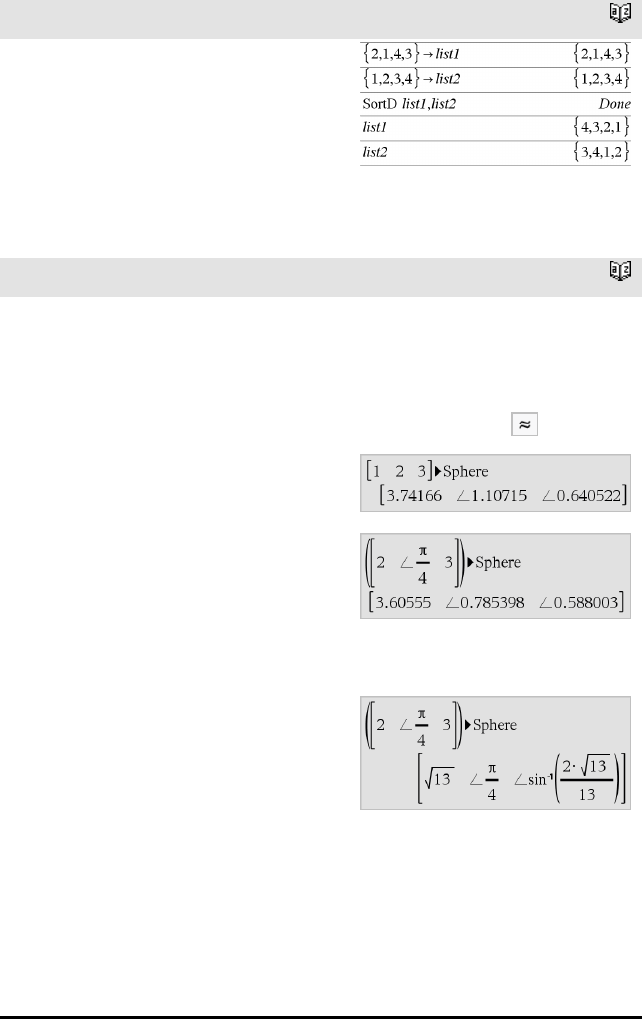
SortD (SorterSy) Katalog >
SortD Liste1[,Liste2] [,Liste3] ...
SortDVektor1[,Vektor2] [,Vektor3] ...
Identisk med SortA, bortsett fra at SortD sorterer
elementene i fallende rekkefølge.
Tomme (åpne) elementer innenfor det første utsagnet
flyttes til bunnen. For mer informasjon om tomme
elementer, se side 217.
4Sphere (sfærisk) Katalog >
Vektor 4Sphere
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @>Sphere.
Viser rad- eller kolonnevektor i sfærisk form [r ±q
±f].
Vektor må være av dimensjon 3 og kan enten være en
rad- eller en kolonnevektor.
Merk: 4Sphere er en visningsformat-instruksjon, ikke
en omregningsfunksjon. Du kan bare bruke den på
slutten av en kommandolinje.
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .
Trykk på ·
Alfabetisk oversikt 161

162 Alfabetisk oversikt
4Sphere (sfærisk) Katalog >
sqrt() (kvdrt) Katalog >
sqrt(Uttr1)⇒uttrykk
sqrt(Liste1)⇒liste
Returnerer kvadratroten til argumentet.
For en liste, returneres kvadratroten til alle
elementene i Liste1.
Merk: Se også Kvadratrot-sjablon, side 5.
stat.results (stat.resultats) Katalog >
stat.results
Viser resultater fra en statistisk beregning.
Resultatene vises som et sett av navn-verdi-par. De
spesifikke navnene som vises er avhengige av den
aller siste brukte statistikkfunksjonen eller
kommandoen.
Du kan kopiere et navn eller en verdi og lime den inn i
andre posisjoner.
Merk: Unngå å definere variabler som bruker de
samme navnene som de som brukes for statistisk
analyse. I noen tilfeller kan det oppstå feilbetingelse. I
tabellen nedenfor finner du en liste over variabelnavn
som brukes for statistisk analyse.

stat.a
stat.AdjR²
stat.b
stat.b0
stat.b1
stat.b2
stat.b3
stat.b4
stat.b5
stat.b6
stat.b7
stat.b8
stat.b9
stat.b10
stat.bList
stat.c²
stat.c
stat.CLower
stat.CLowerList
stat.CompList
stat.CompMatrix
stat.CookDist
stat.CUpper
stat.CUpperList
stat.d
stat.dfDenom
stat.dfBlock
stat.dfCol
stat.dfError
stat.dfInteract
stat.dfReg
stat.dfNumer
stat.dfRow
stat.DW
stat.e
stat.ExpMatrix
stat.F
stat.FBlock
stat.Fcol
stat.FInteract
stat.FreqReg
stat.Frow
stat.Leverage
stat.LowerPred
stat.LowerVal
stat.m
stat.MaxX
stat.MaxY
stat.ME
stat.MedianX
stat.MedianY
stat.MEPred
stat.MinX
stat.MinY
stat.MS
stat.MSBlock
stat.MSCol
stat.MSError
stat.MSInteract
stat.MSReg
stat.MSRow
stat.n
stat.Ç
stat.Ç1
stat.Ç2
stat.ÇDiff
stat.PList
stat.PVal
stat.PValBlock
stat.PValCol
stat.PValInteract
stat.PValRow
stat.Q1X
stat.Q1Y
stat.Q3X
stat.Q3Y
stat.r
stat.r²
stat.RegEqn
stat.Resid
stat.ResidTrans
stat.sx
stat.sy
stat.sx1
stat.sx2
stat.Gx
stat.Gx²
stat.Gxy
stat.Gy
stat.Gy²
stat.s
stat.SE
stat.SEList
stat.SEPred
stat.sResid
stat.SEslope
stat.sp
stat.SS
stat.SSBlock
stat.SSCol
stat.SSX
stat.SSY
stat.SSError
stat.SSInteract
stat.SSReg
stat.SSRow
stat.tList
stat.UpperPred
stat.UpperVal
stat.v
stat.v1
stat.v2
stat.vDiff
stat.vList
stat.XReg
stat.XVal
stat.XValList
stat.w
stat.y
stat.yList
stat.YReg
Merk: Hver gang applikasjonen Lister og regneark beregner statistiske resultater, kopierer den “stat.”-
gruppevariablene til en “stat#.”-gruppe, der # er et tall som økes automatisk. På den måten kan du
bevare tidligere resultater mens du utfører flere beregninger.
stat.values (stat.verdier) Katalog >
stat.values
Viser en matrise av verdiene som er beregnet for siste
behandlede statistikkfunksjon eller kommando.
Se stat.results -eksemplet.
Alfabetisk oversikt 163

164 Alfabetisk oversikt
stat.values (stat.verdier) Katalog >
I motsetning til stat.results utelater stat.values navnene som
assosieres med verdiene.
Du kan kopiere en verdi og lime dette inn i andre posisjoner.
stDevPop() (stAvvPop) Katalog >
stDevPop(Liste[, frekvListe])⇒uttrykk
Returnerer populasjonens standardavvik for
elementene i Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
Merk: Liste må ha minst to elementer. Tomme (åpne)
elementer ignoreres. For mer informasjon om tomme
elementer, se side 217
I radian-vinkelmodus og automatisk modus:
stDevPop(Matrise1[,FrekvMatrise])⇒matrise
Returnerer en radvektor av populasjonens
standardavvik i kolonnene i Matrise1.
Hvert frekvMatrise element teller antallet
forekomster av det tilsvarende elementet i Matrise1.
Merk: Matrise1 må ha minst to rader. Tomme (åpne)
elementer ignoreres. For mer informasjon om tomme
elementer, se side 217.
stDevSamp() (UtvstdAvv) Katalog >
stDevSamp(Liste[,frekvListe])⇒uttrykk
Returnerer utvalgets standardavvik av elementene i
Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
Merk: Liste må ha minst to elementer. Tomme (åpne)
elementer ignoreres. For mer informasjon om tomme
elementer, se side 217
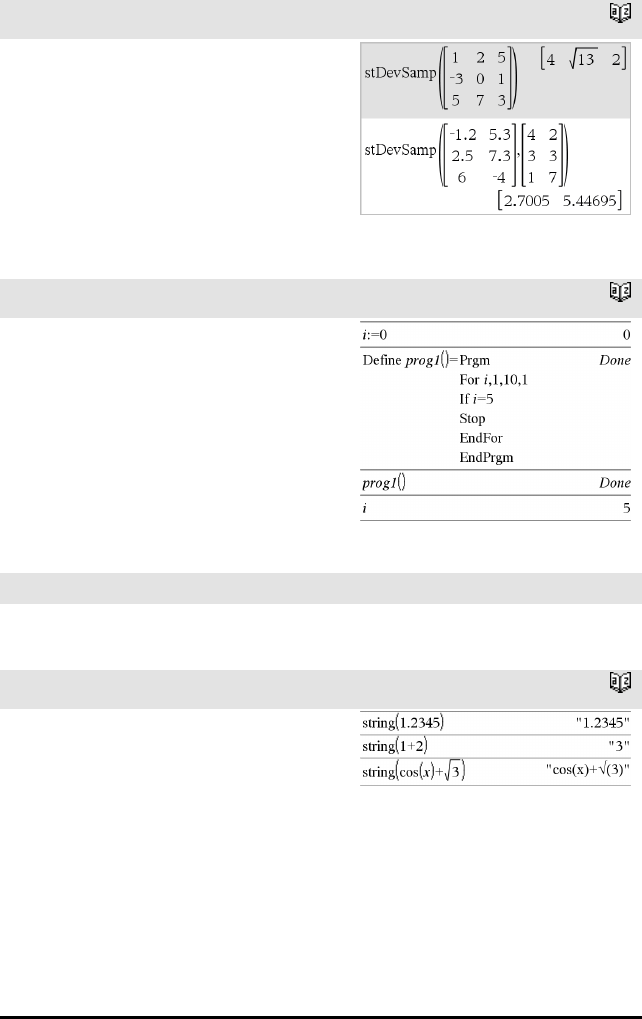
stDevSamp() (UtvstdAvv) Katalog >
stDevSamp(Matrise1[,frekvMatrise])⇒matrise
Returnerer en radvektor av utvalgets standardavvik
av kolonnene i Matrise1.
Hvert frekvMatrise element teller antallet
forekomster av det tilsvarende elementet i Matrise1.
Merk: Matrise1 må ha minst to rader. Tomme (åpne)
elementer ignoreres. For mer informasjon om tomme
elementer, se side 217.
Stop (Stopp) Katalog >
Stop
Programmeringskommando: Avslutter programmet.
Stop er ikke tillatt i funksjoner.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Lagre Se &(lagre), side 215.
String() (Streng) Katalog >
string(Uttr)⇒string
Forenkler Uttr og returnerer resultatet som en
tegnstreng.
Alfabetisk oversikt 165
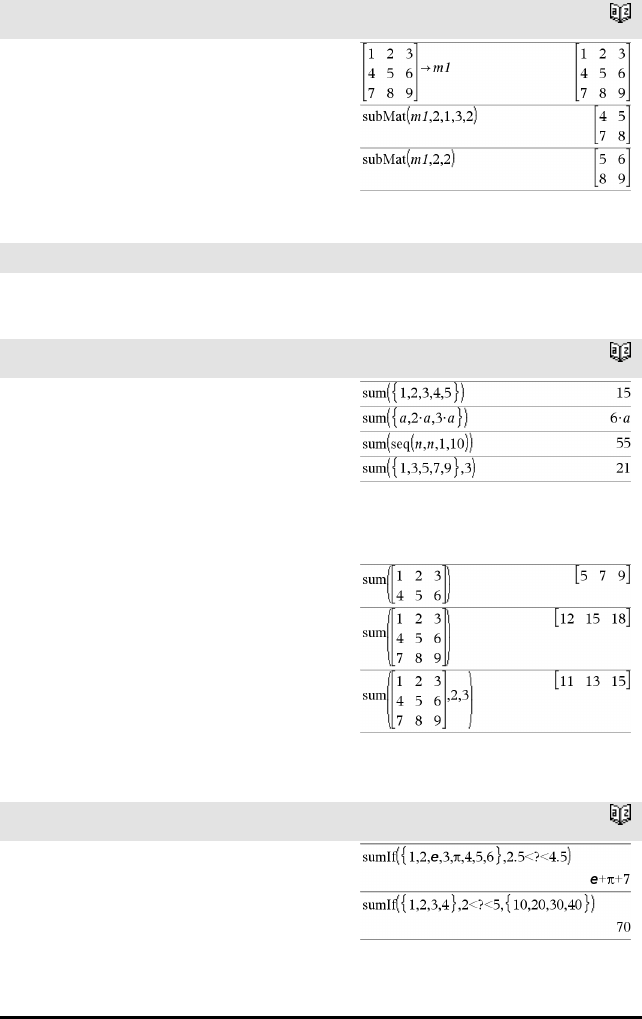
166 Alfabetisk oversikt
subMat() (undermatrise) Katalog >
subMat(Matrise1[,startRad] [,startKol] [,endRad) [,
endKol])⇒matrise
Returnerer den spesifiserte undermatrisen til
Matrise1.
Grunninnstillinger: startRad=1, startKol=1,
endRad=siste rad, endKol=siste kolonne.
Sum (Sigma) Se G(), side 206.
sum() Katalog >
sum(Liste[,Start[,Slutt ]])⇒uttrykk
Returnerer summen av elementene i Liste.
Start og Slutt er alternativer. De spesifiserer et
elementområde.
Et tomt utsagn produserer et tomt resultat. Tomme
(åpne) elementer i Liste ignoreres. For mer
informasjon om tomme elementer, se side 217.
sum(Matrise1[,Start[,Slutt]])⇒matrise
Returnerer en radvektor som inneholder summene av
elementene i kolonnene i Matrise1.
Start og Slutt er alternativer. De spesifiserer et
radområde.
Et tomt utsagn produserer et tomt resultat. Tomme
(åpne) elementer i Matrise1 ignoreres. For mer
informasjon om tomme elementer, se side 217.
sumIf() Katalog >
sumIf(Liste,Kriterium[, SumListe])⇒verdi
Returnerer samlet sum av alle elementene i Liste
som møter de spesifiserte Kriterier. Eventuelt kan
du spesifisere en endringsliste, sumListe, for å hente
de elementene som skal samles (akkumuleres).
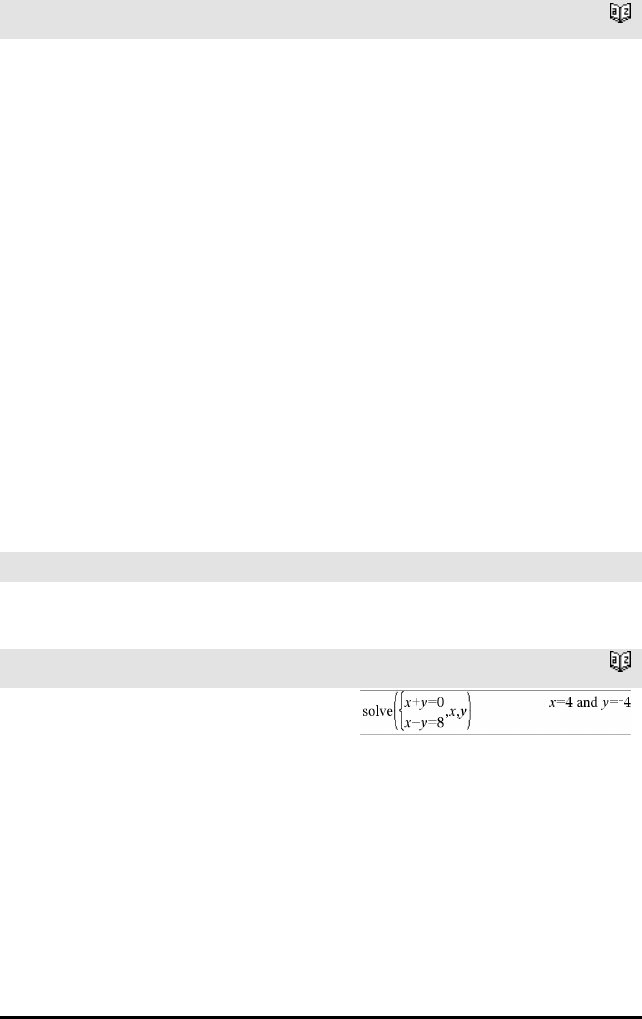
sumIf() Katalog >
Liste kan være et uttrykk, en liste eller en matrise.
SumListe, hvis spesifisert, må ha samme dimensjon
(er) som Liste.
Kriterium kan være:
• En verdi, et uttrykk eller en streng. For
eksempel, 34 samler kun de elementene i Liste
som forenkles til verdien 34.
• Et boolsk uttrykk som inneholder symbolet ?
som plassholder for hvert element. For
eksempel, ?<10 samler kun de elementene i
Liste som er mindre enn 10.
Hvis et Liste-element møter Kriteriene, legges dette
elementet til den samlende summen. Hvis du
inkluderer sumListe, legges tilsvarende element fra
sumListe til summen istedenfor.
I applikasjonen lIster og regneark kan du bruke et
celleområde istedenfor Liste og sumListe.
Tomme (åpne) elementer ignoreres. For mer
informasjon om tomme elementer, se side 217.
Merk: Se også countIf(), side 38.
sumSeq() Se G(), side 206.
system() Katalog >
system(Uttr1 [,Uttr2 [,Uttr3 [,...]]])
system(Ekv1 [,Ekv2 [,Ekv3 [,...]]])
Returnerer et ligningssystem, formatert som en liste.
Du kan også opprette et system med en sjablon.
Merk: Se også Ligningssystemer, side 7.
Alfabetisk oversikt 167

168 Alfabetisk oversikt
T
T(transponert) katalog >
Matrise1T⇒matrise
Returnerer den komplekse konjugerte transponerte
av Matrise1.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @t.
tan() µtast
tan(Uttr1)⇒Uttrykk
tan(Liste1)⇒liste
tan(Uttr1)returnerer tangens til argumentet som et
uttrykk.
tan(Liste1)returnerer en liste over tangensene til alle
elementene i Liste1.
Merk: Argumentet tolkes som grader, gradianer eller
som radianer, avhengig av aktuell vinkelmodus. Du
kan bruke¡,G, eller Rfor å hoppe over vinkelmodusen
midlertidig.
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
tan(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisetangensen av kvadratMatrise1.
Dette er ikke det samme som å beregne tangens for
hvert element. For mer informasjon om
beregningsmetode, se under cos().
I Radian-vinkelmodus:

tan() µtast
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
tan/() µtast
tan/(Uttr1)⇒Uttrykk
tan/(Liste1)⇒liste
tan/(Uttrykk1)returnerer vinkelen med tangens lik
Uttr1, som et uttrykk.
tan/(Liste1)returnerer en liste over de inverse
tangenser til hvert element i Liste1.
Merk: Resultatet returneres som en vinkel i enten
grader, gradianer eller radianer, avhengig av aktuell
vinkelmodus-innstilling.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arctan(...).
I Grader-vinkelmodus:
I Gradian-vinkelmodus:
I Radian-vinkelmodus:
tan/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse tangens til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers tangens til hvert element. For mer
informasjon om beregningsmetode, se under cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:
tangentLine() katalog >
tangentLine(Uttr1,Var,Punkt)⇒uttrykk
tangentLine(Uttr1,Var=Punkt)⇒uttrykk
Returnerer tangentlinjen til kurven som er
representert av Uttr1 i punktet som er spesifisert i
Var=Punkt.
Sørg for at den uavhengige variabelen ikke er definert.
Hvis for eksempel f1(x):=5 og x:=3, vil tangentLine(f1
(x),x,2)returnere “false” (“usant”).
Alfabetisk oversikt 169

170 Alfabetisk oversikt
tanh() Katalog >
tanh(Uttr1)⇒Uttrykk
tanh(Liste1)⇒liste
tanh(Uttr1)returnerer hyperbolsk tangens til
argumentet som et uttrykk.
tanh(Liste1)returnerer en liste av hyperbolske
tangenser til hvert element i Liste1.
tanh(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens hyperbolske tangens til
kvadratMatrise1. Dette er ikke det samme som å
beregne hyperbolsk tangens til hvert element. For
mer informasjon om beregningsmetode, se under cos
().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I Radian-vinkelmodus:
tanh/() Katalog >
tanh/(Uttr1)⇒Uttrykk
tanh/(Liste1)⇒liste
tanh/(Uttrykk1)returnerer invers hyperbolsk tangens
til argumentet som et uttrykk.
tanh/(Liste1)returnerer en liste over invers
hyperbolsk tangens til hvert element i Liste1.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive arctanh(...).
I rektangulært, kompleks format:
tanh/(kvadratMatrise1)⇒kvadratMatrise
Returnerer matrisens inverse hyperbolske tangens til
kvadratMatrise1. Dette er ikke det samme som å
beregne invers hyperbolsk tangens til hvert element.
For mer informasjon om beregningsmetode, se under
cos().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
I radian-vinkelmodus og rektangulært, kompleks
format:
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.

taylor() Katalog >
taylor(Uttr1,Var,Orden[,Punkt])⇒uttrykk
Returnerer etterspurt Taylor polynom. Polynomet
inkluderer ikke-null-ledd med grader i heltall fra null til
Orden i (Var minus Punkt). taylor() returnerer seg selv
hvis det ikke er noen kuttet potensrekke av denne
orden, eller hvis den krever negative eksponenter eller
brøk-eksponenter. Bruk substitusjon og/eller
midlertidig multiplikasjon med en potens av (Var
minus Punkt) for å bestemme mer generell
potensrekke.
Punkt grunninnstilles til null og er “utvidelsespunktet”.
tCdf() Katalog >
tCdf(nedGrense,øvGrense,df)⇒tall hvis nedGrens og øvGrens
er tall, liste hvis nedGrens og øvGrens er lister
Beregner student-t-fordelingens sannsynlighet mellom
nedGrense og øvGrense for spesifisert grader av frihet df.
For P(X {øvreGrense), sett nedreGrense =.ˆ.
tCollect() (tSlåSmn) Katalog >
tCollect(Uttr1)⇒uttrykk
Returnerer et uttrykk der produkter og
heltallspotenser av sinus og cosinus er omregnet til
en lineær kombinasjon av sinus og cosinus med
flersifrede vinkler, vinkelsummer og vinkelforskjeller.
Transformasjonene omregner trigonometriske
polynomer til en lineær kombinasjon av deres
harmoniske ekvivalenter.
Noen ganger vil tCollect() oppnå en ønsket forenkling
når den grunninnstilte trigonometriske forenklingen
ikke gjør det. tCollect() kan omgjøre endringer som ble
gjort med tExpand(). Noen ganger kan et uttrykk
forenkles hvis du bruker tExpand() på et resultat fra
tCollect(), eller omvendt, i to separate omganger.
Alfabetisk oversikt 171

172 Alfabetisk oversikt
tExpand() (tUtvid) Katalog >
tExpand(Uttr1)⇒uttrykk
Returnerer et uttrykk der sinus og cosinus av
flersifrede heltallsvinkler, vinkelsummer og
vinkelforskjeller er utvidet. På grunn av identiteten
(sin(x))2+(cos(x))2=1, er det mange mulige
ekvivalente resultater. Derfor kan et resultat være
forskjellig fra fra et resultat som vises i andre
publikasjoner.
Noen ganger vil tExpand() oppnå målene dine når den
grunninnstilte trigonometriske forenklingen ikke gjør
det. tExpand() kan omgjøre endringer som ble gjort
med tCollect(). Noen ganger kan et uttrykk forenkles
hvis du bruker tCollect() på et resultat fra tExpand(),
eller omvendt, i to separate omganger.
Merk: Grader-modus-skalering med p/180 kommer i
konflikt med tExpand() sin evne til å gjenkjenne
uttrykk som kan utvides. For beste resultater bør
tExpand() brukes i radian modus.
Text Katalog >
TextpromptStreng[,VisFlagg]
Programmeringskommando: Stopper programmet og viser
tegnstrengen promptStreng i en dialogboks.
Når brukeren klikker på OK, fortsetter programmet å utføre.
Det valgfrie flagg -argumentet kan være et hvilket som helst
uttrykk.
• Hvis VisFlagg utelates eller behandles til 1, blir
tekstmeldingen lagt til i Kalkulator-loggen.
• Hvis VisFlagg behandles til 0, blir tekstmeldingen ikke lagt
til i loggen.
Hvis programmet trenger et skrevet svar fra brukeren, kan du se
etter på Request, side 138 eller RequestStr, side 139.
Merk: Du kan bruke denne kommandoen inne i et brukerdefinert
program, men ikke inne i en funksjon.
Definer et program som stopper for å
vise hver av de fem tilfeldige tallene i en
dialogboks.
Innenfor malen Prgm...EndPrgm
fullfører du hver linje ved å trykke på @
istedenfor på ·. På tastaturet på
datamaskinen, hold nede Alt og trykk på
Enter.
Define tekst_demo()=Prgm
For i,1,5
strinfo:=”Random number “& string
(rand(i))
Text strinfo
EndFor
EndPrgm
Kjør program:
tekst_demo()
Text Katalog >
Eksempel på dialogboks:
Then (Så) Se If, side 81.
tInterval katalog >
tInterval Liste[,Frekv[,CNivå]]
(Dataliste-inndata)
tInterval v,sx,n[,CNivå]
(Oppsummerende statistikk-inndata)
Beregner et t-konfidensintervall. En oversikt over resultatene
lagres i stat.resultater-variabelen. (Se side 162.)
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall for et ukjent populasjonsgjennomsnitt
stat.xUtvalgets gjennomsnitt av datasekvensen fra normal tilfeldig fordeling
stat.ME Feilmargin
stat.df Grader-av-frihet
stat.sx Utvalgets standardavvik
stat.n Lengde av datasekvensen med utvalgsgjennomsnitt
tInterval_2Samp Katalog >
tInterval_2Samp Liste1,Liste2[,Frekv1[,Frekv2[,CNivå
[,Felles]]]]
(Dataliste inndata)
Alfabetisk oversikt 173
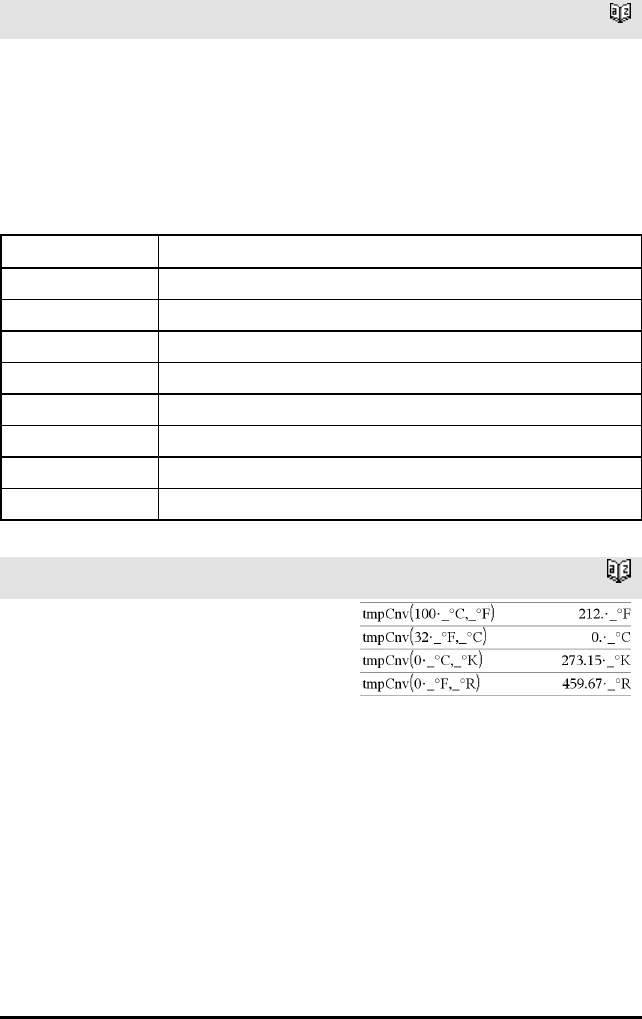
174 Alfabetisk oversikt
tInterval_2Samp Katalog >
tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,CNivå,Felles]
(Summering statistikk inndata)
Beregner et to-utvalgs tkonfidensintervall. En oversikt over
resultatene lagres i stat.results-variabelen. (Se side 162).
Felles=1fellesvarianser; Felles=0gjør ikke fellesvarianser.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall som inneholder konfidensnivå-sannsynligheten for en fordeling
stat.x1-x2 Utvalgsgjennomsnitt av datasekvensene fra normal tilfeldig fordeling
stat.ME Feilmargin
stat.df Grader-av-frihet
stat.x1, stat.x2 Utvalgsgjennomsnitt av datasekvensene fra normal tilfeldig fordeling
stat.sx1, stat.sx2 Utvalgets standardavvik for Liste 1 og Liste 2
stat.n1, stat.n2 Antall utvalg i datasekvenser
stat.sp Det felles standardavviket. Beregnet når Felles=JA.
tmpCnv() Katalog >
tmpCnv(Uttr_¡tempEnhet1, _¡tempEnhet2)⇒
uttrykk _¡tempEnhet2
Omregner en temperaturverdi spesifisert av Uttr fra
en enhet til en annen. Gyldige temperaturenheter er:
_¡C Celsius
_¡F Fahrenheit
_¡K Kelvin
_¡R Rankine
Velg fra symboler i katalogen for å skrive ¡.
for å skrive _, trykk på /_.
For eksempel, 100_¡C omregnes til 212_¡F.
For å omregne et temperaturområde, bruk @tmpCnv()
istedenfor.
Merk: Du kan bruke katalogen for å velge
temperaturenheter.

@tmpCnv() Katalog >
@tmpCnv(Uttrykk_¡tempEnhet, _¡tempEnhet2)
⇒uttrykk _¡tempEnhet2
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive deltaTmpCnv(...).
Konverterer et temperaturområde (forskjellen mellom
to temperaturverdier) som er angitt ved Uttrykk fra en
måleenhet til en annen. Gyldige temperaturenheter er:
_¡CCelsius
_¡FFahrenheit
_¡KKelvin
_¡RRankine
Hvis du skal sette inn ¡, kan du velge det fra
symbolpaletten eller skrive @d.
For å skrive _, trykk på /_.
1_ ¡C og 1_¡K har samme størrelse, og det har også
1_¡F og 1_¡R. Men 1_¡C er 9/5 så stor som 1_¡F.
For eksempel, et 100_¡C-område (fra 0_¡C til 100_
¡C) er ekvivalent til et 180_¡F-område.
For å omregne en spesiell temperaturverdi istedenfor
et -område, bruk tmpCnv().
Velg fra symboler i katalogen for å skrive @.
Merk: Du kan bruke katalogen for å velge
temperaturenheter.
tPdf() Katalog >
tPdf(XVerd,df)⇒tall hvis XVerd er et tall, liste hvis XVerd er en
liste
Beregner sannsynlighetstetthetsfunksjonen (pdf) for Student-t-
fordelingen ved en spesifisert x-verdi med spesifiserte grader av
frihet df.
trace() katalog >
trace(kvadratMatrise)⇒uttrykk
Returnerer diagonalsummen (summen av alle
elementene på hoveddiagonalen) til kvadratMatrise.
Alfabetisk oversikt 175

176 Alfabetisk oversikt
Try Katalog >
Try
blokk1
Else
blokk2
EndTry
Utfører blokk1 med mindre det oppstår en feil.
Programmet overfører til blokk2 hvis en feil oppstår i
blokk1. Systemvariabelen feilKode inneholder
feilkoden, dermed kan programmet utføre retting av
feil. For en liste over feilkoder, se “
Feilkoder og
feilmeldinger
,” side 223.
blokk1 og blokk2 kan enten være et enkelt utsagn
eller en sekvens av utsagn som er adskilt med tegnet
“:”.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Eksempel 2
For å se kommandoene Try,ClrErr og PassErr i drift,
legg inn egenverdier() -programmet som vist til høyre.
Kjør programmet ved å utføre hver av følgende
uttrykk.
Merk: Se også ClrErr, side 28, og PassErr, side 122.
Define egenverdier(a,b)=Prgm
© Programmet egenverdier(A,B) viser egenverdier
av A·B
Try
Disp "A= ",a
Disp "B= ",b
Disp " "
Disp "Egenverdier av A·B er:",egVd(a*b)
Else
If feilKode=230 Then
Disp "Feil: Produkt av A·B må være en
kvadratmatrise"
ClrErr
Else
PassErr
EndIf
EndTry
EndPrgm
Try Katalog >
tTest Katalog >
tTest m0,Liste[,Frekv[,Hypot]]
(Dataliste inndata)
tTest m0,x,sx,n,[Hypot]
(Summering statistikk inndata)
Utfører en hypotesetest for ett enkelt ukjent
populasjonsgjennomsnitt mnår populasjonens standardavvik ser
ukjent. En oversikt over resultatene lagres i stat.results-
variabelen. (Se side 162).
Test H0:m=m0, mot ett av følgende:
For Ha:m<m0, sett Hypot<0
For Ha:m ƒ m0 (standard), sett Hypot=0
For Ha:m>m0, set Hypot>0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.t (x N m0) / (stdev / sqrt(n))
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader-av-frihet
stat.xUtvalgsgjennomsnitt av datasekvensen i Liste
stat.sx Utvalgets standardavvik av datasekvensen
stat.n Utvalgenes størrelse
tTest_2Samp Katalog >
tTest_2Samp Liste1,Liste2[,Frekv1[,Frekv2[,Hypot[,Felles]]]]
(Dataliste inndata)
tTest_2Samp v1,sx1,n1,v2,sx2,n2[,Hypot[,Felles]]
(Summering statistikk inndata)
Alfabetisk oversikt 177
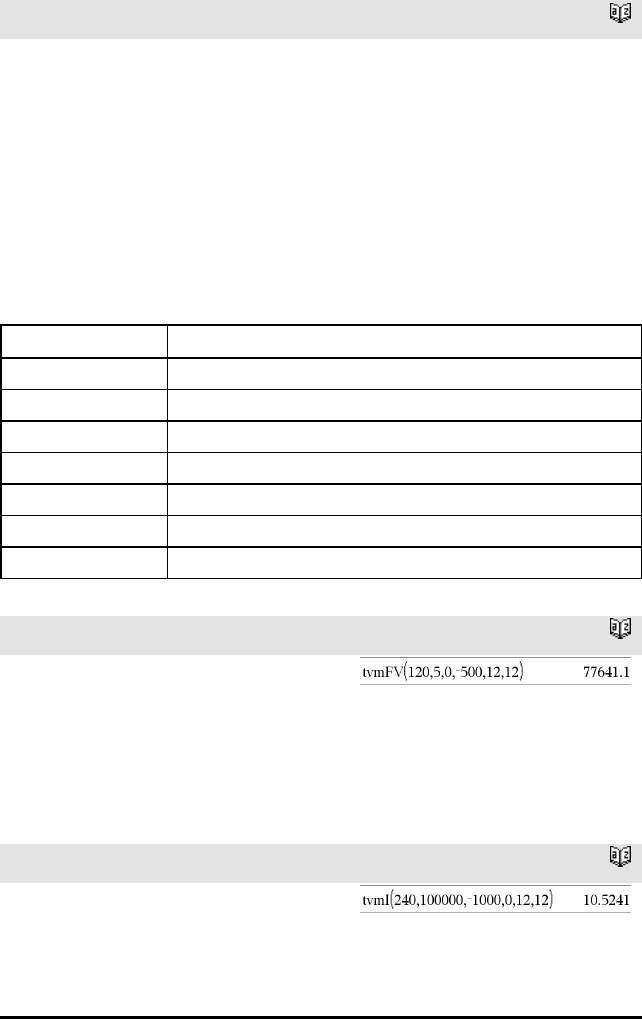
178 Alfabetisk oversikt
tTest_2Samp Katalog >
Beregner en to-utvalgs t-test. En oversikt over resultatene
lagres i stat.results-variabelen. (Se side 162).
Test H0:m1 = m2, mot ett av følgende:
For Ha:m1< m2, sett Hypot<0
For Ha:m1ƒ m2 (standard), sett Hypot=0
For Ha:m1> m2, sett Hypot>0
Felles=1fellesvarianser
Felles =0gir ikke fellesvarianser
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.t Standard normalverdi beregnet for forskjellen i gjennomsnitt
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.df Grader av frihet for t-statistikken
stat.x1, stat.x2Utvalgets gjennomsnitt av datasekvenser i Liste1og Liste2
stat.sx1, stat.sx2 Utvalgets standardavvik til datasekvenser i Liste 1og Liste2
stat.n1, stat.n2 Utvalgenes størrelse
stat.sp Det felles standardavviket. Beregnet når Felles=1.
tvmFV() Katalog >
tvmFV(N,I,PV,Pmt,[PpY],[CpY],[PmtAt])⇒verdi
Finansiell funksjon som beregner fremtidig verdi for
penger.
Merk: Argumenter som brukes i TVM-funksjonene er
beskrevet i tabellen over TVM-argumenter, side 179.
Se også amortTbl(), side 12.
tvmI() Katalog >
tvmI(N,PV,Pmt,FV,[PpY],[CpY],[PmtAt])⇒verdi
Finansiell funksjon som beregner rentefoten per år.
Merk: Argumenter som brukes i TVM-funksjonene er

tvmI() Katalog >
beskrevet i tabellen over TVM-argumenter, side 179.
Se også amortTbl(), side 12.
tvmN() Katalog >
tvmN(I,PV,Pmt,FV,[PpY],[CpY],[PmtAt])⇒verdi
Finansiell funksjon som beregner antallet
betalingsperioder.
Merk: Argumenter som brukes i TVM-funksjonene er
beskrevet i tabellen over TVM-argumenter, side 179.
Se også amortTbl(), side 12.
tvmPmt() Katalog >
tvmPmt(N,I,PV,FV,[PpY],[CpY],[PmtAt])⇒verdi
Finansiell funksjon som beregner beløpet for hver
betaling.
Merk: Argumenter som brukes i TVM-funksjonene er
beskrevet i tabellen over TVM-argumenter, side 179.
Se også amortTbl(), side 12.
tvmPV() Katalog >
tvmPV(N,I,Pmt,FV,[PpY],[CpY],[PmtAt])⇒verdi
Finansiell funksjon som beregner nåverdien.
Merk: Argumenter som brukes i TVM-funksjonene er
beskrevet i tabellen over TVM-argumenter, side 179.
Se også amortTbl(), side 12.
TVM-
argument* Beskrivelse Datatype
N Antall betalingsperioder reelt tall
I Årlig rente (rentefot) reelt tall
PV Nåverdi reelt tall
Pmt Betalingsbeløp reelt tall
Alfabetisk oversikt 179

180 Alfabetisk oversikt
TVM-
argument* Beskrivelse Datatype
FV Fremtidig verdi reelt tall
PpY Antall betalinger pr. år, grunninnstilling=1 heltall > 0
CpY Antall renteperioder pr. år, grunninnstilling=1 heltall > 0
PmtAt Betaling som forfaller ved slutten eller begynnelsen av hver
periode, grunninnstilling=avslutt
heltall (0=avslutte,
1=begynne)
*Disse tidsverdi-for-penger-argumentnavnene likner TVM-variabelnavnene som f.eks. tvm.pv og
tvm.pmt) som brukes av Calculator applikasjonens finansløser. Men finansielle funksjoner lagrer ikke
argumentverdiene eller resultatene til TVM-variablene.
TwoVar Katalog >
TwoVar X,Y[,[Frekv] [,Kategori,Inkluder]]
Beregner 2-variabels statistiske observatorer. En oversikt over
resultatene lagres i stat.resultater-variabelen. (Se side 162.)
Alle listene må ha samme dimensjon bortsett fra Inkluder.
Xog Yer lister av uavhengige og avhengige variabler.
Frekv er en valgfri liste med frekvensverdier. Hvert element i
Frekv angir hvor ofte hvert korresponderende datapunkt Xog Y
forekommer. Standardverdien er 1. Alle elementene må være
heltall0.
Kategori er en liste over kategorikoder for de tilsvarende Xog Y-
dataene..
Inkluder er en liste med én eller flere av kategorikodene.
Baredataelementene med kategorikode som er i listen blir
inkludert iberegningen.
Et tomt (åpent) element i enhver av listene X,Frekv eller
Kategori resulterer i et tomt (åpent) element for det tilsvarende
elementet til alle disse listene. Et tomt element i enhver av
listene fra X1 til X20 resulterer i et tomt (åpent) element for det
tilsvarende elementet i alle disse listene. For mer informasjon om
tomme elementer, se side 217.
Utdata-variabel Beskrivelse
stat.vGjennomsnitt av x-verdier
stat.Gx Sum av x-verdier
stat.Gx2 Sum av x2 verdier
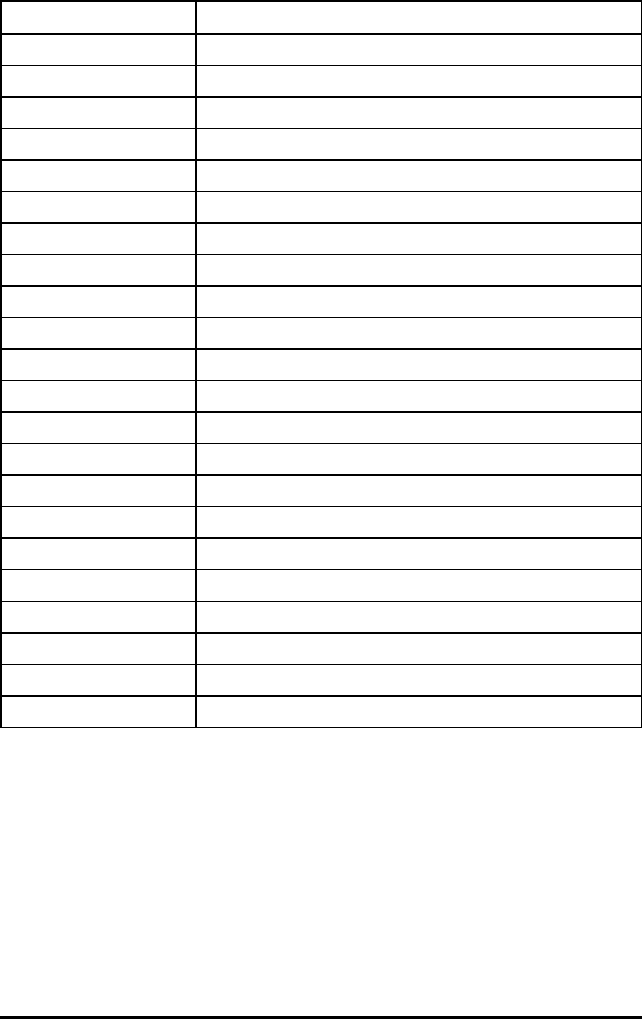
Utdata-variabel Beskrivelse
stat.sx Utvalgets standardavvik til x
stat.sx Populasjonens standardavvik til x
stat.n Antall datapunkter
stat.wGjennomsnitt av y-verdier
stat.Gy Sum av y-verdier
stat.Gy2Sum av y2-verdier
stat.sy Utvalgets standardavvik til y
stat.sy Populasjonens standardavvik til y
stat.Gxy Sum av x·y -verdier
stat.r Korrelasjonskoeffisient
stat.MinX Minimum av x-verdier
stat.Q 1X Første kvartil av x
stat.MedianX Median av x
stat.Q 3X Tredje kvartil av x
stat.MaxX Maksimum av x-verdier
stat.MinY Minimum av y-verdier
stat.Q1Y Første kvartil av y
stat.MedY Median av y
stat.Q3Y Tredje kvartil av y
stat.MaxY Maksimum av y-verdier
stat.G(x-v)2Sum av kvadratavvik fra gjennomsnittet av x
stat.G(y-w)2Sum av kvadrat for avvik fra gjennomsnittet av y
Alfabetisk oversikt 181

182 Alfabetisk oversikt
U
unitV() (enhetsV) Katalog >
unitV(Vektor1)⇒vektor
Returnerer enten en rad- eller kolonne-enhetsvektor,
avhengig av formen på Vektor1.
Vektor1 må være enten en enkel-rad-matrise eller en
enkel-kolonne-matrise.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
unLock Katalog >
unLockVar1 [,Var2] [,Var3] ...
unLockVar.
Låser opp spesifisert variabel eller variabelgruppe.
Låste variabler kan ikke modifiseres eller slettes.
Se Lock, side 98, oggetLockInfo(), side 77.
V
varPop() Katalog >
varPop(Liste[,frekvListe])⇒uttrykk
Returnerer populasjonsvariansen for Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
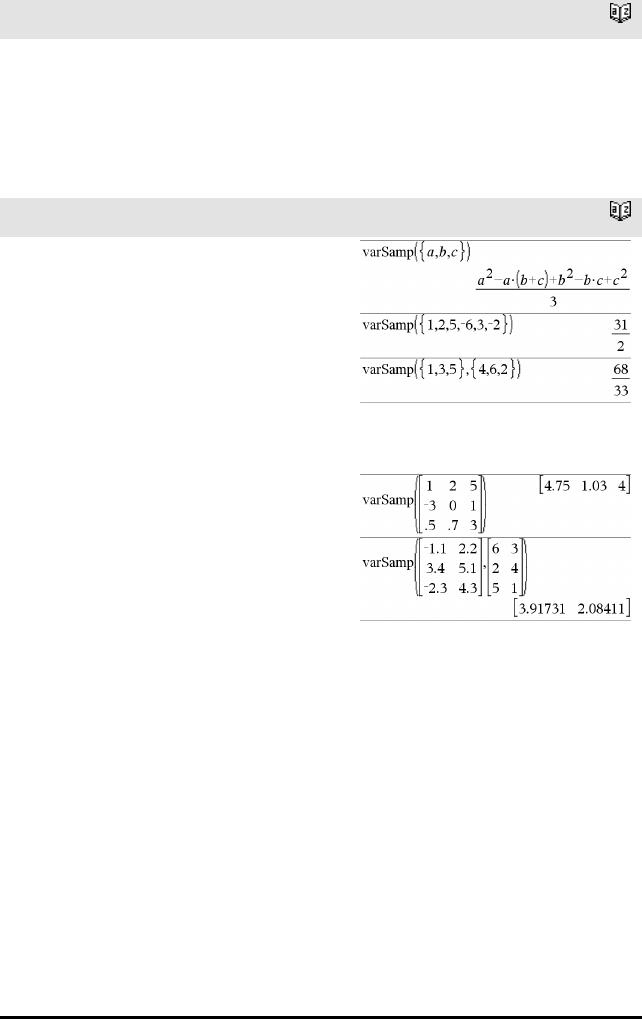
varPop() Katalog >
Merk: Liste må inneholde minst to elementer.
Hvis et element i en av listene er tomt (åpent),
ignoreres dette elementet, og det tilsvarende
elementet i den andre listen ignoreres også. For mer
informasjon om tomme elementer, se side 217.
varSamp() (utvalgets varians) Katalog >
varSamp(Liste[,frekvListe])⇒uttrykk
Returnerer utvalgets varians for Liste.
Hvert frekvListe element teller antallet forekomster
av det tilsvarende elementet i Liste.
Merk: Liste må inneholde minst to elementer.
Hvis et element i en av listene er tomt (åpent),
ignoreres dette elementet, og det tilsvarende
elementet i den andre listen ignoreres også. For mer
informasjon om tomme elementer, se side 217.
varSamp(Matrise1[,frekvMatrise])⇒matrise
Returnerer en radvektor som inneholder utvalgets
varians for hver kolonne i Matrise1.
Hvert frekvMatrise element teller antallet
forekomster av det tilsvarende elementet i Matrise1.
Hvis et element i en av matrisene er tomt (åpent),
ignoreres dette elementet, og det tilsvarende
elementet i den andre matrisen ignoreres også. For
mer informasjon om tomme elementer, se side 217.
Merk: Matrise1 må inneholde minst to rader.
Alfabetisk oversikt 183

184 Alfabetisk oversikt
W
warnCodes () Katalog >
warnCodes(Uttr1,StatusVar)⇒uttrykk
Behandler uttrykk Uttr1, returnerer resultatet, og
lagrer kodene for alle genererte varsler i
listevariabelen StatusVar. Hvis ingen varsler er
generert, tildeler denne funksjonen StatusVar en tom
liste.
Uttr1 kan være et hvilket som helst gyldig
matematisk uttrykk i TI-Nspire™ eller
TI-Nspire™CAS. Du kan ikke bruke en kommando
eller tildeling som Uttr1.
StatusVar må være et gyldig variabelnavn.
Se side 230 for en liste over varselkoder og assosierte
meldinger.
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
when() (når) Katalog >
when(Betingelse,santResultat [,usantResultat][,
ukjentResultat])⇒uttrykk
Returnerer santResultat,usantResultat, eller
ukjentResultat, avhengig av om Betingelse er sann,
usann eller ukjent. Returnerer inndata hvis det er for
få argumenter til å spesifisere korrekt resultat.
Utelat både usantResultat og ukjentResultat for å
definere et uttrykk bare i det området der Betingelse
er sann.
Bruk et udef usantResultat for å definere et uttrykk
som bare plotter grafen på et intervall.
when() er nyttig for å definere rekursive funksjoner.

While Katalog >
While Betingelse
Blokk
EndWhile
Utfører utsagnene i Blokk så lenge som Betingelse er
sann.
Blokk kan enten være et enkelt utsagn eller en
sekvens av utsagn som er adskilt med tegnet.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
X
xor (enten ...eller ...) Katalog >
BoolskUttr1xorBoolskUttr2 returnerer Boolsk uttrykk
BoolskListe1xorBoolskListe2 returnerer Boolsk liste
BoolskMatrise1xorBoolskMatrise2 returnerer Boolsk
matrise
Returnerer sann hvis BoolskUttr1 er sant og
BoolskUttr2 er usant eller omvendt.
Returnerer usann hvis begge argumentene er sanne
eller hvis begge er usanne. Returnerer et forenklet
Boolsk uttrykk hvis ikke noen av argumentene kan
avgjøres som sanne eller usanne.
Merk: Se or, side 120.
Heltall1 xor Heltall2 ⇒heltall
Sammenlikner to reelle heltall bit-for-bit med en xor -
handling. Internt er begge heltallene omregnet til 64-
biters binære tall med fortegn. Når tilsvarende biter
sammenliknes, er resultatet 1 hvis en av bitene (men
ikke begge) er 1; resultatet er 0 hvis begge bitene er 0
eller begge biter er 1. Returnert verdi representerer
bit-resultatene og vises i grunntall-modus.
Du kan skrive inn heltallene med hvilket som helst
grunntall. Hvis du skriver inn en binær eller
I heksades grunntall-modus:
Viktig: Null, ikke bokstaven O.
I binær grunntall-modus:
Merk: Et binært innlegg kan bestå av opptil 64 siffer (i
Alfabetisk oversikt 185

186 Alfabetisk oversikt
xor (enten ...eller ...) Katalog >
heksadesimal verdi, må du bruke hhv. prefiks 0b eller
0h. Uten slik prefiks blir heltall behandlet som
desimalt (grunntall10).
Hvis du oppgir et desimalt heltall som er for stort for et
64-bit binært tall med fortegn, vil en symmetrisk
modulusoperasjon bli brukt til å konvertere tallet inn i
gyldig verdiområde. For mer informasjon, se 4Base2,
side 21.
Merk: Se or, side 120.
tillegg til prefikset 0b). Et heksadesimalt innlegg kan
bestå av opptil 16 siffer.
Z
zeros() (nullpkt) Katalog >
zeros(Uttr,Var)⇒liste
zeros(Uttr,Var=Forslag)⇒liste
Returnerer en liste med kandidater til reelle verdier av
Var som gjør Uttr=0. zeros() gjør dette ved å beregne
exp4liste(solve(Uttr=0,Var),Var).
Noen ganger kan resultatformen for zeros() være mer
praktisk enn den for solve(). Men resultatformen for
zeros() kan ikke uttrykke implisitte løsninger,
løsninger som krever ulikheter, eller løsninger som
ikke involverer Var.
Merk: Se også cSolve(),cZeros() og solve().
zeros({Uttr1,Uttr2}, {VarElForslag1,VarElForslag2
[,… ]})⇒matrise
Returnerer alternative reelle nullpunkter for simultane
algebraiske uttrykk, der hvert VarElForslag
spesifiserer en ukjent som du vil finne verdien til.
Alternativt kan du spesifisere et startforslag for en
variabel. Hvert VarElForslag må ha formen:
variabel
– eller –
variabel =reelt eller ikke-reelt tall
For eksempel er x gyldig, og det er x=3 også.

zeros() (nullpkt) Katalog >
Hvis alle uttrykkene er polynomiske og hvis du IKKE
spesifiserer noe startforslag, bruker zeros()
Gröbner/Buchbergers leksikale eliminasjonsmetode
for å prøve å bestemme alle reelle nullpunkter.
La oss for eksempel anta at du har en sirkel med
radius r om origo og en annen sirkel med radius r
midtstilt der hvor den første sirkelen krysser den
positive x-aksen. Bruk zeros() for å finne
skjæringspunktene.
Som vist med r i eksemplet til høyre, kan simultane
polynomiske uttrykk ha ekstra variabler som ikke har
noen verdi, men som representerer gitte numeriske
verdier som kan legges til senere.
Hver rad i resultatmatrisen representerer et alternativt
(annet) nullpunkt, med komponentene plassert som i
VarElForslag -listen. For å trekke ut en rad, pek på
matrisen med [rad].
Trekk ut rad 2:
Du kan også (eller istedenfor) inkludere ukjente som
ikke forekommer i uttrykkene. For eksempel kan du
inkludere z som en ukjent for å utvide det forrige
eksemplet til to parallelle gjennomskjærende sylindre
med radius r. Sylindernullpunktene viser hvordan
løsningsfamilier av nullpunkter kan inneholde
vilkårlige konstanter i form av ck, hvor k er et heltall
fra 1 til 255.
For polynomiske systemer kan beregningstiden eller
plassen i minnet sterkt avhenge av hvilken rekkefølge
du setter de ukjente i. Hvis startforslaget bruker opp
minneplassen eller tålmodigheten din, kan du prøve å
flytte om på variablene i uttrykkene og/eller
VarElForslag-listen.
Hvis du ikke inkluderer noen forslag og hvis et uttrykk
er ikke-polynomisk i en vilkårlig variabel men alle
uttrykkene er lineære i alle ukjente, bruker zeros()
gaussisk eliminasjon for å prøve å bestemme alle
reelle nullpunkter.
Alfabetisk oversikt 187

188 Alfabetisk oversikt
zeros() (nullpkt) Katalog >
Hvis et system er verken polynomisk i alle variablene
eller lineært i de ukjente, bestemmer zeros() som
regel ett nullpunkt med en tilnærmet iterativ metode. I
så fall må antallet ukjente være lik antallet uttrykk, og
alle andre variabler i uttrykkene må forenkles til tall.
Hver ukjente starter ved foreslått verdi hvis den er
spesifisert; ellers starter den ved 0.0.
Bruk forslagene til å finne andre løsninger en etter en.
For konvergens kan det hende at et forslag må være
ganske nært et nullpunkt.
zInterval Katalog >
zInterval s,Liste[,Frekv[,CNivå]]
(Dataliste inndata)
zInterval s,v,n[,CNivå]
(Summering statistikk inndata)
Beregner et zkonfidensintervall. En oversikt over resultatene
lagres i stat.results-variabelen (side 162).
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall for et ukjent populasjonsgjennomsnitt
stat.xUtvalgets gjennomsnitt av datasekvensen fra normal tilfeldig fordeling
stat.ME Feilmargin
stat.sx Utvalgets standardavvik
stat.n Lengde av datasekvensen med utvalgsgjennomsnitt
stat.sKjent populasjons standardavvik for datasekvens Liste
zInterval_1Prop Katalog >
zInterval_1Prop x,n [,CNivå]
Beregner et en-proporsjons zkonfidensintervall. En oversikt over
resultatene lagres i stat.results-variabelen. (Se side 162).

zInterval_1Prop Katalog >
xer et ikke-negativt heltall.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall som inneholder konfidensnivå-sannsynligheten for en fordeling
stat.ÇBeregnet andel (brøkdel) av suksesser
stat.ME Feilmargin
stat.n Antall utvalg i datasekvens
zInterval_2Prop Katalog >
zInterval_2Prop x1,n1,x2,n2[,CNivå]
Beregner et to-proporsjons zkonfidensintervall. En oversikt over
resultatene lagres i stat.results-variabelen. (Se side 162).
x1 og x2 er ikke-negative heltall.
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall som inneholder konfidensnivå-sannsynligheten for en fordeling
stat.ÇDiff Beregnet differanse mellom andeler (brøkdeler)
stat.ME Feilmargin
stat.Ç1Beregnet andel av suksesser i utvalg 1
stat.Ç2Beregnet andel av suksesser i utvalg 2
stat.n1 Utvalgsstørrelse i datasekvens 1
stat.n2 Utvalgsstørrelse i datasekvens 2
zInterval_2Samp Katalog >
zInterval_2Samp s1,s2,Liste1,Liste2[,Frekv1[,Frekv2,
[CNivå]]]
(Dataliste inndata)
zInterval_2Samp s1,s2,v1,n1,v,,n2[CNivå])
Alfabetisk oversikt 189

190 Alfabetisk oversikt
zInterval_2Samp Katalog >
(Summering statistikk inndata)
Beregner et to-utvalgs zkonfidensintervall. En oversikt over
resultatene lagres i stat.results-variabelen. (Se side 162).
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.CLower, stat.Upper Konfidensintervall som inneholder konfidensnivå-sannsynligheten for en fordeling
stat.x1-x2 Utvalgsgjennomsnitt av datasekvensene fra normal tilfeldig fordeling
stat.ME Feilmargin
stat.x1, stat.x2 Utvalgsgjennomsnitt av datasekvensene fra normal tilfeldig fordeling
stat.sx1, stat.sx2 Utvalgets standardavvik for Liste 1 og Liste 2
stat.n1, stat.n2 Antall utvalg i datasekvenser
stat.r1, stat.r2 Kjent populasjons standardavvik for datasekvens Liste 1 og Liste 2
zTest Katalog >
zTest m0,s,Liste,[Frekv[,Hypot]]
(Dataliste inndata)
zTest m0,s,v,n[,Hypot]
(Summering statistikk inndata)
Utfører en z-test med frekvens frekvliste. En oversikt over
resultatene lagres i stat.results-variabelen. (Se side 162).
Test H0:m=m0, mot ett av følgende:
For Ha:m<m0, sett Hypot<0
For Ha:m ƒ m0 (standard), sett Hypot=0
For Ha:m>m0, sett Hypot>0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.z (x N m0) / (s/ sqrt(n))
stat.P-Verdi Minste sannsynlighet som null-hypotesen kan forkastes ved

Utdata-variabel Beskrivelse
stat.xUtvalgsgjennomsnitt av datasekvensen i Liste
stat.sx Utvalgets standardavvik av datasekvensen. Returneres kun for inndata Data.
stat.n Utvalgenes størrelse
zTest_1Prop Katalog >
zTest_1Prop p0,x,n[,Hypot]
Beregner en en-proporsjons z-test. En oversikt over resultatene
lagres i stat.results-variabelen. (Se side 162).
xer et ikke-negativt heltall.
Test H0:p = p0 mot ett av følgende:
For Ha:p > p0, sett Hypot>0
For Ha:pƒp0 (standard), sett Hypot=0
For Ha:p < p0, sett Hypot<0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.p0 Hypotesisk populasjonsandel
stat.z Standard normalverdi beregnet for andelen
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.ÇBeregnet andel av suksesser
stat.n Utvalgenes størrelse
zTest_2Prop Katalog >
zTest_2Prop x1,n1,x2,n2[,Hypot]
Beregner en to-proporsjons z-test. En oversikt over resultatene
lagres i stat.results-variabelen. (Se side 162).
x1 og x2 er ikke-negative heltall.
Test H0:p1 = p2 mot ett av følgende:
For Ha:p1 > p2, sett Hypot>0
For Ha:p1 ƒp2 (standard), sett Hypot=0
Alfabetisk oversikt 191

192 Alfabetisk oversikt
zTest_2Prop Katalog >
For Ha:p < p0, sett Hypot<0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.z Standard normalverdi beregnet for differansen av andelene
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.Ç1Beregnet andel av suksesser i utvalg 1
stat.Ç2Beregnet andel av suksesser i utvalg 2
stat.ÇBeregnet samlet andel av suksesser
stat.n1, stat.n2 Antall utvalg som er tatt i forsøk 1 og 2
zTest_2Samp Katalog >
zTest_2Samp s1,s2,Liste1,Liste2[,Frekv1[,Frekv2[,Hypot]]]
(Dataliste inndata)
zTest_2Samp s1,s2,v1,n1,v2,n2[,Hypot]
(Summering statistikk inndata)
Beregner en to-utvalgs z-test. En oversikt over resultatene lagres
istat.results-variabelen. (Se side 162).
Test H0:m1 = m2, mot ett av følgende:
For Ha:m1 < m2, sett Hypot<0
For Ha:m1ƒ m2 (standard), sett Hypot=0
For Ha:m1 > m2, Hypot>0
For informasjon om effekten av tomme elementer i en liste, se
“Tomme (åpne) elementer” (side 217).
Utdata-variabel Beskrivelse
stat.z Standard normalverdi beregnet for forskjellen i gjennomsnitt
stat.PVal Minste signifikansnivå som null-hypotesen kan forkastes ved
stat.x1, stat.x2Utvalgets gjennomsnitt av datasekvenser i Liste1og Liste2
stat.sx1, stat.sx2 Utvalgets standardavvik til datasekvenser i Liste 1og Liste2
stat.n1, stat.n2 Utvalgenes størrelse

Symboler
+ (addere) +tast
Uttr1 +Uttr2⇒uttrykk
Returnerer summen av de to argumentene.
Liste1 +Liste2⇒liste
Matrise1 +Matrise2⇒matrise
Returnerer en liste (eller matrise) som inneholder
summene av tilsvarende elementer i Liste1 og Liste2
(eller Matrise1 og Matrise2).
Dimensjonene i argumentene må være like.
Uttr +Liste1⇒liste
Liste2 +Uttr⇒liste
Returnerer en liste som inneholder summene av Uttr
og hvert element i Liste1.
Uttr +Matrise1⇒matrise
Matrise1 +Uttr⇒matrise
Returnerer en matrise med Uttr addert til hvert
element på diagonalen til Matrise1.Matrise1 må
være kvadratisk.
Merk: Bruk .+ (prikk pluss) for å addere et uttrykk til
hvert element.
N(subtrahere) -tast
Uttr1 NUttr2⇒uttrykk
Returnerer Uttr1 minus Uttr2.
Symboler 193

194 Symboler
N(subtrahere) -tast
Liste1 NListe2⇒liste
Matrise1 NMatrise2⇒matrise
Subtraherer hvert element i Liste2 (eller Matrise2) fra
tilsvarende element i Liste1 (eller Matrise1), og
returnerer resultatene.
Dimensjonene i argumentene må være like.
Uttr NListe1⇒liste
Liste1 NUttr⇒liste
Subtraherer hvert Liste1 element fra Uttr eller
subtraherer Uttr fra hvert Liste1 element og
returnerer en liste over resultatene.
Uttr NMatrise1⇒matrise
Matrise1 NUttr⇒matrise
Uttr NMatrise1 returnerer en matrise av Uttr hver
gang identitetsmatrisen trekkes fra Matrise1.
Matrise1 må være kvadratisk.
Matrise1 NUttr returnerer en matrise av Uttr hver
gang identitetsmatrisen subtraheres fra Matrise1.
Matrise1 må være kvadratisk.
Merk: Bruk .N(prikk minus) for å subtrahere et uttrykk
fra hvert element.
•(multiplisere) rtast
Uttr1 •Uttr2⇒uttrykk
Returnerer produktet av de to argumentene.
Liste1•Liste2⇒liste
Returnerer en liste som inneholder produktene av
samsvarende elementer i Liste1 og Liste2.
Dimensjonene i listene må være like.
Matrise1•Matrise2⇒matrise
Returnerer matriseproduktet av Matrise1 og
Matrise2.
Antallet kolonner i Matrise1 må være likt antallet
rader i Matrise2.

•(multiplisere) rtast
Uttr •Liste1⇒liste
Liste1•Uttr⇒liste
Returnerer en liste som inneholder produktene av Uttr
og hvert element i Liste1.
Uttr •Matrise1⇒matrise
Matrise1•Uttr⇒matrise
Returnerer en matrise som inneholder produktene av
Uttr og hvert element i Matrise1.
Merk: Bruk .•(prikk multipliser) for å multiplisere et
uttrykk med hvert element.
à(divider) ptast
Uttr1 àUttr2⇒uttrykk
Returnerer kvotienten av Uttr1 dividert med Uttr2.
Merk: Se også Brøk-sjablon, side 5.
Liste1 àListe2⇒liste
Returnerer en liste som inneholder kvotientene av
Liste1 dividert med Liste2.
Dimensjonene i listene må være like.
Uttr àListe1 ⇒liste
Liste1 àUttr ⇒liste
Returnerer en liste som inneholder kvotientene av
Uttr dividert med Liste1 eller Liste1dividert med Uttr.
Matrise1 àUttr ⇒matrise
Returnerer en matrise som inneholder kvotientene av
Matrise1 àUttr.
Merk: Bruk ./(prikk divider) for å dividere et uttrykk
med hvert element.
Symboler 195

196 Symboler
^ (potens) ltast
Uttr1 ^Uttr2 ⇒Uttrykk
Liste1 ^Liste2 ⇒liste
Returnerer det første argument opphøyd i det andre
argumentet.
Merk: Se også Eksponent-sjablon, side 5.
For en liste, returneres elementene i Liste1 opphøyd i
tilsvarende elementer i Liste2.
I reell grunnmengde bruker brøkpotens som har
forkortet eksponent med oddetall i nevner en rell
forgreining i motsetning til hovedforgreining for
kompleks modus.
Uttr ^Liste1 ⇒liste
Returnerer Uttr opphøyd i elementene i Liste1.
Liste1 ^Uttr ⇒liste
Returnerer elementene i Liste1 opphøyd i Uttr.
kvadratMatrise1 ^heltall ⇒matrise
Returnerer kvadratMatrise1 opphøyd i heltall -
potens.
kvadratMatrise1 må være en kvadratmatrise.
Hvis heltall =L1, beregnes invers matrise.
Hvis heltall <L1, beregnes invers matrise opphøyd i
en korrekt positiv potens.
x2(kvadrat) qtast
Uttr1 2⇒Uttrykk
Returnerer kvadratet av argumentet.
Liste12⇒liste
Returnerer en liste med kvadrater av elementene i
Liste1.
kvadratMatrise1 2⇒matrise
Returnerer matrisens kvadrat av kvadratMatrise1.
Dette er ikke det samme som å beregne kvadratet av

x2(kvadrat) qtast
hvert element. Bruk .^2 for å beregne kvadratet av
hvert element.
.+ (prikk adder) ^+ taster
Matrise1 .+ Matrise2 ⇒matrise
Uttr .+ Matrise1 ⇒matrise
Matrise1 .+ Matrise2 returnerer en matrise som er
summen av hvert par av samsvarende elementer i
Matrise1 og Matrise2.
Uttr .+ Matrise1 returnerer en matrise som er
summen av Uttr og hvert element i Matrise1.
.−(prikk subt.) ^- taster
Matrise1 .−Matrise2 ⇒matrise
Uttr .−Matrise1 ⇒matrise
Matrise1 .−Matrise2 returnerer en matrise som er
differansen mellom hvert par av samsvarende
elementer i Matrise1 og Matrise2.
Uttr .−Matrise1 returnerer en matrise som er
differansen av Uttr og hvert element i Matrise1.
.•(prikk mult.) ^rtaster
Matrise1 .•Matrise2 ⇒matrise
Uttr .•Matrise1⇒matrise
Matrise1 .•Matrise2 returnerer en matrise som er
produktet av hvert par av samsvarende elementer i
Matrise1 og Matrise2.
Uttr .•Matrise1 returnerer en matrise med produkter
av Uttr og hvert element i Matrise1.
Symboler 197

198 Symboler
. / (prikk divider) ^p taster
Matrise1 ./ Matrise2 ⇒matrise
Uttr ./ Matrise1⇒matrise
Matrise1 ./ Matrise2 returnerer en matrise som er
kvotient av hvert par av samsvarende elementer i
Matrise1 og Matrise2.
Uttr ./ Matrise1 returnerer en matrise som er
kvotienten av Uttr og hvert element i Matrise1.
.^ (prikk potens) ^l taster
Matrise1 .^ Matrise2⇒matrise
Uttr . ^ Matrise1⇒matrise
Matrise1 .^ Matrise2 returnerer en matrise, der hvert
element i Matrise2 er eksponenten for samsvarende
element i Matrise1.
Uttr .^ Matrise1 returnerer en matrise, der hvert
element i Matrise1 er eksponenten for Uttr.
L(negere) vtast
LUttr1 ⇒Uttrykk
LListe1 ⇒liste
LMatrise1 ⇒matrise
Returnerer argumentets negasjon.
For en liste eller matrise returneres alle elementene
negert.
Hvis argumentet er et binært eller heksadesimalt
heltall, gir negasjonen komplementet til to.
I binær grunntall-modus:
Viktig: Null, ikke bokstaven O
For å se hele resultatet, trykk på £og bruk så ¡og¢
for å bevege markøren.
% (prosent) /k taster
Uttr1 %⇒Uttrykk
Liste1 %⇒liste
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
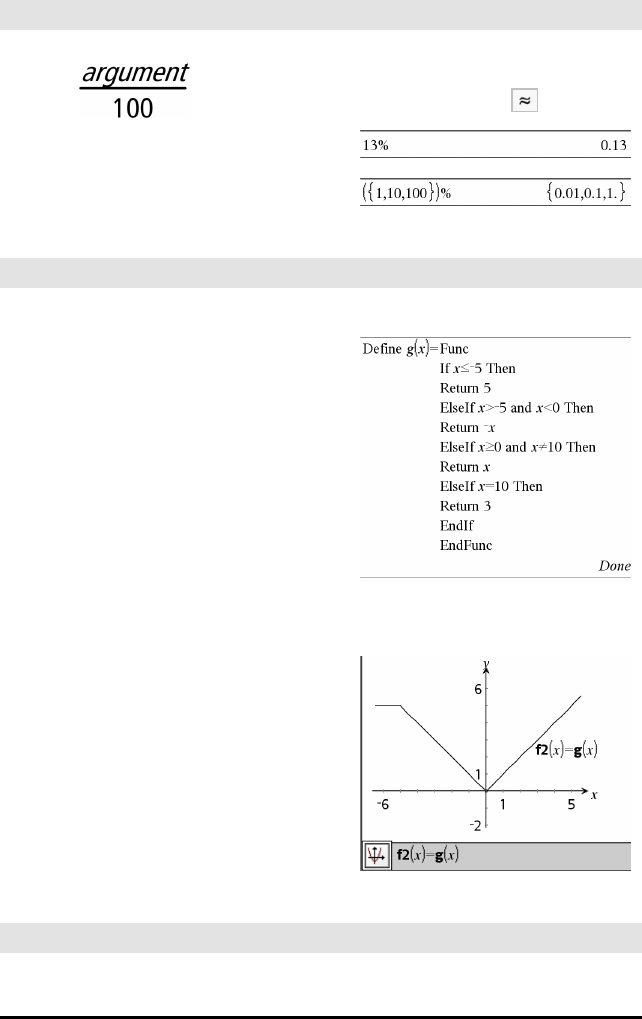
% (prosent) /k taster
Matrise1 %⇒matrise
Returnerer
For en liste eller matrise, returneres en liste eller
matrise med hvert element dividert med 100.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .
= (er lik) =tast
Uttr1 =Uttr2⇒Boolsk uttrykk
Liste1 =Liste2⇒Boolsk liste
Matrise1 =Matrise2⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være lik
Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være ulik
Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger
element for element.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
Eksempel på funksjon som bruker matematiske
testsymboler: =, ƒ,<,{,>,|
Resultat av grafisk fremstilling g(x)
ƒ(ulik) /= taster
Uttr1 ƒUttr2 ⇒Boolsk uttrykk Se “=” (er lik) eksempel.
Symboler 199

200 Symboler
ƒ(ulik) /= taster
Liste1 ƒListe2 ⇒Boolsk liste
Matrise1 ƒMatrise2 ⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være ulik Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være lik Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger element for
element.
Merk: Du kan sette inn denne operatoren fra tastaturet ved å
skrive /=
< (mindre enn) /= taster
Uttr1 <Uttr2 ⇒Boolsk uttrykk
Liste1 <Liste2 ⇒Boolsk liste
Matrise1 <Matrise2 ⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være mindre enn Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være større enn eller lik
Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger element for
element.
Se “=” (er lik) eksempel.
{(mindre enn eller lik) /= taster
Uttr1 {Uttr2 ⇒Boolsk uttrykk
Liste1 {Liste2 ⇒Boolsk liste
Matrise1 {Matrise2 ⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være mindre enn eller lik
Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være større enn Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger element for
element.
Merk: Du kan sette inn denne operatoren fra tastaturet ved å
skrive <=
Se “=” (er lik) eksempel.

> (større enn) /= taster
Uttr1 >Uttr2 ⇒Boolsk uttrykk
Liste1 >Liste2 ⇒Boolsk liste
Matrise1 >Matrise2 ⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være større enn Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være mindre enn eller
lik Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger element for
element.
Se “=” (er lik) eksempel.
|(større enn eller lik med) /= taster
Uttr1 |Uttr2 ⇒Boolsk uttrykk
Liste1 |Liste2 ⇒Boolsk liste
Matrise1 |Matrise2 ⇒Boolsk matrise
Returnerer sann hvis Uttr1 er bestemt å være større enn eller lik
Uttr2.
Returnerer usann hvis Uttr1 er bestemt å være mindre enn eller
lik Uttr2.
Alt annet returnerer en forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger element for
element.
Merk: Du kan sette inn denne operatoren fra tastaturet ved å
skrive >=
Se “=” (er lik) eksempel.
⇒(logisk implikasjon) /=-taster
BoolskUttr1 ⇒BoolskUttr2 returnerer Boolsk uttrykk
BoolskListe1 ⇒BoolskListe2 returnerer Boolsk liste
BoolskMatrise1 ⇒BoolskMatrise2 returnerer Boolsk
matrise
Heltall1 ⇒Heltall2 returnerer Heltall
Behandler uttrykket not <argument1> or <argument2>
og returnerer sann, usann eller en forenklet form av
ligningen.
Symboler 201

202 Symboler
⇒(logisk implikasjon) /=-taster
For lister og matriser, returneres sammenlikninger
element for element.
Merk: Du kan sette inn denne operatoren fra
tastaturet ved å skrive =>
⇔(logisk dobbel implikasjon, XNOR) /=-taster
BoolskUttr1 ⇔BoolskUttr2 returnerer Boolsk
uttrykk
BoolskListe1 ⇔BoolskListe2 returnerer Boolsk liste
BoolskMatrise1 ⇔BoolskMatrise2 returnerer Boolsk
matrise
Heltall1 ⇔Heltall2 returnerer Heltall
Returnerer negasjon av en XOR Boolsk handling på
de to argumentene. Returnerer sann, usann eller en
forenklet form av ligningen.
For lister og matriser, returneres sammenlikninger
element for element.
Merk: Du kan sette inn denne operatoren fra
tastaturet ved å skrive <=>
! (fakultet) ºtast
Uttr1! ⇒Uttrykk
Liste1!⇒liste
Matrise1!⇒matrise
Returnerer argumentets fakultet.
For en liste eller matrise, returneres en liste eller
matrise av elementenes fakulteter.
& (legg til) /k taster
Streng1 &Streng2 ⇒streng
Returnerer en tekststreng som er Streng2 lagt til
Streng1.

d () (derivert) Katalog >
d(Uttr1,Var[,Orden])⇒uttrykk
d(Liste1,Var[,Orden])⇒liste
d(Matrise1,Var[,Orden])⇒matrise
Returnerer den første deriverte av det første
argumentet med hensyn på variabel Var.
Orden, hvis inkludert, må være et heltall. Hvis orden
er mindre enn null, vil resultatet være en anti-derivert.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive derivative (...).
d() følger ikke normal behandlingsmekanisme når det
gjelder å forenkle argumentene fullstendig og deretter
bruke funksjonsdefinisjonen til disse fullstendig
forenklede argumentene. Istedenfor utfører d()
følgende trinn:
1. Forenkler det andre argumentet kun slik at det
ikke fører til en ikke-variabel.
2. Forenkler det første argumentet kun slik at det
ikke henter frem noen lagret verdi for variabelen
som ble bestemt ved trinn 1.
3. Bestemmer den symbolske deriverte av
resultatet av trinn 2 med hensyn på variabelen fra
trinn 1.
Hvis variabelen fra trinn 1 har en lagret verdi eller en
verdi som er spesifisert av begrensningsoperator (“|”),
settes denne verdien inn i resultatet fra trinn 3.
Merk: Se også Førstederiverte, side 9;
Andrederiverte, side 10; eller N-tederiverte, side 10.
‰() (integral) Katalog >
‰(Uttr1,Var[,Nedre,Øvre])⇒uttrykk
‰(Uttr1,Var[,Konstant])⇒uttrykk
Returnerer integralet av Uttr1 med hensyn på
variabelen Var fra Nedre til Øvre.
Merk: Se også Bestemt eller ubestemt integral-
sjablon, side 10.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive integral(...).
Symboler 203
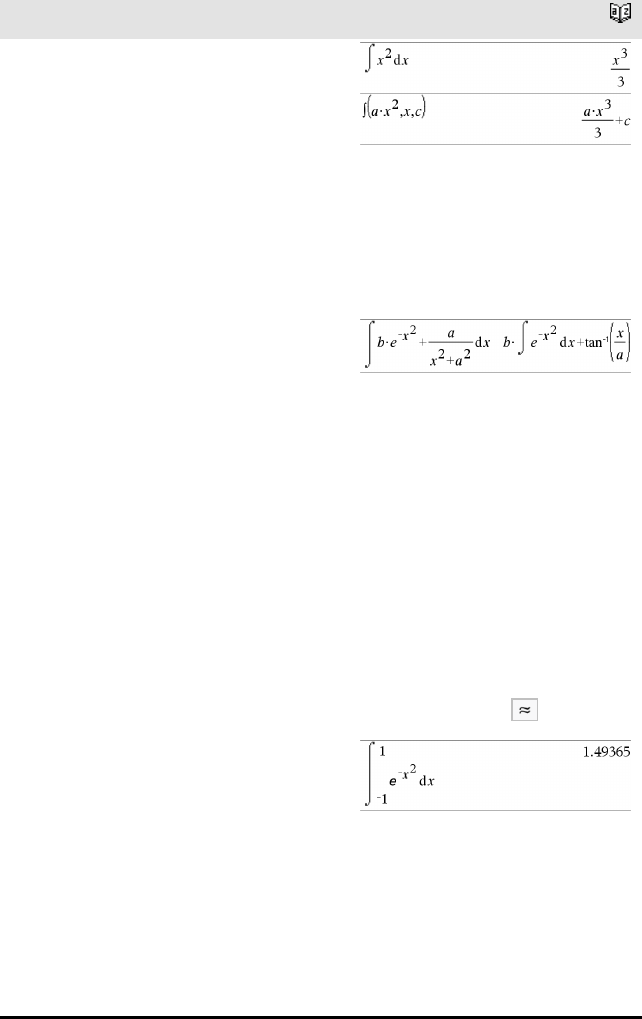
204 Symboler
‰() (integral) Katalog >
Returnerer en antiderivert hvis Nedre og Øvre
utelates. En symbolsk integrasjonskonstant utelates
hvis ikke du oppgir argumentet Konstant.
Like, gyldige anti-deriverte kan variere med en
numerisk konstant. Særlig kan en slik konstant være
skjult, dersom en anti-derivert inneholder logaritmer
eller inverse trigonometriske funksjoner. Dessuten
blir noen ganger stykkevis konstante uttrykk lagt til
for å gjøre en anti-derivert gyldig over et lengre
intervall enn den vanlige formelen.
‰() returnerer seg selv for stykker av Uttr1 som ikke
kan bestemmes som en eksplisitt endelig
kombinasjon av innebygde funksjoner og operatorer.
Hvis du oppgir både Nedre og Øvre, gjøres det et
forsøk på å finne eventuelle diskontinuiteter eller
diskontinuerlige deriverte i intervallet Nedre <Var <
Øvre, og dele opp intervallet på de stedene.
For autoinnstilling av modusen Auto eller Tilnærmet,
brukes numerisk integrasjon hvis mulig, dersom en
anti-derivert eller en grense ikke kan bestemmes.
For innstilling i Tilnærmet, prøves numerisk
integrasjon først, hvis mulig. Anti-derivert søkes bare
der hvor slik numerisk integrasjon ikke er mulig eller
ikke lykkes.
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .
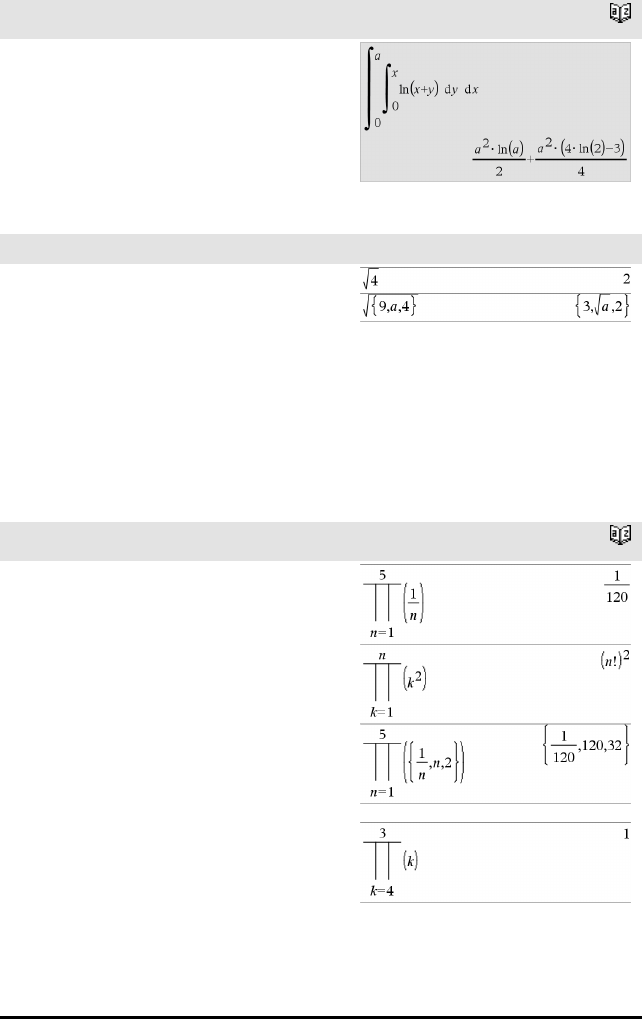
‰() (integral) Katalog >
‰() kan nestes for å danne flere integraler.
Integrasjonsgrensene kan avhenge av
integrasjonsvariabler utenfor dem.
Merk: Se også nInt(), side 113.
‡() (kvadratrot) /q taster
‡(Uttr1)⇒Uttrykk
‡(Liste1)⇒liste
Returnerer kvadratroten til argumentet.
For en liste, returneres kvadratroten til alle
elementene i Liste1.
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive sqrt(...)
Merk: Se også Kvadratrot-sjablon, side 5.
Π() (prodSeq) Katalog >
Π(Uttr1,Var,Nedre,Øvre)⇒uttrykk
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive prodSeq(...).
Finner Uttrykk1 for hver verdi av Var fra Nedre til
Øvre, og returnerer produktet av resultatene.
Merk: Se også Produkt-sjablon (Π), side 9.
Π(Uttr1,Var,Nedre,NedreN1)⇒1
Π(Uttr1,Var,Nedre,Øvre)⇒1/Π(Uttr1,Var,
Øvre+1,NedreN1)hvis Øvre <Nedre 1
Produktformlene som er brukt er hentet fra følgende
referanse:
Symboler 205

206 Symboler
Π() (prodSeq) Katalog >
Ronald L. Graham, Donald E. Knuth, og Oren
Patashnik. Concrete Mathematics: A Foundation
for Computer Science. Reading, Massachusetts:
Addison-Wesley, 1994.
G() (sumSeq) Katalog >
G(Uttr1,Var,Nedre,Øvre)⇒uttrykk
Merk: Du kan sette inn denne funksjonen fra
tastaturet ved å skrive sumSeq(...).
Behandler Uttrykk1 for hver verdi av Var fra Nedre til
Øvre, og returnerer summen av resultatene.
Merk: Se også Sum-sjablon, side 9.
G(Uttr1,Var,Nedre,NedreN1)⇒0
G(Uttr1,Var,Nedre,Øvre)⇒LG(Uttr1,Var,Øvre+1,
NedreN1)hvis Øvre <NedreN1
Summeringsformlene som er brukt er hentet fra
følgende referanse:
Ronald L. Graham, Donald E. Knuth, og Oren
Patashnik. Concrete Mathematics: A Foundation
for Computer Science. Reading, Massachusetts:
Addison-Wesley, 1994.
GInt() Katalog >
GInt(NPmt1,NPmt2,N,I,PV,[Pmt],[FV],[PpY],
[CpY],[PmtAt],[avrundVerdi])⇒verdi

GInt() Katalog >
GInt(NPmt1,NPmt2,amortTabell)⇒verdi
Amortiseringsfunksjon som beregner rentesummen i
løpet av en spesifisert rekke av betalinger.
NPmt1 og NPmt2 definerer start- og sluttgrensene for
betalingsrekken.
N,I,PV,Pmt,FV,PpY,CpY og PmtAt er beskrevet i
tabellen med TVM-argumenter, side 179.
• Hvis du utelater Pmt, grunninnstilles den til
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Hvis du utelater FV, grunninnstilles den til
FV=0.
• Grunninnstillingene for PpY,CpY og PmtAt er de
samme som for TVM-funksjonene.
avrundVerdi spesifiserer antallet desimalplasser for
avrunding. Grunninnstilling=2.
GInt(NPmt1,NPmt2,amortTabell)beregner
rentesummen basert på amortiseringstabell
amortTabell. Argumentet amortTabell må være en
matrise i den form som er beskrevet under amortTbl
(), side 12.
Merk: Se også GPrn(), nedenfor, og Bal(), side 21.
GPrn() Katalog >
GPrn(NPmt1,NPmt2,N,I,PV,[Pmt],[FV],[PpY],
[CpY],[PmtAt],[avrundVerdi])⇒verdi
GPrn(NPmt1,NPmt2,amortTable)⇒verdi
Amortiseringsfunksjon som beregner summen av
hovedbetalinger i løpet av en spesifisert rekke av
betalinger.
NPmt1 og NPmt2 definerer start- og sluttgrensene for
betalingsrekken.
N,I,PV,Pmt,FV,PpY,CpY og PmtAt er beskrevet i
tabellen med TVM-argumenter, side 179.
• Hvis du utelater Pmt, grunninnstilles den til
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Hvis du utelater FV, grunninnstilles den til
FV=0.
Symboler 207
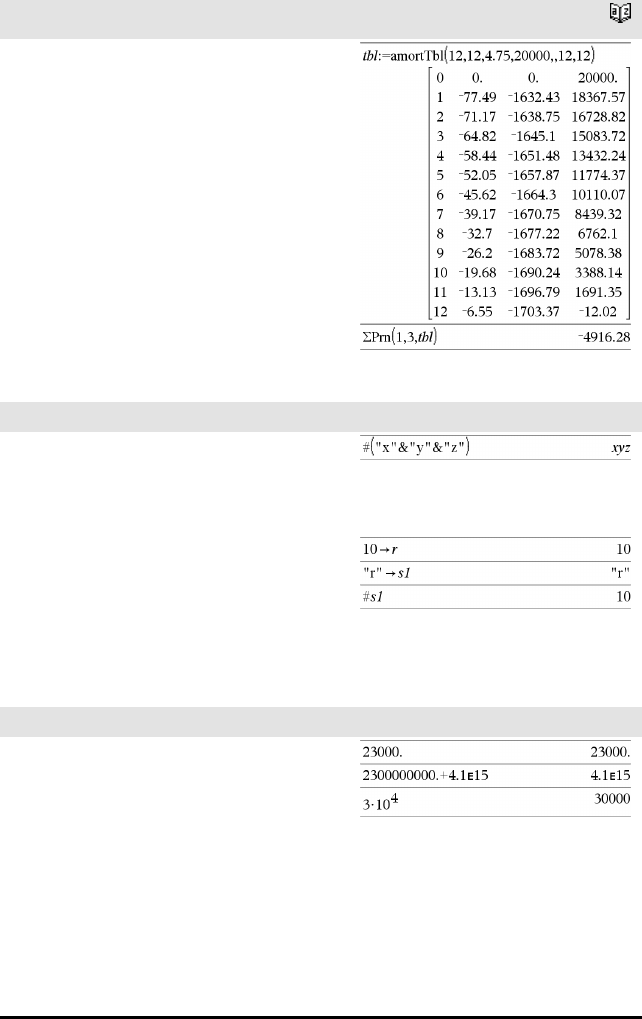
208 Symboler
GPrn() Katalog >
• Grunninnstillingene for PpY,CpY og PmtAt er de
samme som for TVM-funksjonene.
avrundVerdi spesifiserer antallet desimalplasser for
avrunding. Grunninnstilling=2.
GPrn(NPmt1,NPmt2,amortTabell)beregner summen
av hovedbetalinger basert på amortiseringstabell
amortTabell. Argumentet amortTabell må være en
matrise i den form som er beskrevet under amortTbl
(), side 12.
Merk: Se også GInt(), over, og Bal(), side 21.
# (Indir.ref) /k taster
#varNavnStreng
Refererer til variabelen med navnet varNavnStreng.
På denne måten kan du bruke strenger for å opprette
variabelnavn “innenfra” en funksjon.
Oppretter eller refererer til variabelen xyz.
Returnerer verdien av variabelen (r) som har et navn
som er lagret i variabel s1.
E(vitenskapelig tallnotasjon) itast
mantissaEeksponent
Legger inn et tall i vitenskapelig fremstilling. Tallet blir
tolket som en mantissa × 10eksponent.
Tips: Hvis du vil legge inn en potens av 10 uten å
forårsake desimale verdier i resultatet, bruk
10^heltall.
Merk: Du kan sette inn denne operatoren fra
datamaskintastaturet ved å skrive @E. Eksempel:
Skriv 2.3@E4 for å legge inn 2.3E4.
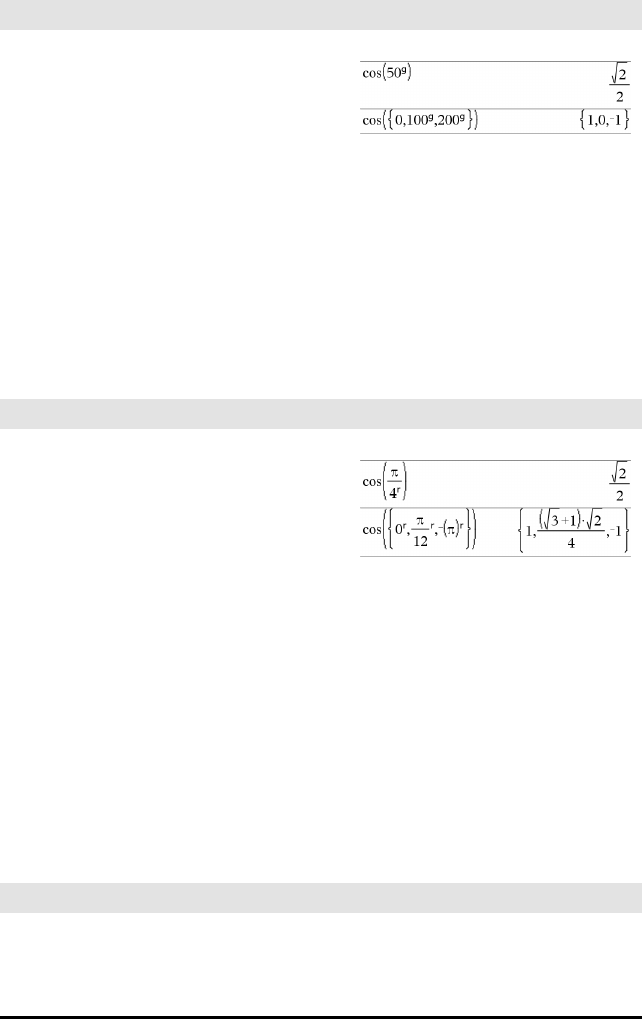
g (gradian) ¹tast
Uttr1g⇒Uttrykk
Uttr1g⇒Uttrykk
Liste1g⇒liste
Matrise1g⇒matrise
Denne funksjonen gir deg en mulighet til å spesifisere
en vinkel i gradianer mens du er i grader- eller gradian-
modus.
I radian-vinkelmodus, multipliseres Uttr1 med p/200.
I grader-vinkelmodus, multipliseres Uttr1 med g/100.
I gradian modus, returneres Uttr1 uendret.
Merk: Du kan sette inn dette symbolet fra
datamaskintastaturet ved å skrive @g.
I grader, gradian eller radian modus:
R(radian) ¹tast
Uttr1R⇒Uttrykk
Liste1R⇒liste
Matrise1R⇒matrise
Denne funksjonen gir deg en mulighet til å spesifisere
en gradian vinkel mens du er i grader- eller radian-
modus.
I grader-vinkelmodus, multipliseres argumentet med
180/ p.
I radian-vinkelmodus, returneres argumentet uendret.
I gradian modus, multipliseres argumentet med 200/
p.
Tips: Bruk Rhvis du vil tvinge radianer inn en
funksjonsdefinisjon uavhengig av hvilken modus som
er i bruk når du bruker funksjonen.
Merk: Du kan sette inn dette symbolet fra
datamaskintastaturet ved å skrive @r.
I grader, gradian eller radian modus:
¡(grader) ¹tast
Uttr1¡⇒Uttrykk
Liste1¡⇒liste
I grader, gradian eller radian modus:
Symboler 209
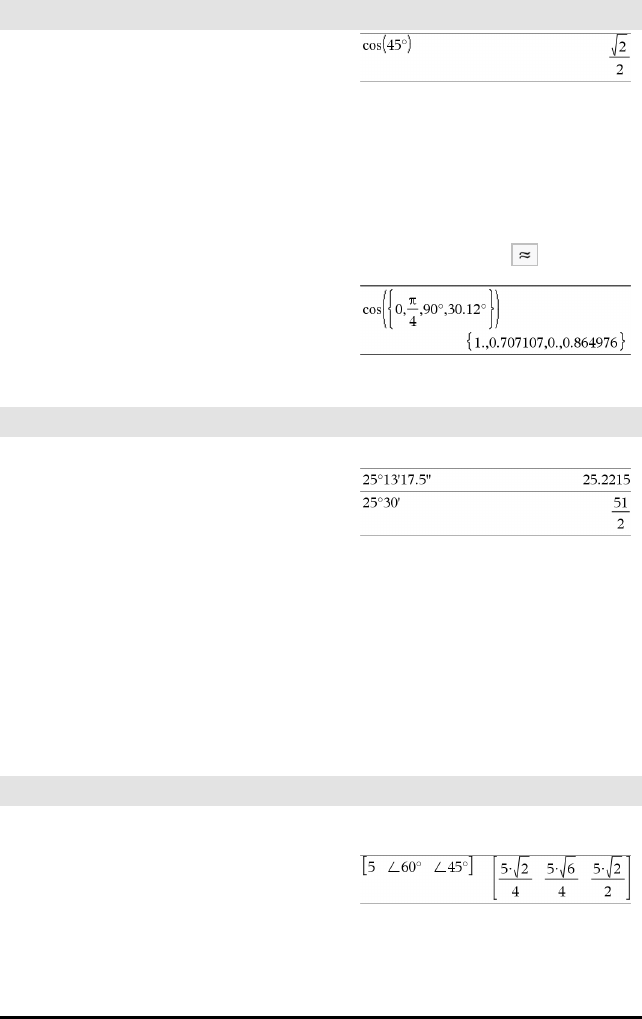
210 Symboler
¡(grader) ¹tast
Matrise1¡⇒matrise
Denne funksjonen gir deg en mulighet til å spesifisere
en grader-vinkel mens du er i gradian eller radian
modus.
I radian-vinkelmodus, multipliseres argumentet med
p/180.
I grader-vinkelmodus, returneres argumentet uendret.
I gradian-vinkelmodus, multipliseres argumentet med
10/9.
Merk: Du kan sette inn dette symbolet fra
datamaskintastaturet ved å skrive @d.
I radian modus:
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .
¡, ', '' (grader/minutter/sekunder) /k taster
gg¡mm'ss.ss''⇒Uttrykk
gg Et positivt eller negativt tall
mm Et ikke-negativt tall
ss.ss Et ikke-negativt tall
Returnerer gg+(mm/60)+(ss.ss/3600).
Dette grunntall -60-formatet lar deg:
• Sette inn en vinkel i grader/minutter/sekunder
uten hensyn til aktuell vinkelmodus.
• Sette inn tid, som timer/minutter/sekunder.
Merk: Sett to apostrofer ('') etter ss.ss, ikke et
anførselstegn (").
I Grader-vinkelmodus:
±(vinkel) /k taster
[Radius,±q_Vinkel]⇒vektor
(polar inndata)
[Radius,±q_Vinkel,Z_Koordinat]⇒vektor
(sylindrisk inndata)
[Radius,±q_Vinkel,±q_Vinkel]⇒vektor
(sfærisk inndata)
I radian modus og vektorformat innstilt på:
rektangulær
sylindrisk

±(vinkel) /k taster
Returnerer koordinater som en vektor, avhengig av
vektorformatets modusinnstilling: rektangulær,
sylindrisk eller sfærisk.
Merk: Du kan sette inn dette symbolet fra
datamaskintastaturet ved å skrive @<.sfærisk
(Størrelse ±Vinkel)⇒kompleksVerdi
(polar inndata)
Setter inn en kompleks verdi i (r±q) polar form.
Vinkelen tolkes avhengig av aktuell vinkelmodus-
innstilling.
I radian-vinkelmodus og rektangulært, komplekst
format:
Merk: For å tvinge frem et tilnærmet desimalresultat,
Grafregner: Trykk på / ·.
Windows®: Trykk på Ctrl+Enter.
Macintosh®: Trykk på “+Enter.
iPad®: Hold på enter, og velg .
' (merke) ºtast
variabel '
variabel ''
Setter inn et derivertsymbol i en differensialligning. Et
enkelt derivertsymbol markerer en førsteordens
differensialligning, to derivertsymboler markerer en
annenordens, osv.
_ (senket strek som et tomt element)
Se “Tomme (åpne) elementer” |,
side 217.
Symboler 211

212 Symboler
_ (senket strek som enhetsbetegnelse) /_ taster
Uttr_Enhet
Markerer enhetene for et Uttr. Alle enhetsnavnene
må begynne med en senket strek.
Du kan bruke forhåndsdefinerte enheter eller opprette
dine egne enheter. For en liste over forhåndsdefinerte
enheter, åpne Katalogen og vis Enhetsomregner-
fanen. Du kan velge enhetsnavn fra katalogen eller
skrive inn enhetsnavnet direkte.
Merk: Du kan finne omregningssymbolet, 4, i
katalogen. Klikk på , og klikk så på Matematiske
operatorer.
Variabel_
Hvis Variabel ikke har noen verdi, blir den behandlet
som om den representerer et komplekst tall. Ved
grunninnstilling, uten _, behandles variabelen som
reell.
Hvis Variabel har en verdi, ignoreres _ og Variabel
gjenopptar opprinnelig datatype.
Merk: Du kan lagre et komplekst tall til en variabel
uten å bruke _. Men for best resultat i beregninger,
som cSolve() og cZeros(), anbefales_.
Assuming z is undefined:
4(omregne) /k taster
Uttr_Enhet1 4_Enhet2⇒Uttr_Enhet2
Omregner et uttrykk fra en enhet til en annen.
Senket strek-tegnet_ markerer enheten. Enhetene
må være i samme kategori, som f.eks. Lengde eller
Areal.
For en liste over forhåndsdefinerte enheter, åpne
Katalogen og vis Enhetsomregner-fanen:
• Du kan velge et enhetsnavn fra listen.
• Du kan velge omregningsoperatoren, 4, fra
øverst på listen.
Du kan også skrive inn et navn manuelt. For å skrive
inn “_” mens du skriver inn enhetsnavn på
grafregneren, trykk på /_.
Merk: For å omregne temperaturenheter, bruk
tmpCnv() og @tmpCnv(). Omregningsoperatoren 4
behandler ikke temperaturenheter.

10^() Katalog >
10^ (Uttr1)⇒Uttrykk
10^ (Liste1)⇒liste
Returnerer 10 opphøyd i argumentets potens.
For en liste, returneres 10 opphøyd i elementenes
potens i Liste1.
10^(kvadratMatrise)⇒kvadratMatrise
Returnerer 10 opphøyd i potensen av
kvadratMatrise1. Dette er ikke det samme som å
beregne 10 opphøyd i potens av hvert element. For
mer informasjon om beregningsmetode, se under cos
().
kvadratMatrise1 må kunne diagonaliseres.
Resultatet inneholder alltid flytende desimaltall.
^/(resiprok) Katalog >
Uttr1 ^/⇒Uttrykk
Liste1 ^/⇒liste
Returnerer den inverse verdien av et argument.
For en liste, returneres den inverse verdien av
elementene i Liste1.
kvadratMatrise1 ^/⇒kvadratMatrise
Returnerer den inverse verdien av kvadratMatrise1.
kvadratMatrise1 må være en ikke-singulær
kvadratisk matrise.
| (begrensningsoperator) /k-taster
Uttr |BoolskUttr1 [and BoolskUttr2]...
Uttr |BoolskUttr1 [or BoolskUttr2]...
Begrensningssymbolet (“|”) fungerer som en binær
operator. Operanden til venstre for | er et uttrykk.
Operanden til høyre for | spesifiserer en eller flere
relasjoner som kan ha innvirkning på forenklingen av
Symboler 213
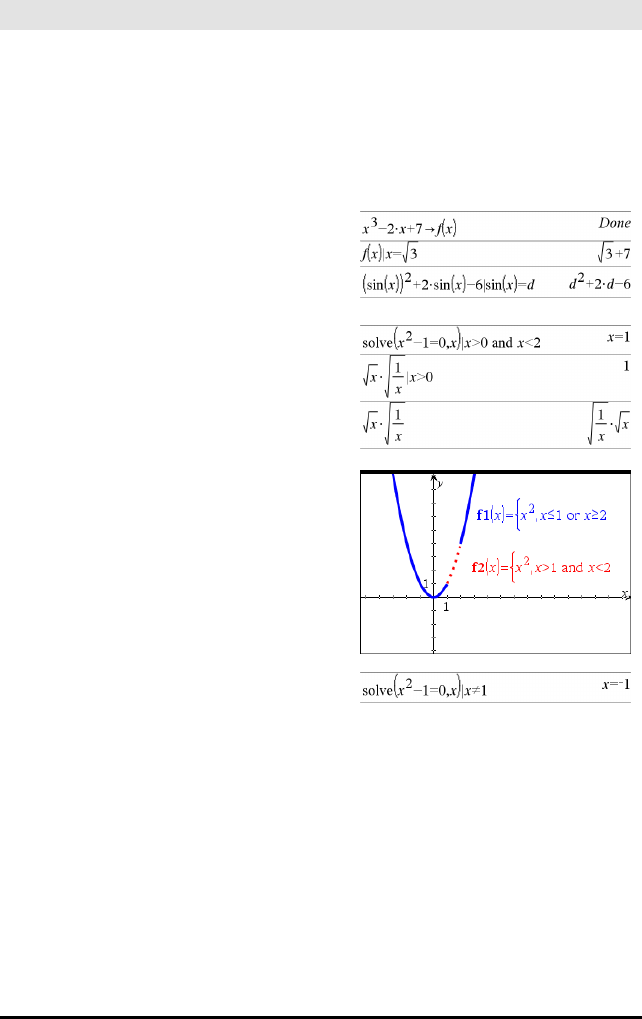
214 Symboler
| (begrensningsoperator) /k-taster
uttrykket. Flere forbindelser etter | må sammenføyes
av logiske “and” eller “or” operatorer.
Med begrensningsoperatoren har du tre utgangstyper
av funksjonalitet:
• Erstatninger
• Intervallbegrensninger
• Eksklusjoner
En erstatning har form som en ligning, som x=3 eller
y=sin(x). For at den skal være mest effektiv, bør den
venstre siden være en enkel variabel. Uttr |Variabel
=verdi vil erstatte verdi for hver forekomst av
Variabel iUttr.
Intervallbegrensninger tar form som en eller flere
ulikheter som er føyd sammen av logiske “and” eller
“or” operatorer. En intervallbegrensning tillater også
forenkling som ellers kan være ugyldig eller ikke mulig
å beregne.
Eksklusjoner bruker relasjons-operatoren “ulik” (/= or
ƒ) for å ekskludere en spesifikk verdi fra å komme i
betraktning. Den brukes først og fremst for å
ekskludere en eksakt løsning når du bruker cSolve(),
cZeros(),fMax(),fMin(),solve(),zeros(), osv.

&(lagre) /h tast
Uttr &Var
Liste&Var
Matrise &Var
Uttr &Funksjon(Param1,...)
Liste &Funksjon(Param1,...)
Matrise &Funksjon(Param1,...)
Hvis variabel Var ikke eksisterer, opprettes Var og
initialiserer den til Uttr, Liste, eller Matrise.
Hvis Var allerede eksisterer og ikke er låst eller
beskyttet, erstattes innholdet med Uttr,Liste, eller
Matrise.
Tips: Hvis du skal til å gjøre symbolske beregninger
med udefinerte variabler, bør du unngå å lagre dem
under de mest vanlig brukte en-bokstavs variabler,
som a, b, c, x, y, z og så videre.
Merk: Du kan sette inn denne operatoren fra
tastaturet ved å skrive =: som en snarvei. Eksempel:
Skriv pi/4 =: minvar.
:= (tildele) /t taster
Var := Uttr
Var := Liste
Var := Matrise
Funksjon(Param1,...) := Uttr
Funksjon(Param1,...) := Liste
Funksjon(Param1,...) := Matrise
Hvis variabel Var ikke eksisterer, opprettes Var og
initialiserer den til Uttr,Liste, eller Matrise.
Hvis Var allerede eksisterer og ikke er låst eller
beskyttet, erstattes innholdet med Uttr,Liste, eller
Matrise.
Tips: Hvis du skal til å gjøre symbolske beregninger
med udefinerte variabler, bør du unngå å lagre dem
under de mest vanlig brukte en-bokstavs variabler,
som a, b, c, x, y, z og så videre.
Symboler 215

216 Symboler
© (kommentar) /k taster
©[tekst]
©fremstiller tekst som en kommentarlinje som lar deg
kommentere funksjoner og programmer som du
oppretter.
©kan plasseres ved begynnelsen eller hvor som helst
på linjen. Alt som er til høyre for ©, til slutten av linjen,
er kommentaren.
Merk for å legge inn eksemplet: For anvisninger om
hvordan du legger inn flerlinjede program- og
funksjonsdefinisjoner, se avsnittet Kalkulator i
produkthåndboken.
0b, 0h 0B taster, 0H taster
0b binærTall
0h heksadesimalTall
Markerer hhv. et binært eller heksadesimalt tall. For å
sette inn et binært eller heksadesimalt tall må du sette
inn prefikset 0b eller 0h uavhengig av
grunninnstillingsmodus. Uten prefiks blir et tall
behandlet som et desimaltall (grunntall10).
Resultatene vises i forhold til grunntall-modusen.
I desimalt grunntall-modus:
I binær grunntall-modus:
I heksades grunntall-modus:

Tomme (åpne) elementer
Når du analyserer reelle data, kan det hende at du ikke alltid har et komplett datasett.
TI-Nspire™CAS tillater tomme eller åpne dataelementer, slik at du kan fortsette med data
som nesten er komplette istedenfor å måtte starte på nytt eller forkaste oppgaver som ikke er
fullført.
Under “
Plotte graf fra regnearkdata
” ikapitlet Lister og regneark finner du et eksempel på
data som involverer tomme elementer.
Med funksjonen delVoid() kan du fjerne tomme elementer fra en liste. Med funksjonen isVoid
() kan du teste for et tomt element. For detaljer, se delVoid(), side 51, og isVoid(), side 87.
Merk: For å legge inn et tomt element manuelt i et matematisk uttrykk, skriv “_” eller nøkkelordet void.
Nøkkelordet void konverteres automatisk til et “_” -symbol når uttrykket blir behandlet. For å skrive inn
“_” på grafregneren, trykk på / _.
Beregninger som involverer åpne elementer
De fleste beregninger som involverer et åpent (tomt)
innlegg, vil produsere et åpent (tomt) resultat. Se
spesialtilfeller nedenfor.
Listeutsagn som inneholder åpne (tomme) elementer
Følgende funksjoner og kommandoer ignorerer
(hopper over) åpne (tomme) elementer som blir funnet
i listeutsagn.
count,countIf,cumulativeSum,freqTable4list,
frequency,max,mean,median,product,stDevPop,
stDevSamp,sum,sumIf,varPop, og varSamp, samt
regresjonsberegninger, OneVar,TwoVar og
FiveNumSummary statistikk, konfidensintervaller og
statistikktester
SortA og SortD flytter alle åpne (tomme) elementer
innenfor det første utsagnet til bunnen.
Tomme (åpne)elementer 217
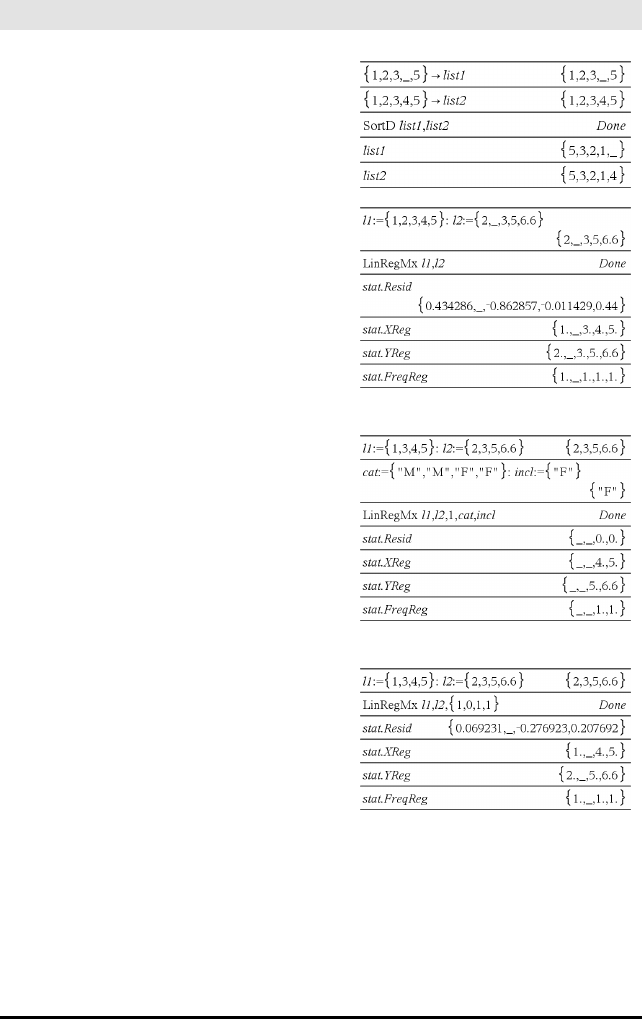
218 Tomme (åpne)elementer
Listeutsagn som inneholder åpne (tomme) elementer
I regresjoner introduserer en åpning i en X- eller Y-liste
en åpning for det tilsvarende elementet i en rest.
En utelatt kategori i en regresjon introduserer en
åpning (tomt element) for det tilsvarende elementet i
en rest.
En frekvens på 0 i en regresjon introduserer en åpning
(tomt element) for det tilsvarende elementet i en rest.

Snarveier/hurtigtaster for å legge inn
matematiske uttrykk
Hurtigtaster lar deg legge inn matematiske uttrykk ved å skrive istedet for å bruke katalogen
eller symbolpaletten. Eksempel: Når du skal legge inn uttrykket ‡6, kan du skrive sqrt(6) på
kommandolinjen. Når du trykker på ·, endres uttrykket sqrt(6) til ‡6. Noen hurtigtaster
kan brukes både fra kalkulatoren og fra tastaturet på datamaskinen. Andre er først og fremst
nyttige fra tastaturet på datamaskinen.
Fra kalkulatoren eller datamaskintastaturet
Hvis du skal legge inn dette: Skriv dette:
ppi
qtheta
ˆinfinity
{<=
|>=
ƒ/=
⇒(logisk implikasjon) =>
⇔(logisk dobbel implikasjon,
XNOR)
<=>
&(lagre-operator) =:
|| (absoluttverdi) abs(...)
‡() sqrt(...)
d() derivative(...)
‰() integral(...)
G() (Sum-sjablon) sumSeq(...)
Π() (Produkt-sjablon) prodSeq(...)
sin/(),cos/(), ... arcsin(...),arccos(...), ...
@List() deltaList(...)
@tmpCnv() deltaTmpCnv(...)
Snarveier/hurtigtaster for å legge inn matematiske uttrykk 219

220 Snarveier/hurtigtaster for å legge inn matematiske uttrykk
Fra tastaturet på datamaskinen
Hvis du skal legge inn dette: Skriv dette:
c1,c2, ... (konstanter) @c1,@c2, ...
n1,n2, ...
(heltallskonstanter)
@n1,@n2, ...
i(imaginær konstant) @i
e(naturlig log-grunntall e) @e
E(vitenskapelig notasjon) @E
T(transponert) @t
R(radianer) @r
¡(grader) @d
g(gradianer) @g
±(vinkel) @<
4(konvertering) @>
4Decimal,4approxFraction
(), osv.
@>Decimal,@>approxFraction(), osv.

EOS™ (Ligningsoperativsystem)-hierarkiet
Dette avsnittet beskriver Equation Operating System (ligningsoperativsystem) (EOS™) som
brukes av TI-Nspire™CAS -teknologien for undervisning i matematikk og realfag. Tall,
variabler og funksjoner legges inn ien enkel, ukomplisert sekvens. EOS™ -programvaren
behandler uttrykk og ligninger ved hjelp avparentetisk gruppering og isamsvar med de
prioriteringene som beskrives over.
Rekkefølge av beregning
Nivå Operator
1 Parentes (), hakeparentes [], buet parentes {}
2 Omregning (#)
3 Oppkalling av funksjon
4 Postoperatorer: grader-minutter-sekunder (-,',"), fakultet (!), prosent (%),
radianer (QRS), senket skrift ([]), transponert (T)
5 Eksponensiering, potens-operator (^)
6 Negasjon (L)
7 Sett sammen streng (&)
8 Multiplikasjon (¦), divisjon (/)
9 Addisjon (+), subtraksjon (-)
10 Likhetsrelasjoner: lik (=), ulik (ƒeller /=), mindre enn (<), mindre enn eller lik ({
eller <=), større enn (>), større enn eller lik (|eller >=)
11 Logisk not
12 Logisk and
13 Logiske or
14 enten...eller,verken ...eller,ikke både ...og
15 Logisk implikasjon (⇒)
16 Logisk dobbel implikasjon, XNOR (⇔)
17 Begrensningsoperator (“|”)
18 Lagre (&)
EOS™ (Ligningsoperativsystem)-hierarkiet 221

222 EOS™ (Ligningsoperativsystem)-hierarkiet
Parenteser, hakeparenteser, buede parenteser
Først behandles alle beregninger som står i parentes, hakeparentes eller buet parentes. I
uttrykket 4(1+2) behandler EOS™ -programvaren for eksempel først den delen av uttrykket
som står i parenteser, 1+2, og multipliserer deretter resultatet, 3, med 4.
Antallet åpne- og lukkeparenteser, åpne- og lukke-hakeparenteser og buede åpne- og
lukkeparenteser må være det samme innenfor ett uttrykk eller én ligning. Hvis ikke, vises en
feilmelding, som angir det manglende elementet. For eksempel vil (1+2)/(3+4 vise
feilmeldingen “Mangler ).”
Merk: Siden TI-Nspire™CAS -programvaren gjør at du kan definere dine egne funksjoner, blir et
variabelnavn fulgt av et uttrykk i parentes betraktet som en “oppkalling av funksjon” istedenfor halvveis
skjult multiplikasjon. For eksempel i a(b+c) blir funksjonen a beregnet for verdien b+c (av den variable).
For å multiplisere uttrykket b+c med variabelen a, må du bruke eksplisitt multiplikasjon: a*(b+c).
Omregning
Omregnings-operatoren (#) omregner en streng til et variabel- eller funksjonsnavn. For
eksempel oppretter #(“x”&”y”&”z”) variabelnavnet xyz. Omregning lar deg også opprette og
modifisere en variabel mens du er inne iet program. Hvis for eksempel 10"r og “r”"s1, så er
#s1=10.
Postoperatorer
En postoperator er en operator som kommer direkte etter et argument, som f.eks. 5!, 25%,
eller 60¡15' 45". Et argument som er fulgt av en postoperator blir behandlet ved fjerde
prioritetsnivå. I uttrykket 4^3! blir blir for eksempel 3! behandlet først. Resultatet, 6, blir så
eksponenten av 4 for å oppnå 4096.
Eksponensiering
Eksponensiering (^) og element-for-element-eksponensiering (.^) blir behandlet fra høyre til
venstre. Uttrykket 2^3^2 blir for eksempel behandlet som det samme som 2^(3^2) for å
produsere 512. Dette er forskjellig fra (2^3)^2, som er 64.
Negasjon
For å legge inn et negativt tall, trykk på vfulgt av tallet. Postoperasjoner og eksponensiering
utføres før negasjon. Resultatet av Lx2er for eksempel et negativt tall, og L92=L81. Bruk
parenteser for å opphøye et negativt tall i annen potens, som f.eks. (L9)2for å produsere 81.
Begrensning (“|”)
Argumentet som følger etter (“|”)-operator gir et sett av begrensninger som påvirker hvordan
argumentet som står foran operatoren blir behandlet.

Feilkoder og feilmeldinger
Hvis det oppstår en feil, er koden knyttet til variabel feilKode. Egendefinerte programmer og
funksjoner kan undersøke feilKode for å bestemme årsaken til feilen. For et eksempel på
bruk av feilKode, se eksempel 2 under kommandoen Prøv, side 176.
Merk: Noen feilforhold gjelder kun for TI-Nspire™ CAS-produktene, og noen gjelder kun for
TI-Nspire™-produktene.
Feilkode Beskrivelse
10 En funksjon returnerte ingen verdi
20 En test ga ikke resultatet SANN eller USANN.
Vanligvis kan udefinerte variabler ikke sammenliknes. Testen If a<b vil for eksempel forårsake enten
at a eller at b ikke er definert, dersom utsagnet If blir utført.
30 Argumentet kan ikke være et mappenavn.
40 Argumentfeil
50 Uoverensstemmelse i argument
To eller flere argumenter må være av samme type.
60 Argumentet må være et Boolsk uttrykk eller et heltall
70 Argumentet må være et desimaltall
90 Argumentet må være en liste
100 Argumentet må være en matrise
130 Argumentet må være en streng
140 Argumentet må være et variabelnavn.
Pass på at navnet:
• ikke begynner med et tall
• ikke inneholder mellomrom eller spesialtegn
• ikke bruker senket strek eller punktum på ugyldig måte
• ikke overgår tillatt lengde
Les mer om dette i Kalkulator-avsnittet dokumentasjonen.
160 Argumentet må være et uttrykk
165 For lite strøm i batteriene til å sende/motta
Legg i nye batterier før sending eller mottak.
170 Grense
Den nedre grensen må være mindre enn den øvre grensen for å definere søkeintervallet.
180 Avbryt
Feilkoder og feilmeldinger 223

224 Feilkoder og feilmeldinger
Feilkode Beskrivelse
Det ble trykket på tasten deller cunder en lang beregning eller mens et program ble utført.
190 Sirkulær definisjon
Denne meldingen komme til syne for å unngå at du slipper opp for minne under uendelig erstatning av
variable verdier. For eksempel vil a+1->a, der a er en udefinert variabel, forårsake denne feilen.
200 Ugyldig begrensningsuttrykk
For eksempel vil løs(3x^2-4=0,x) | x<0 eller x>5 produsere denne feilmeldingen, fordi begrensningen
er skilt med “eller” istedenfor “og”.
210 Ugyldig datatype
Et argument er av feil datatype.
220 Avhengig grense
230 Dimensjon
En liste eller matriseindeks er ikke gyldig. Hvis for eksempel listen {1,2,3,4} er lagret i L1, så er L1[5]
en dimensjonsfeil, fordi L1 kun inneholder fire elementer.
235 Dimensjonsfeil. Ikke nok elementer i listene.
240 Dimensjonsfeil
To eller flere argumenter må være av samme dimensjon. For eksempel er [1,2]+[1,2,3] en
dimensjonsfeil, fordi matrisene inneholder ulikt antall elementer.
250 Divisjon med null
260 Grunnmengdefeil
Et argument må være i en spesifisert grunnmengde. For eksempel er tilf(0) ikke gyldig.
270 Duplikatnavn på variabel
280 Else og ElseIf ugyldig utenfor If...EndIf-blokk
290 EndTry uten tilhørende Else-uttrykk
295 For mange iterasjoner
300 Forventet 2- eller 3-elements liste eller matrise
310 Det første argumentet av nSolve må være en ligning i én variabel. Det kan ikke inneholde noen annen
variabel enn den variabelen som vi er interessert i.
320 Det første argumentet til løs eller kLøs må være en ligning eller ulikhet
For eksempel er løs(3x-4,x) ugyldig fordi det første argumentet ikke er en ligning.
345 Inkonsistente enheter
350 Indeks utenfor gyldig område
360 Indireksjonsstrengen er ikke et gyldig variabelnavn
380 Udefinert Svar
Enten opprettet ikke den forrige beregningen noe Svar, eller det ble ikke lagt inn noe forrige beregning.

Feilkode Beskrivelse
390 Ugyldig tildeling
400 Ugyldig tildelingsverdi
410 Ugyldig kommando
430 Ugyldig for de gjeldende modusinnstillingene
435 Ugyldig gjetning (startverdi)
440 Ugyldig “skjult” multiplikasjon
For eksempel er x(x+1) ugyldig; derimot er x*(x+1) korrekt syntaks. Dette skal forhindre forvirring
mellom halvveis skjult multiplikasjon og oppkalling av funksjon.
450 Ugyldig i en funksjon eller gjeldende uttrykk
Det er kun visse kommandoer som er gyldige i en egendefinert funksjon.
490 Ugyldig i Try..EndTry-blokk
510 Ugyldig liste eller matrise
550 Ugyldig utenfor funksjon eller program
Et antall kommandoer er ikke gyldige utenfor en funksjon eller et program. For eksempel kan ikke
Lokal brukes hvis den ikke er inne i en funksjon eller et program.
560 Ugyldig utenfor Loop..EndLoop-, For..EndFor- eller While..EndWhile-blokk
For eksempel er Avslutt-kommandoen kun gyldig inne i disse loop-blokkene.
565 Ugyldig utenfor program
570 Ugyldig banenavn
For eksempel er \var ugyldig.
575 Ugyldig polar kompleks verdi
580 Ugyldig programreferanse
Det kan ikke refereres til programmer inne i funksjoner eller uttrykk, som f.eks. 1+p(x), der p er et
program.
600 Ugyldig tabell
605 Ugyldig bruk av enheter
610 Ugyldig variabelnavn i Lokalt utsagn
620 Ugyldig variabel- eller funksjonsnavn
630 Ugyldig variabelreferanse
640 Ugyldig vektorsyntaks
650 Kommunikasjons-forbindelse
En kommunikasjon mellom to enheter er ikke fullført. Kontroller at forbindelseskabelen er koplet godt
til i begge ender.
Feilkoder og feilmeldinger 225

226 Feilkoder og feilmeldinger
Feilkode Beskrivelse
665 Matrisen kan ikke diagonaliseres
670 Lite minne
1. Slett noen data i dette dokumentet
2. Lagre og lukk dette dokumentet
Dersom 1 og 2 mislykkes, ta ut batteriene og sett dem inn igjen
672 Ressursbegrensning
673 Ressursbegrensning
680 Manglende (
690 Manglende )
700 Manglende “
710 Manglende ]
720 Manglende }
730 Manglende start eller slutt på blokksyntaks
740 Manglende Then i If..EndIf-blokken
750 Navnet er ikke en funksjon eller et program
765 Ingen funksjoner er valgt
780 Fant ingen løsning
800 Ikke-reelt resultat
Hvis for eksempel programvaren er i Reell innstilling, er ‡(-1) ugyldig.
For å tillate komplekse resultater, endre “Reell eller Kompleks” modusinnstilling til REKTANGULÆR
eller POLAR.
830 Overflyt
850 Fant ikke programmet
Det ble ikke funnet en programreferanse i et annet program i oppgitt bane under utføring.
855 Rand-funksjonstyper ikke tillatt i grafer
860 Rekursjonen for dyp
870 Reservert navn eller systemvariabel
900 Argumentfeil
Median-median-modell kunne ikke brukes på datasettet.
910 Syntaksfeil
920 Fant ikke teksten
930 For få argumenter

Feilkode Beskrivelse
Funksjonen eller kommandoen mangler et eller flere argumenter.
940 For mange argumenter
Uttrykket eller ligningen inneholder for mange argumenter og kan ikke behandles.
950 For mange indekser
955 For mange udefinerte variabler
960 Variabelen er ikke definert
Variabelen er ikke tildelt noen verdi. Bruk en av følgende kommandoer:
• sto &
•:=
•Define
for å tildele variablene verdi.
965 Ulisensiert OS
970 Variabel er i bruk, så referanser eller endringer er ikke tillatt
980 Variabel er beskyttet
990 Ugyldig variabelnavn
Pass på at navnet ikke overgår tillatt lengde
1000 Grunnmengde for vindusvariabel
1010 Zoom
1020 Intern feil
1030 Overtredelse av beskyttet minne
1040 Ustøttet funksjon. Denne funksjonen krever Computer Algebra System. Prøv TI-Nspire CAS.
1045 Ustøttet operator. Denne operatoren krever Computer Algebra System. Prøv TI-Nspire CAS.
1050 Ustøttet egenskap. Denne operatoren krever Computer Algebra System. Prøv TI-Nspire CAS.
1060 Innlagt argument må være numerisk. Bare innlegg som inneholder numeriske verdier er tillatt.
1070 Trig-funksjonsargument for stort for nøyaktig reduksjon
1080 Ustøttet bruk av Svar. Denne applikasjonen støtter ikke Svar.
1090 Funksjonen er ikke definert. Bruk en av følgende kommandoer:
•Define
•:=
• sto &
for å definere en funksjon.
1100 Ikke-reell beregning
Hvis for eksempel programvaren er i Reell innstilling, er ‡(-1) ugyldig.
Feilkoder og feilmeldinger 227

228 Feilkoder og feilmeldinger
Feilkode Beskrivelse
For å tillate komplekse resultater, endre “Reell eller Kompleks” modusinnstilling til REKTANGULÆR
eller POLAR.
1110 Ugyldige grenser
1120 Tegn ikke endret
1130 Argumentet kan ikke være en liste eller matrise
1140 Argumentfeil
Det første argumentet må være et polynomisk uttrykk i det andre argumentet. Dersom det andre
argumentet utelates, prøver programvaren å velge en grunninnstilling.
1150 Argumentfeil
De første to argumentene må være polynomiske uttrykk i det tredje argumentet. Dersom det tredje
argumentet utelates, prøver programvaren å velge en grunninnstilling.
1160 Ugyldig banenavn for bibliotek
Et banenavn må være av formen xxx\yyy, der:
• Delen xxx kan bestå av mellom 1 og 16 tegn.
• Delen yyy kan ha 1 til 15 tegn.
Les mer om dette i Bibliotek-avsnittet dokumentasjonen.
1170 Ugyldig bruk av banenavn for bibliotek
• En verdi kan ikke tildeles et banenavn som bruker Define,:= eller sto &.
• Et banenavn kan ikke erklæres som en lokal variabel eller brukes som
parameter i en funksjonsdefinisjon eller programdefinisjon.
1180 Ugyldig variabelnavn på bibliotek
Pass på at navnet:
• Ikke inneholder punktum
• Ikke begynner med senket strek
• Ikke består av mer enn 15 tegn
Les mer om dette i Bibliotek-avsnittet dokumentasjonen.
1190 Bibliotek-dokumentet ble ikke funnet:
• Kontroller om biblioteket er i mappen MittBibl.
• Oppdater biblioteker.
Les mer om dette i Bibliotek-avsnittet dokumentasjonen.
1200 Bibliotek-variabler ble ikke funnet:
• Kontroller om bibliotek-variablene eksisterer i den første oppgaven i biblioteket.
• Forsikre deg om at bibliotek-variabelen er blitt definert som BiblOff eller
BiblPriv.
• Oppdater biblioteker.
Les mer om dette i Bibliotek-avsnittet dokumentasjonen.
Feilkode Beskrivelse
1210 Ugyldig navn på snarvei til bibliotek.
Pass på at navnet:
• Ikke inneholder punktum
• Ikke begynner med senket strek
• Ikke består av mer enn 16 tegn
• Ikke er et reservert navn
Les mer om dette i Bibliotek-avsnittet i dokumentasjonen.
1220 Grunnmengdefeil:
Funksjonene tangentLinje og normalLinje støtter kun funksjoner med reelle verdier.
1230 Grunnmengdefeil.
Trigonometriske omregningsoperatorer støttes ikke i Grader- eller Gradian-vinkelmodus.
1250 Argumentfeil
Bruk et system av lineære ligninger.
Eksempel på et system av to lineære ligninger med variablene x og y:
3x+7y=5
2y-5x=-1
1260 Argumentfeil:
Det første argumentet til nfMin eller nfMax må være et uttrykk i én variabel. Det kan ikke inneholde
noen annen variabel enn den variabelen som vi er interessert i.
1270 Argumentfeil
Den deriverte må være av orden 1 eller 2.
1280 Argumentfeil
Bruk et polynom på utvidet (ekspandert) form i én variabel.
1290 Argumentfeil
Bruk et polynom i én variabel.
1300 Argumentfeil
Koeffisientene i polynomet må være numeriske verdier.
1310 Argumentfeil:
En funksjon kan ikke behandles for ett eller flere av dens argumenter.
1380 Argumentfeil:
Nestede oppringinger til område() funksjon er ikke tillatt.
Feilkoder og feilmeldinger 229

230 Varselkoderog meldinger
Varselkoder og meldinger
Du kan bruke funksjonen warnCodes() for å lagre varselkodene som ble generert da et
uttrykk ble behandlet. Denne tabellen opplister hver numeriske varselkode og dens
assosierte melding.
Se warnCodes() på side 184 for et eksempel på lagring av varselkoder.
Varselkode Melding
10000 Kommandoen kan gi falske løsninger.
10001 Derivasjon av en ligning kan gi en ugyldig ligning.
10002 Tvilsom løsning
10003 Tvilsom nøyaktighet
10004 Kommandoen kan utelate løsninger.
10005 KLøs kan spesifisere flere nullpunkter.
10006 Løs kan spesifisere flere nullpunkter.
10007 Flere løsninger kan eksistere. Prøv å angi passende øvre og nedre grenser, og/eller en gjetning.
Eksempler ved bruk av solve():
• solve(Ligning, Var=Forslag)|nedGrens<Var<øvGrens
• solve(Ligning, Var)|nedGrens<Var<øvGrens
• solve(Ligning,Var=Forslag)
10008 Grunnmengden til resultatet kan være mindre enn grunnmengden til innlegget (inndata).
10009 Grunnmengden til resultatet kan være større enn grunnmengden til innlegget (inndata).
10012 Ikke-reell beregning
10013 ˆ^0 eller udef^0 erstattet av 1
10014 udef^0 erstattet av 1
10015 1^ˆeller 1^udef erstattet av 1
10016 1^udef erstattet av 1
10017 Overflyt erstattet av ˆeller Lˆ
10018 Kommando krever og returnerer 64-biters verdi.
10019 Ressursbegrensning, forenkling kanskje ufullstendig.
10020 Trig-funksjonsargument for stort for nøyaktig reduksjon.
10021 Inndataene inneholder en udefinert parameter.
Resultatet kanskje ikke gyldig for alle mulige parameterverdier.

Varselkode Melding
10022 Å spesifisere riktig nedre og øvre grense kan gi en løsning.
10023 Tallstørrelsen er multiplisert med identitetsmatrisen.
10024 Resultat oppnådd ved bruk av tilnærmet aritmetikk.
10025 Ekvivalens kan ikke verifiseres i EXACT-modus.
10026 Avhengighet kan være ignorert. Spesifiser avhengighet i formen "\" 'Variabel MatteTestSymbol
Konstant' eller en forbindelse av disse formene, for eksempel 'x<3 og x>-12'
Varselkoderog meldinger 231

232 Generell informasjon
Generell informasjon
Informasjon om service og garanti på TI-produkter
Informasjon om service for
TI-produkter
Nærmere informasjon om service for TI-produkter fås ved
henvendelse til TI via elektronisk post eller ved å slå opp på TI
hjemmeside på Internett.
Elektronisk post: ti-cares@ti.com
Internettadresse: education.ti.com
Informasjon om service og
garantibetingelser
Du kan lese mer om garantibetingelser, garantitid samt om
produktservice på garantierklæringen som medfølger dette produkt.
Du kan også henvende deg til din lokale forhandler/distributør for
Texas Instruments.

236 Stikkordregister
►Polar, vise som polar vektor[Polar] 123
►, omregne enheter[*] 212
►, omregner til gradian vinkel[Grad] 80
►approxFraction() 17
►cos, vise uttrykt ved cosinus[cos] 33
►DD, vises som desimalvinkel[DD] 48
►Desimal, vise resultat som desimal[Decimal] 48
►DMS, vise som grader/minutter/sekunder[DMS (GMS)] 55
►exp, vis uttrykt ved e[exp] 63
►Grunntall10, vise som desimalt heltall[Grunntall10] 23
►Grunntall16, vise som heksadesimal[Grunntall16] 23
►Grunntall2, vise som binær[Grunntall2] 21
►Rad, omregne til radian vinkel[Rad] 133
►Rect, vise som rektangulær vektor[Rekt] 135
►sin, vise uttrykt ved sinus[sin] 153
►Sphere, vise som sfærisk vektor[Sfære (kule)] 161
→
→, lagre 215
⇒
⇒, logisk implikasjon[*] 201, 219
⇔
⇔, logisk dobbel implikasjon[*] 202
©
©, kommentar 216
°
°, grader fremstilling[*] 209
°, grader/minutter/sekunder[*] 210
0
0b, binær indikator 216
0h, heksadesimal indikator 216
1
10^(), tier-potens 213
2
2-delers stykkevis funksjon
sjablon for 6
2-utvalg F test 73
A
abs(), absoluttverdi 12
Absoluttverdi
sjablon for 8
addere, + 193
amortiseringstabell, amortTbl() 12, 21
amortTbl(), amortiseringstabell 12, 21
and, Boolsk operator 13
andrederivert
sjablon for 10
angle(), vinkel 14
ANOVA, enveis varians-analyse 14
ANOVA2-veis, toveis varians-analyse 15
Ans, siste svar 17
antall betingede elementer i en liste , tellIf() 38
antall elementer i en liste, antall() 38
antall(), antall elementer i en liste 38
approx(), tilnærmet 17
approxRational() 18
arccos() 18
Stikkordregister 237

238 Stikkordregister
arccosh() 18
arccot() 18
arccoth() 18
arccsc() 18
arccsch() 18
arcLen(), buelengde 18
arcsec() 19
arcsech() 19
arcsin() 19
arcsinh() 19
arctan() 19
arctanh() 19
argumenter i TVM-funksjoner 179
augment(), utvid/sett sammen 19
avgRC(), gjennomsnittlig endringshastighet 20
avrund, round() 143
avslutt
funksjon, EndFunc 74
avslutt, Exit 62
B
begrensningsoperator "|" 213
begrensningsoperator, rekkefølge av beregning 221
behandle polynom, polyEval() 125
behandling, rekkefølge av 221
bestemt integral
sjablon for 10
bibliotek
lage snarveier til objekter 89
BiblOff 50
BiblPriv 49
binomCdf() 24
binomPdf() 24
binær
indikator, 0b 216

vise, ►Grunntall2 21
Boolske operatorer
⇒201, 219
⇔202
and 13
eller 120
enten ... eller ... 185
ikke 116
ikke både...og 110
verken ... eller 114
brøker
ekteBrøk 129
sjablon for 5
buelengde, arcLen() 18
C
c 2 2-veis 27
c 2 Pdf() 28
Cdf() 68
ceiling(), øvre 24
centralDiff() 25
cFactor(), kompleks faktor 25
char(), tegnstreng 26
charPoly() 26
χ²Cdf() 27
χ²GOF 27
ClearAZ 28
colDim(), matrisens kolonnedimensjon 29
colNorm(), matrisens kolonnenorm 29
comDenom(), fellesnevner 30
completeSquare(), complete square 30
conj(), kompleks konjugert 31
constructMat(), konstruer matrise 31
cos⁻¹, invers cosinus 34
cos(), cosinus 33
Stikkordregister 239

240 Stikkordregister
cosh⁻¹(), hyperbolsk, invers cosinus 36
cosh(), hyperbolsk cosinus 35
cosinus
vise uttrykk med hensyn på 33
cosinus, cos() 33
cot⁻¹(), invers cotangens 36
cot(), cotangens 36
cotangens, cot() 36
coth⁻¹(), hyperbolsk invers cotangens 37
coth(), hyperbolsk cotangens 37
cPolyRoots() 39
crossP(), kryssprodukt 39
csc⁻¹(), invers cosekans 40
csc(), cosekans 40
csch⁻¹(), invers hyperbolsk cosekans 41
csch(), hyperbolsk cosekans 40
cSolve(), kompleks løs 41
CubicReg, kubisk regresjon 43
cumulativeSum(), kumulativ sum 44
cycle, Løkke 45
Cycle, løkke 45
cZeros(), komplekse nullpunkt 45
D
d (), første deriverte 203
dager mellom datoer, dbd() 47
dbd(), dager mellom datoer 47
Define, definer 48
Definer 48
Definer BiblOff 50
Definer BiblPriv 49
definer, Define 48
definere
felles (offentlig) funksjon eller program 50
privat funksjon eller program 49

deltaList() 50
deltaTmpCnv() 50
DelVar, slett variabel 51
delVoid(), fjern gamle elementer 51
derivative() 51
deriverte
første deriverte, d() 203
numerisk derivert, nDeriv() 113
numerisk derivert, nDerivative() 112
deriverte eller n-te deriverte
sjablon for 10
desimal
heltall vise, 4Grunntall10 23
vinkel-visning, ►DD 48
deSolve(), løsning 52
det(), matrisedeterminant 54
diag(), matrisediagonal 54
dim(), dimensjon 54
dimensjon, dim() 54
dividere heltall, intDiv() 84
dividere, / 195
dominerende ledd(), dominerende ledd 56
dominerende ledd, dominerende ledd() 56
dotP(), prikk produkt 57
E
e eksponent
sjablon for 6
e i en potens, e^() 58, 63
E, eksponent 208
e, vise uttrykk uttrykt ved 63
e^(), e i en potens 58
eff ), omregn nominell til effektiv rente 58
effektiv rente, eff() 58
egendefinerte funksjoner 48
Stikkordregister 241

242 Stikkordregister
egendefinerte funksjoner og programmer 49-50
egenvektor, eigVc() 58
egenverdi, eigVl() 59
eigVc(), egenvektor 58
eigVl(), egenverdi 59
eksakt, exact() 62
ekskludering med "|" operator 213
eksponensiell regresjon, ExpReg 65
eksponent, E 208
eksponenter
sjablon for 5
ekte brøk, propFrac 129
eliminasjonsform, ref() 136
eller (Boolsk), eller 120
eller, Boolsk operator 120
else if, ElseIf 60
else, Else 81
ElseIf, else if 60
en-variabel-statistikk, OneVar 119
end
For…EndFor 71
if, EndIf 81
stigningstall, EndLoop 101
while, EndWhile 185
end if, EndIf 81
end stigningstall, EndLoop 101
end while, EndWhile 185
endfunksjon, EndFunc 74
Endret internrente av retur, mirr(), 107
EndTry, avslutt prøv 176
EndWhile, end while 185
enhetsvektor, unitV() 182
enten ... eller ..., Boolsk eksklusiv eller 185
EOS (Equation Operating System) 221
Equation Operating System (Ligningsoperativsystem) (EOS) 221

er lik, = 199
erstatning med "|" operator 213
etikettNavn, Lbl 88
euler(), Euler function 61
exact(), eksakt 62
Exit, avslutt 62
exp(), e i en potens 63
exp►liste(), uttrykk til liste 63
expand(), utvid 64
expr(), streng til uttrykk 99
expr(), streng til uttrykk 65
ExpReg, eksponensiell regresjon 65
F
factor(), faktor 66
faktor, factor() 66
fakultet, ! 202
feil og problemløsing
send feil, SendFeil 122
slett feil, SlettFeil 28
fellesnevner, comDenom() 30
Fill, matrise fylle 68
finansielle funksjoner, tvmFV() 178
finansielle funksjoner, tvmI() 178
finansielle funksjoner, tvmN() 179
finansielle funksjoner, tvmPmt() 179
finansielle funksjoner, tvmPV() 179
FiveNumSummary 68
fjerdegrads regresjon, QuartReg 131
fjern
åpne elementer fra liste 51
floor(), nedre 69
fMax(), maksimalpunkt for funksjonen 70
fMin(), minimalpunkt for funksjonen 70
For 71
Stikkordregister 243

244 Stikkordregister
for, For 71
For, for 71
fordelingsfunksjoner
binomCdf() 24
binomPdf() 24
c 2 Pdf() 28
c22-veis() 27
invNorm() 86
invt() 86
Invχ²() 85
normCdf() 115
normPdf() 116
poissCdf() 122
poissPdf() 123
tCdf() 171
tPdf() 175
χ²Cdf() 27
χ²GOF() 27
format(), formatstreng 71
formatstreng, format() 71
fortegn, sign() 152
fpart(), funksjonsdel 72
frekvens() 73
fremstilling i grader/minutter/sekunder 210
fremstilling minutter, 210
fremstilling sekunder, " 210
freqTable() 72
Frobenius-norm, norm() 115
Func, funksjon 74
Func, programfunksjon 74
funksjoner
del, fpart() 72
egendefinere 48
maksimalpunkter for, fMax() 70
minimalpunkter for, fMin() 70
programfunksjon, Func 74
funksjoner og variabler
kopiere 32
første deriverte
sjablon for 9
G
G, gradianer 209
gcd(), største felles divisor 75
geomCdf() 75
geomPdf() 76
getDenom(), lesNevner 76
getLangInfo(), hent/returner språkinformasjon 76
getLockInfo(), tester låsestatus av variabel eller variabelgruppe 77
getNum(), les/returner teller 78
getType(), get type of variable 78
getVarInfo(), les/returner variabelinformasjon 79
gjennomsnitt, mean() 103
gjennomsnittlig endringshastighet, avgRC() 20
Goto, gå til 80
grader fremstilling, ° 209
grader/minutter/sekunder-visning, ►DMS 55
gradian fremstilling, G 209
grafregnere
omregne 212
grupper, låse og låse opp 98, 182
grupper, teste låsestatus 77
gå til, Goto 80
H
heksadesimal
indikator, 0h 216
vise, 4Grunntall16 23
heltall, int() 84
Stikkordregister 245

246 Stikkordregister
heltallsdel, iPart() 86
hent/returner
variabelinformasjon, getVarInfo() 76, 79
hurtigtaster 219
hyperbolic (hyperbolsk)
invers tangens, tanh⁻¹() 170
hyperbolsk
cosinus, cosh() 35
invers cosinus, cosh⁻¹() 36
invers sinus, sinh⁻¹() 156
sinus, sinh() 155
tangens, tanh() 170
høyre, right() 140
I
identitetsmatrise, identity() 80
identity(), identitetsmatrise 80
if, If 81
If, if 81
ifFn() 82
ikke både...og, Boolsk operator 110
ikke, Boolsk operator 116
imag(), imaginær del 83
imaginær del, imag() 83
ImpDif(), implisitt derivert 83
implisitt derivert, Impdif() 83
Indir.ref, # 208
inndata, Input 83
innenfor streng, inString() 84
innstillinger, les aktuell 77
Input, inndata 83
inString(), innenfor streng 84
int(), heltall 84
intDiv(), dividere heltall 84
integral, ∫ 203

interpolate(), interpolate 85
invers cosinus, cos⁻¹() 34
invers kumulativ normalfordeling (invNorm() 86
invers sinus, sin / () 155
invers tangens, tan⁻¹() 169
invers, x⁻¹ 213
invF() 85
invNorm(), invers kumulativ normalfordeling) 86
invt() 86
Invχ²() 85
iPart(), heltallsdel 86
irr(), internrente av retur
internrente av retur, irr() 86
isPrime(), primtallstest 87
isVoid(), test for åpen 87
K
kolUtvid 29
kombinasjoner, nCr() 111
kommentar, © 216
kompleks
faktor, cFactor() 25
konjugert, conj() 31
løs, cSolve() 41
nullpunkt, cZeros() 45
konstant
i løs() 158
konstanter
hurtigtaster for 220
i dlLøs() 52
i kLøs() 43
i kNullp() 47
i løs() 159
konstruer matrise, constructMat() 31
kopiere variabel eller funksjoner, CopyVar 32
Stikkordregister 247

248 Stikkordregister
korrelasjonsmatrise, corrMat() 33
korrMat(), korrelasjonsmatrise 33
kryssprodukt, crossP() 39
kubisk regresjon, CubicReg 43
kumulativ sum, cumulativeSum() 44
kvadratisk regresjon, QuadReg 130
kvadratrot
sjablon for 5
kvadratrot, √() 205
kvadratrot, ‡ () 162
L
lagre
symbol, & 215
Lbl, etikettNavn 88
lcm, minste felles multiplum 88
left(), venstre 88
legg til, & 202
lengde på streng 54
les
modus, lesModus() 149
les/returner
lesNevner, getDenom() 76
lesTeller, getNum() 78
lesModus(), les modus 149
lesModus(), les modus-innstillinger 77
libShortcut(), lage snarveier til bibliotekobjekter 89
ligningssystemer (2-ligning)
sjablon for 7
ligningssystemer (N-ligning)
sjablon for 7
lim
lim() 90
limit() 90
sjablon for 11

limit() eller lim(), grense 90
lineær regresjon, LinRegAx 91
lineær regresjon, LinRegBx 90, 92
LinRegBx, lineær regresjon 90
LinRegMx, lineær regresjon 91
LinRegtIntervals, lineær regresjon 92
LinRegtTest 94
linSolve() 95
Δlist(), differensliste 95
list►mat(), liste til matrise 95
liste til matrise, list►mat() 95
liste, antall betingede elementer i 38
liste, antall elementer i 38
lister
differens, @liste() 95
differenser i en liste, @list() 95
kryssprodukt, crossP() 39
kumulativ sum, cumulativeSum() 44
liste til matrise, list►mat() 95
maksimum, max() 103
matrise til liste, mat Δliste() 103
midtstreng, mid() 105
minimum, min() 106
nye, newList() 112
prikk produkt, dotP() 57
produkt, product() 128
sorter fallende, SortD 161
sorter stigende, SortA 160
summering, sum() 166
tomme elementer i 217
uttrykk til liste, exp►liste() 63
utvid/sett sammen, utvid() 19
ln(), naturlig logaritme 96
LnReg, logaritmisk regresjon 97
Local, lokal variabel 98
Stikkordregister 249

250 Stikkordregister
Logaritme
sjablon for 6
logaritmer 96
logaritmisk regresjon, LnReg 97
logisk dobbel implikasjon, ⇔202
logisk implikasjon, ⇒201, 219
Logistic, logistisk regresjon 99
LogisticD, logistisk regresjon 100
logistisk regresjon, Logistic 99
logistisk regresjon, LogisticD 100
lokal variabel, Local 98
lokal, Local 98
Loop, stigningstall 101
LU (lower-upper), matrisens nedre-øvre dekomposisjon 102
løs, solve() 157
løsning, deSolve() 52
Lås, lås variabel eller variabelgruppe 98
låse opp variabler og variabelgrupper 182
låse variabler og variabelgrupper 98
M
maksimum, max() 103
mat►list(), matrise til liste 103
matrices (matriser)
undermatrise, subMat() 167
matrise (1 × 2)
sjablon for 8
matrise (2 × 1)
sjablon for 8
matrise (2 × 2)
sjablon for 8
matrise (m × n)
sjablon for 8
matrise til liste, mat Δliste() 103

matriser
determinant, det() 54
diagonal, diag() 54
dimensjon, dim() 54
egenvektor, eigVc() 58
egenverdi, eigVl() 59
eliminasjonsform, ref() 136
fill, Fylle 68
identitet, identity() 80
kolonnedimensjoner, colDim() 29
kolonnenorm, colNorm() 29
kumulativ sum, cumulativeSum() 44
liste til matrise, list►mat() 95
maksimum, max() 103
matrise til liste, mat Δliste() 103
minimum, min() 106
nedre-øvre dekomposisjon, LU (lower-upper) 102
nye, newMat() 112
prikk addisjon, .+ 197
prikk divisjon, .P 198
prikk multiplikasjon, .* 197
prikk potens, .^ 198
prikk subtraksjon, .N 197
produkt, product() 128
QR faktorisering, QR 129
radaddisjon, rowAdd() 143
raddimensjon, rowDim() 144
radhandling, mRow() 108
radmultiplikasjon og addisjon, mRowAdd() 108
radnorm, rowNorm() 144
radskift, rowSwap() 144
redusert eliminasjonsform, rref() 144
summering, sum() 166
tilfeldig, randMat() 134
transponert, T 168
Stikkordregister 251

252 Stikkordregister
undermatrise, subMat() 166
utvid/sett sammen, augment() 19
max(), maksimum 103
mean(), gjennomsnitt 103
med (gitt at), | 213
median-median linjeregresjon, MedMed 104
median(), median 104
median, median() 104
MedMed, median-median linjeregresjon 104
mid(), midtstreng 105
midtstreng, mid() 105
min(), minimum 106
mindre enn eller lik, { 200
minimum, min() 106
minste felles multiplum, lcm 88
mirr(), endret internrente av retur 107
mod(), modul 107
modul, mod() 107
modus-innstillinger, lesModus() 77
moduser
lesing, lesModus() 149
mRow(), matrise radhandling 108
mRowAdd(), matrise radmultiplikasjon og addisjon 108
multiplisere, * 194
Multippel lineær regresjon ttest 109
MultReg 108
MultRegIntervals() (MultRegIntervaller) 108
MultRegTests() (MultRegTester) 109
N
n-te rot
sjablon for 5
naturlig logaritme, ln() 96
nCr(), kombinasjoner 111
nDerivative(), numerisk derivert 112

nedre, floor() 69
negasjon, legge inn negative tall 222
netto nåverdi, npv() 117
nevner 30
newList(), ny liste 112
newMat(), ny matrise 112
nfMax(), numerisk funksjonsmaksimum 113
nfMin(), numerisk funksjonsminimum 113
nInt(), numerisk integral 113
nom ), omregn effektiv til nominell rente 114
nominell rente, nom() 114
norm(), Frobenius-norm 115
normal-linje, normalLine() 115
normalLine() 115
normCdf() 115
normPdf() 116
nPr(), permutasjoner 117
npv(), netto nåverdi 117
nSolve(), numerisk løsning 118
nullpunkt, zeroes() 186
numerisk
derivert, nDeriv() 113
derivert, nDerivative() 112
integral, nInt() 113
løsning, nSolve() 118
ny
liste, newList() 112
matrise, newMat() 112
når, when() 184
O
objekter
lage snarveier til bibliotek 89
omregne
4Grad 80
Stikkordregister 253

254 Stikkordregister
4Rad 133
grafregnere 212
omregnings-operator (#) 222
område(), områdefunksjon 56
områdefunksjon, område() 56
OneVar, en-variabel-statistikk 119
operatorer
rekkefølge av behandling 221
ord(), numerisk tegnkode 121
Overfører øyeblikkelig kontroll til den neste iterasjonen i aktuell løkke (For, While, eller Loop). 45
P
P►Rx(), rektangulær x-koordinat 121
P►Ry(), rektangulær y-koordinat 121
Pdf() 72
permutasjoner, nPr() 117
poissCdf() 122
poissPdf() 123
polar
koordinat, R►Pr() 132
koordinat, R►Pθ() 132
vektor-visning, ►Polar 123
polyEval(), behandle polynom 125
polyGcd() 125-126
polyGrader() 124
polyKoef() 124
polynomer
behandle, polyEval() 125
tilfeldige, randPoly() 134
PolyRoots() 126
potens, ^ 196
potensregresjon, PowerReg 126, 138-139, 172
PowerReg, potensregresjon 126
Prgm, definer program 127
prikkP
addere, .+ 197
divisjon, ./ 198
multiplikasjon, .* 197
potens, .^ 198
produkt, dotP() 57
subtraksjon, .- 197
prime, 211
primtallstest, isPrime() 87
prodSeq() 128
product(), produkt 128
produkt, P() 205
produkt, product() 128
programmer
definere felles (offentlig) bibliotek 50
definere privat bibliotek 49
programmer og programmering
slett feil, SlettFeil 28
try, Try 176
vis I/O skjerm, Vis 55
programmering
definer program, Prgm 127
send feil, SendFeil 122
vis data, Vis 55
propFrac, ekte brøk 129
prosent, % 198
Q
QR faktorisering, QR 129
QR, QR faktorisering 129
QuadReg, kvadratisk regresjon 130
QuartReg, fjerdegrads regresjon 131
Stikkordregister 255

256 Stikkordregister
R
R, radian 209
R►Pr(), polar koordinat 132
R►Pθ(), polar koordinat 132
radian, R 209
randMat(), tilfeldig matrise 134
randNorm(), tilfeldig norm 134
randPoly(), tilfeldig polynom 134
RandSeed, tilfeldig startverdi 135
real(), reell 135
redusert eliminasjonsform, rref() 144
reell, real() 135
ref(), eliminasjonsform 136
regresjon
fjerdegrads, QuartReg 131
kvadratisk, QuadReg 130
lineær regresjon, LinRegAx 91
lineær regresjon, LinRegBx 90
logaritmisk, LnReg 97
Logistisk 99
logistisk, Logistic 100
median-median-linje, MedMed 104
MultReg 108
potensregresjon, PowerReg 126
sinus, SinReg 156
Regresjon
lineær regresjon, LinRegBx 92
regresjoner
eksponensiell, ExpReg 65
kubisk, CubicReg 43
potensregresjon, PowerReg 126, 138-139, 172
rekke(), rekke 148
rekke, rekke() 148
rektangulær vektor-visning, ►Rect 135

rektangulær x-koordinat, P►Rx() 121
remain(), rest 137
Request (Forespør) 138
RequestStr (ForespørStr) 139
resiprok, x⁻¹ 213
rest, remain() 137
resultat
vise uttrykt ved cosinus 33
vise uttrykt ved e 63
vise uttrykt ved sinus 153
resultat verdier, statistikker 163
resultater, statistikk 162
retur, Return 140
Return, retur 140
right(), høyre 140
right, right() 30, 61, 85, 140, 184
rk23(), Runge Kutta function 140
rotate(), rotere 142
rotere(), rotere 142
rotere, rotate() 142
rotere, rotere() 142
round(), avrund 143
rowAdd(), matrisens radaddisjon 143
rowDim(), matrisens raddimensjon 144
rowNorm(), matrisens radnorm 144
rowSwap(), matrisens radskift 144
rref(), redusert eliminasjonsform 144
S
sannsynlig normalfordeling, normCdf() 115
sannsynlig student- t -fordeling, tCdf() 171
sannsynlighetstetthet for student- t, tPdf() 175
sannsynlighetstetthet for student-t, tPdf() 175
sannsynlighetstetthet, normPdf() 116
sec⁻¹(), invers sekans 145
Stikkordregister 257

258 Stikkordregister
sec(), sekans 145
sech⁻¹(), invers hyperbolsk sekans 146
sech(), hyperbolsk secant 146
sekvens, seq() 146
send feil, SendFeil 122
SendFeil, send feil 122
senket strek, _ 212
seq(), sekvens 146
seqGen() 147
seqn() 147
sequence, seq() 147
sfærisk vektor-visning, ►Sphere 161
shift(), skift 151
sign(), fortegn 152
simult(), simultane ligninger 152
simultane ligninger, simult() 152
sin⁻¹(), invers sinus 155
sin(), sinus 154
sinh⁻¹(), hyperbolsk invers sinus 156
sinh(), hyperbolsk sinus 155
SinReg, sinusregresjon 156
sinus
vise uttrykk uttrykt ved 153
sinus, sin() 154
sinusregresjon, SinReg 156
sjabloner
(∏), produkt 9
2-delers stykkevis funksjon 6
Absoluttverdi 8
andrederivert 10
bestemt integral 10
brøk 5
deriverte eller n-te deriverte 10
e eksponent 6
eksponent 5

første deriverte 9
kvadratrot 5
ligningssystemer (2-ligning) 7
ligningssystemer (N-ligning) 7
lim 11
Logaritme 6
matrise (1 × 2) 8
matrise (2 × 1) 8
matrise (2 × 2) 8
matrise (m × n) 8
n-te rot 5
stykkevis funksjon (N-delers) 7
sum (G) 9
ubestemt integral 10
skift, shift() 151
slett
feil, SlettFeil 28
åpne elementer fra liste 51
slettAZ 28
slette
variabel, DelVar 51
SlettFeil, slett feil 28
slå sammen trigonometrisk, tCollect() 171
snarveier, tastatur 219
solve(), løs 157
SortA, sorter stigende 160
SortD, sorter fallende 161
sorterer
fallende, SortD 161
stigende, SortA 160
språk
hente språkinformasjon 76
sqrt(), kvadratrot 162
standardavvik, stdDev() 164, 182
stat.resultater 162
Stikkordregister 259

260 Stikkordregister
stat.verdier 163
statistikk
en-variabel-statistikk, OneVar 119
fakultet, ! 202
gjennomsnitt, mean() 103
kombinasjoner, nCr() 111
median, median() 104
permutasjoner, nPr() 117
standardavvik, stdDev() 164, 182
tilfeldig norm, randNorm() 134
tilfeldig startverdi, RandSeed 135
to-variable resultater, TwoVar 180
varians, variance() 183
stdDevPop(), populasjonens standardavvik 164
stdDevSamp(), utvalgets standardavvik 164
stigningstall, Loop 101
Stoppkommando 165
streng
dimensjon, dim() 54
lengde 54
strenger
brukes for å opprette variabelnavn 222
format, format() 71
formatering 71
høyre, right() 140
Indir.ref, # 208
innenfor, InString 84
legg til, & 202
midtstreng, mid() 105
rotere, rotate() 142
rotere, rotere() 142
skift, shift() 151
streng til uttrykk, expr() 65, 99
tegnkode, ord() 121
tegnstreng, char() 26

uttrykk til streng, string() 165
venstre, left() 88
string(), uttrykk til streng 165
strings
right, right() 30, 61, 85, 140, 184
stykkevis funksjon (N-delers)
sjablon for 7
stykkevis() 122
større enn eller lik med, | 201
større enn, > 201
største felles divisor, gcd() 75
subMat(), undermatrise 166-167
subtrahere, - 193
sum (G)
sjablon for 9
sum av hovedbetalinger 207
sum av rentebetalinger 206
sum(), summering 166
sum, Σ() 206
sumIf() 166
summering, sum() 166
sumSeq() 167
svar (siste), Ans 17
T
T , transponert 168
t test, tTest 177
tan⁻¹(), invers tangens 169
tan(), tangens 168
tangens, tan() 168
tangentLine() 169
tangentlinje, tangentLine() 169
tanh⁻¹(), hyperbolsk invers tangens 170
tanh(), hyperbolsk tangens 170
Taylor polynom, taylor() 171
Stikkordregister 261

262 Stikkordregister
taylor(), Taylor polynom 171
tCdf(), sannsynlig student t-fordeling 171
tCollect(), slå sammen trigonometrisk 171
tegn
streng, char() 26
tegnkode, ord() 121
tegnstreng, char() 26
Tekstkommando 172
teller dager mellom datoer, dbd() 47
tellIf(), antall betingede elementer i en liste 38
test for åpen, isVoid() 87
Test_2S, 2_utvalg F test 73
tExpand(), utvide trigonometrisk 172
tidsverdi for penger, antall betalinger 179
tidsverdi for penger, betalingsbeløp 179
tidsverdi for penger, Fremtidig verdi 178
tidsverdi for penger, nåverdi 179
tidsverdi for penger, Rente 178
tier-potens, 10^() 213
tilf(), tilfeldig tall 133
tilfBin, tilfeldig tall 133
tilfeldig
matrise, randMat() 134
norm, randNorm() 134
polynom, randPoly() 134
startverdi, RandSeed 135
tilfeldig utvalg 135
tilfInt(), tilfeldig heltall 134
tilfUtv() 135
tilnærmet, approx() 17
tInterval, t konfidensintervall 173
tInterval_2Samp, toutvalg t konfidensintervall 173
ΔtmpCnv() [tmpKnv] 175
tmpCnv() 174-175
to-variable resultater, TwoVar 180

tomme (åpne) elementer 217
trace() 175
transponert, T 168
Try, feil håndteringskommando 176
try, Try 176
Try, try 176
tTest, t test 177
tTest_2Samp, to-utvalgs t-test 177
TVM-argumenter 179
tvmFV() 178
tvmI() 178
tvmN() 179
tvmPmt() 179
tvmPV() 179
TwoVar, to-variable resultater 180
U
ubestemt integral
sjablon for 10
ulik, ≠ 199
undermatrise, subMat() 166-167
unitV(), enhetsvektor 182
unLock, lås opp variabel eller variabelgruppe 182
uttrykk
streng til uttrykk, expr() 65, 99
uttrykk til liste, exp►liste() 63
utvid, expand() 64
utvid/sett sammen, augment() 19
utvide trigonometrisk, tExpand() 172
V
variabel
opprette navn fra en tegnstreng 222
Stikkordregister 263

264 Stikkordregister
variabler
lokal, Local 98
slette alle enkelttegn 28
slette, DelVar 51
variabler og funksjoner
kopiere 32
variabler, låse og låse opp 77, 98, 182
varians, variance() 183
varPop() 182
varSamp(), utvalgets varians 183
varselkoder og meldinger 230
vektorer
enhet, unitV() 182
kryssprodukt, crossP() 39
Overfører øyeblikkelig kontroll til den neste iterasjonen i aktuell løkke (For, While, eller
Loop). 45
prikk produkt, dotP() 57
venstre, left() 88
verken ... eller, Boolsk operator 114
vinkel, angle() 14
vis data, Vis 55
Vis, vis data 55
vise som
binær, 4Grunntall2 21
desimalt heltall, 4Grunntall10 23
desimalvinkel, ►DD 48
grader/minutter/sekunder, ►DMS 55
heksadesimal, 4Grunntall16 23
polar vektor, ►Polar 123
rektangulær vektor, ►Rect 135
sfærisk vektor, ►Sphere 161
sylindrisk vektor, ►Cylind 45
W
warnCodes(), Warning codes 184

when(), når 184
while, While 185
While, while 185
X
x⁻¹ , resiprok 213
x², kvadrat 196
XNOR 202
Z
zeroes(), nullpunkt 186
zInterval, z konfidensintervall 188
zInterval_1Prop, en-proporsjons z konfidensintervall 188
zInterval_2Prop, to-proporsjons z konfidensintervall 189
zInterval_2Samp, to-utvalgs z konfidensintervall 189
zTest 190
zTest_1Prop, en-proporsjons z-test 191
zTest_2Prop, to-proporsjons z-test 191
zTest_2Samp, to-utvalgs z-test 192
Ø
øvre, ceiling() 24-25, 39
Å
åpen, test for 87
åpne (tomme) elementer 217
åpne elementer, fjern 51
Stikkordregister 265





